Автор: Айзенберг И. Грайнер В.
Теги: ядерная, атомная и молекулярная физика физика ядерная физика
Год: 19755
Текст
И.АЙЗЕНБЕРГ - В ГРАЙНЕР
МОДЕЛИ ЯДЕР
КОЛЛЕКТИВНЫЕ
И ОДНОЧАСТИЧНЫЕ
ЯВЛЕНИЯ
Перевод с английского
кандидатов физико-математических наук
С. П. КАМЕРДЖИЕВА и Б. А. ТУЛУПОВА
МОСКВА АТОМИЗДАТ 1975
УДК 539.144
NUCLEAR THEORY
volume 1
NUCLEAR MODELS
Collective and Single-Particle Phenomena
Judah M. EISENBERG, Professor of Physics.
University of Virginia, Charlottesville, Virginia, U. S. A.
Walter GREINER, Professor of Theoretical Physics.
Johann Wolfgang Goethe Universitat, Frankfurt am Main,
Germany
1970
North-Holland Publishing Company Amsterdam — London
Айзенберг И., Грайнер В. Модели ядер. Коллектив-
ные и одночастичные явления. Пер. с англ. М., Атомиз-
дат, 1975, 456 с.
Книга посвящена рассмотрению важнейших совре-
менных моделей, используемых для описания сферических
и деформированных ядер. Рассматриваются две группы
моделей — одночастичные и феноменологические, или кол-
лективные, модели. Авторы—известные теоретики, ак-
тивно работающие в этой области ядерной физики. В част-
ности, Грайнер внескбольшой вкйад в развитие динамиче-
ской коллективной модели. Много места в книге отведено
описанию гигантскогоХ резонанса в рамках этой модели и
применению моделей яйра к рарсеянию тяжелых ионов,
т. е. вопросам, гго которым на/русском языке не имеется
обзорной литературы. ' \
Таблиц 24, рисунков 16U библиография 397.
—""j4
20402—017
А------------
034 (01) — 75
17—75
© Перевод на русский язык, Атомиздат, 1975
ОГЛАВЛЕНИЕ
Предисловие переводчиков ................................... . 7
Предисловие..................................................... 9
Введение........................................................12
Глава 1. Виды коллективных движений.............................17
§ 1.1 Квадру пол иные моменты ядер.........................19
§ 1.2. Электромагнитные переходы............................26
1.2.1. Предварительные сведения о радиационных переходах 26
1.2.2. Обсуждение экспериментальных данных............30
Глава 2. Коллективные координаты 36
§ 2.1. Поверхностные переменные оД1.........................37
§ 2.2. Коллективные переменные gW, описывающие колебания
плотности ядра.............................................43
§ 2.3. Канонически сопряженные импульсы и операторы рождения
и уничтожения фононов.......................................46
Глава 3. Структура коллективного гамильтониана ядра ............50
§ 3.1. Квадрупольные колебания поверхности ядра............51
§ 3.2. Гармонические колебания поверхности ядра............53
3.2.1 Построение собственных функций оператора углового мо-
мента .....................................................57
3.2.2. Мультипольные операторы в пространстве коллективных
переменных . ..............................................63
3.2.3. Построение оператора углового момента в пространстве
коллективных переменных....................................66
§ 3.3. Простейшие применения модели гармонического осцилля-
тора ......................................................69
3.3.1. Среднеквадратичная деформация .................69
3.3.2. Среднеквадратичный радиус распределения заряда
в возбужденном состоянии ......................71
3.3.3. Электромагнитный распад вибрационных квадруполь-
ных состояний .........................................74
3.3.4. Квадрупольные моменты возбужденных состояний 75
Глава 4. Потенциальная энергия коллективных колебаний ядра 77
§ 4.1. Внутренняя система координат.......................78
§ 4.2. Свойства симметрии потенциальной энергии квадруполь-
ных колебаний..............................................86
§.4.3. Схематическая модель для потенциальной энергии квадру-
польных колебаний......................................88
4.3.1. Случай С2 >0...................................88
4.3.2. Случай С2 0...................................93
3
Глава 5. Квантовая механика ротатора............................97
§ 5.1. Углы Эйлера, лабораторная и собственная системы коор-
динат ................................................... 98
§ 5.2. Составляющие оператора углового момента относительно
лабораторной и внутренней систем координат ..... 101
§ 5.3. Временные производные D-функций.....................107
§ 5.4. Коллективная кинетическая энергия как функция углов
Эйлера и внутренних переменных............................109
§ 5.5. Матричные элементы составляющих оператора углового
момента относительно внутренних осей..................... 113
5.5.1. Собственные значения оператора L2.............117
5.5.2. Матричные элементы операторов углового момента 119
§ 5.6. Преобразования собственных функций оператора углового
момента при конечных поворотах............................121
§ 5.7. Связь между конечными и бесконечно малыми поворотами 125
§ 5.8. (0р как собственные функции оператора углового
момента............................................. 127
§ 5.9. Симметричный волчок................................ 129
Глава 6. Колебательно-вращательная модель . . 132
§ 6.1. Гамильтониан колебательно-вращательной модели . 133
§ 6.2. Квантование в криволинейных координатах.............140
§ 6.3. Решение уравнений колебательно-вращательной модели 147
§ 6.4. Симметризация волновых функций . . ...............151
§ 6.5. Эффекты колебательно-вращательного взаимодействия 156
Глава 7. Модель асимметричного ротатора . 170
§ 7.1. Гамильтониан модели асимметричного ротатора . . 170
§ 7.2. Вероятности электрических квадрупольных переходов во
вращательных полосах..................................... 178
§ 7.3. f-Колебания асимметричного ротатора 179
Глава 8. Одночастичные модели ................... . 184
§ 8.1. Одночастичные состояния сферических ядер ... . 185
8.1.1. Собственные функции и собственные значения одно-
частичного гамильтониана для бесконечной прямо-
угольной ямы .......................................186
8.1.2. Собственные функции и собственные значения одноча-
стичного гамильтониана гармонического осцилля-
тора......................... . . . 189
§ 8.2. Спин-орбитальная связь............................. 193
§ 8.3. Реалистические одночастичные потенциалы............ 199
§ 8.4. Распределение нуклонов в ядре.................. .... 201
§ 8.5. Спаривание и предельная одночастичная модель . 203
8.5.1. Предсказания квадрупольных моментов . . 207
8.5.2. Предсказания магнитных моментов...............213
§ 8.6. Экспериментальное доказательство существования силь-
ной спин-орбитальной связи................................220
§ 8.7. Движение частицы со спином 1/2 во внешнем поле; реляти-
вистский вклад в спин-орбитальное взаимодействие . . . 222
Глава 9. Модель оболочек для деформированных ядер и обобщенная
модель ...... . 229
§ 9.1. Слабая связь...................................... 231
§ 9.2. Гамильтониан модели сильной связи...................235
§ 9.3. Структура и свойства симметрии волновых функций мо-
дели сильной связи .... ......... ... 239
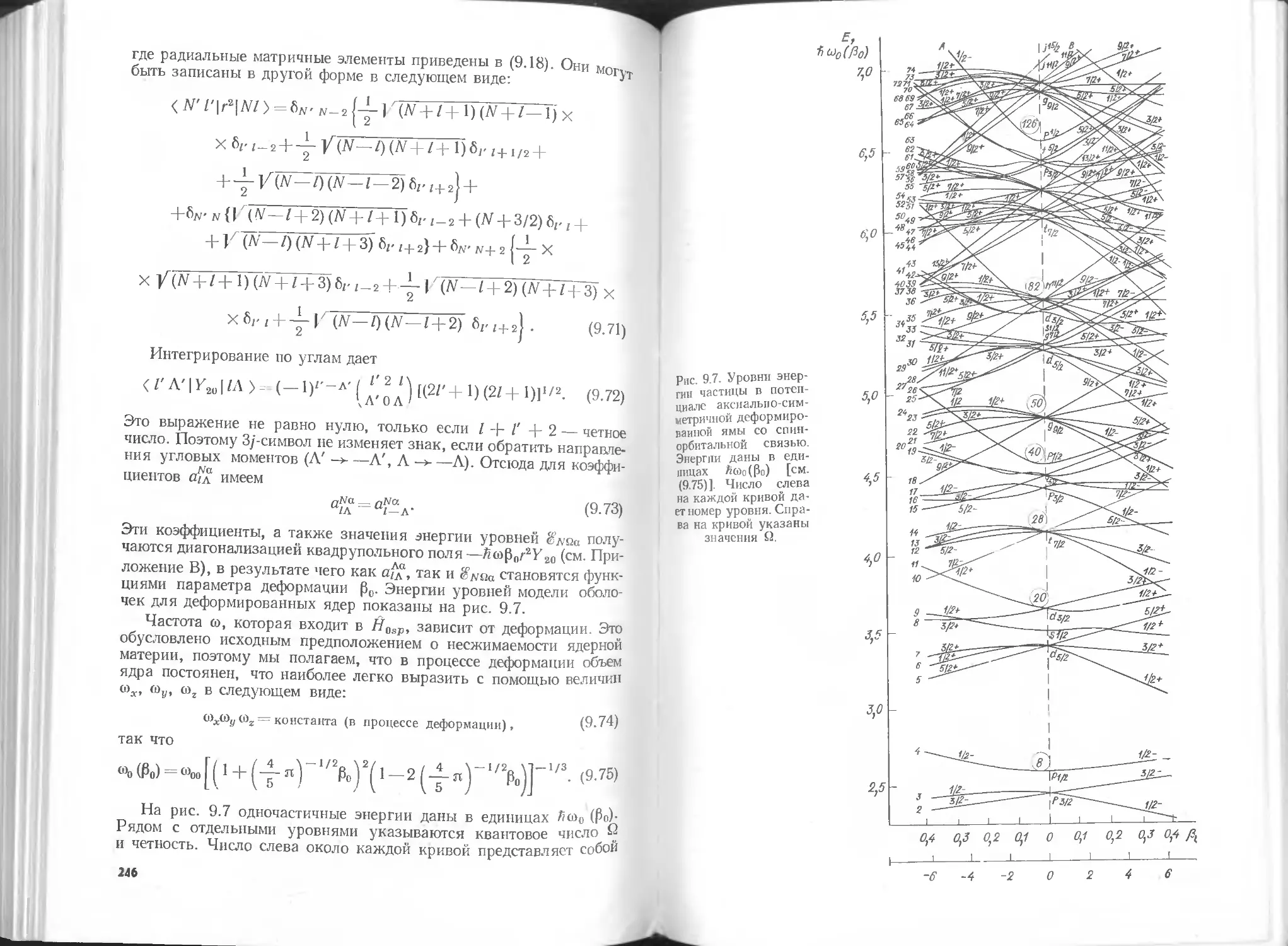
§ 9.4. Модель оболочек для деформированных ядер...........243
§ 9.5. Спектры нечетных деформированных ядер...............250
§ 9.6. Неадиабатические эффекты............................255
4
11
9.6.1. Кориолисовы силы................................255
9.6.2. Отклонение от аксиальной симметрии..............259
§ 9.7. Магнитные моменты нечетных деформированных ядер 263
§ 9.8. Дальнейшее развитие модели оболочек для деформирован-
ных ядер......................................................268
§ 9.9. Нечетно-нечетные деформированные ядра.................271
Глава 10. Гидродинамическая модель ядра . . .... 275
§ 10.1. Введение.................................... . 275
§ 10.2. Краткий обзор фотоядерных реакций....................278
§ 10.3. Гидродинамическая модель.............................282
§ 10.4. Классические дипольные решения гидродинамических
уравнений для случая сферического ядра.................294
§ 10.5. Сечение фотопоглощения в классической гидродинамиче-
ской модели............................................. 299
§ 10.6. Уточнения модели...............................302
§ 10.7. Классификация собственных колебаний плотности . . . 306
10.7.1. Различные представления тензоров...............306
10.7.2. Природа нормальных колебаний...................307
10.7.3. Ортогональность нормальных колебаний .... 310
10.7.4. Нормировка колебаний плотности.................311
§ 10.8. Полная энергия гигантских мультипольных резонансов 311
§ 10.9. Квантовая гидродинамика; квантование гигантских муль-
типольных резонансов......................................315
§10.10. Мультипольные операторы в пространстве коллективных
координат.................................................316
§ 10.11. Сечение фотопоглощения в квантовой гидродинамиче-
ской модели..............................................318
§ 10.12. Микроскопическое обоснование гидродинамической мо-
дели ядра............................................... 322
Глава 11. Динамическая коллективная модель 329
§ 11.1. Взаимодействие колебаний плотности со степенями сво-
боды поверхности ядра.....................................329
§ 11.2. Нормальные колебания плотности в деформированном
ядре и параметры связи....................................331
§ 11.3. Оператор Гамильтона для деформированного четно-чет-
ного ядра.................................................340
§ 11.4. Волновые функции и энергии гигантских дипольных ре-
зонансов в четно-четных ядрах.............................344
§ 11.5. Волновые функции и энергии гигантских квадрупольных
резонансов в четно-четных ядрах...........................349
§ 11.6. Оператор Гамильтона для нечетного деформированного
ядра......................................................351
§ 11.7. Волновые функции и энергии гигантского дипольного
резонанса в нечетном деформированном ядре.................353
§ 11.8. Зависимость дипольных и квадрупольных операторов
от коллективных переменных................................354
§ 11.9. Анализ экспериментальных данных для деформированных
ядер......................................................357
11.9.1. Эрбий..........................................358
11.9.2. Гольмий........................................361
§ 11.10. Динамическая коллективная модель сферических четно-
четных ядер...................................................368
11.10.1. Структура гамильтониана.......................369
11.10.2. Расщепление гигантского резонанса в сферичес-
ких ядрах .................................371
11.10.3. Экспериментальные сечения поглощения . . . 376
11.10.4. Анализ экспериментальных данных для сфери-
ческих ядер........................................378
5
Глава 12. Рассеяние тяжелых ионов ..................383
§ 12.1. Эффекты деформации ядер в реакциях с тяжелыми ионами 384
§ 12.2. Некоторые предварительные сведения...............385
§ 12.3. Рассеяние сферических ядер.......................390
§ 12.4. Рассеяние деформированных ядер...................395
§ 12.5. Квазимолекулярные состояния — экспериментальные
данные....................................................399
§ 12.6. Энергии связи ядер — полуэмпирическая массовая фор-
мула......................................................402
§ 12.7. Описание ядер конечных размеров в теории типа Томаса-
Ферми.....................................................406
§ 12.8. Квазимолекулярный ядерный оптический потенциал . . 413
§ 12.9. Сечение упругого рассеяния 1еО на 1вО.............420
Приложения
Приложение А. Классическая энергия поверхностных колебаний
ядра в гидродинамическом приближении..........................425
Приложение Б. Матрицы конечных вращений.......................428
Приложение В. Диагонализация одночастичного гамильтониана
трехосного ядра в цилиндрических координатах . . . 434
Приложение Г. Распределение плотности в ядрах [вывод дифференци-
альных уравнений (12.35)—(12.37)].............................436
Список литературы.............................................440
Алфавитно-предметный указатель................................451
ПРЕДИСЛОВИЕ ПЕРЕВОДЧИКОВ
Предлагаемая вниманию советского читателя книга И. Айзенберга
и В. Грайнера «Модели ядер» является первым томом трехтомной мо-
нографии авторов «Теория ядра».
В книге рассматриваются важнейшие модели ядра — оболочеч-
ная, коллективная и обобщенная, а также их применение для описа-
ния некоторых явлений в области ядерной физики. Оболочечная
модель в настоящее время все в большей степени становится одной из
основ понимания свойств ядра, так сказать, одной из основ ядерно-
теоретического мировоззрения. На наших глазах она превратилась
в такую же неотъемлемую часть физической науки, как и теория
относительности, хотя и уступает последней в красоте и обосно-
ванности. Думается, что в недалеком будущем старшеклассники
будут изучать модель оболочек так же, как сейчас они изучают
теорию относительности и модель атома Бора.
Какой-либо конкретный вариант модели оболочек всегда приме-
няется в многочисленных методах расчетов свойств ядер, в которых
используется остаточное или эффективное взаимодействие квазичас-
тиц. В более глубоких подходах, где нуклон-нуклонное взаимодей-
ствие определяется из данных о рассеянии свободных нуклонов, мо-
дель оболочек часто присутствует незримо, ибо одной из задач этих
методов является обоснование ее результатов. К сожалению, в пред-
лагаемой книге модель оболочек по сравнению с коллективными мо-
делями изложена недостаточно полно. Это объясняется, по-види-
мому, личными интересами авторов и общей направленностью кни-
ги, большая часть которой посвящена изложению коллективных
моделей.
Коллективные модели, рассмотренные в книге, разделяются
на два класса — модели для описания низколежащих уровней и мо-
дели гигантских резонансов. В разработку последних большой
вклад внес В. Грайнер, который известен как один из создателей
динамической коллективной модели. Эта феноменологическая мо-
дель, основанная на простых физических предположениях, является
в настоящее время, по-видимому, единственной моделью, которая
позволяет довольно подробно описать свойства гигантского резо-
нанса в широкой области сферических и деформированных ядер.
7
Предлагаемый том доступен читателям, изучившим обычный
одногодичный курс квантовой механики. Особенностью и достоин-
ством книги является обстоятельное (иногда даже чрезмерно) изло-
жение материала и выводов основных результатов. Некоторые
вопросы квантовой механики разбираются подробнее, чем в обычных
учебниках. По сравнению со вторым томом книга в целом требует
меньшего знакомства с квантовой механикой и может быть частично
использована при изучении общего курса ядерной физики. Вместе
с тем изложение доведено до такого уровня, что читатель, изучивший
интересующий его вопрос по данной книге, сможет свободно ориен-
тироваться в оригинальной литературе. Книга может быть исполь-
зована в качестве учебного пособия для студентов старших курсов
и аспирантов; она будет также полезна и специалистам — теорети-
кам и экспериментаторам. Прежде всего это связано с тем, что в на-
шей литературе нет книг, в которых рассмотрены коллективная мо-
дель гигантских резонансов и проблемы, связанные с рассеянием
тяжелых ионов.
В книге изложены основы моделей, а численные результаты в
основном являются лишь иллюстрацией их применения. Поэтому
мы не сочли целесообразным доводить изложение до современного
уровня и делать какие-либо добавления, что привело бы к увеличе-
нию объема и нарушению цельности книги.
Авторы снабдили книгу большим списком оригинальной лите-
ратуры, а работы [1 — 6] рекомендуются ими читателям для общего
ознакомления с основными проблемами физики ядра. При переводе
использованы следующие названия остальных томов монографии
Айзенберга и Грайнера: т. 2— Excitation mechanisms of the nucleus.
Amsterdam, North-Holland, 1970 (см. пер.:Механизмы возбуждения
ядра. M., Атомиздат, 1973) и т. 3 — Microscopic theory of the
nucleus. Amsterdam, North-Holland, 1972.
Камерджиев С. Л.,
Tулупов Б. A.
ПРЕДИСЛОВИЕ
Теория структуры ядра долгое время была одной из наиболее
трудных для преподавания областей физики. Дело в том, что методы,
применяемые для изучения ядер, весьма разнообразны, и среди них
невозможно выделить достаточно широкие общие темы. Например,
экспериментально исследовались такие различные явления, как
(d, п)-реакции и захват мюонов. Даже те экспериментальные методы,
которые связаны друг с другом в силу своей физической природы
(например, кулоновское возбуждение, фотоядерные реакции и мюон-
ные атомы, имеющие в основном электромагнитную природу), осно-
вываются на совершенно разных свойствах ядерной динамики или
статики. Вследствие этого экспериментальная информация в опре-
деленной степени имеет тенденцию к фрагментации, а не к интегра-
ции. Подобная же картина наблюдается и в работах по теории ядра.
В попытках описать свойства ядер с помощью феноменологических
моделей привлекалось много различных областей физики, которые
часто очень далеки друг от друга: классическая гидродинамика, вра-
щающиеся молекулы, модель оболочек, сверхпроводимость и т. д.
В такой ситуации большинство попыток представить физику яд-
ра в более или менее законченном виде сводилось к написанию обзо-
ров основных результатов в ее разных областях. Читателю же пре-
доставлялась тяжелая работа понять, как первопринципы теории
превращаются в детальные количественные предсказания свойств
ядер. Эта работа становится все более трудной по мере того, как лите-
ратура по ядерной физике, обширная и хаотическая уже в настоящее
время, увеличивается с устрашающей скоростью, тогда как некото-
рые наиболее фундаментальные принципы теории весьма кратко из-
лагаются в оригинальных журнальных статьях. Нам кажется, что
настало время попытаться представить накопленный материал
в компактном виде и рассмотреть его с единой точки зрения.
В соответствии с этим мы попытались дать замкнутое изложение
физики ядерной структуры, которое отражало бы главные достиже-
ния теории и развивало бы их разумным образом. Нашей целью
было представить материал так, чтобы все результаты, которые мы
рассматриваем, были бы последовательно выведены друг из друга.
Мы полагали, что физик, который хорошо знаком с главными на-
9
правлениями развития теоретической мысли, сможет относительно
легко применить основные методы и в других областях ядерной фи-
зики. Выполнению указанной программы очень помогли успехи
последних лет, которые привели к большему пониманию того, как
несвязанные на первый взгляд попытки описания свойств ядер в
действительности оказываются тесно связанными, если при этом
систематически применяют первопринципы теории.
Настоящее изложение теории структуры ядра состоит из трех
томов, каждый из которых, как предполагается, является отдельной
книгой, но все вместе они дополняют друг друга. Содержание рас-
пределяется по томам следующим образом.
1. Ядерные модели (коллективные и одночастичные явления).
В этом томе рассматриваются феноменологические способы описания
коллективных вращательных и колебательных свойств ядер, а также
эмпирически обоснованные аспекты модели оболочек для сфериче-
ских и деформированных ядер.
2. Механизмы возбуждения ядра (электромагнитное и слабое вза-
имодействия). Здесь рассматриваются главные методы исследова-
ния ядра, которые не приводят к усложнениям, связанным с сильно
взаимодействующими «пробными» частицами.
3. Микроскопическая теория ядра. Том посвящен описанию
ядерных свойств, исходящему из «затравочного» нуклон-нуклонно-
го взаимодействия. Он включает обсуждения двух- и трехнуклонных
систем, ядерной материи, приближения Хартри—Фока, частично-ды-
рочного формализма, спаривания и их связи с более феноменологи-
ческими подходами.
Эти книги написаны на таком уровне, который делает их полез-
ными для тех, кто прослушал обычный одногодичный курс кван-
товой механики и немного знаком с ядерными явлениями. Они могут
служить учебниками по теории ядра для студентов старших курсов,
причем для изучения каждого тома требуется приблизительно один
семестр. Это предполагает, конечно, что при работе в аудитории часть
материала в каждом томе будет опущена. Мы думаем, что это долж-
но быть именно так: ведь раньше преподаватели ядерной физики нес-
ли тяжелую ношу разработки весьма скудного теоретического мате-
риала, даваемого в стандартных учебниках. По нашему мнению, лек-
тору лучше было бы сосредоточиться на физической стороне дела,
представляющей интерес в его курсе, а на долю учебника оставить
задачу информирования студентов и подготовки их к чтению жур-
нальной литературы. Мы надеемся, что эти книги могут быть также
использованы для аналогичных целей специалистами по ядерной фи-
зике, которые найдут в них дополнительный материал в областях,
связанных со сферой приложения их главных интересов. В частно-
сти, мы думаем, что многие экспериментаторы-ядерщики будут себя
чувствовать более уверенно с книгой, в которой выполняются про-
межуточные выкладки, чем с той книгой, в которой они опущены, —
ведь детали опускаются под предлогом простоты, но это обычно при-
водит лишь к мистификации читателя.
ю
Настоящий том является первым в задуманной серии книг. Вна-
чале описываются коллективные координаты, строится коллективный
гамильтониан ядра и рассматривается потенциальная коллективная
энергия. Затем обсуждается квантовомеханическая теория ротатора,
которая используется в качестве отправной точки для подробного
рассмотрения колебательно-вращательной модели и модели асиммет-
ричного ротатора. Изучается соотношение между этими двумя мо-
делями. Далее описывается модель оболочек для сферических и де-
формированных ядер в отдельности и вводится обобщенная модель,
которая позволяет рассмотреть взаимодействие одночастичных и кол-
лективных степеней свободы. Возвращаясь к феноменологическому
коллективному способу описания, мы рассматриваем предмет ядер-
ной гидродинамики и подготавливаем почву для обсуждения динами-
ческой коллективной модели для деформированных и сферических
ядер. В конце книги рассмотрено применение ядерныхмоделей для
описания рассеяния тяжелых ионов. Таким образом, этот том дает
обширный обзор феноменологического описания ядерных свойств.
Он также подготавливает почву для микроскопического описания,
поскольку здесь выявляются существенные свойства, которые затем
должны быть объяснены в рамках более фундаментальной теории.
В этом томе шляпкой обозначаются операторы, действующие
в конфигурационном пространстве, например Q, но соответствую-
щие классические величины таким образом не обозначаются (на-
пример, О).
В написании книг нам помогало много людей, и мы хотим вос-
пользоваться предоставившейся возможностью, чтобы выразить им
глубокую благодарность. Мы очень обязаны многим физикам за по-
лезные обсуждения, которые привели к прояснению и лучшему от-
бору материала в этой книге и в остальных томах, — докторам Аке-
ру, Альбрехту, Даносу, Финку, Фриске, Фульчеру, Гаю, Келли,
Ле-Турне, Маршаллу, Риттеру, Шайду, Шопперу, Спайсеру, Што-
ку, Веберу и Вайтхеду. Один из нас (В. Г.) хочет поблагодарить док-
тора Кабрера за гостеприимство, оказанное им в Университете шта-
та Виргиния (США). Также хотелось бы выразить особую благодар-
ность доктору Вайтхеду, а через него Центру современных исследо-
ваний Университета штата Виргиния за решение трудных админи-
стративных проблем, которое сделало возможным наше сотрудниче-
ство. Мы также благодарим в этой связи Немецкое исследователь-
ское общество, Федеральное министерство научных исследований
и Гессенское министерство по делам культов.
Мы очень признательны редакторам The Physical Review,
Physical Review Letters и Review of Modern Physics за любезное
разрешение использовать иллюстрации, которые опубликованы
в этих журналах. Наша работа по подготовке рукописи к печати
была значительно облегчена благодаря неизменной заботе и терпе-
нию многих людей, которые занимались размножением материала.
Шарлоттесвилле, Виргиния, И. Айзенберг, В. Грайнер
Франкфурт-на-Майне
Январь 1970 г.
11
ВВЕДЕНИЕ
В последние два десятилетия наши знания о структуре ядер
чрезвычайно пополнились благодаря развитию моделей ядра. Прос-
тые математические предположения и лежащие в их основе простые
физические представления были очень полезны для систематической
интерпретации огромного количества экспериментальных данных.
При этом благодаря непрерывным усилиям по улучшению моделей
очень часто оказывалось возможным получить не только качествен-
ное описание наблюдаемых явлений, но и количественно объяснить
их. Развитие физических представлений об атомных ядрах часто
сопровождалось постоянным обменом идей с другими областями
физики, в частности с атомной и молекулярной физикой, физикой
твердого тела и элементарных частиц. Даже гидродинамика играла
важную роль в ядерной физике. Типичными примерами такого сход-
ства между разными областями являются: модели оболочек атома
и ядра, которые привели к глубокому пониманию одночастичного
движения; теория вращений и колебаний ядер, сформулированная
в полной аналогии с теорией спектров вращательного и колебатель-
ного движения в молекулах; наконец, недавно развитые представ-
ления о ядерных молекулах и квазимолекулярных потенциалах
между ионами очень похожи на обычное описание двух взаимодейст-
вующих атомных молекул.
Конечной целью физики ядерной структуры является, разумеет-
ся, объяснение свойств сложных ядер исходя из взаимодействия
между двумя нуклонами (естественно, если были бы найдены
убедительные доказательства существования трехчастичных или
других многочастичных сил, то это привело бы к появлению нового
важного эффекта, который затем следовало бы последовательно
учесть в теории структуры ядра). Эта цель — микроскопическое
описание, выражающее свойства ядра через свойства его составных
частей, — определяет направление, в котором развивается физика
ядерной структуры в поисках фундаментальной теории ядра.
Современные исследования в области микроскопической теории
обычно связаны с моделью оболочек ядра. Наиболее ранние работы
по модели оболочек [36, 37, 163] предвосхитили ее последующее
12
развитие. В частности, большое значение имели работы Шмидта
(312,3131, в которых предсказывались магнитные моменты ядер в
основном состоянии. Бурное развитие этой модели началось
с работы Майер, в которой были собраны экспериментальные
доказательства существования оболочечной структуры в ядрах
[139, 246, 285]. Это непосредственно привело к возникновению
динамической модели с сильными спин-орбитальными силами, раз-
витой Майер, Йенсеном, Xакселем, Сьюессом, Финбергом и Норд-
геймом, которая достигла больших успехов в описании спинов и
четностей основных состояний ядер [139,141,179,180, 247—249]*.
В настоящее время оболочечная модель ядра — фундамент большин-
ства современных теоретических работ по физике ядра. Тем не менее
следует иметь в виду, что оболочечное описание является все еще
в основном феноменологическим и нуждается в более глубоком мик-
роскопическом обосновании.
Несмотря на огромные успехи модели оболочек в предсказании
спинов и четностей основных состояний, магических чисел, систе-
матики свойств а- и |3-распадови т. п., область ее применения ока-
залась довольно ограниченной. Например, экспериментальные
значения квадрупольных моментов ядер в большинстве случаев
намного больше, чем значения, предсказываемые в модели оболочек,
в особенности для ядер с сильно незаполненными оболочками [ 165,
360]; вероятности переходов с низколежащих уровней очень часто
превышают одночастичные оценки в 10—100 раз; в ядрах наблю-
даются характерные вращательные и колебательные полосы, кото-
рые нелегко объяснить в рамках этой модели. Наконец, большим
стимулом для использования моделей, отличных от модели оболочек,
было открытие в 1947 г. фотоядерного гигантского резонанса [28,
29]. Вначале его наблюдали в виде большого и широкого максимума
в сечениях фотоделения, а затем обнаружили, что это свойство яв-
ляется общим для всех ядер. Довольно быстро стало ясно, что для
его объяснения можно использовать представление о коллективных
колебаниях протонов относительно нейтронов под действием элект-
рического поля налетающего фотона, что уже подразумевало кол-
лективное описание явления.
Эти и многие другие эксперименты привели к развитию различ-
ных коллективных моделей. Фактически было разработано два су-
щественно отличающихся друг от друга класса моделей. В первом
из них рассматриваются коллективные поверхностные (деформацион-
ные) степени свободы, т. е. низкоэнергетические коллективные коле-
бания и вращения ядра. Потребность в таком подходе появилась
уже давно, начиная с первых попыток объяснить деление ядер.
В 1939 г. Фннберг [ 138] и Бор и Уилер [49] исследовали форму и ста-
бильность деформируемой заряженной жидкой капли. Они рассмат-
ривали полную энергию ядра как функцию деформации сферической
* Прекрасное описание развития физических представлений, лежащих
в основе модели оболочек, дано Йенсеном в его Нобелевской речи [207].
13
равновесной формы. Финберг рассмотрел стабильность ядер по от-
ношению к спонтанному делению, а Бор и Уилер подробно исследо-
вали теорию этого процесса. Следуя предположениям, ранее введен-
ным Вайцзекером [381], полную энергию ядра они представили
в виде суммы объемного члена, поверхностной энергии, обусловлен-
ной постоянным поверхностным натяжением,и кулоновской энер-
гии. При изменении формы ядра первое слагаемое увеличивается,
второе уменьшается. Отсюда пришли к заключению, что форма ос-
новного и низколежащих состояний четно-четных ядер должна быть
сферической.
Очень важный шаг (в настоящее время основательно забытый)
в развитии коллективной модели для низких энергий возбуждения
был позже сделан Флюгге [146], который впервые рассмотрел поверх-
ностные колебания и вращения ядер. Им было указано на важную
роль поверхностного натяжения для понимания динамических и ста-
тических свойств ядер. Флюгге также понял, что вращение ядра
может привести к появлению вращательных спектров.Однако он не
считал, что поверхностные колебания и вращения могут быть свя-
заны друг с другом.
Анализ причин появления больших квадрупольных моментов
привел Рейнуотера [302] к пониманию того, что одна нечетная час-
тица может поляризовать остов ядра. Им было показано, что одна
частица может иметь более низкую энергию, если ее потенциальная
яма деформирована. Таким образом, впервые было указано на то,
что ядерная система, состоящая из остова и связанной с ним час-
тицы (или, возможно, нескольких частиц), может перейти в состоя-
ние с меньшей энергией, если остов изменяет сферическую форму*.
Большой заслугой О. Бора, а позднее О. Бора и Моттельсона
[50, 51 ], было указание на то, что статическая форма и ориента-
ция деформированного ядра и переменные коллективной деформации
взаимосвязаны. Как было отмечено еще Флюгге, эти переменные мо-
гут играть роль динамических переменных. В то время это был важ-
ный шаг от классической картины Флюгге к квантовому описанию
Бора. Это квантовое коллективное движение сильно влияет на дви-
жение индивидуальных частиц. Оказалось, что динамика ядер во
многом совершенно аналогична динамике молекул. Независимые час-
тицы играют роль электронов, а деформированное ядро как целое
играет роль молекулярного (внутреннего) остова. Разумеется, в от-
личие от молекул остов ядра сам создается нуклонами.
Следует подчеркнуть, что введение коллективных степеней сво-
боды ни в коем случае не должно рассматриваться как противопо-
ставление модели независимых частиц [51]. Фактически само эф-
фективное поле модели независимых частиц является коллективным
по своей природе (см. [204]). Наиболее отчетливо это было показано
в работах Нильссона [283], Готфрида [167] и Мошковского [262],
* Представление о деформированном остове было также введено Шмид-
том [313] на десять лет раньше.
14
которые обобщили сферическую модель оболочек на деформирован-
ные ядра.
В вышеупомянутой работе Бора и Моттельсона рассматрива-
лись как коллективные, так и одночастичные явления и были зало-
жены принципиальные основы для дальнейшего развития такого
подхода. Теоретическое применение и развитие основных физи-
ческих представлений было осуществлено как этими авторами,так и
другими. А. С. Давыдов и его школа [89], исходя из коллек-
тивного гамильтониана Бора, с большим успехом исследовали
неаксиальные ядра. В итоге были объяснены вероятности многих
£2-переходов и отклонения от энергетических спектров простых
ротаторов. Вскоре после этого были получены решения уравнений
динамической модели с учетом р- и у-колебаний для аксиально-
симметричного остова ([129—131, 133], см. также [42]), указано на
важность колебательно-вращательного взаимодействия в ядрах и
установлена эквивалентность с моделью асимметричного ротатора,
в особенности для основного состояния и для у-полос.
Второй, совершенно отличный от первого, класс коллективных
моделей стал развиваться вскоре после открытия фотоядерного
гигантского резонанса. Чтобы объяснить это явление, Гольдхабер
и Теллер [164] предложили несколько моделей, в которых для опи-
сания энергетической зависимости сечений фотовозбуждения они
учитывали коллективные дипольные эффекты. В одной из таких
моделей введены твердые протонная и нейтронная сферы, каждая из
которых совершает гармонические колебания около своего положе-
ния равновесия. Энергия резонанса в этом случае оказывается про-
порциональной ~ А-1/6, где R — радиус ядра, А — атом-
ный номер. Во второй модели сжимаемые протонные и нейтронные
жидкости совершают колебание друг относительно друга. В пред-
положении, что возвращающие силы пропорциональны градиенту
плотности, было получено, что резонансные частоты пропорциональ-
ны Д1 ~ А~ ’/з. Эта модель была подробно изучена, и ее пол-
ное математическое описание дано Штейнведелем, Д. Йенсеном и
Р. Йенсеном [347, 348] и Даносом [86]. Эти авторы рассмотрели
двухжидкостную задачу для сферического ядра и получили следую-
щую формулу, связывающую резонансную энергию Ет с фазо-
вой скоростью второго звука в ядерной материи ш
Em = 2,08utiR~1.
Таким образом, они предсказали, что энергия гигантского резонан-
са должна быть пропорциональна А-'/3. Данос [88] и Окамото
[292] обобщили эту модель на случай ядер с аксиально-симмет-
ричной статической деформацией. Этими авторами было предсказано
расщепление гигантского резонанса, пропорциональное деформации
ядра и обусловленное различием периодов колебаний звуковых волн
вдоль большой и малой осей ядра. Указанный эффект был экспери-
ментально обнаружен в работах [152, 344].
15
Оба класса коллективных моделей — для низких и высоких
энергий — сосуществовали до 1964 г., когда они были объединены
для того, чтобы изучить тонкую структуру гигантских резонансов
[96, 234, 3251. В деформированных и сферических ядрах на звуковые
волны, соответствующие гигантскому резонансу, накладываются по-
верхностные колебания. Таким образом, в области максимума гигант-
ского резонанса появляется несколько сателлитов, на которые
приходится заметная доля дипольной силы. Это приводит к появле-
нию тонкой структуры (промежуточной коллективной структуры).
Впоследствии она была обнаружена во многих ядрах. Несколько
удивительным в этой связи было обнаружение расщепления гигант-
ского резонанса в сферических ядрах [230, 376, 377].
Структура гигантских резонансов в легких и магических ядрах
подробно изучена в рамках модели оболочек с учетом взаимодействия
нуклонов. Этот подход является микроскопическим подходом, аль-
тернативным к коллективной модели гигантских резонансов, кото-
рая описана выше. Фактически гигантский резонанс может быть
легко описан как в рамках коллективного, так и в рамках микро-
скопического подходов. Это делает гигантский резонанс особенно
ценным для описания коллективного движения в рамках микроско-
пического подхода, что, разумеется, является важнейшей проблемой
в теории ядерной структуры.
Различные ядерные модели, описанные выше, широко приме-
няются для объяснения свойств ядерных реакций при низких энер-
гиях, поляризационных эффектов в мюонных атомах, рассеяния эле-
ктронов и фотонов и кулоновского возбуждения. Многообещающим
является недавнее применение этих моделей в физике тяжелых
ионов. Использование процессов с участием тяжелых ионов дает
возможность получить короткоживущие ядерные молекулы*. Ква-
зимолекулярные нуклон-нуклонные потенциалы могут быть объ-
яснены на основе весьма правдоподобных представлений и, по-
видимому, смогут дать сведения о такой важной величине, как
сжимаемость ядра [318]. Еще более заманчивым было бы открытие
сверхтяжелых элементов (Z » 114 или 164), которое может ожидать
нас в будущем.
Настоящий том посвящен систематическому изложению теории
феноменологических ядерных моделей. Особое внимание уделено
выяснению физики явлений, одновременно дано полное математи-
ческое описание моделей, что позволяет легко выполнить подробные
расчеты свойств ядер, необходимые в любой количественной теории.
Наконец, мы надеемся продемонстрировать, что в рамках рассмат-
риваемых моделей можно связать большое количество экспери-
ментальных фактов. Это поможет создать нам правильное представ-
ление об истинных свойствах ядер.
* Такие эффекты, по-видимому, были обнаружены в работах Бромли
с сотр. [65, 337].
16
Глава 1. ВИДЫ КОЛЛЕКТИВНЫХ
ДВИЖЕНИЙ
Существует много фактов, которые указывают на то, что ядер-
ное движение не сводится только к простым одночастичным воз-
буждениям, как можно было бы предполагать в модели оболочек.
Имеется несколько явлений, существование которых подразуме-
вает коллективное движение. Последнее означает, что много нук-
лонов движутся когерентно с хорошо определенными фазами.
Чтобы понять этот вид когерентного движения нуклонов, рассмотрим
некоторые типичные примеры. Существуют четыре важных вида
коллективного движения.
1. Поверхностные колебания формы ядра представляют собой
движение нуклонов из одной области ядерной сферы в другую. Это
коллективное направленное движение показано стрелками на
рис. 1.1,о. На рис. 1.1,6 стрелки указывают периодические колеба-
Рис. 1.1. Схематическое изображение поверхностных (а) и компресси-
онных (б) колебаний ядра:
а\ слева — сферическое ядро, справа — искажение сферической формы; б — ради-
альные колебания поверхности; это коллективное движение, соответствующее сжа-
тию и разрежению ядра, приводит к колебаниям ядерной плотности.
ния радиуса ядра вокруг его равновесного значения До. Плотность
ядра в этом случае также периодически уменьшается или увеличи-
вается (компрессионные, или «дыхательные», колебания).
2. Другим примером когерентного синфазного движения ядер-
ной материи является вращение деформированных ядер. В этом слу-
чае вокруг остова ядра движется некая приливная волна (рис. 1.2).
17
3. Деление ядра как вид коллективного движения нуклонов
схематически показано на рис. 1.3. Нуклоны движутся в разные сто-
роны относительно друг друга так, что ядро делится на две части.
На рисунке указаны различные стадии этого процесса при переходе
Рис. 1.2. Схематическая картина вра-
щения деформированного ядра. Остов
может также вращаться, но с мень
шей угловой скоростью.
от одного сферического ядра к
двум сферическим ядрам. Стрел-
ки указывают направление пото-
ка ядерной материи.
Три рассмотренных выше
процесса происходят в более
или менее поверхностной обла-
сти ядра Даже в случае враще-
ния внутренний сферический
остов (заштрихованное прост-
ранство на рис. 1.2) в основном
может считаться находящимся
в покое, а движущейся может
считаться лишь та часть ядер-
ной материи, которая находит-
ся вне остова. Это происходит
потому, что потенциальное поле
-остова не меняется во время вращения и, следовательно, нуклоны
остова не испытывают воздействия внешних нуклонов и не дают
вклада в энергию движения в отличие от нуклонов в приливной
волне (см. также замечания в связи с рис. 1.16).
Рис. 1.3. Схематическая картина деления ядра.
4. В коллективном движении, соответствующем гигантскому
дипольному резонансу, принимают участие уже внутренние области
ядра. Электрическое поле фотона Е действует только на протоны,
и, поскольку центр тяжести ядра должен оставаться в покое, нейт-
роны должны двигаться в направлении, противоположном направ-
лению движения протонов. В этом процессе поверхность ядра остает-
18
Рис. 1.4. Схематическое описание
движения, соответствующего воз-
буждению гигантского дипольного
резонанса в ядрах.
Электрическое поле Е фотона вынуж-
дает протоны двигаться вверх. Нейтро-
ны при этом движутся вниз, чтобы со-
хранить неподвижным центр тяжести
ядра.
ся в покое, в то время как протоны и нейтроны движутся когерентно,
но в противоположных направлениях (рис. 1.4).
Этих примеров достаточно,чтобы получить представление о раз-
личных видах коллективного движения в ядрах.
Рассмотрим теперь, какие экспериментальные факты указывают
на их существование. Если некоторая совокупность эксперименталь-
ных данных может быть объяснена в рамках коллективной теории,
построенной на основе рассмотренных выше физических представ-
лений, то это уже, разумеется, подтверждает коллективную при-
роду наблюдаемых возбуждений.
Однако существуют некоторые
общие признаки, типичные для
коллективных спектров, которые
дают возможность сразу же по-
нять степень коллективности изу-
чаемых возбуждений. Фактически
в ядрах не существует только
коллективных или только одноча-
стичных уровней, но всегда име-
ются оба вида уровней. Впоследст-
вии мы увидим, что чисто коллек-
тивное и чисто одночастичное дви-
жение — это идеализация. В дей-
ствительности оба вида движения
смешаны, и поэтому иногда бывает
трудно понять природу ядерного
состояния. Можно назвать следующие эффекты, которые дают
некоторые прямые указания на существование коллективного
движения.
1. Большие квадрупольные моменты, наблюдаемые в ядрах,
далеких от магических.
2. Большие вероятности переходов между коллективными
уровнями.
3. Некоторые свойства низкоэнергетических возбуждений (вра-
щательные и колебательные спектры) или возбуждений с большой
энергией (гигантские резонансы).
Обсудим теперь эти эффекты более подробно.
§ 1.1. КВАДРУПОЛЬНЫЕ МОМЕНТЫ ЯДЕР
Оператор электрического мультипольного момента имеет вид.
2^ = 24^^), (1.1)
k=i
гДе суммирование выполняется по всем протонам ядра. Электри-
ческий квадрупольный момент Q ядра в состоянии определяется
1»
как среднее от оператора Q20 в состоянии | jM > = |//>, умножен-
« - лл /16 V/2
ное на обычный коэффициент I — лJ :
= (1'2)
Квадрупольный момент характеризует отклонение ядерной плот-
ности от сферической симметрии. Если разложить величину
ф/1 (г) ф^ (г) по сферическим гармоникам
(г) Ф;у (г) = Ад (Г) + А, (г) Г10 + А2 (г) У2Я + Д (г) Езо Е... , (1.3)
то квадрупольный момент будет характеризовать долю ядерной
плотности, которая пропорциональна Е20. Дипольный и октуполь-
ный моменты характеризуют долю ядерной плотности, пропорцио-
нальную Е10 и У30 соответственно.
Рассмотрим простейшую модель ядра с нечетным протоном,
в которой ядерные свойства определяются одним протоном, движу-
щимся в поле, производимом всеми нуклонами. Тогда волновая функ-
ция ядра имеет вид
tjm (п, 0 = U (О (Ш I V'/ц (1-4)
ц.а
Здесь и (г) —радиальная волновая функция протона, цот) —
коэффициент Клебша — Гордана, который связывает собствен-
ную функцию орбитального момента Yim и спиновую функцию
%1 /2а в функцию | jm > с полным угловым моментом j и его проек-
цией т. В этой предельной одночаспшчной модели (см. гл. 8) предпо-
лагается, что нуклоны связаны в пары с угловым моментом, равным
нулю, и образуют остов ядра. Последняя нечетная частица одна
определяет основные свойства ядра, если энергии возбуждения
не слишком велики. Это приближение обсуждается значительно
более подробно в гл. 8 и 9. Используя формулу (1.4), можно полу-
чить одночастичное значение для квадрупольного момента (1.2):
QsP = J “*ri и dr-
(1.5)
Последний множитель — среднеквадратичный радиус нуклона. Вы-
ражение (1.4) получено для нечетного протона.
Для нечетного нейтрона квадрупольный момент может также от-
личаться от нуля благодаря отдаче остальной части ядра: смещение
нейтрона на величину гп по отношению к положению центра масс
приводит к смещению заряда Z остальной части ядра на расстояние
гп/(Д — 1) от центра масс (рис. 1.5). Тогда эффективный квадру-
польный момент
2
О"1 = (Д_ 1)2
(1.6)
20
Если предположить однородное распределение заряда, то
(г2) = (3/5) R2, где R — радиус ядра (R = г0 Л'/3). В резуль-
тате получаем значение Qsp (ядра с нечетным протоном), которое
пропорционально Л2/3 и составляет 10~26—5-10-25 см2. Для ядер
с одним нечетным нейтроном соответствующая величина приближен-
но пропорциональна Л~1/3 и равна 10“23—10 26 см2.
Эти результаты следует сравнить с экспериментальными значе-
ниями квадрупольных моментов, представленными на рис. 1.6. Сра-
зу же видно несколько явных расхождений
с экспериментом. Во первых, все знаки од-
ночастичных квадрупольных моментов, да-
ваемых формулами (1.5) и (1.6), отрицатель-
ны, тогда как экспериментальные значения
преимущественно положительны, и лишь
несколько ядер с числом нуклонов, немно-
го превышающим магические числа, имеют
отрицательные квадрупольные моменты. Во-
вторых, предсказываемые значения значи-
тельно меньше экспериментальных. В-третьих,
в тех случаях, когда Q довольно велики, нет
заметных различий в значениях моментов
ядер с нечетным протоном и нечетным нейтро-
ном. Эти расхождения указывают на то, что
Рис. 1.5. Ядро с нечет-
ным нейтроном. Ука-
заны положения не-
четного нейтрона гп и
остатка гп/(Л—1) по
отношению к центру
масс (ц. м.).
вклад в величину квадрупольных моментов
может давать не только один протон, но и
большее их число. Нечетный нейтрон тогда
дает лишь малую добавку к большому мо-
менту протонов. Однако можно возразить,
что более совершенная одночастичная модель
могла бы быть более успешной в описании
экспериментальных данных. Тот факт,
что в модели независимых частиц угловой момент ядра определяет-
ся всеми частицами, находящимися вне замкнутых оболочек, сразу
же указывает на возможность объяснения того, что ядра с нечетным
нейтроном имеют большие электрические квадрупольные моменты.
Рассмотрим более общий случай п эквивалентных протонов,
находящихся на одночастичном уровне с моментом /. Для вычисления
Q воспользуемся антпсимметризованными волновыми функциями,
соответствующими полному угловому моменту / и (м—1) нук-
лонам, связанным с угловым моментом, равным нулю (схема связи
с квантовым числом сеньорити). В § 8.5 будет получено следующее
выражение для Q:
Q=Qsp (1
2п— 2 \
~2/~1 ) ’
(1-7)
где 1 2 /. В частности, для дырки (и = 2/) получаем Q =
= — Qsp- Для всех п, отличных от 1 и 2/, Q< Qsp. Оно отрица-
тельно для ядер с оболочками, заполненными более чем наполовину.
it
Это лишь отчасти улучшает согласие с экспериментом, так как на-
блюдающегося преобладания положительных квадрупольных мо-
ментов не получается. Кроме того, не может быть объяснен и порядок
величины больших моментов (см. рис. 1.6). Все это указывает на то,
что простая одночастичная модель является слишком грубой и что
в коллективных движениях,связанных с отклонением от сфериче-
ской симметрии, может участвовать весьма большое число частиц.
Можно оценить число частиц, дающих вклад в большие квадру-
польные моменты, если рассмотреть заряженный сфероид. Для этого
Рис. 1 6. Экспериментальные значения электрических квадруполь-
пых моментов как функция числа протонов (X) или нейтро-
нов (•) [288].
Значения моментов, равные нулю, указывают на то, что соответствующие
ядра имеют сферическую форму. Большие квадрупольные моменты указы-
вают па наличие асимметрии ядра. На рисунке отмечены положения маги-
ческих чисел.
аппроксимируем форму сфероида в сферических координатах сле-
дующим образом:
Я = Яо(1+₽иУ2о), (1-8)
где Re — радиус «эквивалентной» сферы того же объема (в нижай-
шем порядке по |30). Тогда получаем
Qo = ( — Y/s — к По f {г* dr j dQ =
k 5 ) AnRl J Ц J
= (? Г ^4- Яо (14 Po По)5 По dQ « 3 (5л)~% zpo. (1.9)
Из экспериментальных значений Qo (см. рис. 1.6) можно получить
Ро ~ 0,24-0,3. Эти значения 0О весьма велики, поэтому для того,
11
чтобы создать сфероидальное распределение плотности, для многих
ядер необходимо участие большого числа нуклонов. Действитель-
но, разность объемов эллипсоида и внутренней сферы (рис. 1.7)
равна dV = (5л)1/2 7?о₽0 и, следовательно, число нуклонов в этом
объеме dA = (А V) dV = (5/л)1/2 ЛР0, где V — объем, А —чис-
ло нуклонов ядра. Мы видим, что dA/A « 0О-
Другим интересным свойством кривой квадрупольных момен-
тов, изображенной на рис. 1.6, является то, что она проходит через
нуль для некоторых значений N и Z. Q меняются от больших поло-
жительных до малых отрицательных значений, не противоречащих
величинам одночастичных моментов. Затем Q снова довольно быстро
увеличиваются до больших положительных значений. Нули появ-
ляются для Д' или Z = 8, 14, 20, 28, 40, 50, 82, 126. Следовательно,
ядра с этими значениями Z или N являются сферическими и если
добавляются один или два нуклона, то сферический остов дефор-
мируется не сильно. Предсказания модели независимых частиц
[см. выражение (1.7)], по-видимому, справедливы для нескольких
ядер, находящихся вблизи этих «.магических» ядер. Например, хо-
рошо согласуются с экспериментом противоположные знаки квад-
рупольных моментов ядер, имеющих одну частицу или дырку.
Однако по мере того, как увеличивается число дополнительных нук-
лонов, ядра, по-видимому, принимают сфероидальную форму.
Целесообразно кратко описать различные экспериментальные
методы определения квадрупольных моментов ядер [ 121, 123, 217].
Например, их можно измерять по наблюдаемым отклонениям от
правила интервалов в энергии уровней внешних электронов. Пра-
вило интервалов обусловлено тем, что энергия взаимодействия
электронов и ядер пропорциональна величине IJ, где I — спин
ядра, J — спин электрона. Полный угловой момент атома
F=I + J. (1.10)
Применяя правила сложения угловых моментов, получаем возмож-
ные значения F:
f —(7+7), (7+7— 1).... ,(7—7), если 1 „ ц.
Л = (/ +7), (7 ф7—Г),...,(/ —7), если 7^7.)
В первом случае мы имеем (2/ + 1), во втором — (27 + 1)
различных значений F. Энергии состояний с разными значениями
F различаются за счет магнитного диполь-дипольного взаимодействия
между ядром и электронами. Поскольку магнитный момент ядра зна-
чительно меньше магнитного момента электронов, это взаимодейст-
вие мало, что в свою очередь приводит лишь к малым различиям
в энергии этих состояний. Электронный уровень с угловым момен-
том 7 расщепляется на (2/ I) или на (27 + 1) близко располо-
женных уровней в зависимости от того, какое неравенство выпол-
няется: 7 > 7 или 7 > 7. Это расщепление называется сверхтонкой
23
структурой уровня. Его следует отличать от тонкой структуры, обус-
ловленной связью орбитального и спинового моментов электрона.
Каждый уровень тонкой структуры может иметь свою сверхтон-
кую структуру.
Как уже упоминалось, энергия магнитного взаимодействия про-
порциональна скалярному произведению угловых моментов I n J,
которое инвариантно относительно вращения
1Г = Д1Л (1.12)
Рис. 1 7 Заштри-
хованный участок
характеризует часть
объема ядра, свя-
занную с коллек-
тивным движением.
Рис. 1.8. Процессы, имеющие
место при кулоновском воз-
буждении первого 2+-уровня
ядра. Прямой переход ука-
зан двойной стрелкой. Ука-
зан также реориентацион-
пый эффект ( т? ).
Среднее от этого выражения в состоянии | F (I, J)>, где обозначение
F (I, J) указывает на то, что I и J связаны в угловой момент F,
равно
<Е(/, J) | А1J\F(I, /)> = -^Д(Е(/, J)|E2—I2—j2|F(/, J)> =
= 1/2Л(Е(Е+1)-/(/+1)-/(/+1)). (1.13)
Подставляя сюда значения F из (1.11), получаем, что разности
между последовательными состояниями мультиплета составляют
Л(7 + У), Л(7 + У—1), Л(7 + У—2),... , Л(7 —J), (1.14)
т. е. разности энергий пропорциональны значениям F из (1.11).
Этот результат и называется правилом интервалов. Если I < J,
то можно определить спин ядра 7, пересчитывая уровни, на которые
расщепляется уровень с данным J. Если I > J, то пересчитывая
уровни сверхтонкой структуры, находим J, a F получаем с помощью
правила интервалов, если известно относительное разделение уров-
ней. Это позволяет снова определить /. Однако если кроме магнит-
ного имеется также электрическое взаимодействие, обусловленное су-
ществованием квадрупольного момента ядра (энергия квадруполь-
ного взаимодействия пропорциональна Q/r3), то это приводит к от-
клонению от правила интервалов. По величине этого отклонения
можно определить квадрупольный момент. Если переход совер-
24
шается между двумя уровнями, каждый из которых имеет сверх-
тонкую структуру, то соответствующее расщепление спектраль-
ных линий будет значительно более сложным, чем расщепление
каждого из этих двух уровней. В этом случае необходимо выбрать
два электронных уровня, один из которых имеет значительно
более сложную сверхтонкую структуру, чем другой. Тогда рас-
щепление спектральной линии будет в основном обусловлено только
расщеплением этого уровня.
Очень точные измерения квадрупольных моментов стали воз-
можны после открытия мюонных атомов [11, 326]. Если мюон за-
хватывается ядром на атомную орбиту после испускания атомом
электрона, то энергетический спектр мюона будет похож на спектр
электрона в одноэлектронном атоме. Из-за большой массы мюона
(m!t = 270 те) его боровская орбита частично находится внутри
ядра, как что мюон является хорошей «пробной» частицей для из-
мерения свойств ядра. Сначала мюон захватывается на высоко
лежащую орбиту, затем, в результате каскадных переходов, он
переходит в 1 s-состояние. Испускаемые рентгеновские лучи можно
измерить с высокой степенью точности. Тогда из расщепления линии,
соответствующей мюонному переходу 2 -> 2 рз/2, можно полу-
чить даже знаки так называемых внутренних квадрупольных мо-
ментов четных ядер*.
Наиболее современным методом определения квадрупольных
моментов «перехода», так же как и квадрупольных моментов возбуж-
денных состояний ядра, является кулоновское возбуждение [62, 104,
105, 111, 117, 173]. Тяжелый ион, приближающийся к ядру, воз-
буждает его, например, квадрупольной составляющей кулоновского
поля. Пусть ядро переходит при этом из основного 0+-в первое
2+-состояние. Имеется несколько возможных механизмов такого
процесса (рис. 1.8):
а) прямой £2-переход (электрический квадрупольный переход);
б) £2-переходы в более высокие состояния с последующей раз-
рядкой и переходом в первое 2+-состояние;
в) реориентация ядра в первом 2+-состоянии (о связи с квадру-
польным моментом возбужденного состояния см. [61, 117, 119,
245)].
Реориентация ядерной оси вызывается электрическим полем
налетающей частицы, которая возбудила ядро. Изменение направ-
ления спина ядра оказывает влияние на угловое распределение ис-
пускаемых рентгеновских лучей или рассеянных частиц.
Если налетающие частицы имеют малую энергию, малую массу
и заряд, то наибольший вклад дает прямой переход. Однако для
тяжелых заряженных частиц начинают давать вклад эффекты
второго порядка. Можно получить выражение для вероятности пе-
рехода во втором порядке теории возмущений:
Р w|<2/M|Q[0>+a<2M |Q|2M'><2M'|Q|0>|2, (1.15)
* Более подробно см. т. 2, гл. 8.
25
где второй член с множителем а описывает реориентационный эф-
фект, соответствующий тому, что ядро, первоначально находившее-
ся в состоянии |2ЛГ>, затем«реориентируется» в состояние 12Л4>.
Если оператором перехода является компонента Q20 квадруполь-
ного оператора (1.1), то
Р « | <2М |Q20|0> |2 + 2tz<2M |Q20|0> <2M | Q20 ( 2M> <2Al|Q2O|0> +
+ ... = |<2M|Q2O|0> |2(1-|-2а (2Л4 |Q20| 2Л4>) + ... ,
т. е. эффекты второго порядка позволяют определить знак и величину
квадрупольного момента возбужденного состояния.
Эксперимент выполняется путем сравнения вероятностей куло-
новского возбуждения различными ионами, например 4Не и 1ВО.
Энергии подбираются так, чтобы оба иона двигались по одинаковой
траектории. Поскольку 4Не имеет малый заряд, он вызывает только
прямые переходы, тогда как 1еО вызывает также и эффекты второго
порядка. Де Боер с сотр. [1051 были первыми, кто таким образом
определил статический квадрупольный момент первого 2+-уровня
в 114Cd. Они нашли, что эта величина равна 0,7 ± 0,2 барн*. В ра-
ботах [33, 321 I был точно определен квадрупольный момент первого
2+-СОСТОЯНИЯ в 24Mg, равный Q = — 0,26 барн.
§ 1.2. ЭЛЕКТРОМАГНИТНЫЕ ПЕРЕХОДЫ
1.2.1. Предварительные сведения
о радиационных переходах
Одночастичная модель не может объяснить свойства многих
электромагнитных переходов в ядрах примерно по тем же причинам,
по которым она оказывается неспособной предсказать статические
квадрупольные моменты. Естественно, что вероятность перехода
будет намного больше для тех переходов, в которые дают когерент-
ный вклад много нуклонов (одновременно «прыгают» много нукло-
нов), чем для переходов, в которых изменяет конфигурацию только
один нуклон (одночастичные переходы). Эти идеи должны быть
количественно сформулированы, в частности, следует сравнить
экспериментальные матричные элементы электромагнитных пере-
ходов с предсказаниями одночастичной модели. В данном разделе мы
дадим краткий обзор результатов такого сравнения. Таким путем
можно также снова продемонстрировать коллективные свойства ядер.
Математические детали теории радиационных переходов в яд-
рах подробно рассмотрены в т. 2, так что здесь нет необходимости
останавливаться на этом. Поэтому начнем прямо с формул для ве-
роятностей электромагнитных переходов. Вероятность перехода
ядра из начального состояния | i> в конечное | /> с испусканием
* 1 барн = 10~24 см2.
2Ь
фотона электрического (а = е) или магнитного типа (а — ni)
с энергией /но и угловым моментом X имеет вид
Tfi(K Ц, Q)= -8л^ 11 4-(—ГХ+’|</|^Лц|»>Г- (1-16)
f X [(2Х4-1)!!]2 Л к с I 11 * 1 4
Здесь Q обозначает электрический (Qxy.) или магнитный (Мхи)
мультипольный оператор, которые даются следующими выраже-
ниями*:
(е) = Qxg = 2 [о г Яц (Йу) +
/
+ igsj Но (<о/с) (А ф I)-1Оу X rr V (г* ЯДФ, (1-17)
Йм (т) = -ip02 (gsj Sy ф2 (Аф I)-1 Sl] 1y) V (г* Яц)у, (1-18)
/
где сумма пробегает по всем нуклонам. Матрицы Паули и спиновые
матрицы обозначаются а и s соответственно, g, и gt—гиромагнитные
отношения спинового и орбитального угловых моментов, р0—
ядерный магнетон. Обычно не интересуются ориентацией ядра в на-
чальном и конечном состояниях, поэтому следует просуммировать
по магнитным квантовым числам конечного состояния Mf и усред-
нить по магнитным квантовым числам начального состояния
Тогда приведенная вероятность перехода определяется следующим
образом:
В(а, A; = 1— V |<ТуМу|^|^Л1г>|2 =
= |y^-KfPA||i>l2- (1.19)
Здесь были использованы теорема Вигнера — Эккарта
{J, Mf | ЙХи | J£ М£>= (Л AJ, | Mt цМ{) (Ji ,| йх || J£>, (1.20)
где (J/1| Йу. || J ty — приведенный матричный элемент, и усло-
вие нормировки коэффициентов Клебша — Гор дана. Вероятность
перехода можно теперь записать в виде
Т(Х; П)=т^ги^4(—Г'+'В(а’ Х)- (1-21)
А |(2Аф1)!!]2 Ъ, \ с )
Свойства ядра содержатся в приведенном матричном элементе
в выражении (1.20). Остальные множители в формулах (1.19) и
(1.21) являются лишь статистическими или геометрическими фак-
* Вт. 2 электрический и магнитный мультипольные операторы обозначе-
ны (е) и Яц (ш). Здесь для краткости они обозначены Q и М.
27
торами. Полученные общие формулы можно использовать в любой
модели ядра. Для этого необходимо получить волновые функции и
операторы перехода в соответствующих координатах (например,
в коллективных, см. гл. 2),а затем вычислить приведенные матрич-
ные элементы. Получим теперь обычные оценки вероятностей одно-
частичных переходов, пользуясь формулой (1.19). Для этого ядерные
вотновые функции возьмем в виде (1.4), а в электрическом мульти-
польном операторе (1 17) учтем лишь главный член,пропорцио-
нальный (ДУдц). В общем случае, когда спин начального состояния
ядра есть Jt, а конечного состояния — Jf, вклад в переход обычно
дают несколько электрических мультиполей. Например, согласно
закону сохранения углового момента, разрешены следующие зна-
чения мультиполей: к = = (J) + Jf)... (J} — J,)- Эти правила
отбора содержатся в коэффициентах Клебша — Гордана в формуле
(1.20). Некоторые из этих возможностей могут не осуществиться
из-за действия закона сохранения четности. Для EZ-переходов, как
следует из (1.17), четность изменяется по закону (—1)х, и посколь-
ку она определяется орбитальным угловым моментом I, то полу-
чаем, что (/, — If) должно быть четным, если Z четное. Однако и
после этого могут остаться еще несколько мультиполей.
Рассмотрим здесь лишь наиболее важные мультиполи с данным
Д7 и ограничимся случаем X = Д/ = Д/. Такой переход является
единственно возможным, если Jf — 0, как видно из примера на
рис. 1.9, где показан переход из состояния с J = к и четностью
( —1)х в состояние с Jn = 0+. При этом в переходе участвует
только мультиполь с к = J. Такие случаи часто встречаются,
в частности, для переходов в основное состояние в четно-четных яд-
рах, у которых спин основного состояния равен нулю. Учитывая
сделанные упрощения, легко вычислить вероятности одночастич-
ных переходов. Получаем из (1.21)
Т(Ек; Ы = Ы---к) = - 2(^+1) . (j х, Jf)RK,
' ’ к [(2Z ’ I)!!]2 Нс \ с ' 7
где
(1.22)
(1-23)
— радиальный матричный элемент, aS — комбинация коэффициен-
тов Клебша — Гордана, которая в нашем случае сводится к выра-
жению
S(J х (27> + 1)(7>-1/2)!(2Х+1)!!(27<)!!
” ’ f (27; + 1)(27>)!!А!(7<-1/2)!
(1 24)
Здесь J и J — большее и меньшее значенья 7, и J} соответственно.
Необходимо теперь оценить величины вероятности (1.22) для
одночастичных переходов. Воспользуемся для этого грубым приб-
28
лиженпем в формуле (1.23), полагая радиальные функции констан-
тами и нормируя их на единицу по объему ядра. В результате по-
лучим
/?х = (3/(^ + 3))2. (1.25)
После этого в формуле (1.22) остаются лишь две величины, ко-
торые связаны с конкретным ядром -— статистический множитель
S и радиус ядра Е. Введем удобные единицы для измерения времени
жизни, положив 5 = 1, тогда
Р- 2(X+D / 3 V е2 -1 /1 осх
1 (£M = -------------- ----- — со сек \ (1.26)
А.[(2Х+1)!!]2 U+3 ' hc\ с ) 7
*7 О
Рис. 1.9. Переход с уров-
ня с угловым моментом
X и четностью (—I)7’ в
СП-состояние может осу-
ществляться с испускани-
ем излучения мультиполь-
ности £Х.
Индексом W обозначают единицы Вайскопфа, который впервые их
ввел в работе [382]. В качестве единицы заряда здесь используется
заряд электрона е. Было бы неверным ожидать, что это справедливо
лишь для протонов в ядре и что нейтроны имеют заряд, равный нулю.
Если учесть эффекты отдачи, то нуклоны приобретают эффективный
заряд, который зависит как от мультипольности перехода, так и от
природы одночастичной волновой функции. Протонные и нейтрон-
ные переходы здесь не различаются, поскольку величины (1.26)
используются для сравнения со всеми экспериментальными перехо-
дами безотносительно к тому, в рамках какой модели рассматри-
ваются ядерные состояния. Для этого лишь необходимо знать выра-
жение для радиуса ядра, которое обычно выбирается в виде R а;
~ 1,2 У11/3 ферми.
Численные результаты часто полезно представить в виде зна-
чений ширин у-распада, определяемых по формуле
ГУ = АТ. (1.27)
Если энергия у-квантов Е, то величина (Ел), определенная по
аналогии с формулой (1.27) с помощью (1.26), пропорциональна
1. Чтобы читатель получил представление о порядке ве-
личин Гущ, приведем некоторые их численные значения для пере-
ходов различной мультипольности: = 6,8- 10-2эв (А = 1); Г?«7=
= 4,9-10 8 эв (X =2); rvllz =2,3-10“14 эв (А=3).
Для сравнения'с экспериментом следует использовать парциаль-
ные ширины у-распада. Поэтому должны быть сделаны поправки для
Учета конкурирующих процессов, например внутренней конверсии
или испускания частиц (если рассматриваемое состояние ядра лежит
выше порога вылета частиц).
29
1.2.2. Обсуждение экспериментальных
данных
а Электрические дипольные переходы. Поскольку электрические
дипольные и электрические квадрупольные переходы — весьма раз-
личные характеристики ядра, обсудим их свойства отдельно. Срав-
нивая эти величины между собой, можно наглядно убедиться в том,
как коллективные свой-
L 1 J i I J J J_J 1 । 1 J 1 I t ,
10 е 10 5 10"4 10 310 2 10 1 1 Т^/Т^
Рис. 1.10. Распределение вероятностей
£/-перехода (измеренных в единицах
Вайскопфа) для легких ядер. Заштрихо-
ванная гистограмма — то же для Е1-пе-
реходов, запрещенных по изоспину [338].
8 -
е -
Е1- переход
4 -
2 -
О ----1—i I
10~9 10е 101 10е 105 10* IO^Tj/Tjw
Рис. 1.11. Распределение вероятностей
£7-переходов в тяжелых ядрах [388].
ства ядер проявляются в
£2-переходах. Статистиче-
ское рассмотрение различ-
ных переходов особенно
удобно, поскольку оно
выявляет характерную
«гросс-структуру» свойств
электрических переходов
в ядрах. На рис. 1.10 от-
ложена частота появления
различных времен £/-пере-
ходов, измеренных в еди-
ницах Вайскопфа. Здесь
гистограмма представлена
только для легких ядер,
так что можно ожидать,
что в данном случае при-
менима одночастичная мо-
дель и, следовательно, од-
ночастичные оценки Вайс-
копфа для £/-переходов
должны давать правильный
порядок величины. Однако
все эти переходы являют-
ся более медленными, чем
дают оценки Вайскопфа:
среднее отношение состав-
ляет 0,055. Если учесть
эффективные заряды нукло-
нов, равные е!2 для прото-
нов и — е/2 для нейтронов
[202], это число изменится
в четыре раза и будет сос-
тавлять 0,2. Поскольку в вероятности перехода (1.16) входит квад-
рат матричного элемента, то полученный результат указывает на то,
что ядерные матричные элементы в среднем приблизительно в два
раза меньше, чем те, которые используются в единицах Вайскопфа.
Это расхождение является относительно небольшим ввиду грубости
используемой модели, и следует ожидать, что более детальное рас-
смотрение улучшит согласие с опытом. Такие улучшенные расчеты
зо
были сделаны Куратом [219,
220, 223].
На рис. 1.11 показана ста-
тистика ГУ-переходов в тяже-
лых ядрах. Они оказываются
значительно слабее, чем в
легких ядрах. Это, возмож-
но, указывает на то, что мно-
гие состояния с отрицатель-
ной четностью имеют значи-
тельно более сложную струк-
туру, чем та, которая пред-
полагается в одночастичной
модели. Соответствующие эф-
фекты подробно рассмотрены
в третьем томе.
Существуют, однако, так-
же уровни, для которых Е1-
переходы в основное состоя-
ние значительно усилены.
Это — гигантские дипольные
резонансы, которые встре-
чаются во всех ядрах в обла-
сти энергий 10—25 Мэв. Они
имеют типично коллективную
природу и подробно рассмот-
рены в гл. 10 и 11.
Основной механизм, обус-
ловливающий этот вид ядер-
ного движения, был уже
схематически описан в нача-
ле главы. Гигантские диполь-
ные резонансы представляют
собой вид ядерного движения,
в котором все протоны дви-
жутся в одном направлении,
а все нейтроны — в противо-
положном. Это создает самые
большие дипольные моменты,
которые возможны в ядре, и,
следовательно, возбуждение и
распад гигантских резонансов
характеризуются очень боль-
шими вероятностями у-пере-
ходов.
б. Электрические квадру-
польные переходы. На рис.
•12 и 1.13 представлена ста-
Рис. 1.12. Распределение вероятностей
электрических квадрупольных переходов;
в тяжелых ядрах [388].
Рис. 1.13. Распределение вероятностей
электрических квадрупольных переходов
в легких ядрах [388].
3t
тистика электрических квадрупольных переходов для тяжелых
и легких ядер соответственно. В противоположность Е/-пере-
ходам Е2-переходы часто очень усилены: в 10—103 раз по срав-
нению с единицами Вайскопфа. Это указывает на то, что суще-
ствует коллективное движение квадрупольного типа. Мы уже
знаем о существовании больших квадрупольных моментов, и не-
трудно понять, что эти два факта связаны между собой. Действи-
тельно, как будет показано ниже (гл. 6), большие внутренние ква-
друпольные моменты обусловливают вращение ядер и большие ве-
роятности переходов между ротационными уровнями.
Результаты данного раздела показывают, каким образом, изме-
ряя квадрупольный момент ядра и вероятности различных переходов,
можно установить коллективную природу ядерных состояний. В сле-
дующем разделе будет рассмотрено еще одно свойство ядер, кото-
рое поможет определить природу состояний, а именно энергии низ-
колежащих уровней, соответствующих возбуждению поверхност-
ных степеней свободы ядра.
в. Низкоэнергетические спектры (колебания и вращения). Вообще
говоря, модель оболочек предсказывает возбуждения одного нуклона
с энергией порядка 5—6 М.эв, что соответствует энергетическому ин-
тервалу между главными оболочками. Могут появиться возбужде-
ния с более низкой энергией (> 1 Мэе), соответствующие переходу
нуклона между подоболочками, однако согласно модели оболочек
такие возбуждения должны наблюдаться только у нескольких со-
седних изотопов и изотонов. Как только нуклоны заполнят подобо-
лочку, частицы должны перейти на следующую, более высокую
подоболочку, которая обычно отделена интервалом в несколько ме-
гаэлектронвольт. (Модель оболочек подробно обсуждается в гл. 8 и 9.)
Экспериментальные данные категорически противоречат этим
предсказаниям одночастичной модели. В четных ядрах, соседних
с теми, оболочки которых заполнены, систематически наблюдаются
низколежащие 2+-уровни с энергией возбуждения 0,5—1 Мэв.
Ботеетого, если все больше заполнять протонами и нейтронами одно-
частичные состояния так, что числа протонов и нейтронов будут
сильно отличаться от магических, то эти 2+-уровни опустятся до
энергий, меньших 100 кэв.
Для большей конкретности экспериментальные данные обычно
представляются следующим образом. В четно-четных ядрах наблю-
даются два вида низколежащих состояний положительной четно-
сти*. Один из них может быть назван колебательным, поскольку его
типичный спектр таков, что, как видно из рис. 1.14, энергия трипле-
та уровней 0+, 2+, 4+ почти равна удвоенной энергии первого
2+-уровня. Это наводит на мысль о гармонических колебаниях**,
для которых каждый из квантов колебаний имеет угловой момент,
* Существуют также низколежащие уровни отрицательной четности.
Они будут рассмотрены в гл. 9.
** Более подробно о квадрупольном вибраторе см. гл. 3.
32
равный 2h. Наблюдаемые состояния тогда представляют собой два
кванта с суммарным спином и четностью 0+, 2+, 4+.
Другой вид низколежащих коллективных состояний называют
враигргпельным. В этом случае, как показано на рис. 1.15, энергии
уровней приближенно описываются законом 1(1 +1). Такая за-
висимость положения энергетических уровней от спина по аналогии
с физикой молекул сразу же наводит на мысль о вращательной при-
роде этих уровней. Симметричный ротатор имеет вращательные энер-
гии е/ = I (I + 1) где — момент инерции.
-------------------------:
Рис. 1.14. Типичный спектр квад-
рупольиых колебаний поверхности
ядра.
Триплет уровней 0+, 2+, 4+ имеет энер-
гию приблизительно в два раза боль-
шую энергии первого 2+-уровня. Эго
указывает на то, что соответствующие
состояния представляют собой гармо-
нические колебания.
__________________2*
---------------- 0+
Рис. 1.15. Типичный
спектр вращающегося
ядра. Энергии уровней
вращательной полосы
описываются законом
/ (/+1).
Оба рассмотренных вида спектров не похожи на спектры модели
оболочек и интерпретируются как спектры коллективной природы
(см. в этой связи рис. 1.1 и 1.2); в особенности это справедливо для
вращательной схемы уровней. Ядра, имеющие колебательный спектр,
являются сферическими, т. е. совершают колебания вокруг сфери-
чески равновесной формы. Если же наблюдаются вращательные
спектры, то такие ядра являются деформированными, так как толь-
ко деформированные ядра могут иметь момент инерции, отличный
от нуля. Действительно, нуклоны, движущиеся в сферическом
потенциале, все еще движутся в том же самом потенциале, даже
если он поворачивается на некоторый угол. Следовательно, нук-
лоны не испытывают никакого сопротивления во время такого пово-
рота. Для деформированных потенциалов это не так (рис. 1.16).
С физической точки зрения можно ожидать, что ядра, близкие
к магическим, являются сферическими. Деформированные ядра
появляются, если вне замкнутых оболочек имеется достаточно боль-
шое число нейтронов и протонов, такое, что сферические оболочки
исчезают и вместо них возникают деформированные оболочки. На
Рис. 1.17 показано распределение магических чисел протонов и
нейтронов для ядер, там же указаны долины стабильности, для ядер,
2 Зак. 1218 33
наблюдавшихся в природе. Пересечение протонных и нейтронных
магических линий дает дважды магическое ядро. Можно ожидать, что
вдоль магических линий и поблизости от них расположены сфери-
ческие ядра, т. е., согласно сказанному, вибрационные ядра. Вдали,
как от протонных, так и от нейтронных магических линий следует
ожидать появление деформированных ядер с вращательным спект-
ром (заштрихованные области
Рис. 1 16 Схематическая картина движе-
ния нуклонов в сферической и деформи-
рованной потенциальных ямах.
Только вращение деформированной ямы приво-
дит к изменению потенциала, действующего на
нуклон и орбиты нуклона.
Рис. 1.17. Зоология ядер. Магические
числа протонов и нейтронов указаны
прямыми линиями.
Заштрихованные области указывают деформи-
рованные ядра. Следует ожидать, что ядра
с числом нуклонов, близким к магическому,
являются сферическими. Ядра известные в при-
роде, имеют Z<J |01 и < 150 [143].
на рис. 1.17).
В периодической таблице
имеются три или, возможно,
четыре экспериментально об-
наруженные области дефор-
мированных ядер, а именно:
А = 194-28, А = 1504-190,
А 222, и, возможно, вблизи
А == 8. На рис. 1.17 схе-
матически представлена пе-
риодическая таблица ядер, в
которой области деформиро-
ванных ядер указаны заш-
трихованными участками.
Вплоть до А « 40 числа
протонов и нейтронов ненам-
ного отличаются друг от дру-
га. Поэтому первые области
деформации с 2< N, Z<C 8
it8<N, Z< 20, указанные
на рис. 1.17, имеют N~Z
Однако при А > 40 линия
P-стабильности сдвигается в
сторону увеличения отноше-
ния числа нейтронов к числу
протонов. Этот сдвиг обуслов-
лен кулоновской энергией.
Таким образом, здесь про-
тонные и нейтронные оболоч-
ки частично не совпадают
вплоть до области редких зе-
мель и актиноидов, где наблю-
дается обширная область де-
формированных ядер, по-
скольку в них попадают ядра
с 50< Z< 82, 82 < N<
<126 и с 82<Z<126, 126<
</V<184. Однако и области,
отмеченные на рис. 1.17 циф-
рами 1 и 2, также должны
содержать деформированные
34
ядра [331 ]- В этих областях находятся сильно нейтронодефицит-
H[je (и> следовательно, нестабильные) ядра с N > Z.
Систематическое появление низкоэнергетических колебательных
и вращательных спектров, которые обсуждались выше, прямо ука-
зывает на существование коллективных форм движения в ядрах.
Эти низкоэнергетические возбуждения обусловлены коррелирован-
ным движением большого числа нуклонов. Рассмотрим вкратце
интерпретацию этих возбуждений на микроскопическом языке.
Предположим, что можно точно решить многочастичную задачу,
т. е. задачу N нейтронов и/протонов, движущихся по орбитам одно-
частпчной модели оболочек и взаимодействующих друг с другом по-
средством остаточного взаимодействия V (rit г}). Тогда после диаго-
нализации этого взаимодействия мы получим, что некоторые состоя-
ния сильно опустились вниз по энергетической шкале, а некоторые
сильно поднялись, так что центр тяжести всех уровней приблизи-
тельно сохранился. Обе группы состояний содержат коллективные
уровни. В первую группу войдут низкоэнергетические уровни,
рассмотренные выше, во вторую — высокоэнергетические коллек-
тивные уровни. Ниже мы увидим, что последние относятся к уров-
ням типа гигантского разонанса.
* * *
В этой главе была сделана попытка качественно обсудить наи-
более характерные экспериментальные свойства коллективного дви-
жения в ядрах. Рассмотренные вопросы также обсуждаются в книге
Престона [301] и в обзорной статье Дэвидсона [100]. Другую по-
лезную литературу по этому вопросу можно найти в статьях
[211] и [278].
2*
Глава 2. КОЛЛЕКТИВНЫЕ
КООРДИНАТЫ
Вместо того чтобы описывать ядро с помощью ЗА степенен сво-
боды, часто бывает не только удобным, но и необходимым ввести
новые координаты оД1 (х1( хза), которые являются функция-
ми ЗА координат ядра (хъ х3д). Назовем эти новые координаты
коллективными. Модель ядра (гамильтониан), сформулированная
с помощью коллективных координат, называется коллективной, мо-
делью ядра. Одним из недостатков такой коллективной модели яв-
ляется то, что функции оЯ (xr, ..., хзд) неизвестны*. Другими
словами, зависимостью оДМ от координат нуклонов в большинстве
случаев полностью пренебрегают. Коллективные координаты
обычно вводятся на основе классических представлений о ядре, на-
пример при использовании представления о поверхностных колеба-
ниях, вращении ядра или о колебаниях плотности протонов. Свой-
ства величин получаются непосредственно из этих определений.
Затем с помощью общих свойств инвариантности коллективный га-
мильтониан выражается через а*М. Разумеется, правильный выбор
коллективных координат имеет то преимущество, что он делает
проблему более простой и наглядной и, следовательно, приводит
к лучшему пониманию физической стороны задачи. Кроме того, это
уменьшает математические трудности. Естественно, что apriori не-
известно, правильно ли выбраны коллективные переменные. Имен-
но это следует установить, пытаясь получить правильное описание
свойств ядра.
Что касается использования классических представлений при
введении коллективных переменных, то в действительности такой
путь используется всегда, даже в так называемых «фундаменталь-
ных» подходах в нашей сложной многочастичной проблеме. То, что
называют «фундаментальным» подходом, в действительности являет-
ся весьма упрощенной моделью, которая описывает несколько взаи-
модействующих друг с другом точечных частиц с массой, отличной от
* Имеются многочисленные работы, посвященные обоснованию введе-
ния коллективных координат |51, 83, 204, 205, 231, 239—241, 253, 276, 277,
319, 356, 361, 367—369]. Частично они рассмотрены в т. 3.
36
нуля. Мы всегда конструируем гамильтониан, имея в виду более или
менее классическую картину. Квантовый аналог нашей классиче-
ской картины получается после применения соответствующих пра-
вил квантовой механики. Из атомной и молекулярной физики хоро-
шо известны соответствующие примеры: планетарная модель атома,
в которой атомное ядро играет роль Солнца, а электроны — роль
планет, модель ротатора для двухатомных молекул и т. д.
Рассмотрим два класса коллективных переменных, а именно
переменные описывающие движение поверхности ядра, и пе-
ременные описывающие флуктуации ядерной плотности.
§ 11. ПОВЕРХНОСТНЫЕ ПЕРЕМЕННЫЕ а[Х]
Коллективные координаты описывающие движение поверх-
ности ядра, определяются с помощью разложения отклонения по-
верхности ядра от сферической формы радиуса /?0 в ряд по сфери-
ческим гармоникам:
r(в, <р, /)=/?е[1+ <p)i. (2.D
1 Х,ц J
В классической картине [49, 50, 142, 146] сферические тензоры*
с/РЛ = {сс?.р.}, где р = Л, Л — 1, .... — Л, зависят от времени,
т. е. «хц = “Хц (()• и> следовательно, согласно (2.1) описывают
колебания поверхности ядра. Из инвариантности выражения (2.1)
по отношению к вращению следует, что «хц являются компонентами
неприводимого тензора ранга X и преобразуются по (2Z + 1)-мер-
ному представлению группы SO (3), т. е.
^ = 2^(0;) «XV. (2.2)
где величины Схц определяют поверхность ядра во вращающейся
системе способом, аналогичным выражению (2.1); 07- — утлы Эйлера,
связывающие обе системы координат (рис. 2.1). Это можно показать
следующим образом. Выражение для поверхности ядра в лаборатор-
ной системе дается формулой (2.1), во вращающейся системе оно
имеет вид
W', ср', О = /?оГ1+ V (-1)^х-ц(0^(6', Ф')1 . (2.3)
L X, ц J
Где углы 6', ср' определены во вращающейся системе (см. рис. 2.1).
Хорошо известно, что сферические гармоники при вращениях
преобразуются по формуле [306]
Гхц(0', ФЭ = 2£>Ш)Кхт(е, ф).
V
(2.4)
Более подробно о тензорных обозначениях см. б начале гл. 3.
37
Так как из свойств инвариантности поверхности относительно вра-
щения системы координат следует, что Л (6', ср', t) = Я (6, <р, t),
то из (2.1) и (2.3) имеем для каждого X
2(_])вал_м(/)уЛ(г(е, <P) = V(-I)vaz_v(oyzv(e', <р'); (2.5)
И V
подставляя (2 4) в (2.5), получаем выражение (2.2).
Поскольку радиус R (6, ср) является действительной величиной,
то
Отсюда, учитывая, что
Рис. 2.1. Связь между
двумя системами коор-
динат:
Оси xr, z' внутренней систе-
мы координат совпадают с
главными осями ядра. Схе-
матически указаны углы
Эйлера в/ (их определение
см. на рис. 5.1).
В модели оболочек
2(-im_uy^=2(-im_vHv. (2.6)
Ц V
Иц = ( — I)’1 П-ц, получаем
а1ц = (-1)^ах-ц. (2-7)
Это свойство можно рассматривать как
преобразование относительно обращения
времени, поскольку в данном случае опе-
рация обращения времени сводится только
к комплексному сопряжению. Кроме того,
поскольку R (в, <р) — скаляр, то из опре-
деления алц (2.1) следует, что их четность
должна быть ( —1)Л, т. е. совпадать с чет-
ностью сферических гармоник Ули. Таким
образом,
Р(а3щ)Р-1 = (-1)^, (2.8)
где Р — оператор пространственного отра-
жения. Формы ядерной поверхности
для квадрупольной, октупольной и гек-
садекапольной деформаций показаны
на рис. 2.2.
щра предполагается, что нуклоны движутся
более или менее независимо в среднем поле, которое имеет сфери-
ческую симметрию. Эквипотенциальными поверхностями являются
сферы R = 7? о- Такое среднее поле обусловлено замкнутыми обо-
лочками. Нуклоны вне замкнутых оболочек поляризуют сфериче-
ски симметричное поле остова. По мере увеличения количества та-
ких нуклонов этот эффект увеличивается, приводя к появлению де-
формированного ядерного среднего поля, эквипотенциальные поверх-
ности которого могут быть описаны выражением (2.1). В этом слу-
чае координаты R, 6, ср обозначают положения точки на эквипо-
тенциальной поверхности, описываемой параметрами о^ц.
Можно описать любое коллективное движение поверхности ядра,
если считать, что величины «хц меняются во времени, т. е. «хц =
= Kzii (0- Эти величины рассматриваются в качестве обобщенных ко-
ординат и являются коллективными динамическими переменными.
Как следует из представленного в предыдущей главе обсуждения
38
ебательного и вращательного спектров слагаемые с А = 2 (квад-
К°польные члены) в выражении (2.1) играют главную роль в ядерной
троскопии. Члены с X = 0 (монопольные члены) соответствуют
С менению объема ядра. Они обусловливают появление так называе-
компрессионных, или «дыхательных» колебаний [88] Можно
ожидать, что эти колебания соответствуют большим энергиям возбуж-
ения поскольку ядерная материя, по-видимому, является отно-
сительно несжимаемой. Члены с А = 1 обычно исключаются из
пазложения (2.1), потому что для малых а1|Хони соответствуют
перемещению всего ядра. Это легко показать, если рассмотреть ча-
стный случай а10 ф 0, «ц = ax-i = 0. Тогда форма ядра дается
выражением
R = Ro (1 + а1О1'1о) = Rn (1 + а10 (3/4л)^ cos 6). (2.9)
Рис. 2.2. Формы поверхности ядра различных видов де-
формаций.
Из (2.9) видно, что для малых а10 сфера сдвигается на величину
а10 (3/4 л)1/2, как показано на рис. 2.3. (Для больших а10 центр масс
также сдвигается, но, кроме того, деформируется поверхность ядра.)
Движение центра масс тривиально и, таким образом, члены с А = 2
являются первыми членами, которые представляют интерес. Члены
с А = 3 соответствуют октупольным колебаниям и связаны с 3_-сос-
тояниями. Они также представляют большой интерес (см. гл. 7).
Значения А в разложении (2.1), описывающем поверхность ядра,
имеют верхний предел. Так как представление о ядерной поверхно-
сти более или менее основывается на идее, что ядерную материю
можно рассматривать как континуум, то каждый максимум кривой,
описывающей поверхность ядра, должен содержать по крайней мере
один нуклон. Число максимумов кривой, описываемой выражением
= (1 + 2аХц^хц)> пропорционально А3. Отсюда получаем,
ц
что А < Д’/з, где /| — число нуклонов в ядре.
Рассмотрим теперь более подробно вопросы о движении центра
масс и о сохранении объема ядра. Как уже упоминалось, радиус
в формуле (2.1) выбирается так, чтобы были равны объемы де-
формированного и исходного, недеформированного ядра с радиу-
м = R 0; это предположение соответствует представлению о не-
39
сжимаемой ядерной материи. Следовательно, необходимо перенор-
мировать величину R0 для деформированного ядра, заменив ее
величиною Ro, такой, что объем (4'3) nR3 был бы равен объему ядра
с радиусом R = Ro (1 +2 ( — l)’1 «х-ц Ухц)- Это можно сделать
Х,ц
двумя способами. Либо ввести Ro, о котором говорилось выше, тогда
Ro будет зависеть от Ro и от параметров деформации аХц. Либо
сохранить исходное Ro в формуле (2.1), что приведет к соотношению
между параметрами «> м. В последнем случае будем иметь
(4/3)jiRg= J = =
Деформированное О
ядро
= (1/3) R30 J dQ (1 +2 (—1)х (27, + 1)54 [а[МхУ[М][01)3, (2. 1Q)
Рис. 2.3. Поверхность яд-
ра, описываемая малым
аю=А0 (ац=а|_|=0) со-
ответствует лишь смеще-
нию сферы (----------).
Большие а10 соответству-
ют тому, что центр тяже-
сти сдвигается и сфера
деформируется
(--------------)
где R=Ro(l + 2(—1)Цах-цУхц^. С точностью до членов второ-
\ X, ц J
го порядка по (aW 1) получаем
О = X (— 1 )х (2А + 1)14 [alM X У^ X yiojjio] +
х J
+ 2 (— 1)K+V (27, 4- 1)54 (2Г + 1)54 5 dQ [a™ X yiM][0] x
X X yix'l][o] x y[°]]I°J,
что можно легко свести к соотношению
О = «[Л + (4л)-54 £ (_ 1)X (2Х 1)*/. [И[Х] х а1М][0]. (2.11)
х
Аналогично можно получить ограничение, связанное с движе-
нием центра масс, если потребовать, чтобы начало системы коор-
динат и центр масс ядра находились в одной и той же точке:
р(г)гс/т = О. (2.12)
Объем
ядра
Здесь р (г) — распределение плотности ядра, которое для простоты
предполагается однородным. Вектор г = xlx + z/l2 -f- zl3 следу ю-
40
щим образом выражается через сферические координаты:
г=— (4л)*/« г[У[ЧхуЧ][о), (2.13)
т-пр Ё11] — единичный сферический вектор:
I в
Ь =----кйх+Щ), £о=13. ^=-^(1!-^).
} 2 Д/2
Для постоянной плотности условие (2.12) принимает вид
д
О = $ far [У[11 X У’ 1JI0] = J [У[ 1 ] х у 1 ]][0] $ гз dr, (2.14)
О
где
\ X. н )
Выполняя вычисления, аналогичные тем, о которых говорилось
выше, получаем
0 = а1П_з/2(4я)-% 2 (2Х+1)*/Д2Х' + 1)^(^ X
Л, X' \и и и/
X [cdzl X (2.15)
т. е. тензорное уравнение, справедливое для каждой компоненты р.
тензора первого ранга.
Если в разложении (2.1) имеются только четные мультиполи
(четные Z), то условие (2.15) выполняется всегда. В общем случае
условия (2.11) и (2.15) должны учитываться при рассмотрении ди-
намики системы (см. гл. 3 и 4). К счастью, в большинстве случаев
величины odx! << 1, поэтому если а!°1 = 0, то условие (2.11) выпол-
няется с точностью до малых членов порядка (cd1!)2. Аналогично,
условие (2.15) выполняется с той же точностью, если cd1! = О,
т. е. если в разложении (2.11) не учитывается дипольная дефор-
мация.
Если рассматриваются только члены с Л = 2, то разложение
(2.1) принимает вид
« = /?о(1+1]^У2ф (2.16)
где мы пока опустили индексX (=2) у переменныха. Полезно запи-
сать это уравнение поверхности в прямоугольной системе коорди-
нат:
(у2 tl2
1 + ахх + ауу — +
+ “zz 7? +2а^+ 2ttxz уг2<Zyz' (2-17)
Прямоугольные а-координаты подчиняются условию
ахх + + a2Z = 0. (2.18)
41
Эти формулы сразу же получаются из (2.16), если функции
У2ц(6, ф) выразить через х, у, z и г = (х2 + у2 + г2)'^:
(2-19)
Используя эти соотношения, находим
(2.20)
Мгновенные значения а описывают форму ядра или форму сред-
него поля ядра. Удобно перейти к системе, в которой осями коор-
динат являются главные оси симметрии ядра. Форма ядра в этой
системе имеет вид
/ , х'2 , и'2 , г'2 \
R=Ro ( 1 + а*х — + аиу — + ~ ) •
у г2 г- г- )
(2.21)
В а'-системе, или системе главных осей, а'ху = а'уг = <х'хг = 0.
Поэтому, согласно (2.2) и (2.20), имеем
аг = а_± = 0;
= Я_2,
Оц = 2^(61, 02, оз) av.
(2.22)
Таким образом, две величины а0 и с2 = °-2 описывают форму
ядра во внутренней, или собственной, системе координат, а три
угла Эйлера описывают его мгновенную ориентацию в пространст-
42
ве Вместо fl0 ий2О. Бор [50, 52] ввел два параметра 0 и у, свя-
занные с а0 и аг соотношениями
1/Т
c0 = pcosy, а2 = -^—psiny. (2.23)
Удобство
значения
тогда
их использования становится ясным, если рассмотреть
ядерного поля на главных осях. Введем
К, = R (О' = 90°, ср' = 0) = Ro (1 + бгж);
R2 = R(0' = 9O°, <p' = 90°) = Ro(l+6r!/);
R3 = R(0' = 0°) = Ro(l+6r2),
(2.24)
(2-25)
аксиально-
где k = 1, 2, 3 для х, у, z. В частности, ядро является
симметричным, если 7 = 0, 60, 120° ... Оно имеет вытянутую форму,
если а0> 0, и сплющенную, если а0<2 0. (См. также рис. 2.1, на
котором показана мгновенная ориентация внутренней системы
координат.)
В заключение перечислим результаты этого раздела. Сущест-
вуют два альтернативных способа описания квадрупольной дефор-
мации ядра. Можно использовать:
1. Пять переменных аг, alt а0, a_Jt а_2, которые определены
на равноправной основе, и особенно удобны в качестве коллектив-
ных динамических переменных в тех ядрах, для которых характерны
малые мгновенные отклонения от сферически симметричной равно-
весной формы. Это имеет место в так называемых вибрационных
ядрах, в которых совершаются малые квадрупольные колебания
вокруг равновесной сферической формы.
2. Внутренние координаты а0 и а2 (или, что эквивалентно, па-
раметры р и у), которые характеризуют форму ядра во внутренней
системе координат, и три угла Эйлера 0Ъ 62, 03, характеризую-
щие ориентацию внутренней системы координат в пространстве.
Этот набор переменных особенно удобен в качестве коллективных
динамических переменных для тех ядер, которые обладают ста-
тической деформацией. В обоих случаях мы имеем пять степеней
свободы. (Величиныа2ц в лабораторной системе являются комплекс-
ными числами, но так как они подчиняются дополнительным усло-
виям а2ц = ( — 1)ца2-ц> то и в этом случае мы имеем пять неза-
висимых параметров.)
§ 2.2. КОЛЛЕКТИВНЫЕ ПЕРЕМЕННЫЕ (/|? |-
ОПИСЫВАЮЩИЕ КОЛЕБАНИЯ ПЛОТНОСТИ ЯДРА
Коллективные переменные для описания ядерного движения,
НО(2БеТствУЮ1цего возбуждению гигантского резонанса мультиполь-
и л, определяются с помощью мультипольного разложения велп-
43
Ро
рп(°)
Рр(°1
R
Рис. 2.4. Распределение плотности
нейтронов и протонов в равновес-
ном состоянии Предполагается од-
нородное распределение.
чины 11 (г, t), которая характери-
зует отклонение плотности ядра от
ее равновесного значения. Восполь-
зуемся гидродинамическим под-
ходом, в котором ядро описывает-
ся сферой, заполненной прони-
кающими одна в другую протонной
и нейтронной жидкостями. В рав-
новесном состоянии обе эти жид-
кости равномерно заполняют объем
ядра. Но как только начинает дей-
ствовать возмущающее поле (на-
пример, кулоновские силы между протонами или внешнее электро-
магнитное поле), протонная и нейтронная жидкости разделяются.
Это разделение и описывается флуктуацией плотности т] (г, t).
Более точно, в гидродинамическом подходе, плотности протонов и
нейтронов описываются формулами
Рр(г. 0 = Рр(0)11 +П(г, /)];
рпИ. 0=Pn(0)[i-^-n(r. о]. (2,26)
где рр(0) и рп (0) =-р рр (0)— равновесные протонная и нейтрон-
ная плотности соответственно (рис. 2.4), а ц (г, /) — отклонение
плотности от равновесного значения. Как видно из (2.26), для
любого момента времени t выполняется условие
Рр(г> 0 + Рп(г» /) = Рр(0) + рп(0) = ро = const, (2.27)
т. е. суммарная плотность является величиной, не зависящей от
координат и времени. Это соответствует пренебрежению компрес-
сионными колебаниями (сжатием и разрежением ядра).
Флуктуацию плотности т] (г, /) можно представить в виде
ц (г, t) = ц (г) ехр (— iQ/), (2.28)
где Q — частота колебаний плотности, являющихся, как предпо-
лагается, гармоническими. Действительно, это предположение всег-
да с хорошей степенью точности выполняется в ядерной гидродина-
мике (см. гл. 10). Мы увидим, что ц (г) удовлетворяет уравнению
Гельмгольца
V2r] (г) + &2т] (г) = 0 (2.29)
с однородным граничным условием
n-Vn(r)|noEepXH = 0, (2.30)
где п — вектор, нормальный поверхности ядра. Из уравнения
(2.29) следует, что колебания плотности в ядре описываются вол-
44
(2.31)
вым уравнением. Волны плотности являются своего рода звуко-
Н й волной в ядерной материи. Волновое число k следующим об-
азом связано с константой энергии симметрии х в формуле Бете —
Вайнзекера для масс ядер и с эффективной массой нуклона М*
(см- гл. Ю):
= k2»u2 = k2 — —
М* Л2
Граничное условие (2.30) означает, что радиальная скорость vr,
пропорциональная Vr ц (г), исчезает на поверхности ядра, так как
поток через нее равен нулю. Нормальные решения уравнения (2.29),
удовлетворяющие условию (2.30), имеют вид
(г) = Нп) Д (М"> г) Гхв (0, <р), (2.32)
где п характеризует обертоны; X — мультипольность колебаний;
—нормировочные константы. Волновые числа этих нор-
мальных мод (2.32) получаются из граничного условия (2.30), ко-
торое теперь принимает вид
dlK (*ь г)
dr
= 0.
r = R
(2.33)
Решения этого трансцендентного уравнения легко получаются чис-
ленно. Они приведены в табл. 2.1 вплоть до четвертого обертона и
гексадека пол ьной мультипольности (X = 4).
Т а б'л ищ а 2.1
Собственные значения Z-/n k'^R для гигантских резонансов
различной мультипольности
п х=о Х=1 Х=2 Х = 3 Х=4
1 4,493 2,081 3,342 4,514 5,646
2 7,725 5,940 7,289 8,583 9,840
3 10,904 9,205 10,613 11,972 13,295
4 14,066 12,404 13,846 15,244 16,609
Таким образом, общее решение временной задачи дается выра-
жением
оо оо X
П(г, 0= £ Z Ё (-lW-n(Mp(r). (2.34)
п=1 Х = 0 ц = —X
Компоненты образующие сферический тензор д*'1) РД явля-
О^Ся Коллектиеными координатами для колебаний плотности.
Нпе еД?оеН"е (2 34) полезно сравнить с соответствующим определе-
м (2.1) для поверхностных переменных а[Х1. Используя тот
45
факт, что колебания плотности должны быть действительными и ин-
вариантными по отношению к вращениям, и повторяя те же рас-
суждения, которые привели к формулам (2.7) и (2.8), получаем
Л1--(-и-Л; I ,235.
где Р — оператор пространственного отражения.
Некоторые виды распределений плотности иллюстрируются на
рис. 2.5. Дипольные колебания (X = 1) соответствуют движению
Квадрупольные
Монопольные
Рис. 2.5. Графическое представление колебаний плотности для ги-
гантских резонансов различной мультипольности:
— — недостаток протонов и избыток нейтронов; + — избыток протонов и
недостаток нейтронов. Эти распределения изменяются во времени.
протонов (указанных знаком плюс) в одну сторону ядра, а нейтро-
нов — в другую. Квадрупольные колебания соответствуют кон-
центрации протонов на полюсах сферы, а нейтронов — на экваторе.
Наконец, монопольные колебания соответствуют сферически сим-
метричному движению протонов к поверхности, а нейтронов —
к центру ядра. Конечно, эти распределения являются динамиче-
скими, т. е. протонная и нейтронная жидкости проникают друг в дру-
га и периодически обмениваются местами.
§ 2.3. КАНОНИЧЕСКИ СОПРЯЖЕННЫЕ ИМПУЛЬСЫ
И ОПЕРАТОРЫ РОЖДЕНИЯ И УНИЧТОЖЕНИЯ
ФОНОНОВ
Канонически сопряженные импульсы лРД соответствующие
переменным должны удовлетворять обычным коммутацион-
ным соотношениям
[w> ах'ц'] = — 6fl|V ; (2.36а)
[лхц, = [аХц, ах'ц-] =0. (2.366)
Введенные здесь канонические импульсы являются квантовомеха-
ническими операторами. Выражения в правой части соотношений
46
c eg) инвариантны по отношению к вращениям и пространственному
отражению. Отсюда можно получить трансформационные свойства
пцчин по отношению к вращениям в пространстве. Для этого
рассмотрим соотношение (2.36) для частного случая Z = Z', р, = р':
•П'Хц = \h. (2.37)
Очевидно, это означает, что лХц, действуя на аХм, дает — ik, т. е.
(лхцахц) = — \h. (2.38)
Это соотношение не зависит от системы координат, следовательно,
величина при вращении должна преобразовываться контра-
градиентно по отношению к аХц> т- е. с помощью матрицы враще-
нийД[Х]*. Поскольку соотношение (2.38) инвариантно по отношению
к действию оператора пространственного отражения Р, то из свойства
Р(ахц) Р-1 = ( — 1)Л «хц следует:
(«Ли)^1 = (—l)x«Xu- (2.39)
Свойства канонического импульса по отношению к обращению
времени можно получить также непосредственно из соотношения
(2.38). Операция обращения времени в данном случае является ком-
плексным сопряжением. Выполняя операцию комплексного сопря-
жения для соотношения (2.38) и используя (2.7) получаем
(л£ц а£ц) = (лхц (— 1 f ах-ц) = + ^. (2.40)
Сравнивая это с соотношением (2.38) для компоненты с индексом
— р, имеем
(лх-мах-ц) = — (2.41)
и
Лм=-(-1Г^-ц, (2.42)
т. е. при обращении времени канонические импульсы изменяют фазу
и меняют знак второго индекса на противоположный. Мы получили
несколько важных свойств канонических импульсов: величины
л[Х] образуют неприводимый тензор ранга X четности (— 1)\ т. е.
при поворотах системы координат преобразуются согласно соотно-
шению
Лхц = 2 D^, (0у) rtxv , (2.43)
где — тензор импульсов во вращающейся системе. Эту фор-
мулу полезно сравнить с формулой (2.2). Поскольку мы требуем
выполнения перестановочных соотношений (2.36а), (2.366), то
величины и оД-] должны теперь рассматриваться как опера-
47
торы. Эти соотношения сразу же позволяют перейти к квантовоме-
ханическому описанию, если выразить гамильтониан ядра через
и Подобным же образом можно ввести тензор импульсов,
канонически сопряженных координатам Обозначим его
jy(n)[X]_ Разумеется, эти операторы должны удовлетворять тем же
перестановочным соотношениям (2.36а), (2.366) и преобразовывать-
ся согласно (2.39), (2.41), (2.43).
Иногда очень полезно ввести вместо операторов и a[,-l
операторы рождения и уничтожения фононов — и рхц соот-
ветственно. Это можно сделать с помощью канонического преоб-
разования:
«Лц = —Vх (Рм» +(—
лхм= i ((—IFPx'-u—₽хц)-
(2.44)
Выражая рхц и через аХц и лХ11 [см. ниже (2.46)] и используя
соотношения (2.36), легко получить коммутационные соотношения
для новых операторов:
Рх'ц' Рхц.— РхцРх'ц'
[Рмо Ржи'] = [Рлц. Рх'ц']=О-
(2.45)
Это обычные коммутационные соотношения для бозонов. Так как
операторы
о + 1 Г/ \—‘4 " • [ 1 л- о "4
z у / \ z /
(— 1)м
(2.46а)
и
Рхц = 4-
,Л(—l^ax-jx + i 1/2 Яхц
(2.466)
преобразуются по отношению к вращениям в пространстве с по-
мощью матриц D[Z1 и соответственно [см. формулы (2.2)
и (2.43) ], то эти фононы имеют полный угловой момент Л с проек-
цией р на ось z. Согласно (2.8), (2.39) и (2.46), их четность опреде-
ляется соотношением
P(Pxt)^"1 = (-l)xPxt« (2.47)
так как оператор л^ц, согласно формуле (2.39), имеет ту же чет-
ность, что и оператор aKll.
Трансформационные свойства операторов рождения и уничто-
жения по отношению к обращению времени легко получаются из
соотношений (2.46). Выполняя соответствующую операцию комп-
48
лексного сопряжения, получаем
т<)
— i 1/2
М-) “
"J = (-1)“₽\+_ц,
(2.48}
Гце f’ — оператор обращения времени. Аналогично
^(Рлц)Т-1 = ₽;м = (-1)^х-ц- (2.49)
С помощью (2.47), (2.48) и (2.42) легко проверить, что это согла-
суется с трансформационными свойствами по отношению к обра-
щению времени для операторов aKll и
Аналогично можно ввести операторы рождения q^ и операторы
уничтожения <7хц для фононов, соответствующих гигантскому муль-
типольному резонансу (гионов — см. гл. 10.11):
(П) _ / (~+(Ю , / 1Щл<П) 1-
п£’= и (4-/<вГ>йГ))“((-i)"
(2.50)
Повторяя те же самые рассуждения, что и выше, можно получить,
что операторы qj^ описывают бозоны четности ( — 1)х с полным
угловым моментом X и проекцией на ось z, равной р.
Множители (*/2 ^/Вх°Н)1/2 и + i (х/2 ^Вх<ох)1/2 в формулах (2.44) и
(2.50) определены таким образом, чтобы, во-первых, операторы унич-
тожения были нормированы на единицу [см. (2.45)] и, во-вторых,
гамильтониан гармонического осциллятора был бы диагональным.
Как будет показано в следующей главе, параметры В-, и харак-
теризуют гармонический осциллятор.
❖ * *
Общие свойства коллективных координат обсуждаются в рабо-
тах [43, 93, 100, 211]. Некоторые вопросы их обоснования рас-
сматриваются в [367].
Глава 3. СТРУКТУРА КОЛЛЕКТИВНОГО
ГАМИЛЬТОНИАНА ЯДРА
В предыдущих главах обсуждались различные виды коллектив-
ных движений в ядрах, были даны определения и рассмотрены свой-
ства коллективных переменных. Обратимся теперь к формулировке
ядерных моделей, иными словами, попытаемся найти коллективные
гамильтонианы, которые в полной мере соответствуют словам
«коллективная модель ядра». Весьма существенно, что структура
различных коллективных гамильтонианов определяется наиболее
легко и в наиболее общем виде с помощью трансформационных
свойств коллективных переменных по отношению к вращению, об-
ращению времени и преобразованию пространственной инверсии.
Неопределенными остаются лишь несколько констант в различных
членах, содержащих коллективные координаты. Эти константы бу-
дут входить в виде произвольных параметров, зависящих, вообще
говоря, от JV и Z. Их значения должны быть найдены впоследствии
либо подгонкой рассчитываемых значений к определенным экс-
периментальным данным, либо с помощью анализа на более глу-
боком уровне, например с помощью микроскопического рассмотре-
ния коллективного движения. Несколько примеров применения та-
кого подхода даны в гл. 10 и Приложении А.
Введем обозначения для различных операций со сферическими
тензорами. Определим здесь, что означают эти сокращенные обозна-
чения. Произведение двух сферических тензоров
= (3.1а)
В[^]=(ВХ'м'}, (3-16)
дающее новый сферический тензор
(?[*"] = (3.2)
где {АХ|1} обозначает набор сферических компонент тензора, сим-
волически записывается в виде
(3.3)
50
и означает, что
Сх,"ц"= 2 (лл/х" |ни'мя) АцВл'ц'-
м.ц'
(3.4)
Здесь (M/Z,"| ИН Н”) — коэффициент Клсбша — Гордана. Сокращен-
ное обозначение (3.3) позволяет избежать явной записи сумм в (3.4).
Более длинные обозначения часто крайне утомительны, в особен-
ности, когда связываются более чем два сферических тензора.
Вернемся теперь к построению коллективного гамильтониана.
Для того чтобы сохранялись угловой момент и четность, ядер-
ный гамильтониан Н оДД должен быть инвариантным по
отношению к вращению в пространстве и пространственному отра-
жению. Следовательно, должны рассматриваться лишь те комбина-
ции операторов и которые инвариантны относительно
вращения и преобразования пространственной инверсии. Кроме
того, в силу инвариантности гамильтониана по отношению к обра-
щению времени выражение для кинетической энергии Т (л[*Д а[?4)
должно содержать произведения лишь четного числа канонических
импульсов П*ХЕ Согласно (2.42) имеем
(3.5)
Здесь Т — оператор обращения времени (комплексного сопряже-
ния). Соотношение (3.5) может быть записано в сокращенной форме
Т(л[М) +„[xr. (3.6)
Теперь подробно обсудим один важный случай, а именно га-
мильтониан низколежащих квадрупольных колебаний поверхно-
сти ядра.
§ 3.1. КВАДРУПОЛЬНЫЕ КОЛЕБАНИЯ ПОВЕРХНОСТИ ЯДРА
Единственными коллективными переменными, которые нам необ-
ходимы в данном случае, являются величины ctI2l, т. е. предпола-
гается, что деформация поверхности ядра имеет квадрупольную
симметрию. Гамильтониан состоит из двух слагаемых — кинетиче-
ской и потенциальной энергий:
Н = al2)) + V (а[21). (3.7)
Предполагая, что эти слагаемые можно разложить в ряд по малым
величинам cJ2l и л42Е получаем
T(nt2J, a[2)) = ^-L]/5/B2j[n[2]x ni2)]<°) +
+ вз [[л[21 X cd2)][2] х л12)][О(3.8)
V(«[2J) = [а[2] х а[2]][0] _|_ Cs | [а[2] х а[2]][21 х а[2]][0] +
+ с4 [а!21 X CJ2]][0]. [а[2] х а[2]j[0] + _ (3.9)
51
Связывание различных тензоров в формулах (3.8) и (3.9) в пол-
ный угловой момент, равный нулю, т. е. в скаляр, обеспечивает вра-
щательную инвариантность гамильтониана. Назовем параметры Bv
в слагаемых кинетической энергии в (3.8) массовыми параметрами,
а параметры Cv в слагаемых потенциальной энергии — параметра-
ми жесткости. Они характеризуют инерцпальность коллективного
движения и деформируемость ядра соответственно. Структура
выражений (3.8) и (3.9) остается единственной до тех пор, пока
мы ограничиваемся разложением в степенные ряды и не рассматри-
ваем полюсные слагаемые, например ((с<Л21 X а[21][0])-1. Это, по-
видимому, неочевидно для члена четвертого порядка в разложении
(3.9), поскольку могут быть другие варианты связывания тензоров
а[21, например
[[а[2] X X [cd2] X «E2l][/]j С°], (3.10)
где I =1, 2, 3, 4. Легко видеть, что члены с нечетным I тождест-
венно равны нулю из-за свойств симметрии al2J: если, например,
поменять местами две величины а! 21 в первом множителе, то появит-
ся фактор (— I)2, но в остальном выражение (3.10) не меняется.
Более того, члены с четным I пропорциональны члену с I = 0, кото-
рый входит в выражение (3.9). Это можно показать прямым вычис-
лением или с помощью следующих рассуждений.
Рассмотрим общий случай, когда четыре тензора «C/'vl (v = 1,2,
3, 4) связаны в скаляр. Ранги /\ этих тензоров не должны равняться
друг другу. Инвариант четвертого порядка в этом случае имеет
вид
[cJ/‘] х аБЛ]П'] X [cJ/’l X сс1Л][7'] [о]. (3.11)
В этом выражении тензор о&БЛ связан с тензором так, что
образуется промежуточный тензор с угловым моментом J’\ ана-
логичным образом связаны тензоры а[Л и аЬЛ. Промежуточные
тензоры ранга J' связаны в скаляр (вращательный инвариант)
нулевого ранга. Можно, однако, осуществить другую схему связи,
а именно а[,11 и a[/J связать в тензор ранга J", а а[Л и «1Л —
в тензор ранга J" и эти промежуточные тензоры связать в скаляр:
[[oJ/Л х х [аБЛ х аБЛ]17*]](0]. (3.12)
Как известно, существует унитарное преобразование между
двумя схемами связи (3.11) и (3.12), которое имеет следующий
общий вид:
[[а!/Л х X [о4/Л х =
= _ ((А /г) J 12 Оз /4) А-й J I (/1 /з) Аз (/г /4) А1> А X
J24
X [[a[/11 X аБЛ][Лэ] х [аБЛ х аЬ\]][Л4]][-/]>
(3.13)
52
где
вол
матрица унитарного преобразования выражается через 9/-сим-
[357]:
C(/i /2) 12 О'3 i&) *^34’ I (Л I3) ^13 (1'2 *^24’
[(2Jj2+ 1) (2J84+ 1) (2Лз+1) (2J24+ 1)]1/2
А /г
/з ii
Аз А4
J12
Ai
J
(3-14)
g /-символ может быть легко найден с помощью таблиц* [307]. В на-
шем случае J = 0 и, следовательно, J12 = J3i = J' и J13 = J2i =
== J". Матрица унитарного преобразования (3.14) равна
<(Л /з) J' (/з А) 01 (л /з) J" (j2 Г; о> =
А /г J
= (2./' + 1)(2Г+1)
/з /4 >'
J" J" 0
(3.15)
9/-Символ сводится к 6/-символу по формуле
/1 /2
/з /4 J
J" J" 0
i/2+/3+j'+j"[(2J'+1)(2J"+1)]_1/2|{1 /а Jп
I ii /з J
(3.16)
и преобразование между двумя схемами связи (3.11) и (3.12) можно
записать в явном виде:
[[alA] X 1 X [al,3l X J'J][oj =
= V(— i)^+A+J'+J" [(2J'+ 1)(2J" + 1)11/Z
j"
X [[«IM X al^U"]] [[od/sl X «[/’«J]!7"!]!0!. (3-17)
/1 /2 J' ] x
!i is J I
Отсюда следует, что в частном случае а1й! = а[/*1 = а[/з1 =
= а[2) соотношение (3.17) сводится к системе линейных одно-
родных уравнений для различных возможностей связи в (3.10).
Легко показать, что определитель преобразования (3.17) в указанном
частном случае равен нулю, и следовательно, выражения (3.10) для
I = 2 и 4 линейно связаны с выражением (3.10) для I — 0.
§ 3.2. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ ПОВЕРХНОСТИ ЯДРА
До тех пор, пока мы ограничиваемся только квадрупольной
Деформацией поверхности ядра, вид гамильтониана, даваемый фор-
мулами (3.8) и (3.9), является совершенно общим. Массовые пара-
. * Свойства 3/
А т. 2.
6/- и 9/-СИМВОЛОВ кратко рассмотрены в Приложении
53
метры Bv и параметры жесткости Cv должны рассматриваться
как параметры теории, которые могут быть получены или подгон-
кой по экспериментальным данным, например, энергий уровней
вероятностей перехода, или рассчитаны в рамках другой, более
сложной, модели ядра. Как будет видно из § 10.8 и из Приложения А,
эти параметры можно рассчитать в гидродинамической модели ядра
(с использованием приближения безвихревого течения или без
него). Они могут быть также получены в рамках так называемых
микроскопических моделей (см. в т. 3 описание модели оболочек
и сверхтекучей модели ядра). Таким образом, гамильтониан (3.7)
не подразумевает какую-либо конкретную модель ядра. Эта формула
лишь выражает гамильтониан через переменные а[2Т В ней со-
держатся и кинематические свойства этих переменных, т. е. она опи-
сывает поверхностное движение квадрупольного типа с положитель-
ной четностью и т. п. Очевидно, что энергетический спектр, соот-
ветствующий такому гамильтониану, зависит от значений параметров
Bv и Cv, так что для разных наборов этих параметров будут
получаться совершенно различные спектры. Мы увидим, что в за-
висимости от вида потенциальной энергии V (а[21) этот гамильто-
ниан описывает колебания около равновесной сферической формы
ядра, вращения деформированного ядра, а также вращения и коле-
бания деформированного ядра. Свойства и различные физические
следствия общего выражения для потенциальной энергии (3.9) под-
робно рассмотрены в гл. 4.
Рассмотрим важный частный случай гамильтониана (3.7),
а именно гармонические колебания поверхности ядра. Это также не-
обходимо для ознакомления с методами, используемыми при реше-
нии задачи на собственные значения для коллективного гамильто-
ниана. Вообще, чтобы получить правильное динамическое описание
квадрупольных поверхностных степеней свободы, следует учесть
несколько членов в формулах (3.8) и (3.9). Предположим, однако,
что для некоторых ядер первые слагаемые в формулах (3.8) и (3.9)
дают главный вклад, а членами более высокого порядка по л^2! и
cJ2J можно пренебречь. В этом случае мы имеем гамильтониан
квадрупольного осциллятора*
HHQ= — (±/5/Вг) [л!2] х 4- (-А- J/5GJ [ai2Jx a[2l][°J =
= (2BJ-1 л2ц л2ц + 4- с2 2 а*ц а2ц, (3.18)
и 2 ц
где в последнем выражении использована формула для коэффициен-
та Клебша — Гор дана (//0 | р — рО) — ( — 1)/+**/(27 + 1)1/2-
* Формализм для описания поверхностных колебаний другой мультиполь-
ности в гармоническом приближении полностью аналогичен случаю гармо-
нических квадрупольных колебаний. Необходимо заменить лишь индекс муль-
типольности 2 на X, если рассматриваются колебания с мультипольностью X.
54
учитывая, что
Л2ц= — (—
«2р = (—1)^«2-ц.
и вводя в (3.18) фононные операторы согласно (2.44), получаем
Яно = Л®22(р2+/р2м+1/2), (3.19)
И
где _____
co2=J/G/B2 (3-20)
__частота гармонического осциллятора.
Введем далее оператор числа фононов
И2ц=Р2цр2ц. (3.21)
Используя коммутационные соотношения (2.45), легко показать, что
{HHQ, п2ц] = 0, (3.22)
т. е. собственное значение оператора п2(1 является хорошим кванто-
вым числом. Гамильтониан (3.19) можно выразить через оператор
Ян<2 = Й<о21(«2И 4-1/2). (3.23)
в
Найдем теперь спектр и соответствующие собственные функции
гамильтониана (3.19). Определим фононный вакуум |0> соотно-
шением
р2(1|0> = 0; (3.24)
отсюда
»2ц I 0 > — 0.
Это означает, что в вакуумном состоянии фононы отсутствуют.
Волновая функция, описывающая N фононов с индексом р, имеет
вид
Ч = °> = (₽2+в)"м I 0>. (3.25)
У'/ц раз
Индекс N указывает, что в этом состоянии находятся N ц фононов
вида р. С помощью коммутационных соотношений (2.45) легко най-
ти, что
ПгцРгц = 02ц (1 4" °2ц)> (3.26)
тогда
П2ц Фдгц = /12ц02ц ••• 02 ц | 0> = фд?ц 4* 02цИ-2ц 02ц • 041 | 0>- (3.27)
раз (Мц — 1) раз
55
(3 ДС,ЮЛЬЗУЯ ЭТ° соотношение —1) Раз’ получаем с учетом
(3-28>
Из соотношения п2м-Р2+м = Рг^Щр' имеем
п2ц'11^ = 0 для р#=р'. (3.29)
Выражение (3.28) и (3.29) можно записать в виде
VVVW (3-30)
Таким образом, название «оператор числа фононов» для п2„ впол-
не оправдано. Если имеется более общее состояние с N_2 фонона-
ми с р = — 2, AL, фононами с р = — 1 и т. д. до Af2 фононов
с р = 2
^w-22V-iNowiiV2 = ••Рг-г) (Р^-1 ...p^-i)...
W_2 раз /V раз
(р+...р+)|О>, (3.31)
Л'2 раз
то, как следует из (3.30),
п2р%г_2....¥2 = Лр%г_2...м2 (3.32)
и
Wv_2...w2 = v n2(l^w_2...N2 =
ц= —2
= (ЛС2 + AL, + Л'о + N, + TV2) ^w_2...n2 = 2_.(3.33)
Следовательно, сумма
2 „
2 «2ц = N (3.34)
H=-2
описывает полное число фононов, находящихся в состоянии ... n2
независимо от индекса р. Гамильтониан (3.23) можно теперь за-
писать в виде
Hhq = (N + 5/2) Йсо2. (З.Зб)
Из уравнения (3.33) следует, что фдг_2 ... является собственной
функцией оператора Hhq, соответствующей энергии Nh(o2:
Hhqn2 = GV+ 5/2) S©2tpw_2...N2, (3.36)
где N = ^_2 + ^_1 + ^ + /^4-/^2 — полное число фононов.
Следовательно, каждый фонон имеет энергию Н<в2. Основное состоя-
ние, которое находится ниже всех по энергии, совпадает с ваку-
56
умным
денное
Х₽2>1
РгцР-че
состоянием. Оно имеет энергию (5/2) Й<о2. Первое возбуж-
состояние является однофононным состоянием (W = 1)х
О > с энергией (1 + 5/2) Й<о2. Второе возбужденное состояние
, —двухфононное с энергией (2 ф- 5'2) Йсо2 и т. д.
3.2.1. Построение собственных функций
оператора углового момента
До сих пор мы не рассматривали угловые моменты различных
собственных функций tpw_2jv_1 ... дг2. Начнем с нижайшего со-
стояния.
а. Вакуумное состояние | 0). Оно описывает основное состояние и
по определению имеет угловой момент, равный нулю, и положитель-
ную четность для четно-четных ядер. Для четно-нечетных и нечет-
но-нечетных ядер вакуум может быть определен как состояние,
имеющее угловой момент /, его проекцию т и четность л, т. е. | jm >я.
Однако более удобно определить фононный вакуум в этих случаях
так же, как и для четно-четных ядер. Основное состояние тогда опре-
деляется в виде |0>- \jm >п, где |/т>л описывает состояние по-
следней нечетной частицы (частиц). Выберем это последнее опреде-
ление, так как в основном состоянии четно-четные ядра имеют нуле-
вой спин и положительную четность, тогда как для остальных ядер
благодаря наличию нечетных нуклонов основное состояние может
иметь угловой момент, неравный нулю, и отрицательную четность.
Ниже будут рассматриваться четно-четные ядра*. В этом случае
L2|0> = 0; (3.37а)
Р|0>=ф-|0>, (3.376)
где L и Р обозначают операторы углового момента и четности со-
ответственно. Следует подчеркнуть, что соотношения (3.37) вместе
с (3.24) определяют вакуум. Определения (3.37) для четных ядер
выбираются с учетом наших эмпирических знаний об основных
состояниях четно-четных ядер.
б. Первое возбужденное состояние РффО>. Поскольку оператор
рождения фонона при вращении в пространстве преобразуется с по-
мощью матрицы конечных вращений [см. (2.2), (2.43), (2.46)]
= (3.38)
где b}v — оператор рождения фонона во вращающейся системе,
то состояние р^|0> преобразуется совершенно аналогично (3.38).
Следовательно, функция Ргц | 0> описывает состояние с угловым мо-
ментом 2 и проекцией момента на ось z, равной р. Соотношение
[ о8) можно интерпретировать в том смысле, что фонон обладает
Нечетные ядра обсуждаются отдельно в гл. 9.
57
угловым моментом 2 и проекцией на ось z, равной р. Это заключе-
ние следует непосредственно из трансформационных свойств вол-
новой функции и операторов по отношению к вращению в прост-
ранстве*. Следовательно, можно записать
L2₽2+u|0> = 2(2+1)S2₽2+|0>; 1 (3 зд)
4₽2^|0> = рГф2^|0>, )
где L — оператор углового момента.
в. Нижайшие возбужденные состояния гармонического квадру-
польного осциллятора. Теперь мы можем получить нижайшие воз-
бужденные состояния. Введем для них обозначения
\a,N,IM>, (3.40)
где N — число фононов, I — полный угловой момент, М — его про-
екция на ось z. Индекс а описывает дополнительные квантовые чис-
ла, которые, как будет видно, необходимы для состояний с боль-
шим числом фононов. Однофононное состояние имеет угловой момент
/ = 2:
|W=1, 2Л1> = рЙч|0>. (3.41)
Оно нормировано, т. е. <Рглг | Рглг> = 1-
Двухфононное состояние и его полный угловой момент нетрудно
получить с помощью соотношения (3.38), из которого следует, что
фононы имеют угловой момент I = 2 и проекцию момента М = р.
Следовательно
|2V—2, IM> = Ar S (22/| т, т2ЛД рг1™, ргт21 0 >, (3.42)
nii т2
где А/ — нормировочный множитель. На первый взгляд кажется,
что I может принимать значения 0, 1,2, 3, 4. Рассмотрим, однако,
нормировку состояний (3.42):
| Л I2 ( Z (22/ | т1ш2Л1) р2+ , 02+ 21 0 >\+ X
\т1т2 '
X 2 (22/т^М) Р^ Р^21 0 > =
т4т2
* В общем случае, если угловой момент волновой функции фут есть /,
то волновая функция при вращениях преобразуется по формуле
'ф;т=
т'
где — волновая функция во вращающейся системе. Однако, если по-
казать (как например, сделано выше), что волновая функция, угловой момент
которой еще неизвестен, преобразуется с помощью матрицы конечных враще-
ний то можно сделать вывод, что эта волновая функция соответствует
состоянию \jrny с угловым моментом /. Более подробно см., например, [306]-
58
(3.43)
= | Л/12 У, (22/ | т1 m2 M) (2211 т1 т2М) X
X <01 РгтаРгст! Ргт, Р2™210).
Среднее по вакууму от фононных операторов легко рассчиты-
вается, если, используя коммутационные соотношения (2.45), пе-
реставить операторы уничтожения справа от операторов
рождения. Тогда оператор уничтожения, действуя на вакуум, со-
гласно (3.24) даст нуль. В результате получаем
<01 P2mj P2miР21(A, 10> = 6mi- + 6mi- . (3.44)
Подставим это в (3.43)
<W = 2, IM]N = 2, IM> =
= | Л |2 У (2211 тхт2М.) (2211т1 т2М) (fiCT1^t +
mt, mt
tnt, тя
4А^А^) = 1Л'12 2 (22/1 mfri2M) [(221 \mim2M) +
mz
+ (221 |m2m1 Л4)].5 (3.45)
Используя свойства симметрии коэффициента Клебша — Гордана
(jij2I \тгт2М) — (—l)/i+i*-1 (jzjj \т2т1М) для одного из сла-
гаемых в квадратных скобках, получаем окончательно
(2V =2, IM\N=2, 1МУ —
= 1 Л/12(1 Ч-(—1/) 2 (221\т1т2М)(221\тгт2М) =
т>. тя
= 1 ЛИ2(1 +(-1)0. (3.46)
Следовательно, двухфононные состояния с / = 1,3 не могут быть
нормированы. Их волновые функции тождественно равны нулю. Это
обусловлено симметрией волновой функции по отношению к пере-
становке фононов (бозонов!) и коммутационными соотношениями
(2-45). Действительно, в (3.45) стоит сумма, одно из слагаемых кото-
рой получается перестановкой двух бозонных индексов другого
счагаемого. Нормировочный множитель для неисчезающих двухфо-
нонных волновых функций не зависит от спина и равен Л / = J/2/2.
Кратко остановимся на трехфононных состояниях. Здесь воз-
никает уже задача определения генеалогических коэффициентов,
которая обсуждается в разделах учебников, посвященных рассмот-
рению системы фермионов (см., например, [306, 357]). В нашем
Учае нужно решить совершенно аналогичную задачу для системы
зонов. Необходимо построить волновую функцию, которая харак-
ризуется хорошим квантовым числом углового момента и симмет-
59
Рис. 3.1. Энергетический спектр
квадрупольного гармонического
осциллятора.
4 2,505
6*2,286
2*2,159
рична относительно перестановки
всех пар бозонов. Это можно сделать
пользуясь суперпозицией состояний'
соответствующих различным схемам
связи фононов. В табл. 3.1 пред,
ставлены волновые функции для од-
но-, двух- и трехфононных состояний
[168].
Трехфононных состояний с угло-
выми моментами 1 = 1 или 5 не
существует по причинам, анало-
гичным рассмотренному выше слу-
чаю двухфононных состояний. Для состояний с большим числом фо-
нонов необходимо учитывать состояния пары фононов с суммарным
угловым моментом, равным нулю. Для этого вводится новое кван-
товое число сеньорита V, которое определяется как
v = N—1/2 сг= число фононов — число пар,
где N — полное число фононов, о — число фононов, связанных в па-
ры с угловым моментом, равным нулю. Теоретико-групповую клас-
сификацию состояний с большим числом фононов и использование
квантового числа сеньорита можно найти в соответствующей лите-
ратуре [183, 3771.
На рис. 3.1 показан спектр гармонического квадрупольного
осциллятора. Видно, что три двухфононных состояния и пять трех-
фононных состояний являются вырожденными. Для того чтобы
понять, в какой степени модель гармонического квадрупольного
осциллятора описывает ядерные спектры, на рис 3.2 и 3.3 показа-
ны некоторые из наиболее характерных примеров эксперимен-
тальных колебательных спект-
ров. Первое систематическое
сравнение модели гармоническо-
го осциллятора с экспериментом
было проведено Шарф-Гольдха-
бером и Венезером [314].
Следует отметать, что двух-
фононные триплеты появляют-
ся при энергиях, близких к
удвоенной энергии однофонон-
ного 2+-уровня. Эти триплеты
в общем случае не вырождены,
в некоторых случаях (78Se) от-
сутствует один из его уровней,в
других (11,5Cd)— рядом с уров-
нями триплета имеются два
дополнительных уровня (0+, 2+).
Что касается квинтета трехфо-
нонных уровней, то до настояще-
2* 1.307
2+1,552
0,615
2
------о
78Se
------О'
£0Ni
Рис. 3.2. Типичные экспериментальные
спектры колебательного движения
ядер [288]. Указаны спины и энергия
(в Мэв) уровней.
60
61
N Jft Е,Мэв R N Jn
EjMaff R
3
3(3,4+)
2
3(3,4*)
4
0
2.754 5,35
2,868
534
4(3,4*)
4(3,4+)
2,349 4,58
,2,304 4,50
(W
2,574
4,62
(W,2)
2,393 4,25
2
2
2
Рис 3 3. Схема уровней 1C6Pd и I14Cd; данные взяты из работ [340, 341]
(см также [393]).
Числа у стрелок показывают относительные значения В(Е2). Толстые и тонкие линии
показывают переходы, относительные интенсивности которых больше 10 и меньше
10% соответственно. С учетом наблюдаемых энергий и способов распада некоторыс
уровни могут рассматриваться как колебательные (указывается число фононов Л/)
Другая попытка идентификации трехфоионных состояний предпринята в эксперимен-
тальной работе [323]. Особенностью схемы уровней для ,06Pd являются сильные кас-
кадные Е2 переходы с AW=1, что характерно для колебательных спектров.
времени идентификация соответствующих уровней не является
Одежной. Отсутствие одного из уровней триплета, возможно, связа-
с несовершенством экспериментальной техники. Однако существо-
ание дополнительных уровней в этой области может дать допол-
нительные сведения о свойствах потенциальной энергии ядра
/см гл- 4). Верхние 0+- и 2+-уровни в 114Cd с энергией 1,305 и
1 363 Мэе соответственно являются, вероятно, членами вращатель-
ной полосы, построенной на возбужденном уровне, который соот-
ветствует появлению деформации ядра. Тем не менее расщепление
триплетных состояний и отклонение их энергий от удвоенной энер-
гии однофононного уровня является отчетливым указанием на су-
ществование ангармонических членов (третьего и четвертого по-
рядков по а[2]) в гамильтониане (3.7). Гармоническое приближение
для этих ядер, по-видимому, является лишь нулевым приближе-
нием.
3.2.2. Мультипольные операторы в пространстве
коллективных переменных
Операторы в квантовой механике обычно выражаются через ко-
ординаты частиц гг. Например, все электрические и магнитные муль-
типольные операторы (1.17) и (1.18) выражаются через rt и Y (6г, <р;),
где i = 1, 2, ..., А (А — число нуклонов). Возникает вопрос, каким
образом эти операторы могут быть выражены через коллективные
переменные. Соответствующую общую процедуру и используемые
при этом приближения мы рассмотрим на примере электрических
мультипольных операторов (1.17). Поскольку спиновые координа-
ты при описании коллективных колебаний до сих пор не учтены, мы
не будем принимать во внимание второй член в (1.17), который во
всяком случае мал по сравнению с первым членом. Таким образом,
электрический мультипольный оператор в одночастичных коорди-
натах имеет вид
^ = £(^Пц(^))- (3-47)
I
Это тензорный оператор ранга X и четности ( — 1)\ £2г— краткое
обозначение углов 6г и <р;. В пространстве коллективных поверх-
ностных переменных этот оператор должен выражаться в виде
Qxo" = /axa + 2 <7k»(Z'X"ZllAW)aA'Bavv + -> (3.48)
X', X"
p.v
где не выписаны члены более высокого порядка по Величины
rT .7' г" ЯВЛЯ1°тся константами, которые необходимо найти.
РУктура мультигсльного оператора в пространстве коллективных
^ременных полностью определяется выражением (3.48). Очевидно,
в СУмма по и Должна быть ограничена таким образом, чтобы
Дили лишь тензоры ранга X' и X", которые могут быть связаны
6?
в тензор ранга X так, чтобы при этом выполнялись требования, обуг
ловленные законом сохранения четности, а именно полная четность
произведения cJz'W?-"] должна быть ( — 1)\
Как определить константы q? Это можно сделать следующим
образом. Пусть ф (хХ1 хг> •••> Хд, а[?])—многочастичная волновая
функция основного состояния ядра. Она зависит от коор.
динат отдельных частиц, а также от коллективных переменных
Поскольку коллективное движение является медленным по срав-
нению с одночастичным движением, то можно предположить, что
эта волновая функция определена для каждого произвольного, но
фиксированного набора переменных а1*] (адиабатическое прибли-
жение). Далее необходимо обойти трудность, связанную с наличием
слишком большого числа степеней свободы. В адиабатическом пре.
деле оД] является набором не зависящих от времени параметров, и
поэтому они не описывают каких-либо степеней свободы. Рассмотрим
величину
<Ф(х1, •••, хд, а[К]) I I ф(хп ..., Хд, <ДМ)> =
А
= ^<Ф(Х1, —, Хл, | Si rb У*.ц (Qj) I ф (хх.Хд, cJ4)) =
i=i
л
= V ( ф* (хх,.... х;,.... хд, аРЛ)ф(хп ..., х;,..., хд, аХМ) х
i=lJ
X dxx... dx/_1 dxi+1... t/хд et r^Y^iQ^dxt. (3.49)
Требуя, чтобы коллективные мультипольные операторы получа-
лись путем усреднения этого выражения, в котором индивидуальные
частицы находятся в основном состоянии, мы пренебрегаем некото-
рыми членами, связанными с интерференцией между одночастичным
и коллективным движениями. Причина появления этих членов
заключается в том, что заряды частиц, участвующих в одночастич-
ных переходах, в общем случае не равны усредненным зарядам
(см. ниже). Однако это приближение согласуется с адиабатическим.
Определим одночастичную плотность:
р (хь cJxI) =
= Ф*(х1, ..., х;,..., хд, сДО-1)ф(Х1,..., х£,..., хл, оХИ) dxh; (3.50)
k^i
тогда
<Ф (Х1..Хд, °-[М) I | ф (хр ..., х„, сс1М)> =
л
= v С р (Xi, aW^y^Q.)^, (3.51)
i=iJ
т. е. среднее значение полного мультипольного момента выражает'
ся через сумму по всем частицам ядра. Это суммирование можно
44
легко выполнить. В результате имеем
= <Ф (xv •••> хл, аИ) | Q& | ф (xn хл, aW)) =
= J Pp (x, aP-1) r*Y^ (Q) dx, (3.52)
ne было использовано, что заряд протонов et = 1, заряд нейтро-
нов е, = Величина рр (х, — плотность протонов в основном
состоянии ядра. Формула (3.52) строго выполняется лишь в адиа-
батическом пределе. Ее правая часть зависит от коллективных пере-
менных а[Х], что и указывает на зависимость мультипольного опе-
ратора от коллективных координат сДЕ Следует подчеркнуть, что
* (к, а[?-]) является зарядовым распределением в основном состоя-
нии. Распределение заряда в возбужденном многочастичном со-
стоянии 4'v (*i> х2.... вообще говоря, отлично от его
распределения в основном состоянии. Поэтому коллективное сос-
тояние, построенное на возбужденном многочастичном состоянии,
должно иметь не только другие массовые параметры В-, и параметры
жесткости Ск в коллективном гамильтониане (3.8) и (3.9), но и
другие мультипольные операторы. Этой зависимостью коллективных
величин от состояния обычно пренебрегают. Однако иногда она мо-
жет быть существенной. Например, поверхностные колебания ядра,
которое находится в возбужденном состоянии, соответствующем
возбуждению гигантского резонанса, могут несколько отли-
чаться от обычных поверхностных колебаний ядра (см. гл. 10
и И).
Чтобы продвинуться дальше, необходимо теперь воспользо-
ваться какой-либо моделью для описания протонной плотности
рр (х, aW). Для этого имеются несколько возможностей, напри-
мер модель однородного распределения плотности с радиусом вида
R = Ro (1 + 2а;.цЕхр) или распределение Ферми
х. и
р (г) =--------£<>------ , (3.53)
1-|-ехр{(г— с)/а}
где с = с0 (1 + S «хи^Хц) — радиус, соответствующий плотно-
X, в
сги, равной половине ее значения в начале координат; а характе-
ризует толщину поверхности. После этого константы дк и д^ х"
можно легко вычислить. Разумеется, они до некоторой степени
зависят от используемой модели зарядового распределения.
Возьмем первую из упомянутых моделей, т. е. модель однород-
ного распределения плотности. Имеем
R
<&°“ dx = f rW drdV, (3.54)
0
Где /^ = (1 + 2 <%хц Кхц)- Этот интеграл может быть взят с лю-
бой 11
и степенью точности по сщ.ц, однако формулы становятся при этом
3 ,
Зак. 1218 65
весьма громоздкими. Рассмотрим случай квадрупольного оператора
R
= = (3.55)
о
и воспользуемся
лагая в ряд по
хранения объема
формулой R = Ro (1 +а00 Уоо + 2а2и Пц), раз.
малым величинам cd 1 и пользуясь условием со
(2.П)
аоо = — (4^)-1/2 Va2ua$(l, (3.56)
получаем с точностью до третьего порядка по а2ц
(1 - ( ) [«[2J х а12]]10Й -
4л I \ \ л / /
\ у « uj i / \Л1*£ = 0 2.4
Х (о о о У(- 1)11 [1“[21 х aI21]IL1 х а[2]]-н}- (3'57>
С помощью (2.1) можно в общем случае получить коллективные муль-
типольные операторы с точностью до членов второго порядка по
по al^l;
QeoU = Г +_£ (Х + 2) {(2Х+ (2Л1 +
4л L 2 х".
^2»
х(2Х2+1)/(4л)}1/2(^1У;') (3-58)
\ О 0 0 / \ V] v3 |1 ' J
Аналогично могут быть получены и другие величины, например
магнитные мультипольные операторы. Характерно, что общий вид
их зависимости от «В1 и лР-1 можно определить довольно легко.
Но для вычисления различных констант, таких, как q'- в выражении
(3.48), необходимо использовать конкретные предположения (мо-
дели) для распределений заряда и тока в ядре. Имеется одно ис-
ключение из этого правила, а именно выражение для оператора пол-
ного углового момента в пространстве коллективных координат.
Перейдем к рассмотрению этого вопроса.
3.2.3. Построение оператора углового момента
в пространстве коллективных переменных
Иногда бывает полезно выразить оператор углового момента
L1(i через операторы рождения и уничтожения фононов. В част-
ности, это дает возможность сразу же получить угловые моменты
бб
пичных волновых функций, которые приведены в табл. 3.1.
Имеем, как обычно,
£1ц = (гхр)ц. (3.59)
леке 1 здесь указывает на векторный характер оператора угло-
момента, который при вращениях в пространстве преобразует-
Б°ГС помощью матриц конечного вращения DM, индекс ц характе-
isveT соответствующую сферическую компоненту. Запишем выра-
жение (3.59) в другом виде:
С1?. = 2(~ 1)V(1]1 |раЖ) W-v = Z (41 |pvX)rup*, (3.60)
H.V и-v
из которого следует, что для того, чтобы получить тензор ранга 1,
связываются два других тензора того же ранга (т. е. векторы) Здесь
также подразумеваются сферические компоненты для радиус-
вектора г и импульса р. Заметим, что р* связано с г в том смысле,
что р преобразуется контраградиентно по отношению к г, тогда как
р* преобразуется аналогично тому, как преобразуется г по отноше-
нию к вращениям. Более точно г и р* преобразуются по представ-
лению D19, в то время как р преобразуется по представлению
ЙИМ*. [См. также (2.43) для случая коллективных переменных.]
Это обусловлено тем, что если для получения нового сферического
тензора необходимо связать два сферических тензора, то исход-
ные тензоры должны иметь те же самые трансформационные свой-
ства по отношению к вращениям в пространстве.
Обобщая выражение (3.60) для тензоров ранга 2,можно записать
Lctf = М 2 (2211 ervp.) а2о n‘2v. (3.61)
a, v
Это означает, что оператор углового момента всегда получается свя-
зыванием координат и сопряженных импульсов в тензор ранга 1
(векторный оператор). Здесь М — нормировочный множитель,
который будет найден ниже. Выражая а2о и n*v через операторы
рождения и уничтожения фононов (2.44), получаем
= М 2 (221 I OVH) ± in [ р+ + (-1 fp2 _а] [ р+ _ (-1 )'₽2 _ v] =
и, v 2
= ~1Ш2(22! [ cfvji) [p+j^.-(-lf+vp2_o₽2_v +
Z О. V
+ (-l)°P2-OP2t(-l)V₽2t₽2-v]. (3-62)
н,ЛаГае™е- пРопоРЦиональные р+ р+ и рр, тождественно равны
Mv.ru. /ч л можно показать способом, аналогичным получению фор-
у ы (3-46). Поэтому
Т ‘^2(221 I OVJ1) [(- If р2_ор+_(_ l)vp2+p2_v], (3.63)
^'=_|
3*
67
Применяя коммутационные соотношения для и замечая
что
2(221 |сг—стО) (—1)° = 0, (3.64)
получаем
= у (22! |ctvh) [(-ir₽2_a^v-(-l)vP2-vp2+a]. (3.65)
2 о, v '
Перестановка индексов суммирования в первом члене дает
= ± i [(221 I W(l) (- 1)V p2_vp2+a-
— (221|ovp,)(—l)vp2-v₽2+al =
= 2- i h M У (— 1)* p2_v 02+o [(— l)1 (2211 ovp) — (2211 crvp.)] =
= — ihM S(221|CTVH)(-l)vp2_vp2+o. (3.66)
O, V
Определим, наконец, нормировочный множитель. Для этого
потребуем
£“о" Йн 10> = и ti р2+ц | 0>, (3.67)
т. е. в соответствии со свойствами преобразования фононного опе-
ратора проекция момента на ось z в однофононном состоянии
Рзц 10> должна равняться р,.
Поскольку полученный результат является весьма изящным и
вместе с тем, по-видимому, не очень хорошо знакомым читателю,
обсудим его более подробно. Ранее [см. (3.38) и (2.47)] было доказа-
но, что операторы преобразуются по представлению БИЧ
Более того, в разд. 3.2.1 мы определили фононный вакуум для чет-
но-четного ядра таким образом, что выполнялись соотношения
(3.37). Это означает, что вакуумное состояние имеет угловой мо-
мент нуль и, следовательно, преобразуется по отношению к вра-
щениям системы координат по представлению £>1°Б Поэтому со-
стояние Йн 10 > преобразуется по представлению £>[21 X £>[°] =
— £H2J. Хорошо известно [306], что если волновая функция при
вращении системы координат преобразуется с помощью матриц
[см. (5.128) и (5.141)], т. е. если
Ф'Хт = 2 Dfn'tn (0j) Флт'>
гп'
где ф' — волновая функция во вращающейся системе, то полный
угловой момент соответствующего состояния есть X, а его проекция
на ось z равна т. Иначе говоря, трансформационные свойства
волновых функций по отношению к вращениям системы коорДИ"
нат полностью определяют угловой момент состояния. Таким
68
образом,
из доказанных выше трансформационных свойств состояния
следУет:
(I/0")2 | о> = 2 (2 + 1) К р2+ц I о>;
ЬГо"Р2+ц|О> = рАр2+ц|О>.
Используя явное выражение для соответствующего коэффициента
Клебша — Гордана
(LlL|p + v—vp.) =
= (£(£+1))~’/!
%
для
-^(£ + ц)(£-цф1)]'/2
v= 1
v = 0
v— -1
(3.68)
И
можно получить из соотношения (3.67), что М = i ] 10, тогда
L{°“ =ti /ТО 3 (2211 ovp) (- l)v p2_v p2V (3.69)
a, v
Это выражение для оператора углового момента совершенно не за-
висит от модели. При его получении были использованы лишь самые
общие соображения типа соотношений (3.60) и (3.61) и свойства
коллективных переменных (свойства углового момента, коммутаци-
онные соотношения и т. и.). Таким образом, оператор углового мо-
мента всегда выражается формулой (3.69) безотносительно к виду
конкретных предположений, касающихся распределения заряда
ядра (однородное, распределение Ферми, гауссиан и т. п.).
§ 3.3. простейшие применения модели
ГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА
Чтобы сравнить модель гармонического осциллятора с экспе-
риментом, необходимо вычислить несколько ядерных характеристик,
которые могут быть предсказаны в рамках этой модели. Такими
характеристиками являются, например, среднеквадратичные ра-
диусы различных возбужденных состояний, вероятности переходов
жду состояниями гармонического осциллятора и квадрупольные
оменты возбужденных состояний.
3.3.1. Среднеквадратичная деформация
Деформация ядра определяется средним от выражения
= + (3.70)
\2В2 w2 /
69
В основном состоянии гармонического осциллятора
<0|а2ц|0>= V/2<0| Йи + (- 1)^2_ц|0> = О, (3.7П
т. е. среднее значение а2и в основном состоянии равно нулю. Анало-
гичный результат получается и для N-ro возбужденного состояния
поскольку из-за ортогональности состояний с различным числом
фононов N
<0|£^р(р^ + (-1И2_и)₽+ ... р+|0> = 0. (3.72)
N раз N раз
Для того чтобы можно было количественно характеризовать ам-
плитуды колеблющегося ядра, определим среднеквадратичную де-
формацию р2 как среднее по основному состоянию от величины
S|a2fl|2. Используя выражение (3.70), имеем для TV-фононного со-
в
стояния
Рм — <а, N, IM | v а2ц а2ц | «, N, 1Му =
в
= <«• N, /7И|У(-1)ч(р;_и+(-1)чр2ц) х
Z£>2 ^2 Ц
X (р2ц + (— 1)и Р2_и) | а, /V, IМУ =
= -^-<а, N, /ТИ|2(-1^(р2+_цр2_и +
Z£>2 Ц
+ Ргц р2ц) | a, N, 1Му =
= N, IM 12(2р2+цр2ц + бцц) | а, N, 1МУ.
£.02 Mg д
С помощью соотношений (3.33) и (3.34) и учитывая, что 2биц = 5,
и
получаем
р&=<а, N, /Mf Уа2ца2и|а, N, 1МУ =-^— (5 + 2ЛТ). (3-73)
Ц 2В2 (||2
Как и можно было ожидать, среднеквадратичная деформация зави-
сит от числа фононов. В частности доя основного состояния имеем
р2 = 5Л,2Д2со2, для однофононного состояния р2 = 7Л/2Д2иг
и для двухфононного состояния Р2 = 9А/2Д2о>2.
Обсудим теперь, по крайней мере для некоторых ядер, как найти
изменение среднеквадратичной деформации однофононного со-
стояния по сравнению с основным состоянием.
3.3.2. Среднеквадратичный радиус распределения
заряда в возбужденном состоянии
Среднеквадратичный радиус распределения заряда можно выра-
ь через коллективные координаты ядра с помощью электричес-
кого монопольного оператора
<2оо= $ Р/Мт,
Объем
ядра
(3-74)
01 _ Как обычно, плотность заряда ядра, которая снова пред-
полагается постоянной. Интегрирование выполняется по объему
ядра, т. е. в пределах от г = 0 до г = R = Ro (1 + аОо^оо +
। £а2цУ2ц), где аоо определяется из условия сохранения объема
(2.11) соотношением (3.56). Тогда
Q7 R
4nR30 J J
(3.75)
Q7 Л
— V^drdQ^
= - • -- Я2 V1 + «„о Коо + 2 dti,
4л 5 ц
и после интегрирования получаем
Qoo = 4 ZRl + 4 ZRi 2
5 4л ц
Второе слагаемое зависит от состояния ядра. Этот член пропор-
ционален введенной выше квадратичной деформации, что является
весьма естественным, поскольку изменение среднего радиуса долж-
но быть пропорционально амплитуде колебаний ос2ц-
Теперь нетрудно вычислить изменение среднеквадратичного ра-
диуса в различных возбужденных состояниях гармонического квад-
рупольного осциллятора. Определим
>возб.СОСТ= КI | >возб. сост (| f |)осн. сост].
С помощью формулы (3.73) находим
fi<k2|>w, ш = ^R12N
4л 2В2 (02 5 4л
!?е Ро среднеквадратичная деформация основного состояния.
™м образом, изменение среднеквадратичного радиуса зависит
। °’ Кот°рая для различных ядер изменяется в пределах от не-
льких сотых до нескольких десятых (табл. 3.2).
сост еРВЬЮ измерения среднеквадратичного радиуса возбужденных
СОм°™ийяДРа выполнены Кистнером и Суньяром [214] и Брик-
ность ^ИНли 1^9, 185]. Они использовали следующий метод. Плот-
вероятности атомных s-электронов конечна в начале коорди-
(3.76)
(3.77)
71
Таблица 3.2
Некоторые характеристики вибрационных ядер [224 , 288, 375]
Ядро Энергия одно- фононного уровня, Мэв 4- о t + CM о со. Энергии двухфонон- ных состояний, Л£эв Ядро Энергия одно- фононного уровня, Мэв + о t + CM . Энергии Двухфонон- ных состояний, Мэв
о+ г+ 4 + о+ 2 + - 4 +
64Fe 1,41 0,18 , 11(iCd 0,513 0,201 1,217
66 Fe 0,845 0,23 .— — 2,085 120Те 0,560 0,170 — —
68Fe 0,805 0,27 — 1,664 — 122Те 0,564 0,183 — 1,250
64Zn 0,990 0,250 2,29 1,78 — 124Те 0,603 0,174 — 1,326 1,248
66Zn 1,039 0,227 2,37 1,87 — 12вте 0,667 0,163 — 1,41 1,36
68Zn 1,078 0,205 — — — 128Те 0,743 0,142 — —
7°Zn 0,887 0,229 — -—- — 130Те 0,840 0,127 — — .
74Se 0,635 0,337 —. — 142Nd 1,570 0,104 — —
76Se 0,559 0,326 — 1,216 — 144Nd 0,695 0,111 — — 1,31
78Se 0,614 0,287 (1,44) 1,307 (1,44) i«Nd 0,455 0,161 — (1,20) 1,07
80Se 0,666 0,240 1,455 — 148Nd 0,300 0,197 — —.
s6Rn 0,833 0,159 .— — — 1880s 0,155 0,193 — 0,633 0,479
il8Rn 0,654 0,215 — (1,41) 1,42 ISOQS 0,186 0,185 — 0,557 0,546
1TORn 0,540 0,232 1,14 1,36 — 192PI 0,316 0,179 — 0,613
l02Rn 0,473 0,264 .— 1,105 1,105 l',4Pt 0,328 0,156 -— 0,622
lo4Rn 0,358 0,288 — 0,893 — 196p| 0,356 0,125 — 0,687
loapd 0,555 0,212 — 1,33 — 198pf 0,405 0,134 — —
loepd 0,512 0,224 1,137 1,125 — iMiHg 0,426 0,129 — —
lonpd 0,434 0,243 1,049 0,942 1,156 198Hg 0,412 0,109 — 1,089 —.
uopd 0,374 0,252 — 0,812 — 200JJg 0,368 0,098 — — 0,947
106Cd 0,633 0,186 — — — 202Hg 0,440 0,086 — 0,965 .—
108Cd 0,633 0,195 — 1,473 1,509 2MHg 0,430 0,047 — — —
11(lCd 0,658 0,183 — 1,474 1,541 204pb 0,899 0,048 — — 1,563
112Cd 0,617 0,186 1,23 1 ,31 1,41 206p|j 0,803 0,037 — — —.
114Cd 0,558 0,193 1,15 1 ,21 1,278
нат, поэтому будет отлична от нуля и вероятность нахождения
s-электронов внутри ядра. Кулоновское взаимодействие этих элект-
ронов с зарядом ядра приводит к сдвигу ядерных уровней. Этот
сдвиг может быть измерен с помощью эффекта Мёссбауэра. Более
точно: почти постоянная плотность заряда электронов |ф (0) |2,
где ф(0) — волновая функция всех s-электронов, вычисленная в на-
чале координат, создает дополнительный кулоновский потенциал
И(г) = |ф(0)|2 $ —l—dT.
Объем I Г Г I
ядра
(3.78)
Потенциал, зависящий от координат, создается лишь электронным
зарядом внутри ядра. Сферическое распределение заряда вне ядра
создает постоянный (не зависящий от координат) потенциал.
Используя разложение
Ц = 4л У _L_y?m(Q)yfm(Q') JL.,
| Г— Г'| !,m2l 1
(3.79)
72
находим
V (г) = 2л ^-±^1^(0) |2.
(3.80)
Отсюда в первом порядке теории возмущений получаем, что ядер,
ный уровень с волновой функцией сдвигается по энергии на по-
ложительную величину
AEV = < Tv | — Ze2V (г) | Т v> =
= +^nZe2^(0)|2<Yv|r2|Yv>. (3.81)
о
Следовательно, энергия ядерного у-перехода из состояния [ t > в ос-
новное состояние | f > = 10 > изменится на величину (рис. 3.4)
ДЕ-АЕ, —АЕУ = + — nZe2fi<r2>i|i]?(0)|2, (3.82)
3
гдеАЕ; и-АЕ/ — сдвиги уров-
ней начального и конечного
состояний соответственно. АЕ
настолько мала, что ее не-
возможно измерить непосред-
ственно. Однако в работе
Хюфнера и др. [2001 был
использован следующий ме-
тод. В кристалле находятся
Соединение I СоединениеЕ
Рис. 3 4 Сдвиг начального и конечного
уровня ядра, обусловленный взаимодей-
ствием электронов атомной оболочки с
зарядом ядра. Этот сдвиг различен для
различных соединений. Значение Л£
[см. (83)] соответствует разности энер-
гии у-квантов, каждая из которых обо-
значена волнистой линией.
два различных иона, напри-
мер Еи2+ и Ей3 . Плотность
электронов в начале коорди-
нат для Еи2+ описывается
величиной | фл (0) |2; для Еп3+
соответствующая величина
уже другая, поскольку в
этом ионе недостает трех, а
не двух, как в Ей42, электронов. Обозначим плотность электро-
нов для Еп3+ |фи(0)|2. Таким образом, поскольку сдвиг энер-
гии у лучей АЕ пропорционален плотности электронов в начале
координат, то в этих двух случаях он будет различным (см. рис.
3-4). Тогда величина
6Е = (АЕ)1-(АЕ)Н,
(3.83)
где индексы I и II относятся к двум соединениям, легко получается
из (3.81) и (3.82):
ЙЕ = -j- л Ze211 ф, (0) I2—| фи (0) |2] 6 <г2>г. (3.84)
О
Ры'Т энеРгетнческий сдвиг, называемый изомерным сдвигом (кото-
рен Весьма мал 11 составляет « 5 • 10-6 эв для 1БЗЕп) был изме-
с помощью эффекта Мёссбауэра. Соединение I использовалось
73
в экспериментах Хюфнера как излучатель, а соединение II— Как
поглотитель. Как видно из формулы (3.84), величина 6 < г2 >. может
быть определена, если для обоих соединений известна плотность
электронов в начале координат. Считается, что достаточно надеж-
ную информацию об этом можно получить из данных об изотопи-
ческом сдвиге [691. Однако неопределенность, связанную с необхо-
димостью определения плотности электронов, можно исключить
если вместо электронных атомов воспользоваться мюонными ато-
мами. Это обусловлено тем, что волновые функции мюона извест-
ны с очень хорошей точностью. Более того, эффект в этом случае
становится настолько большим, что его можно измерить непосред-
ственно, т. е. сравнивая энергию ядерных у-лучей для двух слу-
чаев — когда на орбите находится мюон и когда его там нет*.
3.3.3. Электромагнитный распад вибрационных
квадрупольных состояний
Вероятности переходов между состояниями гармонического квад-
рупольного вибратора легко рассчитать с помощью формулы (1.16).
В данном случае преобладают электрические квадрупольные пере-
ходы. Соответствующий квадрупольный оператор дается формулой
(3.57). Если ограничиться членом, линейным по a2(i, то оператор
перехода просто выражается через операторы рождения и уничто-
жения фононов:
С2ц'= ^(-^У/2(р2м+(-1)^Й-ц)- (3.85)
4 71 У 2d 2 ^2 '
Отсюда видно, что в этом приближении существуют лишь переходы
между состояниями, которые различаются одним фононом. Ве-
роятность перехода из первого возбужденного 2+-состояния в ос-
новное имеет вид
(£2) - лЬг' f 2J<° I °> Г “
Z^I-0-OJ \п^) Г" [Л, м
__ 8л (Ао>2)5 е2 / 3ZRIV о2
2-3-52 ’ (Ас)5 А ( 4л J °’
Таким образом, из данных о распаде первого вибрационного состоя-
ния может быть определена величина среднеквадратичной дефор-
мации Ро- Оказывается, что вероятность кулоновского возбуждения
однофононных состояний также определяется тем же самым мат-
ричным элементом, который входит в формулу (3.86). Следователь-
но, для измерения РВ можно использовать также и кулоновское
возбуждение. Для того чтобы получить количественные представ-
ления об энергиях возбуждения (Асо2) и среднеквадратичных де-
формациях для разных ядер, следует обратиться к табл. 3.2.
Более подробное рассмотрение мюонных атомов см. в т. 2.
74
3.3.4. Квадрупольные моменты
возбужденных состояний
Выражение для квадрупольного оператора через квадруполь-
поверхностные переменные a2(i можно получить, полагая
1 _ 2 в формуле (3.58):
Первый член линеен по операторам рождения и уничтожения фоно-
нов второй член квадратичен по этим операторам. Поскольку,
по определению, квадрупольный момент есть [см. (1.2)1
Q = fyn)’/2</V, z/|Q20^, //), (3.88)
то в рамках гармонической осцилляторной модели вклад может да-
вать лишь второй член в (3.87). Имеем
+ (- 1)* ₽2- v) (₽2+-v+ (- 1)V p2v )| =
= , 16V/.3ZW |0[± ,2 2 2\ J х
\ 5 / 4л \ 5 / \ 0 0 0 / 2В3 со3
//|У(2 2 2V-1)v(2₽2+v₽2v+1)|/V, /А . (3.89)
1 “*7 \ V —v 0 / ' z
Легко видеть, что
2(2 2 2 | V —v 0) (—l)v = }/ГУ(2 2 2 | v — v0) X
V Т
X (2 2 0|v—v0) = 0 (3.90)
и, следовательно,
(J=(16n\»^10(A„V«/2 2 2'|^_x
\ 5 ) 4л \ 5 ] \0 0 0 / 2В3 о3
X-|l Г<М, п | 2 (2 2 2|v—v0)(— 1)v₽2+v₽2v|/V, //>. (3.91)
° V
Для получения конкретных результатов, необходимо теперь
^Р^делить волновые функции \N, I, М). В случае однофононного
4 / 2 2 2\ А _
— Л -----X
5 / \0 0 0 /2В3ыг
Фоднофон
3 3Z^10
4л
2 _
х - ]/5 2 (2 2 21V-V 0) (- 1)V <01₽22 р2% ₽2v 10).
° V
75
Так как <01 ₽г2 02v₽2v ₽22 I 0> = 6V2, то окончательно имеем
'16 V/23Z/^1n/4 \-’/./2 2 2\ А ч
— Л -----10—Л ----X
,5 / 4л \5 / \OOO/2B2io2
^однофон--
X |/5 (2 2 212-2 0) = - (| л)"1 pg Z^.
(3.92)
Например, для 114Сс1 р0 = 0,193 (см. табл. 3.2), Z = 48, Ro = 1, 2\
хЛ’^3 = 5,82 ферма и <2ОВНОфоП (114Cd) » 2-10-2 барн, что намного
меньше экспериментального результата (около 0,7 барн), получен-
ного путем измерения реориентационного эффекта (см. гл. 1).
Это указывает на то, что для ядерных состояний рассматриваемого
типа приближение чисто гармонического осциллятора является
очень грубым и иногда может быть совершенно непригодным.
В действительности, как будет видно из обсуждения потенциальной
энергии коллективного движения в следующей главе, даже низко-
энергетические колебания большинства ядер являются ангармони-
ческими. Для таких ангармонических колебаний число фононов не
является хорошим квантовым числом и, следовательно, в выражение
(3.87) для квадрупольного оператора будет давать большой вклад
первый член. Смешивание фононных состояний, обусловленное на-
личием ангармонических колебаний, в основном и приводит к рас-
хождению между теорией и экспериментом.
* * *
Некоторые полезные вопросы теории квадрупольных колебаний
рассмотрены в [168].
Глава 4.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
КОЛЛЕКТИВНЫХ КОЛЕБАНИЙ ЯДРА
Индивидуальные свойства ядра определяются в основном по-
тенциальной энергией коллективных колебаний. Знание этой ве-
личины позволяет ответить на вопрос, является ли ядро гармони-
ческим или ангармоническим вибратором, имеет ли оно деформиро-
ванные возбужденные состояния, деформировано ли оно в основном
состоянии или, может быть, является сферическим для некоторых
возбужденных состояний и т. д. Она также определяет «мягкость»
ядра по отношению к колебаниям и его делимость. В общем случае
потенциальная энергия коллективных колебаний зависит от набора
коллективных переменных, т. е. V = V а^2!), и, следо-
вательно, является очень сложной функцией. Для того чтобы вы-
полнялись законы сохранения углового момента и четности, эта
функция должна быть инвариантной по отношению к пространст-
венным вращениям и отражениям. Мы также знаем, что для малых
оД1 она должна описывать некий потенциал, который имеет свя-
занные состояния; для больших параметров деформации, т. е.
для cd4->oo, эта функция должна обращаться в нуль. Потен-
циальный барьер между значениями а[Ч = 0 и = оо в ос-
энергия
природу
новном определяет процессы деления. Потенциальная
V (аИ) для малых «1’4 определяет спектры ядер, т. е.
различных низколежащих возбужденных состояний.
Чтобы получить представление об основных свойствах
Чтобы получить представление об основных свойствах функции
V (сДД и соответствующих поверхностях потенциальной энергии,
мы рассмотрим здесь простейший нетривиальный случай, а именно
‘’отенциэльную энергию коллективных квадрупольных колебаний
(3.9). Иначе говоря, предположим, что квадрупольные поверх-
ностные координаты Д21 являются единственными коллективными
к2?РДИНатами, которые определяют структуру ядра. Для больших
Деформаций это, разумеется, несправедливо. Поэтому можно ожи-
пТЬ’ ЧТо ВЬ1Ражение для потенциальной энергии (3.9) годится лишь
я качественного описания низкоэнергетических спектров ядер.
Но к будет показано ниже, в значительной степени дело обстоит имен-
обс?аК Ограничиваясь выражением (3.9), мы тем самым исключаем
уждение процессов деления. Причина этого заключается в том
77
что функция V (а[2]) (3.9) становится бесконечной при больших
а[21. (Она будет положительно или отрицательно бесконечной в за-
висимости от знака коэффициента С4.)
Мы не будем обсуждать здесь вопрос о получении потенциаль-
ной энергии (3.9) в рамках каких-либо микроскопических моде-
лей* (например, модели оболочек со взаимодействием). Наш под-
ход — более феноменологический. Рассмотрим, какие типы поверх-
ностей потенциальной энергии соответствуют формуле (3.9). Каковы
максимумы и минимумы этой поверхности для различных наборов
параметров С2, С3 и С4? Что означает появление различных «холмов»
на поверхности, получаемой из формулы (3.9)? После того как
будут изучены эти свойства, а также качественное поведение со-
ответствующих энергетических спектров, каждому ядру будет сопо-
ставлена «его» поверхность потенциальной коллективной энергии.
Она будет рассматриваться в качестве важнейшей характеристики
конкретного ядра. Исследование свойств этой поверхности позво-
лит понять многие свойства ядер.
§ 4.1. ВНУТРЕННЯЯ СИСТЕМА КООРДИНАТ
В гл. 2 было указано, что для квадрупольных коллективных
координат можно определить новую систему координат К', оси
которой совпадают с главными осями ядра. В этой системе поверх-
ность ядра в декартовых координатах имеет вид
/ , х'2 u'2 z'2\
R' = R0 1 + ^хх—+а^и^- + а^-г . (4.1)
I rZ гй I
Поэтому выражение для поверхности в данной системе координа
инвариантно по отношению к любому из преобразований
х'-э—х',
у'-+—у',
z'-^>—z’,
(4.2)
т. е. инвариантно при зеркальных отражениях в плоскостях х'у',
x'z' и y'z'. Условие того, чтобы координатные оси были главными
осями поверхности ядра, есть а'ху = а'хг = <х'уг = 0 [ср. формулы
(2.17) и (2.21) между собой). Вместе с формулами (2.20) это приво-
дит к следующим условиям доя сферических компонент (Д21 тензо-
ра cd2! во внутренней системе координат:
1/8 \'/* . , , .
= а-2 — ~ I ~ л I \а*х Я-yyh
Z \ 1О /
а1 = а_г — 0;
1 /16 .
— ( ЭТ ) (2cc2z CLxx
b \ 5 J
(4.3)
* Это будет сделано в т. 3.
78
м образом, во внутренней системе координат поверхность ядра
(4^) выражается через сферические координаты
R' (6Z, <pz) — Ro [1 + «0^20(6Z, ф/)Н~
+ «2^22(6'. <Рz) + 2 (6z, <₽')}]•
(4.4)
Как и в гл. 2, мы опустили ненужный первый индекс у квадруполь-
ных переменных av и оставили лишь второй индекс, т. е. а20 =
== а0, «22 = °2-
Следует подчеркнуть необходимость понимания нескольких осо-
бенностей преобразования от лабораторной системы к внутренней
системе координат. Это преобразование не приводит к однознач-
ному соответствию между переменными в лабораторной системе и
новыми координатами, выраженными через углы Эйлера и внутрен-
ние координаты. Так как это очень часто приводит к неверному по-
ниманию и трудностям, обсудим указанное преобразование подроб-
но Обозначим
(хД = {х, у, z}— координаты точки в лабораторной системе;
= {%', у’, г'} — координаты во внутренней системе, поворот которой
описывается углами Эйлера;
j Xj } = { X, у, Z ) — координаты х' =х, у' = у, г' —г для данной точки
во внутренней системе.
Это графически проиллюстрировано на рис. 4.1.
Вместо декартовых координат {х, у, г} введем соответствующие
сферические координаты гт [см. (2.13)]:
г пг = О
^(x-iz/) щ^-1
=г(улУ/>г1т(е>
(4.5)
где 0, ср — полярные углы в лабораторной системе. Аналогично
введем сферические координаты г'т точки {х’, у', z'} во внутрен-
ней системе:
т = 1
т = О
m = — 1
= Г(з’Л) 2 ф (4’6
где 6 , ф' — полярныеТуглы во внутренней системе. При этом
г = |/х2ф-«/2 + г2 — ^х'2+ у'2-\-z'2 (4.7)
79
и гт выражается через г'т (см. [306], гл. 5):
Гт = о2, ()3)<.
V
(4.8)
Углы Эйлера обычно определяются из условия, чтобы во вра-
щающейся системе точка имела фиксированные координаты г' =
= rv, где rv — фиксирован-
ные числа. При таком опре-
делении соотношение (4.8) со-
храняет степени свободы: име-
ются три степени свободы с
левой стороны, а именно х, у,
Z, и три степени свободы с пра-
Рис. 4.1. Требование, чтобы
точка Р, движущаяся в ла-
бораторной системе (указа-
но сплошными линиями),
имела фиксированные пере-
менные х, у, г во внутрен-
ней системе (указано штрих-
пунктирными линиями), оп-
ределяет углы Эйлера, свя-
зывающие обе системы ко-
ординат. Углы Эйлера сим-
волически указываются в
виде Т 6j V
Рис. 4.2. Четыре способа выбо-
ра внутренней системы коорди-
нат
В каждом из способов меняется
лишь ориентация внутренней систе-
мы. Если оси внутренней системы
на рис. а совпадают с главными
осями ядра (обозначенными стрел-
ками длиною х, £/, z), то и в слу-
чаях б—г эти оси также совпадают
с главными осями.
СО
вой стороны, а именно три угла Эйлера 0Х, 02, 03. Фиксированные
числа ~х,~У, z характеризуют, так сказать, внутренние координаты
точки. Если точка движется в лабораторной системе, т. е. х = х (/),
w = у (f), z = z (t), то требование г'ч = rv для всех времен опреде-
ляет углы Эйлера 0г = 0; (/) как функции времени.
Углы Эйлера могут быть также определены и другим, более упот-
ребляемым способом. Это определение использует тот факт, что
оси х', у' и z внутренней системы координат должны совпадать
с главными осями ядра (или молекулы). Но тогда преобразование
(4.8) от координат гт к новым координатам 0Х, 02, 03, не является
однозначным преобразованием: данному набору координат гт со-
ответствуют различные наборы координат 0Х, 02, 03, Гу. Это можно
показать следующим образом. Существует 24 различных способа вы-
бора внутренней системы координат, совпадающей с главными ося-
ми описывающей ту же самую точку х, у, z в лабораторной систе-
ме. Некоторые из этих способов показаны на рис. 4.2, на котором
лабораторная система не показана, а указывается лишь внутрен-
няя система координат вместе с фиксированными координатами
точки. Рис. 4.2, а соответствует самому простому случаю. Внутрен-
няя система х', у’, z' является той же самой, что и на рис. 4.1, и
повернута на углы 0Х, 02, 03 по отношению к лабораторной системе.
В этом случае фиксированная точка имеет координаты
х'=х, у'= у, z'—z. (4.9)
На рис. 4.2, б показан другой способ выбора внутренней системы ко-
ординат. Этот способ получается из случая, показанного на
рис. 4.2, а вращением системы координат на угол л 1,2 вокруг оси z'.
Точка имеет то же положение в лабораторной системе, если в новой
внутренней системе, указанной на рис. 4.2, б:
х' — у, у' — —х, z' = z. (4.Ю)
Аналогично новые внутренние системы координат, указанные на
рис. 4.2, виг получаются вращением старой системы на рис. 4.2, а
соответственно на углы л и 3/2 л вокруг оси z'. Положение точки
останется неизменным, если внутренние координаты одновременно
меняются по закону
х' -=—х, у’ = —у, z' — z (4.11
и
х'= —у, у' =х, z'—Z (4.12}
соответственно. Очевидно, что кроме четырех случаев, показанных
Рис. 4.2, существуют также следующие возможности:
’ В каждом из случаев, показанных на рис. 4.2, можно поменять
местами оси х' иг'.
8»
2. Ось z может быть выбрана вдоль осей z', х' или у' как в поло-
жительном, так и в отрицательном по сравнению с рис. 4.2, а на-
правлении этих осей.
Таким образом, имеется всего 4 X 3 X 2 = 24 способа выбора
системы координат х', у', z', совпадающей с главными осями*.
Для большинства из этих 24 способов углы Эйлера 01( 62, 03 и
«внутренние координаты» х' = х, у' = у, z' = z будут различными.
Однако нетрудно видеть, что все 24 способа могут быть выражены
с помощью произведения трех основных преобразований R ъ Д 21
определенных следующим образом:
ДДх, у, z, 0П 02, 03) = (х, —у, — z, 0L + n, л—е2, -
Д.,(х. у, z, 0„ 02, 03)= (у, —х, z, 0П 02, 03 4-2-л) ;
Я3(*, У’ ®1> ®2> ®з) = ZI Xt 01» 0J 4" ~ 03 4" ~ 31
При этом очевидно, что
Д2 = 1, £*=1, Д*2 = 1. (4.14)
Эти преобразования можно представить графически (рис. 4.3).
Видно, что 7?! соответствует одновременному отражению осей у' и
z и соответствующему изменению внутренних координат (х, у, z);
Д2 описывает поворот на угол л/2 вокруг оси z' и одновременно из-
менение внутренних координат х' -> у, у' —х и z' -> z. Наконец,
Яз описывает циклическую перестановку осей х', у', z' и соответст-
вующую перестановку внутренних переменных х, у, z. Из определе-
ния углов Эйлера (см. гл. 5) можно видеть, что координаты {х/} во
вращающейся системе следующим образом связаны с координатами
{xj лабораторной системы:
з
x'i = 2 Ды-(01, 0,, 03)Х;, 1=1, 2, 3. (4.15)
/= 1
Элементы матрицы преобразования Дг7- зависят от трех углов Эйлера
и имеют вид [см. (5.22)]
Ry
/ cos В-, cosBz cosB3 -sin B1 slnBj
I - cos B1 cos в2 sin B3-sinB1 cos B3
\ cosB1sinBz
sin 8r cos 8z cos B3+cos Btsin B3
-sin 61 cosBz sinB3+cosB, cosB3
sin В., sin Вг
-sin Вг cos В;
sin B2 sinB3
COS В2
(MS)
* Если имеется симметрия относительно оси вращения (например, симме-
трия вокруг оси г' на рис. 4.2, а, в случае х = у), то система координат К
будет всегда совпадать с главными осями при повороте на любой угол вокруг
оси симметрии. Таким образом, в этом случае существует бесконечное число
способов для выполнения условия, чтобы К' совпадала с главными осями.
82
Подставляя изменения углов Эйлера согласно (4.13), можно не-
едственным вычислением проверить интерпретацию величин/?1(
n°C R даваемую на рис. 4.3. Например, легко видеть, что при под-
становке 0J 61 + Л, е2^ л — е2, ез^ — 63 г'- и «/'-компо-
ненты [согласно (4.15)1 меняют знак, тогда как х'-компонента его не-
Рис. 4.3. Три основных преобразования Ri, R2, R3 внутренней
системы координат х', у', г'; х, у, z обозначают координаты
точки, фиксированной в пространстве.
меняет. Это в точности соответствует преобразованию показан-
ному на рис. 4.3. Легко также проверить, что операции, соответст-
вующие преобразованию R3, приводят к циклической перестановке
внутренних осей.
Три преобразования R2, R3 названы основными преобразо-
ниями потому, что, как следует из рис. 4.3, все 24 способа осуще-
8J
ствления совпадения внутренней системы координат с системой глав-
ных осей могут быть получены последовательным применением пре-
образований Rlt R2, R3, т. е. произведений вида
R^R^R^R^, (4.17)
где nk — положительные целые числа.
Теперь необходимо рассмотреть, как операции, указанные
в (4.13), выражаются на языке коллективных координат. Величины
х', у', z' описывают внутренние декартовы координаты частицы
например, по отношению к вращающейся системе (системе главных
осей). Как следует из соотношений (4.3), в системе главных осей
коллективными переменными являются о0, а2. Поверхность ядра
во внутренней системе выражается через декартовы координаты фор-
мулами (4.1) и (2.21):
R = RO(1 +ахх^- + аод^— + (4.18)
I r2 r2 r2 I 7
Используя преобразования (4.13), получим
&ХХ = tyxxi ахх ~ ^уу. ^з &хх = ^уу\
R1 <*УУ = ^УУу ^2 ^УУ = ^xxt Щу = ^zz»
&ZZ = ^ZZ, “ ^ZZ, ^zz ~ ^хх*
Отсюда с помощью (4.3) имеем
К1а2 = «2. —а2, — у ]/б а0—уа2;
/?1о0 = ц0, 7?.,а0 = й(), R3a0= — у«о+ — Кб а2,
или, введя согласно (2.23) коллективные параметры [> и у:
- 2
^1Т = Т. RzV=— У, Я3у = у—— л.
о
(4-19)
(4.20)
(4.21)
Тогда три основных преобразования можно записать в виде, часто
встречающемся в литературе [50]:
Ri (Р. V, бы 02, Оз) - (₽, Т, 0j + л, л —02, -03), Rl = 1;
4 (₽, Y, е1( е2,63) = (₽, -У, o1F о2, е3 +1 = 1;
«3 (₽, У > 0j, 02, ()3) =
= (р. т—|-л,е1,е2 + 1л,е3+^л), к>2 = 1.
\ ‘J /
(4.22)
34
Следует подчеркнуть, что как преобразование (4.8) координат от
бэпаторной системы к внутренней системе, так и преобразование
(см. (2-22)1
«2н= 2^(01,02. e3)«v
(4.23)
являются инвариантными по отношению к преобразованиям Rlt
п и, следовательно, по отношению ко всем 24 преобразованиям
3’ пабораторной системы к системе главных осей. Поэтому наши
результаты можно выразить следующим образом. Пусть имеется
однозначная функция f (xit а2ц) лабораторных координат {xj и
(а» т- е- каждому набору переменных соответствует одно и только
одно'значение f (хг, a2(i). Если, подставляя (4.8) и (4.23), выразить
эту функцию через углы Эйлера и внутренние переменные, то мож-
но получить новую функцию
f (х1> Х2, Х3, &2ц) =
= f (Xi = ^ (01> ®2' 03) Xj t а2Ц = 2 (01 > 021 03) av\ =
\ j V >
= f (9ц 02, 03. х', у', а„, а2). (4.24)
Теперь можно сделать два важных заключения:
1. Поскольку соотношения (4.8) и (4.23) инвариантны по отно-
шению к преобразованиям Rlt R2, R3, то новая функция f (01,
0-2, 03, х , У’, а', а0, а2) также инвариантна по отношению к этим
преобразованиям и, следовательно, инвариантна по отношению ко
всем 24 преобразованиям, рассмотренным выше.
2. Если выполняется какой-либо расчет, использующий внут-
ренние координаты {0 j, 02, 03, х', у', z', а2, а0}, например решается
уравнение Шредингера, записанное в этих координатах, то, вообще
говоря, получаются решения ф„ (0!, 02, 03, х', у', г’, а2, а0), ненн-
вариантные по отношению к преобразованиям R±, R2, R3. Однако,
если требуется, чтобы та же самая волновая функция фп (х, у, z, а2|1),
выраженная в лабораторных координатах, была однозначной функ-
цией, то необходимо симметризовать функцию ф„ по отношению
к преобразованиям Rlt R.2 и R3. Только таким образом можно обес-
печить однозначность волновой функции в лабораторной системе,
что является основным требованием квантовой механики.
Эта многозначность при использовании внутренних переменных
делает обязательной симметризацию волновых функций и автома-
тически порождает свойства симметрии функций во внутренней
системе координат. Совершенно необходимо помнить происхожде-
ние, различных свойств симметрии, иначе можно легко прийти
неверным выводам. Как будет видно из дальнейшего, нсполь-
ание параметров а0, а2 для описания поверхностей коллективной
Анальной энергии с помощью эквипотенциальных кривых не
Ял„ЬКо Удобно для исследования свойств симметрии поверхности
Р но также отражает особую роль внутренних координат.
85
§ 4.2. СВОЙСТВА СИММЕТРИИ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ
КВАДРУПОЛЬНЫХ КОЛЕБАНИЙ
Потенциальная энергия квадрупольных коллективных колеба-
ний как функция квадрупольных координат имеет вид [см. (4.39) [
V (а!2]) = — /5 С2 [«[21 X сс12]][0] + сз [[«[2] х ссГ2]]г21X а!21] 1°] +
4-С4[сс[2] X а[2]][0] [а[2] х а[2]][0]+ ... (4.25)
Это ротационно инвариантная функция координат oJ2] в лабора-
торной системе. Если выразить V (а[21) через углы Эйлера и внут-
ренние координаты, то новая функция V (а0, а.2) будет обладать
свойствами симметрии, которые обсуждались в предыдущем раз-
деле. Кроме того, необходимо помнить,что преобразованная потен-
циальная энергия V (а0, п2) вообще не зависит от углов Эйлера,
поскольку V (а[23) — скаляр. В новой системе координат, напри-
мер в системе главных осей, скалярная функция имеет в точности
тот же самый вид, что и в старой системе, а ее координаты преобра-
зуются в координаты новой системы, например в нашем случае
а[2] а[2]_ Поэтому имеем
V (а0, а2) - — /5 С2 [at2! х а[2]][0] + Сд [[о[2] х а[2]][2] х а[2]][0] +
+ С4[а[2] х af2]j[0].[Q[2] х a[2]j[0]( (4.26)
или в явном виде
V (п0, п2) = у С2 («о + 2а1) +
+ у ]/ 5 С3 [По {(2221 000) а* + (22212- 20) а2 _|_ (2221220) а^} +
+ п2 {(22210 - 2 - 2) п0 «2 + (2221 - 20 - 2) п2 о0} +
+ а2 {(2221022) а0 а2 + (2221202) а2 с0}] +
+ ±С4(п2 + 2<. (4.27)
О
После подстановки значений всех коэффициентов Клебша —
Гордапа получаем
V (а0, п2) = у С2 (п2 + 2п2) +
+ 1^^C3a0(Gal-al)+ ± Q (п2 + 2п2)2. (4.28)
F ОО О
Для функций V (а0, а2), которые зависят только от а0 и а2 и не
зависят от углов Эйлера, из 24 видов симметрии остается только 6.
Именно, имеется только 6 преобразований вида (4.20) или (4.21),
которые действуют на внутренние координаты а0, а2 или, что экви-
86
валентно, на Р> Т- Эти преобразования могут быть получены с по-
, ю двух основных преобразований 7\ и Т2, определенных сле-
дящим образом [160]:
Tj (а0, а2) = (ап, —а2), Т* = 1;
/ 1 , I г- 1 1 \ , f (4.29)
f2(flo. af) = ( 2 + 2 1 6 °2’ 4 ^6g° 27’ — ’
или
Л (₽.?) = (₽> -V).
ТгФ,т) = ^,Т-ул),
f2 = l;
fi = l.
(4.30)
Шесть различных преобразований, которые могут быть получены
из 7\ и Т2, имеют вид
Т2(а0, а2)=(— уа« + у ^6й2, — -1^6 а0— у«2); (4.31а)
ТЦа^ а2) = (—^-«о— у Кб а2, у /ба0—уй2) ; (4.316)
Т2 (а0, а2) — (п0, а2) (тождество); (4.31в)
Т1Т2(а0, а2) = (—уяо + уКба2, уКб а0 + у й2) (4.31г)
Л fl («0, а2) = (-у а0- у Кб а2, - у Кб «о + у «2) 1 (4.31д)
Ti fl (а0, а2) - (а0, -о2) = Т, (а0, а2). (4.31е)
приведена
Графическая иллюстрация этих 6 преобразований
на рис. 4.4. Линии а2=0, а2 = ^-]Лб а0, а2 = —~ 1/б а0 разбивают
плоскостьаоа2 на шесть областей. Одна из этих областей, например
1, может полностью покрыть плоскость а0а2 при преобразованиях
симметрии (4.31). Необходимые преобразования указаны на обла-
стях. Буквы gy и g2 обозначают границы области 1. Буквы g!, g'[ и
g-2, g'2 соответственно обозначают преобразования этих границ в гра-
ницы новых областей
Таким образом, если выводы о свойствах ядра должны быть по-
лучены с помощью коллективной потенциальной энергии, то обсуж-
дение следует ограничить только одной из шести областей. Каждая
из них содержит все соответствующие физические свойства, и в силу
свойств внутренних переменных рассмотрение других областей
излишне.
Каждой точке аи, а2 в одной из шести областей на рис 4.4
физически соответствует одна из возможных форм поверхности ядра
во внутренней системе координат. Функции, определенные в такой
ВрЛаСТИ’ напРимер потенциал V (а0, а2), дают информацию о соот-
ствующем свойстве ядра, например коллективном потенциале,
87
для данной формы ядра, описываемой параметрами а0, а2. Вознц.
кает вопрос, каким наиболее легким и простым способом рассмотреть
физические свойства в одной из областей плоскости а0о2. Это будет
Рис 4.4 Действие операций
симметрии Ti, Т2 в плоскости
аойг-
Каждая точка (ас, а2) в одной из.
шести областей этого рисунка опи-
сывает возможную форму ядра
Функции, определенные в этой об.’
ласти, дают информацию о кон-
кретных свойствах ядра, форма ко-
торого определяется данными пара-
метрами («о, а2) [например, кол-
лективная потенциальная энергия
V (яо, а2)].
сделано с помощью изучения экстремумов поверхности потенциаль-
ной энергии, ее седловых точек и нахождения эквипотенциалов
потенциальной энергии.
§ 4.3. СХЕМАТИЧЕСКАЯ МОДЕЛЬ ДЛЯ ПОТЕНЦИАЛЬНОЙ
ЭНЕРГИИ КВАДРУПОЛЬНЫХ КОЛЕБАНИЙ
Потенциальная энергия, даваемая формулой (4.28), соответст-
вует очень упрощенной модели квадрупольных колебаний. В общем
случае следует ожидать, что потенциальная энергия будет намного
более сложной функцией, инвариантной по отношению к вращению
и пространственному отражению. Более реалистическая функция
рассчитана и исследована в т. 3. Тем не менее схематическое опи-
сание потенциальной энергии с помощью выражения (4.28) уже дает
все важные свойства, которые могут иметь ядра в некоторых обла-
стях периодической таблицы. Поэтому целесообразно кратко об-
судить различные виды потенциальной энергии, даваемые формулой
(4.28). Приобретенный опыт будет полезен для исследования более
сложных и более реалистических функций. В дальнейшем обсуж-
дении мы используем внутренние координаты а0 и а2.
Потенциальная энергия, (4.28), зависит от трех параметров С2,
С3 и С4. Вначале исследуем случай С2 > 0 [13].
4.3.1. Случай С2>0
Параметр С3 можно без потери общности выбрать положитель-
ным. Отрицательное значение С3 соответствует зеркальному преоб-
разованию функции V (а0, а2) по оси а2. Как видно из рис. 4.4,
это дает ту же самую динамику, но пр и этом вытянутые ядра (а 0 > О,
а2=0) превращаются в сплюснутые (а0< 0, а2 = 0). Параметр С4
88
пжен быть положительным, поскольку в противном случае для
б°чьших деформаций V->--—оо, что соответствовало бы делению.
Зта возможность может существовать лишь для трансурановых и
сверхтяжелых ядер.
Теперь можно легко найти экстремумы поверхности V (а„, а2)
плоскости а0а2. Приведем здесь результаты анализа.
а Наибольшую роль для понимания свойств потенциальной
энергии (4.28) играет параметр
С2 ct
б. При С2 > о потенциал V (а0,
а2) всегда имеет минимум при а0 =
~а =0 независимо от значений С3
и С*. В частности, V (0, 0) = 0.
в. V (п0, аг) не имеет экстрему-
мов во всей плоскости а0а2 за
исключением границ шести обла-
стей, показанных на рис. 4.4. Это
можно легко увидеть, переходя от па-
раметров а0, а2 к параметрам р, у.
Для р Ф 0 необходимое условие
экстремума есть сЖ/йр = йЙ/йу =
=0. Это уравнение имеет решение для
у = и • у, где п = 0, 1,2, ..., что
соответствует границам различных
областей на рис. 4.4. Поэтому до-
статочно рассмотреть только частный
случай V (а0, а2 = 0).
г. Необходимое и достаточное
условие появления второго мини-
мума на оси а0, кроме точки а0 = а2 = 0, имеет вид
х>—= 6,222... (4.33)
9
Рис. 4.5. Схематическое пред-
ставление потенциальной кри-
вой V (а0, 0) разрез вдоль оси
а0 в плоскости ао“2 для ядра,
имеющего сферическую форму
в основном состоянии и дефор-
мированную форму в возбуж-
денном состоянии.
Д. Второй минимум появляется в точке а0 — ро (рис. 4.5), где
ь=1/1И[х+/ 4х-?)]- (4-34)
е- Высота второго минимума по сравнению с минимумом, соот-
ветствующим сферической форме, равна
I ’ /о лх 45 С2 3 о ।
"Ь'т]/ х(х—— — х 1 х(х— — 'j—— . (4.35)
з Г \ 9 ? 28 I \ 9 J 9 ' '
89
ж. Второй минимум глубже, чем центральный минимум Ппи
а0 = а2 = 0, т. е. V ((30, 0) < 0, если
х>7- (4.36)
Таким образом, ядро принимает аксиально-симметричную форму
в основном состоянии при Х>7. Отсюда получаем, что условие су-
ществования второго минимума 1см. (4.33)] с энергией, большей
центрального минимума, имеет вид
6,222 < х <7. (4.37)
Рис. 4.6. Поверхность потенциальной энергии V(a0, а2) для гармо-
нического квадрупольного осциллятора.
з. Поверхность V (а0, а2) не имеет максимума, однако кривая
V (ао, 0), соответствующая разрезу вдоль оси а2 = 0, имеет мак-
симум, если х> 6,222. Он появляется при а0 — где
(4.38>
Максимум функции V (а0, 0) соответствует седловой точке поверх-
ности V (а0, а2).
и. Высота максимума этой кривой по сравнению с минимумом
в центре равна
(4.39)
90
Рис 4.7. Типичная поверхность потенциальной энергии для слегка ангар-
монического квадрупольного осциллятора.
₽!1с. 4.8. Поверхность потенциальной энергии для ядра, которое имеет
сферическую форму в основном состоянии и деформировано в возбуж-
денном состоянии (см. также рис. 4.5). Расстояние между эквипотен-
циальными кривыми составляет 1 Мэв.
к. Разность А между седловой точкой р, и вторым минимумом
в точке р0 равна (см. рис. 4.5)
л ., а т / /о л\ 45 Cf f [ 56 \ Г 3 4 ] ,
л. Имеется также точка поворота для потенциальной кривой
0) при
V («о,
14
х— —
3
4,67.
(4.41)
Преимущество параметризации
коллективной потенциальной энер-
гии с помощью параметров С2, Сч
и С4 заключается в том, что таким
образом можно описать все слу-
чаи: сферические ядра (гармони-
ческие вибраторы), слегка ангар-
монические сферические вибрато-
ры с деформированным возбуж-
денным состоянием, ангармониче-
ские «сферические» ядра, ядра,
которые не могут быть ни сфери-
ческими, ни деформированными,
а также деформированные ядра со
сферическими возбужденными со-
стояниями.
Представим теперь поверхно-
сти потенциальной энергии с по-
мощью эквипотенциальных кривых
Рис. 4.9. Кривая потенциальной
энергии У(в0> 0) для ядра, одно-
временно сферического и деформи-
рованного в основном состоянии.
Пунктирная кривая указывает ос-
цилляторный потенциал, прибли-
женно соответствующий сфериче-
скому минимуму
в плоскости а0а2 для нескольких
типичных случаев. На рис. 4.6 показаны поверхности потенциальной
энергии для гармонического вибратора. Шесть эквивалентных обла-
стей указаны прямыми, проходящими через начало координат.
В правом верхнем углу рис. 4.6 показана потенциальная кривая
V (а0, 0) т. е. разрез через вершину вдоль оси а0.
Случай слегка ангармонического осциллятора показан на
рис. 4.7. Можно видеть растягивание эквипотенциальных кривых
вдоль оси с0, а также вдоль направлений у = 120“ и у — 240 .
Это действует на соответствующие волновые функции таким обра-
зом, что деформация ядра увеличивается.
На рис. 4.8 показана поверхность потенциальной энергии ядра
со сферическим основным состоянием и сильнодеформированным
возбужденным состоянием. Потенциальный барьер А между двумя
минимумами составляет около 3 Мэв.
Ядро, которое обладает свойствами и сферического и деформи-
рованного ядра, может быть описано потенциалом, показанным на
рис. 4.9. Такое ядро должно иметь одновременно вибрационный и
92
отационный спектр низкоэнергетических возбуждений. Возможно,.
цТо такими свойствами обладают некоторые ядра в переходной
области между вибраторами и ротаторами.
Наконец, на рис. 4.10 представлена поверхность потенциаль-
ной энергии для ядра, деформированного в основном состоянии.
н0 имеющего сферические возбужденные состояния. В области
малых энергий возбуждения такие ядра должны обладать враща-
тельным спектром.
Рис. 4.10. Поверхность потенциальной энергии для ядра, де-
формированного в основном состоянии и сферического в воз-
бужденном состоянии. Соответствующая потенциальная кри-
вая У(до, 0) показана в правом верхнем углу.
Следует помнить, что, введя условие С3 > 0, мы ограничили
себя рассмотрением вытянутых ядер; случай Ся<_ 0 соответственно
дает нам поверхности коллективной энергии ядер, сплюснутых в ос-
новном состоянии.
4.3.2. Случай С2 <0
Как и ранее, экстремумы поверхности (4.28) могут быть легко
найдены из условий
ЗУ (д0, а2) дУ (а0, са) = р.
д2У (д0, а2) . д2У (а0, а2) /д2У (а0, а2) \ 2 > Q • (4 42)
да^ да^ \ da0 da2 '
^>0.
dal
He теряя общности, можно снова ограничиться случаем
> 0. Как видно из (4.28), рассмотрение случая С3< 0 соот-
тствует переходу от вытянутого ядра к сплюснутому и наоборот.
93
Параметр С4 должен быть также всегда положительным. Решая
уравнения (4.42), получаем следующие результаты 11691.
а. В начале координат (а0 = 0, а2 = 0) всегда существует от-
носительный максимум.
б Минимум появляется только вдоль оси а0 при
15 Л_2_ Сз , _5
8 |/ 35 С4 ' 8
ао — Ро: -
1 1 Г18 „2 16„ ~
’ С4 V 35^1^ ’ (4ЛЗ)
а2 = 0
в. Для случая С3 = 0 минимума нет. Однако в этом случае вок-
руг начала координат в плоскости а0а2 существует «минимальное
Рис. 4.11. Поверхность потенциальной энергии для ядра, деформиро-
ванного в основном состоянии и не имеющего квазистабильного сфе-
рического возбужденного состояния. Параметры выбраны так, чтобы
воспроизвести спектр ядра 166Ег.
кольцо» радиуса а0 = у lZ5 (| С2| ICJf1*. В плоскости Ру это кольцо
соответствует значениям {р = у 5 (| С2| 1СУ1г, у}, где у изменяется
во всей области 2л. Говорят, что ядро с такой поверх-
ностью потенциальной энергии является у-нестабильным, поскольку
потенциал не зависит от у.
94
г Разложение потенциала V (а0, а2) в области минимума
ао = ₽о+<. а2 = 0 + < (4.44)’
дает
ч tz/o л\ ! 1 (d2V -2 , d2V <2) г
V(a.. O!) = V(₽.. 0)+-5Г^“. +sf0-| +
1
3!
W , з
----- a0
da30 °
+ 3
w
daedal
,2 9 . dfV ,4
a° “2+й°2
(4.45>
Рис. 4.12. Потенциальная кривая V(ao, 0)
для 166Ег. Пунктирная линия соответствует
гармоническому приближению.
W ,4 , c
°
Производные берутся в точке равновесия а0 = р0, а2 = 0 и выра-
жаются через С2, С3 и С4:
(4.46)
95
Для дальнейшего обсуждения удобно выразить производные
Солее высоких порядков через Со, С2 и |30:
1 d-V 1 тг. 1
-- л»
2 dal 2
2 dal
1 &V С2-|-9С0
6 da?, ~ 18(3О ’
1 эн' c2-icT
2 daodal Ро
1 d*V С24-ЗСо
24 dag “ 24pg ’
J_ d*V C2-|-3C0
4 dlda* 6₽g ’
1 d*V С2+ЗС0
24 dag ~ 6₽§
(4.47)
Эквипотенциальные кривые такой потенциальной энергии по-
казаны на рис. 4.11. Видно, что аксиально-симметричный минимум
при а0 = р0, а2 = 0 повторяется при у = 120 и 240°. На рис. 4.12
показана потенциальная кривая V (а0, 0), соответствующая разре-
зу вдоль оси а0 через вершину поверхности У (a0, а2). На этом
рисунке показано также гармоническое приближение. Параметры
(деформации, энергии p-колебаний Ер и у-колебаний Е,,, см. гл. 6)
на этих рисунках выбраны так, чтобы воспроизвести низкоэнерге-
тический спектр ядра lfi6Er. Видно, что гармоническое приближе-
ние может объяснить структуру потенциальной энергии вблизи по-
ложения равновесия для деформированного ядра только весьма
грубым образом. Более подробно эти вопросы будут рассмотрены
в гл. 6 при обсуждении колебательно-вращательной модели.
г „яв a 5. КВАНТОВАЯ МЕХАНИКА
I л О О ₽ -*•
РОТАТОРА
Простейший коллективный квадрупольный гамильтониан ядра
имеет вид [см. (3.8) и (3.9)]
// = В„ V 012ц а,ц I V (Огц), (5.1)
И
где вместо сопряженных импульсов* введены производные по вре-
мени от коллективных координата2ц. Это сделано для более удобно-
го предстоящего обсуждения ядерных вращений. Для простоты
в формуле (5.1) использован лишь первый член кинетической энергии
(3.8). Однако этот гамильтониан обладает всеми важными свойст-
вами вращательных и колебательных спектров ядра. Фактически
здесь мы встречаемся с одной из труднейших проблем современной
теоретической ядерной физики — проблемой определения истинного
коллективного гамильтониана ядра. Эго можно сделать прагмати-
чески: начать с самого простого подхода к решению задачи, т. е.
с формулы (5.1), в которой величина У(а2ц) дается (3.9), и выяснить,
как такой подход описывает экспериментальные данные. Если воз-
никнет расхождение между теорией и экспериментом, то как к ки-
нетической, так и к потенциальной энергии можно добавить более
сложные члены высших порядков. И снова мерой правильности выб-
ранного коллективного гамильтониана будет являться согласие
теоретических предсказаний с экспериментом. Другой возможный
подход заключается в микроскопическом получении и обосновании
коллективного гамильтониана. Однако поскольку в этом подходе
имеются математические трудности, а также трудности, связанные
с основными принципами, то становится более или менее необходи-
мым решить сначала феноменологическую проблему. Например,
одно из принципиальных затруднений заключается в том, что нам
неизвестен вид правильного микроскопического гамильтониана,
Соотношение между сопряженными импульсами и производными коор-
динат по времени имеет вид йД/йа, в нашем случае из уравнения (5.1)
^Учаем: л2ц
4
Зак 1218
97
из которого следует исходить. Единственное,что мы знаем, — это то
что входит средний потенциал (вероятно, типа Вудса — Саксона)
и остаточное взаимодействие. Конкретный вид среднего потенциала
и остаточного взаимодействия должен быть определен из сравнения
с экспериментом.
По этим причинам мы предпочитаем здесь описанную выше праг-
матическую точку зрения. Ниже будут рассмотрены способы полу-
чения модельных решений гамильтониана (5.1). Следует подчерк-
нуть, что даже проблема нахождения решений этого простого кол-
лективного гамильтониана математически очень сложна. Точные
решения могут быть получены лишь путем диагонализации в про-
странстве собственных функций пятимерного гармонического квад-
рупольного осциллятора. Если потенциальная энергия имеет де-
формированный второй минимум [т. е. удовлетворяет условию
(4.33)J, то эта процедура требует диагонализации матриц очень
большого порядка. Тем не менее такой точный подход, рассмотрен-
ный в работах Кумара и Баранжера [221] и Ньюса и др. [160—1621,
дает очень интересные результаты. Они будут обсуждаться в т. 3.
Вначале мы рассмотрим решения для случая деформированных
ядер. В этом и последующем разделах будут получены модель-
ные решения в области, близкой к минимуму потенциальной энер-
гии для сильнодеформированных ядер, например, такому, кото-
рый показан на рис. 4.12. Такой подход чрезвычайно физичен и
дает хорошую количественную основу для изучения динамики
явлений, связанных с вращением ядра.
§ 5.1. УГЛЫ ЭЙЛЕРА, ЛАБОРАТОРНАЯ
И СОБСТВЕННАЯ СИСТЕМЫ КООРДИНАТ
Чтобы записать кинетическую энергию, входящую в формулу
(5.1) во внутренней системе координат, необходимо получить про-
изводные по времени от величины
а2Н = (61, 62, ®з) (5.2)
V
т. е.
а2п = 2 (Oj, 02, 08)nv+ 2^й^(61, 0-2, 63) av. (5-3)
V V
В этой связи полезно вспомнить определение углов Эйлера. Две
ортогональные системы координат хг- и х/ могут быть преобразова-
ны в линейном векторном пространстве одна в другую поворо-
том на углы Эйлера 0; (/ = 1, 2, 3). Величины хг и х/ являются
единичными векторами трех осей этих двух систем координат.
Углы Эйлера определяются следующим образом (рис. 5.1).
1. Поворот на угол 0х (0 0Х <; 2л) вокруг исходной осн z
с единичным вектором х3, что приводит к изменению положения
осей х и у.
98
2 Поворот на угол 02 (О =С 0а < л) вокруг новой оси у (направ-
еНПе которой совпадает с направлением единичного вектора е2
а рис- 5.1). Единичный вектор х3 оси z переходит в вектор Хз.
Н з. Поворот на угол 03 (0 03 < 2л) вокруг новой оси z с еди-
ничным вектором Хз. Единичными векторами осей х и у становятся
векторы х[ и х2 соответственно.
Введем, кроме этого, единичные векторы ег (i = 1, 2, 3), ко-
торые указывают направление осей поворотов на углы Эйлера
(см рис. 5.1). Тогда три указанных выше поворота могут быть оп-
ределены относительно системы координат хг. Первый поворот 0Х
совершается вокруг первоначальной оси z, поэтому
ei=x3. (5.4)
Второй поворот 02 совершается вокруг новой оси у, тогда
е2=—Xj sin 014 X2COS0J. (5.5)
Третий поворот 03 совершается вокруг новой оси z с единичным
вектором Хз, т. е.
е3 = х, cos 0Х sin 0.2 х2 sin 0Х sin 02 + х3 cos 02. (5.6)
Рис. 5.1. Определение углов
Эйлера Од
xi(i==l,2, 3) — единичные векторы
лабораторной системы координат;
3) — единичные векторы
конечной системы координат, полу-
ченной в результате поворота на
углы Эйлера; c-(Z==l, 2, 3) — еди-
ничные векторы промежуточных
осей поворота.
Соотношения (5.4)—(5.6) можно записать в виде
i
(5-7)
где
/О —sin0x
С'/, (01( 02) = I 0 cos 0]
\1 о
cos 0х sin 02
sin 0Х sin 0,
cos 02
(5.8)
99
Аналогично векторы ег можно выразить через векторы х/ повеп-
нутой системы координат
(е2. ез)*/- (5.9)
Легко найти (см. рис. 5.1)
/—sin02 cos 03 sin 03 °\
Vy, (6.2, e3) = | sin02 sin 03 cos03 ° 1 ’ (5.10)
\ cos 62 0 1/
Матрицы, обратные матрицам вид / cos 0t cos 02 U и V, имеют соответственно sinOjCos02 —sin03\
(t/-1)ij = — sin-1621 sin sin 02 - — cos 01sin 02 0 | (5-H)
\ —COS 0j и / cos 03 — sin 0j — sin 03 0 ) ° \
(V“1)iy =—sin-102| —sin02sin03 — sin 02 cos 03 0 (5.12)
\ — cos 02 cos 03 cos 02 sin 03 — sin 02/
Используя эти результаты, можно легко выразить векторы х,
через ег. Согласно (5.7) имеем
= 3 ({/-%• ег (5.13)
i
и аналогично, согласно (5.9),
= 1 (!/-%• ег. (5.14)
i
Подставив (5.7) в (5.14), можно выразить единичные векторы вра-
щающейся системы Ху через единичные векторы Ху лабораторной
системы:
х/=--Z Hmi(C-%-xm ^VU7m;(B1>e2,e3)xm, (5.15)
i, т m
где
wmj (01( 02, e3) =-- 1 umi (6,, e2) (r1 (02, e3));7, (5.16)
i
или в явной форме
f.cosB1 cosB2 cosB3-sinBi sinBj
sinBf cosB2 cosBj+cosBiSinBj
-sinB2 cosB3
-cosB, cosB2 sinB3-sinB1 cosBj
- sin 6f cos B2sinB3+ cos B1 cos B3
sin в2 sinB3
cos Bi sinB2
sinBfsinB2
cos В2 /
(5.17)
100
к
Используя трансформационные свойства векторов по отношению
вращению, имеем
= (5.18)
/ i
где Hi и У‘ —компоненты вектора, например радиус-вектора, в си-
стеме базисных векторов х7 и х/ соответственно. Скалярное умно-
жение равенства (5.18) на х< дает
У/=2Е(х/-ху)уу. (5.19)
Скалярное произведение (х,'-Х;) можно легко найти, скалярно
умножая (5.15) на хг и используя соотношение ортогональности
(Х; -Xm) =
/?!> = (х;.х7-) = гя(е1,е2,е3). (5.20)
Подставляя это выражение в (5.19), окончательно получаем
У( - Rtj (0i, 02, 03) Уз — — Уз-
i i
(5.21)
Отсюда следует, как и должно быть, что координаты yt преобра-
зуются контраградиснтно к базисным векторам х; и матрица пре-
образования Rn транспонирована по отношению к матрице
Следовательно, матрица RtJ имеет вид
5ij{By,B:,B3) •=
' cos By cosB2 cosBj-sinB-f sinB3
-cosBy cos8z sinBj-sinBy cosB3
cos Bf sin62
sinBy cos8yCOsB;+cosBySine}
-sin By cos62 sinB3+ cosBy cosB3
sinBy sinBy
-slnB2 cosB3
sin В2 sin В3
COS В2 .
{5.22)
Это в точности та же самая матрица преобразования, которую мы
использовали ранее [см. (4.16)].
§ 5.2. СОСТАВЛЯЮЩИЕ ОПЕРАТОРА УГЛОВОГО МОМЕНТА
ОТНОСИТЕЛЬНО ЛАБОРАТОРНОЙ И ВНУТРЕННЕЙ
СИСТЕМ КООРДИНАТ
Вектор поворота может быть разложен по компонентам в си-
стеме х;, т. е. если выполняется зависящий от времени поворот вну-
ренней системы х/ по отношению к фиксированной системе хг, то
У лы Эйлера будут зависеть от времени: 0> = Оу (О- [ц описывают
РаЩение вокруг х/. Для бесконечно малого поворота имеем
2 ег(/0£=^х; ф-- (5.23)
« /
101
и после подстановки (5 14) получаем
(5.24)
А-
(5.25)
Компоненты оператора углового момента по отношению к вну-
тренним осям определяются следующим образом:*
Lk=— i ——, k -1,2,3.
ОРд
Используя (5.24) и (5.25), эти компоненты можно легко выразить
через углы
(5.26)
или
С помощью
7-2 =
Эйлера:
0 00a vi a
opb " ^’opT “o07=^(V
(5.27)
(5.28)
(5.12) получаем их явный вид:
cos 03 д . . о д . , п п д )
-—Г + sin 03 ——|- etg е2 cos ез —— ;
Sin 02 00! 002 003 )
. f sin 0» д гх 0 , „ . п 0 )
11-----------9 cos 0,------ctg09 sinOo----I;
I sin 0.2 00! O02 2 003 /
(5.29)
и
1
Т-з =
'з
Отсюда можно получить коммутационные соотношения для компо-
нент углового момента во внутренней системе:
Щ(0,), L;(eJ)]_=-iL'(e>);
[£з(е7), Lje^^-iL'^.),
что можно записать более коротко
L (^)XL' (0j)=-iL (0>).
(5.30)
(5.31)
Подчеркнем еще раз: в этих формулах штрих обозначает, что
оператор углового момента определяется по отношению к внутрен-
ней системе координат. Как следует из (5.31), компоненты углово-
* Операторы углового момента определяются здесь без обычного множи-
теля tv. Это удобно для геометрической иллюстрации, рассматриваемой ниже.
102
ro момента по отношению к внутренним осям подчиняются обычным
коммутационным соотношениям за исключением знака минус, сто-
ящего с правой стороны*.
Чтобы пояснить это важное свойство, получим компоненты опе-
ратора углового момента по отношению к осям лабораторной си-
стемы. Обозначим эти операторы Lk, k = I, 2, 3. Они могут быть
получены либо из соотношения (5.21)
1к = (5.32)
либо, более просто, следующим путем. Пусть вектор поворота раз-
ложен на компоненты щ в лабораторной системе (т. е. <ч описывает
повороты вокруг Xj и т. д.). Тогда по аналогии с (5.23) имеем
У ег Mi — У х7 daj. (5.33)
i i
Подставляя (5.7) и (5.13), находим
(5.34)
/
и
daj = 'ZUjidVi. (5.35)
Компоненты оператора углового момента по отношению к осям
лабораторной системы имеют вид
Lh—— i — , k = 1,2,3. (5.36)
dctfc
Из (5.34) следует, что
——— = У(67-1) Л —, (5.37)
dah dah 56,- ,Jh dQj ’
тогда
, k= 1,2,3.
Используя (5.11), находим
/ ; f л । л д . п 0 , cos t)i д 1
Li -—11COS 0, ctg 0,------sin 0,------------1---- ;
I 501 502 sin02 503 J
£„___ ; ( . n i л д , п д , sin 0, д ]
*----11 — sinB.ctgO,--------- cos 0,----------1---- ;
1 1 6 2 501 1 502 sin 02 503 J
I 00i I
(5.38)
(5.39)
Это было впервые отмечено в теории молекул Клейном [216].
103
Легко проверить, что коммутационные соотношения для компонент
в лабораторной системе имеют вид
£(е;)х£(е;) = идеу). (5.40)
Выразим оператор полного углового момента через углы Эйле-
ра (это понадобится в дальнейшем)
ь2 = £? + Ц+Ьз = М2+122+1з2 =
-ctges-^------!_(—+^-1 +
I -xg йо2 в1пгеД ае| )
+ 2£^_JL_\ (5.41)
sin2 02 dGjdGs J V ’
Важно понять смысл изменения знака в коммутационных соот-
ношениях для углового момента во вращающейся (внутренней)
Рис. 5.2. Некоммутативность вращений проявляется при сравие-
нии двух различных последовательностей поворотов.
а — выполняется поворот сначала вокруг осн х, а затем вокруг оси у, б —
те же повороты, но в обратном порядке. Различие в положениях точки Р
после этих операций эквивалентно повороту вокруг первоначальной осн z.
системе по сравнению с коммутационными соотношениями в лабора-
торной системе. Причина этой особенности заключается в том, что
компоненты в лабораторной системе определены по отношению
к осям, фиксированным в пространстве, т. е. операторы углового
момента не поворачивают лабораторную систему — она все время
фиксирована. Однако для внутренней системы это не так. В этом слу-
чае операторы углового момента фактически поворачивают систему,
по отношению к которой они определены. Отсюда и получаются раз-
личные коммутационные соотношения. Это положение иллюстри-
руется на рис. 5.2 и 5.3. Как известно [306], поворот на угол
вокруг оси х совершается в результате действия оператора
ехр (—icCiLJ, а поворот на угол а2 вокруг оси у — в результате
действия оператора ехр (—ia2£2). На рис. 5.2 показаны два бес-
104
конечно малых поворота на da± и da2 соответственно, выполняе-
те в различном порядке. На рис. 5.2, а сначала выполняется
поворот вокруг оси х, а затем второй поворот вокруг оси у. Чтобы
определить конечную ориентацию, например, оси х, введена фикси-
рованная точка Р с декартовыми координатами (1, 0, 0), т. е. точка
с единичным расстоянием по оси хот начала координат. На рис. 5.2, а
показан результат двух поворотов, выполненных сначала вокруг
оси х, а затем вокруг оси у, т. е. поворот ехр (—ida2l2) ехр (—
Первый поворот, конечно, не меняет оси х, но меняет ось у. Сле-
дует отметить, что второй поворот вокруг оси у выполняется во-
кпиг старой оси у, определенной в системе с фиксированными ося-
ми а не вокруг новой оси, полученной после поворота вокруг оси х
на угол cfai-
Рис. 5.3. Та же последовательность поворотов, что и на рис. 5.2, но выполня-
емая для компонент, определенных во вращающейся внутренней системе:
а “ за поворотом вокруг оси х' следует поворот вокруг новой осн у"; б — первый по-
ворот выполняется вокруг оси у, второй — вокруг новой оси х". Различие в положени-
ях точки Р эквивалентно повороту вокруг оси z", но в направлении, противоположном
соответствующему направлению на рис. 5.2.
На рис. 5.2, б показаны два поворота, выполненные в обратном
порядке. Сначала был выполнен поворот на угол da2 вокруг оси
У> а затем на угол da1 вокруг оси х. Оператор суммарного поворота
есть ехр (—ida^j) ехр (—ida2L2). Необходимо снова подчерк-
уть, что вращение всегда выполняется вокруг старых осей, фикси-
рованных в пространстве, т. е. вокруг осей у и х соответственно
V не вокруг оси х', которая также указана на рис. 5.2, б).
двух ри сРавнении рис. 5.2, а и 5.2, б видно, что разностью
У последовательностей поворотов является смещение, перпен-
105
дикулярное к первоначальной оси г, фиксированной в пространстве-
величина этого смещения имеет второй порядок малости. Отсюда
следует хорошо известное утверждение, что бесконечно малые пово-
роты коммутируют в первом порядке.
Суммарное смещение, перпендикулярное к оси х, эквивалентно
повороту на величину daYda2 вокруг старой оси г, фиксированной
в пространстве. Мы имеем
ехр( — irfa]1l1)exp(—ida2L2) - exp ( iJa2L2)exp(—idajLj)
= exp(—it/aj da2 £3)--1. (5.42)
Разложим экспоненты с точностью до второго порядка по беско-
нечно малым dat и da2:
р — ic/ajlj---^-(rfai)2ZiJ 1 — ida2L2---^-(da2)2L?2 —
— p — ida2 L2—- ~ (da2)2Ll p — idccj, L±---~ (da^Lj j =
= — idc^ da2 L3. (5.43)
Линейные члены с левой стороны сокращаются и для членов вто-
рого порядка получаем
— dat da2 L2—L2 LJ = —ida1 da2 L3. (5.44)
Поскольку это равенство справедливо для любых значений dat и
da2, мы находим обычное коммутационное соотношение для угло-
вых операторов L± и L2 в системе координат, фиксированной в про-
странстве, т. е. соотношение (5.40):
= ^Дз» (5.45)
Рассмотрим теперь коммутации тех же самых поворотов, совер-
шаемых вокруг осей вращающейся системы координат. Рис. 5.3, а
и 5.3, б аналогичны соответственно рис. 5.2, а и 5.2, б. На
рис. 5.3, а показан поворот, выполняемый вокруг оси х' на угол
с/Pi, за которым следует второй поворот вокруг новой оси у" на угол
dfi2. Важным отличием от случая, рассмотренного выше и соот-
ветствующего поворотам по отношению к фиксированной в простран-
стве системы координат, является то, что повороты всегда выпол-
няются вокруг новых осей, связанных с вращающимся телом. Дело
в том, что сами повороты изменяют систему координат, по отноше-
нию к которой они определяются. Поэтому на рис. 5.3, а показан
поворот ехр (—idf}2L2) exp (—ic/pxLJ). Штрих у компонент и L2
означает, что операторы определяются по отношению к вращаю-
щейся системе.
На рис. 5.3, б показан поворот на угол сф2 вокруг оси у >
за которым следует второй поворот на угол с/0х вокруг новой оси х".
106
Оператор поворота в этом случае есть exp (—ic!pxLi) exp (—idfi2L'2).
Из рисунков видно, что разность двух последовательностей пово-
ротов эквивалентна повороту вокруг оси z" на угол (—c/p2^Pi)-
(Это становится особенно очевидным, если сравнить операции, ука-
занные на рис. 5.2, с теми, которые указаны на рис. 5.3.) Имеем
exp (— it/Pi Л) exp (— it/₽2Ц)—exp (— id₽2 Ц) exp (— idpx Ц) =
= exp[—i (-J₽x ф2)£;]-1. (5.46)
Как и раньше, разлагая экспоненты до второго порядка по беско-
нечно малым, получаем
— dpx t/p2(L1 2-2 — £2-7-1) "К(5-47)
Отсюда следуют коммутационные соотношения для проекций угло-
вого момента на оси вращающейся внутренней системы координат
L\L2—L2L\- iZ-з. (5.48)
Таким образом, из нашего рассмотрения совершенно отчетливо
видно, что изменение знака в соотношении (5.48) по сравнению
с (5.45) полностью обусловлено тем фактом, что компоненты £/;
описывают повороты относительно системы координат, фиксиро-
ванной в пространстве, тогда как компоненты L’k порождают пово-
роты относительно вращающейся внутренней системы. Иначе гово-
ря, вращения Lh не поворачивают систему координат, в которой
они действуют, в то время как вращения L’k это делают.
§ 5.3. ВРЕМЕННЫЕ ПРОИЗВОДНЫЕ £)-ФУНКЦИЙ
Величины Dmm’ (0J, 02, 03) определяются через оператор конеч-
ных поворотов R, который совершая повороты на углы Эйлера, пре-
образует лабораторную систему координат во внутреннюю систему
(см. § 5.6)
R (°п Т-о (х)) = exp (— iO1 £3 (х))ехр (—i02 £2 (х)) ехр(—i03 L3 (х)).
(5.49)
Заметим, что операторы углового момента Lh (х) действуют здесь
в координатном пространстве лабораторной системы, но не дей-
ствуют на углы Эйлера.
Матрица конечных вращений D‘mm' (Ох, 02, 03) определяется
как совокупность матричных элементов оператора R между со-
стояниями 11т (х)> и 11т' (х)> следующим соотношением (аргу-
мент х указывает, что волновые функции 11т) определены в коор-
динатном пространстве):
D'mm' (Oj, 02, 03) = (1т | R11т') =
= (1пг\ ехр (—iOj L3) ехр( — iO2£2)exp (— iO3£3) I Im'). (5.50)
107
Как видно из формулы (5.3), для того чтобы выразить коллек-
тивную кинетическую энергию через внутренние координаты, не-
обходимо знать временные производные от функций Чтобы
получить их, запишем
-±- Dmm’ (6;) = У [-4- D'™' (01’ 62> 0з) ] - (5.51)
dt [ О0у J dt '
Операция d/dQt может быть выражена через составляющие угло-
вого момента относительно внутренних осей. Из (5.25) и (5.26)
имеем
— = i у17йДб(0г). (5.52)
Аргументы операторов L'k (0;) указывают, что эти операторы дейст-
вуют в пространстве эйлеровых углов. Тогда
-4-D™' (еЭ = I I ^'> = i 214/ </m I й (6£) RI Im'> =
uvj dVj k
= —Vhj<Jm\Lk(xi)\Im”><Jm"\R\Im'>, (5.53)
k. m"
где использовано соотношение (5.166) L'k (Oy) R (Оу) =
= —L'k (x'i) R (Оу), доказываемое ниже в § 5.7. На последнем этапе
матричный элемент произведения LkR был разложен на произве-
дение матричных элементов сомножителей. Подстановка (5.53)
в (5.51) дает
-^-П^(бу) =
dt
= -i 2 Vkl<Im\Lk(xl)\Im")am"\R(ei,Lo(<x))\Im')^- ,
/, k, m" dt
(5.54)
где аргументы оператора R явно указывают на то, что он зависит
от La (х) и 0г [см. (5.49)]. Тогда, определяя величину
aj>JL = Vyw-^ (5.55)
dt dt
как угловую скорость вокруг (внутренней) оси, связанной с телом,
имеем
108
в формуле (5.53) можно также воспользоваться соотношением
ЙДег)й(еь М*)) = — Й(бг, La (х)) Lk (xt), (5.57)
которое будет доказано ниже [см. (5.179)1, и с помощью (5.56)
найти другое выражение для искомой производной:
— D'inm> (О,) = — i У D',nnz- (60 (Im" | Lk | Im'}a'k. (5.58)
ot A
§ 5.4. КОЛЛЕКТИВНАЯ КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
КАК ФУНКЦИЯ УГЛОВ ЭЙЛЕРА И ВНУТРЕННИХ
ПЕРЕМЕННЫХ
В лабораторной системе коллективная кинетическая энергия
в нижайшем порядке по коллективным переменным дается выра-
жением
Т = (5.59)
и
Ограничиваясь этим простейшим видом, рассмотрим метод преобра-
зования кинетической энергии от координат лабораторной системы
к углам Эйлера и внутренним координатам. Другие члены, входя-
щие в выражение (3.8), могут быть рассмотрены аналогично. Под-
ставляя (5.3), получаем
V (-iHi^Gv + D^v] (5.60)
Н. V, о
что сводится к выражению
Т -~Т В 2 (-l)wKvD2-*MaavCa + O^DL\loav«o]. (5.61)
Ц. V, о
Покажем, что перекрестные члены не дают вклада в (5.61).
Имеем
2 (-1)“ [ЙД* О2_*цо av ао + Й2_% ЙД$ av «о! =
ц. V. а
= 2 (-1)к(ЙД?О2_*ца + ОД^Й^)а^о =
Ц, V, о
= 2 ^ ( - 1)м (D2? О2ДШ) av ао =
Ц» V, G
= 2 £ (- I)° ВД ОД- о) av ао. (5.62)
|Л» V» о
С помощью (5.58) получаем
2 2 (-1)°(Й^ОД-а)^«а =
Ц. V, G
1С9
= +2i Z (-l)°D^<2/n"|4(x)|2v>’<^^_a«vfl’a. (5.63)
|i. v, a, k, m” '
Использование соотношений ортогональности для D-матриц
Dm'm (0J|, 62, 6a) D'm"m (6j , 62 , 03) = (5.64a)
^D^n- (elt e2, e3)dL,-(e^ e3, e3) =_(5.646)
tn '
дает
2 3 (-1)°(D-D“_a)av«a
Ц. V, о
= +2i 5 (-1)°<2—o|Lfe(*)|2v>*flvOa(^. (5.65)
k, v', a
Поскольку aY = o_1 = 0, то индексы пит принимают значения 0
и 2. В § 5.5 будет показано, что операторы Lj и L2 имеют неисчезаю-
щие матричные элементы <2 — o|£(x)|2v> только для v =
= —о ± 1. Следовательно, члены с k = 1 и й = 2 в (5.65) равны
нулю. Единственный оставшийся член — (2 — a| La (х) 12v> =
= v6_ov (см. § 5.5). Учитывая, что а2 = а_2, легко видеть, что сум-
ма равна нулю. Таким образом, все перекрестные члены в выражении
(5.62) обращаются в нуль. Заметим, что причина этого заключается
главным образом в свойствах внутренних переменных, т. е. в том,
что = 0, так как главные оси ядерного эллипсоида совпадают
с осями внутренней системы координат.
Соотношение ортогональностей (5.64) позволяет упростить по-
следнее слагаемое в (5.61), так что выражение для кинетической
энергии принимает вид
Т = ~В [ У (-lFD^DL%Gvfla+ V(- l)v«v a-v]- (5.66)
2 p,, v. G V
Рассмотрим первое слагаемое. Воспользуемся соотношениями
(5.56) и (5.58), тогда
4-В V (-l)<TD^D^_a0vGo
Ц, V, о
= У (-1)0П^(2/п"|4(х)|2т>*^х
2 k, tn"
Ц. V
х S Didn't, {2m"'\Lk- (Л')|2—о> со/'-nv ao. (5.67)
k' . m
Учитывая соотношение ортогональности (5.64) и эрмитовость опе-
ратора Lk, получаем
~В (-l)‘’(2v]C&(x)|2/H"><2/7?''|LA.(A-)|2-o>(1)Z^ova0
k, k', in"
V, G
110
— В 2 ( — 1)CT <2v|£ft(x) £ft'(*)|2—(5.68)
2 k. k'
v, a
В этом выражении члены ск^= k' равны нулю, поскольку v и о
принимают только четные значения. В результате получаем зна-
комое выражение
Т = 4-1Х2гМ«о,а2)+4-в2^, (5.69)
2 k 2 у
где
В V.( -l)o<2v|£l(x)|2-o>avao (5.70)
V, о
можно назвать моментами инерции.
Матричные элементы составляющих углового момента относи-
тельно внутренней системы получены в § 5.5. Их явный вид опре-
деляется из соотношений (5.123) и (5.124):
<2v|£2(x)|2q> = v26vo;
<2v | Lj (x) 12v> = <2v 1£2 (x) 12v> = A [2 (2 + l)-v2];
<2v + 21 £2 (X) 12v> = -<2v + 21 £2 (x) 12v> =
= (l-v)(2-v)(3 + v)(4 + vj;
4
<2v—21 £2 (x) 12v> = — <2v—21 £| (x) [ 2v> =
= 4- f(l-bv) (2 + v)(3-v)(4-v).
(5.71)
Если эти выражения подставить в (5.70) и воспользоваться (2.22)
и (2.23), то получатся следующие формулы для моментов инер-
ции 150]:
(Qo> п2) = В (За2 + 2 ]<6 а0 а2 4- 2а2) = 4Вр2 sin2 | л j
^2 («о, а2) = В (За2— 2 ]/б а0 а2 + 2а2) = 4Bp2sin2^y-л
^3(a2) = 8Bal = 4B₽2sin2y,
(5.72)
или
У-к = 4Вр2 sin2 —k л
k=\, 2, 3.
(5.73)
Моменты
Ции р.
инерции пропорциональны квадрату параметра деформа-
111
Введем эксцентриситеты ядра
Р Р
t-jj « t-o ' « L -| 1
где Rt — полуоси
выразить ek через
Rl “ Rf
эллипсоида. Используя (2.24) и (2.25), можно
параметры р и у:
л) ,/2psinH>—/г-—л'), Л= 1,2,3. (5.75)
Тогда моменты инерции ядра можно записать в виде
Ул = ~ яВеЬ (5.76)
15
Таким образом, мы получили важный результат: если кинети-
ческую энергию Т = ~ ВХа^а^ выразить через углы Эйлера и вну-
тренние переменные, то она будет состоять из двух слагаемых. Пер-
вое слагаемое в (5.69) можно назвать энергией вращения, хотя
в него также входит взаимодействие с колебаниями поверхности
«внутреннего» ядра. Последнее обусловлено тем, что моменты инер-
ции (5.72) явно зависят от поверхностных переменных а0 и а2. Второе
слагаемое (5.69) легко интерпретируется как кинетическая энергия
колебаний поверхности ядра.
Выделение в полной кинетической энергии энергии вращения и
кинетической энергии колебаний является совершенно формальной
процедурой. Как будет показано в дальнейшем, в тех случаях, когда
потенциальная коллективная энергия такова, что возникает дефор-
мированное равновесное состояние ядра, такое разделение весьма
реалистично. Однако в случае гармонического осциллятора коле-
бательно-вращательное взаимодействие так сильно изменяет выра-
жение (5.69), что разделение энергии вращения и кинетической энер-
гии колебаний становится невозможным. Важно помнить при этом,
что наше определение углов Эйлера (2.22) таково, что вращающаяся
система координат совпадает с главными осями ядра, т. е. равенства
аг = = 0 приводят к диагональному виду энергии вращения
в (5.69). Если бы углы Эйлера были определены так, что а^О, то,
как легко видеть из (5.68), появились бы члены вида (а„, а.^'
xw'ktok', т. е. составляющие были бы не равны нулю.
До сих пор рассматривалось лишь простейшее выражение для
кинетической энергии в лабораторной системе, а именно Т =
= Теперь нетрудно преобразовать и более сложные
слагаемые, т. е. члены третьего и более высокого порядков по а
и а. Приведем результат вычисления кинетической энергии с уче-
том членов второго и третьего порядков [12—14, 330, 332]
Т’ = + V ( 2 2 2J av ах. (5.77)
2 и н. V. Л \ И V X '
112
следующим образом выражается через углы Эйлера
переменные:
= 4 Z Tk («0, а2) «>1+4 Bal (1 + 2ВЧ) +
2* 2
+ Bal (1 — 2В'а0)—4ВВ'ага0 а2,
где В' — —V 2/35 В3/В и
</* = 4/Е?(32 Г 1 — 2В'Р cos I у—k — 4] sin21 у
Эта величина
и внутренние
Т'
(5.78)
Лул'). (5.79)
Здесь снова получаем формальное разделение на энергию вращения
и энергию колебаний. В последнюю величину теперь входит массо-
вый параметр, зависящий от а0 и аг.
§ 5.5. МАТРИЧНЫЕ ЭЛЕМЕНТЫ СОСТАВЛЯЮЩИХ ОПЕРАТОРА
УГЛОВОГО МОМЕНТА ОТНОСИТЕЛЬНО ВНУТРЕННИХ ОСЕЙ
В этом разделе мы получим матричное представление операто-
ров L[, L’2, L'3. Эти операторы определены коммутационными соот-
ношениями (5.30). Для составляющих углового момента Llt L2, L3
относительно лабораторной системы, определяемых коммутацион-
ными соотношениями (5.40), процедура получения матричных эле-
ментов хорошо известна. Здесь будет описана эта процедура как для
Lk, так и для L’k- Такой подход позволит определить, где возникает
различие в матричном представлении, обусловленное разными ком-
муташ юнными соотношен и ями.
Вместо трех операторов Lh обычно вводят повышающий и пони-
жающий операторы L+ и £_, соответственно и оператор проекции
момента на 3-ю ось:
L+ £_ £| + i L2, = Ц — i £2 или В'+ Ll = £х + i £2, = £i • £2> (5.80)
£о 4
Тогда квадрат оператора углового момента записывается в виде
L2 = ц + ц + LI = 4 (£+ £_ + £_ £+) + £2 =
=£;2+£;2+£;2 = 4 (£; ll + ll £;.)+£-. (5.81)
Используя соотношения (5.30) и (5.40), легко можно получить
новые коммутационные соотношения:
[L2, £+]=0, [L3, £+]=£+;
L2, Г0]=о, [£3, £_] =-£_;
[l2, £_]=о, [£+,£_] = 2£3
(5.82а)
113
и
[1Л £;] = о,
[L\ Lo]=0,
[l2, Г] = о,
[Z;, £;] = -£?,
[i;, //]=£?,
[£;, L_] = — 2L3.
(5.826)
С помощью (5.29) и (5.39) можно также получить, что операторы
£з (0;) и £3 (0,) коммутируют друг с другом:
Рис. 5.4. Графическая интерпретация
коммутационных соотношений (5.82)
и (5.83).
Вектор углового момента L прецессирует
вокруг оси z лабораторной системы коор-
динат, что соответствует определенному
значению т. В то же время ось ядра, изо-
браженная на рисунке, прецессирует вокруг
вектора L, что одновременно соответст-
вует определенному значению Л'.
£з]=--0. (5.83)
Как видно из рис. 5.4, по-
следнее коммутационное соотно-
шение имеет простую графиче-
скую интерпретацию. Угловой
момент состояния с фиксиро-
ванными квантовыми числами
£ и т можно представить как
прецессию вектора L вокруг
фиксированной оси z (см. рис.
5.4). Отсюда сразу же видно,
что величины Lx и £у не имеют
фиксированных значений, что
является графической интер-
претацией коммутационных со-
отношений [£3, £j = +i£2 и
[£г, £3] = +Щ- Из рис. 5.4
также следует, что проекция век-
тора L на внутреннюю ось имеет
определенное значение одновре-
менно с £3. Это связано с тем,
что внутренние оси, как и угло-
вой момент, прецессируют во-
круг оси z и, кроме того, во-
круг самого углового момента,
что формально и выражается в
[£3, 1'Л = 0.
коммутационном соотношении
В качестве базиса нашего представления выберем нормирован-
ные собственные функции операторов L'2 = L2, £' и £3. Обозначим
их и (j, т, п), где /, т, п находятся в однозначном соответствии
с собственными значениями L2, £3, £3. Различные символы /,
т, п будут соответствовать различным собственным значениям
операторов L2, £3, £3, и наоборот. Следовательно, собственные
функции и (j, т, п) с различными значениями j и (или) т, п орто-
гональны. Кроме того, если имеются другие операторы Г, которые
одновременно коммутируют с L2, £3 и £', то все элементы рассма-
114
триваемого базисного набора обладают тем же самым набором соб-
ственных значений по отношению к операторам Г.
Любой оператор А в представлении функций углового момента
определяется соотношением
4(н(/, /«> «>) = 2 ч(!'. т’> n')<j' т’ n'\A\jmn>, (5.84)
' /' , гп', п'
где предполагается ортогональность функций и (j, tn, ri):
<jmti | j'tn’ n'y = 6/p 6n„'. (5.85)
Пусть Xy, tn и n — неизвестные пока собственные значения опе-
раторов L2, L3, L'3 соответственно. Тогда
L2u (j, т, п) = Ху и (j, т, п); (5.86а)
L3 и (j, т, п) = mu (j, т, п)\ (5.866)
£'н(/, т, n) = nu(j, т, п). (5.86в)
Так как все операторы углового момента Lh и L'k коммутируют
с L2, имеем для любого k
L2 Lh и (j, т, п) = LkL2u (j, т, ti) = Ху Lk и (j, т, п)
и
L2 L’k и (j, т, п) = Li L2и (j, т, п) = Ху L'k и (j, т, п). (5.87)
Эти уравнения справедливы для любой функции и (j, т, п). Можно
ограничиться лишь набором и (j, т, п) с одним и тем же значением
j для всех состояний, поскольку действие операторов L'k или L*.
не приводит к набору с другими значениями j.
Рассмотрим теперь матричные элементы соотношений
L3 L_|_—L^. L3 — La (5.88)
и
ZU;—(5.89)
Имеем
(m' -tn) (jm'n11 Lv | /mn) = < jtn' ti'\ L^ | jmtt) btm- (5.90)
и
^тт- (n’—n) <jtn' n' | L'+\ jinn) -= — (jtn' ti' | L'+ | jtntiy . (5.91)
Следовательно, отличны от нуля лишь матричные элементы от L+
для щ' — т = } и от L'+ для п'—п = — 1, т. е. можно записать
L+u(j, т, ti)-= хти (j, mA-1, п) (5.92)
и
Z.; и (], т, п) — х,'г и (j, т, /г— I). (5.93)
115
Аналогично
£_ и (j, т, п) = хт и (j, т— 1, п) (5.94)
и
т, n) = XnU(j,m, /1+ 1). (5.95)
Используя определение L+ и L_ (5.80) и эрмитовость Llt L„
и L[, L'2, нетрудно проверить, что
хт+1=-х*т (5.96)
и
Хп—1 = хп . (5.97)
Отсюда для коммутационных соотношений L+L_ — L_~L+ = 2L3
и L'+LL — L'—L'+ = —2L3 получаем соответственно
(jmn\L+1 jm—1/? > (jm— l/i|L_ | jmn)—
— < jmnI L_ I jm +1 n> (jm + 1 n | L+| jmn) = 2 <jmn | L31 jmn) (5.98)
или
Xm-l xm— 1 — XmXm = 2m
И
(jmnI L'+ I jmn+ 1> (jmn-j-11 L'_ | jmn) —
— (jmn ILL I jmn — I> (jmn — 11 L'+ | jmn) —
= — 2(jmn IL' I jmn) (5.99)
или
xn-j~ 1 Xn-f- i Xn X/i = 2n.
Уравнение (5.98) является разностным уравнением для |xm|2:
km-il2-krnl2=2m, (5.100)
а уравнение (5.99) — разностным уравнением для | х’п |2:
\x'n+l\-\x^=-2n. (5.101)
Общие решения этих уравнений имеют вид
|xm|2 = C-m(m+l) (5-102)
и
|%п|2 = С'—п(п — 1) (5.103)
соответственно. При любом конечном значении каждой из констант
правая часть становится отрицательной для достаточно больших
положительных или отрицательных значений т или п. С другой
стороны | хт |2 и | — неотрицательны. Указание на то, как раз-
решить это противоречие, можно получить, если проверить полу-
ченные решения с помощью соотношений (5.90) и (5.91). Нетрудно
116
видеть, что эти соотношения удовлетворяются для любых значений
/и (или п), когда матричный элемент от L+ (или £ф) равен нулю, т. е.
когда | хт |2 (или |Хп|2) равен нулю. Следовательно, величины | хт |2
и |хл|2 отличны от нуля лишь для ограниченной области значений
m и и соответственно, т. е.
/77=/77 + 1, т + 2.т — 2, т—1, т; (5.104)
п = п, п+1, п+2, п—2, п—1, 5.105)
где верхние и нижние границы т и т или (п и п) отличаются на це-
лое число. Можно также сказать, что собственные функции и (j, т, п)
имеют значения т, равные т + 1, т + 2, ..., т — 1, т, и значения
п, равные п, п + 1, п + 2, ..., п — 1. Граничные значения т, т и
,7, п можно найти, решая квадратные уравнения, полученные
соответственно из (5.102) и (5.103):
0 = С—/п(пг+1) (5.106)
и
0 — С'— п(п—1). (5.107)
Получаем
/п=—i—^П+4С, т~ —L + -L/T+4C (5.108)
и
п=-1----L/ 1+4С', п=-’+^-|ПМС'. (5.109)
Отсюда
С=тп(пг + 1) и т =—т—1 (5.110)
в первом случае и
С—п(п—1) и n= 1— п (5.111)
во втором. Поскольку тит отличаются на целое число, т — т =
~ 2т + 1, то 2т — неотрицательное целое число и т может при-
нимать только значения т = 0, 1/2, 1, 3/2, 2, ...Аналогично 2п —
положительное целое число, т. е. n = 1, 3/2, 2, ...
5.5.1. Собственные значения оператора L2
Согласно (5.81), оператор L2 выражается через L3, L+, L_ или
через £з, £ф, Поэтому собственные значения этого оператора
можно вычислить, пользуясь полученными выше результатами.
Мы должны найти величину А/ в (5.86а)
L2 и (j, т, n) = А,- и (j, т, п), (5.112)
117
где т принимает одно из значений (5.104), ап — одно из значений
(5 105). Используя (5.866), (5.86в), (5.92—5.97), (5.106), (5.107)
(5.110) и (5.111), находим
^ = -у(1|2) + m2=-|-lm (m+ 1) —
— (m—l)m + m(m+ 1) — l)] + m2 = щ(тЦ- 1). (5.113)
Аналогично можно получить
= \!mn | ~~ U+ L'_ + t’_L'+) + jmn'y =
= |/mn+ 1> <jmn-]-1 |L1 |/mn> +
4- <jmn | L’_ | jmn —1> (join— 11 L'+ | /nm> + n~ 1'
= 1 x'+ , |2 + -j-1 x'n |2 + n2 = ± [2C - n (n + 1) - (n- 1) n] + n2 =
= -y [2n(n-1)] =n(n— 1).
Поскольку L2 = L'2, to
m (/«+ 1) =n(n— 1),
t. e. m = n — 1. Вместе c (5.110) и (5.111) это дает
n ——m; n--=—m.
(5.114)
(5.115)
Следовательно, квантовые числа n, удовлетворяющие условию —
п п < п, имеют интервал изменений одинаковый с интервалом
для квантового числа т. Как и следовало ожидать, (5.113) и (5.114)
не зависят от т и п. Теперь можно отождествить т с символом /,
который использовался для обозначения собственных функций опе-
ратора L2.
Таким образом, задача построения представления операторов
углового момента решена. Мы получили следующие результаты.
Базис для представления операторов углового момента составляют
собственные функции и (j, т, п) операторов L2, Ls и £з, где /, т, п
определяются из решения уравнений
L2и (j, т, п) = j (j + 1) и (/, т, п);
L3 и (j, т, п) = mu (j, т, п);
L'3 и (j, т, п) = пи (j, т, п).
(5.Н6)
Квантовые числа /, т, п имеют следующие ограничения.
118
1. Для данного представления / фиксировано и принимает зна-
чения
1- 0, -j-, 1, -j-, 2,... (5.117)
2. Для каждого / и каждого п существует (2/ 4~ 1) значений,
которые может принимать т, а именно
т j, /— 1, -/+1, -/. (5.118)
3. Для каждого j и каждого т также существует (2/ + 1) зна-
чений и, которые могут принимать те же значения, что и т, а именно
п 1, !— 1.......................... —/+1. —/• (5.119)
Мы получили, таким образом, (2/ + 1) X (2/ + 1)-мерное
представление операторов L2, L3, L3. Базис этого представления
составляют (2/ + 1) X (2/ + 1) собственных функций и (j, т, п).
Для любого фиксированного значения п = п' (2/ + I) собствен-
ных функций и (j, т, п') образуют базис (2/ + 1)-мерного пред-
ставления двух операторов L2 и L3. Аналогично для любого фикси-
рованного т = т' (2/ ф- 1) собственных функций и (j, т , п)
образуют (2/ + 1)-мерное представление двух операторов L2 и £з-
Последовательно используя операторы L+ и можно преобразо-
вать любую функцию из набора и (j, т, п') в любую другую функ-
цию из того же набора. Аналогично последовательное применение
операторов L'+ и LL преобразует любую функцию из набора и (j, т', п)
в другую функцию из того же набора с теми же j и т'.
5.5.2. Матричные элементы операторов
углового момента
Матричные элементы операторов L+ и £_ определяются из урав-
нений (5.92) и (5.94) соответственно, с помощью соотношений (5.96)
и (5.102). Однако величины хт, необходимые в (5.92) и (5.94), полу-
чаются из (5.102) только с точностью до фазового множителя. Выбор
этого множителя произволен, но, разумеется, он должен быть сде-
лан последовательно. Мы используем условие выбора фазового
множителя Кондона и Шортли [78], которые выбрали его рав-
ным Д1:
хт + УС —/и (m+1) =+}//(/+1) —/и (/и-[-1) (5.120)
и аналогично
<= +] ГС' —п(п— 1)= + У/(/+ 1)—н(п—1) . (5.121)
Отсюда
и (i, т, п) = -ф ]//(/+!)—m(m+i) и (j, т+1,п) (5.122а)
119
и
£- и (j, т, м) = + I У(/+ 1) — т(т — \)и (j, т— 1, п). (5.1226)
Так как £х = у (£+ + £_) и £2 = — у i (£+ — £_), то легко
получить, что отличные от нуля матричные элементы операторов
£j и £2 имеют вид
(jm + 1м | Lx | jmn) = -|-У7(/4- 1)—т (/??+ 1);
<jm— In | | jmn) = ~ /;(/+ 1) —m(m—1)
и
< jm+ ln|£2| jmn) =----£-i] j(j + 1) — m (m+ 1);
(jm — \n | £2| jmn) = “i V/'(/+ B—m (m— 0-
(5.123)
(5.124)
С помощью (5.93), (5.95) и (5.121) аналогично получаются ма-
тричные элементы составляющих углового момента относительно
внутренних осей, т. е. £[ — у (£ф + LL) и £2 i (£4- — £-)•
Имеем
L'+ u(j, т, ri) — +]£/(/ + 1)—п(п— 1) «(/, т, п — 1),
L'_ и (j, т, ri) — 4- У/(/+ 1)—м(м+ 1) и (j, т, п + 1). (5.125)
Отсюда
(jmn + 11£; | jmn) = J, /(/4-1) —и(«+ 1);
(5.126)
(jmn— 11 £; | jmn) = -у J z/(/4-l) —п(м—1)
и
(jmn + 11 £; I jmn) = i //(/4-!)—n(n4~ D ;
(5.127)
(jmn— 11L’2\jmn)=----l- i K/(/+ 1)—n(n—1) .
Мы видим, что матричные элементы операторов £j и £[ [см. (5.123)
и (5.126)] формально одинаковы, но матричные элементы L2 и Аг
отличаются знаком [см. (5.124) и (5.127)].
120
§ 5.6. ПРЕОБРАЗОВАНИЯ СОБСТВЕННЫХ ФУНКЦИЙ
ОПЕРАТОРА УГЛОВОГО МОМЕНТА ПРИ КОНЕЧНЫХ
ПОВОРОТАХ
В последнем разделе было получено, что (2/ + 1) собствен-
ных функций углового момента и (j, т,п')ст= j,j — 1, .... —j +
if —j образуют базис неприводимого представления операто-
ров V, L3, Llt L2, определенных в лабораторной системе коорди-
нат. В дальнейшем можно опустить фиксированный индекс п', т. е.
обозначить собственные функции и (j, т). В этом параграфе мы
рассмотрим преобразования этих собственных функций при конеч-
ных поворотах системы координат. Полезно напомнить читателю
основные свойства преобразований волновых функций и матема-
тические свойства D-функций. Конечной целью нашего рассмотре-
ния является доказательство того, что матрицы D'mn (0Ъ 02, 03)
как функции углов Эйлера являются собственными функциями
гамильтониана симметричного ротатора. Будут также получены
различные свойства симметрии D-функций, необходимые для ис-
пользования свойств симметрии волновых функций коллективного
гамильтониана при преобразованиях (4.13) и (4.22).
Рассмотрим вращение системы координат на угол 0 вокруг
оси, заданной единичным вектором п. Волновая функция ф в исход-
ной системе связана с волновой функцией ф' во вращающейся си-
стеме преобразованием R, которое должно быть унитарным, по-
скольку волновая функция нормирована в обеих системах. Имеем
ф' = £(п, 0)ф. (5.128)
В общем случае операторы унитарного преобразования зависят от
трех углов, в качестве которых наиболее удобно выбрать углы
Эйлера. В нашем случае два из этих углов можно использовать для
определения направления вектора п, а третий угол 0 — для опре-
деления величины поворота. В пределе 0 -> О R (п, 0) должно стре-
миться к единице, поэтому можно записать
R(n, 0) = ехр( — i S (п, 0)), (5.129)
где при 0 -> О имеем 5 (п, 0) -> 0 и S должно быть эрмитовым опе-
ратором, поскольку R (п, 0) унитарно.
Чтобы определить оператор R (п, 0), необходимо найти S (п, 0).
Это можно сделать, если рассмотреть бесконечно малые повороты,
т- е. повороты на бесконечно малый угол dO. Так как 5 в этом слу-
чае становится бесконечно малой, то можно написать
R (п, dO) = 1 — i S (п, с?0) (5.130а)
и
ф' = 7?ф = (1 — 15)ф. (5.1306)
121
Рассмотрим теперь бесконечно малые повороты вокруг осей
х, у, z лабораторной системы. Используя разложение в ряд Тейчо
ра, получаем
ф—ф = — 1й(0£1ф;
/?2 ф — ф = — i d0£2 ф;
RзФ— Ф= — i d&L3 ф,
(5.131)
где
4 = — i (" d d \ Z dy ) ’
dz
L2 = — i (z d X —h
dx dz )
Ls = -i d -y д \
\ дУ dx) ;
(5.132)
Таким образом, три эрмитовых оператора Llt L2, L3, которые опре-
деляют бесконечно малые повороты, совпадают с тремя составляю-
щими оператора углового момента относительно осей лабораторной
системы. Очевидно, что для произвольной оси поворота п
Яф ф —Цп-ЦЛОф. (5.133)
Сравнивая это с соотношением (5.130), находим оператор поворота
для бесконечно малых вращений
5 —(n-L)ilO. (5.134)
Любой конечный поворот на угол 0 может быть получен последо-
вательным применением бесконечно малых поворотов, т. е.
7?ф = ехр(—Ю(п-Ь))ф. (5.135)
Это соотношение является определением операторов углового мо-
мента для произвольного поля ф, иными словами, изменение поля
при поворотах определяет оператор углового момента.
Если конечный поворот характеризуется тремя углами Эйле-
ра, то оператор поворота будет произведением трех операторов
поворота на углы Эйлера 01, 03, 03 (см. §5.1):
7?(п, 0) - Re3 RetRet. (5.136)
Согласно (5.135), операторы Re- выражаются через три угла
Эйлера
R = Re3 Re, Ret = ехр (— i 03 L") ехр (—i 02 £') ехр (— i0r £3), (5.137)
где штрихи у операторов соответствуют тому, что поворот на угол
02 совершается вокруг новой оси у, полученной из старой оси у
122
поворотом на угол 0t вокруг старой оси z, а поворот на угол 03
совершается вокруг результирующей оси z. Второй и третий пово-
рот в (5.137) желательно выразить через повороты вокруг осей ла-
бораторной системы координат. Хорошо известно, что унитарное
преобразование V переводит оператор Г в оператор Г' по закону
= Оператор /?ег = ехр (—i02L') является преобра-
зованием величины ехр (—102£2), полученной в результате действия
предыдущего поворота ехр (—iOjL3) (L2 определено по отноше-
нию к фиксированной оси у лабораторной системы координат).
Поэтому
ехр(—i02^2) = exP(—*01^з)ехр(—i624)exp( + i01L3) . (5.138)
Аналогично ехр (—103£3) является результатом преобразова-
ния величины ехр (—i03£'), полученным при предыдущем повороте
ехр (—i02Z2). Учитывая (5.138), имеем
ехр (—i 03 L3) = ехр (— i 02Ц) ехр (—i 0313) ехр (+ i 0212) =
= ехр (— i ОДз) ехр (— i 02 Z2) ехр ( + i 0А L3) ехр ( — i 0j Z3) X
Xexp (— i 03L3) exp (i 61/.a)exp (+ i 02 L2). (5.139)
И, подставляя это выражение в (5.137), получаем
R(eit 02, 03) = exp(—i 01£3)exp(—102£2)ехр(—i03L3). (5.140)
Этот вид оператора поворота мы будем использовать при рассмо-
трении эйлеровских поворотов. Порядок поворота здесь является
обратным: вначале совершается поворот на угол 03, последним —
поворот на угол 0Г Это обусловлено тем, что все повороты вокруг
осей вращающейся системы (5.137) выражены через повороты отно-
сительно лабораторной системы.
Рассмотрим теперь, как влияет вращение системы координат,
описываемое углами Эйлера, на собственные функции и (j, т).
Оператор R (0ъ 62, 03) (5.140) преобразует набор функций и (j, т),
где т = /, .... —/, в тот же самый набор, так как в соответствии
с результатами последнего раздела последовательное применение
любого из операторов Llt L2, L3 порождает волновые функции из
того же самого набора и (j, т):
R (01. 02. 03) « (/, Ш) = У Dln' т (61, 02, 03) « (/. т") >
т'
(5.141)
где матрица D определяется соотношением
D'm' т (01( 02, 03) = <jm' | R (0J, 02, 03) | /7п> =
С/га'| ехр (—i01£3)exp(—i62£2)exp( — i03£3)|/ra>. (5.142)
123
Используя соотношение [exp (—i61L3)]+ = exp (+i61L3) и то
что и (j, т) являются собственными функциями оператора £3, ц0.
лучаем
D'm-щ (6^ 02, 03) = exp (—i ©j in) х
X <jm’ [exp (—i02Z2) | jm} exp (—i63m). (5.143)
Введем новую матрицу
d'm m (62) = < /ш' [ exp (—i 02 L2) | /m), (5.144)
что позволяет записать D-матрицу в виде
D'm' mt®!, 02, 03) = ехр(— iO1rn')J/n'm(02)exp(—103/л). (5.145)
Матрицы d'm-m (62) были вычислены Вигнером [383, 387]:
dm' т (62) = [(/ + ш)! (/—т)! (/-|-т')1 (/—т')1 ]1/2 х
х У_________________( -‘)v__________________ х
(j— tn'~v)! (j-pm—v)! m)l v!
I 1 n \ 2j+m—m' — 2v ' . 1 \m'— m-|-2v , ,
x/cos —621 [—sin —02j (5.146)
(см. Приложение Б). Индекс v пробегает все целочисленные зна-
чения, для которых аргументы, стоящие под знаком факториала,
больше или равны нулю. Этот результат можно выразить через
гипергеометрическую функцию
2Л(а, Ь-. с; х) = 1+—х + — °(а И)Ь(Ь-Н) (5 147)
с 2! с(с+1)
и получить
(I \2j-\-m— т'/ [ \т'— т
. „ _________________ ”5те-) Нпте-)
тК 2> L(/ + "2')! (/—m)!-l (т'- ту.
X2Fv[m' — j, —m — j\ tn'—т F F, —tg2-i-02j, m'^m. (5.148)
Два первых аргумента гипергеометрической функции, а именно
т' — j и —т — j, — всегда отрицательные целые числа. Функ-
ции F (—п, —т\ с; х) для этого случая представляют собой полино-
мы Якоби степени п и ортогональны на интервале 0 х < 1 с ве-
совой функцией xc~l (1 — х)-т~с~п, т. е.
1
^7(—п, —т\ с; x)F(~n’, —т; с; х) х"7-1 X
о
Х(1— х)-т~с-п(1х=^пП'. (5.149)
В выражение (5.148) входят полиномы Якоби степени | т' — j | или
। т + j | в зависимости от того, какое из этих двух чисел меньше.
124
§ 5.7. СВЯЗЬ МЕЖДУ КОНЕЧНЫМИ
И БЕСКОНЕЧНО МАЛЫМИ ПОВОРОТАМИ
Получим некоторые полезные коммутационные соотношения
между оператором R (0П 62, 03) и операторами углового момента.
Это позволит определить важные свойства функций D!m-m (0Ъ 02, 6з)-
В частности, с помощью этих соотношений можно будет доказать,
что Dm'm (0i, 6-2, 63) являются собственными функциями симме-
тоичного ротатора (см. § 5.8 и 5.9).
Вначале рассмотрим еще раз соотношение (5.128), которое мож-
но записать в виде
Ф (Х^, Х2, Х3) = R (01, 02, 0з) Ф (Д, Х2, Х3). (5.150)
Здесь
Ф'(*1, х2, л-3) = ф«, х2, хф) = ф(/?х). (5.151)
Координаты во вращающейся системе х/ получаются из координат
лабораторной системы с помощью преобразования (5.21), т. е.
4 = 2^(О1,02,Оз)хз-, (5.152)
/
где Rtj (01, 02, 03) дается выражением (5.22).
Найдем соотношение между операторами R (0j, 02, 03), опи-
сывающими конечные повороты системы отсчета, и операторами
бесконечно малых поворотов. Для этого в волновой функции перей-
дем от декартовых координат xt к полярным координатам г, 0, ф,
т. е. ф(хь х2, х3) = ф (г, 0, <р) и ф (х', х', х') = ф (г, 0', <р') (по-
лярные утлы 0', ф' определены по отношению к вращающейся
системе). Соотношение (5.150) можно переписать в виде
ф' (г, 0, ф) = R (0Ь 02, 03) ф (г, 0, ф) = ф (г, 0', Ф'). (5.153)
Рассмотрим поворот системы отсчета в положительном направ-
лении вокруг оси z на угол 03, т. е. (0, 0, 03). Точка Р с координатой
Ф в старой системе (рис. 5.5) во вращающейся системе (х' у') имеет
азимутальный угол
Ф' = Ф—03. (5.154)
Таким образом, имеем
R (0, 0, 03) ф (г, 0, ф) = ф' (г, 0, ф) =
= ф(г, 0, ф') = ф(г, 0, Ф — 03). (5.155)
Это соотношение можно записать в дифференциальной форме
д . л -»
Х’ Ф (г, е, ф) = — Ф (г, о, ф-03)=4- R (0lt 02, 03) Ф (г, 0, ф) =
--^-ф(г,0,ф_ 03) = -^^(01,02,0з)Ф(/-,0, <р). (5.156)
125
Здесь уже имеется в виду общий случай — поворот {61( 02, 0а}
Таким образом, получено следующее важное соотношение:
4- (01> е2- ез) = —Л К (01. 02, 63). (5.157)
Ооз Офз '
где Фз указывает на угол, от которого зависит волновая функ-
ция ф. Этот угол соответствует вращению вокруг третьей эйлеров-
ской оси е3. Аналогично можно получить
03) = -^/?(е1,02.Оз);
002 д<р2
(5.158)
~ R (61, е2, Оз) = R (01, о2, 03/,
или в более общем виде
R(O1, 02 , 03) = —7? (01, о2. 03). (5.159)
Рис. 5.5. Влияние на координаты точ-
ки Р поворота системы координат на
угол 03 вокруг оси z.
полнительный бесконечно малый
полнить конечный поворот, за ко
Подобно тому, как опреде-
ляется обычный полярный угол
Ф при повороте вокруг оси г,
углы ф1э ф2, Фз в этих соотно-
шениях определяются как по-
лярные углы при поворотах во-
круг эйлеровских осей е2, е3
(см. рис. 5.1) в пространстве
аргументов волновых функций
х1( х2, х3. Соотношение (5.159)
выражает тот факт, что можно
либо выполнить конечный по-
ворот, описываемый углами
Эйлера 01, 62, 0з, а затем до-
поворот на угол dQj, либо вы-
юрым последует бесконечно ма-
лый поворот на угол (—dtp,).
Как было показано ранее (см. (5.38) и (5.39)1, оператор угло-
вого момента выражается через углы Эйлера:
4(01,б2,0з)==-(2(^-%^-, й= 1,2,3. (5.160)
Используя (5.159), получаем
Ц (01, е2, 0з) R (61, 02. е3) = -i 2 4- R (0lt 02, 03)
/ OVj
= tf(0i.e2,03). (5-16D
i O'fj
126
Очевидно, что величина
— • _ ~--— Lh (Л’1> X2t хз) (5-162)
i ^4>J
является оператором углового момента, действующим на волновые
функции ф (л'1, х2, х3). Таким образом, мы получаем важный ре-
зультат
L(, (0р 02, 03) R (01. ©2. 0.з) = -Lh (Xlt X2> Л'з) (®1> ®2> 6з)- (5- 163)
Напомним еще раз, что величины Lh (Op 02. ®з) являются операто
рами углового момента, действующими на углы Эйлера, тогда как
Lh (A'i> х2, хз) — это операторы углового момента, действующие на
волновые функции.
Аналогично, пользуясь соотношением (5.159), получаем из (5.28)
и (5.29)
Lh (61. 02. ез) R (61- 0з. 6з) = - i 2 (V-x)a " 0з) =
i ии j
= i3(V-1b -/-R (6i, 62. 63). (5.164)
/ d<Pj
Поскольку величины
L'k «, <, х’) = -i v (V-% , k = 1,2, 3, (5.165)
i a(Pj
являются операторами углового момента, действующими на волно-
вые функции во вращающейся системе координат, то
L'k (61, 62 , 63) R (61, 62, 03) = -L'k (ху, х2, х3)R (б,, 02, 0я). (5.166)
Кроме того, так как L2 = L'2, то с помощью (5.163) и (5.166) полу-
чаем
L2 (0р 02, 03) R (Op 02, 03) = + L2 (ху, х2, Хз) R (Ор 62> 03). (5.167)
Эти «коммутационные» соотношения обычно приводятся в обозна-
чениях, которые не указывают аргументы операторов углового мо-
мента, что приводит к большой путанице. Подчеркнем еще раз, что
операторы Lh (0,) и Lh (х}) действуют в разных пространствах:
первый действует на углы Эйлера, второй — на координаты.
§ 5.8. Dlm,m (64 КАК СОБСТВЕННЫЕ ФУНКЦИИ
ОПЕРАТОРА УГЛОВОГО МОМЕНТА
Соотношения (5.163), (5.166) и (5.167) позволяют получить очень
простое доказательство того, что матрицы Dlm’m (0j) как функции
Плов Эйлера являются собственными функциями оператора угло-
127
вого момента L2 (Оу). Из (5.142) и (5.167) имеем
L2 (Оу) Dlm- т (0у) = L2 (Оу) </т' (ху) | R (бу) 11т (ху)> =
= </т' (хг) | L2(6y) R (Оу) | Im (xz)> =
= + </m' (xz) | L2(xz) R (0y) | Im (xy)>. (5.168)
Запись | Im (xy) > указывает на то, что функции | 1т > зависят
от xit а не от углов Эйлера. Согласно (5.116),
L2 (Оу) О1т- т (Оу) =-]-/(/-[- 1) Dlm • т (Оу). (5.169)
Записывая оператор L2 (Оу) в явном виде [см. (5.41)J, получаем
f-4_ctg02^—1—
I ао2 ь ае2 sin2 о2 ае2 ае2 J
+ '2С?пг яЛа-----/(/+ 1))с^т(0?=--О. (5.170)
sm2 02 ае^Оз / v '
Из уравнений (5.169) или (5.170) следует, что величины Dlm-m (бу)
как функции углов Эйлера являются собственными функциями
оператора L2 (Оу), соответствующими собственным значениям
I (I + 1).
Докажем теперь, что D!m-m (Qj) есть также собственные функции
оператора L3 (Оу). Используя соотношение (5.163), получаем
4 (Оу) Dlm-m (Оу) = £3 (Op < 1т' (xj | R (Оу) 11т (х{) > =
= < 1т' (xz) | L3 (Оу) R (Оу) 11т (xz) > =
= — < Im' (Xi) | L3 (xt)R (Оу) 11т (xz)>. (5.171)
Поскольку Ls (ху) | Im' (ху) > = m' | Im' (xy)>, то
4 (Оу) D‘m-m (Оу) = —m' Dlm-m (0y), (5.172)
t. e. Dlm-m (0y) — собственная функция оператора L3 (Оу) с собст-
венным значением, равным —т'.
Совершенно аналогичным способом можно также доказать, что
Dm-т (0у) являются собственными функциями оператора Ьз (Оу) —
проекции оператора углового момента на ось z вращающейся вну-
тренней системы координат. Для этого воспользуемся (5.166)
и получим
7<з (Оу) Dlm-m (Оу) = Ь'з (Оу) </т' (ху) | Д(0у) | Im (xt) ) =
= <-/m' (х^ | Ц (Qj)R (0y) | Im (xt) > =
= -< Im' (х^) | Ц (x[) R (0j) | Im (xt) >. (5.173)
128
функции I Im (Л',)> — собственные функции оператора L3 (хг), но
не оператора £3 (*'/)• Собственные функции L'3 (х[) даются выраже-
нием
11т' (х) У — R(0;) 11т (л) >. (5.174)
Отсюда
< Im' (Xi) | U (х[) R (О,-) 11т (лу) > =
= < 1т' (х^ | R (0,-) l3 (х^ R-1 (Gs) R (0,) | Im (xt) > =
= < Z/n' (x^ | R (Gj) L3 (x^ | Im (x^ > =
= m < Im' (x^ | R (Qj) | Im (x.) > = rnDlm-m (Oj). (5.175)
Следовател ьно,
L'3 (0,) Dlm.m (0j) = -mDlm.m (0j), (5.176)
t. e. Dm’m (0у) является собственной функцией также и составляю-
щей Ьз оператора углового момента относительно оси г' вращающей-
ся системы координат. В выводе, который приведен выше, было
использовано соотношение
U Ы) = R (0У) L3 (х^ R~' (0;). (5.177)
Заметим также, что легко получить
U (0,) R (6/) = -U (х-) R (0,-) = - R &)Ь3 (х^
или
и (^)^^) = ~Н^)13(Х1)
и аналогично для любой составляющей
^(6;)^(6>)= -R(^)h(Xi).
Кроме того можно получить соотношения
Ц(х!)^(^) = ^(е})ьь(х{)-,
Ц(е})^(е}) = ^(е})1к(еу).
(5.178)
(5.179)
(5.180)
«Коммутационные» соотношения (5.179) были использованы ранее
при получении выражений для моментов инерции [см. (5.53)—
§ 5.9. СИММЕТРИЧНЫЙ ВОЛЧОК
Кинетическая энергия твердого тела, которое имеет три момен-
та инерции ^2, ^з и вращается вокруг центра масс, имеет вид
л л
Б Зак. 1218 129
где coj, ci>2, юз — угловые скорости вокруг осей х', у', z вращаю-
щейся системы координат, жестко связанной с телом. Поскольку
составляющие оператора углового момента относительно внутрен-
них осей даются выражением
M = (5.182)
то предыдущую формулу можно записать в виде
М\2 М'22
~ 2^! + 2^2
^з2 у W
2^з "k
(5.183)
Симметричный жесткий ротатор имеет два одинаковых момента
инерции: = $-2 = ось г' в этом случае является осью сим-
метрии и
Мз2 _ М2—Лф Лф
2^0 + ЗУ3 ~ 2^0 + 2^3 ’
(5.184)
До сих пор мы просто повторяли классическую механику. Т ста-
нет оператором, если мы потребуем, чтобы угловые моменты кван-
товались, а составляющие относительно внутренних осей удовлет-
воряли коммутационным соотношениям (5.826) или составляющие
относительно осей лабораторной системы подчинялись бы коммута-
ционным соотношениям (5.82а). В этом случае, согласно результа-
там последнего раздела, (0,) являются собственными функция-
ми оператора, получаемого в (5.184). Имеем
L2 (0>) Омк (б;) = I (/ + 1) d'mk (61);
4(б;)^мк(01)=^мк(е1);
£з(9^^*к(0;) = КО^к(0>),
(5.185)
где использовано соотношение
Р'ж <е>) - (- 1)”-к (в,). (5.186)
которое доказано в Приложении Б. Отсюда легко получить*
собственные значения оператора Т:
\ 0 । Мз2 2^з - j D~mk (9j) -
/ А2£2-Й.3£з2 к 2^0 A2 L'32 ' 2^з ) D'mk (0;)
_ / /(/ + 1) А2-кА2 Л 2^0 . К2 А2 2^з 1 D/ak (6j) ’ / (5.187)
Оператор углового момента М = Al [см. (6.16)].
«30
Поскольку проекция углового момента на ось z' внутренней
системы координат должна быть всегда меньше углового момента,
т. е. К < I, то уровни симметричного ротатора разделяются на
вращательные полосы, соответствующие различным значениям Д’,
а уровни каждой полосы удовлетворяют известному правилу
I (I + 0- Как будет показано ниже, волновые функции должны
быть симметризованы относительно преобразований Rlt R2, R3
Jcm. (4.22)], что приведет к правилам отбора для I и К (см. §6.4).
Собственные функции симметричного волчка были впервые полу-
чены Райхе и Радемахером [303] и независимо от них Кронигом и
Раби Г218].
* * *
Статья Казимира [74] является первой работой, посвященной
рассмотрению свойств жесткого ротатора. Эти свойства также об-
суждаются в книгах об угловых моментах в квантовой механике
[66, 116, 306].
5*
Глава 6. КОЛЕБАТЕЛЬНО-ВРАЩАТЕЛЬНАЯ
МОДЕЛЬ
В гл. 3 были рассмотрены свойства гармонического квадруполь-
ного вибратора, гамильтониан которого является простейшим при-
мером общего коллективного гамильтониана ядра (3.7) для низко-
энергетических возбуждений. Существенно, что в этом случае кол-
лективная потенциальная энергия V («[21) имеет минимум при
а[2] = 0 и, следовательно, может быть представлена в виде V (cd2!) да
да4- СХа2|1а2|1- Это всегда справедливо для ядер с замкнутыми
в
оболочками или близких к ним, поскольку в основном состоянии
такие ядра являются сферическими. В ядрах, далеких от магиче-
ских, внешние нуклоны связаны менее сильно, поэтому эти ядра
имеют тенденцию к деформируемости. Коллективный потенциал
тогда усложняется и может быть представлен в виде разложения
такого же типа, какое качественно обсуждалось в § 4.2 и 4.3.
Его структура показана на рис. 4.10. В этом случае становится на-
много более удобным выразить полный гамильтониан через внутрен-
ние координаты а0, а2 и углы Эйлера 07-. Потенциальная энергия
разлагается в ряд вблизи точки минимума, соответствующего де-
формации, отличной от нуля (ср. рис. 4.12), что позволяет при-
ближенно описать динамические свойства системы. Таковы общие
идеи, имеющие отношение к моделям, которые будут обсуждаться
в этой и следующей главах, а именно к колебательно-вращательной
модели и модели асимметричного ротатора.
Впервые внутренняя (собственная) система координат была
введена О. Бором в 1952 г. [50]. А. С. Давыдов и его школа [891
первыми получили решения уравнения Шредингера с гамильтониа-
ном Бора для ядер со статической неаксиальной деформацией. По-
следовательные решения для аксиально-деформированных ядер
с учетом |3- и у-колебаний (т. е. решения уравнений колебательно-
вращательной модели) были позже получены Фесслером и Грайне-
ром [129—131, 1331.
132
§ 6.1. ГАМИЛЬТОНИАН КОЛЕБАТЕЛЬНО-
ВРАЩАТЕЛЬНОЙ МОДЕЛИ
Колебательно-вращательная модель рассматривает ядра, кол-
ективная потенциальная энергия которых имеет минимум, соот-
ветствующий аксиально-симметричным деформированным ядрам.
Эта коллективная потенциальная энергия разлагается в ряд
вблизи точки равновесия
а0=Ро4-^ = Р0+1; (6 J.
а. = 0 ф- а 2 = 0 ф-1]
и таким образом, имеет вид
V (ai, а'2) = -j- Соао2 + С2 а'22 = -^ СД2 + С2 г)2. (6.2)
Классическая кинетическая энергия в первом приближении берет-
ся в виде
4" В S «2ц «2ц-
2 в
Выражая ее через углы Эйлера и внутренние переменные, полу-
чаем
'2 1
7'=?^Гк>+Тв<“г + 2^ <6-3’
где моменты инерции даются выражением (5.72). Как будет видно
из дальнейшего, эти выражения для моментов инерции должны быть
разложены в точке равновесия (6.1) с точностью до членов второго
порядка. Чтобы последовательно описать члены более высокого по-
рядка, необходимо учесть слагаемые более высоких порядков уже
в исходном выражении для кинетической энергии в лабораторной
системе координат, что соответствовало бы добавлению следующих
членов.
В3 На121 ,a[2Y21 ха[2]][0] -|-В4 [а[2 W2]]t0] X [а[2] X <x[2]]t0] +...
Выражение для кинетической энергии (6.3) является все еще
классическим, поэтому необходимо рассмотреть вопрос о кванто-
вании классической функции Гамильтониана, заданной в общих
криволинейных координатах. Для этого существует хорошо из-
естный метод, который будет рассмотрен отдельно в§6.2. Приведем
десь лишь наиболее существенные необходимые результаты.
усть классическая кинетическая энергия задана как били-
иеиная форма координат qv\
т = l/22;9Mv(9a)9u ?v, 1,2, (6.4)
133
где g^v (7с) = gw Ofc) являются функциями только координат.
Элемент длины в криволинейном пространстве определяется в виде
ds2 = 27 (dt)2 = X (7<т) dq^ dqv. (6.5)
p,,v
Квантовое выражение для кинетической энергии имеет вид
„13 д
, (6.6)
где G — определитель матрицы g^ и (g'1)^ обозначает матрицу,
обратную матрице g^v Элемент объема равен
dr = | | G | dqr... dqN. (6.7)
Для квантования выражения (6 3) воспользуемся формулой (6.6).
Перепишем (6.3) в форме
Т = 4- 2 (с0, с2) (2 Vhi (бп е2,63) У+
2 k \ i at )
+ _1_В(й§ + 2^), (6.8)
где использованы формулы(5.69) и (5.55). Координаты q^ в данном
случае записываются так
<7i = c0, 9г = с2, 7з = е1. ?4 = е2. ?5 = ез- (6-9)
Отсюда
gn-B, ^гг = 2В;
^=^1 = ° для Ь
^"=Яй2 = 0 ДЛЯ
= 2 («о. с2) (0Z) Vkv (0j), JX, v > 3. (6.10)
k
Явное выражение для этой матрицы таково
£ ос, аг)~ ВО 0 0 2В 0 ^,slnZв2 C0S2а7 + 0 0 !-Jzsin2 егз1п:63 +$3св!гег 0 0 -^1sin6zcose3sine3^ +^г sin в2 sin в3 cos 83 0 0 j3C0S^z 0 0 sin ег cos в3 sin е3+ + r^2 sin 82 sin 83 cos 83 ^sin283+J2cos'O3 0 0 0 J3cos82 0 (В. 11)
Легко вычислить определитель матрицы
G = det Ы = 2Д2 sin2 02 2Д Оз =
= 16B5a!(3«§— 2al)2sin202. (6-12)
134
Обратная матрица равна
G/В П О
О G/2B О
' 0
^sinle3^zcos е3)
о 0 -ibzj3
x^s'in Вг cosB3sinB3
+jz sin в2 sin e3 cos e3)
о 0 -2.B2J3C0se2
^(J1sinzB^JlcoszB3)
0
0
x(~T sin Bz cos B3 sin 63
+J2 sin В2 sin B3 cos B3)
xtysin 8z COS2В3
+ JzSinZBZSinZe3)
+2BZJ3 cos ег
*(- 7, sin Bz cos B3 sin 63
+j2sinBzcosB3sine3')
В
0
-zbzTcosbz
*(isinze3
4гсо5ге3)
+ZB2lcosB2
^(-Ъс'т Bz cos 83 sin 83
+J2 sin 8Z sin B3 cos B3)
+JiJ3cos2e2SLnZe3
(6.13)
После длительных, но простых вычислений согласно (6.6) полу-
чаем квантовомеханический оператор для кинетической энергии (6.3):
t = TTOt + Tvib, (6.14)
где вращательная энергия дается выражением
Тто1 =- - А2 Г_____?--( — + Sin ез ±-
[2^! («о. "2) V sino2 «Эбх ао2
, „ Q д V . 1 / sin03 д
+ ctg 6о COS 0.,--- Н----------------------------1
о63 / 2^2(а0,а2) \ sin 02 30!
, п д , д . Q д \2 . 1
+ cos ез -------ctg е2 sln 6з -дг- + -----7
д02 2^з (#0, G2)
__ -у Mk2
k^T.2,3 2^h(a0,a2)
k 503 I J
(6.15)
Здесь введены компоненты оператора углового момента:
(6.16)
где L'k (0,-) даются формулами (5.29). Формула (6.15) для квантовой
вращательной энергии получена ранее в § 5.9 более изящным спо-
собом. Здесь она выведена на основании общих правил квантования
в криволинейных координатах.
Энергия колебаний относительно легко вычисляется с помощью
(6-6) и (6.13):
Sr _____ А2 Г d2 , 1 д2 . 6а0 д
J vib — -------—----------1---------------------------------
2В [ да^ 2 да2 За§ — 2а| да0
__________3 (ag —4а^)__________\ д 1
2а2 (g§-}-2а|) (3gg — 2g|)_____' да2 J
(6.17)
135
Это выражение легко записать через параметры |3 и у, связанные
с а0 и а2 соотношениями (2.23). В результате получим формулу
используемую копенгагенской школой 150, 51]:
* А2 г I а а , 1 1 д . „ д 1
Tvti I „ _ Р 4~ . Sln3y . (6.18)
2G [ р4 др др р- sin Зу ду ду J '
Согласно (6 7), элемент объема имеет вид
dr = | ] G | da0 da2 с/0г d62 d63 =
= 4B5/2 | a211 За?—2c?211 sin 021 da0da2dQ1 dO2dO3. (6.19)
Можно, конечно, опустить постоянный множитель в этом выражении
поскольку он не будет влиять на все соотношения нормировки и
ортогональности. Сначала [50] элемент объема выбран так, что
dr = dr (а0, cQ dfi, (6.20)
где
dQ = | sin 021 d0x d02 d03 = sin 02 d0t d02 d03 (6.21)
является элементом объема в пространстве углов Эйлера, а величина
di (с?0, а2) = У 2 | с?211 Зс?о—2а21 daoda2 = р41 sin3y | d|3dy (6.22)
есть элемент объема в пространстве внутренних координат. В этом
случае условие нормировки волновой функции ф (о0, с?2), описы-
вающей колебания поверхности ядра, принимает вид
§ф* (с?0, с?2) ф (с?0, с?2) У 2 I а211 Зс?о — 2cz| | da2 da0 =
= ф* (а0, а2) ф (czp, а2) D (с?0, cz2) da0 da2 = 1, (6.23)
где D (с?0, а2) = У 21 а2113czg — 2а221.
Более удобно [129, 130] ввести новую волновую функцию
ф (а0, а2) = У D (с?0, с?2) ф (с?0, с?2), (6.24)
которая нормируется с простым элементом объема
с/т (с?0, cz2) = da0 da2, (6.25)
т. е.
V Ф* (с?0, с?2) ф (с?0, cz2) da0 da2 = 1 (6.26)
благодаря тому, что множитель [ D (с?0, с?2) входит в новую волно-
вую функцию ф (с?0, с?2). При этом необходимо помнить, что при
вычислении матричных элементов от дифференциальных операторов
по волновым функциям ф дифференциальные операторы должны
быть соответственно преобразованы, прежде чем действовать на
волновые функции ф Недифференциальные операторы могут ис-
пользоваться без этого преобразования.
136
Рассмотрим теперь дифференциальное уравнение, решениями
торого являются волновые функции q (о0, а2). Волновая функция
4>°(а0> °г) удовлетворяет уравнению Шредингера
Tvib (а0, а2) ф (а0, а2) = Еф (а0, а2), (6.27)
где T'vtb — дается выражением (6.17) или соответствующей частью
выражения (6.6). Подставляя ср (а0, а2), согласно (6.24) имеем
тм(»„«,) ~ Е . (6.28)
у D (oq> °s) I D (а0, а2)
Умножим это выражение слева на ) D (а0, а2), тогда
Tvib (а0 а2) ср (av а2) = У (tvib (а0, а2) ~^а°’ ] =
V D \aQi ^2/ /
= Е<р(сг„, а2\ (6.29)
Таким образом, ср (о0, «2) удовлетворяет уравнению Шрединге-
ра с кинетической энергией колебаний, которая может быть полу-
чена из (6.29). Полезно выполнить эту процедуру, применяя схему
квантования, описанную в начале этого раздела (формулы (6.4)—
(6.7)1. Кинетическая энергия колебаний, соответствующая волновой
функции ф с элементом объема* di — D (а0, а2) da0da2, имеет вид
с- 1 1 х’ а д
Tvib= — —1 n d E(g )хх д . (6.30)
л# Л л Д,
Волновая функция ср = У D ф удовлетворяет уравнению
Tvib4>(a0,a2) = Eq>(a0,a2), (6.31)
где
Tvib= =
I „ д д
+КЙ(М. (6.32)
z и,Х = 0,2 оаК
Кинетическая энергия является теперь не только дифференциаль-
ным оператором, но содержит «дополнительный потенциал»
4D ид
dD д(8~1)у.-ь d2D
дак дах
2D дак дак J
(6.33)
Напомним,
зависящей от а0
что D2 (а0, а2)
и а2.
являются частью
определителя G (6;-, ov),
V _
v add —
137
Поскольку субматрица (2 X 2), соответствующая «колебатель-
ной» части матрицы (G-1) [см. (6.13)1, является диагональной, вы-
ражение для дифференциального оператора Tvib теперь значитель-
но упрощается. Эга простота, так же как и простота нормировочного
интеграла (6.26) и матричных элементов, достигнута ценою появ-
ления дополнительного потенциала Vadd (а0, а2). Теперь легко
получить соответствующий квантовомеханический оператор для
классической кинетической энергии (6.3). Он имеет вид
м'к1 2
2^k(ao> «г)
fr2 Г d2 1 d2 (3a02+6aj)2
2В [dag ~ 2 да2 8a2 (3ag —2a2)2
(6.34)
при этом dx = d(Jdauda2 = sin 02dB1d02d^3daoda2.
Выражение для кинетической энергии колебаний значительно
упростилось по сравнению с выражением (6.17), но при этом по-
явился «дополнительный потенциал» — последнее слагаемое в (6.34).
Как будет показано ниже, его учет является довольно простым.
Если вместо квантования выражения (6.3) необходимо выполнить
процедуру квантования более сложного выражения (5.78) для кине-
тической энергии, содержащего члены второго и третьего порядков
по и в лабораторной системе координат, то аналогичным
образом можно получить
у Mk2____________А" | д l-2g'a0__________д
k 2Д (а0, а2) 2В | da0 (1 — 4g'2 (ag - |-2а|)) да0
1 д_________1 +25' ао_______d , d____________4g' а2 д
2 da2 (1 —4g'2 (ag+2ag)) da2 1 da0 (1 — 4g'2 (ag +2ag)) da2
+-T- „ J.B,' °’,, - -T-l+<6 *-35’
да2 (1—4g “ (ag-f-2ag)) da0 |
где dr = dSida0da2. Дополнительный потенциал в этом случае
дается выражением
, _ _ А2 ( 9 (ag-|~2a2)2-j-2g' (ag-|-2ag) a0 (ag —6a2)
аМ~' 2Ви (8 a2(3a2 — 2a2)2
, Д'2 j__9__________g'2 (2-5g'2 (ag+2a2))________
+ и ‘ 4 1 —3g'2(ag-|-2a2) —2g'3 * *a0(ag —6a2)
I 2gg'2 (ag+2a^) —2g'a0(ag—6fl^) ) (6.36)
u2 I
где и — 1 —4B'2 (ng + 2g2). Моменты инерции ty'k (g0, a2) и пара-
метр В' определены в (5.78) и (5.79). Заметим, что, как это и должно
быть, в предельном случае В' — 0 получается выражение (6.34).
Добавляя к оператору кинетической энергии (6.34) потенциаль-
ную энергию колебаний V (gq, a2), получаем коллективный квадру-
польный гамильтониан, выраженный через углы Эйлера и внутрен-
не
ние переменные:
гу. У Mk________________________I д
2^ь(а0, a2) 2C [ dal
i a2
2 3fl|
(3a2-{-6a2)2
8a2 (3a2-2a2)2
j +1/ (a0, a2)
(6.37)
с элементом объема dx = dilda0da2. Полученное выражение можно
записать через параметры |3 и у:
,, = у Aife2________А2 г1 а ,,4 а 1 1 э х
Т127й(Р,у) 2В [ р« ар ар р2 sin3? а?
х sin Зу+ V (р, у). (6.38)
Элемент объема в этом случае есть dx — p4|sin 3y|d0dydfi.
Формула (6.38) впервые была получена О. Бором в 1952 г. в его
известной работе 150] о связи поверхностных колебаний ядра с дви-
жением индивидуальных нуклонов. Она была отправной точкой
для развития коллективной модели в области низких энергий и
использовалась многими авторами. В настоящее время она также
является исходным пунктом различных вариантов этой модели,
рассматривающих свойства низколежащих возбуждений ядра.
Формула (6.37) полностью эквивалентна гамильтониану Бора.
Однако она имеет более простое выражение для элемента объема
и энергии колебаний. Видно, что члены, описывающие вращение
и колебания, связаны друг с другом благодаря тому, что моменты
инерции зависят от av. Если сделать предположение, что потен-
циальная энергия поверхностных колебаний имеет глубокий сим-
метричный минимум, соответствующий аксиально-деформированным
ядрам, так что можно пользоваться разложениями (6.1) и (6.2), то
выражение для моментов инерции (5.72) можно разложить в ряд
с точностью до членов второго порядка по отношению а\У|30:
1 1 Г1 I 2Q22 2 -.г~б 2а! За!21
М р§ - 2 у 6 ——s Ро2 V О— 'Ч — ; 3 Ро Ро PS J
1 =^[>+2^ -2 /6 1 <g а2 2^0 I Sflp2 "1
» 2 1 ^oL pg 1 р2 3 Ро Ро ро2 1’ (6.39)
8Ва'2 ’
= зед
пол fTIIbIH тРет™ момент, конечно разложить нельзя). Выполняя
Полу 1 Разложение также для дополнительного потенциала в (6.34),
учаем гамильтониан колебательно-вращательной модели (а'о =
-S> «2 st)) [129—135]:
Н -Hrot-1!- Н + Hvlbrnt >
(6.40)
139
где
Н vib
м;2 м? м'2 _ м*-/й'3 m's- .
2^о 22% i6Bfl'2 22% 16Щф ’
1 d21+-^c0g2+c2l]2-
2211 — 2-L + 3 IL
₽o pg
+/^~ Г2 l/(Fil — l/б”-2L
42% fig 3 po
2 di]3
- _ м3—M'2
‘‘vibrot
&lr о
h2
16Дг|3
42%,
₽0
(6-41)
(6.42)
(6.43)
с элементом объема di = dQd£,dn\. Здесь введены обозначения
M+=M'i + iM?, ml=M'l—iMo, мГ—=
= ^-(Л4+ + Л422) (6.44)
и колебательно-вращательное взаимодействие обозначеноHVibrot- По-
следнее слагаемое в Hvib обусловлено дополнительным потенциа-
лом (6.34).
Собственные значения и собственные функции колебательно-
вращательной модели будут получены в § 6.3. В следующем парагра-
фе более подробно рассмотрено то, что ранее было принято без до-
казательства, а именно квантование классической кинетической
энергии в криволинейных координатах.
§ 6.2. КВАНТОВАНИЕ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
Квантовомеханическое описание любой классической системы
можно получить, если найти соответствующую классическую функ-
цию гамильтониана, выразить уравнения движения через некоторые
канонические переменные qi, pt и сделать соответствующую замену
классических скобок Пуассона
^ = -^ + {F, Н\, (6.45)
dt ot
где
F = F(?i,..., ..., ру; 0 (6-46)
является функцией динамических переменных qp, pt и И — класси-
ческая функция Гамильтона. Классические скобки Пуассона
{F, Н} определены в виде
{F, v ™0F\ , (6.47)
г±1 W dpi dqt др^ ) ’
а уравнение (6.45) является классическим уравнением движения
для F. Квантовый аналог классических уравнений движения по-
140
„учается, вообще говоря, заменой скобок Пуассона коммута-
ционными скобками, деленными на iA, т. е.
{F, Н}^± [F, Й] = -±r(FH— HF). (6.48)
17г i/ь
Канонические переменные при этом подчиняются квантовым соот-
ношениям [315]
[<7{. Pi] = [<7f. 7;]^ °- [Pt, P/]=0- (6.49)
Этот метод полезен при квантовании классических полей и клас-
сических частиц. Существуют однако две трудности, которые воз-
никают при его применении. Во-первых, в этом методе координаты
и импульсы должны быть выражены через декартовы координаты.
Во-вторых, должна быть устранена неоднозначность в порядке не-
коммутирующих величин. Это обычно делается путем использования
симметричных выражений, являющихся средними от произведений
величин, взятых в различном порядке. Указанные трудности иллю-
стрируются на следующем примере.
Рассмотрим атом водорода в сферической системе координат.
Если записать уравнение Шредингера сначала в декартовых коор-
динатах
VW. У. г) + |^Е + -у-)ф(*, у, z) = 0, (6.50)
а затем переписать его в сферических координатах, то получим
_LJL (г2 е, <р) \ 1 д е, Ф)
г2 dr dr F r2sine ае I аФ / +
Заметим, что ф, рассматриваемая как функция координат х, у, z
в уравнении (6.50) и как функция г, 0, <р в уравнении (6.51), яв-
ляется одной и той же функцией положения точки, так что для со-
ответствующих значений координат
ф(х, у, г) = ф(г, 0, <р). (6.52)
Уравнение (6.51) является обычной формой уравнения Шредин-
геРа Для атома водорода.
коордТ^ еСЛИ исходить из Функции Гамильтона в сферических
1
г2 sin2 0
Рг =
А___д_
i dr
и
положить
~ А д Кд
Рй . да ’ Рф — . "Т- ’
1 ае 1 а<р
(6.53)
(6.54)
141
то коммутационные соотношения (6.49) выполняются, но при этом
получается следующее уравнение:
дая|?(г, 6, у)
5г2
1 д2 я|) (г, 6, ф)
г2 дв2
1 д2 ф (г, 6, <р)
г2 sin2 6 dtp2
+ 0j ф) = 0>
(6.55)
которое отличается от (6.51).
Частично эта трудность может быть обусловлена различием в спо-
собах нормировки яр (г, 0, ф) и яр (г, 0, ф). Для яр (г, 0, ф) мы имеем
§яр*(х, у, з)я[:(х, у, z)dxdydz =
= §яр*(г, 0, ф)яр(г, 0, ф) г2 dr sin Od()d(f= 1, (6.56)
в то время как функцию яр (г, 0, ф) можно было бы считать норми-
рованной так же, как это делается в предыдущем разделе, где мы
перешли к элементу объема, являющемуся произведением лишь бес-
конечно малых рассматриваемых координат. В нашем случае dr =
= drdQdtp, и условие нормировки имело бы вид
§ яр* (г, 0, ф) яр (г, 0, ф) dr df) dtp = 1.
(6.57)
Отсюда можно получить соотношение между яр и яр [см. (6.24)]:
яр (г, 0, ф) = — 1 яр (г. О, ф). (6.58)
Д/ г2 sin 6
Подставляя (6.58) в (6.51), можно найти правильное уравнение для
функции яр (г, 0, ф), которое, однако, все еще не согласуется с урав-
нением (6.55).
Таким образом, мы приходим к заключению, что функция
Гамильтона (6.53) не является верной для квантовой механики.
Действительно, формулу (6.53) можно записать во многих классиче-
ски эквивалентных формах, которые будут сильно различаться
при переходе к квантовой механике. Например, величину р2
можно записать в виде г~гртгрг, г~1ргг3ргг~1, гртг~&ртг2 и т. д.»
но эти записи не эквивалентны, если рг не коммутирует с г.
Изложим теперь, следуя работе Подольского [300], метод полу-
чения правильного квантовомеханического оператора Гамильтона
в произвольной системе координат. Для этого рассмотрим кон-
сервативную систему N частиц, имеющую 3N степеней свободы-
Обозначим декартовы координаты частиц
•^1» ^2’ " ’ •^'З/V,
(6.59)
а соответствующие импульсы
Р1> р2> ••• . P3N-
(6.60)
142
ф} нкция
Гамильтона всей системы частиц имеет вид
3W 2
= + x3N).
, , 2т
(6.61)
Потенциальная энергия V (хъ .... х3л') не зависит от импульсов и,
следовательно, совпадает с ее классическим выражением. Урав-
нение Шредингера в декартовых координатах хорошо известно:
# + ^L + 5(£-V(x1,..., х3к))Ж- . Л'зл/) = О, (6.62)
ах! дх™ А
при этом предполагается, что ф (лу...x3W) нормирована в декар-
товом пространстве так, что
... §ip*(Xi,... , x3W)i])(Xi, ... , x3N)dx1... dx3N = 1. (6.63)
Рассмотрим теперь нашу задачу с 37V координатами для N ну-
клонов в конфигурационном пространстве. Перейдем к новым коор-
динатам, которые включают коллективные координаты и остальные
степени свободы. Новая система координат
{tz} = u1, и2,..., ит,.... u3N (6.64)
может быть охарактеризована коэффициентами grs, которые по-
являются в выражении, связывающем квадрат элемента длины дуги
с координатами ит:
ds2 = gndu2i + 2gl2 du1du2 + ... + 2glm dut dum + .. .
3N
g3N3N dusN du3u — V gT sdurdus, (6.65a)
r, s= 1
при ЭТОМ
grs = gsr- (6.656)
В качестве коллективных переменных могут, например, рассматри-
ваться первые т координат, в то время как остальные координаты
um+i> u3N описывают дополнительные внутренние «одночастич-
ные», степени свободы системы N частиц*. Определитель матри-
цы grs обычно обозначают g:
g—det{grs}, (6.66)
а матрицу, обратную матрице grs — (g~1)rs-
Запишем теперь формулы (6.62) и (6.63) в системе координат
(и}- При этом, поскольку мы интерпретируем выражение фйф как
плотность вероятности, потребуем, чтобы оно было инвариантной
ми ол С‘педУет подчеркнуть, что последние координаты не являются обычны-
коопди°ЧаСТИЧНЬ1МИ К00РДинатами и не должны отождествляться с какими-либо
м коо"аТаМИ Xi' Однако в гл- 9 будет рассмотрена приближенная связь с эти-
к важ!тД”ИНаТа«И ДЛЯ тяжелых нечетных ядер. Это непосредственно приводит
описки,,,? пРоблеме «духовых» состояний, возникающей при коллективном
ии ядер. Она будет рассмотрена в т. 3.
143
функцией координат. Выразим координаты х1г х2, ... в функции
ф (хъ ..., л'зд?) через координаты и, т. е.
ФСЧ,..., x3N) =>ф («lf... , ит,, u3N). (6.67)
Формулы для преобразования величин, входящих в (6.62) и (6.63)
таких, как лапласиан V2 в TV-мерном пространстве, известны в об-
щей теории криволинейных координат (см., например, [345] или
Г2601). Имеем
S,
3N___L ,
2 г>/-
r=l OUT
dus '
2т [E — V(ult..., u3N)) ф («!,... , Пзл-) = 0
Л2
(6.68)
и
1
§... §ф*(«1, ..., «злОФ(иг,, U3N) Ig2 u3N)\du1...du3N=l.
(6.69)
Таким образом, новый элемент объема есть
1
dx = \g2 u3N)\du1.,.du3N. (6.70)
Если же работать с элементом объема
dx = du1... du3N, (6.71)
то необходимо ввести волновую функцию
Ф(ы1( и2,.... u3w) = |g-2 (“1,...» M3w) I2 ф(«1,... , u3N), (6.72)
так, чтобы
§... §ф*ф(«!,..., w3W)Ig2 |d«1...dH3№
= § ... §Ф*Ф(Н1,... , u3N) du±... du3N . (6.73)
Подставляя (6.72) в (6.68) и умножая полученное уравнение на
g* («!, ..., u3n), находим волновое уравнение для волновой функции
Ф (щ, ..., u3N):
У £ 4 U3N) +
2tn r i диг 1 ous
+ (Е-Е)Ф («!,..., «3W) = 0. (6.74)
В предыдущем разделе (см. выражение (6.32)1 мы использовали
именно этот результат в конкретном случае криволинейного про-
странства внутренних переменных а0 и а2.
144
Воспользуемся общим правилом замены дифференциальных опе-
аторов (Л/i) (д/дик) соответствующими импульсами pk и получим
давильное квантовомеханическое выражение для гамильтониана
в криволинейных координатах:
3N !_ —-
//==1 < Prg* (g-^P.g 2 +У(иг....... U3N). (6.75)
В классическом случае, когда порядок множителей несуществен,
это выражение принимает обычную форму
1 3N
Н"п (g-1)r,PrP' + V(ul............. u3N). (6.76)
Г. S=1
Рассмотрим теперь случай, когда первые т координат и1г ...,
являются коллективными координатами, а координаты ит+1, ...,
u3n описывают внутренние. степени свободы ядра. Легко видеть
что разделение волновых функций на части, соответствующие кол-
лективному и внутреннему движению, означает, что матричные
элементы
для г<т и s>т,
(6.77)
для г>т и s^m,
grS = 0 {
т. е. матрица grs должна иметь следующий вид:
gll ё12 • • • Sim 6 ........О
&21 ....
gml • • -grrim 6 ...........О
О 0 g^m+lm+l Sm+lm+2 • • • Sm+1 3N
• • ёт+2т+1
(6.78)
_ о 0 g3Wm4-l...............g3N3N
Таким образом, чисто коллективная модель подразумевает, что
внутренняя волновая функция является одинаковой для всех кол-
лективных состояний. В действительности это справедливо лишь
отчасти, так как, вообще говоря, коллективные и внутренние степе-
и свободы взаимодействуют между собой. В этом общем случае
еобходима большая осторожность при получении правильного
145
квантовомеханического гамильтониана в соответствии с формулами
(6.75) или (6.68), рассмотренными в этом параграфе.
В качестве примера, в котором не используются коллективные
координаты, применим полученные результаты к сферическим ко-
ординатам. Это даст возможность увидеть, как выполняется кван-
тование для случая более общих координат. Имеем
ds2 dr2jt-r2dQ2-\-r2sm2Qd(f2, (6.79)
т. е.
£u = 1. £22 = г2, gS3 --= г1 sin 6,
£ift = 0 для i^k. (6.80)
Отсюда
(£ г)н — 1 • (£ ^22 = ~ , (£ 1).чл = ' ,
г2 г2 sin2 6
(£-1)iA = 0 для i=£k. (6.81)
Определитель системы g = г4 sin2 0.
Таким образом, волновая функция ф (г, 0, <р), определенная
в пространстве с элементом объема dr = r2dr sin OdOdtp, удовле-
творяет волновому уравнению (6.68), которое в нашем случае имеет
вид
( А2 Г 52 . 2 д , 1 д / . Q д \ , 1 д2 1 ,
J-----------1--------1-----------Sin 0----- II------------4-
( 2т | dr2 г dr г2 sin 0 50 \ 50 ) г2 sin2 0 5<p2J
+ V(r, 0, ф)—Е|ф(г, 0, ф) = 0 (6.82)
в то время как волновая функция Ф (г, 0, ф), определенная в про
страпстве с элементом объема dx = drdOdq, удовлетворяет волново-
му уравнению (6.74), имеющему в нашем случае вид
(-ИрГ-ь—1_Л(5|ПеА)_!_+ „ Л1+
( 2т[дг2 r2sin%0 V 50 ) sin%e Г2 Sin% 0 5<p2J
+v(r, e, ф)+го^-е)ф(г, e, ф) = о. (6.83)
Операторы импульса в первом случае даются общей формулой
^Ф = — g~'A^g^, (6-84)
1 duk
в частности
D А 1 5
= -------—г,
1 г or
Рв = — —1—- — sin% 6; (6.85)
i sin*/,e 50
р
146
Во втором случае они даются обще й формулой
' .. А д ,
Pk® = ~- Ф.
1 OUh
В частности для сферических координат
Рг = ~/, Ре = -^, = —
1 дг 1 dQ 1 ci
§ 6.3. РЕШЕНИЕ УРАВНЕНИИ
КОЛЕБАТЕЛЬНО-ВРАЩАТЕЛЬНОЙ МОДЕЛИ
(6.86)
(6.87)
Рассмотрим теперь решение уравнения Шредингера с колеба-
тельно-вращательным гамильтонианом (6.40)—(6.43). Решение урав-
нения Шредингера с гамильтонианом Hrol + Hvib может быть
полечено точно. Поскольку Hvibroi является малым возмущением
(по крайней мере для малых угловых моментов), то эту величину
можно учесть по теории возмущений. Преимущество такого подхода
заключается в том, что можно получить явные выражения для
энергии уровней и волновых функций. Для больших угловых мо-
ментов необходимо использовать второй метод— метод диагонали-
зации.
Будем исходить из уравнения Шредингера с гамильтонианом
f М'2 М'2—fe2 А2 / д2 1 ,
I 2^0 16Вц2 2В \<Э£2 2 ди2/ +
+ у С0^ + С2»]2^ (6Ь g, t)) = £^(67-, £, т]) (6.88)
и искать волновую функцию в виде
5 (6,-, £, л) = D%K (6,-) <р (I, Т]), - (6.89)
тогда, так же как и для собственных функций симметричного рота-
тора [см. (5.187)], получаем
1 (/ (/ + !)—/С2) А2 (Д2—1)Л2 _ Л2 В2 1_ ,
I 2^0 + 16Вт]2 ~ 2В\д^+ 2 +
+ |ШС2Л2)ф& т)) = £Ф(^ г]). (6.90)
Это означает, что гамильтониан Hroi 4~ Hvib диагоналей по К-
Функцию ф (|, т|) можно представить в сепарабельном виде
<₽(£, 11) = Хк(П)£п0 (£). (6-91)
^Т°^)РИведе^ к следующим дифференциальным уравнениям для
f-EU+l)-#2) А2 (№—1)Л2 А2 д2 . r 2 ,р р .I , . п
-----—lfiR 2-----+ С2 Л2— Хк 01) = О,
16Вт)2 4Вдт)2 J
(6.92)
о
147
и
(Й2 д2 1 \
- Тв h + т С°?-Ео Ш = °. (6.93)
Таким образом, для а0 (или |-)-колебаний* мы получаем решения
гармонического осциллятора, которые легко выразить через опе-
раторы рождения и уничтожения а0-фононов:
+ + (6.94а)
= Po)=-i«oy(-|?+ + ₽o); (6.946)
____/ А \ % q (38 \ % л. Сл _ г
у==\2в^) ’ Е=?7’£р=д У Т’ *°=зв^
(6.94в)
Эти операторы удовлетворяют коммутационным соотношениям для
бозонов
Ро₽+-р+₽о=1-
Следовательно, g (|) можно записать как |п0>, Где
£по (I) = I «о > = (/г0!)-^ Р+... Р+|О>
п0 раз
(6.95)
(6.96)
и 10> — вакуумное состояние.
Для энергии До а0-колебаний имеем
До = («о + 1 /2) fia0 = («р +1 /2) ti (п0 +1/2) Др,
• но = О, 1, 2,... (6.97)
Обратимся теперь к уравнению (6.92). Очевидно, что величина
(№ — 1) А2/16Вг]2 представляет собой своего рода «центробежный
потенциал», который оказывает сильное влияние на решения ХкС1!)-
После простых преобразований уравнение (6.92) можно записать
следующим образом:
- xv-ММ1)+Л (Т]) = 0> (6.98)
(dr)2 + |
где
ха -= |(Д - Д„) - (I (Г + 1) -№)е/2];
е = /к(/к+1) = 1/4(№-1), V = (6.99)
/о S2
* а0-Колебания иногда называются £- или p-колебаниями, з то время
как а2-колебания называются тр или у-колебаниями.
148
и, в частности,
/к1.к1=1/2(±К-1), К>0.
(6.100)
Уравнение (6.98) для аг (или 1]-)-колебаний формально совпа-
дает с волновым уравнением для сферического осциллятора. Кван-
товые числа / и Д', описывающие вращение, обусловлены ротаци-
онным слагаемым 1/2 (М'2 — 7И'2)/^и и колебательно-вращатель-
ным членом М'2/16Вг]2, которые были включены в гамильтониан
// t. Асимптотическое поведение и поведение волновой функции
^.колебаний вблизи т] = 0 описываются выражениями
о(т]),
т)— ‘к* е~'/гКг1‘ w (т])_
X/<(»]) =
(6.101а)
(6.1016)
Используя подстановку t = Хц2, из уравнения (6.98) получаем
конфлюэнтные дифференциальные уравнения для v и w.
<6Л03>
решения которых имеют вид [20, 149, 260]
»<>!) /'<.+т-х”2]+
(6.104)
»<ч)=с;Л[ф(-/к.+ф-^), -/к.+ф. w]+
+ Gn(2^+1)1A1 vK+v-S-'l ’ + M- (6J05)
z \ z zA, / z J
Таким образом, мы получаем два решения для Хк (т]). Однако при
Л = 0 волновые функции (ц) должны равняться нулю для
К #= 0, следовательно, в этом случае С2 — С'г — 0 [потенциальный
барьер (К2 — 1)/т]2 непроницаем при rj —0]. Подстановка /Л1 и 1Кг
из (6.100) в выражения (6.104) и (6.105) показывает, что оба решения
в действительности тождественны. Поэтому имеем окончательно
Хл 01) -= Сг т] 1*+1 e~'^\F
1 / , , 3 х2 \ , 3 21
'k+V м’
(6.106)
где lK = -i- (| К| — 1). Для К — 0 нельзя полагать С2 = С' = 0,
поскольку в этом случае 1К1 — 1К1 = —1/2 и, следовательно, v и w
^тановятся тождественными. Этот же результат получается, если
выражение (6.101а) подставить функцию, пропорциональную Cit
149
и функцию, пропорциональную С2. Таким образом, случай К = Q
уже содержится в выражении (6.106). Условие нормировки функ-
ций (г]) дает собственные значения для энергий (см., например
[129, 1491):
E-E0=(lK +-|-+2п2)й(й2 + (/(/ + 1)-№^е, (6Л07)
где п2 = 0, 1, 2, ..., ^со2 = А (С2/В)>/2 = Еу, 1К = у (| К] — 1).
Функции XxOl) могут быть легко нормированы на интервале
0 т] <; оо. Это достигается с помощью формулы [339]
$ е-^^яГвЦа), (й); Kt]AFB- [(«'). (^'); K't]dt =
о
оо
-s-'rw V rf+«; <П f
m=Q \и)тп.т-ъ L 5
(6.108)
где
(a)nl = a(a+ l)(a + 2)... (a-|-/n—1),
и величина
лРв[(а), <b), zJ-^b!^, a2,..., aA; blt b2, ... , bB; z] =
= V = i . а^...аА z
n^0((b)B)nnl~ b1b2...bB 1! '
(ax +1) a, +1) • • -«а («д +1) z2 . j
+ М*1 + 1)Ы^ + 1) ..М*в+1) 2! ’
является обобщенной гипергеометрической функцией. Функции
Ущ (»]), нормированные таким способом, имеют вид
Г МК + ~2~ "Ь "2 ) I
хк, п2 уф =-----------------—------X
(п2!),4г^//<+—)
XT)'«+1e-’/2X,,'1F1(— п2,1к + -~-, , (6.110а)
где lK = -j- (K-l). (6.1106)
Согласно (6.23) и (6.24), волновые функции ХкСп)» которые
должны совпадать с функциями ф (6.24), содержат множитель
1 1
|а2|2 = | т] | 2 . Подставим его в выражение (6.110а), тогда
{X к / Г (/^-|-3/2-|-п2)}%
Хк . пг (Т1) = -------Х
(пг!)/гГ(//<+3/2)
X I Т] е-%^г (_ п2, 1К + 3/2; М]2) (6.111)
150
Пополнительный индекс п2 в функциях хк, л, обозначает число
^'..колебательных квантов.
Таким образом, используя (6.91), (6.96) и (6.111), можно
записать полную волновую функцию (6.89) в виде
Ф (fij, е, й) = ND'mk (6>) Хк. п. (Ц) | «о>> (6-112)
где ц __ нормировочный множитель полной волновой функции,
который будет определен ниже. Эти волновые функции должны
удовлетворять свойствам симметрии, которые обсуждались в общем
виде в § 4.1.
§ 6.4. СИММЕТРИЗАЦИЯ ВОЛНОВЫХ ФУНКЦИИ
В § 4.1 были подробно рассмотрены свойства симметрии волно-
вых функций, выраженных через углы Эйлера и внутренние коорди-
наты. Волновые функции (6.112) еще не удовлетворяют этим свой-
ствам. Напомним, что свойства симметрии по отношению к преобра-
зованиям (4.22) обусловлены требованием, чтобы волновые функции,
которые с помощью (2.22) выражаются через лабораторные коорди-
наты а2ц1 (что практически является очень трудно выполнимой за-
дачей), были однозначными функциями а2ц. Это можно получить,
если функции (6.112) будут симметричны по отношению к пре-
образованиям (4.22).
Начнем с преобразования R2 из (4.22). Действуя оператором R2
па волновую функцию (6.112), получаем
^2 ф (°j. t, i]) = R2 Dm к (Oj) 7.K. n, (л) | n0> =
°2. 63+1/2л)%7<> „2 (—T])irt()>. (6.113)
Согласно определению D'MK (6;) [см. (5.143)1
Dmk («r. e2, 03 + 1 /2л) = e^nK D'mK (0lf 02, 03), (6.114)
и используя выражение (6.111) для Хк(>1)» находим
Хк. «И —11) = (—1)%кХк, п2 (т]). (6.115)
Таким образом,
I, п)=(-1)хф(е;, g, п). (6.П6)
Следовательно, <р инвариантно по отношению к преобразованию R2
только в том случае, если R является четным целым числом:
К 0, ±2, +4,... (6.117)
Поэтому значения углового момента I также должны выражаться
Целыми числами, поскольку его проекция К — целое число. Более
того, так как угловой момент не может быть меньше его проекции
<\, то
/ = |К|,|К| + 1. IKI + 2,... (6.118)
151
Рассмотрим теперь преобразование Rr из (4.22). Оператор R
действует только на углы Эйлера, поэтому можно ограничиться
изучением величины
RiDmk(^< 62, 03) (0г-} л, л-j-02, —63), (6.119)
которая может быть получена следующим образом. В гл. 4 (см.
рис. 4.3) было показано, что R, соответствует повороту на угол л
вокруг внутренней оси х'. Следовательно, волновая функция
фк, определенная во внутренней системе, преобразуется согласно
(5.141):
Ri^K = ^DlK-к (л, л, 0)фк-, (6.120)
так как поворот на угол л вокруг оси х' выражается на языке уг-
лов Эйлера в виде (0х, 02, 03) = (л, л, 0). Значение D'K-K(xt, л, 0)
можно найти из (5.145) *
/^к'к(л, л, 0) = (—1)~к ^к'к(л1- (6.121)
Поскольку (cos л/2)2С1т-т'-2^ = 0, кроме случая 2; + т —
— т' — 2v, то из (5.146) следует, что
d'm'm (л) =
_ [(/ +т)! (/—т)! U + т'у. Ц—т'у.]'7’ (— 1)2/+/+% Цп-т')
(4-( — т -m')V (4" (m! (/ + 4(т'—т))\(/-)- 4 (m—т'))!
(6.122)
Из вида двух первых множителей в знаменателе заключаем, что
^т'т(л) — 0, как для 1/2 (т + т') > 0, так и для 1/2(т + т') <
< 0, т. е. dm’m (л) =4= 0 только для т + т' = 0; отсюда полу-
чаем
^т(л) = (-1)3/-т'бт_т,. (6.123)
Следовательно,
D'K’K^, п, 0) = (-1)з^-2/<'6/<._к==(_1убк,_/(; (6.124)
тогда, согласно (6.120),
/?гфк = (-!)'Ф-к- (6-125)
* Здесь использовано условие, что верхняя граница области периодич-
ности экспоненциальной функции принадлежит этой области периодичности.
152
ренней оси это
получаем
Если взять ф« = (—1)м KD~M_K, то при вращении вокруг внут-
выражение образует тензор ранга I, и для (6.119)
R±D'mK (6;) = (-I)'"2* D^K (©,). (6.126)
волновая функция, инвариантная по отношению
к преобразованию имеет вид
D^K (6>) + (- О'"2* £>м-Д (бу). (6.127)
Таким образом, мы нашли полную волновую функцию гамиль-
тониана Hrot + H„ib, которая инвариантна по отношению к
и R2. Она записывается следующим образом:
| ШКп2 По> =
,с +(-0'd*-k(е>)) Хд. п2(П) |п0>
16ла (14-Одо) /
^|/Ж>Хд.«2(11)1«о>, (6.128а)
где
К 0, 2, 4,...
/ = 0, 2, 4, ... для К 0,
/ = Е, К + 2,... для Е=/=0.
(6.129)
Соответствующие энергии даются выражением
EiKn2 по = (1 (/ + 1)—№) — е+ f — | К | + 1 + 2/г2) £v4-(n0+ — j Ер.
(6.1286)
Нормировка получается с помощью формулы
$ Оца т, (бу) т£ (Оу) Dg, m, (Оу) dQ =
~7 (/i Ё /з I l’i И2 Из) (A h /з I "h m2 m3). (6.130)
Правила отбора (6.129) для вращательных квантовых чисел
были получены только из требования, что волновые функции долж-
ны быть симметричны* по отношению к вращениям /?1 и R2.
Подчеркнем, что для всех полос с К = 0 спины только четные,
поскольку для нечетных I вращательная часть волновой функции
(6.128) тождественно равна нулю, так как D'Mo (07) =D^_q(6j).
гловой момент / никогда не может быть меньше величины его
проекции поэтому последнее правило в (6.129) вполне коррект-
Преобразование R3 будет рассмотрено ниже.
153
ft- полоса
л т,
_______ne~°i
_______n0=0
' K=2,
n2=o, 2-я//-полоса
n0=0
------— 2+
------0+
K=0,
n2=1,
no=O
в-я J-пол оса
K-0,n2=0,
no=o
Основная
//-полоса
6
полоса
Рис. 6.1. Типичная структура полос деформированного четно-четного ядра
Рпс. 6 2 Графическая иллюстрация
о'0(Р-)-и (Y-)-колебаний, о,'-Ко-
лебания увеличивают и сокращают
эллипсоид вдоль большой оси; у-
колебания делают это вдоль ма-
лой оси.
но. Заметим также, что симметризация (6.127) по отношению
к преобразованию /?2 возможна только потому, что в соответствии
с формулой (6.1286) для энергий уровней функции (6.112) вы-
рождены для К и —К-
Любой набор квантовых чисел
К, п2, п0 называется «полосой'».
Поскольку для данного набора
К, п2, п0 квантовое число углового
момента пробегает значение I =
К, ..., оо, то различные значе-
ния чисел этого набора дают раз-
личные вращательные полосы. Как
видно из (6.128 б), уровни в преде-
лах полосы удовлетворяют обыч-
ному7 правилу 1 (I + 1). Типич-
ная структура полос деформиро-
ванного ядра показана на рис. 6.1
Полоса основного состояния за-
писывается в виде | /000>. |3-Ко-
лебательная полоса записывается
в виде | /001>, она расположена выше основного состояния на
энергию = h (С01В)1/2 = Ер. Эксперимент дает, что для
162Sm Ер « 800 кэв, а в середине области редкоземельных элемен-
тов Ер может быть даже больше 1,5 Мэв. у-Колебательпая полоса
записывается как 11 200>. Соответствующее состояние называется
у-колебанием, даже если п2 = 0, потому что благодаря сильному
влиянию колебательно-вращательного слагаемого 7Из2/16В1]2, ко-
154
е включено в Нго1, у-колебания дают вклад в возбужденное
отстояние для К #= 0. Действительно, энергия состояния 12200>
ше основного состояния на величину (£v F е) (£у = Й (С2/В)'/2).
На рис. 6.1 показаны также более высокие у-полосы 11400> и
I I 010>-' Этот рисунок нетрудно распространить и на случай более
высоких энергий, где колебательно-вращательный спектр стано-
вится более сложным.
му исчезает необходимость накладывать требованья симметрии,
связанные с преобразованием 7?3. Аксиально-симметричный мини-
мум потенциальной энергии при у=0° повторяется при 120 и 240°.
На рис. 6.2 показана графическая иллюстрация а0- и а2-коле-
баний. P-Колебания растягивают и сокращают эллипсоид вдоль
оси симметрии, тогда как у-колебания делают это в направлении,
перпендикулярном большой оси. Эта интерпретация становится
понятной, если вспомнить основные определения (2.3) и (4.4) для
внутренних квадрупольных координат а0 и а2 соответственно.
Продолжим теперь рассмотрение свойств симметрии волновой
Функции и исследуем симметрию относительно преобразования
из (4.22). Это преобразование оставляет инвариантным как
оператор кинетической энергии Т в (6.3), так и потенциальную
энергию V (а0, а2) в (4.28). Однако оно не оставляет инвариантным
155
исходный гамильтониан колебательно-вращательной модели
(6.41)—(6.43). В разложении вращательно-инвариантной потен-
циальной энергии около точки аксиально-симметричного мини-
мума [см. (6.2)1 один из трех минимумов в выражении для V(a0, а2)
является особенно характерным — это минимум на оси а0 (обла-
сти 1 и 6 на рис. 4.4, см. также рис. 4.10). Поэтому колебательно-
вращательная модель описывает только область 1 на рис. 6.3.
Можно выполнить подобные разложения вращательно-инвариант-
ной функции V (а0, а2) в точках минимума и в областях II и Ш,
Таким образом, можно получить гамильтониан во всей плоскости
на рис. 6.3:
то + я"^', п')+#ш(Г, П"), (6.131)
где Н1 (g, т]) совпадает с (6.40), а координаты (£', т]') и (£", rf) оп-
ределяются из рис. 6.3. Если действовать таким образом, то необ-
ходимо использовать симметрию относительно преобразования R3.
Однако мы ограничимся исходным выражением (6.2) и таким об-
разом выделим минимум на оси а0. Это будет эффективно соот-
ветствовать ограничению только областью I в плоскости (а0а2)
на рис. 6.3 и мы получаем однозначное соответствие между вол-
новыми функциями, которые выражены через координаты ла-
бораторной системы а2(1 и через внутренние координаты а0 и а2
[см. (4.24)1. Следовательно, при таком определении нет необходи-
мости в симметрии, связанной с преобразованием Ra.
§ 6.5. ЭФФЕКТЫ КОЛЕБАТЕЛЬНО-ВРАЩАТЕЛЬНОГО
ВЗАИМОДЕЙСТВИЯ
Одна очень важная часть колебательно-вращательного взаи-
модействия — член Л4'2/16Вц2— уже содержится в решениях
(6.128). Это слагаемое действует подобно центробежной силе и
«оттягивает» •ц-колебательную волновую функцию от центра коор-
динат. На рис. 6.4, а этот эффект показан для полосы с К = 2.
Следует отметить, что благодаря члену — Д2/16Вт]2 в H,.ib (6.42)
такой эффект имеется даже для туколебательной волновой
функции основного состояния. «Центробежный эффект» в этом слу-
чае обусловлен только элементом объема в пространстве колеба-
ний, который пропорционален [ а21 для функции %(т])[см. (6.19)1.
Таким образом, даже если мы стартуем от аксиально-симметрич-
ного туосциллятора (с2=0), динамические причины приводят к от-
клонению волновой функции от начала координат (см. рис. 6.4)
и делают ядро эффективно трехосным.
Рассмотрим теперь роль слагаемого Hvibrot (6.43). Первый член
диагоналей по Л’ и, следовательно, имеет неисчезающие матричные
элементы только внутри полос с одинаковым К. Он смешивает
также [3-полосу и полосу основного состояния. Второй член
156
в (6 43) смешивает полосы с различными Дг. В гл. 5 мы нашли (см.
(5-125)):
М'+ D'm = Ы'+ d'm = £ V Z(/+1)-K(K-1) D'm- |
M—Dmk = = У?/ (4+1)—К (К + 1) Dm+ 1 • I
Теперь можно легко получить вращательные матричные элементы:
(/Д7И|М+ + M-l/'fCM') /г21(1 1 6/<о)(1+6к'о)],/«Х
Х[6к'Д-+2 !(/-/<)(Л К+1)(/- /<—!)(/ 4 К + 2)}^ +
+ 6к'К-2{(/ + /<)(/-/< + 1)(/4 К-1)(/-К + 2)}’/']бщбж,
(6.133)
Рис. 6.4. Примеры «центробежных эффектов», ко-
торые приводят к отклонению волновой функции
от начала координат:
а — влияние члена Мз 2/1бВ»1г для полосы с К=2, б —
влияние члена — ^2/16Вц2 для волновой функции основ-
ного состояния.
выражение (6.128). Аналогично с помощью
где использовано
(6.108) и (6.128) можно получить матричные элементы по ^-коле-
бательным функциям:
<хк«1(п)|¥|хк’п'(п)>=4-
1-, -ЮЖ ]
Г(1/2А-|-1+иг) Г(1/2К'+1+л0]%
n2! n2! J
Г {1 /2 (1/2/С + 1/2А + d + 2)} х
Г(1/2К- 1)Г(1/2К' + 1)2^ V/
х у» ( —n2)m {1/2 (1/2/С'-) 1/2К-Н Ь2);„, ч<
(l/2K + l)mm!
*2^1 [—п2, 1/2(1/2/<'Н1/2/<-|с/ + 2)фт; 1/2К'+1; 1]- (6-134)
Используя эти общие выражения, нетрудно получить все матрич-
ные элементы оператора HvibTot по состояниям (6.128). Матрич-
ные элементы, зависящие от аг„ рассчитываются тривиально с по-
мощью (6.96) способом, аналогичным тому, который применялся
при вычислении матричных элементов в фононном представлении
гармонического осциллятора в гл. 3.
157
Для получения точных решений гамильтониана (6.40) необхо
димо диагонализировать оператор Hvibrot. Однако сейчас мы
используем метод теории возмущений, справедливый для малых
угловых моментов. Для больших угловых моментов возмущение
Hvibrot увеличивается пропорционально I2 (7 + I)2 и, следова
тельно, быстро становится очень большим. Ниже мы обсудим ре-
зультаты точной диагонализации.
Рассмотрение в рамках теории возмущений имеет то преиму-
щество, что в этом подходе получаются явные формулы, полезные
для физического понимания колебательно-вращательного взаимо-
действия. Мы рассмотрим по теории возмущений только смешивание
основной полосы | 7000>, у-полосы 11 200> и p-полосы | 7 001>.
Введем более краткие обозначения для этих полос:
Ф1 = | /000>; <р2 = | /200>; Фз | 7001 >. (6.135)
Из (6.132), (6.133) и (6.134) легко получить
<Ф1|Д|ф1>=6/; о,2,4, ...[/(/+1)1 1/2е (x^ + S^+l);
<Ф11 Н | ф2>=6/: 2, 4, 6. - [I (I |-1) (7+2) (7—1)]% 1/2е (—1/Зх /б I;
<Ф11^1Фз>=6/; о, 2, 4, ••• [7(7+ 1) —2] 1/2е( — 2у),
<Ф2| 77|ф2>=6/; 2. з. 4. .• [{7(7 + 1)-4} l/2e(2x2 + 3i/2+ 1)+ £VJ;
<Ф21 Н | Фз> = б/; 2, 4, 6. • - [7 (7 + 1) (I -1) (7 + 2)]!4 1 12ехУ /б?
<Фз|77|Ф3>=б/; о, 2,4, ...[/(/+1)1/2в(х2 + 9у2+1) + £р],
(6.136)
где 6/;о,2, 4,...—обобщенный символ Кронекера, т. е. величина
равная 1 для 7 = 0, 2, 4, и т. д. и равна 0 в остальных случаях.
Далее
(6.137)
Обозначим \ 1МКп2п0> возмущенную волновую функцию, воз-
никающую из невозмущенного состояния | 1МКп2п0>\
11МКп2 п0> = 1I МКп2 п0> +
। Пд | Hvjb rot I IMKn-z I IMK'tiy (g 138)
K'.n'2,no^ EIKn2n0 Е1К-П'2П^
» ^2 » 7Z0
Соответствующие возмущенные энергии ЕщПгП1) имеют вид
ElKn2n„ — ElKn, nQ + (IMKn2 n0 I Hvib roi I IMKn2 ПдУ +
158
К’,«2•«От*
1 С ^0 1 Hvib rot | ftp
P , __p , .
IKn2 n0 IKrri2 710
(6.139)
Если смешиваются только основная, |3- и у-полосы, то
щью (6.136) получаются следующие результаты*:
а. Основная полоса
| /Л4000> = А, <f х 4- А2 <р2 + А3 <р3,
с помо-
где
Д =1;
/ =. e —
Л £v-2e
V
(6.140)
£0
0
и
E/ooo = 7(7 l-l)l/2e[l+3^-4--^ + 2 6
\ bv 2 c₽
— /2(Z+l)2e/ ---------b —
2 £v ET -2e 2
Член, пропорциональный /2(/+1)2, удобно записать
Вге/2(7+1)2, где
В2е = Е
е
£Р
\ 2 \
е
(6.141а)
в виде
е
1 е е . 3
ТЁ7 £v-2e +-2
2
(6.1416)
б. у-Полоса
| /7И2ОО> = В± + В2 Фг + ^зЧз>
где
в1 =
Б
Ет~2е
е
х/(/ + 2)(/ + 1)/(7-1)6/;2,4>6.
в2 = 1;
(6.142)
Вч =----е----
£v-2e -£(1
и
-МЗ/2 । 3)Х
£Р
х/(/ + 2) (/ + 1) / (7-1)6/; 2. 4. 6, ...
£/2oo = £v + /(/ + 1) 1/2е/1 + 6-^-+-5-Г-2ТГ
е
£v 2 Ер Ev £v-2e
Детальные сведения можно найти в литературе, см. [131].
159
8
; 2. 4, 6. ••• — 27
Еу £р —-2s Е,, Е(
27 е е
8
1)2е/1/2---- .
к Еу Еу 2б 4 Еу Ер Еу—Ер— 2е
— 2efl + 6 —+——V
к Еу 2 £Р)
6/; О, 2, 4
(6.143)
в. ft-Полоса
| /Л1001> = С1ф14-Сгср24 С3ф3,
где
Сг =
и
Еу
-~УЗ /(/+ 2)(/ + !)(/-ГН
(6.144)
£/оо1 — £р+7 (7+1) е
1+— —+3 —
2 Ер Ет
81 е е е
2 Ер Еу Ер—Е?+2е
+ 12/—]2| + /2(/+D2e/'—— --------
к£₽// к 4 Еу Ер Ер-Е? + 2е
(6.145)
Наличие члена, пропорционального 7 (7 + 1), в формуле
(6.141) указывает на то, что эффективный момент инерции +,ф
состоит из двух слагаемых — момента инерции $-0, соответствую-
щего основному состоянию ядра, и поправки, обусловленной
Р- и у-колебаниями. Существование такого члена указывает на
то, что колебательно-вращательное взаимодействие дает поправ-
ку к моменту инерции, также зависящую от спина:
:'/Эф = г(о^ + /(7 + 1)^, (6.146а)
где
ДУ 1 е е 3 / е \2
У ТЁ7 Ет- 2е hT^EpJ
(6.1466)
Эта величина имеет простую физическую интерпретацию. В процес-
се вращения ядро растягивается благодаря действию центробеж-
ных сил, что приводит к увеличению момента инерции, который
пропорционален I (/ f- 1). Поэтому в выражении для энергии по-
является член, пропорциональный /2 (/ + I)2. Величину центро-
160
Таблица 6.1
Экспериментальные значения параметров колебательно-
вращательной модели
Ядро z A Мэв 2 + ', Мэв e, кэв EV- кэв кэв ₽o
62 152 0,122 1,086 32,31 1040 685 0,28
Gd 61 154 0,123 0,998 32,35 950 680 0,33
64 156 0,089 1,154 25,49 1122 1050 0,41
64 158 0,0795 — 23,55 1154 (1500) 0,46
64 160 0,075 — 22,31 957 (1800) 0,47
Dv 66 160 0,0867 0,966 25,34 934 (1600) 0,35
66 164 0,073 0,761 21 17 735 1764 0,41
Er 68 166 0,0806 0,788 23,37 757 1460 0,33
68 168 0,0798 0,822 23,61 793 — 0,33
Yb 70 168 0,087 0,987 25,29 955 (-1500) 0,30
70 172 0,0787 1,093 23,24 1065 (=1500) 0,31
Hf 72 178 0,0931 1,480 27,72 1447 1700 0,31
w 74 182 0,100 1,285 28,50 1224 1122 0,26
74 184 0,111 0,904 31,17 863 (=1500) 0,24
74 186 0,122 0,730 33,02 684 ( = 1300) 0,24
Os 76 186 0,137 0,768 36,85 716 (=1500) 0,20
76 188 0,155 0,633 40,45 571 1766 0,18
76 190 0,187 0,557 46,22 477 1585 0,16
Th 90 230 0,053 0,783 15,29 764 634 0,23
90 232 0,050 0,790 14,58 770 725 0,25
U 92 232 0,047 0,868 13,86 851 693 0,26
92 234 0,044 0,922 13,20 906 811 0,25
92 238 0,0147 — 13,67 1047 994 0,28
Pu 94 238 0,044 1,030 13,34 1014 937 0,27
94 240 0,043 0,942 12,97 926 858 0,28
бежного параметра Bze (6.1416) можно легко вычислить и срав-
нить с экспериментом. Он приводит к понижению вращательных
уровней основной полосы по сравнению со значениями, вычислен-
ными согласно правилу I (I + 1) и был впервые введен Бором
и Моттельсоном [51] в качестве феноменологического параметра.
Прежде чем сравнивать предсказания теории с экспериментом,
перечислим четыре параметра колебательно-вращательной модели,
которые должны быть определены из эксперимента. Этими пара-
метрами являются;
параметр е - Й2/^-0, который определяется из эксперимен-
тальной энергии первого вращательного состояния;
2) параметр равновесной деформации ядра 0О, который полу-
чается из ветичины В (Е2) для первого вращательного уровня
1или из расщепления гигантских резонансов (см. гл. 11)1;
3) энергия у-колебаний Ev, которая подгоняется к энергии
второго возбужденного 2+-уровня;
4) энергия 0-колебаний Ер, определяемая из данных о первом
возбужденном 0+-уровне.
6 Зак. 1218 161
На рис. 6.5 показаны величины, определяемые из эксперимен-
та. Остальные энергии уровней и вероятности переходов предска-
зываются теоретически. В табл. 6.1 представлены найденные зна-
чения параметров для некоторых ядер редкоземельной и транс-
урановой областей.
Величины Bze теперь можно легко рассчитать и сравнить с экс-
периментом. Это показано на рис. 6.6. Видно, что как общее пове-
дение, так и отдельные значения довольно хорошо описываются
теоретически. Увеличение значений
и Os обусловлено мягкостью ядра
0
2
Г
2
В(Е2)
Bze в областях Sm — Gd
по отношению к £- (малые £₽)
и у-колебаниями (малые £т)
соответственно. Изотопы Sm
и Os представляют собой пе-
реходную область от сильно-
деформированных ядер к
ангармоническим вибраторам.
Как следует из краткого
рассмотрения в § 4.2 и 4.3
(см., например, рис. 4.12),
минимумы, соответствующие
равновесной деформации, ста-
новятся весьма плоскими и,
следовательно, ядро будет
мягким по отношению к р- и
у-колебаниям. Для таких переходных ядер, т. е. для сильно
ангармонических осцилляторов, удовлетворительной теоретической
модели пока не существует (см. гл. 4)*.
Нетрудно вычислить и поправки более высокого порядка,
такие, как параметр С в формуле для энергий уровней:
Рис. 6.5. Иллюстрация определения
из
эксперимента значений параметров коле-
бательно-вращательной модели е, ро, Ev
и £р.
E = AI (I + \)—BzJ2(I+ 1)2 + С/3(/+ 1)3 + ... (6.147)
Сравнение с экспериментом показано на рис. 6.7. Выводы оказы-
ваются такими же, как и для центробежного параметра Bze.
Рассмотрим кратко предсказания колебательно-вращательной
модели для состояний с большими угловыми моментами. Для боль-
ших I необходимо диагонализировать гамильтониан HvibTCt.
Вращательные уровни с большим моментом в деформированных яд-
рах и многофононные состояния в сферических ядрах систематиче-
ски наблюдаются в (аь и)-реакциях, исследование которых было
начато в работе {266]. Более подробную экспериментальную и тео-
ретическую информацию можно найти в литературе [133—135,
267, 226, 350]. На рис. 6.8 показано сравнение предсказаний коле-
бательно-вращательной модели с экспериментом для основных по-
лос ядер 160Dy, 166Ег и 1860s.
* Ньюс и др. [161] развили перспективный метод рассмотрения произволь-
ных коллективных потенциалов. Этот метод основан на диагонализации гамиль-
тониана в базисе сферического осциллятора.
162
Рис. 6.6. Значения параметра центробежного растяжения Вге (в кэв) для раз-
личных ядер предсказываемые колебательно-вращательной моделью (сплош-
ная линия) и найденные из эксперимента.
Штрих-иуиктирная линия — предсказания теории, в которых не учитывается смешивание
0-полосы с основной полосой. Штриховая — предсказания модели асимметрич-
ного ротатора (см. гл. 7) [131].
ис. 6.7. Значения параметра С в формуле (6.147) для энергии уровней, пред-
казываемые колебательно-вращательной моделью (сплошная линия) и найден-
ные из эксперимента.
3-п§ло;ПУНКТИрная „линия — предсказания теории, в которой не учитывается смешивание
осы с основной полосой. Штриховая — предсказания модели асимметричного рота-
тора (см. гл. 7) [131].
6’
163
Эксперимент Теория Эксперимент Теория Эксперимент Теория
1еоПу ™0s
Рис. 6.8. Сравнение экспериментальных значений уровней основных полос для трех ядер
с предсказаниями колебательно-вращательной модели.
Обсудим теперь приведенные вероятности Е2-переходов между
овнями различных вращательных полос. Формула (3.57) дает
УРдпупольный оператор в лабораторной системе. С помощью (5.2) он
вырз^ается чеРез Углы Эйлера и внутренние переменные:
с-«=з^.Г^(е)Ро/
4л \
2
7
+«S(e/)s(i+v|/7-₽»)+«<е,) А |/A(?_2nS)+
+{оЗ(в/)+^лел{(1-А|/
(6.148)
Здесь учтены члены второго порядка по коллективным переменным,
так как они важны для получения вероятностей перехода между
разными полосами. Приведенная вероятность £2-перехода опреде-
ляется в виде
В(Е2; /г^//) = Л2^±1|</г||С™«||7/>|2, (6.149)
I А
где А = 3//?б/4л, &°“ = А~Ч%“.
Приведенные матричные элементы рассчитываются с использо-
ванием волновых функций (6.140), (6.142) и (6.144):
<li IIQ?" \\If> = ₽о К (h) <h (If) (If 2It I 000) (1 + а + ау*-ах*) +
+ «1 (h) а2 (If) (Ifili 12-20) х (1 -2а) +
+ fli (h) as (If) (Ifilt | ООО) у (1 + 2а) +
+ «2 (li) ai (If) (If^lt 1022) x (1 - 2а) +
4- a2 (/f) a2 (If) (lf2It | 202) (1 + а + 2t/2- 2ax2) +
+ «2 (li) aAlf) (If^Ii 1022) x (—2ayx) +
+ as (Ц) O1 (I,) (Ifllf | 000) у (1 -J- 2a) +
+ as (Ц) a2 (If) (If21112—20) (—2ayx) +
+ a3(It) as (If) (If2Ii | 000) (1 + a + За^-ах2)}. (6.150)
Величины щ (I) совпадают с коэффициентами Bv или Cv в фор-
мулах (6.140), (6.142) или (6.144) в зависимости от того, принадле-
ит ли начальное состояние основной, у- или p-полосе соответствен-
°- Кроме того, здесь введены следующие обозначения:
а = Т|/~~Ро ~ 0,36po; х= i/(6.151)
ког РассмотРим вначале несколько простых переходов для случая,
Тог коле^ательно-вращательное взаимодействие отсутствует.
д х 0, у = о и av (I) равно 0 или 1 в зависимости от кон-
165
кретного рассматриваемого состояния. Для £2-переходов внутри
различных полос имеем
В (Е2-, I, -> 7У)ОСН. полоса = Л2 р2 (/, 2/г | ООО)2 (1 -|-а)2;
-j- 1
В(Е2; 7^ Полоса =Л24гТТ₽о(//2/И2О2)2(1+«)2; 1(6.152)
В(Е2- -полоса — Л2ДГ±Г₽о2(//2/«-1000)2(1 +а)2-
2/г- +1
Для переходов между уровнями различных полос получаем
при отсутствии колебательно-вращательного взаимодействия
В (£2; Полоса = Л2|^±1рО(//2/И022)2х2(1-2а)2;
£(£2; /г-^Л)р .осн. полоса = Л2р§(7/27г|00)2г/2(1 + 2а)2.
(6 153)
Заметим, что при вычислении первой из величин В (Е2) в (6.153)
следует рассмотреть очень важную часть 7Из2/16£г]2 колебательно-
вращательного взаимодействия, учет которой сильно меняет резуль-
тат. Таким образом, переходы между уровнями различных полос мо-
гут быть рассчитаны лишь при последовательном учете колебательно-
вращательного взаимодействия. Для переходов внутри вращатель-
ной полосы формулы (6.152) для В(Е2) соответствуют случаю сим-
метричного ротатора со статической деформацией ро. Поправки
к полученным выражениям, обусловленные колебательно-враща-
тельным взаимодействием, рассчитываются с помощью общей фор-
мулы (6.150). Например, учитывая колебательно-вращательное
взаимодействие в нижайшем порядке теории возмущений, можно
получить для приведенной вероятности перехода внутри основной
полосы:
£(£2; 7^7.)
осн полоса {^2/И000)х
Х(1 + а + а^_ах2) + г-£^-^-^±] 2 ) X
X V\lf+2)(IJ+i)If(If+l) (1,2Ц 12-20) х (1 -2а) +
+ ^|/ 2^Z/(Z/+l)(7/27i|000)t/(l+2a)} +
V i (т^)]2л+2)(Л+1)/<-(/г"Г) х
X (1,21,1022) х (1 - 2а) + 1/ I, (Д +1) (7,2/г | ООО) у (1 +2а)}-
Р Г Р (6.154)
1бб
видим, что колебательно-вращательное взаимодействие эффек-
тно приводит к изменению деформации^основной полосы, которое
зависит от спина:
₽эФ (Л, //) = Р2о{-}2(Л2Л|000)-2(1+а)Л (6.155)
г 1 обозначает величину, заключенную в скобки, в формуле
Уб 154). Предпринимались усилия, чтобы измерить эту зависимость
^’формации от углового момента с помощью многократного куло-
15i6d i58Gd 160Dy к8Ег 1е8УЪ mtif 1860s 190OS S32Th 238Pu
Рис. 6.9. Сравнение отношения значений В(Е2) для распада у-ко-
лебательного 2+-состояния в 0+- и 2+-состояния основной полосы
с предсказаниями колебательно-вращательной модели (сплошная
линия) it модели асимметричного ротатора (штриховая линия),
рассмотренной в гл. 7 [135].
новского возбуждения [104]. Однако ввиду трудности выполнения
подобных экспериментов эти попытки не позволили сделать каких-
либо окончательных заключений.
Обсудим теперь переходы между полосами с учетом колебатель-
но-вращательного взаимодействия. Так же как и в предыдущем
случае, соответствующие формулы получаются из общего выражения
1 -150). Их явную запись можно найти в литературе (см. [129—135]).
ассмотрим здесь конечные результаты*. На рис. 6.9 показано от-
ношение величин В (Е2) для распада у-колебательного 2+-состояния
И 2+-с°стояния основной полосы (коэффициент ветвления). На
Р сунке также указаны рассматриваемые переходы. Без учета ко-
тельно^0ДР°бнь‘й анализ экспериментальных данных и предсказаний колеба-
вращатсльной модели можно найти в работах [7—9].
167
5
3
2
1
152Sm 15B6d 1B0Gd 16iDy ™Er 172Yb 182w 1B6w 1BB0s 230n 232u 238u ™Pu
15i0d 15e6d ie°Uy ieeEr 1SBYb mHf 18e0S 19°OS 232Th 23iV 238Ru
Рис. 6.10. Сравнение отношения значений В (£2) для распада у-ко-
лебательного 3+-состояния в 2+- и 4+-состояния основной полосы
с предсказаниями колебательно-вращательной модели (сплошная
линия) и модели асимметричного ротатора (штриховая линия),
рассматриваемой в гл. 7 [135].
лебательно-вращательного взаимодействия для этой величины полу-
чается следующее значение:
В (£2; 2+' 2+) _ (222 I 022)2 10 _
В (£2; 2+' -> 0+) (0221022)2 7 ’ ' ’ '
которое известно как правило Алаги. Смешивание полос, обусловлен-
ное колебательно-вращательным взаимодействием, приводит к ре-
зультатам, описываемым сплошной верхней кривой. Даже если
согласие с экспериментом находится в пределах 10—20%, общее
поведение экспериментальных результатов удивительно хорошо
предсказывается теорией.
0,8
0,6
0,2
0/
i52Sm 1566d ie°Gd 16% ,BBEr mYb 182W 1BBW 18BOS 23°П 232U 238U ™Pu
™&d 1586d 1B0Hy 1№Er 168Yb 178Hf 189W188Os ,9°0s 232Th 238U 238Pu
Рис. 6.11. Сравнение отношения значений В (£2) для перехода у-ко-
лебательного 2+- в 2+-состояине основной полосы и для перехода
между 2+- и 0+-СОСТОЯННЯМИ основной полосы с предсказаниями
колебательно-вращательной модели (сплошная линия), и модели
асимметрнчногро ротатора, рассматриваемого в гл. 7 [135].
168
П vrue коэффициенты ветвления показаны на рис. 6.10—6.12.
этих случаях предсказания колебательно-вращательной мо
Во ВСпасходятся с экспериментом не более чем на 10—20% и общее
ДеЛИ ение экспериментальных данных воспроизводится очень хоро-
п0Бе5т0 разумеется, указывает на то, что колебательно-вращатель-
1110 рдёль удовлетворительно описывает основные физические свой-
НЭЯ ^ядерной динамики. Однако при изучении таких тонких эффек-
СТВЭ как изменение среднеквадратичного радиуса в возбужденном
^стоянии, наблюдаются более значительные отклонения от пред-
0,14
0,11
0,10
0,08
0,06
0,04
0,01
1520 156 160 184 172,,. 182lt, 186,,, 188пЯ0 232 23В 240
Sm (rd Gd Dy Er Y6 W W Os Th U U Pa
™Gd 15e6d 160Dy ™Er 16SYb 178Hf ieeOs W'u 236Pu
Рис. 6.12. Сравнение отношения значений В (Е2) для перехода у-ко-
лебательного 2+-состояния в 0 ’ -состояние основной полосы и для
перехода между 2+- и 0+-состояниями основной полосы с пред-
сказаниями колебательно-вращательной модели (сплошная линия)
и модели асимметричного ротатора (штриховая линия), рассмат-
риваемой в гл. 7 [135].
сказаний этой модели. Мы не будем обсуждать здесь эти эффекты.
Упомянем лишь о том, что они, по-видимому, указывают на новое
важное свойство динамики коллективных движений ядра. А именно,
до сих пор мы рассматривали протоны и нейтроны, которые колеб-
лются в фазе и с одинаковыми амплитудами. Упомянутые выше рас-
хождения, так же как вероятности 714/-переходов и уменьшение
вращательных гиромагнитных отношений gR, по сравнению со зна-
чением ZIA, указывают на то, что протоны могут колебаться с ам-
плитудами, меньшими, чем амплитуды нейтронов ([171, 172], см.
также § 9.7).
* * *
Основой для обсуждений в этой главе был гамильтониан, впер-
вые введенный О. Бором [50]. Свойства гамильтониана были также
рассмотрены в обзорах [43, 100, 186, 211]. Колебательно-вращатель-
леб М0дель п°дробно обсуждалась в работе [133]. Октупольные ко-
сформированных ядер были рассмотрены в работах [94,
Глава 7. МОДЕЛЬ АСИММЕТРИЧНОГО
РОТАТОРА
Первоначальная модель Бора—Моттельсона [50, 51] была не
в состоянии объяснить параметры Bze и С в формуле для энергий
уровней (6.147), а также большие отклонения (иногда в 2—4 раза)
от правила Алаги (см. рис. 6.9, 6.10). Это привело Давыдова и Фи-
липпова [89] в 1958 г. к совершенно другому подходу при обобщении
коллективного описания колебаний в сферических ядрах на слу-
чай деформированных ядер. Давыдов и Филиппов постулировали
существование неаксиальных ядер, т. е. ядер с фиксированными
значениями параметров а0, а2 #= 0. Исходя из представления об
асимметричном ротаторе, они рассчитали энергетический спектр
и вероятности Е2-переходов*. Хотя некоторые физики высказывали
сомнение ** в теоретическом обосновании этой гипотезы, расчеты по
модели Давыдова — Филиппова привели к весьма впечатляющему
согласию с экспериментальными данными. Мы обсудим здесь модель
асимметричного ротатора, а также ее интерпретацию с точки зрения
колебательно-вращательной модели. Кроме того, в § 7.3 будет рас-
смотрено обобщение модели асимметричного ротатора, сделанное
Давыдовым и Чабаном [92].
§ 7.1. ГАМИЛЬТОНИАН МОДЕЛИ
АСИММЕТРИЧНОГО РОТАТОРА
В своей первой работе [89] Давыдов и Филиппов предположили,
что ядро является асимметричным ротатором, гамильтониан кото-
рого имеет вид [см. (5.183)]
у М'к2
Т ^h(av) ’
(7.1)
где моменты инерции описываются формулами (5.72) и (5.73) . Эта
модель, в которой пренебрегается поверхностными степенями сво-
боды, предполагает весьма специальный вид коллективной потен-
* Предположение об асимметричном ротаторе было раньше сделано Мар-
ти [242], но не было им детально разработано.
** См., например, работу О. Бора [53].
170
ной энергии. Поскольку она должна описывать, вообще гово-
ЦИЭ асимметричный ротатор, т. е. случай #i=/=#2 =/= #’з, необходимо,
Ря’бы а2 0- Таким образом, коллективная потенциальная энер-
ЧТ° должна иметь резко выраженный минимум в плоскости (а0,
ПхЯПри конечных значениях а0 и п2 (рис. 7.1). Этот минимум должен
быть очень глубоким, таким, чтобы разложение
V (а0, а2)= 1/2С0(о0—а0)2 + С2(п2—п2)2 (7.2 а)
привело бы к большим значениям параметров жесткости Со и С2
пая поверхностных колебаний. Тогда энергия поверхностных коле-
баний станет очень большой и,
следовательно, их влиянием можно
будет пренебречь.
Подставляя значения моментов
инерции (5.73) в формулу (7.1),
получаем
"=7^2-------------—
* sin2 (у—-д-Лл)
(7.2а)
Рис. 7.1. Схематический вид кол-
лективной потенциальной энергии
трехосного ротатора.
где Р и у определяют точку мини-
мума, соответствующую трехосному
ядру:
a0 = Pcosy; а2= 1/2] 2psiny.
(7-26)
Таким образом, гамильтониан модели асимметричного ротато-
ра содержит три параметра: массовый параметр В и фиксированные
значения р и у. Фактически в формулу (7.2) входят лишь два дейст-
вительных параметра — произведение Вр2 и у. Однако для вычисле-
ния приведенных вероятностей перехода В (Е2) значение р должно
быть известно отдельно. Фиксированные параметры Р и у опреде-
ляют значения величин k — 1, 2, 3.
Решение уравнения Шредингера с гамильтонианом (7.1) не-
трдуно получить из (5.187) и условий симметрии по отношению к пре-
образованиям (4.22). Гамильтониан (7.1) можно представить в виде
суммы гамильтониана симметричного ротатора и остатка:
Л/2
и = (м -7 - ме) (1 жг’ +1М72)++
27 з
4 (Л412-М22)(1/4^Г'-1/4Н2). (7.3)
Волновая функция симметричного ротатора, симметризованная
надлежащим образом по отношению к преобразованиям и Д’2,
Дается выражением [см. (6.128а)]
I = |/ ^1+^ (D^(e>) + (-l)U-K(e>)), (7.4а)
171
где
К, К+1, К + 2,... для К+=0,
0,2,4,... для К = 0. (7Лб)
Третье слагаемое в (7.3) должно быть диагонализовано в базисном
наборе функций (7.4). Наиболее общее решение имеет вид
Ф/м,- = >2 А‘к (?) | /МК>, К = 0, 2, 4.I, (7.5)
где коэффициенты Ак зависят от параметра асимметрии у (для у = 0
третье слагаемое в (7.3) равно нулю). Индекс i у волновой функции
ф/дн указывает, что, вообще говоря, могут встречаться несколько
состояний с данным спином I. Сумма по К в (7.5) берется по всем
четным целым числам, меньшим или равным I для данного полного
углового момента I. Однако для нечетных I значение К — 0 исклю-
чается, поскольку в (7.4) нет нечетных значений спина. Для част-
ного случая I = 0, К = 0 получаем основное состояние 1000>.
Так как в этом случае существует только одна базисная функция
(7.4) с / = 0, решение уравнения Шредингера с гамильтонианом
(7.3) дает только одно состояние с I = 0, которое совпадает с основ-
ным состоянием ядра.
Поскольку К — 0, 2, 4, ... и спины I ограничены значениями,
указанными в (7.46), в базисном наборе не встречается состояний
с / = 1. Поэтому среди соответствующих решений уравнения Шре-
дингера нет решений с I — 1. Легко видеть также, что в базисном
наборе (7.4) имеется лишь одно состояние |ЗЛ42> с / = 3. Это со-
стояние диагонально и, следовательно, является решением уравне-
ния Шредингера с гамильтонианом (7.3), что легко можно проверить
непосредственно.
В общем случае следует взять все возможные базисные состоя-
ния (7.4), которые необходимы для данного полного углового
момента /, и диагонализировать гамильтониан (7.3) в этом базисе.
В итоге имеем для
четных I: | IM0), (/7И2>,....
нечетных / (/> 3): | IM2), |/М4>,..., \IMI- 1>. ( ’
Таким образом, для состояний с четным I мы имеем всего + 1)
базисных функций, а для состояний с нечетным I, где I 3, —
х/2 (/ — 1) базисных функций.
Для нахождения коэффициентов А1К (у) в (7.5) необходимо ре-
шить уравнение Шредингера
Г 3 .^,2
у м k
-А W*
(7.7)
'Ф/ЛН — 0"
172
п Я этого умножим уравнение (7.7) слева на < /Л4Е| и подставим
разложение (7.5):
1МК
IMK'\ = O. (7.8)
К'
Пользуясь матричными элементами от M'k2 [см. (5.185) и (6.132)],
получаем после простых преобразований
Д^+2(лЛ-?/1)^[(/-/<)(/-/<-1)(/ + /<+1)(^ + ^ + 2)]1/2 +
+ Л'к [2 СУ1 + $2) 2М' (/ + 1)~Л2} + & /е-8 (Е/Й2) &] +
+Л^-2(У2-^)^[(/+Ю(/+/<-1)(/-^+1)(/-/<+2)]1/2=0.
(7-9)
Условием существования решений является равенство нулю опре-
делителя системы (7.9). Это дает уравнение для энергии Е степени
(1/2/ 1) для четных / и г/2(/—1) для нечетных I, если 7^3.
Например, для I = 2 уравнения имеют вид
А2 ]6 СЛ-^) + А2 [6 (^ + &) 4 (ЕМ2) $2 П = О,
АI [2 (& + &) &+8^ 2 - 4 (Е/Й2) #2 &] +
КШ~Ш = О. (7.10)
Отсюда получаются два состояния, энергия которых является
корнями уравнения
Решения этого уравнения даются выражением
3 (У1-У2)2
8 ЯЯ
' 1/2
ЯЯ'.
з { -!—+— 1 1
k I?52 ^1^3
(7-12)
Для аксиально-симметричного ядра и В этом СЛУ‘
чае корни уравнения (7.11) есть Е = ЗЙ2/^ и Е = 2А2/^3. Первый
из них является решением (Л2/2^и)7(/ + 1), соответствующим зна-
ению I = 2 [см. (5.187)] для симметричного готатора. Второй ко-
Р нь стремится к бесконечности при #3 0-
173
Как уже упоминалось, система уравнений (7.9) для I = 3 сво-
дится к одному уравнению. Соответствующий коэффициент А3„
определяется из условия нормировки. Решение с I = 3 совпадает
с функцией |ЗЛ42>- Подставляя это в (7.7), получаем энергию
3+-состояния:
Е(3+) = Е/=з = 2^(2
(7-13)
(при этом использовано соотношение М'+2\ЗМ2) — М'_2\ЗМ2) =
= 0). Учитывая (7.12), находим, что для энергий всех (двух)
2+-уровней и одного 3+-уровня
Рис. 7.2. Зависимость энергии уровней
асимметричного ротатора в единицах
Л2/45р2 от параметра деформации у.
Значения угловых моментов уровней
указаны справа.
асимметричного ротатора спра-
ведливо соотношение
Е1(2+) + Е2(2+)=Е(3+), (7.14)
которое может быть легко про-
верено экспериментально (см.
ниже).
В общем случае решения
уравнений (7.9) зависят от па-
раметра у. Они получаются чи-
сленно как функция у с помощью
диагонализационной процедуры,
описанной выше. На рис. 7.2
показаны результаты для энер-
гий уровней (в единицах
А2/4Вр2). Случай у — 0 соответ-
ствует симметричному ядру,
энергии уровней основной по-
лосы которого удовлетворяют
правилу I (I + 1). По мере
того как асимметрия увели-
чивается, энергия «аномальных»
вращательных состояний, ко-
— 0, приближается к энер-
тора я была бесконечной при
гии соответствующих состояний основной полосы. Модель асиммет-
ричного ротатора предсказывает небольшие отклонения энергий
нормальных 2+-,*’4+-, 6+, ... состояний от правила /(/+1). Этот
эффект аналогичен центробежному растяжению ядра, предсказы-
ваемому колебательно-вращательной моделью. Соотношение (7.14)
также приближенно выполняется в этой модели. Соответствующие
экспериментальные данные приведены в табл. 7.1. Кроме того, в ней
вычисляются отношения
(Е. (2+) + Е2 (2+)—Е (3+))/(£х (2+) + Е2 (2+)),
(4Ег (2+) + Е2 (2+)-Е (5+))/(4Е1 (2+) +Е2 (2+)).
174
Таблица 7.1
Отношения (£i (2+)+£2 (2+)—£ (3+))/(£i (21-)-|-£2 (2+))
и (4£!(2+) + £2(2+)—£(5+))/(4£i(2+)H-£2(2+)) Л™ яДеР
с двумя измеренными уровнями с 7=2 и одним измеренным
уровнем с 7=3 или 7=5 [100]
Ядро Et (2+). Мэв E, (2 + ). Мэв E (3+), Мэв E (5+). Мэв 1 + oj, + + 04 «Р + 04 U? + "o4 (+S) 3- (_pS) !3+(+ZJ) . % 4 E, (2+) + E, (2+)
21 Mg 1,368 4,24 5,22 6,9
26Mg 1,83 2,97 3,97 (?) — 17
42Са 1,52 2,42 (?) 2,751 (?) — 30
ьбре 0,845 2,660 3,445 3,84 (?) 17 3 4
82Кг 0,777 1,475 2,094 — 70
»«Мо 0,770 1,524 1,850 (?) 2,730 19,3 4
102Ru 0,475 1,105 1,525 — 3 ,5
loopd 0,5116 1,1285 (?) 1,5575(?) 2,7569 (?) 5,0 13
134Ва 0,604 1,168 l,760(?) — 0,68
160Sm 0,334 1,167 1,508 — —0,47
132Sm 0,122 1,087 1,236 — —2 ,2
154Gd 0,123 0,998 1,129 — —0,71
156Gd 0,089 1,154 1,248 (?) 1,622 (?) —0,40 —7,4
160Dy 0,0867 0,966 1,049 — 0,38
i6«Er 0,0806 0,788 0,861 — 0,92
188ЕГ 0,0798 0,822 0,897 (?) — 0,55
172Yb 0,0787 1,4675 1,5502 — —0,26
182yy 0,1001 1,258 1,331 — 2,0
184\V 0,111 0,904 1,006 — 0,89
186\y 0,122 0,730 0,85 (?) — 0
184Os 0,125 1,085 1,215 — —0,41
1860s 0,13715 0,76738 0,91033 1,27530 —0,64 +3,1
188(JS 0,15503 0,63307 0,78999 (?) — —0,24
190Os 1,,2Os 0,1867 0,2057 0,5572 0,4891 0,755 0,6909 .— -0,5 +0,56
lS2pt 0,3165 0,6129 0,9208 0,92
0,3285 0,6220 0,9227 (?) — 2,9
0,356 0,689 1,001 (?) — 4,2
200Hg 0,368 1,575 1,776 ' — 8,6
214Po 0,609 1,281 1,544 — 18
—8Th 232U 234U 238Pu 0,058 0,047 0,044 0,044 0,969 0,868 0,922 1,030 1,023 0,913 0,965 1,071 1,087 (?) 0,39 0,22 0,10 0,28 1,0
Cl 2MFm 0,041 1,032 (?) 1,074 (?) — —0,093
0,044 0,692 0,734 — 0,27
175
также должно равняться нулю в модели асимметричного
Как видно из табл. 7.1, в пределах областей деформи-
ядер (от 152Sin до 19°0s и за Th) соотношение (7.14) вы-
очень хорошо, но вне этих областей оно не выполняется.
Последнее
ротатора,
рованных
полняется
Таблица 7.2
Коэффициенты разложения AIyi (у), определяющие волновые
функции состояний (7.5) со спином 2 и 4
у, град 0 10 20 25 30
* Дб1 1 1 000 0,996 0,974 0,866
0 7,8-Ю-з 0,0872 0,227 0,500
Л 2 0 —7,5-10-3 —0,0867 -0,226 —0,500
12 • 1 о 9 1 1,000 0,996 0,975 0,866
44i 1 0,999 0,955 0,852 0,739
1 0 0,030 0,296 0 522 0,661
дд 0 10-4 0,010 0,043 0,125
Дог 0 —0,030 —0,296 —0,523 —0,559
Д?2 1 0,999 0,954 0,842 0,500
ДД 0 0,004 0,043 0,128 0,661
Из таблицы можно также видеть другую характерную черту ука-
занных областей, заключающуюся в том, что энергии нижайших
2+-уровней быстро увеличиваются на границах и достигают весьма
больших значений вне этих областей.
В табл. 7.2 представлены значения коэффициентов А'м (у) вол-
новых функций (7.5) с/ = 2и/ = 4 для различных значений у.
Хотя К не является хорошим квантовым числом, при малых у сме-
шивание по К мало. Даже при больших значениях у уровни с более
низкими энергиями для каждого I в основном являются уровнями
с К — 0. Значения у и Вр2 обычно находятся из энергии второго
2+-уровня (который в колебательно-вращательной модели опреде-
ляется как у-колебательный уровень) и из энергии первого 2+-
Уровня соответственно.
Зависимость величины у от А показана на рис. 7.3. Поскольку,
согласно (7.12) и (5.73), отношение Е± (2+, у)/В2 (2+, т) является
Функцией параметра у, значения у могут быть получены из экспери-
ментальных данных о первом и втором 2+-уровнях. Видно, что для
сильно-деформированных ядер асимметрия мала, в то время как
Для осцилляторов, таких, как 76Se, 114Cd и186Р1, она, по-видимому,
максимальна (у = 30°).
177
§ 7.2. ВЕРОЯТНОСТИ ЭЛЕКТРИЧЕСКИХ КВАДРУПОЛЬНЫХ
ПЕРЕХОДОВ ВО ВРАЩАТЕЛЬНЫХ ПОЛОСАХ
Приведенная вероятность электрического квадрупольного пе-
рехода между состояниями асимметричного ротатора, описывае-
мыми волновыми функциями (7.5), дается формулой
В(Е2- Л^//) = Л2^±1|<Л.ц(?2||//>|2, л = (7.15)
i ~г 1 43Т '
Е,
КЗв
1™0S
1SS0S
3000
3562
2000
2868! <
+28042807'—! !
2511'
— • I
2095! '!
1*20592052 ’]
2841
2286 2288;
10+ 2590 2632''
3428
2244
1643 ''\167е
1000 14051^,7 \ ^584
е \1259
~6+869_ S£1 877 ^836
1859
1589 15311566Г^
—.434 435 439 557 434
4-------------------
2+137 137 137 137 137
Г —— "—~~—
'----— h
*1297
«---
94 g Q4e 966 1218
-----
479 483 489 516 479
155 155 155 155 155
- 17631795'
16601—----’
8*—'
10461090^'
\932
™ 523 \892
,t54D 564_573^____.546
1^071
2+137 187 187 187
0+ ~~
187
О
Рис. 7.4. Сравнение различных моделей в переходной области для изотопов Os.
В первом столбце слева приводятся экспериментальные значения энергий, во втором —
предсказание колебательно-вращательной модели, в третьем — предсказание модели асим-
метричного ротатора, в четвертом и пятом — результаты расчета по формулам /4/(/+1)
и АЦ1+1)—В/2(/-)-1)2 соответственно. В последнем столбце дополнительный центробежный
параметр В подгонялся по 4+-уровию. Видно, что наблюдается нарушение простого раз-
ложения энергии в ряд по степеням спииа [135].
где квадрупольный оператор получается из выражения (3.57)
<?2ц = [D2* (6,) а0 + (D& (67) + D^2 (Oj)} а2] =
= ₽ [ПЙО (6j) COS у + {D^2 (6,-) + D?- 2 (6;)} (у ) si .'
sin у . (7.16)
Теперь нетрудно вычислить приведенный матричный элемент в (7.15).
Так как волновые функции (7.5) должны быть найдены численно
путем диагонализации, то какие-либо аналитические выражения
получить нельзя. Результаты расчетов различных отношений вели-
чин В (Е2) в модели асимметричного ротатора были уже показаны
штриховой линией на рис. 6.9—6.12.
Можно заключить, что модель асимметричного ротатора качест-
венно и количественно дает то же самое поведение этих величин, что
178
ебательно-вращательная модель. Это же справедливо и для
И К°гий уровней. Последнее хорошо видно на рис. 7.4 для изотопов
энер также представлены результаты расчетов по формуле / (/+
и по феноменологической формуле, учитывающей центробеж-
+ поправку /2 (/ + О2*- Мы видим, что дая мягких у-вибраторов,
НУЮ1МИ являются изотопы Os, предсказания колебательно-враща-
КЙКьной модели и модели асимметричного ротатора очень похожи
Те vr на друга и хорошо согласуются с экспериментом. Расчет же по
£муле I (Z + 1) даже с феноменологическим учетом центробеж-
ного растяжения не в состоянии описать эксперимент. Это указывает
на важность корректного учета колебательно-вращательного взаи-
модействия и на то, что обе модели эквивалентны в его учете, по край-
ней мере для нижайших вращательных полос (см. следующий пара-
граф).
§ 7.3. р-КОЛЕБАНИЯ АСИММЕТРИЧНОГО
РОТАТОРА
Мы видели, что модель асимметричного ротатора предсказывает
только одно 0+-состояние, являющееся основным состоянием ядра.
Однако, как указывалось при обсуждении колебательно-вращатель-
ной модели в предыдущей главе, во многих ядрах существует по
крайней мере одно возбужденное О'-состояние, которое в предыду-
щей главе интерпретировалось как p-колебание. Таким образом, же-
лательно обобщить модель асимметричного ротатора так, чтобы по-
следовательно учесть по крайней мере p-колебания ядра. Это было
сделано Давыдовым и Чабаном [92], которые предположили, что
трехосное ядро является жестким по отношению к у-колебаниям, а
по отношению к p-колебаниям оно таковым уже не является. Мы
опишем здесь упрощенный вариант [134, 135} подхода Давыдова—
Чабана, основанный на колебательно-вращательном гамильто-
ниане [(6.40) — (6.43)].
Коллективная потенциальная энергия, разложенная в точке
минимума а0 — а0 — р0, а2 = а2 (см. рис. 7.1), соответствующего
неаксиальному ядру, имеет вид
а2) = -^С0(а0-а0У+С2(а2-а2)\ (7.17)
где предполагается, что С2 > Со. Это предположение является очень
важным. Оно означает, что ядро является очень жестким по отноше-
нию к п2-колебаниям и, следовательно, ими можно пренебречь при
рассмотрении низколежащих уровней. Поэтому величина а2 в (6.40)—
(6.43) может быть заменена его равновесным значением а2 и нет не-
судимости рассматривать динамические степени свободы, связан-
ные с а2. Это приводит к гамильтониану
________ н = но + н'0, (7.18)
ВопРосы, связанные с экспериментальным изучением изотопов Os,
нуждаются в работах [59, 125].
179
где
М2-Л1?, Л4§ А-2 дг 1
2^0 + 16Bb| 2В dtf + 2
и
М2—М2
2^о
А1++М1
/ 2g 3g2 2а2 \
\ ₽о ₽§ ₽§ /
. _L 1А6 —i/б— в)
\ 3 ₽0 pg 7
(7.19)
(7.20)
Здесь предполагается, что п2, g < ро, т. е. статическая асимметрия
и амплитуды P-колебаний вокруг положения равновесия малы по
сравнению с деформацией ро. Такое предположение соответствует
реальности, особенно для сильнодсформированных ядер. Коорди-
ната g есть динамическая переменная, описывающая Р-колебания
тогда как координата а2 — статический параметр, который характе-
ризует отклонение от аксиальной симметрии. Собственные значения
и собственные функции гамильтониана Яо получаются из (6.128а):
| Ю^(е,)+(-1)'оСл-(е,)| х
X^-’^p^J + IO, (7.21)
п0 раз
И
£,K^(„.+±)£f + (/(f+l)-K’)ie + ^F.
no = 0, 1, 2,...
Здесь Ро, Ер и К имеют тот же смысл, что и ранее [см. (6.96), (6.97)
и (6.129)1. Жесткость P-колебаний описывается величиной Со. Ког-
да Со бесконечна, ядро является жестким и вращательная структура,
показанная на рис. 7.2, остается неизменной. По мере того как Со
уменьшается, поверхность ядра становится более эластичной и коле-
бательно-вращательное взаимодействие, которое описывается сла-
гаемыми, зависящими от g, в формуле (7.20), становится более важ-
ным Последнее справедливо для легких Р-осцилляторов.
Вариант модели асимметричного ротатора, предложенный
Давыдовым и Чабаном, эквивалентен колебательно-вращательной
модели в той мере, в какой речь идет о нижайших вращательных
полосах. Обе модели имеют одинаковое число параметров, а именно:
е, Ер, Еу, ро в колебательно-вращательной модели и п2, е> £₽>
в модели асимметричного ротатора с учетом p-колебаний. Эти пара-
метры в обоих случаях определяются из одних и тех же экспери-
ментальных данных, т. е. из энергии 2+-, 2+'- и 0+'-состояний и вели-
чины В (Е2, 2+-> 0+). Поэтому необходимо более глубоко попять,
почему эти две модели эквивалентны для нижайших полос и где
их предсказания различаются.
180
в § 6.5 было показано, что к «отталкиванию» волновой функции
т>. колебаний от начала координат приводят два эффекта — элемент
объема в соответствующем пространстве и колебатсльно-вращатель-
нос взаимодействие, описываемое слагаемым (где rj =— а \
Это еще раз продемонстрировано на рис. 7.5, где изображены вероят-
ности | <рк. (л) I2 Для основного (М = 0) и у-колебательного (К = 2)
состояний, предсказываемые колебательно-вращательной моделью
Видно, что эти величины имеют несколько сдвинутые максимумы
в районе ц = «а- Следовательно, в этой области колебательно-вра-
Р11С. 7.5. Вероятности |<Рк(т])12 Для основного состояния
(Д'=0), первого у- (Л'=2) и второго у-колебаний (п2=1,
А=0), предсказываемые колебательно-вращательной мо-
делью. Модель асимметричного ротатора аппроксимирует
первые две волновые функции дельта-функцией в точке
т)~Щ.
щательная модель предсказывает динамическую асимметрию. Мы
приходим теперь к важному полуколичественному заключению:
модель асимметричного ротатора по существу заменяет динами-
ческую функцию распределения вероятности |<р (ц)|2_ддя основного
и ^-колебательного состояний дельта-функций б (т] — т]). Поскольку
величины е и т[ определяются из условия совпадения с экспериментом
энергий первых двух 2+-уровней, не удивительно, что обе модели
Дают практически одинаковые предсказания о свойствах полос ос-
новного, у- и Р-колсбательных состояний (величина Ер в точности
совпадает в обеих моделях). Однако для высоких вибрационных по-
лос эти модели должны значительно различаться. Например, второе
возбужденное 0+-состояние | 00010 > с п2 = 1, являющееся вторым
у-колебательным уровнем* с К = 0, должно иметь функцию распре-
деления вероятности, показанную на рис. 7.5 штриховой линией.
* Энергия этого уровня приближенно совпадает с энергией у-колебания
с А = 4 (см. рис. 6.1).
181
В этом случае имеются два максимума, которые значительно смеще-
ны по сравнению с максимумами для случаев К =~0, м2 = 0 и К~2
и2 = 0. В модели асимметричного ротатора это может быть описа-
но изменением асимметрии ротатора, т. е. введением дополнитель-
ного параметра.
Как указывалось выше, кроме основной полосы и однофононных
колебателяных полос в деформированных ядрах следует ожидать
также полосы, построенные на двухфононных колебательных со-
стояниях. Они соответствуют состояниям колебательно-вращатель-
ной модели, в которых преобладает одно из базисных состояний
| /44400), | /Л4002) или | /Л1201). В модели асиммитричного ротато-
ра соответствующими состояниями являются состояния | /Л140)
| 7М02) или |/Л421>.
Интересно отметить, что в ядрах Os имеются 0+- и 4+-уровни,
которые естественно интерпретировать как указанные состояния
с большим числом фононов. 0+-уровень с энергией 1086 кэв в 1880s
расположен слишком низко для того, чтобы быть началом 0-поло-
сы, которую следует ожидать примерно при 1700 кэв. В расчетах
в рамках колебательно-вращательной модели предполагается, что
0+-уровень с энергией 1766 кэв является нижайшим уровнем 0-
полосы, а уровень с энергией 1086 кэв является состоянием 100010).
Колебательно-вращательная модель предсказывает этот уровень
при энергии 1140 кэв, т. е. с точностью 5%. Это предположение под-
тверждается также значением отношения вероятности из состояния
1086 кэв на у-колебательный 2+-уровень и на 2+-уровень основной
полосы. Экспериментальное значение этого отношения л?3,5. Это
примерно в 100 раз больше, чем если считать указанный уровень
0+-уровнем 0-полосы. Если же предположить, что уровень при
1086 кэв является двухфононным у-колсбатсльным состоянием, то
колебательно-вращательная модель дает для указанного отношения
величину »25. Согласно этой модели в данной области энергии не
может быть 0+-уровней, если значительно не нарушать относительно
хорошее согласие с данными об основной полосе.
В ядре 180Os 4+-уровень с К = 4 и энергией 1163 кэв, по-види-
мому, является состоянием 140400), даваемым колебательно-враща-
тельной моделью. Эта модель предсказывает его при энергии 1193 кзв,
т. е. с точностью 3%. В модели Давыдова с учетом 0-колебаний ни-
жайшее состояние с I = Д = 4 лежит при энергии 2084 кэв. По-
этому динамическая колебательно-вращательная модель, по-види-
мому, имеет явные преимущества при объяснении колебаний с боль-
шим числом фононов*.
Поскольку двухфононные состояния особенно критичны к ангар-
моническим членам в потенциальной энергии, то следует с удовлетво-
рением отметить тот факт, что колебательно-вращательная модель
* Состояние с большим числом фононов в изотопах Os экспериментально
исследовалось в реакциях захвата нейтрона в работах [59, 209].
182
может также описать несколько экспериментально наблюдаемых
двухфононных состояний.
Однако следует также отметить, что при больших энергиях ста-
новится важным большое число дополнительных эффектов, таких,
как смешивание коллективных состояний с одночастичными возбуж-
дениями, антиспаривательный эффект кориолисовых сил [134, 135]
для больших значений вращательного углового момента и, наконец,
блокинг-эффскт [134, 135] для слабо коллективизированных вибра-
ционных состояний. Все эти эффекты могут быть причиной заметных
отклонений от предсказаний данной простой модели и привести
к необходимости использовать микроскопический подход. Следо-
вательно, значение таких моделей заключается в их простоте, боль-
шой наглядности и возможности почти количественного описания
ядер при малых энергиях возбуждения.
* * *
Свойства асимметричного ротатора рассмотрены в обзоре [100].
Они также обсуждались подробно в оригинальных статьях Давыдо-
ва и сотр. [89—92]* и в работах Боша и др. [9, 10].
* См
атоми. ’ также монографию А. С. Давыдова. Возбужденные состояния
х ядер. М., Атомиздат, 1967.—Прим. пер.
Глава 8 ОДНОЧАСТИЧНЫЕ
МОДЕЛИ
До сих пор мы рассматривали только коллективные эффекты
в четно-четных ядрах. Для того чтобы обобщить модель на случай,
когда кроме коллективных колебаний, явно учитывается одна (или
несколько) частица, -— кратко обсудим оболочечные модели для сфе-
рических и деформированных ядер.
Совершенно очевидно, что полную информацию о структуре ядра
можно получить, если мы знаем истинную ядерную волновую функ-
цию. Однако хорошо известно, что теоретического описания поведе-
ния всех степеней свободы таких сложных динамических многочас-
тичных систем, какими являются тяжелые ядра, практически полу-
чить невозможно. Даже если бы удалось получить явные выражения
для указанных волновых функций, оказалось бы, что все еще оста-
ется очень желательным и необходимым развить упрощенную мо-
дель, которая содержала бы все существенные свойства динами-
ки ядра и тем самым давала описание ядра на более простом
языке.
До сих пор мы рассматривали некоторые чисто коллективные
аспекты поведения ядра. Теперь необходимо попытаться объединить
это в одну картину с другим предельным случаем описания ядерной
динамики, а именно с одночастичным описанием. Коллективные мо-
дели, которые обсуждались выше, мало связаны с числом нуклонов
и едва ли в состоянии предсказать особенности, связанные с маги-
ческими числами (см. гл.1).
В одночастичной модели оболочек отдельные нуклоны рассмат-
риваются как движущиеся по стационарным орбитам. При этом
предполагается, что все парные нуклоны, в том числе нуклоны незапол-
ненной оболочки, образуют инертный остов со спином равным нулю,
так что значения многих ядерных характеристик определяются
только последним непарным нуклоном. Поэтому одночастичная
модель не содержит в себе коллективного движения двух или трех
нуклонов.
Однако она является фундаментальной моделью, которую
мы можем в дальнейшем обобщить (см. т. 3) так, чтобы она содержа-
ла такие корреляции.
§ 8.1. ОДНОЧАСТИЧНЫЕ СОСТОЯНИЯ
СФЕРИЧЕСКИХ ЯДЕР
В физике очень часто оказывается полезным применение извест-
методов, зарекомендовавших себя в близких областях, к еще
НЬизвестным областям исследования. Ранний период развития тео-
Не ядра является подтверждением справедливости этого положе-
Рия В процессе решения проблемы структуры атома было выяснено,
чтсГдвижение электронов в основном определяется кулоновским про-
тяжением центрального ядра и что кулоновское отталкивание между
электронами можно рассматривать как возмущение этого поля при-
тяжения. Следовательно, в качестве волновой функции нулевого
порядка системы электронов можно взять антисимметризованное
произведение волновых функций каждого электрона и затем учесть
взаимодействие электронов в первом порядке теории возмущений.
Однако в проблеме структуры ядра положение существенно иное.
В этом случае нет центрального поля, создаваемого внешним источ-
ником, а существует лишь сильное взаимодействие между нуклона-
ми. Тем не менее не кажется слишком некорректным считать, что
нулевое приближение при описании движения нуклонов в ядре мож-
но получить, если предположить, что движение одного нуклона под
действием всех других нуклонов аналогично движению в централь-
ном поле. Таким образом, можно рассчитать спектр ядра, исходя из
центрального потенциала, который образуется в результате действия
сил между частицами. В настоящее время это среднее поле рассчи-
тывается для легких ядер с помощью процедуры Хартри — Фока.
Однако на более ранней стадии развития модели оболочек оно
только постулировалось.
Благодаря короткодействующему характеру ядерных сил
соответствующая потенциальная яма должна иметь резкие границы,
определяемые границей распределения ядерной материи в ядре.
По практическим соображениям такая яма должна быть достаточно
удобной для расчетов. Мы рассмотрим здесь бесконечную прямо-
угольную потенциальную яму
V (г) = — Vo для г < R,
V (г) = оо для г > R
и бесконечную яму гармонического осциллятора
V(r)= — Vo + ^-Ako2r2.
(8.1)
(8-2)
Значения энергий одночастичных уровней, получаемые для этих
Двух ям, очень похожи. Эксперименты по рассеянию нуклонов ука-
зывают [389] на то, что первая яма более реалистична для тяжелых
яДер, а вторая — для легких. Однако большая простота потенциала
гармонического осциллятора привела к преимущественному исполь-
ванию этого потенциала в большинстве оболочечных расчетов. Мы
риведем здесь одночастичные решения для обоих потенциалов, но
185
в основном будем использовать оснилляторные волновые функции
Как было указано Двайер и Йенсеном [249], большинство реалисти-
ческих одночастичных схем уровней соответствует яме, промежуточ-
ной между осцилляторной и прямоугольной.
8.1.1. Собственные функции и собственные значения
одночастичного гамильтониана для бесконечной
прямоугольной ямы
Для бесконечной прямоугольной ямы (8.1) собственные функции
должны обращаться в нуль при г > R, поэтому следует рассматри-
вать только решения внутри ядра, исчезающие при r — R. Уравне-
ние Шредингера для частицы в яме имеет вид
V2 + V(r)ju(r) = £a(r). (8.3)
Полагая
M(r) = /?ni(r)^im(0. <Р). (8.4)
для величин R получаем радиальное уравнение для центрального
поля:
jr+f <8-5)
В случае прямоугольной ямы воспользуемся подстановкой
, •> 2МЕ ,о
Р = £г = |/ -^-г (8.6)
и получим
+ '«+>],;(р) = 0. (8.7)
dp2 р dp [ р2
Это уравнение очень похоже на уравнение Бесселя. Функцию R (р)
можно выразить через сферические функции Бесселя /г (р), регу-
лярные при р = 0 [2591:
Я(Р) = /г(р)= |/|р/+1/2(р), (8-8)
где J обозначает обычную функцию Бесселя полуцелого порядка.
Аналогично нерегулярные решения уравнения (8.7) являются сфе-
рическими функциями Неймана
МР) = (-1)'+,1 ^J-/_i/2(p). (8-9)
Известно [372], что функции J/+i/2 (р), где I — положитель-
ное или отрицательное целое число или нуль, можно выразить через
сумму произведений sin р и cos р на полиномы нечетного порядка
по р-1/2. Выпишем несколько явных выражений для функций j и п-
186
/о(Р) = sin р . Р sin р z v cos р «о(р)= р ; cosp . , v_ cosp sin p
/1 (р) - Р2 p p p
t 3 1 \ . 3
/2(р) = рз — sin p cos p; P P2
1 з 1 \ 3 .
«2 (Р) = (р- ) cos p sin p. p ' p2
(8.10)
Часто необходимо знать асимптотическое поведение этих функций
/ Ой—> р
« vr'P->o 1.3.5...,-(2/4-1) ’ (8.Н)
t х 1-1.3-5.....(2/— 1)
П‘(р) р.О р'+1
и
'><р)л17-С05 (р у(*+1)лУ 1 \ (8-12)
«г(р)-^ —sin | р--Ь(/4-1)л .
р>оо р 2 J
Приведем также некоторые свойства функций j и п:
pl (р) р2 Ф=у р3 t/о (р)+п0 (р) /1 (р)1;
[ «2 (р) р2^р = у р3 («о (р)—/о (р) ni (р)1;
«1-1 (р) /1 (р)—rii (р) /г ! (р) = у-, I > 0;
ii (р)у-«г(р)—«i(p) уМР) =4--
dp dp р4
(8.13)
Следующие свойства справедливы как для функций /, так и для
функций и:
/i-i (р) +ji+i (р)= 7<(р)» Z>°’>
~ = 77Т7 f//z 1 (Р)-(' + /'+1 (Р)Ь
-у 1Р/+‘/г(Р)] = Р/ + 1/г-1(р). z>°i
~ [р~г it (р) ] =—р-' ii+i (р);
f /1 (р) ф=—/о (р); f /о (р) р2 dp = р2 /1 (р)>
f it (р) р2 dP=JL рз [;-2 (р)—/-г_1 (р) /г+1 (р)], I > о.
(8.14)
187
Таблица 8.1
Одночастичиые состояния бесконечной прямоугольной ямы*
Орбита (и/) Xnl Wnl= =2 (2 г+1) й Н С Орбита (nZ) Xnl Nnl= =2(2 Z+I) ? M 1 3 /
1 S 3,142 2 2 2 d 9,095 10 '— 68
1 Р 4,493 6 8 1 h 9,356 22 90
1 d 5,763 10 18 3 s 9,425 2 92
2 s 6,283 2 20 2 f 10,417 14 106
2 f 6,988 14 34 1 i 10,513 26 132
2 р 7,725 6 40 3 P 10,904 6 138
1 g 8,183 18 58 2 g 11,705 18 156
* В первом столбце указаны состояния бесконечной прямоугольной ямы, во втором -
значения Хп^ в формуле (8.16) Для определения собственных значений энергии, в треть-
ем— число частиц на соответствующих уровнях, в четвертом—полное число частиц [141].
Граничные условия
/г(р)= 0 для р = /г/? (8.15)
в случае бесконечной прямоугольной ямы приводят к одночас-
тичным энергиям
_ ^2 __ & Х"1
nl 2М^п‘ 2м' R2 ’
(8.16)
где Хп1 являются нулями трансцендентного уравнения (8.15), кото-
рые, вообще говоря находятся численно. Некоторые из них приве-
дены в табл. 8 1
Таким образом, согласно (8.4), (8.8) и (8.16), нормированные вол-
новые функции в случае прямоугольной ямы имеют вид
“nlm (Кп1г) = Ani it (Kni г) Ylm, (8.17)
где
3),/2
_____1____
/i+i (KniR)
(8.18)
Третий и четвертый столбцы табл. 8.1 дают соответственно число
нуклонов Nnl в различных подоболочках и полное число нуклонов,
включая последнюю заполненную подоболочку. Мы использовали
здесь обычное правило и назвали оболочками или подоболочками
одночастичные состояния, характеризуемые квантовыми числами
пи/. Более строгие определения будут даны в следующих раз-
делах.
188
8.1.2. Собственные функции и собственные значения
одночастичного гамильтониана гармонического
осциллятора
Сферическая система координат. Для случая гармонического
иллятора в сферической системе координат радиальное уравне-
ние (8-5) после подстановки (8.2) принимает вид
НИ dzR 2 dR — ’ .....
2МЕ М2 со3 2 f(Z+l)
Й’ Й3 Г г2
]т?(г) = 0. (8.19)
dr2 г dr
Нормированные решения этого уравнения можно записать еле
дующим образом
U (г.1)»/А-</-X
Х^^-п, 1 + 3/2, 7.r2)Y,m- (8.20)
Еп1 Йы(2п +1 + 3/2) = Jw>(N + 3/2), п = 0, 1,2,...,
где Z Mm/ti. Фазовое условие (—1)" выбрано так, чтобы все
матричные элементы от Е были положительны. Заметим, что для
данного главного квантового числа N = 2п + I, т. е. для одного
уровня с энергией Е = Асо (Л' + 3/2), существует несколько
собственных функций. Если N — четное, то I может принимать все
четные значения от 0 до N (например, для N = 6 возможны значения:
I = 0, п = 3; I = 2; п = 2; b = 4, п = 1; I = 6, п = 0). Таким
образом, для четного Д' имеется 4- N + 1 вырожденных решений.
Если W — нечетное, то I может принимать все нечетные значения от
1 до N (например, для N — 5 возможные значения: I = 1, п ~ 2;
I =3, п 1, I 5, н 0) и в этом случае имеется-* (IV + 1) вырож-
денных решений. В приведенных числах еще не учтено вырождение
по т, поскольку для каждого значения / имеется 21+1 различных
решений с разными т.
В табл. 8.2 указаны все возможные значения чисел частиц
(ср. с табл. 8.1).
б. Декартовы координаты. Часто вместо сферической системы
координат более удобно работать в декартовой системе, например
в случае потенциала деформированного осциллятора, который будет
рассмотрен в гл. 9. Приведем здесь соответствующие результаты.
Уравнение Шредингера для случая трехмерного гармонического
осциллятора в декартовых координатах имеет вид
[S Н^-*2х2)«] + [^ +(^-*V)«] +
+ f_?!+ + (/<3_-X2z2) «1 = 0, (8.21)
L dz2 I
Они получены, например, в работе [149].
189
Таблица 8,2
Одночастичные состояния бесконечной осцилляторной ямы*
N EN. ha Орбита (п, 1) 2 2 (2/4-1) п,1 Полное число час- тиц Еы, hit) Орбита (п. 0 + n И e Полное I число час-/ тиц /
0 1 2 3/2 5/2 7/2 1 S 1 р 2 s, 1 d 2 6 12 2 8 20 4 5 11/2 13/2 3s, 2d, 1 g 3p,2f,\h 30 42 70 112
3 9/2 2 Р, И 20 40 6 15/2 4s, 3d, 2g, 1 i 56 168
* В четвертом столбце приводится число частиц, находящихся на соответствующих
подоболочках.
где
nr Ть
Записывая и (х, у, г) в виде
и(х, у, z) = f(x)g (y)h(z),
(8.22)
получаем три совершенно аналогичных уравнения для одномерного
гармонического осциллятора. Например, дифференциальное урав-
нение для f (х) имеет вид
^L + (/<j_Vx2)/(x) = 0. (8.23)
Решения этого уравнения хорошо известны [149]. Энергия Е =
— Ao (tii + 1/2), где пг — целое число. Волновые функции имеют
вид
е 2
/(*) =
-----г,
хе 2 .F,
— п, — , Хх2 , если пх = 2п четно;
2 ' (8.24)
' —п, —, Хх2\ если пу = 2п 4-1 нечетно.
Таким образом, полная энергия Е равна:
£ = ^(0^ + 1/2)4-Йм(п2+ 1/2) +Йо» (п3+ 1/2). (8-25)
Исследуем теперь решения уравнения (8.19) в сферической систе-
ме координат и выясним, чему они соответствуют в декартовых коор-
динатах. В качестве примера выберем решение ип1 Ую с п = 1
и I = 2. Согласно (8.20), соответствующая энергия
£ = Йо) (4+ 3/2), (8-26)
а произвольно нормированная собственная функция имеет вид
V2
Р2 (cos 0) =
190
r2e-i/2Xr>(i__|-V2'j«3/2)cos2e—1/2). (8.27)
бственная функция должна быть линейной комбинацией таких
^(хИп. для которых
' n1 + n2 + n3 = (2n + Z) = 4. (8.28)
Очевидно, что каждое слагаемое содержит множитель exp (—V2/2)=
еХр (—’(1/2) А. (х2 + У2 + г2)), входящий в и. Поэтому в дальней-
шем его можно опустить. Кроме того, имеем
f/0, у, И = 1: F(-!’ у’ Хх2) = 1-2Хх2;
F| — 2, — , = 1— 47х2 + — Х2х4;
V 2 1 3
xFl 0, у , 7.x2 = х;
(8.29)
Легко показать, что условие (8.28) можно удовлетворить 15
различными способами, которые указаны в табл. 8.3. Из этих 15 ре-
шений необходимо сконструировать такую линейную комбинацию,
которая дает функцию (8.27). Это можно сделать, если выразить
функцию (8.27) через х, у, г:
(_lCos20 —y) = ^-|-z2—у г2) (1 — у^2) =
= ± Хх4 + у Xz/4 — у Хг4 + у Хх2 //2—у W г2—у Та2 z/2 —
-±х2—1у2 + г2. (8.30)
Поскольку сюда входят только четные степени х, у, г, то из 15 воз-
можных слагаемых, указанных в табл. 8.3, следует опустить те,
которые содержат нечетные степени х, у, г, т. е. те, где по крайней
мере одно из квантовых чисел nr, п2, ns является нечетным. Множи-
тели, на которые должны умножаться различные собственные функ-
ции в декартовых координатах, приведены в последнем столбике
табл. 8.3. В нашей суперпозиции остается теперь только шесть соб-
ственных функций. Сравним соответствующие коэффициенты при
членах х4, у4, z4, х2у2, y2z2, г?х2, х2, у2, а2 в (8.30) и в табл. 8.3. В ре-
зультате получаем десять линейных уравнений для шести неизвест-
ных коэффициентов. Следовательно, в последовательном расчете
с21Ыре из П0ЛУченных линейных уравнений должны линейно зави-
ь от шести остальных уравнений.
Рассмотренная процедура является примером. Ее нетрудно обоб-
НТь, в результате чего произвольное решение в сферических коор-
191
динатах может быть всегда выражено через собственные функци
в декартовых координатах*. В гл. 9 мы увидим, что удобно исполь^
зовать оба эти представления при рассмотрении модели оболоче'
для деформированных ядер. Поэтому важно помнить об эквивалент-
ности обоих представлений волновых функций при использований
их в качестве базиса.
Таблица 83
Собственные функции ямы гармонического осциллятора
в декартовых координатах
«1 «2 «3 Собственные функции в декар- товых координатах с точностью до общего множителя ехр (—‘/я X г)2 ——J Множитель
0 0 4 4 1 — 4Хг2 +— X2z4 - — Х-1
3 14
0 1 3 / 2 \ yz 1 — — X г3 V 3 1 0
0 2 2 (1 — 2 Xz/2) (1 — 2Хг2) - 1 Х-1 28
0 3 1 2 \ —^J/2) 0
0 4 0 4 1- 4Х//2 + — О + —Х-1 т 28
1 2 \
1 0 3 xz(l-—Xz2) 0
1 1 2 ху (1 — 2 Хг2) 0
1 2 1 хг (1 — 2 Хт/2) 0
1 3 0 ху (1 — ^у2} 0
2 0 2 (1 —2Хх2)(1 —2Хг2) — — х-1 28
2 1 1 г/г(1 — 2Хх2) 0
2 2 0 (1 — 2 Хх2) (1 — 2Хг/2) +- х-i 14
3 0 1 хг^1—— Хх2) 0
3 1 0 ху 1 —-|-Хх2) 0
4 0 0 4 1 — 4Хх2-;-—Х2х4 3 + — х-1 т 28
* В дальнейшем также представляют интерес решения в цплиядр,1'1£
ских координатах, они приводятся в Приложении Г.
192
§ 8.1. СПИН ОРБИТАЛЬНАЯ СВЯЗЬ
, рассмотрели два вида модели оболочек. Однако ни чисто
МЬ\то1ьная, ни чисто осцилляторная яма не годятся в качестве
прямо} ическоГо потенциала модели оболочек. Реалистический по-
Реа1й потжен воспроизводить экспериментально наблюдаемые
теНЦ“еёки<? ‘шсла 2’ 8)1 20’ 28> 40> 50’ 82, 126’ Как УказЬ1ваЛ0СЬ
(1i,2g,3d,4s) (56) 61ш (1h,2f)3p) (42)5fw [168] [112] <[^1i[l38] , 72f[106]^ < 1h[32] S.3pm [132] 1[(26) — 25E
(Igjdjs) (30) [70] 3S[70][^ 2d[68] ' \lff[58] № 33(2) _ ^-1S(S) — 20E
(WP) (20) Jficu [40] V'.. 2p[4Q]''' X 1f[34F~ ^-2p(6) - 15Ё
(id, 2s) (12) 2Pw [20] 2s[20]''' '' ' 1d[l8]" — 1f(14)~ ltf2S(2) 10Ё
(1P) (6) 1fiu [8] 1p[8] — 1d(10)_ — 1P(G) - 5Ё
(W (2) OP 0) r 7 [2] 1S[2] 1s (2)
Рис. 8.1. Схемы уровней ямы гармонического осцилля-
тора (слева), бесконечной прямоугольной ямы (справа)
и потенциала, изображенного на рис. 8.2 и являющеюся
интерполяцией между этими двумя поедельными случая-
ми (в центре). Числа нуклонов в каждом случае указаны
в скобках. Спектр прямоугольной ямы дан в единицах
£=2Д2/Л17?2, частота осциллятора равна h <в = 3/(С0£)
[249].
в гл. 1 (см. рис. 1.6) ядра, в которых как число протонов, так и число
нейтронов совпадают с одним из этих магических чисел, не имеют
Квадрупольного момента в основном состоянии. Следовательно, та-
кие ядра характеризуются сферическим распределением заряда,
ксперимент также показал, что эти ядра имеют относительно боль-
шую энергию связи нуклона (т. е. энергию, которую необходимо
тратить для того, чтобы один нуклон оставил ядро) (см. § 12.6).
и эмпирические факты указывают на то, что магические числа
ответствуют замкнутым заполненным оболочкам. Поэтому модель
7 Зак. 1218
193
Рис. 8.2. Потенциалы гармонического
осциллятора и прямоугольной ямы и
интерполяция между ними (штрихо-
вая линия).
оболочек должна быть феноменологически построена таким образ0м
чтобы воспроизводить вышеупомянутые магические числа.
На рис. 8.1 показаны схемы уровней гармонического осцилля-
тора и прямоугольной ямы. Можно было бы ожидать, что интер.
полиция между этими двумя предельными случаями (см. рис. 8.2)
дает магические числа. Спектр уровней для такого проме-
жуточного потенциала приво-
дится в центре рис. 8.1, на ко-
тором указываются также чис-
ла нуклонов, заполняющих
уровни этой интерполирован-
ной модели оболочек. Из рисун-
ка отчетливо видно, что во всех
трех рассмотренных моделях
воспроизводятся лишь несколь-
ко первых магических чисел,
тогда как остальные магические
числа таким способом не полу-
чаются.
Для того чтобы получить
остальные магические числа, к
потенциалу гармонического ос-
циллятора следует добавить фе-
номенологический спин-орби-
тальный потенциал. Таким обра-
зом, улучшенный одночастичный потенциал имеет вид
V(r)= — Vo+— Mco2r2--g-(bs). (8.31)
2 1ъ
где
1 .s = -L{(i -ps)2— I2-—s2)=y(f2—I2—s2) (8.32)
и j = 1 + s — полный угловой момент, равный сумме орбитального
углового момента 1 и спинового момента нуклона s. Собственные
функции |/т> полного углового момента имеют вид
|/т > = /?„, (г) V (8.33)
"Ч- ms 4
где обозначает спиновую функцию, Дп/ — радиальная
волновая функция. Из выражения (8.32) следует, что матричные эле-
менты оператора l-s по функциям |/ш> диагональны, тогда
1 •s|jm>
±^(/(/-+i)_s(s + i))|/m>: (8.34)
194
Для двух возможных случаев j = 1± 4>- получаем
1. s | jm > = -^h2
, 1 , 1
I ДЛЯ / = I + —
-(/+1) для / = /-у.
| jm), (8.35)
пая / ~ 0 спин-орбитальной связи, конечно, не существует. Учитывая
(8 35), получаем для потенциала (8.31)
V(r)=:=+ y/Исо2г2 для / = /±у. (8.36)
Поскольку в исходных предположениях о спин-орбитальной
связи а считается постоянной величиной, не зависящей от г, то ос-
цилляторные волновые функции не изменяются от добавления 1-s-
члена. В соответствии с формулой (8.36) собственные значения
Eni в (8.20) изменяются на аддитивное слагаемое, зависящее от
Z и /
+ Для/’ = /± 4’ (8-37)
I * i 1 J
или в явном виде
Enii — ha ^2n-pZ-p—^-)-а
— Z для / = / + — ,
Z+ 1 для j = l—~ .
(8.38)
В частности, для энергий, отсчитываемых от нижайшего уровня,
имеем
Enii i-i/2 — £ooi/2 — Й<в(2п-р Z)— al,
Eni z — i/2—Eoo i/2 = (2n-p I) -p a (I -j- 1).
Таким образом, вырождение осцилляторных уровней частично сни-
мается. Для положительного а состояния с 1, антипараллельным
s (1 I-----сдвигаются вверх, а состояние с 1, параллельным
s (/ Z + у), сдвигается вниз. Однако вырождение по т функций
/т} все еще сохраняется. Имеем
(2/ -р 1) = 2 l^l -j- — 'j -Р 1 = 2 (Z -р 1) СОСТОЯНИЙ ДЛЯ j = I _р — ;
(2/л 1) = 2(Z----L -р 1 = 2Z состояний для j =-Z-2-. (8.40)
Следовательно, центр масс энергий уровней Епц есть
-(aZ)2(Z+l) + a(/-pl)(2Z)=0, (8.41)
7*
195
т. е. введение 1-s-связи не приводит к изменению центра масе
энергии одночастичных уровней.
Таблица 8.4
Состояния одночастичного гамильтониана (8.31), содержащего
потенциал гармонического осциллятора с энергетическим па-
раметром Йю и спин-орбитальное взаимодействие с параметром а
N п 1 Состояние 2 N . J —. i J
6 3 0 4 sx/2 6 Йо 2 —-
2 2 3 45/2 6 fitii — 2 a 6
1 4 2 Ss/2 6 — 4 a 10
0 6 1 *12/2 6 Йо — 6 a 14 126
5 0 5 1 hg / 2 5 fico -| 6 a 10
1 3 2 fs/г 5 fe)-| 4 a 6
2 1 3 Р1/2 5 ~|~ 2 cc 2
2 1 3 Р3/2 5 fiti) - a 4
1 3 2 К/2 5 tia -3 « 8
0 5 1 ftn/z 5 Йо —5 a 12 82
4 0 4 J §7/2 4 Йо 5 a 8
1 2 2 4g/2 4 Йо 3 a 4
2 0 3 s1/2 4 Йо 2
1 2 2 45/2 4 Йо -2 a 6
0 4 1 £9/2 4 Йо— 4 a 10 50
3 0 3 • /5/2 3 Йо к 4 a 6 40
1 1 2 P1/2 3 ti(S) |- 2 a 2
1 1 2 P3/2 3 tun—a 4
0 3 1 /7/2 3 Йо —3a 8 28
2 0 2 1 43/3 2 Йо ' 3 a 4 20
1 0 2 S1/2 2 h(A 2
0 2 1 45/2 2 Йо -2 a 6
1 0 1 1 Pi/2 Йо + 2 a 2 8
0 1 1 P3/2 Йо—a 4
0 0 0 1 SJ/2 0 2 2
В табл. 8.4 протабулированы одночастичные состояния осцил-
ляторной модели оболочек со спин-орбитальной связью. Квантовое
число N = (2п + /) характеризует различные оболочки гармони-
ческого осциллятора. Число нуклонов в данной /-оболочке обозна-
чается через Nj, a N = j дает полное число нуклонов, при усло-
вии, что все оболочки ниже рассматриваемой заполнены. Так
как для первых трех оболочек (N = 0, 1, 2, ) I • s-расщепление весьма
мало, то в этом случае схема уровней практически совпадает с преж-
ней схемой, в которой не учитывалась спин-орбитальная связь.
Однако для более высоких оболочек имеет место существенная пере-
196
иповка уровней, которая сильно зависит от параметра а,
ГР пеаяющего величину спин-орбиталыюй связи. Вообще говоря,
°П кже как и со (осцилляторный параметр), может зависеть от N
а Кроме того, а может зависеть от главного квантового числа п
И орбитального момента I. Экспериментально было найдено [79],
П °ТПРИ фиксированном п параметр а несколько уменьшается с уве-
ЧТ<чением /. Эта эмпирическая закономерность получена в результа-
Л тщательнС)Г0 анализа возбужденных одночастичных состояний
^различных ядрах. Полученные значения параметра а приведены
в табл. 8.5.
Таблица 8.5
Эмпирические значения параметра спин-орбитального
расщепления а как функция оболочечных квантовых чисел
п, I [79]
п г=1 1=2 /=3 1=4 1=5 1=6
0 1,15 0,93 0,76 0,46 0,44
1 0,68 0,58 0,26 0,28 — —
2 0,39 0,19 —• — — —
Как видно из табл. 8.4, благодаря действию спин-орбитальной
связи уровни с наибольшими значениями / всегда сильно опускают-
ся вниз и обычно попадают уже в более низкую группу уровней.
Из этой таблицы также видно, что экспериментально наблюдаемые
магические числа возникают как числа частиц в замкнутых подобо-
лочках, однако они не соответствуют отчетливо разделенным глав-
ным замкнутым оболочкам. Этот результат можно получить, если
либо подгонять значения а от оболочки к оболочке, либо сделать
осцилляторную яму более плоской (см. рис. 8.2). В последнем случае
получится схема уровней модели оболочек, показанная на рис. 8.3,
которая воспроизводит экспериментально наблюдаемые магические
числа 2, 8, 20, 28, 50, 82, 126. Радиальные волновые функции такого
потенциала являются промежуточными между функциями осцил-
ляторной и прямоугольной ям и не могут быть получены в явном
виде. Это неудобство будет преодолено в следующем параграфе
в результате использования более реалистического потенциала моде-
ли оболочек, который понижает преимущественно состояния с боль-
"1ИГ?, УГЛОВЬ1М моментом.
Мы уже обсуждали некоторые экспериментальные данные, сви-
ельствующие о существовании магических чисел. Теперь для
лноты картины перечислим основные экспериментальные факты,
ПоказываЮщИе существование магических чисел*. Эти результаты,
Ученные для широкого круга ядерных явлений, таковы:
Детальные сведения см. в литературе, например [249].
197
1) разрывы в графиках, изображающих зависимость энепг I
связи от N и Z, при значениях этих чисел, которые соответс rnv^*1
магическим (см. § 12.1);
(-48------
' 6tiW
Четный
5 бы
Нечетный
-dp-
~2f-
4Ии
Четный'
Г- 38-
\-2d-
'--1J,5/2-
' 7s
~5^ *-
.__ц
~11,S 5^-
29g/s
-----------1Чз/2
ЗРз!2~
_____2f _
1h Гу/2
1П9/2----------
,(16)_[184]____184
(4)
(2)
-(8)
-(12)
(6)
-(10
(14)_[126]____126
(2)
(4)
(6)
(8) — [100]
(Ю)
(12)—[82]-----82
(2)
-(4)
(6)-[64]
-(8)
3sni 1h,,li
-^-'9^
ЗИы\—2р.
Нечетный
W 9П
2рз/ё
1р7/2
(10)— [50]--50
(2)-[40]
(6)~ [38]
(4)
(8)—[28]----28
28 1d3/2
Четный \~1d---------------------------——
1 /d5(2
(4) -[20]---20
(2)- [16]
(6)~ [14]
-1p—1pi/2
Нечетный 'P3/2
(2)'- [8]--8
(4)-[6]
0 -18----------18
(2)- [2]---2
Рис. 8.3. Схема одночастичных уровней гамильтониана, состоя-
щего из центрального потенциала, промежуточного между по-
тенциалом гармонического осциллятора и потенциалом прямо-
угольной ямы, и из спин-орбитального взаимодействия.
В круглых скобках дано число частиц [249].
2) пики в кривых, которые описывают относительную распро-
страненность изотопов и изотопов, при значениях чисел протонов
и нейтронов, соответствующих магическим числам;
3) увеличение энергии первого возбужденного уровня по мер
приближения к магическим числам;
198
., заметное уменьшение сечений захвата нейтронов ядрами с
м протонов или нейтронов, близким к магическим;
число^очень малые квадрупольные моменты ядер, соседних с маги-
„ескими ядрами (см рис. 1.6)
4 Существование оболочечной структуры в ядрах стало нссомнен-
пп меое того как накапливались измерения ядерных моментов
ЦЬ1М по ’
и свойств спектров ядер-.
§ 8.3. БОЛЕЕ РЕАЛИСТИЧЕСКИЕ
ОДНОЧАСТИЧНЫЕ ПОТЕНЦИАЛЫ
Осцилляторный потенциал и потенциал прямоугольной ямы яв-
ляются двумя чрезвычайно схематическими одночастичными потен-
циалами. В предыдущем разделе мы видели, что ни один из них не
может должным образом воспроизвести магические числа. Магиче-
ские числа могут быть получены при использовании потенциала,
состоящего из потенциала, промежуточного между осцилляторной
и прямоугольной ямами, и спин-орбитального слагаемого. Другой
путь заключается в использовании I-s-члена, который заметно ме-
няется от оболочки к оболочке. Ясно, что оба подхода не очень хоро-
ши. Для практических целей требуется простой феноменологический
потенциал, одночастичные решения которого могут быть получены
явно, и схема уровней которого более или менее воспроизводит маги-
ческие числа.
Как видно из табл. 8.4, различные замкнутые подоболочки уже
дают магические числа. Необходимо еще получить более значитель-
ное энергетическое разделение главных оболочек. Просматривая
табл. 8.4, нетрудно убедиться, что это можно получить, если опу-
стить вниз подоболочки с большим орбитальным угловым моментом /.
Представленная выше интерполяция между осцилляторной и пря-
моугольной ямами фактически дает именно этот эффект. Для боль-
ших I осцилляторныс оболочки слишком высоки по энергии, в то
время как в прямоугольной яме такие оболочки расположены слиш-
ком низко. Это происходит потому, что в результате действия боль-
шого центробежного момента нуклоны с большим I проводят боль-
шую часть своего времени вблизи края прямоугольной ямы, пока-
занной на рис. 8.2. Таким образом, уровень в прямоугольной яме
оказывается лежащим слишком глубоко, а в случае, когда исполь-
зуется потенциал гармонического осциллятора той же глубины,
что и потенциал прямоугольной ямы, притягивающие силы имеют
слишком малую величину. Интерполированный потенциал дает
н ЖнУ,ю глубину уровня при больших расстояниях для таких состоя-
с большим орбитальным угловым моментом.
тат”ИЛЬСС°Н ^31 показал, что можно получить такой же резуль-
> если к осцилляторному потенциалу со спин-орбитальной связью
легкиДп клеРиментатоРы подробно изучают свойства одночастичных уровней
в обляг! 297’ 304] и средних [44, 80, 127, 189, 208, 280], а также ядер
асти 08РЬ [72, 188, 237, 268].
199
добавить член, пропорциональный I2, т. е. использовать следуюши’'
потенциал*:
V(t)=-1-M^ + C1.s+D12. (842)
Здесь константа С — —2а й2 характеризует силу спин-орбитальной
связи, параметр D — степень отклонения осцилляторного потен-
циала от более реалистического потенциала. Для легких ядер £>
' 19в12 2р . 2РЦ2 "'-1^-'' 2pJls lfy/2 1 N=6 i 4S , 3d3/2 1 / ^S1I2 - 297/2 \\ 29 X 'X5/i \ ' 4 y.5/2 \ V ~ №
N=2 1d2s , 1йз/2 <- — 23ц2 195/2 .. ' . / 29s/2 N=5 \ 1i / 3P1!2 — w \\ 2f Sp.3/2 \ iX'2 \ ™
N=1 1Р 1Р1/2 1Pi/2 N=4 3S "" 1Qhii/2 —X—-<= \ 1g / 2d,5/2 l9S/2
N=0 13
15^2
Рис. 8.4. Уровни модели оболочек для сферического ядра, полученные для
чисто осцилляторного потенциала (слева), для осцилляторного потенциала
с учетом 12-члена (в центре) и для потенциала (8.42), в котором учтены
12-член и спин-орбиталыюе взаимодействие.
приближенно равен нулю, в то время как, например, для одно-
частичных состояний в 209РЬ [272]
D= —(0,056 ± 0,043) Мэв/П2.
Для осцилляторного потенциала параметр D всегда отрицателен,
тогда как для прямоугольной ямы он был бы всегда положительным.
* В работе [177] это слагаемое было модифицировано так, что вместо опе-
ратора I2 использовалось выражение (I2 — <UV| I2 |JV>) = (I2 - - -% N 3))>
т. е. отклонение оператора I2 от его среднего значения в /V-оболочке. Такой пун-
дает возможность сохранить центр масс осцилляторных оболочек и обо
тись без подгонки параметров для различных оболочек (см. Приложение /
я цис. 8.4 показаны уровни модели оболочек для потенциала
ридно, что магические числа хорошо воспроизводятся. Слева
(8' уровни в чисто осцилляторном потенциале. Спектр в се-
п°ка получен с учетом расщепления, обусловленного членом,
Ре опциональным I2. Справа показан окончательный спектр,
олучеННЬ™ с Учетом члена с I2 и спин-орбитального взаимодей-
CTB[T работе Роста 13091 подробно изучался реалистический
оболочечный потенциал Вудса-Саксона, который первоначаль-
был введен в качестве оптического потенциала для описания
нуклонного рассеяния. Этот потенциал имеет вид
I7 (г) =-----,
1 + ехр {(г—с)/а}
(8.43)
где с радиус ядра (расстояние, на котором абсолютное значение
потенциала уменьшается до половины его значения в центре). Тол-
щина поверхности характеризуется параметром а. Типичный набор
параметров в потенциале (8.43) таков:
с СоЛ1/3, Vo « 50 Мэв, аш 0,5 ферма, с0 х 1,1 ферма.
§ 8.4. РАСПРЕДЕЛЕНИЕ
НУКЛОНОВ В ЯДРЕ
Рассмотрим пространственное распределение ядерной плот
ности. Известно, что плотность ядра приблизительно постоянна
внутри ядра и довольно резко обрывается на поверхности. Потен-
циал сферического осциллятора дает плотность, которая спадает
к нулю на поверхности ядра
более плавно. Это видно на
рис. 8.5, где показана полная
плотность ядра
А
(8.44)
рассчитанная с использованием
осцилляторных волновых функ-
ций. Хотя таким путем с по-
мощью потенциала гармоничес-
кого осциллятора нельзя описать
Детали наблюдаемой ядерной
плотности, представляет инте-
Рес выяснить, какие значения
онстанты ы0 дают правильное значение радиуса ядра.
Ной УДем измеРять среднее значение кинетической и потенциаль-
энергии для ямы гармонического осциллятора от дна ямы. Тогда
Рис. 8.5. Ядерная плотность для раз-
личных заполненных оболочек, рас-
считанная в модели гармонического
осциллятора.
201
сумма одночастичных энергий всех нуклонов есть
= Л4со2 <i | г21i> = Mw2 А (г2),
4=1
где
<г2> = Л-1 Е<4|г*|»>
4= 1
(8.45)
(8.46)
— средний квадрат радиуса. Для однородного распределения
плотности нуклонов он равен
<''2>=-^-Я2, (8.47)
где
/? = г0Л1/3л 1.2711 /3 ферми.
А
Нетрудно получить приближенное выражение для суммы ^Е, в ос-
4=1
новном состоянии ядра [2631. Рассмотрим ядро с одинаковым чис-
лом протонов и нейтронов и предположим, что все осцилляторные
состояния с главным квантовым числом N No заполнены прото-
нами и нейтронами. Тогда имеем [см. текст, следующий после
формулы (8.20)]
А = 2 2J((V+l)((V+2)
л = о
(8.48)
и, согласно (8.20),
Л’о
= 2 2(^+ 1) (N+2) (N + 3/2). (8.49)
л/=о
Суммирование дает
Л^4(До + 2) + 0«(Лу,
О
(8.50)
где предполагается, что No велико и меньшими степенями No можно
пренебречь. Аналогично
Йю0 Ц- ((Vo + 2)‘-A (No + 2)4 (8.51)
Сохраняя только члены наивысшего порядка по
исключая (No + 2) из (8.50) и (8.51), получаем
£Ег = — (—4/3 л4/3 0,86Йюо А4/3.
1 2 \ 2 ' 0 0
(?V0+ 2) и
(8.52)
202
впяя (8.52) и (8.47) в (8.45), находим расстояние между уров-
^Д^ямы гармонического осциллятора:
Йсоо^41Л“1/3 Мэв.
(8.53)
В заключение этого параграфа отметим, что имеются более север-
ные расчеты распределения заряда ядра (см., например, [124,
в которых использовались более реалистические потенциалы
пели оболочек. Эксперименты по рассеянию нейтронов указывают
маДто что зарядовые радиусы различных подоболочек не зависят
над [190, 191]. Это, по-видимому, приводит к необходимости при-
ять какую-то ступенчатую функцию при описании зависимости
Йш от А вместо слабой зависимости от А в формуле (8.53).
§ 8.5. СПАРИВАНИЕ И ПРЕДЕЛЬНАЯ
ОДНОЧАСТИЧНАЯ МОДЕЛЬ
Модель оболочек предсказывает одночастичные орбиты в ядре.
Однако в эксперименте измеряются состояния всего ядра. Следова-
тельно, необходимо выяснить, при каких обстоятельствах одно-
частичные состояния могут рассматриваться как состояния всего
ядра. В этой связи одним из основных вопросов является вопрос
о спаривании нуклонов в ядре. Экспериментально найдено, что
энергия спаривания 26 двух эквивалентных нуклонов (протонов или
нейтронов, см. § 12.6) приближенно описывается формулой [3741
6= 11,2Л —1/2 Мэв, (8.54)
Рис. 8.6. Распределение плотности ве-
роятности для нуклона в данном маг-
нитном подсостоянии и схематическое
перекрытие этих распределений.
Перекрытие нуклонов в под состояниях т=2
кпТ*1 Или ° очевь мало. Только в случае.
м ™ значеннс1671 у нуклонов одинаково,
жду ними имеет место сильное взаимо-
действие.
тг=±2^±1
Т‘ еА~ДЛя легких ядер 6^3 Мэв, тогда как для тяжелых
220) б -----------
ядер (А
0,75 Мэв. Существование спаривания в ядрах можно
опять, если предположить, что кроме среднего поля модели обо-
н°Чек в ядРе действуют относительно короткодействующие остаточ-
ж е бИЛЫ междУ нуклонами. В этом случае два нуклона одной и той
оболочки всегда будут находиться в таком (двухнуклонном) се-
янии, которое имеет наиболее низкую энергию. Оказывается, что
203
таковым является состояние, в котором спины двух нуклонов, нах
дящихся в одночастичных состояниях | /гл> и | jm'), складывав'
ся в полный угловой момент, равный нулю:
100 > = у, (//01 тт’ 0) | jm> | jm’>.
тт'
(8-55)
То, что это состояние будет иметь наименьшую энергию для корот
недействующих остаточных сил, можно качественно понять очень
просто. На рис. 8.6 показаны распределения плотности для состояний'
\jtri) и |/—т). Кроме того, показаны распределения плотности для
одночастичных состояний с т', отличных как от т, так и от____т
Если взаимодействие является предельно короткодействующим, оче-
видно, что волновые функции двух нуклонов, один из которых на-
ходится в состоянии | jm), а другой в состоянии | / --- т), будут
75/2
S1/2 \f?/2 ^^5^1/299/2^5/297/2 S1/2h11/2 ^3/2 47/2 h9/2 Рз/2р5/2Р112 L13/2 ।
РЦ2 d3/2
0 8 20 28 50 82 126
Рпс. 8.7. Сравнение экспериментальных значений спинов
ядер, имеющих нечетное число нейтронов, с предсказа-
ниями одночастичной модели оболочек:
О — спины, предсказываемые одночастнчной моделью; X — наблюда-
емые значения спинов, не согласующиеся с одночастичной мо-
делью [122].
иметь наибольшее перекрытие. Это означает, что энергия взаимодей-
ствия
ДЕ = <(/, т\, (j, —т).2| V(1, 2) | (/, т)х; (/, — т).2), (8.56)
где V (1, 2) — остаточные двухчастичные силы, намного больше,
чем соответствующая энергия взаимодействия между двумя нукло-
нами, когда один из них находится в состоянии | jm), а другой
в состоянии | jm') с т’ =/= т, —т. Таким образом, отсюда становит-
ся ясным, что спаривание нуклонов существует в состояниях | Т7 >
204
• — т> т. е. когда их угловые моменты складываются в полный
мпмент, равный нулю [248].
М Следовательно, можно заключить, что при заполнении одночас-
нЫх уровней модели оболочек нуклонами происходит попарное
ТИЧывание нуклонов с образованием пар с угловым моментом, равным
се' ю и только последний нечетный нуклон будет иметь спин, от-
Н^чный от нуля. Это значение спина и считается полным спином
лИ а в основном состоянии. Отсюда также следует, что все четно-
четные ядра (т. е. ядра с чет-
ным числом протонов и ней-
тронов) должны иметь в ос-
новном состоянии угловой
момент, равный нулю. Это пра-
вило выполняется всегда, в
действительности, именно оно
п привело к идее о спарива-
нии нуклонов. Попарное свя-
8
6
a
Возбужденное
состояние
Основное
состояние
Нечетные
ядра
зывание нуклонов называет-
ся схемой связи синьорити,
или иногда схемой связи
Майер Йенсена.
На рис. 8.7 представлены
предсказываемые одночастич-
ной моделью значения угло-
вых моментов и четностей для
ядер с нечетным нейтроном.
Внизу указаны также пред-
сказываемые значения I
(четность основного состояния
определяется как (—1)')- Хо-
Основное
состояние
Четные
ядра
Возбужденное
состояние
Рис. 8.8. Схематическая иллюстрация
основного и возбужденного состояний
в нечетных и четных ядрах согласно
предельной одночастичной модели
оболочек.
тя, как видно из рисунка,
модель дает очень хорошее общее согласие с экспериментальными
значениями спинов, все же наблюдается заметное число случаев
расхождений с экспериментом. Более того, многие из этих расхож-
дений имеют систематический характер. Для некоторых ядер, по-
видимому, невыгодно иметь большой спин после того, как запол-
нена оболочка с малым спином. Это особенно заметно для оболо-
чек/1ц/2 и t'13/2, которые начинают заполняться после заполнения
оболочки с j = 1/2, аналогичный эффект наблюдается также
и для оболочек йд/2 и ^7/2. Для объяснения этого эффекта было
постулировано эмпирическое правило, согласно которому энер-
гия связи пары частиц увеличивается с увеличением их значения
/, так что, например, конфигурация (81/2)2йц/2 имеет меньшую
энергию связи, чем sI/2 (йц/2)2.
Другие отклонения от предсказаний одночастичной модели
людаются в ядрах с числом нейтронов между Д/=82 и N =126.
(1 асть ядеР соответствует области редкоземельных элементов
~ 170), в которой, как известно, наблюдаются большие дефор-
205
Рис. 8.9., Спектр протонов при^ угле 25 в реакции 11 'Sm (d, р) 150Sm [212]. Хорошо заметно резкое увели-
чение числа возбужденных состояний при энергии протонов около 15,8 Мэв. Это соответствует энергиям возбуждения
ядра 1MSm выше щели 1,8 Мэв.
sonowodu о ironh
ядер (и большие квадрупольные моменты — см. рис. 1.6).
Ча 111 ольку эти ядра находятся вдали от ядер с замкнутыми оболоч-
П°с' ‘ естественно, что одночастичная модель здесь менее всего
каМ ^на. В самом деле последовательные оболочечные расчеты
надТой области ядер являются наиболее трудоемкими, поскольку
В j должны учитывать взаимодействие большого числа конфигура-
°Hft обусловленное остаточными силами. Этот случай лучше всего
Шисывается моделью оболочек для деформированных ядер и кол-
лективной моделью (см. гл. 9).
На рис. 8.8 показана схема образования возбужденных состояний
нечетно-четных и четно-четных ядрах. Нечетная частица в нечет-
ном ядре может подняться на следующий или более высокий уро-
вень. Но можно возбудить также и частицу из заполненной оболоч-
ки которая может перейти на последнюю частично заполнен-
ною подоболочку или на другую незаполненную подоболочку
(см. рис. 8.8, в).
Для того чтобы четное ядро могло перейти в возбужденное состоя-
ние, необходимо разорвать связанную пару (см. рис. 8.8, д). Это
можно сделать, если энергия возбуждения больше, чем энергия
спаривания (ct 1 Мэв). Имеется также другой способ образования
возбужденного состояния, показанный на рис. 8.8, е, когда вся пара
поднимается на более высокий уровень. Ясно, что для образования
состояний, подобных изображенным на рис. 8.8, д, существует мно-
го других возможностей. Следовательно, в четно-четных ядрах сле-
дует ожидать появление относительно малого числа возбужден-
ных состояний при низких энергиях возбуждения и очень большого
числа состояний при энергиях возбуждения, больших, чем энергия
спаривания 6. Эта закономерность особенно проявляется для тяже-
лых ядер. В качестве типичного примера на рис. 8.9 показаны возбуж-
денные состояния ядра 150Sm, наблюдаемые в реакции (d, р) [212].
Спариватечьная щель отчетливо проявляется при энергии протонов,
равной 15,8 Мэв, что соответствует приблизительно 1,8 Мэв по
энергии возбуждения ядра.
8.5.1. Предсказания квадрупольных моментов
Электрический квадрупольный момент ядра характеризует
отклонение распределения заряда ядра от сферической формы. Рас-
смотрим квадрупольный момент ядра с нечетным числом протонов
и четным числом нейтронов N в схеме связи синьорити. Среднее
значение оператора
<?20=(4яУ/2 1 r"Y^k) (8.57)
\ 5 ' л=I
Должно быть получено для состояния Z протонов, которое представ'
новцС°фОВ антиснмметРизованное произведение одночастичных вол"
207
Ф>Шт = Rnl (Г) V / I _L j | pn/n'j У/ц X2/,
il rr\ '
(8.58)
u, <л
Предположим для простоты, что все Z протонов находятся ца
одном и том же /-уровне, т. е. имеют одинаковые квантовые числа
п, I, j. Магнитные квантовые числа т пробегают значения
т1, 1П2, •••> mZ-
Ограничение одной / оболочкой не приводит к потере общности
Мы покажем, что заполненная /-оболочка имеет квадрупольный мо-
мент, равный нулю, и, следовательно, можно всегда ограничиться
последней неполностью заполненной оболочкой. Легко показать
что среднее значение любого оцночастичного оператора |каковым]
является оператор (8.57)1
О = 2 о (rh)
k
(8.59)
по антисимметризованному состоянию
4z (т^ т2, ..., mz) = (Z!) 1 /2 2 (— 1 (1) 41 т2 (2)... (Z)
(8.60)
выражается через сумму одночастичных средних по состояниям
Символ Р обозначает перестановку переменных, описываю-
щих частицы и обозначенных 1, 2, ..., Z. Докажем, что
<^z (ггц, т2, ..., mz) | О | (т 1, т2, ..., mz))
(8.61)
где сумма пробегает по всем v. Это соотношение наиболее легко до-
казывается, если записать волновую функцию (8.60) в виде определи-
теля. Тогда соотношение (8.61) принимает вид
208
где
Фп,г(»
Фт,(2) — Ф^-1)
Фт^-1)
4>np) — iP^v-1)
Фп,,(^)-- <J)m,(z)
Фтг(^’" Ф^
ф„ ,(Z)
(Pmjv+I) •" Фтг^
(8.63)
ч
является минором, полученным из исходного определителя вычер-
киванием /Нц-й строки и v-ro столбца. Поскольку AmV не содержит
аргументы v в одиочастичных волновых функциях, имеем
• ••> ^2)101^(0?!, ..., mz))
7?^ S <4,mJv)|o(v)|i|>n (v))</m vM v>. (8.64)
Z I V= 1 Ц. p,'
В силу ортогональности одночастичных функций, содержащихся
в Лт^, получаем
A^vlA^-v) (Z-l)!6ll(l-, (8-65)
следовательно, правая часть соотношения (8.64) принимает вид
7?Т ^Ч w 10 (v) 1 ^Ч ^Z~~ 1)!
(8.66)
Таким образом, соотношение (8.61) доказано.
Теперь необходимо вычислить квадрупольный момент согласно
•8.61). Используя волновые функции (8.58) и выражения для коэф-
фициентов Клебша— Гор дана и коэффициентов Рака, которые можно
иаити в литературе (например, 1306]), нетрудно найти
Q'/! C/m|(L4yS^20|j>H >. 'm- <И1>- (8.67)
В частном случае m j получается старый результат (1.5). Сумма
2 2 Q'j' (8.68)
209
дает квадрупольный момент заполненной оболочки. Учитывая соот
ношение
2 ^2=-!-/(/+1)(2/+1), (8б9
т=‘/2 о 1
легко получить
1 07 = 0. (8.70)
Таким образом, мы доказали высказанное ранее утверждение о том
что квадрупольный момент заполненной оболочки равен нулю'
Это, в частности, означает, что магические ядра (имеющие пол-
ностью заполненные оболочки) сферически симметричны.
Волновая функция (8.60) антисимметрична по всем Z протонам.
Однако, вообще говоря, она не имеет определенного углового мо-
мента, за исключением случая заполненной оболочки, когда пол-
ный угловой момент равен нулю, и случая Z = 1 (только один
протон в оболочке), когда полный угловой момент есть j. Следо-
вательно, мы должны определить соответствующие линейные ком-
бинации функций ..., тг), угловой момент которых будет
хорошим квантовым числом. В схеме связи сеньорита (схеме связи
Майер — Йенсена) это осуществляется путем попарного связы-
вания моментов двух протонов в спин, равный нулю, так что спин
ядра с нечетным протоном определяется спином последнего неспа-
ренного протона [311].
Для лучшего понимания указанной процедуры рассмотрим сна-
чала две частицы в /-оболочке, суммарный момент которых равен
нулю. Их волновая функция есть
Ч'Шо == 2 (7/01 т-т 0)ф;т(1) ф;_т(2). (8.71)
т
Верхний индекс (2) обозначает число частиц. Эта волновая функ-
ция еще не антисимметрична. Соответствующая антисимметризо-
ванная волновая функция имеет вид
1 —\ '
= ( — V2 ) У (//0 | т—т0)¥г(т, —т), (8.72)
\ 2 / т = -— j
где использована функция (8.60). Коэффициент Клебша—Гордана
равен
(// 01 tn—т 0) = -tr1)' , (8 73)
У2/ + 1
и, следовательно, не учитывая общий множитель (—1)', можно
записать нормированную волновую функцию (8.71) следующим
210
образом:
Ч'И’о 1 тЛг (-l)«Va(/n, -m). (8.74)
I 2/ + 1 m = y2
житель i 2/(2/ + 1), определяемый коэффициентом вектор-
' ° сложения, можно интерпретировать как нормировочный ко-
^шшиснт, тогда как множитель (—I)"1 ответствен за связывание
в спин, равный нулю.
Рассмотрим теперь случаи трех протонов, два из которых имеют
ымарный момент нуль, а для третьего т = j. Полная волновая
жуНКция имеет тогда полный угловой момент j и проекцию полного
спина на ось z, также равную /:
w<3) _
* H -
2 (-1)-T3(m, —т, j). (8.75)
— 1 m = '/,
Каждое слагаемое в этой сумме нормировано и ортогонально ко
всем другим. Отметим также изменение в нормировочной констан-
те. Это обусловлено тем, что, так как '1% (mj, m2, m3) полностью
антисимметрична, члены с т = ± / тождественно равны нулю,
а все остальные слагаемые входят с одинаковым весом. Квадру-
польный момент ядра в этом случае дается формулой
Q(3) S <^з(т. — tn, /)|<?20|'К3рп, (8.76)
2/ —1
Аргумент в Q (3) указывает на число частиц. Перекрестные члены
исчезают, поскольку одночастичный оператор Q20 может одно-
временно изменить состояние только одного протона, тогда как
в волновых функциях Y3 (т, —т, j) в выражении (8.75) всегда
меняются значения т двух протонов. Для вычисления Q (3) ис-
пользуем соотношение (8.61):
<Уз(т, -т, /)|Q2o|V8(/7i, -т, /)>=$+2<?7- (8.77)
Подставляя (8.77) в (8.76), получаем
7-1
<2(3)=0+-^- = (8.78)
т='/г ' 1 )
где использовано соотношение
(8-79)
m=%
Которое следует из (8.70).
211
Рассмотрим теперь более сложный случай, а именно Z = 5*
Две пары протонов теперь имеют угловой момент, равный нулю
а нечетная частица снова находится в состоянии с т = j. дНт '
симметризованная волновая функция имеет вид
ЧУ5) ----------- V % (_])(«+«') х
"|/(2/—1) (2/—3) т^/г = % 7
х ¥5(от, — т, т', —т, j). (8.80)
Нормировочный множитель обусловлен тем, что все состояния
входят с равным весом, за исключением состояний с т — j, т' == ;
и т = ±т', которые тождественно равны нулю в силу принципа
Паули. Квадрупольный момент в этом состоянии выражается
формулой
(2(5) = —-------------X
(2/-1)(2/-3)
/-)
X S <^b(m,—m,m',—m',j)\Q20\yVb(m,—m,m',—m',i\\.
т, т' — '/2 '
(8.81)
Индексы т и т’ изменяются от 1/2 до / — 1. Штрих означает, что
в сумму не входят члены с т = т'. Используя (8.61) и (8.67), на-
ходим
<^ъ(т, —tn, tn’, —tn', j) I Q.2014rs(m, —m, tn', — m', j)> =
-2Qf + 2Qr’ + Qj:- (8.82)
Подставим это в (8.81):
Q(5)-Q}+ ,„- в , Г (<?;+«') =
(Д—l)(^] — 6) т.т'=%
-Cf+ „ 3 , W+«F)-2 s' or] <8 83>
(штрих в последней сумме по т, т' отсутствует). Пользуясь соот-
ношением (8.79), получаем окончательно
(2(5)= Г1-_1_|(2':. (8.84)
L ч — * J
Полученные результаты теперь легко обобщить. Если имеются
Z = 2v + 1 протонов, то вместо соотношения (8 83) можно запи-
сать
2v+i
Q(Z)-Q ,
' ' (2/-1Д2/-3) ... (2/-2v+l)
* Для четных Z волновые функции получаются весьма просто.
212
i— I
x У 1<27' + <2",2-|-... + Q7Z), (8-85a>
m2, . , m^=y2 }
m- принимают значения 1/2, ..., (/'— 1). Штрих в сумме по-
ГДзывает, что в ней не содержится двух равных значений m;. С по-
КЗщью соотношения (8.79) можно снова легко показать, что
Q(Z) Г1-2^УУ|$, Z=l, 3, 5.. 2/. (8.856)
L 2/ 1 J
Мы получили формулу (1.7),
Из нее следует:
Q < 0 для
Q = 0 для
Q > 0 для
которая уже обсуждалась в § 1.1.
1^Z</——;
2
7 ,1
Z = I Н-;
2
j + s/2^Z^2j.
(8.86)
Таким образом, одночастичная модель предсказывает, что
квадрупольные моменты изменяют знак в середине любой протон-
ной оболочки и при любом магическом числе протонов (запол-
ненная оболочка). Квадрупольный момент ядра, в котором не хва-
тает лишь одного нуклона в заполненной оболочке (одна протон-
ная дырка), можно легко получить, если положить Z = 2/:
Q(Z = 2/) = -Q’f. (8.87)
Подробное обсуждение экспериментальной информации о квад-
рупольных моментах см. в § 1.1. Из рис. 1.6, в частности, отчет-
ливо видно, что для магических чисел 50 и 82 квадрупольные мо-
менты меняют знак с положительного на отрицательный. Эту тен-
денцию можно также проследить и для других магических чисел.
Однако существуют и значительные отклонения от предсказаний
одночастичной модели для квадрупольных моментов. Это связано
с пересечением различных протонных и нейтронных подоболочек
в ядре редкоземельных элементов (150 А < 190) и для актинои-
дов (Д ^ 220). Как уже обсуждалось в § 1.1, большие расхожде-
ния с предсказаниями одночастичной модели показывают, что для
указанных ядер сферическая модель оболочек несправедлива, по-
скольку эти ядра являются деформированными. Модель оболочек
Для деформированных ядер будет рассмотрена в гл. 9.
8.5.2. Предсказания магнитных моментов
Магнитный момент р. определяется как среднее по подсостоя-
Нию с М = J От оператора
МП]==р, = роу1р4-^p,nQn+(8-88)
р п р
213
где [лр = 2,793 (eh/2Mc) и р„ . =— 1,913(е/?/2Л4с). Единица ц0
= eTillMc называется ядерным магнетоном. Суммирование в пеп-
вом слагаемом выполняется только по угловым моментам прото-
нов 1Р, так как нейтроны не заряжены и поэтому не дают вклада
в орбитальные магнитные моменты. Спиновые операторы Паули
а имеют собственные значения ±1. Для единообразного описания
протонов и нейтронов в операторе магнитного момента соотноше-
ние (8.88) можно переписать в виде
МП] = р, = popgnT Р-СПИН =
А
= Ро 2 (gft ’ lft + g*s) sft), (8.89)
где введены гиромагнитные отношения, или g-факторы:
&=!-, gkZ, = O;
Sp ’ = 2Рр/р«; gn ’ = 2pn/p0; р0 = еЛ/2Л1с. (8.90)
Оператор р является векторным оператором. Средние значе-
ния его проекций на оси х и у равны нулю. Следовательно, маг-
нитный момент определяется выражением
p = <//n = /|pz|/m = />. (8.91)
Для вычисления этого матричного элемента воспользуемся об-
щей теоремой о том, что для изолированной системы со спином /
и проекцией на ось а, равной т, среднее значение векторного опе-
ратора А можно представить в виде
</т| А | jm) = </m| j | /т> , (8.92)
< jm | j21 jm>
где j = 1 + s — оператор полного углового момента. Эта теорема
называется теоремой о проекциях (см. [3061 с. 94) и утверждает,
что вклад в матричный элемент дает только компонента вектора
А, параллельная вектору j. Компонента А, перпендикулярная
j, при усреднении дает нуль (рис. 8.10). Взяв в (8.92) проекцию
на ось z для т = j, получаем
(jm = /\А21 jm = j> = дтууу <jm = j | A j | jm = />. (8.93)
Заменяя А на р, находим
р=</т==/|рг|/т==/> =
= =/1 н i I itn i>-
(8.94)
214
ьку в простой одночастичной модели оболочек вклад дает
Поскол п^следняя нечетная частица, сумма в выражении (8.89)
Удится ЛИШЬ к одному члену. Поэтому
n=^(^i+^>s), I (8 95)
р j = 9o(g(Z) ' +g(s) s)-(f+s). )
Используя тождества
2(j-l) j24-l2-s2, |
2 (j • s) j2-l2+s2, [
получаем из (8.94)
yg(s)j Ио ДЛЯ / /+у,
р= -L^(/ + 3/2)g('>-yg's)>)Mo Для /=/~у-
(8.96)
(8.97)
Рис. 8.10. Компоненты вектор-
ного оператора А, перпендику-
лярные полному угловому мо-
менту j системы, при усредне-
нии дают пуль.
Эти значения магнитных моментов называются значениями (преде-
лом) Шмидта, а кривые, описывающие их поведение в зависимости
от j, — линиями Шмидта. Шмидт [312] получил эти соотношения,
использовав одночастичную модель, задолго до открытия модели
оболочек.
На рис. 8.11 и 8.12 показаны экспериментальные значения маг-
нитных моментов в зависимости от / для нечетных ядер*. Сплош-
ные кривые — линии Шмидта, определенные, согласно соотношениям
(8.97). Отметим некоторые общие особенности диаграмм Шмидта:
1- Моменты большинства ядер отклоняются от линий Шмидта
на величину, лежащую в пределах от р0/2 до Зр0/2.
2. Большинство значений магнитных моментов заключено меж-
ду линиями Шмидта. Только магнитные моменты легких ядер 3Н,
Не, 13С, 15N являются исключением из этого правила.
3. Если провести кривые, которые дают средние отклонения
от линий Шмидта, то полученные линии будут приблизительно
параллельны линиям Шмидта. Они показаны штриховыми линиями
в верхней части рис. 8.11.
Описание экспериментальных методов измерения магнитных моментов
Довольн° полную библиографию см. в обзорах Боденштедта [55, 56] и Грод-
инса [174].
215
Рис. 8.11. Экспериментальные значения магнитных моментов [55 122 174] *
диаграммы Шмидта для ядер с нечетным числом нейтронов. Пунктирные ли-
нии на верхних рисунках — линии Шмидта, в которых использованы магнп
ные моменты «голых» нуклонов.
4 Средние отклонения для ядер с нечетным числом протонов
скотъко больше (примерно на 20%), чем для ядер с нечетным
Числом нейтронов.
5 Лишь очень немногие ядра имеют магнитные моменты, ко-
’ отклоняются от линий Шмидта меньше чем на 0,2 р0. Этими
ядрами (кроме А = 1 и А = 3) являются 17О, 39К, 41К и все ядра
р,/2-обОЛОЧКИ.
1/2 3/2 5/2 7/2 9/2 j
Рис 8.12. Экспериментальные значения магнитных моментов и диа-
граммы Шмидта для ядер с нечетным числом протонов.
217
Все это ясно указывает на хорошую качественную корреляцию
между предсказаниями одночастичной модели и наблюдаемым!
моментами, а также и на существование значительных отклонений
от линии Шмидта. Можно указать несколько эффектов, которые
приводят к изменениям в нужном направлении и частично объяс-
няют наблюдаемые расхождения. Например, некоторыми авторами
(45, 106, 2521 был предложен другой выбор значений р„ и рр По
сравнению с их значениями для свободных нуклонов в формуле
(8.88). «Голые» нуклоны, т. е. нуклоны без мезонной «шубы», долж-
ны иметь gp = 2 для протона и g^s) = 0 для нейтрона. Отклоне-
ние g-факторов свободных нуклонов (8.90) от этих значений обя-
зано существованию облака мезонов, окружающих «голые» ну-
клоны. Аналогично следует ожидать, что, когда нуклоны собраны
вместе в ядре, сильные ядерные силы, обусловленные взаимодей-
ствием с мезонным полем и действием принципа Паули, приведут
к изменению виртуальных мезонных токов и, следовательно, к
изменению магнитных моментов. Этот эффект называют эффектом
подавления магнитных моментов. Если мезонное облако имеет
большие размеры для нуклона внутри ядра, следует ожидать,
что наблюдаемые значения моментов лежат между линиями Шмид-
та и аналогичными линиями, полученными для магнитных момен-
тов «голых» нуклонов. Последние величины показаны пунктир-
ными линиями в верхней части рис. 8.11. Для протонов эти линии
весьма близки, а для нейтронов они даже совпадают. Таким обра-
зом, не имеется, по-видимому, хорошего объяснения для обсуж-
даемого эффекта*.
Возможно, что наиболее реалистическим и разумным способом
объяснения указанного расхождения одночастичной модели с экс-
периментом является предположение, что коллективное движение
нуклонов может оказать влияние на одночастичное движение и
таким образом привести к более значительному отклонению от
линий Шмидта. Предположим, что некоторая часть углового момен-
та обусловлена коллективным движением других нуклонов. По-
скольку в магнитный момент дают вклад только протоны, то обыч-
ный g-фактор коллективного движения относительно мал — поряд-
ка ZIA. Поэтому учет коллективного движения мог бы до некоторой
степени объяснить расхождение с экспериментом. Положение здесь
не является еще полностью понятным, но совершенно очевидно,
что одной из важнейших причин этого расхождения является пе-
реупрощение, связанное с использованием одночастичных волно-
вых функций.
Мы видим, что коллективные эффекты могут быть важны для
объяснения ядерных магнитных моментов. С другой стороны, су-
* В работе [24] был рассмотрен еще один способ описания эффекта псдав_
ления — учет смешивания возбужденного состояния нуклона (N*) с его основ
ными состояниями (N).
218
тву1от также доказательства того, что нечетная частица в
шеС при этом играет важную роль. В периодической таблице
*ДРе 0 около 12 ядер с нечетным Z, которые имеют по нескольку
ИЗВтопов. Эти изотопы обладают одинаковым' спином и отличают-
И3°лруг от друга на четное число нейтронов. Магнитные моменты
ядер почти равны между собой. Исключение из этого пра-
Типа составляют 151Еи и 163Eu, 81Rb и 87Rb, 69Ga и nGa. Имеются
в ‘ е трИ случая двух изотопов с нечетным числом нейтронов
= 65, 85 и 117), в которых измерены магнитные моменты.
Рис. 8.13. Величина (щ—ц)/(щ—цс) как
функция N или Z для ядер с нечетным
N и нечетным Z [249].
Магнитные моменты этих изо-
топов также почти одина-
ковы. Следовательно, можно
заключить, что для ядер с
нечетным Z четное число ней-
тронов оказывает незначи-
тельное влияние на магнитный
момент. Аналогично и для
ядер с нечетным N четное чис-
ло ротонов также мало вли-
яет на магнитный момент.
Эти результаты приведены
на рис. 8.13 для ядер с Z,
N < 50, где отложена без-
размерная величина (p.s —
— p)/(ps—Цо) как функция Z
или N в зависимости от того,
какое из них нечетно. Здесь
ц — наблюдаемый магнитный
момент, ps — его шмидтовское
значение. Величина ц8 — ц
делится на ps — цс, где
Цс — момент Дирака (цо =1
для протона и Цо = 0 для
нейтрона) лишь для того, чтобы получить безразмерную величину.
Видно, что две кривые — одна для ядер с нечетным А, другая
для ядер с нечетным Z — близки друг другу во всей области N,
Z<50. Этот факт является весьма удивительным, поскольку срав-
ниваются ядра с совершенно различными массами. Например, при
значении Z, N — 25 двумя сравниваемыми ядрами являются 47Ti
(Z = 22, N — 25) и б5Мп (Z = 25, N = 30). Оба ядра имеют оди-
наковый спин, равный 5/2, так как спин всегда определяется чис-
лом нечетных частиц. Этот пример наглядно показывает важность
учета конфигурации четной частицы для вычисления магнитных
моментов, что и учитывается в модели оболочек.
Наконец, следует указать на небольшую поправку к маг-
нитным моментам, возникающую благодаря наличию спин-орби-
тальных сил [206]. Любые силы, зависящие от скорости, например
спин-орбитальные силы
219
f(r)(s-l) A 'f(r)(s-[r Pi), (8.98)
дают вклад в эффективный магнитный момент заряженной частицы
Для незаряженных частиц этого эффекта нет.
Рассмотрим этот вопрос более подробно. Гамильтониан взаи-
модействия заряженной частицы с электромагнитным полем, опи-
сываемым векторным потенциалом А (г), получается с помощью
замены
р->р—^-А(г). (8.99)
Таким путем обеспечивается выполнение требования калибровоч-
ной инвариантности. Эта замена должна выполняться везде, где
в гамильтониан входит величина р, т. е. не только в кинетической,
но также и в потенциальной энергии, если она зависит от р. Под-
ставляя (8.99) в (8.98), получаем дополнительную энергию взаи-
модействия с электромагнитным полем:
— 4~f (r)s-[rX А]. (8.100)
Ле
Обычно при измерении магнитных моментов используется по-
стоянное магнитное поле Н. Векторный потенциал такого маг-
нитного поля есть А = 4 [И Хг]. Тогда энергия взаимодействия
(8.100) может быть записана в виде —р • Н, где
р, — 4-f(r)[—ras + (r-s)rl. (8.101)
2Лс
Легко видеть, что поправка к одночастичному магнитному момен-
ту равна
А для / = /±±. (8.102)
ti2/M 2j-h2 2Мс 2
Здесь <Zr2f (r)>ni — среднее значение величины r2f (г) по одно-
частичному состоянию | п, 1>:
^f{r}ynl=^f(r)Rh(r)dr.
Это выражение можно легко оценить, в результате чего имеем
£~_L.?Z+L.A для ; = Z±_L. (8.103)
4 2/ + 2 2Мс 1 2
§ 8.6. ЭКСПЕРИМЕНТАЛЬНОЕ ДОКАЗАТЕЛЬСТВО
СУЩЕСТВОВАНИЯ СИЛЬНОЙ СПИН-ОРБИТАЛЬНОЙ СВЯЗИ
Мы видели, что, для того чтобы объяснить магические числа и,
следовательно, получить правильную одночастичную схему уров-
ней, в потенциал модели оболочек необходимо ввести сильное спин-
220
аПЬное взаимодействие. В ранний период развития модели
очек это было сделано в виде гипотезы ad hoc. Однако в на-
°^оЛШее время можно прямым экспериментом доказать, что в ко-
СТ°ной ядерной материи существуют спин-орбитальные силы. Та-
НеЧ1 образом, наличие спин-орбитальных сил должно рассматри-
Каться как теоретическое предсказание одного из свойств ядерной
МаТДва ядра БНе и 3Li очень полезны для экспериментальной про-
пки существования спин-орбитальной связи. Предполагается,
то пятый нуклон связан со сферически симметричным остовом,
представляющим собой а-частицу. Нуклоны, входящие в ее состав,
в основном создают потенциал модели оболочек.
а-Частица является дважды магическим ядром, нуклоны ко-
торого находятся на s-оболочке (N = 2, Z = 2), поэтому нечет-
ный пятый нуклон находится в соседней р-оболочке в очень слабо
связанном состоянии. Фактически в этом случае нечетный нуклон
не связан вообще, поскольку вНе и BLi нестабильны. Эти ядра мо-
гут проявляться только как квазистабильные ядра (резонансы)
в экспериментах по рассеянию нейтронов или протонов на 4Не.
Действительно, в соответствующих поперечных сечениях имеются
заметные резонансы при 0,95 Мэв (вНе) и 1,80 Мэв (6Li) (рис. 8.14).
С помощью фазового анализа можно показать [15], что этот резо-
нанс соответствует оболочке р3/2 и что примерно на 3—5 Мэе выше
находится второй резонанс, обусловленный оболочкой р1/2. Этот
второй резонанс проявляется как плоский резонанс в реакциях
6Li (n, d) вНе и 6Li (у, п) 3Li. Появление такого дублета уровней
Рз/s и р1/2 с расщеплением в несколько мегаэлектронвольт ука-
зывает на наличие сильных спин-орбитальных сил, что согласуется
с предсказаниями модели оболочек для основного и первого воз-
бужденного состояний ядер BLi и 3Не (см. рис. 8.3).
Еще более убедительное доказательство существования спин-
орбитальных сил в ядрах было получено в экспериментах Хен-
синкфельда и Фрайера [182]. Авторы использовали пучок неполя-
ризованных протонов с энергией 1,8 Мэв, проходящий через щель
в камеру, наполненную газообразным 4Не (рис. 8.15). Протон, рас-
сеянный в точке а, имеет угловой момент 1 =-- [г X р|, который перпен-
дикулярен плоскости рисунка. Поскольку рассеяние происходит
при энергии 1,8 Мэв, то из рис. 8.14 нетрудно понять, что рас-
сеяние совершается преимущественно с возбуждением уровня р3/2-
Е этом случае векторы 1 и s параллельны, поскольку j = I + х/2 =
~ 3/г- Поэтому вектор s также перпендикулярен к плоскости ри-
сУнка, и так как вектор 1 направлен от плоскости рисунка, то и s
направлен так же. После того как рассеянные протоны проходят
вторую щель, происходит рассеяние частично поляризованных
Ротонов на 4Ые. Так же, как и в первом акте рассеяния, опре-
деляем величину 1 и находим, что в детекторе А должно регистри-
роваться больше протонов с s, параллельным 1, тогда как в детек-
221
торе В должно регистрироваться больше протонов с s, антипа
лельпым 1. Это справедливо, если предположить, что во время Э*'1'
рого акта рассеяния направление вектора s не меняется. Поско
речь идет об упругом рассеянии, второй акт рассеяния также
исходит при энергии 1,8 Л4эе, т. е. в основном с s, параллельным^
Следовательно, в детекторе А должно быть зарегистрировано бол '
ше протонов, чем в детекторе В. В опыте было найдено, что э!”
отношение равно 2:1. '
исходит при энергии 1,8 Мэв, т. е. в основном с s, параллельным f
Следовательно в пвтрктлпр А nnnwun Лиги оапошк™™________ _ ' '•
в детекторе В. В опыте было найдено, что^д
Рис. 8.14. Резонансы в ядерных си-
стемах а+п(БНе) и a+p(sLi) [16].
Рис. 8.15. Схема эксперимента по двой-
ному рассеянию, подтверждающего суще-
ствование спин-орбитальных сил в яд-
рах [249].
Аналогичные эксперименты по двойному рассеянию были так-
же выполнены при большой энергии (выше 100 Мэв) и на тяжелых
ядрах. Ферми [137] показал, что спин-орбитальное взаимодействие,
наблюдаемое в этих экспериментах, имеет тот же знак и ту же ве-
личину, что и взаимодействие, используемое в модели оболочек.
В экспериментах по рассеянию нейтрона на протоне и протона
на нейтроне при энергиях между 50 и 150 Мэв также проявляются
спин-орбитальные силы двухнуклонного взаимодействия [335,
3361. Как мы увидим в следующем разделе, это согласуется с дан-
ными о взаимодействии частицы (нуклона) со спином 1/2 с другими
полями.
§ 8.7. ДВИЖЕНИЕ ЧАСТИЦЫ СО СПИНОМ 1 I ВО ВНЕШНЕМ
ПОЛЕ; РЕЛЯТИВИСТСКИЙ ВКЛАД В СПИН-ОРБИТАЛЬНОЕ
ВЗАИМОДЕЙСТВИЕ
В этом разделе мы более подробно рассмотрим спин-орбиталь-
ные силы, которые появляются для частицы со спином 1/2, движу~
щейся во внешнем поле. Так как нуклоны имеют спин V2. они под
чиняются уравнению Дирака
(8.104)
dt
222
где
(8.105)
fl =Hd—e[a-A (г) — Л0(г)],
//« = c(ap) + mc2p.
Здесь fld — гамильтониан Дирака для свободных частиц, а и
а — обычные матрицы Дирака. В гамильтониан Н входит взаимо-
действие частиц Дирака с внешним электромагнитным полем,
которое задается векторным потенциалом А и кулоновским потен-
циалом (г); е — заряд частиц Дирака, равный нулю для нейт-
рона; P — вектор импульса.
р Сведение уравнения (8.104) к уравнению Шредингера в нере-
лятивистском пределе является хорошо известной процедурой
(см., например, [102]), при этом спин-орбитальная связь возникает
автоматически. Взаимодействие в этом случае характеризуется
электрическим зарядом е в потенциале. Однако известно, что эле-
ментарные частицы могут взаимодействовать так, что гамильто-
ниан взаимодействия может не зависеть от электрического заряда.
Наиболее простым примером в данном случае являются силы между
нуклонами, обусловленные взаимодействием нуклонов с мезонным
полем. В этой связи можно упомянуть также и о слабом взаимо-
действии нуклонов с электронным и нейтринным полями, которое
изменяет свойства нуклонов в ядрах.
Таким образом, необходимо рассмотреть общий случай движе-
ния частицы со спином 1/2 в произвольном внешнем поле. Наи-
более общее уравнение имеет вид
[' 2тиРм + тсН= — ip.
1 Ц J С а
(8.106)
Здесь уц—матрицы, которые выражаются через матрицы а и 0:
/0 — с \
у — i Р« = i , у4 = ₽, (8.107)
\о 0 J
где a—матрицы Паули и
(I — единичная матрица 2 X 2). Величины Qa в уравнении (8.106)
являются операторами, характеризующими различные типы взаи-
модействия частицы с внешними полями. При этом возможны
следующие случаи:
1- Взаимодействие с внешним скалярным полем. Соответствую-
щий оператор Ьп равен
Qs = V(r). (8.Ю8)
2. Взаимодействие с внешним векторным полем описывается
оператором
Qv • ТцВц — (В, i Во),
в
(8.109)
223
где Вц — 4-вектор. В качестве примера этого типа взаимодейств
рассмотрим случай электромагнитного поля в формуле' (8.1оч\Я
Это поле определяется потенциалом '•
(A, 1Д). (8.110)
Сравнивая (8.110) и (8.105), находим, что
— еАр,. (8.1Ц)
3. Взаимодействие с тензорным полем описывается выражением
Qt _ Th Tv Сцу. (8.112i
fl, V '
Примером такого взаимодействия является взаимодействие недн-
раковского магнитного момента с электромагнитным полем
Av — дА^/дх,,—дАу,/дхц. (8.113)
В этом случае
Cmv ygPoA-p, (8.114;
где ро = еЛ/2/nc; т — масса электрона; g—константа связи.
Для электронов g = 0, для нуклонов g 0.
Рассмотрим теперь случай, когда частицы взаимодействуют
одновременно со скалярным и векторным полями. Подставляя
(8.108) и (8.110) в (8.106) и выделяя временные производные в урав-
нении (8.106), получаем
*^'л7==[са' ( Р ~ ~в(п) +₽ (me2—V(r)) + B0(r)| ф. (8.115)
at [ \ с
Следующий шаг заключается в том, чтобы получить нерелятн-
вистский предел этого уравнения. Это можно сделать, используя
преобразование Фолди — Вутхайзена*. Однако мы воспользуемся
более простым методом. Возьмем ф в виде
ф(г,/) ф(г)ехр[ — i (EltAt]. (8.116)
и запишем четырехкомпонентный спинор в следующем виде
Цг)., (’<'>). (8.117)
где <р (г) и х (г) — двухкомпонентные спиноры, т. е. векторы в виде
столбца из двух компонент. Выберем также для простоты
В(г)х0, (8.П8)
* В т. 2 этот метод подробно обсуждается при рассмотрении теории взя
имодействия ядер со слабым и электромагнитным полями.
оставим в уравнении (8.115) V' (г) и Ви (г). Подстановка выра-
жений (8.П6) и (8.117) в (8.115) дает
|Е- В0(г)—(тс2— V(r))]q (г) - с(о р)х(г); (8.119а)
[Е Вп (г) -) (тс2 -1(г))] х (г) о (о р)<| (г). (8.1196)
уравнения являются точными. Рассмотрим движение частицы
со спином 1/2 во внешних полях Вп (г) и V (г), ограничиваясь чле-
нами порядка иЧс2. Полагая Е = Е' + тс2, т. е. выделяя энергию
массы покоя из полной энергии, находим
[£' — (г) + V (г)] <р (г) = с (<г р) х (г),
f2mc2 + E' — Во (г)-- Р(г)1х(г) - с(о р)ф (г).
(8.120а)
(8.1206)
Из последнего уравнения получим х (г) с точностью до первого по-
рядка по величине (Е' — Во (г) — V (г))/2тс2
х(г) = Г1-^-д».-(-Ч~1-г) (8121>
L 2тс3 2тс
и подставим это выражение в уравнение (8.120а). Тогда получаем
уравнение, содержащее только двухкомпонентную функцию <р (г):
(Е'—В0(г) + И(г))ч (г)
- У ( 1 ~ — (а р) q (г). (8.122)
2т \ 2тс2
Воспользуемся теперь соотношениями
(о-АДаВ) (A B)-j-i (о(А В]) (8.123)
и
(o-P)f (г) (ар) -7(г)(а-р) (О-Р)—iA(o-v/)(a.p) =
=-f(r)P2—iA[(v/P)4-iolv/Xp]l. (8.124)
Тогда уравнение (8.122) можно записать в виде
Я'<р(г) E'q(r), (8.125)
где
А(а-|уД„ ,р]) A(a fvlz(r)XP])
4т‘- с2 4т2 с2
ГТГ^'(г)-Р). (8.126)
с Чтобы построить последовательную теорию, справедливую
точностью до ц2/с2, необходимо получить соответствующую нор-
8 ч
За«- 121а 225
мировку для величины <р. В теории Дирака плотность заряда
р = е(<р+<р + х+Х) (8.127)
нормируется на единицу
$pdr=l. (8 Л28)
Оставляя в выражении (8.121) для у, члены нижайшего порядка
т. е. 1
а р
<8.129)
и пользуясь соотношением (8.123), получаем
р «р+ (1 + р2/4т2с2) ср. (8.130)
Таким образом, имеем нормировочный интеграл
$pdr = §ф+(1 + р-/4пг2с2)ф dr = 1. (8.131)
Это правильная нормировка для ф (г). С другой стороны, известна
нормировка для волновой функции
§ip+ipdr=l. (8.132)
Поэтому вместо ф удобно использовать другую волновую функцию
Ф = Й, (8.133)
так что
§ ф+ ф tlr — § ф+ g+ gcp dr = 1. (8.134)
Отметим, что величина g может быть оператором. Сравнивая
(8.134) и (8.131), находим
g — [1 + р2/4т2с2]‘4 « 1 -|- р2/8гп2с2. (8-135)
Чтобы найти гамильтониан для функции ф, умножим уравне-
ние (8.125) слева на g, тогда
gH'g~* g<P = E'gq> (8.136)
или
Дф = £'ф, (8.137)
где Н с точностью до членов v2lc2 дается выражением
И = I 1 + Д' I 1-----------=
\ 8т-с2 I \ 8т2с2 '
226
+ Во (г) - И (г) - 1Ё'~ Ёп{г)][ v^- +
2т 2тс2
. А(с-[УД0 (г) Р|) , А(а-[УУ(г) <Р])
4т2с2
£2
z4rVV(r).
8m2 с-
4m2c2
/,2
Лт^вс(г) +
8/?z2 с2
(8.138)
Здесь использованы соотношения
p'V(r) — V (г) р2 = —A2V2V(r) —2 i h : (Vl (r)-p)
- g0 (r) + V (О p2 рг _ - Bq (r)F Vj(£) (8 J39)
\ 2mc2 i ca
Первые три слагаемых в выражении (8.138) дают нерелятивист-
ский гамильтониан. Остальные слагаемые являются релятивист-
скими поправками порядка v2/c2. Их можно записать ч виде
U = U. + U. + U,. (8.140)
Первый член
t/i= -^V2B0(r) +-^VW) (8.141)
8m2c3 8m-c2
обусловлен кулоновским потенциалом и впервые был введен Дар-
виным [85]. Для кулоновского поля Во (г) = +Z#lr. Поскольку
W 1 - —4л6 (г), то в этом случае
(^)кул= (8.142)
2т2 с*
Второй член
U — №’-в° (r)]^ V- (г)
2 2тс2
является поправкой к кинетической энергии и обусловлен зави-
симостью массы частицы от скорости. Последний член
ц = А(с-[УВ(, (Г)хр]) А (з -[У1/ (г) X Р1) ,8 |44ч
3 4/га2с2 4т2 с2
есть спин-орбитальное взаимодействие. Для сферически симмет-
ричных полей имеем
VBc(r) = -
r dr
VV(r)= —
' г dr
(8.145)
Учитывая, что величины Й1=[гхр] и s = являются опера-
т°ром углового момента и спиновым оператором соответственно,
й подставляя (8.145) в (8.144), получаем
// = (Г) 8 I I *2^У(г) s~ * о
3 dr 2m2c2r ' dr 2m2c2r' (8-146)
Первое слагаемое является спин-орбитальным взаимодействием
возникшим от электромагнитного поля, второе обусловлено полем
ядра. Поскольку на малых расстояниях ядерное взаимодействие
намного больше, чем электромагнитное, второе слагаемое в выра-
жении (8.146) будет давать главный вклад. Таково происхождение
релятивистской части ядерной спин-орбитальной связи.
Оценим теперь ее величину для осцилляторной модели. В этой
модели V (г) = -^-Л4ю2г2, dVldr = Мсо2г, поэтому оценка второго
слагаемого в (8.146) дает
yL2dV(r) S-I
dr 2m2c2r
(Aw)3 (6 Мэв)2 nim ил ,
- - » - ——— & 0,02 Мэв. (8.147)
2mc2 2000 Мэв ’
Таким образом, спин-орбитальные силы, обусловленные реля-
тивистской поправкой к центральному потенциалу, возникающему
из-за обмена мезонами, значительно меньше по сравнению с теми,
которые требуются для объяснения спин-орбитальных сил в модели
оболочек*. Оболочечная спин-орбитальная связь должна быть по-
лучена непосредственно из мезонной теории ядерных сил. В на-
стоящее время эти теории не настолько развиты, чтобы достаточно
надежно подтвердить или исключить существование спин-орби-
тальных сил. Спин-орбитальное слагаемое в нуклон-нуклонном
взаимодействии дает соответствующий член в оболочечном потен-
циале, который растет с увеличением числа нуклонов [120]. Это
согласуется с эмпирическим фактом, заключающимся в том, что спин-
орбитальная связь, по-видимому, сильнее в почти полностью за-
полненной оболочке, чем в том случае, когда начинает запол-
няться новая оболочка. Более подробно различные виды ядер-
ного взаимодействия будут рассмотрены в т. 3, в котором будут
обсуждаться микроскопические подходы в теории структуры ядра.
* * *
Хорошее общее введение в модель оболочек дано в книге Майер
и Йенсена [249] и в большой обзорной статье Эллиотта и Лейна
[120]. Очень полное описание формализма модели оболочек пред-
ставлено в книге де Шалита и Талми [357]. В работе Майер,
Йенсена и Курата [2501 сделан обзор оболочечных расчетов для
сферических ядер. Роль и место модели оболочек в физике ядра
рассматриваются в книгах А. С. Давыдова [95] и Престона [31И-
См. также обсуждение этого вопроса Розенфельдом [305].
ва 9. МОДЕЛЬ ОБОЛОЧЕК
ДЛЯ ДЕФОРМИРОВАННЫХ ЯДЕР
И ОБОБЩЕННАЯ МОДЕЛЬ
Предыдущее рассмотрение модели оболочек совершенно не было
связано с коллективным движением в ядрах. В действительности,
эти два вопроса близко связаны между собой. Основным предполо-
жением в последней главе, посвященной модели оболочек, было
предположение о том, что среднее поле ядра является сферически
симметричным. Однако хорошо известно, что в зависимости от вида
коллективной потенциальной энергии в ядрах имеются медленные
поверхностные колебания и существуют статически деформирован-
ные ядра. Очевидно, что одночастичные орбиты должны зависеть
от формы поверхности ядра, т. е. от пространственного распределе-
ния нуклонов. Это приводит к взаимодействию между коллектив-
ными и одночастичными степенями свободы. Можно думать, что
такая связь является слабой в почти сферических ядрах с очень
малыми амплитудами поверхностных колебаний. В этом случае
говорят о пределе слабой связи. В деформированных ядрах указан-
ная связь может быть очень сильной, и тогда говорят о пределе
сильной связи.
Таким образом, необходимо одновременно рассматривать одно-
частичцое и коллективное движения. Соответствующий гамильто-
ниан имеет вид
H = Hcoll + Hsr + Hint. (9.1)
Если для простоты ограничиться рассмотрением только коллектив-
ных квадрупольных переменных то вид гамильтониана Нсо11
дается выражением (3.18) или (6.40) в зависимости оттого, являются
Ди ядра сферическими или деформированными. Слагаемое Hsp
представляет собой гамильтониан модели оболочек:
Hsp= ^{^ + Е(п, h,s;)}, (9.2)
i
ГДе Г'„— кинетическая энергия, Vt — потенциал модели оболочек
Для z-ii частицы. В силу вращательной инвариантности взаимодей-
229
ствие одночастичных и коллективных степеней свободы должно имрт
формулу
Hint=, (93)
где опущены члены более высокого порядка по а2(Х. Один из способов
определения вида функции f (г) состоит в следующем. Известно, что
движение отдельных нуклонов является очень быстрым по сравне-
нию с коллективным движением. Действительно, время, которое
нужно нуклону с кинетической энергией 40 Мэв для того, чтобы
пройти ядро, равно
Т = = 10 ФеРми ~ 1 п-22 грк
нукл у2Екин/Л1 с У80 Мэв/Мс2
тогда как полный период поверхностного колебания с энергией
« 0,5 Мэв есть
УПоврРхн = Мэв 9 -10-21 сек.
Таким образом, за время одного периода поверхностных колебаний
нуклон может пересечь ядро примерно 100 раз. Поэтому можно
предположить, что в каждое мгновение нуклоны подстраиваются
к коллективному движению. Иными словами, среднее поле ядра
претерпевает те же деформации, что и распределение ядерной ма-
терии. Если форма ядра описывается выражением R — Ro (1 +
+ Swa?MY2ц), то можно предположить, что эта поверхность и яв-
ляется эквипотенциальной поверхностью ядерного поля
Если оболочечный потенциал сферического ядра с ть Уо (г,
1, s), то эквипотенциальными поверхностями потенциала
V (a2U, г, I, s) = V ( у ’ 1>
\ 1 “'ll “2ц 1 2Ц /
являются поверхности г = R = Ro (1 + £ца2мУ2(Х). Выражение
(9.4) можно разложить в ряд по коллективным параметрам с точ-
ностью до членов первого порядка:
У(а2ц, г, U) = V(0, r, Vs) + 2( Дг) а2*ц + -.
= V0(r, 1, S) + 2 ( 1 ( dr ’ (ду; l+Sva2*y2V \a^+-
... = V0(r, 1, 8)-Ц^)2а*2цУ2ц = ..., (9.5)
где Vo (г, 1, s) = V (0, г, 1, s). Таким образом, мы получили выраже-
ние (9.3), в котором
f(r)^_ г — (9
' dr ’
230
в более общем случае, если в выражение для поверхности ядра
р (1 + Ухц) включить мультипольпые деформации
И лее высокого порядка, то f (г) по-прежнему будет выражаться фор-
туной (9.6), но в (9.3) вместо суммы по р войдет сумма
2 «хцЪ.ц.
X, ц
Поскольку величина 1/0 (г, 1, s) обычно имеет форму потенциала
Вудса__Саксона, то производная отлична от нуля только в области,
близкой к поверхности ядра. Следовательно, величина rdV^ldr
представляет собой связь с поверхностью, которая является, вооб-
ще говоря, слабой связью. В частном случае, когда Уо (г) является
потенциалом прямоугольной ямы глубиной Vo и радиуса Ro, имеем
Hr) = 7?oVofi(r-7?o)- (9-7)
В общем случае f (г) является функцией типа функции Гаусса
с максимумом вблизи поверхности ядра. Разумеется, при этом воз-
никает вопрос, каково точное определение ядерной поверхности.
Для прямоугольной ямы это-— радиус ямы R = Ro (1 -I
+ 2а2ЦУ2ц). Для потенциала типа потенциала Вудса —Саксона
радиус поверхности ядра можно отождествить с радиусом с —
= с0 (1 + SoC(iy2|1), т. е. с расстоянием, на котором потенциал
спадает до половины его значения в центре ядра. Таким образом,
какого-либо одного определения поверхности ядра указать нельзя.
§ 9.1. СЛАБАЯ СВЯЗЬ
Как уже упоминалось, можно ожидать, что в сферических
ядрах (квадрупольных вибраторах) взаимодействие одночастичного
и коллективного движений является относительно слабым. В этом
случае гамильтониан четно-нечетного квадруполыюго вибратора
имеет вид
H = Hcoll + Hsp + Hint, (9.8)
где
нсоЦ - ^S|n2u|2 + 4cSr«2ul2; (9-9)
ZD ц 2 ц
/7sp= p2/2M + (l/2)War2 + Cbs + Di2; (9.10)
Я,п,= -М<о2г2За2%У2(1. (9.11)
и
Решение уравнения Шредингера с этим гамильтонианом мы полу-
чим по теории возмущений. Если Hint действительно мало, то сум-
м7 7fCi,zz Hsp можно рассматривать в качестве невозмущенного
гамильтониана, собственные функции и собственные значения кото-
рого обсуждались в гл. 3 и 8. Коллективные волновые функции есть
' (см. табл. 3.1), одночастичные— | (см. (8.33)]. Волно-
731
вые функции с полным угловым моментом J и его проекцией Л1
соответствующие гамильтониану Нсоц + HsP, имеют вид
\NIjJM) = У J\mlm2M)\NIm1)\jm2). (919,
mlt rnz )
В основном состоянии квадрупольных фононов нет ^=0), и не-
четная частица находится в состоянии | jM), т. е.
|00/ЛИ> = |0>|/М>. (9.13)
Основное состояние соседнего четно-четного ядра представляет
собой фононный вакуум | 0>. Первое возбужденное состояние яв-
-----------------о+---------------------------!Jm>
Четна-четное ядро Нечетно-четное ядро
Рис. 9.1. Снятие вырождения в случае, когда нуклон связан с поверхност-
ными колебаниями и взаимодействие между частицей и фононом не равно
нулю. Указаны различные угловые моменты однофононного мультиплета.
ляется однофононным 2+-состоянием 112/И!> = | 0>. Это соот-
ветствует следующему состоянию нечетного ядра:
|12/ЛМ>= У (2/^|тхта M)p2+mi|0>|/rn2>, (9.14)
mltmt
где полный угловой момент равен
(/4-2)... (/ — 2) для />2;
(2 + /)... (2 — /) для /<2
(9.15)
(см. рис. 9.1). Однофопонное состояние четно-четного ядра превра-
щается в нечетном ядре в мультиплет пяти (если / > 2) или (2/ + 1)
(если / < 2) состояний. Если Hint = 0, то этот мультиплет вырож-
ден. На рис. 9.1 показан случай, когда /?г,„ #= 0 и вырождение уже
снято. Подобные же мультиплеты имеются и для двухфононных
2+- и 4+-СОСТОЯНИЙ, но, разумеется, не для двухфононного (^-со-
стояния.
Когда учитывается взаимодействие Hint, то смешиваются, вооб-
ще говоря, все мультиплеты с одинаковым спином и четностью. Это
в особенности справедливо, в том случае, когда Hint содержит кроме
членов первого порядка по а2(1 [как в формуле (9.11)] еще и члены
232
-„ее высокого порядка поа2м. Если взаимодействие является доста-
очно слабым, т. е. если величина | a2|J, | = (bh!2B2 со2)'/2 очень
т„аа, то смешиваться будут лишь те состояния (9.12), которые отли-
\ются ДРУГ от ДРУга одним квадрупольным фононом. Это происхо-
вследствие того, что операторы рождения и уничтожения фоно-
нов входят в гамильтониан взаимодействия (9.11) только линейно.
Например, основное состояние смешивается со всеми состояниями
। 12/'/М', для которых матричный элемент
U2/'/M|/yini|00/7/l4>
(9.16)
не равен нулю, т. е. с основным состоянием смешиваются лишь одно-
фононные состояния с нечетной частицей, находящейся в той же или
в другой /-оболочке.
Матричные элементы (9.16) можно легко рассчитать. Результат
имеет вид
<12/747 |Йш|00//7И> =
/Л/2Вг й2 </' ||У21| /> | Меа2г21 nly, (9.17)
где двойными вертикальными линиями отмечены приведенны
матричные элементы сферической гармоники У2М,. Первый множи-
тель связан со среднеквадратичной деформацией ро соотношением
(Й/2В2ю2)1/2 = [см. (3.73)]. Используя осцилляторные
радиальные функции (8.20) и формулу (6.108), можно вычислить
радиальные матричные элементы:
<и'Г 17И(о2г21 ill) —
f/ + 2n + 3/2
~-]/2n(2n+2l+l)
~ V(2n + 2Z + 1) (2n + 2/ —
V (2n + 2)(2n + 2/+l)
~ V2n(2n-2)
0
для n', I' n, l\
для n', Г — n— 1, I;
для n’, Г = n, I—2;
(9.18)
для n', l' = n-\-l, I—2;
для n', I'=n—2, /-|-2;
в остальных случаях.
Для типичных осцилляторных квантовых чисел, например п = 3
и = 2, эти матричные элементы составляют 30—40 Мэв.
Волновая функция основного состояния в первом порядке теории
возмущений имеет вид
%сн.сост=100Ж> —
У ( й V'2 </'11М/> । i2j’jM>. (9д9)
\ 2^2 СО2 /гС02“1“^у' — j
233
Если учитывается связь с фононами более высокой мультипопы
сти (А > 2), то суммирование в этой формуле должно выполнять*0"
также и по индексу А. Следует отметить, что формула (9.19) соде*4
жит смешивание по j' в основном состоянии. Возможные значени*"
j' определяются приведенным матричным элементом </'||У2|./) ТакЯ
чтобы | j — / | = 2,1,0. Из вида энергетического знаменателя еле’
дует, что в основном смешиваются состояния с малой энергией"
0+______________1,137
2*--------------1,125
2+--------------0,513 _
} 5/2 -------------
3/2~--------------
//J2+ -----------
(S)
(2+)
1,509
1,473
2*------------0,632
0,423
0,324
0,094
46 Pd60 47 Ад60
48 Са'во
Рис. 9.2. Низкоэиергетические спектры трех ядер с М=60
и 2=46, 47 и 48. Два четно-четных ядра имеют колеоатель-
ные спектры, тогда как спектр ядра l07Ag можно рассматри-
вать как результат связи протона в оболочке 2р^2 и одио-
фононного 2 '-состояния [288].
4 ---------— °,76 4*---------2,37Q
9/2~--------1,813
+ 11/2———1,609
2 ------------1,56 _ 2*----------1,434
3/2 ---------0,930
5/2~---------0,320
0 ------------ 7/2"------------ /----------------
50 ; 51 52
22 L28 23^28 24Cf28
Рис. 9.3. То же, что и на рис. 9.2, но для Д'=28 [288].
Смешивание зависит от данной оболочечной конфигурации и
коллективных свойств ядра, т. е. от эффективной деформации Ро —
— (57/2B2w2)1/2 и коллективной частоты. Это хорошо проявляется
в эксперименте. На рис. 9.2 показаны низкоэнергетические спектры
ядер 1“бР<1, “zAg, 14gCd, имеющих одинаковое число нейтронов
и разные числа протонов. Согласно схеме уровней модели оболочек
(см. рис. 8.3) протонная конфигурация основного состояния 10<’Ро
есть (lg9/2)e- Спаривание в оболочке gg/г приводит к опусканию
^э/2-конфигураций ниже 2/ц^-конфигурации. Поэтому нечетный
протон в 107Ag находится на оболочке 2pi/2- Тогда состояния 3/2
234
5/2", по-видимому, можно интерпретировать как результат связи
"фононного 24-состояния с протоном в оболочке pi/2 в резуль-
тате чего образуются сложные состояния 3/2~ и 5/2". На рис. 9.3
показан аналогичный низкоэнергетический спектр ядер 60Ti,51V и
52Q в которых, как и раньше, число нейтронов одинаково, а число
протонов увеличивается. Протонная конфигурация основного со-
стояния 61V есть (1/т/з)3 (см. рис. 8.3). Возбужденные состояния
этого ядра можно интерпретировать как однофононные конфигу-
рации (2+ X 7/2 )J. Очевидно, что они сильно расщепляются.
Состояние J — 7/2 отсутствует. Можно ожидать, что оно лежит
выше 1,8 Мэв.
Приведенные примеры показывают важность частично-фононной
связи, а также свидетельствуют о том, что действительная ситуация,
по-видимому, никогда не бывает очень ясной, т. е. всегда возможно
смешивание чистых одночастичных или однодырочных состояний
с фононными состояниями четных ядер. Например, в последнем
примере на рис. 9.3 частица может находиться на одночастичных
уровнях 2р3/2, 1/5/2, 2р1/2 и lgg/2, что может дать состояния яд-
ра 3/2", 5/2", 1/2" и 9/2+ соответственно. Поэтому в каждом отдель-
ном случае необходимо специальное исследование*.
§ 9.2. ГАМИЛЬТОНИАН МОДЕЛИ
СИЛЬНОЙ СВЯЗИ
Для ядер с постоянной деформацией взаимодействие (9.3) между
индивидуальными нуклонами и коллективными колебаниями яв-
ляется большим и использованные теории возмущений больше не
являются справедливыми. Поэтому связь с деформированным осто-
вом ядра следует рассматривать точно. Это приводит к модели обо-
лочек для деформированных ядер, т. е. к одночастичным оболочкам
в деформированном потенциале. Полный гамильтониан, как и рань-
ше, имеет общую структуру, даваемую выражениями (9.1). Однако
коллективный гамильтониан теперь представляет собой соответ-
ствующий коллективный гамильтониан деформированного ядра,
а именно колебательно-вращательный гамильтониан (6.40). Исполь-
зуемая нами модель схематически иллюстрируется на рис. 9.4,
где показано, что два нуклона движутся вокруг деформированного
остова, в то время как сам остов согласно колебательно-вращатель-
ной модели может колебаться и вращаться.
Разумеется, можно рассматривать другие модели для нечетных
яДер, основанные, например, на модели асимметричного ротатора.
Поскольку, как было видно в гл. 6 и 7, для низкоэнергетических кол-
лективных возбуждений обе модели дают почти одинаковые резуль-
таты, мы предпочитаем динамический подход колебательно-враща-
тельной модели.
* Связь дырочных состояний с октупольными фононами эксперименталь-
0 изучалась для ядер вблизи РЬ в работах [175, 176, 343].
235
В гамильтониан колебательно-вращательной модели (6.40) вхо-
дит вращательный угловой момент остова М. Полный угловой момент
системы I состоит из углового момента остова и углового момента
внешних частиц j (рис. 9.5):
1=v=r2.b’ (9-2°)
где]\—угловые моменты индивидуальных частиц. Таким образом*,
Рис. 9.4 Схема, иллюстрирующая
физический смысл модели сильной
связи. Показаны два нуклона, дви-
жущиеся вокруг деформированно-
го остова по орбитам О, и По-
Вращение остова по отношению
к лабораторной системе показано
углами Эйлера 0; и двойными
стрелками.
Рис. 9.5. Схема сложных угловых
моментов в модели сильной связи.
Угловые моменты экстрануклонов скла-
дываются в момент J, который в сум-
ме с угловым моментом остова М дает
полный момент I. Проекции моментов
j н I на ось z' ядра, приближенно
являющиеся константами в пределе
сильной связи, обозначаются соответ-
ственно Н и К.
U = M + jA.
(9.21)
Составляющие полного углового момента I системы относительно
внутренних осей подчиняются коммутационным правилам
KH-h.k -i/xxv (9.22)
Однако составляющие момента j относительно внутренних осей
подчиняются другому правилу:
7х /х— 71 Ух - i/xxX- (9-23^
* Операторы АГ, М и Aj обозначают угловые моменты.
236
Поскольку операторы j и I действуют в различных пространствах
— в одночастичном пространстве, I — в пространстве углов Эй-
лера)» имеем
К 0. (9.24)
Спедует отметить различные знаки в правых частях равенств (9.22)
j (9.23). Это вытекает из того факта, что составляющие полного
углового момента генерируют вращения вокруг вращающихся осей,
тогда как операторы не изменяют вращающуюся систему отсчета.
(Подробное обсуждение этого вопроса см. в конце § 5.2.)
Подставляя М = I — j в колебательно-вращательный гамиль
тониан (6.40) легко получить Йсо11 для деформированных ядер,
в которых имеются несколько дополнительных частиц сверх остова.
Результат имеет вид
Йсои— ^rot^r Hvibrot, (9.25)
где
fr _ (г-г)2^2 (/;-Л)2^ . (/з-Л)^ .
Tot 2^0 16S113
Н vib
Hvib rot —
Й2 Г d2 . 1 d2 1 1 р t2 j г a tl2 .
2 di]2] 2 -11 165ч]2 ’
(Г-Г)Ч2 (/з /,;)2й2 г2 211 2 _L л - з -^-1
2^0 [ ₽? ₽<> 1 ₽3 J
I П+ 7+)2^ I (/- /_)-/' 2 1 л6 1/ 6 21
4^о [ 3 ₽„
(9.26)
Ф
(9.27)
и элемент объема в пространстве коллективных переменных
dx — dQd’^di].
Согласно (9.10) и (9.11), гамильтониан дополнительных частиц
в осцилляторной модели оболочек имеет вид
+iiint=v AW v г ;2 + с v i; • s; +
+ D 2 if - Mo>2 Z г/2 [«о У20 (0 + a2 (Y22 (!) + У2_2 (!))], (9.28)
‘-вязанной с лабор
Суммирование по !
где a0 |30 + g и o2 = ip Здесь все координаты частиц рассматри-
ваются во вращающейся системе координат, поэтому и функция Й2|Х
в выражении (9.28) также определена в системе x'y'z' (см. рис. 9.4),
аторной системой с помощью углов Эйлера 0?-.
выполняется по всем индивидуальным частицам,
которые учитываются явно. Мы рассмотрим только одну частицу,
ваходящуюся вне остова, тогда сумма по ! в (9.28) сведется к одному
237
лену. Общий случай можно всегда получить, заменяя одг.очастич-
ный оператор в гамильтониане соответствующей суммой по рас-
сматриваемым частицам.
В нашем случае удобно записать полный гамильтониан в еле-
дующем виде:
Н = ^Осоп+ + (9.29)
где
Н^„ [|!-Щ-Й)!] + ^ КЧ-ЙГ-И-
2В [д£2 2 di]2J 2 '
tfOs„ = + -L Мы2 Г'2 + СГ - s' + D1'2 —MwV2 р0у20 (9.31)
os' ИИ 2 ’
и
н' -^-Г2-^['4/- + /-/++2/зЛ] +
2/о 2уи
-2('/;/;+ад][2 /6 |-Гб ^-1-
L Ро Ро J
-M<oV'2 lgr20 + T] (У22 + У2_2)]. (9.32)
Здесь использованы хорошо известные определения 7± =7( ± i?2
и /± = /J ± i/2- 7з —проекция оператора полного углового момен-
та на ось z' вращающейся системы отсчета. Оператору 7з соответст-
вует квантовое число К. Аналогичный оператор для нечетного нук-
лона есть /з, ему соответствует квантовое число й (см. рис. 9.5).
Величина Н0соЦ описывает вращение и колебания остова и тесно
связана с суммой Hrot + Hvib, даваемой выражениями (6.40)
и (6.88). Если пренебречь членом, пропорциональным /з, то Н0соц
совпадает с Hrot + Hvib (6.40). Колебательно-вращательное взаи-
модействие содержится в слагаемом, пропорциональном А2/16Вт]2 и
связанным с третьим моментом инерции. Дополнительный нуклон из-
меняет полный угловой момент [см. (9.21)1 и таким образом модифи-
цирует колебательно-вращательное взаимодействие.
Величина H0Sft представляет собой оболочечный гамильтониан
частицы, движущейся в деформированном аксиально-симметрич-
ном потенциале ядра. Он состоит из гамильтониана сферической
модели оболочек (8.42) и дополнительного квадрупольного потен-
циала, пропорционального РоГ2К2о- Последняя величина обусловле-
на деформацией ядра и, естественно, пропорциональна р0.
238
Величина Н' состоит из нескольких малых слагаемых. Первое
ниХ1 пропорциональное j2, представляет собой чисто одночастич-
й g член. Поскольку, как будет видно ниже, он не диагоналей
в представлении одночастичных функций, соответствующих гамиль-
тониану HOsP, мы включили его в Н'. Второе слагаемое описывает
связь вращения с одночастичным движением и пропорционально
произведению 21'-j' = (l+jL + Д-/4-+ 2/3/3). В классическом слу-
чае это соответствует силам Кориолиса, так как в классической меха-
нике потенциальная энергия кориолисовых сил для частицы, дви-
жущейся во вращающейся системе, может быть записана в виде
где ы — угловая частота вращающейся системы. Третье и чет-
вертое слагаемые в выражении (9.32) описывают взаимодействие
частицы с колебаниями и вращением ядра, обусловленное измене-
нием моментов инерции благодаря поверхностным и ^-колеба-
ниям. Наконец, последний член в И' содержит взаимодействие ва-
лентного нуклона с поверхностными колебаниями.
Сначала в § 9.3 и 9.4 мы обсудим решения, соответствующие
невозмущенному гамильтониану Но соц + Но sp, а затем в § 9.6
кратко рассмотрим влияние взаимодействия И' на невозмущенный
спектр. .
§ 9.3. СТРУКТУРА И СВОЙСТВА СИММЕТРИИ
ВОЛНОВЫХ ФУНКЦИЙ МОДЕЛИ СИЛЬНОЙ связи
Для получения несимметризованных решений, соответствую-
щих гамильтониану Н0со11, можно воспользоваться выражением
(6.112) и написать
<Р (°;, L П) = NDmk Хк-fi пг 01) | л0>. (9.33)
Единственное отличие от (6.112) состоит в том, что квантовое число
К в волновой функции, описывающей ц-колебание, заменено на
К — й:
Й. (9.34)
Это обусловлено тем, что сравнивая гамильтониан (9.30) с (6.41) и
(6.42), нетрудно получить
(9.35)
Таким образом, сильное колебательно-вращательное взаимодей-
ствие, связанное с третьим моментом инерции, в данном случае оп-
ределяется собственными значениями оператора /3 — /3, т. е. К — й.
Здесь Q — собственное значение оператора /з, являющееся проек-
цией углового момента частицы на ось симметрии ядра (ось г' на
рис. 9.5). Отсюда следует, что Й — хорошее квантовое число гамиль-
тониана H0coll -J- Hosp, так как этот гамильтониан описывает
239
вращения, колебания и одночастичные движения аксиалъно-сц
метричного ядра, в котором ось z' является осью симметрии,
ствительно, как мы знаем из обсуждения в гл. 6, это справедливо дд^
Н0сои- Из (9.31) видно, что гамильтониан HOsl, также аксиально-
симметричен [части, которые нарушают аксиальную симметрию
включены в последнее слагаемое гамильтониана Н' (9.32)]. Таким
образом, для решений, соответствующих гамильтониану НОа 7, уГЛо
вой момент вообще говоря, не является хорошим квантовым чис-
лом, но /з таковым является. Следовательно, можно написать
(9.36)
где фа<г и ^а<1 — нормированные волновые функции и энергии о но-
частичных орбит в деформированных ядрах. Индекс а обозначает
дополнительные квантовые числа, которые конкретизируются в сле-
дующем параграфе.
Полные волновые функции невозмущенного гамильтониана
Но - Н0соц-\- HOsp. (9.37)
имеют вид
Ф НDmK (Оj) yvK_ Qtl2 (i]) | ПдХрощ. (9.38)
Согласно (6.1286) и (9.36), соответствующие энергии даются выра-
жением
Е1каПг„с а = сТай + ^7 (7 + 1) - (К - Q)2) е +
+ f-L|K-fi|+l + 2n^Ev+(n0+±')Ep. (9.39)
Волновые функции (9.38) должны быть симметричны по отноше-
нию к преобразованиям Rlt /?2, R3 (4.13) и (4.22). Рассмотрим вна-
чале симметрию по отношению к преобразованиям R± и Т?2, так же
как это сделано в § 6.4 для четно-четных ядер. Начнем, как и там,
с преобразования R2, которое соответствует поворотам вокруг оси
z на угол -^-л и одновременной замене а2 на —а2 (или т] на - т]). Из
соотношений (6.114) и (6.115) известно, как действует оператор R-z
на функции DmK (0у) и (»]) соответственно:
е2, е3)=£»^^е1, о2, е3+-±л) =
= exp(-i-i£njD^(Gi, 62, 63) (9.40)
и
/?2 Хк-йл, (Т)) = Хк-йл, (—Л) = (— 1),/г Хк-йле (л)- (9-41)
240
Далее, поскольку компоненты оператора j относительно непод-
<жной системы координат подчиняются обычным коммутационным
соотношениям (9.23) или (5.82а) [в противоположность соответст-
вующим компонентам I, которые имеют коммутационные соотно-
шения, аналогичные соотношениям (9.22) или (5.826)], можно заклю-
чить, что зависимость функции <pas от азимутального угла имеет
вид
<р«п(т, fl, q) = 4a(r, fl)exp(—i<2([). (9.42)
Отсюда
Т?2фай(г, °, ф) = фаЦт, 6, ф+уЯ) =
= exp ----у <paQ(/-, 0, <p). (9.43)
Следовательно, полная волновая функция будет инвариантна по от-
ношению к преобразованию R2, если
(— 1)%к (__ 1)-/2 (К-В) (— 1)-%а = ( — 1)Д-й = 1, (9.44)
что дает
Л—Q = 2v, v = 0, ±1, ±2,... (9.45)
Это аналог соотношения (6.117).
Рассмотрим теперь симметрию волновой функции (9.38) по отно-
шению к преобразованию Оператор действует только на углы
Эйлера и координаты нечетной частицы 1см. (4.13) и (4.22)]. Это
соответствует вращению на угол л вокруг оси х' вращающейся
системы. С помощью (6.126) имеем
^х7)л/к(61, 02, 6з) = ^мк (0j 4- л, л—62, —63) =
= (-i)/-2K£);;_K(ei( е2, е3). (9.46)
Чтобы понять, как Rl действует на функцию <paQ, следует помнить,
что в выражение (9.31) входит аксиально-симметричный потенциал
И поэтому величина j2 не является константой движения. Однако во
многих задачах более удобно иметь дело с состояниями, которые ха-
рактеризуются квантовым числом углового момента, поэтому вве-
дем величину
= (9.47)
!
где <р,-о — функции сферической модели оболочек без слагаемого
Рог2У2о в (9.31), являющиеся собственными функциями оператора j2.
Найдем величину R^jo, используя тот факт, что определяет-
ся во внутренней системе координат х'у'г'. Сначала выразим
Чэрез функции (р-т, которые определены в лабораторной системе
241
х, у, z (см. рис. 9.4). Квантовое число т здесь является собственным
значением оператора jz — проекции вектора j на ось z лабораторной
системы координат. Согласно (5.141) имеем
Ф>й (л ) — Dmti (0) (р/т (л). (9.48)
Оператор не действует на функции ф/,„ (х), так как они опреде-
лены в лабораторной системе и не зависят от выбора осей внутрен-
ней системы координат. Так как D'^q = (—l)m-S2DLm_fi, то из
(9.46) следует, что
О/„й (0) (- 1)«-й О'*м-а =
= (-1)1+ 2й (-!)'«-й£)Гтй = (-l)/^_Q. (9.49)
Отсюда
Л1Ф^и = (“1),ф/-й- (9.50)
Полная симметризованная волновая функция должна иметь вид
ф + где ф дается выражением (9.38). После нормировки полу-
чаем окончательно
| IMKQn2 п0 а> = 1/ i {Олж (6j) фай +
1/ 16л2
+ (- 1)'~2КD'm-k (67) У (-1)/С$ ф,_й} % к-й |л, (Л) I «о>, (9.51)
/
где использовано (—1)4й = 1 и явно выписан результат действия
оператора Rt на <рай.
В наиболее общем случае, когда учитывается возмущение Н',
даваемое выражением (9.32), Дг, Q, п2, «о и а больше не являются
хорошими квантовыми числами. Полная правильно симметризован-
ная волновая функция в этом случае есть
фш= 2 АКаП2Пса\1МК£}п2п0а'>, (9.52)
К.Й.п,, л„, а
где коэффициенты смешивания АкаПгпеа определяются по теории
возмущений или путем диагонализации гамильтониана Н. Вол-
новая функция (9.51) является совершенно общей в том смысле, что
<рай может быть также и многочастичной волновой функцией. Если
она описывает только одну частицу, то можно воспользоваться
другим представлением фай через одночастичные волновые функции
Ф/лй, которые характеризуются орбитальным угловым моментом
/, его проекцией Л на ось z' и проекцией спина S на ось z':
S = Q—Л (9-53)
и вместо (9.47) записать
Фай = 2А^’йФ/Лй. (954)
Z, л
242
Поскольку четность является хорошим квантовым числом, то значе-
1 я I в этой формуле будут либо все четными, либо все нечетными.
Функции <р/ли связаны с функциями <р/й в разложении (9.47) соот-
ношением
= S (I 4" 11Л 2 Фмй, (9.55)
А. X к 2 )
и следовательно,
= 2 ( /4-/|л2£ЙС$
/ \ 2 /
или
,-(«) V
Ь/Я = —
Л, X
(9.56а)
(9.566)
сЙ’й-
В следующем параграфе мы докажем важное соотношение
Фла - О/—л—а (9.57)
Используя свойство коэффициентов Клебша—Гордана
(/1/2/3= (— l)z*+z«-Za (/i/2/3|—rrii—m3) и соотноше-
ния (9.57) и (9.566), находим
С/й.-(-1)'+1Л-7С/_й. (9.58)
Учитывая, что (—1)' = лф есть четность состояния <pia, получен-
ный результат можно записать по-другому:
С/й = (-!)*/•-/лфС,_й. (9.59)
Подставим это во второе слагаемое в выражение (9.51) и получим
окончательно
1IMKQn2 ноа> =
= 1 / +<- 2)'+Уг _2К х
р 16л2
х£>м-к(0у) лф<ра_й} %iK~a1na(i'])l»o>- (9-60)
§ 9.4. МОДЕЛЬ ОБОЛОЧЕК
ДЛЯ ДЕФОРМИРОВАННЫХ ЯДЕР
В предыдущем разделе были рассмотрены структура и свойства
симметрии волновых функций модели сильной связи. Теперь необ-
ходимо получить решения уравнения Шредингера с одночастичным
гамильтонианом (9.31) для деформированной ямы:
,2
4- + 4-Мш2(1-2роУ20)г'2 +
2М 2
+ СГ- s' + £>r2) <рой = %оа фай, (9.61)
243
где штрих показывает, что соответствующие операторы берутСя
во вращающейся (внутренней) системе. Эта задача была впервые
подробно исследована Нильссоном [283] в 1955 г., менее подробно
она рассматривалась также Готфридом [167] и Мошковским [262].
Уравнение (9.61) описывает движение одной частицы в трехмерной
анизотропной гармонической осцилляторной яме со спин-орбиталь-
ной связью. Слагаемое, пропорциональное Г2, обеспечивает интер-
поляцию между потенциалами гармонического осциллятора и пря-
моугольной ямы (см. § 8.3). Эквипотенциальные поверхности ани-
зотоопного осциллятора представляют собой эллипсоиды. Это
Рис. 9.6. Эквипотенциальные поверхности (эллипсоиды) для одночастпч-
ного потенциала (9.62). На рисунках изображены сечения в плоскости
x'z' и у'г'.
легко видеть, выражая величину У2о через декартовы координаты
[см. (2.19)]:
H°sP = 2M ' ~ТМ [(ю*,х'2 + (гоХг/'2~Ь +
Cl'-s' + ГЛ'2, (9.62)
где
со2 = <о2 соЦ 1 + (А л ₽0 ) (9.63а)
и
(Ob Ш1-21-±лГЧ)- (9.636)
Таким образом, если деформация (30 положительна, частица колеб-
лется быстрее в экваториальной плоскости {х'у'), чем вдоль оси сим-
метрии г' (рис. 9.6).
Вводя безразмерные координаты
г = 1/^гЧ
|/ h
(9.64)
244
уравнение (9.61) можно переписать
в виде
Hosl> <рая = (Й<оо (—V2 + г2)—Й<оо Д,г2 У20 +
+ Cl'-s' + Dl'2
фай — 8ай фай-
(9.65)
Определим новый оператор — гамильтониан сферического гармо-
нического осциллятора
Н° = + ко0 (—V2 + г2) (9.66)
Соответствующие волновые функции см. (8.20) и энергии имеют вид
|A/AV>=A0(— 1)"/'ехр( — r2/2)iFi п, / + -|- , г2) Y [Л fa;
(9.67а)
^=(2Г(п+/ + 3^. (9.67б)
(nl)% Г (/ + 3/2)
Ем = Йсо(А + 3/2); А = 2» + /, n = 0, 1, 2, .. (9.68)
Здесь мы добавили спиновую функцию Хх- Решения фаа, соответ-
ствующие гамильтониану Н0<т>, получаются диагонализацией га-
мильтониана Hosp в базисе собственных функций (9.67а) гамильто-
ниана Но.
Собственные функции гамильтониана HOsp можно характеризо-
вать собственным числом Q 3-й компоненты оператора одночастич-
ного углового момента, которое является хорошим квантовым чис-
лом. Это обусловлено тем, что в HOsp входит аксиально-симметричный
член ядерного квадрупольного поля. Вообще говоря, это квадру-
польное поле рпг2У2о смешивает квантовые числа N в выражении
(9.67). Однако в редкоземельной области ядер, где значения ро ле-
жат в пределах от 0,15 до 0,35, это смешивание мало и им обычно
пренебрегают. Поэтому деформированные состояния можно харак-
теризовать и числом N. Запишем
HOs]) | АПа> = g’jvQa | №a>,
|M2a>==2S«?kO|A7A2). (9.69)
Для рассматриваемых квадрупольных сил матричные элементы
по базисным состояниям (9.67) равны
<А7'А'2|г2У20|А7Л2>-
= <A7'|r2|A/><A'|y20|A>6z-z,
(9.70)
245
где радиальные матричные элементы приведены в (9.18). Они могс
быть записаны в другой форме в следующем виде:
< N' I' | г2 \Ш > = . N- 2 {-L-1 > + /+l)(7V + /-lj х
х 6/.2 + A Y(N-l)(N + l+\)8г 1+1 /2 +
+ -у 8r Z+ 2} +
+6N' n {Г (V-Z + 2)(N + /+1) 8г t_ 2 + (N + 3/2) 8r t +
+ К (А'--О (А + I + 3) 8г 1+ 2} + бл” N+ 2 {-£- X
X /(N + Z+l)GV + / + 3)8г 1-2 + ~J<(N-Z4-2)(ZV + Z + З) х
X 8г , 4--j- Г (A-i) (А-1 + 2) 8г /+2} - (9.71)
Интегрирование по углам дает
<Z'A'|/20|ZA>= (-1)''-A'(^^[(2Z'+1)(2Z+1)]*/2. (9.72)
Это выражение не равно нулю, только если Z + Г + 2 — четное
число. Поэтому З/’-символ не изменяет знак, если обратить направле-
ния угловых моментов (А' —> А', А -э А). Отсюда для коэффи-
циентов й/л имеем
^л“ = «Г“л- <9-73)
Эти коэффициенты, а также значения энергии уровней полу-
чаются диагонализацией квадрупольного поля —Л®рпг2У20 (см. При-
ложение В), в результате чего как aff, так и (+<_>« становятся функ-
циями параметра деформации р0. Энергии уровней модели оболо-
чек для деформированных ядер показаны на рис. 9.7.
Частота со, которая входит в HOsp, зависит от деформации. Это
обусловлено исходным предположением о несжимаемости ядерной
материи, поэтому мы полагаем, что в процессе деформации объем
ядра постоянен, что наиболее легко выразить с помощью величин
(Од., <»ь., сог в следующем виде:
wz= константа (в процессе деформации), (9.74)
так что
Ч(₽о)=Чо[( 1/2Ро)2( 1— 2 1/2Ро)]”1/3- (9,75^
На рис. 9.7 одночастичные энергии даны в единицах АсоС) (Ро)-
Рядом с отдельными уровнями указываются квантовое число W
и четность. Число слева около каждой кривой представляет собой
Рис. 9.7. Уровни энер-
гии частицы в потен-
циале аксиально-сим-
метричной деформиро-
ванной ямы со спин-
орбитальной связью.
Энергии даны в еди-
ницах ЙЫо(Ро) [см.
(9.75)]. Число слева
на каждой кривой да-
ет номер уровня. Спра-
ва на кривой указаны
значения й
номер уровня В табл. 9.1 в качестве примера приводятся некстовк
одночастичные энергии и волновые функции. В первом ряду дане
энергии в единицах Лсоо (ро) для каждого состояния. Три др\ГиЫ
числа в столбце дают коэффициенты fi/д в разложении (9.69) ДдХ
значения параметра деформации, указанного вверху таблицы Я
Таблица 9.1
П римеры энергий и собственных функций (9.69) для Д' 5
Q=-^- [283]. Базисные векторы | 553 1 > , | 533 ф > , | 554 |
Первая строка дает энергии в единицах Аю0 (0О). Следующие
три строки дают коэффициенты разложения а, в форму-
ле (9.67). Параметр деформации т] связан с [30 соотношением
11=2 ("пгл) 7
1]=— 6 —4 —2 0 2 4 6 Too
— 16,090 —0,615 —0,583 0,531 — 15,493 —0,485 —0,723 0,493 — 14,007 —0,214 —0,954 0,210 — 11,400 0,000 1,000 0,000 —8,393 0,094 —0,994 —0,055 —5,255 0,144 —0,987 —0,067 —2,055 0,177 —0,982 —0,068 [503]
—20,498 0,082 —0,717 —0,692 — 18,153 0,254 —0,655 —0,712 — 16,194 0,432 —0,285 —0,856 —15,000 —0,426 0,000 0,905 —13,961 —0,372 —0,086 0,924 — 12,885 —0,321 —0,111 0,941 — 11,757 —0,279 —0,117 0,953 [514]
—27,812 0,784 —0,382 0,489 —26,755 —0,837 0,220 —0,501 —26,199 —0,876 0,092 —0,473 —26,000 0,905 0,000 0,426 —26,046 —0,924 -0,066 —9,378 —26,260 —0,936 —0,114 —0,333 —26,588 —0,944 —0,149 —0,295 [523]
Результаты расчетов, разумеется, зависят от значения парамет-
ров (о00, С, D и Ро- В § 8-4 было найдено, что осиилляторная кон-
станта <оО() связана с размерами ядра следующим образом: Йо)00 =
= 41у4 ^3 Мэв [см. (8.53)]. Величины С и D были выбраны в §8.3
так, чтобы получилась правильная модель оболочек для сфериче-
ского ядра. В нашем случае используются параметры
х = С/2^сооо, р = 2О/С. (9.76)
Первый из них изменяется в пределах и = 0,05 (для N > 50)
и и = 0,08 (для N < 20), ар — в пределах от 0 до 0,70 в зависи-
мости от оболочки.
На рис. 9.7 различные уровни в деформированном потенциале
характеризуются квантовым числом Q, четностью и порядковым
номером. В литературе довольно часто используются также дрУгие
обозначения для одночастичных состояний с помощью квантового
числа Q, четности и тройки чисел [АнзА]. Здесь А — главное кван-
товое число осцилляторной оболочки [см. (8.20)1. п3 дает число
осцилляторных квантов вдоль оси / [см. (8.62)]. Очевидно, что в рас-
248
сматриваемом представлении оно не является константой движения.
Однако для очень больших деформаций оно становится очень близ-
ким к константе движения (является асимптотическим квантовым
числом), так как, согласно (9.63), разность — Йсо2 для коле-
баний, перпендикулярных к оси симметрии ядра и параллельных ей,
увеличивается с увеличением деформации.
6,50
6,25
6,00
5,75
1/2' [501]
5/2' [503]
3/2' [501]
1312+[606]
9/2" [505]
11/2* [615]
7/2~[503]
3/2'[512]
1/2'[510]
9/2t[624]
7/2'[514]
5/2'[512]
7/2+[633]
1/2 [52]
11/2~[505]
5/2'[523]
3/2~ [521]
5/2+[б42]
3/2^[65]
1/2+[660]
3/2 /532]
1/2 [530]
1/2'[541]
О 0,1 0,2 0,3 6
О 2 4 6 О
। I___________________________I_________________L__________________L________
Рис. 9.8. Иллюстрация табл. 9.1. Нейтронные одиочастичпые
уровни как функции деформации ядра.
Поясним теперь использование таблиц типа табл. 9.1 на примерах
Для нескольких нильссоновских оболочек. Рассмотрим первое со-
стояние в табл. 9.1, которое обозначается как:
а. |йп/Уп3Л> = |7/2~ 503>. При деформации рс = 0 (сфе-
рическое ядро) оно имеет энергию £ = —11,400 и волновую функ-
цию
<Р7/2(₽о--О)^_ О-|553 ф > +1 -|533 ф >4-0-| 554 ф >, (9.77)
т- е. это — базисное состояние | WZAS) = | 533 f >, являющееся со-
стоянием /7/2 сферической модели оболочек с проекцией полного
249
углового момента tn = 7/2 на ось z. При деформации* ц — 6
уровень имеет энергию Е = —2,055 и волновую функцию
этот
<Р7/2 (Л = 6) = 0,177 | 553 f > — 0,9821 533 ф >— 0,0681 554 ф >. (9 78)
Таким образом, опа становится довольно сложной суперпозицией
сферических базисных состояний |Л//Л2>. Состояние (9.78) харак
теризуется квантовыми числами N = 5, 9 = 7/2 и четностью л ='
б. Состояние | 9лЛ+3Л> = | 7/2’ 514>— второе состояние в
табл. 9.1. В сферическом ядре оно имеет энергию Е = —15 и сод.
новую функцию 1
Ф7/2(₽о=О) = —0.426| 553 f > + 0-| 533 | > + 0,905-| 554 j >, (9.79)
т. е. оно является состоянием сферической модели оболочек й9/2
(т = 7/2, так как представляет собой суперпозиции двух состояний
|/ = 9/2т = 7/2> = (5-|- 3±1) У6з(е,Ф) Х1/а+
+(5 тт| 4-Т т)ys4(Gl4,) х-1/2‘ (9-8°)
Мы видим, что два коэффициента функции (9.79) являются просто
коэффициентами Клебша—Гор дана.
На рис. 9.8 показана часть схемы Нильссона, которая включает
состояния, приведенные в табл. 9.1. С помощью этого рисунка мож-
но легко проиллюстрировать примеры, которые были рассмотрены
выше.
§ 9.5. СПЕКТРЫ НЕЧЕТНЫХ
ДЕФОРМИРОВАННЫХ ЯДЕР
Деформированное ядро с данной деформацией имеет хорошо
определенный одночастичный спектр, который можно получить из
рис. 9.7. Как и в модели оболочек для сферических ядер индиви-
дуальные орбиты заполняются парами нуклонов, имеющих проекции
углового момента /3, равные +9 и —Q. Таким образом, различные
пары имеют полную проекцию углового момента на внутреннюю
ось, равную нулю, и свойства основного состояния нечетных ядер
определяются последней нечетной частицей.
Обозначим одночастичную орбиту, определяющую основное со-
стояние нечетного ядра Хо„- Энергию основного состояния примем
равной нулю. Более высокие одночастичные орбиты обозначим
Xs,, Хо2. а их энергии $2, Согласно (9.39) и (9.60), каждое из
* Параметр деформации г] был введен Нильссоном. Эта величина связана
с обычным параметром деформации соотношением т)=2|— л) P0Act>0 (Ри)/С'
250
их одночастичных состояний является основанием вращательной
поюсы. Полоса основного состояния характеризуется квантовыми
числами
K = Q0, щ,-.0, л0 0, (9.81)
й угловые моменты различных вращательных состояний принимают
значения
/ = П0, Q0+l, Qo + 2,... (9.82)
Для возбужденных одночастичных состояний картина аналогич-
на Их вращательные полосы определяются условиями
/<-Qv = 0; v = 1,2,3; |
Z = | Qv |; |QV| +1; |Qv| + 2. |
Рис. 9.9. Схематическая
иллюстрация одночастич-
ных орбит и вращающе-
гося остова:
а — нуклон в основном со-
стоянии б — нуклон перешел
в возбужденное состояние.
Такие состояния можно наглядно представить так, как они изобра-
жены на рис. 9.9, а, где схематически показаны остов и несколько
одночастичных состояний |аП0), |а£2т>, |аП2)-
На каждом из этих одночастичных состояний строится вращатель-
ная полоса, угловые моменты которой определяются правилом
(9.82). Возбужденные одночастичные состояния схематически пока-
заны на рис. 9.9, б.
Разумеется, кроме одночастичных возбуждений могут также
существовать Р- и у-колебания остова. Первые характеризуются
значением п0 = 1, вторые описываются следующим соотношением
между проекциями угловых моментов:
Д'—Qv=±2
и значениями спинов
/ = |Л|, |К|4-1, IKI + 2,...
Их энергии даются формулами [см. (9.39)1
£’k = qv+2 = (4Qv + 2) е Jr£v,
2 = (— 4Qv—2) ~ е + ^v-
(9.84)
(9.85)
251
Мы получили важный результат: в нечетных ядрах всегда сущес
вуют два у-колебательных состояния. Колебательные возбуждении '
состояния схематически иллюстрируются на рис. 9.10. В обои*6
случаях р- и у-колебаний частица находится на орбите, соответст
Рис. 9.10 Схематическая
иллюстрация одпочастпч-
ных орбит II возбужде-
ния остова ядра:
а — P-колебание, б — у коле-
бание.
вующей основному состоянию ядра | aQ()>. В первом случае воз-
буждаются поверхностные колебания вдоль оси симметрии остова
(p-колебания), во втором — вдоль короткой оси (у-колебания).
Несколько типичных спектров нечетных ядер показаны на
рис. 9.11—9.13. На них указаны различные деформированные одно-
частичные орбиты, на которых построены вращательные полосы.
4,60---5/2
4,04 — 9/2 1/2
3,44 — 9/2 ’ ' 3,72—7/2
3.09----3/2
2,73----7/2 9,70--3/2
2,50---1/2
1.81 __5/2
1,61----7/2
Мэв °,95--------------3/2
0,45----- 1/2
0----5/2
К=5/2+ К=1/2+
[202] [211/
К-1/2+
[200]
К-1/2 К-3/2*
[330] [211]
Рис. 9.11. Экспериментальные уровни 27А1, представленные
так, чтобы показать различные вращательные полосы [288]
Для подробного ознакомления с уровнями модели оболочек в дефор-
мированных легких ядрах см. работы [30, 63, 232, 233, 279, 293, 329],
а для деформированных тяжелых ядер — работы [35, 213, 257,
258, 264].
Так как 25А1 имеет 13 протонов и 12 нейтронов, последний нечет-
ный протон находится на уровне 5/2+ деформированного потенциала
252
(орбита № 5 на рис. 9.7). Действительно, все следующие возбуж-
денные одночастичные состояния: у (№ 9), у (№ 11), у (№ 8),
1Д (№ 14), имеются в экспериментальном спектре на рис. 9.11 и соот-
ветствуют уровням, на
ные полосы.
которых построены различные вращатель-
9/2 -554)2
7/2'
7/2~-412/1
ф- —MJ W
3/2' -208,8 7/2 -207i°
3[2 [5121
5/2 ------99,1
3,2 ------40)5
1)2 1/2'[5Ю]
453/1
9/2+-----309,5
7/2 Г503] 9/2*[б24]
Рис. 9.12. Экспериментальные уровни l83W и классификация
полос, основанная на учете связи вращений остова с одно-
частичным движением. Энергия дана в кэв [288].
483 512
‘ 434 К~5/2+
388 9/2 --------9/2 7
392------7/2
331 -----7/2 К=7/2~
28 Б------5/2
193 _____11/2 К 5/2
164 -----9/2
76_____ 7/2
57-----=5/2
8-- з/о
о 1/2
К = 1/2*
Рис. 9.13. Уровни энергий 239Ри, представлен-
ные так, чтобы показать вращательные полосы.
Энергия дана в кэв.
Интересно отметить, что предсказания модели оболочек для де-
формированных ядер, касающиеся различных одночастичных уров-
ней, являются почти правильными. Большинство из предсказанных
возбужденных уровней найдены в эксперименте, даже если их
энергии не согласуются с теорией. Спины основных состояний очень
хорошо объясняются в рамках этой модели. Это показано в табл. 9.2.
253
Таблица 9.2
Спины основных состояний тяжелых ядер, предсказываем
в модели деформированной ямы Ые
Ядро Предполагае- мая деформа- ция р0 'теор 'эксп Ядро Предполагае- мая деформа- ция po ^теор ^KCtl
^Еи 0,16 3 2 ±’ 5 2 ± 5 2 155Cd 0,31 5 2 +, 3 2 ~ 3 2
Ч!Еи 0,30 5 2 3 2 ' 5 2 W’Cd 0,31 3 2 » 5 2 + 3 2
MsTb 0,31 3 2 + ’ 5 2 + 3 2 0,31 5 2 ~
16в?Но 0,30 7 2 ~’ 1 2 ~t" 7 2 lee?Er 0,29 1 2 —, 7 2 + 7 2
lees9Tm 0,28 1 2 +'’ 7 2 1 2 1?JYb 0,29 7 2 +, 1 2 ~ 1 2
4?Lu 0,28 7 2 5 2 + 7 2 S’gYb 0,29 5 2 ~ 5 2
18^Та 0,23 5 2 +’ 7 2 + 7 2 177Rf 72П1 0,26 7 2 ”
>URe 0,19 го | со J 5 \ 2 "* ) 5 2 S’gHf 0,27 9 2 —
‘,%’Re 0,19 г СП | сч to 1 СЛ + s 5 2 0,21 J 2 — 7 ’ 2~ 3 ’’ 2~ 1 2
isijr 77 1Г 0,14 з 2 11 2+’ 2 + ’ 2~ 3 2 ^Os 0,18 1 2 — 3 ’ 2~ 9 ’’ 2 —
193Tr 77 1Г 0,12 3 1 11 2-г. 2 2 3 2 0,15 1 2 3 2— 11 2 + 3 2
Однако теоретические предсказания основываются на точном зна-
нии деформации ядра, которая, так же как и в четно-четных ядрах
[см. (6.152) и рис. 6.5], должна получаться из данных о значениях
В (Е2) для переходов в пределах основной полосы. Деформация,
полученная таким способом, всегда связана с экспериментальными
погрешностями, и одночастичный спектр можно подогнать лишь
в пределах этих погрешностей*.
* Обзор, посвященный наблюдаемым одночастнчным уровням деформи-
рованных ядер, см. в работе [278] .
254
Если установлены нильссоновские уровни для последней нечет-
ной частицы, то можно попытаться рассчитать другие свойства де-
формированных ядер, используя знания о соответствующих одно-
частичных волновых функциях. Например, можно попытаться пред-
сказать вероятности Е1-, Ml- или ЕЯ-переходов, изменение сред-
него квадрата радиуса в возбужденных состояниях, магнитные мо-
менты и т. п. Большинство из этих величин, так же как возбужден-
ные одночастичные уровни, зависит от различных членов в гамиль-
тониане Н' (9.32). Поэтому необходимо подробно рассмотреть влия-
ние гамильтониана Н' на одночастичные уровни деформированных
ядер.
§ 9.6. НЕ АДИАБАТИЧЕСКИЕ ЭФФЕКТЫ
9.6.1. Кориолисовы силы
Вернемся теперь к рассмотрению гамильтониана возмущения
И' в формуле (9.32). Одним из важнейших членов в Н' является
кориолисово взаимодействие
Hcoriolis= -*Wo(/+ /_ + /_/+ + 2/3 /3) = -(Ш) (I j )• (9.86)
Матричные элементы этого выражения легко рассчитываются
с помощью волновых функций (9.60):
< IMK' П' п2 ii0 а | Hcoriolls | /МК&п2 п0 а > =
= —2 С^: с$ {[6К. к_, 6Q,Q_. 4- (-1) '-Н X
х (_ 1)/-1/2 6К,_(К_1)ЙЙ,_(Й_1)] [(/ + /<) (/_/<+ 1)Х
X(/+Q) Q--Q+l)]i/2| + [6K,K + lfifi.fi+1 + (_l)/+i/2(_i)/-i/2X
Хбк'-(К+1)6й'_(й+1)][(7-^(/ + 7<+1)(/-О)(/ + П + 1)]1/2}-
--^-2№6л^6а.а. (9.87)
о
Здесь были использованы коммутационные соотношения (9.22)—
(9.24) для операторов /v и /v, которые, согласно соотношениям
(5.122) и (5.125), приводят к матричным элементам
< IMK i /± | IMK ± 1 > = ТЛ(/+Ю(/±К+1) (9.88)
и
< /О | /т | /О ± 1 > — J (/ + Й)(/ ±0 + 1). (9.89)
Заметим, что во втором из этих матричных элементов знаки ± обра-
щены по сравнению с первым.
255
Зависимость от углового момента / в выражении (9.87) содер-
жится только в той части, которая пропорциональна члену в фигур-
ных скобках. Он дает вклад в диагональные матричные элементы
с К' = К и Q' = Q только для полосы с К = 1/2. Этот матричный
элемент обычно принято записывать в виде
— так называемый параметр развязывания.
Рис. 9.14. Зависимость энергии вращательных
уровней от параметра развязывания а для полосы
сЛ'=*/2.
Это название он получил потому, что соответствует частичному
нарушению связи одночастичного и вращательного движений.
С учетом кориолисового члена в первом порядке теории возму-
щений формула (9.39) принимает вид
Е1КиПг naa = %aQ + (J(J+ l)-(K-Q)2) -у- в +
+ f-i-IK—Я| + 1 + 2пг) £т+('л0 + -МЕ|}_аГ(_1)'11х
— еб !—2№— . (9.92)
2 2
2S6
ртияние кориолисовых сил на полосы с К = 1/2 может быть очень
значительным: при больших значениях параметра развязывания
может измениться даже порядок уровней во вращательной полосе.
Это показано на рис. 9.14, где отложена зависимость энергии уровней
вращательной полосы от параметра развязывания а. Для а = О
уровни располагаются согласно правилу /(/ +1). При больших поло-
жительных или отрицательных значениях а порядок уровней ста-
новится совершенно другим.
В общем случае гамильтониан Hcorioiis смешивает две враща-
тельные полосы, для которых АД = ±1. Очевидно, что этот эффект
будет мал, если невозмущенные полосы сильно разделены по энер-
гии- Однако если нечетная частица связана слабо, то эти полосы
сильно перекрываются и поправка от кориолисовых сил важна.
В этом случае можно получить аналитическое выражение, описы-
вающее влияние кориолисовых сил на собственные энергии двух
таких полос, простой диагонализацией матрицы 2x2:
£/KQn0n2a — Е ( /Д£2п2 tl0 а ' ^Coriolis 1IК 162 ф- 1н2 п0 <%)> _Q
( !К~\~ 1 £2 —|— 1 п2 п0 <х | Нcarious I £/к+ш+ ins п„ а Е
(9.93)
Соответствующие решения равны
£± (7ДЙ«2Поа) -|-|£7КЦп2п0а-|-£/К+1й+1л2 лоа ±
। л Р 1 1 । л I С/Д~| Ш| п,, а |/7corfo;;g |/KQzta а> 1 /п
где АЕ -^= £/к<,„2„оа — Е/а: , ц, । Матричные элементы, входя-
щие в эту формулу, получаются из выражения (9.87) и могут быть
записаны в более удобном виде:
</МД + 1Q+ ln2 иоа| Hcoriolis | IMKQn., п0 а) =
- Лк[(/-Д)(/ + Д+1)]'/2, (9.95)
где
---U [(/_Д) (у + Д+ I)]1'2. (9.96)
2 /
Очевидно, что Д больше не является хорошим квантовым числом,
даже если остов все еще обладает аксиальной симметрией. Только
в случае, если нечетная частица связана сильно, величина А£
становится большой и Д будет приближенно хорошим квантовым
числом.
Влияние кориолисовых сил на уровни ядер впервые рассмотрел
Керман для ядра 183W [210]. В этом ядре наблюдаются две довольно
большие полосы с Дя = 1/2“ и Дл = 3/2 ” и два уровня, являющиеся
основанием полос Дл = 7/2" с энергией 0,453 Мэв и Дп = 9/2+
9 Зак. 1218 257
Таблица 9з
Спины и моменты инерции для некоторых нечетных ядер
В случае К = 1/2 приводятся также значения параметра раз
вязывапня а. В четвертом столбце даны моменты инерций
соседних четно-четных ядер
Ядро /о КЗв кэв а Ядро К кэв кэв
15о!Еи 5 9
2 71 122 2 66 90
15elGd 3 2 72 123 ^iTa 7 2 91 93
lseIGd 3 2 66 89 1 2 78 100
156£Tb 3 5
2 70 79 2 108 112
16ЛНо 7 2 63 73 *?s7Re 5 2 116 123
1 2 74 80 —0,77 2»iu 5 2 5 45
7 7
4JLu 2 76 78 2351 1 92b 2 31 45
7 2 75 89 2^Np 5 2 28 44
•„Pu 1 2 37 43
0,19
0,58
при энергии 0,309 Мэв (рис. 9.15). Основная полоса Кг- = 1/2 ',
за ней следует полоса с = 3/2 у начинающаяся при энергии
2,088 Мэв. Согласно предыдущему рассмотрению, кориолисово взаи-
модействие будет смешивать две нижние полосы. На рис. 9.15 пока-
зано сравнение между измеренными значениями энергии уровней
и энергиями, рассчитанными по формулам (9.94) и (9.92). Однако
следует помнить, что в этих расчетах подгонялись пять параметров,
а именно, моменты инерции полос 1/2~ и 3/2, основной уровень
полосы 3/2“, параметр развязываниями параметр смешивания Л1/2-
Поэтому в данном случае нельзя придавать большого значения со-
гласию с экспериментом.
В табл. 9.3 приводятся данные о спинах, моментах инерции и
параметрах развязывания а для некоторых нечетных вращаю-
щихся ядер. Для того чтобы показать влияние нечетной части-
цы на моменты инерции, в четвертом столбце приведены моменты
инерции соседних четно-четных ядер. В третьем столбце даны мо-
258
менты инерции возбужденных состояний с Д' — К + 1. Все пара-
метры были получены из эксперимента. Возникает вопрос, как хо-
рошо теоретически определяется параметр развязывания с помощью
формулы (9.91). Оказывается, что имеются случаи, когда встре-
о-)'----554,2
' (556.4)
----412,1
{/>29127 9/2—308,9 9^—309,5
512 ~ (23? 8) -
312 — 208,87/2-(206,0)
(208,8) . 99,1
г/2---(99,02)
3/2/512] 1/2~[510j 7/2~[503] 9/2 [62]
7/2~-----453,1
Рис. 9.15. Сравнение эксперимен-
тального спектра ,83W с теоретиче-
скими предсказаниями по форму-
лам (9.92) и (9.94). Теоретические
результаты даны в скобках.
чаются большие расхождения. По-видимому, это связано с тем, что
так называемые деформированные одночастичные состояния в дей-
ствительности являются более сложными конфигурациями. Доволь-
но подробные исследования этой возможности проводились в рабо-
те 12581.
9.6.2. Отклонение от аксиальной симметрии
Связь одночастичного движения с коллективным в деформиро-
ванных ядрах, описываемая гамильтонианом Н', исследовалась
Фесслером [132]. Он диагонализировал полный гамильтониан воз-
мущения Н' (9.32) в базисе собственных функций оператора НсВц +
Ь Н°р (9.60). Величины К и Q больше не являются хорошими
квантовыми числами и значительно смешиваются. Волновые функ-
ции гамильтониана Н (9.29) являются суперпозицией базисных
функций (9.60):
Ф/млр=-- Z A^w\lMK^n2n^ (9.97)
К. R
пг, п„, а
и определяются диагонализацией гамильтониана Н. Для таких со-
стояний были рассчитаны энергии и вероятности электромагнитных
переходов. В этом подходе магнитный дипольный оператор ЛДМ
и электрический квадрупольный оператор Q2m состоят из двух час-
тей. Первые части М‘щ и Qc2°Jl соответственно представляют собой
колтективные мультипольные операторы, обусловленные возбуж-
дением остова ядра. Вторые части М\рц и соответственно связа-
ны с нечетной частицей. Имеем
Л'11.л = Л4Г'' + Л4^; (9-98)
9*
159
ношения приведенных вероятностей £2-переходов (9/2 -> 5/2)'(7/2-»-
5/2) внутри основной вращательной полосы в 1мЕп (рис. 9 IfT
Видно, что эта величина в обоих подходах почти одинакова. В дву
следующих строках приведены отношения вероятностей £2-перех*Х
дов из полосы с = 3/2+ в основную полосу с йя - 5/2+ к вероят'
ности перехода внутри основной полосы. Переход «= 3/2+ *'
—— 5/2+ (см. рис. 9.16) является одночастичным переходом
В этом случае теория Феслера дает хорошее согласие с эксперимен-
том, тогда как одночастичная модель дает расхождение примерно
в 103 раз.
1289 23/2
165,,
67il°
1067 21/2
861 19!2 815 13/2
636 7/2
566 .5/2
514-------3/2
1-я [-полоса
672 17/2
499 15/2
345 13/2
209,8 11/2
94,7 9/2
О 7/2
687 11/2
361 3/2
2-я д'-полоса
К=3/2=7/2-2
[523 7/2]
К=7/2 5=11/2 = 7/2+2 К=3/2+
[523 7/2]п2=0 [523 7/2] [4113/2]п2=0
Рис. 9.17. Спектр ядра 1СГ>Но, в котором наблюдаются
две у-полосы. Приведенные вероятности перехода
между основным состоянием и у-колебательнымч
уровнями равны В (£2) =0,050 для 7/г-»-3/2, 0,040 для
'/г-’-’Чг и 0,08 для 0-1-2. Энергии даны в кэв [108].
Подобные эффекты можно найти и в других ядрах. Причина уси-
ления одночастичных переходов заключается в том, что второй,
третий и четвертый члены в гамильтониане И' (9.32) смешивают
малые компоненты коллективных конфигураций (т]-колебании)
с одночастичными конфигурациями. Эти малые коллективные при-
меси могут увеличить вероятности одночастичных £2-переходов на
порядки величины, тогда как на чисто коллективные переходы та-
кие поправки влияют мало (например, на отношение вероятностей
переходов внутри основной полосы, табл. 9.4)*.
* Коллективное усиление одночастичных переходов в легких ядрах О,
16N наблюдалось в работе Роуза с сотр. [159].
262
Еще одним важным результатом единой теории коллективных
пебаний, вращений и одночастичного движения является пред-
сказание существования двух у-вибрапионных полос [см. формулы
/0 84) и (9.85)]. Они экспериментально обнаружены Даймон-
м Элбеком и Стефенсоном 1108] в ядре 165Но и показаны на
д°’ 9 17. Видно, что и величина энергетического расщепления, и зна-
чения спинов уровней с энергиями 514 и 687 кзе подтверждают
их интерпретацию как у-полос, построенных на основном состоянии
1499 23/2 isg
---- В5™
1285 21/2 ''-1280
1102 7/2
1053 19/2 1086=5/2.
------ 97?_Л?
862 17/2 V2
у 678 5/2 668 15/2
617 —~3/2
580 1/2 510—1312 429 7/2
352 11/2 5/2
1-я /- полоса 24[__912 2-я полоса
137,0 7/2
58.0 5/2
О 3/2
К=1/^=3/2-2 К=3/2* K=7/2+=3/2i-2 К=5/2* К=1/2+
[4113/2] [4113/2]п2=0 [411 3/2] [413 5/2]п2=0 [4111/2]п^0
Рис. 9.18. Спектр ядра 159ТЬ, в котором наблюдаются две у-по-
лосы. Энергии даны в кэв [108].
К. = 7/2. Такие же данные существуют и для 159ТЬ (рис. 9.18). Та-
ким образом, наличие у-полос в деформированных нечетных ядрах
указывает (согласно самой природе этих у-полос) на динамические
отклонения этих ядер от аксиальной симметрии.
§ 9.7. МАГНИТНЫЕ МОМЕНТЫ НЕЧЕТНЫХ
ДЕФОРМИРОВАННЫХ ЯДЕР
Магнитные моменты сферических ядер были рассмотрены в § 8.5.
Но аналогии с формулой (8.91) магнитные моменты различных со-
стояний деформированных нечетных ядер определяются как сред-
ние от z-компоненты магнитного дипольного оператора (9 101) по
состоянию | 1МК&п2п0а) (9.60), взятые для подсостояния с М = Г.
Р Ро | gn lo -|-G0| III[Qn2n0a). (9.102)
Оператор 7Й1Ц в выражении (9.101) записан в лабораторной си-
теме. Для вычисления матричного элемента в (9.102) необходимо
263
выразить его через углы Эйлера и внутренние координаты. Инцек
р в формуле (9.101) обозначает сферические компоненты векторного
оператора Мг В частности, сферические компоненты вектора G
выражаются через декартовы координаты по обычному правилу
= 2(G\.±iGy), Gu — Gz. (9.103)
Преобразование компонент G^ в лабораторной системе к компонен-
там Gv во внутренней системе выполняется с помощью соотношения
ёц = 2 D.v (0;) Gv. (9.1 Q4j
Первое слагаемое матричного элемента (9.102), т. е. матричный
элемент от /0, можно получить легко:
Но (ПК^п2 п0 а | gR 10 | ПК&п2 п0 а) = р0 gR I, (9.105)
так как = М | IMK). Для дальнейшего будет необходим
матричный элемент общего вида
</' М' К' й' п2п0а| 1IMKDn2 поа.) —
= (ГМ' К' й' п2 /гоа] v (0,) Gv lMKDn2nu а>, (9.106)
V
который содержит второе слагаемое матричного элемента (9.102)
как частный случай. Пользуясь функциями (9.60), получаем
( Г М' К' й' п? поа| У (0j) Gv | /7ИДЙи2 zi0 а>
= [^+i)(2/;+i)]v^. 2 {<J^., D.:! Л >
X <afi'|Gv|at2> + (—1)/+,/2-2д'1Тфй <7?ЛГК. \D1111\DImk'> >’
X <ай' | Gv | а— й) + (— 1)/' + 1/2-2К' х
X лф£2< (Dw’_K-1|Пмк> <а—Й' | Gv | ай> +
+(— 1/ Лфй- (Dm- —к.- | Pjv | Dm—к) <а— И' | Gv | ct—й>).
(9.107)
Здесь лФа — четность состояния q>n [см. (9.59)1. Теперь легко вы-
полнить интегрирование по углам Эйлера [см. (6.13)]. Используя
(9.58) и учитывая, что G( являются сферическими компонентами
векторного оператора, имеем для матричного элемента
<ай'| G{,| аЙ> = — (a—Й' |Glv|cc—Q>, (9.ЮЮ
который отличен от нуля, если v = Q' — й. Используя это свой-
ство и симметрию коэффициентов Клебша—Гордана при обруше-
нии знаков магнитных проекций квантовых чисел, находим для мат
ричного элемента (9.107):
</' М' К' й' п2 ггосх| дц | IMKSln2 п0 а> =
264
=т ]'/2 (Л 1 1 Mfx (1 + Лф£3 Яфо') х
X |(/1/' | Д7С—КК') <а£2' | Go- _<> I +
X a-F| Gi | сх---• (9.109)
Дчя частного случая магнитного момента
м=/, К’ = КЛ
K = Q, Q'- Q, р = 0. )
Требование /< = £2 показывает, что рассматриваются магнитные
моменты вращательной полосы, в которой у-колебания не возбуж-
даются. Это всегда имеет место для основного состояния Подстав-
ляя (9.100) в (9.109), находим
р- p0!g« М- 1 [К <aF I Go | «Ю + бд-1 /2бд-'1/2 X
X (_1/н12-6/2л<1)к(2/+1)/а^-|д;|а-^-\]}. (9.111)
Матричные элементы <a/<|G6| «/<> рассчитываются с помощью
формулы (9.101):
(«К I (ёг~gR)j0 + (gs—gi) «о | «К> =
K{g —gR)A-{gs— gi) <aK\s0\aK>. (9.112)
Как н для разложения (9.69), имеем
I «Ю = 2 «/.л | М/Л2 >, (9.113)
l,A
где 2 /< — Л. Таким образом,
<«/<|s0|a/<> = ^-Z(|a(z“,_J2-|^+i/2|2) (9-114)
и из выражения (9.111) получаем
ll = Ho{g« + gR)K + ~^ (gs~gi)X-
X2(1F“’ 1|2-|C,1|2)1). F^l/2.
Z ZK-5 JJ
(9.115)
Для уровня, являющегося основанием вращательной полосы, I = К
н этот результат сводится к следующему:
Iх — 1*о ; ।[gj +gR + ~~ (gs—gi) 2 (| а\к-1/212—
265
Таблица 95
Магнитные моменты ядер с нечетным протоном
Ядро J [WnzAKJ Предполагае- мое значение 6 Расчет p, Эксперимент ц
4F 1 2 1 220 V =0,4 2,7 — 2,63
5 1
l»F<a> T 220 T =0,4 3,7 3,5
3 1
??Na T 211 V =0,5 2,4 2,22
5 5
2зА1 T 202 ~2~ =0,3 3,7 3,64
5 5
i6aEu T 532 V 0,16 3,1 3,4
5 5
lt33Eu ~2~ 413V 0,30 0,9 1,5
3 3
ЧГГЬ 2 411V 0,31 2,2 ±1,5
7 7
*S?Ho ~2~ 523 V 0,30 4,5 ±3,3
1 1
16eCTm V 4HV 0,29 —0,2 —0,21
7 7
T 404 V 0,28 1,4 2,0
7 7
41Ta V 404 2 0,23 1,5 2,1
1^Та<б) 5 2 5 402 V 0,23 3,7 з,з
4|Re 5 2 5 402 V 0.19 3,7 3,14
5 2 5 402 V 0,19 3,7 3,18
197?Ir 3 2 3 402-g- 0,14 0,0 0,2
4flr 3 2 3 402 V 0,12 0,0 0,2
2l?Ac 3 2 i 530 у =0,2 2,9 1,1
2?’3Np 5 2 5 642 V 0,25 3,0 ±(6±2,5)
*37Np(B> 5 2 5 523 у 0,25 1,0 = 1,4
2ilAm 5 2 5 523 у 0,27 1,0 1,4
2h3Am 5 2 сл ND Co 0,27 1,0 1,4
<а) Изомерное состояние ,,F с энергией 197 кэв.
<б> Изомерное состояние 181Та с энергией 482 кэв
<в> Изомерное состояние 23’Np с энергией 60 кэв.
266
—1 С/К М /2 I2) j ,
(9.116)
2
Целесообразно указать другой способ записи полученного выра-
жения Некоторые авторы определяют гиромагнитное отношение
gK соотношением
<аК | Go | аК> = К (gt—gid-
(9.117)
Подставляя это в (9.111), находим
|.(/,Ю *H»fo'(Ti-i^g«7+r) мя <9118)
И для основного состояния (/ = К)
И -j-T^-(gR+ fgK)-
(9.119)
Таблица 9.6
Магнитные моменты ядер с нечетным нейтроном
Ядро £ < e Предполагав мое значение 6 Расчет ц. Эксперимент Ц Ядро N e Предполагае- мое значение 6 Расчет ц Эксперимент Ц
iiNe 3 2 3 211T -0,5 —0,8 —0,66 7 2 7 514 - 2 0,27 1,4 0,6
_5_ 2 5 202 — 2 ^0,4 —1,1 —0,86 B?Hf 9 2 9 624 — 0,26 —i,o —0,47
iBtGd 3 2 3 521 — 2 0,31 —0,5 —0,30 lg39W 1 2 1 510 — 2 0,21 0,8 0,12
‘esGd 3 n 3 521 — 2 0,31 —0,5 —0,37 H?Os 1 2 510y 0,18 0,8 0,12
ЧРу 5_ 2 5 642 — 2 0,31 —0,6 —0,37 3 2 3 512 — 2 0,15 0,9 0,65
\6?Dy 5 2 5 523 — 2 0,30 1,1 0,51 2 5 633 у 0,23 0.7 0,51
^Er 7 2 7 633 — 2 0,29 -0,8 ±0,5 iltu 7 2 7 743 T 0,24 - 0,6 —0,34
loiYb 1 2 1 521 — 2 0,28 0,7 0,46 2fsSPU 1 2 631T 0,26 —o,i ±0,02
lo’Yb _5_ 2 512 — 2 0,28 —0,8 —0,65 5 2 5 622— 0,27 —0,5 ±0,1
267
Обычно gK рассматривается как эмпирическая константа, однак
легко видеть, что, сравнивая соотношения (9.112) и (9.114) с опреде°
лением (9.117), эту величину можно выразить через коэффин/
енты о/л- и‘
Полученное выражение для магнитного момента справедливо
если К =/= 1/2. Для К = 1/2 возникает дополнительный вклад [См’
формулу (9.111)) от матричного элемента (oy|Gi |а — -1>. в этом
случае магнитный момент уровня со спином I дается выражением
И = Ноуу {(gs~gz)[y 2(az2o—az2i) + (—!);-I/2 X
ХлФ1/2^-(27+1)^а?о14 (gz-gK)|4- + (-l)'’1/2X
х у (2/+ 1) а]+ £«/(/Д1)| (9.120)
Здесь а — параметр развязывания (9.91). Полученные теоретиче-
ские результаты, т. е. формулы (9.116) и (9.120), были впервые
сравнены с экспериментом Моттельсоном и Нильссоном [264]. Коэф-
фициенты О/д были получены из одночастичных волновых функций
деформированных ядер, коллективные гиромагнитные множители
gii приближенно брались равными ZIA (см. об этом в § 9.6). Однако
в действительности меньше, чем ZIA на 20—30% [172].
В табл. 9.5 и 9.6 сравниваются данные теории и эксперимента.
Учитывая неопределенности, связанные с gR и с поправками, кото-
рые могут возникнуть благодаря конфигурационному смешиванию,
согласие является довольно хорошим. Вообще, согласие с экспери-
ментом для ядер с нечетным протоном несколько лучше, чем для ядер
с нечетным нейтроном.
§ 9.8. ДАЛЬНЕЙШЕЕ РАЗВИТИЕ МОДЕЛИ ОБОЛОЧЕК
ДЛЯ ДЕФОРМИРОВАННЫХ ЯДЕР
Можно рассмотреть несколько возможностей обобщения модели
оболочек для деформированных ядер. Во-первых, бесконечный
деформированный осцилляторный потенциал в действительности не
является реалистическим. Как уже подробно обсуждалось в случае
оболочечной модели для сферических ядер (см. § 8.2 и 8.3), бо-
лее реалистическим, по-видимому, является конечный потенциал ти-
па Вудса — Саксона со спин-орбитальным взаимодействием. (Факти-
чески слагаемое с I2 в потенциале (9.62) было введено, чтобы описать
эффект потенциала Вудса—Саксона по крайней мере для одночастич-
ных энергий.) Расчеты такого рода выполнялись в работе [3621,
в которой в соответствии с работой Готфрида [167] использовался
потенциал деформированной прямоугольной ямы. Готфрид исполь-
зовал разложение по степеням параметра деформации ро, в то время
как в работе [362] необходимые матричные элементы вычислялись
точно.
268
Деммер и Грин [228] выполнили расчеты одночастичных уровней
зависящего от скорости несферического потенциала с диффуз-
ным краем*. Они использовали очень короткодействующий нело-
кальный потенциал указанного вида, который допускается теорией
ядерной материи. Их волновое уравнение эквивалентно следующе-
му:
f—Г—— Р2 + 2Р V- Р + Р2 -т—-1 + Го1 • —+
| 4 [ 2т 2т 2т J И+2ца2цУ2ц/
+ С1 • s| ф = Еф, (9.121)
где использованы соображения, приведшие к соотношению (9.4).
Здесь Го (г) — локальный средний потенциал типа Вудса—Саксона,
т — эффективная масса:
т ------------,------,
1 — (а3 Л4/2Д2) Уо Г)
м
(9.122)
и а — размер области нелокальное™ потенциала. Собственные
функции и собственные значения, соответствующие одночастичным
уровням в потенциале этого типа, были найдены авторами с помощью
теории возмущений по отклонению от сферической симметрии. По-
лученные результаты очень похожи на результаты Нильссона [283].
Было показано, что дополнительные члены с оператором импульса
р в уравнении (9.121) приводят почти в точности к таким же эффек-
там, что и член в I2, который был введен феноменологически [229].
Это, в особенности, справедливо для больших деформаций.
Расчеты Деммера и Грина были улучшены в работе [310] введе-
нием более сложной энергетической зависимости потенциала. В ней
также был учтен эффект спаривания, обусловленный остаточным
взаимодействием. Сравнение рассчитанных одночастичных возбуж-
денных состояний с экспериментальными низкоэнергетическими
спектрами нечетных ядер показало, что даже эта сложная модель
не дает удовлетворительного количественного согласия с экспери-
ментом.
В работе Феслера и Шелайна [136] были рассчитаны собственные
функции для сферического и деформированного потенциала Вудса—
Саксона со спин-орбитальной связью типа связи Томаса. Волновые
функции деформированного ядра разлагались по осцилляторным
Функциям, а зависимость от деформации коэффициентов разложе-
ния и энергий была протабулирована подобно тому, как это
сделал Нильссон [283]. Подобные расчеты выполнялись также Ро-
стом [308]. Эти расчеты не дали значительных улучшений в одно-
частичных энергиях и вероятностях переходов.
Влияние потенциала, зависящего от скорости на связанные одночастич-
ые состояния сферических ядер, рассматривалось в работах [251, 308, 391].
269
Модель оболочек для деформированных ядер можно также обоб-
щить на случай ядер со статической неаксиальной деформацией'
Это приводит к модели асимметричного ротатора для нечетных ядеп
Соответствующие расчеты были выполнены Ньютоном [281, 282]
Он ввел последнее слагаемое в гамильтониане возмущения Н' (9 32)
-Мео2 г'2 [т] (У23 (6', ер') + У2_2 (6', ер'))]
в гамильтониан HOsp и рассматривал координату г] не как динами-
ческую переменную, а как статический параметр, характеризующий
трехосное ядро [см. гл. 7 и, в частности, (7.2)]. Поэтому оболочечный
потенциал трехосного ядра формально совпадает с выражением
(9.62)
HBsp -—-н’-мпх'2- +
2т 2
+ C1-S+D12 (9.123)
с тем существенным отличием, что все три частоты соя, ео,;, ео раз-
личны:
где
(9.124)
(9.125)
Таким образом, частоты обратно пропорциональны соответствую-
щим ядерным осям [см. (2.24)]. Условие (9.74), вытекающее из пред-
положения о несжимаемости ядра, приводит к выражению, анало-
гичному выражению (9.75), а именно
(9.126)
Одночастичные состояния, полученные в модели оболочек трех-
осного ядра, будут использованы в дальнейшем для расчетов
коллективной потенциальной энергии. Более подробное обсуждение
этих вопросов см. в т. 3.
270
§ 9.9. НЕЧЕТНО-НЕЧЕТНЫЕ
ДЕФОРМИРОВАННЫЕ ЯДРА
Свойства нечетно-нечетных ядер в значительной мере определяют
нечетными протоном и нейтроном. Протон и нейтрон движутся
реформированном потенциале. Если пренебречь всеми эффектами
взаимодействия, то гамильтониан нечетно-нечетной системы можно
записать в виде [см. (9.25)—(9.28)]
н°=н°со11+й°р.
(9.127)
[I2—(/з—/а,!)—7з(2)>21 Ч- .^ГХ
2Уо IbnT]
< \2 1, л-3 г <э2 . 1 д2 i ,
Х[Нз-./з(1) -! (2)) +
+ -^СО^ + С2Т12 (9.128)
н° = у M(o2r'24ci;-s;+ni1'2-
[ 2Л1 2
-A4o)2p(1r'2E2O(r')j . (9.129)
Штрих показывает, что соответствующие величины относятся к внут-
ренней системе координат.
Гамильтониан возмущения легко получить по аналогии с выра-
жением (9.32). Одночастичный гамильтониан разделяется на га-
мильтониан протона и нейтрона до тех пор, пока пренебрегается
остаточным взаимодействием между двумя нечетными нуклонами
и вышеупомянутым гамильтонианом возмущения. Пусть протон
находится на одночастичной орбите фцр с энергией &’а а нейтрон —
на орбите с энергией %о . Тогда волновые функции и энергии,
соответствующие гамильтониану Н°р, имеют вид
или Ф+Щ = гР+орФ+£2п, й’й1 = й,£2р + ^’оп (9.130)
Фньс2 ф±£2р Фт% , + (9.131)
В первом случае проекции углового момента на ось г' склады-
ваются, во втором — они вычитаются. Так как коллективный га-
мипьтониан зависит от суммы /з (1) + /з<2), то конфигурации (9.130)
и (9.131) приведут к невырожденным состояниям, отличающимся
энергией вращения. Обычно эта энергетическая разность мала по
сравнению с одночастичными энергиями $qv. Таким образом, одна
из конфигураций (9.130) или (9.131) будет описывать основное со-
стояние, тогда как другая — низколежащее возбужденное состояние.
Полная волновая функция гамильтониана Неон + Н%Р и соот-
271
ветствующие энергии получаются аналогично
чаю
(см. § 9.3). Результат имеет вид
одночастичному еду.
~6л" {Dmk (бу) Чайу Фа£2п
( 2К Dm—К (0/)Яфйр •П'<Р£2,1 Фа — йр фа— пп| х
х Х|к-Пр-пл |щ(л)|»о>,
11MKQV л2 п0
(9.132)
7/2 [523] 7/2^633]
330 -
----
7/2[523] 1/2[521] 7/2[523] 5/2[512]
।------------1 г---------------,
—6 421 .
-----7
373 +
348 ±-----4
-----5
260
-----4
294
------6
181 4-
168~~~3~151
----8
1S1
— 3
82
53 ---Г?
----2
О _ 9____
----О --------7
с. 9.19 Экспериментальный спектр ядра |ССНо, в кото-
ром указаны различные вращательные полосы [349].
где
К—— Q„- 0, ±2, ±4, ....
/ I*'1, |К|+1, |Л'| + 2, ... (9.133)
и
E/KQp Qn П2 п„а ~ ^айр + ^апп 4“ (^ (/ + 1) —
-(/С-йр-^пЯ±е+[±| /c-fip_Qn| +
Z \ z I
-|-1+2n2j Ev + ^п0+— j Ер. (9.134)
В этих формулах представлен только случай, соответствующий
(9.130), для конфигурации (9.131) все полностью аналогично. Ана-
логия соотношений (9.39) и (9.134), а также (9.60) и (9.132) оче-
видна.
272
Интересный частичный случай возникает при К = 0, когда
волновые функции (9.132) принимают вид
I IMQ Qp — «2 «О «> = | (е>) <fa- Op -
- (-1/ Ф^-СрФЙР] Хоп, (11) I «о>- (9.135)
Две волновые функции в скобках не одинаковы, поэтому нельзя
сделать вывод о том, что возможны только четные или нечетные спи-
ны что имело место для четно-четных ядер [см. условие (6.129)1;
мы'должны заключить, что для состояний (9.135) возможны все
значения спинов I = 0, 1, 2, ... Как будет показано ниже, между
нечетными нуклонами действует остаточное взаимодействие. Сред-
ние от этого взаимодействия различаются для четных и нечетных
спинов вращательной полосы состояний (9.135), так как функции
(9.135) зависят от фазового множителя (—I)7. Поэтому можно ожи-
дать сдвига «нечетной полосы» (нечетные спины уровней) по отно-
шению к «четной вращательной полосе» (четные спины уровней).
Эго подтверждается в эксперименте и показано на рис. 9.19, на ко-
тором представлен экспериментальный спектр ядра 166Но, получен-
ный Страблом и сотр. [349]. Хорошо видны сдвиги уровней с чет-
ными и нечетными значениями спинов, обусловленные остаточным
взаимодействием и фазовым множителем (—I)7 в волновой функ-
ции (9.135). Над двумя полосами, которые построены согласно
правилам (9.139), указаны одночастичные состояния нечетных нук-
лонов. Такое смещение уровней с четными и нечетными значениями
спинов во вращательных полосах с К = 0 впервые наблюдал Азаро
в ядре 242Ат [26].
В общем случае квантовые числа одночастичных уровней Qp
и определяют основания двух низколежащих вращательных по-
лос с последовательностью спинов:
/Х=^|ПР—Qn |, |ПР—йп|+1, + ...; g
/2 = |Qn + Qp|, |Qn + QP|-! 1, l^ + QJ + 2, ...
Как было предположено Бором и Моттельсоном [51], можно ожи-
дать, что для данного нечетно-нечетного ядра одночастичный уро-
вень нечетного протона будет тем же уровнем, что и в соседнем не-
четном ядре с одинаковым числом протонов (аналогично для нейт-
ронов) Это было подтверждено экспериментально. В работе Пекера
1295] было также показано, что, если нечетно-нечетное деформиро-
ванное ядро может иметь спин основного состояния /а или /2, то
первое возбужденное состояние часто имеет спин 12 или соответ-
ственно.
Ответ на вопрос о том, какое значение спина, /х или /2, является
спином основного состояния, зависит от остаточных сил между не-
четными нуклонами. В сферической модели оболочек эта задача
решается правилами Нордгейма [286, 287], которые гласят, что спин
273
нечетно-нечетного ядра с нечетными нуклонами на одночастичных
уровнях jn и jp есть
i=\in—ip\ для
Z Z
И
in—ip\^l ^in+ip для /n = /n±-^-; jp^lp±~ (9.137)
z z '
Первое из этих правил называется сильным правилом Нордгей-
ма. По-видимому, эти правила утверждают, что внутренние спины
последнего протона и последнего нейтрона имеют тенденцию взаим-
но сокращаться. Эти эмпирические результаты были теоретически
обоснованы де Шалитом [107] и Бринком [60], которые показали, что
если учесть остаточные силы конечного радиуса действия вида
= — (1 — а4- <т7) Vo f (r,j), (9.138)
то для а, больших 0,1, состояние со спином / = | jn — jp | энерге-
тически лежит значительно ниже других возможных состояний не-
четно-нечетного ядра, при условии, что величины (Д — /р) и (/„ —
— /„) противоположного знака. Если эти величины имеют одинако-
вый знак, то энергия состояния с /=/'₽ + jp понижается. Для
очень больших а этот уровень может оказаться даже ниже уровня
с | jp — jn |. Однако расстояние между двумя конфигурациями очень
мало и слабое возмущение может легко изменить порядок уровней.
Эта модель была обобщена Галахером и Мошковским [156] на
случай деформированных ядер. Они предположили, что нечетные
нуклоны всегда связаны так, что проекции их внутренних спинов
на внутреннюю ось 2пи параллельны. При этом предполагается,
что ядро имеет достаточно большую деформацию, поскольку только
для больших деформаций и А, и 2 становятся хорошими квантовы-
ми числами. (Для реального случая это выполняется только прибли-
женно.) Отсюда получаем правила связи для деформированных ядер:
I = | Qp—йп |, если Йп = Ап ± у; Ц, = А,, + j- (9.139)
и
/ = |йр + йп|, если Qn = An±y, QP = AP+-J-
При рассмотрении всех нечетно-нечетных ядер (не только дефор-
мированных, но также и сферических) было найдено, что эти пра-
вила связи в общем объясняют спины основных состояний. Они
нарушаются в основном для ядер вблизи замкнутых оболочек. Ти-
пичный спектр нечетно-нечетного ядра был показан на рис. 9.19
для 166Но, где указаны полосы, соответствующие конфигурациям
(9.139). Видно, что для полосы с К = 0 наблюдается специфическая
структура, а для полос с 0 этот эффект, зависящий от спинов
частиц, отсутствует.
Глаза Ю. ГИДРОДИНАМИЧЕСКАЯ
МОДЕЛЬ ЯДРА
§ 10.1. ВВЕДЕНИЕ
В 1947 г. Болдуин и Клайбер [28, 29] обнаружили, что сечение
реакции фотоделения ядер имеет четко выраженный максимум (ги-
гантский резонанс) в области энергий порядка 15—20 Мэв. Подоб-
ные максимумы были вскоре найдены в сечениях других реакций,
происходящих под действием фотонов: (у, и), (-р, р) и т. п. Поэтому
Рис. 10.2. Типичный спектр тор-
мозного излучения.
ПучОН
налетающих щотоноб
Рис. 10.1. Схема типичного экспе-
римента для исследования фото-
ядерных реакций.
можно считать, что гигантские резонансы в сечениях фотоядерных
реакций являются общим характерным свойством всех ядер.
На рис. 10.1 изображена схема типичного эксперимента для оп-
ределения сечений фотоядерных реакций с вылетом частиц. Если
бы пучок падающих фотонов был монохроматическим, то измеряе-
мый выход частиц Y удовлетворял бы соотношению
Y=jo, (10.1)
гДе / — поток фотонов, а о — сечение рассматриваемой реакции.
Однако обычно используемые пучки у-квантов представляют собой
тормозное излучение электронов, ускоренных с помощью цикли-
ческих или линейных ускорителей. Поскольку при торможении
электронов могут испускаться фотоны разных энергий, спектр соот-
ветствующего излучения имеет вид, подобный кривой, изображенной
275
на рис. 10.2. Таким образом, в экспериментах, выполненных с тор-
мозным излучением, измеряются энергия электронов Ео и выход
Е<,
Y(E0) = J /(£, E0)o(E)dE. (10.2)
Е = 0
Чтобы определить сечение, необходимо решить данное интеграль-
ное уравнение. Эго легко было бы сделать, если бы спектр фотонов
/ (Е, Ео) имел простую форму, подобную представленным на
рис. 10.3.
В случае спектра прямоугольной формы (рис. 10.3, a), j (£)_
= с = const, решение уравнения (10.2) имеет вид
Рис. 10.3. Схематическое
представление спектра
тормозного излучения.
о(£0) = ±
с
dY (Ев)
dEu
(Ю.З)
В случае спектра треугольной формы
(рис. 10.3, б), j (Е) = с + ЬЕ, где Ео =
= —с/b, имеем соответственно:
а(Е0)
£ d* Y (Е„)
b dE%
(Ю-4)
ные от выхода реакции
Кривая / (Е), описывающая действи-
тельную форму спектра тормозного излу-
чения (см. рис. 10.2), в области больших
энергий лежит между кривыми а и b рис.
10.3 и неограниченно возрастает в области
малых энергий фотонов. Поэтому, чтобы
правильно определить вторые производ-
[уравнение (10.4)], необходимо иметь до-
статочно точные экспериментальные данные. Особенно трудно
этого добиться в области энергий Ео > 25 Мэв. Для определения
сечения реакции с помощью соотношения (10.4) были развиты
различные методы [83, 296].
Чтобы обойти трудности, связанные с использованием сплошного
спектра, Гольдемберг [166] и Аксель с сотрудниками предложили
метод «монохроматизации» фотонов, основанный на измерении энер-
гии электрона, испустившего тормозной квант. Зная эту энергию,
можно определить энергию фотона, вызвавшего ядерную реакцию.
В описываемом методе электрон наблюдается на совпадениях с про-
дуктами реакций независимо от того, являются ими рассеянные
фотоны [290] или фотонейтроны [222]
Наиболее современный метод получения «монохроматических»
у-квантов был разработан Тзара с сотр. [254, 255] и Фульцем с сотр.
[154]. В этом методе монохроматические фотоны получаются при
аннигиляции налету позитронов, имеющих небольшой разброс по
энергии.
На рис. 10.4 представлен типичный пример гигантского резонан-
са в сечении реакции 40Са (у, п). Можно видеть, что этот резонанс
276
I
ndD^‘anHahdQ
имеет ярко выраженную структуру, обусловленную его расщепле-
нием на ряд отдельных максимумов. Механизм возникновения этой
структуры обсуждается в гл. 11.
§ 10.2. КРАТКИЙ ОБЗОР ФОТОЯДЕРНЫХ
РЕАКЦИЙ
Рис. 10.5. Схематическое изобра-
жение уровней четно-четного ядра.
В области ниже порога имеется не-
большое число уровней, плотность
которых возрастает с увеличением
энергии возбуждения.
Основные фотоядерные реакции — реакции с испусканием нук-
лонов. В средних и тяжелых ядрах порог этих реакций лежит в об-
ласти энергий около 8 Мэв. На рис. 10.5 схематически представлены
уровни четно-четного ядра. В области низких энергий имеется не-
большое число уровней. По мере увеличения энергии возбуждения
возрастают как плотность уровней,
так и их ширины, что приводит
к быстрому перекрыванию уров-
ней при энергиях, превышающих
энергию отделения нуклона. Наи-
более характерные свойства сече-
ний фотопоглощения наблюдают-
ся в области энергии возбуждения
ядер от 12 до 20 Мэе, где располо-
жен сильный резонанс (гигантский
резонанс) шириной Г = 3 -j-
-4-4 Мэв* (рис. 10.6). В области низ-
ких энергий существует лишь не-
большое число слабо возбуждаю-
щихся уровней 1“ (дипольных со-
стояний). В области между поро-
гом отделения частицы и гигант-
ским резонансом находится ряд более широких уровней.
Так как состояния непрерывного спектра (Е > 0; области II
и III на рис. 10.6) распадаются главным образом с испусканием
частиц, а не у-квантов, ширины уровней, расположенных в областях
II и III, значительно превышают ширины уровней области I. Струк-
тура сечения фотопоглощения в областях / и II сильно зависит от
свойств уровней, между которыми происходят переходы, вслед-
ствие чего эта структура заметно меняется от ядра к ядру**. В про-
тивоположность этому, сечения фотопоглощения в области гигант-
ского резонанса характеризуются следующими свойствами***:
1 . Во всех ядрах эти сечения имеют широкий максимум.
2 . Средняя энергия Ео резонанса медленно меняется с Л:
для средних и тяжелых ядер Ео » А—'Е. Заметные отклонения от
* Такую ширину гигантских резонансов имеют ядра сферической фор
мы. — Прим. пер.
** См., например, работы [197, 198].
*** См., например, работы [261, 275].
278
этого правила наблюдаются лишь в области легких ядер (рис.
10 7)*-
3 Ширина резонанса меняется от 3 (ядра с заполненными обо-
лочками) до 6 Мэв (сильно деформированные ядра).
4 Поглощение в области резонанса очень велико. Интеграль-
ное сечение fo (E)dE обычно исчерпывает с погрешностью от 10 до
20% классическое дипольное правило сумм, если интеграл берется
по области гигантского резонанса.
Рис. 10.6. Схематическое изображение спектра фотопогло-
щения. В области 1 наблюдаются дискретные уровни; в об-
ласти II происходит поглощение фотонов с возбуждением
уровней, расположенных в непрерывном спектре; III— об-
ласть гигантского резонанса [197].
О 50 100 150 200 А
Рис. 10.7. Зависимость энергии гигант-
ского резонанса £ся от А.
При более высоких энергиях вплоть до порога рождения мезо-
нов (~140 Мэв) сечение поглощения, по-видимому, очень мало. Од-
нако выше порога рождения мезонов сечение снова возрастает. Как
уже упоминалось, наиболее важ-
ный вклад в сечение фотопогло-
щения дает электрическое ди-
польное (Е1) поглощение. Этот
результат можно грубо объяс-
нить следующим образом. Сог-
ласно уравнениям (1.16) и (1.17)
матричные элементы, описываю-
щие дипольные и квадруполь-
ные переходы, пропорциональ-
ны соответственно kR и (kR)3.
Для фотонов с энергией 20 Мэв и радиусом ядра, равным
5 ферма, kR «г 0,5. Это означает, что в рассматриваемой области
* В настоящее время нельзя считать твердо установленным, что зависи-
мость средней энергии £0 гигантского резонанса от А описывается соотноше-
нием Ео ~ Д-1/3. Так> например, в книге Е. Hayward. Nuclear Structure and
Electromagnetic Interactions, Plenum Press, New York, 1965, указывает-
ся, что экспериментальные данные о положении максимума гигантского резо-
нанса в средних и тяжелых ядрах достаточно хорошо описываются соотноше-
нием £0~ Д-0.165. _ПриМ' пер_
279
энергий квадрупольные переходы, вообще говоря, значительно мене
интенсивны, чем дипольные. Ниже будет показано, что интеграть
ные сечения для Е2-переходов составляют примерно 10% соответ'
ствующего значения для случая Е/-резонанса.
В области энергий возбуждения, лежащей выше гигантского ре-
зонанса, могут существовать переходы других мультипольностей
(рис. 10.8). Непосредственно за гигантским дипольным резонансом
следует ожидать поглощение Е2- и М/-излучения, а выше порога
рождения мезонов основной вклад в сечение фотопоглощения доп.
жен давать процесс фоторождения мезонов М]-излучением.
Попытаемся теперь понять природу механизма возбуждения ги-
гантских резонансов. Гигантские резонансы являются совокуп-
ностью состояний, сильновозбуждающихся при поглощении у-кван-
Рис. 10.8. Схематическая иллюстрация расположения резонан-
сов высших мультипольностей в зависимости от энергии воз-
буждения.
тов. Процесс поглощения фотона, приводящий к испусканию ну-
клона, представляет собой следующую последовательность событий:
1. При поглощении фотона внутри ядра электрическое поле
падающей волны вызывает когерентное движение протонов ядра
в направлении Е (рис. 10.9). Благодаря сохранению движения центра
масс это приводит одновременно к движению нейтронов в противо-
положном направлении. Так как длина волны X ^> /?, электриче-
ское поле Е (/) является практически однородным в области ядра
и зависит только от времени.
2. Вследствие взаимодействия нуклонов друг с другом энергия
когерентного состояния распределяется между другими степенями
свободы ядра (процесс, аналогичный трению). Ниже этот механизм
затухания будет рассматриваться как трение между протонной
и нейтронной жидкостями внутри ядра. Можно также сказать, что
на второй стадии рассматриваемой фотоядерной реакции происходит
превращение энергии упорядоченного движения в тепловую, что
приводит к исчезновению когерентного колебания и возникновению
других типов возбужденных состояний. Микроскопическое описа-
ние этого процесса было дано Даносом и Грайнером [98].
280
3 Образовавшееся сложное состояние гигантского резонанса
аспадается с испусканием нейтронов или протонов- происходит
ппоцесс остывания ядра. Благодаря тому что эти нуклоны вылетают
из ядра вследствие испарения, их энергетический спектр имеет ста-
тистический характер. При увеличении энергии фотонов спектр
вылетающих нуклонов фактически не меняется. Это является ти-
пичным указанием на про-
цесс нагревания ядра. Рас-
смотренный механизм фото-
ядерной реакции с испуска-
нием нуклонов представлен
схематически на рис. 10.10.
физические процессы, про-
Рпс. 10.9. Схематическое изображение
механизма возбуждения гигантского
резонанса. Под действием электриче-
ского поля фотона протоны (+ + +)
двигаются вверх; благодаря сохране-
нию импульса центра масс нейтроны
(------) движутся в противополож-
ном направлении.
исходящие в ядре при по-
глощении фотонов в области
за гигантским резонансом,
аналогичны атомным явле-
ниям при фотоионизации. В
этом случае промежуточное
сложное состояние не обра-
зуется, а находящийся внут-
ри ядра нуклон большой энергии сразу же вылетает из него. Оста
точное ядро обычно образуется в возбужденном состоянии, которое
затем высвечивается («остывает»). Подобные прямые процессы мо-
гут быть разделены на две группы:
Коллективное Термализация
возбуждение
Ядерное ____
взаимен =
действие
iph --,---- ==^>
^-Поглощение
Процессы
охлаждения
2ph
Испускание
частицы
Основное состояние ядра-мишени
Рис. 10.10. Схематическое изображение трех стадий
процесса поглощения фотона и испускания частицы.
1 - Прямая фотоионизация, полностью аналогичная атомному
фотоэффекту. В этом случае из ядра вылетает нуклон большой энер-
гии, а импульс отдачи передается остаточному ядру. Можно также
сказать, что фотон непосредственно взаимодействует с одним из
нуклонов ядра и выбивает его в состояние непрерывного спектра.
Поэтому при увеличении энергии фотона энергия прямых фотонук-
лонов также увеличивается в противоположность обсужденному
281
выше процессу испарения, при котором спектр вылетающих час-
тиц всегда имеет статистический характер.
2. Квазидейтонный процесс, в котором фотон взаимодействует
со сталкивающейся внутри ядра парой протон —нейтрон. Этот слу-
чай можно рассматривать как фоторасщепление виртуального дей-
тона, образующегося внутри ядра. Так как импульс фотона очень
мал, протон и нейтрон (только такая пара нуклонов имеет диполь-
ный момент) должны вылетать из ядра в противоположных направ-
лениях, при этом импульс отдачи остаточного ядра обычно мал.
Рассматриваемый процесс описывается матричным элементом вида
(flexp liqr|A]/i>, где q— импульс фотона, из которого следует, что
заметный вклад в этот матричный элемент могут давать только те
ядерные волновые функции, которые исчезают на малых расстоя-
ниях между протоном и нейтроном. К таким короткодействующим
корреляциям приводит нуклон-нуклонный потенциал с твердой
сердцевиной. Таким образом, при изучении квазидейтонного про-
цесса можно исследовать короткодействующие корреляции [118,
178, 199].
§ 10.3. ГИДРОДИНАМИЧЕСКАЯ МОДЕЛЬ
Вскоре после открытия Болдуина и Клайбера Гольдхабер и Тел-
лер 1164) предложили несколько возможных объяснений явления
гигантского резонанса. Так, согласно одному из предложенных ва-
риантов, гигантский резонанс связан с колебаниями жесткой про-
тонной сферы относительно нейтронной (рис. 10.11). В этой очень
простой по своей структуре модели зависимость энергии гигант-
ского резонанса от массового числа определяется соотношением
Дсо ~ А~1/в, в то время как экспериментальные данные указы-
вают, что Aw ~А~*/а*. Вскоре после появления работы Гольдхабсра
и Теллера Штейнведель и Йенсен 1347] детально развили одну из
предложенных ими моделей — гидродинамическую модель ядра,
состоящего из двух жидкостей. Именно на основе этой модели была
позднее создана динамическая коллективная модель [96, 97], ко-
торая привела к пониманию многих важных свойств гигантского
резонанса.
Согласно гидродинамической модели, ядро состоит из протон-
ной и нейтронной жидкостей, плотности которых равны соответ-
ственно р;,(г, t) и рп (г, /), причем предполагается, что полная плот-
ность ядерного вещества
Ро(г) - Р„(г, 0 + рп(г, 0 (10.5)
не зависит от времени. Это предположение эквивалентно предполо-
жению о несжимаемости ядерного вещества, или, более точно,
пренебрежению связью гигантского резонанса с колебаниями, воэ-
* См. примечание на стр. 278.
282
икающими при сжатии ядра (см. гл. 12). Уже из основной идеи
'той модели, которая рассматривает ядро состоящим из двух жид-
Э стсй следует ее ограниченность. Для легких ядер, содержащих
пишь небольшое число нуклонов, рассматриваемая модель, разу-
меется, не является хорошим приближением.
Вследствие того что внешнее возмущение, электромагнитное
поте зависит от времени, плотности протонов и нейтронов также
зависят от времени. В отсутствие возмущения ядро находится в рав-
новесном состоянии; равновесные плотности протонов и нейтронов
обозначим соответственно р(рв> (г) и (>,?’ (г). В дальнейшем эти величи-
ны считаются постоянными внутри ядра (рис. 10.12). Наблюдаемая
экспериментально толщина поверхностного слоя ядра учитывается
в динамической коллективной теории введением поверхностных ко-
Рис. 10.11. Схематическое
описание возбуждения ги-
гантского резонанса в фото-
ядерных реакциях в модели
Гольдхабера — Теллера.
Рис. 10.12. Равновесные распределе-
ния плотностей проникающих друг в
друга протонов п нейтронов. Колеба-
ния поверхности, изображенные стрел-
ками, приводят к размыванию грани-
цы ядра.
лебаний, которые на рис. 10.12 изображены стрелками. Очевидно, что
в результате подобных колебаний поверхность ядра размывается*.
При возникновении локальных отклонений плотностей от равно-
весных значений протонная и нейтронная жидкости оказываются
разделенными. В рассматриваемой модели предполагается, что сила,
препятствующая такому разделению, обусловлена энергией симмет-
рии. Как следует из формулы Бете-Вайцзекера для массы ядра,
энергия связи ядер с N ф Z характеризуется дополнительным
членом (см. гл. 12)
и -
8 А
х ж 20 Мэв.
(10.6)
Можно предположить, что эта энергия связана с потенциалом
энергии симметрии
Us = х С (рр(г’ dr, (10.7)
J Ро(г)
Поверхность ядра является размытой даже в ядрах с очень малой ам-
плитудой колебаний поверхности. Поэтому учет этих колебаний в динамиче-
ской коллективной модели может объяснить лишь небольшую часть эффек-
тов, обусловленных размытостью ядерной поверхности. — Прим, пер.
283
имеющим минимум при рр (г) = рр0) и рп (г) = рА0), т. е. при равно-
весных значениях плотностей. Подставляя в (10.7) однородные
распределения плотностей, изображенные на рис. 10.12, получаем
соотношение (10.6). Величина потенциальной энергии, определен-
ной соотношением (10.7), зависит только от локального разделения
ядерных жидкостей.
Получим теперь уравнения движения протон-нейтронной системы
с учетом потенциала энергии симметрии. Используем для этой цели
следуя Даносу [93], принцип Гамильтона
6$ЛЛ=0, (Ю.8)
где лагранжиан L для случая консервативных сил определяется
соотношением
L-T-U. (Ю.9)
Здесь Т и U—кинетическая и потенциальная энергии соответствен-
но. В гидродинамике движение характеризуется зависимостью от
времени координат s (t) элемента объема жидкости. Скорость эле-
мента объема дается в этом случае соотношением
v(0 = s(0- (10.10)
Будем считать, что sp (/) и sn (/) описывают положения, соответ-
ственно, протонов и нейтронов в элементе объема, находящемся
в точке s (/).
Используемые нами локальные скорости и плотности опреде-
ляются как средние значения по достаточно малым элементам объ-
ема. Эти элементы должны быть малыми по сравнению с объемом
всего ядра и в то же время должны содержать достаточно большое
число частиц. Это обстоятельство еще раз указывает на то, что тео-
рия применима лишь к средним и тяжелым ядрам.
Варьирования в (10.8) должны выполняться следующих дополнительных условий: при соблюдении
р0 = const; (10.11)
-~+V-(Ppvp)- 0; ot (10 12)
^ + V-(pnvn)= 0; Ol (10 13)
n'VP I г = д (6,<P) =' 0’ (10.14)
n vn I r = R (fi,<p) = (10.15)
где п — вектор нормали к поверхности ядра Д (0, <р).
Соотношения (10.12) и (10.13) являются уравнениями непрерыв-
ности, описывающими соответственно сохранение чисел протонов
и нейтронов. Соотношения (10.14) и (10.15) означают отсутствие
284
ТОКОВ протонов и нейтронов через поверхность ядра. Кинетиче-
ская энергия системы, состоящей из двух жидкостей, имеет вид:
Т = j(Ppv£+p„ 'Vnjd't. (10.16)
Объем
ядра
Вводя относительную скорость
v = vp-vn, (10.17)
приведенную плотность
pr£d=P^ (10.18)
Ро
и скорость центра масс
V = — (ppVp + p„vn), (10.19)
Ро
можно переписать Т в виде суммы двух членов, описывающих ки-
нетическую энергию движения центра масс и кинетическую энергию
относительного движения:
Т = ±М f(pnV2 l-rwv2)^T. (10.20)
Объем
ядра
Используя (10.19), из уравнении непрерывности (10.12) и (10.13)
можно получить соотношение
V-(pnV)=-A(p +Pn)= (10.21)
dt at
Так как полная плотность ядерного вещества постоянна во времени
и по объему ядра, то
VV = 0. (10.22)
Это соотношение характеризует движение несжимаемой жидкости.
Используя снова уравнения непрерывности, получаем
^=-V.(Pndv)-V-(p;,V). (10.23)
dt
Учитывая (10.22), последнее соотношение можно переписать в виде
^r- + v-vPp=-V-(Predv). (10.24)
ot
Полная потенциальная энергия является суммой энергии симметрии
и кулоновской энергии:
+ Ц.1Рр-~Pn)2 dx + ± e2j j* PP<r)Pp(r,)-efTrfT\ (10.25)
Объем Объем
ядра ядра
285
Чтобы учесть сохранение полного числа частиц, необходимо
к соотношению, описывающему принцип Гамильтона
0 = 8^Ldt= \di (8T—8U)
(10.26)
добавить член
7 § dt8N = 8^dx dCK (рР + р„),
(10.27)
где X — множитель Лагранжа.
Для классического описания возбуждения и затухания гигант-
ских резонансов в вариационную процедуру необходимо включить
еще два члена
6Л= §(—MrprCdv-(6sp—6sn) + рр К • 6sp) </т. (10.28)
Объем
ядра
Первый из них описывает затухание, причем предполагается, что
неконсервативные силы трения пропорциональны относительной
скорости и приведенной массе. Из последнего условия следует, что
силы трения исчезают, если одна из плотностей рр или рп равна нулю.
Это означает, что рассматриваются силы трения, обусловленные
только движением жидкостей друг относительно друга. В дальнейшем
соответствующие эффекты мы будем называть шириной разброса
(spreadingwidth) гигантского резонанса. К ней относится та часть ши-
рины, которая связана с нагреванием ядра, т. е. с передачей энергии
когерентного коллективного состояния большому числу некогерент-
ных возбуждений. Второй член в правой части (10.28) описывает
взаимодействие протонов с электромагнитным полем:
К = еЕ+ — vp X Н,
С
(10.29)
где Е и Н — напряженности электрического и магнитн ого полей со-
ответственно.
Для удобства дальнейшего изложения необходимо сделать нес-
колько замечаний относительно операций интегрирования, входящих
в вариационную процедуру. Часть из них должна быть выполнена
в предположении, что поверхность жидкой капли не зависит от вре-
мени*. Кроме того, в соответствии с уравнениями (10.14) и (10.15)
вариации 6sp и 6s,г траекторий соответствующего элемента объема не
будут содержать на поверхности ядра никаких компонент, перпен-
* В гл. 11 обсуждаются эффекты, обусловленные влиянием колебании
ядерной поверхности на структуру гигантских резонансов. Однако поскольку
движение поверхности происходит значительно медленнее, чем колебания,
соответствующие гигантским резонансам (адиабатичность), сделанное выш
предположение оправдано.
286
-учярных к этой поверхности. Следовательно, все поверхностные
еграл'ы, пропорциональные нормальным компонентам 6sp и 6s,г,
вращаются в нуль. В частности, из теоремы Гаусса
Jv-Wdx = §W-rfa, (10.30)
Объем Поверхность
п„ ____бесконечно малый вектор нормали к поверхности, следует,
где его
что
V-(P(r)6sp)dr = 0 (10.31)
Объем
ядра
И
$ V -(Q (г) 6sn) с/т = 0,
Объем
ядра
(10.32)
где Р (г) и Q (г) — произвольные скалярные функции.
После этих общих замечаний вернемся к вариационной проблеме
сформулированной в виде уравнений (10.26) и (10.27). Имеем
6vp= = (10.33)
и аналогичное соотношение для 6vn. Из уравнений непрерывности
(10.12) и (10.13) следует:
6рр=—ppV-6sp (10.34)
6pn=-pnV-6s„. (10.35)
Используя (10.5) и (10.11), имеем
брр - — брп. (10.36)
Вычислим теперь член, содержащий вариацию кинетической энергии
Т (10.16). Имеем
§ dt&T - М dt dt {Рр Vp 6vp +
+ Pn v„ 6v„ у v2p брр + -y v26p„ +
+ у Pe vp v ' Ssp + у P„ v2 V 6s„}
M Jd/drJppVp y-6sp + pn v„y- 6s, j =
= —Al i (PpVp)-6sp + (p„ v„)-6s,l —
J I dt dt )
~M \dt tlr{pp6sp-Vp V-Vp + p„6sn-vn V-vn}, (10.37)
287
так как
f dx — = — f dxF— f dxF V v. J dt di J J
Из урави ений непрерывности следует, что Vp„=^ + dt dt dt + V-(ppVp)—ppV-vp=—ppV-Vp, (10.38)
а также 7r=7T + ^-V)v- <10-39)
Аналоги! образом, 1ные соотношения имеют место для dpjdt и dvjdt. Таким имеем j dtFT = — М dt dx |pp + (vp • V) Vpj X X6sp+p„[ ,l +(vn-V)vnl-fisn|. (10.40) L dt j J
Вычи< Рассмотр :лим теперь вариацию потенциальной энергии U (10.25). им сначала энергию симметрии Us. Обозначим Е = х[ p7'~~p,t V=»z 1 р" ~2рр Г- (10.41) \ Ро \ Ро
Тогда Е'= — - — 4xIp»ZZ^lj (10.42) dpp Ро Е"_^Е 8х (1043) dp2P Ро2
и VE E'Vop= — E'Vp„. (10.44)
Для вар нации Us теперь имеем dt8p Us - dt dx р0 (Е' брр 4- Е V 6sp) Jd/dT-^-p0(E — PpE')V-6sp. (10.45)
Для формулу дальнейшего преобразования этого уравнения используем (10.31). Тогда получим: J dtSp lds = рв di dxfisp • V (рр Е' — Е).
По анал эгии Сdt^nUa= — у Ро Jdtdi8sn-V(рпЕ' + Е).
288
Таким образом, используя (10.44), имеем
$d/fil/e- \dt(6pUs + 6nUs) =
= Jd/dr-i- р0 [ррfiSp-VE'—p„6sn-VE'] =
= ^dfdrpppnE"(Vpp)-(6sp—Ssn) +
+ $ dt dx [Pp (VE) • 6sp + pn (VE) fisn]. (Ю.46)
Вычислим теперь вариацию кулоновской энергии:
J dt8Uc = f dte21 J drfipp (r) J dr' +
+ JJd'tdt'pp(г)рр(r')6 2r, । +
-pjdrpp(r) V-6sp Jdr'. (10.47)
Введем кулоновский потенциал
Ф = е С dr' Рр(г ,
J |г~г'|
а также используем соотношение
6—?— = 6sp.V 1(10.48)
|Г — Г'| | г — г'|
Подставляя эти выражения в (10.47), спомощью (10.34) получаем:
dtfiUc = § dt dxe [Ф6р7, + Рр ФV • 6sp + рр 6sp • УФ] =
= ^dtdxepp (УФ)-6sp. (10.49)
Преобразуем теперь к более удобной форме дополнительное условие
(10.27):
5 dt8N =\dt dr {7. (брр + 6pn + PpV-6sp + pnV-6s„) +
+ (Ppfisp + pn6sn)-VZ} --^dtdr'Vl-(pp6sp + pn6sn). (10.50)
Последний член, включаемый в вариационный принцип для полу-
чения уравнений классической гидродинамической модели, запишем
в форме:
§d/6.4= ^dtdr{(—Л4Гргей v + ppK)-6Sp + 7VirpredV-6sn}. (10.51)
С учетом соотношений (10.27) и (10.28) принцип Гамильтона прини-
мает вид:
0 = $d/{6r — 8U + 8N + 8A}. (10.52)
10 Зак. 1218
289
Так как вариации 6sp и 6s,, независимы, то из (10.52) с учетом (10 40^
(10.46) и (10.49) — (10.51) получаем: ’
0 = Wr + (Vp• V) Vpj—рр рп Е" Vpp—рр VE —
— eppVO + ppVX—Mrprcdv + ppK (10.53)
и
0 = -Мрп + (vn• V) vn] + рр pn Е" Vpp-Рп VE +
4-Рп VZ + AfTp^v. (10.54)
Вычитая (10.54) из (10.53), имеем
0 = (vp • V) vp-(vn • V) v„ + VPp +
+ ^-¥Ф + 7г + Гу-77К- (10.55)
М dt М '
Складывая уравнения (10.53) и (10.54) и учитывая уравнения не-
прерывности (10.12) и (10.13), получаем
0= — {pp(Vp-V)Vp + vpV-(ppVp) + pn(vn-V)vn +
Ро
+ v„V‘(PnVj}+^ + ^V(E-Z) +
+ — Р£ уф_ Р£ J-K. (10.56)
М р0 ро М
Уравнения (10.55) и (10.56) являются точными уравнениями движения
системы из двух жидкостей, характеризующихся различным поведе-
нием по отношению к внутренним и внешним силам. Член V(E — 7)
описывает гидродинамическое давление. Входящие в эти уравнения
члены вида (v-V)v, нелинейные по скорости, приводят к возникно-
вению в жидкости завихрений.
Линеаризуем полученные уравнения, отбросив нелинейные
члены. Легко показать, что соответствующие эффекты составляют
по порядку величины 10~3 от эффектов, обусловленных линейными
членами [99]. Линеаризованные уравнения имеют вид:
+ VpP + Tv--------К+— УФ (10.57)
<)/ Л1р0 |рт м м
и
0= — + — V(E — Х)+ — ^-УФ— — К. (10.58)
dt М М р0 р0 М
В этом приближении уравнение непрерывности также принимает
более простую форму
dpp/dt=—plr°e^-v, (Ю.59)
290
^следствие того, что члены v-Vpp, V"Vpret| и (pred Pred)V’^
В юют второй порядок по флуктуациям плотностей. В этих соот-
HMe*vi I
ношениях
о(0)_ о(0) (0),
Ргеа — Рр Рп I Ро*
Применяя оператор (V-) к уравнению (10.57) и используя (10.59),
получаем:
п_______1 д2рр , 8х у2_______Г дрр
„(0) ^МРо 1р „(0) dt
lJred Vred
V-K.+— У2Ф. (10.60)
м м
С помощью уравнения (10.57) граничные условия (10.14) и (10.15)
можно записать в более удобном виде. Поскольку из (10.14) и (10.15)
следует, что
n.^bZLl = 0,
dt |г=«(е,ф)
граничные условия эквивалентны условию
Л1ро |г = Ц(0, ф) М |г = /?(0,ф)
+ — n-vol =0.
М |г = К(6,ф)
(10.61)
Взаимодействие рассматриваемых жидкостей с электромагнитным
полем описывается в этом уравнении двумя членами V Е и
V(vp j'H). Первый член в случае электромагнитной волны тож-
дественно равен нулю вследствие отсутствия источников поля. Вто-
рой член мал, так как он пропорционален vp и магнитному полю
Н, которые малы по величине. Кроме того, для простоты пренебре-
жем эффектами электростатических кулоновских сил. Тогда отбра-
сывая в уравнении (10.60) соответствующие члены, имеем:
1 й2 . 8х „2
р(0) й/2 Рр Л4р0 Рр
Г йрр =()
Р<°2 dt '
(10.62)
Полученное уравнение описывает волновой процесс с затуханием.
Его решения определяются с помощью граничного условия
— n-VpJ =—пК| • (Ю.63)
Л1ро |г-Д(6,Ф) М |г=Ц(0,Ф)
Заметим, что электромагнитное поле входит только в граничное
условие (10.63) и не входит в само волновое уравнение (10.62). Если
те же самые приближения использовать в случае уравнений (10.57)
и (Ю.58), получим
^+-^-VpP + rv = 0 (10.64)
dt Л'1р0
10*
291
и
^ + J_V(E-4=0. (10.66)
Из последнего уравнения следует, что V(E — Z) описывает гидроди-
намическое давление.
С помощью уравнения (10.65) можно исследовать движение цент-
ра масс. Так как V-V = 0 [см. (10.22)1, то, применяя оператор (V-)
к (10.65), получаем
V2(E —Л) —0. (10.66)
Таким образом,
Е (10.67)
Следовательно, уравнение (10.65) сводится к следующему уравне-
нию:
dV/dt = 0. (10.68)
Применяя к (10.65) оператор rot, имеем
VxV = C, (10.69)
где С — постоянный вектор, значение которого определим ниже.
Подобным образом, применяя к (10.64) оператор rot, находим
уравнение
-^-Vxv + rVx v = 0, (10.70)
решение которого имеет вид
Vxv = A(r)exp(— Г(), (10.71)
где А (г) — некоторый вектор. Следовательно, возникающие в си-
стеме завихрения должны затухать согласно уравнению (10.71).
Не ограничивая общность результатов, будем в дальнейшем рассмат-
ривать собственные колебания системы, удовлетворяющие условию
Vxv = 0, (10.72)
которое соответствует безвихревому движению жидкости. Вводя
потенциал скоростей
v = —Vq> (10.73)
и дифференцируя (10.64) по времени, находим
_ 8х РгЛ v2Г^Р _0 (10.74)
dt2 М р<0> * dt
Соответствующее граничное условие имеет вид
n-V<pl —------------— п-к| - (10.75)
|г=Н(0,Ф) /И |г=Д(0,ф)
292
Ниже будут детально исследованы решения уравнения (10.74),
ймеющие форму
Ф (г, /) = ф(г)ф(/). (10.76)
Однако уже сейчас можно заключить, что
^||v. (10.77)
Этот результат будет использован ниже.
Из уравнения (10.72) следует
Vxvp = Vxvn. (10.78)
Используя (10.69), находим:
р0 С ру V X V = Рр V х Vp -f-
+ [Vpp X Vp] + р„ v X v„ + [Vp„ X vn], (10.79)
Так как pn = р0 — рР и Vpn = —Vpp, то
PoC = PovXvn + ppVxv+]VppX v]. (10.80)
Из уравнений (10.64) и (10.77) получаем
[VPpXv] = 0. (10.81)
Отсюда с помощью (10.78) и (10.80) находим:
VxVp = Vxvn = C. (10.82)
Таким образом, вихревые свойства движения центра масс совпа-
дают с соответствующими свойствами движения протонной и ней
тропной жидкостей. Разумно предположить, что движение жидко-
стей происходит без завихрений, т. е. С = 0. Отсюда следует, что
V X V = 0. Таким образом, V — постоянный вектор. Поэтому
в дальнейшем мы не будем рассматривать движение центра масс,
которое в области физики фотоядерных реакций существенно лишь
для томсоновского рассеяния (см. т. 2).
Итак, рассматриваемая система из двух жидкостей описывается
только двумя величинами рр (г, t) и ф (г, /), которые удовлетворяют
следующим уравнениям:
V2pp—Г^ = 0, й/2 dt (10.83)
_^_рц2у2ф—Г-^ = 0 й3 dt (10.84)
и граничным условиям
n-vPp| =тгп-к| |г = Д (0, ф) 8и |г = Д (6, ф) (10.85)
п-\7ф| = ^-п-к| |г = Л(0.Ф) Л1 |г —Д(0. ф) (10.86)
293
Эти величины связаны друг с другом благодаря уравнению не-
прерывности (10.59), которое можно записать в виде
д-~—p(r^V2q> = 0. (10.87)
Выше мы ввели скорость и, определяемую соотношением
,= 8к Ргй =8и NZ_
М р0 МА2
(10.88)
которая аналогична скорости звука и характеризует скорость
распространения в ядре колебаний плотности.
Дальнейшее изложение будет посвящено двум главным про-
блемам. Во-первых, мы должны найти полные решения классиче-
ских гидродинамических уравнений (10.83)—(10.87) и получить клас-
сическую формулу для сечения поглощения. Во-вторых, мы должны
выразить функцию Гамильтона через величины, характеризующие
колебания плотности, и сделать переход к квантовой механике.
§ 10.4. КЛАССИЧЕСКИЕ ДИПОЛЬНЫЕ РЕШЕНИЯ
ГИДРОДИНАМИЧЕСКИХ УРАВНЕНИЙ
ДЛЯ СЛУЧАЯ СФЕРИЧЕСКОГО ЯДРА
Найдем решения уравнений (10.83)—(10.87) для сферического
ядра. В этом случае поверхность ядра описывается уравнением
Д (0, ср) = До, что означает равенство нулю всех переменных а?,ц
в соотношении (2.1): = 0- Это простейший случай, который
можно точно исследовать. В данной главе мы будем пренебрегать
связью колебаний плотности с движением ядерной поверхности,
которая во многом определяет структуру гигантских резонансов.
Эти вопросы детально обсуждаются в гл. 11, посвященной динами-
ческой коллективной модели.
Чтобы получить решения уравнения (10.83), удобно представить
полную плотность протонов рр (г, t) в виде суммы равновесной плот-
ности рр (0) и плотности флуктуаций рр (0)-т] (г, t):
Рг (г> 0 = Рр (0) [1 + »] (г,/)]. (10.89)
В этом случае волновое уравнение принимает вид
«2V2n (г, /)— д2|1(г- f) _г-Т)(г’ Z) = 0. (10.90)
'' ' dt2 dt
Соответственно для граничного условия имеем:
n-vJ = р0 п-к| . (Ю.91)
|г = Д0 8крр (0) |г = 7?0
Используя подстановку
т) (г, t) = ц (г)ехр (—i со/), (10.92)
получаем
V2T](r) + ^2T] (r) = 0,
(10.93)
Aj2=^fi+i_L\ (10.94)
и2 V <jj /
Будем искать решения уравнения (10.93), описывающие колеба-
ния которые возбуждаются электрическим дипольным полем
(рис. 10.13). Стационарные решения в рассматриваемом случае
должны удовлетворять граничному условию (10.91), имеющему вид
I = е£р0 _ cos 0, (10.95)
dr |r = R0 8хрр (0)
где Q — уГОл между Е и г (см. рис. 10.13). Будем искать общее реше-
ние уравнения (10.93) в форме:
т](г)= <р). (10.96)
1т
Используя граничные условия, получаем
Л ('') = Go Ji (kr) У1о (0, <р) = С]\ (kr) cos 0, (10.97)
где
С _ е£р0 Га/i (kr) I 1“1 = с£Ро 11
8ирР(0) L dr L=fl0J 8ирр (0) /i(z)—z/2(z)
z = kR0. (10.98)
Заметим, что постоянное в пространстве электрическое поле
приводит к возбуждению только дипольных колебаний. В самом
деле, учет граничного условия (10.95) приводит к тому, что в разло-
жении (10.96) остается только член, пропорциональный У1о. Более
систематическое исследование нормальных типов колебаний плот-
ности будет дано в разд. 10.5.
Амплитуда С в выражении (10.98) имеет резонансный характер.
Она имеет полюса в точках г, определяемых из условия обращения
в нуль знаменателя:
/1 W = z/2(z). 0°-")
Используя явный вид функций Бесселя, уравнение (10.99)
можно переписать в форме
tgz = 2z/(2—г2). (10.100)
Решения этого уравнения представлены в табл. 10.1.
Из уравнения (10.94) получаем
2 п2
= = ®_(1-pi —) (10.101)
и2 \ к>п /
295
или
где
(10.102)
(10.103)
Таким образом, система из протонной и нейтронной жидкостей ха-
рактеризуется собственными колебаниями, частоты которых опреде-
Таблица 10.1
Кории трансцендентного
уравнения tg z =
= 2z/(2—z2)
1 2,08
2 5,95
3 9,20
4 12,42
Рис. 10.13. Координаты, исполь-
зуемые в гидродинамической
модели. Е указывает направле-
ние электрического поля.
Большие п пх
ляются уравнением (10.103). В резонансах амплитуда С неограни-
ченно возрастает, если электрическое поле Е имеет конечную вели-
чину.
Оценим резонансные энергии, пренебрегая Г и полагая ANZIA2
» 1. Имеем
fan = hVn = h^zn = -^l/ =
п RB п___Ro V М И2
= zп |/_2^_А (Ю.104)
п I /Ис2 е2 Ro
причем
е2 е2 тс2Л-1/з
Ro ГоА^ г0
Для n=l, zn = 2,08 и х«20 Мэв
= Мэв. (10.105)
Экспериментально было найдено, что энергии гигантских резо-
нансов можно описать с помощью соотношения fa:>exp^№A~'!‘Мэв.
Таким образом, согласие теоретических и экспериментальных
результатов является достаточно хорошим. Тот факт, что резонанс-
ные энергии пропорциональны Д—*/», обусловлен пропорционально-
296
ыо частоты колебаний обратной величине характерного размера
Сбласти (радиуса ядра), в которой происходят колебания.
До сих пор мы предполагали, что дипольный тип (и = 1) коле-
баний плотности может быть отождествлен с гигантскими резонан-
сами. Это предположение оправдано тем, что нормальный тип коле-
баний с п = 1 характеризуется, как будет видно ниже, наибольшей
величиной сечения поглощения.
Вычислим дипольный момент D системы, который нам понадо-
бится в дальнейшем. Так как, согласно рис. 10.13, электрическое
поле Е направлено вдоль оси z, то
D2 = ерр (0) drzt] (г) = ерр (0) (j dtr cos 0т] (г) =
= еСрр (0) (j dxrj1 (kr) cos2 0 =
~ • -^Pp(°)lWb(^)lr=«0 =
= -y-^-PP(0)/2(^o). (10.106)
Учитывая (10.98), получаем:
c2 ER* A . /2 (z)
8x z/, (z) —z2/2 (z)
Здесь мы использовали соотношение (4л/3)Д(03)р0 = А. Составляю-
щие Dx и Dy дипольного момента равны нулю, так как в рассматри-
ваемом случае направление индуцированного дипольного момента
совпадает с направлением электрического поля.
Рассмотрим теперь более детально резонансные свойства инду-
цированного дипольного момента. С этой целью исследуем меро-
морфную функцию
fl?1 Л/ ы-Х w ’ г~кк‘- (10-107>
Для конечных k единственными особыми точками этой функции яв-
ляются нули знаменателя. Точка z = оо — существенно особая
точка. Представим f (z) в виде разложения
f(z) = V__£n_< (10.108)
п z—гп
коэффициенты которого определяются с помощью теоремы Коши:
+^-^f(z')dz'. (10.109)
контур вокруг 2п
Так как f (г) имеет только простые полюса, ее можно записать в виде
f(z)=g(z)lh(z\ (10.110)
где g(z) и h (z) — соответственно числитель и знаменатель уравне-
ния (10.107). Отсюда
Г g(z)
, f . X
h' (z)
(10.111)
Используя явный вид функций Бесселя (уравнение (8.10)], легко
находим:
1 sin гп — zn cos zn 1
Сп = _П-------------------^ = -r-(tgzn-zn). (10.112)
Zn COS Zn Zn 1
Величины zn являются нулями знаменателя h (z) уравнения
(10.107) и, следовательно, совпадают с полученными ранее положе-
ниями резонансов, которые представлены в табл. 10.1. В частности
из уравнения (10.100) следует, что zn удовлетворяют соотношению
Подставляя (10.113) в (10.112), сразу же получаем
с __________________________!_
” zn 2-z£ ’
Отсюда следует
/И=2(— -у-М—
П \ zn Z—Zn ) Z~zn
(10.113)
(10.114)
(10.115)
В разложении (10.115) суммирование производится как по поло-
жительным, так и по отрицательным значениям zn. Так как корни
уравнения (10.113) симметричны относительно нуля, zn = ±а,
то (10.115) можно преобразовать к виду
yi 2 —1
Т гп—2 z2—Zn ’
(10.116)
где суммирование проводится только по положительным значениям
Zn-
Выразим теперь z и zn через со и vn. По аналогии с уравнением
(10.101) можно написать
z2 = ft2/?2 = -^L((D2 + irw). (10.117)
и2
Из уравнения (10.103) находим
298
пеЛичина г комплексна, a zn — действительна. Подставляя полу-
ченные для них выражения в (10.115), получаем:
.. ._ ч2 у —2 . ____________J________
' * /?2 Zn—2 о)2—Vn-pi Гео ”
и п
и1 2 у —2 со2— Vn— i Гео ПО 11
" R2 г2 _2 (co2-Vn)2+r2co2
формула (10.118) полностью определяет резонансные свойства
индуцированного дипольного момента (10.106). Ниже мы исполь-
зуем ее при выводе выражения для классического сечения поглоще-
ния.
§ 10.5. СЕЧЕНИЕ ФОТОПОГЛОЩЕНИЯ В КЛАССИЧЕСКОЙ
ГИДРОДИНАМИЧЕСКОЙ МОДЕЛИ
Сечение поглощения определяется как отношение средней по-
глощенной энергии в единицу времени к потоку падающей энергии:
ст = (Е • D)cp/Scp, (10.119)
при этом поток электромагнитной энергии дается соотношением
5сР=~Е2- (Ю.120)
Эти формулы справедливы в тех случаях, когда электрическое поле
и дипольный момент описываются действительными величинами.
Если, как в настоящем изложении, используются комплексные обо-
значения, то сечение имеет вид
CT=-l-Re(E*-Ь)/5ср. (10.121)
Подставляя в это выражение соотношения (10.106) и (10.118)
и предполагая, что электрическое поле и индуцированный диполь-
ный момент изменяются во времени по гармоническому закону
с частотой со (Е ~ ехр (—ico/), D ~ ехр (—ico/)), легко находим:
1 8л е2 ERo А с п f £ ,
ст =------- ----—£Re{ —i<of(z)} =
2 сЕ2 8и 1
__ 4ле2 _________Гео2_____ ,1Q 122'.
сМ А г2п — 2 (Vn—со2)2-р Г2со2 ’ ' ‘ '
п
Таким образом, классическое сечение поглощения имеет типич-
ную резонансную структуру, причем формы отдельных резонансов
описываются кривыми Лоренца. Чтобы отождествить гигантский ре-
зонанс с одним из этих резонансов, характеризующихся частотами
vn, очень важно знать, какое из рассматриваемых дипольных коле-
бании наиболее сильное. Для решения этой проблемы найдем ин-
299
тегральное сечение поглощения. Рассмотрим сначала интеграл
/ — Г Гсо2Дсо _ Г у2 dy
J (со2—Vn)2-|-Г2 со2 “ .1 ({/2-а2)2-р»2 ’ (Ю.123)
о о
где у = <о/Г на = vn/r. Сделав замену у = а2/х, получаем
оо
у___ Г_____a2 dx
J (х2—а2)2+х2 ’
о
Отсюда следует
оо СЮ
I _ С У2 dy О с2 dy
J (</2~а2)2 + «/2 J (|/2-а2)2 + «/2
о о
1 С (y2+a2)dy
2 .) (у2—а2)2+у2
О
1 * ( а2 \
= —arctg (у-----
2 \ У 1
С Гг’'2' [' Гсо2Фо 1
.1 (со2—ч2) + Г2со2 ,) (со2—vn) -1- Г2 со2 ~ ~2
о о
Используя этот результат, находим
? , . , 2л2 е2
I о (со) аа =------
J Мс
(10.124)
(10.125)
(10.126)
(10.127)
NZ v 2
А z2—2
п
Как известно (см. т. 2, гл. 5), так называемые силы осциллято-
ров fn определяются соотношением
оо
o(co)dco = ^±2^- (10Л28)
о п
Сравнивая (10.127) и (10.128), находим, что в классической гид-
родинамической модели
Z"=JT'^V' <10J29)
/1 Zn — z
Можно показать (см. т. 2, § 5.6) на основании самых общих предпо-
ложений, что
^fn = NZ/A. (10.130)
п
Интересно поэтому посмотреть, в какой степени это соотношение,
называемое классическим дипольным правилом сумм, выполняется
в классической гидродинамике. Для этой цели приравняем друг
другу правые части уравнений (10.107) и (10.116)
300
____/г (г) = V 2 . 1
z/\(z) — гг/г(г) —J г„—2 z„—г2
(10. 131)
• шожим обе части полученного соотношения на (—г2) и перейдем
пределу г-> оо. Используя асимптотическое поведение функций
Бесселя (8.12), находим
V-#—= И (10.132)
п —
Полученный важный результат показывает, что интегральное
сечение поглощения, вычисленное по гидродинамической модели,
полностью исчерпывает классическое правило сумм. Так как, соглас-
но табл. Ю.1, вклад дипольного колебания с п — 1 в правило сумм
(10.130) равен 84%:
----- = --= 0,84,
г2-2-----------------(2,08)2—2
(10.133)
то это дает основание отождествить дипольное колебание с п - 1
с экспериментально наблюдаемым сильным гигантским резонансом.
Таким образом, можно заключить, что вычисленное положение ги-
гантского резонанса согласуется с экспериментальными данными, а
полученный результат не противоречит тому факту, что эксперимен-
тальная величина интегрального сечения почти совпадает со зна-
чением, полученным с помощью правила сумм.
Найдем теперь поляризуемость а ядра, которая классически
определяется с помощью соотношения
а (со) = D (со, t). (10.134)
Используя (10.106) и (10.118), имеем
/ \ С2 NZ X1 2 1 /1А1ОСХ
а (со) =--- • - > —г----------т--------- (10.135)
Л1 А z^—2 vn—со2—(Гео х
п
и, в частности, в статическом случае
а(0) = — --- • -4-. (10.136)
' ’ М А Zn—2 v2n V ’
п
На основании уравнения (10.127) можно найти
а (0) —— С g((0)rft0 __ с2 . NZ у____2 . _L_ (Ю 137)
2л2 J Ю2 м А г2_2 V2 • '
п
Полученные соотношения дают нам второе полезное правило
сумм. Согласно (10.131) и (10.103),
V 2 1 = R2 х 2 1 =
4- z2 —2 v2 «2 z2-2 z2 =
= _R|_ . --Mf)-------1 = 0>2 . (ю. 138)
«2 zjl (z) — Z2 /2 (z) |г = 0 и2
301
Легко показать, что первый член этой суммы равен 0,1947?о/п2. Этот
результат еще раз доказывает, что колебание с п — 1 наиболее су-
щественно.
Подведем теперь краткие итоги. Классическая гидродинамиче-
ская модель достаточно хорошо описывает положение гигантского
резонанса и исчерпывает практически полностью классическое ди-
польное правило сумм, 84% которого приходится на долю первого
дипольного колебания (и = 1). Гидродинамическая модель пред-
сказывает также [см. (10.105)1 экспериментально наблюдаемую за-
висимость (Л-1/3) энергии гигантского резонанса от А (см. рис. 10.7).
§ 10.6. УТОЧНЕНИЯ МОДЕЛИ
Гидродинамическая модель, которая до сих пор рассматривалась,
нуждается в уточнениях, из которых наиболее существенны сле-
дующие:
а. Обменные поправки. Как известно, заметную долю ядерных
сил составляют обменные силы, благодаря которым между прото-
ном и нейтроном происходит обмен зарядами, или виртуальными ме-
зонами. Существование обменных сил приводит к изменению диполь-
ного момента системы, не связанному с механическим движением
нуклонов*. Этот эффект можно учесть, вводя эффективную массу [93]
М* = МЦ\ +а). (10.139)
Введение этой величины соответствует тому, что в колебаниях за-
ряда эффективно участвует лишь часть нуклонной массы. Параметр
а зависит от величины обменных сил. Его можно определить, исходя
из условия точного равенства теоретических и экспериментальных
значений энергии гигантского резонанса. В этом случае а = 0,2 4-
— 0,3. С учетом поправки на обменные силы интегральное сечение
поглощения [уравнение (10.128)] в области гигантского дипольного
резонанса принимает вид
= ^-(1+а). (10.140)
о
Подставляя = 2,08 и используя экспериментальные значения
для интегрального сечения, снова находим а « 0,2 4- 0,3. Этот
результат согласуется с результатами выполненных БетеиЛевинд-
жером расчетов поправки к правилам сумм, обусловленной обмен-
ными силами (см. [127] и т. 2, гл. 5).
б. Граничные условия. До сих пор мы предполагали, что ядро
представляет собой жесткий шар с постоянной плотностью вещест-
* Относительно концепции эффективной массы квазичастиц см. т. 2,
§9.6.
302
На самом деле распределение плотности вещества внутри ядра
ваеет вид, подобный распределению Ферми (рис. 10.14). Можно
пМепполож'ить, что колебания поверхности приведут к размытию
нРдерхности ядра. В какой-то мере подобный эффект был действи-
тетьно обнаружен в мезоатомах [298]. Существуют, однако, указа-
ния на то, что поверхность ядра является размытой даже в отсутст-
вие таких колебаний. Тем не менее, учет колебаний поверхности
ядра весьма существен для объяснения структуры гигантского ре-
зонанса. Детально этот вопрос обсуждается в гл. 11.
Рис. 10.14. Распределение Ферми, используе-
мое для описания распределения плотности
заряда в ядре. Размытость ядерной поверх-
ности в основном связана с колебаниями по-
верхности, изображенными стрелками.
в. Кулоновские поправки. В предыдущем изложении мы прене-
брегали для простоты эффектами кулоновских сил. Данос и Штейнве-
дель [86, 87] показали, что учет этих сил приводит к увеличе-
нию резонансной частоты, которое для тяжелых ядер составляет
2—3%.
г. Деформированные ядра. До сих пор мы обсуждали гидроди-
намическую модель в случае сферических ядер. Известно, однако,
что ядра, имеющие вращательный спектр, обладают статической
деформацией. Данос [88] и Окамото [292] изучили следствия гидро-
динамической модели для ядер, имеющих форму аксиально-сим-
метричного эллипсоида. В сферическом ядре существуют три вырож-
денных дипольных колебания (см. следующий раздел). В случае
эллипсоида эти колебания разделяются на две группы: одна группа
колебаний соответствует колебаниям вдоль оси симметрии эллипсо-
ида, другая — двум вырожденным колебаниям в плоскости, перпен-
дикулярной к оси симметрии (рис. 10.15). Так как гигантские ре-
зонансы представляют собой стоячие волны внутри ядра, то можно
ожидать, что длины волн нормальных колебаний ~ где А*,- —
полуоси эллипсоида. Отсюда следует, что частоты сог ~ У?;-1, т. е.
энергии гигантских резонансов обратно пропорциональны радиу-
сам. Точные расчеты Даноса показывают, что эти соотношения, дей-
ствительно, являются хорошим приближением. Согласно Даносу
188]
Eh/Ea — 0,91 \а/Ь + 0,089
или
(Еь—Еа)/Еа — 0,911 (а-Ь)/Ь. (10.141)
303
Для аксиально-симметричного ядра, характеризующегося дефор.
мацией квадруполыюго типа [уравнение (2.25) с у — 0], имеем'
(Ю.142а)
Рис. 10.15. Ядро, имеющее форму эллипсои-
да вращения, характеризуется двумя макси-
мумами в сечении гигантского резонанса,
связанными с двумя различными частотами
колебаний вдоль большей и меньшей осей
эллипсоида соответственно.
где ро — параметр деформации ядра. Таким образом, в случае де-
формированных ядер, сечение поглощения в области гигантского
резонанса имеет два пика, расстояние между которыми пропорцио-
нально деформации |30. Если ядра ориентированы хаотически, пол-
ное сечение поглощения дается выражением
Рис. 10.16. Влияние ориентации деформированного ядра па
характер возбуждающихся колебаний.
1 9
(w-i43>
где ва и <уь — сечения поглощения фотонов, поляризованных
вдоль осей а и b соответственно (рис. 10.16). Этот результат
есть следствие того факта, что в аксиально-симметричном ядре две
оси из трех равны, что учитывается статистическими факторами
304
„ и 2/3- Чтобы получить <то либо оь, необходимо ядра выстроить
|аК, как показано на рис. 10.16.
Так как
сто«аь, (10.144)
сечение поглощения в деформированном ядре должно иметь форму,
изображенную на рис. 10.17.
В деформированных ядрах вытянутой формы, для которых |30 > 0
(или а > см Рпс’ 10-17), интегральное сечение поглощения
в области верхней компоненты гигантского резонанса вдвое превы-
Рис. 10.17. Схематическое изображение связи между
видом сечения фотопоглощения и формой ядра:
а — сферическое ядро, б — вытянутое ядро, в — сплюснутое
ядро. Пунктиром изображены силы переходов в коллектив-
ной модели.
шает интегральное сечение в области нижнего максимума. В ядрах
сплюснутой формы (см. рис. 10.17, в) имеет место обратная ситу-
ация. Таким образом, форма сечения поглощения в области гигант-
ского резонанса дает прямую информацию не только о величине, но
и о знаке ядерной деформации.
Расщепление гигантского резонанса в деформированных ядрах
независимо наблюдали Фуллер, Вейсс и Хейвард [151—153] и Спай-
сер и др. [344]. Как оказалось, все исследованные до сих пор дефор-
мированные ядра [67, 76, 255, 294] имеют вытянутую форму. Наблю-
дение расщепления гигантского резонанса вследствие деформации
ядра оказалось первым случаем, в котором наблюдалась сильная
связь дипольных колебаний с формой ядерной поверхности. Далее
мы увидим, что такая связь имеет очень общий характер и что можно
предсказать (и обнаружить) более богатую структуру в спектре
возбуждений, если перейти от статического случая к учет}' колеба-
нии ядерной поверхности. Более полное теоретическое исследование
этой проблемы будет дано в следующей главе.
305
§ 10.7. КЛАССИФИКАЦИЯ СОБСТВЕННЫХ
колебаний плотности
В предыдущих разделах была развита классическая гидродина-
мическая модель ядра. В частности, на основе этой модели были ис-
следованы процессы поглощения. Квантовомеханическая трактов-
ка этой модели является не только более полной, но и необходимой,
так как ядро представляет собой по сути дела микроскопическую
систему, подчиняющуюся законам квантовой механики. Для пере-
хода от классического описания к квантовому нам потребуются
в дальнейшем более систематическое описание и классификация ос-
новных решений гидродинамических уравнений, что будет сделано
в этом параграфе.
10.7.1. Различные представления тензоров
Для целей дальнейшего изложения рассмотрим преобразование
составляющих какого-либо тензора от сферических координат к де-
картовым. В качестве частных случаев такого преобразования кол-
лективных координат можно привести уравнения (2.20) и (4.5),
описывающие соответственно преобразования коллективных коор-
динат ядерной поверхности и радиуса-вектора. В общем случае
если qlm являются компонентами тензора в сферических коор-
динатах, его компоненты в декартовых координатах определяются
с помощью соотношений:
Qlm=--/2 (9z_m_(-l)m9jm);
Qlo = ?(0>
2 (?Z-m + (—tn>Q.
(10.145)
Для случая сферических функций будет использоваться несколь-
ко отличное определение:
-у Г2" (^т+(-1ГУг..т); |
®го — Г/о,
(10.146)
(Dz_m=-LiT2 ^-(-Ijmy^j, m>0,
где Ф;,п — сферические функции в декартовых координатах. Со-
отношения (10-145) и (10.146) различаются знаками индексов т и ко-
эффициентами. Используя (10.145) и (10.146), легко показать, что
выражение
2 (-1)"1 Ylm = 2 (-1Г Qt-m Фгт (10.147)
т tn
является скаляром.
306
10.7.2. Природа нормальных колебаний
Поскольку мы интересуемся собственными колебаниями протон-
„ „онной системы, опустим в соответствующих уравнениях чле-
Не описывающие взаимодействие с электромагнитным полем и тре-
Ние Тогда уравнения (10.89)—(10.91) принимают вид:
Рр(г,/) = Рр (0) (J+т] (г,/)); (10.148а)
и2 V2 т] (г, /)—= 0; (10.1486)
п- V-n |,= ко = 0.
(10.148в)
Решения этих уравнений, периодические во времени, будем ис-
катьв форме 1] (г, t) = т] (г) ехр (—i®/). Тогда нормальные колебания
определятся как соответствующие решения уравнений (10.148).
Они удовлетворяют уравнению Гельмгольца
V2t] (r) + ^2i] (г) = 0. (10.149)
Очевидно, что совокупность функций (/г (k\n} г) Yim (0, ср)} с лю-
быми возможными п, /, и т является полной системой* собственных
функций оператора Лапласа с собственными значениями —.
Эти собственные функции ограничены в начале координат. Разумеет-
ся, система функций {/г (k^r) Ф/т (0, <р)}, где Ф/Го (0, <р)—опре-
деленные выше компоненты сферических функций в декартовых
координатах, есть также полная система функций. Поэтому любое
решение уравнений (10.149) может быть разложено по одной из этих
систем функций.
Покажем теперь, что инвариантное относительно вращений раз-
ложение
-»1(г. 0= Z ill (И 0>
1=0
где
тц(г, 0 s^i/i(^n) г)(—1)' (21+ 1)1/2[9[г](/)хГ[/]][0],
(10.150)
(10.151)
удовлетворяет граничному условию (10.148), если поверхность ядра
представляет собой сферу, т. е. R (0, <р) = А’ц. Входящие в (10.151)
величины Ft являются нормировочными множителями, которые
будут определены ниже. Из структуры тц (г, t) ясно видно, что коле-
бания плотности описываются функциями, инвариантными отно-
сительно вращений**. Используя (10.150) и (10.151), получаем урав-
Эта система функций является полной для описания функций, регуляр-
х в начале координат.
(2 11 общем случае, когда поверхность ядра описывается уравнением
),величины г); (г, 0 зависят также от коллективных координат поверхности
Лр. и выражение (10.151) заменяется более сложным (см. работу [351]). Этот
Ший случай кратко обсуждается в § 11.2.
307
пение
° ° а''(ГГ)|,..я.1‘,1'1('>ХУ''1|‘Ч О0-152а)
Так как gt'J и не равны тождественно нулю, заключаем, ЧТо
Полученное уравнение имеет бесконечное число решений ==
= k\n}R0. Первые четыре решения для некоторых значений I пред,
ставлены в табл. 10.2.
Мы обозначили различные значения k как k\n\ Заметим, что
частный случай дипольных колебаний (см. табл. 10.1) также
Таблица 10.2
Значения zjn
п /=о 1=1 1=2 1=3 Z=4
1 4,4934 2,0815 3,3421 4,51409 5,64670
2 7.7252 5,9404 7,2899 8,58375 9,84045
3 10,9041 9,2058 10,6138 11,97273 13,29556
4 14,0662 12,4044 13,8461 15,24451 16,60934
содержится в уравнениях (10.152). Разложение (10.150) можно
теперь записать в виде
т](г, /) = 2 П/"’(г, 0, (10.153)
т
где
П/"’ (г, /) = Л(п) /, (С> г) (- 1)' (2Z+ 1)V2 х
X [<7<п>П1(/)хПО][0]. (10.154)
Нормировочные множители F/n) будут определены позднее
(10.168). Решения, соответствующие I — 0, 1, 2, 4, .... описывают
гигантские монопольные, гигантские дипольные, гигантские квадру-
польные и гигантские гексадекапольные колебания соответственно.
Индекс п характеризует различные обертоны этих колебании.
Будем называть колебание, описываемое т)/п>, n-м гигантским коле-
банием 2'-польного типа. Таким образом, как следует из обсужде-
ния, проведенного в последнем разделе, т])1’, т. е. первое гигантское
дипольное колебание, называется обычно просто «гигантский ре-
зонанс». Уже отмечалось, что каждый гигантский 2г-мультиполь
2/ + 1 раз вырожден соответственно 21 + 1 различным значением
308
ндекса т сферических функции, так как Е\п} = (llu/R0)z\n\ а
(п) = /?(1п) Ro ие зависит от т-
21 Интересно отметить, что энергия гигантского монопольного
ебания больше энергий дипольного и квадрупольного коле-
Ая ий и близка к энергии гигантского октупольного колебания
гм табл. 10.2). Начиная с дипольных колебаний, энергия резо-
анса при фиксированном п увеличивается при увеличении мульти-
Ночьности. Схематическое изображение гигантских мультипольных
колебаний было дано на рис. 2.2.
До сих пор мы интересовались только решениями уравнений
110 88) или (10.148), описывающих колебания плотности. Однако,
\пя того чтобы получить кинетическую энергию этих колебаний
(W 20), нам необходимо также знать решения уравнения для по-
тенциала скоростей, которое имеет вид [см. уравнение (10.84)]:
скоростей, которое имеет вид [см. уравнение (10.84)]:
----+ц2у2(Р<г’ 0-0- (10.155)
Разделяя переменные, т. е. полагая <р (г, I) = <р (г) ехр (—ico/),
получаем
Va<p(r) + F<p(r) = 0.
Соответствующее граничное условие имеет вид:
п • Vcp(r,/)|г=до = 0 (10.156)
или
— icon - V<p(r)|r=/?o = 0. (10.157)
Сравнивая эти уравнения с дифференциальными уравнениями
(10.148) для т) (г, /), видим, что мультипольные компоненты т) (г, /)
и ср (г, /) могут отличаться только множителями или аддитивными
постоянными. Однако поскольку физический интерес представляет
только \7<Р (г, /) [см. (10.73)], аддитивные постоянные можно не
рассматривать. Включая постоянные сомножители в коэффициенты
разложения, можно тогда написать:
<р(г, /) = 2<р1п)(г,/)= ^(-l)mS^’cp/(-m. (10-158)
nl nlm
причем
ср}н)(г, /) = Д<'‘>Д(^'ОГ)(_1)С(2/+ 1}1/2
X |s(n,w(/) X YU]][01 = i(— Ifslm’cpjl’m. (10.159)
т
Благодаря тождественности граничных условий (10.148в) и
(10.157), величины ^п) в точности совпадают с аналогичными вели-
чинами, входящими в выражение (10.154), описывающие колеба-
плотн°сти В соотношениях (10.158) и (10.159) (/) означает
сферические тензорные амплитуды, аналогичные введенным выше
величинам функции ср (г) и т) (г) не являются независимыми
309
друг от друга, так как они связаны уравнением непрерывности
(10.87). Функции <р‘п) (г) удовлетворяют уравнению
V2q><"> (г) = - (fe<">)2 (pt"> (г). (10.160)
Используя (10.87), можно получить:
П(О)
рр А(») — <?<") /10
Pl°d(Mn))2 Clm (*0-161)
Таким образом, тензор S'™, входящий в выражение (10.159)
для потенциала скоростей, с точностью до множителя совпадает
с производной по времени от тензора/Д' (/), входящего в выражение
(10.154), которое описывает колебания плотности.
10.7.3. Ортогональность нормальных колебаний
Докажем теперь, что нормальные колебания (г, t)
см. (10.154)1 удовлетворяют соотношениям ортогональности вида
$ П/('г)*(г)'пГ)(г)^=И<">бп,блп„ (10.162)
Объем
ядра
где Ип) — постоянные. Из дифференциального уравнения (10.149)
следует
J ф'>* V2nJn)dT= — (fe|n>)2 тД) dr, (10.163a)
а также
J T]|") V2T]t?')*dT= —тДМт. (10.1636)
Используя теорему Грина, получаем обычным образом
((/?<?'))2—(^n))2) J Ti^dT =
Объем
ядра
= J (11‘?')* ?2тД>— »li(n) V2n|"'>*)d'r =
Объем
ядра
= J (T]j? )* V'nj")—т]|п) do. (10.164)
Поверхность
ядра
Так как благодаря граничным условиям (10.148) интеграл по по-
верхности ядра обращается в нуль, то
|(Л(?'’)2—(&|n))2] f тД4* T]<'l)dT = 0. (Ю. 165)
310
I =£ l' ортогональность т]/"’ немедленно следует из свойств
ЛлЯ гоХтьностп сферических функций. Рассмотрим поэтому, урав-
орТ° (10.165) дчя I = /' Тогда, так как /г\п) #= для п #= п',
НеНП0 165) и ортогональности сферических функций сразу же можно
1,3„учпть соотношение (10.162). Поэтому функции т]/л) образуют
П°тему ортогональных и линейно-независимых нормальных реше-
CHft гидродинамических уравнений. Эта система функций является
также полной. Те же результаты, разумеется, имеют место для по-
тенциалов скоростей (г, 0-
10.7.4. Нормировка колебаний плотности
Скажем теперь несколько слов о нормировочных множителях.
Мы доказали единственность разложения •»] (г, I) или ср (г, f) по
нормальным колебаниям. Нормируем функции
Л{",(г) = ^п)/г(^п)г)Ьт, (10.166)
определяющие нормальные колебания плотности (10.154), для удоб-
ства сравнения амплитуд q^m в тех случаях, когда нужно знать меру
интенсивности, с какой возбуждается определенное нормальное
колебание (гигантский мультипольный резонанс). Нормировочные
множители определяются из условия
До
[ ’Ч/т* = (^(П))2 j? (k^ г) Г2 dr = 1. (10.167)
Объем *0
ядра
Для случая сферического ядра* имеем:
f(zn) = [4-(^n))“3z/3n(/'^n)-/z-1(г1п)/г+1М] 1/2- (Ю.168)
Множители нормировки потенциалов скорости qjm = Fzn) X
X ii г) Y 1т имеют, конечно, тот же вид, что и в случае
нормальных колебаний плотности. Однако в следующих разделах
мы увидим, что в действительности нормировка нормальных коле-
баний не является обязательной, так как все окончательные ре-
зультаты никогда не зависят от нормировки.
§ 10.8. ПОЛНАЯ ЭНЕРГИЯ ГИГАНТСКИХ
МУЛЬТИПОЛЬНЫХ РЕЗОНАНСОВ
В предыдущих разделах было показано, что колебания плотно-
сти жидких компонент ядра удовлетворяют волновым уравнениям,
ри этом функции т|)п) (г) описывают собственные коллективные
чт Лля сферического ядра нормировочные множители не зависят от т,
е имеет места для деформированного ядра.
311
колебания нуклонов, которые называются гигантскими резонанс
ми. Чтобы дать общий анализ коллективного движения, >келате%*
но выразить полные энергии различных гигантских мультипольны'
резонансов с помощью коллективных переменных. Как следует и
(2.34), величины q^, определяемые соотношением
оо эо I
п(г. 0 = V 2 V (- (0С> (г)
»=! 1 = 0т = — 1
= v V (_ 1)1 (2/+ 1)>/2 [ZJ х п(„) [^[0], (10 16
п=11 = 0 '
можно рассматривать как коллективные координаты гигантских
мультипольных резонансов. Если пренебречь кулоновскими силами
и трением, то полная энергия Е рассматриваемой системы из двух
жидкостей дается, согласно (10.20) и (10.25), выражением
Е = 7+ U = -i-Л4р>°Л f v2c(t + — Г (рр—рп)2с/т.
2 J Ро J
Объем Объем
ядра ядра
Так как
Рр-=Рр(0)(1+п(г. 0)
и
Рп = Рп(0)(1 —-^Т)(г, /)],
(10.170)
то энергия симметрии равна
L,_ *Р£(О) f
Ро «)
Объем
IV
1 — — + 2т] (г, f)
2
dt.
(10.171)
ядра
При выводе соотношения (10.171) мы не учитывали постоянное
слагаемое
-(рР(О)-рЛ(оф.
Ро J
Входящий в (10.171) член, линейный по т] (г, f) и имеющий вид
4^(0) Г (Ю.172)
Ро \ ' J
Объем
ядра
равен нулю, так как
У, f Т]<">6?Т= —2(fe("))-2 f v2T]jn)dT =
In J in
==— 2(fe<n,)-2$VT)z(")dT = 0. (10.173)
312
Поп доказательстве этого результата были попользованы теоре-
Гопна и граничное условие (10.148в). Разумеется, равенство нулю
_ . > т €1 ТТ £1
Съемного интеграла
(' т] (г, t) di
Объем
ядра
есть просто следствие
j] (г, /). Действительно,
Z, то
поляризационного характера плотности
так как полный заряд постоянен и равен
Z = $ Рр
Объем
ядра
(0) [ 1 + и (г, /)] dr =
5 Рр (°)dr + Рр (°) f
Объем Объем
ядра
ядра
(10.174)
Отсюда
Объем
ядра
Следовательно, в выражении для энергии симметрии нужно учиты-
вать только члены, квадратичные по т] (г, t).
Таким образом, для полной энергии получаем:
Д = -1-Л1р^ Г v2dT_|__±Lp=(0) Г |т](г, 0|Мт. (10.175)
2 J Ро J
Объем Объем
ядра ядра
Рассмотрим отдельно каждый из членов. Используя (10.169) и со-
отношение ортогональности (10.162), потенциальную энергию можно
записать в виде:
Ро J Ро inm
Ооъем
ядра
f (10.176)
J Ро
Объем
ядра
„ Для вычисления кинетической энергии вспомним, что, согласно
/III 1 Го\ 1 1 1
v = — V<p = — 2 (Г, /).
Inm
Используя теорему Грина, находим
J (v^;>-r-v^dT
Объем
ядра
J (10.177)
Объем
ядра
313
так как
J sW V<> -do = 0.
Поверхность
ядра
На основании (10.160) и ортогональности функций tpffl имеем-
J w'm-r-J фГгМ,п^т=
Объем Объем
яДРа ядра
= (Ji^y2 6ПП- 6/(- 6mm' . (10. 17g}
Отсюда можно заключить, что не только cpffi, но и Vcp}"’ образуют
систему ортогональных функций. Используя (10.158) и Получен-
ные выше результаты, находим
$ | v I* dr = 21 I2 J I V<> |2 Л = V (fe(«))2£ | S<£)|2. (10.179)
Объем nlm nl m
ядра
Таким образом, с помощью (10.161) получаем следующее выражение
для полной энергии (10.175):
£=v^S^2l«i! + -^2ICT-
Pred nl Vе/ ) m 10 nlm
которое легко записать в виде
2 (т в'п) (~ 1)|(2/+о1/2 ^<л) ш <п) [/]1[0]+
т 1
+ -i-C'(—1)/(2Z+1)1/2^(,i>w х (?(") П1][0]} , (10.181)
где
Д(п) ^Рр(О) .
С1 = -8^-(0) . (10.182)
Ро
Коэффициенты Ch как видно из (10.182), не зависят от I. Вы-
ражение (10.181) ясно показывает, что гигантские мультипольные
резонансы соответствуют системе несвязанных гармонических ос-
цилляторов, описываемых коллективными координатами q\m - В сле-
дующем параграфе мы опишем процедуру квантования выражении
(10.180) и (10.181).
314
_ _________________________J
S 10.9. КВАНТОВАЯ ГИДРОДИНАМИКА;
КВАНТОВАНИЕ ГИГАНТСКИХ МУЛЬТИПОЛЬНЫХ
РЕЗОНАНСОВ
Чтобы совершить переход к квантовому описанию системы,
обходимо согласно изложенному в гл. 2 ввести величины П^’,
которые являются импульсами, канонически сопряженными коор-
динатами qtt- По определению,
П$= = (10.183)
где кинетическая энергия Т дается первым слагаемым в (10.181).
Исключая q'im с помощью (10.183), получаем следующее выражение
для полной энергии:
£ _ V (—Д)г (2^+1 )‘/г щ(п) [/] х П(П) [Z]][O]
*ni 2B/n)
+ — V C<n> (_ iy (2/+ 1)% [?(") И! х ?(«) Ш]Ю1,
2 nl
(10.184)
или
е = X 4 “12 п{">* п{"> +
nl 2 m
I 1 v Нп) у ДЮ*Дл)
+ z.qim qim’
Z nl m
(10.185)
Далее квантование выполняется непосредственным образом с по-
мощью метода, детально описанного в гл. 2, к которой мы отсылаем
читателя. Вводя на основе (2.50) операторы q\^+ и q\m, описывающие
фононы гигантского мультипольного резонанса, получаем
Но«= 2ЫП)(?/т)+^П)+4-)- <10-186>
где
^> = ^1/ £Ц. = ^П) = Й1/(10.187)
I B(zn Г м A Ro
Значения zln даны в табл. 10.2. Формула (10.187) была получена
на основе соотношений (10.182), (10.103) и (10.88).
Решение уравнения Шредингера с гамильтонианом (10.186)
совершенно аналогично решению задачи о гармоническом осцилля-
торе квадрупольного типа, обсужденному в гл. 3. Основное состоя-
ние (вакуум) четно-четного ядра обозначим |0>. Тогда состояния
гигантских мультипольных резонансов можно обозначить как
?Й)+|0>. (Ю.188)
31S
Из трансформационных свойств операторов qfm относительн
пространственных вращений (гл. 2) следует, что фононы мультц°
польного гигантского резонанса <?/т + |0> имеют угловой момент
и его проекцию на ось г, равные / и т соответственно. Четность этих
фононов (гионов) равна (—I)2. Пусть L — оператор углового мо
мента. Тогда
|о>=/(/+1)^)+|о>,1
Ч W f (,О|89>
Сам оператор углового момента в рассматриваемом случае стро-
ится в полной аналогии с оператором углового момента квадру.
польных фононов, описывающих колебания ядерной поверхности:
в выражении (3.69) операторы [3, р+ необходимо заменить опера-
торами q и q+ п использовать соответствующие значения I н т.
Помимо однофононных состояний существуют также и много-
фононные состояния | 1Мп>, которые строятся путем векторной
связи из состояний с меньшим числом фононов подобно тому, как
мы строим многоквантовые волновые функции гармонического квад-
рупольного осциллятора, представленные в табл. 3.1. Например,
состояния с двумя дипольными фононами имеют вид
|/Л42>+= £(ll/|pvM)^k|0>. (10.190)
(IV
Четность таких состояний положительна. Полный угловой момент
I может принимать только два значения: 0 и 2. Значение I = 1 ис-
ключается по аналогии со случаем состояний, содержащих два
квадрупольных фонона [уравнение (3.46)1.
§ 10.10. МУЛЬТИПОЛЬНЫЕ ОПЕРАТОРЫ В ПРОСТРАНСТВЕ
КОЛЛЕКТИВНЫХ КООРДИНАТ
Поскольку мы перешли к кваптовомеханическому описанию мо-
дели, нам необходимо выразить операторы электрических мульти-
польных моментов (а также, возможно, некоторые другие опера-
торы) с помощью коллективных переменных. Следуя изложенному
в разд. 3.22 общему методу выражения мультнпольных операторов
с помощью коллективных координат, получаем для операторов
электрических мультнпольных моментов формулу
С- $Р7>гЧ\(1Л, (10.191)
Объем
ядра
где
Рр(г,о = Рр(О)(1+1](г,о). (Ю-192>
Поскольку мы не рассматриваем степени свободы, соответствующие
движению ядерной поверхности, т. е. cJH = 0 для любого X, т0
316
интеграл (10.191) дают только флуктуации плотности
ВКЛ(0р1 (г z)- П°ЭТОМУ с П0М0Ш'ЬЮ (Ю.169) легко получить
^=Рр(0)2 2 2 нгЛх
n=I 1=0 m= — l
X T)/m (0 Пр. dt.
Объем
ядра
(10.193)
Используя (10.166), находим
Q^=Pp(0) 2
11= 1
оо
2 4ЯЧГ,
п= 1
(10.194)
где fM дается выражением (10.168), а
° ।
G^ <5 А<’0^2^-1?}+3-^/Ан(еЧ). (10.195)
о «Л Ко
Таким образом, в оператор EZ-мультиполя дают вклад только
2х-польные гионы. Используя, наконец, выражение (2.50), полу-
чаем окончательно
2 4П) 1/жйяг(^ + (-1)^ГД)- (10.196)
п = 1 * ztJ}. "’к
Величины В[п) и col"1 определяются соотношениями (10.182) и
(10.187) соответственно. Оператор мультипольного момента линей-
но зависит от операторов рождения и уничтожения фононов. По-
этому его отличные от нуля матричные элементы связывают состоя-
ния, числа фононов (гионов) в которых различаются на единицу.
Мы рассмотрели квантовую гидродинамическую модель в слу-
чае жесткого сферического ядра, не имеющего других степеней сво-
боды, кроме тех, которые связаны с колебаниями плотности. Однако
это чрезвычайное упрощение делает более ясным основные идеи
модели и позволяет легко найти пути ее дальнейшего усовершенст-
вования. Наиболее существенное уточнение модели связано с уче-
том взаимодействия гигантских мультнпольных резонансов с дви-
жением ядерной поверхности.
Чтобы более полно ознакомить читателя с квантовой гидроди-
намикой ядра, мы дадим в следующем разделе последовательный
квантовомеханический вывод выражения для сечения фотопоглоще-
ния и сравним полученные результаты с результатами классических
расчетов.
317
§ 10.11. СЕЧЕНИЕ ФОТОПОГЛОЩЕНИЯ В КВАНТОВОЙ
ГИДРОДИНАМИЧЕСКОЙ МОДЕЛИ
Как было сказано в начале данной главы, гигантские резонан
обычно изучаются в реакциях поглощения фотонов путем измерен
поглощения пучка тормозного излучения, падающего на мщцен^
Исследуем эту проблему [97], предположив, что в момент t = п
включается электромагнитное поле Е (t) частоты со. Рассмотрим
поведение системы после включения поля в течение промежутка
времени, большого по сравнению с временами жизни возбужденных
состояний. Пусть ф; — волновая функция основного состояния
(состояние 10> вакуума фононов, соответствующих гигантскому
резонансу), а ф/ — волновая функция возбужденного состояния
(однофононное, или одногионное, состояние). Основное состояние
системы является стабильным и не распадается. В противополож-
ность этому возбужденное состояние распадается с переходом ча-
стично в состояния непрерывного спектра и главным образом в кон-
фигурации, отличные от конфигураций резонансного типа. В преды-
дущих разделах при рассмотрении классической гидродинамической
модели для описания распада гигантских резонансов вводилось
трение, качественной характеристикой которого служил параметр
ширины Г. При исследовании нормальных типов колебаний, необ-
ходимых для квантования системы, мы не рассматривали трение
для того, чтобы получить стабильные нераспадающиеся состояния.
После того как мы произвели квантование системы, нам необходимо
вновь ввести ширины состояний, что будет сделано ниже с помощью
гамильтониана
Будем описывать полную систему с помощью гамильтониана
H^f^+th + Hrad. (10.197)
В этом выражении Но — сумма членов, описывающих обсуждавшие-
ся выше гигантские резонансы и другие степени свободы ядра, кото-
рые здесь не будут конкретизироваться; Нг описывает распад со-
стояний гигантского резонанса: недиагональные отличные от нуля
матричные элементы связывают эти состояния с другими возбуж-
денными состояниями, например с многочастичными конфигурация-
ми типа состояний модели оболочек.
Мы будем предполагать, следуя идеям метода хаотических
фаз*, что усредненное взаимодействие различных уровней гигант-
ского резонанса, обусловленное гамильтонианом Jfj, близко к ну-
лю, т. е.
у <%|^|%><%|^| V ~ 0 (j0 198)
Метод хаотических фаз в теории ядра обсуждается в т. 3.
318
где фа 11
гягмое в (Ю
____________состояния гигантского резонанса. Последнее сла-
197), Hrcd, есть взаимодействие системы с электромаг-
нитным полем:
Hrad = e[ —) *E(/)D, (10.199)
Е__напряженность электрического поля, D — оператор ди-
потьного момента, т. е. е — заряд электрона. Будем считать,
что зависимость электрического поля от времени определяется вы-
ражением
E = £Eosin<o/, (10.200)
где е _ вектор поляризации.
Если at и af — амплитуды состояний ф,- и ip/, a ipv — полная
система ортонормированных собственных функций гамильтониана Но
(некоторые из ipv являются волновыми функциями состояний ги-
гантского резонанса, описываемых Hgr), то с помощью обычной
теории возмущений, зависящей от времени, получаем:
at Of еХ|Р (l
и
П/ = — ^-l- ai ехР о о +
+ > щ,ехр (i Юр,/). (10.201)
При выводе первого уравнения мы пренебрегали переходами из
основного состояния в «нерезонансные» возбужденные состояния.
Так как по определению гамильтониан Нг не имеет матричных эле-
ментов, связывающих основное состояние с другими состояниями,
во втором уравнении в сумме отсутствует член с v = i.
Образно говоря, эта сумма описывает превращение энергии возбуж-
денного состояния ф/ в тепловую (трение в гидродинамической мо-
дели). Следуя Вайскопфу и Вигнеру [379J, мы учтем эту диссипацию
энергии в среднем, предполагая, что члены с разными фазами ком-
пенсируют друг друга. Тогда имеем:
«/ = ^^ехрО^-ш)/)- (10.202)
Таким образом, амплитуды д{ и af удовлетворяют системе свя-
Усло1ЫХ диФФеРенциальных уравнений и следующим начальным
319
которые означают, что в момент включения электромагнитного
ля (I = 0) система должна находиться в основном состоянии. По°'
ставляя в (10.202) вместо а; его начальное значение, находим Д*
п (j\ __ ____Hrad\ t>_______
2iA[i(coyi—co) — Г//2&] X
X exp (i (co,—<o) /)—exp (—Гу//(2£)). (10.204)
Соответственно вероятность обнаружить возбужденное состояние
фу через длительный промежуток времени после включения поля
дается выражением
| af (t = оо) |2 = \ ------------
г 4&2 (On__W)2+r2/4A2
(10.205)
Сечение поглощения у-квантов о (со) определяется’ как отноше-
ние энергии, поглощенной за время жизни Й/Гу возбужденного со-
стояния, к величине потока электромагнитной энергии, падающего
на систему. Используя (10.120), находим:
ст (£) = ' \2Efi _
(El с/8л) (Й/Гу)
= f I </ WraJ | О |2--------E,iTf 1— . (Ю.206)
ft El с (Efi-E)*+ -Iff
Полученное выражение показывает, что сечение фотопоглощения
имеет резонансный характер, определяемый формулой Брейта -
Вигнера.
Вычислим теперь матричный элемент взаимодействия системы
с электрическим полем. В качестве примера рассмотрим случай
гигантских дипольных резонансов; для мультиполей высших по-
рядков вычисления производятся аналогичным образом. Конечное
состояние является состоянием гигантского дипольного резонанса,
начальное — основным состоянием системы
(10.207)
Ф/ = ?|(,п)+|0>, фу = [О>.
Рассматриваемый матричный элемент имеет вид
(10.208)
где скалярное произведение
е-D =2(—1)ц е-иЦ.
в
записано в сферических координатах, а для оператора дипольного
момента Qip. использовано выражение (10.196). Благодаря
тому что операторы ц и q удовлетворяют бозевским коммутацион-
ным соотношениям, сумма, входящая в (10.208), сводится к един-
ственному члену с п = N. Поэтому имеем:
//AN
с п = N. Поэтом)' имеем:
LP(^y/2£.>Z(-i)’ie-r
I \ ^ / ц
7 4л \ 7г „ .,... , f i
= е(т) £о^ет|/ —, (10.209)
1Й1\
«7i(£)+1 + (-1? 10> = (- 1)"!бт-ц.
Беря квадрат модуля матричного элемента, суммируя по кван-
товым числам проекции полного момента и учитывая, что У | ет |2 =
т
= 1, находим
2к^’+ ° 0>Г =
т । Х \ 3 / / |
<10-210)
Подставляя (10.210) в (10.206), получаем следующее выражение
для сечения фотопоглощения:
(т (р\ = 32jtS е2 7 Д(МП2 ____Ед Г/_____
' ЗА ’ с 1 7 2B(1,V> <b<w> ’ (E‘W)—£)2 + Гу/4
о(£) = — •
/2 (Z1.V)
Используя (10.168), (10.182), (10.194) и (10.195), получаем:
е- p°red х
с М ’ ’ ш(*) '
. Л "' ‘-. (10.211)
/?(2iw) /o(2iw)/2(2in)__________________(Е("» -E)4i1/4
Так как zN удовлетворяют уравнению
М.= ^.[//1_1(г)-(/ + 1)/у+1(г)] 0, (10.212)
то
— —h+i(Z|w)- (10.213)
11 Зак. 1218 321
320
Учитывая далее соотношение
/^(z) Pj,+1(2)^ Z Ё(2). />о,
получаем окончательно:
16л 2 е2 NZ о (Е) = — • — • — Ро - R3 2 В- х
3 Me2 A2 со’"'
у Еп Г/
(£’<w>-£)2 + rf2/4 •
(’0.214)
(’0.215)
Это выражение совпадает с классическим результатом (Ю 122)
для случая возбуждения колебаний типа q^+ |0>; сечение поглоще-
ния в области гигантского дипольного резонанса соответствует
М = 1. Единственное различие заключается в форме кривой погло-
щения: в квантовой гидродинамической модели форма сечения фото-
поглощения описывается формулой Брейта—Вигнера, в то время
как в классической теории — формулой Лоренца. Однако в слу-
чае малых ширин Г формы обеих кривых совпадают. Кроме состоя-
ний классического типа, q^^ 10>, в квантовомеханической модели
существуют состояния более сложной природы, q+q+...q+10}, не
имеющие аналога в классическом случае. Можно понять, почему
классическая гидродинамика дает результаты, достаточно хорошо
согласующиеся с экспериментом. Причина этого в том, что опера-
торы мультипольных моментов (10.196), в частности операторы ди-
польных моментов, линейно зависят от операторов рождения и унич-
тожения соответствующих фононов. Вследствие этого отсутствуют
переходы из основного в многофононные состояния. Другими сло-
вами, полная сила перехода исчерпывается вкладом однофононных
состояний, являющихся аналогом классических колебаний.
§ 10.12. МИКРОСКОПИЧЕСКОЕ ОБОСНОВАНИЕ
ГИДРОДИНАМИЧЕСКОЙ МОДЕЛИ ЯДРА
Может показаться, что возникает довольно затруднительная
ситуация. С одной стороны, имеется модель оболочек, в которой
все частицы движутся в общем потенциале и испытывают действие
остаточных взаимодействий. С другой, мы имеем коллективную
модель, в которой ядро характеризуется лишь небольшим числом
степеней свободы, описываемых классическим образом с помощью
нормальных координат. Естественно, возникает очевидный вопрос,
существует ли связь между этими двумя способами описания ядра,
или, более точно, может ли быть обоснована коллективная модель
в рамках модели оболочек? Мы изложим здесь некоторые сообра-
жения в пользу такого обоснования для случая ядерной гидроди-
намики*.
* Обоснование других коллективных степеней свободы будет рассмотрс
но в т. 3.
322
Рассматриваемая проблема не является тривиальной. Она вклю-
в себя как составную часть проблему описания высоковозбуж-
чаеТ х СОСтояний системы многих частиц. Довольно простое и яс-
ДеННхотя и громоздкое, ее решение было дано Уайлдом [386]. Общая
н ’ а обоснования коллективного подхода такова:
С 1 Определяется микроскопический (оболочечный) многочастич-
нЫй гамильтониан Н.
9.
Н по
Классический гамильтониан находится как среднее значение
подходящим волновым функциям. Обозначим символически
Нка---<\Н\У. (10.216)
3. Классический гамильтониан, являющийся функционалом от
используемых волновых функций, выражается с помощью класси-
ческих величин (наблюдаемых), таких, как локальные плотности,
локальные скорости и т. п. Символически его можно записать
в виде:
^кл = ^л(Ф)^^кл(р(Ф). У(ф),...). (10.217)
4. Нкл сопоставляется с классической функцией Гамильтона
гидродинамической модели (10.180).
5. Устанавливается справедливость уравнения непрерывности.
После того как доказана справедливость коллективного описания
системы, можно использовать все результаты, полученные в преды-
дущих разделах: определение нормальных колебаний и нормальных
частот, квантование классической функции Гамильтона и т. п.
Рассмотрим теперь несколько подробнее перечисленные выше пять
пунктов.
1. Квантовомеханический гамильтониан имеет вид:
„ _ , п-2 .
... (10.218>
гДе Hint — взаимодействие с электромагнитным полем, a Vij —
двухчастичное ядерное взаимодействие:
Vo(ro) = (W + HPrif P°1 + MPru+ ВР?,} Го (гм). (10.219)
Здесь Prtj — оператор перестановки пространственных координат:
О)-Ф(О. П). (10.220)
а 1 (. , ।
ч ~ 2Ф1 I Gt • ар —оператор перестановки спиновых пере-
менных. Оператор РцР^,, меняющий местами как спиновые, так
Ространственныг координаты, называется также обменным опе-
ратором I ейзенберга Рц. Его действие эквивалентно перестановке
арядовых координат нуклонов. Действительно, Рц = —Рц =
11
323
= —2 (1 + т;т>), так как благодаря антисимметрии волновой фуНк
ции ядра относительно перестановки пары частиц i и j Р^р*
= —1. Величина W характеризует долю сил Вигнера [384, 385]
Первоначально это название применялось к любым короткодейст
вующим силам, однако в настоящее время оно используется исклю
чительно для обозначения обменно-независимых сил. Аналогично
другие члены взаимодействия (10.219) называются по именам фн.
зиков, внесших большой вклад в развитие теории ядерных сил-
В обозначает силы Бартлетта [271, Н — силы Гейзенберга [187]
и М — силы Майораны [2381.
2. Определим теперь нужную нам волновую функвию. Наиболее
естественно и просто предположить, что основное состояние, ядра
Рис. 10.18. Схематическое изображение пзоспиновых (а)
и спии-спиновых (б) возбуждений ядра. Вертикальными
стрелками указаны направления спинов.
с заполненной оболочкой описывается оболочечной волновой функ-
цией
где фа (г) — одночастичные волновые функции модели оболочек.
Попытаемся теперь описать возбужденное состояние ядра, соот-
ветствующее в гидродинамической модели локальным колебаниям
плотности. Это может быть сделано путем следующего изменения
одночастичных функций:
Фа (У)-><fa (/) ==фа(/)ехр(Кб к*)-Х; X
х exp [ifh (Xj, t)} Vgh (Xj, t). (10.222)
Индекс k здесь означает тип частицы, например протон со спином>
направленным вверх, протон со спином вниз, нейтрон со спинов
вверх и, наконец, нейтрон со спином вниз. Модель формулируется
в таком общем виде, чтобы в ней имели место не только коллектив-
ные колебания протонов относительно нейтронов, но также и дрУ11,с
типы когерентных движений, такие, как спин-изоспиновые колеса
324
которых протоны со спином вверх и нейтроны со спином
Н,,Я’ колеблются совместно относительно протонов со спином вниз
вН113“тпонов со спином вверх. На рис. 10.18 схематически изобра-
И Пе?г изоспнновые колебания (обсуждавшийся до сих пор гигант-
резонанс) и спин-изоспиновые колебания*.
фактор exp [i (6k/) -xj вводится для того, чтобы учесть изме-
импульсов, возникающие при колебаниях плотности. Если
н-' в котором находятся частицы какого-либо одного типа (на-
име’р. протоны со спином вверх), сжимается, то импульсы этих
частиц должны увеличиваться, так как уменьшение объема вызы-
вает уменьшение длин волн находящихся в нем частиц, что приво-
дит в конечном счете к увеличению импульсов. Можно также ска-
зать, что уменьшение объема вызывает расширение сферы Ферми.
Так как числа частиц, движущихся направо и налево, одинаковы,
то ферми-сфера расширяется равномерно во всех направлениях.
Это означает, что
(10.223)
т. е. чистое течение жидкости отсутствует.
Возможность возникновения течения жидкости учитывается
дополнительным фактором exp (ifh (xjt /)), где fh (х,, t) связано
с локальной скоростью частицы k-ro типа. Амплитудный фактор
gk (xj. 01/2 вводится для того, чтобы принять во внимание общие
колебания плотности. В зависимости от выбора gh (х/, t) можно
описать либо волны плотности, либо спиновые волны. Это дает воз-
можность рассматривать движение протонов относительно нейтро-
нов, частиц со спином вверх относительно частиц со спином вниз
п т. д.
Если мы предположим, что возбужденное состояние описывает-
ся детерминантом Слетера, построенным из модифицированных одно-
частичных волновых функций <ра (у), то мы столкнемся с тем фак-
том, что, вообще говоря, <ра (у) не образуют подобно фа (у) ортонор-
мированной системы функций. Однако для малых колебаний плот-
ности различие между фа (j) и <ра (у) также мало. Можно поэтому
ожидать, что отклонение системы функций <ра (у) от условия орто-
нормированности мало, пока колебания плотности невелики. В
том случае для среднего значения кинетической энергии имеем;
Т= — ^2$<Ра(7) VJ<po(y)dT =
2т j е
— — L !) фа (/) gh 0 V/? Фа (/) dx +
Zm j
~ 2 J (Vf;,)2 2 (ф£ (/) gh (Xj, t) Фа (/)) dr +
k ih
* См. также т. 2, гл. 7 и И.
325
+ TZ i f (“T Z O') Sk (*j, О Фа (/)) dr +
bm k J \ gh J jk
+ $V-(...)dr. (10.224)
В этом выражении индекс jh обозначает /-частицу Л-го типа. Ча-
стицы, относящиеся к типу k', не совпадающему с k, не дают вклада
в сумму Последнее слагаемое в (10.224), содержащее операцию
дивергенции, возникает вследствие интегрирования по частям дв\х
предшествующих членов. Следуя изложенной выше программе
(10.1)—(10.5), выражение (10.224) можно рассматривать как клас-
сическую кинетическую энергию, которую теперь необходимо вы-
разить с помощью классических величин, таких, как плотности
скорости и т. п. Л4ы произведем эту операцию лишь с кинетической
энергией; обсуждение потенциальной энергии будет дано ниже.
3. Локальная плотность частиц k-ro типа дается выражением
2 Ф* (У) gh I) Ф (j) = Ph-
hi
Далее, вводя скорости
A .
Vh = —V/д.
i m
(10.225)
(10.226)
которые можно интерпретировать как локальные скорости частиц
/?-го типа, получаем кинетическую энергию в виде
т = + ( phvldT +
k z J
(10.227)
Здесь To — средняя кинетическая энергия в основном состоянии,
модифицированная благодаря фактору gh (х;, /). Она отличается
от истинной средней энергии в основном состоянии То лишь во
втором порядке малости, так как (gh (xit /))'/» имеет вид ]/ gb » 14
+ а, где а — величина первого порядка по малым отклонениям
от основного состояния.
4. Итак, мы подошли к моменту, когда нужно установить соот-
ветствие с классическим описанием. Ясно, что слагаемое l/2fflPhv*
в (10.227) может быть интерпретировано как классическая кинети-
ческая энергия колебаний плотности. Третий член в (10.227) не
зависит от скорости, так как он содержит лишь величины, описы-
вающие плотность системы. Поэтому при переходе к классической
гидродинамической модели он должен интерпретироваться как по-
тенциальная энергия. Подобный член, зависящий от градиента
локальных плотностей, использовал Вайцзекер в работах 13°
3811, посвященных выводу массовой формулы.
326
сих пор мы обсуждали только то слагаемое гамильтониана
которое соответствует кинетической энергии. Потении
^ная энергия может быть рассмотрена подобным образом,
есЛИ вычислить ее среднее значение
2S <Ч>«1 Vuka).
(10.228)
~ означает детерминант Слетера, составленный из волновых
дикций (10.222) аналогично выражению (10.221). Средняя потен-
альная энергия (10.228) также может быть записана в виде функ-
ции от локальных плотностей рй. Однако наряду с обычными чле-
нами в соответствующем выражении появляются обменные силы,
которые не могут быть классически интерпретированы столь же
непосредственным образом, как прямые члены. Эти обменные члены
могут быть сведены к прямым, если ввести функцию двухчастичных
корреляций [386].
5. Чтобы вывести уравнение непрерывности для колебаний плот-
ности, заметим, что
др
dt
-ТД'Ф + 'Ф 47
dt dt
(10.229)
и
dip
dt
(10.230)
Используя эти уравнения для волновых функций (10.222), мож-
но получить для компоненты /г-го типа уравнение непрерывности
в следующей форме:
г) г»
=—У • (Ph Vft) + обменные члены. (10.231)
dt
Это уравнение показывает, что изменение локальной плотности
частиц данного типа может быть вызвано как конвекционными
токами [первое слагаемое в (10.231)], так и обменными силами.
В действительности, обменные поправки компенсируют друг друга,
если рассматривать изменение полной плотности р = У ph. Тогда
имеем k
др
dt
- V- (2 Ра vft).
k
(10.232)
Первоначально при выводе массовой формулы Бете—Вайцзекке-
Р (см. гл. 12) гамильтониан Нкя был найден Уайлдом для основ-
выб СОСТОЯНия- Входящие в расчеты различные параметры сил
коэ^аЛИСЬ таким образом, чтобы получить правильные значения
ного нциентов в массовой формуле. Для избежания коллапса ядер-
вещества, при этом предполагалось, что при больших плотно
327
стях существует сильное отталкивание (см. гл. 12). Полученн
таким образом силы были использованы в дальнейшем УайлдЬ№
для исследования гигантского резонанса. Хотя схема выполнен^'
им расчетов довольно проста, ввиду громоздкости вычислений м3
приведем здесь лишь некоторые результаты. Единственное формаль*
ное различие между подобным микроскопическим подходом и из'
ложенной выше гидродинамической моделью заключается в появ
лении в уравнениях непрерывности обменных членов, которые
приводят к возникновению эффективной массы
т = ’ (10.233)
где
1 ,
«=уРо(Р1з + |Д4),
а
И13=-^С13(/И+Я),
р14 = -^-с14/И,
Cih = (s) р (S) 4- s2ti (s) tk (s) ds.
Здесь p(s) и t (s) — функции двухчастичных корреляций. Как можно
показать, Cik положительны. Поэтому для притягивающих ядер-
ных взаимодействий р, а следовательно, и а также положительны.
Таким образом т* < т, что совпадает с тем, что было отмечено
выше [см. уравнение (10.139)]. В заключение этого раздела отметим,
что исследование гигантского резонанса может быть, конечно, вы-
полнено и в рамках частично-дырочного формализма. Мы обсудим
это в т. 3 данной серии.
* * *
Представленное в данной главе изложение гидродинамической
модели было основано главным образом на лекциях Даноса [93]
и диссертации Штока [351]. Общие аспекты физики фотоядерных
реакций и их связь с этой моделью обсуждаются в статьях Даноса
и Фуллера [101], Шевченко и Юдина [333] и в недавнем обзоре
Спайсера [346].
r пав a 11. ДИНАМИЧЕСКАЯ
' КОЛЛЕКТИВНАЯ МОДЕЛЬ
Излагая в предыдущей главе гидродинамическую модель ядра,
мы ограничились лишь случаем сферических ядер, предположив,
что их поверхность не меняется во времени. Однако существование
колебаний ядерной поверхности и ее деформация указывают на
то что это приближение не удовлетворительно. Таким образом,
для изучения рассматриваемых свойств ядер требуется более по-
следовательная теория, принимающая во внимание коллективные
степени свободы поверхности ядра. Данная глава посвящается из-
ложению такой теории. Сначала рассмотрим общий бид взаимодей-
ствия колебаний ядерной поверхности с движением, соответствую-
щим гигантскому резонансу. Определение этого взаимодействия
во многом производится таким же образом, что и определение
коллективной потенциальной энергии (см. гл. 4). Далее мы увидим,
что взаимодействие колебаний плотности со степенями свободы по-
верхности ядра является очень сильным, поэтому оно существенно
сказывается на структуре гигантских резонансов. Излагая динами-
ческую коллективную модель, мы будем следовать истории ее раз-
вития. Поэтому сначала рассмотрим эффекты этого взаимодействия
в ядрах с вращательным спектром, а затем обобщим модель на слу-
чай сферических ядер, в которых происходят квадрупольные коле-
бания поверхности.
§ 11.1. ВЗАИМОДЕЙСТВИЕ КОЛЕБАНИЙ ПЛОТНОСТИ
СО СТЕПЕНЯМИ СВОБОДЫ ПОВЕРХНОСТИ ЯДРА
Наиболее важными типами колебаний плотности являются ги-
гантские дипольный и квадрупольный резонансы, которые описы-
ваются соответственно коллективными координатами (/j? и q(^
см. уравнения (2.34) и (10.153)]. Поскольку мы ограничимся обсуж-
дением ^только этих двух типов движения, опустим в дальнейшем
ерхний индекс (1). Сферические тензоры* и имеют соот-
---------
колеб ^еРхние индексы типа (1), (2) и т. п. обозначают различные обертоны
облои?НИИ’ в то время как верхние индексы [1], [2] и т. д. используются для
начения ранга тензоров.
329
ветственно отрицательную и положительную четности. Степеи
свободы, соответствующие квадрупольный деформациям повел И
ности ядра, описываются тензором а[21 положительной четности
Так как взаимодействие И гигантских резонансов с поверхностью
ядра должно сохранять как четность, так и полный угловой мо
мент, оно должно быть тензором нулевого ранга положительной
четности. Таким образом, наиболее простое взаимодействие гигант-
ского дипольного резонанса с квадрупольными колебаниями поверх-
ности ядра имеет следующий вид:
//('>=. /<(<) [«[2] х |<у'Ч X <?111][2]1[0]_|_
+ /<<'„) [cc[2I X al21Ц0] [t/in X ?1П]Ю] +
+ ') X a[21l[2] X [<7[1] X rytЧ]Е2]] ЮЗ
+ К‘‘> [cd2] X 1Г1ГЧ х ninplJ^+K^) [al-9l X anilol х
X [ШП X П1П][0] + К<2'2) [ [al2l X ccf 2]][2I X
X [П(Ч x П1П](2]]Ю1_|_ ... (Ц Л)
Первая часть этого выражения, содержащая q, описывает по-
тенциальную энергию, в то время как вторая часть, зависящая от
канонических импульсов П[*], характеризует связь кинетической
энергии дипольных состояний с движением ядерной поверхности.
Ниже мы увидим, что для гармонических дипольных колебаний
члены с 4-го по 6-й выражения (11.1) равны соответственно членам
с 1-го по 3-й. Благодаря требованию инвариантности относительно
обращения времени рассматриваемое взаимодействие должно быть
квадратичным относительно импульсов П. Возникает вопрос: по-
чему в выражении (11.1) отсутствуют члены, содержащие л[2]—
канонические импульсы, описывающие движение поверхности ядра?
Такие члены могли бы, например, иметь вид
[[ЛИ! X ЭТЮЗ]12] х (</[ 1] х q[ I ]](21]О]
или
[Л121Х л12]]1°] [П[|1 х П1Ч](0] (11.2)
Члены первого типа опущены вследствие условия адиабатич-
ности. Энергия йсо2 возбуждений поверхности имеют величину
порядка 1 Мэв, в то время как энергии ЙИ состояний гигантского
резонанса больше 15 Мэв. Поэтому
д»2<до. О1-3)
Другими словами, в каждый момент времени колебания, соот-
ветствующие гигантскому резонансу, происходят как бы при фикси-
рованной форме ядерной поверхности. Ясно, что в адиабатическом
пределе (со2 -> 0) члены рассматриваемого типа должны обращаться
в нуль. Члены, содержащие четыре канонических импульса,
являются релятивистскими и имеют поэтому очень малую величину-
330
гигантских квадрупольных резонансов со степенями сво-
бо ^^поверхности ядра описывается выражением, аналогичным
Н(2) К™ [а[2] X [cd23 X [</[2] у ^J^JgO] _|_
° + [ccf 2J X «[2]][0] [<Д 2] X ?[2]][0] +
_|_ [[«121 Х «[2]][2] X [^2I X ^С2]][2]] [0] _[_
+ К£> [[а[2] х «[2JJI41 X [</[2] X 9[2]][4]][°] +
+ К<2) [«[2] X [П12] X ПГ21][2]][°]-р
К^2) («[21 X a[2J][°] [ПС23 х П[2]]10] +
+ MV [[“[21 Х «[2]][2] X [ГК2] X П12]][2]]I°I +
+ К<2> [[«(2] X а<2Л™ х [П12] X П12]][41][°] +... (11.4)
В противоположность (11.1) это взаимодействие содержит члены,
линейные по квадрупольным координатам q!2] в случае гигантского
дипольного резонанса подобные члены отсутствуют благодаря со-
хранению четности и углового момента. Ниже мы увидим, что куло-
новское отталкивание протонов в ядре приводит к появлению чле-
нов вида [а[2] X (?12]][0].
Мы установили структуру взаимодействий, исходя из общих
условий инвариантности. Теперь необходимо определить значения
параметров связи К$, входящих в выражения (11.1) и (11.4).
§ 11.2. НОРМАЛЬНЫЕ КОЛЕБАНИЯ ПЛОТНОСТИ
В ДЕФОРМИРОВАННОМ ЯДРЕ И ПАРАМЕТРЫ СВЯЗИ
Относительно просто параметры связи, входящие в и /7<2),
могут быть найдены в адиабатическом пределе, т. е. при со2 0.
В этом случае ядро характеризуется мгновенной деформацией
и поэтому очень важно установить вид нормальных колебаний
плотности и их частот в деформированном ядре. Решение этой проб-
лемы, а именно определение нормальных решений уравнения Гельм-
гольца
V2 т] (г) 4- k2 Т) (г) = 0
с граничным условием
(П-5)
где
n-VTj(r) |г=й=-0,
(11.6а)
/? = (1 + X ( — 1)х (2Х + 1)’/« [cdM X УР^Ю]), (11.66)
не являете тривиальным, так как граничные условия должны удов-
воряться согласованным образом относительно параметров де-
формации а[Ч. уже из общей формулировки проблемы видно, что
331
в рассматриваемом случае колебания
новятся зависящими от т. е.
плотности и их частоты
ста.
Т] = Т] (г, atM);
k = k (а[Л1).
(U.7)
Общее решение этой задачи, которое довольно сложно и громозл
ко, было найдено Штоком [351, 353]. Ради простоты и ясности
изложения мы дадим здесь менее последовательное решение, кот0
рое, однако, позволит легче понять основные идеи метода [364]'
Это приближенное решение может быть найдено для ядра в форме
произвольного эллипсоида с помощью вариационной процедуры
[203]. Умножая уравнение (11.5) на т]* (г) и интегрируя по объему
(поверхность, ограничивающая этот объем, может быть деформиро-
ванной), получаем:
§ rj*¥2т)с[т4-А2 § ri*i)dT = 0. (П.8)
V V
С помощью теоремы Грина находим
т]* V2qdr = .f' т]* Vr]-c/s— Vi]*-Vr)dr. (П 9)
vs v
Отсюда, используя (11.8), имеем
JVT)* Vi]dT— J T)*VT)-ds
k2=*-------------------------
f t] dx
V
Если бы т] (г) было точным решением уравнения (11.5), удов-
летворяющим граничному условию (11.6), тогда второй член в чис-
лителе формулы (11.10) равнялся бы нулю и эта формула определяла
бы точные собственные значения k2. В общем случае, однако, такие
точные решения трудно найти. Поэтому мы будем исходить из ва-
риационного принципа
f IVt)/ I2 dx
/c2 = rnin —--------, (11.11)
f | T]t |2 dx
v
где T)f (r) — пробная функция, которая может зависеть от пара-
метров, т. е. т]( (г) == гр (A.J, Х2, ...; г). В качестве пробных функции
в уравнении (11.11) могут также использоваться функции, которые
не обязательно удовлетворяют краевому условию (11.6).
Очевидно, что нормальные колебания, происходящие в сфериче-
ском ядре, при увеличении деформации непрерывным образом пере-
ходят в нормальные колебания ядра эллипсоидальной формы, т. е
т) (г> Ро) -* Л (г) при р0 —>0. Так как в действительности деформации
332
ядер относительно невелики, 0 < ₽0 0,35, нормальные коле-
бания деформированных ядер не очень сильно отличаются от
нормальных колебании сферических ядер, определяемых выра-
жением (Ю.154). Кроме того, поскольку (2Л + 1) нормальных
колебании сферического ядра являются вырожденными можно
no-видимому, использовать в качестве пробных функций п, линей-
ные комбинации этих колебаний: н «
Що (flo> fla) ~ (°о, °з)'Ф-м (г). ° — 1. 2, ..., (2Я,ф-1), (11.12)
Рис. 11.1. Схематическое изображение нормальных дипольных колебаний в де-
формированном ядре согласно (11.13): (+ + +)—протоны, (--------—)—ней-
троны.
где ijXa (а0, а2) — (2Z, + 1) нормальных колебания деформирован-
ного ядра. В общем случае коэффициенты разложения ДОц (а0, а2)
зависят от параметров деформации а0 и а2, описывающих форму
эллипсоида во внутренней системе координат. Минимизация соот-
ношения (11.11) позволяет в этом случае получить (2Z + 1) линей-
ных однородных уравнений для определения (а0, а2) и, сле-
довательно, нормальных колебаний деформированного ядра.
Однако описанная выше процедура все еще слишком трудоемка.
Поэтому мы предпочтем следующий метод. Известно [260], что
с помощью вариационного принципа собственные значения обычно
определяются с точностью на порядок лучшей, чем собственные
Функции т]г. Кроме того, согласно определению, параметры связи,
входящие в выражения (11.1) и (11.4), не зависят от параметров
°о и а2. Поэтому для вычисления параметров связи достаточно рас-
смотреть только случай очень малых (бесконечно малых) деформаций
°0 и «2- Тогда, используя в качестве пробных функций для уравне-
333
Рис. 11.2. Схематическое изображение нормальных квадрупольных колебаний в деформированном ядре согласно
(11.14). Обозначения те же, что и на рис. 11.1.
1 ц\ функции, описывающие нормальные колебания сфери-
Н11Я ^'ядра, можно получить достаточно хорошие значения k2,
чес*01"0 вен’но вычисляя интегралы, входящие в формулу (11.11).
цепоср Л‘ ическнх соображений очевидно, что нормальные диполь-
I 3 ,1ебания плотности в трехосном эллипсоиде представляют
нь>е ^колебания, соответствующие стоячим звуковым волнам вдоль
С°х главных осей. Эти колебания плотности описываются выра-
жениями - г)ф1ль м = 1,0, -1, (11.13)
где Ф|«__компоненты сферических гармоник в декартовых коор-
натах [см. (10.146)1, a Fi — нормировочный множитель. Нормаль-
ные колебания плотности (11.13) схематически изображены на
11 .1. В упомянутой выше работе Штока можно найти строгое
доказательство того, что выражение (11.13) действительно является
хорошим приближением для описания собственных дипольных коле-
баний в деформированном ядре.
Аналогичная ситуация имеет место и для гигантских квадру-
польных резонансов. В этом случае распределения нормальных
колебаний плотности в деформированном ядре имеют вид
^M = F2j2(k2r)®2M, М----2, 1, 0, -1, — 2, (11.14)
схематически изображенный на рис. 11.2. Видно, что колебания
видат]21 и т]2-1 происходят соответственно вдоль осей 0~ , <р = 0
и 0 ~ = Позднее этот факт окажется довольно важным, так
как мы увидим, что измерения энергий указанных квадрупольных
гигантских резонансов могут дать информацию о размерах ядер
вдоль этих осей.
В общем случае нормальные колебания плотностей в слабо
деформированном ядре приближенно описываются выражением
(см. (10.147) и (10.151)]:
П (г, 0 = 2 Л г) 2 (- l)m ;
In т
= 2(-Л/ш,
(11-15)
1пт
из структуры которого видно, что являются коллективными
координатами, описывающими соответствующие гигантские резо-
нансы в деформированном ядре. Знак~ указывает, что эти коорди-
ты относятся к внутренней системе отсчета. Величины q и Q обоз-
иают соответственно компоненты тензоров в сферических и де-
картовых координатах.
3Hen*“ опРеДеления с помощью вариационного принципа (11.11)
ргии гигантских резонансов в слабодеформированных ядрах под-
-овимв (11.11)
выражения для нормальных колебаний:
= (П.16)
335
и вычислимом?. В результате длинных, но простых расчетов поле
следующие выражения для волновых чисел гигантских диполь *
и квадрупольных колебаний: ‘ |,Ь|>
2,08 / R —R \
м^)('-| 0’08Лг}' |,=1Л“| (и.,?)
и
(«о. а2) -= [1 + 4 (В2-2) 0,284 (ап-
/\о L
— вб|ц| 1 + ] '6 ) — Л^о]. Р - —2, - 1, о, 1, 2, (П 18)
где
Fo=O,186; F±i = 0,077; F±2 =—0,058; (11.19)
(а0, а2)—длины главных полуосей ядерного эллипсоида. Если
поверхность ядра описывается уравнением
I ' +1 20 ~Ь °2 (^22 4~ 1^2-2))’ (1 1.20)
то [см. (2.24) и (2.25)]
/?и=^о|1 + (----,/2(°о+)]• (11.21)
Формула (1117) была впервые получена Инопиным [2031, кото-
рый показал, что это приближенное соотношение очень хорошо
описывает точное решение Даноса [88] для случая аксиально-сим-
метричного эллипсоида. Аналогичные выражения легко также полу-
чить для всех других нормальных колебаний плотности. Однако мы
не будем рассматривать здесь высшие мультиполи, так как в физике
фотоядерных реакций наиболее важную роль играют дипольные
и квадрупольные резонансы.
Энергии этих резонансов в слабодеформированном ядре имеют
вид:
E^-huk^. (11.22)
Подставляя в это выражение числовые значения и учитывая члены
второго порядка малости по параметрам деформации [3641, получаем,
используя (11.17):
О,58ОЗао +0,3661а?};
Е1 ± I = Eg {1 + О,29О2ао +0,7107а2 + (11-23)
+ 0,0915а? + 0,4483аоа2 + 0,5491а|},
и, используя (11.18),
Е20 = Eg {1 — 0,2848а.,—0,1872а? — 0,2456а22};
Е2±1 =£«{!~°, 1424«о ± 0,3488а2—0,0775а? +
+ 0,0262а2 + 0,222аоа2},
336
£2±2 £2(14-0,2848^^0,0584^-^’7369^2^ (Ц.24)
где
*'0
/ 8х NZ
|/ М* А2
=йах
н
первый корень J,6055£* = ЙЙ.,. (11.25)
Ео - первый корень /J ° 2,0816 “
пажения (11.23) и (11.24) определяют энергии резонансов в соб-
°енной системе координат, жестко связанной с ядром, и их за-
^спмость от параметров деформации а0 и а2. В адиабатическом
ппиближении эти параметры являются фиксированными.
Сферические компоненты координат гигантских резонансов во
внутренней системе отсчета определяются выражением
7xp=l^(6;)^v. (11.26)
В адиабатическом приближении
-- У Dvg (0>) <7zv + S (0/) « У (0,-) qKv, (11.27)
v v V
так как благодаря малости энергий (частот) вращения ядра по
сравнению с энергиями гигантских резонансов, Лс£>го1 ' ЙЙ,
можно пренебречь членом, пропорциональным Ьуц.
По аналогии с уравнением (10.145) введем декартовы компоненты
коллективных координат гигантских резонансов по отношению
к внутренней системе отсчета:
__Li । 2 (<n^-(-l)>.J;
Q?.o q^o;
Qx-н у) 2-(9х-ц4-(— iWxJ, p>o.
(11.28)
а также операторы рождения и уничтожения соответствующих
фононов (гионов)
—±- i I Г(^-и-(- 1)Н );
Qxo =<?zo;
г(0*_м+(-1Ня+м)
(11.29а)
337
и
&n = y-i| 2 (— 1)н^ц);
Q?.o = <?ло;
&-и = уГ2 ^л-ц-Н— 1)»‘^).
Теперь мы можем очень просто установить форму гамильтониана
описывающего гигантский резонанс в слабодеформированных я ’
рах. Подведем предварительно краткие итоги. Мы показали, что
нормальные колебания таких ядер хорошо описываются выражения-
ми (11.13) и (11.14); в этом случае соответствующие коллективные
координаты определяются уравнением (11.15). С помощью варца.
ционного принципа были вычислены энергии резонансов (11.23)
и (11.24). В собственной системе отсчета слабодеформированного
ядра искомый гамильтониан в адиабатическом приближении мо-
жет быть поэтому представлен в виде суммы гармонических осцил-
ляторов различных мультипольностей:
Иод+ //int=X^xn(«o. «з) -у) (11.30)
Вид этого гамильтониана определяется с помощью метода, ана-
логичного используемому в 'молекулярной физике и основанному
на адиабатическом приближении методу Борна—Оппенгеймера [48].
Следуя основным идеям этого метода, можно предположить при
выводе выражения (11.30), что форма ядра, характеризуемая пара-
метрами а0 и а2, является фиксированной. После того как вид га-
мильтониана (11.30) установлен, параметры а0 и а2 рассматриваются
как обычные динамические переменные, определяющие коллектив-
ное движение поверхности ядра.
Гамильтониан (11.30) содержит как невозмущенный член Hgr,
описывающий гигантские резонансы, так и взаимодействие Hint
этих резонансов с движением ядерной поверхности. Очевидно, что
(11.30) должно совпадать с (11.1) и (11.4), если их записать в соб-
ственной системе отсчета:
Hint = Hint(a0, а2, Ql'\ Q[2]) = j
= а2, ql'\ Y^) + H%(a0, а2, q™ (H-3D
Как видно из (11.31), Нш и H^t являются функционалами °т
а0, а2 и Пхм. Взаимодействие Hint может быть получено с по-
мощью (11.30), если рассматривать только члены, зависящие оТ
а0 и а2. Так как взаимодействие является скаляром, выражения
(11.1) и (11.4) преобразуются к собственной системе отсчета просто
338
Замен°й
а[2]^й[2];
ПР-]-> ГР-]
(11.32)
ппяя из этих замен возможна лишь в адиабатическом при-
Г°С>кении [см. выражение (11.27)]. Подставляя (11.28) и (11.29)
Н1 30) выражая с помощью (2.50) координаты и импульсы через
В еоатор'ы рождения и уничтожения и сравнивая соответствующие
°Пены в левой и правой частях выражения (11.31), получаем систему
з'инейных уравнений для определения неизвестных параметров
связи Kfcv- Мы не будем выписывать здесь эти уравнения вследствие
их громоздкости; заметим лишь, что они имеют единственные ре-
шения:
М*> _А_+к(1) 2-hB jfi 2В!Й! 1 2 11 1 BjQi -0,794E£
л(,) *'20 MV—h в, Qj MV A 2В!Й! -° 2 Вг Й! 0,354E£
/((П /Х22 +MV — й =M V = 2ЙХЙ! 22 2 1 1 22 BiQ, - 0,468E£
(11.33)
K{02) 0;
k<2) 1 2В2 Q2 +7((2) 4- Ьв2 п2 = М2)А = °’596^ Z £>2 ““2
Ю(2) 20 2В2Й2 4-MV -Ub2Q2 = M20> А = -°’081£9о; Z £>2 ““2 (11.34)
M2V — 2В2Й2 +MV 4tlB^ А = -°-355£s;
К<2) - 24 2В2Й2 + MV 4 ^2^ = М2) А =-°’188£0’ Z £>2 ^2
где В, и В2 — массовые параметры дипольных и квадрупольных
резонансов, определяемые формулой (10.182). Как уже указывалось
выше, определенные таким способом параметры М и Кк, харак-
теризующие соответственно потенциальную и кинетическую энергии
взаимодействия, имеют единственные значения. Факторы ^/2B?Qx
и ~2 ^В^Ц^ входящие в соотношения (11.33) и (11.34), связаны
00 £груКТурой выражений (2.50).
явл аК КаК колебания, соответствующие гигантским резонансам,
Из П?ТпЯ почти гармоническими, это дает возможность исключить
' 1) и (11.4) члены, связанные с кинетической энергией. По-
339
скольку в рассматриваемом приближении кинетическая и по
циальнаяэнергии равны, можносохранитьв (11.1) и (11.4) лищь°Те11'
потенциальной энергии, изменив соответствующим образом цЧ1е11
метры связи: аРа-
1/(^) _ /
V |iv - (11.35)
Эти значения параметров связи будут использованы в разд. 11 ю j
В адиабатическом приближении взаимодействия типа [ссО]
X для гигантских квадрупольных резонансов отсутствую
так как в этом приближении выражение (11.30) содержит тольк’
квадратичные члены относительно операторов рождения и унпчто°
жения гионов. Однако благодаря наличию кулоновского взаимо
действия протонов параметр связи Mj,2’ не равен нулю (109].
В принципе подобный метод может быть также использован для
вычисления параметров связи, характеризующих взаимодействия
высших порядков. Хотя мы ограничились рассмотрением только
членов второго по а2(1, следует указать, что взаимодействия
высших порядков, а также ангармоничность колебаний по-
верхности ядра могут оказать довольно заметное влияние на струк-
туру гигантских резонансов в сферических ядрах [377].
§ 11.3. ОПЕРАТОР ГАМИЛЬТОНА
ДЛЯ ДЕФОРМИРОВАННОГО ЧЕТНО-ЧЕТНОГО ЯДРА
Мы будем следовать историческому ходу развития динамической
коллективной модели, которая была впервые предложена для де-
формированных ядер [97, 325]. Гамильтониан, описывающий раз-
личные коллективные степени свободы ядра, в общем случае имеет
вид
Н — Hcoll+Hgr-Ь-н inf (11.36)
В частном случае деформированного четно-четного ядра Нссц со-
держит члены, определяющие вращение ядра, HToi, [3- и у-колеба-
ния, Hvib, а также колебания октупольного и других типов, кото-
рые мы не будем в дальнейшем рассматривать. Поэтому
ficoll = Hrot + Hvib, (П-37)
где
HTot = t - (/ц- /в? = Hrot 4- Hroivib + Hcoriolis + -
Подобное представление Hrot можно получить, основываясь н
соображениях, аналогичных тем, которые были использованы в сЛ
чае ядра с нечетной частицей [см. выражение (9.25)]. Связь гио№>
340
б ждений, соответствующих гигантским резонансам, с дви-
т е. в°3 УерНОй поверхности, рассматривается в полной аналогии
жением ДЯ, ильной связи внешней частицы с ядерным остовом,
со сЛУ и (Ц.38))gZ) — компоненты углового момента, соответст-
В ВЬ'Р Х-польному гигантскому резонансу, а Д — компоненты
вуюШеГО ,ювого момента системы. Заметим, что наиболее сущест-
вую роль в правой части (11.38) играет член
(f-i/.-h11)2)-
2Уо
Гамильтониан Hvib описывает, как обычно [см. выражение
(6 42)1, колебания поверхности ядра:
1+—с0£Ч-с21]
2 ат)2] 2 оь 21
(11.39)
HBib 2B [d£2 2
.2
A2
. (11.40)
16Bt)2
Моменты инерции (L й) определяются выражением (5.72).
Следует заметить, что гамильтониан (11.37), описывающий степень
свободы поверхности ядра, может быть определен из свойств низко-
энергетического спектра ядра (основная вращательная полоса, вра-
щательные полосы Р- и у-колебаний и т. п. — см. гл. 6). Появление
JU) в (11.38) обусловлено сильной связью (f — М + j(X), где М —
угловой момент вращения остова) гигантских резонансов с поверх-
ностью ядра. В дальнейшем мы будем пренебрегать [96, 97] различ-
ными малыми членами, такими, как взаимодействие вращений и
колебаний, кориолисово взаимодействие и т. п. Как уже указывалось
выше, параметры, входящие в (11.37), непосредственно связаны
с характеристиками низкоэнергетических возбуждений ядра. Де-
формация ядра р0 определяется с помощью приведенной вероятности
перехода В (£2; 0+ 2+) в первое вращательное состояние, Еу =
h {С^В)'В — энергия у-колебаний, £р А (С0/В)'В — энергия
P-колебаний, а е = h2lty определяет величину энергии первого
вращательного уровня (см. рис. 6.5).
В общем случае гамильтониан, описывающий гигантские резо-
нансы в собственной системе координат, дается выражением (11.30),
+ = т])(<2хц+^и + • (Н.41)
(Н 41) отсутствуют обертоны гигантских резонансов (н _> 1);
нью^А Д^Т РассматРиваться лишь дипольные (1 = 1) и квадруполь-
лее = 2) колебания. Чтобы сделать дальнейшее обсуждение бо-
Зап ЯСНЫМ’ РассмотРим эти Два случая независимо друг от друга.
Hgr + нш = ч Н\1п] + 4- .
(11.42)
341
где
и
Н^+Й<М.= V Ай1ц (g, П) ( Q1^1u + -L')
2 Eltl(g, п)(&Ж+44
Ц= —1 * 2 '
+ Й% = £ (В, ц) (& йн + 4-1
= е2ц(|, п) (&Ж+44
ц = —2 к 2 '
1
(11.43)
Здесь фщ, Q2h и ф1ц, ф2)11 — соответственно операторы рождения
и уничтожения дипольных и квадрупольных гионов в собственной
системе координат. Как было упомянуто выше, обертоны (п > 1)
в (11.43) не учитываются вследствие малости соответствующих сил
переходов (см. § 10.5). Частоты Qut и Q2>i были вычислены ранее
с помощью гидродинамической модели и определяются формулами
(11.17), (11.18) и (11.22), в которые надо подставить величины
«о = ₽о + I и о2 = г)-
Напомним еще раз, каким образом возникает связь гигантских
резонансов с колебаниями поверхности ядра. Частоты Q]tl и Й2(1
зависят от деформации поверхности ядра и, следовательно, от пере-
менных £ и т], описывающих колебания поверхности. Гамильтониан
(11.43) и частоты (11.17) и (11.18) были определены в адиабатическом
приближении. Так как Ер/ЛПг ж ж то колебания по-
верхности являются очень медленными по сравнению с колебания-
ми, соответствующими гигантским резонансам. Благодаря этому
частоты могут быть вычислены в предположении, что форма
ядра является неизменной. После того как частоты определены
в статическом приближении, величины Н и т] снова рассматриваются
как переменные, описывающие движение поверхности. Подобная
процедура полностью аналогична методу Борна—Оппенгеймера
[48], используемому в молекулярной физике. Разлагая Пх(1 (В. т1)
в ряд относительно положения равновесия £ = 0, г] = 0 и ограничи-
ваясь линейными членами, получаем
^/г£М0)(^Ж+4~) ; (1Ь44)
1
Ц = -2
(0) ( Фг^фзцф——;
(11.46)
342
V йй2и (0)6^15 Ц6|(1|1Т]1 6 + (11.47)
r.ie
X
G^l> (- 1 /2)'и) (4л/5)-’/«х
1__________________( 0,08
1+( 1 /2)1 1 (4л/5)-у= ₽„ 1+0,08( -l/2)i u 1(4л/5Г’/2ро
есть факторы,
зависящие от статической деформации ядра 0О, а
/,Й10 (0) ЙЯ (0){1 —О,58О30о + 0,36610g + ..};
Д£2, (0) Ди-2,08^* = 70х Л-*/3 Мэв;
&>1±1(0) (0) {1 + О,29О20о -ф 0,09150g+ ...}
(11.48)
—частоты гигантского резонанса в ядре, имеющем только стати-
ческую деформацию.
Аналогично
G‘2> ° (0)’ Q2 (°) = » X 3,3437?-»;
£Q20 (0) ДЙ2 (0) (1 — 0,28480o—0,18720о + •••);
Ш2±2 (0) = ДО2(0)(1 + О,28480о+О,О5840§+ ...);
ДИ2± i (0) ДП2 (0) (1 — 0,14240о — 0,07750g + • • )
(11.49)
— коэффициенты разложения и частоты квадрупольных гигантских
резонансов, зависящие только от статической деформации ядра 0О.
Гамильтонианы (11.45) и (11.47) описывают влияние гигантских
резонансов на колебания поверхности и наоборот. Поскольку харак-
терные амплитуды колебаний g, т) « 1/10, то, пользуясь (11.45)
и (11.47), легко показать, что взаимодействие колебаний поверх-
ности деформированного ядра с гигантскими резонансами имеет
величину порядка Hint «14-2 Мэв. Таким образом, взаимодей-
ствие Hint ведет к расщеплению дипольных колебаний типа Qn
и Qt-i, а также квадрупольных колебаний Q21 и Q2-i на величину
порядка 1—2 Мэв*. Первые из этих колебаний являются диполь-
ными колебаниями плотности в плоскости, перпендикулярной
ко «ЬШ°^ °СИ ядРа> в то вР^я как вторые — квадрупольными
иИй^МИ плотности в направлении 0 = л/4 (см. рис. 11.1
И3.3 г,то явление может быть также описано следующим образом
щее Я БЗаим°Действия, которое линейно зависит от tj, ядро, являю-
.__я аксиально-симметричным в основном состоянии, принимает
ф+ Вывод авторов о расщеплении возбуждений и QJ-!, а также и
этот1 воппл СВязи с У-колебаниями является неправильным. Подробно
т. 19 г с«Ф’,с обсУждается в работе Орлина В. Н. «Ядерная физика», 1974,
’ ' OZI- — Прим. пер.
343
форму трехосного эллипсоида при возбуждении гигантских дН1] 1
ных резонансов Qt±i |0>. Вследствие этого происходит расщеп 4,1
двух первоначально вырожденных колебаний (?i±i|0>. ।
В добавление к трем основным типам гигантских дипольных к
баний возникают также серии (сателлиты) вращательных и к 1
бательных полос, т. е. состояний, которые связаны с возбужден'16
как дипольных, так и поверхностных фононов. Это явление
более детально разобрано в следующих разделах.
§ 11.4. ВОЛНОВЫЕ ФУНКЦИИ И ЭНЕРГИИ ГИГАНТСКИХ
ДИПОЛЬНЫХ РЕЗОНАНСОВ В ЧЕТНО-ЧЕТНЫХ ЯДРАХ
Собственные функции полного гамильтониана
Й{ 1 } = И rot Ц- Hvib 4- И or + Н (I з + (j з11j2) > (11.50)
описывающего спектр состояний гигантского дипольного резонанса
являются произведениями волновых функций ротатора £>мк(6),
р- и у-колебательных волновых функций Unos (В) и (ц) и вол-
новых функций дипольных возбуждений Qis I 0>. Полная волновая
функция должна удовлетворять условиям симметрии, определяе-
мым операциями Rlt R2 и R3 (4.22). Условие симметрии, связанное
с удовлетворяется, если в произведении
^(0j)&|O> (И. 51)
К—S всегда равно четному числу, т. е.
К—S = 2v, v = 0, ± 1, ±2,.... (11.52)
Этот результат получается точно таким же образом, что и соотноше-
ние (9.45) в случае одночастичной модели оболочек в деформирован-
ном ядре. Действительно, поскольку связь колебаний дипольного
типа Qts 10> с вращениями и поверхностными колебаниями ядра
формально полностью эквивалентна связи внешней частицы с осто-
вом, мы можем использовать соответствующие результаты гл. 9-
Под действием операции R2 функция (11.51) преобразуется при
S =# 0 по закону
D'mk (О,) Qfs 10> -> А (_ 1/-I-K-PX+S D'^ K (0j) QK+ s ] о>. (11.53)
Id I
Используя (11.52) и (11.53) и методы построения должным обр®
зом симметризованных полных волновых функций (6.128) и (9° )’
344
чить следующие выражения для искомых волновых функ-
м°ЖНостояний дипольного резонанса [96, 97]:
/ 2ТЙЙ
| /МКП2110
l+K + — S (S+D
-(-II
_L(K-S (S-D)
• (-1)2
ч92/1 )Л ч ^.^)[№(0;)-
32л2(1 ] Ько)
Dm-к (0j)) Ч>Кп2 s (— ц) Qfisl 0) +
;+К+ —S(S-l)
№(0j)-(-i)
X Фкп2 s (n) Qi^-S I 0>],
d'm-k^)} X
(11.54)
гДе / и А' удовлетворяют следующим условиям [96, 97]:
K = |S|, |S| + 2, |S| + 4,...: (11.55)
S = 0, + 1;
/= 1, 3, 5, ... для К = 0;
1 = К, К+1, К + 2,... для К>о.
Волновые функции Р-колебавий имеют вид:
Un.s® ]/ 2“ exp[-4-a2(E-Wl Кл.(а(£-Ь|)).
I 2п«п0!+л L 2 J
(11.56)
где
а2 2£₽/Зер§; £р--=Й) QB?
ЗЙй,,с,(0) , (11.57)
e=AW = A2/3Bp§; g|S|----------1^112 G?>pg,
а КПо (5) — полиномы Эрмита.
Волновые функции у-колебаний могут быть получены аналити-
чески лишь в случае S 0, т. е. для дипольных колебаний, проис-
ходящих вдоль оси симметрии ядра. Эти функции имеют вид:
ЧКп, о(»])
+ (К4-2) / 1 \
2А2 г(^(К + 2) + п2) t
"2! Г 2))
х+(к+1)
-2- К+1; для ц^О;
для ц<0,
(11.58)
345
где
X 2Ev/3b0§, Еу й, | С2/В, П1
a jFi — конфлюэнтная гипергеометрическая функция.
Волновые функции у-колебаний определены только для пол Л
тельных значений аргумента, т. е. при т] 0 . В то же время поп^11
волновая функция (11.54) состоит из двух частей, одна из кото''3’
зависит только от отрицательных значений т], другая — от nontj
тельных. Фазовое соотношение между этими частями определяй*1'
условием симметрии, связанным с R2. f
Благодаря тому что ЯЙ/ содержит члены, линейные по i] СсГ
ственные функции фдП! ± i Сп)» удовлетворяющие уравнению
((0)01'’и 0.
(11.60)
не могут быть определены аналитически.
Так как входящий в эти уравнения потенциал обращается в бес
конечность при q = 0, решения (11.60) могут быть определены толь-
ко в областях г; > 0 или т] 0. Функции фк„, s (ц) выбираются
[21—23] таким образом, что
ЧточзО]) 0 при ц <: 0. (Ц.61)
Шек [3161 показал, что для п2 = 0,1 хорошие приближенные
решения могут быть получены вариационным методом. Для боль-
ших значений н2 эта процедура становится слишком громоздкой
и не очень точной. Так как в дальнейшем будут учитываться у-ко-
лебательные состояния вплоть до п2 = 3, то более предпочтительными
являются численные решения уравнения (11.60). Следует также за-
метить, что с помощью волновых функций (11.54) можно диагонали-
зировать только один член вращательной энергии (11.38), а именно
«и®
16Ят)2 16Zh]2 8Вт)3
Уравнение (11.50) содержит лишь первое слагаемое из правой
части этого выражения. Благодаря соотношению
7зФщ= — (рФ1-ц ,
(11.63)
следующему из (10.146), член —(^/SBi]2)/^1’ смешивает состояний
с S = ± 1. Так как матричные элементы этого взаимодействи
f /о
8Вт]2 3 3
= 6//- 6мм- бкк- 6п0 П' 6s'_s iS <фк-п
ГМ'К'п? tioS'
*> | IMKn2 п0 S }
;'-з| 1]“2|фКп,3>
(11.64)
346
„ния порядка 0,1—0,2 Мэв, то сильно смешиваются толь-
цмеют зна 11Я, которые разделены энергетическим интервалом,
ко те с0 q 2_0,4 Мэв. Поскольку энергия дипольного состояния
меныиим ' q 1—2 Мэв меньше энергии состояния S = —1,
*> 0 то только состояния типа S = 1, п2 > 0 могут заметным об-
п2 и’смещиваться с основным гигантским резонансом 5=1,
разом Более того, большие ширины (~1—2 Мэв) различных
Яз = пых состояний уменьшают вклад такого смешивания в сече-
дцполы ^ощения и рассеяния. Вследствие этого в дальнейшем мы
НИЯ П ппенебрегать соответствующими эффектами. Как показывают
б'^ьные расчеты [235], такое приближение оправдано.
^Энергии различных состояний дипольного спектра определяются
выражением
Е,КПгп.э (/ (/ + S|) т е+ +
4 (и-65)
\ £р /2
Ер +
где
Ецп, о — 2пгН—— К + 1 j Еу,
а ЕКп,± i определяются посредством численного решения уравнения
(11.60).
Обсудим теперь полный спектр гигантского дипольного резонан-
са в деформированном четно-четном ядре. Как показывают получен-
ные результаты, максимум гигантского резонанса, расположен-
ный при более высоких энергиях, соответствует возбуждениям, про-
екция угпового момента которых на ось симметрии ядра равна ±1.
Другими словами, возбуждения типа Q{±i|0> расположены в верх-
ней части гигантского резонанса, что связано с наличием в выраже-
нии (11.65) члена /(Q1S (0). Так как для положительных значений де-
формации р0 (0) < AQ1±1 (0) 1см. (11 48)], то энергия возбуж-
дений с X — ± 1 больше энергии возбуждений с S = 0.
Связь дипольных и поверхностных колебаний приводит к появ-
лению в выражении (11.65) члена Екпгэ- Так как Е101 — Е10_г ~ 2
7 3 Мэв [971, то первоначально вырожденные дипольные колебания
Qi±i |0) (колебания в плоскости, перпендикулярной оси симметрии
сдРа) оказываются расщепленными благодаря взаимодействию
Колебаниями*. Качественно это можно объяснить следующим
СкРазом- Как было показано, у-колебания являются ангармониче-
ИМи- Вследствие этого, вероятность распределения значений у
ет максимум при у 0 и даже в основном состоянии обращается
<неа Ь ПРИ = 0. Поэтому ядро становится в динамическом смысле
спальным», что отличается от случая модели Давыдова—Филип-
См. примечание переводчика на с. 343.
347
пова (см. гл. 7), в которой ядро имеет постоянную неаксиальну^!
форму. При возбуждении «поперечного» колебания Qi_ 1 | о у н
спальная форма ядра стабилизируется. В результате вырожде315’
верхнего дипольного резонанса снимается и появляются два
нанса, соответствующих колебаниям вдоль осей, перпендикуляр.,30’
оси симметрии ядра. Согласно (11.65), на каждом дипольном сосго**
нии возникает совокупность колебательных и вращательных по-/
(рис. 11.3). Таким образом, дипольные состояния ведут себя по
ностыо аналогично состояниям нечетной частицы в области малы
энергий возбуждения (см. гл. 9). Этот результат не является удцВиХ
тельным.
-----5~
К=0 К=2 К=1 К=1
3 По~1^п2-0 fiQ~0^r2~i
f S=0 S-1 s=-1
к=о____________________________________________________к=а <=r к=1
По~О,П2жО no=O,n2~O
S=0 S=0 S=1 S-=-1
Рис. 11.3. Схема уровней гигантского дипольного резонанса в деформи-
рованном ядре с учетом вращений и колебаний.
Три 1—-СОСТОЯНИЯ [К—О, «0=0. «2=0, <S=0 И К=1, «0=0, «2=0, S= ±1] могут быть
отождествлены с типами дипольных колебаний в модели Окамото - Даноса
(см. § 10.6).
В § 11.8 будут найдены выражения для дипольного оператора
и вероятностей соответствующих переходов. Покажем, что наряд)
с обычными дипольными состояниями с довольно заметной вероят-
ностью возбуждаются также такие состояния, в которых помимо по-
перечных дипольных колебаний присутствуют колебательные воз
буждения. Таким образом, поперечные дипольные состояния имекя
«сателлиты», расположенные выше на 0,8 Мэв и имеющие кванто
вые числа {К = 1, и0 = 0, л2 = 1, S = 1} и {К = L п» = , ’
п2 = 1, S = —1} (см. рис. 11.3). На первый взгляд могло бы п°я
заться, что переходы в эти состояния подавлены согласно правя )
348
алогичному правилу отбора по К, имеющему место в об-
0Тбора. энергий возбуждения. Однако из-за ангармоничности
ласТ|1 ^а‘ £ и их сильной связи с поперечными дипольными возбуж-
т колсба п1Эавило отбора нарушается, что приводит к заметному
сагом"™'
§ 11.$. ВОЛНОВЫЕ ФУНКЦИИ И ЭНЕРГИИ ГИГАНТСКИХ
КВАДРУПОЛЬНЫХ РЕЗОНАНСОВ В ЧЕТНО-ЧЕТНЫХ ЯДРАХ
Согласно выражениям (11.36) — (11.40), (11.46) и (11.47), га-
ьтониан, описывающий гигантские квадрупольные резонансы,
М^₽т быть записан следующим образом:
,,П . rr tj(2) I fj(2) i 'l2
H(i} Hrot\-nvib-: Hgr-\ Hint I
(11.66)
Собственные функции этого гамильтониана соответственно имеют
вид *: __________
1IMKn^ п0 D = 1/— <4. т Ш {(D'mk +
Г 32лг (14-бК0)
+ sign Т (- 1 )'+*+’ d'm - к] <№, т 10> +
— (K-ITI)
-Н—I)2 (£>л1к + sign Т(— \)'+KDM_K) <ркп2т( — л)Х
X^-i/rlO». (11.67)
Квантовые числа, входящие в (11.67), удовлетворяют условиям:
К |Т|, |ТЦ-2, |ТЦ 4,...;
I 1, 3, 5,... для К' 0, Т —2;
I 0, 2. 4, ... для 0, Г=# —2; (11.68)
/ К, К + 1, К + 2 для К>0;
— 2, —1, 0, 1, 2.
идно, что квантовое число Т — аналог квантового числа S, опи-
сывающего состояния гигантского дипольного резонанса. Соответ-
ственно функции <рл?/2т- (i]) являются решениями дифференциаль-
°го уравнения, аналогичного уравнению (11.60):
и С ! Ачкч Л-1)
I 4Д <9т)2 2 Г" 16В1]2
-J 6 Тб1|Г)О?’^о?-ЕКП!т }<р)гЛ7 <П) - 0. (11.69)
вы/щЯ = 0’ ±2 это уравнение описывает радиальные волно-
тРехмеРн°го осциллятора с центробежным барьером,
Детальный вывод этого выражения см. в работе [236].
349
соответствующим угловому моменту
/«—ф+ф» КЧГГ (,ч
Собственные значения и собственные функции имеют в рассматои
мом случае следующий вид: F Вае'
ФКп, т
Екп2т |Т|=7^1; (Н.71
I ) * *3)
-
аГЛ' гг('«'"-+~т) ч,гк1, х
> »='! (<«+ф) (11.7|а
Х/Ц —Щ, 1ткЛ-~\ ^т]2) ДЛЯТ]>О, |Т|#=1,
О для т] < О,
Рис. 11.4. Направления различных
квадрупольных колебаний в деформи-
рованном ядре.
где X. = 2Ev/3epo-
В случае Т = ± 1 уравнение
(11.69) содержит дополнительный
линейный по г] член, который об-
условлен связью гигантских квад-
рупольных колебаний с у-колеба-
ниями [см. (11.47)1. Отсюда можно
заключить, что в случае квадру-
польных резонансов только воз-
буждения типа ^2±1|0> связаны
с у-колебаниями*. Этот результат
легко понять с помощью рис. 11.2
и 11.4, из которых видно, что коле-
бания Q$±210> связаны с обеими
осями ядерного эллипсоида и пото-
му не^могут быть связаны су-колебаниями. В то же время возбужде-
ния(2^±1|0> соответствуют колебаниям вдоль направлений 0- л/4,
Ф=0и 0 = л/4, <р — л/2 соответственно. Благодаря этому такие
состояния взаимодействуют с у-колебаниями, так как энергии воз-
буждений <?2±| | 0> зависят от обратной величины радиусов ядерного
эллипсоида в указанных направлениях.
Энергетический спектр квадрупольных возбуждений изображен
на рис. 11.5. Каждое квадрупольное колебание служит основанием
_ * Благодаря у-колебаниям происходит смешивание колебаний тиЛ'
QJo | 0> и (?2±2 | 0>, которое приводит к дополнительному уширению сооТ
ветствующих максимумов. Однако, величина этого уширения весьма незначи
тельна. — Прим. пер.
350
ку11ности колебательных и вращательных полос. При квад-
д.тя с0Е х Г1ереходах из основного состояния 0+ четно четного ядра
р}по-пьн б ждаться только 2+-СОСТОЯНИЯ этих полос. Интенсивности
могут в переходов определяются толщиной стрелок. Дальнейшее
разл»4” гигантского квадрупольного резонанса дается в § 11.9
обсуЖДени
Рис. 11.5. Спектр гигантского £2-резонанса в четно-четном ядре.
§ 11.6. ОПЕРАТОР ГАМИЛЬТОНА ДЛЯ НЕЧЕТНОГО
ДЕФОРМИРОВАННОГО ЯДРА
В предыдущих разделах была изложена полная коллективная
теория ядра, объединяющая низкоэнергетические и высокоэнерге-
тические коллективные степени свободы, т. е. вращения и колеба-
ния поверхности ядра и гигантские резонансы. Однако до сих пор
в рамках этой теории рассматривались лишь ядра, спин которых
в основном состоянии равен нулю. Настоящий раздел мы посвятим
обобщению теории на случай ядер с отличным от нуля спином, для
чего попытаемся объединить обобщенную модель ядра с динамической
коллективной моделью четно-четных ядер.
Можно привести целый ряд доводов в пользу такого обобщения
теоРии. Во-первых, значительное число экспериментов было выпол-
нено с ядрами нечетного А, спин которых в основном состоянии не
Р вен нулю. Неоднократно высказывалось утверждение, не под-
цепленное количественными оценками, что последняя нечетная
ГиСТица оказывает пренебрежимо малое влияние на общую структуру
важНТСКОГо Резонанса- Доказательство этого утверждения особенно
топ Н° ВвидУ того, что ядра с нечетным А часто являются моноизо-
ными. Поэтому в экспериментах с такими ядрами можно изучать
Н11"3 е Тонкие детали фотоядерных реакций, например форму кривой
ИЗо ВГо максамума, чем в экспериментах, выполненных со смесью
ков. Во-вторых, введение'нечетной частицы совершенно не-
351
обходимо для последовательного описания эффектов, связ
с ориентацией ядер. В частности, тензорная поляризуемость
(см. т. 2, § 5.5) равна нулю, если спин основного состояния
нулю. Кроме того, свойства упругого и комбинационного рассе ЗВе"
фотонов (см. там же) также существенно зависят от спина осноп
состояния ядра. Наконец, при наличии дополнительного угч0Н°Г<)
момента, т. е. углового момента нечетной частицы, появляется б °Г°
шое число возможностей для связи угловых моментов составных 1Ь
стей системы в данный полный момент. Вследствие этого возмю?а' I
существенное обогащение структуры спектра нечетных ядер
сравнению с уже достаточно богатой структурой спектров чети*10
четных ядер. 1
Рассмотрим ядро с нечетным А как систему из четно четно
остова с одной внешней частицей. Для описания остова будем ио
пользовать коллективную модель, а для дополнительной нечетной
частицы — модель оболочек с деформированным потенциалом (си
гл. 9) и приближение сильной связи с остовом. Таким образом, пол
ный гамильтониан ядра с нечетным А состоит из коллективного га-
мильтониана остова, Нсиц, одночастичного гамильтониана нечет-
ной частицы, HVarl и взаимодействия частицы с остовом, HCBll PaTl (gg] -
art 4“ Неон part' (11.72)
Здесь HPurt — гамильтониан модели оболочек с деформированным
потенциалом (модель Нильссона), имеющий вид
HPart = ~ (- V2 + k2r2) - р0 г2У20 + CI • S + П12, (11.73)
где Асо — энергетический параметр одночастичной модели оболочек.
Собственные функции гамильтониана (11.73) где Q--проекция
углового момента / частицы на ось симметрии ядра, были получены
в гл. 9, в которой также было детально обсуждено взаимодействие
частицы с остовом. Ниже мы будем учитывать только часть этого
взаимодействия, имеющую вид
А2 -.2 , А2
---- / з
2/0---------16Вг|2
/з-
(11.74)
Остальные члены оказывают лишь очень малое влияние на коллек-
тивные состояния. Разумеется, в такой модели одночастичные со-
стояния описываются весьма грубо. Используя, наконец, в качеств
коллективного гамильтониана остова полученный нами гамильто-
ниан четно-четного ядра, можно записать динамический коллектив
ный гамильтониан ядра с нечетным А в следующем виде:
352
ti2 j d^_
2B Ug2
-^4-1
2 dr]2) 2
t]2+
+ Й& + 4- HParl.
(11.75)
Входящие в это выражение члены, описывающие гигантские резо-
нансы, определены формулами (11.44)—(11.47). Решения уравнения
Шредингера с гамильтонианом (11.75) могут быть получены с по-
мощью гГг'о?об1с)Г1°1 исп°льзованному в случае четно-четных
ядер (см- 197], (991 и § 11.4 и 11.5).
§ 11.7. ВОЛНОВЫЕ ФУНКЦИИ И ЭНЕРГИИ ГИГАНТСКОГО
ДИПОЛЬНОГО РЕЗОНАНСА В НЕЧЕТНОМ
ДЕФОРМИРОВАННОМ ЯДРЕ
Будем искать рассматриваемые волновые функции в виде про-
изведений вращательных волновых функций, волновых функций
поверхностных колебаний, гигантских дипольных колебаний и одно-
частпчных волновых функций. Благодаря дополнительным одно-
частпчным функциям симметризация полной волновой функции
несколько отличается от симметризации волновой функции, опре-
деляемой выражением (11.54). Искомая симметризованная полная
волновая функция имеет вид 121, 23, 99]:
| /МКЯап2 п0 S', = 1 /^±1 s (g) х f №<fafi -
I/
i+i+K+a+-L(s+i) ~
~( 0 2 Дм-К<Г’а-и) X I K-п I n2s (ц) Qis | 0>+
. / + / + K + B+±S(S-1)
-(-I)2 (^MK<faQ-(-l)~ 2 X
X Xik-й i n2s (л) Qri-s | o>], (11.76)
где I и К удовлетворяют условиям, аналогичным (11.55):
|S|, Q—|S| + 2, Q—|S| + 4,
/ = 1^1, Kl+l, IKI-4 2, ... (11.77)
(11 И Xl K~a |n2,s определяются выражениями
__g, P (И-58) и (11.60), в которых К должно быть заменено | Д' —
ных - 1'ак 11 прежде, X|K-fi|n2s01) определена лишь для положитель-
значений аргумента (rj 0). Соответствующие энергии равны
Е' ал2n0 s = [/ (/+ 1)—Af2-S2— Й2] уе+ ^г0 + у) Ер—
—. ^Qis(Q) (|.\2 з
\ £ Gs j — ePo + Ei/c-ni n2s + &Qis(0)-|-Ena> (11.78)
где 4 р > 2
12 Зак- 1218
£IK-Q I пг о = ( 2/г3 4- у | Д' — У 14- 1 Еу
353
a £[к~ Q|n2s Для S = ±1 должно определяться с помощью числе
решения уравнения, подобного уравнению (11.60). Так как ЭТа1,11ого
решения задачи полностью аналогична соответствующему ре. Час4
для случая четно-четных ядер, мы отсылаем читателя к разд
где также обсуждается член (А2/8В2) (73—/3) }'з1). который ана1 1
чен последнему члену в выражении (11.62). Это взаимодейсг
смешивающее состояния с S ± 1, имеет величину того же пороЯ
что и (11.64), и поэтому может считаться пренебрежимо ма-цЯ
§ 11.8. ЗАВИСИМОСТЬ ДИПОЛЬНЫХ И КВАДРУПОЛЬНЫХ
ОПЕРАТОРОВ ОТ КОЛЛЕКТИВНЫХ ПЕРЕМЕННЫХ
В предыдущих разделах мы рассмотрели динамическую кет?
тивную модель гигантских резонансов и получили их волновые ф\Нк
ции и энергии. Для того чтобы определить сечения различных п₽
акций, например сечения фотопоглощения, необходимо вычислить
матричные элементы переходов для электромагнитных операторов
различных мультипольностей. Коллективная часть мультипольньп
операторов, связанная с распределением заряда ядра
РД, /) = рр(0)(Ц-т](г, t)},
в лабораторной системе координат должна иметь вид
A1qill + B1[q^xa^ + ... (11.79)
и
Q2K- 4<7гц +W2’X + (11-80)
в
Постоянные Л 2 и Л 2 определяются с помощью выражения (10.196),
котором верхний индекс (п) обозначает обертоны колебаний. Так
как эти обертоны для нас здесь не представляют интереса, то верхний
индекс в дальнейшем будет опускаться. Величины В,, В2, а также
коэффициенты при членах более высокого порядка в (11.79) и (11-80)
могут быть в принципе определены с помощью метода, использован-
ного при выводе выражения (10.196). Однако в этом случае необхо-
димо знать зависимость колебаний плотности т) (г, I, а[?]) от ко-тлек-
тивных координат поверхности ядра [см. уравнение (11-7)1-
Можно, однако, получить интересующие нас величины значительно
более простым путем, если совершить переход в собственную систем!
отсчета и использовать для колебаний плотности выражение (П-
В этом случае, чтобы получить последовательным образом чле
первого порядка по аШ в выражениях для мультипольных опера
* Гигантские квадрупольные резонансы в ядрах с нечетным A м°г- [10вЬ'
рассмотрены по аналогии с гигантскими дипольными резонансами. в°' ве?.-
функции и энергии этих резонансов в ядрах рассматриваемого типа nj
ны, например, в работе [236].
354
бхот.им° подставить в (11.15) функции, описывающие распре-
ров>ие0 „потностей нормальных колебаний в деформированном ядре:
де пени я п*
q/л ~ Pl ji. (ki-м г) Флм. M = L, —L, (11.81)
(а ad определяются формулами (11.17) и (11.18) для
где kl " "соответственно.
Ь Н -обходимо ясно представлять себе различие между выражениями
1 ЯП и (11-13), (1114). В первом случае аргументами функций
I1 сет я являются произведения ki.u («о. «2) г, в которых волновые
ЬеС ’завцсят как от типа колебаний во внутренней системе отсчета,
ЧИС и от координат поверхности. В противоположность этому волно-
та* числа, входящие в выражения (11.13) и (11.14), являются волно-
ВуМИ числами kb для случая сферического ядра (см. табл. 10.2). Это
оазтичне обусловлено тем, что функции (11.13) и (11.14) являются
пробными функциями нулевого порядка. Поправки первого порядка
могут быть получены заменой kb на /гьм («о, я2)- Если разложить
функции Бесселя jL (kLM («о> «2) г) в ряд по степеням а0 ип2, то для
колебаний плотности получится выражение, совпадающее с (11.12)
с точностью до членов первого порядка относительно а0 и а2.
Компоненты мультипольных операторов во внутренней си-
стеме координат могут быть теперь легко вычислены с помощью
формулы
Qxh = Рр (0) $ Л (г, /, а0, а2) г7- dr =
= Рр (0) J (2 (— 1)”' Q,-m Fiit (klm (а0, а2) г) <р1т) г*- Y}^ dr, (11.82)
Im
где черта над знаком оператора означает, что его компоненты рассма-
триваются во внутренней системе отсчета. Опуская длинные, но не-
сложные вычисления, приведем окончательные результаты.
Дипольные операторы [21, 22, 98, 99]:
X (1 +Si ।M| |)-|- [ilni (Qhpi + Quhi) + p (<2i-IhI +
+ Qi-U]|H /6S1||t|T]|, (11.83)
где
= ЙД (0,925 + 0,050 p0 + 0,26 pg);
di ’ = (- 0,654 + 0,018 ₽0—0,18 p02);
5П1л| = (—2)-1н10,349; ‘
f1= I /^Z(l-pg) 1 3
1 V 2AM /j,Qx(O) 4л
(11.84)
12*
355
Квадрупольные операторы [234, 235]:
{[($Ыц|+<?2 |ц1)---------------------------------------------------------(1—6|ц| о) Sign Ц [0^'_||11|_|_
Q2-|(i|)] X [ 1 S2 щ] с]— [(С?22-|ц| + Q22— 1 mi J
+ ^lnl 1 sign p IQ21HI—2 + Q21 ml—2)] V6 6|P.| 1 0,497т]} , (Ц g^
где
^) = 2^2(l+0,497p2);
^2) 1-^2(1 +0,248 p0 +0,42 ₽2);
d<2> = й/2(1-0,497 po +0,29 p2);
S2|(l| = y(2-|p|2)0,497,
(И.86)
f2 = O,311tfo|/
6A'Z(1| a)
nAM
1
К й2 (0)
Используя матрицы конечных вращений, можно выразить
компоненты мультипольных операторов в лабораторной системе
координат через компоненты во внутренней системе:
$J=Mv(v,)^. (11.87)
V
Именно такая форма мультипольных операторов используется
в случае деформированных ядер, описываемых с помощью углов
Эйлера 6; и внутренних координат. Заметим, что эти операторы
линейно зависят от операторов рождения и уничтожения гионов.
Поэтому действие рассматриваемых мультипольных операторов на
основное состояние (вакуум) (этому соответствует, например, опи-
сание процесса поглощения фотонов) приводит к возбужден! к
только тех состояний гигантских резонансов, которые содержат
один гион. „
Теперь довольно просто определить постоянные Вг 11 ;
в выражениях (11.79) и (11.80), если преобразовать
внутреннюю систему координат. Такое преобразование j&nae
простой заменой и а2(г->- а2|1. Выражая далее с
мощью декартовых компонент ф/.ц [см. (И 28)], вводя оператор
рождения и уничтожения |см (11.29) и (2.51)] и сравнивая чл
линейные по aIL и не содержащие а(1 в выражениях (11.83) и (
и соответственно в (11.85) и (11.80), можно определить единс
356
,м образом коэффициенты Alt В
0,925, / 6 NZ
B1= —0,246 р0Д;
и A 2, В 2 [21, 236]. Имеем:
1
л А W A (0) ’
3104/? 1 / — — —— —- ’
'dlU Г л A MM Afi2(0) ’
B.,= — /^7 0,4967 A.
2
(11.88)
A
Выражения (11 -79) и (11.80) для мультипольных операторов осо-
бенно полезны при исследовании вибрационных ядер. Детальное
обсуждение этой проблемы будет дано в § 11.10. Волновые функ-
ции ядер такого типа могут быть выражены с помощью операторов
рождения гионов qi^, взятых в лабораторной системе координат,
и операторов рождения фононов поверхностных колебаний Ргц
без использования углов Эйлера и внутренних переменных. Пер-
вые члены в (11.79) и (11.80) характеризуют мультипольные опе-
раторы для сферических ядер, в то время как последующие члены
учитывают изменение колебаний плотности в деформированном
ядре.
§ 11.9. АНАЛИЗ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ ДЛЯ
ДЕФОРМИРОВАННЫХ ЯДЕР
Фотоядерные реакции могут быть разделены на два типа: реак-
ции поглощения и реакции рассеяния фотонов. До настоящего вре-
мени оба типа реакций исследовались только для четырех тяже-
лых деформированных ядер Ег, Но, ТЬ и Та. Мы попытаемся дать
возможно более полный анализ для первых двух ядер, являющих-
ся типичными примерами четно-четных и нечетно-четных ядер. На
основе динамической коллективной модели этот анализ произво-
дится следующим образом. Три параметра е, Еу, Ер из числа пара-
метров, определяющих теоретические сечения, находятся с по-
ощью данных, описывающих свойства низкоэнергетического
^чектра ядер (см. рис. 6.5). Деформация ядра [30 также может быть
принципе определена из таких данных. Однако определение
Дефо П°МОи*ЬЮ КУЛОНОВСКОГО возбуждения ядер не позволяет найти
тетьнМаШ1Ю С Такой точностью- какая требуется для удовлетвори-
нейше Г°к'ПИСаНИЯ сечен,,й гигантских резонансов. Поэтому в даль-
тальнь* йо Рассматриваться как переменный параметр. Ос-
сеченщ” паРаметРы определяют положение, абсолютную величину
Различи И Ши₽инУ резонансов. Мы будем предполагать, что ширины
б)Жден ЫХ Дипольных состояний зависят только от энергии воз-
197, 98]- ’ пРИЧСм эта зависимость описывается степенным законом
Г,, ГО(ЕП/ЕО)6, (11.89)
357
где Гп и Еп — соответственно ширина и энергия п-состо
гигантского дипольного резонанса, а Го и До = Ай, (0)
логичные величины для некоторого произвольного дипОльа,1а'
состояния. В качестве этого состояния удобно выбрать низ*
состояние гигантского дипольного резонанса в деформирован*
ядре, описываемое квантовыми числами | /Л40000 > [см. (1 ] g,?.
Таким образом, все ширины определяются двумя параметр ’
Го и 6. Рами
— энергии
интегральному
Детали выбора двух оставшихся параметров:
состояния | /Л10000 > и а — обменной поправки к
сечению, описаны в работе [21].
Для ядер с нечетным А не всегда удается определить нужные
параметры из данных, относящихся к низкоэнергетическим спект-
рам. В таких случаях обычно используются параметры, определен-
ные для соседних четно-четных ядер. Разумеется, такой метод
связан с некоторыми неопределенностями, что особенно относится
к определению энергии у-колебаний Еу. Поэтому в подобных слу-
чаях Еу может также рассматриваться как переменный параметр
[21, 22]. С наилучшей точностью определяются /ДД(0) (погреш-
ность менее 1%) и Го и р0 (погрешность ~ 5%).
11.9.1. Эрбий
В эксперименте, выполненном Фульцем и др. [154], изучалось
поглощение фотонов естественной смесью изотопов эрбия, в которой
содержатся главным образом четно-четные изотопы: 33,4% 166Ег,
27,1% 16вЕг и 14,9% 170Ег. Хорошо известны низкоэнергетиче-
ские спектры 16вЕг и 168Ег, в то время как спектр 170Ег изучен
Рис. 11.6. Сеченне фотопоглощения в ядре 166Ег:
точки — экспериментальные данные, сплошная кривая — теоре-
тический расчет (96].
358
аТОчно полно. Как следует из имеющихся данных, два пер-
цеДР^1 а характеризуются практически одинаковыми значениями
«U1X ИДг -- пттттто пэпсшртплп rTosrrniuv ПЯСПАТЫ бы.ПИ ПЫПОЛ-
₽lJ птпенных выше параметров. Поэтому расчеты были выло л-
рассМс набором параметров, соответствующих наиболее распрост-
йенЫнНому изотопу 16<!Ег. Сечения вычислялись с помощью фор-
Ра" (10.206), в которой в качестве начального состояния исполь-
^тось основное состояние ядра 10 > , а в качестве различных
3°ВрЧНЫХ состояний — состояния, волновые функции которых
К°оеделя1отся выражением (11.54). Полученная кривая изображена
°оис. П-6; использованные в вычислениях параметры таковы:
На= 11 68 кэв-, Еу — 758 кэв; Др = 1460 кэв; Е10000 = 12,1 Мэв;
*' 2$ Мэв; Ро = 0,29; 6 — 1,5; а = 0,09.
£ -
Го
Мэв; Ро = 0-29; 6 = 1,5; а = 0,09.
Рис. 11.7. Схема уровней и силы дипольных переходов в области
гигантского дипольного резонанса в ядре 166Ег. Указаны кванто-
вые числа I, К, п2, п0, S основных состояний.
На рис. 11.7 изображена схема состояний гигантского диполь-
ного резонанса и силы переходов. Пунктирная линия указывает
положение и силу перехода для случая поперечных колебаний при
Условии, что взаимодействие дипольных колебаний с колебаниями
ЖН°СТИ отсУтствУет (эффект Окамото — Даноса; см. также
ны ° Основной эффект, обусловленный взаимодействием диполь-
Шр Колебаний с колебаниями поверхности, заключается в рас-
лИЧаении попеРечных колебаний | IM100+1 > |см. (11.54)1, ве-
Шое на которого ~ 2 Мэв*. Помимо этого возникает также боль-
хапаЧИСЛо вибрационных сателлитов, однако лишь один из них
Д ТеризУется заметной величиной интенсивности перехода.
ли _^РУгое важное применение динамической коллективной моде-
Читате^еДСКа3аНие Различных свойств сечений рассеяния фотонов.
г~—интересующегося детальной теорией таких процессов,
Г-м- примечание переводчика на с. 343.
359
мы отсылаем к т. 2, гл. 5 и к работам [21—23]. Нил^е мы
лишь основные результаты. °6сУди-4
На рис. 11.8 приведены полученные описанным выше Сп 1
сечения упругого и наиболее важных реакций неупругого n°6°'1
ния фотонов. В рассматриваемом случае упругое рассеяние ^ассея-
8 10 12 14 16 18 20 22 Е, Мэв
Рис. Н.8. Сечения упругого и пеупругого рассеяния фотонов
в области гигантского резонанса на ядре 166Ег:
кривая 0+-сечение упругого рассеяния, кривые 2+- и 2'+ — сечения не-
упругого рассеяния с возбуждением первого уровня вращательной поло-
сы и первого уровня у-полосы, соответственно (см. рис. 11.9).
ся чисто скалярным рассеянием, так как спин основного состояния
равен нулю. Тензорное рассеяние ведет к возбуждению первого
вращательного состояния 2+ и состояния 2'+, являющегося ос-
нованием у-полосы. Эти процессы рассеяния схематически изобра-
Г
г
__ Неупругое
рассеяние
С возбуждением
полосы
2*'
Неупругое
рассеяние
с возбуждением
первого
+ вращательного
* уровня
Рис. 11.9. Схематическое изображение
различных процессов упругого и ие-
упругого рассеяния.
жены на рис. 11.9.
Большой интерес представ-
ляет неупругое рассеяние с
возбуждением уровня 2+, сече-
ние которого примерно на по-
рядок превышает сечение рас-
сеяния с возбуждением других
колебательных состояний [22].
Причина этого связана с тем,
что амплитуды рассеяния со-
держат интегралы перекрытия
от у-колебательных волновых
функций (см. рис. 11.9). В об-
щем случае эти интегралы очень
малы, а при отсутствии связи
между вращениями, коле0
ниями и дипольными возбужД
ниями они должны тождестве
но обращаться в нуль.
360
„пявЯ члену (/| + Д1)2)/(16 Вт]2) в (11.50) дифференциаль-
Б.чагод н ? волновЫХ функций ^-колебании имеет разный
ное УРаВвазнЫх вращательных полос [см. (11.60)1. Однако даже
вид ДлЯ Р ае ИНТегралы перекрытия малы для тех волновых функ-
в эТом слу были бы ортогональными в отсутствие указанного
цнй, к0Т°[а; Как следует из квантовых чисел 1 = 2, К = 2, п2 = 0,
БЫ11|С чл гаЯНИя, являющегося основанием у-колебательной по-
п0 состояние в действительности не содержит у-колебатель-
10СЬ'\ ^нонов*. На самом деле из-за действия центробежных сил,
НЬ’Х овленных отличием К от нуля, ядро растягивается и приобре-
°б)СформУ трехосного эллипсоида (см. рис. 6.4 и 7.5).
Рис. 11.10. Полное сечение кназиупругого рассеяния фото-
нов на угол 140°:
точки — экспериментальные данные; сплошная кривая — теорети-
ческий расчет.
На рис. 11.10 приведено суммарное сечение квазиупругого рас-
сеяния фотонов на угол 140°. Экспериментальные точки взяты из
работы Ланжевена и др. [225]. Согласие измеренного и вычислен-
ного сечений следует считать отличным, особенно если учесть, что
в расчетах не было варьируемых параметров: все параметры под-
бирались таким образом, чтобы объяснить данные о сечении по-
глощения фотонов.
11.9.2. Гольмий
Роны° -?!аннени|° с эрбием ситуация в данном случае, с одной сто-
То г’ б()лее ясна,так как рассматриваемое ядро является моноизо-
не ческ,1м> а с Другой, более неопределенна, поскольку пока еще
спект'1)1еС|(.!^е'1 Д°статочно надежного анализа низкоэнергетического
Р Имеющиеся данные, по-видимому, указывают на существо-
ной nonocf,HJIbHAe яазывать это состояние основанием аномальной вращатель-
“• Прим. пер.
361
вание двух уровней со спинами 3/2 и 5/2 и энергиями соот'ветст
514 и 687 кэв (см. [1081 и рис. 9.17), которые можно считать ВеН8°
ваниями у-полос. Это означает, что параметр Ev, определи 0Сд
энергию соответствующих уровней, должен лежать в предад1®®
500 до 700 кэв. Такая оценка £v не противоречит систематике Х 01
лебательных уровней в соседних ядрах (см. обсуждения в n
9.6.2). Вследствие указанной неопределенности Ev в расч
рассматривается как свободный параметр. етах
На рис. 11.11 показаны вычисленное сечение поглощения т-кв.
тов и соответствующие экспериментальные данные, получею?*1'
Брамблеттом и др. [67, 681, которые свидетельствуют о существ^
Рис. 11.11. Сечение поглощения у-квантов ядрами i65Ho:
сплошная кривая — теоретический расчет [236].
вании гигантского квадрупольного резонанса в области энергий
20—26 Мэв. Ниже приведены параметры, использованные в рас-
четах, а на рис. 11.12 — распределение интенсивностей диполь-
ных переходов: в = 10,5 кэв; Ev = 1000 кэв; Е10000 = 12,0 Мэв;
Го =2,3 Мэв; ро = 0,24; 6 = 1,6; а = 0,25.
Спектр дипольных состояний, как и следовало ожидать па ос-
новании изложенного в § 11.6 и 11.7, существенно обогащается,
хотя распределение сил переходов остается практически неизмен-
ным по сравнению со случаем четно-четных ядер. Так, отношение
сумм сил переходов для основных групп уровней, изображенных
на рис. 11.12 и 11.7, равно 86 : 51 : 20 : 79 для 1В5Но и 86 : 58 : 1' •
: 80 для 166Ег. Этот результат количественно подтверждает вы
сказанное выше предположение о слабом влиянии нечетной частин
на распределение дипольных сил в гигантском резонансе. В то
время сила перехода оказывается распределенной между несК°иИ
кими компонентами, очень тесно расположенными по энер
На рис. 11.13 приведены схемы уровней гигантских 1<ва^оК
польных резонансов в Ег и Но [236]. Без учета обменных попр
интегральное сечение поглощения в области квадрупольного
зонанса составляет около 7 ?6 от интегрального сечения Д1
ного поглощения. Так как Е2-резонанс расположен в облает .
362
поглощение еще играет существенную роль, то экспери-
дцП°льН°ре изучение этого резонанса встречается с заметными труд-
мента-пьно^еы не менее эксперименты ливерморской группы [67, 68],
hoct”mH- дают некоторые указания на существование гигант-
по-виД,1Г‘ ’ 1ОЛЬНОГО резонанса в сечении фотопоглощения*. Ре-
сього к исследования угловых распределений быстрых фотонейт-
зУдьТ j 42] также согласуются с предположением о существовании
Р°Н упольного поглощения в области энергий выше 20 Мэв.
Рис. 11.12 Состояния гигантского дипольного резонанса в
нечетном ядре :б5Но. Указаны квантовые числа /, К., Щ, п0,
S основных состояний.
Недавно Спайсер и др. [346] смогли обнаружить подобную струк-
туру в сечении реакции (у, 2п) в 166Но. Уровни гигантских квад-
рупольных резонансов разделяются на четыре группы, соответст-
вующие различным значениям квантового числа Т = ±2 ±1,0
'см § 11.5). Состояния с Т = ±2 почти вырождены, в то время как
?Н^?ГИи состояний с Т — ±1 различаются на величину порядка
Мэя. Этот результат уже обсуждался нами в связи с рис. 11.4.
в Спектр квадрупольных состояний в ядрах с нечетным А, как и
случае дипольного резонанса, существенно обогащен по сравне-
нию № спектром четно-четных ядер (см. рис. 11.13). Состояния
_ । ~ о расщепляются на три компоненты, а состояния с К =
р ’ на шесть [236]. Однако из-за очень малой величины
Ние епЛения„и конечных ширин каждого из этих состояний влия-
значи1едеТН°й частиЦы на сечение поглощения оказывается не-
* см. также [155, 366].
363
На рис. 11.14 и 11.15 изображены сечения некоторых
рассеяния фотонов. Так как спин основного состояния ядр-
отличен от нуля, упругое рассеяние содержит как скалярную
и тензорную часть. На рис. 11.14 вклад скалярного рассеяния в’ Так
ное сечение изображен пунктирной линией. При неупругом П0,п'
сеянии фотонов могут возбуждаться два уровня основной вр ^ac'
тельной полосы, так как при поглощении нечетным ядром со
ном / дипольного излучения могут возбуждаться состояния СПИ’
гантского резонанса со спинами j, j ± 1. Схематически эти nJ
цессы изображены на рис. 11.16, соответствующие количественн°'
результаты приведены на рис. 11.14.
На рис. 11.15 представлены сечения комбинационного рассея
ния фотонов с возбуждением состояний у-полосы в ядре с нечет"
ным А. В низшей у-полосе (К = 3 2) могут быть возбуждены пять
вращательных состояний.
На рис. 11.17 изображен общий случай неупругого рассеяния
фотонов и представлены шесть первых состояний низшей у-полосы
с К = | / — 21 и возможные переходы. Для случая ядра 167Но
на рис. 11.15 приведены соответствующие сечения рассеяния за
исключением сечения рассеяния с переходом в состояние I — Ц 2,
К = 3/2, величина которого очень мала. Благодаря правилам от-
бора для дипольных переходов при неупругом расстоянии фотонов
может возбуждаться лишь одно состояние (/ = j ф- 2, К = j + 2)
верхней вращательной полосы. Интересно отметить, что суммарное
рассеяние с возбуждением всех возможных уровней двух у-полос
в нечетном ядре соответствует в случае четно-четных ядер рассея-
нию с возбуждением состояния, являющегося основанием у-по-
Рис 11.13. Схема уровней и силы квадрупольных переходов в
гантского квадрупольного резонанса в ядре 166Ег (а) и в ядре г
Указаны квантовые числа основных состояний.
364
к> 11/2 3/2 0,1 ±2> к —— 9/2 3/2 0,1 ±2> 1 7/2 3/2 0,1 12> ——I 5/2 3/2 0,1 ± 2>
11/2 11/2 0,1 ±2> I 3/2 3/2 0,1 t 2>
-= Л 11/2 3/2 0,0 *2> 'i 9/2 3/2 0,0 12> "У 7/2 3J2 0,0 ±2> § 5/2 3/2 0,0 ±2> 11/2 11/2 0,0 t 2>
165Но J I I i li i II I I 3/2 3/2 0,0 ± 2> 11/2 5/2 0,1 * 1> 9/2 5/2 0,1 + 1> г- 1 11/2 9/2 0,1 т /> 7/2 5/2 0,1 + 1> 9/2 9/2 0,1 -f 1> 5/2 5/2 0,1 f 1> 11/2 5/2 0,1 -1> 9/2 5/2 0,1 -1> Г—-| 11/2 9/2 0,1 - 1> 1 7/2 5/2 0,1 -1> <~~-1 9/2 9/2 0,1 -1> 5/2 5/2 0,1 -1> А 11/2 5/2 0,0 +/> Х\ 9/2 5/2 0,0 + 1> 11/2 9/2 0,0 + 1> 7/2 5/2 0,0 + /> 9/2 9/2 0,0 + 1>
- о, 5/2 5/2 0,0 + 1> 11/2 5/2 0,0 - 1> <_| 9/2 5/2 0.0 - 1> --^S| 11/2 9/2 0,0 - 1> =-~ 1 7/2 5/2 0,0- - 1> ^74 9/2 9/2 0,0 - 1 > 5/2 5/2 0,0 ~1> \11/2 7/2 0,0 0> । 9/2 7/2 0,0 0> § 1 7/2 7/2 0,0 0>
*——1
Рис. 11.14. Предсказания теории для сечений упругого и неупру-
гого рассеяния фотонов на ядре ,65Но с возбуждением уровней
основной вращательной полосы.
лосы. Сечения комбинационного рассеяния с возбуждением уров-
ней p-полосы и более высокой у-полосы имеют значительно мень-
шую величину [21, 22].
На рис. 11.18 представлены полное сечение квазиупругого рас-
сеяния фотонов и известные в настоящее время экспериментальные
данные. Более подробное изложение рассмотренного вопроса чи-
татель может найти в работах [21, 22].
Рис. 11.15. Вычисленные сечения пеупругого рассеяния
фотонов на ядре |65Но с возбуждением уровней дв}-<
у-полос.
366
чение. Как мы видели, имеется довольно хорошее со-
3аКЛЮжду экспериментальными данными и соответствующими
гласив м^ияМИ теории. Значения получаемых в модели ядерных
предсказ противоречат их значениям, вытекающим из анали-
napaMeTPgH етических спектров. Можно также сказать, что дан-
за HH3K°DaMeTpe затухания гигантского резонанса Го и & согласуют-
нь'е ° П петическимп оценками ширины размазывания коллективных
сясте°Р„ [gg]_ Следует, однако, заметить, что значение параметра
с0СТ0Я1ац11л р0, получаемое из анализа спектров высокоэнергети-
дефор* ^збуж’дений, по-видимому, меньше соответствующей ве-
Рис. 11.16. Различные процессы упругого
I: неупругого рассеяния фотонов на де-
формированном ядре с возбуждением
уровней основной вращательной полосы.
Дипольные
гигантские
резонансы
Пгнобное состояние
J-2
'-2/ Низшая полоса
Рис. 11.17. Процессы неупругого
рассеяния с возбуждением уровней
нижней у-полосы в деформирован-
ном нечетном ядре.
личины, определяемой из свойств низкоэнергетического спектра
121, 22]. К этому выводу можно прийти, если сравнить значения
Ро, приведенные в табл. 11.1 и 11.2, со значениями, полученными
из данных об интенсивностях переходов в области низких энергий.
Гак, в случае Ег эти величины соответственно равны 0,29 и 0,33.
Использованная нами модель все еще не является достаточно
совершенной. В частности, в ней не рассматриваются нерезонанс-
Механизмы поглощения, например, процессы прямого фото-
эффекта и квазидейтонный эффект (см. § 10.2), на существование
оторых указывают, по-видимому, результаты экспериментов
нь ' ЛеРа и ДР- 1191 по изучению поглощения фотонов поляризован-
ных'1 ЯдРами’ К сожалению, точность экспериментов, выполнен-
ра с неполярнзованными мишенями, не позволяет определить
лИч',1ИЧ11я в Форме сечений, которые могли бы быть связанными с на-
этимцМ ДОполнительной скалярной компоненты, обусловленной
комп неРез°нансными процессами. Вклад этой дополнительной
оненты должен составлять около 15%.
367
Небольшие нерегулярности на подъеме сечения вероятнее
объясняются структурными особенностями отдельных состо
В схематической модели Брауна — Болстерли* [641 благ Hll®‘
этим особенностям возникают коллективные состояния. • хаРакЙ”
зующиеся большим значением силы перехода. В коллективной »
ли подобные состояния могут быть, по-видимому, описаны с'0^'
мощью спин-изоспиновых волн, рассмотренных впервые УайлЯ
[3861, а позднее Юбералем [363]. Если отвлечься от указанных в*Д°М
Рис. 11.18. Полное сечение квазиупругого рассеяния фото-
нов на ядре |65Но:
крестики — экспериментальные данные из работы [359]; точки дан-
ные работы [225].
недостатков теории, то можно признать, что динамическая коллек-
тивная модель достаточно хорошо описывает свойства гигантских
резонансов в области деформированных ядер. В последнее время
были сделаны попытки обьединить частично-дырочную и динамиче-
скую коллективные модели [112, 113, 3271*. Введение коллектив-
ных корреляций позволяет даже в случае легких ядер более полно
понять природу структуры гигантского резонанса.
§ 11.10. ДИНАМИЧЕСКАЯ КОЛЛЕКТИВНАЯ МОДЕЛЬ
СФЕРИЧЕСКИХ ЧЕТНО-ЧЕТНЫХ ЯДЕР
часто
по-
14 изкоэнергетические спектры сферических ядер очень
представляют собой типичные спектры почти гармонических
верхностных колебаний квадрупольного типа. Из данных о СТР^
туре спектров таких вибрационных ядер и вероятностях ^2-пер
ходов между соответствующими состояниями следует, что кол
См. т. 3 этой серии.
368
оНой поверхности имеют довольно большую амплитуду. Дей-
янЯ я^еР очень часто среднеквадратичная деформация
^вительно, _______________
₽о=/<0|2а2*йа2ц|0>, (11.90)
,аютая вследствие колебаний поверхности ядра, сравнима
в°зН1,к 11не со статической деформацией деформированных ядер
1,0 Б-Л0 15—0,3, см. табл. 3.2 и работу [349]). Поэтому следует ожи-
(Р" "что в ядрах подобного типа взаимодействие гигантских резо-
ДаТЬвых колебаний с колебаниями поверхности ядра очень важно,
^противоположность случаю силыюдеформированных ядер, где
В е учет статических эффектов ядерной поверхности приводит к ка-
'Нтвенно правильном} описанию расщепления гигантского ре-
нанса, в рассматриваемых ядрах взаимодействие полностью
вызвано динамическими эффектами. Кроме того, нужно ожидать,
что благодаря большой амплитуде поверхностные колебания не
являются с большой степенью точности гармоническими. Однако
разложения по степеням амплитуды этих колебаний должны схо-
диться достаточно быстро.
Необходимость выхода за рамки гармонического приближения
стедует также из анализа свойств низкоэнергетических спектров
ядер. В четно-четных чисто вибрационных сферических ядрах двух-
фононные состояния должны были бы образовывать вырожденный
триглет 0+, 2+, 4+, энергия которого вдвое превышает энергию
первого возбужденного состояния 2+ (см. гл. 3). На самом же деле
то многих ядрах в этой области энергий имеется большое число
ссстояний, причем часто расщепление мультиплета имеет тот же
порядок величины, что и энергия гармонических колебаний. Еще
более сложный характер имеют спектры нечетных ядер. Следует
также заметить, что до настоящего времени практически не имеет-
ся данных о трехфононных состояниях. Представляется целе-
сообразным предпринять систематическое развитие теории и срав-
нить ее результаты с экспериментальными данными. Динамическая
коллективная модель сферических ядер была развита Ле Турне
[2301 и Вебером, Хубером и Грайнером [376, 377]. В настоящем
параграфе мы ограничимся рассмотрением только гигантского ди-
польного резонанса. С деталями исследования квадрупольного
резонанса читатель может ознакомиться по работе [365].
11.10.1. Структура гамильтониана
Гамильтониан, описывающий квадрупольные колебания поверх-
дв\ ’ гигантсКне дипольные резонансы и взаимодействия этих
образом°ЛЛеКТНВНЫХ движенив> может быть записан следующим
Н = Н quad + Hdip + Hint. (11.91)
36»
Обсудим каждый из этих членов по отдельности. Гами'льто 1
Hquad, описывающий квадрупольные колебания поверхности На|1
согласно (3.18) имеет следующий вид: я^Ра,
(119!
Как было показано в гл. 3, гармоническое приближение до нек
рой степени применимо для описания свойств сферических че™°
четных ядер в области малых энергий. Однако почти во RH°
вибрационных ядрах наблюдаемые двухфононные состояния
являются вырожденными. Для описания этого эффекта к выраж*6
нию (11.92) необходимо добавить ангармонические члены, кою
рыми для простоты в дальнейшем мы будем пренебрегать. Пара
метры В 2 и С2 могут быть получены из данных о низкоэнергетиче-
ских спектрах исследуемых ядер. Вводя операторы рождения и
уничтожения квадрупольных фононов, можно записать (11.92)
в виде:
Hquad— 1 (11.93)
Ц \ 2 ' 1
Гамильтониан, описывающий гигантские дипольные резонансы,
в гидродинамической модели ядра имеет вид
ЯЛр= — уУТ (В?1 [?U1X<7[14[O1)> (П-94)
где Вг и С\ определяются с помощью формулы (10.182):
в = Mpg (O)Z?g с = 8xpg(0)
1 ' р<«] (2,08)« ’ 1 Ро
(11.95)
Как мы видели выше, гигантские резонансы с очень хорошей
точностью могут рассматриваться как гармонические колебания.
Используя операторы рождения и уничтожения, можно предста-
вить (11.94) в форме:
Hdip = 2
И
у) .
(11.96)
где
2,08
Ro '
(11.97)
Вспомним теперь, что связь гигантских резонансов с кол
ниями поверхности обусловлена, в сущности, граничными У^®^.
ми для гигантских резонансов, следствием которых является -1
ношение
*n7? = zn.
(11.98)
370
„дерн011 ПнымИ переменными квадрупольных колебаний а2ц,
коллекти^ (] + 2а*мугц). Поэтому полный гамильтониан
как R " 0 „„„ „
держи1
женнем
образом, энергия резонанса AQn = зависит от формы
Таким ерХН0Сти, которая, в свою очередь, характеризуется
И I ___ - -у.» ITTT Т1г¥1 Tzn п Tt •*» Ж ГТТГХ-» ТТТ ТТТ TV ТГГ\ ТТ Г\£~1П TTTITI *га К
2и). Поэтому полный гамильтониан со-
члены взаимодействия, вид которых определяется выра-
(11.1):
V20
I- kU1
X|r<7fllX9t,]Ht0] +
Vo’[aC21Xa[2]][O] [?fllX?fI1][°] +
’ [ [a[Z1 X a[2]]f2J X [q 01 X ^,]][2]][0J. (11.99)
п выводе (П-99) мы использовали соотношение (11.35), которое
I Р1 я следствием гармоничности гигантских резонансных коле-
(Гнпй Константы связи VgV легко определяются с помощью (11.33):
у(» = — 1,588 С\;
уи) = _ 0,708 Сг;
ун)=—0,936 Cv
(11.100)
Подставляя в (11.99) выражения (2.44) и (2.50), получаем:
Him = Нг + /Ло + Н2, --= — 0,16 £1 р0 { £ (— 1 > (1! 2 | vp—vp) X
liv
X [(—1)*х—v*7v z/v„g + ( l)v9 -v<7tx—v] [pip.4~(
-0,05s ft 2 (-1)Л,Х
1 = 0,2 tivit'v'M
X (22/1 pvM) (11/1 p'v' — M) [(— l)v' Q-v' +
+ (-1Г?-ц' P^+(-lFPg p_v +
(-l)Hp_gP1 + (-l)Aip_(ip_v]), (11.101)
где
/0 = 1,58; f2 = 0,94; £x = = 70Л-’/3 Мэв; ’ (11.102)
Р^ = <0|2а2*ца2и|0> = 5^(2В.2С2)->/2= -||^. (11.103)
Эффективная деформация po связана с вероятностью £2-пе-
рехода в области низких энергий соотношением (3.86). При выводе
выражения (11.101) мы опустили члены, которые не коммутируют
с оператором числа гионов, т. е. члены, пропорциональные qf qt
и ?i9i- Позднее они будут учтены с помощью теории возмущений.
11 .10.2. Расщепление гигантского резонанса
в сферических ядрах
Решение уравнения Шредингера с гамильтонианом (11.91) про-
пий°ДПТСЯ пУтем Диагонализации Hint на основе собственных функ-
и гамильтониана
Н° = Hquad Y Hdip-
(11.104)
371
Собственные значения Н° определяются соотношением
£(7V1,.V2)= Гу1 +AUq,
+ (д', + А
к 2
где Л' j — число гионов, a N 2 — число фононов. Собственные ь
ции гамильтониана (11.104) будем обозначать как ФУНк-
<11.105,
ГГ
Г Г
| Zj', N2v2l2, IM}, /ц .
*1U6)
где квантовые числа и /2 определяют угловые моменты дипоть
гионных и квадрупольных фононных состояний соответс НЫХ
г __________________________но- Символ обозначает
синьорити квадруг10льны.Т
?ХЯНИЙ (см Разд‘ 3-2-1),а
J J I и м — полный угловой мо
мент и его проекцию на ось 2
В этом разделе мы будем
рассматривать лишь состоя-
Рис. 11.19. Схема собственных состояний
гамнльтонпана Н°.
Низшие состояния — состояния квадрупольного
типа, верхние — дипольного типа
ния гигантского дипольного
резонанса в четно-четных
ядрах, спин которых в ос-
новном состоянии равен ну-
лю. В этом случае Д11 = '11
/1=1, 1 = 1- Вообще гово-
ря, трехгионные состояния
(Л\ = 3, 1А = 1,3) также
входят в состав полного ба-
зиса для состояний отрица-
тельной четности и I = 1.
Однако энергии этих со-
стояний (больше 30 Мэв) зна-
чительно превышают энергию
гигантского резонанса, и по-
этому соответствующие эф-
фекты будут . малы. Мы не
будем пока рассматривать конфигурации подобного типа, а затем
учтем их с помощью теории возмущений. Поэтому базис (11.106)
строится из таких многофононных состояний, для которых /2 ~
= 0 и 2. На рис. 11.19 представлен спектр невозмущенных со-
стояний рассматриваемой задачи. Низкоэнергетическая часть этого
спектра представляет собой хорошо известную схему уровней квад-
рупольного осциллятора, в то время как высокоэнергетическа
часть состоит из одно-, двух-, трех- и т. д. фононных возбуждении,
построенных на базе состояния, соответствующего дипольным
лебаниям. На рисунке изображены только такие фононные сост^
ния, которые могут быть связаны с дипольными колебаниями в
стояния, полный момент которых / = 1. На рис. 11.19 показ
также, что при дипольных переходах в невозмущенной системе
372
состояний 1“ может возбуждаться лишь состояние с наи-
вссХ энергией т. е. состояние qt^ | 0 > . Этот результат легко
><Ь ecZ вспомнить форму дипольного оператора, определяе-
лонять» жеШ1ем (Ц.19), и учесть тот факт, что в невозмущенной
муЮ ^отсутствует связь дипольных колебаний с колебаниями
^Взаимодействие (11.99) [или (11.101)1 имеет величину порядка
9 Мэв Так как разность энергий соседних невозмущенных со-
шй Tiwo = 0,54-1,2 Мэв, то это взаимодействие является силь-
сГОЙ и не может рассматриваться с помощью теории возмущений,
потому, как указывалось выше, мы произведем диагонализацию
рззлмодействия, используя в качестве базиса собственные функ-
(11.106) гамильтониана Н°. В то же время примесь трехгион-
ных состояний к однотонным состояниям, которые являются обыч-
ным гигантским резонансом, может быть определена с помощью
теории возмущений, так как SQj значительно превышает по вели-
чине как энергию взаимодействия, так и энергию /ко2 квадруполь-
ных колебаний. Поэтому мы отбросили выше в гамильтониане
Hint [см. (11.101)] все те члены, которые пропорциональны q+q+
и qq, рассчитывая в дальнейшем ввести соответствующие поправки
с помощью теории возмущений.
Гамильтониан взаимодействия H'int имеет как диагональные,
так и недиагональные матричные элементы. Диагональные эле-
менты оператора Н2В [см. (11.101)1 приводят к следующим эффек-
там. После интегрирования по координатам, соответствующим ди-
польным колебаниям, они принимают форму, аналогичную форме
потенциальной энергии в операторе Hquad. Это означает, что дейст-
вие гигантских дипольных резонансов на колебания поверхности
ядра приводит к изменению параметра «жесткости». Поэтому па-
раметр С2, обычно определяемый из экспериментальных данных,
должен быть перенормирован. Для случая отсутствия гионов,
Vi = 0, имеем:
^ = ^ + 0,547 А Пр (11.107)
где 0“ — перенормированный параметр потенциальной энергии
колебаний поверхности. Для состояний 1~ (см. рис. 11.19), в ко-
торых имеется один дипольный квант, получаем:
CVf = C|w +0,368 АЙр (11.108)
результаты означают, что в состояниях, в которых имеются
имррЛ г1Ме кванты< параметр жесткости квадрупольных колебаний
а ет большую величину, чем в состояниях основной полосы. Для
^°<> дсТ'^Д)||ЯЛеР значение эффекта перенормировки составляет от
Рассмотрим теперь недиагональные матричные элементы га-
ониана взаимодействия Hint, которые связывают состояния
373
с различным числом поверхностных фононов и различными
орити. Взаимодействие Нг смешивает состояния, в которых СИНЬ'
квадрупольных фононов и синьорити различаются на eniЧ11С;1а
в то время как Н.2П и Нгг изменяют ЛД на 2, a v на 0 или 2 Я
ственно [376 , 377]. ТВет-
На рис. 11.20 представлено схематическое изображение Мя
цы энергии, на котором вклады различных частей гамильтони^"
0 1 2 3 4 .5 6
V 0 1 0 2 1 3 0 2 4 1 1Ф 0 I 2 |c |ff
0 0 Но Vi V
1 1 Но Vi V
2 0 2 v2o Vl2 w V1 HgW20Vi V22 v20^22 V/
1 2 VIO 'J22 w Vi ttovsow ve2 Vi
4 0 2 4 vso v22 w Vi Ho V20 w v22 Vi V20 v22 W
5 1 2 5 V20 v22 w Ho V20W V22 Vi
6 0 2 4 6 v20 V22 <4 Ho V20 W v22
Рис. 11.20. Схематическое изображение энергетической
матрицы. Прямоугольники н квадраты содержат матрич-
ные элементы, не равные нулю. Вклад различных частей
гамильтониана взаимодействия обозначен соответству-
ющими константами связи [Н° и IP — соответственно
гамильтониан (11.104) и взаимодействие (11109)].
взаимодействия обозначены соответствующими параметрами связи.
Поскольку взаимодействие Hint является сильным, то для диа-
гонализации требуется большое число многофононных состоянии.
Так, для случая «мягких» ядер необходимо учитывать фононные
состояния вплоть до N.2 = 14 [21, 22]. Классификация многофонон-
ных состояний и вычисления матричных элементов довольно слож^
ны, хотя получающиеся алгебраические выражения имеют отно
сительно простой вид. Детали соответствующих расчетов мож
найти в литературе [183, 230, 377].
Часть гамильтониана Hlnt, некоммутирующая с операторе^
числа дипольных фононов, может быть представлена в виде су
374
х членов W1 и W3:
(11.109)
.„хся соответственно линейной и квадратичной функциями
ЯВ’7ДадиМ приближенную оценку энергетического сдвига, обуслов-
тенного W?
Г,
+ [[4+
- 0,356 А Ц Ро { [I? + х 4+][2] X р +](0]+
+ [ к х91 ][2] хр][0]}. (11.110)
Как указывалось выше, это взаимодействие может быть рас-
смотрено с помощью теории возмущений. Для энергетического сдви-
га в этом случае имеем
l<f|^i|i>l3
Et-Ef
АЕ = J
f
<i|^|i>
2А Qt
(11.111)
используя приближение Et— Ef^ —2EiQx. Грубая оценка
показывает, что | ДЕ | < 0,4 Мэв. Этот результат a posteriori оп-
равдывает как применение теории возмущений, так и пренебреже-
ние взаимодействием W72, так как вклад его меньше соответствую-
щего вклада на фактор порядка Ро, величина которого 0,1—0,01.
Точные формулы для вклада в различные матричные элементы
даны в работе Вебера и др. [377J.
Вследствие взаимодействия дипольных и квадрупольных фоно-
нов происходит смешивание базисных состояний (11.106). Резуль-
тирующие векторы состояний имеют вид:
Фш = 4Ю Я\м 10) + а\К} [</+ X Р+]м | 0> +
+ 4? [<7+Х [р+Хр+]10,]м|0> +
Ф X [р+ X р+] 12]]м | 0> + ... (11.112)
Таким образом, чистое гионное состояние q\M | 0 > «размазано»
по большому числу состояний, благодаря чему появляются допол-
нительные дипольные переходы, интенсивности которых опреде-
ляются главным образом коэффициентом (гфю)2- Действительно,
используя выражение (11.79) для дипольных операторов, легко
показать, что матричный элемент перехода из основного состояния
состояние гигантского резонанса (11.112) имеет следующий вид;
<Ф1м* | | 0> = А г ( ар ф А, <рк. (11.113)
375
Как следует из (11.88), | BJAi 1, что доказывает сдел
выше утверждение. UaHHoe
Сечение поглощения у-квантов может быть получено с по
формулы (10.206), которую легко привести к виду м°Щью
(Е-Е^+Г^/4 ’ О1-114)
где
/ f 2 \
«Rl°> )' (И.Н5)
Подставляя (11.113) в (11.115) и используя (11.88), получаем око
чательное выражение для сечения поглощения:
о(Е) 0,0095(1+a)— V ---------------Е*------ ш
' л Г (Е-Ел)2+Г^/4 ’(И !16'
где суммирование происходит по всем состояниям ф(1д/ гигантского
резонанса, определяемым выражением (11.112). В формуле (11.116)
энергии выражаются в Мэв, а о — в барнах.
11.10.3. Экспериментальные сечения поглощения
Перед тем как сравнивать предсказания теории с- эксперимен-
тальными данными, необходимо сказать несколько слов о сече-
ниях поглощения, измеряемых в экспериментах. Сечение поглоще-
ния фотонов* дается выражением:
u°bs = о (у, н) + о (у, р) + о (у, р/г) + о (у, 2р) +
+ о(у, 2п) + ... (11.117)
По энергетическим причинам в большинстве ядер испускания
более двух частиц обычно не происходит (рис. 11.21). В средних
и тяжелых ядрах испускание протонов сильно подавлено из-за
кулоновского барьера. За исключением изотопов Ni вклад реакций
с вылетом фотопротонов в полное сечение поглощения составляет
менее 10% [181]. По этой причине мы не рассматривали в преды-
дущих разделах (см. § 11.9) такие реакции. Ниже мы также будем
пренебрегать вкладами процессов, связанных с эмиссией протонов.
В этом случае получаем
oflbs = u(y, н) + а(у, 2н). (11.118)
Помимо резонансных процессов существуют прямые переходы
в непрерывный спектр, которые ведут к испусканию быстрых фото-
нейтронов. Учитывая это, имеем
о (у, и) = осо11 (у, n) + od‘rcc/(y, и). (Н.П®)
* Экспериментальное исследование полных сечений фотопоглощения про.
изводилось различными группами; см. например, работы [41, 73, НО, По.
394, 395].
376
получить сечение возбуждения коллективных дипольных
Чт°бь нй, необходимо вычесть из полного сечения поглощения
с°сТ0 этОго нерезонансного процесса:
odip — QColl (у, и) 4-о (у, 2п) = Oobs — odirect (у, п). (11.120)
К сожалению, сечение оЛгес* очень ПЛОхо известно. Ис-
я имеющееся небольшое число экспериментальных данных
можно заключить, что его вклад в интегральное сечение
тощения составляет менее 15?о. Мы будем, кроме того, предпо-
Пагать, что это сечение плавно зависит от энергии. Неопределен-
Рис. 11.21. Схема распада состояний гигантского резонанса:
Заштрихованные области — непрерывный сиекгр; стрелки — испускание ча-
стицы (протона или нейтрона), волнистые линии — иопускание ^-кванта;
Еу — энергия поглощенного фотона.
ности, связанные с таким предположением, обычно не превышают
погрешностей эксперимента.
Чтобы получить из измеряемых на эксперименте сечений выхода
фотонейтронов
оехр - а<°и (у, п) + 2о (у, 2п) + odirect (у, и) (11.121)
полные сечения поглощения, необходимо ввести поправку F (Е)
на множественность нейтронов, определяемую с помощью соотно-
шения
Gd‘p -Oexp — (^direct (у, — О'(у, 2п) =
= {о£-ч>—orf,fec<(y, n)}F(E). (11.122)
мошНЧИНа ЭТ°й попРавки может быть рассчитана, например, с по-
ю статистической теории испарения нейтронов. В этом случае
377
F(E) =
1
2—(1-J-x) e~*
1
для E>E^;
для E < E'/‘,
tH.123)
где x = (E — E'n)/0, a E2hn — порог энергии для вылета двух -
тронов (рис. 11.22). Температура 0 выбирается в пределах 0*^1
1 Мэв. На рис. 11.22 представлены результаты расчетов F (Е]^~
различных температур. Видно, что небольшие неопределенно'"'151
в 0 мало сказываются на величине этой поправки. В заключен™
Рис. 1122. Поправка на множественность нейтронов.
F(Е) —фактор, связывающий величину выхода с полным
сечением фотонейтронных реакций [198].
этого раздела заметим, что в настоящее время имеются результаты
непосредственного измерения сечений реакции (у, 2и) с помощью
совпадений. В частности, подобная методика использовалась ли-
верморской группой при измерениях сечений поглощения [67, 68],
результаты которых обсуждались в § 11.9.
11.10.4. Анализ экспериментальных данных
для сферических ядер
Поскольку в литературе можно найти большое число очень де-
тальных обсуждений результатов исследований сечений поглоще-
ния у-квантов в сферических ядрах [32, 81,84, 144, 145,256,346,
376, 378], мы представим здесь лишь некоторые типичные данные
для ядер Сг и Zn, а также теоретические предсказания для реак-
ций рассеяния фотонов. Параметры теории определяются следу-
ющим образом. Энергия Лсо2 равна энергии первого возбужден-
ного состояния 2+, а р0 связана с величиной приведенной вероят-
ности перехода в это состояние. Точное значение энергии дипольных
колебаний определяется отождествлением основного пика в теоретп
ческом сечении поглощения с соответствующим экспериментальная
максимумом. Ширины различных состояний гигантского Р®
нанса считаются равными одной общей ширине Г, величина к°
рой, равная 1—2 Мэв, выбирается таким образом, чтобы она
впадала с шириной первого основного максимума в сечении
378
«я Детальное обсуждение этих вопросов дано в работе
«Р°береаИДР- [377]'
л ла спектра дипольных состоянии очень сильно зависит от
пн параметров tia>2 и |30. На рис. 11.23 приведены типичные
веДИЧОы вычисленные для их различных значений 1197, 198].
Ля’сь рисунком, легко получить полуколичественную оценку
^оЛреДеления интенсивностей дипольных переходов в произволь-
рЗС сферическом ядре в рассматриваемой области значений А.
к уже указывалось выше, подлежащая диагонализации матрица
нергий является в принципе бесконечной. Для практических це-
а
Ро 0,150 .
1 0,200- 1 1 1 1., Il ..I.."
Li_J । 0,250- । iL il । <j ।. < -
Ll 1 I 0,300 - —1 il 11 li »l 11
0,2
О
Ор
О,2
О
о,2
о
0,2
О
W 16 18 20 22 24
Е, Мэв
5
Рис. 11.23. Силы дипольных переходов для различных значений Р, вычис-
ленные с учетом восьми квадрупольных фононов, S£2i = 18 Мэв:
а—Д <02=0,6 Мэв, б — Д<02= 0.5 Мэв, в — Д<о2=1,2 Мэв.
лей необходимо рассматривать матрицу конечного порядка. Число
учитываемых фононных состояний зависит от численных значений
Ро И //О 9.
На рис. 11.24 и 11.26 изображены теоретические и эксперимен-
тальные сечения поглощения Поскольку для ядер Сг и Zn отсутст-
вуют данные о (у, н)-реакциях, для сравнения с теорией исполь-
зовались экспериментальные данные для соседних ядер 51V и Си со-
ответственно. При этом предполагалось, что последняя нечетная
частица не изменяет существенно структуру гигантского резонанса
Соответствующие сечения упругого рассеяния, а также неупругого
рассеяния с возбуждением первого и второго состояний 2+
(см. рис. 11.19) изображены на рис. 11.25 и 11.26. Сечение неупруго-
го рассеяния с возбуждением второго уровня 0+, принадлежащего
Вадрупольному триплету, на порядок меньше величины сечения
Другого рассеяния. Как и следовало ожидать на основании опти-
ской теоремы (см. гл. 5 т. 2) и дисперсионных соотношений, сече-
другого рассеяния и поглощения во всех случаях имеют по-
ЛУЮ структуру. Интересно отметить, что связь дипольных и
^Рупольных колебаний приводит к относительно интенсивному
379
для этих сферических ядер неупругому рассеянию фотонов с во г.
дением первого и второго 2+-состояний. Этот результат_____Зб^-
ствие большой величины тензорной поляризуемости ядер. мС'1ед'
сказать, что благодаря связи дипольных и квадрупольных" к0 Жн°
ний ядро становится оптически анизотропным (см. т. 2 гл. 5) х '
этот эффект экспериментально еще не наблюдался, обнаруж °Тя
его возможно, так как энергия возбуждения первого 2+-уп0ИИе
составляет для рассматриваемых ядер от 0,4 до 1,4 Мэв, что пНЯ
Рис. 11.24. Вычисленное сечение фотопоглощения в ядре
52Сг в области гигантского резонанса. Точками изображены
экспериментальные данные.
Рис. 11.25. Вычисленные сечения упругого (сплошная кри-
вая) и неупругого рассеяния фотонов на ядре 52Сг. Пунк-
тирная и штрих-пунктирная кривые-—сечения неупругого
рассеяния с возбуждением первого и второго 2J-состояний
соответственно.
воляет выделять неупругую компоненту в рассеянии [221. Даже
в том случае, когда процессы упругого и неупругого рассеянии не
могут быть экспериментально разделены по энергии, вклад тензор-
ного рассеяния должен проявиться в угловых распределениях.
Очевидно, изучение реакций неупругого рассеяния дает дополни
тельные возможности исследования волновых функций динамиче^
ской коллективной модели, т. е. коэффициентов разложения а,
в уравнении (11.102). ^0.
Заключение. Как можно было видеть, теория достаточно
рошо описывает распределение интенсивностей дипольных nePcfl,._
дов и структуру сечений, в частности, в жестких сферических
380
5iy 55Мо, 2GfiPb [198]. Однако в некоторых случаях низко-
РаЧ ти'ческая часть резонанса, т. е. область, лежащая ниже ос-
энеРге ппка> обладает структурой, которая не объясняется тео-
н°бНО ^араК14рным примером подобного рода является ядро D0Zr
P,ieIRl 334, 346]. Чтобы понять причины успехов и неудач теории,
’ рассмотреть обсуждаемые проблемы с точки зрения более
яментальной теории, например с точки зрения модели оболо-
Ф}нд^ак гигантский резонанс, так и колебательные состояния яв-
че^тся 1р1/1-состояниями (одна частица — одна дырка) (см. т. 3).
Рис. 11.26 Рассчитанное се-
чение фотопоглощения в
ядре 64Zn.
В ннжней части рисунка изо-
Лражеиы: сплошная кривая —
сечение упругого рассеяния фо-
т 'Нов (теория); пунктирная и
1трнх-пунктирная кривые — се-
чения неупругого рассеяния фо-
т нов с возбуждением первого и
второго 2+-состояний соответст-
венно (теория).
Говоря более точно, однофононное состояние есть lpl/t-состояние,
двухфононное — главным образом 2р2/1-состояние (две частицы —
две дырки) и т. д. В области сферических ядер периодической сис-
темы частично-дырочные состояния, связанные с поверхностным
возбуждением и гигантским резонансом, довольно сильно разли-
чаются, хотя и не полностью. Разумно поэтому считать, что эти два
типа возбуждений могут существовать в ядре одновременно и взаи-
модействовать главным образом благодаря граничному условию
для гигантского резонанса. Это означает, что дипольные колеба-
ния «настраиваются» па форму поверхности ядра и, в свою очередь,
адиабатически влияют на нее.
Совершенно другая ситуация имеет место, когда рассматривают-
ся многофононные состояния поверхностных колебаний. Одно-
фононное состояние является линейной комбинацией соответствую-
щих 1р1/г-состояний. В гармоническом приближении двухфононное
состояние поверхностных колебаний является 2р2/1-состоянием,
состоящим из двух невзаимодействующих 1р1/i-состояний. Нет
никаких оснований предполагать, что две частицы или дырки этих
'Щух lpl/i-состояний не взаимодействуют. Напротив, следует ожи-
дать, что две 1р1 /г-компоненты двухфононных состояний взаимодеи-
381
ствуют очень сильно. Подобные аргументы играют еще бо
щественную роль в случае многофононных состояний. ’ее СУ-
Чтобы учесть эти взаимодействия в коллективной модед
обходимо добавить к гамильтониану (11.91) ангармонические ч'’ Не'
так как до сих пор мы рассматривали лишь потенциалы, квадп еНЬ*’
ные по а[21. Однако совершенно не очевидно, будет ли достаточ1"4'
такое изменение гамильтониана. Может оказаться, что мног^И
ионные состояния совершенно не обладают свойствами фононов R
же, по-видимому, в некотором приближении поверхностные к Се
бання сохраняют фононный характер, так как в противном слсц6
было бы трудно объяснить полуколичественные согласия резу/6
татов расчетов в гармоническом приближении с эксперимента-ц,'
ными данными о сечениях. Во всяком случае, для того чтобы почт'
чить более точное количественное согласие между теорией и экс"
периментом, необходимо сначала дать достаточно точное описание
низкоэнергетического коллективного спектра. Это относится
в первую очередь, к состояниям 0+ и 2+, которые влияют на
структуру спектра дипольных состояний.
Однако наиболее заметное расхождение между теорией и экс-
периментом связано со структурой низкоэнергетической части ре-
зонанса. Весьма вероятно, что превышение экспериментального
сечения над теоретическим вызвано переходами в некоторые из
тех состояний, которые в схематической модели [64] не возбужда-
лись при дипольных переходах. Такое предположение ведет к идее
коллективных корреляций [112, 113]. На языке коллективной модели
гигантский резонанс является изоспиновой волной. Связь этого
возбуждения со спином и появление спин-изоспиновой волны могут
привести к расщеплению гигантского резонанса, что подтверждает-
ся, например, расчетами для ядра 16О, в котором возникают два
интенсивных дипольных перехода, причем переход с большей энер-
гией происходит с переворачиванием спина. Возможно, что эта же
связь является причиной структуры в низкоэнергетической части
гигантского резонанса.
* * *
Связь между результатами динамической коллективной модели
и экспериментальными данными обсуждается в статьях Шевченко и
Юдина [333], Даноса и Фуллера [101] и Спайсера [346]. Резуль-
таты исследования рассеяния фотонов на основе этой модели даны
в работе [231.
а 12. РАССЕЯНИЕ
глав ТЯЖЕЛЫХ ИОНОВ
В последние годы физика тяжелых ионов стала чрезвычайно
интересной и многообещающей областью ядерных исследований.
Образно говоря, в ядерной физике соответствующие явления пред-
ставляют собой явления микрокосмического типа. В настоящее
время интенсивно изучаются самые разнообразные реакции с уча-
стием тяжелых ионов: рассеяние, реакции переноса, кулоновское
возбуждение, деление и т. п. Большой интерес представляют также
многочисленные приложения этих реакций в ядерной химии.
Наиболее важной характеристикой тяжелых ионов в ядерных
взаимодействиях является их классическая природа. Поскольку
этот факт весьма важен для понимания физики рассматриваемых
реакций, проанализируем его более подробно. Если протяжен-
ность волнового пакета, описывающего ион, существенно меньше
расстояний, характерных для данной ядерной реакции, то можно
использовать полуклассические или даже классические прибли-
жения. Если использовать в качестве характерной длины наимень-
шее расстояние, на которое приближается ион к ядру при лобовом
соударении, т. е. 2а = ZrZ2e2IE, а в качестве размера волнового
пакета — длину волны \ = t'^v, то соударение можно будет рас-
сматривать классически при условии
т] = п/Х = Zx Z2 e2!tiv » 1. (12.1)
Здесь eZj и eZ2 — заряды сталкивающихся ядер (е — заряд элект-
рона), v — абсолютная величина их относительной скорости и
•о = рс2 2 — относительная энергия двух ионов. Другими сло-
вами. под классическим столкновением мы понимаем такое столкно-
вение, при котором взаимодействующие ядра движутся по куло-
новским траекториям. Очевидно, что это предположение во многих
случаях существенно упрощает вычисления.
с другим важным свойством взаимодействия тяжелых ионов
ядрами является возможность передачи очень больших угловых
п*ентов пРи малых энергиях возбуждения. В качестве примера
ожно привести реакцию рассеяния на золоте ионов кислорода
v энергией 160 Мэв, в которой играют существенную роль угловые
383
моменты вплоть до 90 Й. Ясно, что такое большое значение
ваемых угловых моментов может оказать существенное в'еРе4а-
на механизм ядерной реакции. Иянце I
Одна из наиболее заманчивых перспектив в области яде
реакций с тяжелыми ионами — получение новых изотопов^ р!Ь'Х
более важным для этого процесса является образование состав*1'
ядра в рассматриваемых реакциях. Можно ожидать, что слия°Г°
ядер будет происходить при относительно малых скоростях ХоНие
как мы увидим в следующем разделе, это предположение’ ВесТЯ’
лишь частично. Чтобы подобное слияние ядер стало возможнь °
необходимо преодолеть кулоновский барьер. Однако сильное э-р
ктростатическое взаимодействие может вызвать заметную дефолт/*
цию и поляризацию ядер в течение процесса столкновения, что"
в свою очередь, может эффективно увеличить высоту кулоновского
барьера и сделать процессы слияния менее вероятными. Эти очень
интересные и важные явления будут обсуждены с помощью рас-
смотренных моделей в § 12.1—12.5, в которых мы также постара-
емся описать основные представления физики реакций с тяжелыми
ионами.
К сожалению, мы не можем рассматривать здесь все разнообра-
зие явлений этой области физики. Поэтому мы ограничимся лишь
общим изложением метода исследования реакций, в которых проис-
ходит деформация тяжелых ионов, а также обсудим последние
очень интересные идеи, касающиеся ядерных молекул, или, более
точно, ядерных молекулярных состояний. Эти состояния из двух
ионов, скажем, система 16О — 16О, не образуют составного ядра,
а являются состояниями молекулярного типа. В § 12.7—12.9 бу-
дут рассмотрены квазимолекулярные оптические потенциалы. Об-
суждение других проблем физики реакций с тяжелыми ионами чи-
татель может найти в работах [18, 54, 126, 150, 170, 358, 3961.
§ 12.1. ЭФФЕКТЫ ДЕФОРМАЦИИ ЯДЕР В РЕАКЦИЯХ
С ТЯЖЕЛЫМИ ИОНАМИ
Как уже указывалось выше, одно из наиболее интересных бу-
дущих направлений в физике тяжелых ионов связано с реакцией
слияния атомных ядер, ведущей к образованию сверхтяжелых
ядер с Z « 114, а также, возможно, с Z « 164 [143, 269, 271, 2841.
Во время столкновения тяжелых частиц их кулоновское отталки-
вание будет возбуждать как в мишени, так и в налетающей частице
вращательные и колебательные состояния и гигантские резонансы.
Наиболее удобно эти внутренние степени свободы рассматривать
с помощью коллективных переменных и так как мпкроско
пическое описание этих эффектов слишком трудоемко. При возС)У
дении этих внутренних степеней свободы происходит уменьше
энергии относительного орбитального движения. Кроме того,
годаря изменению формы ядер и распределения зарядов, вели41
384
некого барьера будет отличаться от значения, определяемого
£сто°й формулой:
пр Uc = ZxZ2e*lR, (12.2)
„__расстояние между центрами масс двух ионов. Чтобы про-
гДе к слияние двух ядер, относительная энергия ионов должна
1130111 вавна высоте кулоновского барьера. При больших энергиях
бЬ1Тет произойти диссоциация системы.
"0>В первых работах, посвященных исследованию кулоновского
содействия тяжелых ядер[157, 39Э, 319], использовалось адиа-
®за' ческое приближение. В этом приближении расстояние между
Еами считается фиксированным и ищется минимум полной энер-
Я п системы как функции коллективных переменных двух ядер,
п'пи этом Гейликман [157] рассматривал квадрупольные и окгу-
рольные деформации, Уонг[390]—только квадрупольные, а Шарн-
веб’Р [3171 — квадрупольные деформации и гигантские мульти-
польные резонансы. Первые очень упрощенные расчеты динами-
ческих эффектов были сделаны в работах [39, 244]. Здесь мы бу-
дем следовать наиболее полному динамическому исследозанию
этой проблемы, данному Холмом и др. [193—195]. Для этой цели
определим полную функцию Гамильтона классической двухион-
ной системы, состоящей либо из двух сферических, либо из двух
деформированных ядер. Для изучения возбуждения внутренних
степеней свободы как функции времени, получим уравнения Га-
мильтона, описывающие сильную связь орбитального и внутрен-
него движений, и найдем их численные решения. Это даст нам воз-
можность определить деформацию ядер, характер их движения и
распределения зарядов в произвольные моменты времени. Зная
эти характеристики ядер, можно получить интересующую нас ин-
формацию об изменении кулоновского барьера, возбуждении раз-
личных степеней свободы и изменении траекторий движения.
§ 12.2. НЕКОТОРЫЕ ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
Одним из самых важных членов в полной функции Гамильтона
является энергия орбитального движения. Взаимное расположение
Двух ядер характеризуется их относительными координатами R,
"> <р. Рассмотрим две фиксированные в пространстве координат-
ные системы, центры которых совпадают с центрами масс ионов
•Рис. 12.1). Чтобы вычислить кулоновское взаимодействие, необ-
ходимо знать величину | гг — г2 | -1 = гГг1, которая для
дается абсолютно сходящимся рядом вида [75]
ходи МО
ri - '2< R
ХУ/,, (6, ф)У;1т,(е1,ф1)У/г„гг(е2,(р2), (12.3)
Зак. 1218
385
где
,, тг = ())>». 4 m, (4л)3/2 '
{(2/j + 1)(2Z2 1)(2/14 2/2Н I)}1/2
(/i + Za + ffti+?п2)! (11 + 1° — wt — т2)! 11/2
(/i+«*i)!(/i— m^l (/2 + т2)! (/2 — т2)! j
<12.4,
Так как мы рассматриваем рассеяние в плоскости, то
положить ср = 0. Тогда для функции Гамильтона относитет'0*^
движения получаем льного
ногЬ- А+Л
2ц 2ц/+
(12.5)
где ц = МГМ2 (Мг + Л42) —приведенная масса двух ядер Дя1Рр
для угла рассеяния х (рис. 12.2) имеем: ‘ ‘ ее'
X |л—26О|.
Полная функция Гамильтона системы из двух сферических
ядер содержит помимо НогЬ члены, описывающие поверхностные
колебания, гигантские резонансы, электромагнитное взаимодействие
налетающей частицы с мишенью и взаимодействия гигантских ре-
зонансов с колебаниями поверхности [см. выражение (11.1)1-
Кулоновское отталкивание ядер приводит к их динамической
деформации; это означает, что в результате взаимодействия возни
кают поверхностные колебания. На рис. 12.3 изображены таки
колебания для случая квадрупольных и октупольных деформаЦ11 ’
Энергии квадрупольных и октупольных колебаний поверхно
равны 0,3—1,2 и 1—2,5 Мэв, а периоды этих колебаний и ыь
изменяются соответственно в пределах 2 • 10-20 — 4 • 1и
386
21 _ । 6 10~21 сек. Для дальнейшего изложения важно
4 • 1® ч[1аТь «время кулоновского взаимодействия». Чтобы найти
'3*'я'е [я рассмотрим центральное столкновение и определим
Зто ВР наибольшего сближения а с помощью соотношения
flapaMeTP
Zj Z2 e\a.
l 2
—
(12.7)
Рис. 12.2. Связь между углами рассе-
яния х п 6о (р — параметр удара).
Рис 12.3. Квадрупольные и октуполь-
ные деформации ионов, возникающие
вследствие их кулоновского отталки-
вания.
Для некоторого произвольного расстояния Л1 между двумя
ионами имеем соответственно:
1 = (12.8)
Л Л /\
Отсюда для скорости од на расстоянии R получаем
dR Zi Z2^~“ / 1 1 \_I 1_______
d/jl 1 \ a R ) | a R ’
I
(12.9)
r^e A 12Z1Z2e2/p.
Определим теперь время кулоновского столкновения Тс как
время, которое требуется иону, чтобы приблизиться к мишени на
расстояние а с расстояния а • х и вернуться в прежнюю точку
ах
Тс(х)^ f------------ =
а
2Д^аЗ/2(|/ -р ln(/x +/х— 1)}. (12.10)
13*
387
Выбирая в качестве примера х « 3, получаем для случа
новения тождественных ионов: Тс « 2,8 • КУ21 сек п,1 Ст°‘Чк-
и Тс « 2,78 • 10~21 сек для 122Sn. Так как Тс т . ” П
квадрупольные колебания не следуют адиабатически за движ"’’ т°
иона. Вместо этого некоторое количество энергии передан-6НИем
иона рассматриваемому колебательному движению повепхГСЯ °т
которое продолжается и после столкновения, так как ионы °СТ11,
вают удалиться друг от друга на достаточно большое расстоящ СПб'
того, как энергия квадрупольных колебаний превратится обп*6 Д°
в энергию орбитального движения. Ратно
Рис. 12.4. Модель механизма возбуждения различных
степенен свободы ядер.
Эта ситуация становится более понятной, если обратиться
к представленной на рис. 12.4 простой механической модели, изо-
бражающей гармонический осциллятор, на который действует
внешняя сила. Аналогом времени столкновения является время Т.
в течение которого колесо поворачивается из положения 1 в поло-
жение 2. Если Т у Tosc, то осциллятор не успевает следовать за
изменением внешней силы. При Т « Tosc осциллятор может пе-
редать обратно внешней силе часть полученной им энергии. Ана-
логом этого случая является возбуждение октупольных резонансов.
Если Т 3> Tosc, то осциллятор следует без сдвига по фазе за изме-
нениями внешней силы, не получая от нее энергии. Точно такая
же ситуация имеет место при возбуждении гигантских резонансов.
Деформация и поляризация ядер уменьшают их кулоновскою
энергию, что, казалось бы, должно привести к понижению куло-
новского барьера. Однако из-за деформации центры масс обоих
ионов должны сблизиться сильнее, чтобы могло произойти их слия-
ние (см. рис. 12.3). Поэтому эффективно это приводит к увеличению
высоты кулоновского барьера. Степень адиабатичности этого про-
цесса определяется отношением Tvib!Tc.
Аналогичная ситуация, причем, возможно, даже более отчетли-
вая, имеет место для деформированных ядер. В этом случае состоя-
ние поверхности проще описывать не колебательными амплитудам’1
а2м, а внутренними координатами а0, а2 и тремя углами Эйлера
0,- : ах = (0(, 0,, 03) a2h [см. формулу (2.2)]. Углы Эйлер
описывают ориентацию собственной системы отсчета относптель
но лабораторной системы. Движению подобного рода будет соо
388
ва'гь в функции Гамильтона член, характеризующий вра-
ретство ю энерГИЮ как мы видели в гл. 6, вращательные энер-
1ца’геЛ ер имеют величину порядка 40—200 кэв. Мы можем, таким
гп11 Я м заключить, пользуясь сделанными выше оценками харак-
0браз х ’ядерНЬ1х времен, что ни мишень, ни налетающая частица не
Рис. 12.5. Иллюстрация вращения двух деформированных ядер:
с — столкновение ядер полюсами, б — экваториальное столкновение. В последнем слу-
чае движение ядер происходит в направлении, перпендикулярном к плоскости чертежа.
могут занять путем вращения энергетически наиболее выгодного
положения, так как действующие в течение краткого времени со-
ударения внешние силы поворачивают ядра лишь на несколько
градусов (рис. 12.5).
Рис. 12.6. Поляризация зарядов ядер
(возбуждение гигантских резонансов)
при их сближении, вызванная куло-
новским отталкиванием.
Как в деформированных, так и в сферических ядрах при их
сближении возникают эффекты, вызванные поляризацией распреде-
ления зарядов (рис. 12.6). Отталкивание протонов в обоих ядрах
будет происходить главным образом вдоль линии, соединяющей
их центры. Из самых общих свойств гигантских резонансов сле-
дует (см. гл. 10 и 11), что такое разделение протонов и нейтронов
означает просто возбуждение в обоих ядрах гигантских резонансов,
особенно гигантских дипольных резонансов. Период колебании,
соответствующий энергии этих резонансов в средних и тяжелых
яДРах (12—17 Мэв), составляет (2,4—3,4) • 10 2' сек. Отсюда
можно заключить, что соответствующие колебания адиабашчески
меняются при движении тяжелых ионов.
13В
Зак. 1218
389
§ 12.3. РАССЕЯНИЕ СФЕРИЧЕСКИХ ЯДЕР
Полная функция Гамильтона системы из двух сфещ
ядер может быть записана в виде: 1Чес«их
Н = Нorbit 4- Hvlb (1) + HgR (1) + HcRtib (1) +
+ HVib (2)-Г Hgr (ty + HcRtib (2) + Hint, Ц2
где представлены орбитальное движение, поверхностные кол г
ния, гигантские резонансы и кулоновское взаимодействие н'
Различные коллективные гамильтонианы, входящие в это выпа-'"
ние, обсуждались в §3.2, 10.8 и 11.10. Рассмотрим более подроби'
Hint. Этот член связан главным образом с электростатически0
взаимодействием ядер, так как магнитные взаимодействия малы
(начальные скорости ионов имеют порядок 3-109 см'сек и ста-
новятся очень малыми для малых расстояний /?). Поэтому И-
можно записать в виде:
Я(1) R (2)
Рр Hi.nCl)) X Рр (г2, т](2)1 ch2~, (12.12)
0 0 Г12
где /?(>) = (01>(Р11 а /?<2> = А<2> (02, ч2, aW(2)).
При этом г12 определяется формулой (12.3), плотности распределе-
ния протонов в ядрах рр (г, р) — выражениями (10.148а) и (10.150),
а зависящие от коллективных координат поверхности оД] гра-
ничные радиусы (0v, <pv, cJH (v))—формулой (2.1). Вы-
числение интеграла (12.12) является довольно простой, хотя и
очень громоздкой процедурой; детали этого расчета могут быть
найдены в литературе [193]. Заметим также, что из H!nt может быть
выделен член ZxZ2e2'R-.
Hlnt = H,lnt + Z1Z2e2IR, (12.13)
который описывает кулоновское взаимодействие точечных зарядов.
Это взаимодействие совместно с Horblt определяет резерфордовские
траектории сталкивающихся ионов.
Будем рассматривать импульсы л1Н, П[И, pR и рв как обоб-
щенные импульсы, а координаты сДИ, qW, R и 0 как обобщен-
ные координаты. Тогда с помощью уравнений Гамильтона
dHldqK=—pK, dHldpK = qK (12l4)
легко получить систему уравнений, описывающих столкновение
двух тяжелых ионов. При учете квадрупольных и октупольных к
лебаний поверхности, а также гигантских дипольных Резо^ПСн.
уравнения (12.14) приводят к системе из 34 связанных диффере^
циальных уравнений, которые могут быть относительно легко Р
шены численно с помощью метода Рунге— Кутта [397].
390
Особый интерес представляет седловая точка
фрьера, определяемая соотношением
E’c = Z1Zae2/(/?<oi) + ^(2)).
Она может быть достигнута в процессе рассеяния,
налетающих ионов EN удовлетворяет условию
кулоновского
(12.15)
если энергия
(12.16)
в дальнейшем параметром
е&я'н"йя представляет собой расстояние между центрами ядер
Гмомен’т их соприкосновения.
В данном разделе мы не рассматриваем ядерные силы, введение
которых приведет к понижению кулоновского барьера (см. § 12.7—
12 9) и изменению энергии деформации [271].
При учете внутренних степеней свободы соотношения (12.15) и
(12 16) видоизменяются, так как в этом случае радиусы ядер зави-
сят от времени. Если t — т — момент времени, в который проис-
ходит соприкосновение ионов, то соответствующее расстояние
равно
Величина R(ol) 4 /?(02),
EN = EC.
называемая
^МИН — А<’)(т) + А<2)(т).
(12.17)
Обсудим теперь два примера: рассеяние 118Nd на U8Nd и
l22Sn на 122Sn. В табл. 12.1 представлены характеристики этих
ядер. Чтобы сделать исследование этих реакций возможно более
ясным, ограничимся изучением центральных столкновений, в ко-
торых рассматриваемые эффекты играют наибольшую роль.
Параметры 183Nd и 122Sn
Таблица 12.1
I Ядре Квадрупольные ко- лебания Октупольные коле- бания Гигантский диполь- ный резонанс Е(у Мэв 1пг<1оф ‘(г°)а4-(т^
Энергия Период Г2, сек Энергия Eb—fittis, Мэв Период Та, сек Энергия Мэв Период 71. сек
l22Sn 0,300 1,14 1,38-10“2° 3,62.10-21 1,03 2,50 4,01-10-21 1,65-10-21 15,5 16,6 2,66-10-22 2,49-10“22 408,9 302,8 12,75 11,90
l48Nd — ,48Nd-pacce»HHe. Если два иона достаточно удалены друг
друга (/? ~ 15q ферми), то внутренние степени свободы не воз-
Уждаются, т. е. все соответствующие амплитуды равны нулю.
возбуждения внутренних степеней свободы кулонов-
номИ|1 РЬеР Дожигается при расстоянии А*мин между ионами, рав-
сбл 1 Ферми. Это означает, что до соприкосновения ионы могут
'зиться на расстояние меныпее, чем параметр касания. В мо-
13В*
391
мент соприкосновения амплитуды различных возбуждений
равны: 1 Ядер
а20(1) (2) = -0,078;
а30(1)= — «30 (2) =-0,034;
9ю(1) = —<7ю (2) = —0,691.
Отрицательный знак квадрупольной деформации указывает
при касании ядра имеют сплюснутую форму.
чт0
На рис. 12.7 изображено распределение энергий внутрент
степеней свободы в зависимости от времени; т означает момент нам
Рис. 12.7. Зависимость от времени энергии, приходящей
ся на различные внутренние степени свободы при лобо
вом столкновении ядер l4SNd.
большего сближения. В момент времени t = т энергия распреде-
ляется следующим образом:
E2j.(t) = 1,94 Мэв-,
Е3-(т) 0,382 Мэв-, (12.19)
Ех- (т) 0,997 Мэв.
Соответственно после столкновения (/ -> оо)
Е2+(оо) = 8,01 Мэв (~ 25 фононов);
£3-(оо)- 0,93 Мэв (« 2 фонона); (12 20)
7Г]-(°о) = 0 (нет возбуждении).
Следовательно, в рассматриваемой реакции в обоих ядрах возбу»
даются квадрупольные и октупольные колебания, а возбуждения
гигантского дипольного резонанса не происходит. Этот вывод по.
ностью согласуется с изложенным в § 12.2 этой главы.
392
ПолУче1ШЬ1е результаты показывают, что энергия коллективных
*, рдений тяжелого составного ядра, образующегося в момент
В°3 ени / = т> невелика. Поэтому реакции подобного типа можно
БРеМпь3овать для получения сверхтяжелых элементов при слиянии
"сП°.'сталкивающихся тяжелых ионов (см. также сноску на следую-
щей*странице).
Ш рассмотрим теперь рассеяние ядер lzzSn на ядрах L-Sn. Так
к это ядро является более «жестким» относительно колебаний по-
капХности, чем 148Nd, часть энергии квадрупольных и октуполь-
uv колебаний после столкновения превращается обратно в энергию
орбитального движения (рис. 12.8). В момент столкновения ядер
(i = т, RM11H = 10,47 ферма) амплитуды и энергии коллективных
возбуждений равны
а20 (1) — а20 (2) — 0,046;
а30(1) = -а30(2) = -0,119;
?10(1) = -<7ю(2)--0,646;
£2+ (т) =1,01 Мэв;
£3-(т)=1,39 Мэв;
£1-(т) = 0,892 Мэв.
После столкновения имеем:
(12.21)
Е2+ (оо) —2,84 Мэв (~ 3 фонона);
Ея- (оо) = 1,60 Мэв («г 1 фонон);
(12.22)
Ег- (оо) =0 (нет возбуждений). ’
Вообще говоря, кулоновский барьер зависит от R, 0 и от ха-
рактера сближения ионов. Так, например, он является разным
Для падающей и удаляющейся частиц благодаря возбуждению внут-
393
Е,Мэв
1,6
О
12.10. Изменение траектории
0,8
0,6
°>4
°,2
°’4
Время. 10 тсек
0,6 0.8
,-20
Рис. 12.9. Понижение кулоновского барь-
ера вследствие возбуждения внутренних
степеней свободы ядра ,22Sn. Однако в
действительности кулоновский барьер
оказывается эффективно увеличенным па
40 Мэв из-за того, что ядра могут ближе
подойти друг к другу (расстояние между
центрами равно Р(т), а не
/?(0v)—поворотная точка возмущенной
резерфордовской орбиты.
р = 0,
l22Sn.
орби-
Рис.
Ек=Ес при столкновении ионов
Верхняя кривая — невозмущенная
та, нижняя — возмущенная орбита.
ренних степеней свободы. На
рис. 12.9 показано измен?
ние кулоновского барЬепа
вследствие возбуждения к
лебаний поверхности и г°*
гантских резонансов, рж'
отсутствии возбуждений сед
ловая точка находилась ?
на расстоянии /?<*,’ * /^>(2)
В действительности, однако
ядерные силы могут действо',
вать между ионами только в
том случае, если расстояние
между ними близко к вели-
чине параметра касания:
Rmhh R СО- Поэтому оче-
видно, что в результате это-
го седловая точка эффектив-
но увеличится на величину
порядка 40 Мэе*. Следова-
тельно, для данной началь-
ной энергии и данного пара-
метра удара р орбиты ионов
будут искажены по сравне-
нию с резерфордовскими ор-
битами.
В качестве примера на
рис. 12.10 представлена из-
мененная орбита ядра 1=2Sn
для р = 0 и En = Ес- В
рассматриваемом случае из-
менение зависимости расстоя-
ния между ионами от вре-
мени оказывается незначи-
тельным. Однако при р Ф 0
этот эффект может существен-
но увеличиться, что приве-
дет к заметному изменению
сечения. Как известно, ча-
стицы, имеющие параметры
удара в области между Р 1
р + dp, рассеиваются в оо-
* В работах [194, 195]I
показано, что на малых ра т
пнях ядерные силы неитРа п.,т к
кулоновские силы, что при г0
заметному уменьшению
эффекта.
394
I углов между у и у 4- dy. Отсюда для дифференциально-
^сечения получаем
do = 2ло dp = 2лр (у) I -(>—ZL I dy
I |
(12 23)
и> следовательно,
do P (x)
dfi sin %
I dp (X)
I d%
(12. 24)
Значение p (у) может быть вычислено аналитическ к только для
езерфордовского рассеяния. В общем случае эта функция должна
быть определена численно [193].
§ 12.4. РАССЕЯНИЕ
ДЕФОРМИРОВАННЫХ ЯДЕР
В случае взаимодействия двух деформированных ядер анало-
гом (12.11) является выражение
Д = Horbit + Hrot (1) + Hvib (1) + Hrctvib (1) +
4" HqR (1) + HcRvib (1) + Hrot (2) + Htib (2) 4-
+ нrotvib (2) 4 Hgr (2) 4* HGRvib (2) + Hint. (12.25)
Операторы Гамильтона, описывающие вращательные возбуждения
ядер и гигантские резонансы, были рассмотрены выше [см. урав-
нение (6.3) и гл. 11]. Взаимодействие Hint определяется выраже-
нием (12.12), в котором интегрирование происходит по объемам
деформированных ядер. Детальное решение уравнений Гамильтона,
полученных с помощью (12.25), описано в работе [193]; мы обсудим
здесь лишь полученные результаты, ограничившись несколькими
типичными случаями.
В качестве первого примера рассмотрим реакцию с участием
двух ядер 168Gd. Параметры этого ядра приведены в табл. 12.2,
где также даны соответствующие параметры ядра 23eU.
Таблица 12.2
Параметры ядер 158Gd и 238U
Ядро е, кэв Ро кэв Еу, кэв Е(у Мэв ферма Acot, Мэв
158Gd !38и 26,5 14,9 0,358 0,292 1700 994 711,9 627 455,2 808,1 12,97 14,87 15 15
Будем, как и прежде, рассматривать лишь лобовые столкнове-
ния. Динамика столкновения деформированных ядер очень сильно
395
зависит от начальной ориентации ядер относительно друг
Поэтому сначала рассмотрим случай, изображенный на рис ^о^3,
который соответствует О1/’ = —л/2, О?1’ = л/2
е«г> = О, е!,2’ = л/2, е?> = 0; р = О при t = 0. Если начТ
ная энергия Ем = 467,5 Мэв, то полная энергия возбужпе 1Ь
£ (оо) = 22,5 Мэв, а минимальное расстояние между понрпНИя
стями 7?мин = 1,75 ферми. рхн°‘
С другой стороны, при начальных условиях б'/' — ___
“ ...... " Т=я/2. 0?'= 0; р18о
момент соприкосновения рас
ферми, а их ориентация Прн
о?> = л/2, е^1’ = о;' е?» = л/8, е?’ =
(см. рис. 12.5, б), En = 511,8 Мэв в
стояние между ядрами £мин = 10,67
t — х определяется соотношениями:
Рис. 12.11. Начальная ориентация двух деформи-
рованных ядер гадолиния.
QU) = —6(2)=----22,9°;
<(1) = < (2) = 0,053;
о/(1) = а; (2) = —0,107;
9и (0 911 (2) = 1,07.
Эти результаты показывают, что к моменту наибольшего сбли-
жения, t — т, ядра поворачиваются на очень малый угол (A0t =
= 0,4 ).
Наконец, рассмотрим лобовое столкновение ионов, при котором
ядра сближаются своими полюсами. В этом случае седловая точк
барьера достигается при энергии £д = 428,9 Мэв, так как ядра
соприкасаются уже при /?мип = 15,43 ферми. Если в начальны)
момент времени существует небольшой угол между осями яд р
(рис. 12.12, б), б^1’ = — 6(22' = — 3° (это означает существова-
ние вращающего момента), то в момент наибольшего сближе
возбуждения различных степеней свободы характеризуются
396
дуютиМИ
значениями параметров:
е(‘) = -0(а2) = —4,35°;
(2)=-0,051;
<(!) = < (2) = —0,0002;
?н(1) = ?и (2) = 0,038;
?;0(1) = -?ю(2)=-0,513.
Рис. 12.12. Начальная ориентация двух деформированных
ядер при лобовом столкновении полюсами (а); ориентация,
при которой возникает момент сил (6).
(12.27)
Таким образом, к моменту t = т ядра поворачиваются на неболь-
шой угол Л02 = — 1,35 . Как показывают расчеты, наибольший
поворот ядер к моменту наибольшего сближения, t = т, имеет место
0.3 0.4 0.5 0,6 0,7 0,8 0,9 1.0 L1
11111 -ОО '
В рем я, 10 сек
Рис. 12.13. Зависимость от вре-
мени полной энергии возбужде-
ния налетающего иоиа и ядра-
мишенп при рассеянии lssGd на
И8и. £с=609,7 Мэв, Ея =
= 565,5 Мэв. EGr — функция
возбуждения гигантского резо-
нанса.
началыюй ориентации ядер, изображенной на рис. 12.5, а.
этом случае Л0^ 14°. Совершенно аналогичная ситуация имеет
Сг° Для системы 23eU — 238U, которая представляет большой
397
интерес с точки зрения образования сверхтяжелых элементов
акциях с тяжелыми ионами. в
На рис. 12.13 изображены в зависимости от времени эне
возбуждения мишени и налетающей частицы при рассеянии uIq1
Рис. 12.14. Возбуждение различных сте-
пеней свободы при столкновении ионов
158Gd.
на 238Н. Видно, что энергии возбуждения обоих ядер очень велики
(16 и 18 Мэв соответственно), причем возбуждение носит чисто вра-
щательный и р-, у-колебательный характер. Гигантские резонансы
в этой реакции, как и в ранее рассмотренных, не возбуждаются.
Рис. 12.15. То же, что на рис. 12.14, для
ядер 23eU.
Следует отметить другой интересный результат: в момент наиболь-
шего сближения полное возбуждение ядер достаточно велико
(от ~ 5 до 6 Мэв), что делает весьма вероятным деление отдельных
398
На рис- 12.14 и 12.15 приведена зависимость энергии возбуж-
яДеР", ядер от времени в реакциях Gd — Gd и И — U. Наибольший
^и^рес представляют большая величина энергий возбуждения и
litI ольно слабое возбуждение [З-колебаний. В случае последней
*°BI1H эти энергии равны 8; 7 и 0,4 Мэв соответственно. Это озна-
ет что в рассматриваемой реакции возбуждаются вращательные
частояния вплоть до 7 - 324-35 и у-колебательные состояния, со-
евжащие от 10 до 15 фононов. Однако этот очень интересный ре-
зультат весьма существенно зависит от свойств ядер, участвую-
щих в реакции.
§ 12.5. КВАЗИМОЛЕКУЛЯРНЫЕ СОСТОЯНИЯ —
ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ
Сечения ряда реакций, происходящих при бомбардировке ядер
углерода ионами углерода, обладают весьма отчетливой структу-
рой. Первые данные подобного рода были получены Бромли и др.
[65], измерившими сечения упругого рассеяния на 90° ядер 12С
на 12С и 16О на 1£О. При энергиях в системе центра масс порядка
6 Мэв в реакции 12С — 12С наблюдается довольно интересное явле-
ние. На рис. 12.16 изображены функции возбуждения этой реак-
ции с образованием протонов, у-квантов, а-частиц и нейтронов.
Как видно из рисунка, каждая из этих кривых обладает ярко выра-
женной структурой в области энергий около 6 Мэв, лежащей чуть
ниже кулоновского барьера. Детальный вид этой структуры пред-
ставлен на рис. 12.17, из которого следует, что наиболее отчет-
ливые пики находятся при энергиях 5,64, 6,00 и 6,36 Мэв.
Совершенно аналогичная ситуация имеет место при упругом
рассеянии 12С на 12С, 12С на 16О и 16О на 16О. Результаты соответ-
ствующих измерений приведены на рис. 12.18. Несколько лет назад
были получены данные о сечении последней реакции в области
энергий вплоть до 35 Мэв [337] (см. рис. 12.28), которые показали
наличие заметной структуры при энергии выше 17 Мэв. В случае
— 12С-рассеяния такая структура появляется при меньших
энергиях (около 8 Мэв)-, мы увидим ниже, что этот результат может
^bi6Q ^^Чствием относительной мягкости ядра 12С в сравнении
Алмквист и др. [18] выполнили весьма детальное исследование
реакции 12C (12С, a) 20Ne с образованием 20Ne в пяти различных
конечных состояниях. Угловые распределения а-частиц, образую-
щихся в реакции, показывают, что наблюдающиеся в 12С — 12С-си-
стеме резонансы с энергией 5,6 и 6 Мэв имеют спины 2 и 4 соответст-
венно. Таким образом, эти состояния являются состояниями со-
ставного ядра 21Mg. Из данных об упругом рассеянии можно заклю-
чить, что ширина распада составного ядра с испусканием 12С,
в. путем деления молекулы, составляет примерно 10% полной
ирины. Кроме того, оказалось, что приведенная ширина для рас-
ада с испусканием 12С примерно в 10 раз превышает приведенную
399
Рис. 12.16. Зависимость функций возбуждения для образо-
вания протонов (/), у-квантов (2), а-частиц (<?) и нейтро-
нов (4) при столкновении ионов 12С от энергии в с. ц. м. [17].
ширину для испускания сс-частиц и в 100 раз превышает нуклонную
приведенную ширину. Все это показывает, что в рассматриваемой
реакции, по-видимому, образуется система, весьма сильно напоми-
нающая молекулу 12С — 12С. Это предположение подтверждается,
в частности, большим значением приведенной ширины распада сос-
тавного ядра с испусканием 1?С.
400
Рис. 12.17. Зависимость функции возбуждения для образова-
ния у-квантов при столкновении ионов 12С от энергии в систе-
ме центра масс [65].
Уже с момента появления первых результатов исследования
реакции 12С —- 12С, и особенно после опубликования данных измере-
ний Йельской группой сечения упругого рассеяния 16О 16О
[337], был предложен ряд теоретических моделей для объяснения
экспериментальных данных [70, 71, 77, 274, 318, 320, 370]. Поведе-
ние функции возбуждения вблизи кулоновского барьера (< 15 Мэв)
401
Рис. 12.18. Зависимость сечений упругого рассеяния ядер углерода и кисло-
рода от энергии в системе центра масс [65].
было исследовано с помощью действительного потенциала, полу-
ченного из расчетов по теории ядерной материи [65]. В этой области
энергий поглощение не оказывает существенного влияния на ве-
личину эффектов в канале упругого рассеяния. Однако выше 17 Мэв
экспериментальная функция возбуждения для реакции 1ЬО —
1СО [337 ] характеризуется регулярной резонансной структурой
(см. рис. 12.28). Как эти, так и другие результаты [274] указы-
вают на необходимость учета абсорбционного (мнимого) потенциала
для объяснения сильного уменьшения функции возбуждения
(см. пунктирные кривые рис. 12.18, изображающие моттовское рас-
сеяние). Ниже мы обсудим предложенную Шайдом и Грайнером
модель [318, 320] для вычисления действительной и мнимой частей
потенциала, описывающего взаимодействие тяжелых ионов.
§ 12.6. ЭНЕРГИИ СВЯЗИ ЯДЕР —
ПОЛУЭМПИРИЧЕСКАЯ МАССОВАЯ ФОРМУЛА
Поскольку для последующего изложения нам потребуются д
ные об энергиях связи ядер, а также полуэмпирическая массо
формула, рассмотрим кратко соответствующие вопросы.
402
g основной характеристикой ядра является его полная
«я или масса в основном состоянии. Можно ожидать, что
9неРг1 а> содержащего Z протонов и N нейтронов, близка к сум-
маС7Л1 + ’ММП, где Мр и М„ — массы протонов и нейтронов соот-
твенно. Отклонения от этой величины имеют очень большое
I Срние. Наиболее просто найти экспериментально массу ней-
з1,апьного атома М (A, Z). Тогда энергию связи можно определить
^помощью соотношения
В (A, Z) = ZMH + NMn — М (A, Z),
(12.28)
д,.^, — масса атома водорода. Очевидно, что два эффекта дают
Гклад в это соотношение: энергия связи ядра и различие между
нергией связи электронов в нейтральном атоме с зарядом Z и
соответствующей величиной для Z атомов водорода. Величина
электронных эффектов, как правило, пренебрежимо мала*.
Массы ядер обычно измеряются посредством масс-спектрометри-
ческого определения отношения заряда к массе. Основная идея
таких измерений заключается в следующем. Ионизованные атомы
исследуемого вещества вводятся в масс-спектрометр в смеси с ядра-
ми известной массы, характеризующимися близким значением
удельного заряда. Это приводит к появлению в масс-спектрограм-
ме «массового дублета», связанного с ядрами неизвестной и извест-
ной масс. Таким способом были измерены массы очень большого
числа ядер [114].
Иногда можно определить массы изотопов непосредственно, если
известна масса одного из них. В этом случае ядро исследуемого изо-
топа вводится в состав молекулы, что приводит к изменению ее
момента инерции. Измеряя частоты молекулярного спектра, можно
найти изменения энергий вращения, а следовательно, и момента
инерции. Однако с помощью этого метода были измерены массы
лишь очень небольшого числа ядер [158]. Верхняя граница энер-
гий p-спектров (поправленная на две электронные массы в случае
позитронного распада) также позволяет определить разность масс
родительского и дочернего ядер. Однако в этом случае необходимо
твердо установить, что |3-распад идет на основное состояние дочер-
него ядра. В противном случае в баланс энергий нужно включать
у-кванты, сопровождающие распад. Аналогичным образом а-рас-
пад может быть использован для определения массы ядра (А — 4,
Z — 2), образующегося из ядра (A, Z), если учесть поправки на от-
дачу дочернего ядра и энергию связи а-частицы.
Для определения масс ядер может быть использовано очень боль-
шое число других ядерных реакций. Вапстра и Хьюзенга [196,
* Иногда вместо энергии связи используют другие величины:
,,..а) дефект массы М—А, выражаемый в массовых единицах (м. е.). 1м. е.
' ‘'—931,44 Мэз) равна 1/12 массы нейтрального атома 13С;
б) упаковочный коэффициент (Л—М)/Л;
в) До I960 г. практически во всех работах использовалась другая массо-
мяг едини„ца — атомная единица массы (а.е.м.). 1 а.е.м. определяется как 1/16
сы нейтрального атома 16О.
403
373, 374] проанализировали данные измерений для почти
ядер с целью установить их совместимость. Еще более потп
точные таблицы дефектов масс, выраженных в массовых и ато?'е 11
массовых единицах, были опубликованы Вапстрой с сотр. [128 243 Х
Рис. 12.19. Энергии связи на нуклон для Р-стабпльных изобар
(точки — четно-четные ядра, крестики — нечетные ядра), полу-
ченные путем усреднения данных для нескольких соседних ядер.
На рис. 12.19 представлены энергии связи ядер, рассчитанные
на один нуклон. Наиболее интересным свойством этих величин
является их приблизительное постоянство для всех ядер за исклю-
чением самых легких. Как видно из рисунка, значение В; А изме-
няется в пределах от 7,4 до 8,8 Мэв. Именно этот результат имеют
в виду, когда говорят о насыщении ядерной материи. Впервые мысль
об этом свойстве ядер была высказана при анализе измерений Ас-
тона [25] Гейзенбергом [187], предложившим для объяснения этого
эффекта существование обменных сил между нуклонами. Вайцзеккер
[381 ] и Бете [38] для описания данных об энергиях связи предло-
жили полуэмпирическую формулу, основанную на модели жидкой
капли. В настоящее время эта формула записывается в виде [3281:
В (А) Го А — уА2/3 —0,864 г-1 Z2 А ‘/з [1—0,76361 Z -2/3-
— 2,453 г--2 А—2/3] (г]Д-4/з_.рА-1) (A —Z)z4
+ 6А- >/2 (0, ±1) +7 ехр (—61 A—Z | А-’) 4
+ 14,33-10-6Z2-39. (12.29)
Первый член в этом соотношении, пропорциональный А, отражает
факт насыщения ядерной материи, а второй, пропорциональны!
404
, з описывает энергию поверхностного натяжения. Предполагая,
А' радиус ядра определяется соотношением 7? = г() А1/3, можно
^тать, что третий член в (12.29) связан в основном с кулонов-
С<1-ой энергией, которая пропорциональна Z2 R. Однако этот член
Рис. 12.20. Дефект массы (в а. е. м. для двух систем с А = 124
(а) (нижняя кривая — четно-четное ядро, верхняя — нечетно-
нечетное ядро) и для ядер с А = 125 (б) (по данным, приве-
денным в книге Престона [С]).
содержит две поправки, обусловленные обменными поправками
к кулоновской энергии и размытостью ядерной поверхности. Чис-
ленные значения параметров, определяющих размытость поверх-
ности, получены из данных о рассеянии электронов [328]. Четвер-
тый член в соотношении (12.19) — энергия симметрии, которая иг-
рает важную роль в изложенной в гл. 10 гидродинамической модели
ядра. Это слагаемое содержит также поправку на поверхностные
эффекты, которая пропорциональна тр
Эффекты спаривания, обусловленные силами спаривания меж-
ду нуклонами в ядре (см. § 8.5), описываются в (12.29) членом,
пропорциональным 6, который равен нулю для ядер с нечетным А,
положителен для четно-четных ядер и отрицателен для нечетно-
нечетных ядер. На рис. 12.20 изображены типичные примеры подоб-
ных эффектов для случая дефектов масс в ядрах с А = 124 и
А — 125. Попытаемся понять представленные результаты, а также
причину параболического вида изображенных кривых. Если бы
в выражении (12.29) отсутствовал член энергии симметрии, про-
порциональный (7V— Z)2, то В (А) достигала бы максимума
при Z = 0, т. е. все ядра состояли бы из нейтронов. Однако если
заменить в ядре 124Те 52 протона 52 нейтронами, то эти нейтроны
не смогут разместиться на 26 низших энергетических уровнях, заня-
тых протонами, и расположатся на уровнях с 37-го по 62-й, так как
первые 36 уровней уже заняты нейтронами. Таким образом, обра-
405
зуя ядро целиком из нейтронов, мы исключаем полностью купон
скую энергию, существенно увеличивая при этом полную энео °В~
в силу принципа Паули |301 ]. Другими словами, исходя из ус ю Н1°
N = Z, мы приходим к выводу, что кулоновские эффекты вел'151
к уменьшению Z, в то время как действие принципа Паули веч
к увеличению энергии. Эта добавка к энергии известна как энепш
симметрии. Из изложенного ясно, что в массовой формуле долже^
содержаться член, пропорциональный (N — Z)2.
Именно этот результат находит свое отображение в параболиче-
ской формуле кривых, изображенных на рис. 12.20. Легко видеть'
что парабола для ядер с нечетными А лежит между соответствующий
ми кривыми для нечетно-нечетных и четно-четных ядер, которые
сдвинуты относительно первой параболы на ± 6А~,/2. Этот эф-
фект, разумеется, связан со спариванием нуклонов: в четно-четных
ядрах в результате спаривания достигается выигрыш в энергии
равный — в то время как в нечетно-нечетных ядрах соот-
ветствующее количество энергии теряется.
В заключение приведем численные значения параметров, вхо-
дящих в формулу (12.29). Они получены сопоставлением по методу
наименьших квадратов, вычисленных по формуле (12.29) энергий
связи с 1127 соответствующими экспериментальными данными
1243, 3281:
^0= 15,645 Мэв;
у = 19,655 Мэв;
р = 30,586 Мэв;
т) = 53,767 Мэв;
6= 10,600 Мэв;
r0 1,2025 фермы.
(12.30)
§ 12.7. ОПИСАНИЕ ЯДЕР КОНЕЧНЫХ РАЗМЕРОВ
В ТЕОРИИ ТИПА ТОМАСА — ФЕРМИ
Рассмотрим систему, состоящую из двух ядер 1SO, в качестве
примера, на котором будет разработана теория оптических потен-
циалов, описывающих взаимодействие тяжелых ионов. Обобщен116
на случай систем, состоящих из ионов других типов, может быть
сделано довольно просто.
Если два ядра 1ЯО преодолевают кулоновский барьер, то они
проникают друг в друга, в результате чего происходит бэльш
число неупругих, или необратимых, реакций, таких, как испУсК^а
ние частиц или образование составной системы 32S, в которой о
иона теряют свою индивидуальность. Поэтому необходимо Pa3\.
чать два основных процесса, которые происходят одновремен
обратимое взаимное проникновение ионов 1вО друг в друга и Р
406
пение их оболочечной структуры. Оба процесса характеризуют-
Р 'примерно одной и той же временной характеристикой т = 5 X
С” 10 22 сек’ К0Т0Рая определяет, с одной стороны, время столкно-
' 1Я а с другой—время обращения нуклона в ядре по классиче-
ской орбите. Таким образом, мы имеем здесь дело с процессом рас-
с ния, который не является ни адиабатическим, ни мгновенным,
обладает некоторыми промежуточными свойствами. В данном
алгчае «адиабатичность» означает энергетически выгодное измене-
ние ядерных орбит в каждый момент времени в течение процесса
столкновения. С другой стороны, приближение мгновенного рассея-
ния может быть применено в том случае, когда процесс проникнове-
ния ионов происходит настолько быстро, что изменение структуры
ядер 1СО слишком мало для образования составной системы 32S.
Следуя работе [318], выберем в качестве отправного пункта для
дальнейшего изложения приближение мгновенного столкновения.
Считая в первом приближении, что структура ядер 16О остается
неизменной в процессе рассеяния, вычислим действительную
часть оптического потенциала, предполагая, что плотности ядер-
ного вещества аддитивно складываются в каждый момент времени.
В феноменологической картине область перекрывания плотностей
представляет собой область, объем которой увеличивается в про-
цессе взаимодействия, что приводит к возникновению неупрутих
реакций. Соответствующие эффекты можно учесть, вводя мнимую
часть потенциала, которая описывает затухание процесса в канале
упругого рассеяния. Это затухание вызвано вытеканием ядерной
материи из областей сильного сжатия (см. рис. 12.24). Таким обра-
зом, для вычисления потенциальной энергии взаимодействия двух
ядер необходимо иметь феноменологическую теорию ядерной мате-
рии. Основная идея развиваемой здесь теории схожа с идеями теорий
конечных ядер, предложенных в последние годы Бете [40] и Брак-
нером |71]. А4ы предпочтем схематический подход, преимуществом
которого является то, что он позволяет найти плотности ядерного
вещества в отдельных ядрах посредством решения линейных диф-
ференциальных уравнений. Поэтому сначала мы должны определить
эти плотности. Для этой цели предположим, что энергия связи ядра,
состоящего из А нуклонов, следующим образом зависит от плот-
ности распределения ядерного вещества р:
Е (р) = Wo А + f (р-р0)2 (К +
2 Ро J
2
V Ц Г ( , ехр(-|г,-г,|»,) (pW_p(r,))rfl,rf,,+
i=i «л J |п -«Д
— ( — V С
2 I А ' J
Р (ri) Р (£г) _р
|Г1—г2|
(12.31)
407
Такой вид зависимости Е от р достаточно правдоподобен
зический смысл первого члена, пропорционального числу нукз
весьма очевиден; второе слагаемое описывает энергию сжатия 'и В’
следующих члена — взаимодействия Юкавы, а последние слага ^Ва
описывают энергию кулоновского взаимодействия и обычную эМые
гию симметрии, обсуждавшуюся в гл. 10 при исследовании н
ронной и протонной жидкостей*. Для упрощения модели предпг>НТ"
гается, что плотность заряда пропорциональна плотности ядещ Э"
материи. Хотя ради общности в выражение (12.31) включень: °И
взаимодействия Юкавы, в дальнейшем мы ограничимся исследи^3
нием случая, когда оба взаимодействия совпадают.
Пренебрегая кулоновской энергией и энергией симметрии
можно легко вычислить энергию связи нуклона в бесконечной ядёп-
ной материи. Поскольку в этом случае плотность ядерной материи
однородна, то
£/Л = й70 + е/2)С-^(р/р0-1)2. (12.32)
Последнее уравнение позволяет определить смысл различных пара-
метров: W70 — энергия связи нуклона в ядерной материи, находя-
щейся в состоянии равновесия. В этом случае плотность р равна
равновесному значению р0. Параметр С связан с модулем сжатия.
Согласно определению, модуль сжатия К описывает сжимаемость
ядра постоянной плотности относительно равновесного радиуса R:
К2
dR”- k А /
(12.33)
Вычисляя модуль сжатия
р0, легко находим:
для равновесного значения плотности
К = 9С.
(12.34)
Для малых плотностей р р0 энергия связи, определяемая
соотношением (12.32), неограниченно возрастает, что противоречит
физическому смыслу. Поэтому выражение (12.31) является правиль-
ным лишь для достаточно больших плотностей, скажем, рЭ’РоЗ-
Для малых плотностей это выражение должно быть модифициро-
вано. Однако этот случай здесь рассматриваться не будет.
Найдем теперь систему дифференциальных уравнений и соот-
ветствующих граничных условий, определяющих распределение
плотности в ядре конечных размеров. С этой целью вычислим ва-
риацию энергии связи в зависимости от плотности р, предположив
в качестве дополнительных условий, что ядро ограничено поверх*
* Если плотности распределения протонов и нейтронов различаются, т0
энергия симметрии в (12.31) должна быть записана в виде jyGpyXQpp Р”^
408
ю r R vi полное число частиц Л Jрс/т является постоян-
й°с Используя процедуру, описанную в § 10.3 (см. Приложение Г),
мучаем следующую систему уравнений [318, 320]:
I—+ —(24-1П р+
к Ро Ро к А ' }
+ Ф1 + 4-2 + 4 Ч’ = const’
/1
(12.35)
где
У2Фг—2Ф; = - У,Р>
(12.36)
а кулоновский потенциал ср удовлетворяет уравнению
V2 ф = —4neZp/A.
(12.37)
Соответствующее граничное условие для р на поверхности ядра
имеет вид
р (R) = пр0,
(12.38)
где
-4=1-{У1^+у2н1)-7г+(24-1У“7-- (12-39)
vJ С \ А / С
Эти уравнения должны быть дополнены, разумеется, условием
нормировки плотности. Уравнение (12.35) содержит все потенциалы
и соответствует гидродинамическому уравнению Бернулли. Как
мы увидим ниже, при выборе реалистических значений параметров
энергии на поверхности ядра плотность р (R) достаточно мала по
сравнению с р().
Полученная выше система уравнений имеет единственное реше-
ние для равновесной плотности. Легко видеть, что при отсутствии
энергии симметрии, кулоновской энергии и взаимодействия Юкавы
плотность распределения внутри ядра имеет постоянное значение
Р = р0. Силы притяжения Юкавы (Уг< 0) приводят к появлению
поверхностных эффектов; в частности, из-за этих сил происходит
уменьшение плотности в области поверхности ядра. Этот результат
следует из граничного условия (12.38). Общее решение для плот-
ности может быть записано в виде (см. Приложение Г):
з
Р= 2 «г/о(««/•)• (12.40)
1= 1
Для данного числа нуклонов радиус ядра R и другие параметры,
входящие в выражение для р, имеют фиксированные значения.
Постоянные а, представляют собой корни кубического уравнения,
Которые в общем случае — комплексные числа [318, 320].
В дальнейшем мы будем учитывать в выражении (12.31) только
одно взаимодействие Юкавы притягивающего типа. Определим те-
409
верь значения входящих в (12.31) постоянных 1Е0, С, р у
Часть из них, а именно №0, С, р() и G, приближенно извег/ И G‘
работ, посвященных изучению ядерной материи [40, 71J н ТНа Из
ных о массах ядер [328]. Постоянная G выбирается таким об'3 Аан'
чтобы воспроизвести правильное значение Z/А вдоль линии PR3°M’
бильности [320]. Для выбора 1Г0, р0 и V обычно используются^'
ные о среднеквадратичном радиусе какого-либо ядра (HanoiДЭН'
32S) и энергиях связи двух произвольных ядер (например м?’
64Сп). Таким образом, для определения рассматриваемых парам И
Рис. 12.21. Энергия
связи на нуклон для
случая бесконечной
ядерной материи, со-
держащей равное чис-
ло протонов и нейтро-
нов. Кулоновское вза-
имодействие отсутст-
вует:
/ — результаты расчеши
Бракнера; 2 и 3 — резу*.
тэты расчетов по форму-
ле (12.32) с набором па-
раметров (12.41).
ров, общих для всех ядер, необходимо использовать лишь неболь-
шое число данных о свойствах двух ядер. Два оставшихся пара-
метра, С и pi, определяются непосредственно из данных о сечении
упругого рассеяния 16О на 10О. Чтобы показать зависимость ре-
зультатов от С и pi, приведем два набора различных значений па-
раметров.
1. Если С = 100/9 Мэв, pi = 0,8 ферма, то
1Е0= — 16,0 Мэв; ро = 0,188 ферми~3; ] (1241а)
У = —469 Мэв-ферми; G = 70 Мэв. )
2. Если С = 80 9 Мэв, pi = 0,3 ферма, то
1Е0= — 15,3 Мэв; ро = 0,1767 ферма-3; ] (12 416)
V= — 13012 Мэв-ферма; G = 70 Мэв. j
Используя эти значения параметров, можно рассчитать РаЗЛ“
ные характеристики ядер. Во-первых, пользуясь соотношени
(12.32), можно построить график зависимости энергии связи ЯД Р
ной материи от плотности. Эта зависимость изображена на рис. 1 • ’
на котором для сравнения представлены также результаты расч
Бракнера [70]. Видно, что для не очень малых плотно
410
О 06 фермиг3) отклонение результатов расчетов по схемати-
(Р 'Cjf модели от результатов Бракнера составляет около 20%.
^С.5ВНзна кривых в точке р0 (сжимаемость) также различна, при-
м сжимаемость ядра в схематической модели несколько меньше.
Однако можно сказать, что выражение (12.31) достаточно хорошо
воспроизводит свойство насыщения ядерной материи.
^Для данного А можно вычислить изменение энергии связи в за-
висимости от Z. На рис. 12.22 и 12.23 изображены в виде функций
от А рассчитанные для двух на-
боров параметров (12.41) энер-
гия связи В/A и число прото-
нов Z. Хотя параметры (12.41)
выбирались таким образом,что-
бы воспроизвести значения энер-
гий связи ядер с А =•= 34 и
12 22. Зависимости энергии связи
нуклон, числа протонов Z, коэф-
фициента поверхностного натяжения
фквивалентпого радиуса Req и диф-
•1оцНОСТ1И 110веРхп<)сти t от числа нук-
делр11 Нижний рисунок — распре-
nBVvH,le пл°™ости по радиусу для
вь!п0 ЯДеР С = Ю 11 21 = 250. Расчеты
лнепы с набором параметров
(12.41а).
Рис. 12.23. То же, что па рис. 12.22,
для набора параметров (12.416).
411
A - 36, все вычисленные энергии связи, включая область
зи А = 250, отклоняются от экспериментальной кривой на Вбли~
чину порядка 4%. Различие теоретических и эксперимента
результатов становится еще меньше, если не использовать поеНЬ1Х
ложения о пропорциональности плотностей распределения^ ДП°'
тонов и нейтронов и производить оптимальное описание 4^°"
периментальных значений энергий связи выбором параметр'
1FO, р0 и V с помощью данных для ядер с сильно различающими^
А, например А = 32 и А = 250.
На рис. 12.22 и 12.23 представлены также результаты расчетов
коэффициентов поверхностного натяжения с помощью выражения
учитывающего эффекты конечной протяженности ядра:
7„=Д-2/зГВ_й70Л-±-«-(2^—1Г ГрМт-
1 Ро \ л / J
е_£\2 С Р (Г 1) Р (1-2)
А ' J |Г1—г2|
(12.42)
При выводе этой формулы мы не рассматривали поверхностные
эффекты, обусловленные энергией симметрии. Чтобы их включить,
необходимо найти энергию связи бесконечной ядерной материи при
ее насыщении, учитывая эффекты энергии симметрии. Минимизируя
обобщенное таким образом выражение (12.32), а именно
— = IFO+ — — 1Г + — G (2 — — 1 V-P- (12.43)
А ° 2 р I Ро ) 2 \ А । ро '
в зависимости от р, находим искомую величину энергии связи:
Отсюда получаем следующее выражение для коэффициента поверх-
ностного натяжения с учетом эффектов энергии симметрии:
Как видно из рис. 12.22 и 12.23, коэффициент поверхностно^
натяжения является медленно меняющейся функцией Л. Из эм
рической массовой формулы, полученной в работе [328], следу »
что у„ ж 19,6 Мэв [см. (12.30)1. Это значение находится в ХОР°^В_
согласии с предсказаниями теории. На рис. 12.22 и 12.23 пред
412
ны также плотности распределения ядерной материи, эквивалент-
•ч ]е радиусы и диффузность ядерной поверхности. Эквивалентный
Я с определяется соотношением
г; р
|Л-1 j г2рД. (12.46)
В качестве меры диффузности ядерной поверхности t обычно при-
нимается толщина слоя, на котором плотность ядерного вещества
уменьшается от 90 до 10% значения плотности в центре ядра р (0).
Как следует из полученных результатов, кулоновское взаимодей-
ствие существенно при А > 100. В результате действия кулонов-
ских сил происходит уменьшение плотности во внутренней обла-
сти ядра из-за того, что протоны выталкиваются на поверхность
ятра. Поэтому при А > 100 радиус г0 — RA- 1/3 слегка увеличи-
вается с ростом А, в то время как диффузность поверхности умень-
шается. Величина эффекта зависит от сжимаемости ядра, так как
при больших значениях С ядерное вещество становится более «же-
стким» и, следовательно, менее подверженным действию кулонов-
ских сил. Значения параметров С и ц, для которых плотность ядер-
ной материи резко уменьшается на поверхности ядра, т. е. при
v ' 1 [см. (12.38)], приводят к слишком малой величине сжимае-
мости. Поэтому кулоновские силы оказывают гораздо большее влия-
ние на диффузность поверхности и эквивалентный радиус в случае
v 1, чем при больших v. Этот результат может быть, конечно,
существенно исправлен, если в выражение (12.31) включить нелиней-
ные члены, которые обеспечивали бы правильное поведение Е (р)
при малых плотностях [320].
§ 12.8. КВАЗИМОЛЕКУЛЯРНЫЙ ЯДЕРНЫЙ
ОПТИЧЕСКИЙ ПОТЕНЦИАЛ
Выше мы представили некоторые экспериментальные данные
о рассеянии тяжелых ионов и развили теорию типа Томаса —
Ферми для ядерной материи, которую теперь мы попытаемся приме-
нить для расчета ион-ионных потенциалов. Как уже упоминалось
в начале предыдущего раздела, мы имеем дело с ситуацией, когда не
применимы ни адиабатическое приближение, ни приближение мгно-
венного столкновения. Следует ожидать, что при упругом рассея-
нии тяжелых ионов могут играть существенную роль сильные мни-
мые потенциалы. Поэтому сначала рассмотрим приближение мгно-
венного столкновения, учитывая все адиабатические процессы с по-
мощью мнимого потенциала.
В первом приближении два ядра ИО проникают друг в друга
663 образования составной системы 32S, т. е. без существенного
изменения своей структуры. Другими словами, это означает, что
пРи расчете действительной части потенциала мы можем аддитивно
вкладывать плотности обоих ядер 10О. Аддитивное сложение плот-
413
ностей ведет к образованию нестабильного состояния, которое
падается. Распад этого состояния с уходом из упругого KaJ.>ac'
описывается мнимой частью потенциала. Используем теперь вы^3
жение (12.31) для энергии системы и полученную выше плотно^'
ядерной материи в ядре 16О (12.40) для определения потенциадСТЬ
В рассматриваемом приближении плотность вещества в систе
1еО — 1СО определяется соотношением
Р — Р1во (ri) Pieo (гг)-
Н2.47)
Рис. 12.24. Схематическое изображе-
ние процесса проникновения ядер
друг в друга:
а— и и г2 — координаты, отсчитываемые,
от центров ядер; г —относительное рас-
стояние между этими центрами; б — плот-
ности ядер 1 и 2 перекрываются в заштри-
хованной области 3, в которой вещество
находится в сжатом состоянии; в — распре-
деление плотности в плоскости, проходя-
щей через центры обоих ядер ,6О.
Рис. 12.25. Энергии связи ядра 32S,
системы ,еО + 1СО и действительная
часть потенциала. Вдоль оси абсцисс
откладывается относительное расстоя-
ние между двумя ядрами |6О.
Плотности вещества в отдельных ядрах являются функциями
расстояний г, и г2, отмеряемых соответственно от центров масс
каждого из ядер. Расстояние между центрами масс обозначим
г (рис. 12.24). Действительная часть потенциала может быть запи-
сана в виде разности полной энергии связи системы 1GO + 16О>
плотность вещества в которой определяется выражением (12.47),
и энергий связи 5.«о ядер 16О:
V(r) = £ (р16о (г1) + р16о(г2))-2В16о, (12.48)
(12.49)
где
Bi6O---£,|Pi6o)-
414
Таким образом, потенциал взаимодействия ионов зависит толь-
оТ относительного расстояния между центрами масс ионов.
о°том случае, когда плотность распределения вещества определяется
° пажением (12.40), все интегралы, входящие в соотношение (12.48),
в рут быть найдены в аналитическом виде, причем все они выра-
жаются через один основной интеграл
I (г, а, р, ц) =
R
= J_ C j0 {аГ1) ехР (-1 П-Ч-Н/Н) jo (k2) dTi (12.50)
4л J In— r2— г |
вЫЧисленный в работе [320]. Используя (12.40), (12.47) и (12.50),
получаем следующее выражение для потенциала V (г):
3 I с г 1 3
V(г) —J — I ah р) 4-
.^. 1РоГ21Р JB “0
4/ — 1
2 е2 2 }
+ i VftZ(r, “i. ai. 1Ч,)~1-4л ) /(r, ait ajt ц -> оо) -
k=i \ А I
+ (12.51)
где
1 для х>0;
0 для х < 0.
Если ядра не перекрываются, то их взаимодействие определяется
только кулоновскими силами. Учет притягивающих сил Юкавы
приводит к понижению кулоновского барьера. При возрастании
степени перекрытия отталкивающие силы, а следовательно, и по-
тенциал взаимодействия быстро увеличиваются.
Значение потенциала в точке полного перекрытия, т. е. при
г — 0, является мерой сжимаемости составной системы 32S. Энер-
гия, необходимая для сжатия ядра 32S до размеров ядра 1СО, опре-
деляется соотношением
= V (г = 0)-(S32s-2Bi6O). (12.52)
Разность энергий связи равна —16,6 Мэв.
На рис. 12.25 изображен вид действительной части потенциала и
энергии связи. Определим эффективный модуль сжатия составной
системы 32S, предположив, что зависимость объемной энергии от
Радиуса — квадратичная. Для R — й?1.о разность энергий равна
Используя (12.33), находим:
(12.53)
гДе /?32S и £)]в0 — радиусы ядер 32S и 16О соответственно. Вы-
численный по формуле (12.53) эффективный модуль сжатия при-
415
мерно в два раза превышает значение К = 9 С. Д.)ф зависит
пределения ядерной материи, кулоновского взаимодействия °Т ^ас'
же от радиуса действия сил Юкавы. ’ а Так-
Важным свойством потенциала, изображенного на рис 19 о
является наличие минимума глубиной около 5 Мэв. физи “
это связано с притягивающими ядерными силами, которые начни0*'1
сказываться в момент соприкосновения ионов. Однако дово1а1°Т
быстро их действие подавляется сильной несжимаемостью ядепЬН°
материи, проявляющейся в момент, когда область перекрывай01'
ионов становится достаточно большой.Таким образом, изображенн'1”
на рис. 12.25 потенциал имеет типичную форму известных в молеку"
лярной физике потенциалов, описывающих взаимодействие моле-
Рис. 12.26. Модель для вы-
числения мнимой части по-
тенциала, описывающего
взаимодействие тяжелых
ионов.
Сжатое вещество вытекает из
области повышенного давления,
заштрихованной на рисунке
Стрелки указывают направление
потока. С правой стороны ри-
сунка изображен цилиндр посто-
янной высоты h и радиуса S,
расширяющийся в радиальном
направлении до размеров, ука-
занных пунктиром.
кул. Это дает нам основание говорить о ядерных молекулах-, напри-
мер, в рассматриваемом специальном случае мы имеем дело с моле-
кулой 16О — 1СО.
До сих пор мы рассматривали приближение мгновенного слия-
ния и предполагали, что основная структура отдельных ядер остает-
ся неизменной в течение процесса рассеяния. В действительности,
эта структура начинает разрушаться в области перекрывания, в ко-
торой ядерная материя сильно сжата и поэтому находится в не-
стабильном состоянии, стремясь выйти из этой области в область
меньшего сжатия. В микроскопической картине этот процесс может
быть интерпретирован как разрушение оболочек ядер 1ВО и обра-
зование составной системы 32S*.
Очень маловероятно, что после образования большой области
перекрывания плотностей, т. е. после образования составной систе-
мы 32S, произойдет восстановление оболочек и ядер 10О. Поэтому
в данном случае мы можем использовать приближение абсолютно
неупругого рассеяния, которое означает, что проникновение ядер ДРУГ
в друга (рис. 12.26) вызывает неупругие процессы, сильно подав-
* Оболочечная структура ядер 16О остается неизменной до тех пор, п<)^
эти ядра могут рассматриваться как раздельные кластеры. В этом случае
имеем дело не с составным ядром, а с системой типа молекулы. Составная
стема 32S представляет собой сложное оболочечное состояние ядра ^’Впя.
тором оба иона 16О более или менее сильно слились друг с другом и потер
ли свою первоначальную индивидуальность.
416
ющие процесс восстановления оболочек 16О*. Перемещение
г щества из области сильного сжатия можно рассматривать как
В чальную стадию всех неупругих процессов.
В Влияние этих процессов на упругое рассеяние можно описать
помощью мнимой части потенциала. Для ее определения вычис-
, сначала характеристическое время затухания процесса в упру-
гом канале, в качестве которого будем рассматривать время выте-
кания ядерной материи из области сжатия.
Связь между временем затухания и мнимой частью потенциала
можно определить следующим образом. Если зависящая от времени
волновая функция убывает экспоненциально с постоянной вре-
мени Т
фф* « ехр (—t/T), (12.54)
то, используя уравнение Шредингера, легко найти следующее со-
отношение для неопределенности энергии:
1Г(г)= — Щ2Т(г). (12.55)
Этот же результат может быть также получен с помощью соот-
ношения неопределенностей Гейзенберга, согласно которому время
Т и неопределенность энергии W связаны условием
|№Т1>£/2. (12.56)
Так как время вытекания зависит от степени сжатия, а следова-
тельно, и от степени проникновения ядер друг в друга, мнимый
потенциал W является функцией расстояния между центрами ядер
16О (см. рис. 12.24 и 12.26). Для определения времени вытекания
сделаем ряд упрощающих предположений, которые позволили
бы решить аналитически соответствующую гидродинамическую
задачу. Предположим, во-первых, что ядерная материя вытекает
из области увеличенной плотности в направлении, перпендику-
лярном к направлению относительного движения ядер. Действи-
тельно, в этом случае поток ядерного вещества встречает наимень-
шее сопротивление. Во-вторых, область перекрывания, ограничен-
ную двумя сферическими поверхностями, мы заменим на цилиндр,
как показано на рис. 12.26. Поскольку предполагается, что выте-
кание вещества происходит в радиальном направлении, то во вре-
мя рассматриваемого процесса высота цилиндра остается постоян-
ной, а радиус увеличивается.
Высота цилиндра h определяется из условия равенства его объ-
ма объему области перекрывания до начала вытекания ядерного
* Выполненные в работе [322] исследования тонкой структуры в сечениях
Рассеяния тяжелых ионов указывают, что это предположение, по-видимому,
Не является достаточно справедливым. Как следует из систематического ана-
лиза различных данных [291, 371], в рассматриваемых реакциях имеет место
ильное поверхностное поглощение, что может быть связано с реакциями пере-
носа. См. также работу [ЮЗ].
417"
вещества. Величина этого объема зависит от относительного
стояния между двумя ядрами следующим образом:
Рас-
— л/?3| 1 —
3 к
(12.57)
Если мы возьмем в качестве начального момента
чай, изображенный на рис. 12.26, то
расширения слу
(12.58)
Можно получить довольно реалистическое описание распределе-
ния вещества внутри рассматриваемой цилиндрической области
вводя простую функцию распределения, зависящую только от ра1
диальной координаты г' и нормированную на число нуклонов в об-
ласти перекрывания:
р(''>=-гйИ1-4ГСО5(т’'т)’ <12-59>
где
N = \ р dx.
Область
перекрывания
Как показано в работе [320], окончательные результаты в дей-
ствительности слабо зависят от вида плотности распределения. Ядер-
ная материя, находящаяся в выделенном объеме, совершает ком-
прессионные колебания с частотой со относительно положения рав-
новесия, которое определяется минимумом потенциальной энергии
в зависимости от S.
Рассматриваемая модель не позволяет описать вытекание ве-
щества из области сильного сжатия как апериодический процесс.
Поэтому согласно используемому нами приближению будем счи-
тать, что время вытекания, т. е. время затухания процесса в упругом
канале, равно половине периода колебаний с частотой со:
Т — л/со. (12.60)
Упростим вычисления со, предположив, что можно пренебречь
вкладом короткодействующих сил Юкавы и кулоновского взаимо-
действия в потенциальную энергию колебаний. В этом случае
£рр« = 4" ~ f (Р —Ро)2^- (12.61)
‘ Ро J
Подставляя (12.59) в (12.61), получаем:
EpOt (S) =
1 с [ W
2 ( 32/iS2 рй
— 2N+nhS2p0
(12.62)
418
Равновесное распределение плотности соответствует минимуму по-
теНЦиальной энергии, который находится в точке S = Хо, причем
N 1 / 1 1 4-2/л
йро 4 у 2 1—2/л
(12.63)
Таким образом, рассматриваемый цилиндрический объем по-
стоянной высоты h должен совершать колебания относительно по-
ложения равновесия So. Для малых амплитуд колебаний, т. е.
в приближении гармонического осциллятора, потенциальную энер-
гию можно записать в следующем виде, разложив ее в ряд относи-
тельно положения равновесия и сохранив лишь члены второго по-
рядка малости:
Epot = const + 2Ср0 hn (S—So)2. (12.64)
Распределение скоростей можно найти, используя уравнение
непрерывности. Полагая
v=-^S, (12.65)
получаем следующее выражение для кинетической энергии колеба-
ний:
Т = — М f po2dx= — NM 1 6(2/ft)2+6(Wl s2. (12.66)
2 J 2 1 —2/л
Используя (12.64) и (12.66), легко вычислить искомую частоту
колебаний плотности:
(Асо)2 = Л2___4л<1-.2/я)----- =
1 — 6 (2/л)2 4-6 (2/л)3 МИ
16л / 1 г \ . 1 г
---(1 —2/л) 1 — ----— !+— —
_ 3 \ 2 \4 R> х
1-6 (2/л)2 4-6 (2/л)3 1 Д(1/2)(г/7?)
x ffp0 Cfe2c2 (12.67)
NMc*
где NM — масса нуклонов, находящихся в области перекрыва-
ния ядер; г — расстояние между центрами сталкивающихся ионов
и 7? — радиус отдельного иона.
Вблизи точки соприкосновения вещество в области перекрыва-
ния оказывается несжатым. Так как в этом случае вытекание ядер-
ной материи отсутствует, то в рассматриваемой области мнимая часть
потенциала равна нулю. Однако если область перекрывания в на-
чальном состоянии имеет меньший объем, чем в точке равновесия
$о, т. е. если ядерное вещество в этой области оказывается сжатым,
41»
Рис. 12.27. Действительная и мнимая
части потенциала, описывающего уп-
ругое рассеяние ядер 16О друг на
друге.
При г=0 действительный потенциал равен
115 Мэв. Для иллюстрации высоты центро-
бежного барьера и положения квазисвязан-
ных молекулярных состояний пунктирными
линиями изображен потенциал с учетом
центробежной потенциальной энергии для
угловых моментов Z=8; 12; 16.
то мнимая часть потенциала с
лична от нуля. В сжатом состоя'
нни рассматриваемый цитцнчп
имеет форму, изображенную и
рис. 12.26. Поэтому согласно ис-
пользуемой модели, ядерное ве
щество может вытекать из об'
ласти перекрывания только в
том случае, если выполняется
следующее неравенство:
R2-~r<Sl (12.68)
В начальный момент сопри-
косновения распределение ядер-
ной материи находится в состоя-
нии равновесия. По мере уве-
личения степени проникновения
ядер друг в друга увеличивается
масса вытекающего вещества,
что, по-видимому, приводит к
возрастанию времени вытека-
ния. Поэтому, согласно выра-
жению (12.55), при все более
тесном сближении ионов мнимая
часть потенциала уменьшается.
Это качественное поведение W (г)
легко проследить на рис. 12.27.
§ 12.9. СЕЧЕНИЕ УПРУГОГО РАССЕЯНИЯ 16О НА 16О
Ядра 1GO подчиняются статистике Бозе, и поэтому система
16О ф 1СО должна описываться симметричной волновой функцией.
Поскольку в рассматриваемом случае нельзя отличить рассеиваемую
частицу от рассеивающей, сечение рассеяния является симметрич-
ной функцией относительно угла 90° в системе центра масс. Чтобы
вычислить это сечение, необходимо определить амплитуду рассеяния.
Амплитуда кулоновского рассеяния имеет вид
fc(O) = — exp (— i т] In (sin2 (6/2) )ф i л-[-2 i o0). (12.69)
a (.i — приведенная масса. Обозначая фазы кулоновского и ядер-
ного рассеяния через о( и 6( соответственно, можно записать пол-
ную амплитуду рассеяния следующим образом [315]:
f(0)-fc(6) + fc(n-e)+
ф — Z (2/ф 1)ехр (i (2o^6z))sin6zPz(cos0). (12-70)
2k 1= о, четные
Д20
vaK следует из этого выражения, амплитуда рассеяния зависит
TOibKO от четных значений углового момента. Фазы рассеяния ё,,
явчяющиеся из-за наличия мнимой части потенциала комплексны-
ми' числами, должны быть определены численно.
Следует заметить, что для определения мнимой части потенциала
не требуется новых параметров. Таким образом, единственными па-
раметрами, необходимыми для расчета потенциалов, являются па-
раметры, входящие в выражение (12.31). Так как ядра 10О и 32S
содержат равное число протонов и нейтронов, параметр энергии
симметрии G не входит в рассматриваемую задачу. Если ограни-
читься случаем лишь одного взаимодействия Юкавы, то для вы-
числения потенциалов нужно определить пять параметров 1Е0, р0,
С, р и V. Хотя ранее уже был найден набор параметров (12.41),
который описывал целый ряд свойств большого числа элементов,
более удобно использовать параметры, позволяющие точно воспро-
изводить энергии связи ядер 10О и 32S и их эквивалентные радиу-
сы. Поскольку мы изучаем сечение рассеяния 1еО на 1СО в зави-
симости от радиуса действия р и сжимаемости С, только три вели-
чины из указанных выше экспериментальных данных могут быть
использованы для определения р0, V и IFO. Если мы выберем, на-
пример, С = 100/9 Мэв и р = 0,3 ферма, то используя =
=—127,6 Мэв, В™,=—271,8 Мэв и Req (32S) = 4,10 ферма, по-
лучим:
1Е0 = — 14,6 Мэв-, р0 = 0,14 фермат3',
V = —13616 Мэв-ферма.
(12.71)
При этом
Req (1ВО) = 3,33 ферма
(экспериментальное значение — 3,42 ферма), а диффузности поверх-
ности равны
/)6о= 1,99 ферма, /32s = 2,20 ферма
(экспериментальные значения—1,8 и 2,6 ферма соответственно).
Вычисленные для этого набора параметров действительный и мни-
мый потенциалы изображены на рис. 12.27.
Положение основных максимумов функции возбуждения
определяется главным образом действительной частью потенциала
(рис. 12.28). Действительный потенциал является также причиной
появления виртуальных состояний. С классической точки зрения
стационарные орбиты возникают в том случае, когда угловой момент
В и радиус орбиты b удовлетворяют следующему условию:
— [V(r) + —
dr \
(12.72)
I =0.
\г=Ь
В квантовой механике такие стационарные орбиты соответст-
вуют квазисвязанным состояниям. В рассматриваемом случае бла-
Л21
годаря условиям симметрии угловые моменты этих состояние! м
принимать только четные значения. Число состояний ограничено
за того, что наибольшее значение углового момента удовлетвовИ3
соотношению L2 — pfe3 (dV/db) и, следовательно, определяется м еТ
симальной величиной положительного наклона V (г).
На рис. 12.27 приведен ряд эффективных потенциалов V
= V (г) + L2/2 рг2 для различных значений углового момента
Видно, что в области энергий до 28 Мэв могут появляться квазисвя
20 25 30 35
Энергия в С.Ц.М., Мэв
Рис. 12.28. Сечение упругого рассеяния 16О на 1ВО на
угол 90°.
Точками изображены экспериментальные данные, полученные
Йельской группой [337]. Сплошная кривая в верхней части ри-
сунка — результаты расчета без учета мнимой части потенциала;
нижняя кривая — расчет с мнимым потенциалом. Расчеты выпол-
нены с набором параметров (12.71).
занные состояния, максимальное значение углового момента которых
равно примерно 18. Эти виртуальные состояния частично ответст-
венны за общее поведение структуры сечений рассеяния в обзасти
энергий выше кулоновского барьера. В равной степени резонансы
в сечениях могут быть приписаны эффектам интерференции волн,
отраженных от остова ядра и барьера, связанного с кулоновским
потенциалом.
При изменении радиуса действия ядерных сил р высота куло-
новского барьера также изменяется: при увеличении р высота ку-
лоновского барьера понижается, и наоборот. Высота этого барьера
определяет значение энергии, при котором форма сечения рассея-
ния начинает отклоняться от формы сечення чисто кулоновского
рассеяния. Поэтому можно выбрать р,исходя из поведения сечения
при малых энергиях (< 17 Мэв). В то же время величины различ-
ных максимумов в сечении при более высоких энергиях могут быть
объяснены выбором соответствующего значения С, определяющего
422
веЛичину мнимой части потенциала и, следовательно, степень
поглощения ионов. Именно таким способом из данных об упругом
рассеянии 16О на 16О было определено значение С, равное 100/9 Мэв.
Для данного С эффективная сжимаемость А.,ф (12.53) составной
системы :12S равна 201 Мэв. Таким образом, из данных о рас-
сеянии тяжелых ионов можно не только получить сведения о ква-
зимолекулярной структуре, но и определить сжимаемость ядра.
Как видно из рис. 12.28, теория не объясняет тонкую струк-
туру сечения упругого рассеяния 1GO на 1еО, имеющую ширину
около 0,5 Мэв. Эта структура, по-видимому, связана со структурой
самих ядер 16О*. К такому выводу можно прийти, сравнивая рас-
сматриваемые сечения с сечением упругого рассеяния 12С на 12С
(см. рис. 12.18). Так как 12С не является дважды магическим ядром,
то вероятность прямых неупругих реакции в этом случае значитель-
но больше, чем в случае ядер 16О. Поэтому сечение рассеяния ядер
12С имеет более богатую структуру. Однако недавно Йельской груп-
пой в сечении этой реакции при больших энергиях была обнаружена
регулярная резонансная структура, подобная структуре в сече-
нии 16О — 16О-рассеяния. По-видимому, такое регулярное пове-
дение сечений является следствием когерентного коллективного
рассеяния, связанного с образованием квазимолекулярных состоя-
ний, играющих роль входных состояний. Эти входные состояния
могут содержать примесь внутренних возбуждений отдельных ядер,
что приводит к появлению такой структуры в сечениях.
Микроскопической теории рассеяния тяжелых ионов пока еще
не существует. Весьма вероятно, что создание такой теории следует
начать с изучения «-кластерных свойств легких ядер. Так, напри-
мер, поведение сечения упругого рассеяния 12С на 16О на большие
углы, по-видимому, полностью определяется передачей «-частицы
[571.
В § 12.5 мы видели, что резонансы в сечении рассеяния 12С на
12С появляются до того, как ядра начинают проникать сквозь куло-
новский барьер [18]. Этот эффект мог бы появиться вследствие гомо-
полярной связи двух ядер i2C, обусловленной двумя валентными
а-частицами. В этом случае между ядрами 12С могли бы возник-
нуть силы притяжения большего радиуса действия, в результате
чего потенциал взаимодействия ионов имел бы небольшой минимум
в области непосредственно перед кулоновским барьером [320].
Аналогичный потенциал был также предложен Алмквистом и
Др. [18].
Следует отметить, что рассеяние тяжелых ионов очень тесно свя-
зано с обратным процессом, а именно с делением ядер. Эти два
* Недавно Шайд и др. [S22] предположили, что благодаря неупругим ка-
налам типа (16О—16*О) квазисвязанные молекулярные состояния, появляю-
Н1иеся в потенциалах, изображенных на рис. 12.27, могут привести к возник-
новению тонкой структуры резонансов. Этот эффект подобен механизму, пред-
ложенному Иманиши [2011 для объяснения молекулярных состояний в систе-
ме 12С— i2C при энергиях ниже кулоновского барьера.
423
процесса развиваются во времени совершенно по-разному: в то
мя как процесс рассеяния происходит более или менее мгновец^"
деление является адиабатическим процессом. Однако потенция0’
описывающий взаимодействие ионов, по-видимому, совпадает с п
тенциалом, описывающим процесс деления, в той области, г е °
мнимая часть равна нулю. Так, для тяжелых ядер минимум ион°
ионного потенциала сил притяжения находится на расстоянии'
приблизительно равном сумме радиусов двух фрагментов*.
Таким образом, мы видим, что физика тяжелых ионов охваты
вает чрезвычайно широкую область явлений. Одним из ее наиболее
интересных будущих аспектов явится, по-видимому, возможность
образования довольно стабильных сверхтяжелых элементов при
столкновении очень тяжелых ионов. Этот вопрос будет подробно
рассмотрен в третьем томе настоящей серии.
* * *
Различным аспектам физики тяжелых ионов посвящен ряд об-
зорных статей [54, 126, 150, 170, 358, 396]. Состояние исследований
в данной области наиболее полно освещается в трудах конференций
по этой тематике, в частности конференций в -Брукхейвене в 1965 г.
[192] и Гейдельберге в 1966 и 1969 гг. [184, 58].
* Этот результат можно было бы рассматривать как альтернативное и
более удовлетворительное объяснение природы так называемого второго ми-
нимума кривой потенциальной энергии, предсказанного Струтинским [352J-
Этот минимум барьера деления подобен второму минимуму, изображенному
на рис. 4.5. В этом случае недавно обнаруженная в сечении деления ярко вы-
раженная промежуточная структура может рассматриваться как следствие об-
разования в процессе деления долгоживущих промежуточных квазимолеку-
лярных состояний.
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ Д
Классическая энергия поверхностных колебаний ядра
в гидродинамическом приближении
В этом разделе мы дадим пример вычисления на основе классической мо-
дели ядра массовых параметров и коэффициентов жесткости, входящих в вы-
ражение для коллективного гамильтониана поверхностных колебаний. В ка-
честве такой модели выберем модель безвихревого движения ядерного вещест-
ва, которая явилась исторически первым подходом к решению рассматривае-
мой проблемы [142, 146J. Предположим, следуя этой модели, что коллективное
движение нуклонов в ядре может быть описано как безвихревое движение
жидкости постоянной плотности р. Так как поверхность ядра описывается
выражением (2.1), то отклонение формы ядра от сферической может быть за-
писано в виде
Д/? = /?(6, <Р)~Ro-RoZaXn Чц(в’ ?) (А.1)
Предположим далее, что изменение формы ядра связано с рассматривае-
мым безвихревым движением ядерной материи. В этом случае скорость эле-
мента объема ядра может быть выражена через потенциал скоростей Ф с по-
мощью соотношения
v=V®. (А. 2)
Для случая постоянной плотности получаем уравнение
V • v = V2® -О, (А.З)
общее решение которого, конечное при г = 0, имеет вид
(А.4)
Здесь г, 0, <р — полярные координаты произвольного элемента объема внутри
ядра.
На поверхности сферы должно выполняться условие:
(0, <р)
Отсюда, используя (А.1) и (А.4), получаем:
(А-6)
। Кинетическая энергия поверхностных колебаний определяется выраже-
Т =—— р [| ¥Ф|Мт. (А.7)
2 J объем ядра
14 Зак. 1218
42S
Интегрируя по объему ядра и учитывая формулу [306]
I/ Z-|-l / du и \
21 + 1 \~d7~1 Т'- +
1/ I I du . . . и \
2i + l ( dr +U 1 ~ ) Т/- т>
(А. 8)
(А.9)
где
Tj. L-, м = S I М-ттМ) YLM_m (0, ф)
т
есть векторные сферические функции, легко находим:
7’ = 'У/?ор2^|ЛХц|2. (А. 10)
Используя (А.6), получаем
Г=У 2 fizl“Zul2, (А. 11)
где массовые параметры определяются следующим образом:
вх=Р^о/Х- (А. 12)
Рассмотрим теперь потенциальную энергию, связанную с изменением
формы ядра. Эта энергия состоит из двух членов:
V' = VS+VC. (А. 13)
В этом выражении — изменение энергии, связанное с изменением поверх-
ности ядра AS при его деформации:
Vs = oAS, (А. 14)
где о — коэффициент поверхности натяжения; Vc — изменение кулонов-
ской энергии протонов ядра.
При деформации ядра (Ro —> Ro AR) его поверхность изменяется на
величину
AS=-7-R«2(X-1)^ + 2)l“^|2- <А 15)
Z Хр.
Поэтому
2)|аХмр. (А. 16)
2 ?.ц
Изменение кулоновской энергии, обусловленное деформацией ядра, мо-
жет быть записано в виде
где Ф — кулоновский потенциал, а Рр — плотность заряда.
Для случая ядра сферической формы плотность заряда внутри ядра Да'
ется выражением
Ze
рр(0) =-----------.
₽ (4/3) nRs
(А. 18)
426
Вне ядра плотность заряда, разумеется, равна нулю. Следовательно, изме-
нение плотности заряда, вызванное изменением формы ядра, равно
А/?
«Рр = Рр (0) Ro 6 (г- Ro) ~ - (А. 19)
АО
Легко проверить, что
[ брр di = 0,
объем ядра
как и следовало ожидать.
Чтобы вычислить изменение потенциала 6<р, разложим его в ряд по сфе-
рическим функциям:
г ^0’
лц 'о
г»?-
r>Ro-
Хр г 1
(А. 20)
Коэффициенты разложения определим из
условия [см. (А.19)]:
^Ll - 1 _4„рР<0)Л₽.
dr о or |r=/?0+ о
Используя (A.l) и (A.20), легко находим:
4лрр (0) Rj t
vxu 2X+ j “Хц.
Отсюда следует:
1 С
~ 6<p6ppdT =
9Z2e2 уз|аХц I2
8л7?0 2Z. | 1
(А. 21)
(А. 22)
(А. 23)
Чтобы вычислить второй интеграл в выражении (А. 17), запишем потен-
циал в тонком поверхностном слое в виде
Отсюда eZ ~ eZ (' АТ? \ Ф“ Z?0(H-AZ?/Z?0) ~ Ro V Ro J' 2J.p6ppdT- 2l“Xul2- (А'24>
Используя (А. 17), (А.23) и (А.24), получаем следующее выражение для пол-
ного изменения кулоновской энергии:
6Vr=—-3e2-2 V-—- 1 а 12 (А.25) с 4п/?„ -W2X+1 1 V
Таким образом, потенциальная энергия поверхностных колебаний может
быть записана в виде
V- 2 22Сх1 “хр|2, (А-26) Хц
pp fitpdx —0,
14*
427
где коэффициент жесткости Су определяется выражением
Сх= (Х-1) (Н-2) RI о
3e2Z2
2л(2Х+1)7?о
(А. 27)
Аналогично могут быть вычислены члены более высокого порядка
а?(1, которые весьма существенны при определении кулоновской энергии
в тяжелых и сверхтяжелых ядрах. Однако в этом случае необходимо исполь
зовать более точный метод расчета [269—271].
ПРИЛОЖЕНИЕ Б
Матрицы конечных вращений
В гл. 5 мы видели, что матрицы вращений играют очень важную роль
в теории углового момента. Желательно поэтому дать точный вывод выраже-
ния (5.146), что может быть сделано несколькими способами. Мы будем следо-
вать здесь удобному методу, который состоит из двух этапов. Сначала пока-
жем, что существует соответствие между унитарными двухмерными матрица-
ми и трехмерными вращениями, а затем получим (2/ + 1)-мерное представле-
ние унитарной группы, которое может быть отождествлено с (2/ + 1)-мерным
представлением группы вращений.
Б.1. Рассмотрим унитарные преобразования двух переменных Zx и Z2:
Zi — йц Zj + flj2 Zg!
(Б.1)
Z2 — й21 Zi -J- o22 Z2,
где aij — комплексные числа, удовлетворяющие условиям отонормирован-
ности = &ij и Преобразования (Б.1) можно запи-
си о
сать в матричной форме
где унитарная матрица
Числа а и b могут быть
Z' = WZ,
W должна иметь следующий вид:
/ а
W =
I ~Ь*
также записаны в виде
а = exp (i £) cos to, Z> = exp (i т]) sin co,
(Б.2)
(Б.З)
(Б.4)
b
а
из которого непосредственно следует условие нормировки | а |2 + | b |2 = 1-
Таким образом, любое унитарное унимодулярное преобразование зависит
от трех параметров £, г] и со.
Рассмотрим теперь действие унитарного преобразования, определяемого
матрицей W, на произвольную двухмерную матрицу. Такая матрица может
быть представлена в виде линейной комбинации единичной матрицы и трех
матриц Паули {ох, оу, ог} = о. Имеем:
- 1«п “12 \ у . ~ , - I т + z х— if/\ <Б5)
а- = у/Ч-хОс + f/ay+zoz = •
\.сс21 at2J \x + ij/ у—г )
428
Отсюда следует:
у = 2 (ки+а2а);
1
х= —(а21 + «22);
Г/= — — («21-«1г);
г = —(йц—а22).
(Б.6)
Преобразованная матрица а' имеет вид
a’=Wa,W~1 = у' I + х'ох | -у’ ъу + г'сг. (Б.7)
Ясно, что у' = у. Этот результат — следствие инвариантности шпура матри-
цы относительно унитарных преобразований. Величины х', у', г' зависят от
х, у, г согласно соотношению
х'=Мх, (Б. 8)
где х — вектор с компонентами х, у, г, а х'— вектор с компонентами х', у', г'.
Используя соотношение
Z4 ~ (О* -Ь\
Г-1 = Г+= ( , (Б.9)
^6* а)
легко найти элементы матрицы УЙ:
Л1ЖЖ= ~~~ (а2—b2-f-a*2— 6*2) = cos2 со cos 2g—sin2co cos 2tj;
Myy = (a2|-fc2a*2-|6*2) —cos2 co cos 2g + sin2 CO cos 2tj;
Alzz = | a |2— I b |2 = cos2 co—sin2co = cos 2co;
7Hxy =(a*2—a2-j-b*2—fe2) = cos2co sin 2g-|-sin2co sin 2tj;
Л1уж = — (a2—a*2-f-b*2—fe2) = —cos2 co sin 2g-|-sin2co sin 2tj;
Alyz = i (a* b*—ab) = sin 2co sin (g-J-"»]);
Alzy = i (a* b—afe*) = sin 2cosin (g—t]);
Mzx=a6*+ta*=sin 2(0 cos (g—i]);
Atxz = — (a* b* l-ab) = — sin 2cocos(g-|-T)). )
Определитель матрицы не изменяется при унитарных преобразованиях.
Поэтому из условия
det (а') = det (а) (Б. 11)
следует
x2 + t/2 + z2 = x'2+f/'2+z/2.
(Б. 12)
Согласно соотношению (Б. 12), матрица М соответствует операции вра-
щения. Мы можем исключить из рассмотрения операции отражения, также
Удовлетворяющие условию (Б.12), поскольку при а2 = 1 и Ь == 0 det (/И) = I,
429
что соответствует преобразованиям вращения. Легко найти связь используе
мых параметров с углами Эйлера бу. Полагая со О (Ь 0), получаем- '
cos 2g
sin 2g
0
M =
м =
— sin 2g cos 2g 0 1, 0 0 1/ (Б.13)
ta угол 2g относительно оси г. При g = г) = о
/cos 2(0 0 —sin2(o\ I ° 1 0 ] \sin 2® 0 cos 2(0 / (Б. 14)
что соответствует повороту
матрица
совпадает с матрицей поворота на угол 2со вокруг оси у.
В общем случае элементы матрицы М могут быть представлены в виде
Mih = -^-Sp(Oi W oh Г-»), (Б. 15)
где i, k = 1, 2, 3 обозначают соответственно х, у, г. Так как М является дей-
ствительной ортогональной матрицей, то матрица Л1-1 получается транспо-
нированием матрицы М: М~г= М. Из (Б.3) и (Б.9) следует, что это эквива-
лентно замене а —» а* и Ь —» —b или g —» —g и т) —> —т). Этот результат
можно проверить с помощью выражений (Б. 10), (Б. 13) и (Б. 14).
Очевидно, что для каждой матрицы W может быть найдена матрица М.
Единичная матрица U” = / соответствует единичной трехмерной матрице
М = 7.
Докажем теперь следующее утверждение: если Mj соответствует U"i,
а М2 —то соответствует IV/21V’1. Термин «соответствует» означает,
что преобразование
с?= №'1а№1“1=т/ + х' • о, (Б. 16)
где
?7 + х б, (Б. 17)
определяет матрицу М, такую, что
х' =Мх. (Б. 18)
Применяя последовательно два рассматриваемых преобразования, полу-
чаем:
a'' = fi/2a'W'^,=W'2W'1 а 1 1 =№2 Fi а(Г2 (Б.19)
Кроме того,
а' =у7-|-х' • с == -у/-|-Л4j х о;
(Б. 20)
а" = б = у/+М2 х' - 5=у7-|-Л42 Л1, х-в,
откуда следует, что МгЛД соответствует W2W±.
Полученный результат означает, что двухмерные матрицы IV' и трехмер-
ные матрицы М являются представлениями одной и той же группы, а именно
группы вращения.
430
Это соответствие не является взаимно однозначным, что легко увидеть из
(Б-10). Действительно, при одновременном изменении знаков а и Ь матрица М
остается неизменной. Таким образом, W и —W определяют одну и ту же ма-
трицу М, т. е. одно и то же вращение. Рассмотрим, например, случай М = /.
Тогда, согласно (Б. 10), со и | кратны л, аг] — произвольное. Используя (Б.З)
и (Б.4), получаем W = ±1. Отсюда следует, что каждому элементу группы
вращений соответствует два элемента рассматриваемой унитарной группы.
Этот результат можно также получить с помощью выражений (Б. 13) и
(Б. 14), которые показывают, что значения углов Эйлера вдвое превышают зна-
чения углов, определяющих элементы матриц W [см. (Б.З) и (Б.4)]. Следова-
тельно, изменение этих последних углов на л приводит к изменению углов Эй-
лера на 2л, что соответствует тому же самому вращению.
Б.2. Построим теперь совокупность (2/ + 1)-мерных матриц А1, кото-
рые образуют представление рассматриваемой унитарной группы, т. е. сово-
купность матриц A' (j = 0, 1/2, 1, 3/2, ...), обладающих теми же самыми груп-
повыми свойствами, что и №. В случае j = 1/2 можно положить А1^2 “ №.
Еще более просто найти А1 для j = 0: 'А0 = /. Основная проблема состоит
в определении (2/ + 1)-функций от Zj и Z2, которые подвергаются унитарным
преобразованиям, если Zi и Z2 преобразуются согласно (Б.1). Очевидно, что
при преобразованиях (Б.1) (2/ + 1)-одночленов
z/+mz/-m m<j (Б 21}
линейно преобразуются друг через друга.
Введем величины
Fjm = NjmZ{+m Zi2-m (Б. 22)
и определим коэффициенты Njm таким образом, чтобы линейные преобразова-
ния величин Fjm являлись унитарными. Для этого построим одночлены
Fjm - NjmZt,+mZii-m, (Б. 23)
где Z{ и Z2 определены согласно (Б.1)—(Б.З). Если преобразование величин
Fjm является унитарным, то выполняется условие
У, Fjm Fjm = У I Fjm Fjm- (Б. 24)
m = — j m = — j
Согласно (Б.23),
Z I Fim |2 = Z I I2 (Л zf )' + m (Z; Zf (Б. 25)
m m
Заметим, что единственным инвариантом преобразования (Б.1) является
величина
|21P + |Z2|2=|Z;|2+|Z^|2. (Б.26)
Таким образом, для выполнения условия (Б.24) необходимо выбрать | Njm |2
так, чтобы выражение (Б.25) являлось функцией | Z[ |2 + | Z2 |2. Это, очевид-
но, можно сделать только в том случае, если (Б.25) является полиномом от
| Z{ |2 -ф | Z2 |2. Поэтому необходимо положить
|/V;m |2~ [(/+«)! (j-m)!]-1- (Б. 27)
Используя формулу биномиального разложения, имеем:
2 I F<™ I2 = -ДД7 (I z; I2 +1 г' I2)2/ = (| Z, I2+1 Z2 |2)21? = V |Е . (Б. 28)
т \~J)* иг
431
Поскольку фазы Fjm не играют существенной роли, то можно записать F
в виде
Fjm —
2'(+m Z'2~m
(Б. 29)
Аналогичное выражение имеет место для Fjm. Подставляя (Б.1) в (Б.23)
получаем
f' = У A' F - УУ ( К/'+>»)1(/—т)!]у«
«г s" s!s'!(/+m—з)!(/-m—s')!
Xa/+'”-sa*s'b*'-m-s' 6SZ?Z-S-S' Zs+s' . (Б.30)
В этом выражении можно не определять точно пределы суммирования и сум-
мировать по всем целым положительным и отрицательным числам, так как
биномиальные коэффициенты равны нулю, когда s, s' лежат вне области сум-
мирования. Полагая т' = / — s — s , имеем:
р' у у , рм’ + s—m /П)1]^
sl (/ —s—m')l (/4-m —s)! (m'+s—m)\
Xa’ + m-s a*'~m'-s b*m'+s~ m bsZ{+m' Z'2~m'. (Б.31)
Используя (Б.29), окончательно находим:
p' \ \ ..m'+s-rn l(/+m)! (/—mY U+m'y. (j- m')!]%
1 im = ’ > ( — 1) 1 -------------------------------— x
“ T s! (/—s—rn')l (j+m—s)I (m'+s—m)!
Xa'+m-sa*/-m'-s6*'n'+s-m bsFjm. . (Б. 32)
Таким образом, коэффициенты преобразования А'т,т, определяемые
соотношением (Б.30), имеют следующий вид:
т у , ! „ К/'+т)! (у —т)! (/Ч-гга")! (/—т')!]!4
s\(j——s)!(m'+s—т)!
Xa'+"!~sa*/-m'-s b*m'+s~m bs, (Б.ЗЗ)
л^,те=(-1Г'
где —j < tn < j, —j < tn' ... j. Следовательно, матрицы A^ являются
(2/ + 1)-мерными матрицами. Используя полученное выражение для случая
а = 1, 6=0, находим очевидный результат:
А{п'т= (Б-34>
На основании (Б.ЗЗ) можно также заключить, что каждой двухмерной
матрице W, определяемой выражением (Б.З), соответствует одна и только одна
(2/+ 1)-мерная матрица А. Кроме того, если две матрицы Aj и Л2 получены
с помощью (Б.ЗЗ) из матриц и VZ2 соответственно, то аналогичная связь
существует между матрицами Л3Л2 и Однако соответствие между
матрицами W и А не является взаимнооднозначным. Если а и 6 меняют знак,
то все элементы матрицы А умножаются на фактор (—1)2Л который равен
+ 1 для целых / и (—1) для полуцелых /.
Вспомним теперь полученный нами результат, согласно которому для
целых j существует одна матрица А для каждого вращения. Неоднозначность
W не играет роли, если речь идет о вращениях. Таким образом, в данном слу-
чае мы имеем взаимнооднозначное соответствие матриц А1 и вращений в трех-
432
мерном пространстве, определяемых тремя углами Эйлера 0П 02 и 03. Однако
для полуцелых значении / имеются две матрицы А1 и —А1, соответствующие
матрицам W и —W соответственно. Это означает, таким образом, что две ма-
трицы А соответствуют одной и той же матрице преобразований М, которая
определяет углы Эйлера с точностью до целого числа 2л. Другими словами,
в рассматриваемом случае две матрицы А1 соответствуют одному вращению.
Именно такими свойствами обладают матрицы вращений D1. Можно поэтому
написать
= U A}U~\
(Б. 35)
где
U — унитарная матрица. Полагая
е2
cos ехр
. е2
sin ехр
(Б. 36)
и U — 1, получаем:
02. е3) = е--'е*е-'"*е’ X
* v ( ~1)' [(7+^)! Ц — т)1 и+т')\ (/ —
s! (/ — s—m')l (j-\-т — s)! (т' +s—т)\
I 02 \2/+т—т’ — 2s 02\m'— m-p2s
X COS --- I — sin----
k 2 ) \ 2 J
(Б.37)
что в точности соответствует (5.143) и (5.146).
Из (5.146) и (5.148) может быть получено важное соотношение
<т(02)=^_т_т.(О2). (Б. 38)
которое означает, что элементы матрицы инвариантны относительно пере-
становки индексов т и т' с одновременным изменением их знаков. Кроме того,
используя унитарные свойства оператора вращения ехр (—i02£2), можно
показать, что
4-m(02)=<m, (-02). (Б. 39)
Заменяя в (5.148) 02 на —02, получаем еще одно соотношение:
<т(-02) = (-»т'-т^т(0«)- (Б-40)
Комбинируя (Б.39) и (Б.40), имеем:
4'т(02)=(- 1)т'~т4п,'(02)- (Б-41)
Наконец, используя (Б.38) и (Б.41), находим
<«т(02)=(- l)m’-'ndLm._„1(02). (Б. 42)
Оператор, обратный оператору вращения R (5.140), можно записать в виде
Д-1(01. 02, 03) = exp (i 03L3) ехр (i 02£2) exp(i OjLj). (Б. 43)
433
Из унитарности оператора вращения R следует, что матричные элементы
оператора R-1 совпадают с матричными элементами эрмитово сопряженного
оператора Д+, т. е.
</т' | R-1 ] /т> = <jm |/?| (Б 44)
Используя определения D-функций (5.50) и (5.142), можно переписать
(Б.44) в виде
^>т(-0з, — 02, -e1)=D^.(e1, е2, ез). (Б.45)
Другое важное соотношение для D-функций, которое мы часто использовали
в гл. 5—7, можно получить с помощью выражения (Б.42). Имеем:
е2, ез) = exp (i т^) d’inm, (62)exp(im' 63) =
= (— I)"1-'”' exp (im6i) (62)e(im' 03) =
= DLm_m. (0i, 02, Оз). (Б. 46)
Отсюда
^и(0/)=(- i)m'-moL„1._„I(e>)- (Б.47)
ПРИЛОЖЕНИЕ В
Диагонализация одночастичного гамильтониана
трехосного ядра в цилиндрических координатах
Рассмотрим модельный оператор Гамильтона, определяемый выражения-
ми (9.5) и (5.62):
Й 2 1
+“^'2+“гг'2) +
+СГ-s'+D(I'2-<|1'2|>n), (В.1)
где в последнем члене будут учитываться лишь эффекты отклонения квадрата
орбитального момента от его среднего значения в TV-й оболочке осциллятора
(см. § 8.3). По аналогии с (9.63) во внутренней системе отсчета, используя (9.4),
имеем:
£Ох_Ио/ж(ао, а2) 1_(1бл;/5)-1/2а0-|-(8л/15)-,/га2 ’
- “° fy (й0’“2) = 1 — (16зг/5)-^ао—(8^/15)-% а2 ’
. К>о
o>z = «о fz (До, а2) = -- -----.
1+(4л/5)-1а0
Используя условие сохранения объема (9.74), легко находим соотношение
<Oo=Wo(kMz)~,/% (В-3)
являющееся обобщением (9.75).Вводя безразмерные координаты
х= х'V, у = у'Утыу/ti; г = г'Утыг/Ь, (В.4)
434
можно преобразовать (В.1) к виду
1 , Г I д2 \ I д2 \
HSP = — А«о [Ц - — + х2 )+/,(-—+ у2 ) +
id2 \1 „
+fz - — +г2 +С1 -s +£>(Р- <|121>„).
\ дг2 IJ
(В. 5)
При выводе выражения (В.5) мы заменили оператор орбитального момен-
та Г, определенный в системе координат х', у', г', аналогичным оператором 1
в системе координат х, у, г. Это приближение, детально обсуждавшееся Ниль-
ссоном [283], может быть оправдано чисто модельным характером членов, за-
висящих от Г.
Преобразуем (В.5) к цилиндрическим координатам (р, г, <р) и положим
fp=4"^ + W> (В.6)
Тогда получим
1 . Г / д2
HsP= — &Oo[M-Vp+p2) I Ц- ^r+z2 )] +Н' +
+ С1 •s + D(P-<|P|>jV), (В.7)
где
I - д2 д2 X
//' — —+—+*2~i/2i- <в-8)
2 \ дх2 ду2 )
Первое слагаемое Hsp диагонально на базисе состояний
|ДрД2Л2> = | ДрЛ>|Л>| Дг>|2>, (В.9)
где —собственная функция оператора проекции спина на ось г, а
| Л > = (2п)—1/1 exp (i Л<р);
I Дг > = [|/ц Дг| 2W< ~1 /2 ехр - y г2) (г)=
|^л>-[~г<|лГ++Д.>яГ'г"1’("Т’’)L-'(В-101
Здесь п = -у (7Vp — | Л I), Т„Л| — полиномы JIareppa, a HN (г) — поли-
номы Эрмита (см. §8.12,6).
Используя волновые функции (В.9), легко получить следующие выражения
для матричных элементов операторов, зависящих от 1:
- <А -2Л/г-|-2Д|12^рАгЛ> = [(Ар-Л)(Ар4-Л)Х
X (A/z 1)(Л7г ]-2)]1/2;
<(Vp + 2Az-2A|f*|WpAzA> =
[(Ар-|-Л + 2)(Ар--Л -\-2)Nz(Nz- 1))1/2;
(Ар Nz Л | Р! Др Nz Л> = Л® -I- 2Дг Др + 2Дг+Nр;
(Др-1Дг + 1Л± 12'11 • s|ApAzA2> =
= -у^ртЛ)(^+1)11/2:
(В.11)
435
<Wp + lWz-lA± 12'11 .S|ApAzAZ> =
=4“K/vp±a+2)^]i/2-.
<NpAzAS|l • s|ApAzAS>=AS,
где 2' = X ф 1. Все остальные матричные элементы равны нулю.
Из полученных выражений, в частности, следует, что для операторов I2
и I • s величины
W=Ap4-Az и Й=Л+Е (В. 12)
являются хорошими квантовыми числами. Оператор Н', определенный выра-
жением (В.8), смешивает состояния с разными О, но сохраняет неизменным N.
Вычислим матричные элементы Н' на базисе состояний (В.9), размерность
которого (1/2) (N + 1) (N + 2). Используя теорему вириала, легко получить
следующее выражение:
<А' а' |Н' |Аа> fd <Na' | х2 — z/2 [ Na>. (В. 13)
Преобразуя х2 — у2 к цилиндрическим координатам, имеем
1»'I (- Тх
X {бл'Л+2[(^р-А)(Ар+Л+ 2)]’/*+бл,л_21(Ар-Л+2)(Ар + Л)^} .
(В.14)
Базис, определенный выражениями (В.9) и (В. 10), имеет два существен-
ных преимущества по сравнению со сферическим базисом, использованным
в § 9.4. Во-первых, в этом базисе аксиально-симметричная часть гамильтониа-
на (В.1), включая члены, зависящие от I', диагональна по А. Во-вторых, ис-
пользование базиса (В.9) позволяет получить очень простые выражения для
матричных элементов (В. 11) и (В. 14), не связанные с вычислением коэффициен-
тов Клебша—Гордана. В результате этого для диагонализации Я£р с по-
мощью ЭВМ в цилиндрических координатах требуется примерно в десять раз
меньше времени, чем в случае использования сферических координат.
ПРИЛОЖЕНИЕ Г
Распределение плотности в ядрах
[вывод дифференциальных уравнений (12.35) — (12.37)]
Найдем изменение энергии связи (12.31)
+ +₽?)« +
If eZ Г
+ — J Р Ol’i+’M dt]+ — j ptpdT
(Г.1)
в зависимости от плотности р. В формуле (Г. 1) ф,- и <р — соответственно потен-
циалы Юкавы и Кулона, определяемые выражениями
V'i Р ехр ( —| г—г'|/р,-)
’Мг) = ’^г. --------lr-r-1
(Г. 2а)
436
eZ С р (г')
(Г. 26)
Предполагая, что границей ядра является сфера радиуса т = /?, полу-
чаем:
6£= f Р+Ж+’Рг + “~Г <p^pdr +
J \ Ро f A J
(С eZ \
+ [^р(/?)+’1’1(/?)+1р2 (/?)+— <f(R)]p(R)4nR4R +
+ тМ Ро2 - ~Т Р2 Щ ) № 6R.
2Ро \ v2 I
(Г.З)
Примем теперь во внимание дополнительное условие постоянства числа
частиц
Л=|р^т (Г. 4а)
и соотношение
JCpdr^—р(7?) 4л7?267?. (Г.46)
Тогда условие SE = 0 приводит к следующему уравнению для потенциа-
лов:
С eZ
---ГР + ’1)14-'1’2+—г <P = const (Г.5)
Ро»2 А
и граничному условию
р(/?) = цр0. (г-6)
Используем систему уравнений (Г.2), (Г.4)—(Г.6) для вычисления распре-
деления плотности ядерной материи. Общее решение этих уравнений имеет
вид
3
Р = У аг/0(а/г). (Г.7)
z= 1
Подставим теперь (Г.7) в (Г. 5), учитывая при этом следующее соотно-
шение, которое имеет место при г < R:
R
1 fexp(— I г—- г'1/и) . , ,
— о «Иdx =
4л J |г—г' |
О
= —2~Г г{7о(«г)—exp(--7?/p)(cosaR + (l/pa)sina/?)7o(i'’/P)}- (Г.8)
Первое слагаемое в правой части выражения (Г.8) может быть использо-
вано для определения решения неоднородного дифференциального уравнения
(12.36), второе слагаемое удовлетворяет соответствующему однородному урав-
нению. Входящие в соотношение (Г.5) суммы решений однородных и неодно-
родных уравнений должны порознь обращаться в нуль. Условие обращения
437
в нуль суммы решений неоднородных уравнений приводит к следующему урав
нению третьей степени относительно величин а?:
с , Vi Vz / ez у i „
РоО2 + Иг2 + а? + Н22 + «? +4я1 А 1 а/ =°'
(Г.9)
Корни этого уравнения, вообще говоря, являются комплексными числами.
Требуя, чтобы сумма решений однородных уравнений также обращалась
в нуль, получаем два уравнения для определения параметров а,;
з
а«)=°. fe = 1. 2, (Г. 10)
i = 1
где
1 / 1 \
F(u, а) =---——— cosaRH---------sinaRJ.
р~2 + а2 \ р.а )
Третье уравнение для at может быть получено на основании граничного
условия (Г.6):
з
2 ai/o(“iR)=4>o-
1 = 1
(Г. И)
Решая линейные уравнения (Г. 10), (Г. 11), можно найти величины а,
в виде функций от радиуса ядра R. Наконец, подставляя (Г.7) в условие нор-
мировки (Г.4), мы получаем следующее уравнение для определения радиуса
ядра:
з
71 = 4nR3
i = l
ai /1 (at R)
a; R
(Г. 12)
Решение этого уравнения может быть найдено с помощью метода итераций.
Распределение плотности (Г.7) может быть получено в простом виде
для следующих случаев:
Z = 0 I Z 0
И2 = 0, a2 = as = 0
Р2 =£ 0, «з = 0
а3 0
а, =/= 0
В качестве примера и для более ясного понимания проблемы найдем рас-
пределение плотности ядерной материи в том случае, когда имеется лишь один
потенциал Юкавы, а кулоновская энергия и энергия симметрии равны нулю.
При этих предположениях уравнение (12.38) принимает вид:
^-=1-У1Фо/С-
(Г.13)
Для плотности распределения можно использовать следующее выраже-
ние, которое автоматически удовлетворяет граничному условию на поверх-
ности г = R:
p(r) = pov
1 — Р (sh ar)!ar
1 — P(shaR)/aR
(Г. 14)
438
Согласно (Г.9) и (Г. 10), параметры а и Р должны удовлетворять соотношениям
(Г. 15а)
C/Ро о2 + Е/(р-2 — а2) = О
и
р2(1+/?/р)
откуда следует, что
v
а =—
И
P
-----:-(ch al? + sh aR/pa) = 0,
pi-2—a2
р (1+W(l~t>2)
ch (yR/p) +— sh (yR/ц)
(Г.156)
(Г. 16)
Если ограничиться в дальнейшем рассмотрением случая достаточно боль-
ших радиусов R, то выражение для распределения плотности может быть
упрощено и записано в виде
1 - (1 +р/1?) (1 — о)ехр (о (г—1?)/р)
1 — р(1- v)/(Rv)
Параметр диффузности t, определяемый как толщина слоя, в котором
плотность уменьшается от 90 до 10% своего значения в центре ядра р (0), в рас-
сматриваемом приближении равен
(Г. 17)
Р (г) = Ро
— (1п10 + 1п(1 — о)). (Г. 18)
V
Соответственно энергия связи может быть записана в виде суммы объемной
и поверхностной энергий:
Е=1Г0Л+с[4- А -£^+4-Ро^л/?3-л1«№о4+тЛ2'3, (Г. 19)
[2 ро 2 о J
причем параметр у, определяющий величину поверхностной энергии, равен
3 1 — о / 4 \1/з
С-------р — лр0 . (1-20)
Л V \ о /
СПИСОК ЛИТЕРАТУРЫ
1. Де Бенедетти С. Ядерные взаимодействия. Пер. с англ. Под. ред.
А. О. Вайсенберга. М., Атомиздат, 1968.
2. Блатт Дж., Вайскопф В. Теоретическая ядерная физика. Пер. с англ.
М., Изд-во иностр, лит., 1954.
3. Давыдов А. С. Теория атомного ядра. М., Физматгиз, 1958.
4. Eder G. Kernkrafte. Karlsruhe, Verlag G. Braun, 1965.
5. Hertz G. Lehrbuch der Kernphysik I, II, Hanau/Main, Werner Dausien
Verlag, 1961.
6. Престон M. Физика ядра. Пер. с англ. М-, «Мир», 1964.
7. Abecasis S. М., Bosch Н Е., Heras С. A «Nuovo cimento», 1967, v. 51В,
р. 310.
8. Abecasis S. М., Bosch Н. Е. «Nuovo cimento», 1968, v. 53В, p. 147.
9. Abecasis S. M., Bosch H E., Plastino A. «Nuovo cimento», 1968, v. 54Б,
p. 245.
10. Abecasis S. M., Bosch H. E., Plastino A. «Nucl. Phys.», 1969, v. A129, p.434.
11. Acker H L. e. a. «Nucl. Phys.», 1965, v. 66, p. 477.
12. Acker H. L., Marschall H. «Phys. Lett.», 1965, v. 19, p. 127.
13. Acker H. L. Zur Theorie der Rotations—Vibrations—Wechselwirkung in
gg-Kernen. Dissertation. Phys. Inst. Univ. Freiburg/Breisgau, 1965, unpub-
lished.
14. Acker H. L. Zur Theorie der Rotations—Vibrations—Wechselwirkung in
Atomkernen. — Thesis, Univ. Freiburg/Breisgau, 1965.
15. Adair R. K.«Phys. Rev.», 1952, v. 86, p. 155.
16. Ajzenberg F., Lauritsen T. «Rev. Mod. Phys.», 1955, v. 27, p. 77.
17. Aimquist E., Bromley D A., KuehnerJ. A. «Phys Rev. Lett.», 1960, v. 4,
p. 515.
18. Almquist E. e. a. «Phys. Rev.», 1968, v. 130, p. 1140.
19. Ambler E., Fuller E. G., Marshak H. «Phys. Rev.», 1965, v. 138, p. Bl 17.
20. Арфкеи Г. Математические методы в физике. Сокр. пер. с англ. М., Атом-
издат, 1970.
21. Arenhovel Н., Danos М., Greiner W. «Phys. Rev.», 1967, v. 157, p. 1109.
22. Arenhovel H., Weber H. J. «Nucl. Phys.», 1967, v. A91, p. 145.
23. Arenhovel H., Greiner W. Theory of Photon Scattering by Nuclei and the
Dynamic Collective Model. — «Progr. Nucl. Phys.», 1968, v. 10.
440
24. Arenhovel H., Danos M., Williams H. T. «Phys. Lett.», 1970, v. 31 В, p. 109.
25. Aston F. W. «Proc. Roy. Soc.», 1926, v. Al 15, p. 487.
26. Asaro F. e. a. «Phys. Rev.», 1960, v. 120, p. 934.
27. Bartlett J. H., Jr. «Phys. Rev.», 1936, v. 49, p. 102.
28. Baldwin G. C., Klaiber G. C. «Phys. Rev.», 1947, v. 71, p. 3.
29. Baldwin G. C., Klaiber G. C. «Phys. Rev.», 1948, v. 73, p. 1156.
30. Batchelor R. e. a. «Nucl. Phys.», 1960, v. 16, p. 38.
31. Baglin J. E. E., Spicer В. M. «Nucl. Phys.» 1964, v. 54, p. 549.
32. Bacin G. e. a. «Nucl. Phys.», 1965, v. 67, p. 178.
33. Bamberger A., Bizetti P. G., Rovh B. «Phys. Rev. Lett.», 1968, v. 21, p. 1599.
34. Baranger M., Kumar K- «Nucl. Phys.», 1968, v. Al 10, p. 490.
35. Backlin A. e. a. «Phys. Rev.», 1967, v. 160, p. 1011.
36. Beck G. «Z. Phys.», 1928, Bd 47, S. 407; 1928, Bd 50, S. 548.
37. Beck G. «Z. Phys.», 1930, Bd 61, S. 615.
38. Bethe H. A. «Rev. Mod. Phys.», 1936, v. 8, p. 82.
39. Beringer R. «Phys. Rev. Lett.», 1967, v. 18, p. 1006.
40. Bethe H. A. «Phys. Rev.», 1968, v. 167, p. 879.
41. Bezic N. e. a. «Nucl. Phys.», 1969, v. A128, p. 426.
42. Birbrair B. L., Peker L. K., Sliv L. A. «Soviet Phys. JETP», 1959, v. 9,
p. 566.
43. Biedenharn L. C., Brussaard P. J. Coulomb Excitation. Oxford, Univ. Press,
Oxford, 1965.
44. Bjerregaard J. H. e. a. «Phys. Rev. Lett.», 1967, v. 24B, p. 568.
45. Bloch F. «Phys. Rev.», 1951, v. 83, p. 839.
46. Блатт Дж., Вайскопф В. Теоретическая ядерная физика. М., Изд-во
иностр, лит., 1954.
47. Black J. L.. Tanner N. W. «Phys. Lett.», 1964, v. 11, p. 135.
48. Born M., Oppenheimer R. «Ann. Phys.», 1927, v. 84, p. 457.
49. Bohr N., Wheeler J A «Phys. Rev.», 1939, v. 56, p. 426.
50. Bohr A. «Kgl. Danske Videnskab. Selskab Mat.-Fys. Medd.», 1952, Bd 26,
N 14. (См. пер. в сб.: Проблемы современной физики. М., Изд-во иностр,
лит., 1955, вып. 9.)
51. Bohr A., Mottelson В. «Kgl. Danske Videnskab. Selskab Mat.-Fys. Medd.»,
1953, Bd 27, N 16. (См. nep. в сб.: Проблемы современной физики. М.,
Изд-во иностр, лит. 1955, вып. 9.)
52. Bohr A. Rotational States in Atomic Nuclei (Thesis, Copenhagen, 1954).
(См. пер. в сб.: Проблемы современной физики. М., Изд-во иностр, лит.,
1956, вып. I.)
53. Bohr A. Proc. Intern. Conf, on Nuclear Structure. Kingston, Ontario, 1960,
University of Toronto Press, p. 807.
54. Bodansky D. «Ann. Rev. Nucl. Sci.», 1962, v. 12, p. 79.
55. Bodenstedt E. «Fortschr. Phys.», 1962, v. 10, p. 321.
56. Bodenstedt E., Rogers J. D. In Perturbed Angular Correlations. North Hol-
land, Amsterdam, 1964.
57. Bock R. Max Planck Inst. f.Kernphysik Heidelberg, Internal Rept., 1968.
58. Bock R. Proc. Intern. Conf, on Physics with Heavy Ions, Heidelberg, North
Holland, Amsterdam, 1969.
59. Bohm E., Stelzer K- Proc. Intern. Symp. on Neutron Capture Gamma-Ray
Spectroscopy. Intern. Atomic Energy Agency, Vienna, 1969.
60. Brink D. M. «Proc. Phys. Soc.», 1954, v. A67, p. 757.
441
61. Breit G., Glucks tern R. L., Russel J. E. «Phys. Rev.», 1956, v. 103, p. 103
62. Breit G., Gluckstern R. L., Russel J. E. «Phys. Rev.», 1957, v. 105, p. 112/
63. Bromley D. A., Gove H. E., Litherland A. E. «Canad. J. Phys.», 1957, v 35
p. 1057.
64. Brown G. E., Bolsterli M. «Phys. Rev. Lett.», 1959, v. 3, p. 472.
65. Bromley D. A. e. a. «Phys. Rev. Lett.», 1960, v. 4, p. 365.
66. Brink D. M., Satchier G. R. Angular Momentum. Oxford Univ Рге«=
Oxford, 1962. s’
67. Bramblett R. L. e. a. «Phys. Rev.», 1963, v. 129, p. 2723.
68. Bramblett R. L. e. a. «Phys. Rev.», 1964, v. 133, p. B869.
69. Brix P. e. a. «Phys. Lett.», 1964, v. 13, p. 140.
70. Brueckner K. A. e. a. «Phys. Rev.», 1968, v. 171, p. 1188.
7i. Brueckner K. A., Buehler J. R , Kelly M. M «Phys. Rev.», 1968, v. 173
p. 944.
72. Von. Brentano P. e. a. «Phys. Rev. Lett.», 1968, v. 26B, p. 666.
73. Бургов H. А. и др. «Ж- эксперим. и теор. физ.», 1959, т. 37, с. 1811 1962
т. 43, с. 70; 1963, т. 45, с. 1693.
74. Casimir Н. В. G. Rotation of a Rigid Body in Quantum Mechanics. Disserta-
tion, Leiden, 1931.
75. Carlson В. C-, Rushbrooke G. S. «Proc. Cambridge Philos. Soc.», 1950, v. 46,
p. 626.
76. Carver J. H., Turchinetz W. «Proc. Phys. Soc.», 1959, v. A73, p. 69.
77. Chatwin R. A. e. a. «Phys. Rev.», 1969, v. 180, p. 1049.
78. Коидон E., Шортли Г. Теория атомных спектров. Пер. с англ. М., Изд-во
иностр, лит., 1949.
79. Cohen R. С. е. a. «Phys. Rev.», 1962, v. 127, р. 1678.
80. Coulon Т. W-, Bayman В. F., Kashy E. «Phys. Rev.», 1966, v. 144, p. 941.
81. Costa S. e. a. «Nuovo cimento», 1967, v. 48, p. 460.
82. Coester F. «Phys. Rev.», 1955, v. 99, p. 170.
83. Cook В. C. «Nucl. Instrum, and Methods», 1963, v. 24, p. 256.
84. Cook В. C. e. a. «Phys. Rev.», 1966, v. 143, p. 530.
85. Darwin C. G. «Proc. Roy. Soc.», 1928, v. Al 18, p. 634.
86. Danos M., Steinwedel H. «Z. Nafurforsch.», 1951, Bd 6a, S. 23.
87. Danos M., Steinwedel H. «Z. Nafurforsch.», 1951, Bd 6a, S217.
88. Danos M. «Nucl. Phys.», 1958, v. 5, p. 23.
89. Davydov A. S., Filippov G. E. «Nucl. Phys.», 1958, v. 8, p. 237.
90. Davydov A. S-, Rostovsky V. S. «Nucl. Phys.», 1959, v. 12, p. 58.
91. Davydov A. S. Soviet Phys. JETP 1959, v. 36, p. 1103.
92. Davydov A. S., Chaban A. A. «Nucl. Phys.», 1960, v. 20, p. 499.
93. Danos M. Photonuclear Physics. Univ. Maryland Dept. Phys. Tech. Rept.
v. 221, July 1961.
94. Davidson J. P. «Nucl. Phys.», 1962, v. 33, p. 664.
95. Давыдов А. С. Теория атомного ядра M., Физматгиз, 1958.
96. Danos М., Greiner W. «Phys. Lett.», 1964, v. 8, p. 113.
97. Danos M., Greiner W. «Phys. Rev.», 1964, v. 134, p. B284.
98. Danos M., Greiner W. «Phys. Rev.», 1965, v. 138, p. B876.
99. Danos M., Greiner W., Kohr С. B. «Phys. Rev.», 1965, v. 138, p. B1055.
100. Davidson J. P. «Rev. Mod. Phys.», 1965, v. 37, p 105.
101. Danos M., Fuller E. G. «Ann. Rev. Nucl. Sci.», 1965, v. 15, p. 629.
442
102. Давыдов А. С. Квантовая механика. М., «Наука», 1973.
103. Davis R. Н. Proc. Intern. Conf, on Nuclear Structure. Tokyo, 1967.
104. De Boer J., GoldringG., Winkler H. «Phys. Rev.», 1964, v. 134, p. B1032.
105. De Boer J. e. a. «Phys. Rev. Lett.», 1965, v. 14, p. 564.
106. De Shalit A. «Helv. Phys. Acta», 1951, v. 24, p. 296.
107. De Shalit A. «Phys. Rev.», 1953, v. 91,- p. 1479.
108. Diamond R. M. e. a. «Nucl. Phys.», 1963, v. 43, p. 560.
109. Donner W., Greiner W. «Z. Phys.», 1966, Bd 197, S. 440.
110. Долбилкин Б. С. «Труды ФИЛИ», 1966, т. 36, с. 18.
111. Douglas A. C., MacDonald «Phys. Lett.», 1967, v 24B, p. 477.
112. Drechsel D., Seaborn J. B., Greiner W. «Phys. Rev. Lett.», 1966, v. 17, p. 488.
113. Drechsel D., Seaborn J. B., Greiner W. «Phys. Rev.», 1967, v. 162, p. 983.
114. Duckworth H. E. «Rev. IVfod. Phys.», 1957, v. 29, p. 767.
115. Dular J. e. a. «Nucl. Phys.», 1959, v. 14, p. 131.
116. Эдмондс A. P. В сб.: Деформация атомных ядер. Пер. с англ. М., Изд-во
иностр, лит., 1958, с. 305.
117. Eichler J «Phys. Rev.», 1964, v. 133, p. Bl 162.
118. Eisenberg J M., Le Tourneux J. «Nucl. Phys.», 1967, v. B3, p. 47.
119. Eichler J., De Boer J. «Adv. Nucl. Phys.», 1968, v. 1, p. 1.
120. Elliott J. P., Jane A. M. «Handb. der Phys.», 1957, Bd 39, S. 332.
121. Elton L. R. B. Introductory Nuclear Theory. Pidman, London, 1959.
122. Elliott J. P. The Shell Model (review article in Nuclear Reactions, P. M.
Endt and M. Demeur, eds. North-Holland, Amsterdam, 1959). (Cm. nep.
в сб.: Ядерные реакции, т. I. Под ред. П. М. Эндта и М. Демера. Пер.
с англ. М., Госатомиздат, 1962.)
123. Элтон Л. Размеры ядер. Пер. с англ. М., Изд-во иностр, лит., 1962-
124. Elton L. R. В., Swift A. Proc. Williamsburg Conf, on Intermediate
Energy Physics. College of William and Mary, Williamsburg, Va., 1966.
125. Emery G. T. e. a. «Phys. Rev.», 1963, v. 129, p. 2597.
126. Ericson T. «Advances Phys.», 1960, v. 63, p. 479.
127. Erskine J. R. «Phys. Rev.», 1966, v. 149, p. 854.
128. Evening F. e. a. «Nucl. Phys.», 1960, v. 18, p. 529.
129. Faesslcr A., Greiner W. «Z. Phys.», 1962, Bd 168, S. 425.
130. Faessler A., Greiner W. «Z. Phys.», 1962, Bd 170, S. 105.
131. Faessler A., Greiner W. «Z. Phys.», 1964, Bd 177, S. 190.
132. Faessler A. «Nucl. Phys.», 1964, v. 59, p. 177.
133. Faessler A., Greiner W., Sheline R. «Nucl. Phys.», 1965, v. 80, p. 417.
134. -Faesslcr A., Greiner W., Sheline R. «Nucl. Phys.», 1965, v. 62, p. 241.
135. Faessler A., Greiner W., Sheline R. «Nucl. Phys.», 1965, v. 70, p. 33.
136. Faessler A., Sheline R. K. «Phys. Rev.», 1966, v. 148, p. 1003.
137. Fermi E. «Nuovo cimento», 1954, v. 11, p. 407.
138. Feenberg E. «Phys. Rev.», 1939, v. 55, p. 504.
139. Feenberg E. «Phys. Rev.», 1949, v.. 75, p. 320.
140. Feenberg E., Hammack К- C., Nordheim L. W. «Phys. Rev.», 1949, v. 75,
p. 1968.
141. Feenberg E. Shell Theory of the Nucleus. Princeton Univ. Press, Prince-
ton, New Jersey, 1955.
142. Fieri M. «Helv. phys. acta», 1943, v. 16, p. 365.
443
143. Fink В., Mosel U. Contribution to Memorandum der Hessischen Ker
physiker, Darmstadt — Frankfurt — Marburg, 1966.
144. Fielder D. S. e. a. «Phys. Rev. Lett.», 1965, v. 15, p. 33.
145. Fielder D. S., Min K-, Whitehead W. D. «Phys. Rev.», 1968, v. 168
p. 1312.
146. Fliigge S. «Ann. Phys.», 1941, Bd 39, S. 373.
147. Fliigge S. «Z. Naturforsch.», 1946, Bd 1, S. 121.
148. Fliigge S. «Z. Naturforsch.», 1948, Bd 3a, S. 97.
149. Fliigge S., Marschall H. Rechenmethoden der Quantentheorie. Springer
Berlin-Goettingen—Heidelberg, 1952.
150. FlerovG. N., Karnoukhov V. A. Compt. Rend. Congr. Intern. Phys. Nucl
Paris, 1946, v. 1, p. 373.
151. Fuller E. G., Hayward E. «Phys. Rev. Lett.», 1958, v. 1, p. 465.
152. Fuller E. G., Weiss M. S. «Phys. Rev.», 1958, v. 112, p. 560.
153. Fuller E. G., Hayward E. «Nucl. Phys.», 1962, v. 30, p. 613.
154. Fultz S. C. e. a. «Phys. Rev.», 1962, v. 128, p. 2345.
155. Fultz S. C. e. a. «Phys. Rev.», 1970, v. 186, p. 1255.
156. Gallagher C. J., Moszkowski S. A. «Phys. Rev.», 1958, v. Ill, p. 1282.
157. Geilikman В. T. Proc. Intern. Conf, on Peaseful Uses of Atomic Energy,
1955, v. 2, p. 201.
158. Geschwind S. «Handb. der Phys.», 38/1, S. Fliigge, ed. Berlin, Springer,
1958.
159. Gill R. D. e. a. «Nucl. Phys.», 1968, v. A106, p. 678.
160. Gneuss G. Zum Studium der kollektiven Potentialenergie Flachen in
Atomkernen. Diplomarbeit, Inst. Theoret. Phys. Univ. Frankfurt/Main,
1967, unpublished.
161. Gneuss G., Mosel U., Greiner W. «Phys. Lett.», 1969, v. 30B, p. 397.
162. Gneuss G. Struktur der kollektiven Potentialflachen von Atomkernen.
Thesis, Inst. Theor. Phys. Univ. Frankfurt/Main, 1970.
163. Goldschmidt V. M. Skrifter Norske Videnskaps—Akad. Oslo I: Mat. Na-
turv. KI. 4 (1937).
164. Goldhaber M., Teller E. «Phys. Rev.», 1948, v. 74, p. 1946.
165. Gordy W. «Phys. Rev.», 1949, v. 76, p. 139.
166. Goldemberg J. «Phys. Rev-», 1954, v. 93, p. 1426.
167. Gottfried K- «Phys. Rev.», 1956, v. 103, p. 1017.
168. Grechukhin D. P. «Nucl. Phys.», 1961, v. 24, p. 576.
169. Greiner W. «Z. Phys.», 1963, v. 172, p. 386.
170. Greider K. R. «Ann. Rev. Nucl. Sci.», 1965, v. 15, p. 291.
171. Greiner W. «Phys. Rev. Lett.», 1965, v. 15, p. 559.
172. Greiner W. «Nucl. Phys.», 1966, v. 80, p. 417.
173. Greiner W., Arenhovel H. «Nucl. Phys.», 1968, v. A107, p. 225.
174. Grodzins L. «Ann. Rev. Nucl. Sci.», 1968, v. 18.
175. Grosse E. e. a. «Z. Phys.», 1969, Bd 218 , S. 213.
176. Grosse E. e. a. «Z. Phys.», 1969, Bd 219, S. 75.
177. Gustafson e. a. «Arkiv. fys.», 1967, Bd 36, S. 613.
178. Guy R., Eisenberg J. M., Le Tourneux J. «Nucl. Phys.», 1968, v. Al 12,
p. 689.
444
179. Haxel О., Jensen J. H. D., Suess H. E. «Phys. Rev.», 1949, v. 75, p. 1766.
[80. Haxel O., Jensen J. H. D., Suess H. E. «Z. Phys.», 1950, Bd 128, S. 295.
181. Hayward E. Photonuclear Reactions. Scottish Univ. Summer School, 1964.
182. Hensinkfeld M., Freier G. D. «Phys. Rev.», 1952, v. 85, p. 80.
183. Hecht К- T. «Nucl. Phys.», 1965, v. 63, p. 177.
184. Hering W. R. Proc. Symp. on Physics with Tandems. Heidelberg, 1966.
185. Henning W. «Z. Phys.», 1968, Bd 217, S. 438.
186. Heras C. A., Abecasis S. M., Bosch H. E. U. S. Atomic Energy Commi-
sion, Div. Tech. Inf. Rept. No. NP-17506.
187. Heisenberg W. «Z. Phys.», 1932, Bd 77, S. 1.
188. Hinds S. e. a. «Phys. Rev. Lett.», 1965, v. 17, p. 302.
189. Hinds S., Middleton R. «Nucl. Phys.», 1966, v. 84, p. 651.
190. Hintcrberger F. e. a. «Nucl. Phys.», 1968, v. Alli, p. 265.
191. Hinterberger F. e. a. «Nucl. Phys.», 1968, v. Al 15, p. 570.
192. Hollaed G., Steiglitz R. Proc.’Summer Study Group on the Physics of the
Emperor Tandem van de Graaf Region, v. Ill, Brookhaven Natl Lab.,
Upton, N. Y., 1965.
193. Holm H. Diploma thesis Inst. Theoref. Phys. Univ. Frankfurt/Main, 1969.
194. Holm H. e. a. «Z. Phys.», 1970, Bd 231, S. 450.
i95. Holm H., Greiner W. «Phys. Rev. Lett.», 1970, v. 24, p. 404.
196. Huizenga J. R. «Physica», 1955, v. 21, p. 410.
197. Huber M. G. «Amer. J. Phys.», 1967, v. 35, p. 685.
198. Huber M. G. e. a. «Phys. Rev.», 1967, v. 155, p. 1073.
199. Huber M. G. Habilitationsschrift. Inst. Theoret. Phys. Univ. Frank-
furt/Main, 1968.
200. Huefner S. e. a. «Z. Phys.», 1965, Bd 187, S. 67.
201. Imanishi B. «Nucl. Phys.», 1969, v. A125, p. 33.
202. Inglis D. R. «Rev. Mod. Phys.», 1953, v. 25, p. 390.
203. Инопин E. В. «Ж- эксперим. и теор. физ.», 1960, т. 38, с. 992,
204. Inglis D. R. «Nucl. Phys.», 1962, v. 30, p. 1.
205. Inglis D. R. «Rev. Mod. Phys.», 1962, v. 34, p. 165.
206. Jensen J. H. D., Mayer M. G. «Phys. Rev.», 1952, v. 85, p. 1040.
207. Jensen J. H. D. Zur Geschichte der Theorie des Atomkerns, Les Prix No-
bel en 1963. Norstedt, Stockholm, 1964.
208. Jones K. W. e. a. «Phys. Rev.», 1966, v. 145, p. 894.
209. Kane W. R., Emery G. T. «Bull. Amer. Phys. Soc.», 1967, v. 12, p. 597.
210. Kerman A. K- «Kgl- Danske Videnskab. Selskab Mat.-Fys. Medd.», 1956,
Bd. 30, N 15.
211. Kerman A. K. Nuclear Reactions. P. M. Endt and M. Demeur, eds. (North-
Holland, Amsterdam; 1959). В сб.: Ядерные реакции. Под ред.
П. М. Эндта и М. Демера. Пер. с англ. М., Госатомиздат, 1962.
212. Kenefick R. A., Sheline R. К. «Phys. Rev.», 1964, v. 133, р. В25.
213. Kern J. e. a. «Phys. Rev.», 1968, v. 173, p. 1133.
214. Kistner О. C., Sunyar A. W. «Phys. Rev. Lett.», 1960, v. 4, p. 412.
215. Kisslinger L. S., Sorenson R. A. «Kgl- Danske Videnskab. Selskab Mat.-
Fys. Medd.», 1960, Bd 32, N 9.
216. Klein O. «Z. Phys.», 1929, Bd 58, S. 730.
445
217. Kopfermann H. Kernmomente. Akademische Verlagsgesellschaft, Frank.
furt/Main, 1956.
218. De Kronig R. L., Rabi I. I. «Phys. Rev.», 1927, V. 29, p. 262.
219. Kurath D. «Phys. Rev.», 1956, v. 101, p. 216.
220. Kurath D. «Phys. Rev.», 1957, v. 106, p. 975.
221. Kumar K., Baranger M. «Nucl. Phys.», 1967, v. A92, p. 608.
222. Kuchnir F. T. e. a. «Phys. Rev.», 1967, v. 161, p. 1236.
223. Kurath D. Proc. Rehovoth Conf, on Nuclear Structure, North-Holland
Amsterdam, 1968, p. 46.
224. Landolt—Bornstein. Neue Serie V. 1, Springer, Berlin, 1961.
225. Langevin M., Loiseaux J. M., Maison J. M. «Nucl. Phys.», 1964, v. 54
p. 224.
226. Lark N. L., Morinaga H. «Nucl. Phys.», 1965, v. 63, p. 466.
227. Levinger J. S., Bethe H. A. «Phys. Rev.», 1950, v. 78, p. 115.
228. Lemmer R. H., Green A. E. S. «Phys. Rev.», 1960, v. 119, p. 1043.
229. Lemmer R. H. «Phys. Rev.», 1960, v. 117, p. 1551.
230. Le Tourneux J. «Kgl- Danske Videnskab. Selskab Mat.-Fys. Medd.», 1965
Bd 34, N 11.
231. Lipkin H., de Shalit A., Talmi I. «Phys. Rev.», 1956, v. 103, p. 1773.
232. Litherland A. E. e. a. «Canad. J. Phys.», 1958, v. 36, p. 378.
233 Litherland A. E. e. a. «Canad. J. Phys.», 1959, v. 37, p. 53.
234. Ligensa R., Greiner W. «Nucl. Phys.», 1966, v. 77, p. 577.
235 Ligensa R. Thesis. Univ. Frankfurt/Main, 1966, unpublished.
236. Ligensa R., Greiner W. «Nucl. Phys.», 1967, v. A92, p. 673.
237. Lilley J. S., Stein N. «Phys. Rev. Lett.», 1967, v. 19, p. 709.
238. Majorana E. «Z. Phys.», 1933, Bd 82, S. 137.
239. Marumori T., Yukowa J., Taneka R. «Progr. Theoret. Phys.», 1955, v.13,
p. 442.
240. Marumori T., Yamada E. «Progr. Theoret. Phys.», 1955, v. 13, p. 1557.
241. Marumori T. «Progr. Theoret. Phys.», 1955, v. 14, p. 608.
242. Marty C. «Nucl. Phys.», 1956, v. 1, p. 85.
243. Mattauch J. H. E., Thiele W., Wapstra A. H. «Nucl. Phys.», 1965, v. 67,
p. 1.
244. Maly J., Nix J. R. Proc. Intern. Conf, on Nuclear Structure p. 678,
Tokyo, 1967.
245. MacDonald N. «Phys. Lett.», 1964, v. 10, p. 334.
246. Mayer M. G. «Phys. Rev.», 1948, v. 74, p. 235.
247. Mayer M. G. «Phys. Rev.», 1949, v. 75, p. 1969.
248. Mayer M. G. «Phys. Rev.», 1950, v. 78, p. 22.
249. Майер M. Г., Иеисеи И. Г. Д. Элементарная теория ядерных оболочек.
Пер. с англ. М., Изд-во иностр, лит., 1958.
250. Mayer М. G., Jensen J. Н. D., Kurath D. Alpha-, Beta- and Gamma-Ray
Spectroscopy. K. Siegbahn, ed. (North-Holland, Amsterdam, 1965). Cm.
Альфа-, бета- и гамма-спектроскопия. Под ред. К- Зигбана. Вып. 2.
Пер. с англ. М., Атомиздат, 1969.
251 Meldner Н., Siissmann G., Ulrici W. «Z. Naturforsch.», 1965, Bd 20a,
S. 1217.
252. Miyazawa H. «Progr. Theor. Phys.», 1951, v. 6, p. 263.
253. Miyazawa H., Tamura T. «Progr. Theor. Phys.», 1956, v. 15, p 255
446
254. Miller J. e. a. «J. Phys. Radium», 1960, v. 21, p. 296.
255. Miller J , Schuh I C., Tzara C. «Nucl. Phys.», 1962, v 32, p 236.
256. Min K-, White T. A. «Phys. Rev. Lett.», 1968, v. 21, p. 1200.
257. Michaelis W. e. a. Proc. Intern. Symp. on Neutron Capture Gamma-Ray
Spectroscopy. Intern. Atomic Energy Agency, Vienna, 1969.
258. Michaelis W. e. a. «Nucl. Phys.», 1970, v. A143, p. 225.
259. Морз Ф. Колебания и звук. Пер. с англ. М —Л., Гостехтеориздат, 1949.
260. Морз Ф., Фешбах Г. Методы теоретической физики. Пер с англ. М.,
Изд-во иностр, лит., 1958.
261. Montalbetti R., Katz L., Goldemberg J. «Phys. Rev.», 1953, v. 46, p. 598.
262. Moszkowski S. A. «Phys. Rev.», 1955, v 99, p. 803.
263. Moszkowski S. A. «Handb. Phys.», 1957, v. 39, p. 411 (Springer, Berlin).
264. Mottelson B. R., Nilsson S. G. «KgL Danske Videnskab. Sclskab Mat.-
Fys. Skrifter», 1959, Bd 1, N 8
265. Mottelson B. R., Valatin J. «Phys. Rev. Lett.», 1960, v. 5, p. 511.
266. Morinaga H., Gugelot P. C. «Nucl. Phys.», 1963, v. 46, p. 210.
267. Morinaga H., Lark N. L. «Nucl. Phys.», 1965, v. 67, p. 315.
268. Moore C. F. e. a. «Phys. Rev.», 1967, v. 164, p. 1559.
269. Mosel U. Thesis Inst. Theor. Phys. Univ Frankfurt/Main, 1968.
270. Mosel U., Greiner W. «Z. Phys.», 1968, Bd 217, S. 256.
271. Mosel U., Greiner W. «Z. Phys.», 1969, Bd 222, S. 261.
272. Mukherjee P., Cohen B. L. «Phys. Rev.», 1962, v. 127, p. 1284.
273. Mutchler G. Ph. D. thesis. Messachusetts Inst. Tech., 1965, unpublished.
274. Munn R. J., Block B., Malik F. B. «Phys. Rev. Lett.», 1968, v. 21, p.159.
275. Nathans R., Halpern J. «Phys. Rev.», 1954, v. 94, p. 659.
276. Nataf R. «Compt. rend.», 1955, v. 240, p. 2510.
277. Nataf R. «Compt. rend.», 1955, v. 241, p. 31.
278. Nathan P. and Nilsson S. G. Alpha-, Beta- and Gamma-Ray Spectro-
scopy, K- Siegbahn, ed. (North-Holland, Amsterdam, 1965). См.: Альфа-,
бета- и гамма-спектроскопия. Под ред. К- Зигбана. Вып. 2. Пер. с англ.
М., Атомиздат, 1969.
279. Nann Н. е. a. «Z. Phys.», 1969, Bd 218, S. 190.
280. Newman E. e. a. «Phys. Rev. Lett.», 1966, v.16, p. 28.
281. Newton T. D. «Canad. J Phys.», 1959, v. 37, p. 944
282. Newton T. D. «Canad. J. Phys.», 1960, v. 38, p. 700.
283. Nilsson S. G. «Kgl. Danske Videnskab. Selskab Mat.-Fys. Medd.», 1955,
Bd 29, N 16. (См. nep. в сб.: Деформация атомных ядер. М., Изд-во
иностр, лит., 1958.)
284. Nilsson S. G. е. a. «Nucl. Phys.», 1968, v. А115-, р. 545.
285. Nordheim L. W. «Phys. Rev.», 1949, v. 75, p. 1894.
286. Nordheim L. W. «Phys. Rev.», 1950, v. 78, p. 294.
287. Nordheim L. W. «Rev. Mod. Phys.», 1951, v. 23, p. 322.
288. Nuclear Data Sheets (Nuclear Data Group, Oak Ridge Natl Lab., Oak
Ridge, Tenn. 1966).
289. Obst E., Rauch F., Rossie E. «Phys. Lett.», 1966, v. 21, p. 50.
290. O’Connel J. S. e. a. «Phys. Rev.», 1962, v. 126, p. 228.
291. Von Oertzen W. On the Interaction Induced by the Exchange of Nucleons
between Two Identical Nuclear Cores (Max Planck Inst., Heidelberg, 1970).
447
292. Okamoto К. «Phys. Rev.», 1958, v. 110, p. 143.
293. Paul E. B. «Philos. Mag.», 1957, v. 2, p. 311.
294. Parsons R. W., Katz L. «Canad. J. Phys.», 1959, v. 37, p. 809, 1344.
295. Peker L. K. «Bull Acad. Sci. USSR Phys. Ser. English Transl.», 1957
v. 21, p. 1030.
296. Penfold A. S., Leiss J. E. «Phys. Rev.», 1959, v. 114, p. 1332.
297. Pelte D., Povh B., Scholz W. «Nucl. Phys.», 1966, v. 78, p. 241.
298. Pieper W., Greiner W. «Nucl. Phys.», 1968, v. A109, p. 539.
299. Plastino A., Abecasis S. M., Bosch H. E. «Nuovo cimento», 1968, v. 56B
p. 38.
300. Podolsky B. «Phys. Rev.», 1928, v. 32, p. 812.
301. Престон M. Физика ядра. Пер. с англ. М., «Мир», 1964.
302. Rainwater J. «Phys. Rev.», 1950, v. 79, p. 432.
303. Reiche F., Rademacher H. «Z. Phys.», 1926, Bd 39, S. 444.
304. Ritter R. C., Sheldon E., Strang M. «Nucl. Phys.», 1970, v. A140, p. 609.
305. Rosenfeld L. Nuclear Forces, North-Holland, Amsterdam, 1948.
306. Rose M. E. Elementary Theory of Angular Momentum. Wiley, N. Y., 1957
307. Rotenberg M. e. a. 3/-, 6/- and 9/-Symbols. Mass. Inst. Tech. Press. Cam-
bridge, Mass, 1959.
308. Rost E. Princeton Univ. Rept. PUC-937-66-202, 1966.
309. Rost E. «Phys. Lett.», 1968, v. 26B, p. 184.
310. Roeper P. «Z. Phys.», 1966, Bd 195, S. 316.
311. Sachs R. G. Nuclear Theory. Addison—Wesley, Reading, Mass., 1953
312. Schmidt Th. «Z. Phys.», 1937, Bd 106, S. 358.
313. Schmidt Th. «Naturwissenschaften», 1940, Bd 35, S. 565.
314. Scharff-Goldhabcr G., Weneser J. «Phys. Rev.», 1955, v. 98, p. 212.
315. Шифф Л. Квантовая механика. Пер. с англ. М., Изд-во иностр, лит.,
1957.
316. Scheck F. «Nucl. Phys.», 1966, v. 77, p. 577.
317. Scharnweber D. Diploma thesis Inst. Theor. Phys. Univ. Frankfurt/Main,
1968.
318. Scheid W. e. a. «Phys. Rev. Lett.», 1968, v. 21, p. 1479.
319. Scheid W., Greiner W. «Ann. Phys.», 1968, v. 48, p. 493.
320. Scheid W., Greiner W. «Z. Phys.», 1969, Bd 226, S. 364.
321. Schwalm D., Povh B. «Phys. Lett.», 1969, v. 29B, p. 103.
322. Scheid W. e. a. «Phys. Rev. Lett.», 1970, v. 25, p. 176.
323. Sen Gupta A. K-, van Patter D. H. «Phys. Rev.», 1968, v. 131, p. 318.
324. Segel R. E. e. a. «Phys. Rev. Lett.», 1963, v.10, p. 345.
325. Семеико С. Ф. «Ядерная физика», 1965, т. I, с. 414.
326. Sens J. C. High Energy Physics and Nuclear Structure, G. Alexander, ed.
North-Holland, Amsterdam, 1967.
327. Seaborn J. B. «Phys. Rev.», 1969, v. 179, p. 958.
328. Seeger P. A. Preprint. Los Alamos Sci., Lab. Univ. California LA-DC-
8950a.
329. Sheline R. K- «Nucl. Phys.», 1956, v. 2, p. 382.
330. Shakin C. Thesis. Harvard Univ., 1961.
331. Sheline R. K. e. a. «Phys. Rev. Lett.», 1961, v. 7, p. 446.
332. Shakin C. «Phys. Lett.», 1962, v. 1, p. 151.
448
333. Shevchenko V. G., Yudin N. P. Atomic Energy Review, 1965, v. 3, p. 3.
334. Shafroth S. M., Legge G. J. F. «Nucl. Phys.», 1968, v. AJ07, p. 181.
335. Signell P. S., Marshak R. E. «Phys. Rev.», 1957, v. 106, p. 832.
336. Signell P. S., Marshak R. E. «Phys. Rev.», 1958, v. 109, p. 1229.
337. Siemssen R. H. e. a. «Phys. Rev. Lett.», 1967, v.19, p. 369.
338. Skorka S. J. e. a. «Nucl. Data», 1966, v. 2, p. 347.
339. Slater L. J. Confluent Hypergeometric Functions (Cambridge Univ
Press, Cambridge, 1960).
340. Smith W. G. «Phys. Rev.», 1961, v. 122, p. 1600.
341. Smither R. K. «Phys. Rev.», 1961, v. 124, p. 183.
342. Сорокин Ю. И., Шевченко В. Г., Юрьев Б. А. «Ж- эксперим. н теор.
физ.», 1962, т. 43, с. 1600.
343. Solf J. е. a. «Phys. Lett.», 1969, v. 28В, р. 413.
344. Spicer В. М. е. a. «Austral. J. Phys.», 1959, v. 18, р. 298.
345. Spiegel М. R. Vector Analysis. Schaum, N. Y., 1959.
346. Spicer В. M. «Advances in Nuclear Phys.», 1969, v. 2, p. 1.
347. Steinwedel H., Jensen J. H. D. «Z. Naturforsch.», 1950, Bd 5a, S. 413.
348. Steinwedel H., Jensen J. H. D. «Phys. Rev.», 1959, v. 79, p. 1019.
349. Stelson P. H., Grodzins L. «Nucl. Data», 1965, v. 1, p. 21.
350. Stephens F. S. e. a. «Nucl. Phys.», 1965, v. 63, p. 82.
351. Stock H. Zur Theorie der Quantenhydrodynamik in Atomkernen Diplo-
marbeit Inst. Theoret. Phys. Univ. Frankfurt/Main, 1967.
352. Strutinsky V. M. «Nucl. Phys.», 1967, v. A95, p. 420.
353. Stock H., Arenhovel H. «Z. Phys.», 1968, Bd 212, S. 83.
354. Suessmann G. «Z. Phys.», 1954, Bd 139, S. 543.
355. Swift A., Elton L. R. B. «Phys. Rev. Lett.», 1966, v. 17, p. 484.
356. Tamura T. «Nuovo cimento», 1956, v. 4, p. 713.
357 Talmi 1., de Shalit A. Nuclear Shell Theory. Academic Press, N. Y.,—
Lond., 1963.
358. Thomas T. D. «Ann. Rev. Nucl. Sci.», 1968, v. 18, p. 343.
359. Tipler P. A. e. a. «Phys. Rev.», 1963, v. 129, p. 2096.
360. Townes С. H., Foley H. M., Low W. «Phys. Rev.», 1949, v. 76, p. 1415.
361. Tolhoek H. A. «Physica», 1955, v. 21, p. 1.
362. Toepffer C. Einteilchenzustande in deformierten Kernen. Diplomarbeit,
Phys. Inst. Univ. Freiburg/Breisgau, 1966.
363. Oberall H. «Nuovo cimento Suppl.», 1966, v. 4, p. 781.
364. Urbas T. D., Greiner W. «Z. Phys.», 1966, Bd 196, S. 44.
365. Urbas T. D. The Quadrupole Giant Resonances in Spherical Nuclei.
Thesis, Inst. Theor. Phys. Univ. Frankfurt/Main., i970.
366. Urbas T. D., Greiner W. «Phys. Rev. Lett.», 1970, v. 24, p. 1026.
367. Villars F. «Ann. Rev. Nucl. Sci.», 1957, v. 7, p. 185.
368. Villars F. «Nucl. Phys.», 1957, v. 3, p. 240.
369. Villars F. «Ann. Phys.», 1958, v. 5, p. 244.
370. Vogt E. W., McManus H. «Phys. Rev. Lett.», I960, v. 5, p. 518.
371. Voos U. C., von Oertzen W., Bock R. «Nucl. Phys.», 1969, v. A135, p. 207.
372. Ватсон Дж. Теория бесселевых функций. Пер. с англ. М., Изд-во
иностр, лит., 1957.
373. Wapstra А. Н. «Physica», 1955, v. 21, р. 367, 385.
449
374. Wapstra А. Н. «Handbuch Phys.», Springer, Berlin, 1958, v. 38, p. |
375. Warburton E. K. e. a. «Phys. Rev.», 1963, v. 129, p. 2180.
376. Weber H. J. e. a. «Z. Phys.», 1966, Bd 190, S. 25.
377. Weber H. J. e. a. «Z. Phys.», 1966, Bd 192, S. 182.
378. Webb D. V. e. a. «Phys. Rev.», 1967, v. 164, p. 1397.
379. Weisskopf V„ Wigner E. «Z. Phys.», 1930, Bd 63, S. 54.
380. Von Weizsacker C. F. «Z. Phys.» 1935, Bd 96, S. 461.
381. Von Weizsacker C. F. «Z. Phys.», 1935, Bd 96, S. 431.
382. Weisskopf V. F. «Phys. Rev.», 1951, v. 83, p. 1073.
383. Wigner E. P. Gruppentheorie. Vieweg, Braunschweig, 1931.
384. Wigner E. P. «Phys. Rev.», 1933, v. 43, p. 252.
385. Wigner E. P. «Z. Phys.», 1933, Bd 83, S. 253.
386. Wild W. Sitz. ber. Math. Naturw. KI. Bayer. Akad. Wiss, Miinclien, 1955.
387. Вигнер E. Теория групп и ее применение в квантовой механике атомных
спектров. Пер. с англ. М., Изд-во иностр, лит., 1961.
388. Wilkinson D. Н. In Nuclear Spectroscopy, F. Ajzenberg-Selove ed. (Aca-
demic Press, N. Y., 1960).
389. Woods R. D., Saxon D. S. «Phys. Rev.», 1954, v. 95, p. 577.
390. Wong C. Y. «Phys. Lett.», 1968, 26B, p. 120.
391. Wyatt P. J. e. a. «Phys. Rev», 1960, v.119, p. 1031.
392. Wyckoff J. M. e a. «Phys. Rev.», 1965, v. 137, p. 576.
393. Yoshizawa V. «Phys. Lett.», 1962, v 2, p. 261.
394. Ziegler B. «Z. Phys.», 1958, Bd 152, S. 566.
395. Ziegler B. «Nucl. Phys.», 1960, v. 17, p. 238.
396. Zucker A. «Ann. Rev. Nucl. Sci.», 1960, v. 10, p. 27.
397. Zurmuhl R. Praktische Mathematik, 5. Aufl. Springer, Berlin, 1965.
АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Адиабатичность в реакциях с тя-
желыми нонами 388, 407, 413
Аксиальная симметрия 43, 139,
173, 174, 240
Алаги правило 168
Анализ экспериментальных данных
для сферических ядер 378
Ангармонические эффекты в гигант-
ских резонансах 382
Ангармоничность квадрупольных
колебаний 63
Асимметрия ядер 156, 170, 259
Асимптотические квантовые числа
248
Атомная единица массы 403
Безвихревое движение 425
Бета-колебания 148, 344, 345
----- асимметрического волчка 179
Бета-колебательная полоса 154,
366
Борна—Оппенгеймера приближе-
ние 338, 342
Брента—Вигнера резонанс 320,
322
Вайскопфа единицы 29
Вакуум фононов 57
Взаимодействие дипольных коле-
баний с движением поверхности
329
Возбуждение фононов и гионов в фо-
тоядерных реакциях 372
----— — при столкновении тя-
желых ионов 392
Волновые функции динамической
коллективной модели 344
— — колебательно-вращательной
модели 147
— — коллективного движения,
симметрии 151
Волновые функции модели асим-
метрического волчка 172, 177
— оболочек для деформиро-
ванного ядра 243
- — — сильной связи, симметрии
239
модифицированной одночас-
тичной модели 324
- — трансформационные свойства
57, 68
Вращательная полоса нечетная 273
— — основного состояния 154
— — четная 273
Вращательно-колебательная модель
132, 147
Вращательный гидромагнитный фак-
тор 169, 261
- спектр 33
Вращение бесконечно малое 101,
104, 121, 125
— ядра 17, 33
Время взаимодействия 387
— столкновения 387
Вудса—Саксона потенциал 200
деформированный 268
Гамма-колебательная полоса 360
Гамильтона принцип 284, 286
— уравнения 390
Гамильтониан асимметрического
волчка 154
— деформированных нечетных ядер
351
— деформированных четно-четных
ядер 340
— коллективного движения 51
Гельмгольца уравнение 44, 307, 331
Гигантские мультипольные резо-
нансы 46, 308, 337
Гигантский квадрупольный резо-
нанс 308, 335, 349, 363
— резонанс 18, 43
Гидродинамическая модель 282
Гидродинамические уравнения Дви-
жения 290, 291
451
Гидродинамическое давление 290,
292
Гион 49, 337, 340, 356, 371
Гидромагнитный фактор 214, 219,
261
Гипергеометрические функции 124,
149
Гольдхабера—Теллера модель 282
Гомополярная ядерная связь 424
Граничные условия для плотности
распределения 409, 437
— — — системы двух жидкостей
284, 293, 331
Двухфононные состояния 57, 58,
61, 62
Деление ядерных молекул 399
ядра 18, 384
Дефект масс 403
Деформация тяжелых ионов 384,
388
Деформированные ядра, нечетно-
нечетные 271
— — нечетные 351
— — четно-четные 340, 344 , 349
Динамическая коллективная модель
329
— — — волновые функции и энер-
гии 344, 349, 353
— — — деформированные ядра 331
— — — сферические ядра 368
D-функции 107, 128, 428
Жесткости параметр 52, 373, 428
Зависимость частот гигантских ре-
зонансов от А 278, 296
— энергии связи от А 411
Затухание молекулярных состояний
417
Изомерный сдвиг 73
Испарение нуклонов 281
Испускание быстрых нейтронов 376
Квазидейтрон 282
Квазимолекулярные состояния 399
Квазимолекулярный ядерный оп-
тический потенциал 413
Квадрупольные гармонические ко-
лебания 53
— движения поверхности ядра 53
— - моменты 19, 22, 23, 207
— — возбужденных состояний 26,
75
Квадрупольный момент одночастич-
нын 20, 210
Квантовая гидродинамика 315
— механика ротатора 97
Квантовое число К 130, 131, 348
Классическое правило сумм зр]
Колебания поверхности 53, 425
— — кинетическая энергия 119
425, 426
— — потенциальная энергия 88, 426
Колебательные полосы 154
Колебательный спектр 33, 60
Коллективное движение 17
— — кинетическая энергия 51, 109
— — потенциальная энергия 88
Коллективные координаты 36, 312
— — гигантских мультнпольных
резонансов 329, 337
— — поверхности ядра 37
— корреляции 368
Конечные вращения 107, 121, 125
Константы связи колебаний поверх-
ности и гигантских резонансов
331, 339, 371
Кориолиса сила 239, 255
Короткодействующие корреляции
282
Кулоновские поправки к гигант-
ским резонансам 303
Кулоновский барьер 385
Кулоновское взаимодействие слож-
ных ядер 385
Лоренцева форма резонанса 299
Магические числа 34, 193, 198
— ядра 23, 34
Магнитные моменты 214
— — деформированных нечетных
ядер 263
Майер—Йенсена схема связи 204,
210
Массовая формула 403
Массовый дублет 403
— параметр 52
• — — для гигантских резонансов
314, 370
— — — колебаний поверхности
426
Матрицы вращений 428
Модель асимметрического волчка
170
— обобщенная 229
— оболочек, деформированные ядра
243
--- сферические ядра 185
— — трехосные деформированные
ядра 190, 270, 434
— одночастнчная 203
Модуль сжатия 408
•--эффективный 415
Молекула С12 —С12 401
Моменты инерции 111
Мультнпольность гигантских резо-
нансов 308
452
Насыщение ядерной материи 404
Неадиабатические эффекты 255
Нейтронная жидкость 282
Несжимаемость ядерной материи
282
Нильссона модель 244
Нордхейма связь 273
Обменные поправки 302
Оболочечная стуктура 184
— — потенциал гармонического ос-
циллятора 189
— — бесконечной прямоугольной
ямы 186
— — с (I • s)-взаимодействием 193
Одночастичные орбиты сферические
185
— переходы 28
Октупольный момент 20
О16—О16-система 414
Оператор гионный 337
— — коммутационные соотношения
48
— импульса 46
— коллективных мультнпольных
моментов 63, 316, 354
— магнитного дипольного момента
214
— монопольный 71
— обменный 323
— одночастичный 207
— поворота 104
— углового момента 101
— — — коммутационные соотно-
шения 102, 103
— •— — — — в лабораторной сис-
теме 107
— — — — — в собственной сис-
теме 101
— — — собственные функции 57,
127
— — — трансформационные свой-
ства 113
— фононный 48, 55
— — коммутационные соотношения
48
— числа фононов 55
— - электрического квадрупольного
момента 19, 354
Остаточные двухчастичные силы 35
Относительные вероятности 167, 260
Параметр касания 391
— развязывания 256
Периодическая таблица элементов 34
Переходы между квадрупольными
колебательными состояниями 74
— прямые 376
— электрические дипольные 30
- — — квадрупольные 31
— электромагнитные 26
Поверхностное натяжение, коэф-
фициент 411, 426
Поляризация тяжелых ионов 384
Поправки на множественность нейт-
ронов 377
Потенциал у-нестабильный 94
— деформированный 93
зависящий от скорости 269
— — — деформированный 269
— квазимолекулярный действи-
тельный 415, 420
— мнимый 417, 420
скоростей 292, 425
- центробежный 148
Потенциальная энергия квадруполь-
ных колебаний 77, 86, 88
Правило интервалов 23
Приближение абсолютно неупруго-
го рассеяния 416
Приведенная плотность 285
Протонная жидкость 44, 282
Пуассона скобки 140
Равновесная плотность 409
Распределение нуклонов 201
— плотности в ядрах 201, 411, 437
Рассеяние деформированных ядер
395
— кулоновское 420
— — амплитуда 420
— полная амплитуда 421
сферических ядер 390
— тяжелых ионов 383, 424
— упругое 420
— фотонов 364, 380
Расщепление у-полос в нечетных
ядрах 252
— гигантского резонанса 305, 343,
371
Реалистические одночастичные по-
тенциалы 199
Релятивистские эффекты в спин-
орбитальных силах 223
Реориентации эффекты 25
Рунге—Кутта метод 390
Сателлиты гигантского резонанса
344, 348
Сверхтяжелые ядра 384
Связь между конечными и бесконеч-
но малыми вращениями 125
Связь сильная 235
— слабая 231
— спин-орбнтальная 193, 221
Сечение выхода нейтронов 377
- поглощения у-излучения 279,
318, 347, 358, 362, 380
магнитного дипольного излу-
чения 280
453
— — электрического дипольного
излучения 280, 320, 376
— — — квадрупольного излуче-
ния 280, 363
— упругого рассеяния 420
— фотоядерных реакций Но 361
------- Ег 358
Сжимаемость ядра 411
Симметричный волчок 129
Скорость звука в системе из двух
жидкостей 294
Слияние тяжелых нонов 384
Синьорити 204, 210
Смешивание полос вследствие взаи-
модействия вращений и колеба-
ний 156, 159, 167
— — — кориолисовых сил 257
Спаривание нуклонов 203
Спектр вращательного движения 33
— гармонического квадрупольного
вибратора 33, 57
— гигантского дипольного резо-
нанса, деформированные ядра
347
— — — — сферические ядра 379
— колебательного движения 33
Среднеквадратичная деформация 69
Спин-изоспиновые волны 368
Струтинского минимум в барьере
деления 424
Теорема о проекциях 214
Томаса—Ферми модель ядра 406
Тормозное излучение 276
Трение в системе двух жидкостей
286, 319
Угловой момент 10
— — гионов 49, 316
— — остова 236
— — реакции с тяжелыми ионами
384
— — фонона 48
— — частицы 236
Унитарные преобразования 428
Упаковочный коэффициент 403
Уравнение непрерывности 284
Фонон 48
Фотоделение 275
Фотоионизация 281
Фотоядер ные реакции 278
Функция Гамильтона, асимметри-
ческий волчок 170
— — деформированные ядра 219.
395
- — орбитальное движение 385
сферические ядра 390
Центробежный параметр 159, 163
- эффект 157
Шмидта линии 215
Ширина гигантского резонанса 278
— разброса 286
Штейнведеля—Йенсена модель 282
Эйлера углы 98, 356, 388, 430
Эквивалентный радиус 413
Энергетическая щель 207
Энергия вакуума 57
- вращательного движения 111, 112
гигантских мультипольных ре-
зонансов 311, 336, 344, 349,
353, 372
деформации 391
- колебательного движения 425
— связи 193, 403
сжатия 408
симметрии 283, 313, 405, 408
спаривания 203, 405
- фононов 55, 56
Эффект блокировки 183
Эффекты входных состояний 423
Эффективная масса 302, 328
Юкавы взаимодействие 408
Ядерная молекула 416
— поверхность 425
Иуда Айзенберг
Вальтер Грайнер
МОДЕЛИ ЯДЕР
КОЛЛЕКТИВНЫЕ И
ОДНОЧАСТИЧНЫЕ ЯВЛЕНИЯ
Редактор В. И. Безрукова
Художественный редактор
А. Т. Кирьянов
Художник А. М. Шавард
Технический редактор
И. И. Подшебякин
Корректоры Л. С. Тимохова и
И. А. Смирнова
Сдано в набор 5/XI 1974 г.
Подп. к печати 1 3/V 1975 г.
Формат 60X90 Vie Бумага типографская № 1
Усл. печ. л. 28,5. Уч.-изд. л. 29,11
Тираж 3330 экз. Зак. изд. 71350
Зак. тип. 1218 ЦенаЗр. 15 к.
Атомиздат, 103031. Москва, К-31,
ул. Жданова. 5.
Московская типография № 4 Союзполиграф-
прома прн Государственном комитете Совета
Министров СССР по делам издательств,
полиграфии и книжной торговли.
Москва, 11-41. Б. Переяславская ул., 46
ВНИМАНИЮ ЧИТАТЕЛЕЙ!
На базах и складах Союзкниги и издательства имеется
следующая литература:
Денисов Ф. П., Мехедов В. Н.
Ядерные реакторы при высоких энергиях. 1972, 232
стр., 1 р. 42 к.
Коэффициенты перевода единиц измерения физико-тех-
нических величин. 1967 г., 40 стр., 8 к.
Заказы принимают все книжные магазины, распростра-
няющие научно-техническую литературу.
В Москве обращайтесь по адресу: Москва, Центр,
ул. Петровка, 15, магазин № 8, отдел «Книга—почтой».
Атомиздат