Курс математического анализа. Том 1 - Камынин Л.И.

Автор: Камынин Л.И.
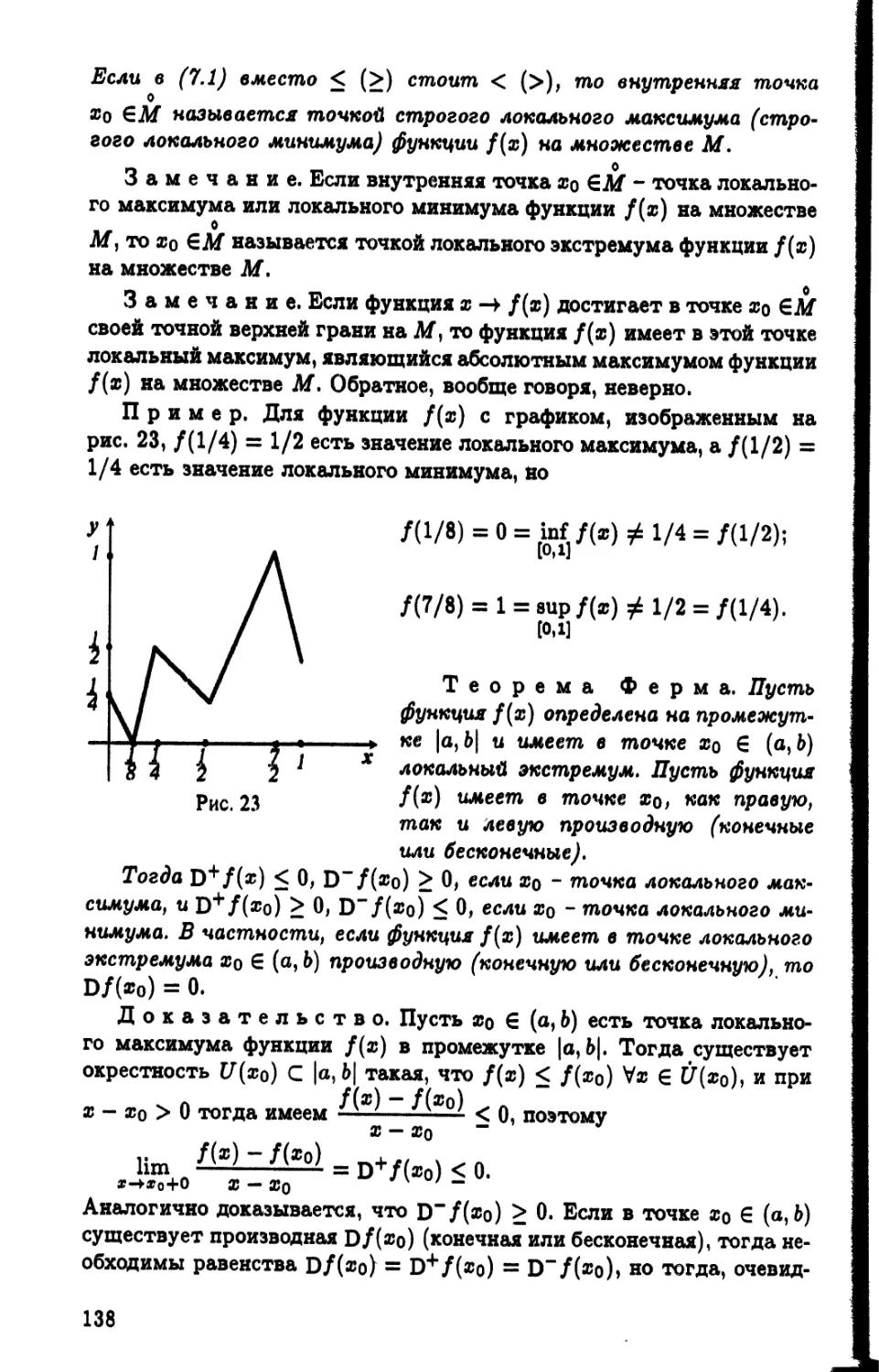
Теги: анализ математический анализ функциональный анализ математика
ISBN: 5-211-04483-5
Год: 2001
Похожие
Анализ линейных дифференциальных операторов с частными производными. Том 1. Теория распределений и анализ Фурье
Анализ линейных дифференциальных операторов с частными производными. Том 2. Дифференциальные операторы с постоянными коэффициентами
Анализ линейных дифференциальных операторов с частными производными. Том 4. Интегральные операторы Фурье
Пучки на многообразиях
Текст
                    Л.И.Камынин
КУРС
МАТЕМАТИЧЕСКОГО
АНАЛИЗА	I
Л. И. Камынин
КУРС
МАТЕМАТИЧЕСКОГО
АНАЛИЗА
Том I
2-е издание, исправленное и дополненное:.
Допущено Министерством образования Рос-
сийской Федерации в качестве учебника для
студентов высших учебных заведений, обуча-
ющихся по направлению 510100 «Математика» и
специальности 010100 «Математика»
ИЗДАТЕЛЬСТВО МОСКОВСКОГО УНИВЕРСИТЕТА
2001
УДК 517
ББК 22.161
К18
Федеральная программа книгоиздания России
Рецензенты:
академик РАН Ю. Г. Решетняк,
доктор физико-математических наук Я Я Фельдман,
доктор физико-математических наук В. Я Буренков
Камынин Л. И.
К18 Курс математического анализа. Т. 1.- 2-е изд., испр. и доп. -
М.: Изд-во МГУ, 2001.- 432 с.
ISBN 5-211-04483-5 (Т. 1)
ISBN 5-211-01941-5
Учебник написан на основе лекций, читаемых автором на механико-
математическом факультете Московского университет. В книге отражены следую-
щие темы: теория пределов и дифференциальное исчисление функций одного пере-
менного, интегральное исчисление функций одного переменного, дифференциаль-
ное исчисление функций многих переменных, ряды, бесконечные произведения и
несобственные интегралы, кратные интегралы Римана и интегрирование дифферен-
циальных форм. Материал излагается на современном уровне, теоретические поло-
жения иллюстрируются примерами, допускающими простое наглядное истолкова-
ние.
Для студентов математических специальностей вузов.
УДК 517
ББК 22.161
ISBN 5-211-04483-5(Т. 1)
ISBN 5-211-01941-5
О Издательство Московского
университета, 2001
ПРЕДИСЛОВИЕ
Математический анализ — основа математи-
ческого образования. В том или ином объеме эта
дисциплина изучается практически во всех учеб-
ных заведениях, и ей посвящено большое количе-
ство книг, адресованных различному кругу чита-
телей.
Естественно, наиболее основательно предмет
математического анализа изучается в университе-
тах и институтах, по уровню математической под-
готовки близких к ним.
Тем не менее местом, где выдерживается эта-
лон преподавания этой дисциплины, являются ме-
ханико-математические (математические) факуль-
теты университетов. На них возложена особая
роль — сохранить лучшие традиции в подходах к
изучению, восходящие ещё к Ньютону и Лейбни-
цу, выработать новый взгляд, развить новый со-
временный математический язык, обогатить этот
предмет новыми идеями и дидактическими наход-
ками. Именно на ученых, закончивших универси-
теты, работающих в них или связанных с ними,
ложится также задача создания новых учебников
по математическому анализу.
У нас имеется много первоклассных учебни-
ков по математическому анализу, каждый из них
— большое достояние высшей школы. Поэтому
создание нового учебника — трудная и ответст-
венная задача.
Предлагаемый читателю двухтомный учеб-
ник «Курс математического анализа» профессора
Л. И. Камынина — удачная попытка создать хо-
роший учебник по университетскому курсу.
Автор этого двухтомника — профессор ка-
федры математического анализа механико-
математического факультета Московского универ-
ситета — многие годы читал этот курс на механи-
ко-математическом факультете МГУ, издал его
ранее в виде четырех ротапринтных выпусков.
Этот учебник характеризуют прежде всего
глубина и основательность изложения. В некото-
ром смысле в нем есть все, что может понадобить-
ся студенту при изучении предмета. А с другой
стороны, этот материал реально прочитывается за
два года обучения студентам, т. е. это практически
лекции профессора Л. И. Камынина.
Строгость изложения, современный язык,
полная логическая «замкнутость» изложения —
стиль учебника.
В учебнике имеется очень много находок в
подходах к изложению материала, в том числе тех,
которые иногда позволяют и по-новому взглянуть
на целый раздел классической дисциплины.
Нет нужды перечислять разделы и главы
учебника, можно только с уверенностью сказать,
что, изучив этот учебник, найдет для себя много
полезного и начинающий штудировать математи-
ческий анализ, и уже знакомый с этим курсом, и
профессионал в этой области.
Ректор
Московского государственного
университета,
академик РАН	В. А. Садовничий
Часть!
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИЙ ОДНОГО ПЕРЕМЕННОГО
Глава 1
ОСНОВНЫЕ ПОНЯТИЯ
МАТЕМАТИЧЕСКОГО АНАЛИЗА
§ 1. Некоторые понятия теории множеств
и математической логики
Понятие множества на совокупности объектов является одним из
самых фундаментальных в математике. Множества определяются не-
которым свойством 01, которым должен или обладать, или не обладать
каждый из рассматриваемых объектов: те объекты, которые облада-
ют свойством 01, образуют множество А,
Пример. Пусть рассмотрены совокупность целых чисел Z и свой-
ство 01, заключающееся в том, чтобы «быть простым числом». Тогда
соответствующее свойству 01 множество А состоит из всех простых
чисел 2, 3, 5, 7, 11, 13,...
Основным в математическом исследовании множеств является то,
что множества, комбинируясь между собой в результате выполнения
некоторых операций, образуют новые множества - так же, как числа,
комбинируясь между собой с помощью операций сложения и умноже-
ния, образуют новые числа (например, 2 + 3 = 5, 2 - 3 = 6 и т.д.). Из-
учение операций над множествами приводит к «алгебре множеств»,
которая имеет много общего с обычной числовой алгеброй, хотя кое в
чем и отличается от нее.
Будем в дальнейшем рассматривать множества, входящие в неко-
торое определенное «универсальное» множество объектов Е, и обозна-
чать через А, В, С, X, У и т.д. некоторые подмножества из Е.
Пример. Пусть No - множество всех неотрицательных целых
чисел 0, 1, 2, 3, 4,... . Пусть тогда N - множество положительных
целых чисел 1, 2, 3, 4, 5,..., А - множество всех простых чисел, В -
множество всех четных чисел 2, 4, 6,..., С - множество всех нечетных
чисел 1, 3, 5, 7,...
Пример. Пусть Е - совокупность всех точек на плоскости и А
5
- множество точек, лежащих внутри какого-либо круга, а В - множе-
ство точек, лежащих внутри некоторого треугольника.
Объекты, из которых состоит данное множество А (т. е. объек-
ты, обладающие свойством St), называются элементами множества
А (или его точками) и обозначаются а, Ь, с. Запись а = Ъ означает,
что элементы а я Ъ совпадают. Запись а Ъ означает, что эти эле-
менты различны. Если а - элемент множества А, то пишут a 6 А
(элемент а принадлежит множеству А) или А Э а (множество А со-
держит элемент а). Запись а $ А или её А означает, что элемент а не
принадлежит множеству А (т. е. не обладает свойством St).
Пример. Если Z - множество всех целых чисел, а А - множество
всех простых чисел, то 3 € А, но 10€А.
Определение. Если А есть множество элементов а € Е,
обладающих свойством %, то пишут А = {а € Е|21}.
Пример. Если Е = R - множество всех действительных чисел,
то множество X всех действительных чисел, удовлетворяющих нера-
венствам -1 < х < 3, записывается в виде X = {® € R| - 1 < х < 3}.
Определение. Если АиВ - множества из Е и каждый эле-
мент а множества А принадлежит множеству В, то множество
А называется подмножеством множества В. Символически это за-
писывается в виде АС В или В D А, где знак С называется символом
включения.
Замечание. Отношение А С В означает, что в А нет элементов,
не принадлежащих В.
Пример. Пусть Е = Z - множество всех целых чисел, А - множе-
ство целых чисел, делящихся на 10, а В - множество всех целых чисел,
делящихся на 5, тогда А есть подмножество В, т. е. А С В.
Пример. Пусть А - подмножество Е я а € А - элемент из А.
Тогда множество {а}, состоящее из одного элемента а, есть подмно-
жество А, т. е. {а} С А.
Определение. Если множество А не сдержится во мно-
жестве В, то пишут А £ В.
Замечание. Если А С В « В С А, то множества А я В
содержат одни те же элементы и тогда пишут А = В.
Отношения включения А С В между множествами напоминает
отношение а < b между действительными числами. Отношение вклю-
чения обладает следующими свойствами, непосредственно вытекаю-
щими из определения операции включения С:
1)	А С А (т. е. всякое множество А есть подмножество самого
себя);
2)	если А С В я В С А, то А = В;
3)	если АсВиВсС, тоАсС (транзитивность отношения
включения).
б
Замечание. В силу свойств 1)-3) отношение включения Ас В
иногда называют отношением порядка. Основное отличие рассматри-
ваемого отношения Л С В от отношения а < Ъ из теории чисел заклю-
чается в том, что между любыми двумя заданными действительными
числами а 6 R и 6 6 R непременно осуществляется хотя бы одно из
отношений а < Ъ или b < а, тогда как для отношения Ас В аналогич-
ное утверждение неверно, например, при А = {1,2,3} и В = {2,3,4}
не имеет места ни отношение А С В, ни В С А. Множество Е называ-
ется поэтому частично упорядоченным отнощением А С В, в отличие
от множества R действительных чисел, являющегося, как говорят,
вполне упорядоченным отношением а < Ь.
Рассмотрим множество объектов из универсального множества В,
обладающих свойством а а. Такое множество, очевидно, не содер-
жит ни одного элемента и называется пустым множеством. Пустое
множество обозначается символом 0. Итак, по определению 0 = {а €
В|а -ф. а}. Далее заметим, что само универсальное множество Е мо-
жет быть определено как множество объектов, обладающих свойством
а = а, т. е. Е = {а € Е\а = а}.
Замечание. Если А 0 0, то это означает, что множество А
не пусто, т. е. содержит хотя бы один элемент из Е.
Пример. Пусть Е = R - множество действительных чисел,
тогда А = {« € R|® < 2, х > 5} = 0, но В = {« € R|« < 2} 0.
Отметим свойства:
4)	0 С А для любого множества А из В.
В самом деле, если бы отйошение 0 С А не имело места, то это
означало бы, что в множестве 0 существует элемент а, не принад-
лежащий множеству А, но 0 пусто, а поэтому вообще не содержит
никаких элементов. Противоречие.
5)	А С В для любого множества А из В.
Замечание. Согласно свойству 1) всякое множество А есть
подмножество самого себя, а в силу свойства 4) пустое множество так-
же является подмножеством А. Множества А и 0 называются несоб-
ственными подмножествами множества А, остальные подмножества
множества А называются собственными подмножествами А. Таким
образом, В есть собственное подмножество А, если В 0, В С А и
В/ А.
Определим теперь две операции над множествами, формально об-
ладающие многими алгебраическими свойствами сложения и умно-
жения чисел, хотя по своему внутреннему содержанию совершенно
отличные от этих арифметических операций.
Определение. Пусть АиВ - множества из Е. Объединением
(или суммой) АиВ множеств АиВ называется множество всех
элементов, каждый из которых принадлежит хотя бы одному из
множеств АиВ, т. е. х € A U В, если х € А, но х£В, или х Е В,
7
но х£А, или, наконец, х 6 А и х 6 В.
Таким образом, АОВ = {хЕ Е\х 6 А или х G В}.
Пример. Пусть Е = N - множество натуральных чисел и
А = {1,2,3}, В = {2,3,4}, тогда A U В = {1,2,3,4}.
Пример. Пусть Е = Z - множество всех целых чисел, тогда
N = A U В, где N - множество всех натуральных чисел, А - множес-
тво всех четных натуральных чисел, В - множество всех нечетных
натуральных чисел.
Обобщение. Если {Аа} - совокупность множеств Аа из Е, то
U Аа есть объединение всех Аа, так что (JAa = {® G Е\х 6 Аа хотя
а	а
+оо
бы для одного a}, (J Ап = Ai U А2 U ... U Ап U ... = {® 6 Е\х G Ai,
П = 1
или х G Аг,..., или х G Ап,...}.
Определение. Пусть АиВ - множества из Е. Пересечением
А О В множеств АиВ называется множество всех элементов,
каждый из которых принадлежит и А и В, т. е. х 6 АП В, если
одновременно х G А их еВ. Таким образом,
асу в = {х е е\х е А и х е в}.
Замечание. Если у множества А или В нет общих элементов,
то АаВ = 0.
Пример. Если Е = N и А = {1,2,3}, В = {2,3,4}, то А А В =
{2,3}.
Обобщение. Если {Аа} - совокупность множеств из Е, то
Ч-оо
Q Аа = {ж G Е\х G Аа при каждом a}, Q Ап = {х G Е\х 6 Ап для
а	п=1
любого П 6 N}.
Пример. Пусть Е = Q - множество всех рациональных чисел
и Qn - множество всех рациональных чисел, абсолютные величины
1	f	11	+°°
которых < -, т. е. Qn = < q € Q| |g| < - ?• Тогда Q Qn = {0}.
n	I	nJ	n=1
Пример. Пусть E = Q и Q+ = Q|g > 0, q < Тогда
I	n J
4-00
n <2+ = 0.
n = l
Операции объединения и пересечения обладают следующими ал-
гебраическими свойствами:
б)	A U В = В U А (коммутативность объединения);
7)	АА В = В П А (коммутативность пересечения);
8)	AU(BUC) = (AUB)UC = AUBUC (ассоциативность объ-
единения);
9)	АП(ВПС) = (АПВ)ПС = АПВПС (ассоциативность пере-
сечения);
8
10)	AuA = A; 11) AnA = A; 12) (AUB) ПС = (АЛС) U (В ПС)
и вообще ((J Aa) П В = |J(Aa n (дистрибутивность пересечения
a	a
относительно объединения);
13)	(АПВ)иС = (AUC) Л(ВиС) и вообще (Q Aa)UC = П(АаиС)
а	а
(дистрибутивность объединения относительно пересечения);
14)	A U 0 = А; 15) А А Е = А;
16)	A U Е = Е; 17) А А 0 = 0;
18)	отношение А С В эквивалентно каждому из двух отношений
AUB -В, А ГУ В = А.
Проверка этих свойств проводится с помощью элементарной логи-
ки. Приведем в качестве примеров доказательств свойств 10) и 12).
Доказательство свойства 10) A U А = А. Пусть х 6 A U А,
тогда х 6 А или х 6 А, т. е. х 6 А. Таким образом,
АиАсА.	(1.1)
Пусть теперь х € А. Тогда, очевидно, х 6 A U А, т. е. имеет место
включение
АсАиА.	(1.2)
Из (1.1) и (1.2) вытекает свойство 10) A U А = А.
Доказательство свойства 12). Обозначим левую и правую
части равенства 12) через F и G соответственно. Пусть х 6 F. Тогда
х 6 С и ® Е АиВ, т. е. х Е А или х Е В (или то и другое), поэтому
х Е А О С или х Е ВС\ С так, что х Е G. Но тогда имеем включение
F С G.	(1.3)
Пусть теперь х Е G. Тогда х Е А А С или х Е В А С, т. е. х Е С и
х Е A U В так, что х Е F. Поэтому имеем
G С F	(1.4)
Из (1.3) и (1.4) следует F = G, чем свойство 12) доказано.
Задание. Провести самостоятельно доказательство остальных
свойств 1)-18).
Замечание. Свойства 6)-9) и 12) внешне тождественны с хо-
рошо известными свойствами коммутативности, ассоциативности и
дистрибутивности операций сложения (+) и умножения (•) в обычной
алгебре чисел. Отсюда вытекает, что все правила обычной алгебры
чисел имеют место и в алгебре множеств. С другой стороны, свойства
10), 11) и 13) не имеют аналогов в обычной алгебре и они придают
алгебре множеств более простую структуру. Например, вместо фор-
мулы «квадрата суммы» (а 4- 5)2 = а2 + 2аЬ 4- Ь2 из обычной алгебры
чисел в алгебре множеств в силу свойства И) имеем более простое
9
равенство (A U В) П (A U В) = A (J В. Свойства 14), 15) и 17) гово-
рят о том, что свойства множеств 0 и Е по отношению к операциям
объединения U и пересечения Г) весьма похожи на свойства нуля 0 и
единицы 1 по отношению к операциям сложения (+) и умножения (•)
в числовой алгебре.
Замечание. Утверждения 1)—18) обладают замечательным
свойством двойственности в следующем смысле: если в одном из зако-
нов 1)—18) символы (С и Э), (0 и Е), (U и О) переставляются между
собой (поскольку они встречаются), то в результате получается опять
один из тех законов, а именно свойство 1) переходит в Г) A D А, свой-
ство 2) переходит в свойство 2*): если A D В и В D А, то А = В, свой-
ство 3) переходит в свойство транзитивности включения D, свойство
4) переходит в свойство 5), а 5) переходит в 4); закон коммутативнос-
ти объединения U 6) переходит в закон коммутативности пересечения
И 7) и, наоборот, 7) переходит в 6); закон ассоциативности объедине-
ния U 8) переходит в закон ассоциативности пересечения 9) и обратно,
9) переходит в 8); свойство 10) переходит в И), а 11) переходит в 10);
закон дистрибутивности пересечения П относительно объединения U
12) переходит в закон 13), а 13) переходит в 12); 14) переходит в 15),
а 15) переходит в 14); 16) переходит в 17), а 17) переходит в 16); на-
конец, закон 18) переходит в «двойственный» закон 18*), отношение
A D В эквивалентно одному из отношений А П В = В,A U В = А.
Замечание. Из двойственности законов 1)—18) вытекает, что
каждой теореме, которая может быть выведена из законов 1)—18), соот-
ветствует другая «двойственная теорема», получающаяся из первой
указанными выше перестановками символов. (В самом деле, посколь-
ку доказательство первой теоремы состоит в последовательном при-
менении некоторых законов 1)—18), то, применяя на соответствующих
этапах «двойственные законы», получаем доказательство двойствен-
ной теоремы.)
Определение. Пусть АиВ - множества из Е. Разностью
А\В множеств АиВ называется множество всех элементов, при-
надлежащих А, но не принадлежащих В, т, е, х € А\В, если х € А,
но х^В. Таким образом,
А \ В — {х 6 В|х € А и x'ZB}.
Замечание. В определении разности А \ В, вообще говоря, не
предполагается, что A D В,
Пример. Пусть Е = N и А = {1,2,3), В = {2,3,4,5). Тогда
А\В = {1}, В \ А = {4,5}.
Определение. Пусть А - множество из Е. Дополнением
СА множества А (относительно Е) называется множество Е\А.
Очевидно, что СА = {х € В|х?А}. Символ С называется символом
операции дополнения.
10
Пример. Пусть Е = N и А - множество всех простых чисел,
тогда С А есть множество, состоящее из всех составных чисел и числа
1.
Операция перехода от А к СА, для которой нет аналога в обычной
алгебре чисел, обладает следующими свойствами:
19)	A U СА = Е\ 20) А Л СА = 0; 21) С0 = Е\
22)	СЕ = 0; 23) ССА = А; 24) отношение А С В, эквивалентное
отношение СВ С СА;
25)	С(А U В) = СА Л СВ и вообще C(|J А«) = f) САО;
а	а
26)	С(А Л В) = СА U СВ я вообще C(f) А«) = (J СА«.
а	а
Докажем для примера формулу 26) C(Q Аа) =
а	а
Пусть х € С(р|Аа), тогда х не может принадлежать всем
а
т. е. х Е САа хотя бы для одного а, но тогда х Е (JCAa, откуда
а
имеем C(QAe) С |JCAe. Пусть теперь х Е |jCAe, т. е. х € САа
а	а	а
хотя бы для одного а, но тогда	т. е. х € С((")-Аа), откуда
а	а
С С(р|Аа), но тем самым формула 26) доказана,
а	а
Задание. Доказать остальные свойства 19)-25) самостоятельно.
Замечание. Законы 19)—26), как и законы 1)—18), облада-
ют «двойственностью» относительно указанных ранее перестановок
символов.
Замечание. Для операции вычитания можно отметить следу-
ющие свойства:
(А \ В) Л С = (А Л С) \ В = (А Л С) \ (В Л С);
А\В = А\(АЛВ); А = (А ЛВ) и(А\В).
Если А С В, то А Л СВ = 0. (Доказательство этих свойств провести
самостоятельно.)
Пусть А и В - множества (из Е) и а Е А, Ъ Е В - элементы этих
множеств. Рассмотрим упорядоченную пару с = (а, 6). Тогда равен-
ство (а, Ь) = (а , b ) означает, что а = а и 6 = 6 ; в частности, равен-
ство (а, Ь) = (Ь, а) приводит к а = Ъ. Первый (соответственно второй)
элемент упорядоченной пары с = (а, 6) называется первой (соответ-
ственно второй) проекцией пары с и обозначается символом а = рг3 с
(соответственно 5 = рг3 с).
Определение. Пусть АиВ- множества из Е. Тогда де-
картовым произведением множеств АиВ называется множество
Ах.В, состоящее из всех упорядоченных пар (в,Ъ), где а Е А и b Е В.
Таким образом, А х В = {с = (а,Ь)|а Е АиЬ Е В}.
Из определения декартова произведения вытекают следующие его
свойства:
И
1)	отношение А х В = 0 эквивалентно отношению А = 0 или
В = 0;
2)	если Ах В 0 (это означает, что А ф 0 и В ф 0), то отношение
А х В С А х В эквивалентно отношению А С А и В С В;
3)	(А х В) U (А' х В) = (A U А'} х В;
4)	(А х В)Н(А' х В ) = (АПА ) х (ВПВ').
Докажем, например, равенство 4). Введем обозначения
F = (AxB)n(A' хВ'), G=(AHA') х(ВПВ').
Пусть z = (ж, у) Е F, тогда включение z 6 А х В дает х Е А
и у 6 В, а включение z 6 А х В дает х Е А и у 6 В , поэтому
х 6 АП А и у Е В АВ , откуда z Е G, т. е.
F С G.	(1.5)
Далее, пусть z = (ж, у) Е Gr тогда х Е АП А и у Е В П В . Но из
х Е А и у Е В имеем z Е Ах В, а из х Е А ну Е В имеем z Е А х В ,
откуда z Е F и поэтому
G С F.	(1.6)
Из включений (1.5) и (1.6) имеем равенство 4).
Пример. Пусть А = {1,2,3} С N и В = {1,2} С N. Тогда
(1,2) ф (2,1), так как ах = 1 / 2 = a2, ЬХ = 2 / 1 = Ь2? (1? 2) ± (1,1),
так как хотя ах = 1 = а2, но i>x = 2	1 = i>2, (2,2) = (2,2).
Пример. Пусть XOY - декартова двумерная плоскость, где
ОХ - ось абсцисс, a OY - ось ординат. Пусть А = {ж Е R|0 < х < 1},
В = {у Е R|0 < у < 1}. Тогда множество А х В = {(®,j/) Е XOY|0 <
®<1,0<у<1} есть квадрат на плоскости XOY.
Обобщение. Декартовым произведением множеств Ах, Аг, ...,
Ап называется множество (обозначаемое символом Ах х Аг х ... х Ап)
всех упорядоченных систем из п элементов (ах,аг,... , ап), где ах Е
Ах, а2 Е А2,..., ап Е Ап, т.е. АххА2х...хАп = {(ах, а2,... , ап) |а< Е
А,; г = 1,2, ...,п}. Если с = (ах, а2,... , ап), то а* = prtc есть г-я
проекция элемента с.
Рассмотрим некоторые понятия математической логики. Любая
теорема, доказываемая в математике, состоит в том, что задается не-
которое свойство А, называемое условием, и из него с помощью логи-
ческих рассуждений выводится свойство В, называемое заключением.
Отметим некоторые логические операции, не вдаваясь в их математи-
ческое обоснование, поскольку это будет серьезно рассмотрено в курсе
математической логики.
1.	Логическая операция импликация. Обозначение =>. А => В
означает, что свойство А влечет свойство В.
Пример. Пусть х Е R. Рассмотрим свойства А : х < 3 и В:
х < 4. Тогда А => В.
12
Замечание. Если А => В, то обратная теорема записывается
в виде В => А.
Из приведенного выше примера следует, что обратная теорема,
вообще говоря, может и не быть справедливой. Далее, пусть X = {ж 6
R|A} и Y = {у G R|B}, тогда А => В соответствует отношению
X С Y.
Замечание. Операция импликации => вполне аналогична
операции включения С из алгебры множеств.
2.	Логическая операция тождество. Обозначение <£>. Если для
данной теоремы А => В справедлива и обратная теорема В => А, то
свойства АиВ эквивалентны, что и записывается в виде Л В, а
словами выражается в форме: «для того чтобы было справедливо Л,
необходимо и достаточно выполнения В».
Замечание. Логическая операция тождества <=> вполне ана-
логична операции = в алгебре множеств.
3.	Логическая операция отрицание. Обозначение ~ или
Утверждение, противоположное некоторому свойству Л, записывает-
ся в виде «не Л» или Л, или ->Л.
Пример. Пусть х 6 R. Рассмотрим свойство Л: х < 3. Тогда
свойство -»Л = Л : х > 3. Вводя множества X = {ж 6 R|A}, Y = {ж 6
R| Л}, видим, что У = СХ = R \ X. Вообще, если х^ЕтХ СЕ, то
свойству Л : х G X соответствует ->А : хЁХ.
Замечание. Логическая операция отрицания вполне анало-
гична операции дополнения С в алгебре множеств.
3 а м е ч а н и е. Всегда справедливо утверждение: не не Л <=> Л,
т. е. -«-IЛ = Л, (Л) = Л.
Замечание. Имеет место принцип исключенного третьего,
т. е. для любого свойства Л справедливо утверждение: «или Л или не
Л».
Т е о р е м а. (Л => В) <=> (-«В => -»Л).
Доказательство. 1. Пусть имеет место Л => В и пусть при
этом имеет место -vB. Тогда в силу принципа исключенного треть-
его должно быть справедливо ->Л (иначе, в силу Л => В, было бы
справедливо В, а не —<В), т. е. ->В => -пЛ.
2. Пусть имеет место -чВ => ->Л. Тогда по доказанному выше имеем
«Л) => -•(-'В) , т. е. Л => В.
4. Логическая операция «или». Обозначение V. Если некото-
рый объект обладает свойством Л или свойством В, то пишут что оно
удовлетворяет «Л или В» и иначе в символическом виде Л V В. Отме-
тим, что утверждение «Л или В» вовсе не исключает одновременного
выполнения и Л и В.
Пример. Пусть ж 6 R и Л : -1<®<0, В : 0 < ж < 3.
Тогда Л V В : — 1 < х < 3. Заметим, что если X = {ж 6 R|A} и
Y = {х е R|B), то	€ R|AVB}.
13
Замечание. Операция V вполне аналогична операции объеди-
нения (J из алгебры множеств.
б. Логическая операция «и». Обозначение А (&). Если имеют
место одновременно свойства А и В, то это записывается в виде АЛВ
или же «А и В», или же А&В.
Замечание. Операция логического «и» вполне аналогична
операции пересечения f"| в алгебре множеств.
Докажите самостоятельно следующие свойства введенных выше
логических операций:
AVB = AAB, AAB = AVB
или
avb = ^кв,Акв = avb.
Будем в дальнейшем использовать знакомые по школьному курсу
кванторы 3 и V. Квантор существования 3 означает выражение «су-
ществует» или «существуют». Квантор общности V заменяет слова
«для любого», «для каждого».
Пусть дано множество X и свойство А(®) (где х е X). Тогда сим-
волическая запись (Ух € X) (А(х)) означает: для любого элемента
х, принадлежащего множеству X, имеет место А(х) (т. е. выполнено
свойство А). Символическая запись (3® € X) (А(®)) означает: сущест-
вует элемент х из множества X, для которого выполнено свойство А.
Используя операцию отрицания, имеем
(V® 6 Х)(А(«)) & (3® 6 Х)(А(®)),
а также
(3® 6 Х)(А(х)) & (V® € Х)(А(х)).
$ 2. Понятия отображения и функции
Определение. Пусть АиВ - два непустых множества.
Отображением А в В или функцией) определенной на А со значени-
ями в В, называется соответствие ff которое каждому элементу
х € А соотносит (ставит в соответствие) единственный элемент
у ЕВ, обозначаемый через f(x).
Обозначения для отображения (функции): А В; f : А В;
f : У = /(®), ® € 4, у € В; f : х € A, f(x) Е В\ у = /(®), х € А,
у Е В; х —> /(®). Элемент f(x) при отображении х f(x) называ-
ется значением функции f(x), принимаемым в точке х. Множество А
при отображении f : А —> В называется областью определения или
областью существования отображения (функции) /. Множество всех
значений функции f называется ее областью значений (или множест-
вом значений). Таким образом, если Y - множество значений функции
f : А В, го Y = {у Е В|3® € А такое, что/(х) = у}. Следует раз-
личать отображение f и элемент /(х), соответствующий х при этом
отображении.
14
Примеры. 1. Равенство у = х3 ставит в соответствие любому
х € R единственное число у € R. Например, если х = 2, то у =
4, если х = —3, то у = 9. Это равенство задает функцию х -> х3,
определенную на множестве X = {ж € R| — оо < х < +оо} с областью
значений У = {у € R|0 < у < 4-оо}.
Если же обозначить эту функцию символом /, то имеем /(2) = 4,
/(-3)=9.
2.	Равенство N = п! ставит в соответствие любому п € N един-
ственное натуральное же число JV. Например, если п = 3, то N = 6,
если п = 5, то N = 120. Таким образом, это равенство задает функ-
цию, определенную на множестве натуральных чисел N с областью
значений, являющейся подмножеством N : п -4 п!.
3.	Функция у = sin х, —оо < х < +оо, у € [-1,1]. Если /(х) = sin х,
то /(0) = 0, /(ir/2) = 1; х -> sinx.
4.	Пусть А есть множество треугольников х на плоскости, а В = R.
Поставим в соответствие любому треугольнику х 6 А длину его пери-
метра у, тем самым будет задана функция, определенная на множест-
ве всех треугольников плоскости. Аргументом этой функции будет х,
значениями аргумента будут различные треугольники, а значениями
функции - периметры треугольников.
5.	Любому числу n € Z поставим в соответствие точку (п, п). Тог-
да получим отображение множества всех целых чисел Z в множество
всех точек плоскости: п -> (п, п).
Определение. Пусть дано отображение f : А -4 В. Тогда
множество Г = {(х, у) € А х В|х € А, у = /(х) € В} называется
графиком отображения f.
6.	Пусть А есть отрезок [—1,1] оси абсцисс ОХ, а В есть ось ор-
динат OY координатной плоскости XOY, причем Г есть дуга полу-
окружности единичного радиуса с центром в начале координат. Тогда
Г есть график отображения
А -^4В, где f :у = VI -ха, -1 < х < 1, у € В; х -4 т/1 - х*.
7.	Функция, ставящая любому элементу х своей области определе-
ния А одно и то же число с, называется постоянной функцией. Гра-
фиком постоянной функции х -> с является множество Г = {А} х {с}.
Постоянная функция х -4 с иногда обозначается этой же буквой с.
Определение. Отображение f : А -4 А, определенное
равенством f(x) = х Vx € А, называется тождественным.
Замечание. Если А С В, то отображение А В, опреде-
ленное равенством f (х) = х, называется канонической инъекцией А в
В.
Определение. Вели Ах В - декартово произведение мно-
жеств А и В, то отображение ргА : А х В -4 А (или (х, у) -4 х),
ставящее в соответствие любой паре (х,у) € А х В элемент х €
15
А, называется проекцией на А. Аналогично определяется проекция
(ж, У) У на В.
Определение. Пусть f : А В - отображение множества А>
в множество В. Если X С А, то множество тех элементов у € В>
которые в силу отображения f поставлены в соответствие хотя
бы одному элементу х Е X, называют образом множества X при
отображении f и обозначают через f(X). Итак, f(X) = {у 6 В|Эх €
X такое, что/(х) = у}.
Замечание. Очевидно, f(A) - это область значений отобра-
жения f : А В.
Пример. Пусть f : у = х2, х € [—4,4], у € [0,16] и X = [-1,1].
Тогда /(X) = [0,1] С В = [0,16].
Определение. Пусть дано отображение f : А В. Пусть
у есть любой элемент множества В. Полным прообразом элемента
у при отображении f называется множество всех х Е А таких,
что f(x) = у. Полный прообраз элемента у Е В обозначают через
Л1 (у). Тогда f~l(y) = {« € А|/(х) = у}. Аналогично, если У С В,
то полным прообразом множества У при отображении f : А В
называется множество всех х Е А таких, что f(x) Е У, т. е. У~Х(У) =
{ж Е А\3у Е У такое, что/(х) = у}.
Пример, f - у = sinx, х Е [0,2тг], у Е [—1,1] (график функции
изображен на рис. 1). Тогда
Г»(0) = {0} U {*} U {2тг}, /-^([-1/2,1/2]) =
= [0,тг/6] U [5тг/6,7тг/6] U [11Я-/6,2тг].
Определение. Отображе-
ние f : А В называется вза-
t	имнооднозначным, или инъектив-
ным, если полный прообраз f~r(y)
0-	«..-у.»х каждого элемента у Е В состо-
1 % хЛ/2” ит не более чем из одного элемен-
|	та множества А. Другими слова-
рис ।	ми: отображение f множества А
в В называется взаимнооднознач-
кие два различных элемента
ным, или инъективным, если ника-
из А не имеют одинаковых образов в
В; или отображение f : А В есть инъекция, если Vzi, Х2 6 А
имеем (я?1 / «2) <=> (/(zi) # /(хг)); «ли если xi,X2 6 А, то
(Х1 = х2) & (/(*1) = /(ж2)).
Замечание. Каноническая инъекция х -> х, А -> В (А С В)
является взаимнооднозначным отображением.
Определение. Если область значений отображения f : А
В совпадает с множеством В, то говорят, что f отображает А
на В. Отображение х -4 f(x) называется при этом сюръективным.
Замечание. Отображение f : А -4 В есть отображение А на
/(А), причем /(А) С В.
16
Определение. Отображение f : А-¥ В называется биектив-
ным, если отображение f является взаимнооднозначным отображе-
нием А на В (т. е. биекция является одновременно инъективным и
сюръективным отображением),
П р и м е р ы. 1. Пусть отображение f : А В задано своим
графиком Г = {(®, у) Е Ах В|® Е А, у = f(x) Е В}, изображенным на
рис. 2, тогда имеем /(А) С В, но /(А) В.
Заметим, что если отображение f сюръективно, т. е. отображает
А на В, то /(А) = В, поэтому наше отображение не сюръективно.
2.	Пусть отображение f : А —> В задано графиком, изображенным
на рис. 3. Тогда /(А) = В, т. е. отображение f сюръективно, т. е.
отображает А на В.
Рис. 4
Рис. 5
3.	Отображение / : А -> В с графиком, изображенным на рис. 4,
есть инъекция А в В, так как любая прямая, параллельная оси Ох
и проходящая через точку (0, у), где у = У(х), пересекает график Г
отображения / только в одной точке (х, у) и поэтому любой у € У(А)
имеет полный прообраз У-1 (у), состоящий из единственной точки х €
А. Отметим, что отображение / : А —> В не сюръективно и поэтому
y-x(y) = 0Vy€B\y(A).
4.	Отображение / : А -> В с графиком, изображенным на рис. 5,
есть биекция, поскольку У(А) = В (т. е. f сюръективно) и Уу € В
существует единственный прообраз х = f~l(y) € А (т. е. У инъектив-
но).
5.	Отображение f : у = х2, х £ [-1,1] = А, у £ [0,1] = В не
является инъективным, поскольку, например, У(-1) = /(1) = 1, од-
нако отображение д : у = х2, х € [0,1], у £ [0,1] уже инъективно и
даже биективно, так как у([0,1]) = [0,1] = В и Ухх, х2 £ [0,1] имеем
(хх £ х2)	(х? xl).
Определение. Пусть отображение f : А -> В есть биекция
и у € В = /(А). Тогда полный прообраз У-1 (у) состоит из един-
ственной точки х £ А такой, что У(х) = у. Введем отображение
f"1 : у —> х =	(у) множества В на А. Отображение f~* вновь
является биекцией и называется обратным отображением (обрат-
ной функцией) или биекцией к у.
Замечание. Итак, если отображение f : А -4 В есть биекция,
то обратная биекция У-1 : В -> А ставит в соответствие любому
у € В его единственный прообраз х £ А.
Замечание. Вели отображение f : А -> В не является биекцией
(т. е. не является взаимнооднозначным отображением А на В), то
обратного отображения не существует.
----------------- У ---------------
• х = у-х(у)	->	-У = У(х)
А = У'Х(В)	<-	В = У(А)
-------------- -----------------
Замечание. Если f : А -4 В - биекция и У-1 : В —> А -
обратная биекция, то имеем
У"х(У(х)) = xVxe А = у-х(В),
f(f~Hy)) = yVy€B = f(A).
П р и м е р. У : у = х2, х £ [0,1], у £ [0,1], (х -4 х2), тогда
У"1 : х = y/у, у £ [О,1], х £ [0,1], (у -4 ^/у).
Пусть f •. А В и X С A, Y С В. Отметим некоторые важные
соотношения для образов и полных прообразов при отображении f.
1.	У(0) = 0.
2.	(Xi С Хг С А) =► (У(Х1) С У(Х2) С В). (Доказательства про-
вести самостоятельно).
3.	У(Хх UX2) = У(Хх) uy(X2)VXi,Х2 С А.
18
Доказательство. Пусть сначала у € /(Хх U Хг). Тогда
существует х € Xi U-Xj такое, что /(®) = у. Но х € Хх UX2 означает,
что или х € Хх, или х € Хг. В случае х € Хх имеем у = f(x) € /(Хх);
в случае х Е Хг имеем у = f(x) € /(Хг), т. е. в обоих случаях имеем
включение у Е /(Хх) U /(Хг), откуда а) /(Хх UX2) С /(Хх) U /(Хг).
Пусть теперь у € /(Хх) U /(Хг). Тогда или у Е /(Хх), или у €
/(Хг). В случае у € /(Хх) 3® € Хх такое, что /(®) = у, и поскольку
Xi С Xi U Х2, то (® € Xi U Ха) =► (у = /(®) Е /(Хх U Х2)).
В случае у € /(Хг) 3® Е Хг С Хх U Хг такое, что /(®) = у, т. е.
У Е /(Хх U Хг). Итак, в обоих случаях имеем у € /(Хх U Хг), т. е.
имеет место включение б) /(Хх) U /(Хг) С /(Хх U Хг).
Из а) и б) вытекает утверждение 3.
4.	/(Хх Л Хг) С /(Хх) Л /(Хз)УХ1,Хз С А. (Доказать самостоя-
тельно.)
Замечание. Равенства /(Хх Л Хг) = /(Хх) П /(Хг) может и
не быть, например, если / : А -4 В есть постоянное отображение, т.
е. /(®) = 6 V® Е А и Хх, Хг С Л, но Хх ЛХг = 0. Тогда /(Хх ПХг) =
/(0) = 0, однако /(Хх) Л /(Х2) = {6} # 0, т. е. /(Хх) П /(Х2) #
/(ХхПХ2).
5.	/~х(0) = 0.
Замечание. Может оказаться, что ЗУ С В такое, что /-Х(У) =
0, хотя У 0.
Пример. Рассмотри отображение / : R. -4 R, где / : ® -4 ®2,
тогда /-х(-1) = 0.
6.	/-1(УХ) С /-1(У2) УУХ С Уг С В. (Доказать самостоятельно.)
7.	/“Х(УХ иУ2) = /’ЧУх) и/-х(У2)УУх, Уг С В. (Доказать само-
стоятельно.)
8.	/-Х(УХ ПУг) = /-Х(УХ) П /-х(Уг) УУХ, У2 С В.
Доказательство. Пусть сначала ® € /”Х(У1 ЛУг). Тогда у =
/(®) G УХЛУ3, но (у Е Ух) < (® € f'HYi)), а (у £ Уг) < (® € Гх(Уз)),
т. е. х € /-х(У1)Л/-х(Уг), откуда в) /"Х(УХ ЛУ2) С /-1(^)Н/-х(Уа).
Пусть теперь ® € /”Х(У1) Л /"х(Уг)	0. Тогда (® € /~Х(УХ))
(У = /(®) € Ух), а (® € /-х(Уг)) =>(у = /(®) € Уг), т. е. у = /(®) Е
Ух ЛУ2, откуда имеем ® € /-Х(УХ ЛУг), так что г) /”Х(УХ) Л/"х(Уг) С
/-Х(УХ Л Уг). Из в) иг) вытекает справедливость 8.
9.	/-Х(СУ) = С/"Х(У)УУ С В.
Д о ка зате л ьс тв о.Имеем В = УиСУ, А = /-Х(В) = /-х(Уи
СУ). В силу свойства 7 имеем равенство /~Х(У U СУ) = /-1(У) U
/-Х(СУ). Заметим, что /~Х(У) Л /-Х(СУ) = 0, так как в противном
случае Эх Е А такое, что /(®) Е У Л СУ = 0. Это невозможно. Итак,
имеем А = /-х(У)и/“х(СУ), причем /-Х(У) Л/-Х(СУ) = 0, но тогда
/~Х(СУ) = А \ /”Х(У) = С/“Х(У).
10.	/"х(/(Х)) DXVXC А.
19
Доказательство. Пусть х 6 X, тогда /(®) 6 f(X) = У и
в силу определения полного прообраза х Е У*"1 (У) = 7"1(/(Х)), т. е.
X с ГЧНХ)).
п./(/-х(у))су уу св.
Доказательство. Пусть у G /(У-1 (У)), тогда существует
xq 6 У"1 (У) такое, что /(®о) = У- Поскольку xq G У-1(У), то в силу
определения полного прообраза f(xo) = у € У => /(/-1(У)) С У.
Определение. Если f : А В есть отображение с областью
определения А и X С А - подмножество А, то сужением функции
f на X называется функция fx'-X~+ В, область определения ко-
торой есть X, и такая, что /х(®) = У(х) V® 6 X. Для сужения fx
используется также обозначение f\X.
Замечание. Если fx является сужением функции f : А —> В на
X С А, то функцию f называют продолжением функции fx * X —> В
на множество А.
Пример, f : у = х2, х Е [-1,1] = А, у Е [0,1] = В. Пусть
X = [0,1] С А, тогда имеем f\X :у = х2,хЕ [0,1], у Е [0,1].
Определение. Пусть Е, F и G - непустые множест-
ва и f : Е —> F; g : F -> G. Тогда композицией (суперпозици-
ей) g о f называется отображение Е в G, определенное формулой
(д о /)(ж) = g(f(x)) V® 6 В. Заметим, что запись д о f производится в
порядке, обратном тому, в котором производятся операций д и /. При
исследовании композиций полезны диаграммы
Е f F g G
g°f
Таким образом, в математическом анализе принято правило, со-
гласно которому в композиции операций д о f нужно начинать с опе-
рации /, расположенной справа.
Замечание. Если А С Е, то (д о /)(А) = g(f(A))> если В С G,
TO(5o/)-x(B) = f-1(ff-1(B))cB.
Замечание. Композиция отображений ассоциативна, т. е. если
f : Е -> F; д : F -> G; h : G Я, то (hog) о f = ho(g о /), что проще
записывается в виде hog о f.
На диаграмме это выглядит так:
20
Замечание. Если f~r является биекцией, обратной к f : Е —> F,
то /-1 о f = где Ie ~ тождественное отображение Е (на Е) и
/о У"1 = 1р, где If ~ тождественное отображение F (на F).
Пример. Пусть д : у = и2, и G (—оо, 4-оо), f : и = х 4- 1,
х G (—оо, 4-оо), и € (—оо, +оо), тогдаро/ : у = (ж4-1)2, х G (—оо, +оо),
у е [о, +оо).
При рассмотрении числовых функций f : А В, где В С R вы-
деляют класс числовых (или действительных) функций одного дейст-
вительного- переменного, т. е. функции /(ж) вида f : А —> В, где А
и В являются подмножествами множества действительных чисел R
(ACR,BCR).
Замечание. Функция п —> /(п), определенная на множестве N
всех натуральных чисел, называется (числовой при f(n) 6 R) после-
довательностью. Ее значение, или член последовательности, для дан-
ного п 6 N обычно обозначают через ап, а сама последовательность
обозначается символами (ап) или ai, аг, •••, ап, ... . Таким образом,
(ап) есть отображение п —> ап, п G N.
Определение. Скажем, что числовые функции f : у = f(x),
X е Xf, у Е Yf =Z f(Xf) и д : у = р(ж), х G Хд, у е Yg = д(Хд)
совпадают, если: 1) совпадают их области определения Xf = Xg и
2) f(x) = р(ж) Уж G X = Xf = Xg.
Простейшими элементарными функциями одного действительного
переменного будем называть следующие- функции:
Рп(х)
1)	рациональные функции f(x) =	- , х Е R \ (Ji®/}, гДе
Qm(x)	t
п	т
Р«(®) = ak%k и Qm(x) = 52	“ многочлены и xi - действи-
*=0	к=0
тельное число, такое, что Qm(xi) = 0;
2)	степенная функция у = жа, 0 < х < 4-оо, а 6 (-оо, +оо); 0 <
х < 4-ос, a 6 (0,4-оо);
3)	показательная функция у = а*, —оо < х < 4-оо, а > 0, а ф 1;
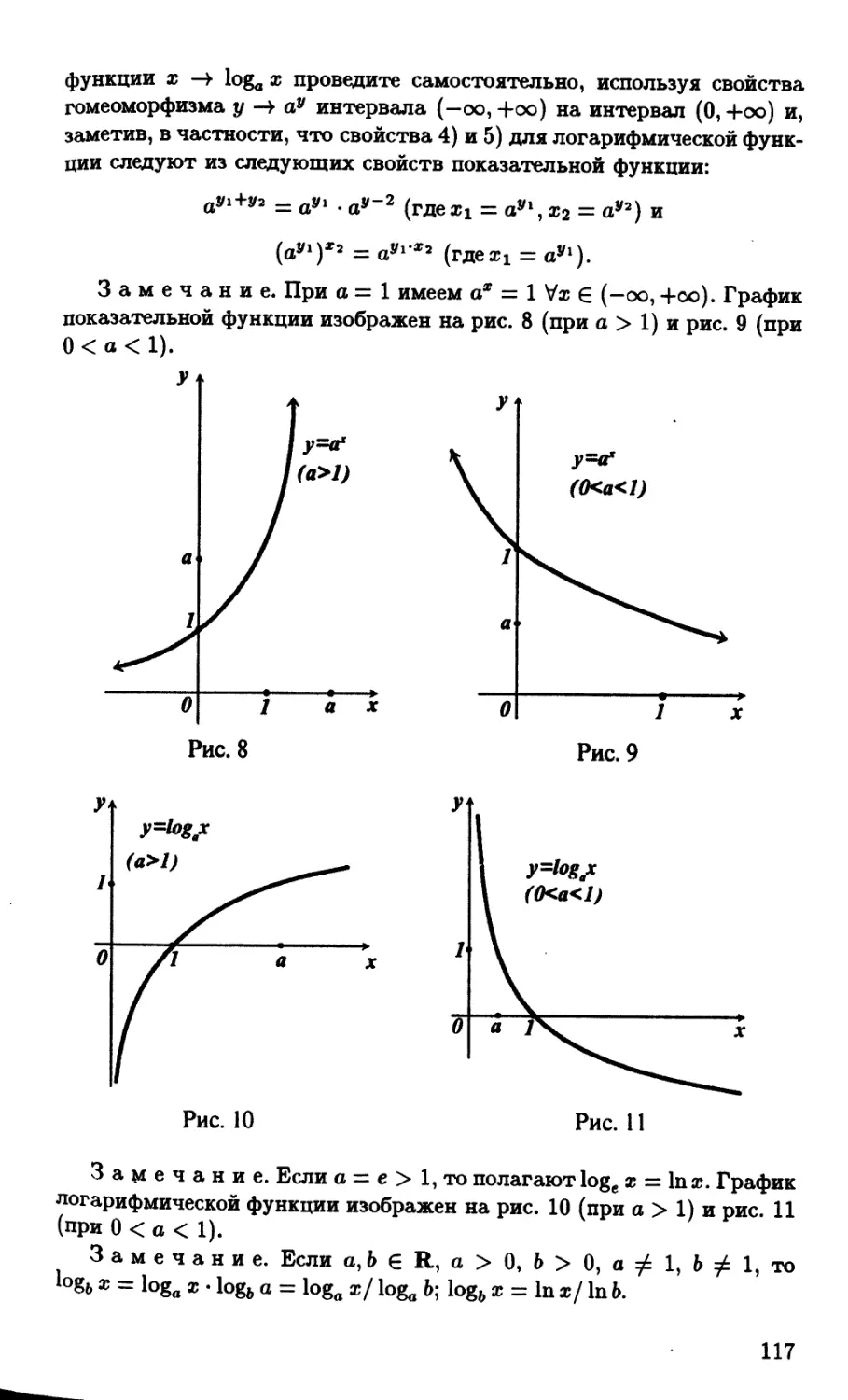
4)	логарифмическая функция у = loga ж, 0 < х < 4-оо, а > 0, а / 1;
5)	тригонометрические функции:
у = sin ж, —оо < ж < 4-оо, — 1 < у < 1;
у = cos ж, —оо < ж < 4-оо, — 1 < у < 1;
У = tgx, (2Л-1)£ < X < (2* + 1)^ (к = 0,±1,±2,±3,...);
у = ctgх, kir < х < (А:+ 1)тг (fc = 0,±1,±2,±3,...);
6)	обратные тригонометрические функции:
у - arcsiu ж, -1 < х < 1, -- < у <
у — arccos х, — 1 < х < 1, 0 < у < тг;
тг
2
7Г
2;
21
у — arcctg ®, -оо < х < +оо, 0 < у < к.
Определение. Элементарными функциями называются
функции, получающиеся из простейших элементарных функций по-
средством конечного числа арифметических действий или компози-
ций этих функций.
Пример. Функция у = |®|, х € (-оо; +оо) элементарная (|®| =
у/х*).
ГТ	Л.	Г! \	®	( 1>® > О,
Пример. Функция j(x) = т-г = <	.	\ элементарная.
|ф|	х < и
Пример. Функция sgn х не элементарная.
§ 3.	Счетные и несчетные множества
Определение. Пусть АиВ- непустые множества.
Если существует биекция (т. е» взаимнооднозначное отображение
на) f : А —> В множества А на В, то множества АиВ называются
равномощными» Запись: А~ В.
Отношение ~ обладает следующими свойствами эквивалентности:
1) А ~ А (рефлексивность); 2) (А ~ В) => {В ~ А) (симметричность);
3) (А ~ В) Л (В ~ С) => (А ~ С) (транзитивность).
Определение. Если Зп € N такое, что А ~ Jn = {1,2,..., п},
то непустое множество А называется конечным, в противном слу-
чае непустое множество А называется бесконечным»
Пример. Множество А = {2,4,6,...,2п} конечно, так как
отображение k -> 2k (k = 1,2,..., п) множества Jn на А есть биекция
и поэтому А ~ Jn.
Определение. Непустое множество А называется счетным,
если А ~ N (где N - множество натуральных чисел)»
Примеры:
а)	Пусть А = {2,4,6,..., 2п,...} = множество всех четных нату-
ральных чисел. Тогда отображение п -> 2п множества N на А есть
биекция, и поэтому А ~ N, т. е, А счетно;
б)	рассмотрим множество всех целых чисел Z. Тогда отображение
п ап, п € N, где
_ (	п/2 при п четном,
n " \ (1 - п)/2 при п нечетном
есть биекция N на Z, поэтому Z ~ N, т. е. множество Z счетно;
в)	пусть Д1И Аг - любые два отрезка. Построим прямоугольник
со сторонами Ai и Аг. Тогда диагональ Г С Ai х Аз этого прямо-
22
угольника будет являться графиком отображения
/ : Д1 Дз
|Л»1
|Дх|
Очевидно, f отображает Д1 на Дз, и притом взаимнооднозначно, т. е.
является биекцией. Но тогда Дх ~ Дз.
Следствие. Если множество А счетно, то по определению
существует биекция N на А, и поэтому элементы множества А можно
записать в виде последовательности си, аз,..., ап,..., причем (п ф т)
(ап / ат Ут,п € N). Иными словами, элементы счетного множес-
тва можно занумеровать в последовательность сц,аг,... , ап,... так,
что различные элементы получат и различные номера. Обратно, ес-
ли элементы множества А можно занумеровать таким способом, то
множество А счетно.
Определение. Бесконечное множество, не являющееся
счетным, называется несчетным множеством.
Теорема. Всякое непустое подмножество счетного множес-
тва либо конечно, либо счетно.
Доказательство. Пусть непустое множество А счетно
(т. е. А - N), тогда его элементы можно расположить в последова-
тельность
• • • ?	• • •»	(3.1)
причем (п т) <=> (ап ф ат). Пусть В ф 0, В С А и аПг - первый
элемент последовательности (3.1), являющийся элементом В, так что
ani 6 В. Пусть аПа - второй такой элемент последовательности (3.1),
так что Пз > их и аПа € В и т. д. Возможны лишь два случая: 1)
после конечного числа шагов! все множество В будет исчерпано; 2)
получим бесконечную последовательность аПх, аМа,..., аПй,...; п* >
ni при k > Ц состоящую из всех элементов множества В. В случае 1)
множество В конечно. В случае 2) положим bk = аПй, тогда множество
В оказывается расположенным в последовательность , Ьз, • • • ,	...,
причем (Л ф I) & (nk # п/), и поэтому (bk = ank # ani = bi) <=> (Л /).
Отображение k bk есть биекция N на В, поэтому В ~ N, т. е. в
случае 2) множество В счетно.
Следствие. Любое бесконечное подмножество счетного мно-
жества счетно.
Определение. Множество А^ 0 называется не более чем
счетным, если оно конечно или счетно.
Теорема. Объединение счетного множества счетных мно-
жеств счетно.
Доказательство. Пусть {An} (n g N) - семейство
+<х
сметных множеств и S = (J Ап. Расположим каждое множество Ап в
последовательность	•.. ,ajj.n\... и рассмотрим бесконечную
таблицу
	-> 4м	а(1) а3	а™
а(х2)	Z £	а(2) “3	
4-			
		„(3) а3	
в которой элементы множества Ап образуют n-ю строку. Эта таблица
содержит все элементы множества S. Эти элементы можно располо-
жить в последовательность, как это указано стрелками:
Jl) Jl) J2) Л(3) (2) (1) (1)
, а2 >	> °2 »°3 > а4 > • • • •
Полученной последовательности соответствует некоторая нумерация
h, Ьг,..., Ьп,... (Ьх = Ьг = а<х),...)	(3.2)
элементов из S, задающая отображение п Ьп множества N на S.
При этом отображение п Ьп может не быть взаимнооднозначным,
если какие-либо два множества Ак и Ai (при к / I) имеют общие эле*
менты (поскольку эти общие элементы появятся в последовательности
(3.2) более одного раза). Однако, перебирая один за другим элементы в
последовательности (3.2) и оставляя в (3.2) при этом только различ-
ные элементы, видим, что существует подмножество Т С N такое,
что S ~ Т, Поскольку Т есть подмножество счетного множества N,
то множество Т, а стало быть, и множество S ~ Т не более чем счет-
но. По условию Ai счетно и потому бесконечно. Но S D Ai, поэтому и
S бесконечно. Итак, S бесконечно и не более чем счетно, т. е. счетно.
Следствие. Объединение не более чем счетного множест-
ва не более чем счетных множеств не более чем счетно. (Доказать
самостоятельно.)
Теорема (Кантора). Пусть множество А состоит из всех по-
следовательностей вида (ап), т. е. ai,аг, • • • ,• • • > ап = { ®
Тогда множество А несчетно.
Доказательство. Допустим противное, т. е. предположим,
что все такие последовательности можно занумеровать:
(1)	а™	а™	...,	<£>,	...
(2)	а™	а?....... а<?>,	...
(п)	а<п),	а<п),	....	а£п),	...
Докажем, что в множестве А есть последовательность, не входя-
щая в нумерацию. Возьмем последовательность, где первый элемент
24
отличен от второй отличен от и т. д. Обозначим построенную
последовательность через &i, 62,••• , in, • •• • Эта последовательность
отличается от всех пронумерованных хотя бы одним элементом. В са-
мом деле, если бы она имела номер (fe), то имели бы Ък = но по
построению Ьк / <4*\ Таким образом, множество А не может быть
счетным, т.е. А (будучи бесконечным) несчетно.
Глава 2
ПОЛЕ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
§ 1. Поле, упорядоченное поле, полное
упорядоченное поле
В арифметике было введено понятие множества натуральных чи-
сел N = {1,2,3,4,... , п,...}. Понятие натурального числа будем счи-
тать первичным. Обоснование теории натуральных чисел можно най-
ти в книге Э. Ландау [1]. Приведем два утверждения из теории нату-
ральных чисел, которые будут часто использоваться в нашем курсе.
Принцип минимума. В любом непустом множестве
натуральных чисел существует минимальное число» Скажем, что
р G N является минимальным для множеств А С N, если р € А и
р<т Ут Е А.
Принцип минимума является одной из аксиом теории натуральных
чисел.
Принцип математической индукции. Пусть не-
которое множество А натуральных чисел (А С N) удовлетворяет
следующим двум условиям: 1) 1 Е А; 2) если п Е А, то (п + 1) Е А.
Тогда множество А содержит все натуральные числа, т. е. А = N.
(Заметим, что если принцип минимума взят в качестве аксиомы, то
принцип математической индукции доказывается в качестве теоремы,
при этом верно и обратное утверждение.)
Доказательство. Допустим от противного, что С А =
N \ А / 0. Тогда С -А Л А = 0 и А ^4 0. В силу принципа минимума
Зп0 Е СА такое, что Ут Е С А => т > по, п0ЕА. В силу условия 1)
по > 1, но тогда (по — 1) Е N, и, кроме того, поскольку (по — 1)ЕС А,
то (по - 1) Е А. Но тогда в силу условия 2) (по — 1) + 1 = no Е А, что
противоречит отношению поЕА. Итак, С А = 0, т. е. А = N.
25
€ N| £ k2 = |n(n + l)(2n + 1) 1.
fc=i 0	J
=> fl2 = |(1 • (1 + 1)(2 •1 + 1)Y t. e. IeA.
\ о	/
TO
Пример. Докажем, что Vn Е N имеет место равенство
п	1
52 = g»(n + l)(2n + 1).
k=l	°
Пусть
n
Заметим, что (n = 1)
Далее, если п € А,
£ А2 + (« + I)2 = “»»(п + l)(2n + 1) + (п + 1)а =
Л=1	°
= ~(n + 1) (2п2 + п + 6п + 6) = -(п + 1)(п + 2)(2п + 3) =
О	и
= g (n + 1)[(n + i) + Ц [2(n + i) +
откуда следует, что и (n + 1) £ А. В силу принципа математической
индукции имеем А = N, т. е. наша формула справедлива Vn € N.
Натуральные числа N, нуль и отрицательные натуральные числа
образуют множество целых чисел Z. Отношения вида — (где т 6 Z,
п
п Е N) образуют рациональные числа. Множество всех рациональных
чисел будем обозначать через Q. Очевидно, N С Z С Q. В элементар-
ной математике были введены операции сложения и умножения рацио-
нальных чисел, правило сравнения этих чисел и указаны некоторые
свойства этих операций и отношений. Множество рациональных чи-
сел Q, в котором определены сложение и умножение, образуют так
называемое поле. Дадим определение поля.
Определение. Непустое множество 7 называется полем,
если наТ определены две (бинарные) операции, называемые сложени-
ем и умножением (так, что Vx, у €	= х+у GF u3v = х*у € 7),
причем
I. Для сложения: 1) справедлив закон ассоциативности х + (у +
z) = (х + у) + z Vx,y,z £	2) 3 элемент 0 множества 7 такой,
что х + 0 = х Vx Е 3) V® Е Я 3(-х) Е Я такой, что х + (-х) = 0;
4) справедлив закон коммутативности х + у = у + xVx,y £
IL Для умножения: 1) справедлив закон ассоциативности х> (у* z)
= (х • у) • z Vx,y,z Е 2) существует элемент 1 множества F
такой, что 1	0 и х • 1 = xVx Е Г; 3) Vx £ Т, х 0 Зх"1 Е
26
7 такой, что х • ®-1 = 1; 4) справедлив закон коммутативности
х-у = У'Х^х,уЕ F.
III. Для сложения и умножения: 1) справедлив закон дистрибу-
тивности умножения относительно сложения x-(y+z) = x-y+x-z
Vx,y,z G T.
Замечания. Элемент 0 поля 7 из I называется нулем поля 7.
Элемент (—®) поля 7 из I называется противоположным для элемента
х, причем, очевидно, (—0) = 0 и -(-ж) = х V® G F- Бинарная операция
х — у определяется формулой х — у = х + (-у) У®, у € 7 и называется
вычитанием. Пользуясь законом III, легко доказать дистрибутивность
вычитания относительно умножения, т. е. (® - y)z = xz - yz V®, у, z €
7. В самом деле, используя закон III и определение вычитания, имеем
x-z- ((®-y) + y)*z = (x-y)-z+y-z, т. е. (®-y)-z+y-z = x-z, что и
означает равенство (®—y)-z = x-z—y-z, откуда вытекает, что х• 0 = 0
V® € (В самом деле, ® • 0 = ® • (у — у) = х • у - х • у = Q.) Элемент
1 из II называется единицей поля 7. Элемент ®-1 из II называется
обратным для х 0, причем, очевидно, I”1 = 1 и (ж"1)"1 = ® V® € 7\
если ® 0 0. Бинарная операция -, определяемая формулой - = х - у-1
У 1 У 1
V®, у G F, где у 0, называется делением. Очевидно - = 1 и - = ж-1
1	2D
У®#0.
Замечание. Пользуясь законами I, II и III, можно доказать (это
будет сделано в курсе алгебры), что (-х)-у = -(®-у); (-«) = (-1)*®;
(-®) • (-у) = ® • у У®, у G 7,з частности, (-1) • (-1) = 1. (Например,
в силу закона III имеем (-®) • у + ® • у = ((-®) + ®)*у = 0- у = 0=>
(-®) .у = —(® .у) Ух, у е 7.)
Пример. Множество натуральных чисел N с арифметическими
операциями сложения и умножения не есть поле, так как оно не содер-
жит 0 и Уп € N не существует элементов (-п) и п'1 (если n 1) из
N.
Пример. Множество Z всех целых чисел с арифметическими
операциями сложения и умножения не является полем, так как для
® € Z, ® 1, ® 0 не существует элемента ®-1 из Z.
Пример. Множество Q рациональных чисел с арифметическими
операциями сложения и умножения является полем.
Определение. Упорядоченным полем называется поле 7, в
котором определены отношения <, =, >, обладающие следующими
свойствами:
1)	Ух, у Е 7 справедливо и притом только одно из следующих
утверждений: х < у, х = у, х > у;
2)	(® > у) Л (у > z) => (® > z) У®, у, z Е 7 (транзитивность отно-
шения >), (® = у) Л (у = z) => (® = z) (транзитивность отношения
=);
27
3)	(х > у) (х 4- z > у 4- г) V®, у, z Е
4)	(х > у) Л (z > 0) => (х • z > у • z) Vx,y, z Е J7.
Замечание. Можно показать, что (® > у) <=> (у < ®).
Следствие!, (х > у) h(z > и) => (x + z > у + и) Vx,y,z,u Е
Доказательство. Из (х > у} l\{z > ti) => (x + z > у + z)
nyiz>y + u, откуда ввиду транзитивности отношения > имеем
® 4- z > у 4- и.
Следствие 2. (® > 0) => (—х < 0) V® Е J7.
Доказательство. Если ® > 0, то из закона 3) имеем ((—®)4-
® > (-®) 4- 0 = -®)	(0 > — ®).
Следствие 3. (® > 0) Л (т/ < 0) => ® • < 0.
Д о к а з а т е л ь с т в о. Пусть ®, у Е ® > 0 и у < 0, тогда
-у > 0, поэтому ((® > 0) Л (-у > 0)) => (® • (-у) > 0) => (~® • у > 0)
=> ((я -у) < 0).
С л е д с т в и е 4. г2 > 0 Vi € 5, ®	0, в частности, 1 = I2 > 0.
Доказательство. Пусть ® Е J7, ® / 0. В случае ® > 0 из
закона 4) имеем ®2 > 0. В случае ® < 0 имеем -® > 0 и поэтому
х2 = (—®) • (—®) > 0.
Следствие 5. ®-1 > 0 V® Е Т х > 0.
Доказательство. Поскольку ® • ®-1 = 1>0, тоиз®>0
следует ж""1 > 0.
Следствие 6. V®, 2/ Е Я, х > у > 0 => х"1 < у""1.
Доказательство. Если ® > у > 0, то ® • tf"1 > у • у~1 =
1 > 0, откуда (®~1(® • J/”1) > ®-1) => (j/”1 > ж”*1).
Замечание!. Поле рациональных чисел Q D Z становится
упорядоченным полем, если, используя естественную упорядоченность
„	7П1 ТП2 _
Z, ввести отношения >, =, < следующим образом: пусть —, — Е Q,
П1 П2
т. е. тп1,т2 Е Z и ni,n2 Е N, тогда — > —, если пцпг > тг^И, и
П1 П2
mi m2
— = —, еСЛИ ТП1П2 = УП2П1.
Замечание 2. Упорядоченное поле рациональных чисел Q
плотно в себе, т. е. для любых двух рациональных чисел х,у Е Q,
таких, что ® < у 2z Е Q, для которого х < z < у.
Доказательство. Пусть ®, у Е Q и ® < у, тогда z = (® 4-
у)/2 Е Q таково, что ® < z < у, В самом деле,
(® < у) => (® + х < у 4- ®) => I х < -  -
\
f ® | U
(х < у) (® + у < у + у) => I ——- < у
\ Z
► => X < Z < у.
Замечание 3. Если (® > у) V (® = у), то пишут ® > у.
28
Определение. Если Т - упорядоченное поле, то абсолют-
ная величина (модуль) |х| элемента определяется следующим
образом:
. ,	( х при х > О,
Ж = <	” Л
11	[ — х при х < 0.
Отметим свойства абсолютных величин:
1)	|®| > 0 V® Е причем (|х| = 0) <=> (х = 0) (свойство 1) вытекает
из определения модуля |я|).
2)	|ж-2/| = |®| • М е F.
Доказательство. Если х = 0 или у = 0, то свойство 2)
очевидно. Пусть х • у 0. Рассмотрим два случая:
а)	х • у > 0. Тогда |а? • у| = |(±|аг|) • (±|у|)| = ||я| • |у|| = |я| • |у|;
б)	х • у < 0. Тогда |я • у| = |(±|я|) • (т|у|)| = |-(|я| • |у|)| = |я| • |у|.
3)	Пусть х, е G Т. Если е > 0, то (|я| < е) (—г < х < е).
Доказательство. По определению модуля имеем — |я| <
х < |я|, откуда (—£ < х < г) <=> (|аг| < е). В самом деле, (|я| < г) =>
(-г < —|я| < х < |я| < е) =$ (—е < х < г).
Обратно, пусть — £ < х < е, тогда при х > 0 (|я| = х < е) => (|я| <
г); при х < 0 (—|аг| = х > —г) => (|я| < е), т. е. (-е < х < е) => (0 <
|х|<г).
4)	Чх,у Е Т имеет место «неравенство треугольника» |ж 4- у\ <
|®1 + |у|-
Доказательство. Пусть х,у 6 Т и для определенности
1®1 > |у|- Тогда в случае х • у > 0 имеем |х + у| = |±(|х| + |1/|)| =
||®| + |у|| = |х| + |у|, а в случае х у < 0 имеем |я4- у| = |±(|я| - |у|)| =
11®1-|г/11 = Ы-Ы < |®1 + М-
5)	11®! “ Ml < I® - 2/|, I® - 2/| > 1®1 - l!/| V®, У 6
Доказательство. (|я| = |(я - у) + у| < |я - у| 4- |у|) =>
(I® -2/1 > |®|~ |2/|)- Но |у- я| > |у| - |я|, поэтому |я -у| > ||х|,- |у||.
Обозначения. Пусть - упорядоченное поле и a, b € jF,
причем а < Ь. Тогда будем пользоваться следующими обозначениями:
[а, 6] = {я G а < х < Ъ}, (а, fr] = {х G а < х < Ь},
[а, Ь) = {х G а < х < Ь}, (а, Ь) = {я 6 а < х < Ь},
[а, +оо) = {я 6 Т7! а < я}, (а, +оо) = {я G а < я},
(-оо, Ь] = {я G ^1 х < 6}, (-оо, Ь) = {я G х < 6},
(-оо, -|-оо) = {я| я G Я}.
Все эти множества называются промежутками, причем [а, 6] называ-
ется замкнутым промежутком или отрезком (или иногда - сегментом),
Ъ) (или [а, 6[), (а, Ь] (или ]а, Ь]), [а, 4-оо) (или [а, 4-оо[) и (—оо, Ь] (или
29
] - оо, b]) называются полуоткрытыми промежутками или полуинтер-
валами, а (а, Ь) (или]а, Ь[), (а, +оо) (или ]а, +оо[), (-оо, Ь) (или ]-оо, Ь[)
и (-оо, +оо) (или ] — оо, +оо[) называются открытыми промежутками
или интервалами. Промежутки [а, Ь], (а, Ь], [а, Ь) и (а, Ь) называются
конечными: а и b называются их концами. Остальные промежутки
называются бесконечными. Иногда полезно причислить к отрезкам
также множество [а, а], состоящее из одной точки а.
Определение. Пусть Т - упорядоченное поле. Элемент b €
Т называется верхней гранью непустого множества А С Я, если
Ух € А имеет место неравенство х < Ь.
Определение. Элемент а & F называется нижней гранью
непустого множества А С 7-, если Ух £ А имеет место неравенст-
во х> а.
Определение. Непустое множество Ас 7 называется
ограниченным сверху (снизу), если ЗЬ € 7 (За g Т), являющееся верх-
ней (нижней) гранью множества А.
Определение. Непустое множество А С 7 называется
ограниченным, если оно ограничено и сверху и снизу.
Замечание. (Множество А С 7F ограничено) 4» (ограничено
сверху множество {|®| € х g Л}).
Пример. Если множество А С Т состоит из конечного числа
элементов, то оно ограничено. (Доказать самостоятельно.)
Пример. Интервал (а, +оо) С Р есть множество, ограниченное
снизу и не ограниченное сверху. В самом деле, (а, 4-оо) = {® € F\ а <
х}, a g 7F, поэтому Ух € (а, 4-оо) => х > а, т. е. а € 7 есть ниж-
няя грань множества (а, +оо). С другой стороны, если бы множество
(а, 4-оо) было ограничено сверху, то ЗЬ € являющееся верхней гра-
нью для (а, 4-ос), так что
х < ЪУх g (а, 4-оо).	(1.1)
Из (1.1), в частности, следует, что Ъ > а. Но поскольку 1 > 0, то
®o = b4-l>b>a. Таким образом, существует ®о € (а, 4-оо) такое,
что ®о > Ъ. Противоречие с (1.1).
Замечание. Множество натуральных чисел N С Q не огра-
ничено сверху в упорядоченном поле рациональных чисел Q.
Доказательство. Поскольку п > 0 Уп g N, то достаточно
доказать, что Vq g Q, q > 0	3n g N	такое, что n > q	>	0. Пусть
q € Q и q > 0 фиксировано. Поскольку	0,1/q g Q и 0 < 1/q,	то в силу
. _m _	Л	m	1
плотности поля Q в себе 3—	g Q такое, что 0 < — <	-,	но тогда
п	п п
0<i<-)=>q<n.
п «/
Теорема Архимеда (для поля рациональных чисел).
Ух, у g Q таких, что х > 0, у > 0 3n g N, для которого п-х > у.
30
Доказательство. Пусть ®, у е Q, ® > 0, у > 0, тогда - € Q
я У. > 0 и в силу неограниченности множества N в Q Зп £ N такое,
X
что (п > |) =* (п •х > у)-
Замечание. Поскольку поле рациональных чисел обладает
свойством, сформулированным в теореме Архимеда, то поле Q назы-
вают архимедовым полем.
Определение. Пусть непустое множество А С J- ограни-
чено сверху. Точной верхней гранью множества А называется эле-
мент М Е? такой, что: 1) М является верхней гранью множества
А; 2) М меньше любой другой верхней грани множества А. Обозна-
чение: М = sup А.
Определение. Пусть непустое множество А С -F ограни-
чено снизу. Точной нижней гранью множества А называется эле-
мент тЕ Т такой, что: 1) т является нижней гранью множества
А; 2) т больше любой другой нижней грани множества А.
Обозначение: М — inf А.
Итак, М = sup А, если М 6 Т и 1) х < М V® € А; 2) УЬ е Т
такого, что b < М Эхо € А, для которого b < xq < М. Аналогично
т = inf А, если т € !F и 1) х > т Vx € А; 2) Va € ? такого, что т < a
3x1 € А, для которого т < ®i < а.
Теорема единственности. Если точная верхняя грань
sup А существует, то она единственна.
Доказательство. Допустим от противного, что Зх = sup А
и у = sup А (®, у 6 F), причем х < у. Тогда 3®о € А такое, что
® < ®о < у, но тогда ® не есть верхняя грань непустого множества А,
вопреки предположению.
Дадим еще одно определение sup A (inf А).
Определение. М = sup А, если М Е F и 1) х < М Ух Е А;
2) Уе > 0, е € Т 3®о € А такое, что М - е < ®о < М.
Определение, т = inf А, если m € Я и 1) т < х Ух Е А;
2)Уе > 0, е € Т 3®i € А такое, что т < ®i < т 4- е.
Пример. Пусть А = {1/n; n € N}, тогда 1 € Q и supA = 1,
inf А = 0. В самом деле, 1 = sup А, поскольку 1 £ Q и 1) - < 1
Vn € N; 2) Ve > 0, e E Q, 1 € А и обладает тем свойством, что
1 “ е < 1. Отметим, что 1 = sup А € А. Далее, 0 = inf А, так как
0 € Q, 1) — > 0 Уп € N, 2) Уе > 0, е, - € Q и в силу неограниченности
fl	€
сверху множества N 3fc € N такое, что к > -, и тогда т € А таково,
1	е	к
что 0 < - < 0 + е. Отметим, что 0 = inf АЗД.
Определение. Полным упорядоченным полем называется
31
упорядоченное поле Т, в котором для каждого непустого множес-
тва, ограниченного сверху в существует точная верхняя грань.
Теорема. Упорядоченное поле рациональных чисел Q не явля-
ется полным.
Доказательство. Прежде всего покажем, что не сущест-
вует рационального числа, квадрат которого равен 2, т. е. покажем,
что число, обозначаемое через д/2, не есть рациональное число. До-
/= т	„	т
пустим противное, т. е. пусть у2 = —, где т 6 Z, п Е N, причем-
п	п
несократимая дробь. Тогда числа т и п не могут быть одновременно
тд2
четными. Возводя в квадрат, имеем —у = 2 или 2п2 = т2, но тогда
п
т есть четное число, т. е. т = 2тх, mi 6 Z, откуда 2n2 = 4m2 =>
(n2 = 2m2) => n - четное. Итак, оказалось, что числа тип оба чет-
ные вопреки предположению. Итак, \/2eQ. Предположим теперь, что
Q - упорядоченное полное поле. Пусть А = {д 6 Q|g > 0,д2 < 2}.
Поскольку 1 Е А, то А / 0. Число 2 Е Q является верхней гранью
множества А, т. е. д < 2 Vg Е А. В самом деле, если бы существовало
до 6 А такое, что до > 2, то до > 1 => q% > до > 2. Противоречие.
Итак, множество А непусто и ограничено в Q сверху. В силу пред-
положения о полноте поля Q существует с Е Q такое, что с = sup А.
Поскольку \/2EQ, то возможны два случая: 1) 1 < с2 < 2 и 2) с2 > 2.
2-с2
В случае 1) положим d = —-Очевидно, dEQnO<d<l, так
2(с+ 1)*
как 0<d<^x(2 — с2) = 1 — ~с2 < 1.
Поскольку с 6 Q, d Е Q, то (с + d) Е Q и d2 < d < 1. Далее,
(c+d)2 = c2 + 2cd+d2 <c2 + 2cd+d = c2 + (2c + l)d<c2 + |(2-c2) =
1 + \<? < 2,
откуда с + d Е А, но с = sup А, поэтому с + d < с. Противоречие. В
с2 _ 2
случае 2) (2 < с2) положим d = —-—т > 0. Очевидно, с — d Е Q,
2(с+ 1г



(с - d)2 = с2 - 2cd + d2 > с2 - d(c+ I)2 > с2 - |
с2 _ 2
Далее, 1 < с = sup А, 0 < d < -• х— = 1/2 — 1
2с£
1
2

Итак, c — d > 0 и (c — d)2 > 2, t. e. (c — d)£A. Но тогда c - d
есть верхняя грань множества А. В самом деле, если бы существовало
до 6 А такое, что до > с — d > 0, то qfi > (с — d)go > (с — d)2 > 2.
Противоречие. Но если с — d Е Q есть верхняя грань А, то неравен-
ство с — d < с = sup А приводит к противоречию. Таким образом,
упорядоченное поле Q не является полным упорядоченным полем.
I
32
Определение. Множеством действительных чисел R на-
зывается полное упорядоченное поле.
Теорема. Любые два полных упорядоченных поля F и
изоморфны в том смысле, что существует биекция Т на Т9, со-
храняющая бинарные операции сложения и умножения и отношение
порядка, т. е. при х € F, х9 € F9 (хх9) => ((ж+у)9 = ж'+з/; (х-у)9 =
х9 • у9); (х < у) <=> (х9 < у9); (х = у) <=> (х9 = у9). (Теорема доказана в
М.)
Замечание. В книге Э. Ландау [1] можно познакомиться с
реализацией поля R с помощью «дедекиндовых сечений», а в книге
В.А. Ильина и Э.Г. Позняка [2] можно найти реализацию поля R с
помощью «бесконечных десятичных дробей».
3 а м е ч а н и е. Из полноты поля R следует, что для любого
непустого множества А С R, ограниченного снизу, существует inf A Е
R. Для доказательства достаточно рассмотреть множество А- = {ж 6
R| — х € А}, ограниченное сверху в R, и убедиться, что inf А =
— sup А_.
Замечание. Пусть дано полное упорядоченное поле R. Эле-
менты из R будем называть действительными числами (или просто
числами). Натуральными числами в R называются определяемые по
индукции числа 1,2=14-1,3 = 2 + 1,4=3 + 1,... . Множество нату-
ральных чисел из R будем обозначать через N. Отметим, что из дан-
ного определения N следует: 1) 1 Е N и 2) п+1 6 N Vn 6 N. Можно до-
казать, что N удовлетворяет аксиоматике Пеано натуральных чисел
(см. [1]) и, в частности, для N имеет место принцип математической
индукции. Натуральные числа {1,2,3,...}, числа {-1, —2, — 3,...} и
число 0 называются целыми числами в R, их множество будем обо-
„ тт -	т	~
значить через Z. Действительные числа вида —, где т G Z, п 6 N,
называются рациональными; множество всех рациональных чисел в
R будем обозначать через Q. Любое действительное число, не являю-
щееся рациональным, называется иррациональным. Например, число
у/2 G R иррационально.
Введем обозначения: если множество X С R не пусто и не ограни-
чено сверху в R, т. е. V6 Е R Зжо Е X такое, что xq > 6, то пишут
supX = +оо. Если множество X С R непусто и не ограничено снизу
в R, т. е. Va G R 3®о Е X такое, что х0 < а, то пишут inf X = —оо.
Теорема. Пусть N - множество натуральных чйсел в R,
тогда множество N не ограничено сверху в R.
Доказательство. Допустим от противного, что множест-
во N ограничено сверху в R. Тогда в силу полноты упорядоченного
поля R 36 = sup N G R, т. е. 1) п < 6 Vn Е N и 2) (б = 1 Е R) =>
(3m е N такое, чтот > Ъ — 1). Но тогда m + 1 Е N и m + 1 > &, т. е.
6supN не есть даже верхняя грань для N. Противоречие.
2 Зак. 860
33
Следствие. Для множества целых чисел Z в R имеем sup Z =
+оо, inf Z = -оо.
Теорема Архимеда. Пусть R - поле действительные
чисел. Тогда Vx, у £ R таких, что х > 0, у > 0 Зп € N, для которого
п-х>у.
Доказательство. Пусть х,у Е R, х > 0, у > 0, тогда
- € R, - > 0 и в силу неограниченности N сверху (в R) Зп € N
такое, что \ п > -, х > 0) => (п • х > у).
Теорема (принцип минимума для N). Если А С N не пустое
множество, то существует т = inf А € А.
Доказательство. Вели Л С N иЛ 0, то А > 1 Vfc € А, т.
е. множество А ограничено снизу в R. Из полноты R =$> За = inf А £
R. Если а?А, то, поскольку а = inf А, имеем: 1) к > а Vfc € А и 2)
для 1 € R Зто € А такое, что а < то < а 4- 1. Кроме того, в силу
опять же свойства 2) из определения точной нижней грани, для числа
mo € А С N, удовлетворяющего неравенству а < mo, 3mi G А С N
такое, что а < mi < mo. Итак, 3mi, mo £ А С N такие, что а < mi <
mo < а 4-1, откуда 0 < mo — mi < 1. Но это неравенство невозможно
при различных натуральных mi и то. Противоречие. Таким образом,
имеем а = inf А € А.
Замечание. Если А С Z - непустое ограниченное сверху
(снизу) подмножество целых чисел, то sup А € A (inf А € А), т. е. в
множестве А существует наибольший (наименьший) элемент.
Следствие. Vx£R множество {fc £ Z| к > х} всех целых
чисел > х имеет наименьший элемент, а множество {А 6 Z| к < х}
имеет наибольший элемент.
Следствие. Vx£R 3m £ Z такое, что m < х < m4-l. Это целое
число обозначается символом [х] и называется целой частью числа х.
Доказательство. Vx g R число т = sup{& £ Z|к < х)
удовлетворяет неравенствам m < х < m 4-1.
Пример.
Теорема. Множество Q плотно в R, т. в. Va, Ъ € R таких,
-4, 3
что а < b 3q € Q, для которого а < g <Ь.
Доказательство. Пусть a, b £ R и а < Ъ, тогда (Ь - а >
0) => (' 1 > 0 | и в силу теоремы Архимеда Зп £ N такое, что
— a J
(п >	j - ' | =►	\Ь — а>	- |	=> ffr > a4- - J •
о-a/	\	nJ \ nJ
Но тогда [an] < ап < [ап] 4-1, и поэтому
[ап] 4-1 ап	[ап] 4-1 ап 4-1	1
g =	----> — = a,q = —<-------<--------= a 4- -
n n	n n	n
34
т. е. 3g = ([an] + l)/n € Q такое, что a < q < b.
Следствие. В любом интервале (a, b) C R содержится беско-
нечное множество рациональных чисел.
§ 2. Принципы полноты поля R
При определении поля действительных чисел R нами был положен
в основу:
I принцип полноты Вейерштрасса. Любое огра-
ниченное сверху непустое множество из R имеет точную верхнюю
грань (в R/
II принцип полноты Дедекинда. Пусть R = Ли В,
где А / 0 и В 0, причем (Va € Л) Л (V6 € В) => (а < Ь).
Тогда или существует с Е А такое, что а < с Va Е А, или
существует с ЕВ такое, что с < bYb Е В,
Доказательство. Поскольку А 0 и Va € А => а < Ь, где
b Е В (В 0), то А - ограниченное сверху непустое множество в R
и в силу принципа полноты Вейерштрасса существует с = sup А Е R.
Поскольку c€R, тосбЛиВ.
Заметим, что А П В = 0. В противном случае существует а$ Е
АГ\В,т тогда (ао 6 Л) Л (ао G В) => (ао < ао), что невозможно.
Поскольку А П В = 0, то либо с Е А, либо с Е В. Если с Е Л,
то (Va G Л) => (а < с), поскольку с = sup Л. Если с Е В, то должно
выполняться неравенство b > cVb Е В. В самом деле, допустим от
противного, что существует Ьо ЕВ такое, что 6о < с. Тогда поскольку
с = sup Л, то из свойств точной верхней грани множества вытекает,
что существует ао € Л такое, что Ьо < ао < с. Но неравенство Ьо < ао
при а0 6 А и Ьо € В противоречит свойству (Va € Л) Л (Vb € В) =>
а < Ь. Итак, в случае сЕ В имеем с < b Vb Е В.
III принцип полноты R (теорема отдели-
мости). Пусть А С R и В С R, причем А/0 иВ/0, а также
(Va е А) Л (Уб € В) => (a < Ь).
Тогда Зс £ R такое, что (Va € А)Л(Уб £ В) => (a < с < б) (точка
с отделяет множества А и В).
Доказательство. Построим разбиение по Дедекинду R =
U Bi такое, что А С Ах и В С Вх. Для этого положим Вх = {бх €
R|36 е В такое, чтоб < Ьх} и Ai = R\ Вх. Докажем, что В С Вх и
А С Ах. В самом деле, Убх € В 35 = бх € В, т. е. bi € Вх, откуда имеем
Д С Вх. Далее, если бы существовало ао € А такое, что ао € Вх, то
в силу определения множества Вх ЗЬо € В такое, что Ьо < ао, но это
неравенство противоречит условию теоремы, согласно которому (Va €
А) Л (Уб 6 В) => (а < Ь). Поэтому ао€Вх вопреки предположению.
Итак, А с R \ Вх = Ах- Таким образом, имеем R = Ах U Вх, где
35
Ai Э A ± 0 и Bi D В 0. Докажем^ что (Vai 6 Ai) A (Vbi E Bi) =>
(ai < bi). В самом деле, в противном случае Зао 6 Ai и ЗЬо 6 Bi такие,
что Ьо < <*0, и тогда в силу определения множества Bi ЗЬ Е В такое,
что Ь < Ьо < ао, откуда следует, что ао 6 Bi = R \ Ai. Противоречие.
Таким образом, множеств Ai и Bi удовлетворяют условиям Дедекин-
да (определяют разбиение R по Дедекинду). По теореме Дедекинда
существует с £ R такое, что
(Vai 6 Ai) A (Vbi Е Bi) => (ai < с < bi).
Но тогда (Va £ Ac AJ Л (Vb Е В С Bi) => (a < с < Ь).
Определение. Система отрезков {[an, Ьп]}, п Е N, назы-
вается вложенной системой, если [an,bn] С R и
[^n+i? ^п+1] С [ап, ЬЛ] Vn Е N.
IV принцип полноты R Кантор а. Пусть в R дана
вложенная система отрезков {[an, Ьп]} так, что Vn Е N [an, bn] С R
и [ап+ь^n+i] С [ап,Ьп].
4-оо
Тогда Q [ап, Ьп] ф 0, т. е. Зс Е R такое, что с Е [an, bn] Vn Е N.
П = 1
Доказательство. Воспользуемся теоремой отделимости.
Пусть А = {a Е R|а = an,n Е N} 0 и В = {Ь Е R| b = bn,n Е
N} 0. Пусть п < т, тогда (ап < ат < Ьт) => (ап < bm), а при
п> т (ап <Ьп < Ът) => (ап < Ьт). Итак, ап < bm Vn, т Е N.
Таким образом, А С R, А 0, В С R, В / 0 и (Va Е А) Л (Vb Е
В) => (а < Ь). В силу теоремы отделимости существует с Е R такое,
что ап < с < bm Vn, т Е N и, в частности, ап < с < bn Vn Е N, т. е.
4-оо
с Е [an, bn] Vn Е N р)	0*
П = 1
Теорема. Если 7 есть архимедово упорядоченное поле, в
котором имеет место принцип полноты Кантора, то J7 = R, т.
е. принцип полноты Вейерштрасса следует из принципа полноты
Кантора в упорядоченном поле с аксиомой Архимеда.
Доказательство. Итак, нужно доказать, что в архиме-
довом упорядоченном поле Т с принципом полноты Кантора любое
непустое ограниченное сверху множество А С Т имеет в F точную
верхнюю грань. Будем при этом предполагать, что для множества
натуральных чисел N из Т справедливы аксиомы Пеано и, в част-
ности, имеет место принцип математической индукции. (Это можно
доказать.) Пусть А С Т, А 0 и А ограничено сверху в Т. Тогда
существует bi Е Т такое, что а < bi Va Е А (поскольку любое число,
большее верхней грани множества А, само является верхней гранью
для А). Выберем какое-либо ai Е А и рассмотрим отрезок [ai,bi]. В
36
дальнейшем при доказательстве этой теоремы отрезок [®, у] будем на-
зывать нормальным, если: 1) существует а 6 А такое, что а 6 [®,2/],
и 2) V& Е Т такого, что Ь > у => ЬеА. Если нормальный отрезок раз-
делить пополам, то по крайней мере одна из его двух половин будет
нормальной. В самом деле, если правая его половина содержит хотя
бы одну точку из А, то эта половина и будет нормальной, в противном
случае нормальной будет его левая половина. Отрезок [сц, fri] норма-
лен. Разделим его пополам и обозначим через [а2, Ь2] его нормальную
половину. Вообще, пусть по индукции [ап+х,Ьп+х] есть нормальная
половина отрезка [ап, Ьп].
Заметим, что длина отрезка [ап, Ьп] есть Дп = Ьп — ап =
(&1 -
В силу принципа полноты Кантора для вложенной системы
+оо
{[а», Ьп]}, П 6 N, имеем Q [ап, Ьп] / 0.
п = 1
Докажем, что у вложенной системы {[ап, Ьп]} только одна общая
точка. Если бы Bq, с2 6 [ап, bn] Vn G N и сх / с2 (ci < с2), то [ci, с2] С
[<Хп4-19 Ьп+iL и поэтому Vn G N ci -с2 < (Ьх — ах)/2п или ——— > 2П
с2 — С1
Vn G N. Но имеет место неравенство 2n > п Vn 6 N, что доказывается
с помощью принципа математической индукции, поскольку 1) 21 > 1
и 2) если 2” > п, то 2n+1 = 2 • 2n > 2п > п 4-1, т. е. 2n+1 > п 4-1.
Итак, (Ьх — txi)/(c2 — ci) > n Vn G N, но это соотношение противо-
+оо
речит архимедовости поля J7. Итак, Q [ап, &п] = {с}, где с 6 7.
п = 1
Докажем, что с = sup А. Если бы с не было верхней гранью для А,
_ +°О
то За0 Е А такое, что с < а, но тогда а06 П Ъп] = {с}, и поэтому
п = 1
Зп0 е N такое, что аПо < с < ЪПо < ао, т. е. отрезок [аПо, ЬПо] не может
быть нормальным. Противоречие.
Итак, 1) а < с Va 6 А.
Далее, Vai 6 Т такого, что ai < с Зпх 6 N, для которого ai <
4-оо
ani < с < ЬП1. (В противном случае имели бы ах 6 П [an,bn] = {с},
П = 1
т. е. ai = с. Противоречие.) Но тогда в силу нормальности отрезка
[annbni] Ba G A, a G	=> (аП1 < а < с < ЬП1) => (ах < а).
Итак, 2) Vai 6 F такого, что ах < с За 6 А, для которого имеем
а1 < а < с. Из свойств 1) и 2) вытекает, что с = sup А. Таким образом,
в упорядоченном архимедовом поле 7 имеет место принцип полноты
Вейерштрасса, а поэтому 7 = R.
37
$ 3. Мощности множеств Q и R
Если Q - множество всех рациональных чисел, a R - множество
всех действительных чисел, то Q С R.
Теорема. Множество рациональных чисел Q счетно.
Доказательство. Поскольку Q = { — €R|m€Z,n€N
m	n
и дробь — несократима}, то множество Q равномощно множеству
п
А = {(m, n)|m € Z,n € N и дробь — несократима}. Но А С В =
п
{(m,n)|m € Z,n € N}, где В - множество всевозможных упорядо-
ченных пар (тп, п) (тп € Z, п € N). Заметим, что А ~ Q будет даже
собственным подмножеством В. Докажем счетность множества В, для
чего построим таблицу
(0,1) -	* (0,2)	(0,3) -> (0,4) ..		•	(0,п)
(-1,1) 1	/	(-1,2)	(-1,3) 7	(-1,4) ••	• (-1,п)
(1,1)	(1,2) '	7	(1,3)	(1,4)	• (1,п)
(-2,1) Ф /	(-2,2)	(-2,3)	(-2,4) ..	• (-2,п)
В этой таблице содержатся все элементы множества В, и каждый
элемент из В входит в таблицу только один раз. Пронумеровав ее
согласно стрелкам, получим биекцию N на В. Итак, В ~ N, т. е.
счетно. Но тогда А С В как подмножество счетного множества не
более чем счетно. Но тогда не более чем счетно и Q А. Заметим,
что Q D N, и поэтому Q бесконечно, а стало быть, и счетно.
Теорема. Множество всех действительных чисел R несчетно.
Доказательство. Допустим от противного, что множест-
во R счетно, т. е. все действительные числа из R можно расположить
в последовательность
П1, аз, аз,... , ап,...	(3.1)
так, что п ф т ап ат. Проведем теперь следующие постро-
ения. Пусть [ai,/?i] - отрезок из R, не содержащий вх. (Например,
[ai,/?i] = [ai + l,ai + 2].) Тогда	Разделим отрезок [ai, fa]
на три равные части и выберем ту его треть [ааь/Зз], которая не со-
держит а2, тогда [а^/ЭД С [ai, fa], ai€[a2, fa]; i = 1,2. Допустим, что
уже построена система отрезков {[од,/%]} (к = 1,2,... , п) такая, что
[Лп,/?п] С [лп~ 1, fa_i] С ... С [ai,/3i],	, fa]5 i = 1,2,... ,п. Раз-
делим отрезок [an,/3n] на трй равные части и выберем ту его треть
38
[an+i> A»+1]> которая не содержит an+i, тогда [an+i,/3n+i] С [an,/3n] С
... С [«1,/?1], а<?[ctn+i, /Зп+1]> i = 1,2,..., n + 1. Тем самым по индук-
ции мы построили вложенную систему {[an,/3n]} n G N такую, что
Vn € N Oi?[«n,/3n] (г = 1,2,, п). По теореме Кантора существу-
+оо
ет с е R такая, что с € П [an,/3„].
П = 1
Но действительное число с не может быть членом последователь-
ности (3.1). В самом деле, если бы существовало т € N такое, что
с = ат, то по построению
+оо
С = aroG[a,n,)3ro] и поэтому Q [ап,/Зп].
П = 1
Противоречие. Таким образом, несчетность R доказана.
Глава 3
ТЕОРИЯ ПРЕДЕЛОВ
$ 1. Топология числовой прямой
Рассмотрим числовую прямую (-оо,+оо) = {®gR|-oo<®<
+оо} и в дальнейшем будем считать R = (-оо, +оо).
Определение. Окрестностью 0(a) (или U(a), или V(a))
точки а € R называется любой интервал (а,/3), содержащий точку
af т. е. 0(a) = (a,/3) = {® G R|a < ® < /3, а < а < /3}. Центриро-
ванной или сферической (с радиусом 6 > 0) окрестностью точки а
называется множество Uj(a) = (a — £, a + £) = {® € R| |® — a| < 5}.
Заметим, что V окрестности 0(a) = (а, (3) Зяо € R и £о > 0 такие,
что 0(a) = U&0(xq). (В самом деле, достаточно взять «о = (а +/3)/2 и
= (/3 - а)/2 > 0, тогда 0(a) = (а, /3) = («о - йь ®о + <fo) = Us0 (®о)-)
Определение. Если U (а) - окрестность точки а € R, то
проколотой окрестностью точки а называется множество U(a) =
Ща) \ {а}. В частности, Oj(a) = {я G R| 0 < |® - а| < 5}.
Отметим некоторые свойства окрестностей на числовой прямой.
1) Если a G R, то любая окрестность 0(a) точки а непуста, в
частности, Us (а) / 0 У<5 > 0. В самом деле, V окрестности 0(a) точки
а имеем
0(a) = (а, /3) = (a, a) U {a} U (а,/3) => 0(a)	0.
2) V окрестности 0(a) точки а € R существует центрированная
окрестность Us (а) такая, что Us(a) С 0(a), при этом радиус 6 >
39
О можно выбрать рациональным. В самом деле, поскольку О (а) -
окрестность точки а Е R, то 3®о € R и <5© > О такие, что О (а) =
Uj0(xQ) и а е Ufi0(xQ), т. е. О < |а - ®0| < <5о- Если xQ = а, то все
доказано. Пусть ®о / а, тогда 0 < |а — ®о| = <51 < <5о- Положим
J = (50 — <5х>0и рассмотрим центрированную окрестность Vi (а)
точки а. Тогда |а — ®о| < 6 Ух 6 Vi (а) и в силу выбора <5 > 0 и нера-
венства треугольника для модуля имеем |я — ж0| = |(®~а) + (а — ®о)| <
I® — а| + |а-®о| < <5+<5i = <5о~= <5о- Таким образом, |®~®о| < <£о
V® G Vi (а), т. е. х G (7<$0 (®о) = О(а) => Vi (а) С О(а). Далее, Q плотно в
R, поэтому 3g G Q такое, что 0 < q < 6 и тогда У<Да) С Vi (а) С 0(a).
3) Для любых двух окрестностей vW(a) и 02Да) точки а Е R
существует окрестность 0(a) такая, что 0(a) С У^(а) А 02Да).
В самом деле, в силу свойства 2) существуют центрированные
окрестности И^Да) точки а, для которых имеем И^Да) С У^(а)
(i = 1,2). Но тогда при 6q = min((5i,(52) > 0 имеем Wi0(a) С ИЪДа)
(г = 1,2), т. е. Wi0(a) С W6l (a) A W*2(a) С У(1)(а) А У<2>(а).
3') (Обобщение). Пересечение конечного числа окрестностей точки
a G R содержит окрестность точки а, т. е. У{У(*Да)} (г = 1,2,... , т)
30(a) С П V^(a).
»=1
4) (Аксиома отделимости Хаусдорфа). Если a, be R
и а / Ь, то 3 окрестности (7(a) и V(b) такие, что U(a) Г}У(Ь) = 0.
В самом деле, если а / Ь, то |а — Ь| = 8 > 0. Рассмотрим окрестнос-
ти IVi(a) и IVi(b) точек а и Ь соответственно. Покажем, что И^/з(а) А
W*/3(b) = 0.
Допустим, что 3®о 6 ИЪ/з(а) A Wi/3(b). Тогда в силу неравенства
треугольника имеем 0 < 6 = |а — Ь| = |(а — ®о) 4- (®о ~ Ь)| < |а — ж0| +
। tl <5	*	2<f
l^o —	< - -h - = —. Противоречие.
О	и	и
5) УЬ 6 О(а) => 0(a) = U(b), т. е. для любой точки b Е 0(a)
множество 0(a) является окрестностью точки b Е R. Кроме того,
если b £ 0(A) и b / а, то существует центрированная окрестность
V^(b) С 0(a) такая, что aGVi(b).
В самом деле, поскольку b Е О(А), то О(А) = (7(b), причем в силу
свойства 2) ЗУ^ (b) С (7(b); если b / а, то |Ь — а| = 62 > 0, и тогда при
О < 6 < пйп(<М2) Vs(b) С Vh(b) С U(b) = 0(a), причем аёУДЬ).
Определение. Точка а Е R называется внутренней точ-
кой множества А С R, если существует окрестность 0(a) точки
а такая, что 0(a) С А.
Пример. А = [0,1), а = 1/2, Oi/^(a) = (1/4,3/4) С А, т. е.
а = 1/2 - внутренняя точка множества А = [0,1).
40
Определение. Совокупность всех внутренних точек мно-
0
жества А называется внутренностью А и обозначается А или А*.
П р и м е р. А = [0,1), А= (0,1).
Определение. Точка а Е R называется внешней точкой
множества А, если существует окрестность 0(a) точки а такая,
что О(а)ПА = 0. В частности, если а - внешняя точка множества
А, то аЕА, т. е. а 6 СА. Обратное утверждение, вообще говоря,
неверно.
П р и м е р. А = [0,1), а = 3/2, 0(a) = (5/4,2), а = 3/2 - внешняя
точка множества А, но b = 1 не является внешней точкой для А, хотя
b Е СА.
Следствие. Внешняя точка множества А является внутрен-
ней точкой для его дополнения СА.
Определение. Совокупность всех внешних точек множес-
тва А называется внешностью А и обозначается через Ае,
П р и м е р. А ~ [0,1), Ае = (-оо, 0) U (1, +оо).
Определение. Точка а Е R называется граничной точкой
множества А С R, если V окрестности 0(a) точки а имеем 0(a) О
А / 0 и 0(a) О СА ф 0.
П р и м е р. А = [0,1), а = О, b = 1 - граничные точки множества
А.
Определение. Границей дА множества А называется мно-
жество всех граничных точек А. Очевидно, дА = 5(СА).
П р и м е р. А = [0,1), дА = {0} U {1}, {0} Е А, {1}ЁА.
Определение. Точка а Е R называется точкой прикосно-
вения множества А С R, если для любой окрестности 0(a) точки
а имеем 0(a) Г\А^0.
Пример. Любая внутренняя точка и любая граничная точка
множества А являются точками прикосновения множества А.
Определение. Совокупность всех точек прикосновения мно-
жества А С R называется замыканием множества А и обознача-
ется через А, при этом А С А.
П ри м е р. А = [0,1) U {2}, А = [0,1] U {2}.
Замечание. (А С В) => (А С В).
Определение. Точка а Е R называется предельной точкой
множества А С R, если для любой окрестности О (а) точки а имеем
О (а) ПА ф 0.
П р и м е р. А = [0,1), а = 1ЁА, но О (1) О [0,1) ф 0 VO(1), т. е.
а — 1 - предельная точка.
Определение. Совокупность всех предельных точек мно-
жества А называется производным множеством и обозначается
через А', при этом Af С А.
41
П р и м е р. А = (0,1), А' = [0,1].	_
3 а м е ч а н и е. Из определений множеств А и А1 вытекает отно-
шение Л U Л' С Л.
Определение. Точка а € R называется изолированной точ-
кой множества А С R, если существует окрестность 0(a) точки
а такая, что 0(a) П А = {а}.
П р и м е р. А = [0,1) U {2}, а = 2 - изолированная точка множес-
тва А.
Теорема. Z = Л U А9 и СА = Ле.
Доказательство. Было отмечено, что всегда имеем A U
А9 С Л. Для доказательства обратного включения заметим, что если
а € Л, то а есть точка прикосновения множества Л, и тогда либо
а - изолированная точка множества Л (и поэтому а € Л), либо_а -
предельная точка для Л (т. е. а € Л'). В обоих случаях имеем Л С
ЛиЛ'. Итак, Л = ЛиЛ'.
Далее, включение Ле С С Л вытекает из определения внешней точ-
ки. Если же а?Л, то а не является точкой прикосновения для Л, a
потому существует окрестность 0(a) точки а такая, что 0(a) П Л =
0 => а € Ле, откуда С Л С Ле. Из обоих включений вытекает равен-
ство С Л = Ле.
3 а м е ч а н и е. Из определений вытекают включения дА С Л и
(а € дА) А (а?Л) => а G Л'.
Замечание. Любая изолированная точка множества Л явля-
ется граничной точкой для Л (т. е. а € дЛ).
Определение. Множество Л С R называется открытым,
о
если все его точки внутренние, т. е, если А =А>
Теорема. Любая окрестность 0(a) точки а € R есть от-
крытое множество.
Доказательство. Рассмотрим любую окрестность 0(a) точ-
ки а € R. В силу свойства 5) для окрестностей в R множество 0(a)
является окрестностью любой точки Ь € 0(a) (т. е. 0(a) = С7(Ь)),
таким образом, любая точка b € 0(a) есть внутренняя точка для мно-
жества 0(a). Но тогда множество 0(a) открыто.
Теорема. Множества Л, и Ае открыты для любого множе-
ства Л.
Доказательство. В силу определения Va € Л, 3 окрест-
ность 0(a) С Л. Но поскольку Vb € 0(a), имеем 0(a) = U(b) С Л,
то Ь есть внутренняя точка для Л, поэтому b € Л,-. Таким образом,
Va € Л,’ 30(a) С Л,, т. е. Л, - открытое множество. Далее, Vа € Ле
30(a) С СЛ, но Vb € 0(a) имеем 0(a) = U(b) С СЛ, т. е. b € Ле. Тем
самым доказано, что Va € Ле 30(a) С Лв, т. е. множество Ле открыто.
Определение. Множество А С R называется замкнутым,
если оно содержит все свои предельные точки, т. е. если А9 С Л.
42
Теорема. Множество А С R замкнуто о А = А.
Доказательство. 1) Пуста А замкнуто^тогда А' С А, но
Я = A U А', поэтому А = А. 2) Пуста А = А, тогда А = A U А' А' С
А, т. е. множество А замкнуто.
Замечание. Пустое множество 0 и все множество R являют-
ся одновременно замкнутыми и открытыми.
Теорема. (Множество А замкнуто)^ (множество СА от-
крыто).
Доказательство. Необходимость: пусть А замкнуто. Тог-
да А = А. Докажем, что Vb € С A 30(b) С С А.
Допустим, что это не так. Тогда 0(b) П А ф 0 VO(b), и поэтому
b G А = А, что противоречит предположению b € СА. Таким образом,
если А замкнуто, то СА открыто.
Достаточность: пусть множество СА открыто. Докажем, что А' С
А. Допустим, что это не так, тогда ЗЬ € А' такая, что_Ь € СА. Но
поскольку СА открыто, то 30(b) С СА, и тогда b € СА, т. е. Ь?А'.
Противоречие. Итак, А' С А, т. е. А замкнуто. Таким образом, если
СА открыто, то А замкнуто.
Пример. Пусть А = [a—S, а+й] = [а,/3] - отрезок в R. Покажем,
что множество СА открыто в R. В самом деле, Vxq € СА = {х €
R| |х - а| > й} => |хо - а| = Йо > 6, но тогда, выбирая h € (0, Йо - 6).
видим, что Vx € Оь(хо), в силу неравенства треугольника имеем
|а — х| = |(а - хо) - (х - хо)| > |а - хо| — |х - хо| > Йо - Л >
> Йо — (Йо — й) = Й > О,
т. е. х € СА, а потому Uh(xo) С СА, т. е. СА = R \ [а, /3] - откры-
тое множество. Но тогда в силу теоремы видим, что отрезок [а, $ -
замкнутое множество в R, причем [а,/3] не является открытым, т. е.
его концы а и /3 не являются внутренними точками.
Следствие. (А открыто) <=> (СА замкнуто). В самом деле,
применяя предыдущую теорему к множеству В = СА, имеем (В = СА
замкнуто) <=> (СВ — ССА = А открыто).
Теорема. Пересечение конечного числа открытых множеств
есть открытое множество. Объединение конечного числа замкну-
тых множеств есть замкнутое множество.
Доказательство. Пусть G = р| G», где G* =G* - от-
к=1
крытые множества при k = 1,2,..., т. Но тогда Va € G =► а €
=G* (к = 1,2,...,т), и поэтому 3 окрестности 0^(а) такие,
что 0<*)(e) с G* (Л = 1,2,... , m). В силу свойства 3) окрестнос-
тей 30(a) С П 0^(a) С G, т. е. (любая a G G есть внутренняя
*=1
точка множества G) => (G =G*), т. е. G открыто. Пусть теперь
43
т
F = (J Fk, где множества Fk замкнуты. Тогда в силу законов алгеб-
к=1
т	т
ры множеств G = CF = С U F* = р| CF*. Поскольку Fk замкнуто,
fc=l	к=1
то CFk открыто при к = 1,2,... ,тп, и поэтому в силу доказанного
т
выше G = р| CFk открыто, а потому F = CG замкнуто.
к=1
Замечание. Теорема перестает быть верной для бесконечного
«числа» множеств.
Пример. Пусть Gk = ( -1 — 7,1 4- 7 ), тогда Gk открыто Vfc G
у к к J
+ оо
N, но р| Gk = [— 1,1] - множество замкнутое, а не открытое.
к=1
Теорема. Пересечение р| Fa любого семейства замкнутых мно-
а
жесте Fa есть множество замкнутое. Объединение (JGa любого
а
семейства открытых множеств Ga есть множество открытое.
Доказательство. Пусть Ga - открытое множество Va и
а 6 G = (J Ga. Тогда существует а© такое, что а 6 Gao, Gao открыто,
си
поэтому существует 0(a) С Gao С G = |JGa, т- е* любая точка а 6 G
а
есть внутренняя точка для G. Поэтому множество G открыто. Далее,
пусть Fa замкнуто Va и F = р| FQ. Тогда CF = С р| Fa = (J CFa, при-
at	at	a
чем Va множество CFa открыто (как дополнение замкнутого множес-
тва Fa). Поэтому в силу доказанного выше множество CF открыто,
а поэтому множество F замкнуто.
Теорема. Для любого множества А граница дА есть замкну-
тое множество.
Доказательство. Пусть a G дА. Тогда 0(a) А дА / 0
VO(a), и поэтому существует b G дАсЮ(а), т. е. Ь 6 0(a) = U(b). Но в
силу определения граничной точки имеем U(b) А А 0 и U(b) А С А /
0, откуда О(а) А А / 0 и 0(a) АСА 0, т. е. a G дА. Таким образом,
имеем дА С дА => дА = 5А, т. е. дА замкнуто.
Теорема. VACF множество А замкнуто.
Доказательство. Ранее было доказано, что СА = Ае. Но
множество Ае (а стало быть, и множество СА) открыто, поэтому А
замкнуто.
Задача. Докажите непосредственно, что (А) = А.
Теорема, (а 6 А' 0) (в любой окрестности 0(a) точки
а 3 бесконечное множество точек из А).
Доказательство. Необходимость. Пусть А' / 0 и a G А',
о
тогда О (а) А А 0 V0(а). Допустим, что существует окрестность
О (а) точки а такая, что в ней содержится лишь конечное число точек
44
из А, тогда О (a) Cl А = {ai,..., а*}	0. Поскольку Л,- = |а - а, | > О
(г = 1,... , к), то имеем h = min(/ii, Л2, • • • > hfc) > 0.
v	о
Рассматривая центрированную окрестность С7л(а), видим, что Uh
(а) П А = 0, но тогда абА'. Противоречие.
Достаточность. Пусть в любой окрестности 0(a) точки а содер-
0
жится бесконечное множество точек из А. Тогда О (а) П А	0 VO(a),
т. е. а Е А'.
Следствие. Конечное множество А С R не имеет предельных
точек.
Теорема. Для любого А С R производное множество А* за-
мкнуто, т. е. А* = А1.
Доказательство. Пусть А С R. Если А' = 0, то А' за-
мкнуто. Пусть А' 0. Заметим, что всегда A' D А'. Покажем, что
7 С А'. Но Va Е А' => 0(a) А А' 0 VO(a), и тогда существует
& Е А' такая, что Ъ Е О(а), поэтому 0(a) = U(b) есть окрестность
точки Ь. Поскольку Ь Е А', то ее окрестность U(b) = 0(a) содержит
бесконечное множество точек из А, но тогда a Е А', т. е. А' С А'.
Итак, А' = А', т. е. производное множество А' замкнуто.
О п р е д е л е_н и е. Множество А С R называется всюду плот-
ным (в R), если A = R.
Пример. Пусть Q -множество рациональных точек, тогда Q =
R, т. е. Q всюду плотно в R. Заметим, что всюду плотное (в R)
множество Q счетно.
Примеры. 1) А = Z С R. Множество А - бесконечное множес-
тво, состоящее из одних изолированных точек, оно не имеет ни одной
предельной точки, т. е. А' = 0. Кроме того, A D 0 = А', т. е. А = Z
замкнуто.
2)	А = {g Е Q|g = 1/п, п Е N}. Тогда 0 есть единственная пре-
дельная точка А, т. е. А' = {0}, причем ОеА.
3)	А = |g Е Q|g = — илид = 1--,пЕЮ С R. Тогда А' = {0}U
(	п	nJ
{1}, при этом О Е А,1 Е А, А' С А, А - замкнутое множество.
4)	А = (g е Q|g = А-илид = ^-± —^-;п, fe G No). Тогда А' =
{о, 1, i,..., А,J с Д т,е, А замкнуто.
Будем рассматривать теперь числовые последовательности вида
(an) в R (п ап, п Е N, ап Е R). Заметим, что каждая по-
следовательность (ап) определяет некоторое множество {an} из R:
{an} = {х Е R|3n 6 Nтакое,что® = an}. Последовательность
ai> а2,... ,an,... всегда «бесконечна», но входящие в нее элементы
не обязаны быть различными, так что соответствующее последо-
вательности (an) множество {an} может оказаться и конечным. На-
45
пример, последовательности (ап), где ап = 1 Vn € N, соответствует
множество {ап} = {1}, состоящее из одной точки.
Определение. Пусть (ап) - числовая последовательность.
Точка (число) а € R называется пределом последовательности (ап),
если V окрестности 0(a) точки a 3N € N такое, что ап € 0(a)
Vn>N.
Если последовательность (ап) имеет пределом точку а € R, то
говорят, что последовательность (ап) сходится к а.
Замечание. Последовательность (ап) сходится к а, если, како-
ва бы ни была окрестность 0(a) точки а, все элементы последователь-
ности (ап), за исключением, быть может, конечного их числа, принад-
лежат окрестности 0(a). Если использовать свойство 2) окрестностей
в R, то имеем
Определение. Последовательность (ап) сходится к точке
а € R, если Ve > 0 3./V(e) € N такое, что ап € Ue(a) Vn > N(e).
Пример. Последовательность ( - ) сходится к 0. В самом деле,
\П/
Ve > 0 по аксиоме Архимеда 3No G N такое, что No > - > 0, но тогда
11 е
- < е Vn > No, т. е. - € 17* (0). В частности, показано, что Ve > 0
SN(e) е N такое, что Ui/n(0) С 17.(0) Vn > N(e).
Теорема (единственности предела последовательности). Если
последовательность имеет предел, то этот предел единствен.
Доказательство, Допустим, что последовательность (ая)
имеет два различных предела а / b (a, b Е R). Тогда в силу акси-
омы отделимости Хаусдорфа (см. свойство 4) для окрестностей) су-
ществуют окрестности U(a) и У(Ь) такие, что 17(a) П V(b) = 0. По-
скольку последовательность (ап) сходится к а, то для U(a) 3Ni Е N
такое, что ая € U(a) Vn > Ni. С другой стороны, поскольку после-
довательность (ая) сходится к 6, то для окрестности V(b) 3N2 € N
такое, что ая € V(b) Vn > Nj. Но тогда Vn > No = max(Ni,N2)
ая g 17(a) A V(b) = 0. Противоречие.
Теорема, (а € А) <=> (3 последовательность (ая), ап € А
(Vn Е N) такая, что (ая) сходится к а).
Доказательство. Достаточность. Если существует после-
довательность (an) элементов A (an € A Vn € N), сходящаяся к а,
то V окрестности U(a) 3No € N такое, что an € Ща) Vn > No, т. в.
U(а) А А 0 4U(a), поэтому, согласно определению точки прикосно-
вения, имеем a € А.
Необходимость. Пусть a € А. Рассмотрим центрированные окрест-
ности I7i/n(a) Vn Е N. Тогда по определению точки прикосновения
имеем I7i/n(a) А А 0 Vn g N, так что Vn g N Зая € I7i/n(a) А А.
Рассмотрим последовательность (ая). Очевидно, an € A Vn € N. Кро-
46
ме того, Ve > О 3JV(e) > - такое, что Vn > JV(e) имеем ап € Ui/n (а) С
У<(а). Но это и означает сходимость последовательности (ап) к точке
а.	_
Замечание. Итак, замыкание А множества А есть множество
пределов всех сходящихся последовательностей из А.
Следствие. Для того чтобы множество А было замкнуто, не-
обходимо и достаточно, чтобы А содержало пределы всех своих схо-
дящихся последовательностей.
Т е о р е м а. (а € А' ф 0)0 (существует последовательность
(ап), сходящаяся к а, такая, что ап € А \ {a} Vn 6 N и От
Vn ф т).
Доказательство. Достаточность. Пусть последовательность
(ап) сходится к а £ R, причем On € А \ {а} Vn € N и а„ £ ат при
п т. Тогда VO(a) ЭЛГо € N такое, что an € 0(a) Vn > Nq, т. е. лю-
бая окрестность 0(a) точки а содержит бесконечное множество точек
ан € А, но тогда, как было доказано ранее, a € А'.
Необходимость. Пусть А' 0 и a € А'. Тогда любая окрестность
0(a) содержит бесконечное множество точек из А. Рассмотрим семей-
ство центрированных окрестностей {I7i/n(a)}, п € N. Тогда сущест-
вует ai такое, что ai € £7i(a) Г) А, Заз <*1 такое, что аг € 17х/а(а)НА,
Заз / ai, аз аг такое, что аз € 17х/з(в)ПА и вообще Vn > 1 Зап а*
(k = 1,2,..., п -1) такое, что an € ^1/п(«) П А. Построенная последо-
вательность (an) такова, что an € А\ {a} Vn; ап / ат1 п/т, причем
Ve > 0 ЗЛ7Ь(г) € N такое, что an € Ui/n(a) С К (a) Vn > No(e), т. е.
последовательность (an) сходится к а.
Определение. Точка а £ R называется точкой сгущения
(или частичным пределом) последовательности (ап), если любая окрест-
ность U(а) точки а содержит бесконечное множество злементов
из (а„).
Замечание. Если последовательность (an) сходится к а, то ее
предел а является точкой сгущения последовательности (ап). Обрат-
ное, вообще говоря, неверно.
Пример. Последовательность (an), где an = (—l)n Vn € N,
имеет две точки сгущения (-1) и 1 и не имеет (проверьте это само-
стоятельно) предела. Между прочим, множество {an} = {-1,1} пре-
дельных точек не имеет.
Замечание. Точка сгущения последовательности (an) может
не быть предельной точкой множества {an}, хотя и будет всегда точ-
кой прикосновения множества {an}.
Определение. Пусть (an) - последовательность. Рассмот-
рим строго возрастающую последовательность натуральных чисел
(п*) такую, что пх < пг < пэ < ... (п/, < п/ при к < I), пь > к Vfc.
47
Тогда последовательность (ank) называется подпоследовательнос-
тью последовательности (ап).
Замечание. Полагая для (an) Пк = fc, видим, что последова-
тельность (аь) является подпоследовательностью для самой себя.
Теорема, (а является точкой сгущения последовательности
(аЛ)7 последовательности (ап) можно выделить подпоследо-
вательность (anh), сходящуюся к а).
Доказательство. Необходимость. Пусть а есть точка сгу-
щения последовательности (ап). Тогда в любой центрированной окрест-
ности Ui/k(a) G N) существует бесконечное множество значений п
таких, что ап € C/i/fc(a). Рассмотрим такое ni > 1, что аП1 е Ui(a).
Далее возьмем П2 > nx > 1 такое, что аП2 е СЛ./г(<*)> при этом
пг > 2, затем выберем пз > Пг > 2 таким, что апз € СЛ/з(а), причем
пз > 3. Шаг за шагом получим последовательность к Пк такую,
что Пк > Пк-ъ аПк € Ui/k(a)> nk > Л- Очевидно, п* Д и п* > fc, так
что последовательность (ank) есть подпоследовательность последова-
тельности (аЛ). Положим Ьк = аПк. Тогда Ve > 0 SNq € N такое, что
No > и поэтому Ьк = аПк € Ui/k(a) С Ve(a) Vk > Nq. Но это озна-
чает, что последовательность (Ък)9 а стало быть, и (anjb), сходится к
а.
Достаточность. Пусть из последовательности (ап) можно выде-
лить подпоследовательность (аП||), сходящуюся к а. Тогда в любой
окрестности 0(a) содержится бесконечное множество элементов под-
последовательности (anjk), а тем самым и последовательности (ап). Но
тогда а есть точка сгущения последовательности (ап).
Теорема. Множество точек сгущения последовательности
(ап) есть замкнутое множество.
Доказательство. Пусть А есть множество всех точек сгу-
щения последовательности (an). Пусть a € А', тогда в любой окрест-
ности 0(a) точки а содержится хотя бы одна точка сгущения Ь, и по-
скольку 0(a) = U(6), то по определению точки сгущения в окрестнос-
ти U(b) = 0(a) содержится бесконечное множество элементов последо-
вательности (an), т. е. а € А1 есть точка сгущения последовательности
(ап). Тем самым показано А1 С А, т. е. множество А замкнуто.
§ 2.	Понятие предела функции в точке
Пусть дана действительная функция одного действительного пе-
ременного f : у = /(«), я € А С R, |/ С R и точка а € R. Введем
сначала понятие предела функции f(x) (при х а) для точек a € А',
т. е. только для предельных точек области определения А функции
f(x). В дальнейшем будут рассмотрены обобщения понятия предела
48
функции на случаи (ж -> а + 0), (ж а - 0), (ж -> +оо), (ж -> -ос),
(ж -> оо). Будет рассмотрено также понятие предела функции по «ба-
зису фильтра».
Отметим следующие свойства проколотых окрестностей точки а:
1) {/(а)	0 Vl7(a) (a GR) и, в частности, Vh(a) 0	> 0;
2) Vl/^^a) и СЛ2)(а) 3V(a) С (/^(а) О 1Л2)(а) и, в частности,
tff7hl(a),l7h2(a) 3^(а) С 141(а)пик2(а).
Замечание. Очевидно, имеют место даже более точные утверж-
дения:
^(а) ГИ7<2>(а) = Й(а)и17Л1(а) П1Д2(«) =
где кз =	/12) > 0.
Определение (окрестностное определение предела функции
в точке). Пусть дана функция f : х Е А С R, у = /(ж) Е R и a Е А9 -
предельная точка области определения А. Точка (число) Ь Е R на-
зывается пределом функции /(ж) в точке а, если для любой окрест-
ности Vfb) точки b существует окрестность Ufa) точки а такая,
что ffx) Е Vfb) Ух eUfa)C\ А. Запись: b = lim ffx).
Замечание. Итак, b = lim /(ж) (а 6 А9), если W(b) 317(a)
х-+а
такая, что ffUfa) П А) С V(i>). Окрестностному определению предела
эквивалентно следующее (e, <J) определение предела функции в
точке по Коши:
Пусть функция /(ж) определена на множестве А С R и а 6 А1.
Тогда b = lim ffx), если Уе > 0 3<5 > 0 такое, что Ух Е А, удовле-
х—¥а
творяющего неравенствам 0 < |ж — а| < 6 => |/(ж) — Ь| < е. Отметим
еще одно определение предела функции в точке.
Определение. Пусть функция /(ж) определена на множес-
тве А С R и а 6 А9. Тогда b = lim ffx), если Уе > 0 существует
х-+а
окрестность Ufa) точки а такая, что |f (ж) — Ь| < е Ух 6 Ufa) П А.
Пример, /(ж) = [ж], ж G А = [0,п), очевидно, п Е А'. Покажем,
что lim ffx) = n — 1. В самом деле, Уе > 0 3<5 = 1/2 > 0 такое, что
Ух Е А, удовлетворяющего неравенствам 0 < |ж — п| < 1/2 (п — 1/2 <
ж < п) => |[ж] - (п - 1)| = |(п - 1) - (п - 1)| = 0 < е.
Замечание. Пусть ffx) определена на множестве А и а Е А'.
Введем систему В множеств {В} таких, что В = Ufa) О А. Тогда
система В обладает свойствами: 1) В = Ufa) П А 0 У В Е В (в силу
определения предельной точки а Е А' и свойства 1) для проколотых
окрестностей 17(a)) и 2) VBi,B2 Е В ЗВ3 Е В такой, что В3 С В1ПВ2
(в силу свойства 2) для проколотых окрестностей 17(a)).
Тогда b = lim ffx), если Уе > 0 существует множество В Е В
такое, что |/(ж)< е Ух Е В.
49
Рассмотрим числовую последовательность п -> ап, п € N, ап € R.
Вспомним введенное ранее понятие предела последовательности.
Определение. Пусть п ап, п € N, есть числовая после-
довательность. Число о € R называется пределом последователь-
ности (an)f если VU(d) BNq € N такое, что ап € U(a) Vn > No.
Запись: a = lim an. Или
n—>4-oo
Определение. Число a € R называется пределом последо-
вательности (ап), если Ve > 0 Э-/Уо(е) € N такое, что |an - a| < е
Vn > No.
Замечание. Итак, если числовая последовательность (an) схо-
дится к а, то а = lim ап.
п-44-00
Замечание. Введем систему В множеств {Вп}, где Вп =
{т 6 N|m > п}. Очевидно, В обладает следующими свойствами (ср.
свойства системы В из определения lim /(®) = Ь):
я-4 a
1)	Вп * 0 Vn е N;
2)	VBm, Вп € В ЗВ/ € В такое, что В/ С Вт П Вп (1 = тах(т,п)).
Тогда a = lim an, если Ve > 0 ЗВх0 € В такое, что |ап - а| < е
п->4-оо
Vn е Вх0.
То общее, что есть в определениях lim /(х) и lim ап с помощью
я-4 а	п—>4" оо
системы В, послужит нам в дальнейшем для введения общего понятия
предела функции по «базису фильтра».
П р и м е р ы. 1). Пусть (an), где an = с Vn € N, тогда *lim* an = с,
так как Vn € N => |an — с| = |с - с| = 0 < е Ve > 0.
2)	. Пусть an = (~1)п. Последовательность (an) не имеет предела
(хотя у нее и есть два частичных предела -1 = ^lim*a2n+i и 1 =
lim азп<) В самом деле, допустим, что 3 lim ап = а и а < 0, тогда
n-44-oo	n-44-oo
'in = 2k е N => an -a = 1-a > 1 |an-a| > 1. Аналогично при a > О
in = 2k +1 e N => a„ - a = -1 - a < -1 |an - a| > 1. При 0 < e < 1
получаем противоречие с определением предела lim an = a.
n-+4-oo
3)	. Вели 0 < a < 1, то lim an = 0. В самом деле, ip > 0 и in € N
n-44-oo
п-1	п-1
имеем (1 + р)п > (1 +р)п -1 = Р S (1 +р)* > Р S 1 = пр. Поскольку
*=о	” fc=o
1 1
О < a < 1, то для р =---1 имеем р > 0 и a = 7——. Тогда имеем
а	1+р
/ 1 \п 1 1
О < a" = I -----I = г.------гт < —• В силу теоремы Архимеда
\1+р/	(1 + р)п пр
Ve > 0 BJVq € N такое, что No > —, откуда in > No => |an - 0| =
1 *
|an I < — < е => lim ап = 0 при 0 < a < 1.
Пр	п->+оо
50
n	1
4). Если q 6 R, |g| < 1, to lim IT g* = ---------. В самом де-
«-♦+<* *ж0	1 —9
ле, Vg € R имеем (1 - g) £ qk = 1 - g"+1, поэтому при g 1
*0
(Ee* =
\*=0
при g = 0
n
£g‘-
k>0
-g"+l
1-9
9
i-g
(n	1 \
52 g* = ,-) • Используя доказанное ранее соотношение
k=o L-qJ
lira |g|n = 0 при 0 < |g| < 1, имеем (Vg € R, 0 < |g| < 1) Ve > 0
П-4Ч-00
BNo € N такое, что |g|n <
e  9 • -—- = e Vn > No, t. e. lim 52 9* = , * 
i - g g	fw+oo	i - g
Замечание. Рассмотрим числовую последовательность (ап) и
n
построим еще одну последовательность (вп), где вп = 52 °* называг
к=1
ется n-й частичной суммой бесконечного числового ряда
+оо
(2.1)
Определение. Если 3 lim вп = в € R, то ряд (2.1) козы-
П-44-00
вается сходящимся, а число 8 называется его суммой. Если lim вп
П-4+00
не существует, то числовой ряд (2.1) называется расходящимся.
5). Пусть a* = g*”1 (k = 1,2,...) есть член геометрической про-
n	1 — д’*
грессии со знаменателем д. Тогда при д # 1 вп = 52 д*-1 = т—
*1	1 - д
1	t2P .	1
и поэтому а) при |д| < 1 3 Um вп = т-~ > так что 52 д*-1 = ;-
п-++оо 1 — д	Г— д
(ряд сходится), б) при |д| > 1 ряд расходится (доказать самостоятель-
но).
в). Рассмотрим функцию х -+ х, х € А, причем а € А1. Тогда
1™ х = а. В самом деле, полагая f (x) = х V® € А, из определения
предела функции в точке по Коши имеем Ve > 0 3d = е > 0 такое,
что V® е Л, удовлетворяющего неравенствам 0 < |® - a| < S = е, <
|/(®) - а| = |® - а| < е, 3 lim /(®) = а.
§ 3. Теоремы о пределах функций
и последовательностей
Будем рассматривать функцию вида f : ® 6 М, /(®) € R (причем
a € М') и числовые последовательности (оп) (п -+ an,n € N). Будут
51
доказаны «дуальные» теоремы о пределах как для функций, так и для
последовательностей.
Теорема единственности предела функции.
Если функция /(®), определенная на множестве М, имеет предел в
точке a Е Mf, то этот предел единствен.
Доказательство. Допустим от противного, что
3 lim f(x) = bi и Slim f(x) = b2, причем b± ф b2 (b^b2 E R).
x-+a	x-+a
В силу аксиомы отделимости Хаусдорфа существуют окрестнос-
ти U^(bi) и U(2\b2) такие, что U^(bi)	= 0. Поскольку
lim f(x) = bi, то в силу окрестностного определения предела функции
х—
в точке а существует окрестность У^)(а) такая, что f(x) Е U^(bi)
V® 6	П М. С другой стороны, поскольку lim f(x) = b2,
х—+а
то существует окрестность у(2)(а) такая, что f(x) Е U^(b2)
V® Е V<2)(a) AM.
Но тогда, используя свойство 2) для проколотых окрестностей,
видим, что 31У(а) С 0хЦа) П У^2^(а), и тогда V® Е ТУ (а) А М
f(x) Е U^(bi) A U(2\b2) = 0. Противоречие.
Замечание. Теорема единственности предела последователь-
ности была доказана в § 1 главы 3 данной книги.
Теорема 1. Пусть существует lim /(®) = А и А > В, Тогда
х—¥а
существует U(a) такая, что /(®) > В V® Е (7(a) А М.
Доказательство. Положим А — В = во > 0* Тогда по
определению предела функции в точке а Е Mf BU(a) такая, что V® Е
(7(a) А М => (|/(®) ~ 4[) < £о) => (-£о < /(®) - А < во), откуда
/(®) > А - во = В Ух Е U(а) А М.
Замечание. Пусть существует lim f (®) = А и А < С, Тогда
х-ьа *
существует (7(a) такая, что /(®) < С Ух Е U(a) А М.
Т е о р е м а 1'. Пусть существует lim ап = а и а > Ь. Тогда
п—>+оо
существует No 6 N такое, что ап > ЬУп> Nq. .
Доказательство. Пусть а — b = во > 0, тогда в силу опре-
деления а = lim ап для во > 0 3No(eo) Е N такое, что |an — a| < во
Уп > No(eo), откуда —во < ап—а < во, т. е. ап > а—во = bУп > No(so)-
Замечание. Пусть существует lim ап = а и а < с. Тогда
п—>+оо
существует^ Е N такое, что ап < с Уп> Nq.
Определение. Функция f(x), определенная на множестве
М С (—оо, 4-оо), называется ограниченной на этом множестве, если
существует К > 0 такое, что |/(®)| < К Ух Е М.
Определение. Функция /(®), определенная на множестве
М, называется локально ограниченной в точке а Е М (которая либо
принадлежит М, либо является предельной точкой для М), если
существуют U(a) и К > 0 такие, что |/(®)| < К Ух Е U(a) А М.
52
Определение. Функция f(x) (f : М -> R) называется ло-
кально ограниченной на множестве М± С М, если f(x) локально
ограничена в каждой точке множества Mi.
Замечание. Из ограниченности функции f(x) на множестве
М следует ее локальная ограниченность на М, но из локальной огра-
ниченности f(x) на М ее ограниченность на множестве М, вообще
говоря, не следует.
Пример. Пусть f : х ~> ®, ® Е Af = (—оо, 4-оо). Тогда Va Е М
имеем |/(®)| < |a| + 1 V® Е (71(a) (т. е. f(x) локально ограничена на
множестве М), однако функция f(x) не ограничена на множестве М.
В самом деле, VN > 0 3a Е М такое, что |/(®)| = |а| > К.
Теорема (о локальной ограниченности функции, имеющей пре-
дел). Пусть существует lim f(x) = A (a Е М'). Тогда функция f(x)
х—¥а
локально ограничена в точке а.
Доказательство. Пусть существует lim fix) = А, где a Е
т->а
М'. Выберем числа В и С такими, что В < А < С. Тогда в силу
теоремы 1 (и замечания к ней) существует 17(a) такая, что В < f(x) <
CV® Е Ща)ГУМ. Полагая К = тах(|В|, |С|, |/(а)|) (если функция f(x)
не определена при х = а, то |/(а)| нужно убрать), имеем |/(®)| < К
\/х EU{a)f} М, т. е. f(x) локально ограничена в точке а.
Определение. Числовая последовательность (ап) (п —>
an,n Е N) называется ограниченной, если существует С > 0 та-
кое, что |ап | < С Vn Е N.
Определение. Числовая последовательность (ап) называ-
ется финально ограниченной, если существуют С > 0 и No Е N
такие, что |an| < С Vn > No.
Замечание. Очевидно, если последовательность (аЛ) ограни-
чена, то она и финально ограничена. Верно и обратное утверждение.
Теорема. Если числовая последовательность (ап) финально
ограничена, то (ап} - ограниченная последовательность.
Доказательство. Пусть (an) финально ограничена, тогда
существуют Ci > 0 и Ni Е N такие, что |an| < Ci Vn > Ni. Положим
C2 = max(Ci, |ai|,... , la^-il). Тогда, очевидно, |an| < C2 Vn E N,
т. e. последовательность (an) ограничена.
Теорема. Любая сходящаяся последовательность ограничена.
Доказательство. Пусть существует lim ап = а, тогда
Для е = 1 > 0 3No Е N такое, что Vn > No => (|an — a| < 1) =>
danI = |a + (an — a)| < |a| + |an — a| < |a| 4- 1). Таким образом, (an)
финально ограничена, а потому в силу предыдущей теоремы (an) -
ограниченная последовательность.
Теорема 2. Пусть а Е М* и существует окрестность 17(a)
такая, что /(®) > В \fx Е (7(a) А М. Тогда если существует
= А, то А>В.
53
Доказательство. Допустим, что А < В» Тогда поскольку
А = lim /(®), то в силу теоремы 1 существует V(a) такая, что f(x) <
В V® € У(а) ПМ. Но в силу свойства 2) для проколотых окрестностей
существует W(a) С 17(а)П V(a), и поэтому /(®) < В V® € W(a)C\M С
U(d) П М, что противоречит условиям теоремы 2.
Т е о р е м а 2'. Если существуют lim* ап = а и No G N такое,
что ап >ЬУп> No, то а>Ъ. Доказать самостоятельно.
Доказательство. Допустим от противного, что а < Ь.
Тогда поскольку lim ап = а, то в силу теоремы 1' существует
П-+Ц-00
JVj € N такое, что ап < b Vn > Ni, но тогда an < Ъ Vn > Nt =
тах(Ло, Ni)> Nth что противоречит условию теоремы 2'.
Определение. Если lim /(х) = 0, еде а € М', то функция
/(х) называется бесконечно малой в точке а (или при х —¥ а). За-
пись: /(х) -> 0 (х -4 а).
Определение. Числовая последовательность (ап) называ-
ется бесконечно малой, если существует lim ап = 0.
п-++оо
Теорема (о представлении функции, имеющей предел в точке).
Пусть функция /(х) определена на множестве М и а 6 М'. Тог-
да (существует Нт/(х) = А)& (существует окрестность U(a)
точки а, в которой имеет место представление /(х) = А + а(х)
Vx € U(a) Г) М, где функция а(х) (определенная на множестве
U(a) О М) - бесконечно малая при х -> а).
Доказательство. Необходимость. Пусть существует
Hm/(x) = Л, а € М'. Полагая а(х) = /(х) - A Vx € АГ, видим, что
Ve > 0 ЗС7(а) такая, что |/(х) - А| = |а(х)| < е Vx е 17(a) Л М, т. е.
существует lima(x) = 0. Таким образом, для любой окрестности
17(a) имеет место представление /(х) = А + a(x) Vx € 17(a) П М, где
а(х) -4 0 (х —> а).
Достаточность. Пусть существует окрестность U(a) такая, что
имеет место представление
/(х) = А + a(x) Vx € 17(a) Л М,
где а(х) —> 0 (х —> а). Тогда поскольку
lima(x) = 0,
*-го
то Ve > О 3V(a) С 17(a) такая, что
|a(x)| = |/(х) - А| < eVx € V(a) Л М,
т. е. существует lim f(x) = А.
Теорема (о представлении сходящейся последовательности).
(Существует lim^an = а) & (существует бесконечно малая по-
следовательность (ап) такая, что an = a + ап Vn 6 NJ. (Доказать
самостоятельно.)
Теорема (о пределе суммы функций). Пусть функции f(x) и
д(х) определены на М иа€ М*. Пусть существуют lim/(®) = А и
lira g(x) = В. Тогда существует lim (/(®) + g(x)) = А + В.
х-+а	®-4а
Доказательство. Пусть существует lim /(®) = А, тогда
Уе > 0 317(a) такая, что |/(®)-А| < е/2 V® € 17(a) ЛМ. Но существует
lim д(х) = В, поэтому для выбранного е > О ЗУ (а) такая, что |$(®) -
а? "4 в	•
Д| < е/2 V® € У (а) Л М. Но в силу свойства 2) для проколотых
окрестностей существует ТУ (a) С 17(a) Л У (а), и тогда в силу выбора
окрестностей 17(a) и У (а) имеем
|(/(х) + 9Ю) - (А + В)| < (/(®) - А| + |р(®) - В| <
<e/2 + e/2V®6 IF(a) ЛМ,
т. е. 3 lim (/(®) + д(х)) = А + В.
Следствие. Пусть функции h(x) (k= 1,2,... ,m) определе-
ны на М и a 6 М'. Пусть существует lim /*(®) = A* (k = 1,2,..., т).
я-4 a
т	т	т
Тогда 3 lim 2 Л(®) = Е Ит Л(®) = Е Ль (Доказать по индук-
ции.)
Теорема (о пределе суммы сходящихся последовательностей).
Пусть существуют ^lim^an = а и ^lim^ bn = b. Тогда существует
^lim^(an + bn) = a + b. (Доказать самостоятельно.)
Доказательство. Пусть 3 lim On — a. Тогда Ve > О
П-4-f-OO
3M € N такое, что |an - a| < e/2 Vn > Ni. Ho 3 n lim^ bn = b, поэтому
для того же е > 0 3JVj 6 N такое, что |bn - b| < е/2 Vn > Nj, то тогда
Vn > N3 = max(jVi,N3) => (|(an + bn) - (a + b)| < |an - a| + |bn - b| <
e/2 + e/2 = e) => (3 lim (an + b„) = a + b).
П-4Ч-00
Следствие. Сумма конечного числа бесконечно малых функ-
ций (при х -> а) (или бесконечно малых последовательностей) есть
бесконечно малая функция при ® -> а (бесконечио малая последова-
тельность).
Теорема (о пределе произведения локально ограниченной
Функции на функцию бесконечно малую). Пусть функции f(x) и а(®)
определены на М u a € М'. Пусть функция f(x) локально ограниче-
но в точке а, а функция а(®) - бесконечно малая при х -+ а. Тогда
Функция f(x) *a(®) - бесконечно малая при х -> а.
55
Доказательство. Поскольку f(x) локально ограничена в
точке а Е АГ, то существуют К > 0 и U(a) такие, что |/(®)| < К
Ух Е 17(a) А М. Поскольку 3 lima(x) = 0, то Уг > 0 3V(a) такая,
х—
что |а(®)| < — Ух Е V(a) А М. В силу свойства 2) для проколотых
К	...
окрестностей видим, что ЗТУ(а) С 17(a) AV (а), но тогда в силу выбора
17(a) и V (а) |/(х)а(ж) | = |/(х) | |а(ж) | < К •	= г Ух Е ТУ (а) А М, т. е.
А
существует lim(/(®)a(®)) = 0.
т—>а
Теорема (о сходимости произведения финально ограниченной
последовательности на бесконечно малую последовательность). Про-
изведение финально ограниченной последовательности на бесконеч-
но малую последовательность есть бесконечно малая последова-
тельность. (Доказать самостоятельно.)
Доказательство. Пусть для (an) существуют С > 0 и
No Е N такие, что |an| < С Уп > NQ. Поскольку существует
lim (an) = 0, то Уг > 0 3Ni Е N такое, что |an| < г/С Уп > т.
П-4-+ОО
е. |an«n | <7r-C = £Vn>N2 = тах(М, N2) => 3 lim (anO!n) = 0.
С	п—>+оо
Теорема (о пределе произведения функций). Пусть функ-
ции f(x) и д(х) определены на М и а Е М'. Пусть существуют
lim/(ж) = А и Нт^(ж) = В. Тогда существует Нт(/(ж) • д(х)) =
х—Ъа	х—+а	х~+а
А-В.
Доказательство. Поскольку существуют lim fix) = А и
х—>а
lim д(х) = В, то по теореме о представлении функции, имеющей пре-
х—Ьа,
дел, существует V(a) такая, что f(x) = А4-<*(ж) Ух Е V(a)C\M, a(®) —>
0 (х -4 a); д(х) = В 4- 0(х) Ух Е V(a) A Af, (3(х) -4 0 (ж -4 а). Тогда
имеем f(x)-д(х) = А-В4- (<*(ж) -В+/3(х) • А4-а(ж) -@(х)) = АВ + у(х)
Ух Е V(a) А М. Из существования lim а(ж) = 1пп/3(ж) = 0 следу-
ет, в частности, что /3(х) локально ограничена в точке а, но тогда
функции а(х) • В, /3(х) • А и а(х) • /3(®), по теореме о пределе произ-
ведения локально ограниченной функции на бесконечно малую, есть
функции бесконечно малые при х -4 а. Но функция 7(ж) как сумма
трех бесконечно малых функций есть функция бесконечно малая при
х -4 а. Из представления f(x) • д(х) = АВ 4- 7(®) Ух Е V(a) Г) Af, где
lim у(х) = 0, по теореме о представлении функции, имеющей предел,
х—
видим, что существует lim (/(ж)(/(ж)) = АВ.
Следствие. Пусть функции fk(x) (k = 1,2,... , т) определе-
ны на множестве М и а 6 Af'. Пусть 3 lim А (ж) = А* (к = 1,2,... , т).
х—±а
m	т
Тогда 3 lim А(®) = П At- (Доказать самостоятельно.)
*-*ак=1	fc=i
56
Теорема (о пределе произведения сходящихся последователь-
ностей). Если существуют lim ап = а и Ит Ъп = Ъ, то сущест-
п—>4-оо	п—>-Ьоо
вует lim (ап • Ъп) = а • Ь. (Доказать самостоятельно.)
п—>-|-оо
Доказательство. Положим апЬп—аЬ = (an—а)Ьп4-а(Ьп—Ь),
поскольку существуют lim ап = а и lim Ъп = 6, то Ve > О 3N G N
п—>4-оо	п—>4-оо
такое, что |ап - а| <	|Ь„ - Ь| <	Vn - N' Т°ГДа
Vn > ЛГ IM = |Ь + (Ьп - 01 < 10 + |Ьп - 0 < 10 + е/2 = (2|6| + е)/2;
Мп-аЬ| < М«„-а| + |а||Ьп-0 < (1^1+е/2)9|.f • +1«|9Г|~ Г <
+ г 2(|а| 4-1)
е/2 4- е/2 = е => 3 lim (ап • Ьп) = а • Ъ.
Пример, lim [(1 + (—1)п/п) (1 + 1/(п 4-4))] = lim (1 4*
п—>4-оо	п—>4-оо
(—1)п/п) • „ limjl 4- 1/(п 4- 4)) = 1 • 1 = 1.
Следствие. Произведение конечного числа бесконечно малых
функций при х -4 а (бесконечно малых последовательностей) есть бес-
конечно малая функция при х —> а (бесконечно малая последователь-
ность).
Лемма. Пусть функция д(х) определена на М и а Е М'. Пусть
существует lim д(х) = В, причем В / 0. Тогда существует U(a)
х—±а
такая, что д(х) / О Vx Е U(a) О М и существует lim -~-г =	.
х—>а д\Х)	В
Доказательство. Поскольку существует lim д(х) = В
х->а
О, то для Ео = |В|/2 > 0 3V(a) такая, что |^(®) — В\ < EqVx Е V(a)C\M
или |g(x)| = |B+(g(®)-В)| > |В|- \д(х)-В| > |В|- |В|/2 = |В|/2 > О
В2е
Va: g	. Далее, Ve > О ЗТУ(а) С У(а) такая, что |</(а;)—В| < ——
V® g W(а) П М, и поэтому для тех же х имеем оценку — — =
В(®) В
М®) - В|	В2е	2	1	1	1	п^п
т-, —г=п < —— •	= г, т. е. 3 hm -т—? = — при Bi 0.
|<z(®)| • |В|	2	|В|	|В|	д(х)	В
Лемма (для последовательности). Если Ъп / 0 Vn Е N и
3 lim bn = Ъ 0, то 3 lim — = т. (Доказать самостоятельно.)
П—>4-00	п-> + оо Ъп b
Доказательство. Поскольку существует lim Ъп = Ъ, то
п—>4-00
Ve > О 3N g N такое, что |i>n — В| < тш(гЬ2/2, |6|/2) Vn > N. Тогда
поскольку Ьп 0 Vn g N и b / 0, то Vn > N |ЬП| = |Ь + (Ьп - Ь)| >
|Ь|-|6„-6|>|Н-|ф2=|Ц/2>0;	<
2 Ь2
?2 • е • — = е, т. е. 3 lim 1 /Ьп = 1/Ь.
и	2	п->4-оо
Пример, lim 1/(1 4- (—l)n+1/n) = 1/ lim (1 4- (—l)n+1/n) =
_ t	п—>4-оо	п—>4-оо
1/1 = 1.
57
Теорема (о пределе частного двух функций). Пусть функ-
ции f(x) и д(х) определены на М и а Е М'. Пусть существуют
lim /(®) = A u limp(s) = В, где В ^0. Тогда lim f(x)/g(x) = А/В.
х-~>в	я—>о
Доказательство. При выполнении условий теоремы из
леммы (для функций) вытекает, что существует 17(a) такая, что
\д(х)\ > О V® Е 17(a) П Af, и тогда = f(x) • —V® Е 17(a) П М.
Применение теоремы о пределе произведения и леммы (для функ-
.	_ ..	/(®)	V X V	1	л	1	А
ции) дает d lim -7-4* = lim fix) • lim	-7—г	=	A	•	—	=	—.
’	®->a g(®)	®->a	®->a	g\X)	В	В
Теорема (о пределе частного двух последовательностей).
Пусть существуют lim ап = а и lim Ьп = Ъ, причем Ъп уЬ О
п->4-оо	п->4-оо
Vn € N и Ь / 0. Тогда существует lim ап/Ьп = a/Ь. (Доказать
п—>4-оо
самостоятельно.)
Замечание (о пределе разности двух функций (последова-
тельностей)). Пусть функции f(x) и д(х) определены на М и а Е 1И'.
Если 3 lim f(x) = А и 3 lira д(х) = В, то 3 lim(/(®) — д(х)) = А — В.
®—>а	аг—>a	аг—>а
Аналогично, если 3 lim an = а и Э lim bn = 6, то 3 lim (an -
n—>4*oo	n—>4-oo	n—>4*oo
bn) = a — (Доказать самостоятельно с помощью представлений
/(®) - д(х) = /(®) + (~1)д(х) Ух € М иап-Ьп=ап + (-l)5n Vn Е N.)
Теорема (о предельном переходе в неравенстве для функций,
имеющих пределы). Пусть функции f(x) и д(х) определены на М
и а Е Af'. Если 3U(a) такая, что f(x) > д(х) V® Е U(a) П М и
3 lim /(®) = А, 3 lim д(х) = В, то А> В.
Доказательство. Рассмотрим вспомогательную функцию
h(x) = /(®) — ^(®) V® Е Af. Тогда в силу условий нашей теоремы
Л(®) > О V® Е 17(a) П М и в силу замечания о пределе разности двух
функций 3 lim h(x) = A-В. Но тогда в силу теоремы 2 имеем А—В >
аг->а	~
О => А > В.
Теорема (о предельном переходе в неравенстве для сходящихся
последовательностей). Пусть существуют lim ап = а и lim Ьп =
п—>4*оо	п—>4*оо
Ь, причем ЭЛГо € N такое, что ап > bn Vn > Nq. Тогда а > Ъ,
(Доказать самостоятельно.)
Доказательство. Рассматривая последовательность (сп),
где сп = ап - Ьп Vn Е N, видим, что сп > 0 Vn > Nq и, кроме того,
3 lim сп = а — Ь. В силу теоремы 2' имеем a-6>0=>a>6.
п—>4*оо
Замечание. Если ап > Ьп Уп > Nq т 3 lim an = a,
“	n->4-oo
3 lim bn = 6, то, вообще говоря, нельзя утверждать, что имеет
п—>4*оо
место строгое неравенство а > Ь (вместо а > Ь). Пусть, например,
an = 1/п, Ьп = 0 Уп Е N, тогда ап > Ъп Уп Е N, lim ап = a = О,
п->4-оо
lim bn = b = 0, но а = b = 0.
п->4-оо
58
§ 4. Признаки существования предела функции
в точке и предела числовой последовательности
Определение. Числовая последовательность (ап) называ-
ется строго монотонно возрастающей (монотонно возрастающей),
если ап < an+i (an < an+i) Vn € N.
Запись: ап ТТ («п t)-
Аналогично определяются монотонно убывающая (ап ф) и строго
монотонно убывающая (ап Ц) последовательности.
Теорема (критерий сходимости монотонной последователь-
ности). Пусть (ап) - монотонно возрастающая (монотонно убы-
вающая) числовая последовательность. Тогда (3 lim ап)
П-+4-0С
(последовательность (ап) ограничена сверху (ограничена снизу));
при этом если 3 lim ап = а, то а = sup ап для ап f (соответ-
ственно а = inf ап для ап J,)).
N
Доказательство. Необходимость. Пусть существу-
ет lim ап. Тогда последовательность (ап) сходится, а потому
п—>4-оо
ограничена (и, в частности, ограничена как сверху, так и снизу).
Достаточность. Пусть числовая последовательность (ап) монотон-
но возрастает и ограничена сверху. Тогда имеем
an<an+itfn€N	(4.1)
и ЗС > О такое, что
ап < СУп е N.	(4.2)
Рассмотрим множество А = {ап; п € N}. В силу оценки (4.2) мно-
жество А будет ограниченным сверху непустым множеством из R. В
силу полноты R из принципа полноты Вейерштрасса вытекает, что
существует а = sup А = sup ап € R, причем по определению точной
N
верхней грани а = sup А имеем: 1) ап < а Vn € N; 2) Уе > 0 3Nq € N
такое, что а-е < адг0 < а. Но тогда в силу оценки (4.1) имеем ап > а#0
Уп > NQ, т. е. а - е < ап < а Уп > ЛГ0. Итак, Уе > 0 32Vo € N такое,
что |ап - а| < г Уп > No => 3 lim ап = а.
““	п->4-оо
Замечание (критерий сходимости знакоположительного чи-
4-оо
елового ряда). (Ряд а* с неотрицательными членами а* > 0 Vfc
fc=i
сходится) Ф> (последовательность его частичных сумм (sn) ограни-
чена сверху). В случае сходимости ряда для его суммы в имеем
4-оо
я = L а* = supen.
fc=l N
В самом деле, если а* > 0 Vfc G N, то sn+i = зп + an+i > sn Vn,
т- е- «nt- Но критерием сходимости монотонно возрастающей числовой
59
последовательности (sn) является ее ограниченность сверху, причем
+оо
если существует lim sn = з, то s = supsn = ак.
n->4-oo	n
+oo 1
Пример. 0< 52 T2 < +°°- В самом деле, имеем sn =
fc=l *
n 1	1	»+l 1
52 -rx. Тогда 1) aj = г; > 0 Vfc € N. Далее, sft < 1 + 52	<
fc=l	*	к=2 *
n + 1	1	n + 1 ✓ 1	-I \	>*+1 -1	1
1 + 52 k(k -1)	= 1 + 52 (itt	 ь)	= 1 + 52 fezy	~ 521	=
к=2 V '	fc=2 x	7	к=2	к=2
" 1	n+11	1
у = 1 + 1------ < 2 Vn G N, т. e. 2) sn < 2 Vn G N. В
&k n + 1
силу установленного критерия сходимости знакоположительного ряда
+оо 1
видим, что ряд 52 сходится.
к-1 к
Т е о р е м а (формула бинома Ньютона). Для любых п € N
и любых a,b е R (а + Ь)" = £ Скап~кЬк, где Ск = (£) =
к=0
n(n-l) ...(n- fc+1) n!
—---------г-------~ = VT7--rv7, nPu этом полагают 0! = 1! = 1
I»l	If* ( *П   Ifi 1 I
так, что Cg = (») = 1 = (“) = C”.
Доказательство. Пусть A = {n 6 N| (a 4- b)n =
n
52 C„an~kbk}. Заметим, что для n = 1 формула бинома Ньютона
к=0
верна, так что имеем 1) 1 6 А. Докажем 2) п 6 А => (n + 1) 6 А.
(a + b)n+1 = (а + 6)п(а + Ь) = (а + Ь) Скап~кЬк =
= 12 Сп«п+1-*Ь* + 12 Cn«n-fe^+1 = C°an+1 + Ckan+l~kbk+
к=0	к-0	fc=l
п —1
+ Ckan~kbk+1 + C”bn+1 = {Ая = к + 1 => к = ki - 1} =
к-0
= (7°an+1 + 2jC'*an+1-4‘ + Ckl~1an+1~k'bkl + C%bn+1 =
k=zl	fci=l
= {c°=i = c«+1,c» = i=c:+1i,fc1 = fc} =
= Cg+1an+1 + 2(C* + Ск~1)ап+1~кЬк + C^bn+1 =
k=l
60
= {но Сп + Сп = щп_ку + (fe_i)!(n_fc + i)i =
_ n!(n - fe + 1 + ft) _ (n + 1)!	_ k 1 _ k n+j_fc,k
" fc!(n-fc + l)! fe!(n + l- *)! Gn+1J £lCn+1
В силу принципа математической индукции из 1) и 2) вытекает А =
N.
П
(In —
ример. Число е. Рассмотрим числовую последовательность
/ 1\”
(14— 1 , n Е N. Применяя формулу бинома Ньютона, имеем
\ п/
в>п — 14-1 +
п(п — 1)
2п2
п(п — 1)(п — 2)
+	3!^
+ ••• +
Очевидно, ап < an+i Vn 6 N, т. е. ап1Т* Кроме того, ап < 2 +	+
---F ~ < 2+.£ + ^Н----------F 2^1 < 3, Vn G N. В силу критерия
сходимости для монотонных последовательностей имеем
/	1 \ п
3 lim ап = lim (14— ) «=/ е,
п->+оо	п—>+оо \ nJ
причем, очевидно, в силу теоремы о предельном переходе в неравен-
ствах 2 < е < 3.
Теорема (оценочный признак существования предела функции
в точке). Пусть функции fi(x), д(х) и f2(x) определены на множестве
М и а Е Mf. Если существует U(a) такая, что fi(x) < д(х) < /г(®)
V® е Ща) А М и 3 lim Д(ж) = lim f2(®) = A, mo 3 lim g(x) = A.
x->a	T->a	x-+a
Доказательство. Поскольку существуют lim Д (x) = А и
f2(x) = A, to Vs > 0 3V(a) C U(a) такая, что A — e <
/2(2?) < A + s Vx G V(a) П M или в силу условий теоремы А — е <
Л(«) < д(х) < Л(®) < А + е, т. е. \д(х) — А| < е Vx 6 V(a) ПМ, откуда
имеем 3 lim д(х) = А.
х->а
61
Теорема (оценочный признак сходимости числовой последова-
тельности). Пусть для числовых последовательностей (ап), (Ьп) и
(cn) BNo € N такой, что ап < сп < bn Vn > No и существует
lim ап = lim bn = а. Тогда существует lim сп = а,.
п—>+оо	п—>4*00	п—>4-оо
Доказательство. Поскольку существуют # lim^ ап = а и
lim Ъп = Ь, то Ve > О BNi € N такое, что Ni > No и Vn > Ni
n->4-oo	""
a-e < an', bn < a +e пти в силу условий теоремы а - е < ап < сп <
Ъп < а + е Vn > Ni. Но тогда Ve > 0 BNi € N такое, что |сп - а| < е
Vn > Ni => 3 lim сп = а.
““	П«44*00
Теорема. 1) lim sin а = 0; 2) lim сое а = 1; 3) lim tga = 0;
*	z ti-rt	’ ' я->0	’ z °
.. .. sina	.. tga
4) hm------= 1; 5) lim -£— = 1.
«-►о x	®->o x
Доказательство. Пусть ZAO В = a, 0 < a < g. Рас-
смотрим (см. рис. 6) круг радиуса 1. Пусть ОМ = 1, MN = sina,
АВ = tg а,
Рис. 6
тогда £±ОАМ С сектор 0AM С ДО АВ,
откуда для площадей имеем неравенства
S&QAM < 5сежторОЛЛГ < S^oab, т. е.
/1 . а 1 \	. .
I-вша < - < jjtga I => (эта < а <
\ 2i	£l	A	/
tg а), деля на sin а, имеем 1 < — <--
'	.	вша сова
или сов а <	< 1 Va € (О, -Я-/2).
а
.Заметим, что сов(-а) = сова;
sin(—a)	sina	sina	,
.	. =------, поэтому cos а <---< 1
(—а)	а	а
при 0 < |а| < к/2. В частности, |sina| <
|а|, 0 < |а| < ff/2 (и даже при 0 < |а| <
тг/2), но |sina| < 1 < ff/2 < |а| для |а| >
ff/2, так что окончательно имеем оценку
|sina| < |а| Va 6 (-оо, +оо). Возвращаясь
к случаю 0 < laI < тг/2, имеем 1 - cos а > 1 - —— > 0, но 1 - cos а =
2sins(a/2) < 2|sin(a/2)| < 2(|а|/2) = |а|, откуда получаем оценки
О < |sina| < |а|, 0 < 1 - сова < |а|, 0 < 1 - —— < |а| V|a| € (0,ir/2).
X
Поэтому из оценочного признака существования предела в силу
существования lim |а| = 0 имеем lim sin а = 0, lim(l - cos а) = О,
а?—>0	а?—>0
1* 1л	81П X |	-	а-	и
hm I 1-------) = 0, откуда, поскольку 3 hm 1 = 1, по теореме о пре-
йр—>о у	х у	>о
62
деле (алгебраической) суммы имеем
sin® ,
3 lim cos х = 1, 3 lim----------------= 1.
®-f0	ar-fO X
Используя теоремы о пределе произведения и частного, имеем
lim tg® = lim = (lim sin®)/(lim cos®) = 0/1 = 0,
j->0 ar-+o cos ®	' ®->o
lim(tg®)/® = lim (sin®/®)/cos ® = lim(sin®/®)/limcos® = 1/1 = 1.
>0	.	ar—>0	ar—>0
Определение. Пусть функция f(x) определена на множес-
тве М, а Е Mf. Скажем, что lim/(®) = +оо (соответствен-
но Xvcaf(x) = -со), если УК > 0 317(a) такая, что fix) > К
в-+а
V® € 17(a) П М (соответственно /(®) < -К V® € U(a) П М).
Определение. Пусть функция /(®) определена на множес-
тве М и а € Mf. Скажем, что lim /(®) = оо, если УК > 0 317(a)
аг—
такая, что |/(®)| > К V® € 17(a) П М.
Замечание. Если lim f (®) = оо, то функция /() называется
бесконечно большой при х -> а.
Теорема (о связи бесконечно большой и бесконечно малой
функций). Пусть функция f(x) определена на М и а € М'. Если
3 lim /(®) = оо, то 3U(a) такая, что |/(®)| > О V® € U(a) П М и
3 lim -77-7 = 0 (т. е. если f(x) бесконечно большая при х -> а, то
х-*а J(X)
функция l/f(x) есть бесконечно малая функция при х —> а).
Доказательство. Поскольку 3 lim f(x) = 00, то Уе > 0
ar-ta
3t7(a) такая, что
|/(®)| > 1/е > 0V® е U(а) П М,
и тогда для тех же ® имеем оценку |1//(®)| < е, но это и означает,
что существует lim(1//(®)) = 0.
аг—>а
Теорема (о связи бесконечно малой и бесконечно большой
функций). Пусть функция /(®) определена на множестве М и а €
М', Если 3 lim /(®) = 0 и 31Г(а) такая, что |/(»)| > 0 V® 6 Е7(а)ПМ,
то 3 lim(l//(®)) = оо.
Доказательство. Поскольку 31im/(«) = 0, то Уе =
1/К > 0 3V(a) С U(a) такая, что 0 < |/(®)| < l/K V® € U(a) П М, но
тогда для тех же ® имеем |1//(®)| > К, т. е. 3 lim(1//(®)) = оо.
Пример. Поскольку Jim ® = 0, то lini (1/®) = оо, но неверно было
бы писать ни lim(1/®) = +оо, ни lim(l/®) = —оо. В самом деле, УК >
О 3d = 1/К > 0, для которого |1/®| > К У® € (7<(0) => 3 lim(l/®) = оо,
63
однако V<5 > 0 3xi > О, Х2 < 0 такие, что Ж1, Х2 G (0) и вместе с тем
l/xi > 0 и 1/®2 < 0. Поэтому lim(l/x) +оо или lim(l/x) ф -оо.
Определение. Пусть функция f(x) определена на множес-
тве М, не ограниченном сверху. Скажем, что lim f(x) = b Е R,
если Ve > 0 ЭК > 0 такое, что \ f(x) - Ь| < е V® 6 (К, +оо) П М.
Задание. Сформулировать самостоятельно определения:
lim f(x) = 6; lim f(x) = 4-оо; lim f(x) = +oo; lim f(x) =
x->-oo v	x->4-oo v 7	x->-oov 7	x->+oo v
—oo: lim f(x) = — oo; lim f(x) = oo; lim f(x) = oo.
x->-oo 7	T->+oov	x->-oo
Определение. Пусть функция f(x) определена на множес-
тве М, а - предельная точка множества (—оо, a) Cl М. Тогда ска-
жем, что функция f(x) имеет левосторонний предел b в точке а,
если Ve > 0 36 > 0 такое, что Vx 6 М, удовлетворяющего условию
а — S < х < а => |f(ж) - 6| < е.
Запись: lim (х) = b f(a — 0).
Определение. Скажем, что функция f(x) имеет право-
сторонний предел в точке a: lim f(x) = b = f(a 4- 0), если a ~
x->a+O
предельная точка множества M О (а, +оо) и Че > 0 36 > 0 такое,
что |f (ж) — &| < е Vx Е М П (а, а 4- 6).
Пример. Пусть f (х) = sgn х, где
sgn ж = <
1 при х > 0,	( lim f (х) = -1,
0 при х = 0,	=> 3 < т-^°“0
„	Л	1 lim f(х) = 1.
—1 при х < 0	I я-ю+о v
Теорема (критерий существования предела функции в точке).
Пусть функция f(x) определена на множестве М и а Е М'. Тогда
(3 limf(x) = А) & (3 lim f(x) = f(a — 0), если а - предельная
х-+а	х—>а—О
точка множества (—оо, а) П М, 3 lim f(x) = f(a 4- 0), если а -
л->а+О
предельная точка множества МП(а, 4-оо) и f(a — 0) = f(a4-0) = А).
Доказательство. Необходимость. Пусть 3 lim f (х) = А.
х-ьа
Тогда в силу (е, ^-определения предела функции в точке a Ve > 0 36 >
0 такое, что Vx Е М, удовлетворяющего неравенству 0 < |х — а| < 6,
|f (х) — А| < е, но это означает:
а)	что Vx Е М, удовлетворяющего неравенству а — 6 < х < а,
|f (х) — А| < е, т. е. (если а - предельная точка множества (—оо,а) ГУМ)
3 lim f(ж) = f(а — 0) = А;
х—— О
б)	что Vx Е М, удовлетворяющего неравенству а < х < а 4- 6,
|f (х) — А| < е, т. е. (если а - предельная точка множества ЛТП (а, 4-оо))
3 lim f (ж) = f (а 4- 0) = А. Откуда f (а — 0) = f (а 4- 0) = А.
64
Достаточность. Пусть 3 lim f(x) = f(a — 0), если a - предельная
x—>a—О
точка множества (—оо,а) П М и 3 lim f(x) — f(a + 0), если а -
г—>а+О
предельная точка множества М CI (а, +оо) и /(а — 0) = /(а 4- 0) = А.
Поскольку 3 lim f(x) = А, то Vs > 0 3<Ji > 0 такое, что \f(x) —
т—>а—О
А| < s V® Е (а — Ji, a) Q М. Поскольку 3 lim f(x) = А, то для того
х—>а-|-0
же е > 0 3<5г > 0 такое, что \f(x) — А| < е V® 6 М П (а, а 4* <5г)» но
тогда для 6 = min(<5i,<52) > 0 имеем \f(x) — А| < € V® G Ut(a) Cl М,
т. е. 3 lim f(x) = А.
х-+а
Определение. Функция f(x), определенная на множестве
М, называется возрастающей на множестве М, если V®i, х2 6 М
таких, что Xi < х2 У(®1) < /(®г)« Обозначение: f(x) f на М. Ес-
ли при этом xi < х2 => /(®i) < У(®2); nio функция f(x) называется
строго возрастающей на множестве М. Запись: f(x) Д на М. Ана-
логично определяется функция, убывающая или строго убывающая на
множестве М (запись: f(x) | на М или f (ж) Ц на М).
Определение. Функция возрастающая или убывающая на
множестве М называется монотонной на множестве М.
Определение. Пусть функция f(x) определена на множес-
тве М, тогда р = sup f(x) Е R, если 1) f(x) < pVx E M; 2) Vs > 0
3®o € M такое, что p — e < /(®o) < A*-
Задание. Дать определение и = inf^ f(x).
Теорема (о существовании односторонних пределов у монотон-
ной функции). Пусть f(x) | на интервале (а,/?) (—оо <«</?<
4-оо). Тогда 1) Va Е (а,/?) существуют конечные односторонние пре-
делы f(a — 0) = lim f(x) = sup f(x); f(a 4- 0) = lim f(x) =
0	a<x<a	x—>a+0
inf f(x), причем —oo < f(a - 0) < /(a) < f(a 4- 0) < 4-oo;
a<x<0
%) 3	+ 0) = inf /(x); 3 lim f(x) = f(/3 - 0) =
s-*a+0	(a,/3)	x-4-0-0
sup f(x), причем — oo < /(a 4- 0) < /(/? - 0) < 4-oo; 3) Va,b E (<*,/?)
таких, что a < a < b < (3, имеем —oo < /(a 4- 0) < f(b — 0) < 4-oo.
Доказательство. 1) Пусть a E (a,/3) и A = sup f(x). В
(a,a)
силу монотонного возрастания f(x) имеем f(x) < f(a) Vx E (a, a),
t. e. — oo < A < f(a) < 4-oo. Докажем, что A = f(a — 0) = lim f (®).
ar->a—0
В самом деле, по определению точной верхней грани А = sup f(x)
(a,a)
имеем a) f(x) < А V® Е (a, a); б) Vs > 0 3®о 6 (ct,a) такое, что
A — s < /(®o) < А. Но тогда, полагая xq = a — 6 E (a, a), в силу
монотонного возрастания f(x) имеем А — s < /(®о) < /(®) < А V® Е
(а—<5, а) = (хо,а) => |/(®) —А| < sV® Е (а—<5, а), но это и означает, что
Зак. 860
65
A — lim /(x) = f(a - 0), причем -oo < f(a - 0) < /(а). Аналогично
доказывается, что 3/(a4-0) = inf /(х) > f{a) и /(а) < /(а+0) < +оо.
(<Ь0)
Тем самым все утверждения 1) теоремы доказаны.
2) Пусть А = sup /(х). Нужно различать случаи А < 4-ос и
М
А = 4-оо, а также для интервала (а,/3) : /3 < 4-оо и /3 = +оо. В
случае /3 < +оо и А < +оо доказательство, проведенное выше, сра-
зу дает А = lim 0/(®) = f(P ~ 0). Рассмотрим случай А < 4-оо и
/3 = +оо, тогда по определению А = sup /(х) имеем а) /(х) < А
(а,+оо)
Ух € (а, 4-оо); б) Уе > 0 Эхо € (а, 4-оо) такое, что А - е < /(®о) < А.
В силу монотонного возрастания /(х) имеем А—е < /(хо) < /(х) < А
Vx > хо, т. е. 3 lim /(х) = /(4-ос) = А.
>4-оо
Рассмотрим теперь случай /3 < 4-оо и А = 4-оо. Тогда по опре-
делению sup /(х) = 4-оо видим, что УК > 0 Эхо € (а,/3) такое,
(«3)
что /(хо) > К, откуда в силу монотонного возрастания /(х) имеем
/(х) > /(х0) > К Ух € (/3- <5,/3) = (х0,/3), »• е. 3 lim /(х) = 4-оо.
4Г——О
Случай (3 = 4-оо и А = 4-оо рассмотреть самостоятельно.
Аналогично доказывается, что 3/(а 4- 0) — inf^f(x). Но тогда
-оо < /(а 4- 0) = inf /(х) < sup /(х) = /(/3 - 0) < 4-оо, тем самым и
(а-0)	(а,/3)
утверждения 2) теоремы доказаны.
3) Пусть а < а < b < (3. Тогда по доказанному выше Э/(а 4- 0) =
inf /(х) и 3/(Ь—0) = sup /(х). В силу монотонного возрастания /(х)
(а,0)
на (а,(3) Ухо € (а, Ь) имеем -оо < /(а 4- 0) = inf /(х) < /(хо) <
sup f(x) = f(b - 0) < +оо; -оо < /(а + 0) < f(b - 0) < +оо. Тем
самым утверждения 3) теоремы также доказаны.
Задание. Сформулируйте и докажите теоремы о существовании
односторонних пределов у монотонно убывающей функции, заданной
на интервале.
Следствие. Монотонная на интервале (а,/3) функция f(x)
имеет в каждой точке а € (а,/?) конечные односторонние пределы
/(° - 0) и /(а 4-0).
Пусть f iy = f(x), х ЕЩа), причем 3 lim f(x) = А.
аг—>а
Пусть : х = 9>(у), у Е V(A) и 3 lim <р(у) = В.
Пусть, наконец, f(U(а)) С V(A). Тогда можно рассмотреть ком-
позицию функций /(х) и <р(у) F = <ро f : z = ^[/(х)], х € 17(a). Можно
ли утверждать, что 3 lim F(x) = Bl
66
Пример. Пусть а = О, А = О, В = О и /(®) = О V® € (-оо, +оо),
= 1 0 при у * 0 (Vy € R\ {°})’
Г'*'	[ 1 при у = 0.
р(у) определена в У(А), но ф(А) ф В, f(U(O)) = {Л} = {0} С У(А),
но £ У(А). Тогда 3 lina f(x) = 0 = A, 3 lim <p(y) = 0 = В, но
F(®) = (фо/)(®) = p[/(®)] = IV® G (-oo,+oo),
T. e. 31imF(®) = 1^0 = B.
t—>0
Пример. Пусть a = 0, A = О, В = 0 и /(®) = О V® G (—oo, +oo),
(ja _ Г Оприу O(Vy € R\ {0}),
| не определена при у = 0.
/(C7(a)) = {А} = {0}(=V(A), <р(у) определена лишь на У(А). Тогда
3 lim f(x) = А = 0. Э lim <р(у) = В = 0, но композиция (сложная
sr—>О=а	у—>О=Л
функция) Г(®) = (<р о /)(®) вообще не определена ни при каких ®, так
что не имеет смысла говорить о lim F(®).
Теорема (о пределе композиции двух функций или о преде-
ле сложной функции). Пусть функция f(x) определена на множес-
тве М, a € ЛГ', 31im/(®) = А. Пусть при этом существует
х-ta
окрестность Ща) такая, что /(®) А V® € й(а) П М (т. е.
Agf(U(a) П М). Пусть функция <р(у) определена на множестве Y,
A G У и 3 lim <р(у) = В. Пусть Y D f(U(a) П М). Тогда компози-
ция <р о f определена на множестве й(а) Л М (ф о f : z = ф[/(«)],
® G Ща) П М, z € R) и 3 lim(p о /)(®) = В.
Доказательство. Поскольку A G У' и 3 lim <р(у) = В, то
Ve > 0 ЗУ (А) такая, что |^(у) - В| < е Уу € V(A) Л Y. Далее, ае М’
и 317(a) такая, что Y D f(U(a)C\M), причем А^/(С?(а) Л М), поэтому
композиция F = <р о> f определена на множестве U(a) Г) М так, что
F : z = ^[/(®)], х е Ща) Г) М, z € R. Из существования lim f(x) = А
в силу окрестностного определения предела f (®) в точке а е М' выте-
кает, что для ранее выбранной окрестности У(А) существует окрест-
ность (а) С Cf(a) такая, что f(U^(a) Г) М) С У(А). Но поскольку
Аб/(Й'(1)(а) Г1 М) и Y D f(U^(a) Л М), то это соотношение можно
переписать так: f(U^(a) Л М) С У(А) Л У, т. е. у = /(®) € У(А) Л У
V® е U’(1)(a) Л М. Но тогда для функции F(®) = (ipo f)(x) имеем
при у = /(®), z = <р(у) = ^[/(®)] = F(®), поэтому в силу выбора
окрестности V(A) (l^y) - В| < е) (|F(®) - Ь| < е).
3*
67
Итак, Уб > 03 окрестность U^(a) С U(a) такая, что |F(x) — В\ < е
V® G U^(a) А М, но это и означает, что 3 lim(y> о /)(ж) = В.
х—>а
Замечание. Если функция y>(j/) определена в точке А Е У',
причем р(А) = В (где В = lim y>(j/)), то требование AGf (17(a) П М)
у-+л
в условиях теоремы о пределе сложной функции можно отбросить.
Попытайтесь доказать теорему о пределе сложной функции в из-
мененной формулировке. Впрочем, это замечание будет рассмотрено
в одном из параграфов главы 4 о непрерывных функциях.
„	_	sin ах	..	_ _	Л
П р и м е р. 3 hm---- = а Уа G R. В самом деле, при а = 0
х—>0 X
это очевидно. Пусть а / 0. Рассмотрим функции: f : у = ах,
х 6 (-оо,+оо), х / 0;	: z = у g (—оо,+оо), у 0. Тогда
У
3 lim f(x) = lim ах = 0 = А и 3 lim и>(у) = lim Sln^ = i — В. По-
х—>0	х—>0	у—>А=0	у
скольку а^0=>ах^0Ух54 0, тоА = 0g/((7(0)) У17(0). По теореме
о пределе сложной функции имеем
\ г sin(a®) 1	sina®
3 hm(^ о fMx) = hm —----= 1, откуда 3 hm----=
x->o	x->o ax	x->o x
(sin ax \	.. sin(ax)
a -----I = a • hm ——— = a • 1 = a.
ax /	x—>o (ax)
§ 5. Предел по Коши и предел по Гейне функции
в точке
Понятие предела последовательности несколько проще понятия
предела функции в точке, поэтому естественно попытаться свести
(б, J) определение предела функции в точке к пределу числовой по-
следовательности.
Определение. Пусть М С R, М1 / 0 иаЕ Мг. Последова-
тельностью Гейне, связанной с точкой a G Af', называется после-
довательность (£п), сходящаяся к точке а, и такая, что £n 6 М,
# а Уп G N.
Замечание. Пусть Af' 0, тогда Уа G Af' 3 последователь-
ность Гейне (£п), связанная с точкой а (причем последовательность
(£п) состоит из попарно различных элементов). В самом деле, если
М' ф 0 и a G М', то, как было доказано в § 1 (о топологии числовой
прямой) главы 3, всегда существует последовательность (£п), сходя-
щаяся к а и такая, что £п Е М \ {а} Vn Е N и / £т Уп ф т.
Определение (предела функции в точке по Гейне). Пусть
функция f(x) определена на множестве М и а Е Mf. Тогда А
68
является пределом функции f(x) в точке а по Гейне, если V по-
следовательности Гейне (£п), связанной с точкой а 6 М', имеем
3 lim f(£n) = А. Запись: f(x)	А(х —> a), lim f(x) <= А.
п—>+оо	х—>а
Теорема (об эквивалентности (s, (5) определения предела по
Коши и предела по Гейне). Пусть функция f(x) определена на мно-
жестве М и a G Mf. Тогда (3 lim f(x) == А) (3 lim f (х) <= А).
х—+а	х—+а
Доказательство. 1) (К) => (Г). Пусть 3 lim f(x) <= А.
х—+а
Тогда Vs > О 3<5(s) > 0 такое, что |/(®) — А| < s V® G М C\Uf(a). Пусть
(£п) ” любая последовательность Гейне, связанная с а 6 М* так, что
3 lim £п = а, £п 6 М и £п 54 a Vn 6 N, поэтому для выбранных е > О
п—>+оо
и <5 > О 37V((5) G N такое, что £п 6 U$(a) А М Vn > N(6), но тогда в
силу выбора <5(б) имеем \f (£п) — А| < е.
Итак, V последовательности Гейне (£п), связанной с a G Af', имеем:
Vs > 0 3N G N такое, что |/(£п) — А| < е Vn > N, т. е. 3 lim f(£n) =
n—>4-оо
(Г)
А. Таким образом, 3 lim f(x) = А, т. е. показано, что (К)=^(Г).
х—+а
2) (Г)=>(К). Доказательство проведем от противного. Пусть
(Г)
3 lim f(x) = А, но А не есть предел /(®) в точке а по Коши.
х—¥а
Тогда 3so > 0 такое, что Vl7(a) 3®о 6 17(a) А М, для которого
|/(«о) - А| > Со > о.
Рассмотрим систему проколотых окрестностей Ui/n(a) = {® 6
R|0 < |® — а| < 1/n} Vn G N. Тогда по предположению Vn 6 N
о	о	о
(7i/n(a)HAf такое, что |/(£п)-А| > е0 > О, т. е. А^ lim /(4П).
п—>4"°°
о ,	о
Но £ng I7i/n(a) И М Vn. G N => 3 lim £n= a, £п 6 М, £n / а
п—>4-оо
о
Vn е N, т. е. по построению (£п) есть последовательность Гейне, свя-
(Г)
занная с точкой а 6 Mf. Поскольку 3 lim fix) = А, то должно быть:
х-+а
о
nlim^/(£n) = А. Противоречие. Итак, (Г)=>(К).
/ 1V
Пример. Число е. Ранее было доказано, что 3 lim ( Ц— ) =
п->4-оо у п J
е. Забегая несколько вперед, рассмотрим показательно-степенную
Функцию f : х (1 4- х)1/*, х е М = (—1,0) U (0,+оо) и докажем,
что 3 Ит(1 4- х)1^ = е. Точнее, докажем сначала, что существуют
односторонние пределы
lim (14-х)1^х = еи lim (14-®)1^ = е,
®->o+ov	'	®->o-ov	1
воспользовавшись определением односторонних пределов функции по
Гейне.
69
Будем различать два случая: а) (®п) - любая последовательность
Гейне, связанная с 0, являющимся предельной точкой (0, +оо), так
что ®п > 0 Vn € N и 3 lim хп = 0; б) (хп) - любая последователь-
п->4-оо
ность Гейне, связанная с 0, являющимся предельной точкой множества
(-1,0), так что -1 < хп < Vn € N и 3 lim хп = 0.
п->4-оо
В случае а) имеем lim хп = 0 и хп > 0 Vn € N. Но тогда Vn € N
п—>4-оо
Зпц, = [1/®п] € N такое, что Шп < 1/хп < тп + 1 Vn € N, поэтому
Р- > хп > —Vn е n) => ((1 + l/(m„ + 1)Г“ <
\ГПп	тп +1	/
< (1 +	< (1 + l/mn)™»*1) =► (1 + 1/m,, + 1)т"+1/(1+
+l/(mn + 1)) < (1 + х,,)1/’» < (1 +	• (1 + I/т»).
Но
(3 lim хп = 0) Л (хп > OVn G N) => ( lim (1/®п) = +оо),
п—>4*оо	п—>4*оо
откуда
(mn + 1 > 1/хп) => lim (пц, + 1) = lim пц, = +оо.
,	п->4-оо	п->4-оо
Докажем, что lim (1 + l/mn)nia = е. В самом деле, поскольку
n->4-oo	j
3 lim (1+1/fe)* = е, то Ve > 0 3feo € N такое, что |(l+l/fco)k°—е| < fi.
k->+oo
Но lim тп = +оо, поэтому для выбранного ко > 0 Зп € N такое,
П-4+00
что тпп > ko Vn > N. Но ah = (1 + 1/fc)* ft, причем а* < е Vfc € N
так, что (е - а*) Ц, и поэтому |е — а,п„| < |е - а*| Vm„ > к. Но тогда
в силу выбора ко имеем при пц, > ко оценку |(1 + l/mn)mn - е| < е,
т. е. 3 lim^Jl + 1/тп)та“ = е. Доказательство того, что 3+
l/(nin + l))mn+1 = е проводится аналогичным образом.
Итак,
lim (1 + l/(m„ + l))m«+t/(l + l/(«n + 1)) = e/1,
n—>4*00
„lira [(1 +	• (1 + 1/ran)] = e
n—>4*00
и в силу оценочного признака существования предела последователь-
ности имеем в случае а) 3 lim (1 + фп)х^п = е. По теореме об экви-
п->4-оо
валентности определений (одностороннего) предела функции в точке
по Гейне и по Коши имеем 3 lim (1 + ж)1/® = е.
jp->O4*Ov 7
В случае б) можно, без ограничения общности, считать, что
3' lim = 0 и хп < 0 Vn € N. Положим хп = тогда
п->4-оо
70
lim Уп = 0, уп > О Vn € N. В силу теоремы V из § 3 главы 3 видим,
n-f+oo
что (1 > 0 = lim уп) => (ЗЛГ0 такое, что 0 < уп < 1 Vn > No). Пола-
71—>Ц-00
гая 2п = Уп/(1 - Уп) Vn > No, получаем lim zn = 0, zn > 0 Vn > No,
n—>4-oo
при этом Уп = zn/(zn + 1).
Итак, Vn > No имеем (1 + xn)1/Xn = (1 - yn)~^Vn = (1 + l/n/(l -
yn))1/Un = (1+zn)1+1/,n = (1+«п)1/,п-(1+гп). Поскольку ^lirn^Zn = 0
и zn > 0 Vn > No, то по доказанному в случае а) имеем 2 lim [(1 +
n—>4*00
zn)1^n*(l+«n)] = e*l = e так, что ив случае б) 3 lim (14-Bn)1/®" = е,
т. е. 3 lim (1 + х)1^ = е.
аг—>0—0 V
Итак, 3 lim (1 4- ж)1/® = lim (1 + ж)1/® = е, но тогда в силу
хн-о+о' '	®->о—о'	'
критерия существования предела из § 4 главы 2 имеем
3 lim(l 4- х)1^ = е.
аг—>0
lim (Ьп — ап) = 0 (т. е. длина отрезка Дп стремится к нулю
—>4" оо
§ в. Дополнения к принципам полноты поля R
Теорема Вейерштрасса. Если числовая последова-
тельность (ап) монотонно возрастает и ограничена сверху, то она
сходится, причем lim ап = sup ап.
n->+oo n€N
Доказательство было проведено в § 4 главы 3.
Определение. Система отрезков Дп = [an,bn], п € N,
называется стягивающейся, если 1) она является вложенной сис-
темой, т. е. С Дп Vn € N (tin < &п4~1 < ^n+i < bn Vn € N)/
2>3,.
при n -> +oo).
Теорема Кантора (о стягивающейся системе отрезков).
Стягивающаяся система отрезков имеет, притом только одну, об-
щую точку.
Доказательство. По теореме Кантора для вложенной
системы отрезков {Дп} Зс € R такое, что с € [ап, Ьп] Уп € N.
4-оо
Докажем, что П Дп = {с}. Допустим от противного, что 3ci, сг €
n=1
ci < С2 такие, что ci,C2 € Дп Vn € N. Тогда (ап < ci < сг <
ьпУп € N) => (Ьп “ an > С2 - ci > OVn G N), что противоречит
условию lim (bn - ап) = 0.
п-^4-оо
На числовой прямой R существуют бесконечные множества, не
имеющие предельных точек. Таковым, например, является множес-
тво N с R. Однако на отрезке каждое бесконечное множество имеет
71
хотя бы одну предельную точку. Это свойство отрезка называется
свойством секвенциальной компактности, и оно отличает отрезок от
всей прямой.
Теорема Больцано-Вейерштрасса (для
множеств). Если М С [а, Ь] есть бесконечное подмножество отрез-
ка [а, 6], то множество М имеет по крайней мере одну предельную
точку, принадлежащую этому отрезку.
Доказательство. Если М С [а, Ь] и М бесконечно, то хотя бы
одна из половин отрезка До = [а? Ч содержит бесконечное множество
точек из М. Обозначим эту половину через Дх. Тогда Дх С До? Д1ПА£
бесконечно и |Д11 = —Через |Д| = (3 — а будем обозначать длину
отрезка Д = [а, /?].
Разделим отрезок Дх пополам и выберем ту его половину Д2, ко-
торая содержит бесконечное множество точек из М: Д2 С Д1 С До?
Л	V Г	I А I	П ГТ
Д2 П М бесконечно, |Д2| = --у. Продолжая процесс, получим вло-
женную систему отрезков {Дп}, для которой Дп С Дп-1 С ... С
Ъ — а
Дх С До? Дл Cl М бесконечно и |Дп| = ——. Очевидно, lim |Дп| =
2п	п->+оо
Ь — а
lim - = 0 (по индукции легко доказывается неравенство 2” > п
Vn Е N). Но тогда вложенная система отрезков {Дп} оказывается
стягивающейся. По теореме Кантора о стягивающейся системе от-
+оо
резков Зс Е R такое, что р| Дп = {с}, причем (с Е Дп С [а, 6]
П = 1
Vn Е N) => с Е [а, Ч- Далее, lim (Ьп — ап) = 0, поэтому V<5 > О
п—>+оо
3m((5) Е N такое, что 0 < Ът — ат < 6 Vm > т(6). Но с Е Дт? и по-
скольку |®-с| < Ът-ат < 6 Vx Е Дт? то Дт С Us(c) (при т > тп(6)),
причем в силу построения системы {Дп} множество М П ДП1 беско-
нечно.
Итак, > 0 ЗДт С U&(c), т. е. V6 > 0 окрестность Us (с) содержит
бесконечное множество точек из М, поэтому с Е М'.
Следствие. Любой отрезок числовой прямой обладает свой-
ством секвенциальной компактности.
Теорема Больцано-Вейерштрасса (для
числовых последовательностей). Любая ограниченная числовая после-
довательность имеет хотя бы одну точку сгущения (хотя бы один
частичный предел).
Доказательство. Пусть (an) (п —> an, п Е N, ап Е R) -
ограниченная числовая последовательность, тогда Зс > 0 такое, что
|ап| < с Vn Е N. Пусть М — {an} = {ж Е R| ж = ап,п Е N}.
Тогда М С [—с, с]. Отрезок [—с, с] секвенциально компактен, поэто-
му если М С [—с, с] - бесконечное множество, то М' П [—с, с] / 0
72
и ЗЬ € Mf П [—с, с]. Но тогда в любой окрестности U(b) содержится
бесконечное множество элементов последовательности (ап), поэтому
Ъ 6 [—с» с] есть точка сгущения числовой последовательности (ап). Ес-
ли М = {an} =	Ап} € [-с, с] - конечное множество, то
существует точка bi = Ь 6 [—с, с] такая, что равенство ап = b име-
ет место для бесконечного множества индексов п = пх, п2,..., п&,...
(nk TMfc > fcVfc 6 N). Но тогда lim ank = b 6 [—с, с], т. е. b есть
v	fc—>4-оо
точка сгущения последовательности (ап).
Следствие. Из любой ограниченной числовой последователь-
ности можно выделить сходящуюся подпоследовательность.
Замечание. Для бесконечного ограниченного множества
М С [а, Ь] имеем Мг / 0 и М' С [а, Ь]. В самом деле, утверждение
Mf Ф 0 вытекает из теоремы Больцано - Вейерштрасса о секвенци-
альной компактности отрезка, а в силу замкнутости отрезка имеем
М С [а,Ь] => (М С [а,Ь] = [а, Ц) => (М' С М С [а, 6]).
Следствие. Если (ап) - ограниченная числовая последо-
вательность и S множество всех ее точек сгущения, то S / 0 и S
ограничено.
Определение. Пусть А С R и Ма С R Va. Система мно-
жеств {Ма} называется покрытием множества А, если D А,
а
Определение. Будем говорить, что из покрытия {Mrt} мно-
жества А можно выделить конечное подпокрытие, если существу-
ет конечное число множеств из системы образующих покры-
тие А.
Пример. Система всех интервалов вида (® — 0,1, х 4- 0,1), где
х Е [0,1], образует покрытие отрезка [0,1].
Определение. Множество К С R называется компакт-
ным, если из любого покрытия множества К интервалами можно
выделить конечное подпокрытие.
Лемма Бореля-Лебега. Из любого покрытия отрезка [а, Ь]
интервалами можно выделить конечное подпокрытие, т. е. любой
отрезок [а, 6] С R компактен (в R/
Доказательство. Пусть [а, Ь] С R и система {Ма} =
{(/^a,7a)} есть покрытие отрезка [а, 6] интервалами, т. е. [а, Ь] С
U Мл- Предполагая, что система {Mrt} бесконечна, допустим, что от-
резок До = [а, Ь] не допускает выделения конечного подпокрытия. Раз-
делим отрезок До пополам: если бы обе его половины допускали ко-
нечное покрытие интервалами из системы {Ма}, то и весь отрезок До
Допускал бы конечное покрытие. Поэтому хотя бы одна из его половин
Д1 не допускает выделения конечного подпокрытия: Д1 С До» Ai не
Допускает конечного покрытия интервалами из {Ма}, | Д11 = (Ь—а)/2.
Делим отрезок Д1 пополам и выбираем ту его половину Д2, которая
73
не допускает конечного покрытия: Д2 С Ai С До, Дз не допускает
конечного покрытия, |Дг| = (Ь- а)/22. Продолжая процесс, получаем
систему отрезков {Дп} : Дп С Дп-1 С ... С Д1 С До, Дп не допускает
конечного покрытия интервалами из {Ма} |ДП| = (Ь-а)/2п. Система
отрезков {Дп} (п € N) стягивающаяся, и по теореме Кантора Зс € R
4-оо
такое, что П Дп = {с} или с € Дп[а, Ч Vn € N. Но с € [а, Ч> поэтому 3
П = 1
интервал Ма = (/3,7) Э с (при этом/3 < с < 7 => (с-/3 > 0,7-с > 0)).
Выберем m G N таким, что |Дгп| = (Ь - а)/2т < |min{c - /3,
7 - с}, тогда Дт С (/3,7) (в противном случае было бы, например,
(ат < /3 < с < Ът) => (Ът - ат > с - /3 > 0) вопреки выбору
О < Ът - ат < (с -/3)/2), т. е. оказалось, что отрезок Дт не допус-
кающий по построению конечного покрытия интервалами из системы
{Мл}, покрыт одним интервалом из системы {Ма}. Противоречие.
Замечание 1.В условиях леммы Бореля - Лебега нельзя
заменить отрезок [а, 6] на интервал (а, Ь), т. е. интервал не компактен
в R.
Пример. Пусть (а, Ь) = (0,1), Мп = (1/п, 2), п G N, тог-
4-оо
да (0,1) С (J Мп, а выделить конечное покрытие из системы {Мп}
П = 1
нельзя (почему?).
Замечание 2. В условиях леммы Бореля - Лебега нельзя
вместо (открытого) покрытия интервалами рассматривать покрытие
отрезками: Ма = [0ft,7a].
Пример. Пусть [а, Ь] = [0,1], Mi = [0,1/2], Мп = [1/2 + 1/n, 1],
+оо
п = 3,4,..., тогда [0,1] С Mi U (J Мп, но выделить из системы {Мя}
п=3
конечное подпокрытие нельзя.
§ 7. Критерии существования предела числовой
последовательности, предела функции в точке
Теорема (критерий существования предела числовой после-
довательности). Пусть (ап) - числовая последовательность. Тогда
((ап) сходится) <=> ((ап) ограничена и имеет только одну точку
сгущения).
Доказательство. Необходимость. Пусть (ап) сходится, т. е.
существует lim ап = а, тогда последовательность (ап) ограничена
п->4-оо
и ее предел а есть точка сгущения для (ап).
Докажем, что других точек сгущения у (ап) нет. Допустим от про-
тивного, что у (ап) есть еще одна точка сгущения Ь ф а. Тогда по ак-
сиоме отделимости Хаусдорфа существуют окрестности U(a) и V(b)
74
такие, что U(a) П V(b) = 0. Поскольку а =	то для окрест-
ности U(a) 3Nq € N такое, что ап € U(a) Vn > No, т. е. в окрестности
У(&) может содержаться не более Nq—1 элементов последовательности
(ап), что противоречит определению Ь как точки сгущения последоваг
тельности (ап). Тем самым необходимость критерия доказана.
Достаточность. Пусть (ап) - ограниченная числовая последова-
тельность. Тогда по теореме Больцано - Вейерштрасса (ап) имеет
хотя бы одну точку сгущения. Пусть в соответствии с условием те-
оремы (ап) имеет единственную точку сгущения а € R. Докажем,
что а = lim ап. Допустим от противного, что (ап) не сходится к
n-44-oo
числу а. Тогда существует ео > 0 такое, что вне Ut0(a) существует
бесконечное множество элементов из последовательности (ап), т. е.
Эт > 1 такое, что |аП1 — а| > во > 0; Зпз > 2, пз > пх такое, что
|аПз - а| > во > 0 и вообще Vfc € N Зпд. > к и (при fc > 2) пд. > п*_х
такое, что |аЛй — <х| > во > 0, т. е. n* ff и supn* = +оо. Поэтому после-
к
довательность (Ьк) (где = ank) является подпоследовательностью
ограниченной последовательности (ап). Ограниченная последователь-
ность (Ьк) по теореме Больцано - Вейерштрасса имеет хотя бы одну
точку сгущения Ь, являющуюся тем самым и точкой сгущения для
последовательности (ап). Поскольку (ап) имеет единственную точку
сгущения а, то b = а. Но тогда в окрестности UtQ(b) (Ь = а) точки Ь,
являющейся точкой сгущения последовательности (Ьк)} должно содер-
жаться бесконечное множество элементов из (Ь&), в то время как по
построению Ьк = anitEUt0(a) = 17<0(Ь) Vfc € N. Противоречие. Итак,
а= lim ая.
п->4-оо
Следствие. Если последовательность (ап) сходится к а, то и
любая ее подпоследовательность (аПй) также сходится к а.
Теорема. Пусть (ап) - ограниченная числовая последователь-
ность и S - множество всех точек сгущения последовательности
(ап). Тогда 1)5^ 0; 2) множество S ограничено; 3)~8 = S, т. е.
множество S замкнутое; 4)	= eupS € S, ао = inf S € S.
Доказательство. Утверждения 1)-2) были доказаны ра-
нее. Доказательство 3): (а € 5) => (U(a) П S 0 я ЗЬ € U(a) П S),
и поскольку С7(а) = U(b), то U(a) содержит бесконечное множество
членов (ап), т. е. а € S, откуда (S С S) => (3 = S), т. е. множество
S замкнуто. Для доказательства 4) заметим, что из ограниченности
множества S в силу полноты R имеем За0 = sup S, ао = inf S Е R.
Докажем, что а0 € S. (Доказательство включения ао € S провести
самостоятельно.) В самом деле, пусть а0 = sup S € R. По определению
supS = а0 имеем: а) а < а° Va € S и б) Ve > 0 ЗЬ Е S такое, что
а°~е<Ь<а°=>ЬЕ U,(a°). Итак, S П С7((а°)	0 Ve > 0, другими
словами, S П U(a°) # 0 Vtf(a°), т. е. а0 € Я = S.
75
Следствие. Если (ап) - ограниченная числовая последова-
тельность и S - множество ее точек сгущения, то а0 = supS Е S
есть самая правая точка сгущения последовательности (ап), а ао =
inf S Е S есть самая левая точка сгущения (ап).
Определение. Пусть (ап) - ограниченная числовая после-
довательность и S - множество точек сгущения (ап). Тогда числа
aQ = sup S uaQ = inf S называются соответственно верхним и ниж-
ним пределами последовательности (ап).
Обозначения:
а0 = lim ат = lim sup ап d— lim sup an,
n—>4-00	n->+oo ,n>n	n->+oo
a© = lim am = lim inf an	lim inf an.
n->4-oo m>n	n->4-oo
Замечание. Пусть (an) - ограниченная числовая последова-
тельность и S - множество ее точек сгущения. Из следствия к теореме
о свойствах множества S вытекает, что верхний предел a0 = lim ап
п->4-оо
и нижний предел ао = lim ап можно определить следующими экви-
п—>4-оо
валентными способами:
I.	a0 = lim ап есть наибольший частичный предел (самая пра-
п->4-оо
вая точка сгущения) последовательности (an), ao = lim ап есть наи-
П->4-ОО
меньший частичный предел (самая левая точка сгущения) последова-
тельности (an);
II.	a0 = lim an, если Ve > 0 правее точки a0 + е имеется не более
п->+оо
конечного числа элементов из (an), но правее точки а0 — е содержится
бесконечное множество элементов из (ап). Аналогично ао = lim ап,
п—>4-оо
если Ve > 0 левее точки ао—е имеется не более конечного числа элемен-
тов из (ап), но левее точки ао + е содержится бесконечное множество
элементов из (ап);
III.	а0 = lim ап, если 1) Ve >0 32V 6 N такое, что ап < а0 4- е
п—>4-оо
Vn > N* 2) Ve > 0 и Vfc Е N Зп£ > к такое, что а0 — е < аПк.
Аналогично ао = lim ап, если 1) Ve > О 32V 6 N такое, что ап >
п—>4-оо
ао — е Vn > N; 2) Ve > 0 и Vfc Е N Зп& > к такое, что ао + г > аПк.
Следствие (критерий сходимости ограниченной числовой по-
следовательности). Пусть (an) - ограниченная числовая последова-
тельность. Тогда ((an) сходится) <=> ( lim ап = lim an).
n->4-oo	n->4-oo
Доказательство. Условие lim ап = lim ап для огра-
п->4-оо	п->4-оо
ниченной числовой последовательности (an) означает, что S = {а},
76
так что у последовательности (ап) имеется единственная точка сгу-
щения. Но тогда применим доказанный ранее критерий сходимости
числовых последовательностей.
3 а м е ч а н и е. Не нужно смешивать понятия верхнего (нижнего)
предела и точной верхней (нижней) грани для последовательности.
Пример. Пусть ап = (—1)п(1 4- 1/п). Тогда lim ап = 1,
п —>+оо
lim ап = —1, supan = 3/2, inf ап = -2.
п->+оо	п	п
Определение. Последовательность (ап) называется после-
довательностью Коши, еслиУе > О 3N 6 N такое, что |an —ат| < е
Уп > N, т > N.
Теорема (критерий Коши существования предела у числовой
последовательности). (Числовая последовательность (ап) сходится)
<=> ((^п) есть последовательность Коши).
Доказательство. Необходимость. Пусть (ап) сходится,
т. е. 3 lim ап = a G R. Тогда по определению предела последо-
п->4-оо
вательности Уе > О 3JV 6 N такое, что |ап — а| < е/2 Vn > N и
|а.п - а| < е/2 Vm > N, откуда |ап - а»п| = |(«п - а) + (а - ага)| <
|ап — а| + |«т — а| < е/2 + е/2 = s, т. е. числовая последовательность
(ап) есть последовательность Коши.
Достаточность. Пусть числовая последовательность (ап) есть по-
следовательность Коши. Тогда Уе > О 3N 6 N такое, что |an — ат| < е
Уп, m>N. Пусть го = 1 > 0, тогда BNq 6 N такое, что |an — am| < 1
Уп, т > Nq. Зафиксируем по > Nq, тогда |аПо - aw| < 1 Ут > Nq
или аПо — 1 < ат < аПо 4- 1 Ут > Nq, т. е. последовательность (ат)
финально ограничена, но тогда она и просто ограничена. По теоре-
ме Больцано - Вейерштрасса ограниченная последовательность (ап)
имеет хотя бы одну точку сгущения а. Поскольку (ап) есть последо-
вательность Коши, то Уе > О 37V 6 N такое, что |ап — ат| < е/2
Уп, т > N. Из того, что а есть точка сгущения последовательности
(ап), вытекает, что для е/2 > 0 3ni > N такое, что |аП1 - а| < е/2.
Но тогда
|ат — tz| = |(aw “Ащ) 4- (пП1 — а)| <
< |«m - аП1| 4- |аП1 - а| < еУт > N,
т- е. 3 lim ат = а.
т->+оо
С л е д с т в и е (критерий Коши сходимости числового ряда).
4-сю	» п
(Ряд £ а* сходится) (Уе > О 32V G N такое, что £	< е
fc=i
Уп > m > N).
к
Доказательство. Если 8п = ^2 ак ~ п-я частичная сумма
fc=i
fc=m+l
77
+00	L
ряда £ а*, то сходимость ряда эквивалентна сходимости последова-
к=1
тельности (sn). Применяя к этой последовательности критерий Коши
п
существования предела, имеем в силу равенства вп - зт = а*
fc=m+l
наше следствие.
Теорема (критерий существования предела функции в точке).
Пусть функция /(х) определена на множестве М и а € Mf. Тогда
(3 Jim f(x) = А Е R) <=> (Ve > 0В<5 > 0 такое, что |/(®х) - /(®г)| < е
V®i, € Lfy(a) n М).
Доказательство. Необходимость. Пусть 3 lim f(x) = А.
Тогда в силу (е, 6) определения предела функции в точке Ve > О В<5 > О
такое, что /|(®х) — А| < е/2 V®x € Us (а) П М и |/(®г) — А| < е/2
V®2 € Ut(a)r\M, но тогда |/(®х)-/(®г)| = |(/(®х)-А) + (А-/(х2))| <
|/(®х) - А| + |/(®2) - А| < е V® 1,х2 € U*(a) П М.
Достаточность. Пусть для функции f(x) и точки а Е М' выпол-
нены условия Коши. Пусть (£п) - любая последовательность Гейне,
связанная с точкой а, т. е. lim £п = n, in € Af, in a Vn € N.
Положим f(in) = ап и докажем, что числовая последовательность
(ап) есть последовательность Коши. Пусть е > 0 любое. Тогда в силу
условия Коши Э£(е) > 0, а в силу свойств последовательностей Гейне
3JV(J) Е N такие, что: 1) поскольку lim £п = а и in Е М, in / а
п->+оо
Vn € N, то	DM Vn,m > N(6), и тогда 2) в силу вы-
бора 6(e) > 0 по условию Коши имеем |/(£п) - /(6n)| = l“n - “ml < е
Vn,m > N(6).
Таким образом, числовая последовательность (ап) есть последо-
вательность Коши, сходящаяся в силу критерия Коши для последо-
вательностей. Итак, V(£n) ~ последовательности Гейне, связанной с
точкой а € Af', 3 lim f(£n) = -А».
Пусть (£п) и (tyn) - две любые последовательности Гейне, связан-
ные с точкой а € М', и пусть lim f((n) = Aj и lim f(r}n) — Аг.
П-4Ц-00	n—>4" ОС
Рассмотрим последовательность (£„), где (п = & при п = 2fc и £п = щ
при n = 2fc - 1 (к € N). Очевидно, имеем
(6 е мVfc е N) л (ъ € MVfc е N) =► е MVn е N);
(6 0 a Vfc € N) Л (ъ # “Vfc € N) => «п '0 aVn € N);
(3 lim & = lim щ = а) => (3 lim (п = а).
fc—>4"00	1?<*^4"Оо	п—>4"Оо
Таким образом, последовательность (Сп) есть последовательность
Гейне, связанная с точкой а € Mf. Если сп = /(Сп), то последова-
тельность (сп) имеет две точки сгущения Ах и Аг. Но выше было
78
показано, что последовательность (сп) обязана быть последователь-
ностью Коши, а потому 2 lim сп = Л. Стало быть, Ai = А] = А.
n-4+oo
Итак, V последовательности Гейне (£п), связанной с точкой a g ЛГ',
существует один и тот же единственный предел lim (£п) = А, т. е.
J	п-44*оо
(Г)
3 lim /(х) — А. Но тогда по теореме об эквивалентности определений
0-40
предела функции в точке по Гейне и по Коши имеем
(3 lim /(х) А) => (3 lim /(х)	А), т. е. 3 lim /(х) = А.
0-4а	аг-4 а	х-4а
Замечание. Если функция /(х) определена на М и sup М =
+оо, то для х + +оо критерий Коши формулируется следующим
образом: (3^Km^/(х) = А € R) (Уе > О ЗД > О такое, что |/(xi)-
У(хг)| < е Vxi, xj € М П (К, +оо)).
Пример. Для У(х) = 1/х, х 0, при х —> +оо выполнен критерий
Коши, поскольку Уе > О ЗД = 2/е > О такое, что Ух,- 0 (г = 1,2)
таких, что Xi > Д, Хг > К, |l/xi - 1/ха| < |l/xi| + |1/хз| < 2/К = е.
§ 8. Сравнение асимптотического поведения
функций
Знания того, что функции стремятся к пределам на множестве М
при х -> а g М', равно как и знания значений самих пределов, еще не
достаточно для решения всех задач о переходе к пределу в выражени-
ях, составленных из этих функций. Например, при х -> +оо каждая из
трех функций х, х2 и ч/® стремится к +оо, однако если рассмотреть
выражения
(х + 1) - X, (х + I)2 - X2 и V® + 1 - ч/®> то
JfeoK* + 1) - х] = 1; Кт [(х + I)2 - X2] = Кт (2х + 1) = +оо;
0-44*00	в—>4-оо	9-44*00
Кт [ч/х + 1 - ч^) = Кт 1/(ч/х + 1 - у/х) = 0.
0-44*00	0-4"hOO
Поэтому важно знать не только предельные значения функций при
® -> а (если эти пределы существуют), но нужно знать и асимпто-
тику поведения функций, т. е. «способ стремления» функций к своим
пределам. Для этого необходимо установить классификацию во мно-
жестве функций, стремящихся при х -> а к одному и тому же пределу,
причем а может быть как числом, так и одним из символов -оо, +оо,
00.
Определение. Пусть функции /(х) и д(х) определены на
множестве М и а € М'. Скажем, что f = 0(g) (х —>а), если су-
ществуют постоянная С > 0 и окрестность U(a) точки а такие,
что 1/(1) | < С|у(х) | Ух g 17(a) Л М.
79
Замечание. Если функция f(x) определена на М и а 6 М', то
f = 0(1) (х -4 а) означает локальную ограниченность функции f(x) в
точке а 6 М'.
Замечание. Если supМ = Ч-оо, то равенство f = 0(1)
(х -4 +оо) означает финальную ограниченность f(x) при х -4 +оо,
т. е. существование С > 0 и К >0 таких, что |/(®)| < С V® G
МП (К, +оо).
Примеры, sin® = 0(1) (®-4 0), так как |sin®| < 1 V® 6
(—оо, +оо); sin ® = О(®) (® —> 0), так как | sin®| < |®| V® 6 (—оо, +оо);
sin2 ® = O(sin®) (® -4 +оо), так как | sin2 ®| < | sin ®| V® 6 (—оо, 4-оо).
Теорема (о свойствах символа О). Пусть функции Д(®),
Д(®), Д(®), <71(®)> 02 (®), Л(®) определены на М и a G М'. Тогда
1) (fi = O(f2) (х а)) Л (f2 = О(Д) (х -4 а)) => (Д = О(Д) (х а))
(транзитивность символа О); 2) теорема сложения (fi = 0(h)
(х -4 a) (i= 1,2)) => (А + /2 = 0(h) (х -4 а)); 3) теорема умножения
(fi = O(g<) (х -> а) (г = 1,2)) => (Л • /2 = 0(gi • g2) (х -> а)).
Доказательство. 1) Пусть Д = О(Д) (® -4 а) и Д =
О(Д) (® -4 а). Тогда из определения Д = О(Д) (® -4 а) => 3Ci >
О и BU(a) такие, что |Д (®)| < С1|Д(®)| V® G U(a) П М. Далее, из
Д = О(Д) (® -4 а) => ЗС2 > 0 и 3V(a) такие, что |Д(®)| < С2|Д(®)|
V® 6 V(a) П М. Но тогда для С = Ci • С2 > 0 и 1Г(а) С U(a) П V(a)
имеем |Д(®)| < С|Д(®)| V® G 1Г(а) П М, т. е. Д = O(fz) (х -4 а).
2) Из условий fi = 0(h) (х -4 a) (i = 1,2) имеем 30, > 0 и BU^(a)
(i = 1,2) такие, что |Д(®)| < С||Л(®)| V® 6 U^(a)C\M (i = 1, 2), откуда
для С = Ci + С2 > 0 и V(a) С U^(a) П U™(a) имеем |Д(®) + Д(®)| <
C\h(x)I V® е V(a) П М, т. е. Д + Д = 0(h) (х -4 а).
3) Из условий fi = O(gi) (х -4 a) (i = 1,2) => 30,- > 0 и 3U^(a)
(i = 1,2) такие, что |/,(®)| < С«|0«(®)| V® 6 U^(a)C\M, откуда для С =
0x02 > 0 и V(a) С U^(a)C}U^) имеем\fi(x)-f2(x)\ < C\gi(x)-g2(x)\
V® € V(a) П M, т. е. Д • Д = 0(gr • g2) (х а).
Следствие. Пусть функции /(®), gi(x), g2 (х) определены на
М и а е М'. Тогда 1) O(O(f)) = 0(f) (х а); 2) £ X;O(f) = 0(f)
(® -4 а) (А, = const); 3) 0(£i) • 0(g2) = 0(дг • д2) (х -> а).
П р и м е р ы. 1) (sin® = 0(х) (х -4 0);® = 0(1) (® -4 0)) => sin® =
0(1) (® -4 0); 2) (® + 1 = О(х) (х -4 +оо), у/х = О(х) (х -4 +оо))
=> х + у/х + 1 = О(х) (х -4 4-оо).
Определение. Пусть функции f(x) и д(х) определены на
множестве М и а 6 Mf. Если f = 0(g) (® 4 а) и д = 0(f) (х -4 а),
то скажем, что функции f(x) и д(х) подобны при х -4 а. Обозначе-
ние: f х д (х -4 а).
Замечание, f х д (® 4 а), если существуют постоянные
80
Ci > 0, Сг > О и окрестность 17(a) такие, что
С11Ф)1 < 1/(*)1 < G|<7(s)|Vx Е 17(a) AM.
Замечание, f д (х а) означает, что существуют С± > О,
С2 > 0 и 17(a) такие, что 0 < С± < \f (®)| < С2 < +00 V® Е 17(a) А М.
Замечание. (3 lim /(®) = с 0) => (/ х 1(® -> а)),
х—>а
Пример, sin2® = O(sin®) (® -> +оо), но sin® O(sin2 ®)
(ж —> 4-оо), поэтому отношение sin2 ® х sin® (® —> 4-оо) неверно.
Теорема умножения (для отношения подобия). Пусть
функции fi(x), gi(x) (i = 1,2) определены на множестве М и а Е Af'.
Пусть fi х gi (® -> а) (г = 1,2). Тогда fa- f2~9i- 92 (® -> а).
Доказательство следует из теоремы умножения для символа О.
3 а м е ч а н и е. Из А х gi (® а) (г = 1,2), вообще говоря, не
следует А+А х 01+02 (® —> а) (т. е. теорема сложения для отношения
подобия х неверна). Например, если А(®) = 0i(®) = ®2, А(ж) = — (®2+
х), 0г(®) = ~(®2 + 1), тогда /, х д< (® -> +оо) (г = 1,2). Но Л(®) +
А(ж) = -ж, д±(х) + д2(х) = -1. Очевидно, -® / О(-1) (®->+оо),
хотя -1 = О(х) (® -> +оо), т. е. отношение А+ /2 ~ 01+02 (® +оо)
неверно.
Определение. Пусть функции f(x) и д(х) определены на
множестве М и a Е Mf. Скажем, что f = о(д) (® -> а), если Уе > 0
317(a) такая, что |/(®)| < е|0(®)| V® Е [7(a) А М.
Замечание. Если f = о(д) (® —> а), то f = 0(g) (® —> а).
Замечание. Пусть функции /(®) и д(х) определены на мно-
жестве М и а Е М'. Если существует 17(a) такая, что д(х) ф 0
V® Е U(a)f}M, то отношение f = о(д) (® —> а) означает, что су-
f(x) о(^(®)) Л
ществует hm - = hm 	— 0.
х—>a д(х)	x->a д(х)
Замечание. Если функция /(®) определена на множестве М,
a Е М' и f = о(1) (® —> а), то lim /(®) = 0, т. е функция /(®) = о(1)
х—>а
(х -> а) есть бесконечно малая функция при ® —> а.
Пример. Поскольку limsin® = 0, то sin® = о(1) (® —> 0).
Пример. Пусть а,Р Е R и а < /3. Тогда ®а = о(х&) (® —> +оо);
= о(®а) (®	0). В самом деле, при а < [3 имеем а— (3 < 0, /3—a > 0,
откуда lim ха/х^ = lim ®a~^ = 0; lim ®^/®a = lim x^~a = 0.
x->+oo	x->+oo	x->0	x~>0
Замечание. Пусть функции /(®), g(x) и a(®) определены на
множестве М и а Е Mf. Если а(®) - бесконечно малая функция при
® а и существует 17(a) такая, что f(®) = а(х)д(х) V® Е 17(a) А М,
= о(д) (х а).
Теорема (о свойствах символа о). Пусть функции fi(x), А(®)^
91{х), 0г(®), Л(®) определены на множестве М и a Е Mf-
81
Тогда Iа) (ft = 0(f2) (x -4 a))A(ft = o(ft) (® -4 <*)) => (ft = o(ft)
(® -> a)); 6) (fi - o(ft) (® -4 a)) A (ft = 0(f3) (x -4 a)) (ft = o(ft)
(x -4 а)); в) (теорема транзитивности) ((ft = o(ft) (x -4 a)) A (ft =
o(ft) (x -4 a))) =► (ft = o(ft) (x -4 a));
II теорема сложения (ft = о(Л) (x -4 a) (i = 1,2)) => (ft+ft = o(h)
(x -4 a));
III теорема умножения {fi = o(gt) (x -4 a) (*' = 1,2); (ft = O(gi)
(x -4 a)) A (ft = o(g2) (x -4 a)); (ft = o(gi) (x -4 a)) A (ft = 0(g2)
(x -4 a))} => (ft • ft = o(gi • g2) (x -4 a)). (Доказательство провести
самостоятельно.)
Докажем, например, I а). Пусть ft = O(ft) (х -4 а) и ft = o(ft)
(х -4 а). Тогда существуют С > 0 и U(a) такие, что |ft(x)| < C|ft(x)|
Vx € U(а) П М. Далее, поскольку ft = o(ft) (х -4 а), то Ve > О 3V(a)
такая, что
|ft(®)| < 7;lft(®)|Vx G У(а)ПМ.
и
Но тогда Ve > 0 3W(a) С U(a) Г) V(a) такая, что
|Л(®)| <	< <4|/з(®)| = e|ft(x)|Vx G W(a) ПМ,
и
т. е. ft = o(ft) (х -4 a).
Следствие. Пусть функции f (х) и д(х) определены на мно-
жестве М и а € М'. Тогда:
1)	О(о(/)) = o(f) (х -4 a); o(O(f)) = o(f) (х -4 а); о(о(/)) = o(f)
(х -4 а);
2)	-o(f) = o(f) (х-4 а);
i-i
3)	o(f) • о(д) = o(f • д) (х -4 a); o(f) • 0(g) = o(f • д) (х -4 а).
Пример, (sinx = о(1) (х -4 0); sinx = О(х) (х -4 0)) => (х •
ein х = о(х) (х -4 0); sin2 х = о(х) (х -4 0)).
Теорема. Пусть функции f(x) и д(х) определены на М и а €
М'. Тогда (f(x) - g(x) = o(f(x)) (х -4 а)) => (f(x) - g(x) = o(g(x))
(x -4 а)), причем f = 0(g) (x -4 a) ug = 0(f) (x -4a).
Доказательство. Пусть f(x) — g(x) = o(f(x)) (x -4 a).
Тогда Ve € (0,1) 317(a) такая, что
Vx G U(a) П M => (e|/(x)| > |/(x) - p(x)| >
> l/(®)|- lf(«)l) => ((l-e)l/(®)l < 1Ф)1 =>
=> (l/(®)<	e. f = O(g) (xa).
Итак, (f(x) - g(x) = o(f(x)) (x -> a)) => (f = O(g) (x -4 a)), но
o(O(0)) = o(g) (x -4 a), поэтому f(x) - g(x) = о($(х)) (x -4 a).
82
Определение. Пусть функции f(x) и д(х) определены на
множестве М и а € М'. Скажем, что функции f(x) и д(х) эквива-
лентны при х -> а, если f(x) - д(х) = o(f(x)) (х -4 а). Запись: f ~ д
(х -4 а).
Замечание. Если f(x) и д(х) определены на М и а Е М', то
(/ ~ д(х <*)) => (/ х в(х -4 а))>но не наоборот. В самом деле, (/ ~ д
(х -> а)) => (/ = 0(g) (х -4 а)) Л (д = 0(f) (х -4 а)) =►(/ ~ д(х -4 а)).
Замечание. Если функции f(x) и д(х) определены на М и
а Е М', то (/ ~ д (х -4 а)) <=> (/ = д + о(д) (х -4 а)).
Замечание. Если функции f(x) и д(х) определены на М а
а€ М' и существует U(a) такая, что д(х) ф 0 Ух € U(a) П М, то f ~ д
(х -4 а) означает, что существует lim —$ = 1. В самом деле, (f ~ д
'	д(х)
(х -4 а)) => (f(x) = д(х) + о(д(х)) (х -4 а)), откуда в й(а) И М имеем
Д— = 1 + о(1) (х —> а) => 3 lim = 1. (Обратное утверждение
р(х)	«-*««(«)
доказать самостоятельно.)
3 а м е ч а н и е. Из f ~ д (х -4 а) не следует 3 lim(/(x) - д(х)) —
0.
Например, (х2 + х) ~ х2 (х -4 +оо), но (х2 + х) — х2 = х -4 +оо при
х -4 +оо, т. е. эта функция даже не ограничена.
Пример. Пусть f(x) определена на М, а € М' и / ~ с (х -4 а),
где с - постоянная. Тогда существует lim f(x) = с.
В самом деле, (/ ~ с (х —> а)) => f(x) = с + о(с) = с + о(1) (х -4 а),
откуда 3 lim f(x) = с.
х-ta
n
Пример. Пусть Рп(®) = S <**®п“* ~ многочлен степени п, при-
ksO
чем ао 0, тогда Рп(х) ~ <*о®п (® -4 +оо). В самом деле,
Рп(х) -aoxn = ^a*xn“fc = У^о(х") = о(х") (х -4 +оо).
Ь=1	к=1
Пример. (1 + 1/х) sinx ~ sinx (х -4 +оо), так как имеем (1 +
1/х) sinx — sinx = (1/х)einх = o(sinx) (х -> +со).
Замечание. Если функции fc(x) и gi(x) (i = 1,2) определены
на множестве М, а Е М' и fi *- gt (х -4 а), то функции fi(x) + fa(x)
111 9i(x) + дз(х) могут и не быть эквивалентными при х -4 а (т. е.
Для отношения эквивалентности ~ теорема сложения, вообще говоря,
неверна).
Например: 1) fi(x) = х2 ~ х2 = gi(x) (х -> +оо); /г(х) = -(х2 +
®) ~ —(х2 + 1) = дг(х) (х -> +оо), но функции Д(х) + Л(х) = -х и
91(х) + рг(®) = -1 не эквивалентны при х -4 +оо;
2) Л(®) = х + х2 ~ х + х3 = gi(x) (х -> 0); /г(®) = -х + х2 ~ -х =
®г(®) (х -4 0), но функции fi(x) + /j(x) = 2ха и fli(x) + 0а(х) = х3 не
83
эквивалентны при х —> 0.
Теорема умножения (для эквивалентных функций).
Пусть fi(x) и gi(x) (г = 1,2) определены на множестве М иа Е М'.
Тогда если fi ~ gi (х -4 а) (г = 1,2), то Д • Д ~ 01 • 02 (®	а).
Доказательство.	(1 а) (i = 1,2)) (Д = <7i+o(<h)
(ж -4 а) (г = 1,2)), но тогда имеем Д • Д = (91 + o(gi))(g2 4- o(g$)) =
gi • 92 + fol • o(g2) + 92 • о(дг) 4- о(дг) • о(^2)] = 01 • 02 + о(дг • д2) (х -4 а)
=> Д • Д = 01 • 02 + о(дг • д2) (х -4 а), т. е. Д • Д ~ 01 • 02 (® -4 а).
Теорема о знаке. Пусть f(x) и д(х) определены на М, а Е
Mf и существует окрестность 1Д(а) такая, что д(х) > 0 (< 0)
V® 6 МГУ(а, <x-F(5) (или Vx Е МС\(а—6, а)). Тогда если f ~ д (х -4 а 4- 0)
(или при х-^а — 0), то существует окрестность Vs1(a) С Us(a)
такая, что f(x) > 0 (< 0) Vx Е М А (а, а 4-£i) (соответственно
Vx Е М О (а — Ji, а)).
Доказательство. Пусть f~g(x->a + 0)n д(х) > 0
Vx Е М А (а, а + (5), тогда f = д 4- о(д) (х —> а 4- 0), и поэтому Ve Е
(0,1) ЗУ^Да) С Щ(а) такая, что |/(®) -£(®)| < е|0(®)1 = е9(х) Vх €
М А (а, а 4- <5i), откуда f(x) > д(х) - ед(х) = (1 - е)д(х) > 0 Vx Е
М А (а, а 4* <5i).
Теорема о пределе частного. Пусть функции
fi(x), 9i(x) (♦ ~ 1»2) определены на множестве М, а Е Mf и
существует окрестность U(a) такая, что f2(x)	0, д2(х} / 0
Vx Е 17(a) А М. Пусть 3 lim = А и Д ~ gi (х -4 a) (i = 1,2).
Д(®)
Тогда
Доказательство. Поскольку 3 lim j-т-г = А, то имеет
х->а f2(x)
место представление fi(x)/f2(x) = А4-о(1) (® —> а) в U(a) А1И, откуда
Д = АД 4- о(Д) (ж -4 а), но Д ~ д2 (х -4 а), поэтому Д = д2 4- о(д2)
(® -4 а) и Д = О(д2) (х -4 а), откуда Д = А^24-[А-о(^2)4-о(О(02))] -
А02 4- о(д2) (х -> а) и, в частности, Д = О(д2) (х а). Далее, д^ Д
(х -4 а), поэтому fl! = Д 4 о(Д) (х а) или дг = Ад2 4- [о(^2) 4-
°(О(д2))] = Лд2 4- о(д2) (х -4 а), т. е. Vx Е U(a) А М gi(x)/g2(x) =
А 4- о(1) (х -4 а) => 3 lim gi(x)/g2(x) = А.
т—>а
Пример. sin® = ®4- о(х) (® -4 0) => sin х х (® -4 0); sin 2х =
. 2	2
2® 4- о(®) (® —> 0) => sin 2® ~ 2® (® —> 0) => lim —. -   = lim —— =
х->о ® sin 2®	х-*о х • 2®
1
2*
Пусть функции а(®) и (3(х), определенные на множестве М, яв-
ляются бесконечно малыми при ® -4 а (где а Е М'), т. е. а = о(1)
(® -4 а); /3 = о(1) (® -4 а).
84
Определение. Бесконечно малые при ж -4 а функции а (ж) и
называются бесконечно малыми одного порядка при х -4 а, если
fl (ж -4 а).
Пример. Бесконечно малые а(ж) = 1/ж и fl(x) = 3/ж (при
х —> 4-оо) одного порядка, так как /3(ж)/3 = 1/ж < а(ж) = 1/ж <
/3(х) = 3/ж \/ж / 0.
Определение. Бесконечно малые функции а(ж) и fl(x) на-
зываются эквивалентными при х -4 а, если а ~ fl (ж -4 а).
Пример. Поскольку 3 lim —ПЖ = 1, то sin ж ~ ж (ж —> 0).
х—>0 X
Определение. Бесконечно малая функция а(ж) при ж -4 а
называется бесконечно малой более высокого порядка, чем беско-
нечно малая (при х -4 а) функция fl(x), если а = o(fl) (ж -4 а).
Пример. Пусть а(ж) = sin2 ж и fl(x) = ж \/ж G (—оо,4-оо),
• 2	/ X Z	sin2 ж	(ж4-о(ж))2
тогда sin ж = о(ж) (ж —> 0), так как 3 пт- = hm ---  =
т-4-0 Ж х->0 X
lim----------= 0.
дг—>0	X
Приведем следующие девять простейших разложений при х -4 0.
1)	sin® = х 4- о(ж) (ж -4 0) (в самом деле, Slim sin х/х = 1 =>
х —>0
(sin®/® = 1 + о(1) (® -> 0)) => (sin® = х + о(х) (х -> 0)));
1 —~ COS X
2)	cos® = 1 — ®2/2 + о(®2) (® —» 0) (в самом деле, 3 lim-z-y-— =
' '	®->о ®2/2
2sin2(®/2)	4(®/2 + о(®))2	®2(1+о(1))
iim —тйН- = 1шл ——2~v	=11т —-—5-^ -х);
®,—>0	Х2/2	х->0 X2	>0 х2
3)	tg х = х 4- о(ж) (х -4 0) (в самом деле, 3 lim tg xfx = 1 => tg x =
x—>0
4)	arcsin x = x 4- о(ж) (ж -4 0);
5)	arctg x = x 4- о(ж) (ж -4 0);
ln( 1 4- x)
6)	ln(l 4- a?) = x 4- o(x) (x -4 0) (в самом деле, 3 lim —---- =
x
limln[(l 4* ж)1/*] = Ine = 1;
7)	ex = 1 4- x 4- о(ж) (ж -4 0) (в самом деле, ех — 1 = z, ж = 1п(1 4- z)
=> 3 lim------- = lim Z—- = lim---------= 1);
x «->o ln(l 4* z) z->o z 4-o(z) '
8)	ax = 1 4- x In a 4- о(ж) (ж -4 0), a > 0, a 1. (ax = ехр{ж1па} =
9)	(1 4- х)а = 1 4- ах 4- о(ж) (ж -4 0) (в самом деле, (1 4- х)а
е*р{а1п(1 4* ж)} = ехр{а(ж 4- о(ж))} = 14- а(ж 4- о(®)) 4- о(х 4- о(ж))
II II
85
$ 9. Предел числовой функции по базе
При рассмотрении теорем о пределах была отмечена двойствен-
ность формулировок ряда теорем для числовых функций и для число-
вых последовательностей, причем и доказательства этих теорем ока-
зывались вполне аналогичными. Для выяснения этого явления проана-
лизируем определения предела функции в точке и предела числовой
последовательности. При окрестностном определении предела число-
вой функции /(®) (заданной на множестве М) в точке а € М':
Jim /(®) = А требовалось, чтобы Уе > 0 существовало множество
= U(a) П М такое, что |/(®) - А| < е V® € В*. При этом в доказа-
тельствах всех теорем о пределах функции от системы множеств {В* }
требовалось выполнение только двух свойств: 1) В* = Us (а) Г) М 0
V<J > О это свойство обеспечивалось тем, что а € М' и СТ* (а) есть
окрестность точки а; 2) V<5i > 0,	> О ЭВ*, = 17*, (а) П М такая,
что В*, С В*, П В*,, т. е. В*,(а) Л М С (17*, Л 17*,(а)) Л М (напри-
мер, V63 € (0, гшп(^1,^г))) (это свойство следует из указанного ранее
свойства 2) проколотых окрестностей).
Аналогично в определении предела числовой, последовательности
lim an = а требовалось, чтобы Уе > О Э множество натуральных
п-++оо
чисел Bn0 = {т € N|m > JVb} такое, что, |an — a| < е Vn € Bn0.
При доказательстве всех теорем о пределах последовательностей ис-
пользовались только два свойства системы {Bn}: 1) Вп ф 0 Vn € N
и 2) Vn, т € N 31 € N такое, что Bi С Вп П Вт (например,
V/> тах(т, п)).
Определение. Пусть дано множество М. Система мно-
жеств В = {В} (где В С М суть подмножества М) называется
базисом фильтра (или предфильтром, или просто базой) во множес-
тве М, если: 1) В ± 0 VB € В и 2) VBi, В2 € В ЗВз € В такое, что
В3 С Bi П В2 •
Множества В из базы В будем называть элементами базы.
Примеры:!) Если а € Мто система множеств В = U(a) П М
VU(a) есть база в М, она обозначается символом х а;
2)	если а € М, то система множеств В = 17(a) П АГ V17(a) есть база
в АГ:
3)	если а € где М+ = М П (а, +оо), то система множеств
Bf = (а, а + <5) П М Vi > 0 есть база в М, она обозначается символом
х —> а + О?
4)	если а € где М~ = (-оо,а) П Af, то система множеств
Bs = (a - i, а) П М Vi > 0 есть база в АГ, она обозначается символом
х а - 0;
5)	система множеств Вп = {n, п + 1, п + 2,...} Vn € N есть база в
N, она называется базисом фильтра Фреше и обозначается символом
п -> +оо;
86
6)	если sup М = +оо, то система множеств Вк = М П (К, +оо)
УК > 0 есть база в М, она обозначается символом х -> +оо;
7)	если inf М = —оо, то система множеств Вк = (-оо, -К) П М
УК > 0 есть база в М, она обозначается символом х -4 —оо;
8)	если sup |®| = +оо, то система множеств Вк = {® € М)|®| > К)
УК > 0 есть база в М, она обозначается символом х -> оо;
9)	если [а, b] С (-оо,+оо) - заданный отрезок, то система всех
окрестностей {(а,0)}, содержащих отрезок [а, Ь] ([а, Ь] С (а,/3)), есть
база в R.;
10)	множество всех окрестностей В = {(а,/3)} Va,/3 € (-оо,+оо)
(а < 0) не является базой в (-оо, +оо), так как, например, (0,1) € В
и (-1,0) € В, но (0,1) О (-1,0) = 0, т. е. не выполнено требование 2)
из определения базы.
Замечание. Из определения базы В в М следует, что если
Во € В, то система множеств {В} всех элементов В € В таких, что
В С Во, также есть база в М.
Определение. Пусть (числовая) функция f(x) определена
на множестве М и В есть база (предфильтр) во множестве М.
Скажем, что число А € R есть предел функции f(x) по базе В
(вдоль предфильтра В), если Уе > 0 существует элемент В € В
такой, что |/(®) — А| < е Ух € В.
Обозначение: А = lim/(®).
Все доказанные ранее теоремы для пределов функции в точке мо-
гут быть сформулированы и доказаны для пределов функции по базе.
Задание. Переформулируйте и докажите теоремы из § 3, 4 и
8 этой главы для пределов функции по базе.
Пример.
Теорема о пределе с у м м ы. Пусть функции /х(®) и
/з(®) определены на множестве М и В - база во множестве М,
причем 31im/i(®) = (г =1,2). Тогда
в
31im(/i(®) + /2(®)) = Ai + Аа.
В
Доказательство. Поскольку 31im/,(®) = А,- (г = 1,2), то
Ve > О ЗВ, е В (г = 1,2) такие, что |/Д®)-Л<| < е/2 V® € В, (» = 1,2).
По свойству 1) базы В,: 0, а в силу свойства 2) базы существует
элемент Вз G В такой, что Вз С Bi П Ва, но тогда |(/i(®) + /2(®)) -
(Ai + Л2)| < |Д(®) - А| + |/2(®) - А| < е/2 + е/2 = е V® е В3, т. е.
^^(/i(®) +/2(®)) = Л1 + Л2.
Определение. Пусть функция /(®) определена на множес-
тве М и В = {В} - база в М. Функция /(г) называется локально
87
ограниченной по базе В, если существуют постоянная С > 0 и эле-
мент Bq Е В такие, что |/(®)| < С У® Е Во.
Теорема (о локальной ограниченности функции, имеющей пре-
дел по базе). Пусть f(x) определена на М и В - база в М. Если
31im/(®) = А, то функция f(x) локально ограничена по базе В.
Доказательство. Из определения предела lim/(®) = А вы-
текает, что для го = 1 > 0 ЗВо 6 В такой, что |/(®) — А| < 1 У® Е Во,
т. е. |/(®)| < С = |А| 4-1 V® 6 Во, где Во 6 В, что и означает локаль-
ную ограниченность функции /(®) по базе В.
Лемма. Пусть функция /(®) определена и ограничена на мно-
жестве М. Тогда VB С Во, имеем
sup |/(®1) - /(®г)| = sup f(x) - inf f (x).
^h^iEB	В	®
Доказательство. Положим I = sup /(®) — inf /(®). Заме-
в	B
тим, что V®i,®2 E В С Во => —оо < inf/(®) < /(®t) < sup/(®) < 4-oo
B B
(i = 1,2), откуда имеем 1) |/(®i) — /(®г)| < sup/(®) — inf/(®) = I
в B
V®1, ®2 6 B.
Далее, в силу определений sup f(x) и inf f(x) имеем Уг > О 3®$, ®° Е
в в
В такие, что /(®?) > sup/(®) — г/2 и /(®§) < inf/(®) 4- г/2, т. е.
в	в
/(®1) — /(®§) > Но тогда 2) Уг > О 3®?,®° 6 В такие, что
1/(®1)““/(ж2)1 > Из 1) и 2) вытекает, что I = sup |/(®i)—/(®г)|-
ЕВ
Теорема. Пусть числовая функция /(®) определена на мно-
жестве М и В - база в М. Пусть f(x) ограничена на элементе
базы Bq Е В. Тогда УВ1,Вг Е В таких, что В± С Bq, В2 С Bq,
имеем —оо < inf/(®) < sup/(®) < 4-оо.
В2
Доказательство. В силу свойств базы В имеем В, / 0
(г = 1,2), BiClB2 / 0, причем В, С Во (г = 1,2), B1QB2 С Во. Но тог-
да, очевидно, (—оо < inf/(®) < inf/(®) < inf /(®) < sup f(x) <
Bq	B\	B1QB2	В1Г\В2
sup/(®) < sup/(®) < 4-oo) => (—00 < inf/(®) < sup/(®) < 4-oo).
B2	Bo	B1	B2
Теорема. Пусть числовая функция f(x) определена на мно-
жестве М и В - база во множестве М. Пусть /(®) ограничена
на элементе Bq Е В. Тогда существуют числа ао,а0 Е R та-
кие, что ао = sup inf f(x), а0 = inf sup/(®), причем
всвОувевхеВ
—оо < ао < а0 < 4-оо.
Доказательство. В силу ограниченности функции /(®) на
элементе Во Е В имеем —оо < inf /(®) < sup f (®) < 4-оо. Рассмотрим
В°	В0
88
следующие множества Ао и А0 из R. Ао = {у G R|j/ = mf f(x),B С
Во, В G В}, А° = {z Е R|z = sup f (ж), В С Во, В G В}. Поскольку
inf/(ж) € Ао и sup f(x) Е А0, то Ао ^4 0, А0 0. Кроме того, в силу
Во	Во
теоремы, доказанной выше, имеем —оо < inf f (х) < sup f(x) < 4-оо
Bi	в2
VBi С В, Bi С Bq (i = 1,2), откуда
(Уу€Ао)л№еАо)=*(у<г),	(9.1)
т. е. непустое числовое множество Ао ограничено сверху, а непус-
тое множество А0 ограничено снизу в R. В силу полноты R Зао =
supAo Е R и За0 = inf А0 Е R, причем из неравенства (9.1) вы-
текает: 1) любое z Е А0 есть верхняя грань для множества Ао, т. е.
«о = sup Aq < z Vz е А0. Но тогда имеем: 2) ао есть нижняя грань для
множества А0, и поэтому (ао < а0 = inf А0) => (—оо < ао < а0 < +оо).
Замечание. Числа а° = inf sup f(x) = Ит/(ж) и ао =
ВСВо>ВбВд.^д	В
sup inf f(x) = lim f(x) называются соответственно верхним и
BCBo,B€B*GB	в
нижним пределами функции f(x) по базису фильтра В.
Доказать самим эквивалентность определений а) и б), где
а)	а0 = lim ап (старое) и
п->+оо
б)	а0 = lim ап = inf sup .
n->+oo VmeNVn>m
Теорема (критерий Коши существования предела числовой
функции по базису фильтра). Пусть числовая функция f(x) опре-
делена на множестве М и В - базис фильтра на множестве М.
Тогда (Slim/(ж) = А) (Vs > 03 элемент B(s) Е В такой, что
- /(®г)| < е Ух!,х2 G В(е)).
Доказательство. Необходимость. Пусть 3limf(x) = А,
тогда в силу определения предела числовой функции по базису фильт-
ра В видим, что Vs > 0 3Bi Е В такой, что |/(®<) — А| < е/2
Ух, 6 Bi (» = 1,2), т. е. - У(х2)| = |(/(xi) - А) + (А - /(х2)| <
- А| + |/(х2) - А| < £ V®i,a;2 G В2.
Достаточность. Пусть выполнены условия критерия Коши, тогда
для е0 = 1 > 0 ЗВо Е В такой, что |/(ж) — /(жо)| < 1 Уж,жо G Во
=> 1/(ж)I < 1/(ж0)| + 1 = С Уж Е Во, т. е. /(ж) ограничена на эле-
менте Во Е В (и, в частности, /(ж) локально ограничена по ба-
зе В). Но тогда по предыдущей Теореме За0 = inf sup/(ж),
ВСВо,В€В х^В
ао = sup inf f(x), причем —оо < <ю < а0 < +оо и, в частности,
всв0,вев®ев
89
УВ C Bq, В € В имеем
—оо < inf /(х) < ао < а0 < eup/(x) < +оо.	(9.2)
•В	в
Докажем сначала, что ао = а0. В самом деле, в силу условия Коши
Vf > О 3Bi е В такое, что
|/(®1) —/(®г)| <eV®i,x2 GBj.	(9.3)
Но в силу свойства (9.2) базы В ЗВ2 € В такое, что В2 С Bi Г) Во,
используя лемму и (9.3), имеем
е> sup |/(хх) -/(х2)| = sup/(x)-inff(x). (9.4)
Но тогда из (9.2) получаем оценки 0 < а0 — ао < sup f(x) - inf f(x) <
Въ	в*
бив силу произвольности е > 0 имеем ао = а0 = А, причем из
(9.2) следует оценка inf/(®) < А < sup/(®). Кроме того, очевидно,
В3	в3
inf f(t) < f(x) < sup/(t) V® € B2, т. е. V® Е В2 => |/(®) - А| <
в3	в3
sup/(t) —inf f(t) = sup |/(®i) — /(®з)|. Но в силу выбора (по е > 0)
Вз	*з	®1,®з€В2
элемента В2 € В из (9.4) имеем |/(®) — А| < е V® Е В2, но это и
означает, что А = lim/(®).
Пусть теперь во множестве L заданы два базиса фильтра В = {В}
и D = {D}.
Определение. Базисы фильтра В и D во множестве L на-
зываются эквивалентными, если: 1) VB € В 3Do Е D такой, что
2>о С В, и 2) VD € D ЗВо Е В такой, что Bq С D.
Замечание. Если базисы фильтра В = {В} и D = {©}, за-
данные во множестве £, эквивалентны, то VB Е В и VD Е D 3Si Е В
и Е D такие, что Bi С В П D, С В А D.
Доказательство. Пусть В Е В и D Е D. Поскольку базы
В и D эквивалентны, то ЗВо € В такое, что Во С Я и 3D0 6 D такое,
что 1>о С В. Но тогда имеем BAD D В АВо и BAD D D ADo- В силу
свойства 2) базы 3Bi Е В такое, что Bi С В АВо С В AD, и 3Di Е D
такое, что Di С Р С В DD, что и требовалось доказать.
Замечание. Класс эквивалентных баз В во множестве L на-
зывается фильтром в L.
Примеры. Пусть ®о € L С R. Тогда следующие базисы фильтра
во множестве L эквивалентны: 1) А = {А}, где А = [а,/3] AL У(а,/3) Э
®о; 2) В = {Bj}, где В$ = Дд(®о) A L, Д$(®о) = [®о — ®о + £] Vrf > 0;
3) D = {£}, где D = Е7(®о) П L VC7(®0) = (а,/3) Э ®0.
Докажем, например, эквивалентность баз АиВ (эквивалентность
баз А и D доказать самостоятельно). В самом деле, VA Е А имеем
90
A = [a, /3] П L D (a, /3) Л X, где a < xo < /3, но тогда 3<5o > 0 такое, что
а < ®о ~ *о < ®о < ®о + <5о < Д Bt0 = Д^о (х0) Л L С [се, /3] Л L = А.
Итак, УА € A 3Bj0 G В такое, что В/о С А. С другой стороны,
Уб > 0 из хо - 6 < ®о < ®о + 6 вытекает существование его» А) таких,
что 0 < хо - ао < 0 < А) - ®о < ®о - £ < «о < ®о < А) < ®о 4-
А = [ао, А)] Л L С В{, т. е. У Вл G В ЗАо € А такое, что Ао С Bt, что
и завершает доказательство эквивалентности баз А и В.
Теорема. Пусть числовая функция /(х) определена на мно-
жестве L и базисы фильтра В u D (во множестве L) эквивалент-
ны. Тогда (31im/(x) = А) (31im/(x) = А).
Доказательство. Пусть 31im/(x) = А. Тогда Уе > О
ЭВо(е) € В такой, что |/(х) - А| < е Ух € Во(е).
Но база D эквивалентна базе В, поэтому 31>о € D такой, что Фо С
В0(е), откуда
|/(х)-А| <еУх€Ф0СВо(е),
т. е. 31im/(x) = А. Итак, доказано включение (31im/(x) = А) =>
(31im/(x) = A).
Обратное утверждение доказывается аналогично.
Следствие. Пусть числовая функция / (х) определена на мно-
жестве L и базы В и D (во множестве L) эквивалентны. Тогда условия
критерия Коши существования предела /(х) по базам В и D выпол-
няются одновременно.
Теорема. Пусть числовая функция f(x) определена на мно-
жестве L и базы А и В (во множестве L) эквивалентны. Если /(х)
локально ограничена по базе А, то она локально ограничена и по
базе В, причем ЭЛ/, m G R такие, что
М = inf sup /(х) = inf sup f(x);
m = sup inf f(x) = sup inf /(x),
aca»6* b6b«6B '
причем -oo < m < M < 4-oo.
Доказательство. Пусть числовая функция /(х) локально
ограничена по базе А, тогда существуют постоянная С > 0 и элемент
Ао G А такие, что |/(х)| < С Ух G Ао, и, в частности, УА 6 А такого,
что А с Ао, имеем
-оо < sup /(х) < sup /(х) < +оо.
х£А	x^Aq
Но база В эквивалентна базе А, и поэтому ЗВо € В такой, что
Во С Ао, и тогда |/(х)| < С Ух € Во С Ао, т. е. функция f(x) локаль-
но ограничена по базе В, причем УВ € В такого, что В С Во, имеем
91
неравенства sup f(x) < sup/(ж) < sup/(ж) < +oo. В силу ранее дока-
В	Bq	Aq
занной теоремы о существовании предела функции
За0 = inf sup f(x) Е R,
ACA0,A€Ax6A
36° = inf sup f(x) e R.
Рассмотрим теперь любые A C Aq и В С Во такие, что А Е А
и В 6 В. Поскольку базы АиВ эквивалентны, то в силу замечания
к определению эквивалентных баз ЗА1 6 А и 3Bi 6 В такие, что
AiCAClBcBC Во; Bi С А П В С А С Ао, откуда имеем
sup f(x) < sup f(x) < sup f(x) (VB C Bo),	(9.5)
rgAi	AnB .	x£B
sup f(x) < sup f(x) < sup f(x) (VA C Ao).	(9.6)
xEBi	АГ\В	x€A
a° < b° 1
Но из (9.5) и из (9.6) =>	~ ^o > => a0 = 5° = Af 6 R. В самом
деле, поскольку VB С Во 3Ai Е А такое, что sup/(ж) < sup/(ж), то
Ai	В
a0 = inf sup/(ж), а0 < sup/(ж), так что а0 < sup/(ж) VB С Во, и
АСАо A	Ai	В
поэтому а0 - нижняя грань чисел sup/(ж).
в
Тогда а0 < Ь°, поскольку 5° - точная нижняя грань (т. е. наиболь-
шая из всех нижних граней).
Заметим, что число М 6 R на самом деле не зависит от выбора
элементов Ао и Bq. Аналогично доказывается, что существует т =
ао = bo Е R, при этом всегда имеем —оо < т < М < +оо.
Следствие. Если базы А и В (во множестве L) эквивалентны
и функция /(ж) локально ограничена по этим базам, то
Пт f(x) = lim f(x),
lim /(ж) = lim /(ж).
А	В
Глава 4
НЕПРЕРЫВНЫЕ ФУНКЦИИ
§ 1. Непрерывность функции в топке.
Точки разрыва функции
Будем рассматривать функцию /(х), определенную на множестве
М С R. Введем понятие непрерывности функции в точке хо 6 М. Уже
этим понятие непрерывности функции в точке отличается от понятия
предела функции в точке, поскольку предел lim f(x) определялся для
X—
а Е Mf, причем точка а могла и не принадлежать множеству М.
Определение (окрестностное определение непрерывности
функции в точке). Пусть функция f(x) определена на множестве М.
Функция f(x) называется непрерывной в точке xq Е М, если для лю-
бой окрестности V(/(xo)) существует окрестность U(xq) такая,
что f(x) Е V(/(®o)) Ух Е U(xq) О М. Запись: f Е С(хо).
Определение ((б,5)-определение (по Коши) непрерывнос-
ти функции в точке). Пусть функция f(x) определена на множестве
М С R. Функция f(x) называется непрерывной в точке хо € М, если
Уб > 0 3(5 > О такое, что \/х Е М, удовлетворяющего неравенству
(|® - ®о| < <5) => (|/(ав) - /(хо)I < е).
Замечание. Для того чтобы функция /(х) была непрерывна
в точке хо Е М (f Е С(хо)), необходимо, чтобы функция /(х) была
определена в точке х0, т. е. должно существовать /(х0).
Определение. Пусть функция /(х) определена на множес-
тве М и хо 6 М. Функция /(х) называется непрерывной в точке
х0 Е М, если Уб > 0 существует окрестность U(xq) такая, что
|/(х) - Д®о)| < е Ух Е Щх0) О М.
3 а м е ч а н и е. Из определения непрерывности функции f(x) (за-
данной на множестве М) в точке х0 Е М следует, что lim/(x) =
f(x0), где в качестве базы В в М рассмотрена система множеств
В = U(xo)f} М (подчеркнем, что U(xq) полная, а не проколотая окрест-
ность точки хо Е М). Итак, имеем (f Е С(хо)) <=> (31imf(x) = f(x0)).
Определение. Пусть функция f(x) определена на множес-
тве М С R и хо Е М. Если функция /(х) не является непрерывной в
точке xq, то говорят, что функция f(x) разрывна в точке xq Е М.
Замечание. Функция /(х), определенная на множестве М, не-
прерывна в любой изолированной точке xq Е М. В самом деле, если
6 М - изолированная точка области определения М функции /(х),
то существует С7(х0) такая, что U(xo)0 М = {хо}. Но тогда Уб > О
93
ЗСЛ1)(®0) С U(xq) такая, что ® = ®0 V® € U^(xq) П Af, я поэтому
для «тех же» х имеем |/(®) - /(®о)| = |/(®о) - У(®о)| = 0 < е, т. е.
/ € 0(®о). В частности, тогда 31im/(®) = /(®о), где В = {В} - база
во множестве М с элементами В = 1/(®о) Л М VU(xd).
Замечание. Область определения М функции /(®) можно
представить в виде М = Me О Мр, где Мс - множество всех то-
чек из М, где функция /(®) непрерывна, а М-р - множество всех то-
чек разрыва функции /(®). Очевидно, Мр С М' П М, т. е. точками
разрыва функции /(®) могут быть только предельные точки области
определения М (принадлежащие М).
Теорема. Пусть функция f(x) определена на множестве М и
®о € М Г\М'. Тогда (/ € С(®о)) <$=> (Э ^lim /(®) = /(®о))-
Доказательство. Необходимость. Пусть ®о € М П М' и
f € С(®0). Тогда существуют /(®о) и lim/(®) = /(®о), где В = {В} -
база в М с элементами В = U(xq) Л М VC7(®o). Поскольку ®о € М', то
Й(®о) Л М 0 и U(xq) Г) М С U(xq) Л М = В, но тогда 31im/(®) =
В
/(®о), т. е. Ve > О существует элемент Bi = U^(xo) Л АГ базы В
такой, что |/(®) - /(®о)| < е V® € U^(xq) Л М С Bi = tMl>(®o) Л М,
откуда и следует, что существует lim /(®) = /(®о).
Достаточность. Пусть ®о € М Л М' и 3 lim /(®) = /(®о)- Тогда
V? > 0 существует проколотая окрестность 17(®о) такая, что
|/(®) —/(®о)| < eV® € П(®о) Л М.
Но для® = ®о € М также имеем |/(®)-/(®о)| = |/(®о)—/(®о)| = 0 < е.
Таким образом, Ve > 0 существует полная окрестность 17(®о) такая,
что
(|/(®) - /(®о)| < eV® 6 В = П(®о) Л М) =► (3lim/(®) = /(®0)),
В
Т. е. f € С(®о).
Проведем классификацию точек разрыва ®о € М Л М' функции
/(«), определенной на множестве М С R. Вели ®о € Мр С М Л М', то
возможны случаи: 1) ®о € М Г\М', 3^1пп /(®), но *Нт /(®)	/(®о)-
В этом случае точка ®о € М называется точкой устранимого разрыва
функции /(®); 2) ®о € М Л М’ и не существует lim /(®).
Определение. Пусть функция f(x) определена на множес-
тве М и ®о € М Л М' есть тонка разрыва функции f(x). Если ко-
нечные односторонние пределы /(®о - 0) = lim /(®) и f(xo + 0) =
lim /(х) существуют, то говорят, что функция /(®) имеет в
94
точке xq Е М разрыв 1-го рода. В противном случае точка ®о € М
называется точкой разрыва (функции fix)) 2-го рода.
_	т/ \ Г ® Ф 0,® € (—оо, +оо),
Пример, fix) = < «	_ а	Очевидно,
I 1, х — и»
lim f(x) = 0^1 = /(0), так что точка ®о = О есть точка устра-
$р—>0
нимого разрыва функции f{x). Если переопределить функцию f(x) в
точке ®о = 0, рассмотрев функцию
\ Г /(®)< ® Ф О, X 6 ( —00, +00),	.	и/ \ в
F(x) = < л _а '	то функция Г(х) будет непре-
1 и, X —• и,
рывной в точке ®о = О-
Пример.
Для функции sgn х =	0, х = О,
рыва, при этом 3 lim sgn х = 1 ф — 1
20 = 0 есть точка разрыва 1-го рода.
точка ®о = 0 есть точка раз-
= lim sgn х, поэтому точка
/(®) = (
Пример.
1, х - рационально,
О, х — иррационально.
Тогда V® € (—оо, +оо) не существует односторонних пределов /(®о—0)
и /(®о + 0), т. е. любая ®о € (-оо, +оо) есть точка разрыва 2-го рода
функции f(x). В самом деле, воспользуемся критерием Коши сущест-
вования lim f(x) и заметим, что множество всех рациональных
чисел Q плотно в R. Кроме того, множество всех иррациональных
чисел R \ Q также плотно в R (в R плотно, например, такое множе-
ство Р = {г € R \ Q|r = q + у2/п Vq € Q, Vn G N}). Тогда 6 > 0
=€ Q и 3ri E R\ Q такие, что qi, rj. € (®o,®o + <f), и поэтому
l/(?i) ~ /(ri)l = 1 > 0, т. e. не выполнены условия критерия Коши
для существования /(®о+0). Аналогично доказывается, что не может
существовать /(®о — 0).
Пример. f(x) = ( о’ д е R \ Q Тогда Ve > 0 3<5 = е > О
такое, что |/(®) -/(0)| < |®| < 6 = е V® 6 U/(0), т. е. f € С(0). Однако
любая точка ®о Ф 0 является точкой разрыва 2-го рода функции /(®).
В самом деле, пусть ®о > 0, тогда V®o > 26 > 0 3ri € R \ Q и Bqi € Q;
ri,9i € (®о-^®о), для которых |/(ri)-/(«i)| = qi > хо-6 > ®о/2 > О,
т. е. опять условия критерия Коши не выполнены и поэтому не может
существовать /(®о — 0). Аналогично показывается, что и /(®о + 0) при
®о 0 не существует.
Введем теперь полезное для дальнейшего понятия колебания функ-
ции на отрезке и в точке. Пусть числовая функция /(®) определе-
на на множестве L С R и локально ограничена в точке «о € L
так, что существуют постоянная С > 0 и окрестность ЭДо(®о) та-
95
кие, что |/(®)| < С V® 6 Ug0 (®о) П£. Будем рассматривать отрезки
[а,/?] С Uio(xo) и такие, что хо € (<*,0) П L. Положим
Af(/; [«,$) =	sup	f(x),
m(f-,[a,0\)=	inf	f(x).
r€[a,/3]nL
Определение. Колебанием функции f(x) на отрезке [а,/3]
называется величина o>(f; [а,/3]) = Af (/; [а,/?])—m(/; [а,/?]). Заметим,
что в силу леммы из § 9 гл. 3 имеем
<*>(/; [<*,$) = sup |/(®i) - /(®2)|.
аг1,х2€[а,/3]п£
Замечание. V(a/,/?') С (at, /?), xq 6 (а',/?') имеют место оцен-
ки
-оо < m(/; [а,/3]) < m(f; [а',/3']) < M(f; [а',/3']) <
< Af (/; [а, /3]) < +оо;
О < ^(/; [<Л(3‘]) <	[а,0]) < +оо.
Положим М(6) = Af(/; Д$(®о))> тгь(6) = m(f; Aj(®0))? Д$(®о) =
[®о — <J, ®о 4- <J] V<5 6 (0, <Jo). Тогда VO<<J1<<J2< <Jo имеем —оо < —С <
m(<J2) < m(<Ji) < Af (<Ji) < Af(<J2) < C < +00, т. e. функция M(<J) f на
(0, <Jo) и ограничена как сверху, так и снизу, а функция m(<J) | на (0, <Jo)
и ограничена как снизу, так и сверху. В силу критерия существования
предела у монотонных функции имеем 3 lim Af (<J) = inf Af(<J) =
6—>+O	O<4<£o
Af(/;«o); 3 lim m(<J) = sup m(<J) = m(/;®o)*
Очевидно, при этом имеют место оценки (V<J G (0, <Jo)) —00 <
m(f; Aj(®0)) < m(/;®0) < Af(/;®0) < Af(/; Д^(®0)) < 4-oo.
Определение. Если функция f(x) определена на множестве
L и локально ограничена в точке xq 6 L, то величина w(f;«o) =
М(/;®о) ~	называется колебанием функции f(x) в точке
Xq 6 L.
Замечание. Очевидно, w(/;®o) = ^limow(/;Д4(®°)), причем
V<J 6 (0, <Jo) имеем 0 < о>(/, ®0) < ^(/; Д^(®0)) < +оо.
Введем во множестве L два. эквивалентных базиса фильтра В =
{В} и А = {А}, где Вл = Д^(®о) О L V<J G (0,<Jo) и А = [а,(3] П L
V[a,/3] С Us0(xq) и таких, что [а,/3] D (а,/3) Э ®о-_
Тогда имеем M(J,xq) = inf sup f(x) = lim/(ж), m(/;®o) =
0<J<£0 x^B6	В
sup inf f(x) = lim f(x). Поскольку базы В и А эквивалентны, то
о<л<$охеВ«	в
из последней теоремы § 9 гл. 3 имеем
М(f-, Хо) = Пт f(x) = inf sup f(x) d= Йт f(x),
A	[*>/4Ct^o(®°)*6[<»,le]nL	»->0
96
тп(/;хо) = lim f(x) = sup inf f(x) d= lim /(x),
V л Мс^о(*о)же1“-Яп1
w(/;«o)=f lim f(x) - lim f(x).
#~>#0	X-*XQ
Замечание. Традиционное обозначение x -> xq здесь неудач-
но, поскольку рассматривается не база {17(®о)ПL}, а база {U(®0)nL},
эквивалентная АиВ. Отметим, что У[а, /3] С U&0(xq) при «о Е (а,/3)
имеем
-оо < m(/; [а,/?]) < пг(/;а:о) < M(f;x0) < M(f-, [а,/3]) < +оо;
О < ы(/; х0) < w(/; [<*,/?]) < +оо.
Теорема (критерий непрерывности Бэра). Пусть функция
f(x) определена на множестве М, xq Е М и f(x) локально огра-
ничена в точке xq. Тогда (f Е С(ж))	(о>(/; жо) = 0)).
Доказательство. Необходимость. Пусть f Е C(xq). Если
xq Е М - изолированная точка множества Af, то, очевидно, М(f; xq) =
m(f; ®о) = /(®о) => ^(/; ®о) = 0. Если xq Е М П Af', то f Е С(жо) =>
3 lim f(x) = /(®о), и поэтому функция f(x) локально ограничена
в точке ®о € Af, причем Ve > 0 36i > 0 такое, что V<J 6 (0, <5i) и
Уж Е A$($o)ClAf С Us1(xQ)r\M => |/(ж) — /(®о)| < £, но тогда V®i,®2 G
Д$(ж0)ПА/ имеем |/(ж1) ~/(ж2)| < |/(®1)-/(®о)| + |/(ж0)-/(ж2)| < 2е
т. е.
w(/; Aj(®0)) = sup |/(®i) - /(ж2)| < 2е,
2 6 Дз(хо)пл/
а потому Ve > 0 и V<5 Е (0, <5i (е)) получаем оценки
0 < о>(/; ж0) < w(/; Aj(®o)) < 2е.
В силу произвольности е > 0 имеем o>(f; жо) = 0.
Достаточность. Пусть f(x) локально ограничена в точке xq Е Af
и w(/;®o) = 0. Поскольку о>(/;®о) =	Д^(жо)), то Ve > 0
3J > 0 такое, что 0 < w(/; Aj(®o)) < е, но тогда \f(x) — /(жо)| <
Уж 6 Us(xq) О Af С Д^(жо) П Af, т. е. / G С^жо)-
Пусть функция f(x) определена и монотонна на интервале (а, Ъ) и
xq Е (а, Ь). Тогда, как было доказано, 3 Jim±o/(x) = /(жо±0), причем
/(®о-0) < /(жо) < /(®о+0), если f(x) f на (а, Ь), и /(жо —0) > /(®о) >
/о(®о + 0), если f(x) 4, на (а, Ь). Пусть /(ж) 4, на (а, Ь), тогда УД^(жо) С
(а, Ь) при ж© Е (а, Ь) имеем а>(/; Д^(хо)) = /(жо+£)”/(жо—<5), и поэтому
w(/; я0) =	Aj(®o)) = /(жо + 0) — /(жо — 0). Аналогично если
/(ж) 4, на (а, Ъ) и ж0 G (а, Ь), то а>(/; ®0) = /(®о — 0) - /(xq 4- 0).
4 Зак. 86(»
97
Замечание. Монотонная на интервале (а,Ь) функция может
иметь разрывы только 1-го рода.
Замечание. Если функция f(x) монотонна на интервале (а, Ъ)
и хо € (а,Ь), то (ш(/; х0) = 0) 4* (/(х0 - 0) = /(х0 + 0) = /(х0)).
Из этого замечания в силу критерия непрерывности Бэра имеем:
Теорема (критерий непрерывности монотонной функции).
Пусть функция f(x) монотонна на (а,Ъ) и хо € (а, Ь). Тогда (f €
С(хо)) (/(®о — 0) = /(хо + 0) = /(хо)). В самом деле, в си-
лу критерия непрерывности функции в точке имеем f € С(х)
(3 lim /(х) = /(хо)) О (3 lim /(х) = /(х©))	w(/;x0) = 0 для
®-+®о±О
монотонной функции.
Теорема (о мощности множества точек разрыва монотонной
функции). Пусть функция f(x) монотонна на интервале (а, Ь). Тогда
множество точек интервала (а, Ь), в которых функция /(х) разрыв-
на, не более чем счетно.
Доказательство. Пусть, для определенности, /(х) f на
(а, Ь) и Мр С (а, Ъ) - множество точек разрыва функции /(х). Тог-
да /(х - 0) < /( + 0) Vx € Мр. Любой точке х € Мр поставим в
соответствие рациональное число q(x) € Q такое, что /(х - 0) <
д(х) < /(х + 0). Это возможно, поскольку множество Q плотно в R.
Пусть xi,X2 € М-р, Xi Х2. Для определенности, пусть Xi < хз, тог-
да /(хХ - 0) < «(xi) < /(xi + 0) < /(х2 - 0) < в(х2) < /(х2 + 0),
т. е. (xi х2)	(з(®1) / ifa)). Тем самым установлена биекция
х -> q(x) между множеством Мр и подмножеством множества рацио-
нальных чисел Q, которое не более чем счетно. Итак, множество Мр
не более чем счетно.
§ 2.	Локальные свойства функций, непрерывных
в точке
Теорема (о сохранении знака). Пусть функция f(x) опреде-
лена на множестве М и хо 6 М. Пусть f G С(хо) и /(хо) > 0 (или
/(хо) < 0/ Тогда существуют постоянная с > 0 и окрестность
СГ(хо) такие, что /(х) > с > 0 Vx € £7(хо) П М (соответственно
f(x) < -с < 0 Vx € U(xq) Г) М).
Доказательство. Пусть хо € М, /(хо) > 0 и f € С(хо).
Тогда 31шх/(х) = /(хо), где В = {В} - базис фильтра в М с элемен-
тами В = С/’(хо)Г)ЛГ VI7(xo). Но тогда Vc > 0 такой, что 0 < с < /(хо),
видим, что для ео = /(®о) - с > 0 существует окрестность U(xq)
такая, что |/(х) - /(хо)| < ео Ух € Щхо) И М = В € В, т. е.
/(х) > /(хо) - ео = с > 0 Vx € U(xq) П М.
Теорема (о локальной ограниченности функции, непрерывной
в точке). Пусть функция /(х) определена на множестве М, хо € М и
98
f € C(®o)- Тогда функция f(x) локально ограничена в точке ®о £ М.
Доказательство. Пусть f Е С(®о), где хо € М, тогда
31imf(®) = /(®о), где В = {В} - база в М с элементами В = U(xq) П
М VU(xo). Тогда для е0 = 1 > 0 317(®о) такая, что |/(®) - /(®о)| < 1
V® Е U(x) Л М = В Е В, т. е. |/(®)| < |/(®о)| + 1 V® £ В, что и
означает локальную ограниченность функции /(®) в точке ®о € М.
Теорема (о непрерывности линейной функции). Пусть f(x) =
ах + b V® Е М С В u ®о € М• Тогда f £ С(®о)>
Доказательство. Докажем, что существует lim/(®) =
ахо + Ъ, где В = {Bj} - база в М с элементами Bj = %(®о) Г1 М
VS > 0. В самом деле, Ve > 0 3<J = f/(|a| + 1) > 0 такое, что
|/(®)-/(®о)| = |а(®-®о)| < |а| <5 < е V® $ С7а(®0) DAf = Bj Е В, т. е.
f £ С(®о).
Теорема (о непрерывности суммы непрерывных функций).
Пусть функции fi(x) (i = 1,2,... ,п) определены на множестве М,
®о 6 ЛГ, /,• € С(®о) (» = 1,2,..., n) и A, (t = 1,2,... , п) - постоянные.
Тогда £ А,/,(®) Е С(®о), где (£ А./Д (®) = £ А,/,(®) V® £ М.
i=i	\1=1	/	i=i
Доказательство. Поскольку fi £ С(®о) (t = 1,2,..., п),
то 31im/,(®) = /,(®о) (г = 1,2,... ,п), где В = {В} - база в М с
элементами В = U(xq) П М VC7(®o). В силу теоремы о пределе суммы
(по базе) имеем
п	п	п
31imJ2А,/,(®) = 52 Wi(®o), т.е.52А,Л € С(®0).
“ <=1	t=l	4=1
Теорема (о непрерывности произведения непрерывных функ-
ций). Пусть функции Д(®) и f2(x) определены на множестве М,
®о € М и fi Е С(®о)'(* = 1,2). Тогда fi- fi Е C(xq), где (Л • /2)(®) =
fi(x)f2(x) \fx £ М.
Доказательство. Поскольку /, Е С(®о) (i = 1,2), то
31im/,(®) = /<(®о) (» = 1,2), где В - база в М с элементами
В = U(xq) П М V17(®o)- Но тогда в силу теоремы о пределе произ-
ведения (по базе), доказательство которой проводится по схеме § 4
ГЛ. 3, имеем
ЭНт(/1(®) • /2(®)) = lim/i(®) • lim/2(®) =
В	в	в
= Л(®о) • Л(®о) => fi • fi е С(х0).
Пример. Функция /(®) = ®n, ® Е (-оо, +оо), непрерывна V®
п
и Vn G N. Более того, многочлен ?»(«) = Е akXn"k непрерывен в
fc=o
любой точке х Е (-оо, +оо).	*
4*
99
Лемма. Пусть функция f(x) определена на множестве М, ®0 6
М и f Е С(®о), причем /(®о) / 0- Тогда у Е С(®о).
Доказательство. Пусть хо 6 М А М' и /(®о) / 0, тогда
по теореме о знаке существуют с > 0 и окрестность U(®о) такие, что
\f(x)\ > с > О V® Е U(®o) п М => 1/|/(®)| < 1/с V® Е U(xQ) А М. Но
тогда, применяя теорему о пределе дроби, имеем
3 lim l//(®) = l/f(®o) => 1/f e С(ж0).
X—
Если хо Е М - изолированная точка М, утверждение леммы оче-
видно.
Пример. Функция /: х -> 1/®, х Е (—оо, 4-оо), х / 0, непре-
рывна в любой точке ®о 0.
Теорема (о непрерывности частного двух непрерывных функ-
ций). Пусть функции f(x) и д(х) определены на множестве М,
хо Е М и f,g Е С(®о), причем д(хо) / 0. Тогда - Е С(®о) (дока-
зать самостоятельно).
Лемма. Пусть функция f(x) определена на множестве М и
f Е С(®о), где xq Е М. Пусть ап Е М Vn Е N и 3 lim ап = ®о.
Тогда 3 lim f(an) = f(®o).
п—>+оо
Доказательство. Поскольку f Е С(хо), то Vs > О 35(e) >
О такое, что |/(®) - /(®о)| < s V® Е Uj(g\(x) А М. Но lim ап = ®о
v '	п->+оо
(an € MVn € N), и тогда для <5(е) > 0 31Vo 6 N такое, что (ап 6
Ui{t](x0) С\М Vn > No) |/(а„) - /(®о)| < е. Итак, Ve > О ЗЛГ0 6 N
такое, что |/(ап) - Л®о)| < Е Vn > No, т. е. 3 lim /(an) = f(x0).
п->+оо
Теорема (о непрерывности композиции двух непрерывных
функций). Пусть функция f(x) определена на множестве М, xqEM
и f Е С(®о). Пусть функция д(у) определена на множестве L таком,
что L D f(M) ug Е С(уо), где уо = /(®о)- Тогда go f Е С(®0).
Доказательство. Поскольку д Е C(j/o), то Vs > 0 35(e). >
О такое, что |^(t/) - д(у0)| < е Чу Е Vi(e)(t/o) A L. Далее, поскольку
f Е С(®о), то для выбранного (по е > 0) (5(г) Зг)(е) > 0 такое, что
|/(х) - /(хо)| < 5(e) V® Е f^(e)(®o) A Af, откуда, полагая у = /(®) Е
/(Af) С L, уо G /(®о) G L, имеем \у - j/0| < J(s) => у Е V^(yQ) A L.
Но в силу выбора <5(г) > 0 имеем \д(у) — д(уо)| < £ или (полагая
-P’(aj) = V® 6 М) |д[/(®)] - д[Дх0)]| = |F(x) - F(x0)| < е.
Итак, Vs > 0 3r?(s) > 0 такое, что |F(®)~F(®o)| < sV® Е t^(e)(®o)A
Af, т. e. F = g о f E C(®o).
100
§ 3.	Глобальные свойства числовых непрерывных
функций
Определение. Пусть X С (—оо, +оо) и М С X, Функция
f(x), определенная на множестве X, называется непрерывной на
подмножестве М множества X (М С X), если она непрерывна в
каждой точке множества М. Запись: f Е С(М).
Таким образом, f Е C(Af), если при любом xq Е М Ve > 0 3(5 > О
такое, что |/(®) — /(®о)| < е V® Е 1^(®о) АХ. При этом 5 = (5(®о,г),
т. е. выбор <5 > 0 зависит как от точки ®о 6 М, так и от е > 0.
Замечание. При М = X получаем определение функции,
непрерывной на множестве X - ее области существования. Пусть
/:Х—>RnAfCX. Рассмотрим /м : М R - сужение функции
/(®) (определенной на множестве X) на подмножество М С X.
Теорема (о непрерывности сужения непрерывной функции).
Пусть функция /(®) определена на множестве X и /м(%) ~ ее суже-
ние на подмножество М С X. Тогда f Е С(Х) => /м Е С(М).
Доказательство. Поскольку f Е С(Х) и М С X, то име-
ем, что V®o Е М и Ve > 0 3(5(®о, е) > 0 такое, что
(\f(x) - /(®0)| < eVx Е Uj(®0) А М С U*(x0) П X) =>
=> (|Ли(®) - /м(яо)| < eV® Е	А М)),
откуда /м Е С(ЛГ).
Замечание. Из того, что /м Е С(М) (при М С X), во-
обще говоря, не следует, что f Е С(Х) (и даже не следует, что
f Е С(М)). Например, при X = R, Af = Q С R рассмотрим функ-
цию /(®) =
1,® Е Q,
0,®ER\Q.
Тогда функция f (®) разрывна в любой
точке ®0 Е (—оо, +оо), хотя ее сужение на Q, т. е. fq(x) = 1 V® Е Q
непрерывна на Q.
Определение. Множество М С R называется (линейно)
связным, если (V®i, ®2 Е Af, ®i < ®г) => ([®i, ®г] С М).
Следующая теорема устанавливает структуру связных множеств
на числовой прямой.
Теорема. Любое связное множество числовой прямой явля-
ется либо отрезком, либо интервалом, либо полуинтервалом: [а, Ь];
(а, 6), [а, Ъ), (а, Ь], (—оо, Ъ), (а, +оо), [а, +оо)? (—оо, Ь], (—оо, +оо).
Доказательство. Пусть множество М С R связно. Поло-
жим а = inf М и b = sup М (заметим, что а = — оо, если множество М
не ограничено снизу в R, и Ъ = +оо, если множество М не ограничено
сверху в R).
Рассмотрим случаи: 1) —оо < а < b < +оо. Тогда если а Е М
и Ь Е М, то в силу определения (линейной связности) множества М
101
[а, Ь] С М. Далее, поскольку а = inf М и b = sup М, то не существует
точек ®i, Х2 G М таких, что xi < а и Х2 > Ь, т. е. [a, Ь] D ‘ЛГ, откуда и
вытекает равенство М = [а, Ь]. Далее, если a Е М, но Ъ^М, то, в силу
определения b = supAf, V®o 6 R, такого, что а < xq < b, G М,
для которого имеем ®о < ®1 < Ь. Но в силу связности множества М :
[a, ®i] С М, и поэтому «о 6 М, т. е. М = {® € R|a < х < Ь} = [а, Ь).
Аналогично если aGM, но Ъ € М, то М = (а, Ь], и, наконец, если
а ЕМ и ЪеМ, то М = (а, Ь).
2)	-оо < а < Ь = +оо. Тогда М = [а, 4-оо) при a G М и М =
(а, 4-оо) при аЕМ.
3)	-оо = а < Ъ < 4-оо. Тогда М = (-оо, Ъ] при b G М и М =
(—оо, Ъ) при bGAf.
4)	-оо = а < b = 4-оо. Тогда М = (-оо, 4-ос).
Теорема (о нуле непрерывной функции). Пусть f € C([a, fr])
u /(a) • f(b) < 0. Тогда существует c G (a, b) такая, что f(c) = 0.
Доказательство, основанное на принципе полноты R
Кантора. Пусть До = [а, Ь], f € С(До) и, для определенности, /(а) > О
и/(<>) < 0. Доказательство проведем методом «деления пополам». Раз-
делим отрезок До пополам и обозначим середину отрезка До через Со-
Возможны три случая: 1) /(со) = 0, и тогда теорема доказана при
с = со € (а, Ь); 2) /(со) > 0 или 3) /(со) < 0. В случаях 2) и 3) выбе-
рем ту из половин До (обозначив ее через Д1 = [ai,bi]), для которой
/(ai) > 0 и f(bi) < 0. Тогда
До Э Д1 = [ai, bi], |Ail = (b - a)/2, /(ai) > 0, /(frx) < 0.
Продолжая процесс, делим отрезок Д1 пополам и т. д. Наш процесс
либо оборвется, т. е. для середины c„_i отрезка Дп-1 = [a„_i, bn_i]
будем иметь /(cn-i) = 0 (и тогда теорема доказана при с = cn-i),
либо Vn > О имеем
До D Д1 D ... D Дп-i Э Дп;
|Д„| = (b- а)/2", Дп = [ап,Ьп],
/(a„)>0,/(b„)<0.
Вложенная система отрезков {Дп} (п = 0,1,2,...) является стя-
гивающейся, поскольку ^lim^ |Дп| = lirn^fb - a)/2" = 0. По теореме
Кантора для стягивающейся системы отрезков следует, что сущест-
+00
вует с е До такое, что П Дп = {с}, причем lim an = lim bn = с,
ns=Q	п—>Ц-оо	л—>Ц-оо
an < с < bn Vn > 0. Поскольку / e C([a,b]) и /(an) > 0, f(bn) < 0
Vn € No, то, используя лемму из $ 2 и теорему о предельном переходе
в неравенствах, имеем
f(с) = lim /(an) > 0, f(c) = lim /(bn) < 0, т. е./(с) = О,
102
причем, учитывая неравенства f(a) > 0 и f(b) < О, получаем а < с <
ь.
I —1 х Е [— 1 0)
Пример. Пусть f(x) = | 1 J [о 1] * Функция f(x) не не-
прерывна на отрезке [—1,1], и хотя /(—1) < 0 и /(1) > 0, не сущест-
вует точки с Е (—1,1) такой, что /(с) = 0.
Пример. Пусть f(x) = {	®	3]^* Множество М = [0,1]U
[2,3], являющееся областью определения функции /(®), не связно, f Е
С(М), и хотя /(0) < 0, /(3) > 0, не существует точки с Е М такой,
что /(с) = 0.
Замечание. Если в условиях теоремы о нуле непрерывной
функции заменить отрезок на несвязное множество М С (-оо,+оо),
то теорема перестает быть верной.
п
Следствие. Пусть Pn(®) = S л*®"”*, ао 0 и п нечетно.
к=О
Тогда существует с Е (—оо,+оо) такое, что Рп(с) = 0, т. е. много-
член нечетной степени с действительными коэффициентами имеет по
меньшей мере один действительный корень.
Доказательство. Без ограничения общности можно счи-
тать, что ао = 1, в противном случае нужно рассматривать многочлен
Qn(®) = Рп(®)/«о- Поскольку
Ф.(,Л -	-> -ОО),
о(®п)(® —► +оо),
к=1
то Рп ~ хп(х —> — оо) и Рп ~ хп(х -> +оо). Но при нечетном п
имеем хп < О V® < 0 и хп > О V® > 0. По теореме о знаке для
эквивалентных функций из $ 9 гл. 3 имеем: 1) поскольку Рп ~ хп(х ->
-оо), то 3ci > 0 такое, что Рп(х) < 0 Vx Е (—оо, -ci), и, в частности,
€ (-оо, ci) такое, что Рп(®1) < 0; 2) поскольку Рп ~ ®п(® -> +оо),
то Эс2 > 0 такое, что Рп(®) > О V® € (сз, +оо), и, в частности, 3®з €
(сз,+оо) такое, что Рп(®г) > 0. Итак, 3®i,®2 такие, что ®i < ®2,
Рп € C([®i,®2]), Рп(®1) < 0, Рп(®з) > 0. Тогда по теореме о нуле
непрерывной функции Зс € (®i, ®г) такое, что Рп(с) = 0.
Теорема Больцано (о промежуточных значениях непре-
рывной функции). Пусть функция f(x) определена на отрезке [а, 6],
/ 6 С([а, Ь]) и f(a) f(b) (например, f(a) = А < В = f(b)). Тогда
для любого числа С, находящегося между f(a) и f(b), (А < С < В)
Зс G (а, Ь) такая, что f(c) = С.
Доказательство. Пусть f Е С([а,Ь]), /(а) = А < В =
f(b) и А < С < В (УС). Фиксируя С, рассмотрим вспомогательную
функцию F(x) = f(x) — С. Тогда имеем F Е С([а, Ь]), F(a) = f(a) -
С = А — С < 0, F(b) = f(b) — С = В — С > О, и по теореме о нуле
непрерывной функции Зс Е (а, Ь) такое, что F(c) = 0, т. е. f(c) = С.
103
Теорема (о сохранении связности при непрерывном отобра-
жении). Пусть функция f(x) определена на связном множестве М С
(—оо, +оо). Тогда если f Е С(М)> то множество f(M) связно в R.
Доказательство. Пусть множество М (линейно) связно
в R, / Е С(М) и Y = f(M) С R. Для доказательства (линейной)
связности множества У в R нужно показать, что VA, В Е У таких,
что А < В => [А, В] С У или, что С Е У VC Е (А, В). Но если А < В
и А, В Е У = то существуют a, b Е Af, для которых имеем
/(а) = А и f(b) = В. Пусть для определенности а < Ь (равенство
а = b при А < В невозможно в силу однозначности отображения
f : М У). Тогда в силу связности (линейной) множества М в R
имеем [а, Ъ] С М и по теореме Больцано о промежуточных значениях
непрерывной функции Зс Е (а, b) С М такое, что /(с) = С, Но /(с) Е
f(M) = У, т. е. С Е У. Итак, множество У = f(M) (линейно) связно
в R.
Теорема Вейерштрасса (об ограниченности функции,
непрерывной на отрезке). Пусть /(®) определена на отрезке [а, Ь].
Если f Е ^([а, Ь]), то функция f(x) ограничена на отрезке [а, Ь].
Доказательство. Поскольку f Е С([а,Ь]), то f Е С(®о)
V®o 6 [а, Ь]. Но в силу локальных свойств непрерывной функции f(x)
локально ограничена в точке xq Е [а, 6], т. е. существуют посто-
янная K(xq) > 0 и окрестность 17(®о) такие, что |f(®)| < К(х$)
V® Е U(xq) А [а, Ь]. Заметим, что [а, b] С (J U(x), т. е. система
х£[а,Ь]
интервалов {U(x);x Е [а, &]} есть покрытие отрезка [а, Ъ]. По лем-
ме Бореля - Лебега отрезок [а, Ь] компактен, т. е. существует ко-
нечное подпокрытие отрезка [а, Ь] интервалами из системы {С7(ж)},
п
т. е. В®, Е [а, Ь] (Р= 1,2, ...,п) такие, что [а, Ь] С (J Щх$. Заме-
«=1
тим, что при i = 1,2,... , п каждой окрестности 17(®>) соответствует
в силу построения такая постоянная К(х{) > 0, что |f(®)| < K(xi)
V® Е U(xi) А [а, Ь]. Положим К = max К(®>) > 0, тогда V® Е [а. 6]
,п
3m (1 < m < п) такое, что ® Е U(m), а потому |/(®)| < К(хт) < К.
Итак, |/(®)| < К V® Е [а, Ь], т. е. функция /(®) ограничена на отрезке
[а,Ь].
Замечание. Если в условиях теоремы Вейерштрасса отрезок
[а, Ъ] заменить на интервал (а, Ь), то теорема перестает быть верной.
Пример. Пусть f (®) = 1/®, х Е (0,1), тогда f Е С((0,1)), но
функция /(®) = 1/® не является ограниченной на интервале (0,1).
Замечание. В теореме Вейерштрасса нельзя отказаться и от
условия f Е С([а, 6]). Например, при
1/®, 0 < х < 1,
О, х = О
/(*)=.{
104
функция f(x) не непрерывна на [0,1] и не ограничена на отрезке [0,1].
Теорема Вейерштрасса (о достижении функцией, не-
прерывной на отрезке, своих точных верхней и нижней граней). Пусть
функция f(x) определена на отрезке [а, Ь] и f Е С([а, Ь]). Пусть
М = sup f(x) ит = inf f(x). Тогда существуют ®i,х2 6 [а, Ь] такие,
[а,Ь]
что f(xi) = М, f(x2) = т.
Доказательство. Поскольку f Е C([a,Ь]), то по преды-
дущей теореме Вейерштрасса функция /(ж) ограничена на отрезке
[а, 6], и поэтому точные грани М и т конечны. В силу определения
точной верхней грани М = sup f(x) имеем f(x) < М Vx 6 [а, Ь], но
[а,Ч
Уб > 0 Зжо G [а, Ь] такое, что М — е < /(жо) < М. Поэтому Vn Е N
Е [а, 6] такое, что М — 1/п < /(ап) < М. По теореме Больцано -
Вейерштрасса из ограниченной последовательности (an) можно вы-
делить сходящуюся подпоследовательность (anfc), а < аПк < Ь, k Е N,
так, что существует х± такое, что lim аПк = при этом, оче-
к—>4“ оо
видно, xi Е [а, 6]. Поскольку / Е С([а, 6]), то f Е C(xi), и поэтому
3 lim f(a„k) = но М — 1/nt < /(an*) < М Vfc Е N, переходя
fc->+oo
к пределу в этом неравенстве (при к —> +оо), имеем М < /(®i) < М,
т. е. /(®i) = М, где xi 6 [а, Ь]. Аналогично доказывается, что
Зх2 Е [а, Ь] такая, что f(x2) = т.
Определение. Пусть функция f(x) определена на множес-
тве М. Тогда точка xq Е М называется точкой максимума функ-
ции f(x) на множестве М, если f(x) < /(жо) Уж Е М. Значение
/(жо) называется при этом максимумом функции /(ж) на множестве
М и обозначается /(жо) = max/(ж). Аналогично определяются точка
м
минимума и минимум функции /(ж) на множестве М (min/(ж)).
Следствие. Функция, непрерывная на отрезке, имеет на этом
отрезке максимум и минимум.
3 а м е ч а н и е. В теореме Вейерштрасса (о максимуме и мини-
муме) нельзя (в условиях) заменить отрезок на интервал.
Пример. Пусть /(ж) = 1/ж, ж Е (0,1), тогда f Е С((0,1)), но
ЛГ = sup (1/ж) = -|-оо.
*€(0,1)
Пример. Пусть /(ж) = ж, ж Е (0,1), тогда М = 1 и т = 0, но
не существует точек Ж1, ж2 Е (0,1) таких, что /(жх) = 1, /(ж2) = 0.
Замечание. В теореме Вейерштрасса (о максимуме и мини-
муме) нельзя отказаться и от условия / Е С([а,Ц).
Пример. Пусть /(ж) = < л’ — п < тогДа М — sup /(ж) =
I U, ж — U,	[0Д]
1» но не существует точки жх Е [0,1] такой, что /(жх) = 1.
Теорема (о Д-свойстве (свойстве Дарбу) для непрерывной
105
функции). Непрерывный образ отрезка есть отрезок.
Доказательство. Пусть / € С([а,6]). Тогда по теореме
Вейерштрасса о достижениях максимума и минимума существуют
®i,®2 G [а,Ь] такие, что /(®i) = М, /(xj) = т, где М = вирУ(х),
(в,Ч
т = inf У(х). Отрезок [а, Ь] есть связное множество в Л, и по теореме
[а,Ц
о сохранении связности при непрерывном отображении следует, что
множество /([а, Ь]) (линейно) связно в R. Поэтому из т, М 6 /([а, Ь])
следует, что [m, М] С /([а, 6]), но т < f(x)	[а, Ь], т. е.
[m, АГ] D /([а, Ь]). Таким образом, У([а,Ь]) = [т, М], т. е. образ отрез-
ка есть отрезок.
Замечание. В случае т = М отрезок [m, М ] вырождается в
точку. Так будет для постоянной функции У(х) = с Vx € [а, 6].
Замечание. Итак, доказано: если / € С(А), где множест-
во А связно в R, то функция У(х) обладает свойством Дарбу, т. е.
(V[a, b] С А) => /([а, Ь]) - отрезок. Обратное утверждение, вообще го-
воря, неверно, так как существуют разрывные на связном множестве
функции, обладающие свойством Дарбу.
Пример. Рассмотрим функцию
.. .	[ вшя72х, 0 < х < 1,
/(ж) = ( 0, х = 0.
Тогда (рис. 7) V[a, Ь] С [0,1] образ /([а, 6])
есть отрезок, и, в частности, /([0,1]) =
[-1,1], однако функция У(х) разрывна при
х = 0.
Теорема (критерий непрерывности
монотонной функции). Пусть функция f (х)
определена и монотонна на связном мно-
жестве М С R. Тогда (У € С(М))
(функция /(х) обладает на множестве М
свойством Дарбу). (Попробуйте доказать
самостоятельно.)
Доказательство. Необходи-
мость. Если / € С(М), то из теоремы
Дарбу вытекает, что функция У(х) облада-
ет Д-свойством.
Достаточность. Пусть для определенности f | на М и обладает на
связном в R множестве М свойством Дарбу. Поскольку М (линейно)
связно в R, то множество М есть либо отрезок [а, 6], либо полуинтер-
вал [а, Ь) или (а, Ь], либо интервал (а, Ь) (при этом полуинтервал или
интервал могут быть неограниченными).
Пусть для определенности М — (а, Ь]. Покажем, что Vx0 € (a, b]
имеют место равенства У(хо-О) = У(хо) и У(хо) = У(хо+0) (если хо
Ъ). Докажем, например, равенство У(хо - 0) = У(хо). Итак, хо € (а, Ь].
106
Пусть ®i € (а,®о). Поскольку /(®) | на (а, Ь], то /(®i) < /(®0 - 0) <
у(®о). Если при этом /(®i) = /(®о), то равенство /(®о - 0) = /(®о)
доказано.
Пусть /(®i) < /(®о)> В силу монотонного возрастания функции
f(x) на (а, Ь] и свойства Дарбу имеем /([®i, ®о]) = [/(®1),/(®о)]- Но
тогда Ve > 0 такого, что /(®i) < /(®о) - е < /(®о), имеем /(®о) - е €
/([®1,®о]), т. е. существует ®2 Е (®i,®o) такое, что /(®г) = /(®о) - £-
Но тогда V® Е (®2, ®о) С Af => f(xo) -е = /(®г) < /(®) < /(®о).
Переходя в этом неравенстве к пределу при ® -> ®о — 0, получаем
/(во) _ е < /(®о — 0) < /(®о) и в силу произвольности е > 0 име-
ем равенство /(®о — 0) = /(®о)- Аналогично доказывается равенство
/(®о) = /(®о + 0), если ®о # Ъ. Итак, /(®о - 0) = /(®о) = /(®о + 0)
V®o € М, т. е. в силу ранее доказанного критерия непрерывности мо-
нотонной функции / Е С(®о) V®o 6 М, т. е. f Е С(М).
Определение. Функция f(x), определенная на множестве
М С (-ОО) +оо), называется равномерно непрерывной на множестве
М, если Ve > 0 2<5(е) > 0 такое, что V®i,®2 Е М, для которых
|®i - ®2| < 6 => |/(®1) - /(®з)| < е. „
Подчеркнем, что £(е) > 0 в определении равномерной непрерыв-
ности функции /(®) на множестве М зависит только от е > 0 и не
зависит от выбора точек ®i, ®г Е М.
Замечание. Если функция /(г) равномерно непрерывна на
множестве М, то f Е С(М). Обратное, вообще говоря, неверно.
Напомним определение f Е С(М) для функции /(®), заданной на
множестве М : Ve > 0 и V®o € М 3£(®о,е) > 0 такое, что |/(®) -
/(®о)| < е V® £ М П Ui(®о). В этом определении величина <$(®о,е) > 0
зависит не только от е > 0, но и от выбора точки ®о € М.
Пример. Пусть /(®) = 1/®, ® Е (0,1], тогда / Е С((0,1]), но
функция ® -> 1/® не является равномерно непрерывной на (0,1], так
как Зео = 1 > 0 такое, что V<5 > 0 3®^ = 1/n, ®n2^ = l/(n -I-1), для
которых при любом п > 2/6 |®^ - ®«2)| < 2/п < 6, но
1/(4п) - /(42)) I = 11/4х) -1/42) I = |(п+1) - п| = 1 = ео > 0.
Определение. Пусть функция f(x) определена на множес-
тве М и f € С(М). Функция f(x) не является равномерно непре-
рывной на множестве М, если Эво > 0 такое, что У<5 > 0 су-
ществует пара точек х^\х^ € М таких, что	< S,
1/(4П) - /(®$а))I > е0 > 0.
Теорема Кантора (о равномерной непрерывности функ-
ции, непрерывной на отрезке). Пусть функция /(®) определена на от-
резке [а, Ь] и f € С([а, Ь]). Тогда f(x) равномерно непрерывна на от-
резке [а, Ь].
107
Доказательство. Допустим, что / Е С([а, Ь]), но при этом
функция /(ж) не является равномерно непрерывной на отрезке [а, Ь].
Тогда Збо > 0 такое, что Vn Е N существует пара точек аП1/Зп Е [а, Ь]
таких, что |ап -(Зп\ < 1/п, но \ f(an) - f(/3n)\ >	> 0.
Рассмотрим числовую последовательность (аЛ). Поскольку а <
ап < b Vn Е N, то последовательность (ап) ограничена и в силу теоре-
мы Больцано - Вейерштрасса существует сходящаяся подпоследова-
тельность (anfc) lim = so» причем а < аПк < Ъ Vk => xq Е [а, 6].
к—>+оо
Заметим также, что Vfe Е N имеем
|Д»к - ®о| < lanfc - ®о| + |/3nk - <*nk| < |аЯк - ®о| + 1/nfc,
откуда вытекает, что 3 lim (3Пк = х0. Но f G С([а, Ь]) => f 6 C(xq),
fc->4-oo
поэтому 3 lim f(anit) = lim f(j3nk) = /(®o) и, в частности, пере-
fc—>-hoo	к—>+оо
ходя к пределу при к -> 4-оо в неравенстве |/(anfc) ~ f(0nk)\ > £о > О,
имеем |/(®о) — /(®о)| > £о > 0. Противоречие.
Замечание. Ранее рассмотренный пример показывает, что в
условиях теоремы Кантора нельзя заменить отрезок на полуинтервал.
Замечание. В условиях теоремы Кантора нельзя заменить
отрезок на неограниченное связное множество [а, +оо).
Пример. Пусть f(x) = ж2, х Е [0, +оо), тогда f Е С([0, +оо)), но
для €o = 1>0hV(5>0 Зж^ = у/п, ж^ = у/п 4-1 так, что при любом
n > 1/<52 => |ж,(2) — Жп1)] = у/п 4-1 — у/п = 1/(л/п 4-1 + \/п) < 1/у/п < <5,
|/(жп2)) — /(жп1))! = |(п 4-1) - n| = 1 = £0 > 0, т. е. функция ж -> ж2 не
является равномерно непрерывной на [0,4-оо).
Замечание. В условиях теоремы Кантора отрезок можно за-
менить на любое секвенциально компактное или компактное (в R)
множество. Напомним определение из § 2 гл. 1.
Определение. Пусть М С R, L С R и функция f : М —> L
есть биекция. Пусть у Е L = f(M), тогда полный прообраз f~r(y)
состоит из единственной точки х Е М, такой, что f(x) = у. Если
ввести функцию f~r : у —> ж = (у), то она отображает множес-
тво L на множество М взаимно однозначно и называется обратной
биекцией. При этом имеют место соотношения
/-1(/(®)) = xVx G М =	=y^yeL = f(M).
Определение. Гомеоморфизмом множества М С R на
множество L С R называется любая биекция М на L, непрерыв-
ная вместе со своей обратной биекцией.
Итак, если биекция f : М —> L осуществляет гомеоморфизм М на
L, то f Е С(М) и Л1 Е C(Z).
108
Теорема (о существовании и непрерывности обратной функ-
ции для строго монотонной непрерывной функции). Пусть функция
f(x) определена, строго монотонна и непрерывна на промежутке
|а, &| (являющемся интервалом, полуинтервалом или отрезком чи-
словой прямой). Тогда: 1) отображение f : |а, Ь| —> /(|а, Ь|) есть би-
екция, причем множество /(|а, Ь|) есть промежуток |ск,/3| и обрат-
ная биекция : |а, /?| —> |а, Ъ\ есть строго монотонная функция на
|а> f}\; 2) образ /(|а, Ь|) = |а,/3| есть промежуток в R того же вида,
что и промежуток |а, Ъ\ (так что, например, при
f П на |а, Ъ\ : (а G |а,/?|) <=> (а G |а,Ь|); (/? G |<*,/?|) <=> (b G |а, Ь|));
3) обратная биекция /-1 6 С(|а,/3|), т. е. биекция f : |а, 6| ->
|а,/?| осуществляет гомеоморфизм промежутка |а, Ь| на промежу-
ток
Доказательство. Будем для определенности считать, что
f(x) П на la, Н* Доказательство теоремы проведем поэтапно.
1)	Поскольку промежуток |а, Ъ\ есть (линейно) связное в R множес-
тво, то из условия f 6 С(|а, Ь|) в силу теоремы о сохранении связнос-
ти (при непрерывном отображении) вытекает, что образ /|а, Ъ\ есть
(линейно) связное множество в R, т. е. /(|а, Ь|) = |а,/?|, где |а,/?| -
промежуток в R. Докажем, что отображение f : |а, Ь| -> |а, /?| есть би-
екция, для чего покажем, что V®i, 6 |а, Ь| /(®1) = /(®г) <=>	= ®2«
Допустим от противного, что существуют ®i,®2 6 |а, 6| такие, что
xi < а?2, но /(®i) = /(®2)« В силу условия f |Т на |а, Ъ\ имеем < х2
(»i,®2 Е |сц Ь|) => (/(si) < /(®2))« Противоречие.
Итак, отображение f : |а, 6|	|ск,/?| есть биекция, а потому су-
ществует обратная биекция /-1 : |а,/?|	|а, Ь|.
Докажем, что /-1(j/) П на |а,/3\. Пусть уиу2 Е |а,/3| и у± < у2.
Тогда существуют хх,х2 Е |а, 6| такие, что /(®i) = Ух и f(x2) = у2,
так что хх = /“1(j/i) и х2 = /“х(ф). Поскольку отображение f есть
биекция, то yi у2 => хх х2. Неравенство хх > х2 невозможно, так
как тогда из условия f(x) Д на |а, 6| имели бы /(®i) = Ух > у2 = /(®г)
вопреки предположению.
Итак, xi < х2, т. е. /~1(j/i) < У"1 (3/2)* Тем самым показано, что
< /-1(!/2) ЧУ1,У2 6 У1 < У2, Т- е. /-1(у) ТТ на |а,/3|.
2)	Докажем теперь, что а 6 |а,/?| <=> а 6 |а, Ь|. Пусть а 6 |а, Ь|,
тогда yQ = /(а)	|а,/3|. Если а yQ, то, поскольку а = inf |а,/?|
имеем а < у0. Но тогда в силу определения точной нижней гра-
ни е /(|а, Ь|) такое, что а < у^ < уо. Но у^ 6 /(|а, Ь|), т. е.
3«1 G |а, Ь| такое, что /(®i) = у±. По доказанному в п. 1) обрат-
ная биекция У”1 на |а,/3|, поэтому из yi = /(®i) < уо = f(a)
< а = inf|a, Ь|, что невозможно, поскольку х± 6 |а, Ь|. Итак,
/(а) = а, т. е. а 6 /(|а, Ь|) = |а,(3\. Утверждение а 6 |а, Ъ\ => а G
109
доказано. Обратное утверждение a G |а,/3| => а € |а, 6| доказывает-
ся аналогично с использованием условия f(x) ТТ |а, Ь|. (Провести
это доказательство самостоятельно.) Итак, если f(x) П на то
(а G |а,/3|) (а € |а, Ь|); (/9 € |а, р\)	(/3 € |а,Ь|) (что доказывается
аналогичным образом). Но тогда промежуток |а;/3| имеет тот же вид
(интервал, полуинтервал или отрезок), что и промежуток |а, Ь|.
3)	Докажем теперь, что У-1 € С(уо) Vyo G |а,/3|. Пусть хо =
f~l(yo) € |а, Ь|. Пусть сначала хо - внутренняя точка промежутка
|а, Ь|, т. е. существует интервал (®i, х2) С |а, такой, что xq € (®i, х%).
По доказанному выше в п. 2) образ любого интервала из |а, Ь| при би-
екции f есть интервал, лежащий в промежутке |а, /3|. Но тогда Ve > О
такого, что U,(х0) С (®i,®2) С |а,Ь|, имеем У(17*(®о)) = V(yo) С (а,Х?|,
причем поскольку / есть биекция окрестности Ut(xo) на окрестность
V(yo), то имеем
ГХ№)) = Ut(x0),
а поэтому х = f~l(y) € Ut(х0) Vy € V(yo).
Итак, для любой окрестности 17<(У“1(уо)) С (®i,x2) существует
окрестность V(yo) С |а,/3| такая, что У-1(у) €	^У € У(Уо),
т. е. f~l е С(уо).
Пусть теперь хо = /“1 (уо) € |а, Ь| - граничная точка промежутка
|а, Ь|, например xq = а, тогда, как было показано в п. 2), уо — f(a) =
а € |а,/3| и, кроме того, биекция f переводит любой полуинтервал
(®о,®1) С |а, Ь| в полуинтервал [уо, У1), содержащийся в промежутке
|а,/?|. Но тогда Ve > 0 такого, что хо + е < Ь, имеем /([хо, ®о + е)) =
[уо, Уо+S) С |а,/9|, причем поскольку / - биекция, то f~1 ([уо, уо+£)) =
[х0, х0 + е) и х = У-1 (у) 6 [®о> ®о + е) Vy € VJ(yo) П |а,/3| = [уо, уо + 6).
Итак, Ve > 0 (хо + е < b) > 0 такое, что У-1 (у) € 1Л(У-1(уо))
Уу€Уе(уо)П|а,/9|,т.е. У-1 € С(уо).
Таким образом, У-1 G С'(уо) Vy € |а, /3|, т. е. У-1 € <7(10, /?|).
Замечание. В силу п. 2) доказательства теоремы об обратной
функции следует, что отображение х -> У(х) переводи любую внут-
реннюю точку хо € |а, Ь| во внутреннюю точку уо = У(®о) € У(|а, 6|) и
обратно, отображение у -> У-1 (у) переводит любую внутреннюю точ-
ку Уо € У(|а, Ь|) во внутреннюю точку х0 G У-1(уо) € |а, Ь|, а потому
при гомеоморфизме f промежутка |а, Ь| на промежуток гранич-
ные точки (если они есть) переходят в граничные.
Теорема (о гомеоморфизме). Пусть |а,Ь| - промежуток из
R. Для того чтобы биекция f промежутка |а, Ь| на У(|а, Ь|) была
гомеоморфизмом, необходимо и достаточно чтобы f была строго
монотонной и непрерывной на |а, Ь|.
Доказательство. Достаточность следует из теоремы об
обратной функции.
ПО
Необходимость. Пусть отображение х -> f(x) осуществляет гомео-
морфизм промежутка |а, Ь| на /(|а, Ь|). Тогда отображение f : |а, Ь| —>
/(|а, Ь|) есть биекция, причем f 6 С(|а, Ь|). Докажем, что отображе-
ние f : х -> f(x) строго монотонно на |а, Ь|. Допустим от противного,
что функция f(x) не является монотонной на |а, Ь|. Тогда существуют
G |а, Ь| такие, что xi < хъ < хз, причем /(хз) не заключено
между /(®i) и У(®з). Пусть, например, f(xt) > /(®i) и /(®2) > /(®з).
Поскольку / биективно отображает |а, Ь| на /(|а, Ь|), то (®i	х3) =$
(/(®1) # /(®з)).
Допустим, что /(®i) < /(®з)- Но (®2 / ®з) => (/(®з) ф /(®з))»
так что (/(»2) > /(®з))	(/(®г) > /(®з))- Таким образом, /(х2) >
/(®з) > Поскольку / € С(|а, &|) => / € C([®i, ®г]), то в силу
теоремы Больцано (о промежуточных значениях непрерывной функ-
ции) 3®о Е (®1,®з) такое, что /(®о) = /(®з), причем, очевидно,
®о ®з* Противоречие со взаимной однозначностью отображения
У : |а, Ь| -> /(|а, Ь|). Итак, функция /(®) монотонна на промежутке
|а, Ь|, и в силу биективности отображения / функция /(®) строго мо-
нотонна.
Замечание. Если / : |а,Ь| —> /(|а,Ь|) есть гомеоморфизм, то
в силу теоремы об обратной функции образ /(|а, Ь|) есть промежуток
|а, Ь| того же вида, что и |а, Ь|.
Замечание. Если отображение ® -> /(®) есть биекция |а,Ь|
на /(|а, Ь|), но /?С(|а, Ь|), то функция /(®) может и не быть строго
монотонной на |а, Ь|.
Пример. Пусть /(®) = < *’ х 6	тогда существу-
А X, X с **• \ Ч)
ет У”1 (10 = | 1-^ R \ Q ПрИ ЭТ0М Функция является
биекцией (-оо, +оо) на (-оо, +оо), не будучи ни непрерывной, ни мо-
нотонной.
Замечание. Если отображение х -» У(х) осуществляет
гомеоморфизм интервала или полуинтервала |а, Ь| на промежуток
|а,/?| = /(|а, Ь|) (являющийся также интервалом или полуинтерва-
лом), то ограниченность (соответственно не ограниченность) проме-
жутка |а, Ь|, вообще говоря, не сохраняется для промежутка |а, /3\ =
fM.
Пример. Отображение х —> tg х осуществляет гомеоморфизм
ограниченного интервала (—тг/2,%/2) на неограниченный интервал.
Пример. V(a, Ь) С (—оо, +оо) отображение х -> /(х), где /(х) =
— | 1----1_ —L_ | есть гомеоморфизм (а, Ь) на (—оо, +оо). (Доказать
\х — а х — Ь/
самостоятельно, что / G ^((а, Ь)) и /(®) И на (а,Ь).)
111
§ 4. Элементарные функции и их непрерывность
Ранее были доказаны непрерывность степенной функции х —>
хп (Vn 6 N) и непрерывность многочлена Рп(®) = £
fc=o
V® G (—00,4-00). Из теоремы о непрерывности частного (от деле-
ния двух непрерывных функций) следует, что функция х —> 1/хп
(Vn G N) непрерывна на (—оо, 0) U (0,4-оо) и рациональная функция
х -> Pn(x)/Qm(x) непрерывна на (-00,4-оо) \ U{a7}, где aj - дейст-
з
вительный корень знаменателя.
Теорема (о степенной функции с натуральным показателем).
Степенная функция ® —> ®n (Vn G N) осуществляет гомеоморфизм
промежутка [0,4-оо) на себя, при этом:
1)	хп 6 С([0, 4-оо)); 2) 0п = 0, lim хп = 4-оо; 3) хп Д на [0, 4-оо).
х—>+оо
Далее, существует обратная функция у —> уг1п, обладающая
свойствами:
1)	у1/” е С([0,4-оо)); 2) О1/” = 0, lim у^п = 4-оо; 3) у^п ТГ па
у->+оо
[0, 4-оо).
Доказательство. Свойство 1) хп 6 С([0,4-оо)) было дока-
зано ранее.
2)	Равенство 0п = 0 (Vn G N) очевидно, и поскольку п > 1 Vn 6 N,
то хп > х V® > 1, т. е. lim хп = 4-оо.
х->+оо
3)	Имеем (V®2 >	> 0) => (®J ~	— (®2 ~ ®i) x2®i> 0),
fc=o
т. e. xn Д на [0,4-oo).
Теперь все утверждения теоремы, в том числе и свойства 1)-3)
обратной функции у —> у1^п, вытекают из теоремы об обратной функ-
ции.
Замечание. Из теоремы (о степенной функции с натуральным
показателем) следует, что Vn G N и Va > 0 существует, и притом
единственное, число х > 0 такое, что хп = а. Это число обозначается
через а1/” или д/а.
Замечания. Меняя обозначения х и у, называют обратной к
функции х —> хп (на [0,4-оо)) функцию х -> х^п (на [0,4-оо)). Введем
обозначение х~п = (1/®)п Vn G N и V® 0. Тогда, очевидно, функция
® -> х~п (Vn G N) непрерывна на (-оо, 4-оо) \ {0}.
Теорема (о степенной функции с отрицательным натураль-
ным показателем). Степенная функция ® —> ®-n (Vn Е N) осущест-
вляет гомеоморфизм интервала (0,4-оо) ма себя, причем: 1) х~п Е
С((0,4-оо)); 2) limo®“n = 4-оо, lim ®”n = 0; 3) х~п jj, на (0,4-оо).
Доказательство. Утверждения 1) и 2) докажите сами.
Для проверки свойства 3) заметим, что хп ТТ на (0,4-оо), поэтому
112
VO < Xi < имеем "* ®in = (xi “ xz)/(xix2) < 0, t. e. x~n JJ, на
(0.4-oo).
Введем обозначения Va E R, a > 0, V9 E Q, где q = —, m E Z,
71
n e N; a° = 1, a1 = a, cfl = am/n = (a1/")™, a“« = (l/a)«.
Лемма. Если a E R, a> 0 uq 6 Q, то имеем:
1)	(aq')q* =aq'q* Vqi,q26Q;
2)	a9 • i>9 = (a • b)q V9 E Q, a > 0, b > 0;
3)	aq' • a92 = a91+92 V91, q2 E Q, a > 0;
4)	aq > 1 = a0 V9 E Q, q > 0, a > 1.
Доказательство. Утверждения 1) и 2) проверьте сами.
3)	Пусть 91 = 7П1/п1, 92 = тъ/пъ, где тП1,т2 6 Z, ni,n2 Е
N. Тогда, учитывая, что mi • п2, тп2 • ni Е Z, имеем а91 • а92 =
ami/ni , am2/n2 —- (al/nin2jmin2 , (al/fiin2)m2ni = (al/nin2^т1п2+т2п1 __
a(inin2+in2n1)/n1n2 = flmi/ni+m2/n2 _ agi+g2
4)	Пусть а Е R, а > 1, и q Е Q, причем q = т/п > 0. Допустим от
противного, что ат!п < 1, тогда очевидно, что (а7П//п ... ат1™ < 1... 1)
п	п
=> (ат < 1), с другой стороны, (а > 1) => (а^а > К^Л) => (aw > 1)-
т	т
Противоречие.
Итак, aq > 1 V9 > 0, q Е Q.
Теорема (о степенной функции с рациональным показателем).
Степенная функция х —> xq (V9 Е Q \ {0}) осуществляет гомеомор-
физм интервала (0, 4-оо) ма себя, причем:
1) xq Е С((0, 4-оо)); 2) lim^x9 = 0 (9 > 0), lirn^x9 = +оо (9 < 0),
lim xq =
(0,4-оо) при 9 < 0. (Доказательство провести самостоятельно.)
3 а м е ч ан и е. ®° = 1 V® Е (0,4-оо).
Замечание. Vn Е N все решения уравнения хп = а, где
ж, а Е R, можно выразить с помощью символов а1/" = у/a. Если
п = 2k (четное), то х2к > 0, и поэтому уравнение х2к = а имеет реше-
ние только в случае а > 0. Но если жо есть решение, то и (—жо) ~ тоже
решение уравнения х2к = а, поэтому при а > 0 единственным поло-
жительным решением уравнения х2к = а будет а1/2*, другим (отри-
цательным) решением будет число —а1/2*. Для записи обоих решений
уравнения х2к = а применяется символ ± 2^/а, где а > 0 и 2^/а > 0.
Если п = 2к + 1 (нечетно), то а Е R может быть и отрицательным.
Поскольку функция х —> x2fe+1, х Е (—оо,4-оо) возрастает от —оо до
+оо, то уравнение ж2*+1 = а имеет единственное решение Va Е R.
Если a > 0, то таким решением будет 2к+^/а > 0, если же a < 0, то,
полагая a = —Ь, имеем ж2*+1 = —Ь или (-ж)2*+1 = b => — х = Ь1/2**1,
т. е. х = — 2fc-tyZa есть решение уравнения ж2*+1 = а для a < 0.
3) xq Д ма (0,4-оо) при q > 0 и xq Д на
113
Теорема (о показательной функции на множестве Q). Функ-
ция х а* определена на множестве Q С R и Va € R, a > О,
обладает следующими свойствами: 1) ах ft на Q, если а > 1, и
a* Ц на Q, если 0 < а < 1; 2) lim а® = (	°’ ® > 1’ ,
®->-оо	+00) и < а < 1,
lim а® = | П+Т’ “ > lim а” = 1; 3) а” € C(Q).
«-►+<»	( 0, 0 < а < 1, *-м>	7	' ’
Доказательство. 1) Пусть а > 1 и ®i,xj € Q любые та-
кие, что < ®2, тогда в силу 4) леммы имеем (®г - ®1 > 0)
(a®’”*1 > 1) => (а’^а*’-®1 - 1) > 0) => (а®’ > а®1), т. е. при а > 1
а® П на Q. Пусть теперь 0 < а < 1. По доказанному выше имеем
(1/а)® П на Q, и тогда, очевидно, для функции а® = 1/(1/а)® имеем
а® Ц на Q.
2) Пусть сначала a > 1. Ранее было доказано важное неравенство
(1 + р)п > 1 + пр Vp > 0 Vn € N. Поскольку а > 1, то а = 1 + р, где
р > 0, и поэтому ап > 1 + пр Vn G N. Но а® П на Q при a > 1, откуда
а* > ап Vx > п, х € Q.
Заметим, что в силу теоремы Архимеда VN € N Зпо G N та-
кое, что 1 -I- pno > N. Но тогда V^ € N Зпо € N такое, что
a* > а"° > 1 + рпо > ЛГ Vx > По (х € Q), т. е. lim а® = 4-оо.
г—>4-оо
Очевидно, lim а* = lim 1/а~® = 0. При 0 < а < 1 по доказанно-
г-44-оо	Г-ф-00
му имеем lim a® = lim (l/a)“®; lim a® = lim (l/a)“® = +oo.
x—^4-00	г-фЦ-оо	г—ф — оо	Г4~оо
Далее, пусть опять a > 1, тогда a = (1 -I- p)n, где p = a1/” - 1 > 0,
поэтому из нашего неравенства имеем оценку a > 1 + n(a1/" - 1) =>
(О < a1/” — 1 < -—- |, откуда lim a1/” = 1, а также lim а’1^ =
П J	п4-oq	п—>4*00
1.
Докажем, что lim а* = 1, воспользовавшись определением предела
по Гейне. Пусть (gn) - любая последовательность Гейне, связанная с
О, такая, что qn € Q, qn £ 0 Vn G N и lim qn = 0 (такие последовав
п->4-оо
тельности существуют в силу плотности Q и R). Но по доказанному
выше lim а1/п = 1и lim a-1/" = 1, поэтому Ve > 0 Зпо G N такое,
п->4-оо	п->4-оо
что 1 - е < a-1/n° < a1/”0 < 1 + е. Далее, (*lim^ gn = 0) => (3^ € N
такое, что — 1/по < qn < 1/по Vn > N), но тогда поскольку ая ТГ на
Q, то 1 — е < a-1/”0 < a?n < а1/"0 < 1 + е, т. е. (-е < аЯп — 1 < е) =>
(|а,п — 1| < е) =#> (3 lim аЯк = 1).
(Г)
Итак, lim ах = 1. В силу эквивалентности определений предела
лг—>0
по Гейне и по Коши в случае a > 1 имеем 3 lim a* = 1, но тогда и при
г-фо
О < a < 1 3 lim a® = 1.
Г-40
114
3) Пусть ®о € Q, где ®о - любая (фиксированная) точка. Тогда
V® G Q имеема®-а*° = а10(а1-®0-1), откуда, используя 2), получаем
(3 lim а*"'0 = 1) => (lim а® = а’0) => (а* € C(®o)Vxo 6 Q) =>
а® € C(Q).
Замечание. Если а = 1, то а* = 1 V® € Q. Если а = 0, то
а® = О V® G Q\{0}; значение 0° не определено.
Определение. Пусть aGR, a>lu®GR. Положим а* =
sup а9. При 0 < q < 1 имеем b = 1/а > 1, и поэтому определен
символ If V® € R, тогда полагаем а* = Ъ~* Ух € R, где введено
обозначение b~* = 1/lf.
Замечание. Если ®о = то/по € Q, где то € Z, по € N, то,
очевидно, а*0 = ат°'/п° = (а1/"0)"*0 и в соответствии с ранее введен-
ными обозначениями имеем, в частности, a0 = 1, а1 = а.
Теорема (о показательной функции, определенной на R). По-
казательная функция х a® (a > 0,a l,a G R) осуществляет
гомеоморфизм интервала (—оо, +оо) на интервал (0,+оо), при этом
обратная функция у = log, у называется логарифмической функцией.
Показательная функция обладает следующими свойствами:
1)	a* ТТ на (-оо, +оо) при а > 1 и а* Ц на (-оо, -Нэе) при 0 < a < 1;
2)	lim of = (	°’ ° > lim of = ( n+n°° “ > 1’1
'	+ oo 0 < a < 1, a?->+oo	Оу 0 < a < 1;
3)	a® G C((-oo, +oo));
4)	(a®1)®’ = a®1®’ V®i,®2 € (-oo,+oo);
5)	a®  bx = (a • Ь)® V® € (-oo, +oo), V6 > 0, b # 1;
6)	a®1 • a®’ = a*1+*’ V®i, ®2 6 (-oo, +oo);
7)	a“® = 1/a®, (1/a)® = 1/a®, a®‘/a®’ = a«>“«’ V®,®i,®2 € (-oo,+oo);
a0 = 1, a1 = a.
Логарифмическая функция ® —> log, x (a G R, a > 0, a / 1) осу-
ществляет гомеоморфизм интервала (0,+oo) на интервал (-оо, +оо)
и обладает свойствами:
1)	log, х ТТ на (0, +оо) при a > 1 и log, в Ц на (0, +оо) при 0 < a <
1;
2) lim =(	» lim =( +“’“>T'1
*->4-0	( +оо, 0 < а < 1	®->4-оо	( -оо, 0 < а < 1;
3) log, ® G С((0,+оо));
4) log,(a;1 • ®2) = logo ®2 4- log, ®2 V®i, ®2 G (0, +oo) и, в частности,
log, (1/х) = -log,® V® G (0,+oo);
5) loga[(®i)®2 3 4 5] = ®2 log, ®i V®i, ®2 G (0, +oo).
Доказательство. Сначала рассмотрим показательную
Функцию х -> a*. 1) Пусть ®2,®2 G (—оо,+оо), ®2 < ®2. Тогда в
силу плотности Q в R 3gi, д2 G Q такие, что ®i < gi < д2 < ®2, и
поскольку а® ТТ на Q, то, используя определение символа a® V® G R,
115
имеем aX1 = sup aq < aqi < a92 < sup aq = aX2 => aXl < a®2,
«€Q,g<*i	g€Q,g<®2
т. e. функция ax Д на (—oo, 4-oo).
2)	V® G (—00,4-00) => (mn = [x] < x < mn 4- 1), но тогда по-
скольку функция ах П на (—оо,4-оо), то ах > а™п. По ранее дока-
занному lim атп = 4-оо => lim ах = 4-оо. Далее, lim ах =
mn—> 4-сю	х—>4-оо	х—>-оо
— lim l/a“® = 0.
я—> —сю
3)	Пусть ®о Е R - любое, но фиксированное. Докажем предвари-
тельно лемму.
Лемма. Если ®о G R, то У г > 0 3gi,g2 6 Q такие, что q± <
хо < q2 иО < aq2 — aqi < г.
Доказательство. В силу плотности Q в R Vn 6 N
2?n,«n € Q такие, что q'n < х0 < «" < х0 + 1, 0 < g" - q'n < 1/п,
но тогда в силу свойств показательной функции q aq\ определенной
на Q, имеем 0 < aq” — aq‘n = a9n(a9«-9n — 1) < aXo+1(a1/n — 1). Но,
как было доказано ранее, существует lim a1/” = 1, поэтому У г > О
п—>4-оо
Зпо G N такое, что aXo+1(a1/n° — 1) < в, откуда, полагая qi = q„0,
q2 = g"o, имеем оценки 91 < ®о < 92 и 0 < a92 — a91 < г.
Теперь воспользуемся определением предела функции в точке по
Гейне. Рассмотрим любую последовательность Гейне (хп), связанную
с точкой хо, так что хп 6 R, хп / ®о Vn G N и lim хп = ®о- По
п->4-оо
лемме Уг > 0 3gi, 92 6 Q такие, что qi < xQ < 92 и 0 < а92 — а91 < г.
Поскольку lim хп = хо, то 3N G N такое, что 91 < хп < q2 Уп > N,
п—>4-оо
и тогда поскольку ах ТТ на (—оо, 4-оо), то имеем оценки а91 < ах° < а92
и а91 < аХп < а92 Уп > N, откуда в силу выбора 91,92 6 Q получаем
(Г)
оценки |аГл — а*°| < а92 — а91 < г, т. е. 3 lim аХп — ах° => 3 lim ах =
п->4-00	х->х0
ах°.
Итак, Ухо 6 R 3 lim ах = ах°, и поэтому, используя (предельный)
критерий непрерывности функции в точке, имеем ах 6 0(®о) V®o 6 R
=> ах G C(R).
Свойства 4)-6) для показательной функции проверяются единооб-
разно с помощью 3). Проверим, например, свойство 4).
Пусть ®i, ®2 6 (—оо, 4-оо) - любые, но фиксированные, и пусть по-
следовательности (an) и (вп) (ап,0п 6 Q Уп) таковы, что lim ап =
п->4-оо
®i, lim 0п = ®2 (выбор таких последовательностей возможен в си-
п->4-оо
лу плотности Q в R). В силу свойств функции 9 —> а9, определенной
на Q, имеем аап • а^п = aaft+/,ft. Поскольку ах 6 С((—оо, 4-оо)), то
в этом равенстве можно перейти к пределу при п —> 4-оо. Но тогда
аХ1 • аХ2 = аХ1+а?2. Свойства 7) для показательной функции вытека-
ют из свойств 1)-6). Проверку свойств 1)-5) для логарифмической
116
функции х —> loga х проведите самостоятельно, используя свойства
гомеоморфизма у —> ау интервала (—оо, 4-оо) на интервал (0,4-оо) и,
заметив, в частности, что свойства 4) и 5) для логарифмической функ-
ции следуют из следующих свойств показательной функции:
ayi+y2 _ ayi , ау-2 (ГдеЖ1 = а»1, Х2 = аУ2) и
(аУ1р	(гдея^а*1).
Замечание. При а = 1 имеем ах = 1 Vx 6 (—оо, +оо). График
показательной функции изображен на рис. 8 (при а > 1) и рис. 9 (при
Рис. 11
Замечание. Если а = е > 1, то полагают loge х = In ж. График
логарифмической функции изображен на рис. 10 (при а > 1) и рис. 11
(при 0 < а < 1).
Замечание. Если а,Ъ 6 R, а > 0, Ъ > 0, а ф 1, b / 1, то
log6 х = loga х • log* а = loga х/ loga b; log* x = In x/ In 6.
117
В самом деле, V® > 0 имеет место тождество х = alog«®, откуда
logb х = logo х • logb а, а стало быть,
logo x = logb X • logo b => logb a • loga 6=1.
Определение. Обозначим через х -+ ха функцию, которая
любым х > 0 и а € R ставит в соответствие число ха. Эта функ-
ция называется степенной функцией.
Замечание. Поскольку при а > 0, а / 1 имеем х = aloguх,
(а®х)*э = то ®а = аа10&»® и, в частности, ха = exp{aln®}.
Таким образом, степенная функция х ха, определенная на ин-
тервале (0,+оо), является композицией логарифмической функции
х —> loga х и показательной функции у -> aay.
Теорема (о степенной функции с действительным показате-
лем). Степенная функция х —> xQ (а € R, а 0 осуществляет
гомеоморфизм интервала (0, +оо) на интервал (0, +оо) и обладает
следующими свойствами:
1)	ха Tf на (0,+оо) при а > 0 и ха Ц на (0,+оо) при а < 0;
2)	lim ха = [ °’ а>^.'	и lim ха = ( +п°°’ *> °’
' «-.+0	[ 4-оо, а < 0	®-.+оо	( 0, a < 0;
3)	ха € С((0,4-00)) Va Е R, а # 0;
4)	(ха)0 = ха^ V® > 0, Va,0 6 R;
5)	х° • х% = (®i • ®2)a V®i > 0, ®г > 0; Va Е R;
в) ха • х? = ха+^ 'ix > 0; Va,0 € R.
Доказательство. 1) и 2). Пусть (®„) - любая последова-
тельность Гейне, связанная с 0, причем ®п > 0 Vn Е N и lim°° хп = 0.
Тогда из свойств логарифмической я показательной функций имеем
lim ln®n = —oo^ lim exp{aln®n} = I °	’
п->+оо "	П-.+ОО	п> ( 4-00, a<0.
3) Заметим, что ®“ = Г(®), ® € (0,4-оо), где F = ро/,
причем /(®) = In®, х Е (0,4-оо); /((0,4-оо)) = (-оо,4-оо); f Е
С((0,4-оо)); <р(у) - е"», у Е (-оо,4-оо); р((-оо,4-оо)) = (0,4-оо),
Е С((-оо, 4-оо)).
В силу теоремы о непрерывности композиции непрерывных функ-
ций имеем F = р о / Е ^((0,4-оо)) => ха Е С((0,4-оо)).
Свойства 4)-6) проверяются единообразным способом. Например,
Ха -х? = е"1п® .	= e(a+3)ln® = Х«+И ух > о, ya)0 G R.
Замечание. При a = 0 => ха = 1 V® Е (0,4-оо). График сте-
пенной функции изображен на рис. 12 (при a > 0) и рис. 13 (при
а < 0).
Определение. Тригонометрическими функциями назыеа-
ются функции: у = sin®, ® Е (-оо,4-оо); у = cos®, ® Е (-оо,4-оо);
у = tg® (= sin®/cos®), х (2k 4- 1)тг/2; у = ctg® (= cos®/sin®),
® kir (k = 0,±1,±2,...).
118
Отметим некоторые свойства тригонометрических функций, из-
вестные из школы (к этим свойствам мы вернемся во 2-м томе курса
математического анализа при изучении степенных рядов):
1) sin(® + 2Ляг) = sin®; cos(® + 2kir) = cos®; tg(® + fcir) = tg®;
ctg(® + ктг) = ctg x (k = 0, ±1, ±2,...);
2) sin(®i + ®2) = sin®i • cos ®2 + cos®i -sin®2; cos(®i + ®2) = cos®i •
cos ®2 - sin ®i • sin ®2; sin2 ® + cos2 ® = 1;
3) sin(-®) = - sin®; cos(-®) = cos® V® € (—oo, +oo);
4) sin®, cos® € C((-oo, oo)).
Для доказательства свойства 4) заметим, что sin® — sin®о =
2 cos . sin^-y^, откуда |sin® - sin®o| < 2|sin(® - ®o)/2| <
2|® - ®o|/2 = |® - ®o|- Таким образом, Ve > 0 3d = e > О такое, что V®,
удовлетворяющего неравенству |® - ®о| < d, имеем | sin® - sin ®о| < е,
т. е. (sin® € 0(®о) V®o € -оо,+оо)) => (sin® € С((-оо, +оо))).
Для доказательства непрерывности функции ® cos ® использу-
_	л . ® 4" ®0 . ®	®0 «
ется равенство cos ® - cos ®о = -2 еш —-— • sin —-—. Заметим, что
в силу теоремы о непрерывности частного (от деления двух непре-
рывных функции) функции х -4 tg® и х -+ ctg as также непрерывны в
своих областях определения.
Графики функций у = sin х и у = сое х изображены на рис. 14, а
Функций у = tg х и у = ctg х - на рис. 15.
Теорема (об обратных тригонометрических функциях). Функ-
ция х -> sin® осуществляет гомеоморфизм отрезка [—тг/2,7г/2] на
отрезок [-1,1], причем обратная функция у —> arcsin у такова, что
(меняя обозначения х и у):
1)	arcsin х ТТ на [-1,1];
2)	lim arcsinх = -я72, lim arcsin® = тг/2;
3)	arcsin® € C((-l, 1]).
119
Функция х —> cos х осуществляет гомеоморфизм отрезка [0, тг] на
отрезок [—1,1], причем для обратной функции у —> arccost/ имеем:
1)	arccos® Л на [—1,1];
2)	lim arccos® = тг/2 и lim arcsin® = 0;
' я-4-l+O	х-И-0
3)	arccos® 6 C([-l,1]) -
Функция х —> tg® осуществляет гомеоморфизм интервала
(—тг/2, тг/2) на интервал (—оо, 4-оо), причем для обратной функции
у —> arctg у имеем:
1/ arctg® И на (-оо,+оо);
2) lim arctg® = —тг/2 и lim arctg® = тг/2;
т—>•—оо	х—>+со
3) arctg® Е С((-оо, 4-ос)).
Функция х —> ctg ® осуществляет гомеоморфизм интервала (0, тг)
на интервал (—оо, 4-оо), причем для обратной функции у —> arcctg т/
имеем:
1)	arcctg® 11 на (—оо,4-оо);
2)	lim arcctg ® = тг u lim arcctg ® = 0;
X—► — оо	я—> —оо
3)	arcctg® Е С((-оо, +оо)).
Доказательство. Рассмотрим функцию ® —> sin х. Пусть
-тг/2 <	< тг/2, тогда 0 < ®2 —	< тг, и поэтому (—тг <
4-	®2 < тг) => (sin®2 — sin®i = 2sin(®2 — ®i)/2 • cos(®i 4- ®з)/2 > 0)
=> (sin®2 > sin®i) => (sin® TT [—уг/2,тг/2]). Таким образом, sin® Е
С([-тг/2,тг/2]), sin([—тг/2,тг/2]) = [—1,1] и sin® ТТ на [-тг/2,тг/2]. В
силу теоремы об обратной функции видим, что функция ® -> sin®
осуществляет гомеоморфизм отрезка [—тг/2, тг/2] на отрезок [—1,1]
и существует обратная функция <р(у) такая, что <р(у) ТТ на [—1,1],
<р(—1) = —тг/2, у>(1) = тг/2 и (р Е С([— 1,1]). Эта функция обозначает-
ся через arcsin j/, для которой (меняя ® и у) имеем:
1)	arcsin® ТТ на [—1,1];
120
2)	lim arcsinx = —тг/2 и lim arcsin» = тг/2;
' x—> —14-0	x—>1—0
3)	arcsin» 6 C([— 1,1]).
Остальные утверждения теоремы докажите самостоятельно.
Графики обратных тригонометрических функций изображены на
рис. 16—19.
Замечание. Итак, все простейшие элементарные функции:
1)	рациональная функция » —> Pn(®)/Qm(®)> m = 0,1,2,...;
2)	показательная функция » —> а®;
3)	логарифмическая функция » —> loga »;
4)	степенная функция » —> »а;
121
5)	тригонометрические функции х —> sin», х -> cosx, х tgx и
х -> ctgx;
6)	обратные тригонометрические функции х —> arcsin®, х —>
arccosx, х —> arctgx и х —> arcctgx являются непрерывными функ-
циями в своих естественных (т. е. максимальных) областях сущест-
вования.
Напомним, что элементарной функцией называется функция, полу-
ченная из простейших элементарных функций посредством конечного
числа арифметических действий и композиций. Вспоминая теоремы об
алгебраических действиях над непрерывными функциями и теорему
о непрерывности композиции непрерывных функций, имеем теорему.
Теорема. Любая элементарная функция непрерывна в своей
естественной области определения.
гг	a	\	\ 1 ПРИ х > О,
Примеры. Функция f(x) = |	ж < q является эле-
ментарной, поскольку /(») = -Д V» 0, причем |х| = у/х$, х О,
|®1
1 при х > О,
поэтому f е C(R \ {0}). Функция sgn х =	0 при х = 0, не явля-
—1 при х < 0
ется элементарной. Функция х —> sgn х разрывна в точке xq = 0.
Глава 5
ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ (ОДНОЙ
ПЕРЕМЕННОЙ)
§ 1. Дифференцируемость функции в точке
Пусть функция х -> f(x) определена на множестве М С (—оо, +оо).
Рассмотрим открытое множество М, т. е. множество всех внутренних
точек х из М. Введем понятие дифференцируемости функции /(») во
о
внутренней точке х0 6 А/.
Определение. Пусть функция f(x) определена в окрест-
о
ности U(xq) С М точки xq ЕМ> Функция f(x) называется диф-
ференцируемой в точке х0, если существует число А такое, что
имеет место представление
f(xQ + Дж) — /(ж0) = ААх + а(Дж) • |Дж| V»o + Д® € U(x0), (1.1)
где функция а(Дж) является бесконечно малой при Дж —> 0, так что
122
в проколотой окрестности U(xq) имеем а(Дх) = о(1) (Д® —> 0).
Запись: f Е Р(®о)«
Замечание!. При фиксированном ®о ЕМ число А не зависит
от «приращения» Дх. (Но, вообще говоря, А = А/(®о), т- е- зависит
как от функции /, так и от точки ®о.)
Поскольку а(Дх) = о(1) (Д® -> 0), то имеем
Определение. Функция f : М -> R называется дифферен-
о
цируемой в точке xq ЕМ, если существует число А такое, что в
проколотой окрестности Щхо) С М имеет место представление
/(®о + Дх) - /(®о) = Л • Дх + о(Дх) (Д® -> 0).
Замечание 2. Функция а(Дх) из представления (1.1) при
Дх ф 0 определена однозначно равенством а(Дх) = (/(®о + Дх) -
/(®о) ~ АД®)/| Д® |. При Дх = 0 значение а(0) может быть любым,
но мы в дальнейшем будем считать а(0) = 0, так что функция а(Дх)
становится непрерывной при Дх = 0 (а € С(0)).
Пример. Пусть /(®) = ®2, х Е (-оо, +оо), тогда V®o имеем
(хо+Дх)2-х§ = 2хо-Дх+(Дх)2 (А = 2®о, (Дх)2 = о(Д®)(Д® -> 0)),
т. е. функция ® -> ®2 дифференцируема V®o 6 (-оо, +оо).
Замечание 3. Если функция /(®), определенная в окрестнос-
ти С7(хо), дифференцируема в точке ®о, то в окрестности £7(®б) ото-
бражение х -> /(®) с точностью до о(х - ®о) (х —> хо) можно заме-
нить линейным (аффинным) отображением ® —> /(®о) -Н(х - ®о), где
I : h -> А • h есть линейное отображение (линейная форма) в R. Та-
ким образом, приходим к следующему (эквивалентному) определению
дифференцируемости числовой функции в точке.
Определение. Функция f : U(xq) —> R дифференцируема в
точке xq, если существует такое линейное отображение I: R —> R,
что
.	|/(а?0 + Да;) - f(x0) - ЦАа?)|
д““о	|Да;|
Замечание 4. Линейное отображение I : h -4 А • h из опреде-
ления дифференцируемой функции /(®) в точке хо называется диффе-
ренциалом функции У(х) в точке хо и обозначается символом с!/(®о)
(так что df (хо) : h -> А • Л). Итак, имеем
Определение. Функция f : U(xq) -4 R дифференцируема в
точке хо, если существует линейное отображение (линейная фор-
ма) df(xo) : h —> A* h такое, что в окрестности U(xq) имеет место
представление /(xq + Дх) - /(®0) = d/(®o) (Дх) + о(Дх) (Дх -4 0),
при этом число й/(хо)(Дх) есть значение дифференциала df(xo) (как
линейной формы) при h = Дх.
123
Теорема (единственности дифференциала). Пусть функция
f(x), определенная в окрестности U(xq), дифференцируема в точке
xq. Тогда число А (соответственно дифференциал *• h A-h)
определяется единственным образом.
Доказательство. Пусть функция /(ж) определена в
окрестности U(xq), дифференцируема в точке xq и в U(xq) имеют мес-
то два представления:
/(®о + А®) ~ /(®о) = А, Дж + о(Дж), (Дж —> 0); i = 1,2.
Тогда (Ai—Аг) Дж = о(Дж) (Дж —> 0) и при Дж 0 имеем А±—Аг =
о(1) (Дж —> 0) => Ai = Аг. Таким образом, число А (а стало быть, и
линейная форма df(xo) : h -> А • h) определяется однозначно.
Замечание. Если ввести понятие приращения функции Дг/ =
/(жо + Дж) — /(®о)> соответствующее приращению аргумента Дж
(в точке жо), то для функции /(ж), дифференцируемой в точке жо,
имеем представления Дт/ = А • Дж + о(Дж) (Дж —> 0) или Д$/ =
<//(ж0)-(Дж)+о(Дж) (Дж —> 0), т. е. при А 0 Д$/ ~ АДж (Дж —> 0) или
Ду ~ <//(жо)(Дж) (Дж —> 0). Таким образом, значение дифференциа-
ла <£/(жо)(Дж) (при А ф 0) есть главная линейная часть приращения
функции t±y.
Теорема (о непрерывности дифференцируемой функции).
Пусть функция f(x) определена в окрестности U(xq) и дифферен-
цируема в точке жо- Тогда f € С(жо).
Доказательство. Поскольку /(ж) дифференцируема в точ-
ке жо, то в проколотой окрестности (7(жо) имеем представление /(ж) —
/(ж0) = А(ж-жо)+о(ж-ж0) (ж -> ж0), откуда (3 lim (/(ж)-/(ж0)) = 0)
X—
=» (3 lim /(s) = /(so)) => (/ 6 С(®о)).
Замечание. Если /(ж) определена в Е7(жо) и f G С(жо), то
функция /(ж) может и не быть дифференцируемой в точке жо.
Пример. Пусть f : ж -> |ж|, ж G (—оо,+оо). Тогда f 6
С((-оо,+оо)), но функция ж -> |ж| не дифференцируема в точке
жо = 0. В самом деле, для ж0 = 0 Ду = |Дж|, и если бы функция
/(ж) = |ж| была дифференцируема в точке жо = 0, то по определению
ЗА такое, что Д3/ = |Дж| => |Дж| = АДж + о(Дж) (Дж -> 0), причем
в силу теоремы единственности дифференциала число А определено
единственным образом. В частности, при Дж > 0 => (Ду = Дж) =>
А = 1, а при Дж < 0 => (Ду = -Дж) => А = -1. Противоречие.
§ 2. Производная функции в точке
Определение. Пусть функция /(ж) определена в некоторой
окрестности С7(жо). Производной функции f(x) в точке жо называ-
f(x\__________________________________^(жо)
ется предел (если он существует) lim ------. Производная
х-^хо Ж — Жо
124
функции f(x) в точке xq обозначается символами f(xo) = D/(®o) =
df(xp)
dx
Итак,
fM = ita, /w-zw
х->л?о X — Xq
Теорема (критерий дифференцируемости функции в точ-
ке). Пусть функция f(x) определена в окрестности U(xq). Тогда
(функция f(x) дифференцируема в точке ®о) <=> (в точке xq сущест-
вует (конечная) производная /'(®о)).
Доказательство. Необходимость. Пусть функция /(ж),
определенная в U(xq), дифференцируема в точке «о- Тогда имеем
представление Ау = АД® 4- о(Д®) (Д® -4 0), откуда ввиду Д® 0
имеем = А 4- о(1) (Д® -4 0) => fs lim = А^ => 3/'(®о) = А.
Д®	v х	\ Ах->оД® у v 7
Достаточность. Пусть f(x) определена в U(xq) и существует пре-
..	/(®о 4-Д®) - №о)	,// х г,,	a ./
дел lim --------------—- = f (®о). Тогда, полагая Ду = /(®о 4-
Дх->о А®
Д®) — /(®о), имеем в проколотой окрестности U(xq) представление
= /'(^о) 4- о(1) (Д® -4 0) => Ду = /'(®о)Д® 4- о(Д®) (Д® -4 0).
Таким образом, функция f(x) дифференцируема в точке ®о.
Следствие. Если функция /(®), определенная в (7(®о), диф-
ференцируема в точке ®о, то в U(xq) имеем представление Ду =
/'(®о)Д® 4- о(Д®) (Д® -4 0) и df(xQ) : h -4 fz(®o) • Л» в частнос-
ти, для значения дифференциала функции f(x) при h = Д® имеем
df(xQ)(Ax) = /'(®о)Д® (заметим попутно, что из теоремы единствен-
ности дифференциала вытекает, что А = fz(®o))-
Пример. Пусть р : ® —> ® - тождественное отображение R на R.
Тогда функция р(х) дифференцируема V® Е (—оо, 4-оо). В самом деле,
—- = 1 \/Д® / 0 => р'(®) = 1 V® Е (—оо, 4-оо) и в
силу критерия дифференцируемости р(х) дифференцируема, причем
для дифференциала dp имеем dp: h -4 1 • h.
Положим dx = dp. Тогда дифференциал (независимого переменно-
го) dx : h -4 h есть линейная форма, для которой при любом h Е R
dx(h) = h.
Пусть теперь функция f(x) дифференцируема в точке ®о, тог-
да для ее дифференциала <//(®о) имеем представление df (®0) : h -4
/'(®о)Л и, в частности, с1/(®о)(Л) = У'(®о)Л = fz(®o)d®(h), поэтому
имеет смысл запись для линейной формы df(®o) = /z(®o)d® или, по-
лагая у = f(x) и dy = df(x), получаем часто употребляемую форму
записи для дифференциала dy = ff(x)dx, dy =	• dx (tf = f(x)).
Отметим также обозначение для производной /z(®) =
125
Определение. Пусть функция f(x) определена Vx G Щхо)Г)
[®о, +оо) (или V® е 17(®о) п (-оо, ®о]).
Если существует правосторонний (левосторонний) предел
•-♦•о+о X — ®о
(•-♦•о-о)
то этот предел называется правой (левой) производной функции
/(®) в точке ®о и обозначается символами Д(®о) = D+/(®o) (соот-
ветственно /1(®о) = D“/(®o))-
Из критерия существования предела функции в точке имеем:
Теорема (критерий существования производной). Пусть функ-
ция f(x) определена в U(®o). Тогда (3/'(®о)) (В (конечные)
D+/(®o)> D~/(®o)> причем D+/(®o) = D“/(®o) = /'(®о))-
Пример. Пусть f : ® -> |х|, ® € (-оо, +оо). Тогда, очевидно,
D+/(0) = 1 и D”/(0) = -1, но производная D/(0) не существует (еще
одно доказательство недифференцируемости функции ® -> |®| в точке
®о = 0).
Замечание. До сих пор для функции /(®), определенной в
{/(®о), рассматривались лишь конечные производные /'(®о)-
Иногда удобно пользоваться понятиями бесконечной производной,
полагая /'(®о) = +оо (-оо), если f € С(®о) и
3 lim (/(х) - /(®о))/(® - ®о) = +оо (-оо).
(Отметим, что при D/(®o) = +оо (-оо) функция /(«) не является
дифференцируемой в точке ®01).
Аналогичным образом вводятся бесконечные односторонние про-
изводные
D+/(®o) = +оо, D"/(®o) = +оо (-оо)
(если /(®о) = /(®о + 0), /(®о) = /(®о - 0) соответственно).
Пример. Пусть f : ® -> ^Д®|, х G (-1,1). Тогда
D+/(0) = lira \/|®[/® = +оо; D+/(0) = lim x/\x\/x = -oo.
Замечание. Если функция f(x) определена на интервале (а, Ь)
и V® € (а, Ь) существует конечная производная /'(х), то говорят, что
/(х) дифференцируема на интервале (а, 6). Запись: f Е 1>((а, Ь)). Если
/ € 1>((а, 6)) и f € С((а, &)), то говорят, что функция /(х) непрерывно
дифференцируема на интервале (а, Ь). Запись: / € С^((а, Ь)),
Замечание. Если функция /(х) определена на промежутке
|а,Ь| (полуоткрытом или замкнутом), / € 1>((а,Ь)) и при а G |а, Ь|
существует конечная правосторонняя производная D+f (а), и при Ь €
126
|а, Ь| существует конечная левосторонняя производная T)~f(b), то гово-
рят, что функция f(x) дифференцируема на промежутке |а, Запись:
/ g U(|a, fr|). Если / € 2>(|а, Ь|) и функция
Г(а:) =
D+/(a), х = а (если |а, Ь|),
D/(®), ® € (а, 6),
D"/(b)> ® = Ъ (если Ь € |а, Ь|)
непрерывна на промежутке |а, Ь|, то говорят, что функция f(x) непре-
рывно дифференцируема на промежутке |а, Ь|. Запись: / € С^(|а, Ь|).
Определение. Пусть функция /(®) определена на [а,6] и
имеет на отрезке [а, 6] разрывы только первого рода. Пусть сущест-
вуют точки а = ао < ai < <*з	am-i < am = Ь щакие, что
функции
{/(щ+0), ® = а(,
/(«), а,' < х < а<+и » = 0,1,... ,т-1,
/(а,+1 - 0), х = а<+1
непрерывно дифференцируемы на отрезках [а,',а,ч.1] (пг. е. /,• €
С№((а<, a<+i]); i = 0,1,..., т — 1). Тогда говорят, что функция /(®)
кусочно-непрерывно дифференцируема на отрезке [а, Ь] (рис. 20).
Замечание. Очевидно, / € 1>(|а,Ь|) => / € С(|а,Ь|), но су-
ществуют функции, непрерывные на (-оо, +оо) и не имеющие произ-
водной ни в одной точке ®о € (-оо, +оо) (см. пример Ван-дер-Вардена,
приведенный в учебнике [3]).
§ 3. Касательная к графику функции
Пусть дана функция f : (a, b) -+ R и множество Г = {(®,у)|у =
/(®), х € (а, Ь)} С RxR = R есть ее график. Тогда, очевидно, ((®, у) G
Г) =* (у = /(®),® € (а, Ь)).
127
Определение. Если существует конечная производная
/'(хо), то касательной к графику Г функции f в точке (хо,/(хо)) 6
Г называется график функции х /(®о) 4- /'(хо)(х — ®о), определен-
ной Ух 6 (—оо, 4-оо).
Замечание. Касательная к графику Г является прямой, про-
ходящей через точку (®о,/(хо)) и имеющей уравнение у = /(хо) +
У'(хо)(ж — хо), при этом значение производной /'(®о) будет угло-
вым коэффициентом касательной в точке Mq = (хо, /(хо)). Если точ-
ки Mq, М 6 Г, где Г - график функции /, то прямая, проходя-
щая через точки Mq и М, называется секущей, ее уравнение, как
- У ~ Уо х — хо
известно из аналитической геометрии, будет —-- = —-- или
Лу Дх
А 2/
у = J/0 + --—(х — хо) (рис. 21, где введены обозначения Mq = (®о,з/о),
Дх
М = (х0 4- Дх, Уо 4- Дз/), Уо = /(х0), Аз/ = /(®о 4- Дх) - /(х0)).
Теорема (о касательной как предельном положении секущей).
Если функция f : U(xq) R дифференцируема в точке хо, то
предельным положением секущей, проходящей через точки Mq =
(®о,3/о), М = (х0 4- Дх, j/о 4- Дз/) пРи Ах 0, будет касательная
к графику Г функции х —> /(х) в точке Mq = (хо, /(®о)) 6 Г.
Аз/
Доказательство. Из уравнения секущей у = j/0 4- — (х —
Дх
хо) следует, что = tg^(Ax), где ^?(Дх) - угол, образованный се-
Дх
Дз/
кущей MqM с осью абсцисс Ох, так что у>(Дх) = arctg Поскольку
Аз/
f Е 2>(х0), то Э/'(хо) = Ит —, и в силу непрерывности функции
Ах->0 Дх
х —> arctg х видим, что
3 lim у>(Дх) = lim arctg = arctg/'(xo) = ^o-
Aa?->0	At->0
Итак, при Дх -> 0 существует предельное значение угла накло-
на секущей MqM, а стало быть, существует и предельное положение
секущей, проходящей через точку Mq (при М -> Mq). Для отыска-
ния предельного положения секущей перейдем к пределу в уравнении
секущей у = уо + ~^-(х — хо) при Дх -> 0. Получаем уравнение каса-
Дх
тельной к графику Г функции х —> f(x) в точке Mq = (хо, /(®о)) • У —
/(х0) 4-/'(х0)(х -х0).
Определение. Если /'(xq) = +оо(—оо), то касательной к
графику Г функции f в точке (®о,/(хо)) 6 Г (при f Е С'(хо)) назы-
вается множество {(х,у) Е R2|x = хо, — оо < у < 4-оо}. Касатель-
ная в случае /'(хо) = +оо(—оо) есть прямая с уравнением х = х0,
128
Определение. Если существует конечная правая произ-
водная D+ f'(xo)> то правой полукасательной к графику Г функ-
ции f в точке (жо,/(жо)) 6 Г называется график функции х —>
f(xo) + D+ /(®о)(® ~ ®о), определенной Vx > ж0.
Определение. Если существует конечная левая производ-
ная D” /(жо), то левой полукасательной к графику Г функции f
в точке (жо,/(жо)) G Г называется график функции х -> /(ж0) +
D“ f(xo)(x ~ ®о), определенной Vx < xq.
Определение. Если D+ 7(®о) = 4-оо(—оо), то правой полу-
касательной к графику Г функции f в точке (жо,/(ж0)) € Г назы-
вается множество точек (х,у) таких, что х = жо, у > /(®о) (у <
/(«о))-
Аналогично определяется левая полукасательная в случае
D- /(®о) = +оо(-оо) : х = х0, у < /(®о) (у > /(«о))
(рис. 22).
$ 4. Правила дифференцирования
Теорема. Пусть и(х) и v(x) определены в U(xq) uu,v Е Р(жо).
Тогда:
1)	(и 4- v)' = и'4- v';
2)	(c-u)f = с* и' для постоянной с ф 0;
3)	(и • v)f = и1 • v 4- и • vf;
(и\ uf - v - u-vf . . . Л
U)= —у—’ссли * °-
Доказательство. Давая аргументу приращение Дх, име-
ем:
1)	Д(и 4- v) = (и + Ди 4- v + Дг>) — (и 4- v) = Ди 4- Дг>, откуда
(Д(и4- v)/Ax = Ди/Д®4- Av/Дж (=>) (u4-v)' = и'4- v');
2)	(Д(с*и) = с* Ди) => (Д(с*и)/Дж = с-Ди/Дж) => ((с*и)' = с*и');
5 Зак. 860
129
3)	(A(u> v) = (u +Au) • (v + Av) — u- v = v • Au + uAv + Au • A v) =>
(A(u*v)/Ax = v^Au/Дх+u-Av/Дх+Av-Au/Ax) => ((u-v)' = u'«v+u>v'
(поскольку v G 2>(xo)) =► ((v € C(xo))) => (Av -> 0 при Ax -> 0), a
Jim^ Au/Ax = u');
4)	A(u/v) = (u + Au)/(v + Av) — u/v = (vAu-uAv)/v • (v +Av) =>
A(u/v)/Ax = (v • Au/Ax — u • Av/Ax)/v • (v + Av).
Если v(xo) 0, to v G (xo) => v(xo)+Av 0 при достаточно малом
Ax, а потому, переходя к пределу при Ах —> 0, имеем
(u/v)1 = (v • и' — и • v')/v2.
Теорема (о дифференцируемости композиции дифференци-
руемых функций). Пусть f : U(xq) -4 V(yo) (где у0 = /(хо)) «
д : У(уо) -> R. Пусть f G ®(хо) u д G 1>(уо). Тогда h = gofe ©(хо),
причем D Л(хо) = Dy(/(®o)) • D /(®о)-
Доказательство. Поскольку / G 2>(хо), то в окрестности
'СГ(хо) имеет место представление (Ду = /(xq + Ах) - /(®о))'-
Ду = D /(хо)Дх + а(Дх)|Дх|,
где a G С(0) и JimQa(Ax) = а(0) = 0.
Заметим, что при ®о + Ах G U(®o) имеем уо + Ду € V(yo), где
У(уо) - область определения функции я = -д(у). Далее, д G ®(уо),
поэтому в окрестности У(уо) имеет место представление (Ах = у(уо +
Ду) - д(Уо))-	= Dy(yo) • Ду + /?(Ду) • |Ду|, где 0 G С(0) и
д11то/3(Ду) = /3(0) = 0. Заметим, что f G 1>(®о) =► f € С(хо), поэто-
му lim Ду = 0 => ( lim /3(Ау) = lim /3(Ду) = /3(0) = 0) (обратите
Дг-40	Аг-+0	Ду-4О
внимание на то, что при Ах 0 может быть Ау = 0, и тогда в силу
нашего соглашения /3(Ду)|д9=о = /3(0) = 0). Но тогда в окрестности
£/(хо) имеет место представление
А® = Dy(yo) -D/(®o) • Дх+ [Dy(yo) ‘«(Д®)  |Д®|+
+/3(Ду) • |Ду|] = Dy(yo) -D/(®o) • Д® + 1(Д®).
Но
|1(Д®)| < (| Dy(yo)| • |а(Д®)|+ |/3(Ay)|(|D/(®o)|+
+|а(Ах)|)|Ах| = г(Дх) • |Дх|,
откуда в силу соотношений lim а(Ах) = 0, lim /3(Ду) = 8(0) = 0
имеем lim г(Дх) = 0, т. е. 7(Дя) = о(Дх) (Дж -> 0).
А&-+О
Итак, в проколотой окрестности U(xq) имеет место представле-
ние (h(x) = g(f(x)), h(xQ 4- Д®) — Л(®о) = Дя) Л(®о + Д®) — Л(®о) =
130
Dy(/(®o)) ' 0/(®о) • A® + о(Дх) (Дх -> 0), t. e. h = g о f E 2>(x0),
причем в силу теоремы единственности дифференциала имеем
DЛ(®о) = Dff(/(®o)) -D/(xo).
Замечание. В дифференциальных обозначениях теорема о
производной сложной функции выражается следующим образом: по-
скольку f G то дифференциал функции f имеет вид dy =
ff(x)dx, далее, поскольку д 6 то дифференциал функции д имеет
вид dz = g'(y)dy.
В силу доказанной теоремы видим, что дифференциал сложной
функции h = д о f получается из дифференциала функции если за-
менить у на /(®), a dy на дифференциал ff(x)dx, т. е. dz = hf(x)dx =
/(/(»)) • /'(»)<*»•
Замечание (об инвариантности формы 1-го дифференциа-
ла). Если у Е D(y), то первый дифференциал функции д записывается
в форме dz = g'(y)dy (при этом аргумент у есть независимая пере-
менная). Пусть теперь у = f(x), f 6 2>(х) и dy = /'(x)dx, тогда по
теореме (с производной сложной функции) для 1-го дифференциала
функции д имеем запись: dz — tf(f(x)) • f'(x)dx => dz = g'{y)dy^ т. e.
1-й дифференциал функции z = д(у) и в случае у = /(х) записывается
в (прежней) форме dz = g'(y)dy.
Замечание. Форму для вычисления производной сложной
функции у = у(х), где х = x(t), можно записать в виде
dy _ dy dx
dt dx dt'
Теорема (о производной обратной функции). Пусть функция
/(®), определенная на промежутке |а, Ь|, строго монотонна и непре-
рывна на |а, Ь|. Тогда если функция f(x) имеет производную в точке
®о € (а, Ъ) и /'(®о) Ф О, то обратная функция <р(у) = f~1(y), опреде-
ленная на промежутке |c,d| = /(|а, Ь|), имеет производную в точке
Уо = /(хо) G (c,d), причем <р'(уо) = 1//'(®о).
Доказательство. Поскольку функция /(х) строго моно-
тонна и непрерывна на промежутке |а, 6|, то в силу теоремы об об-
ратной функции обратная функция ^(у) = /-1(у) определена, строго
монотонна и непрерывна на связном множестве /(|а, Ь|), являющемся
промежутком |с, d| того же вида, что и |а, Ь|. Пусть хо, хо+Ах € (а, Ъ).
Положим уо = /(®о), ®о = <р(Уо), тогда
Уо = /(?(уо)) € (с, d), уо + Ду = №(уо + Ду)) € (с, d),
откуда Ду = f(<p(y0 + Ду)) - /(^(уо)). Заметим, что в силу строгой
монотонности обратной функции = /-1 имеем
(Ду 0) (у>(уо + Ду) - <р(у0) 0 0),
5*
131
причем поскольку <р = f 1 G Cdc, d|), то
lim Myo + Ду) - <р(уо)) = 0.
Ду->0
Но тогда при Дт/ 0 Vj/o + &У 6 (с, d) имеем
y>(i/0 + Ду) - У>(уо) _ х /_Ду__________
Ду	/ ¥>(уо + Ду) - ¥>(уо)
_ х / /(у(уо + Ду)) - /(у(уо))
/	<р(у0 + Ду) - р(уо)
Но f G поэтому существует
„ = W( ( н=„
AWO <p(yQ + Дт/) - ^(т/0)	7
и, стало быть,
Т. е. </> е 2>(х/о), причем <р'(уо) = 1//'(ж0), где yQ = /(®о).
Замечание. Формулу для вычисления производной функции
х = ж(т/), обратной функции у = т/(ж), можно записать в виде
dx __ I dy
dy J dx*
Следствие. Пусть функция х —> /(ж) осуществляет гомео-
морфизм промежутка |а, Ь| на промежуток |с, d| = f (|а, Ь|), а у —> ^>(т/)
есть обратный гомеоморфизм. Если функция f(x) дифференцируема в
точке xq G (а, Ь) и /'(жо)	0, то функция <р(у) имеет в точке т/о = f(%o)
производную </>'(уо) = l/ff(xQ).
Доказательство. Из того, что х -> f(x) есть гомеомор-
физм промежутка |а, 6| на промежуток |с, d| = /(|а, Ь|), следует, что
внутренняя точка xq 6 (а, Ь) переходит во внутреннюю же точку
J/o = /(®о) 6 (с, d), причем / 6 С(|а, Ь|) и функция f(x) строго мо-
нотонна на |а, Ь|. Теперь остается применить теорему о производной
обратной функции.
§ 5.	Производные элементарных функций
1.	Если с - постоянная, то (рассматривая постоянную функцию
х —> с) имеем с' = 0.
2.	(жп)/=пжп“1 VneN.
3.	(sin®)' = cos®.
132
4.	(cosx)' = — sin®.
5.	(tg x)f = 1/ cos2 ®, x тг/2 4- тгп (n = 0, ±1, ±2,...).
6.	(ctg®)' = —1/sin2®, x irn (n = 0, ±1, ±2,...).
7.	(arcsin®)' = l/\/l — ®2, —1 < ® < 1.
Для доказательства формулы 7 воспользуемся теоремой о произ-
водной обратной функции ® = sin у, у 6 (—тг/2, тг/2), заметив, что
cosy > 0 Vy Е (-тг/2,тг/2), тогда
= 1/со8у = 1/\/1-sin2!' = .
8.	(arccos®)' = —1/л/1 — ®2, ® Е (—1,1). В самом деле, ® = cosj/,
у Е (0,7г), причем sin у > 0 Vy Е (0, тг), тогда по теореме о производной
обратной функции имеем
3^ = 1 /= — 1 /sin у = —1 /у/1 ~ cos2 = —1/\/1 ~ ®2*
dx / dy	/
9.	(arctg ®)' = 1/(14- ®2).
10.	(arcctg ®)' = —1/(1 4- х2).
11.	(In®)' = 1/®, х > 0. В самом деле, (у = In®, ® > 0)
1	1	/ Дж\
=> (у1 = lim ——(1п(® 4- Д®) — In ®) = lim 3— In I 1 4-----------I =
Дя?->0 Д® v '	7	д®->о Д® у х J
-.	1 I ^Х t А V |	.
hm —— (--------|-о(Д®) 1 = 1/®).
Дт->0 Д® у х	J
12.	(а*)' = ах • Ina, ® Е (—оо,4-оо), 0 < a, а / 1; (ех)' = ех.
В самом деле, у = ех => ® = In у, и по теореме о производной обратной
dy I dx /1
функции имеем — = 1 / — =1 / - = w = е .
dx / dy /у
13.	(®a)' = a®a-1, a E R, x E (0,4-oo).
В самом деле, у = ха => у = еа 1пяг, и по теореме о производной сложной
функции имеем
у/ _ (e«lnxy = e«to*(alna;)' = еа1“® • а/х = а®"’1.
§ в. Производные и дифференциалы высших
порядков
Определение. Пусть функция х —> /(®) определена на мно-
жестве М С (-оо,4-оо). Полагаем /^(®) = f(x), f^(x) = ff(x) =
D/(®) для тех х Е Mf для которых функция f(x) дифференцируема,
и, вообще, Vn Е No (если функция х —> f^n\x), где f^(x) = Dnf(x),
133
определена в некоторой окрестности U(x) СМ точки х ЕМ) пола-
о
гаем Dn+1/(®) = D(Dn/(®)) для тех точек х ЕМ, в которых функ-
ция Dnf(x) дифференцируема.
Замечание. Для того чтобы n-я производная /(п)(ж) сущест-
вовала в точке ®о ЕМ, производная f^n~x\x) должна существовать в
некоторой окрестности Е7(азо) точки xq и должна быть дифференцируе-
мой в точке хо- При этом функция /<п”2)(х) должна быть дифференци-
руемой в окрестности 17(®о) (где существует производная
Пример. Пусть у = 1/ж V® 0. Тогда у^ = (-1)п • п! • ж"”"1
Vn Е N. Доказательство проводится по индукции: у^ = ж"1, у1 =
(-1)1®-2, ...,	= (y^Y = ((-l)n • n! •	= (-1)"*1. (n +
1)! • art”*2).
Теорема. Если существует Dnfi(x) (i = 1,2,... , m) и с, -
постоянные (г = 1,2,... , т), то существует
(7П	\
»=1	/
причем
(т	\	т
•=1	/	1=1
Доказательство. При а = 1 теорема была доказана в § 4
гл. 5. При п > 2 по индукции имеем
D" (2>Л(®)] = D Dn-X
\»=1 / . \»=1
= D (f>Dn-7,(x)) =	(D"-7i(x)) =
\»=1 / 1=1 1=1
Теорема (формула Лейбница). Если существует Dnu(x),
D"v(®), то D"(u • v) = £ C*Dku • D"-‘v, где C” = C° = 1,
k=0
C" = Jb!(n - fc)!' 0! = 1! = L
Доказательство. При n = 1 имеем
i
D(u • v) = Du • D°v + D°u • Dv = 52 С&и • Dx"*v.
*=o
Далее, проводим по индукции переход от п к п + 1:
Dn+1(u- v) = D(Dn(u-v)) = D [52C'"D*W,D"'*V) =
\k=0	/
134
= S c'nDfe+1u • D”"*v + £C«D*U • Dn+1-*v =
k=0	k=0
= (делаем замены &-|-1 = тий = т) =
n + l	n
2 C™-xD’nu • Dn+1-mv + 52 C™Dmu • Dn+1-TOV =
m=l	m=0
= C°D°u • Dn+1v + 52 (C'n'‘“1 + Cn) Drau • D”+1"”*H-
n=l
+C„Dn+1u • D% (C° = C°+x = 1,	= Cffl = 1,
—x*vm	71»!	71.
/Чш—1 I /1ТП __	।	_
n n “ (7п-1)!(п-7п+1)!	т!(п-тп)! "
_ n!(m+ (n+ 1 - m)) _	n!(n+ 1)	_ m \
тп!(п + 1 — тп)! m!(n+l — m) n+1) ’
поэтому
n + l
D"+1(U • v) = 52 C'n'l+iDmu • Dn+1"rav.
rn=0
Пусть числовая функция f(x) определена и дифференцируема в
окрестности С7(®о) (т. е. f 6 D(C7(®o))? так что V® 6 17(®о) существует
линейная форма (1-й дифференциал функции f(x)) df(x) : h —> D/(®)x
h => D/(x) • h = df(x)(h) (df(x) = ff(x)dx), являющаяся функцией x в
окрестности U(xо).
Определение. Функция f(x) называется дважды диффе-
ренцируемой в точке xq (запись: f 6 T№(xq)), если f G ®(t/(®o))
и линейная форма df(x) = D/(®)d® дифференцируема (по х) в точ-
ке xQf т. е. если существует постоянная Az такая, что Vh € R
в окрестности U(xq) имеет место представление V®o + k € 17(®о)
df(xQ + k)(h) - df(xQ)(h) = (A2k + o(k))h = A2 - h • k + h • o(k) (k -> 0).
Билинейная форма d2/(®o) J (Л, k) —> A2 • h • к называется при этом
2-м дифференциалом функции f(x) в точке ®о*
Замечание. Если f € T>^(xq)} то из представления
D/(®o + Д®)Л - D/(®o)^ = (ЛзД®+
+о(Дх))Л (Дх -+ 0) V®o + Д® € U(xq)
легко получаем
=	D/(»o + Ax)-d/(xo) = 2
Л-_кЛ	Am
135
Следствие. Если / Е	то существует билинейная
форма d2/(«o) • (Ь, fc) —> D2/(®o) • h • к такая, что для 1-го диффе-
ренциала функции /(®) в окрестности U(xq) (VA Е R) имеет место
представление V®o 4- к Е U(xq):
df(xQ + k)(h) - df(x0)(h) = D2/(®o) • h • к 4- h - o(k) (fc -> 0).
Поскольку dx : h 1 • h (dx : fc —» 1 • fc), то применяется запись
d2/(x0) = D2/(so)d®2.
По индукции вводится следующее определение n-раз дифференци-
руемой функции.
Определение. Функция f(x), определенная в окрестнос-
ти U(xq), называется п-раз дифференцируемой в точке а?о, если
f е Р^п"1)(17(®0)) « существует полилинейная п-форма (п-й диффе-
ренциал) dnf(xQ) : (fci,... , Лп) -> Dnf(xQ) -hi...hn (dnf(x0) : Rn
R) такая, что в окрестности U(xq) для (п — 1)-го дифференциала
dn~1f(x) имеет место представление
(dn-7(xo + hn) - dn-7(®o))(fci,. . . , fcn-l) =
= Dn/(®o) • Л1 • • • Лп 4- Ai • • • hn-i • o(hn) (hn —> 0)
V(fci,... , E Rn \ ®o 4- hn E U(xq).
Очевидно, имеет место следующий критерий.
Теорема (критерий дифференцируемости). Пусть функция
f(x) определена в окрестности U(xq). Тогда (f Е 'D^(xq))
(существует конечная Dnf(®o))*
Замечание. Если х - независимая переменная, то линейная
форма dx : h 1 • h не зависит от х и поэтому (р : х ®, р9(х) = 1,
р"(х) = 0) d2x : (Л, fc) -> 0 • h • fc, т. е. dmx = 0 Vm > 2.
Замечание. Если u, v Е 2>(®о), то
d(u • v) = du • v 4- и • dv (d(u • v) = (и • v)fdx =
u'dx • v 4- и • vfdx = du>v 4- u> dv).
Формальное правило. Пусть функция х —> f(x) определена
в окрестности U(xq) и х Е U(xq). Тогда полагают у = f(x)-, d°y = у,
dry = dy, d2y = d(dy), ..., dny = d(dn~’1)y, n E N.
Для x, независимого переменного, имеем dkx = 0 Vfc > 2, и тогда
dy = y'dx, d2y = d(y,dx) = d(yf)dx 4- t/'d2® = y"dx2, t. e. dny = y^dxn
Vn E N. Таким образом, в случае х, независимого переменного, и у =
у(х) имеем обозначение

136
Замечание (об неинвариантности формы дифференциала
высшего порядка). Если х = x(t) есть дифференцируемая функция,
то формула dny = y^dxn при п > 2, вообще говоря, не имеет места.
Например, d2y = d(dy) = dtf • dx +	• d2x = y"dx2 4- yfd2x, где d2x =
x"(t)dt2 / 0, t. e. d2y = y"dx2 4- tfd2x, а не d2y = y"dx2.
Замечание. Если u, v, щ 6 7>^(xq) и q (г = 1,2,... , m) -
/ m \
постоянные, то при ж, независимой переменной, имеем dn I 52 c«u« ) =
\t=i /
тп	п
у* c,Jnu,, а также dn(u • v) = 52 Ckdku • dn~kv (формула Лейбница).
»=i	fc=o
Пример.
и = х3, V = е*; dn(x3 • ех) = ^С*<1к(х3)  <Г*-*(е’),
fc=o
но
dmex = e*dxmVm е N; d(x3) = 3x2dx,d2(x3) = 6xdx2,
d3(x3) = 6dx3, dk(x3) = OVfe > 4, => dn(x3e’) =
/ 3 л 2 6n(n-l) 6n(n — l)(n - 2)\ _ n
= e ( ж3 4- Зпж2 4“ — ~x + — ---------#------- ) dx *
Определение. Пусть функция f(x) определена на (а,Ъ).
Скажем, что f(x) т-раз непрерывно дифференцируема на (а,Ъ)
(запись: f е С<т>((а,Ъ))), если f е 2><т)((а, 6)) и Dmf Е С(а,Ь)).
Определение. Пусть функция f(x) определена на отрезке
[а, 6]. Скажем, что функция f(x) кусочно т-раз непрерывно диффе-
ренцируема на [а, 6], если функция f(x) может иметь на [а, Ь] разры-
вы только 1-го рода и существуют такие точки а = ао < ai < аг <
... < an-i < ап = Ъ, что функции

f(ai 4- 0), х = а,-,
/(ж), х е (а,-,а,+1),
/(а,+1 - 0), х = ai+i; i = 0,1,
n - 1,
таковы, что fi G С^т)([а,, a,+i]) (г = 0, l,...,n— 1) (в концах а,
w а1+1 отрезка [a,, ai+i] нужно рассматривать соответствующие
односторонние производные порядка к (к = 1,2,... , т)).
§ 7. Теоремы о конечных приращениях
Определение. Пусть функция f(x) определена на множес-
0
тве М, тогда внутренняя точка xq ЕМ называется точкой локаль-
ного максимума (локального минимума) функции f(x) на множестве
если существует окрестность U(xq) С М такая, что
f(x) < /(жо) (/(Ж) > /(жо)) Уж G (7(жо).	(7.1)
137
Если в (7.1) вместо < (>) стоит < (>), то внутренняя точка
о
хо ЕМ называется точкой строгого локального максимума (стро-
гого локального минимума) функции f(x) на множестве М.
о
Замечание. Если внутренняя точка хо €М ~ точка локально-
го максимума или локального минимума функции f(x) на множестве
о
М, то хо €М называется точкой локального экстремума функции f(x)
на множестве М.
о
Замечание. Если функция х -> f(x) достигает в точке xq ЕМ
своей точной верхней грани на М, то функция f(x) имеет в этой точке
локальный максимум, являющийся абсолютным максимумом функции
f(x) на множестве М. Обратное, вообще говоря, неверно.
Пример. Для функции f(x) с графиком, изображенным на
рис. 23, /(1/4) = 1/2 есть значение локального максимума, а /(1/2) =
1/4 есть значение локального минимума, но
Рис. 23
х
/(1/8) = 0 = mf/(х)	1/4 =/(1/2);
/(7/8) = l = sup/(x)#l/2 = /(l/4).
(ОД]
Теорема Ферма. Пусть
функция f(x) определена на промежут-
ке |а, Ь| и имеет в точке xq Е (а, Ь)
локальный экстремум. Пусть функция
f(x) имеет в точке xq, как правую,
так и левую производную (конечные
или бесконечные).
Тогда D+/(®) < 0, D"/(xo) > 0, если хо “ точка локального мак-
симума, и D+/(®o) > О, D"/(®o) < 0, если хо - точка локального ми-
нимума. В частности, если функция f(x) имеет в точке локального
экстремума xq € (а, Ь) производную (конечную или бесконечную), то
D/(®o) = 0.
Доказательство. Пусть xq € (а, Ь) есть точка локально-
го максимума функции f(x) в промежутке |а, Ь|. Тогда существует
окрестность U(xq) С |<х, Ь| такая, что f(x) < /(хо) V® € U(xq), и при
/(х) — f(xn)
х - х0 > 0 тогда имеем	———- < 0, поэтому
X — Хо ”
Hm zAfo.} - D+/(®o) < 0.
а?—X Xq	““
Аналогично доказывается, что D_/(®o) > 0. Если в точке ®о 6 (а,Ъ)
существует производная D/(®o) (конечная или бесконечная), тогда не-
обходимы равенства D/(®o) = D+/(®o) = D"/(®o), но тогда, очевид-
138
но, (Г(®о) < о) Л (Г(®о) > о) => f'(x0) = 0.
Замечание. Если функция f(x) дифференцируема в точке
хо € (0>^) и имеет в «о локальный экстремум, то /'(®о) = 0 я ка-
сательная к графику функции в точке (хо, /(хо)) параллельна оси аб-
сцисс Ох; обратное, вообще говоря, неверно.
Пример. Функция у = х2, х € (-оо, +оо), график которой из-
ображен на рис. 24, имеет в точке xq = 0 локальный минимум, и
касательная к графику этой функции в точке (0,0) есть ось Ох.
Пример. Функция у = хэ, х € (-оо, +оо) (график которой из-
ображен на рис. 25) такова, что ось Ох является касательной к ее гра-
фику Г в точке (0,0). Однако наша функция не имеет в точке хо = 0
локального экстремума.
Теорема Ролля. Пусть непрерывная на отрезке [а, 6]
функция /(х) имеет в каждой точке интервала (а, Ь) производную
f'(x), конечную, или равную +оо, или равную -оо. Если при зтом
f(a) = f(b) = 0, то существует, по крайней мере одна, точка с €
(а, 6) такая, что /'(с) = 0.
У*
Рис. 24	Рис. 25
Доказательство. Если /(х) = 0 на [а, 5], то теорема Рол-
ля очевидна. Пусть функция /(х) не является тождественным нулем,
тогда /(х) принимает по крайней мере одно значение > 0 или хотя
бы одно значение < 0.
Рассмотрим, например, первый случай. Тогда / € С([а, 6]) => М =
eup/(x) > 0. Поскольку / € С([а, 5]), то по теореме Вейерштрасса
1«,Ч
существует с 6 [а, 5] такая, что /(с) = М > 0. Но в силу условия
/(в) = /(Ь) = 0 имеем с € (а, 6). Но тогда точка с € (а, Ь) есть точка
локального максимума функции /(х) на отрезке [а, 6], причем в силу
условий теоремы Ролля существует f'(c) (конечная или бесконечная).
По теореме Ферма имеем f(c) = 0.
139
Замечание. Условие о существовании конечной или бесконеч-
ной производной у непрерывной функции в условиях теоремы Рол-
ля нельзя заменить на существование односторонних производных
D+/(®) и	В самом деле, пусть f(x) = 1 — |®|, х 6 [—1,1] (рис.
26). Тогда /(-1) = /(1) = 0 и V® G (—1,1) 3D+/(s), D~/(s), причем
р+/(0) = —1, D”/(0) = 1. Однако не существует точки с Е (—1,1)
такой, что D+/(c) = D”/(c) = D/(c) = 0.
Следствие. Между двумя соседними нулями дифференциру-
емой на интервале функции лежит по меньшей мере один нуль ее про-
изводной (рис. 27).
п
Следствие. Если Рп(х) = £ (ап # 0) ~ многочлен п-й
fc=O
степени, то уравнение Рп(ж) = 0 имеет не более п решений.
У
Рис. 27
Доказательство. Допустим от противного, что уравнение
Рп(®) = 0 имеет не меньше п + 1 (действительных) решений gi < д2 <
• • • < qn < Яп+i, Pn(gi) = 0 (г = 1,2,... ,n + 1). Тогда производная
п
DPn(®) = 52 ^akXk~1 является многочленом степени n — 1 и по теоре-
fc=i
ме Ролля Vi (i = 1,2,..., п) ЗЬ, такое, что д,- < Ь, < g,+i и DPn(M = 0,
т. е. уравнение DPn(z) = 0 имеет не меньше п действительных реше-
ний. Продолжая дифференцировать и применять теорему Ролля, ви-
дим, что для т < n DmPn(x) = £ к(к - 1)... (к - т + 1)акХк~т,
к—тп
причем уравнение DmPn(®) = 0 имеет не меньше n+1 — т решений. В
частности, при т = п это уравнение должно иметь не меньше одного
решения, в то время как DnPn(®) = п! • ап 0, поэтому уравнение
DnPn(®) = 0 вообще не имеет решений. Противоречие.
Таким образом, уравнение Рп(®) = 0 имеет не больше п решений,
п
Следствие. Если Рп(®) = 52 акхк, ап Ф 0, п > 2, и уравнение
fc=O
Рп(«) = 0 имеет ровно п различных (действительных) решений, то
уравнение DPn(®) = 0 имеет точно п — 1 (действительных) решений.
140
Доказательство. Производная DPn(®) есть многочлен
степени п—1 и в силу предыдущего следствия имеет не больше n—1 ну-
лей. Поскольку Рп(ж) имеет ровно п нулей gi < дг <••• < Qn-i < Qn,
а по теореме Ролля между двумя соседними нулями д, < <7*4-1 (i =
1,2,... ,п - 1) многочлена Рп(а?) существует по меньшей мере один
нуль bi Е (gi, g*+i) производной DPn(s), то этих нулей не меньше п — 1,
т. е. п - 1.
Теорема Лагранжа (о формуле конечных прираще-
ний). Пусть функция f(x) определена на отрезке [а, b], f Е С([а, Ь]) и
Ух Е (а,Ь) существует конечная или бесконечная производная f
Тогда существует с Е (а,Ь) такая, что ff(c) = ^7—
о — а
Доказательство. Введем вспомогательную функцию
F(ж) = f(x) - f(a) - А(ж - а). Тогда F(a) = 0. Выберем постоян-
ную Л так, чтобы иметь F(b) = 0, т. е. f(b) - f(a) — X(b - а) = 0
=> А = (/(b) - /(a))/(b - а). Тогда F Е C([a,b]), F(a) = F(b) = 0 и
Ух Е (а, Ь) существует (конечная или бесконечная) F'(x) = ff(x) — А.
По теореме Ролля Зс Е (а,Ь) такая, что F'(c) = 0 => (/'(с) = А) =>
fr(c) = ZM .
у	о — а /
Замечание. Формула конечных приращений из теоремы Ла-
гранжа часто записывается в виде
f(x + h)-f(x) = Df(x + 9h)h,
0 € (0,1); х, х + h € [а, Ь].
Пример. f(x) = tfx, х € [-1,1], f € C([-l, 1]); Vx / 0 3d/(x) =
|х-2/3, D/(0) = lim — = +oo; /(1) - /(-1) = D/(c) • 2, где c =
О	®—>0 x
±3~3/2.
Замечание. В теоремах Ролля и Лагранжа условие о су-
ществовании конечной или бесконечной производной (равной +оо или
-оо) Ух Е (а, Ь) нельзя заменить на условие существования конечной
или бесконечных односторонних производных (D+/(s) = +оо (—оо),
D~/(s) = -оо (+оо), причем D+/(s) / D”/(s)).
Пример (рис. 28). f(x) = а/я2, х Е [-1,1], D/(s) =
Чя О, D+/(0) = +оо, D“/(0) = -оо; /(1) - /(-1) = 0 и не сущест-
вует точки с Е [—1,1] такой, что D/(c) = 0, т. е. ни теорема Ролля,
ни теорема Лагранжа не верны для рассматриваемой функции /.
Из теоремы Лагранжа вытекает следующая
Теорема (обобщенная теорема Ролля). Пусть f Е С([а,Ь])
иУх е (а,Ь) существует (конечная или бесконечная) производная
Г(х), причем f(a) = /(b). Тогда существует с Е (а,Ь) такая, что
/'(с) = 0.
141
Замечание. Если f £ С(С7(®о)) и V® Е £/(®о) существует ко-
нечная или бесконечная производная f(x), то V® = ®о + Д® £ U(xq)
Эч? € (0,1) такое, что Ду = D/(®o + 1? • Д®) • Д®.
Доказательство. Пусть Ду = /(®о + Д®) - /(®о)> причем
[®о, ®о+Д®] С U(xq) при Д® > 0 или [®о+Д®, ®о] С 17(®о) при Д® < 0.
Применяя теорему Лагранжа, найдем при Д® > 0 с € (®о, ®о + Д®)
(т. е. с = ®о + $Д® при 0 <	< 1 такое, что Ду = /'(с)Д®) =»
Ду = D/(®o 4- 1?Д®) • Д® (при Д® < 0 рассуждения аналогичны).
Замечание (о геометрическом смысле теоремы Лагранжа).
Если функция /(®) удовлетворяет на отрезке [а, 6] всем условиям те-
оремы Лагранжа, то на графике Г = {(®, у) Е R2 |у = /(®), а <х <Ь}
функции /(®) существует точка С = (с, /(c)) Е Г (где а < с < Ь) та-
кая, что касательная к графику Г в этой точке параллельна секущей,
соединяющей точки А = (а, /(а)) £ Г и В = (Ь, /(b)) Е Г (рис. 29).
Следствие 1. Если / € С([а, Ь]) и / Е 1>((а, Ь)), причем су-
ществует постоянная L > 0 такая, что |2?/(®)| < L V® Е (а, Ъ), то
|/(® 1) - /(®г)| < £|®1 - ®з| V® 1, ®2 € [а, Ь].
Доказательство. Достаточно применить к функции /(®)
на отрезке [®2, ®2] С [а, Ь] теорему Лагранжа, в силу которой сущест-
вует с Е (®х, ®2) такая, что /(®2) - /(®2) = D/(c)(®2 - ®i)> но тогда
(|D/(®)| < L V® 6 (a,b)) =► (|/(®2) - /(«1)| < £|®1 - ®г|).
Следствие 2. Пусть / Е С([а,Ь]) и /(®) дифференцируема
V® £ (а, Ь) \ Кп, где Кп С (а, Ь) - множество, состоящее не более
чем из п точек. Пусть существуют постоянные т и М такие, что
m < /'(®) < М V® Е (а, Ъ) \ Кп< Тогда имеет место оценка
“ Ь-а ~
Доказательство. Пусть Кп = {®i,..., ®n} С (а, Ъ), при-
чем а = ®о < ®х < ... < ®п < ®n+i = Ь. Заметим, что / £ С([а, Ь])
=> / Е С([®й®,+1]) (t = 0,1,... ,п) и V® Е (®,-,®,+i) 3f(x) (причем
142
т < f'(x) < М)- Применяя к функции f(x) на отрезке [®<, ®i+i] тео-
рему Лагранжа, видим, что Зс< € (®<, ®<+i) (* = 0,1,... , п) такие, что
/(®<+i) - f(xi) = f (с<)(®<+1 - ®<), и в силу оценки т < ffa) < М
имеем неравенства m(®<+i - ®<) < /(®<+i) - /(®.) < Af(®<+i - ®<)
(: = 0,1,..., п), откуда, суммируя по i, получаем оценки
т £ (®«+1 “ ®<) = т(6 - а) < £ (/(®<+1) “ /(®<)) = /(ь) “ /(°) <
4=0	1=0
< М £(®4+i -®<) = M(b-a) => m(b-a) < f(b)-f(a) < M(b-a).
Теорема (формула Тейлора с остаточным членом в форме Ла-
гранжа). Пусть f € Ctm)(U(xo)) u V® 6 U(xo) существует конечная
или бесконечная производная Dm+1/(®). ТогдаУх € 17(®о) Зс € (®о, ®)
(или Вс € (®,®о)) такая, что имеет место представление
т 1
/(®)-/(®o) = S^(®-xo)‘D*/(®o)+
Доказательство. Введем вспомогательную функцию
w 1	1
F(t) = /(®) - /(<) - р ~ <)‘D‘/(*) - (х - <)m+1A-
Тогда, считая для определенности х > хо, [®о» ®] С U(xq), имеем
F € С([®о» ®]) и Vt € (®о> ®) IF'(t) = -/'(<)+
w 1
-Йи(г",)‘/<‘+11,<) + Я(1”<ГА =
fc=l
= -nt)+гм+Ej I® -	(«)-
- Е ^|(« -<)fc/(fc+1)(0 - ±(Х -	+ ^(® -i)mA,
fc = l	*
т. е. существует (конечная или бесконечная) производная
Df,{<) =	(® “ *)mDm+1/(<) + (® - <)”*А.
143
Далее, F(x) = 0. Выберем постоянную А так, чтобы иметь F(x$) =
0. Тогда в силу теоремы Ролля, примененной к функции F(t) на от-
резке [®о, х], видим, что существует с G (®о, такая, что DF(c) = 0,
откуда имеем
-с)т-Х = ±(х - c)TODm+1/(c) => А = Dra+7(c).
Теперь формула Тейлора (с остаточным членом в форме Лагран-
жа) вытекает из равенства F(xq) = 0 при А = Dm+1f(c).
Замечание. Формулу Тейлора с остаточным членом в форме
Лагранжа часто записывают в виде (V® 4- Л 6 17(®))
"L hk . Лт+1
f(x + Л) = f(x) + £	+
k\	(m+ 1)!
где - некоторое число из интервала (0,1).
Теорема (формула Тейлора с остаточным членом в форме
Пеано). Пусть f е ^"-^(хо)) (т = 1,2,...) и f е ©<т>(х0). Тогда
в проколотой окрестности U(хо) имеет место представление
™ (г _ ~.\к
f(x) = /(хо) + £ .., о; d7(*o) + о((х - х0)го) (х -> хо).
к-1
Доказательство. При т = 1 формула Тейлора справедлива,
поскольку / е Т>(х0) => /(х) = /(хо) + D/(x0)(x - хо) + о(х - х0)
(х ->• хо).
При т > 2 введем так называемый многочлен Тейлора
Яп(х; /, хо) = /(х0) + £ ^ ~*о)*в7(хо)
к=1
и отметим, что при 1 < р < т
Олп / Л \ ’t-л — 1) . . . (fc — р+ 1) /	\
У» ®о) —	(® — ®о)	У(®о)*
к=р
Но при р < к < т имеем
ХО) |х=хо - | Oj к
т. е., полагая х = ®о> имеем
TF?m(x0\ f, ®о) =	= Iffixo) (р = 1,2,... , тп)
р!
и Лп(®о;/,®о) = У(®о)«
144
Таким образом, если ввести вспомогательную функцию
ff(®) = Д®)	X е U(x0),
Tofe (U(xq)) =^де р(т-1)(С7(а;о)) (т. е. д G С<т-2\Щх0)) <
^m'1\U(x0))), afe Ъ<т\хо) =>д£ ®<т)(Жо), причем Вр^(жо) =
О (р = 0,1,... , т). Применим к функции д(х) в окрестности U(xq)
формулу Тейлора (с заменой т > 2 на т — 2) с остаточным членом в
форме Лангранжа. Тогда при т > 2 имеем представление в U(xq)
(т —
ff(®) = “7---7Т7—Dra-1ff(®0 +	- Хо)), 0 < 1? < 1,
(m — 1J!
где 19 = 19 (ж) зависит от (ж — ®о)-
Но д 6 ^т\хо) => 'Dm~1g G 2>(жо), и поэтому имеем представление
Вт“1р(ж0 4- 19(ж - а?о)) = Dm~1^(®o) + $ (ж - so)Dw0(®o)+
• 4-о(ж - Жо) (® -» Жо),
отсюда в силу отмеченных ранее равенств Втп-1<7(жо) = Втр(жо) = 0
имеем в 17(жо)
Вт-1£(жо 4- 19(ж - ®о)) = о(х - xq) (х ®о),
т. е. в 17(жо) имеет место представление д(х) = о((ж — жо)т) (ж —>
жо). Но тогда доказано, что в проколотой окрестности 17(жо) имеет
место представление f (ж) = Рт(ж; /, жо) + о((ж —жо)т) (ж —> ®о)« Итак,
формула Тейлора с остаточным членом в форме Пеано доказана.
Приведем основные асимптотические разложения по формуле Тей-
лора (с остаточным членом в форме Пеано) для простейших элемен-
тарных функций.
п
1И = 1+Етг + °(а:")
fc=l
В самом деле, пусть /(ж) = е®, тогда В*Дж) = ех => B*f(0) = 1
Vfc е n0.
Применение формулы Тейлора с остаточным членом в форме Пеано
дает искомое разложение.
n	x^+i
2)	sinx= £	+ °(® + ) (ж -> 0)-
fc-о	4- 1)!
В самом деле, /(ж) = sin®, Bsinx = cos® = зш(ж 4- тг/2), Dkf(x) =
i /л\	• т7Г ( (—l)fc притп = 2fc 4-1,
»ш(* + Ьт/2), D /(0) = «п — = | ‘ np'„m = ik
fl
3)	cos X = 1 + £ (-1)‘	+ o(x2n) (x 0).
* = 1
145
В самом деле, /(®) = сое®, D/(®) = — sin® = соз(® + тг/З), Dm/(®) =
.	Г (-1)*,т = 2Л,
сов(® + ттг/2), Dm/(0) = coe(mff/2) = | q, „J _ 2fc + 1,
4)	1п(1 + ®) = 52	+ Д®п) (® “* 0)*
*=1 «
В самом деле, /(®) = ln(l + ®), D/(®) = (1 + ®)“х> Da/(®) = (-1)1 х
1!(1 + ®)"2, Dm/(®) = (~1)т-1(т - 1)1(1 + ®)"т (т > 1), Dm ДО) =
(-1)т-1(т - 1)! (т > 1), /(0) = 0.
5)	(1 + ®)“ = 1 + t а{а~1}“,\а~-+1)хк + о(®п) (® -> 0).
*=i	*!
В самом деле, /(®) = (1 + ®)“, D/(®) = а(1 + ®)“-1, D*/(®) = «(« -
1)... (а - к + 1)(1 + ®D* ДО) = а(а - 1)... (а - к + 1) (к > 1).
п 2.2*+!	.	,
в)sh ж = S3 7ЙТГ1М +
*=О
В самом деле, Deh® = ch®, Dch® = eh®, Da*sh® = eh®, Da*+1sh® =
ch ®, eh(0) = 0, ch(0) = 1.
7) ch ® = 1+ £ ®2*/(2*)! + o(®2n) (® -> 0).
*=i
В самом деле, Da* ch ® = ch ®, Dafc+1 ch ® = eh ®, f(x) = ch ®, Dm Д®) =
( 1, m = 2fe,
( 0, m = 2k + 1 (m > 1).
Теорема Коши (о конечных приращениях). Пусть функции
f(x) и д(х) определены на отрезке [а, 6], причем:
1) f € (7([а, 6]) u V® € (а, Ь) существует конечная или бесконечная
производная D/(®);
2?0€С([а,Ч)Л1>((а,Ь));
3) Dp(®)	0 V® € (а, Ь). Тогда Зс 6 (а, Ь) такое, что
D/(c)/Dff(c) = (ДЬ) - Да))/(ДЬ) - Да)).
Доказательство. Из условия 3) Dy(®)	0 V® € (а, Ь) при
выполнении условия 2) d € С([а, &]) Л 1>((а, Ь)) в силу теоремы Ролля
(в обобщенной формулировке) имеем д(а) д(Ь). Введем вспомога-
тельную функцию F(x) = f(x) — Хд(х) и выберем постоянную А так,
чтобы выполнялось равенство F(a) = F(b). Тогда
(/(а) - АДа) = ДЬ) - АДЬ)) => (А = (/(Ь) - /(а))/(ДЬ) - Да))),
и поскольку F € С([а, Ь]), F(b) = F(a) itVt € (а, Ь), в силу условий
1) и 2) существует конечная или бесконечная производная D-F(®) =
D/(®) - АОД®).
По теореме Ролля (в обобщенной формулировке) Зс € (а, Ь) такая,
что DF(c) = 0, т. е. (D/(c) - АоДс) = 0)	(D/(c)/Dp(c) = А) =#>
(D/(c)/Dp(c) = (ДЬ) - /(а))/(ДЬ) - Да))).
Замечание. Условия 1) и 2) в теореме Коши (о конечных при-
ращениях) можно заменить на условия 1') / € С([а, Ь]) ЛР((а, 6)) и
146
2') в C([ai Ч) и Vs G (a, b) существует конечная или бесконечная
производная Dg(x) (при выполнении условия 3)). Однако при выпол-
нении условий 1), 2') и 3) проведенное выше доказательство теоремы
Коши не проходит (почему?).
§ 8. Правила Лопиталя раскрытия
неопределенностей
Теорема 1 (правило Лопиталя раскрытия неопределенности
вида 0/0). Пусть функции /(s) и д(х) определены на интервале (а, Ь),
причем: 1) 3 lim f(x) = lim д(х) = 0; 2) f,g€ D((a, b)) и Dg(®) #
»-+a4"O	®-4a+O
0 Vs G (a.b); 3) 3 lim — 4 где А конечно или символ +oo
»->a+o Dfl(s)
(-oo). Тогда Э lim = A.
»-+a+o p(s)
Доказательство. Воспользуемся определением предела
функции (при х -4 a + 0) по Гейне. Пусть (sn) - любая последова-
тельность Гейне, связанная с точкой а, т. е. а < хп < b 'in € N и
f(x )
lim хп = а. Докажем, что Э lim —--у = А.
п^+оо	п-Ц-оо p(sn)
Рассмотрим отрезок [a, sn] и доопределим функции / (s) и д(х) в
точке s = а, положив /(а) = д(а) = 0. Тогда функции /(s) и д(х)
определены на отрезке [a, sn] и удовлетворяют следующим услови-
ям 1) - 3): 1) f,g € С([а, sn]). В самом деле, поскольку Vs G (а, Ь)
3/'(®),ff'(s), то f,g € С((а, Ь)), а из соотношений ( lim /(s) = 0 =
Ла)> = 0 =	* ^9 е (f>9 € c<M)))i
2) Vs G (a,sn) 3Df(®), Dff(®); 3) D$(®)	0 Vs G (a,b) и, в част-
ности, по теореме Ролля (в обобщенной формулировке) ff(sn) 0.
На отрезке [a, sn] к функциям f(t) и g(t) применима теорема Ко-
ши (о конечных приращениях), поэтому Vn G N 3cn € (a, sn) та-
кое, что	Но последовательность
. . ff(®n) 5(®n)-5(a) D0(cn)
(Cn) удовлетворяет условиям a < cn < sn < b in G N, lim cn =
..	»4+co
n-i?oo = a’ П0ЭТ0МУ (cn) есть последовательность Гейне, связанная с
точкой а. В силу условия теоремы 3 lim D/(s)/Dp(s) = А, поэтому
-	®-»а+0
3 n-i+^j D/(cn)/Dl/(cn) = А. Но тогда при п -> +оо существует предел
lim	lim PZ<C")
”“+«> д(хп) ЛТоо Dff(cn)
147
т. е. 3 lim = А.
®->а+о д(х)
Замечание. Теорема 1 остается справедливой и для а =
—оо < Ъ < 0. В самом деле, введем вспомогательные функции F(z) =
/(®), G(z) = д(х), где х = 1/z. Тогда 3	= *Пт°/(®) = 0,
3 limoG(z) = lim д(х) = 0, 3dF(z) = -z“2D/(®)> 3dG(z) =
-z“2Dtf(®) Vz E (1/6,0), 3 lim DF(z)/DG(z) = lim D/(®)/D^(a?) =
2—>—О	X—> —OO
А. Поэтому к функциям F(z) и G(z), определенным на интервале
(1/6,0), можно применить теорему 1.
Теорема2 (правило Лопиталя раскрытия неопределенностей
вида оо/оо). Пусть функции f(x) и д(х) определены на (а, Ь), причем:
1) 3 lim |^(®)| = 4-ос; 2) f,g Е 2>((а, Ь)) и Dg(x) / 0 V® Е (а, Ь);
х—>а+0
3) 3 limoD/(®)/D^(®) = А (где А конечно или символ 4-оо (—оо)).
Тогда 3 lim f(x)/g(x) = А,
х->а+0
Доказательство. Отметим, что V» Е (а, а 4- <5о) С (а, Ь)
имеет место (основное) равенство
/(х)/^(х) = (1 -р(а +<5о)/ф))(/(®)-
-/(« + <50))/(р(х) - д(а + <50)) + /(а + 60)/д(х).
В самом деле, V® 6 (а, а 4- <5о) имеем
= (/(®) - Да + &о))/д(х) + /(а + S0)/g(x) =
= (р(®) - д(а + 6o))/g(x)(f(x) - f(a + 60))/(д(х) - д(а + <50))+
+/(а + S0)/g(x),
откуда и следует основное равенство.
Будем различать случаи: 1) А = 0; 2) А 0 и, конечно, 3) А = 4-оо
(-оо).
1)	А = 0. Поскольку lim D/(<)/Dp(t) = 0, то Ve > 0 3<5q > 0
такое, что
\Df(t)/Dg(t)\ < eVt Е (а, а 4- <50) С (а, 6).
Поскольку lim |^(t)| = 4-оо, то для выбранных е > 0 и <5о > 0 3(5 6
(0,(5о) такое, что V® Е (а,а4-<5) С (а,а4-<5о) имеют место оценки |^(а4-
<*о)/0(®)| < 1 (так что |1-^(а4-<50)/^(®)| < 2) и \f(a+60)/g(x)\ < е. Для
любого ® Е (а, а4-<5о) к функциям f(t) и g(t) на отрезке [®, а4-<5о] С (а, Ъ)
применима теорема Коши о конечных приращениях, в силу которой
(f(x) - f(a + <5o))/(ff(®) - д(а + <50)) = D/(c)/Dff(c),
148
где с Е (а, а 4- Jo), так что имеет место оценка |D/(c)/D<j(c)| < £• Но
тогда V® Е (а, а 4- J) С (а, а 4- Jo) в силу основного равенства имеем
оценку
|/(x)/ff(®)| = |1 - д(а + 60)/д(®)| |Df(c)/Dg(c)|+
+|/(а + 80)/д(х)| < 2 • £ 4- е = е.
Итак, Уе > О Э<5 > О такое, что \f(x)/g(x)| < г У® G (а,а + <$), т. е.
3 lim f(x)/9(x) = О-
х—>а+0
2)	А / 0 (конечное). Введем вспомогательную функцию F(x) =
f(x) — А • д(х). Тогда Ух Е (а, Ь) существует конечная про-
_/ ч л/ ч	ч	DF(x)
изводная DF(x) = Df(x) - А • Dfif(«), причем hm - ' =
л-4-а+О
( D^(®)	\
lim I —т—г — A 1 = 0. Но тогда по доказанному в случае 1) видим.
x-hi+o\dp(®)	/
что
/	f(x) \	f ^(®)	\
I 3 lim	—т~г = 0 J =>	( 3 lim —7-7	= А	)	(где А	—	конечное).
у ®->а+о	д(х) /	у яг->а+о д(х)	/
3)	А = +оо. Поскольку	* lim.oD/(^)/D^(t)	=	4-оо, то УК > 0 3<5о > 0
такое, что D/(t)/D<?(tf) > К4-1 yt Е (а, а4-Jo)- Поскольку lim |^(^)| =
t—>а+О
4-оо, то для фиксированного К > 0 и выбранного Jo > О 3J Е (0, Jo)
такое, что Ух Е (а, а 4- J) С (а, а 4- J), имеют место оценки \д(а 4-
<*о)/я(®)1 < V2 (так что 1 4-^(а 4- &о)/д(х) > 1/2) и |/(а 4- Jo)/fir(®)| <
1/2. Применяя к функциям f(t) и g(t) на отрезке [ж, а 4-Jo] С (а, Ь)
(при х Е (а, а 4- J)) теорему Коши в конечных приращениях, имеем
оценку
/(x)-/(a4-Jo)_D/(c)
g(x)-g(a + 6Q) Dg(c) +
где с Е (ж, а 4- Jo)- Но тогда в силу основного равенства Ух Е (а, а 4- J)
получаем оценку снизу
Лж) = А _ д(а 4- Jp)\ D/(c) f(a + Jp)
\ g(x) J Dg(c) g(x)
> (K 4-1)/2 - 1/2 = K/2.
Итак, УК > 0 3J > 0 такое, что	Ух Е (а,а 4- J)
д(х) 2
^x2jJlI}.0A®)/^(ai) — (Случаи А = — оо рассмотрите самостоя-
тельно.)
Замечание 1. Теорема 2 остается справедливой и для а =
< Ь < 0. В этом случае достаточно ввести функции F(z) = /(ж);
= д(х) (где х = 1/х;), определенные на интервале (1/6,0), и при-
менить теорему 2.
149
Замечание 2. Применение теорем Лопиталя требует обяза-
тельной проверки всех условий этих теорем. Формальное применение
правил Лопиталя может привести к неверным результатам.
Пример 1. Пусть f(x) = x2sin(l/x) и д(х) = sinx. Тогда
Нт/(®) = Нтф) = 0 и 3 lim/(®)/$(®) = lim(®2ein(l/®))/(® +
ар—>и	аг—>и	аг—>и	аг—>и
о(®)) = 0, во предел lim D/(®)/Dff (®) = lim(2®ein(l/®) -
cos(l/®))/co8® не существует.
Пример 2. Пусть /(«) = е-2® (cos® 4-2 sin®), д(х) = е“*(сов®4-
sinz). Тогда lim f(x) = lim д(х) = 0 и 3 lim D/(®)/Dff(«) =
аг->+оо	®—>4*оо	ар—>4° оо
lim (-5е-2® sin®)/(-2e_®sin®) = 0. Но для ДД = е~* • Х
»-4+оо'	и\	/	1 + tg®
предела при ® —> 4-оо не существует (не выполнено условие Т)д(х) О
V® > 0).
ха	ха~1
Пример 3. Va>03 lim ®“е“® = lim — = а lim —— =
аг->4*оо	ар—>4"оо g*	ар—>4-оо в*
Д.Л-П
... = а(а - 1)... (а - п 4- 1) lim —— = 0(п-1<а<п)^®“ =
ар—>4"0о в*
о(е®) (® —> +оо). Таким образом, показательная функция е* растет
при ® -> +оо быстрее любой степенной функции ха.
Пример 4. Va > О
,. 1па®	In"”1®
hm -------= a hm -----------
аг->4-oo x ар->4-оо X
lna"n ®
= a(a — 1)... (a - n 4-1) lim ------= 0
ар->4-оо x
(n - 1 < a < n) => lna z = o(®) Va > 0.
Пример 5. Va > 0
lim ln®/®“ = lim (l/®)/a®“-1 = lim l/a®a=O,
аг—>4"Oo	ар—>4*oo	аг—>4*oo
t. e. Inx = o(xft) (x —> 4-oo) Va > 0. Таким образом, логарифмическая
функция In х растет при х -» 4-ос медленнее, чем любая степенная
функция ха (при a > 0).
1-я теорема Ш т о л ь ца (§). Пусть числовые последова-
тельности (ап) и (Ьп) таковы, что
1)3 lim ап = lim Ьп = 0;
п—>4*оо	п—>4*оо
Ю (Ьп) U 0 (так что Ьп > Ъп+1 > 0 Vn € N);
3) 3 lim тг—— i (г^в [ конечно или символ 4-ос или -оо).
п-++оо оп — on+i
Тогда
3 lim 2^ = 1.
n->4*oo bn
150
Доказательство. Отметим лемму из алгебры.
Лемма. Если А <	< В (к = 1,..., т), где /Эь > Q Ук =
Pk
1	., тп, то
т
S «»
А<к-^—<В.	(1)
Е/з*
fc=l
Доказательство. Поскольку Д > 0 Vfc = 1,...»m, то
< jg- < В\ fc = 1)...)	fc = 1» • • • i
откуда имеем
mm	m
ЛХ><5>*<ВХ>-
*!=i	*=1	fc=i
m
Вновь, учитывая, что £ 0k > О, получаем оценки (1).
k=l
При доказательстве 1-й теоремы Штольца рассмотрим сначала
случай а) I конечно. Поскольку Ъп U 0, то Ьп - Ь„+1 > 0 Vn £ N
и, учитывая условие 3), 3 lim	—5*±1 - ц видим, что Ve > О
п-*+оо Оп — 0п+1
3N(e) € N такое,что Vn > N(e) и Vfe > О
I _ е °и+* ~ а»+*+1 г г . 6
2^ U»“in+»+i	2’
где bn+k - bn+k+i > 0. В силу (1) леммы, учитывая, что
"Ь-l	т-1
S (^*п+к ~ ^n+fc+1) =	~ &п+т» 52 (®n+* “ °n+k+l) = ®п ~ Пп+т,
k=0	fc=0
имеем оценки
<2>
Переходя при фиксированном п > .АГ(е) к пределу в оценке (2) при
+оо и учитывая условие 1) 1-й теоремы Штольца
lim ап+т = lim bn+m = 0,
ш->+оо	т-ФЦ-оо
получаем из (2) оценки
l-f<^<i+|Vn>JV(e),
Ti «• Э lim = 1, если I конечно.
п-»+оо Ьп
151
Рассмотрим теперь в условии 3) случай б) I = 4-оо, так что
3 iim	= +оо.
п->+оо ьп - Ьп+!
Тогда 3No G N такое, что ап — an+i > bn — bn+i > 0 Vn > No, т. е.,
учитывая условие 1) lim ап = 0, имеем ап > an+i Vn > No, т. е.
П->4-ОО	—
ап Я 0 (п —> 4-оо), и, в частности, ап > 0 Vn > т > Nq. Но тогда в
силу условия 3) (при I = 4-оо) имеем
3 lim bn ~h+l = о,
п-»+оо ап - ап+1
и поэтому в силу доказанного в случае а) видим, что 3 lim — = О,
откуда, учитывая, что	п
> 0 Vn > mo > No,
Ьп
имеем
3 lim = 4-оо,
п->+оо Ьп
чем 1-я теорема Штольца полностью доказана.
2-я теоремаШтольца (^-). Пусть числовые последова-
тельности [ап) и (Ьп) таковы, что
1) Ьп ТТ +оо е. t>n-i < bn Vn 6 N и 3 lim Ьп = 4-оо);
п->+оо
2) 3 lim ~= I (где I конечно или символ 4-оо или —оо).
П->+ОО Ьп — Ьп-1
Тогда
3 lim = I.
п->+оо Ьп
Доказательство. Будем различать три случая: а) I = О,
б) I ф 0 конечно и в) I = +оо (—оо).
а)	I = 0. Поскольку Ъь ТТ» то Ь* — bk-i > 0 Vfc 6 N и в силу условия
1) lim bm = 4-оо Зтпо Е N такое, что Ьт > 0 Vm > mo-
rn—>оо
Поскольку в случае а) 3 lim	= 0, то Vs > 0 32V(s) 6 N
fc->+oo bk — bk-1
такое, что Vfc > N(e) и Vp > 1 имеют место оценки
< &к+р —	< £
2 bk+p — bk+p-i 2
Но Ьк+р - bk+р-! > 0 Vp > 1 и
m	т
~ ак+р—1) = afc+m —	Ьк+р-1) — Ьк+т ~ Ьк,
р=1	р=1
152
поэтому в силу (1) леммы имеем Vfc > N(e) и т > 1 оценки
2 Ъь+т — Ък 2
или
Qn Q’fc
bn - bk
< bn > bk > 0 Vn > к > mo > N(e).
&
(3)
Отметим тождество Vn > к:
О"п. _ Qfc _i_	__
KT"	\ “ К
an ~~ Qfc
bn “ bk
(В самом деле, — =
On
Qn ~~ Ofc
bn — bk
1-r <
On
l-£
&n ,
оценки
On “ Ofc
ak । On ~ Ofc
bn bn bk
bn — bk _ ak
= +
1 Vn > fc, откуда, учитывая оценку (3), имеем
On < | Ofc | | On ~ Ofc
bn bn bn — bk
b
n
+ =
e e
an
2 ' 2
b,
Но в силу условия 1) lim bn = +oo при фиксированном к > tyiq >
n->+oo
N(e) видим, что Зпо(е) > к > mo > Nq(c) такое, что < - Vn >
оп 2
По (б).
Итак, Зб > О Зпо(г) > к > то > N(e) такое, что < | 4-1 = е
On 2	2
Vn > п0(е), т. е. 3 lim = 0.
п->4-оо Ьп
б)	I / 0 конечно. Введем вспомогательную последователь-
ность (сп) = (аЛ — 1Ьп), для которой имеем 3 lim	=
fc->oo Ofc — Ofc — i
lim ( ~_ l) = 0, и тогда по доказанному в случае а) имеем
*-» + <Х) \frfc - б*.! J	’
Гз lim = lim (r~ —	=0^ Гз lim	= IV
\ n->4-00 bn П-4-+ОО	/	/	\ П-4- + ОО bn /
в)	I = 4-oo. В силу условия 2) 2-й теоремы Штольца имеем
^nlj^oo _ fr”"1 = +°°’ и П0СК0ЛЬКУ в СИЛУ условия 1) Ъп ТТ +оо,
ЭАГ0 G N такое, что ап - an-i > bn - bn~i > 0 Vn > No, т. е.
ап > ап_! Vn > No, а потому ап ТТ на No,+oo и, в частности,
ь кг \ак ~ ak~i) = ап — o.No-1 > 52 (bk — bk-i) = bn - bjfa^i, t. e.
*=л»	*=N0
153
ап > bn + (ax0_i - 6w0-i) Vn > No. Но тогда	= +oo) =>
( lim an = +oo), и поэтому Это > No такое, что an > 0, bn > О
n-44-oo
Vn > mo > No-
Итак, для последовательностей (an) и (i>n) имеем:
V) °n ТТ +оо (Ьп ТГ +°°) и 3 lim ап = lim bn = +оо, причем
п->4-оо	п—>4-оо
ап - an-i > 0 Vn > mo-
В силу условия 2) (при I = +оо) 2-й теоремы Штольца имеем
2') 3 lim Ьп ~ Ьп~1 = О,
n->4-oo <Zn “ &п-1
поэтому из условий Г) и 2’) по доказанному в случае а) 2-й теоремы
Штольца имеем 3 lim — = 0, и поскольку > 0 Vn > то > ЛГо
п-44-00 ап	Ьп
то 3 lim 7— = +оо, чем 2-я теорема Штольца полностью доказана.
n-44-oo оп
Следствие 1 (о среднем арифметическом). Ес-
ли 3 lim ап = I (где I конечно, или +оо, или -оо), то
п-4 4-оо
з lim о1 + о» + -" + °п =
п->4-оо	n
В самом деле, полагая во 2-й теореме Штольца (—) ап =	+
оо
.	»	-ip &п Лп-1 г	ап
... + ап, Ьп = п, имеем 3 hm -т-------г---- = lim -----------— =
n-44-oo Ъп - bn-i п-44-оо П - (п - 1)
lim ап = Ц откуда по 2-й теореме Штольца
П-4 4-00
3 lim = lim °1 + "- + °" -
п->4-оо Ьп п-44-оо п
Следствие 2 (о среднем геометрическом). Если ап > 0 Vn €
N и 3 lim ап = I (где I > 0 конечно или +оо), то
п-4 4-оо
3 lim i/ai • аг •... • an = I > 0.
п->4-оо	"*
В самом деле, полагая ап = 1пап, где ап > 0, видим, что З^Нт^йп =
In I, где I > 0 (или +оо), так что 1п/ = —оо при I = 0 и 1п1 = +оо при
I = +оо. Тогда в силу следствия 1 (о среднем арифметическом)
3 Um ai+«» + ...,. +an s Um lna1 + ... + lnan=lni|
n-44-oo	n	n->4-oo	n
t. e.
3 lim «/ai • aj •... • an = I > 0.
n-44-oo
Примеры.
154
,	.. an — a”"1
1) При a > 1 имеем lim -----------—
an 1 - -
\ a J
lim (ап - а”-1) =
и поэтому в силу 2-й теоремы Штольца
lim
н-*4"с e	.
ап	/	- \
3 lim — = +оо (а > 1).
п-*+<» п
v Inn-ln(n-l)
2) bm ---------Г"..i "
' n-Ц-оо n “ (n “ 1)
n
n - 1
lim In----г = 0, и поэтому в силу
п-^+оо *» — 1
___.	, Inn
2-й теоремы Штольца 3 hm ------= 0.
n->+oo п
ч	\/п!
3) Вычислим предел hm ------.
'	п-*+оо п
__	_ Ш
Полагая f/On = -------, имеем an
п
(n+l)!-nn nn _	1
(n + l)“+1-n! (n + 1)»	(1 + 1)»
v п
в силу следствия 2 ко 2-й теореме Штольца имеем
п! тт	вп + 1
= —. Но тогда —— =
Пп	Оп
«• ОП+1	1
lim —— = и поэтому
п-и-оо ап	е
3 lim —
n->+<x> у ax
= lim = lim —~ = -
an_i n->+oo	n->+oo n e
§ 9. Свойства производных дифференцируемых
функций
Определение. Пусть функция f(x) определена на множес-
тве М. Скажем, что функция f(x) возрастает (строго возраста-
0
ет) в точке Xq ЕМ, если существует окрестность U(xq) С М
такая, что Vx G U(xq), при х > хо имеем оценку /(х) > /(хо)
(Л®) > У(®о)) « при х < хо имеем оценку /(х) < /(хо) (/(х) < /(х0)).
Аналогично определяется понятие убывания (строгого убывания)
функции в точке.
Теорема. Пусть функция /(х) определена Чх € [®о> ®о + <5о)
(или Vx е (хо — So, xoV и имеет (конечную или бесконечную) правую
производную D+/(®o) (имеет левую производную D“/(«o)?) 8 точке
®о< Пусть при этом D+/(xo) > 0 (соответственно D“/(®o) > 0/
Тогда существует окрестность VJ(xo) С 17<0(хо) такая, что Vx €
«о, «о + S) имеем оценку /(х) > /(®о) (соответственно Ух G (хо - £>
®о) имеем оценку f(x) < f(xo)).
Доказательство. По определению правой производной
*Д^+0(/(®) “/(®°))/(® -®о) = D+/(®o) > 0. Но тогда в силу теоремы
0 знаке (при конечной D+/(xq)) видим, что существует окрестность
155
Vi(®o) C Uj0 (®o) такая, что
(f(x) - f(x0))/(x - Xq) > 1/2 • D+/(®o) > О V® E (®o,	+ <5),
откуда в силу неравенства х — ®о > 0 получаем
/(®) > /(®о) v® Е V(®o) а [®о,+оо).
Следствие (достаточное условие строгой монотонности
функции в точке). Если функция /(®) определена в окрестности
17(®о) и в точке ®0 существует конечная или бесконечная производная
D/(®o) > 0 (D/(zo) < 0), то функция /(®) строго возрастает (строго
убывает) в точке ®о.
Замечание. Из того, что функция /(®), определенная в
окрестности (7(®о), строго монотонная в точке ®о, вообще говоря, не
следует, что функция /(®) будет монотонной хотя бы в некоторой
окрестности V(®o) С U(xq).
Пример. Функция
ч f х + 2®2sin(l/®), х / 0,
/w = l о, . = 0
имеет производную
| 1 + 4®sin(l/®) — 2cos(l/®), х 0,
Очевидно, в любой достаточно малой окрестности нуля производ-
ная D/(®) имеет как положительные, так и отрицательные значе-
ния, т. е. функция /(®), строго возрастая в точке ®о = 0 (поскольку
D/(0) = 1 > 0), тем не менее не будет монотонной в любой достаточно
малой окрестности U(xq). (В самом деле, если бы /(®) была монотон-
но возрастающей в окрестности U(xq), то /(®) была бы возрастающей
в любой точке ® € U(xq), что невозможно для точек ® Е U(xq), где
Df(x) < 0.)
Теорема Д а р б у (о промежуточных значениях производ-
ной). Пусть функция f(x) определена на отрезке [а, Ь], / Е 1>((а, Ь)) и
существуют конечные односторонние производные D+/(a) u D~ f(b)
в концах отрезка [а, 6], причем D+/(a) / D“/(5)« Тогда V постоян-
ной С, находящейся между числами D+/(a) и D~ f(b), существует
точка с Е (а, Ь) такая, что Df(c) = С.
Доказательство. Пусть сначала D+/(a) • D" f(b) < 0. На-
пример, D+/(a) > 0 и D~f(b) < 0. Из условий теоремы Дарбу вы-
текает, что / Е С([а, Ь]). В самом деле, поскольку существуют одно-
сторонние производные D+/(a) и D"/(b), то / Е С (а) и f Е С(Ь),
кроме того, / Е D((a,b))	/ 6 С((а,Ь)), т. е. / Е С([а, 6]). Но
156
тогда по теореме Вейерштрасса существует с Е [а, Ь] такая, что
f(c) = М = sup f(x). Отметим, что с / а, так как в противном слу-
[а,Ь]
чае имели бы /(ж) < /(а) = f(c) = М Ух Е [а, 6]. Но D+/(a) > О,
и по предыдущей теореме существует окрестность U(a) такая, что
f(x) > f(a) = supf(t) = М Ух Е U(а) О [а, Ц. Противоречие. Анало-
[а,Ч
гично доказывается, что с ф Ъ. Таким образом, с Е (а, Ь), и в силу тео-
ремы Ферма в точке локального максимума жо = с имеем D/(c) = 0. В
случае D+f(a) > С > D" f(b) рассмотрим вспомогательную функцию
F(x) = f(x) — Сх, для которой имеем DF(x) = Df(x) — С Ух Е (а, Ь);
D+-F(a) = D+/(a) — С > 0, D“F(b) =	— С < 0. По доказанному
выше ЗсЕ (а, Ь) такое, что D-F(c) = 0, откуда D/(c) = С.
Замечание. Теорема Дарбу показывает, что производная
D/(x) дифференцируемой функции f Е Р([а, Ь]), подобно непрерывной
на отрезке функции, принимает все промежуточные значения на от-
резке, однако производная Df (®) может и не быть непрерывной функ-
цией.
тт	тт	а \ f ®2sm(l/x), х ± 0,
Пример. Для функции f[x) = <	2 л	имеем
I и, ж — и
г zn// .	\\	х f 2жзт(1/ж) — соз(1/ж), х ± 0,
f Е Р((—оо, 4-оо)), причем Df(x) = < п __ л
I и, X — и,
очевидно, D/EC(0).
Теорема (о пределе производной). Пусть f Е С([жо, ®о 4- <5о])
и f Е Р((жо, xq 4- (5о)). Пусть 3 lim Df(x) = А, где А конечно или
х->х0+0
символ 4-оо (—оо). Тогда в точке xq существует правая производная
D+/(«o) = А. (Попробуйте доказать сами.)
Доказательство. 1) Пусть сначала А конечно. Посколь-
ку 3 lim Df(x) = А, то Ve > 0 3<5 Е (О, <50) такое, что |D/(*) -
яг—>®о+О
А| < в yt Е (®о>®о + <5)« Тогда Ух Е (жо, ®о + <£) рассмотрим вы-
У(ж) — /(ж0)
ражение------------А. По теореме Лагранжа о конечных при-
Ж Жо
ращениях (примененной к / б <7([асо» ®]) А Т>((жо, ®))) Зс б (®о,®)
такая, что D/(c)
_ /(®) - /(®о) „ „________
— -------------, и поэтому
X — Xq
Итак, W > 0 3(5 > 0 такое, что Ух Е (жо,жо +
--------------А < е, из которой следует, что
У(ж) - /(а?0)
® ®о
<0 имеем оценку
X Xq
3 lim ZfeV" - а => D+/(®o) = А.
®->®о+О х - хо
2) Если А = 4-оо (или А = — оо), поскольку 3 lim Df(x) = 4-оо,
jp др 0
то УК > 0 3(5 Е (О, <50) такое, что Df(t) > К УЬ Е (ж0, жо 4- <5), и
вновь, применяя теорему Лагранжа на отрезке [жо, видим, что Ух Е
157
(®о, ®о + £) Эс € (®о, ®) такое, что	—£12°) _ р/(с) > К, т. е.
X — ®о
(3 lim	—Л^о) — -j-qq) (d+/(®0) = 4-00).
®-4®o*l"O X Xq
Пример. Пусть /(®) = ®arcsm® + VI - ®2> ® € [-1,1]. Тог-
да f е С([-1,1]) Л -Р((-1,1)), причем V® € (-1,1) 3D/(®) =
arcsin® -I- ® / VI - ®* — ®/Vl - ®2 = arcsin® я 3 lim^D/f®) = w/2,
3 lim D/(®) = -?r/2, поэтому в силу теоремы о пределе производ-
ноГзп+/(-1) = -ff/2, D'/(l) = */2.
Теорема (о разрывах производной). Если функция f (х) диф-
ференцируема в окрестности U(xq), то производная D/(®) не мо-
жет иметь в окрестности U(xq) точек разрыва 1-го рода.
Доказательство. Пусть f € 2>(17(®о))» так что V® €
С7(®о) существует конечная D/(®)> Допустим от противного, что
®i € U(xo) есть точка разрыва 1-го рода для функции D/(®). Тог-
да 3 lim D/(®) Ф lim D/(®)« Но / € С(У(®о)), и в силу теоре-
мы о пределе производной 3D+/(®i) = *_lim+oD/(®) и 3D“/(®i) =
lim D/(®). Ho (/ € D(I7(®o)) => (/ £ 2>(®i)), поэтому 3D/(®i),
"0
причем D/(®i) = D+/(®i) = D“/(®i). Противоречие. Итак, функция
D/(®) не может иметь точек разрыва 1-го рода.
Замечание. Как показывает ранее рассмотренный пример
.	./ , f ®2ein(l/®), ® О,
функции /(®) = < g — 0	производная может иметь раз-
рывы 2-го рода.
§ 10. Формула Тейлора
Теорема (формула Тейлора для многочлена). Пусть Р(х) =
п
J2 а*®* - многочлен п-й степени. Тогда У®о € (—00, +00) сущест-
во
вует, и притом единственный, многочлен Тейлора *РП(®;Я, ®д) =
22 тт(® - ®о)* (где ck = DfcP(®o)) такой, что Р(х) = Рп(®;Р,®о)
ksO Л1
V® € (-оо,4-оо).
п
Доказательство. Положим Р(х) =	<4* (х фо)* и най-
fc=O
дем коэффициенты Ak при k = 0,1,2,... ,п. Для любого т (т =
0,1,... , п) m-кратное дифференцирование дает
D’nP(®) = £ к • (k - 1) •... • (к - т 4- l)Afc(® - ®o)*-m.
fc=m
158
Полагая х = ®о, имеем DwP(®o) = m!Am, т. е. коэффициенты
дт = -iyDmP(®o) определяются единственным образом через мно-
гочлен Р(®). Полагая ст = DmP(®o)» получаем единственное пред-
ставление Р(х) = Pn(®;P,®o) V® € (-oo^-l-oo).
Определение. Пусть функция f(x) определена V® G (а, Ь)
и хо Е причем 3Dn/(®o)« Тогда многочленом Тейлора степе-
ни п в точке ®о для функции f(x) называется многочлен Рп(®) =
w 1
Pn(x;f,xo) такой, чтоРп(х) = £ r;Dk f(xQ)(x - х0)к.
*=о
п
Замечание!. Для любого многочлена Р(®) = £3 а*®* и У®о €
к=0
(-оо, +оо) в силу теоремы о формуле Тейлора для многочлена имеет
место точное равенство
Р(®) = Рп(®;Р,®о) У® е (-оо,+оо).
Замечание 2. Если f € С(®о)> то в окрестности U(xq) име-
ем представление /(®) = /(®о) + о(1) (® -> ®о)> так что /(®) —
Ро(®;/,®о) + г0(®,®о)> где Ро(®;/,®о) = /(о)(®о) и г0(®,®о) = о(1)
(® —> ®о)‘
ЗамечаниеЗ (формула Тейлора с остаточным членом в форме
Лагранжа). Если f €	(Е7(®о)), то У® € Z7(®o) имеем представле-
ние /(®) = Рп(®; /, ®0) + гп(®, ®о)> где
гп(®, ®0) = •^-щПп+1/(с)(® ~ ®о)п+1с е 17(®о).
Замечание4 (формула Тейлора с остаточным членом в форме
Пеано). Если / € 2><п"1)(С/'(®0)) и f €	(®о), то в окрестности 17(®о)
имеем представление /(®) = Рп(®;/, ®о) + г„(®, ®о), где гп(®, ®о) =
о((® - ®0)п) (® -> ®0).
Теорема (единственности многочлена Тейлора). Пусть f €
D<"-1)(17(®o)) и f € D<п)(®о), причем в окрестности Й(®о) име-
ет место представление /(®) = Qn(®) + о((® — ®о)п) (® —> ®о),
г^е Qn(®) - многочлен п-в степени относительно ® — ®о. Тогда
Qn(®) = Рп(®;/,®о).
, Доказательство. По условию теоремы в окрестности
П'(яо) имеет место представление
/(®) = Qn(®) + о((® - ®0)п) (® -> ®0),	(10.1)
но по теореме Тейлора (о формуле Тейлора с остаточным членом в
Форме Пеано) имеем представление
/(®) =,Pn(®;/,®o) + o((®-®o)n) (®->®о).	(Ю.2)
159
Представляя функцию Qn(x) с помощью ее многочлена Тейлора
Рп(®;Ф»м®о), имеем
Qn(®) = ^2 Tt (® ®о)**
fe=o к‘
Докажем, что с* = D*f(®о) (fc = 0,1,2,... , п). Допустим от против-
ного, что Вк (0 < к < п) такое, что с* 54 D*/(®o)> и пусть fco = min{fc}.
Тогда Pn(s; /, ХО) - Qn(x) = £ (Dm/(s0) - ст) ——. Заметим,
m=fco
что при п > т > fco (® - ®о)т = (® — хо)к°(х — ®0)m“*° = о((® ~ ®о)*°)
(х ~4 Хо), поэтому
Pn(®; f, Хо) - Qn(x) = ^(D*°/(so) - Cfc0)(® - s0)*°+
KQ\
+o((a; - so)*0) (s -> so).
(x —
Вычитая (10.2) из (10.1) почленно, имеем (Dfe°/(®o)~cfc0)~—Fi — =
fco’
o((x- ®o)fe°) + °((:c"'®o)n) = o((x -x0)fe°) (® -> ®o), откуда D*°/(®o) -
cjg0 = o(l) (x -4 xq) => cjg0 = D*°/(®o)? вопреки предположению. Итак,
Qn(x) = ^n(®j ®o)-
Пример. Пусть f(x) = arcsin®. Найдем Dn/(0) Vn G N. Оче-
видно,
D/(s) = (1 - я2)’1'2, sG(-l,l).
По	формуле Тейлора	с остаточным	членом в	форме Пеано для
бинома имеем (1 —	х2)-1/2	= 1	4- тт (	) ( —z — 1 ) • • •
fc=i fc! \	2/ \ 2 /
—fc + 1^ (—х2)к 4- о(х2п)	(х ->	0)	или (1	- ж2)"1/2 = 14
» ЬЗ’...’(2к-1) 2fc z 2пч /
> л ----хь—г;-----х +о(® ) (х -4 0). В силу локальной теоремы
к=ь
Тейлора имеем D/(®) = Ргп(®; D/, 0) 4* о(х2п) (х -4 0), где
2п
P2n(s;D/,0) = ^(l/m!)Dm+1/(0)s’“.
7П=0
В силу теоремы единственности многочлена Тейлора имеем
D2fc/(0) = 0, D2*+1/(0) = (l/2*fc!) • 1 • 3 •... • (2fc - 1) • (2fc)l
ИЛИ
D2fc+i/(0) = l-3-...-(2fc-l)-b2-3-4-...-(2fc-l)-2fc =
160
= [(2fc —I)!!]2 (ft = 1,2,...), D/(O) = 1.
Теорема (о формуле Тейлора). Пусть f G C^n)((a,t>)) и
Ух Е (а, Ъ) \ {®о} существует конечная или бесконечная произ-
водная Dn+1/(®)' Пусть ф(1) - любая функция, такая, что ф G
С([ж, ®о])Л^((жо,®)) (где С (а,Ь)) или ф G С([ж, ®о])Л2>((®, ж0))
(где [ж, х0] С (М)), причем Вф(1) О V* G (®о,®) (yt G (х,х0))-
Тогда Ух G (а, Ь) \ {®о} имеет место формула Тейлора f(x) =
Pn(x-,f,x0)+rn(x,xQ), гдегп(х,х0) =	•Р	-(x-c)n,
причем хо<с<х(х<с< жо).
Доказательство. Введем вспомогательную функцию
n 1
y?(i) = f(x) - f(t) - й • Dkf(t)(x — t)k 'it e [®o, и отметим равен-
fc=i
ства ч>(х) = 0, <р(х0) = rn(®,®o); Dy>(t) = -D/(t)- 22 TiD*+1/(*)-(®-
fc=i fc!
<)* + E	= -D^W- E (l/m!)Dm+1/(t) • (X -
k=l	'*	m=l
t)m + Ё (l/w!)Dm+1/(t)(® -t)m = -D/(t) - (l/n!)Dn+1/(«)(® -t)n +
m=O
D/(t) = -(l/n!)Dw+1f(t)(x~t)n, т. e. yt G (®o> ®) существует конечная
или бесконечная производная D^) = “(l/n!)Dw+1/(£)(® — t)n.
Рассмотрим на отрезке функции <p(t) и ф(1), для которых
имеем: 1) <р G С([а?о? ®]) и yt G (®о? ®) существует конечная или бес-
конечная производная Dy>(t); 2) ф G С([жо,®]) ЛР((®о>®))? причем
3) DV’(^) 0 yt G (®о, ®)«
Таким образом, для функций <p(t) и ф(1) на отрезке [®о, вы-
полнены все условия теоремы Коши о конечных приращениях, в
w _	. ч	(ф(х\ — <р(хо) Dy>(c)\
силу которой Эс G (хо, ®) такая, что I -77-^-——= —> I =>
\УЦж) - У>(ж0)	DV’(c)/
(,ы=_ж=^).в₽(с)),т.в.
г.(», 10) =	.(>-«)", «о <С< *.
DV^c)	п!
Аналогичная формула имеет место и для отрезка [х, хо]» причем
х < с < а?о»
Следствие! (формула Тейлора с остаточным членом в форме
Коши). Полагая ф(1) = х — t, получаем остаточный член формулы
Тейлора в форме Коши: гп(ж,ж0) = Dn+1/(c)^—go)(g—£)_,
6 Зак. 860
161
с < ®, или, полагая с = ®о + 19(® - ®о)» где 0 < 19 < 1,
гп(®, хо) = D"+1/(®o + tf(x - хо))(1 - 1>)п (х - xo)n+1.
В самом деле, имеем = х -t, ^(хо) = х - хо, ^(х) = О, DV’CO =
-1, и подстановка в формулу Тейлора дает остаточный член в форме
Коши.
Следствие? (формула Тейлора с остаточным членом в форме
Лагранжа). Полагая = (х — t)n+1, получаем остаточный член
формулы Тейлора в форме Лагранжа
Гп(х,®о) =	+	- ®o)"+1, Хо<С<х(х<С< Хо).
В самом деле,
У>(4) = (х - t)n+1, V>(®) = 0, V(®o) = (® - ®o)"+1,
Dtf>(*) = -(n + l)(x-i)n, DV’(c) = ~(n+ l)(x -c)n.
Замечание. Пусть при выполнении условий теоремы Тейлора
функция f (х) удовлетворяет дополнительному условию
Mn+i = sup |Dn+1/(®)l < +oo.
(e,»)\{»o}
Тогда /(х) = Pn(x;f, хо) + Го(®>®о), причем для остаточного члена
имеет место оценка
1М®.®о)|<7^|®-®о|"+1.
(п+ 1)
В самом деле, представляя остаточный член формулы Тейлора в фор-
ме Лагранжа, имеем оценку
kn(®,®о)| = |D"+1/(c)(® -®o)n+1/(n+ 1)!| <
<Мп+1|х-х0|п+7(п+1)!.
Теорема. Пусть f,g е D<"\(®o) u D*/(®o) = D*j(®o) (к =
0,1,..., п). Тогда в окрестности U(xq) имеет место представление
f(x) - g(x) = о((х - хо)п) (х -> х0).
Пример. Рассмотрим функции
_ J ехр{-1/х2}, х О,
'' '	| 0, х = 0 и д(х) = 0.
162
Тогда D’MO) = 0 Vn € No, т. e. Pn(x;g, 0) = 0.
Докажем, что D"/(0) = 0 Vn € N. Пусть x 0, тогда D/(x) =
J- exp I —-71 = Рз(1/®) ехр{-1/®2}. Допустим, что
0!3 I » J
D*7(®) = Рэп(1/») exp{-l/®2} (® # 0),
тогда
D"+7(®) = (DP3n(l/»)(-l/®8) +Рэ»(1/®)(2/®3))ехр{-1/®2} =
= Язп+з(1/®) exp{—I/®2}.
Очевидно, Рзп(1/®) = о(ехр{-1/®2}) (® -> 0), так что
Э lim Dn/(®) = lim	= 0,
х-ю '' ’	®-+o exp{l/®2}
и по теореме о пределе производной имеем Vn € N Dn/(0) =
limD*‘/(®) = 0, т. e. f e C<°°)((-oo, +oo)). Но тогда Pn(®;/,0) =
x—>0
Pn(®;p,0), откуда f(x) -g(x) = o(®") (® -> 0) Vn e N.
Глава 6
ИССЛЕДОВАНИЕ ФУНКЦИЙ С ПОМОЩЬЮ
ПРОИЗВОДНЫХ
§ 1. Условия монотонности функции
Теорема 1 (критерий монотонности функции). Пусть f €
С((а, b)) u V® G (а, Ь) существует конечная или бесконечная произ-
водная D/(®). Тогда (/(®) f на (а,Ь))	(D/(®) > О V® € (а,6));
(/(®) | на (а, 6))	(D/(®) < 0 V® € (а,Ь)).
Доказательство. Необходимость. Пусть f G С((а,Ь)) и
V® € (а, Ь) существует конечная или бесконечная D/(®). Пусть /(®) f
яа (а, Ь). Рассмотрим любую точку ®0 € (а, Ь). Тогда V® е (а, Ъ) \
{®о} в силу условия /(®) | на (а, Ь) имеем	> 0, т. е.
X — ®о ~
D/(®) = Jjm	> 0 (если производная D/(®o) бесконечна,
то, очевидно, D/(®o) = +оо). Итак, (/(®) t яа (а, Ъ)) =► (D/(x) > 0
v®e(«,b)).
Достаточность. Пусть f € С((а, Ь)) и V® € (а, Ь) существует конеч-
ная или бесконечная производная причем D/(®) > 0. Для лю-
бых ®х, Х2 € (а, Ь) таких, что ®i < по теореме Лагранжа о конечных
б-
163
приращениях, примененной к функции f(x) на отрезке [®i, х2] С (а, 6),
Зс 6 (®i,х2) такая, что f(x2) — f(x±) = Df(c)(x2 — а?х), но D/(c) > О,
поэтому (f(x2) - f(xr) > 0) => (f(x2) > f(xi)). Итак, (D/(x) > 0
Va? E (a, b)) => (f(x) f на (a, b)).
Следствие 1 (критерий монотонности для дифференцируе-
мой функции). Если f Е V {(а,Ь)), то (f(x) | на (a, b))	(D/(®) > 0
Va? Е (а, Ь)) и (f(x) J, на (a, b))	(D/(a?) < 0 Va? Е (а, Ь)).
Следствие 2. Пусть f Е С((а, Ь)) и xq Е (а, Ь). Пусть Va? Е
(а, Ь) \ {®о} существует конечная или бесконечная производная D/(a?),
причем D/(®) > 0. Тогда f (х) | на (а, Ь).
Доказательство. В силу теоремы 1 (Va?x,х2 Е (a,xq) или
Va?i, х2 Е (а?о, Ь) таких, что х± < х2) => (/(a?i) < Да?2)) и Va?x, х2 Е (а, Ь)
таких, что а < a?i < xq < х2 < b по теореме Лагранжа о конечных при-
ращениях, примененной к функции f (х) на отрезках [а?х, а?о] и [а?о,
3ci Е (а?х,а?0),с2 Е (а?0,а;2) такие, что /(а?0)-/(а;х) = D/(ci)(®o-®i) >
0, f(x2) - /(а?0) = Df(c2)(a?2 - ®о) > 0, откуда f(a?x) < f(a?0) < f(x2).
Таким образом, (Va?x,a?2 Е (a,i>), а?х < х2) => (/(а?х) < f(x2)) => (/(а;) |
на (а, Ь)).
Теорема 2 (достаточное условие строгой монотонности функ-
ции). Пусть f Е С((а, Ь)) и Va? Е (а, Ь) существует конечная или
бесконечная производная D/(®), причем D/(a?) > 0. Тогда f(x) ТТ на
(а,Ь).
Доказательство. Va?x,х2 Е (а,Ь), а?х < х2 по теореме Ла-
гранжа, примененной к функции /(ж) на отрезке [а?х,а?2], Зс Е (а?х,а?2)
такая, что (Да?2) - /(а?х) = D/(c)(a?2 - a?i) > 0) => (/(а?2) > /(а?х)). Но
тогда /(а?) ТТ на (а,Ь).
Следствие 1. Если / Е Р ((а, Ь)) и Df(x) > 0 Va? Е (а, Ь), то
/(а?) ТТ на (а,Ь).
Следствие 2. Пусть f Е С((а, Ь)) и а?0 Е (а, Ь). Пусть Va? Е
(а, b) \ {а?о} существует конечная или бесконечная производная D/(a?),
причем D/(a?) > 0 (если D/(a?) бесконечная, то Df(x) = +оо). Тогда
f(x) ТТ на (а,Ь).
Доказательство. Рассмотрим любые точки a?i, а?2 Е (а, Ь)
такие, что а?х < а?2, тогда при а < а?х < а?2 < а?о или а?о < a?i < х2 < b
по теореме 2 имеем /(a?i) < /(а?2). При а < a?i < а?о < а?2 < b по теореме
Лагранжа о конечных приращениях, примененной к функции /(а?) на
отрезках [a?i,a?o] и [а?о, а?2], Зсх Е (a?i,a?o) и Зс2 Е (а?о?®г) такие, что
/(®o)-/(®i) = D/(ci)(a?0~a?i) > 0, /(а?2)-/(а?0) = Df(c2)(x2-x0) > 0,
т. е. (/(a?i) < f(a?0) < f(a?2)) => (/(а?) ТТ на (а,Ь)).
Теорема 3 (критерий строгой монотонности функции, име-
ющей производную). Пусть f Е С((а, b)) u Va? Е (а, Ь) существу-
ет конечная или бесконечная производная D/(a?). Тогда (/(а?) ТТ
(а, Ь)) (выполнены два условия: 1) D/(a?) > 0 Va? Е (а, 6) и 2)
V(a,/?) С (а, b) 3a?o Е (<*,(3) такое, что D/(®o) > 0).
164
Доказательство. Необходимость. Пусть f Е С((а,Ь)) и
Уж Е (а, &) существует конечная или бесконечная производная В/(ж) и
функция f(x) П на (а, Ь). В силу теоремы 1 (критерия монотонности
функции) имеем В/(з) > 0 Уж Е (а, 5), т. е. условие 1) выполнено.
Рассмотрим любой интервал (а,/3) С (а, Ъ). Если бы В/(®) = О
Уж € (а,/3), то по теореме Лагранжа, примененной к функции /(ж)
на (любом) отрезке [жх, ж2] С (а,/3), с Е (жх,ж2) такая, что (/(ж2) -
/(Ж1) = В/(с)(ж2~Ж1) = 0) => (Д®1) = Я®2)), и функция /(ж) не была
бы строго возрастающей на (а, Ъ) (вопреки предположению). Поэтому
Зжо € (а,/?) такая, что В/(®о) > 0, т. е. условие 2) также выполнено.
Достаточность. Пусть f Е С((а, Ъ)) и Уж Е (а, Ъ) существует конеч-
ная или бесконечная производная Df (я) и выполнены условия 1) и 2)
теоремы 3.
Из условия 1) В/(®) > 0 Уж Е (а, Ъ) в силу теоремы 1 (критерия
монотонности) вытекает, что /(ж) | на (а, Ъ).
Допустим, что функция /(ж) не является строго возрастающей на
(а, &). Тогда 3а,/3 6 (а, Ь), а < /3 такие, что f(a) = f(/3). Поскольку
f(x) t на [а,/3], то /(а) < f(x) < f(j3) Vx е (а,0), т. е. f(x) = f(a)
Уж Е [а,/3], но тогда В/(®) = 0 Уж 6 [«,/?], что противоречит условию
2). Таким образом, /(ж) П на (а, 5).
Следствие (критерий строгой монотонности дифференциру-
емой функции). Пусть f Е 1>((а, Ъ)). Тогда (/(ж) |Г на (а, Ь)) (вы-
полнены два условия: 1) Df (ж) > 0 Уж Е (а, Ь) и 2) множество точек
жо Е (а, Ь), где D/(^o) > 0 плотно на интервале (а, Ъ)).
Пример. Пусть /(ж) = ж3, ж Е (-1,1) (см. рис. 25). Тогда /(ж) П
на (—1,1) (почему?), но В/(0) = 0.
§ 2. Экстремумы функции
В § 7 гл. 5 была доказана
Теорема Ферма (необходимый признак существования ло-
кального экстремума для дифференцируемой функции). Пусть функ-
ция f(x) определена на множестве М и имеет локальный экстремум
о
во внутренней точке xq ЕМС М. Тогда если /(ж) дифференцируема
в точке xq, то В/(жо) = 0.
Теорема 1 (достаточный признак существования строгого ло-
кального экстремума). Пусть функция f(x) определена на промежут-
ке |а, 6|, ж0 е (а, Ъ) и f Е С(жо), причем существуют конечные или
бесконечные односторонние производные В*"/(®о) и В+/(жо). Если
Б“/(ж0) > 0 и В+/(ж0) < 0, то функция f(x) имеет в точке жо
строгий локальный максимум. Если В“/(®о) < 0 и В+/(®о) > 0, то
Функция f(x) имеет в точке xq строгий локальный минимум.
Доказательство. Пусть f Е С(ж0) и В”/(®о) > 0, а
165
D+f (®о) < 0, тогда в силу теоремы из § 9 гл. 5 ч. 1 существует S > О
такое, что /(х) < f(x0) Ух е (х0-£, х0) и f(x) < f(xQ) У € (х0, х0 + <5),
т. е. f(x) < f(xo) Ух € Us(bq) С (а,Ь), так что хо - точка строгого
локального максимума функции /(х).
Теорема (достаточный признак существования локального
экстремума). Пусть функция f(x) определена на промежутке |а, Ь| и
хо € (а,Ь). Пусть существует окрестность Us(xq) С |а, Ь| такая,
что /(х) f (ТГ) на полуинтервале (хо — хо] и f(x) ф (Ц) на полуин-
тервале [х0, xo+i). Тогда в точке х0 функция f(x) имеет локальный
максимум (строгий локальный максимум).
Доказательство. При выполнении условия теоремы
/(х) < /(®о) Vx G Us(xq) (соответственно /(х) < /(хо) Ух Е Us(x0))
видим, что хо € (а, Ь) есть точка локального максимума (строгого
локального максимума).	Ц
Замечание. Обратное утверждение, вообще говоря, неверно,	|
т. е. из того, что в точке хо € (а, Ь) функция /(х) имеет локальный 1
экстремум, вообще говоря, не следует, что в полуинтервалах [хо, хо + I
<5) и (хо - 6, хо] функция /(х) монотонна.	|
Пример. Рассмотрим функцию	|
ч _ / x2sin(l/x) + 2х2, х ф О,	I
f(X> - t О, х = О,	I
тогда f(x) = хг(2 + sin(l/x)) > х2 > 0 = /(0) V® 0, т. е. хо = 0 есть
точка локального минимума функции /(х).	(
Однако (D/(x) = 2®(2 + sin(l/®)) - cos(l/x) = ^i(x) + рз(х)) => t
(|y>i(x)| = 2|х(2sin(l/x))| < б|®| < 1/2 V® € 171/1г(0)), поэтому имеем |
Vn > 12/ir	j
=(-D"«+22kk+ь I
Таким образом, при x > 0 (соответственно при х < 0) функция /(х)	|
не является монотонной.
Следствие 1 (достаточный признак существования локаль-
ного экстремума - по знаку 1-й производной). Пусть функция /(х)
определена на промежутке |а, Ь|, ®о € (а, Ъ) я существует окрестность
Ui(®o) С |а,Ь| такая, что / G C(Us(xq)) и Vx € l)i(®o) существу-
ет конечная или бесконечная производная D/(x), причем D/(®) > 0
(D/(®) > 0) V® € (®о - <5, ®о) и Df(x) < 0 (D/(x) < 0) Vx € (х0, ®о + ^)-
Тогда точка ®о € (а, Ъ) есть точка локального максимума (строгого
локального максимума) функции f(x).
В самом деле, пусть х € U/(x0) С (а,Ь). Тогда при х < х0 имеем
f G С([х,хо]) и Vi € (х, хо) существует конечная или бесконечная
производная D/(i) > 0 (D/(i) > 0), так что в силу теоремы Лагранжа
166
о конечных приращениях 3ci € (х, х0) С (xq —£, ®о) такая, что /(х0) -
/(ж) = D(ci)(x - ®о) > 0 (> 0).
При х > Xq аналогично в силу теоремы Лагранжа, применен-
ной к функции f G С([хо,®])> видим, что Зег € (хо,х) такая, что
/(х)-/(х0) = D/(c2)(x-x0) < о (< 0), т. е. имеем /(х) < /(х0)(/(х) <
/(хо))	€ l4(xo) С (а, 6), и поэтому точка Хо G (а, Ь) является точ-
кой локального максимума (строгого локального максимума) функции
/(х).
Замечание. Условие / € C(U (хо)) существенно для справедли-
вости следствия 1 и не может быть отброшено, как показывает пример
функции f (с графиком, изображенным на рис. 29) f € 'D(U(xo))y но
{>0 х <с 0
п’ п’ Но хо = 0 не есть точка
v U, х и»
локального максимума.
Пример. Пусть f(x) = |х|, -оо < х < +оо, тогда f €
С((-оо, +оо)) и D/(®) = |	так что точка хо = 0 есть
точка строгого локального минимума нашей функции.
Следствие 2 (достаточный признак существования локаль-
ного экстремума - по монотонности 1-й производной). Пусть функция
/(х) определена на промежутке |а, Ь|, xq € (а, b) тл. существует окрест-
ность 17(хо) С |а, Ь| такая, что f € 1>(С7(хо))• Пусть D(®o) = 0 и первая
производная D(®) убывает (строго убывает) в точке хо. Тогда точка
®о 6 (а, Ь) есть точка локального максимума (строгого локального
максимума) функции f(x).
Доказательство. Пусть производная Df(x) строго убывает
в точке ®о € (а,Ь). Тогда 3Vi(®o) С С7(®о) такая, что V® € V^(xo)
D/(x) > D/(®o) = 0 при х € (®о-^ ®о), кроме того, D/(®) < D/(®o) =
О при х € (хо, ®о+<5)• Наконец, f € 2?(17(хо)) => f € C(Vi(x0)), поэтому
в силу следствия 1 точка азо € (а» Ь) есть точка строгого локального
максимума функции /(х).
Замечание. Пусть функция f(x) определена на промежут-
ке |а, Ь|, ®0 е (а, Ь) и существует окрестность U(xq) С (а, Ь) такая,
что f £ 7?([7(хо)). Пусть в точке хо выполнен необходимый признак
существования локального экстремума (для дифференцируемой функ-
ции), т. е. D/(®o) = 0. Тогда если в окрестности U(xq) при переходе
через точку хо производная D/(®) меняет знак с плюса на минус, то
точка а?о € (а, Ь) есть точка строгого локального максимума.
Аналогично, если при переходе через точку хо производная меня-
ет знак с минуса на плюс, то точка х € (а, Ь) есть точка строгого
минимума функции /(х) (рис. 30 и табл. 1).
167
Таблица!
х
У
Xq
max
.yg.
О
a?i
min
-У!-
О
+
Следствие 3 (достаточное условие существования строгого
локального экстремума - по знаку 2-й производной). Пусть функция
f(x) определена на промежутке |а, Ь|, xq 6 (а, Ь) и f € ®(2)(жо). Пусть
D/(®o) = 0 и D2/(®o) < 0 (D2/(®o) > 0). Тогда точка xq Е (а, Ъ) есть
точка строгого локального максимума (строгого локального миниму-
ма) функции f(x).
Доказательство. Из условия D2/(®o) < 0 (D2/(®o) > 0)
в силу теоремы о достаточном условии строгой монотонности функции
Пример. Пусть f(x) = —;
-2ж, D2/(x) = —2 < 0, D/(0) =
в точке, примененной к про-
изводной D/(®), следует, что
D/(®) строго убывает (строго
возрастает) в точке жо 6 (а, Ъ).
Поскольку D/(®o) = 0, то про-
изводная Df(x) при переходе че-
рез точку xq меняет знак с плюса
на минус (с минуса на плюс), и
поэтому (см. замечанием следст-
вию 2) точка xq Е (а, Ь) есть точ-
ка строгого локального макси-
мума (строгого локального ми-
нимума) функции f(x).
ж2, х Е (—оо, +оо). Тогда D/(«) =
0, поэтому точка жо = 0 есть точка
локального максимума функции.
Теорема. Пусть функция f(x) определена на промежутке
|а,Ь|, ж© G (а, Ъ) и f Е Р^п^(жо) для п > 2, причем D*(®o) = 0;
k = 1, 2,... , п — 1, но Dn/(®o)	0. Тогда:
1) если п = 2т (четное) и D2m/(®o) > 0 (D2m/(®o) < 0), то точ~
ка xq Е есть точка строгого локального минимума (строгого
локального максимума) функции /(ж);
2) если п — 2тп+1 (нечетное) и В2т+1/(ж0) > 0 (D2m+1/(®o) < 0),
mo функция /(ж) строго возрастает (строго убывает) в точке жо-
Доказательство. Из условий теоремы следует сущест-
вование окрестности С7(ж0) С |а, Ъ\ такой, что f Е D(n“1)(t/(a?o))
и f 6 D^n)(®o)* Тогда по теореме Тейлора имеет место формула
Тейлора с остаточным членом в форме Пеано, т. е. в окрестнос-
ти (7(жо) имеем /(ж) = Рп(ж;/, жо) + о((ж — ®о)п) (® жо), при-
чем в силу условий ПЛ/(ж0) = 0 (к = 1,2,... ,п - 1) Рп(ж;/,ж0) =
168
(х ~~~
у(хо) + T>nf(xo)~—^5---’ т- е- имеем представление /(х) — /(хо) =
52^(!С—(х - х0)п + о((х - х0)п) (х -+ Хо).
п|
Поскольку Dn/(®o) / 0, то по теореме о знаке для эквивалентных
функций (допускающих представление вида f = д + о(д) (ж -> жо±0))
следует, что > 0 такое, что знак разности f(x) — /(а?о) совпадает
со знаком функции Dn/(xo)(x - хо)п в полуокрестностях (жо - й ®о),
(жо, жо + <5) CZ Щхо). Поэтому если п = 2т (четное), то
(D2m/(®o) > 0) => (/(х) - /(х0) > 0) => (/(х) > /(x0)Vx G Us(x0))
(аналогично (D2m/(®o) < 0) => (/(х) < /(x0)Vx G Ug(x0))). Таким
образом, при n = 2т xq - точка строгого локального минимума (стро-
гого локального максимума) функции /(х). Если же п = 2т + 1 (не-
четное), то (D2ra+1/(®o) > 0) => (f(x) - f(xQ) < 0 Vx G (х0 - <f,®o)
и f(x) — /(хо) > 0 Vx G (хо, ®о + £)), т. е. функция f(x) строго воз-
растает в точке xq 6 (а, Ъ) (аналогично при D2m+1/(®o) < 0 такое же
рассуждение показывает, что функция f(x) строго убывает в точке
Xq 6 (а, 6)).
Пример 1. Пусть f(x) = ж4, х 6 (—оо, +оо) (рис. 31). Тогда
D/(x) = 4ж3, D2/(x) = 12ж2, D3f(x) = 24ж, D4/(x) = 24 > 0, D*/(0) =
0 (k = 1,2,3), т. е. точка жо = 0 есть точка строгого локального
минимума функции /(х).
Пример 2. Пусть (рис. 32)
fl3.\ - I ехр(-1/х2), х / 0,
\ 0, х = 0.
Тогда Dfc/(0) = 0 Vfc > 1 и теорема не применима, хотя xq = 0 есть
точка строгого локального минимума функции /(х), так как производ-
иая D/(x) = 2х-3ехр(—ж-2) при переходе через точку жо = 0 меняет
знак с минуса на плюс.
169
§ 3. Направление выпуклости. Точки перегиба
Определение. Пусть функция f G С((а,Ь)) и ®о € (а,Ь).
Пусть f G ®(®о) п у = L(x, xq) есть уравнение касательной к гра-
фику Г = {(®,у) € R2|y = /(®), х G (а, Ь)} функции f(x) в точке
(®о,Д®о)) € Г. Скажем, что функция f(x) выпукла (строго выпук-
ла) вниз в точке xq, если существует окрестность U(xq) С (а, Ь)
такая, что f(x) > 1(®,®о) (/(®) > 1(®,®о)) V® € 17(®о)-
Аналогично, функция f(x) выпукла (строго выпукла) вверх в точ-
ке хо, если существует U(xq) С (а,Ь) такая, что f(x) < L(x,xo)
(/(®) < L(x,xq)) V® € U(x0).
Замечание. Если функция f(x) строго выпукла вниз (вверх) в
точке ®о € (а, Ь), то в некоторой окрестности этой точки U(®o) С (а, Ь)
график Г = {(х,у) € R2|y = f(x), х G С7(®о)} функции /(®) нахо-
дится над (под) касательной, проходящей через точку (®ch/(#o)) 6 Г
(рис. 33)..
Определение. Пусть f Е С((а, Ь)) и ®о € (а, Ъ). Пусть f £
Р(®о). Точка (®о>/(®о)) € Г называется точкой перегиба графика
функции /(®), если существует окрестность U(®o) С (а, Ь) такая,
что Vx Е £7(®о) /(®) < Ь(®,®о) (/(®) > Ь(®,®о)) для х < ®о и f(x) >
1(®, ®0) (/(®) < Ь(®, ®о)) для х > ®q.
Определение. Пусть f Е С((а, b)) uxqE (а, Ь) и 3D/(®o) =
+оо (—оо), тогда точка (®<ь/(®о)) € Г также называется точкой
перегиба графика Г функции f(x).
Замечание. Если точка (®о,/(®о)) € Г есть точка перегиба
графика Г функции /(®), то в некоторой окрестности CZ(®o) С (а, Ь)
точки ®о 6 (а, Ь) график Г переходит с одной стороны касательной на
другую (рис. 34).
Заметим, что точки с, € Г (i = 0,1,2) являются точками перегиба
графика Г, в то время как точка сз Е Г не является точкой переги-
ба, поскольку в точке сз нет вертикальной касательной (хотя и есть
170
вертикальные правая и левая полукасательные).
Пусть f € С((а, Ь)), х0 € (а,Ь) и f € ®(®о)- Если у = 1(®, ®о) есть
уравнение касательной к графику Г функции f(x) в точке (®о, /(®о)) €
Г, то имеем £(®, ®о) = /(®о) + D/(®o)(® “ ®о)>	® < +оо.
Введем при х € (а, Ь) функцию Д(®) = f(x) - £(®,®о), так что
д(х) = /(®) - /(®о) “ D/(®o)(® “ ®о) V® € (а, Ь), и заметим, что Д €
С((а,Ь)) Л®(®о), причем Д(®0) = 0 и ОД(®о) = D/(®o) - D/(®o) = 0.
Теорема (критерий выпуклости дифференцируемой функции
в точке и критерий существования точки перегиба графика диффе-
ренцируемой функции). Пусть f € С((а,Ь)), ®0 € (а, Ъ) и f € 2>(®о)-
Тогда:
1)	(функция /(®) выпукла (строго выпукла) вниз в точке ®о) <=>
(функция Д(®) имеет в точке ®о локальный минимум (строгий ло-
кальный минимум));
2)	(функция f(x) выпукла (строго выпукла) вверх в точке ®о)
<=> (функция Д(®) имеет в точке ®о локальный максимум (строгий
локальный максимум));
3)	(точка (®о, /(®о)) Е Г есть точка перегиба графика Г функции
f(x)) <=> (функцйя Д(®) строго монотонна в точке ®о).
Доказательство. 1) Если функция f(x) выпукла (строго
выпукла) вниз в точке ®о, то существует окрестность U(xq) С (а, Ь)
такая, что Д(®) > 0 = Д(®о) (Д(®) > 0 = Д(®о)) V® 6 U(xq), т. е. ®о -
точка локального минимума (строгого локального минимума) функ-
ции Д(®).
Обратное утверждение докажите самостоятельно. Очевидно,
утверждение 2) нашего критерия доказывается так же, как и утверж-
дение 1).
Далее,
3)	если точка (®о,/(®о)) € Г есть точка перегиба графика Г функ-
ции /(®), то ВС7(®о) С (а, Ь) такая, что V® € U(xq) Д(®) > 0 = Д(®о)
(Д(®) < 0 = Д(®о)) при ® < ®0 и Д(®) < 0 = Д(®о) (Д(®) > 0 = Д(®о))
при х > ®0, т. е. функция Д(®) строго монотонна в точке ®о.
Обратно, если функция Д(®) строго монотонная (например, строго
возрастает) в точке ®о € (а, Ь), то ЭЩ®о) С (а, Ь) такая, что V® €
U(xq) Д(®) < Д(®о) = 0 при ® < ®о и Д(®) > Д(®о) = 0 при ® > ®о, но
это и означает, что точка (®о, /(®о)) € Г есть точка перегиба графика
Г функции /(®).
Теорема 1 (достаточный признак выпуклости функции в точ-
ке и существования точки перегиба у ее графика - по первой произ-
водной). Пусть f GT)((а, Ь)) и ®о € (а, Ь). Тогда:
1)	если D/(®) t (ТТ) в точке ®о, то функция f(x) выпукла (строго
выпукла) вниз в точке ®о;
2)	если D/(®) I (It) в точке ®о, то функция f(x) выпукла (строго
выпукла) вверх в точке xq;
171
3)	если производная D/(x) имеет в точке xq строгий локальный
экстремум, то точка (хо, /(хо)) 6 Г является точкой перегиба гра-
фика Г функции f(x).
Доказательство. При выполнении условий теоремы 1
Va? Е (а, Ъ) ЗвД(х) = В/(х) - В/(х0), причем ВД(хо) = 0.
1) Если производная Df(x) Т (ТТ) в точке хо, то ЗС7(хо) С (а, Ь)
такая, что Va? Е 17(а?о) ВД(х) < 0 = ВД(х0) (ВД(х) < 0) при а? < xq
и ВД(х) > 0 = ВД(хо) (ВД(х) > 0) при х > а?о, причем вД(хо) = 0.
Поэтому функция А (а?) имеет в точке х = а?о локальный нулевой мини-
мум (строгий локальный нулевой минимум), т. е. Д(х) > 0 (Д(х) > 0)
Va? Е U(xQ), и поэтому в окрестности С7(а?о) график Г функции /(а?)
находится над касательной, так что функция /(х) выпукла (строго
выпукла вниз) в точке хо- Утверждение 2) теоремы 1 доказывается
аналогично.
3) Пусть, например, производная Df(x) имеет в точке хо строгий
локальный минимум. Тогда существует окрестность U(xq) С (а, 6)
такая, что (В/(х) > Bf(x0)) => (ВД(х) > 0) Vx Е U(xq). Но тогда
в силу следствия из теоремы о строгой монотонности дифференциру-
емой функции функция Д(х) Т| на U(xo), и поэтому функция Д(х)
при переходе через точку xq меняет знак с минуса на плюс, так что
график Г переходит с одной стороны касательной на другую в точке
(хо, /(хо)) 6 Г, являющейся тем самым точкой перегиба Г.
Следствие (необходимое условие существования точки пе-
региба). Если f Е Р((а, Ь)), хо Е (а, Ь) и ЗВ2/(хо), то равенство
D2/(®o) = 0 является необходимым условием существования точки
перегиба (хо, /(хо)) 6 Г графика Г функции f(x).
В самом деле, если (хо, /(хо)) Е Г есть точка перегиба графика Г
функции /(х), то функция Д (х) строго монотонна в точке х0 и поэтому
меняет знак при переходе через точку хо, причем Д(хо) = ВД(хо) = О
и В2Д(®о) = В2/(хо). Если бы D2/(®o) / 0, то функция Д(х) имела бы
в точке хо строгий локальный нулевой экстремум и поэтому не могла
бы менять знак при переходе через xq. Противоречие, т. е. В2/(хо) =
0.
Замечание. Обратное утверждение, вообще говоря, неверно.
Так, график функции f : х х4 (см. рис. 31) не имеет точку (0, /(0)) Е
Г точкой перегиба, хотя В2/(0) = 0.
Теорема 2 (достаточный признак выпуклости функции в
точке и существования точки перегиба у ее графика - по производным
высшего порядка). Пусть f Е Р<п-1)((а, Ь)) при п > 2 хо Е (а, Ъ) и
f £ р(п)(ж0). Пусть В*/(®о) = 0 (1 < к < п), но Вп/(хо) ф 0- Тогда:
1) если п = 2т (четное), то функция /(х) в точке xq строго вы-
пукла вниз при В2т/(хо) > 0 и строго выпукла вверх при В2т/(хо);
2) если при т > 1 п = 2т + 1 (нечетное) и В2т+1/(х0)	0, то
точка (хо,/(®о)) Е Г есть точка перегиба графика Г функции /(х).
172
Доказательство. Из условий теоремы 2/6 р(Л-1)((а, 5))
и / 6 Р<п)(®о)- Тогда по теореме Тейлора имеет место формула
Тейлора с остаточным членом в форме Пеано, причем в силу усло-
вий В*/(жо) = 0 (1 < к < п) имеем представление f(x) = /(®о) 4-
D/(xo)(® - ®о) + —(ж - ®о) + о((® - Хо)п) (® -> Хо ± 0), отку-
да f(x) - L(x,x0) = В	~ Шо)П + °((ж ~ Ш°)П) (® -> ®о ± 0).
Поскольку Dn/(®o)	0, то по теореме о знаке для эквивалентных
функций, допускающих представление / = д 4- о(д) (х -> жо 4: 0), сле-
дует, что 3<5 > 0 такое, что знак разности /(ж) — Ь(ж, х — 0) совпадает
со знаком функции Вп/(жо)(ж — ®о) в полуокрестностях (жо — <5, жо),
(жо, жо + <5) С (а, Ъ). Поэтому если п = 2т (четное), то (B2w/(®o) > 0)
=> (/(ж) — Ь(ж,жо) > 0) => (/(ж) > Ь(ж, жо) Уж 6 U(xq)). Аналогично
(Э2ш/(жо) < 0) => (/(ж) < £(ж,ж0) Уж 6 Щжо)), т. е. при п = 2т
функция /(ж) строго выпукла вниз (вверх) в точке жо 6 (а, 5).
Если же п = 2тп4-1 (нечетное), причем т > 1, то (В2т+1/(ж0) > 0)
=> (/(ж) - £(ж,ж0) < 0) => (/(ж) < £(ж,жо) Уж 6 (ж0 - <5, ж0) и /(ж) >
L(x, жо) Уж 6 (ж0, жо 4- <5)).
Аналогично при В2т+1/(ж0) < 0 имеем /(ж) > Ь(ж, жо) Уж 6 (жо —
<5, жо) и /(ж) < £(ж, жо) Уж 6 (жо, жо 4- <5), т. е. при п = 2т 4-1 (т > 1)
точка (жо, /(®о)) Е Г является точкой перегиба графика Г функции
/(*).
Следствие 1 (достаточный признак существования точки
перегиба у графика функции - по 3-й производной). Пусть / 6
р(2)((а, Ь)), жо Е (а, Ъ) и / 6 1>(3)(ж0). Если В2/(ж0) = 0, но В3/(ж0) /
0, то точка (жо, /(®о)) € Г есть точка перегиба графика Г функции
Ж).
Пример. Пусть / : ж -> ж3 (см. рис. 25). Тогда В/(ж) = Зж2,
В2/(ж) = 6ж, В3/(ж) = 6 > 0, В2/(0) = 0, В3/(0)	0, поэтому точка
(0, /(0)) Е Г есть точка перегиба графика Г нашей функции.
Следствие 2 (достаточный признак строгой выпуклости
функции в точке - по 2-й производной). Пусть / 6 2>((а, 6)), жо 6 (а, Ъ)
и / 6 Р(2)(ж0). Тогда если В2/(жо) > 0 (В2/(жо) < 0), то функ-
ция /(ж) строго выпукла вниз (вверх) в точке жо. В самом деле,
/(ж) - £(ж,ж0) = 2|В2/(ж0)(ж - ж0)2 4- о((ж - ж0)2) (ж -> ж0) и при
В2/(ж0) > 0 /(ж) — £(ж, жо) > 0 Уж 6 (7(ж0), т. е. функция /(ж) строго
выпукла вниз в точке жо.
Теорема. Пусть f 6 2>((а, Ь)), причем В/(ж) Д (Д) на
(а, Ъ), тогда У[ж1,ж2] С (а, Ъ) - хорда, соединяющая точки =
(®i,/(®i)) 6 Г и М2 = (ж2,/(ж2)) Е Г, лежит выше (ниже) куска
графика Гмгм2 = {(Х,У) G R2|j/ = /(ж), ж 6 (Ж1,ж2)} функции /(ж)
(рис. 35).
173
Доказательство. Пусть Mi = (х<,f(xt)) € Г (t = 1,2),
где а < ®1 < ха < Ъ, тогда уравнение секущей, проходящей через
у — f(®l) X — ®1
точки Mi € Г и М2 € Г, имеет вид .	.. . =-----или у =
/(®а)-/(®1)	®а-®1
/(х), если положить l(x) = /(xi) + ——^11(х - Xi). Утверждение
Х2  Х1
теоремы сводится к доказательству неравенства
Пусть Xq € (xi, xj) - любая, но фиксированная точка, тогда
Цх0) - /(хо) = —[(/(«г) - /(®1))(®о - ®1)+
®2 ““ ®1
+(/(®i) - /(®о))(®а - ®i)] = —Ц-[(/(®а) - /(«о)(®о - ®1)+
®2 — ®1
+(/(®о) - /(®1))(®0 - ®1 - ®а + ®i)] => (/(®о) - /(®о) =
= Т [(/(*>) “ /(»о))(®о - ®1) - (/(®о) - /(®1))(®2 - ®о)]).
®2	®1
Применяя к функции /(t) теорему Лагранжа о конечных прира-
щениях на отрезках [xi,xo] и [х0, хг], видим, что 3ci € (®i, ®о) и
Эс2 € (х0, х2) такие, что /(х2)-/(х0) = D/(c2)(x2-xo), /(®o)-/(®i) =
D/(ci)(xo - xi). Но тогда имеем а < ®i < ci < хо < C2 < хг < b
Ц®о) ~ /(®о) = —-—(D/(c2) - D/(ci)](x0 - ®i)(®2 - ®о),
®2 ~ ®1
откуда в силу условия D/(®) ТТ (И) на (xi,®2) и C2 > ci имеем
(D/(c2) - D/(ci) > 0 (< 0)) => (/(хо) > /(хо) (/(хо) < /(®о))). что
и требовалось доказать.
Замечание 1. Если D/(®) ТТ (а> ^)< утверждение теоре-
мы аналитически выражается неравенством /(х) > /(х) Vx € (®i, Х2)
174
и V[® - 1,®г] С (а, 6), которое в свою очередь эквивалентно сле-
дующему неравенству (условию выпуклости): /(A®i + (1 - А)®г) <
A/(®i) + (1 - А)/(®з) VA € (0,1).
В самом деле, V[®i, ®г] С (а, Ь) пусть Ао € (0,1), тогда при Ао =
(®2 - ®о)/(®2 “ ®1)> 1 - Ао = (®о - ®1)/(®2 - ®1) имеем ®о = Ао®1 + (1 -
Ло)®2 € («1, ®г)> и тогда
Ц®о)>/(«о)=>	- ®1) + /(®х) > /(®о)) =>
\	®2 "" ®1	/
—7^ + /(®2)	~	> /(®о)) =>
\	®2 "" ®1	®2 “ ®1	/
=> (/(Ао® 1 + (1 - Ао)®г) < Ao/(®i) + (1 - Ао)/(®г)).
Определение. Функция f(x), определенная на интервале
(а,Ь), называется выпуклой (строго выпуклой) вниз на интервале
(а,Ь), если V отрезка [®i,®2] С (а, Ь) u VA G (0,1) выполнено нера-
венство f(X%i + (1 — А)®з) < A/(®i) + (1 — А)/(®г) (соответственно
f(Xxt + (1 - А)®3) < А/(®1) + (1 - А)/(®2)).
.Замечание. Если в определении V® € (®1, ®э) положить A®i +
(1-А)®2 = ®, то получаем А = ——— и 1-А = ———, где 0 < А < 1,
®2	®1	®2 “ ®1
0<1-А<1, и тогда /(A®i + (1 — А)®г) = /(®), так что
А/(®х) + (1 - А)/(®2) = 1(х) = /(хх) +	_ Xi),
®2 ““ ®1
где у = 1(х) есть уравнение секущей, проходящей через точки М\ =
(®1)/(®1))) М2 = (®2)/(®г)) € Г = {у = /(®)|®1 < ® < ®г}- Та-
ким образом, неравенство из (глобального) определения выпуклости
(строгой выпуклости) вниз функции f(x) эквивалентно неравенствам
/(®) < *(®) (/(®) < К®)) V® € [®1,®г] С (а,Ь).
Аналогично определяется выпуклость (строгая выпуклость) вверх
функции f(x) на интервале (а, Ь).
Следствие! (достаточный признак строгой выпуклости диф-
ференцируемой функции). Если / е 1>((а, 6)) и первая производная
D/(®) ТТ (И) на (а, Ъ), то функция /(®) строго выпукла вниз (вверх)
на интервале (а, Ь).
Следствие 2 (достаточный признак выпуклости для дваж-
ды дифференцируемой функции). Пусть / G l?W((a, Ъ)) и D2/(®) > 0
(D2/(x) > 0) V®G (a,6), тогда функция f(x) выпукла (строго выпук-
ла) вниз на интервале (а, Ь).
176
Пример 1. Функция f(x) = ха, х Е (0,4-оо) строго выпукла
вниз на (0, +оо) при (а < 0) Л (а > 1) и строго выпукла вверх на
(0,4-оо) при 0 < а < 1. В самом деле, имеем Уж > 0	*
D2(®°) = а(а - 1)жЛ"2 ( ;2ПрИ°5п<1’
v ’	( > 0 при а < 0 или а > 1.
Пример 2. Функция /(ж) = — In |ж| Уж / 0 строго выпукла вниз
как на (—оо,0), так и на (0, +оо), поскольку D2(—1п|®|) = D(—1/ж) =
I/®2 > 0 Уж / 0.
Замечание. Если функция /(ж) выпукла (строго выпукла)
вниз на (а, 6), то для функции «наклона» ^>(ж; жо) =	—Я^о) уж
Ж ®о
(а, Ь) \ {жо} имеем у>(х; х0) t (ТТ) на (а, Ъ) \ {ж0}.
В самом деле, пусть для определенности f(x) строго выпукла вниз
на (а, Ъ), так что l(x) > f(x) Ух € (®х,®2) С (а, Ъ) и, в частности,
Ух е (жх, ж2) ^!Е2--—^1^12 . (ш _ ЗС1) -j.	- /(ж)) > 0, т. е.
Ж2 — Ж1
/(ж) - f (жх) /(ж2) - /(ж)	.
-----------<--------------£ г®х, Х2) С (а, о).
X Ж1	Ж2 “* ®
Тогда в случае а < Ж1 < жг < ®о> полагая ж = жо, имеем
, Ч /(®х) - Лжо) . Лш2) - Дяо) ,	.
р(жх;ж0) = -1— ----< -д—;--------—- = <р(х2;х0).
®1 — ®0	®2 ~ ®0
В случае а < жо < ®i < ®2, полагая ж = ®о, имеем
Шо) = Aflb/W <	= „(Г]!Io),
®1 “ ®0	®2 - ®0
и, наконец, в случае а < Ж1 < жо < ®2, полагая ж = жо, имеем
г{11.1о) = Д?хЬ < /(*,) - /ы = (
®1 ~ ®0	®2 - ®0
т. е. у>(ж; жо) ТТ на (а, Ъ) \ {ж0}.
Теорема (о непрерывности выпуклой вниз функции). Пусть
функция f(x) выпукла вниз на (а,Ь). Тогда Ужо 6 (а, Ь) существуют
конечные односторонние производные —оо < D”/(®o) < D+/(®o) <
Ч-oo, так что f Е С((а, Ъ))> причем У[ж1, Ж2] С (а, Ь) имеем
D~/(xx) < D+/(acx) <	< о"/(ж2) < D+f(x2),
Ж2 — ®1
так что D“/(®) t на (а>&), D+/(®) t на (а»^)«
176
Доказательство. Пусть функция f(x) выпукла вниз на
(а,Ь); тогда <р(х-, а?0) Т на (а, Ь) \ {ж0}, так что при х < ж0 <
(f(x; Xq) <	®о)«
Тогда в силу существования ограниченного предела монотонной
. А 3 г / ч 1- Лж) - f(xo)
ограниченной функции 3 hm <р(х; а?о) = hm --------------- =
ж—>т0—О	т->®о-О	X —
D"/(a:o) < р(®2;®о) =	И lim а>(х2;х0) = D+/(®o) >
«2 ~ ®0	®->а?о+О
D-f(x0) = Ит р(®;жо)> так что Vzo G (a, b) 3D"/(®o) < D+/(®o),
I—>Tq— О
и поэтому f Е С(®о) V«o 6 (а, Ь).
Далее,
/, . т х _ /(*1) - Лж2) _ f(x2) - f(Xi)
^(®1,#2) —	—	— ^(®2)а'1)>
«1 — «2	$2 ~ Ж1
откуда имеем
lira y>(®i;х2) = D-/(®2) < D+f(x2),
так что имеем D"/(®i) < D+/(®i) <	< D“/(®2) <
Ж 2 Ж 1
D+/(®2) и, в частности, D- f(x) | на (а, Ъ) и D+/(®) t на (а, Ь).
Можно доказать следующий критерий.
Теорема (критерий выпуклости вниз функции на интервале).
(Функция х -> f(x) выпукла вниз на интервале (а,Ъ)) <=> (функция
f(x) обладает двумя свойствами: 1) f Е С((а,Ъ)) и 2)Vx Е (а,Ь) су-
ществуют конечные односторонние производные D+/(®) u D-/(ж),
где равенство D+f(x) = D“f(®) = D/(®) имеет место всюду, за ис-
ключениему быть может, счетного множества точек на (а,Ъ), при
этом D“/(®) < D+ f(x) Vx E (a,b),
D+f(x2) < f-^~ Я*1) < D-/(x2), X1 < x2,
®2 ““
и, в частности, D~ f(x) t «в (a,b) и D+/(®) t Ha (a?^))-
Теорема (критерий выпуклости вниз для дифференцируемой
функции). Пусть f Е 2>((а, Ь)). Тогда (функция f(x) выпукла (строго
выпукла) вниз на (а, Ь)) <=> (D/(®) t (ТТ) на (а,Ъ)).
Доказательство. Достаточность критерия вытекает из
следствия 1 ранее доказанной теоремы.
Необходимость. Пусть, например, f(x) строго выпукла вниз на
интервале (а, Ь) и а < Xi < «2 < Ь. Тогда, вспоминая неравенство
^(ж) > f(x) Vx Е (®i,#2), характеризующее строго выпуклую вниз
Функцию /(ж), имеем
—— ^(ж - Xi) 4- f(xi) > f(x) Vx Е (a?i,х2)
177
или (У(®2) - /(®i))(® - ®i) + (/(®i) - /(®))[(®2 - х) + (® - ®i)] > 0, ,»г. е.
(/(х2) - /(®))(х - ®i) + (/(®I) - /(®))(®г - ®) > О V® € (®1, ®2), откуда
№)-/(».)	(.„»,)	(3.1)
X - ®1	®2 - ®
Переходя в этом неравенстве к пределу сначала при х ®i+0, а затем
при ® ч ®2 - 0 и вспоминая, что f € 2>((а, Ь)), получаем D/(®i) <
—— -----1—- < D/(®2) V®1 < ®2, так что доказано D/(®) t на (а> &)•
®2	®1	""
Вновь возвращаясь к строгим оценкам (3.1), применяя теорему
Лагранжа для функции f(t) на отрезках [®i,x] и [®, ®2], видим, что
3ci € (®х, ®) и Зс2 Е (х, ®2) (так что ®i < ci < ® < с2 < ®2), для
которых имеем
X — Xi	Х2 — х
Но по доказанному ранее D/(®) t на (а, Ь), поэтому из оце-
нок ®i < ci < С2 < ®2 имеем D/(®i) < D/(ci) < В/(сг) < D/(®s)» т. е.
D/(®i) < D/(®2) V®1 < ®2 => (D/(®) ТТ на (а, Ь)).
Замечание 1. Для функции f € С((а, Ь)) из г л о б а л ь -
ной выпуклости функции на интервале следует локальная
выпуклость функции в каждой точке интервала.
Замечание 2. Если функция f(x) строго выпукла вниз на
(а, Ь), то попутно доказанное неравенство (3.1) показывает, что угло-
вой коэффициент хорды MiMq меньше углового коэффициента хорды
М0М2 (здесь Mi = (®i,/(®i)) € Г),
Мо = (®о,/(®о)) € Г, М2 = (®2»/(®г)) в Г (см. рис. 35).
Следствие (критерий выпуклости вниз для дважды диффе-
ренцируемой функции). Пусть f € Т№((а,Ь)). Тогда (функция f(x)
выпукла вниз на (а, Ь)) <=> (D2/(®) > О У® € (а, Ь)).
Теорема (критерий строгой выпуклости вниз для дважды диф-
ференцируемой функции). Пусть f € I>W((a, Ь)), тогда (функция
f(x) строго выпукла вниз на (а,Ь)) <=> (выполнены два условия:
1) D2/(®) > О У® € (а, Ь) и
2) множество точек xq € (а, Ь), для которых D2/(®o) > 0, плот-
но на (а, Ь)).
Для доказательства теоремы достаточно воспользоваться крите-
рием строгой монотонности производной D/(^) для дважды диффе-
ренцируемой функции У € 1?(2)((а, 5)). Условия 1) и 2) необходимы и
достаточны для того, чтобы D/(®) П на (а, Ь) (ср. теорему 3 из § 1
гл. 6).
178
Теорема (неравенство Йенсена). Пусть функция /(®) выпукла
вниз на (а, Ъ). Тогда V®i, «г, •.., хп € (а, Ь) и Va< > 0 (t = 1,2,..., п)
таких, что 52	= 1 имеет место неравенство
1=1
f(aixi + ... + ап®п) < ai/(®i) +... + anf(xn).
Доказательство. При п = 2, полагая а = А и ад =
1 - А, А € (0,1), поскольку функция /(я) выпукла вниз на (а, 6), имеем
оценку V®i,®3 € (а, b) /(ai®i + «2®з) <	+ аз/(«з), так что
неравенство Йенсена для п = 2 справедливо.
Дальнейшее доказательство проведем по индукции переходом от
n = m - 1 и n = tn. Пусть а, > 0 (i = 1,2,..., п) и, например ап > 0.
Тогда Аг = аг + ... + а» > 0,
<*з ,	. ап ,	, х ,
-—h ... + т“ = ai + Аз = 1.
Aj	Аз
m
Заметим, что при Z( е (а,Ь),	> 0 (» = 1,2,... ,т) и £74 = 1,
1=1
очевидно, имеем оценки
т	т	т
° = 527(0 <	< 527<г>=
i=i	i=i	i=i
так что поскольку ®2,®з>>*. >®п € (а,Ь) и а*/Аг € [0,1] (» > 2), то
2J т-®1 € (а, Ь). Используя предположения индукции, имеем
1=2 Л2
= J I «1®1 + Аг >< Т-
\	\|=2
<Л1/(®1)+
чем неравенство Йенсена доказано.
Замечание. Если функция /(®) выпукла вверх на (а, Ь), то
^«1, ®г,... , ®п € (а, b), Votj >0 (t = 1,2,.... п) таких, что £	= 1,
~	i=i
имеет место неравенство Йенсена
(п	\ п
1=1	/	<=1
179
Пример. Функция f(x) = In х строго выпукла вверх на (0,4-оо),
п
поэтому в силу неравенства Йенсена > 0, а» = 1, «» > 0, имеем
i=i
«1 lna?i + .. .4-<*п 1п®Л < ln(aia?i + .. .H-an®n) или х"1 •.. .-ж*п < «1X14-
... 4- апжп. В частности, при а, = 1/n ^/«i ...хп < —(®i 4- ... 4- хп)
п
(соотношение между средним геометрическим и средним арифмети-
ческим) .
§ 4. Условия постоянства функции. Первообразные
функции
Теорема 1. Пусть f Е С([а, Ь])Л2>((а, Ъ)). Тогда (/(ж) = const
на [а, Ь]) & (f Е 2>((а, Ъ)) и D/(«) = 0 Vx Е (а, 6)).
Доказательство. Необходимость. Пусть f(x) = с Vx Е
[а, 6], тогда, очевидно, f Е С([а, Ь]) и Df(x) = 0 Vx Е (а, Ь).
Достаточность. Пусть f Е С([а, 6]) и Df(x) = 0 Vx Е (а, Ь). Тогда
|D/(I)|=£ = O Vx Е (а, 6), и в силу следствия 1 из теоремы Лагранжа
о конечных приращениях V«i, ж2 Е [а, Ь] имеем оценку (условие Лип-
шица) (0 < |/(ж2) - /(®i)| < L\x2 - «1| = 0) => (/(ж2) = Л®1)) и, в
частности, при ж0 Е [а, Ь] имеем /(«) = /(«о) = с Vx Е [а, 6].
Следствие. Пусть Д, Д Е С([а, Ь]) А 2>((а, Ь)), причем
D/i(«) = D/(«2) Vx Е (а, b).
Тогда Д («) — Д (ж) = const на [а, Ь].
Доказательство. Рассмотрим вспомогательную функцию
^(®) = /1(я)-/2(®) Vx Е [а, Ь], тогда Е С([а, Ь])АР((а, Ъ)) и Vx Е (а, Ъ)
3D^>(«) = 0. В силу теоремы 1 <р(х) = const на [а, Ь], т. е. Д(ж)—Д (ж) =
const на [а, Ъ].
Определение. Пусть функции f(x) и F(x) определены на
интервале (а,Ъ). Если Vx Е (а, Ь) 3D^(«) = /(«), то функция F(x)
называется точной первообразной (точной примитивной) функции
f(x) на интервале (а,Ъ).
Теорема 2. Если функция f(x)f определенная на интервале
(а, Ь), имеет на этом интервале точную первообразную Fq(x), то
множество всех точных первообразных функции f(x) на интервале
(а, Ь) совпадает с множеством (функций) F(x) = Fo(x) 4- С, где С -
любая постоянная.
Доказательство. 1) Пусть Fq(x) есть точная первообраз-
ная функции f(x) на интервале (а, 6), так что Vx Е (a, b) 3DFo(x) =
/(«). Тогда для функции F(x) = Fq(x) 4- С при постоянной С имеем
Vx Е (а, Ь) 3T)F(x) = /(ж), т. е. функция F(x) = Fq(x) 4- С при любой
постоянной С есть точная первообразная функция /(ж) на (а, Ь).
180
2) Пусть Fq(x) и F(x) являются точными первообразными для
функции f(x) на (а, Ь), т. е. Vx G (а, b) 3DF0(a?) = /(ж), 3dF(x) = f(x),
яо тогда в силу следствия из теоремы 1 имеем Fq(x) — F(x) = const
на [а, Ц.
Замечание. Если F(x) есть точная первообразная для функ-
ции f (х) на интервале (а, 6), то (F € ®((а, 6))) => (F € С((а, Ь))).
Замечание. Для того чтобы функция F(x) была точной пер-
вообразной для функции f(x) на (а, Ь), нужно, чтобы функция /(ж)
удовлетворяла довольно жестким условиям: функция /(ж) должна об-
ладать на интервале (а, Ъ) свойством Дарбу (т. е. принимать все про-
межуточные значения), далее, если существуют односторонние пре-
делы f(xQ — 0) и /(жо 4- 0), то необходимо выполняются равенства
f (жо “ 0) = f (жо 4- 0) = У(жо), т. е. функция /(ж) не может иметь в
(а, Ъ) точек разрыва 1-го рода.
Пример. Рассмотрим функцию (рис. 36)
{-1, —1 < ж < 0,
О, ж = О,
1, 0 < ж < 1.
Функция /(ж) = sgn ж не может служить производной ни для какой
функции, непрерывной на (-1,1), т. е. функция sgn ж не имеет на
интервале (—1,1) точной первообразной. В то же время, если F^) =
|®|, х е (—1,1) (рис. 37), то Уж 6 0 3DFM = /(ж) и естественно было
бы назвать функцию F(x) = |ж| первообразной для функции f(x) =
sgn ж, хотя функция F^) = |ж| не является точной первообразной для
sgn ж.
Определение. Пусть функция f(x) определена на |а,Ь|.
Тогда функция F^), определенная на промежутке |а, Ь|, называет-
181
ся первообразной (примитивной) для функции /(®) на промежутке
|а, Ь|, если F € С(|а, Ь|) и V® 6 (а, Ь) \ Кп (где Кп - множество, со-
стоящее не более чем из конечного числа точек) 3DF(®) = /(®).
С точки зрения этого определения функция F(®) = |®|, х € (—1,1)
является первообразной для функции f(x) = sgn х на (—1,1), причем
Kt = {0}.
Пример. Функция F(x) = sgn xf х € [-1,1] не является пер-
вообразной для функции f(x) = 0 на [-1,1], хотя V® € (-1,1) \ {0}
3DF(®) = /(®) = 0, поскольку FeCQ-l, 1]).
Теорема 3. Пусть F Е С( |а, Ь|) и существует конечное число
точек Xi Е (а, Ь) (г = 1,2,... ,п) таких, что DF(x) = 0 V® Е (а, Ь),
х ®t*. Тогда F(x) = const на |а, Ь|.
Доказательство. В силу условий теоремы 3 V® € (а, Ь) \
Кп, где Кп = {®х, ®2,... , ®п}, имеем т < DF(x) < М для т = М = 0.
Поскольку F € С(|а, Ь|), то в силу следствия 2 к теореме Лагранжа
о конечных приращениях V$x,*2 € |а, Ь| (tx < имеем оценки (0 =
т < (F(t2) - F(tx))/(t2 - h) < М = 0) => ((F(t2) - F(ti) = 0)) =>
((F(®) = const на |a, b|)).
Следствие. Пусть Fi, F2 6 C(|a, Ь|) и существует конечное
число точек ®, Е (а, Ь) (г = 1,2,... , п) таких, что D«Fi(®) = DjF^®)
V® 6 (а, Ь), х 7^ Xi. Тогда Fx(®) = F2(x) + С V® € |а, Ь|.
Доказательство. Рассмотрим вспомогательную функцию
Ф(®) = Fx(®) — F2(x) и применим к ней теорему 3.
Теорема 4. Пусть функция f(x) определена на промежутке
|а, Ь|. Если /(®) имеет на |а, Ь| первообразную Fq(x), то множество
всех первообразных функции f(x) на |а, Ь| совпадает с семейством
функций F(®) = Fq(x) + С, где С - постоянная.
Доказательство. 1) Если Fq(x) - первообразная для /(®)
на |а, Ь|, то по определению первообразной Fq Е С(|а, Ь|) и ЗЛ^ С (а, Ь)
такое, что V® € (а, Ь) \ КПо 3DFo(®) = /(®), поэтому если F(®) =
Fo(®) + С, где С - постоянная, то F Е С(|а, Ь|) и V® Е (а,Ь) \ Кпо
BDF(x) = D(Fo(®) + C) = DFo(®) = f(x), т. e. функция F(x) = Fo(®) +
C есть первообразная функция /(®) на |a, b| при любой постоянной С.
2) Пусть функции Fq(x) и Гх(®) являются первообразными для
функции /(®) на |а, Ь\, т. е. F, € С(|а, Ь|) (г = 0,1), и существуют
конечные множества КП{ С (a, b) (г = 0,1) такие, что V® Е (a, b) \ Kni
1
3DFi(®) = f(x) (i = 0,1), но тогда V® € (a,b) \ (J Kni 3dF0(®) =
i=0
DFx(®), и в силу следствия к теореме 3 имеем Fx(®) = Fq(x) + С
V® Е |а, Ь|.
Замечание 1. Из теоремы 4 следует, что если функция /(®)
имеет на |а, Ь\ одну примитивную Fo(®), то f(x) имеет на |а, Ь| беско-
нечное множество примитивных.
182
Замечание 2. Теорема 4 устанавливает общий вид первооб-
разной F(x) = Fq(x) + С для функции f(x) на |а, Ь|, если Fq(x) - одна
из первообразных функции f(x) на |а, Ь|.
Замечание 3. Из общего вида первообразной Г(х) — Fq(x)+C
следует, что первообразные для функции f(x) на |а, Ь| определяются
«с точностью до аддитивной постоянной».
Пример. Примитивная функция f(x) = хп (п > 0) на (0, +оо)
равна Fo(®) = -ут®п+1
п +1
и любая другая примитивная имеет вид
§ 5. Центр кривизны, радиус кривизны и кривизна
графика функции
Если функция /(х), определенная на (а, Ь), дифференцируема в
точке xq € (а, Ь), то существует касательная к графику Г функ-
ции f(x) в точке Mq = (хо,/(хо)) € Г и ее уравнение имеет вид
У = /(®о) + D/(x0)(x - ®о), -оо < х < +оо.
Назовем в этом случае нормалью по к графику Г функции f(x) в
точке Мо = (х0, /(®о)) € Г прямую с уравнением у = /(«о) —
X — Xq
Df(x0)’
-оо < х < +оо (если D/(®o) = 0, то нормаль будет вертикальной пря-
мой с уравнением х = хо). Очевидно, нормаль (рис. 38) ортогональна
касательной.
Замечание 1. Если f(x) = Ах + В, х € (а,Ъ), - линейная
функция, то ее график Г есть отрезок прямой с уравнением у = Ах +
В, х Е (а, Ь), и в любой точке графика Г существует касательная (к
графику) с уравнением у = Ах + В, совпадающая с графиком Г Vx 6
(а, 6), при этом существует также и нормаль. Все нормали к графику
линейной функции параллельны между собой (т. е. «пересекаются» в
одной бесконечно удаленной точке).
Замечание 2. Если /(х) = yo±(R2-(x-xq)2)1/2, х е (хо-Я,
®о 4- Я), то графиком Г этой функции будет верхняя (при +) или
нижняя (при -) половина окружности с центром в точке (xb, j/o) и с
радиусом Я > 0.
В любой точке Мо € Г существуют касательная и нормаль, причем
все нормали к Г пересекаются в одной точке - центре окружности (рис.
39) и на одном расстоянии (равном радиусу окружности Я) от точки
пересечения нормалей с графиком Г, при этом величина
1/Я =
.. Да .. Да
1Ш1	;  .т, = НШ л ------7ГГ
Af-кМо |MoM| Аа->0 2Явш(Да/2)
характеризует искривленность дуги окружности Г и называется кри-
183
визной окружности Г. Заметим, что точка пересечения нормалей к
окружности С - центр кривизны - совпадает с центром окружнос-
ти, лежит на нормали по = Мопо и находится с графиком Г по одну
сторону от касательной MQtQ к графику Г в точке Mq, При R = +оо
окружность «переходит» в прямую, имеющую кривизну 1/R = 0.
Замечание 3. Если график Г функции f(x) отличен от ду-
ги окружности, то нормали к Г не будут, вообще говоря, пересе-
каться в одной точке, однако точка пересечения нормалей, проходя-
щих через две «близкие» точки графика Mq = (®о,/(®о)) G Г и
М = (®о + Д®, /(®о) + Д/(®о)) G Г, будут характеризовать искрив-
ленность графика Г в окрестности точки Mq G Г.
Определение. Пусть Г = {(ж, у) G R2\у = /(®), а < х < Ь} -
график функции f G D((a,b)). Пусть Mq = (®о,/(®о)) 6 Г, М =
(®о + Д®,/(®о) +Д/(®о)) е Г U С(Д®) = (Х(Д®),У(Д®)) есть точка
пересечения нормалей Мопо и Мп к графику Г. Центром кривизны
графика Г в точке Mq G Г называется предельное положение (если
оно существует) точки С(Дж) при Д® —> 0. Ятак, центр кривизны
Cq = (Хо,Уо) графика Г в точке Mq Е Г определяется формулой
Cq = lim С(Д®).
Теорема (формулы для вычисления координат центра кри-
визны). Пусть f G 2>(2)((а,Ь)), причем D2/(®) # 0 V® G (а,Ъ). Тогда
для любой точки Mq = (®о,/(®о)) Е Г существует центр кривизны
Со = (Хо,Уо), где
Хо = хо - D/(x0)(l + (Df(xo))2)/D2/(x0),
Yo = уо + (1 + (D/(x0))2)/D2/(x0),
Уо = /(х0), причем центр кривизны Со = (Хо,Уо) « график Г (в неко-
торой окрестности точки Mq 6 расположены по одну сторону
184
от касательной к графику Г в точке Mq € Г.
Доказательство. Пусть Mq = (xq, уо), М = (xq 4- Д®, уо +
Дуо) € Г, где уо = Д®о)> &У = /(®о + А®) — /(®о)- Уравнения нор-
малей Mono и Мп в точках Mq, М 6 Г имеют вид Mono: Y — уо =
-(X-®o)/D/(®o) и Мп-. Y—(уо+Ау) = -(X-(®o+Aa:))/D/(®o+A®).
Точка Со(Х(Да:), Y(Дх)) пересечения нормалей Mono и Мп имеет ко-
ординаты Х(Дх) и У(Дх), удовлетворяющие системе уравнений
У(Д®) - уо = -(Х(Дх) - xo)/D/(®o),
У (А®) - (у0 + Ду) = -(Х(Дх) - (х0 + Ax))/D/(®o + А®)
или
Х(Дх) - хо = -П/(®о)(У(Д®) - Уо).
Х(Дх) - х0 - А® = -D/(®o + Д®)(У(Д®) - уо - Ду).
Вычитая, получаем Да: = —Df(®o + Дх)Дх + (D/(®o + Аа:) —
В/(®о))(У(Д®) — Уо) или, деля на Дх / 0, имеем
1	, л > D/(®o + А®) - D/(®o) tv, Л ,	,
1 = —D/(®o + Ах) — + Ь-----------------—-(У(Да:) - уо).
Но (/ Е Р((а, Ь))) => (D/ G С((а, Ь))), и поэтому имеем
Э lim
д»-»о	Дх	v ’
3 lim Ду = 0, 3 lim Ду/Да: = D/(®o),
Дт-4-0	Дх->0
3 lim D/(®0 + д®) = D/(®o)>
Д®->0
откуда, переходя к пределу при Дх —> 0 в нашем равенстве, имеем
3 lim У(Дх) = Уо, (1 = -(D/®o))2 + 02/(®о)(У - Уо)) =>
Дя?—>0
=> (Уо = Уо + (1 + (D/(®o))2)/D2/(®o))>
откуда, используя уравнение нормали Mono, видим, что
3 lim Х(Дх) = Хо; (X - х0 = -ОЛ®о)(У - Уо)) =>
Дж—>0
=> (Хо = ®0 - D/(®o)(l + (D/(®o))2)/D2/(®o)).
Утверждения о расположении центра кривизны и графика Г относи-
тельно касательной MqIq к Г в точке Mq G Г вытекают из рис. 40 - 45.
Очевидно, при D2/(® — 0) / 0 график Г и центр кривизны Cq в некото-
рой окрестности точки Mq 6 Г лежат по одну сторону от касательной
к Г в точке Mq.
185
Определение. Если график Г функции f € С^2^((а, Ь)) име-
ет центр кривизны Со точки Mq € Г, то окружность с цент-
ром в Cq, имеющая общую касательную Moto с графиком Г в точ-
ке Мо € Г, называется соприкасающейся окружностью (в точке
Мо € Г), а ее радиус Ro = (1 + (^)2)3/2/|j/o I Уо = /(®о),
З/о = D/(®o), Уо = D2/(®o)) называется радиусом кривизны графи-
ка Г в точке Мо € Г. При этом величина ко = л/о/(1 + (j/o)2)3^2
называется кривизной графика Г в точке Мо € Г.
Замечание. Если D2/(®o) = 0, то кривизна ко графика Г в
точке Мо € Г равна нулю.
Пример. Если Мо € Г - точка перегиба графика Г дважды
дифференцируемой на (а, Ь) функции f(x), то кривизна ко = 0.
Определение. Если f € D<2)((a» Ч) « Г - график функции
f(x), то геометрическое место центров кривизны графика Г на-
зывается эволютой графика Г. В параметрическом виде уравнения
эволюты имеют вид
Х = х- D/(®)(1 + (D/(®))2)/D2/(®)>
Y = Дх) + (1 + D/(®))2)/DaД®), х € (а, Ъ).
Пример. Найдем кривизну и эволюту параболы: у = х2, х €
(—оо, +оо). Очевидно, f(x) = х2, Df(x) = 2х, D2/(®) = 2, откуда
k(x) = 2(1 +4х2)~3/2, а уравнения эволюты в параметрическом виде
(X = х - 2х(1 + 4®’)/2, Y = х2 + (1 + 4х2)/2,
( V = — 4д3
ХЕ (-оо,+оо))=> I Y = Зх2 + 1/2,хе(-оо,+оо).
Но тогда (х = (-Х/4)х/з, х = ±((у - l/2)/3)V2) => (±((У -
l/2)/3)V2 =	(X/4)V3) => (У - 1/2 = 3 • 2~*'3Х3/3) =>
(13	\
эволюты параболы изображен на
рис. 46.

lim |Acd/|Af0Af | =
Дх-^0
Замечание. Пусть функция
f € 2>(2>((«, fr)) и Мо = МЫ) е г,
М = (®о + А®,/(®о) + Д/(®о)) € Г.
Обозначим (см. рис. 38) через Да угол
между нормалями Mqtiq и Мп (рав-
ный, очевидно, углу между касатель-
ными MQtQ и Mt). Заметим, что для
хорды М0М имеем \MqM| - ((Аж)2 +
(Aj/)2)1/2, где Дт/ = /(жо + Д®)-Л®о)-
Очевидно, отношение |Да|/|ЛГоМ| ха-
рактеризует искривление графика Г
вблизи точки Mo G Г.
Покажем, что существует
Иш |Да|/|МоЛГ| = |fc0|, где ко -
Дяг->0
определенная выше кривизна графика
Г в точке Мо 6 Г. В самом деле, имеем
| arctg D/(®o + Дж) - arctg D/(®o) I
Д™о |Дх| • (1 + (Ду/Д®)2)2^
_ u |A(arctgPf(®0))/A®| _
дЛо (1 + (ДЛхоУДа:)2)1/2
= |D(arctgD/(a;o))|/(l + (D/(»o))2)1/2 =
= |D2/(xo)l/(l + (D/(xo))2)3/2 = |fco|
(где k0 = Р2/(®о)/(1 + (P/(®o))2)3^2 - кривизна графика Г в точке
Мо G Г).
ЛИТЕРАТУРА
1.	Л а н д а у Э. Основы анализа. М.: ИЛ, 1947.
2.	И л ь и н В. А., П о з н я к Э. Г. Основы математического анализа.
М.: Наука, 1965.
3.	Фихтенгольц Г. М. Курс дифференциального и интегрального
исчисления. Т. II. М.-Л.: ОГИЗ, 1948.
188
Ч а с т ь II
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ
ОДНОГО ПЕРЕМЕННОГО
Глава 1
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. Неопределенный интеграл
Основной задачей интегрального исчисления является задача об
отыскании функции f(x) по заданной производной Df(x) (или отыс-
кание функции f (х) по заданному дифференциалу df(x)).
Очевидно, эта задача является обратной к задаче дифференциаль-
ного исчисления.
Пример. Пусть s = s(t) - закон движения материальной точки
по прямой, т. е. s(t) - длина пути, отсчитываемого от некоторой на-
чальной точки Afo, где t - время, за которое пройден путь s(t). Пусть
М - положение точки в момент а М' - в момент t4- At и Да - длина
пути от точки М до Af', так что As = s(t 4- At) — s(t). Тогда Аз/At
есть то, что называется в механике величиной средней скорости дви-
жения на участке от Af до Af', a v(t) = Jim Да/Д$ есть величина
мгновенной скорости движения точки Af в момент t. Таким образом,
ds _
для величины мгновенной скорости имеем v = —. По определению
dt
дифференциала ds = v(t)dt видим, что значение дифференциала пу-
ти ds(At) = v{t)dt, соответствующее приращению времени At, равно
расстоянию, которое прошла бы точка М за промежуток времени от
момента t до момента t 4- At, если бы она двигалась равномерно со
скоростью, равной мгновенной скорости v(t) точки в момент t. Ве-
личина же Аз действительного перемещения точки (за промежуток
времени At) будет Аз = ds(At) 4- o(At) (At -> 0). Таким образом,
с механической точки зрения замена Аз на значение дифференциала
ds(At) означает, что движение на рассматриваемом участке считает-
тт
ся равномерным. Наряду со скоростью v(t) = можно ввести и
dt
ускорение a(t) = как предел среднего ускорения аср = Av(t)/At
при At —> 0. Таким образом, ускорение точки Af в момент t есть
a(t) = —если s\4 ” закон движения.
ОТ
189
Задача. Найти путь, пройденный точкой за время t при свобод-
ном падении в пустоте, если ускорение силы тяжести есть д. Посколь-
de	dv
куи = —то нужно решить так называемое дифференциаль-
at	at
8	i ds i
ное уравнение = д I зт = 04 > («(<) = 0<2/2) при условиях
at* . \dt J
s(0) = v(0) = 0.
Напомним определение точной первообразной и первообразной
функции /(х) на промежутке |а, 6| (см. ч. I, гл. б, § 4).
Определение. Пусть функции f(x) и F(x) определены
на (а, 6). Функция F(x) называется тонной первообразной (точной
примитивной) функции f(x) на (а, Ъ), если Vs € (а, Ъ) 3D-F(s) = f(x).
Замечание. Если F(x) есть точная первообразная для f(x) на
(а, 6), то F € С((а, 6)) (поскольку F(x) дифференцируема на (а, &)).
Определение. Пусть f(x) определена на промежутке
|а, Ь|, тогда функция F(x), определенная на |а, Ь|, называется пер-
вообразной (примитивной) для функции f(x), если F € С(|а, Ь|) и
Vs € (а, Ь) \ Кп (где Кп - множество, состоящее не более чем из п
точек) 3DF(x) = /(в).
Замечание. Можно было бы еще обобщить понятие первооб-
разной, считая исключительное множество К не более чем счетным.
Пример. Напомним, что функция F(x) = |s| не есть точная
первообразная для функции /(s) = sgn s на (-1,1), однако F(s) =
|s| является первообразной для функции sgn s на (-1,1), при этом
исключительное множество Ki = {0}.
В дифференциальном исчислении было доказано, что если /(s)
дифференцируема, то существует D/(®) и при этом (конечная) произ-
водная D/(x) единственна. В отличие от производной первообразная
не обладает свойством единственности. В самом деле, ранее (см. ч. I,
гл. б, § 4) была доказана
Теорема. Пусть функция /(s) определена на |а, Ь|. Если
/(s) имеет на |а, 6| первообразную Fo(s), то множество всех пер-
вообразных функции /(s) на |а, Ь| совпадает с множеством функций
F(x) = Fq(x) -I- С, где С - любая постоянная.
Замечание. Из этой теоремы следует: 1) если функция /(s)
имеет на |а, Ь| одну первообразную Fo(x), то /(s) имеет на |а, Ь| бес-
численное множество первообразных;
2) формула F(x) = Fo(s) + С устанавливает общий вид первооб-
разной для /(s) на |а, 6|, если fo(s) - одна из первообразных функции
/(s) на |а, Ь|;
3) из общего вида первообразной следует, что первообразная для
/(s) на |а, Ь| определена с точностью до аддитивной постоянной.
Замечание. Если /(s) имеет на |а, 6| примитивную Fq(x) и
so € (а, Ь), то для любой фиксированной постоянной Со существует, и
190
притом единственная, примитивная F(x), удовлетворяющая условию
Г (®о) = Со-
В самом деле, F(x) = Fo(x) + С, где С - любая постоянная,
тогда условие F(xq) = Со дает равенство (Со = Fo{xq) +.С) =>
(С = Со - Fo(®o))> откуда искомая примитивная дается формулой
F(x) = Ро(®) + (Со—Го(®о))- В частности, существует, и притом толь-
ко одна, примитивная G(x) функции f(x) на |а, Ь| такая, что G(xq) = 0.
Для любой другой примитивной F(x) имеем G(x) = F(x) — F(xo),
G(®o) = 0.
_	d2e	... de (dv \	...	,	_ .
Пример. ^2=5,	v(t)	= —, I — = gJ	=> (v(t)	=gt + Ci)	=>
(e(t) = gt2/2 + Cit + Сг). Для выделения единственного закона дви-
жения нужно задать начальные условия: начальное положение точки
з(0) = «о и начальную скорость v(0) = «о, которые и дадут возмож-
ность определить постоянные Сд и Cf. (v(t) = gt + Ci) => (Ci = dq);
(e(t) = gt2/2 + Dot + Сг) => (C2 = во). Таким образом, для искомого
закона движения имеем s(t) = gt2 (2 + vot + во.
Определение. Пусть функция f(x) определена на [а, Ь|. Не-
определенным интегралом от функции f(x) на |а, Ь| называется лю-
бая первообразная F(x) (если она существует) функции f(x) на |а, Ь|.
Неопределенный интеграл от f(x) (если он существует) на |а, Ь| обо-
значается символом J f(x)dx; f(x) называется при этом подынтег-
ральной функцией.
Замечание. Таким образом, если Fq(x) является первообразной
функции f(x) на |а, 6|, то имеет место формула J f(x)dx = Fo(x) + С,
где С - постоянная, надлежащий выбор которой дает возможность
получить любую из первообразных F(x) функции /(г) на промежутке
|а, Ь|.
Замечание. Пусть Fi(x) и Fi(x) - первообразные функции
f(x) на |а, Ь|,тогда / f(x)dx = Д (x) + Ci = Fi(x) + Сг- Эти равенства
эквивалентны, причем 2*1 (хе) - Гг(х) = С.
Замечание. В дальнейшем будут использоваться равенства
вида
У f(x)dx + У g(x)dx = j h(x)dx,	(1.1)
означающие, что функции, стоящие слева и справа в (1.1), отличаются
постоянной, так что (1.1) эквивалентно равенству
У f(x)dx + У g(x)dx = j h(x)dx + С.
Пример.
У У = In 1x1 +С.	(1.2)
191
Функция F(x) = In |ж| 6 C(|a, 6|) есть примитивная для функции
f(x) = 1/ж на любом промежутке |а, 6|, не содержащем 0, поскольку
функция In |ж| разрывна в нуле, поэтому: а) при ж > О J = 1пж 4- С
dx
и б) при ж < О J — = 1п(—ж) + С.
Формально (1.2) есть объединение формул а) и б).
§ 2. Основные свойства неопределенного интеграла
В дальнейшем будет доказана
Теорема (о существовании точной примитивной для непре-
рывной функции). Пусть f G С((а, Ь)). Тогда на (а,Ь) существу-
ет точная примитивная F(x) для функции f(x), т. е. Уж 6 (а, Ь)
3D-F(®) = f(x). Таким образом, для функции f G С((а, 6)) на (а,Ь)
3J f(x)dx.
Теорема (о связи дифференцирования и интегрирования).
Пусть функция /(ж) имеет на |а, 6| первообразную F(x) с исключи-
тельным множеством Кп С так что 3 J f(x)dx = F(x) 4- С.
Тогда Vx 6 (а, Ь) \ Кп имеем d(J f(x)dx) = f(x)dx> D (J f(x)dx) =
f(x),JdF(x) = F(x).
Доказательство. Поскольку f f(x)dx = F(x) 4- С, где
F(x) - примитивная для /(ж) на |а, Ь| (с исключительным множес-
твом Кп С (а,Ь), то Уж G (a,b) \Кп D (J f(x)dx) = В(/Р(ж) 4* С) =
В-Р(ж) = /(ж), откуда d(J f(x)dx) = dF(x) = f(x)dx, кроме того,
(jDF(®)d® = F(®)4-C) => (рГ(ж) = Г(ж) + С).
Теорема (о линейности операции интегрирования). Пусть на
|а, 1>| существуют неопределенные интегралы J f(x)dx и fg(x)dx.
Тогда для любых постоянных а и 0 на |а, Ь| существует неопреде-
ленный интеграл J(af(x)+0g(x))dx, причем
(af(x) + 0g(x))dx = a j f(x)dx+0 J g(x)dx.
Доказательство. В силу линейности операции дифферен-
цирования и теоремы о связи дифференцирования и интегрирования
имеем D (<* J f(x)dx + 0 f g(x)dx) = D (<* J f(x)dx ) + D (0f g(x)dx) =
af(x) + 0g(x) для любого x G (a, b) \ (Kni U КП2)> т. e. функция
af(x) + 0g(x) имеет на |a, 6| примитивную a J f(x)dx + /3 f g(x)dx G
C(|a,fr|), откуда
(af(x) + (3g(x))dx = a I f(x)dx+0 I g(x)dx. (2.1)
192
Замечание. Равенство (2.1) означает, что линейная комбинация
(с коэффициентами а и /?) каких-либо первообразных функций /(®) и
д(х) является первообразной для функции а/(®) 4- (Зд(х) и что всякая
первообразная функция af(x)+Pg(x) является линейной комбинацией
(с коэффициентами а и /3) некоторых первообразных функций f (®) и
Следствие. Пусть на |а, 6| 3 J fi(x)dx (i = 1,2,... , n). Тог-
/ п	\
да для любых постоянных (i = 1,2,..., п) 3 / ( £ с«/«(®)) dx =
fi(x)dx.
«=1
Т е о р е м а (об интегрировании по частям). Пусть на |а, Ь| су-
ществуют функции uf(x), vf(x) и f u(x)v'(x)dx (с исключительным
множеством Кп С Тогда существует f v(x)uf(®)d® с исклю-
чительным множеством Кп, причем
л=1
и
Д о к а з а т е л ь с т в о. V® 6 (а, Ь) \ Кп имеем
х
т. е.
u(x)vf(x)dx Е С(|а, Ь|).
Следствие. Пусть u', г>' 6 С((а, Ь)). Тогда в силу теоре-
мы (о существовании точной примитивной у непрерывной функции)
функции u(®)t/(®) и v(x)u'(x) имеют точные примитивные на (а, Ь) и
формулу интегрирования по частям, справедливую V® 6 (а, Ъ), можно
записать в виде
и • v
Теорема 1(о замене переменной в неопределенном интеграле).
Пусть функция F(t) определена Vt Е [ок, /?] и является точной прими-
тивной для функции f(t) на т. е. 3 / f(t)dt = F(t) + С. Пусть
Vx Е определена функция t = о>(®), где ш Е С([а, Ь]) Л1>((а, Ъ))
и си([<х,Ь]) С [а,/?], так что V® Е (а, Ь) Зо/(®). Тогда на [а,Ь]
3 f f(u(x))u'(x)dx = f /(w(x))dw(x) = F(w(x)) + C
7 Зак. 860
193
Доказательство. Для сложной функции F[w(®)] = (F о
о>)(х), определенной на [a, b], V® € (а, Ь), выполнены условия теоремы
о существовании производной сложной функции, в силу которой
V® G (a,6)3-^F(w(®)) =	= /(а>(®)), w'(®),
ах	at
но это и означает существование точной примитивной
/(w(®))w'(®)d® = F(w(®)) + С.
Замечание. В теореме 1 из существования неопределенного
интеграла J f(t)dt = F(t) + С следует существование неопределенно-
го интеграла J/(w(®))wz(®)d®. Если f € С([а,/3]), то существование
функции F(t) следует из теоремы о существовании точной примитив-
ной у непрерывной функции.
Теорема 2 (о замене переменной в неопределенном интегра-
ле). Пусть функцияt = ы(®) определена на [а, 6], причем ш € С([а, £>]) А
D((a, 6)) u V® € (а, b) wz(®) > 0 (либо ы'(®) < о) u ы(а) = а, ш(Ь) = (3
(либо ы(а) = (3, ы(Ъ) = а). Пусть функция f(t) определена на [a, /3],
причем существует точная примитивная Ф(®) = //(w(®))wz(®)d®.
Тогда на (а,/3) существует точная примитивная F(t) = f f(t)dt,
причем f f(t)dt = Ф(С1(<)) + С, где ® = П(<) - функция, обратная к
функции t = ш(х).
Доказательство. Из условий теоремы 2 относительно
функции ы(х) следует, что для нее существует обратная функция
® = O(t), причем по теореме о производной обратной функции име-
ем Oz(4) = l/wz(®). Тогда
1ф(Пй) = «А = *'(»)/«'(«) =
at	ах at
= /(ш(х))ш'(х)/ш’(х) = /(w(®)) = f(t),
Vt Е т. е. функция Ф(О(4)) есть точная примитивная для функ-
ции f(t) на (а,0), но тогда / f(t)dt = Ф(П(4)) + С.
Замечание. В теореме 2 из существования неопределенного
интеграла J /(w(®))wz(®)d® вытекает существование неопределенного
интеграла J f(t)dt.
§ 3. Таблица основных неопределенных интегралов
Ранее (см. ч. I, гл. 4, § 5) была введена таблица производных прос-
тейших элементарных функций, представляющая собой вычислитель-
ный аппарат дифференциального исчисления. Каждая формула этой
194
таблицы, устанавливающая, что та или иная функция F(x) имеет про-
изводную, равную /(®), приводит в силу определения неопределенно-
го интеграла к соответствующей формуле интегрального исчисления
J* f(x)dx = F(x) + С. Таким образом, приходим к следующей таблице
основных точных примитивных (неопределенных интегралов):
1.	fO-dx = С;
2.	f 1 • dx = х + С;
3.	J xQdx = —— + С (a / -1);
41 f T = ln l»l + C (» °)!
a®
5.	f atdx =	+ C (0 < a £ 1), f eedx = e« 4-C;
In a
6.	J ein xdx = - cos® + C;
7.	/ cos xdx = sin x + C;
8.	J = tg x + C (x ir/2 + nw, n = 0,±l,±2,...);
9.	/ -r-т— = - ctg x + C (x ± nir, n = 0, ±1, ±2,...);
sin x
in f — I arcs*n® + Ci
’	- x^ ~ t “ arccos x + C (-1 < x < 1);
11 f — / arct8 X + C,
‘ 1 + x2 — I - arcctg x + C;
dx	t.....
= In |x + vx2 ± 1| + С (в случае знака «-> |x| > 1);
x - 1
x +1
12.	f . .
\/х2 ± 1
Ч Л f dx 1 .
13.	/ -5-Г = A ln
J х2 - 1	2
14.	/ eh xdx = ch x + C;
15.	J ch xdx = eh x + C;
/dx .
—j— = th x + C;
ch x
17- J “ГТ" = “ cth x + C (x 0).
sn X
Замечание. В дифференциальном исчислении было показано,
что операция дифференцирования не выводит из класса элементарных
функций.
Замечание. Интеграл от элементарной функции не обяза-
тельно является также элементарной функцией.
Пример. Можно доказать, что интегралы /ехр(—®2)dx,
f cos(a?)d®, /sin(®2)d®,	(0 < x 1), J ^^-dx (x ф 0), /
0) не являются элементарными функциями.
Теорема. Если R(x) - рациональная функция, то интеграл
f R(x)dx выражается через элементарные функции, причем кроме
Рациональных функций ничего худшего, чем логарифм или арктан-
генс, не появляется.
7*
+ С(|х|#1);
195
Глава 2
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ РИМАНА
§ 1. Определение интеграла Римана
Пусть числовая функция f(x) определена на отрезке [а, Ь]. Опреде-
лим разбиение Т отрезка [а, Ь] заданием конечной системы точек {ж,}:
а = ®0 <	< • • • <	< %i < • - - < хп = Ь. Диаметром d(T) раз-
биения Т отрезка [а, 6] назовем число d(T) = max (®t — ®,-i) > 0.
,n
Очевидно, для любого разбиения Т отрезка [а, Ь] имеем 0 < d(T) <
Ъ — а. При заданном разбиении Т отрезка [а, Ь] рассмотрим любую
систему точек & Е	(i = 1,2, ...,п) и введем обозначение
£ =	• • • >6»} (а = ®о <	< • • • <	< & < Xi < ... <
xn-i < < хп = Ъ). Разбиение Т отрезка [а, Ь] вместе с выбранной
системой точек £ = {£1,£г, • • • , £п) назовем размеченным разбиением
отрезка [а, Ь] и будем обозначать символом Т£ = р. Множество всех
размеченных разбиений {Т£} = {р} отрезка [а, Ъ] будем обозначать
через Р. Таким образом, Р = {р = Т£|0 < d(T) < b~a}.
Введем во множестве Р систему множеств В = {В^}, где В$ = {р =
Т£ Е Р|0 < d(T) < J}, 6 6 (0, Ъ — а]. Для системы В = {В^} выполнены
условия: 1) V<5 Е (0, Ъ — а] Bj С Р => В$ 0; 2) VJi, 62 Е (0, Ь - а]
В$ С Bdh ПВ,2 Vcf Е (O,min((5i,<52))-
Тем самым показано, что система В = {Bj} есть базис фильт-
ра в Р. Будем обозначать этот базис фильтра (или базу) символом
d(T) -> 0.
По заданной функции f : [а, 6] —> R и размеченному разбиению Т£ с
диаметром d(T) > 0 построим так называемую «интегральную сумму
def ”
Римана»: Sy(T^) =	” ®«-1) (индекс f в дальнейшем будет
« = 1
часто опускаться). При фиксированной функции f(x) на множестве Р
(всех размеченных разбиений отрезка [а, Ь]) определим отображение
F : Р R, положив F(p) = Sy (Т£), где р = Т£ Е Р. Используя'базу
В = {Bj}, т. е. d(T) —> 0, введем
Определение. Интегралом Римана функции f(x) на от-
резке [а, Ь] называется такое число J (если оно существует), что
lim F(p) = JftMU lim Sf(T£) = J).
d(T)->0 v '	d(T)—>o	'	7
Замечание. Напомним, что запись J = lim Sf (Tf) означает
d(T)—>0
Vs > 0 ЗВ^ E P такое, что для любого размеченного разбиения Е
В$ (так, что разбиение Т имеет диаметр d(T) < 6) => \S/(T^) — J\ < s.
ъ
Обозначается интеграл Римана следующим образом: J = f f(x)dx,
а
196
при этом а называется нижним пределом, b - верхним пределом, а
ъ
f(x) - подынтегральной функцией. Интеграл Римана J = J f(x)dx =
а
Ф(а, 6; /) зависит от а, b и /, но не зависит от ж. являющейся «немой»
переменной (переменной интегрирования), в то время как неопреде-
ленный интеграл / f(x)dx = F(x) 4- С зависит от х.
Определение. Если для функции f : [a. b] —> R существует
интеграл Римана на отрезке [а, Ь], то говорят, что функция f(x)
интегрируема по Риману на отрезке [а, 6]. Обозначение: f 6 Л[а, Ь].
Замечание. Класс функций, интегрируемых по Риману на
отрезке [а, Ь], будем обозначать через R[a, Ь].
Расшифровывая понятие предела по базе d(T) -4 0 из определения
интеграла Римана, имеем
(г, <5) - определение интеграла Римана. Число J 6 R на-
зывается интегралом Римана функции f(x) на отрезке [а, 6], если
Vf > 0 35 > 0 такое, что V разбиения Т (отрезка [а, Ъ\) с диамет-
ром d(T) < 6 и¥£ выполняется неравенство \Sf(T£) — J| < г.
Замечание. Геометрически
интегральная сумма Римана (при
f е С([а,Ч), f(x) > О V» G
М) sf(Tt) = Е№)(х. -х.-1)
4 = 1
имеет (рис. 47) простой смысл: это
сумма площадей прямоугольников,
аппроксимирующих криволинейную
трапецию. Поэтому интеграл Рима-
ъ
на R f f(x)dx =	^/(^) можно
рассматривать как «площадь» этой
криволинейной трапеции.
Теорема (единственности интеграла Римана). Для функции
f(x), определенной на отрезке [а, Ь], может существовать не более
одного числа J из определения интеграла Римана. Теорема единст-
ъ
венности интеграла Римана J — f f(x)dx = lim Sj(T£) есть след-
а	d(T)-+O
ствие общей теоремы единственности предела по базе.
Пример. Пусть / : хчс,® € [а,^ тогда для любого разме-
ченного разбиения Т£ отрезка [а, Ь] имеем
S(T&=~ ®«-1)=c(t-a)>
1=1	4=1
Т. е. число J = с(Ь — а) удовлетворяет определению интеграла Римана
197
ь
для (постоянной) функции f : х -> с. Поэтому с € Я[а, 6] я J cdx =
с(Ъ — а).
Пример. Пусть / : х —> х, х € [а, 6], рассмотрим размеченное
разбиение Т( отрезка [а, 6] с диаметром d(T) = t > 0.
Пусть Д®, = Xi - Xi-i, тогда 0 < Д®, < t (i = 1,2,..., п). Далее
S(Tt) = £ /(б)д®< = £ 2£^=1Да)<+
1=1	1=1	z
+ £ (б -	А*. = 5 Ь°?-«?->)+
•=1 4	/	1=1
п /	.4
•=1 ' '
+ 53((» ~ (®« + ж«-1)/2)Дж|.
i=i
Но имеют место неравенства —Дж^/2 = Xi-i — (ж,- 4- ®»-i)/2 <	—
(ж,- + Xi-i)/2 < Xi —	4- ж,-1)/2 = Дж,/2, откуда
\S(Tt) - (Ъ2 - а2)/21 < I £ (Д®.)2 < |	- Х.-1) = t(b - а)/2.
4 1=1	1=1
2в
Но тогда, полагая Ve > 0, 6 = и J = (Ь2 - а2)/2, имеем при
0 < t = d(T) < S |$(Т{) - J| < е, т."е.°
ь
У xdx = (Ь2 - а2)/2 =► х € Я[а, 6].
а
Теорема (необходимое условие интегрируемости по Риману).
Если f € R[a, b]f mo функция f(x) ограничена на отрезке [а, Ь].
Доказательство. Пусть f € Я[а, Ь]. Но тогда
ъ
BJ = I f(x)dx = dlimoSf(Tt),
а
и поэтому при во = 1 Э<Уо > 0 такое, что для любого размеченного
разбиения с d(T) < 6q имеем |S(T£) - J\ < 1. Зафиксируем раз-
биение Т = {®о, ®i,... , жп} с диаметром d(T) < £о, тогда У£ имеем
is(re)i < и+1.
198
Допустим, что функция f(x) не ограничена на [а, 6], тогда
существует отрезок [®*_i,®*] с концами ®*_j, ®* € Т такой,
что на нем функция /(®) также не ограничена. Выберем £ =
{®1> • • • ,®*-1, (к, ®*+i,..., ®п} и положим S(T() = S*(T£)+/(&)A®fc.
В силу неограниченности функции /(®) на отрезке [®k-i,®s] Э& €
[®k-i,®t] такое, что |/(^k)|A®k > 1 + |J| + |S*(T^)|, т. е. сущест-
вует размеренное разбиение Т£ с диаметром d(T) < 60 такое, что
|5(Т4)| > |/(&)Д®к| - |5*(Т£)| > |<7| + 1. Противоречие.
Замечание. Из ограниченности функции /(®) на отрезке
[а, Ь], вообще говоря, не следует, что / € Л[а, 6].
Рассмотрим, например, функцию Дирихле на отрезке [0,1]:
...	/О,®- рационально,
j (а?) “ 1 1
' 7	[ 1, х — иррационально.
Тогда в силу плотности множеств рациональных и иррациональных
чисел в R (Q = R, R \ Q = R) при любом разбиении Т отрезка
[0,1] на любом частичном отрезке [®k-i,®k] существует как рацио-
нальная 9k, так и иррациональная г*, откуда для любого разбиения Т
отрезка [0,1], полагая q = {gi, 92,... , 9п} и г = {гх, гг,... , гп}, имеем
S/(Tq) = 0, S/(Tr) = 1, т. е. ^Шп ^Sf(T() не существует. (В самом
деле, если бы Э^Ит (Т£) = J, то в силу критерия Коши сущест-
вования предела числовой функции по базе d(T) -> 0 Ve > 0 3Bj € Р
такое, что VT£, Тг) g Bf |Sy (Т£) - Sf (Гт?)| < £, но при 0 < е < 1 имеем
|S?(T9) - S?(Tr)| = 1. Противоречие. Итак, /?Я[0,1]).
§ 2. Суммы Дарбу и критерий Дарбу
интегрируемости по Риману
Если / € Я[а, 6], то 3 ^Нт ° Sf (Т£) = J € R.
Пусть Т - некоторое разбиение отрезка [а, 6], тогда возможный
разброс интегральных сумм Римана S/(T{) при различном выборе 4
и ? определяется величиной sup \Sf(T£) - Sf(T£')\. Ранее (см. ч. I,
гл. 3, § 9) была доказана
Лемма. Пусть Е С R u w = sup 2? - inf Е. Тогда ы =
sup |®i — ®г|.
Таким образом, sup \S/(T£) - Sf(T£')\ = "Sf(T) - Sf(T), где
У/(Т) = etipS,(Т{), £ДТ) = inf
199
Величина Sj(T) называется верхней суммой Дарбу функции f(x) для
разбиения Т отрезка [а, Ъ], a Sf(T) называется нижней суммой Дар-
бу.
Теорема (формулы Дарбу). Пусть функция f(x) определена
и ограничена на [а, 6]. Пусть Т - разбиение отрезка [а, 6] и Mk ==
sup f(x), ть = inf f(x). Тогда имеют место формулы Дарбу
[arfc_i,xfc]	[*к-1Лк]
S/(T) = Y'Mkbxt, Sf(T) = Ymkbxk.
k=l	k=l
Доказательство. Для заданного разбиения Т отрезка [а, Ь]
и G	имеем m* < f(£k) < Af*, откуда для любого £
получаем оценку
п
S(Tt) <^Mkbxk.	(2.1)
fc=l
Поскольку Mk = sup /(®), то Vs > 0	6	такое, что
[rfc-i,Xfe]
f(£k) > Mk — ^/{Ь — а), т. e. для выбранного таким образом размечен-
ного разбиения имеем оценку
S(Tl)>Yl{Mk--^—}^xk = YlMk^xk-e (2.2)
k=i '	° а)	k=i
п
(где использовано равенство £ &хк ~ Ь — а). Из (2.1) и (2.2) имеем
fc=i
п
VMfcAa;fc = supS(T£) = S(T).
Аналогично доказывается равенство
^mk&Xk = irfS(T£) = S(T).
fc=l	*
Замечание. Если f 6 C([a,Ь]), то верхняя и нижняя суммы
Дарбу являются интегральными суммами Римана, так как для не-
прерывной на отрезке функции по теореме Вейерштрасса существуют
точки £*,£* G [ж*. 1, xk] такие, что Mk = /(?*), ю* = и поэтому
S(T) = S(T£), S(T) = S^T^). В случае, когда f(x) только ограничена
на [а, Ь], таких точек и £* может не существовать, поэтому суммы
Дарбу S(T) и S.(T), вообще говоря, не являются интегральными сум-
мами Римана для f(x).
200
Замечание. Для данного разбиения Т отрезка [а, 6] положим
и к = Mfc—mfc, тогда Шк = w(/;	есть колебание функции f(x)
<ief —
на отрезке	Положим Оу (Г) = Sy(T) - SAT) = £
fc=i
Тогда для любого разбиения Т имеем
sup |$у(Т£) - Sf (ТЩ = Sf (T) - Sy(T) = Oy(T).
u'
Определение. Пусть Т иТ' - два разбиения отрезка
[а, Ь]. Раз биение Тг называется продолжением разбиения Т, если лю-
бые точки деления, входящие в Т, входят и в Т*, т. е. разбиение
Т' получас тея из разбиения Т добавлением дополнительных точек
деления отрезка [а, Ь]. Если Т' - продолжение Т, то пишут Т' -<Т
(Т = {®о,	• • • , Т = {®о,	• • • } пх > п) =>
—((X —- ®0 ~ ®0 <	< ®1 = ®2 < • • • <	“
= Х1 < х1+1 < • • • < ®п =	~ &)•
Теорема 1. Пусть функция f(x) определена и ограничена на
отрезке [а, Ь] и Т, Т' - два разбиения [а, Ь], причем Tf -< Т. Тогда
S(T') < S(T), S(T') > S(T). Более того, если \f(x)\ < М Vx G [а,Ь]
и разбиение Tf содержит не более р дополнительных точек деления
по сравнению с разбиением Т, имеющим диаметр d(T), то
S(T) - 2pMd(T) < S(Tf) < S(T),
S(T) 4- 2pMd(T) > S(Tf) > S(T).
Доказательство. Пусть T = {®o>	• • • , и T' =
Tf ~<Тнт. — n — p> 1. Без ограничения общ-
ности будем считать р = 1. Пусть дополнительная точка деления
разбиения Т' попала на отрезок	разбиения Т так, что
xk-i = ®{_х <	< ®{+1 = Xk- Тогда Д®* = Д®{ 4- где Д®{ -
длина	®{], а Д®{+1 - длина [®{, ®*]. В силу свойств точных верх-
ней и нижней граней имеем
Mk = sup f(x) > <
[xfe- 1 ,Xfc]
м; = sup f(x),
Af('i = sup /(x),
ТП* <
tn{+1.
Поэтому, учитывая неравенство |/(x)| < Af Vx G [а, Ц и 0 < Дх^ <
<ЦТ) для k = 1,2,..., п, получаем оценки
О < S(T) - S(T') = MfcAxfc - (Af/Дх, + М/+1Дх{+1) =
201
= (Мк - M/fAxf + (Мк - М/+х)Д®}+1 < 2М(Д®{ + Д®{+1) =
= 2МД®* < 2Afd(T),
откуда S(T) - 2pMd(T) < S(T') < S(T).
Аналогично доказывается £(Т) + 2pMd(T) > S.(Tf) > £(Т).
Следствие. Если Т' Ч Г, то Q(T') < П(Т) и, более точно,
ад - 4pd(T) < ад) < ад.
Теорема 2. Пусть функция /(®) определена и ограничена на
отрезке [а, 6] и Тх,Та - любые два разбиения [а, 6]. Тогда S(Ti) <
S(Ta).
Доказательство. Наряду с разбиениями Ti и Тг введем
новое составное разбиение Т' = {Тх,Та}, определяемое точками деле-
ния как разбиения Тк, так и разбиения Та. Тогда Т' ч Тх и Т' Ч Та и
в силу теоремы IjiMeeM оценки: S'(T') <	£(Т') > £(ТХ), откуда
(£(Т1) < ад') < S(T') < ада)) => (£(Т1) < S(Ta)).
Следствие 1. eup£(T) < infS(T) или, если ввести поня-
т т
ь def _
тия 7 = U f f(x)dx = inf S(T) - верхний интеграл Дарбу и Z =
а
Lj f(x)dx d= eup£(T) - нижний интеграл Дарбу, то для функции
а	т
ь
/(®), ограниченной на отрезке [а,6], имеем оценку J = L f f(x)dx <
а
Ъ
U j f(x)dx = 7.
а
Следствие 2. Для любого разбиения Т отрезка [а, Ь] имеем
ад)<2<7<ад)ио< 7-2<ед.
.Замечание. Рассматривая на множестве всех разбиений Р* =
{Т} отрезка [а, Ь] отображение П : Т -> П(Т), Т еР*, выберем в Р*
базис фильтра (базу) В* = {Bf} с элементами = {Т €	=
d(T) < J} (будем в дальнейшем обозначать базу В* символом t -> +0).
Тогда можно ввести понятие предела lim (2(Т).
Теорема (предельный критерий интегрируемости по Рима-
ну). Пусть /(®) определена и ограничена на отрезке [а, Ь]. Тогда
(/ € Я[а,Ь]) (ЭДтад = 0 (d(T) = i)).
Доказательство. Необходимость. Пусть / € Я[а,6] и
ь
J = f f(x)dx. Тогда J = lim S(T£). Вспоминая критерий сущест-
а	<<(Т)-»О
вования предела (числовой) функции по базису фильтра (d(T) -> 0),
видим, что в силу необходимости этого критерия Уе > 0 3<5 > 0
такое, что для любых двух размеченных разбиений отрезка [а, &]
202
Ti,TC e Bi = {f-4 6 P|d(f) < <5} => \S(T£) - S(Tf)| < e, t. e.
8up|S(W-S(Tf)l = n(T)<e.
Итак, показано, что Ve > 0 3<5 > 0 такое, что для любого разбиения
Т € в; = {Т' е P*|d(T') < <5} => (О < П(Т) <е)=»
=>(ЗДтП/(Т) = 0).
Достаточность. Пусть функция f (®) определена и ограничена на
отрезке [а, 6] и B^lim^T) = 0. Следствие 2 из теоремы 2 этого пара-
графа для любого разбиения Т отрезка [а, 6] дает оценки 0 < J — 2, <
О(Т), откуда ((limoD(T) = 0) => (J = Z = J).
ь
Докажем, что J = lim S(T£), т. е. J = / f(x)dx. Пусть е > 0
d(T)->0	_	о
любое, тогда из соотношения (limo(S(T) - £(Т)) = 0 следует, что
35(e) > 0 такое, что VT € В% (так что t = d(T) < 6(e)) имеем
оценки 0 < ?(Т) - £(Т) < £. Но при фиксированном Т имеем
оценки £(Т) < S(T() < "S(T) и, кроме того, для любого разбиения
Г £(Т) < J <1(Т). Из оценок
£(Т) < S(T£) < 3(Т), £(Т) < J < ~8(Т)
имеем |$(Т{) - J| < 3(Т) - £(Т) = П(Т), так что Ve > 0 35(e) > 0
такое, что VT € Bf при любом выборе £ (так что Т( € Bi) имеем
оценку |S(T£) - J| < е, т. е. 3^ Hm^/pTf) = J.
Замечание. Если f(x) ограничена иа [а, 6] и 3 lim П(Т) = 0,
_	ь
то J = / = J = J f(x)dx и, в частности, (/ € Д[а, Ь]) =» ( lim П/(Т) =
4	t">+0
b	ь	ъ
0) =► (Uff(x)dx = Ljf(x)dx = f f(x)dx).
a	a	a
Теорема (критерий Дарбу интегрируемости по Риману).
Пусть функция f(x) определена и ограничена на отрезке [а, Ь]. Тогда
(/€ Я[а,Ь]) (inf П(Т) = 0).
Доказательство. Необходимость. Пусть f G Я[а, Ь], тог-
да в силу «предельного критерия интегрируемости по Риману» име-
ем 4Н1ПоП(Т) = 0, так что, учитывая, что П(Т) > 0 VT, имеем
infn(T)°=0.
Достаточность. Пусть inf S i (Г) = 0. Тогда по определению точной
нижней грани видим, что Ve > 0 3 разбиение Ti = {хо, ®i,...,
отрезка [а, Ь] с р+ 2 точками деления такое, что 0 < Q(Ti) < е/2. В
203
силу ограниченности функции f(x) на отрезке [а, Ь] ЭМ > 0 такая,
что |/(ж)| < Af Va? Е [а, t>]. Положим 6 = е/&рМ и пусть Т - любое
разбиение отрезка [а, Ь] с диаметром d(T) < (5. Пусть Т2 = {Ti, Т} - со-
ставное разбиение [а, Ь] такое, что Т2 -< и Т2 -< Т, причем разбиение
Тг имеет не более р дополнительных точек по сравнению с Т. Тогда в
силу следствия к теореме 1 (учитывая неравенство d(T) < 6 = e/SpM)
имеем
(Т2 -< Ti) => (Й(Т2) < O(Ti)) => (Й(Т2) > О(Т) - 4pMd(T) >
> Q(T) - е/2) => (0 < П(Т) < П(Т2) 4- е/2 < П(ТХ)4-
+е/2 < е/2 + е/2 = е).
Итак, Ve > О В<5 > 0 такое, что VT 6 имеем оценку 0 < О(Т) < е,
т. е. 3 lim П/(Т) = 0. Но тогда из достаточности предельного кри-
терия интегрируемости по Риману следует, что f Е Я[а, Ь] и даже
_	ь
равенство J — J_— J — f f(x)dx.
а
Теорема (критерий интегрируемости по Риману). Пусть f(x)
определена и ограничена на отрезке [а, Ь]. Тогда
ъ
ъ

j* f(x)dx
а
= L I f(x)dx = J).
Доказательство. Необходимость. Пусть f Е Я[а,Ь], тог-
да в силу замечания к «предельному критерию интегрируемости по
_ ь
Риману» имеем J = J = f f(x)dx.
а
Достаточность. Пусть J = J = J, но J = inf S(T) и J = supS(T),
Т
поэтому Ve > 0 3 разбиения и Т2 отрезка [а, Ь] такие, что S(Ti) <
J + е/2, S(T2) > J - е/2. и для составного разбиения Т = {Ti,T2} в
силу теоремы 1 имеем
(S(T) < S(Ti), S(T) > S(T2)) => (0 < O(T) = S(T) - S(T) <
< S(Ti) - S(T2) cJ + efr-y- e/2) = e).
Итак, Ve > 0 существует разбиение T отрезка [а, Ь] такое, что 0 <
О(Т) < е. т. е. inffi(T) = 0. В силу достаточности критерия Дарбу
_	ь
имеем / Е R[a, Ь] и, как показано выше, J = J = J = J* f (x)dx.
204
$ 3. Множества из R меры нуль и длины нуль
В этом параграфе будут использованы определения числового ря-
да (см,- ч. I, гл. 3, § 3) и критерий сходимости для знакопостоянных
числовых рядов (см. ч. I, гл. 3, § 4).
Определение. Множество А С R имеет меру нуль, если
Уб > О существует такое не более чем счетное покрытие множес-
тва А отрезками Ik = [а*,Ь&] (к = 1,2,...), что:
-boo	4-оо
1)АС U «2)£>| < е,
к-1	к=1
где |Д| = Ьк — ак ~ длина отрезка Ik- Обозначение: mes А = 0.
Замечание. В определении множества меры нуль вместо от-
резков [а^, bk] можно рассматривать интервалы (ак,Ьк).
Теорема. Пусть А, В С R и В С А. Тогда (mes А = 0) =>
(mes В = 0).
Доказательство. Поскольку mes А = 0, то Уб > 0 3 не
4-оо
более чем счетная система отрезков (Д) такая, что А С (J Ik и
к=1
4-оо
52 \h \ < но тогда
4-оо
(В с А) => (В с U /*) => (mes В = 0).
*=1
4-оо
Теорема. Пусть А, Ак С R (к = 1,2,...) и А С U Ак. Тогда
к=1
(mes Ак = О УЛ) => (тез А = 0).
Доказательство. Поскольку mes Ак = О УЛ, то Уб > О 3
4-оо
совокупность отрезков (Д) (Л,Z = 1,2,...) такая, что (J Ikj D Ак и
1-1
+оо	4-оо 4-оо
52 |А,/| < б/2*. Но тогда Ac U ( U Л,<)* Таким образом, счетная
/=1	к=1 1=1
система отрезков (Z* j) покрывает множество А. Эту счетную систему
можно перенумеровать, обозначая через Is отрезки Z*,/, расположен-
ные в порядке возрастания к + I, а для одинаковых к + I - в порядке
N	N / N \
возрастания Л. Тогда УТУ > 1 имеем оценку J2 |4| < 52 (52 |Z*,d )>
5=1	k=i \/=1	’ /
N	4-оо
но в силу построения (Z&,/) имеем 52 lA,d < 52 lA,d < €/%к поэ-
1=1	’	1=1
N	N
тому, очевидно, 52 |Л| < £ • 52	< £ VN > 1, и в силу критерия
«=1	к=1
205
сходимости для знакоположительных числовых рядов имеем
(4-оо	.У	\
22|Д| = sup£ |Д| < е) => (шее А = 0).
1=1	N «=1	/
Следствие 1. Если множество А С R состоит из конечного
или счетного числа точек, то mes А = 0.
Следствие 2. Множество Q всех рациональных точек из R
имеет меру нуль.
Определение. Множество А С R имеет (одномерный объ-
ем) длину нуль, если Ve > О существует такое конечное покрытие
множества А отрезками Ik = [сц, Ь&] (А; = 1,2,..., т(е)), что:
т	т
1)AC |jA«2)£|/fc|<e.
fc=sl	* = 1
Замечание 1.В определении множества длины нуль можно
считать, что покрытие (Д = [a*, bk]) состоит из попарно не перекры-
вающихся отрезков.
Замечание 2. В определении множества длины нуль вместо
о
отрезков Ik = bk] можно брать интервалы Ik= (a*, bk).
Замечание 3. Если В С А и множество А имеет длину нуль,
то и множество В имеет длину нуль.
Теорема. Пусть (Ik) (k = 1,2,... , т) - любое конечное по-
м
крытие отрезка [а, Ь] отрезками Ik так, что [а, Ь] С (J Л • Тогда
к=1
т
Е |Д| > Ь-а > 0.
k=i
m
Доказательство. Пусть [а,ЭД С (J h, где Д = [а*,
t=i
тогда при т = 1 теорема справедлива, поскольку (Д = [аi, /31] D [а, ЭД)
=> (|Д | = /31 — «j > Ь — а > 0). Рассуждая по индукции, переходя от т
к т+1, допустим, что теорема верна для покрытий, составленных из
т4-1
т отрезков, и пусть [а, ЭД С IJ Д. Изменяя в случае необходимости
*=1
нумерацию, будем считать, что а € [ai,/3i] = Д. Тогда ai < a <
(3i. Если при этом 6 < 01, то |Д| = /31 - ai > 6 - a > 0, если же
/31 < Ь, то система (Д, Д,..., Im+i} образует покрытие отрезка [/31, ЭД,
состоящее из т отрезков, и поэтому в силу предположения индукции
т4-1	т4-1
S |Д| > 6-/31 > 0. Но тогда Е |Д| > (01 - а) + (6-/31) = b-а > О,
k=2	k=l
что и завершает доказательство теоремы.
Следствие 1. Отрезок [а, ЭД С R не может иметь длины нуль
в смысле данного выше определения.
206
Следствие 2. Если множество А С R имеет длину нуль, то
4= 0. В самом деле, если бы A# 0, то 3®о €4, причем 3(а,/3) СА
тако!, что ®о € (а,Р) С А, и поэтому существует отрезок [а, Ь] С
(а,/3) С А. Но тогда отрезок [а, Ь] имел бы длину нуль, поскольку
множество А имеет длину нуль. Противоречие.
Следствие 3. Пусть Т = {®о,®1,• • •,®п} - разбиение от-
резка [а,6] с частичными отрезками Д = [®k-i,®*] (к = 1,2,... ,п).
Пусть {Ji} (I = 1,2,..., тп) - конечная система отрезков Д, такая, что
mm	m	р
и Ji э и тогда Ё 1^1 > Ё Н*.1-
/=1	«=1	1=1	»=1
Замечание. Если множество А С R имеет длину нуль, то
множество А имеет и меру нуль. Обратное утверждение, вообще го-
воря, неверно.
Замечание. Если множество А С R не ограничено, то оно не
может иметь длину нуль.
В самом деле, если множество А не ограничено в R, то Vfc € N
3®* € А такие, что |®*| > к и |®к - ®<| > 1, к > », а поэтому не
может существовать конечного покрытия множества А отрезками 1п
(имеющими конечные длины |Д|), т. е. множество А не может иметь
длину нуль.
Теорема. Если К С R - замкнутое и ограниченное множес-
тво, то К компактно в R.
В дальнейшем в ч. III этого тома будет доказана более общая тео-
рема для пространства R, поэтому попробуйте доказать эту теорему
самостоятельно по схеме доказательства леммы Бореля - Лебега о
компактности отрезка (ч. I, гл. 3, § 6).
Доказательство. Поскольку множество К ограничено в
R, то существует отрезок Д = [а, 6] D К. Дальнейшее доказатель-
ство воспроизводит доказательство леммы Бореля - Лебега о ком-
пактности отрезка. Допустим, что множество К не компактно, тогда
существует покрытие множества К бесконечной системой интерва-
лов {АД} = {(а7,/37)}, из которой нельзя выбрать конечного под-
покрытия для К. Применяя метод деления отрезка Д = [а, 6] попо-
лам, получаем по индукции систему отрезков {Д} (п = 0,1,2,...):
Д С Д-i С ... С А С Д = [а, 6]; множество Д П К 0 не допускает
выделения конечного покрытия из системы {АД} и |Д| = (Ь- а)/2п.
Система отрезков (Д) (п € No) стягивающаяся, и по теореме Кантора
3{с} ж +п д.
н=0
Заметим, что для любой окрестности U(c) Зпо € N такое, что
17(c) D 7Яд О (7Яд О АС), т. е. С7(с) О 0, поэтому с €	* По мно-
жество К замкнуто, т. е. К' С К, поэтому с € К, и тогда существует
интервал (а,(3) из системы {АД} такой, что с € Но, как уже
было замечено, тогда Зпо такое, что (а,/3) D До D (До П К), т. е.
207
множество 1По П К 0) оказалось покрытым одним интервалом из
системы {Му}. Противоречие.
Теорема. Пусть К С R компактно и mes К = 0. Тогда мно-
жество К имеет длину нуль.
Доказательство. Пусть множество К С (—оо, +оо) ком-
пактно в R и mes К = 0. Тогда Уг > 0 3 не более чем счетное покрытие
о	+оо 4-00 о
множества К интервалами Ik= такое, что (J Ik D IJ IkD К
fc=i k-i
4-oo
и 52 |Д| < £• В СИЛУ компактности К из нашего (открытого) по-
fc=i
т 0	т
крытая можно выделить подпокрытие U . D К, причем $2 !•(?• I <
i=i	J=i 3
4-оо
\h | < £> тем самым показано, что множество К имеет длину нуль.
fc=i
Следствие. Если mes А = 0, то А= 0- В самом деле, до-
0	о
пустим, что mes А = 0 и	0. Тогда существуют точка ®о €А и
интервал (а,/3) такие, что	G (а,Ь) С А. Но тогда существует и
отрезок [а, Ь] такой, что xq 6 [а,/3] С (а,/3) С А. Но (mes А = 0) =>
(mes [а, Ь] = 0) и в силу компактности отрезок [а, 6] имеет длину нуль,
что невозможно.
Следствие. Любое счетное ограниченное замкнутое множес-
тво из R имеет длину нуль. В самом деле, счетное множество имеет
меру нуль, кроме того, будучи замкнутым и ограниченным, оно ком-
пактно в R, а тогда в силу доказанной теоремы оно имеет и длину
нуль.
Теорема. Если множество А С (—оо, 4-оо) ограничено, то его
граница дА компактна (в R/
Доказательство. Поскольку множество А ограничено в
R, то существует отрезок [a, b] D А. В силу замкнутости отрезка
[а, 6] = I имеем I = [а, Ь] Э А. Но (дА С А) => (дА С [а, 6]). Поэтому
множество дА ограничено в R. Но как было доказано ранее (см. ч. I,
гл. 3, § 1), граница дА всегда замкнута. Итак, множество дА замкнуто
и ограничено в R, т. е. компактно в R.
Замечание. Если множество А С R имеет длину нуль, то и
граница дА множества А имеет длину нуль.
В самом деле, поскольку множество А имеет длину нуль, то А
ограничено и Уг > 0 существует конечное покрытие А отрезками { Д }
(Д = bfc]) (k = 1,2,... ,т(г)) такое, что Fm = Q Ik D А, при-
fc=i
m
чем 52 И*1 < Но множество Fm как объединение конечного чис-
fc=i
ла замкнутых ограниченных множеств само замкнуто и ограничено,
причем (Fm D А) => (Fm = Fm D A D дА). Итак, Уг > О 3{Д}
208
f	m(e) m
(k = 1,\2,... , т(г)) такое, что дА C (J Д и |Z*| < г, т. е. граница
fc=i fc=i
дА имеет длину нуль.
Замечание. Если множество А С R не компактно, то из того,
что оно имеет меру нуль (mes А = 0), вообще говоря, не следует, что
оно имеет длину нуль (даже если оно ограничено).
Пример. Пусть Q = Q П [0,1] С R - множество всех рацио-
нальных точек отрезка [0,1]. Множество Q ограничено и счетно, так
что mes Q = 0. Если бы Q имело длину нуль, то и его граница dQ (по
доказанному выше) также имела бы длину нуль. Однако dQ = [0,1],
а отрезок [0,1], как было доказано, не может иметь длину нуль.
§ 4. Критерий Лебега интегрируемости по Риману
Ранее (см. ч. I, гл. 4, § 1) были введены понятия колебания функ-
ции на отрезке и в точке. Пусть функция f(x) определена и локально
ограничена на множестве А С R и ®о 6 А. Для любого интервала
(а,/?) Э ®о положим
ЛЛ/; [«,/?]) = sup f(x),
[а,0]АА
т(/;[а,$) = inf /(*)•
[а,Д]ПА
Колебанием функции f(x) на отрезке [а,/?] была названа величина
w(/; [«,/?]) = Af(/; [а,/?]) - тп(7; [а,/?]). Было доказано, что
w(/; [«,$) = sup 1Л®1) - /(®г)|.
Xi
Далее, при любых (а', /?') С (а, /5), ®о 6 («',/?') имеют место оценки
-оо < m(f; [а, /3]) < т(/; [а',/3']) < М(/; [а', /?']) <
< М(J; [а, /?]) < +оо;
0 < w(f; [ot',/3']) < w(f; [а,$) < +оо.
Полагая при
ДИшо) = [®о - <5, ®о + Я], M(f; xq) = lim M(f; Af(®o)) =
= inf sup fix) = lim /(as);
<*>Од,(«о)пл	^*o
Tn(/; ®o) = lim m(f; Aj(a;o)) = sup inf f(x) = lim f(x),
^->0	4>оД«(«о)ПА
209
вводим понятие колебания функции f (®) в точке ®о 6 А как величину
w(/;®o) = Af(/;®o) - m(/;®0), при этом w(/;®o) = Дт^/; ДД®о))
и 0 < а>(/;®о) < w(/;Aj(®o)) < +<*> Vi > 0, а также w(/;®o) <
«(/; [а, $) < +<ю V(a, /3) Э х0.	!
Ранее (см. ч. I, гл. 4, § 1, 3) были доказаны теоремы:
Теорема (критерий непрерывности Бэра). Если f € В(А),
®о € А, то (f G С(®о)) & (w(f*,®o) = 0).
Теорема Кантора (о равномерной непрерывности). Если
f(x) определена и ограничена на отрезке [а, Ь] и w(f\ ®) = 0 V® G [а, Ь],
то функция /(®) равномерно непрерывна на отрезке [а, Ь].
Обобщим теорему Кантора на разрывные функции.
Теорема Кантора. Пусть функция f : [а, b] -> R ограни-
чена на [а, Ь] и 3w > 0 такое, что 0 < w(/;®) <w V® € [а, Ь]. Тогда
Ve > 0 3 разбиение То = {®o,®i?... ,®п} отрезка [а,Ь] такое, что
Щ = w(/;	®л]) < ш + е (k = 1,2,...,п).
Доказательство. Пусть е > 0 - любое, но фиксирован-
ное. Поскольку 0 < w(/;®) < ш V® € [а, Ь], то V® €_[а, Ь] 3 интервал
= (® - i(®),® + i(®)) Э ® такой, что w(/;U^(a.)(®)) < ы + е,
причем [а,i>] С |J	В силу компактности отрезка [а, Ь] су-
я?€[а,Ь]
шествует конечное подпокрытие
т
(®*)} = {(<**, MJ (fc = 1,2,... ,m), [а, 6] С [J (ак, Ьк).
k=i
Пусть То - такое разбиение отрезка [а, Ь], что все точки вида х =
а*, х = Ьк (к = 1,2,... , т), принадлежащие отрезку [а, Ь], входят в
разбиение То, и любой частичный отрезок_[®i-i, х(] из разбиения То
содержится в некотором отрезке [а*,Ь&] = Ujk(xk). Тогда, очевидно,
<w + e Vi.
Следствие. При выполнении условий теоремы Кантора Ve >
0 Э такое разбиение То отрезка [а, Ь], что П/(То) < (ы + е)(Ь — а).
Теорема. Пусть F С (—оо, +оо) - замкнутое множество и
функция f : F -» R определена и ограничена на множестве F, Пусть
Е(е) = {х € F|w(/;x) > е > 0}. Тогда:
1) Е(е2) С E(et) VO < Ei < е2; i) Е'(е) С Е(е) Ve > 0, т. е.
множество Е(е) замкнуто в R Ve > 0.
Доказательство. Утверждение 1) очевидно. Для доказа-
тельства утверждения 2) предположим, что xq € Е'(е)у тогда Vd > 0
3xj 6 Е(е) П Uj(хо), причем w(/; F П С/е(х0)) > ы(/; хд] > е > 0. Но в
силу замкнутости множества F имеем (F D Е(е)) => (F = F Э Е(е) D
^(е))	(®о € F). Но тогда поскольку w(/;xo) = iimw(/;Fnt/i(xo)),
то («(/; хо) > е > 0) (хо €	(Е'(е) С Е(е)), т. е. множество
Е(е) замкнуто в R.
210
Замечание. Если Е - множество всех точек разрыва функ-
ции /(®), определенной и ограниченной на замкнутом множестве F С
4-ос / 1 \
(-00,-1-00), то Е = и ЕЦ — |.
т=1	\т/
Теорема (критерий Лебега интегрируемости по Риману).
Пусть функция f(x) определена и ограничена на отрезке [а, 6] и Е -
множество точек разрыва функции f(a) на [а, 6]. Тогда
(f € Я[а, Ь]) & (mes Е = 0).
Доказательство. Необходимость. Пусть f € Я[а, Ь] и Е С
[а, Ь] - множество точек разрыва функции /(®) на [а, Ь]. Поскольку
+<Ю
Е = (J Е(1/т), то достаточно доказать, что mes Е(1/т) = 0 Vtn 6
m=l
N. Тогда множество Е как объединение счетного множества меры
нуль само будет иметь меру нуль. Будет доказано, что множество
Е(1/т) имеет длину нуль Vm £ N. Поскольку f € Я[а, 6], то в силу
критерия Дарбу (интегрируемости по Риману) имеем inf fly (Т) = О,
т. е. при фиксированном т € N Че > 0 существует разбиение Т =
{®о, ®х,... , ®„} отрезка [а, Ь] такое, что 0 < П/(Т) < е/2т.
Рассмотрим совокупность {/*} = {г»]} (k = 1,2,..., п) всех
частичных отрезков, соответствующих выбранному разбиению Т. По-
ложим Ё(1/т) = Я(1/т) П (J h в Ё(1/т) = Е(1/т) П (J 5Д. По-
*=i	k=i
скольку граница dh = {®k-i}U{®j.} есть совокупность двух точек, то
А	Л
91k имеет длину нуль. Но поскольку Е(1/т) с U ЯД, то и множес-
fc=i
тво Ё(1/т) имеет длину нуль. Но тогда для зафиксированного е > О
существует конечная система отрезков {Л) (1 = 1,2,..., 1(e)) такая,
-	Х,(<)	Д(<)
что Е(1/т) С и Л « £ 1<Я1 < е/2«
i=i 1=1
Рассмотрим теперь множество Ё(1/т) С (J I*. Возьмем любую
точку ®0 € Ё(1/т)	0. Тогда существует ко такое, что ®о € Ло, и
в силу определения множества Ё(1/т) имеем €Л0= (®*0-i, ®*'о),
и поэтому 3<5 > 0 такое, что Aj(®o) С /*в => (w*0 = w(/j/*0) >
w(/; Aj(®o)) > w(/;®o) > 1/m > 0).
Таким образом, J&(l/m) С (J Л, где суммирование (к) распростра-
(*)
няется на те частичные отрезки Д из Т, на которых шь	>
1/m. Но в силу выбора разбиения Т отрезка [а, Ь] по заданному е > О
211
имеем	•
1 11
— 52 lZfcl - 1’2Ык' I2*! - 52W^’[®>-1,®*1)A®*=
(fc)(wk>l/m)	(fc)	j=l
= П/(Т) < г/2т => | 52 l2*l < е/2 (w* > V™) ) •
\(к) /
А	Ь(И
Итак, Е(1/т) = Е(1/т) U Е(1/т) С U h U U Ji, где £|Д| +
(fc) i=i	(fc)
L(e)
53 I < s/2 + e/2 = e. В силу произвольности e > 0 вытекает, что
/=1
множество 2?(1/тп) имеет длину нуль, чем и завершается доказатель-
ство необходимости критерия Лебега интегрируемости по Риману.
Достаточность. Пусть Е С [а, Ь] - множество точек разрыва функ-
ции f (ж), определенной и ограниченной на отрезке [а, 6]. Заметим, что
W > 0, имеем Е(е) = {х е [а, Ь]|о>(/; ж) > е > 0} С Е С [а, Ь], т. е.
Е(е) ограничено. Но, как было доказано, множество Е(г) замкнуто,
но тогда замкнутое и ограниченное множество Е(е) компактно в R
при любом е > 0.
Пусть ines Е = 0, тогда (Е(г) С Е) => (mes Е(е) = 0). В силу ком-
пактности множество Е(г) имеет и длину нуль Ус > 0. Итак, Уб > 0
множество Е(г) имеет длину нуль, т. е. для того же е > 0 3 конеч-
ная система J отрезков {У/} (I = 1,2,... , т) такая, что система ин-
тервалов {У/} покрывает Е(е), т. е. |J Ji D |J J’/D Е(е), причем
/=1 /=1
т
Е1У/|<г.
1=1
Пусть Т = {xo,xi,... , жп} - разбиение отрезка [а,Ь], состоящее
из точек a, Ъ и всех концов отрезков У/ (I = 1,2,... , т), лежащих на
[а, Ь]. Пусть Ik = [ж*_ 1, ж&] (к = 1,2,... ,п) - частичный отрезок из
о
разбиения Т. В силу построения интервал (xk-uXk) —Ik не содержит
концов отрезков Ji из системы J, поэтому возможны лишь два слу-
чая: 1) существует индекс Iq такой, что Д С Ji0; эту группу отрезков
(из Т) будем обозначать через I' = {Д'}; 2) Xk) П J\ = 0 VZ. В
этом случае конец Xk-i (или конец Xk) может быть концом некоторого
отрезка из системы У, но даже и в этом случае Xk-i€E(e) (xkEE(e)).
В самом деле, если бы Xk-i Е Е(е), то, поскольку система интерва-
0
лов {J*/} покрывает множество Е(е), существует индекс 1± такой, что
Е Jix, и тогда, очевидно, (ж*-1, ж*)П Jix / 0 вопреки построению
разбиения Т.
212
Итак, Xk) C\Ji = 0 (I = 1,2,... , m)) => (1кГ\Е(г) = 0). Эту
группу отрезков будем обозначать через Z" = {/*«}.
Тем самым показано, что каждый из отрезков Ik разбиения Т со-
держится либо в группе Z', либо в группе Z". Поскольку f(x) ограни-
чена на [а, 6], то существует постоянная М > 0 такая, что \f(x) | < М
Ух € [а, 6], и тогда Шк = ^(/; Д) < 2Af VZ& из Г. В частности, если
m
1к, б I', то (J Д' С (J Ji и в силу следствия 3 из § 3 имеем оценку
(*')	1=1
]>>НД-1<2М£|Л|<2Ме.
(*')	Ь
Пусть теперь Ik" G Z". Тогда Ik" С\Е(г) = 0, и поэтому o>(f; х) < г
Ух G Ik"- Применим к отрезку Ik" = [ж*»-i, ж*»] следствие из теоремы
Кантора (полагая в нем ы = е). Тогда существует разбиение Т^к >
отрезка Ik": Т^к ) =	,Уп(к“) = ^к"} с частичными
отрезками zjfc = [эд_ ь yi] такое, что	}
*(*")
$2	< 2е|Д»|.
1=1
Образуем теперь составное разбиение Т° отрезка [а, 6] с помощью
разбиений Т и Т^к ), обозначив через Z® его частичные отрезки. Тогда
имеем оценки
о<«/(т°)=	52 “>гЦ?1+
+ 52	i^i < 2еМ+
и»СД»€1")
+ 522е-|А»1<2е(М + 6-а).
(*")
В самом деле, поскольку |/(ж)| < М Ух 6 [а, Ь], то шг < 2М Уг, при-
чем	1^?1 = 52 l^fc'l < так что	52	шг|Z°| < 2Ме.
(к»)	(1?С1к'£Г)
Далее, для любого г из группы (Z® С Ik" 6 Z") имеем шг < 2е, причем
S |J?I = 52 1Д"1 < Ь - а’ так что 52 шг\1г\<2е(Ъ-а).
Итак, при е > 0 существует разбиение Т° отрезка [а, 6] такое,
что 0 < Qy(T°) < 2г(М 4- Ъ — а). В силу произвольности е > О
имеем infQy(T) = 0, откуда в силу достаточности критерия Дарбу
f € Я[а, Ь], что и требовалось доказать.
213
§ 5. Классы функций, интегрируемых по Риману
Теорема 1. Если функция f(x) определена и ограничена на
отрезке [а, Ь] и имеет на нем не более счетного множества точек
разрыва, то f Е R[a, Ь].
Доказательство. Пусть Е С [а, Ь] - множество точек раз-
рыва функции /(®) на отрезке [а, Ь]. Если множество Е не более чем
счетно, то mes Е = 0, а потому в силу критерия Лебега интегрируе-
мости по Риману f Е R[a, Ъ].
Следствие 1. (/ Е С([а, Ь])) =Ф> (/ Е R[a, Ь]).
Замечание. Ввиду важности следствия 1 приведем еще одно
доказательство интегрируемости непрерывной функции по Риману,
не опирающееся на критерий Лебега.
Доказательство. Поскольку f Е С([а,Ь]), то по теореме
Кантора о равномерной непрерывности функции, непрерывной на от-
резке, следует, что Уе > 0 3<5 > О такое, что V разбиения Т отрезка
[а, Ь] с диаметром d(T) < 6 => (w* = w(/; [®*-i, ®*]) < е/(Ь - а) VA).
Но тогда УТ £ BJ (т. е. при t = d(T) < <f), П/(Т) =	<^Д®* <
fc=i
е А е
7---\ , Д®* = 7--(Ь - а) = е, так что 3 lim ГЪ(Т) = 0, и поэто-
му в силу предельного критерия интегрируемости по Риману имеем
/€Я[М].
Следствие 2. Если функция f(x) определена и монотонна на
отрезке [а, Ь], то / G Я[а, Ь].
В самом деле, если f(x) монотонна на отрезке [а, Ь], то она огра-
ничена на [а, Ь] и имеет на [а, Ь] не более счетного множества точек
разрыва. Но тогда в силу теоремы 1 / Е Я[а, Ь].
Замечание. Приведем еще одно доказательство интегрируе-
мости монотонной функции, не опирающееся на критерий Лебега.
Доказательство. Пусть для определенности f f на [а, Ь],
тогда /(а) < f(x)	< f(b) V® £ [а, Ь], т.	е.	существует	постоянная
М > 0 такая, что	|/(®)| < М V® Е [а, Ь].	В	силу монотонности /(®)
для любого разбиения Т отрезка [а, Ь] имеем щ = ы(/; [®*-1,®*]) =
“ /(®fc-i) >	О VA, но тогда Уе >	0	3<5 = е/2М	такое, что
VT Е Bj (так что	i = d(T) < <5) П/(Т)	=	£	£ w* <
fc=i	fc=i
- /(«->)) =	- /(«)) <	= £, Т. е.
fc=l
= 0, откуда в силу предельного критерия интегрируе-
мости по Риману имеем / € Я[а,Ь].
Замечание. Помимо классов С([а,6]) и 2?[а,6] введем классы
214
JB[a,b] и Af[a, Ь], где B[a, Ь] - множество всех функций /(®), опреде-
ленных и ограниченных на [а, Ь]; М [а, Ь] - множество всех функций
/(®), определенных и монотонных на [а, Ь]. Тогда по доказанному вы-
ше имеем
Замечание (о вычислении определенного интеграла Римаг
ь
на). Пусть f € B[a, Ь]. Для того чтобы вычислить f f(x)dx, нужно
а
проверить, что f € Я[а, Ь], и в случае f € Л [а, Ь] в силу теоремы о един-
ственности интеграла Римана можно вычислить предел
по какой-нибудь последовательности размеченных разбиений Т(п>£(п)
с d(T^) -> 0, полагая, например, hn = (b - а)/п. х* = а + khn
(к = 1,2,..., п).
Ь	п
Тогда f f(x)dx = lim £ f((xk-i + xk)/2)hn.
a	"->+00fe=l
Определение. Пусть A C R, тогда характеристической
функцией Ха множества А называется функция
= { J: ’г/
Определение. Ограниченное множество А С R, граница
дА которого имеет меру нуль (тег дА = 0), а стало быть (в силу
компактности границы дА), и длину нуль, называется измеримым
по Жордану.
Теорема (критерий измеримости по Жордану). Пусть А С
[а, 6]. Тогда (множество А измеримо по Жордану (т. е. тег дА = 0))
(ХА £ Я[а,Ь]).
Доказательство. Покажем, что дА = Е = {® Е
R|w(XA; ®) > 0}, V®o € (-оо, +оо) имеем ®о GA UA. U дА. Но:
1)	®о ЕА. Тогда ЭДл(хо) САС А, так что XA(®) = 1 V® € Д<(®о),
т. е. ХА £ С(®о) ^®о 6 А-
2)	®0 G Ае. Тогда ЗД<(®0) С С А, так что ХА(х) = О V® € Д*(®о),
т. е. ХА £ С(®0) У®о е Ае.
3)	®о 6 дА. Тогда V<5 > О Э®1 £ Да(®о) Г) А и 3®2 £ Д<(®о) О С А,
т. е. XA(xt) = 1, Хл(®г) = 0, так что (о>(Хл; Д$(®0)) = 1 Vtf > 0)
(w(XA,®0) = 1 > 0), т. е. ХлЁС^о) V®o G дА.
Итак, дА = Е. Но (А С [а, Ь]) => (дА = Е С [а, Ь]). Таким образом,
в силу критерия Лебега имеем
(ХА £ Я[а, Ь]) => (mes Е = mes дА = 0)
215
(А С [а, 6] — измеримо по Жордану).
Определение. Если множество А С [а,Ь] измеримо по
ъ	def
Жордану, то интеграл Римана f Хд(х)(1х = |А| называется дли-
а
ной множества А в R.
Замечание. Ранее определение множества длины нуль было
введено с помощью конечных покрытий множества отрезками. Вы-
ше введена длина |А| множества А с помощью интеграла Римана от
характеристической функции Хд. Необходимо поэтому рассмотреть
вопрос об эквивалентности этих двух определений.
Теорема (об эквивалентности двух определений множества
длины нуль). Пусть А С [а,Ь]. Тогда (|А| = 0) <=> (множество А
имеет длину нуль (в старом определении)).
Доказательство. Необходимость. Пусть |А| = 0. Тогда
ь	о
Ха Е R[a, 6] и / Хд(ж)с/ж = 0. Докажем, что А= 0. В самом де-
а
о
ле, если А/ 0, то существует интервал (а,(3) С А, и тогда мож-
но было бы указать разбиение То отрезка [а, 6] такое, что для неко-
торого к, (а,/3) D 4 =	1, ж*], причем |Д| = 6 > 0. Но тогда
тк = т(Хд;1к) = 1, и поэтому SXa(Tq) > тк£±хк = <5 > 0, откуда
ь	ъ
|А| — J Ха(х)(1х = Lf Хл(х)дх = sup SXa(T) > 6 > 0. Противоречие
а	а	Т
с условием |А| = 0.
Итак, А= 0. Но тогда А С дА. Далее, (Ха Е R[a, Ь]) => (множество
А измеримо по Жордану, а потому mes дА = 0). В силу компактности
граница дА имеет длину нуль (в старом определении). Но А С дА,
поэтому и множество А имеет длину нуль в старом определении.
Достаточность. Пусть А С [а, Ь] есть множество длины нуль (в
старом определении). Тогда Уб > 0 существует конечная система J
т о tn
отрезков {У/} (I = 1,2,... ,?п(б)) такая, что Ac J У/С U Ji, при-
/=1 /=1
т
чем |У/| < е. Теперь, следуя ходу доказательства достаточности
1=1
критерия Лебега, рассмотрим разбиение Т отрезка [а, Ь], составлен-
ное из точек а, b и всех концов отрезков У/ (из системы У), лежащих
на отрезке [а, Ь]. Тогда, как было доказано, любой частичный отрезок
h =	разбиения Т содержится только в одной из двух групп
Т и Z": Z') существует индекс такой, что Д С Ji0\ I") 1к О А = 0.
Рассмотрим теперь для характеристической функции Ха верхнюю
сумму Дарбу Sx(T) на отрезке [а, 6]. Очевидно,
(0 < Мк. = М(Хл;/р) < 1, Мкп = М(ХА;1к") = 0) =>
216
in
=> (0 < Sxa(T) = £ Mfc<Azv <	1Я1 < £)-
(к<)	(к*)	J=i
Итак, Уе > О ЗТ такое, что 0 < SxA (Т) < £ Но тогда inf SxA (Т) =
_ ь
О = J = U f XA(x)dx. Но (Хл(х) > О V® € [<*, &]) =>(</> 0), поэтому
а
из0<У<7 = 0=> ХА €Я[в,Ч« (jXA(®)<fe = o| =► (|А| = 0).
\ а	/
Пример. Пусть Q = Q А [0,1], тогда Q как счетное множество
имеет меру нуль (mes Q = 0), однако ее характеристическая функция
{1 я Е О	_
’ — есть функция Дирихле, поэтому XqE-R[0, 1],
v,
т. е. множество Q не измеримо по Жордану и не имеет длины. В
частности, множество Q не имеет длины нуль.
Замечание 1. При доказательстве теоремы об эквивалент-
ности определений множеств длины нуль в старом и новом смысле
попутно было показано, что при А С R (|А| = 0) => (А= 0), так что
множество длины нуль не может иметь внутренних точек.
Замечание 2. Если А С (—оо, 4-оо), то (|А| = 0) => (|5А| =
|А| = 0).
В самом деле, ранее было доказано, что (|А| = 0)	(|5А| = 0),
но_тогда А = A U дА имеет длину нуль (в старом определении), т. е.
(|А| = 0).
Теорема. Пусть множества Ai, А2 С [а, Ь] измеримы по Жор-
дану, Тогда: 1) множество Ai U А2 измеримо по Жордану; 2) мно-
жество Ai А А2 измеримо по Жордану; 3) множества [а, Ъ] \ А, =
CAi А [а, Ь] (г = 1,2) измеримы по Жордану; 4) множества Ai \ А2 и
А2 \ Ai измеримы по Жордану.
Доказательство. 1) Поскольку множества Ai,А2 С [а,6]
измеримы по Жордану, то mes дА, = |0А»| = 0 (г = 1,2). Но легко
видеть (докажите это самостоятельно), что д(А± U А2) С дА\ U дА2,
откуда mes д(А± U А2) = |5(Ai U А2)| = 0. Но (Ai,a2 С [а,Ь]) =>
(Ai U А2 С [а, Ь]), поэтому множество Ai U А2 измеримо по Жордану.
2)	Очевидное включение 3(Ai А А2) С дАг U5A2 позволяет тем же
путем доказать измеримость множества Ai А А2 С [а, Ь].
3)	Если множество А С [а, Ъ] измеримо по Жордану, то mes дА =
1<ЭА| = 0, но (дСА = дА С [a,b]) => (mes дСА = |5СА| = 0). Для
отрезка [а, 6] имеем 3[а, 6] = {а} U {Ь}, так что |3[а, Ь] — 0, т. е. отрезок
[а, 6] измерим по Жордану, причем (см. пример 1 из § 1 этой главы)
ь	ь
|[а, Ь]| = У Х[а^](ж)с/ж = у Idx = b — а.
а	а
217
Но тогда [а, Ь] \ = СА, А [а, Ь] С [<*, Ч> (5([а, Ь] \ Д) С dCAi U 0[а, Ч)
=> (|д([а, Ь] \ Д)| = 0), т. е. множество [а, Ь] \ А измеримо по Жордану.
(Заметим, что множество СА< не ограничено, а потому и не измеримо
по Жордану, хотя mes dCAi = |5СА| = 0.)
4)	(Ai, Аг € [а, Ч) => (Ах \ Аг С [а, Ь]), причем Д \ Аг = САг А Л*.
В силу измеримости множеств Ai, Аг глее ЗА, = |дД| = 0 (t = 1,2).
Поскольку д(А1 \ Аг) С дСАг U dAi = дАг U АД, то mes 3(Ai \ Аг} =
|5(А1\Аг)| = 0, т. е. множество Ai\Aj С [а, Ь] (атакже Aj\Ai С [а, Ч)
измеримо по Жордану.
Следствие. Пусть множества А, С [а, 6] (i = 1,2,... , т) из-
m	m
меримы по Жордану. Тогда множества Q А, и U А, также измери-
i=i	i=i
мы по Жордану.
Замечание. Приведенное следствие не распространяется на
счетные объединения множеств, измеримых по Жордану, например,
-Ьоо
множество Q = Q П [0,1] не измеримо по Жордану, хотя Q = U {gt},
fc=i
где Q = {g*; к = 1,2,...} и каждое множество {qk} (точка) измеримо
по Жордану: |{д*}| = 0.
Теорема. Система а всех множеств А отрезка [а, Ь], из-
меримых по Жордану, образует алгебру, т. е. выполнены условия:
а) [а,Ь] € ст; б) (VAX, А2 G а) => (AXUA2, АХПА2 € а); в) (VA G <т) =>
(САп[а,Ь] = [а,6]\А€а).
§ 6.	Свойства интеграла Римана
Определение. Непустое множество Г называется (ком-
мутативным) кольцом, если на Т определены две бинарные опера-
ции - сложение и умножение, обе коммутативные и ассоциативные,
а также связанные законом дистрибутивности, причем сложение
обладает обратной операцией - вычитанием.
Рассмотрим класс Я[а, Ь] и введем в нем бинарные операции сло-
жения и умножения следующим образом:
V/,0 е Я[а, Ч (/ + д)(х) = /(®) +?(х);
(/ •	= f(x)g(x) V® G [а, Ч.
так что ^(®) = О V® G [а, Ь] есть «нуль» в Я[а, Ь], а е(х) = 1 V® € [а, Ь]
есть «единица» в Я[а, Ь].
Теорема. Класс Я [а, Ь] есть (коммутативное) кольцо функ-
ций с обычными действиями сложения и умножения.
Эта теорема вытекает из нижеследующих теорем 1 и 2.
Теорема 1. Если fj € Я[а, 6] и cj - постоянные (j =
т
1,2,..., т), то 2 cjfj 6 Я[0, Ч, причем
i=i
218
fj(x)dx.
Доказательство. Пусть fj € Я[а, 6] (j = 1,2,..., m) и
h(x) = £ Тогда для любого размеченного разбнения Tf от-
j=i
резка [а, Ь] имеем представление
Sh(Tf) =	= Е (Ес'Л«*> ) Да!* =
fc=l	fc=l \j=l	/
m	/ n	\	m
=Е/ЛЫД»» =
j=l \fc=l	J j=l
откуда в силу теоремы о «пределе суммы» получаем
т
m
= Е ci‘ rf/feo Sfi	h G flfa’
j=l
причем
m f
Cjfj(x)dx =	/ fj(<e)dx.
a
Следствие. Если множества А, В C [a, 6] измеримы по Жор-
дану и А П В = 0, то множество A U В измеримо по Жордану и
|АиВ| = |А| + |В|.
В самом деле, как показано в § 5 этой главы, система всех мно-
жеств отрезка [а, Ь], измеримых по Жордану, есть алгебра а, поэтому
(А,В G <т) =► (A U В € а) и, в частности, Хд, Хв, ХАив € Я[а, Ь].
Поскольку А П В = 0, то Хдив(®) = Ха(х) + Хв(х) Ух € [а, Ь], и
тогда по теореме 1 получаем
ь	ь
|AUB|= [ XAuB(x)dx= f(XA(x) + XB(x))dx =
ь	ь
У* XA(x)dx + у* XB(x)dx = | А| + |В|.
a	a
219
w
Теорема 2. (/, g 6 Я[а, Ч) (/ • д 6 R[a, Ц).	I
Доказательство. (/,^6 Я[а, Ч) => (f,g 6 В[а, Ч) => (f-g Е I
В[а,Ъ]).	I
Пусть Ef, Ед и Efg - множества точек разрыва функций /(®), д(х) |
и f(x) • д(х) соответственно, тогда имеем	I
Ef.gCEfEg,	(6.1) I
В самом деле, поскольку |/(®)| < Mj, |^(®)| < Мд V® 6 [а, Ь], то V®, у Е I
[а, 6] имеем	I
1/(®)р(®) - f(y)g(y)\ = 1/(®) • (»(®) -д(у)) + д(у) • (/(®) - №))1 <	|
t
< 1/(®)1 • |5(я) - р(1/)1 + 1^(у)1 • 1/(®) - №)1>
т. е. VJ > 0 и V® Е [а, 6] получаем оценку w(f • д; Uf(x)) <
Mjw(g-, Lfy(®)) + Mgw(f-, Lfy(®)), откуда, переходя к пределу при <5 —> О,
имеем 0 < w(f • д;х) < Mfw(g;x) 4- Мдш(/;х) V® G [а,Ь], т. е. имеет *
место (6.1).	4
В силу критерия Лебега интегрируемости по Риману имеем
I
(/, д Е R[a, Ч) => (mes Ef = mes Ед = 0),	\
но тогда из (6.1) получаем mes Ef.g = 0 й вновь, применяя критерий
Лебега, имеем f • д Е Я[а, Ц.
Теорема 3. Пусть f Е Я[а,Ь] и Эр > 0 такое, что |/(®)| >
р > 0 V® G [а, Ь]. Тогда 1// 6 R[a, Ь].
Доказательство. (/6 R[a, Ч) => (/ Е В[а, Ь]), но тогда из j
условия |1//(®)| < 1/р V® 6 [а, Ъ] имеем 1// 6 В[а, 6]. Далее, V®, у Е Й
[а,Ч имеем |1//(х) - 1//(у)| = |/(х) - /(у)|/(|/(х)| • |/(у)|) < |/(х) - '
/(у)1/р21 откуда У<5 > 0 и Vx е [а, 6] имеем
^(1//;^(х)) < lw(/;C7,(x))) => ^(1//;х) < ^(/;х)) •
Пусть Ef и E1/f - множества точек разрыва функций /(®) и 1//(®)
соответственно. Тогда из нашей оценки вытекает Ei/f С Ef. Приме-
нение критерия Лебега интегрируемости по Риману дает (/ G R[a, Ь])
=> (mes Ef = 0) => (mes E^f = 0) => (1// 6 Я[а, Ц).
Следствие. Пусть f,g Е R[a, 6] и Эр > 0 такое, что |^(®)| <
р > 0 V® 6 [а, Ь]. Тогда f/g Е R[a, Ц.
Теорема 4. (f Е R[a,b]) => (|/| Е R[a,b]).
Доказательство. (/ Е R[a, Ч) => (/ 6 В[а, Ч) => (|/| Е	(
В[а, Ь]). Но ||/(х)| - |/(з/)|| < |/(х) - /(у)| V®, у G [а, Ц, т. е. VJ > 0
и Vx G [а,Ь] имеем оценку w(|/|;Us(x)) < u(f',Us(x))	(w(|/|;х) < j
w(/;®))-	I

220
Пусть Ef и E\j\ - множества точек разрыва функций f(x) и |/(ж)|
соответственно. Тогда из нашей оценки имеем ^|/| С Ef, и примене-
ние критерия Лебега интегрируемости по Риману дает (/ Е Я[а, Ь])
=> (mes Ef = 0) => (mes Ещ = 0) => (|/| Е R[a, Ь]).
Замечание. Из |/| Е R[a, Ц, вообще говоря, не следует, что
f е Я[а,Ь]. Например, /(ж) = { 7,«€lt\Q. Т°ГДа ~ 1 6
Д[а, Ь], но fER[a, Ь].
До сих пор предполагалось, что а < Ь.
а
Определение. При а = Ъ положим f f(x)dx = 0, при а > b
а
b	а
положим f f(x)dx = — f f(x)dx, если один из интегралов существу-
а	Ъ
ет.
Теорема 5. Пусть f(x) определена на [а, 6] и а < с < Ь. Если
Ъ	с
f Е Я[а, с] и f Е R[c, Ь], то f Е R[a, Ь], причем f f(x)dx = f f(x)dx +
а	а
ff(x)dx.
С
Доказательство, (f Е R[a, с] A R[c, Ь]) => (/ Е В[а, с] А
В[с, Ь]) => (/ Е В[а, 6]). Поскольку f Е Я[а, с], то для множества всех
точек разрыва функции f на [а, с] Ef[a, с] = {® Е [а, c]\w(J;x) >
0} в силу критерия Лебега интегрируемости по Риману имеем
mes Ef[a, с] = 0. Аналогично (f Е R[c, Ь]) => (mes Ef[c, Ь] = 0). Но
поскольку Ef[a,b] С Ef[a,c] U Ef[c, b] U {с}, то mes Ef[a,b] = 0, и в
силу того же критерия Лебега интегрируемости функции по Риману
ъ
имеем f Е R[a, Ь], так что 3 J f(x)dx =
а
Рассмотрим любое разбиение Т отрезка [а, 6], содержащее точку
с. Тогда Т = {71, Тг), где 71 = {а =	< ®1 < • • • <	= с} есть
разбиение отрезка [а,с], Т2 = {с = хк < xk+i < ...<xn = b} есть раз-
биение отрезка [с, Ь]. В силу следствия 2 из теоремы 2 § 2 имеем оценки
$[а,е](Т1) + S[e,'b](T2) = ^^(Т) > J = J = J > ^(Т) = (Тх) +
£[с,ь](22), т. е. S[a,c](7i) + S[C16](T2) > J > S[a)Cj(7i) + S[c 4(7г), откуда
e	6
[ f(x)dx + [ f(x)dx = inf (S(T1) + S(T2)) =
J	J	VI,T2}
a	c
~ ^£5[а,о](Т1) +i“f5’M](32) > J >
* i	T2
> вир^о>с](Т1) + supS[Ci6](T2) = sup |5(Тг) + S(T2)| =
t2	{T„T5}
221
e	b \
= у* f(x)dx + У f(x)dx j =>
/г	г г \
=» I / f(x)dx d= J = I f(x)dx + I f(x)dx j .
\«	«	Jc /
»
Следствие. Полагая Jf(x)dx = J[a,Ь], имеем при a < c <
a
b: J[a, b] = J[a, c] + J[c, Ь], т. e. интеграл Римана есть аддитивная
функция отрезков.
Теорема б. Пусть a<a</3<6u/€ Я[а, Ц. Тогда f €
«[a.fl.
Доказательство. (/ € Я[а,Ь]) => (/ € В[а,6]) ^ (/ €
J3[ot, /?]). В силу необходимости критерия Лебега (/ € Я[а, Ь]) => (мно-
жество Я[а, 6] = {® € [а, Ь]|ы(/;®) > 0} всех точек разрыва функ-
ции f(x) на отрезке [а, 6] имеет меру нуль, т. е. mes Я[а, 6] = 0). Но
([а, /3] С [а, 6])	(Я[а,/3] с 2?[а, Ь]), поэтому множество Я[а,/3] всех
точек разрыва функции f(x) на отрезке [а,/3] также имеет меру нуль,
т. е. mes E[a, /3] = 0, а потому в силу достаточности критерия Лебега
имеем f € Я[а,/3].
Следствие. Пусть а<с<Ьи/б Я[а, 6], тогда f € Я[а, с] Л
Я[с, Ь] и
Ь	с	b
У f(x)dx = У f(x)dx + У f(x)dx.
а	а	с
Теорема 7. Пусть f е Я[а,Ь] и т < /(®) < М V® € [а,Ь].
ъ
Тогда при а <Ь имеет место т(Ь — а) < J f(x)dx < М (Ь - а),
а
Доказательство. Для любого размеченного разбиения Т£
отрезка [а, 6] в силу неравенств т < /(^k) < М Vfe имеем т(Ь — а) <
< М(Ъ — а), и поскольку f €• Я[а, 6], то Э lira Sf(T() =
6
/ f(x)dx, причем
а
Ъ
т(Ь — а)< У f(x)dx < М(Ъ — а),
а
Теорема 8. Пусть f € Я[а,Ь] и /(®) > 0 V® €• [а,Ь]. Тогда
J f(x)dx > 0. Теорема 8 следует из теоремы 7.
а
222
Следствие (интегрирование неравенств). Пусть f,g € Я[а, Ь]
ь	ь
и /(®) < »(*)	€ Ч- Тогда / /(«)<*« < /g(x)dx.
а	а
Следствие (монотонность «меры Жордана»). Если множес-
тва А, В С R измеримы по Жордану, то (А С В) => (|А| < |В|).
В самом деле, (А С В) => (Ха(®) < Хв(х) V® € (-оо, +оо)).
Из измеримости множеств А и В по Жордану в силу критерия из-
меримости по Жордану видим, что существует отрезок [а, Ь] D В D А
и Хл,Х& € Я[а, Ь], но тогда по теореме об интегрировании неравенств
ъ	ъ
имеем |А| = /Хд(®)й® < JХв(х)(1х = |В|.
а	а
* Следствие. Пусть f € Я[а,6]. Тогда имеет место оценка
а
Ъ
< J |/(®)|d®.
а
Доказательство. (/ G Я[а, 6]) => (|/| е Я[а, Ь]). Из нера-
венств -|/(®)| < /(®) < |/(®)| V® € [а, 6] в силу теоремы об интегриро-
ь	ь	ъ
вании неравенств имеем оценки - / |/(®)|d® < / f(x)dx < J |/(®)|d®,
a
a
откуда
/ f(®)d®
a
< J|/(x)|d®.
a
Следствие. Пусть f G Я[а, Ь] и |/(®)| < L V® G [а, 6]. Тогда
ь
f f(x)dx
a
< L(b-a).
Теорема 9. Если f € Я[а, fr], то множество всех точек не-
прерывности функции f(x) всюду плотно на отрезке [а, Ь].
Доказательство. Пользуясь критерием непрерывности
Бэра, достаточно доказать, что на любом отрезке [а, [3] С [а, Ъ] 3 точка
®о 6 [а,/3] С [a,i>] такая, что о>(/;®о) = 0.
Допустим от противного, что 3[a,/3] С [а,Ь] такой, что о>(/;®) >
0	€ [ск,/3]. Тогда [a,/?] С В, где Е - множество точек разрыва
/(ж) на [а, Ь]. Но f 6 Я[а, Ь] и в силу необходимости критерия Лебега
интегрируемости по Риману mes Е = 0, и поэтому отрезок [а, /3] С Е
также должен иметь меру нуль, а в силу компактности и длину нуль.
Но отрезок не может иметь длину нуль. Противоречие.
Лемма. Пусть f € Я[а,Ь] и f(x) > 0 V® 6 [а, Ь], причем су-
ществует точка xq Е [а, Ь] такая, что f g С(®о) и /(®о) > 0* Тогда
f f(x)dx > 0.
а
Доказательство. Поскольку / е С(®о) и /(®о) > 0, то
в силу локальных свойств непрерывных функций существует такой
отрезок [a, fi], что ®0 G [a, fi] С [а, Ь] и /(®) > 1/2>/(®0) > 0 V® G [а,/3].
223
Но (/ Е R[a, Ч) => (/ Е Я[а,а], f е Я[ск,/?], f Е R\j3, Ь]). В силу
аддитивности интеграла Римана и теоремы 8 имеем
f(x)dx
> 1/2 •/(®0)(/3 — а) > 0.
Теорема 10. Пусть f Е R[a, 6] и f(x) > 0 V® 6 [а, 6]. Тогда
ъ
ff(x)dx>0.
а
Доказательство. По теореме 9 3®о Е [а, Ь] такая, что f Е
С(®о), /(®о) > 0, f(x) > 0 V® Е [а, Ь], но тогда оценка теоремы 10
вытекает из нашей леммы.
Теорема И. Пусть f Е Я[а, Ъ] и f(x) > 0 V® Е [а, 6]. Тогда
(ь	\
f f(x)dx = 0 j => (mes 5 = 0, где £ = {® Е [а, Ь]|/(®) > 0}).
а	/
Доказательство. Рассмотрим множество Е - множество
всех точек разрыва функции /(®) на [а, Ь] и покажем, что £ С Е.
Допустим от противного, что 3®о Е £ такая, что f Е С(®о), тогда
ъ
/(®о) > 0 и по лемме J f (x)dx > 0 вопреки предположению теоремы.
а
Итак, £ С Н. Но в силу необходимости критерия Лебега (/ Е
Д[а, 6]) => (mes Е — 0) (mes £ = 0).
Теорема 12. Пусть f Е Л[а, Ь] и £ = {® Е [а, 6]|/(®) # 0}.
(6	\
J f(x)dx = 0 1.
а	/
Доказательство. (/Е Я[а, Ь]) => (|/| Е R[a, 6]) => £ = {ж Е
[а, 6]11/(®)| > 0}. Поскольку |/(®)| > 0 V® Е [а, 6], то для любого разби-
ения Т отрезка [<х, Ь] имеем S|y| (Т) > 0. Докажем, что на самом деле
S|y|(T) = 0 VT. Допустим от противного, что существует разбиение
То отрезка [а, Ь] такое, что S|/| (То) > 0. Тогда в разбиении То сущест-
вует такой частичный отрезок До длины <5 > 0, что inf |/(®)| > 0. Но
^ко
тогда (|/(®)| > 0 V® Е 1к0) =» (1к0 С 5), так что £ / 0. Но по условию
mes £ = 0, поэтому, как было доказано ранее, £= 0. Противоречие.
Итак, для любого разбиения Т отрезка [а,6] имеем S^(T) = 0,
ъ
откуда J = supS|y|(T) = 0. Но |/| Е Я[а, 6], поэтому f |/(®)\dx = J =
ч	а
0, и поскольку
ь	ъ
У f(x)dx < У |/’(aj)|dsc = 0,
а	а
224
ь
то J f(x)dx = 0.
а
Следствие. Если f,g G Я[а, 6], 8 = {ж G [а, 6]|/(ж) / #(ж)}, то
(ь	ь	\
J* f(x)dx = J* g(x)dx j.
a	a	J
Лемма. Пусть Ai, А2	С (—оо, 4-оо),	тогда
XA1UA2(x) = Xaj(®)	4-Ха2(ж)	- Ха1Па2(ж) Vx G (-00,4-00)	(6.2)
Доказательство. Пусть ж0ЕА1 U А2, тогда жоЕА, (г = 1,2)
и жо?А1 А Аг, т. е.
X’a1ua2(®o) = XaJxo) = Хд2(®о) = XAinA2(®o) = 0,
так что соотношение (6.2) имеет место при жбА1 U Аг.
Пусть хо Е Ai U Аг, тогда Хд1ил2(®о) = 1» причем возможны
случаи:
а)	жо 6 Ах, но жоЕАг (или ж0 Е Аг, но Ж0ЁА1). Тогда ХА1 (®о) = 1,
Хд2(«о) = Ха1ПЛ2(ж0) = 0 (илиХд2(ж0) = 1, Хд^Жо) = Хд1Па2(®о) =
0), т. е. (6.2) имеет место и в случае а).
б)	жо G Ai П А2. Но тогда XAl(®o) = Хд2(ж0) = Ха1Па2(®о) = 1,
т. е. (6.2) имеет место и в случае б).
Следствие 1. Пусть множества Ai, Аг С [а, 6] измеримы по
Жордану, тогда измеримы по Жордану множества Ai U А2 и Ai А А2,
причем |Ai U Аг| 4-1Ai А А21 = | Ai | 4-1Аг| и, в частности, |АХ U Аг| <
|А1 + |Л2|.
Доказательство. Поскольку множества, измеримые по
Жордану на отрезке [а, Ь], образуют алгебру, то из измеримости по
Жордану Ai, Аг следует, что множества Ai U А2 и Ai А А2 также
измеримы по Жордану. В силу критерия измеримости по Жордану
имеем тогда ХА1, Хд2, Xajua^ ХА1г\а2 Е Я[а, Ь], откуда по теореме 1
Xajua2 4- Ха1Па2, ХА1 4- Ха2 Е R[a, Ь], причем
ь	ъ
|Ai U Аг| 4- |Ai А А2| = JXa1ua2(®)^«4- f XAinA2(x)dx =
а	а
Ь	Ь
/(Xa1ua2(®) + XA1rtA2(x))dx = У(Хд1 (ж) 4- XA2(x))dx =
а	а
8 Зак. 860
225
Поскольку Хл1Пл3(х) > О V® € [а,Ь], то (|АХ П Аа| > 0) => (|АХ U
Л2| < |ЛХ| + |А3|).
Следствие 2. Пусть множества А< С [а, 6] (/ = 1,2,..., т)
т
измеримы по Жордану. Тогда множество |J А» также измеримо по
1=1
Жордану, причем
m	m
iLh'i<DA'i-
i=i	i=i
Следствие 3 (усиленная аддитивность меры Жордана).
Пусть множества Ai, Аа С [а, Ь] измеримы по Жордану и |АхПА2| = 0.
Тогда множество Ai U Аа измеримо по Жордану, причем |Ai U А21 =
I-A1I +1 Аа|.
В самом деле, в силу следствия 1 имеем |АХ U А2| = |АХ| + |А2| -
|Ai П Аа|, откуда (|АХ П Аа| = 0) => (|Ai U А2| = |АХ| + |Аа|).
Следствие 4. Пусть множества Ay С [а, Ь] (j = 1,2,..., т)
т
измеримы по Жордану, причем |Aj П А*| = 0 Vj к. Тогда | |J Aj| =
j=i
m
Е И,|.
у=1
Следствие 5 (свойства меры Жордана). Пусть на отрезке
[а, Ь] рассмотрена система а множеств {А}, измеримых по Жордану
(т. е. таких, что mes дА = 0 VA € <т). Тогда на системе а, образую-
щей алгебру (множеств), определена неотрицательная функция «мера
ъ
Жордана»; д : А	|А| = / Хд(х)<2ф > 0, обладающая свойствами:
1)	|А\ > 0 VA € <г,
2)	|Ai U А21 < |Ai| + |А2| VAi, А2 €
3)	VAi, Аг € а таких, что Ai П А2 = 0 (или |Ai П А2| = 0) =>
|AiUA2| = |A1| + |A2|;
4)	если [а,/3] С [а, Ь], то |[а, /3]| = (3 - а.
Заметим, что свойства 2) и 3) выражают конечную аддитивность
меры Жордана. Заметим также, что мера Жордана не обладает свой-
ством счетной аддитивности.
Теорема (1-я обобщенная теорема о среднем). Пусть g Е
Я[а, Ь] и д(х) > 0 V® € [а, Ь]. Пусть f Е В[а, Ь] и т = inf f(x),
[а,Ь]
М = sup/(®). Пусть f'gE Я[а, Ь]. Тогда существует число р, такое,
MJ
ь	ъ
что т < д < М, причем f f(x)g(x)dx = g/g(x)dx.
a	a
b
Если f € С[а, 6], то Эс € [а, Ь] такая, что J f(x)g(x)dx =
226
b
f(c)fg(x)dx.
Доказательство. Поскольку g(x) > О V® € [а, Ь], то
тд(х) < f(x)g(x) < Мд(х) Ух € [а, Ь]. Но д, f • д € Я[а,Ь], поэтому,
применяя теорему об интегрировании неравенств, имеем
ъ
т / g(x)dx <
a
b	b
У f(x)g(x)dx < M у* g(x)dx.
а	а
b
Если / g(x)dx = 0, то при любом /х € [m, М] имеем
a
о
ъ	ь	/ ь
Если же /g(x)dx > 0, то m < / f(x)g(x)dx / /g(x)dx < М, т. е. су-
a	a	/ °
b	lb
ществует число /х = f f(x)g(x)dx / f g(x)dx^ удовлетворяющее усло-
a	I a
b	b
вию m< p,< M hl такое, что / f(x)g(x)dx = /х $ g(x)dx>
a	a
Если f € C([a,t]), то в силу теоремы Вейерштрасса (о мак-
симуме и минимуме) существуют точки ®i,®2 € [a,b] такие, что
/(®i) = М и /(®г) = т> Поскольку т < /х < М, то в силу тео-
ремы Больцано о промежуточных значениях функции, непрерывной
на отрезке, существует точка с € [а, Ь] такая, что /(с) = /х, и тогда
ъ	ъ
j f(x)g(x)dx = f(c) Jg(x)dx.
a	a
1-я теорема о с p e д н e м. Пусть fE Я[а, Ь] и т = inf f(x)f
[a,b]
М = sup/(®). Тогда существует число /х € [m, М] такое, что
[a,b]
b
f f(x)dx = pi(b - а), если же при этом f Е С ([а, Ь]), то существует
а
b
точка с Е [а, Ь] такая, что f f(x)dx = f(c)(b — a),
a
Замечание. Если f E C([a, Ь]), то можно считать, что Зсо €
(a, b) такая, что
b
= /(c0)(b-a).
a
8*
227
Определение. Если функция д(х) определена на [а, Ь] и су-
ществуют постоянные К > 0 и a Е (0,1] такие, что |^(®i) — 0(®2)| <
Kj®i — ®г|а	6 [а, 6], то говорят, что функция д(х) удовлетво-
ряет на отрезке [а, Ь] условию Гельдера с показателем а и посто-
янной К. Запись: g Е HQ[a, Ь]. При а = 1 говорят, что функция д(х)
удовлетворяет на отрезке [а, Ь] условию Липшица: g Е Lip[a, 6] =
Я1[а,Ь].
Замечание, (g Е На[а, Ь]) => (д 6 С[а, 6]). В самом деле, V®o 6
[а, Ь] и VA® (а < ®0 4- А® < Ъ) (д Е Яа[а, Ь]) => (|^(»о + А®) ~ tf(®o)| <
Я|Д®|а) => (3 lim д(х0 4- А») = g(xQ)) => (д Е С(®о) V®o Е [а, Ъ]) =>
Дт—>0
(jec[a,4).
Замечание. Если д Е Яа[а, 6] при a > 1, то д(х) = const на
[а,Ь].
В самом деле, VA® / 0 имеем V®, х + A® 6 [а, Ь] (0 < |д(® +
А®) - д(х)|/|А®| < 2C|A®|°'-1, где а — 1 > 0) => (3 lim (д(х + А®) —
Дх—>0
р(®))/Д® = 0) => (D#(®) = 0 Vx Е [a, i>]) => (д(х) = const на [а, 6]).
Пусть f Е R[a, Ь], тогда f Е Я[а, ®] V® 6 [а, 6], и поэтому имеет
х	а
смысл функция Ф(®) = J причем Ф(а) = J f(t)dt = 0.
а	а
Теорема (о непрерывности определенного интеграла Римана
X
как функции верхнего предела). (/ 6 R[a, Ь]) => (Ф(®) = J f(t)dt Е
C([a, Ь])) (точнее, Ф Е ЯЦа, Ь])).
Доказательство. V®, х 4- А® 6 [а, Ь] имеем в силу
х+Дх
аддитивности интеграла Римана Ф(® 4- А®) — Ф(®) = / f(t)dt —
а
f f(t)dt = f f(t)dt (при A® > 0) и Ф(®4- А®) — Ф(®) = — J f(t)dt
(при А® < 0). Но (/ Е R[a, Ь]) => (/ Е В[а, Ь]) => (М = sup |/(®)| <
[a,b]
4-оо), поэтому
ЯГ + Дя?
|Ф(® 4- А®) — Ф(®)| <
X
<Af|A®|,
т. е. Ф Е Я1[а, Ь], откуда Ф Е С([а, 6]).
Лемма (тождество Абеля). Пусть даны последовательности
(а*), (а*), (б*), где = Gk — Gk-i- Тогда при т> п имеет место
тождество Абеля
т	т-1
afcttfc = Gfc(ajs - Offe+l) + Gm«m - Gn-ian
k=n	k=n
228
к
и в частности, тождество Абеля при Gk = $к = ^2 аЬ ак = 8к —
’ /=1
$к_1? з0 = 0 имеет вид
п	п — 1
52 акак ~ У?	~ а* + 1) + Зп«п-
fc=l	fc=l
Доказательство. Полагая а* = Gk - Gfc-i, имеем
т	т	т	т
52 aitafc = 52	~ Gk-i) = 52 ак@к - 52 akGk-i =
к=п	к=п	к=.п	к—п
т	тп—1	тп— 1
= 52 ак^к — 52 а/+1Ф = 52	— аН1) + Gmam — Gn-iotn-
к=п	l=n — 1	/=п
Замечание. Итак, имеем тождества Абеля (т > п)
т	тп—1
52	~ Gk-i) = 52 &к(ак ~ a*+i) + Gmam — Gn-iOLn
к=п	к=п
И
т	т
52 ak(Gk-l — Gk) = 52(“а*)(^* ~~	=
к=п	k=zn
т—1
= 52 ^**(а*+1 “ ак) ~ GmOLm + Gn-iOln-
к=п
Следствие. Если Qi > &2 > ...> ап > 0 и существуют
постоянные тп, М такие, что т < Gi < М (I = 1,2,... , п), то при
Gq = 0 имеем оценку
п
«1ГП <52(<?fc-Gft_ i)afc < ахМ.
fc=i
Аналогично если 0 < Qi <	< • • • < <*п> то при Gn = 0 имеем
оценку
п
ап»п < 52 “fe(Gfc-i - Gk) < апМ.
к=1
В самом деле, в силу тождества Абеля при п = 1 и т = п имеем
п	п
52(^fe “ Gk-i)ock = 52^(«fe ~ «k-i) 4- Gn<*n — Goai,
k=l	fc=l
229
откуда, поскольку Go = 0, т < Gk < М и ед - ед+х > 0, имеем
mai = т I 52 (а* “ а*+1) + а" ) - 52(^к -	-
\к=1	/	к=1
(П-1	\
52 (а* - а&+1) + ап j = Mai.
fc=i	/
2-я интегральная теорема о среднем. Пусть
f G Я[а, Ь] и д € М[а, Ь]. Тогда существует точка с € [а, Ь] такая,
что
b	с	Ъ
У f(x)g(x)dx=g(a) j f(x)dx+g(b) f f(x)dx.
a	a	c
Доказательство. Рассмотрим сначала случай д(х) ф на
[а, Ь] и д(х) > О V® € [а, Ь]. Тогда
(д е м[а, Ь]) => (д € Я[а, 6]),
(/ G R[a,b}) => (/ • д € Я[а,Ь]),
причем
ъ
3 Hm Sf.g(T() = J = [ f(x)g(x)dx.
a
Рассмотрим специальное размеченное разбиение Т(°, где (° = {а =
Хо, Х1, . .. , Хп-1}I и положим
S/s(T£°) = Sfg(T) =
fc=l
Тогда 3 lim Sfg(T) = J. Положим
mk(f) =	= Mk(f),
тогда при любом выборе д«, G [пгь(/), Mk(f)] имеем
|/(ед_1) - цк\ < w(/;Ik) = uk(f).
п
Положим Зцд(Т) = g(xk-i)p>k&Xk> Тогда поскольку 0 < д(х) <
&=1
д(а) V® 6 [а, Ь], то для любого разбиения Т отрезка [а, Ь] имеем оценки
|S/s(T) -SM(T)| <	<g(a)Slf(T).
fc=l
230
Ho f 6 Я[а, Ь], и поэтому в силу предельного критерия интегриру-
емости по Риману имеем ^1нпоП/(Т) = 0, так что
3ilimS„(T) = (limS,s(T) = /.
Поскольку (/ € Я[а,Ь]) => (/ G ®*]), то в силу 1-й интеграль-
ной теоремы о среднем Здь € [т* (/), ЛГ*(/)] такое, что
Вк
У* f(x)dx = ДкД®к,
Як-1
и тогда при указанном выборе р>к имеем


Введем функцию Ф(®) = / f(t)dt, Ф(а) = 0. В силу теоремы о
а
непрерывности интеграла Римана по верхнему пределу имеем Ф 6
С([а, Ь]) и, в частности, Ф € В[а, 6], так что
-оо < т = inf Ф < Ф(®) < sup Ф = М < -Foo.
[®»Ь]	[а,Ь]
Но тогда J f(t)dt = Ф(®&) - Ф(®*-1), причем Ф(®о) = Ф(а) = 0.
ЯЛ-1
Имеем
5М(Т) = £- Ф(^_1)).
fc=l
Полагая &к =	видим, что д(а) = ai > аг > . • • > ап =
р(®п-1) > 0. Полагая Ф(®*) = G* (fc = 1,2,..., п) и Ф(®о) = Go = 0,
имеем в силу оценки т < Gk = Ф(®й) < М и следствия к тождеству
Абеля оценку тд(а) <	< Мд(а) VT.
Переходя в ней к пределу по базе t +0, имеем
ъ
т9(а) < У f(x)g(x)dx < Мд(а).
а
В случае д(а) > 0 имеем оценку
ъ
т < / f(x)g(x)dx/g(a) < М.
231
Но Ф E C([o,fc]), и поэтому в силу теоремы Вейерштрасса (о мак-
симуме и минимуме непрерывной функции) 3ci,2G [а, i>] такие, что
Ф(с1) = тп < М = Ф(с2), и тогда по теореме Больцано о про-
межуточных значениях непрерывной функции Зс 6 [а, Ь] такое, что
ъ
ф(с) = f f(x)g(x)dx/g(a), т. е. имеем
а
Ъ	с
j f(x)g(x)dx = д(а) j f(x)dx.	(6.3)
а	а
В случае д(а) = 0 равенство (6.3) имеет место Ve Е [а, Ь].
Пусть теперь д(х) j, на [а, 6], причем д(х) может иметь и отрица-
тельные значения на [а, Ц. Тогда для функции h(x) = д(х)— д(Ъ) имеем
h(x) | на [а, 6] и h(x) > 0 Va? Е [а, Ь]. Тогда по доказанному выше (см.
(6.3)) видим, что существует точка с Е [а, Ъ] такая, что
откуда имеет место равенство
Ъ	с	Ъ
/ f(x)g(x)dx = д(а) f f(x)dx+g(b) f f(x)dx, (6.4)
а	ас
что и доказывает 2-ю теорему о среднем в случае д(х) | на [а, Ь].
Если д(х) f на [а, Ь], то применяем 2-ю теорему о среднем в виде
(6.4)	к функции (-д(х)) | на [а, Ь].
Замечание 1. Пусть f Е Я[а, 6], д(х) | на [а, Ь] и д(х) > О
Va? Е [а, 6], тогда Зс Е [а, Ь] такая, что имеет место равенство (6.3).
Замечание 2. Пусть / Е Я[а,Ь], д(х) f на [а,Ъ] и д(х) > О
Va? Е [а, 5], тогда Зс Е [а, Ь] такая, что
ъ	ъ
j f(x)g(x)dx = g(b) f(x)dx.	(6.5)
а	а
232
Для доказательства равенства (6.5) полагаем
п	п
Sfg(T) = '£ig(xk)f(xk)Axk, так что 5Д9(Т) = ^0(ж*)/^Дач =
fc=l	fc=l

b
где G(a?) = / Учитывая, что G(xn) = G(b) = 0, m < G(xk) < M
X
(k = 1,2,... , n) и 0 < g(xk) < g(b) (k = 1,2,... , n), и применяя след-
ствие к тождеству Абеля, получаем оценки тд(Ь) < 8^д(Т) < Мд(Ь)
ъ
и тпд(Ь) < J f(x)g(x)dx < Mg(b), после чего, учитывая, что <?(с) =
а
Ь
f f(x)dx, доказательство (6.5) завершается, как и при доказательстве
основной 2-й теоремы о среднем.
Теорема (о дифференцируемости интеграла Римана по верх-
нему пределу). Пусть f 6 Я[а, t>] и f Е С(а?о), где xq Е (а, Ь). Тогда
X
для функции Ф(а?) = $ f{t)dt ЗвФ(а?о) = /(®о)-
а	« .
Замечание. Если в теореме f Е С(а) (соответственно f 6
С(Ь)), то ЗВ+Ф(а) = /(а) (соответственно ЗВ“Ф(&) = f(b)) (доказать
самостоятельно).
Доказательство. Поскольку f Е Я[а, Ц, то функция Ф(ж)
существует Va? Е [а, Ь]. Далее, VA® > 0 такого, что ®о 4- А® Е [а, 6],
имеем
Ф(ж0 4- Да?) - Ф(а?о) =
то+Д®	я?о+Дя
У f(t)dt; f(x0)  Ах = у* f(x0)dt,
Xq	Xq
поэтому
Хо+Дх
(Ф(®0 + Ах) - Ф(х0))/Ах - f(x0) =	[ (f(t) - f(x0))dt.
1ЛХ J
Xq
Аналогично при Да? < 0 (а?о 4- Да? Е [а,Ь]) имеем равенство
(&О	\
-	[ (f(t)-f(x0))dt\.
J	I
хо+Дх	/
233
Но / € C(xq), поэтому Ve > 0 35 > 0 такое, что Vt 6 [а, Ь], удовлетво-
ряющего неравенству |t - ®о| < 5, имеем |/(t) - У(®о)| < в.
Пусть 0 < |Д®| < 6, тогда |/(t) - /(®о)| < е V|t - ®о| < |Д®|, т. е.
|(Ф(®о + Д®) - Ф(®о))/Д® - У(®о)| <
0о+Д0
<i^i / 1/(0 - /(®0)|Л < е/|Д®| •
0о+Д0
lett
= €,
00
а>0
откуда
(3 lim (Ф(®0 + Д®) - Ф(®о))/Д® = У (®о)) * (ЭПФ(®о) = /(®о)).
Д0-4О
Теорема (о существовании точной примитивной у непрерыв-
ной функции). Пусть f € С([а, Ь]), Тогда функция f(x) имеет точную
0
примитивную Ф(®) = / f(t)dt на отрезке [а, Ь], причем Ф(а) = 0.
а
Доказательство. (/ € С ([а, Ь])) =► (/ € Я[а, &]) => (Ф €
С([а,Ь])) и в силу предыдущей теоремы V® € (а, Ь) ЗПФ(®) = /(®).
Теорема (о существовании первообразной у кусочно-непре-
рывной функции). Пусть f € В(о, Ь] и f € С(®) V® € [а, Ь] \ Кп (где
X
Кп - конечное множество). Тогда функция Ф(®) = j является
а
первообразной для функции /(®) на отрезке [а, Ь], причем Ф(а) = 0.
Доказательство. / € В[а, Ь], причем множество точек раз-
рыва функции /(®) на [о, Ь] совпадает с Кп, т. е. конечно, поэтому
У € Я[а, 6]. Далее,
(У 6 Я[в,Ч) => (Ф(®) = J f(t)dt € С([а,Ь])иФ(а) = 0).
а
Наконец, из теоремы о дифференцируемости интеграла Римана по
верхнему пределу видим, что V® € [а, Ь] \ Кп ЗпФ(®) = У(®). Таким
образом, функция Ф(®) является первообразной для У(®) на отрезке
(», ч-
Теорема (формула Ньютона - Лейбница для кусочно-непре-
рывной функций). Пусть f € В[а,Ь] и f € С(®) V® € [о, Ь] \ Кп (где
Кп конечно). Пусть F(x) = f f(x)dx - неопределенный интеграл от
X t
функции f(x) на [а,Ь]. Тогда j f(t)dt = F(®) - F(a) V® € [а, 6], u, в
а
b
частности, / f(x)dx = F(b) - F(a).
234
Доказательство. Из условий теоремы вытекает, что
функция Ф(®) — j f(t)dt является первообразной для f(x) на [а, Ь]. Из
теоремы об общем виде первообразной следует, что F(x) = Ф(®) + С,
где F(x) = J f(x)dx, х € [а, 6], но при х = а Ф(а) = 0 => С = Г(а),
т. е. Ф(®) = F(®) - F(a) Vx € [а, Ь].
Итак, / f{t)dt = F(®)-F(a), где F(x) - любая первообразная функ-
а
ции /(®) на отрезке [а, 6].
Замечание. Формулу Ньютона - Лейбница записывают в ви-
де
I f(x)dx = F(®)|* = F(5) - F(a), гдеГ(®) = j f(x)dx.
a
Пример.
J -д = In (® + \/l + ®a)|o = ln(l + Vi) - In 1 = ln(l + Vi)-
Замечание. Если функция F(x) есть примитивная для функ-
ции f(x) на отрезке [а, Ь], то из этого, вообще говоря, не следует, что
f € Я[а, 6]. Например, функция
р/_\___J 0, ® — О,
' ’ 1 ®2sin®“2, х О
есть точная примитивная на отрезке [-1,1] для функции
/(«О = {
2® sin “2 - 2®-1 сое ®“2, а О,
О, х = О,
но	1], и поэтому /?Я[-1,1].
Пример. Рассмотрим на отрезке [а, 6] функцию Римана.
{б при ® иррациональном,
1/дпри® = p/q рациональном (p/q — несократимая
дробь, q € N).
Очевидно, / е В [а, Ь].
Докажем, что функция Римана непрерывна в любой иррациональ-
ной точке и имеет разрывы 1-го рода в любой рациональной точке. В
самом деле, пусть ®о € [а, Ь] фиксировано. Ve > 0 существует лишь
конечное число q € N таких, что 0 < q < 1/е, поэтому на отрезке [а, 6]
имеется лишь конечное число рациональных точек p/q, для которых
f(.p/q) = 1/g > е.
235
Но тогда 3(5 (г) > 0 такое, что множество Us{e)(^o) П [а, Ь] не со-
держит ни одной рациональной точки р/g, для которой 1/q > г, т. е.
О < /(х) < € V® 6 IZy(e)(®o) П [а, 6]. Тем самым доказано, что
V®o Е [а, Ъ] 3 lim f(x) = f(xo ± 0) = О,
т. е. функция Римана может иметь разрывы только 1-го рода.
Поскольку /(®о) = 0 для xq иррациональной, то f Е (7(®о)
V®oOoo = Q А [а, Ъ]. В случае ®0 = p/q Е Коо f(xQ) = 1/q > О,
т. е. /ЕС(®о) V®o Е Koq.
Итак, функция Римана ограничена и множество ее точек разрыва
Коо счетно, а потому mes Коо = 0. Но тогда в силу критерия Лебега
f Е Я[а, 6], причем в силу теоремы 12 § 6 гл. 2
X
Ф(х) = / f(t)dt = О V® 6 [а, ь].
а
Заметим, что ВФ(я) = 0 = /(®), УхёКоо и D$(®o) = 0	У(®о) V®o Е
-Коо, где множество Коо не является конечным, поэтому Ф(х) не может
быть первообразной функции Римана (в нашем определении).
Замечание. Если функция f(x) кусочно-непрерывна на отрезке
[а, Ь], т. е. У Е С([а, Ь] \ Кп) А В[а, Ь], то f Е Я[а, Ь] и функция Ф(х) =
X
$ всегда есть ее первообразная.
а
Теорема (формула Ньютона - Лейбница). Пусть функция
F Е С([а, Ь]) и является первообразной для функции f Е Я[а, fr]. Тогда
имеет место формула Ньютона - Лейбница
ь
У f(x)dx = F(b)-F(a).
а
Доказательство. Пусть функция F(x) есть первообразная
для функции f(x) на отрезке [а, 6], тогда F Е С([а, Ь]) и существует
множество Кт = {ai,... , am} такое, что V® Е (а, Ь) \ Кт 3dF(x) =
f(x). Для любого разбиения Т отрезка [а, Ь] построим продолжение
Т Т, добавив точки -Кт, и пусть Т =	,®п}. Тогда по
теореме Лагранжа о конечных приращениях существуют точки ту, Е
такие, что Г(х,) — F(x/-i) = /(qt-)A®t-, и поэтому
п	п
F(b) - F(a) = £№) - F(®i-1)) = £№,)Дш. = Sf(Tr)).
t=l	:=1
236
b
Ho f E Я[а,b], и поскольку существует ^Пт= f f(x)dx,
то в силу критерия Коши существования предела числовой функции
по базе (d(T)_2> 0) Ve > О В<5 > 0 такое, что VT£, Ttj G В$, имеем
\S/(T£) — Sf(TT})\ < е, и поскольку	= F(b) — F(a), то имеем
lim	= F(b) - F(a), t. e. J f(x)dx = F(b) - F(a).
a
x
Замечание. Функция Ф(®) = J*будет при этом перво-
а
образной для функции f(x) на отрезке [а, Ь].
В самом деле, если F(x) - первообразная для f Е Я[а, Ъ], то по
доказанной теореме Ньютона - Лейбница Ф(ж) = F(x) — F(a), т. е.
функция Ф(ж) также является первообразной для f(x) на [а, Ъ].
X
Замечание. Если f Е Я[а,Ь] и Ф(ж) = /f(t)dt Vx Е [а,Ъ], то
а
Ь
Ф Е С([а, Ь]) и имеет место равенство J f(x)dx = Ф(Ь) — Ф(а) (где
Ф(а) = 0).
Однако Ф(ж), вообще говоря, не является первообразной для функ-
ции f Е Я[а, b], поскольку множество ее точек разрыва £ = {х 6
[а, b]|w/(®) > 0} может не быть конечным (хотя бы в силу критерия
Лебега mes £ = 0). Так будет для функции Римана, введенной выше,
для которой £ = Q П [а, Ь] счетно.
Теорема 1(о замене переменной в определенном интегра-
ле Римана). Пусть f(x) G С([А,В]), <p(t) Е	/?]), причем
*>([«,$) с [А,В], <р(а) = а, = Ь; [a, ft] С [А,В].
Тогда
ь	р
У f(x)dx = У f(<p(t))D<p(t)dt.
а	а
Доказательство. Поскольку f 6 С([А,В]), то на отрез-
ке [А, В] для функции f(x) существует точная примитивная F(x) и
ъ
в силу формулы Ньютона - Лейбница J f(x)dx = F(b) - F(a). Да-
а
лее? Функция (/ о <р) Е С([а,/?]) и поэтому также имеет точную
примитивную, равную в силу теоремы о производной сложной функ-
ции F[y>(tf)]. Но тогда, вновь применяя формулу Ньютона - Лейбница,
имеем
/з
/ fMt))D<p(t)dt = ВМ<)]|£ = F(ft) - F(a),
Л
237
т. е.
ь	0
У f(x)dx = У f(<p(t))T)<p(t)dt.	'
а	а	1
Теорема 2 (о замене переменной в интеграле Римана). Пусть
f € R[a> Ь], <р € Р([а,/3]) и D<p € Я[а,/3], причем <р : [ос,/3] -> [а, Ъ] =
¥>([«,/?]) есть строго монотонная функция (<р П или Ц на [а,/?]),
для которой ^>(а) = а, <р(/3) = Ь (или соответственно <р(а) = Ъ,
р(/3) = а). Тогда fop* € Я[а,/3] и
ъ	И
j f(x)dx = У
а	а
Доказательство. Пусть для определенности ТТ на [а, /?].
Тогда отображение t —> p(t) осуществляет гомеоморфизм отрезка
[о£,/3] на отрезок [а, Ь] = у>([а,/3]), так что существует обратный го-
меоморфизм х -> причем <р~* G С([а, Ь]) и <р~г ТГ на [а, Ь]. Для
любого размеченного разбиения Т£ отрезка [а, 6]
Т = {а = х0 < ®i < ... < хп = 6},
6 €	(» = 1,2,... ,п)
рассмотрим точки t, =	€ [а,/3], т< = ^”х(6) €
Тогда Тот *= р-1(Т£) (где То = {а = to < ti < ... < tn = /3},
Ъ = y>-1($,)) есть размеченное разбиение отрезка [а,/3], «индуци-
рованное» (с помощью гомеоморфизма (р-1) размеченным разбиени-
ем Т£. Аналогично, любому размеченному разбиению Тот отрезка
[ее, /3] можно поставить в соответствие «индуцированное» (<р) разме-
ченное разбиение Т( d= р(Тот) отрезка [а, Ь] по правилу ®,- = <p(t{),
& = р(т<) (i = 1,2,... , п). Поскольку	ТГ на [а,/?] и р-1 ТГ на [а,Ь],
то Дх,- =	— <f>(ti-i) > 0 и Д<< =	> 0, и тог-
да для Т = <р(То) d(T) = тахД®< = max(p(t«) —	> 0, а для
То = у>—Х(Т) d(T0) = max At, = max(^-x(®,) - y>“x(®,_i)) > 0.
Поскольку ip e C([a,0]) и <p~l € C([a, /3]), то по теореме Кантора
функция <p(t) равномерно непрерывна на [а,/3], а ^-1(х) равномерно
непрерывна на [а, 6], и тогда при Т = <р(То) имеем lim d(T) = 0 и
<ЦТо)->О
при То = ^Um °d(To) = 0. Если использовать базы d(T) —> 0 и
d(To) —> 0, то имеем:
1)	обозначение (d(T) -> 0) ’=» (d(To) -> 0) означает, что для любого
элемента Ач = {Tor|d(To) < г]} базы (d(To) -> 0) существует элемент
238
Bs = {T£\d(T) < <f} базы (d(T) -4 0) такой, что Тот = p-1(T£) G А,
VT^GB,;
2)	обозначение (d(T0) -4 0) => (d(T) -4 0) означает, что VBj ЗА,
такой, что Т( = <fi(Tor) € Bg VTor G Ап. В силу условия / G Я[а, i>]
»
3	lim Sf(T£) = J f(x)dx = J, поэтому Ve > 0 существует элемент
d(T)-»O	a
Bj(e) (базы d(T) -4 0) такой, что
\Sf(Tt)-J\<e/2VTteBt{t).	(6.6)
Для доказательства утверждения (/op) Фр G Я[а, /3] рассмотрим лю-
бое размеченное разбиение Tqt отрезка [а, /3] и соответствующее ему
ггиипупированное» размеченное разбиение Т( = ф(Тот) отрезка [а, Ь].
Поскольку <р G 2>([а, /3]), то в силу теоремы Лагранжа о конечных при-
ращениях, примененной к функции <p(t) на отрезке [ti-i, <,], сущест-
вует точка 1? €	такая, что Д®< = p(t,) - p(t<-i) = Dp(tf)A*i,
и тогда имеем представление (при Т£ = р(Тот), & = р(-г,-),	= р(М)
sf(Tt) = ^/(б)д®< = £/(p(n))DpWA*i =
»=1	1=1
= Е	+ /(Тот),	(6.7)
1=1
где положено
/(Тот) = E№(t,))(DpOM - Dp(t<))A«<.
1=1
Поскольку f € Я[а, Ь] А В[а, Ь], то существует постоянная М > 0
такая, что |/(®)| < М Ух 6 [а, 6], и, полагая w,(D^) =	[<•-1,$»•]),
имеем оценку
|/(Тот)| < М^W<(D^)A<i = MSlDip(T0).
1=1
Но Dp G Д[а, /3], я поэтому в силу предельного критерия интегрируе-
мости по Риману o^D¥>(To) = 0, а потому q/(Tot) = 0 и
для фиксированного в (6.6) е > 0 существует элемент Ап(») (из базы
°ЦТо) -4 0) такой, что
|/(Т0т)| < е/2 VT0r € An(t).	(6.8)
Из представления (6.7) имеем (при Т£ = р(Тот)) представление
В/^(Тот) = 5/(Те)-/(Тот),
239
дающее оценку
|5/о^(Тот) - J\ < \Sf(T£) - J| + \I(TQr)\.	(6.9)
Рассмотрим сначала элемент А^е) (базы d(To) 0), для которого
выполнена оценка (6.8). Поскольку (d(To) -> 0) Л (d(T) —> 0) (где
Т£ = у>(Тот)), то для элемента (базы d(T) -> 0) из оценки (6.6)
существует элемент Ащ с Д,(е) такой, что
Т£ = р(Тот) е BJ(e) VTor е а^.	(б.ю)
Но тогда W > 0 (фиксированного в оценках (6.6) и (6.8)) существует
элемент (базы d(7b) —> 0) такой, что имеет место (6.10), и поэтому
выполнены оценка (6.8) и оценка (6.6), т. е. из (6.9) в силу (6.6), (6.8)
имеем оценку
< ^/2 + s/2 = е VTor G Afj1,
т. e.
ъ
3 lim
<f(To)->o J * *
так что f о <p • D^> 6	0] и
£	ь
/	= / f(x)dx.
a	a
Теорема (о среднем в интегральной форме). Пусть функция
f(x) имеет на отрезке [а, Ь] первообразную F(a?) и f 6 Д[а, 6]. Тогда
1
F(b) - F(a) = (b-a)f f(a 4- t(b - a))dt,
о
и, в частности, если F(x) есть точная примитивная на [а, Ь] для
функции f(x) = DF(®), то
1
F(b) - F(a) = (b - a) DF(a + t(b - a))dt.
о
Доказательство. По теореме Ньютона - Лейбница имеем
ь
У f(x)dx.
а
240
Сделав в интеграле Римана, стоящем справа, гомеоморфную замену
$ = а 4- (Ь — a)t, имеем в силу теоремы 2
ъ
F(b) — F(a) = (b — a) J f(a 4- t(b — a))dt.
a
Замечание (по поводу интегрирования сложной функции).
Пусть /(®) € Я[а, Ч и <p(t) Е Я[а,/3], причем р([а,/3]) С [а, &]. Будет
ли F = f o<f> 6 .R[at, /3]?
Контрпример. Рассмотрим функции
/(®) = | J’ 1 о “ 11 (так что f Е Я[0,1]),
, v _ ( 1/дпри£ = p/q 6 Q — несократимая дробь,
[ 0 при t иррациональном.
Функция Римана <p(t) разрывна в каждой точке вида t = p/q и не-
прерывна в каждой иррациональной точке. Но тогда множество
точек разрыва функции счетно, а потому имеет меру нуль. В силу
критерия Лебега (интегрируемости по Риману) <р G Я[0,1]. Однако
для функции
„ г	/ 0, tGQn[0,1],
^ = /^имеемГ(<) = |
т. е. F = f о есть функция Дирихле, не интегрируемая на [0,1].
Можно доказать следующую теорему.
Теорема (достаточное условие интегрируемости по Риману
сложной функции). Пусть f(x) G С([а, b]), <p(t) G Я[а,/3] и у>([а,/3]) С
[а, Ь]. Тогда F = f о <р G Я[а,/3].
Теорема 1 (об интегрировании по частям). Пусть uf v 6
2>([а, Ч) и Du, Dv G Я[а, Ь]. Тогда
а	а
Доказательство, (u, v,Du, G R[a, Ь]) => (uv^u'v G
Я[а, б]). Далее, ((u(®) • v(®))' = uf(x)v(x) 4- u(»)v'(®) V(® G [a, b]) =>
((u • vy e Я[а, Ч). По формуле Ньютона - Лейбница
ь
У(и(х) • v(x))fdx = [u(«)v(»)]|a
a
241
и, кроме того,
ь	ъ
У (u(x)v(x))fdx = У (u(x)vf(x) + uf (x)v(x))dx =
а	а
Ъ	Ь
= f u(x)vf(x)dx + У v(x)uf(x)dx,
а	а
откуда
ъ	ъ
и(®)и(®)|д = У	+ У
а	а
Теорема 2 (об интегрировании по частям). Пусть а < b и
X	х
f,g 6 Д[а, Ь]. Пусть F(x) = / f(t)dt + A, G(x) = f g(t)dt + В, где А и
а	а
В - любые постоянные. Тогда
ъ
F(x)G(x)\b- J f(x)G(x)dx.
а
Доказательство. (/,$€ Д[а, 6]) =► (/, g € В[а, 6]). Далее,
(F, G € С([а, fe])) => (F, G € В[а, 6]), поэтому существует постоянная
М > 0 такая, что
|Г(®)| < М, |G(®)| < MV® € [а,Ь].
Наконец, (Г, G € Я[а, 6]) => (f-G,g-F Е Л[а,6]). Для любого разбиения
Т отрезка [а, Ь] имеем
F(®)G(®)|^ = £(F(®*)G(xfc) - Ftxk-JGtx^)) =
к=1
= Y, F(^)(G(xk) - G(®fc_i)) + £С(®к_!)(Г(®*) - F(®*_i)) =
fc=l	k=l
= £Г(®*) 7	g^dt	+ ^G^) 7	f(t)dt =
fc=1 , a?fc-i	fc=1	xj.-i
(так как (G(®) = f g(t)dt + B) => (G(®*) - G(®*_i) = / g(t)dt),
a
(F(®) = у f(t)dt + A) => (F(®*) - F(®*_i) = J f(t)dt)) =
a	»*-i
242
= i/ + £ 7 G(t)f(t)di+
+ E 7 (F(xk)-F(t))g(t)dt + j2 7 (G(x»-1) - G(t))f(t)dt.
Ho
1/(01 < Mf Vt € [a,4,
|F(®fc) - -F(01 < w(^; [®k-i> ®*]) = w*(F),
|G(®*_i) - G(t)| < w(G; [®t-1, ®k]) = w(G)Vt € зд],
т. e.
< Mg £Ui(F)^xk + Mf %\>k(G)Axk = MgilF(T) + MftoG(T).
k=l	k=l
Ho (F,G € Я[а, Ь]) => ((Пт,Пк(Т) = ^Ит^ПвСТ) = 0), так что, пере-
ходя к пределу по базе (t -> +0), имеем искомое равенство
&	ь
F(®)G(x)|„- у* F(x)g(x)dx- f G(x)f(x)dx = 0.
а	А
Следствие. Пусть а < Ь и функции F(x) и G(x) являют-
ся соответственно первообразными для функций f,g € Я[а, Ь]. Тогда
имеет место равенство
ъ	ъ
У F(x)g(x)dx = Г(®)бг(®)|д - У f(x)G(x)dx.
а	а
В самом деле, Ф(®) = J f(t)dt и У(®) = /g(t)dt есть первообразные
а	а
Для функций /(®) и д(х) соответственно, причем F(®) = Ф(®) + F(а),
G(®) = У(х) + G(a).
2-я теорема о среднем. Пусть f € О([а, Ь]), д G С^Ца, Ь]),
D$(®) > 0 (Dff(x) < 0) V» € [а, Ь]. Тогда существует с € [а, 6] такое,
что J f(x)g(x)dx = д(а) / f(x)dx -I- g(b) J f(x)dx.
а	ас
243
X
Доказательство. Полагая Ф(®) = Jf(t)dt, видим, что
а
D$(z) = /(®), поскольку f G С([а, ft]) и Ф(а) = 0. Применяя формулу
интегрирования по частям, имеем
ъ
ь
= f g(x)d$(x) = д(Ъ)Ф(Ъ) - д(а)Ф(а)-
а
Ъ
J $(x)Dg(x)dx (Ф(а) = 0).
Но Ф G С[а, ft]; D^(®) > 0 V® G [а, Ъ] и Dtf 6 С[а, Ъ] С Л[а, Ъ]. Тогда по
1-й обобщенной теореме о среднем существует с 6 [а, ft] такое, что
Ф(с)
T)g(x)dx
f(x)dx •	- g(a))
(}	Г	f
=> I / f(x)g(x)dx = g(b) I f(x)dx - (g(b) - g(a)) I f(x)dx =
\a	a	a
/6	c	\	c
= g(b) I у f (x)dx - у f (x)dx j 4- g(a) f f(x)dx =
\a '	a	/	a
c	b	\
= g(a) У f(x)dx 4- g(b) ) f(x)dx j .
a	c	/
Определение. Пусть E есть множество (линейное про-
странство) функций f(x), определенных на отрезке [а, ft]. Функци-
оналом F(f) называется отображение F : Е 4 R.
Примеры функционалов. Fi(f) = sup/(®), fz(/) =
[a,b]
inf /(x); F3(f) = /(x0), x0 € [a, 6]; F4(f) = Df(x0), x0 G (a, b).
[a,b]
Пример. Пусть E = B[a,ft], тогда отображение F : f J(f)>
b
где J(J) = J f(x)dx 6 R есть функционал на Я[а, ft].
а
Определение. Функционал F(f), определенный на (линей-
ном пространстве) Е, называется:
1)	аддитивным, если F(f + g) = F(f) 4- F(g) Vf, g € E;
2)	однородным, если F(a • /) = a • F(f) Vf G Va e R;
3)	неотрицательным, если F(f) >QVfeE, f(x) > 0 V® 6 [a, ft];
244
I) положительным, если F(f) > OVf € Е, f(x) > О У® G [а, Ъ].
Определение. Аддитивный однородный функционал на (ли-
нейном пространстве) Е называется линейным функционалом на Е.
Определение. Пусть Е = R[a, Ь] и ||/|| d= sup \f(x) | V/ G Е.
[а,Ь]
Линейный функционал F(f) на R[a, Ь] называется ограниченным, если
существует число К > 0 такое, что |F(/)| < К||/|| Vf G R[a, Ь].
ъ
Теорема. Функционал J(f) = J f(x)dx есть линейный, огра-
а
ничейный, положительный функционал на Я[а, Ь].
Доказательство. В силу теорем 1, 2 этого параграфа
R[a, Ъ] есть кольцо, поэтому J(a • f + /3 • g) = а • J (J) + /3 • J(g)
Vf,g G R[a, 6], Va,/3 G R, так что J(f) есть однородный и аддитивный
функционал на R[a, Ь], т. е. J(f) есть линейный функционал на R[a, Ь].
В силу следствия к теореме 8 имеем оценку сверху |J(/)| < #||/||
V/ G Л[а, Ь], где К = Ъ — а > 0, т. е. <7(/) есть ограниченный, линей-
ный функционал на R[a, Ъ]. Из теоремы 8 имеем
(V/ G R[a, b], f(x) > ОУ® G [а, Ь]) => (/(/) > 0),
причем если f(x) > 0 V® G [а, Ь], то в силу теоремы 10 J(f) > 0, т. е.
/(/) - положительный линейный функционал на R[а, Ь].
§ 7.	Понятие о мере множеств.
Длина числового множества как мера.
Площадь криволинейной трапеции
Понятие меры /х(Л) множества А является естественным обобще-
нием понятий длины отрезка, площади многоугольника, объема мно-
гогранника. Пусть некоторым множествам {Е} = £ из R, R2 и т. д.
соотнесено понятие меры. Такие множества будем называть измери-
мыми, а их мера будет обозначаться через /х(Е). Будем считать, что
мера /х(Д обладает следующими свойствами:
1)	для любого измеримого множества е G £ => (м(^) 6 R и ^(Е) >
2)	(монотонность меры) для любых измеримых множеств Е±, Е2 G
£ таких, что Ег С Е2, д(Д) < Р>(Е2)\
3)	(аддитивность меры) если множества Ei, Е2 G £ измеримы и
Д А Д = 0? то /х(Д U Д) = д(Д) 4- р(Е2) (в частности, имеет место
конечная аддитивность меры:
(УД G £ (г = 1, 2,... ,п), Д П Д = 0 Уг / j) =>
=>(hQ^)=E^.))-
«=1	1=1
245
Пример. Рассмотрим интервалы 1= (а, b) С R и положим
0	0	о
д(I) = Ъ - а. Пусть Е = {/, I}. Тогда свойства 1) и 2) для меры д(/)
выполнены, что касается свойства 3), то заметим, что (для любых ин-
тервалов /1,12, таких, что h П 12= 0) => (m(/i U /2) = м(11) + м(/г)).
О	0	0
Пусть теперь 1= (а,Ь) и а < с < Ь. Положим Л= (а, с), /а= (с, 6),
тогда д(1) = Ъ - а = (с - а) + (6 - с) = д(Ь) + д(/а), но, с другой
стороны, I=Ii U 1з КД, где А = {с}, причем множества /i, /2 и
А попарно не пересекаются, и поэтому при выполнении свойства 3)
должно быть (д(/) = д(Л) + д(/а) + д(Д)) => (/х(Д) = 0).
Итак, если любой точке {с} приписать меру /х(с) = 0, то условие
3) для меры /<(/) будет выполнено. Но в этом случае для отрезка
о
I = [а, Ь], интервала 1= (а,Ь) и полуинтервалов Л [а, 6), /а = (а, Ь]
0	0 о
имеем д(1) = д(7) = дщ) = ц(1з) = b-а. Из следствия 5 (о свойствах
меры Жордана) к теореме $ в вытекает
Теорема. Пусть £ = {А} - множество всех измеримых по
Жордану множеств из [а, 6]. Тогда длина множества ц(А) = |Л| =
ь
J Хд(х)дх есть мера, удовлетворяющая условию нормировки: ц(1) =
рГ| =0 —а V/= [а,0] С [в(Ц.
Определение. Пусть f G С([а,i>]) u f(x) > 0 Vx € [а,Ь].
Тогда V(a,0) С [а, Ь] криволинейной трапецией назовем множество
£(а,0) = {(х, у) € Ra|a <х<./3,0<у< /(х)} и положим D[a,0] =
2>(а,0).
Теорема. Если f € С([а, 6]), /(х) > 0 Vx, G [а, 6] и £ =
ъ~
{1>(а,0)}, то д(1>(а,0)) = д(1>[а,0]) = / f(x)dx есть мера (пло-
а
щадь) на £, удовлетворяющая условию нормировки: ц(1£) = Л>(0—а)
VIg = 1>Л[а,/3] с f(x) = h > 0.
Доказательство. Учитывая условие /(х) > 0 Vx € [а, Ь],
имеем в силу теоремы 8:
1)	VP = 1>(а,0) € £ (где (/ € С([а, 6])) => (/ € Я[а, 6])), тогда
= I f(x)dx > 0;
а
2)	(монотонность меры д(1>)) V2>i,	€ £ при l>i = D(ai,0i) С
^(аа./Зз) = ®2, тогда (ai,/?i).C («а,0а) С [а, Ь], откуда
01	0з
д(®1) = У* /(x)dx < / f(x)dx = д(02),
«1	<*3
246
т. е. p(Zh) < М(^а)-
По поводу аддитивности меры д(Р) заметим, что при Р = Р(а,/3)
V7 б (а,0) имеем Р = Pi UP2 U Д, где T>i = Р(а,7), T>t = 2>(-у,уЗ),
Д = {(®,1/) 6R2|® = 7, 0 < у < и поэтому в силу теоремы 1 $ 6
имеем
Д	1	И '
ц(р) = У f(x)dx = У f(x)dx + У f(x)dx = д(Р1) + д(Р2),
а	а	у
при этом, очевидно, д(Д) = J f(x)dx = 0, и поэтому
1
ц(Р) = n(Pi UP2 и Д) = д(®1) + м(®а) + /4А)=	ж) + м(®з)-
Итак, VPi, Р2 б £, где Pi = P(ai,/3i), Ра = ©(«а,/За). при Pi П
Dj = 0 имеем а < «х < /31 < а2 < /32 < Ь (или а < а2 < /За < оц <
Pi
< Ь)> откуда, полагая g(Px UPa) = j f(x)dx + J /(®)d®, имеем
“	a,	at
3)	д(Рх U P2) = д(1>1) + д(2>а) VT>i,P2 € £, Vi П P2 = 0,
т. e. мера /i(P) обладает свойством аддитивности на £.
Наконец, условие «нормировки» 4) также выполнено, поскольку
У/£ = Р[а, /3] с f(x) = h > 0, имеем
И
PUb) = y^d® = A(/3-a),
a
что совпадает с величиной площади /д, принятой в школьной геомет-
рии.
В силу доказанной теоремы можно ввести понятие площади кри-
волинейной трапеции Р = {(®,у) € R8|a < х < Ь, 0 < у < /(«)} при
f б С([а, Ь]) с дополнительным условием /(®) > О V® € [а, Ь]. Обобщим
понятие площади трапеции на случай функции /(®), меняющей знак
на отрезке [а, Ь], считая (рис. 48), что площадь трапеции также имеет
знак. Далее, если D {(®, у) € R2|o < ® < Ъ, /1(®) < у < /а(®)} и
Л б C([a, b]) (i = 1,2), то можно ввести понятие «площади» и для
множества Р, полагая
М(^) = У(fa(®) - A(®))d®.
247
Можно таким же способом определить «площадь» и для более слож-
ных фигур, представимых в виде объединения конечного числа не пе-
рекрывающихся областей вида Д (г = 1,2,... , тл), каждая из кото-
рых имеет такую границу dZ),, что любая прямая, параллельная оси
От/, пересекает ее не более чем в двух точках или по целому отрез-
ку (рис. 49). Общая теория измерения площадей плоских фигур будет
построена в дальнейшем с помощью двойных интегралов Римана.
§ 8. Замечания о некоторых геометрических и
механических приложениях интеграла Римана
1. Объем тела вращения. Пусть f е С([а,Ч) и /(х) > о
V® 6 [а, Ь]. Рассмотрим любое разбиение Т отрезка [а, Ь] и на каж-
дом частичном отрезке I* = [®*_1,®*] построим два прямоугольника
с высотами Мк = sup f(x) и mk = inf f(x) соответственно. При вра-
ik	I*
щении трапеции = {(х,у) 6 R1 2|a < х < Ь, О < у < /(«)} вокруг оси
Ох видим, что тело вращения заключено между двумя ступенчатыми
телами, составленными из цилиндров с объемами
п	п
тг$/г(т) = j^ax*, =^м^хк-
fe = l	* = 1
Поскольку / G С([а, Ь]), то (/2 6 С([а, Ь])) => (/2 6 R[a, 6]), и поэтому
ъ
zMimo7rSy2(T) = \Hn^Sf2(T) = % f f2(x)dx.
a
Назовем «объемом» тела вращения число
ъ
V = тг у* f2(x)dx.
а
248
2. Масса и центр тяжести неоднородного тела. Рассмотрим
неоднородный стержень, расположенный на отрезке [а, 6] оси Ох с ли-
нейной плотностью р(х) так, что р(х) = lim Дтп(х)/Дх, где Дтп(х)
w	Дх—>0
есть масса части стержня, расположенного на отрезке [®,® 4- Дх].
рассмотрим любое размеченное разбиение отрезка [а, Ь]. Тогда
п
g = 52	приближенно есть значение массы стержня.
р *=1
ъ
Если р Е ^([а, 6]), то 3Af = Jp(x)dx. Величина М называется мас-
а
сой неоднородного стержня с линейной плотностью р(х). Для опре-
деления координаты центра тяжести нашего неоднородного стерж-
ня вспомним, что для конечной системы материальных точек {х,}
(г = 1,2,... ,п) с массами m(xi) = тп, координата центра тяжести
вычисляется по формуле
п	п
хс = ^Хк/^Хк.
к=1	к=1
Рассмотрим любое разбиение Т отрезка [а, Ь]. Тогда масса тп*
стержня [xjb-i,®*] есть
7	п Г
mk = I p(x)dx, причем Af =	= / p(x)dx
Xk-i	к=1	а
есть масса всего стержня. Поскольку р Е С([а,/?]), то по теореме о
среднем 3£* Е [х&-1, х&] такая, что пц = р(£*)Дх*. Тогда
п
2 £кр(£к ) A^fc/Af.
к = 1
Поскольку р Е С([а, Ь]), то, переходя к пределу по базе (d(T) —> 0),
ь	/ ъ
имеем хс = f xp(x)dx / /p(x)dx.
a	I а
3. Работа переменной силы. Пусть материальная точка пере-
мещается из точки а в точку Ь оси Ох под действием переменной силы
F(x), параллельной оси Ох. Рассмотрим любое размеченное разбие-
ние отрезка [а, Ь], тогда работу А силы F(x) на отрезке [а, Ь] можно
п
приближенно считать равной величине Sf(T£) =	если
р	fe=1
£ с([а, Ч), то определим работу А силы F(x) на отрезке [а, Ь] по
ъ
Формуле А = HmoSF(T^) = jF(x)dx.
249
$ 9. Формула Тейлора с остаточным членом
в интегральной форме
Теорема. Пусть f €	Ь]) и D^n+1^/ € Я[а,Ь]. Пусть
xq € (a, b)t тогда имеет место формула Тейлора с остаточным чле-
ном в интегральной форме
f(x) = /(®o) + 52^-=^^-(®-®o)fc + rn(®)®o)Vx € [а, Ь],
где
гп(х - ®0) = Л А® - <)" Dn+1 f(t)dt.
п\ J
Xq
(9-1)
Доказательство. Поскольку f € D<n+1> ([a, ft]), то функция
D*-1/(x) есть точная на [a, Ь] примитивная для функции Dfc/(x) при
к = 1,2,..., п + 1, причем D*/ € С([а, 6]) С Я[а, 6] при к = 1,2,..., п.
Но тогда в силу формулы Ньютона - Лейбница имеем
X
/(®) = /(®о) + / D/(i)<ftVx€[a,4,
Xq
полагая u(t) = D/(<)» dv(t) = dt = d(-(x-t)) и интегрируя по частям,
имеем
X
л®) = /(®о)+[-(х - <)D/(t)] i:=;0+J(x -
Xq
t. e.
X
f(x) = /(x0) + D/(®o)(® - ®o) + y*(® - t)D3f(t)dt.
Xq
Вновь интегрируя по частям при u(i) = D2/(t), dv(t) = d[-(x -t)2/2],
получаем
X
J(x~ ^)D2 f(t)dt =
Xq


+
X
+^f(x-t)2D3f(t)dt,
Xq
250
т. е.
2 к	X
/(*) = /(хо) + £	- ®о)* + /(® - *)2D3/(t)dt,
JPQ
тем самым по индукции доказана формула
/(X) = /(хо) + £ ^Ц^(® - хо)к + f(X- t)-^f(t)dt.
Но Dnf(t) является точной первообразной для Dn+1/ € Я[а, Ь], так
что, вновь интегрируя по частям при u(t) = Dnf(t), v(t) = -(x—t)n/n,
получаем
x
/ (х-t)n~1jf*f(t)dt =
Xq
Xq
чем и доказана формула Тейлора
f(x) = /(хо) + £ 5Ц^(х - хо)* + -, [(х- t)nDn+1f(t)dt.
£1 к' nlJ
Xq
Следствие 1. Пусть f € С([а,Ь]), причем производная
Dn/(®) является на отрезке [а, Ь] первообразной для функции д €
Я[а, 6]. Пусть ®о € (а, Ь). Тогда имеет место формула Тейлора с остаг
точным членом вида
х
гп(®, ®о) = Д Л® - t)ng(t)dt.
ni j
Хо
В частности, если Dn/(®) имеет кусочно-непрерывную (ограничен-
ную) на [а, 6] производную, т. е. при D"+1/ € С([а, 6] \ Кт), то
X
гп(х,хо) = Д- f (х -t)"Dn+1/(t)dt.
71! J
Xq
251
В самом деле, поскольку Dn/ 6 С ([а, Ь]) - первообразная для д Е
Я[а, Ь], то по формуле Ньютона - Лейбница V®o 6 (а, Ъ)
Dnf(t) = Dn/W +
t
У g(z)dz,
аг0
— a?n)n
и тогда, полагая Dnf(t) = G(t) и F(t) = —(ж — t)n/п = —------------h
71
t
+ f (х — z)n~rdz, применяя обобщенную теорему об интегрировании
®о
по частям, имеем
\n^G(t)dt =
х0
Хо
= [_(^r.C(()
п
t—XQ
4(X-trg(t)dt =
п J
Хо
=	+ - А®-t)ng(t)dt,
п	nJ
Xq
что и доказывает формулу Тейлора в рассматриваемом случае.
Следствие 2. Если f Е С^п+1)([а, Ь]), то в силу 1-й обобщен-
ной теоремы о среднем 6 [®о? такое, что (см. (9.1))
Гп(х,хо)_ (п+1)! D
т. е. получаем остаточный член формулы Тейлора в форме Лагранжа.
Можно считать, что £ Е (жо, ®).
Замечание 1. Пусть f Е 2>(п+1)([а, Ь]) и Dn+1/ 6 Я[а, Ь],
тогда, делая замену z — t — xq в (9.1), имеем
х—х0
тп(х, Хо) = ~ / (ж - Хо - z)nDn+1/(®o 4- z)dz,
о
откуда после еще одной замены z = (ж — ®о)А имеем
гп(х, х0) = ...aft”*1 Al - A)"Dn+1/(®o + А(® - ®o))dA.
n! J
0
252
Замечание 2. Если f G C<n+1)([a, t>]), то, полагая x — Хо = fc,
в силу замечания 1 имеем (при п 4- 1 > р > 1)
1
Тп(х, хо) = —Г- / (1 - A)n+1-' . (1 - А)'-1 . Dn+1/(®0 + Afc)dA.
П: J
О
Применение 1-й обобщенной теоремы о среднем дает равенство
/1П+1	г
г„(®, хо) = —Hl - #)n~p+1Dn+1f(xo 4- г9Л) / (1 - A)p-1dA,
п!	J
О
так что
г„(х, шо) = *-----------D"+1/(®o + №)/in+1 (0 < 19 < 1),
p • n!
откуда получаем остаточный член формулы Тейлора при р = 1 в
форме Коши
гя(х, х0) =	+ 19Л)Лп+1 (0 < 19 < 1)
п'
и при р == п 4-1 в форме Лагранжа
’») =	(0 < * < !)•
Можно считать, что 0 < 19 < 1.
253
Часть III
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
Глава 1
НЕПРЕРЫВНЫЕ ОТОБРАЖЕНИЯ ИЗ Rn В Rm
§ 1. Линейные, евклидовы, нормированные
и метрические пространства
Определение. Непустое множество Е называется линей-
ным (или векторным) пространством, если в Е определены операции
сложения элементов из Е и умножения на числа из поля R, причем:
1) (Ух, у € Е) => (х+у € Е) и операция сложения ассоциативна, ком-
мутативна и обладает обратной операцией вычитания; 2) (Vx Е Е,
Уа,/3 Е R) => (а ' (/3 ' х) = а/3 • х, 1 • х = х). Операции сложения и
умножения на числа (из R) связаны законом дистрибутивности.
Пример 1.1) JE7 = R — числовая прямая с обычными арифмети-
ческими операциями сложения и умножения есть линейное простран-
ство. 2) Пространство Rn становится линейным пространством, если
для векторов х = (xi, хз,..., xn) Е Rn ввести операции сложения и
умножения на числа (из R) следующим образом:
(Vx = (®1, ®2, • • • , ®п), У = (j/1, 1/2» • • • t Уп) G Rn) =>
=> (х + у) = (®х+ {/!)•••,Хп + уп) 6 Rn);
(Va € R, Vx € Rn) =► (а • х = (a®i,..., an®n) G Rn). ’
Пример 2. Множество С([а, Ь]) с обычными операциями сложе-
ния функций и умножения их на действительные числа есть линейное
пространство непрерывных функций.
Определение. Элементы Xi, хз,..., хп линейного про-
странства Е называются линейно зависимыми, если Эс,- Е R (г =
п
1,2,... ,п), не все равные нулю, такие, что J2 c, Xi = 0. Если же
i=i
п
из равенства £2 с»х» = 0 (г$е # 0 Vi) следует, что Ci = 0
i=i
254
= 1,2,... ,n), то элементы xi,x2,... ,хп € Е называются ли-
нейно независимыми.
Определение. Если в линейном пространстве Е можно
найти п линейно независимых элементов, а любые n + 1 элементы
этого пространства линейно зависимы, то говорят, что простран-
ство Е имеет размерность п. Если же в пространстве Е можно
указать систему из произвольного числа линейно независимых эле-
ментов, то Е называется бесконечномерным.
Примеры. Пространство R одномерно. Пространство Rn п-
мерно. Элементы е,- = (0,... , 0,1,0,..., 0) (i = 1,2,..., п) из R” ли-
tf
нейно независимы. Пространство С([а, Ь]) бесконечномерно, так как
элементы 1, ®, х2,... , ®п,... G С*([а, Ь]) линейно независимы Vn 6 N.
Определение. Скалярным произведением на линейном про-
странстве Е называется положительная билинейная форма (х, у),
которая любой паре элементов х, у € Е ставит в соответствие
действительное число (х, у), причем: 1) (х,у) = (у,х) Vx,y € Е;
2) (aixi + a2xa,y) = ai(xi,y) + a2(xa,y) Vxi,xa,y е Е, Vai,a3 € R;
S) (х,х) > 0 Vx € Е, причем ((х,х) = 0) (х = 0).
Определение. Линейное пространство Е со скалярным
произведением (х,у) называется евклидовым пространством.
Определение. Нормой на линейном пространстве Е на-
зывается неотрицательная функция х —> ||х||, которая каждому
элементу х € Е ставит в соответствие действительное неот-
рицательное число | |х|| Е R+, причем: 1) (положительность нормы)
||х|| > 0 Vx Е Е, причем (||х|| = 0) <=> (х = 0); 2) (выпуклость нормы)
1|х + у|| < INI + НуII Ух» У е Е; 3) ||а • х|| = |а|- ||х|| Vx € Е, Va е R.
3 а м е ч а н и е. Из свойств 2) и 3) легко выводится обобщенное
п	п
условие выпуклости || 53 х,-1| < 52 ||х<||, также неравенство
i=i	i=i
,1|х-у|| > 11|х|| — ||у11 I Ух»у еЕ.
Замечание. Если функция х -> ||х||, определенная на Е, обла-
дает свойствами 2) и 3) нормы, а вместо свойства 1) обладает свойст-
вом Г) ||х|| > 0 Vx Е Е, то функция х —> | |х|| называется полунормой
в Е,
Определение. Линейное пространство Е, в котором зада-
на норма х —> ||х||, называется нормированным пространством.
Теорема. В евклидовом пространстве Е со скалярным про-
изведением (х,у) лсожко ввести норму: х —> ||х|| = ^/(х,х).
Доказательство. Норма ||х|| = ^/(х,х), очевидно, обла-
дает свойствами 1) и 3). Свойство 2) следует из неравенства Минков-
ского, которое будет доказано ниже.
255
Теорема (неравенство Коши - Буняковского). Если Е -
евклидово пространство, то |(х, у)| < ||х|| • ||у|| Ух, у 6 Е (где
||х|| = у/(х, х)).
Доказательство. Пусть
р(А) = (Ах + у, Ах + у) VA G R.
Тогда
у?(А) — А2 • ||х||2 4- 2А • (х,у) + ||у||2 > О VA G RnVx,y G Е
и, в частности, при ||х{| > 0 имеем VA € R оценку 0 < ^(А) =
(А • ||х|| + (х,у)/||х||)2 + (||х||2 • ||у||2 — (х, у)2)/||х||2. Выбирая А та-
(х, у)
КИМ, что А • ||х|| + *	= 0, видим, что
||х||
(^(А) > 0)	(||х||2 • ||у||2 - (х,у)2 > 0)	(|(х,у)| < ||х|| • ||у||).
Теорема (неравенство Минковского). Если Е - евклидово
пространство, то, полагая ||х|| = ^(х, х), имеем неравенство
Нх + у|| < l|x||+||y||Vx,y ЕЕ.
Доказательство. С помощью неравенства Коши - Буня-
ковского имеем
||(х + у)||2 = (х + у,х + у) = (х,х) + 2(х,у) 4- (у,у) =
= ||х||2 + 2(х,у) + ||х||2 < ||х||2 + 2||х|| • ||у11 + ||у||2 = (||х|| + ||у||)2,
т. е. ||х+ у|| < ||ХН+ 11x11-
Следствие. Из неравенства Минковского следует выполнение
свойства выпуклости 2) для нормы х —> ||х|| = ^/(х, х).
Замечание. Наличие в евклидовом пространстве Е скаляр-
ного произведения (х, у) позволяет определить в этом пространстве
не только норму ||х|| (т. е. длину) вектора х 6 Е, но и угол между
двумя векторами х, у 6 Е, В самом деле, поскольку из неравенства
Коши - Буняковского вытекает оценка |(х,у)/||х|| • ||у||| < 1, то угол
между двумя векторами х =4 0 и у / 0 можно ввести по формуле
cos = (х, у)/||х|| • ||у||. Векторы х, у е Е, для которых (х, у) = 0 (а
стало быть, у? = 7г/2), называются ортогональными.
Примеры. 1) В п-мерном векторном пространстве Rn для
векторов а = (ai,... , an), b = (bi,... , bn) введем скалярное произ-
п
ведение по формуле (а, Ь) = ^2 а« * &«• (Очевидно, все свойства 1)-3)
«=1
256
скалярного произведения выполнены.) Тогда норма ||а|| =
n
на-
зывается евклидовой нормой в Rn. Неравенство Коши - Буняковского
|(а,Ь)1 < 1|а||- 1|Ь|| дает
Неравенство Минковского ||а+ Ь|| < ||а|| + ||Ь|| дает
причем
Отметим также неравенство
вытекающее из оценки
п	\ 2	п	п
£i“’i) =I2a«?+Sia’i‘iaji^52a«?-
,.=i /	.=1	i&	.=i
2) В линейном пространстве С([а, 5]) С Л[а, Ь] для х = ®(t), у = y(t) Е
ь
С([а, Ь]) положим (х, у) = f x(t) • y(t)dt. Условия 1)~3) для скалярного
а
произведения, очевидно, выполнены. В частности, V®(f) Е С([а, Ь]),
/ ъ	\
имеем (x(t) = 0) I Jx2(t)dt = 0 I. Тогда функция х ||х|| =
\ а	/
/ь	у/2
I fx2(t)dt 1 есть норма в С([а, Ь]). Неравенство Коши - Буняков-
\ а	/
ского |(х,у)| < ||х|| • ||у|| дает
Ь
I x(t)y(t)dt <
Зик. 5:60
257
а неравенство Минковского ||х + у||<||х|| + ||у|| дает
Определение. Метрическим пространством называется
пара {X, р}, состоящая из множества (пространства) X и рас-
стояния р, т. е. неотрицательной действительной функции р(х,у),
определенной на любых х и у из X и удовлетворяющей условиям:
1) (положительность) р(х,у) > 0 V®,j/ € X, причем (р(х,у) = 0) <=>
= у); Л) (симметрия) р(х,у) = р(у,х) Vx,y G X; 3) (неравенство
треугольника) р(®, z) < р(®, у) + р(у, z) Vx, y,z 6 X.
3 а м е ч а н и е. Из неравенства треугольника вытекают неравен-
ства p(x,z) > \р(х,у) - p(y,z)\ нр(х!,хт) < p(®i,®2)+?(®2,®з) + ...
®m) V®1, ®2, . . • , Хт € X.
Метрическое пространство будем в дальнейшем обозначать либо
как R = {X, р}, либо просто X.
Теорема. Евклидово пространство Е со скалярным произве-
дением (х,у) является метрическим пространством при р(х,у) =
Цх-У||-
Доказательство. Vx, у, z € имеем:
1)	р(х.У) = II» “ У|| > 0, (11* “ У|| = Р(х»У) = 0) (х = у);
2)	р(х,у) = ||х-у|| = ||у - х|| = р(у,х);
3)	p(x,z) = ||x-z|| = Н(х-У) + (У-»)П < 1|К-У|| + 11У-»Н =
р(х>У) + р(У.з)-
Следствие. Нормированное пространство Е с нормой х ->
||х|| является метрическим пространством с расстоянием р(х,у) =
||х - у ||, обладающим двумя дополнительными свойствами: а) (инва-
риантность относительно сдвига) р(х — а, у — а) = р(х,у) Vx, у, а €
Е\ б) р(ах,ау) = |а| -р(х,у) Vx,y € Е, Va е R.
Примеры. Числовая прямая R есть метрическое пространст-
во с расстоянием р(х, у) = |® - j/| (эту метрику называют естест-
венной в R). Евклидово пространство Rn с расстоянием р(х,у) =
/ п	\ V2
Е(®1 -!Л)г	, где ® =	,®п)> У = ({/!,-•. ,Уп) е R”, есть
\| = 1	/
метрическое пространство (с естественной метрикой).
§ 2. Дифференцирование и интегрирование (векторных)
функций одного действительного переменного
Определение. Пусть (числовые) функции х -> fi(x) (i =
1,2,... ,п) определены на отрезке [а, Ь]. Тогда (векторная) функция
258
f : [a,6] -4 Rn (x -4 f(x) = (A(x),... ,/п(®)) отображает отрезок
[a, i>] в п-мерное евклидово пространство Rn.
Положим: 1) f € C([a,b]), если ft E C([a,b]) (i = 1,2,... ,n) и, в
частности, lim f(®) = ( lim /i(®),..., lim /„(®)) (®o € [a, b );
2)	f € P(xo) (®o € (a, 6)), если fi G 2?(®o) Vi, причем Df(®o) *—
(D/i(®o,--- ,D/n(®o));
3)	f e C<m)((a,b)), если /,• G C(m)((a,6)) Vi, причем Dmf(s)
(Dro/i(®o),...,D"7n(®o));
4)	f G Я[а, Ь], если fi G R[a, 6] (i = 1,2,... , n), причем
b	/ ь	ъ \
У f(x)dx*^ I У fa.(x)dx,... , f fn(x)dx\ ;
a	\a	a	/
5)	(векторная) функция F(®) есть первообразная для (вектор-
ной) функции f(®) на |а,Ь|, если F G С(|а, Ь|) и V® G (а, Ъ) \ Кт
3dF(®) = f(»).
Теорема 1. Пусть f <*> : [a, i>] —> Rn, f (*) е Я[а, J] и c* G R
m
постоянные (k = 1,2,...,m). Тогда E € Л[а,6], причем
k=i
x)dx.
Теорема 2 (формула Ньютона - Лейбница). Если F : [a, b] -4
Rn u F G C([a, b]) есть первообразная для f : [a, 6] -4 Rn, причем
b
f G R[a, b], mo jf(®)d® = F(b) - F(a).
a
Для f : [a, 6] -4 Rn (® -4 f(®) = (/i(®),... , /п(®)) введем обозначе-
ния if (®)i=iif(®)n=4/(f(®),f(®))=(e
\» = 1	/
Теорема 3. Пусть f : [a, b] -4 R" u f G R[a, Ь]. Тогда ||f|| G
b
j f(®)d®
a
b
<	m- e-
й[а, Ц, причем
Доказательство. Поскольку fi : [a, b] 4 R и /,• G R[a, 6] Vi,
то множество точек разрыва (числовой) функции fi (®) на [а, 6] (т. е.
9*
259
Ef. = {ж 6 [а, Ь]| о>(Л;®) > 0}) в силу критерия Лебега интегри-
руемости по Риману имеет меру нуль mes Е/. = 0 Vi. Далее, если
fi Е С(®о) (®о 6 [а,Ь]) Vi, то, учитывая равенство |f(®)| = ||f(®)|| =
/ п	\ 1/2
( 52 fi(x) )	» видим, что (числовая) функция ||f|| G С(®о), то тогда,
\»=1	/
очевидно, имеем
п
^1П1 = {®е[а,Ч1^|г||;а!)>0}сигл
«=1
и поэтому (mes (ify. = OVi) => (mes ^цг|| = 0)- Замечая, что (Л 6
В[а,Ь] V») => (||f|| 6 В[а, Ь]), и применяя еще раз критерий Лебега к
числовой функции I|f(ж)II, имеем ||f|| 6 Я[а, Ь]. Теперь для любого раз-
меченного разбиения отрезка [а, 6] в силу обобщенного неравенства
/п	\ 1/2
Минковского (для нормы f —> ||f|| = I fi(x) I > имеем оценку
\«=i	/
ll*(WII =
m
= (2Л)
k=l
В силу свойств евклидовой нормы имеем
Но (f е Я[а, 6]) => (Л 6 Я[а, 6] (i = 1,2,... , п)), так что
lim Sfi(T£)
d(T)->Q J
и поэтому существует
lim
<f(T)-+O
l|Sf(WII-
т. e.
3 lim ||Sf(T^)|| =
d(T)-+O
260
Далее,
(ъ	\
Э4Пто%|,(Тг) = У ||Г(Х)|М® I ,
но тогда можно перейти к пределу по базе d(T) -4 0 в неравенстве
(2.1), что и дает оценку
ь
ъ
\х.
§ 3. Векторные функции ограниченной вариации
Определение. Пусть (векторная) функция f : [а, 6] -4 Rn
(ж —> f (ж) = (fi(ж),... , /п(®)) определена на отрезке [а, Ь] и Т = {а =
жо < xi < ... < хт = Ь} - любое разбиение отрезка [а,Ь]. Тогда
Ь	т
величина \jf = sup	11 Aft lb г^е Aft = f(ж*) — называется
а Т k=l
полной вариацией (векторной) функции Г(ж) на отрезке [а,Ь]. Если
ъ
У f < 4-ос, то говорят, что Г(ж) - (векторная) функция ограничен-
а	' ;
ной вариации на отрезке [а, Ь]. Запись: f Е \/[а,Ь]. В частности, для
числовой функции ж -4 /(ж) Е R, определенной на [а, Ь], получаем
V / = sup Е |Aft |, где Aft = f(xk) - f(xk-i). Запись: f Е Vla, Ъ].
а Т к=1
Замечание!. Если f : [a, 6] -4 R и f Е ЯЦа, Ц, то f Е \/[а, Ч-
В самом деле, для любого разбиения Т отрезка [а, Ь] имеем
m
(/ G Ях[а,Ч = Lip[a,6])	(J2 |/(®fc) - /(х*_х)| <
к=1
<к£лхк = К(Ъ - а) < +оо) => (V/ < К(Ь - а) < +оо) =>
к=1	а
=H/eVM)-
Замечание 2. Если f : [а, Ь] -4 R и f Е М[а, Ь], то f Е \/[а> Ч-
В самом деле, пусть f Е М [а, Ь], тогда для любого разбиения Т отрезка
[а, 6] имеем
/
(52 ia®*) -
m
= |/(Ь) - /(а)|
fc=l
261
b
=>(\ff = l/W - /(a) I < +oo) => (/ G V[«*. Ч)-
a
Замечание 3. Пусть f : [a, b] -» R, тогда (/ € \/[a, 6]) =>
(/€В[а,Ц).
ъ
В самом деле, (|/(x)| < |f(a)| + |/(х) - f(a)| < |/(a)| + V f < +oo
V«€[e,4)=>(/eB[a,4).
Замечание 4. Из f G C([a, Ь]), вообще говоря, не следует, что
/€VM-
Пример. Для функции
,, . _ Г ®вт(тг/®), 0 < х < 2,
!(Х)~ I 0, х = 0, (/ G С([0,2]))
рассмотрим разбиение
Гп = {0,2/(2п - 1), 2/(2п - 3).2/5,2/3,2},
так что
Xk = 2/(2n + 1 - 2k) (k = 1,2,..., п - 1), ®о = О-
Тогда имеем
El/(®*)-/(®*-il = 2/(2n- 1)+
*=1
+(2/(2п - 1) + 2/(2п - 3)) +... + (2/5 + 2/3)+
+(2/3 + 2) > 1/2 + 1/3 + ... + 1/П.
Но по теореме Лагранжа о конечных приращениях
ln(k + 1) - Ink = l/(k +1>) < 1/k, G (0,1),
поэтому
( V f > E V* > E (H* + 1) - Ink) = ln(n + 1) - In2 ) =►
\0	k=2	*=2	/
/	n	\	2
=»( lim £ l/k = +oo =>(V/ = +oo)=>(/?V[0,2]).
\n->+00	/	0
Теорема. Пусть числовые функции f,g G Vta» 4 u G R.
Тогда Л • f + ц-g, f • g € Vla> Ч» причем
ь	ь	b
V(A/+^)<|A|V/ + lMlVff-
a	a	a
262
В частности, \/[а, Ь] есть кольцо относительно обычных операций
сложения и умножения.
Доказательство. Поскольку f,g 6 \/[а, 6], то для любого
разбиения Т отрезка [а, Ь] имеем
(т	m
£|Д(Л./ + д.у)к| =£|АДЛ + дДу*|<
fc=l	Л=1
т	т	b	Ъ \
< |А| Е |АЛI + 1м1 S |Ау*| < |А|V/ + ИV?) =>
fc=l	fc=l	а	а /
Ъ	Ъ	Ъ
=> (V(V + w) < IА| V f + |д| V«Z < +оо) => (А/ +	€ Vfc Ч)-
а	а	а
Далее, поскольку f и д - числовые функции, то определена числовая
функция f-g, причем (/, д € Vta» Ч) (А 9 € В [а, 6]), т. е. существуют
постоянные Ап В такие, что |/(х)| < A, |®(®)| < В V® G [а, 6], откуда
(т	т
521д(/ • s)k I = 53A»k + д/k | <
к=1	*=1
£ |Affk| + в £ |ДД| <A\/g + B\/f} =►
fc=l	fc=l	а	а /
b	Ъ	Ъ
=> W(f • 9) < А Уд + В V f < +оо) => (/ • 9 G V [<*, Ч).
а	а	а
Замечание. Класс М [а, i>] не образует кольца относительно
сложения и умножения. В самом деле, хотя х,х2 € Af [0,1], но х -
®2^ЛГ[0,1], далее, х € ЛГ(-1,1], но х2^М[-1,1].
Теорема Жордана. Пусть f : [а, 6] -> R. Тогда (f € V[a» Ч)
<=>(/ = А - Л, г^е Л f u ft f на [а, &]).
Доказательство. Достаточность. Пусть / = А - /г, где
числовые функции Д tи A t на [а, Ь]. Тогда (Л, h G Af [а, Ч С V(a> Ч)
=> (/ = А - А € У[а, Ь]), поскольку V[а, Ь] есть кольцо.
Необходимость. Пусть f : [а, Ь] —> R и f € V[a> Ч* Положим Vf (х) =
Я?
V f при а < х < b и Vf(a) = 0. Далее, положим А(®) = ;(”/(®)+/(®))>
а	а
А(®) = g(v/(®) - /(®)). Очевидно, f = А" А- Докажем, что A t и
A t на [а, 6]. Пусть ®i, xt € [а, 6] любые, причем ®i < ®г> тогда имеем
оценку
Я>2
«/(®1) + 1/(®з) — /(®1)| < У f = Vf(x3).
263
В самом деле, поскольку
т
Vf(x!)= sup VlA/fcl,
T[a,«i]t=x
то Ve > О существует разбиение Ti отрезка [a, ®i] такое, что
М®1) < 521дЛ1 + е,
*=1
и тогда
w/(®i) + 1/(®г) - /(®i)| < £ +	1Д/*1+
*=1
+|/(®г) - У(®1)I < е + V f = « + «/ (®г)-
а
В силу произвольности е > 0 получаем оценку, из которой имеем
|/(®г) — /(®i)| < Vf(x2)
Но тогда
2(/i(®2) - Л(®1)) = Vf(x2) - vy (®i) 4- /(®2) - /(®1) >
> vj(x2) - vy(®i) - \f(x2) - f(Xi)\ > О,
т. е. А | на [а, Ь]. Аналогично
2(Л(®2) ~ А(®1)) = vf(x2) - vy(xi) - (/(®2) - /(®i)) >
> Vf(x2) - vf(x1) - \f(x2) - /(zi)| >0,
т. e. f2 f на [a, 6].
Следствие. Если числовая функция f € Vla> Ч» то она может
иметь разрывы только 1-го рода, причем множество ее точек разрыва
не более чем счетно.
Следствие. V[a> Ч С Я[а, Ь].
Перейдем теперь к (векторным) функциям f : [d, 6] -> R" (® ->
f(®) = (А(®),... , fn(x)) ограниченной вариации.
Теорема 1. Пусть f : [а, Ь] —> Rn. Тогда
(f е vk Ч) (А е \/[а, Ч (* = 2,., п)),
где f(®) = (А(®),... , fn(x)), причем
Ъ Ь п Ь
a a	a
264
Доказательство. Для любого разбиения Т = {а =	<
$!<...<	= &} отрезка [а, Ь] в силу неравенства
/ п	\ V2	п
\i=l /	t=l
имеем оценки Vi
n
|Л(хк) - /,(^-1)1 < ||f(xk) — f(®k-i)|| < £|Л(як) -
J=1
откуда и вытекают утверждения теоремы 1.
Теорема 2. Пусть f : [а,Ь] -> Rn, а < с < b uf е Vta>cb
b	с	b
f 6 VIе’ Ч- Тогда f € V(a> Ч> причем \/f = \/f + \/f.
a	a	c
Доказательство. Поскольку f 6 V[a’e] и f € Vte’ Ч> то для
любого разбиения T' = {a = ®o < ®i < • • • < ®n = с < ®p+i < ... <
xm = b} отрезка [a, Ь], содержащего точку с, имеем
т	р	т	с	b
Е ||Af*||= Е ||Affc||+ Е im< Vf+Vf-
fc=l	fc=l	Л=р+1	a	С
Но V разбиения Т отрезка [а, Ь] при добавлении точки с в качестве
точки деления получаем Т' -< Т и при xp-i =	< с = х'р <	=
хр имеем оценку сверху
llf(xF) - f^-xjn < Ilf (®;+1) - f(4)ii+Ilf (x'p) -
откуда
c b	b c b
E IIAffcll < E AM < Vf+Vf. T.e. Vf < Vf+Vf-
T	Tf	a c	a a c
Далее, Ve > 0 существуют разбиения T[[a,c] и T^c, Ь] такие, что
с	ь
Е ||Afk|| > \/f - е/2 и Е IIAf»ll > Vf - е/2- Поэтому для со-
т;[«.с]	а	т'[с,Ц	с
ставного разбиения Т'[а, 6] = {Т{, TJ} имеем
Ь	с	b
Vf> Е IIAffcll > (Vf+ Vf)-e,
а	Т'[а,6]	®	с
откуда в силу произвольности е > 0 имеем оценку снизу
/ Ь	с	b \	/ b	с	Ъ \
(Vf >Vf+Vf) => (Vf = Vf+Vf)-
\a	а	с/	\a	a	с/
265
Теорема 3. Пусть (векторная) функция f : [а, 6] —> R”
является первообразной на отрезке [а, Ь] для (векторной) функции
» ъ
g G Я[а, 6]. Тогда \/f = /1|g(®)||d®, f € \/[а, 6].
а а
Доказательство. (g € Я[а, Ь]) => (||g|| G Я[а, Ь]). Далее,
поскольку f € С([а, b]) есть первообразная для (векторной) функции
g € Я[а, 6], то для любого разбиения Т отрезка [а, Ь], применяя обоб-
щенную формулу Ньютона-Лейбница к частичным отрезкам разбие-
ния Ik = [®*-х, ®ь] (k = 1,2,..., m), имеем
m	m
fc=l	fc=l
m 9Jf
b
/ l|g(*
a

b	b
откуда Vf < J l|g(*)ll<it Далее, (g = (pt..gn) € Л[а, &]) => (д €
a	a
Я[а, 6])Vt и в силу критерия Дарбу интегрируемости по Риману Уе > О
существуют разбиения Т<'> отрезка [а,Ь] такие, что	<е (i =
1,2,..., п). Очевидно, для составного разбиения То = {Т^\..., Т<п>}
имеем То -<	(» = 1,2,..., п) и поэтому
Ов(Т0) = ^ы»(0<)Д®ь < еЫ.
к = 1
Используя формулу Ньютона-Лейбница и неравенство Минковского,
имеем (||а - Ь|| > ||а|| - ||Ь||) оценку снизу


||f(«*)-f(®t_x)l| =
У* g(«)dt = / (g(«*)-(g(®k)-g(t)))^ =
Pfc-l

Xh	Xk
! %(3>k)dt- j (g(®fc) - g(<))d«
Pfc-l	®fc-l
У (g(®*)-g(on
Гй-1
Xh
> I |g(®*)l I A®* - У I |g(®fc) - «(t) I =
®fc-l
Xk	Xk	Xk
= у iig(»*)ii<fc- y.iig(®k) -g(*)ii^= у iig(*)-(g(*)-
Xk-\	Xh^i	fffc-i
266
Sb	Sk
-g(«*))ii«tt- y* iig(®»)-gwii«K> / iig(oii<**-
®fc-l	Я?Л-1
“2 / ||g(t) - g(x*)||dt.
Ho
n	n
iig(*) - g(®*)ii < 52м*)	< 52w*(^)v< e
1=1	1=1
где Uk(ffi) = ш(д,-; [«*-1, »*]), откуда
IIAftll >
Пв^цл-г^ы*^)- д®*.
Поэтому в силу выбора разбиения То имеем оценку снизу
b	m	Ъ
Vf> Е IIAffcll >/llg(t)ll*-
a	fc=l	а
2пе,
откуда в силу произвольности е > 0 имеем
ъ ь \	/ ь ь
Vf>/llg(«)ll^ => I Vf=/llgG)ll^
а а	/	\ а а
Следствие. Если f : [а, 6] —> Rn и f € Р([а, 6]), причем Df €
ь	ь
Я[а,Ь] (где Df(®) = (D/i(®),..., D/n(®))), то \/f = / ||Df(®)||d® (в
а	а
частности, это равенство имеет место, если функция f € С([а, 6]) име-
ет ограниченную кусочно-непрерывную производную Df(г) на [а, Ь]. § *
§ 4. Пути и кривые в Rn
Рассмотрим евклидово пространство R” с декартовой системой
прямоугольных координат {г} = {(si,... ,гп)}. Пусть промежуток
Л С R1 является или интервалом 1= (а, Ь), или отрезком / = [а, 6].
Определение. (Непрерывным) путем (1-путем) <р в R"
называется непрерывное отображение : Л -> Rn, где t € Л, >p(t) =
267
(^1	,¥>n(t)); ж = <p(t) e Rn, Xi - C R (i = 1,2, ...,n)?
так что (p 6 C(It)- Образ Г = <р(Л) C Rn называется носителем
или следом этого пути. Если It = [а, Ъ] есть отрезок, то путь (р
называется замкнутым, а точки (р(а) и (р(Ъ) (из TLn) называются
соответственно началом и концом пути (р.
Определение. Пусть It = | а, Ь| и 1Т = |а, /3\ - два промежут-
ка из R1, причем оба они или открыты, или оба замкнуты. Тогда
функция t : 1Т —> It, t = £(т), t E Ir называется допустимым преоб-
разованием параметра (от 1Т к It), если 1) отображение t : IT It
есть гомеоморфизм, так что существует обратное отображение
г = t-1 : It -> Ir, причем t Е C(IT), т ~ t~r Е C(It); 2) It = t(Ir) и
Ir = r(It); 3) t(r) П на Ir, r(t) JT на It, причем t(a) — a и t((3) = b,
если Ir и It есть отрезки.
Замечание. Если отображение t : IT It является до-
пустимым преобразованием параметра (от 1Г к It), то обратное ото-
бражение г = tT1 : It —> 1Т является допустимым преобразованием
параметра от It к 1Т- Если отображения t : Ir —> It и А : It —> /д -
допустимые преобразования параметра, то композиция А о t : IT —> It
также является допустимым преобразованием параметра (от 1Т к Д).
Следствие. Если <р : It -ь Rn есть путь в Rn и функция
t : IT It осуществляет допустимое преобразование параметра (от
1Т к It), то отображение ip : IT R”, где ip = <р ot, ip = 1р от есть
(непрерывный) путь в Rn, причем ip(Ir) = ^(Л) = Г С R”, так что
носители обоих путей <р и ip совпадают как множества в Rn. (Если
путь (р замкнут, то и путь ip замкнут, причем для It = [а, Ь],1Т = [а, Д]
имеем ip(a) = ^ot(oi) = у>(а), ip((3) = <pot((3) = </?(6), т. е. в этом случае
пути <р и ip имеют общее начало и общий конец).
It = ip от ф
т = t~r t	Г
IT ip = (pot t
Определение. Пути (в Кп) <р : It Г С Rn и ip : 1Т Г С
Rn называются эквивалентными (запись: (р ~ ip), если существует
допустимое преобразование параметра t : Ir It, такое, что ip =
<pot, (р = ip оt-1.
Замечание. Введенное отношение ~ является отношением эк-
вивалентности, поскольку оно обладает свойствами: 1) рефлексивнос-
ти (р ~ <р\ 2) симметричности (<р ~ ip) => (ip ~ (р) и 3) транзитивности
(^ ~ ip) Л (ip ~ д) => (<р ~ д). (Проверить самостоятельно.)
Но тогда введенное отношение эквивалентности путей в Rn разби-
вает множество всех непрерывных путей в Rn на классы эквивалент-
ности: классу эквивалентности произвольного пути <р принадлежат те
пути, которые ему эквивалентны. Таким образом, каждый путь в Rn
268
принадлежит одному из классов эквивалентности и пересечение двух
различных классов эквивалентности пусто.
Замечание. Если отображения (пути) <р : It —> Г и У ‘ 1т -> Г
биективны и ~ то допустимое преобразование параметра t : 1Т ->
для которого ф = <р о t, определяется однозначно. В самом деле,
если А : 1Т —> It - также допустимый гомеоморфизм, то, используя
биективность отображения у>, имеем ф(т) = (pot(r) = у>оА(т), откуда
(<р о t = <р о А) => (t(r) = tp"1 о(ро А(т)) =>
=> (t(r) = А(т) Vr 6 Zr) => (f = А).
Пример. Рассмотрим следующие пути в Rn:
: [0,1] = А [0,1],® = А;
<	р2 : [0, тг/2] = 12	[0,1], х = sint2;
<	рз : [О, 7г/2] = Z3	[0,1], х = cosf3;
<	Р4 : [0, тг] = Ц —> [0,1], х = sin£4.
Заметим, что <pi(Ii) = [0,1] = Г (г = 1,2,3,4), т. е. все пути имеют
в R1 один и тот же носитель. Далее, при t2 : Zi = [0,1] —> [0, тг/2] = Z2,
t2 = arcsinfj, имеем t2 E C([0,1]), t2(ti) ТТ на Zi = [0,1] и t2(Zi) = Z2,
поэтому t2 : Zi —> Z2 дает допустимое преобразование парамет-
ра (от Zi к Z2), кроме того, <pi = <р2 о t2, т. е. (pi ~ <р2. Далее,
*з : Zi = [0,1]	[0,7г/2] = Z3, t3 = arccosfi, t3 e C([0,1]), *з(*1) U
на Zi = [0,1], поэтому отображение t3 : Zi —> I3 не является допусти-
мым преобразованием параметра (от Zi к 13) и, хотя <pi = <p3ot3, тем
не менее в силу биективности отображений и пути <pi и <р3 не
эквивалентны (иначе в силу замечания гомеоморфизм t3 был бы до-
пустим преобразованием параметра). Аналогично показывается, что
^4 / И <р3.
Определение. Кривой (1-поверхностью) Ф в R” называ-
ется класс эквивалентности 1-путей (с представителем 1-путем
<Р : It -> Г = <p(It) С Rn/
Замечание. Понятие носителя (следа) данной кривой Ф в R”
определяется однозначно, так как все пути, входящие в класс эквива-
лентности Ф, имеют один и тот же носитель. Аналогичным образом
понятия «замкнутая» кривая, начало и конец кривой Ф не зависят от
выбора пути (т. е. не зависят от выбора «параметризации»).
Определение. Пусть <р : It —» Rn и ф : IT -> Rn - два
пути в R”. Будем писать <р = —ф или ф = — <р> если существует
такой гомеоморфизм t : Ir —> Ц, что: 1) t Е C(Ir) t = t(r) 6 Zt,
t = f-1 G C(It); 2) t(Ir) = It! 3) t(r) Ц на It и 4) Ф =	4> =
Замечание. Поскольку <p(It) = V>(f“1(Zt)) = ф(1Т) = Г C Rw,
то носители обоих путей <р и ф = —<р совпадают как множества в Rw.
Если путь ip замкнут (т. е. 1Т = [а, 6]), то путь ф = —<р также замкнут
(т. е. I = [а,/?]), причем У^(ск) = y>ot(a) = <р(Ъ); ф((3) = <pot((3) = <р(а)
269
так, что начало ^>(а) пути является концом <р((3) пути 0 = ф,
наоборот, конец <р(Ъ) пути <р совпадает с началом 0(a) пути 0 =
Замечание. Если отображение <р : It -» Г С Rn не биек-
тивно, то возможно равенство <р = —0. Так будет для постоянного
отображения (пути) <р : It -> с С Rw и для пути <р4 из приведенного
ранее примера. (В самом деле, если (р4 : [0, тг] —> [0,1], <p4(t) = sint
и ф : [0, тг] —> [0,1], <ф(т) = sin(7r — т), то при гомеоморфизме t = т
имеем = 0, а при гомеоморфизме т = тг — t, т : [0, тг] -> [0, тг] имеем
<р4 = -0.)
Следствие. Если для двух путей <р и 0 имеем <р = -0, то для
любых путей и 0* таких, что ~ и 0* ~ 0, имеем <р* = —0*.
(Докажите это самостоятельно.) Но тогда можно говорить о кривых
Ф и Ф таких, что Ф = -Ф.
Замечание. Если Ф = -Ф, то скажем, что кривые Ф и Ф име-
ют противоположную ориентацию, отметим, что при этом носители
в Rw кривых Ф и Ф = -Ф совпадают как множества в Rn.
Пример. Пути <pi : [0,1] -» [0,1], х = ti и <рз : [0, яг/2] -> [0,1], а? =
costs, рассмотренные ранее, имеют противоположную ориентацию,
так как /з • [0,1] -> [0, яг/2], 1з = arccosti, 1з € С([0,1]), 1з Ц на [0,1] и
^>1 =	©t3, т. е. <рз = “^1-
Пусть "замкнутые пути <pi и <р2 таковы, что щ : Д = [at*,0i] -> Rn,
причем <pi([k) = р2(а2), т. е. конец пути <pi совпадает с началом пути
<Р2' Для того чтобы определить «сумму» путей ^i+y>2, введем отрезок
1*2 = [01,01 + (02 - «г)] и допустимое преобразование параметра т —>
t(r) (от Г2 к I2) t : Г2 -> I2, t(r) = т - 0i + а2, t(0i) = а2. Тогда
I = Л UI2 = [ai,0i + 02 - <*2]« Положим теперь
_ / Pi(r), r€/i,
I (^2 0t)(r), Т€Д.
Тогда (рх € С(Л)) => (р G С(Л)), (р2 о i G ОД) 4 (р G ОД), и
поскольку y?i(0i) = (у>2 ot)(0i) = ^2(^2), то <р € C(0i), откуда имеем
<р € С(1). Но тогда <р : I —> Rn есть путь в Rn, причем начало пути
<р совпадает с началом пути pi, а конец пути <р совпадает с концом
пути <р2, причем для носителя пути <р имеем
Г = <p(I) = <pi(Л) U (рз(Ь) = Гх U Г2.
Кривую Ф будем называть суммой кривых Ф1 и Ф2 и обозначать через
Ф = Фх 4- Ф2. По индукции можно определить сумму конечного числа
кривых Фх, Ф2,... , Фш при условии, что для к = 1,2,... , m — 1 конец
кривой Ф& совпадает с началом кривой Ф&+1-
Определение. Замкнутая кривая Ф называется замкну-
тым контуром (в Rn/ если ее конец совпадает с ее началом.
270
Определение. Пусть отображение <р : I —> Г С Rn (где
9? € С(1)) биективно, тогда путь <р называется жордановым. Кри-
вая Ф при этом также называется жордановой (или простой ду-
гой)-
Определение. Замкнутый контур Ф называется жордано-
вым (или простым), если для кривой Ф существует замкнутый путь
р : [а, 6] —> R” (представитель кривой Ф) такой, что отображение
ip : [а, Ъ) —> Г \ <р(Ъ) биективно, причем <р(а) = <р(Ъ).
Положим r(t) =	, xn(t)) € Rw, t € I и через r(t) =
п
2 «,(/)е» обозначим вектор из линейного пространства Rn.
i=i
Определение. Путь г : I —> Rn называется непрерывно
дифференцируемым, если г € С№(1).
Определение. Непрерывно дифференцируемый путь г : I
Rn называется гладким, если
/ п	\ W
1Ю^)н=	>0V*€L
\i=l	/
Определение. Кривая Ф называется гладкой, если сущест-
вует хоть один гладкий путь <р, входящий в класс эквивалентности,
определяемый кривой Ф.
Определение. Кривая Ф называется кусочно-гладкой, если
т
Ф = 22 где Фк. - гладкие кривые Vk.
л-=1
Замечание. При введенном ранее определении отношения эк-
вивалентности ~ гладкая кривая Ф может иметь своим представите-
лем непрерывно дифференцируемый, но не гладкий путь г : 7 -> Rn.
Пример. Рассмотрим путь г : [-1,1] —> R2, г(*) = (М),
так что, полагая х = I, у = t, имеем г : у = ®, -1 < х < 1. По-
скольку Dr(J) = (1,1) Ф (0,0), то путь г - гладкий, с другой сто-
роны, допустима замена t : [-1,1] -> [-1,1], t(r) = т3, приводящая
к пути р : [-1,1] —> R2 (г ~ р), где р(т) = (rot)(r) = (т3,т3),
Dp(r) = 3(т2,т2), причем Dp(0) = (0,0), т. е. путь р - непрерывно
дифференцируемый, но не гладкий.
В дальнейшем при рассмотрении гладких кривых в Rn мы изме-
ним данное ранее определение «допустимого» преобразования пара-
метра (от 1Т к It), заменив в нем условие 3) t(r) на Ir на более
жесткое условие 3’) Vt Е 1г 3D^(t) > 0.
271
$ 5. Длина кривой в Rn
f
Определение. Пусть г : [а, /3] Rn есть замкнутый путь
в Rw (r(t) =	... , Для любого разбиения Т = {а = to <
ti < ... < tm = /3} отрезка [а,/3] положим Tk = r(tfc) 6 г([а,/3]) С
R”. Тогда длиной «ломаной» в Rn с вершинами в точках Tk (к .=
0,1,... , т) называется величина
т	т
1т(г) = 53 Нг* - г*-*н= ZL 11
k=l	fc=l
(где Гк - точка в аффинном пространстве Rn, а г* — rt-i - век-
тор в линейном пространстве Rn с началом в точке rk-i и концом
fi
в точке Гк). Очевидно, suplr(r) = \/г (где вектор г из линейного
Т	а
пространства R” соответствует точке г = О 4- г из аффинного
пространства Rn).
Определение. Длиной замкнутого пути г : [а,/?] —> Rw
fi
называется величина Цг) = У г. Путь г называется спрямляемым,
а
если 1(г) < +оо.
Теорема (критерий спрямляемости замкнутого пути). Пусть
в Rn задан замкнутый путь г : [а,/3] -> Rn, где r(t) =
,xn(t)). Тогда (l(r) < +оо) (ж,- Е (*=1,2,... ,п)).
(Утверждения теоремы следуют из теоремы 1 §3.)
Теорема. Пусть r : [а,/3] -> Rn есть непрерывно дифферен-
цируемый путь в R”, т. е. r(<) =	,x„(t)) и г е С*1)([«,/?]).
Тогда путь г спрямляем и для его длины имеем формулу
Рг	1 ( п \1/2
Z(r) = у ||Dr(t)||<ft = у I 5>х.(<))2 j dt.
(Утверждения теоремы следуют из теоремы 3 §3.)
Пример. Пусть f : [а, Ъ] —> R1, причем f Е С^)([а, 6]). Тогда
г : [а, 6]	R2, где г(х) = (ж,/(ж)) есть непрерывно дифференциру-
ъ
емый путь в R2 с длиной Z(r) = J(1 4- (D/(®))2)x^2d« (длина пути в
декартовых координатах).
Пример. Пусть т : [а,/3] —> R2, где
= (pGp) COS <р, p(ip) sin ч>) е С(1)([а,^]).
Тогда
(Dr(^) = (р'(р) cos ~ p{v) sin p'fa) sin V> + р(р)cos *>)) •=►
272
=* (l|Dr(^)||2 = p2(^) + (^Й
\	у aip ) j
и поэтому
1/2
dip
- длина непрерывно дифференцируемого пути в полярных координа-
тах.
Теорема (об инвариантности длины для эквивалентных пу-
тей). Пусть <р : [а,/3] = I -> Rn и ip* :	= Z* —> Rn - эк-
вивалентные пути в Rn. Пусть путь <р спрямляем. Тогда путь <р*
также спрямляем, причем 1(<р*) =
Доказательство. Поскольку <р ~ ip*, то существует до-
пустимое преобразование параметра t : г —> Цт) (от Z* к I) такое,
что t е C(Z*), t(r) П на Z*, ЦГ) = Z, причем т = t"1 Е С(1),
r(t) ТТ на I, т(1) = Г и <p(t) = (<р* oi_1)(i), <р*(т) = (<р о t)(r).
Пусть Т = {а = to < ti < ... < tm = /3} - любое разбиение от-
резка [а,/3] = Z. Положим = t-1(tfc), тогда в силу условия t-1(t) Д
на [а,/?] видим, что разбиение Т отрезка [а,/?] = I индуцирует раз-
биение Т* = {а* = то < л < ... < тт = /?*} отрезка Г = [«*,/?*], и
поскольку tk = то имеем
т	т
= 22	- ¥’(<*-i)ii=22 IK*» ° /)('г*) - (¥> ° <)(n- j 11 =
fc=l	fc=l
m
= 22 Н*’*(т*) - ¥’*(n-i)|| = It* (<?*)
k=l
С другой стороны, любое разбиение Т* отрезка /* индуцирует раз-
биение Т отрезка I с точками разбиения tk — t(r*) и опять имеем
равенство 1т* (у>*) = 1т (у>), но тогда sup/j(y>) = supZy(y>*), т. е. путь
т	т*
<р* спрямляем и 1(<р*) = Z(y>).
Замечание. Пусть <р = —ф - замкнутые пути. Если <р спрям-
ляем, то и У; спрямляем, причем Z(V>) = 1(<р).
Замечание. Все пути, входящие в класс эквивалентности,
определенный кривой Ф, имеют одну и ту же длину (если хотя бы
один из путей, входящих в этот класс эквивалентности, спрямляем).
Поэтому можно ввести понятие спрямляемой кривой и длины кривой.
m
Следствие. Пусть дана кривая Ф =	Ф&, где Ф& - спрям-
fc=i
m
ляемые кривые в Rn. Тогда кривая Ф спрямляема и /(Ф) =	К^к)-
к=1
273
Доказательство. Поскольку Ф = 2 Ф^, то можно вы-
к=1
брать пути <pk :	—> Rn (к = 1, 2,... , т) так, чтобы /3* = а^+1
(к = 1,2,... ,m - 1). Тогда имеем путь <р : [ai, /Зт] —> Rn, где
= <?*(*), * € [<**,&] (к = 1,... ,тп), причем
Ч>к(Рк) = ¥>fc+i(afc+i)(&= 1,2,... ,m-1).
Поскольку путь <рь спрямляем Vfc, то <рк 6 \/[а*>Рк] и в силу теоремы
2 §3 об аддитивности полной вариации имеем
(ft™	т fth \	/	m	\	/	т \
I V Р =	S V 4>к I	=> (1(<р)	- L	)	=Ф> (1(Ф)	= Z	1№к) )	•
fc=l «й ) X к=1	/	\	fc = l	/
ш
Следствие. Если кривая Ф = £ Ф*, где Ф* - непрерывно
Js=l
дифференцируемые кривые, то
т Рр	Ру
!(*)’£ / ||Dr*(t)||dt = / ||Dr(t)||dt,
*=1«й	«1
где Тк - непрерывно дифференцируемые пути - представители кривой
Фь аг- кусочно-непрерывно дифференцируемый путь, являющийся
представителем кривой Ф.
Пусть дан спрямляемый путь г : [а,/3] -> Rn, где r(t) =
(®i(<),... , xn(t)). Положим (Vr € [а,/3]) ут : [а,т] Д Rn, тогда длина
«дуги» i(7r) = з(т) есть функция параметра т на отрезке [а,/3]. Если
путь г - гладкий, т. е. г € С^)([а,/3]) и ||Df(t)|| > 0 Vr € [а, /3], то
/ тг / п \ 1/2	;	\
(в(т) = /(7Г)) =$- I з(т) = у I 22(D»i(O)2 I dt= I llDr(t)||cft I ,
\	a '<=1	'	a	/
откуда для функции s : г -> я(т) имеем s(r) g ([а,/?]),
= ||Dr(r)|| > OVr е [а,/3], ds = ||Dr(r)||dT.
Итак, з € С(1)([а,/3]), »(т) П на [ot,/?] и в([а,/3]) = [0, я0], где в0 = Цг).
Но тогда функция $ : [а,$	[0, $о] определяет допустимое преоб-
разование параметра (от [а,/3] к [0, зо]), причем обратная функция
т = л-1 : [0, «о] -> [<*>/?] также является допустимой заменой пара-
метра (от [0, .$о] к [а,$). Более того, в силу теоремы о производной
обратной функции имеем
= 1	= 1/llDr(r)|| > 0Vs 6 [0, so].
as / ат
274
Положим теперь р(в) = (г о т)(в), тогда г(т) = (р о я)(т) и путь
р ; [0, зо] -> Rw таков, что р ~ г, причем, очевидно, р - гладкий
путь. Используя теоремы о производной для сложной функции и для
обратной функции, имеем
= D((r о т)(з)) = Dr(r) • Dt(s) =
as
= Dr(r)/Ds(r) = Dr(r)/||Dr(r)||,
откуда для пути р получаем ||Dp(*)|| = 1. Параметризация р : [0, so] —>
Rn (кривой R с представителем г) называется натуральной парамет-
ризацией (при натуральной параметризации параметр 8 с точностью
до постоянного слагаемого совпадает с длиной дуги на пути г), при-
to	*о
У ||Dp(*)||^ = У 1. de = «о =/(г).
о	о
§ 6. Касательная к кривой в Rn
Пусть Ф есть кривая в Rn, тогда для пути <р : I Rn, принад-
лежащему классу эквивалентности, определенному кривой Ф, отобра-
жение <р : I -> Г = <р(Г) С Rn отрезка I на носитель Г (кривой Ф)
может и не быть взаимно однозначным (если кривая Ф не жорданова),
поэтому кривую Ф нельзя определять как множество Г = <р(1) в Rn, а
следует определять как отображение <р : I Г С Rn отрезка I на Г с
последующим установлением условий, при которых два отображения
(два пути) pi : Д 3 Г и рз : /j 3 Г считаются эквивалентными
(принадлежащими одной кривой).
Определение. Путь А : R Rn называется параметризо-
ванной прямой в Rn, если отображение Л аффинно и невырождено,
т. е. имеет вид X(t) = ®о + * • г, еде ®о " точка, а г - постоянный
вектор из Rn, для которого ||г|| > 0.
Определение. Пусть А : R -> Rn и А* : R -4 Rn - две пара-
метризованные прямые в Rn. Скажем, что А ~ А*, если существует
аффинное преобразование параметра g : R —> R вида д(т) = ат + Ь,
т Е R, где а, Ь € R и а > 0, такое, что А*(т) = (А о^)(т).
Замечание. Если А ~ А* и A(i!) = xQ + i-r, А*(т) = Xq + t-г*,
то, поскольку (А* = Ао0) => (®5 + т-г* = хо+(ат+Ь)-г),	= ®0+Ь-г,
г* = а • г (а > 0), поэтому векторы гиг* «одинаково» направлены в
Rn (рис. 50).
Замечание. Введенное отношение ~ является отношением эк-
вивалентности, которое разбивает множество всех параметризован-
ных прямых в Rn на классы эквивалентности.
275
Определение. Ориентиров анной прямой Л в Rn называет-
ся класс эквивалентности параметризованных прямых (с предста-
вителем А : R —> Rn/
Теорема. Пусть г : (а,/?) -> Rn (где r(t) =	,xn(t)))
есть гладкий путь в Rn. Тогда отображение г : (а,/3) Г =
г(а,/3)) локально взаимно однозначно, т. е. Vto 6 (а,/?) существует
окрестность Us(to) С (а,/3) такая, что отображение т : ЭД (to)
r(t^(^o)) С Г С Rn взаимно однозначно.
Доказательство. Пусть to 6 (а, /3) - любая точка. Поскольку
г - гладкий путь, то ||Dr(to)|| > 0, но
П	*0
I|Dr(fo)112 = ^2(D®fc(*o))2 >0, I 1 • dz = s0 = ЦН,
*=i	{
поэтому существует номер i такой, что D®«(to) # 0. Пусть, для опре-
деленности, D®«(^o) > 0. В силу гладкости пути г De, G С (to) и тог-
да теоремы о локальных свойствах непрерывной функции позволяют
утверждать, что существует окрестность Us (to) С (ol,/3) такая, что
De, (t) > 0 Vt 6 Us(to)- Из теоремы о существовании обратной функции
у строго монотонной функции отображение е,- : Us (to) R1 инъек-
тивно (и даже осуществляет гомеоморфизм Us (to) на е,(ЭД(^)) С R,
т. е.	= E,(t2)) <=> (ti = t2 в ЭД(/о))- Но тогда, поскольку
(r(tx) = r(t2)) <=> (||r(ti)-r(t2)|| = 0), то в силу оценки ||r(tx)-r(t2)11 >
|е«(^1) ~ E,(t2)| имеем (r(tx) = r(t2)) => (®.-(ti) = E<(t2) Vi) => (ti = t2).
Обратное включение (ti = t2) => (r(tx) = r(t2)) очевидно. Итак, ви-
дим, что отображение г : Us (to) -> г (Us (to)) С Г также взаимноодно-
значно.
Пусть теперь R - некоторая гладкая кривая в Rn и хо 6 Г - точка
носителя Г. Пусть г : I = (а,/?) -> R” (где r(t) = (xi(t),... ,xn(t)))
есть гладкий путь - представитель кривой R так, что г 6 С^(1)
276
и ||Dr(t)ll > 0 Vt G /• Пусть х0 = r(t0), t0 е I, тогда по преды-
дущей теореме существует окрестность Ug (to) € I такая, что ото-
бражение г : Ug(t0) -> r(Ug(t0)) С Г взаимно однозначно. Пусть
Г1 = r(ti) G r(Ug(t0)) С Г и ri r0 = r(t0), так что ti / t0. Формула
X(t) = ®0 + -——-(ri — го) определяет некоторую параметризованную
' ’ ti - to
прямую (секущую) А, проходящую через точки r0 = A(t0) и n = A(tj).
Поскольку путь г - гладкий, то (г G C(1>(t0)) => (®< G C(1)(t0) Vi),
т» е»
3 lim	=В»,(М-
*1—>to	ti — to
Полагая по определению
r(ti) - r(t0)
hm -L-^—
ti —Ho	tj — to
Srfti) - Si(tp)
ti — to
цт — Xn(tp)
<1—Ho	tj — to
видим, что
3 lim	= В»
ti—Ho tj — to ti-Ио ti — to
= Dr(to).
Введем параметризованную прямую Ao : R —> Rn, полагая Ao(t) =
s0 + (t — to) • Dr(to), t 6 R. Эту прямую можно рассматривать как
предел положения секущей А (к пути г), проходящей через точки го =
Xq Е Г и 7’1 Е Г при 7*1	7*0 = Xq.
Определение. Прямая Ао называется касательной к пути
г в точке xq Е Г.
Докажем, что касательная не зависит от выбора гладкого пути г
(т. е. не зависит от параметризации кривой R). Для этого достаточно
рассмотреть натуральную параметризацию кривой R р : Iq Rn,
так что р ~ г и r(t) = (р о s)(t), где я = s(t) - натуральный па-
раметр, т. е. дифференцируемая и строго возрастающая длина дуги.
Положим = s(to), xq = p(sq). Тогда касательная к пути р опре-
деляется параметризацией p,Q, где pq(s) = ®о + (s - «о) • Dp(«o)? но
r = Р ° «, откуда Dr (to) = Dp(so) •	, причем > 0, так что
at	at
Ao(t) = Xo 4- (t - to)ds^  Dp(so) И при t = g(s) = to + (e - »o)/Ds(to),
где Ds(to) > 0, имеем po = Ao од. Заметим, что g : s -> t - допустимое
аффинное преобразование параметра, так что ро Ао, чем показано,
что касательная в точке xq Е Г к кривой R не зависит от выбора
представителя г. Итак, гладкая кривая R в любой точке xq своего но-
сителя имеет касательную, которую будем обозначать через тХо. Если
277
существует единственное значение tolT I такое, что r($o) = хо G Г, то
касательная определена единственным образом. Если же существует
несколько значений tk 6 I таких, что г(^) = хо € Г, то в точке хо € Г
может быть (рис. 51) несколько касательных.
Если ориентированная прямая (в R") А определена аффинным ото-
бражением A(t) = xo+t*r, то отображение (-А) : t -» xo+t*(—г) опре-
деляет противоположно ориентированную прямую (—А). Касательной
к гладкой кривой (-Л) в точке xq € Г является прямая, ориентиро-
ванная противоположно касательной тХо к кривой Я в точке хо 6 Г.
Пример. Пусть т : х (х, /(х)), где f Е С^((а, Ь)). Тогда г
есть гладкий путь в R^J/Dr(t) = (1, D/(®)) и касательная к кривой R
в точке Mq = (®о»/(®о)) € Г = г((а,Ь)) имеет параметризацию х
Ао(х), где Ао(х) = (х, Уо + (х- ®o)D/(®o))> т. е. уравнение касательной
имеет вид у = j/о + (® “ ®o)D/(®o), ® € (-оо, +оо), j/0 = /(®о)«
Пример. Пусть р : t -> (pi(tf),... , рп(t)) - гладкий путь в Rg,
так что pi €	(г = 1,2,... ,п),
llD^)||2 = S(^r)2>ov<e(a^),
тогда, полагая хо = ^(<о) € Г = р((а,/3)), имеем для параметризован-
ной касательной Ао
A©(t) = р(*о) + (t - *o)Dp(*o) = (Pi(*o) + (t - *o)Dpi(*o), • • 
..., ^pn(^o) + (^ — ^o)D^n(^o)),
или
®,- - x? = (i - to)Dp,(to)> ®° = {i = 1,2,... ,n),
или, исключая параметр t, получаем уравнения касательной в точке
®о =	€ Г = у>((а,/3)) С R” к кривой Ф в виде
Д-1 Д*1  	_ Д*п ~
Dpi(to)	DPn(*o)’
Замечание (о вычислении площади поверхности вращения).
Пусть кривая Ф - жорданова и задана (в R2,v) уравнением у = у(х),
а < х < Ъ, причем у G С^\[а, Ь]) и у(х) > 0, Vx g [atb]. Для любо-
го разбиения Т отрезка [а, Ь] заменим часть поверхности, полученной
вращением носителя Г,- = {(х,у)|у = y(x),x,_i < х < х,} вокруг оси
Ох, усеченным конусом. Тогда площадь полученной фигуры равна
п
ад = я SMx^x) + у{х<))((Ьх<)* + (Ду,)2)1'2.
i=i
278
Но ((A®.)2 + (Д1Л)2)1/2 = (1 + (D!/(£i))’)1/aA®i, поэтому, переходя к
пределу по базе d(T) -> 0, получаем величину
ь
S - 2?гу у(®)(1 + (Dy(®))2)1/2d®,
а
которую естественно назвать площадью поверхности вращения Г во-
круг оси Ох. (Теория измерения площадей будет развита в т. 2.)
§ 7.	Топология метрического пространства
Пусть Я = {X, р} - метрическое пространство. Если Х\ С X есть
подмножество X, то Ri = {Xi, р} есть метрическое пространство с
тем же расстоянием р. Ri называется подпространством метрического
пространства R.
Определение. Пусть a€XuO<r< +оо. Открытым
шаром с центром е точке а и радиусом г > 0 называется множество
Шг(а) все® точек х € X, для которых р(®, а) < г, т. е. Шг(а) = {х Е
Х|р(х,а) < г}. Множество Шг(а) = {х Е Х|р(х,а) < г} называется
замкнутым шаром с центром в точке а и радиусом г > 0. Сферой с
центром в точке а и радиусом г > 0 называется множество
Sr(a) = {х € Х|р(®, а) = г}.
Определение. Окрестностью U(a) (или У(а), ТУ (а) и т. д.)
точки а £ X будем называть любой открытый шар 1Щ(®о) (где
хо GX), содержащий точку а. Окрестность вида Ш«(а) с центром
в точке а € X называется центрированной окрестностью точки а.
Определение. Если U (а) - окрестность точки а, то про-
колотой окрестностью точки а называется множество вида
U(a) = U(a)\{a}.
/ п	\ 1/2
Пример. Пусть R = R" и р(х, 1/) = I S (®< ~ 1Л)2) » тогда
\i=i	/
Uf(a) = 1П*(а) = {® € R"|0 < р(®,а) < <5} # 0V<5 > 0.
Проколотая окрестность 17(a) точки а € X метрического пространст-
ва {X, р} может оказаться пустым множеством. Если Ri = {Х2, р},
ГДе p(®i, ®2) = |S1 _ а;а|, Хх = (0,1) U {2}, то (71/2(2) = Ш1/2(2) = 0 в
Л1.
279
Отметим следующие свойства окрестностей в метрических про-
странствах. Пусть R = {X, р} - метрическое пространство, тогда:
1)	Если а Е X, то любая окрестность 17(a) точки а непуста, в
частности Ш^(а)	0 V5 > 0.
В самом деле, a G 17(a) V окрестности 17(a) точки а Е X, поэтому
U(a) # 0.
2)	Для любой окрестности 17(a) точки а Е X существует центриро-
ванная окрестность Ш;(а) такая, что Ш$(а) С 17(a), при этом радиус
6 > 0 можно выбрать рациональным.
В самом деле, поскольку 17(a) есть окрестность точки а Е X, то
3®0 Е X и 35о > 0 такие, что 17(a) = IIIjo(®o) и a Е 1Що(®о), т. е.
0 < р(а, ®о) < <5о* Если ®о = а, то все доказано. Пусть xq ф а, тогда 0 <
р(®о, a) = Ji < (50- Положим 6 = 5о—51 > 0 и рассмотрим Шд(а). Тогда
р(х, а) < 5 V® Е 1Щ(а) и в силу выбора 6 и неравенства треугольника
имеем
р(®, ®0) < р(ж,«) 4- р(а, ®о) <	= <5о - <51 + <51 = 50.
Итак,
(V® Е ПЬ(а)) => (р(®, ®о) < 50) =>
(® Е 1Що(®о) = U(a)) => (1Щ(а) С 17(a)).
3)	Для любых двух окрестностей 17(a) и V(a) точки а Е X су- ’
ществует окрестность VT(a) такая, что VT(a) С 17(a) Л V(a). В самом
деле, в силу свойства 2) существуют центрированные окрестности '
Ш^(а) С 17(a) и 1Щ2(а) С У(а), но тогда при 5 = min(5i,52) > 0
имеем
W(a) = ПЬ(а) С Ш^(а) П 1Щ2(а) С U(a) П У(а).
3') Обобщение. Пересечение конечного числа окрестностей
точки а Е X содержит окрестность точки а:
W(fc)(a)(k = 1,2,... ,m)3V(a) С Q U(fc)(a).
к=1
4)	Аксиома (отделимости Хаусдорфа). Если a, b Е X и а / Ь, то I
существуют окрестности U(a) и V(b) такие, что U(a) Cl V(b) = 0.	I
В самом деле, если а Ь, то р(а, Ъ) = 6 > 0. Рассмотрим окрестное-	|
ти Шд(а) и Ш$(Ь) точек а и Ъ соответственно и покажем, что Ш4/з(а) А
Ш^/3(Ь) = 0. Допустим от противного, что 3®о 6 Ш^/з(а) П Ш^/з(Ь),
тогда в силу неравенства треугольника имеем
0 < 6 = р(а, Ъ) < р(а, ®0) 4- р(«о» Ъ) < 5/3 4- 5/3 = 25/3.
Противоречие.
280
5)	(V6 6 Ufa) С X) => fUfa) = У(Ь)), т. e. для любой точки b G Ufa)
^тожество Ufa) является окрестностью точки b б X. Кроме того,
если b G Ufa) и b а, то существует центрированная окрестность
Шл(&) С 17(a) такая, что абШд(Ь). В самом деле, 1-е утверждение
свойства 5) следует из определения окрестностей точек а, Ь 6 X. Для
доказательства 2-го утверждения свойства 5) заметим, что a, b G X и
(а^Ь) =► fpfa,b) = <5 >0).
Пусть U(а) - окрестность точки а G X, являющаяся при b G U\a)
окрестностью и точки Ъ 6 X (U(a) = V(b)). Тогда в силу свойства 2)
окрестностей ЭШд0(Ь) С V(t>), где Ло > 0. Выберем h = min(h0, <5) > О,
тогда, очевидно, Шд(Ь) С Шд0(Ь) С V(b) = 17(a), но (р(а, Ь) = <5 > h >
0) => (аёШЛ(Ь)).
Теперь все определения и теоремы, использующие понятия окрест-
ностей (см. ч. 1, гл. 3, §1), для числовой прямой, полностью перено-
сятся без каких-либо изменений (с очевидной заменой R на I) на
метрическое пространство Я= {X, р}. (Проверьте это самостоятель-
но.) Ниже для полноты изложения приведены (без доказательства) все
основные факты, касающиеся топологии метрического пространства
R= {Х,Р}.)
Определение. Пусть А С X, тогда точка а Е X называ-
ется внутренней точкой множества А, если существует окрест-
ность U(а) точки а такая, что U(а) С А.
Определение. Совокупность всех внутренних точек мно-
0
жества А С X называется внутренностью А и обозначается А или
д.
Определение. Точка а Е X называется внешней точкой
для множества А, если существует окрестность U(a) такая, что
U(a)C\A— 0. В частности, если а - внешняя точка для множества
А, то аЁА, т. е. а 6 С А. Обратное, вообще говоря, неверно.
Следствие. Внешняя точка для множества А является внут-
ренней точкой его дополнения С А = X \ А.
Определение. Совокупность всех внешних точек для мно-
жества А называется внешностью множества А и обозначается
Ае.
Определение. Точка а Е X называется граничной точкой
множества А С X, если (VU(a)) => (17(a) А А 0 и U(a) АС А 0).
Определение. Границей дА множества А называется мно-
жество всех граничных точек А. Очевидно, дА = 5(С А).
Определение. Точка а Е X называется точкой прикосно-
вения множества А С X, если U(a) А А 0 717(a). В частности,
любая внутренняя точка ЕА и любая граничная точка х% 6 дА
множества А являются точками прикосновения множества А.
Определение. Совокупность всех точек прикосновения
281
множества А С_Х называется замыканием множества А и обо-
значается через А, при этом А С
Замечание. (А С В) => (А С В).
Определение. Точка а € X называется предельной точкой
множества AqX, если U(a) П А 0 VC7(a).
Определение. Совокупность всех предельных точек мно-
жества А С X называется производным множеством и обознача-
ется А9, при этом Af С А.
Замечание. AU А'С А.
Определение. Точка а € X называется изолированной
точкой множества А С X, если 317(a) такая, что 17(a) П А = {а}.
Теорема. A = AU А1, С А = Ае. (Доказать самим.)
Замечание. Из определений вытекает, что дА С А и (а €
дА) Л (а^А) => (а е А').
Замечание. Изолированная точка а множества А С X может
не быть граничной точкой для А.
Пример. Рассмотрим метрическое пространство, X = [-1,1] U
{2} и множество А = (-1,1) U {2} С X. Тогда а = 2 - изолированная
точка множества А, но а$дА = {-1}и{1}.
Определение. Множество А С X называется открытым,
о
если все его точки внутренние, т. е. если А =А>
Теорема. Любая окрестность U(a) точки а € X есть от-
крытое множество. (Доказательство провести самостоятельно, ис-
пользуя свойство б) окрестностей в метрическом пространстве R =
Замечание. (Для любого множества А С X) => (множества
А, и Ае открыты). Доказать самостоятельно по схеме, указанной в
ч. 1, гл. 3, § 1.
Определение. Множество А С X называется замкнутым,
если оно содержит все свои предельные точки, т. е. если А* С А.
Теорема. (Множество А С X замкнуто) (А = А). (Дока-
зать самостоятельно.)
Замечание. Пустое множество 0 и все множество X являют-
ся одновременно замкнутыми и открытыми.
Теорема. (Множество А С X замкнуто) & (множество С А
открыто). (Доказать самим, пользуясь свойствами 1)-5) окрестнос-
тей в метрическом пространстве по схеме, указанной в ч. 1, гл. 3,
§1.)
Пример. Покажем, что множество {® G Х|р(х,а) > £} =
С Шt (а) есть открытое множество в метрическом пространстве R =
{X, р}. В самом деле, (V®o € C^(a)) => (р(хо,а) = Jo > £), но тогда,
выбирая h € (0, Jo — £), видим, что V® € Шь(хо), в силу неравенства
треугольника имеем p(x,a) > р(а, хо)-р(®>®о) > 6—h> 6o — (6q—8) =
282
s > О, T. е. х е СШНа), а потому Шл(®0) С СШДа), т. в. СПЬ(а) -
открытое множество. Но тогда в силу теоремы видим, что замкнутый
шар Шл(а) есть замкнутое множество в метрическом пространстве
R={X,p}-
Теорема. Пересечение конечного числа открытых множеств
есть множество открытое. Объединение конечного числа замкну-
тых множеств есть множество замкнутое. (Доказать самостоя-
тельно.)
Замечание. Теорема перестает быть верной для бесконечного
числа множеств.
Теорема. Пересечение QFa любого семейства замкнутых
а
множеств Fa С X есть множество замкнутое. Объединение (J Ga
а
любого семейства открытых множеств Ga С X есть множество
открытое. (Доказать самостоятельно.)
Теорема. Граница дА любого множества А С X есть замк-
нутое множество. (Доказать самостоятельно.)
Теорема. (VA С X) => (множество А замкнуто). (Доказать
самостоятельно.)
Теорема (критерий принадлежности точки производному мно-
жеству). (а € А1 ф 0) <=> (в любой окрестности Ufa) точки а € X
существует бесконечное множество точек из А). (Доказать самим.)
Следствие. Конечное множество А С X не имеет предельных
точек.
Теорема. Для любого_множества А С X производное мно-
жество А' замкнуто, т. е. А* = А1. (Доказать самим.)
Определение. Пусть R = {X, р} - метрическое пространст-
во и (рп) (п-+ pn,n € N) - последовательность точек (элементов)
рп е X. Точка р € X называется пределом последовательности
(Рп)> если для любой окрестности U(p) точки р Э.У € N такое, что
Рп 6 U(p) Vn > N. Если последовательность (рп) имеет пределом
точку р € X, то говорят, что последовательность (рп) сходится
к точке р.
Итак, последовательность (рп) из X сходится к р € X, если, какова
бы ни была окрестность С7(р) точки р € X, все элементы последовав
тельности (рп), за исключением (быть может) конечного их числа,
принадлежат окрестности U(p).
Если использовать свойство 2) окрестностей в метрическом про-
странстве R = {X, р}, то имеем
Определение. Точечная последовательность (рп) из X
сходится к точке р € X, если Ve > О Э.У(е) € N такое, что рп €
ш«(р) Vn > ДГ(е).
Теорема (единственности предела точечной последовательнос-
ти). Если последовательность (рп) (рп € X Vn € N) имеет предел р
283
(в R — {X, р}), то этот предел единствен. (Доказать самостоятель-
но, используя аксиому отделимости Хаусдорфа.)
Теорема (критерий принадлежности точки замыканию мно-
жества). (р 6 А) <=> (существует последовательность (рп),Рп € А С
X такая, что (рп) сходится к точке р). (Доказать самим.)
3 а м е ч а н и е. Из доказанного критерия следует, что замыкание
А есть множество пределов сходящихся последовательностей из А С
X.
Следствие. Для того чтобы множество А С X было замк-
нутым, необходимо и достаточно, чтобы А содержало пределы всех
своих сходящихся последовательностей.
Теорема (критерий принадлежности точки производному мно-
жеству). (р Е А' / 0) <=> (существует последовательность (рп)> схо-
дящаяся к точке р Е X, такая, что рп € А \ {р} Vn Е N и рп / рт
Чпф т). (Доказать самостоятельно.)
Определение. Точка р Е X называется точкой сгущения
(или частичным пределом) последовательности (рп) точек из X,
если любая окрестность U(p) точки р содержит бесконечное мно-
жество элементов из последовательности (рп)-
Замечание. Если последовательность (рп) точек из X сходит-
ся к точке р Е X, то ее предел р является точкой сгущения последова-
тельности (рп). Обратное утверждение, вообще говоря, неверно.
Замечание. Точка сгущения последовательности (рп) может
и не быть предельной точкой множества А = {pn Е X|n Е N}, хотя
всегда будет точкой прикосновения множества А.
Определение. Пусть (рп) - последовательность точек из
X. Рассмотрим строго возрастающую последовательность нату-
ральных чисел (njb) такую, что < пг < пз < ... (п* < п/ при
fc < Z) u nfc > fc Vfc Е N. Тогда последовательность (pnk) называется
подпоследовательностью последовательности (рп)»
Замечание. Полагая для (pn) n& = fc, видим, что последова-
тельность (pfc) является подпоследовательностью самой себя.
Теорема (критерий того, что точка является точкой сгуще-
ния точечной последовательности). (Точка р Е X является точ-
кой сгущения последовательности (рп)) <=> (пз последовательности
(Рп) можно выделить подпоследовательность (рПк)} сходящуюся к
р). (Доказать самим.)
Теорема. Множество точек сгущения последовательности
(Рп) (пространства {X, р}) есть замкнутое множество. (Доказать
самим.)
Рассмотрим теперь линейное нормированное пространство Е с
нормой х —> ||х||. Как было доказано в §1 этой главы, пространство
Е при введении метрики (расстояния) р(х,у) = ||х — у|| становится
метрическим пространством.
284
Определение. Пусть Е - линейное пространство, в кото-
ром заданы две нормы: х -> ||x||i и х -> ||х||2. Нормы || ||х и || ||2 на-
зЫваются эквивалентными, если существуют положительные по-
стоянные сх > 0 и с2 > 0 такие, что ci||x||i < ||х||2 < с21|х||х Vx Е Е
(откуда ± • ||х||2 < ||х||х < 1 • ||х||2 Vx € Е).
Теорема. Пусть Е - линейное пространство, в котором за-
даны две нормы: || ||х и || ||2. Пусть Ri = {E,pi} - метрические про-
странства с расстояниями р,(х,у) = ||х - у||» (г = 1,2). Если нор-
мы || ||1 и IIII2 ^вивалекшкы и a Е Е - любая точка, то для лю-
бой окрестности Ш^(а) = {хЕ-Е|рх(х, а) < <fx} из Rx существу-
ет окрестность Ш^(а) = {х 6 1?|р2(х, а) < 62} из R2 такая, что
Ш^(а) С Ш^(а), и, обратно, УШ^(а) из R2 существует Ш^(а)
из Ri такая, что Ш^(а) С Ш^(а).
Доказательство. Поскольку нормы || | |i и )| ||2, эквива-
лентны, то существуют ci > 0, с2 > 0 такие, что Vx 6 Е имеем
оценки ci||х||i < ||х||2 < с2||хЦ1, с^1 • ||х||2 < ||х||х < с^1 • ||х||2. Пусть
a Е Е и Ш^(а) - любая окрестность точки а из Лх. Тогда
рх(х,а) = 1|х - а||х ^с^Пх-аПг = с”1р2(х,а),
поэтому при 62 = сх • £х, имеем Ш^(а) С Ш^(а).
Второе утверждение теоремы доказывается аналогично.
Следствие. Пусть метрические пространства {Е,рх} и
{Е,р2} (где Е - линейное пространство) построены с помощью эк-
вивалентных норм 111 |х и ||||2. Тогда:
1) (точка а Е Е - внутренняя, внешняя, граничная, предельная,
точка прикосновения множества А С Е в Дх) (точка а Е Е - (соот-
ветственно) внутренняя, внешняя, граничная, предельная, точка при-
косновения множества А С Е в Д2);
2) (множество А С Е открыто, замкнуто в Ях) <=> (множество
Aq Е (соответственно) открыто, замкнуто в Д2).
Введем в линейном пространстве Е = R” «нормы» х —» ||х||р, где
Vx=(®i,...,xn)ERn (х= f>,eiERw
\ t=i
/ п \ l/р
НХНр = (52l®»|P|	(р= 1,2,...), ||х||оо = sup |a?j|(p=oo),
\i^l /	t=l,2,...,n
причем, полагая |®*| = sup |ж>| (так что |a?t|/|®fc| < 1, i k),
i=l,2,... ,n
имеем
/ n	\ i/P
11x1100= lim (521ж*1₽)
p->+oo \	*	/
\»=1	/
285
/	/	\ \ 1/р
= »li5ino 11+S(i®'i/i®*i)p 11 =ы= «чр i®d-
Р-*+оо I I “	I I	1 = 1,2,...,»
(так как 1+52(l®d/l®*l)p < п и п^р = !)•
Р->+оо
Замечание. Можно доказать, что «норма» х —> ||х||р удовле-
творяет всем аксиомам определения нормы из §1 и любые две нормы
||х||Р1 и ||х||Рз эквивалентны.
/п	\1/2
Норма ЦхЦг = ( $2 l®d2 1 называется евклидовой нормой в Rn.
\»=1	/
Теорема. Нормы II ||2 « lllloo в евклидовом пространстве
Е = Rn эквивалентны.
Доказательство. В §1 этой главы было доказано, что
функция х ||х||2 является нормой в Rn. Проверим аксиомы нор-
мы для функций X -> ||х||1 и х -> ||х||оо.
1)	INI1 = Е |х.-| > OVx G R" и (||х||1 = £ |®,| = о)	(|®,| = О
»=1	\	1=1	/
Vi, т. в. х = 0).
2)	||х+у||1 = £ |xi+l/i| < Е |х.|+Е 1»1 = l|x||i+||y||iVx,y G Rn.
i=l	i=l t=l
3)	ll<* • x||i = E la •	= |a| • IW11 Vx G R” Va G R.
1=1
Далее, для функции x -> ||x||oo имеем
1)	||x||oo = sup I®*| > 0 Vx G R", (||x||oo = sup |®*| = 0) & (®< = 0
k	k
Vi);
2)	||x + y||oo =sup|®k + I/fcI < sup(|®t| 4- |y*I) < sup I®*) + sup |yi| =
h	k	k	I
||x||oo + ||y||oo Vx,y G R";
3)	||a • x||oo = sup |a • ®*| = sup(|a • |®*|) = |a| • sup |®*| = |a| • ||x||oo
fc	k	k •
Vx G Rn, Va G R.
Теперь рассмотрим вопрос об эквивалентности норм || ||i, || ||г и
|| ||оо> Очевидно, Vx G Rn, имеем
п
IMI1 = У? |®<I < nsup |®*| = п||х||оо,
Ы	*
||х||оо = SUp |®fc| <	1®»1 = IMIb
k	i=l
т. е. ||х||оо|| < х||1 < nllxllooi п"1 • ||х||1 < ||х||оо < ||х||1, откуда
вытекает эквивалентность норм || ||1 и || ||оо- Далее,
/П \1/г
||х||оо = sup |®*| < I 1®<12 )	= I|х||а,
286
так как если максимальное из чисел |xj|, |и2|,... , |хп| есть |®,|, то
|®,12 < Е 1Ж* I2- С ДРУГ0Й стороны,
’	““ 1. —1
Поскольку £ |®,|2 < n(sup|x*|)2, и поэтому имеем ||х||оо < ||х||2 <
i=i	k
п1/2 • IMloo, п"1/2 • ||х||2 < ||х||оо < ||х||2, т. е. нормы ||||2 и ЦП»,
также эквивалентны. Наконец, из полученных оценок Vx 6 Rn имеем
п"1 • ||х||1 < ||х||2 < п1/2 • ||х||1, п"1'2 • I|х||2 < ||х||1 < п • ||х||2, т. е. и
нормы II 111 И II ||2 эквивалентны.
Замечание. Можно доказать (см. [2], с. 17, теорема 1.6.2), что
в Rn любая норма эквивалентна евклидовой норме
/ п	\
1|х||2 = I Sl®il2) •
\»=1	/
Замечание. Рассмотрим в Rn нормы ||х| |i, | |х| |2 и ||х||оо.
Тогда для окрестностей в этих нормах имеем: Ш^2\а) = {® €
Rn| ||х-а||2 < J} - есть открытый шар с центром в точке а и с радиу-
сом S > 0. «Шар» Ш^(а) = {® € Rn| ||x-a||i < 5} при п = 2 есть от-
крытый квадрат с центром в точке а и диагоналями, параллельными
осям 0®i и 0x2» Наконец, «шар»	= {® € Rn| ||х - а||оо < 5}
есть n-мерный открытый куб с центром в точке а и со сторонами,
имеющими длину 2d и параллельными осям координат.
$ 8. Пределы в метрическом пространстве
Пусть R = {Х,р} - метрическое пространство и п -> рпу п € N,
~ последовательность в X. В §7 было дано окрестностное определе-
ние предела (сходящейся) точечной последовательности, из которого
вытекает
Определение. Точка рЕ X называется пределом точечной
последовательности (рп), если 3 lim^ р(р,рп) = 0. Таким образом,
Р = п	Рп> если Ve > 0 32У(е) € N такое, что p(p,pn) < е Vn > N(e).
Определение. Множество А С X называется ограничен-
ным в метрическом пространстве R = {X, р}, если существуют
К > 0 и a G X такие, что р(®, а) < К V® € А, т. е. А С Шх(а).
Т е о р е м а (об ограниченности сходящейся последовательности
в метрическом пространстве). Если точечная последовательность
287
(рп) сходится в метрическом пространстве, то она ограничена в
нем. (Доказать самостоятельно.)
Определение. Точечная последовательность (рп) из мет-
рического пространства R = {Х,р} называется последователь-
ностью Коши (или фундаментальной последовательностью), если
Vs > О 3N(s) Е N такое, что р(рп,Рт) < £ Чп,т > N(e).
Из ч. 1 (гл. 3, §7) известно, что если (ап) есть последовательность
Коши в R1, то она сходится. Таким образом, это свойство последова-
тельности является основным, поскольку оно позволяет ответить на
вопрос о том, является ли последовательность сходящейся, даже ес-
ли мы не знаем предела, к которому последовательность (ап) может
сходиться. Однако имеет место
Замечание. Последовательность Коши (рп) не обязана быть
сходящейся в метрическом пространстве R = {X, р}.
Пример. Пусть R = {X, р}, где X = {1/n Е Rx|n Е N} и
р(х,у) = |® - у\. Тогда (рп) = (1/п) есть последовательность Коши в
R = {X, р), но она не сходится в X, поскольку ОЕХ.
Рассмотрим некоторые общие свойства последовательностей Коши
в метрическом пространстве.
Замечание. Если последовательность (рп) сходится в метри-
ческом пространстве к р, то (рЛ) фундаментальна.
Теорема. Пусть (рп) - последовательность Коши в метри-
ческом пространстве R = {X, р}. Тогда последовательность (рп)
ограничена и любая ее подпоследовательность (рПк) также являет-
ся последовательностью Коши.
Доказательство. Поскольку (рп) - последовательность
Коши, то Зпо Е N такое, что p(pn>Pm) < 1 Vm, п > п0. Но тогда (pn) Е
nii(Pno) Vn > По, откуда при г = max(p(pno,pi),... , р(рПо,Рпо-1), 1) >
О видим, что рп Е Шг(рп0) С X Vn Е N (т. е. (рп) ограничена в X).
Далее, рп - последовательность Коши, поэтому Vs > О 32V(s) Е N
такое, что p(pn,Pm) < £ ¥тп,п > N(s). Рассмотрим любую подпо-
следовательность (pnfc) (где njc Tf и пк > к), тогда (VZ, к > N(e)) =>
(nk,nt > N(e)) => (р(рПк,рП1) < £), т. е. последовательность (рПк)
также фундаментальна.
Теорема. Пусть (рп) - последовательность Коши и р Е X -
точка сгущения для (рп)- Тогда последовательность (рп) сходится
к р.
Доказательство. Поскольку (рп) фундаментальна, то
Vs > 0 BNq(€) Е N такое, что p(pn,Pm) < £/2 Vm,n > Nq. Но р - точ-
ка сгущения для (рп), поэтому существует хотя бы одно тп© > Nq(c)
такое, что р(р,р,По) < £/2. Откуда в силу неравенства треугольника
имеем
p(Pn,p) < p(Pn,Pmo) + p(pmo,p) < £/2 + s/2 = sVn > No(e),
288
т. е. 3 lim рп = р.
. П-4 + 0О
Следствие!. Любая последовательность Коши (из метричес-
кого пространства R = {X, р} либо не имеет (в X) точек сгущения,
либо имеет только одну точку сгущения, к которой она и сходится.
Следствие 2. Если для последовательности Коши (рп) су-
ществует хотя бы одна сходящаяся ее подпоследовательность (pnfc),
то и сама последовательность (рп) сходится.
В самом деле, если 3 lim рПк = р, то точка р 6 X является точкой
fc->+oo
сгущения для (рп), а тогда в силу фундаментальности последователь-
ности (рп) 3 lim рп=р.
п->+оо
Определение. Метрическое пространство R = {X,р} на-
зывается полным, если в нем сходится любая последовательность
Коши.
Определение. Нормиров анное векторное пространство Е,
полное относительно метрики р(х, у) = ||х — у||, определяемой нор-
мой ||||, называется банаховым пространством.
П р и м е р. R1 есть полное метрическое пространство, оно также
и банахово пространство.
Теорема. Пусть Ri = {Е, р,}, где ‘Е - линейное простран-
ство, в котором введены две || ||« и метрика pi(x,y) = ||х — у||®
определена нормой х -> ||х||,- (г = 1,2). Тогда если нормы || ||i и
|| Цг эквивалентны, то любая сходящаяся последовательность (лю-
бая последовательность Коши) (рп) в Ri является сходящейся по-
следовательностью (последовательностью Коши) в R2 и наоборот.
(Таким образом, если нормы || ||i и || ||з эквивалентны, то понятия
предела последовательности в метрических пространствах Ri и R%
совпадают.)
Доказательство. Поскольку нормы || ||i и || ||2 эквива-
лентны, то существуют постоянные ci > 0 и с2 > 0 такие, что Vx Е Е
С1 • IMI1 < 1|х||2<С2-11x111,
«г'1 -IMI2 < ||Х||1< ef1 -||х||2.
Пусть п —> р„ g Е - последовательность Коши в Ri = {Е, pi}. Тогда
Уе > О е N такое, что
(Vm,n > N(e)) => (pi(pn,Pm) = llPn -qm||i < e/c2)
=> (P2(Pn,P,n) = HPn - Pmlh < C2 • ||pn “ Pm||l < C2 • (e/c2) = fi),
T- e- (Pn) есть последовательность Коши в Я2 = {Е, р2}.
10 Зак. 860
289
Теорема. Пусть R = {Rn,p}, где р есть метрика, опреде-
ляемая любой из трех эквивалентных норм || ||j, || ||j, || ||оо Тогда
для
р»(а|*\ 4* , • • • ’ 4*>) € Rn, р = (<*1 >	«•») €
€ Rn( lim Pk=p)<=>( Вт =a<; i= 1,2,... ,n).
fc->+oo	fc-*+oo
Доказательство. Необходимость. Пусть 3, lim рь = p,
k-++oa
тогда fcHmop(p*,p) = 0) => (* lim* ||p* - p|| = 0), t. e. Ve > 0 3W € N
такое, что ||p* - p||oo < e Vfe > N, но тогда
(Пр* “ plloo = sup |ajfc) - aiI < e) =>
1=1,2,...,n
=> (|ajfc) - a,| < ||р* - р||те < eV») =>
=> (Э * lim aj*) = a,; i = 1,2,..., n).
Достаточность. Пусть 3 lim aj*^ = a,; i = 1,2,... , n. ТогдаVe >
fc-++oo
0 3M € N (* = 1,2,..., n) такие, что |aj*^ - a,-1 < e Vfc > Ni. Но тогда
(VA: > maxNi) => (|ajfe) -а<|<е;» = 1,2,...,п)^-
=>>(l|pfc-p||oo= sup |a(fc) - Oil < e) ^-( lim p(p*,p) = 0) =>
<=1,2,... ,n	*-++oo
=>(3 lira Pl, =p).
Теорема (о полноте Rn). Пусть Rn - п-мерное евклидово
пространство и k -» рп € Rn - последовательность в Rn. Тогда
(3*lim pig) <=> ((рл) есть последовательность Коши (в Rn/J.
Доказательство. Необходимость. Пусть 3 lim р* = р,
fc-> + <X)
где pjg € Rn Vfc € N и p € Rn. Тогда поскольку *lim р(р*,р) = 0, то
Ve > 0 3N € N такое, что р(р*,р) < е/2, р(рт?р) < е/2 УЛ,т > N. В
силу неравенства треугольника имеем
p(Ph,Pm) < p(pk,p) + p(p,Pm) < eVfc.m > N,
t. e. (ph) есть последовательность Коши в R*.
Достаточность. Пусть k -> р* € R.n - последовательность Коши в
Rn, причем ph = (a^*\...,a^). Тогда из неравенств |a{*^ — а{т^| <
I Ip* - Pmlloo = p(p*,Pm) (*' = 1,2,..., п) следует, что числовая после-
довательность k aj*’ € R V» есть последовательность Коши в R.
290
в силу полноты R имеем 3fclim^a(fc) = <ц (i = 1,2,... ,n), а,- е R.
Пусть р = (ai, аг,... , ап) ё R", тогда из предыдущей теоремы имеем
(aj = lim ajfc) Vi) => (p = lim рк (в Rn)).
Л->+оо	fc->4-oo
Следствие. Евклидово пространство Rn полно в любой из
эквивалентных норм || ||i, || ||2, || ||оо-
Замечание. Пусть Я = {X, р) - метрическое пространство и
А С X, р € Af С X, тогда система множеств {U(р) П А} есть база во
множестве А (которую будем обозначать х -> р).
В самом деле, поскольку р - предельная точка множества А, то:
1) й(р) А А 0 для любой окрестности С7(р); 2) в силу свойства 3)
окрестностей в метрическом пространстве Я для любых двух окрест-
ностей U(p) и У(р) существует окрестность И7(р) С V(p), и
тогда в силу 1) имеем ТУ(р) А А С (Щр) А А) A (V(p) А А), т. е. система
множеств {Е7(р) А А} есть база во множестве А.
Определение (предела отображения по Коши). Пусть R =
{X, р} и Ях = {Xi,pi} - метрические пространства. Пусть А С X
и f : А С X -4 Xi есть отображение множества А в Хх. Пусть
а е А1 С X. Тогда точка ai € Xi называется пределом (по Коши)
отображения f по базе х —> а, если для любой окрестности V(ai) С
Xi существует окрестность U(a) С X такая, что f(x) € V(ai)
V® € a A 17(a); или ai = lim f(x), если Ve > 0 > О такое, что
Ух € А, удовлетворяющего неравенствам 0 < р(®,а) < 6, имеем
Р1(/(®),ai) < е.
Определение (предела отображения по Гейне). Точка ai £
Xi называется пределом (по Гейне) отображения f : А С X -4 Хк
(®	/(®)) при ® -4 а, а € А' С X. если для любой последовательнос-
ти Гейне (ха), связанной с точкой а€ А' (т. е. такой, что хп € А,
хн a Vn 6 N и lim ®п = а) 3 lim /(®п) = <*!•
п->+оо	ц->4-оо
Теорема (об эквивалентности определений предела отображе-
ния по Коши и по Гейне). Определения пределов отображения (в
точке) по Коши и по Гейне эквивалентны, т. е. если х —> f(x)
есть отображение множества А С X в Xi и а е А' С X, то
(3 lim f(x) = ai) <=> (3 lim f(xn) = ai для любой последовательное-
;r->a	П-++00 v '
mu Гейне (xn), связанной с точкой a € А'). Доказательство прове-
дите самостоятельно по примеру доказательства об эквивалентности
определений предела числовой функции в точке по Коши и по Гейне
из ч. I; см. также [2] (с. 94, теорема 4.2).
Теорема (единственности предела). Если отображение х
/(«) (/ : А С X -4 Xi, где R = {X, р} и Ях = {Хх , pi} - метрические
пространства) имеет предел в тючке а € А' С X по базе х -4 а, то
этот предел единствен.
Доказать самостоятельно, используя свойство 4) (аксиому отдели-
Ю*
291
мости Хаусдорфа) окрестностей в метрическом пространстве Ri.
Важный частный случай. Пусть R = {X, р} - метрическое про-
странство, a Hi = {Rm,pi} - m-мерное евклидово пространство с
метрикой pi, построенной с помощью любой из эквивалентных норм
II Hi, ННгилиННоо.
Пусть McXnf:McX-+ RTn есть отображение М в Rm.
При т = 1 отображение х —> f(x) будем называть (числовой) функ-
цией, а при т > 2 отображение х —> f(x) будем называть (векторной)
функцией, определенной на множестве М С X метрического про-
странства R. Пусть ei,e2,... ,ет - канонический базис в Rm, т. е.
,н.. .	т
е,- = (0,..., 0,1,0,..., 0), тогда f(а?) =	-₽»(®) • еи где отображе-
S	V	Z	1 = 1
т
ния fi : М С X —> R (г = 1,2, ...,т) называются координатны-
ми функциями (векторной) функции f(x). Полагаем по определению
f(x) = (/if®), • • • , /т(®)), считая f(x) точкой в аффинном простран-
стве Rm.
Рассмотрим любой у G Rm, тогда у = £ !/№, j/ = (j/i,... , yw).
i=i
Введем в Rm отображение р,- : у -> у,- (i = 1,2,... ,тп), называемое
г-й проекцией (в Rm), так что р,(у) = у,-. Очевидно, отображение
Pi : у -> у,- линейно да Rm, т. е. Уу(1),у(2) 6 Rm и Vai,«г 6 R
p,(aiy<x) +a2y(2)) = aip^yt1)) + a2p,(y(2)).
Заметим, что если f : М С X -> R”1 и f(x) =	... , fm(x)),
(т	\
f(®) =	/«(®)е« ). Из полученных результатов о
«=1	/
пределах в метрических пространствах имеем:
Теорема. Пусть aeM'cXuf-. МсХ-^ R™, причем
f(x) = (А(®),-«-	А = (А1,...,Ат). Тогда (3Jim/(®) = А)
<=> (3 lim f)i(x) = Ai Vi, 3 lim р,- о f (x) = p,(A) Vi).
я?->а
Замечание. Пусть f : M С X -> Rro и g : M С X —> R*n -
два отображения, тогда поскольку Rm - линейное пространство, то
можно определить отображения f ± g : М С X -> Я'п и А • f : М С
X -> Rm (VA G R), положив V® G M С X (f ± g)(x) = t(x) ± g(x),
(A • f)(®) = A • f(®).
Теорема. Пусть R = {X, p} - метрическое пространст-
во, M с X и а е М‘. Пусть f : М С X -> Rm, g : М -> Rm и
3 lim f(x) = А, 3 lim g(x) = В. Тогда при т> 1:
х-+а	х-+а	~
1) 3 lim(ai >f(®) + а2 • g(®)) = ах • А + а2 • В VaHa2 Е R;
^3jg(f(x),g(x)) = (A,B);
3) при т = 1 и В ф 0 3 Цт f(x)/g(x) = А/В. (Доказать самим.)
Замечание. Важным случаем метрического пространства
292
R =л{Х, p} являются евклидовы пространства R = R1 и R = Rn (п >
2). Тогда отображение f : М С R1 -> R’n есть (векторная) фуйкция
одного действительного переменного, а отображение f : М С Rn —>
Rm
есть (векторная) функция n-переменных, при этом если Г(ж) =
т
2 Л(ш)е,-, /(ж) =	,/т(®)), ТО для координатных функций
»=1
fi(x) принята запись fi(x) = Л(®1,... , хп) (г = 1,2,... , т).
Пусть М G Rn и f /. М С Rn -> R1. При п = 2 z = f(x,y)
есть функция двух переменных. Пусть ро = (жо,2/о) 6 Af' и су-
ществует проколотая окрестность U(ро) С М С R2. Тогда если
3 lim f(p) = lim f(®,p), то этот предел называется двойным пре-
делом функции /(ж, у) в точке (жо, Уо) (или пределом функции по со-
вокупности переменных х и у).
Пусть при фиксированном у ро 3 lim f(x,y) = <р(у) и при фик-
сированном ж / ж© 3 lim /(ж,*р). = У>(ж). Тогда пределы (если они
существуют)
lim <р(у) = lim ( lim fix,у)) = lim lim fix, у), lim i>(x) =
SfT^J/O	у—*уо X—IXq	, y-+yQ
= lim (lim f(x,y)) = lim lim f(x,y)
X-¥Xq у—^Уо	X-^Xq y-+yo
называются повторными пределами функции f(x,y) в точке (жо, ро)-
Пример 1. Двойной предел существует, а повторные пределы
могут и не существовать:
_ f х • sin(l/y) + У • sinfl/x) при х - у О,
- ( 0прих-у = 0.
Из неравенства |/(ж,р)| < |ж| 4- |р| => (3 lim /(ж, р) = 0). Но при
(х,у)->(о,о)
ж 0 не существует lim /(ж, р), а при у 0 не существует lim /(ж, р).
у-+о	®->о
П р и м е р 2. Двойной предел не существует, а повторные пределы
существуют и различны.	1
fix «1 - /	~ У2Жх2 + У2) пРия;2 + У2‘> °-
- I 0при® = 2/ = 0. .
Тогда в любой 17((0,0)) существуют точки pi = (а, 0), ръ = (0, а)
такие, что /(pj = 1, f(p2) = -1.
Таким образом, двойной предел f(x,y) при (ж,р)-~> (0,0) не су-
ществует. Но при ж / 0 (^(®) = Кт/(ж,р) = 1) => (3	= 1),
у—>0	т—>0
а при (<р(у) = lim/(ж, у) = -1) =3> (3 lim <р(у) = -1), т. е.
х—>0	у—>0
lim lim f(xYy) = 1 =£ —1 = lim lim /(ж, p).
293
Пример 3. Двойной предел не существует, а повторные пределы
существуют и одинаковы.
ti \	/	*1 2 ДРи!ра + Уг > 0>
/(®, у) = 4 х2 + у2
( 0 прих = у = 0.
Тогда в любой U(Q, 0) существуют точки pi = (а, а), рг = (0, а) такие,
что /(pi) = 1/2, /(рг) = 0. Таким образом, двойной предел f(x, у) при
(х, у) -> (0,0) не существует. Но при у 0 (9 lim f(x, у) = <р(у) = 0) =>
(9 lim р(у) = 0), а при х 0 (9 lim /(х, у) = V>(x) = 0) => (91im^(z) =
у 0	j/~^0
0). Таким образом,
lim lim f(x, у) = lim lim f (x, y) = 0.
Теорема (достаточное условие существования повторно-
го предела). Пусть функция f : (х,у) —> /(х,р) € R определена
Vp = (х,р) € U(po)f где ро = (хо, ро). Пусть существует двойной
предел lim f(p) = А иУу ф уо 3 lim f(x}y) = <р(у)> Тогда сущест-
®-4®0
вует повторный предел
lim <р(у) = lim lim f(x,y) = А.
у->уо	У-*Уо
Доказательство. Поскольку 3 lim f(p) = А, то Ve > 0
р-4ро
3i > 0 такое, что Vp € U*(po) (т. е. при 0 < р(р,ро) <	~
А| < е. Заметим, что в силу свойства 5) окрестностей в метрическом
пространстве Vp ро такого, что 0 < |р — ро| < <5/2, существует
окрестность V(xo,p) С Us(po) и поэтому функция /(р) определена в
V(®o,p). Поскольку по условию Vp ро 3 lim /(х,р) = ^>(р), то в
неравенстве \f(x,y) - Л| < е (х,у) € Uf(po) можно перейти к пределу
при х —> ®о» где у - любое такое, что 0 < |у - у0| < 6/2. Но тогда для
любого у, удовлетворяющего неравенству 0 < |у - уо| < 6/2, имеем
оценку |р(у) - А| < е, т. е. 9 lim <р(у) = А.
У^Уо
Следствие. Пусть функция f(x, у) определена в 17((®о> Уо)) в 1)
существует двойной предел lim /(р); 2) существуют оба повторных
р->ро
предела *lim ^Ит У(х, р) и Пт lim /(х, у). Тогда повторные пределы
равны двойному пределу.
294
§ 9.	Непрерывные отображения в метрических
пространствах
Несколько обобщим понятие окрестности точки а € X в метричес-
ком пространстве R = {X, р}. Напомним (см. §7 о топологии метри-
ческого пространства), что множество G С X называется открытым в
метрическом пространстве Я = {X, р}, если Va € G существует цент-
рированная окрестность (шар) Ш$(а) = {х 6 Х|р(х,а) < 5} такая,
что 1Щ(а) С G.
Определение. Открытой окрестностью точки G X на-
зывается любое открытое множество G С X, содержащее точку
а. Обозначение U(a), V(a), 1У(а) и т. д. - открытая окрестность
точки а € X.
Замечание. Открытые окрестности обладают следующими
свойствами:
1)	если a € X, то любая окрестность 17(a) точки а непуста;
2)	для любой окрестности 17(a) точки а € X существует центри-
рованная окрестность 1Щ(а) С С7(а);
3)	пересечение любых двух окрестностей 17(a) и V(a) точки а € X
является открытой окрестностью точки а (доказать самостоятельно);
3') об о бщ ени е. Пересечение конечного числа открытых окрест-
ностей точки о € X является открытой окрестностью точки а;
4)	аксиома (отделимости Хаусдорфа). Для любых точек а, b Е
X таких, что а Ь, существуют окрестности U(a) и V(b), для
которых U(a) C\V(b) = 0;
5)	(W Е 17(a)) => (U(A) = V(b)).
Очевидно, в силу свойств 1)-5) окрестностей вида 17(a) во всех ре-
зультатах §7 о топологии метрического пространства под 17(a) можно
понимать открытые окрестности в новом определении.
Пусть даны два метрических пространства Я = {X, pr), S =
{У, ру}. Пусть f : М С X У (х -> f(x) = у € У) есть отобра-
жение множества М в У.
Определение. Отображение f : М С X —> У называется
непрерывным в точке хо € М (запись: f € С(хо)), если Че > 0 3<5 > О
такое, что Vx € М, для которого рх(х,хо) < <5 имеем
Рг(/(®),/(®о)) < е.
Определение. Отображение f : М С X —> У, непрерывное
в каждой точке х £ М, называется непрерывным на множестве М.
Запись: f G С(М).
Замечание. Если хо - изолированная точка М С X, то для
любого отображения f : М С X -> У имеем f £ C(xq).
295
Замечание. Если ®о 6 М* сХи/:Л£сХ—>У, то можно
говорить о пределе (по базе х —> ®о) Hm f(x).
X~+Xq	‘ ‘s'-
Теорема (предельный критерий непрерывности отображения
в точке). Пусть f : М С X Y и xq 6 М. Для того чтобы f Е
C(xq), необходимо и достаточно выполнения одного из следующих
двух условий: 1) xq - изолированная точка множества М; либр 2)
если xq Е М С\ Mf, то	с
3 lim f(x) = f(xQ).
X—^Xq
Доказать самим, используя соответствующую теорему из ч. I.
Теорема (о непрерывности композиции двух непрерывных
отображений)* Пусть R = {Х,рх}> S = {У,ру} и f : М С X -> У.
Пусть Т,— {Zypz} и существует множество N С У такое, что
N D f(M) и <р : N CY 4 У. Пусть f Е С(®о) и <р Е С(уо),, где
xq Е М и уо = /(®о) 6 N- Тогда композиция F=<pof:.McX-tZ
такова, что F Е C(xq). Доказать самим, используя, схему доказа-
тельства, теоремы о непрерывности сложной функции (см. ч* I, гл. 4,
§2).
Пусть R = {Х,рх} и S = {У,ру} - метрические пространства и
f : М С X —к У - отображение множества М в У. Пусть Ух С У,
тогда множество /-1(Ух) = {ж Е M\f(x) Е У1} называется полным
прообразом множества Ух При отображении /. Ниже нам понадобятся
свойства образов и полных прообразов, отображения f (см. § 2 гл. 1
Ч. I).
Перефразируя (г, «^-определение непрерывности отображения / :
М С X —> У, получаем
Определ е н и е. Пусть R =. {Х,рх} и S = {У,ру} - мет-
рические пространства. Отображение f : М С X —> У называет-
ся непрерывным в точке xq Е М, если для любой центрированной
окрестности Ver(/(®о)) С У точки /(®о) существует центриро-
ванная окрестность U*(%о) С X точки xq такая, что
f(u^xo)ryM)cveY(f(Xo)). .	,
В силу свойств 1)-5) окрестностей из (е, «^-определения вытекает
следующее эквивалентное ему (проверить самим)
Определение (окрестностное). Пусть R = {X,рх}, S =
{У,ру} - метрические пространства. Отображение f : М С X ->
У называется непрерывным в точке xq Е М, если для любой
окрестности Vr(/(®o)) С У точки /(®о) существует окрестность
Ux(®о) С X точки xq такая, что /(С7х(®о) ПМ) С Vy(J(xq)).
296
Теорема .(критерий непрерывности отображения, определен-
ного на открытом множестве). Пусть R = {Х,рх}, S = {У,ру} -
метрические пространства uG С X - открытое (в R) множество.
Пусть f : G С X У - отображение G в Y. Тогда (/ 6 C(G)) <=>
(для любого открытого (в S) множества V С Y полный прообраз
f~x(V) С G открыт в R).
Доказательство. Необходимость. Пусть f Е 0(G), где
G С X - открытое в R множество. Пусть V С Y - открытое в S мно-
жество. Докажем, что множество /“X(V) открыто в R. Если /“1(У) =
0, то множество /-1(У), очевидно, открыто в R. Пусть /-1(У) # 0.
Рассмотрим любую точку xQ Е /“’1(У) С G, тогда /(ж0) 6 V С Y. Но
множество V открыто в S, и поэтому V = Оу(/(жо)) есть (открытая)
окрестность точки /(а?о) (в S). В силу окрестностного определения
непрерывности отображения в точке из f 6 С(жо) вытекает, что для
окрестности Оу(/(а?о)) существует окрестность Ux (жо) С X точки
х0 такая, что f(Ux(xp) П G) С Оу(/(жо)). Поскольку множества G и
Ux («о) открыты и содержат точку ж0, то оба они являются (открыты-
ми) окрестностями точки xq и в силу свойства 3) (для окрестностей)
их пересечение GO Ux(xq) = РГА(жо) есть окрестность точки но
тогда f(Wx(xo)) С 0Y(f(xo)) = V, откуда ТГ^жо) С /“Х(У). Таким
образом, Ужо 6 /-1(У) существует окрестность 1Гх(жо) С /-1(У),
т. е. множество /”1(У) открыто в R.
Достаточность. Пусть для любого открытого (в S) множества
V С У его полный прообраз /~1(У) С G открыт в R. Рассмотрим
любую точку хо Е G, тогда /(ж0) Е У. Рассмотрим любую (откры-
тую) окрестность OY(/(жо)) = V С У точки /(жо). Тогда множество
/-1(У) С G открыто в Я, причем (/(ж0) Е V) => (х0 Е /-1(У)),
т. е. /-1(У) = С7а(жо) С G есть (открытая) окрестность точки
жо. Заметим, что /(/-1(У)) С V. Итак, для любой окрестности
Оу (/(ж0)) = V С У существует окрестность Vх(жо) = /-1(У) С G
точки хо такая, что (/(t7x(®0)) С Оу(/(ж0))) => (/ Е С(ж0) Уж0 Е G)
=>(/eC(G)).
Теорема (критерий непрерывности отображения). Пусть R =
{Х'Рх} и S == {У,ру} - метрические пространства. Пусть f : X
У. Тогда (f Е С(Х)) (для любого замкнутого (в S) множества
F С У его полный прообраз f~1(F) С X замкнут в R). Доказать
самим, переходя к дополнениям и используя соотношение f~1(CF) =
Cf-\F).
Замечание. В предыдущих критериях непрерывности ото-
бражения нельзя в формулировках заменись полные прообразы на
прямые образы. Например, при постоянном отображении / : G —> У,
/(ж) = Уо Уж Е G, очевидно, имеем / Е C(G), однако для любого от-
крытого множества U С G его образ f(U) = {1/0} 6 У есть точка, но
точка, вообще говоря, не является открытым множеством в метричес-
297
ком пространстве S = {У,/>у}.
Определение. Пусть R = {X, рх}> S = {У, ру } - метрические
пространства и множество G С X открыто в R. Отображение
/ : G С X —> У называется открытым, если для любого открытого
множества U CG его образ f(U) С У открыт в S.
Следствие. Пусть R = {X, рх}, S = {У, ру) и G С X,
0 С У, где G открыто в R, а 0 открыто в S. Пусть отображение
f : G “ 0 есть биекция. Тогда существует обратная биекция :
0 G, причем: 1) (/ Е 0(G)) (отображение f~l открыто); 2)
(отображение f открыто) 4» (/-1 € С(0)).
Замечание. (Биекция / : G Ч 0 = f(G) является гомео-
морфизмом открытого множества G на открытое множество 0)
(отображения f и f~l - открыты).
Следствие. Норма х ||х|| в нормированном линейном
пространстве Е, рассматриваемая как отображение Е в прямую R с
естественной метрикой, является непрерывной функцией.
В самом деле, из неравенства | ||х|| - ||а|| | < ||х — а|| Vx, а Е Е
вытекает, что Ve > О 3<J = е > 0 такое, что из неравенства ||х-а|| < <5
имеем |||х||-||а|||<£.
Теорема. Пусть R = {X, р} - метрическое пространство, а
S =	- т-мерное евклидово пространство. Пусть f : М С
X -> Rm (® -> /(®) = (Л(®),... ,/то(®)). Тогда (f € С(М)) (Л €
C(M);i = 1,2...т).
Доказательство вытекает из предельного критерия непрерывности
отображения и теоремы о пределе (векторной) функции.
Теорема. Пусть fug- (векторные) функции, отображающие
множество М С X в Rra. Пусть f, g € С(М) и а € R. Тогда f ± g,
(f, g), a-f € C(M). Если при зтом т = 1 и 0(®о) Ф О,7710 f/д € С(®о).
(См. теорему о пределах (векторных) функций.)
§ 10. Компактность в метрических пространствах
Пусть R = {X, р) - метрическое пространство и К С X. Напом-
ним, что система открытых множеств {С?а} из X называется откры-
тым покрытием множества К С X, если |J Ga D К.
а
Определение. Множество К С X метрического про-
странства R = {X, р} называется компактным, если из любого его
открытого покрытия можно выделить конечное подпокрытие.
Определение. Множество А С X называется предком-
пактным или относительно компактным в Я = {X, р}, если замы-
кание А компактно в R.
Теорема. Пусть Ki С X (г = 1,2,... ,тп) и множества К,
298
т
компактны в R Vi. Тогда множество К = |J Ki компактно в R.
1=1
Доказательство. Пусть система {Ga} есть открытое no-
tn
крытие. множества К = (J Ki. Тогда, очевидно, |jGn D Ki (i =
1,2,... ,т) и в силу компактности Ki Vi из системы {Grt} можно вы-
делить конечное подпокрытие {Gj,,} (j = 1,2,... ,i,;i = 1,2,... ,m),
it
так что (J Gj,i D Ki (i = 1,2,... ,m). Но тогда система открытых
j=i
множеств {Gj,,} (j = 1,2,... ,i,;i = 1,2, ...,m) конечная образует
(конечное) покрытие множества К : |J (J Gj,i D К, т. е. К компакт-
но в R.
Следствие. Объединение конечного числа предкомпактных
множеств из R предкомпактно в R.
Пример. Если множество К состоит из конечного числа точек,
то оно компактно.
Замечание. Любое неограниченное множество А С X метри-
ческого пространства R = {X, р} не компактно. В самом деле, пусть
точка а € А С X. Рассмотрим систему открытых шаров (Шп(а)}
+<Ю
(n = 1,2,...). Очевидно, IJ Шп(а) Э А. Если бы множество А было
nsl
компактно в Л, то из открытого покрытия {Шп(а); п = 1,2,...} мож-
tn
но было бы выделить конечное подпокрытие (J ШП((а) D А, но тогда
А С Ш„|(|(а) (при то =	п<), т- е* множество А ограничено
вопреки предположению.
Теорема. Пусть К Q X компактно и К С (J Gi, где {€?»•} -
i=i
возрастающая последовательность (Gi С Gt С ... С Gn С Gn +1 С
...) открытых множеств. Тогда Зпо такое, что К С Gno.
Доказательство. Очевидно, система {GJ есть открытое
покрытие множеств^ К. В силу компактности К из системы {Gt-}
можно выделить конечное подпокрытие {С?ц, Gi2,... , Gim}, но тогда
при no = max(ii,... , im) имеем К С Gno.
Замечание. Если при выполнении условий теоремы К =
+оо
U , то Зпо такое, что К = Gno.
i=i
Теорема. Пусть К С X компактно и {FJ (г = 1,2,...) -
убывающая последовательность (Fi D F2 D ... D Fn D Fn+i D ...)
+00
замкнутых множеств таких, что Fi С К Vi и Q Ft- = 0. Тогда Зпо
i=i
такое, что Fno = 0.
299
Доказательство. Введем открытые множества G, QFi-
Тогда (Fi D F2 D ... D Fn Z> ...) => (Gx C G2 C C Gn
Кроме того, ( p| Fi = 0) => ( p| CG, = C |J G, = 0), т/ e. Jf =
«=i	»=i	«=i	1
+oo
U Gi D К. Но тогда из предыдущей теоремы следует, что Эпо такое,
»=1 ’ < •
что К С Gno = GFno, но по условию Fno С К, поэтому Fno =‘0.
Теорема Кантора. Пусть R = {X, р} - метрическое про-
странство и множество К С X компактно. Тогда любая вложен-
ная система непустых замкнутых множеств из К имеет непустое
пересечение (т, е, если К Э Fi D ... D Fn D ..., где Fi ф 0, Ft = Ft
+°°
Vi, mo AF(^0).
t=l
Следствие. Пусть R = {X,p} - метрическое пространство
и множество К С X компактно. Тогда любая стягивающаяся систе-
ма замкнутых непустых множеств из К имеет единственную общую
точку (т. е. если К D Л D ... D Fn D ..., Ft 0,Ft- = Ft Vi и
lim di = 0, где di = sup p(®, у), то существует точка a 6 К такая,
-boo
что p) Fi = {a})<	/
t=i
Определение. Множество К С X метрического про-
странства R = {X, р} называется секвенциально компактным, если
каждое его бесконечное подмножество М С К имеет хотя бы од-
ну предельную точку, принадлежащую К (т. е. множество К СХ
секвенциально, компактно, если (для любого бесконечного подмно-
жества М С К) => (Mf С К 0)).
Теорема. Пусть множество К С X компактно в метрическом
пространстве R = {X, р}. Тогда К секвенциально компактно.
Доказательство. Если множество К С X состоит из
конечного числа точек, то теорема верна. Пусть множество К С X
компактно и бесконечно. Допустим, что К не является секвенциально
компактным в R. Тогда существует бесконечное множество М С К
такое, что М' П К = 0. Но тогда для любой точки х 6 К сущест-
вует окрестность U(x) С X такая, что U(х) А К содержит лишь ко-
нечное число точек из М. Очевидно, К С (J U(x), поэтому система
хек
{U(x), х 6 К} есть открытое покрытие множества К. В силу компакт-
ности К из этого открытого покрытия можно выделить конечное под-
rn
покрытие (J Ufa) Э К Э М. Но в окрестности С7(ж>) (i = 1,2,... , m)
»=i
Vi содержится лишь конечное число точек из множества М, т. е. мно-
жество М конечно, вопреки предположению. Итак, компактное мно-
жество К секвенциально компактно.
300
Определение. Пусть М С X есть множество метричес-
кого пространства R = {X, р} и е > 0. Множество А С X называ-
ется Е-сетью для множества М, если V® Е М За 6 А такое, что
р(х, а) < £•
Определение. Множество М С X метрического про-
странства R = {Х,р} называется вполне ограниченным, если для
него при любом е > 0 существует конечная е-сеть.
Замечание. Если множество М С X вполне ограничено, то
М - ограниченное множество.
В самом деле, поскольку М С X вполне ограничено в Я, то при е =
1 для множества М существует конечная 1-сеть А = {ai,... , ат} С
Пусть у Е М фиксировано, тогда V® 6 М За», ay Е М такие, что
p(®,at) < 1 и р(у, aj) < 1, откуда в силу неравенства треугольника
V® 6 М имеем
р(х, у) < р(х, ai) + p(ai, a,) + p(aj,y) < 2 + d(т.е. M C HI2+<i(y)).
Замечание. Если множество М С X вполне ограничено в
метрическом пространстве R = {®,р}, то для множества М Че > 0
существует конечная е-сеть В = {bi,... , Ьт] такая, что bi 6 М (г =
1,2,... ,пг).
В самом деле, если множество М С X вполне ограничено, то Че > 0
существует конечная е/2-сеть А = {ai,... ,am) С X, но тогда Va, Е А
36,i е М (г = 1,2,... , т) такое, что р(а», 6,) < е/2, и поэтому множест-
во В = {bi,... ,bm} С М есть конечная г-сеть для множества М,
поскольку V® Е М Baj Е А и Bbj Е М такие, что p(®,aj) < е/2,
P(aj,bj) < е/2, откуда, применяя неравенство треугольника, имеем
ьз} < Р(х^	< е-
Замечание. В произвольном Метрическом пространстве
R = {X, р} из ограниченности множества М С X, вообще говоря,
не следует его вполне ограниченность в Я.
Пример. Рассмотрим метрическое пространство т = {Е,р},
где х Е Е, если х = (®i, ®2,..., ®„,...), ®< ER и ||х||оо =
sup|®i| < -f-оо, с метрикой р(х,у) = ||х — у||оо. Тогда множество
& = {е1> е2,... , еп,...}, где еп = (0,... , 0,1,,...), ограничено, так
п
как p(et-,e7) = 1 Vi 54 j, но при 0 < е < 1/2 для F не существу-
ет конечной г-сети, т. е. множество F не является вполне ограни-
ченным в пространстве т. Допустим от противного, что F впол-
не ограничено, тогда для любого е > 0 существует конечная е-сеть
301
В = {е,!, е1з,... , е,т} С F. В силу бесконечности множества F и ко-
нечности множества В С F существуют ej € F и elfc € В С F такие,
что p(ey,elfc) < € и ejе<й, но в силу построения F р(е^е^) = 1
и при 0 < е < 1/2 получаем противоречие. Итак, F не может быть
вполне ограниченным в метрическом пространстве тп, будучи ограни-
ченным в нем. Попутно заметим, что F* = 0, т. е. множество F — F
замкнуто в тп.
Замечание. Если множество М С Rn ограничено, то оно
вполне ограничено в R”.
В самом деле, для ограниченного множества М С Rn существует
куб 1п такой, что М С 1п> Но Уе > 0 можно разбить куб 1п на ма-
лые кубики с ребром 2е/\/п. Тогда вершины этих кубиков образуют
конечную е-сеть как для куба Г1, так и для множества М С
Теорема. Пусть R = {X, р] - метрическое пространство и
множество К С X секвенциально компактно. Тогда множество К
вполне ограничено (а стало быть, и ограничено) в Л.
Доказательство. Пусть множество К С X секвенциаль-
но компактно. Допустим, что К не является вполне ограниченным в
R. Тогда существует ео >0 такое, что для множества К в X нет
конечной €о-сети. Пусть точка ai € К - любая, но фиксирована.
Множество {а,} С X не есть £о-сеть, поэтому Заз € К такая, что
p(ai,aa) > во > 0. Множество {01,02} не может быть ео-сетью для
К, поэтому Э03 G К такое, что ^(о^оз) > £q > 0 (г = 1,2). Конечное
множество {01,03,03} также не может быть ео-сетью для К, тогда
З04 € К такая, что />(01,04) > ео > 0 (г = 1,2,3) и т. д. Постро-
ением по индукции получаем множество М = {ох,... , оЛ,...} С К
такое, что p(o<,oj) > €0 > 0 V: ф j. Но для бесконечного множест-
ва М имеем тогда М' = 0 (в самом деле, если ЛГ 0 и а € Mf -
предельная точка, то в окрестности UtQ/2(а) существуют, по меньшей
мере, две различные точки a,,aj € М (г j) и тогда по неравенству
треугольника < p(<*i,<b) < р(а^,а) + р(а,а^) < е0/2 + £о/2 = во,
противоречие), что противоречит секвенциальной компактности К.
Итак, К вполне ограничено в Я.
Теорема. Пусть множество К С X секвенциально компакт-
но в Я = {X, р} и F С К - замкнутое множество. Тогда множество
F секвенциально компактно в F.
Доказательство. Пусть М С F - любое бесконечное мно-
жество. Поскольку М С X, то в силу секвенциальной компактности
К имеем М' П К 0. В силу замкнутости F из С F получаем
М С F = F. Тогда (М* С М С F С К) => (Mf П F = М' П К ± 0).
Итак, (для любого бесконечного множества М С F) => П F 0),
т. е. множество F секвенциально компактно в Я.
Теорема. Пусть множествоKQX секвенциально компактно
в метрическом пространстве Я = {X, р}. Тогда К замкнуто в Я.
302
Доказательство. Пусть множество К С X секвенциаль-
но компактно в R и ®о € Kf. Тогда существует последовательность
попарно различных точек (®<) (® € К Vi) такая, что ,	= я о- Но
тогда бесконечное множество М = {®i,... , xnt...} С К и Mf = {хо}•
В силу секвенциальной компактности К имеем (Mf П К 0) =>
хо € К) => (К' С X), т. е. К замкнуто в R.
Следствие. Пусть множество К С X компактно в метричес-
ком пространстве Jt = {X, р}, тогда множество К вполне ограничено
и замкнуто в Я.
Теорема. Пусть множество F С X замкнуто и вполне огра-
ничено в метрическом пространстве R = {X, р}. Тогда Ve > О
имеет место представление F = (J Fi, где Fi = Fi С F (i =
i=i
1,2,... , rn(e)) - непустые замкнутые множества диаметра d(Fi) <
е.
Доказательство. Поскольку F С X вполне ограниче-
но в Я, то Ve > О для множества F существует конечная е/3-сеть
т(е)
{ai,... ,ат(е)} С Я. Но тогда U Ше/3(а,) э F. Положим Fi =
__	i=i
Ш(/э(а,) nF 0, Очевидно, Г,- являются непустыми замкнутыми
т(«)
подмножествами F диаметра < 2е/3. Итак, Vs > О F = (J F,, где
Fi * 0, Ft = Fh d(Fi) < е Vi.
Следствие. Пусть К С X секвенциально компактно в R =
"»(<)
{X, р}. Тогда Ve > О имеет место представление К = (J Ki, где Ki -
1=1
непустые замкнутые секвенциально компактные множества диаметра
d(Ki) < е.
Теорема. Пусть Я = {X, р} - метрическое пространство и
множество секвенциально компактно в Я. Тогда К компактно в R.
Доказательство. Пусть множество К С X секвенциально
компактно в Я. Допустим от противного, что К не является компакт-
ным в Я, т. е. существует бесконечное открытое покрытие {С?Л} :
^C|jGn,H3 которого нельзя выделить конечного подпокрытия для
а
К. Поскольку К секвенциально компактно, то оно замкнуто и вполне
т(с)
ограничено, т. е. Ve > 0 существует представление К = U Х,(е), где
i=i
Х, (е)	0 Vi, замкнуто и имеет диаметр < е, причем К,(е) С К. Но
тогда хотя бы одно из множеств К{в (е) не допускает выделения конеч-
ного подпокрытия из открытого покрытия {(?«} и, в частности, мно-
жество Kio (е) бесконечно. По индукции показывается, что существует
система непустых бесконечных замкнутых множеств {Кп} такая, что
303
К D Ki D ... D Kn D Kn+1 D ..., d(Kn) < 1/n, причем множеств^
Kn Уп не допускает выделения конечного подпокрытия из открыто 1
го покрытия {Ga}. Но тогда система {Кп} есть стягивающаяся сис- *
тема непустых, замкнутых, бесконечных множеств из секвенциально
компактного множества ^.Поскольку множество Кп бесконечно для
любого п, то во множестве К существует последовательность («п),
состоящая из попарно различных точек (хп хт при п / тп) и та- :!
ких, что хп Е Кп Vn Е N. Но d(Kn) < 1/п, поэтому Ve > 0 Зп0 > 1/е
такой, что (Vm,n > п0(е)) (хп,хт Е КПо) => (р(жп,ж,п) < г), т. е. ?
(хп) есть последовательность Коши. В силу секвенциальной компакт- |
ности К для бесконечного множества М = {®i,	, жп,...} С К
имеем М' Cl К ф 0, поэтому последовательность Коши (жп) имеет (и
притом единственную) точку сгущения а Е К. В силу замкнутости
4-оо
Кп Vn из xm Е Кп Ут > п имеем а Е Кп Уп, т. е. а Е U Кп, но сис-
П = 1
4-оо	-
тема {Хп} - стягивающаяся, поэтому Q Кп = {а}. Поскольку а Е К,
П = 1
то существует открытое множество G«o из системы {G«} такое, что
a Е Gao, но а - внутренняя точка Gaoi поэтому существует открытый J
шар 1Щ(а) С X такой, что ИЦ (а) С Gao. Поскольку lim d(Kn) = О
n—>-hoo	;
(и а Е Кп Vn), то Эпо такой, что КПо С ШДа) С G«o, т. е. мно- •
жество КПо оказалось покрытым одним элементом GQq из системы
{Ga}. Противоречие с построением множества КПо. Итак, секвенци-
ально компактное множество К компактно в R.
Следствие. В метрическом пространстве понятия компакт-
ности и секвенциальной компактности совпадают.
Теорема Больцано-Вейерштрас с а.
Пусть множество К С X компактно в метрическом пространст-
ве R— {X, р}. Тогда из любой последовательности (рп) точек из К
можно выделить сходящуюся подпоследовательность (рпк)> причем
lim рПк =ро Е К.
k ->4-оо	'I
Доказательство. Пусть М = {рх,р2, • • • ,р»? • • •} С К.
Множество К компактно, а потому и секвенциально компактно в R.
Если М С К - бесконечное множество, то MfC\K /0н Зро 6 MfC\K.
Но тогда ро 6 К есть точка сгущения последовательности (рп), и по-
этому существует сходящаяся к точке р0 Е К подпоследовательность
(pnJ. Если множество М = {pi,P2,... ,рп,...} = {ах,... , aw} С К
конечно, то существует точка ai = ро Е К такая, что равенст-
во рп = ро имеет место для бесконечного множества индексов п =
ni, п2,... , пк,... (пк {Г пк > к), но тогда lim рПк = р0 Е К, т. е.
fc->4-oo
опять из последовательности (рп) можно выделить сходящуюся под-
последовательность (рПй).
304
о:: Теорема (критерий компактности в полном метрическом про-
странстве). Пусть R = {Х,р} - полное метрическое пространство
и К С X. Тогда (множество К компактно в R) (К замкнуто и
вполне ограничено в R).
Доказательство. Необходимость. Пусть множество К С
X компактно в R. Тогда К секвенциально компактно в Я, а потому
замкнуто и вполне ограничено.
Достаточность. Пусть множество К С X замкнуто и вполне огра-
\ ничено в полном метрическом пространстве R. Докажем, что множе-
ство К секвенциально компактно в Я, для чего достаточно доказать,
что из любой последовательности (р&), состоящей из попарно различ-
ных точек множества X, можно выбрать сходящуюся подпоследова-
тельность. Заметим, что ранее было доказано, что если замкнутое
множество К С X вполне ограничено, то Vs > О существует Представ-
ите)
ление К = |J где С К - непустые замкнутые множества с
i=i
диаметрами d(K^ < е Vi, причем существует К('°\ содержащее бес-
конечное множество членов из последовательности .(р*). Рассмотрим
последовательность гп = 1/n Vn Е N и, пользуясь сделанным замеча-
нием, построим по индукции стягивающуюся систему непустых замк-
нутых множеств {Хп} такую, что К D Kr D ... D Кп D Кп+\ D ...;
d(Kn) < еп — 1/п, причем множество Кп С К Vn содержит бесконеч-
ное множество точек из последовательности (pt). Пусть
Pki G Ki,Pfc2 G K2(k2 > ki),pk1 ф pk2,
и, вообще, pkn E Kn Vn (fcn H,fcn > n), pkn ± pkm Vn / m. Тогда
подпоследовательность (p*n) является последовательностью Коши. В
самом деле, поскольку lim d(Kn) = 0, то Vs > О 3n0 Е N такой, что
п->+оо
«.о) < £ и (VmJ > п0) => (Pfcm,p*, G Яп0) => (p(Phm,Pkt) < е).
В силу полноты метрического пространства Я 3 lim pk = р0 Е
n->+oo n
X. Но множество К С X замкнуто, поэтому (pkn Е К) => (ро Е К).
Итак, множество К секвенциально, компактно, а поэтому и компакт-
но.
Теорема (критерий компактности в R”). (Множество К С
Rn компактно) <=> (К замкнуто и ограничено).
В самом деле, применим общий критерий компактности множест-
ва в полном метрическом пространстве, поскольку Rn - полное, а
ограниченное в Rn множество вполне ограничено.
Задача. (Множество К С X компактно в полном метрическом
пространстве Я = {X, р}) (множество К замкнуто и Vs > 0 для К
существует компактная s-сеть).
Пусть Я1 = {X,рх} и Яг = {У,ру} - метрические пространства.
Введем метрическое пространство Я = R±xR2 = {Z, р}, где Z = ХхУ
305
(так что (z = (х,у) 6 Z) (® £ Х,у € У)), а метрика p(zi, г2)
определена одним из следующих расстояний:
/>1(«1, «2) = Рх(®1,®2) +Ру(1/1,!/2);
Poofzi'Zi) = тйх(рх(х1,Х2),ру(У1,У2))',
/>2(21,22) = (Рх(®1,®2)+|4(1/1,1/2))1/а-
Проверим свойства метрики для p2(zj,,z2) :
1)	P2(Z1,Z2) = (/>^(®1,®2) + Ру (1/1, Sfo))1/2 > о И (Р2(®1,2з) = 0)
(рх(®1,®2) = 0,py(i/i,j/2) = 0)	(®х = ®2,yi = уз) («1 = ®г);
2)	(симметрия)./>2(22,21) = p2(zi,z2). Очевидно,
3)	(неравенство треугольника) рз(г1,z2) < p2(zi,z) + p2(z,z2)
V®i, z2, z & Z — X x У.
В самом деле, используя неравенство треугольника для метрик
рх и ру, имеем p%(zi,z2) = ргх(хих2) + ffy(yi,y2) < (рх(®1,®г) +
рх(х,х2))2 + (ру(У1,у) + ру(у,уз))2 = (Рх(®1,®) + Ру(1/1, у)) +
(Рх (»> ®2) + 4 (1/, ЗЛг)) + 2(рх (® 1, ®) • рх(в, х2) + РУ (j/1, у) 'РУ {у, 1/2)) <
(но в силу неравенства Коши-Буняковского 2(ai&i + a2b2) < 2(а? +
а2)1/2 • (6i + &2)1/2 Va< > 0, &/ > 0; г = 1,2) < (р^(®х,®) + $(1/1,1/)) +
(Рх(®,®2)) +‘Pyfolfe)) + 2(р^(®1,г) + $(l/i,l/))1/2(Px(®,®2) +
$(1/,1/г))1/2 = Р2(«1>«) + Рз(&ъ) + ^P2(zi,z)p2(z,z2) = (p2(z2,z) +
p2(z,z2))i, т. е. p2(zi,z2) < P3(zi,z)+P2(z,z2).
Замечание. Свойства метрики для pi и рте проверьте само-
стоятельно по схеме § 8 (для норм || ||i и ||
Замечание. Поскольку имеют место оценки rpi(^i,22) <
it
/>00(21,2:2) < Р1(21,22); ^=/>2(21,22) < />«,(2:1,22) < />2(21,22) V21,22 €
Z, то «топологии» метрического пространства R = Ri х Яг» определя-
емые этими тремя метриками Pi, рг и роо, эквивалентны. В дальней-
шем под метрикой р метрическом пространстве R = {X х У; р} будем
понимать любую из метрик pi, рг. Рос
Теорема. Пусть 2?i = {Х,рх}, Яг = {ISpy} и Я = {Z,p} -
метрические пространства, где Z = X х У, а метрика р определя-
ется любой из трех эквивалентных метрик pi, рг и роо. Тогда для
Zk = (хк'Ук) EZ (к = 1,2,...), zq = (®о»1Л)) € Z:	= «о)
(3 lim ХкЕхо, 3 lim ук = г/о)-
fc—>Ц-оо	fc—
Доказательство. Необходимость. Пусть 3 lim z* = zq в
fc->+oo
R = Ri x Яг, тогда Ve > 0 3&o € N такое, что pi(zh,го) < eVk > ko.
306
Но тогда имеем
Г рх(®к,®о) 1 < pttZk Zo) < gVfc > fc0 т.е.З lim = xq,
l РУ(!/Ы/О) J“rV	-
3, liin yk = уо-
k-t+vo
Достаточность. Пусть lim Xk = ®о (в Ях), Hm Ук = j/o (в
fe-ч+сю	- fc-ч+оо
Я2), тогда Ve > 0 3fc< G N такие, что px(®fc>®o) < s/2 Vfc > fcx
и ру(ук,Уо) < ё/Ъ Vk > fc2, но тогда Vfc > max(fci, fc2) pi(zfc,z0) =
px(xkiyk) + рг(ук,Уо) < е/2 + е/2 = е, т. е. 3 lira zk - zo (в
Л’—>+оо
R = Ri х Яг).
Следствие. Пусть Ri и Яг ~ полные метрические простран-
ства, тогда метрическое пространство Я = Я1 х Яг также полное.
Следствие. Поскольку R - полное пространство, то вновь
получаем полноту пространства Rn = R х R х ... х R.
Теорема. Пусть Ях = {X,рх}> Яг = {У, ру} - метрические
пространства и Ki С Xf К2 CY - секвенциально компактные мно-
жества. Тогда множество К = К\ к KzCZ^XxY также сек-
венциально компактно в метрическом пространстве Я = Ях х Яг =
{Z,p}.
Доказательство. Для доказательства секвенциальной
компактности множества К = Ki х К2 в R = Ri х Я2 покажем, что из
любой последовательности (гп) точек множества К (zn = (хп,уп) €
Ki х К2) можно выбрать сходящуюся (в Я) подпоследовательность.
Итак, пусть (zn) = ((®п, уп)), где ®n € Кх, уп eKi'inE N. Поскольку
множество Ki секвенциально компактно в Ях, то из последовательнос-
ти (®n) (an € Ki Vn) можно выбрать сходящуюся (в Ях) последова-
тельность fa) = (®,,fc) такую, что 3 lim $* = ®о € Кх. Рассмотрим
последовательность (%) = (уп*), где г)к € К2 Vfc G N. Поскольку мно-
жество К2 секвенциально компактно в Яз, то из последовательности
(гд.) можно выбрать сходящуюся подпоследовательность (т?*,) такую,
что Цшх r)kt = уо € К2. Но рассматривая последовательность (£<),
где 0 = (tkh'Okt) = zn*p видим, что Ci € К VI и в силу доказанной
выше теоремы З^Дш^С = (®о,уо) = «о G К, т. е. (0) = (z,U|) есть
сходящаяся (в Я) подпоследовательность последовательности (zn) из
множества К. Таким образом, множество К = Кх хК2 секвенциально
компактно в Я = Ях х Я2.
Определение. При а = (ах,...,On), b = (Ьх,..., bn) G R" и
а* < Ьк (fc = 1,2,..., п) множество /п[а, 6] = [ах, Ьх] х ... х [ап, Ь„] на-
зывается замкнутым п-мерным брусом в R", а множество 1п (а, Ь) =
(а1> Ьх) х ... х (ап,Ьп) называется открытым п-мерным брусом в Rn.
307
При bi — ai = 6 > 0 (г = 1,2,..., п) брус называется п-мерным кубом.
Заметим, что открытый куб 1п(а,Ь) является открытым шаром
1П$/2(с) С Rn (по норме || ||оо7 в Rn с с, = (а, + Ь»)/2 и bi — а, = <5 > О
(г = 1,2,... , п).
ТеоремаБольцано-Вейерштрасса в Rn.
(Ограниченный) замкнутый брус Zn[a, Ь] секвенциально компактен в
Rn (с метрикой, индуцированной любой из эквивалентных норм || ||х,
||||2 « IHloo).
Доказательство. По определению Zn[a, Ь] =. [ах,bi] х
[«nj^n] С Rn. Но отрезок [а*,6*] С R секвенциально компактен в
R для любого k в силу теоремы Больцано-Вейерштрасса из [1] (ч. I,
гл. 3, §6). Поэтому в силу доказанной выше теоремы замкнутый брус
Zn[a,b] секвенциально компактен в Rn.
Следствие. Пусть множество К С R” замкнуто и ограниче-
но, тогда множество К секвенциально компактно в Rn.
Доказательство. Поскольку множество К С Rn ограни-
чено, то в Rn существует замкнутый брус Zn[a, Ь] D К. Но по теореме
Больцано - Вейерштрасса брус Zn[a, Ь] секвенциально компактен в Rn
и тогда множество К, будучи замкнутым подмножеством секвенци-
ально компактного множества Zn[a, Ь], само секвенциально компактно.
ТеоремаБореля-Лебега в R”. Если множество
К С R*1 замкнуто и ограничено, то оно компактно в Rn.
Доказательство (не основанное на общей теореме об эк-
вивалентности компактности и секвенциальной компактности в пол-
ных метрических пространствах). Поскольку замкнутое множество К
ограничено в Rn, то существует замкнутый куб Zn[a, b] с диаметром
<5о > 0 такой, что К С Г1 [а, Ь]. Докажем, что множество К компактно
в Rn. Допустим, что К не компактно в R”, тогда для него существу-
ет открытое покрытие {G«} (К С из которого нельзя выбрать
конечного подпокрытия.	а
Заметим, что Vf > О можно получить (например, последователь-
ным делением пополам каждого ребра [a,, Ы] куба Zw[a, Ь]) разбиение
куба Zn[a, Ь] на частичные кубы Z"(e) (d(Z"(f)) < е). Тогда, полагая
m(e)
Ki(e) = KnZp(e), получаем представление К = (J Ki(e), где К,(е) -
«=1
непустые замкнутые множества с диаметром d(Ki(e)) < €. Поскольку
Ki (г) С К, то хотя бы одно из К,о (г) не допускает выделения конечно-
го подпокрытия из открытого покрытия {G*}. Но тогда по индукции
получаем, что существует стягивающаяся система замкнутых непус-
тых множеств {Кт} такая, что
К D Ki D ... D Кт D Km+i D ... , d(Ktn) < 1/т,
причем каждое из Кт не допускает выделения конечного подпокрытия
308
из укрытого покрытия ,{G«}. Поскольку ограниченное, замкнутое (в
множество К секвенциально компактно (по теореме Больцано -
Вейерштрасса для Rn), то дальнейшее доказательство совпадает с
приведенным в теореме о компактности секвенциально компактного
множества в общем метрическом пространстве Я, в силу которого су-
ществует последовательность Кощи (жт) такая, что хт £ К1П С К
€ N.B силу полноты Rn последовательность Кощи (рт) сходится
к точке xq е Rn. Но xi 6 Кт VZ > т, поэтому в силу замкнутости Кт
+сю	'	.
хо G Кт € N, так что х0 G П Кт. Но lim d(Km) = 0, поэто-
: -	;т=1 . г	-
му П Кт = {®о} С.К = К CljGa и тогда 3Grttl Э ®о- Поскольку
>' т=1	• 	‘ ‘	; а	г-
множество Gao открыто, то x-о -внутренняя точка Ga„ и поэтому
ЗШЯя-о) С Gaa. Поскольку хо 6 К,п Ут gNh lim d(Km) = 0, то
m->4-oo
3?n0 G N (?по > 1/<5) такое, 4td/fm'o С 1Щ(®о) С Gao, т. «. множество
KWti покрыто одним элементов Ga'o из системы {G«}. Противоречие с
построением множества KWn. Итак, множество К (замкнутое й огра-
ниченное в Rn) компактно в Rn.'
Следствие (критерий компактности в Rn). Пусть множество
К CR*. Тогда (if компактно в'Ип) <=> (К замкнуто и ограничено).
Дока з а т ё л ь с т в о (не опирающееся на общий критерий
компактностйв полном метрическом пространстве). Необходимость.
Пусть К компактно в Rn, тогда оно секвенциально компактно, а по-
тому замкнуто и вполне ограничено (т^ е. ограничено).
Достаточность. Пусть множество К С Rw замкнуто и ограничено
в Rn. тогда в силу теоремы Б орел я-Лё бега оно компактно в Ru.
Замечание. Обратите внимание на отличие критерия ком-
пактности в Rn (замкнутость и ограниченность) от обпхего критерия
компактности в полном метрическом пространстве “Я/( замкнутость и
вполне ограниченность).
Пример. Ранее было показано, что в метрическом бесконеч-
номерном пространстве т (элементами которого являются последо-
вательности х = (жп) с ||х||ьо < 4-оо) множество (всех ’’ортов”)
F ~ {еь • • • , е,,...} (где et = (^>)) замкнуто и ограничено, но не яв-
ляется вполне ограниченным. Поэтому множество F не может быть
секвенциально компактным, а потому и компактным в пространстве
т' . • '
§ 11. Связность в метрических пространствах
Определение. Метрическое пространство R = {X,р} на-
зывается несвязным, если существуют два открытых непустых
множества G± и G2 из X, таких, что Gi UG2 и Gi H G2 = 0-
ао9
Определение. Метрическое пространство R = {X,р} на-
зывается связным, если не существует двух непустых открытых
множеств Gi и G% из X таких, что Gi U G2 = X и Gi Cl G2 = 0-
Замечание. Пространство R = {X, р}, состоящее из одной
точки, связно.
Определение. Множество М С X метрического про-
странства R = {X, р} называется связным, если не существует
двух непустых открытых (в R) множеств Gi и G2 таких, что
Gi Г\ М 0 (г = 1,2), Gx U G2 D М, Gi Г) G2 = 0»
Замечание. Можно дать эквивалентное определение несвяз-
ного метрического пространства с помощью замкнутых множеств:
метрическое пространство Я = {Х,р} называется не связным, если
существуют два непустых замкнутых множества Fi и Fz таких, что
Fi П 2*2 = 0 и Fi U 2*2 = X.
Теорема (о сохранении связности при непрерывном отображе-
нии). Пусть R = {X,px}f S = {У,ру} - метрические пространства
и G С X - открытое в R множество. Пусть f : G С X -> Y -
отображение G в Y. Если f Е 0(G) и множество М С G связно в
R, то образ f(M) С Y связен в S.
Доказательство. Допустим от противного, что множест-
во М С G С X связно (в Я), f € C(G), но множество f(M) С У не
связно (в S). Тогда существуют открытые множества 0Х, 02 из У
такие, что 0< П f(M) 0 (i = 1,2), 0Х U 02 D /(Af), 0Х П 02 = 0-
Рассмотрим полные прообразы Gi = /“x(0i) С G. Поскольку
f Е C(G) и множества 0i открыты в У, то в силу критерия непре-
рывности отображения видим, что множества Gi открыты в X. Но в
силу свойств прообразов имеем
(01 П 02 = 0) => (0 = П 02) = п /" х(®з) =
= Gi П G2) => (Gi П Gi = 0), (0i U 02 Э f(M)) =►
=► f-х(01 и 02) = /-1(01) и /-J(02) D f-4f(M)) D М) =>
=► (Gi U Gi D M).
Наконец, 0,- П f(M) 0, поэтому 3®,- € М такое, что f(xi) Е 0<,
откуда (®i е Gi = /"1(0i)) => (О, П М ф 0;г = 1,2). Таким образом,
для множества М С G С X существуют открытые множества Gx и
G3 из X такие, что Gi П М ± 0 (г = 1,2), Gx П G2 = 0, Gx U G2 D М.
Но тогда множество М С X не связно в X вопреки условию теоремы.
В ч. I, гл. 4, § 3 для множеств числовой прямой было введено по-
нятие линейной связности.
Определение. Множество М С R называется линейно
связным, если V®, 2/ Е М (® < у) имеем [®, у] С М.
310
Теорема. Пусть М С R. Тогда: (множество М не связно в
RJ (множество М не связно линейно в R/
Доказательство. Необходимость. Пусть множество М С R
не связно. Тогда существуют открытые не пустые множества G± и G2
из R такие, что Gi А М = Mi / 0 (2 = 1,2); Gi A G2 = 0, Gi U G2 D
Af. Поэтому Эя Е М\ и Эу 6 Л£г. Пусть для определенности х < у.
Рассмотрим множество Go = Gi А (—оо, у) = Gi А (-оо, у] (поскольку
2/EGi), и пусть z = sup Тогда х < z < у, причем (z Е Go) => (z Е
__
Gi). Докажем, что zeGt- В самом деле, если бы z Е G2, то поскольку
Gt открыто, то существует (открытая) окрестность U(z) С G2. Но
(Gi A Gt = 0) => (U(z) A Gi = 0), т. е. zE^i. Противоречие. Таким
образом, ZGG2, но
(у € М2 С Gt) => (z < у), ((z^Gt) => (zeM2)).
Докажем, что z?Gi. В самом деле, если бы z € Gi, то поскольку Gi
- открытое множество, то существует окрестность V(z) С Gi и в силу
неравенства z < у 3zx Е Gi такое, что z < zi < у, но тогда z не может
быть верхней гранью множества Go = Gi А (-00, j/). Итак, zEGi. Но
х Е М1 С Gi, поэтому (ж < z) => (я < z,z?Afi). Окончательно имеем
Эя Е М, Эу Е Мт 3z^Mi (i = 1,2), т. е. z?Af, откуда имеем я < z < у.
Но тогда множество М не связно линейно в R.
Достаточность. Пусть множество М С R не связно линейно в R.
Тогда Эя,?/,z Е R такие, что х,у Е Af, z$M т х < z < у. Положим
М1 = М А (-оо, z) 0, Mt = М A (z,+oo) / 0. Тогда множества
Gi = (-оо, z), Gt = (z, +00) непусты и открыты в R, причем G, AAf =
Mi ф 0 (i = 1,2), Gi U Gt D Af, Gi A Gt = 0, т. е. множество М не
связно в R.
Следствие. Множество М С R связно в R тогда и только тог-
да, когда Af является одним из следующих множеств (а < 6; а, b Е R);
(-оо,Ь), (-оо,&], [а, +оо), (а,+оо), (-оо,+ос), (а, 6), [а, 6), (а, 6], [а, 6].
(Доказательство было проведено для линейно связного множества в
ч. I, гл. 4, § 2).
Теорема Больцано (о промежуточных значениях не-
прерывной числовой функции). Пусть R = {X, р} - метрическое про-
странство uG С X - открытое множество. Пусть / : G С X —> R
и f Е G(G). Тогда, если множество М С G связное, то функция
/(я) принимает на множестве М все промежуточные значения.
Доказательство. Поскольку f Е G(G) и множество М С G
связно в X, то образ f(M) С R есть связное числовое множество. Но
тогда множество f(M) линейно связно в R и потому V?/i, у2 Е f(M)
таких, что ?/i < yt и (Vy Е [?/i,yt]) => (у Е /(Af)), т. е. Эя Е Af такое,
что /(я) = у.
311
Определение. Множество М С R” называется линейно
связным в Rn, если любые две точки из М можно соединить не-
прерывным путем : [а,/?] —> Г = у>([а,/ЭД) С Rn с носителем
Г = у>([ац/ЭД), целиком лежащим в М (Г С М).
Опред е л е н и е. Множество М С Rn называется выпуклым,
если (Уж,т/'Е М) => ([ж, у] С М), где [ж, j/] = {z 6 Rn|z = (1 — t)x 4-
ty,t € [0,1]} есть отрезок, соединяющий точки х и у.
Замечание. Любое выпуклое в Rn множество линейно связно.
Замечание. Открытый шар Й1^(а) С R” является выпуклым
множеством при любой из трех эквивалентных норм || ]| 1, II IMIIloo В
R”.
В самом деле, пусть ж, у Е Ш$(а) и z = (1 — t)x4-*y> * ё [0,1], тогда
z — а<= (1 — t)(x - а) 4- t(y - а), откуда Vt Е [0,1] имеем
(||z- а|| < (1 - i)||x - а||.+t||y - a|| < (1 ~ t)6 + tS = <5) =>
=>(||z - a|| < S) => (z E IIIj(a)) => ([x,y]) С Ша(а)).
Замечание. Любой открытый (замкнутый) брус 1п(а, Ъ) х
(1п [а, ЭД) является выпуклым множеством в Rn.
В самом деле/ пусть ж, у Е 1п[а, ЭД; тогда а, < ж, < ЭД, а, < yi < bi
(i == 1,2,... ; п), и поэтому для z — (1 — t)x 4- ty при 0 < t < 1 имеем
(а, = (1 — t)di 4~ tai < % = (1 - t)xi 4- tyi < (Г — t)bi 4- tbi = ЭД:
i = 1,2,... ,.n) => (z E Тп{а, ЭД), т. e. [ж, у] С 1п[а, ЭД.
Теорем а. Пусть М С R” - линейно связное множество. Тог-
да М связно в R”.
Д о к а з а т е л ь с т в о. Пусть множество М С R9 линейно связ-
но. Допустим от противного, что множество М не связно в Rn. Тогда
существуют открытые множества Gi и G2 такие, что Gi А М / 0
(i = 1) 2), Gi A G2 — 0 и Gi U G2 D М. Пусть ж* Е Gi А М и
ж2 Е G2 А Тогда ж1, ж2 Е Af, и поскольку множество М линей-
но связно, то существует путь : [а,/ЭД Gi U G2, соединяющий
точки ж1 и с носителем, целиком лежащим в Af, т. е: таким, что
ж1 = у>(а), х2 = Е С([а^]) и Г = y>[(a,/J)] С Af, Заметим, что
пут$» у? : [а,/3] —> Rn, где Е. C([a,j9]), можно продолжить на путь
Ф(а — 6, /3 + J) Rn, где Ф Е С((а — 5, (д 4- £)), положив,
Ф(*)
(р[а) = ж1, t Е (а — ЭД а),
= < <p(t\ t E [а,/ЭД,
^(/?) = ж2,*Е(А^ + <5).
Тогда отображение Ф : (а — ЭД/J-h £) —> Rw определено на открытом в
R множестве G = (а ~ ЭД/34- d), Ф Е G(G) и отрезок [а,/ЭД С G связен,
поэтому применима теорема о том, что «непрерывный образ связного
множества у связен», в силу которой множество Ф([а,/ЭД) = у>(а,/ЭД) =
312
I4 С M связно в Rn. Однако х' € Г А б?, (г = 1,2), так что Г A G,0
(г = 1,2), причем Г С М С Gi U G2, Gi A G2 = 0, т. е. множество Г
не связно. Противоречие,
Определение. Ломаной в Rn называется. непрерывный
путь <р в R" : [«,/?] -> Rn, t т->	... , t e[a,/3],
(p € C([a,/3]), для которого существует разбиение Т = {а = to <
< ... <	= /3} отрезка [а,/3] такое, что на любом частичном
отрезке [tk-i,tk] (1 < к < т) сужение отображения <р имеет вид
4>[t) =	[**-13*],
т. е. является аффинным, так что Носитель Г* =	есть
отрезок в Rn.	, (	.
Теорема (критерий связности открытого множества в Rn).
Пусть G С Rn - открытое множество. Тогда следующие условия
эквивалентны: а) множество G связно в Rn; б) множество G линей-
но, связно в Rw; в) любые две точки из G Можно соединить ломаной,
целиком лежащей в G.	•
Д ок аза те л ь с т в о. Очевидно, в) б). Из доказанной вы-
ше теоремы вытекает, что б) а). Осталось доказать, что а) => в).
Пусть непустое открытое множество G связно в R” и ж0 6 G. Обо-
значим через U С G множество всех точек х 6 G. таких, что точки
ж0 и х могут быть соединены ломаной I, целиком лежащей в G. По-
скольку G - открытое множество, то ж0 € G - внутренняя точка, для
которой существует шар 1Щ(ж°) 6 G, но в силу выпуклости шара
(Va: е Illj(ж0)) => ([ж0, ж] 6 1Щ (ж0) С G), т. е. U 0< Будет доказано,
о
что U =U (т. е. что множество U открыто). Будет также доказано,
что U D Uf П G (т. е. что множество U замкнуто в G). Докажем,
что тогда в'силу связности G имеем G = U. В самом деле, допустим
от противного, что G \ U 0, т. е. G = U U (G \ U), и положим
Gi ±= U, G2 = G \ U. Тогда G, 0 (г = 1,2). Далёё, множество
Gi = U открыто, поскольку открыто 17: Но из условия U D U' П G
имеем G \ U = G\U = G A CU (в самом деле, поскольку (17 С 17)
=> (G \ U Э G \ С7), то условие U D U* A G дает U D U A G, откуда
получаем G \ U С G \ (U C\_G) =• G А 0(47 A G) = GO (CU U<7G) =
(GAC17)U(<GACG) = GACC7 = G\U, т. е. G\U C С\СЛ_но тем самым
доказано G \ U = G\U). Поскольку множества G и CU открыты, то
и множество G2 = G A CU открыто. Но тогда имеем G = Gi U G2,
Gi 0 (i = 1,2), Gi A G2 = 0, т. е; множество G не связно в R”,
вопреки условию а) теоремы. Итак, G = 17, где множество U постро-
ено с помощью точки ж0 6 G. Покажем, что тогда для множества G
выполнено условие в). В самом деле, пусть х\х2 G G = 17. Тогда
существует ломаная соединяющая точки ж1 и ж° и лежащая в G.
Существует также ломаная /2» соединяющая точки жа и ж2 и лежащая
в G. Очевидно, ломаная /1 UI2 соединяет точки ж^ и ж2 и лежит в G,
313
т. е. для G выполнено условие в). Докажем теперь, что U =U. Пусть
а 6 U - любая, но фиксированная точка, тогда существует ломаная
/[х°, а] С G, соединяющая точки х° и а. Но а € U С G есть внутренняя
точка (открытого) множества G, так что существует шар 1Щ(а) С G.
В силу выпуклости шара V» € 1Щ(а) имеем [а, ж] С Ш<5(а) С G, но
тогда ломаная /[ж0, a]U[a, х] = /[х°, х] С G соединяет точки х° и х, т. е.
х 6 U. Итак, 1Щ(а) С I/, т. е. любая точка а 6 U является внутренней
точкой множества 17, что и означает, что U =Ц.
Докажем, наконец, что U D Uf П G. Пусть а € Uf A G - любая,
но фиксированная. Тогда существует шар ШДа) С G, для которого,
поскольку a G Uf, имеем ШДа) A U 0, т. е. ЭЬ € U А 1Щ(а). Но
тогда существует ломаная /[х°, Ь] С G. В силу выпуклости шара 1Щ (а)
имеем [Ь, а] С Ш;(а) С G, так что ломаная Z[x°, b] U [b,a] = i[x°,a] С
G, но тогда а 6 U. Тем самым показано, что U D U' A G, чем и
завершается доказательство теоремы.
Замечание. Открытое связное множество называется облас-
тью.
Замечание. Для произвольного (не открытого) множества из
а), вообще говоря, не следует б), т. е. существуют связные, но не ли-
нейно связные множества.
Пример. Пусть множество М С R^y есть объединение графика
функции у = sin(7r/x), х ф 0 и вертикального отрезка х = 0, \у\ < 1.
Тогда множество М не является линейно связным, поскольку точки
(0,0) и (а,вш(тг/а)) при а ф 0 нельзя соединить непрерывным путем
(из М). Докажем, что множество М связано (в R2). Введем множества
Mq = {(х,2/)|х = 0, М<1},
= {(х,$/)|у = вш(тг/х), -оо < х < 0},
М± - {(х, у)\у = вт(тг/х), О < X < +оо}.
Очевидно, множества Af-, Mq til Af+ линейно связны, т. е. связны.
Пусть существуют непустые открытые множества Gi, Gi С R2 такие,
что Af = Af_ U Mq U М+ С Gi U G2, причем Gi A G% = 0. В силу
связности Af-, если Af- AGj 0, то Af_ С Gi. Но Mq С Af _, поэтому
Mq A Go = 0 и в силу связности Mq имеем АГо С Gi. Но Mq С Af-н
поэтому М+ A Gi 0 и тогда в силу связности М+ имеем М+ С Gi.
Итак, доказано, что в случае Af- A Gi / 0 имеем Af С Gi. Но это и
означает связность М (почему?).
Замечание. Для произвольного множества М С RM из б), во-
обще говоря, не следует в). (Например, для окружности на плоскости
условие б) выполнено, а условие в) не выполнено.)
314
§ 12. Непрерывные отображения на компактных
множествах
Замечание. Пусть Я = {X, рх} - метрическое пространство.
Если множество К С X компактно в Я, то в силу секвенциальной
компактности множества К любая последовательность Коши (®п) из
К (хп € КУп) будет сходящаяся (причем 3 lim хп = ®о € Я), т. е.
'	п->4-оо
подпространство Лх = {Я, рх} - полное.
Теорема (о сохранении компактности при непрерывном отобра-
жении). Пусть Я = {X, рх} u S = {У,ру} - метрические простран-
ства. Пусть множество К С X компактно в Я и отображение
f : К С X У непрерывно (/ € С(К)). Тогда образ f(K) С У
компактен в S,
Доказательство. Пусть /:ЯсХ->У, / € С(Я) и
множество К С X компактно в Я. Рассмотрим любое открытое (в S)
покрытие {G«} множества f(K) С У, так что |JGa D /(Я), где Grt
а
открыты в S Va. Компактность множества f(K) будет доказана, если
показать, что из системы {Ga} можно выделить конечное подпокры-
тие для f(K). Поскольку /(®) € f(K) V® 6 Я, то существует индекс
а(®) такой, что f(x) € Ga(x). Поскольку множество Ga(T) открыто
(в S), то Ga(x) = V(f(x)) есть открытая окрестность точки /(®). По
условию (/ 6 С(К))	(/ € С(®)) и в силу окрестностного опре-
деления непрерывности отображения в точке существует (открытая)
окрестность U\x) С X точки х € К такая, что Ga(x) D f(U\x) П К).
Система открытых окрестностей {U(®),® 6 К} образует открытое
покрытие множества Я, т. е. К С (J U(x). Но в силу компактнос-
ти К (в Я) существует конечное подпокрытие {С7(®,); i = 1,2,..., т}
такое, что
m	/ т	\
(К с и и(Xi)) => (f(K) = f U№.) ПК) =
•=1	\i=l	/
m	m
= |J/№.) пк) c|J <?«<)»
i=i	i=i
т. e. система {Gfti, i = 1,2,..., m} есть конечное открытое покрытие
множества f(K). Таким образом, множество f(K) компактно в S.
Следствие. Если множество К С X компактно в R = {X, рх }
и отображение f : К С X -4 Y непрерывно на К (/ € С(К)), то образ
/(К) с Y замкнут, вполне ограничен и ограничен в метрическом
пространстве R = {Y,py}.
Определение. Пусть R = {Х,рх} - метрическое про-
странство, М С X. Тогда (векторная) функция f : М С X -> R"1
315
называется ограниченной на множестве М, если существует по-
стоянная А > 0 такая, что ||f(ж)|| < А Ух 6 М, т. е. если образ
f(Af.) С Rw ограничен в R”1.
Следствие (теорема Вейерштрасса). Если R == {Х,р} - мет-
рическое пространство, множество К С X компактно в R и f : К С
X —>‘Rm - непрерывная на К (векторная) функция (f Е С (К)), то об-
раз f (К) С Rra замкнут и ограничен в Rm и, в частности, (векторная)
функция f(x) ограничена на К.
С л е д с т в и е (теорема Вейерштрасса). Пусть R = {X, р} - мет-
рическое пространство, множество К С X компактно в R и f : К С
X —> R - числовая функция, непрерывная на К (/ 6 С'(К’)), при-
чем М = sup/(ж), т = inf/(ж). Тогда существуют точки ж2 6 К
к	к
такие, что /(®i) = m, /(®г) = М.
В самом деле, поскольку f Е С(К) и множество К С X компактно
в R = {X, р}, то множество f(K) С R также компактно, т. е. f{K)
есть замкнутое и ограниченное множество числовой прямой. Тогда
—оо < т < М < 4-ос. По определению точных граней числа т и
М есть точки прикосновения замкнутого множества /(X), но тогда
m, М Е /(л) = /(X). Далее, из m, Af Е f(K) следует, что 3«i, Х2 6 К
такие, что f (®i) = тп, /(ж2) — Af.
Следствие. Пусть множество К С X. компактно в метричес-
ком пространстве R = {X, р} и / : К R - числовая функция. Пусть
f Е С (К) и f(x) > 0 Ух Е К. Тогда существует <5 > 0 такое, что
/(ж) >^>,о Ухе к.
В самом деле, в силу теоремы Вейерштрасса 3®о 6 К такое, что
/(ж0> = injf /(?), но тогда f(®o) = $ > 0 и поэтому f(x) > 6 > О
Ухе К; А*.............
п
Замечай й е’ Пусть (Ах,х) = aijXiXj - (симметрическая)
м=1,
квадратическая положительно определенная (в Rn) форма, так что
(Ах, х) > 0 Vx ф 0, х Е Rn. Тогда существует постоянная ао > О
такая, что (Ах,х) > а0 НхП* Vx Е R”.
В самом деле, положим /(у) = (Ау,у) Vy Е К = 51П1(0) = {у Е
Rn| НуШ — Ц- Тогда f е С(Х) и7(у) > 0 Vy Е К. Поскольку мно-
жество К замкнуто и ограничено, то оно компактно в Rn, и поэто-
му в силу следствия из теоремы Вейерштрасса Зао > 0 такое, что
/(у) > а0 > 0 Vy Е К. Но тогда, полагая у = х/||х||2 Vx О,
имеем (Ах,х)/(х,х) = (Ах, х)/||х||| = (Ау,у) > ао > 0, поскольку
у = х/1|х||2 6 5Ш1(0) = К, откуда
г‘ г (Ах,х) > a0||x|||Vx Е Rn.
Определение. Пусть R == {X, р} - метрическое простран-
ство, М С X - множество, а х Е X - точка. Тогда расстояни-
ем
ем от точки х до множества М называется величина р(х,М) =
inf р(®, а). Очевидно, V® Е X р(х, М) > 0 и р(х, М) = О V® 6 М.
Теорема. Пусть F С X - замкнутое в метрическом про-
странстве R = {Х,р} множество и f : X —> R+, где f(x) = p(®,F).
Тогда f Е С(Х) и р(®, F) > О У®ЁГ.
Доказательство. Пусть множество F С X замкнуто
и точка уЁР- Допустим от противного, что р(®, F) = 0, тогда
inf р(®, а) = 0, и поэтому V<5 > О имеем IIIj(®) П F / 0, т. е.
a£F
х Е F = F. Противоречие. Итак, р(®,Г) > О V®EF. Введем функ-
цию /(®) = p(®,F) > О V® Е X. Пусть ®i,®2 € X - любые, тогда
Уе > 0 За Е F такое, что р(®1? а) < p(®i, F) + е, и в силу неравенства
треугольника имеем
р(®2, а) < р(х2, ®i) + p(®i, а) < p(®i, ®2) + p(®i, F) + е,
откуда
р(®2, F) < р(®2, а) < р(®ь ®2) + p(®i, F) + е.
Итак, Ve > 0 имеем p(x2,F) < p(®i,F) + p(®i, х2) + е или, в силу
произвольности е > 0, p(®2,F) < p(®i,F) + p(®i, х2). Меняя ®i и х2
местами, имеем p(®i, F) < р(х2, F) + р(®1, х2), откуда
(|р(® 1, F) “ р(®2, Л1 <	®г)) =>
=> (“ /(®г)| < p(®i, х2) V®x, ®2 Е X).
Но из этой оценки вытекает, что f Е С(Х). В самом деле, пусть ®i Е
X, тогда Уг > 0 3(5 = е и при р(® i, ®2) < 6 = е => |/(®i) - f(x2)| < г. ’
Определение. Пусть R = {X, р} - метрическое простран-
ство и Mi,M2 С X - непустые множества, тогда расстоянием
между множествами Mi и М2 называется величина
р(М1,Л2) = г inf „ р(®1, ®г) > 0.
3 а м е ч а н и е. p(Mi,M2) = inf p(xi,M2)= inf p(x2,Mi).
В самом деле, пусть 6 = р(Мг,М2) = inf p(l/i,!/2) > 0,
yiGMi,y2€Af2
S1=	P(2/1>-^г) > 0.
yiGMi
Отметим, что V®i E Mi и V®2 E M2, имеем
р(®1, x2) > inf p(®i, y2) = p(xi, M2) > inf p(j/i, M2) = 51 > 0.
УзеМ2	У16Л/1
Итак, <5i есть нижняя грань величин p(®i, х2), где ®i Е Mi и х2 Е
М2. Но тогда <5 = inf	> <51 (так как точная нижняя
х 1 ЕЛ/, )Д?2€Л/2
грань есть наибольшая из нижних граней). Итак, 6 > S2.
317
С другой стороны, Ji = inf p{yi, М2), и поэтому Ve > 0 3xi 6 Mi
|Г1€М1
такое, что р(хх, М2) < <$i +е/2, но р(хх, М2) = inf р(хх, 2/2)» т. е. для
Уэ€Мз
того же е > 0 Зх2 € М2 такое, что р(хх, х2) < р(®ь М2) + е/2 < £х +е.
Но тогда ((5 = inf p(xi,x2) < <5i + е Ve > 0) => (<5 < <5i). Тем
® 1 €М 1,® з€ Л/з
самым показано, что 6 =
Замечание. Пусть Fi и F2 - замкнутые множества из метри-
ческого пространства R = {X, р}. Тогда, даже если FiClF2 = 0, может
случиться, что p(Fi,F2) = Q. Так будет, например, для гиперболы и
ее асимптоты на плоскости.
Теорема. Пусть множество F Q X замкнуто, а множество
К С X компактно в R = {X, р}. Пусть FC\K = 0, тогда p{F,K) >
0, причем Зхх € К такое, что p{FK) = p(F, хх) > 0.
Доказательство. Пусть F П К = 0 и p(F, К) = 6 > 0.
Тогда 6 = inf р(х, F). Рассмотрим функцию f{x) = p(x, F). Как было
доказано, f € С (К). Поскольку К компактно, то по теореме Вейер-
штрасса 3®i е К такое, что /(хх) = (5, но F замкнуто и xi?F, поэтому
p(xi, jF) > 0, т. е. ((5 = /(®1) > 0) => (p(F,X) = p(xi,F) > 0).
Следствие!. Пусть G С Rn - открытое множество, а К С
G С Rn - компактное множество. Тогда р(Х, dG) > 0, если dG 0.
В самом деле, граница dG 0 замкнута, а К компактно, причем
XcGcRnH0GriG=0, но тогда {dG П К = 0) => {p{dG, К) > 0).
Следствие 2. Пусть F С Rn замкнуто и xq^F. Тогда 3xi € F
такое, что р(хо, F) = р(®о, ®1)«
В самом деле^пусть xo€F, тогда p(xo,F) = 6 > 0. Рассмотрим
замкнутый шар Ш44.1 (&о) С R”, он компактен в Rn, а потому К =
Ш<5+1(яо) nF 0 есть замкнутое ограниченное множество в Rn,
поэтому К компактно, но тогда xq^K и {хо} есть замкнутое множест-
во. Поэтому 3®i € К С F такое, что р(хо, ®1) = р(®о, К) < 6 4-1. Но
(V® € F\K) => (р(х, жо) > <Н1 > р(®о, К), поэтому p{xQ, К) = р(ж0, F),
т. е. 3®1 6 F, такое, что р(хо, хх) = p(xo, F) = 6.
Следствие 3. Пусть F,К С Rn, где F замкнуто, а К ком-
пактно и F П К = 0. Тогда Зхо 6 К и 3xi 6 F такие, что
/>(Г, К) = р(х0, S1) > 0.
В самом деле, по теореме Зхо G К такое, что р(хо, F) = р{К, F) >
0, но xqGF и F замкнуто в Rn, поэтому в силу следствия 2 3xi € F
такое, что р(хо, xi) = р(хо, F) = р{К, F) > 0.
Определение. Пусть R — {X, рх} и S = {У, ру} - метри-
ческие пространства и множество М С X. Отображение f : М С
X —> У называется равномерно непрерывным на множестве М С X,
если Ve > 0 3i(e) > 0 таков, что Vx, х2 € М, удовлетворяющих усло-
вию рх(х1, х2) < 6, имеем ру (/(хх),/(х2)) < е.
Теорема Кантора (о равномерной непрерывности отобра-
318
жения, непрерывного на компактном множестве). Пусть R = {X, рх}
и S = {У,ру} - метрические пространства, множество К С X
компактно eRuf •. KCX-+Y. Если f € С (К), то отображение
f равномерно непрерывно на К.
Доказательство. Пусть К С X компактно в R и f € С(К}.
Тогда f € С'(х) Vx G К, я поэтому Ve > О существует окрестность
(шар) Шп(е,®)(х) С X с радиусом т/(е,х) > 0 такая, что
(Ve е Ш,(М)(*)ПХ) < (ру(/(4),/(®)) < £).
Пусть е > 0 - любое, но фиксированное. Тогда, полагая т)(е, х) = »?(х)
в силу предыдущего, видим, что существует открытый шар
Ш,(.)/2(х) = U(x) С Ш,(г)(х) С X.
Система {С7(х);х € К} образует открытое покрытие компактного
множества К : |J U(x) D К. Поэтому из этой системы можно выде-
лить конечное открытое подпокрытие
{tf(®fc);fc = l,2.m}:	(J U(xk) D К.
k=l
Положим 6 = - min % и покажем, что Vx,£ € К таких, что рх(х,£) <
2 k
6 имеем py(f(x), /(£)) < 2е. В самом деле, поскольку (J U{xk) Э К,
к=1
то существует индекс i такой, что £ € U(xi) = Шт?1/2(х,), так что
< гц/2 < гц. Используя неравенство треугольника, имеем
Px(x.aJi) <	+/>х(6 ®<) <б + гц/2 < гц, т. е. х е Ш,((х,). Итак,
х,( € ШЧ((х<) П К, но в силу выбора шара Шч(<1Г<)(х<) имеем
Ру (/(®), /(»,)) < е, ру (/(£), /(»<)) < е,
откуда, вновь используя неравенство треугольника, получаем
Pv(/(®), /(€)) < py{f{x),f(xi)} +py(f(x<),f(t)) < 2е.
Итак, Ve > О 3<5 > О такое, что V£, х G К, удовлетворяющих нера-
венству рх(х,£) < 6, имеем py(f(x),/(£)) < 2е, т. е. отображение /
равномерно непрерывно на компактном множестве К.
§ 13. Сжимающие отображения в метрических
пространствах
Определение. Пусть R = {X, р} - метрическое простран-
ство. Отображение f г X X пространства R в себя называ-
ется сжимающим, если существует такое число 0 < а < 1, что
^(/(®1), У(®2)) < otpfxi, ®2) V®i, ®2 € X.
319
Замечание. Любое сжимающее отображение / метрического
пространства R = {X, р} в себя непрерывно, т. е. f 6 С(Х). В самом
деле, если xQ G X, то (/ G С(а?о)) <=> (3 lim f(x) = /(®о))« Но из
X—
оценки p(f(x),f(xo))ap(x,xo) следует, что Ve > 0 при р(а;,®о) < в
имеем p(f(x),f(xo)) < ар(а;,®о) <«£<£, т. е. 3 lim f(x) = /(®о).
X—>Xq
Теорема (принцип сжимающих отображений). Пусть R =
{X, р} - полное метрическое пространство и f : X —> X - сжима-
ющее отображение R в себя, т. е. /(X) С X. Тогда существует
и притом единственная неподвижная точка этого отображения,
т. е. уравнение f(x) = х имеет одно и только одно решение из R.
Доказательство. Единственность. Пусть существуют две
неподвижные точки ®i,®2 Е X отображения f : X —» X, т. е. /(ж.) =
Xi (г = 1,2). Тогда в силу сжимаемости отображения f : X —> X
имеем p(®i, Х2) = p(/(«i),/(ж2)) < ар(ж1,ж2). Но 0 < а < 1, поэтому
р(®1, Х2) = 0, т. е. xi = ®2-
Существование. Применяя метод последовательных приближений,
рассмотрим произвольную точку Xq 6 X и положим Xi = /(жо),
®2 = /(®i)? ..., жп = /(®п-1)- Тогда получим последовательность (жп)
из X. Докажем, что (хп) есть последовательность Коши. Поскольку
отображение / : X —> X - сжимающее (с коэффициентом сжатия
О < а < 1), то имеем
р(®2,®1) = р(/(®1),/(®о)) < ар(ж1,жо),
р(®з, х2) = p(f(x2), /(®i)) < ар(®2, ®1) <
< а2р(жь ж0), • • • , />(®п+ь хп) < апр(хи х0),... ,
откуда в силу обобщенного неравенства треугольника имеем оценку
Vp : р(хп+р, хп) < р(хп+р, жп_|_р_1) 4- p(xn+p-i, Жп+р-г) 4-... 4-
+р(®п+1, ®п) <	4- ар“2 4-... 4- а 4- l)p(®i, ®о) <
< ап/(1-а) -p(a?i,a?0),
т. е. Vp > 1 3 lim р(хп+р, хп) = 0, т. е. (хп) есть последовательность
п—>+оо
Коши в полном метрическом пространстве R. Но тогда (жп) сходится
к некоторому пределу ® 6 X, т. е. 3 lim хп = х. В силу непрерыв-
п—>4-00
ности отображения /(/ G С(Х)), переходя к пределу (при п —> 4-оо) в
равенстве жП4-1 = f(xn), имеем х = f(x). Таким образом, х 6 X есть
неподвижная точка отображения /.
Замечание. При выполнении условий теоремы о сжимающих
отображениях имеем оценку
p(®n,a;)= lim p(®n,®n-tp) < an/(l-a)-p(®i,a:o)Vn G N-
р->4-оо
320
3
оценку скорости сходимости последовательных приближений (жп) к
неподвижной точке х.
Замечание. Предположение 0 < а < 1 необходимо в прин-
ципе сжимающих отображений, поскольку условие 0 < а < 1 не яв-
ляется достаточным ни для единственности, ни для существования
неподвижной точки.
Пример 1. Тождественное отображение I : х —> х метри-
ческого пространства R = {Х,р} в себя удовлетворяет условию
p(Z(#i), 1(®г)) < <*р(ж1, ®2) V®i,a?2 е X при а = 1. Но для отобра-
жения I любая точка х G X является неподвижной, т. е. нарушена
единственность неподвижной точки.
Пример 2. Отображение «сдвига» / :s4x + 1bR также
удовлетворяет условию p(f(®i), /(жг)) < <*p(®i,®2) V®i,®2 Е R при
а = 1, однако для отображения f нет ни одной неподвижной точки
(нет существования неподвижной точки).
Глава 2
ДИФФЕРЕНЦИРУЕМЫЕ ОТОБРАЖЕНИЯ ИЗ
Rn В Rm
§ 1. Частные производные функций многих
переменных
Рассмотрим точечное аффинное n-мерное пространство Rn, в ко-
тором введена декартова система координат, так что х = (хх,... , хп)
- точка в Rn. Рассмотрим присоединенное линейное n-мерное про-
странство Rn с каноническим базисом {ei,e2,... ,еп}, где орт е7 =
п
(р> • • • , 0,1,0,..., 0) (j = 1,... , п). Тогда для вектора х £ R” име-
j
п
ем представление х = xjej =	, ®п). Таким образом, х =
7=1
(®1,... , хп) - точка из аффинного пространства Rn, ах = (®1?... , хп)
(п	\
= 2 xjej I “ вектор из присоединенного линейного пространства
7=1	/
Rn. Отметим, что для двух точек х и у из аффинного пространства
п
Rn можно ввести вектор у - х = 52	~®»)е> =	~ ®1,... , уп - хп)
7=1
из присоединенного линейного пространства Rn с «началом» в точке
х = (#1,-.. ,хп) и с «концом» в точке у = (i/i,... ,уп). Далее, для
точки а = (ai,... ,ап) (из аффинного пространства Rn) и вектора
i 1 Зак. 860
321
х = (®х,.,. , xn) (из линейного пространства Rn) можно ввести точку
b = а 4- х = (ai +	, ап + ®п) из аффинного пространства Rn.
Введем в присоединенном линейном пространстве скалярное про-
п
изведение (а, Ъ) = 22 аз ' Va, b Е R" (так что Rn становится
3=1
евклидовым пространством) и евклидову норму ||х|| = у/(х, х) =
/ п	\	п
I 52 I Vx = 52 xiej = (®ъ • • • , хп) 6 Rn. В аффинном простран-
V=1 /	>=1
стве Rn введем евклидову метрику р(ж, у) = ||х-у || (так что аффинное
пространство R” становится метрическим пространством).
Аналогично рассмотрим аффинное m-мерное пространство Rm с
декартовой системой координат {у = (уь... , ут)} и присоединенное
m-мерное линейное (евклидово) пространство Rm с каноническим ба-
rn
зисом {е'х,... , е(п}, где е< = (0,..., 0,1,0,..., 0) (г = 1,... , т), так
что точке у — (yi,..., ут) соответствует вектор у = (yi,... , ут) =
m
Е У<ер
1=1
п
Замечание. Если f : х G Rn —> f (х) = 2 /• (®)®i “ векторная
1=1
функция, определенная в аффинном пространстве Rn со значениями в
линейном пространстве Rm, то ей соответствует отображение f : х Е
R"->/(®) = (/i(®),... , /т(®)) С Rw из аффинного пространства Rn
в аффинное пространство Rm.
Рассмотрим векторную функцию одного переменного f : 17(a) С
R Rm. В гл. 1 ч. III было введено понятие производной векторной
функции f в точке а по формуле
Df(a) = lim(f(a + Л) - f(a))/ft € Rm.
Л-чО
m
В координатной форме имеем f(x) = 22 Л(®)е< = (Л(®), • • • > /т(®))>
1=1
т
Df(a) = £ D/,(«)e< = (D/i(a),.... D/m(a)).
1=1
Рассмотрим теперь (векторную) функцию п переменных f : 17(a) С
R« Где а = (ai,..., ап) - точка в Rn. Пусть 1 = (fi,... , 1п) -
вектор из Rn.
Определение. Производной (или частной производной)
функции f в точке а вдоль вектора 1 называется производная (если
она существует) функции t f(a 4- Й) при t = 0. (Обозначение:
Dif(a).)
322
Итак, Dif(a) =	+ й) “ f(a))/*- Очевидно, производная
D1f (а) е R”1 есть вектор.
Замечание. Если 1 = О G Rw - нуль-вектор, то из данно-
го выше определения следует, что производная вдоль нуль-вектора
всегда существует и равна нулю.
В координатной форме имеем для f(x) =	• • • > Лп(®))
Dif(a) = (Di/i(a),...,Di/m(a)),
где
Di/»(a) = lim(/j(а 4-1 • 1) - fi(a))/t(i - 1,2,... , тп).
Замечание. Если f : Ufa) С Rn Rw и 3Dif(a), то VA € R
BDA if(«)> причем DA if(n) = A • Dif(n). В самом деле, при А = 0 это
очевидно. Для А 0 положим в = t • А, тогда (i -4 0) =Ф> fs -4 0), но
(f(a +1 • А • 1) - f(a))/t = А • (f(a + в • 1) - f(a))/a, поэтому, переходя к
пределу при t -4 0, получаем
(3 lim(f(а + i • А • 1) - f (а))/t = А • Dif(а)) => (Dx.if(а) = А • Dif (а)).
Пусть f : Ufa) С Rn -4 R - числовая функция п переменных и ej
- J-й координатный орт в Rw.
Определение. Производная функции f в точке а вдоль ор-
та ej : D«,/(a) = djf(a) = Djf(a) =	= lim(f(a + te,) - /(a))/i
называется j-й частной производной функции f в точке а. Очевид-
но’ ~	-	,°n) - /(ai,... ,an))/i.
Uibj	l-rU
Замечание. Определение первых частных производных функ-
ции многих переменных не требует введения новых понятий по сравне-
нию с дифференциальным исчислением функции одного переменного.
Пример. Пусть /(®,у) = sin(®2 + y/у), тогда
‘2Ш; ~~^ду	= С°8^2 +	°)-
Определение. Пусть f : Ща) С R" -> —	_ _
(“!>••• ,а„) 6 R’1, тогда j-й частной производной (векторной)
Функции f в точке а называется вектор djffa) = Djf(a) = lim(f(a +
<ej)“-f(<x))/i. В координатной форме djf(a) = Dyf(a) = 2 е* =
dfm(a)\
\ dxj ’	’ Qx. J *
= cos(®2
Rw и а
11*
323
Определение.mxn - матрица, составленная из частных
д
производных —---- (i = 1,2,... j = 1,2,... ,п), т. е.
OXj
/	d/i(a)	g/i(a)	\
дх±	*’*	дхп
dfm(a)	dfm(a)
\	Oxi	* * *	дхп	/
называется матрицей Якоби для (векторной) функции f в точке
а. Если т = п, то определитель матрицы Якоби называется яко-
бианом (векторной) функции f в точке а и обозначается символом
* ** —(а) =	* * * *	(а). Из определения частных произ-
водных вдоль вектора вытекает
Теорема (о линейности частного дифференцирования). Пусть
f : U(a) С Rn Ч Rm, g : U(a) G Rn -> R,n, 1 = (h,
м 3Dif(a), Dig(a) (3Djf(a),Dig(a)). Тогда в точке x = а имеем:
1) Di(f4-g) = Dif+Dig, (Dj(f+g) = Djf+Djg); 2) Di(a-f) = a-Dif
Va e R; 3) при m = 1 Di(/ • g) = g • Di/ 4- f • Di£.
Замечание. Пусть f : 17(a) C Rn R и 3Dj/(a) Vj, тог-
да для функции одного переменного /(ai,... , aj_i, Xj, ay+i,... , an) =
gj(xj), очевидно, имеем gj 6 C(aj) Yj, но утверждение f 6 C(a), вооб-
ще говоря, неверно.
Пример. Пусть
О, х — 0, — оо < у < 4-оо,
№ и) =	0, -оо < х < 4-ос, у = О,
J ’У’	1, для точек (ж, у) G R2, не лежащих
на координатных осях.
Тогда ^-/(0,0) = -^-/(0,0) = 0, но при р0 = (0,0) VC^(po) 3pi, р2 G
Ст®	оу
Uf(po),_Pi = (р,р), Р2 = (0,р), р / 0 такие, что f(pi) = 1, /(рг) = О,
т. е. /еС(ро).
Использование теоремы о производной сложной функции для функ-
ций одного переменного (ч. I, гл. 5, §4) дает теорему:
Теорема (о частных производных композиции двух функций).
Пусть f : U(xq) С Rn -> R и (у> : (a,/3) С R —> R, причем (a,/3) D
/(С7(жо))« Тогда существует композиция <рof : U(q) С Rn —> R. Если
при этом существуют частная производная D»/(®o) « производная
В<р(уо), где yQ = f(xQ) G (а,/?), то 3D»V ° /(®о) = Dy>(3/o) -D«f(®o)«
Для простоты будем теперь рассматривать числовую функцию п
переменных f : 17(a) С Rn -> R. Допустим, что Vx G 17(a) 3D»f(«b
324
тогда в окрестности U(a) С Rn определена функция Г,- : 17(a) С Rn —>
R где Fi(x) —	Пусть функция F{(x) имеет в точке а j-ю част-
ную производную DjFi(a).
Определение. Частной производной второго порядка
DjDi/(a) функции f(x) в точке а называется частная производная
vt Fi(a), га. €- DjDi/(a) = Dj(Dif(®))|®=а- Обозначения: смешанные
f(a)
производные (г # j) DiDjf(a) =	= дх qx , чистые производ-
„ X , X 92f(a)
ные второго порядка D.D./(a) = fxiXi(a) = ~g^2~~‘
Пример. Пусть f(x, у) = arctg(a:/2/). Тогда
Di/(®, у) = у/(х2 + у2), D2/ = -х/(х2 + у2),
DiDi/ = -2ху/(х2 + у2)2, D1D2/ = (®2 -3/2)/(ж2 + у2)2 = D2D1/,
D2D2/ = 2ху/(х2 + у2)2(х2 + у2 > 0).
Пусть f : G С Rn —> R, где G С R” - открытое множество.
Определение, тп-й производной функции f(x) в точке а Е G
называется функция, определяемая по индукции
DimDim^ • -.Dh/(а) = DUD.^,... , Dtl f(x))\x=a,
где ik = 1,2,... , n; k = 1,2,... , m (в предположении, что все част-
ные производные, участвующие в определении, существуют).
Теорема Шварца (достаточное условие равенства смешан-
ных частных производных второго порядка). Пусть f : G С Rn —> R,
Е G и G С R” - открытое множество. Пусть существует
окрестность 17(®о) С G такая, что \/х Е 17(жо) Зв7(ж), Djf(x)
(i / j) и 3DjDi7(®), причем DjDif 6 С(ж0). Тогда 3D«Dj/(®o) и
D«Dj/(a?o) = DjDi/(®o)-
Доказательство. Без ограничения общности рассмотрим
функцию двух переменных f(x,y). Пусть Vp Е U(ро) С G
D2/(p), D2Di/(p), причем D2D1/ Е С(ро), Ро = (xQ,yo). Положим
Дж = h, Др = fc, причем (3O4-/i,Po4-fc), (®o4-fe,2/o), (xo,yo+k) Е U(р0).
Положим А = Дх Ду/(ро) = /(ж0 4- h, yQ + к) - f(xQ + Л, р0) - /(®о, Уо +
+ f(xQ,yQ), если ¥>(ж0) = /(жо,Ро 4- fc) - /(ж0, J/o), то
А = ч>(х0 4- h) - у>(ж0).
Применяя теорему Лагранжа о конечных приращениях, имеем А =
^/(ajo4-i91/i) = Л(В1/(ж04-г91Л, !/о4-Л)-В1/(жо4-1?1/1,Ро)), 0 <	< 1.
Поскольку Vp Е 17(ро) 3D2Di/(p), то можно еще раз применить те-
орему Лагранжаи получить Di/(®o4-i?ift,Po4-fc)-Dif^o4-$i/i,Уо) =
D2Di/(®0 4- dih, Уо + ^2^) • к, 0 <	< 1, поэтому
= D2Di/(xo + i9ih, Уо + iM) • h • к, 0 <	< 1 (г = 1,2).
325
Поскольку D2D1/ € С(ро)> то
DaDi/(®o + tf 1Л, уо + tfafc) = DaDi/(®o> уо) + °(1)
(p=(A2 + ^)1/2->0h
откуда A = DaDi/(«o, Vo)h -k + o(h-k)(p-> 0), t. e.
G?(®o + h) — <p(xc))/hk = DaDi/(®o,!/o) + o(l) (p 0).
Таким образом, Ve > 0 3<Ji > 0, St > 0 такие, что при любых h,
к, удовлетворяющих неравенствам 0 < |Л| < <Ji, 0 < |fe| < <5а, имеет
место оценка
|(р(®о + Л) - <p(x0))/hk - DaDi/(po)| < £•	(1-1)
Полагая <р(х0) = /(®0) Уо + к) - /(®0, Уо) = ¥>(®о, к), имеем
|(^(®о + М)Д- <p(xo-,k)/k)/h-ThDif(po) \ < е,
но поскольку <р(хо', к)/к = (/(®0, Уо + к) - f(x0, Sfo))/k> то
lim у>(®0; к)/к = Da/(®o, Уо),
«—>0
lim <р(х0 + h',k) = Da/(®o + h, Уо),
К-4 О
поэтому, переходя в неравенстве (1.1) к пределу при к -> 0, имеем при
О < |Л| < Ji(e) оценку
|(Da/(®o + Л, уо) - Da/(®o»yo))/h - DjDif (®о> Уо)| < е>
которая и означает, что существует
lim(Da/(®o + h, Уо) - Da(®о, 1/о))/Л = DaDi/(®o, Уо)-
Л-40
Таким образом, 3DiDa/(po) и DiDa/(po) = DaDi/(po)-
.Замечание. Теорему Шварца обычно применяют в следующей
ослабленной форме: пусть существует окрестность U(xq) С R” такая,
что V® € <7(®о) 3D*/(®), Dy/(«), D<D//(«), D^D</(«), (» # j), причем
DiD^/(«), DjD</(®) € C(®0). Тогда DiD^/(«o) = DjDi/(«o).
Теорема. Пусть f : G C Rn -> R, где G C Rn - открытое
множество. Пусть функция f(x) имеет в G всевозможные частные
производные до (т — 1)-ео порядка включительно и смешанные про-
изводные т-го порядка, причем все эти производные непрерывны в
G. Тогда значение т-й смешанной производной не зависит от того
порядка, в котором производятся последовательные дифференциро-
вания. (Теорему можно доказать по индукции.)
326
Пример функции, имеющей различные смешанные производные:
,, ч _ f ху(х2 - у2)/(хг + у2), х2 + у2 > О,
Кх’У>-\ 0, ®2 + у2 = 0,
_ tl ,	( у(х4-у4 + 4х3у2)/(х2 + у2)2, х2 + у2 > О,
0,	®г + у2 = 0,
откуда
D2D1/(0,0) = lira (Di/(0, у) - Dif (О,0))/у = -1,
n -1 ж(®4 _ у4 ~ ^у2)/^2 + у2)2, ®2 + у*> о,
Da/( > У) ।	q,	х2 _|_ у2 _ q
поэтому
DiD2/(0, 0) = lim(D'2/(®,0) -D2/(0,0))/® = 1,
>0
т.е.
D2Di/(0,0) = -1^1 = DiD2/(0, 0).
§ 2. Некоторые сведения из линейной алгебры
Определение. Отображение А : Rn —> R’" называется ли-
нейным (или гомоморфизмом, или морфизмом), если Vxi,x2 € R" и
Vai, «2 G R A(aixi + a2x2) = aiAxi + a2Ax2. В частности, АО = 0.
Пусть А : Rn —> R"‘ - линейное отображение, тогда матрицей
морфизма А (относительно стандартных базисов {в;} (j = 1,2,..., п)
в Rn и {е<} (4= 1,2,..., т) в R"*) называется mxn матрица (Ay) (г =
m
1,2,... , m; j = 1,2,..., n) такая, что Aej = 2 Aij*i (» = 1» 2,..., n),
»=1
n
У = Ая., yi = 22 AijXj (i = 1,2,...,tn), или в векторно-матричной
.	i-i
форме
Замечание. Между линейными отображениями А : Rn -> R’n и
tnxn матрицами (Ay) существует взаимно однозначное соответствие,
327
поэтому в дальнейшем линейное отображение и его матрицу будем
обозначать одной буквой А (А = (Ау)).
Определение. Пусть £(Rn, Rm) - множество всех линей-
ных отображений А : Rn —> Rm. Тогда £(Rn,Rm) становится ли-
нейным пространством, если положить: 1) \fA±,A2 Е £(Rn,Rw)
(Ai = А2) (Aix = А2х Vx Е Rw); Ю Vai,a2 Е R и VAX,A2 Е
£(Rn,Rm) (aiAi 4- а2А2)х = axAix 4- а2А2х Vx Е Rn, при этом
aiAi+a2A2 e£(Rn,Rm).
Замечание. Если Ах,А2 Е £(Rn,R,n) и Afc = (А^) (fc =
1,2) - матрицы, соответствующие морфизмам Ai и А2, то линейному
отображению a^Ai 4-а2А2 Е £(Rn, Rw) соответствует т х п матрица
(aiAt-p 4- а2А^). Таким образом, линейное пространство £(Rn, Rw)
изоморфно линейному пространству всех т х п матриц, т. е. имеет
размерность т • п.
Определение. Пусть А Е £(Rn, Rw) и В Е £(Rm, Rp).
Рассмотрим отображение В о А : R” —> Rp, определенное с помо-
щью равенства (В о А)х = В(Ах) Е Rp VxRn (AxR,n). Очевидно.
В о A G £(R'\RP)-
Замечание. Пусть А Е £(Rn, R,n) и А = (А,,) т х п матрица
морфизма А, а В Е £(RW, Rp) и В = (В*/) рхт матрица морфизма В.
Тогда отображению В о А Е £(Rn, Rp) соответствует р х п матрица
т
С = (С/Х1/), где С/Х1/ = 52 Atlz, т. е. для матриц А, В и С имеем
i=i
С = В • А.
Определение. Пусть A £ £(R”, R”‘), тогда положим
1ИН = sup (||Ax||m/||x||n) = sup ||Ax||,n = sup ||Ax||m.
IHI»>o	IMI»=i	1Н1п<1
Для доказательства написанных равенств заметим, что в силу ли-
нейности А и свойства нормы ||||,n Vx 0 О имеем (Ах)/||х||п =
^(х/Цх||п) = Ау, где ||у||п = ||х/||х||п||п = 1, т. е. ||А|| =
sup ||Ау||то. Далее, очевидно, sup ||Ax||m > sup ||Ах||,„ =
ll»ll»=i	IMIn<i	lkll»=i .
||А||, но в силу линейности А при 0 < ||х||„ < 1 имеем |(Ах||,„ =
||х||п • ||A(x/||x||n)||m < ||A(x/||x||n)||m = ||Ау||го < ||А|| (так как
||у||п = 1), откуда sup ||Ах||го = ||А||.
1Н1»<1
Замечание. Норма ||А|| зависит от выбора норм || ||п и || ||т
в линейных пространствах Rn и R"1.
Замечание. Пусть А Е £(Rn,Rw) и ||А|| < 4-оо. Тогда
||Ах||w < ||А|| • ||х||п Vx Е Rn. В самом деле, для нулевого вектора
х = 0 это очевидно, а при х / 0 имеем
(||Ах||,п/||х||п < sup (||Ax||,n/||x||n)) => (||Ах||„, <
' 1Н1п>о
328
< ||A||-||x||„VxeRn).
Замечание. Пусть A G £(R",Rm) и а > 0 таково, что
1|Лх||т < «IKIIn Vx G Rn. Тогда ||А|| < а.
В самом деле, при х 0 (||Ах||,п/||х||п <<*)=> (||А|| =
sup (11Ах||,п/1|х||п) < а).
^Теорема. Пусть A 6 £(R",Rm)- Тогда: 1) ||А|| < +оо;
2) ||АХ1 - Ах2||т < ||А|| • ||xi - х2||„ Vxi,x2 G Rn, так что лю-
бое линейное отображение А : Rw -+ Rm равномерно непрерывно на
Rn.
Доказательство. Морфизму A 6 £(Rn, R,n) соответству-
ет т х п матрица А = (A,j) (г = 1,2,... ,m;J = 1,2,... ,п), при-
чем если у = Ах Е Rm, х = (х’Ь... ,хп) Е R”, то у{ = AijXj
j=i
(J = 1,2,... ,т). Очевидно, координатные функции yi(x) непрерыв-
ны в Rn Уг. Как было замечено в §7 гл. 1 ч. III (и доказано для
норм || ||1 и ||||оо), любая норма в Rw (Rm) эквивалентна евклидо-
вой норме, так что (см. §9 гл. 1 ч. III) непрерывность отображения
А : Rn —> R’n эквивалентна непрерывности координатных функ-
ций yi(x) (г = 1,2,... ,т), поэтому для функции f(x) = Ах име-
ем f Е C(Rn). Но тогда в силу теоремы Вейерштрасса (об огра-
ниченности векторной функции непрерывной на компактном мно-
жестве) имеем ||А|| = sup ||Ax||m < 4-оо, поскольку множество
1М1п = 1
К = {х Е Rn|||x||n = 1} компактно в Rn (в любой норме). Итак,
при любом выборе норм || ||п и || ||тп имеем 1) ||А|| < +оо. Далее, в си-
лу линейности отображения А : Rn R”1 имеем 2) 11Axi - Ах21 |т =
||(A(xi -х2)||т < ||А|| • ||х1-х2((п Vxi,x2 Е Rn, откуда, в частности,
следует равномерная непрерывность морфизма А на Rn.
Следствие. Пусть нормы ||||п и || ||,п евклидовы и A G
/ т п \ 1/2
£(Rn, Rm). Тогда ||А|| < I £ 52 I > гДе (А*у) _ матрица мор-
физма А.
п
В самом деле, поскольку г/, = 52 Aijxj> то, используя неравенство
7=1
Коши-Буняковского и рассматривая евклидовы нормы || ||п и || ||w,
имеем
т п
.=1 j=i
329
т. е.
1/2
(т п \
.-iwinVxeR*
1=1 j=l J
откуда имеем
Теорема. Функция А -4 ]|А||, определенная VA G £(Rn, R"*),
есть норма в линейном пространстве £(R**,RTO).
Доказательство. По доказанному выше 0 < ||А|| =
sup | |Ах||,п < +оо. Тогда имеем:
11*11»=!
1) ||А|| > О VA G £(Rn,R"‘), (А = 0) => (Ах = 0 Vx G Rn) =>
(||А|| = 0), если же 11А|| = 0, то (||Ах||,„ < ||А|| • ||х||п, Vx G R”) =>
(||Ах||,п = 0 Vx G R") => (Ах = 0 Vx G R") => (А = 0) (т. е. (А = 0)
^(||А|| = 0));
2)(VA1,A2G£(Rn,Rm))=>(||A1 + A2||= sup ||(A1 + A2)x||,n =
11*11»=!
sup ||Aix+A2x||„, < sup (||Aix||rn + ||A2x||m) < sup ||Aix||w +
||®||n = l	||a?||n=l	||®||n = l
sup I|A2x||m = HAill + ||A2|I) => (||АХ + A2|| < ||AJ| + ||A2||):
ll*ll«=i
3) (Va € R, VA € £(Rn,R’n)) => (||a • A|| = sup ||(a • Ax||m =
= |a|. sup ||Ax||m = |a| • ||A||) => (||a • A|| = |a| • ||A||).
Il®ll»=i
Следствие. Нормированное линейное пространство
£(R”,Rm) становится метрическим пространством, если в нем
ввести метрику, индуцированную нормой ||А||, т. е. положить
p(Ai, А2) = ||Aj - А2|| VAi, А2 G £(R",R"‘).
Замечание. Пусть А 6 £(Rn, R”*) и В € £(R"‘, R₽). Тогда
BoAe£(R",R»>), ||В о А|| < ||В|| • ||А||.
В самом деле, (Vx € R") => (Ах € Rw) (В(Ах) € R₽), (||В о
А)х||р = ||В(Ах)11„ < ||£|| • ЦАх||,„ < ||В11 • ||А|| • ||х||„) => (||В о-А|| <
11ВЦ-ЦАЦ).
Пример. Рассмотрим пространства R, Rm и £(R, R”*). Далее
Vy € R”‘ рассмотрим отображение Ау : R -4 R’" такое, что Ау •
h = h • у V/i 6 R. Очевидно, Av € £(R, R’") есть морфизм c m x 1
(У1 \
! I и нормой ||A«|| = sup ||h • y||„, = sup (|4| 
' I	IM=i	W=i
Ут I
llxllm) = llyllm, так что ||Ay|| = ||y||m, при этом aiyi + a2y2 ->
aiAPi + а2АУз, т. e. указанное отображение у -> Av пространства
R"‘ в £(R, R"‘) линейно и сохраняет норму ||у||т = ||АУ[|. Обратно,
330
любому морфизму А 6 £(R, Rm) А : h -> Ah, где Ah 6 R"‘, можно
поставить d соответствие вектор А • 1 = у € R”* такой, что А : h ->
/i • (Л • 1) = • У- Это соответствие А -> у = А • 1 также линейно:
а1Л1+«2^2 -* «1У1+«2У2 = aiAi>l+ot2A2*l'. Тем самым установлен
1	и»
—>
изоморфизм линейных пространств Rm £ £(R,Rm).
Теорема. Пусть В € £(Rn, R'1) и ||В|| < 1. Тогда уравнение.
х _ Вх = у однозначно разрешимо Vy G R".
Доказательство. Рассмотрим полное метрическое про-
странство R = {R",p} с точками х € R" и метрикой p(xi,x2) =
цХ1 _ х2||п и введем отображение f : х -> Вх + у пространства R в
себя. Поскольку В G £(R", Rn), то Vxi,x2 € R” имеем оценку
p(/(xi),f(x2)) = ||В(Х1-Х2)||„ < ||В||- ||Х1-Х2||П =
= 1|Я|| • р(Х1,Х2),
но по условию ||В|| < 1, поэтому f есть сжимающее отображение
полного метрического пространства R в себя. В силу принципа сжи-
мающих отображений существует единственная неподвижная точка
х € R” отображения /, так что (/(х) = х) => (х - Вх = у) и при
этом х = lim xrn, где ®о = у, xm = /(xm-i) (m = 1,2,...), так что
т-
Х1 = у+Ву, х2 = у+Ву+В2у,..., х,„ = у+ £ Вку, X = у+ £ Вку,
k=l	fc=l
m	\
у + 22 Д*У ) II» = 0. Заметим, что в
fc=i	/
силу следствия к теореме о принципе сжимающих отображений имеем
оценку скорости сходимости (при а = ||В|| < 1 и хо = у, х2 = у + Ву,
Il-ВуНп = p(xo,xi)) р(х,х,п) = Цх-Xmlln < ||В||’"р(Хо,Х1)/(1-||В||) <
1|в||",+11|у||п/(1 - ||В||).
Следствие (лемма Неймана). Пусть В € £(R", R") и ||В|| <
1. Тогда I - В € £(Rn,R’‘) является биекцией R" на R", причем
обратная биекция (/ - B)~l € £(Rn, R") такова, что
+(Х)
(I - В)-1 = I + £ Вк и I|(Г - В)-111 < 1/(1 - ||В11).
к=1
Доказательство. В силу доказанной выше однозначной
разрешимости уравнения х - Вх = у Vy € R” вытекает, что ото-
бражение / — В : х —> у = х — Вх есть биекция и поэтому сущест-
вует обратная биекция (/ - В)-1 : у —> х = (I — В)“1у, являющаяся
гомоморфизмом из £(R",Rn), как показано в линейной алгебре. (В
самом деле, пусть С € £(Rn,Rn) есть линейная биекция, так что
“У1>У2 9 Rn Эх1,х2 6 Rn, для которых Cxi = ух, Сх3 = у2 или
lim p(x,xm) = lim ||х-
331
xi = С~гу1} x2 = С-1у2 и тогда C(«iXi 4- «2X2) = «iCxi 4- а2Сх2 =
«1У1 4- «2У2, T. e. C-1(aiyi 4- «2Уг) = <*1*1 4- «2X2, откуда имеем
C'"1(aiyi 4-а2У2) = «1С'"1У1 4-О!2С_1у2, т. е. С"1 Е £(Rn,Rn). В
силу единственности неподвижной точки имеем представление
х= lim х,„ = lim (у + 52-В‘у | d= у + У2вку =
in—>4-оо	т—>4-оо	\	*—*	/	'
\	к=1	/	к-1
(4-оо \
/ + £в‘ у,
Л = 1	/
т. е. х = (I—В)-1у d= (l + 52 Я*4) У? так что (I—В)-1 d=
\	к=1	/	к = 1
Напомним, что х = liin хт означает lim ||х —xw||n = 0, причем,
как показано ранее, ||x-xm||n < ||B||m+1 • ||у||п/(1 - ||В||). Но
т	т
||х,„||„ = ||у + £в‘у||» < ПуII» + ЕI 1^*у11» <
к=1	к=1
(т	\
1 + LllBll* ||y||n<||y||n/(l-||B||),
k=l	/
Т. е. ||x„i||„ < ||y||n/(l - ll-SID- Поскольку lim хто = x, то в силу
m—>4-оо
непрерывности нормы || ||п в R”, переходя к пределу при т -> 4-оо,
получаем оценку ||х||п < ||у1|„/(1 - | |В| |), т. е.
||(/- В)"1?)!» < ||у||„/(1 - ||B||)Vy € Rn,
откуда имеем оценку ||(-Г - •В)-1|| < 1/(1 - ||В||). Заметим, что фор-
мально эта оценка может быть получена из формального представле-
4-оо
ния (I — В)-1 = I 4- 52 дающего
fc=i
4-оо	4-оо
||(Z - В)-111 = ||/+ £в‘ц < 1 + £ ||В||‘ = 1/(1 -1 |В||).
fc=l	к-1
Теорема (о линейном возмущении). Пусть А, С G £(R”, Rn),
причем ЗА-1 Е £(Rn,Rn) и ||А-1|| < а. Пусть ||А — С|| < где
а(3 < 1. Тогда ЗС”1 Е £(Rn, Rn), причем |It?-1!| < а/(1 - ар).
Доказательство. Заметим, что А~ХС = I — (I — А-1С) =
I - А'1(А - С). Но ПА-1^ - С)|| < 11А"111 • 11А - С|| < ар < 1, так
что, полагая D = А-1 С, в силу леммы Неймана видим, что ЗВ”1 Е
£(R\Rn), причем ||2>-1||< 1/( 1 — 11А~х(А—С7)11) < 1/(1-а/?). Далее,
332
(p-Pp = /) => ('D~1A~1C = /), т. e. ЗС"1 =	e £(Rn,Rn),
причем
|\C-41 = ||2>“1A-1|| < ||T>“1||. 11 A-111 < a/(l - a/3).
Пусть G C Rm - открытое множество и V® E G C Rm опреде-
лен морфизм A(x) E £(Rn,Rn), тогда отображение x Л(®) есть
отображение G C Rm —> £(Rn, Rn).
Теорема (о нелинейном возмущении). Пусть G C Rm - откры-
тое множество и xq Е G - точка. Пусть А : G С Rm -> £(Rn, Rw)
(х А(ж)), где А(х) Е £(Rn,Rn) и А Е C(xq), причем для морфизма
А(«о) существует обратный морфизм А“х(®о) 6 £(Rn,Rn). Тогда
существуют шар 1Щ(®о) С G С Rw и постоянная у > 0 такие,
что Vx Е Ш^(®о) С G С Rm морфизм А(х) Е £(Rn,Rn) имеет об-
ратный А-1(х) Е £(Rn,Rn), причем ||А“’1(х)|| < у и отображение
А-1 : Ш^(жо) С G —> £(Rn, Rn) непрерывно в точке xq Е G.
Доказательство. Положим а = 11 А~ 1(хо) 11 и выберем
О < fl < 1/а. Поскольку А Е С(®о)> то для /3 > 0 существует шар
1Щ(яо) С G такой, что ||А(ж0) - А(®)|| < /3 V® Е ШД®о) С G, но
поскольку 0 < a fl < 1, то в силу теоремы о линейном возмущении
(где А = Л(®о), С = А(х)) видим, что морфизм А(®) Е £(Rn,Rw)
есть биекция и для обратной биекции А“х(®) Е £(Rn, Rn) имеет место
оценка ||А“Х(®)|| < а/(1 - afl) = 7. Далее, V® Е Ш^(®0) С G имеем
1|А-1(хо) -	= ||А"1(х0)(А(х) - А(хо))А-1 (х)|| <
< ||А-1(х0)|| • ||А-1(х)|| • ||А(х) - А(х0)|| < а • 7 • ||А(х) - А(х0)||.
Но А Е С(®о), поэтому Ve > 0 З61 Е (0,6) такое, что ||А(®) — А(®о)|| <
е/ау Vx Е Ш^(®0), а потому ||А“х(®0) - А“х(®)|| < е, т. е. А-1 Е
С(х0).
§ 3. Понятие дифференцируемости отображения
из Rn в Rm
Пусть G С Rn - открытое множество и а Е G. Тогда существует
окрестность U(а) С G. Пусть / : G С R" -> Rm. Вспомним определе-
ние дифференцируемости в точке а Е G С R для числовой функции
/(«) одного действительного переменного.
Старое определение. Числовая функция f(x), опре-
деленная на G С R, называется дифференцируемой в точке а Е G,
если существуют окрестность U(a) С G и число А Е R такие, что
(Va + Л G U(a)) => (/(х + А) = /(а) + АА + г(А)|А|, где r(h) = о(1)
(Л -> 0)), при этом число A G R определялась единственным обра-
зом и называлось производной функции f в точке а : А = Вводя
333
линейное отображение А G £(R1,R1) по формуле А : h f'(a) • h,
можно дать эквивалентное определение дифференцируемости функ-
ции f в точке а.
Новое определение. Функция f : G С R -4 R называется
дифференцируемой в точке а Е G, если существуют окрестность
U(а) С G и морфизм A G £(RX, R1) такие, что Va 4- h 6 U(a) имеем
f(a 4- h) = /(a) + Ah 4- r(h)|h|, где lim r(h) = 0 (m. e. r(h) = o(l)
|Л|->0
(h —> 0)), при этом морфизм A : h —> f (a) • h определяется единст-
венным образом и его естественно назвать производной (или диф-
ференциалом) функции f(x) в точке а € G. Этот морфизм также
обозначается символом /'(а) или df(a).
В конце §2 этой главы был доказан изоморфизм пространств R1 и
£(RX, R1), поэтому производную функции f в точке а, т. е. f(a), мож-
но считать как числом из R (старое определение), так и морфизмом
df(a) : h -4 /'(a) • h из £(R\ Rx) (новое определение).
Рассмотрим теперь (векторную) функцию одного действительного
переменного f : G С R -4 Rm, тогда f(®) = (Л(®),... , /т(®)). Ранее
мы по определению положили /'(a) = lim(f(а + h) — f (а))/Л, так что
Л—>0
Г(а) = (Л(а),...,/иа))или
Старое определение. (Векторная) функция f : G С
R —> Rm называется дифференцируемой в точке a G G С R, если в а
дифференцируемы все координатные функции fi(x) (г = 1,2,... , т),
т. е. если существует вектор А = (Ai,... ,Am) € Rm и окрест-
ность U(а) С G С R такие, что Va 4- h € U(a) имеем fi (a 4- Л) =
/i(a) 4- Aih 4- п(Л)|Л| (i = 1,2,... ,m), где limrt(A) или в векторной
форме f(a 4- h) = f(a) 4- A • h 4- r(h)|Л|, где r(h) = (ri(h),... , rm(h)
и lim ||г(Л)||т = 0. Вектор A € Rw определяется при этом един-
|Л|—>0
ственным образом и называется производной (векторной) функции f
в точке а : А = fz(a) = (/{(a),... ,/,'n(a)) € Rw. Если ввести мор-
физм А € £(R, Rm) по формуле А : h -4 Г(а)Л, то можно дать иное
(эквивалентное) определение.
Новое определение. (Векторная) функцияf : G С R-4 Rrn
называется дифференцируемой в точке а € G С R, если существу-
ют морфизм A G £(R, Rm) и окрестность U(a) С G С R такие, что
Va -|- Л € C7(a) f(a 4- h) = f(a) + A - h + г (Л)\h\, где lim | |r(h) | |w = О,
|Д|->0
при этом морфизм А : h fz(a) • h (определяемый единственным
образом), называется производной (или дифференциалом) функции f
в точке а Е G и обозначается символом f'(a) (или df(a)).
и*
—>•
В силу доказанного в §2 изоморфизма Rm £(R, Rm) производ-
ную fz(a) (векторной) функции f в точке а Е G можно считать как
334
вектором из Rm (старое определение), так и морфизмом df(a) : h —>
f'(a) . h из пространства £(R, Rm) (новое определение). В обоих слу-
чаях Rm = R и Rm (тп > 2) пространства Rm и £(R, Rm) изоморфны
и, в частности, имеют одну размерность тп.
Перейдем теперь к определению понятия дифференцируемости
отображения f : G С Rn Rm в точке а 6 G. В этом случае (при
п > 2) размерность £(Rn,Rm) будет тп • п, не равной размерности
Rw. Напомним, что пространство Rn является как векторным про-
п
странством векторов х = xjeh гДе {еЛ (i = 1,2,... ,п) - кано-
>=1
нический базис Rn, так и точечным аффинным пространством точек
х = (xi,... ,®п) (с присоединенным векторным пространством Rn),
но тогда имеет смысл запись а + h = Ъ для точки Ъ 6 Rn, являющейся
концом вектора h = b — а Е R” с началом в точке а и концом в точке
6.
Определение. Отображение f : G С Rn -> Rm диф-
ференцируемо в точке а Е G, если существуют линейное отобра-
жение А € £(Rn,Rm) и окрестность U(a) С G С Rn такие, что
f(a+h) = /(a)+Ah+r(h)||h||n, Va+h е U(a), где lim ||r(h)||ro = 0,
ll*l|n“*O
при этом морфизм A € £(Rn,R,n) называют производной (или диф-
ференциалом) отображения f в точке atG. Запись: А = D/(а) или
А = df(a). Если отображение f дифференцируемо в точке а € G, то
будем писать f € ©(a).
□	\ ж /и\ f(a +h)-f(a) - Ah
Замечание. (Векторная) функцияr(h) = —-----------liTTi ------
определена единственным образом при h 0. Будем считать, что
г 6 С(0), т. е. положим г(0) = 0. Подчеркнем, что вектор h € Rn и
для точки а + h € 17(a) С G вектор f(a + h) — f(a) € Rm. Поскольку
A e £(Rn, Rm), to Ah есть вектор из Rm так, что для любой точки
a + h£t7(a) С G С Rw вектор f (a + h) — f (a) — Ah € Rm. Дифферен-
цируемость отображения f в точке a € G C Rn можно истолковать
так: при фиксированной точке а 6 G и малом (по норме || ||т) векторе
h Е Rn вектор разности Af (a) = f (а + h) — f (а) 6 RTn приближенно
равен вектору D/(a)h (т. е. значению морфизма А = D/(a) = df(a) на
векторе h Е Rw).
Замечание. (/€ ©(a)) <=> (выполнено одно из двух эквива-
лентных утверждений:
iJjm п НЛа+ h) - f(a) - Ahm/||h||„ = 0;
||Л| I n—>0
2)	существует окрестность U(a) C G C Rn такая, что в 17(a) имеет
место представление
/(a + h) = /(а) + Ah + о(||h||n)(h -+ 0)).
Определение. Пусть f : G С R” Rm, где С С Rn -
335
открытое множество. Скажем, что функция f дифференцируема
на G (запись: f Е 7>(G)), если / Е Z>(x) Vx Е G.
Теорема (о единственности производной). Пусть G С Rn -
открытое множество, a Е G и f : G С Rn —> Rm. Если f Е П(а),
то линейное отображение А = Df(a) Е £(Rn,Rw) из определения
производной единственно.
Доказательство. Допустим, что 3Ai, А2 Е £(Rn, Rm)
такое, что Va 4- h Е U(a) С G имеет место представление /(а 4- h) =
/(а) 4- A,h 4- r,(h)||h||n, где Hm ||r,(h)||m = 0 (г = 1,2). Пусть В =
Л1 — А2 Е £(Rn,Rm). Тогда для любого вектора X Е Rn (X 0),
полагая (при i Е R) h = t • X, видим, что для достаточно малых
i / 0 a4t- X Е (7(a), поэтому ||В(/ • X) | |m = | |Ai(t • X) — A2(tf •
X)||w = 11(f(a + t • X) - f(a) - n(* • X) • \\t • X||n) - (f(a 4-1- X) -
f(a) - r2(* • X)\\t • X||n)I|m = H • I|X||n • I|n(t • X) - r2(* • X)I|m, откуда
||B(t • X) 11 ,n/(|i I • ||X| |„) = ||BX||m/||X||n = I|n(t • X) - r2(t • X) I |ra. Ho
(limrj(t • X) = 0 (i = 1,2)) => (| |BX| |TO = 0
VX e R") => (I|B|| = 0) => (B = Ai - A2 = 0) => (ai = A2).
Следствие. Если f : G C R" Rm, a € G и f G D(a),
то существует окрестность 17(a) C G такая, что Va: € U(a) имеем
/(a:) = /(a)+D/(a)(x-а)+г(х-а)-||х-а||п, где lim ||r(x-a)||m = 0
х—>a
(x — а есть вектор с началом в точке а и концом в точке х).
П р и м е р ы. 1) Пусть f(x) = с = {с} Е Rm V® Е G С Rn есть
сужение на G постоянного отображения Rn на Rm. Тогда / Е B(G)
и De = 0. В самом деле, (V®,® 4- h Е G) => (/(х 4- h) = f(x) = с),
т. е. f (x4-h) = /(х) Ч-oh, и в силу единственности производной имеем
De = 0 Е £(Rn, Rm), т. е. De = 0.
2)	Пусть А Е £(Rn, Rm) nf:x—>O4-A(J2 xjej I > гДе x =
V=1	/
(xi,... , xn) E Rn. Тогда Df (ж) = А. В самом деле, Vx 4-h E Rw имеем
(f (x 4- h) = 0 4- f (x) 4- Ah) => (Df (x) = A Vx E Rn).
3)	Пусть A E £(Rn,Rm) и/:х->Ь4-А1^3 xjej L гДе x =
V=1	/
(xi,... , xn) E R”, 6 E Rm. Тогда D/(®) = A E £(Rn, Rm). В самом
деле, (Vx 4- h E Rn) => (/(x + h) = /(x) 4- Ah) => (3D/(x) = A).
4)	Пусть pi : Rn -> R есть i-я проекция, так что для х =
(xi,... ,xn) Е R”, Pi* = Xi, тогда Dpi = Pi Е £(Rn,R). (Доказать
самим.)
Теорема (о непрерывности дифференцируемой функции).
Пусть f : U(a) С Rn Rm и f Е Р(а). Тогда имеем f Е С(а)
и, более точно, 3£ > 0 и с > 0 такие, что Va 4- h Е 1Щ (а) С U(а)
336
||f(a + h) — f(a)||m < c||h||n (таким образом, если f E mo f
непрерывна no Липшицу в точке a).
Доказательство. Поскольку / Е 3?(а), то существует мор-
физм D/(a) G £(Rn, Rm) такой, что Va 4- h Е U(a) С Rn имеет место
представление
f(a + h) - f(а) = D/(a)h + r(h) • ||h||n,
где lim | |r(h) | |w = 0, причем, как показано в §2, для морфизма D/(a)
h—►О
имеем ||D/(a)|| < +оо. Но тогда Va 4- h Е 17(a) имеем оценку ||f(a +
h) -f(a)||w < (||D/(a)11 +1|r(h)||w) • ||h||n. Поскольку lim ||r(h)||w = 0,
to Wo > 0 3(5 > 0 такое, что ||r(h)||w < го V||h||„ < <5, и тогда,
полагая с = ||D/(a)|| 4- во, имеем оценку ||f(a 4- h) - f(a)||w < c||h||n
Va 4- h E ПЫа) C 17(a) и, в частности, f E C(a).
Теорема (о существовании производной вдоль любого вектора
у дифференцируемой вектор-функции). Пусть f : 17(a) С R" -+ R”‘
п
и 1 = ^2 IjCj - вектор из Rn. Пусть f Е 32(a), тогда существует
i=i
частная производная (векторной) функции f в точке а вдоль век-
тора 1, причем Djf(a) = Df(a)l.
Доказательство. Поскольку f Е 32(a), то, полагая h =
t • 1 Е R” при достаточно малом t / 0, имеем а 4-1 • 1 Е Ща) и тогда
ввиду f Е 32(a) имеем представление f(a 4-1 • I) — f(a) =	• 1) 4-
Г (< • 1) • 11* • 1| In = t(Df (a)l + (|t|/t) • r(t • 1) • 111| |n), (f (a + «•!)- f (a))/t =
Df|(a)l+ (|i|/<) -r(t -1) • ||1||„, откуда в силу условий ||t|//| = 1 (t / 0),
lim r(t • 1) = 0 видим, что
t->0
31im(f(a4-* - I) —	= D/(a)l,
t. e. 3Dif(a) = Df(a)l.
Следствие (необходимое условие дифференцируемости
вектор-функции в точке). Пусть f : 17(a) С Rw -4 Rw. Если f Е 32(a),
то для функции f в точке а существуют все j-e частные производные
D>f(a) = D/(a)ei = £^e<.
Теорема (о представлении производной дифференцируемой
функции в координатной форме). Пусть f : U(a) С Rn —> Rw и
f Е 32(ж) (f(x) = (/1(ж),... , /,п(ж))). Тогда производной D/(a) Е
£(Rn, Rrn) как морфизму соответствует в качестве матрицы мат-
рица Якоби
/ дЩа)	дМа) \
dfm(a)	dfm (a)
\ dxi ’ * ’ dxn /
12 Зак. 860
337
Доказательство. Пусть {«у} (j — 1,2,..., п) - канони-
ческий базис в Rn и {ej} (i = 1,2,..., m) - канонический базис в Rm.
Поскольку / € то существует морфизм D/(e) € £(Rn,Rm).
Пусть (Ац) (i = 1,2,j = 1,2,...,n) m x n матрица мор-
m
физма D/(a). Тогда из линейной алгебры имеем D/(a)ej =
1 = 1
(i = 1,2,..., m). Но в силу необходимого условия дифференцируемос-
ти функции в точке а существуют частные производные Dj/(a) =
D/(a)ej (j = 1,2,..., п), так что в координатной форме имеем
DiA‘») = E^e<0, = 1.2.........п),
поэтому
	„)К
\i=l	1=1	3./
=	= 1» 2,..., m; j = 1,2,... , п)^ .
В силу теоремы о единственности производной у дифференцируе-
мого отображения имеем
Определение. Пусть f : 17(a) С Rn R™ и /(®) =
(Л(®)} • • • 1 fm (®)). Тогда f € если е окрестности U(a) имеет
место представление
fi(a + h) = /Да) +	D/M<»)fy+
;=i
+о(||h||n)(h -> 0)(i = 1,2,..., m); h =
j=i
В частности, для числовой функции
/ : U(a) С Rn -► R
утверждение f € D(a) означает, что в 17(a) С Rn имеет место пред-
ставление
+Л1,...,an + hn) = /(ai,..., an) + У?.Ч-----~hj+
j=i
+o(||h||n)(h-> 0).
338
Теорема (критерий дифференцируемости (векторной) функции
в точке). Пусть f : 17(a) С Rn -» Rm, f(s) = £ /•(»)«{> Тогда
1=1
(f6D(a))^(AeP(a)(* = l,2...m)).
Следствие (выражение производной вдоль вектора через
п
частные производные). Пусть f : 17(a) С Rn -> R’n и 1 = £ hej “
i=i
вектор из Rn. Пусть f G D(a) (гдеГ(ж) = £ Л(®)в< )• Тогда
Dif (a) = D/(a)l = D/(a) | j = X?iDf(a)eJ =
V=1	/
m / n
i=l
т. e.
Di/i(a) —	Dj/»(a)/j (i — 1,2,..., m).
i=i
В частности, для числовой функции f : tf (a) C Rn -> R и орта 1q =
(cog ai,... , cosan) имеем (при f G l>(a))
5/(a) A df(a)
Замечание. Пусть / : U(a) C Rn -> R и f G C(U’(a)). Тогда из
существования даже всех частных производных (j = 1,2,..., п)
(п > 2)> вообще говоря, не следует, что f G Т>(а).
Пример (непрерывной функции, имеющей все частные произ-
водные в точке, но не дифференцируемой в точке). Пусть /(®,у) =
И® • J/I, (®> У) € R’, ро = (0,0), р = (Д®, Ду), тогда f G C(R2) и
^/(0,0) = lim (/(Д®, 0) - /(0,0))/Д® = 0,
Ду)  /(0’О))/Ду = 01
Покажем, что /?1>(ро). Допустим от противного, что / G Р(ро)> тог-
да из единственности производной имеем представление Д/(ро) =
12*
339
/(Дх, Др)-/(О,О) = 0-Дх + 0-Др4-о(р) (р = ((Дх)2 + (Др)2)1/2 -> 0).
Но Д/(ро) = |Дх • Др|1/2 # О(р) (р -> 0), поскольку при Ду = Д®,
р = х/2Д® и |Д® • Ду|1^2 = |Д®| = р/\/2, т. е.
(|Ах • Аз/р/2 о(р)(р _> о)) => (/ё©(ро)).
Теорема (достаточное условие дифференцируемости функции
в точке). Пусть f : G С Rn -> Rw, где G - открытое множество и
а Е G. Пусть существует окрестность U(a)cG такая, что Ух Е
17(a) 3Dj/i(x) (i = 1,2,	= 1,2,...,п). Тогда (Djfi E C(a)
=> (f 6 ®(a)).
Доказательство. Поскольку (/ E 2>(a)) <=> (fi E P(a),
(i = 1,2, ...,m)), то достаточно доказать, что (Dj/« e C(a) (j =
1, 2,... ,n)) => (fi E 2>(a) Vi). Без ограничения общности будем счи-
тать, что т = 1 и п = 2, т. е. положим fi(x,y) = f(x,y). Пусть
Ро = (®о,Уо) и р = (х,у) Е U(ро) С G С R2, причем Vp Е U(p0)
^Djf(p) и Dj/ Е C(pq) (j = 1,2). Тогда Уе > 0 3<5(г) > 0 такое, что
\Djf(p) - Djf(po)\ < е/2 Vp Е 1Щ(ро) С U(po) С G, но Д/(р0) =
Л®, у) - /(®о, Уо) = (/(х, у) - f(x, Уо)) + (/(х, уо) - /(х0, Ро)). Рассмот-
рим при фиксированном уо функцию <p(z) = f(z, у0) на отрезке [®о, х].
Поскольку TPp(z) = Di/(^, Уо) Vz Е [х0, х], т. е. tp Е 2>([®о, х]) и, в част-
ности, <р Е С([®о, х]), поэтому к функции ip(z) на отрезке [®о, х] приме-
нима теорема Лагранжа о конечных приращениях. Аналогично, пола-
гая ^(z) = /(®, z), видим, что из существования Вг/(р) Vp Е U(po) вы-
текает, что Е 1>([уо, у]), V' Е С([ро,р]) и Di>(z) = Вг/(х, z), так что
и к функции tl>(z) на отрезке [уо, у] применима теорема Лагранжа о ко-
нечных приращениях. Но тогда имеем представление Д/(ро) = (у—уо)
D2/(х, Ро 4-191 (р - ро)) 4- (х — xo)Di/(xo 4- д2(х - х0), уо), 0 < 19, < 1
(i = 1,2).
Положим Pl = (х,ро4-#1(р-ро)),Р2 = (хо4-^г(х-хо),Ро) 6 1Щ(ро),
тогда из неравенства p(po,Pj) < 6 (j = 1,2) в силу выбора (5(г) > 0
имеем |Di/(Po) - Di/(p2)| < е/2, |Пг/(Ро) - Пг/(Р1)| < е/2, т. е.
|Д/(Ро) - (Di/(po)(x - хо) 4- Пг/(ро)(р - Ро)| < е(|® - х0|4- •
4-|р - Ро|)/2 < ep(p,po)Vp Е ПЬ(Ро) => (/ Е 2>(ро))«
Теорема Юнга (достаточное условие равенства вторых
смешанных частных производных у функции многих переменных).
Пусть f : U(a) С Rn -> R, причем Vx Е U(a) существует Di/(x)
и Dif 6 P(a) (i = 1,2, ...,n). Тогда yi,j = 1,2, ...,n 3D«Dy/(a) и
DiDjf(a) = DjDif(a) при i / j.
Доказательство. Без ограничения общности будем
считать п = 2 и положим ро = (хо,ро), Р = (х,р) Е U(p), так что
Ур G U(ро) 3Dj(p) и Dif 6 D(po) (i = 1,2). Заметим сначала, что
340
= 1,2,... ,n 3D<Dj/(po)- Пусть h таково, что (x0 + A,y0 + A),
(хо+^,уо), (®o,J/o+A) G Щро) С R2. Тогда при А® = Ду = h положим
А = f(xo + h, уо + А) - f(x0 + h, уо) - f(x0, уо + А) + f(x0, Уо)- Вводя
обозначения х = ®о+Д®, У = Уо+Ду, Д»/(®о, Уо) = f(x, yo)~f(xo, уо),
&я/(хо,Уо) = f(xo,y)-f(xo,yo), имеем А = Д9Дх/(ро) = AxAj,/(po).
Пусть <р(х0) = f (xo,yo + h) - f(xo,yo) = Ayf(xo,yo)- Тогда A =
AxA,,f(po) = Д«Н®о) = <fi(xo + h) — y>(xo)> По теореме Лагранжа о
конечных приращениях i G (0,1) такое, что у>(зсо + А) - Н®о) =
D^>(®o + ^1А) • А. Но Dy>(®o + $1А) = Di/(®o + $iA, уо + А) — Di/(®o +
i?iA, уо)-Таким образом А = (Di/(®o+^iA, !fo+A)-Di/(®o+^iA, yo)h).
Но
(Di/ 6 1>(ро)) =>• (Di/(®o + $1А, уо + A) = Di/(a;o) S/o)+
+DiDi/(®o, Уо) -191А + D2Dif(®o,!/o) • A + oi(|A|)(A —> 0))
и
(Dif (®o + 1A, yo) = Dif(®o> Уо) + DiDi/(x0, yo) • #iA+
+o2(|A|)(A-> 0)),
поэтому
A = D2Dif(a;o, lfo)A2 4- (oi(|A|) + o2(|A|)) • A(A -> 0)
или
Д*Д»/(Ро) = D2Di/(®o, Уо)А2 + o3(A2)(A -> 0).
Аналогичным образом полагая А = AvAx/(po) = V’O/o + A) — ^(уо),
где У>(у0) = f (®о + А, уо) - f(x0, у0), имеем
А = DiD2/(®o, Уо)А2 + о4(А2)(А —> 0),
т. е. при А 0 0
(DiD2/(®o>1/o)A2 +оз(А2)) = D2Di/(a;o,!/o)A2+
+о<(А2)(А —» 0)) => (DiD2/(®o> Уо) = D2Di/(®0) Уо))-
Определение. Отображение f : G С Rn -> Rm, где G -
открытое множество, называется непрерывно дифференцируемым
на G с Rn (запись: f G C<X>(G)), если (при f(x) = (fi(x),, fm(x)),
VxeG 3Dj/,(a:) (i = 1,2,... ,m;y = 1,2,... ,n) u Djfi G C(G)
Можно дать иное, не связанное с координатными функциями опре-
деление.
Определение. Пусть f : G С Rn —> Rra, где G - открытое
множество. Пусть f G H(G). Тогда отображение f называется не-
прерывно дифференцируемым на открытом множестве G С Rn, ес-
ли отображение D/ : G С Rn -> £(Rn,Rm) (D/ : х -> Df(x)) есть
341
непрерывное отображение множества G С Rn в нормированное про-
странство £(Rn,Rm). Итак, f € C^(G), если Че > 0 и У®о € G
3<У(е, ®о) > О такое, что, ||D/(®) - D/(®o)|| < е Чх € Шо(®о) С G.
Теорема (критерий непрерывной дифференцируемости функ-
ции на открытом множестве). Пусть f : G С Rn -> Rw, где G -
открытое множество. Тогда (f 6 CW((?)) <=> (выполнены два усло-
вия:
1) Чх 6 G3Dj/i (®) (i = 1,2,... , тп; j = 1,2,... , п);
2) Djfi 6 C(G) (i = 1,2,... ,m; j = 1,2,... ,п).
Доказательство. Необходимость. Если f €
(в смысле второго определения), то Чх € G существует морфизм
D/(®) € £(Rn,Rw) с матрицей Якоби (Dj/i(®)) (i = 1,	=
1,... , п) при канонических базисах {ej} (j = 1,2,..., п) в Rn и {o'-}
(i = 1,2,..., m) в Rw. Тогда в силу правила умножения матриц име-
m
ем D/(®)ey = 2 D//<(x)e{, откуда Vi, J (i = 1,2,... ,m; j = 1,2,... ,п)
1=1
и V®, ®0 € G С R" получаем оцевки
|Djfi(®) - Dj fi(®о)| < ||D/(®)ej - D/(®o)eJ|m = ||(D/(®)—
-D/(®o))e, ||TO < ||D/(®) - D/(xo)|| • ||е^||Л = ||D/(®) - D/(xo)||
(поскольку ||ej||n = 1 в евклидовой ворме || ||п). Но тогда
(/ 6 C^(G)) =► (D/ € C(G)) => (D/ € C(«o)) =►
=► Qis l|D/(x)D/(xo)|| = 0) => ( lim |Dj/,(®)-
-Dj/<(®o)| = OVi, j) => (Djfi € C(®o)V®o € G,Vt, j) =>
=* (Djfi e C(G), i = 1,2,... , m; j = 1,2,... , n).
Достаточность. Пусть Djfi € C(G) Vi,j, тогда, используя доста-
точное условие дифференцируемости функции в точке, имеем (fi е
P(G) Vi) => (f € Ь(С)). Далее, для матрицы Якоби (Djfi(x)) (г =
1,2,... ,m;j’ = 1,2, ...,п) производной Df(x) € U(R",Rm) имеем
оценку
С\ 1/2
ЕЕ(М(«)-М(®о))’|	V®,®o€G,
i=ij=i	/
из которой Vi, j имеем
(Djfi е C(G)) =► (Djfi e c(®o)) => (lim |D,/,(®)-
X—>Xo
—Dj/«(®o)| = 0; i = 1,2,... ,m-,j = 1,2,... ,n)
342
=> ( lim ||D/(x) - D/(®o)11 = 0) =>
T—
(D/ € C(x0)Vx0 € (?) => (/ € C^(G)).
Пусть f : U(a) C Rn -> R и / 6 ®(a). Тогда, пользуясь общим
определением дифференцируемости отображения f из Rn в R, видим,
что существует морфизм df (a) G £(Rn, R), который мы назвали диф-
ференциалом функции f в точке а, такой, что df(a) : Rn -> R, и для
любого вектора h = hjCj такого, что а + h € 17(a) имеет место
i=i
представление
f(a + h) = f(a) + fd(a)h + o(||h||n)(h -4 0).
Морфизм df(a) € £(R", R) есть линейная форма (линейная функция),
определенная в линейном пространстве Rn, а число
п
#(а)Ь = £п//(а)Л€Л
>1
есть значение линейной формы на векторе h = 52	€ R". Таким
i=i
образом, дифференциал df(a) € £(Rn, R) функции f в точке а есть не
число, а символ линейной формы.
Рассмотрим, в частности, линейную форму pj € £(Rn,R) (j-ю
n
проекцию) такую, что pjx = Xj Vx = 52 Тогда в силу ранее
i=i
доказанного видим, что pj € t>(R") и dpj = pj, поэтому имеем
D,P'(X)_ dxi '3~ t
Следуя классическим традициям записи, положим dpj = dxj Vj. Тогда
дифференциал (независимого переменного xj) dxj : Rn -> R есть не
число, а линейная форма dxj € £(R", R) такая, что
(п	\
Vh = £ е Rn I => (dxj(h) = dpj(h) = pj(h) = hi) =►
3=1	/
=> (dxj(h) = hj 0 = 1,2,...,n)).
Но тогда отмеченное ранее равенство df(a)h = £ &jf(a)hj дает
з=1
возможность записать дифференциал df(a) как линейную форму из
343
n
£(R”,R) в виде df(a) = £ Djf(a)dxj. Итак, первый дифференциал
3=1
п
функции f в точке а : df(a) = 52	есть не число> а символ
5=1
линейной формы, определенной на векторах h 6 Rn, причем для ее
п
значения на любом векторе h = 52 hjej € Rn имеем
5=1
п	п
df(a)h = £>/(а)<МЬ) =
5=1	5=1
Вспоминая основное представление для функции / Е D(a) в окрест-
ности U (а) Е Rn:
п
bf(a) = f(a + h) - f(a) = £>/(а)Л; + o(||h||n)(h -> 0),
5=1
видим, что значение дифференциала df(a) на векторе h Е Rn df(a)h =
п
52 Dj/(a)/iy есть главная (при df (а)	0) линейная часть приращения
5=1
функции f(x) в точке а, соответствующая приращению h Е Rn. Итак,
для f Е Р(а) в окрестности 17(a) С Rn имеем представление Дд/(а) -
d/(a)h = o(||h||n) (h 0).
Определение. Пусть f : 17(a) С R" 4 Rm, f E C(l7(a)),
f E ©(а) и Г = {(x,y) E Rn+m|z E U(a)y = f(x) E R’n} C
Rn+m есть график отображения f. Пусть b = /(a) E Rm. Тог-
да касательной п-мерной плоскостью в Rn+m к графику Г в точке
Е Г называется аффинное подпространство с уравнением
у = /(а) 4- D/(a)(x — а) или в координатной форме
Vi = /.-(а) + 22- aj) (» = 1,2,...,m).
3=1
Пример. Пусть Г = {(ж,2/, z) G R3|(x,!/) е U((x0,y0)),
= fx,y)} - график функции f : U((xo,yo)) С R2 -> R1 и / G
®((®Ot!/o))> f € C(U). Тогда уравнение касательной плоскости к Г
в точке (®0, Уо, f(xo, уо)) G Г имеет вид z = £(®, у), где
У) = /(®о, Уо) +	Уо)(х - х0) +	Уо)(у - Уо)-
Далее, поскольку f G Уо)), то в окрестности U((xq, уо)) С R2
имеем f(x, у) - Цх,у) = о(р(р,ро)) (р = (®,у) -> Ро = (»о,Уо)), это
344
представление является геометрической характеристикой касатель-
ной плоскости. Заметим, что частная производная — f(xQ,yo) есть
их
угловой коэффициент касательной прямой к графику Г i = Г А {у = уо}
функции <71 : х -> f(x,yG) в точке Ро = (®o> 2/о, f(xo, Уо)) € Гх. Анало-
д fi \
гичныи смысл имеет и частная производная
cty
Пример. Пусть f : (а,^) С R -> R2 (® -> (y(x),z(x)) х G
(а,[3)). Тогда касательная прямая к графику
г = {(®,!А*) 6 R3|?/ =	= z(x),x & (а,р)}
этого отображения f в точке (a, j/(a), z(a)) Е Г имеет уравнения
Г у-у(а)= у'(а)(х — а),
( z — z(a) = z'(a)(® — а).
Рассмотрим числовую функцию f : U(a) С Rn —> R, где f Е
2>(а). Тогда Df(a) € £(Rn,R) есть линейная форма. Рассмотрим Rn
как евклидово пространство, тогда существует вектор 1 Е R” такой,
что D/(u)h = (1, h) Vh 6 Rn. В самом деле, D/(a)h = Db/(a), где
Dhf (и) ~ производная функции f вдоль вектора h в точке а, но тогда
в каноническом базисе {е/} (j = 1,2,... , п) для Rn имеем D/i/(a) =
12	откуда получаем D/(a)h = (1,h), где 1 = £ Vjf(a)ej-
7=1	’	7=1
Используя канонический базис в Rn, положим 1 = grad f (а), тогда
. V- э	_ (Of (а)
ЯГ„Л /(«) = £,	=	.
7 = 1 J
df(a)\
дхп / ’
D/(a)h = (grad f(a),h)Vh € Rn.
n
Попутно заметим, что если е = ^2	есть орт в Rn и f Е D(Rn),
7=1
то для производной функции f(x) по направлению е (вдоль вектора
е) имеем
п д
ИеДж) = 52 ^f^cosai = (Sradf(x),e).
7=1
В частности, модуль производной функции f(x) по направлению
= \gradf(x), е)| > 0 имеет максимальное значение при
е = Л • gradf(x) (т. е. направление вектора градиента grad f(x) есть
направление наибольшего изменения функции f(x)) и равно нулю,
df(x)
де
345
если орт е ортогонален вектору градиента. Заметим, что линейной
» д
форме 4f(a) = 2 -z—f(a)dxj € £(Rn,R) можно поставить вектор
j=i
п д
grad f (а) =	Ч—/(A)ej, получающийся формальной заменой (в
j=i dxj
df(a)) линейной формы dxj на орт е7.
Определение. Отображение f : G С Rn -> Rw (где G -
открытое множество) слабо дифференцируемо (по Гато) в точке
а Е G, если существует линейное отображение A G £(Rn,Rm) и
окрестность U(a) С G С R” такие, что аth € U(a) имеет место
представление f(a+th) = f(a)+t' Ah+t’r(t’h), где lim ||r(t’h)|| = I).
при этом морфизм A E £(RM,RHI) называется производной Гато
(или слабой производной) отображения f в точке а Е G.
Запись: f Е De (а), А = Do/(а).
Замечание. Векторная функция
r(H• h) =	~*'Ah e Rm
определена однозначно при t / 0. Будем считать, что г € С(0), поло-
жив г(0 • h) = 0 е Rw.
3 а м е ч а н и е. (/ € De (и)) => (выполнено одно из двух эквива-
лентных утверждений:
1) Пш llf(« + ^)-f(g)-<-Ah||„, =
' t-»o	t
2) существует окрестность U(a) С G С R" такая, что Va + f.h €
U (а) имеет место представление
/(а 4- /h) = /(а) +1 • Ah + o(t • h) (f. -4 0)
(o(f • h) = f. • o(l) (t-> 0)).
Замечание. Если f € Dc(«), то для любого вектора 1 =
п
IjCj € R" существует производная вектор-функции f вдоль век-
j=i
тора 1
_ fl х .. f(a + t-h) -f(a)
Dif(a) = hm -J----,
f ==-#0	/J
причем
Dif(a) = Dc/(a)l,
где Dc/(«) € £(R",R"‘) - производная Гато.
Замечание. Из того, что отображение f : U(a) С R" -4 R’n
имеет для любого вектора 1 € R" производную вдоль этого вектора
Dif(a), вообще говоря, не следует, что f € De (а) по Гато, так как,
хотя производная Di/(a) однородна (по 1) (т. е. Dxif(a) = ADif(a)
346
VA ё R), но аддитивности (по 1) Di+hf(a) = Dif(«)+Dhf(a) VI, h Е Rn
может и не быть.
Пример.
У(®> У) =
X3 - Зх{/2	2	2
V+?-'1 +!?>0
О, х2 + у* = 0.
Тогда
/(о,о) = ^ = «М.о
м ’ ' <Эх ду
и если бы / Е Dc((0,0)), то имели бы Dc/(0,0) = 0 € £(R2,RX)
и, в частности, Di/(0,0) = Dc/(0,0) = 0. Однако Di/(0,0) =
th-5o t “JUS “ fl + Jj ^Опри|1^°-
Теорема (о единственности производной Гато). Пусть f :G С
RM -4 R’H, где G - открытое множество и а € G. Если f € Dc(a)>
то линейное отображение А € £(Rn,R"‘) из определения производ-
ной Гато единственно.
Доказательство. Допустим, что ЗА1, Аг € £(Rn, R"‘) и
окрестность 17(a) С G такие, что Va +1 • h € U(a) C G имеет место
представление
/(a +1 • h) = /(а) +1 • A,h +1 • r,(t • h) (t = 1,2),
где lim ||r,(t • h)||„, = 0 (i = 1,2).
Пусть В = A1-A2 € £(R", R”‘). Тогда для любого вектора х Е Rn
(х 0) видим, что при достаточно малых 0 имеем а 4-1 • х £ 17(a)
и поэтому
||B(i-x)||,n = ||Ai(i-x)- A2(«-x)||m =
= ||(f(a + < • х) - f(a) -1 • ri(i • x))-
—(f(a + tx) - f(a) -1 • r2(* • x))||,n =
= |<l’||ri(<ix)-r3(t-x)||w,
откуда
= ||Bx||m = ||n(< • x) - r3(t • x)||,„.
Ho
lira ||ri(* • x) -r2(* •x)||m = 0<
t. e. ||Bx||,„ = 0 Vx E Rn и поэтому В • x = 0 Vx E R", так что
(В = Ai - A3 = 0) => (Ai = Аг).
347
Замечание. Если f : U(a) С Rn —> Rm и f E Defa), то из
этого, вообще говоря, не следует, что f 6 С(а).
Пример.	(
f(x V) = J 1 при у = ®2. х + 0
J [0 для остальных (ж, у) Е R-
Тогда /(0,0) = 0 и /ЕС((0,0)). Однако при достаточно малых t
имеем f(tli,tl2) = 0, причем ^£12121 =	= 0 и VI Е R2
ох	оу
ЗПт^у^ = 0, т. е. 3Dc/(0,0) = 06 £(R2,RX)	=
/(0,0) +1 • (o/i 4- ol2) +1 - o(l) (t -> 0), где t  o(l) = 0 Vi / 0), t. e.
/ € Dc((0,0)).
Следствие. Если f : G C Rw —> Rm, где G - открытое мно-
жество, a E Си / 6 Dc(a), то существует окрестность U(a) C G C Rn
такая, что Va +1 • h 6 U(a) имеет место представление
/(a 4- th) = /(a) 4-1 • Dc/(a)h 4- o(t • h) (t -> 0),
где Dc/(a) G £(Rn, Rnl) - производная Гато.
Следствие (необходимое условие существования производной
Гато). Если / Е Dc/(a), то V/ = 1,...,п 3^^- = Dc/(«)e, =
1П
ww = S и тогда производной Гато Dc/(a) Е £(Rn, Rm)
t=i dx*
как морфизму соответствует матрица Якоби (Dj/j(a)) Е Мтхп при
т
f(*) = Е Л(х)е<-
1=1
В самом деле, поскольку 3Dc/(«) € £(Rn,Rra), то морфизму
Dc/(a) соответствует матрица (Atj) G Мтхп, для которой
т
Dcf(a)ej = £2 Aye'.
»=i
„ „ .. . п .. . df(a) ^дЦа)	л df,(a)
Но Dc/(a)ey = D.,f(a) =	• е^, откуда
Vj = 1,... , n; i = 1,... , m, так что морфизму Dc/(«) (производной
Гато) соответствует матрица Якоби.
Теорема. Если /: 17(a) С Rn -> R,rl и f е D(a) в смысле
Фреше, то f е Dc(a) в смысле Гато и D/(a) = Dc/(a) 6 £(Rn,RTn)
(с матрицей Якоби).
В самом деле, поскольку / G D(a) (в смысле Фреше), то Vh Е Rn
имеем, в частности, Va 4-1 • h Е 17(a) представление
f(a 4-1 • h) - f (a) = tD/(a)h 4- o(t • h) (t —> 0),
348
что и означает дифференцируемость отображения f в точке а Е G в
смысле Гато, причем в силу единственности производной Гато име-
ем 'Def(«) = Df(a) Е £(Rn,Rw) (с матрицей Якоби) и Dhf(a) =
т ( п	т
Df (a)h = Dcf(a)h = £	£	e<, (где f(x) = £ ЛЖ).
t=i \j=i uxj /	«=1
В силу теоремы единственности слабой производной и замечания о
представлении производной Гато Def (а) в координатной форме имеем
Определение. Пусть f : U(а) С Rn Rm u f(®) =
(fi(®),... ,/т(®))» Тогда f Е De(«), если в окрестности Ща) С R’1
имеет место представление Va 4-t • h 6 U(a)
fi(a 4-1 • h) = fi(a) + t- ^Djfi(a)hj 4* t • o,(l) (t -> 0), i = 1,... ,m.
j=i
В частности, для числовой функции f : 17(a) С Rn —> R утверж-
дение f Е De (а) означает, что Va 4-1 • h E [7(a) C Rw имеет место
представление
/(ai+t/ii,... ,an+th2) =	,an)+t-Y' hj+t-o(l) (t -> 0).
j=i 0Xj
Теорема (критерий слабой дифференцируемости вектор-
функции). Пусть f : U(a) С Rn -> R,n, где f(®) = £ Л(®)ер Тогда
(f Е Dc(a)) (f« Е Dc(a) Vi= 1,... ,m).
Замечание. Ранее была доказана теорема о связи производ-
ной Фреши и производной Гато: (f Е D(a) в смысле Фреше) =>
(f Е Dc(a) в смысле Гато, причем Def (a) = Df(a) Е £(Rn,R,n).
Обратное утверждение (f Е Dc(a)) => (f G D(a)), вообще говоря,
неверно.
Пример.
/(*,!/) = ( ^Т^,х2 + у2>°
( 0, х2 4- у2 = 0.
Очевидно, f (0, 0) =	= 0 и при h = hrei 4- h2e2
ох	оу
имеем
НтЖ1,^2)-Ло,о)
t —>0
-Г *4' h*h2 - n
t™t2(r-h* + h22)-t ~ ’
T. e. f E Dc(0,0) и Dc/(0,0) = 0 6 £(R2,R). Однако /€D(0,0), так
как при у = х2 имеем
/(*, У) ~ /(0,0) =	=	/ о(\/х2 4- у2) = о(|зс| • \/1 4- х2) (х -> 0),
349
т. е.
/(®,1/)-(/(0,0)+о-® + о-р) = f ч И о(>/®2 + у2) (\/®2 + у8 -» 0).
аг +
Замечание. Теорема о производной сложной функции для
слабых производных, вообще говоря, неверна.
Пример.
0(®,у) = | ^^^2 + у2>0
I 0, ®2 + у2 = 0,
где р(0,0) = ^в’° =	= 0, д € О((0,0)) Л Dc((0,0)), причем
Dcff(0,0) = 0 € £(R2,R) (как было показано выше). Пусть f : t ->
t • ei +t2 --ej = ®(t)ei + y(t)ej, так что = 1,	= 2t.
at at
t
Тогда для сложной функции F = po/:t-> —т = z видим, что
MV	40
3D^(t) = Vt. Однако формула (из теоремы о производной сложной
.	.	dF(0)	fy(0,0) d®(0) др(0,0) di/(0) п п , п
dt ox dt оу dt
2t|t=o = O0 5.
Теорема (достаточное условие сильной дифференцируемос-
ти). Пусть f : О С Rn -> Rm, еде G - открытое множество,
®о € G и BU(xq) С G такая, что f € Do(®) V® € U(xq) С G
(так что 3Dc/(®) € £(R**,Rm) (с матрицей Якоби) Ух € U(xq))
и Def € С(®о) (т. е. Ve > 0 ЭШ(®о) С 17(®о) такой, что ||Do/(®) -
Do/(®o)|| < е Ух € Ш«(с)(®о). Тогда f 6 D(®o) е смысле Фреше и
D/(®o) = Do/(®o).
Доказательство. Поскольку (/ € D(a) или / € Dc(a) &
(fi € D(a), * = 1,... ,m или fi € Dc(a), i = 1,... ,m), то достаточно
рассмотреть случай m = 1, полагая f : G C Rn -* R. Итак, f €
Do(®) V® € U(xq) C G C Rn, причем De/ € C(®o), t. e. ||Dc/(®) -
Dc/(®o)|| < e V® € ШЛ(е)(®о) C U(x0).
Пусть ®o + h € Ш;(е)(®о) С 17(®о). Введем функцию
w(®o,h) = /(®о + h) - /(®о) - Dc7(®o)h.
Нужно доказать, что
W(®o,h) = 0(||h||n)(||h||n -4 0).
350
Введем числовую функцию F(t) = f(xo +1 • h) на отрезке [0,1].
Тогда имеем F(l) = f(xo + h), Г(0) = /(®o), причем, посколь-
ку f € Dc(®) V® € Ш4(Г)(®О) С 17(®о), то W € [0,1] 3^^ =
д11то +	д^) ~	+	= Do/(®o +1 • h)h, т. е. F €
D([0,1]) и, в частности, F 6 С([0,1]). Но тогда в силу теоре-
мы Лагранжа (о конечных приращениях) 3tf € (0,1) такое, что
F(l) - F(0) =	= Dc/(®o + tf • h)h, что дает равенст-
во w(®o,h) = [Dc/(®o + tf • h) - Do/(®o)]h, где Do/(®o + tf • h) -
Do/(®o) € £(Rn,R), причем в силу выбора Ш$(,)(®о) при ®о + tf • h,
®о € Шл(е)(®0) С U(xq) С R” имеем оценку |w(®o,h)| < ||Do/(®o + tf •
h) - Dc/(®o)|| • ||h||n < e • ||h||n, t. e. w(®oh) = 0 (||h||n) (||h||n -> 0),
что и означает существование производной Фреше
D/(®o) s Dc/(®o) 6 £(Rn,R)
в силу теоремы единственности для сильной производной.
§ 4. Теорема о производной сложной функции и ее
следствия
Теорема (о производной сложной функции). Пусть f : U(xq) С
Rn -4 Rm и уо = /(®o) € Rm. Пусть g : V(i/o) C Rm -+ Rp, etfe
/(17(®o)) C V(lto) C Rm. Пусть f € Z>(®o) u 9 € P(l/o). Тогда для
композиции F = go f : U(xq) C Rn -> Rp имеем F € P(®o), причем
DF(®o) = D0(l/o) © D/(®o) 6 £(Rn,R”).
Доказательство. Поскольку / € P(®o) и 17(®о) C Rn, то
в силу липшицевости функции / в точке ®о видим, что существуют
окрестность Ш«(®о) С U(xq) и постоянная с > 0 такие, что
||f(®o+h)-f(®o)||m <C*||h||n
V®o + h € Ш<(®о) C U(xq).
Положим /(®о + h) = уо + к, где к = f(®0 + h) - f(®0) 6 Rm, тогда
||k||m < c||h||n V||h||n < <5 и, в частности, lim ||k||m = 0. Кроме
||п||п-Ф0
того, поскольку f(U(x0)) С V(j/0) С Rm, то /(®о + h) € V(i/o) С Rm,
так что F(®o+h) = j(/(®0+h)) = s(i/o+k) V®0+h e 1Щ(®о) C U(xo).
Поскольку / € 'D(x), to
3D/(®o) € fi(Rn,Rm)H||D/(®o)|| < +oo.
Аналогично
(g € T>(i/0)) * (3Dp(|/o) € £(Rro, R*) и ||Dff(|/o)|| < +oo),
351
причем Dg(2/o) о D/(®o) G £(Rn, Rp). Но тогда
V®o + h G lil^(®o) C U(xq)
имеем
||F(x0 + h) - F(s0) - (Dsr(yo) ° Df(®o))h||„/||h||„ =
(поскольку f(so + h) -f(so) = D/(®o)h + a(h) • ||h||n, где	!
„lim Jla(h)llm = 0) = llg(y° + k)-g(!fo)-	'
-Dp(j/o)(f(®o + h) -f(so) + a- ||h||n)||P/||h||n =	|
= l|g(l/o + k) -g(j/0) -Dff(!fo)k + Dff(yo)(a!(h) • ||h||n)||p/||h||n =	j
(ho g e D(yo), t. e. g(j/0 + k) - g(y0) = Dff(yo)k+
+/?(k) • ||k||m, где lim ||/3(k)||p = 0) =
||k||m—>0
= ||/?(k) • ||k||ra + DS(yo)(a(h) • ||h||„)||p/||h||„ < A(h) + /2(h),
где ||k||,n < c||h||n,
0</i(h) = ||/3(k).||k||m||p/||h||n<
<||/3(k)||p.||k||m/||h||n<c.||^(k)||p,
и поскольку
ton ||k||ra = 0, TO lim ||/3(k)||p = lim ||/?(k)||p = 0,	. '
INIn-*0	||h||n—>0	||k||m—>Q
T. e. lim Д(Ь) = 0. Далее, 0 < /2(h) =
ПЛ11л“>°	|
= ||Dff(lto)(a(h) • ||h||„)||p/||h||n < ||Dfl(yo)«(h)||p <	|
< llD5(lto)||-||a(ft)||m, но
( lim ||a(fe)||m = 0) => ( lim J2(h) = 0).
Таким образом, существует морфизм Dfl(l/o) ° D/(so) 6 £(Rn,Rp)
такой, что
lim ||F(s0 + h) - F(s0) - Ыуо) ° D/(®o)h||p/||h||n = 0,
t. e. F G (®o) и в силу единственной производной
DF(s0) = Dp(yo) о Df(x0) е £(Rn,R₽).
352
Замечание. Если ввести дифференциальные обозначения у =
f(x), z - д(у), dx = (d®i,... ,dxn), dy = (dyu... ,dym), dz =
(dzi,... ,dzp), то имеем dy = Df(x)dx, dz = Dp(y)dy и тогда (из тео-
ремы о сложной функции) видим, что дифференциал сложной функ-
ции F = д о f получается из дифференциала функции д, если заме-
нить у на f(x) и dy на дифференциал D/(®)dx, т. е. dz = T)F(x)dx =
Dp(/(®))(D/(®)dx).
Замечание. 'Поскольку DF(®o) = D<z(i/o) ° D/(xo)> где
Df(®o) € £(Rn,Rm) и Dff(l/o) € £(Rm,IU’), то матрица Якоби
для морфизма DF(®o) € £(Rn,R₽) есть p x n матрица (Dj.fi (®o))
(I = 1,2,...,p‘,j = 1,2,Она получается как произведение
матриц Якоби (Dift(i/o)) G = l,...,p;t =	и (DjA(®o))
(* = 1,... ,т; j = 1,... ,п) у0 = /(®0), т- е.
/ Diffi(yo) • ••
Dm<71(i/o) \ / Dl/l(®o)
Dn/l(®o)
Р ................
\ Diffp(yo) ...
Dmffp(j/o) / \ Dl/mC^o) •••
m =
Dn/m(-To) /
Di^i(®o)
< Di-fp(®o)
Dnfi(®o) \
............. P
... Dn^p(®o) ;
где Dj^Kso) = EDiPi(yo) • DjA(®o) (I = 1,2,... ,p,j = 1,2,... ,n).
Последнюю формулу можно записать короче, вводя не совсем коррект-
ные, но очень удобные обозначения: пусть
/ : х -> у(х) = (У1(х),... , Ут(х)), д-.у-+ z(y) =
= (^i(y),... ,М»))»
F = д о f : х -> z(y(x}) = («i(y(®)),... , zp(y{x))),
тогда
dzi _	dzi dyt
dxj ~	9yt dXj
,p\j = 1,2,... ,n).
353
Если n = m = p, то якобиан сложной функции F = g о f в точке ®o
равен произведению якобиана отображения f в точке хр на якобиан
отображения д в точке ур = /(го), т. е.
D(zi,... ,zn) _ D(zi,... ,zn) ф Р(У1,-.. ,!/n)
D(®i, • • •, ®u) D(yi, • • •, Уп) D(®i,  • •, ®n)
Следствие 1 (цепное правило вычисления частных произ-
водных сложной функции). Пусть / : U(xp) С Rn —> R’" и / G 7?(®0).
Пусть д : V(y0) С Rm ч R, где f(U(x0)) С V(yo) С Rm, Уо = /(®о)
яде Р(у0). Тогда сложная функция F = до f : U(xp) С R" -> R,
•F(®) = y(/i(®),.. •, /m(®)) дифференцируема в точке ®0 (F € 2>(®o))
и
m
DjF(xo) = 22 Dtf(tt)) • Dj/i(®o) (j = 1,..., n),
или
или
dF(x0) _ А dg(yp) 0/.(®о) __ t 2 д)
5® j	dyi dxj
dz ___ dz dyi
dXj ~ ££ dyi dXj
»п),
Следствие 2 (теорема о полной производной сложной функ-
ции). Пусть / : / С R -+ Rn ufe 2?(®о), ®о € I = (a, b) С (-оо, +оо).
Пусть д : V(y0) С Rn -* R, где f(I) С V(yo) С Rn, Уо = /(®о) и
д € ®(уо). Тогда сложная функция F = g о f : (а, b) -> R дифферен-
цируема в точке хо (F € Р(®о))> причем
п
DF(»o) =
1=1
или
—F(x 1 = V dg^ •	_ V dyi)
dx ' °	dyi dx ’ dx dyi dx
Замечание. В теореме о производной сложной функции важ-
но, что F = g о f есть композиция дифференцируемых функций f и
д. Одного существования частных производных у функций f и д не-
достаточно для справедливости формулы DF(®o) = D<j(3/o) °D/(®o)-
Пример. Пусть F(t) = (д о /)($), где f(t) = (t,t) и
а(х	+	®2 + У2 > 0.
о, ®2 + у2 = 0.
354
Очевидно,	= 0 и /{(0) = /а(0) = 1, при этом
(/?($) = i3/2i2) =» (F(t) = i/2) => (F'(0) = 1/2). Вычисление же по
формуле теоремы о производной сложной функции дает неверный ре-
зультат
Л°) = ^(0,0)Л(0) + ~й(0,0)/i(0) =
= 0 • 1 + 0 • 1 = 0 # 1/2.
Все дело в том, что функция д(х, у) не дифференцируема в точке (0,0).
В самом деле, д(Дх, Ду)-д(0,0) = (Дх)2Ду/(Дх)2+(Ду)2) = r(h) при
h = (Дх, Ду). Но при Ду = Дх, р = -\/2 • |Дх|, т. е. r(h) = Дх/2 о(р)
(р-> 0).
Теорема (о линейности дифференцирования). Пусть f : G С
Rn -4 R u д G С Rn -4 R, где G - открытое множество. Пусть
f,g € 1>(х), х G G. Тогда ^а,/3 € R илееж а • f + (3 • g G 1>(х),
f • g € 2>(х), причел
O®i	uXi	OXf UX{
= f--^- + 9'^(i= 1,2,...,п)
UXi uXi
U
d(af + fig)(x) = a • df (x) + /3 • dg(x) € £(Rn, R),
d(f • P)(®) = /(x) • dy(x) + y(x)  (x) € £(Rn, R).
dflx)
Доказательство.Поскольку f,g G®(x),то
^g(g) w,
’ dxi
и равенства для частных производных функций a-f+ft-g и f-g следуют
из соответствующей теоремы о линейности дифференцирования для
функций одного переменного (см. ч. I, гл. 5, § 4). Для доказательства
дифференцируемости функций a-f+/3-g и f-g воспользуемся теоремой
о производной сложной функции, для чего введем вспомогательные
функции F : G С Rn -4 R2, Г(х) = (/(х), р(х)), щ : R2 -4 R (i = 1,2),
Pi(l/i, Уз) = а • Ух + /з • Уз, Рз(У1, Уз) = У1 • Уз- Тогда (/,у G D(x)) =>
(F G D(x)) и <£>,• G D(R2) (i = 1,2). Но очевидно, а  f + /3  g = <pi° F,
f • 9 = <Рг ° F, и по теореме о производной сложной функции имеем
a-f+V-g €1>(х), f-g£T)(x).
Задача. Пусть f : G С R” -4 R; g : G C Rn -4 R, где G
~ открытое множество. Пусть f,g G ^(x), x G G, причем p(x) 0.
Тогда f/g G D(x) и «^-(//g) = (яуг- - f jr-} /g2 Vi, так что
uXi	\ UXi	uX{ J
d(f/9)(x) = (g(x)df(x) - /(x)dp(x))/y2(x) G £(R”, R).
355
(Доказать самим.)	<
Теорема. Пусть f : Rn -> R, f E P(Rn); (J : R,n -> Rn, 9 €
D(RW), причем f : x —» f(x); t —> g(t) = x, где x — («1,... ,xn) 6 Rn,
t =	... , tm) E Rw. Тогда для композиции и = f о g : Rm -> R (u :
t -> f(gi(t),... имеем и = fog E P(Rm), du(t) = Dif(x)dxif
1=1
m
где dxi = J3 Tfjgi(t)dtj i = 1, 2,... , n).
>=i
Доказательство. Применяя теорему о производной слож-
ной функции, имеем (/ Е 2>(Rn)i 9 Е P(R”1)) => (и = f о g е 2>(Rm),
D(/ о g) = D/(x‘) о Dp(^) 6 £(Rm,R)), откуда, вспоминая правило
умножения матриц Якоби, имеем
п
Е>>(/од) = 52Dif(x)Djg(t) (j = 1,2,... ,т),
i=l
т. е.
т	т п	п
= 52 ° y)dti = 52 52 D,^a')D^’= 52D,^(®)x
>=i	j=i «=1	t=i
I m	\	m
x I 53	], однако при ж, = gi(t) имеем dxi = £ T)jgi(t)dtj,
\j=i	/
71	/	П	\
поэтому (du(t) = 53 Dif(x)dxi) I d(f og) = 52 Dif(x)dxi ).
1=1	\	»=1	/
3 а м e ч а н и e (об инвариантности формы первого дифференци-
ала). Пусть у = /(®1,... , жп), где числовая функция f : G С R" —> R
п 3/(ж)
дифференцируема (/ Е П(х) Vx Е G), тогда dy = У* —-^—^dxi. Пусть
t=l ^xi
Xi = Xi(t), t = (ti,... ,^w), где Xi E 2>(t) - дифференцируемые функ-
m dx (t)
ции, тогда dxi =	—-dtj, С другой стороны, по теореме о про-
j = l <"'3
изводной сложной функции функция у — f(x(t)) дифференцируема,
причем
m

\ .. _
>=i
dtj
п
т. е. форма записи 1-го дифференциала dy = ^2
: = 1
от того, являются Xi независимыми переменными или дифференциру-
емыми функциями Xi = Xi(t);
df(x)
—----dxi не зависит
UXi
356
Замечание (формулы для вычисления дифференциалов). Пусть
f : G С Rn -> R, где G - открытое множество и х 6 G. Если f 6 (ж),
п
то поскольку df(x) = 52 Dif(x)dxi Е £(Rn,R) и частные производ-
«=1
ные Di/(®) сами являются линейными операторами по отношению к
функции, то Vu, v Е Р(ж) имеем:
1)	d(c • и) = с • du Ve Е R;
2)	d(u ±v) = du ± dv,
3)	d(u • v) = udv — vdw,
4)	d(u/v) = (vdu — udv)/v2 (v(x)	0).
Для примера докажем равенство 3). Пусть w = и • v. Тогда w диф-
ференцируема как функция и и v, поскольку ее частные производные
— = v Е C(R ) и -д— = и Е C(R ) непрерывны в R и поэтому
(JU	(JX
t dw . dw . dw dw	,	,	.
dw = тг— du+ -z—av, но -r— = v, = u, так что dw = vdu+udv. В си-
du dv du dv
лу инвариантности формы 1-го дифференциала выражение vdu 4- udv
будет дифференциалом функции и • v и в случае, когда и и v сами
являются дифференцируемыми функциями других переменных.
Теорема (об обратной биекции). Пусть G С Rn и 0 С Rm - от-
крытые множества и f : G ™ & - биекция G на так, что сущест-
вует обратная биекция f”1 : 0 G. Пусть f Е Р(а) и У"1 Е Т>(Ь),
где b = f(a) Е 0, а Е G. Тогда морфизм D/(a) G £(Rn,Rm) явля-
ется биекцией Rn ма Rm и его обратная биекция (DZ(a))”1 явля-
ется производной в точке b = /(а) для обратной биекции т. е.
(Dj(a))”1 = D/”1(b), при этом размерности тип совпадают, т. е.
т = п и матрица Якоби обратной биекции f'1 в точке Ь = /(а) яв-
ляется обратной матрицей для матрицы Якоби отображения f в
точке а, т. е.
д(У1, • • • , уп) ( . д(хг,... , хп)
«(.,....^)(о) • эй,:"./;,.)7'0» -L
Доказательство. Поскольку f : G ™ 0 - биекция и f"1 :
0 G - обратная биекция, то (/”1о/)(ш) = х Vx Е G, (f o/“1)(j/) = у
Vy Е 0, т. е. o/4-1g, /о/"1 = где Ig : G™ G -тождественное
отображение (G на G) и I© : 0 Ц 0 - тождественное отображение
(0 на 0). Очевидно, D/c(a) = In Е £(Rn,Rn) и D/©(i>) = Im е
£(Rm,R"1)), где In : Rn Rn и Im : Rw ™ Rw - тождественные
отображения Rn на Rn и Rm на Rm соответственно. Поскольку f E
^(a) и У-1 E ^(i>), где b = /(а), то в силу теоремы о производной
сложной функции имеем (f о f'1 = 1$) => (D(/ о /“1(Ь)) = DI& = 1п)
=> D/(a) oD/-1(&) = 1т и D/"1(b)oD/(a) = 1п, т. e. морфизм D/(a) :
Rn Rm есть линейная биекция Rn на Rm, а морфизм D/”1(i>) :
357
Rm —> Rn есть обратная линейная биекция Rm на Rn. Но тогда из
линейной алгебры имеем т = п и D/-1(b) = (D/(a))-1, откуда и
следуют все утверждения теоремы об обратной биекции.
$ 5. Теорема о среднем для отображений из Rn в R’"
и ее приложения
В дифференциальном исчислении функций одного переменного до-
казана (ч. I, гл. 5, § 6) важная теорема Лагранжа о конечных прира-
щениях: если / 6 D((a, Ь)) А С([а, Ь]), то существует точка £ Е (а, Ъ)
такая, что /(Ь) - /(а) = D/(€)(Ь - в).
Замечание. Теорема о среднем в указанной выше форме,
вообще говоря, неверна для отображений / : R” -> Rm при т > 2.
Пример. Пусть f : R2 -4 R2, где / : (а, у) -4 (а3, а2), тогда не су-
ществует точки ( = (ао, Уо) на отрезке {(а,у) Е R2| у = а, 0 < ж < 1}
такой, что f(l, 1) - f(0,0) = D/(®o,lfo)h (h = (1,1)). В самом деле,
D/(®, l/)h = (За2,2у), и, допустив, что такая точка (ао, уо) сущест-
вует, мы бы имели 1 = За§, 1 = 2уо, но уо = 1/2	1/\/3 = ао,
т. е. точка (®о,Уо) не может лежать на отрезке, соединяющем точ-
ки (0,0) и (1,1). Для обобщения теоремы о среднем на отображение
f : G С Rn -4 Rm а -4 /(а) = (Д(а),..., /,п(а)) при т > 2 возможны
три пути: 1) применение теоремы Лагранжа к координатным (число-
вым) функциям Л (а) (г = 1,2,... ,т); 2) вывод теоремы о среднем
для отображения f в интегральной форме; 3) замена точного равен-
ства f(6) - f(a) = D/(£)(b - а) на неравенства
||f(b)-f(a)||m < М(/) • ||Ь —а||п,
где 0 < M(f) < +оо.
Теорема (о среднем для числовой функции многих переменных).
Пусть / : G С R" -4 R, где G - открытое множество и отрезок
[а, Ь] С G. Пусть f € С([а, Ь]) А 2>((а, Ь)), тогда существует число
д 6 (0,1) такое, что имеет место формула конечных приращений
f(b) - /(а) = £Dj/(a + I?(b - a)) (bj - а,).
>=i
Доказательство. Рассмотрим вспомогательную функ-
цию (одного переменного) F{t) = f(a + t(b - а)). Поскольку отрезок
[а,Ь] = {а € G|a = а + i(b - a),i € [0,1]} С G, то функция F(t)
определена на отрезке [0,1], причем Г(0) = /(о) и F(l) = f(b). По-
скольку f Е С ([а, 5]), то в силу непрерывности линейной функции
t -4 а + t(b - а) на отрезке [0,1] имеем F Е С([0,1]). Поскольку
358
f 6 ®((a, b)) (где (a, b) C G), то по теореме о производной сложной
функции (используя дифференцируемость линейной функции) видим,
что Vi Е (0,1) у функции F(t) = f(a + t(bi - ax),..., an + t(bn - an))
существует производная
i=i }
Но тогда к функции одного переменного F(t), удовлетворяющей усло-
виям F € С([0,1]) Л D((0,1)), применима теорема Лагранжа о конеч-
ных приращениях из ч. I, гл. 5, §7, в силу которой 319 € (0,1) такое,
что F(l) - F(0) = DF(i9)(1 - 0) или
W) " /(«) = L Dj/(a + 4(Ъ - а))(5, - ц).
J=1
Теорема (о среднем для отображений из Rn в Rw). Пусть f :
G С RM —> R”‘ и отрезок [а, Ь] С G (где G - открытое множество).
Пусть f G С([а, b])AD((a, b)) и Ц/Л(®) Vi, j ограничены на интервале
(a, Ь), причем
/ ,» п	\ 1/8
М(П = O8UP lDi/.(a + t(b-a))|)2
°<«<1 /
Тогда имеет место оценка
l|f(b)-f(a)llm < M(f). ||b-a||n
Доказательство. Полагая /(х) = (/i(x),... , /,п(®)), имеем
/ е С([а, &]) Л 2>((а, 5))) => (Л 6 С([а,Ь]) Л Р((а,Ь)) (» = 1,2.тп)),
где [а, 6] С G. Тогда в силу теоремы о среднем для числовых функций
существуют числа $, € (0,1) (г = 1,2,..., т) такие, что имеют место
равенства
/,(Ь) - А(а) = £Djfi(a + й(Ь -	- 0/) (» = 1,2,..., т).
i=i
Но тогда в силу неравенства Коши-Буняховского имеем
||ф)-Г(а)||’> = £(Л(Ь)-Л(а))’ =
359
2
= E (^DJf.(a+^(b-a))(6>-aj) j <
»=1 V=1	/
m n	n
< ES (!W.(a + tf,(b - a)))2 • ^(bj - aj)2 < M2(f)  ||b - a||?.
t=lj=l	j=l
так, что
||f(b)-f(a)||ra<M(f).||b-a||n.
Замечание. Указанная теорема о среднем существенно ис-
пользует координатное представление отображения f : G С Rn —>
Rm, а потому неинвариантна. Доказательство аналогичной теоремы
о среднем в инвариантной (не координатной) форме значительно слож-
нее и приведено, например, в книге [3].
Следствие 1. Пусть f : G С Rn —> R,n, где G - открытое
множество, f Е 'D(S) (причем Djft(x) ограничены на S где
S С G - выпуклое множество и имеет место оценка
1/2
т п	\
ЕЕ^^)2 <M*xes.
1=1 j=l	/
Тогда отображение / удовлетворяет на S условию Липшица
||f(ati) - f(ж2)||«г < М  ||xi - x2||n Vail, ш2 € S.
Следствие 2. Пусть f : G С Rn -> Rm, где G - открытое
множество, и / Е ЯЯ где S С G - выпуклое множество, причем
частные производные	(i = 1,2,...	= 1,2,... , п) ограни-
чены на S. Тогда для любых точек x,y,z Е S имеет место оценка
||f(y) - f(z) - D/(*)(y - z)||„, <
/m „	\1?2
< I EE sup (Dj/«(y + *(z “У))-’Djfitx))2 I -||y-z||n. (5;1)
Доказательство. Для фиксированного x E S рассмотрим
функцию F(w) = f(w) — D/(»)w, w E S. Тогда F E 2>(S), причем
ГДго) = fi(w) - 5? Dt/,(a:)wfc, D2F,(w) = Dy /•(«’)-
fc=i
-Dj fi(®) (j = 1,2,... , n; i = 1,2,... , m).
Поскольку множество S выпукло, то Vy, z 6 S отрезок [у, z] C S C G
так, что F G C([y, z]) AP((y, z)). В силу ограниченности всех частных
360
производных Dy/» на множестве S, применяя теорему о среднем для
отображений (из Rn в Rw), получаем оценку
l|F(W)-F(z)||m<M(F)-||y-z||n
где
(\ х/2
тп	\
52 52sup +*(z - у)))21
52 52 sup +^z - у)) - Dj/.(®)2	< +oo,
откуда и вытекает оценка (5.1), поскольку
F(y) - F(z) = f(y) - f(z) - D/(x)(y - z).
Теорема. Пусть f : G C Rn R,n, где G - открытое
множество и f G D(G), причем D/ € C(xo) (где ®o E G). Тогда
W > 0 3<J > О такое, что шар ИЦяо) С G и имеет место оценка
||/(у) - /(х) - О/(ж0)(у - х)||,„ < е||у - х||п Ух,уе Шл(ш0).
Доказательство. Поскольку f G 1>(G) и D/ 6 С(хо), где жо
- внутренняя точка G, то Vf > 0 3<5 > 0 такое, что шар ШДжо) С G и
|Dj fi(w) - Dj/»(a:o)| < els/m-n'iw G Шл(жо).
Но тогда имеем оценку
525>>/«(w) - Dj A(o--o))2 < е2 Vw G Ш7(хо).	(5.2)
<=1 }=1
В силу выпуклости шара Шл(ж0) С G для любых точек х,у G Ш^жо)
отрезок [ж, j/] С ПЪ(ж0) так, что w = х + t(y - х) G ШДж0) Vt G [0,1],
и поэтому в силу .(5.2) имеем
М2 ~ 52 5^ sup + *(У ~ х)) - Dj fi(ж0))2 < е2.
Но тогда в силу оценки (5.1) следствия 2 имеем из оценки (5.2)
||f(?/) - Г(ж) - О/(ж0)(у - х)||,„ < М • ||у - х||п <
361
< е||у - x||nVx, у € Ш* (®о) С G с R”.
§ 6. Формула Тейлора для (векторных) функций
Будем в дальнейшем использовать следующие обозначения с муль-
тииндексом
п
fc = (Л1,	• • • >	|^| =	0 <	< |^| (^i € No|
1=1
i — 1,2,..., n),
Определение. Пусть f : G C R" -> R, где G - откры-
тое множество и хо € G. Функция f(x) называется т раз диффе-
ренцируемой в точке хо при т > 2, если существует окрестность
U(x0) С G С R" такая, что функция f(x) дифференцируема (т - 1)
раз на U(xq) и все ее частные производные D*/(х) (|&| = т — 1)
дифференцируемы в точке xq. Запись: / € 2>(т)(хо).
Замечание. При т = 2, f € D^(xo), если ЭС7(хо) С G С R**
такая, что f € T>(U(xo)), причем Di/ € 2>(®о) (» = 1,2,..., п). Тогда
по теореме Юнга 3D»D;/(®o) (hi = 1,2,... ,п), причем DjDi/(®o) =
DiDj/(®o) » j- Вообще, если f € T>^(xo), to Dkf € 2>(®o) при
|fe| = m - 1 и значение Г/Дхо) =	(W = m) не зависит
от порядка частных дифференцирований.
Определение. Если f € “D^ (х) Vx € G С Rn, то говорят,
что функция /(х) т раз дифференцируема на G. Запись: / €
Определение. Если f € lXm>(G) и Dfc/ € C(G) V|A| = т,
то говорят, что функция /(х) т раз непрерывно дифференцируема
на G. Запись: f G C<TO>(G).
Определение. Пусть f : G С Rn —> R’n, где G - от-
крытое множество, xq € G и в каноническом базисе Rm имеем
/(®) = (Л(®), • • •,/т(®)). Тогда
(f Е ®w(x0))	(Л € ©W(x0) (г = 1,2,..., т)),
(/ G V^(G))	(ft G V^(G) (i = 1,2,..., m)),
(/ 6 C^(G))	(fi € C^(G) (i = 1,2,... , m)).
362
Замечание. Проведенные определения классов (®о)>	(б?)
й C^(G} существенно используют координатную запись отображе-
ния /из R" в R”1, т. е. не инвариантны.
Лемма (обобщение формулы бинома Ньютона). Пусть х =
(#1,• • • ,Яп) €	fen) - мультииндекс (ki е No;
i — 1,2,... , п), причем |fc| = fci + &2 + • • • + fcn u fc! = fci! • k2l..
xk = «J1 • «j2.. .®£n = П Тогда Vm 6 N имеет место обобщен-
«=1
ная формула Ньютона
(®1 + ®2 + • • • + ®n)m = тр * я* =
|Л|=т
Доказательство. Рассмотрим однородный многочлен т-й
степени
(®1 + «2 +...+ »n)w =	52	....*.’«х* -«IS
fci+fca+.•.+&!»=»!»
дт
Беря производную	(где v = (1/1,... ,i/n), |i/| = m) от
обеих частей этого тождества, имеем
m! = £ Afcl.........*„ • П • (kt - 1)... (ki - Vi + 1)®	,
|fc|=m	i=l
причем, очевидно, справа сохраняются лишь те индексы для ко-
п „ п
торых имеем fc, > ц* Vi. Но т =	S поэтому ki < (i =
i=i i=i
1,2,... , п), т. е. сохраняются лишь индексы k, = Vi (i = 1,2,..., п). Но
тогда имеем m! = AV1,„.)|Zb • Pi!.. т. e. AVl<„.tVn = m!/(vi!.. .pn!),
откуда AjCli„.ikn = m!/fcl, что и доказывает обобщенную формулу би-
нома Ньютона.
Замечание. При п = 2 имеем, полагая ki = I a k2 = т — I,
m	।
fci+h=«	/=0	'	'
- обычный бином Ньютона.
Лемма. Пусть f : Ш^(го) С Rn -> R и f е ©^(Illffxo))- Пусть
хо +1 • h е Ш<(ш0) С R" так, что t е [0,1]. h = £2 u НЧ1п < &
i=i
363
Положим F(t) = f(xQ 4-1 • h). Тогда Vm 6 N такого, что 1 <m<p,
имеет место (V/ 6 [0,1]) формула
^Л<)= Е ~kih -Dfc/(®o + <-h) =
|fc|=m
Е rr^r7-^*--.^-Dj1...D‘"/(a:o + <-h) =
«1. . . . кп.
|fc|=m
f(®0 +t -h).
Доказательство. Очевидно, имеем /(«о + t • h) =
/(zj+t-hi, • •. ,Xn+t-hn), причем f G №(x0)), поэтому, приме-
няя теорему о производной сложной функции из §4 к функции одного
переменного F(t) = f(xQ 4-1 • h), получаем
= E	+ * • Ь) Л s ( E I /(®o +1 • h)
dt >=1	V-1	/
и вообще для любого натурального т 6 N, 1 < т < р имеем пред-
ставление
^(1) = £ Вк1.......кя • Л‘‘...	• DJ* • • • D‘V(*0 +1 • h).
|»|=m
Заметим, что коэффициенты	в этом представлении, очевид-
но, не зависят от вида функции /, поэтому их можно вычислить, беря
в качестве функции /, например, функцию = ехр{®1 4*. •. 4- ®п}.
Но тогда
Ф(*) = р(®о 4-1 • h) = ехр{(®$ -I-1 • Лх) 4-... 4- (®п + ‘ М) ~
= ехр{(®$ + ... 4- ж°) 4- *(Л1 4-... 4- hn)}.
Очевидно, DJ1 • • .D„n^(a?) = и поскольку <р € С(1Щ(®о))> то, ис-
пользуя формулу Ньютона в обобщенной форме, имеем в силу теоремы
о производной сложной функции представление
dm	dm
—Ф(<) = ехр{®$ + ... +	• — exp{f(Лг + ... + hn)} =
Сьъ	ил
= ехр{(а;$ 4-... + ж°) 4- t(hk 4- • • • 4- /in)}(^i 4- • • • 4- hn)m =
364
= ^o+t.h). 52 -^L-.hk^...h^ =
iki=»i 1"" "
= 52 Bk>>••• •*» • /ii' • • • л«” • oi1 • • • dJ;v(®o+1- ь) =
|A*|=m
= ^xo + t-h). 52 Bkl..kn-hk'...hk^
1*1=»»
откуда
Bk.....kn = m!/(&i!... kn\), |fe| = fci 4-... 4- kn - m.
(Метод доказательства леммы сообщен автору Н.И. Фельдманом.)
Замечание. Поскольку f € Т>^ (Ш^(ж0)) (р > 1), то, полагая
«	,	6	6
h = 52 hjGj и выбирая 0 < д'о < <5 и €о € (0, -— 1) так, что 14-во <
/ = 1	до	до
видим, что Жо 4- th е Ша(,(ж0) С 1Щ(ж0) V|t| < 1 4- £о и ||h||n < <50 < д
(так как (1 4-^о)д'о < д'). Тогда функция F(t) = f(x0 4-th) определена
Vi Е (—1 — fo? 1 4- £о), причем в силу теоремы о производной сложной
dtn
функции (F е р(р)((1 - бо, 1 4-го)) 3—F(t) Vt е (-1 - г0,14-во) Vm,
CLZ
1 < т < р, и, в частности, (ср. с. 134, 170) F € D^([0,1]), причем Vm,
, ,	(ZmF(0)	dm f .	dmF(l)	dmF(t)	.
1 < m	< p, имеем	—------=	-—F(t) L-o	и	———	=	———	L-,.
dtm	dtm ' 1 1	dtm	dtm	1
Теорема (формулы Тейлора для числовой функции многих пе-
ременных). Пусть f : 1Щ(я0) С R” и f е Р(р+1)(Ш<5(ж0)) при р > 0.
Тогда Ужо 4~ h € ШДжо) С Rn имеет место представление
(\ Ь
11	\
У2	+гр(ж°’ h)’
>=i	/
причем. Eh9 G (0.1) такое, что
(\ р+1
П \
52Л>о>1	л®о+0-ь)
~ остаточный член формулы Тейлора в форме Лагранжа; если, кроме
того, f е С^+1)(Ш*(®0)), то
1	/	\	р+1
If	/ п	\
rp(xa, h) = - / (1 - А)Н 52 hjDj f(Xo + А • h)dA-
Р' о	М=1	/
т-.таточный член формулы Тейлора в интегральной форме.
365
Доказательство. Рассмотрим сложную функцию (одного
действительного переменного t) F(t) = f(xo+t-h), t € [0,1]. Заметим,
что в силу выпуклости шара Ш4(жо) С R." при ||h||n < S имеем хо +
t • h € Ш{(го) С Rn Vi € [0,1], поэтому функция одного переменного
F(t) определена Vt € [0,1], причем f(0) = /(®о)> F(l) = f(xo + h).
Поскольку f €	(Ш*(®о)), то в силу леммы, приведенной выше,
имеем представление
(\ *
ЕМ)/| /(xo + t-h)(fe = l,2,...,p),
i=i /
так что
(\ к
£мъ| /(®о)(^ = 1,2,...,р).
j=l /
В случае / € 2>(+1) (Ш<(®0)) имеем F € CW([0,1]) и F^ Е Р((0,1))
и по формуле Тейлора с остаточным членом в форме Лагранжа (для
функции одного переменного из §10 гл. 5), примененной к функции
F(t) на отрезке [0,1], видим, что 30 € (0,1) С (-1 - ео, 1 + Со) такое,
что
F(t) = Г(0) + £ 1 • F(*)(0)t* + F(p+I)(tf . «),
и при t = 1 имеем
*
n	i
$2	1	+h)’
j=l	/
где
r>’(®0’h)“ (р+1)|
\₽+1
/(®о + 0 • h), 0 < 0 < 1.
J=i /
В случае / G С'(₽+1) (Ш«(го)) формула Тейлора с остаточным членом
в интегральной форме (из §9 гл. 2 ч. II), примененная к функции F(t)
на отрезке [0,1], дает
1	/р+1	/*
^(0 = ^(0) + £	+	А)₽^(,,+1)(А • t)dX,
366
откуда при t — 1 имеем
где
С\ fc
л	\
/(®о) +M®o>h),
j=i	/
гр(хо,Ь) = ^
р+1
f (®о + А • h)dA.
Замечание. При доказательстве теоремы Тейлора существен-
ное значение имела выпуклость шара 1Щ(жо) С G С Rn, для которого
f е (1Щ(®о))* Поэтому при разложении функции f(x) по фор-
муле Тейлора в точке xq 6 G необходимо, чтобы отрезок [®о> ®], соеди-
няющий точки xq и х из G, целиком содержался в G. Таким свойством
обладают области G, звездные относительно точки «о G G, т. е. такие
области, что [яо, С G V® 6 G. Поэтому для звездных относитель-
но точки xq областей G С Rn справедливо разложение по формуле
Тейлора при выполнении прочих условий (гладкости).
Следствие (теорема о среднем для числовой функции многих
переменных в интегральной форме). Пусть f : G С RM -> R, где G -
открытое множество и отрезок [a, b] С G. Пусть f € С^)([а, Ь]), тогда
имеет место представление
п
л=1 о
Замечание. Используя обобщенную формулу бинома Ньютона,
формулу Тейлора можно переписать в виде
мп
/(.о+ h) = /(»,)+ £
+Гр(®о> h)V®o + h € Ш<(х0) С G,
где при f еТ><₽+1)ПМ®о))
rp(xo,h)= Е ^D"7(®o + i?-h)
|m|=p+l
(остаточный член формулы Тейлора в форме Лагранжа) или при
/€С(»,+1)(Ш,(®о))гр(хо,Ь) =
367
1
мп Г
= (p+1) E ^J(l-WDmf(x0 + X-h)dX
|m|=p+l	* q
(остаточный член формулы Тейлора в интегральной форме).
Теорема (формула Тейлора с остаточным членом в форме
Пеано). Пусть f : Ш^(®о) С Rn -> R и f 6 ТЯ*”1) (Ш^жо)), при-
чем f Е '&(р}(хо) (р > 1). Тогда имеет место формула Тейлора с
остаточным членом в форме Пеано V®o -h h Е 1Щ(а?о)
(\ к
п	\
ЕМЪ /(xo) + o(||h||₽)(h -> 0),
>=1	/
или
Р кт
/(xo+h) = /(xo)+	D-/(a;o) + o(||h||P)(h->0).
|m|=l
Доказательство. При р = 1 формула Тейлора справедлива,
поскольку
(/ G 2>(хо)) => (f(x0 + h) = f(x0) + £ DjfMhj + o(||h||n) (h -> 0)).
J=1
При p > 2 положим
p,(i;/w) = /w+ £	-o’-fM,
отметим, что при к = (&i, fc2> • • • , кп), 1 < |&| < р имеем
|m|=p	/ п
DkPp(x-,f,x0) =	I Цтп, -(т, - 1)...
,mn=fcn м=1
... (mi - fci 4- l)/(m! • m2!.. .mn!)x
х(ш, - x?)m<-ki) • D’ini • D”2.. .D™"/(xo),
откуда, полагая x = xq, имеем
DkPP(xo-, f, »o) = ( П *‘!) /(fcl! •••*"’)• DkKx°) = VkfM
\»=1 /
Таким, образом, если ввести вспомогательную функцию g(x) = f(x) —
Pp(x-,f,x0), р > 2, X 6 ш,(хо), то (/ 6 ^-^(ШИхо))) => (д 6
368
рЬ’-^ШИхо))), причем (/ G ©^(хо)) ^(j 6 ^(х0)) => (dM*o) =
0; |fc| = 0? 1,... ,p). Применим к функции д(х) в Ш<у(я?0) формулу Тей-
лора (с заменой р > 2 нар—2) с остаточным членом в форме Лагранжа.
Тогда при > 2
5f(x0 + h)= 52 —rDmff(xo + ^ • h), 0 < i? < 1,
. . HI!
|m|=p-l
но (д Е ^^р^(а?о)) => (Dmg Е 2>(®о) при |тп| = р — 1 > 1), и поэтому при
|?п( = р — 1 имеем
Dmff(x0 4-tf-h) = Dmff(x0) +	+ o(||h||n) (h -> 0),
j=l
откуда в силу отмеченного ранее равенства Dm^(®o) = DjDm#(®o) = 0
при |m| = р — 1 > 1 имеем
D”‘g(x0 + 0 • h) = o,„(||h||n) (h -4- 0), |тп| = - 1 > 1,
фо + Ь)=	(Л"*/т!) • o(||h||n) = o(||h||£) (h —» 0),
|т|=р-1
т. е. при р > 2
f(xo + h) = Рр(х0 + Л; /, хо) + o(||h|К) (h -> 0),
что и завершает доказательство формулы Тейлора с остаточным чле-
ном в форме Пеано.
Теорема (формулы Тейлора для (векторных) функций). Пусть
f : ПМжо) С Rn -> Rw. Тогда:
1) если f Е (1Щ(а?о)) и f Е Р^р\а?о) (при (р > 1), то в про-
колотой окрестности Ш^(азо) С R” имеет место формула Тейлора
с остаточным членом в форме Пеано
(\
п	\
f(xo) + o(||h||₽)(h->0),
y=i	/
2) если f Е (1Щ(я?о)) прир> 0, то V«04-h Е Ш^(»о) имеет
место представление
(\ ь
п	I
$2 hi I f (x°) + гр (®o, h),
>=i	/
13 Зак. 860
369
где
rp(®0,h)- (p+1)i
f(®o + 0 * h), 0 = (0i,

причем 0 <	< 1 (i = 1,2,... , m) и
f (®o + 0 * h) = Г Л(®0 + di • h)ej
i=i
(остаточный член формулы Тейлора в форме Лагранжа), если же
f еС<'+1’(ПМ®0)) (р>0), то
rp(®o,h) =
1
р!
1	/	\
i	/ п	\
/(l-A)*	f(®o + A*h)dA
о	V=1	/
(остаточный член формулы Тейлора в интегральной форме).
Доказательство. Достаточно применить уже доказанные
теоремы Тейлора для каждой из координатных функций (®о + Л) =
Pi of(x0 + h). Заметим, что, применяя формулу Тейлора с остаточным
членом в форме Лагранжа для fi(xo + h) (i = 1,... ,m), получаем
числа di 6 (0,1), вообще говоря, различные при разных г, так что в
отличие от формулы Тейлора для числовой функции многих перемен-
ных нельзя выбрать d = di одинаковыми для всех г = 1,2,... , т,
Следствие (теорема о среднем для векторной функции).
Пусть f : G С R” 4 Rw, где G - открытое выпуклое множество
и f € ©(G). Тогда для любого отрезка [а, ft] С G 3d = (191,... , dm),
О < 19, < 1 (г = 1,2,... , m) такое, что
f(ft) - f(а) = D/(a +19 * (Ь - a))(b - а),
н
или в координатной форме fj(ft)-fi(а) = 52 Dj/»(a+^i(b-a))(ftj-ctj),
J=i
(г = 1,2,..., m), при этом все 19 € (0,1), вообще говоря, различны, и
хотя точки а +19,(Ь - а) € (a, ft) (i = 1,... , т), но D/(ct +19 * (b — а))
не является производной функции f в некоторой промежуточной точке
отрезка [а, Ь].
Следствие (теорема о среднем для векторной функции в ин-
тегральной форме). Пусть f : G С Rn —> Rw, где G - открытое вы-
пуклое множество и f € C^^(G). Тогда для любого отрезка [а, ft] С G
имеет место формула конечных приращений
1
f (ft) - f (а) = I Df(a + A • (b - a))(b - a)dA,
о
370
или в координатной форме
Л	1
fi(b) - fi(a) =	- aj) / Djfi(a + A • (b - a))dA (i = 1,2,...,m).
i-l {
Следствие (формула Тейлора для векторной функции одного
переменного). Пусть f: (а,/3) С R1 -4 Rm. Тогда:
1) при хо б (а,/3), f € ^“^((а,/?)), f € 2>^(хо) (р > 1) имеем в
(а,/3) \ {®о}
f (х) = f(хо) + S	(хо) + о(|х - хо|р) (х -4 хо);
k=i *!'
2) если f €	((а, /3)) при р > 0, то Vx € (а, /3) имеем
f(x) = f(хо) + 52 ^r^-D^xo) + г„(х,хо),
к=1	*•
где
гр(х, хо) =	' • f(,,+x)(xo + 0 * (х - хо)),
1? = (я?1, • • •, i?m), 0 <	< 1 (i = 1,2,..., тп),
f<₽+i)(x0 + д * (x - хо)) = 52 /<F+1)(®o + i9i(® “ ®o)) • eI
i=l
(остаточный член формулы Тейлора в форме Лагранжа), если же при
P>of ec^ifK/J)), то
г₽(х, ®о) = (Ж ~р>!)(Р+1) J(t- А)” • D₽+1f(x0 + А(х - x0))dA
о
(остаточный член формулы Тейлора в интегральной форме).
Лемма. Пусть f : G С Rn -4 R, где G - открытое связное
множество. Тогда (/(х) = const в G) <=> (/ € D(G) u Vx € G 4f(x) =
О € £(R", R), т. е. D,/(x) = 0 Vx 6 G (j = 1,2,...,п)).
Доказательство. Необходимость. Пусть /(х) = const в
G, тогда / G D(G) и (tf(x) = 06 £(Rn,R) Vx 6 G) =► (D^/(x) = 0
Vx€G;; = l,2.......n).
Достаточность. Пусть f 6 U(G) и c(f(x) = 0 Vx € G, тогда
Dj/(x) = 0 Vx 6 G (j = 1,2,..., n). Зафиксируем точку хо G G и рас-
смотрим любую точку х 6 G. Поскольку открытое множество G связ-
но в R’*, то в силу критерия из §11 гл. 1 точки хо, х 6 G можно соеди-
m
нить ломаной /[хо, х] = (J [а*, Ьь] (ах = хо, а* = bk-i, bm = х) с носите-
к=1
лем, целиком лежащим в G. Поскольку [а*, Ь*.] с G (k = 1,2,..., m),
13*
371
то в силу теоремы о среднем для числовой функции f Е £!([«*,&*])
существуют точки с* 6 (а*,Ь*) С G (к = 1,2, ...,тп) такие, что
f(bk) - f(ak) = Е D>/(c*)(6<fe> - «<*>), но (ск Е G) => (Dj/(cfc) = 0),
поэтому (/(а*) = f(bk) (fc = 1,2,... ,m)) => (/(®) = f(xQ) V® G G) =>
(f(x) = const в G).
§ 7. Локальные экстремумы числовой функции
многих переменных
Определение. Пусть f : М С R” —> R, тогда внутренняя
о
точка xq ЕМ называется точкой локального максимума (локаль-
ного минимума) функции f(x) на множестве М, если существует
окрестность U(xq) С М такая, что
/(х) < f(x0)(f(x) > /(so)) Vs € й(х0),	(7.1)
О
(если в (7,1) вместо < (>) стоит < (>), то точка xq ЕМ называ-
ется точкой строгого локального максимума (строгого локального
минимума) функции f(x) на множестве М).
Замечание. Если xq ЕМ - Фочка локального максимума или
о
локального минимума функции f(x) на множестве М, то xq ЕМ на-
зывается точкой локального экстремума функции f(x) на множестве
М.
Теорема (необходимое условие существования локального эк-
стремума для дифференцируемой функции). Пусть f : М С Rn —> R
о
и xq ЕМ есть точка локального экстремума функции f(x) на мно-
жестве М. Тогда если f Е 7)(xq), то D«/(®o) = 0 (г = 1,2,..., п).
Доказательство. Пусть f Е 7)(xq) и существует
шар 1Щ(®о) С М такой, что, например, f(x) < /(®о) V® G 1Щ(®о).
п
Докажем, что для любого ненулевого вектора 1 — $2 им?ем
i=i
Di/(®o) = 0. В самом деле, пусть F(t) = /(®о +1 • 1) Vt 6 (—£i,<5i),
где xq 4-1 • 1 6 IIIj(®o), тогда F(t) < F(0) Vt 6 (—<5i, <У1), и посколь-
ку f E 1>(®о), to 3Fz(0) = Di/(®o)« Но тогда в силу необходимого
условия существования локального экстремума у дифференцируемой
функции одного переменного (см. ч. I) имеем (F'(0) => (Di/(®o) = 0)
и, в частности, Dj/(®o) = Ве,/(®о) = 0 (j = 1,2,... , п).
Замечание. Доказанное необходимое условие существования
локального экстремума для дифференцируемой функции ни в коем
случае не является условием достаточным.
Пример. Пусть М = R2, ®о = (0,0) и /(®i, ®г) =	““ xv Тог-
да Dj/(0,0) = 0 (j = 1,2), но функция /(®i, 0) = —®2 имеет в точке
372
xi = 0 локальный максимум, а функция /(О, ®г) = х% имеет в точке
Х2 = 0 локальный минимум, функция У(х1,хг) =	не имеет
в точке (0,0) локального экстремума, поскольку точка (0,0) является
«седлом* для графика функции z =
кий параболоид, см. рис. 52).
Прежде чем приводить доста-
точные условия существования ло-
кального экстремума для числовой
функции многих переменных, на-
помним некоторые сведения из ли-
нейной алгебры (см. [4]). Рассмот-
рим квадратическую форму
Ф(х) = £ а,,®,®,,
•>i=i
х = £	€ Rn
>=i
/(®1, ®г) (график - гиперболичес-
с симметрической матрицей (а,-,) (г, j = 1,2,...,п) (так что ау = а,,
V» / j).
Определение. Квадратическая форма Ф(х) называется по-
ложительно (отрицательно) определенной, если Ух G Rn, имеем
Ф(х) > 0(< 0) при ||х||п > 0
(7.2)
Замечание. Если в (7.2) знак > (<) заменить на > (<), то
квадратическая форма Ф(х) называется положительно (отрицатель-
но) полуопределенной.
Определение. Квадратическая форма Ф(х) называется не-
определенной, если Ф(х) может принимать как положительные,
так и отрицательные значения при различных Х1,Хг € R”.
Ранее в $ 12 гл. 1 ч. III была доказана
Лемма. Если квадратическая форма Ф(х) - положительно (от-
рицательно) определенная, то существует постоянная с > 0 такая,
что Ух G Rn
Ф(х) = £ aijXiXj > с||х||2 (< -с||х||2).
»J=1
Теорема (признак Сильвестра определенности квадратической
п
формы). Пусть Ф(х) = aijx*xj ” квадратическая форма и А =
м=1
(aij) (*» i = 1» 2,... , п) соответствующая ей симметрическая (atj =
373
aji j) nx n матрица с главными минорами
Ai = ац, Az =	«11 «21	«12 «22	, Аз =	«11 «21 «31	012 022 Оз2	«13 «23 «33
	•, Ап	«11 • • •		«1п		
		«П1		«пп		
Тогда:
1) (квадратическая форма Ф(х) является положительно опреде-
ленной) & (Ai > 0, Ai > О, ..., Ап > О);
2) (квадратическая форма Ф(х) является отрицательно опреде-
ленной) & (Ai < О, Аг > О, Лз < О, ... , (-1)"ЛП > 0). (Доказатель-
ство теоремы Сильвестра приводится в курсах линейной алгебры, см.,
например, [4].)
Пусть / : М С Rn -> R, ®о и f € Т№(хо), тогда су-
ществует окрестность С7(хо) С М такая, что / € 1>(17(®о)), е. в
любой точке х € U(xq) существует первый дифференциал df(x) =
22 T)jf(x)dxj € £(Rn,R), причем Dj/(®) € 2>(а?о) (j = 1,2,... ,n),
i=1
так что Vxo + h € Й(®о) имеет место представление Dj/(®o + h) -
Dj/(®o) = SD«Dj/(®o) +Oj(||h||n) (h-> 0) (j = 1,2,... ,n). Рас-
•=1
смотрим при Xq + h € U(xo) и Vk € R" разность
4f(«o + h)k - d/(x0)k = 52(Dj/(®o + h) - Dj/(®o))fy -
i=i
=	(DiD^/(®o)A, + oj(||h||n))fcj =
i,j=i
= £ DiDjflxo^ + Oj(||h||„)*j (h -4 0).
•j=i
В силу теоремы Юнга D,Dj/(®o) = DjDi/(®o) V* j, так что, вводя
def
билинейную форму d2/(®o) == 52 D<Dj/(®o)d®< dxj : (h,k) € Rn x
«j=i
Rn —> R имеем представление V®o + h € U(xq) и Vk € Rn
(®O + h)k - d/(xo)k = d2/(®o)(h, k) + o(||h||n)||k||n (h -> 0). (7.3)
Равенство (7.3) можно принять за определение того, что f €
Итак, если для функции f 6 ®^2^(®о) Л2>(Щ®о)) окрестность U(xQ) С
374
М, то существует второй дифференциал d2/(®o) G £(Rn х Rn,R),
участвующий в представлении (7.3), и тогда билинейная форма
п
B(h, к) = d2/(®0)(h,k) = £ D,DJ/(x0)fe.*j
М=1
является значением второго дифференциала d2f(xo) =
/ п	\ 2
( 52 D»d®i ) /(®о) на паре векторов (h, к) G Rn х Rn. Билиней-
\*=1	/
ной форме B(h, к) соответствует квадратическая форма
п
Ф(Ь) = B(h,h) = d2/(®0)(h, h) = £ DiDy/(®o)Mi,
i,j=l
причем матрица Гессе (D,Dj/(®o)) (м = 1,2, ...,п) квадратичес-
кой формы Ф(Ь) - симметрическая, поскольку в силу теоремы Юнга
DiDy/(®o) = DjD«/(®o) Vi
Теорема (достаточное условие существования локального эк-
стремума для дважды дифференцируемой функции). Пусть f : М С
О
R” -> R, ®о и существует шар 1Щ(®о) С М такой, что
f € 2>(Ш*(хо)) Л2><2)(®о)" Пусть df(xo) = 0 (так что Dif(xo) = 0;
г = 1,2,..., п). Тогда:
п
1)	если квадратическая форма Ф(Ь) = d2/(®o)(h,h) = 52 Di х
ij=l
- положительно (отрицательно) определенная, то
о
функция f(x) имеет в точке ®о ЕМ локальный минимум (локальный
максимум);
2)	если квадратическая форма Ф(Ь) = d2/(xo)(h,h) - неопреде-
о
ленная форма, то функция f(x) не имеет в точке xq ЕМ локального
экстремума.
Доказательство. Поскольку f € Р(1Щ(®о)) и f 6 2>(2)(®о)>
то к функции f(x) в окрестности 1Щ(жо) С М применима теорема о
формуле Тейлора с остаточным членом в форме Пеано, в силу которой
имеем
f(x0 + h) = /(®о) +	+ | • 52 D«Dj/(®o)M,+
i=i	м=1
+°(l|h||n) (h —> 0) V®o + h € liltf(aco)
или в силу условий теоремы D>/(®o) = 0 (j = 1,2,... , n) V®o + h €
Ш«(®о) имеем представление
п
/(®о +h) - /(®о) = 1/2 • £ DiDjfMhihj + 0.(1 |h||2) (h -> 0).
»j=i
375
1) Пусть теперь Ф(Ь) = d2/(a?o)(h,h) = £2 DiDjf(%o)hihj - по-
»J=i
ложительно определенная квадратическая .форма, тогда по лемме су-
ществует постоянная с > 0 такая, что Vh 6 Rn имеет место
п
£аОУ/(хо)М;>с.||Ь||2
»,j=i
(и, в частности, для h G Rn таких, что хо 4- h G nij(xo))- Но тогда
Vx 6 Ш<(хо) имеем оценку f(x) - /(хо) > 1/2 • (с + о(1)) р2{х, х0)
(х —> хо)- Но по определению символа о(1) (ж —> хо) 3<5х > 0 такое,
что с + о(1) > с/2 > 0 Vx G lilj, (хо) С 1П4(х0), и тогда f (х) — /(х0) >
°
ср2(х, хо)/4 > 0 Vx G ШлДхо), т. е. хо GAf есть точка (даже строгого)
локального минимума функции /(х).
2) Пусть квадратическая форма Ф(Ь, h) = d2f(xo)(h, h) - не-
определенная форма. Тогда ЗЬ1,Ьг G R" такие, что ||h|||n > О
(I = 1,2) и Ф(Ь1) = Ci > 0, Ф(Ьг) = сг < 0. Но тогда Bio > 0
такое, что хо + t • h< G Ш«(®о) Vt G (-<5o,<5) G = 1,2), откуда
/(x0 +1 • h,) - /(x0) = t2/2 • £ D<D//(*o)M° •	+ <2ot(l) (t -> 0),
•J=l
t. e. f(xo 4- th/) - f(xo) = t2(c/ 4- o/(l))/2 (t -4 0). В силу определения
символов о/(1) (t -4 0) 3(5i 6 (0, (Уо) такое, что ci 4- oi(l) > q/2 > О,
с2 4- 02(1) < с2/2 < 0 V|t| < Ji, и тогда f(x0 4-t • hi) - f(xQ) > О,
/(®o 4-t • h2) - /(®0) < 0 V»o 4-1 • h/ G lib(®o) G = 1,2), т. e. точка
о
xq EM не может быть точкой локального экстремума функции f(x).
Замечание. Если квадратическая форма
Ф(Ь) = d2/(xo)(h,h)
является полуопределенной квадратической формой, то функция f(x)
о
в точке xq GAf, где D«/(®o) = 0 (г = 1,2,... , п), может иметь локаль-
ный экстремум, а может и не иметь его (это сомнительный случай,
требующий дополнительного исследования).
Пример. Исследовать на экстремум функцию /(ж, у) = х2 4-
(у - ®)2. Очевидно, имеем Di/(®,!/) = 2®, D2/(®,!/) = 2(у - 1),
D2/(®,!/) = 2, DiD2/(®,!/) = D2Di/(®,!/) = О, D2/(®,!/) = 2. Тогда
Di/(0,1) = D2/(0,1) = 0 и d2/(0,1)(h, h) = 2(h2 + h2) > 0 V||h||2 > 0
- положительно определенная квадратическая форма, т. е. точка (0,1)
есть точка локального минимума /(0,1) = 0 = min/(x,j/) (это даже
точка абсолютного минимума этой функции).
376
§ 8. Обратные функции
В §2 гл. 2 изучался вопрос о решении линейного уравнения вида
Ах = у, где А Е £(Rn, Rn).
Замечание. Пусть А Е £(Rn, Rn) и А = (Ay) (г = 1,2,... , п) -
матрица морфизма А. В линейной алгебре было доказано утверждение
(ЗА”1 Е £(R”, Rn)) <=> (det А # 0).
Теперь рассмотрим вопрос о решении нелинейных уравнений вида
/(») = у, где f : G С Rn -+ Rn.
Теорема (достаточное условие существования гомеоморфизма).
Пусть f : G С Rn -> Rn, G - открытое множество, f Е C(G) и
Зс > 0 такое, что | |f (жх) -f(®2)||n > с - |[xi-x2||n Ужъ х2 Е G. Тогда
отображение f осуществляет гомеоморфизм G на f(G), так что
существует обратная биекция f"1 Е C(f(G)), причем выполнена
оценка Липшица -f~1(3/2)||n < 1/с-||yi~y2||n Чуъуг Е f(G).
Доказательство. Поскольку ||Г(ж1)— f (ж2) | |п > с-Цхх-хгЦп
ж2 Е G, то (/(®i) = f (®2)) <=> (®i = ®2), поэтому отображение f :
G С Rn -> /(G) С Rn есть биекция и существует обратная биекция
/-1 : /(G) -> G. Далее Vj/i, у2 Е /(G) Зжг, х2 Е G такие, что /(®i) = у±
и /(®2) = У2. но тогда имеем оценки ||f“1(?/1) - f"1(j/2)||n = ||xi -
x2||n < l/c-||f(®i)-f(«2)||n = l/c-||yi—у2||п, т. е. ||f"1(t/i)-f(!/2)||n <
1/с - ||yi — у2||Л Vt/i, У2 Е /(G) и, в частности, Z”1 Е C(/(G)). Но
/ Е G(G), и поэтому отображение / : G -> /(G) есть гомеоморфизм.
Уточним теорему о принципе сжимающих отображений из §13 гл. 1
ч. III.
Теорема (о принципе сжимающих отображений). Пусть ото-
бражение f : G С Rn —> Rn - сжимающее на замкнутом множестве
F С G, причем f(F) С F. Тогда отображение f имеет единствен-
ную неподвижную точку в F.
Доказательс тво. Применим метод последовательных
приближений для решения уравнения /(ж) = ж, положив жо Е F и
®т = /(®т-1) (т = 1,2,3,...). Поскольку /(F) С F, то хт Е F
\/т. Но тогда, поскольку отображение / - сжимающее на F С Rn, то
последовательность (жт) фундаментальна, и поэтому в полном про-
странстве R” 3 lim хт = ж Е F. Но множество F замкнуто, так
тп—>+оо
что ж Е F. Переходя к пределу при т —> 4-оо в рекуррентном соот-
ношении хт — f(xm_i) и учитывая, что / Е C(F) (в силу того, что
/ - сжимающее на F), имеем ж = /(ж), т. е. ж Е F есть неподвижная
точка отображения /, единственная в силу сжимаемости /.
Замечание. Если условие /(F) С F не выполнено, то отобра-
жение /, сжимающее на F, может не иметь в F неподвижной точки.
Например, отображение / : R1 -> R1, где /(ж) = 1 + ж/2 - сжи-
мающее (с коэффициентом сжатия 1/2) на отрезке F = [0,1], но не
377
имеет на этом отрезке неподвижной точки, поскольку (/(®о) = ®о) =>
(®о = 26[0,1]). (Заметим, что /([0,1]) = [1, 3/2] £ [0,1].)
Теорема (о нелинейном возмущении). Пусть А € £(Rn, Rn) и
существует обратный морфизм А"1 € £(Rn, Rn) (с нормой ||А~1|| =
а > 0). Пусть для отображения g : G С Rn Rn (где G - откры-
тое множество) для внутренней точки xq € G существуют шар
Ш^(«о) С G и постоянная (3 > 0 (где 0 < а -/3 < 1) такие, что име-
ет место оценка Липшица ||g(x‘i) - g(®2) I In < /3||xi ” X2Hn E
ПЫхо) C G. Тогда отображение f = А-^_^Ш^(®о) C G_C Rn
(x —> Ax — g(x)) осуществляет гомеоморфизм 1Щ(®о)	/(П1$(®о))>
причем:
a)	||f(®i) -f(®2)||n > ((1/а) -/3) • ||xi -x2||n V®i,®2 € Ш^(®0);
б)	Ур € Ш<у(/(®о))^ где а = ((1/а) - /3) • 6 > 0, уравнение
f(x) = у имеет единственное решение х € ШЩяо), т. е. Ша(/(®о)) С
/(шн»о)).	_
Доказательство. Поскольку f(x) = Ах — g(x) Vx 6 nij(®o)>
то Ах = f(g)+g(g), и поскольку ЗА”"1 6 £(Rn,Rn), то х = A~1(f(®) +
g(®)) Vx € Ш$(®о)‘ Но тогда, используя линейность морфизма А-1 и
условие Липшица для отображения д, имеем V®i, х2 6 Шд(хо)
||Х1 - Хз||п = 11Л“Х(Г(®1) + g(®i)) - A-1(f(®2) + g(«2))I In =
= IIA-Wi) - f(®2)) +	- g(®2)||„ <
< 11A"111 • (||f(xi) - f(®2)1|„ + ||g(xi) - g(®2)||„) <
< a • ||f(®i) - f(®2)1|„ + afi • ||xi - x2||n,
t. e. (l-a/3)-||xi~x2||n < a-||f(®i)-f(®2)||n, тем самым оценка а) дока-
зана. Из оценки а) в силу теоремы (о достаточном условии существовав
ния гомеоморфизма) видим,_что отображение / = А — д осуществляет
гомеоморфизм 1Щ(®о) на /(IUj(®q)). Для доказательства утверждения
б) выберем любое (но фиксированное) у € Ш^(/(®о)) и рассмотрим
отображение h : ШДхо) С R" 4 Rn (® -> h(x) = О + h(®)), положив
h(x) = A-1(g(x) -I- у). Покажем, что тогда (/(х£= у) & (х = Л(х)).
В самом деле, поскольку д = А - /, то Vx G inj(xo) имеем h(z) =
A“x(Ax-f(x) + y) = x + A-1(y-f(®)), т. е. h(x) = ® +A-1(y-f(®)),
откуда (® = Л(®))	(А-1(у - f(®)) = 0) и (поскольку гомоморфизм
Л-1 обратен к А) (у - f(®) = 0) (f(®) = у) (/(®) = у).
Докажем, что функция h осуществляет сжимающее отображение
замкнутого шара Ш;(®о) в себя. Учитывая, что ||А—1|| = а, имеем
V®i, ®2 € Ш«(®о) оценки
I|h(«i) - h(®2)11„ = ||A"1(g(®1) - g(®2))||n < a • ||g(®i) - g(®2)||„ <
< a/3 • ||xi — x2||n>
378
где 0 < aft < 1. Итак, h является сжимающим отображением на замк-
нутом шаре Ша(®о) С Rn. Докажем, что Л(Ш^(®о)) С В самом
деле, поскольку h(®o) — *о = А"1 (у - f(®o))> то V® € 1Щ(®о) имеем
оценки
I|h(®) - xo||n < I|h(x) - h(®0)||n + ||h(®0) - x0||n < «0 • Iх ~ *oI|n+
+l|A~1(y - f (®o)) | |n < a/3 • ||x - x0|ln + <* • Ну - f (®o) I In-
Ho ||x-x0||n < S в (у G 1Щ(®о))) => (||y-f(®o)||n < ff), поэтому имеем
строгое_неравенство ||Ь(®)-ХоЦп < аЪ5+сит = a/W+a((l/a)-/3)J = <5,
т. е. Л(Ша (®о)) С Ш<(®о). Но тогда в силу уточненного принципа ежи-
мающих отображений видим, что сжимающее отображение h должно
иметь единственную неподвижную точку х в замкнутом шаре
но, на самом деле, х = h(x) Е 1Щ(®о), так что f(x) = у. Итак,
Vy Е Ш<г(У(®о)) существует единственная х G 1Щ(®о) такая, что
/(®) = у, т. е. имеет место утверждение б) Ш<т(/(®о)) С /(Ша(®о))-
Определение. Отображение / : G С Rn 4 Rn называет-
ся локальным гомеоморфизмом в точке ®о € G, если существуют
окрестности U(xQ) С G С Rn и V(/(®0)) С /(G) С Rn такие,
что сужение f : U(xq) —> V(/(®o)) есть гомеоморфизм (так что
П/(®о)) = /(СЛ(®о))).
Следствие (теорема о локальном гомеоморфизме). Пусть / :
G С Rn —> Rn, где G - открытое множество и ®о € G. Пусть су-
ществует морфизм А € £(R”,R”) такой, что для него существу-
ет обратный морфизм А-1 € £(Rn,Rn) с нормой ||А-1|| = а > 0.
Пусть существуют 6 > 0 и /3 > 0 (где 0 < а[3 < 1) такие, что
V®i, ®з € Ш«(®о) С G имеет место оценка ||f(®i) - f(®2) - A(xi -
хг)11п < /3 * IIх! ~ хг||п> Тогда отображение f является локальным го-
меоморфизмом в точке ®о, т. е. существуют окрестности Щ®о) С G и
V(/(®o)) С f(G) такие, что отображение f : П(®о) -4 V(/(®o)) С /(G)
есть гомеоморфизм, при этом имеет место оценка
Ilf(®i) -f(®3)||n > ((1/a — /3) • ||xi - x2||n V®1, ®2 € У(®о)-
Доказательство. Полагая g = f - A : Ш<(®о) -> Rn,
видим, что V®i,®2 € Ш«(®о) C G имеет место оценка Липшица
||g(®i) - g(®2)||n < 0ПХ1 - ха||п, где 0 < afi < 1, a = ||А-11| > 0, но
тогда в силу теоремы о нелинейном возмущении отображение / яв-
ляется гомеоморфизмом шара Ш;(®о) С G С Rn на /(ЙЩ®о)) С Rn,
причем существует открытый шар Ш<г(/(®о)) = V(/(®o)) такой, что
НМ/(®о)) С /(IIIj(®o)). Далее, поскольку при непрерывном отобра-
жении / : Ш{(®о) —> /(Ш;(®о)) «прообраз открытого множества -
открыт», то множество U(xq) = /-1(V(/(®o))) С Ш*(®о) являет-
ся окрестностью точки ®о € Ш$(®о) С G С R", и поэтому су-
жение / : П(®о) -> У(/(®о) = /(С/(®о)) = /(/-1(^(/(«о))) (W
379
U(xo) С 1Щ(ж0), V(/(®o)) С /(IIh(®o))) есть гомеоморфизм, т. е.’ f
локально гомеоморфно в точке xq G G. Кроме того, в силу а) тёоремы
о нелинейном возмущении имеет место оценка
||f(*i) -f(®2)||n > ((1/a) -/?) • ||xi -Х2||ПУЖ1,Я2 G U(x0).
Определение. Отображение f : G С R” -> 0 С R” (где G и
0 = /(G) - открытые множества) называется диффеоморфизмом
(класса ), если f является гомеоморфизмом G на 0, причем f 6
C<X)(G) и Л1 G С<х)(0).
Определение. Отображение / : G С Rn -> R” называется
локальным диффеоморфизмом (класса CW) в точке xq G G, если
существуют окрестности U(xq) С G С Rn и V(/(®o)) С f(G) С
Rn такие, что сужение f : U(xq) —> У(/(а?о)) есть диффеоморфизм
(класса С^), так что, в частности, У(/(жо)) = f(U(xo)).
Теорема (о локальном диффеоморфизме). Пусть f : G С Rn -»
Rn и f G G^^(G), где G - открытое множество. Пусть Xq € G и
detDf(®o) Ф О* Тогда отображение f является локальным диффео-
морфизмом в точке xq, т. е. существуют окрестности U(xq) С G и
V(/(®o)) = f(U(xQ)) такие, что сужение f : 17(®о) —> V(/(®o)) есть
диффеоморфизм (класса С^), причем f G С^)(17(®о))
/-1 G C™(V(f(x0))),	= (D/(x))-x(!/ = /(*)) Vx G С7(х0),
detDf(x) • detD/-1(y) = 1 (у = /(x))Vx G У(х0)
(“»=1 M •
Доказательство. Поскольку detD/(«o) / 0, то
для морфизма D/(®o) Е £(Rn,Rn) существует обратный морфизм
(D/fao))"1 6 £(Rn,Rn). Пусть ||D/(®o))“111 = а0 > 0. Поскольку
/ G C^)(G), то в силу теоремы из §5 этой главы для > 0 (та-
кого, что_0 < (Зо < 1/a) существует шар 1Що(®о) С G такой, что
V®i, ®2 6 Ш4о(»о) имеет место оценка
||f(®i) - f(®2) - D/(so)(xi - x2)||n < /Зо • I|*i - x21|n.
Но тогда в силу теоремы о локальном гомеоморфизме существуют
окрестности и(1)(ж0) С 1Що(®о) С G и V^)(/(®o)) С /(G) такие,
что сужение / : U^(x0) -> V^(/(®o)) = f(U^(xo)) есть гомео-
морфизм, являющийся, в частности (поскольку f~! G C(V^(f(xQ))
и /	C(U^(xq))), открытым отображением, причем имеет место
оценка
||f(xi) -f(x2)||n > ((1/ao) -/?))• I|X1 -x2||„Vxi,x2 G U^(x0).
380
Поскольку (D/ 6 C(G)) => (D/ G C(U^(xq)) и морфизм D/(®o) имеет
обратный (D/(®o))-1 G £(Rn,Rn), то по теореме о нелинейном воз-
мущении из §2 этой главы существуют шар Ш^Дхо) С U^(xq) и по-
стоянная а > 0 такие, что V® G Ш^Дхо) морфизм Df(®) G £(Rn,Rn)
имеет обратный (БД®))"1 G £(Rn,R”), причем ||(В/(®))~1|| < а,
и, в частности, имеет место оценка ||(В/(®1))-1 — (Bf(®2))-111 =
||(В/(®2))-1(В/(®2) - B/(®i))(B/(®i))"1|| < а2||ВД®2) - D/(®i)ll
V®i, X2 G	Ho D/ G C(G), и поэтому из полученной оценки
вытекает, что (В/)"1 G (7(111^(®o))« Положим
<Т(®о) = Ш41 (so) С U^(x0).
Напомним, что гомеоморфизм f : U(xq) ->	(/(®о)) является от-
крытым отображением, поэтому множество V(/(®o)) = f(U(xo)) яв-
ляется окрестностью точки f(xo). Итак, существуют окрестности
U(xq) С U^(x0) и V(/(®o)) С V^(/(®o)) такие, что сужение f :
U(xq) -> V(f(x0)) осуществляет гомеоморфизм У(®о) на V(f(®o))> для
которого / € C^(U(xo)) и Vx б U(xq) существуют морфизм Df(x) б
£(R",Rn), а также обратный морфизм (D/(®))-1 6 £(Rn,R"), при-
чем Df € С(Щхо)), (D/)"1 G С№о)), ||Df(*))’1ll < * и V®,
®4-h б U(xq) имеет место оценка ||f(®4-h)-f(a;)||n > ((1/а0)~A))||h||n.
Докажем, что /-1 б D(j/) Уу б У(/(®о)), причем для у = f(x) име-
ет место равенство D/-1(y) = (D/(®))-1. Пусть у б V(/(®o)) - лю-
бое, но фиксированное, тогда Уу 4- к б V(/(®о)) в силу биективности
отображения / : Z7(®o) —> V(/(®o)) 3s, х 4- h б U(xq) такие, что
у = f(x) и у 4- k = f(x 4- h), откуда х = /-1(j/), х + h = /~х(у 4- к) и
к = f(s4-h)-f(s), причем ||h||n < ||к||п/(1/а0) ~@о), т. е. (||к||п -> 0)
=> (||h||n -> 0). Поскольку f б D(s), то Ух 4- h б U(xo) = О(х) име-
ет место представление f(® 4- h) - f(ж) - D/(®)h = r(h) • ||h||n, где
lim ||r(h) ||n = 0. Но тогда Уу, у 4- k 6 V(f(x0)) имеем
h—>0
llf-^y + k)	- (D/(x))-1k||n =
= ll(p/(x))-1(-k + Df(x)(f-1(y + k)	’
< 11 (DA®))-111 • Ilf (x + h) - f (x) - D/(®)h||n < a • ||r(h)||n • ||h||n <
< (a/((l/a0)-&)) • ||r(h)||„. |k||„.
Ho Hm ||r(h)||n = Uni ||r(h)||n = 0, поэтому
3 lim(l/Hk||„) • ||f-1(y 4-k) — f-1(y) - (D/MHkH,, = 0,
т. e. /-1 б D(y), где у = f(x). В силу единственности производной
имеем равенства р/_1(у) = (D/(x))-1, т. е. D/-1(y) = (D/(®))-1 °
/-1(у) (где у = f(®)), но f б C(U(so)) и /-1 б C(V(f(x0))), поэтому
381
((Df(®))-1 G C(U(xq))) => (при x = Г'(У)) (Df-1 € C(V(f(x0)))),
t. e. /-1 € C^(V(f(xo))), я поскольку
f G CM(U(x0)),
то гомеоморфизм / : U(xq) -> V(/(®o)) является диффеоморфизмом
класса C^1*. Наконец, поскольку
(D/-1)(/(®)) = (D/(®))~x V® G t^(®o)>
то при у = f(x) имеем равенство для якобианов
det D/(®) • detD/“x(t/) = IV® G 17(®о)
или
...................^W)) = i *• e иы-
0(®i,... , ®Л)	^(2/1, • • • , Уп)
Замечание. Теорему о локальном диффеоморфизме обычно на-
зывают теоремой об обратной функции. Отметим попутно, что метод,
использованный при доказательстве теоремы о локальном диффеомор-
физме, позволяет доказать следующую теорему об обратной функции.
Т е о р е м а (об обратной функции). Пусть / : G С Rn
f € ®(G), ®о € G и D/ € C(®ob причем detD/(®o) 0. Тогда ото-
бражение f является локальным гомеоморфизмом в точке xq, т. е.
существуют окрестности U(xo) С G и У(У(®о)) С f(G) такие, что
сужение f : Е7(жо) -> У*(У(®о)) является гомеоморфизмом и для об-
ратной биекции f"1 : И(У(®о))	17(®о) имеем У"1 € ®(У(У(®о))),
причем bf~*\y) = (D/(®))“1, где у = У(х) и D/“x € С(?/о). (Попро-
буйте доказать эту теорему самостоятельно.)
Замечание. Условие det D/(®o) £ 0, фигурирующее в тео-
ремах об обратных функциях, является лишь достаточным условием
для существования обратной функции У*"1. Обратная функция У“х в
окрестности точки j/o = У(®о) € f(G) может существовать и в случае
det D/(®o) = 0. Например, для функции f : х -+ я3 имеем D/(0) = 0,
но обратная функция У-1 : у —> tfy существует.
Замечание. Если якобиан det D/(xo) = 0, то обратная функ-
ция У"1, если она и существует, не может быть дифференцируемой
в точке уо = f(xo). В самом деле, если бы У"1 G ®(j/o)? то из тео-
ремы об обратной биекции из § 4 этой главы имели бы равенство
для якобианов det ВУ(®о) • det ВУ~х(з/о) = 1, противоречащее усло-
вию det ВУ(®о) = 0.
Следствие. Пусть f : G С Rn -> 0 = f(G) С Rn есть диф-
феоморфизм класса C'W, тогда det ВУ(®) 0 V® 6 G.
В самом деле, если бы 3®o G G такая, что det ВУ (® о) = 0, то в силу
предыдущего замечания имели бы У"1 G В(У(®о))> что противоречит
условию У”1 G из определения диффеоморфизма.
382
Следствие (из теоремы о локальном диффеоморфизме).
Пусть f : G С R" -> 0 = /(G) С Rn, / G C<X)(G), где G - от-
крытое множество, det D/(x) / 0 Vx 6 G. Тогда, если / биективно на
G, то отображение / осуществляет диффеоморфизм (класса С^) G
на 0 = /(G).
§ 9. Неявные функции
Пусть / : G = Gi х G2 С Rn х R’n -> Rm (где / : (х,у) -> /(х,у),
х € Gi С R”, у € Gt С Rm /(х, у) G Rm), Gi, Gt и Gi х Gi - откры-
тые множества в R”, Rm и Rn+m соответственно. Пусть уравнение
f(xo, у) = 0 имеет решение у = уо» т. е. /(хо, Уо) = 0. Исследуем вопрос
о решении уравнения f(x,y) = 0 в окрестности V(yo) точки уо € G2.
Определение. Пусть f : G = Gi х Gi С Rn х Rp ->
Rm, где Gi С Rn, G2 C Rp - открытые множества, xq € Gi,
Уо € Gi, (x0,yo) € G, f(x,y) = (/i(x,y),... ,fm(x,y)). Пусть g :
Gi C R₽ -> Rm, где g(y) = f(xo,y). Тогда частной производной
^/(xo,yo) отображения f в точке (хо, Уо) € G называется мор-
физм Dy(yo) € £(Rp,Rm), где Dg(yo) есть производная отображе-
ния g в точке уо € G2.
Замечание. Если / € 1>((хо,уо)), то, очевидно, существуют
^/(®о,Уо) 6 £(R",Rm) и ^/(хо,уо) € £(R₽,Rm).
Замечание. Пусть /(х, у) = (Л(х, у),..., /т(х, у)) и сущест-
вует частная производная •«—/(хо,1/о) € £(Rp,Rm), тогда морфиз-
Оу
0	/ Q	\
“У а“/(®о, Уо) соответствует т х р матрица Якоби (•?—Л(хо,Уо) 1
Оу	\ ayi	)
(i = 1,2,..., m; j = 1,2,...,р). Если при этом р = т, то частной про-
Q
изводной ^/(®о, Уо) 6 £(Rm, Rm) соответствует квадратная т х т
(д	\
л—fi(хо, Уо)) (*'| / = 1,2,..., тп) с якобианом
^Уз	/
0(/1» • • • > /т) /	\ _
...
• • • • • •
^/т(®0,|/0)	...
д . .	.
д~/т(хо, Уо)
ОУт
причем условие	'^т\(хо,уо)	0
5(1/1,... ,Ут)
физм ^-/(х0,!/о)	€ £(R’n,RTO) имеет
оу
означает,
обратный
что мор-
морфизм
383
(о	\	о
Уо))	€ £(Rm,R"*), т. е. морфизм -^-f(xo,yo) явля-
оу	/	оу
ется изоморфизмом Rm на Rm.
Теорема (о неявной функции в случае п > 1, т = 1). Пусть
f : G = Gi х G2 С R”*1 -> R1, f Е G(G), где Gi, G2 и G - откры-
тые множества, (®о,3/о) 6 G, /(®о>3/о) = 0 и V(®,j/) 6 G = Gi х G2
д	df	д
Э^/(®,т/), причем G С((®о,3/о)) и ^/(®о,3/о) / 0. Тогда сущест-
вуют окрестности U(xq) CGiCR" u V(t/o) = (з/о — Уо 4- <f) С G2 С
R1 такие, что V® 6 17(®о) уравнение /(®i,... , хп; у) = 0 имеет един-
ственное решение у = Л(®1,... , ®п) 6 V(yo) такое, что Л(®о) = З/о,
f(x,h(x)) = 0 V® G U(xq), и для функции h : С7(®0) С Rn-> V(yo) С
Л f
R1 имеем h 6 G(U(®o)). Если при этом 3—(®о,з/о) € £(Rn,Rx), то
ох
h 6 Р(®о) и
ОЛ(®о) =
(«о, уо)

так что
ч
• ^(хо>Уо)Ц = 1,2,... ,п).
О £	fi£
Если, наконец, V(®,у) 6 G существует —(®,у) € £(Rn,Rx) и
их	их
е G(G), то he C^(U(xQ)).
оу
д f
Доказательство. Пусть, для определенности, — (®о, уо) =
ду
Q £
2ао > 0. Поскольку — € С((®о,1/о)), то в силу локальных свойств
непрерывной функции существуют окрестность U^(xq) С Gi С Rn
и 6 > 0 такие, что —	> а0 > 0 V® € U^Uxq) С Gi и Vj/ G
оу
[уо - З/о + <5] С G2. Поскольку
у) > «о > OVy G [3/0 - <5>3/о 4-<f],
то функция (от у) f(x,y) Tf на [2/0 — <5,1/о 4- и, учитывая условие
/(®о,з/о) = 0, имеем /(®о,3/о - <J) < 0, /(®о,1/о 4- <f) > 0. Но f € C(G),
так что, вновь используя локальные свойства непрерывной функции
/(®,2/), видим, что существует окрестность U(xq) С U^(xq) С Gi
такая, что f(x,yQ - 5) < 0, /(®,з/о 4- £) > 0 V® G С7(®о) С Gi. Но
тогда при фиксированном ® € 17(®о) функция g(y) = f(x,y) такова,
384
что д 6 С([1/о - <5,1/0 + <Ч), у(у) ТТ на [у0 - 6,Уо + <5] и д(у0 - 5) < О,
д(уо 4- <5) > 0. Тогда по теореме Больцано о промежуточных значениях
непрерывной (числовой) функции By = h(x) 6 (j/o — S, уо + <5) такое,
что д(у) = 0. В силу строгой монотонности функции д(у) это значение
у = h(x) единственно, так что, в частности, при х = xq имеем у = уд
(поскольку д(у0) = f(xQ,yQ) = 0). Итак, доказано, что существуют
окрестности U(xQ) С <?i и V(j/o) = (уо - &,Уо + С G2 такие, что
уравнение f(x,y) = 0 V® G U(xq) имеет единственное решение у =
h(x) G V(yo) такое, что Л(®0) = Уо и /(®,Л(®)) = 0 V® 6 17(®о)» где
h : С7(®0) -> У(уо), причем Л(®о) = Уо-
1) Докажем, что h G C(U(xq)). Пусть ®, х 4- Дх 6 17(®о), где поло-
п
жено Дх = 52 ^хз ‘ ез* Поскольку
i=i
> <*о > о У(®, у) G Щшо) х V(yo),
то, применяя теорему о среднем к числовой функции д(у) = f(x 4-
Дх, у) на отрезке [Л(®), h(x 4- Дх)], имеем представление
f(x + Дх, h(x + Дх)) - f(x 4- Дх, Л(®)) =
= -^-/(® 4- Дх, h(x) 4- 19Дй(®)) • ДЛ(®)
&у
(где ДЛ(®) = h(x 4- Дх) — Л(®), 0 < 19 < 1), откуда получаем оценку
снизу
|/(® 4- Дх, h(x 4- Дх)) - f(x 4- Дх, Л(®))| > а0|ДЛ(®)|,
что в силу равенства /(®4-Vx, Л(®4-Дх)) = 0 имеем V®, ®4-Дх 6 С7(®о)
оценку сверху
|Л(® + Дх) - Л(®)| < (1/а0) • |/(х + Дх, Л(®))|.	(9.1)
Но f € C(G), так что 3 lim f(x 4- Дх, h(x)) = /(®, Л(®)) = 0 и из
(9.1) тогда следует, что 3 lim Л(® 4- Дх) = Л(®), т. е. h G С(®)
||Дх||л-И)
V® 6 17(®о)? и поэтому h G C(U(xq)).
2)	Пусть теперь 3-r—/(®о, j/o) 6 £(Rn,Rx). Докажем, что тогда
ох
Л G 2>(®о), причем
D^(®o) = ~	‘	€ £(Rn,R1)
и, в частности,
dh(x0) df(xQ,yQ) /df(xQ,yQ)
=----------------------ST- (, = 1’2....................n)-
385
Замечая, что
Л(®о) = Уо, /(®о + Дх, h(x0 + Дх)) = /(®о, Уо) = О,
и полагая ДЛ(®о) = h(xo + Дх) - Л(®о), имеем V®o + Дх € U(xq) С Gi
(где Дх € Rn) оценки
Л(«о + Дх) - Л(®о) - /_д/(вО’У°)\	* *	•
\ ОУ /	”хз
(-Jj(’o.w)
Оу	ох
= (1/2а0) У(®о + Дх, уо) - /(®о, Уо) -
1 +
о® Jx
+ [/(®о + Дх, Л(®о + Дх)) - /(®о + Дх, Л(®о))-
~f(*o, У°) ’ ДЛ(®°)] - (1/2«о)(Л + А)-
Поскольку	€ £(Rn,Rx), то имеем Д = О1(||Дх||п)
(||Дх||п -+ 0) и, в частности, /(®о + Дх, Л(®о)) - /(®о>Л(®о)) =
Ах + О1(||Аж||ст) (||Дх||п -> 0), откуда
= (1/ао)
|ДЛ(®о) < (1/ао)|/(®о + Дх,Л(®0))| =
= (1/“о)|/(®о + Дх,Л(®о)) - /(®о> Л(®о))| =
^(то’и,)Дх + о.(||Дх||.) = О(||Дх||„) (||Дх||.	0).
дх
о/	а/
Поскольку V(®,y) € U(x0) х V(y0) Э--(х,у) и € C((®o,Vo)), то по
Оу	Оу
теореме Лагранжа о конечных приращениях (для числовой функции
многих переменных) 3i9 € (0,1) такое, что
h
* Q£	Qf
^(®о + Дх, Л(®0) + 1?Л(®о)) - 0~(®о, h(x0)) ДЛ(®0) =
= О2(|ДЛ(®0)|) = 02(О(||Дх||п)) = о3(||Дх||п)(||Дх||п -4 0).
Но тогда из нашего представления имеем
А + h = oi(||Дх||п) + оз(||Дх||п) = о4(||Дх||п)(||Дх||п -4 0),
386
т. е. V® + Дх € U(хо) получено представление
Л(®0 + Дх) - Л(х0) - Уо}) '	У<№* =
= о(||Дх||п)(||Дх||п-> 0),
означающее, что h 6 2?(хо), Причем
(д
fyf(xo,yo)
df(xo,yo) e<C(Rn Rl)
Ox
д
3)	Пусть теперь V(x,j/) € G существуют морфизм -т— f(x,y) €
их
£,(‘R.ntR1) и < причем	€ C(G). Докажем, что тогда
Л G C^(U(xq)). Заметим, что V®, х + Дх €-17(®о)> имеем /(®, Л(®)) =
/(® + Дх, h(x + Дх)) = 0. Далее,	> а0 > 0 и |ДЛ(®)| <
Оу
(1/а0)|/(х + Дх, Л(х))|, причем € С((х, у)) (у = Л(х)) и, как было
показано выше (в 1)), h € C(U(x$)). Но тогда, как показано в 2) (при
хо = ®), имеем h € D(x) Vx € С7(хо), причем
D*(») = (•’1;^®’»)) '• ?7(®,1/) e^RMt1)
\ Оу / Ох
(у = Л(®), ® € 17(®о)).
Но тогда (поскольку у = Л(а), h € C(U(xq))) имеем Dft G С(С7(®о)),
т. е. h € C^(U(xo)). Тем самым теорема о неявной функции случае
n > 1, т = 1 доказана полностью.
Теорема (о неявной функции в случае п > 1 и т > 2). Пусть
f : G = Gi х Gi С RJ —> RJ* —> Rm, где G, Gi и Gt - открытые
множества, f € C^(G), (®о, уо) € G, /(®o,!/o) = 0 и
л. df(x0, уо) _ 0(Л,..., fm),
Тогда существуют окрестности 17(х0) C Gi C Rn и V(yo) C G2 С
Rm такие, что Vx = (xi,... , хп) С U(xq) С Rn система т уравне-
ний с (п + т) переменными
fi(®1» • • • ? ®п, 1/1, • • • , Ут) — 0 (i — 1,2,, т)
имеет единственное решение у = Л(х) С V(l/o) такое, что Л(хо) =
З/о, Л(х,Л(х)) = 0 (г = 1,2,... ,m) Vx € U(xq), причем h Е C^(U(xq))
и
Dft(x) = - (£ £(Rn, R"»)
\ Оу / Ох
387
при у = h(x).
Доказательство. Доказательство проведем по индукции (по
т, где т > 2), следуя схеме Юнга, изложенной в [5]. Предполагая, что
теорема верна для системы из т — 1 уравнений, рассмотрим якобиан
3(»,») -	......(»,„) = det а-^- =
^(j/l, . . . , Ут)	&У
dfi dfr
dyi ” ‘ дут
= ................
dfm
dyi ‘ “ дут
Пусть 311? З21, ••• }3mi - алгебраические дополнения элементов 1-го
т dfi
столбца определителя 3} так что 3 = 52 Ъ—3«1- Поскольку по усло-
i=l
вию 3(^0} Уо) 7^ 0, то хотя бы одно из алгебраических дополнений
3«i(®0} З/о) (£=1,2,..., т) отлично от нуля. Пусть, для определеннос-
ти, 311(®о, Уо) # 0. Поскольку 311 Е C(G), то существуют окрестности
С^х)(®о) С Gi и И1) С G2 такие, что
у) 0V® е U™(x0), Vy G V<1)(Jft>).
Рассмотрим систему т— 1 уравнений /,(®, у2,у1) = 0 (г = 2,3,... , тп),
где положено у* = (ух,... , ут). Поскольку
Зи(хо, уо) = |!~;2~	Ух, Уо) # О,
О\У2, • • • , Ут)
то по предположению индукции для этой системы уравнений верна
теорема о неявной функции, в силу которой существуют окрестности
U^(x0) С U^(x0) С Gx,
(у? - *2, У? + <м X 02>(j/o) с g2 с
и существует отображение у :	(®о) х (у? — <52, У? + <52) С ->
^(2)(Уо) С R”-1 такое, что g 6 C^(U^(x0) х (у? - <$2,Ух + <52)),
У(®о,Ух) = Уо, причем
А(»,У1,У(®,У1)) = 0(г = 2,3,... ,т).	(9.2)
Рассмотрим теперь функцию /i(a5,t/i,j/) и докажем, что для одного
уравнения
А(®,У1,у(®,У1)) = Ф(ж,У1) =0
388
выполнены условия теоремы о неявной функции (в случае т = 1),
доказанной ранее. Отметим равенство
Ф(«о,У?) = fi(xo,y^,g(xo,yi)) = fi(xo,yo) = О
и заметим, что поскольку fi G C^^(G) и д G C^U^^xo) х (у$ —
<5г,!/? + <М)> то в силу теоремы о производной сложной функции имеем
Ф G C^(U^(x0) х (у° - 62, £ + J2)).
Проверим, что -—Ф(®о»3/1)	0. В самом деле, поскольку Ф(®, ух) =
ОУх
A(®,!/1>0(®,3/1)), то
=	,_L
dyi ^yi dyj dyi
(9.3)
и, дифференцируя по ух тождества (9.2), имеем
Q=dfL + ^dfL.dgL(i = 2
dyi дУ] <hn
(9-4)
Умножая (9.3) на алгебраическое дополнение 31» а (9.4) на 3«1 и скла-
дывая, получаем равенство
ЭФ	dfi
' Эух	дУ1
m л
Q9j
hdyl

3,1 •
Но из алгебры известно, что сумма произведений элементов данного
(О f • \
т—) на соответствующие алгебраи-
uyj /
ческие дополнения 3«fc (элемента ^-^) вычисляется по формулам
иУк
hdy>
Zik = 3 • &;к, Т.е. V . 3,1 = Зи V . 3.4 = о
dyi ду>
при j = 2,3,... , тп, откуда имеем равенство
Зи(®о, Уо) • ^-ф(хо, Уо) = 3(®о, уо).
Поскольку Зп(®о, Уо) Ф 0, 3(®о, Уо) 0, то доказано неравенство
•т—Ф(®0, Ух) 5^ 0, позволяющее применить ранее доказанную теорему
иУ1
389
о неявной функции к одному уравнению Ф(®, yi) = 0, в силу которой
существуют окрестности U(xq) С (®о) С Gi С R", (у?—5, у°+<У) С
(у? - $2, Ух + £г) и отображение <р : U(®о) С Gi -> (у° - 6, $ + 6) такое,
что <р € <7<1>(Z7(®o))» р(®о) = У? (Ф(®о,У?) = 0), причем
Ф(®, у>(®)) = 0 V® G U(xq).	(9.5)
Но тогда, вводя отображение h : U(xo) -> V(jfo) = (у° — S,yi + 6) x
V^KVo) C G2, где h(x) = (p(®),g(x,<p(x))) (так что hi(x) = <p(x),
hj(x) = gj(x,<p(x)) (j = 2,3,... ,m), в силу непрерывной дифферен-
цируемости функций tp и д имеем по теореме о производной слож-
ной функции Л € C^(U(xo)), причем Л(®о) = (¥’(®о),у(®о,¥>(»о))) =
(у°, j/о) = уо, а также (вспоминая (9.2), (9.3)) имеем V® € Я(®о) С Gi
/1(®, Л(®)) = /1 (®, ¥>(®),у(®, р(®))) = Ф(®, у>(®)) = 0,
Л (®, Л(х)) = fj (®, у>(х), д(х, р(®))) = 0 (j = 1,2,3,..., т),
т. е. /(®, Л(®)) = 0 V® G U(®o), Л(®0) = уо, h G С^(17(®о)), чем доказа-
на теорема о существовании неявной функции для системы f (®, у) = 0.
Докажем единственность решения у = h(x). Допустим от против-
ного, что в окрестности U(®о) существуют две не тождественно рав-
ные функции Н, he CW(l7(®o)) такие, что Я(®о) = Л(®о) = уо;
я(®), Л(®) е У(уо), /(», Я(®)) = /(®, Л(®)) = оV® е я(®0).
Поскольку / е C^(G), то, считая окрестности 17(®о) € Gi и V(yo) С
Gt выпуклыми, можно применить теорему о среднем в интегральной
форме, в силу которой имеем V® е Щ®о)
0 = /(®,Я(®))-/(®,Л(®)) =
1
= [ |-/(®,ft(®) + A(H(®)-h(®)))(H(®)-h(®))dA,
о
или в координатной форме V® € Я(®о) (» = 1,2,..., т)
-М®))-
к=1
Таким образом, функция Н(®) - h(®) при любом фиксированном ® е
Я(®о) является решением однородной алгебраической системы (9.6).
Поскольку Я(®о) = Л(®о) = уо и Я, Л € С(Я(®о)), то имеем
Э lim (Л(®) + А(Н(®) - h(®))] = уо VA £ [0,1].	(9.7)
j ^(®, Л(е) + А(Н(®) - h(»)))dA = 0. (9.6)
о
390
a Z,
Поскольку € C(U(x0) х V(j/o)); Л, Я € С(Я(®о))> то, исполь-
ОУк
зуя выпуклость окрестности V(yo), в силу (9.7) видим, что Ve > О
ЗШ*(®о) С Я(®о) такой, что
^-(х, h(x) + А(Н(х) - h(x))) -	Уо) | <
< eV® Е Ше(®о) (г,к = 1,2,... ,т),
откуда
о
Чх, Л(х) + A(H(s) - h(»)))dA - уо) =
Ъ	иУк
о
(х, h(x) + А(Н(х) - h(x))) - Ж0,Уо)1 dX < е,
°Ук
т. е.
Э lim / ^-(x,fc(x) + A(H(x)-h(®)))dA =
J Wk....................  '
0
1
= [ Vo)dX = yo) (i, к = 1,2,...,
J ОУк	ОУк
О
так что
1
Э lim det f ^(х,Л(х) + А(Н(®)-Ь(®))Ш =
J Qy
0
= det |£(хо, Уо) # 0.
Но тогда окрестность U(xq) С Gi можно считать столь малой, что
для определителя системы (9.6) имеет место
1
det f y-/(®,A(®) + A(H(®)-h(®)))dA^0,
о
Vs E U(xq) C Gi и поэтому однородная линейная система (9.6) при
любом фиксированном х Е 17(®о) может иметь только нулевое реше-
ние, так что Н(х) = h(x) в U(xq) С Gi. Противоречие, доказывающее
единственность неявной функции у = h(x).
391
Замечание (о вычислении частных производных неявной
функции). Для вычисления частных производных -—hi(x) (i =
OXj
1,2,... ,m;j = 1,2,... ,n) функции h E С^(17(®о)) продифференци-
руем no Xj (j = 1,2,..., n) тождества fi(x, h(x)) = 0 (i = 1,2,... , m),
что дает
M^Ofi dhk,._. 9	„
dxi t^dyk ' dx, (t 1>2>----”M-1>2>
П £	A £
и поскольку существуют гомоморфизмы — Е £(Rn,Rm), -г- Е
ох	оу
£(RW, R’n), Dh Е £(Rn, RTn), то имеем равенства
А	А
•д-Л®, Цх)) +	М®)) ° Dh(s) = 0.
Ох	оу
д	f 8 \
Вспоминая, что в силу det —/(ж,</)	0 3 I —f ) Е £(Rm,Rw),
оу	\иу /
имеем при у = h(x)
еС№0))
их
и, в частности, для h 6 (7<х>(17хо)) имеем
0(А,
_d_hk =________________________________________________
1	,yk-i,xj,yk+i,... ,yn) / d(yi,... ,ym) ’
(k = 1,2,... ,m;j = 1,2, ...n).
Замечание. Сравнение условий (гладкости) двух теорем о
неявной функции, доказанных выше, показывает, что требование (в
случае п>1ит>2)/Е C^^(G) является более жестким, чем
О £
требования f Е C(G) и — Е C(G) (в случае п > 1 и т = 1). Ни-
оу
же будет приведена основная теорема о неявной функции (в случае
Я f
п>1ит>1)с условиями гладкости f Е C(G) и Е C(G),
оу
метод доказательства которой сходен с проведенным в теореме о ло-
кальном диффеоморфизме из § 8. Отметим, впрочем, что, как показы-
вает лекционная практика, эта современная методика воспринимается
студентами-первокурсниками как более трудная в сравнении с клас-
сическим методом Юнга.
Предварительно докажем теорему.
392
Теорема. Пусть f : G = Gi x G2 C Rn x Rp —> Rm, где
Gi C Rn, G2 C Rp и G C Rn+p - открытые множества (®о>3/о) 6 G
(xo e Gi, Уо 6 G2/ U У(®,т/) e VF((®o,!/o)) c G существует морфизм
Я	д
у) Е £(RP, Rm), причем — Е C((so, Уо)). Тогда Уг > О 3(5.- > О
ду	ду
(i = 1,2) такие, что имеет место оценка
||Г(®,У1) ~Цх,у2) - ^/(хо,!/о)(У1 -Уг)||т <
< е||У1 - Уг||рVx е Ш^(х0) С GinVyn у2 G Ш^уо) С G2,
где Ш<;>(х0) х Ш^уо) С РГ((хо,Уо)) С G.
Доказательство. Поскольку — f Е С((®о, 2/о))> то Уг > О,
Э(5> > 0 (г = 1,2) такие, что
ш£>(х0) х Ш^(уо) С Ж((х0,уе))н
у) -	Уо) <	у) €
dyj
€ Ш<;>(хо) х Ш^уо) (г = 1,2,..., т; j = 1,2,..., п).
Для фиксированного х G Ulj"\xo) определим функцию g : Ш^(уо) ->
Rw, положив g(y) = f(x,y) -	2/о)у так, что
р д
9i(y) = Л(®,У)-52^-Л(®о,Уо)Ук(» = 1,2,... ,тп),
д , . д г . . д Г1 . m
откуда д—у<(у) = д— fi(x,y) - •=— /,(®о,Уо). Тогда имеем оценку
ayj	oyj	oyj
т р / д \ 2	/ \
12 Z2 I Л-у«(у) ) < «2 Vy G Шг’(уо) и по теореме о среднем из
•=1 >=1 \ОУз /
§ 5 этой главы имеем оценку ||g(yi) - g(y2)||m < М(у)||yi - у2||р <
е*||У1-Уг||р Vyx,y2 € Ш^Суо), т. е. ||f(x,yi)-f(®, у2)-^/(х0, Уо)(У1~
У2)||т < е • ||У1 - у2||р Vx G ш£>(хо) С Glt Vylty2 е Ш^(уо) С G2.
Основная теорема (о неявной функции (см. [7] ч. II
5.2.4, с. 128)). Пусть f •. G = Gr х G2 С Rn+m -> Rw, f E C(G)
(где Gi C Rn, G2 C Rm и G C Rn+Tn - открытые множества).
Пусть (xo,yo) Е G (®о Е Gi С R”, уо 6 G2 С Rm) /(®о,Уо) = О
Q
u V(x,y) G G существует морфизм —f(x,y) 6 £(Rm,Rm), причем
393
д	Э
-x~f € C^Xq^q)) и det -^/(xo^o) # 0. Тогда существуют окрест-
Оу	Оу
кости U(xq) С Gi С Rn и V(ya) С G2 С Rm такие, что Vx € U(x0)
уравнение f(x,y) = 0 имеет единственное решение у = h(x) G V(j/o)
такое, что Л(®о) = Уо, f(x,h(x)) = 0 Ух € U(xq), и для отобра-
жения h : U(xq) —> V(i/o) имеем h Е C(U(xq)). Если, кроме того,
существует морфизм -5-/(®о,Уо) 6 £(R",Rm), то h G T>(xq) и
ОХ
o^/(®o,yo)e£(Rn,Rm).
OX
д	д	д
Наконец, ec4uV(®,y) € G существует -g-f(x,y) и &-/, -^-f € C(G),
ОХ	ОХ	Оу
mo he C^(U(x0)).
Доказательство. 1) Поскольку det а~7(®о, Уо) # 0, то для
д	V
морфизма s~f(xi,yo) € £(R’",Rm) существует обратный морфизм
Оу
-1
(д	\
(хо,уо) I € £(Rm, Rm). Пусть
vj/	/
Q
Поскольку	€ С((хо, Уо)), то в силу предыдущей теоремы для/Зо > 0
такого, что 0 < /Зо < 1/ао существуют <5, > 0 (i = 1,2), для которых
имеет место оценка
g
f (®< Vi) - f(x, Vt) - lto)(yi - ya)
= ао > 0.
</V ||У1-У2||т, (9.8)
m
V® G Ш^(хо) C Gi C R" и Vj/i.w e ш£>(и>) C G2 C Rm, причем
inj")(®o) x C G = G\ x G2 C Rn+’n. Для фиксированного x €
inj")(®o) C Gi определим отображение ge : inj’sn)(tfo) C Rra -> Rm,
положив = ^f(xo,yo)y-f{x,y) + f(x,yo) Vy e ш£п)(уо) C R"‘.
Но тогда, полагая Ft(y) = f(®, y) - f(x,y0), имеем Ft = A - gx :
Ш^И)) C Ga -> RTO V® € ш£>(®0) C Gx (причем A = ^f(x0,y0)
и ||A-1|| = ao > 0). Заметим, что Fa(yo) = 0. Из оценки (9.8) для
нелинейного возмущения дх имеем оценку
1ЫУ1) -0®(Уа)||т = ||J^(®o,yo)(yi -Уг)-
“(Г(х,У1) - f(x, Уа))||т < /Зо||У1 - Уз||т,
394
где 0 < ао • A) < 1- Замечая, что /(®o,lfo) = О I (/ € С(С?)) =>
(J £ С((®о, Уо))), видим, что <51 > 0 можно выбрать столь малым, что
имеет место оценка
||f(®, Уо)||т = ||f(®> Уо) - f(®0, lfo)||m < <T = ((l/a0) -/Зо) • $2 > о,
т. е. f (х, уо) € шУ (0) V® G (®о). Но тогда в силу теоремы о нели-
нейном возмущении, примененной к отображению Fx = А—дх, видим,
что отображение Fx = А — дх : Ш^(ро) С <?2 -* Rm Vx € Illj"\®o) С
Gt осуществляет гомеоморфизм окрестности V(j/o) =
на F®(V(j/o)) С Rm, причем:
a)	||F«(l/l) -F«(l/2)||m = ||f(®,Vl) - f(®,l/2)||m > ((l/«o) ~ 0o) *
||yi - yallm Vj/1,1/2 G	C G3, V® € Ш^(®0) C Gx;
б)	V® €	= Ш^О) C Rm, где <7 = ((1/а0)-Д>)-^2 > 0,
уравнение Fx(y) = z имеет единственное решение в V(j/o) С G3 'ix €
U(xo) = Ш^(хо) C Gi, и тогда, полагая z = ~/(®,1/о) G ш£*>(0),
видим, что уравнение Fx{y) = -/(®,уо) имеет единственное решение
V® € U(xo) С Gi. Но (Fx(y) = -/(®,уо))	(/(®,у) = 0). Таким
образом, в силу б) доказано, что существуют окрестности U(xq) С
Gi С Rn и V(i/o) С G3 С RTO такие, что V® € Cf(®o) С Gi существует
единственное решение у = h(x) € V(|fo) С G3 уравнения f(x,y) =
0, так что /(®,А(®)) = 0 V® € Щ®о) и, в частности, при ® = ®о
имеем У(®о,А(®о)) = 0, но f(xo,yo) — 0, т. е. в силу единственности
(решения) А(®о) = Уо- Вводя отображение h : U(xo) С Gi С R" -4
Y(y0) С G2 С Rm, где у = А(х), А(х0) = уо, /(®, А(®)) = 0, докажем,
что Л € С(С7(®0)).
Пусть х,® + Дх € U(xo) С Gi, тогда, полагая j/i = А(® + Дх)
и у3 = А(®), имеем из оценки a) ||f(x + Дх,ух) - f(x + Дх,{/2)||т >
((l/aoj-^oj’llyi-yallm оценку (учитывая, что/(®+Дх, А(х+Дх) = 0)
||Г(х-|-Дх, А(® + Дх))-С(® + Дх, А(®))||то > ((1/а0)-/Зо)||Ь(® +Дх)-
h(®)||m> откуда, учитывая равенство /(®, А(®)) = 0, получаем оценку
в)	||h(x + Дх) - h(®)||m < a0/(l - ao/3o) • ||f(® + Дх,А(х)) -
f(x,h(x))||m.Ho (/ € C(G))=>» (3Jimo||f(x+Ax,A(x))-f(®,A(x))||m =
0) => (3 lim ||h(x + Дх) - h(®)||m = 0) => (A e C(x) V® € Щ®о)) =►
Д®—>0
(h G С(17(хо)))- Теорема о существовании и единственности неявной
функции у = А(х), определяемой уравнением f(xby) — 0, доказана.
2) Пусть существует морфизм ^-/(жсЗ/о) € £(Rn,Rro). До-
ох
кажем, что h G ©(®о) и Dft(®o) = -
д-/(®о,Уо) G £(Rn,Rm). Замечая, что /(®o,!fo)
их
' д V1
^/(®o,yo)J	°
= 0, А(®о) = !/о>
395
( д Л"
(^/(*o,yo)J
Дх 6 Rn) оценки
= ао > 0, имеем Ужо 4- Дх 6 17(®о) С G±
h(®0 4- Дх) - h(®0) -
-^/(ж°,Уо)Дх
' д \ д
-d-f(x0, уо)) о д-/(®о, Уо)Дх
У	/ох
т

0
~dyf(x<h yo^h(®° + Дх) ~ ь(жо))-
< ао ||[фо + Дх, h(xo + Дх))-
т
q
-f(жо + Дх, Л(®о))) - д^/(жо, yo)(h(®o + Дх) - h(ac0)) +
+
f (®О + Дх, л(®о)) - f (®о, h(xo)) - -£-f(xQ, уо)Дх
их
т
< ао(А(Дх) + /2(Дх)),
Q
. Но в силу предположения 2) 3—/(®о,2/о) 6
т
где/х(Дх) = ||f(®0 + Дх, Л(хо + Дх))- Г(®о+Дх,Л(х0))--Дл®о,Уо)
иу
(h(x0 + Дх) - h(®o))||„,, /г(Дх) = ||f (®о + Дх, Цх0)) - f(x0, h(x0))~
Уо) Дх
£(R",Rro), поэтому имеем f(®o + Дх, Л(®о)) — f(®о> ^(®о)) =
Уо)Дх + 7(Дх) • 11Дх||п, где lim 117<Дх)||га = 0. Пусть £ > 0
ОХ	Дф-+о
- любое, но фиксированное, тогда 3<5о(е) > 0 такое, что в силу оценки
(9.8) (где > 0 заменено на £ > 0 и yi = Л(х0 + Дх), у2 = h(x0) Е
с ^(Уо)) Ч|Дх||» < <5о имеем, учитывая оценку в), 0. <
А(Дх) < е||Ь(®о+Дх)-Ь(®)||то <£ао/(1-аоД))-||Г(®о + Дх,Л(жо))-
f(®o,4®o))||m = «*о/(1 - аоА>) • ^/(хо,Уо)Дх + 7(Дх) • ||Дх||п .
Поскольку д11т0 П'У(Дх)||т = 0, то можно считать ^о(е) > 0 столь ма-
лым, что ||7(Дх)||т < £ V||Ax||n < <5о(е)- Но тогда У||Дх||„ < <50(е)
имеем оценки 0 < Л(Дх) < еа0/(1 — аоРо)
д £(	.	\
ДЖО, ?/о) 4- € 1 •
||Дх||п и 0 < /2(Дх) < ||7(Дх)||т • ||Дх||п < е  ||Дх||„. Итак,
У||Дх||„ < <f0(e) имеем оценку Л(Дх) + /2(Дх) < е(ао/(1 — аоРо) 
^f(x0,y0) +г + 1) • ||Дх([
|п, т. е.
396
3 lim ||h(a;o +Дх) — h(«o) —
Дх~>0
Уо) J	°
o-^f(x0,y0) Дх
Но это и означает, что h G причем в силу единственности
производной имеем равенство
D^(®0) = - (~^f(^o, Уо)\ ° я~/(®(Ь Уо) 6 £(Rn, Rm),
\ оу / ох
чем утверждение 2) также доказано.
3) Пусть V(x,y) 6 G существует морфизм
ох
ЗВ	д
причем —G C(G). Тогда, поскольку det — f < 0, то в сн-
ег® dy	оу “
лу теоремы о нелинейном возмущении из §2 этой главы существу-
ют окрестность Vr((®o>3/o)) С G и постоянная а > 0 такие, что
V(as, у) 6 Vy((x0, уо)) существует обратный морфизм

причем

<аи(^-Л	eC(VF((®o,J/o))).
\оу /
Но тогда из рассуждений, проведенных в 1) и 2), вытекает, что неяв-
ная функция h : U(xo)	V(yo) С G2 (определяемая уравнением
/(ж, У) = 0) такова, что при U(х0) х V(y0) С ^((жо, Уо)), Vx G U(xQ)
(при у = h(x))
3Dfc(r) = - (у)} 1 о у) е £(Rn, Rm),
\ оу / ох
причем поскольку

397
то Dh G С(С7(®о)), т. е. h € C^(U(xo)), чем утверждение 3) доказано.
Отметим важные частные случаи теоремы о неявной функции.
Следствие 1. Пусть / : G С R2 -> R, (®о,Уо) € G, при-
чем /(®о> Уо) = 0, / € C^(G) а тг-/(х(ъУо) 0. Тогда существу-
оу
ют окрестности Е7(®0) С R1 и V(yo) С R1 такие, что W((®o,yo)) =
U(xo) х V(yo) С G, и существует единственная неявная функция
h : U(xq) -» V(yo), h € C([7(®o))> являющаяся решением уравнения
/(®, у) = 0 в окрестности W, т. в. f(x,h(x)) = О V® € С^(®о)> при-
чем Л(®0) = уо и (считая, что -^f(x,y)	0 V(®, у) 6 W((»o,yo)))
Л'(х) = -Di/(»,fc(®))/Djf(®,ft(®)) V® € U(xo).
Пример. Рассмотрим f (®, у) = ®2 + у2 -1, тогда 4-/(», у) = 2у.
Оу
Пусть /(®о, !/<) = 0, причем у< 0 (» = 1,2). Тогда ^-/(®о, У<)	0 и по
Оу
теореме о неявной функции существуют (рис. 53) окрестности Wt =
U х Ц, в которых,уравнение ®2 + у2 - 1 = 0 однозначно разрешимо,
т. е. Эу = Л,(®), х G U, причем /(®, Л,-(®)) = 0 V® € U, hi(x) € И-
Очевидно, hi(x) = (-1)<+1(1 - ®2)*/2
V® € U (» = 1,2). При ®о = -1 или
®о = 1 теорема о неявной функции не-
применима, поскольку (/(±1, уо) = 0)
=> (Уо = 0) => ~/(±1,0) = 0), и, в
оу
самом деле, для точек (±1,0) не су-
ществует окрестности WJ, в которой
уравнение ®а + уа - 1 = 0 было бы
однозначно разрешимо. Итак, уравне-
ние ®2 + у2 - 1 = 0 даже при выпол-
нении условия ^/(®o,lto)	0 разре-
шимо, вообще говоря, не однозначно,
но при выполнении всех условий тео-
ремы о неявной функции можно ука-
зать окрестности Wi и Wi, в каждой
из которых это уравнение разрешимо
однозначно.
Следствие 2. Пусть / : G С Rn+1 -» R1, (®о»Уо) € G,
/(®о.Уо) = 0, f € CM(G) и ^/(®о,Уо) 0 0, где ®о = (®°,... ,®°)-
Тогда существуют окрестности U<n)(®o) С Rn и V^^(yo) С R1 та-
398
кие, что W(n+1>((®o, Sto)) = U^(xo) x 0х)(уо) C G, и существует
единственная неявная функция h : (7<">(®о) С R" —> У^цуо) С R1,
h € C^(U^n\xo}), являющаяся решением уравнения f(x,y) = О
в окрестности Wr'n+1)((®o,lfo))> т. е.	,®n;A(®i,... ,xn)) = О
V® € I7(n)(®o)> причем h(®o) = Уо и
al/w = - Д/(1>	/ ^/(1’
Vx€tf(n)(®o)(» = l,2,...,n).
Следствие 3 (теорема о неявных функциях, определяемых
системой уравнения). Пусть /,• : G С R3 -> R (i = 1,2), (®о> Уо> го) € G,
/.(®о,Xto,«о) = о, fi € C(D(G) (» = 1,2),
Тогда существуют окрестности СГ(®о(С R1, Vi(j/o) С R1, У2(го) С R1
такие, что W^((xoilfo»«o)) = U(xq) х Vi(jfo) х VS(®o) С G, и сущест-
вует единственная пара функций
hi: U(x0) С R1 -> У, hi € C^(U(x0)) (i = 1,2),
являющихся решением системы уравнений
/1(®,У,г) = О
/2(®,1/,я) = 0,
в окрестности 1Г^((®о, Уо>«о))> т. е.
Г /1(®,А1(®),Л2(®)) = 0
1 /2(х, Л1(®),А2(®)) = 0V® е G(xo)>
причем
A'i(x) =
л;
г0(л,л)
д(у,г) ’
д(у, z) ’ •
Для проверки последних формул продифференцируем, пользуясь цеп-
ным правилом, тождества
/,(®,Л1(а:),Л2(®)) = 0, х Е U(xQ) (t = 1,2),
тогда
Di/i + D2/i •	+ D3/1 • Л2 = 0,
399
Di/z + D2/2 • Л! + D3/2 • h2 = О,
откуда в силу правила Крамера и вытекают формулы для
Замечание. Основная теорема о неявной функции является,
очевидно, теоремой о существовании системы неявных функций
yi =	, ®n) G = 1,2,... , тп),
X = (хХ, .. . , Хп) е У(п)(хо), У = (У1,.. • , Ут) 6 И’П)(!/о),
являющихся единственным решением системы уравнений
,ХП',У!,... ,Ут) = 0(г = 1,2,... ,т)
в окрестности
Иг(п+го)((а;о, Уо)) = 17(п)(хо) х 0т)(2й)) С G = Gx х G2 С Rn+ro.
§ 10. Условный экстремум функции многих
переменных
Пусть (р : G С Rn -> Rm, где G С Rw (тп < п) - открытое
множество.
Определение. Множество М = {ж 6 G С Rn|y>(x) —
0} называется (п — тп) - мерным многообразием класса (к =
1,2,... , 4-оо) в точке xq Е М, если существует окрестность
U(xQ) С G такая, что <р Е C^(U(xq)) и ранг матрицы Якоби
(Dj^i(eo)) (j = 1,2,... ,n;j = 1,2,... ,тп) равен т.
Замечание. Далее будет доказана теорема о ранге, в силу
которой существует окрестность У<т)(0) С p(U^(xq)) С Rm.
Определение. Множество М С Rw называется (п — т)-
мерным многообразием класса С^к\ если М является (п—т)-мерным
многообразием класса \/х Е М.
Теорема (о существовании касательной плоскости). Пусть
М = {ж Е G С Rn|y>(x) = с} есть (п — т)-мерное многообразие
класса ti xq Е М. Тогда Dy>(®o)(x — Хо) = 0 есть уравнение ка-
сательной (п — т)-мерной аффинной плоскости к многообразию М
в точке xq Е М.
Доказательство. Поскольку xqEMhM={xEGc
Rw|y>(x) = с} есть (п — т)-мерное многообразие класса в точке
жо 6 М, то матрица Якоби (Dj^,(®o)) (j = 1,2,..., п; г = 1,2,... ,m)
имеет ранг тп. Пусть, для определенности,
400
и положено ®' = (®i,... , ®то), я" = (®m+i,... , ®п). Тогда в силу теоре-
мы о неявной функции, примененной к уравнению <р(х', х") — с = 0 (где
^(жо»жо) “ с = 0), видим, что существуют окрестности СЛп“т)(2?о) С
R”7m и	С R™ и отображение h : C7(n“w)(xg) -> V*”1)^)
такие, что в окрестности V0n)(®o) = С^Л“то)(®о) х ^то)(жо) сущест-
вует единственное решение xf = h(x"} уравнения ^(я',®") — с = 0,
так что ^>(Л(®"), ®") — с = 0 V»" 6 и(п~т)(хо), причем h(®o) = x'Qi
hec^u<n-m\xf')),
Dh(x%) = - (^7^0)) о 2L^(®0).
Таким образом, многообразие М допускает в окрестности V0n)(®o)
представление М П И^п)(®о) = Г = {(ж',®") Е RTO х Rn-W =
Rn|a?' = Ь(х"),х" Е lj(n-m)(®")}, Но график Г C Rn имеет в точке
®о = (^(®о),®о) 6 Г (п — т)-мерную аффинную касательную плос-
кость с уравнением х' — Xq = D^(®o)(x// “ жо)> которую и естественно
назвать аффинной касательной (п — тп)-мерной плоскостью к много-
образию М в точке а?о 6 М. Но тогда имеем
х' - хо = -	° aJ77*’(®°)(x" “ хо)’
и поскольку гомоморфизм -у>(®о) 6 £(Rm,Rm) имеет обратный
охг
/ Q	\ —1
I 7^(®о) I 6 £(Rm,Rw) (т. е. осуществляет изоморфизм RTO на
\	/
Rw), то имеем
^*>(®о)(х' - Xq) + ^7*>(*о)(х" - xg) = 0,
что эквивалентно (проверить самим) уравнению
D^(®0)(x - хо) = 0.
Замечание. Если т = 1, то многообразие М = {® Е G С
Rn|/(a?) = /(а?о)} является поверхностью уровня для числовой функ-
ции / : G С Rn —> R и тогда уравнение касательной гиперплоскости
к (п — 1)-мерному многообразию М класса в точке ®о 6 М имеет
вид
(D/(a?o)(x - х0) = 0)	= 0
14 Зак. 860
401
так что, как это следует из аналитической геометрии, вектор-
градиент
п д
grad /(хо) = 52
является нормалью в точке хо € М к касательной гиперплоскости.
Замечание (о замене переменных в представлении для мно-
гообразия). Пусть М = {х € G С Rnlp(x) = 0} - (п - т)-мерное мно-
гообразие класса С^1). Тогда <р € С^цС?) и матрица Якоби (DjPi(®o))
(j = 1,2,... , n; i = 1,2,... , m) имеет ранг m Vxo € G, поэтому для
фиксированной точки xq € М имеем при выборе надлежащей ну-
Л /	\
мерации координатных осей	— -— (х0) / 0. Но поскольку
о(®1,..., хт)
Dj^i € C(G) Vi, j, то существует окрестность U^(xq) С G такая,
что
ОУх е и^(х0),
СЦХ1, ... , Xw)
и тогда, в частности, линейные формы
cty>(x0) = 52 T>j<f>i(x0)dxj € £(Rn, R) (t = 1,2,..., m)
3=1
линейно независимы. (Отметим попутно, что имеет место и обрат-
ное утверждение: если в точке xq Е М линейные формы d^(xo)
(г = 1,2,... , т) линейно независимы, то при т < п множество М =
{х € G С Rn|^(x) = 0} будет (п - т)-мерным многообразием класса
С(х) в точке хо € М.) Введем обозначения xf = (xi,... ,xm) 6 Rw,
x" = (xm+i,... , xn) G Rn”m, x = (x\ x") € R”, у = (j/i,..., ym) € Rm
и в окрестности VF((O,x0)) = Ит)(0) x U^(xq) C R™®1 (где в силу
«теоремы о ранге» из [8] т. 2, ч. VI, гл. 2 § 3) существует окрестность
= V0(w) с p(U^(xo)) рассмотрим уравнение у = ^(х',х") или
(в координатной форме) систему т уравнений с п + т переменными
!/•’ =	• • • » ®m5 ®m+li • • • » ®n) (i = 1, 2,... , ш),
для которой при хо € М имеем ^(хо) = ^>(®о> жо) = 0 (l/o = 0). По-
скольку
=d“ * °vi е и‘п>ы’
то в силу теоремы о неявной функции, примененной к уравнению
- У = 0 (где р(®о,®о) -0 = 0), видим, что существу-
ют окрестности Щ = C7<’n)(xG) С R$, Ug = tf<"-’n)(xg) С R",7’n,
402
Vo = V(m)(0) C RJ\ Uo = UJ x Ug C €7<n)(®0) C R" и отображение
h : Vo x Uq C R" -> U'Q C Rm такие, что уравнение <p(x', ®") - у = О
V(y, x") € Vo x Uo имеет единственное решение x' = h(y, x") € Uq та-
кое, что h e C(X)(VO x U£), <p(h(y, ®"), ®") - у = 0 V(y, x") € Vo x US C
Rn, причем (Л(0, ®'о') = ®b) => (р(Л(0,®8)>®о) = ¥*(®o, ®o) = 0) =>
(yo = 0)- Тем самым доказана возможность перехода в окрестнос-
ти Wo = Vo х Uo х Uo C R^t>'' от переменных (®', ®") к новым
переменным (у, ®") по формулам (®' = h(y, ®")) <=> (у = р(®', ®")),
причем многообразия М имеем (при U = Uq х Uq С G) представ-
ления М пи = {(®',®") € Uq х и^'М®',®") = 0} = {(у,®") €
Vo х и^|р(Л(у,®")»®") = 0} = {(у, ®zz) 6 Vo х Utf\y = 0} (так как
<p(h(y,х"),х") — у). Многообразие М в новых координатах (у,®")
имеет в окрестности Vo х US точки (0, ®о) € М простое уравнение
у = 0.
Пусть f : G С R" -> R и <р : G С Rn -4 Rro, где G С Rn (1 <
т < п) - открытое множество, и множество М = {® € <?|у>(®) = 0}
является (п — т)-мерным многообразием класса С^1’.
Определение. Точка ®о € М называется точкой условно-
го локального минимума (максимума) функции f на множестве М,
если существует шар Ш^п\®о) С G такой, что /(®) > /(®о)(/(®) <
/(®о)) V® € Ш^п)(®0) ПМ.
Замечание. Если существует шар (®о) С G такой, что
/(®) > /(®о) (/(®) < Д®)) V® € UIj*\®o) ПЛГ, то точка ®о £ М на-
зывается точкой строгого локального условного минимума (максиму-
ма) функции f на множестве М. Отметим при этом, что если точка
®о € М является точкой локального условного минимума или мак-
симума функции / на множестве М, то ®о € М называется точкой
локального условного экстремума функции f на множестве М.
Теорема (необходимое условие существования локального
условного экстремума). Пусть /:GcRn-»Ru^:GcRn-> R™,
где G С Rn (при 1 < т < п) - открытое множество. Пусть мно-
жество М = {е € G|p(®) = 0} С Rn является (п - тп^-мерным
многообразием класса в точке ®о € М, причем ®о - точка ло-
кального условного экстремума функции f на множестве М. Пусть
f G C^(G). Тогда существуют постоянные € R (t = 1,2,..., т)
т
такие, что dffa) = 2	tuu в координатной форме
•’=1
т
Dj/(®o) = 22 xiVj<pi(xo) (j = 1,2,..., n).
isl
Числа Л, называются множителями Лагранжа, соответствующи-
ми точке локального условного экстремума &о Е М.
14*
403
Доказательство. Поскольку М—(п—т)-мерное многообразие
в точке xq 6 М, то линейные формы
d4>i(xQ) е £(Rn, R) (i = 1,2,..., m)
линейно независимы и существует окрестность U = U^(xq) С G
такая, что в ней (при надлежащей нумерации координатных осей)
имеем
д(/1’ * * * *	(д) = det	0V® е и.
,хго)	дх' ' ' '
Но тогда, как было замечено ранее, в окрестности РУ(т+п)((0, жо)) =
0т)(О) х Uq х Uq С R™ х R™ х R"/7m можно совершить замену пере-
менных (ж', ж") —> (у, х") по формулам (ж' = Л(у, ж")) <=> у = р(х', х")),
причем h : Vo х Ug С Rn -> Щ С Rm, h е CW(V0 х Uq) и
у>(Л(т/,ж"),®") = у V(j/, ж") Е Vf) х Uq, Л(0,Жо) = Жд. В новых коор-
динатах (у, х") имеем представление М П U = {(y,xff) G Vb х Uq С
G\y = 0}. Подставляя ж' = h(y, ж") в функцию /(ж', ж"), получаем ра-
венство f(h(y, ж"), ж") = F(yi, ...ут\хто+1,... , жп), причем поскольку
f е C'WfG) и ЛЕ C'WfVf) х CZ"), то F е С^(У0 х U"). Заметим, что
если точка жд Е М была точкой локального условного экстремума
функции /(ж) на множестве М, то точка (0, Жд) 6 М является точкой
локального экстремума функции F(y, х”) на множестве
м п и = {(у, х") е Vo х U''ly = 0}.
Таким образом, функция F(y, хн) при (у, х") 6 М имеет вид F(0, ж")
и имеет локальный экстремум в точке (0, Жд). Но тогда в силу необхо-
димого условия существования локального экстремума у дифференци-
руемой функции имеем —Г(0, ж£) = 0 (Л = m +1,... , п). Вычислим
дифференциал функции F(y, ж") в точке (0, Жд) € М
т	п
|(у,а?")=(о,я?") = DtF(0, a?g)(fyi -Ь } * D&F(0, ж0)с!ж*
»=1
и, полагая А, = D«F(0, Жд), имеем (учитывая, что Вл^(0,Жд) = 0 при
т
к = тп+ 1,... , п) <1Г(0,ж£) = Xidyi. Вспоминая, что F(y, х") =
«=1
f(h(y, ж"), я") = (/° h)(y, ж"), перейдем к старым переменным (ж', ж")
с помощью замены (у =	ж")) <=> (Л(т/, ж") = ж'). Тогда (Ро^)(ж) =
Г(у>(ж',ж"), ®") = /(Л(т/, х"), ж") = /(ж', ж"), т. е. (F о <р)(х) = /(ж),
но тогда в силу инвариантности формы первого дифференциала име-
т
ем (при yi = y>i(x) (i = 1,2,... ,m)) dF о ^>|1=Ло = £ Ajd^j(a:o), где
«=1
404
n	n
d(pi(xo) = 52 DkPi(x0)dxk, t. e. df(x0) = 52 ^id(P = (®o), что и требо-
Jt=i	«=1
валось доказать.
Замечание (о геометрическом смысле необходимого условия
существования условного экстремума). Пусть (п — тп)-мерное много-
образие М С R” класса С*1) определяется уравнениями <Pi(x) = О
(г =? 1,2,... ,пг) (1 < т < п). Тогда уравнения Dy>i(®)(x — Хо) = О
(г = 1,2,... ,т) или
п
52	- х?) (г = 1,2,... , тп)	(10.1)
i=i
являются уравнениями касательной аффинной (п — тп)-мерной плос-
кости к многообразию М в точке xq € М. С другой стороны, урав-
нение f(x) = /(®о) определяет гиперповерхность в Rn, для которой
уравнение Df (®о)(х — хо) = 0 или (в координатной форме)
п
— Xj) = 0	(10.2)
i=i
является уравнением касательной гиперплоскости к этой гиперпо-
т
верхности в точке xq. Соотношение D/(®o) = £2 AiDy>t (®o) озна-
i=i
чает, что гиперплоскость (10.2) содержит (п — тп)-мерную плос-
(т	\
D/(®o)(x - хо) = J} A»Dw(®o)(x - хо) = 0 I =>
(D/(®o)(x — х0) = 0).
Замечание. Пусть f : G С Rn -> R и : G С R" -> Rm,
где G С R” (при т < п) - открытое множество. Пусть множество
М = {ж 6 G С Rn|^(®) = 0} является (п — т)-мерным многообра-
зием класса С^1). Рассмотрим отображение F : G С Rn —> R, где
F(x) = /(ж) - 22 А<р,(ж), причем <р = (v>i,... , <рт) и Ах, Л2,... , Аго -
1=1
некоторые постоянные. Тогда для любой точки xq локального услов-
ного экстремума функции f на множестве М имеем dF(®o) = 0 при
некотором выборе постоянных (Лагранжа) Ах, Л2,... , Ат. Тем самым
задача об отыскании точек условного экстремума xq G М сводится к
решению следующей системы п 4- тп уравнений с п 4- т неизвестны-
rn
ми:	• • • , Ai,... , Ато : Dfc-F(®) = Dfc/(®) “ 52 AjDfc^i(®) = 0
t=i
(к = 1,2,... ,n),	= <рДх) =0 (j =
Замечание. Если f, G C(2)(G), то можно показать (проде-
лайте это самостоятельно), что для отыскания локального условного
405
экстремума функции /(г) на (п - пг)-мерном многообразии М = {® €
G С Rn|^(®) = 0} класса С'2» нужно исследовать на обычный ло-
m
кальный экстремум функцию Лагранжа F(x) = f(x) — 52 А^Дх), где
»=i
Ai,... ,Ат - найденные ранее множители Лагранжа. Рассматривая
(в соответствии с достаточным признаком существования локального
экстремума для дважды дифференцируемой функции) второй диффе-
n Q2
ренциал функции Лагранжа d2F(®o) = У? *3—5—F{xa)dxi dxj> нуж-
•J=l OXiOXj
но заметить, что из уравнений (®) = 0 (i = 1,2,... , т), определяю-
щих (п—т)-мерное многообразие М, следует, что при х = хо должны
выполняться соотношения d^t(®o) = 0, т- е-
п д
52 о—= О (г = 1,2
j=i axi
и в силу условия
0(Р1,
5(®i,
—г (®о)	0 можно выразить dx{
®m)
(при i = 1,2,... ,m) линейно через «независимые» дифференциалы
dzm+n • • • »dxn. Найденные дифференциалы d®i,... , dxm нужно под-
ставить в d2F(xo} и исследовать полученную квадратическую форму
от dzm+i,... , dxn как обычно.
п
Пример. Пусть Ф(х) = £ aijxixi (аи = °i« V* 3) ~ квад-
М=1
ратическая форма (в Rn) и М = {® € Rn|p(®) = 0} (где <р(х) =
п
52 ж2 — 1) - (п - 1)-мерное многообразие (единичная сфера) класса
i=i
С?*. Найдем точки х^,х^ G М такие, что Ф(х^Ь = min Ф(х) и
Цх||п=1
Ф(х<2)) = max Ф(х), т. е. найдем точки x^t х^ € М локального
П»11»=1
условного минимума и максимума квадратической формы Ф на еди-
ничной сфере М. Составим функцию Лагранжа F(x) = Ф(а) -
для которой имеем (1/2)—f’(x) = ад®1+.. .+(оду - X)xj+.. .+ajn®n
о® у
(j = 1,2,... , п). Использование необходимых условий существования
локального условного экстремума дает систему (n +1) уравнений для
определения ®i, ®2, • • • »и А
(l/2)Aj?(a!) = 0(j = l,2,...,n),	(10.3)
||х||’ = £>? = 1.	(10.4)
i=i
406
Система (10.3) является однородной линейной системой п уравнений
для определения ®i, ®г,..., ®п, которая имеет нетривиальное решение,
если для ее определителя выполнено условие
<*ii - А
Д(А) =
апп ““ А
= 0.
В алгебре показывается, что уравнение Д(А) = 0 имеет только дейст-
вительные корни (собственные значения квадратической формы Ф)
Ai < Аг < ... < Ап. Каждому из собственных значений А* соот-
ветствует точка = (®^\... 'Хп^) € М, являющаяся решением
системы (10.3), (10.4), при этом только в точке х^ Е М возмож-
но достижение локального условного экстремума функцией Ф на М.
Пусть точке х^ € М соответствует собственное значение Afc, тогда
из (10.3), (10.4) имеем
(l/2)f>jfc) AF(a!(*)) = ф(х<*>) - А*||х<*>||» = 0,
i=i 1
т. е. Ф(х<*>) = А* (так как ®<*> £ М => ||х<*)||* = 1), откуда попут-
но получаем формулы для вычисления наименьшего и наибольшего
собственных значений для квадратической формы Ф
Л* = и Тп 1	~ ф(х(М)> Л" = ф(х) = *<х(п))-
IWI»=i	||*||п=1
§ 11. Зависимые функции
Определение. Пусть / : G С Rn -> Rm (где т < п)
(f = (Л, /г,... ,/m) « f € CW(G) (где G - открытое множест-
во в Rn). Скажем, что числовая функция fm зависима от число-
вых функций fi, fi,... , fm-i на открытом множестве G С Rn, ес-
ли существует функция Ф : 0 С Rm-1 —> R, Ф Е С^'(0) (где
0 - открытое множество в Rm-1 и 0 D /1(G) х ... х fm-i(G)),
причем fm(x) = Ф(/1(®),... ,/m-i(®)) Vx € G. Система функций
fit fit • • • , fm называется в этом случае зависимой на множестве
GcRn.
Теорема 1 (необходимое условие зависимости функций). Если
система функций fi, fi,... ,fm зависима на множестве G С R”, то
ранг матрицы Якоби (Djfi(x)) (* = 1,2,... ,m;j = 1,2,... ,n) (2 <
т < п) меньше т.
Доказательство. Пусть функция fm(x) зависима от
Функций /1(®),... , fm-i(x) на множестве G С R". Тогда существует
407
числовая функция Ф 6 С^Ф), Ф : 0 С Rw 1 —> R такая, что fm(x) =
Ф(Д(х), Д(х),... ,/m_i(x)) Va? Е G. Но тогда ^-/т(х) = У^ЩФ-
0Х>	fc=i
Dj fk (®) (J = 1,2,... , п), что означает, что m-я строка матрицы Якоби
(Djfi(x)) (i = 1,2,... ,m;J = 1,2,... ,п) есть,линейная комбинация
т — 1 первых ее строк, так что ранг матрицы Якоби не может быть
равен тп, а потому меньше т.
Теорема 2. Пусть f : G С Rn —> Rm (2 < m < n),
f E	(где G C Rn ~ открытое множество) и ранг мат-
рицы Якоби	(г = 1,2, ...,m;J = 1,2, ...,п) для системы
, /т(ж) Vx 6 G равен р, причем 1<р<т и
и(Х1, .. • , Хр)
Тогда существует окрестность U(xq) С G такая, что система
не является зависимой на U(xq) и в то же время функ-
ция fj при любом j = р+ 1,... , т зависима от функций Д, Д, • • • , fp
на С7(хо).
Доказательство. Поскольку f Е CW(G) и
то в силу локальных свойств непрерывных функций существует
окрестность О^л^(хо) С G такая, что
но тогда в силу теоремы 1 система Д,... , fp не является зависимой в
окрестности СИп)(хо) С G. Введем обозначения х = (х',х") Е Rn, где
х' = (xi,..., Хр) Е Rp, х" = (хр+1,... ,xn) Е Rn~p, у = (У1,...,уР) Е
Rp и хо = (хо,Xq), уо = (Д(х0),... ,Д(хо)). Рассмотрим систему р
уравнений yi — Д(х', х") = 0 (г = 1,2,... ,р) в окрестности О^р\уо) х
О(»)(х0) С Ry+n. Поскольку Д,..., fp е C^(G) и	±
О, то существует окрестность U[xq) С О^(хо) С G такая, что
»(£:::: :£)w ^•vie иы-
Положим Fp = (Д,... , fp) : U(xq) С Rw -> Rp, тогда в силу теоремы
о ранге (из ч. VI, т. II) существует окрестность V^p\yo) С Fp(U(xq)) С
Rp. Тогда i/о = Fp(xo) и к уравнению yi —fi(x\ х") = 0 (г = 1,2,... , р),
рассматриваемому в окрестности V^(yo) х U(xq) С Rp+n, применима
408
теорема о неявной функции, в силу которой существуют окрестности
Uq = и^(х'о) с RF, Ug =	С R"_p и Vo s K>₽)(j/o) C RF
такие, что Uq х Uq С.17(жо), Vb С O^(j/o) и в окрестности W6 =
V6 х Щ х Uq С R£ х R£, x R”/7P существует единственное решение
h : Vo x Uq C Rn —> Uq C Rp нашего уравнения такое, что h €
C(1)(Vb x ZZ"), Л(ро,®о) = ®o и
yi =	x"), x") V(p, x") e Vo x tf" (i = 1,2,... ,p).	(11.1)
Рассмотрим Vt > 1 функцию fP+i(x',xff) и сделаем в ней замену х' =
Л(г/, ж"). Тогда получим (при I = 1,2,... , т — р) функцию Ф(р, x,f) =
/p+i(h(i/, х"),х"). Докажем, что
&
®") = о (j = Р + 1,... , n; I = 1,2,... , т - р).
Но
х") = Dkfp+i • -^hk + Djfp+i (j = р+ 1,... ,n).
Дифференцируя тождества (11.1) по х; (при j = р+1,... , п), получаем
соотношения
р	л
52Bkfi  g^hk + Djfi = 0 (i = 1,2,... ,р).	(11.2)
Следуя С. М. Никольскому [6], введем при фиксированном j = р +
1,... , п векторы
a(i) = (Difi,.... Dpfi, Djfi) > b =	• • • ,	1) •
у uXj	uXj J
Тогда из (11.2) имеем
(a<*\b) =0(г= 1,2, ...,p).	(11.3)
По условию теоремы имеем
••• ’/р’Л+О^) = 0 Vi; е g,
, . . . , ®р, Xj)
но тогда последняя строка этого определителя есть линейная комби-
р
нация предыдущих р строк, т. е. а(р+/) = j} и поэтому в силу
«=1
(11.3) имеем
(a^+'),b) = 2/t,(aW,b) = 0.
»=i
409
Но легко видеть, что

q
Таким образом, доказано, что =—$i(y,х") = 0 {j = р+ 1,... , п).
V® j
Применяя теорему Лагранжа о конечных приращениях к числовой
функции Ф|(у, ®")> имеем V®" € 17о(®о) (ПРИ Iм €	-
n Q
Ф|(16®о) = S я—~ ®?) = 0- Тем самым доказано, что
;=р+1 OXj
функция $i(y, х") = Ф,(у) не зависит от х". Но тогда при любом
I = 1,2,... , т — р имеем равенства fP+i(h(y,х"),х") = Ф|(у), отку-
да, учитывая равенства у,- = /,(х) (при i = 1,2,... ,р), имеем
. • • , ®п) = /Р+<« ®") = ff+i(h(y, х"), х") =
= Ф«(У1,... , Ур) = Ф|(А(х),..., Ш) V® € СГ(п)(хо) = X
т. е.
fp+t(x) = ФНЖ®),... ,4(®))V® е и^(х0),
откуда и следует, что функция fP+i(x) (при р + I = р + 1,... ,тп)
зависима от системы функций /х(®),..., fp(x) на U^(xq) С G.
§ 12. Разбиение единицы
Определение. Семейство множеств {Ва} пространст-
ва R” называется локально-конечным, если V® € R” существует
окрестность Шр(®) такая, что ШД®) П Ва = 0 для всех индексов
а, кроме конечного их числа ах, аг,, вт(®)’
П р и м е р ы: 1) система {Вп}, где Вп = [—n,n] (n = 1,2,...), не
является локально-конечной;
2) система {Вп}, где Вп = [n, п + 1], локально-конечна при п =
0,1,2,..., так как V®o > 0 имеем no < ®о <	+ 1 и Шх(®о) ПВП 0
только при п = по - 1, По, По + 1.
Замечание. Если система множеств {Ва} локально-конечна
в Rn, то для любого компактного множества К С Rn существует не
более конечного числа индексов ах,... , ат таких, что К П Ва = 0
при а a, (г = 1,2,...,m). В самом деле, поскольку система
{Вл} локально-конечна в R”, то V®o € К ЗШРо(®о), такой, что
Ш^0(®0) П Во = 0 Va ах,... ,ат(Хо) и тогда С U шро(®о)-
В силу компактности множества К существует конечное подпокры-
м
тие {Шя(®|); I = 1,2,... ,М} такое, что К С U ШР1(®(), и поэтому
1=1
К ПВп = 0 Va ф ок*, где i = 1,2,... ,L = max m(xi).
/=1,2,,.. ,Л/
410
Замечание. Если {F,,} Jn = 1,2,...) - локально-конечная
система замкнутых множеств (Fn = Fn Vn € N), то множество
+00	_	_
F = (J Fn также замкнуто (F = F). В самом деле, пусть хо € F,
П = 1
тогда Ш₽о(®о) П F 0 (V/>o > 0), и поскольку система {Fm}
локально-конечна, то существуют тпо € N и шар ШР1 (хо) такие, что
ШР1 (®о)Г|Д. = 0 Vfc > mo- Но хо € F, поэтому хо € U Fm. Поскольку
т=1
множество Ftn = Ftn замкнуто, то множество |J Fm также замкну-
		т=1
то_____________то	то	+оо
ТО, т. е. U Fm = U Fm. Таким образом, х0 € U F,n С (J F,n = F,
т=1	т=1	__ т=1	т=1
т. е. ®о € F, так что множество F = F замкнуто.
Определение. Пусть f : Q С R” —> R (где Q - открытое
множество). Носителем (supp f) функции f(x) называется замы-
кание множества всех точек х Е П, для которых f(x) 0, т. е.
supp f = {® € П|/(®)	0). Функция f Е C(fl) называется при этом
финитной, если supp f - компактное множество.
тт	1 \	«	\ I |®| I,
Примеры:!) для функции /(®) = < 1	.'. ’1 имеем
{х G R'*|/(x) 0} = (-1,1); supp / = [-1,1], т. е. / финитна;
2) 1>(х) = ( 3’ Тогда {х е R|2>(x) # 0} = CQ и supp Р =
(-оо, -Foo) не компактен, т. е. D(®) не является финитной.
Определение. Пусть множество AcR" и {П«} - откры-
тое покрытие А (т. е. А С г^е ” открытое Va). Разбиени-
ем
ем единицы класса (k = 0,1,2,..., +оо) для множества А, под-
чиненным этому покрытию, называется система функций {et(®)}
(i = 1,2,...), е, € С^^(П) (где П D А - некоторое открытое мно-
жество) такая, что:
I)	0 < ei(®) < 1 V® 6 П и Vi, причем е»(ж) = 1 V® € А;
t=i
2)	Vi носитель (supp ej) функции et(x) является компактным
множеством, причем семейство {supp е,} (i = 1,2,...) образует
+ <Х)
локально-конечное покрытие множества А (т. е. А С (J supp е,),
i=i
так что каждая точка ®о € А имеет окрестность Шр(®о), в ко-
торой лишь конечное число функций е<(х) не равно тождественно
нулю;
3)	Vi Эа такое, что supp е< С
Замечание. В определении разбиения единицы фигурирует
411
+оо
рад 53 в|(зс) V® 6 А и возникает вопрос о сходимости этого ряда.
«=1
Однако в силу локальной конечности покрытия множества А систе-
мой {supp е,} (г = 1,2,3,...) любая точка xq Е А (и даже некото-
рая ее окрестность в силу свойства 2)) может принадлежать лишь
конечному числу (носителей) supp etfc (к = 1,2,... , m(&o))? а пото-
му лишь конечное число функций eik(x) (к = 1,2,... ,m(«0)) из сис-
темы {е,(®)} (г = 1,2,...) отлично от нуля в точке «о, т. е. ряд
4-оо	т(хо)
52 еДжо) = 53 е»*(®о) = 1 Для любой точки жо Е А содержит лишь
»=1	к=1
конечное число отличных от нуля членов, а потому всегда сходится.
Лемма 1. Для любого открытого множества G С Rn и для
любого компактного множества К С G существует функция <р Е
C(°°)(R.") такая, что у>(х) = { J’ * | Rn \ g V>(x) < 1 Vx G
Rn, причем носитель supp <р компактен и К С supp <р С G.
Доказательство. Рассмотрим сначала частный случай,
когда G = Шя(0) = {х Е Rn|||x||n < R} и К = Шг(0) = {ж Е
Rn 11lxlIn < т*}, причем 0 < г < R < 4-ос. Пусть 0 <r < Rq < R< 4-оо.
Построим вспомогательные функции
a(f\_ Г ехр{-1/(< - г2)} • ехр{— 1/(Д§ -t)}, r2<t<R%< R2,
9( I 0, t G (= оо.+оо) \ [г2,Я§]
и
«о	,«0
= [ 9(т)<*г / I g(r)dr , t G (-00,4-00).
t	' r2
Очевидно, h E C^°°)((—oo, 4-oo)), причем
= { J: яГЛ 0 - - 1 v< 6 (-o°’+oo)-
Тогда для нашего частного случая двух концентрических шаров име-
ем
?(х) = Л(||х||2) = { J’ 0 < <p(t) < lVx G R",
К C supp <р С ШЛо(0) С Шл(0),
причем носитель supp (р С G = Шд(0) компактен (как замкнутое и
п
ограниченное в Rn множество). Отметим, что функция ||х||„ = 53
«=1
бесконечно дифференцируема, поэтому <р Е C^°°)(Rn).
Пусть теперь К С G С Rn, где К - любое компактное множество,
a G - любое открытое множество. Тогда V® Е К С G существует от-
крытый шар Шр(х)(ж) такой, что Шр(т)(ж) С Шр^Дж)) С G, причем
412
G D U ^p(®)(®) Э В силу компактности множества К сущест-
® € К
вует открытое подпокрытие {1ПГ{(®>)} (г = 1,2,... , т) множества К
такое, что G D (J Шг.(ж>) D (J Шг.(ж,) D К. Положим Ki = Шг.(ж|)
1=1	«=1
(г = 1,2,... ,тп), где, очевидно, 0 < г, < p(x,,5G). Выберем Д- > О
так, чтобы 0 <	< Ri < р(ж,, dG). Тогда
G D ШЛ1. (ач) Э	D Я,- (г = 1,2,... , т).
Для пары концентрических шаров {К,,	построим функцию
/ \	/ 1, х 6 Ki,
^х} ~ t 0, х G Шл<(х,), <Р G C(°°)(R"),
О < <pi(x) < 1 Vx G Rn, Ki C supp у, С Шд,.(х,) C G (i = 1,2,...,m).
Тогда искомая функция <p(x) имеет вид
m
<p(x) =1 - IB1 ~ (H®)) ='
m ___
i,хеке |jnir,(®<),
t=l
m
0, xG U ШдДх,),
так как (xG U Шя<(х,)) => (x G C (J Шд,^) = Q СШдДх;)) =>
(®GCIIIjl<(a;’j’vi = l,...,rn),
0 < H«) < 1Vx G R", <f> G C(oo,(Rn),
m	m
причем supp <p С U П1я< (®t) C G, т. e. К C supp <p C U ШдД®,) C
«=i	t=i
(J ШнД®|) C G, так как supp <p = {x G Rn|y>(«) / 0} C U Шд.(ж,) C
i=l	» = i
m __
(J ШдД®»), носитель supp <p C G компактен (как замкнутое и огра-
i=i
ниченное в Rn множество) и К С supp <р С G.
Следствие. Пусть f : (ai,l>i) -> R, f G GW((ai, l>i)) и
(ai, bi). Тогда Эф G C<°°)((-oo, 4-co)) такая, что
_ / 1, ® € [a, 6],
V[> ~ | 0, x?(a,/?), 0 < tf>(®) < IV® G (-oo,+oo),
[a, 6] C supp <p C (at,/?), причем для финитной функции F(x) = f(x) •
i/>(x) имеем F G C^*((—oo, 4-oo)),
n* P(r\ — 1 ^/(ж), ® G [a, 6],
D F[X> "{О, xG(a,/?),
413
supp d'F C (a,(i) (J = 0,1,2,..., fc).
Теорема (о существовании разбиения единицы). Пусть мно-
жество А С R” и {Па} - любое открытое покрытие множества
А. Тогда существует разбиение единицы {е<(®)} (г = 1,2,...) для
множества А (класса С^), подчиненное этому покрытию.
Доказательство теоремы основано на следующей лемме:
Лемма 2. Пусть множество А С Rn и {Пл} - открытое
покрытие множества А. Пусть существует не более чем счет-
ное локально-конечное открытое покрытие {Ui} (i = 1,2,...) мно-
жества А такое, что: 1) для любого i существует компактное
4-оо	4-оо
множество Ki С Ui; 2) (J Ui D |J Ki Э A; S) Vi За такое,
issl	t=l
что Ki C Ui С Тогда существует разбиение единицы {е;(®)}
(i = 1,2,...) для множества А (класса С^), подчиненное покры-
тию {Па}, причем Kt С supp е,- С Ui, Vi.
Доказательство. Для любой пары (Ki, Ui) в силу леммы
1 существует функция щ € C(oo)(Rn) такая, что
<Pi(x) = | J’ 0 < <п(х) < IV® € R",
Ki С supp <fi С. Ui, причем носитель suppy»,- компактен. Поскольку
<Pi € С (Ki) и pi(®) = 1 V® € Ki, то в силу локальных свойств непре-
рывных функций V®o € Ki С Ui существует окрестность 0(®о) С Ui
такая, что щ(х) > О V® € 0(®о). Но тогда множество V, = |J 0(®о)
открыто, Ki С И С Ui и, очевидно, ^i(®) > О V® G V,. Поло-
4-оо	4-оо
жим О = (J И- Тогда множество П открыто и А С (J Ki С О С
1=1	1=1
4-оо	4-оо
U supp <pi С U Ui, причем в силу локальной конечности покрытия
1=1	1=1
{U,} системы {Ki}, {Vj} и {supp е<} также локально конечны. Рас-
смотрим функцию <р(х) —	*Р<(Х) V® G П. В силу локальной конеч-
1=1
кости покрытия {supp <pi} supp <pi V®o € П существует шар ШРо(®о)
такой, что nifO(®o) П supp ipih 0 лишь при k = 1,2,..., т(®о), так
т(®о)
что <р(х) = £ <pik (®) > О V® € ШРо(®о), т. е. функция р(®) определе-
fe=l
на в некотором шаре ШРо(®о) для любой точки ®о Е П и, в частности,
V®o € А, причем ШРо(®о) П V, = 0, если j ф ц при к = 1,2,..., т(®о).
4-оо
Далее, если ®о G □, то из того что П = |J V, вытекает существование
1=1
fco (1 < too < m(®o)) такого, что ®о € Цйо, и поэтому (^i\o(®o) > 0)
414
=> (у>(®о) > 0 V®o € Л). Но тогда на открытом множестве Q Z) А
для любого i определена функция е<(®) = щ(х)/р(х) Е
причем 0 < е<(®) < 1 V® Е П и е<(®) = 1 V® € П (и, в част-
•=1
ности, V® € Л). Очевидно, носитель supp е, = supp С Ui ком-
пактен, причем Ki С supp щ = supp е, с U, , а система множеств
{supp е,}, как и система {Ui} (t = 1,2,...), локально-конечна, причем
4-оо	4-оо
AC U Ki С U supp е;. Система функций {е<(®)} (» = 1,2,...) и
•=1	•=!
есть искомое разбиение единицы для множества А, подчиненное его
открытому покрытию {Па}.
Продолжая доказательство теоремы о существовании разбиения
единицы, рассмотрим 4 случая:
1)	А = К, где К компактно в R”;
+оо	О
2)	А = U К/, где Ki компактно и К/ CKi+i VI;
/=1
3)	А = G, где G - открытое множество из Rn;
4)	А - любое множество из Rn.
Итак, 1) пусть множество А = К С R" компактно. По условию
{Пп} - открытое покрытие множества К. В силу компактности К
можно выделить конечное подпокрытие {Па|} (I = 1,2,..., т) такое,
m
что К С (J ПО). Положим Ui = (t = 1,2,... , m). Тогда К С
/=1
m	m
U Ui. Рассмотрим компактное множество Wi = К\ |J Ui С Ui. Тогда
(=1	1=2
p(Wi,dUi) > 2pi > 0. Воспользуемся следующим определением.
Определение. Открытой окрестностью 0(B) множества
В С Rn называется любое открытое множество, содержащее В. В
частности, ^-окрестность множества В называется множество
Ot(В) d— (J Рассмотрим множества
Ki= OPl(Wi) СК1 = С U1.
Поскольку компактное множество W\ ограничено, то и ее р\-
окрестность ограничена. Тогда множество Ki компактно и
о т	m m
К CKi U U Ui С К1 и U Ui С U и,.
i=2	1=2 i=l
(1—1 о mN
U Ki U U и, С Ui. В силу ком-
i=i i=i+i у
пактиости множества Wi имеем p(Wi, dUi) > 2pi > 0. Положим теперь
416
Ki= Op,(Wi) С к + 1 = Op, (Wi) C Ui, где Кt C Ui и Kt компакт»017
причем	эж.>!
r#
/	m	I	m	m
kc|Jk,u (J h.cJk.u J t/,c|J I7i.
i=l i=/4-l	»=1 i~/4-1	»=1	'•учж
in 0 m	m
Но тогда при I = m имеем К C |J KiC |J К,- C U Uh где
i=i	t=i	»=i
KiC Ki C 17», причем Ki компактно при i = 1,2,... ,m. Итак, для
любого компактного множества А = К С Rn такого, что К С IJfla,
а
построено (по индукции) конечное (а потому и локально-конечное) от-
крытое покрытие {Ui} (i = 1,2,... , тп), такое, что:
1)	для любого i существует компактное множество Ki такое, что
Ki С
т 0 т	тп
2)	к с и KiC и я. С и Ui',
1=1	t=l	1=1
3)	Vi За = а,- такое, что Ki С Ui = Па. = Оа. В силу леммы 2
для компактного множества А = К существует разбиение единицы
{е,(«)} (i = 1,2,... , т) класса С^°°\ подчиненное открытому покры-
тию {Оа}, причем supp е» С J7» Vi. Разбор случая 1) закончен.
+оо	0
Случаи 2). Пусть А = (J Кц где Ki компактно, причем Ki СК1+1
/=1
V/. Пусть А С (Jfla (где множества открыты). Положим С2 =
а
t о
Кг = Ki U Кг, Ci = Ki\ К1-1 при I > 3. Тогда Ci компактно VZ > 2 и
А = (J Ki = (J Ci С (J причем (рис. 54) С)Г1С,+2 = 0 Vs > 2. По-
1=1	1=2 а
(2)	®	/по
ложим	Кз и введем открытый слой = ПаП(К/+1 \#/-2
при I = 3,4,.... Тогда С/ С IJwcP VI > 2, т. е- “ откры-
а
тое покрытие множества Cj. В силу рассмотренного выше случая
1) для компактного множества Ci существует открытое покрытие
{17/,»} (i = 1,2,... , m(I)), подчиненное открытому покрытию {а>сР} и
удовлетворяющее условиям леммы 2. Более того, открытое покрытие
{l7/,i} (i = 1,2,... , m(i)) компактного множества Ci обладает свойст-
вами: а) для любых I,i существует компактное множество Cii С 17/,»
т(/)	т(/)
(i = 1,2,... ,т(/)); б) С/ С U C/,j G (J С7/}|-; в) VI, i 3wa такое, что
»=1	»=1
Ul,i С Ша)- Поскольку СК1+1 \К|-2, ТО (рис. 55) Ul,i П U,+2,j = 0
4-оо	4-оо m(/)
Vs > I и Vi. Очевидно, A = |J Ci C (JU Ui,,. Поэтому {С7)Д
1=2	1=2 i=l
(i = 1,2,...	= 2,3,...) есть не более чем счетное открытое
416
скрытие множества Л, подчиненное открытому покрытию {Па}. До-
'м, что система {С/ц} локально-конечна. В самом деле, Vzo € А
такое, что xq Е Cj0, т. е. xq Е 17/о,«о. Но тогда Vs > Iq и VJ име-
еь. 44о,»о	т. е- любая точка ®о 6 А обладает окрест-
'тью С/}о3о, пересекающейся не более чем с конечным числом мно-
жеств Ui,i (г = 1,2,... , m(0; 1 < fo + 2), т. е. открытое покрытие {17},,}
+оо
(г =; 1,2,... , m(/); I = 1,2,...) множества А = (J Ci счетно, локально-
1=2
+оо т(/)	+оо т(/)
конёчно и обладает свойствами: а) и г) А С U IJ C/,t С (J U ^,<5
1=2 •=!	1=2 »=1
д) 30а такое, что СТ},.- С С Оа. Таким образом, открытое по-
крытие {С7}}|} локально-конечно и удовлетворяет всем условиям леммы
2. Разбор случая 2) закончен.
Случай 3). Пусть А — G - открытое множество из Rn. Тогда
G = (J Ki, где = {® Е G|||x||n < I, p(x,dG) > 1/1}. Очевидно,
i=i
о
множества Kj компактны и Ki CKi+i Тем самым показано, что
для открытого множества А = G имеет место разобранный выше
случай 2).
Случай 4). Пусть, наконец, А С Rn - произвольное множество и
{Оа} - его открытое покрытие. Тогда множество G = (Jfia открыто
а
и G D А. В силу рассмотрений, проведенных при работе случая 3),
для открытого множества G существует разбиение единицы {е,(®)}
(г = 1,2,...), подчиненное открытому покрытию {йа}. Но система
{е, (х)} будет, очевидно, разбиением единицы и для множества А С G.
Теорема о существовании единицы доказана полностью.
Замечание. Если К С А С Rn и множество К компактно, а
{е, (®)} (г = 1,2,....) - разбиение единицы для множества Л, подчинен-
417
вое локально-конечному открытому покрытию {£/)} (г = 1,2,...) (так
что supp е, С U* Vt), то лишь конечное число функций е,-(®) не равно
нулю V® € К, т. е. К П supp е; 0 лишь для t = ц (к = 1,2,..., тп),
причем £ е,й(») = 1 V® € К.
к=1
В самом деле, поскольку система {supp е,} (t = 1,2,...), образу-
ющая покрытие К, локально-конечна, то, как было замечено ранее, в
силу компактности К существует не более конечного числа индексов
ikm таких, что К П supp е, = 0 Vt / ц, и тогда равенство
4-оо	m
£ е,(®) = 1 V® € К С А дает £ е,* (®) = 1 V® € К.
i=i	*=1
Теорема. Пусть G и 0 - открытые множества из Rn и ото-
бражение ffi : G С R? -> 0 = <p(G) С RJ является диффеоморфизмом
4" оо
класса Пусть 0 = U 17), где {£/)} - открытое покрытие мно-
1=1
жества 0 и {е,(®)} (i = 1,2,...) - разбиение единицы для 0 класса
(к > 1), подчиненное этому покрытию, причем supp е, С Ui Vi.
Тогда G = |J Vi, где {VJ =	- открытое покрытие мно-
»=1
жества G и система {(е,* о p)(t)} (i = 1,2,...) является разбиени-
ем единицы для G класса подчиненным открытому покрытию
{Ц}, причем supp(е,- op) С И Vi.
Доказательство. Поскольку отображение : G С R" ->
0 С RJ есть диффеоморфизм класса С^1), то это отображение биек-
тивно, так что существует обратное отображение <р~* : <В -> G =
^”1(0), причем € C'W(G), <р~г € СМ(0). Множество Vi как прооб-
раз открытого множества Ui = р(Ц) при непрерывном отображении <р
является открытым множеством Vt. Докажем, что система {(е, о <р) (t)}
(t = 1,2,...) есть разбиение единицы (класса б^1)) для G, подчинен-
ное открытому покрытию {V)}-
1)	Очевидно, 0 < еДр(<)) < 1 Vt € G и Vt, причем если ® = <p(t) €
0, то t = <p~l(x) € G и Vt € G имеем 2 е<(^(^)) = S е»(®) — 1
1=1	i=i
(т. е. G С U supp(e, о ^)) в силу свойства 1) определения разбиения
1=1
единицы {е<(®)} (t = 1,2,...) для 0, при этом поскольку <р € C^(G)
и е{ € С<*)(0) (k > 1), то е< о <р € C™(G).
2)	supp (в; о р) С V, Vt, причем носитель supp (е,- о <р) компактен
Vt. В самом деле, поскольку носитель supp е,- = £Я С Ui компактен
в R" и € С(ЗД), то множество Ki = ^-1(9%) как непрерывный
образ компактного множества компактен в R”, и в силу биективнос-
ти отображения имеем (£)% С Ui) (Ki С И). Пусть теперь
to^Ki, но to € К-, тогда ®о = p(to)?£R< = supp е<, ®о € Ui в си-
418
лу биективности отображения р, и поэтому существует окрестность
0(®о) С Ui такая, что O(xq) П ЗЯ,' = 0, и тогда V® € 0(®о) име-
ем е,(®) = 0, т. е. е,(у>(<)) = 0 Vi € ТУ (ip) = у>-1(0(®о)), и тогда
to € supp е, о <р = {t € G|(е< о p)(t) ф 0}. (Если бы to € supp (е< о р), то
в любой окрестности ТУ (to) должно было бы существовать ti € ТУ (to)
такое, что (е, о p)(ti) ф 0.) В силу биективности и <р~1 име-
ем ТУ (to) С У- Но ТУ (to) П Ki = 0 (так как (0(®о) Ай, = 0)
=> (р-1(0(®о) И ЗЯ,) = р-1(0(®о)) П <р~ 1(9Я,) = 0) и поскольку
to?8upp(e,- о <р), то supp(e,' op) с Ki С У. Множество supp е,' о <р
замкнуто, а в силу ограниченности Ki и ограничено, т. е. компактно
(в *")
+оо
3)	Из свойства 1) следует, что G С (J supp(e, о <р). Докажем,
1=1
что покрытие {supp(e, о р)} локально-конечно. В самом деле, пусть
to € G ” любая точка, тогда ®о = <p(to) Е 0 = U supp е, и в си-
i=i
лу локальной конечности системы {supp е,} существует окрестность
0(®о) С <б такая, что е,(®) = 0 V® € 0(®о) при i = t'i,... , г,п(®0)- Но
тогда (е, о p)(t) = 0 Vi G Ty(to) = р-1(0(®о)) (где t = р-1(®)) при
» # »з,	• • • > »т(«о)> причем ТУ (io) С G есть окрестность точки to € G.
Таким образом, система {supp (е, о у>)} локально-конечна и {(е,- о у>) (t)}
(г = 1,2,...) есть разбиение единицы (класса £<*>) для G, подчинен-
ное открытому покрытию {У } (i = 1,2,...), причем supp (е,' ор) с У
V».
ЛИТЕРАТУРА
1.	К а р т а н А. Дифференциальное исчисление. Дифференциаль-
ные формы. М.: Мир, 1971.
2.	Р у д и н У. Основы математического анализа. М.: Мир, 1966.
3.	Ш в а р ц Л. Анализ. Т. I. М.: Мир, 1972.
4.	Кострикин А. И., Манин Ю. И. Линейная алгебра и
геометрия. М.: Наука, 1986.
5.	Валле-Пуссен Ж.-Ж. Курс анализа бесконечно малых.
П.: Н.К., 1922. Т. I.
6.	Никольский С. М. Курс математического анализа. Т. I.
М.: Наука, 1973.
7.	О р т е г а Дж., Рейнболдт В. Интегральные методы
решения уравнений со многими неизвестными. М.: Мир, 1975.
8.	К а м ы н и н Л. И. Курс математического анализа. Т. 2. М.:
Изд-во Моск, ун-та, 1995. 624 с.
ОГЛАВЛЕНИЕ
Предисловие.............................  3
ЧАСТЬ I. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИЙ ОДНОГО ПЕРЕМЕННОГО ........... 5
Глава 1. Основные понятия математического анализа ...	5
§1	. Некоторые понятия теории множеств и математической логики. 5
Законы алгебры множеств (7—11). Свойства декартовых произве-
дений (12). Некоторые понятия математической логики (12, 13,
И).
§2	. Понятия отображения функции........................ 14
Основные соотношения для образов и полных прообразов (18,
19).
§3	. Счетные и несчетные множества...................... 22
Теорема о мощности подмножеств счетного множества (23). Те-
орема о счетности объединения счетного множества счетных
множеств (23). Теорема Кантора о существовании несчетного
множества (24).
Глава 2. Поле действительных чисел...................... 25
§1	. Поле, упорядоченное поле, полное упорядоченное поле. 25
Принцип минимума (в N) (25). Принцип математической ин-
дукции (25). Определение поля (26). Определение упорядоченно-
го поля (27). Теорема Архимеда для поля рациональных чисел
(30). Определение полного упорядоченного поля (31). Теорема
о неполноте поля рациональных чисел (32). Теорема о неогра-
ниченности сверху множества N в R (33). Теорема Архимеда в
поле действительных чисел (34). Теорема о принципе минимума
для N (34). Теорема о плотности Q в R (34).
§2	. Принципы полноты поля R............................ 35
Принцип полноты Вейерштрасса (35). Принцип полноты Деде-
кинда (35). Принцип полноты Кантора (36). Теорема о справед-
ливости принципа Вейерштрасса в архимедовом упорядоченном
поле с принципом Кантора (36).
§3	. Мощности множеств Q и R............................ 38
Теорема о счетности множества рациональных чисел (38). Тео-
рема о несчетности множества действительных чисел (38).
Глава 3. Теория пределов............................. 39
§1	. Топология числовой прямой.............................. 39
§2	. Понятие предела функции в точке ....................... 48
§3	. Теоремы о пределах функций и последовательностей....... 51
421
Теорема о единственности предела (52). Теорема 1 о знаке для
функции, имеющей предел (52). Теорема о локальной ограничен-
ности функции, имеющей предел (53). Теорема об ограниченнос-
ти финально ограниченной последовательности (53). Теорема об
ограниченности сходящейся последовательности (53). Теорема 2
о переходе к пределу в неравенстве (53). Теорема о представле-
нии функции, имеющей предел (54). Теорема о пределе суммы
функций (55). Теорема о пределе произведения локально ограни-
ченной функции на функцию бесконечно малую (55). Теорема о
пределе произведения функций (56). Теорема о пределе частного
двух функций (58). Теорема о предельном переходе в неравенст-
ве для функций, имеющих пределы (58).
§4	. Признаки существования предела функции в точке и предела
числовой последовательности................................. 59
Критерий сходимости монотонной последовательности (59).
Формула бинома Ньютона (60). Число «е» (61). Теорема об оце-
ночном признаке существования предела функции в точке (61).
Оценочный признак сходимости числовой последовательности
(62). Теорема о пределе отношения синуса бесконечно малого ар-
гумента к аргументу (62). Теорема о связи бесконечно большой
и бесконечно малой функций (63). Теорема о связи бесконечно
малой и бесконечно большой функций (63). Критерий существо-
вания предела функции в точке (64). Теорема о существовании
односторонних пределов у монотонной функции (65). Теорема о
пределе композиции двух функций (67).
§5	. Предел по Коши и предел по Гейне функции в точке....... 68
Теорема об эквивалентности определений предела по Коши и по
Гейне (69). Число «е» (69).
§6	. Дополнения к принципам полноты поля R.................. 71
Теорема Вейерштрасса о сходимости монотонной ограничен-
ной последовательности (71). Теорема Кантора о стягивающей-
ся системе отрезков (71). Теорема Больцано-Вейерштрасса (для
множеств) (72). Теорема Больцано-Вейерштрасса (для число-
вых последовательностей) (72). Лемма Бореля-Лебега (о ком-
пактности отрезка) (73).
§7	. Критерии существования предела последовательности, преде-
ла функции в точке.......................................... 74
Критерий существования предела числовой последовательности
(74). Теорема о свойствах множества точек сгущения ограни-
ченной последовательности (75). Критерий Коши существова-
ния предела у числовой последовательности (77). Критерий Ко-
ши существования предела функции в точке (78).
§8	. Сравнение асимптотического поведения функций........... 79
Теорема о свойствах символа О большого (80). Теорема умно-
жения для отношения подобия (81). Теорема о свойствах сим-
вола о маленького (81). Теорема умножения для эквивалентных
функций (84). Теорема о знаке для эквивалентных функций (84).
Теорема о пределе частного для эквивалентных функций (84).
Таблица разложений простейших элементарных функций (85).
422
§9	. Предел числовой функции по базе........................ 86
Теорема о пределе суммы (87). Теорема о локальной ограничен-
ности функции, имеющей предел по базе (88). Теорема о сущест-
вовании верхнего и нижнего предела функции по базису фильтра
(88). Критерий Коши существования предела числовой функции
по базису фильтра (89). Теорема о пределах функции по экви-
валентным базисам (91).
Глава 4. Непрерывные функции....................... 93
§1. Непрерывность функции в точке. Точки разрыва функции . . 93
Предельный критерий непрерывности функции в точке (94).
Критерий непрерывности Бэра (97). Критерий непрерывности
монотонной функции (98). Теорема о мощности множества точек
разрыва монотонной функции (98).
§2.	Локальные свойства функций, непрерывных в точке....... 98
Теорема о сохранении знака (98). Теорема о локальной огра-
ниченности функции, непрерывной в точке (98). Теорема о не-
прерывности линейной функции (99). Теорема о непрерывности
суммы непрерывных функций (99). Теорема о непрерывности
произведения непрерывных функций (99). Теорема о непрерыв-
ности частного двух непрерывных функций (100). Теорема о не-
прерывности композиции двух непрерывных функций (100).
§3.	Глобальные свойства числовых непрерывных функций .... 101
Теорема о непрерывности сужения непрерывной функции (101).
Теорема о структуре связного числового множества (101). Те-
орема о нуле непрерывной функции (102). Теорема Больцано
о промежуточных значениях непрерывной функции (103). Те-
орема о сохранении связности при непрерывном отображении
(104). Теорема Вейерштрасса об ограниченности функции, не-
прерывной на отрезке (104). Теорема Вейерштрасса о достиже-
нии функцей, непрерывной на отрезке, своих точных верхней
и нижней граней (105). Теорема о свойстве Дарбу для непре-
рывной функции (105). Критерий непрерывности монотонной
функции (106). Теорема Кантора о равномерной непрерывности
функции, непрерывной на отрезке (107). Теорема о существова-
нии и непрерывности обратной функции для строго монотонной
непрерывной функции (109). Теорема об общем виде гомеомор-
физма (ПО).
§4.	Элементарные функции и их непрерывность...............112
Теорема о степенной функции с натуральным показателем (112).
Теорема о степенной функции с отрицательным натуральным
показателем (112). Теорема о показательной функции на мно-
жестве Q (114). Теорема о показательной функции, определен-
ной на R (115). Теорема о степенной функции с действительным
показателем (118). Теорема об обратных тригонометрических
функциях (119).
423
Глава 5. Дифференцируемые функции (одной переменной). 122
§1	. Дифференцируемость функции в точке...............  122
Теорема единственности дифференциала (124). Теорема о непре-
рывности дифференцируемой функции (124).
§2	. Производная функции в точке........................124
Критерии дифференцируемости функции в точке (125). Крите-
рий существования производной (126).
§3	. Касательная к графику функции......................127
Теорема о касательной как предельном положении секущей
(128).
§4	. Правила дифференцирования..........................129
Теорема о производной суммы, произведения, частного (129). Те-
орема о дифференцируемости композиции дифференцируемых
функций (130). Теорема о производной обратной функции (131).
§5	. Производные элементарных функций...................132
§6	. Производные и дифференциалы высших порядков........133
Формула Лейбница (134).
§7	. Теоремы о конечных приращениях......................137
Теорема Ферма (138). Теорема Ролля (139). Теорема Лагранжа
о конечных приращениях (141). Теорема (обобщенная теорема
Ролля) (141). Теорема (формула Тейлора с остаточным членом
в форме Лагранжа) (143). Теорема (формула Тейлора с остаточ-
ным членом в форме Пеано) (144). Таблица основных асимпто-
тических разложений для простейших элементарных функций
(145). Теорема Коши о конечных приращениях (146).
§8	. Правила Лопиталя раскрытия неопределенностей........147
Теорема 1 (правило Лопиталя раскрытия неопределенности ви-
да 0/0) (147). Теорема 2 (правило Лопиталя раскрытия неопре-
деленности вида оо/оо) (148).
§9	. Свойства производных дифференцируемых функций.......155
Достаточное условие строгой монотонности функции в точке
(156). Теорема Дарбу о промежуточных значениях производной
(156). Теорема о пределе производной (157). Теорема о разрывах
производной (158).
§10	. Формула Тейлора....................................158
Теорема (формула Тейлора для многочлена) (158). Теорема
единственности многочлена Тейлора (159). Теорема (о форму-
ле Тейлора) (161).
Глава в. Исследование функций с помощью производных . 163
§1	. Условия монотонности функции.......................163
Теорема 1 (критерий монотонности функции) (163). Теорема
2 (достаточное условие строгой монотонности функции) (164).
Теорема 3 (критерий строгой монотонности функции, имеющей
производную) (164).
§2	. Экстремумы функции.................................165
424
Необходимый признак существования локального экстремума
для дифференцируемой функции (165). Теорема (достаточный
признак существования локального экстремума) (165). Следст-
вие 1 (достаточный признак существования локального экстре-
мума - по знаку 1-й производной) (166). Следствие 2 (доста-
точное условие существования локального экстремума - по мо-
нотонности 1-й производной) (167). Следствие 3 (достаточное
условие существования локального экстремума - по знаку 2-й
производной) (168). Теорема (достаточное условие существова-
ния локального экстремума и монотонности в точке по произ-
водным высшего порядка) (168).
§3	. Направление выпуклости.............................170
Точки перегиба. Теорема (критерий выпуклости дифференци-
руемой функции в точке и критерий существования точки пе-
региба графика дифференцируемой функции) (171). Теорема 1
(достаточный признак выпуклости функции в точке и существо-
вания точки перегиба у ее графика - по 1-й производной) (171).
Следствие (необходимое условие существования точки перегиба)
(172). Теорема 2 (достаточный признак выпуклости функции в
точке и существования точки перегиба у ее графика по произ-
водным высшего порядка) (172). Следствие 1 (достаточный при-
знак существования точки перегиба у графика функции - по 3-й
производной) (173). Следствие 2 (достаточный признак строгой
выпуклости функции в точке - по 2-й производной) (173). Тео-
рема (достаточный признак выпуклости функции на интервале)
(177). Теорема (критерий выпуклости вниз для дифференцируе-
мой функции) (177). Следствие (критерий выпуклости вниз для
дважды дифференцируемой функции) (178). Теорема (неравен-
ство Йенсена) (179).
§4	. Условия постоянства функции. Первообразные функции.... 180
Критерий постоянства для дифференцируемой функции (180).
Теорема об общем виде точной первообразной (180). Теорема
(достаточное условие постоянства функции) (182). Теорема об
общем виде первообразной (182).
§5	. Центр кривизны, радиус кривизны и кривизна графика функции183
Теорема (формулы для вычисления координат центра кривиз-
ны) (184). Кривизна и эволюта параболы (186).
Литература...................................188
ЧАСТЬ II. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНК-
ЦИЙ ОДНОГО ПЕРЕМЕННОГО................  189
Глава 1. Неопределенный интеграл.......................189
§1	. Неопределенный интеграл...........................189
§2	. Основные свойства неопределенного интеграла.......192
425
Теорема о связи дифференцирования и интегрирования (192).
Теорема о линейности операции интегрирования (192). Теорема
об интегрировании по частям (193). Теорема 1 о замене пере-
менной в неопределенном интеграле (193). Теорема 2 о замене
переменной в неопределенном интеграле (194).
§3. Таблица основных неопределенных интегралов..........194
Глава 2. Определенный интеграл Римана...................196
§1	. Определение интеграла Римана.......................196
Теорема единственности интеграла Римана (197). Теорема о не-
обходимом условии интегрируемости по Риману (198).
§2	. Суммы Дарбу и критерии Дарбу интегрируемости по Риману. 199
Теорема о формулах Дарбу (200). Теорема 1 о свойствах сумм
Дарбу (201). Теорема 2 о свойствах сумм Дарбу (202). Теоре-
ма о предельном критерии интегрируемости по Риману (202).
Теорема о критерии Дарбу интегрируемости по Риману (203).
Теорема о критерии интегрируемости по Риману (204).
§3	. Множества из R меры нуль и длины нуль...............205
Теорема о мере подмножества множества меры нуль (205). Тео-
рема о мере счетного множества множеств меры нуль (205). Тео-
рема о длине отрезка (206). Теорема о компактности замкнутого
ограниченного числового множества (207). Теорема о длине ком-
пактного множества меры нуль (208). Теорема о компактности
границы ограниченного множества (208).
§4	. Критерий Лебега интегрируемости по Риману...........209
Теорема о критерии непрерывности Бэра (210). Теорема Канто-
ра для разрывных функций (210). Теорема о колебаниях функ-
ции (210). Теорема о критерии Лебега интегрируемости по Ри-
ману (211).
§5	. Классы функций, интегрируемых по Риману.............214
Теорема 1 об интегрируемости ограниченной функции со счет-
ным множеством точек разрыва (214). Следствие 1 об интегри-
руемости непрерывной функции (214). Следствие 2 об интегри-
руемости монотонной функции (214). Теорема о критерии изме-
римости по Жордану (215). Теорема об эквивалентности двух
определений множества длины нуль (216). Теорема о свойствах
множеств, измеримых по Жордану (217). Теорема - множества,
измеримые по Жордану, образуют алгебру (218).
§6	. Свойства интеграла Римана...........................218
Теорема 1 (об интегрируемости суммы) (218). Теорема 2 (об
интегрируемости произведения) (220). Теорема 3 (об интегриру-
емости частного) (220). Теорема 5 (об аддитивности интеграла)
(221). Теорема 6 (об интегрируемости по подотрезку) (222).
Теорема 7 (об оценках интеграла) (222). Теорема 8 (об оценке
интеграла) (222). Следствие (об интегрировании неравенств)
(223). Следствие (о монотонности «меры Жордана») (223).
426
Теорема 9 (о множестве точек непрерывности интегрируемой
функции) (223). Теорема 10 (о положительности интеграла
от положительной функции (224). Теорема И (224). Теорема
12 (224). Теорема (1-я обобщенная теорема о среднем) (226).
1-я теорема о среднем (227). Теорема о непрерывности ин-
теграла Римана хак функции верхнего предела (228). Лем-
ма (тождество Абеля) (228). Следствие (к тождеству Абеля)
(229). 2-я интегральная теорема о среднем (230). Теорема о
дифференцируемости интеграла Римана по верхнему пределу
(233). Теорема о существовании точной примитивной у непре-
рывной функции (234). Теорема (о существовании первообраз-
ной у кусочно-непрерывной функции) (234). Теорема (формула
Ньютона-Лейбница для кусочно-непрерывной функции) (234).
Теорема (формула Ньютона-Лейбница (236). Теорема 1 (о за-
мене переменной в интеграле Римана) (237). Теорема 2 (о за-
мене переменной в интеграле Римана) (238). Теорема о среднем
в интегральной форме (240). Теорема 1 (об интегрировании по
частям) (241). Теорема 2 (об интегрировании по частям) (242).
2-я теорема о среднем (243). Теорема об интеграле Римана хак
линейном функционале (245).
§7	. Понятие о мере множеств. Длина числового множества хак
мера. Площадь криволинейной трапеции..................245
Площадь криволинейной трапеции (246).
§8. Замечания о некоторых геометрических и механических при-
ложениях определенного интеграла Римана....................248
Объем тела вращения (248). Масса и центр тяжести неоднород-
ного тела (249). Работа переменной силы (249).
§9	. Формула Тейлора с остаточным членом в интегральной форме.250
Теорема о формуле Тейлора с остаточным членом в интеграль-
ной форме (250).
ЧАСТЬ III. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ ....................254
Глава 1. Непрерывные отображения из R” в Rm......254
§1	. Линейные, евклидовые, нормированные и метрические про-
странства .......................................254
Теорема (неравенство Коши-Буняковского) (256). Теорема (не-
равенство Минковского) (256).
§2	. Дифференцирование и интегрирование (векторных) функций
одного действительного переменного...............258
Теорема 1 (об интегрировании суммы) (259). Теорема 2 (фор-
мула Ньютона-Лейбница) (259). Теорема 3 об оценке нормы ин-
теграла от (векторной) функции через интеграл от нормы этой
функции (259).
§3. Векторные функции ограйиченной вариации................261
Теорема о полной вариации суммы и произведения функ-
ций (262). Теорема Жордана (263). Теорема 1 (о свойствах
427
векторной функции ограниченной вариации) (264). Теорема 2
(об аддитивности полной вариации) (265). Теорема 3 (266).
§4	. Пути и кривые в Rn ................................ 267
§5	. Длина кривой в Rn.........................<.........272
Теорема (критерий спрямляемости замкнутого пути) (272), Те-
орема (об инвариантности длины для эквивалентных путей)
(273). Натуральная параметризация кривой (274).
§6	. Касательная к кривой в Rn.............................275
Теорема 6 локальной взаимнооднозначности (276). Замечание о
вычислении площади поверхности вращения (278).
§7	. Топология метрического пространства...................279
Теорема об эквивалентных нормах (285). Теорема об эквива-
лентности норм || ||1, || ||г и || ||оо в Rn (286).
§8	. Пределы в метрическом пространстве....................287
Теорема (об ограниченности сходящейся последовательности)
(287). Теорема о подпоследовательности последовательности
Коши (288). Теорема о сходимости последовательности Коши,
имеющей точку сгущения (288). Теорема о пределе последова-
тельности в пространствах с эквивалентными нормами (289).
Теорема (о полноте Rn) (290). Теорема об эквивалентности
определений предела отображения по Коши и по Гейне (291).
Теорема о единственности предела (291). Теорема (критерий
существования предела у векторной функции) (292). Теорема
о пределах (292). Теорема (достаточное условие существования
повторного предела (294).
§9	. Непрерывные отображения в метрических пространствах . . . 295
Теорема (предельный критерий непрерывности отображения в
точке) (296). Теорема (критерий непрерывности отображения,
определенного на открытом множестве) (297).
§10	. Компактность в метрических пространствах..............298
Теорема (о компактности объединения конечного числа ком-
пактных множеств) (299). Теорема Кантора (300). Теорема о
секвенциальной компактности компактного множества (300).
Теорема о полной ограниченности секвенциально компактно-
го множества (302). Теорема о замкнутости секвециально ком-
пактного множества (302). Теорема о представлении замкнутого
вполне ограниченного множества в метрическом пространстве
(303). Теорема о компактности секвенциально компактного мно-
жества в метрическом пространстве (303). Теорема Больцано-
Вейерштрасса (304). Теорема (критерий компактности в полном
метрическом пространстве) (305). Теорема (критерий существо-
вания предела последовательности в декартовом произведении
метрических пространств) (306). Теорема Бореля- Лебега (308).
Следствие (критерий компактности в R”) (309).
§11	. Связность в метрических пространствах.................309
428
Теорема о сохранении связности при непрерывном отображении
(310). Теорема об эквивалентности топологической связности и
линейной связности на числовой прямой (311). Теорема Больца-
но о промежуточных значениях непрерывной числовой функции
(311). Теорема о связности линейно связного множества (312).
Теорема (критерий связности открытого множества в Rn) (313).
§12	. Непрерывные отображения на компактных множествах . . . . 315
Теорема о сохранении компактности при непрерывном отобра-
жении (315). Теорема Вейерштрасса (316). Замечание о поло-
жительно определенной квадратической форме (316). Теорема
о расстоянии точки до замкнутого множества (317). Теорема
о расстоянии между замкнутым и компактным множествами
(318). Теорема Кантора о равномерной непрерывности (318).
§13	. Сжимающие отображения в метрических пространствах . . . 319
Теорема о принципе сжимающих отображений (320).
Глава 2. Дифференцируемые отображения из R” в Rm . . . 321
§1.	Частные производные функций многих переменных.321
Теорема о линейности частного дифференцирования (324). Тео-
рема о частных производных композиции (324). Теорема Швар-
ца (достаточное условие равенства смешанных частных произ-
водных второго порядка) (325).
§2.	Некоторые сведения из линейной алгебры...............327
Теорема о равномерной непрерывности линейного отображения
(329). Теорема о норме линейных отображений (330). Теорема
об однозначной разрешимости линейного уравнения (331). Лем-
ма Неймана (331). Теорема (о линейном возмущении) (332). Те-
орема (о нелинейном возмущении) (333).
§3.	Понятие дифференцируемости отображения из Rn в Rm . . . 333
Теорема о единственности производной (336). Теорема (о не-
прерывности дифференцируемой функции) (336). Теорема (о су-
ществовании производной вдоль любого вектора у дифференци-
руемой функции) (337). Следствие (необходимое условие диф-
ференцируемости функции в точке) (337). Теорема (о представ-
лении производной дифференцируемой функции в координатной
форме) (337). Теорема (критерий дифференцируемости вектор-
ной функции в точке) (339). Теорема (достаточное условие диф-
ференцируемости функции в точке) (340). Теорема Юнга (до-
статочное условие равенства вторых смешанных частных про-
изводных у функции многих переменных) (340). Теорема (кри-
терий непрерывной дифференцируемости функции на открытом
множестве) (342). Уравнение касательной гиперплоскости к гра-
фику функции (344). Градиент функции (345). О производной
Гато (346).
§4.	Теорема о производной сложной функции и ее следствия . . . 351
429
Теорема (о производной сложной функции) (351). Следствие
1 (цепное правило вычисления частных производных сложной
функции) (354). Следствие 2 (теорема о полной производной
сложной функции) (354). Теорема о линейности дифференци-
рования (355). Замечание (об инвариантности формы первого
дифференциала) (356). Теорема (об обратной биекции) (357).
§5. Теорема о среднем для отображений из Rn в Rm ..........358
Теорема (о среднем для числовой функции многих переменных)
(358). Теорема (о среднем для отображений из R” в Rm) (359).
Теорема (об оценке) (361).
§6. Формула Тейлора для (векторных) функций................362
Теорема (формулы Тейлора для числовой функции многих пере-
менных) (365). Теорема (формула Тейлора с остаточным членом
в форме Пеано) (368). Теорема (формулы Тейлора для вектор-
ных функций) (369). Следствие (теорема о среднем для вектор-
ной функции в интегральной форме) (370). Следствие (форму-
лы Тейлора для векторной функции одного переменного) (371).
Лемма (критерий постоянства дифференцируемой функции на
открытом связном множестве) (371).
§7	. Локальные экстремумы числовой функции многих переменных. 372
Теорема (необходимое условие существования локального эк-
стремума для дифференцируемой функции) (372). Лемма (о по-
ложительно определенной квадратической форме) (373). Теоре-
ма (достаточное условие существования локального экстремума
для дважды дифференцируемой функции) (375).
§8	. Обратные функции..................................377
Теорема (достаточное условие существования гомеоморфизма)
(377). Теорема (об уточненном принципе сжимающих отобра-
жений) (377). Теорема (о нелинейном возмущении) (378). След-
ствие (теорема о локальном гомеоморфизме) (379). Теорема (о
локальном диффеоморфизме) (380). Теорема об обратной функ-
ции (382). Следствие (382).
§9. Неявные функции......................................383
Теорема (о неявной функции в случае п > 1 и т ® 1) (384).
Теорема (о неявной функции в случае п > 1 и т > 2) (387). За-
мечание (о вычислении частных производных неявной функции)
(392). Теорема (об оценке) (393). Основная теорема о неявной
функции (393). Следствие 1 (398). Следствие 2 (398). Следствие
3 (теорема о неявных функциях, определяемых системой урав-
нений) (399).
§10	. Условный экстремум функции многих переменных.........400
Теорема (о существовании касательной плоскости) (400). Теоре-
ма 1 (необходимое условие существования локального условного
экстремума) (403). Замечание (о геометрическом смысле необ-
ходимого условия существования условного экстремума) (405).
Замечание (о собственных значениях квадратической формы)
(405).
§11	. Зависимые функции....................................407
Теорема 1 (необходимое условие зависимости функций) (407).
Теорема 2 (достаточное условие зависимости функций) (408).
430
§12	. Разбиение единицы ................................410
Лемма 1 (412). Теорема (о существовании разбиения единицы)
(414). Лемма 2 (414). Теорема (о разбиении единицы, индуциро-
ванном диффеоморфизмом) (418).
Литература...............................................420
431
Учебное издание
КАМЫНИН Леонид Иванович
КУРС МАТЕМАТИЧЕСКОГО АНАЛИЗА
Том 1
Зав. редакцией Г. С. Савельева
Художественный редактор Ю. М. Добрянская
Технический редактор Н. И. Смирнова
Корректоры: Н. И. Коновалова, В. В. Конкина, Г. В. Сибирцева
Изд. лиц. №> 040414 от 18.04.97.
Подписано в печать 14.12.2001. Формат 60x90 ’/ i6. Бумага офс. № 1.
Офсетная печать. Усл. печ. л. 27,0. Уч. изд.л. 27,5. Тираж 3000 экз.
Заказ .v Изд. № 7253
Ордена “Знак Почета”издательство Московского университета.
103009, Москва, ул. Б. Никитская, 5/7.
Отпечатано с готового оригинал-макета в ООО
“Типография ИПО профсоюзов Профиздат”.
109044, Москва, Крутицкий вал, 18.
ЪБН
к-ies