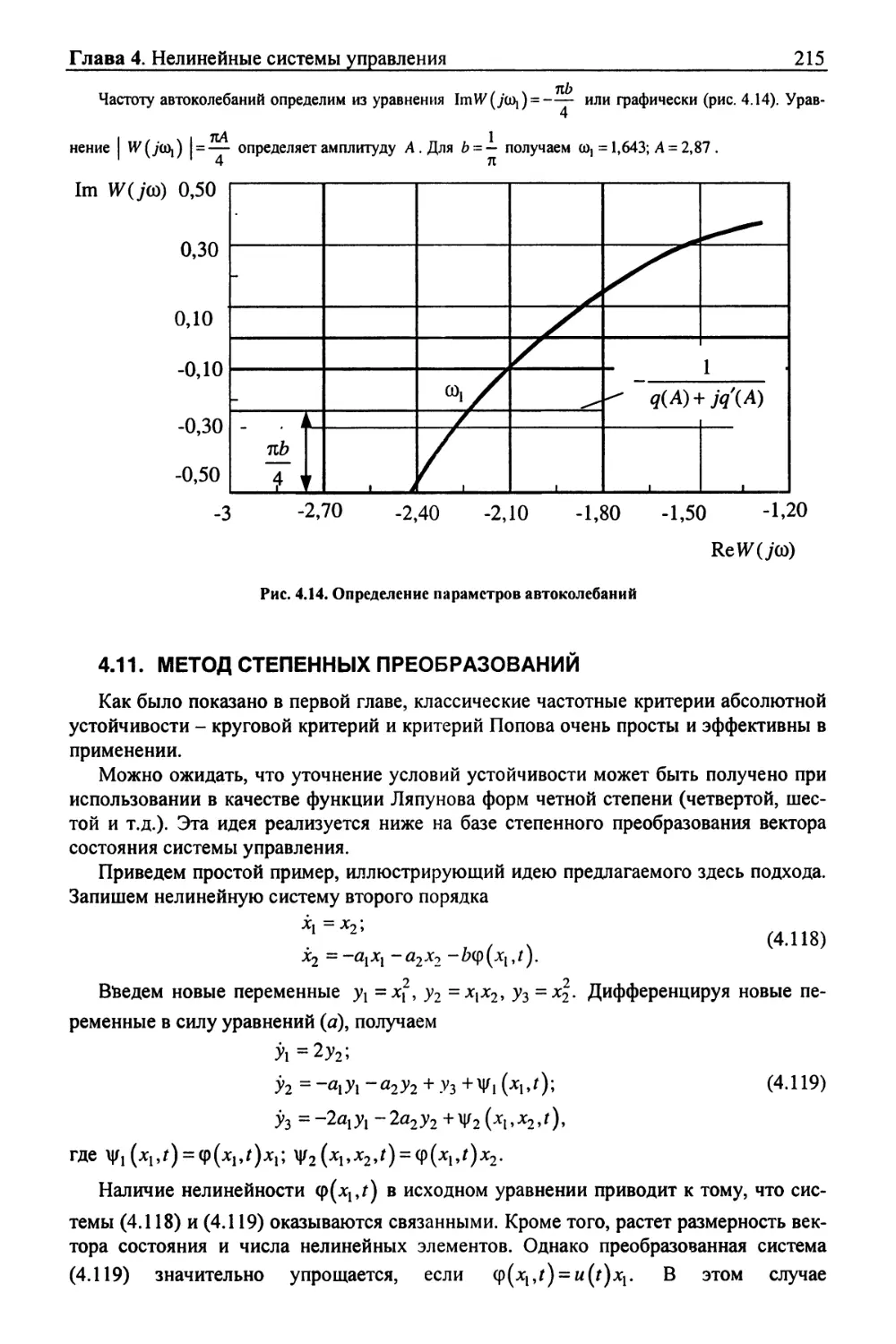
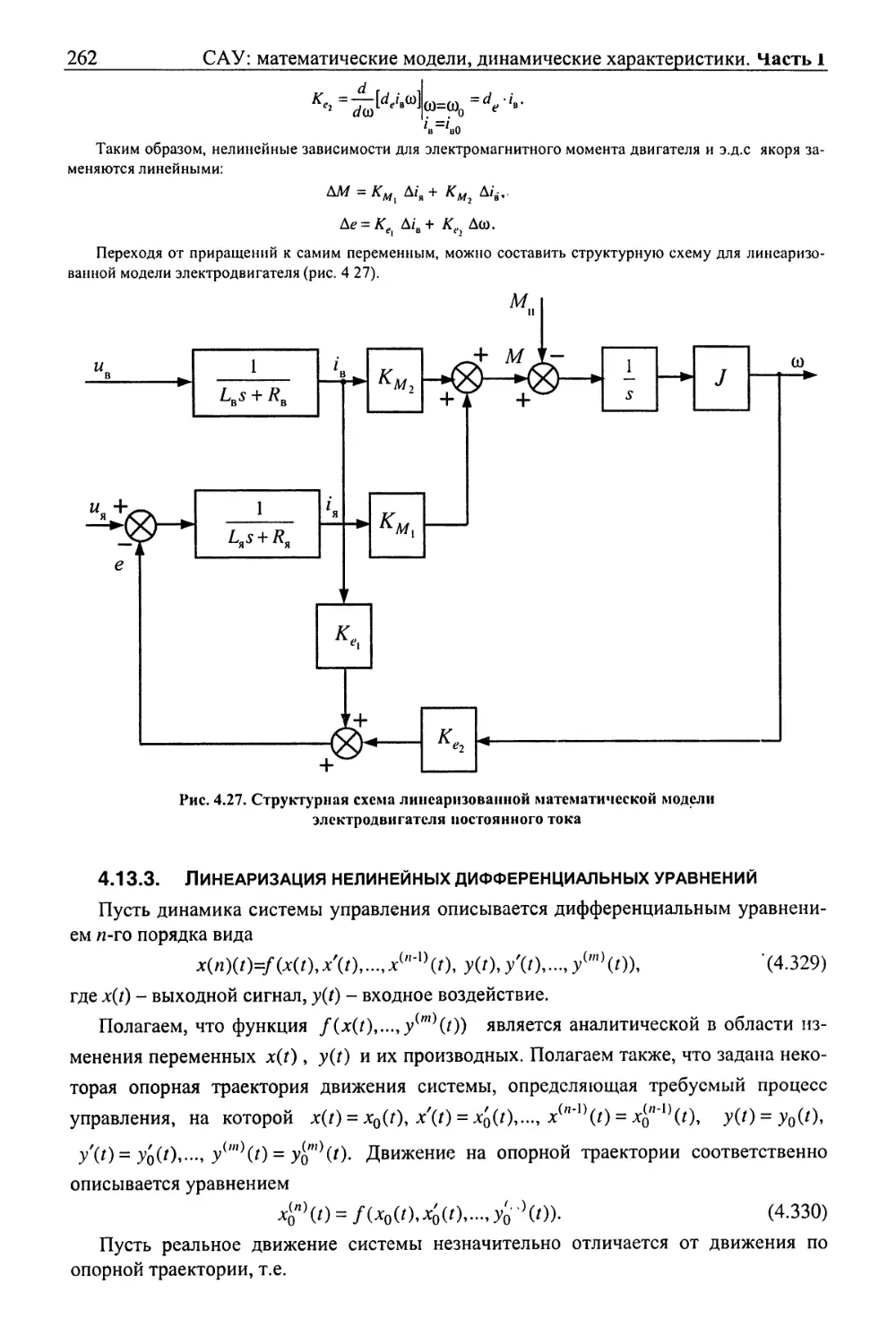
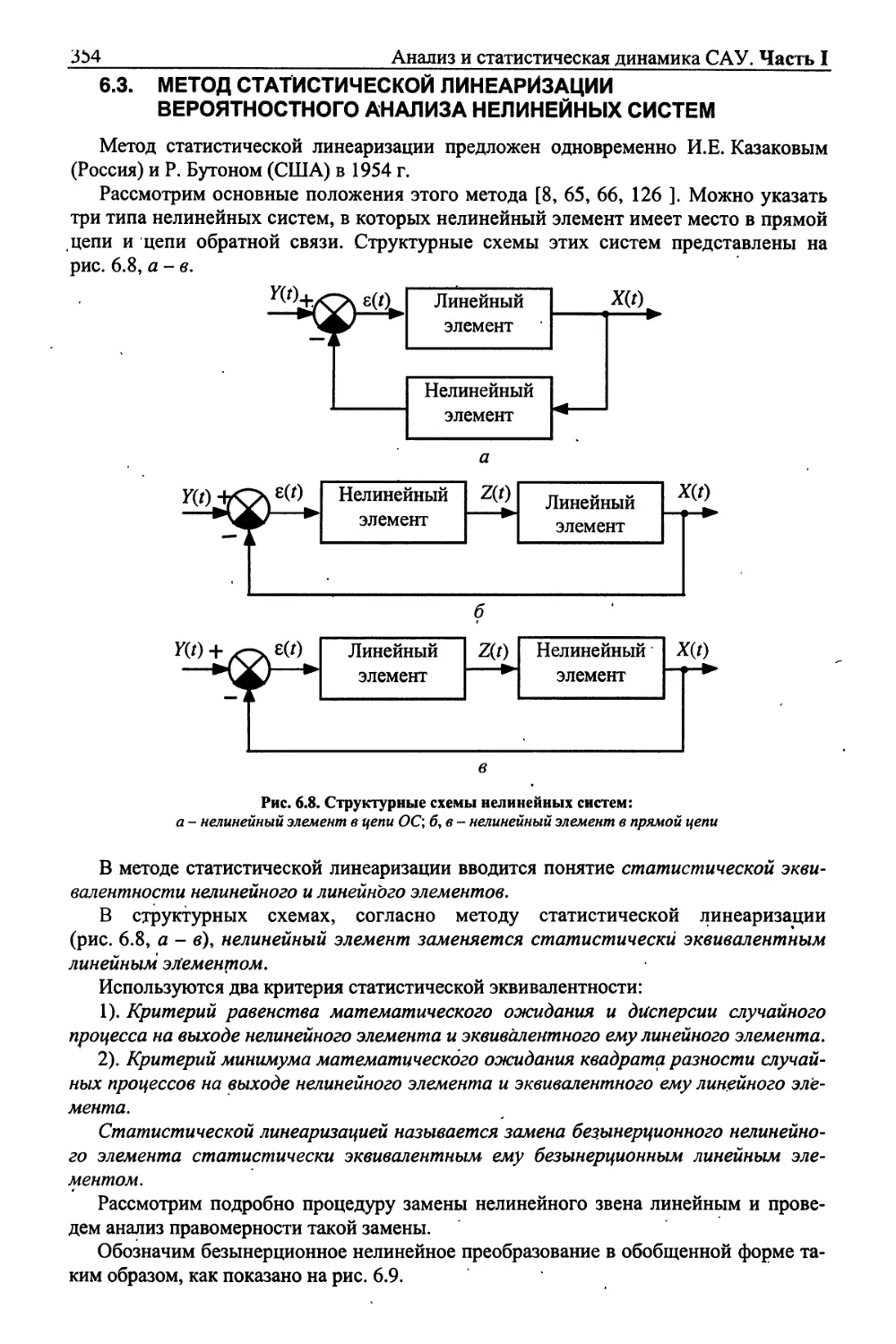
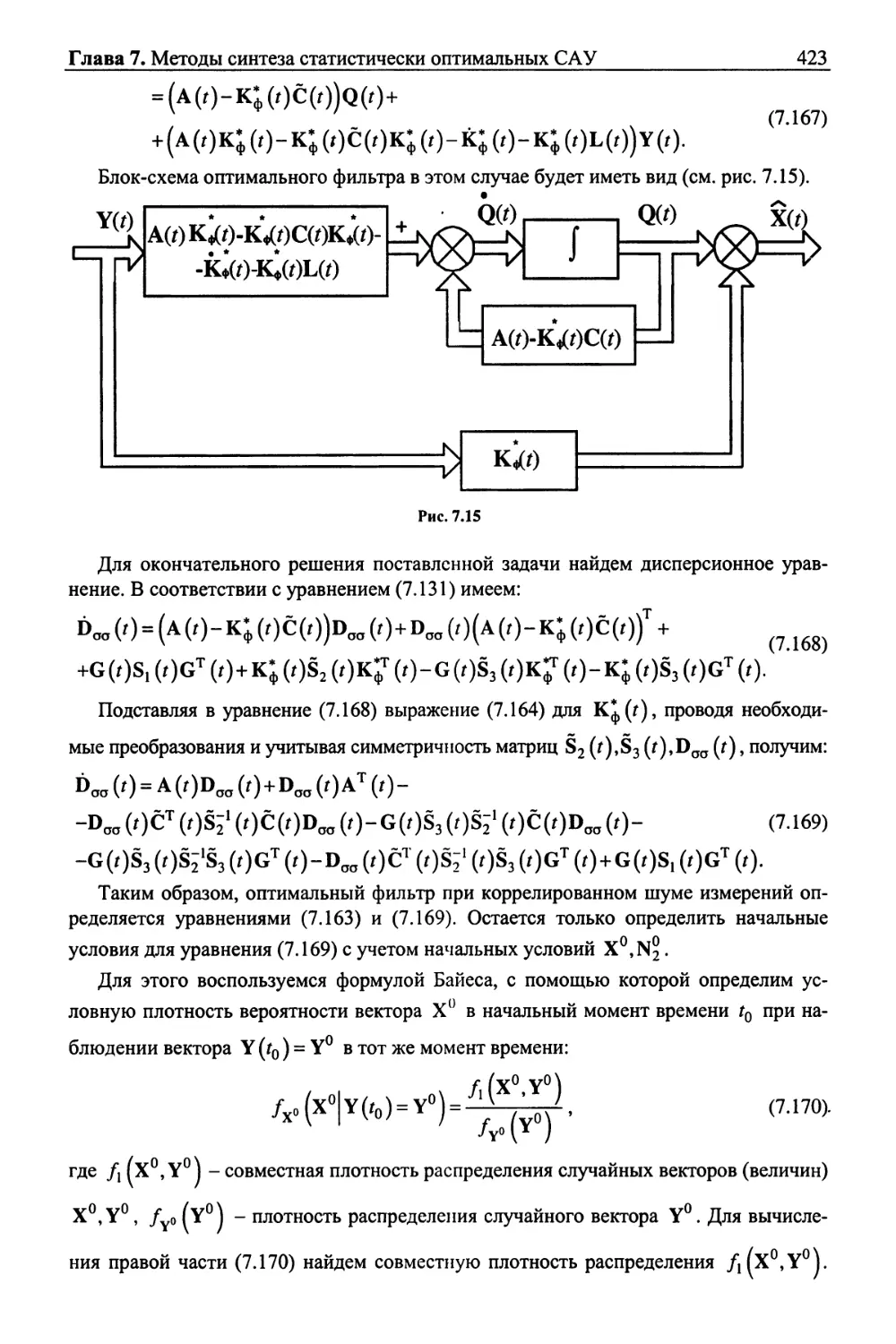
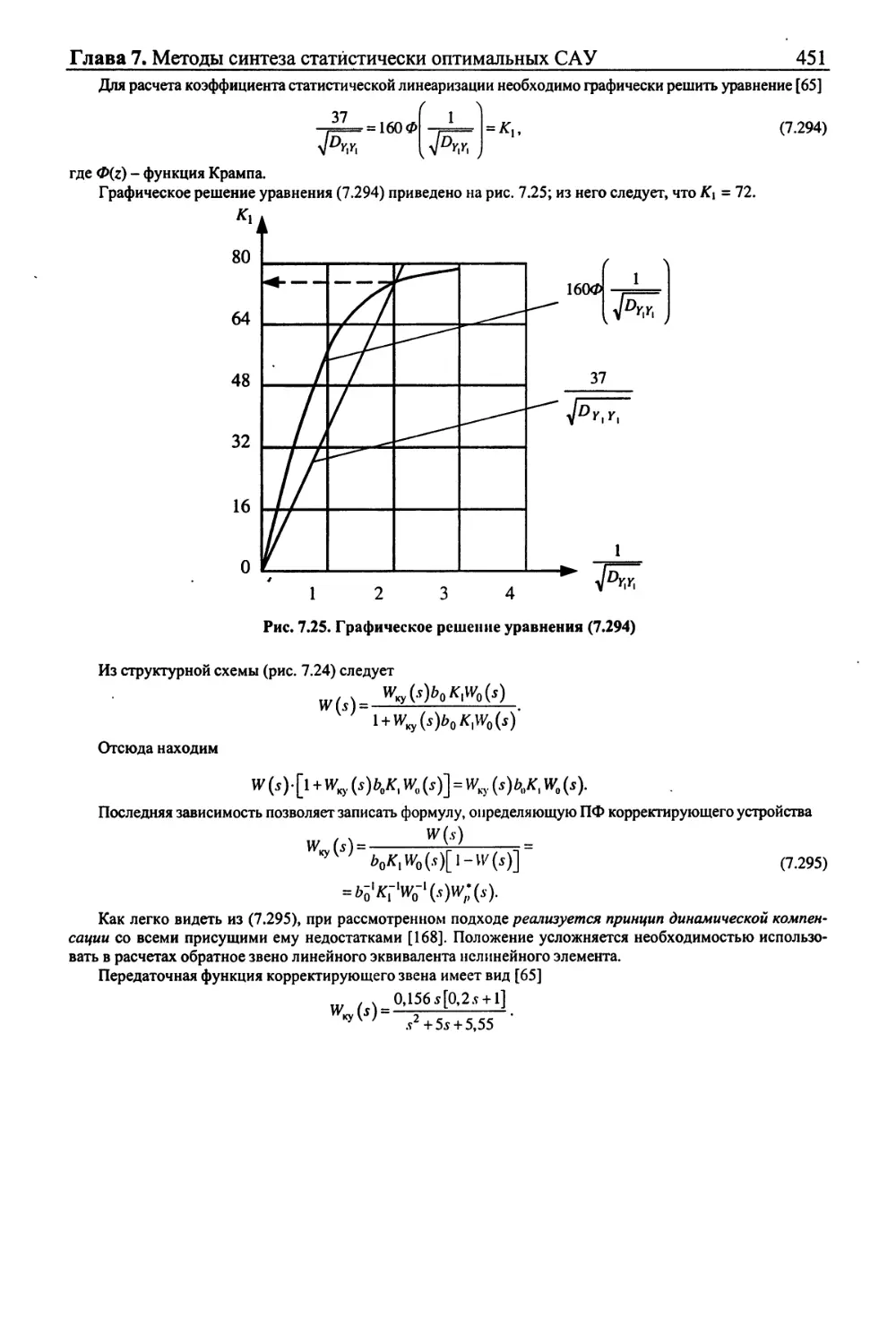
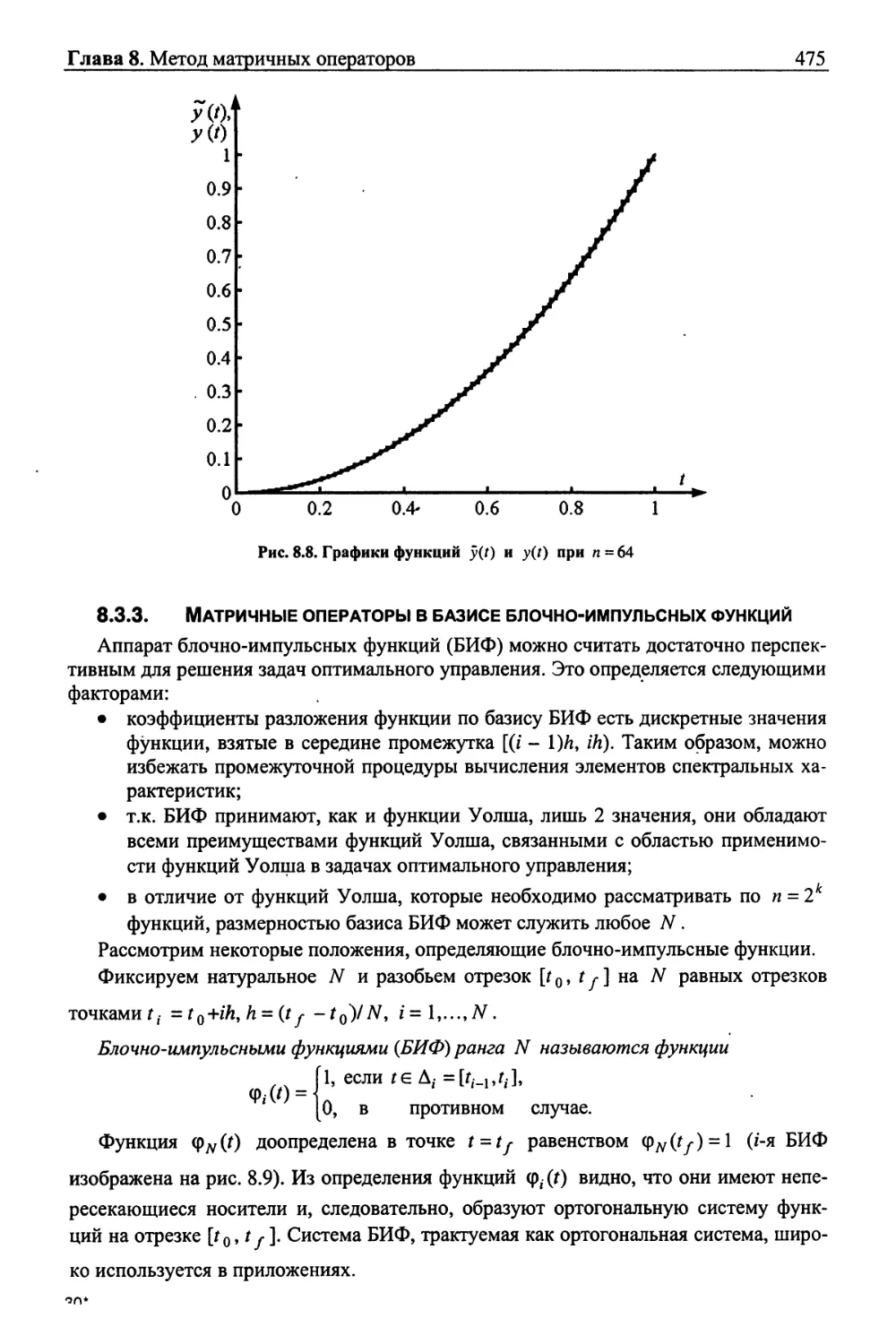
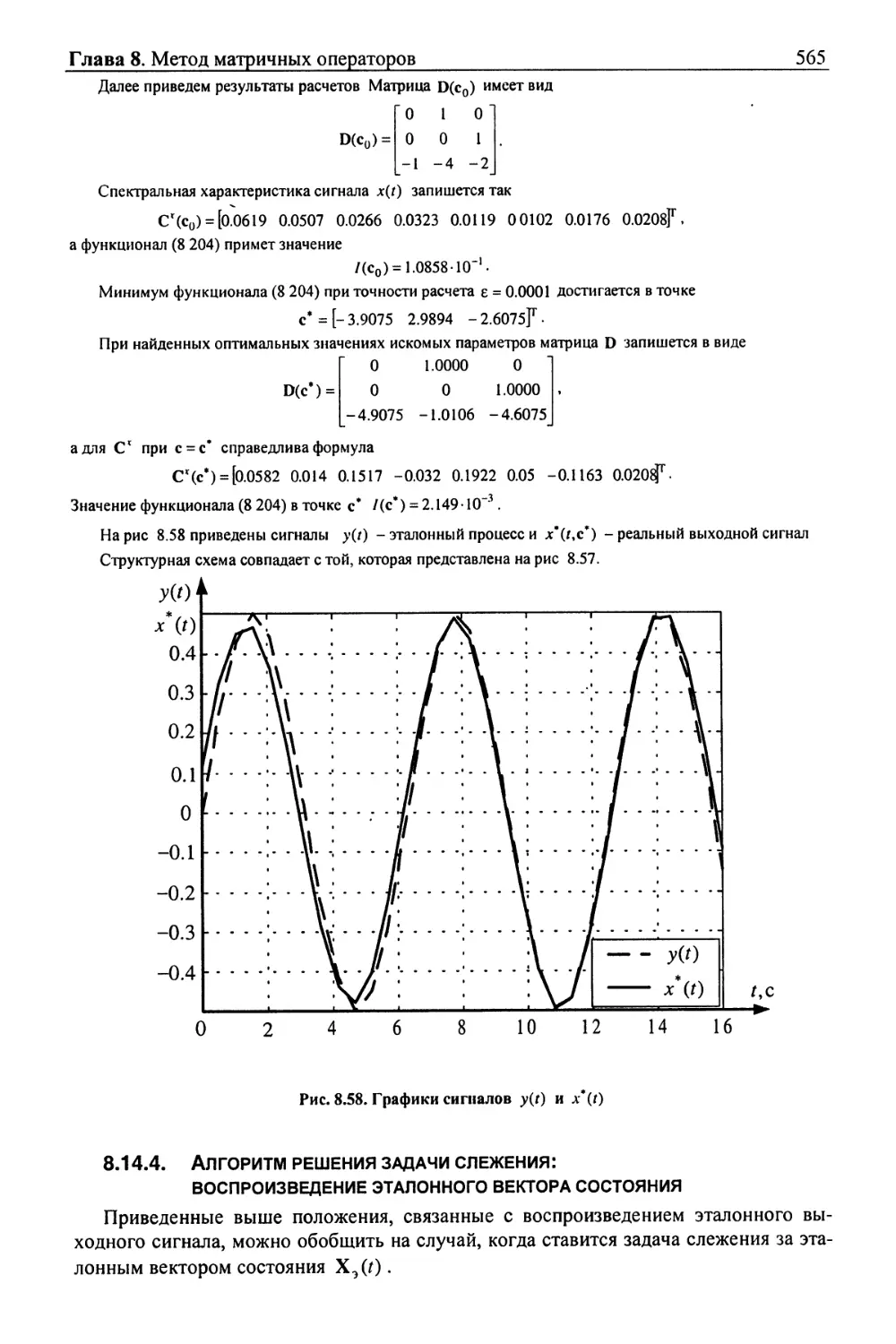
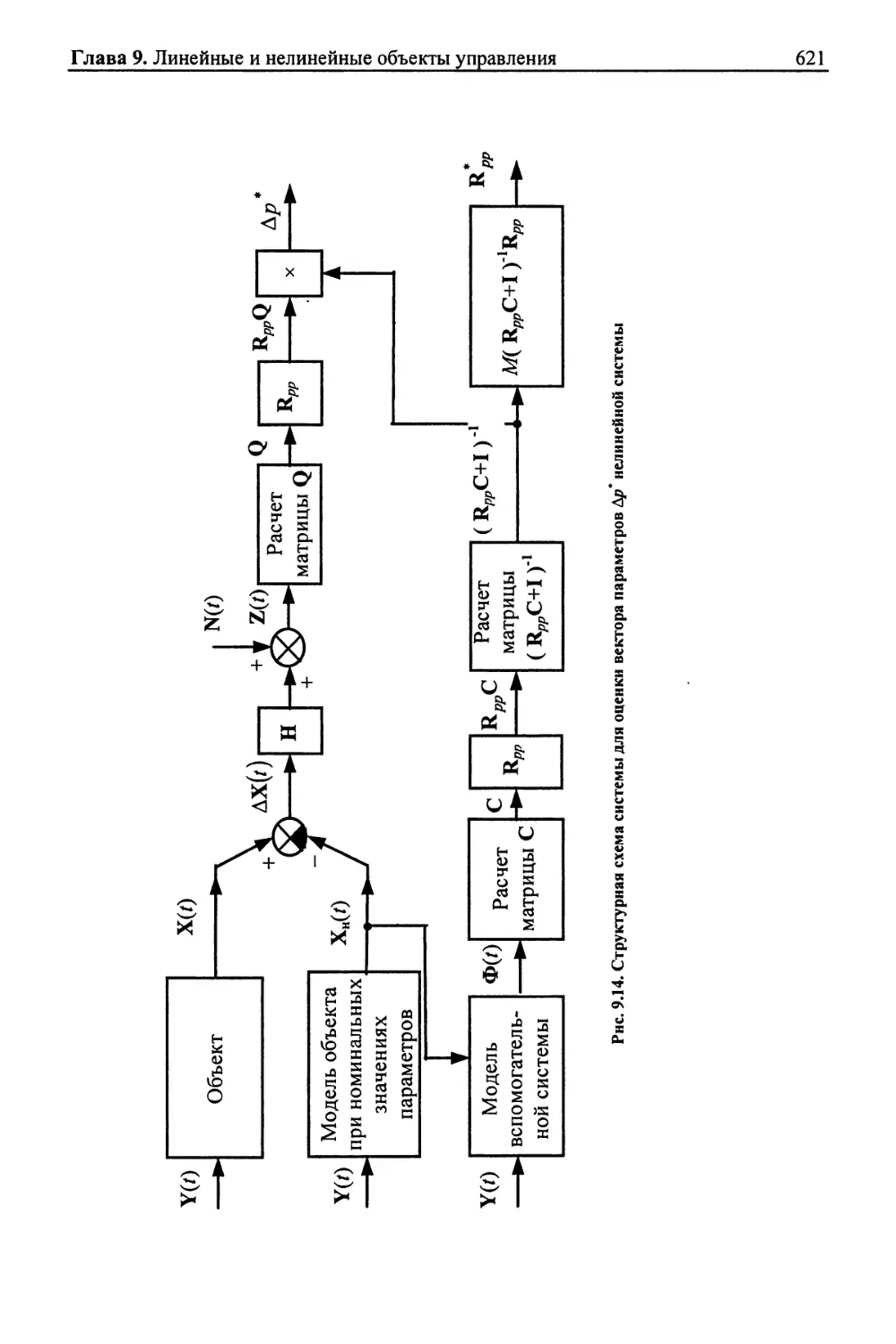
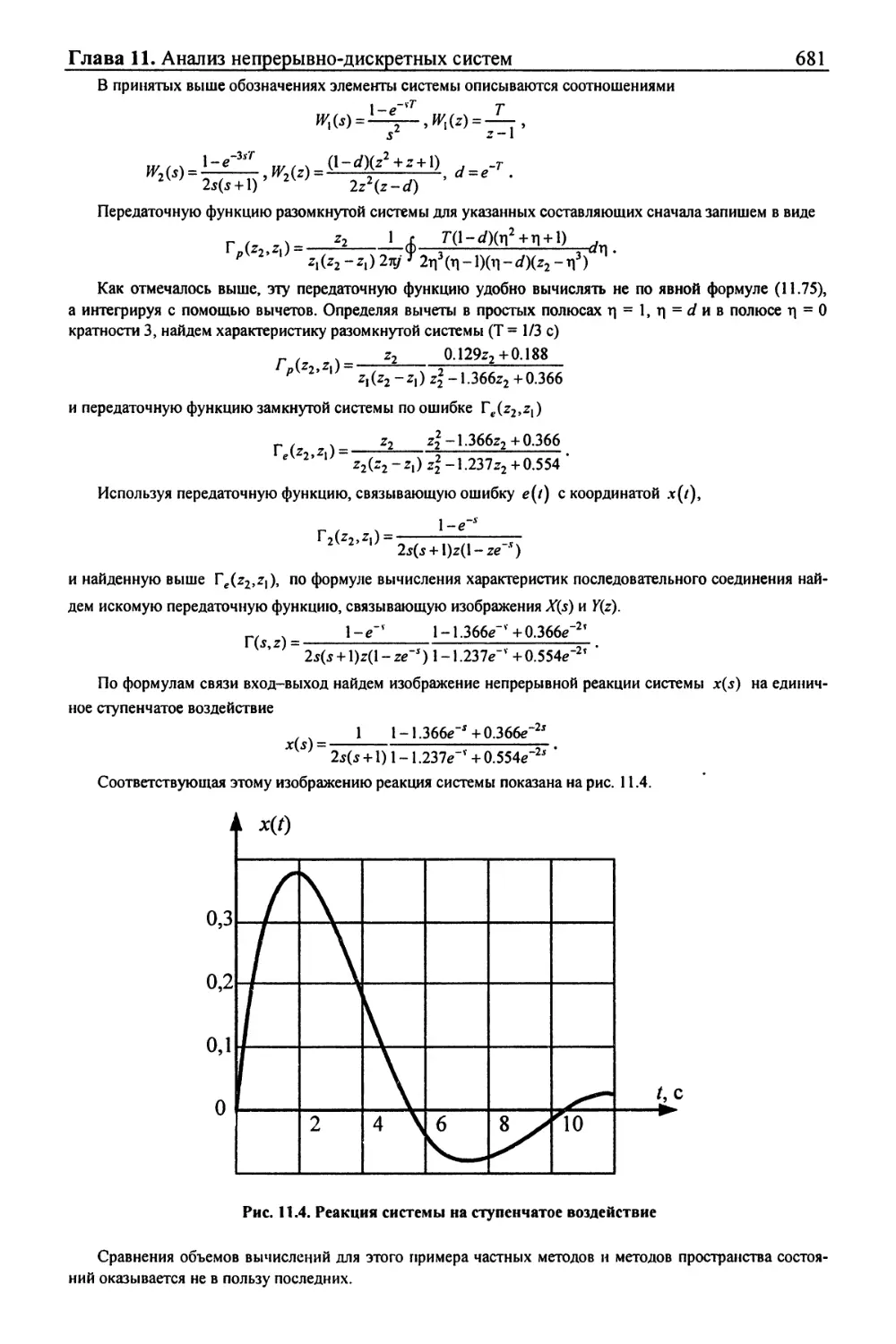
Текст
МЕТОДЫ ТЕОРИИ
АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ
Цикл учебников и учебных пособий
основан в 1997 г.
Под общей редакцией заслуженного деятеля науки РФ,
доктора технических наук, профессора
К.А. Пупкова
МЕТОДЫ КЛАССИЧЕСКОЙ
И СОВРЕМЕННОЙ ТЕОРИИ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Учебник в трех томах
Т0М1
АНАЛИЗ И СТАТИСТИЧЕСКАЯ ДИНАМИКА
СИСТЕМ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ
Под редакцией заслуженного деятеля науки РФ,
доктора технических наук,
профессора Н.Д. Егупова
Рекомендовано Министерством образования Российской Федерации
в качестве учебника для студентов высших учебных заведений,
обучающихся по машиностроительным
и приборостроительным специальностям
Москва
Издательство МГТУ им. Н.Э. Баумана
2000
УДК 681.5:681.3(075.8)
ББК 14.2.6
М54
Рецензенты:
1. Академик РАН Е.П.Попов;
2. Кафедра автоматических систем Московского института радиотехники,
электроники и автоматики (заведующий кафедрой, член-корреспондент
РАН ЕД. Теряев).
Авторы:
Д-р техн. наук, проф. К А. Пупков, д-р техн. наук, проф. АЖБаркин,
д-р техн. наук Е.М. Воронов, д-р техн. наук, проф. НД, Егупов, канд. техн.
наук, доц. ВТ. Коньков, канд. техн. наук, доц. В.Н, Пилишкин, канд. техн.
наук, доц. В.И. Сивцов, д-р техн. наук, проф. А.И. Трофимов, д-р техн.
наук, проф*. Н.В. Фалдин
М54 Методы классической и современной теории автоматического управления:
Учебник в 3-х т. Т. 1: Анализ и статистическая динамика систем автоматического
управления / Под ред. Н.Д. Егупова. - М: Изд-во МГТУ им. Н.Э. Баумана, 2000,
- 748 с, ил.
ISBN 5-7038-1578-9 (T.I)
ISBN 5-7038-1579-7
В первом томе учебника изложены основные положения классической теории
автоматического управления: основные понятия и принципы управления, методы математического
описания стационарных, нестационарных и нелинейных непрерывных систем и исследования их
устойчивости и качества процессов управления; подробно рассмотрен метод пространства
состояний. С необходимой степенью глубины приведены разделы статистической динамики
линейных и нелинейных систем и описаны методы фильтрации сигналов (фильтры Колмогорова -
Винера, фильтры Калмана - Бьюси). Значительное внимание уделено построению алгоритмов
для ЭВМ, рассчитанных на применение при решении задач расчета и проектирования сложных
САУ. Показана возрастающая роль функционально-аналитических методов, языка и результат
тов функционального анализа.
Отдельная глава посвящена изложению методов идентификации линейных и нелинейных
объектов управления. Большинство глав сопровождается задачами, решение которых помогает
глубже усвоить излагаемый материал.
С достаточной полнотой изложен материал, связанный с описанием и анализом непрерывно-
дискретных систем. Материал является частью общего курса теории автоматического управления,
читаемого студентам МГТУ им. Н.Э. Баумана, ТулГУ, ОИАТЭ и других вузов,
Учебник предназначен для студентов вузов. Может быть ^полезен аспирантам и инженерам,
а также научным работникам, занимающимся автоматическими системами,
УДК 681.5; 681.3 (075.8)
ББК 14.2.6
TCDiNj с тп*в 1 сто о/тп © Пупков К.А., Баркин А.И., Воронов Е.М. и др., 2000
lbBJN Э-7О38-1378-У (1.1) о мггу им н э Баумана> 2000
ISBN 5-7038-1579-7 © Издательство МГТУ им. Н.Э. Баумана, 2000
Нашим учителям
посвящается.
ОБЩЕЕ ПРЕДИСЛОВИЕ К УЧЕБНИКУ
I. Особенности учебника.
Учебник издается в трех томах, состоящих из четырех частей и заданий для
самостоятельной работы. Для него характерно следующее:
1. Учебник охватывает основные положения, составляющие содержание
теории автоматического управления. Изложение материала начинается с
основных понятий и определений (сущность проблемы автоматического управления,
определение системы управления, фундаментальные принципы управления, основные
виды и законы автоматического управления и др.) и заканчивается детальным
рассмотрением содержания некоторых современных направлений теории
автоматического управления.
Поскольку курс теории автоматического управления включен в учебные планы
различных инженерных специальностей и является одним из важнейших элементов
общетехнического образования, учебник может быть рекомендован студентам,
заново приобретающим знания в области теории автоматического управления, и
специалистам, которым приходится эти знания восстанавливать. Учебником могут
пользоваться также студенты тех специальностей, для которых-курс является
профилирующим, определяющим квалификацию инженера.
При изучении курса студент или специалист должен сделать выборку материала,
определяемого конкретной задачей и возможностями общего плана обучения.
2. Содержание учебника имеет инженерную направленность, поэтому
изложение ведется с инженерной точки зрения, подчеркиваются главные идеи, лежащие в
основе методов, но не всегда приводятся строгие математические доказательства.
Учитывая, что без освоения технического аспекта изучение методов теории автоматического
управления не приводит к нужному результату (часто имеют место трудности в
постановке и решении инженерных задач даже при хороших знаниях теоретических
положений), физическая и содержательная сторона дела подчеркивается в течение
всего курса. Более того, значительное внимание уделено рассмотрению конкретных
промышленных систем управления. Например, в главе 6 тома 2 рассмотрены
системы управления теплоэнергетическими параметрами атомных электростанций; в
заданиях для самостоятельной работы описаны системы управления, применяемые в
атомной промышленности. Примеры, иллюстрирующие теоретические положения и
методы расчета, тесно связаны с решением конкретных инженерных задач в таких
отраслях, как атомная энергетика, производство летательных аппаратов и др.
3. Методы теории автоматического управления, рассмотренные в учебнике, в
большинстве своем ориентированы на применение ЭВМ.
Интенсивное развитие процессов автоматизации проектирования систем
автоматического управления, обусловленное развертыванием высокопроизводительных
вычислительных комплексов в проектно-конструкторских организациях,
перемещение центра тяжести процесса проектирования от аппаратного обеспечения к
алгоритмическому и программному обеспечению приводят к необходимости разработки
нового методологического обеспечения, включая соответствующие вычислительные
технологии [156].
Предисловие
Для содержания книги характерна, в известной мере, «вычислительная окраска»,
поскольку возможности современных ЭВМ позволяют значительно ускорить сроки
проектирования САУ и, таким образом, налагают свой отпечаток на вычислительную
часть ТАУ. Успех в решении поставленных задач расчета и проектирования с
использованием ЭВМ зависит от многих факторов, основными из которых являются:
степень адекватности математической модели системы; степень эффективности
численных методов ТАУ, используемых в алгоритмическом обеспечении; наличие
высококачественного программного обеспечения, от того, насколько успешно
используется творческий потенциал исследователя-проектировщика. При этом решающий
фактор остается за человеком, который может решать многие неформализованные
задачи.
Поскольку систе,\Я>1 автоматизированного проектирования (САПР) являются в
настоящее время одним из наиболее эффективных средств повышения
производительности инженерного труда и научной деятельности, сокращения сроков и улучшения
качества разработок, то в главе 8 (том 1) кратко отражены соответствующие положения, в
том числе изложены численные методы (аппарат матричных операторов).
Рассмотренное в трехтомнике методологическое обеспечение, ориентированное
на применение ЭВМ, может служить базой для решения весьма сложных задач
инженерного проектирования САУ.
4. В учебнике с единых позиций изложены как основные методы классической
ТАУ, так и положения, определяющие содержание некоторых современных
направлений теории управления.
При рассмотрении материала учитывался тот факт, что периодизация развития
ТАУ не является установившейся и общепринятой [156].
К классическим можно отнести положения, базирующиеся на рассмотрении ли=
нейных и нелинейных дифференциальных и разностных уравнений с постоянными и
переменными коэффициентами применительно к описанию систем, исследованию их
устойчивости и качества процессов.
К классическим положениям также можно отнести и описание процессов в
пространствах состояний, поскольку в классической теории широко применялось
описание движения в фазовом пространстве.
В конце пятидесятых - начале шестидесятых годов появились известные работы
Л.С. Понтрягина, Р. Белмана, Р. Калмана, в которых заложены основы теории
оптимального управления: принцип максимума, динамическое программирование,
функционально-аналитические методы и др. Хорошо известно, что многие идеи теории
оптимального управления сформировались на инженерном уровне в классический
период ТАУ.
Важнейшие результаты теории оптимального управления можно отнести к
классическим положениям ТАУ.
Все указанные положения с необходимой глубиной и полнотой изложены в
первых двух томах учебника.
Методы современной ТАУ, интенсивно разрабатываемые в настоящее время и
включающие аппарат синтеза грубых систем автоматического управления в про^
странстве состояний, Я00 -теорию оптимального управления, задачи оптимизации
многообъектных многокритериальных систем с использованием стабильно*
эффективных компромиссов, синтез систем автоматического управления
методами дифференциальной геометрии (геометрический подход), а также задачи
исследования и проектирования адаптивных систем отражены в 3-м томе учебника,
Таким образом, учебник охватывает наиболее важные разделы теории
автоматического управления, вместе с тем он не претендует на всесторонний охват
проблематики теории автоматического управления. Не затронуты такие важные направления,
как инвариантность, теория чувствительности, методы и алгоритмы оценивания ди-
Предисловие
намических процессов, идентифицируемость и методы и алгоритмы идентификации
(отражены лишь содержание проблемы и подходы к ее решению), системы со
случайной структурой, стохастические системы, теория нелинейной фильтрации, теория
хаоса.
5. Основное содержание и структуру учебника определил коллектив авторов,
включающий представителей разных российский школ науки об управлении:
К.А.Пупков (МГТУ им. Н.Э.Баумана), А.И.Баркин (Институт системного анализа
РАН), Е.М. Воронов (МГТУ им. Н.Э. Баумана), Н.Д. Егупов (МГТУ им. Н.Э. Баумана),
В.Г. Коньков (МГТУ им. Н.Э. Баумана), А.П. Курдюков (Институт проблем
управления РАН), Л.Т. Милов (Московский государственный автомобильно-дорожный
институт (МАДИ)), В.Н. Пилишкин (МГТУ им. Н.Э. Баумана), В.И. Рыбин (Московский
государственный инженерно-физический институт (МИФИ)), В.И. Сивцов (МГТУ им.
Н.Э. Баумана), Я.В. Слекеничс (Обнинский институт атомной энергетики (ОИАТЭ)),
А.И. Трофимов (Обнинский институт атомной энергетики (ОИАТЭ)), Н.В. Фалдин
(Тульский государственный университет); этими авторами написана большая часть
трехтомника.
И. Методические вопросы. Необходимо указать, что никакой учебник не может
дать окончательных рецептов для решения широчайшего спектра задач,
порожденных практикой проектирования сложных систем автоматического управления;
Изложенный в книгах материал призван служить базой, фундаментом,
позволяющим с большей скоростью и эффективностью находить пути для решения задач
практики.
Вместе с тем материал излагается таким образом, чтобы читателю были видны
пути практического применения рассматриваемых методбв. В большинстве своем
методы доведены до расчетных алгоритмов, приводятся таблицы и другой
вспомогательный материал, облегчающий их применение. Положения, изложенные во всех
разделах, иллюстрируются подробно рассмотренными примерами, связанными с
задачами расчета и проектирования конкретных систем.
Весьма важным является вопрос методики изучения курса «Теории автоматического
управления» с целью стать специалистом в этой области, пользуясь циклом учебных
пособий и учебников, издаваемых указанным выше коллективом авторов.
Весь цикл учебников и учебных пособий можно условно разбить на три серии:
1 серия - базовая; эта серия включает три тома настоящего учебника.
2 серия - базовая повышенного уровня, в которой основное внимание уделено
глубокому и достаточно полному изложению методов, определяющих, содержание
современных направлений теории автоматического управления.
3 серия - серия учебных пособий, посвященная полному и глубокому изложению
теоретических положений конкретных направлений ТАУ, например, статистической
динамике нелинейных САУ и др.
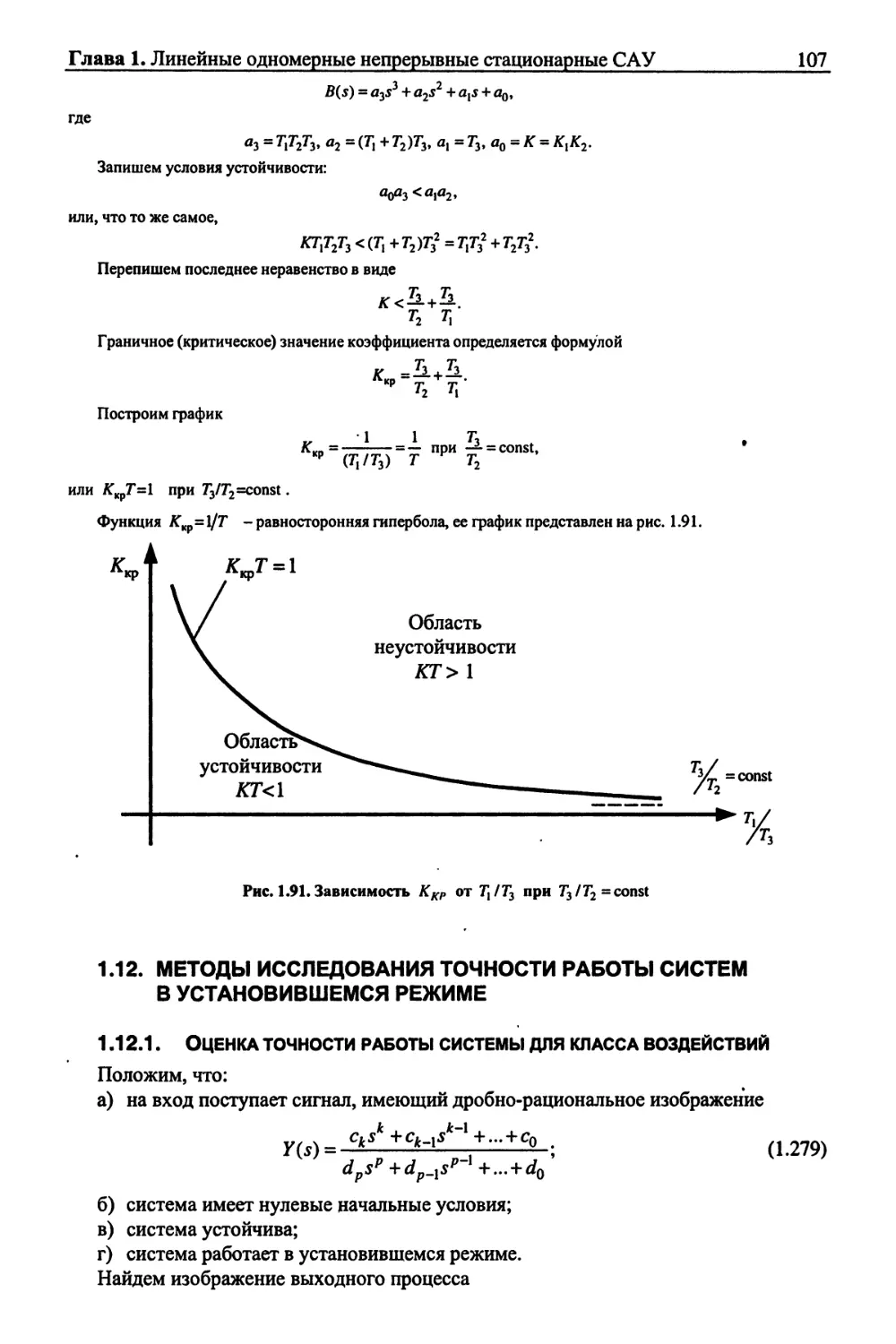
Сказанное выше иллюстрируется рис. В.1.
Базовый уровень приобретается изучением предлагаемого учебника, в котором
систематически изложены методы классической и современной теории управления и дано
достаточно полное представление о проблематике и путях развития науки об
управлении техническими объектами.
Содержание каждого из томов учебника серии базового уровня иллюстрируется
рис. В.2.
После освоения базового уровня можно приступить к специализации в той или
другой области теории автоматического управления, изучая соответствующие тома 2-й
серии, а также статьи и монографии по специальным проблемам теории управления.
Цикл: Методы теории
автоматического управления
1
i
Том 1: Анализ и статистическая
динамика систем автоматического
управления.
М: Изд-во МГТУ, 2000. - 748 с.
♦
Том 2: Синтез регуляторов
и теория оптимизации систем
автоматического управления
*
Том 3: Методы современной теории
автоматического управления
1-я серия учебников "Методы
классической и современной теории
автоматического управления" - серия
базового уровня
1
Том 1: Методы синтеза
оптимальных систем автоматического
управления. М.: Изд-во МГТУ, 2000.- 512 с.
♦
Том 2: Оптимизация многообъектных
многокритериальных систем
*
и интеллектуальные системы
автоматического управления
2-я серия учебников - серия
повышенного базового уровня
1
К.А. Пупков, Н.Д. Егупов,
А.И. Трофимов. Статистические
методы анализа, синтеза и
идентификации нелинейных систем
автоматического управления.
М.: Изд-во МГТУ, 1998.- 562 с.
К.А. Пупков, Н.Д. Егупов,
В.Г. Коньков. Методы анализа,
синтеза и оптимизации
нестационарных систем
автоматического управления.
М.: Изд-во МГТУ, 1999.- 684 с.
3-я серия - серия учебных пособий,
в которых отражены конкретные
направления ТАУ
(специализация)
Рис В.1
Предисловие
1 том: Анализ и статистическая динамика
систем автоматического управления
1
Математическое описание классов систем, отраженных
на приводимой ниже структурной схеме
1. САУ; 2. Линейные САУ; 3. Нелинейные САУ; 4. Непрерывные САУ;
5. Дискретные САУ; 6. Непрерывно-дискретные САУ; 7. Стационарные САУ;
8. Нестационарные САУ; 9. САУ с сосредоточенными параметрами;
10. САУ с распределенными параметрами
±
Анализ и статистическая динамика САУ
Детерминированный анализ систем:
1. Устойчивость,
2. Качество в
переходном
режиме,
3. Качество в
установившемся
режиме и др.
Статистический
анализ систем
Линейная
фильтрация
(фильтры Винера -
Колмогорова,
фильтры Калмана
- Бьюси);
нелинейная
фильтрация и
статистический
анализ систем
Идентификация
объектов
управления
t
2 том: Синтез регуляторов и теория оптимизации
систем автоматического управления
- Методы и задачи —.
Синтез систем по заданным показателям
качества.
Методы синтеза регуляторов:
1. Группа методов, основанная
на принципе динамической
компенсации;
2. Группа методов, использующая
аппарат математического
программирования;
3. Частотный метод;
4. Модальное управление;
5. Метод моментов и др.
Синтез оптимальных систем.
Методы оптимизации:
1. Вариационное исчисление;
2. Принцип максимума;
3. Динамическое программирование;
4. Аналитическое конструирование
регуляторов;
5. Нелинейное программирование;
6. Метод моментов
I
3 том: Методы современной теории автоматического управления:
1. Методы синтеза грубых САУ;
2. Оптимизация многообъектных многокритериальных систем;
3. Я"- теория оптимального управления;
4. Адаптивные системы;
5. Синтез систем методами дифференциальной геометрии, понятия о теории
катастроф, фракталах и теории хаоса;
6. Интеллектуальные системы
Рис. В.2
_10 Предисловие
Если специализация предусматривает расширенное изучение статистической
динамики нелинейных систем автоматического управления, то можно воспользоваться
учебным пособием К.А. Пупкова, Н.Д. Егупова, А.И. Трофимова «Статистические методы
анализа, синтеза и идентификации нелинейных систем автоматического управления». -
М.: Издательство МГТУ им. Н.Э. Баумана, 1998. - 562 с. (под редакцией д-ра техн. наук,
проф. Н.Д. Егупова), в котором систематически изложено содержание основных
положений статистической теории нелинейных систем, методов их анализа, синтеза,
оптимизации и идентификации.
При специализации в области систем автоматического управления с переменными
параметрами полезным может оказаться учебное пособие К.А. Пупкова, Н.Д. Егупова,
В.Г. Конькова, Л.Т. Милова, А.И. Трофимова «Методы анализа, синтеза и оптимизации
нестационарных систем автоматического управления». - М.: Издательство МГТУ
им. Н.Э. Баумана, 1999. - 684 с. (под редакцией д-ра техн. наук, проф. Н.Д. Егупова).
Этот труд представляет собой первое учебное пособие в отечественной литературе,
специально посвященное рассмотрению методов математического описания,
детерминированного и статистического исследования, синтеза и оптимизации
нестационарных систем. Работа включает две части: в первой части изложена теория линейных
систем с переменными параметрами; вторая часть посвящена разработке алгоритмов
исследования, синтеза и оптимизации сложных нестационарных систем, поведение
которых описывается скалярными и векторно-матричными дифференциальными
уравнениями высокого порядка. Алгоритмы предназначены для решения задач, имеющих
место в повседневной инженерной, практике при расчете и проектировании систем
управления одноконтурными и многоконтурными сложными объектами с переменными
параметрами.
Авторы выражают глубокую благодарность рецензентам - академику РАН
Е.П. Попову и коллективу кафедры «Автоматические системы» (Московского
государственного института радиотехники, электроники и автоматики (МИРЭА)), руководимой
членом-корреспондентом РАН Е.Д. Теряевым, за ценные замечания, способствовавшие
улучшению содержания книги. Авторы благодарят заслуженного деятеля науки и
техники РФ, д-ра техн. наук, проф. А.С. Шаталова, заслуженного деятеля науки и техники
РФ, д-ра техн. наук, проф. Б.И. Шахтарина (МГТУ им. Н.Э. Баумана), которые своими
советами позволили значительно улучшить структуру учебника, углубить изложение
отдельных теоретических положений, улучшить окончательный вариант рукописи.
Авторы благодарят концерн «Росэнергоатом», научно-исследовательский центр
космической системотехники, департамент образования и науки Правительства
Калужской области, а также Издательский Дом «Манускрипт» за помощь в издании учебника.
Большой объем книги и широта охваченного материала вызвали большие трудности
при ее написании. Конечно, эти трудности не всегда удавалось преодолеть наилучшим
образом. Читатели, вероятно, смогут высказать много замечаний и дать свои
предложения по улучшению книги.
Авторы заранее признательны всем читателям, которые не сочтут за труд указать
на замеченные неточности, ошибки, на пути совершенствования структуры учебника
и его содержания.
К.А. Пупков
Н.Д. Егупов
Предисловие 11
ПРЕДИСЛОВИЕ К 1-МУ ТОМУ
Настоящая книга представляет собой 1-й том учебника «Методы классической и
современной теории автоматического управления», который охватывает основные
разделы классической теории автоматического управления, относящиеся к
математическому описанию систем автоматического управления, исследованию их
устойчивости и качества процессов управления (детерминированный анализ), их работы
при случайных воздействиях (статистический анализ), фильтрации сигналов в
классе линейных и аналитических нелинейных систем. Одной из важнейших проблем
теории управления является проблема построения математической модели системы
(идентификация), под которой понимается оператор, характеризующий ее поведение и
описывающий все ее информационные свойства. Изложению содержания проблемы и
некоторых подходов к её решению посвящена глава 9 настоящего тома. Кратко
изложены основы автоматизированного проектирования систем автоматического
управления. Разработаны конкретные алгоритмы, в основе которых лежит метод
матричных операторов (глава 8). Алгоритмическое обеспечение, приведенное в
учебнике, является эффективным средством повышения производительности
инженерного труда, сокращения сроков и улучшения качества разработок.
Определенная часть содержания книги нетрадиционна, и методы, изложенные в
соответствующих параграфах, направлены на эффективное решение инженерных
задач. Поэтому можно надеяться, что знакомство с указанным материалом
представит интерес для научно-технических работников.
В приложении к книге даны необходимые материалы, носящие как справочный,
так и теоретический характер. Например, построение и теоретическое обоснование
вычислительных схем, применяемых для исследования сложных систем, имеющих
высокую размерность при детерминированных и случайных воздействиях, а также
решение классов операторных уравнений (например, уравнения Винера - Хопфа) не
обходится и не может обойтись без широкого использования языка и результатов
функционального анализа. Возрастающая роль функционально-аналитических
методов в приложениях к теории управления объясняется возможностью глубокого
теоретического обоснования построенных на их основе алгоритмов расчета и
проектирования САУ. В связи с этим в приложениях 2 и 3 приводятся некоторые положения
функционального анализа и зависимости, определяющие конкретные ортонормиро-
ванные базисы, используемые в методе матричных операторов.
Для лучшего уяснения излагаемого материала приведено значительное число
примеров по описанию и исследованию систем автоматического управления,
используемых в атомной энергетики, машиностроении и др.
Соавторами отдельных разделов 1-го тома являются д-р техн. наук, проф..
Л.Т. Милое, (пщвз 2), д-р техн. наук, проф. ЮЛ. Корнюшин (§ 4,13), канд. физ.-мат.
наук, доц. СВ. Лапин (§§ 8.2, 8.3, 8J, 8.12, приложение 2), инженер ДД Мельников
(§ 6.4), канд. техц. наук М.О. Гдбибулаев (§§ 6.1, 6.3, 8.9 - 8,11), инженер
А.Н. Бурлакин (§ 8.3), канд. техн. наук Д.А. Акименко (§ 8.14), канд, техн. наук, доц.
A.M. Макаренков (§§ 8.15, 8.16), канд. техн. наук, доц. А.К. Карышед (глава 5), канд.
техн. наук, доц, СИ. Николаенко (§ 8.13), канд. техн. наук, доц, Я.В. Слекеничс
(§ 1.1), § 7.3 написан канд. техн. наук, доц. В.И. Краснощеченко.
Авторы выражают признательность сотрудникам редакционно-издательского
отдела Калужского филиала МГТУ им. Н.Э. Баумана К.И. Желнову, СН. Капранову,
М.П. Трубачеву, К.Ю. Савшченко за подготовку рукописи к изданию и создание
оригинал-макета учебника.
ЧАСТЬ I
АНАЛИЗ И СТАТИСТИЧЕСКАЯ ДИНАМИКА
СИСТЕМ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ
Список используемых аббревиатур и обозначений
13
СПИСОК ИСПОЛЬЗУЕМЫХ АББРЕВИАТУР
АСУ - автоматизированная система управления
АФЧХ - амплитудно-фазовая частотная характеристика
АЧХ - амплитудно-частотная характеристика
АЭС - атомная электростанция
БИФ - блочно-импульсная функция
БПУА - быстрое преобразование Уолша - Адамара
БПФ - быстрое преобразование Фурье
БПФ-У - быстрое преобразование Фурье - Уолша
БШ - белый шум
ВЧХ - вещественная частотная характеристика
ГД -г гидродвигатель
ГС - генератор сигналов
ГФВН - генератор функций вибрационных нагружений
ГОС - гибкая обратная связь
ДЗ - дифференцирующее звено
ДЗР - дифференциальный закон распределения
ДП - датчик перемещений
ДЧХ - действительная частотная характеристика
ДУ - дифференциальные уравнения
ЗУУ - золотниковое управляющее устройство
ИЗ - интегрирующее звено
ИСТ - инверсно-сопряженная система
ИЗР - интегральный закон распределения
ИПФ - импульсная переходная функция
ИУ - исполнительное устройство
ИУр - интегральное уравнение
ККФ - кусочно-кубическая функция
КЛА - космический летательный аппарат
КЛФ - кусочно-линейная функция
КПФ - кусочно-параболическая функция
КС - критический стенд
КЧХ - комплексная частотная характеристика
КУ - корректирующее устройство
КФ - корреляционная функция
ЛАЧХ - логарифмическая АЧХ
ЛНС - линейная нестационарная система
ЛП - линейное программирование
ЛС • -линейная система
ЛСС - линейная стационарная система
ЛФЧХ - логарифмическая ФЧХ
ЛЧ -линейная часть
МБПФ - матричная бичастотная передаточная функция
МИПФ - матричная импульсная переходная функция
ММ - математическая модель
14
Анализ и статистическая динамика САУ. Часть I
МНК - метод наименьших квадратов
МНПФ - матричная нормальная передаточная функция
МО - математическое ожидание
МП - математическое программирование либо матрица перехода
МППФ - матричная параметрическая передаточная функция
МПФ - матричная передаточная функция
МПЧХ - матричная параметрическая частотная характеристика
МЧХ - мнимая частотная характеристика
МСИ - метод статистических испытаний
НЭ - нелинейный элемент
НП - нелинейное программирование
НПФ - нормальная передаточная функция
НЧ - неизменяемая часть
О - пространство оригиналов •
ОБИФ - обобщенная блочно-импульсная функция
ОК - основной канал в многомерных системах
ОНБ - ортойормированный базис
ОНС - ортонормированная система
ОС - обратная связь
ОУ - объект управления
ПС - перекрестная связь в многомерных объектах
ППФ - параметрическая передаточная функция
ПФ - передаточная функция
ПХ - переходная характеристика
ПЧХ - параметрическая частотная характеристика
Р - регулятор
РЛС - радиолокационная станция
САУ - система автоматического управления
САР - система автоматического регулирования
СВ - случайная величина
СВИ - система вибрационных испытаний
СВН - система вибрационных нагружений
СКО - среднеквадратическое отклонение
СНАУ - система нелинейных алгебраических уравнений
СП - случайный процесс
СПл - спектральная плотность
СПФ - стандартная передаточная функция либо сопряженная
передаточная функция
СРП - система с распределенными параметрами
ССП - система с сосредоточенными параметрами
СУЗ - система управления и защиты
СФ - случайная функция
СХ - спектральная характеристика относительно ОНБ
ТАР - теория автоматического регулирования
ТАУ - теория автоматического управления
ТПВ - тракт преобразования вибраций
ТП - технологический процесс
УСО - усилитель сигнала ошибки
ФВН - функции вибрационных нагружений
Список используемых аббревиатур и обозначений 15^
ФС - фундаментальная система
ФФ - формирующий фильтр
ФЧХ - фазочастотная характеристика
ЦАП - цифро-аналоговый преобразователь
ЭГСВ - электрогидравлический следящий вибратор
ЭГУ - электрогидравлический усилитель
ЭМП - электромагнитный преобразователь
ЯР - ядерный реактор
ЯЭУ - ядерная энергетическая установка
16 Анализ и статистическая динамика САУ. Часть!
СПИСОК ИСПОЛЬЗУЕМЫХ ОБОЗНАЧЕНИЙ
Непрерывные САУ
А - оператор системы
y{t) - входной скалярный сигнал
Y(/) - входной векторный сигнал
x(t) - выходной скалярный сигнал
Х(/) - выходной векторный сигнал
W(s) - передаточная функция скалярной системы
W(s) * - передаточная функция системы в пространстве
состояний
W(s, t) - параметрическая передаточная функция
F(s) " - преобразование Лапласа функции^/)
Цх) . - импульсная переходная функция скалярной
стационарной системы
К(т) - матричная импульсная переходная функция
k(t, т) - импульсная переходная функция скалярной
нестационарной системы
К(/, т) - матрица ИПФ нестационарной системы в
пространстве состояний
Ко - коэффициент статистической линеаризации по
математическому ожиданию
К\ - коэффициент статистической линеаризации
по центрированной составляющей
А((й) - амплитудная частотная характеристика
/>(со) - действительная частотная характеристика
Q((o) - мнимая частотная характеристика
L((o) - логарифмическая амплитудная частотная
характеристика
у((й) - фазовая частотная характеристика
A (j(q\ - амплитудно-фазовая частотная характеристика
е(/) - сигнал ошибки системы
хс (/) - свободная составляющая выходного сигнала
(свободные колебания)
xu(t) - вынужденная составляющая выходного сигнала
(вынужденные колебания)
х (t) - установившаяся составляющая выходного сигнала
xn(t) - переходная составляющая выходного сигнала
h(t) - переходная характеристика
я(0 - помеха
m(t) - полезный входной сигнал (управляющее случайное
воздействие)
I - единичная матрица
.•_ ГГу - мнимая единица
К - коэффициент усиления системы или элемента
Список используемых аббревиатур и обозначений 17_
т - порядок числителя передаточной функции
п - порядок знаменателя передаточной функции
Tyjp - время переходного процесса
5(/) - дельта-функция
Т - постоянная времени
W0(s) или WH4{s) - передаточная функция объекта или неизменяемой
части системы
Wp(s) - передаточная функция разомкнутой системы
Wyyis) - передаточная функция корректирующего устройства
(регулятора)
E(s) - преобразование Лапласа для сигнала ошибки
£ - коэффициент демпфирования
Xt - корни характеристического уравнения
со - частота среза
Ск - коэффициенты ошибок
р(ХуУ) - метрика
L [0,Г], С[0,Г] - функциональные пространства
II х II - норма элемента х
F = {fj^t): к = 1,2,...} - линейно независимая система
Ф={(р*(/): к =1,2,...} - ортонормированный базис или ортонормированная
система
U - матрица ортогонализации
rf - коэффициенты Фурье функции^/)
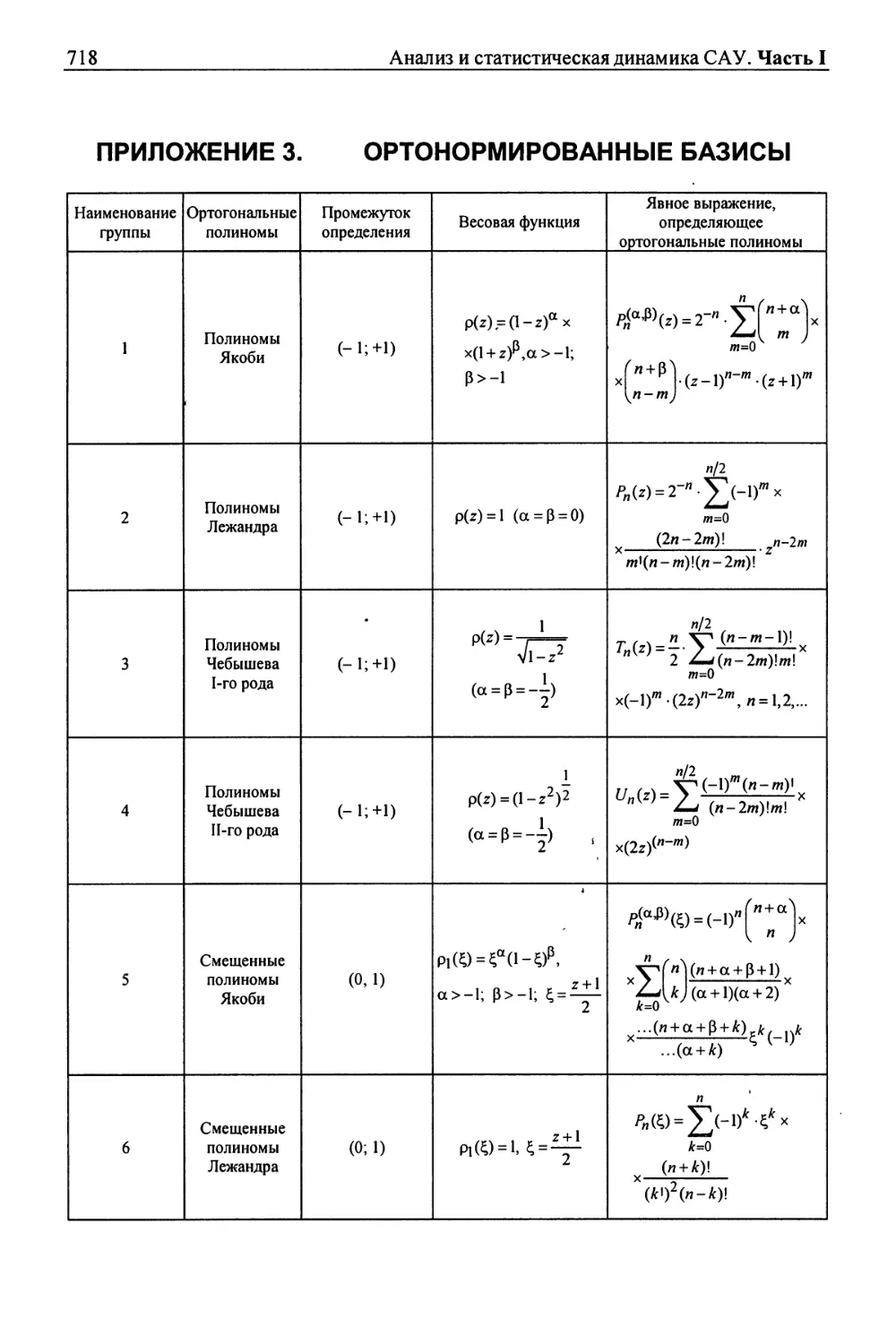
p(a$)(z) - полиномы Якоби
р (z) - полиномы Лежандра
f (z\ - полиномы Чебышева 1-го рода
U (z\ - полиномы Чебышева 2-го рода
С/ - одностолбцовая матрица коэффициентов Фурье
функции ДО
Wal(k,t) - *-я функция Уолша
Х(0 - вектор-функция состояния
X (0 - транспонированная вектор-функция
Хв (/) • - вектор-функция выхода
А(0, В(/) - матрицы коэффициентов векторно-матричного
дифференциального уравнения
Хф(/) - фундаментальная матрица
М - оператор математического ожидания
&хх (*i»h) ~ корреляционная функция случайного процесса X(f)
&xyih>h) ""взаимная корреляционная функция случайных
процессов ДО и ПО
Dxx (t) - дисперсия СП X(f)
mx(t) - математическое ожидание СП X(t)
Sxx (t) - спектральная плотность случайного сигнала X(t)
Асо - эффективная полоса пропускания системы
сх (t) - среднеквадратическое отклонение случайного сигнала
X(t)
3 Зак. 232
J_8 Анализ и статистическая динамика САУ. Часть I
<j(t) - случайный сигнал ошибки системы
C(t) - матрица уравнения наблюдения
р - вектор оптимизируемых параметров
р - вектор оптимальных параметров
К (А) - число обусловленности оператора А
Fx(x) - интегральный закон распределения случайной
величины Jf
fx(x) - дифференциальный закон распределения случайной
величины X
М \х\ ~ математическое ожидание случайной величины X
Dxx - дисперсия случайной величины X
ах - среднеквадратическое отклонение случайной
величины^
гхх (f j, t2) - нормированная корреляционная функция случайного
процесса ДО
DCTCT (t) - дисперсионная матрица векторного сигнала ошибки
фильтрации
Ан - спектральная характеристика линейного
нестационарного элемента или системы, описываемой векторно-
матричным дифференциальным уравнением
д - спектральная характеристика нелинейного элемента
ко по математическому ожиданию
д - спектральная характеристика нелинейного элемента
кх по центрированной составляющей
Ф(/?,/), W(syt) - параметрическая передаточная функция
W (ц, s) - бичастотная передаточная функция
N{\i,x) - нормальная передаточная функция
H(p,t) ~ сопряженная передаточная функция ЛНС
k (t,i) - нормальная ИПФ линейной нестационарной системы
k h, т) - ИПФ сопряженной линейной нестационарной системы
дс /^ т\ _ нормальная ИПФ сопряженной линейной
нестационарной системы
А - матричный оператор (спектральная характеристика)
линейного элемента или системы, либо матрица
коэффициентов векторно-матричного ДУ (стационарный
случай), либо матрица условий, либо матрица
состояния стационарной системы
А - СХ корректирующего устройства
Ад - матрица оператора дифференцирования (спектральная
характеристика дифференцирующего звена)
Рт = Аи - матрица оператора интегрирования (спектральная
характеристика интегрирующего звена)
А (/) = U^ = Uw (/) - операционная матрица умножения на функцию /(/)
(спектральная характеристика множительного элемента)
W (/, t0) - матрица перехода
Список используемых аббревиатур и обозначений 19_
Дискретные САУ
S(s) - спектральная плотность непрерывного стационарного
случайного сигнала
S(z) - спектральная плотность дискретного стационарного
случайного сигнала
S(s, p) - двумерная спектральная плотность нестационарного
непрерывного случайного сигнала
S(zu z2) - двумерная спектральная плотность дискретного
нестационарного случайного сигнала
W(s) - передаточная функция стационарной непрерывной
системы
W{z) - передаточная функция стационарной дискретной
системы
V(s, т) - обобщенная передаточная функция непрерывной
системы
V(s, nT) - обобщенная передаточная функция дискретно-
непрерывной системы
K(z, т) - обобщенная передаточная функция непрерывно-
дискретной системы
V(z, nT) - обобщенная передаточная функция дискретной системы
И (/, s) - сопряженная передаточная функция непрерывной
системы
Н(пТ, s) - сопряженная передаточная функция непрерывно-
дискретной системы
Я(/, z) - сопряженная передаточная функция дискретно-
непрерывной системы
Н(пТ, z) - сопряженная передаточная функция дискретной
системы
Дя, р) - бичастотная передаточная функция непрерывной
системы
I\z, s) - бичастотная передаточная функция непрерывно-
дискретной системы
I\s, z) - бичастотная передаточная функция дискретно-
непрерывной системы
f\zu z2) - бичастотная передаточная функция дискретной системы
А(/) - матрица состояния нестационарной непрерывной
системы
А(л7) - матрица состояния нестационарной дискретной системы
В - матрица управления стационарной системы
В(г) - матрица управления нестационарной непрерывной
системы
В(я7) - матрица управления нестационарной дискретной
системы
I? (-оо, 0], I? [О, оо), ~ пространства Лебега квадратично интегрируемых
2 л (или суммируемых) и ограниченных сигналов соот-
L (-оо,оо),/,00(~оо,0], ветственно на интервалах (-оо,0], [0,оо), (-оо,оо)
Г[0,оо),ГНо,оо)
^2 £«> _ пространства Лебега для функций, определенных
в частотной области
7Q Анализ и статистическая динамика САУ, Часть I
ГЛАВА 1. ЛИНЕЙНЫЕ ОДНОМЕРНЫЕ НЕПРЕРЫВНЫЕ
СТАЦИОНАРНЫЕ СИСТЕМЫ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ:
МАТЕМАТИЧЕСКИЕ МОДЕЛИ,
ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ,
УСТОЙЧИВОСТЬ, ТОЧНОСТЬ ОТРАБОТКИ
СИГНАЛОВ
Под математической моделью (ММ) понимается оператор, характеризующий
поведение реальной системы и отражающий все ее информационные свойства [156].
В соответствии с этим определением выделяются наиболее существенные
свойства и признаки системы, они представляются в такой упрощенной форме, которая
необходима для последующего теоретического и экспериментального исследования.
Теория автоматического управления - точная наука, она оперирует количествен*
ными характеристиками. Поэтому за качественным описанием системы следует
вторая фаза абстрагирования - количественное описание системы. Известно
высказывание Иммануила Канта: «... во всякой науке столько истины, сколько в ней мате'
матики». Эту же мысль подтверждают слова Давида Гильберта: «Математика - осно*
ва всего точного естествознания». В этой главе будут рассмотрены проблемы
количественного описания систем.
Математическая модель САУ отражает в той или иной мере свойства реальной
системы, в том числе ограничения, существующие в реальных условиях [85, 156].
Математическая модель разрабатывается в математических терминах и имеет
количественное описание. Математические модели могут быть представлены
различными математическими средствами: действительными или комплексными
величинами, векторами, матрицами, геометрическими образами, неравенствами, функ~
циями или функционалами, множествами, алгебраическими, разностными,
дифференциальными и интегральными уравнениями и т.д.
1.1. СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ:
ОСНОВНЫЕ ПОНЯТИЯ, ЦЕЛИ И ПРИНЦИПЫ УПРАВЛЕНИЯ
ОПЕРАТОР СИСТЕМЫ
1.1.1. Примеры систем автоматического управления
Введем основные понятия, позволяющие сформулировать цели и принципы
управления и рассмотреть вопросы математического описания на примере
конкретных автоматических систем.
Прежде всего, дадим некоторые пояснения и определения.
При реализации технологических процессов параметры, которые характеризуют
эти процессы, должны изменяться по определенным законам (или быть
постоянными). Необходимость изменения параметров в соответствии с требуемым законом
возникает в самых разнообразных отраслях техники. Функциональные элементы'
Глава 1. Линейные одномерные непрерывные стационарные САУ
21
технологического процесса будем обозначать квадратиками, а сигналы^
поступающие на эти элементы, - стрелками (рис. 1.1).
Дадим определение сигнала.
Сигналами называются физические процессы, параметры которых содержат
информацию. Например, в телефонной связи при помощи электрических сигналов
передаются звуки разговора, в телевидении - изображение.
Параметры, содержащие информацию, называются информационными
параметрами. Например, сигнал - электрическое напряжение, информационный
параметр - амплитуда сигнала.
Входной
сигнал
элемента.
Функциональный
элемент
Выходной
сигнал
элемента
Рис. 1.1. Функциональный элемент
ъ
а
[
{
f
►
Рис. 1.2. Аналоговый сигнал ДО
Сигнал называется аналоговым, если его информационные параметры могут
принимать любые значения в заданном промежутке (рис. J..2).
Сигнал называется дискретным, если его информационные параметры
принимают только дискретные значения (конечное множество). Перейдем к рассмотрению
конкретного технологического процесса.
Регулирование температуры в электропечи для закалки металла [112]. Для
реализации рассматриваемого процесса электропечь снабжается управляющим (или
регулирующим) органом, с помощью которого можно управлять процессом
закаливания (изменять температуру в соответствии с заданным законом).
Создание условий, обеспечивающих требуемое протекание процесса закаливания,
т.е. поддержание необходимого режима, называется управлением. Оно может быть
ручным или автоматическим. При ручном управлении воздействие на управляющий
орган осуществляет человек, наблюдающий за ходом процесса.
Введем определение: функциональной схемой системы называется
символическое изображение всех функциональных элементов технологического процесса и
связей между ними; в функциональной схеме отражена последовательность процессов
в системе.
22
Анализ и статистическая динамика СЛУ, Часть I
Представим с помощью функциональной схемы технологический процесс
закаливания металла в электропечи (рис. 1.3).
Требуемый процесс
изменения температуры y(f)
Реостат
u(t)
Разность между
требуемым и реальным
процессами измерения
температуры
Прибор для
фиксирования
температуры в
электропечи
Термопара
(датчик,
измерительный
элемент)
j
Электропечь
для закалки
металла
Реальный процесс
изменения
температуры
в электропечи
Рис. 1.3. Функциональная схема технологического процесса
Сиетема предназначена для поддержания необходимого режима, т.е, для
изменения температуры y(t) в электропечи по заданному закону. Для обеспечения
необходимого изменения температуры электропечь снабжается двумя элементами: термо-
парой, выходом которой является электрическое напряжение x(t)t пропорциональное
температуре в электропечи, и реостатом, с помощью которого меняется
сопротивление в цепи нагрева печи. При увеличении сопротивления ток в цепи нагрева
уменьшается и температура в электропечи уменьшается. При уменьшении сопротивления
ток возрастает и температура увеличивается. Оператор, которому известен нужный
закон изменения температуры y(t), наблюдает за показаниями прибора (на котором
фиксируется реальная температура в электропечи). В зависимости от того, в какую
сторону температура отклонилась от требуемого ее значения, оператор перемещает
движок реостата таким образом, чтобы реальная температура в электропечи мало
отличалась (на величину е(0) от требуемого значения. Имеет место так называемая
обратная связь (ОС). Важнейшим элементом рассмотренного технологического
процесса является человек-оператор, наличие которого делает систему ручной. При
автоматическом управлении воздействие на управляемый орган (реостат) осуществи
ляет специальное управляющее устройство. Построим схему, осуществляющую
реализацию технологического процесса без участия человека. Назначение оператора ~
перемещение движка реостата в зависимости от наблюдаемого отклонения
температуры. Эту операцию можно реализовать с помощью двигателя (привода), Поскольку
на выходе термопары имеет место сигнал очень небольшой мощности (ее
недостаточно для питания даже небольшого приводного двигателя), то вводят
промежуточное звено - усилитель мощности. Реализация процесса закаливания металла в
электропечи может быть представлена с помощью функциональной схемы (рис. 1.4).
Глава 1. Линейные одномерные непрерывные стационарные САУ
23
Сигнал y(t) {заданная температура в печи) называют управляющим, а сигнал x(t)
(реальная температура) -управляемой переменной.
устройство
(задает нужное
изменение
температуры)
f идеальная температура
в электропечи
y(t)
Ster
1 \
Усилитель
мощности
^ошибка (расе
обрат*
) - реальная тем
в электропе
—>
оглас
1ая се
nepai
чи
Привод
ование)
$язь
ура
Т
Реостат
еомопаоа
u(t)
Электропечь лля
закалива
ния
металла
элемент вычитания
(сравнения)
Рис. 1.4. Функциональная схема системы, реализующей процесс закаливания металла в электропечи
Систему, реализующую процесс закаливания, называют системой
автоматического управления. Таким образом, система автоматического управления (САУ)
представляет собой совокупность объекта управления (ОУ) и управляющего
устройства, включающего в себя усилитель, реостат, измерительное устройство
(датчик), элемент сравнения. Объектом управления является электропень,
выходные переменные которой (температура), называемые в данном случае управляемыми,
подлежат управлению. Под управляющим устройством подразумевается
устройство, обеспечивающее процесс управления, т.е. целенаправленное воздействие,
приводящее к желаемому изменению управляемой переменной (температуры закаливания).
Итак, введены новые термины: объект управления - электропечь, управляемая
переменная - температура закаливания, управляющий орган - реостат, обратная
связь (ОС). Для улучшения качества управления (например, уменьшения ошибки е(г),
уменьшения степени колебательности и т.д.) в систему вводят дополнительный очень
важный элемент - регулятор. С учетом этого элемента САУ, представленная на
рис. 1.4, принимает несколько иной вид (рис. 1.5).
x(t)
г
У
E{t)
з я
II
u(t)
4
ос
I
5
6
8
7
Рис. 1.5. Функциональная схема системы автоматического управления процессом закаливания:
/ - задающее устройство; 2 - сравнивающее устройство; 3 -регулятор; 4 -усилитель мощности;
5 - привод (двигатель); 6 -реостат; 7 - электропечь; 8 - измерительное устройство (датчик);
I'- неизменяемая часть САУ; II-регулятор (изменяемая часть САУ)
При проектировании САУ параметры элементов 4-8 остаются неизменными,
поэтому часть САУ, включающая в себя 4-8 носит название неизменяемой. На
практике неизменяемую часть часто называют объектом, а к управляющему устройству
относят лишь регулятор. Именно его параметры изменяются в процессе
проектирования САУ.
24
Анализ и статистическая динамика САУ. Часть I
Рассмотрим еще несколько примеров конкретных систем.
Многие САУ, используемые в атомной энергетике, предназначены для
автоматического регулирования уровня жидкости. К таким системам относятся, например,
автоматические регуляторы уровня в парогенераторах (ПГ), конденсаторах,
компенсаторах давления (КД), барабанах-сепараторах (БС) и др.
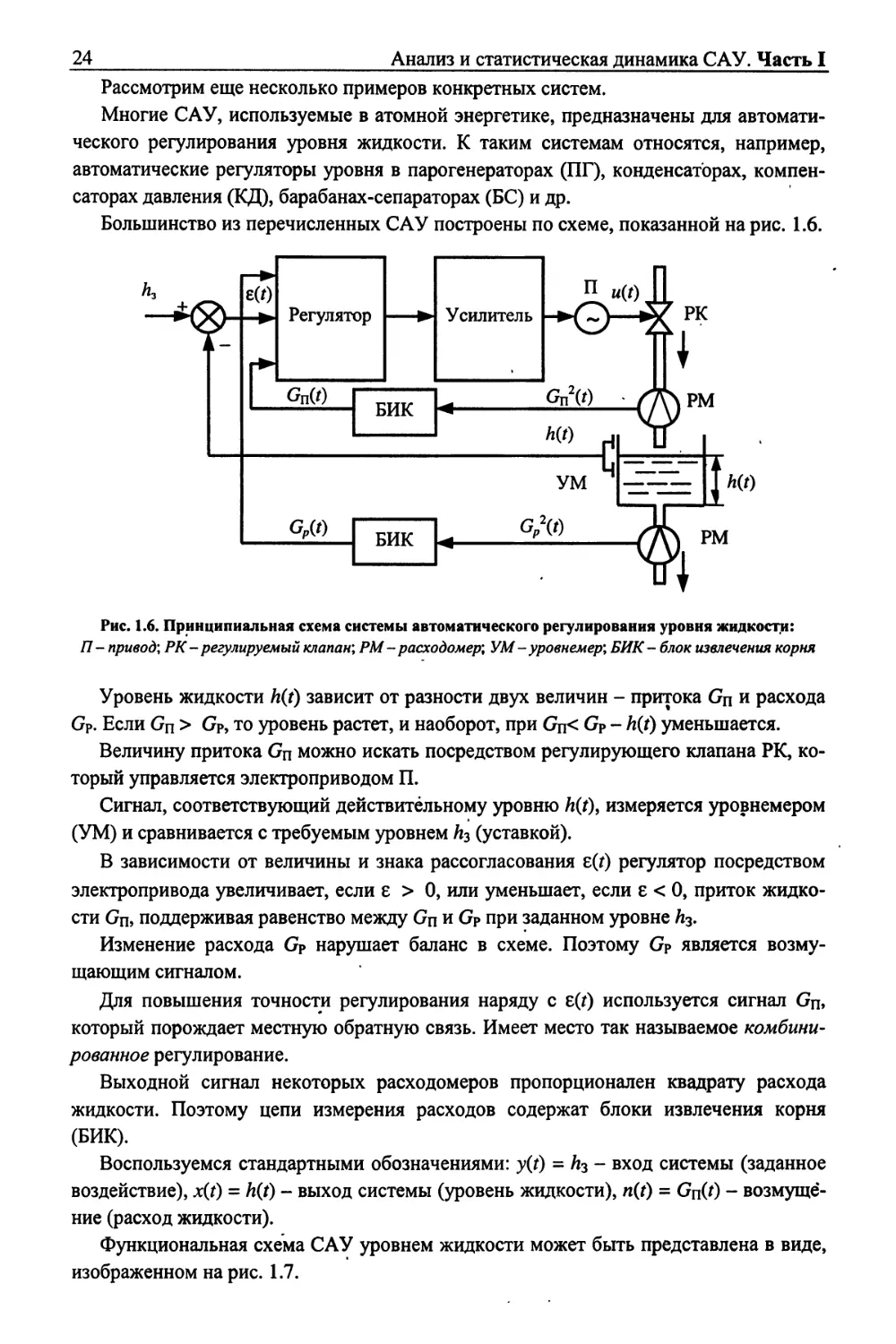
Большинство из перечисленных САУ построены по схеме, показанной на рис. 1.6.
^-*®-~
Рис. 1.6. Принципиальная схема системы автоматического регулирования уровня жидкости:
П- привод; РК- регулируемый клапан; РМ - расходомер; УМ - уровнемер; БИК- блок извлечения корня
Уровень жидкости h(t) зависит от разности двух величин - притока Gn и расхода
GP. Если Gn > Gp, то уровень растет, и наоборот, при Gn< Gp - hit) уменьшается.
Величину притока Gn можно искать посредством регулирующего клапана РК,
который управляется электроприводом П.
Сигнал, соответствующий действительному уровню h(t), измеряется уровнемером
(УМ) и сравнивается с требуемым уровнем А3 (уставкой).
В зависимости от величины и знака рассогласования е(г) регулятор посредством
электропривода увеличивает, если 8 > 0, или уменьшает, если 8 < 0, приток
жидкости Gn, поддерживая равенство между Gn и Gp при заданном уровне Л3.
Изменение расхода Gp нарушает баланс в схеме. Поэтому Gp является
возмущающим сигналом.
Для повышения точности регулирования наряду с е(г) используется сигнал Gn,
который порождает местную обратную связь. Имеет место так называемое
комбинированное регулирование.
Выходной сигнал некоторых расходомеров пропорционален квадрату расхода
жидкости. Поэтому цепи измерения расходов содержат блоки извлечения корня
(БИК).
Воспользуемся стандартными обозначениями: y(t) = h3 - вход системы (заданное
воздействие), x(t) = h(f) - выход системы (уровень жидкости), n(t) = Gn(0 -
возмущение (расход жидкости).
Функциональная схема САУ уровнем жидкости может быть представлена в виде,
изображенном на рис. 1.7.
Глава 1. Линейные одномерные непрерывные стационарные САУ
25
2
к
и(0
"(О
г - £
9
► А -ш
*• ц. -т
<*
„ С л
* Э *
- 8
*. £ -•
^ О
•*» 7 •
*(0
Рис. 1.7. Функциональная схема САУ уровнем жидкости:
/ - задающее устройство; 2 - сравнивающее устройство: 3 -регулятор;
4 -усилитель мощности; 5 - привод; 6 - регулирующий орган {клапан);
7 - объект управления; 8 -уровнемер; 9,10- линейные расходомеры
Рассмотрим ядерную энергетическую установку (ЯЭУ). Простейшая схема
установки приведена на рис. 1.8.
Рис. 1.8. Простейшая схема двухконтурной ядерной энергетической установки
с паротурбинным циклом
В установке основными элементами являются ядерный реактор ЯР и
теплосиловое оборудование. Первый контур включает ядерный реактор ЯР, парогенератор ПГ,
циркуляционный насос Нь трубопроводы горячего (от реактора) и холодного (к
реактору) теплоносителя.
В теплосиловое оборудование входят турбина Т с электрическим генератором ЭГ,
конденсатор отработанного пара К, циркуляционный насос Н2 и т.д. Это
оборудование образует второй контур ядерной энергетической установки.
В первом контуре наряду с основным оборудованием имеется различное
вспомогательное оборудование: система очистки теплоносителя, система подачи
теплоносителя в первый контур (компенсаторы уровня, система аварийного расхолаживания
реактора, система поддержания давления в контуре и т.д.).
2 Зак. 232
26
Анализ и статистическая динамика САУ. Часть I
Рассмотрим подробнее основные элементы конструкции ядерного реактора
(рис. 1.9).
Ядерный реактор - это устройство, в котором обеспечиваются условия для
протекания управляемой самоподдерживающейся реакции деления ядер, а также съем
тепла. Получаемое в процессе цепной реакции тепло в реакторе отводится
циркулирующим теплоносителем и используется в паросиловой части ЯЭУ для получения
электрической энергии. Несмотря на большое разнообразие реакторов, можно
выделить ряд элементов и систем, присущих большинству из них.
'^
Рис. 1.9. Основные элементы ядерного реактора:
/ -управляющие стержни\ 2 - отражатель', 3 - теплоноситель', 4 - биологическая защита',
5 - активная зона\ 6 - замедлитель', 7 - ядерное топливо
Активная зона - та часть реактора, в которой осуществляется цепная реакция
деления. В активной зоне размещаются ядерное топливо (уран и его сплавы, плутоний
и т.д.), замедлитель (графит, бериллий, вода и пр.), который служит для снижения
энергии нейтронов деления. Отвод тепла от тепловыделяющих элементов активной
зоны обеспечивает теплоноситель (вода, жидкие металлы, газы и пр.). В активную
зону реактора также входят различные конструкционные материалы: материалы
труб, по которым подается теплоноситель, материалы оболочек тепловыделяющих
элементов и т.д.
Отражатель используется для уменьшения потери нейтронов за счет утечки
через поверхность активной зоны. Обычно в качестве материала отражателя
применяются те же материалы, что и для замедлителя.
Биологическая защита. Работающий ядерный реактор является мощным
источником различного рода излучений (нейтронов, у-квантов, а- и (3-частиц и т.д.).
Биологическая защита предохраняет персонал от действия этих излучений.
Система загрузки и выгрузки топлива. В процессе работы реактора происходит
выгорание ядерного горючего, накопление продуктов цепной реакции, являющихся
поглотителями нейтронов, и т.п. В связи с этим необходимо осуществлять замену
тепловыделяющих элементов. Эта замена может производиться при выключенном
Глава 1. Линейные одномерные непрерывные стационарные САУ
27
реакторе либо на работающем реакторе. Для осуществления операций по замене
выгоревших блоков горючего используется комплекс механизмов и устройств,
объединенных в систему загрузки и выгрузки топлива.
Органы системы управления. Для управления цепной реакцией в активную зону
ректора вводятся, как правило, специальные регулирующие элементы,
воздействующие на процесс образования или исчезновения нейтронов. Эти элементы являются
исполнительными органами системы управления.
Аппаратура систем контроля, управления и защиты - это комплекс
механизмов, приборов, регулирующих устройств, предназначенный для обеспечения
безаварийной эксплуатации-ядерной установки, т.е. исключения самопроизвольного
разгона реактора или отклонений технологических параметров установки от
заданных значений.
Основную роль в обеспечении безопасности эксплуатации ЯР призвана сыграть
система управления и защиты (СУЗ), на которую возлагаются функции по
управлению цепной реакцией при пуске, переходе с одного уровня мощности на другой и
остановке ЯР, а также быстрому прекращению реакции деления в случае
возникновения аварийной ситуации.
Системы автоматического управления ЯР являются подсистемами СУЗ и
предназначены для автоматического регулирования реактора во время его разгона (пуска) и
стабилизации на данном уровне мощности. Функциональная схема САУ ЯР,
осуществляющая алгоритм пуска по периоду со стабилизацией заданного уровня по
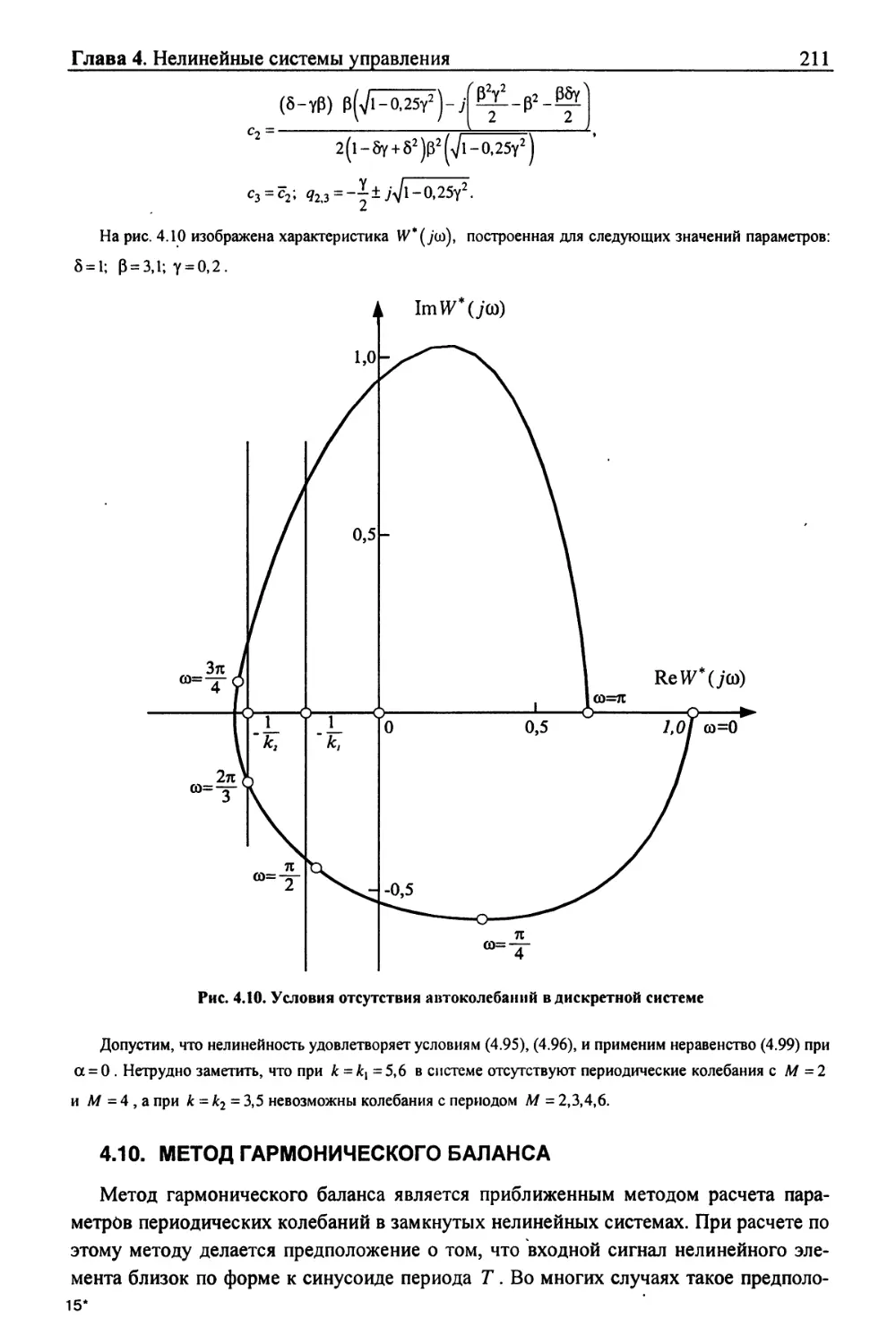
сигналу измерителя мощности, представлена на рис. 1.10, где обозначено: АР -
автоматический регулятор, ЭП - электропривод, ЯР - ядерный реактор, АК - аппаратура
контроля ЯР, N3u N- заданный и действительный (выходной) сигналы мощности
соответственно, К, и К - заданный и действительный сигналы обратного периода (период
Тр - время, за которое мощность ЯР увеличивается в е раз; обратный период -
величина, обратная периоду, т.е. 1/ГД £/- выходной сигнал АР, N и Y - сигналы
оценки мощности и обратного периода соответственно, р — реактивность.
Рассматриваемая САУ работает следующим образом. Пусть требуется перевести
ЯР с уровня мощности Af0 на уровень N39 причем N3 > No. После включения АР
происходит увеличение реактивности р до достижения заданного значения Y3 обратного
периода, после чего в течение разгона ЯР осуществляется режим стабилизации
периода (сигнал мощности игнорируется). При подходе к заданному уровню мощности,
АР автоматически переключается от режима стабилизации периода на режим
стабилизации мощности (установка по обратному периоду автоматически изменяется от У3
до нуля).
i
АР
i i
i
и
N
/\
Y
ЭП
АК
Г)
к
n(t)\
яр
lnN
1
1 Т
v
1
Рис. 1.10. Функциональная схема САУ ЯР
2*
28
Анализ и статистическая динамика САУ, Часть I
Качество регулирования и надежность САУ ЯР существенно зависят от
электропривода, выбор которого определяет закон регулирования. На практике широкое
распространение получил релейный закон регулирования - в.этом случае статическая
характеристика ЭП подобна характеристике трехпозиционного реле. Релейные САР
ЯР имеют высокую надежность, быстродействие и универсальность, а также
меньшую чувствительность к флуктуациям входных сигналов из-за наличия зоны
нечувствительности.
Выше рассмотрены замкнутые системы, в которых имеет место обратная связь,
т.е. сравнение входного сигнала (эталона) с выходным сигналом (реальное значение
регулируемой величины). Кроме них встречаются системы разомкнутого типа и
комбинированные системы. В разомкнутых системах для выработки управляющего
воздействия u(t) (сигнал с выхода регулятора) используется только информация о
цели управления y(t), а действительное значение выходной управляемой переменной
x(t) не контролируется.
Система автоматического управления (САУ) числом оборотов
электродвигателя постоянного тока [153].
Функциональная схема системы представлена на рис. 1.11.
0
Рис. 1.11. Функциональная 'схема разомкнутой САУ;
1 - потенциометр', 2 -усилитель', 3 - электродвигатель; 4 - тахогенератор со стрелочным прибором
В варианте ручного разомкнутого управления оператором задается путем
перемещения движка потенциометра 1 нужное число оборотов двигателя (оно
пропорционально напряжению на входе усилителя). С выхода 1 сигнал подается на
усилитель 2, что приводит к изменению тока в якоре электродвигателя. Последнее
приводит к изменению угловой скорости двигателя, которая измеряется тахогенератором
и стрелочным прибором, но не используется для замыкания системы.
Из-за старения и износа элементов, при колебаниях температуры, из-за
неточности исполнения элементов, градуировка системы нарушается (каждому положению
движка потенциометра должно соответствовать заданное число оборотов двигателя в
установившемся режиме). Поэтому системы, работающие по разомкнутому циклу,
часто не могут обеспечить высокого качества работы (высокую точность). Эту
схему можно автоматизировать, причем система будет функционировать по
замкнутому циклу, т.е. по принципу обратной связи. Качество ее работы повышается.
Функциональная схема такой системы представлена на рис. 1.12.
Система замкнутого цикла отличается от системы разомкнутого цикла тем,
что в системе с ОС имеет место сравнение реального числа оборотов двигателя с
Глава 1. Линейные одномерные непрерывные стационарные САУ
29
требуемым. Рассогласование (ошибка) поступает на регулятор 2 и усилитель 3;
управление осуществляется сигналом ошибки е(г). Структура и параметры
регулятора 2 выбираются таким образом, чтобы обеспечить высокую точность работы
системы. Замкнутая система не требует точной градуировки: точность сохраняется и при
«уходе» параметров системы от эталонных из-за старения или по другим причинам.
Рис. 1.12. Функциональная схема замкнутой САУ:
1 - потенциометр; 2 -регулятор; 3 -усилитель; 4 - электродвигатель; 5 - тахогенератор
Сделаем дальнейшие пояснения и уточнения, связанные с сущностью проблемы
автоматического управления с использованием рассмотренных выше конкретных
САУ.
САУ является кибернетической системой в соответствии с определением
кибернетики:
кибернетика - наука об управлении, передаче и переработке информации.
В САУ присутствуют основные понятия, составляющие содержание кибернетики:
управление, информация, система.
Элементы САУ связаны между собой информационными каналами, линиями
управления, по которым передаются.управляющие сигналы.
Отметим важное свойство системы: система обладает свойствами и выполняет
функции, которые существенно отличаются от свойств и функций ее отдельных
элементов.
Отличительной чертой рассмотренных САУ является поступление на вход
системы так называемой «обратной информации», которая необходима для контроля
(обратная связь). ОС замыкает канал управления (поэтому такое управление называют
замкнутым).
Таким образом, при управлении с ОС значение управляющей переменной
постоянно сопоставляется с ее заданным (эталонным) значением. Цель управления -
сделать эти величины близкими (в известном смысле), несмотря на различные помехи.
Контур управления - это система, состоящая из объекта управления и регулятора
(управляющей системы, с помощью которой добиваются нужного качества
управления).
К основным функциям контура управления относятся: измерение, сравнение и
реагирование (выработка команды управления u(t) на объект), которые должны, по
возможности, выполняться, в известном смысле, оптимально; в этом случае контур
управления, несмотря на различные помехи, постоянно поддерживает управляемую
переменную близкой к ее заданному значению.
^0 Анализ и статистическая динамика САУ, Часть I
..1,2. Цели и принципы управления
Уже на основе рассмотрения указанных примеров можно сформулировать,
например, задачу управления: изменять протекающие в объекте управления процессы
путем воздействия на него соответствующими командами таким образом, чтобы
была достигнута поставленная цель.
Существует теория, рассматривающая общие принципы проектирования систем
автоматического управления (САУ), которая получила название теории
автоматического управления (ТАУ), в основе которой лежат математические модели,
отражающие связь элементов САУ друг с другом и с внешней средой.
Теперь можно расширить определение САУ: системой автоматического
управления называется система, представляющая собой совокупность объекта управления и
управляющего устройства, обеспечивающего процесс управления, т.е.
целенаправленное воздействие, приводящее к желаемому изменению управляемых переменных.
Фундаментальными принципами управления являются (их содержания
становится ясным на основе рассмотрения приведенных выше примеров) [161]:
• принцип разомкнутого управления;
• принцип компенсации (управление по возмущению: если возмущающие
воздействия в системе велики, то для повышения точности разомкнутой системы
на основе измерения возмущений в алгоритм управления вводятся
коррективы, компенсирующие влияние возмущений);
• принцип обратной связи (ОС);
В дальнейшем будут рассматриваться системы, работающие по принципу
обратной связи.
Для САУ этого класса характерно следующее:
• наличие обратной связи;
• слабые управляющие сигналы на входе, идущие от измерительного
устройства, преобразуются в достаточно мощные воздействия на объект (ток в цепи
нагрева);
• ошибка 8(0 является движущим сигналом для системы, работающей на
уменьшение этой ошибки;
• САУ является замкнутой системой, замыкание осуществляется через обратную
связь (ОС), которая, в свою очередь, реализуется с помощью измерительного
устройства (термопары); измерительный (чувствительный) элемент служит не
просто для регистрации температуры, а для формирования рассогласования
8(г), являющегося входом усилителя и, таким образом, реализующего процесс
управления.
Использование принципа ОС позволяет дать еще одно определение САУ,
делающее акцент на особом значении указанного принципа [153]: САУ называется
система, стремящаяся сохранить в допустимых пределах отклонения
(рассогласования) ошибки 8(0 между требуемыми y(t) и действительными x(i) измерениями
управляемых переменных при помощи их сравнения на основе принципа ОС (замкну*
того цикла) и использования получающихся при этом сигналов для управления
источниками энергии.
1.1.3. Типовая функциональная схема САУ. Классификация систем
Рассмотренные примеры САУ позволяют представить типовую функциональную
схему (рис. 1.13). Функциональное назначение каждого из элементов типовой схемы
состоит в следующем [153].
Глава 1. Линейные одномерные непрерывные стационарные САУ
31
1
1
v(t)
%
г
до
л
ч
wi(0 5
1 "2(0
/:
О
о
о
7
/
(r)i
1 1
11
10
Рис. 1.1Э. Типовая функциональная схема САУ:
1 - задающее устройство; 2,5- сравнивающие устройства', 3 - преобразующее устройство;
4,8- корректирующие устройства (регулятор); б - усилительное устройство; 7 - исполнительнок
nrtiifmarr О — илюптаипюпииию или ччилегштепииме ъпрклриты' 10 — ъпрклеит рппаипи nfinnmunii гая
, о — корректирующие устройства крегулятору, и — усилительное устройства, / — исполнительное
устройство; 9 - чувствительные или измерительные элементы; Ю- элемент главной обрап
И - объект управления; n(t) - помеха
хтной связи;
Задающее устройство преобразует воздействие в сигнал y(i), а сравнивающее
устройство путем сравнения сигнала y(t) и регулируемой величины x(t) (предполагается,
что 9 и 10 не искажают сигнал x(t)) вырабатывает сигнал ошибки s(t). Иногда
сравнивающее устройство называют датчиком ошибки, отклонения или рассогласования.
Преобразующее устройство 3 служит для преобразования одной физической
величины в другую, более удобную для использования в процессе управления (во
многих системах преобразующее устройство отсутствует).
Регулятор 4, 8 служит для обеспечения заданных динамических свойств
замкнутой системы. Например, с его помощью .обеспечивается высокая точность работы в
установившемся режиме, демпфируются колебания для сильно колебательных
объектов (например, летательных аппаратов). Более того, введение в систему регулятора
позволяет устранить незатухающие или возрастающие колебания управляемой
величины. Иногда регуляторы вырабатывают управляющие сигналы (команды) в
зависимости от возмущающих воздействий, что существенно повышает качество работы
систем, увеличивая их точность.
Из схемы САУ видно, что в хорошо спроектированной системе ошибка е(г)
должна быть мала. Вместе с тем на объект должны поступать достаточно мощные
воздействия. Мощности же сигнала 8(0 совершенно недостаточно для питания даже
небольшого двигателя. В связи с этим важным элементом САУ является усилительное
устройство, предназначенное для усиления мощности сигнала ошибки е(г).
Усилитель управляет энергией, поступающей от постороннего источника. На практике
широко используются электронные, магнитные, гидравлические, пневматические
усилители.
Следующим важным элементом САУ является исполнительное устройство, оред-
назначенное для воздействия на управляющий орган. В системах управления
используются следующие типы исполнительных устройств: пневматические,
гидравлические и электрические, подразделяемые, в свою очередь, на электромоторные и
электромагнитные.
Пневматические исполнительные устройства имеют сравнительно малые
габариты и массу, но требуют большого расхода сжатого газа.
Гидравлические исполнительные устройства способны преодолевать большие
нагрузки и практически безынерционны. Недостаток - большая масса. Электрические
исполнительные устройства достаточно универсальны в применении и отличаются
простотой канализации подводимой к ним энергии. Вместе с тем их использование
32 Анализ и статистическая динамика САУ. Часть I
требует наличия достаточно мощного источника тока. В некоторых САУ
исполнительный механизм как таковой отсутствует и воздействие на объект осуществляется
изменением состояния какой-либо величины (тока, напряжения) без помощи
механических устройств.
Чувствительные или измерительные элементы (датчики) необходимы для
преобразования управляемых переменных в сигналы управления (например,
преобразования вида: «угол - напряжение»).
Элемент, который подвергается управлению, называют объектом управления.
При проектировании систем объектом управления считают всю неизменяемую часть
системы (все элементы, кроме регулятора). Им может быть электрическая печь для
закаливания металла, самолет, ракета, космический аппарат, двигатель, ядерный
реактор, станок для обработки металла и т.д. В связи с большим разнообразием объектов
управления разными могут быть и управляемые переменные: напряжение, число
оборотов, угловое положение, курс, мощность и т.д. Изучением конструкций объектов
занимаются специальные дисциплины: электротехника, авиация и космонавтика,
самолетостроение, энергетика, ядерная техника, турбостроение, двигателестроение и т.д.
Из рассмотрения рис. 1.13 можно сделать вывод, что САУ представляет собой
замкнутую систему, обладающую свойством однонаправленности и реагирующую
на сигнал ошибки z(t).
Напомним определения сигналов, представленных на рис. 1.13.
Сигнал y(t) называют воздействием (задающим воздействием, входом).
Процесс x(t) называют управляемой переменной (выходом системы, реакцией).
Сигнал 8(0 называют сигналом ошибки (сигнал рассогласования).
Сигналы u\(t)u u2(t) - команды управления.
Дадим несколько определений.
Система, у которой сигнал y(t) - известная функция (детерминированный
сигнал) на всем промежутке управления, называется системой программного
управления.
Система, у которой задающее воздействие y(t) = const называется системой
стабилизации.
Система, у которой задающее воздействие y(t) - случайная функция, называется
следящей системой.
Таким образом, одномерные системы могут быть" системами программного
управления, системами стабилизации и следящими системами.
Кроме этого на практике имеют место [153]:
• системы с поиском экстремума показателя качества;
• системы оптимального управления;
• адаптивные системы.
1.1.4. Математические модели систем; оператор системы
На первом этапе расчета и проектирования систем автоматического управления
(САУ) ограничиваются качественным описанием систем и в связи с этим
рассматривают их функциональные схемы. Такое описание называют содержательным или
неформальным. Неформальным описанием САУ называется вся имеющаяся
совокупность сведений о ней, достаточная для построения фактического алгоритма ее
работы. Неформальное описание системы содержит информацию, достаточную для
построения ее функциональной схемы. Последняя же служит основой для разработки
формального (математического) описания системы.
Недостаток содержательного или неформального описания систем в том, что
такой подход не оперирует количественными характеристиками и, таким образом, нау-
Глава 1. Линейные одномерные непрерывные стационарные САУ 33_
ка, в основе которой лежит неформальное описание, не является точной наукой. Для
решения же задач исследования и проектирования систем необходимо оперировать
количественными характеристиками, определяющими качество ее работы. В связи с
этим центральным понятием теории систем является математическая модель или
оператор системы.
Под математической моделью САУ понимают количественную формализацию
абстрактных представлений об изучаемой системе. Математическая модель — это
формальное описание системы с помощью математических средств:
дифференциальных, интегральных, разностных, алгебраических уравнений, а также неравенств,
множеств и т.д. [85]
Пользуясь понятием системного оператора, можно на единой основе рассмотреть
понятие математической модели САУ.
Пусть Y и X- множества входных и выходных сигналов САУ. Если каждому
элементу yeY ставится в соответствие определенный элемент хе X , то говорят,
что задан системный оператор А.
Связь между входом и выходом системы задается посредством системного
оператора А:
Ах = у и х = А'1 у = By.
Операторное уравнение (или уравнение с оператором А) Ах = у следует
считать математической моделью САУ, поскольку оно устанавливает количественную
связь между входом y(t) и выходом x(t) системы.
Принципиально важным является ответ на вопрос: как построить оператор
системы А?
Важным положением ответа на поставленный вопрос является следующее: в
подавляющем большинстве случаев операторное уравнение системы принадлежит к
классу дифференциальных уравнений или эквивалентных им интегральных уравнений.
Для получения дифференциального уравнения системы в целом обычно составляют
описание её отдельных элементов, т.е. составляют дифференциальные уравнения для
каждого входящего в систему элемента (например, для САУ (рис. 1.4) составляются
дифференциальные уравнения усилителя, привода, реостата, электрической печи,
термопары и элемента сравнения).
Совокупность всех уравнений элементов и дает уравнение системы в целом.
Уравнения системы определяют ее математическую модель, которая для одной и
той же системы в зависимости от цели исследования может быть разной [153].
Полезно при решении одной и той же задачи на разных этапах строить разные
математические модели: начинать исследование можно с простой модели, а затем ее
постепенно усложнять, с тем, чтобы учесть дополнительные физические явления и
связи, которые на начальном этапе не были учтены как несуществующие.
Задать оператор системы — это значит задать правило определения выходного
сигнала этой системы по ее входному сигналу.
В этой главе будем изучать системы, операторами которых являются линейные
дифференциальные и интегральные операторы.*
В зависимости от того, какими классами дифференциальных уравнений
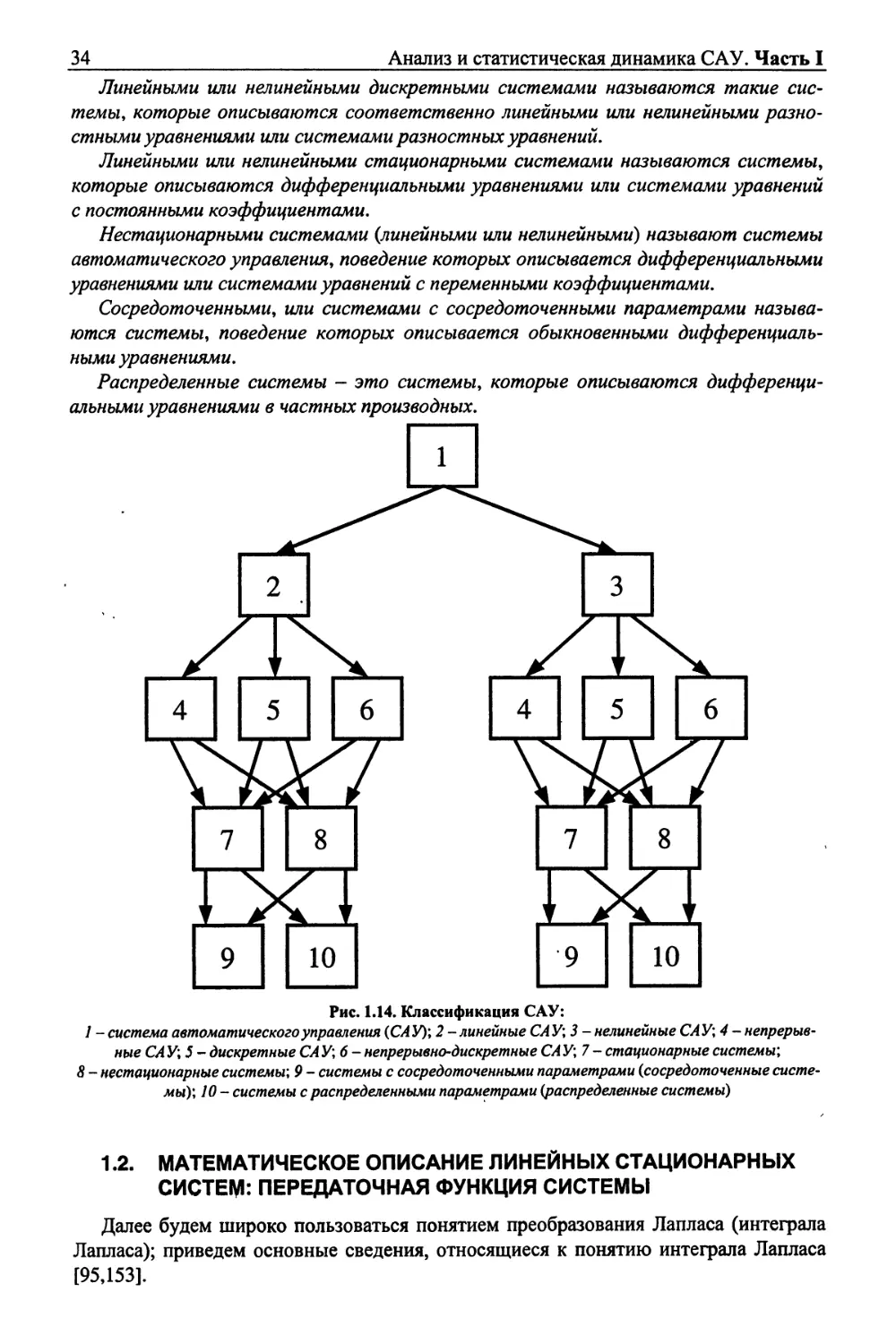
описываются САУ, их можно укрупненно классифицировать так, как показано на рис. 1.14 [153].
Линейными называют класс систем, описываемый линейными операторными
уравнениями (например, линейными дифференциальными уравнениями или их
системами), в противном случае система входит в класс нелинейных систем.
* Предполагается, что читатель знаком с основными положениями теории дифференциальных
уравнений (см., например, [45]).
34
Анализ и статистическая динамика САУ. Часть I
Линейными или нелинейными дискретными системами называются такие
системы, которые описываются соответственно линейными или нелинейными
разностными уравнениями или системами разностных уравнений.
Линейными или нелинейными стационарными системами называются системы,
которые описываются дифференциальными уравнениями или системами уравнений
с постоянными коэффициентами.
Нестационарными системами (линейными или нелинейными) называют системы
автоматического управления, поведение которых описывается дифференциальными
уравнениями или системами уравнений с переменными коэффициентами.
Сосредоточенными, или системами с сосредоточенными параметрами
называются системы, поведение которых описывается обыкновенными
дифференциальными уравнениями.
Распределенные системы - это системы, которые описываются
дифференциальными уравнениями в частных производных.
4 i
\%
7
9
>
) 6
f/
8
<-
10
4 i
7
v >
9
■Ч
5 6
YJ
8
<-
10
Рис. 1.14. Классификация САУ:
1 - система автоматического управления (САУ); 2-линейные САУ; 3 - нелинейные САУ; 4-
непрерывные САУ\5- дискретные САУ; 6- непрерывно-дискретные САУ; 7- стационарные системы;
8 - нестационарные системы; 9 - системы с сосредоточенными параметрами (сосредоточенные
системы); 10- системы с распределенными параметрами (распределенные системы)
1.2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ
СИСТЕМ: ПЕРЕДАТОЧНАЯ ФУНКЦИЯ СИСТЕМЫ
Далее будем широко пользоваться понятием преобразования Лапласа (интеграла
Лапласа); приведем основные сведения, относящиеся к понятию интеграла Лапласа
[95,153].
Глава 1. Линейные одномерные непрерывные стационарные САУ 35^
Множество функций x(t), удовлетворяющих условиям: 1) x(t) = 0 при г<0;
2) 3 М и с: \x(t)\ < Mect; 3) имеет место не более чем счетное число точек
разрыва первого рода на [0,°°), называется пространством оригиналов и обозначается О.
Введем понятие интеграла Лапласа, пользуясь определением интеграла Фурье.
Прямое одностороннее преобразование Фурье определяется формулой:
Х(7Ю) = /х(0е-***. 0.1)
о
Как известно, преобразование Фурье может быть применено к функциям x(t),
для которых интеграл
оо
\\x{t)\dt
о
существует (условие абсолютной интегрируемости). Этому условию не
удовлетворяют многие функции, используемые при исследовании систем: l(r), Asin(r), еш,
Acos(0, некоторые решения дифференциальных уравнений.
Для того, чтобы иметь возможность подобную функцию x(t) преобразовать по
Фурье, предварительно ее надо умножить на функцию e~at, где вещественное число
а > а0 выбрано таким образом, чтобы интеграл
j\x(t)\e~atdt (1.2)
о
был сходящимся,
В результате приведенных рассуждений запишем
Х(7(о,с) = jx(t)e~ate-jmdt = Х(а+ №. (1.3)
• о
Введем новую комплексную переменную s = а + ./со; получим
оо
X(s) = jx(t)e~stdt. (1.4)
о
Функция X(s), определяемая зависимостью (1.4), где x(t) -оригинал, 5 = а+7'со,
называется изображением x(t) и обозначается
xU)^X(s) иди X(s) = L{x(t)}.
Часто интеграл (1,4) называют интегралом Лапласа. Ему присущи следующие
двойства.
Линейность:
4£М*(о} = 2М*М, meXk(s) = L{xk(t)}9 * = U.
Смещение в комплексной рблдсти:
пусть x(t) t*X(s), тогда jc(r)^ ш о X(s + a).
Смещение в действительной области:
пусть x(t) <-^ X(s), тогда д:(г-т) ^-> е~5'Х (.$•).
36 Анализ и статистическая динамика САУ. Часть I
Изображение производной:
L{x'(t)} = sX(s)-x(fl),...,
L{xin) (/)} = snX (s) - sn'lx(0) - sn-2x(O) -... - xin"l) (0).
Изображение от интеграла:
l|J*(t)</tI = ±X(5).
Дифференцирование изображения:
^-(-l/ifA*)}.
Изменение масштаба во временной области: если x{t) о X(s), то
L{x(at)} = (l/a)X(s/a).
Свертка функций в действительной области:
L\
]xl{x)x2{t-x)dxUXl{s)X2{s).
№
Свертка в комплексной области:
C+joo
1 ь-гу«"
L{xl(t)x2(t)} = — J Xl(q)X2(s-q)dq.
J C-joo
Далее изложим содержание второй теоремы разложения, позволяющей находить
оригинал по изображению. Эту теорему удобно применять, если X(s) есть дробно-
рациональная функция вида
x(s) = bmsm+bm_lS^+...+bo=m
sn+an_lSn-l+... + a0 B(s)
причем т<п и коэффициенты {а,} и {bt} действительные. Если известны корни
многочлена B(s) = 0, то зависимость (1.5) можно переписать в виде
' Xit)m ь^+ьп.^+...+ь0 '
где ц, - кратность корня st.
Известна формула
x(t) = L-l{X(s)} = %BbviX(s)es'\_ . (1.7)
v=l s Sy
а). Пусть (sn+an_lsn~l+...+a0) = (s-sl)(s-s2)...(s-sn)9rne sl9s2,...,sn
-различные вещественные и комплексные корни. Тогда оригинал находят по формуле
*(0=!£8е"'- (18>
б). Если изображение имеет вид
X(s) = 4£t' (L9>
sB(s)
то
Глава 1. Линейные одномерные непрерывные стационарные САУ 37^
fi(O) faskB'(sk)
в). Случай кратных корней. Пусть X(s) = A(s)/B(s), где B(s) = (s - s^1 x
x(s-s2yi2.~(s-sr)*ir, Ш +Цг +—+Ит = п • Тогда оригинал находят по формуле
^'^j?e"+^'(£Sj]e'"+-+^'e"+
vm / W4 ; (1 n)
+^т£^^'+^ ra**+-+v'+-+
^(£^^+^(£^eV+"-+^-
Коэффициенты Лд определяются зависимостью
4*"С=щ£К'"<к1Р'Н. ■ (112)
Структурная схема алгоритма построения оригинала представлена на рис. 1.15.
Входные
данные
I
*
±
] д<0
>►
Рис. 1,15. Структурная схема алгоритма построения оригинала:
7 - нахождение корней полинома B(s) = 0=> sl,s2,...,sn ; 2 -расчет коэффициентов Ajk ;
3 - построение оригинала jt(f)
Пример 1.1. Имеем
Найдем корни характеристичеекога. ураэнения:
Формула для оригинала им§§Т ЭВД:
5(0) Й'/^Х*,)
Имеем:
^)=4§+i4^^'. (1.14)
38
Анализ и статистическая динамика САУ. Часть I
А(0) = 100, 5(0) = 100, Д(0)/Я(0) = 1,
B\s) = 2s + 10;
В^2) = 2(-5 + 7Ч/75) + 10 = -10 + 27Ч/75 + 10 = 2>У75;;
B'(s3) = 2(-5 - У>/75) + Ю = -10 - 2;775 +10 = -2775;;
s2B\s2) = ("5 + jjT5)(2jl5j) = -10775; -150;
s3B\s3) = (-5 - jJJ5)(-2sll5j) = 10775; -150.
Итак, можно записать:
Найдем С2 и С3:
x(t) = \ + C2eS2' +C2eSi*.
100 100(-150 + 10775j) ^^775.
: ?==—= - = -0,5 + /:
-150-10775; 30000 30
100 100(-150-1(К/75;) 7т5 . Л,
___ = i L- 1—0,5.
-150 + 10775; 30000 30
(1.15)
С,=
Отсюда
JC(/) = 1 +
= 1 + е"
.-5/
I-0,5 +—; I(cos775r + ;sin775/) +
J_0)5-—;|(cos775r-;sin775r) =
L 30 J J
= l-*-5'| cos775/ + — sin775r |.
Пример. 1.2. Положим, что изображение имеет вид
(s-lf(s + lf
(1.16)
(1.17)
Здесь 5-1 = 1 — кратность 3; $2 = - 1 - кратность 3. Тогда jii = 3, Ц2 = 3. Формула для оригинала имеет вид
x(t) = AllLie' + All^e' + A3iel + Al2j;e-+A22^e-'+Ai2e-. (1.18)
Найдем коэффициенты Л,>:
or
(,-1)3(,+1)3
5=J,=I
(*,+1)3 8
-3(^ + 1)2^2
J=8=i4li;
= 1 d Г 52 1 _2j(.e + 1)3
^l 1!^L^ + 1>3JL (5 + 1)°
25 1 З^2 I =J_ = A
= (, + l)3L|"(, + l)4L|=16= 2"
= l["2(5 + l)3-3(5 + l)225 6^ + l)4-4(5 + l)33521
= l[" 2 б£_
6^ 12^
+ •
"2 [(5 +I)3 (5 +I)4 (5 +l)4 (5 + 1У
Глава 1. Линейные одномерные непрерывные стационарные САУ
39
^■^-^(J^tfL-u^L-?
(1.19)
Ам"Тб;/Ц2"1б'
Оригинал определяется формулой
U2 , 1
If2
1 .-'
jt(f) = *' +—te е е +—te +—е .
8 2 16 16 8 2 16 6
Рассмотрим замкнутую автоматическую систему. Предварительно дадим
определение: схема системы, в которой указаны математические модели ее элементов
(например, в форме дифференциальных уравнений), называется структурной схемой.
Представим структурную схему в виде, изображенном на рис. 1.16.
Поскольку полагаются известными дифференциальные уравнения ДУЬ ДУ2, ДУз,
ДУ4, ДУ5 всех элементов, то, пользуясь каким-либо из методов, можно построить
одно уравнение, связывающее вход системы с ее выходом.
Положим, что уравнение имеет вид
5>v;c(v)=5>v?(V)-
v=0 v=0
(1.20)
y(t) e(r)
*(0|
ДУ1
2
ДУ2
з
ДУз
4
ДУ4
ДУ5
Рис. 1.16. Структурная схема системы:
1 -регулятор; 2 - усилительное устройство; 3 - исполнительное устройство;
4 - объект управления; 5 - измерительная система
САУ является одномерной линейной стационарной, поскольку ее поведение
описывается скалярным линейным дифференциальным уравнением с постоянными
коэффициентами.
Найдем изображение выходного сигнала системы.
Воспользовавшись формулой
L{fik\t)} = skF(s)-sk-lf(0)-sk-2fX0)-...-fik-l)(0\ (1.21)
из (1.20) получим
aJ^X^)-^"1^)^
+an_l[sn-iX(s)-(sn-2x(0) + sn-3xm + ... + x(n-2\0)^ (1.22)
+д0* (*) = bmsmY{s) + bm_xsm-lY{s) +... + V4*)-
Из (1.22) следует:
an/x(s) + an_ls"-lX(s) + ... + a0X(s)-
-хф^а^^а^-^а^^-^^а^
iy(5)a±W."-a тц-l^ т...-г«ц (126)
40 Анализ и статистическая динамика САУ. Часть I
-x\0)[ansn-2+an.lsn-3 + an.2sn-4+...+a2]-...-x^l\0) a^ =
' Б^ ' D^(s) (1-23)
= bmsmns) + bm.lSm-lY(s) + ... + b0Y(sy.
Перепишем последнюю зависимость в виде
k*" +an.ls"-l+...+a0]x(s)-x(0)D0(s)-xX0)Dl(s)-...-
г , (1.24)
-^"-"(О)^.,^) = [bmsm + Bm.lsTl +...+bo\Y(Sy.
Отсюда легко записать формулу, определяющую изображение выходного сигнала
ans»+an^+... + a0 (j ^
|x(0)^)(J) + xt(0)AW + .-+Jc(ll"1)(0)P>l-iW
e^'+^V1"1+••• + <%
Положим в (1.25) х(0) = х\0) = ... = х{п-1)(0) = 0, т.е. Х° =[jc(O),jct(O),...,Jc(/I-1)(O)] =
= 0 . Тогда зависимость (1.25) можно записать в виде
_X(j)_Vm4^VW-1+... + fr0
Y(s) ansn+an_xsn-{+... + a0
Дадим одно из стержневых в теории автоматического управления определений:
передаточной функцией (ПФ) САУ называется отношение преобразования Лапласа
X(s) сигнала x(t) на выходе системы к преобразованию Лапласа Y(s) сигнала на входе
y(t) при нулевых начальных условиях X °= 0.
Зависимость (1.26) позволяет записать важное соотношение
X(s) = W(s)Y(s). (1.27)
т.е. изображение выходного сигнала равно изображению входа {воздействия),
умноженному на ПФ системы.
Приведем некоторые свойства и показатели передаточных функций [172]. ПФ
представляет собой дробно-рациональную функцию (см. (1.26)), причем в реальной
системе порядок числителя т не превышает порядка знаменателя я, т.е. т<п .
Коэффициенты ПФ av, v = 0,n; bk, k = 0,m вещественны, поскольку они представляют
собой функции от вещественных параметров системы.
Значения s, при которых ПФ обращается в нуль, называются нулями ПФ. Нули
являются корнями уравнения
bmsm+bm.lsm-l+...+bo=O. (1.28)
Значения s, при которых ПФ обращается в бесконечность, называются
полюсами ПФ. Полюсы являются корнями уравнения
ansn+an_lSn-l+... + a0=0. (1.29)
Передаточная функция W(s) имеет, таким образом, т нулей и п полюсов. Как
нули, так и полюса могут быть действительными или комплексно-сопряженными,
поэтому их можно изобразить на комплексной плоскости (рис. 1.17).
Нули и полюса называются левыми (правыми), если они расположены в левой
(правой) части комплексной плоскости, и нейтральными или нулевыми, если они
лежат соответственно на мнимой оси или в начале координат.
Глава 1. Линейные одномерные непрерывные стационарные САУ
41
(
(
Левые
>
нули
Левые
Мнимая ■
ось
0
0
0
ч
полюса :
: Нейтральные
полюса .
^Нейтральные
нули
)
к
0 #"
•
I
г
0
<
<
I
' Пр
Сомплексная
шоскость
ТТриртнитр ттт.
ОСЬ
Травые нули
авые полюса
Рис. 1.17. Нули и полюса на комплексной плоскости:
* —полюса\ • —нули
К показателям ПФ относятся [172]:
1) порядок ПФ я, равный степени знаменателя ПФ;
2) степень гс, равная разности степеней знаменателя п и числителя т ПФ;
3) индекс апериодической нейтральности sa, равный числу нулевых полюсов ПФ;
4) индекс колебательной нейтральности sKi равный числу мнимых полюсов ПФ;
5) индекс неустойчивости sHi равный числу правых полюсов ПФ;
6) индекс неминимально-фазовости янф, равный числу правых нулей ПФ.
Рассмотренные показатели содержат ценную информацию о свойствах
исследуемой САУ.
На основе понятия передаточных функций в теории автоматического
управления (ТАУ) построен аппарат структурных преобразований, позволяющий находить
ПФ замкнутых систем, заданных структурными схемами. Любая структурная схема
включает последовательно и параллельно соединенные элементы, а также элементы,
соединенные обратной связью. Рассмотрим последовательное соединение (рис. 1.18).
W\(s)
W(s)
W(s)
X\{t)
W2(s)
x(t)
Рис. 1.18. Последовательное соединение
Для него характерны зависимости вида
Xx(s) = ^,(5)У(Д X(s) = W2(s)X,(*) = W2(s)Wl(s)Y(s).
Отсюда имеем
W(s) = Wl(s)W2(s).
(1.30)
(1.31)
42
Анализ и статистическая динамика САУ. Часть I
Для произвольного случая
W(s) = Wx(s)W2(s)...Wn(s). (1.32)
Следовательно, передаточная функция последовательного соединения звеньев
равна произведению передаточных функций отдельных звеньев. Перейдем к
параллельному соединению (рис. 1.19).
y(t)
II/ /_\
W\(S)
W (?\
yVn{S)
*i(0
/ V к
W(s)
Рис. 1.19. Параллельное соединение
Для параллельного соединения
x(t) = xl(t) + x2(t) + ...+xn(t).
Тогда
X(s) = X1(s) + X2(s)+...+Xn(s),
но
Х,(5) = 1У,(5)У(5);
X2(s) = W2(s)Y(s);
(1.33)
(1.34)
(1.35)
Xn(s) = Wn(s)Y(s).
Отсюда
(1.36)
(1.37)
X(s) = Wl(s)Y(s)+W2(s)Y(s)+...+Wn(s)Y(S) =
= (Wl(s)+W2(s) + ...+Wn(s))Y(s),
или, что то же самое, X(s) = W(s)Y(s), где
W(s) = W1(s)+W2(s) + ...+Wn(s).
Из последнего равенства следует, что передаточная функция параллельного
соединения равна сумме передаточных функций отдельных элементов.
На рис. 1.20 представлено соединение с обратной связью. Для такой системы
справедливы соотношения:
E(s) = Y(s) - Хх (s); X (s) = W, (s)E(s); X, (s) = W2 (s)X{s)
Отсюда
X(s)
или
Тогда
Окончательно получим
■ = Y(s)-W2(s)X(s),
X(s) = Wl(s)Y(s)-Wl(s)W2(s)X(s).
X (s) [1+Wi (s)W2 (s)] = W, (s)Y(s).
(1.38)
(1.39)
(1.40)
(1.41)
Глава 1. Линейные одномерные непрерывные стационарные САУ
43
X(s)
ВД
(1.42)
Y(s) 1ЩШ2(з)
Очевидно, что передаточная функция соединения с обратной связью равна
дроби, числитель которой - передаточная функция прямой цепи, знаменатель -
\-\-W\(s)W2(s) (если имеет место положительная обратная связь, то знаменатель имеет
вид 1 - W\{s)W-As)).
y(t)
[
V /Л
x\{t)
Wi(s)
ТХ7 / \
W(s)
x(t)
Рис. 1.20, Соединение с обратной связью
Аналогичным образом легко найти так называемую передаточную функцию
ошибки, определяемую формулой
Els)
WJs) =
Y(s)
Имеем
Отсюда
E(s)*ns)-W2(s)X(s)\X(s) = Wx(s)E(s).
(1.43)
(1.44)
(i.45)
(1.46)
Y (s) l+Wl(s)W2(s)
. При структурных цреобразоэання^ ЧЗРТО используются различные
преобразования (табл. 1.1). Если известна ртруктурная ехема и параметры дистемы, то можно,
пользуясь аппаратом структурных преобразований, найти ПФ замкнутой САУ, а
затем и ее дифференциальное уравнение.
E(s) = Y(s)rWl(s)W2(s)E(s)\E(sl(l+Wl(s)W2(s)) = Y($l
Окончательно получим
E(s)_
1
Преобразования
Пепенос учла
через звено
Перенос узла
через
сумматор
Исходное
Xl
Xl
ЭкРИвале
W" 'wi \
1 UWi \
;ht
X2
т
J
Исходи
—Ha)—
юе
Xi
I *r
I—►
1
-r
L
Таблица J.I
Эквивалент
Г 1 *2
1 i*2
44
Анализ и статистическая динамика САУ. Часть I
Продолжение табл. 1.1
Перенос
сумматора
через звено
нЯН^ГУ
Перенос
сумматора
через
сумматор
JC4
Г*з
Перенос
сумматора
через узел
I X2
xi Т хъ
Х2
XI
хг
\хг
Х\ 1 ХЪ
-j-Hg)—►
TJC1
хг
Последовательное
включение
звеньев
-4WW2
/=1
Параллельное
включение звеньев
"4^1+^2
^экв(*) = №*)
Включение
обратной
связи
W=-
W-.
' \±w.
Аппарат передаточных функций оказался весьма эффективным при исследовании
линейных стационарных систем, имеющих сложные структурные схемы.
На рис. 1.21 показаны полезные при решении инженерных задач эквивалентные
преобразования структурных схем [153].
Глава 1. Линейные одномерные непрерывные стационарные САУ
45
W)(s) |-»>
+\W2(s)
*2
l/Wts) \-+^{*T[-*»
ж
Рис. 1.21. Эквивалентные преобразования структурных схем
Приведем некоторые примеры.
Пример 1.3 [153]. Схема многоконтурной (четырехконтурной) САУ показана на рис. 1.22, а.
Передаточная функция Wm(s) элемента W4(s), охваченного отрицательной обратной связью Z«(.?)t находится по
формуле
W (,)„ Ш?1 .
При этом четырехконтурная система может быть сведена к трехконтурной системе (рис. 1.22, б),
y(t) x(t)
Рис. 1.22. Пример преобразований четырехконтурной САУ
46
Анализ и статистическая динамика САУ. Часть I
Далее последовательно соединенные структурные элементы с передаточными функциями W3(s) и
WuC?), охваченные обратной связью Z3(», могут быть заменены эквивалентным структурным элементом с
передаточной функцией
W3(s)W^s)
W33(s) =
W33(*) = :
\ + Z3(s)W3(s)Wu(s)
W3(s)W4(s)
\ + Z4(s)W4(s) + Z3(s)W3(s)W4(s)
В этом случае трехконтурную схему можно свести к двухконтурной схеме (рис. 1.22, в), которая,
в свою очередь, может быть приведена к одноконтурной схеме (рис. 1.22, г).
Для схемы, показанной на рис. 1.22, г, передаточная функция
W2(j)W33(j)
W22(s) =
\ + Z2(s)W2(s)W33(s)
W2(s)W3(s)W4(s)
1 + Z4(s)W4(s) + Z3(s)W(s)W4(s) + Z2(s)W2(s)W3(s)W4(s)
Передаточная функция всей системы с разомкнутой главной обратной связью имеет вид
W/,(^) = Zl(^(^)W22(^) =
1 + Z4(s)W4(s) + Z3(s)W3(s)W4(s) + Z2(s)W2(s)W3(s)W4(s)'
Передаточная функция системы в замкнутом состоянии
1 WJs)
W(s)--
Zx{s) l + WJs)
W^sW^sW^sW^s)
1 + Z4(s)W4(s) + Z3(s)W3(s)W4(s) + Z2(s)W2(s)W3(s)W4(s) + Z, (^(^)И'2(^)^з(^)^4(^)
Если структурная схема САУ имеет вид (рис. 1.23), то, последовательно преобразуя структурную
схему с вычислением соответствующих передаточных функций, получим ПФ замкнутой системы
W(s) =
1 + Z, (s)W2 (s)W3 (s) + Z2 (.9)W, (s)W2 (s)
y(t)
-►OH ^tw 1
I lM> 1
^[^У^Щ—f4 w^ \++*
Us) [^-
x{i)
Глава 1. Линейные одномерные непрерывные стационарные САУ
47
y(t)
x(t)
-^OMj^iLrHj^i
Us)
«* 1
Phc. 1.23. Пример преобразования структурной схемы САУ с двумя цепями ООС
Пример* 1.4. Построим структурную схему САУ числом оборотов двигателя постоянного тока [153].
«(0 1
_L_N(0 = *(0
Рис. 1.24. Функциональная схема САУ:
1 - элемент сравнения; 2 - электронный усилитель; 3 - электромашинный усилитель;
4 - двигатель; 5 - тахогенератор
Как уже отмечалось, для обеспечения заданного качества управления в систему вводится регулятор.
Кратко остановимся на значении регулятора в рассматриваемой САУ. Внешние воздействия, поступающие
на систему, делятся на два класса - задающие воздействия y{t) и возмущающие воздействия n(t). Задающие
воздействия определяются тем законом, по которому должна изменяться управляемая величина. В
рассматриваемом случае (система стабилизации) задающее воздействие постоянно, оно устанавливается или
вырабатывается задающим устройством.
Для систем стабилизации основным является возмущающее воздействие (изменение нагрузки).
Возмущающее воздействие n(t) может изменяться по вполне определенным законам, а может изменяться и
случайно. Часто характерным является скачкообразное изменение возмущающего воздействия (рис. 1.25),
соответствующее мгновенному увеличению 1 или уменьшению 2 нагрузки. Задачей регулятора является
устранение или уменьшение до необходимых пределов отклонения управляемой величины от заданного
значения, вызванного возмущающим воздействием n(t). Принципиально невозможно сделать управляемую
величину независимой от всех возмущающих воздействий, ибо по самому принципу работы САУ
регулятор может прийти в действие лишь тогда, когда появится отклонение регулируемой величины от
заданного значения (рис. 1.26). При увеличении нагрузки на валу электродвигателя n(t) число оборотов, а
следовательно, напряжение на выходе тахогенератора упадет. Сигнал u(t), а следовательно, сигналы u\{t) и м2(0
возрастут, а это приведет к увеличению скорости вращения вала электродвигателя. Регулятор улучшает
качество управления.
n(t)
■О
t
Рис. 1.25. График возмущающего воздействия
*В параграфе 1.1 рассматривался вопрос построения оператора Л замкнутой системы. Этот пример
иллюстрирует алгоритм нахождения математической модели замкнутой системы, если известны
дифференциальные уравнения ее звеньев.
48
Анализ и статистическая динамика САУ. Часть I
Дифференциальные и алгебраические уравнения элементов системы имеют следующий вид:
1) элементы сравнения
и(') = ;уо-иг2(О; и,(О = и(О-Ис(');
2) электронный усилитель
3) электромашинный усилитель
и2(0 = *эМ1(0;
4) электродвигатель
5) регулятор
deB{t)
'~dT
д dt
«МО
+ ев(0 = Куи2«); Тп -^р + ея(1) = АГуев(О;
Л
Ы«) = Каея«);иТг(1) = КТгЫ(1);
duc
:~dt
+ uc(t) = Kc
de^t)
dt
(1.47)
(1.48)
(1.49)
(1.50)
(1.51)
У(О=УО 1 U(t) l UX(t)
«2(0
n{t)
^я(0 | N(t)=x(t)
Рис. 1.26. Функциональная схема САУ с регулятором в цепи ОС:
7 - элемент сравнения; 2 - электронный усилитель; 3 - электромашинный усилитель;
4 - двигатель; 5 - тахогенератор; 6-регулятор
Зная уравнения элементов и переходя от последних к передаточным функциям, построим структурную
схему системы (рис. 1.27).
—TQ
1
> ^ /С
ГО
«Г2(0
5\ ^
Ис(0
1
Tys +
Kcs
Tcs +
- К
- Лг,
1
1
eB(t)
Гп* + 1
W
д«)=ад
i=
Рис. 1.27. Структурная схема системы управления числом оборотов двигателя
с математическими моделями в форме передаточных функций
Воспользовавшись структурными преобразованиями, найдем ПФ внутреннего контура, охваченного
местной обратной связью (регулятором)
КЭКУКП
bjs + lj
W,(.s) = -
1 +
л з Лу К л Кq s
[(V+i)(rn*+i)(rcf+i)]
«з^3 + a\s2 + a\s + uq '
(1.52)
где
а\ = ГУ7ПГС; а\ = (ТУТС + ТПТС + ТПТУ); а\ =ТУ+ТП+ТС + КЭКУКПКС;
al0 = \;bl = КЭКУКПТС; % = КЭКУКП.
Глава 1. Линейные одномерные непрерывные стационарные САУ
49
Теперь легко найти ПФ замкнутой САУ
W(s) =
V + fr)
aAsA + a3s3 + a2s2 +а^ + а0'
(1.53)
где
b{ -b{K^\bQ= ЬОКУ;
а4 = а\Тл; аъ = (а^Гд + а\); а2 = (а|7д + в£ );
«1 = (во^д + <*\ + */*д *г2); а0 = Ц + Ь0КдКТг).
Подставляя численные значения параметров, получим ПФ в виде
49,7(1 + 0,5.*)
W(s)--
(1.54)
" 0,015/+ 0,215^3 +10,9^ + 25,9^ + 49,7*
Ясно, что последнее выражение является дробно-рациональной функцией, причем коэффициенты ПФ
- действительные числа.
Найдем нуль системы: 1+0,5$ = 0 =* s = - 2.
Рассчитаем полюса системы, которые являются корнями уравнения
0,015/+0,215$3+10,9$2+25,95 + 49,7 = 0. (1.55)
Корни последнего уравнения: s\2 = - 1,2 ±./1,83; 53,4 = -6 ±./25,6. Нанесем значения нулей и полюсов на
комплексную плоскость (рис. 1.28). О системе можно сказать следующее: 1) порядок системы - 4; 2) гс = 3;
3) индекс апериодической нейтральности равен нулю; 4) индекс колебательной нейтральности равен нулю;
5) индекс неустойчивости равен нулю; 6) индекс неминимально-фазовости равен нулю.
Мнимая
ось
+4
Действительная
ось
►
Рис. 1.28. Нули и полюса системы с ПФ (1.54)
Все нули и полюса системы - левые (поскольку лежат в левой полуплоскости). Если известна ПФ
замкнутой САУ, то, используя известную формулу
5*F(5)<->/(ft)(0. (1.56)
легко получить дифференциальное уравнение этой системы. В самом деле,
bs + bb =*X£) (157)
a4s4 + a3s3 + a2s2 + axs + Oq Y(s)
Тогда
a4s4X(s) + a3s3X(s) + a2s2X(s) + alsX(s) + a0X(s) = blsY(s) + b0Y(s). (1.58)
Переходя в пространство оригиналов, запишем:
а4*(4)(0 + a3x{i)(t) + a2x(t) + а{х«) + aox(t) = b^t)+boy(t). (1.59)
Рассматриваемый подход справедлив при исследовании САУ любой степени сложности.
Введем понятия вынужденных и свободных колебаний системы. Если на вход
системы, описываемой уравнением (1.20) при t = 0 поступает воздействие y(t), а система
при t = 0 имела ненулевые начальные условия, то изображение выхода и сам выход
имеют вид
5 Зак. 232
^0 Анализ и статистическая динамика САУ. Часть I
X(s). bmsm +...+b0 ns) + mD0(s) + ...+X^(Q)Dn_i(s) ^ (160)
-y- a^"+...+g0 ^ ansn+...+a0
' I ' ' I '
f
x(t) = jk(t->c)y(>c)dT+xc(t,x(0),xX0),...,xin-{)(0)). (1.61)
0
Р1ли, в развернутой форме,
40 = }^(г-х)Ях)Л + д:(0)хДО + ^1(0)х2(0 + ... + д:('1"1)(0)^(0, (1.62)
о
где jci(O, ..., xn(t) - элементы нормальной фундаментальной системы.
Последние формулы позволяют заключить, что имеют место два фактора,
вызывающие колебания на выходе системы:
1) наличие воздействия на входе y(t);
2) наличие в системе ненулевых начальных условий Х° =fx(O),...,x(/I~1)(O)J^O
(наличие в системе запасенной энергии, порожденной действием предыдущего
сигнала, поступившего на систему до t = 0).
А теперь дадим два важных определения:
Сигнал у определяемый формулой
t
xB(t) = jk(t-T)y(x)dx (1.63)
о
и порожденный воздействием y(t), поступившим в систему при t = 0, называется
вынужденным сигналом (вынужденными колебаниями системы);
Сигнал, порожденный ненулевыми начальными условиями Х°*0 или, что то же
самое, порожденный воздействием, поступившим в систему на промежутке
(-°°,t = 0), называется свободным сигналом (свободными колебаниями).
Выходной сигнал системы при te (- °°, t) можно записать в виде интегрального
соотношения
/ о t
x(t)= J k(t-T)y(i)dT= J k(t-T)y(x)dT+jk(t-T)y(T)dx, (1.64)
где
t
\k(t-T)y(x)dx (1.65)
- полный процесс на выходе системы;
о
xc(t)=\k(t-x)y(x)dz (1.66)
- свободные колебания системы;
t
xb(t)^\k(t-x)y(x)dx (1.67)
о
- вынужденные колебания системы.
Глава 1. Линейные одномерные непрерывные стационарные САУ 51_
1.3. ПЕРЕХОДНЫЙ (ДИНАМИЧЕСКИЙ) И УСТАНОВИВШИЙСЯ
(СТАТИЧЕСКИЙ) РЕЖИМЫ РАБОТЫ СИСТЕМЫ;
ПЕРЕХОДНАЯ ХАРАКТЕРИСТИКА СИСТЕМЫ
Введем понятия установившегося (статического) и неустановившегося
(динамического) режимов работы системы, рассматривая частный случай, когда y(t) = 1(0
(рис. 1.29).
s
t
Рис. 1.29. Входной ступенчатый сигнал
В связи с тем что отклонение управляемой величины существенно зависит от
вида воздействий, места их приложения (которые могут быть различными), то обычно
при рассмотрении конкретных автоматических систем приходится задаваться
типовыми, наиболее характерными для данной системы воздействиями y(t). Обычно в
качестве такого типового воздействия принимают воздействие вида скачка y(t) = l(f),
являющегося во многих случаях наиболее неблагоприятным. Если в этом случае
выходной сигнал удовлетворяет определенным условиям, то часто можно считать, что
он тем более будет удовлетворять им и при иных характерных воздействиях.
Примерами ступенчатых сигналов могут быть сброс или увеличение нагрузки,
отказ двигателя в системе двухмоторный самолет - автопилот курса [153].
Типовое воздействие можно задать в виде 8-функции (дельта-функции).
Например, внезапное вхождение самолета в струю воздуха, движущегося перпендикулярно
траектории движения самолета.
При исследовании следящих систем типовым управляющим воздействием может
являться полином
y(t)=yo + yit + y2t2+--- + y/> *>0. (!-68)
В отдельных случаях типовое воздействие может быть сложной формы,
например, при исследовании следящих систем управления антенной РЛС используется
функция [153]
y(f)=arctg(PO, (1.69)
которая отражает изменения азимутального угла между направлением на цель и
некоторым фиксированным направлением в случае прямолинейного и равномерного
движения сопровождаемого объекта (рис. 1.30). Часто типовые воздействия
определяются экспериментальным путем. На основе формулы (1.60) имеем зависимость для
изображения выходного процесса (начальные условия считаем нулевыми, т.е.
Х°=ОпризЧО = 1(О)
x{s) b-i-+W^+^;1 = 4\. (1.70)
(апз»+ап_^+... + а0) ' sBW
Выходной сигнал, соответствующий изображению (1.70), имеет вид
jc(f)= CoeSot +CxeSlt+C2eS2t +... + C/Ie5"', (1.71)
5*
52
Анализ и статистическая динамика САУ. Часть I
где sl9s2,...9sn - корни уравнения B(s) = 0 (полюса системы ); s0 = О - нулевой
корень, порожденный воздействием y(t)'= 1(г).
Из (1.71) следует важный вывод: полюса системы sl9s2,...,sn определяют закон
изменения во времени выходного сигнала; постоянные же коэффициенты С{,С2,...,Сп
(формула для расчета Ck имеет вид: Со = А(о)/#(о), Ck = A(sk)/skB'(sk), k = l,n )
зависят в соответствии с приведенной формулой как от полюсов, так и от нулей
системы и определяют величину амплитуды каждой из составляющих, определяющих
сигнал x(t).
Перепишем (1.71) в виде
*(0=*,(0+*п(0. (1-72)
где
y{t) = W
MO=Q'v=^ji(')=coi(<);
xn(r)=C1^'+C2^'+... + Cn^-'.
Я') = 5(0
У«)=Уг?П
y(t) = arctg (P0
(1.73)
(1.74)
Рис. 1.Э0. Виды типовых воздействий
Составляющая ху (t) порождена полюсом воздействия y(t) = 1(0, и, следователь
но, 5 = 0, т.к. Y(s) = 1/5. Составляющая xn(t) порождена полюсами ПФ, т.к
s{,s2,...,sn являются корнями
ansn+an_lSn-l+... + a0=0. (1.75
Эта составляющая определяет динамические свойства системы. Итак, имеет мест
картина: y(t) = 1(0 - вход системы;
Глава 1. Линейные одномерные непрерывные стационарные САУ
53
jc(r)=C0l(r)+C1^/+C2^24... + C^v
- выход системы.
Очевидно, в работоспособной системе, если на вход подается ступенчатый сигнал
1(0, то и выход также должен быть постоянной величиной, т.е. Col(r). Этому
«мешает» составляющая хп (t). Отсюда ясно, что в работоспособной системе
*п('Нц—>0. (1.76)
Система, для которой выполнено условие (1.76), называется устойчивой.
Если выполняется условие (1.76), то на выходе системы можно наблюдать два
случая (после затухания хп (?)):
1) co*i и *(0=coi(0«i(0;
2) Со=1 и x(t)=y{t)=l(t).
Таким образом, характер изменения выходного сигнала (управляемой
величины) может иметь вид, приведенный на рис. 1.31 (первый случай) и рис. 1.32 (второй
случай).
Максимальное
динамическое
(1-77)
х(0,
Максимальное
статическое
отклонение
Рис. 1J1. Выходной сигнал системы при y(t) = 1(0 и Сф 0
Максимальное
динамическое
отклонение
Рис. 132. Выходной сигнал системы при y(t) = 1(0 и С = 0
Вводимые ниже понятия имеют важное значение для характеристики качества
работы системы.
Составляющая вынужденного сигнала xn(t) называется переходной
составляющей.
Переходная составляющая, с физической точки зрения, порождена
инерционностью системы (например, в системе управления кораблем момент инерции отличен
от нуля и, в связи с этим, изменение курса происходит с некоторым запаздыванием).
_54 Анализ и статистическая динамика САУ. Часть I
Составляющая вынужденного сигнала ху (г) называется установившимся
сигналом.
Таким образом, вынужденный процесс хв (t) состоит из двух составляющих:
переходной, порожденной полюсами ПФ системы, и установившейся, порожденной
полюсами воздействия (в данном случае s0 = 0).
Режим, при котором составляющая хп (t) отлична от нуля (не затухла),
называется неустановившимся или переходным (динамическим) режимом.
Режим, при котором xn(t)**O (составляющая xn(t) затухла), называется
установившимся или статическим режимом.
Разность между входом y(t) = 1(0 и выходом в установившемся режиме
называется статическим отклонением или установившейся ошибкой (см. рис. 1.31);
Разность между максимальным отклонением при хп (t)^0 и статическим
отклонением, характеризующая величину так называемого перерегулирования,
представляет собой динамическое отклонение. Время, по истечении которого динамическое
отклонение, порожденное наличием д:п \t) Ф 0, становится и далее остается меньше
некоторой заданной малой величины, представляет собой время управления Ту .
Часто говорят, что время управления Ту (или, что то же - время затухания хп (t))
характеризует быстродействие автоматической системы: чем меньше время
затухания хп (t), тем более быстродействующей является система.
Система, у которой статическое отклонение (ошибка в установившемся
состоянии) e(f)*O при y(t) = l(t), называется статической.
Система,у которой статическое отклонение e(f)sO при y(t)-\(t), называется
астатической.
Для статической системы характерно следующее [161]:
1) равновесие системы имеет место при различных значениях регулируемой
величины x(t) (отработка входа с ошибкой);
2) контур управления состоит из статических (безынерционных) звеньев,
реализующих безынерционное преобразование
^вых(0=/кх(0). ^ (1.78)
Для астатической системы равновесие системы достигается при единственном
значении выхода, когда x(t) = y(t) (отработка входа без ошибки). Любое воздействие,
поданное на систему, вызывает в ней динамический режим, по окончании которого
система переходит в новое установившееся состояние. При статическом отклонении,
не равном нулю, можно выделить следующие типы переходных процессов (они
определяются составляющей xn(t)) (рис. 1.33) [161]: колебательные (кривая 1), в
которых имеет место два и более число перерегулирований; малоколебательные (кривая
2), в которых число перерегулирований равно единице; без перерегулирования
(кривая 3), в которых x(t)<x(oo) для всех te [0,«>); монотонные (кривая 4),
характеризующиеся тем, что скорость изменения выхода не меняет знака в течение всего
времени Ту.
Глава 1. Линейные одномерные непрерывные стационарные сау
jj
0
i
/-
/ 1
^ 4
/ А
Рис. 1.ЭЭ. Основные типы переходных процессов
Реакция системы на единичное ступенчатое воздействие y(t) = 1(0 при нулевых
начальных условиях называется переходной характеристикой (ПХ) системы (для
нее существует специальное обозначение h(t)).
Приведем основные параметры ПХ (рис. 1.34) [153, 161]:
но1
flyer
/
Лтах2/
1
1 Т
/
•/max
\;
\
\
Т
/ V
/
1 / 2А
t
Рнс. 1.34. Переходная характеристика системы
• время управления Ту (время переходного процесса) - минимальное время, по
истечении которого выходная величина будет оставаться близкой к
установившемуся значению с заданной точностью
t)-h
уст
<А \ft>TD;
• перерегулирование с, %, определяется выражением
К
a=kmaxl ^уст100%;
►уСТ
в реальных системах обычно
а = (10-30)%,
но в некоторых случаях допускается до 70 %;
• статическое отклонение
(1.79)
(1.80)
(1.81)
(1.82)
ЪЬ Анализ и статистическая динамика САУ. Часть I
• частота колебаний процесса h(t)
© = —, (1.83)
где Т- период колебаний;
• время установления Тн - абсцисса точки пересечения с уровнем
установившегося значения hyCT (иногда Гн называют временем нарастания);
• декремент затухания
«=Ь=^Ц; (1.84)
Р*тах2"~Луст|
• число колебаний п (число максимумов hit)).
При анализе систем рассчитывают параметры ПХ и делают вывод о качестве
работы системы.
При синтезе систем обычно задаются допустимыми значениями параметров
переходной характеристики, например
с<сД0П; Ту <Гудоп; ж< хдоп. (1.85)
1.4. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ
СИСТЕМ: ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ СИСТЕМЫ
Ранее уже отмечалось, что если известны изображения входа Y(s) и передаточная
функция W(s), то по формуле (1.27) можно найти изображение выхода, а путем
обратного преобразования - и сам выходной процесс.
Таким образом, передаточная функция полностью характеризует динамические
свойства системы (при нулевых начальных условиях).
Введем понятие дельта-функции 8(0.
Дельта-функцией называется функция, которая обладает следующими
свойствами:
8(0 = |Г ПРИ' = °; Ь(0А = 1. (1.86)
w [0 при г * 0, ^ w
Иногда 8(0 вводят как производную от единичной функции 1(0, т.е.
в(0-1'(0«|1(0- (1-87)
Дельта-функция имеет производные любого порядка. Поскольку L{l(r)} = l/s , то,
учитывая (1.87), имеем L{8(0} = 1, т.е. изображением 8(0 является единица.
Теперь найдем изображение выхода, если входом является 8(0 - дельта-функция.
Реакцию САУ на единичное импульсное воздействие, т.е. на 8(0 на входе при
нулевых начальных условиях называют импульсной переходной или весовой функцией
(ИПФ) системы K(t).
Найдем изображение ИПФ
L{k(t)} = W(s)L{8(t)} = W(sy\ = W(s). (1.88)
Отсюда следует важный факт: передаточная функция равна изображению по
Лапласу от ИПФ и соответственно
k(t) = I7l{w(s)}. (1.89)
Глава 1. Линейные одномерные непрерывные стационарные САУ
57
ИПФ, как и передаточная функция, является исчерпывающей характеристикой
САУ при нулевых начальных условиях. ИПФ имеет вид, представленный на рис. 1.35.
Рис. 135. ИПФ системы
Найдем соотношение, связывающее входной сигнал y(t)9 выходной процесс x(t) и
ИПФ.
Имеем
Г'{Х(.)}=Г1{И'(5)У(5)}. (1.90)
Зависимость (1.90) представляет собой изображение вынужденного сигнала
системы; формула для вынужденного процесса во временной области имеет вид:
x(t) = jk(T)y(t-x)dT = k(t)*y(t). (1.91)
о
Эта формула, как и зависимость (1.90), справедлива при нулевых начальных
условиях.
Изложим алгоритм построения fc(f-x) по известному ДУ системы вида
Х«,*(У) = Я').
v=0
учитывая, что с математической точки зрения к (г - х) - это решение однородного ДУ
E<VC(V)=O
v=0
при следующих начальных условиях
*r>(,-x)|f=T=i.
Найдем частное решение (1.92) для любого те [0;Г] по формуле
*(f-x) = q (x)Xl(t)^c2 (т)х2(г)+... + сЛтК(0>
где xk(t), к = 1,п - фундаментальная система.
Пусть
В (X) = Хп + ап^Хп~1 +...+а{Х + а0 = 0
4 Зак. 232
(1.92)
(1.93)
58
Анализ и статистическая динамика САУ. Часть I
- характеристическое уравнение ДУ (1.92), А,,,А,2,...,А.П т- корни характеристического
уравнения (простые, кратных нет). Тогда фундаментальная система имеет вид
ф(') = {** (0яе**': * = Ц-. (1-94)
Поскольку /fc,v(f-xM =0, v = 0,>i-2; ^"""(f-x)! =1, то общая формула для
расчета с„ (т) запишется так
х,(х) *j(t)
*,'(х) д£(т)
дГ>(х) д^>(т)
v(«-l)
(х)
С2(х)
=
'(Г
0
1
Но т.к.
*(0-fc(0-eV: * = 1>4
то система имеет вид
«Л*
рХ2х
А,т
Х.е^ \гех*
А..е*-Т
=
0
1
(1.95)
(1.96)
(1.97)
Или
Х(«-1)еХ,т X(2«-DeM ... х<«-1)еХ,.т
с, (т)ех'т + с2 (т)еХ2Т +... +'с„ (т)Лт = 0;
с, (т)*,^'+с2 (т)Х2е^т + ...+с„ (т)А.„Лт =0;
(1.98)
с, (x)A.rV'T+с2 (т)Г2-2^ + ...+ся (т)ХГ2**"* = 0;
с, (х)ЛГ'ех'т + с2 (т) А.Г1 вХгТ + -+с„ (х)^'1 Лт = 1.
Для решения этой системы уравнений умножим предпоследнее уравнение на Х„ и
вычтем из последнего. Этим мы исключим из последнего уравнения неизвестную
с„(х). И вообще, если мы вычтем по очереди из каждого последующего уравнения
предыдущее, умноженное на Х„, то мы исключим с„(х) из всех уравнений, начиная со
второго. В результате получим систему (и - 1) уравнений. Далее исключается
неизвестная с„. i(x), ся_2(х),..., с2(т). В результате получим следующие зависимости
(после некоторых преобразований)
^•щ^-^-щ^*" С"(Т)-^ГЧ
Г^ех"=У—1^('-т>
Таким образом, ядро
к=\ Ы\В\Кк) k=\ti КАк)
Напомним структуру фундаментальной системы (имеются кратные корни):
(1-99)
(1.100)
5'
.5'
Глава L Линейные одномерные непрерывные стационарные САУ
59
Тогда, используя предыдущие рассуждения, получаем зависимость
-1У-
где
(1.101)
(1.102)
lx=xA
Можно рассуждать и следующим образом. Поскольку av= const, v = 0,n-l;
йл 2= 1, то имеет место следующая зависимость
*(6)-сЛ(5)+ад(5)+-.-+^л(§). (I-"»)
где § =ь t - х (положим t« 0), причем
*(«U a *4 (§)U - - - kt2) («U - о; *Г (^,=o=! • (U04)
Постоянные ci, c^ . • •♦ сй определяются из системы
Г 1 1 - 1 ^
}2 л2
Aj A2
Л1
л-1 л л-1
.» х\
п-1
(1.105)
Если Xi,X2,..'.,XK - простые корни, то q =l/B'(Xt). Отсюда имеем
Так как ^ = г - т, то можно записать общее выражение для k(t - х)
*(*-х)-х
- 1 AM
Расчетная формула для построения вынужденных колебаний имеет вид
0 t=lB \Kk) 0 *=1
(1.106)
(1.107)
(1.108)
(1.109)
Интегральное соотношение (1-91) называют интегралом свертки или
интегралом Дюамеля. Для него справедливы следующие основные свойства:
коммутативный закон f\{t)*f2(i) = f2(t)*fl{t)9 т.е.
J/iW/2(^xyT = f/2(x)/1(r-x)Jx; (1.110)
о о
ассоциативный закон
/1(0*[/2(')*/з(0]=[/|(0*/2(0]*/з(0; ' а-»"
дистрибутивный закон
4*
60
Анализ и статистическая динамика САУ. Часть I
М*)*Ш*)+М*)]=Ш*М*)+М*)*М*)- (1Л12)
Графическое представление свертки входного сигнала y(t) и ИПФ к(х) изображено
на рис. 1.36.
i
со
(2)
/—-\
(?)
©
©
©
©
©
y(t) t
y(t) т
у(х)
у(т) т —.
}*(»,-т)у(х
0
1
)dx = x(tl)-
*(т:
--—■
/
Ц
т)
*(
— ■ ■—
t
т
т
ti-T)y(x)
Рис. 1.36. Графическое изображение свертки
Найдем связь между ИПФ и ПХ. Имеем
H(s) = W(s)i.
(1.113)
Отсюда находим
sH(s) = W(s). (1.114)
Так как при нулевых начальных условиях умножению изображения на s
соответствует дифференцирование в области времени, то из (1.114) следует
Л(0 = *(0- О-115)
Пример 1.5. Рассмотрим RLC-цепочку (рис. 1.37).
L R
-О
Уравнение цепочки
или стандартная форма записи
Рис. 1.Э7. Схема tfLC-цепочки
LCx' + RCx' + x = Ky(t),
T2x" + 2Tfy' + x = Ky(t),
Глава 1. Линейные одномерные непрерывные стационарные САУ 61_
причем Г = yfLC; \ = R>fc/2yfL , где Г - постоянная времени цепочки; £ - коэффициент демпфирования;
К - коэффициент усиления.
Входные данные: Г = 0,3; 5 = 0,2; К = 1; y(f) = 4e~2t cos8f. Необходимо записать выражение для
вынужденного колебания на выходе системы в форме интеграла свертки.
1). Характеристическое уравнение
5(Х) = Х2+1,ЗЗХ +11,11 = 0.
2). Корни уравнения определяются формулой
Ч, - ~2П*У -4Г2 --I*^Д Ч, -0.6666. Д2659 ■
3). Построение ИПФ: имеем Я'(Л) = 2А,+ 1,33, тогда
*w=^eX"+ifeeX!l=0-304e"a6666'sin3'2659i-
4). Выходной сигнал определяется зависимостью
t
X(t) =4-a304je-0'6666(/"T)sin3,2659(/-T)e-2Tcos8Ti/T.
о
Рассмотрим уравнение вида
jc' + jc = 1(0.
Входные данные: Г= 1; § = 0; y(t) = l(f).
1). Характеристическое уравнение X2 +1 = 0.
2). Корни уравнения X, 2 = ±У .
3). Таккак Я(Х) = Х2 + 1,то В'(\) = 2\ . Поскольку B'(+j) = 2j; B'(-j) = -2j,то
= — i/(cosr + ;sinr) + -./(cosr-i/sinr) = sinr.
4). Выходной сигнал, выраженный через ИПФ системы
x(t) = f sin (r - i)l(x)dx = f [sinf cost - cosrsinxjl (x)di.
0 • 0
Изложим второй подход, использующий фундаментальную систему. Так как Xl = j\ X2 = ~j ~ корни
характеристического уравнения, которым соответствуют следующие элементы фундаментальной системы:
jcj(/) = cosr, Jt2(f) = sin/,TO
k(t-z) = cl(x)xl(t) + c2(z)x2(t).
Составим систему алгебраических уравнений
с{ (x)cosx + c2 (x)sinT = 0;
-c1(x)sint + c2(T)cosT = l.
Отсюда находим
cosx sinxyc^xJ^fO
-sinx cosxllc2(x
A,(x)=
0 sinx
1 cosx
= -sinx; A2(x) =
cosx 0
-sinx 1
Отсюда
, v sinx . / ч cosx
c1(x) = = z—= -smx; c2(x) = = cosx.
1V ; cos2x + sin2x 2V ; 1
ИПФ определяется соотношением
fc(f-x) = -sinxcosf + cosxsinf .
Рассмотрим уравнение вида x"+x'+x = \(t), дс(О) = О, дс'(О) = О . Входные данные: Т = 1;> § = 0,5 ;
У (О = Н0.
JS2 Анализ и статистическая динамика САУ, Часть I
1). Характеристическоеуравнение Я(А,) = А,2+А- + 1я0.
2). Корни характеристического уравнения А,12 = -1/2 ± /V5/2.
3). Построим ИПФ; учитывая, что
B'(\) = 2\ + U
имеем
k(Л = _* e(-i/2+7V3/2)/—1 е(-1/2-у>/з/2)/ =
W ;7з % 7V3
= 1 /e(-l/2+;V3/2)r+ 1 /е(-1/2-Ул/3/2)г ^ 2 -^6inTf t
Тз-7 7зу л
4). Вынужденный сигнал на выходе системы имеет вид
*(O-J^'^rin^(i-t)l(T)rff.
1.5. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ
СИСТЕМ: ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМЫ
При рассмотрении вынужденных колебаний систем при подаче на вход
гармонических колебаний важную роль играют частотные характеристики, Их роль особенно
заметна при исследовании устойчивости, а также при синтезе корректирующих
устройств (регуляторов). Особую роль при разработке частотных методов сыграл
В.В. Солодовников [153].
Передаточная функция W(s) определяется зависимостью:
]k(ty*<h = ]k(t)e-"t-*"dt*W(s). ' (1.И6)
о о
Пусть k(t) абсолютно интегрируема, тогда можно записать (можно положить
ст = 0)
|*(r)e->'^ = W(;(o) = |M, (U17)
где
X(ja) = ]x(tyjmdt
о
- одностороннее преобразование Фурье выхода;
Y{ja) = ]y(t)t-*»dt
О
- одностороннее преобразование Фурье входа.
Выражение (1.117) запишем так:
■^H'Wl'r-'gp*»- «-us,
Глава 1. Линейные одномерные непрерывные стационарные САУ 63^
Обозначим | W (усо) | = А (со); | X (усо) | = Ах (ш); | Y (jw) | = Ау (со) - модули
соответствующих функций.
Тогда
Теперь можно записать
АН=7Т^; Ф(а))=ФлН-фЛ(0)- (112°)
Если
ап(7а))п+ап.,(уа)Г'+...+а0 с(а>)+#(а>) (j ^
c2((o)+d2((o)
то
A(o)) = Jp2(o))+G2(co); (1.122)
9((o) = arctg
"СИ"
(1.123)
P(O))J
Дадим некоторые определения.
Комплекснозначная функция JV(J(ui) называется комплексной частотной
характеристикой системы (КЧХ) или ймплитудно-фазовой, частотной характеристикой
(АФЧХилиАФХ).
Функции Р((О) и Q((O) называются соответственно действительной и мнимой
частотными характеристиками.
Функции А((й) и ф((0), определяемые зависимостями (1.122) и (1.123), называются
соответственно амплитудно-частотной (АЧХ) и фазочастотной (ФЧХ)
характеристиками.
На рис. 1.38 представлены типовые АЧХ и ФЧХ системы.
Частотные характеристики определяются следующими показателями:
• показатель колебательности М = Amax(co)/A(0) (этот показатель характеризует
склонность системы к колебаниям; чем выше М, тем менее качественна систе-1
ма; как правило, в реальных системах 1,1 < М < 1,5);
• резонансная частота сор (частота, при которой АЧХ имеет максимум; на этой
частоте гармонические колебания имеют наибольшее усиление);
• полоса пропускания системы (интервал от со = 0 до Сйо, при котором
выполняется условие
А(ооь)£0,707А(0); (1.124)
• частота среза соСр - частота, при которой АЧХ системы принимает значение,
равное А(0),т.е.
д(соср) = Д(О) (1.125)
(на рис. 1.38 условно принято А(0) = 1).
Частота среза косвенно характеризует длительность переходного процесса;
справедливо соотношение
64
Анализ и статистическая динамика САУ. Часть I
Гу«0 + 2>
271
(О,
(1.126)
ср
А(со)
0,707Д(0)
ф(со)
Авах(СО)
> А(0)
АЧХ
О)р О)ср ш0
(О
Рис. 1.38. АЧХ и ФЧХ системы
Таким образом, можно сделать важный вывод: чем шире полоса пропускания, тем
система является более быстродействующей.
Если же полоса пропускания является постоянной для всех частот на (-<»,+<»)
(рис. 1.39), и, следовательно, 0)ср = «>, то система является безынерционной, у
которой Ту = 0. Этот вывод следует из формулы (1.126). Поскольку система с
бесконечной полосой пропускания (рис. 1.39) безынерционна, то ИПФ такой системы равна
8(0, а ПХ равна l(t) (т.е. входные сигналы отрабатываются без искажения).
Далее рассмотрим закон преобразования гармонических сигналов линейными
системами, имеющими А(со) - АЧХ и ф((о) - ФЧХ (рис. 1.40).
А(ш)
-О) +0)
Рис. 1.39. Бесконечная полоса пропускания системы
Глава 1. Линейные одномерные непрерывные стационарные САУ 65
y(t) = y0cos
Gty
W(jto) = А((й)еМ(й)
*«-?
-►
Рис. 1.40. Преобразование гармонических сигналов
Имеем (рассматриваем установившийся режим работы системы, для чего верхний
предел интегрирования берется равным <*>)
у(0=л—Y'—'
тогда
х(0 = /*(т)у(^т)Л = ^/*(т)[еЛ(«)+е-^м>]л =
о о
= ^e^Jit(x)e-^Tdx+^e-^Jit(x)e^Tdx =
2 о 2 о
= у0А((00)^—| +)ИМ j = (».127)
* / \С С ТС С
= )ИЫ 2 =
еУ(оу+Ф(«ь))+e-y(«v+4K«b))
= Jo A (coo) = у0А (ш0 )cos (щг+ф (соь)).
. Результат имеет вид
Л:(г)=^0А((00)сО8(0)0Гтф((00)) = Л0СО8(0)0Гтф(0)0)).
Результат (1.128) можно трактовать так: если на вход системы подается косину-
соидалъный сигнал с амплитудой у& то на выходе в установившемся режиме имеет
место также косинусоидальный сигнал с той же частотой, но уже с другими
амплитудой и фазой: амплитуда выхода равна х$ = )>оА((00), а сигнал имеет сдвиг
фазы ф((00).
Полученный факт используют для экспериментального определения А(со) и ф(ш).
Для определения одной точки А(сйо) и ф((00) на вход системы надо подать
гармоническое воздействие
y(t) = y0costo0t, (1.129)
имеющее конкретную угловую частоту соо.
В результате в системе возникнет переходный процесс (имеет место составляющая
Xa(t)) и установившиеся колебания с частотой Сйо. После затухания переходного
процесса (т.е. в установившемся режиме), если система устойчива xn(t)—»0 (t—»°°), на
выходе будут иметь место установившиеся колебания с частотой (Оо, равной частоте
воздействия, но отличающиеся по амплитуде и фазе. Одна точка АЧХ (А(сйо) и ф(сйо))
определяется зависимостями
66
Анализ и статистическая динамика САУ. Часть I
1 Уо
Ф(о>о) - сдвиг фазы выходного сигнала .по отношению ко входу. Аналогично можно
построить все точки АЧХ и ФЧХ (рис. 1.41).
y(t)
Динамическая
система
или звено
x(t)
x(t)
Xq = А((Оо)уо
фЛ-ф =ф((00)
Рис. 1.41. Экспериментальное определение частотных характеристик динамической системы
(динамического звена):
а - система или звено; б - процессы на входе и выходе
Логарифмической амплитудно-частотной характеристикой (ЛАЧХ или ЛАХ)
системы называется график функции L (со) вида
L(o)) = 201gA((o) = 201g|w(;co)|, (1.130)
где ^
W(jco) = >/P2(o))+Q2((o); (1.131)
P(co) = ReW(./co); Q(v) = ImW(jv>). (1.132)
Единицей измерения является децибел. По оси абсцисс откладывается частота
0)[1/с] в логарифмическом масштабе (рис. 1.42). Равномерной единицей на оси
абсцисс является декада. Декада представляет собой промежуток, на котором значение
частоты увеличивается в 10 раз (рис. 1.42).
Частота cOq,, на которой До) пересекается с осью абсцисс, называется частотой
среза* Поскольку lgl = 0, то начало координат чаще всего берется в точке со = 1
(исключая точку (0 = 0, т.к. lgO = -«>). Таким образом, начало координат можно брать в
любой точке (в зависимости от интересующего нас диапазона частот, например:
со - 0,05, (0 = 0,1,со=1,со = 10 или другие), исключая точку со = 0. Обычно начало
координат помещают в точке со = 1.
Логарифмической фазовой частотной характеристикой (ЛФЧХили ЛФХ)
называется график зависимости ф (со) = Arg W (jco).
Глава 1» Линейные одномерные непрерывные стационарные САУ
67
Цдб] ▲
Промежуток усиления
А>1 амплитуды входного сигнала
Промежуток
ослабления
амплитуды
входного сигнала
ф[град] ^
90°
0f0l ОД оо
1 10 100 1000
«90°
со
сек]
Рис, 1.42. Логарифмические частотные характеристики
При построении логарифмической фазовой частотной характеристики отсчет
углов ф идет по оси ординат в обычном масштабе в угловых градусах. По оси
абсцисс откладывается по-прежнему частота со в логарифмическом масштабе.
Важно иметь s виду, что ось абсцисс соответствует значению А •■ 1, т.е.
прохождению амплитуды входного сигнала через звено в натуральную величину. Верхняя
полуплоскость ЛАЧХ соответствует значениям А > 1 (усиление амплитуды), а
нижняя полуплоскость - значениям А < 1 (ослабление амплитуды).
1,6. ЭЛЕМЕНТАРНЫЕ ЗВЕНЬЯ СТАЦИОНАРНЫХ СИСТЕМ
И ИХ ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ
Структурную схему системы можно представить как соединение типовых
элементарных звеньев, порядок дифференциальных уравнений которых не выше второго.
Цель настоящего параграфа - рассмотрение динамических характеристик
типовых звеньев; они строятся с использованием тех алгоритмов, которые изложены в
предыдущих параграфах,
Усилительное зэено, Уравнение звена имеет вид
*(г)-*у(О. (1.133)
Передаточная функция; имеем X(s) = KY($), откуда
Y(s)
(1.134)
68
Анализ и статистическая динамика САУ. Часть I
ИПФ: k(t) = Kb(t) = L~l{W(s)\9
ПХ: h(t) = Ux I - W(s)\ = К -1(0 .
Частотные характеристики:
КЧХ: W( ja) = К ; АЧХ: A(w) = К ; ФЧХ: ф(ш) = 0.
ЛАЧХ: L((0) = 201g*:.
Интегрирующее звено. Это звено имеет следующую передаточную функцию
(1.135)
W(s) = ±.
s
Примеры интегрирующих звеньев приведены на рис. 1.43 [153].
x(t)=e(t)
О . ^
м=т
а б
Рис. 1.43. Примеры интегрирующих звеньев:
а - электродвигатель постоянного тока; б -резервуар с входным трубопроводом
Очевидны следующие зависимости для динамических характеристик:
ИПФ имеет вид
t(0 = if-1(0;
ПХ запишется так:
h(t) = Kt. (1.137)
Графики k(t\ h(t) приведены на рис. 1.44 и 1.45.
(1.136)
КО i
К
i
КО i
К
Рис. 1.44. ИПФ интегрирующего звена
Рис. 1.45. ПХ интегрирующего звена
Построим частотные характеристики. Имеем передаточную функцию:
W(s) = -.
s
Отсюда
JL = -*L = -jL = Р(со) + jQ(co), где С(ю) = —.
7*0) (о со (о
(1.138)
Глава 1. Линейные одномерные непрерывные стационарные САУ
69
Амплитудно-фазовая характеристика W(j(o) определяется формулой
.... , ч л. л. J~
Щ/со) =— = —е 2.
усо со
При изменении частоты со от 0 до «> конец вектора W(j(u) движется по
отрицательной части мнимой оси от -«> до 0 (рис. 1.46).
со = °° Р(со)
W(ja)
Рис. 1.46. АФХ интегрирующего звена
Интегрирующее звено создаёт отставание выходного гармонического сигнала на
90° на всех частотах (рис. 1.47); амплитуда выходного сигнала уменьшается с
возрастанием частоты (рис. 1.47).
Д(со) | ФМ
-90°
СО
(О
Рис. 1.47. АЧХ и ФЧХ интегрирующего звена
АЧХ имеет вид:
А(со) = >2(со) + (22(со) = }^- =—; ф(со) = -90°.
(1.139)
со" со
Графики А(со) и ф(со) приведены на рис. 1.47.
Выражение для логарифмической частотной характеристики запишется так:
Дсо) = 20 lg А(со) = 201g— = 20 lg К - 201gco. (1.140)
со
В зависимости (1.140) - график прямой линии, поскольку Д(0) = Ко + К{ lgco, т.к.
ось абсцисс —lgco. Построим (1Д40). Имеем со = 1; тогда 201gAT — 201gl = 20lgAT.
Пусть со = 10 ; находим значение ЛАЧХ:
Z.(10) = 201g AT - 201g 10 = (lg 10 = log1010 = 1) = 201g AT -20. (1.141)
Таким образом, имеем график (рис. 1.48).
70
Анализ и статистическая динамика САУ. Часть I
201gA((o),flBi k
Наклон = - 20 дБ/дек.
(l,201g/0
Ф(со) i
0
-90°
20igX^;
0 '
,0,1
20 ^^С^
1 1 декада
1 1
[10;
"*>
0
201g£-20)
Рис. 1.48. ЛАЧХ и ЛФЧХ интегрирующего звена
Из этого рисунка видно, что при изменении частоты на одну декаду значение
ЛАЧХ изменится на - 20 дБ. Следовательно, она имеет вид прямой.
Апериодическое звено.
Дифференциальное уравнение имеет вид
a{x+aox = boy. (1.142)
Примеры апериодических звеньев представлены на рис. 1.49.
х(0=т2(0
y(t)=Px(t)
-о
Вен
тиль
x(t)=
у(О=т,(О
Рис. 1.49. Примеры апериодических звеньев:
а - электрический RC-филътр; б-резервуар с сжатым газом; в - процесс закалки детали в жидкости
Получим передаточную функцию
alsX(s) + a0X(S) = b0Y(s).
Отсюда
X(s)_ b0 _ bo/ao _ К
(1.143)
(1.144)
Y (s) a{s + a0 (ajao)s + l Ts + l
Величины КиТ соответственно называются коэффициентом усиления и
постоянной времени апериодического звена.
По известным формулам достаточно просто получить зависимости,
определяющие импульсную переходную функцию и переходную характеристику:
К —
k(t) = L-l{W(s)}=^e T,t>0;
h(t) = irll±W(s)\ = K
1-е Т
, f>0.
(1.145)
(1.146)
Глава 1. Линейные одномерные непрерывные стационарные САУ
71
Функции k(t) и h(t) изображены на рис. 1.50 и 1.51.
Ш) \ h(t) *
т
Рис. 1.50. ИПФ апериодического звена
Рис. 1.51. Переходная характеристика
апериодического звена
Найдем частотные характеристики. Имеем следующую зависимость:
К _К K(T(-jto) + l)
W(s) = -
Ts + l T/w+1 (r(jo)) + l)(r(»j(o) + l)
^-KT(j(Q) + K^ К . -КТ(й
rV+i "гУ+i jtW+i
- = P(0)) + ;Q((0).
(1.147)
АФХ апериодического звена определяется формулой
W(» =
К
Т/со+1
-yarctgr©
и имеет вид (рис. 1.52).
;Q(o>)
Рис. 1.52. АФХ апериодического звена
Выражение для АЧХ имеет вид:
А(со)
1 \(TW
К2Т2(О2
К
7' оо о-оо „! + Г2(О2=-/
+ 1)2 (Г2о2 + 1)2 Г2ш2 + 1 VrV+l
ФЧХ определяется формулой
ф(о) = AigW(j(u) = -arctgcor.
Графики А (со) и ф(со) изображены на рис. 1.53.
(1.148)
(1.149)
72
Анализ и статистическая динамика САУ. Часть I
А(<ю),
к
0
ф((0)-
0
-45°
-90°
\
\. АЧХ
со=1/г\^
О), 1/с
< ФЧХ
Рис 1.53. АЧХ и ФЧХ апериодического звена
ЛАЧХ определятся формулой
со*
201gA((o) = 201g^-201gVl + rW=201gA:-201gJl + ^r,
щ
где щ = частота сопряжения. Рассмотрим три случая:
(1.150)
1). (0« 0)!; тогда можно записать
(О
(1.151)
201gA(w) = 201g£-201gJl + ^ = 201gA:-201gl = 201g*:.
На частотах ©«(ty ЛАЧХ представляет собой прямую, параллельную оси
абсцисс.
2). со»(Of, тогда
20lg А((0) = 20lg К - 20lg—.
(1.152)
3). Рассмотрим, чему равна Цш) при (й = щ и (0 = 10(0!. Пусть (й = (д{, тогда из
(1.152) находим
201gA((01) = 201g^-201g^L = 201gAT-201gl = 201gA:.
Пусть (о = 10©!, тогда
201gA(10co1) = 201gtf-201g^- = 201gtf-201gl0 = 201g*:-20.
ЛАЧХ представлена на рис. 1.54 и рис. 1.55.
20 lg А((о) = L((0) | Прямая с наклоном
-20дБ/дек.
(1.153)
(1.154)
О)! =1/7 10(0! ^*(0, 1/С
Рис. 1.54. Приближенная (асимптотическая) ЛАЧХ апериодического звена
Глава 1. Линейные одномерные непрерывные стационарные САУ
73
Ц(й),
Ф(со),
-45°
-90°
201ёК
(й«Щ
co^l/Г
Точная L(co)
Приближ
>' (асимпто
^(0, 1/с
со, 1/с
— —
Рис. 1.55. ЛАЧХ и ЛФЧХ апериодического звена
Колебательное звено. Имеем уравнение
a2x"+alx'+a0x = b0y(t). (1.155)
Примеры звеньев, описываемых уравнением (1.155), приведены на рис. 1.56 [153].
L R
&
V
Рис. 1.56. Примеры колебательных звеньев:
а - RLC - колебательный контур; б - механическая система (т - масса, ку - коэффициент упругости
пружины, £ - коэффициент демпфирования)
Звено, описываемое уравнением (1.155), называется колебательным. Найдем ПФ;
имеем
(1.156)
a2s2X(s) + axsX(s) + aoX(s) = boY(s).
Тогда
/4
Анализ и статистическая динамика w\y. iacib i
bo
bo/ao
К
(1.157)
где
X(s)=
Y (s) a2s2+axs + a0 (a2/a0)s2+(a{/a0)s + l Г252+2£7Ъ + Г
a0 a0 a0
Параметры К,Ти% называются соответственно коэффициентом усиления,
постоянной времени и коэффициентом демпфирования (колебательности)
колебательного звена.
При различных значениях i; имеют место следующие звенья: £ = 0 -
консервативное; £>1 - апериодическое 2-го порядка; ^ 6(0,1) -колебательное звено.
Запишем выражения для ПХ и ИПФ колебательного звена (рис. 1.57 и 1.58)
-1
h{t) = Ul №s)
M-'t'-T'MH]
где
r = Vl-£2; q> = arctg(r/£).
ИПФ определяется выражением (рис. 1.57)
t(0 = ^-*^sin^r>0.
k(f) = h'(t)
/Л О
0,8
U,o
04
v,t
02
0
-0,2
-0,4
-0,6
С
г
И
I /\
Г
) 2
V
V
1
1
=0,1
25
1,5
f
У
1,0
/
(г
) i
\
т
1 1
*
Г
(1.158)
(1.159)
(1.160)
Рис. 1.57. ИПФ колебательного звена (t =— )
Частота
г
(00 = — = -
1-е
называется частотой собственных колебаний системы.
С учетом введенного определения,
Глава 1. Линейные одномерные непрерывные стационарные САУ
75
Пусть i; = 0, тогда
кг
£(0 =—е~^/т sin city, t > 0.
К 1 К
k(t) = jsmjt =—sina>of,
(1.161)
где 0)0 = 1/Г - собственная частота системы, или
jfc(f) = Кщ sino)or. (1.162)
Положим, что внешняя сила (воздействие) определяется так
y{f) = Asin(G)or+cc). (1.163)
Тогда
x{t) = jsin(co^r + а —) = At sin(Gty + ф)
- амплитуда выходного сигнала линейно растет, с ростом t и может стать сколь
угодно большой. Это явление называется резонансом. Для многих систем явление
резонанса является вредным или даже разрушительным.
Если y(t) = Asin((or + cc), и со* со0, но |(0-(00| - достаточно мало, то имеют дое-
сто колебания в форме биений.
V)
i
1 О
1,о
1 (L
1,0
1 И
1,4
1 *>
1 л
1,U
П Q
U,i5
U,D
0 ^1
П 0
u,z
i
/
/
V
1 /
/
f
/
"\
>
V-
=1,0
= 0,1
-0,
\
25
>
J
/
J
L
r
3BBB
0123456789
- t
Рис. 1.58. ИПФ колебательного звена (t = — )
T
Перейдем к рассмотрению частотных характеристик.
Найдем АФХ звена:
К К
W(j(0) =
Г2(уш)2 + 2Г£(;(0) +1 -Г2(02 + у2Г§ш+1
А:[(1-Г2(О2)-у2Г^(о]
[(-Г2о>2 +1) + у2Г£(о]+[(1 - Г2(02) - ;2Г^(о]
/и
/\нал*и и сшшничакал динамика w\.у. ~iaciь i
= K(l-T2a>2)-j2T$K(u^ £(1-Г2(О2)
(1-Г2со2)2 +4Г242Ю2 (1-Г2о2)2 + 4Г2£2со2
2Г£ЛГо>
-7
г2,.ч2ч2
■2к2/л2
(l-rV)z+ 47^(0
= Р((0) +7(2(ш).
АФХ колебательного звена представлена на рис. 1.59.
;G(to)ik
(0 = оо
tf
(О
Рис. 1.59. АФХ колебательного звена
Найдём АЧХ звена
Л(со) = V^2(co)+Q2(co) = |W(jco)| =
r(i-rV)
2^2ч2
4r2|^V
= л:
[(l-rV)2+4r4V]2 [(l-rV)2 + 4rWf
I (1-Г2ш2)2+4Г2^2о>2 ^
|[(1-7'2а)2)2+4гЧ2(02]2 7(1-Г2(О2)2+4П20)2
л:
>/[1-(а)/(о1)2]2 + 4^2(о)/(о|)2
где
(1.164)
(1.165)
со, 4
Частота ofy как в случае апериодического звена, так и в случае колебательного
звена называется сопрягающей частотой.
ФЧХ имеет вид (£е (0,1)):
ф(0)) =
^ при0)4:
2Гео$ I
-n-arctgirW,npH(O>-.
(1.166)
Графики А((о) и ф((0) изображены на рис. 1.60.
Глава 1. Линейные одномерные непрерывные стационарные САУ
77
1=0,4
Рис. 1.60. АЧХ и ФЧХ колебательного звена
Построим асимптотическую ЛАЧХ; рассмотрим несколько случаев.
1). Пусть ««(Oj; в этом случае имеем А((0)« К\ 201gA((0) = 201g£. При
со » €&!, ЛАЧХ представляет собой постоянную величину, равную 20 lg AT.
2). Если со» щ , имеем
А(<£>) = -
гаженные значения ЛАЧХ:
20lg А(со) = 20lg К - 201g( — 1 =. 201g К - 401g| — |.
Отсюда находим приближенные значения ЛАЧХ:
\2
L(G)) = 201gA(G>)
[рямая с наклоном
^Ю дБ/дек.
Ф(СО);
-90°
-180(
Рис. 1.61. Асимптотическая ЛАЧХ и ЛФЧХ колебательного звена
Возьмем две точки: (й = (й{ и (0 = 10(0!. Присело)! имеем 201gA((01) = 201g£;
при о = 10(0!
201gA(10(01) = 201gAT-401g^^ = 201g^-40.
78
Анализ и статистическая динамика САУ. Часть I
Асимптотическая ЛАЧХ при (д>(й{ представляет собой прямую с наклоном
- 40 дБ/дек. Эта ЛАЧХ представлена на рис. 1.61.
Асимптотическая ЛАЧХ не имеет значительных ошибок при 1 > £ > 0,7 ;
практически же при 0,5<£<1 можно пользоваться асимптотической ЛАЧХ; при £<0,5
необходимо учитывать «горб» (рис. 1.62). Кривые поправок представлены на
рис. 1.64.
1
Цсо),дБ
10
0
1П
-1U
-20
{
•
ш
-*-
i
{
**•
/у
1
1
\ 5=0,05
\_^0,10
л^:о,2о
^L^O0,25
«
^-0,80
Д=1,0
ч
ч
ч
ч
ч
ч
S
ОД 0,2 0,3 0,4 0,50,6 0,8 1,0 2 3 4 5 6 8 о)Г
Рис. 1.62. ЛАЧХ колебательного звена при различных значениях £
-20
-40
-60
-80
-100
-120
-140
-160
-180
Г!
Щ
о/
Ш
Ш
0,4
0,5
Г/
v
^-4=0,05
^"U,1U
_^0,15
^Z-0,20
^0,25
Is.
\^
ii
i
ш
ш
1
d
0,1 0,2 0,3 0,4 0,5 0,6 0,8 1,0 2 3 4 ' 5 6 соГ
Рис. 1.63. ЛФЧХ колебательного звена при различных значениях \
Глава 1. Линейные одномерные непрерывные стационарные САУ
79
Ят,дБ
16
12
8
-8
>
*^
-».
i
s
1
V
у
/
«*^
*ч,
ч
S
S
i>
\
S
ч
\
1—-
5=0,05
.0,10
-0,15
.0,20
,0,25
J0.3O
0,40
-0,50
"
«^
0,60
0,80
$=1,0
0,2 0,3 0,40,5 0,6 0,8 1
3 4 5 6 8 о)Г
Рис. 1.64. Кривые поправок Нт для асимптотических частотных характеристик
колебательного звеиа
Дифференцирующее звено. Передаточная функция имеет вид
W(s) = Ks. (1.167)
Импульсная переходная функция и переходная характеристика определяются
зависимостями
k{t) = Kb(t)\ А(0 = ЛГ8(0.
Частотные характеристики выражаются формулами:
W(jw) = jKw; P((0) = 0; Q(co) = £о>; А(со) = Км;
Ф(ш) = 7i/2;L((O) = 201gtf+ 201gw. (1.168)
АЧХ и ФЧХ изображены на рис. 1.65.
А(ю) ' >
ф((0)'
л/2
/л
и
(О
Рис. 1.65. Частотные характеристики дифференцирующего звена
Логарифмические частотные характеристики изображены на рис. 1.66. ЛАЧХ
дифференцирующего звена - прямая, проходящая через точку с координатами
80
Анализ и статистическая динамика САУ. Часть I
(0 = l,L((o) = 201g£ и имеющая наклон +20дБ/дек; До) увеличивается на 20 дБ
при увеличении частоты на одну декаду.
Доэ)
<р(а>)
я/2
г20 дб/дек.
Г
20\gK
0 1 а>
Рис. 1.66. Логарифмические частотные характеристики дифференцирующего звена
Запаздывающее звено. ПФ имеет вид
W(s) = Ke"s\
Очевидны следующие соотношения:
k(t) = Kb(t-i);h(t) = Kl(t-x).
АЧХ и ФЧХ определяются зависимостями
W(jv>) = Ke~Jm; А(ш) = К; ф(ш) = -сот. (1.171)
В табл. 1.2 приведены основные динамические характеристики элементарных
звеньев.
Таблица 1.2
(1.169)
(1.170)
X
Вид характеристики
Уравнение
Передаточная функция
Передаточная
характеристика h{t)
ара
I
i
ктерр
ТрОПОрь
(усилн
безыне]
jc(O
i
[стики эле
щональное
тельное,
эционное)
= *?(')
L
L
г
ме
i
нтарных звенье
Тип звена
Интегрирующее
at
1
Ts
/arctg^r r
7
i
Апериодическ
(инерционное
*
7i + l
^H |
oe
0
КО
Глава 1. Линейные одномерные непрерывные стационарные САУ
81
т
+
j
i
(
КЧХ W
АЧХ W
ФЧХ ф
Колебате
2 « X{t) ,
J А2 ''
дс(О = Ау(0
Г0У+7
/ А: 1
« * ,
(./со)
(со)
(со)
льное
5 + 1
►
L
i
i
)
х(
1
i
к
4
1
1
кр(о>)
Иде
^иффере
1-го
Г
г) = *|г
h{t)
i
it
Q)
(0 =
)
—►
i
;аль
:нци
пор
r/vff
))
> on
P((0)
CO
►
(0
Тип:
ное
рующее
ядка
4 "I
14
►
1
1
fP(co)
к
1
i
шен
i
i
\
' \<
i А(ш)
1
i
it
a.
Иде
деффере
2-го
Y(t\ _ Л./
dt
K{1OS
ih(t)
ki
k 7fi(o
JO —> <■
C0=l
Продо
>)
P«a)
to
альное
нцирующее
порядка
Г2^2У(О ,
0 *Л
dt
+ y(t))
I , 7»p ,i\
+ IS + I)
! ^
t
3)
it
i
i
q
;
(0 =
'7"Q(
^
^0):
it4
>(0))i
c\
n/
/4
^2
Sana
x(t
X
4 ►
Q(co)
M 0
ft
e mat
a»
^
= oo i
co =
здываю!
) = y(t-
e
i
к
Л
J
(0 =
л. 7.2
|P(co)
1—.
CO
►
Yt
CO
дее
•
т)
P(co)
7 Зак. 232
82
Анализ и статистическая динамика САУ. Часть 1
J
к (
ф((
-я/
/2
—1
iA
Г
(со) |
I ^"^^^»
1 Ui
1 »
1
,ф
к А((0)
/
Ш
(со)
к^
i
п/
/2
i
.Я
■-
Продо
кА«в)
1—^ (0
Ш»=Хо
>(w)
лэн
i
i
71
2
^Ф<
ч
tg
ие табл. 1.2
i A(co)
(0
:ш)
ч/а со
а = т\
1.7. НЕКОТОРЫЕ ВЫВОДЫ, ОСНОВАННЫЕ НА АНАЛИЗЕ
ЧАСТОТНОЙ И ВРЕМЕННОЙ ФОРМ ОПИСАНИЯ СИСТЕМ
Выше были получены формулы, являющиеся стержневыми в теории
стационарных систем.
Одной из таких формул является
X(ju) = W(ju)Y(j®)9 (1.172
где
Y(ju) = ]y(ty*»dt; X(jti>) = ]x(tyjl0tdt; W(jv>) = ]k(tyj™dt
0 0 0
- односторонние преобразования Фурье функций y(t), x(t) и k{t).
Если же комплекснозначные функции Х(/со), У(/(°) и W(/co) представить в показа
тельной форме
К(;ш) = Ау((0)е^(а)); X(jW) = A,(a))e;<(>»; W(y©) = А(о))е^т),
то справедливы зависимости
Л^(о)) = А((о)А),((о), ф(ю) = Фх(со)-Фу(со). (1.173
Из (1.173) следует, что модуль I X (усо) I = Ах (ш) выходного сигнала равен произ
ведению А ЧХ системы на модуль | Y (j(u) | воздействия.
Из (1.173) следует, что система изменяет спектральную характеристику на вхо
де, действуя как фильтр, изменяющий частотные составляющие.
В области, где А(со) > 1, частотные составляющие входа усиливаются по ампли
туде, на промежутке же А(ш) < 1 они ослабляются, при А(ш) = 1 частотные состав
ляющие остаются без изменения.
Подобным же образом, в соответствии с зависимостью (1.173), изменяются фазовьк
сдвиги каждой частотной составляющей сигнала при прохождении через систему.
Пример 1.6. Рассмотрим цепь (рис. 1.67).
Реакция на импульс, АЧХ и Y(j(u) представлены на рис. 1.68 - 1.70.
Глава 1. Линейные одномерные непрерывные стационарные САУ
83
10м
*—С
y(t)
1ф
**-
x(t)
Рис. 1.67. Схема цепи
X(t)
2 4
Рис. 1.68. Реакция на импульс
На рис. 1.70 показана спектральная функция входного сигнала (модуль ее очевиден).
Формула Y(j(o) может быть получена исходя из следующих соображений.
Л(со) =
-0)
-я -тт/2 я/2 п
Рис. 1.69. АЧХ системы
+0)
Y(/co)^
-0) -П
Рис. 1.70. Г(/со) входа системы
Пусть имеется функция (рис. 1.71).
П СО
84
Анализ и статистическая динамика САУ. Часть I
(1 при |г|<т/2;
y(t'~[0 при |г|>т/2.
(1.174)
-t
2
'2
т
2:
Рис. 1.71. Стробирующая функция
Найдем преобразование Фурье
У(уш)= ? e-^rfT=-i-(e-^'2-e^'z) = T^^.
' J >Vrtv ' ((ОТ/2)
(1.175)
уш, .........
Функция Y(j(u) - действительная функция; ее график представлен на рис. 1.72.
Из рисунков можно заключить, что цепочка значительно ослабляет высокочастотные составляющие
входного сигнала и почти не ослабляет низкочастотные (в области | W(y(o)|«1); в связи с этим она может
служить простейшим фильтром нижних частот.
Y(/co) -
» -tt/^S-S-
-со -nlx^s -2nl% 2я/т ^^-^ nix со
Рис. 1.72. Спектральная функция стробирующего сигнала
На рис. 1.68 представлен выход x{t)\ он представляет собой искаженную копию входа y{t). Искажения
вызваны тем, что цепь неодинаково пропускает все частотные составляющие входного сигнала. Сильно
ослабляются высокочастотные составляющие. Это проявляется в более медленном нарастании и спаде
выхода по сравнению со входом.
Рассмотрим условия неискаженной передачи сигнала. Положим, что допускается следующее: 1)
различие в амплитуде (но не в форме), т.к. важна форма, а не величина отклика; 2) выходной сигнал может
запаздывать во времени относительно входа.
Тогда
x{t)=Ky{t-%). (1.176)
Отсюда имеем
ХО'со) = W(ju)Y(j(u) = Ke-jmY(j(u). (1.177)
Следовательно, неискажающая система должна иметь передаточную функцию
*<*>-Л-м-7$-
(1.178)
АЧХ и ФЧХ неискажающей системы представлены на рис. 1.73.
Глава 1. Линейные одномерные непрерывные стационарные САУ
85
\W(j(o)\ = Kt
\
[
0
к ►
\
(О
\
ф(ю) = - ют \
Рис. 1.73. АЧХ и ФЧХ ненскажающей системы
Как следует из предыдущего, для неискаженной передачи сигнала система
должна иметь бесконечную полосу пропускания. В силу физических ограничений такую
систему создать невозможно. В действительности удовлетворительное неискаженное
преобразование можно получить в системе с ограниченной, но весьма широкой
полосой пропускания. Энергия любого физического сигнала убывает с увеличением
частоты, поэтому достаточно, чтобы система пропускала лишь те частотные
составляющие, в которых содержится наибольшая часть энергии сигнала.
Рассмотрим идеальный фильтр нижних частот; его АЧХ и ФЧХ изображены на
рис. 1.74. В идеальном фильтре частоты выше 0)ср полностью подавляются.
А((о), ф(о>) J
0
-О) -ЮСр
ф(СО) = -СОТ Х
©
Рис. 1.74. АЧХ и ФЧХ идеального фильтра нижних частот
Воспользовавшись обратным преобразованием Фурье, можно найти ИПФ
идеального фильтра нижних частот (рис. 1.75).
Как видно из рис. 1.75, ИПФ отлична от нуля при отрицательных значениях т, в
то время как 8(0 - входная единичная дельта-функция приложена в момент х = 0.
Из этого можно заключить, что реакция на импульс появляется раньше
воздействия (система как бы предвосхищает воздействие). Такие системы физически нереали-
зуемы; создать систему с предсказанием невозможно. Следовательно, идеальный
фильтр нижних частот физически нереализуем. Аналогичным образом можно
показать, что идеальные фильтры верхних частот или полосовые фильтры также
физически нереализуемы (рис. 1.76).
При решении практических задач пользуются фильтрами, характеристики
которых близки к идеальным. В качестве примера на рис. 1.77 приведен фильтр нижних
частот, а на рис. 1.78 - его АЧХ и ФЧХ.
Передаточная функция фильтра нижних частот имеет вид (рис. 1.77)
i/[(i/*)+;coc] 1
v ' j(0L+l/[(l/R)+jaC] l-co2LC + 7"(o(L/J?)
ИПФ определяется формулой
(1.179)
86
Анализ и статистическая динамика САУ. Часть I
»W-*^»*(£v).
Входная дельта-функция 8(0
ВДА
я/со.
'ср
-t
\~s
+t
Рис. 1.75. ИПФ идеального фильтра нижних частот
|W(/<o)|
N
|W(/<o)| к
Ш
т
-СО -СО,
'ср
\чсоср со
-0>о \^0)о. О)
(1.180)
ф((О) = -(ОТ ^ч ф(СО) = -СОТХ
Рис. 1.76. Частотные характеристики фильтра верхних частот и полосового фильтра
y(t)
-ЯГ
x(t)
Рис. 1.77. Принципиальная схема фильтра нижних частот
|W(/co)|,,l
Ф(со)
+71 J.
-СО
Рис. 1.78. АЧХ и ФЧХ фильтра нижних частот
Глава 1. Линейные одномерные непрерывные стационарные САУ
87
Желательно найти признак, по которому можно было бы различать физически
реализуемые и физически нереализуемые системы. Таким признаком является
критерий Пэйли - Винера. Еще раз напомним, что в физически реализуемой системе не
может иметь места реакция {отклик), начинающаяся раньше момента приложения
воздействия. Это положение известно под названием условия причинности.
Очевидно, отклик на единичный импульс в физически реализуемой системе должен быть
равен нулю при t < 0.
Ш)
In
са
ер,
Рис. 1.79. ИПФ фильтра нижних частот
Критерий Пэйли-Винера формулируется так: для физической реализуемости
системы необходимо и достаточно выполнения условия
г
|1п1У(7С0)|
1 + ОГ
<ico<«>.
(1.181)
Если АЧХ не удовлетворяет критерию Пэйли - Винера, то система имеет
непричинную ИПФ, т.е. реакцию, существующую до того, как к системе приложено
воздействие.
1.8. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ, ИМПУЛЬСНЫЕ
ПЕРЕХОДНЫЕ ФУНКЦИИ, ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
СИСТЕМ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
И С ЗАПАЗДЫВАНИЕМ
Все введенные выше понятия, а именно: понятия передаточных функций, ИПФ и
ПХ, частотных характеристик (АЧХ, ФЧХ и др.) - обобщаются на другие классы
стационарных систем: системы с запаздыванием и системы с распределенными
параметрами.
Рассмотрим класс систем с запаздыванием. Он описывается дифференциальным
уравнением (ДУ) с запаздывающим аргументом [45]
E*v*(V) + 5 V(V)('-x) = yif). (1.182)
v=0 v=0
Решение x(t) должно удовлетворять исходному ДУ при положительных значениях
аргумента t и условиям:
х(0 = §(0;*<=[-т,0];
х(0) = х0; х\0) = хх; ...; х(п-{)(О) = хп_1. (1.183)
Полагаем, что начальная функция £(0 дифференцируема т раз на отрезке [-т,0] и
х0 = 5(0); хх = £(0); ...; хт = £Г(0). (1.184)
Анализ и статистическая динамика САУ. Часть I
Введем обозначения
N(x(t)) = XavJc(v)(0;M1(^-x))= ]>>vJc(v)(f-T). . (1.185)
v=0 v=0
При этом полагаем, что п > т (уравнение принадлежит к запаздывающему или
нейтральному типу) [45]. С учетом введенных обозначений исходное ДУ запишется
так:
N(x(t)) + M{(x(i->c)) = y(t).
В [45] показано, что x(t) при известных условиях - оригинал. Поэтому сразу же,
используя этот факт, получаем
оо оо
| N{x{t))e~stdt + $MX (x(t - x))e~stdt = Y(s). (1.186)
о о
Первое слагаемое в (1.186) имеет вид
]NW)e-*A = X(s)\ X<VV -life), (1.187)
О Lv=O J
где Y{(s) - член, учитывающий ненулевые начальные условия.
Если во втором слагаемом выражения (1.186) ввести замену, то можно получить
оо оо
J Mx (x(t - T))e~s'dt = j M, (x(u))e-siu+x)du =
-Т
'О со "I
J Mx{x{u)e-sudu + \Mx{x{u))e-sudu . (1.188)
L-т 0 J
Или, что то же самое,
оо
JM{(x(t-T))e-s'dt =
о
f Г
-sx
= е-"\Х(з)\ УЬ/ -ВД+ M^uW'du}. (1.189)
Г т 1 О
Lv=O J -т
;ависимостей можь
[\ v=0 J \ v=0
На основе полученных зависимостей можно записать:
oV \p'SX
Vs \е
= Y(s) + Yi(s) + e-*tY2(s)+e-tv J М(£,(и))е~*Чи. (1.190)
-X
Вводя обозначения
R(s) = | %avsv ]+[ £ VV V". *(*) = ^(5)+е-ЛУ2(5),
0
(f{s) = e-sx\M{U.u))e~sudu, (1.191)
получим зависимость, определяющую изображение выходного сигнала
ф(,)+ф(,)
Глава 1. Линейные одномерные непрерывные стационарные САУ 89^
Положим, что Yx(s) = 0, Y2(s) = 0, (p(s) = 0. Тогда имеет место зависимость
X(s) = W(s)Y(s),
где W(s) = l/R(s). Обозначим k(t) = L"1 {W(s)}.
Функции W(s) и k{t) называются соответственно передаточной функцией и ИПФ
стационарной системы с запаздыванием.
Частотные характеристики определены теми же зависимостями, что и ДУ систем
без запаздывания.
Если САУ с запаздыванием описывается ДУ с переменными коэффициентами, то
имеют место динамические характеристики, введённые в параграфе.
Далее рассмотрим класс систем с распределенными параметрами [87]
d2x(z,t) , д2хЩ) , d2x(z,t) ,
дг dz otdz
dx(z,t) dx(z,t) / v / v „ ,л^ч
+al-\^ + a2—^-+ax(z,t) = y(z,t). /1.193)
ot dz
Пусть
D = ^-aua22: (1.194)
4
Уравнение (1.193) называется уравнением гиперболического типа, если D > 0;
эллиптического типа, если D < 0; параболического типа, если D = 0 .
Как будет видно из дальнейшего изложения, операционный метод можно
применить лишь для построения решений уравнений гиперболического и параболического
типа, т.е. когда D > 0 или D = 0; зададим условия:
начальные
*(z,O|,=o = *o(z); *)(z.O|,-o = *i(z); (1.195)
краевые
x(z,0|z=o = Л(0; *(z,0|zw = ЗЪ('). (1.196)
Краевые условия часто задаются в виде обыкновенных ДУ, которым должны
удовлетворять функция x(z, t) и ее частная производная dx(z,t)/dz при z = 0 и z = /
(0<z</).
В форме изображений краевые условия можно задать так:
X(0,5) + Gl(^)^^|2=0=G2(5); (1.197)
Х(19*) + С3(5)4Щ^\Ы =G4(j), (1.198)
«г
где G^(^) - известные функции (к = 1,2,3,4).
Рассмотрим более подробно случай (1.196). Предположим, что существуют
изображения от функций
Эх(г,0 d2x(z,t)
dz ' Эг
Преобразуя по Лапласу обе части уравнения, запишем
an[x(z,s)s2-sx(z,0)-x\z,0)y
d2X(z,s) Э
dz oz
6 Зак. 232
x(z,t), ^^, ^F- d-199)
+ои *а +ei2J:[xu.*)*-*U.0)]+
jH) Анализ и статистическая динамика САУ. Часть I
+ai[sX(z,s)-x(z,O)] + a2$?^- + aX(z,s) = Y(z9s). (1.200)
oz
В полученном уравнении дифференцирование X(z, s) производится только по
одной переменной z\ это позволяет знак частной производной заменить на знак полной
производной. Производя соответствующую группировку, запишем последнее
уравнение в более удобной форме
d2X(z,s) , sdX(z,s) , 2 ' 4V/ ч
а22 71~^ + (fli2^ + a2)—3— + (flu* +<V + a)X(z,*) =
* & (1.201)
= jc(z,O)(flnj + fl1) + xi(z,O)fl11+e12^i^ + y(z,j).
Уравнение (1.201) представляет собой обыкновенное ДУ второго порядка
относительно изображения искомой функции X(z, s). Его коэффициенты не зависят от
переменной z, поэтому оно является неоднородным уравнением с постоянными
коэффициентами.
Для его решения можно применить любой известный метод: например, частное
решение неоднородного уравнения можно найти методом Коши, а общее решение
однородного - методом Эйлера. Найдем функции фундаментальной системы.
Из характеристического уравнения
a22k2(s) + (al2s + a2)X(s) + (ans2 + ans + a) = 0 (1.202)
получим
Xl 2 W = ■fa£±gL±JS±gtY-faiija+aiJ + al. (1.203)
2a22 ^ 2a22 J [ a22 J
Теперь можно записать общее решение неоднородного уравнения
X(z,s) = С^е^1 +С2(5)/2(1)г + X0(z,s). (1.204)
Постоянные Cj(5) и C2(s) можно найти, если воспользоваться краевыми
условиями. Это дает возможность записать
Х0(0,5) + С,(5) + С2(5) = К1(5);
XO(U) + C,(V«(1)/ + C2(5)/2W/ =Y2(s),
отсюда
qw- ^ *.„уг.е>--. 21,,
(1.206)
^,WI _/2(^)' lV ; /i(*)' _/гй)'
X0(l,s)-X0(l,s)e^(s)l _
e\{s)l _eX2(s)l
'2
*Ms)l v,_, Y2(s)
* e e * (1207)
X0(l,s)-X0(0,s)eX>Ml
Подставив два последних равенства в зависимость (1.204), получим
X(z,s) = Wl(z,s)Yl(s)+W2(z,s)Y2(s) + W3(z,s), (1.208)
где
Глава 1. Линейные одномерные непрерывные стационарные САУ 91_
W>(z'S)=eW_eW> (L209)
^i(^)z_^A.2(5)z
У3и^) = Х0(г,5)-^|(1у_^(1)/У0(/,5) +
e\{s)ze\2{s)l _eX2{s)ze\{s)l
В предыдущих формулах X0(z,s) - частное решение неоднородного ДУ, оно
зависит от начальных условий и от правой части ДУ (1.201).
Если Y(z, s) = 0, а также имеют место нулевые начальные условия, то выражение
для изображения выходного сигнала имеет вид [87]
X(z9s) = Wl(z9s)Yl(s) + W2(z9s)Y2(s). (1.210)
Анализируя зависимости (1.208), (1.209) и (1.210), легко заключить, что в случае
систем с распределенными параметрами передаточные функции W{(z,s) и W2(z,s)
являются трансцендентными (в отличие от дробно-рациональных для систем с
сосредоточенными параметрами).
Для обращения трансцендентных изображений неприменима вторая теорема
разложения и построение оригинала встречает трудно преодолимые проблемы (в
качестве особых точек изображения (1.210) могут быть точки разветвления, существенно
особые точки и т.д.).
В связи со сказанным выше, разработаны численные методы обращения
трансцендентных изображений [4].
Все выводы, полученные для систем с сосредоточенными параметрами,
справедливы и для систем с распределенными параметрами и запаздыванием. Приведем
соответствующие формулы.
Частотные характеристики определяются выражениями Wj(z,y(o), W2(z,j(O),
A(z,(0) = |W1(z,7(0)|, A2(zM = \W2(zJo»\ ит.д.
ЕслиИ^(г,.у) = 0, то интеграл Дюамеля запишется так (он определяет
вынужденные колебания)
t t
J<Z,0 = J*i(z,T)yia«T)£/T + Jt2(z,T)y2fr"T)£/T> (1.211)
о о
где kx(z,i) и k2(z,i) -ИПФ системы.
Свободные колебания определяются членом W3(z,t).
Установившиеся колебания находят по формуле
оо со
x(z9t) = lkl(z,T)yl(t-x)dx + jk2(z^)y2(t'T)dx. (1.212)
о о
Если коэффициенты уравнения (1.212) зависят от времени (рассматривается
нестационарная система с распределенными параметрами), то выходной сигнал
определяется интегральным соотношением
t t
л(г,0 = /*1(г.^.т)л(т)^т+/*2(г,г,т)у2(т)Л (1.213)
о о
Для нестационарных систем с распределёнными параметрами можно ввести в
рассмотрение параметрические передаточные функции
б*
92 Анализ и статистическая динамика САУ. Часть I
О
W2(s9t9z) = jk2(z,t9x)e-si"*)dT.
о
Тогда
X(s9t,z) = Wx(sj9z)Y{(s) + W2(s^z)Y2(s). (1.214)
Пользоваться приведёнными выше формулами чрезвычайно сложно.
1.9. ИССЛЕДОВАНИЕ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ: ПОСТАНОВКА ЗАДАЧИ
Далее изложены как общие положения, связанные с исследованием САУ, так и
конкретные пути решения задач устойчивости *.
Рассмотрим систему (рис. 1.80).
y(t)
Рис. 1.80. Структурная схема системы
Положим, что при г = 0, т.е. в момент подачи входного сигнала y(t), система
имела ненулевые начальные условия
Х° =(*(0),*'(0) *("-'> (0))*0. (1.215)
Воздействие, поданное при t = 0, имеет преобразование Лапласа
Y(sU с***+с*-/~1+- + 3) . (1.216)
V ' dpsP+dp.ls"-l+... + d0
Тогда изображение выходного сигнала запишется в форме
X
(bmsm+... + b0)(cksk+... + c0) ^
(S)=(ans^^ao)(dps^.^dof (i2i7)
|^(о)^(5)+-+^<в"1)(о)д-1(5)>ст1:л
ansn+an_lsn-l+... + a0
Запишем формулу для выхода, для чего найдем корни уравнений
Vw+^_1^-1+... + a0=0 и dpsp+dp_{sp-l+... + d0=0. (1.218)
Положим, что A.J, Х2, ... Ал - корни первого уравнения (характеристического
уравнения системы), a al9 a2, ... ,ар - корни второго уравнения (полюса
изображения воздействия).
Запишем изображение выхода и соответствующий этому изображению сигнал, но
таким образом, чтобы была ясность в отношении появления каждой из составляющих
выхода (формулы (1.219) и (1.220)):
Методы расчета выходных сигналов рассмотрены в главе 8.-
Глава 1. Линейные одномерные непрерывные стационарные САУ 93^
x{s)= 8m+ks""k+... + g0
(v-+...+*)(</,,'+...+«,) (i2i9)
ix(0)DQ(s)+... + x(n-i\Q)Dn_l(s)_
ansn+an_1s"-i+... + a0
x(t) = c?ex< + ...+c>X"' + c,yea'' + ... + c*A' +
+с^х'Ч... + с„сЛ'
*(') *,(.) (L220)
*c(<)
Таким образом, имеем
x(t) = xn (t)+xy(t) + xc(t), (1.221)
где xa(t) - сигнал, порожденный полюсами передаточной функции системы (он
характеризует динамические свойства системы в переходном режиме); xy(t) -
сигнал, порожденный полюсами изображения; xc(t) - сигнал, порожденный
ненулевыми начальными условиями и определяемый через полюса системы.
Сигнал хП (/) называется переходной составляющей при отработке воздействия
Сигнал xy(t) называется установившейся составляющей при отработке
воздействия у(г).
Определение хс (t) было дано выше (этот сигнал носит название свободных
колебаний системы).
Положим, что входной сигнал имеет вид (он является оригиналом функции Y(s)):
Y(s)=CkSk+- + C° ; (1.222)
V ' dps"+... + d0
y{t) = clea>' +clea* +...+c3pea-'. (1.223)
Теперь можно записать выражения для сигналов y(t) и x{t) в явной форме:
у(1) = с\еа<+с\еа*+... + греа>'
- входной сигнал;
x{t) = с\е^ +...+Су>' + с?ех>' +...+с^Л' + с,с/'' +... + с'Л'
- выходной сигнал.
Сравнивая две последние зависимости, легко записать условия неискаженного
воспроизведения сигнала:
*п(0 = 0; (1.224)
xc(t) = O; (1.225)
cj=cf, i = T^. (1.226)
Эти условия достижимы лишь в статических {безынерционных) системах.
В динамических системах, описываемых дифференциальными уравнениями,
указанные условия достижимы лишь в установившемся режиме.
94
Анализ и статистическая динамика САУ. Часть I
Например, условиями неискаженного воспроизведения входного сигнала y(t) в
установившемся режиме являются
хП(t) = с?ех'' + ...+сУ '-*" )0; (1.227)
хс (t) = с,сЛ +... + сс„ех"' '-*" ) 0; (1.228)
cf=cf, 4=4,...,cl=c;. (1.229)
Легко заметить, что если xn (t)—*~*°° )0, то с течением времени хс (f) также
будет затухать (и наоборот).
Третье условие (1.229) в реальных системах в общем случае не выполняется,
поэтому системы проектируют таким образом, чтобы лгп (г) и хс (г) достаточно быстро
затухали, а с? не сильно отличалось от с?, i = l,p.
Однако для ряда входных сигналов можно обеспечить точное выполнение всех
условий.
Например, если y(t) = l(t) и Х°=0, то условиями точного воспроизведения
входа в установившемся режиме являются (рис. 1.81):
а) ReX, <0, / = 1,л ;
б) в прямой цепи включен один интегратор.
6(0 = 0 точное
воспроизведение
входа y(t)
Установившийся
режим
Рис. 1.81. Отработка ступенчатого воздействия
Приведем еще один пример. Если y(t)=yxt, то условиями точного
воспроизведения этого воздействия являются (рис. 1.82):
а) ReX, <0, i = l,л ;
б) в прямой цепи включены два интегратора.
Если же y(t) = у0 + y2t2 , то условиями точного воспроизведения входа являются:
а) ReX,<0;
б) в прямой цепи включены три интегратора.
Приведем несколько фактов, связанных с одновременным достижением условий
а) и б). Как правило, одновременное достижение условий связано с определенными
трудностями. Поэтому на практике ограничиваются одним-двумя интеграторами.
В связи с этим, в общем случае, когда сигнал, например, имеет вид
y(t) = yo + yxt + y2t2+... + yitl, (1.230)
одновременное выполнение условий а) и б) недостижимо.
Глава 1. Линейные одномерные непрерывные стационарные САУ
95
к
x(t)
ЭКС1
/
L
^^
тонента ^
синусоида
1 е(0 ^0 точное
воспроизведение
входа Х0
** Установившийся
режим
►
Рис. 1.82. Отработка воздействия .у(0 -уit
Приведем два определения:
Ошибка системы, определяемая формулой
е(0 = у(0--*1.(0-^(0-*у(0 d-231)
(при условии, что ^п(0 и *с(0 не затухли), называется переходной ошибкой.
Ошибка системы, определяемая формулой
s{t)=y(t)-xy(t) (1.232)
(при условии, что *n(f) и xc(t) затухли), называется установившейся ошибкой.
А теперь обратимся к формулировке задач анализа:
1) нахождение необходимых и достаточных условий затухания составляющих
xn(t) и хс (г) (анализ устойчивости системы);
2) изучение поведения системы в переходном режиме, когда xn(t) и хс(t) не
затухли (построение переходных процессов и переходных ошибок системы);
3) изучение поведения системы в установившемся режиме, когда xn(t) и xc(t)
затухли (анализ точности в установившемся режиме).
1.10. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ
ОДНОМЕРНЫХ СИСТЕМ. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ
УСЛОВИЯ
Понятие устойчивости является одним из центральных в теории систем.
Система управления постоянно подвергается возмущениям, отклоняющим ее от
заданного закона движения. Действие возмущения сопровождается
восстанавливающим действием регулятора. В системе возникает переходный процесс. Может
оказаться, что система не сможет восстановить требуемый закон движения. Она
будет либо удаляться от желаемого состояния, либо совершать вокруг него
незатухающие колебания. Возможные виды переходных процессов для устойчивой системы
приведены на рис. 1.83, а, для неустойчивой системы - на рис. 1.83, б.
96
Анализ и статистическая динамика САУ. Часть I
Рис. 1.8Э. Виды переходных процессов для устойчивой (а) и неустойчивой (б) систем
Первая задача, которая возникает перед конструктором системы, - ее статический
расчет. Вторая задача - решить вопрос о том, будет ли система устойчива и при
каких условиях.
Чтобы определить, устойчиво ли состояние равновесия какой-либо системы,
обычно изучают поведение этой системы при малых отклонениях от положения
равновесия.
Рассмотрим механическую систему (рис. 1.84, а). Чтобы определить, устойчиво
ли положение шара в углублении, можно задать ему малое отклонение, переместив
в положение В. При этом возникает сила, которая стремится вернуть шар в
положение равновесия. Убедившись, что эта сила возникает при любом малом отклонении,
приходим к заключению, что положение равновесия устойчиво.
Ъ7т9$ ^9^
А
а
А
б
О О
7777777/7
в А
А
г
В
Рис. 1.84. Примеры систем с различной устойчивостью:
а - «устойчивость в большом»', б - «устойчивость в малом»; в - нейтральная', г - неустойчивая
В большинстве практических задач, если система устойчива в малом, она
устойчива и при больших конечных отклонениях, как в приведенном примере. Говорят,
что система «устойчива в большом».
В системе на рис. 1.84, б равновесие шара устойчиво лишь в том случае, если
отклонение не переходит за точку С. В этом случае говорят, что система «устойчива в
малом», т.е. система устойчива, но в ограниченной области. Система на рис. 1.84, в
нейтральная, а система на рис. 1.84, г неустойчивая.
Система обычно находится в состоянии движения, поэтому рассматривают
устойчивость движения. А понятие устойчивости в динамике более сложное, чем
определение устойчивости равновесия в статике.
Пусть заданный режим работы системы характеризуется координатами:
*ю (0» *20 (0' -^зо {г)»•••• Пусть на систему действует возмущение, которое
заставляет ее двигаться по другим траекториям: хх (г), х2 (г), х3 (г),.... Система будет
находиться в возмущенном состоянии. Если система устойчива, то она снова войдет
Глава 1. Линейные одномерные непрерывные стационарные САУ 97^
в заданный режим или в область около этого режима е, =** (*)~*го(0* Заданное
невозмущенное состояние движения устойчиво, если в результате действия
возмущений возмущенное состояние движения с течением времени перейдет в некоторую
конечную область, находящуюся в окрестности невозмущенного состояния,
определяемого координатами:
ei(0 = *i(0-*io(0:
е2(о=*2(0-*2о(0; (1233)
ея(0 = *Л0-*|ю(0-
Конкретизируем введенные выше понятия, рассматривая класс одномерных
стационарных линейных систем.
Выходной сигнал,системы, порожденный входом y(t) и ненулевыми
начальными условиями, можно записать в виде
х(0 = /*(/-т)у(т)Л+д:с(0 = хв(0 + хс(0, (1.234)
о
где
xB{t) = \k(t->c)y(>c)d>c = xn(t)+xy{t). ,(1.235)
о
Сигнал хв (j), который обусловлен входом y(t), будем называть невозмущенным
движением (колебанием) системы.
Ненулевые начальные условия будем считать внешними возмущениями: они
будут действовать на выход и вызовут отклонение реального движения от заданного
Реальное или действительное движение *B(0 + Jcc(0 называют возмущенным
движением.
Таким образом, еще раз отметим, что за невозмущенное движение системы
принимают вынужденную составляющую xB(t) в (1.234), а за отклонение или вариацию
- свободную составляющую xc(t).
Возмущениями являются начальные условия
х°=(*(о),*'(о),...,^-1)(о)).
Заданное невозмущенное движение будет устойчивым, если возмущенное
движение, порожденное возмущением X (возникшим в момент t = О под действием
внезапно приложенных к системе дополнительных внешних сил), по истечении
некоторого времени войдет в заданную область |jcB(f)-*(/)[<£, где е = const - заданная
величина.
В соответствии с определением устойчивости по A.M. Ляпунову, система будет
асимптотически устойчивой, если хс (г)—*~*°° )0.
Понятие устойчивости является чрезвычайно важным, поскольку свойство
устойчивости системы определяет факт ее работоспособности или неработоспособности.
98
Анализ и статистическая динамика САУ. Часть I
А если точнее, то устойчивая система принципиально работоспособна,
неустойчивая лее - неработоспособна. Обсудим этот вопрос более подробно.
Имеем
*c(') = ciC*V +С2**2/ +... + ^Лг. (1.236)
Для асимптотически устойчивой по А.М. Ляпунову системы имеем
cfgX|/+... + cggx<>/ '"*" >0. (1.237)
Зависимость (1.236) будет стремиться к нулю тогда и только тогда, когда
корни X отрицательны (если они действительные) или имеют отрицательную
действительную часть (если они комплексно-сопряженные), и в этом и только в этом
случае имеем
to-^t JL.r**-^
сГе
+ с\е
-+... + cie
fi*-Kt.
(1.238)
Корни характеристического уравнения Х{9 Х2, ... Д„ можно расположить на
комплексной плоскости (рис. 1.85).
Мнимая ось
Область
неустойчивости
О
Действительная ось
Рис. 1.85. Комплексная плоскость
Если корни Я1э Х2, ... Дл лежат строго в левой полуплоскости, то их называют
левыми.
Теперь можно сформулировать условие устойчивости: для того, чтобы система
была асимптотически устойчивой, необходимо и достаточно, чтобы все корни ее
характеристического уравнения
ansn+an_lsn-l+... + a0=0
были левыми.
Запишем две зависимости:
хс (t) = с\ех< +с\ех* + ... + с'Л'; (1.239)
хпк) = с?ех*'+с?ех* +...+с>х«'. (1.240)
В асимптотически устойчивой системе хс (f)—г"^°° >0.
Последнее возможно тогда и только тогда, когда корни Х{9 Х2, ... Дп - левые
(т.е. имеют отрицательные действительные части). Отрицательность же
действительных частей показателей Хх, Х2, ... Дп приводит к тому, что и составляющая хп (г)
также стремится к нулю при t —> «>, т.е.
Таким образом, в устойчивой системе затухают как свободная составляющая,
так и переходные колебания.
Глава 1. Линейные одномерные непрерывные стационарные САУ 99^
Анализируя характеристические уравнения системы, A.M. Ляпунов
сформулировал следующие теоремы устойчивости для нелинейных*, но линеаризованных систем,
т.е. описанных линейными уравнениями:
1). Нелинейная система устойчива в «малом», если отрицательны все
вещественные части корней характеристического уравнения системы (ее линейного
приближения).
2). Нелинейная система неустойчива в «малом», если хотя бы один корень
характеристического уравнения линейного приближения имеет положительную
вещественную часть.
3). Если имеется чисто мнимый корень, т.е. вещественная часть равна нулю, то
система находится на границе устойчивости.
Если линейные системы устойчивы в «малом», то устойчивы и в «большом».
Нелинейные системы могут быть устойчивы в «малом», но не устойчивы в
«большом», т.е. при больших сигналах возмущения.
После затухания хс (t) и хп (t) выходной сигнал линейной системы имеет тот же
вид, что и входной
д:у(г) = с{е°* + с\е** +... + с*Л'. (1.242)
Легко видеть, что в устойчивой системе в установившемся режиме ошибка
определяется формулой
е(') = (с1 -с?)еЩ' +Н -^У2' +-+(ср -clV''- (L243>
Известно, что импульсная переходная функция (ИПФ) системы определяется
полюсами Х{, А,2, ... Д„. Выражение для ИПФ имеет вид
k(t) = L'l{W(s)} = cleXlt +c2ex* +... + слЛ'. (1.244)
Поскольку полюса Х1У Х2, ... ,АЛ -левые, то
оо
j\k(tpt <оо, (1.245)
о
Отсюда следует: для того, чтобы автоматическая система была устойчива,
необходимо и достаточно, чтобы ее ИПФ была абсолютно интегрируемой.
Подводя итог сказанному, приходим к следующей формулировке условий
устойчивости.
Если:
1) в ПФ системы т<п, т.е. степень многочлена в знаменателе ПФ не меньше
степени многочлена числителя (ПФ системы строго реализуема);
2) корни характеристического уравнения являются левыми, т.е.
характеристическое уравнение не имеет других корней, кроме корней с отрицательными
вещественными частями,
то САУ является устойчивой.
Для суждения об устойчивости нет необходимости вычислять корни
характеристического уравнения. Достаточно лишь установить их расположение на
комплексной плоскости. Правила, позволяющие это сделать без вычисления корней,
называются критериями устойчивости.
Критерии устойчивости можно разделить на алгебраические и частотные.
Алгебраические критерии позволяют сделать вывод об устойчивости системы по коэффи-
Теория устойчивости нелинейных систем изложена в главе 4.
100
Анализ и статистическая динамика САУ. Часть I
циентам характеристического уравнения. Частотные критерии позволяют судить об
устойчивости по частотным характеристикам элементов, которые могут быть или
рассчитаны или получены экспериментальным путем.
1.11. АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ
1.11.1. Критерий Рауса
Этот критерий был разработан английским математиком Э. Раусом в 1877 г.
Положим, что найдена передаточная функция замкнутой автоматической системы
в форме
W(s) =
_bmsm+bm_lsm-l+...+b0
aosn +axsn I+... + £iJ
Характеристическое уравнение имеет вид:
B(s) = aosn+alSn-{+... + an.
Составим таблицу, которая называется таблицей Рауса (табл. 1.3).
(1.246)
(1.247)
Таблица 1.3
Коэффициенты/*,
-
-
ГЗ = С,|/С12
Г4 = С12/С|3
/5 = С,з/С,4
*
-Cu-2/Cu-i
Строка
/
1
2
3
4
5
i
•
1
Си =я0
с,2 = ах
с\ъ = с2\ - гъс2г
С|4 = С22 - Г4С23
С\Ь = С2з - Г5С24
•
си-
= C2j-2-r,C2j-l
•
Ctoj
2
С21 = а2
сп = Дз
С23 = Сз| - Г3Сз2
С24 = Cyi - Г4С33
Сгь = Сзз - Г5С34
Сц-
= С3,/-2-Г/Сз,/_|
1бец
3
СЪ\ = <*4
Сз2 = а5
СЗЗ = С4\ - Г3С42
Су4 = С42 - ^4Q3
^35 = Q3 - Г5С44
сз,=
= С4,/-2-'*А./-1
4
С41 = «6
с42 = а7
СЛЗ
Си
С45
С4/
•
Алгоритм составления таблицы Рауса очевиден.
Сформулируем критерии устойчивости.
Для того, чтобы автоматическая система была устойчива, необходимо и
достаточно, чтобы для всех коэффициентов г, было выполнено условие
П> 0,/ = 3,4,..., (1.248)
или, что эквивалентно,
си> 0, / = п+1,(яо>О). (1.249)
Если хотя бы один из коэффициентов характеристического уравнения (1.247)
отрицателен, то система неустойчива.
Обращение в нуль одного из коэффициентов а, (за исключением коэффициента
старшего члена) свидетельствует о неустойчивости системы или о том, что она
находится на границе устойчивости. Число отрицательных коэффициентов си
равно числу правых полюсов.
Обращение ап в нуль приводит к появлению нулевого корня. Если
апЛ = 0, я„_2 = 0,... - это приводит к появлению нулевых корней.
Глава 1. Линейные одномерные непрерывные стационарные САУ
101
Обращение промежуточного коэффициента в нуль свидетельствует о появлении
пары чисто мнимых корней.
Для упрощения расчетов элементы строк можно делить или умножать на
положительную величину.
Если в процессе вычислений появляется отрицательный коэффициент в таблице
Рауса, то это свидетельствует о неустойчивости системы и дальнейшие расчеты
проводить не следует.
Число перемен знака коэффициентов г,-, i = 3,4,... равно числу корней
характеристического уравнения (1.247), расположенных в правой полуплоскости комплексной
плоскости.
Таблица, реализующая алгоритм Рауса, удобна для программирования на ЭВМ,
поэтому с помощью этого метода можно исследовать на устойчивость системы
высокого порядка. Более того, можно исследовать влияние на устойчивость системы
отдельных ее параметров.
Пример 1.7. Пусть характеристическое уравнение имеет вид [161]
0,Ш8*5+0,03*4+136*3+4*2+52Д*+50=0;
сп=0,0008>0; с12=0,03>0; с13=1,25Х);
с14=2,77>0; с15=28,6>0; с,6=50>0 .
Из полученных результатов можно сделать вывод, что система устойчива.
1.11.2. Критерий Гурвица
' Этот критерий предложен немецким математиком Гурвицем в 1895 г.
Если известно характеристическое уравнение системы (1.247), то легко записать
матрицу Гурвица
а\
%
0
0
0
0
аг
а2
«1
*o
0
0
аь
а4
аг
<h
а\
«о
«7
«6
а5
а4
аъ
а2
Од ...
Og ...
а-, ...
а6 ...
а5 ...
а4 ...
0
0
0
0
0
0 0 0 0 0 ... ап
Пример 1.8. Если характеристическое уравнение имеет вид
OqS5+als4+a2s2 +a3s2+a4s+as =0,
то матрица Гурвица запишется так:
'д, аъ а5
.(1.250)
uq а2 аЛ
0
0
0
д, аъ а5
Oq a2 а4
0"!
0
0
0
0 ах аъ а5
При составлении матрицы Гурвица первая строка заполняется коэффициентами
характеристического уравнения с нечетными индексами, а вторая - с четными.
Дальнейшие пары строк получаются смещением вправо первой пары на один, два и т.д.
столбцов. Все коэффициенты с индексами, большими степени, заменяются нулями.
Определитель матрицы Гурвица (1.250) называется главным определителем Гур-
вица.
Он имеет вид
102
Анализ и статистическая динамика САУ. Часть I
А =
«о
0
0
0
а3
Л
а,
%
0
а4
а3
0
... 0
... 0
... 0
... 0
... ап
(1.251)
Из (1.251) получим определители Гурвица низшего порядка:
Д, =а,, Д2
«о
<h.
,А3 =
0
а\
а4
(1.252)
Критерий Гурвица формулируется так:
Для того, чтобы замкнутая автоматическая система была устойчивой,
необходимо и достаточно, чтобы при а0 > 0 все определители Гурвица были
положительны, т.е.
Ai > 0, А2 > 0, А3 > 0,..., Ап.! > 0, Д„ = ап Ап.х > 0. (1.253)
Пользуясь критерием Гурвица, получим условия устойчивости для систем,
порядок характеристических уравнений которых не превышает четырех.
Если B(s) = aos + ах = 0, то условия устойчивости имеют вид а0 > 0, ах > 0 ; для
уравнения B(s) = a0s2 + axs + а2 =0 условиями устойчивости являются: а0>0, а^О,
д2>0.
Для уравнения третьего порядка B(s) = aos3 + axs2 + a2s + a3 = 0 имеем
ax аъ 0
Аз = ао а2 ° •
0 ах аъ
Отсюда следуют условия: а0 > 0, ах > 0, а2 > 0, аъ > 0, а^з ~аоа3 > 0.
И, наконец, если имеется характеристическое уравнение четвертого порядка
B(s) = OqS4 + axs3 + а252 + a3s + а4 = 0, то определитель Гурвица запишется так
ах аъ 0 0
4 0 ах аз °
0 Oq а2 а4
Необходимым и достаточным условием устойчивости является
а0>0, ах > 0, а2 > 0, аъ >0, а4> 0, a3(aia2 "аоаз)"a?a4 > 0.
Практически, поскольку а4 > 0, находят определители Гурвица от Ai до An_i.
Например, для последнего случая имеем:
ах аъ 0
ах>0, А2
а3
= аха2-а0а3>0, А3 =
0
я, а3
>0.
Система находится на границе устойчивости, если все определители Гурвица
низшего порядка положительны, а главный определитель равен нулю, т.е. А! > 0,
Д2>0,..., Ая=овА1|Ч=0. .
Глава 1. Линейные одномерные непрерывные стационарные САУ
103
Если ап = 0, а Ап_х > 0, то один из корней характеристического уравнения равен
нулю (система находится на границе апериодической устойчивости), если же апФ0,
а ДлЧ = 0, то система находится на границе колебательной устойчивости (два
комплексно сопряженных корня находятся на мнимой оси).
Сведем полученные выше результаты в табл. 1.4.
Из табл. 1.4 следует, что необходимым и достаточным условием устойчивости
системы, характеристическое уравнение которой первой или второй степени,
является положительность всех коэффициентов характеристического уравнения.
Таблица 1.4
B(s) = 0
aos + ах = 0
aQs2 + axs + а2 = 0
aos3 + axs2 + a2s + аг = 0
aosA + a{s3 + a2s2 +a$s + a4=0
Условия устойчивости
ao>O, ax >0
a0 > 0, ax > 0, a2 > 0
a0 > 0, ax > 0, a2 > 0, аъ > 0, axa2 -atft*} > 0
a0 >0, ax >0, a2 >0, a3 >0, a4 >0, аъ{аха2 -сщаъ)-аха4 >0
Пример 1.9. Имеется система третьего порядка с характеристическим уравнением [172]:
B(s) = аоУ3+Д|$2+а2-Н-Дз = 0.
Обозначим
Тогда (1.254) перепишется в виде
Или, что то же самое,
«о lVaoJ Vflo
a3]i{ao) fl3Vflo
Обозначив
fl3Vl*oJ лз\до
(1.257) перепишем в виде
T3 + AT2 + Bs+\ = 0.
Необходимые и достаточные условия запишутся так:
А>0, Я>0, АВ>\.
Графически (1.259) представлено на рис. 1.86.
Область
устойчивости
АВ>\
(1.254)
(1.255)
(1.256)
(1.257)
(1.258)
(1.259)
(1.260)
АВ=1
Рис. 1.86. Гипербола Вышнеградского
104
Анализ и статистическая динамика САУ. Часть I
Пример 1.9. Характеристическое уравнение имеет вид:
Д(5)=0,000354+0,033753+0,4352+51,25+24,8=0.
Все коэффициенты характеристического уравнения положительны.
Найдем А з:
A3=a3(flifl2-aofl3)-fl4ai2=51,2(O,O337 • 0,43-0,0003 • 51,2)-24,8 • 0,03372=
=-51,2 • 0,0009-24,8 • 0,03372<0.
Вывод: система неустойчива.
1.11.3. Критерий Льенара - Шипара
В 1914 г. Льенаром и Шипаром был предложен критерий, упрощающий критерий
Гурвица.
Критерий Льенара - Шипара формулируется так: при а0>0, ах >0, а2 >0,...,
ап > 0, необходимые и достаточные условия сводятся к тому, чтобы среди
определителей Гурвица A!,A2,..., Д„ были положительными все определители с
четными индексами^ т.е.
Д2>0,Д4>0,Д6>0, (1.261)
или все определители с нечетными индексами
А,>0,А3>0,А5>0,.... (1.262)
Итак, необходимым и достаточным условием устойчивости системы является:
до > 0, ах > 0,..., ап > 0,
А1>0,А3>0,А5>0,..., - (1.263)
или .
а0 > 0, ах > 0,..., ап > 0,
А2 > 0, Д4 > О, Д6 > 0,.... (1.264)
Рассмотрим систему, структурная схема которой представлена на рис. 1.87.
e(t)
—*ЛХ)—
1
к
x(t)
Пусть
Рис. 1.87. Структурная схема системы
«1 (*) = W"'*1 + «П-а-1^'Ц"' + - + «0.
тогда
s>iBi(s) = an_lisn -an_Ms"4 +-+^ц = B(s).
Найдем ПФ замкнутой системы
W(s) =
l + K/(an_tlsn+... + aos>l)
К
где
an_llstt+an_il_lsn-l+... + aos? + K
а„-а =а»>0, <Vu-i = ап-\ > 0.-. К = а0>0.
(1.265)
(1.266)
(1.267)
(1.268)
Глава 1. Линейные одномерные непрерывные стационарные САУ 105^
Анализ (1.267) показывает, что часть коэффициентов характеристического
уравнения
(1.269)
B(s) = an_Visn+... + aos>i + K = ansn+... + alls*l + K
равна нулю (а\ = 0, аг = 0,..., а^\ = 0).
Таким образом, не выполнено условие положительности всех коэффициентов,
что свидетельствует о неустойчивости системы.
Никакой набор коэффициентов ац, а^\,..., ап стабилизировать систему не в
состоянии [172].
Указанный класс систем носит название структурно неустойчивых.
Справедливо утверждение [172]: системы, для которых степень передаточной
фукнции W(s) равна ее порядку, структурно неустойчивы, если индекс
апериодической нейтральности не меньше двух. Такие системы содержат не менее двух
последовательно соединенных интеграторов.
Для стабилизации структурно неустойчивых систем требуется изменить их
структуру, например, сделать ПФ разомкнутой системы в виде
(1.270)
Степень A(s) выбирается таким образом, чтобы все коэффициенты
характеристического уравнения замкнутой системы были отличны от нуля (степень A(s)
должна быть не меньше ц - 1).
Стабилизация структурно неустойчивых систем достигается либо введением
внутренней связи, охватывающей один из интеграторов, либо введением производной.
Пример 1.10. Рассмотрим систему, структурная схема которой представлена на рис. 1.88 [32].
-Hg^
Л*
Г
h
1 +
К с
лос,
Jp
\ + TMs
1
S
x{t)
Рис. 1.88. Структурная схема системы
Построим область устойчивости в функции коэффициентов усиления Ку^ и Ко , если остальные
параметры равны:
В
Кс = 0,4 В/град; Ку = 5,2; с, = 0,014 -
2 град/с
jp = 297; Тя = 0,06 с; Г„ = 0,1 с.
Передаточная функция разомкнутой системы
КсКухКуг1сцр
Wp(J)--
[(l + Tqs)(l + TMs) + Ky2K0]S
Найдем передаточную функцию замкнутой системы
D .
W(s)--
где
TqTMs* + (Tq+TM)Sz+(l + Ky2K0)s + D
кску. Ку2
(1.271)
(1.272)
D = -
ciJP
1U6
Анализ и статистическая динамика САУ. Часть I
Характеристическое уравнение имеет вид
OoS3 +a,s2 +a2s+a3 =0»
где
aD=TqTM=O,0O6; ax=Tq + 7^=0,06+0,1=0,16;
Пользуясь критерием Гурвица, имеем:
Оо>0, а,>0, д2>0, д3>0 . (1.273)
Д2=а,а2-Яоаз>О. (1.274)
Условия (1.273), (1-274) выполняются при К0>0, Kyt >0.
Воспользуемся условием (1.274); имеем
0,16(1+5,2*0)-0,006.0,5Л:У| >0. (1.275)
Из последнего неравенства следует:
£0>0,0036Л:У| -0,192. (1.276)
Граница устойчивости определяется выражением
АГ0=0,0036/ГУ| -0,192. (1.277)
Область устойчивости в плоскости параметров Ку^ и Ко построена на рис. 1.89.
Ко1
0.8 •
0.6 •
0.4 '
0.2
-0.2 ;
Область
устойчивости
Illf
1 ,llLK
1 llJr
1 ,l/lr
lllr 100 200
,ils
Область
неустойчивости
300 *v,
Рис. 1.89. Область устойчивости в плоскости параметров КУу и Ко
Пример 1.11. Рассмотрим сист
"1
ему (рис. 1
7> + 1
•90) [1
72].
T2s + l
*-
1
Рис. 1.90. Структурная схема системы
Передаточная функция разомкнутой системы имеет вид
КХК2
W(s) = -
(TlS + l)(T2s + l)T3s
Характеристическое уравнение замкнутой системы запишется так:
x(t)
(1.278)
Глава 1» Линейные одномерные непрерывные стационарные САУ
107
B(s) = a$s* + a2s2 + axs + a0,
где
аг = ТхТ2Тг, а2 = (Г, + Г2)Г3, ах = Г3, я0 = К = АГ,А:2.
Запишем условия устойчивости:
аоа3<л,а2.
или, что то же самое,
КТХТ2ТЪ<{ТХ +Т2)Т?=Т1Т32+Т2Т32.
Перепишем последнее неравенство в виде
Граничное (критическое) значение коэффициента определяется формулой
Построим график
^кР - т т т •
'2 'I
К^ = = — при -2. = const,
или КфТ=1 при 73/72=const.
Функция АГкр=1/7 - равносторонняя гипербола, ее график представлен на рис. 1.91.
кр
V=i
Область
неустойчивости
КТ> 1
Облает^
устойчивости
КТ<\
—►у
Рис. 1.91. Зависимость ККР от ТХ1ТЪ при Г3/Г2 = const
1.12. МЕТОДЫ ИССЛЕДОВАНИЯ ТОЧНОСТИ РАБОТЫ СИСТЕМ
В УСТАНОВИВШЕМСЯ РЕЖИМЕ
1.12.1. Оценка точности работы системы для класса воздействий
Положим, что:
а) на вход поступает сигнал, имеющий дробно-рациональное изображение
y,s) = CkSk+Ck_xSk Ч.-. + Ср ш
dpsp+dp_lSp-l+...+d0'
б) система имеет нулевые начальные условия;
в) система устойчива;
г) система работает в установившемся режиме.
Найдем изображение выходного процесса
(1.279)
108 Анализ и статистическая динамика 1АУ. часть 1
(bmsm+...+b°)(cksk+...+c0)
X(s) = W(s)Y(s) = j £ L (1.280)
(ansa+...+a0)(dpsP. + ...+d0)
Переходя в (1.279) от изображения к оригиналу, получим зависимость,
определяющую входной сигнал
y(t) = Гх {Y(s)} = <%е°* +$£* + ... + с^Л'. (1.281)
Для нахождения реакции системы на сигнал (1.279) перепишем (1.280) в виде
X{s) W +-+g0 МП (1.282)
(ansn+...+a0)(dpsl>+...+d0) B(s)
Переходя в последней формуле к оригиналу, запишем
x(t) = с?ех>' +...+сУк' +с?еа>' +с>еа>' +...+с>еа"'. (1.283)
В связи с тем что система устойчива и работает в установившемся режиме,
с^1' +...+с%ек' '^Го. (1.284)
Тогда выходной сигнал системы, работающей в установившемся режиме,
определяется формулой
xy{t) = c{e4 +c2V>' +...+cJea''. (1.285)
Формулы для нахождения коэффициентов сук, к = 1,р имеют вид
^Мь-М,^ (1.286)
B'(s)\s=ak B'(ak)
С учетом последнего выражения, (1.285) примет вид
*=1 В \ак )
' Надо отметить, что, поскольку
Д(5) = (Ьт5т+... + Ь°)(^/+... + с0) = Л(5)(^/+... + с0);
B(s) = (ansn +... + ao)(dpsp +... + do) = B(s)(dpsp +... + </0)> (L288)
т.е. в формулы для A(s) и B(s) входят полиномы A(s) и B(s), определяющие
передаточную функцию системы (поскольку W(s) = A(s)/B(s)), то коэффициенты
с1,к-\,р определяют не только свойства воздействия y(t), но и параметры,
характеризующие свойства собственно системы. Именно в связи с последним фактом, т.е.
с учетом коэффициентами сук,к-\ур свойств системы, последние отличаются от
эталонных коэффициентов с*,£ = 1,р. Поскольку известен вход y{t) и реакция
xy{t) на этот вход, то легко записать формулу, определяющую ошибку работы
системы:
eW-ifc-tf).*' s fic^W^\Vkt' (L289)
*=i м{ B{ak)j
Воспользуемся обозначением
Глава 1. Линейные одномерные непрерывные стационарные САУ 109^
С учетом (1.290) получаем выражение, определяющее точное значение ошибки
воспроизведения входного сигнала y(t) исследуемой системы в установившемся
режиме
е(О = Х^г, (1.291)
1.12.2. Приближенное исследование точности работы системы
в установившемся режиме
Положим, что выполнены условия б), в), г), а также
k(x) = L-l{W(s)}. (1.292)
Тогда выходной сигнал системы в установившемся режиме
оо
x(t) = jk(T)y(t-T)dT. (1.293)
о
Пусть существует разложение воздействия в ряд Тэйлора относительно точки t:
У('--0 = £^ТгЛот*. (1-294)
где
y(*)w = ±3W t = 0,1,2,.... (1.295)
dr
Подставляя (1.294) в (1.293), получаем
*(о=Х-
*=0
Величины
}*(т)тЦ(-1)*^. (1.296)
ц*=(-1)*|т**(т)<*т, Л = 0,1,2,... (1.297)
о
называются степенными моментами к -го порядка импульсной переходной функции
*(т).
Зависимость (1.296) позволяет сделать вывод: установившийся процесс в
линейной стационарной системе полностью определяется моментами ИПФ и
производными воздействия [172].
Моменты \xk легко рассчитываются по передаточной функции замкнутой
системы. В самом деле, справедлива зависимость
^£Ц-1)*7т*.-**(т)Л. (1.298)
ds ■ о
Сравнивая (1.297) и (1.298), легко заключить, что
|djv£) ^ £=(U2j (1299)
L * JL
Если разложим W (s) в степенной ряд по s, то получим
110 Анализ и статистическая динамика САУ. Часть I
„(.)-2№1 А (..зоо,
»Ч Л JL
Отсюда следует, что моменты \хк ИПФ представляют собой коэффициенты
разложения передаточной функции W (s) замкнутой системы вряд по степеням s.
Для дробно-рациональных передаточных функций моменты \лк можно
определить простым делением многочлена числителя передаточной функции на многочлен
знаменателя.
С учетом (1.296) и (1.297), имеем
juo kl *=i *!
Введя обозначения
co=1-Ho' Ск=-Чк> * = 1.2Д...,
запишем (1.301) в компактной форме:
8W = E^ZTTZ. (1.302)
*=о *!
Коэффициенты ск, А: =0,1,2,... называются коэффициентами ошибок системы.
Они могут быть вычислены по формуле
1 J j=0
,t= 0,1,2,.... (1.303)
Передаточная функция WB(s) = l-W(s) называется передаточной функцией
ошибки.
Коэффициенты ошибок ck, ft = 0,1,2,... равны к-м производным от
передаточной функции ошибки при 5 = 0.
Коэффициент с0 называется коэффициентом статической или позиционной
ошибки, коэффициент с{ - коэффициентом скоростной ошибки, с2 —
коэффициентом ошибки от ускорения.
Коэффициенты ошибок определяют зависимость установившейся ошибки от
структуры системы и ее параметров. Поэтому исследование коэффициентов ошибок
позволяет наметить пути уменьшения или полного устранения установившейся
ошибки.
Пусть y{t) = yo\(t), тогда е(г) = соуо, т.е. при постоянных воздействиях
установившаяся ошибка также постоянна (эта ошибка называется статической).
Статическая ошибка пропорциональна значению постоянного внешнего воздействия.
Система, отрабатывающая в установившемся режиме входной сигнал
y(t) = УоКО без ошибки, называется астатической 1-го порядка.
Система, отрабатывающая в установившемся режиме входной сигнал
y(t) = УоКО + V\t + У2*2 + - + У/-/"1 (1.304)
без ошибки, называется астатической порядка I.
Для разомкнутой системы с ПФ вида [153]
W(s) = —) L (1.305)
sv (1 + a{s + a2s +...+ansn)
Глава 1. Линейные одномерные непрерывные стационарные САУ
111
формулы для определения коэффициентов ошибок представлены в табл. 1.5.
Как следует из анализа формул, представленных в табл. 1.5, при увеличении
коэффициента усиления К разомкнутой системы ошибка системы в установившемся
режиме уменьшится.
Однако чрезмерное увеличение коэффициента усиления может привести к
неустойчивости системы (см. параграф 1.11).
Таблица 1.5
Тип системы
Статическая
система
Астатическая
порядка
Астатическая
порядка
Коэффициент
ошибки
со
*э
Со
С\
сг
*э
Со
С\
с2
*э
Формула, определяющая коэффициент ошибки
1
1 + К
(<*,-Р.)*
1 + АГ2
2(a2-p2K|2a1(P1-a1K|
(l + Kf (1 + К)3
|2р1(р1-а,К2
(1 + К)4
^(«з-Рз),
(1 + К)2
ш 6K[2ala2-2KPfi2 + (K-l)(o^l + afi2)] ,
(l + Kf
i6K(al-^l)(al + K^f
(1 + К)4
0
1
К
^ai-ft) 2
к к2
6 ^(ft-o,)
к'1 к2 '
к к
0
0
2
к
6(ttl-pl)
к
112
Анализ и статистическая динамика САУ. Часть I
ГЛАВА 2. ЛИНЕЙНЫЕ ОДНОМЕРНЫЕ НЕПРЕРЫВНЫЕ
НЕСТАЦИОНАРНЫЕ СИСТЕМЫ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ:
МАТЕМАТИЧЕСКИЕ МОДЕЛИ,
ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ,
УСТОЙЧИВОСТЬ
Настоящая глава посвящена краткому изложению теоретических положений
систем с переменными параметрами, следуя [121]. Полное изложение теории
рассматриваемого класса систем приведено в [121]*.
2.1. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ОДНОМЕРНЫХ ЛИНЕЙНЫХ
НЕСТАЦИОНАРНЫХ СИСТЕМ С ПОМОЩЬЮ ИМПУЛЬСНЫХ
ПЕРЕХОДНЫХ ФУНКЦИЙ
2.1.1. Дифференциальные уравнения систем
Система автоматического управления называется нестационарной, если ее
параметры изменяются во времени (часто эти системы называют системами с
переменными параметрами).
При проектировании можно прийти к рассмотрению этого класса систем в
следующих случаях:
1) переменность во времени параметров обусловлена физикой работы систем
(изменение массы летательного аппарата за счет сгорания топлива и др.);
2) переменные коэффициенты дифференциального уравнения появляются при
линеаризации нелинейных дифференциальных уравнений около некоторых
опорных траекторий, являющихся также функциями времени;
3) при использовании статистической линеаризации при нестационарных
случайных воздействиях.
Рассмотрим примеры.
Пример 2.1. Структурная схема контура самонастройки имеет вид, представленный на рис. 2.1 [121].
Рис..
У
гл. ст.
к*
Г„5-
руктурна
i
и
1Я схе
s 2
ма системы с перемен
Cxa{t)
ным парамет]
>ом a{t)
к
Достаточно полная библиография по теории систем с переменными параметрами приведена в
[49,99,100,101,121,143].
Глава 2. Линейные одномерные непрерывные нестационарные САУ 113
Уравнение имеет вид
a2(0^-f+al(t)^- + a0№ = АГВХ (I), (2.1)
at at
где
й (0 = _Zi_, а (,) = _L_+*2££l,
21' К,а(О lW tf,a(O AT, (22)
Пример 2.2. Рассмотрим простейший дифференцирующий /?С-фильтр с изменяющимся по известному
закону R(t) сопротивлением и неизменной емкостью С, ток / которого управляет исполнительным
устройством ИУ (пусть управляющая обмотка ИУ обладает постоянным активным сопротивлением /?иу;
индуктивностью обмотки пренебрегаем) (рис. 2.2).
R(t) 4
п
С
т
о Ь
Рис. 2.2. Дифференцирующий фильтр
Поскольку сопротивление изменяется в зависимости только от времени при неизменных остальных
параметрах, фильтр является системой линейной нестационарной. Структурная схема, соответствующая
фильтру, приведена на рис. 2.3.
Фильтр
Рис. 2.3. Структурная схема дифференцирующего фильтра
Работа фильтра в любой момент времени подчиняется второму закону Кирхгофа
МО+МО+^иу (')=?(').
где y*(f), Ус(*)*Уят (0 ~ паДения напряжения на соответствующих элементах; /?, С, /?иу; у(0 -
приложенное к фильтру извне напряжение. С учетом известных из электротехники закономерностей имеем
*(')'(')+£}'(')*+V(')-y('>
'о
Продифференцировав левую и правую части этого выражения, получим
R 1
dl(t
dt
dl(t
dt
)JdR(')+ 1
[а с
Uflo(;)/(0 =
dt '
dy(t)
dt
(2.3)
где a{ (f), Oo(r) - коэффициенты, представляющие собой известные функции времени. То есть динамика
данной линейной нестационарной системы с сосредоточенными параметрами описывается обыкновенным
дифференциальным уравнением первого порядка с переменными коэффициентами.
Аналогично нетрудно убедиться, что поведение линейной нестационарной
системы общего вида описывается линейным уравнением с переменными
коэффициентами порядка п
аД0^+---+М0*(0=М0^+---+М<Ы<)> (2-4)
9 Зак. 232
114 Анализ и статистическая динамика САУ. Часть I
или
i=O 1=0
в связи с чем теория линейных нестационарных систем в значительной степени
посвящается методам исследования линейных дифференциальных уравнений с
переменными коэффициентами. Эта теория является важным разделом курса
«Управление в технических системах» (УТС), т.к. уравнениями вида (2.4) и (2.5) описывается
очень широкий класс явлений, например, движение почти всех аэродинамических
летательных аппаратов, надводных и подводных судов, работа систем в режиме
«разгона», «разогрева», процессы наведения на цель и т.п.
Распространенность уравнений (2.4) и (2.5) объясняется еще и тем, что к ним в
первом приближении сводится описание многих нелинейных процессов, если
рассматривать их линеаризованные модели в отклонениях от изменяющегося в
зависимости от времени опорного движения xon(t) (здесь *on(f)*const - известная
функция времени).
Пример 23. Пусть задана система, описываемая дифференциальным уравнением
«,(*)^+«о*(<)= *?(')• (2-6>
Здесь ах (х) - коэффициент, являющийся функцией выходной координаты, поэтому уравнение (2.6) -
нелинейное. Пусть, например, на основании какого-то упрощающего предположения исходную систему
удалось преобразовать к новой, у которой легко вычислить выходной сигнал хОП (/) (в общем случае
хоп * const), причем процесс xon (t) близок к x(t). Тогда, выбрав *оп (t) в качестве опорной траектории,
получаем
*(') = *о-(')+М'). (2-7)
где Ах (f) - малая величина.
Уравнение (2.6) примет вид
«,(*)^('i+M<)U[U0+M0]=W
Так как по предположению величина Ax(f) - мала, линеаризуем сначала функцию а^х) , если она
нелинейная,
а потом линеаризуем уравнение (пренебрегая малыми второго и высшего порядков, считая при этом, что
dbx(t\
тоже мала)
at
Нетрудно заметить (см. формулу (2.7)), что выражение [а, (*)]^_0 = а\ (*оп) ~ известная функция
времени (т.к. хоп (/) известна). По той же причине известной функцией времени является и выражение
Обозначим:
l>'WL-o=a'o('):
Глава 2. Линейные одномерные непрерывные нестационарные САУ
115
f
\Шх)] Ло„(') 1 '
^onW+hWU^J^oO).
и уравнение примет вид
М0^+М')Д*(0=*(0+л(0-
Здесь а10 (*)» аоо (0* <Уо (О ~ известные функции времени, т.е. исходная нелинейная система после
линеаризации стала описываться линейным дифференциальным уравнением с переменными
коэффициентами с добавочным известным воздействием Уо('), что не приносит дополнительных принципиальных
трудностей в процесс решения. Действительно, эта система линейна и по отношению к ней справедлив
принцип суперпозиции, поэтому Ajc(r) можно искать следующим образом:
Д*(0 = А*,(|) + А*,о(0.
где &xy(t), &xyo(t) - решения уравнений соответственно:
«.о(0^^+^(0Ч(0-*>(0.
*.о(0^^+М0^о(0=*>(')-
2.1.2. Понятие ИПФ Л НС и ее основные свойства
1). Нормальной импульсной переходной функцией (обозначается kH(t,x)) ЛНС
(2.12) называется реакция этой системы на воздействие вида единичной дельта-
функции, приложенной в момент времени т (рис. 2.4) при нулевых начальных условиях
[*(<.<L=*w=°.
~dx{t,T)~
dt
= i(x) = 0,
Ми
dt
y(t) = 8(t-x)
(«-!)
= jr
-)(x)-0.
(2.8)
ЛНС
x(t,x) =kH(t,x)
►
Рис. 2.4. Линейная нестационарная система
Тогда нормальной ИПФ системы (2.5) должно соответствовать уравнение
1=0 at /=о dt
при начальных условиях (2.8), в которых везде x{t,i) следует заменить на kH (r,x).
Прикладывая дельта-функцию при различных т, получим уравнения для семейства
нормальных ИПФ.
Поскольку нормальные ИПФ ЛНС являются ее реакциями, они представляют
собой функции времени t9 удовлетворяющие принципу причинности
9*
116
Анализ и статистическая динамика САУ. Часть I
Лн(г,т) = О; г<т,
(2.10)
которые в силу переменности параметров при различных моментах приложения
дельта-функции могут иметь разный вид (рис. 2.5).
*„(г,-т
V
.)
/
1
/
[
/
1
0
со)
/
>
>
(?Л,
■—^
*>
)
-
(»,т2)
Рис. 2.5. Нормальные ИПФ ЛНС
2). Таким образом, h зависит от двух переменных г,т. Нормальная ИПФ,
рассматриваемая как функция двух переменных г,т, называется импульсной переходной
функцией системы (2.5) (обозначается k(t,%)) и имеет вид поверхности, участок
которой изображен на рис. 2.6.
Величина k(t,%) в силу принципа причинности (условие (2.10)) равна нулю при
значениях независимых переменных Гит, соответствующих области плоскости f От,
расположенной левее биссектрисы координатного угла Ют (линия t = т),
Замечание 2.1. При отрицательных значениях т (см. пунктир на рис. 2.6.) ИПФ
обычно не рассматривается. Считается, что система при t < 0 не наблюдалась, а
следовательно, и не было возможности ею управлять.
kiK{ux)
Рис. 2.6. ИПФ ЛНС
Глава 2. Линейные одномерные непрерывные нестационарные САУ
117
3). Если ИПФ рассматривать как функцию второго аргумента при различных
фиксированных значениях первого (см. рис. 2.6.), то ей соответствует семейство
кривых, называемых сопряженными ЙПФ и обозначаемых кс (г,т) (рис. 2.7).
i i fcft/c)
Рис. 2.7. Сопряженные ИПФ ЛНС
Такое название объясняется тем, что импульсной переходной функции как
функции второго аргумента-функции kc(tyx) отвечает уравнение [121]
1(УЬ^И.Е(_1у''Г'*Ж'-'>]. (2.н,
i=o d*1' i=o dx
которое по отношению к уравнению для нормальной ИПФ (2.16) является
сопряженным (сопряженные уравнения широко используются в математике, например, для
отыскания первого интеграла исходного уравнения).
Часто по ходу изложения бывает ясно, какая из отмеченных ИПФ фигурирует в
данном случае, тогда индекс при &(г,т) опускается и, таким образом, k{t,x) может
обозначать любую из рассмотренных ИПФ.
Поскольку уравнение нормальной ИПФ (2.9) справедливо при всех допустимых
т, а уравнение сопряженной ИПФ (2.11) - при всех допустимых t, многократно
используя любое из них, можно судить и о &(/,т) (как о функции двух переменных),
в связи с чем и (2.9), и (2.11) можно было бы рассматривать как уравнение для ИПФ,
однако в качестве такового принято считать уравнение (2.9), которое в этом случае
записывают в виде
,-=о dt 1=0 dt
(2.12)
при нулевых начальных условиях.
4). Из рис. 2.6. видно, что сечение ИПФ плоскостями, параллельными плоскости
kOt, представляет собой семейство нормальных ИПФ (рис. 2.5); плоскостями,
параллельными плоскости кОт, - семейство сопряженных ИПФ (см. рис. 2.7).
На рис. 2.8 изображено семейство сечений ИПФ плоскостями, параллельными
плоскости fОт. Если эти сечения параллельны биссектрисе ОА координатного угла
Ют, то ИПФ представляет собой цилиндрическую поверхность с образующей ОА,
что может иметь место лишь в случае, когда форма нормальной ИПФ одинакова при
всех т, т.е. в случае стационарной системы. Для уяснения вопроса о стационарности
системы такие сечения иногда и используются.
118
Анализ и статистическая динамика САУ, Часть I
I I I
Q= const (i= 1,2,3)
I ч Ч
' \ \
\ \
X ir.
Рис. 2.8. Семейство сечений ИПФ плоскостями, параллельными плоскости Ют
5). Ввиду того что для нестационарных линейных систем справедлив принцип
суперпозиции, располагая ИПФ, нетрудно вычислить реакцию системы на произвола
ное входное воздействие y(t)9 приложенное в момент времени Tj. Действительно,
представим y(t) в виде импульсов, ширина которых Д0 выбирается так, чтобы их
можно было приближенно считать для данной системы дельта-функциями (рис. 2.9).
i
0
{
y(t)
/
/
*1
Г
-^
t
А0
<4
1 г
Рис. 2.9. Представление входного сигнала y(t) в виде импульсов
Найдем реакцию в некоторый момент ц > т, на один (произвольный) из этих
импульсов, например, на импульс, который приложен на /Д0, / = 1,/ij, где
nlAe^tl-xl (2ЛЗ)
раньше момента времени tx. Так как импульс этот можно приближенно
рассматривать как дельта-функцию площади y(tx -/А0)ДЭ, приложенную в момент t\ ~/Д®,
реакция на него, очевидно, приблизительно равна значению
Глава 2. Линейные одномерные непрерывные нестационарные САУ П£
умноженному на площадь этого импульса y(tY -/Д0)Д0 (т.к., во-первых, согласно
определению, k(t,x) есть реакция системы в момент t на дельта-функцию единичной
силы, приложенную в момент времени т, и, во-вторых, реакция линейной системы
на короткий импульс пропорциональна площади приложенного импульса).
Приближенное значение реакции системы в момент tx на весь входной сигнал,
согласно принципу суперпозиции, равно сумме значений ее реакций в момент tx на
каждое слагаемое входного сигнала (на каждый из входных импульсов):
^„xOsJy^-iAeJk^.^-iAejAe. (2.14)
/=1
Точное значение реакции может быть найдено, если величину интервалов А0
устремить к нулю, при этом произойдет следующее
Д0-></0; /Д©->0, £-> J
i=l О
(см. формулу (2.13)), и выражение (2.14) примет вид
о
Поскольку моменты времени tx и тх были выбраны произвольно, полученная
формула справедлива для любых гит
*('>т)= J y(*-e)k(fff-e)rfe. (2.15)
о
Более широко используется другая форма этого выражения, к которой легко
перейти, выполнив замену переменной
Г-0 = Х; 0 = r-X; </© = -</Х; 0 = 0; X = f; © = r-r, X = x,
после чего
x(t,<z) = ]y(X)k(a)dX. (2.16)
т
Обычно наблюдение за системой начинают с момента приложения воздействия
(тогда <и = 0), формулы (2.15), (2.16) принимают вид соответственно
x(t)=jy(t-e)k(t,t-e)de, (2.17)
о
t
x{t)^\y(X)k{uX)dX, (2.18)
о
Правая часть соотношений (2.17), (2.18) напоминает интеграл Дюамеля из теории
стационарных линейных систем, однако существенно отличается от последнего: она
не является сверткой входного сигнала и ИПФ, в связи с чем соотношения (2.17),
(2.18) называются интегралом суперпозиции.
Соотношение (2.18) установлено, исходя из физических соображений.
Установим связь между входом ^(г), выходом x{t) ИПФ k(t,x) нестационарной
системы, пользуясь следующими рассуждениями [121].
ИПФ определяется уравнением
120 Анализ и статистическая динамика САУ. Часть I
^av(o47^(r'T)=EbvWTV8(^T)' T€(-oo,+oo). (2.19)
v=0 dt v=0 "*
Умножим обе части (2.19) на у(т) и проинтегрируем по т на промежутке
(-оо,+оо). Результат имеет вид
%аЛ0^1к(1л)у№т=%ЬЛ)-^1у(т)Ь(1-т)с1т. (2.20)
v=o at _„ v=o dt _„
Известно следующее свойство 8-функции
J/(x)5(f-T)dT = /(r). (2.21)
—оо
Тогда
2>v(o-7T f k^x)y (x)dx=S*vW-7ryw • <2-22>
v=0 dt -co v=0 *t
Сравнивая (2.5) и (2.22), получаем
x(t)=\k{u%)y(x)d%. (2.23)
—оо
Анализ уравнения (2.23) показывает следующее:
*(г,т)>>(т) = 0прит<0; (2м)
^(г,т)у(т) = О при т>Г.
Тогда (2.23) перепишем в виде
x(t) = )k{t,x)y{x)d%. (2.25)
о
Таким образом, если в результате проведения соответствующего числа
экспериментов построена поверхность &(г,т) - импульсная переходная функция системы, то
реакция системы на произвольный вход y{t) может быть найдена по формуле (2.25).
Рассмотрим две системы, описываемые соответственно уравнениями
Xev(*)*(v)=XM'>y(v)i с2-26)
v=0 v=0
JTav(')*(v) = :KO. (2.27)
v=0
Вторую систему будем называть укороченной.
Математической основой для получения зависимости, определяющей колебания
на выходе одномерной нестационарной системы, описываемой укороченным
уравнением (2.27), является следующая теорема (теорема Коши) [45].
Если:
1) имеет место линейное ДУ вида
S«v(^(v) = ^(0'x°=0' (2-28>
v=0
2) av (Г) - непрерывна на [0, Т], v = 0, п -1; ап (t) = 1;
3) y(t) - непрерывна на [0,Г];
Глава 2. Линейные одномерные непрерывные нестационарные САУ 121_
4) к (f, т) - решение однородного уравнения, т.е. Lk (г, т) = 0, причем
*^х)Ц^;(лх)Ц=... = Г2)('Д)| =0;
"=т (2.29)
*,(иЧ)М =i.
тогда частное решение неоднородного уравнения, соответствующее нулевым
начальным условиям, имеет вид
t
x(t) = \к (г,т) у (x)d% - формула Коши, (2.30)
о
&(м) -ядроКоши.
Доказательство заключается в следующем.
Уравнение (2.28) перепишем в виде Lx-y . Тогда x = L~ly, L~l - оператор,
обратный линейному дифференциальному оператору L. Таким образом, задача
заключается в нахождении оператора L"1. Поскольку L -линейный дифференциальный
оператор, то ясно, что L"1 -интегральный оператор.
Воспользуемся формулой:
^ J /(*,у)Л= J ^lZ2^+P/(y)/(P(^)^)"-cc/(^)/(a(^)^). (2.31)
Дифференцируя формулу Коши, получаем
*(0 = }*(м>(т)</т;
о
/W = J*;(*.x)y(T)dT+*(»fr)y(«)=j*;(r,T)y(T)dT,
о о
At) = jk't'(t,x)y(x)dx+k'l (t,t)y(t) = \k't'{t,z)y{x)dv, (2.32)
о о
т.к.*(*,о-*;('.о--в*.(""2)('.о=°-
Вместе с тем имеем
t
*«(*) = j*,00 (г,т)у(т)^т+^-1) (г, ОУ (0 = j*r"} ('.*Мт)Л+ Я0, (2.33)
о о
т.к. *,(яЧ)(М) = 1.
Подставляя полученные выражения в исходное ДУ (2.28), находим
^av(0j^(v) (г,т)у (т) Jx+ y(t) = y(0, (2.34)
v=0 о
или, что то же самое,
8 Зак. 232
122
Анализ и статистическая динамика САУ. Часть I
Ч п
л v=n at
0Lv=0
у(т)Л+у(О = у(О.
(2.35)
Последнее равенство равносильно следующему
}[1,*(м)]у(т)Л+у(0 = У(О. (2.36)
о
Но L,fc(f,x) = O, т.к. &(г,т) - решение однородного ДУ, отсюда следует
тождество у (г) = у (г), и, таким образом, формула Коши является решением неоднородного
ДУ. Если в (2.30) известно ядро Коши, то расчет x(t) не представляет особого труда.
*('ДФ)А
Xcv(to)*v(O
v=l
г*
]£cv(*l)Xv(0
(2.37)
Рис. 2.10. Ядро Коши для конкретных х = т0 и т = т,
Построим алгоритм нахождения ядра Коши. Поскольку к(г,т) - решение
однородного уравнения, то
/:(г,т) = с1(т)дс1(г)+с2(ф2(г) + ...+с/1(т)^(г),
(рис. 2.10), где Ф(Г) = \хк (t):k = 1, п\ - фундаментальная система ДУ Lx = 0.
Поскольку
*(r,x)|r=t^;(,,x)|/=T=... = ^-2)(r,x)L=O;
*,(ПЧ)И =1'
1г=х
(2.38)
то
с, (т)х, (т)+с2 (т)дг2 (т) + ... + си (т)*„ (т) = 0;
с1(т)х[(т) + с2(т)х'2(т)+... + с„(т)х'п(т) = О;
qW^W + ^W^W+.-. + c^xJ^W-O;
c1(x)^>(x) + ci(x)4-l)(x) + ... + c11(x)x?-')(x)-l.
Отсюда находим
(2.39)
Глава 2. Линейные одномерные непрерывные нестационарные САУ
123
*,(т) х2(т) ... хп(т)
х[(т) хЦх) ... х'п(х)
,f-2)(x) 4-2)(х) - 4"-2)(х)
Г(Г\
(2.40)
или
W(t)C(t) = X°.
Тогда, умножая (2.40) слева на W"1 (т), находим
W1 (т) W(x)C(x) = W"1 (т)х£. (2.41)
Отсюда следует
C(t) = W4(t)X?, (2.42)
т.к. |w(x)| Ф 0 для любого те [0,Г].
Теперь можно записать выражение
*(*,т)*Ст(т)Ф(/) = (Х^)Т(W"1 (т))ТФ(г) -ядроКоши. (2.43)
Окончательно имеем формулу для расчета вынужденных колебаний
нестационарных систем
^о=}(х2)т(1¥-!(т))тф(Оу(т)л.
(2.44)
Ядро &(г,т) найдено для уравнения (2.27), т.е. для так называемого укороченного
уравнения; обозначим его через ky{t,x). Найдем зависимость, устанавливающую
связь между &(г,т) и ky(tyx). Для этой цели достаточно правую часть уравнения
(2.26) полагать входным сигналом системы с ИПФ ky(ty%). Тогда получим
зависимость
к{их) = \ку{ии)^м{и)№ (2.45)
поскольку правая часть уравнения (2.26) при импульсном входе записывается так
dm ,, v . _ dm~l
*m(0—B^-^+ft^W—г5(г-т) + ... + 46(г)5(г-т).
Подставляя (2.46) в формулу
k(t,x) = ]ky(t,u)Ly&(u-T)d%9
(2.46)
(2.47)
получаем (2.45) (здесь /^8(м-т)= ^bv(u)—-8(и-т)). Поскольку справедливо
v=0
выражение
(_l)V^)=J/(T)5(v)(;_x)^
(2.48)
находим искомое соотношение [143]
8*
124
Анализ и статистическая динамика САУ. Часть I
^^^"(-^^[^(^^Wl+'-'+^^^W-
(2.49)
Введем понятие сопряженных систем, рассматривая при этом для примера
уравнение системы с укороченной правой частью, т.е.
£av(0*(v) = >>(')• (2-50)
v=0
Важность введения этого понятия состоит в том, что для нахождения x(t) по
формуле (2.25) требуется с целью построения k(t,x) многократное приложение к
исследуемой системе 8 -функций в различные моменты времени т и последующая
обработка получающихся при этом кривых.
Функцию &(м), рассматриваемую как функцию второго аргумента X при
фиксированном t, условимся обозначать через к* (*,т).
Ясно, что к(г,т) удовлетворяет уравнению
2ev(o-j7*Me8('-0-
at
(2.51)
v=0
Найдем уравнение, которому удовлетворяет функция к* (г,т).
Предварительно определим сигнал y(t), который надо подать на вход инерцион*
ной части системы, чтобы получить на выходе 5-функцию (рис. 2.11),
у®
t,av(t)xw(t) = y(t)
v=0
S(f-T)
Имеем
Тогда
Рис. 2.11. К определению сопряженной системы
£av(0-£-8(,-T) = ,(')-
v=o dt
8(t-T)=]k(t,$)y(£,)dS.
(2.52)
(2.53)
Рис. 2.12. Последовательное соединение
Подставим (2.52) в (2.53)
Глава 2. Линейные одномерные непрерывные нестационарные САУ 125
8(r-T)-jft(«,$)
X-v(«^7»ft-T)k (2.54)
Lv=o d\
Воспользовавшись свойством 5 -функций
{-\)"Щ^-=\ m^\t~\)dt, (2.55)
из (2.54) найдем
8(^^) = S(-l)V^r[*('^K(x)]. (2.56)
v=0 "т
В последнем уравнении относительно k(t,x) независимой переменной уже
является т, т.е.
E(-1)"7^[*('^)«v(t)] = 5(r-x). (2.57)
v=0 "T
Итак, если для определения &(*,т), когда независимой переменной является Г,
служит уравнение
v=0 «*
то для построения k{t,%) с независимой переменной т надо пользоваться уравнением
Х(-1)^[л(/,т)ау(х)] = 4Л(г,т) = 5(г-т). (2.59)
v=0 "T
Оператор L* называется сопряженным относительно оператора Lx.
2.2. ИПФ ПРОСТЕЙШИХ ЗВЕНЬЕВ И ИХ СОЕДИНЕНИЙ
Как видно из рассмотренных примеров, легко определяется ИПФ только простых
систем - систем невысокого порядка с нестационарностями, описываемыми
несложными функциями. Но многие сложные нестационарные системы удается представить
в виде совокупности стандартных соединений более простых систем. Стандартными
называются последовательное, параллельное, типа «обратная связь» соединения
звеньев в силу того, что эти соединения остаются в классе линейных систем, если
входящие в их состав звенья линейны. Отчего исследование стандартных соединений
звеньев проводится в рамках той же теории, которой подчиняются входящие в состав
этих соединений звенья. Но тогда возникает возможность достаточно просто и
удобно исследовать такие сложные системы, если известны правила, позволяющие
определять по ИПФ соединяемых систем ИПФ их стандартных соединений. Часто
разбиение исходных систем на более простые составные части удается выполнить так,
что все «инерционности»* оказываются стационарными, а все нестационарности -
безынерционными (в виде усилителей с изменяющимися известным образом во
времени коэффициентами усиления - в виде безынерционных нестационарных звеньев).
* Термином «инерционность» здесь условно охвачены динамические звенья, в описание которых
входят в любых комбинациях производные как их выходных, так и входных сигналов.
126
Анализ и статистическая динамика САУ» Часть I
Тогда анализ упрощается еще более, т.к. для его проведения оказывается
достаточным знать ИПФ лишь элементарных стационарных звеньев и ИПФ безынерционного
нестационарного звена.
2.2.1. ИПФ НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ЗВЕНЬЕВ
1). Безынерционное стационарное звено с коэффициентом передачи а = const.
Его передаточная функция
W(s) = a,
которой соответствует уравнение
x{t) = ay(t),
откуда, согласно определению,
к (г, т) = ab (t - т) (см. рис. 2.13).
Замечание 2.2. На рис. 2.13. вдоль линии t = т представлена совокупность
дельта-функций, которая изображена так, будто их амплитуды равны величине а. Это на
самом деле является условным обозначением того факта, что величине а равны
площади соответствующих дельта-функций (амплитуды их, как известно, равны
бесконечности).
*(*,Т)
Огибающая
Рис. 2.13. ИПФ безынерционного стационарного звена
2). Стационарное интегрирующее звено.
Передаточная функция: W (s) = —.
Уравнение звена: —— = y[t).
dt
Уравнение для ИПФ: —м^ ' ' = 5 (t - т), откуда
dt
ku(t,x) = jb(t-x)dt = l, k(t,x) = hl[t-x].
(2.60)
Часть ИПФ представлена на рис. 2.14. ,
Глава 2. Линейные одномерные непрерывные нестационарные САУ
127
* it, X)
Рис. 2.14. Часть ИПФ стационарного интегрирующего звеиа
3). Стационарное апериодическое звено.
Аналогично рассуждениям в п. 2 имеем
dt
'■+kM(t,x) = b{t-T),
откуда, опуская очевидные элементарные выкладки, например, на основе
использования преобразования Лапласа, получаем
t-x
(2.61)
1
*мМ=7* г.
*М=
1
•1[,-т].
(2.62)
Часть ИПФ представлена на рис. 2.15.
k(f,x)
Рис. 2.15. К пояснению понятия ИПФ
4). Безынерционное нестационарное звено с коэффициентом передачи a(t).
Его уравнение x(t) = a(t)y(t),
откуда
*^т) = д(05(г-т) = д(т)8(г-т), (2.63)
с учетом селектирующего свойства дельта-функции (см. рис. 2.16 и замечание 2.2).
128
Анализ и статистическая динамика САУ. Часть I
я(т)
Кит)
a(t)
t = x
Рис. 2.16. К пояснению понятия ИПФ
2.2.2. ИПФ ОСНОВНЫХ СОЕДИНЕНИЙ
1). Параллельное соединение элементов (рис. 2.17).
Здесь k{{tfx)y k2(t,x) обозначены ИПФ соединяемых звеньев. Они известны.
Требуется определить ИПФ соединения.
уО)
S(f-x)
/
lr (t т\
^24*» L/
if, т) = ?
bit,*) Ш/"
x2(t) 1
*2(f.T)
xit)
k(f,T)
Рис. 2.17. Структурная схема параллельного соединения элементов
Подав на вход соединения дельта-функцию в момент t = т при нулевых
начальных условиях, на выходе первого и второго звена получим сигналы в виде ИПФ этих
звеньев, которые на выходе схемы образуют сигнал
*M=*i('>t)h *2M=*iMh M'»t)-
Этот сигнал и есть искомая ИПФ, т.к. он представляет собой реакцию всего
соединения на дельта-функцию при нулевых начальных условиях. Таким образом,
*(*,т) = *,(*,т)(!) *2(м).
(2.64)
2). Последовательное соединение элементов (рис. 2.18).
Рассуждая аналогично предыдущему случаю, на выходе первого звена получим
сигнал
Глава 2. Линейные одномерные непрерывные нестационарные САУ
129
5(м)
к
Ь- (t т\
*К*> Ч
:(г.х) = ?
X\{t)
Ш х)
к (t т\
K2V> Ч
x(t)
Рис 2.18. Структурная схема последовательного соединения элементов
Воспользовавшись формулой (2.18) по отношению ко второму звену (имея в виду,
что сигнал кх (t,x) для него является входным процессом, протекающим во времени t
при фиксированном значении т), нетрудно получить его выходной сигнал, который,
будучи одновременно выходным сигналом всего соединения, представляет собой
ИПФ этого соединения, т.к. возник в результате приложения ко входу последнего
дельта-функции при нулевых начальных условиях
х(их) = к (их) = J*i (X,т)*2 {uX)dX.
о
Согласно условию причинности (2.10), которому должен удовлетворять сигнал
кх (Х,т) (т.к. он является еще и ИПФ первого звена),
&,(Х,т) = 0, Х<т, (2.65)
нижний предел интегрирования необходимо заменить на т, тогда
к(ит) = 1к2(иХ)к{(Кт)с1Х.
(2.66)
Как уже отмечалось, здесь кх (г,т) выступает в роли сигнала, а к2 (*,т) - в роли
ИПФ, в связи с чем формулу (2.66) иногда рассматривают как операцию воздействия
второго звена (представленного его ИПФ) на ИПФ первого звена и обозначают ее
поэтому условно
*^т) = *2(лт)**,(*,т), (2.67)
как воздействие второй ИПФ на первую ИПФ, при этом ясно, что в общем случае
ИПФ последовательного соединения зависит от порядка следования звеньев, т.е,
*1 (*.*)**2 (Г'Т) * к2 ('>Т)**1 (*'Т) •
Замечание 2.3. Замена нижнего предела (формула (2.66)) может показаться
излишней операцией, т.к. интегрирование при X < т все равно, казалось бы, должно
дать нулевой результат - согласно свойству (2.65) ИПФ либо потому, что сигнал
к\ (г,т) в реальной системе станет отличным от нуля лишь при X > т. Однако
следует иметь в виду, что в формуле (2.66) символ кх (Х,т) выступает не как ИПФ, но и не
как сигнал, а как функция, используемая для описания сигнала. Эта функция должна
фигурировать здесь так же, как функция у (X), используемая для описания входного
воздействия в формуле (2.18), (т.к. к{ (Х,т) в формуле (2.66) играет ту же роль, что и
у(Х) в формуле (2.18)). Пусть функция y(t) определена от - оо до +оо. Используя ее
для описания входного воздействия системы, нужно было бы писать
у(*)1[*-с]> (2.68)
1JU
Анализ и статистическая динамика САУ. Часть I
учитывая тот факт, что воздействие у (t) поступило на вход в момент t = т, а до
этого момента оно было равно нулю. Однако в формуле (2.18) этот факт уже учтен
самим алгоритмом ее вывода (см. соотношение (2.13)), отчего в ней фигурирует просто
функция y(t), а не (2.68). Поэтому и в формуле (2.66) должна фигурировать (и
фактически фигурирует) функция кш (Х,т), а не кх (Х,т), несмотря на то, что она там
записана, но тогда нижний предел интегрирования должен быть обязательно т.
8(t-x)
К
t,x) =
bx(t т\
**(*,т)
?
««—
т, т)
Рис. 2.19. Соединение элементов типа «обратная связь»
3). Соединение типа «обратная связь» (рис. 2.19).
Поскольку к нестационарной линейной системе применим принцип
суперпозиции, перенесем первый элемент через элемент сравнения (рис. 2.20). Подав на вход
полученной системы дельта-функцию (при нулевых начальных условиях), из
рис. 2.20 заметим, что
fc(''T) = *i(''Tb*i(''T)>
t
где хх (г,т) = \к{Х,т)к3 (t,X)dX - реакция системы с ИПФ къ (f,x) на сигнал k(t>x);
X
t
здесь &3(f,x) = J*i (г,а)Л:2 (or,x)dfa - ИПФ последовательного соединения второго и
т
первого звена (см. формулу (2.66)).
yit)
Рис. 2.20. Структурная схема соединения элементов типа «обратная связь»
Таким образом, ИПФ замкнутой системы связана с ИПФ замыкаемых звеньев
неявной зависимостью
(2.69, а)
k(t,x) = kl(t,x)-jk3(t,X)k(X,x)dX,
X
*з(а) = }*,(»,о)*2(о,Х)Л»,
(2.69, б)
Глава 2. Линейные одномерные непрерывные нестационарные САУ
131
(2.70)
и для отыскания k(t,%) необходимо решить интегральное уравнение (2.69, а), что и
является основной трудностью на пути использования метода ИПФ для исследования
линейных нестационарных систем.
С учетом обозначения, введенного в формуле (2.67), зависимость (2.69) можно
условно представить так
*(г,т) = *1(лт)-*з(^^)**^^.]
M^ = M'^)**2M' j
после чего она своей структурой очень напоминает известную из стационарной
теории зависимость
/ ч Wl(S)
w(s)= ';J . ч,
W l + W{{s)W2{s)
если записать ее в виде
W(s) = Wl{s)-W3(s)-W(s);
W3{s) = Wl{s)-W2(s).
Здесь W(s); Wx(s); W2(s)\ W3 (s) - соответственно передаточные функции
замкнутой стационарной системы, имеющей структуру (см. рис. 2.19); звена,
стоящего в ее прямой цепи; звена ее обратной связи; разомкнутой стационарной системы.
Формально заменяя в выражении (2.71);
1) знак умножения - на знак * (воздействия ИПФ на ИПФ),
2) передаточные функции стационарных звеньев - на ИПФ нестационарных
звеньев, которые стоят на их месте в структурной схеме, получим выражение
(2.70).
Отмеченнзд формальная аналогия распространяется и на случай
последовательного и параллельного соединений элементов (см. формулы (2.67) и (2,64)).
(2.71)
Пример 2.4. Найти Щ1Ф системы, представляющей собой последовательное соединение
стационарного апериодическогр зрена и двух усилительных нестационарных зреньев с коэффициентами,
изменяющимися по закону е' и е~' (рис. 2.21).
у(0
* 6
*l(',T)
Ш ( г\ —
WoyS)
s + a
k2(t,-c)
*-
i
x(t)
Рцр> 2.21. Структурная схема системы
Согласно формулам (2.62) и (1,63),
*,(*,т) = «~'8(г-т);
*2(г,т) = е-а<'-<>1[,-т]:
*зМ = е'6(/-т).
132 ^ Анализ и статистическая динамика САУ. Часть I
Применив соотношение (2.66) к первым двум звеньям, получим
X
*12(лт)=*-а<'А-ч[,-т].
Применяем соотношение (2.66) к kl2(t9x) и k3(t,x)
*м (м) = j^5(r-X)e"a(X"VT^ =
т
= е'е-т jS(t -Xya{k^d\ = <><'-V0^' L .,=е('-«Х'-^) #
Т
^(м) = Ла)(/-т>1[/-т].
Таким образом, ИПФ системы (рис. 2.21) зависит только от разности м, т.е. данная нестационарная
система ведет себя как система стационарная (как стационарное апериодическое звено с постоянной
времени и коэффициентом передачи ), передаточная функция которого
Иногда рассмотренные методы определения ИПФ (чаще всего в силу сложности
системы) не эффективны. Тогда ИПФ можно находить с помощью моделирования.
2.3. ОПИСАНИЕ И ИССЛЕДОВАНИЕ ЛНС С ПОМОЩЬЮ
ПРЕОБРАЗОВАНИЯ ЛАПЛАСА И ФУРЬЕ
Аппарат интегральных преобразований нашел широкое применение в теории
стационарных линейных систем. Прежде всего, следует отметить преобразования
Лапласа и Фурье. Например, теоретической основой часто используемого частного
метода анализа и синтеза систем с постоянными параметрами, в разработку которого
большой вклад внес В.В. Солодовников, является преобразование Фурье.
Сделаны обобщения некоторых положений теории стационарных систем на
системы с переменными параметрами (работы Л. Заде, В.В. Солодовникова,
Ю.И. Бородина, А.Б. Ионнисиана, И.П. Бриккера, В.А. Карабанова, Б.Е. Рудницкого
и др.). Для некоторых классов ЛНС этот аппарат может оказаться достаточно
эффективным. В общем же случае его применение встречает принципиальные трудности,
порожденные свойствами дифференциальных уравнений с переменными
коэффициентами.
Очень удобное соотношение частотного метода, справедливое для стационарной
линейной динамической системы
ВД=У(*)Щ*), (2.72)
где
W(s)=jk(ne-Stdt = Lt [*(*)] (2-73)
о
- передаточная функция, являющаяся преобразованием Лапласа ИПФ линейной
стационарной системы (индекс при символе преобразования Лапласа здесь и далее
указывает переменную, по которой оно выполнено); X(s)=Lt [*(*)]; Y(s)=Lt [y(t)])9
наталкивает на целесообразность обобщения интегральных преобразований Лапласа и
Фурье для исследования и нестационарных линейных систем. Впервые такая попытка
была сделана в работе В.В. Солодовникова [146] и, далее, в работах Л. Заде [196].
Глава 2. Линейные одномерные непрерывные нестационарные САУ 133
2.3.1. Общее интегральное уравнение Л НС
Пусть в уравнении (2.5) коэффициенты представимы как
flI.(0 = e? + 5I.(0, i = CUl . (2?4)
fcv(O = *J + *v(O. v = <^"4
где д?, fej и а,- (0, £v(0 "" соответственно известные постоянные и функции
времени; для последних существуют преобразования Лапласа: Д (s), Bv(s).
Выполнив над левой и правой частями уравнения (2.5) преобразование Лапласа с
учетом соотношения (2.74), имея в виду, что преобразование Лапласа от
произведения двух функций равно свертке (отсюда и название метода - метод свертки)
изображений сомножителей [163], получим
п , Ci+J- п
i=o 2nj c_jooi=0
= £&vVy(5)+-L J £/?v(X)(*-X)vr(5-X)</X,
v=0 2тУ C2-jooV=0
Re5>max[c5;c6];c5=c1+c3;c6=c2+c4,
где cx,c2 и с3,с4 - абсциссы абсолютной сходимости соответственно функций
5/(0, МОи x(t), y(t), '
Введя в рассмотрение полиномы по s
L°(*) = £e,V;F0(5)=f;bvV,
i=0 v=0
получим
ЭД=4о7ТУ<5>+,оЛ ■ f ЁВУ(Х)(*-Х)УГ(*-Х)Л-
tf(s) L°(s)2njcJ_, £й
1 (2.75)
Г J YJAi{X){s-X)iX{s-X)d%
- интегральное уравнение в комплексной области относительно изображения
искомого выходного сигнала [163], к которому свелось в результате применения
преобразования Лапласа исходное линейное дифференциальное уравнение с переменными
коэффициентами.
Первый член правой части выражения (2.75) характеризует в комплексной
области решение уравнения (2.5) без учета переменности его коэффициентов, второй член
позволяет учесть влияние на решение переменности коэффициентов правой части, а
третий член (который и превращает выражение (2.75) в уравнение) - переменность
коэффициентов левой части. Такая структура выражения (2.75) создает
определенные удобства для исследования влияния на решение уравнения (2,5) переменности
его коэффициентов»
Обозначим Xq(s) изцедтиые члены правой части выражения (2.75)
X0(s)=£^Y(s)+ Q l 2\ %Ву(Х)(5-ХУ¥(5-Х)с1Х;- (2.76)
^ (s) L (s)2nj C2_7oov=0
тогда
134
Анализ и статистическая динамика САУ. Часть I
c\+j~ Л
X(s)=X0(s)—g-i ' Г Уда)(*-А.)'Х(*-Л)<а. (2.77)
J(s)2nj ci^
В случае, когда представимо
где
C(s)
D(s)
Хла)(,-х)- = С(^;-Х),
- дробно-рациональное выражение, порядок полинома числителя которого
меньше порядка полинома знаменателя, решение уравнения (2.77) можно искать в
форме сходящегося ряда [163]
члены ХД.у),(/ = 1,2,...) которого вычисляются по формуле
1 '7
C(X,s-\)
(s)2njetij_ D(X)
)
F°(s)
L°(s)
. B(s) .
X^is-XldX.
MO
(2.78)
(2.79)
x(t)
A(s)
Xl(t)
■o
A(s)
x2(t)
Рис. 2.22. Структурная схема стационарной системы, эквивалентной нестационарной
Если второе слагаемое правой части соотношения (2.76) и правую часть формулы
(2.79), которые после выполнения интегрирования зависят только от s, с помощью
аналитических преобразований удастся представить в виде
• -5-J 7 f,Bv(X)(s-XyY(s-\)dX = B(s)Y(s); (2.80)
Глава 2. Линейные одномерные непрерывные нестационарные САУ 135^
0 . J ХАДХ)(5-Х)%ч(5-Х)<а = А(5)Хм(5), (2.81)
£ (s)2nj c^jooi=0
то исходной стационарной системе, согласно (2.76), (2.78) - (2.81), ставится в
соответствие эквивалентная стационарная система, представленная на рис. 2.22.
Таким образом, преобразование по Лапласу уравнения (2.5) к понятию,
аналогичному понятию передаточной функции (как это было в стационарном случае),
непосредственно не приводит.
2.3.2. Понятие параметрической передаточной функции (ППФ)
В интеграл суперпозиции (2.16), записанный для случая, когда входное
воздействие приложено к системе в минус бесконечности (он тогда описывает
установившуюся реакцию системы на это воздействие)
t
*(*,-<») = xy(t) = J y(T)k(t,T)dT, (2.82)
— CO
подставим функцию y(t), выраженную через ее преобразование Лапласа
1 е'7~
y(t)=— \ y(s)e"ds;
VO = ~tJ*(*.t) 7 esly(s)ds <*т = -^7 J (e"-e-")y(*)x
UJ - УС'Ч~ ) nJc<-J~ (2.83)
x f Л(Г,т)ЛЛ = — f esty(s)ds\ f e~^~x)k{t,x)dx Ids.
V-~ ; J cA-j°° ^-oo )
Обозначим V/{s,t) вьфажение в скобке
W(s,t) = J e's(t~x)k(t,x)dz. (2.84)
Л. Заде [196] назвал его параметрической передаточной функцией (ППФ). Теперь
соотношение (2.83) принимает вид
*y<t) = -Vf e"Y(s)W(s,t)d*\ (2.85)
2nj J.
J CA-J<*>
оно отражает тот факт, что xy(t) связано преобразованием Лапласа с произведением
Y(s) W(s,t), но тогда по аналогии со случаем стационарных систем это произведение
можно обозначить X(s,t):
Y(s)W(s,t)=X(s,t). (2.86)
Соотношение (2.86) по форме напоминает соотношение (2.72) из теории
стационарных систем, что и желательно было получить, однако применимость соотношения
(2.86) ограничивается пока только рамками установившегося режима (см. формулу
(2.85)), что, конечно, существенно снижает его ценность в сравнении с выражением
(2.72), справедливым и для переходного режима.
Выражение для текущей реакции нестационарной системы на сигнал y(t),
приложенный в момент т0 (см. формулу (2.16)),
136 Анализ и статистическая динамика САУ. Часть I
t
x(t,To)=j y(t)k(t,T)dT,
т°
с учетом того, что ;у(0=0 при t < т0, можно представить в виде
t
*('Л0)= J ;у(т)1[т-то]£(г,т)</т.
—оо
Проделав над ним операции, аналогичные тем, которые были проделаны над
соотношением (2.82), получим
*('До) = Т-7 f estns)\ |НгЛ(М)1[х.т0]Л Ids. (2.87)
Выражение в скобках представляет собой интегральное преобразование (2.84), но
уже не от fc(f,x), а от ее части, «обрезанной» плоскостью, параллельной
координатной плоскости Ш, проходящей через точку т = т0 (см. рис. 2.23 (жирные сплошные
линии)). Таким образом, для того чтобы формула (2.86) была справедлива в
переходном режиме, W(s,t) в ней должна отличаться от W(s,t), представленной
выражением (2.84), причем для каждого to,W(s,t) различная, что, конечно, очень неудобно. К
счастью, на практике часто система начинает функционировать с момента времени,
определяемого ее пользователем, например, с момента ее пуска. В этот же момент на
систему поступает входной сигнал и начинается наблюдение за ее реакцией, которая
в этом случае (т0 = 0) представляет собой
*,0)=(у(тЖгд)1[фт. (2.88)
—оо
Для такой реакции справедлива формула (см. выражение (2.87)):
! с4+7~ Г t \
*(r,0) = -i- f esty{s)\ \ е"5('-т)^т)1[т]^т L/5, (2.89)
но fc(r,x)l[x] - ИПФ, обрезанная координатной плоскостью Ш (см. штрих-пунктир
на рис. 2.23), и есть именно та ИПФ, которую принято считать ИПФ системы в
реальных условиях ее эксплуатации (см. замечание 2.1), тогда выражение в скобках
совпадает с выражением (2.84) для ППФ такой системы:
W(s,t) = J <f 5('-x)*(f,x)l[x]dx, (2.90)
—оо
а формула (2.86) описывает в этом случае в области комплексной переменной уже
функцию, связанную не с установившейся реакцией д:(Г,-°°), а с переходным
процессом *(f,0) (см. (2.89)).
Из формулы (2.84) следует, что ППФ есть интегральное преобразование от ИПФ,
но не преобразование Лапласа. Сделав в выражении (2.84) замену переменной
Г-т = 0 (2.91)
(новая переменная имеет смысл временного сдвига),
Т = Г + 0; dX = d&9 Т = ~оо; 0 = -оо; х = Г, 0 = 0,
получим
W(5,O=jV50*(M-0)d©,
Глава 2. Линейные одномерные непрерывные нестационарные САУ
137
т.е.
W(s,t)=Le[k(t,t-e)] (2.92)
- ППФ системы все-таки есть преобразование Лапласа, связанное с ИПФ этой
системы (аналогично тому, как это имеет место в стационарной теории (формула (2.73))),
но не от той функции, которую описывает &(г,т) по переменной т, а от функции,
которую описывает k(t,t-Q)=[k(t,T)] Q попеременной Э (см. рис. 2.23).
kH(t,x0)
*•/
\\/-\
^
Рис. 2.23. К пояснению процедуры вычисления выходного сигнала
2.3.3. Понятие параметрической частотной характеристики (ПЧХ)
В стационарной линейной теории широко используется понятие частотной
характеристики W(/co), которая может быть получена из передаточной функции путем
формальной замены в ней аргумента s на у'со:
Выполнив аналогичную замену в ППФ, получим также частотную
характеристику, но помимо переменной со она зависит еще и от параметра г
W(ja,tHW(s,t)]
(2.93)
поэтому называется она параметрической частотной характеристикой. Легко понять,
что ей соответствует семейство (по параметру t) амплитудных, фазовых,
вещественных, мнимых, амплитудно-фазовых (см. рис. 2.24), логарифмических и тому
подобных параметрических частотных характеристик.
138
Анализ и статистическая динамика САУ. Часть I
Одним из важнейших свойств частотной характеристики W(j(O) является то, что
она может быть получена экспериментальным путем. Для выяснения возможности
экспериментального снятия ПЧХ необходимо установить ее физический смысл.
В выражении (2.90) заменим s на у'со и представим его как
ИЧМ')=-
J «*'*(*, т)1[т]Л
о№
(2.94)
Согласно формуле (2.88), числитель правой части выражения (2.94) есть текущая
реакция ЛНС на сигнал у(г) = е]ш , приложенный в момент т = 0, и тогда ПЧХ
трактуется как отношение текущей реакции системы на сигнал е*ш к этому сигналу.
Однако сигнал этот нереальный, т.к. связан с мнимой единицей.
j
Рис. 2.24. К пояснению понятия параметрической частной характеристики
Представив функцию
WOco,r)=P(w,O+/<2(co,f) (2.95)
через вещественную и мнимую параметрические частотные характеристики,
функцию
ejm =coscof + 7sin(0f
разложением по формуле Эйлера, выражение (2.94) приведем к виду
[P(cD,OcoscDr-6(co,OsincDr]+;[P(cu,Osincor + j2(co,r)cosu)r] =
= f cos(Oxk(tfx)l[x]dz-¥ j J sincox/:(r,T)l[T]dT.
(2.%)
Поскольку интегральные члены правой части представляют собой текущие
реакции ЛНС на воздействия coscor и sincor, приложенные при т = 0(см. (2.88)),
обозначим их соответственно xc(t>0) и xs(t,O), после чего, имея в виду, что равенство
(2.96) возможно, если независимо равны вещественные и мнимые его части, получим
два уравнения
P(co,r)coscor-(2(u),Osin(or = j[:c(r,0);lsincDrlcoscDf,
P(cD,r)sincDr + 6(cD,Ocos(or = Jcs(r,0).jcoscorJ sincof.
Глава 2. Линейные одномерные непрерывные нестационарные САУ
139
Домножим левую и правую части первого из них на sin cor, а второго на cos cor
и вычтем почленно первое уравнение из второго. Имеем (т.к. sin2 cor+cos2 Ш = 1)
£K<0,0=M^)cosC0f-;cc(f,0)sinC0f. (2.97)
Домножив левую и правую части первого из них на cos со г, а второго на sin cor и
сложив их почленно, получим
P(<uyt)=xs(ttO)sin(ut + xc(tyO)cos<ot. (2.98)
Соотношения (2.97) и (2.98) описывают алгоритм экспериментального снятия
мнимой и вещественной частотных характеристик ЛЫС. Схема установки,
соответствующей этому алгоритму, представлена на рис. 2.25. Для ее реализации, как это
видно из рисунка, требуются две одинаковые системы. Квадратами с диагональным
крестом здесь обозначены блоки перемножения. ПЧХ является функцией двух
аргументов: со и t.
РШ)
sin см
cos cor
■* система
xs(t,0
хс(',0)
д
/
/
\
\
/
/
V
\
/
\
/
/
\
/
\
(2Ш)
Рис. 2.25. Структурная схема системы, реализующей алгоритм экспериментального определения
частотных характеристик ЛЦС
Совокупность кривых, снятых с установки при фиксированных значениях со,
представит ПЧХ как семейство (по параметру со) функций времени (см.
рис. 2.26, а). Представление ПЧХ в виде семейства функций частоты (что обычно
имеют в виду, употребляя термин частотная характеристика) по параметру t
требует перестройки экспериментально полученного семейртва (рис. 2»26, б).
Р(ш„О Р(ш2,г)
Рис. 2.26, а. К пояснению понятия частотных характеристик ЛНС
и их экспериментального определения
140
Анализ и статистическая динамика САУ. Часть I
P(<bh)
P((O,t2)
Щ со2 \а)з
б
со
Рис. 2.26, б. К пояснению понятия частотных характеристик ЛНС
и их экспериментального определения
2.3.4. Понятие нормальной и бичастотной передаточных функций
ППФ W(sJ), введенная Л. Заде, является интегральным преобразованием (2.84)
от k(ty%) по второму аргументу, поэтому ее еще называют иногда сопряженной
передаточной функцией (СПФ) и обозначают H(t,s):
t
W(s,t)= ^e~s{t~x)k{t,x)dx = H{t,s). (2.99)
Однако не все операции при исследовании ЛНС могут быть осуществлены только
с её помощью. Например, выполним над левой и правой частями интеграла
суперпозиции (2.16) преобразование Лапласа по переменной t
]x{ux)e^tdt^\e^t{\y{x)k{t^)dx)dt.
0 От
Поскольку ИПФ есть &(Г,т)1|7-т], то фактическая область интегрирования имеет
вид заштрихованной на рис. 2.27 области (порядок фактического интегрирования
указан штрихпунктирными стрелками). Поменяем порядок интегрирования
(см. двойные штрихпунктирные стрелки на рис. 2.27):
оо оо
Х(ц,х0) = J (e^Vt)y(T)(J«-|ltt(r,T)rfT)rfT =
То г
оо оо
= \e-^y{x){\e-^k{ux)dx)dv,
здесь Х(|1,т0) обозначено jxityX^e'^dt = Lt[x(t,z0)].
о
В скобках правой части фигурирует выражение, аналогичное интегральному
преобразованию (2.99) от ИПФ, но выполненное по первой переменной, оно называется
нормальной передаточной функцией (НПФ) и обозначается N(\i,t) :
N(\L,%) = le~*t'*)k(t9T)dt.
(2.100)
Глава 2. Линейные одномерные непрерывные нестационарные САУ
141
О
Рис. 2.27. Графическое представление области интегрирования
Понятие НПФ было впервые введено Бриккером [30].
Для ППФ было показано, что
Я(М) = 1в[*(*,*-в)].
Аналогично можно показать, что
N(H,T) = Le[*(x+Ti,T)].
В некоторых случаях наиболее удобной оказывается так называемая бичастотная
передаточная функция (БПФ) W(vl,s) , которая представляет собой двойное
преобразование Лапласа от ИПФ по ее переменным. Она может быть получена как из
сопряженной, так и из нормальной передаточных функций с помощью повторного
преобразования Лапласа по оставшейся временной переменной:
wfas) = Mtf('.-*)]f-wl (2Л01' а)
W(\i,s) = LaltfQx,т)]М1+ц. J (2.Ю1, б)
Приведенное обозначение t—>s + \i означает, что при выполнении повторного
преобразования Лапласа изображение, соответствующее переменной г, является
функцией комплексного аргумента s + \i'. Этот факт является следствием того, что
Н (г, s) - интегральное преобразование по т, отличное от преобразований Лапласа.
Действительно, выполнив двойное преобразование Лапласа от &(*,т), получим бича-
стотную передаточную функцию:
W(\iys)^]e^tdt\e-sxk{t,x)dx.
о о
Но поскольку k(t,%) = 0 при т > t,
со /
ИЧщ s) = je-^(eue-5t)dtje-nk(t,x)dT. (2.102)
о о
Кроме того, &(f,t) = O при т<0 (см. (2.84)), поэтому
со I
W(\L,s) = \e-ve-stdt \ e-si'-x)k(t,T)dT =
= je~(li*s)lH(t,-s)dt.
142 Анализ и статистическая динамика САУ. Часть I
Поменяем порядок интегрирования в выражении (2.102) (см. двойной штрихпунк-
тир на рис. 2.27, при т0 = 0), тогда
W(\xys) = je'^ie^e^dxje^kdt^dt =
= \e-^s)xdT\e-^-x)k(u>z)dt = \e-^s)xN{\x,x)d>z
От 0
(см. выражение (2.100)), откуда следует равенство (2.101, б).
Согласно равенству (2.101, д), в БПФ входит два типа переменных s: та s,
которая уже была в функции Н (Г, s), и та s, которая вновь появилась после повторного
интегрального преобразования (вместе с |Л). Для W(\x,s) как функции двух
переменных происхождение s совершенно безразлично, но если возникает потребность с
помощью обратного преобразования Лапласа вернуться от W(\i,s) к H{tys) и k(t,T),
то эти переменные нужно различать: из «старой» s должна образоваться переменная
т, а из «новой» (в паре с ц, вида \i+s) - переменная t. Чтобы «новая» s не
«затерялась» предлагается ввести обозначение \x + s = X и записывать результат (2.101, а)
в виде W(kys). В случае использования W(k,s) только в области комплексной
переменной заменяем X = \i+s, в случае же перехода в область вещественной
переменной первое из обратных преобразований проводим по X, а второе - по s.
Аналогичное замечание можно сделать по поводу формулы (2.101, б). Здесь
причиной необходимости подобных операций является «старая» и «новая» переменные \х.
ППФ, НПФ и БПФ являются эквивалентными в том смысле, что по любой одной
из них могут быть определены две другие, а самая широкая распространённость
среди них ППФ объясняется, пожалуй, лишь тем, что ей соответствует наиболее простая
связь с оператором системы, и тем, что она ранее других была введена в обиход.
2.4. ОПИСАНИЕ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ
И НЕСТАЦИОНАРНЫХ СИСТЕМ С ПОМОЩЬЮ
ПРЕОБРАЗОВАНИЯ ЛАПЛАСА (СРАВНИТЕЛЬНЫЙ АНАЛИЗ)
Использование преобразования Лапласа для исследования ЛЫС сопряжено с
возникновением дополнительных (в сравнении со стационарным случаем) трудностей,
существо которых удобно выразить в форме следующих проблем [121].
1. Проблема оригинала. Порядок роста функции x(t), описывающей изменение
выходной координаты ЛНС, может быть выше экспоненты, и тогда преобразования
Лапласа от нее не существует:
где 0 - пространство оригиналов (пространство функций, для которых существует
преобразование Лапласа).
В стационарной теории такая проблема не возникает. Дело в том, что
где xn(t) - переходный процесс, xy(t) - установившийся процесс.
Из теории дифференциальных уравнений с постоянными коэффициентами
известно [121], что xy(t)e 0 , если y{t)e ©. Функция, описывающая переходный про-
Глава 2. Линейные одномерные непрерывные нестационарные САУ 143
цесс, складывается из слагаемых типа А{е '', i = 1, л, где А{ = const: \{ - корни
характеристического уравнения системы - вещественные или комплексные постоянные
числа, поэтому xn(t) имеет степень роста не выше экспоненты, в силу чего
x(t)eQ, если y(t)eQ.
Пример 2.5. Пусть система описывается уравнением
x(t) + a(t)x(t) = y(t)', [*(f)],=T=0.
Его точное решение в квадратурах [121]:
-Jfl(T,)rfT, / /o(T,)rfT,
*(',*) = *' \ех y(k)dX. (2.103)
т
Тогда импульсная переходная функция данной системы
-Jo(x,V/t,
k(t,x) = e * -1(*-т),
и решение дифференциального уравнения в квадратурах примет следующий вид
' -}о(Т|)</х,
*(M) = Je* -Kt-X)-y(X)d\.
т
Пусть a{t) p t, тогда'
х(/,х) = е 2 je 2 • 1(г-Я.)• y(\)d\, (2.104)
т
откуда видно, что преобразование Лапласа от *(/,т) попеременной г можно было бы вычислить с
помощью повторного применения теоремы свертки в комплексной области, теоремы об интегрировании
оригинала и теоремы смещения, если функции, составляющие правую часть выражения (2.104), - оригиналы. Но
г2 60, поэтому £,[*(;,т)] вычислять таким образом нельзя; при этом следует учитывать также, что в
общем случае здесь используются смещённые преобразования Лапласа
X{s,t) = J jc(6 + т,т)<Г *°rfe = Jjc, (6)^-^6
о о
и Y(j,t) = J y(Q+*c)e~sQdQ = jyx (Q)e~sedQt
о о
где
*,{<е)^*(6+тд),
jYM-jte+x).
В случае стационарной системы (a(t) = a = const) выражение (2.103) примет вид
в+т
Xl(Q) = J е-«(в+т-Х). 1(е + т _X)y{X)d\ =
= }е'°(в'ц)-1(в-ц)-у(ц + т)ф =
о
в
= /^в(в"й)-1(в-|л)->'1(ц)ф.
о
Это свёртка в вещественной области, поэтому
Х(5,т) = L{jc,(O)} = L{^fl9 -1(0)}. 1{у,(в)}.
То есть
Х(5,Т) = "^ К(5,Т).
5 + а
144 Анализ и статистическая динамика САУ. Часть I
Учитывая, что
К(5,т) = Y(s,0) • еп = Y(s) • е'\
получаем подтверждение факту независимости формы реакции стационарных систем от изменения
момента приложения входного воздействия (при сдвиге входного воздействия реакция стационарной
системы также сдвигается без изменения формы).
Это свойство позволяет принять, что момент приложения х воздействия равным нулю (т = 0), что
приводит к широко известному соотношению [121]
Х(5)= —K(5) = W(*)K(5),
s + a
где W(s) = передаточная функция апериодического звена с постоянной времени — и коэффициен-
s + a a
том передачи -.
Нестационарная система может быть описана в пространстве состояния
следующим образом [143]:
Х(0 = A(OX(O + B(OY(O, [X(r)],=T = Хх,
ХВ(О = С(ОХ(О,
где Х(0, Y(O>XB(O - векторы, соответственно, состояния, управления и выхода
системы, А(0,В(0,С(0 - прямоугольные матрицы, составленные из заданных функций
времени.
Известно [121], что если
1) B(OY(f)e0,
2) А(О,С(О - ограничены, непрерывны и дифференцируемы на [0,°°] 9 то
Х(у)б0. (2.105)
2. Проблема уравнений системы в комплексной области состоит в том, что
использование преобразования Лапласа для исследования нестационарных систем
приводит в общем случае не к алгебраическим уравнениям (как в стационарном случае),
а к дифференциальным или к интегральным (2.75), которые часто оказываются не
проще исходного.
3. Проблема структурных преобразований состоит в том, что их выполнение
сопряжено с добавочными трудностями, содержание которых определяется
необходимостью пользоваться положениями, изложенными в [121], вместо простых
алгебраических соотношений в аналогичных ситуациях для стационарных систем.
4. Проблема обращения возникает в связи с тем, что XB(s,t) в общем случае
принадлежит к более сложному, чем дробно-рациональное выражение (как это было
в стационарном случае) классу функции, например, XB(sj) может содержать
существенно особые точки, особые точки типа точек разветвления. Тогда теряет силу
теорема вычетов и встаёт задача анализа особых точек и разложения Xu(s,t) в их
окрестности, которая не исчерпывает всех трудностей в связи со спецификой связи
ХвС*,0 и *в(г,т).
5. Проблема нахождения передаточной функции нестационарной системы по
ее дифференциальному уравнению.
В стационарной системе, описываемой уравнением
Глава 2. Линейные одномерные непрерывные нестационарные САУ 145
t^-S^yW, (2.106)
v=0 v=0
передаточная функция определяется очень просто (через коэффициенты
дифференциального уравнения)
' w{s) = bmsm+bm_lS»-+...+b0
ansn+an_lsn-1+...+a0
А теперь запишем уравнение нестационарной системы
£«vG)*(v) = 5;M*)y(v). (2:108)
v=0 v=0
На основе последнего уравнения запишем формулу для определения импульсной
переходной функции системы:
v=o dt v=o dt
Умножим обе части (2.109) на е" и проинтегрируем на (-оо,+<»). В результате
получим
£av(O-^T J *(/.т>"Л = XMO-jV J '"«('"^ С2-110)
V=0 «^ -оо V=0 "^ -оо
Перепишем последнее уравнение в виде
£av(0^J *(*,T>-*<'-V'rfT= £л,(/)^*". (2.111)
V=0 "' -co V=0 "?
С учетом формулы (2.25), зависимость (2.111) перепишется в следующей форме
S^W^[W(5,0^]=S*,(07V^- (2.112)
v=o dt L J v=o dt
Воспользовавшись формулой Лейбница для V -й производной от произведения
двух функций, после элементарных преобразований из (2.112) находим зависимость
£1£а(,.0^>(*.0-*('.<). е-113*
v=oV-ds at
где
А(5,г)= ]|>у(0Л B(5,r)=§fev(05v. (2.114)
v=0 v=0
Эти зависимости получены Л. Заде в 1954 г. Формула (2.113) показывает, что.
для нахождения параметрической передаточной функции необходимо решить
линейное параметрическое дифференциальное уравнение с переменными
коэффициентами. Но исходное дифференциальное уравнение (2.108) принадлежит тоже к
этому классу. Преимущество в нахождении параметрической передаточной
функции состоит в том, что, построив ее один раз, можно на ее основе решать широкий
спектр задач анализа и синтеза рассматриваемого класса систем. Уравнение (2.113)
точно не решается. Для нахождения W(s,t) используется в основном метод
последовательных приближений.
Указанные выше положения сведены в табл. 2.1 [168].
11 Зак. 232
146
Анализ и статистическая динамика САУ. Часть I
Таблица 2.1
Понятие
Дифференциальное
уравнение системы
Правомерность применения
преобразования Лапласа
Формулы, определяющие
передаточные функции
систем
Формула, определяющая
изображение выхода системы
Степень сложности
нахождения оригинала по
изображению выхода
Степень эффективности
применения преобразования
Лапласа к уравнениям с
постоянными и переменными
коэффициентами
Выводы:
Стационарная система
v=0 v=0
Если y(t) -оригинал,то
x{t) - всегда оригинал, и
применение преобразования
Лапласа правомерно
Передаточная функция
определяется по
дифференциальному
уравнению системы
w,s)_bmsm+bm_lsm-l+...+b0
"v"' ansn+an_lSn-l+... + a0'
X(s) = W(s)Y(s)
В подавляющем
большинстве случаев X(s) -
дробно-рациональная
функция, и для нахождения
оригинала может быть
использована 2-я теорема
разложения
Уравнение
v=0 v=0
с помощью преобразования
Лапласа переходит в
алгебраическое
X(s) = W(s)Y(s) и,
следовательно, подход очень
эффективен
Для класса стационарных
систем аппарат очень
эффективен
Нестационарная система
|X(')*(v)' = l>v(Oy(v)
v=0 v=0
В общем случае x{t) - не
оригинал, т.е. не преобразуема по
Лапласу, и, следовательно,
применение преобразования
Лапласа не всегда правомерно
Передаточная функция является
решением дифференциального
уравнения
где
v=0
v=0
X(s,t) = W(s,tms,t)
Для нестационарных систем
X(s,t) не относится к классу
дробно-рациональных (часто имеет
трансцендентный вид). Поэтому
задача перехода к оригиналам
очень сложна
Уравнение
5X(o*(v)=!>«)/> с
v=0 v=0
помощью преобразования Лапласа
переходит или в интегральное, или
дифференциальное в комплексной
области (для полиномиальных
N
коэффициентов Oy,(t) = ^avktk ),
*=о
или в разностное (для
экспоненциальных коэффициентов
N
М0=1Х*<Г*')- Подход
малоэффективен
Для класса нестационарных систем
в общем случае малоэффективен;
эффективен лишь для отдельных
классов систем
2.5. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ НЕСТАЦИОНАРНЫХ СИСТЕМ
(ОСНОВНЫЕ ПОНЯТИЯ)
Характерной особенностью ЛНС является то, что устойчивость по отношению к
начальным условиям (предполагающая затухание свободного движения) не предо-
Глава 2. Линейные одномерные непрерывные нестационарные САУ 147^
пределяет ее устойчивости по отношению к управлению (требующему конечной
реакции на конечное управляющее воздействие при нулевых начальных условиях, как
было в системах стационарных [121]).
Пример 2.6 [121]. Пусть задана ЛНС
Согласно формуле (2.103), при y(t) = 1 [/], [■*(*)],_, = ■*<>• 'о = 0 имеем
x(t) = e»"\+e»x+2)J^2dx.
о
Так как
'(—
e"Jt+2 =g[-ln(t+2)X =^-ln(/+2)+ln2 =e-ln(/+2)^ln2 = 2
, ч 2 2 fi + 2^ 2 Г(т + 2)2Т 2 * + 2 2
^)=7^^+7Ti{^T=7Ti^+[^|=7T2^+—'—г
Отсюда видно, что свободная составляющая движения ЛНС (2.115)
*. (О-Tiro (2Л16)
с течением времени стремится к нулю (т.е. эта система устойчива по отношению к начальным условиям), а
вынужденная составляющая
^Л')~~ (2-Й?)
неограниченно возрастает (по отношению к управлению система неустойчива). Поэтому необходимо
исследовать устойчивость ЛНС не только относительно начальных условий, но и ее устойчивость
относительно управления.
2.5.1. Устойчивость ЛНС относительно начальных условий
Точное исследование вопроса устойчивости относительно начальных условий
ЛНС общего вида
^ = А(г)Х(0 (2.118)
представляет значительные трудности, поэтому чаще пользуются приближенными
методами такого исследования. Рассмотрим некоторые из них.
Метод исследования относительной устойчивости состоит в том, чтобы
представить произвольную ЛНС (2.118) через параметры системы
^ = Az(t)Z(t), (2.119)
at
устойчивость которой известна:
^-[AZ(0+E(0]X(0; (2Л20)
и, исследуя свойства матрицы-добавка E(r) = {e^(r)}, ij = l,n, судить об
устойчивости исходной ЛНС (2.118).
Наиболее выгодно в качестве (2.119) использовать системы стационарные и
периодические. Первые - как наиболее простые и исследованные, в которых с учетом
(2.120)
А(г) = Аст+Е(г); (2.121)
11*
148 Анализ и статистическая динамика САУ. Часть I
вторые - в связи с положениями теории Флоке, в них
A(f) = Ar(f)+E(f), (2.122)
где
Аг(г) = Аг(г + Г); (2.123)
Г- период изменения коэффициентов матрицы.
Если HmE(r)=0, то матрица (2.121) называется почти постоянной, а матрица
(2.122) с учетом (2.123) - почти периодической коэффициентной матрицей, и имеет
место следующий критерий относительной устойчивости [121].
Критерий 2.1. Пусть система (2.119), где Az (г) = АСТ-постоянная или
Az (r) = Аг (г)- периодическая, устойчива относительно начальных условий. Тогда
и система (2.118), представленная как система (2.120), также устойчива относительно
начальных условий, если
оо
J|E(t)|</t<oo, (2.124)
где под нормой матрицы понимается
1|е(т)|=Е£Ы4 <2-125)
1=1 У=1
Критерий 2.1 для матрицы Az (r) общего вида справедлив, если помимо условия
(2.124) выполняется еще и условие
t
limJtr[Az(x1)]d/x1 >-oo (2.126)
п
(здесь символом tr[Az (х{ )1 обозначен след матрицы Az (i!), т.е. ^aZii (x{)).
i=i
Если стационарная или периодическая система (2.119) асимптотически устойчива
относительно начальных условий, то при соблюдении требования (2.124)
соответственно почти стационарная или почти периодическая система также асимптотически
устойчива относительно начальных условий.
Критерий 2.2 [121] - аналитический достаточный критерий устойчивости
относительно начальных условий.
Задана ЛНС типа
i=0 dt
(2.127)
*o(0 = 1'
у которых переменные составляющие коэффициентов дифференциального уравнения
а{ (t) ограничены,
аг(1)\<т{ (2.128)
(рис. 2.28), где ^(г) = аю+а/(г), аю- постоянные составляющие коэффициентов,
го, - известные постоянные положительные числа.
Глава 2. Линейные одномерные непрерывные нестационарные и А У му
1
0
i ai(t)
^ i
та
t
Рис. 2.28. К пояснению понятия устойчивости ЛНС
Чтобы ЛНС (2.127), (2.128) была устойчива относительно начальных условий,
достаточно выполнения соотношения
а + М<0, (2.129)
где а-действительная часть ближайшего к мнимой оси корня характеристического
уравнения линейной стационарной системы (ЛСС)
Х«ю—Н = У(')>*оо = 1; (2.130)
i=o at
r = §m1p'+I, (2.131)
i=0
здесь р- модуль наибольшего корня характеристического уравнения системы
(2.130);
А = £|А|- (2.132)
1=1
В (2.132) А(- коэффициенты разложения передаточной функции ЛСС (2.130) на
элементарные слагаемые относительно ее полюсов s = $,,* = 1,и :
1 ^ А-
»=1 '
^cxW =
sn+at
(п-\)0
Sn Ч.-. + ^о £f S-S;
(2.133)
Смысл условия (2.129) можно понимать так: положительный (см. выражения
(2.131), (2.132)) «добавок» гА, который с некоторым запасом учитывает
переменность коэффициентов уравнения (2.127) (см. формулу (2.131)), не должен переводить
самый близкий к границе устойчивости полюс передаточной функции WCT (s)
устойчивой стационарной системы (2.130) в правую полуплоскость.
Из соотношений (2.129) - (2Л 31) видно, что если ЛСС (2.130) устойчива и
коэффициенты (2.127) изменяются относительно коэффициентов ЛСС (2.130) на малую
величину (числа т{ малы), то ЛНС (2.127) останется устойчивой.
2.5.2. Устойчивость ЛНС относительно управления
Критерий 2.3 - необходимый и достаточный критерий устойчивости ЛНС
(2.127), (2.128) по отношению к управлению:
оо
J|K(r,x)|jx<C<oo. (2.134)
Здесь |К(г,т)| = {|/:0.(м)|}, / = 1,г, 7 = 1,/п - МИПФ этого объекта, в которой на
месте каждого элемента стоит.его модуль; С = \cl}}, i = 1,г, j = 1,/n ; c(j = с = const.
150
Анализ и статистическая динамика САУ. Часть I
В справедливости условия (2.134) можно убедиться следующим образом.
Известно, что
X(f) = jK(r,x)Y(x)</x.
(rxl) ,o (rxm) (тх\)
Пусть воздействие Y(г)ограничено некоторой величиной Ymax , тогда реакция
(mxl)
i-ro компонента выхода системы нау-ю компоненту входа
t
МОвКММт)Л
'о
имеет максимально возможное значение при у7 (г) = ут^\%^хк^ (f,x) (рис. 2.29):
t t
*ymax (0 = Утахf*y O'^sign^y (t,-c)dx = ?max J|fy (г,т)<*т|.
i
jmax
0
"Утт
\
Рис. 2.29. К пояснению понятия устойчивости ЛНС
Отсюда видно, что составляющая Jty(f), а следовательно, и любой компонент
выходного вектора ограничены, если
Улшх J\kij (*>ТН ^ УтчРц < - ,
b(j = const .
(2.135)
Из соотношения (2.135) вытекает условие (2.134), если положить
c = max{ fy}; i = l,r ; ; = l,w ; * = <*>.
2.5.3. Устойчивость ЛНС на конечном интервале
Устойчивость - асимптотическое свойство системы, связанное с ее
поведением в бесконечности. Но большинство реальных систем работает на конечном
интервале времени [0,Гд], в связи с чем возникает вопрос, насколько эффективно
такая характеристика, как устойчивость, может быть использована для оценки
работоспособности системы в этом случае?
Для линейных стационарных систем (ЛСС), если устойчивость гарантирует их
работоспособность в бесконечности, то она гарантирует ее и на конечном
интервале через время Г = Гр после начала работы (здесь Тр - время переходного
процесса). Действительно, устойчивость предполагает затухание переходного про-
Глава 2. Линейные одномерные непрерывные нестационарные САУ
151
цесса в бесконечности, и если установившееся значение удалось сделать равным
желаемому *ycT = д:ж (этого можно достигнуть выбором величины ступенчатого
входного воздействия), что и означает работоспособность системы (в смысле
близости x(t) к д:ж) в бесконечности, то, поскольку (согласно смысла
понятия Тр) А - близость x[t) к *yCT(f) обеспечивается уже после t = Tp (здесь
А = 0,05 *Уст(0)' и П0СК0ЛЬКУ Яуст^) вследствие постоянства параметров не
меняется во времени, близость x(t) после г = Тр обеспечится и к хж, т.е.
обеспечивается работоспособность и на конечном интервале после t = Tp9 если Тр < Гд.
При необходимости оцени работоспособности в переходном режиме пользуются
понятием качества системы, впервые предложенного В.В. Солодовниковым. Например,
можно считать систему удовлетворяющей требуемому качеству, если переходная
функция h (r) не выходит за пределы некоторой области («коробочки») (рис. 2.30, где
*ycT, a%, Гр, е^ -соответственно установившееся значение, перерегулирование,
время переходного процесса, статическая точность - первичные показатели качества
системы, являющиеся параметрами переходной функции [153]).
Таким образом, вопрос исследования работоспособности ЛСС на конечном
интервале принципиальных затруднений не встречал и решался в рамках понятий
обычной устойчивости и качества.
*усг +
i
100
хж
0
at(t)
i \
//////A//////////j
/ \
"/ ^
/ v(t)
/
1
/
/
/
//i
>V
ГР
А
г—
1V
т Л-
t
Еоо
•Куст
Рис. 2.30. «Коробочка» В.В. Солодовникова и качество системы
В случае ЛНС после t = Tp также наступает установившийся режим, однако в
силу переменности ее параметров он не постоянен даже при неизменном воздействии.
В силу чего выполнение условия *yCT = хж при t = <*> никак не связано с его
выполнением при te [Гп/|,Гд], ведь *yCT(f) непостоянен и неизвестен, поэтому результат
исследования на устойчивость не может служить для оценки работоспособности
ЛНС на конечном интервале даже после затухания переходного процесса (как было в
случае ЛСС). В частности, использование результатов исследования на устойчивость
для оценки работоспособности на конечном интервале может привести и к
результатам, противоположным истинным. Например, пусть система должна работать на
интервале [0,Гд] и обеспечивать точность не ниже ед, т.е. процесс не должен
выходить за пределы областей, выделенных жирными линиями на рис. 2.31.
152
Анализ и статистическая динамика САУ. Часть I
i
0
Устойчивая
\ Г^
r\J ед
J ед
t
лн
С
->
Гл
x(t)
V
t
i
\
0
Неустойчивая Ш
1С
/ х
У
; ^
Гд t
Рис. 2.31. К пояснению качества работы системы
Удовлетворительную работу на конечном интервале обеспечивает изображенная
на этом рисунке неустойчивая система,, а устойчивая - нет. Поскольку исследование
на устойчивость не решает вопроса определения работоспособности JIHC на
конечном интервале, нужно ставить новую задачу о невыходе управляемого процесса из
«коробочки» (см. жирные линии на рис. 2.31), определяемой техническими
условиями работы системы. Наличие в системе этого свойства и предполагает понятие
устойчивость на конечном интервале, которое, как это видно, является
разновидностью понятия качества.
Так как устойчивость ЛНС по отношению к начальным условиям не
предопределяет ее устойчивости по отношению к управлению, ниже рассматривается
устойчивость на конечном интервале по отношению и к начальным условиям, и к
управлению.
2.5.4. Устойчивость на конечном интервале по отношению
К НАЧАЛЬНЫМ УСЛОВИЯМ
Определение 2.1. ЛНС
dX(t)_
dt
= A(r)X(0 + B(0Y(0
(2.136)
называется устойчивой на конечном интервале для Г|, б, Тр по отношению к
начальным условиям, если для уравнения
^l = A(t)X(t) (2.137)
выполнение неравенства
означает, что
dt
XT(r0)X(r0)<ri
XT(r)X(0<8
(2.138)
(2.139)
на интервале [f0, t0 + Тр J.
Известно несколько достаточных критериев устойчивости ЛНС типа (2.137) на
конечном интервале. Приведем три из них.
Чтобы ЛНС (2.137) была устойчива на конечном интервале для л» е> Тр по
отношению к начальным условиям, достаточно выполнения одного из следующих
условий:
Критерий 2.4.
1, е
JX^x^-ln— , для всех re[f0, t0 +Гр],
(2.140)
Глава 2. Линейные одномерные непрерывные нестационарные САУ 153
где Хм (t) - максимальное собственное значение симметрической матрицы
Критерий 2.5. Все главные миноры матрицы
а(о4[а(О+ат(О]. <2-141>
-А(0+^гШ^1(0 (2.142)
отрицательны.
Критерий 2.6.
Tfm^K- (2Л43)
Критерий 2.4 наиболее труден, а критерий 2.6 наиболее легок в смысле их
практического использования, однако в таком же порядке они расположены и по степени
точности оценки с их помощью необходимых и достаточных условий устойчивости
на конечном интервале [121].
В качестве примера рассмотрим доказательство наиболее точного из достаточных
критериев - критерия 2.4, ценность которого существенно возрастает в связи с тем,
что после нахождения собственных значений матрицы А (г) можно
неопределенность границ областей устойчивости (явившуюся следствием того, что критерий 2.4
лишь достаточный) существенно локализовать, воспользовавшись еще и
достаточным критерием неустойчивости 2.7.
Критерий 2.7. Чтобы ЛНС (2.137) была неустойчива на конечном интервале для
у\, е, Тр по отношению к начальным условиям, достаточно выполнение неравенства
jMTi)dTi>|Z'l~' Для всех fe[f0, *0+Гр], (2.144)
'о
где Хц(т) - минимальное собственное значение матрицы А (г).
Доказательство критерия 2.4. Из теории квадратичных форм [121] известно,
что
Хт (t)A(t)X(t)<XM(t)XT (t)X(t), (2.145)
где А (г) - симметрическая матрица, все собственные значения которой
действительны. Продифференцируем скалярную функцию Хт (г)Х(г):
С учетом соотношений (2.137) и (2.141)
i[xT(0x(r)]-xT(0AT(0x(/)+xT(0A(r)x(0-
-хт(«)[ат(0+а(0]х(0-2хт(/)а(»)х(0.
Имея в виду неравенство (2.145), получим
£[хт(ох(г)]*2МО*т(Ох(О-
Так как Хт(г)Х(г) -скаляр, то
ЮЗак.232
154
Анализ и статистическая динамика САУ. Часть I
4*т(г)х(о]
dt
■<2Хм(0-
хт(г)х(О
Проинтегрируем левую и правую части последнего неравенства в пределах от t0 до t:
ХТ('о)Х('о) I
После потенцирования
ХТ(')Х(г) ,/1^\
Хт0о)Х(го)"
с учетом формулы (2.138)
2\xJxi)dx]
XT(t)X(t)<T]e'° . (2.146)
Из неравенства (2.146) видно, что соотношение (2.139) имеет место, если
или после логарифмирования
'о Ч
откуда и следует неравенство (2.140), что и требовалось доказать.
Аналогично доказывается критерий 2.7, если исходить из второго широко
известного в теории квадратичных форм неравенства
хт(,)а(,)х(0>М0хт(')х(0-
Пример 2.7. Пусть в системе (2.137), где
Г 0 1]
A(0-^_(1_acos2/) 0J.
требуется найти ограничения на параметр «а», обеспечивающие выполнение неравенства
для всех;, принадлежащих интервалу [0, 2п].
Из условия задачи следует, что здесь требуется обеспечить устойчивость на конечном интервале для
т|, е, Тр по отношению к начальным условиям системы (2.137) и (2.146), где Тр=2п секунд, In —= 2 .
Для этого (см. критерий 2.4) нужно вычислить собственные значения матрицы А (г) (см. формулу (2.141))
0
Ц-(1-«о.20 0j + [l 0 JJ"
A(0-2l|^_(1.flCOs2r) 0
о
<zcos2/
acoslt
В соответствии с известным правилом [121], приравнивая определитель
acos It
|а(г)-Х I 1 =
| V ' (2х2)|
-X
acos Ъ
-X
_ 2 fflcos2rY
Глава 2. Линейные одномерные непрерывные нестационарные САУ 155
нулю, получаем уравнение, корни которого
есть собственные значения матрицы А (/).
Из рис. 2.32, где показано изменение собственных значений матрицы во времени, наглядно следует,
что максимальное собственное значение этой матрицы изменяется во времени по закону
1
Л-
2
0
.J2L
7
V
\4
M0 = ^|cos2f
A.2(f) = -|cos2/
/Xl(t) = -cos2t
M') = ^lcos2'l
Рис. 232. График изменения собственных значений матрицы во времени
Согласно критерию 2.4, для всех re [0,2я] должно выполняться условие (2.140)
'fHJcos2d
j > "*"
откуда
|а| < ? для всех I е [0,2я]. (2.147)
J|cos2x1|^x1
о
Чем больше знаменатель правой части, тем более жесткие ограничения накладывает условие (2.147) на
параметр «а». В заданном диапазоне изменения t знаменатель принимает максимальное значение на
границе интервала:
2я 4 «
J|cos2x,|dT, =8Jcos2t,</t1 =4sin2x1|£ =4 ,
поэтому
\а\<-. (2.148)
1 ' 2
Если для решения этой задачи воспользоваться критериями 2.5,2.6, то результаты соответственно
\а\<-'Аа\<-
11 я м 4
получаются все более просто, но, как это видно, они накладывают ограничения на исследуемый параметр
со все большим запасом.
2.5.5. Устойчивость на конечном интервале
ПО ОТНОШЕНИЮ К УПРАВЛЕНИЮ
Определение 2.2. ЛНС является устойчивой на конечном интервале для г\у 8, 7), по
отношению к управлению, если при ||У(0||< = Лу выполняется ||x(f)||< = e на интервале
|>'о + Гр].
Приемом, аналогичным использованному при обосновании условия (2.134),
нетрудно показать, что необходимым и достаточным критерием такой устойчивости
ЛНС является выполнение условия
156 Анализ и статистическая динамика САУ. Часть I
to+Tp
\ \k{ux)\dx<—, to<t<t + Tp.
'9 %
Существует несколько достаточных критериев устойчивости на конечном
интервале относительно управления, а также несколько достаточных критериев
устойчивости на конечном интервале и относительно начальных условий и относительно
управления [121].
В качестве примера приведем формулировку одного из них.
Критерий 2.8. Чтобы ЛНС (2.136) при В(г) = I была устойчивой на конечном
интервале для т), Tiy(f), е(Г), Тр по отношению и к начальным условиям и к
управлению достаточно, чтобы
JXm(t,)</t, ' Дм(т)</т
Т\е'° +J<ny(*i)«f| dxx<E(t)
to
для всех j
>G(fo,fo + rp]f
где XM(r) - максимальное собственное значение матрицы А(г) (см. формулу (2.141)).
I
/
;
Глава 3. Метод пространства состояний
157
ГЛАВА 3. МЕТОД ПРОСТРАНСТВА СОСТОЯНИЙ:
МАТЕМАТИЧЕСКИЕ МОДЕЛИ
И ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ
В главе отражены основные положения метода пространства состояний;
рассматриваются линейные системы с постоянными параметрами и нестационарные системы.
3.1. ОПИСАНИЕ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ В НОРМАЛЬНОЙ ФОРМЕ
Метод пространства состояний в качестве первичной математической модели
предполагает использование для описания системы дифференциальных уравнений
первого порядка, разрешенных относительно производных. Такую систему называют
нормальной системой, или системой в нормальной форме Коши.
Система ДУ имеет вид
xl=an(t)xl+... + ain(t)xn+bn(t)yi+... + bim(t)ym;
x2=a2l (f)x, +... + a2n (t)xn +b2i (t)yi +...+b2m (t)ym;
*.=*ni(t)*i+- + a,*(t)x»+bAt)yi+-+b*m{l)ym-
Описание САУ уравнениями вида (3.1) называют описанием в нормальной форме,
или описанием в пространстве состояний.
Если ввести следующие обозначения [7]
А(0 =
В(0 =
С(0 =
то систему (3.1) можно:
*2l(0
Л1«)
4i(0
C2l(O
cpi(t)
описать
X
anW ■
«22(0 •
««2(0 •
*12(O ••
*22<0 "
*»2<0 ••
Cl2(0 •
C22(0 •
cp2(t) ■
так
= А(ОХн
■■ a2n{t)
■■ «„„(0,
■ b2m(t)
■ bHm(t)j
■ си«У
■ c2n{t)
■ cpn{t)j
hB(OY.
(P*n),
(3.2)
158
Анализ и статистическая динамика САУ. Часть I
Система, у которой матрицы А(г), В(0 зависят от времени t, называется
многомерной нестационарной системой.
Если же А(Г) = const, B(f) = const, то такая система называется стационарной
системой.
К уравнению (3.2) добавляют уравнение вида
ХВ(О = С(Г)Х. (3.3)
Вектор Х(0 называют фазовым вектором, или вектором переменных состояния.
Координаты х{, я^,..., хп называются фазовыми координатами, или
координатами состояния.
Об остальных терминах дает представление рис. 3.1.
Л1
Фазовое
пространство
Хт— конечное состояние
х° х<<*и
начальное
состояние
Фазовая
траектория Х(/)
Ч.
/ Фазовый вектор,
/ или вектор состояния
в момент t = t.
Рис. 3.1. Фазовое пространстве
Множество векторов Х(*ф) называется пространством состояний. Это
пространство совпадает с координатным пространством Rn.
На основе уравнений (3.2) и (3.3) легко построить структурную схему системы
управления (рис. 3.2).
Y(t)
в(о
—^
X(t)
X—К
^>
f
J
А(А
X(t
V-
rV
C(0
xB(/)
=s>
Рис. 3.2.Структурная схема системы
По схеме, показанной на рис. 3.2, можно сделать следующие пояснения. С
помощью вектора Y(t) осуществляется управление объектом. Вектор X(t) характеризует
состояние объекта в фазовых координатах хх, д:2,..., хп. Поведение и свойства
системы полностью характеризуются понятием состояния, которому соответствует
точка в пространстве Rn (см. рис. 3.1) [7].
Глава 3, Метод пространства состояний 159
Если система описывается векторно-матричным уравнением в нормальной
форме Коши, то размерность пространства состояний равна порядку указанной
системы.
Координатами пространства состояний являются переменные системы уравнений
(3.1), т.е. переменные системы, записанной в нормальной форме Коши (переменные
*ь *2»—> хп)-
Поведение системы (ее движение) характеризуется фазовой траекторией
(см. рис. 3.1), которая определяет изменение координат системы во времени. Каждая
конкретная (фиксированная) точка на фазовой траектории характеризует
состояние системы при t = *ф.
Фазовая траектория полностью определяет состояние системы в пространстве Rn
и во времени.
Траектория состояний системы в течение времени t G [Гф,7] - это
геометрическое место точек конца вектора состояния X(t) в пространстве состояний Rn,
параметрически определяемых временем t e [t^T\. Траектория состояний
однозначна на интервале [t$,T\ для заданного на этом интервале входного сигнала Y(t).
Фазовым пространством скалярной системы п-го порядка с переменной на
выходе x(t) называют п-мерное пространство состояний, координаты которого
представляют собо ~: производные по времени x^k\t), к = 0, и -1.
Число координат пространства состояний равно порядку системы уравнений в
форме Коши.
Координаты jc* вектора состояния - это часто абстрактные величины, лишенные
физического смысла. Они необязательно соответствуют (но могут и соответствовать)
реальным физическим величинам процессов, действующих в системе. Многие из них
вводятся искусственно путем некоторых преобразований [153].
Поэтому координаты х{, х2,..., хп соответствуют не реальной, а
математической модели СЛ У (математические модели разной степени адекватности).
Вектор состояний X(t) образуется с помощью компонент *,-(*), выбранных так и в
таком количестве, что если известно их значение Х(гф) при t = *ф, где Гф -
фиксированный момент времени, то при заданном значении вектора входа Y(f) для t e [fy,7]
вектор Хв(0 может быть определен однозначно.
Ясно, что фазовую траекторию X(t) можно получить с помощью системы
дифференциальных уравнений в форме Коши, описывающей поведение исследуемой САУ.
Уравнения состояния не единственны. Функции же x*(f),x\(f),...,xbp(f) доступны
наблюдению (измерению). Это реальные выходные сигналы, которые можно
наблюдать (измерить).
В связи с этим уравнение (3.2) называют уравнением состояния, а уравнение (3.3)
-уравнением выхода [7].
При решении вопросов проектирования систем (в том числе вопросов синтеза
регулятора, например, в задаче стабилизации объекта) необходимо иметь информацию
о состоянии системы в каждый момент времени.
Эта задача решается с помощью устройства, которое называется устройством
наблюдения (наблюдающее устройство). Указанное устройство, анализирующее
выходной векторный сигнал Хв(0 (который, как уже говорилось, можно измерить),
позволяет получить приближенное значение (оценку) вектор-функции X(t). Некоторые
координаты состояния можно измерить, другие же представляют собой линейные
комбинации выходных сигналов, и, следовательно, их можно рассчитать.
160
Анализ и статистическая динамика САУ. Часть I
Система, у которой по вектор-функции XB(f) можно с помощью специальных
наблюдающих устройств восстановить вектор X(t) (в общем случае размерность
Х(г) больше размерности Х?(0), называется полностью наблюдаемой.
Вопросы проектирования наблюдающих устройств изучает специальный раздел
теории автоматического управления [7].*
Введенное выше понятие проиллюстрируем на примере одномерной (скалярной)
системы управления.
Пусть одномерная система описывается скалярным дифференциальным
уравнением
хМ + ап.хх{п-Х) +... + аох = y(t). (3.4)
Получим векторно-матричное уравнение в нормальной форме Коши,
эквивалентное скалярному уравнению (3.4).
Введем в рассмотрение следующие переменные
х,(0 = *(0,
*2(') = *Ч0, *з(0 = *"(0,.., xn(t) = x(n-l\t).
Последние зависимости можно переписать так
*i(0 = *(0,
*2 (') = *('),
x3(t) = x"\t),...,xn(t) = xin)(t).
(3.5)
(3.6)
Тогда
г(«>/'А-
(л-1)/
х(п) (0 = -*о*(0 - «i*(0 -. • • - °п-\*к (0 + У (0 =
= -воЛ1(0-«Л(0-...-«я-Л(0 + у(0-
С учетом выражений (3.6) и (3.7) можно записать
ii(0 = *2(0,
*2(О = *з(О.
*з(0 = *4(0.-...§*я(0 = -в0Х1(0-вл(0-----^п-Л(0 + У(0-
Последняя система в матричной форме запишется в виде
y(f).
(3.7)
(3.8)
' 0
0
1
0
0
1
-а2
0
0
-аъ
... 0 N
... 0
... -а„_,
*1
х2
Л,
+
0
1
(3.9)
Х(0 А Х(0 В
Матрица А имеет форму, предложенную Фробениусом, и поэтому называется
матрицей Фробениуса, или матрицей сопровождения. Для нее характерно
следующее: элементы над главной диагональю равны единице, а элементы нижней строки
являются коэффициентами дифференциального уравнения. Все остальные элементы
являются нулями.
Таким образом, от скалярного уравнения n-го порядка путем замены переменных
перешли к нормальной форме Коши (3.9), где
Вопросам оптимального оценивания посвящен параграф 7.3.
■Глава 3. Метод пространства состояний
161
А =
О
О
1
О
о
1
о
о
о
о
;В =
(3.10)
у-а0 -щ -аг -аъ ... ~ап_х
В системе (3.?) хх,х2,...,хп - фазовые координаты.
Легко видеть, что выводом этой системы является скалярный сигнал x{i).
Поэтому матрица выхода С имеет вид
С = (1 0 0 0 ... 0).
Тогда
• \
*1
Хв(0 = СХ = (1 0 0 ... 0)
= *,(*)=*(*).
Выше подчеркивалось, что на практике не все координаты состояния доступны
измерению, а только их некоторая часть. В данном случае можно измерить лишь
сигнал x(i) = *i, или первую компоненту вектора состояния.
Остальные компоненты можно получить последовательным дифференцированием
сигналад:(О, поскольку xl(t) = x(t)ix2(t) = xt(t)J...Jxn(t)-xin~l)(f).
Для получения всех координат вектора состояния х\, х2,..., хп надо иметь цепочку
дифференцирующих звеньев (рис. 3.3).
На рис. 3.3 показана структурная схема устройства для восстановления всех
фазовых координат вектора состояния Х(г). Если известна математическая модель
скалярной системы «вход - выход», то для получения уравнений состояний можно
воспользоваться несколькими методами, в частности, методом канонического разложения,
методом разложения на простые сомножители [107].
■ wmmw
\ г
ТУЗ
А*
г
Ь. ... aj^
г
ТТО
Д^
xx(t) x2(t) x3(t) xA(t)
Рис. 3.3. Структурная схема наблюдающего устройства
Последний метод очень прост. Рассмотрим уравнение
*„«)
avx
М_
v=0
= 1Ку
(v)
v=0
Передаточная функция имеет вид
Щ$)=К^±Ш=£
ш-1
+...+1
1-1
K(s-yl)(s-y2)...(s-ym) =K^(s-yj) A
(s-sl)(s-s2)...(s-sn) w (*"*i)jiii*-*»"
1
(3.11)
(3.12)
162
Анализ и статистическая динамика САУ. Часть I
;1 +
*|-Vi _*-*«+*/-У* _*-У/
Имеем
s-s( s-st s-Sj s-St
Структурная схема, соответствующая функции (3.12), имеет вид (рис. 3.4).
I xx(t) + y(t) x2{t) + xx{i) + y{i)
y(t)
*i-Vi
S -Л
J<0
■У2"У2
^(O + jKO
i
s-s,
m+1
1
*i(0
*2» *«W ^+i(0^.i(0
Рис. З.4. Структурная схема системы
К
(3.13)
x(t)
*-»
Систему дифференциальных уравнений получим на примере конкретной системы
W(s) = KT\{S~yi) 1 .
Легко видеть справедливость уравнений (рис. 3.5):
*i=*i*i + (*-Yi)y;
х2 = (^2 -Чг)х\ +s2x2 + (s2 -У2)У,
Хз=(Ь -Чз)х\ +(*з -Чз)хг +s3x3 + (s3 -y3)y;
Х4 = ХХ (0 + Х2 (0 + Х3 (0 + 54*4 + >-(') •
(3.14)
t)
■Si—Y,
s-sx
x{(t)
IIх-
s-s2
+t
"-
s-s3
,(0+x2(0
1
x,(0+JCj(<>h«3(0+>(0
*(0
l
s-sA
x,(0 x2(0 x3(r)
Рис. З.5. Структурная схема системы
Матричная запись последней системы имеет вид
*4«
*1
Х2
хз
х4
X
(s2 ~У2)
О
s2
О 0}
О О
(*з~Уз) (*з-Уз) *з О
1 1 1 54
i^4 ,
s2-y2
S3-Y3
1
y(t).
(3.15)
В
А X
Выход определяется выражением
х(О = (0'0 0 *)(*,(0 x2(t) *j(0 *4(О)Т=Юс4(г).
(3.16)
Идея метода канонического разложения состоит в следующем. Имеем уравнение
(3.11) и изображение выхода.
Представим выход в форме
Глава 3. Метод пространства состояний
163
*(о= S-^ яо=Хед.(о,
/=1 S Si
i=l
где
1
*;(0 = У(0-
Из выражения (3.18) находим
*,(*)(*-*,■) = У(0-
Тогда
*/(О = ЗД(О+У(О.
Система дифференциальных уравнений для определения л;, имеет вид
У(0.
X А X В
Выход находится по формуле (см. рис. 3.6)
x(t) = (схс2с3.. .сЛ ) (ххх2хъ.. .*„ )Т = сххх (0 + c2a:2 (0 +... + спхп (Г).
*Э
/
0
0
0
0
0
0
0
0
0
... ол
... 0
... 0
... sn>
/1
д:2
1
1
1
(3.17)
(3.18)
(3.19)
ЯО
1
s—sl
1
s-s2
1
п
С1
С2
г*
Рис. 3.6. Структурная схема системы
Можно воспользоваться еще одной моделью. Имеем
Тогда
ВД=-^-Г(5).
5Х/(5)-51.Х/(5) = с/У(5),
или
^ =5,^ +с,.у(О;*(О = ^1+^2+^з+-..+л„.
Можно записать векторно-матричное уравнение (3.19), где
A = diag[51,52,...,5/1]; B = [c1,c2,...,cn.f; С = [1,1,...,if.
Структурная схема показана на рис. 3.7.
164
Анализ и статистическая динамика САУ. Часть I
У®
s-s*
x.(t)
s-s~
хМ)
1
1
x(t)
Рис. 3.7. Структурная схема системы
Рассмотрим общий случай, когда ДУ имеет вид
х(п) +а/1_1(Г)*(пЧ) + ... + ao(O* = bm(O/n +...+*o(O>' • (3.20)
Предполагается, что коэффициенты в скалярном уравнении имеют необходимое
число производных. Скалярному уравнению соответствует следующая система
уравнений в нормальной форме
xl=x2 + Fl(t)y;
x2=x3 + F2(t)y;
: (3.21)
xn = -a0(f)*i - ax (0*2 - • • • - an-\ (f)xn + ^i(Or,
где x{ = x - F0(t)y, F(j(r) = bn(t), а функции Ft(f)9i = l,n вычисляются с помощью
рекуррентной формулы
F,(t) = bn.x(t) - g I2c;+1_|.an_),t+i(0^^,
в которой
_(n-i + s)\
(n-i)\s\ '
Нетрудно проверить, что при таком выборе переменных состояния матрицы
системы имеют вид:
Г о i о о
0 0 10
А =
0 ^
0
*
1
,в =
•
F.
(3.22)
0 0 0 0
-а0 -а{ -а2 -а3
Ст=(1 0 ... 0).
Например, если п = 2, т.е. рассматриваемая динамическая система описывается
уравнением второго порядка
d2x dx d2y dy
£-£ + <,,(/)—+ао(О* = Ь2(О—7 + ^(0-г + *ь(0У(0,
dt2 dt dr dt
Глава 3. Метод пространства состояний 165
то в соответствии с приведенной выше формулой имеем
at at
F2(t) = b0-a0F0-a{^-a2—T-a{Fl-a2^j- =
dFx dzF _, dF{
—L-a2—T-axFx-a2—*- =
dt dt dt
и (*db2 и ^Л и dal r,d2b2
^ af ) at dt
Если коэффициенты исходного скалярного дифференциального уравнения (3.20)
постоянны, то векторно-матричное уравнение запишется так
Х = АХ + Ву;
в нем элементы матриц А и В определяются, исходя из следующих формул:
i/=^+i + /!ly;«=l,2>...fn-l;
где
F2=V2-^-1^1-^-2^0;
1-1
Fi = *n-i ~ S an-i+mFm-
m=0
Если степень числителя передаточной функции, соответствующей исходному
дифференциальному уравнению, меньше степени знаменателя, коэффициенты
ЬяА-1»—' полагаем равными нулю.
Начальные условия согласованы следующим образом
^(0) = ^(0),х2(0) = ^Ч0)-Ь,Я0),...,
^(0) = ^(/l"1)(0)-F1/w-2)(0)-...-F/l4y(0).
Переход от структурных схем с передаточными функциями или от скалярных
дифференциальных уравнений к векторно-матричным дифференциальным
уравнениям можно рассматривать в качестве перехода к модели в переменных состояния.
Еще раз подчеркнем, что использование такого перехода позволяет состояние
исходной скалярной системы в каждый момент времени полностью описывать
значениями п координат, называемых координатами, переменными состояния, или
фазовыми координатами.
Векторно-матричное уравнение, соответствующее уравнению второго порядка
(см. пример при п = 2), имеет вид
А =[Ч, al2U0 1
[a2l a22) ^-oo -a,
B=fF0=f Ъх~ахЪг
\рг) \Ъй-аф2-ахЪх-а\Ъг
166
Анализ и статистическая динамика САУ. Часть I
3.2. ФУНДАМЕНТАЛЬНАЯ СИСТЕМА. СВОБОДНЫЕ КОЛЕБАНИЯ
В СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ СИСТЕМАХ
Рассмотрим однородное уравнение
Х = А(г)Х. (3.23)
Решением последней системы называется вектор-функция Х(Г) с компонентами
*i(0v..> xn(t), которые обращают уравнение (3.23) в тождество no t.
Частное решение однородной системы, порожденной начальными условиями,
может быть определено так: заданы начальные условия *i(0),..., *л(0); необходимо
построить jci(O»..., *л(0> удовлетворяющие начальным условиям, указанным выше.
Запишем неоднородное дифференциальное уравнение
X = A(r)X + B(r)Y. (3.24)
Сформулируем теорему существования и единственности системы (3.24).
Если матрицы А(Г) и B(f)Y(f) непрерывны на промежутке [0,7] и задан
произвольный начальный вектор Х(0), то на [0,7] существует единственное решение Х(г)
уравнения (3.24) (интервал [0,7] может быть как конечным, так и бесконечным).
Зададим матрицу начальных условий [45]
|%(0) *12(0) ... *1я(0)>
*2i(0) *22(0) ... *2„(0) (325)
^ni(O) *„2(0) ... *,1Л(0);
Столбцы последней матрицы - начальные условия, такие, что имеет место
соответствие
(^ii(0),^2i(0),...,^i(0))^X1(0 = (a:11(0^2i(0,...,^i(0)T;
(*12(0),*22(0),.. .;*„2(0))<->Х2(0==(*12(0, *22(0,.. .,*„2(0)Т;
K(0)^2«(0),...,^w(0))oXw(0 = (x1^0^2n(0,...,^w(0)T.
Определитель вида
*ll(0 *12(0 - х\п(0
x2{(t) x22(t) ... x2n{t)
(3.26)
det(Xo(r)) =
^nl(0 *n2(0
до
(3.27)
называется определителем Вронского системы вектор-функций (3.26), являющихся
решениями (3.23).
Совокупность п-решений (3.26) уравнения (3.23) называется фундаментальной
системой решений уравнения (3.23), если определитель Вронского этих решений не
обращается в нуль ни в одной точке интервала [0,7].
Если матрица (3.25) является единичной, т.е. имеет вид
(\ 0 0 ... 0Л
0 1 0
о
0 0 0 ... 1
то система (3.24) называется нормальной фундаментальной системой.
Глава 3. Метод пространства состояний
167
x2(t)
*.(0,
x2l(t)
L*.l(O,
+ c2
'xi2{t)s
*22(0
+ ... + C,
*2„(0
Следует подчеркнуть, что если А(г)еС[0,7] и определитель Вронского (3.27)
отличен от нуля в некоторой точке toe [0,7], то он отличен от нуля на всем промежутке
[0.7].
Теперь приведем основную теорему, определяющую общее решение однородного
уравнения.
Если матрица А(Г) непрерывна на интервале [0,7] и определитель Вронского
решений Xi(r), X2(0>-.., Xn(t) уравнения (3.23) не обращается в нуль в некоторой точке
toe [0,7], то общее решение уравнения (3.23), соответствующее произвольным
начальным условиям, всегда может быть представлено в виде разложения по
конечномерному базису, порожденному фундаментальной системой:
Х(г) = с1Х1(0 + с2Х2(0 + ... + с,,Хп(0, (3.28)
или
(3.29)
Из выражения (3.29) сразу же можно записать формулы, определяющие x\(t),
x2(t\...,xn(t):
*\ (0 = сххх, (г) + с2*12 (0 +...+cnxln (Г);
х2 (0 = схх2! (Г) + с2х22 (*) + ...+спх2п (Г);
*„ (Г) = ci*ni (Г) + с2дся2 (0+... + ся*яя (г).
В формулах (3.28), (3.29) и (3.30) си с2,..., сп - скалярные величины, определяемые
при построении частных решений через начальные условия *i(0),..., *n(0).
Положим, что при г = 0 решение Х(г) равно некоторому вектору
Х(0) = (х1(0),х2(0),...,хя(0)). (3.31)
Легко показать, что существуют такие постоянные сь с2,..., спу при которых
решение (3.28) удовлетворяет начальному условию (3.31).
С учетом (3.31) для определения сь с2,..., сп можно записать систему линейных
неоднородных алгебраических уравнений
с{хх! (0) + с2хх 2 (0) +... + ся*1я (0) = хх (0);
схх2! (0) + с2х22 (0) +...+cw jc2w (0) = дс2 (0);
сЛ1(О) + с2дся2(О) + ... + сЛя(О) = дся(О).
Или, что то же самое,
(*ц(0) хХ2(0) ... ^(0)^
*2i(0) х22(0) ... дг2я(0) „2 = ^2VV/
^m(0) ДРя2(0) ... дряя(О)
Определитель этой системы является определителем Вронского решений
Х|(г)>...» Хя(0 в точке / = 0; по нашему предположению он отличен от нуля.
Следовательно, существует единственное решение системы (3.32); оно
определяется выражением
С = Х^(0)Х(0). (3.33)
/ \
с2
=
х2(0)
хп(0),
168
Анализ и статистическая динамика САУ. Часть I
Положим, что матрица является единичной, т.е. имеет место соотношение
(3.34)
'1
0
0
0
1
0
0 ...
0 ...
0 ...
0
1.
1 С{ 1
Сп ,
=
(МО))
*2(0)
*„(0)
Тогда
Ci=*i(0); с2=х2(0)\ ...; ся=*я(0).
Частное решение определяется выражением
X2(t)
*■(').
= *,(0)
%(0N
x2i(t)
+x2(0)
'xl2(tf
+ ...+*„(0)
*2„(')
*2(0
=
'*и(0
*2i(0
*«i(0
xi2(t)
*22(0
*2я
(0
(0,
/ \
(3.35)
Далее, с учетом полученных выше зависимостей, в частности, формул (3.27),
(3.29) и (3.30), запишем выражения, определяющие общее и частное решение
однородного уравнения (3.23).
Перепишем (3.30) в форме
(3.36)
Таким образом, общее решение в матричной форме принимает вид
Х(0 = Хф(0С, (3.37)
где Хф(г) - фундаментальная матрица (о ней подробно будет сказано ниже), С -
вектор произвольных постоянных, определяемых через начальные условия.
Предположим, что заданы конкретные начальные условия, т.е. известен вектор
Х(0). Тогда вектор С определяется зависимостью (3.33). Следовательно, частное
решение, соответствующее начальным условиям Х(0), может быть представлено в виде
Х(/) = Хф(0Хф1(0)Х(0). (3.38)
Если же имеет место нормальная фундаментальная система, то
Хф(0) = 1
и, следовательно, находим
Х(Г) = Хф(0Х(0). (3.39)
Для класса стационарных систем известна зависимость [7]
Хф(0Х^(т) = еА('"т). (3.40)
Воспользовавшись последним выражением, формула для Х(7), порожденной Х(0),
имеет вид
Х(0 = *А'Х(0). (3.41)
Подробно рассмотрим случай, когда A(r) = const, т.е. будем изучать уравнение
Х = АХ. (3.42)
Как и в случае скалярных дифференциальных уравнений, будем искать решение
однородного уравнения в виде [45]
дс1(О = а1вХг,дс2(О = а2вХг.-.дся(О = аявХг. (3.43)
Подставляя (3.43) в (3.42), получаем
Глава 3. Метод пространства состояний
169
-a{keXt + ах хъхех* + ах 2a2eXt +... + alnanekt = 0;
а2 \axeXt - a2XeXt + a22a2eXt +... + a2naneXt = 0;
аЯ1<х,«х' + д„2а2ех' +... - anXeXt+ <*nnaHeXt = 0.
(3.44)
Ju
Сокращая на е , из (3.44) находим
(ап-Х)ах+а12а2+а1Ъаъ + ...+аХпап=0\
а21а1+(а22-Х)а2+а23а3+... + а2/1а/1=0;
(3.45)
ап1а{ +ап2а2 + ... + (*,,« -Х)ая =0.
То же самое можно получить, используя матричную форму. Пусть
X(f) = aeXi,
где а = (ось..., а„) - вектор, X - скаляр, Х(0 = (x{(t),..., xn(t)). Поскольку X = XaeXt, то
из (3.42) находим
-А.а«х'+Аа«х'=0.
Отсюда
-Ха + Аа = 0, или Аа-Ха = 0.
Это уравнение можно записать в виде
(А-Х1)а = 0, (3.49)
где I - единичная матрица. В скалярной форме выражение (3.49) записывается в виде
(3.45). В развернутой форме имеем
(3.46)
(3.47)
(3.48)
'аи-Х ап а13
а21 а22 -X а23
апп "А-
а,
а2
= 0.
(3.50)
ап\ atra апъ
Последняя зависимость представляет собой линейную однородную систему
алгебраических уравнений; необходимым и достаточным условием существования
нетривиального решения является равенство нулю определителя системы (3.50)
(ап-Х) а12 а13 ... аХп
а21 (а22-Х) а2Ъ ... а2п
««1 «Л2 ««з - (<*ля-\)
или в матричной форме
det(A-Xl) = O.
Раскроем последнюю зависимость
det(A-XI) = (К-X,)"'(К-\2)"»...(X-X,)"' =
= (Х"+сп_1Г-'+сп_2Г-2+... + с0) = 0.
Ранее уже говорилось, что уравнение (3.52) называется характеристическим, а
корни Хь..., Хп называются собственными значениями матрицы А (ылм
собственными числами). При проведении дальнейших рассуждений будем полагать, что все
собственные значения отличны друг от друга. Положим, что характеристическое
уравнение решено и найдены собственные значения Хь Х2,..., Хп.
(3.51)
(3.52)
1/U
Анализ и статистическая динамика САУ. Часть I
Подставляя поочередно Хь Х2,.., К в (3.48) и решая однородную систему
алгебраических уравнений
А а, =Х/о1-,
находим
el-=(aHfa2,fa3,,...faIIi).
В развернутом виде имеем
Аа, =
ап ап
а2{ а22
1л
2/1
пп ,
Г а, Л
а2;
«„,•
=
А.,а2,-
или, что то же
Решив систем]
са
'а
-»
мое,
а2,
3.53),
«21
а«1
а,2
а«2
получим еле
= о,; Х2->
... а,
!ДУЮШ
/ \
«12
«22
«„2
«2»
(ие века
= а2; .
fttl'l
«2i
оры
= 0
—>
, / = 1,
[<\
a2»
а„п
п.
=
(3.53)
Векторы а(-, являющиеся решениями уравнения (3.53), называются
собственными векторами. Каждый вектор а,, не обращающийся в нуль и удовлетворяющий
уравнению (A-X/IJa, =0, называется собственным вектором квадратной
матрицы А, принадлежащим собственному значению Xi [45].
Поскольку главный определитель системы (3.50) равен нулю, собственные
векторы определяются не однозначно, а с точностью до постоянного множителя.
Очевидно, что fca, при к Ф 0 удовлетворяют уравнению (3.49) и являются
собственными векторами. Длина собственного вектора часто принимается равной
единице; тогда на векторы а, накладывается ограничение
Для матрицы Асп отличными друг от друга собственными значениями
существует точно п собственных векторов, являющихся линейно-независимыми элементами.
Решения уравнения (3.42), соответствующие корням Хь Х2,..., Хл, могут быть
записаны в виде
Х,(0 =
м
а21
{ \ t \
а2/"
«„/"
=
*2l(0
^nl(');
Глава 3. Метод пространства состояний
171
Х2(0 =
х„(')=
Или, в общем виде,
Х,(0 =
«22
,а»2,
'О
а2и
ач
а2)-
Л' =
ех<' =
а12^'
а2пЛ'
а21./''
«.1^ .
=
=
=
^12(0'
^22(0
^п2(0у
^2ЛС)
ч *».('),
(3.54)
(3.55)
Решения Х|(Г), соответствующие различным корням Ль Хг,.., ^л, линейно
независимы.
Решения Xi(f),..., Xn(0 образуют фундаментальную систему, и, таким образом,
общее решение однородной системы (3.42) может быть представлено так
X(0 = qa^Xir +c2a2e^ +... + cnaneKt. (3.56)
Или, в развернутом виде,
X(f) =
м
<х21
«»1
+ с2
а22
О.2.
^а,^
/г'+...+с„
«2я
аи
/-'.
(3.57)
Из последней формулы можно заключить, что общее решение векторно-
матричного уравнения (3.42) определяется через собственные значения матрицы А
(числа Хи Х2,..., Х„) и собственные векторы ai,..., сс„, соответствующие собственным
значениям.
Перепишем выражение (3.57) в развернутом виде
xl(t) = clauex>' +c2anex>' +...+с„а1пек>;
x2(t) = cla2lex't +с2а22Л' +...+с„а2пЛ';
(3.58)
х„ (t) = qa,,/'' + c2an2e^' +...+cnanneXj.
Или, что то же самое,
'*1('Л fai/'' ачеК' - ос,,/-'4)
x2(t)
a2lex>' a22e^'
<*-2пе
Л.'
*-(0j anlex'1 а„2ех>' ... аи„Л'
Х(0 = Хф(0С.
(3.59)
VIL
Анализ и статистическая динамика l-лу . часть i
Если заданы начальные условия, то (3.59) принимает вид
причем
а,, а12
а21 а22
ап1 ал2
а21
аЛ1
а
а, 2
а22
\*а)
In
2«
/1/1
=
МО))
х2(0)
х„(0)
(3.60)
а12
«22
«„2
- собственные векторы матрицы А, соответствующие собственным значениям Хх,
Я2,..., А*. Из (3.60) имеем
аС = Х(0). (3.61)
Отсюда
С = ёГ1Х(0). (3.62)
Свободные колебания на выходе стационарной системы
Х(0 = Хф(Г)а"1Х(0) = еА'Х(0). (3.63)
Из (3.63) следует равенство
(3.64)
Процессы вида а,еХ;' называются собственными процессами системы [45].
Пример 3.1.
dt
dt
4ДГ£ + 3JC2
Запишем характеристическое уравнение
det(A-Xl)=
, илиХ = АХ, гдеА=[ Х 2].
I4 3J
4 3—Х|
Отсюда Х| = 5, Ха - - 1 - собственные значения матрицы А.
Далее найдем собственные векторы. Имеем
Г1-5 'Y'-'U-4 2Ya"l=o.
I 4 3-5j[a2lJ [4 -2j[a2lJ
Тогда - 4ац + 2a!2 = 0, отсюда a,2 = 1щх. Теперь можно записать
Аналогично имеем
4 4^0^
Тогда 2<Х|2 + Ъхп = 0, а» = - «22. Запишем
Х,(0 =
'" ^w; jjy-a
Общее решение имеет вид
Компоненты вектора Х(/) определяются зависимостями
х2(о=| 1_У'.
4:sm;w-v-
Глава 3» Метод пространства состояний
173
х,(0 = с,е$1 + с2е-; x2(t) = 2с,г5' + (-1)с2в"'.
В этом примере Х| = 5, Х2 = — 1 — собственные значения матрицы А, а векторы Я] = 5 —* (1 2)т и Х2 = — 1
-> (1, - 1)т- собственные векторы, принадлежащие соответствующим собственным значениям.
3.3. ФУНДАМЕНТАЛЬНАЯ МАТРИЦА. ВЫНУЖДЕННЫЕ
КОЛЕБАНИЯ В СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ
СИСТЕМАХ; ВЕКТОРНО-МАТРИЧНЫЙ ИНТЕГРАЛ КОШИ
Рассмотрим векторно-матричное неоднородное уравнение
X = A(f)X+B(OY(r). (3.65)
Наряду с уравнением (3.65) рассмотрим однородное уравнение и построим
фундаментальную систему, задаваясь невырожденной матрицей начальных условий
Xi(/)-(*u(/) *2i(0... xnl(t))<*(xn(0),...,xnl(0));
X2(t) = (x12(t) x22(t)... xn2(t))^(xl2(0),...,xn2(0));
(3.66)
Xn(0 = (*in(0 x2n(0... xnn(t))<*(xln(0),...,xnn(0)).
Система (3.66) является линейно-независимой. Систему (3.66), как говорилось
выше, называют фундаментальной системой решений уравнения (3.65). Составим из
(3.66) матрицу вида
'*h(0 xn(t) ... х^))
*2l(0 X22(t) ... X2n(t)
Хф(г) =
(3.67)
Матрицу (3.67) называют фундаментальной матрицей уравнений (3.23) [45].
Поскольку Х,<0 - решение однородного уравнения, то
^■ = А(/)Х„ / = 1,п.
at
Тогда
dt
-А(г)Хф,
(3.68)
т.к. векторные равенства можно представить как равенства соответствующих
столбцов матричного уравнения (3.68).
Следовательно, задача расчета фундаментальной системы (3.66), определяемой
соответствующими начальными условиями, эквивалентна задаче решения (3.68) при
начальных условиях
'х„(0) *,2(0)
*2l(0) *22(0)
Хф(0) =
^in(0)l
*2„(0)
(3.69)
4*.i(0) ^2(0) - хпп(0)
Известен следующий факт: любая п х п матрица Хф(0> такая, что
det(X+(r))*O
и для которой Хф(О существует при всех te [0,T], определяет векторно-
матричное дифференциальное уравнение, в котором A(t) определяется формулой
А(0 = Хф(г)[Хф(01
-1
(3.70)
174 Анализ и статистическая динамика САУ. Часть I
Далее получим интеграл Коши, для чего запишем очевидное равенство
Продифференцируем (3.71)
Хф(г)Хф1(О = 1. (3.71)
—^Хф1(0 + Хф(0-^^ = 0. (3.72)
Учитывая равенство
^^ = А(ОХф(О, (3.73)
получим
А(0Хф(0Хф1(0 + Хф(0^^ = 0,
или
А(О + Хф(О » = 0. (3.74)
Умножим (3.74) слева на Х^(г)
Хф!(ОА(О+ *t =0- (3.75)
Последнюю зависимость умножим справа на Х(0
Хф!(ОА(ОХ(г)+ J^WX(O = O. (3.76)
Из уравнения (3.65) находим
A(r)X(0 = X(0-B(0Y(r). (3.77)
Подставив (3.77) в (3.76), запишем
X^(/)X(r)-X^(0B(0Y(0+—^Х(0 = 0,
или
Хф'(0^р+^^Х(0 = XjWWit). (3.78)
Последнюю зависимость можно переписать в виде
~.(Хф1(0Х(0) = Хф1(0В(0¥(Г). . (3.79)
Отсюда получаем
ХфЧОХ(Г) = Jx^(t)B(t)Y(t)Jt. (3.80)
о
Окончательно (3.80) можно переписать в форме
t
Х(г) =/хф(ОХф1(т)В(т)¥(т)с/т, (3.81)
о
или
t
Х(г) = Jo(r,T)B(x)Y(T)dx. (3.82)
о
Обозначив
К(/,х) = Хф(0Хф1(т)В(т) = Ф(г,х)В(т), (3.83)
Глава 3. Метод пространства состояний
175
запишем
X(r) = jK(M)Y(T)Jx.
В развернутом виде (3.84) перепишется так
X2(t)
I
(kn(t,T) kl2(t,X)
k2l(t,x) k22{t,x)
*2m('.t)
*«*('.*)
У2(1)
У«(х)
dT.
(3.84)
(3.85)
*„,(*, т) kn2{t,x)
Последняя формула называется интегралом Коши. Матрица К(;,т) называется
матрицей импульсных переходных функций, или матричной НПФ.
Матрица Хф(г)Хф'(т) = Ф(г,т) называется переходной матрицей состояния.
Пример 3.2. Рассмотрим уравнение
Х =
Одна из фундаментальных матриц имеет вид
1
t
2
t2
0
2
t ,
X(f), *>0.
ft 0
хФ(0=I ,2
Вычислим
Переходная матрица имеет вид
Х;!(т) =
г 1
т
1
"7
0
1
7,
Хф(г)Хф1(х) =
- о
l-il il
т т3 т2.
Если имеет место система управления с уравнением
X = A(r)X + Y(0,
то
= Ф(М).
О
.Л.
,х т3 т2.
Линейная однородная система, матрица которой получается из матрицы ||Ду(0||
транспонированием и изменением знака, называется сопряженной системой (3.23)
Ф = -Ат(0*. (3.86)
Дифференциальное уравнение X = A(f)X называется самосопряженным, если
для всех t имеет место равенство
1< А(О = -Ат(г).
Приведем некоторые свойства [168]:
1). Пусть Х(0 = (x\(t), x2(t)>..., xn(t)) - произвольное решение системы X = А(Г)Х,
a Y(0 = (Vi(0. V2W»—» Vn(0) - произвольное решение сопряженной системы
4f = -АТ(Г)У (оба решения определены на [0,Г]).
176 Анализ и статистическая динамика САУ. Часть t
Тогда
* x1(0Vi(0 + *2(0V2(0 + -.. + Jc«(0Ve(0 = const. (3.87)
2). Если Ф(Г,го) = Хф(г)Хф1(^о) - переходная матрица состояния Х = А(г)Х,
тогда Фт(г0,0 - переходная матрица состояния сопряженной системы
* = -Ат(0*.
3). Для самосопряженного дифференциального уравнения справедливо условие:
ФТ(Г,ГО)Ф(МО) = 1. (3.88)
Здесь Ф(г,го) = Хф(г)Хф1(^о).
4). Ф(г,го) = Хф(г)Хф1(го) = 1. (3.89)
5). Ф"1(г,го) = Ф(го;О. (3.90)
В самом деле,
ф-1(г,г0) = (хф(г)Хф1ао))"1=Хф(г0)Хф1(0 = Ф(г0,0.
6). Матрица Ф(*,*о) удовлетворяет условию
Ф(Г,г0) = А(*)Ф(Мо), ф('>'о) = L (3.91)
7). Матрица Фт(Г0,г) удовлетворяет сопряженному уравнению
Фт(*0,0 = -Ат(0ФТ(;0,0. (3.92)
Получим выражение для выходного сигнала. Поскольку
X(0 = A(f)X(f) + B(0Y(0
- уравнение состояния,
Хв(0 = С(0Х(0
- уравнение выхода, то с учетом (3.81) и уравнения выхода, находим
t
Хв(г) = С(0Хф(0Х^(0)Х° + /(Х0Хф(0Х^(т)В(т)У(т)Л
о
Таким образом, формула, определяющая вынужденные колебания на выходе
системы, имеет вид
t t
Х„(0 = /СфХфЮХф'СОВСг) Y(x)dx = J C(t)O(t, x)B(T)Y(x)dx.
Или, что то же самое,
t
XB(O = jKB(r,T)Y(xMx,
о
где Кв(г,т) = С(0Ф(Лт)В(т) - матричная импульсная переходная функция «вход -
выход» системы (ядро системы).
Рассмотрим случай, когда система описывается векторно-матричным
дифференциальным уравнением с постоянными коэффициентами, т.е. имеют место уравнения:
X = AX + BY (3.93)
- уравнение состояния;
ХВ=СХ (3.94)
- уравнение выхода.
Запишем фундаментальную систему
Глава 3. Метод пространства состояний
177
Xi(o =
;Х2(г) =
а12е -
а22ех*
; ...;Х_(г) =
а2пе
К'Л
Л.»
Л'
(3.95)
В системе (3.95) предполагается, что собственные значения матрицы А
различны. Если известка фундаментальная система, то легко записать фундаментальную
матрицу
A'N
Хф(г) =
„ Х.г -, Х,г
аие ' а.пе 2
ai«e
а21ех'' а22ех* ... a2neKt
anleX< an2ex*
а„пе
К'
Переходная матрица состояния определяется выражением
(3.96)
(3.97)
Хф(ОХф1(х) = Ф(г,т) = Ф(г-т).
Далее будет показано, что
Ф(г,т) = Фа-т) = еА('-т). (3.98)
Поскольку фундаментальная система (3.95) не является нормальной, то для этого
случая справедливы формулы для свободных колебаний
(3.99)
(3.100)
-1/
Х(г) = Хф(г)Хф1(0)Х(0)
и для вынужденных сигналов
ХО) = }хф(0Хф1(т)В Y(x)dt = \Ф{1 -T)BY(T)dx.
Перепишем (3.100) в виде
X(O = JkG-t)Y(t)</t,
где
г-1/
(3.101)
К(г-т) = Хф(г)ХфЧт)В=Ф(г-т)В. (3.102)
Матрица К(г - т) называется матрицей импульсных переходных функций «вход -
состояние» системы.
Таким образом, сигнал X(t) стационарной системы, порожденный ненулевыми
начальными условиями, определяется (3.99).
Свободный сигнал и вынужденная составляющая на выходе системы
определяется равенством
i
Хв(0 = СФ(0Х(0)+|СФ(г-т)В¥(т)Л =
о
t
= CO(t)X(0)+jKB(r-T)Y(T)rfT,
(3.103)
где
Кв(г-т) = СФ(г-т)В (3.104)
- матрица импульсных переходных функций «вход - выход» системы. Далее будет
показана справедливость равенства
13 Зак. 232
178
Анализ и статистическая динамика САУ. Часть I
XB(O = CeA'X(O) + JCeA(/"T)BY(x)rfx.
(3.105)
При сравнении последнего соотношения с предыдущим легко сделать вывод о
том, что
СФ(0Х(0) = СеАгХ(0);
СФ(г-т)В = Кв(г-т) = СеА('~т)В.
3.4. ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
К ОПИСАНИЮ МНОГОМЕРНЫХ СТАЦИОНАРНЫХ СИСТЕМ.
ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
Поскольку основное внимание здесь уделяется стационарным системам,
рассмотрим введенное выше понятие применительно к стационарным системам, используя
преобразование Лапласа.
Имеем векторно-матричное уравнение стационарной системы
X=AX+BY, A=const; B=const. (3.106)
Обозначим
l\x}=l
X2(t)
U(0,
= s
X2(s)
xm('h
= sX(s);
L\
(yd»)
У2(О
[ym(t)t
• =
(YiW)
ад
(3.107)
= Y(s).
Преобразовав по Лапласу (3.106) с учетом (3.107), получим
sX(s)-X(0) = AX(s) + BY(s). (3.108)
Отсюда находим
sX(s)-AX(s) = BY (s) + X(0). (3.109)
Или
(jI-A)X(j)=BY(j) + X(0). (3.110)
Последнее уравнение - это уравнение состояний системы в области изображений.
Вектором Х(0) порождаются свободные колебания.
Рассмотрим случай, когда Х(0) = 0 (случай вынужденных колебаний). Из
выражения (3.110) находим
Х(5) = (Л-А)"1ВУ(5). (3.111)
Как указывалось выше, уравнение выхода имеет вид
Хв(0 = СХ(г). (3.112;
С учетом выражения (3.111) и
XB(s) = CX(s) (3.113;
получим
XB(j) = C(5l-A)"lBY(j). (3.114;
'«11
a2l
al2
a22
... a[n
... a2n
••• ann
Глава З. Метод пространства состояний 179
Если уравнение (3.111) является уравнением «вход Y(s) - состояние X(s)», то
уравнение (3.114) представляет собой уравнение «вход Y(s) - выход Хв(.ф. Формулы
(3.111) и (3.114) можно записать в виде
X(5) = W(5)Y(5); (3.115)
XB(s)=WB(s)Y(s). (3.116)
Матрицы W(s) и WB(s) называются передаточными матрицами
соответственно «вход - состояние» и «вход - выход».
Для проведения расчетов по формулам (3.115) и (3.116) необходимо иметь
алгоритм расчета матрицы (Л - А)"1.
Покажем несколько путей расчета обратной матрицы.
Первый путь можно назвать прямым. Он использует понятие присоединяющей
матрицы [36].
Рассмотрим вопрос нахождения обратной матрицы. Пусть
А =
- квадратная матрица. Тогда А^ =(-l)l+jMij называются алгебраическим
дополнением или адъюнктом к элементу a(j, М,у - дополнительным минором элемента atj; он
равен детерминанту матрицы порядка и-1, получаемой после вычеркивания из
матрицы А /-ой строки иу'-го столбца.
Заменим каждый элемент в матрице А его алгебраическим дополнением и
полученную матрицу транспонируем. Получившаяся в результате матрица называется
присоединенной для А, или союзной с А и обозначается А . Таким образом,
а=(а,7)т,
где А/, - алгебраическое дополнение элемента а^ . Тогда
А"1 =|А|"! А. (3.117)
Таким образом, для каждой квадратной матрицы А, такой, для которой det А •& О,
существует обратная матрица А"1, элементы которой 5/у вычисляются по формуле
aij = |А| А ,у,
где А/, - алгебраическое дополнение элемента atj матрицы А. Для рассматриваемого
случая формула для обратной матрицы имеет вид
/ ч-1 Л-А
(Л"А) =det(,I-A)'
где (si - А) - присоединенная матрица; del(sl - А) - определитель матрицы (si - A).
При преобразованиях надо пользоваться следующими равенствами:
1) det(A"1) = (detA)"1;
2) (А-^'^А;
3) (Аха2г{ =а21а;1-
4) (А7)"1 = (А"1)7.
13*
180
Анализ и статистическая динамика САУ. Часть I
Пример 3.3. Для матрицы
'1 -1 Г
А= 2 1 1
1 1 2
найти обратную. Имеем
1 -1 1
detA=A=2 1 1=5*0.
1 1 2
Матрица А неособенная. Составим присоединенную матрицу
Ап A2i A3i
А=
\,2 А22 А32
^13 А23 А33
где
А„ =
А„ = -
-1 1
1 1
А„ =
^4 -,1-х
2 1
1 2
= -3;А22 =
2 1
1 2
= 1;А23 = -
1 -1
1 1
Обратная матрица имеет вид
Пример 3.4. Пусть
А--А.
( 1/5 3/5 -2/5^
-3/5 1/5 1/5
1/5 -2/5 3/5
X = AX + BY,
где
Тогда
Js 0W0 6W. 0 \
[0 .J (*2 -кг) \-кг k^s)
s О I ,- ч (s + k3 О
-ъ k3+fsii*s)-( ]i *з *
Теперь легко найти передаточную матрицу объекта по состоянию
Передаточная функция по выходу запишется так
Изложим метод Фаддеева - Леверье нахождения обратной матрицы [1]. В
соответствии с этим методом имеет место следующее соотношение
Тогда соответственно
(Л-А)-' =
-1 М(5)
m(s)
Глава 3. Метод пространства состояний
181
где
М(5) = Ья"1+М1^"2+... + Мя_1;
m(s) = s -mxs -,..-тп.
Коэффициенты М, и /и,- рассчитываются по следующему алгоритму
Aj = A, mx =-SpA!, Mx =A{ -m{L\
А2=АМ!, /и2=— SpA2, М2 = А2-/n2l;
А3 = АМ2, т3=—SpA3, M3 = А3-/И3Г,
АЯ=АМИ, /nrt=-SpArt, Мя=АЛ-/ия1=0,
п
где Sp A - след матрицы А.
Пример 3.5. Рассмотрим систему X=AX+Y , где
Найдем обратную матрицу по методу Фаддеева - Леверье. Имеем
О 1
А =
А,=
-5 -6
Тогда mi = Sp At = - 6;
Вычислим А2, тг и М2:
В результате получим
(Л-А)
M-i° -Hi № i)
—-С :i-5 :)■(: :>
10 . м (-5 <П Г-5 0)
р 0W6 П (s + 6 О
1у + М,
52 - Ш^ - 7«2 ^" + 65 + 5 52 + 65 + 5
Теперь легко написать изображение для состояния системы и для выхода
X'(5)",2+6,+5C[ -5 4y2(*)J'
Пример З.6. Рассмотрим САУ, описываемую уравнением
*i)
Имеем
А,=А =
^0
0
-1
1
0
-2
(Г
1
-2
, н=3; m, =-SpA! =-2;
/-vngjim n у,lairiiiпчсслал дппамила v»//\ j . тасlь l
M, = A, -m,I =
A2 = AM,
m2=-SpA2 = -2;
M2 = A2-m2I =
A3 = AM2 =
m3=-SpA3 = -l.
'0
0
-1
0
-1
0
1
0
-2
2
-2
-1
0N
1
-2
1
0
-2
/2
-1
I °
+ 2
2
0
-
'1
0
0
1
0
1 0
1
1
(
\
)
2^
0
1
f -
(
(
=
1
'2
-1
0
0
-I
0
2
0
-1
0
-1
г
0
*
Теперь можно записать
M(j) = Ly2+M,5 + M2 =
s2 0 0
0 s2 0
0 0 52
(2s s ti\
0 2s s
-s -2s 0
'2
-\
0
2
0
-1
Г
0
0
=
5+25 + 2 5 + 2
I
-1
52 + 25 5
-25-1 s2
m(s) = s3 + 2s2+2s + l.
Изображение вектора состояния системы имеет вид
Х2(5)
Х3(5)
^52+25+.2 5 + 2
1
53+252+25 + 1
1
-I
52+25 5 II Y2(5)
-25-1 52 Y3(5)
(3.118)
Получим векторно-матричный интеграл Дюамеля. Выше была получена
зависимость
Х(5) = (Л-А)~1ВУ(*) + (Л-А)"1Х(0).
Для скалярных функций справедливы формулы
.ie выражения справедливы и для вектор-функций
L-l\^—) = eAtnAl(s)A2(s)=\Al(t-x)A2(T)dT9
[sI-A\ Jo
(3.119)
Аналогичные выражения справедливы и для вектор-функций и для матриц
где AjCs) и A2(s) - матрицы.
Воспользовавшись приведенными выше зависимостями, получим
Х(г) = ^А(г-т)В¥(т)^т + ^Х(0).
(3.120)
Последнюю формулу можно получить и другим путем. Умножим обе части
исходного уравнения на еА/
Глава 3. Метод пространства состояний
183
e~AtX(t) = e~AtAX(t) + e"A'BY(O.
Справедлива зависимость
Из (3.121) имеем
dt
e~AtX{t) - e~At AX(O = e~AtBY(t).
(3.121)
(3.122)
(3.123)
(3.124)
С учетом (3.122), зависимость (3.123) принимает вид
!(,-A'X(0) = <TA'BY(,).
Отсюда находим
t
*ГА'Х(г) = |<ГАтВУ(т)</т + Х(О).
о
Окончательно получим (3.120).
При работе с матричной экспонентой целесообразно пользоваться формулами [7]:
1). Если А - диагональная матрица
А =
(аи 0 ... 0
0 а22 ... 0
0 0
, то е =
еа" 0
0 еа»
0 0
0
0
2). ektekx =^A(/+T)
3). еАев = еА+в, если АВ = ВА (матрицы перестановочны).
4). *АТ'=(*А')Т.
5).±eAt=eAtA.
dt
Дадим несколько определений.
Функция вида eAt называется экспоненциалом матрицы At, или матрицантом.
Зависимость (3.120) называется векторно-матричным интегралом Дюамеля.
Матрица К(т) = £АтВ называется матрицей импульсных переходных функций
«вход — состояние».
Если учесть, что
хв(г) = сх(0,
то легко записать
t
XB(r) = Jc^A(/"T)BY(T)6/T + C^ArX(0). (3.125)
о
Рассмотрим алгоритм расчета Х(0 и Хв(г) по формулам (3.120) и (3.125).
Используем следующий факт [1].
Пусть:
1). А - квадратная матрица порядка п и Л - ее спектр;
2). Р(А) - функция от матрицы А - многочлен вида
Р(А) = а0Ап+а{Ап-1+... + ап1;
3). /(А) - некоторая функция от А.
104
/\н<и1Ш и ысииыичсычал димамшча v_,/\j . idtib &
Многочлен Р(А) называется интерполяционным многочленом Лагранжа -
Сильвестра для /(А) на Л, еслw Р(А) = /(А) на Л.
Функции от матрицы А Р(А) и /(А) равны на Л, если
/(X|.) = P(X|.),/l(Xi) = Pi(Xl-),...,/a'"l)(XJ.) = P(*'"I)(^),
где X, - элемент множества Л, имеющий кратность Kh
Рассмотрим примеры применения этого факта.
Пример 3.7. Пусть
Г 4 -2}
А =
6 -3
- квадратная матрица, требуется найти е .
Имеем
|4-Х -2
-3-Х
= (4-Х)(-3-Х) + 12 = -12-4Х + ЗХ + 12 + Х2=Х2-Х = 0.
Характеристическое уравнение Х(Х - 1) имеет корни Xi = 0; \г = 1; следовательно, корни 0 и 1 -
собственные значения матрицы А.
Имеем
/(А) = еА;Р(А) = я01 + я,А.
Требуется найти числа а0 и а\\ Л = {0;1} - спектр матрицы А. Как говорилось, /(А) = Р(А), если они
равны на Л. Имеем
ao = ltao + al=ei.
Тогда а0 = 1; ах = е1 - а0 = ^' -1 = е -1 = а{. Отсюда получаем
«A)-i+(.-i)A-(; j)+(e-i)[; :j
Или, что то же самое,
Пример 3.8. Перейдем к рассмотрению еще одного примера, найдем матрицу еА , где
А =
Имеем характеристическое уравнение
4-А. 2 -5
4
6
5
2
4
3
-5'
-9
-7
Ф(Х) =
4-Х -9
= (4-Х)2(-7-Х)-90-90-
6
5 3 -7-Х
-[-25(4-Х) + 12(-7-Х)+(4 + Х)(-27)] =
= (l6-8X-X2)(-7-X)-180+100-25X + 34 + 121 + 108-27X =
= -112+56Х-7Х2-16Х + 8Х2-Х3+62-Х.
Из уравнения следует: X3 - X2 = Х2(Х -1) = 0; получаем Х|,2 = 0; Х3 = 1.
Итак,
/(А) = е\ Р(А) = аА2+ЬА+с1.
Для нахождения неизвестных а, Ь, с воспользуемся равенствами
/(0) = Р(0); /'(0) = Р'(0); /(1) = Р(1).
Далее получаем е° = с , отсюда с = 1;
еА|А=0 = 2аА + ^|А=0=>/7 = 1.
И, наконец, для X =1 имеем а + b + с = е1, отсюдаа = е-с-Ь = е-2 ТогдаеА = (е-2)А2 + А +1.
Поскольку
Глава 3. Метод пространства состояний
185
'3
3
3
1
1
1
зч
—3
-3
А2 =
'Зе-1 с -Зе + Г
еА = Ъе е + 3 -Зе-3 .
3<?^1 е + 1 -Зе
Пример 3.9. Применим интерполяционную формулу Лагранжа - Сильвестра для решения
дифференциальных уравнений.
Решение уравнения
° '■ (3.126)
имеет вид
Х = АХ + У,гдеА=, ,,
Г5 ~6J
X(/) = eA'X°+JeA('-T)Y(x>/T.
Ф(Х) =
1 L^x(-6-X) + 5 = 6X + X2 +5 = 0,
6-А|
Основные этапы:
1). Записывается характеристический полином
-X
-5 -6-
Х2+6Я. + 5 = 0.
2). Находятся собственные значения матрицы А
X2+6X + 5 = 0; (X + i)(X + 5) = 0, X, =-1; Л2 = -5.
3). Записывается интерполяционный полином Лагранжа - Сильвестра
Р(А) = во1 + Я|А.
4). Коэффициенты аоищ находятся из условия равенства /(А) = еА = Р(А) на Spec A:
1=„А
aol + а, А = е при А= - Г; ао1 + а, А=е при А = -5;
aQ-ax=e~x\aQ-5ax=e~5.
Имеем
Получаем
Тогда
-а0 + 5а, = -е~5 -> 4а, = е~х - е~5 => ах - -с"1 —е~5.
4 4
"° • 4 4 4 4
= a0I + a,A= \-е —е \\ \ + \—е —е э =
Отсюда находим
гА' =
12 3ак. 232
4
4^
—^
4
5
-г
4
0
4
4
4
4
0
4 4 J
1 _, 1 .
—с —с
4 4
4 4
1 _, 1 _
-с --<?
4 4
1 _, 5
—е +-с
4 4
+
5 ^
-5
5/
-5/
5 .
~?
% if
ч
0
4
4
6 .
"Г
-5/
4
I 6 _5
V \
-^'+5е~
ekt
186 Анализ и статистическая динамика САУ. Часть I
Изложим еще один подход, для чего воспользуемся следующими положениями.
Матричный экспоненциал можно представить в виде
= |>Х'% (3.127)
/=i
где Х( - собственные значения матрицы A; F, - функции (их вид будет указан ниже).
Зависимость (3.127) базируется на разложении функций eAi в степенной ряд.
Воспользуемся формулой Сильвестра
/(A) = £/(X,)F,, (3.128)
где
Применив формулу Сильвестра к (3.127), получим решение задачи.
Пример 3.10. Рассмотрим уравнение системы «вход - состояние»:
[х2) [-5 -6){хг) [у2
Имеем
0 1
А = 1-5 -6
Найдем собственные значения матрицы А
de,(A-XI) = |:* ^
Тогда А.| = -1; А.2 = -5. Построим функции Ft.
det(A-XI) = |_X \ \ = (\ + б)\ + 5 = \2+6\ + 5.
1остроим функции Fi.
A-X2I_lf 5 {\F =A-XiI_l(rl П
1 X,-X2 4-5 -1/ 2 Я-2-Л, 4-5 -5J
Матричный экспоненциал имеет вид
4[-5е- -e'j 4{-5е-ь -5C-"J
if 5e-'-e-* . .
Пусть ^i(r) = cos aw; ^(0 = sin Gfcf; X°= 0. Тогда выражение для вектора состояния системы запишется
так
U(OJ
Отсюда для компонент вектора состояния имеем
Х|(0 = I }[(5^-(г"т) - ^5(/-т) Jcosco,! + [е'^х) - е-5{"х) )sin ш,т]л.
*2(0 = -}[(-5^"(/"т) + 5е"5(/-т) Jcosco^ + (-е"(/-т) + 5^5('-т) )sin ©jtjrfT.
Глава 4. Нелинейные системы управления 187
ГЛАВА 4. НЕЛИНЕЙНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ:
МОДЕЛИ, УСТОЙЧИВОСТЬ,
ПЕРИОДИЧЕСКИЕ КОЛЕБАНИЯ, РАСЧЕТ
ВЫХОДНЫХ ПРОЦЕССОВ
Первым приближением описания системы автоматического управления является
линейная математическая модель, которая обычно строится в виде системы
линейных дифференциальных или разностных уравнений. Решение таких уравнений может
быть получено в аналитическом виде, что облегчает анализ системы управления и
синтез регулятора.
Многие системы управления содержат, однако, нелинейные звенья. В этом случае
применение линейной теории приводит к неточным или принципиально неверным
результатам. В нелинейных системах обнаруживаются типы движений (например,
автоколебания), которые не могут быть описаны в рамках линейной теории.
Приведены основные модели нелинейных систем. Вводятся классические
определения устойчивости по Ляпунову. Приведена сводка результатов по устойчивости и
неустойчивости нелинейных систем общего вида. Специальный вид моделей
рассматривается в задаче об абсолютной устойчивости. Основное внимание уделяется
связи частотных методов с функциями Ляпунова. Глава завершается некоторыми
результатами по оценке параметров периодических колебаний.
4.1. ОПИСАНИЕ ОСНОВНЫХ МОДЕЛЕЙ
Пусть математическая модель управляемой системы описывается
дифференциальными уравнениями
Хк=/к{хих2>-~хп»*)> * = 1.--.Л, (4.1)
где хк - зависимые переменные, хк - производные зависимых переменных по
времени t, fk - нелинейные функции, удовлетворяющие условиям существования и
единственности решений системы (4.1) при заданных начальных условиях
х10>--->хп0 •
Введем вектор состояния X, элементами которого являются зависимые
переменные •*!,...,хя, и вектор-функцию / с элементами fk, к = 1,...,п . Все векторы будем
трактовать как одностолбцовые матрицы. В векторных обозначениях система (4.1)
будет иметь вид
Х = /(Х,г). (4.2)
Фазовое (п + 1)-мерное пространство системы (4.2) образуют переменные
*i,..., хп, X.
Динамическое поведение нелинейной системы (4.2) определяется разбиением
фазового пространства на траектории, изображающие решения.
Напомним некоторые понятия из теории дифференциальных уравнений.
Рассмотрим автономную систему Rn
Х = /(Х). (4.3)
12*
188 Анализ и статистическая динамика САУ. Часть I
В n-мерном пространстве вектор-функция X(t), координаты которой можно
рассматривать как координаты изображающей точки, описывает фазовую траекторию.
Совокупность всех фазовых траекторий, определяемых начальными условиями,
образует фазовый портрет системы (4.3).
Особыми точками фазового пространства являются точки, удовлетворяющие
уравнению /(X) = 0 . Эти точки могут быть изолированы или составлять некоторую
область. Особые точки являются устойчивыми, если они притягивают окрестные
траектории. Поверхности в фазовом пространстве, к которым притягиваются или от
которых отталкиваются траектории, называются сепаратрисными.
Метод фазового пространства особенно нагляден для систем второго порядка,
когда фазовое пространство представляет собой плоскость с координатами х{у х2.
Пусть в этом случае система (4.3) имеет вид
*l=eil*l+*12*2+*(*l.*2).
*2 = а2 Л +<*22*2 +G(xliX2),
где ciij - постоянные коэффициенты, а1{а22 ~^\г^г\ *0, R[x{,x2), G(x{ix2) -
функции от хх и х2, стремящиеся к нулю при X —»0 как бесконечно малые второго
порядка. Особой точкой здесь является начало координат. Характеристическое
уравнение системы (4.4)
{ап-\)(а22-\)-а12а2{ = 0 (4.5)
имеет два корня Х{ и Х2, определяющие один из следующих типов особой точки.
• Устойчивый фокус, если Х{ и Х2 ~ комплексные с отрицательными
действительными частями. На устойчивый фокус траектории наматываются
спиралями.
• Неустойчивый фокус, если Х{ и Х2 - комплексные с положительными
действительными частями. С неустойчивого фокуса траектории разматываются
спиралями.
• Устойчивый узел, если Х{ и Х2 - действительные отрицательные. К
устойчивому узлу траектории сходятся апериодически (без колебаний).
• Неустойчивый узел, если Х{ и Х2 - действительные положительные. От
неустойчивого узла траектории апериодически расходятся.
• Седло, если Х\ и Х2 - действительные разных знаков. В седло две траектории
входят и две выходят, остальные траектории проходят мимо особой точки.
• Если Х{ и Х2 - чисто мнимые, то возможен фокус или центр - в зависимости
от вида функций RnG. Центр представляет собой особую точку, окруженную
замкнутыми траекториями, вложенными друг в друга.
Изолированные замкнутые траектории называются предельными циклами.
Устойчивые предельные циклы называются автоколебаниями.
В случае линейной системы (4.4) R = G = 0 . При этом сохраняются все типы
особых точек: при чисто мнимых Х{УХ2 получается центр, причем замкнутые
траектории не изолированы.
Применение метода фазового пространства к системе порядка п > 2
наталкивается на большие трудности и теряет наглядность.
Глава 4. Нелинейные системы управления 189^
4.2. УСТОЙЧИВОСТЬ И ФУНКЦИИ ЛЯПУНОВА
В настоящей работе устойчивость понимается в смысле Ляпунова. Некоторое
определенное движение системы (4.2), подлежащее исследованию на устойчивость,
называется невозмущенным движением. Ему соответствует определенное частное
решение X(f) = X(f) системы, отвечающей начальным условиям Х(го) = Хо. Если
изменить начальные условия, положив X (г0) = Хо + Ro, то получим новое движение
системы, отвечающее новым начальным условиям и называемое возмущенным.
Обозначим YB(r) = X(f)-X(f).
Определение 4.1. Невозмущенное движение устойчиво по Ляпунову, если по
любому 8 > 0 можно найти такое 8 > 0, что при R'o Ro < 8 и при любом t > t0 будет
выполнятся неравенство Х'Х < 8.
Определение 4.2. Невозмущенное движение называется асимптотически
устойчивым, если оно устойчиво по Ляпунову и для данного t0 существует такое
положительное число А < 8, что если Rq Ro < 8, то X (Ro, t) —> 0 при t —> <» .
Исследование устойчивости любого решения Х(г) уравнения (4.2) можно свести
к исследованию нулевого (тривиального) решения некоторого другого уравнения.
Действительно, для функции YB (r) имеем
Y.(/) = /(Y1+X,r)-/(X,/) = 7(Y,,0,
причем /(0,f) = 0. В дальнейшем, если не оговорено противное, будем изучать
устойчивость нулевого решения уравнения (4.2) при / (0,r) s 0.
Назовем функцией Ляпунова скалярную функцию V(X,t) от векторного
аргумента Х,г, обладающую следующими свойствами:
- функция непрерывна вместе со своими частными производными первого
порядка в некоторой области, содержащей начало координат;
V(O,f) = O;
V(X,f)>0, Х*0.
Геометрический смысл функции V(X,r) можно пояснить при
t = tx = const, n = 2. Обозначим z = У (х{, х2 Jx) и рассмотрим рис. 4.1.
Так как V (Х,^ ) > 0 для X Ф 0, то поверхность z = V (Х,^ ) напоминает стоящую
на столе (плоскость (^, х2)) чашу.
Если рассечь эту чашу плоскостями, параллельными плоскости стола, то
проекции линий пересечения на горизонтальную плоскость описываются уравнениями
V (*!, х2,Ц ) = h. Эти кривые являются замкнутыми (рис. 4.2).
Чаще всего в качестве функции Ляпунова используется квадратичная форма
1=1 7=1
которая в векторно-матричных обозначениях может быть записана в виде
V(X,t) = X/L(r)X, где матрица L(r) имеет элементы !.Vj (t).
190
Анализ и статистическая динамика САУ. Часть I
V(xvx2)l
-- /
У 1
*2
Рис. 4.1. Примерный вид функции Ляпунова
Простые необходимые и достаточные условия положительной определенности
квадратичной формы (4.6) даются критерием Сильвестра: все последовательные
главные миноры матрицы L > 0 должны быть положительными:
'п>0,
11
2\
-12
122
>0,..., |^да|>0; *>/п = 1>2>...,л.
(4.7)
Рис. 4.2. Линии уровня функции Ляпунова V(*i,xi) = h
Сформулируем теорему Ляпунова об устойчивости. Обозначим скалярную
непрерывную неубывающую функцию со свойствами
Глава 4. Нелинейные системы управления 191
ф(0) = 0, ф(ц)>6, при ji>0.
Назовем производной V функции V(X,f) в силу уравнения (4.2) величину
где -— = grad V - вектор, составленный из частных производных -— .
Э X oxi
Теорема 4.1. (Теорема Ляпунова об устойчивости). Пусть существует функция
Ляпунова V(Xj) такая, что
cp(|x|)<V(X,f), (4.9)
V<0. (4.10)
Тогда тривиальное решение уравнения (4.2) устойчиво по Ляпунову.
Доказательство. Пусть е > 0. Возьмем в качестве 5(е,г0) такое число, что
. max V{X0,t0)^9(z). (4.11)
|Х0|<6(£,Г0)
Из непрерывности V(X,t) и условия У(О,ГО) = О следует, что такое 8(е,г0)
существует. Используя (4.9) и (4.10), получим при |Х0| <5(е,г0)
ф(|Х(0|)<^(Х,0^^(Х0,0^|хтахо^(Х0,г0)<Ф(е).
В силу монотонности функции ф()1) получаем |x(f)|<e. Теорема доказана.
Теорема 4.2. (Теорема Ляпунова об асимптотической устойчивости). Пусть
существует такая функция Ляпунова V (Х,г), что
Ф1(|Х|)<1/(Х,Г)<Ф2(|Х|), (4.12)
\>(Х,г)<-Фз(|х|), (4.13)
где ф, (ц), / = 1,2,3- скалярные неубывающие непрерывные функции со
свойствами ф, (ц) > 0 при \х -> 0.
Тогда тривиальное решение уравнения (4.2) равномерно асимптотически
устойчиво.
Теорема 4.3. (Е.А. Барбашин, Н.Н. Красовский [15]).
Пусть выполнены все условия теоремы 4.2 и, сверх того,
ф,(|ы)--»°о при д-»°°. (4.14)
Тогда решение уравнения (4.2) асимптотически устойчиво в целом (для любых
начальных условий).
Теорема 4.4. (Теорема Н.Г. Четаева о неустойчивости). Пусть для уравнений
возмущенного движения существует такая функция, для которой в сколь угодно малой
окрестности нуля существует область, во всех точках которой V > 0 (или V < 0),
V > 0 (или V < 0). Тогда невозмущенное движение неустойчиво.
4.3. УСТОЙЧИВОСТЬ ЛИНЕАРИЗОВАННЫХ СИСТЕМ
Построим функцию Ляпунова для линейной стационарной системы
Х = АХ, ХеД". (4.15)
192 Анализ и статистическая динамика САУ. Часть Г
в виде квадратичной формы
V(X) = X'LX, L = L'. (4.16)
Дифференцируя V(X) по времени, в силу (4.15) получаем
K(X) = X'(A'L + LA)X. (4.17)
Потребуем, чтобы производная V'(X) была равна произвольной квадратичной
форме -Х'РХ : V (X) = -ХРХ, Р = Р'. Из (4.7) получаем
X'(A'L + LA)X = -X'PX. (4.18)
Тождество (4.18) возможно при всех X тогда и только тогда, когда
A'L + LA = -P. (4.19)
Матричное уравнение (4.19) называется уравнением Ляпунова. Собственные
значения Л,, 1=1,...,п матрицы А определяются как корни уравнения
det(A-Xl) = 0. (4.20)
Теорема 4.5. (A.M. Ляпунова). Пусть все собственные значения X, (А) матрицы
А имеют отрицательные действительные части. Тогда для любой матрицы Р > 0
существует единственное положительно определенное решение уравнения Ляпунова
(4.19), вычисляемое по формуле
оо
L = jV'PeA'</f. (4.21)
о
Обратно: если для какой-нибудь матрицы Р > 0 существует решение L > 0
уравнения (4.19), то матрица А устойчива.
Формула (4.21) доказывается следующим образом. Имеем тождество
d_
dtl
Интегрируя в пределах от 0 до °°, получаем
еА'*РеА'\ -P = A/L + LA,
откуда ввиду устойчивости матрицы А следует (4.21).
Устойчивость линейных нестационарных систем. Рассмотрим нестационарное
линейное уравнение
X(r) = A(r)X(r). (4.23)
Известно, что по собственным значениям X{(t),...,\n(t) матрицы А(г) нельзя
судить об устойчивости системы (4.23), т.е. метод «замороженных коэффициентов»,
вообще говоря, не верен. Однако справедливо следующее утверждение.
Теорема 4.6. Пусть собственные значения ji(f) матрицы A = —(A(f) + A'(j))
отрицательны. Тогда система (4.23) асимптотически устойчива.
Доказательство. Возьмем функцию Ляпунова V(X) = Х'Х. В силу (4.23) имеем
• \>=X/X + XX/ = 2X/AX<2jLimax(r)Vr(X). (4.24)
Поскольку \imSiX(t)<09 то из (4.24) и теоремы 4.2 следует доказываемое
утверждение.
Отметим, что решения неоднородного линейного уравнения Х(г) =
= A(f)X(f) + g(f) устойчивы или неустойчивы в зависимости от устойчивости од-
—(*AW) = A7eAW' +eA''PeA'A . (4.22)
fit \ I
Глава 4. Нелинейные системы управления 193
нородного уравнения (4.23). Действительно, если Z(f) - некоторое решение
неоднородного уравнения, то определим Y (г, Хо - Zo) = X (г, Хо) - Z (r, Zo). Имеем
Y(r) = A(r)Y(r); поэтому из устойчивости (неустойчивости) уравнения (4.23)
следует устойчивость (неустойчивость) решения Z(t).
Устойчивость по линейному приближению. Рассмотрим нелинейную систему
X = AX + fc(X), |&(X)|<4ii|x|1+a, a>0, ц>0. (4.25)
Наряду с (4.25) рассмотрим линейную систему первого приближения
Х = АХ. (4.26)
Теорема 4.7. (A.M. Ляпунова). Тривиальное решение системы (4.25)
асимптотически устойчиво, если асимптотически устойчиво тривиальное решение системы
первого приближения (4.26).
Доказательство. Возьмем функцию Ляпунова в виде V = X'LX. В силу
системы (4.25) имеем
V(X) = X'(A'L + LA)X + 2X'Lfc(X). (4.27)
Пусть матрица L>0 удовлетворяет уравнению Ляпунова A'L + LA = -I. Такая
матрица существует, поскольку система первого приближения устойчива.
Тогда
V<-|X|2+2|L||b(X)|<-|x|2 +
+2|Ь||ХИХГ < 2|Х|2 (l -2ц|Ь||Х|а)< -р|х|2,
если
2ц|Ь||Х|а<1-(3, р>0. (4.28)
Таким образом, при малых |Х|, обеспечивающих выполнение (4.28), система
(4.25) асимптотически устойчива.
4.4. ЗАДАЧА ОБ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ
При всем разнообразии нелинейных систем можно выделить класс таких систем,
которые ведут себя в смысле устойчивости подобно линейным системам. Так,
например, устойчивость имеет место при любых начальных условиях; часто из факта
устойчивости следует асимптотическая и даже экспоненциальная устойчивость.
Этот класс систем будем называть классом абсолютно устойчивых систем.
Наряду с линейными системами в него входят системы как с непрерывными, так и с
разрывными нелинейными звеньями. Как правило, такие системы не могут быть
линеаризованы в малом. Поэтому об их устойчивости нельзя судить по уравнениям
первого приближения.
Опишем некоторые основные модели этого класса.
Любая система автоматического управления содержит объект управления и
регулятор. Во многих случаях объект является линейным, в то время как регулятор
содержит существенные нелинейности. Поэтому в моделях систем управления принято
выделять линейную часть и одно или несколько нелинейных звеньев.
Наиболее распространенной является модель, описываемая дифференциальными
уравнениями в п -мерном действительном пространстве Rn
194
Анализ и статистическая динамика САУ. Часть I
X = AX + B£+Rg, X(O) = XO,
Ъ = ФА (4.29)
<т = СХ,
где вектор-функция Х(г) называется вектором состояния, скалярные функции £(f)
н g(t) называются сигналом обратной связи и внешним сигналом соответственно.
Постоянные векторы-столбцы B,R,C имеют размерность п. Матрицу А будем
считать постоянной. Особо выделим важные частные случаи системы (4.29). Будем
называть эту систему автономной, если внешний сигнал отсутствует, т.е. g (t) = О.
Если функция ф(а,г) не зависит явно от времени, ф(а,г) = ф(а), то такую систему
будем называть стационарной,
В ряде случаев полезно перейти от дифференциальных уравнений к описанию с
помощью одного интегрального уравнения, имеющего вид
o{t) = f{t)+s(t)-fw(t-X)t(\)d\,
(4.30)
где
f(t) = L~l{ C'(pl-A)-lX0},s(t) = L-l{ C(pl-A)-lG(p)},
G(p) = L{ g(t)}.w(t)'L-l{ C(A-pl)-!B}.
L{}, L~l {•} - символы прямого и обратного преобразования Лапласа.
\-ii
Функции w(r) и W(p) = C7(A-pI) В называются соответственно импульсной
характеристикой и передаточной функцией линейной части [39]. Блок-схема,
соответствующая (4.30), показана на рис. 4.3.
ш
Рис. 43. Блок-схема нелинейной системы
Обратимся к описанию нелинейности. Будем предполагать, что ф(ст,г)
удовлетворяет условиям
0<ф(а,г)<*аг\
(4.31)
Глава 4. Нелинейные системы управления
195
На плоскости а,£ кривая £ = ф(а,г) лежит в секторе, образованном прямой £ = &<т и
осью а, причем она может иметь общие точки со сторонам^ сектора и совпадать с
одной из сторон (рис. 4.4). Если нелинейность стационарна, то обычно
предполагается, что функция ф(су) однозначна и непрерывна.
Рассмотренный класс включает в себя такие широко распространенные в
автоматическом управлении нелинейности, как зона нечувствительности, реле без
гистерезиса, насыщение и т.д. Очевидно, что линейные характеристики £(f) = w(f)a(f),
и б [ОД], принадлежат этому же классу.
Ф(о)
Рис. 4.4. Характеристика нелинейности
В дальнейшем рассматривается также дискретный аналог системы (4.29),
описываемый уравнениями
X(f + 1) = AX(O + B£(r), X(0) = X0,
$(0 = ф(а(г),0. (4-32)
с(г) = С'Х(г), /=0,1,2,...,
где Х(г) - вектор-функция размерности п ; А - постоянная матрица; B,R,C
-векторы-столбцы размерности п. Нелинейная функция ф(а,г) удовлетворяет
неравенству (4.31).
Уравнению (4.30) соответствует уравнение
a(0=/(0-2>('-«)&(0. <4-33>
;я=0
где
/(r) = D-l{c'(^I-A)"'^X0},
w(<)=d-i|c'(a-^i)"1b|,
196 Анализ и статистическая динамика САУ. Часть I
D{}, D"1 {•} - символы прямого и обратного дискретного преобразования Лапласа
[39].
Постановка задачи об абсолютной устойчивости принадлежит Лурье и Постникову.
Определение 4.3. Автономная система (4.29) абсолютно устойчива в секторе
[О,/:], если при любой функции ф(<т,г), удовлетворяющей (4.31), тривиальное
(нулевое) решение этой системы асимптотически устойчиво в целом. Это означает,
что нулевое решение асимптотически устойчиво по Ляпунову (определение 4.2) и
областью притяжения точки X = 0 является все фазовое пространство.
Следует отметить, что определение абсолютной устойчивости относится к классу
систем, имеющих одинаковые линейные части, но разные нелинейные звенья,
удовлетворяющие неравенству (4.31).
Для исследования абсолютной устойчивости стационарной автономной системы
(4.29) в работе [2] была использована функция Ляпунова вида
сх
V(X) = X'LX + <? J ф(а>/о, (4.34)
о
где L = L' > 0 - положительно определенная матрица, q - действительное число.
Если нелинейность нестационарная, то полагаем, что q = О.
Покажем, что функция (4.34) удовлетворяет условиям теоремы 4.2. Заметим сна-
а
чала, что Гф(сг) do>0 в силу (4.31). Это следует из теоремы о среднем значении
о
интеграла
а
|ф(а) </а = аф(аи),
о
а
где а* принадлежит отрезку [0,а]. Аналогичным образом |7&а-ф(а)) do>0.
о
Пусть q > О. Тогда имеем
х,|х|2<к(х)<хя|х|2+^1<^„+^с'с]|х|2,
где Х{ и Хп - соответственно наименьшие и наибольшие собственные значения
матрицы L . Пусть q < 0. Тогда возьмем вместо L матрицу L — . При этом
.2 q
2
и
2
V(X) = X'LX-2J^ + qj(p(o)do = X'LX-ql(ko-(po)dG>Q,
Таким образом, для обоих случаев
ф,(|х|И,|х|2-
„,Н)Л.+Ы£%-
Глава 4. Нелинейные системы управления 197.
Найдем теперь условия, при которых в соответствии с теоремой 4.2 V < -ф3 (|х|).
Дифференцируя V (X) по времени, в силу уравнений (4.29) получим
— = X'(A'L + LA)X + 2£X'LB + <£6. . (4.35)
Прибавим к правой части выражения (4.35) и вычтем величину ца-/с~1£1>0.
Тогда получим
^ = -5(Х,£Н(а-*"Ч), (4.36)
где
5(X,^) = y42-2y^U/X-X/(A/L + LA)X,
YU = LB+~ + ^A~.
dV(X)
Производная —- будет отрицательно определенной, если квадратичная фор-
dt
ма от п + 1 переменных S(X,£) является положительно определенной. Описанный
специальный прием построения функции Ляпунова назван 5 -процедурой. Как
показано в [43], 5-процедура обладает свойствами неущербности.
Теорема 4.8. [43] Пусть X - евклидово пространство F(X), p(X) -
произвольные квадратичные формы. Кроме того, существует такой вектор Хо, при котором
р(Х0) > 0. Следующие утверждения равносильны:
а) F (X) > 0 на множестве, где £?(Х) > 0;
б) существует такое число т > 0, при котором
F(X)~T£?(X)>0
для всех возможных Xg X .
dV
В рассматриваемом случае роль ^(Х) играет форма из (4.36), а роль
р(Х) - форма JUa-ifc"1!;). Теорема 4.8 говорит о том, что 5- процедура, несмотря
на видимую искусственность, не приводит к потере какого-либо множества в области
устойчивости.
Как видно из уравнений (4.36), форма 5(Х,^) положительно определена, если
выполнены условия
A/L + LA = -UU/-eP,
LB + ^ + l^ = YU, (4.37)
y = (*-!-9Cb)*,
где Р = Р/>0, е>0. Система (4.37) называется системой уравнений Лурье. Если
уравнения Лурье имеют действительное решение, то
198 Анализ и статистическая динамика САУ. Часть I
— <-еХ'РХ<еХ|х|\ (4.38)
где X - наименьшее собственное значение матрицы Р. При этом выполнены все
условия теорем 4.2,4.3. Следовательно, верен следующий результат.
Теорема 4.9. Для абсолютной устойчивости автономной стационарной системы
(4.29) в секторе [0,к] достаточно, чтобы при некотором е >0 существовало решение
уравнений Лурье в виде действительной симметричной положительно-определенной
матрицы L , действительного вектора U и действительного числа у .
К сожалению, прямая проверка существования допустимого решения системы
(4.37) является громоздкой алгебраической задачей, аналитическое решение которой
в общем виде неизвестно.
4.5. МЕТОД АПРИОРНЫХ ИНТЕГРАЛЬНЫХ ОЦЕНОК
И ЧАСТОТНЫЕ КРИТЕРИИ
Метод априорных интегральных оценок был разработан румынским ученым
В.М. Поповым. Суть метода состоит в получении интегральных оценок изучаемых
систем на конечном интервале времени. Изучение поведения таких оценок дает
возможность сделать вывод о характере движения в системе.
Попов [111] исходил из описания (4.30) и использовал интегральную оценку вида
p(r) = j5(a-*"^ + 96) rfr, (4.39)
о
которая называется функционалом Попова. В случае дискретной системы (4.32)-
(4.33) вместо (4.39) используется сумма
р(*)яХ£(оНН"'$(о)- <4-4°)
Приведем сначала частотный критерий абсолютной устойчивости для дискретной
системы.
Теорема 4.10 (критерий ЯЗ. Цыпкина). Автономная система (4.32) абсолютно
устойчива для всех нелинейностей, удовлетворяющих условию (4.31), если линейная
часть системы И^*(д) = С'(A-eql\ В устойчива; для всех О)е[0,я] выполнено
условие
ReW*(ja>)+k-l>0. (4.41)
Доказательство. Рассмотрим сумму (4.40). Из (4.33) имеем a(f) = /(r)-
t
-^ w(t-ni) £(/n), где f(t) и w(r) являются экспоненциально убывающими
т=0
функциями. Подставив а (г) в (4.40), получим
p(n)=Pi(n)-{>2{n), <4-42)
где
piM-£*(Of(o.
(=0 (4.43)
N
piW-S
г=о
е(02>(»-«)§о».)+*»*2(») •
f=0
Глава 4. Нелинейные системы управления 199
В силу свойств нелинейности ф(с,Г) имеем p(N) > 0, следовательно,
р2(ЛГ)<Р,(#). (4.44)
Из неравенства Коши - Буняковского следует, что
р.И- S52(0|S/a(0 • <4-45>
Введем усеченную функцию
«.м-р;::;
Тогда величина р2 (N) может быть записана в виде
р2(*)=1(мо£"('-'«)мо+*"|&(')]- (4-47>
По формуле Парсеваля
2
P2(A0~J|M-H (ReW^O))**-1)^. (4.48)
Если выполнено условие (4.41), то существует такое А > 0, что
RQW*(j(u)+k~{ >A>0. (4.49)
Из (4.48) и (4.49) получаем
р2 (N) > A J ||w (ytofdco = ДХ^ (Г) = ДХ ^2 (Г). (4.50)
Из неравенств (4.32), (4.33) и (4.38) следует, что
Д|С *«««„• (4.51)
Окончательно получаем оценку
И^^"-!^-' (452)
оо
из которой следует, что ряд ^^2 (t) сходится, а его общий член £2 (г) стремится к
/=0
нулю при t -> ©о. Теорема доказана.
Теорема 4.11. (Критерий В.М. Попова [111]). Автономная система (4.29), (4.31)
абсолютно устойчива, если:
1) линейная часть W(s) = C'(A-sl)~ В устойчива;
2) существует такое действительное число q, при котором для всех ш>0
выполняется неравенство-
P(q,ky(u)=Re(l + qj(o) \У(№)+к~1 >0. (4.53)
Доказательство последней теоремы может быть выполнено по схеме
доказательства теоремы 4.1, но является более сложным.
Обозначим £/(G)) = ReW(./G>), V((o) = (ulmW(j(u). Тогда (4.53) можно
переписать в виде
U(ri)-qV((u) + k-l>0. (4.54)
200
Анализ и статистическая динамика САУ. Часть I
Геометрическая интерпретация (4.54) очень проста: параметрически заданная
кривая U(со),V(со) на плоскости U,V должна находиться правее прямой
U-qV + k~l=0 (рис. 4.5).
V
Рис. 4.5. Критерий 11опова
Для случая нестационарной нелинейности ф(а,г) критерий (4.53) справедлив,
если положить д = 0. Приведем простое обобщение этого критерия для
нестационарной системы на случай, когда нелинейность принадлежит сектору [г, к], т.е.
га2<ф(а)а<£о2. (4.55)
Теорема 4.12. (Круговой критерий). Автономная система (4.29) с нестационарной
нелинейностью устойчива в секторе [гД], если:
1) линейная система с передаточной функцией
2) при всех со>0 выполнено условие
п2
l + rW(j)
устойчива;
[RelV(;a>)+![i+l]] +[lm^(;a,)]2 >i[i-l] . (4.56)
Название критерия (4.56) связано с его геометрической интерпретацией: годограф
частотной характеристики W(j(u) не должен пересекать или охватывать запретный
круг (рис. 4.6). При г = 0 условие (4.56) переходит в неравенство
P(o,£,w)=ReW(;co) + *~l >0. (4.57)
В дальнейшем условие (4.57) также будем называть круговым критерием.
Отметим, что при г -> к запретный круг вырождается в точку и критерий (4.56)
превращается в критерий Найквиста.
Глава 4. Нелинейные системы управления
lmW(j(O)
ReWO'co)
Рис. 4.6. Круговой критерий
(4.58)
4.6. ОБОБЩЕНИЕ ЗАДАЧИ ОБ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ
Со времени появления работы Попова [111] было опубликовано большое количество
результатов, в которых обобщалась постановка задачи об абсолютной устойчивости.
Наиболее общим является квадратичный критерий Якубовича [182],
охватывающий основные частотные условия. Рассмотрим систему с векторной нелинейностью
Х = АХ + В£,1
а = С'Х, J
где X-n-мерная вектор-функция, £(')и a(t) n-мерная и m-мерная вектор-
функции. Предполагается, что функции удовлетворяют г локальным связям
/v(£,c,a)>0, / = п
и s интегральным связям
t
Jf*(S,c,g) dt>-y, * = U,
о
где FhFk - квадратичные формы от трех аргументов. Подобного рода
неравенствами можно описать многоконтурные нелинейные системы, а также системы с
частотной и широтной модуляцией и т.д.
Составим форму
F{bo,a) = rfi%iFifaa,a), т>>0. (4.59)
/=i
Введем следующие преобразования формы F(£,yoyd).
Рассматривая £„О96 как независимые аргументы, распространим форму с
сохранением эрмитовости на комплексные значения аргументов, обозначаемые через
^,д,а>. При этом получим эрмитову форму Fx (|, о, a J = Re F (|, а, а].
В форму F{fe,69d) вместо а и а подставим a = -W(i/(o)|, a = -yo)V^(./co)|,
где W(s) - матричная передаточная функция линейной части системы:
W(s) = C'(A-sI) lB. (4.60)
В результате этих преобразований получим форму Ffyco,|j одного векторного
аргумента |.
Теорема 4.13. [182] Пусть матрица А устойчива и F(0,a,6)>0 для всех X.
Для абсолютной устойчивости системы (4.58), удовлетворяющей неравенству
F(£,a,a)>0, достаточно, чтобы форма F(j(\\Z) была отрицательно определена
при любом со>0.
Кроме абсолютной устойчивости положения равновесия, изучалась также
абсолютная устойчивость вынужденных движений в стационарной неавтономной
системе.
Теорема 4.14. [104, 181] Пусть в стационарной неавтономной системе (4.29)
ф(а) -однозначнаяфункция,удовлетворяющая неравенству
0<vv ч yv ~'<k, (4.61)
и выполнено частотное условие (4.57). Тогда для каждой ограниченной функции
g (t) существует ограниченное асимптотически устойчивое решение c(t).
4.7. СВЯЗЬ МЕТОДА ЛЯПУНОВА С ЧАСТОТНЫМИ МЕТОДАМИ
В работе В.М. Попова [111] было установлено, что частотный критерий (4.53)
является необходимым условием существования действительного решения системы
уравнений Лурье (4.37). Достаточность частотного условия установлена в работах
В.А. Якубовича и Р. Калмана.
Теорема 4.15. Пусть линейная система X = АХ+В£ полностью управляема.
Тогда частотное условие (4.53) является необходимым и достаточным условием
существования действительного решения уравнений Лурье (4.37).
Доказательство.
1. Необходимость. Пусть уравнения Лурье (4.37) имеют действительное
решение. Прибавив к левой части первого уравнения в (4.37) и вычтя из нее y'coL ,
получим
(A4ya>I)L + L(A-ya)I) = ~UU/-eP. (4.62)
Умножим (4.62) слева на матрицу (A' + ycoI)" и справа на матрицу (A-ywl)" .
Эти матрицы не вырождены, потому что А -устойчивая матрица. Имеем
(A4y^)"lL + L(A-;o)I)"1=-(A47CoI)"1(UU4eP)(A-yo)l)"1. (4.63)
С
Умножим (4.63) слева на U' и справа на U и учтем, что LB + — = yU, где
С = С+qA'C. Получим
2yRe и'(А-./со1Г1В+|и'(А-./со1Г1в| +
V J ' I V ' I (4.64)
+eB'(A'+ycol)"lP(A-y(ul)"lB = ReC/(A-y(ol)"'B.
Прибавив к левой и правой частям (4.64) число у2, получим
Глава 4. Нелинейные системы управления lvd
Re(l + ^(o)W(y(o) + it-1 = Y + U^A-ycoiy^Bl +
+еВ/(АЧусо1)'1Р(А-усо1)'1В>О,
что и требовалось доказать.
2. Достаточность. Пусть Re(l + qj(u)W (j(u)+k~l >0. Тогда существует такой
действительный вектор U и такое е>0, что справедливо тождество (4.65), где
Р = Р' > 0. Отсюда получаем
1и'(А-;со1)~1в| +2YReU/(A-7a)l)"1B-ReC/(A-y(0l)"lB +
■ I (4.66)
+eB/(A4ya)l)"IP(A-ycol)'1B = 0.
Определим матрицу L как решение уравнения
A'L + LA = -UU'-eP. (4.67)
Отсюда, как и при доказательстве необходимости,
I _1 I2 • -1
U'(A-ya)l) В +2Re(LB) (A-ycoI) В +
+еВ'(АЧусо1)'!Р(А-;со1)~1В = 0.
Сравнивая это тождество с (4.66), получаем
F(yco)s yU-LB-— (A-7a>l)"lB +
V 2) (4.68)
+B'(A'+;cdI)'1| yU-LB-~ =0.
Тождество (4.68) может выполняться только в том случае, если тождественно
равно нулю каждое слагаемое. Действительно, любая правильная дробно-
рациональная функция F(s), тождественно равная нулю на мнимой оси, равна нулю
при любом комплексном s. Функция y^-LB (A-si) В, не равная
тождественно нулю, имеет, по крайней мере, один полюс s = s{. Однако слагаемые в (4.68)
не имеют одинаковых полюсов и поэтому при s = s{ функция F(s) должна
обращаться в бесконечность. Итак,
I YU-LB— I (А-Л)~1В=0. (4.69)
В силу полной управляемости системы Х = АХ + В£ тождество У'(А-Л)~ ВнО
может иметь место только при V = 0. Отсюда имеем
YU = LB + ~. (4.70)
Следовательно, матрица L удовлетворяет уравнениям (4.70) и (4.67), т.е. уравнениям
Лурье. Теорема доказана.
В общем виде связь функций Ляпунова с частотными методами установлена
Якубовичем и Калманом в форме так называемой частотной теоремы. Ради простоты
рассмотрим ее в следующей формулировке.
Пусть задана пхп устойчивая матрица А, /?хш-матрица В и билинейная форма
р(Х£) векторов Хе R\ §е Д1":
p(X,$) = X'GX + 2X'g$ + m, (4.71)
где G,T - симметричные матрицы порядков пхп, тхт; g - матрица порядка
пхт. Требуется найти условие существования симметричной матрицы Н = Н',
удовлетворяющей соотношению
2Х'Н(АХ + В$)-р(Х,!;)<0, (4.72)
для всех XeRn, §еДт.
Теорема 4.16. [43]. Для существования симметричной матрицы Н,
удовлетворяющей соотношению (4.72), необходимо и достаточно, чтобы
p[(jtoI-A)~!BU]>0, (4.73)
где рГхД] - распространение формы (4.71) до эрмитовой. Если условие (4.73)
выполнено, то существуют такие матрицы H = H'>0, h (порядков, соответственно
пхп, пхт), что справедливо тождество
2X^AX + B$)-g>(X£) = -fe-h'X)rfe-h'X),
матрица А = А + Bh' - устойчива.
Приравнивая матрицы в квадратичных и билинейных формах, получим
обобщенные уравнения Лурье:
A'H + HA-G = -hrV,
HB-8=hr. ■ <474)
Частотная теорема является удобным инструментом при решении многих задач,
т.к. она позволяет легко переходить от функций Ляпунова к частотным критериям
и обратно.
4.8. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ
Как указывалось в параграфе 4.5, частотные критерии устойчивости могут быть
получены на основе изучения интегральных оценок координат управляемой системы.
Однако эти оценки можно улучшить даже в рамках использования принятого
критерия устойчивости.
Наиболее точные оценки получаются при использовании частотной теоремы
(теорема 4.16). Рассмотрим интегральную оценку
се
/ = J X'VXdt, Р = Р' > 0, (4.75)
о
где X = X(f) - вектор состояния в нестационарной системе (4.29). Зададимся
квадратичной формой V = X'LX и вычислим ее производную в силу (4.29):
V = X'(A'L + LA)X + 2X'LB£.
Прибавим к правой и левой частям этого выражения форму еХ'РХ и
проинтегрируем обе части в пределах от 0 до ©°:
Глава 4. Нелинейные системы управления 205
e|x/PXt/r + v(X(oo))~v(x(0)) =
1 <4-76)
= J{X/(A'L + LA + eP)X + 2X/LB4}</f.
о
Полагая систему устойчивой, получаем Vr(x(©o)) = 0. Преобразуем
подынтегральное выражение в правой части (4.76), прибавив и вычтя неотрицательную
величину £(С'Х -£~1£]; при этом подынтегральное выражение преобразуется к виду
Х'(АХ + ЬА + еР)Х + 2Х'(ьВ+-(ф-
-i--§(CX-*-l§).
Пусть уравнения Лурье
A'L + LA + eP = -UU',
yU = LB+-C, (4.77)
имеют действительное решение. Тогда из (4.76) и (4.77) получаем
eJx'PXt/r=v(X(O))-J^(c/X-it"^)^. (4.78)
о о
Поскольку £(СХ -k~lt) > 0, то окончательный результат имеет вид
/<e-lX'0LX0, (4.79)
где L - действительное решение уравнений (4.77).
В силу частотной теоремы уравнения Лурье (4.77) имеют действительное
положительное определенное решение при выполнении частотного условия
ReC(A-7(oI)"1B + it"1-eB/(A47a>l)"lP(A-y(ol)"lB>0, (4.80)
которое одновременно обеспечивает абсолютную устойчивость системы (4.29). Более
того, неравенство (4.80) следует из кругового критерия (4.57) при достаточно малом е.
Решение системы (4.77) можно получить при помощи факторизации левой части
неравенства (4.80). Из (4.65) при q = 0 получаем тождество
ReW(yco)+it"1-eB/(A/+ycol)"lP(A-7a)l)"lBs
2 (4.81)
гк/РЧи'(А-./а)1) 1В
, Va)>0,
где вектор U таков, что передаточная функция \£ 1 +и/(А-Л) В имеет нули
только в левой полуплоскости Re s<0. Далее по известному вектору U решается
уравнение Ляпунова
A'L + LA + eP = -Uir (4.82)
относительно матрицы L , что приводит к оценке (4.79).
206 Анализ и статистическая динамика САУ. Часть I
Пример 4.1. Рассмотрим систему первого порядка
В данном случае IV (s) = .
а + s
Пусть O(j) = -!-(W(j) + W (-*)) + *"' =-( JL+ _!_! +г1.
4 ' 2х ч ' ч " 2{a + s a-s)
Фа^ризуем Ф(,): ф^).^-—^-—^
_ (i+ViTI)/
Отсюда получаем w = v (/г- .
Уравнение Лурье имеет вид 21а = и2.
«■J>f*?, /, ьг
* 2e(l + VT+I)
Поэтому .
2а
4.9. ПЕРИОДИЧЕСКИЕ ДВИЖЕНИЯ И АВТОКОЛЕБАНИЯ
Рассмотрим вопрос о том, как преобразуется периодический сигнал непрерывным
линейным звеном с передаточной функцией W (л). В установившемся режиме вход
£(f) и выход r\(t) этого звена представляют собой периодические колебания перио-
да Т и частоты (0 = —. Разложим функции £(/) и Ti(f) в ряды Фурье:
П=-оо
4(0=1^"". (4-84)
п=-°°
В соответствии с определением частотной характеристики имеем
4n=%nW(j«>n), (4.85)
Л(0= J^OtoiJe^. (4.86)
В формулах (4.85) и (4.86) предполагается, что W(s) не имеет чисто мнимых
полюсов j(un . В силу ортогональности членов ряда Фурье коэффициенты £„
определяются следующим образом
%Л)%{х)е-^\1х. (4.87)
1 о
Перейдем к рассмотрению периодических колебаний в замкнутой нелинейной
системе, изображенной на рис. 4.7, где а = / -т), f(t) - Т - периодическое внешнее
воздействие, ф(а) - однозначная функция, удовлетворяющая условию
принадлежности к сектору [ОД].
Глава 4. Нелинейные системы управления
207
-W(ri\
-w\p)
а
АО
Рис. 4.7. Нелинейная система
Пусть в системе установились периодические движения, представимые рядами
(4.83), (4.84). Если внешний сигнал f{t) разложить в ряд Фурье
/(0= Х/»'ушя'.
П=-оо
то справедлива следующая связь
°п =Л-Л* =/,,-W(ycon)Sn.
Будем оценивать энергию колебания интегралом
(4.88)
(4.89)
(4.90)
Очевидно, что
%о-1?^а-1?+!Г±?.
к " гк
Поскольку нелинейность ф(а) принадлежит сектору [0,Л],топри г>к
получаем неравенство
'^фгА*-1?****
(4.91)
Здесь использовано, что для непрерывной и однозначной функции <р(о)
т °(т)
j^adt= J ф(а)с?а = 0.
о о(о)
Оценку (4.91) можно преобразовать, используя формулу Парсеваля для рядов и
приведенные выше разложения
^(o)+i]+2|{ „/Л.
-|5.|2fRe(lt«j0)n)lV(;«m)+il J.
Пусть для значений частоты con, и = 0,1,2,... выполнено условие
P(g,r,con) = Re(l + </ya)n)W(yo>n)+—>0.
(4.92)
(4.93)
208
Анализ и статистическая динамика САУ. Часть I
Выделяя в (4.92) полный квадрат, окончательно получаем
h<
гк
г-к
/о2
(4.94)
Режиму автоколебаний соответствует предельный случай fn = 0. При этом из
(4.94) получаем /^ < 0, что противоречит предположению о существовании
периодических колебаний в исследуемой системе.
Теорема 4.17. В системе (рис. 4.7) отсутствуют автоколебания частоты со, если
выполнено условие (4.93) при п = 0,1,2,
Отметим, что условия этой теоремы отличаются от условий абсолютной
устойчивости (см. теорему 4.11) тем, что:
а) не предъявляется никаких требований к устойчивости линейной части;
б) частотное условие (4.93) проверяется только для ряда частот О,со,2со,..., что
проиллюстрировано на рис. 4.8.
coImWO'co)
ReWO'a))
Рис. 4.8. Критерий отсутствия автоколебательной частоты со
Таким образом, частотные условия вида (4.53), не сопровождаемые
ограничениями на устойчивость линейной части, выделяют класс нелинейных систем без
автоколебаний.
Рассмотрим периодические колебания в нелинейных дискретных системах*
Такие колебания характеризуются относительным периодом М, представляющим
собой отношение периода колебаний Т{ к периоду дискретизации Т, М = —. Будем
Т\
считать М заданным натуральным числом. Пусть W*(q) - дискретная
передаточная функция линейной части системы (рис. 4.9), ф(а) - однозначная нелинейность,
удовлетворяющая условиям
* См. главы 10 и! 1, в которых изложена теория дискретных систем.
Глава 4, Нелинейные системы управления
209
0<ср(а)а<*а2, (4.95)
(Ф(а1)-Ф(а2))(а1-а2)>0. (4.96)
Таким образом, неубывающая, возможно, разрывная функция ф(а) принадлежит
сектору [0,it]. Такими функциями, например, описываются кодирующие и
декодирующие устройства в системах с управляющими ЭВМ.
Пусть в системе существует периодическое движение периода
М: о(п + М) = о(м), £(п + М) = £(М) при всех п . Тогда справедливо
представление сигналов о{п) и £(п) в виде тригонометрических полиномов
(4.97)
2я ._ \М~\ М
где со =—, N = — - целая часть от —.
М [ 2 J 2
Коэффициенты в (4.97) определяются по формулам
271
м-\
271
Л/-1
^~1^УМ^ а,=^2а(у>-^.
М
v=0
М
(4.98)
v=0
-W*(s\
ф(^)
Рис. 4.9. Дискретная нелинейная система
Теорема 4.18. В дискретной системе (рис. 4.9) с нелинейностью,
удовлетворяющей неравенствам (4.95), (4.96), отсутствуют периодические режимы с периодом М,
Ш-
если для всех натуральных £ <
либо существует* такое а > 0, что
ReW* (ja£)[\ + a(l-e-ji»e)yk-1 >0,
либо существует такое а < 0, что
ReW*(ja>t)[l + a(ejl»e -\)Ук-1 >0,
причем хотя бы для одного клевые части (4.99), (4.100) строго положительны.
Доказательство. Рассмотрим выражение
Ф) =4 ^ 5W(a(n)-i»)3 2 5(п>7а(п).
М
п=0
М Mt
(4.99)
(4.100)
(4.101)
п=0
15 3ак. 232
210 Анализ и статистическая динамика САУ. Часть I
где Vo(n) = a(n)-a(n-l) - восходящая разность, a - действительное число. Из
равенства Парсеваля следует
+[l+(l-V<")]+i j.
/-1 ' (4.102)
По теореме о среднем значении интеграла
а(п)
J ф(а)^а = ф(а1)Уа(д2), (4.103)
а(л-1)
где о{ находится на числовой оси между a(/*-l) и а(«). Поскольку ф(ст) -
неубывающая функция, то
ф(а1)<ф(а(п)), если Va(n)>0, . (4.104)
ф(а1)>ф(а(п)), если Va(n)<0. (4.105)
Следовательно, \х(а) > 0 при любом a > 0, что противоречит условию (4.99). Вторая
часть теоремы доказывается аналогично, с заменой (4.101) восходящей разности
нисходящей.
В отличие от непрерывного случая, неравенства (4.99), (4.100) проверяются для
тацию. Обозначим в неравенстве (4.99)
X(co^) = ReW*(ya^), r(co^) = -ReW+ (j(oi){l-e~jloe)j =
= -(l-cos((D/)) RtW*(j(ul) + sin((Ql)lmW*(ja>t).
Тогда (4.99) перепишется в виде
X(a>£)-aY((ui) + k-{ >0. (4.106)
\ М
Для проверки (4.106) при заданном М определяем число —
кости X, Y точки с координатами Х(со^), У(со^); ^ = 0,1,...,
конечного ?<\ — . Для их проверки можно применить геометрическую интерпре-
и отмечаем на плос-
т
Неравенство (4.106) удовлетворяется, если найдется такое неотрицательное число
a, что все отмеченные точки лежат правее прямой X -aY + k~x =0.
Пример 4.2. Пусть передаточная функция непрерывной масти дискретной системы имеет вид
W(s) = r-i г.
(Г15 + 1)(т252+2^ + 1)
Г Г
Обозначим 8 =—, р =—, Y = 2^ . Передаточная функция приведенной непрерывной части записы-
Г, Г2
вается следующим образом
рЧ — 1 pi — I pq — 1
КЧ) leq-e~8 2е«-е<» Ъ е*-г*
где
с- Р2
' a2+p2-P6Y'
Глава 4. Нелинейные системы управления
211
2(l-§y + 82)(32(Vl-0,25Y2)
На рис. 4.10 изображена характеристика W*(j(u), построенная для следующих значений параметров:
5 = 1; р = 3,1; Y = 0,2.
lmW*(j<a)
Рис. 4.10. Условия отсутствия автоколебаний в дискретной системе
Допустим, что нелинейность удовлетворяет условиям (4.95), (4.96), и применим неравенство (4.99) при
а = 0 . Нетрудно заметить, что при к=кх = 5,6 в системе отсутствуют периодические колебания с М =2
и М = 4 , а при к = к2 - 3,5 невозможны колебания с периодом М - 2,3,4,6.
4.10. МЕТОД ГАРМОНИЧЕСКОГО БАЛАНСА
Метод гармонического баланса является приближенным методом расчета
параметров периодических колебаний в замкнутых нелинейных системах. При расчете по
этому методу делается предположение о том, что входной сигнал нелинейного
элемента близок по форме к синусоиде периода Т. Во многих случаях такое предполо-
15*
212 Анализ и статистическая динамика САУ. Часть I
жение оправдывается. Итак, считаем, что при надлежащем выборе начала отчета
времени в автономной (/ (г) s о) системе вида (рис. 4.7)
a(f) = Asin(cof). (4.107)
Выходной сигнал нелинейного элемента £(f) = cp(Asin(Of) является
периодическим с тем же периодом, что позволяет представить его рядом Фурье (4.83), в
котором коэффициенты определяются по формуле
1 т
£„ =— 1е~**п'у(Аь1пш)Ж. (4.108)
Как показано в параграфе 4.8, при подаче периодического воздействия (4.108) на
линейное звено с передаточной функцией W[s) получается периодический выходной
сигнал
Л=-оо
Очевидное противоречие'между формулами (4.107) и (4.109) может быть устранено
только в том случае, если в (4.109) £0 =0, W (у'сог) = 0 при |г| > 1.
Поскольку частота ш до решения задачи неизвестна, то это предположение носит
название гипотезы фильтра. Гипотеза фильтра приводит к уравнению баланса
коэффициентов Фурье:
А = _^(;а)), (4.110)
или, учитывая (4.108) и заменяя т = cor, получаем
1 1 2п
;—г = — f (p(AsinT)(sinT + 7cosxWT. (4.111)
W(j(u) nA JQ ч /ч '
Интегралы
1 «.#!> .
q(A) = -—\ (f>(Asinx)sinxd% ,
nA 0
q'(A) = —j9(Asinx)cosx^x
TLA
nA
L (4.112)
о
называются коэффициентами гармонической линеаризации. Они являются
функциями параметра А и однозначно определяются нелинейной характеристикой ф(о).
Соотношение баланса (4.111) может быть записано в следующем виде
W(j«>) = - \ (4.113)
q(A) + jq(A)
Геометрическая интерпретация уравнений (4.113) приведена на рис. 4.11.
Уравнения баланса упрощаются, если <р(а)- нечетная однозначная характеристика. Тогда
q'(A) = 0,
2 2?
q(A) = —J 9(Asinx)sinT^x (4.114)
nA 0
и уравнения баланса можно записать так
Глава 4. Нелинейные системы управления
213
1
arg W(j(a) = -n.
imW(joi)
(4.115)
(4.116)
ReW(yco)
q{A) + jq\A)
Рис. 4.11. Метод гармонического баланса
Пример 43. Рассмотрим нелинейную систему с идеальным реле и линейной частью третьего порядка
W(,) = -3—£ •
v ' *3+2s2+35 + l
Соответствующая частотная характеристика W(j(u) изображена на рис. 4.12. Идеальное реле
описывается функцией
_ f+1, а>0,
[-1, а<0.
Если предположить, что a = Asino>r, то £(г) является симметричной а/+—]г£(/) и нечетной
функцией. Поэтому ее разложение в ряд Фурье содержит только синусы нечетных гармоник, т.е.
£(0=2^2n+isin((2'l + 1)aV)- Коэффициенты гармонической линеаризации вычисляются следующим
образом
(4.117)
q(A) = — Г s\ntdt = —,
д'(А) = О.
Из уравнения (4.116) получаем расчетную частоту автоколебаний с^ = 1,731, а из уравнения (4.115)
получаем А = —| W(ya)j) | = = 2,546 . Истинные значения этих параметров, полученные при матема-
71 7Е
тическом моделировании, равны с^ = 1,745; А = 2,55.
В данном случае гипотеза фильтра оправдывается, поскольку третья гармоника имеет частоту
3(0=5,235, на которой модуль частотной характеристики близок к нулю.
214
Анализ и статистическая динамика САУ. Часть I
101
10
лг\-\
10
1ГГ2
1U
103
1О"4
ю-5
1 \w(M\
1 1 1 Ш
-
1 1 1 1 1 111
—-^
■ -* ^ ^
Ч
\
>
1 II 1 1 1 1 1
\
\
argW
\
\
S
1 III II 1 1
(У©) (град)
-
-
-
\ -
i i i i 11 \
ю-2
-60
-120
-180
-240
-300
-360
10";
10°
101
102
со (рад/сек)
Рис. 4.12. Частотная характеристика
Пример 4.4. Рассмотрим ту же систему, что и в примере 4.3, но с нелинейностью в виде реле с
гистерезисом (рис. 4.13).
В этом случае
Рассмотрим уравнение баланса в форме (4.113):
b
0
-1
1 '
i
b
G
Рис. 4.1Э. Характеристика реле с гистерезисом
Глава 4. Нелинейные системы управления
215
Частоту автоколебаний определим из уравнения 1т)¥(]щ) = или графически (рис. 4.14).
Уравнение I W(jtuA 1 = — определяет амплитуду Л. Для 6 = — получаем 0)j =1,643; А = 2,87 .
1 4 п
Im W(j(o) 0,50
0,30
0,10
-0,10
-0,30
-0,50
-3
-
-
%ъ
i
i A
щ/
У
i
1
-jq'(A)
-2,70 -2,40 -2,10 -1,80 -1,50 -1,20
ReWO'co)
Рис. 4.14. Определение параметров автоколебаний
4.11. МЕТОД СТЕПЕННЫХ ПРЕОБРАЗОВАНИЙ
Как было показано в первой главе, классические частотные критерии абсолютной
устойчивости - круговой критерий и критерий Попова очень просты и эффективны в
применении.
Можно ожидать, что уточнение условий устойчивости может быть получено при
использовании в качестве функции Ляпунова форм четной степени (четвертой,
шестой и т.д.). Эта идея реализуется ниже на базе степенного преобразования вектора
состояния системы управления.
Приведем простой пример, иллюстрирующий идею предлагаемого здесь подхода.
Запишем нелинейную систему второго порядка
хх =х2\
х2 =-а{хх -а2х2 -by{x{,t).
Въедем новые переменные у{ = xj2, y2 =х{х2, у3 -х\. Дифференцируя новые
переменные в силу уравнений (а), получаем
Ух=2у2;
h = -*1Л -"2У2 + уз + Vi (*ьО; (4Л19)
y3=-2alyl-2a2y2+\\f2(xl,x2,t),
где Vi(*i,0 = 4>(*i'0*i' V2(^i^2»0 = (P(-xi'0-x2-
Наличие нелинейности (f>(x{,t) в исходном уравнении приводит к тому, что
системы (4.118) и (4.119) оказываются связанными. Кроме того, растет размерность
вектора состояния и числа нелинейных элементов. Однако преобразованная система
(4.119) значительно упрощается, если q(xi,t) = u(t)xl. В этом случае
216 Анализ и статистическая динамика САУ. Часть I
Vi(^i»O = M(O^i' V2(Jci»JC2»0 = M(0^2» те- нелинейное преобразование вектора
состояния переводит линейную систему (4.118) в линейную систему (4.119) со сходной
структурой.
Рассмотрим ряд естественно возникающих вопросов.
Каков общий вид преобразования степени р > 1?
Каковы условия эквивалентности исходной и преобразованной систем?
Каким образом можно применить этот подход к нелинейным системам?
4.11.1. Степенное преобразование координат
Степенное преобразование для анализа линейных (в общем случае
нестационарных) систем было развито Р.У. Брокеттом.
Рассмотрим n-мерную систему автоматического управления, фазовые координаты
которого образуют вектор состояния х. Введем вектор у, имеющий в качестве
координат линейно независимые произведения из р (р - натуральное число) элементов
вектора х:
*№■•*„"", £/>,=/>. Pi*0, (4.120)
1=1
причем элементы вектора у упорядочим лексикографически. Размерность вектора у
равна числу сочетаний из п элементов по р с повторениями. Это число определяется
по формуле
Г„ + р-П (п-нр-1)!
( Р ) р!(»-1)!
Назовем степенное преобразование нормированным, если в качестве базовых
взяты элементы
Обозначим нормированное преобразование вектора х через х^. Известно ценное
свойство нормированного преобразования, оправдывающее его название:
(x'x)'=x[pfxW. (4.123)
Выполняется и более общее равенство:
(x'z)p=x[p]'z[pl. (4.124)
Очевидна связь между векторами у и х^:
xW=Mpy, (4.125)
где Мр - диагональная матрица размерности тхт , элементы которой
определяются из (4.123). Поскольку эти элементы положительные, то М^ - положительно
определенная матрица и
у = М;1х[р]. (4.126)
Рассмотрим применение нормированного степенного преобразования к линейным
уравнениям. Если задано уравнение
z = Ax, (4.127)
то имеем
2Ы = АЫх[р]? (4.128)
Глава 4. Нелинейные системы управления
217
где А}р* -mxm-матрица. Например, для п = р = 2 имеем
у[2апап
ап ап
А= ll " |; Ам =
[а21 а22
J21-
<Й
«12
v2aua2i «ii«22+Л12«21 a2la22>J2
4
а2Ха22Л
4
(4.129)
Лр]
Отметим, что элементы матрицы AlPJ нелинейно зависят от элементов матрицы А.
Известны следующие свойства преобразования А^. Пусть А,В-лхп -матрицы/
Тогда:
П 1[р]=1 *
2) (AB)[p] = A[plBW;
3) (а4) =(а'р'| , q-целое, А'существует;
4) (A'/p1=(aW).
Пусть Я,,...ДП - собственные числа матрицы А.
Собственными значениями матрицы А^ являются т произведений Х{Х^.Хк из
р элементов по. различным множествам индексов. Отсюда следует:
а) собственные значения А*-р* лежат внутри единичного круга, если
|А.,| <1, / = UJ;
б) если А' = А>0,то А[р]>0.
Пусть теперь в Rn задано линейное дифференциальное уравнение
x = A(f)x.
Тогда
d [р] . [р]
—хт =АГп ixl^j,
Л • 1р]
(4.130)
(4.131)
где Аг 1 - некоторая mxm-матрица, элементы которой линейно зависят от
элементов матрицы А(0-
Например, матрице
'ап ап
А =
при р = 2 соответствует ее образ
А
а2{ а22
(4.132)
\2]
Л
\ап
0
у/2а21 ап+а22 ЛаХ2 . (4.133)
0 л/2я21 2а22
Отметим соответствие между собственными числами матрицы А и Ar i.
Собственными числами тхт-матрицы Аг i являются т сумм по различным множествам
индексов Я, +Яу +..Ак р членов. Отсюда, в частности, вытекает, что если А - гурви-
цева, то матрица Ar i - также гурвицева.
14 Зак. 232
218
Анализ и статистическая динамика САУ. Часть Г
Приведенных определений степенных преобразований вектора состояния х^ и
связанных с ним верхнеиндексных А^ и нижнеиндексных Ar i преобразований
квадратных матриц оказывается недостаточно для изучения систем с обратной
связью или неавтономных систем. Одним из недостающих звеньев является
нижнеиндексное преобразование br л вектора Ь, которое введем следующим образом.
Определение 4.4. Рассмотрим дифференциальное уравнение в Rn:
х = Ь§(/), (4.134)
где £(f) - скалярная функция. Применяя степенное преобразование, получаем
£xM=h- ^М>"4
где br I - mxl прямоугольная матрица, / =
/2 +/7-2
/7-1
искомым преобразовани
Например,
ем в
(
i
"г
ы
екто]
f i \
ь)
2]
эаЬ
м
=
' и
л/2
0
0
0
. Естественно
[Р]=ЬЫ-
' 2Ь{ 0 N
yf2b2 *Jlbs
0 2b2
\ )
\ 0 С
ь2 4щ с
ft, 0 S
2b2 С
4гъъ V2
0 21
npi
>
\
)
b2
h _
лнятъ также, что
(4.135)
, которую и будем считать
(4.136)
(4.137)
(4.138)
4.11.2. Алгебра степенных преобразований
Принимая за определения матриц А^, А^, Ъ^ уравнения (4.127), (4.130),
(4.132) и используя свойство нормированного степенного преобразования (4.124),
получаем ряд алгебраических соотношений между верхнеиндексными и
нижнеиндексными преобразованиями векторов и матриц. Эти соотношения образуют алгебру
степенных преобразований, являющуюся необходимым математическим аппаратом
для построения новых моделей систем управления.
Рассмотрим соотношения между преобразованиями векторов.
Теорема 4.19. Пусть a, b - действительные вектор-столбцы одинаковой
размерности. Справедливы следующие тождества:
Jp-1]_k' «М. (4.139)
(4.140)
^abVaHbw;
(a + b)[P]=aW + bb];
(4.141)
Глава 4. Нелинейные системы управления 219
(пЪ')1р]=п[р]Ъ[р]/. (4.142)
Доказательство.
1). Продифференцировав тождество (а'х)р = а^х^, в силу уравнения x = b£(f)
получим р(аЪ)а^ч'х^~1^(г) = а^Ь[р]Х^~1^(г). Поскольку вектор х и
функция £(г) произвольны, то выполняется тождество (4.139).
2). По определению (4.130) имеем —х^ =(ba/)r ,х^, если х = Ьа'х. С другой
dt ^
стороны, по определению (4.132) имеем —х^ = Ьг па'хх^"^. Из тождества
dt L J
(4.139) следует (а'х)х'р~^ = —а' х^, что дает в итоге тождество (4.140).
v ' р Ы '
3). Дифференцируя тождество (x'z)p =x^z^', в силу уравнения z = (a + b)£(f)
получаем
Х[Р] ±z[p] =ХЫ (a + b) P(t)z№ = p(x/z)p-Ix/(a + b)t
Использование (4.139) дает тождество
х[р]'(а + Ъ)[р]Ц1)г["-1] = р(х'а+хЪ)х[р-^(1)г[р-1] =
из которого следует (4.141).
Пусть z = ab'x . По определению (4.128)
z[p]=(uW)[p]x[p\
Учитывая, что Ь'х - скаляр, имеем
2ы=аы^х)р=аыьы/хы>
Сравнивая два выражения для т*р*, получаем (4.142).
Следующие результаты демонстрируют свойства нижнеиндексного
преобразования матриц: линейность, перестановочность с транспонированием, преобразование
единичной матрицы.
Теорема 4.20. Пусть А, В - квадратные действительные матрицы одинаковой
размерности. Тогда
(А + В)[Р]=АЫ+ВЫ' <4-143>
(А%гЫ)- <4Л44>
Доказательство. Пусть х = Ах; z = Bz. Дифференцируя тождество
(z'x)p = z*-p* x^, получаем
р (z'x)p-1 (z'x + z'x) = zW (В')[р] хЫ + z[p] A[p]x[pl;
14*
220 Анализ и статистическая динамика САУ. Часть I
pz[p-nxlp-*]z'(A + В)х = & (Aw + (B')[p])xt"l
Свойство (4.139) приводит к тождеству
№ (А + В)[р] ж"- ж"' (а[р] + (В0и)жМ.
Следовательно, (A + B'V , = А[р] + (В')г ^."Положив А = 0, получим Bjp] = (В')г ,,
т.е. свойство (4.144). Поэтому (A + BV , = А[р]+в[р]> те- тождество (4.143)
справедливо.
Теорема 4.21. Нижнеиндексное преобразование единичной матрицы 1„
удовлетворяет тождеству
(Цр] = р1.г (4-145)
Доказательство. Рассмотрим уравнение х = х. В силу определения (4.131)
запишем
d \р] _ \р]
Элементы вектора х*-р* в соответствии с определением (4.122) имеют вид
п
1=1
Дифференцируя каждый элемент, получаем
аР[ П YPl~^Y YP2 YPn 4- YPi П YP2~^Y YPi YPn -4- -4- П YPl YPl YPn~^ Y 1
Поскольку x = x, то ij = jc; и каждый элемент х*-р* имеет вид
( п Л
ПР\ V П \yP* YP4 - nr/PYP* YP"
I W J
Таким образом,
—xL^J = р\1И1.
dt .
Сравнивая два выражения для —х^', получаем тождество (4.145).
А
Теорема доказана.
Невырожденное преобразование у = Вх, det(B)^0, применяемое к
дифференциальному уравнению х = Ах, приводит к уравнению у = ВАВ-1у. Следующий
результат дает преобразование f BAB"1 J .
Теорема 4.22. Пусть А, В - квадратные матрицы одинаковой размерности,
det(B)*O.Tonia
(bAB-)[p] = bWaw(bW)-'. • (4.146)
Доказательство. Пусть х = Ах. Тогда по определению —x^=Ar ix* . Вве-
Л т '
дем линейное невырожденное преобразование у = Вх.
Глава 4. Нелинейные системы управления 221
Имеем
y = (BAB-')y; |yW=(BAB-)[/?]yW.
С другой стороны, у[р]=В[р]х[р\ —уЫ=В[р1А[р](в[р])"1у[р1. Сравнивая два
выражения для —у^\ получаем (4.146). Теорема доказана.
dt
Следующая группа свойств степенного преобразования связывает векторы с
матрицами.
Теорема 4.23. Пусть А - пхп -матрица, a, b - вектор-столбцы размерности п.
Справедливы следующие тождества:
(АЪ^А^-аИЬи; (4-147)
.(АЬ)[р]Ь^ = АыЬ[р]. (4.148)
Доказательство. Пусть x = b£(f),z = Ax. Тогда
*=аь$(0;
±zW = (Ab )[p] *(,)«™ = (Ab)[p] A^V"k(t) •
С другой стороны,
2ы = аых[р]. £zw = AHb[p]X["-^(,).
_ d \р] к •
Сравнивая два выражения для —z , получаем в силу произвольности х и q тожде-
dt
ство (4.147).
Для доказательства (4.148) продифференцируем тождество (b'x)p =b^x^ в
силу уравнения х = А'х. При этом получим р (b'x)p~ Ь'А'х = Ъ, А| лх^ . В
соответствии со свойством (4.139) имеем
b^^b'A^x^^b^A^1,
откуда и следует (4.148). Теорема доказана.
Следствие. Полагая.в (4.148) А = I и используя (4.145), получаем
а[р]а[/7"1] = рп[р]. (4.149)
Применив свойство (4.149) последовательно р-1 раз, разложим
верхнеиндексное преобразование а^ в произведение нижнеиндексных преобразований:
Ряд полезных соотношений связывает преобразования индексов р и р-1.
Теорема 4.24. Пусть А - пхп -матрица, a, b - вектор-столбцы размерности п.
Справедливы тождества:
222
Анализ и статистическая динамика САУ. Часть I
(a'b)l, + __b[p_1]a[p_I] = ^a[p]b[p];
ьыАы=(ь'А)м+А[р-чьы;
аЫЬ[р-Ч=ЬЫа[Р-Ф
р
нения x = b^(f) получаем
а'хх^ + а'х4х1"-Ч4«[Р]Ь[Р^(0.
(4.151)
(4.152)
(4.153)
Доказательство. Дифференцируя тождество а'хх^"1' =— а[р]Х^', в силу урав-
dt
или
aX(Ox[P-n_L_b[p.1]a[p_1]^(r)xt''-1Ula[p]b[;,]x['':^(O)
что в силу произвольности х, £(г) приводит к (4.151). Свойство (4.152)
доказывается аналогично (4.151) с заменой x = b£(f) на х = Ах. Тождество (4.153) является
следствием (4.151) и (4.152) при А = ха'. Теорема доказана.
Соотношения алгебры степенных преобразований приведены в табл. 4.1.
Таблица степенных преобразований
Таблица 4.1
№
п/п
1
2
3
4
5
6
} 7
8
9
10
11
Алгебраические тождества
А. Преобразование квадратных матриц
(AB)(pl = AWBW
(А«) =(aWV, q -целое, А* -определено
(А')М = АМ'
(ЦрГ'1-
(А+в)ы = Аы+вы
(a')w=ah
(вав-111=в1"1аив1"г1
Б. Преобразование векторов (a, b - вектор-столбцы одинаковой размерности)
раЪа|''-1| = Ь|р]а|'>1
Р(аЬ%\ = Х\Ь\р)
(а + Ь)(р] = аЫ + ЬЫ
Глава 4. Нелинейные системы управления
223
12
13
14
15
16
17
18
19
20
21
22
23
Продолжение табл. 4.1
(аЬ')И = аЫЬЫ'
(аЪУ=аЫЬ1р1
а -7!a|'!V"'"a|2ia
а1/']ь[р-Ч = Ь[р]а[р-Ч
7aipib(H=7^Tbi'-1ia'''-li+(a'b)11'
В Связь преобразований матриц и векторов
(Ab^Al'-'l-AWb,,,
(Ab^bM-A,,^
ьыА|,]=(ь'А)ы+А|,-«]ьы
Г. Соотношения для р - 2
(a + b)M=al2l + b'2l + a|2]b
(А + аЬ')(2| = А121 + а|2У2|' + 1а[2]АЬ;2]
4.11.3. Иерархия моделей нелинейной системы управления
Для построения моделей нелинейных систем необходимо иметь общее выражение
для производной вектора х^ (*).
Теорема 4.25. Пусть x(t) - зектор-функция размерности п и производная x(f)
существует, тогда справедливо тождество
±тР(*НЩр]^1](!)- ' (4-154)
Доказательство. По определению имеем
x(f + /*) = x(f) + /zx(f) + 0(/z2).
Применяя верхнеиндексное преобразование (.рр*, получаем
xlp](t + h) = [x(t) + hx(t)f]+0(h2).
По свойству (4.150) имеем
(х(о+ИО)1р1=^Шх(')+Ч')) =
г * Г-О l-rJ
1 1 1
= —-ДХ[г](') + к—№р)Х[р-1)"Х[2]* +
224
Анализ и статистическая динамика САУ. Часть I
+х[р]...(х)[2]х + ... + (х)[р]Х[р_1]...х[2]х}+0(й2).
В фигурных скобках полученного выражения содержится р слагаемых вида
xWx[p_I]...x[r](x)[r_1]x[f_2]...x.
Используя свойство (4.153) степенных преобразований, получаем, что все
слагаемые в фигурных скобках одинаковы и равны
(^)[р]Х[р-1]Х[р-2]-ХИХ-
Применив свойство (4.150), имеем
(x(t)+hx(t)fp]=xM+h(x)[p]^-l\
Откуда
xlp\t + h)-x[p](t) = h(x)[p]x[p-l]+0(h2).
Тождество (4.154) следует отсюда в результате предельного перехода при h —► 0.
Теорема доказана.
Следствие. Пусть х(г) удовлетворяет дифференциальному уравнению
x = F(x,f). (4.155)
Тогда
^x['] = (FM)rix[/'-1].
dt v v ;/W
(4.156)
Формула (4.156) позволяет получить степенные преобразования нелинейных
дифференциальных уравнении. Последовательно применяя (4.156) к уравнению
(4.120) при g (t) = 0, имеем
^ж(0«Ах(0+1*(0;
|ХИ(/) = (Ах(/)+Ь^(0)[2]х(/) =
= A[2]xN(0+b[2]x(r)i;(0;
|хМ(,) = А[р]х^(О+Ь[р]х^(г)^(г).
(4.157)
(4.158)
. (4.159)
Здесь использованы теорема 4.20 (тождество (4.143)) и теорема 4.23 (тождество
(4.147)).
В системе (4.157) - (4.159) каждое последующее уравнение является следствием
уравнения (4.157). Для случая линейной системы с переменным коэффициентом в
обратной связи, т.е. при
£(*) = н(г)с'х (4.160)
Можно сделать уравнение (4.159), не зависящим от х^~'. В соответствии со
свойством (4.139) имеем
= (с'х)х[р-Ч=1с[р]х^.
(4.161)
Глава 4. Нелинейные системы управления 225
Поэтому (4.159) приводится к виду
|хМ^АыДИ(,)Ьыс(р]]ХМ, (4.162)
или в соответствии с (4.140)
-х[р] = (А + и (0ЬсО[р] хЫ- (4Л63>
Наряду с уравнением (4.163) можно рассматривать уравнение в Rm:
|y = (A + M(0bc')[p]y. (4.164)
При согласованных начальных условиях, т.е. при у (0) = Xq , решения уравнений
(4.163) и (4.164) совпадают. При несогласованных начальных условиях решения этих
уравнений различны. Однако можно рассматривать все решения уравнения (4.164)
при всех начальных условиях y(0)e Rm. В этом случае решения уравнения (4.163)
составляют подмножество множества решений уравнения (4.164).
В общем случае систему (4.157) - (4.159) легко развязать, Заменив х'р^ на ye Rm
и х^"1^ на r\eRl. Однако при этом разрывается связь с исходной задачей. Эту
опасность можно в значительной степени уменьшить, если учесть нелинейные, в
частности квадратичные, связи между элементами векторов х'^ и х^"1^. Компактное,
с наименьшим числом свободных параметров описание таких связей является
нетривиальной задачей. Желательно, чтобы это описание было приспособлено к аппарату
теории абсолютной устойчивости и чтобы оно давало возможность улучшить
существующие результаты.
Здесь предлагается использовать в качестве основной связь вида
Л'8с'[р]у = 0, (4.165)
где S = -S' - произвольная кососимметричная 1x1 -матрица.
Равенство (4.165) выполняется тождественно, если
Определение 4.5. Моделью уровня р для уравнения х = Ах + b£ называется
система
У = А[Р]У + Ъ[Р)Ч
Ti'Sc^jy = 0; VS = -S'. (4.166)
Следующим шагом является описание нелинейной обратной связи в новых
координатах. Оно достигается умножением неравенства £(а-&~1£)>0 на произвольную
положительно определенную квадратичную форму
xW]Rx[p-i]r = r^>0>
что приводит к неравенству
VRf~c[p]y-r^j>0. (4.167)
226
Анализ и статистическая динамика САУ. Часть I
Объединяя (4.167) с (4.166), получаем модель уровня/? для исходной системы.
Определение 4.6. Моделью уровня р для системы (4.29), (4.31) называется
система в Rm вида
У = АЬ]у + Ь[р]л;
Л4^с[р]у-^}>О,
(4.168)
где Q = R+S - произвольная несимметричная положительно определенная матрица.
Определение 4.7. Упорядоченная по степени преобразования р совокупность
моделей /7-го уровня называется иерархической системой моделей.
В дальнейшем будут построены модели уровня р для некоторых модификаций
основной системы (4.29), (4.31). При этом наряду с основной связью (4.165) будут
использованы и другие, как локальные, так и интегральные, связи в новых
координатах. В большинстве случаев эти модели целесообразно рассматривать вместе с
исследованием устойчивости, поскольку они отражают специфику применяемых
подходов.
Здесь мы остановимся лишь на случае системы с аддитивным внешним
воздействием g (t)e L2p (0,°°), описываемой уравнением
x = Ax + b£(O + rg(/). (4.169)
При степенном преобразовании (4.169) переходит в уравнение
|хМ=А[р]х^ + Ь[р]Ыр-1] + е(О,
где е(г) = Гг ig (t)x*-p~{*. Для нормы вектора z(t) в L2(0,7) имеем
о
где т - наибольшее собственное значение матрицы г'г i гг ъ
Используя (4.123) и применяя неравенство Гельдера, получаем
(т \УРя „KpiO
Пусть существует интеграл
h=]g2p(t)dt<oo.
(4.170)
(4.171)
Определение 4.8. Назовем моделью р-го уровня для неавтономной системы
следующую систему уравнений и неравенств:
у = аыу+ьыт1+е(г);
z = -c[p]y; л'О(г-Г'л)>0;
Щ\т<ц\\у\\т /p* = J4(P-
(4.172)
Глава 4. Нелинейные системы управления 227
В модели для неавтономной системы наряду с основной связью (4.165) присутст-
(р-у
вует неквадратичная интегральная связь ЦеЦ^ <ц,||;у||г 'р .
Полезность введенной в этой главе иерархической системы моделей не является
очевидной, поскольку модель уровня р> 1 имеет размерность значительно
превосходящую размерность исследуемой системы. Еще более существенный недостаток
состоит в росте размерности вектора нелинейности и появлении неопределенных
параметров (матрица Q). Однако применение к новым моделям метода функций
Ляпунова выглядит интересным, поскольку квадратичная форма от новых координат
является формой степени 2р от исходных координат, т.е. класс функций Ляпунова можно
расширить.
4.11.4. Анализ устойчивости нестационарных моделей
Об устойчивости исходной системы (4.29) будем судить по ее модели р-го уровня:
y = Ab]y + b[p]i1;
' n'Q(z-r'ii)>0; (4.173)
Если модель (4.173) абсолютно устойчива, то у'у —> О при g (t)e h2p (0,°°).
Очевидно, что все свойства устойчивости, присущие модели (4.173) (устойчивость по
Ляпунову, экспоненциальная устойчивость и т.д.), переносятся на исходную систему.
В частности, (х'х) -» 0 при t -> °° .
В дальнейшем будем пользоваться также степенным преобразованием с
единичными коэффициентами в форме (4.120) (ненормированным). При этом получаем
систему
y = Rpy + SpTi;
Tl'Qfz-r^O,
z = Dpy; \ (4.174)
где
D^M^c^M,; (4.175)
Rp=M;iA[p]Mp; (4.176)
t-U
S^M^jM^. (4.177)
Модель (4.173) и эквивалентная ей (4.174) являются линейными Системами с
квадратичными связями. Основной результат по исследованию устойчивости таких
систем сформулируем применительно к системе (4.174).
Теорема 4.26 [16]. Для абсолютной устойчивости системы (4.174) достаточно,
чтобы при всех со > 0 выполнялось неравенство
ReQ(op(70>) + *"lI/)>0, (4.178)
где Фр (усо) - передаточная матрица линейной части,
Op(;u)) = Dp(Rp-;coIm)-'sp. (4.179)
228 Анализ и статистическая динамика САУ. Часть I
Доказательство. Воспользуемся квадратичным критерием Якубовича (теорема
1.14), применив его к линейной системе (4.174) с одной локальной связью. Частотное
условие (4.178) является необходимым и достаточным, для того чтобы F[yco,fi] =
= ffQ(-Op (j(u)-k~ll\f\ < Одля всех г\е Сп. Теорема доказана.
Условие (4.178) означает положительную определенность эрмитовой матрицы
r(o)) = QO(y(o)+0/(-y(o)Q4r1(Q + Q/) . (4.180)
Матрица Г(со) положительно определена, если [182]
Г(оо)>0; (4.181)
detr(co)*O. (4.182)
Для положительно определенной матрицы Q условие (4.181) выполняется
автоматически, поскольку Ф(уа>) —> 0 при со —> оо.
Запишем теперь частотное условие абсолютной устойчивости в терминах
нормированного степенного преобразования. Обращаясь к системе (4.173) и применяя
квадратичный критерий Якубовича, получаем
ReQ(o(yco) + rlI/)>0, (4.183)
где
' Фj» = у[р] (AW - yo>Im)"' ЬЫ. (4.184)
Используя соотношения (4.175) - (4.177), легко показать, что условия (4.178) и
(4.183) эквивалентны при
Q = Mp.1QMp4. (4.185)
Соответствие между Ф(усо) и Фр(у(о) задается тождеством
Ф(;<о) = МнФр (j(o)M-pl_{. (4.186)
Модель (4.174) удобнее модели (4.173) в практических расчетах, поскольку в ней
нет необходимости учитывать коэффициенты в (4.122). Матрицы Dp, Rp, Sp можно
подсчитывать непосредственно по уравнениям, не пользуясь формулами (4.175) -
(4.177). При этом 1хт -матрица Dp имеет вид
~схс2...сп 0 0...0
D 0 схс2...сп 0...0
О с\с2...сп^сп
Если система предварительно приведена (это всегда можно сделать линейным
невырожденным преобразованием) к виду, вкотором с' = (1,0,0,...,0), то D^ может
быть получена из единичнойматрицы Iw отбрасыванием последних т-1 строк.
Рассмотрим примеры применения критерия (4.170).
Пример 4.5. Рассмотрим систему второго порядка с нестационарной нелинейностью:
х, =<!„*,+а12*2 + Ь&
*2=Я21*1+Я22*2 + Ы;
S=<p(<v);
0<(p(altt)a{<ka^
Глава 4. Нелинейные системы управления
229
Введя новые переменные О] = ед + с2х2, о2 = *2, запишем систему в форме
61 = рмо1 + р12а2 + (/1ф(а1,0;
<*2 = P2i°i + Pi2°2 +d2q>(al,t).
Преобразование второй степени дает модель второго уровня
Уг = Рг\У\ + (Рп + Р22 )>2 + Р1зУз + <*гЛ| + 4Л2;
)'з = 2Р21>'2 + 2р22уз + 2(/2Л2, .
где у| = а? ; у2 =a!a2; у3 = <*2 ; Л1 =5 сг,; ti2 =5 <*2 •
Условие устойчивости имеет вид (q2i = 1)
(1е1Г(со) = [^1(Кеф11+Г1) + ^12Кеф21]х
х[ЯеФ22 + ^"1+^21^еф12]-
-~|ftl<Pl2 + Ф21 + 412 (Ф22 + *Ч ) + ^21 (ф!1 + *"' )f > 0.
где (ртл - элемент матрицы Фр(усо), а звездочка означает операцию комплексного сопряжения. Было
принято рп = dx - 0, р12 = 1, (/2 = -1, р2\ = -До»Р22 = -«1 • В этом случае
Ф11(5) = 2(^2Л1)/А(^); Ф12(*Ь4/А(*);
92IW = (^2fll)/AW; Ф22(*)*2/А(*);
A(j) = j3 + Зв^2 + (2a,2 + 4a0)* + 4oofli.
В контрольном примере принято a, = 1, a0 = 2 • При решении на ЭВМ задачи нелинейного
программирования удалось получить максимальную величину к = 5,47 при qu =0,514; qn = 1,193 ; q2\ =-0,206 ;
q21-\. График det Г (о) при этих параметрах приведен на рис. 4.15. Для сравнения укажем, что
критерий Попова в этом случае дает /: < 3,82 .
Г(со)
0,08
3 4 5 6 7 8 со
Рис. 4.15. График det Г (со)
Пример 4.6. Рассмотрим модель третьего уровня для системы, описанной в предыдущем примере,
вводя ее при помощи преобразования третьей степени ух = aj, y2 = ajo2* Уз ~ aia2> У а ~ °2- Для системы
сравнения имеем
R3
Р21
0
0
ЗР12
2А1 + Р22
2Р21
0
0
2/>12
Ai+2ft2
0
0
Pl2
ЗР22.
• С _
36,
0
0
0
26,
2^
0
0
0.
ь,
230 Анализ и статистическая динамика САУ. Часть, I
Область устойчивости по параметру к определялась с помощью ЭВМ для ац=0, а12 = 1,
by = 0, a2i ="2» а22 =-!• Матрица Q имеет вид
1,0 4,075 1,575"
Q =
-0,6508 4,628 2,867
0,4068 0,5683 1,246
При этом максимальная величина к = 5,98.
Пример 4.7. Рассмотрим систему третьего порядка:
х]=х2\
х2 = хъ\
хъ = -20*! -10*2 -10*3 -Юф^ ,г).
Построим модель второго уровня, взяв новые переменные
У\ = *?• Уг = *Л» Уъ = х\хъ> Уа = *2. Уъ = *2*з> Уб = *з»
в результате чего получим систему
>;2 = >;з + >;4;
Уз = -20у, - Ю>;2 - Ю^з + у5- Ют;
>'4 = 2>'5;
у5 = -20^2 -10^4 -}0у5 + у6- 10n2;
у6 = -40^з - 20>;5 - 20Уб - 20ц3,
где T)i=<¥P(ai*O; Л2 = су2ф(а1'0; Лз = азФ(°1»0- По кРитеРию Попова устойчивость имеет место при
к < 2,43. Применив критерий (4.180) и решив соответствующую задачу нелинейного программирования,
удалось получить расширение области устойчивости до к = 3,0.
4.11.5. Сравнение с круговым критерием
Как показано на примерах, критерий (4.178) может давать большую область
абсолютной устойчивости в пространстве параметров, чем круговой критерий (4.57).
Установим соотношение между этими критериями в общем виде.
Теорема 4,27. Пусть выполнено частотное условие кругового критерия (4.57).
Тогда существует симметричная положительно определенная матрица Q , для которой
выполнен критерий (4.178).
Утверждение теоремы говорит о том, что все результаты, которые можно
получить из кругового критерия, можно получить также из условия (4.178), т.е. новый
критерий, во всяком случае, не слабее кругового критерия. Доказательство теоремы
основывается на следующей лемме.
Лемма 4.1. Пусть действительная положительно определенная матрица L = L/ и
действительный вектор и удовлетворяют системе уравнений Лурье (4.47) при q = 0:
A/L + LA = -uu/-sP; (4.187)
Lb + ~c = yu, (4.188)
где А - гурвицева матрица; Р = Р' - действительная4 положительно определенная
матрица; е, у - положительные числа; Ь, с - действительные п-векторы.
Тогда справедливы тождества
A[p]LW + LWA[p] = -iu[p]Lt"-\reF; (4.189)
F = F' = L[p](L-1p)r • (4.190)
Глава 4, Нелинейные системы управления - 231
Доказательство. Пусть выполнены условия леммы. Умножим (4.187) слева на
L"1 и применим к обеим частям полученного тождества нижнеиндексное
преобразование:
(L"lA4]+'^HLMrf-<L'Iplr
Согласно свойству 8 таблицы степенных преобразований имеем
A{p]&K&\r-&\L-uu')[p]-eF,
WF = LW(L-'p)r .
Применив то же свойство, можно убедиться, что F = F'. Согласно свойству 10 имеем
(L"'"»')w-;(L"'u)wui*
а по свойству 18 получаем
(l4]=(lW)~V"-"-
Два последних соотношения показывают, что
L'"(L"1»°'lriuwL['"lni*
что и доказывает тождество (4.189).
Применяя нижнеиндексное преобразование к (4.188) и используя свойство 18,
получаем (4.191).
Доказательство теоремы 4.27. Пусть выполнено частотное условие (4.57).
Тогда согласно частотной теореме Якубовича - Калмана при достаточно малом е > О
справедливы уравнения (4.187), (4.188). По доказанной выше лемме получаем, что
справедливы тождества (4.189) - (4.191). Рассмотрим квадратичную форму
V (У, п) = У'( А'Ы1^ + &\р]) у + 2/&\р]Ц +
(4.192)
Используя (4.189) -(4.191), получаем
+PH'L^[lc[p]y-r'n].
89)-(4.191), получаем
Из свойств степенного преобразования следует, что матрица F = F' - положительно
определенная. Тогда V(y,n) при всех ye R"\ це Rl, |y| + |i]|*0. Поэтому
Ч*Ь^ч|1с'Ыу-*-1ч1<0, (4.194)
при у = (ycolm - А)~ br m, что следует из частотной теоремы. Из (4.194) получаем
RelM jlcf,j (A[p] - рла)"' Ьы + к~% J > 0. (4.195)
Итак, из кругового критерия (4.43) следует выполнение неравенства (4.183) при
Q = L» . Соответственно из (4.57) следует, что выполнено и условие (4.178) при
Q = Mp4L[p-I]Mp.1.
Теорема доказана.
232 Анализ и статистическая динамика САУ. Часть I
Теорема 4.27 свидетельствует о том, что область абсолютной устойчивости в
пространстве параметров системы (4.29), получаемая по круговому критерию, вложена в
область абсолютной устойчивости, получаемую по критерщо (4.178). Поскольку
известны примеры, когда условие (4.178) действительно расширяет область
устойчивости по сравнению с (4.57), то можно утверждать, что вновь полученный критерий
является более сильным, чем круговой.
В примерах разд. 4.11.3 наибольшая область устойчивости получена при
несимметричной матрице Q . Покажем, что нельзя улучшить круговой критерий,
ограничившись в (4.178) использованием только симметричных матриц.
Теорема 4.28. Одним из собственных значений передаточной матрицы
ФМ = у'1р](А[р]-рЛт)1Ъ[р]
является передаточная функция W(.s) = c'(A-.sl)~ b, а соответствующим правым
собственным вектором является вектор
d(,) = [(A-rfn)t'-1]jV'-4 (4.196)
Доказательство. Умножим матрицу Ф(ря) на вектор d(s) справа:
<b(ps)d(s) = ±с'[р] (АЫ - ps\m У Ь[р] [(А - Л„ у1 bf~l]. (4.197)
Обозначим R = А - sin. По свойству 5 из таблицы степенных преобразований имеем
КЫ=АЫ-^1'"=(А-Л'')Ы' <4198)
а по свойству 19 получаем
b[p](R-bf-l]-R[p](R-bf\ (4.199)
<b(ps)d (s) = ic[p] [R-'b]W. (4.200)
Используя в (4.200) свойство 9, имеем
^^(R^bf^c^bJfR^bf-11; (4.201)
Ф (ps)d(s) = с'(А - Л)"1 bd (s), (4.202)
что и требовалось доказать.
Пусть теперь в условии (4.183) Q = Q'. Условие (4.183) эквивалентно неравенству •
QO(py(o) + 0/(-pya>)Q4rl(Q + Q/)>0. (4.203)
При Q = Q', умножая (4.203) слева на d'( - j(o) и справа на d(/a>), получаем
d'(-ja>)Qd (усо)[ф (;со)+Ф (-;со) + 2к~1 ] > 0. (4.204)
Поскольку Q = Q' >0, то из последнего неравенства следует круговой критерий.
Таким образом, круговой критерий не может быть улучшен при Q = <У (или
соответственно при Q = Q' в (4.178)).
4.11.6. УСТОЙЧИВОСТЬ НЕАВТОНОМНЫХ СИСТЕМ
Рассмотрим устойчивость системы (4.29) при наличии исчезающего возмущения
g(t). Для этого введем понятие устойчивости в функциональном пространстве
Ч,(о,~).
Глава 4, Нелинейные системы управления 233
Определение 4.9. Векторная функция x(t) принадлежит L2p (0,°°), если
оо
J(xx)p^<oo. (4.205)
о
Определение 4.10. Система (4.29), (4.31) называется устойчивой в L2/7, если из
условия g(t)sh2p (0,оо) следует, что x(t)y £(f)e L2p(0,«>).
Теорема 4.29. Пусть существует положительно определенная матрица Q, такая,
что для всех со>0 выполнено условие (4.178). Тогда система (4.29), (4.31) устойчива
в L2p(0,со).
Замечание. Если I g(t) |<L<°o, то из устойчивости системы (4.29), (4.31) в
h2p (0,°°) следует ее асимптотическая устойчивость. Действительно, пусть
/(x'x)pA<=o;j42"(0^
о о
Пусть V = х'х. Тогда
—\р =2р(х/х)р'1(х/Ах + хЪ^+х/г^).
dt
Интегрируя, получаем
{x'(t)x(t))P -(х'охо)р =2р\(х'х)р-1 (x'Ax+x1£+x'rgyit. (4.206)
о
/
Оценим слагаемые в правой части (4.206): J(x'x)p l x'Axdt < jij(x'x)2<u, где ц - наи-
0 0
большее собственное значение матрицы — (А + А');
/(х'хГ'хЪ^^Сх'х)"-"2^)1'2^^/^
о
, ч2р-1/2р,/ ч1/2р
, /, Y2p"1)/2pr' V/2/>
}(х'хГ'х'^^г'г)1'2 j(x'x)p</, ]g2p(t)dt .
Приведенные оценки показывают, что
ft N(2P-1)/2P
(x/x)^<(x^xo)p+clj(x^^ + c2 \{x'x)pdt <с3<оо ,
0 1,0 J
(х'х)<М = const.
Оценим теперь V = 2x/x = x/Ax + x/b£+x/r£ . Очевидно, что V<M2<°°, если
g (r)| < L . Используя лемму Барбалата [111], завершаем доказательство.
В силу приведенного замечания теорема (4.128) является частным случаем
теоремы (4.130) при g(t) = O.
234 Анализ и статистическая динамика САУ. Часть I
Доказательство. Очевидно, что для устойчивости системы (4.29), (4.31) в
L2p (0, °о) достаточно, чтобы модель р-го уровня (4.172) была устойчива в L2 (0, «>).
Из (4.172) имеем
y = Rpy + Spn + e(/);
z = Dpy; - (4.207)
r\'Q(z-k-lr\)>0;
1+^1^,11 = const.
Из (4.207) имеем
sY(s) = RpY(s) + SpH(s) + E(s) + y0, (4.208)
где
Y(s) = L{y(t)};
H(s) = L{r](t)};E(s) = L{e(t)}.
Из (4.208) следует
Y(s) = -(Rp-sl)1 SpH(s)+(sl-RpfE(s)+(slm-Rp)~l y0. (4.209)
Обозначим
L-l[(Rp-slm)lSp} = ip(t);
L-l{(slm-RpfE(s)}= /(r);
L-I{(*Im-Rp)"Iyo}=/o(0.
Из (4.209), переходя к оригиналам, получаем
v(t) = -'jip(t-X)r](XyiX + fl (/)+/„ (0- (4.210)
О
Соответственно
О
где
ф(0=в,ф(0; /i(0=Dp/(0; /о(0=»р/о(0-
Введем усеченные вектор-функции
V ; [0, />Г; V ; [0, t>T.
Обозначим zT(t) решение уравнения
zT(t) = -\q>(t-X)4T(X)dX + flT(t)+f0{t), (4.213)
о
где
Глава 4. Нелинейные системы управления 235
Очевидно, что при t < Г выполняется тождество гт (t) = z{t).
Обозначим
т
p{T) = jr\Q(z-k-{4) dt = jr(TQ(zT-k-\)dt>0. (4.214)
о о
Применяя к (4.214) формулу Парсеваля, получаем
p(T) = i- j HHyto)[QVI.(jto)-Q(o/,(7to) + *"lI;)]Hr(jU>)^ (4.215)
где
Ht(s) = L{4t}; VT(s) = L{VT(t)}, vT(0 = /,r(0 + /o(0-
Поскольку р(7) > 0, то
:M HJ. (yo>)QVr (yo>)rfo>>^-J н; (;ш)Г(о>)Нт (Jco)do>, (4.216)
2Я j^ 271 j^
где r(co) = ReQ(op(ya>) + /:~ll)>0 no условию теоремы.
Левую часть (4.216) оценим сверху:
^ / ИГГ (yco)QVr (yo>)do>< ^2||л||т|v||r, (4.217)
где q2 - наибольшее собственное значение матрицы Q'Q .
Для правой части (4.216) справедлива оценка снизу:
^-J НИусо)Г(а))Нг(7со)^а)>с2||л||', (4.218)
—оо
где с2 = min yi(co), yi(co) - наименьшее собственное значение матрицы Г(со).
Сравнивая (4.217) и (4.218), имеем
Иг ^С2!* 1М|Г ^c~2lq2\\Л + /0|г. (4.219)
Оценивая (4.210) в L2(0,7), получаем
|3i *сз|N|T +|/, + /о|| <с4 (Щ+Щ) , (4-220)
где с3 = max уз(со), уз(«)) - наибольшее собственное значение матрицы
Ф(-усо)ф(7Со); с4 =c3c2lq2 +1. Далее имеем
|/i«*Hr. • (4-221>
где с5 = max X2(co), Х2(со) - наибольшее собственное значение матрицы
(-7'(о1ш - R'p) (ycolm - Rp) • Используя (4.221) в неравенстве (4.220), получаем
|4^4с5|е|г+с4|/0|г. ' (4.222)
Принимая во внимание последнее неравенство из (4.220), имеем
1М1т<Иу|Г)/р+с4|14' (4-223)
гдес= JIC4C5.
236 Анализ и статистическая динамика САУ. Часть I
Из (4.223) следует, что \у\\т <°° при любом Т. Действительно, сЛ/А <с0,
поскольку /о(0 - экспоненциально убывающая функция. Поэтому
11у||(р-.)/р(|у|./р_с)<Со (4224)
Возможны случаи:
а) если ||;у||г р < с, то утверждение выполняется;
б) если U^ > с , то lyf0" * с0 /(|,£" -с) < ~ •
Теорема доказана. При конкретных /? неравенство (4.223) может быть решено
аналитически или графически. В частности, при нулевых начальных условиях имеем
\yfT Р < с, а при отсутствии внешнего воздействия |у|| р< с4 /0 .
4.11.7. Устойчивость дискретных систем*
Рассмотрим применение степенного преобразования к дискретным системам вида
*(f + l) = Ajc(f) + b£(f); (4.225)
£(г) = ф(а(0,0; . (4.226)
О < ф(о(/),г)о(/) < ^а2 (г); (4.227)
o(t) = c'x(t). (4.228)
Система (4.225) - (4.228) абсолютно устойчива тогда и только тогда, когда
устойчива линейная система (4.225) с переменным коэффициентом
£(f) = w(f)c'x(f), 0<u(t)<k. (4.229)
Более того, достаточно рассмотреть случай кусочно-постоянной функции u(t)y
принимающей только два значения: 0 и к. Подставляя (4.229) в (4.225), получаем
х (t +1) = (А + и (f)bc')x (г). (4.230)
Отсюда следует
х[р] (/ +1) = (А + и (/)bc')W x[rf (0- (4.231)
Вектор (А + и(*)Ьс') х'р' можно представить в виде
(А + и(0Ьс')Ы х[р] = А[р]х[р] + (S,n(г) + S2u2 (t) +... + Spup (t))z(r), (4.232)
где2(0 = ^с[р]х^(0.
Если w(r) принимает только значение 0 и к, то
(и(0)"=*р-Ч). (4.233)
Используя (4.232) и (4.233), из (4.231) получаем
х[р] (t +1) = А[р]к[р] + и (OSz (t), (4.234)
где
S = ^S^M. (4.235)
i+i
* См. главы 10 и 11, в которых изложена теория дискретных систем.
Глава 4. Нелинейные системы управления
237
Аналогичным образом, применяя ненормированное преобразование (4.120),
получаем
y(/ + l) = Rpy(/)+S,ii(0; • (4.236)
п(0 = и('М0; (4.237)
z(t) = Dpy(t). (4.238)
Для того чтобы исключить (4.237) и получить систему сравнения, введем
неравенство
r\'Q(z-k-lr\)*O. (4.239)
Рассмотрение системы сравнения (4.236) - (4.239) приводит к следующему
результату.
Теорема 4.30. Пусть все собственные числа матрицы А лежат в открытом
единичном круге и существует положительно определенная /х/-матрица Q такая, что для
всех cog [0,7i]
Re Ul)p (Rp - е*Чт)"' Sp + k'% 1J > 0. (4.240)
Тогда система (4.225) - (4.228) абсолютно устойчива. Доказательство теоремы
(4.131) аналогично доказательству теоремы (4.130) с заменой непрерывного
преобразования Лапласа на дискретное и интегралов на суммы.
Следующий пример показывает, что критерий Цыпкина (4.41) является лишь
достаточным условием абсолютной устойчивости нелинейных дискретных систем.
Пример 4.7. Рассмотрим дискретную систему второго порядка
xl(t + \) = auxl(t) + anx2(t) + b£(t)\
x2(t + \) = a2lXl(t) + a22x2(t) + b2^(t).
Применим преобразование второй степени. Тогда
R* =
«fl.
а, ,022
4
2аиа12
a\\<h2+a\2a2\
2а21а22
а\г
а12а22
«2.
S2 =
ТапЬ+кЬ?
2*12*1
«lA+^A+W *12^+в2А
2fl2A+tt|
2а22Ь2
Для аи = 2,07; ai2 = - 2,79; a2i = 0,84; an = - 0,84; Ь\ - 0,1; b2 = 0 в соответствии с теоремой 2.5 получаем
к > 2,98. Критерий Цыпкина дает предельную величину к = 2,51.
Остановимся более подробно на случае квадратичного (р = 2) преобразования.
При этом уравнение (4.231) имеет вид
x[2](r + l) = (A + W(0bc/)[2lx[2](/).
(4.241)
В соответствии со свойством 22 (см. таблицу степенных преобразований)
получаем из (4.241)
гМ
(1 + 1) = (АИ + Л^И ЛиЬ[2]Ас[2] Ь2\
Используя соотношения
и2=ки, с\2]х[2] = (с'х)х.
Т1 = 5 с'х = м(с'х)2=-
MCr,iX'
РГ
[2]
238 Анализ и статистическая динамика САУ. Часть I
с[2]' .
2]„М
Л
2 '
f/Whr J
lr>/+D[2]
л кЪс
Л i
получаем
(4.242)
Полученная модель дает возможность сформулировать следующий критерий
абсолютной устойчивости для дискретных систем.
Теорема 4.31 [18]. Система (4.225) - (4.228) абсолютно устойчива, если
существует такая положительно определенная матрица Q>0, что при всех cog [О,тг]
выполнено неравенство
Re Qfic^fA^-^xfbpjA^^^I^O, (4.243)
Л Л ^
где А{ = А+ .
Доказательство этой теоремы следует из дискретного варианта квадратичного
критерия Якубовича (теорема 1.14) при учете квадратичной связи
n'Q^c[2]Xl2] -*-4|j*0.
Соотношение между критерием (4.243) и критерием Цыпкина (4.41) описывается
следующим образом.
Теорема 4.32. Пусть выполнен критерий (4.41). Тогда матрица
Q = A'LA + L + fccbTLA, (4.244)
где L является действительным положительно определенным решением системы
уравнений
A/LA-L = -ww/-eI, e>0,
A'Lb + - = yw, (4.245)
у2=*~1-ЬХЬ,
обеспечивает выполнение критерия (4.243) для всех cog [0, я].
Таким образом, критерий (4.243) является более сильным, чем критерий Цыпкина.
Нахождение максимальной области устойчивости по критерию (4.243) связано с
численным поиском оптимальной матрицы Q. Этот поиск облегчается, если в
качестве начального приближения взять Q в виде (4.244), (4.245). При этом начальная
параметрическая область устойчивости будет не меньше области устойчивости по
критерию Цыпкина. Отметим, что в отличие от непрерывного случая (теорема 4.27),
начальное приближение (4.244) является несимметричной матрицей.
4.11.8. Квадратичные связи в стационарных системах
Рассмотрим совместно уравнения исходной и преобразованной систем при
квадратичном преобразовании. Опуская индексы, перепишем их в виде (пользуемся
ненормированным преобразованием (4.120))
х = Ах + Ь£; (4.246)
y = Ry + St]; (4.247)
т] = £х. (4.248)
Пусть £ = ср(а), где ср(а) - непрерывная однозначная скалярная функция. В этом
случае результаты разд. (4.122) могут быть усилены за счет учета дополнительных
Глава 4. Нелинейные системы управления 239
квадратичных связей в координатах г\,у, являющихся следствием свойств функций
Ф(а).
Лемма 4.2 [17,18]. Пусть ф(а)-непрерывная однозначная функция,
удовлетворяющая условию (4.31). Тогда справедливы неравенства
jo2 (г )ф(а)сий > -v,, (4.249)
о
|а2(/)[*а-ф(а)]а^>-у2, (4.250)
о
где постоянные Vj и v2 не зависят от t.
Доказательство. Левая часть (4.249) в силу однозначности и непрерывности
ф(а) может быть записана в виде
о(Т) о(Т) о(0)
J а2ф (а)/а= J а2ф(а>/а- J а2ф(а)/а (4.251)
а(0) 0 0
Однако в силу (4.31)
а
Ч/(а) = |а2ф(а>/а>0.
о
Действительно, по теореме о среднем значении
а
Га2ф(а)б/а = аа12ф(а1), а,е[0,а].
о
Поэтому а Gi>0 и (поскольку в\ ф(аО >0) \|/ (а) > 0. Если обозначить V\ = \\f (ao),
то отсюда следует (4.249). Неравенство (4.250) доказывается аналогично с заменой
ф(а) на ко - ф(а).
Лемма доказана.
Для записи неравенств (4.249), (4.250) в новых координатах заметим, что
а2ф(а)а = 'П/сс/ха = Г1сс/(г-Аг-Ьс/т1); (4.252)
а3а = - zWz = z cc'(z - Az - be n). (4.253)
Поэтому при (Xi>0, а2>0 имеем
Тг , -i
J (a1~a2)Ti/cc/(z-Az-bc/Ti) + a2-z/ccz L/r>-v3, (4.254)
где v3 =ol{v{ +a2v2.
Лемма 4.3 [17,18]. Пусть Gb G2, G 3, G4 - неотрицательно определенные пхп-
матрицы; r\, r2, g\, #2 -неотрицательные числа, причем k~l -g/c'b>0. Тогда на
решениях системы (4.246) - (4.248) справедливо неравенство
J{[il'(GI-G2) + (z'-Aii')(G3-G4)](z-Az-bc'Tl) +
О
+^|z'(G3+G4)z + |(P(h1) + P(h2))z'zJ}a^-v, (4.255)
где v = const не зависит от Г;
240 Анализ и статистическая динамика САУ. Часть I
Постоянные ju-i и \Хг являются соответственно наибольшими собственными
значениями матриц Nj =—(М| +Mj J,i=l,2, причем
Mf ^A'Gf+GfA + iw
^=^-[№+6Оь+|г(с+йА/с)];
У?=(*"!-в<сЪ)г,; (4.257)
G! =Gj -G2;
G2 =G3-G4.
Отметим, что N, становится отрицательно определенной матрицей, если G, = L,
/7=1, где L - решение уравнения Лурье:
A'L + LA = -ww'-eP;
Lb+—с+—а-А'с = ум;
2 2*
(4.258)
Доказательство. Обозначим
V^x^x, G,>0, i = p;
У1(а) = |ф(о>/о; (4.259)
о
^2(а) = ^а2-|Ф(аУа.
о
В силу (4.31) имеем
(V1-V2)Tl(a) + (V3-V4)T2(a) + (V4+V2)l/:a2>0. (4.260)
Дифференцируя левую часть (4.260) по времени, а затем интегрируя ее от 0 до Т, по- .
лучаем
J[(V,-V2)V(o)d+(V3-V4)(*a-V(o))d+(VI-V2)'F,(a)+.
О
+(V4-V3)'F2(o)+^['(V2+V4)^.W-v1, (4.261)
где
v, =x^(G1-G2)x0^1(c'x0)+x^(G3-G4)x04'2(c'Xo). (4.262)
Обозначим
V, = V,- V2, V2 = V3 - V4, G, = G, -G2, G2 = G3 -G4.
Для1= 1,2 имеем
^Vi=x'(A'Gi+GiA)x + 2x'Gib^±/;[^(a-rI4+5l.CT)]. . (4.263)
Глава 4, Нелинейные системы управления 241
Выделяя в (4.263) полный квадрат, получаем
4Vi=xtt,x-ft.<p(a)a/;.f (4.264)
at
где N, определено в (4.257). Отсюда
\^{%)^(о)^<\х%х^(а)^-у21, (4.265)
ош о
где
с'х0
v2/ = nSi J <P(°)V; (o)do, (4.266)
0
поскольку
a
$ <p(X)\\fi(X)dX>0. (4.267)
о
Оценивая форму * N>*< ntx x, приходим к неравенству
-v2;,n,<0,
Ц(у()щ(о)^<-
Т /
toj™ Wi(o)dt-v2h ц,->0.
o°
Введя определенную в формулировке леммы функцию |3(и) и учитывая, что
получаем
т d т
J-(Vi)V/(a)^<p(^)JzWr-v2l, (4.268)
о о
Используя (4.268) в (4.261) и подставляя в (4.261) тождества
z = ox, Ti = £x, xa = z - Az - ЬсЧ|,
получаем (4.255). Лемма доказана.
4.11.9. Критерий устойчивости стационарных систем
Рассмотрим устойчивость модели второго уровня, состоящей из уравнений (4.174)
и неравенств (4.31), (4.254), (4.255). Устойчивость этой модели обеспечивает
устойчивость исходной стационарной системы (4.29), (4.31).
Теорема 4.33 [17,18]. Модель второго уровня абсолютно устойчива, если
существуют такие действительные числа a,g! >0, #2^0, г>0, причем k~l -(g{-g2)c'b>0,
и такие действительные п хп -матрицы, Q>0 и G, что при всех о>> 0 выполнено
неравенство
Re{Q(o(y(o) + ^"1l)+^1(G + acc/)[(7(oI-A)0(;co) + bc/]-
—gfii»)®*(;ю)Ф(./<о)}>0 , (4.269)
где Ф(/со) = D(R -у coI)"lS; \i - наибольшее собственное значение матрицы
N = -(M + M/);
2V '
17 3ак. 232
242 Анализ и статистическая динамика САУ. Часть I
М = A G + GA + ии + g2kccA'y
2Yw = (G + G/)b + r(c + gAc); (4.270)
У2=ф'1-£С'Ь), g=g{~g2.
Функция Р(со) описана в лемме 2.3.
Доказательство. Положим в (4.254) а = (Xi-a2 и в (4.255) G3 = G4 = 0, G = Gp-
- G2. Тогда утверждение теоремы получается из квадратичного критерия Якубовича
с использованием связей (4.31), (4.254), (4.255).
Наряду с системой (4.29) - (4.31) можно рассмотреть эквивалентную ей в смысле
устойчивости систему, полученную с помощью преобразования £i = ко - £ :
х = Ах-Ы^ , А = А +кЪс'\
^=kG-q>(G) = <f>x(c); (4.271)
0<<р{(о)о<ко2.
Формальное применение критерия (4.269) к системе (4.271) приводит к еще
одному критерию абсолютной устойчивости преобразованной системы: преобразованная
система абсолютно устойчива, если существуют такие действительные числа
&,#! >0, g2 ^0, г>0 и такие действительные матрицы Qi>0 и Gb что при всех
со > 0 выполнено неравенство
Re{Q1(o(7(o)+rll) + |1(G + acc/)[(7Wl-A)o(70))-bc/]-
-f liP(n)<b* (усо)Ф(7(о)} >0, (4.272)
где
ф(ую) = -(1 + £Ф(70>))~ Ф(./со);
II - наименьшее собственное значение матрицы N = — (М + М'):
М = A'G! + G{ A + ии + £2*сс'А;
2YM = -(G1+G;)b + r(c + gAc); (4.273)
ТГ2=г(*-1-^сЪ), g = gx-g2.
Критерии (4.269) и (4.272), по-видимому, не сводятся друг к другу и поэтому могут
рассматриваться как различные. Связь между ними поясним в следующем разделе.
Пример 4.8. Рассмотрим систему третьего порядка со стационарной обратной связью
г -ч jcj =-101*! +*2+(p(a);
х2=-5хх+хъ\
jc3=-100jc,-(p(a);
0 = *!
и с передаточной функцией линейной части
W(s) = -2 Ц^ .
Годограф видоизмененной частотной характеристики
W,(yco) = RelV(;a))+ jvlmW(ju)
и прямая Попова для наибольшего коэффициента усиления к = 4,85 показаны на рис. 4.16.
Глава 4. Нелинейные системы управления
243
lmW\
Рис. 4.16
Из рис. 4.16 видно, что критерий Найквиста и критерий Попова для данной системы дают различные
области устойчивости по параметру к. Элементы фу передаточной матрицы преобразованной системы Ф(р)
задаются выражениями
Аф, 1 = -2р5 - 404/ - 20430р3 - 4030р2 - 80920р - 4800;
Аф12 = -2р4 - 202р3 - 4р2 + 4р;
Дф13 = -2р3 + 32р + 1608;
Аф21 = 11р4 + 1412р3 + 40р2 - 2420р -160800;
Аф22 = -р5 - ЗОЗр4 - 20404р3 - 402р2 + 404р;
Дф23 = -Р4 " 202Р3 + 16Р2 + 4036Р + 162408р;
Аф31 = р5 + 503р4 + 40622р3 + 3220р2 + 80400р;
Аф32 = р4 + 603р3 + 40622р2 + 1620р;
Дфзз = -р5 - ЗОЗр4 - 20420р3 -1614р2 + 444р + 3240;
Д (р) = Р6 + 404р5 + 5 ЮЗОр4 + 20666857р3 + 447530р2 +
+ 8172900р ++324000.
Нахождение наибольшей области устойчивости по параметру к, при котором выполнен критерий
(4.269), сведено к задаче нелинейного программирования /:—>тах при ограничениях (4.269) и Q > 0 Задача
решалась методом штрафных функций. Значение к = 5,42 получено при следующих величинах свободных
параметров:
1,0000
Q =
-1,7718-1(Г3 -2,9910-Ю"2
-3,5932-КГ2 8,7810-10"4 6,2690-10"3
-4,5513-Ю"2 -5,1960-10"3
г2
0,8910
1,5950-10
-3,0200-Ю"3 -4,9667 -Ю"3
G= 1,0987-10"2 1,4040-10"3 -3,0130 10"3
4,2230-10"3 2,811010"3 1,2500-10"3
г = 0,1310 ; а = -0,1093 ; gl =0,0706 ; g2 = 0.
17*
244 Анализ и статистическая динамика САУ. Часть I
4.11.10. Сравнение с критерием Попова
Покажем, что критерий (4.269) более сильный, чем критерий Попова.
Лемма 4.4 [17,18]. Пусть выполнено частотное условие Попова (4.53). Тогда
существует матрица Q > 0 такая, что для всех со > 0 выполнено неравенство
Re 0{фр {]<&) +к'^ + <7[(;coI-Rp_1)Op (j(o) + DpSp -сЪ1,]}>0. (4.274)
Доказательство. В соответствии с частотной теоремой Якубовича - Калмана при
достаточно малом е > 0 из (4.53) следует существование решения уравнения Лурье
(4.37). При этом мы находимся в условиях леммы (4.1) и теоремы (4.128) с заменой
вектора с на вектор с + q\c при у2 = к~{ - qcb. Поэтому справедливо неравенство
ReL[p-1]U(c + 9A'c)'[p] A[p]- jv> Imy\] + (k-x -«сЪ)1,1>0. (4.275)
Согласно свойству 11 из таблицы степенных преобразований имеем
(c + qA'c)[p]=c{p]+q(cA)[p]. (4.276)
Свойство 20 дает
(cA)[P]=c[p]Aw-Vi]c'w' <4-277>
Элементарными преобразованиями получаем
с(р]АН (А Ы - **« Г Ь[р] = cHbW+ Мр) (А W ~ j(ul- Г ЬЫ- (4'278)
Подставляя (4.277) и (4.278) в (4.275), получаем неравенство
RelP-Ч {(l-9AM)ic[p] (АЫ - МЯУ Ъ[р] + (4.279)
+7cWb["]+ J%C'W Ы ~ М- )"1 Ьы+(к-1 - дсЪ)1(} > о, v»> 0.
Используя соотношение 19, 20 таблицы преобразований, получаем неравенство
(4.274), в Q = M^lMm,.! . Теорема доказана.
Теорема 4.34. [17,18] Пусть существует действительное число q, для которого
выполнен частотный критерий Попова (4.53). Тогда при q >0 выполнен частотный
критерий (4.269), а при q < 0 - критерий (4.272).
Доказательство.
1). Пусть в условии (4.53) q > 0. В соответствии с частотной теоремой Якубовича
- Калмана из (4.53) следует существование действительной симметрично
положительной определенной матрица L, удовлетворяющей уравнениям Лурье (4.37) при
достаточно малом е > 0. Положим в (4.269) Q = G = L, а = 0, gi = #. В силу
замечаний в лемме 4.2 имеем N < 0, Р(ц) = 0. Применение леммы (4.123) завершает
доказательство для этого случая.
2). Пусть в (4.53) q < 0. Используя обозначения
^(усо) = -^(уа>)/(1 + ^(7Со)),
из (4.53) получаем неравенство
RcW{ (j(u)(l-qj(d) + k-l>0. (4.280)
Это неравенство одновременно является условием абсолютной устойчивости для
системы (4.271). Учитывая, что W{(j(o) = -c/(A-./col) b, и используя частотную
теорему, получаем решение соответствующих уравнений Лурье
Глава 4. Нелинейные системы управления 245
A/L1+G1A = -ww/-eP, еР = еР'>0;
уи = -21^ + 0-^'с; (4.281)
yz=k-l-g&.
Из леммы 4.4 следует
ReL1{o(70>) + it-1In-^(7(0l-A)o(;a))-c/bIn}>0. (4.282)
Приняв в (4.272),(4.273) Q^G^Li , a = 0, rx =1, gx = -q9 g2 =0, получим
совпадение левых частей (4.272) и (4.282), что и завершает доказательство.
Из теоремы 4.34 следует, что область устойчивости, соответствующая критерию
Попова, вложена в одну из областей устойчивости, даваемых критериями (4.269) и
(4.272). Практическая проверка этих критериев является задачей нелинейного
программирования. В качестве начального приближения полезно найти такие значения
параметров, при которых критерий Попова выполнен. Поэтому при q > 0 нужно взять
критерий (4.269), а при q < 0 - критерий (4.272).
4.11.11. Оценки качества
Рассмотрим сначала мгновенную оценку состояния системы управления в виде
квадратичной формы
V(x) = xiMx. (4.283)
Любая квадратичная форма вида (4.283) может быть представлена в виде
линейной формы от координат вектора у = х[2]:
V(x) = ay. (4.284)
В соответствии с (4.210) имеем
ъ'у = «'/о " \ct$(t-X)r\{K)dK (4.285)
о
где
9(0=z;i{(r2-.i)-1s2},
/(0 = L-1{(.I-R2)-1yo},
л('К('М0 •
Применяя к интегралу в (4.285) неравенство Коши - Буняковского, получим
1 i
' ft Л! ft \г
]ct$(t-X)r\{\)dX<\ |а/ф(г-Л)ф/(/-Х)о^Х • jr\'(X)r\(X)dX . (4.286)
о [о ) [о )
Отсюда следует
V(x)<a'/(O+H(OH,> (4-287)
V(x)>a'/(0-^i(0lN|,, (4.288)
где
ц(г)= (а'ф((-Х)ф'((-1)^ , (4.289)
246 Анализ и статистическая динамика САУ. Часть I
Таким образом, формулы (4.286) - (4.290) дают двустороннюю оценку для V(x),
если известны величины ц,(0 и Цт^. В качестве оценки для ||т1|г можно использовать
формулу (4.219), положив в ней/! = 0:
Рассмотрим теперь вычисление интегральной оценки
оо
I = fy'Gydt (4.291)
о
для модели произвольного уровня р:
у = А[р]у + Ъ[р]Ц
(4.292)
ц'д[)с[р]у-Г'л]>0.
Зададимся квадратичной формой V = у Ну и вычислим ее производную в силу
(4.292):
V = y'JA^H + НА[р])у + 2у'НЬ[р]П. (4.293)
Дальнейшие рассуждения почти дословно повторяют содержание п. 4.7 с учетом
особенностей модели (4.292). Окончательно получим
ISe-VjHyo, yo=xjrf, (4.294)
где Н - решение обобщенных уравнений Лурье
A'{p]H + HA[p]+eG = -h^h\
1 Q+Q (4295)
В соответствии с частотной теоремой уравнения (4.295) имеют действительное
решение тогда и только тогда, когда выполнено для всех со > 0 частотное условие
KeQ^lKrH'V*-'1)- (42%)
еЬы К)" Н"1 G (A ы - ;ш1Г ьм > °-
При достаточно малом е условие (4.296) эквивалентно условию абсолютной
устойчивости (4.183).
Еще раз подчеркнем, что подинтегральная функция в оценке (4.291) является
формой четной степени от элементов исходного х. Оценка (4.294) может иметь место
и в тех случаях, когда не выполнен круговой критерий (но выполнено условие
(4.296)).
Глава 4, Нелинейные системы управления 247
4.12. МЕТОД ФУНКЦИОНАЛЬНЫХ РЯДОВ
МАТЕМАТИЧЕСКОГО ОПИСАНИЯ И ИССЛЕДОВАНИЯ
КЛАССА НЕЛИНЕЙНЫХ СИСТЕМ
4.12.1. Общие положения
Идейной основой метода функциональных рядов является опубликованная в
1910 г. работа М. Фреше, в которой установлен факт существования некоторого
сходящегося ряда, описывающего непрерывный функционал. На основе этого результата
построена теория нелинейных систем. Эта теория, называемая обычно
аналитической теорией нелинейных систем, имеет целый ряд привлекательных черт: она
применима для решения широкого круга нелинейных задач и опирается на строгий
математический аппарат. Важным достоинством аналитической теории является
возможность обобщения центральных понятий теории линейных систем на
рассматриваемый класс нелинейных систем* В аналитической теории так же, как и в
теории линейных систем, центральными являются понятия импульсной переходной
функции, передаточной функции, частотных характеристик и др. В связи с этим,
используя рассуждения, применяемые при решении конкретных задач в теории
линейных систем, удается получить решения соответствующих задач для класса
нелинейных систем. К таким задачам относятся задачи детерминированного и
статистического анализа, синтеза корректирующих устройств, расчета оптимальных фильтров по
критерию минимума среднеквадратической ошибки, идентификации и др. В отличие
от линейного случая в рассматриваемом подходе используется аппарат многомерных
динамических характеристик (многомерные ИПФ и ПФ) [123].
Первые применения функциональных рядов для описания, исследования и
синтеза нелинейных систем управления связаны с именами Н. Винера, А. Бозе, Л. Заде,
B.C. Пугачева, Г. Ван-Триса, П.И. Кузнецова, Р.Л. Стратоновича, В.И. Тихонова и др.
B.C. Пугачев рассмотрел вопрос преобразования случайных функций, приводимых к
линейным. В [114] отмечено, что класс нелинейных преобразований случайных
функций, приводимых к линейным, очень широк.
В работах ряда авторов (Г. Ван-Трис, Н. Джаган и Д. Редди, Р. Мак-Фи, П. Франк,
Дж. Лаббок, М. Шетцен и др.) рассматривается проблема построения рядов Вольтер-
ра, описывающих поведение замкнутых систем. Используемый аппарат -
многомерное преобразование Лапласа (см. приложение 1). Решению той же задачи во
временной области посвящены работы Р. Флейка, Г. Марчезини, Г. Пикки, М. Килькевича и
др. авторов.
Аппарат рядов Вольтерра широко применяется для синтеза оптимальных
фильтров по критерию минимума среднеквадратической ошибки; получены системы
интегральных уравнений, определяющие оптимальные многомерные ИПФ и рассмотрены
методы решения этих уравнений. Д. Катцнельсон, А. Гулд, М. Лион, Г. Марчезини,
М. Тасинари рассматривают в своих работах итерационные процедуры для
определения многомерных ИПФ оптимальных систем.
Значительное число работ посвящено решению проблемы сходимости
функциональных рядов, а также идентификации динамических характеристик.
Начиная с конца 60-х годов, издаются книги, которые полностью посвящены
решению проблем исследования и проектирования нелинейных систем с помощью
рядов Вольтерра или в которых эта проблема рассматривается частично.
В книге «Техническая кибернетика за рубежом», изданной под ред.
В.В. Солодовникова в 1968 году, помещена совокупность работ, посвященных
описанию и идентификации нелинейных объектов типа Вольтерра [164].
Аппарат рядов Вольтерра и широкий спектр его применения наиболее полно изложен в [72, 123].
248 Анализ и статистическая динамика САУ. Часть I
В 1976 г. была опубликована монография К.А. Пупкова, В.И. Копалина и
А.С. Ющенко «Функциональные ряды в теории нелинейных систем», в которой
систематически и с единых методологических позиций изложена теория нелинейных
систем на основе рядов Вольтерра и ортогональных разложений Винера.
Рассматриваются задачи анализа, синтеза и идентификации нелинейных систем. Для их
решения используются ряды Вольтерра, многомерные преобразования Лапласа и Фурье.
Особое внимание уделено практическому применению указанных методов [123].
В этом же году увидела свет книга Ю.С. Попкова, О.Н. Киселева, Н.П. Петрова и
Б.Л. Шмульяна «Идентификация и оптимизация нелинейных стохастических
систем», которая посвящена вопросам идентификации и оптимизации систем,
информация о которых носит стохастический характер. Вопросы оптимального синтеза и
идентификации излагаются в ней на единой методологической основе, какой
является описание систем функциональными рядами Вольтерра. При решении задач
синтеза особое внимание уделяется структурному синтезу нелинейных систем. Изложение
сопровождается решением конкретных задач [72].
В настоящем параграфе кратко излагаются основные положения метода
функциональных рядов Вольтерра в части описания класса нелинейных систем и решения
задач детерминированного исследования.
4.12.2. Описание нелинейных систем
функциональными рядами вольтерра
Отправным пунктом этого подхода является положение о том, что сигнал на
выходе нелинейной системы можно рассматривать как функционал, заданный на
множестве возможных процессов, действующих на ее вход. Далее используется теорема,
доказанная в 1910 г. французским математиком М. Фреше. В этой теореме М. Фреше
показал, что для любого непрерывного функционала x\y(t)] существует
последовательность функционалов xk \y(t)], которая при &-»«> сколь угодно точно
аппроксимирует x\y(t)] (здесь y(t) и x(t) - детерминированные функции).
Если ДУ, описывающее поведение системы управления, записать в форме
^а.Ы* + F(x,x,x,...) = y(t),
где F(x,x,x,...) - аналитическая функция своих аргументов, то аппроксимирующая
последовательность имеет вид
xdy(t)]-f,j-]h(t^^-^)y^i)y^2)'^k) dxxdx2...dxk , (4.297)
*=io о
где ряд (4.297) называется функциональным рядом Вольтерра, k(t, ть т2, ... , т*) -
многомерные импульсные переходные функции нестационарной системы (ядра
Вольтерра).
Теорема Фреше утверждает, что существует последовательность ядер
k{(t, х{, х2 , ..., т,), при которой x(t) приближается рядом сколь угодно точно. Эту
теорему можно рассматривать как обобщение на функциональное пространство
известной теоремы Вейерштрасса о существовании последовательности
коэффициентов степенного ряда, сколь угодно точно приближающего произвольную
непрерывную функцию.
Таким образом, совокупность ядер ряда однозначно определяет динамические
свойства нелинейной системы, а само ядро k;(t, хх, х2 , ... , х() часто называют
также импульсной переходной функцией i-го порядка [72,123,164].
Глава 4, Нелинейные системы управления
249
Утверждение теоремы Фреше представляет собой теорему существования, т.к.
в формуле (4.297) ядра &,(/, т^ т2 , .., т,) остаются неопределенными, а
гарантируется лишь возможность в каждом конкретном случае найти последовательность
аппроксимирующих функциональных рядов.
Структурная схема нелинейной системы,1 описываемой функциональными рядами
Вольтерра, может быть представлена в виде, показанном на рис. 4.17.
yif)
*,(г,т,)
А2(г,т,,т2)
А,(<,т,,т2)...,т,)
x(t)
Рис. 4.17. Структурная схема нелинейной системы
Для стационарных систем ряд Вольтерра может быть представлен в виде
бесконечной суммы
оо
*(0 = Х *,•(').
;=i
где для i = п
хп(О = |..|^(т1,т2,...д^^-т1Жг-т2)...>;(^т^^т1^т2...^т/1. (4.298)
о о
В данном случае каждая подсистема п-ro порядка (формула (4.298))
характеризуется своим ядром кп(хи х2,.., т„) л-го порядка. Первая подсистема является линейной;
ее выходной сигнал представляет собой свертку входного сигнала y(t) с импульсной
переходной функцией линейной части системы. Вторая подсистема является уже
нелинейной и носит квадратичный характер. Ее выход есть свертка второго порядка
входа с импульсной переходной функцией к2(хи т2). Аналогично третья подсистема
носит кубический характер; ее выход х,(0 представляет собой трехмерную свертку
входа y{t) с импульсной переходной функцией k3(xh Ъ, ^з), которая может быть
названа ядром Вольтерра третьего порядка.
Таким образом, применение рядов Вольтерра является обобщением интеграла
свертки, используемого для описания линейной системы [72].
Этот аппарат обобщается и на случай, когда Y(t) и X(f) - случайные процессы. Для
стохастического случая ряд Вольтерра может быть записан в виде
*О = Ё ]-~]к«^2,.-,%)У(Ъ)У(*2)-- Y(xv)dxxdx2... dxv. (4.299)
v=l 0 О
Покажем, что ряд Вольтерра естественно возникает при описании во временной
области системы, в которой имеется безынерционный нелинейный элемент, предста-
вимый рядом Тейлора или полиномом [72, 123].
Рассмотрим непрерывную нелинейную систему (рис. 4.18), образованную
последовательным соединением линейного инерционного и стационарного
полиномиального безынерционного звеньев.
y(t)
•► k(t,T)
z(t)
+\F[z]\-
x(t)
Рис. 4.18. Структурная схема системы
16 3ак. 232
250 Анализ и статистическая динамика САУ. Часть I
Для такой системы соотношения между сигналами y(t) и x(i) имеют вид (y(t) и x(t)
- детерминированные функции)
z(t) = jk(t9x)y(x)dx9 (4.300)
о
4O = /rU(O] = Sc/z'(O. (4.301)
Общее описание системы можно получить, подставив (4.300) в (4.301)
x(t) = F\jk(t9x)y(x)dx
Lo
N i Г'
N t
= £cJf*^T)>;(T)</T =
/=i lo
^^(«MjWxpftj
Ы y=l LO
N t t i
(4.302)
i=i о о i=i
Если обозначить JJ/:(r,T;) = ^(r,x1,...,T,),/ = l,...,N, то соотношение (4.302)
примет вид ряда Вольтерра
^O = ScJ--j*.?^Ti-T2---Ti0riy(Ty)rfT1..^x/ =
/=1 ° ° • М (4.303)
i=l 0 0
Пусть, например, линейная нестационарная система имеет импульсную
переходную функцию £(/,т) = ехр —(г2-т2) . Это соответствует дифференциальному
уравнению[123]
dx(t) , ч
dt
Тогда ядро порядка / получается в виде
*|-(/,т1,т2,...,х1.) = Пехр ~(г2-т5)[
i=i L z -1
Если линейная система стационарна, то ряд (4.303) может быть записан
следующим образом
^(0 = Ес^...|^(т1,х2,...,т/)П>;а-т7.Мт1...^ =
i=l 0 0 .7=1
= 'Zj..'jki(xX9x2,...9xi)y(t-xl)...y(t-xi)dxl..ulxi9
'=1 0 О
причем его ядра определяются формулами
*?(TifT2 х|.) = П*(ту), / = 1 Л^.
Глава 4. Нелинейные системы управления
251
Если линейная часть системы - апериодическое звено с коэффициентом усиления
К и постоянной времени Г, то
1
к(х) = Кехр( т) и *|?(т1,...,т|.) = К/ехр
~1Ъ
т> 11
1—1
J'~l
Ядро второго порядка для К = 1 и Т= 1 изображено на рис. 4.19.
*2(т„т2)
Д,0
Рис. 4.19. Импульсная переходная функция 2-го порядка
Ядра полинома (4.303) полностью разделимы (сепарабельны), т.е. ядро порядка /
представимо в виде произведения / ядер первого порядка. Другой возможный тип
ядер - это частично разделимые ядра. Частично разделимое ядро порядка /
представимо в виде произведения j ядер (/< /) низших порядков. Например, ядро третьего
порядка вида
*з^т1,т2,т3) = *1^Д|)А:2(/>т2,Хз)
будет частично разделимым.
Если ядра частично или полностью разделимы, то это существенно упрощает
расчет системы. Однако на практике ядра этого типа встречаются редко. Рассмотрим,
например, непрерывную систему (рис. 4.20), образованную последовательным
соединением двух линейных инерционных систем, разделенных безынерционной
нелинейностью.
у(0
й(М)
z(t)
k(t т)
K\ttX)
At)
Рис. 4.20. Структурная схема системы
Ядра этой системы будут уже неразделимыми. Покажем это [123]
x(t) = jk(t,x)i
jh(x,a)y(a)dc
dx =
16*
L2L
/\HdJiHi и Li спин иссекал динамика \^t\ j . -la*, 1 ь а
=}*MX<«
0
J/i(x,a)y(a)Ja
dT =
=Ы*МП
/=i о
N t t
7=1
}*(т,а,),(а,)*а,Л =
(4.304)
(4.305)
i=l 0 0 7=1
В (4.304) для i = 1, ..,N обозначено
g|.(r,a1,...,a|.) = J*(r,x)nfc(T,a/)dT.
0 7=1
Выражение (4.305) определяет неразделимые ядра Вольтерра.
Предположим, что &(г,т) = ехр[-(г-т)]-ехр[-2(/-т)], что соответствует
дифференциальному уравнению второго порядка [123]
d2x(t)dx(t)
dt*
+з^+2*(0=«(0-
dt
Если h(t,x) = exp[-(r-x)], то ядро первого порядка всей системы с учетом условий
причинности получится из формулы (4.305) в таком виде:
t
*i(f-T) = J[exp[-(r-o)]-exp[-2(r-o)]]exp[-(c-T)]do =
= (f-T)exp[-(f-T)]-exp[-(f-T)] + exp[-2(f-T)].
Ядро второго порядка будет таким [123]:
g2(r-T,,f-T2) =
I
тах{т,,т2}
exp[-(f-a)]-exp[ -2(f-a) ]Г1ехр[-(а-ту)] t/a =
7=1
-exp[-a-x1)]expKr-T2)] + exp[-(r-T2)]-
-(/-хОехр^гг + ^+Тг], т^Хз,
-exp[-a-x1)]expHr-x2)] + exp[-(r-x1)]-
-(г-х2)ехр[-2г + т1+т2], т2>х1.
Приведенные примеры являются иллюстрацией к общему положению, согласно
которому любую функциональную нелинейную систему без обратной связи,
образованную соединением инерционных линейных систем и аналитических
безынерционных нелинейностей, можно описать рядом Вольтерра. Одновременно эти примеры
показывают, как это можно сделать практически.
Далее рассмотрим методы построения рядов Вольтерра, описывающих поведение
замкнутых нелинейных систем.
Рассмотрим замкнутую нестационарную нелинейную систему, поведение которой
описывается уравнением
ап (t)x(n) + an_{ (t)x(n-{) +... + ao(t)x + F(x(t)) = y(t), (4.306)
где
F(x) = c2x2 + c3jc3 +... + cNxN = X ckxk (0. (4.307)
k=2
Глава 4. Нелинейные системы управления ; 253
Будем находить решение этого уравнения в виде (4.303).
Поскольку
ап (t)x(n) + ап_{ (0*(""1) +... + ao(t)x = y(t) - F(x(t)), (4.308)
то очевидна справедливость нелинейного интегрального уравнения
оо оо
x(t) = \k(t,x)y(x)dx- jk(t,x)F(x(x))dx. (4.309)
о о
Воспользуемся обозначением
оо
*,(r) = J*(f,T)y(T)dx, (4.310)
о
где k(t, х) - импульсная переходная функция линейной части системы.
Тогда из (4.309) и (4.310) следует
ГN 1
*(O = *i(O-J*(',x) 2>У(т) \dx. (4.311)
0 L^=2 J
Будем находить решение последнего уравнения в виде функционального ряда
[164]
*(0 = f>w(0. (4.312)
Подставляя (4.312) в (4.311), имеем
N
о
Или, что то же самое,
x{(t) + x2(t) + x3(t) + ....=
1ск 5>ию
к=2 [ п=\
dx. (4.313)
2
= xl(t)-c2jk(t,x)[xl(x) + x2(x) + x3(x) + ...] dx-
0
00 з
-c3J^(M)[x1(t) + x2(t) + x3(t) + ...] dx-...-
0
оо
-cpjk(t,x)[xx(x) + x2(x) + x3(x) + ...]Pdx-... .
0
Раскрывая формулы возведения в квадрат, куб и т.д., получим выражение
Ё^(О = ^(О-С2^аД)[Л12(т) + Л-22(т) + Хз2(Т) + ...+
л=1 0
+2х, (т)*2 (т) + 2*, (т)дс3 (т) + 2*1 (т)дс4 (т) +... + .
+2д:2 (т)л3 (т) + 2х2 (т)д:4 (х) +...+2хг (т)хг+1 (х) +... ]dx-
оо
-c3jk(t,x)[xUT:) + ^(x)x2(x) + 3xi(x)xl(T) + xl(x) + ...]dx-
0 (4.314)
-c4J^,T)[x14(T) + ...]rfx-c5J*(/Ix)[^(T) + ...]dT-... .
254
Анализ и статистическая динамика САУ. Часть I
Далее будем строить члены ряда Вольтерра, используя следующие рассуждения.
Эквивалентная нелинейная система, математической моделью.которой является ряд
Вольтерра, может быть представлена структурной схемой (рис. 4.21).
,x(t),
АО
»>
*(/,т)
ь(* Л
k{t,x)
>
►
/
\
/
j
1
2
xx(t)
\
X3(t) //
Xn(t)/
у
Рис. 4.21. Структурная схема нелинейной системы:
У - линейный канал', 2 - квадратичный канал; 3 - канал с характеристикой возведения в куб
Выделим из (4.314) члены, определяющие математическую модель линейного
канала. Она определяется зависимостью
*i(/) = J*(r>T)y(T)rfT = J*1(/fT1)y(Tl)dx1.
о о
Квадратичный канал описывается формулой
оо
x2(t) = -c2jk(t,T)xf(T)dT.
о
Поскольку из (4.314) следует
оо оо
дс,2(х) = /*,(т,т1)у(т1)Л1-/*1(х,х2)у(т2)Л2,
о о
то выражение, определяющее дг2(0» можно представить в форме
(4.315)
*2(O = JJ
О О
-с2 J k(t, x)kx (т, Т! )кх (т, т2 )dx
y(T[)y(x2)dxldx2 =
= J jk2(t,xl9x2)y(xl)y(x2)dxldX29
о о
где
k2(t,x[ix2) = -c2jk(tix)k{(x,x[)kl(x,x2)dx.
(4.316)
(4.317)
Очевидно, третий член в ряде (4.313) представляет собой составляющую
выходного сигнала на выходе кубической ветви системы. Для построения ее
математической модели из правой части (4.314) необходимо выбрать все члены, содержащие в
многомерном интеграле Коши произведение у{(х)у2(х)у3(х).
Из (4.314) имеем
х3(0 = -2c2jk(t,x)x{(x)x2(x)dx-c3jk(t,x)xl(x)dx.
(4.318)
Раскроем зависимости, определяющие х{(х)х2(х) и ^(т).
Глава 4. Нелинейные системы управления
255
Находим
оо оо оо
xi(T)x2(x) = jkl(x,xl)y(xl)dxrjjk2(xix2,x3)y(x2)y(x3)dx2dx3y
о о
^i3(t) = JJJ/:1(t^0^i(^^2)^i(^^3)>;(^)>;(^2)>'(^3MVM^3-
000
Подставив последние две зависимости в формулу (4.318), можно записать
выражение, определяющее x3(t)
*з
o-jjj
00 0
|(-2с2)*(г,т)*1(т,х1)*2(х,т2,т3)Л
ху (*i) у (х2) у (х3 )dx{dx2dx3 +
+]]]\](-C3)k(t,x)kl(x,xl)kl(x,x2)kl(^)dx
oooLo
*У (Ti) У (Т2) У (b )dx{dx2dx3 =
оооооо
= llJk3(t,xl,x2,T3)y(xl)y(x2)y(x3)dxldx2dx3i
(4.319)
ооо
где
k3(t,x{,x2,x3) = |(-2с2)*1(Г,т)А:1(т,т1)*2(т,т2,Тз)Л+
о
оо
+J ("Сз )*i С> T)*i (т> Ti )*i (т> Т2 )*i (т. ^з № •
(4.320)
Поступая аналогичным образом, можно записать формулу, определяющую выход
X4(t)
оо
*4(0 = - c2Jt(r,T)[jc|(T) + 2j:1(T)jC3(T)]dT-
0
-3c3j*(M)jc12(x)jC2(T)dT-c4Jik(r>T)jc14(T)dx.
о о
Подставляя в эту зависимость выражения, определяющие х\(х) , 2х{(х)х3(х\
Х\(х)х2(х) и ^(т), получим
ооооооооГоо 1
^4(0 = JJff М(-^2)*Лт)*2(^Х1,Х2)*2(Х>Хз.Т4)Лкх1)у(Х2)у(Хз)у(Х4)Х
оооо[_о . . J
Х^Т1^Т2^Тз^Т4 +
оо «л» MJ ъя^ I gg
+JJJJ J("2c2)*(r,T)*1(T,T1)*3(T,X2T3,T4)rfT
ooooLo
xdxxdx2dx3dx4 +
y(Ti)^(x2)y(T3)y(T4)x
256 Анализ и статистическая динамика САУ. Часть I
ооооооооГео
■Jff J J(-3c3)ika,T)*1(T>T1)t1(T,T2)*2(T>T3,T4)rfT
о о о о [о
xdxxdx2dx3dx4 +
У^ЫъгМъЫ^А)*
оо оо оо оо I оо
+J J J J J(-C4)*a^)*l(x,T1)t1(x,T2)t1(T>x3)*iCc^4) dx
ooooLo
xdx{dx2dx3dx4.
Или, что то же самое,
У(Т!)у(Х2)у(Хз)у(Х4)Х
оо оо оо оо
X4(O = JJJJ*4^T1^2.T3»T4)y(Tl)y(T2)y(T3)y(T4)rfVMx3dT4.
00 00
где
оо
^4(^T1'T2'T3'T4) = J[(-C2)^(/,T)^2(T,T1,T2)/:2(X,T3,T4) +
0
+(-2с2)*(/,х)*1(х,х1)*3(х,х21х3.'С4) +
+(-Зс3)*(/,х)*1(х,х1)*1(х,х2)*2(х,ХзД4) +
+(-с4)*(г,х)*1(х,х1)«:1(х,х2)«:1(х,Хз)*1(^Х4)]^.
Для составляющей x5(t) справедливы формулы
оо оо
jc5(O = -2c2jA(<,T)jc,(T)*4(x)£/T-2c2J*(r,T)jc2(T)*3(x)rfT-
0 0
оо оо
-3c3fk(t,T)xl(T)xl(T)dT-c5jk(t,x)x5lWT =
о о
оо оо оо оо оо оо
= JJJJJ[J[(-2c2)*(/,t)*1(t,x1)A:4(t,t2,T3,T4,t5) +
0 0 000 0
+(-2с2)'*(г,х)«:2(х,х1,х2)*з(х,ХзД4.т5) +
+(-Зс3)«:(г,х)«:1(х,х1)*2(х>х2,Хз)*2(^Т4.Т5) +
+(-с5)^(М)/:1(т,т1)/:1(т,х2)/:1(т,Тз)^1(т,Т4)^(х,Х5)]^х
Отсюда имеем
оо оо оо оо оо
*5(0 = J J J J J к5(1,х{,х2,х3,х4,х5)у(х{)у(12)у(х3)у(т4)у(х5) dxxdx2dx3dx4dx5,
00 00 0
где
оо
*5^т1.т2^3.^4Д5) = /[(-2с2)«:(Г,Х)*1(Х,Х1)А:4(ХэХ2эХз,Х4,Х5) +
о
+(-2с2)*(Г,Х)*2(Х,Х1,Х2)*3(ХэХз,Х4,Х5) +
+ (-3c3)*(/,X)*l(X,X1)*2(X,X2,X3)*2(^^4.T5) +
+ (-с5)^(г,х)/:1(х,х1')/:1(х,х2)^(х,Хз)/:1(х,Т4)^(х,Х5)]^т-
Аналогичным образом можно получить ядра /:6(r,rh...,x6), A:7(^x1,...,x7) ИТ-Д-
Глава 4. Нелинейные системы управления
257
Структурная схема системы, описываемая рядом Вольтерра, представлена на
рис. 4.22.
*i(0
y(t)
Рис. 4.22. Структурная схема нелинейной системы, описываемой дифференциальным уравнением
(4.306) и эквивалентным ему функциональным рядом Вольтерра
На рис. 4.23 представлена структурная схема эквивалентной нелинейной системы,
поясняющая механизм формирования линейного, квадратичного и т.д. каналов на
основе первичной информации, содержащейся в исходном нелинейном
дифференциальном уравнении.
Воспользовавшись зависимостью (4.312), можно получить решение задачи
расчета выходного сигнала x(t) (детерминированный анализ).
С целью решения задачи анализа рассматриваемого класса нелинейных систем
можно воспользоваться аппаратом многомерного преобразования Лапласа (см.
Приложение 1).
4.13. МЕТОДЫ ЛИНЕАРИЗАЦИИ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Математические модели систем автоматического управления являются, как
правило, нелинейными. В то же время в теории автоматического управления хорошо
обоснованными являются методы анализа и синтеза, ориентированные на класс
линейных систем управления. Поэтому одним из подходов, позволяющих применить
методы теории линейных систем управления* является линеаризация нелинейных
систем.
Сущность линеаризации состоит в том, что нелинейная математическая модель
заменяется некоторой эквивалентной ей линейной моделью. Причем динамические
свойства линеаризованной модели достаточно близки к свойствам нелинейной
модели только при определенных условиях и ограничениях и в рамках решаемой задачи.
Методы линеаризации можно условно разделить на две большие группы:
статическая линеаризация; динамическая линеаризация.
Основным методом статической линеаризации для нелинейных математических
моделей с аналитическими нелинейностями является метод линеаризации
относительно заданной опорной траектории. Примером динамической линеаризации может
служить линеаризация Ньютона - Канторовича, получившая название
квазилинеаризации.
Глава 4. Нелинейные системы управления 259
4.13.1. Линеаризация вблизи опорной траектории
Математические модели систем автоматического управления могут быть заданы:
• в виде структурной схемы;
• в виде одного дифференциального уравнения;
• в виде системы дифференциальных уравнений.
При задании математической модели в виде структурной схемы нелинейные
элементы представляются в виде функциональных преобразователей с одним или
несколькими входами. В этом случае операция линеаризации выполняется для каждого
функционального элемента.
Если математическая модель задана одним дифференциальным уравнением или
системой дифференциальных уравнений, то линеаризуются уравнения системы.
4.13.2. Линеаризация функциональных преобразователей
Рассмотрим нелинейный функциональный преобразователь, описываемый
выражением вида
^/(Л.Уг.-.У,,). (4-321)
Здесь У\,У2*—*Уп ~ входные сигналы, х - выходной сигнал преобразователя.
Относительно функции /(У\,У2,—,Уп) предполагается, что она является аналитической
в заданной области изменения переменных У1,у2,—,У„9 т.е. имеет необходимое
число частных производных.
Полагаем также, что задана некоторая опорная траектория движения системы.
Под опорной траекторией понимается движение, соответствующее режиму
нормальной эксплуатации системы.
Полагается также, что реальное движение системы незначительно отличается от
опорного, т.е.
jc = jco+Ax, (4.322)
причем
Это предположение имеет силу и относительно входных воздействий
|ДУ/|«|У/о|. * = п (4-323)
Разложим нелинейную функцию (4.321) в ряд Тейлора в окрестностях опорной
траектории
ait +...+/„
w<* ^-г-гт^'Т^Т»»
~ ~/, !.../„! Эу,"..^
Ayj1 ..AyJ", (4.324)
У1=УЮ'1= 1»л
где Ду,- = у,-ую.
Ограничимся в ряде (4.324) первыми членами разложения, соответствующими
приращениям в первой степени. Остаточным членом ряда Тейлора, содержащим
приращения переменных в степенях выше первой и произведения приращений,
можно пренебречь в виду его малости. Поэтому
х = /(^i,..., Уп) ~ ДУю.-. Упо) +
Э/(У1,-,уя)
+...+
ду{
ЩУх.....Уп)
Ъп
Ау, +
*=»о.=пГ (4325)
Ду„_
260 САУ: математические модели, динамические характеристики. Часть I
Первое слагаемое в правой части (4.325) соответствует движению по опорной
траектории
*Ь=/(Ло.-.уяо). (4326)
Поэтому выражение (4.325) можно записать в виде
г . Э/(У1 у.)
— Хп =
х-хо
Эй
Луг +...+
Э/(у„-,уп)
ауя
или, что то же самое,
(4.327)
где
g ^ЭЛ^,...,^)
Эу,
- линеаризованный коэффициент передачи по /-му
И=Ло»*= 1»л
входу.
Соотношение (4.327) устанавливает линейную связь между входными
переменными и выходной координатой.
Замена ряда (4.324) его первыми членами геометрически можно
интерпретировать как замену гиперповерхности (4.324) гиперплоскостью (4.325), касательной к
данной гиперповерхности во всех точках опорной траектории.
Коэффициенты передачи Kt{t) являются функциями времени, если опорная
траектория также является функцией времени, или постоянными величинами, если имеет
место опорная точка.
Переход от выражения (4.321) к зависимости (4.327) означает переход к новой
системе координат для переменных х и yh i = 1, л (рис. 4.24).
±x(t),xo(t),Ax(t)
Рис. 4.24. К пояснению процесса перехода к новой системе координат
Часто выражение (4.327) записывают не для упрощений, а для самих сигналов
х = К1У1+К2у2+...+ КпУп. (4.327)
Результат отбрасывания членов высшего порядка малости, т.е. ошибку усечения,
можно оценить с помощью суммы членов второго порядка малости ряда Тейлора.
Пример 4.9. Электродвигатель постоянного тока с независимым возбуждением (рис. 4.25)
описывается следующей системой уравнений (насыщением магнитных цепей и реакцией якоря пренебрегаем)
и. = **-£ + *«•'«+«.
at
fd(O
/_ = Af-AfH,
e-d^-L- со.
Глава 4. Нелинейные системы управления
2Ы
*в
со, а
Рис. 4.25. Принципиальная схема электродвигателя постоянного тока с независимым возбуждением
Индексами «в» и «я» отмечены параметры (индуктивность L, активное сопротивление R) и переменные
(напряжение V, ток i) цепей возбуждения и якоря; М - электромагнитный момент двигателя, е - э.д.с. якоря.
Структурная схема электродвигателя представлена на рис. 4.26.
"в
е
Г
1
LBs-\
л
' ае
-К
1
+ я,
\
ч
>
/
ч
}
\
/
\
ам
Ч
м,
1
.У
т
J
0)
Рис. 4.26. Структурная схема нелинейной математической модели
электродвигателя постоянного тока
Функциональными преобразователями в данной структурной схеме являются умножители, т.е.
элементы, формирующие электромагнитный момент и э.д.с. якоря.
Проведем линеаризацию этих элементов в установившемся режиме -/„ =/я0, /в =/в0, (0 = (00. Эги
значения переменных определяют опорную точку.
Коэффициенты линеаризации для каждого из нелинейных элементов определяются в соответствии с
формулой (4.328):
"1я |'«-'«о
'» ='вО
Км2= — К'Л1 =dM-i
'в='.О
262 САУ: математические модели, динамические характеристики. Часть 1
Таким образом, нелинейные зависимости для электромагнитного момента двигателя и э.д.с якоря
заменяются линейными:
Ае = Кв{ Д/в+ Kei Доз.
Переходя от приращений к самим переменным, можно составить структурную схему для
линеаризованной модели электродвигателя (рис. 4 27).
О)
"в
i
е
г
1
V + ^B
1
V + Яя
К
f
f
1
к
IT..
Y
+1
•d" М 1-
+
1
/
Рис. 4.27. Структурная схема линеаризованной математической модели
электродвигателя постоянного тока
4.13.3. Линеаризация нелинейных дифференциальных уравнений
Пусть динамика системы управления описывается дифференциальным
уравнением я-го порядка вида
Jc(/i)(/)=/(jc(/),/(/),...,jc^^r), y(t\yV)^/m\t)l 44.329)
где x(t) - выходной сигнал, y(t) - входное воздействие.
Полагаем, что функция f(x(t),...,y^m)(t)) является аналитической в области
изменения переменных x(t), y(t) и их производных. Полагаем также, что задана
некоторая опорная траектория движения системы, определяющая требуемый процесс
управления, на которой x(t) = xo(f), x\t) = jco(r) x(n'l)(t) = 4'M)(0, y(0 = yo(t),
y\t)=y'0(t) y°n)(t) = y(om)(t). Движение на опорной траектории соответственно
описывается уравнением
*о°С) = /(*<>('),*&('),..,Уо °(0). (4.330)
Пусть реальное движение системы незначительно отличается от движения по
опорной траектории, т.е.
Глава 4. Нелинейные системы управления
263
х(0(0 = 40(0 + Ах(/)(г),
причем
| Дх(/) (/)|«|4° (0|, i = 0,м-1.
. Те же предположения справедливы и для входного воздействия и его производных
|Ду(О(О|« |уо Ч01,* = 0^.
Разложим функцию в правой части уравнения (4.329) в ряд Тейлора по
переменным х,..., у(т) относительно опорной траектории
хМ(1) = /(хо,х'о,...,х(оп-1\уо,...,уХ) + Щ Ax(t)
Эл1.<.)=.(.»,=-;
'л")=л11),.= 0,П-1
Ьх'\
Ax'(t)
+ ...+
x(i)=4°,i="o^T
3L
>-i)i
^c-»(0 +m
АУ(О
Эх*""0 Эу
+ ...+
О.я-1
■«'^^".^"о^Г
(4.331)
Ду(т)(О +Л2)
х<'>=4'>,,= 0л-1
где Дл:(1)(0 = л:(|)(0-4')(0, г=0,и-1,
Ду(')(О = У(О(О-)'о)(О, i=0,m.
Остаточный член Л2 содержит слагаемые с приращениями переменных в степенях
выше первой и их произведения. Ввиду малости остаточного члена /?2 ограничимся в
ряде (4.331) только линейными членами. Учитывая (4.330), получим
»
.00/
XW(t)-J$»(t)
Введем обозначения
Дх(0
/•>=у<",,="0^
+-+^)i Ау(т)^
(4.332)
= -в»(0.
=w
Ax(")(/) = jc(")(r)-4")(0,
—I
—I
y<'>=.y<'>,i="0^"
Тогда (4.332) можно записать в виде (приближенное равенство заменяем на
точное)
■ Ax(n)(0 + I>,toA*(0(0 = f>(/)Ay(O(O. (4-333)
/=0 1=0
Уравнение (4.333) является линейным дифференциальным уравнением; оно
записано не относительно переменных, а относительно их приращений на опорной
траектории.
264 САУ: математические модели, динамические характеристики. Часть I
4.13.4. Линеаризация систем нелинейных
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Системы управления описываются следующей системой дифференциальных
уравнений в нормальной форме
X(O = F(X(O,Y(O,O, (4.334)
где
X(f) = [*i(O. - .*л(0]Т- вектор состояния,
Y(0 = [y{(t\ ... , ym(t)]T - вектор входа,
F(-) = [/,(•), ...,/;l(-)]T.
Как и ранее, полагаем, что задана опорная траектория движения системы Хо(/),
Yo(0 , а функция F(X(O,Y(O»O является аналитической.
Разложим функцию F(X(0,Y(0,0 в ряд Тейлора по элементам векторов X(f) и
Y(/) относительно опорной траектории движения и ограничимся только линейными
членами. Имеем
X(/)»F(X0(0,Y0(0,0 + X!^
/=1 °xi
™+Ш
х=х()
Y=Y0
ДУ;(О,
х=х0
Y=Y0
или, что то же самое,
(4.335)
где
3F(X,Y,
ЭХТ
3F(X,Y,
ЭУТ
0
0
х=
Y=
х=
Y=
:х„
"Y0
=х0
=Y0
x=x0
V=Y0
x=x0
Y=Y0
n
\-
j =
j =
1
1
X(0 « F(X0(0, Y0(0,0 + A(/) AX(0 + B(OAY(O,
A(0 =
B(/) = -
- якобианы вектора F(X,Y,0 - правой части уравнения (4.334).
Запишем уравнение (4.335) относительно приращений
АХ(О = А(Г)ДХ(О + B(/)AY(r).
Если под приращениями понимать сами переменные, то будем иметь
Х(0 = А(ОХ(О + B(OY(O. (4.336)
Уравнение (4.336) является линеаризованным векторно-матричным уравнением
для нелинейного уравнения (4.334).
Пример 4.10. Кинетика ядерного реактора описывается следующей системой дифференциальных
уравнений
л' = — (р-р)и+Хс,
Л
С' = -Р|!-ХС,
Л
(4.337)
где п - плотность нейтронов в реакторе, с - начальная концентрация предвестника, р - реактивность,
Л, рД - параметры активной зоны реактора, и - управление.
Глава 4. Нелинейные системы управления
265
Первое из уравнений системы является нелинейным. Выполним линеаризацию системы уравнений
(4.337) для установившегося режима работы: л = ло,с = со,р = ро.
Якобианы А и В для правой части уравнений (4 337) будут иметь следующий вид
А =
Эл|_Л
f(«)
on
]
Эр|_Л
J 3cLah J эР[лм J
ОС
Эр
c=c0
P=Po
^■(Po-P) Я
7»
0
-X
0
о
о
в =
Эи|_Л
Р=Ро
Таким образом, линеаризованное уравнение для приращений переменных состояния будет следующим
Дл' = [^-(Ро-Р)]
Ал + X - Ас + —п0 • Ар,
Л
Ас' = — р-Дл-Л-Дс,
Л
Др' = Ди,
или в матричном виде
где
ДХ = А-ДХ + В-«,
(4.338)
(4.339)
ДХ = [Дл, Ас, Ар]т.
Как видно из системы уравнений (4.338), имеют место уравнения с постоянными коэффициентами.
Линейные уравнения (второе и третье) после линеаризации не изменились.
4.13.5. Линеаризация Ньютона - Канторовича
Данный метод линеаризации позволяет выполнить редукцию нелинейного
дифференциального уравнения к последовательности линеаризованных
дифференциальных уравнений, т.е. перейти от нелинейной математической модели системы
управления к последовательности линеаризованных моделей.
Рассмотрим особенности метода Ньютона - Канторовича на примере
операторного уравнения вида
Д* = 0, (4.340)
а затем применим его к нелинейным дифференциальным уравнениям.
Сущность метода Ньютона - Канторовича состоит в том, что если оператор А
дифференцируем по Фреше и найдено приближение хк , то последующее
приближение хк+х находится из линеаризованного в точке хк уравнения
А(хк) + А'(хк)(хк+1-хк) = 0, (4.341)
266 САУ: математические модели, динамические характеристики. Часть I
или модифицированного линеаризованного уравнения
А(хк) + A'(хо)(хк+1 - **) = 0. (4.342)
Линеаризованные уравнения (4.341) и (4.342) принципиально отличаются от
уравнений, линеаризованных относительно опорной траектории. Известно, что если в
шаре Sr(xQ) оператор А ограничен ||Л||<Г|, дифференцируем и его производная
удовлетворяет условию Липшица с постоянной /, оператор А' непрерывно обратим
и существует такое постоянное число т > 0, что (Л')~| < т , то при q = —m2lr\ < 1 и
r' = rnr\£q2 ~l <r итерационные процессы, определяемые уравнениями (4.341) и
*=о
(4.342) и начатые с Xq , сходятся к х*, т.е. хк —» У, хк+1 -хк—>0 при к —> <» и
уравнения (4.341) и (4.342) преобразуются в уравнение
Ах* =0. (4.343)
Для нелинейных уравнений, линеаризованных относительно опорной траектории,
полученные решения не обеспечивают выполнения равенства (4.343). Описанный
подход получил название линеаризация по Ньютону - Канторовичу; он дает
последовательность линеаризованных уравнений. Таким образом, метод Ньютона -
Канторовича позволяет задачу решения нелинейного уравнения представить как задачу
последовательного решения линейных уравнений.
Метод Ньютона - Канторовича может быть применен к различным по структуре
нелинейным уравнениям. Рассмотрим процедуру линеаризации на примере
нелинейного дифференциального уравнения первого порядка, а затем обобщим ее на
уравнения п-го порядка и системы нелинейных дифференциальных уравнений.
Пусть система управления описывается уравнением вида
АО = /WO, у(0,0. *(0) = .т0. (4.344)
Уравнение (4.344) является уравнением самого общего вида, поэтому рассмотрим
применение метода Ньютона - Канторовича именно для него. Полагаем, что функция
f(x,yj) и ее производная по х - непрерывны и ограничены в области
ге[0,оо),хе(-оо,оо).
Рассмотрим два банаховых пространства Х=С'[0,Т] и Z = C[0,T] + £ с нормами
114=^И1+^-
Здесь z(0 = {*(0;*bleZ.
Тогда уравнение (4.344) с учетом начальных условий можно представить в виде
операторного уравнения (4.340)
Ах = 0,
где Ах = АО~ f W0,У(0,0,*(0) = *о •
Для того чтобы воспользоваться методом Ньютона - Канторовича, необходимо
определить А', где А' - производная Фреше оператора А в точке х. Нетрудно
убедиться, что
А\х)и = и'(0 " Л'W0. У(0.0«(0. "(О) = и0 . (4.345)
Таким образом, в соответствии с формулой (4.341) с учетом (4.345) имеем
следующий итерационный процесс:
Глава 4. Нелинейные системы управления 267
4 (о - / (хк (о, у (о, о+*;+i со - /;(** (о, у w, o**+J w - *; со+
+ЛЧ**(О,у(0,0**(0 = 0,
**+i(O) = *>.*= 0,1,2,...,
или
x'M(t) + ak(t)xk+l(t) = dk(t),k =0,1,2,..., (4.346)
где
^0 =-/,'(** (0, у(0,0,
<** (0 = /(** (0, у (О, О - ГЛч (0, у (О, О** (О,
* =0,1,2,....
Уравнение (4.346) является линеаризованным уравнением относительно решения
хк (0 . Оно позволяет найти решение хк+1 (t), которое является более точным
решением исходного нелинейного уравнения (4.344), чем xk(t). Уравнение (4.346)
является линейным по отношению к решению ^+1(0 , т.е. к выходному сигналу системы
управления, но нелинейным по отношению к у(0 - входному воздействию. Если
y(t) входит аддитивно в правую часть нелинейного уравнения, т.е. система
управления описывается уравнением
x'(t) = f(x(t),t) + b(t)y(t), (4.347)
х(0) = л0,
то последовательность линеаризованных уравнений, имеющая вид
х'ы (0 + ** (*)хм (0 = dk (0 + Ь(г)у(О, (4.348)
W0) = *b,*=0fl,2,...,
где
я*(о=-/;и*(о,о,
dk (О = -f'x{xk (0,0хк (/) + /(дс4 (О, О,
будет линейной и по отношению к y(t).
Условия сходимости, определенные для операторного уравнения, применительно
к дифференциальному уравнению (4.344) будут выглядеть следующим образом.
Условию ||Ахо|<Т1 будет соответствовать неравенство
гпах|ль(0-/(^)(0,У(0,0| + (^о(0-^)<Л- (4.349)
Выполнение условия Липшица для производной оператора А гарантируется
в шаре Sr(*o) с радиусом г пространства X для всех x(t)e X, т.е.
ты\т-Хб(0\ + тах\х\0-ъ(0\<г9 (4.350)
[ОТ]1 ' [0,7-1
в случае, если для всех u(t) и v(0 из этого шара выполняется неравенство
|/>(О,у(О,О-/>(О,у(О,ОИ/ИО-КО|, (4.351)
поскольку А'(х)и определено формулой (4.345) и
\А'и - A'v\\ = тю|/>(0, у(0,0 " /;(v(0, У(0,0| •
Так как операторному уравнению А\х)и = z соответствует линейное уравнение
и/(0 = Л/(х(0,у(0.0«(0 + ^(0,
и(О) = дго,
268 САУ: математические модели, динамические характеристики. Часть I
то выполнение оценки
|Н|х<т(||4 + ДЬ) (4.352)
для всех x(t)e Sr(xQ) также приводит к оценке И'] ~| ^ ю в шаре Sr(xQ).
Формулы (4.349) - (4.352) определяют смысл переменных r\J9m и позволяют
оценить условия сходимости итерационных процессов (4.346), (4.348) и оценить
погрешность получаемого решения.
Пусть динамика системы управления описывается линейным дифференциальным
уравнением одного из видов:
X(0 = F(X(/),Y(0,0, (4'353)
Х(/) = F(X(r),/) + B(0Y(0, (4.354)
Х(0) = Х0,
где X(f) = [*i(O» — »*n(*)]T - вектор состояния;
Y(O = [?i(O. —»Уда(0]Т - вектор входных воздействий;
F0 = [ЛО,.....Л0]т, В(о = {tyoEfr;
Х(0) = [JCi(O), ... ,*w(0)]T - вектор начальных условий.
Тогда последовательность линеаризованных векторно-матричных
дифференциальных уравнений, полученных методом Ньютона - Канторовича для каждого из
двух типов уравнений, будет иметь следующий вид:
для уравнений (4.353)
Хы (г) = A* (t)XM (0 + D* (0, (4.355)
Х*+1(0) = Х0,*= 0,1,2,...,
где A*(r) = F^(Xt(r),Y(0,0 - якобиан для вектора F(X(f),Y(f),O.
D* (0 = ¥(Хк (О, Y(r), 0 - Fi (X, (0, Y(r), OX, (г).
Соответственно для уравнения (4.354)
x;+1(o=f(x,(o,y(o,0-fx(x.(o,y(o,Ox^o,
Х*+1(0) = Х0,* =0,1,2,...,
где
A*(O = Fi(X,(O,0'
&(t) = F{Xk(t)j)-rx(Xk(t),t)Xk(t).
Условия сходимости для уравнений, записанных в векторно-матричном виде,
аналогичны рассмотренным выше.
Пример 4.11. Задана колебательная система (маятник в вязкой среде), на которую действует
подталкивающая сила переменной величины. Уравнение, описывающее систему, имеет вид
x\t) + 2^(0 + x(t) = sin(x'(r)), 35?)
jc(0) = 0,a/(0) = 1.
Требуется выполнить линеаризацию, определить коэффициенты линеаризации для каждой итерации и
построить переходный процесс на интервале Т = 9 с.
Для значения 4 = 0,9 имеем
x\t) +1,8*'(0 -sin(*'(O)+ x(t) = 0 . (4.358)
Запишем уравнение (4.358) в нормальной форме Коши
Глава 4. Нелинейные системы управления
269
(4.359)
К(0 = *2(0,
\x2(t) = -*,(*) - l,8*2(O + sin^Cr)).
Применяя метод Ньютона- Канторовича, получим следующую систему линеаризованных уравнений
х;+1 (О = А* (г)Х,+1 (0 + D* (г), (4.360)
где
A*(0 = [f° f°V(O-P!W|.
[ak2l(t) ak2(t)\ [dk(t)\
(4.361)
(4.362)
4(0 = 0; 4(0 = 1;
4(0 = -1; ak22(t) = -1,8 + cos(jc*(0);
4* (0 = 0;
dk(t) = sin(xk(t))-xk2(t)cos(xk(t)).
Учитывая структуру матрицы А* (0 и вид коэффициентов а,*(О, /,У = 1,2; dk{t\ / = 1,2 , систему
уравнений (4.360) можно вновь записать в скалярной форме в виде одного линейного дифференциального
уравнения с переменными коэффициентами
x'(t) + ak(t)x'(t) + x(t) = dk(t\ * = 0,1,2,..., (4.363)
где
AO = -fl22(') = l,8-cos(^(0),
J*(0 = sin(4(0)-^(0cos(^(0).
Коэффициенты ak(t) и dk(t) зависят от решений, полученных на предыдущем шаге итерационного
процесса.
Коэффициенты а*(0 и dk(t) удобно аппроксимировать полиномами 8-й степени
ak(t) = £«,¥.
1=0
(4.364)
(4.365)
^(0 = £^
/=о
Поскольку уравнение (4.357) описывает движение маятника и предполагается, что переходный
процесс будит носить колебательный характер, то в качестве нулевого приближения целесообразно взять
следующие решения:
*0(0 = sin(7tO, *о(О = cos(7tO .
В таблице приведены значения коэффициентов полиномов (4.364) и (4.365) в зависимости от номера
итерации.
Значения коэффициентов полиномов (4.364) и
в зависимости от номера итерации
Таблица 4.2
(4.365)
К
0
1
2
3
4
К
0
1
2
3
4
4
-0,7860
-1,2574
-1,2557
-1,2556
- 1,2556
4
-0,0101
0,3121
0,3081
0,3081
0,3081
ак
- 0,3692
0,6138
0,7236
0,7234
0,7234
di
0,1738
-0,8747
-0,9315
-0,9318
-0,9318
а\
0,9068
0,3144
0,0097
0,0107
0,0107
4
-0,4703
1,0124
1,1844
1,1852
1,1852
-1,0230
-0,9835
-0,6466
-0,6479
-0,6479
4
0,5369
-0,6320
-0,8278
-0,8287
-0,8287
«i
0,6392
0,7109
0,5121
0,5130
0,5130
4
-0,3320
0,2290
0,3476
0,3481
0,3481
-0,2416
0,2635
-0,1934
-0,1937
-0,1937
4
0,1237
-0,0486
-0,0915
-0,0917
-0,0917
0,0575
0,0579
0,0424
0,0425
0,0425
4
-0,0291
0,0056
0,0154
0,0154
0,0154
ак
-0,0087
-0,0079
-0,0057
-0,0057
-0,0057
4
0,0043
-0,0002
-0,0016
-0,0016
-0,0016
4
0,0008
0,0007
0,0005
0,0005
0,0005
4
-0,0004
0,0000
0,0001
0,0001
0,0001
270 САУ: математические модели, динамические характеристики. Часть I
Как видно из таблицы, значения коэффициентов для третьей и четвертой итерации не отличаются.
На рис. 4.28 приведены графики переходного процесса для различных итераций.
1
Рис. 4.28. Графики переходного процесса для различных итераций
и точное решение уравнения (4.357)
Из рисунка (рис. 4.28) следует, что вторая, третья и последующие итерации практически совпали с
точным решением, полученным численным методом.
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 271
ГЛАВА 5. ЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ: СТАТИСТИЧЕСКИЙ АНАЛИЗ
И ОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ
Системы автоматического управления, как правило, работают в условиях помех.
В связи с этим для анализа и синтеза САУ в настоящее время широко привлекаются
вероятностные, или статистические методы.
Начиная с основополагающих работ А.Я. Хинчина в области теории случайных
процессов и работ А. Н. Колмогорова и Н. Винера, посвященных решению проблемы
фильтрации в классе линейных систем, статистическая динамика систем
автоматического управления получила дальнейшее развитие в многочисленных исследованиях
отечественных и зарубежных ученых [6, 8, 59, 64, 65, 66, 79, 84, 85, 87, 92, 93, 109,
114, 116, 117, 121, 123, 126, 133, 144, 145, 149, 151, 154, 157, 163, 171, 172, 174, 178 и
др.]. Основная роль в развитии статистических методов исследования и
проектирования САУ принадлежит B.C. Пугачеву и В.В. Солодовникову, в работах которых
получила развитие теория систем, работающих в условиях помех, и рассмотрены пути
к ее практическим приложениям.
Ценные результаты, связанные со статистическими методами расчета САУ,
получены в работах В.В. Гнеденко, Л. Заде и Дж. Рагоцини, A.M. Пелегрена, Р. Калмана
и Р. Бьюси и др.
5.1. ПРИМЕРЫ СИСТЕМ, РАБОТАЮЩИХ
ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
Пневмосистема с емкостью постоянного давления. На рис. 5.1 представлена
принципиальная схема системы. Кратко опишем ее работу.
Давление в ресивере изменяется в зависимости от положения дроссельной
заслонки, интенсивности потребления воздуха и параметров системы (размер емкости,
протяженность линии раздачи воздуха и др.). Изменяющееся во времени потребление
воздуха из ресивера вызывает отклонение давления от заданного, определяемого за-
датчиком - пружиной чувствительного элемента 4. Чем больше жесткость этой
пружины, тем выше регулируемое давление.
В качестве чувствительного элемента используется мембрана датчика давления 2,
на которую сверху действует сила, пропорциональная давлению воздуха в емкости, а
снизу - восстанавливающая сила пружины. Нарушение равновесия сил, вызываемое
изменением давления, приводит к прогибу мембраны: вверх - при уменьшении и
вниз - при росте давления.
Пружина 4 нижним упором связана со струйной трубкой 5, положение которой
определяется натяжением пружины 4. К струйной трубке через линию 3 под
давлением подводится масло. Струя масла в положении равновесия создает одинаковое
давление в верхней и нижней полостях сервомотора 10, и регулирующий орган -
дроссельная заслонка 12 - остается неподвижной. При смещении струйной трубки от
положения равновесия давления в полостях сервомотора будут различными: в
полости, к которой трубка повернется, - давление возрастет, а в противоположной -
уменьшится.
272
Анализ и статистическая динамика САУ. Часть I
1111
12
<ю
Рис. 5.1. Принципиальная схема системы автоматического регулирования давления
непрямого действия с жесткой обратной связью:
1 - ресивер; 2 - чувствительный элемент давления', 3 - патрубок подвода масла к струйной трубке сер-
вомотора\ 4 — пружина чувствительного элемента', 5 - струйная трубка; 6 - пружина жесткой
обратной связи; 7 - подвижная опора пружины; 8 —рычаг жесткой обратной связи; 9 - шток сервомотора;
10- сервомотор; 11 - дроссельная заслонка; 12 — подводящий патрубок; 13 - патрубок расхода
(подачи воздуха потребителю)
Поршень под воздействием разности давлений будет перемещаться в
направлении, противоположном перемещению струйной трубки, и увеличит проходное
сечение подводящего патрубка 12. Давление в ресивере будет увеличиваться. Роль
жесткой отрицательной обратной связи выполняет рычаг 8, вращающийся вокруг центра
О и воздействующий посредством шарнира на подвижную опору пружины 6. При
этом усилие пружины 6 на струйную трубку уменьшится и скорость ее перемещения
будет меньше.
Положение регулирующего органа 11 будет определяться потреблением воздуха.
При максимальном расходе через патрубок 12 дроссельная заслонка полностью
открыта, при минимальном - частично открыта или закрыта полностью.
Следовательно, положение поршня сервомотора будет определяться потреблением воздуха. В то
же время положение струйной трубки. 5 в состоянии равновесия всегда одинаково.
Это возможно только при различных усилиях на мембрану чувствительного элемен-
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация
273
та, зависящих от давления воздуха в ресивере; это определяет степень
неравномерности регулятора Р = P(Q).
А теперь обратимся к факторам, которые определяют необходимость
исследования этой системы с использованием аппарата случайных функций.
В рассматриваемой системе задающим воздействием служит постоянный сигнал,
соответствующий номинальному расходу воздуха, а возмущающим - непрерывные
колебания <2(0> создаваемые подключением или отключением потребителей. Эти
колебания зависят только от потребителей и заранее не могут быть предугаданы.
Система регулирования частоты вращения автономного генератора
переменного тока. На рис. 5.2 приведена простейшая схема системы регулирования
частоты вращения автономного генератора переменного тока, используемого для
электроснабжения отдаленных малоосвоенных районов.
Рис. 5.2. Принципиальная схема системы регулирования частоты вращения .
автономного генератора переменного тока:
У - пружина\ 2 - чувствительный элемент', 3 -рычаг\ 4 - золотник; 5 — втулка; 6 - поршень;
7 - сервомотор; 8 -регулятор; 9 —рычаг обратной связи; 10 -ротор генератора; 11 — паровая турбина
Любое изменение нагрузки на генератор приводит к изменению момента
сопротивления ротора генератора 10, а значит, и частоты вращения жестко связанного с
19 3ак. 232
274 Анализ и статистическая динамика САУ. Часть I
ним вала привода, в данном случае, паровой турбины 11. Изменение регулируемой
величины - частоты вращения - на Асо приведет к изменению положения муфты
чувствительного элемента 2 на величину Az за счет нарушения равновесия
регулирующей силы (центробежная сила грузов) и восстанавливающих сил (вес грузов,
натяжение пружины). Поворот жестко связанного рычага 3 вокруг оси О вызовет
перемещение поршней золотника 4. В состоянии равновесия отверстия в промежуточной
втулке 5 всегда перекрываются поясками поршней золотника. Давление в верхней и
нижней полостях сервомотора 7 одинаково и регулирующий орган неподвижен. В
зависимости от направления движения золотника будут открываться отверстия для
поступления масла от источника постоянного давления в одну из полостей сервомотора
7, при этом из другой полости будет открываться слив масла. Усилие, возникшее за
счет разности давлений масла в полостях, перемещает поршень 6 и связанный с ним
регулятор 8 подачи рабочего тела в турбину. Изменение положения регулирующего
органа будет происходить до тех пор, пока не будет достигнуто равновесие
крутящего момента турбины и момента сопротивления генератора при требуемой частоте
вращения.
Обратная связь осуществляется с помощью рычага обратной связи 9,
перемещающего промежуточную втулку 5 золотника. При этом втулка всегда движется в
сторону, противоположную перемещению золотника, тем самым уменьшая
проходные сечения подвода и слива масла. Это улучшает качество переходного процесса.
Функции задатчика частоты вращения выполняет пружина 1, обеспечивающая
одинаковое положение муфты регулятора при разных частотах вращения.
Рассмотренный регулятор является статическим, т.к. различному пропуску пара (нагрузке),
определяющей положение поршня сервомотора, соответствуют различные
положения промежуточной втулки и поршней золотника, в состоянии равновесия всегда
перекрывающих впускные и выпускные отверстия для масла.
Интенсивность потребления электроэнергии определяется временем года и суток и,
кроме того, в случайные моменты времени потребители могут изменять нагрузку и
даже включаться в сеть или отключаться из работы. Сказанное позволяет сделать
вывод, что процесс потребления энергии во времени носит заранее непредсказуемый,
случайный характер, и таким образом, система регулирования частоты вращения
автономного генератора подвергается воздействию случайных сигналов. Исследование
этого класса систем может проводиться с использованием аппарата случайных функций.
Теплоэлектростанция блочного типа. На рис. 5.3 представлена упрощенная
принципиальная схема теплоэлектростанции блочного типа, состоящая из
прямоточного котла и паровой турбины с промежуточным перегревом пара.
Работа схемы в упрощенном виде может быть представлена так. Изменение
электрической нагрузки приводит к изменению режима работы турбины,
осуществляемого путем открытия или прикрытия регулирующего органа, определяющего расход
пара через турбину (£/4(0)- Давление и температура пара после пароперегревателя
регулируются путем впрыска питательной воды в редукционно-охладительную
установку (Ui(t)) и изменением режима работы питательного насоса (УгСО)-
Регулирование производительности прямоточного котла производится изменением подачи
топлива к форсункам (6^2(0)» качество распыления которого зависит от параметров пара
перед форсунками (Ui(t)). Контуры регулирования давления и температуры пара за
пароперегревателем и производительности котла являются взаимосвязанными.
Температура пара после вторичного перегрева (U4(t)) также определяется режимом
работы всего агрегата и регулируется впрыском питательной воды.
276
Анализ и статистическая динамика САУ. Часть I
На рис. 5.4 представлены записи основных характеристик прямоточно-котельной
системы мощностью 500 МВт, работающей на сверхкритических параметрах [141]:
Y{(t) - сигнал нагрузки (СН),
Уг(О - давление пара в котле (ДПК),
У3(0 - температура пара в пароперегревателе (ТПП),
Y4(t) - температура пара после вторичного перегрева (ТПР),
U\(i) - поток пара у форсунки (ППФ),
[/3(0 - расход воздуха для горения топлива (ОВК).
Из рассмотрения рис. 5.4 легко сделать вывод, что сигналы теплоэлектростанции
блочного типа относятся к классу случайных и этот факт необходимо учитывать при
расчете и проектировании систем теплоэлектростанции.
Я
и
0 100 200 300 400 500 600 700 800 900
« J
ф$^^1щЩ^^Мч
i | |_
0 100 200 300 400 500 600 700 800 900
С ь
'•VvvVwv^ySva^/^
0 100 200 300 400 500 600 700 800 900
е
с
0 100 200 300 400 500 600 700 800 900
_1 | I | I
i i ^
0 100 200 300 400 500 600 700 800 900
i I
t
0 100 200 300 400 500 600 700 800 900
Рис. 5.4. Записи основных характеристик прямоточно-котельной системы мощностью 500 МВт
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 277
Транспортные системы. Рассмотрим проблему воздействия вибраций на
организм человека. В частности, эта проблема имеет место в транспортных системах,
например, при проектировании автомобилей, самолетов, вертолетов, железнодорожных
и водных средств.
Если в качестве транспортного средства рассмотреть автомобиль, а источником
вибраций - двигатель, то соответствующая функциональная схема может быть
представлена в виде, показанном на рис. 5.5.
Двигатель
автомобиля
ПО
Система, входом которой
являются вибрации
двигателя, а выходом -
1/*Г\ТТ£*^ЯТЛ"1/Ю' ТЛ1Л£*Г*ТТЯ ППТТТ/ТТРТТО'
килеисшия кресла водителя
X(t)
Нолителт»
Реакция
водителя
Рис. 5.5. Функциональная схема системы
С целью изучения этой проблемы проводился соответствующий эксперимент
[141] (рис. 5.6).
Рис. 5.6. Нерегулярные вибрации легкового автомобиля (постоянная скорость 20 км/ч)
На схемах Y(t) - сигнал, являющийся вибрацией двигателя.
На рис. 5.7 представлены графики ускорений вертикальной вибрации двигателя и
кресла в процессе движения легкового автомобиля. Аналогичная ситуация имеет
место при управлении самолетом, вертолетом и другими транспортными средствами.
Очевидно, Y(t) и X(i) - случайные сигналы.
Реакция водителя или пилота на вибрационное воздействие X{t) определяется
индивидуальными особенностями организма, частотой и амплитудой вибрационных
колебаний X(t). Как отмечается в [44], наличие процесса X(t) может вызывать не
только тошноту, повышенное сердцебиение, нарушение зрения, но и кровотечение в
легких и в желудочно-кишечном тракте. Внешние колебания в диапазоне частот
15 - 30 Гц оказывают влияние на сосудистый тонус организма и двигательный
анализатор [44].
Поэтому установлены некоторые количественные критерии допустимости
различных режимов установившихся вибраций конструкции для экипажей, например,
летательных аппаратов. Практика показывает, что работоспособность пилотов
снижается уже при среднеквадратичном значении случайной виброперегрузки выше 0,2.
Затрудняется наблюдение за приборами. Вибрация со среднеквадратичным уровнем
перегрузки, превышающим 0,5, заставляет пилота изменять режим движения (высоту
и скорость полета) [44].
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 279
Рассматривая подобного вида системы, легко заключить, что их исследование
можно проводить только с привлечением аппарата случайных функций, поскольку
Y(t) и X(i) (рис. 5.7) не относится к классу детерминированных функций.
К основным силовым факторам относятся вибрационные воздействия на изделия
при их транспортировке по железной дороге, автомобильными средствами, а также с
помощью водного транспорта. Как показали многочисленные исследования,
вибрационные нагружения на изделия представляют собой случайные функции [141].
Поэтому изучение транспортных систем следует проводить в классе систем,
подверженных не детерминированным, а случайным факторам (рис. 5.8).
Полотно
дороги
Y(t)
Система: шина, система
амортизации, автомобиль
X(t)
Ичлелие
подвергаемое
воздействию
виорации
Рис. 5.8. Система дорога - шина - автомобиль
Обработка металлов шлифованием. На рис. 5.9 представлены результаты
выборочных измерений профиля шлифовальной поверхности [141].
X
-50
250
500
750
1000
Рис. 5.9. Выборочные измерения профиля шлифовальной поверхности
Очевидно, сигнал X относится к классу случайных. Актуальной является задача
не только анализа систем управления процессом шлифования, но и синтеза САУ,
обеспечивающих такой режим, при котором вероятность выхода размеров из поля
допуска (т.е. брака) была бы минимальной. Эту задачу относят к классу задач,
изучающих исследование и синтез систем при воздействии случайных сигналов.
Следящие системы радиотелескопов. В [72] описана следящая система
радиотелескопа, предназначенная для изучения процессов, происходящих во внеземном
пространстве. С помощью этих телескопов проводится исследование объектов,
удаленных от Земли на огромные расстояния, например, слежение за звездами во
внеземном пространстве.
Поскольку поверхностные размеры элементов конструкции радиотелескопа
огромны, на положение его зеркала в пространстве значительное влияние оказывают
всевозможные атмосферные возмущения, а особенно температурные и ветровые.
280
Анализ и статистическая динамика САУ. Часть I
Температурные возмущения возникают из-за разности температур между
элементами конструкции радиотелескопа и могут привести к весьма значительным ошибкам
в положении его осей.
Ветровые возмущения действуют еще более интенсивно. При ветре со скоростью
50 км/ч отклонение осей из-за упругости опор может достигать 18 - 25". Поэтому
следящая система предназначена, главным образом, для компенсации указанных
возмущений.
Следящая система радиотелескопа относится к классу систем, в которых имеют
место сигналы, которые носят случайный, не предсказуемый точно характер.
Система командного телеуправления и самонаведения ракет [74].
Функциональные схемы систем самонаведения и командного телеуправления представлены
на рис. 5.10 и 5.11. Управляющим (входным) сигналом является закон изменения во
времени угла Y(t) между некоторой осью и направлением на цель (рис. 5.12). Ввиду
того что скорость цели, ее высота, ракурс, маневр и т.п. являются случайными, Y(t)
будет случайной функцией времени.
Отраженный от цели сигнал радиолокационной станции (РЛС) модулируется не
только частотой вращения луча, но и флюктуацией коэффициента отражения цели.
Этот эффект проявляется как для наземных целей, так и для воздушных целей.
Эффект флюктуационных помех при облучении РЛС наземных целей создает фон
земли и посторонних предметов. Земную поверхность можно рассматривать как
совокупность хаотически расположенных элементарных отражателей. Флюктуации
отраженных сигналов возникают в том случае, если имеют место колебания
элементарных отражателей или перемещения ракеты или цели. Сигналы, отраженные от
кораблей, зависят от состояния моря. Сигналы, отраженные от лесной местности,
зависят от интенсивности ветра.
Флюктуации сигналов, отраженных от земных ориентиров, зависят от расстояния
до цели, размеров, формы и типа цели, высоты, скорости и курсового угла носителя,
облучающего цель. При этом для различных условий полета ракеты и носителя
ширина спектра флюктуации может меняться в десятки и сотни раз.
Флюктуации сигналов, отраженных от малоразмерных наземных целей (танк,
орудие и др.) могут быть настолько большими, что наведение ракет на подобные
цели будет сопровождаться большими ошибками, а иногда может привести и к
потери цели. Флюктуации коэффициента отражения воздушных целей также
оказывают существенное влияние на точность наведения.
Головка -
самонаведения
У
Устройство
формирования7
команд
\/ППЯКЛРНИЯ
Автопилот
1
К рулям
Рис. 5.10. Функциональная схема системы самонаведения
282
Анализ и статистическая динамика САУ. Часть I
Цель
по
Рис. 5.12. Входной сигнал системы наведения
На рис. 5.13 приведена диаграмма мощности отраженного от самолета сигнала в
горизонтальной плоскости. Многолепестковый характер диаграммы направленности
приводит к тому, что сигналы, отраженные от летящего самолета, будут случайными
функциями времени.
35 дб
Рис. 5.13. Диаграмма мощности отраженного от самолета сигнала в горизонтальной плоскости
Так как ракета и воздушная цель совершают в полете колебания, зависящие от их
скорости полета, высоты, а также от интенсивности ветра, то, строго говоря,
характеристики помех, вызванных флюктуациями коэффициента отражения цели, будут
зависеть от времени, т.е. соответствующие случайные сигналы будут принадлежать к
так называемым случайным нестационарным процессам.
На рис. 5.14 приведена осциллограмма сигнала на выходе приемного устройства
РЛС автоматического слежения за целью. По оси ординат отложена величина
глубины модуляции и эквивалентное отклонение цели в тысячных долях радиана.
Выше были приведены примеры технических систем, подверженных влиянию
случайных факторов. В экономических системах случайная составляющая
вызывается, например, непредсказуемым способом.
К рассматриваемому классу систем относятся биологические системы: система
управления кровообращением, система управления величиной зрачка глаза и др.
284
Анализ и статистическая динамика САУ. Часть I
5.2. СЛУЧАЙНАЯ ФУНКЦИЯ И ЕЕ ВЕРОЯТНОСТНОЕ ОПИСАНИЕ
5.2.1. Одномерные законы распределения, математическое ожидание
и дисперсия случайной функции х(т)
Рассмотрим методы описания случайных сигналов.
Функция, которая при каждом данном значении независимой переменной
является случайной величиной, называется случайной функцией (СФ). Случайные функции,
для которых независимой переменной является время г, называют стохастическими
процессами (СП).
Случайную функцию, зарегистрированную в той или иной форме по результатам
опыта, называют реализацией случайной функции (рис. 5.15): хх (0,^(0 -
реализации случайной функции X(t).
Случайную функцию X(t) можно рассматривать как систему случайных величин
(случайной величиной (СВ) будем называть такую величину, значение которой в
результате одного и того же эксперимента (эксперимента^ проводимого в
одинаковых условиях) может быть различным и заранее неизвестно).
Системой п случайных величин называется совокупность случайных величин
Х{,Х2,..., Хп, совместно рассматриваемых как единое целое (рис. 5.16).
Пример - координаты какой-либо точки, случайным образом расположенной
в пространстве (п = 3).
x(t) f
Рис. 5.15. Случайная функция X(t) (x{(t),x2(t) - реализации СФ X(t))
Ясно, что при рассмотрении лишь одного сечения случайного процесса мы имеем
дело с одной непрерывной случайной величиной X (непрерывной случайной
величиной называется такая величина, возможные значения которой непрерывно
заполняют некоторый интервал (конечный или бесконечный)).
Изложим методы вероятностного описания одной случайной величины X.
Интегральным законом распределения. (ИЗР) случайной величины называется
функция вида
Fx(x) = P[X<x],
т.е. вероятность того, что возможные значения случайной величины X будут
меньше некоторого текущего значения х (рис. 5.17).
Если рассматривать СВ X как случайную точку X оси Ох (см. рис. 5.17), которая в
результате опыта может занять то или иное положение в заданном промежутке, то
Fx (х) есть вероятность того, что случайная точка X в результате опыта попадает
левее точки х, где х - текущее значение.
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 285
х№
*»(0
Рис. 5.16. Рассмотрение СФ X(t) как системы случайных величин
(xl(t),x2(t)y...,xn(t)) -реализацииСФ X(t)
Функция Fx (jc) полностью характеризует СВ X с вероятностной точки зрения.
Очевидны следующие свойства интегрального закона распределения [87]:
1) Fx (х) - является функцией неубывающей;
2) Fx(-oo) = 0;Fx(+~) = l;
3) Р[а < X < Р] = Fx (P)-Fx (a) - вероятность попадания случайной величины
X в интервал [а, Р];
4) функция распределения Fx (x) есть неотрицательная функция, заключенная
между нулем и единицей.
2ЪЬ
Анализ и статистическая динамика САУ. Часть I
ИЗР имеет недостаток, заключающийся в том, что по нему трудно судить о
характере распределения СВ X в небольшой окрестности той или иной точки
числовой оси.
Более наглядное представление о характере распределения непрерывной СВ X в
окрестностях различных точек дается функцией, которая называется плотностью
распределения вероятности, или дифференциальным законом распределения (ДЗР)Ь
Вероятность попадания случайной величины X в заданный интервал (jc,jc+Ax)
определяется формулой (рис. 5.18)
Р(х <X<x + bx)=Fx (x + bx)-Fx (x).
Составим отношение этой вероятности к длине участка Ах :
Fx(x + bx)-Fx(x) (51)
Ах
- средняя вероятность, которая приходится на единицу длины этого участка.
1
0
X
Рис 5.17. К пояснению понятия ЮР
/хЮ
ds = fx(x)dx
х x+dx
Рис. 5.18. определению дифференциального закона распределения
Считая функцию Fx (x) дифференцируемой, перейдем в равенстве (5.1) к
пределу при Ах—»0
Fx(x+&x)-Fx(x)_ ( dFx(x)_
Дифференциальный закон распределения обладает следующими свойствами:
п f (x) dFx{x)-
оо
2) Fx(x)=jfx(x)dx;
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 287
р
3) Fx(fi)-Fx(a) = ]fx(x)dx = Fx(x%=P[a*XSfi\i
ос
- вероятность попадания СВ X на участок [а, Р];
4) ] fx(x)ix = Fx(x)\lo = Fx(^o)-Fx(-oo) = l;
—оо
5) fx[x)>0 (плотность распределения не отрицательна, т.к.. Fx(x) есть
производная от неубывающей функции).
Законы распределения (ИЗР и ДЗР) являются полными характеристиками
случайной величины X.
В некоторых случаях нет необходимости знать законы распределения, а
достаточно ограничиться лишь некоторыми параметрами, определяющими закон
распределения. К таким параметрам относятся математическое ожидание и дисперсия
непрерывной случайной величины.
Основное их назначение - в сжатой форме выразить наиболее существенные
особенности того или иного распределения. С помощью этих параметров (числовых
характеристик) и операций с ними удается в ряде случаев решать широкий круг
вероятностных задач до конца без использования ИЗР и ДЗР.
Математическим ожиданием (МО) неслучайной функции \|/(Х) СВ Xназывают
интеграл от произведения \|/(Х) на ДЗР fx(x) СВ X (предполагается, что функция
\|/(Х) такая, что интеграл существует):
оо
M[v(X)]=\v(x)fx{x)dx. (5.2)
Начальным моментом k-го порядка СВ X называется МО неслучайной функции
у(Х) = Хк
оо
m[xk] = ak = jxkfx{x)dx. (5.3)
Из всех начальных моментов наиболее часто применяются начальные моменты
первого и второго порядка.
Математическим ожиданием СВ X называется число, определяемое (5.2) при
\|/(Х) = Х:
М[Х] = тх = \xfx\x)dx (5.4)
- некоторое среднее значение, около которого группируются возможные значения
СВХ.
В соответствии с формулой (5.4) М[Х\ есть результат вероятностного осреднения
функции \|/(Х) = X , т.е. осреднение с весом, равным ДЗР.
Физическое содержание понятия МО СВ X наиболее наглядно выявляется, если
рассматривать дискретную случайную величину X.
Дискретной случайной величиной называется такая величина, которая при
проведении опыта принимает некоторые заранее неизвестные дискретные значения.
Пусть при проведении экспериментов случайная величина X приняла значения
*i- тх раз;
288 Анализ и статистическая динамика САУ. Часть I
х2 - т2 раз;
х1 - т{ раз.
Найдем среднее значение случайной величины X:
-Л-Л — l—1- = Хг—- + X,—+ ... + JC/ —L =
n n n n
I
= XJI+X2/2+... + XJ* = £*v/v\
v=l
где /v - относительная частота появления случайной величины X со значением л\,.
При проведении большего числа опытов относительная частота стремится к
соответствующей вероятности. Формула для математического ожидания
принимает вид
M[X] = 2>V/V, (5.5)
v=l
где /v - вероятность появления л\,.
Для непрерывной СВ Xравенство (5.5) переходит в (5.4).
Основные свойства математического ожидания случайной величины:
• математическое ожидание неслучайной величины С равняется самой
неслучайной величине С;
• постоянный множитель можно вынести за знак математического ожидания
М[СХ] = СМ[Х]\
• математическое ожидание произведения независимых случайных величин X и
Y определяется формулой
М[ХК] = М[Х]М[У];
• математическое ожидание суммы двух случайных величин определяется
формулой
М[Х+У] = М[Х] + М[Г].
Легко заметить, что математическое ожидание является далеко не полной
статистической характеристикой случайной величины'. Рассмотрим рис. 5.19. В первом
случае случайная величина X может принимать значения X, находящиеся в интервале
At. Во втором случае случайная величина С принимает значения в промежутке А2.
Легко видеть, что математические ожидания случайных величин X и С одинаковы, но
степень разброса относительно математического ожидания у них различна.
Следовательно, с целью более полного вероятностного описания СВ X
целесообразно ввести характеристику, определяющую степень разброса случайной величины
относительно математического ожидания.
Центральным моментом k-го порядка случайной величины X называется
интеграл вида
&-M[(X-M[X])k] = M[(X-mx)k]=](x-mxffx(x)dx.
Наиболее часто находит применение второй центральный момент D[X\, который
характеризует возможные отклонения СВ, т.е. возможный разброс значений СВ
относительно ее МО. Второй центральной момент обычно обозначают Dxx и называют
дисперсией, указывая тем самым, что DXx характеризует возможное рассеивание СВ
X относительно М [X].
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 289
х>У i
;
f
• ту— t
Рис. 5.19. Случайные величины X и С, у которых математические ожидания одинаковы,
а степени разброса относительно МО различны
Таким образом,
Dxx=M[(X-mxfy](x-mxffx(x)dx,
(5.6)
или
J [х2 -2тх х + т\ )fx(x)dx= J x2 fx (x)dx-2mx J xfx (x)dx-
Гоо I2
+m\ j fx{x)dx = a* -m2 = $ x2 fx(x)dx-\ jxfx(x)dx\ .
(5.7)
Дисперсия Dxx имеет размерность квадрата СВ. Во многих случаях вместо
дисперсии Dxx используют положительное значение квадратного корня из нее yJD^ ,
которое имеет размерность самой случайной величины.
Величину yJDxx называют средним квадратическим отклонением (СКО) СВ X
и обозначают ах , т.е.
Gx =y^xx •
МО и СКО или Dxx являются наиболее часто применяемыми числовыми
характеристиками СВ.
Эти числовые характеристики полностью определяют один из наиболее важных и
распространенных законов распределения СВ, а именно нормальный закон
распределения (закон Гаусса), определяемый формулой
оХу]2п
(5.8)
где сх = yjDja - среднеквадратическое отклонение.
Можно показать, что если некоторая случайная величина X является суммой
независимых случайных величин, каждая из которых имеет произвольный закон
распределения, то случайная величина X имеет нормальный закон распределения.
Основные свойства нормального закона распределения:
290
Анализ и статистическая динамика САУ. Часть I
1) максимальное значение нормального закона распределения определяется
выражением \/ах yjln при х = тх ;
2) нормальный закон распределения симметричен относительно тх\
3) изменение математического ожидания приводит лишь к смещению закона
распределения, однако форма не меняется. Дисперсия же при заданном
математическом ожидании изменяет форму закона распределения.
1 П
1,1/
0
Gx\
Gxi < Ъхг
X
fxix) i
Gx\ < GX2
Рис. 5.20. Кривые ИЗР и ДЗР (нормальный закон распределения)
Представим fx(x) в виде (рис. 5.21).
_х тх-2отх-о тх тх+О тх+2о х
Рис. 5.21. Кривая fx(x) нормального процесса
Из рис. 5.21, а также из зависимости (5.8) легко сделать вывод: СВ X
предпочтительнее принимает значения, близкие к тх. Вероятность нахождения СВ X в полосе
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 291
±ах с центром тх составляет 68 %, а в полосе ±2ах - 95 %. Если же рассматривать
полосу ±3сх с центром тх, то вероятность попадания СВ X в эту полосу равна
0.997. Поэтому величину Ъох часто используют в практических расчетах в качестве
верхней границы отклонения СВ X от ее математического ожидания.
Теперь соотнесем приведенные выше рассуждения к случайным функциям. Мы
рассмотрели одно сечение СФ и задача свелась к анализу одной СВ, ее
вероятностному описанию. Но статистические характеристики каждого сечения СФ зависят от
времени t, поэтому как законы распределения, так и числовые характеристики СФ
будут зависеть от параметра t, т.е.
Fx (x,t) - интегральный закон распределения СФ *(*),
fx (*>0 - дифференциальный закон распределения СФ *(*),
тх (*)>£>хх (t),ox(t) - числовые характеристики СФ x(t).
Приведем соответствующие пояснения и определения.
Математическое ожидание СФ в области ее существования представляет
собой совокупность математических ожиданий СВ, равных СФ при всех возможных
текущих значениях ее аргумента t (рис. 5.22).
>>mx(0 + 3ax(0
Y(t)
Рис. 5.22. Графики, иллюстрирующие отклонение СФ X(t) и Y(t) от их МО
(верхние границы отклонений приблизительно равны Зох (/)
при нормальном законе распределения)
Сечения СФ при t = t\, t = ^,... представляют собой СВ Х\9 Х2, ..., каждая из
которых имеет свой закон распределения FX/ (*,,*,) и fXj (*,-,*,•), в связи с этим ИЗР и
ДЗР СФ запишутся так: Fx(x,t) nfx(xyt). На рис. 5.22 показано МО СФ X(t) как
результат вероятностного осреднения.
МО неслучайной величины равно самой неслучайной величине. Поэтому при
значениях аргумента /, для которых СФ является неслучайной величиной, совокупность
этих неслучайных величин образует МО случайной функции.
292
Анализ и статистическая динамика САУ. Часть I
В общем случае МО СФ X(t) зависит от аргумента t и обозначается через тЖ):
оо
mx(t) = M[X(t)]=lxfx(x,t)dx.
Математическое ожидание - это такая неслучайная функция, около которой
группируются все реализации данного случайного процесса и которая полностью
определяется одномерным ДЗР.
Дисперсия СФ в области ее существования представляет собой совокупность
дисперсий случайных величин, равных СФ при всех возможных текущих значениях ее
аргумента,
В общем случае дисперсия СФ X(t) зависит от аргумента t и поэтому обозначается
через Dxxit):
Dxx (O = Af [{X(t)-mx (0)2]= J {x-mx (t)f fx (xj)dx.
Дисперсия представляет собой среднее значение квадрата разности между СФ
и ее МО и характеризует интенсивность отклонений относительно среднего
значения; определяется одномерным ДЗР.
Вывод состоит в следующем: математическое ожидание СФ X(t) представляет
собой некоторую среднюю кривую тх (t), около которой располагаются все
возможные отдельные реализации X (t), а дисперсия Dxx(t) при ox(t) характеризует
рассеяние отдельных возможных реализаций около тх (г) (при нормальном законе
распределения границы отклонений реализаций дгДг) от МО СФ X(t) приблизительно
равны 3ox(t) (рис. 5.21)).
На рис. 5.23 и 5.24 приведены различные виды СФ X(t) [87,126].
Y(t) а
ДО
тКО
тЖ)
Рис. 5.23. Примеры реализации различных случайных функций X{t\ Y(t), Zi$\ имеющих
неодинаковые математические ожидания m^t\ m^$\ mz(t)
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация
Рис. 5.24. Примеры реализации различных случайных функций X(t), Y(t), Z(t\
имеющих одинаковые математические ожидания и разные дисперсии:
а -реализации случайных функций X{t), K(r), Z(i) {сплошныелинии) и математические ожидания этих
функций mx(t)f myit) и т&) (пунктирные линии); б - дисперсии D^ (/), Dn (/) и D^ (/)
случайных функций X(t), Y(t), Z(t)
На рис. 5.25 изображены примеры реализаций различных СФ X(t), У(0, Z(0>
имеющих не только одинаковые математические ожидания т*(0» wiy(0 и тЖ)9 но
одну и ту же дисперсию, т.е. D^ (t) = Dyy (t) = D^ (f).
Ш)
mxit)
my(t)
Рис. 5.25. Примеры реализаций случайных функций X(t\ Y(t) и Z(t)9
имеющих одинаковые математические ожидания и одну и ту же дисперсию,
но разные степени изменчивости (неупорядоченности)
294
Анализ и статистическая динамика САУ. Часть I
Как следует из рисунков, СФ X(t), Y(i) и Z(f) хотя и имеют одинаковые МО и одну
и ту же дисперсию £>(*), по характеру своей изменчивости и неупорядоченности (по
спектральному составу, под которым будем понимать модуль преобразования Фурье
от реализаций СФ) весьма сильно друг от друга отличаются.
Это хорошо иллюстрирует то обстоятельство, что в том случае, когда для
описания СФ используются лишь одни ее числовые характеристики, значение МО и
дисперсии СФ может оказаться далеко не достаточным для суждений о степени ее
неупорядоченности и изменчивости (или, что то же самое, о ее спектральном
составе). Если, например, СФ X(t) (рис. 5.25) при некотором значении аргумента t
приняла значение, лежащее выше тх (t), то почти с достоверностью можно утверждать,
что и ближайшее значение реализации X(t) пройдет выше mx(t). Для функции
Y(t) этого может и не быть, учитывая степень ее неупорядоченности. Разница между
X(t) и У(0 проявляется в характере связи между значениями X(t) и Y(t) для
различных аргументов Ц и t2.
Еще в большей степени разница в указанном смысле имеет место между
сигналами X(t) и Z(0.
Для суждений о ней необходимо знать моменты СФ, связывающие величины ее
при нескольких значениях аргумента t. В частности, весьма важную информацию о
степени изменчивости и неупорядоченности СФ можно получить с помощью ее
корреляционной функции.
5.2.2. Двумерные законы распределения и корреляционная функция
случайного процесса x(f)
В предыдущем параграфе все рассуждения построены на использовании
одномерных законов распределения Fx (x,t) nfx(x,t).
Более полными вероятностными характеристиками СФ X(t) являются ее
двухмерные ИЗР и ДЗР, использующие рассмотрение СФ как системы двух случайных
величин Х\ = X(*i) и Хг = X(t2) при произвольно выбранных значениях аргумента t\ и t2.
Важно то, что здесь уже учитывается связь значений, принимаемых СФ X(t\ -
моменты времени t\ и г2 (рис. 5.26).
x{t) ,
I
\
0
\
>
!
i
1 *1 =
t=t.
X(ti)
Mi
щ
x2 = x(t2)
щ
Рис. 5.26. К рассмотрению случайной функции как системы двух случайных величин
Перейдем к более подробному рассмотрению вопроса.
Введем понятия законов распределения системы двух СВ.
Интегральным законом распределения системы двух случайных величин Х\ и Х2
называется функция Fx (^1,^2) > которая выражает вероятность того, что
случайные величины Х\, Х2 будут принимать значения соответственно меньшие некото-
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 295
рых неслучайных величин х[9х2, т.е. вероятность случайного события,
заключающегося в совместном выполнении двух неравенств
Хх<х{, Х2<х2.
Таким образом (рис. 5.27),
М*1.*2) = ^[(*1<*1)И(Х2<*2)].
^Р\.(.х,<х\)я(хг<х\)[
Рис. 5.27. К определению интегрального закона распределения системы двух случайных величин
Основные свойства интегрального закона распределения:
1) Fx(-K»,+oo) = l;
2) Fx(xl,+~) = FXi(xl);
3) Fx(+~,x2) = FX2{x2);
4) M*i>-°°)=0; <5-9)
5) Fx(-~,*2) = 0;
6) O^FX(^^2)<1;
7) Fx (xx, Х2) - функция, не убывающая по своим аргументам.
Рассуждая так же, как и при рассмотрении одномерного закона распределения,
можно ввести понятие двумерного дифференциального закона распределения и
записать его основные свойства (рис. 5.28):
п f (x хч_Э2М*1>*2).
2) /х(^1,^)>0;
оо оо
3) J j fx(xl>x2)dxldx2=l>
4) Fx (xl,x2)= I j fx (xl,x2)dxidx2;
5) Fx(xvoo)=] ]fx(xl,x2)dxldx2, ^^"^ = J fx (*..*2)<**2 =/x, (^.).
oo
296
Анализ и статистическая динамика САУ. Часть I
Мхи х2) I
Рис. 5.28. Поверхность нормального распределения
Таким образом, если известен двумерный закон распределения, то с помощью
последних формул можно получить одномерный закон распределения каждой из
случайных величин, входящих в рассматриваемую систему. На практике широко
распространены случаи, когда случайные величины Х{ и Х2 независимы.
Тогда можно записать
Fx (*i>*2) = Fxx {х\)гхх (*i); fx {x\**i) = fxx (x\)fx2 {хгУ
Рассмотрим некоторые числовые характеристики системы двух случайных
величин. К таким характеристикам относятся начальные и центральные моменты.
Пусть имеется неслучайная функция системы двух случайных величин Х\ и Х2,
которую обозначим через У¥(Х{,Х2).
Операцией МО функции У¥(Х{,Х2) системы двух случайных величин Х\ и Х2
называется двухкратный интеграл от произведения указанной функции на ДЗР
/х(*1>хг)
M[^(X1,X2)]=ff^(X1,X2)/x(xl^2)^l^2.
(5.10)
Воспользовавшись предыдущим определением, введем понятия смешанных
моментов.
Смешанным начальным моментом k-го порядка называется МО при
оо оо
«U = J I $%h (xl,x2)dxidx2=M[x?,x!?],
где к = к{ + к2 .
Широко применяются начальные моменты 1-го порядка, которые приводятся к
математическим ожиданиям случайных величин Х{ и Х2.
Смешанным центральным моментом к-го порядка называется величина
P*i.*2 = J J (*i ~m*.)' (^ "тх2)2 fx {x\**i)<bi<toi-
Отсюда (пусть к\ =2,к2^ 0)
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 297
\2
Р2о = J (*i ~тхх) fxx 0Ол -дисперсияa:l
Аналогично можно найти дисперсию х2.
Пусть к\ = к2 = 1. Тогда
оо оо
Рх„х2 = J J (*i~тх,)(хг~тх2)fx (*i,*2)<V*2 (5.11)
—оо—оо
-момент корреляции, или корреляционный момент двух случайных величин Хх и Х2,
который характеризует статистическую зависимость между указанными
величинами.
Таким образом, из числовых характеристик системы двух случайных величин
наибольшее употребление нашли:
Ytl\
к, = ]Ч/л:,(*« )<**<> ' = 1.2;
—оо
0ед = J (xi -«х, f fx, (*)<***. * = 1.2;
оо оо
Rxtxj = J J (xi-mxt)(xj-mxt)fx (xiiXjjdXidxj, /,; = 1,2.
Ясно, что Rx.x =^x'. дисперсии СВ Dxx. могут рассматриваться как
частные случаи корреляционных моментов, т.е.
DX)Xi =M[(X,-mXi)(X,r-mXi)] = RXiXi, / = 1,2.
Две случайные величины Х\ и Х2 называются коррелированными, если их
корреляционный момент Rx x не равен нулю. Наоборот, две случайные величины Х\ и Х2
называются некоррелированными, если их корреляционный момент равен нулю:
Rxx =0.
Часто вместо корреляционных моментов рассматривают коэффициенты
корреляции, определяемые соотношением
г =r Rxi*2 - R)CxXl - R)CxXl
ххх2 х2хх
4Rxxxx *х2х2 V^W^A a*i G*2
Корреляционный момент, определяемый формулой (5.11), является
характеристикой не только зависимости СВ х{ и Xj, но и их рассеивания [87]. Величина R при
одной и той же степени связи величин х( и Xj будет различной в зависимости от
того, какими будут отклонения этих величин от своих математических ожиданий -
большими или малыми [87].
Коэффициенты же корреляции характеризуют статистическую зависимость в
«чистом» виде.
Коэффициенты корреляции являются безразмерными величинами, поэтому они
удобны в качестве характеристик степени некоррелированности случайных величин.
Отметим одно важное свойство корреляционного момента [87]:
Г*1 *2 I ~ \IRX\ *1 R*2 *2 = 4^Х\ Х1 ^Х2 Х2 f
298 Анализ и статистическая динамика САУ. Часть I
или
\R
ххх.
^ ах, Gx
Это свойство применительно к коэффициенту корреляции rx х записывается так
'Хх*1
<1, или ±гхх <1.
Коэффициент корреляции rx x определяет степень и характер коррелированно-
сти случайных величин Хх и Х2. Если коэффициент корреляции rXj х^ равен нулю, то
случайные величины являются некоррелированными.
Если абсолютное значение коэффициента корреляции равно единице, то
случайные величины Х\ и Х2 являются полностью коррелированными {связаны линейной
зависимостью).
Значение коэффициента корреляции определяет степень коррелированности
случайных величин. Знак коэффициента корреляции определяет характер связанности
случайных величин. Положительное значение коэффициента корреляции означает,
что при отклонении случайной величины хх от ее математического ожидания
случайная величина Х2 будет иметь в среднем тенденцию к отклонению от своего МО
по знаку в ту же сторону, что и СВ X,. При этом эта тенденция будет проявляться
тем сильнее, чем ближе к единице будет значение rXj х^.
Наоборот, отрицательное значение гх х будет означать, что при отклонении СВ
Х{ от ее математического ожидания СВ Х2 будет иметь в среднем тенденцию к
отклонению от своего МО по знаку в другую сторону по сравнению со случайной
величиной Хх. Эта тенденция будет проявляться тем сильнее, чем ближе к (- 1) будет
значение г^.
Действительно,
_M[(Xx-mXi)(x2-mXi)]
%х2 -"
Поэтому, если rX{ Xi > 0, то
ах, <*х2
M[(X^mXi)(x2-mXi)]>0.
Отсюда получаем, что при rXj Xi > 0 в среднем знаки отклонений X, - тХ| и
Х2 -Щ2 одинаковы. Если же гХ{ Х2 < 0, то
м[(х,-тХ1)(х2-/пХ2)]<0,
и в среднем знаки отклонений Xx-mXi и Хг-тХг различны.
Отметим одно важное обстоятельство: коэффициент корреляции гзд
характеризует степень тесноты линейной статистической зависимости между СВ Хх и Х2, т.е.
такой зависимости, когда при возрастании одной из них другая имеет тенденцию
возрастать или убывать в среднем по линейному закону (рис. 5.29 и 5.30) (в общем
случае равенство нулю корреляционного момента не означает независимости СВ,
однако для нашего изложения эти случаи интереса не представляют) [87,126].
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация
299
°0
о 9*
о
>о
о с/*
р/^ о
о
Х2
х,
о
°Х
*оХ2
Рис. 5.29. К пояснению положительной
корреляции между двумя случайными
величинами Х\ и Х2
Рис. 5.30. К пояснению отрицательной
корреляции между двумя случайными
величинами Х\ и Х2
Соотнесем все рассуждения к СФ Х(г), представленной на рис. 5.31.
Сечения СФ при t = tu t = t2> ..., tn породили СВ Хь Х2, Х3, ..., Хп, ..., являющиеся
значениями СФ. Найдем корреляционные моменты между СВ Xi и СВ Хь Х2,..., Хп; в
результате получим строчку корреляционных моментов:
R
х, х{ t Rxt х2' ^х,х31 Rx^xA '•••» *х. х,, »•••»**
, апСО
Рис. 5.31. Случайная функция Af(l)
Аналогично найдем корреляционные моменты между СВ Х2 и случайными
величинами Хи Х2, Х3,..., Хп; результат имеет вид
Rx2 х,» Rx2 x2 > Rx2 хъ»^х2 хА»• • •»^х2 хп' • • •»^х2 хп •
Продолжая аналогичные рассуждения, найдем корреляционные моменты между
случайной величиной Хп и случайными величинами Хь Х2,..., Х„; запишем результат
R-Y У > **У У > **У У » **У У »#»»>**Y У »»##»**У Y •
лпл1 лпл2 лпл3 ллл4 лпл11 лпли
Запишем всю совокупность корреляционных моментов в виде матрицы:
(Я
1V*1
Rxn
Xi
Xi
x,
lxxx
Rx2
Rx.
x2
x2
x2
"X{
Rx2
Rxn
Хг
Хъ
Хъ
R
xxxn
R
x2xn
R
xnxn
•Rxx^t^R^JJ^lX^^n.
Эта матрица симметрична относительно диагонали, т.к.
RXX [ti'tj ) = RXiXj ~ RXjX{ = RXX \tjJi )•
3UU Анализ и статистическая динамика и А У. часть i
Корреляционная матрица дает информацию о корреляционных моментах лишь
для значений СФ при дискретных значениях аргумента
г = г1э* = г2,/ = /3,...,* = *„,....
А теперь возьмем любые два произвольных сечения СФ X(t) (в отличие от случая,
когда мы брали сечения при t = t\, t2, h, ...) при непрерывном времени t. В этом
случае система «столбиков», порожденная матрицей R, превратится в поверхность
Rxxi^'h)* причем ^£[0,7] и /2€[0,Г]. Эта поверхность представлена на
рис. 5.32.
Rxxifu t2)
/w^ Vl=,2
Рис. 5.32. Графическое изображение корреляционной функции случайного процесса X(t)
Дадим определение. Корреляционная функция СФ X(t) в области ее
существования представляет собой совокупность корреляционных моментов двух СВ X(t\) и
X(t2), равных случайной функции X(t) при аргументах t\ и t2, где значения t\ и t2
представляют собой любые сечения всех текущих возможных значений аргумента t
случайной функции.
Таким образом, согласно определению
/?xx(r1,r2) = M[(x(/l)-mx(r1))(X(r2)-mx(/2))].
Корреляционная функция Rxx(h>h) может быть выражена через двумерный
дифференциальный закон распределения fx (jq,x2,t{,t2):
оо оо
Rxx (h>h)= J J (^i ~mx Ы)(*2 -^дг (h))fx (хиЬ^^сЬс^.
} —OO—OO
/
Ha pkcl 5.25. представлены сигналы X(t),Y(t) и Z(t). Их корреляционные
функции для фиксированных значений Ц представлены на рис. 5.33 [87].
Свойства корреляционной функции:
1). Имеем две зависимости:
оо
Dxx{t)= \{х-тх{$ fx{x,t)<bc,
оо оо
Rxx (hh)= J J (*i ~mx (h))(*2 ~mx {h))fx {x^^t^dx^.
—OO —OO
Из сравнения последних выражений видно, что если аргументы КФ
(корреляционной функции) равны между собой, т.е. t\ = t2 = г, то RxxiU t) = Dxx(t) (рис. 5.34, а).
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 301
Таким образом, необходимость в дисперсии как отдельной характеристики СФ
отпадает, поэтому в качестве основных характеристик СФ достаточно
рассматривать ее МО и КФ.
СФ, у которой МО зависит от времени, а корреляционная функция зависит от
двух аргументов t\ и t2, называется нестационарной.
*хх(*|иЛ)
1
*A*i)
D(t[)
Щ)
Rzz
—*—-^.
^Knfo'A)
Rztil"J2)
RrAt\'\t2)
Рис. 5.33. Дисперсия D(t) случайных функций X(t),Y(t) и Z(t) (рис. 5.25) и их корреляционные
функции Rxx (ti'h) 9 Ryr (ti'h) и Rzz(h'h) при двух значениях /,' и t{ аргумента tx:
D(t[) и D(r() - значения дисперсии D{t) при t=t{ и / = /f; Rxx (K'h) * Rrr (ti'h) u Rzzi^h)
- значения корреляционных функций R^ (t{j2) ♦ Ryy {h*h) u Rzz (h>h) nPu *= *\ »
Rxx i?\*h ) • ^it (*\*1г) u Rzz (*\**2) ~ значения тех лее функций при t = t"
2). Так как корреляционный момент двух СВ X(tx) и X(t2) не зависит от
последовательности, в которой эти величины рассматриваются, то КФ симметрична
относительно своих аргументов, т.е. (рис. 5.34, б)
Rxx {h'h)-Rxx (*2>O-
Rxxih.h) '
i>xx(t) = Rxx(ti>h)\tl^,
1 1
\
B =
R(A
R(U
to.*)
) = R(B)
,h) = R(hA)
X
t{ = t2
= /
6
*
\
h
RxxiUA)
\
Rxxit2A)\
h
Rxxituh)
RxxitiJi)
U = t2=t
(tiji) (ht2) *i = h=t
Рис. 534. К определению свойств корреляционной функции в случаях:
a-nput^^^t Rxx(h'*2) = Dxx0y.6- R^ (r,,/2)= R^^);
«- Rxx (h>h) = Rxx (h>h);^- \Rxx (h>h)|^>jRxx('iA)Rxx{h>h)
302
Анализ и статистическая динамика САУ. Часть I
Если изобразить R^ (tx,t2) B виДе поверхности (рис. 5.34, а), то эта поверхность
симметрична относительно плоскости, перпендикулярной к координатной
плоскости ti0t2 и проходящей через биссектрису угла tfit2.
3). Значение корреляционной функции в любой точке (tu t2) не может
превосходить по модулю среднее геометрическое ее значений на главной диагонали в точках
ее пересечения с прямыми, проведенными из данной точки параллельно осям (t\, t2)
(рис. 5.34, г).
4). Пусть Y(t) = (f>(t)X(t), тогда
%(г„г2) = ф(г1)ф(г2)^(г1,г2).
Когда имеет место система случайных функций, используется понятие взаимной
функции корреляции. Она определяется формулой
оо оо
ЯХ/Х, ('..'2)= J J (*i -mXl (h))(4 -mx. (t2))fx (x^xi^dx^, (5.12)
—oo—oo
где fx (*i\*2,'i''2) ~ смешанный двумерный закон распределения случайных
функций ХДг) и Xj(t).
Случайные функции называются коррелированными, если их взаимная
корреляционная функция не равна тождественно нулю. Случайные функции, взаимная
корреляционная функция которых тождественно равна нулю, называются
некоррелированными.
5.2.3. Стационарные и эргодические случайные сигналы
СФ, имеющая нулевое математическое ожидание, называется центрированной и
обозначается X(i).
СФ X(f) называется стационарной в широком смысле, если ее математическое
ожидание постоянно, а КФ зависит только от разности аргументов x = t2-t{
(рис. 5.35, а)
mx(t) = mx =const; Rxx{h*h) = Rxx{h-h) = Rxx(*)-
X{t)
0
_±rny(t)
0 б t
Рис. 5.35. Стационарный X(t) (а) и нестационарный Y(t) (б) (для сравнения) случайный сигнал
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 303
Дисперсия стационарной СФ согласно формуле D^ (f) = #xx ('i»*2)| равна
Dxx = R\x {h ~h)\ _ _ = ^xx (0)* Следовательно, дисперсия стационарной СФ
постоянна и равна значению КФ в начале координат.
На основании свойства симметрии КФ можно записать
&хх (t\*h) = Rxx ('2 -h) = *xx ('1 -h) = *xx (*) = *» (-*).
где x = r2 -tx.
Таким образом, КФ стационарного СП является четной функцией (рис. 5.35, б).
Поскольку справедлива формула
то для стационарных СФ можно записать
|*ж(ф*;а(0).
т.е. значение КФ стационарной СФ нигде не превосходит по модулю ее значения в
начале координат, т.е. дисперсии. Можно показать, что КФ непрерывной СФ также
непрерывна. Если СФ содержит периодическую составляющую, то КФ также
содержит периодическую составляющую той же частоты. .
Еще раз остановимся на физическом содержании функции R^ (т). Оно состоит в
определении вероятности того, что если СФ X(t) в момент t приняла значение Хь то в
момент времени r + т она имеет значение Х2, т.е. характеризует взаимную связь
между Х(г) и Х(г+т). Если т мало, то связь между X(t) и Х(г + т) велика, т.е. при
очень малых т вероятность того, что значение функции X (t + т) мало отличается от
значения X(t), близка к единице и близка к достоверности. По мере увеличения т
связь между значениями X(t) и X (t + т) ослабевает, они делаются взаимно
независимыми, a Rxx (т) -> 0 . Другими словами, при достаточно больших т вероятность того,
что X (г + т) будет мало отличаться от X(t) практически равна нулю.
Случайный процесс X{t) называют эргодическим, если все его статистические
свойства могут быть определены по одной единственной реализации хг (Г).
Эргодическим также молено назвать такой СП, для которого среднее значение по времени
равно средним значениям по ансамблю.
Для определения статистических характеристик можно ограничиться одним
опытом, проводимым в течение достаточно большого интервала времени, т.е.
ограничиться обработкой одной реализации вместо множества опытов, необходимых
для определения характеристик СФ, не обладающей свойствами эргодичности.
Вместе с тем необходимо иметь в виду, что не всякая стационарная СФ является
эргодической.
Можно показать, что стационарная СФ эргодична, если ее КФ R^ (т)
неограниченно убывает по модулю при |т| -> <» 9 т.е. если Ve > 0 ЗТ0 такое, что
|*xx(*)|<e" Vx>rD.
Таким образом, особенно важное значение эргодическое свойство имеет для
экспериментального определения МО функции Ч^Х^)) стационарной СФ X(t),
т.к. оно дает возможность найти приближенное значение т^ не по множеству pea-
304
Анализ и статистическая динамика САУ. Часть I
лизаций X(f), а по данным одной ее реализации на достаточно большом, но
конечном интервале времени Г, т.е. из зависимости
0
На основе использования свойства эргодичности МО и КФ стационарного СП
вычисляются по формулам
1 т
™х = J xfx (x)dx=\m^-jx(t)dr9
-оо 0
оо оо
R*xx (x)= J J (*i -шх){хг-тпх)fx (x1,x2,i)dxldx2 =
—оо—оо
1 Т-хо о
= lim Г x(t)x(t + T)dt =
г->ооГ-т Jo V
1 г~т
= lim-— J [д:(г)-шх][х(г + т)-шх]Л;
(5.13)
(5.14)
л(г)
дг(;+т)
RXY (т) = lim i ]x(f) y(f)(f + т)Л.
Уменьшение времени интегрирования в формулах и на интервал т обусловлено
тем, что второй сомножитель известен только до (t + т) < Г. (рис. 5.36, а).
Для определения #^х (т) можно воспользоваться формулой
1 тр ° °
RyyM= lim \x(t)x(t-x)dt.
Последней формулой определяется левая ветвь КФ (рис. 5.36, б).
x(t)k
(5.15)
x(t+x)
y/Vvw
^чЛллЛЧЛ^
V4,
v^^
Г-т
(
дс(г+т)
)
л/wV
х б
т
t
t
t
Рис. 5.36. К пояснению формул:
а - (5.13) и (5.14); б- (5.15)
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 305
Для взаимных корреляционных функций RXY (т) и Ryx (т) справедливо
равенство Яхт СО = *»(-*)•
В самом деле,
Лет СО = Hm-J*(r)y(f + T)A;
Г^ооГ
о
7" о
%(T)=limljJ(Oi(r + T)A.
Г-И-Г
-Зто
2т Зт
Я*у(т),/Ыт)
Д*х
-Зто -2т0у -To
\ /
\ /
> /
\ ?
Рхх
/ \
б
Рис. 5.37. График корреляционной функции Rxx (т) стационарной случайной функции X(t)
и взаимных корреляционных функций RXY (т) и Rn (тз) случайной функции ДГ(О
и её производной Y(г) = —^:
а - корреляционная функция R^ (т), б - взаимные корреляционные функции RXY (т) и Лте (т)
Введем во втором равенстве новую переменнуюг + т = Х, dt = dX, г = X-т; в
результате получим
/?w(x)=BmijJ(X-T)*(X)dX.
Теперь вернемся снова к обозначению X = г:
т^юоТ-
21 Зак. 232
306
Анализ и статистическая динамика САУ. Часть I
Сопоставляя последнее равенство с первым, видим, что
На рис. 5.38 показан возможный вид взаимнокорреляционных функций двух
процессов.
у
1
л
4
/
s
Rx,x
/
/
\
V
\
\
N
Рис. 5.38. Возможные графики взаимных корреляционных функций Rx Хк (х) и RXkX( (т)
Еще раз обратим внимание на то, что любая статистическая характеристика,
определяемая в общем случае осреднением по множеству реализаций, для эргодиче-
ских процессов с вероятностью сколь угодно близкой к единице, равна
соответствующей характеристике, определяемой осреднением по времени любой одной,
достаточно продолжительной реализации этого процесса.
Приведем некоторые примеры корреляционных функций.
Если СП содержит постоянную или периодическую составляющие, то эти же
составляющие будут иметь корреляционные функции. При практических расчетах КФ
наиболее часто аппроксимируют выражениями (рис. 5.39 и 5.40):
*« (*) = Dxe-^; Rvc (т) = Dxe-°M cos|3t.
Белый шум - это случайный процесс X(i), который характеризуется
отсутствием какой-либо взаимной статистической связи между любыми двумя
значениями Дг).
ЪМ
Рис. 5.39. График корреляционной функции
Рис. 5.40. Примерный вид корреляционной
функции процесса X{t), содержащего в своём
составе кроме случайной также н
периодическую составляющую
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 307
Яхх(т)
- (т) 0 + (х)
Рис. 5.41. Корреляционная функция белого шума
КФ белого шума равна нулю для любого т, кроме т = 0, и ее можно представить
в виде дельта-функции или практически в виде импульса достаточно малой ширины,
площадь которого равна единице (рис. 5.41).
5.2.4. Спектральная плотность стационарного случайного сигнала
Во временном представлении СП в качестве его характеристики
рассматривалась КФ.
Более наглядным является частотное представление.
Функция Sxx (со), определяемая зависимостью
Sxx(<o)~]Rxx(x)e-^dT, (5.16)
называется спектральной плотностью (СПл) стационарного СП. Тогда
оо
W-0=Kx(<oKJ<OTrfco. (5-17)
Таким образом, КФ и СПл связаны между собой парой преобразований Фурье -
прямым и обратным.
Рассмотрим физический смысл понятия СПл.
Обозначим через ^реализацию СП, определенную на [0, 7]. Тогда
Или
— I Rxx (T)e-j™dT=— I lim - \х\ (t)xT (t + x)dt e'.^dx.
Последнюю зависимость перепишем в виде
— 1 Rxx(x)e-^xdx^ lim-— f xT(t) \xT(t + >z)e-j{»xdtdT.
Тогда, поскольку e~jme+jbix = 1, получим
Sxx (со) = lim IJ- f xT {t)e^dt\xT (t + zy^dT.
-oo 0
Введем замену t + т = Ь; dx = d$, тогда
Sxx (со) = ± j *; {t)e»dt lim IJ,; (t + z)e-""*dx =
0
21*
308 Анализ и статистическая динамика САУ. Часть I
= —lxT (t)e+j<aldt lim - \хт {b)e-iw6db. (5.18)
2п>__ ' w г->~го
*'<-^>) Ит£М+*>)
Из последней формулы имеем
$хх Н = Ит -—Хт (у<й) Хт (-jco) =
= lim ±±(РХ (<a)+JQx (<o)){Px {<*>)-jQx (<в))=- (5.19)
т^тг'пУ к } v " Г-4ООГ27С1 v ;|
Выше введены в рассмотрение функции Хт (./со) и 5ХХ (^) •
Функцию |хт(1/со)| называют спектральной функцией, или спектральной
плотностью амплитуд (амплитудной спектральной плотностью). Спектральная функция
(текущий спектр процесса Xj(t)), являющаяся преобразованием Фурье реализации
СФ X(t), определенной на промежутке [0,Г], характеризует спектральный состав
этой реализации.
В отличие от амплитудной спектральной плотности |xT(i/co)|, определяющей
плотность амплитуд на участке спектра d(u, спектральная плотность Sxx (со)
характеризует распределение мощности составляющих на интервале частот dco.
В самом деле, средняя мощность стационарного СП может быть выражена так
Pcp=ffxUt)d,.
1 о
Или, воспользовавшись равенством Парсеваля, имеем
^ т 1 1 °°
lim - f4 {t)dt = lim -— f \xT (jtof dto.
Обозначим Sxx (со) = lim \ХТ(]{Л .
Отсюда получим зависимость
J Sxx (co)d(D = ij4 (t)dt = Pcp. (5.20)
-*o l 0
Интеграл в левой части характеризует мощность во всем диапазоне частот.
Элементарная же составляющая Sxx (co)t/co = t/P определяет мощность в бесконечно
узкой полосе частот dco, а коэффициент Sxx (со) соответствует крутизне нарастания
с / \ dp
мощности по частоте Sxx (со) = —.
Из формулы (5.19) следует, что функция Sxx (со) тесно связана со спектральнь^
составом СП, характеризующим степень его неупорядоченности.
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 309
Формулы (5.18) и (5.19) являются основными формулами спектральной теории
стационарных СП, впервые математически строго разработанной А.Я. Хинчиным.
Свойства спектральной плотности:
1). СПл является вещественной четной неотрицательной функцией частоты со.
В самом деле, имеем (5.28):
оо 1 °°
Sxx И = ^ J Rxx (t)[coscot-./sinсофт = — f Rxx (x)coscoxrfT-
~ ~ (5.21)
oo 1 °°
-j— f Rxx (T)sincoTdT = — J Rxx (x)cosvndx.
—oo —oo
Из последней зависимости видно, что Sxx (со) - функция вещественная и четная,
т.к. Rxx (t)coscot - четная функция частоты со, a cos сот = cos (-сот):
SxxH = Sxx(-(u).
Неотрицательность Sxx (со) для данного класса СП следует из формулы
Sxx(<») = lim~\XT(j«>f.
Выражение для Sxx (со) можно переписать в виде
sxx (w) = - f Rxx (t)coscot di. (5.22)
n"o
2). Если Rxx (т) - монотонно убывающая функция от т, то Sxx (со) - монотонно
убывающая функция.
3). Интеграл от СПл равен дисперсии или квадрату СКО стационарной СФ.
Имеем
Rxx(*)l=0 = Dxx = ]sxX(<uyJmd(A ,
1т=0
Dxx=Gx = ]Sxx(«>)d(i>, (5.23)
—оо
т.е. дисперсия стационарной СФ пропорциональна площади, ограниченной кривой
СПл Sxx (со) и осью абсцисс.
Пример 5.1. Найти СПл СФ с корреляционной функцией Rxx (т) = Dxxe~a™ (рис. 5.42).
Имеем
2я_
~ ndx
= Rxx\}e™-j™dT + le -at-/
2" [i ' I
-J^^\^£xx. a
я a2+o)2'
Зависимость кривых КФ и СПл от значений а иллюстрируется рис. 5.42. В общем случае, чем шире
график КФ, тем уже график СПл (чем медленнее процесс, тем меньшее значение в СФ имеют высокие
частоты).
310
Анализ и статистическая динамика САУ. Часть I
Sxj№
Dx
Rxx(*)
0 т
Рис. 5.42. Графики спектральной плотности и корреляционной функции
Положим, что КФ СП имеет вид
Найдем Sxx (со):
Имея в виду, что
*xxW = 0*s*~aMcospT.
S*x(<») = iJ Dxxe-a»oos^e-^dz.
cosPx =
получим
Отсюда следует
дует
Пусть Dxx = 40 - дисперсия, a = 0,5 с'1 - параметр затухания, Р = 2 с"1 - резонансная частота.
СПл имеет вид
Sxx И
-Л-
20
20
2я [о, 25+ (2-со)2 0,25 + (2 + со)2 j
Графики Rxx (т) и Sxx (со) представлены на рис. 5.43.
Rxx(t) <
(5.24)
-X
+(0
Рис. 5.43. Спектральная плотность и корреляционная функция случайного процесса
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 311
Часто КФ аппроксимируют зависимостью
*и(т) = Ои«"*(«*Рт+|в1пР|т|\
Тогда спектральная плотность имеет вид
( \_ а n 2P-W 2Р + Ш
Белым шумом называют стационарный СП с постоянной спектральной
плотностью Sxx (со) = 50. Так как
Rxx М = J sxx (<oyjmd(d = Soj ejmda (5.25)
и дельта-функция определяется выражением
8(т) = — lejmd(u, (5.26)
из (5.25) и (5.26) следует, что
Rxx(x) = 2nS08(x) (5.27)
есть корреляционная функция «белого» шума.
Следовательно, корреляционная функция белого шума с точностью до
постоянного множителя представляет собой дельта-функцию (рис. 5.44)
[О при т * 0;
оо при т = 0.
Rxx СО
а2
(
i
-<
)
' sxx(
i
\
т
ш)
►
о т
0
СО
о
б
со
Рис. 5.44. Графики спектральной плотности и корреляционной функции:
а) при белом шуме; б) при постоянной х- а
Из предыдущих рассуждений ясно, что дисперсия белого шума (БШ) равна <», т.е.
Dxx =°°-
Физический процесс типа «белый шум» реализовать невозможно, т.к. мощность
этого процесса должна быть бесконечно большой. БШ является удобной
математической абстракцией. При некоторых условиях в практическом диапазоне частот работы
312
Анализ и статистическая динамика САУ. Часть!
реальной системы «вход» можно аппроксимировать белым шумом, что существенно
упрощает исследование (рис. 5.45).
(Obp 0)
Рис. 5.45. К пояснению понятия «белый шум»
На рис. 5.46 представлены конкретные СФ, их КФ и СПл.
Rx&)
Яхх(т)=А2
-п.^*а1т1
Sx(co) = 2ti^8(co)
со
со
«M)i
Sxx=2DxaJ(a2+(u2)
SxxW
Ях(т) = 5о5(т)
-Щ
t
i
1
i
о
0
Sx
(0))
II
3
со
\
1
1
1
\
.со
~ «О))
= (A2/2)cosc0iT
I
I
X -СО! О СО! СО
Рис. 5.46. Графики спектральных плотностей и корреляционных функций
На рис. 5.47 представлены конкретные виды КФ и соответствующие им
спектральные плотности»
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 313
Dxx
0
а
а.г£а-
а
а
Rxxix)
\ 5i(C0) = .
Jw2(co)
= /Ыт)
3(т)
а а
А^Ых)
7?1(т) = /Ыт)
-£>хх
L5xx(co)
0 2а 4а 6а 8а а
fSi(co) = &(<»>)
,52(0))
и/ Аз(о))
,-/
2Q 3Q 4Q 5Q 6Q
Рис. 5.47. Корреляционные функции, отличающиеся друг от друга масштабом ло оси т,
4 и соответствующие нм спектральной плотности [87]
На рис. 5.48 изображены графики нормированных корреляционных функций
спектральных плотностей.
8хх (<Ь)
%■
J\
У- % %
l
Л, 2,0
0,3/
М
0.2/
У 10/ W
^ = 0.1
-^ = 0,5
щ 20% 3(0^ 4(оо 5(0^
«О
<°Ь
2^ ЗШо 4OJ, 5^ бй^
(0^ 2(оо Зоц, 4вц, 5(0^ бо\,
Рис. 5.48. Нормированные корреляционные функции rxx(*c) = e ^coso^x и соответствующие им
нормированные спектральные плотности g^ (со)
I
Для удобства построения масштаб кривой gxx С®) ПРИ ^Ц) =^Л уменьшен в пять
раз по сравнению с масштабом других кривых gxx (ю) •
20 Зак. 232
Л4 Анализ и статистическая динамика САУ. Часть I
5.3. СТАТИСТИЧЕСКИЙ АНАЛИЗ ОДНОМЕРНЫХ ЛИНЕЙНЫХ
СИСТЕМ С ИСПОЛЬЗОВАНИЕМ ИМПУЛЬСНЫХ ПЕРЕХОДНЫХ
ФУНКЦИЙ (АНАЛИЗ ВО ВРЕМЕННОЙ ОБЛАСТИ)
При решении конкретных задач исследования систем автоматического
управления необходимо получить ответ на ряд вопросов, например:
• какова вероятность того, что в любой момент времени работы системы в
установившемся режиме выходной процесс "не выйдет за пределы допустимого
диапазона [а, |3];
• каковы статистические характеристики выходного сигнала системы в рамках
корреляционной теории, т.е. для СП X(t) вычисляются только его
математическое ожидание и корреляционная функция в переходном или установившемся
режимах в зависимости от постановки задачи.
В общем же случае статистический анализ систем - это изучение законов
преобразования случайных сигналов конкретными классами систем.
Рассмотрим задачу статистического анализа для наиболее простого класса систем
- стационарных.
Положим следующее:
а) имеется стационарная устойчивая линейная система с импульсной переходной
функцией к(т)\
б) на вход системы поступает входной случайный сигнал Y(t)\
в) исследователя интересуют как неустановившийся, так и установившийся
режимы работы системы.
Необходимо найти зависимость, связывающую автокорреляционные функции
входного и выходного сигналов (рис. 5.49).
Y(t)
Случайный
входной
сигнал
*(т)-
ИПФ системы
X(t)
Случайный
выходной
сигнал
Рис. 5.49. К постановке задачи статистического анализа
Получим решение поставленной задачи. Входной и выходной сигналы в
неустановившемся режиме связаны соотношением
t
X(t) = \k{i)Y{t-T)dx. (5.28)
о
Из этой формулы имеем
M[X(t)] = M
1_о
Поскольку МI I («)dT I = I M(-)dx, находим
)k{x)Y{t-x)dx .
}(.)</т =}м(.)</т,]
Lo J о
t
mx (0 = \k(x)mY (t - T)dx. (5-29>
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 315
Последняя формула справедлива для случая, если Y(i) - нестационарный СП. Если
же Y(t) - стационарный СП, то mY (t-x) = mY = const и, следовательно,
t
mx(t) = mYjk(x)dx. (5.30)
о
Полагается, что имеет место неустановившийся режим.
Для установившегося режима имеем
оо
тх (г) = mY \ k(x)dx = mYK = mx = const.
о
Окончательный результат для установившегося режима таков:
mx=KmY. (5.31)
Получим формулы, связывающие корреляционные функции входного и
выходного сигналов линейной стационарной системы.
Положим, что Y{i) - нестационарная СФ.
Из (5.28) и (5.30) имеем
' ;L о
X(t)-mx(t) = jk(x)[Y(t-x)-mY]dx, илиX(t) = ]k(x)Y(t-x)dx.
о о
Запишем последнюю формулу для моментов времени t\ и t2, перемножим правые
и левые части и воздействуем оператором МО:
мГх^ШГг)!^ (5.32)
Поскольку
X{tx)X{t2) \ = Rxx(h,t2);
Y(tx-xx)Y(t2-T2) =*„,(*!-т„г2-т2),
М
м
из (5.32) следует
00
Последняя формула определяет корреляционную функцию СФ X(t), если имеет
место неустановившийся режим, a Y(t) - нестационарный СП.
Пусть Y(t) - стационарная СФ, а режим работы системы - неустановившийся.
Тогда
RYy(*\ -*\>*2 -%) = RYY(h ~Ъ -*l +Tl) =
= Ryy(t2 -tx +т, -т2) = Ryyiu + ъ -т2),
где и = t2-t{,
справедливо выражение
Rxx(t\>h) = |\к(т{)к(т2)Куук2-ц +хх -x2)dxxdx2. (5.34)
00
Теперь рассмотрим установившийся режим, для которого основная формула
(5.28) принимает вид
о °° о
Х(г) = jk(x)Y(t-x)dx. (5-35)
о
20*
316 : Анализ и статистическая динамика САУ. Часть I
Тогда (5.34) перепишется в виде
оооо
Rxx («О = Jf *(Ti)*(t2)%(и + тх -%2)dxxd%2' (5:36)
00
Дисперсия выходного сигнала определяется зависимостью (полагаем и = 0):
оооо ,
Rxx (0) = Dm = J/^Жт^ЛууСс! -T2)dTxd%2. (5.37)
00
Некоторые выводы:
а) если известна ИПФ системы, то МО выходного сигнала определяется как
результат одномерного интегрального преобразования МО входного сигнала,
(формулы (5.29) и (5.30)), а КФ выходного сигнала и его диспероия - как
результат двумерного интегральногр преобразования КФ входного сигнала
(формулы (5.34) и (5.37));
б) для определения дисперсии выходного сигнала требуется задать КФ входного
сигнала. Знание дисперсии входа недостаточно для.расчета дисперсии
выходного сигнала.
В теории стационарных систем можно было выделить такие задачи, которые
связаны только со стационарными, эргодическими случайными процессами [145].
При подаче на вход ЛНС стационарного сигнала на выходе процесс не является
стационарным, поэтому статистическая динамика ЛНС обязательно должна
обеспечивать возможнрсть оперирования с нестационарными случайными процессами.
В силу сложности общей теории нестационарных случайных процессов рассмотрим
здесь некоторые вопросы статистической динамики ЛНС в рамках лишь
корреляционной теории.
Связь корреляционной функции Rxxitu h) выходного сигнала ЛНС с
корреляционной функцией RyAfu h) входного сигнала можно получить следующим образом.
Согласно определению корреляционной функции (5.34), с учетом интеграла
суперпозиции
/^(г^^мГ^Ш^
= |*(г1д)л|шГу(т)У(Х)1[*(г2Д)Л,
т.к. операция математического ожидания линейна. Выражение в фигурных скобках,
согласно определению (5.34), есть Яуу(тД), поэтому
Rxx(hh) = \b(h'№l*M*Mh'Wb. (5.38;
о d
Корреляционная функция установившейся реакции примет вид
*xx('p'2)= f W\*)d*] «ir(TfX)t(r2,X)rfX. (5.39;
Формула (5.39) наглядно иллюстрирует тот факт, что и при стационарном входе
Я1Т(тД) = Л1Т(Х-т) (5.40.
даже установившаяся реакция не представляет собой стационарного сигнала, т.к
Rxxituh) не является функцией, зависящей от t2 -tx.
Наиболее часто (5.39) записывается в виде
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 317
Rxx (h >h) = f } *('i >Ti ЖГ2. T2 )^jt (Ti •> T2 )^i^2,
rr00 (5.41)
^xx(t) = ]]k(t,xl)k(t,x2)RYY(xl9x2)dx{dx2.
oo
На основании анализа приведенных выше формул можно сделать вывод:
выходной сигнал линейной системы представляет собой стационарный СП тогда и
только тогда, когда рассматривается устойчивая стационарная линейная система в
установившемся режиме при стационарном случайном входном сигнале.
В этом случае математическое ожидание и Dxx являются постоянными
величинами, а корреляционная функция выходного сигнала зависит от разности т = t2 -tx.
Нестационарный выходной сигнал может быть порожден одной из трех причин:
а) нестационарностью входного сигнала; тогда для • стационарной системы для
t = оо имеем
оооо
Rxx Ci>h) = f f *(TiЖТ2)ryy(f\ ~Ti.h -T2)dx]dx2;
00
б) нестационарностью системы; тогда корреляционная функция выхода
определяется выражением
Rxx^h)^\\kih,xx)k{t2,x2)RYY{xXyx2)dxxdx2\
оо
в) нестационарностью режима работы системы (переходной режим); тогда для
стационарной системы имеет место зависимость
• %^1^2) = ((^1ЖТ2)%^-^+ТГТ2№А'
00
Рассмотрим случай, если Y{t) - белый шум; тогда
/?кк(т) = 271508(т).
Найдем формулу, определяющую дисперсию выходного Процесса стационарной
системы в установившемся режиме; имеем
оо оо
Rxx(0) = Dxx =2nS0jk(<zx)dxxjk(<z2)6(xx-T2)d<z2.
оо .
Воспользуемся свойством дельта-функции
оо
J7(T)8(f-T)</T = /(0.
о
Тогда
оо
jk(x2mxx-x2)dx2=k(xx).
о
Окончательно найдем
оо
Dxx=2nSojk2(x)dx\
о
Таким образом, установившееся значение дисперсии на выходе линейной
стационарной системы при подаче на вход белого шума характеризуется интегральной
кэадратической оценкой ИПФ.
318
Анализ и статистическая динамика САУ. Часть I
Если же имеет место неустановившийся режим, то дисперсия выходного СП
определяется зависимостью
Dxx(t) = 2nSojk2(x)dx.
В случае воздействия на нестационарную систему белого шума с КФ
Яут('1''2) = £()('2)8('1Т'2)
при S0(t) = 50 = const, получим
Dxx(t) = Sojk2(t,x)dx.
Пример 5.2. На вход системы с передаточной функцией
К
W(s) =
Ts + \
в момент t = 0 поступает случайный центрированный стационарный сигнал с автокорреляционной
функцией Ryy (x) = Опе • Необходимо рассчитать корреляционную функцию и дисперсию выходного
сигнала Dxx в переходном и установившемся режимах.
Исходные данные: К = \0у Г = 10 с, DYY =1, ос=0,05 . Структурная схема системы представлена на
рис. 5.50.
R
ДО
X(t)
Рис. 5.50. Принципиальная схема системы T = RC
Найдем ИПФ системы; характеристическое уравнение имеет вид
1 1
Т RC
Выражение для ИПФ
Далее воспользуемся основной формулой
7 а: _
%W-JV'41^V^^2 =
0
2 -со
- КФ выходного сигнала в установившемся режиме.
Подробно рассмотрим вычисление дисперсии в неустановившемся режиме; имеем
г i
Dxx =*xx('i.'2)|,l=,2=, =llk(xl)k(z2)RYy(xlA2)dTldz2 =
00
(5.42)
о о
Вычислим внутренний интеграл. Здесь необходимо принять во внимание следующее (рис. 5.51):
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 319
,-а|х,-х2|=ка(Т'"Т2) при т^т,;
[<г*(^) притих,.
Т2 <1Х Т2 > Tj
О Tj
Рис. 5.51. Пояснение к вычислению интеграла
Имеем
О
о х,
= —1—\(у + а)е-а^ -2(*Г™ -(y-a)e^e^+a)tl '
Y -orL J
Подставим вычисленные значения внутреннего интеграла в выражение для DXx'.
Dxx =а2х =K2DYY\ye-n-T?rj[(y + a)e-ax> -2ae~^ -
о У О.
-(y-a)e^e^+a>]dzl=^^\l-—\2ye-m-{y + a)e^]Y
v ' J у + а [ y-aL Jj
получена формула, определяющая дисперсию в неустановившемся режиме.
В установившемся режиме, когда t = <», дисперсия определяется соотношением
_ 2 _К2<5уУ _К2<52у1Т KWy
хх ~ах- Y + a - ит + а "1 + 2Г*
Наиболее сложной является задача расчета вероятности нахождения выходного
процесса X(i) в пределах допустимого диапазона [- 8,+ 8].
Наиболее просто она решается в случае, если Y(i) - нормальный СП. Тогда, если
известно, что входной процесс Y(t) является нормальным и центрированным, то
установившаяся реакция также нормальна и центрирована с дисперсией,
вычисляемой согласно формуле (5.42).
Если X(t) - нормальный СП, то ДЗР определяется формулой
f™(x>t)= bj <*exp\-w-T)[x-mx(t)f}- (5-43)
В последнюю формулу входят m^t) и DXx(t), которые определены выше, и, таким
образом, установлен одномерный ДЗР выходного сигнала X(t)..
Если тЖ) = 0,/ЫО = Dxx, то
yJlnDxx [ 2DXX
для рассматриваемого случая ДЗР не зависит от времени г.
Зная /*(,)(*), легко получить ответ на основной вопрос анализа: какова
вероятность Рб того, что в любой момент времени работы системы в установившемся
режиме СФ X(t) не выйдет за пределы отрезка [- 8,+ 8].
Решение задачи дается формулой
° J /ОтгП 9П.„. ГГ..
2D
хх
320 Анализ и статистическая динамика САУ. Часть I
где ох = yjDxx, a
[2Z —
O(z) = J— \е 2 d\ - интеграл вероятностей.
Если 8 = Зсх> то Рь> 0,99.
Если распределение СП X(t) отлично от нормального, то можно воспользоваться
оценкой вероятности выхода из допуска по известным математическому ожиданию и
дисперсии.
Эта оценка следует из классической теоремы Чебышева [108]:
Р[|Х(0-^|>8]<^ = [^]2.
Если 8 = Зстх и тх = 0, то
р[|Х(ф8]<1.
Если известно, что кривая fx(x) симметрична и «одногорба», то [108]
Р[Х(,)>8]<^у.
При 8 = Зах
Р[|Х(г)|>8]<0,05.
Воспользовавшись приведенными формулами, можно дать вероятностную оценку
возможного «размаха» и невыхода его из допуска [108].
5.4. СТАТИСТИЧЕСКИЙ АНАЛИЗ ОДНОМЕРНЫХ ЛИНЕЙНЫХ
СИСТЕМ С ИСПОЛЬЗОВАНИЕМ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
(АНАЛИЗ В ЧАСТОТНОЙ ОБЛАСТИ)
Этот метод можно отнести к основным методам статистического анализа
стационарных систем [145]. Его достоинства - хорошая физическая наглядность,
возможность алгоритмизации и реализации на ЭВМ.
Пусть на вход устойчивой стационарной САУ поступает стационарный СП Y(t)
со спектральной плотностью 5yj<(0). Требуется найти СПл и дисперсию выходного
сигнала системы в установившемся режиме.
Известно, что выходной сигнал в этом случае является стационарным процессом
Х(г). Ранее для рассматриваемого случая была получена формула, определяющая
автокорреляционную функцию выходного сигнала Х(г).
оооо
Rxx 00 = f \k(Tl)k(T2)RYY(x+xl -x2)dxldx2.
00
Поскольку
Sxx«u) = ±] RyyWe-^d-c,
2л
oq
то
Sxx («» ~] J J*(*i)*(T2)Ryy(т+Tj -T2)e-JmdTldx2dx. (5.44)
2Я-оо00
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 321
Так как
то, записывая (5.44) в форме
оо оо 1 °°
Sxx((H) = fk(xl)eJ<m>jk(x2)e-Ju^ — J Л„-(т+т, -т2)х
О 0 ^о
Xe-MT+x,-x2)dTdT]dT2
и учитывая, что
оо оо
Jtec^'dT! =W(-jco); /*(т2)е"^Л 2= Щусо),
о о
получаем
Sxx (со) = WU(uW(-J<o)Syy (w). (5.44л)
Поскольку
WU<*W{-№ = (Р((о) + 7Q(co))(P(co) - 7(2(o))) =
= [P2(o)) + 22(co)] = |WO'(o)|2 = A2(co),
TO
Sxx (©) = |W(yco)|2 Syy (со) = А2 (со)^^ (со). .
Таким образом, СПл выходного сигнала SXx((O) стационарной устойчивой
линейной системы в установившемся режиме при стационарном случайном входном
сигнале равна произведению квадрата АЧХданной системы на СПл входного сигнала.
Теперь легко найти КФ и дисперсию выходного сигнала. В самом деле,
оо оо
Rxx (*) = J sxx (®)eJond<u = J \W(jtii)\2 Syy. (&)ejmda). (5.45)"
Так как Dxx = Rxx(t) при т = 0, из (5.45) находим
оо
Rxx (0) = Dxx = J \ЩУ*со)|2 % (со)^ (5.46)
Имеем: дисперсия выходного сигнала устойчивой линейной стационарной
системы в установившемся режиме определяется как интеграл от
произведения-квадрата АЧХ системы на СПл входного сигнала.
Формулы (5.45) и (5.46) позволяют определить КФ, дисперсию и СКО выхода по
СПл входа и АЧХ системы. DXx и а2* значительно проще выражаются через СПл
воздействия, чем через его КФ.
Кроме трго, при вычислении Dxx^ су2^через Syy(co) в качестве характеристики
системы используется АЧХ А(со) = |W(/a))| системы, которая явным образом может быть
выражена через параметры системы (ИПФ, как правило, явно не выражается через
параметры системы).
Формула
оо
322
Анализ и статистическая динамика САУ. Часть I
весьма широко применяется при вычислении дисперсии и СКО выходного сигнала.
А2(и>У
A2(oS)
Sjofi^rSo
со
Рис. 5.52. АЧХ и СПл входа
Положим, что СПл воздействия 5уу((0) = So, т.е. на вход поступает сигнал типа
белого шума. Тогда
оо
Ом =а2х =2S0j\W(j(O)\2 J(D.
о
При со = 0
где К- коэффициент усиления системы. Представим
W (■/«>)
V / К2
К
Тогда Dxx = а| = 2S0K2A(a, где
Aco = J
W(ju)
К
dco
- эффективная полоса пропускания системы.
Величина Асо имеет размерность частоты. Она является одной из характеристик
системы, связанной с ее АЧХ. Ясно, что если в пределах полосы пропускания САУ
СПл входа постоянна, то такой сигнал можно считать белым шумом по отношению к
этой системе (рис. 5.52).
Обратимся к задаче вычисления дисперсии выходного сигнала X(t) при дробно-
рациональных спектральных плотностях по формуле (5.47). Если ограничиться
классами СФ Y(t), имеющих дробно-рациональные СПл, то
Gyy(O)2)
(5.48)
где Рп{со2) и. QyA®2) - многочлены.
Спектральную плотность, определяемую зависимостью (5.48), можно факторизи-
ровать, т.е. представить ее в виде
Луу((О )- -ayyUCOPyrl-jQ)).
AJTOu))AjT(-./co)
(5.49)
С учетом (5.49) зависимость, определяющую дисперсию выходного сигнала,
можно представить в виде
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 323
-И»
Dxx = J А2(а))5уу(а)Ма) =
£ N(j(u)N(-j(u)Ayy (»А,у (-./со) £ gn (ja))gn (-./со)
(5.50)
где hn(j(u), gn(j(u) - многочлены вида
К (./со) = ^(усо)2"-2 + Ъу{./co)2""4 +... + Ьи-1;
gnU<u) = aoU<u)n +fli(jco)n"1 +... + д„.
Вычисление Дю-по формуле (5.50) сводится к вычислению стандартного
интеграла вида (см. приложение 4).
Теперь можно записать полный алгоритм расчета дисперсий выходных сигналов
систем, заданных своими структурными схемами:
1-й этап. Нахождение ПФ замкнутой системы W(s) по ПФ отдельных элементов.
2-й этап. Нахождение спектральной плотности входного сигнала 5уу<а)).
3-й этап. Представление Спл SVKco) в форме (факторизация СПл)
5yT(a)) = 5jV(ja))5^(-ja)).
4-й этап. Вычисление интеграла
7/2 = 2я J WUtoW(-MS}YU(u)Sw(-j(O)d(u.
—оо
5-й этап. Вычисление дисперсии
Dxx=2nln.
Если АЧХ А(со) и Syr(a)) определены экспериментально, то дисперсия может быть
найдена по формуле
Dxx = J 5xx(w)dG)= J А2(а))5уу(а))^а).
Значение последнего интеграла можно найти графически или вычислить на ЭВМ,
пользуясь известными методами.
Пример 5.3. Найти дисперсию сигнала, имеющего СПл
Перепишем последнюю формулу в виде
bo(-;(O)4-fbi(;o))2-fb2
(ао(уо)) +^1(70)) +а2(Уо)) + аз)
(ao (-70))3 + а\ (-усо)2 + Д2 (-7*0)) + аз j
Ьосо4 - bico2 + Ъг
^"Тх
1
х-т=
(аоО)30)2(-;) + аю)2^;)2 + агаК-;) + аз)
^0(04-^1(02+^2
(-уаосо3 - aid)2 + агЩ + аз)(уао(О3 - aid)2 - 02(0/ + аз)
_ • iboco4 - ^iO)2 + Ъг
Г(аз-а1Ш2)+</(а2о)-аоа)3)Т(аз->а|а)2)-у(а2а)-аоО)3)1
324 Анализ и статистическая динамика САУ. Часть I
boo4 -bio2 +Ьг _Ър(й4 -bi<a2+b2
"(P((u) + </j2(o)))(P((u)-</Q(co))~ Р2(со) + £2((о) f
где Р(о)) = аз - aito2; Q((o) = аг - ао(й3. Тогда
Р2 ((О) + £2((О) = аз - 2aiai<a2 + <ц<а4 + дгсо2 - 2а2ао(О4 + ао(Об =
= до(Об+(а1 -2а2ао)(О4+(а2-2аза1)(О2+лз.
Итак, имеем
^o(04-bi0)2+b2 (О2+2
ао(Об +1 ai - 2агао j(O4 + (Д2 - 2аза1 )а)2 + аз ш + *
Отсюда находим систему алгебраических уравнений
Ьо=О; — bi = 1; Ь2=2; ло=1;
ai - 2агао = 0; аг - 2аза1 = 0; лз = 1.
Значения коэффициентов
Ь0=0; bi =-1; £2 =2; ao = l; ai =2; аг=2; аз = 1.
Далее воспользуемся табличным интегралом
_ -агЬр + apbi - aoaifo /аз _ 5 •
2ао(аоаз-а1Л2) 6
Пример 5.4. На вход системы с передаточной функцией W(s) = K/(Ts+l) поступает сигнал с КФ
%(х) = ^^.
Найти дисперсию выходного сигнала, предполагая, что при t = 0 система имела нулевые начальные
условия, а режим работы - установившийся.
Найдем спектральную плотность
51T(a)) = F{%(x)} = -^-r^-= Г[ао(;со) + а1][ао(-;со) + а1] =
_Руу(Х 1
п (j(u+a)[(-j(u)+aj
Дисперсия выходного сигнала определяется выражением
^nDyyOKi 1
{=1
^Jco
я [ 2я £ [ГОа)) + 1][Г(-;(й) + 1](;о)+а)[(-уо)) + а]
п [гп^ [(Г(У(О) + 1)Оа)+а)][(Г(-./(й) + 1Ж-/со) + a)] J
= 2пРууак(П fr(Jto) rfJa
я [2«ift(jto)^2(-ycD) J
= (^(Усо) = 1;^2(;ш) = Г(;ш)2+(Га+1)Уш+а = ао(Уо))2+а1(</О)) + л2;
^, =0; ^ =1; а0 = Г; а, =(Га + 1); а2 =а) =
2пРууОК Т/а , _ 2яРууЛ: 1 _ 2я^2Руу = КгРуу
п 2Г(Га + 1)". я 2(Га+1)~2я(Га + 1) Га+Г
Для нестационарнь1х систем для частного случая удается получить удобную связь
статистических характеристик входа и выхода в частотной области.
Поскольку корреляционная функция RyyO^ - т) стационарного сигнала есть
обратное преобразование Фурье от спектральной плотности 5ку((о) этого сигнала [56], то
Я (Х-т) = — 7 Syy(co^^ca - (5.51)
2п J
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 325
Выражение (5.39) с учетом формул (5.40) и (5.51) приведем к виду
*jff('i.'2)= f Wi№f ^ f SYY((O)eMX'x)d(o\k(t2iX)dX.
Включив в лодынтегральное выражение сомножители
е)Щ ,£-М =\;ejm2 -e~jmi =1,
а также поменяв порядок интегрирования, получим [56]
" *xx(*\'h)~ J [sYY«uW*(MhW(Mt2)] eMt*-tOd(u. (5.52)
Отсюда видно, что /fofaA) есть обратное преобразование Фурье (в котором роль
временной переменной выполняет сдвиг 0 = t2-tx) от выражения в квадратных
скобках из (5.52). В связи с этим по аналогии с теорией стационарных систем
обозначим через
SYY((o)W*(j(o,ti)W(j(o9t2) = SxxUWuh) (5.53)
текущую спектральную плотность установившегося выходного нестационарного
сигнала, которая в силу формулы (5.52) должна представлять собой преобразование
Фурье.от Rxxituh) по сдвигу 0 = t2 -tx
оо • оо
SxxUWuh) = J RxxOvh)*'**^ f Rxx(h"9^1 + в)^'а)е^0. (5.54)
Формула (5.53), являющаяся своеобразным аналогом формулы (5.44) из теории
стационарных систем [56] показывает, как можно текущую спектральную плотность
выходного установившегося сигнала ЛНС при стационарном входе вычислить с
помощью ее ПЧХ.
Формула для вычисления текущей дисперсии выходного установившегося
сигнала ЛНС при стационарном входе Dxx(t) легко получается из формул (5.52), (5.53) при
tx=t2=t
Dxx(t) = Rxx(t,t) = — \ SjaU^uDddi, (5.55)
—оо
где
Sxx (MM) = 5уу(а))|ЩМ0|. (5.56)
При подаче на вход ЛНС стационарного белого шума интенсивности So с
корреляционной функцией
%('l»'2) = So8('2-'l)
формулы для дисперсии выходного сигнала приобретают наиболее простой вид: из
формулы (5.38) с учетом условия tx = t2 = t
t
Dxx(t) = Sojk2(t,X)dX; . .
о
из формул (5.55), (5.56)
Oxx(0 = |2-f|wCM/)|2duX
Для ЛНС л-го порядка
' L(pyt)X(t) = F(p,t)Y(t) (5.57)
326 Анализ и статистическая динамика САУ. Часть I
связь корреляционной функции выхода и корреляционной функции входа должна
описываться дифференциальным уравнением порядка 2п. Действительно, если бы
удалось найти оператор Ф(р, t) = I7l(p,t)F(p9t), соответствующий уравнению
(5.57), который должен быть также п-го порядка, то
Х(г) = Ф(р,ОГ(О
и
(т.к. операции Л/, ph p$ линейны и выполняются по взаимно независимым
переменным [56]). Таким образом,
где ФвИрьРь *»£) = Ф(Рь*)Ф(р$Л) - оператор связи корреляционной функции входа и
выхода, равный произведению двух операторов п-го порядка, в силу чего его порядок
равен 2п и такого же порядка должно быть дифференциальное уравнение,
связывающее ЯуАФ и Rxx(t£):
Upnt)Upi&R]0C(t,Q = F(ptj)F(pi&RyY(t9Z).
5.5. АЛГОРИТМЫ АНАЛИЗА ДИНАМИЧЕСКОЙ ТОЧНОСТИ
ЛИНЕЙНЫХ АВТОМАТИЧЕСКИХ СИСТЕМ
Количественная оценка качества системы составляет основу задачи анализа и
инженерного расчета.
Для количественной оценки качества системы применяются показатели качества.
Показатель качества - это число, характеризующее в принятой системе единиц
свойство системы. Этот показатель зависит от характеристик системы, ее
параметров, входных функций и возмущений. Различают анализ по априорным и
апостериорным данным. Анализ по априорным данным состоит в определении показателей
качества по известным вероятностным характеристикам входных переменных и
параметров исследуемой системы.
Анализ по апостериорным данным заключается в оценке показателей качества
системы на основании вероятностных характеристик, входных переменных и
параметров, полученных после измерения.
Измерение позволяет уточнить априорную неопределенность характеристик для
конкретных условий наблюдения и тем самым обеспечить более точное решение
задачи.
Основная оценка вероятностных показателей качества динамической системы
начинается с определения сигнала ошибки (рис. 5.53, 5.54).
Пусть m(t) - полезный сигнал; n(t) - помеха; X(t) - выходной сигнал системы.
Сигнал ошибки а(0 - это отклонение фактического выходного сигнала от
полезного сигнала m(i). Сигнал ошибки есть случайная функция времени, а при
фиксированном времени - случайная величина.
Y(t)=m(t)+n(t)
Система
ДО
Рис. 5.53. К постановке задачи анализа точности
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация
С®'
О
327
-6
Рис. 5.54. Сигнал ошибки
На основании понятия сигнала ошибки вводят функцию потерь /(ст(О) = КХ(0*
т(0), характеризующую потери в качестве динамической системы в текущий
момент времени t. Функция потерь также случайная. Поэтому за показатель качества
системы принимают МО функции потерь - средний безусловный риск
-t-oo-t-oo
p = Ml[X(t)MO]= J f l{X{t)Mt))f{x,m)dxdm,
гдеД*, т) - дифференциальный двумерный закон распределения.
При различных формах функции потерь l(X(t), m(t)) получаются конкретные
показатели качества. В практических задачах анализа применяют следующие показатели
качества:
1). СКО - среднеквадратическая ошибка
M[o2(t)] = M[(X(t)-m(t))2];
2). Вероятность превышения ошибкой заданного значения
р = Р{|а(0| = |Х(0-ш(0|>8}.
При решении инженерных задач наиболее часто используется СКО.
Из анализа рис. 5.55 можно сделать вывод, что ошибка состоит из ошибки,
обусловленной неполной «отработкой» полезного сигнала m(t), и ошибки,
обусловленной отработкой сигнала n(f).
snnm
А((0)
V
(О
ср
(О
Рис. 5.55. К постановке задачи анализа точности автоматических систем
Перейдем к соответствующим аналитическим рассуждениям. Имеем a(t) = m(f) -
- X(t) - мгновенное значение сигнала ошибки. Тогда (после формального применения
преобразования Лапласа)
G(s) = M(s)-X(s) = M(s)-W(s)[M(s) + N(s)] =
= M(s)-W(s)M(s)-W(s)N(s) = (l-W(s))M(s)-W(s)N(s)= (5.58)
= Wa(s)M(s)-W(s)N(s).
328 ; Анализ и статистическая динамика САУ. Насть 1
ПФ Wa(s) = 1 - W(s) называют передаточной функцией сигнала ошибки.
Из (5.58) следует структурная схема формирования сигнала ошибки (рис. 5.56).
Имеем ст(г) = X{(t) - X2(t) - мгновенное значение сигнала ошибки.
m(t) t
1 W(S) yV'G(S)
wys)
Xx{t)
\+
/-
X2(t)
Рис. 5.56. Структурная схема системы, формирующей сигнал ошибки а(0
Найдем формулы, определяющие автокорреляционную функцию, спектральную
плотность и дисперсию сигнала ошибки [168]:
/?oo(T) = M[(X1(r)-X2(r))(X1(f + T)-X2(r + x))] =
= (предполагается, что Xl(t),X2(t) центрированы) =
= M[X1(OX1(r + T)-X1(OX2(f + T)-X2(r)X1(r + x)+X2(OX2(r + T)] =
= RxlXl W " Rx,x2 CO " Rx2Xl (x) + Rx2x2 W.
Поскольку m(f) и n(f) не коррелированы, a X^f) и X2(t) порождены
некоррелированными сигналами и, следовательно, сами не коррелированы,
и, таким образом,
^ГО = *ад№ + *хЛ(*) • (5-59)
- корреляционная функция сигнала ошибки.
Преобразуя обе части (5.59) по Фурье, найдем.
- спектральная плотность сигнала ошибки.
Теперь легко записать выражение для дисперсии
Акт = °2 = J 500(со)</со = J [SXlXl (со) + 5ХгХг (соЖох
Ясно, что СПл сигнала ошибки состоит из двух составляющих (рис. 5.55):
1) определяемой выражением
SXtxt («) = \l-W(J(af 5^(0)) = |W0Oco)|2 5^(0))
(эта формула описывает СПл сигнала ошибки через СПл полезного сигнала m(t) и
через передаточную функцию ошибки Wo(/P); данная ошибка определяется тем
фактом, что полезный сигнал m(t) из-за «конечности» и «непрямоугольности» АЧХ
отрабатывается не полностью, с искажениями (рис. 5.57));
2) описываемой выражением
SX2X2((0) = \W(j(0)\2Snn((0)
(эта формула определяет СПл сигнала ошибки через спектральную плотность
помехи Snn((o) и через ПФ замкнутой системы по отношению к возмущающему
воздействию).
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация
ЛИ
329
Ли(со)
Рис. 5.57. К иллюстрации понятия ошибки системы:
/^(со) - АЧХидеальной системы, обеспечивающей отработку сигнала m{t) безошибки\
Лр(со) - АЧХ реальной системы
Лр«о)|5ля(со)
ли(ю)
Л(со)
SJ&
О со
Рис. 5.58. К иллюстрации понятия ошибки o(t)
Ясно, что в идеальной системе сигнал n(t) не должен отрабатываться, но в связи с
тем, что АЧХ Ар((0) реальной системы и Swl(a)) «перекрываются», появляется
составляющая X2(t) в сигнале ошибки (рис. 5.58).
/"
Аи(со)
snnm
со
Рис. 5.59. К иллюстрации понятия ошибки o(t)
Из сказанного выше ясно, что отработка сигнала m(i) без ошибки возможна в
случае, если спектры SWW((D) и S^Cco) не «перекрываются», а АЧХ системы является
прямоугольной (рис. 5.59).
Y(t)=m(t)+n(t) +^ e(Q
wr№
Щ
Рис. 5.60. Структурная схема замкнутой системы
330
Анализ и статистическая динамика САУ. Часть I
На основе изложенного выше выражение для СПл сигнала ошибки имеет вид
5оо((0) = |l-WOo))|2 5mm((o) + |W(yto)|2 5nn(co).
Положим, что рассматривается замкнутая система (рис. 5.60). Тогда
W(s) = - W"
(5.60)
l-W(s) = l-
l + Wp
l + Wp(s)-WB(s)
pvv _
1
1+Wp(s)
l + WJs)
Подставив в формулу (5.60) полученные зависимости, получим
5оо(0)) =
1
1+ВДсо)
$»,«») +
WJM
l+WJJta)
5nn(co).
(5.61)
(5.62)
Последняя формула позволяет определить спектральную плотность сигнала
ошибки 500(со) по заданным спектральным плотностям полезного сигнала Smm((a)
и помехи Sm((ii) и ПФ разомкнутой системы Wp(ja).
Среднее значение квадрата сигнала ошибки (дисперсия) определяется выражением
A,a = °2=J
1
1 + WpOco)
5mm(G))J(0+ J
ВДСО)
l+WD(jco)
Snn((u)da> = G2m+Gl
Анализ динамической точности САУ состоит из следующих шагов:
1). На основании кривых случайного процесса полезного сигнала m(t) и помехи
n(f) определяют соответствующие им корреляционные функции Rmmir) и /?пл(т).
2). По графикам корреляционных функций определяют функции спектральных
плотностей 5mm(co) и 5лп(со) в форме дробно-рациональных выражений.
3). Методом неопределенных коэффициентов представляют ^^„(со) и 5лл(со) в виде
. W<o) = SHMS^,(№ snn(a) = s:n(MS-m(M.
4). Записывают общее выражение для среднего значения квадрата сигнала
ошибки (дисперсии сигнала ошибки) через СПл и ПФ системы.
5). Определяют с помощью таблицы стандартных интегралов составляющие
ст^,а^ (см. приложение 4).
6). Путем суммирования составляющих находят дисперсию сигнала ошибки а2 .
Пример 5.5.
Пусть к системе (рис. 5.61) приложены полезный сигнал m(t) и помеха n{i). Заданы спектральные
плотности сигналов m(t) и n(t):
•• 2Dra, ;£„„(<»))=s0.
г(0=/и(0+л(0 +,
к
*(7i+l)
Щ
Рис. 5.61. Структурная схема системы
Сигналы m(t) и n(t) некоррелированы; их математические ожидания равны нулю. Сигнал X(t) на выходе
системы должен быть близок к полезной составляющей m(t), поэтому ошибка системы равна
O(t) = m(t)-X(t).
Найдем W(j(o) и Wa(ja>):
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 331
W(;a)) =
К
l + WJju>) Ts2+s + K
к
*-jto Г(УшГ + ;ш+ЛГ
Wo(yw) =
1
5(Г5 + 1)
l+wayw) 5(7^+1) + ^
Г(;о))2 + У(О
Г(;а>Г + ;ш+Л:
Найдем спектральную плотность сигнала ошибки
5ОСТ(0)) = W0(yco)Smm(co) + W(ja»SM(<a) =
2
2Dmma
я(оГ+а^)
MTju+l)
T(j<u)z+j(u+K
+s.
T(j(uy + j(u+K
Дисперсия равна
Ara = J 5OCT(0))^0).
Вычислим значение интеграла, пользуясь формулами для стандартного интеграла. Представим Sm^G))
в виде
5mm(co) = S^WS^W - ^^ 1-
я [a + yco][a-yco]
Имеем
о2т = 2я — f Wa(yo))5mm(a))^(o = 4Dmmax
)c 1 7 [Г(;о))24-;о)][Г(-;о))Ч(-;со)]
2я i [ПМ2 + ;о)+ ATJtrc-ycoj2 - ya)+ AT] [a+ ;a)][a + (-;со)]
^/(0
[Г2(О4+СО2]</СО
2я i {[ГСусо)2 + yo)+ K)[ja+a]} {[ГС-уо))2 + (-yco) + АГ][(-;(о) + a)]}
rV+(o2
1 7n J
Запишем:
2я i [ГО'со)3 + (Га + 1)(;ш)2 + (К + а)(у(о) + ATa]g3(-;o))
^зО'а)) = а0(</0))3+а1(У0))2+а2(</а)) + а3,
-^/(0.
где а0 = Г; ах = Га +1; а2 = ^ + а; а3 = Яа, ЛзСУ^) = ^ь(7*со)4 + ^(усо)2 + fe^ причем ^ = Г2; ^ =-1; ^ = 0 .
Запишем табличный интеграл:
где
а3
ао
а4
0
;Л^з =
Ьо
Ь2
ао
а2
а4
0
«3
Тогда
М,=
«3
0
ао
а2
0
0
«3
м,=
= aA:(/i: + a + a2r2);yv:
0
«2
0
0
«3
= ает(1 + аГ + АТ).
При вычислении определителей используется правило Саррюса. Окончательно имеем
"Г _ 20^0(1+ СХ7ЧЛТ)
/Г + а+а2Г2 '
Найдем gz
-1 Л 1
s-H=f
50а:2
2я i (Г(Уо))2 + Усо+ /(Г)(Г(-уо))2 - уш+ АГ)
t/co =
-2rt^Uj
1
^(»
2rc_iegn(ya))gn(-yco)
</© L
332
Анализ и статистическая динамика САУ. Часть I
,2 i т/
где g2U®) = <hU<u) +Л|0'со) + л2, причем
а0 = Г; а, = 1; а2 = АГ; fc0 = 0; Ьх = 1; fc^/to) = b0U<*)2 + ^.
Тогда
а„=2як So—з—
А) а0
А ^2
2я0М2
. °|0 а2
= nS0K.
Дисперсия сигнала ошибки равна
К + а+а2Т2 °
Рассмотрим еще один случай, когда на вход поступает сигнал вида
y(t) = gjt) + n(t),
где g(t) - детерминированный полезный входной сигнал; n(t) - помеха.
Ясно, что расширение полосы пропускания системы приводит к тому, что сигнал g(t) отрабатывается с
меньшей ошибкой, но вместе с тем увеличивается часть ошибки, связанная с отработкой помехи n(t).
Для рассматриваемого случая критерием качества системы может быть
где Eg(0 - установившаяся ошибка отработки полезного сигнала g(0, которая определяется выражением
Здесь Ск - коэффициенты ошибок; для них справедлива формула (рис. 5.62)
C»--j7[1-W(*HL.*-<U2....
as
git)1
Неустановившийся
режим
К.
t) - динамическая
ошибка
Установившийся
режим
Рис. 5.62. К определению е(0
Составляющая aj определяется уже приведенным выше выражением
o2n=j\WU<»)\2Snn ((0)^(0.
Рассмотрим конкретную систему (рис. 5.63). Полезный входной сигнал имеет вид g(t) = hxt, а помеха -
белый шум с нулевым средним и спектральной плотностью 5пп(со) = 50. Динамическая ошибка равна
С0=[1-^)]Ц,
где W(s) - ПФ замкнутой системы.
Y(t)=g(t)+n(t) \
Ж
s(s+2tfon)
щ
Рис. 5.63. Структурная схема системы
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация
Имеем
333
Щз)= <»2пЫ* + 2&п)
*1
1 + со2 / s(s + 2^cow) s(s + 2^con) + со2 s2 + 2£pns + со2
- ПФ замкнутой системы.
Тогда
We(s) = \-W(s) = l—j
о2, = s2+2Z)(i>ns + u>2n -и>2„_ s2 + 2^ns
s2 + 2fyuns + со2 52 + 2^cow5 + coJ s2 + 2Zfuns + to2,
Ясно, что Со = 0 (этот вывод следует из того, что система имеет один интегратор в прямой цепи и,
следовательно, является астатической первого порядка);
Таким образом, динамическая ошибка равна
е(О = С0^(О + С^(О = 0Л1(О+^-Л1=^-.
При отсутствии помех имеем е(0 = g(t)- Xg(t) и, следовательно
Xg(t) = g(t)-E(t).
Найдем ошибку, обусловленную наличием помехи n(t). Имеем
а2= j\W(j(*»\2Snn((i»d<u = 2n
tiSp
_Lf_
2я1[(;со)2 +25cow(yco) + (u2]g2(-yco)
dot
82(№
где
(2nig2(jto)g2(-;(D) J
g2(</co) = 5o(;a))2+a1((/co) + a2; ao = l; a, =2^cow; a2 =co2;
Л2(;со) = Ьо(;а))2 + Jj; Fo =0; b, = 1.
По формулам, определяющим значение стандартного интеграла, находим
. (-0%
" 2а0М2
Дисперсия сигнала ошибки равна
(-1)3
2я0
Ьо
К
"\
«3
а2
а2
-1
2.1(2§и^-0) 4§mJ'
Общая ошибка системы может быть найдена по формуле
5.6. СТАТИСТИЧЕСКИЙ АНАЛИЗ ЛИНЕЙНЫХ СИСТЕМ,
ОСНОВАННЫЙ НА ОПИСАНИИ
В ПРОСТРАНСТВЕ СОСТОЯНИЙ
При описании ЛНС в пространстве состояний
i(0-A(*)X(0+B(0Y(r); 1
XB(0 = C(0X(r);[X(,)],=ro = X<\j
воздействия и сигналы представляют собой вектор-функции - векторы, координаты
которых являются скалярными функциями. Пусть Y(f) - случайная m-мерная вектор-
функция
(5.63)
334 Анализ и статистическая динамика САУ. Часть I
Y(t) = [Yl(t),Y2(t),...,Ym(t)-]T.
Ее полной статистической характеристикой является многомерный закон
совместного распределения всех т случайных функций - компонентов этой случайной вектор-
функции. Даже для вектор-функции невысокого порядка такой закон громоздок и
сложен, поэтому ограничимся рассмотрением только средних значений случайных
функций-компонентов
mYi(t) = M[Yi(t)],i = ui (5.64)
и их авто- и взаимнокорреляционных функций
RYiYj(tX) = M\h(t)Yj(m ij = ui. (5.65)
Если все эти корреляционные функции расположить в виде квадратной
т-матрицы
Ryy {*£) = {V, ('£)}' *J = ^ (5-66>
то с учетом выражения (5.65) легко заметить, что
RYY(^) = M[Y(r)YT(d. . (5.67)
Матрица RYy('/£) называется матрицей корреляционных функций случайной
вектор-функции Y(t).
Если расположить средние значения случайных функций-компонентов случайной
вектор-функции в виде вектора
mY(t) = [mYi (t),mYi (r),. . ,,«у> (г)]Т,
то из выражения (5.64) видно, что
mY(0 = M[Y(,)].
Вектор mY (t) называется средним значением вектор-функции Y(t).
Матрица [Ryy(''£)]c_ = Ryy(*»0 = *Vy(0 называется матрицей
корреляционных моментов вектор-функции Y(f), т.к. компонентами этой матрицы, как это видно
из соотношений (5.65), (5.66), являются корреляционные моменты случайных
величин, получающихся из случайных функций Yfj) при одном и том же фиксированном
значении t их аргумента. По диагонали тогда располагаются дисперсии
^уМ) = м\у .{t)Y .{t)]
случайных функций У,(г), поэтому матрицу PyyW называют еще иногда
дисперсионной матрицей.
Рассмотрим вопрос вычисления среднего значения состояния и выхода ЛИС.
Выполнив над левой и правой частью выражений (5.63) операцию математического
ожидания и учитывая, что операции математического ожидания и
дифференцирования коммутативны, получим
mx(0 = A(0mx(0 + B(0mY(0i
mxB (0=c(0mx (0; [mx (0],=, =mx-
(5.68)
Из сравнения уравнений (5.68) и (5.63) видно, что средние значения состояния и
выхода определяются по средним значениям входа и начальных условий с помощью
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 335
тех оке алгоритмов, которые используются для определения самого состояния и
выхода ЛНС по ее входу и начальным условиям.
Получим уравнение, определяющее дисперсионную матрицу ЛНС. Вычитая из
уравнений (5.63) уравнения (5.68), имеем
X(0 = A(0X(0 + B(r)Y(r)f (5.69)
x.(0=c(r)x(0;[x(0l =х°. (5.70)
Согласно формулам (5.67) и (5.68) получим
•рхх(О=м[х(г)хт(о].
Продифференцировав это выражение, с учетом коммутативности операций
дифференцирования и математического ожидания, имеем
Pxx(f) = M^X(0XT(0J+M^X(0XT(0]. (5.71)
Транспонируем уравнения (5.69), (5.70):
X» = XT(r)AT(f)+YT(/)BT(f), <5Л2>
Хвт(0 = Х»Ст(/). (5.73)
Ф
Подставив теперь в формулу (5.71) выражение для X(t) и X (t) из
соотношений (5.69), (5.72), получим
pxx(O=m^a(Ox(Oxt(O+b(/)y(Oxt(o]+
+м[х(г)ХТ(0Ат(0+Х(0¥Т(/)Вт(0] = А(0Рхх(0+ (5-74)
+pxx(Oat(O+b(Oa/[y(Oxt(o]+m[x(Oyt(o]bt(O.
Поскольку
Х(О = Ф(г,Го)Хо+)ф(гД)В(Х)¥(Я)^, (5.75)
где Ф(г,г0) - матрица перехода ЛНС (5.63), то
м[у(Охт(о1=мГ¥(Ох°(о1фт(г,г0)+
| г. . 1 ' (5'76)
+JM У(г)Ут(г)Ьт(Х)Фт(гД)^ = /к¥¥(гД)Вт(Х)Фт(гД>/Х,
«о •■ J г0
т.к. управляющий сигнал и начальные условия обычно не коррелированы.
Уравнения (5.74) упрощаются для
Y(f) = N(f), (5.77)
т.е. когда управляющий сигнал есть вектор-функция, компоненты которой
представляют собой белые шумы. Если связь между компонентами также «белая», тогда
336 Анализ и статистическая динамика САУ. Часть I
Rnn('A) = S(OS('-*)> (5.78)
где b(t-X) -диагональная /и-матрица, составленная из смещенных дельта-функций;
S(r) = {5/-/ (f)}, Uj = 1,/и - матрица интенсивности векторного белого шума N(f).
Если компоненты пх (t), i = 1,/и взаимно независимы, то матрица S(f) - диагональная.
Если процесс N(r) имеет размерность, например, напряжения (Вольты), то
размерность компонентов матрицы S(r) = |5'/-/(r)}, ij = l,m, равна, в соответствии с
физическим смыслом интенсивности белого шума, квадрату напряжения, поделенно-
(В2 }
го на круговую частоту — = В2с . Дисперсии D компонентов n{(t) равны, со-
(1/с J "
гласно определению понятия белого шума, бесконечности, но если процессы
являются реальными белыми шумами с ограниченным частотным спектром, шириной
Дсо,- 1/с, то
Dnini=S(iA(Oh
где S/, в/?2-с, AcOjB 1/с, следовательно, Dnw в В2.
С учетом формул (5.77), (5.78) выражение (5.76) приводится к виду
MJ^N(0XT(r)j=fs(r)5(r-X)BT(X)OT(a)dX = i[s(0BT(X)OT(a)]x=f.
Множитель — учитывает тот факт, что момент приложения дельта-функции
совпадает с верхним пределом интегрирования [56]. Имея ввиду также, что Ф(г,г) = 1,
получим
m[n(,)xt(o]4s(')bt(O-
Аналогично нетрудно показать, что
j#jx(ONT(OJ-^B(Os(O.
и уравнение (5.74) принимает вид
Pxx(') = A(0Pxx(0+Pxx(0AT(')+B(r)S(0BT(0. (5.79)
Матричному уравнению (5.79) - дисперсионному уравнению - эквивалентно п2
скалярных уравнений, т.к. матрица Рхх(0 имеет размер пхп, но в силу ее
симметричности
п2-п п(л + 1)
следовательно, уравнение (5.7?) эквивалентно системе только +и = -^ -
скалярных уравнений с таким же числом неизвестных.
о
Если сигнал Y(r) небелый (цветной), то построим формирующий фильтр, гене-
о о
рирующий сигнал Y(r) из белого шума N(r) [56]
Y(f) = F(/)Y(/)+N(f), (5.80)
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация
где F(f) - известная матрица формирующего фильтра.
Введя в рассмотрение расширенный вектор состояния
337
*„(')=
х(»)
исходную систему (5.63) и формирующий фильтр (5.80) опишем в виде единой
системы
Здесь матрицы
xp(0=Ap(0xp(0+Bp(0N(0.
(5.81)
На входе системы (5.81), имеющий описание, аналогичное описанию исходной
системы, действует белый шум и, следовательно, методика составления
дисперсионного уравнения (5179) распространяется и на случай цветного воздействия. Правда,
дисперсионное уравнение, записанное для вектора X (г), помимо искомой
информации о Рхх(0 несет не требующуюся в данном случае информацию о матрицах
корреляционных моментов
Rw(O-M[Y(f)YT(o]:Rw(O-^[i(OYT(o}K«(O-[Y(OYT(o].
т.к.
pXpXp(t)=M\kp(t)iTp(t)]=M x{t)\x(t) Y(0
L J |_Y(r)JL
JPxx(') Rxy(')]
LRYX(O Pyy(0J
Это приводит к увеличению расчетной работы, т.к. если размер матрицы F(f)
формирующего фильтра окажется г, то новому дисперсионному уравнению соответствует
(n + r)(n + r + l) ' \ г(г + 1)
■Ц—— скалярных уравнении, т.е. на пг+—- уравнении больше.
Рассмотрим вопрос вычисления матрицы корреляционных функций ЛНС.
Существует несколько примерно равноценных с ^позиции объема вычислений способов
определения матрицы Rxx (г,£). В качестве примера рассмотрим один из них.
Формула (5.75) описывает реакцию в момент t физически реализуемой системы на
начальные условия и сигнал, приложенный в момент г0 (здесь to< t)\ следовательно,
должно быть Х(г) = 0, г < t0.
Чтобы отразить этот факт, формулу (5.75) представим как
. Х(0 = Ф(г,го)1(г-Го)Х(го)+1(г-го)}ф(гД)В(Х)¥(Х)^.
(5.82)
Здесь 1(г - to) = In-1 [г - г0] - диагональная л-матрица, составленная из смещенных
единичных функций
23 Зак. 232
338
Анализ и статистическая динамика САУ. Часть I
(5.83)
l[t-to] = O,t<to,
l[t-to] = l,t>to,
l[t-to] = l/2,t = to.
Согласно определению (5.67) матрицы корреляционных функций, формуле (5.82)
при t > £ > t0, свойству линейности операции математического ожидания, при
условии (5.77) имеем
о о
Rxx(a) = M Х(0Хтф =
=м
O(^)l(/-^)X(^)+l(r-^)Jo(a)B(X)N(X)dX
хтШ
о
т.к. информация о поведении системы на интервале [Г0Д] заключена в сигнале X (£).
С учетом формулы (5.82),
m|V)xt0;)]=
=м\
N(X)
Ф{^0)Щ-к)Х{ф\{%ы0))ф{\ф{хЩх)<1х
= M^)XT(r0)]l(i;-OOT(U)+
+}M[N(X)NT(T)lBT(T)OT(^T)dTl(^-f0) =
'о L ^
= )кщ(Х,т)Вт(т)Фт(^т>/т1(^-г0)(
т.к. входной сигнал и начальные условия обычно некоррелированы
М
\щх)х'
м
= 0.
С учетом условия (5.78),
М
N(X)XT(^)
■1
S(X)6(X-x)BT(x)#T(^T)rfTl^-r0) = 0,
т.к. дельта-функции, приложенные в момент т = X, оказываются приложенными вне
пределов интегрирования этого интеграла, поскольку те Дт = [/0,£] и Хе ДА, = [£,*]
(рис. 5.30).
Глава 5. Линейные САУ: статистический анализ и оптимальная фильтрация 339
Ах
ДЛ
Рис. 5.64. К определению пределов интегрирования
Тогда
Если t0 < г < £ , то из формулы (5.82), при условии (5.77),
X(l) = O(^t)l^-t)X(t)+l^-t)^(^X)B(X)N(X)dX,
t
и аналогично предыдущему случаю нетрудно получить
(5.84)
*хх('Л) = М Х(г)Х
'(*)] =
Pxx(r)I(^-r)0T(iO.'o^^^
(5.85)
Из физического смысла матриц 1(£ - ?). 1(' - ^) (формула (5.83)) видно, что для
получения описания Rxx (t£) во всей области изменения аргументов достаточно
сложить правые части выражений (5.84) и (5.85):
Кхх('^) = Ф('^)1('Ч)Рхх(^)+Рхх(')1(^-0фТ(^0- (5-86)
Формула (5.86) при t = £ с учетом выражения (5.83) дает верный результат
*хх ('.') = рхх (О-
Для вычисления матрицы корреляционных функций в соответствии с алгоритмом
(5.86) нужно располагать дисперсионной матрицей Рхх(0-
Согласно формулам (5.70), (5.73), определению понятия матрицы
корреляционных функций (5.65) и свойству линейности операции математического ожидания
Г\ л
= м с(/)х(охт(^)ст(^) -
Rx.x.(^) = M X,(r)X.(§)
= с(0м x(0xT(^) cT(^)=c(r)Rxx(^)cT(^).
(5.87)
23*
340 Анализ и статистическая динамика САУ. Часть I
ГЛАВА 6. МЕТОДЫ ИССЛЕДОВАНИЯ НЕЛИНЕЙНЫХ
СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
В данной главе изложены методы статистического анализа нелинейных систем
автоматического управления, получившие широкое распространение при решении
конкретных инженерных задач.
К наиболее часто используемым на практике методам принадлежит метод
статистической линеаризации, разработанный И.Е. Казаковым и Р. Бутоном (1954 г.).
Идея метода основана на приближенной замене нелинейных элементов
статистически эквивалентными им линейными звеньями. К полученной после статистической
линеаризации линейной системе могут быть применены хорошо разработанные
методы анализа и синтеза линейных систем. В этом состоит основное достоинство
методов статистической линеаризации. Эти методы обобщены на дискретные системы,
многомерные САУ, на системы с переменными параметрами.
Хотя метод статистической линеаризации и является приближенным, он нашел
широкое применение при инженерных расчетах нелинейных систем
автоматического управления, описываемых дифференциальными уравнениями высокого порядка.
В 1960 г. К.А. Пупковым был предложен метод эквивалентной передаточной
функции. В отличие от метода статистической линеаризации основное внимание в
работах, посвященных данному методу, уделено приближенным исследованиям
сложных нелинейных систем, основанных на представлении нелинейных элементов
статистически им эквивалентными передаточными функциями и соответствующими
частотными характеристиками. Такой подход позволяет распространить на
нелинейные системы частотные методы, широко применяемые для проектирования
непрерывных и дискретных линейных систем.
Характерной чертой [121], в которой изложено содержание рассматриваемого
метода, является ее практическая направленность, наличие подробных таблиц и
графиков, облегчающих применение излагаемого метода для инженерных расчетов.
В начале 60-х годов Н.А. Лившицем и B.C. Пугачевым опубликованы основные
положения метода баланса математических ожиданий и спектральных
плотностей. Последние два метода, в отличие от метода статистической линеаризации,
учитывают обогащение спектра выходного сигнала нелинейного статического
элемента [87].
Широкое распространение при исследовании сложных САУ получил метод
статистических испытаний (метод Монте-Карло). Сущность метода заключается в
непосредственном моделировании работы исследуемой САУ в условиях, близких к
реальным, с учетом всех случайных возмущений. Очевидными достоинствами метода
статистических испытаний являются универсальность и простота. С его помощью
определяются законы распределения выходных координат или, что проще,
отдельные характеристики этих законов. Метод допускает использование не только
математических моделей систем, но также и полунатурных моделей, содержащих отдельные
блоки системы.
К недостаткам метода статистических испытаний следует отнести необходимость
накопления больших массивов информации о выходных координатах системы, что
связано с выполнением значительного объема вычислений. Существенным недостат-
Глава 6. Методы исследования нелинейных САУ 341
ком является громоздкость модели, включающей генераторы случайных
возмущений, и, следовательно, большая трудоемкость. Все это ограничивает применимость
метода [8].
B.C. Пугачевым разработан строго теоретически обоснованный аппарат
представления случайных процессов, исследования нелинейных преобразований случайных
функций и синтеза оптимальных систем, получивший название метода канонических
разложений [114].
Этот метод дает возможность приближенно исследовать весьма общие виды
нелинейных преобразований случайных функций. Он является общим теоретическим
методом прикладной теории случайных функций, дающим возможность решать
основные задачи статистического анализа и синтеза САУ. Он позволяет объединить
статистические методы исследования САУ общей точкой зрения, общим подходом
к решению различных задач и, таким образом, может служить основой для
построения стройной статистической теории САУ [114].
Метод эквивалентных возмущений разработан Б.Г. Доступовым в конце 60-х
годов. Этот метод предназначен для приближенного определения вероятностных
характеристик выходных координат нелинейных САУ по заданным моментам связи
для входных случайных параметров. Существует класс задач, для решения которых
метод эквивалентных возмущений оказывается более эффективным, чем метод
статистических испытаний [55]. Вместе с тем существуют границы, при которых метод
сохраняет свои преимущества. Как указано в [55], прямая попытка применения
метода при большом (порядка десятков и сотен) числе случайных параметров, влияющих
на динамику САУ, приводит к столь сложным вычислениям, что оказывается более
целесообразным использование метода статистического моделирования.
В 60-х годах В.И. Чернецким разработан метод статистического исследования
нелинейных САУ, использующий аппарат интерполирования функций многих
переменных. Метод получил название интерполяционного [174].
В отличие от метода эквивалентных,возмущений, интерполяционный метод
разработан для расчета не только моментов выходных координат, но и
дифференциальных законов распределения на выходе нелинейных систем, т.е. обладает такой же
универсальностью, что и метод статистических испытаний [174]. Интерполяционный
метод можно применять и для решения задачи синтеза оптимальных систем, под
которой понимается определение таких значений конструктивных параметров
элементов систем, при которых вероятность попадания выходных координат САУ в
заданную область достигает своего наибольшего значения. Интерполяционный метод
имеет строгое математическое обоснование.
6.1. ОСОБЕННОСТИ ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ
ПРОЦЕССОВ НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ И СИСТЕМАМИ
Элементы с нелинейными статическими характеристиками вызывают искажение
случайного входного сигнала.
Положим, что на вход нелинейного элемента действует случайный стационарный
сигнал
о
где mY (0 = const - математическое ожидание входного воздействия; Y{t) -
центрированная случайная составляющая входного сигнала. Рассмотрим искажение
процесса Y(t), полагая, что он поступает на вход статического нелинейного элемента с
зоной насыщения (рис. 6.1).
342
Анализ и статистическая динамика САУ. Часть I
При малом уровне помех выходной сигнал равен (сигнал не выходит за пределы
линейного участка)
X(t) = К Y(t) = K[mY+ Y(t)] = ™x+ X(t),
где К = tg a - коэффициент усиления элемента.
ДО
Рис. 6.1. Прохождение синусоидального сигнала через нелинейный элемент
С ростом уровня помех, когда имеет место нелинейный режим работы элемента,
среднее значение выходного сигнала уменьшается, а при очень большом уровне
помех оказывается близким к нулю.
В качестве примера рассмотрим физическую картину прохождения
синусоидального сигнала через нелинейный элемент. Предположим, что на вход нелинейного
элемента с характеристикой F(Y) поступает сигнал вида
Y = ту + sin (01.
Тогда сигнал на выходе нелинейного элемента будет иметь следующий вид
X = F(mY + sin со t).
При прохождении регулярного сигнала (рис. 6.1) (сумма синусоидального и
постоянного) через нелинейный элемент постоянная составляющая на выходе
уменьшается на величину KmY-mx , где KmY - постоянная составляющая при
неограниченной зоне линейности, а тх - действительная постоянная составляющая.
Уменьшение постоянной составляющей обусловлено тем, что синусоидальная
составляющая ограничивается несимметрично, в результате появляется «вредная»
составляющая, усредненная за период синусоиды, которая уменьшает значение К mY .
Если же на вход нелинейного элемента действует полезный сигнал и помеха, при .
нелинейном преобразовании при большом уровне помех эффект действия полезного
сигнала значительно уменьшается.
При прохождении случайного сигнала через нелинейный элемент изменяется его
дифференциальный закон распределения (плотность распределения вероятности).
Рассмотрим этот вопрос более подробно. Положим, что на нелинейный элемент
типа насыщения поступает случайный сигнал, имеющий нормальный закон
распределения (рис. 6.2).
Глава 6. Методы исследования нелинейных САУ
343
Если fY(y) - закон распределения на входе нелинейного элемента, то при
|У(г)| < Ъ ДЗР на выходе нелинейного элемента пропорционален ДЗР на входе. Если
нелинейный элемент работает в нелинейном режиме, то, очевидно, fx (х) = О при
Y(t) > Ъ (рис. 6.3).
-ъ о
-*w
X=F(Y)
Рис. 6.2. Прохождение случайного сигнала через нелинейный элемент
Очевидно, при значениях входного сигнала Y > Ъ или Y <-Ь,Х = В или X = - В,
поэтому вероятность получения величины В или - В на выходе нелинейного
элемента сильно возрастает. Она становится равной величине заштрихованной площади под
участком кривой плотности распределения вероятности входного сигнала fY(у),
лежащей в пределах от Y = Ъ до Y = «> (рис. 6.3) [121]. Это выразится в том, что
плотность распределения вероятности выходного сигнала в точках X = ± В будет
представлять собой 8-функции [121].
Таким образом, выражение для плотности распределения вероятности сигнала на
выходе нелинейного элемента, работающего в нелинейном режиме, можно записать
так
/*<*)=
и
Ь(у±Ъ) при \у\=Ь,
О при \у\>Ь.
Общая площадь под кривой плотности распределения вероятности выходного
сигнала остается равной единице.
Плотности распределения вероятностей сигналов на выходе некоторых
нелинейных элементов приведены в [ 121 ].
344
Анализ и статистическая динамика САУ. Часть I
р =
1/2
-Pi
\
7
/
р\
\
V
>
Р\
7
Р =
1/2
X
-Вов
б
Рис. 63. Плотности распределения вероятности:
а - на входе нелинейного элемента; б-на выходе нелинейного элемента
6.2. СТАТИСТИЧЕСКИЙ АНАЛИЗ НЕЛИНЕЙНЫХ СИСТЕМ,
ОПИСЫВАЕМЫХ ФУНКЦИОНАЛЬНЫМИ РЯДАМИ ВОЛЬТЕРРА
Рассмотрим линейную систему (рис. 6.4).
Y(t)
k(t,x)
X(t)
Рис. 6.4. Линейная нестационарная система
Случайный выходной сигнал системы определяется интегральным соотношением
(начальные условия положим нулевыми, т.е. X ° = 0)
X(t) = jk(t,x)Y(x)dx.
(6.1)
Глава 6. Методы исследования нелинейных САУ 345
Из этой зависимости, пользуясь осреднением по множеству, легко записать формулу,
определяющую математическое ожидание сигнала ДО
mx(t) = jk(t,x)mY(x)dx. (6.2)
о
А теперь положим, что рассматривается нелинейная нестационарная система,
описываемая рядом Вольтерра
ДГ(О = Х|...|*1-(^т1,т2,...,т/)У(т1)Г(т2)...У(т1.)Л1...Л1.. (6.3)
'=1 О О
Для рассматриваемой системы формула, определяющая математическое ожидание
(начальный момент первого порядка) выходного сигнала имеет вид
N г с
а^=А/[ЛО] = А/Щ.../*Д/,т1э...эт/)У(т1)...У(т/)А1...А|.]. (6.4)
'=1 0 ' О
Поскольку интегральный оператор и оператор математического ожидания
перестановочны, то из (6.4) следует
N С С
mx(t) = Y,]--\^,xl,...,Ti)a(ll(xl9x2,...,xi)dxl...dxil (6.5)
'=1 О О
где aty(xl,x2,...,xi) = M[Y(xl)...Y(xi)]-начальный момент /-го порядка
воздействия Y(t).
В формуле (6.5) если mY(t)= yfY(y,t)dy - момент первого порядка, который
определяется через одномерный ДЗР сигнала Y(f), то
+оо+оо +оо
a^(rlfr2f...fr|.)= J J...J ЛУ2--Л/к(л.У2 л;^1 %) dyx...dy{
- начальный момент /-го порядка, определяемый через /-мерный ДЗР.
Начальный момент второго порядка сигнала X(f) определяется так
«1=1*1=10 0 (6-6)
xa^+i2\xl,x29...ixirx[,x2,...ix[)dxl...dx^
При выводе формул (6.5) и (6.6) использовалось свойство линейности оператора
М[(••)] и менялась последовательность операций интегрирования и осреднения.
Начальный момент порядка р сигнала X(t) может быть определен с
использованием рассуждений, которые аналогичны приведенным выше. Записывая (6.3) для
моментов времени t\, t2i ... , tp, перемножая полученные зависимости и используя
осреднение по множеству, находим a^$ (t{, 12,..., tp).
Для рассматриваемого класса нелинейных систем (6.3) корреляционная функция
определяется с помощью таких же рассуждений, как и в случае линейных систем.
Поскольку
/?xx(/1,r2)=M[(x(r1)-/nx(/1))(x(r2)-mx(?2))]=a^(t1,/2)-1
-mx{t,)mx{t2)=a^{tx,t2)-a^{tx)o^{t2),
22 Зак. 232
346 Анализ и статистическая динамика САУ. Часть I
где
а(хх(*\>*2)= J ]x{x2fx(xl,x2,tl,t2)dxldx2,
то
+ ОО+ОО
= J J(^ — mx(г,)){х2 -тх(r2))fx(x{,x2,t{it2)dxxdx2 =
=£XJ-W<i'x' ^J^J^^;..^;2)cx(^2)fc^2^^; т;2)х
'1=1'2=1 0 0 ■
xdtx...dz'h-
-tx}-K( «i.t,.....^) *,• ( >2,т;,..,т;2) (4>^....,т4) а^(т;,...,т;2)х
'l =1 '2 =1 0 0
Xdlp..^ =
N N 'l r2
i,=ii2=ib b
=li2=l о 0
^'(x, t; т;)-а«(т, tJ а<#(т;,...,т;2)] dxx... dx'h.' (6.7)
Если в рассматриваемой системе почти все выборочные функции случайного
входного процесса непрерывны и с вероятностью единица принадлежат области
сходимости этого ряда в пространстве непрерывны* функций, то ряд Вольтерра
сходится рдя почти всех выборочных функций и, значит, по нему можно вычислить
моменты всех порядков выходного сигнала системы.
Вычисления по формулам (6.6) и (6.7) существенно упрощаются, если Y(t) -
нормальный случайный процесс с нулевым средним. В этом случае все моменты
нечетного порядка процесса Y(t) равны нулю:
a(JJ>(T1,...,T/) = 0, / = 1,3,5,... . (6.8)
Моменты четного порядка представимы через корреляционную функцию
следующим образом
а(/>(т1,...,т/) = ХП^(тУ'т^' »' = 2А6,.... (6.9)
В (6.9) суммирование производится по всем разбиениям величин Y{xx),...,Y{xt) на
все возможные пары, а произведение вычисляется для всех пар в каждом разбиении.
/!
Общее число членов суммы равно .
2f'/2(i/2)! '
, Начальный момент порядка/? определяется соотношением
х* it rP тр\ п(^+-+(р)(т1 тр\ /Ут1 ИтР
Глава 6. Методы исследования нелинейных САУ 347
Из последней формулы следует, что для того, чтобы выходной сигнал X(t) имел
конечный момент порядка р, необходимо и достаточно, чтобы входной сигнал Y{t)
имел конечные моменты порядка вплоть до N'p и система (6.3) была устойчива в
пространстве непрерывных функций [123].
Очевидно, если t{ =t2 = ... = tp =tu процесс X(t) - стационарный, то
a^t,...,t) = a^ = jx"fAx)dx.
Даже для линейных систем весьма сложной является задача определения ИЗР или
ДЗР выходного процесса. Только в частном случае, когда процесс на входе линейной
системы нормальный, указанная задача решается просто, т.к. в этом случае закон
распределения процесса на выходе линейной системы остается нормальным и
изменяются только математическое ожидание и функция корреляции. В том* частном
случае, когда ширина полосы пропускания линейной системы мала по сравнению с
шириной спектра входного воздействия, закон распределения процесса на выходе
системы близок к нормальному, даже если входное воздействие имеет распределение,
существенно отличное от нормального. При этом можно приближенно полагать, что
закон распределения выходного процесса полностью определяется его
математическим ожиданием и функцией корреляции.
Весьма сложной является задача построения закона распределения процесса на
выходе нелинейной системы. Для рассматриваемого класса систем можно получить
зависимость, определяющую ДЗР выходного процесса. Известно, что конечномерные
законы распределения (интегральный и дифференциальный) характеризуют «тонкую
структуру» стохастического сигнала. ,
Моментные функции, в частности, начальные моменты k-ro порядка
cc(xkl(h,...,tk) = M[X(tl)X(t2)...X(tk)], * = 1Д...
дают более «грубое» вероятностное описание сигнала и не характеризуют его
однозначно в том смысле, что у двух разных сигналов, ДЗР которых не совпадают, могут
быть одинаковые начальные моменты (до некоторого порядка).
Вместе с тем если известно достаточное число начальных моментов сигнала X(t),
то приближенно можно восстановить ДЗР этого сигнала [123].
С целью рассмотрения этого вопроса введем понятие кумулянтов. Пусть
+ОО
Ч*х (со) = ln[ \fx (x)ejmdx] - кумулянтная функция, (6.11)
—во
+со
где 6Х (со) = fx (x)ej(Oxdx- характеристическая функция.
Кумулянты определяются зависимостью
*к\
(k) _</*Ух(со)
vw —
&ХХ ~
(0=0
, * = 1,2
Рассматриваемый подход используется в тех случаях, когда кумулянтную
функцию можно представить в замкнутой форме. Для численных расчетов часто
используется связь кумулянтов с начальными моментами. Дифференцируя (6.11) по
аргументу со, получим [123]
в^(а)) = ^(со).е^(а)). (6.12)
Повторным дифференцированием находим при со = 0
22* . '
348 Анализ и статистическая динамика САУ. Часть I
ахх - 2j\ • №хх ахх • (0.13)
Из последней зависимости можно получить рекуррентное соотношение для
определения кумулянтов по известным моментам
to, ~ахх 2J[ • гхх ис • 1&.14J
где а^*> = jxkfx{x)dx.
Положим, что сигнал X(t) на выходе анализируемой системы является стационарным.
Тогда, очевидно
а закон распределения не зависит от времени, т.е. fx (jc, t) = fx (x).
Формулы, определяющие первые пять кумулянтов, имеют вид [123]
Ххх ~ахх>
Y(2) _^(2) _f (1) )2 -С\(2)
ахх-^хх v-xx) -Pxx>
v(3) _^(3) 0^(2)^(1) . 9L(1) V-R(3)
Ххх ^ахх~шххахх +zv*xx) -Pxx>
v(4) _ „(3) „(1) oL(2) \2 , 9 (2) L(l) \2 /:L(1) Y _ d(4) _ о(о(2) )2
Ххх -аххахх "Лахх/ +lzccxxlaxx/ -Ьф-хх) -Рхх 5Vxx) »
где р^ - центральные моменты, определяемые формулой .
+оо
№ = j(x-mx)kfx(x)dx,
—оо
где m^ = a^r - математическое ожидание.
Далее воспользуемся рядом Грама - Шарлье [123]
1 -^
fx(х) = —е 2 У с/Я,(х), (6.15)
2п £6
где
cf=-[fx(x)Hn(x)dx,
—ее
причем Нп(х) - полиномы Эрмита; для них имеет место формула
'" .г
Нп{х) = {-\)пех2^е-х\ Л = 1Д....
Полиномы Эрмита можно определять с помощью рекуррентного соотношения
Hn+l(x) = 2xHn(x)-2nHn_l(x)i n>l Н0(х) = 1 Нх(х) = 2х.
Положим, что выходной сигнал нелинейной системы является стационарным, а
/-(*) - ДЗР нормированного случайного процесса X(t). Тогда первые одиннадцать
коэффициентов разложения ДЗР в ряд Грама - Шарлье определяются формулами [87]
Глава 6. Методы исследования нелинейных САУ 349
4=1.^4И+10^'2}'
c/=c/=0,c7/=l(x§+35x^i),
rf _ * VO) rf _ l fv(8) , cfiv(5) (3) .o<L(4) )2^
r/ _ j_Y(4) -/ _ JYYW +»4y<6>v(3) +126v(5)y(4) +28o(v(3) ?1
C4 -^Zxx'c9 -9!^xx+84zxxzJK+120%xif;icxif+Z5UVcxx/ j'
rf _ 1 v(5) ./ _ l fv<10)+nfVv(7)v(3) +?inv(6)v(4) +
+ 126^|>)2+21OOx^(xg)2).
Связь кумулянтов %У~ нормированной случайной величины с кумулянтами х^хх
ненормированной случайной величины определяется зависимостями
v(o _v(o A/L(2) V
Xxy -Kxx/ \\fixx) •
ДЗР /^ (л:) и /х (л:) нормированной и ненормированной случайных величин связаны
соотношением
Ite^j
Путем перегруппировки слагаемых в (6.15) получаем ряд Эджворта, который для
нормированной случайной величины имеет вид
1 _f_ YP;
1 е"2[1 + ±Ж
л/2я 3!
fg(x) = -f=e' 2 [1+J!Lh3(x)+
10^Y(-3)-1 v(5) T?v(4)v(3)
+—-^и-н9М+^-н6(х)+ Л"Л»—^и.я8(*)+
2100y(4) fv(3) \2
+ "Q] та; %(*)+- ]• (6-16)
Если фиксируется максимальный порядок используемых кумулянтов, то ряд
Эджворта, как правило, обеспечивает лучшую аппроксимацию ДЗР, чем ряд Грама -
Шарлье [87], И тот и другой ряды используются при симметричных или слабо
асимметричных ДЗР. /
Пример 6.1 [114]. Пусть система задана структурной схемой (рис. 6.5).
На вход системы поступает центрированный нормальный случайный сигнал Y(t) с корреляционной
функцией Ryyih^l)-
Требуется найти математическое ожидание и корреляционную функцию выходного процесса X(t).
350
Анализ и статистическая динамика САУ. Часть I
' НО
hit т\
1t'
VI/,
квадрато{Г
X(t)
Рис. 6.5. Структурная схема системы
Вход и выход системы, как было показано выше, связаны интегральным соотношением
оо оо
А'(О = Лл2(М1,х2)Г(т1)Г(т2)Л1Л2.
о о
Осредняя обе части последнего равенства по множеству, находим
о о
где Руу (Т|,т2) = М \У(Tj )К(т2 )] = Ryy (TiДг) ~ центральный момент второго порядка.
Окончательно имеем
оо оо
™x(O = J J*2('>T1'OMT1'*2)^1^2-
(6.17)
(6.18)
Для нахождения Rxx^X^l) запишем (6.17) для моментов времени t\ и /2 ♦ перемножим полученные
равенства и осредним по множеству.
Результат имеет вид
0 0 0 0
Момент четвертого порядка Рут(т1>т2»т1»т2) с учетом того, нто сигнал Y(t) имеет нормальный закон
распределения, имеет вид
P$(*i'*2 ,ii Д2)= Ryy^\)Ryy{4^i) + ^«.ti^irW Д2).
А теперь положим, что система, представленная на рис. 6.5, стационарна. Тогда
/ t
mx{t)=\ J k2(tb't2)RYY(Tl-X2)dxidx2y
о о
t t t t
0000
где
= Я>т (^i " Ь )Ryy (< ~ Ь )+Ryy fa - < )Ryy (b ~ *2 )+
+ Ягг(т,-т2)лгк(т2-т;).
Если система устойчива и работает в установившемся режиме, то выражения для математического
ожидания и дисперсии принимают вид
mx=j jk2(Tl,T2)RyY(Tl-'z2)d'zldT2,
о о
Dxx iifi к2к>ъЫ<>ФА{^<,Фъ<1ъ<1<<хг ■ .
0 0 0 0
Пример 6.2 [114]. А теперь рассмотрим случай, когда система имеет стохастическую нелинейность,
т.е. нелинейность имеет случайные параметры. Пусть система имеет структурную схему, изображенную на
рис. 6.6.
Глава 6. Методы исследования нелинейных САУ . 351
Y(t)
ai — oY
до
к(х)
X(t)
Рис. 6.6. Структурная схема системы
Нелинейный элемент описывается зависимостью
Z(t) = aY-bY\
где аиЬ- случайные параметры с дифференциальными законами распределения fa(a) и /ь(Ь).
Кроме этого, положим, что Y(t) - нормальный случайный процесс, имеющий математическое
ожидание mY и функцию корреляции RYY (т). Выражение для выходного процесса имеет вид
X{t) = a\k(x)Y(t-x)dT-b\k(T)Y*(t-T)di. (6.19)
о о
Формула для условного среднего, вычисляемого при фиксированных а и Ь , запишется так
м[х{1)\ауъ]=ату fk(x)dx-b{ k(T)M[Y3(t-T))dx.
о о
Поскольку
Л/[г3(о]=/иу +Ътуо\ , ч (6.20)
то
/
M[x(t)\a,b]=[amY -b{m\ +3mYo2Y)] f k(t)dx. (6.21)
о
Воздействуя оператором М по айв на (6.21), находим абсолютное среднее значение
M[M[x(t)\a,b\ = [M[a)mY -M[b](mY +3mYaj))jk(T)dT .
о
Заменим выражение для условного второго момента
м[х2(ф)б]=а2||*(т1)А(т2К(х2 -т,)+т»К*2 -
о о
г г
-2abjjk(x,)k(^h%,^)d-c,dx2 + ■ (6.22)
о о
0 0-
где
aYY(zl;T2) = mY +3mYaY +3RYY(Tl -T2)(mY +OY)>
aYY (x{, x2) = mY + Зт^а^ (2/я J + За \ )+
+ 9^(1, -x2)(wy +oY)2 + \ZRyy(b -*2)my +6RYY(xl -x2).
Осредняя (6.22)' noanb , получим зависимость, определяющую второй момент
М[М[Х2(ОИ]] = ||/:(т1)Л(т2){Л/[а2][%(т1-т2) + т2] -
00
-2М[а] M[b]ol^(xl,Т2) + М[Ь2) o^(tltt2)]) dxx dz2 =
<=mY[M[a2] -2M[a]M[b](mY+3G2Y) + M[b2](rnY +
+6m2 a2 +9aY)) JJ/rdi)^) dxx dz2 +jj*(T1)*(x2) [M[a2]RYY{x{ -x2)-
00 . 00
-6M[a]M[b] RYY(xx -T2)(m2+G2Y) + M[b2](9<
+\ZRY\(Tl-T2)m$+6RY\('Zl-T2)))d'Cldx2.
-6M[a]M[b] RYY(T{ -Z2){m2 +o2Y) + M[b2](9RYY(xl -T2)(m2 +a?)2 +
Анализ и статистическая динамика и А У. Насть 1
При f=oo результаты будут соответствовать установившемуся режиму. Рассмотрением, ртих
примеров было проиллюстрировано, что аппарат функциональных рядов Вольтерра позволяет получить
конструктивные результаты при решении вопросов статистического анализа классов нелинейных систем,
включая и стохастические нелинейные системы.
Пример 6.3 [114]. Рассмотрим еще один типичный пример - систему, представленную на рис. 6.7.
до
1—►
X
1
КО
1
\
J
г
<
i.
X(t\
X2(t)
Рис. 6.7. Структурная схема системы
Положим, что на вход системы поступает случайный сигнал, задаваемый соотношением
Y(t) = c]q>l(t) + c2q>2(t) + c3q>3(t) + ...,
где с,- - случайные величины с известным дифференциальным законом распределения. Для
определенности положим, что
Y(t) = a + bt, кх (т) = e~Y'T, к2 (т) = e"Y2Tcoso)0x.
Имеем
f -Y.O-t.)
*i(O = Je (a + bxOdx^
о
/ч л -Y2(/-x2)
X2(t)=J e cos[(r-T2)o)0](a + bT2)^T2.
о
Выходной сигнал определяется выражением
X(t) = llk2(Tl,T2)(a + b'Zl)(a + bT2)dxld*c2t
00
где
^2(TI,T2) = e"Y|T|"Y2T2coso)0T2..
Последнюю зависимость можно представить в виде
X(t) = a2Al(t) + abA2(t) + b2A3(t),
где
t i
А'(')=Я е'и"х>)'Ы"Тг) cosKr-^XOolT.rfr.dXj,
00
Л2(,) = Л е-г,<".НМ<-г> cos[(r-T2)(D0]tIrfrIrfT2 +
о о
+ JJ^Yl(/-T')-Y2(/-X2)cos[(r-T2)a)0]x2^I^2,
(6.23)
(6.24)'
(6.25)
о о
^3(0 = JJ^Y|(/"T|)~Y2(/"T2)cos[(r-T2)o)0]TIT2^1^2.,
(6.26)
(6.27)
о о
Поскольку функции А^О, A2{t) и А3(/) случайных составляющих не содержат, та из (6.24) легко
получить зависимость для момента любого порядка сигнала X{t). Полагая известными дифференциальные
Глава 6. Методы исследования нелинейных САУ 353
законы распределения параметров а и Ь, можно определить статистические характеристики выходного
сигнала для Любого t , включая и установившийся режим (f = °°).
Пример 6.4 [114]. Пусть требуется вычислить статистические характеристики выходного сигнала
нелинейной системы, содержащей два канала: линейный и квадратичный. Тогда выходной сигнал
определяется формулой
X(t) = jkl(ttx)Y(x)dx + jjk2(tyxlyx2)Y(tl)Y(x2)dxldx2.
О 00
Положим, что Y(t) - нормальный случайный стационарный процесс с нулевым математическим ожиданием.
Повторяя приведенные выше рассуждения, легко записать зависимости, определяющие
математическое ожидание и автокорреляционную функцию выходного сигнала X(t)
t t
00
Rxx(t\>h) = M[(X(tl)-mx(tl))(X(t2)-mx(t2))) =
= jjkl(tl,xl)kl(t2yx2)RYY(xlyx2)dxldx2 +
г!!!!^^^,^)^^!;,^)^^,^)^^,^)^^^^.
00
+ 2j
0000
Дисперсия DXx(t\ согласно определению, может быть получена, если в последней формуле положить
*i = h ~ t ♦ соответствующая формула имеет вид
/ t
. / \ / \ / \ .
0 0
/ / / /
00
/ / / /
+ 2jJJJ/c2(/,x1,x2)A:2(/,x;,x^>/?KK(x1,x0^Ky'(^2^2)^^i^x2^x^x^.
0000'
В частности, если входной процесс Y(t) - нормальный стационарный белый шум интенсивности So с
нулевым математическим ожиданием и корреляционной функцией /fyy(x) = 2я505(т), то формулы,
определяющие математическое ожидание и дисперсию выходного сигнала, имеют вид
i
тх (О = 2nS0 \ k2(t,-z,T)dTy
о
t t t
Dxx{t) = 2nSQ^kx2{bz)dz^AnSQ^kl{tyzbz2)dz{dz2.
0 .00
Установившееся значение этих характеристик на выходе системы можно получить, если положить
нижний предел равным -°°, т.е. считая, что входное воздействие поступило в бесконечно удаленный в
прошлом момент времени. Для стационарной системы математическое ожидание и дисперсия
неустановившегося процесса принимают вид
со
mx(t) = 2nSojk2(T,T)dT,
о . ,
Dxx(t) = 2nSojkl2(x)dx + 4nSojjk22(xltx2)dTldx2.
0 00
Из теоретических положений и примеров следует, что для определения математического ожидания
выходного сигнала нужно знать N-мерные моменты воздействия, а для определения начального момента
второго порядка - 2М-мерные моменты.
Очевидно, с увеличением N возрастает сложность и трудоемкость вычислений. Поэтому метод
статистического анализа с помощью рядов Вольтерра при больших N с практической точки зрения является
весьма громоздким.
ЗЬ4
Анализ и статистическая динамика САУ. Часть I
6.3. МЕТОД СТАТИСТИЧЕСКОЙ ЛИНЕАРИЗАЦИИ
ВЕРОЯТНОСТНОГО АНАЛИЗА НЕЛИНЕЙНЫХ СИСТЕМ
Метод статистической линеаризации предложен одновременно И.Е. Казаковым
(Россия) и Р. Бутоном (США) в 1954 г.
Рассмотрим основные положения этого метода [8, 65, 66, 126 ]. Можно указать
три типа нелинейных систем, в которых нелинейный элемент имеет место в прямой
цепи и цепи обратной связи. Структурные схемы этих систем представлены на
рис. 6.8, а - в.
Г
I
Линейный
элемент
Нелинейный
элемент
ДО
У(0
е(0
Нелинейный
элемент
2(0
Линейный
элемент
*(0
Y(t) +
8(0
'^ф^
Линейный
элемент
до
Нелинейный
элемент
Рис. 6.8. Структурные схемы нелинейных систем:
а - нелинейный элемент в цепи ОС\ був — нелинейный элемент в прямой цепи
В методе статистической линеаризации вводится понятие статистической
эквивалентности нелинейного и линейного элементов.
В структурных схемах, согласно методу статистической линеаризации
(рис. 6.8, а - в), нелинейный элемент заменяется статистически эквивалентным
линейным элементом.
Используются два критерия статистической эквивалентности:
1). Критерий равенства математического ожидания и дисперсии случайного
процесса на выходе нелинейного элемента и эквивалентного ему линейного элемента.
2). Критерий минимума математического ожидания квадрата разности
случайных процессов на выходе нелинейного элемента и эквивалентного ему линейного
элемента.
Статистической линеаризацией называется замена безынерционного
нелинейного элемента статистически эквивалентным ему безынерционным линейным
элементом.
Рассмотрим подробно процедуру замены нелинейного звена линейным и
проведем анализ правомерности такой замены.
Обозначим безынерционное нелинейное преобразование в обобщенной форме
таким образом, как показано на рис. 6.9.
Глава 6. Методы исследования нелинейных САУ
355
7(0
Нелинейный
элемент
X(t)
Рис. 6.9. Безынерционный нелинейный элемент
Для простоты изложения предположим, что рассматривается нелинейный элемент
с нечетной однозначной характеристикой
X(t) = F(Y(t)),
т.е.
f{-y)=-f(y).
При рассмотрении четных характеристик необходимо учитывать выпрямляющее
свойство нелинейных элементов, которое приводит к отличному от нуля
математическому ожиданию выходного сигнала, если входной сигнал имеет даже нулевое
математическое ожидание.
Случайные процессы на входе и выходе нелинейного элемента представим так
Y(t) = mY(t) + Y(t), ' (6.28)
X(t) = mx(t)+X(t); (6.29)
где mY(t),mx(t) - математические ожидания входного и выходного сигналов
соответственно, ч включающие медленно меняющиеся регулярные составляющие;
о о
Y(t) ,X (г) - центрированные случайные составляющие процессов на входе и
выходе нелинейного элемента соответственно (рис. 6.10).
X(t)=mx(t)+Ht) .
Y(t)=mY(t)+Y(t)
m,
(<)
Н)
к
1 .
тХл (*) = К0тУ
&*.(')•
хл(1)=кЛ1)
Рис. 6.10. Структурные схемы:-
а - нелинейного элемента; б - его линейного эквивалента
Заменим нелинейный безынерционный элемент двумя статистически
эквивалентными линейными безынерционными элементами с передаточными функциями (для
стационарных систем) W0(s)= Ko и Wx(s)= Kx; сигнал на выходе линейного
элемента определяется формулой
*»(')= KomY{t)+KiY{t).
356
Анализ и статистическая динамика САУ. Часть 1
Таким образом, линейный эквивалент с передаточной функцией W0(s)= Ko имеет
отношение только к процессу отработки математического ожидания воздействия, а с
передаточной функцией Wl(s)=Kl - к отработке центрированной составляющей
входного сигнала.
Прэтому часто говорят, что нелинейный безынерционный элемент заменяется
двумя безынерционными линейными элементами: по математическому ожиданию с
коэффициентом усиления Ко и по случайной центрированной составляющей с
коэффициентом усиления К{.
Структурные схемы нелинейного элемента и его статистически эквивалентного
линейного элемента представлены на рис. 6.10.
Коэффициенты Ко и Кх называются коэффициентами статистической
линеаризации соответственно по математическому ожиданию и по центрированной
составляющей.
Рассмотрим решение важнейшего вопроса, связанного с определением
коэффициентов статистической линеаризации.
Воспользуемся первым критерием статистической эквивалентности, в
соответствии с которым математическое ожидание и дисперсия на выходе нелинейного
элемента и эквивалентного ему линейного элемента равны.
Учитывая основное положение сформулированного критерия, имеем
тх(0-тхл(0'
(6.30)
Dxx{t) = DXnXj](t).
Исходя из сказанного, можно записать
DXn>xJt) = Dxx(t)=Kl2DYY(t). (6.32)
Отсюда сразу же запишем соотношения, определяющие коэффициенты Ко и К{
Поясним соотношение (6.32). Имеем
\xY(t)
Отсюда получим
Wx
\DY
.хл.
•=±
м
ах
kit)
f) у!
= м
1
I
= K?Dyy(t).
-fOO
\F\y)fr{y)dy-m2x{t)
1/2
поскольку
°x(f)=
\F2{y)fy{y)dy-m\it)
1/2
(6.33)
(6.34)
(6.35)
(6.36)
где fY(y) - дифференциальный закон распределения случайного процесса Y(t),
имеющего место на входе нелинейного элемента,
Знак в выражении, определяющем коэффициент статистической линеаризации
Kj(1), необходимо выбирать из условия совпадения знаков X(t) и Хя (t).
Глава 6. Методы исследования нелинейных САУ
357
Получим решение задачи нахождения формул, определяющих коэффициенты
статистической линеаризации Ко и Kf' при использовании второго критерия
статистической эквивалентности
£2=мГ (Х(г)-Хл(г))21 = 1шп. (6.37)
Подставляя в последнее выражение зависимости, определяющие X(t) и Хл(г),
получим
г2=М
mx{thh)-KomY(t)-K^°Y{t)
= min.
(6.38)
Отсюда имеем
г2
= М [m2x(t)+ X 2 (0+ Kl ml (t)+ (к^)2 Y2(t)+2mx(t)x(t)- 2K0mY (t)mx (t)-
-2 К\2)тх (t)Y(t)- 2 X(t)K0 mY(t)- 2к\г) X(t)Y{t)+ 2K0 K®mY(t)Y(t)] =
= m2x (t)+ Dxx (t)+ Kim2 it)- 2K0mY {t)mx (t)-
-2K(2kXY(0)+(KU)2 DYY(t).
В последней формуле тх (t) - математическое ожидание случайного процесса на
(6.39)
выходе нелинейного элемента; DYY (t) = M
Y(t)
, Dxx(t) = M\\X(t)
-дисперсии центрированных случайных процессов на входе и выходе нелинейного
элемента соответственно; RXY (0) =М \ X[t)Y[t) \ - математическое ожидание произведе-
|=м|*(г)У(/)]-
ния двух случайных функций X(t) и Y(г), равное начальному значению взаимной
корреляционной функции RXY (О).
При заданных значениях mx(t),DYY(t),Dxx (t),RXY(o) величина е2является
функцией параметров Ко и К^'.
Значения Кои Kf\ при которых выполняется (6.38), найдем, если приравняем
нулю частные производные функции е2 по параметрам Ко и К™.
Найдем частную производную по Ко
Эг2
дКс
• = 2K0mf(t)-2mY(t)mx(t)=0.
(6.40)
Отсюда получаем
KomY(t)=mx{tl К0=^Щ. (6.41)
mY{t)
Таким образом, в случае нечетной характеристики нелинейного элемента
получаем выражение для коэффициента Ко таким же, как и при статистической
линеаризации по первому критерию.
Частная производная от (6.39) по К[2) имеет вид
358
Анализ и статистическая динамика САУ. Часть I
Эе2
дК[2)
= 2K$2)DYY-2RXY(0) = 0.
Тогда
Поскольку
Aj Uyy -КХу{\)), К{ - — .
д
(6.42)
(6.43)
YY
«xr(0)= J (y-%)F(y)/K(y)rfy,
то коэффициент статистической линеаризации К[2) можно выразить через
дифференциальный Закон распределения входного сигнала Y(f) и нелинейную
характеристику F
К\2) = —— \(y-my)F( y)fr (y)dy.
(6.44)
Обычно значение коэффициента К^\ определенное из первого критерия по
• (6.35), является несколько завышенным, a Kf', определенное из второго критерия
по (6.44), - несколько заниженным, поэтому при практических расчетах
рекомендуется брать их среднее арифметическое значение, т.е.
Кх=(к11Кк^)/2. (6.45)
Из приведенных выше рассуждений следует, что формулы, определяющие
коэффициенты статистической линеаризации по математическому ожиданию с
использованием первого и второго критериев статистической эквивалентности, совпадают.
Анализ зависимостей, определяющих коэффициенты статистической
линеаризации по математическому ожиданию и дисперсии, с использованием двух критериев
эквивалентности показывает, что для расчета Ко, К}1' и Kf' необходимо знать
функции F(y(t)) и fy(y). Нелинейная функция F(Y(t)) известна, неизвестным
остается дифференциальный закон распределения. При расчетах полагают
(у-'Пу)2
fY{y)= ) e 2D" , (6.46)
^2nDYY
т.е. предполагается, что закон распределения случайного процесса на входе
нелинейного элемента является нормальным
-(О
(2)
Тогда коэффициенты Ко , К}' и К\' определяются формулами
т„ J ./9.1Г П....
*J')=±
• Va7
KU = -±-](y-mY)F(y
1 e<y-m^l<2b^dy-m\
2% Dyy
1/2
'YY
-h->»r)2feDyy\
>dy
(6.47)
(6.48)
(6.49)
Глава 6. Методы исследования нелинейных САУ
359
Из последних трех зависимостей следует, что при использовании предположения -
о нормальности дифференциального закона распределения fY (у) каждый из
коэффициентов статистической линеаризации зависит лишь от математического
ожидания ту и дисперсии DYY процесса У(г),т.е.
K0 = K0{mY,DYY), K^ = K^{mYiDYYl K[2) = K\2\my,DYy).
Таким образом, справедлива структурная схема, изображенная на рис. 6.11.
Yif)
ffly
+
x{t)=F[Y(t)]=mx+x{t)
е(0 = Х(0-ВД
Рис. 6.11. Схема замены нелинейного элемента статистически эквивалентным линейным элементом
Факт, что коэффициенты Ко и К{ зависят от параметров mY и DYY сигнала на
входе нелинейного элемента, отражен на рис. 6.11 пунктирными линиями [65],
С учетом статистической линеаризации, каждая из нелинейных систем,
структурные схемы которых представлены на рис. 6.8, а - в заменяется двумя замкнутыми
связанными линеаризованными системами: по математическому ожиданию и по
центрированной случайной составляющей (рис. 6.12, а - в).
Рассмотрим решение задачи статистического анализа устойчивых стационарных
нелинейных замкнутых систем с использованием метода статистической
линеаризации. Как и ранее, полагаем, что нелинейный элемент имеет однозначную нечетную
характеристику. Положим, что на вход системы (рис. 6.12) поступает стационарный
случайный сигнал Y(t) с математическим ожиданием mY и автокорреляционной
функцией Дуу(т). Задача заключается в нахождении математического ожидания тх
и дисперсии Dxx выходного сигнала X(t) при предположении, что исследуемая
система работает в установившемся режиме.
Подробно рассмотрим систему, в которой нелинейный элемент находится в цепи
обратной, связи'(рис. 6.12, а). Передаточные функции замкнутой статистически
линеаризованной системы по математическому ожиданию и по центрированной
составляющей можно записать соответственно в виде
l + K0(mx,Dxx)W(sY
W(s)
(6.50)
(6.51)
360
Анализ и статистическая динамика САУ. Часть I
Ht) +
-i
fflv
'"К .
1
1
1
1
h
У
f
1
♦i
-tHK
"T
о
>у£(0
о
/ \
8(0
1
I
» i
A
—►
л
j
л
:0(mxj
V
1
(rn Г
i\mx,L
a
К Am
I*
1
|i-
! ,
f___
г—
) ^
}xx)
DCP)
E£/
Б
D )
К Am
Кх{тг
n
mx
! +'
i i^
1 о
1 w/ \
•I x(0
. J
TI7/ \ ad
Vv(5) и
) ,и
) •
• +f
+
2 k(t)
\ Щ
)
i
mx
op
J
ho
•
nx
Рис. 6.12. Структурные схемы линеаризованных по методу статистической линеаризации
замкнутых систем управления
'XX
Глава 6. Методы исследования нелинейных САУ 361
В связи с тем что рассматривается установившийся режим работы стационарной
устойчивой системы, из (6.50) находим зависимость, определяющую математическое
ожидание выходного сигнала
mx=Wcm(0K _ИФЦ . (6.52)
В последнюю формулу входит коэффициент статистической линеаризации
K0(mx,Dxx) по математическому ожиданию. Численное значение его неизвестно,
поскольку для его расчета по формуле (6.33) необходимо знать математическое
ожидание и дисперсию сигнала на входе нелинейного элемента. В связи с этим
рассчитать математическое ожидание тх по формуле (6.33) не представляется возможным.
Вместе с тем зависимость (6.52) можно рассматривать как уравнение, содержащее
два неизвестных: тх и Dxx . Для получения второго уравнения запишем формулу,
определяющую дисперсию сигнала X (г)
ш 7 у(ар) |2 (ю) 6 53)
где Syy{®) - спектральная плотность воздействия.
Последняя зависимость, как и (6.52), содержит два неизвестных: Dxx и тх .
Выражения (6.52) и (6.53) можно рассматривать как систему двух уравнений с
двумя неизвестными D^ и тх, совместно решая которые, можно приближенно
найти математическое ожидание и дисперсию выходной переменной
рассматриваемой нелинейной системы.
Приближенное решение системы уравнений (6.52) и (6.53) может быть найдено
графоаналитическим методом. Один из таких путей состоит в построении кривых,
соответствующих уравнениям (6.52) и (6.53) в координатах (mx,Dxx), и
нахождении их точки пересечения, которая дает решение указанной системы уравнений.
Изложим достаточно простой метод, основанный на графоаналитическом подходе
нахождения Dxx и тх .
Заменим уравнение (6.52) равноценной системой вида [114]:
W(0)mY ' ,,_.ч
т =п, г| = / ч—т~ч • (6.54)
l + K0(mx,Dxx)w(0)
На графике с координатами {тх,г\) уравнению тх =Г| соответствует
биссектриса координатного угла (рис. 6.13).
Перепишем уравнение (6.54) в виде
4 = /i(m*,O«). (6.55)
Как видно из последней зависимости, функция f{ зависит от двух переменных.
Будем считать аргумент D^ параметром. Задаваясь конкретными значениями
параметра Dxx , рассчитаем семейство кривых
n = /,(mx,Z)W), Л = /,и,Ох2]), Ti = /1(/nx,Df]))... (6.56)
и построим соответствующие графики в координатах {ц,тх) (рис. 6.13).
Поскольку точки пересечения кривых Г) = /Дтх, Djft j с биссектрисой со-
li=l,2,3,...
ответствуют г\ = тх ^ то графики, представленные на рис. 6.13, позволяют построить
кривую Dxx = D^x (mx) в координатах (Dxx ,тх) (кривая 1 на рис. 6.14).
362
Анализ и статистическая динамика САУ. Часть I
А Л
тх=х\ . .
^al
. filpx^D™)
/МхЛ)
«0)
(2) w(3) m(4) m(5)
fflv
my mv mv m
mx
Рис. 6.13. Графики функций
/ifr»x.0j«)
Аналогичным образом поступим с уравнением (6.53).
Полагая
£>хх=Л. Л=|
получим
r\ = f2(mx,Dxx).
5KK(co)do),
>
/
г
У
[mx,L
—-
^ 1
г- 2
£*►
0) ^(2) ^.(3) w(4)
ту т
т\
т\
mf
m
,(')
(6.57)
(6.58)
Рис. 6.14. Кривые, определяющие решение уравнений (6.52) и (6.53)
В последней зависимости полагаем, что тх - параметр; построим функции
ц = f2\Pxx>mx) ПРИ тех значениях параметра тх, которые имеют место на
графиках (6.33) и (6.34) по оси тх . В результате легко построить графики (см. рис. 6.15).
На основе этих графиков можно построить кривую 2, представленную на рис. 6.14.
Глава 6. Методы исследования нелинейных САУ
363
Точки пересечения кривых 1 и 2 определяют математическое ожидание тх и
дисперсию Dxx в установившемся (равновесном) состоянии нелинейной системы.
При проведении инженерных расчетов, связанных со статистическим анализом
сложных нелинейных систем, для нахождения тх и D^ часто используется метод
последовательных приближений.
XI
D1
№
D(i)
- фи**1?}
• фи**®}
► Dxx
XX
В® °% »% *>& .-.
Phc. 6.15. Графики функций /2 [p^ , m^ )
Численное решение задачи целесообразно проводить в следующей
последовательности:
1). Задают, учитывая опыт расчета близких по назначению систем, нулевые
приближения ту и D^ ;
2). Рассчитывают коэффициенты статистической линеаризации Ко и Кх по
формулам (6.33), (6.35) и (6.44);
3). Проводят расчет системы, используя зависимости (6.52) и (6.53); в результате
находят первое приближение ту и D^ .
Далее процесс повторяется до выполнения условий
т
И) _„(.;)
mi
<£i
|n(/+1)_n(0 |<р
\UXX UXX \< е2 t
т.е. до тех пор, пока в итерационном процессе последующие значения
математических ожиданий и дисперсий не будут с достаточной степенью точности совпадать с
предыдущими значениями.
Аналогичным образом проводится статистический расчет нелинейных систем,
представленных на рис. 6.12, б и в.
Метод статистической линеаризации может быть применен к системам с
несколькими нелинейными элементами [66]. В общем случае безынерционные
нелинейные элементы САУ можно рассматривать как многомерные функциональные
зависимости вида
X=F{Y{J2 Гп), (6.59)
где F - произвольная однозначная нелинейная функция. Для статистической
линеаризации рассматриваемой нелинейности выходная переменная представляется в виде
п о
X=F0 + 2jKiYi, / = l,n.
/=1
364
Анализ и статистическая динамика САУ. Часть I
Далее можно воспользоваться вторым критерием статистической
эквивалентности нелинейного элемента и линейного эквивалента
\2~
м
Ffaj^jJ-Fo-^KJi
i=\
= min.
В результате получим уравнения
F0=M[F(YuY29...,Yn)]9
где
п
^K,Dv=DFj, j = l,n,
1=1
Dtj = А#Гу,(г)У;(г )j, DF. = m\f Yj{t)].
(6.60)
(6.61)
(6.62)
(6.63)
Решение последней системы приводит к следующему результату [66]
Ki=y,{-i)i+J^-DF., / = п, (6.64)
где А - определитель системы (6.62),
Д'у - алгебраическое дополнение элемента i -го столбца j -й строки
определителя Д.
Если переменные Y^t)^^),...,Yn(t), поступающие на нелинейный элемент, не-
коррелированы, то
К,=-
M\FYi
Du
, I = 1, И .
(6.65)
Положим, что плотность вероятности совместного распределения переменных
Y{(t),Y2(t) ,...,Yn(t) является нормальной
/,(У1,Г2,...,Гп) = -7_ехр
2А
(6.66)
где А* - окаймленный определитель, получаемый из А путем приписывания одного
(п +1) столбца и (п +1) строки из членов Y{ - mY , Y2 - mY ,..., Yn-hiy ,0.
Если продифференцировать зависимость
F0=Af[F(rlfy2f...fi;)] (6.67)
по mY. при нормальном законе распределения, то можно получить новое выражение
для коэффициентов статистической линеаризации
dmY
(6.68)
Кратко остановимся на вопросе вычисления коэффициентов статистической
линеаризации Ко, К}1' и KfK
При нормальном законе распределения коэффициенты Ко, к[1' и Kf'
выражаются через функцию Крампа (функцию Лапласа)
Глава 6. Методы исследования нелинейных САУ
365
0{x)=JL]e~Z2dz.
(6.69)
Для проведения расчетов достаточно знать математическое ожидание mY и
дисперсию Dyy случайного процесса Y(t) на входе нелинейного элемента и значения
функции Крампа для аргументов, определяемых mY и DYY .
Табулированные значения функции Крампа приведены в табл. 6.1.
С целью упрощения реализации метода статистической линеаризации построены
формулы и графики для расчета коэффициентов статистической линеаризации Ко,
к[1) и К\2) для некоторых типовых нелинейных элементов. Здесь (табл. 6.2)
приведем указанные формулы для некоторых нелинейных элементов с нечетными
характеристиками. Полная информация приведена, например, р [8, 65, 66] и др.
Таблица 6.1
1 г —
Значения функции Крампа Ф(х)=-==\е 2dz
V2*J0
X
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,10
0,11
0,12
0,13
0,14
0,15
0,16
0,17
0,18
0,19
0,20
0,21
0,22
0,23
0,24
0,25
0,26
Ф(х)
0,0000
0,0040
0,0080
0,0120
0,0160
0,0199
0,0239
0,0279
0,0319
0,0359
0,0398
0,0438
0,0478
0,0517
0,0557
0,0596
0,0636
0,0675
0,0714
0,0753
0,0793
0,0832
0,0871
0,0910
0,0948
0,0987
0,1026
X
-
0,41
0,42
0,43
0,44
0,45
0,46
0,47
0,48
0,49
0,50
0,51
0,52
0,53
0,54
0,55
0,56
0,57
0,58
0,59
0,60
0,61
0,62
0,63
0,64
0,65
0,66
Ф(х)
-
0,1591
0,1628
0,1664
0,1700
0,1736
0,1772
0,1808
0,1844
0,1879
0,1915
0,1950
0,1985
0,2019
0,2054
0,2088
0,2123
0,2157
0,2190
0,2224
0,2257
0,2291
0,2324
0,2357
0,2389
0,2422
0,2454
X
-
0,81
0,82
0,83
0,84
0,85
0,86
0,87
0,88
0,89
0,90
0,91
0,92
0,93
0,94
0,95
0,96
0,97
0,98
0,99
1,00
1,01
1,02
1,03
1,04
1,05
1,06
Ф(х)
-
0,2910
0,2939
0,2967
0,2995
0,3023
0,3051
0,3078
0,3106
0,3133
0,3159
0,3186
0,3212
0,3238
0,3264
0,3289
0,3315
0,3340
0,3365
0,3389
0,3413
0,3437
0,3461
0,3485
0,3508
0,3531
0,3554
X
-
1,21
1,22
1,23
1,24
1,25
1,26
1,27
1,28
1,29
1,30
1,31
1,32
1,33
1,34
1,35
1,36
1,37
1,38
1,39
1,40
1,41
1,42
1,43
1,44
1,45
1,46
Ф(х)
-
0,3869
0,3888
0,3907
0,3925
0,3944
0,3962
0,3980
0,3997
0,4015
0,4032
0,4049
0,4066
0,4082
0,4099
0,4115
0,4131
0,4147
0,4162
0,4177
0,4192
0,4207
0,4222
0,4236
0,4251
0,4265
0,4279
366
0,27
0,28
0,29
озо
0,31
0,32
0,33
0,34
0,35
0,36
0,37
0,38
0,39
0,40
1,61
1,62
1,63
1,64
1,65
1,66
1,67
1,68
1,69
1,70
1,71
1,72
1,73
1,74
1,75
1,76
1,77
1,78
1,79
1,80
1,81
1,82
1,83
1,84
1,85
0,1064
0,1103
0,1141
0,1179
0,1217
0,1255
0,1293
0,1331
0,1368
0,1406
0,1443
0,1480
0,1517
0,1554
0,4463
0,4474
0,4484
0,4495
0,4505
0,4515
0,4525
0,4535
0,4545
0,4554
0,4564
0,4573
0,4582
0,4591
0,4599
0,4608
0,4616
0,4625
0,4633
0,4641
0,4649
0,4656
0,4664
0,4671
0,4678
0,67
0,68
0,69
0,70
0,71
0,72
0,73
0,74
0,75
0,76
0,77
0,78
0,79
0,80
1,86
1,87
1,88
1,89
1,90
1,91
1,92
1,93
1,94
1,95
1,96
1,97
1,98
1,99
2,00
2,02
2,04
2,06
2,08
2,10
2,12
2,14
2,16
2,18
-
Анали
0,2486
0,2517
0,2549
0,2580
0,2611
0,2642
0,2673
0,2703
0,2734
0,2764
0,2794
0,2823
0,2852
0,2881
0,4686
0,4693
0,4699
0,4706
0,4713
0,4719
0,4726
0,4732
0,4738
0,4744
0,4750
0,4756
0,4761
0,4767
0,4772
0,4783
0,4793
0,4803
0,4812
0,4821
0,4830
0,4838
0,4846
0,4854
-
зис
татист
1,07
1,08
1,09
1,10
1,11
1,12
1,13
1,14
1,15
1,16
1,17
1,18
U19
1,20
>,20
>,22
>,24
>,26
>,28
>,30
>,32
>,34
>,36
>,38
>,40
>,42
>,44
>,46
>,48
>,50
1,52
>,54
>.,56
>,58
>,60
>,62
>,64
>,66
-
ическая ди
Продо
0,3577
0,3599
0,3621
0,3643
0,3665
03686
0,3708
0,3729
0,3749
0,3770
0,3790
0,3810
0,3830
0,3349
0,4861
0,4868
0,4875
0,4881
0,4887
0,4893
0,4898
0,4904
0,4909
0,4913
0,4918
0,4922
0,4927
0,4931
0,4934
0,4938
0,4941
0,4945
0,4948
0,4951
0,4953
0,4956
0,4959
0,4961
-
намика СА
лжение i
1,47
1,48
1,49
1,50
1,51
1,52
1,53
1,54
1,55
1,56
1,57
1,58
1,59
1,60
2,68
2,70
2,72
2,74
2,76
2,78
2,80
2,82
2,84
2,86
2,88
2,90
2,92
2,94
2,96
2,98
3,00
3,20
3,40
3,60
3,80
4,00
4,50
5,00
-
У. Часть I
пабл. 6.1
0,4292
0,4306
0,4319
0,4332
0,4345
0,4357
0,4370
0,4382
0,4394
0,4406
0,4418
0,4429
0,4441
0,4452
0,4963
0,4965
0,4967
0,4969
0,4971
0,4973
0,4974
0,4976
0,4977
0,4979
0,4980
0,4981
0,4982
0,4984
0,4985
0,4986
0,49865
0,49931
0,49966
0,499841
0,499928
0,499968
0,499997
0,4999997
-
Использование сведений, приведенных в табл. 6.1 и 6.2, значительно упрощает
расчет конкретных систем автоматического управления методом статистической
линеаризации.
Выше были изложены основные теоретические положения метода статистической
линеаризации и алгоритмическая сторона вопроса, связанная с вероятностным
расчетом систем управления.
Далее изложим некоторые положения, которые необходимо учитывать при
использовании этого метода для инженерных расчетов конкретных систем.
Глава 6. Методы исследования нелинейных САУ
367
Таблица 6.2
Формулы и графики для определения коэффициентов статистической
линеаризации некоторых типовых нелинейных элементов
№п/п
' 1
2
3
Типо
И}
-В
х =
Одноз*
т
не
-Я
х=<
Лине*
-В
х = <
ВОР
хеа
хар
j
{'
шч
чу!
-1
В
0
-Я
ша
с н
-ft
/
В
К
-1
IH
пы
>ак
с
?
H3J
ICT
>
0
пр
пр
г
ях
dCi
д
/
ел!
ме
*ая
те
0
пр
*Р
ик
ви
и
и
ipt
ар
/
' С
п
п
1не
нт
ре
)ИС
эй
и з
еле
ас
тел
>
i >
акт
ен1
4
)
ри
ри
ри
йн
ле1
ти
В
У>
/<
йн
301
ьн
В
<
<
epi
ieN
/:=
ft
У
\у
У
ый эле-
2ная
ка
У
0 ;
0
ая харак-
юй
ости
У
у<Ь ;
-ft
лстика
i
= tga
В
У
>ft;
<ft;
<-ft
*-^[
где w,
А' - В [(\
Шут
V2jt
' -iDrr
+ф(1-
{
-(l + n
Фор
стат
кМ =
i-<
г,
кк L
в
ftDyy
4- И7
+ т\)
Г if
( 1-
'. J
».) е
\ + т
^i
мулы для коэффш
истической линеар
lBJ mv )
—ф\ г ;
Пу [ yJDyy J
JDyy 1 1 ф
yJDyylU
B2 { o,
i/l + m Ч2 i/'l
-iii^i] -ifi
^ 4 a> J +e H
ft; a, = yJDyy /ft
°. J -£~4 a, j
^°2/Я^ I I m} i a?
l °l r (1 ffl \
1 v/2i[(1 Щ)
■Hfi
щенто
>изаци
1 ,(
H
_ \2"|
m, ]
^ \ /ftl
b) ^
};
в
и
I/O
1/2
•
-. J
r ^fl + ^ll
Г Ф ■ i-
[ 1 «. J
a« J
368
Анализ и статистическая динамика САУ. Часть I
Продолжение табл. 6.2
Линейная характеристика
с зоной нечувствительности
* = tga
k а у
О Ь
K(y-b) при у>Ь\
О при \у\<Ь;
K(y + b) при у<-Ь
К0 = К{1- —
тху}2п
ifliaf -if Hit 1
Гг{ о, )._е^ о, J К.
^^(1+1±-£.«.|,+Г1±аГи-
а4 л ст4
г1 + т{
{ Ъ
l + nii
fl-m.Yl (1-тЛ 1
1+ L Ф *- ==гХ
*-iHi£M1?!
i»i
Линейная характеристика
с зоной нечувствительности
и насыщением
X
-Ь -а
К
к
а Ъ
= tga
В при > Ъ\
К(у-а) при<;у<£;
О при|^|^а;
К(у + а) прп -Ь<у<-а;
-В при у<-Ь
{ °i J I °i J
{ a, J ч/2я
_И a, J +e 2{ a, J ]J;
I a> J (1-v)2
I a, J (i-vf i a, J
^wi-vf+a? ^wi-v4! a, „
(1-v)2 { a, J (i-vfjbl
x[(l + m,-2v) e 2^ O| J +(l-m,-2v)x
И a' i +(m,+v) e~4 °> i -(m,-v)x
Я-v [ a, J [ o, J
где v = a/b
Глава 6. Методы исследования нелинейных САУ
369
6
7
Куб*
характ
X
0
х = Ку3
Нечетнаяi
характ
X
0
(
х = Ку2 sign
шеская
еристика
свадратичная
еристика
i
J ,
у
*}•>-*
JCp> = 3
k\2)=4kJd
Продолжение
DYy[ 3 + mY/Dyy];
'DYY[ 15 + 36ту/Оуу+9ту/Оуу]
KDyy[ 1 + m^/Dyy]
[DYy J [ V^wJ V2nD,K
IDfy DYy K'Dyy]
ma
1/2.
1 m\
IDyy
бл. 6.2
••
Классы систем. Метод статистической линеаризации особенно эффективен при
анализе стационарного режима работы систем автоматического управления с
постоянными параметрами. В этом случае mY = const, DYY = const и коэффициенты
статистической линеаризации не зависят от времени. Линеаризованная система
является при этом стационарной и ее исследование может быть проведено с
использованием хорошо разработанного аппарата теории линейных систем с постоянными
параметрами.
Положение становится сложным, если рассматривается нестационарный режим
работы системы с постоянными параметрами, вызванный переходным процессом или
нестационарностью воздействия. Аналогичная ситуация имеет место в случае, если
параметры системы меняются во времени. Во всех указанных случаях выходной
сигнал нелинейной системы относится к классу нестационарных и линеаризованная
система оказывается системой с переменными параметрами^ поскольку даже для
стационарной системы коэффициенты статистической линеаризации изменяются во
времени.
Для решения задач, имеющих практический интерес при исследовании процессов
управления в нестационарных нелинейных системах, на которые действуют
случайные возмущения, успешно применяются методы канонических разложений и
интегрирования уравнений вероятностных моментов, основанные на статистической
линеаризации нелинейностей. Однако в этих случаях статистическое исследование
систем значительно усложняется.
Спектральный состав выходного сигнала безынерционного нелинейного
элемента. Метод статистической линеаризации основан на представлении
безынерционного нелинейного элемента эквивалентными безынерционными линейными
элементами.
Если Syy(<u) - спектральная плотность входного сигнала нелинейного элемента,
то спектральный состав случайного сигнала на выходе этого элемента изменяется в
сторону его обогащения как более высокочастотными, так и низкочастотными
гармониками. Поэтому при исследовании точности работы систем автоматического
управления очень важно учитывать искажения спектра, т.к. в сложных системах
25 Зак. 232
370
Анализ и статистическая динамика САУ. Часть I
сразу после нелинейности может быть установлен дифференцирующий фильтр,
который резко подчеркивает высокочастотные гармоники, а это может привести к
дополнительным ошибкам управления.
В связи с этим статистическая линеаризация не отражает достаточно полно
истинную физическую картину прохождения случайного сигнала через нелинейный
элемент, т.к. при рассматриваемой аппроксимации изменяется только амплитуда
сигнала и не изменяется его спектр. В действительности случайный сигнал,
имеющий определенную форму спектральной плотности на входе нелинейного элемента,
изменяет ее на выходе (рис. 6.16).
Из рис. 6.16 можно заключить, что искажение спектральной плотности выходного
сигнала 5^ (со) в полосе [О, соср1, а также факт обогащения спектрального состава,
т.е. Sxx (со) > 0 при со > соср, в методе статистической линеаризации не учитываются.
^5(о))
н-
г
к,2
SYY (со)
- > 5.
Рис. 6.16. Графики спектральных плотностей:
SYY((u) - спектральная плотность входного сигнала Y(t); Sxx (со) - спектральная плотность выходного
сигнала нелинейного элемента; SXjjXjj (о)) = tf^Syy (со) - спектральная плотность на выходе
статистически линеаризованного элемента
Ограничение, связанное с необходимостью принять спектральную плотность
процесса X(t) пропорциональной спектральной плотности воздействия У (г), может
оказаться приемлемым в случае, когда Sxx (со) по характеру своего частотного
распределения мало отличается от SYY (со) или когда указанные спектральные плотности
существенно отличаются лишь в области частот, где линейная часть системы
обладает ярко выраженными фильтрующими свойствами.
Во многих практически важных случаях нелинейный элемент резко изменяет
характер частотного распределения спектральной плотности S^ (со) по сравнению с
5уу(со), т.е. Sxx (со) может сильно отличаться по своему частотному распределению
от SYY((u) и в области частот, где линейная часть системы не обладает достаточными
фильтрующими свойствами [65].
В этих случаях погрешность метода статистической линеаризации может
оказаться чрезмерно большой.
Для устранения указанного недостатка разработаны методы, изложенные в
[8, 115, 116, 117] и др.
Глава 6. Методы исследования нелинейных САУ
371
Аппроксимация дифференциального закона распределения на входе
нелинейного элемента нормальным. Еще одним ограничением метода статистической
линеаризации является требование, чтобы на входе нелинейного элемента случайный
процесс имел нормальный закон распределения.
Следует отметить, что при узкополосном фильтре, установленном за
нелинейностью, закон распределения случайного сигнала после сглаживающего фильтра
стремится к нормальному. Сущность этого явления состоит в том, что после усреднения
случайный процесс с любым законом распределения стремится к нормальному. Это
объясняется условием центральной предельной теоремы: распределение суммы
случайных величин, распределенных по любому закону, стремится к нормальному
распределению.
Однако при расчете следует убедиться в достоверности предположения, что закон
распределения после инерционного фильтра является нормальным, т.к. нормализация
случайного процесса с распределением, отличным от нормального, в сильной
степени зависит от фильтрующих свойств инерционного звена, от глубины его «памяти».
Кроме того, коэффициенты статистической линеаризации Ко , к[1' и К\2'
определяются интегральными соотношениями (6.33), (6.35) и (6.44) и этот факт
уменьшает степени зависимости указанных коэффициентов от вида закона распределения.
Хотя метод статистической линеаризации и является приближенным, он нашел
широкое применение при инженерных расчетах нелинейных систем автоматического
управления, описываемых дифференциальными уравнениями высокого порядка.
Точность метода статистической линеаризации тем выше, чем уже полоса
пропускания линейной части систем и чем больше плотность вероятности на входе
нелинейного элемента приближается к нормальной [161].
Пример 6.5. На рис. 6.17 представлена структурная схема электрогидравлического следящего привода
с нелинейным статическим элементом в обратной связи. Нелинейный элемент реализуется датчиком
перемещений, имеющим зону насыщения. Передаточные функции Wi(s) и W2(s} имеют вид [12, 13]
И^) = 0,2;
W2(s)--
1,548 10"
3,779-Ю"8 53+5,843-10"552+4,78010"45 + 2,337.10-2'
Задача статистического анализа состоит в том, чтобы определить математическое ожидание тх и
дисперсию DXx выходного сигнала устойчивой системы в установившемся режиме, если известны
математическое ожидание ту и корреляционная функция воздействия
mY=2B, /?KK(x)=DKKe"alTl, DYY=9B2, a = 50-.
Y(t)
ул&
w
Wo(s)
YV2\<y/
b - U,Uj
-b
' ft
\/
b
X
= 0,05
X(t)
Рис. 6.17. Структурная схема электрогидравлического следящего привода
25*
372
Анализ и статистическая динамика САУ. Часть I
Получим решение задачи двумя методами: графоаналитическим и методом последовательных
приближений. Используя метод статистической линеаризации, исходную структурную схему (рис. 6.17)
заменим статистически линеаризованной моделью (рис. 6.18).
Для данного типа нелинейности коэффициенты статистической линеаризации пу математическому
ожиданию K0(mXyDxx) и по центрирующей составляющей K\(mXyDxx) определяются следующими
выражениями
К*Ьх**х*)~\Ь + "х)А*^ - (b-mx J*l2t|+-ULx
b + m*
^iK.Oxx)= 4-^-1+
d
Коэффициент статистической линеаризации K\{mx,DXx) определен с использованием второго критерия
статистической эквивалентности.
Передаточные функции по математическому ожиданию и по центрированной составляющей
замкнутой статистически линеаризованной системы можно запивать в виде (см. рис. 6.18)
Wcm{s)= l^0(mx,Dxx)W2{sy
W (-) fifr)^)
mr
Y(fl
Wt(s) \^*ф-М W2(s)
- KoinibDxx)
'XX I
'Щ w,W f1^-^
W2(s)
mx
mx
i
Kiim^D,,)
хЩ
Рис. 6.18. Статистически линеаризованная структурная схема
электрогидравлического следящего привода
Математическое ожидание тх и дисперсия Dxx выходного сигнала системы определяются
следующими выражениями
"*x=Wcm(0)-my =
0,2
Wi(o)iy2(o)
1,548-10"3
2,337 -10"2
1,325-10
.-2
= т-гпу z . ' ч ту,
1 + АгГт n >''548-10 l + 6,6241O-2A:o(mx,Dxx)
2,337-10"2
Глава 6. Методы исследования нелинейных САУ 373
0,2-l,54810~3
3,779-Ю^Осо)3 +5,843-10"5(;О))2 + 4,780- 1О~40*о)+
I2
- - 7 H •5KK((0)^0).
+ 2,337 • 10"2 +1,548 • 10"3 • Kx (mx, Dxx )\
DYY a 9-50 143,24
ПОСКОЛЬКУ Syy = —— z T- = : r- = =■ ,
n a2+co2 3,14-(502+co2) 2500 +со2
U73-10"5
i |з,779 10"80*со)3 + 5,843-10"5(/to)2 + 4,780•10"4(/ш)+
1
+ 2,337 • 10"2 +1,548 • 10"3 • Kx {mx, D^ )|
■T-,
2 2500+O)2
dco =
Таким образом, имеем
mx,Wm(0).mr r^^f -.
1 + K0(mx ,D^ )• 6,624-10"2
-J 4 ^ r*,
Jco.
g30w)3 + g20w)2 + gi0o))+go(^i(wx^xx))| (2500+O)2)
Далее воспользуемся графоаналитическим методом. В соответствии с теоретическими положениями
запишем систему
тх =л,
1,325-КГ2 ,/ п ч
= ; = /Лтх,Dvv );
1 + 6,624-1О-2-/(:о(тх^хх)
Л= : ^ г7 "^=
| 8зЫ?+82и^?+8\{М+8о{^х^хх))\ (2500+со2)
'-fi{mx^xx\
В первой подсистеме параметром является дисперсия Dxx, и по уравнениям этой системы
рассчитывается семейство функций т\, = fi(mx> DJ$ ) при различных фиксированных значениях дисперсий DJ$ . Это
семейство функций строится в виде графиков в координатах (г\,тх) (рис. 6.19). Значения тх и DJ$ ,
соответствующие точкам пересечения этих функций с биссектрисой координатного угла тх = Т|» наносятся
на отдельный график в координатах (mx,DXx) (функция Ьна рис. 6.21).
Во второй подсистеме параметром является математическое ожидание т*, и по уравнениям этой
подсистемы рассчитывается семейство функций fj,- = /2\тх\&хх ) ПРИ различных фиксированных значениях
математических ожиданий mj\
374
Анализ и статистическая динамика САУ. Часть I
Для того чтобы рассчитать семейство функций fj,- = /гуп^^хх) необходимо воспользоваться
стандартным интегралом вида
G4(;co)
, =J_f С
4"2я^40с
))F4(-y(o)
<Ло,
где
F4(/G))=a0(/G))4 + al(j(u)3 + a2{j(u)2 + a3{j(u)+a4,
G4(</O))=bo0'o))6 + bl(ju>)4 + Ь2{]<й)2 + b3.
Стандартный интеграл рассчитывается по формуле
bo{-a{ a4+020^-00^^+00аф2+(а°Ь^\аоа3-а1а2)
4 = / \
2ао(?оаз +«12«4 -«1«2аз
)
Можно записать
fi=J.
~\g3(fi>? +g2W +giM+8o(Kl(mx,Dxx))\2[25OO+m2)
Для рассматриваемого случая
d(u = 2nJ4.
л-5
Отсюда получаем G<
лло-21
2.5
2.
1.5
1
0.5
0
-
-
-
-
/^ i
)=0, bj=O, Ь2=0, ^з =^о = 1373-10"°.
тх=Г\
(1)
ту
(О
ПХ :
(2)
^=1.4-10-3м2
D^=M0"3m2 :
D^ = 0.5-10"3m2
w^ = 2.4-10-2m
m
wx =2.5-10"2m
О) т(^ = 2.6-10-2м
x i
0.5 1
1.5
2.5
т^,10"2м
1.4
1.2
Рис. 6.19. Графики функций первой подсистемы уравнений
Л,10:зм2
л^ = 3-10-2м
D^IO^m2
Рис. 6.20. Графики функций второй подсистемы уравнений
Глава 6. Методы исследования нелинейных САУ
375
' D^,10"3m2
1.4
1.2
. (m.,DAT) = (2.55-10-2; 1.33-10"3)
0.5 1 1.5 2 2.5 3
Рис. 6.21. Графическое решение двух подсистем уравнений
Приведем знаменатель подынтегрального выражения, определяющего fj к стандартной форме
F4(/O))/r4(-7O)), для чего второй сомножитель знаменателя представим в следующем виде
2500 + со2 = ((уо))+ 50)((- усо)+ 50).
Представим первый сомножитель знаменателя в стандартном виде
| £з W3 + 8г 0<»)2 + 8\ Ы+ 8о {К\ (»гх, Dxx ))| =
= (g3(/co)3 + g2{ju)2 + gl(jio)+ SofoK .£>xx )))x
х ( ft(-/»)3 + ft(-/»)2+ft(-^) + &(^iK.Pw)))-
Тогда знаменатель стандартного интеграла можно представить в виде F4(/o)) F4(-j(u), причем
= g3(;w)4 +(50g3 +g2)(>)3 +(50g2 +g1)(yco)2 +
= ao(yo))4 +(?1(y(o)3 +a2(</0))2 +e3Oto)+e4.
Откуда
<*о = 8з> «i=50g3 + g2, e2=50g2+ei. a3=5O^i+^o(^i(OTx»£)xx))»
<>4=5Ogo{Kl(mx,Dxx)).
Семейство функций r\ определится формулой
r\ = 2nJ4= 2я \ / 24 I ■ .
2ао(аоа3 +а{ а4 -а{а2а3)
В последнем выражении коэффициенты аъ и а4 зависят от коэффициента статистической линеаризации
Кх{тх, DXx) (они зависят от коэффициента go(^,(mx ,DXX )))•
Рассчитав семейство функций Л/=/г^х^^^х/» наносим их на график в координатах
\f\,Dxx )(рис. 6.20). Значения т^ и Dlxx , соответствующие точкам пересечения этих функций с
биссектрисой координатного угла, нанесем на отдельный график (функция 2 на рис. 6.21). Точка пересечения
функций 1 и 2 соответствует значению математического ожидания тх и дисперсии DXx выходного сигнала
системы в установившемся режиме
тх =2,5510"2м, Dxx =l,33-10~V.
Получим решение этой же задачи методом последовательных приближений. Заданы те же
статистические характеристики входа: математическое ожидание mY и корреляционная функция воздействия RYy{x)
имеют вид
mY=2B, RYY(x) = DYYe~^x[ DYY=9B2, Ct = 50j/f.
376
Анализ и статистическая динамика САУ. Часть I
Статистический анализ методом последовательных приближений проводится в соответствии со
следующим алгоритмом
1). Задается нулевое приближение математического ожидания ту и дисперсии Djtf на входе
нелинейного статистического элемента. Положим
mf=0MM, Dg=lM2, а^ = Щ = Ы .
2). Определяются при нулевом приближении коэффициенты статистической линеаризации. Для
данного типа нелинейного статистического элемента имеем
#.'|fr..p)ii!#U-.paii£L
„(°)
Jo)
°х
л/2я
'{
Л»
*>
^{(O>O5 + O,O4^M±Mij_(o,O5-O,O4^M5zMJH
>/2я
if 0,03+0,04 У 1Г 0,05-0,04 V
= 3,996 10"2,
^-Jt^Ut^^o^iy
J 0,05 -0,1
-0,04^
= 0,0359 + 0,004 = 0,0399.
3). Находятся нулевые приближения передаточных функций замкнутых систем по математическому
ожиданию и дисперсии
ЗДО 10"
■ i779 -10~V +5,843 -l'0"V+4,780 10^+2,337 Ю"2+1,548 КГ3*^1
шл.Ч')Ч')-
3,096 -10"
5^(ш)
3,779 -10^+5,843 -10~V+4,780 -КГ^+^ЗЗ? 10"2+1,548 -lO"3^''
143,24
4). Находится спектральная плотность воздействия
DYy a _ 9-50
п ос2+(о2 3,14(502+(02) 2500 +со2
143,24
= 5;к(усо) SY-Y(jto) .
((;ш) + 50) ((-Уо)) + 50)
5). Квадрат модуля нулевого приближения передаточной функции по дисперсии представляется в виде
Я(Ж-т
9,585 -10"1
3,779 -Ю"8^)3+5,843 -КГ^»2 +4,780 lO^Jyto)+2,337 -10-2+l,548 Ю-3^о)| '
§1 v .
(йИ 3+82И2+ft(J«>)+&(*io»fi.fl®)))
Глава 6. Методы исследования нелинейных САУ . 377
6). Вычисляется стандартный интеграл первого приближения
jP=±\w®(j<»)w<$(-j<>>)srY(j<»)sYY(-j<»)d<»,
2Я ■_
который представляется в виде
У" -2nJF,,0a))fn(-^)
где
Fn{ju>)=a0(ju>)n +а1(;о))/1-1 +... + «,,
Поскольку в нашем случае л = 4, то вычисление стандартного интеграла производится по формуле
fc0 (- flifl4 + а2дз)~ WA+ aoaib2 + й° у/ Гоаз - а1а2)
у^ * ^ / 2 2—L-V"^ •
2а0 Ц)аз + а\ал ~ а1а2аз /
где
flo=g3/ ai=50g3+^2. O2=50g2+^i. «з=5О^1+^о» «4=50^
^ = Ь,=^=0, b3=fcb.Z>Kr^ = U73.10-5.
Результат расчета
У^1) = 2,223- КГ4!!2.
7). Вычисляется дисперсия (первое приближение)
О^=2яУ4^ = 2-ЗД4-2,22310~4 = 1,396595-1б~3м2.
Среднеквадратическая ошибка (первое приближение) равна
7$ = ^D§h = Vl,396595-10~3 = 5,737105- 10"2м.
ff\
8). Вычисляется математическое ожидание (первое приближение)
Х 2,337 • КГ2 +1,548 • \0~3К^
9). Определяются коэффициенты статистической линеаризации (первое приближение)
+
Л «s> J .Л ^ J
= 0,782957,
& *"* I = 0,4792 + 0,2357 = 0,7149.
x
Далее выполняются пункты 3, 5, б, 7, 8 и 9 (соответственно увеличиваются номера приближений) до
тех пор, пока не выполнится условие
4*о
где i - номер приближения, е - относительная погрешность вычисления дисперсии выходного сигнала
системы.
Задавшись Еотн = 1,2 10"3, получим значения DJ$, d!#, my, tn\,':
D$ =1,331649-10"3м2, т^2) = 2,518808-10"2м,
D^= 1,330076-1О"3м2, т^3) = 2,516696-10"2м.
При этом относительная погрешность вычислений определяется по формуле
24 Зак. 232
378 Анализ и статистическая динамика САУ. Часть I
Их-0иг| 1 1,330076 -10"3-1,331649 10~3|
£>g) 1,330076-КГ3
= 1,18 • 10"3<Еотн= 1,2 10"3.
Таким образом, с относительной погрешностью 1,18-Ю"3 по дисперсии выходного сигнала можно
считать, что в установившемся режиме математическое ожидание тх и дисперсия DXx выходного сигнала
системы принимают следующие значения
тх =/43) = 2,516696-10~2м, Dxx = D$ = 1,330076 10"3м2.
Сравнение полученных значений с результатами расчета графоаналитическим методом позволяет
сделать вывод о быстрой сходимости метода последовательных приближений.
6.4. ЧИСЛЕННО-СПЕКТРАЛЬНЫЙ МЕТОД СТАТИСТИЧЕСКОГО
АНАЛИЗА НЕЛИНЕЙНЫХ НЕСТАЦИОНАРНЫХ
АВТОМАТИЧЕСКИХ СИСТЕМ
Нелинейная нестационарная система со случайными параметрами описывается
системой ДУ вида
^p- = fi(XuX2,...,Xn,Vl,V2 V,;t\ i = u, x(0) = 0, (6.70)
at
где X\(t)9 ... , Xn(t) - фазовые координаты системы, V{, V2, ... , Vi - случайные
параметры, t - время.
Интегралы уравнений (6.70) можно записать в форме
X,.(0=X/fa^2 VrA i=U. (6.71)
Функции (6.71) непрерывны относительно аргументов Vu V2,..., Vh t, если правые
части системы (6.70) непрерывны относительно параметров Vu V*-... Vi и допускают
лишь разрывы первого рода относительно аргумента t.
Функции (6.71) неизвестны и их нахождение связано с большими трудностями.
В связи с этим они служат основой для построения как теоретических положений,
так и алгоритмов исследования нелинейных систем.
В [55, 114, 174] используются приближения функций (6.71), на основе которых
решаются задачи вероятностного исследования. В [114] в качестве аппарата
приближения применяются ряды Маклорена. В этом случае, кроме непрерывности функций
(6.71), необходимо существование их производных до определенного порядка, что
накладывает известные ограничения на функции (6.71). Разложение имеет вид
*,(,)=*(..o,o,...,o)+xiii|...£f_^Lv.vi.
k=\ ;,=1;2=1 jk=l{ h h Jk ) (6.72)
В последней зависимости функции AJiJ2 jk (t) неизвестны, поскольку неизвестна
функция Х((ух,У2 Vi\t).
В [114] показано, что функции Ajj2...jk(t) определяются системой линейных
дифференциальных уравнений.
Для вывода системы уравнений, определяющих функции AJiJ2 jk (t\ достаточно
продифференцировать все уравнения системы (6.72) по случайным величинам
Vj ,—',Vjk после подстановки в них разложений
Ys(t) = lV^is(t) + mYs(t) (6.73)
Глава 6. Методы исследования нелинейных САУ 379
и заменить в полученных таким образом уравнениях все случайные величины V,
нулями [114].
В задачах практики можно производить вычисление указанных коэффициентов,
заменив в формуле (6.72) производные их выражениями через конечные цриращения.
Тогда вычисление коэффициентов разложения Ajj j (t) сводится к
интегрированию системы уравнений (6.70) при различных частных значениях случайных величин
Vj. Это дает некоторое упрощение при решении задачи нахождения вероятностных
характеристик случайных функций хДг,^,...,!^) при помощи цифровых
вычислительных машин.
Это направление в теории нелинейных преобразований случайных функций
развивается Б.Г. Доступовым, который разработал оригинальный метод, позволяющий
существенно сократить число частных значений параметров V,, для которых
необходимо определить реализации исследуемых, случайных функций, чтобы найти их
моменты (см. [55], [66]).
Б.Г. Доступовым в [55] рассмотрен вопрос определения математического
ожидания выходных координат нелинейной системы с помощью разложения интегралов её
уравнений в тригонометрические ряды.
Чернецким В.И. в [174] для приближения функций (6.71) предложено
использовать аппарат интерполирования. Соответствующая формула имеет вид
хдад,..,у,;0=|;£.|>К'Ч>-"'М-Г17—°ЧЧ v
В [117, 168] рассмотрены спектральные методы статистического исследования
линейных и нелинейных систем. Идеология этого подхода обобщается и на
нелинейные системы. В соответствии с этой идеологией решения дифференциальных
уравнений или статистические характеристики решений разлагаются в ряды по
ортогональным базисам.
Положим, что в функциях X,{Vi, V2,..., Vi ; 0 область значений аргументов Vh
V2,..., V/есть промежуток (- 1,+1), т.е. Vre(- 1,+1), г = 1,1. Если же Vre( V™, VrM), то с
помощью замены переменных вида
V +V
V,-
гм гт
о V -V
Ъ—тг^у—ь' (6>74)
v гм v гт Ог
2
— у +V ' у -у —
где Vr= v™^v™ , 8r= rM "",r = U,
всегда можно прийти к промежутку (- 1;+1).
Положим, что
X/(v1,V2,...,V/;OeZ>2((-l,+l)x(-l,+l)x...x(-l,+l)),
т.е. решение X,{Vu V2,..., Vi; t) интегрируемо с квадратом по переменным Vb V2,..., V/.
Такая функция может быть разложена по ОНБ. Полученный ряд будет сходиться
в среднеквадратичном. В качестве ОНБ воспользуемся полиномами Лежандра,
ортогональными на сегменте [- 1,+1] с единичным весом р(у)=.1.'Полиномы Лежандра
определяются зависимостью [159]
^..Lflv.-Of;
24*
380
Анализ и статистическая динамика САУ. Часть I
формула для многочленов Лежандра с единичным старшим коэффициентом
записывается так [159]
Запишем рекуррентную формулу для полиномов Лежандра
(n + l)Pn+i(v)=(2n + l)VPn(v)-nPn_l(v).
Далее будут использоваться ортонормированные полиномы Лежандра,
ляемые соотношением
рп(у)=]Щр;(у).
(6.75)
(6.76)
опреде-
(6.77)
Ортонормированные полиномы Лежандра можно записать в форме
(Po(V))
Pi<Y)
P2(V)
Pi(V)
P(V)
coo
Cm
0
cn
c21
C/1
0
0
c22
Cn
... (Г
... 0
... 0
... cn
V
V
V
V
оЛ
(6.78)
и v
Отсюда находим P(V) = UV ,
где U - матрица ортогонализации полиномов Лежандра.
Формулы, определяющие несколько первых ортонормированных полиномов
Лежандра, имеют вид
P,(v) = clo + cuV,
P2(v)=C70+c2lV + c22V2,
Pvivh^jVl.
Разложим функцию X^Vj.V^v.V,;?) по многочленам Лежандра
х,Ку2 М=££...5Х;,2 ...v/O^fa)^)...?^), (6-79>
vI=lv2=bl v, =1
где
*xt
,-,('>=
V1V2
+1+1 +1
(6.80)
= JJ...Jx^VpV2,...,y/;OPv^VjPv^Vj...PV/(V/VVV2...^
-1-1 -1
- коэффициенты Фурье.
В зависимости от промежутка, на котором изменяются переменные VpV^,...,^,
используются разные ортогональные системы. Если, например, Уге (-<»,+<»),
г = 1,/, то'необходимо применять ортогональные полиномы Эрмита. Если же
Vr e (О,©о), то в качестве ОНБ можно использовать функции Лягерра. Коэффициенты
с*'
Глава 6. Методы исследования нелинейных САУ 381
Фурье (6.80) вычислить не представляется возможным, поскольку функции
хДУрУ'г,...,^;*) неизвестны. Поэтому вычисление коэффициентов Фурье
производится численным методом.
Воспользуемся формулой численного определения значений интеграла (6.80).
Если функция Х( содержит два случайных параметра V{ и У2,т.е. хДУ,,!^;*)»
то по определению двойного интеграла справедлива зависимость [21]
+1+1
<v2 (0= J J*i(Vi,V2;r)PVl (V,)PV2 {v2)dVxdV2 -
"1Ч (6.81)
- ZdsXfas.Vts )PV| (VIS )PV2 (V2S).
5=1
Для /-кратного интеграла можно записать приближенную формулу
2...v, (')- E^^(^i5^25v..,V/5)PVi (Vxs)... PVl (Vfc). (6.82)
5-1
В приведенных соотношениях ds - некоторые постоянные числа, Vls,V2Si...,Vls -
фиксированные значения аргументов Vl,V2,...,Vl9 причем V^5g[-1,+i], Л: = 1,/;
5=п.
Отметим, что (6.82) не является единственным представлением (6.80). Задача
расчета кратных интегралов рассматривалась в ряде работ [21, 34, 62, 67, 76, 98,
166 и др.], в которых выведены формулы, по которым можно определять
численными методами значения ^кратных интегралов для любого /. Однако с
увеличением кратности интеграла резко возрастает число точек, в которых необходимо
рассчитывать численным методом значения подынтегральной функции, чтобы
обеспечить нужную точность.
Если при вычислении однократного интеграла для обеспечения.нужной точности
требуется г узлов, то для вычисления соответствующего Z-кратного интеграла
придется брать примерно г1 узлов. При больших / эти вычисления могут оказаться
трудновыполнимыми. В [98] рассмотрены теоретические положения, Связанные с
проблемой численного расчета значений кратных интегралов.
Обратимся к формуле (6.80). В нее входят решения Х((у18,У23,...,У18и) при
конкретных значениях коэффициентов канонических разложений У15,У25,—,У/5 .
Функции X,-(1^5,^25,...,У/5;t) рассчитываются на ЭВМ численным методом путем
решения системы дифференциальных уравнений (6.70) при фиксированных значениях
аргументов Vx,V2,.->Vl, причем Vx=Vls, S = l,r; V^V^, 5 = l,r;...; Vi=Vls,
S = 1, г. Из сказанного вытекает, что число необходимых интегрирований системы
(6.70) может быть весьма значительным, особенно при больших г и /.
Этап вычисления коэффициентов Фурье по формуле (6.80) является наиболее
трудоемким и при проведении расчетов необходимо изучить пути упрощения
алгоритма вычисления функций с*(, v (t).
Запишем спектральное представление решения X^Vj.V^^V/;*) в базисе
полиномов Лежандра
382 Анализ и статистическая динамика САУ. Часть I
Xl(V1,V2,...,V/;0 =
-tt-ttt-b^e^-^<. v,(0W-..V/' = (6.83)
v,=lv2=l V/=iy,=072=0 7,=0
=is-£EI:-l:<v,..v,(OcL..,,v^-v'.
v,=lv2=l V|=1;,=OJ2=O j,=0
где c*lv v (t) - известные функции, tfj^ - известные постоянные величины,
Vx,V2,...,Vl - независимые случайные величины, дифференциальные законы
распределения которых известны.
Зависимость (6.83) является основой для вычисления статистических
характеристик фазовых координат: математических ожиданий, дисперсий,
корреляционных функций, корреляционных моментов.
Найдем формулу, определяющую математическое ожидание фазовой
координаты X,:
mXi(t)^M\Xtiyxy2 V,;0] =
N N N v, v, v, +~+~
= 2S~Z2 2"2<&v,(0 cihi,\\...
7 ■ (6.84)
... j v/'v2^...v/'/v(vi;v2 v,)<Vv2... dvt =
N I I V, V2 V,
_ v V V V V V rxi (Л гр гу(л+л+-+л)
v,=lv2=l V/=ly,=Oy2=O y,=0
где
+CO+0O +CO
аО,+Л+.+л)= J J ... Jv/.v*...v/'/v(vI,v2,...,v,)<foi*2...rfv/
—oo —oo — oo
- смешанный начальный момент (k = jx + j2 +...+ 7/ )-го порядка.
Если случайные величины VpV^,...,^ независимы, то смешанные начальные
моменты вычисляются по формуле
(4+*+-+л) = ЩуА/у4(^)Л4 =<;va^2...<;V( =П<^. (6.85)
Для расчета дисперсии фазовой координаты X, имеет место зависимость
Яад(') =
^ TV N v, Vl v, / vf (6.86)
yv yv yv v, v, v,
+00+00 +oo y« y« V v V v rx< (A rp J1J2 „л-г-(л+л+-+л)1 v
J J ' *J Lv«=l V2=1 v/=1 >«=0 л=° л=о J
Если воспользоваться обозначением для корреляционного момента между
фазовыми координатами Х,(г)иХу(г)
*Х|Х,(0=м[х|(0М0]=
= r\{Vl9V2 V/;r) = (^(VlfVi Vl^-Affx^O])^;^^ Vt;t)-M[Xj(t)])t
Глава 6. Методы исследования нелинейных САУ
383
то имеет место соотношение
+ОО+СО +СО
*xlXj(t)= I J...j4(V,,V2,....V/:O/v(v,.v2 v/)*yfr2...*'l. (6.87)
—оо —оо —оо
Структурная схема алгоритма расчета математических ожиданий и дисперсий
фазовых координат нелинейной нестационарной системы представлена на рис. 6.22.
Интегрирование сист(
уравнени
у _т/ у _у
Расчет коэффициен
(
Нахождение математич
координаты X i (t J, /
Расчет дисперсии фазово
по фор
5мы дифференциальных
й (6.70) при
в»
тов Фурье по формуле
6.80)
еского ожидания фазовой
= 1, п по формуле (6.84)
г
й координаты Х{ \t), i = 1, п
муле (6.86)
D
nXi(t)
Рис.6.22. Структурная схема алгоритма статистического анализа нелинейной системы
численно-спектральным методом
6.5. ВЕРОЯТНОСТНОЕ ИССЛЕДОВАНИЕ НЕЛИНЕЙНЫХ
НЕСТАЦИОНАРНЫХ СИСТЕМ МЕТОДОМ
СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ
Наиболее общим методом вероятностного анализа нелинейных систем, включая
нестационарные и стохастические, является метод статистических испытаний (МСИ).
Изложим идею метода. Положим, что спроектирована система и создан ее
серийный экземпляр. На серийных экземплярах системы проводится заключительный этап
натурных испытаний. Полученная при этом информация о характеристиках системы
(например, о параметрах, характеризующих точность работы САУ) позволяет
вынести окончательное суждение о соответствии их требованиям технических условий и,
как следствие, техническому заданию на проектирование.
Оценим точность работы системы, проводя соответствующие натурные
испытания серийных экземпляров. В качестве примера можно рассмотреть такие
характеристики точности системы управления летательным аппаратом (ЛА), как вероятность
его попадания в заданную область. Проводя соответствующие эксперименты, каж-'
384 ; Анализ и статистическая динамика САУ. Часть I
дый раз фиксируется попадание или непопадание летательного аппарата в заданное
область. Тогда искомая величина задачи Р(А) - вероятность попадания ЛА в
заданную область - принимается равной относительной частоте
P(A) = min, (6.88)
где т - число случаев попадания ЛА в заданную область, п - общее нисло
экспериментов.
При этом п должно быть выбрано таким, чтобы обеспечить достаточную точность и
надежность в определении оценки искомой вероятности попадания ЛА в заданную
область.
Таким образом, в рассматриваемой задаче искомая величина равна вероятности
появления события А и ее приближенное значение можно принять равным
относительной частоте появления этого события. В общем случае приближенные значения
искомых величин, которые находятся путем статистической обработки результатов
эксперимента, на основании закона больших чисел стремятся к истинным искомым
величинам.
Выше было изложено решение задачи оценки точности работы системы с
помощью натурного эксперимента. Недостатки такого подхода очевидны: дороговизна,
необходимость иметь серийные образцы системы, большой объем испытаний
заставляет совершенствовать испытательную аппаратуру и оборудование, большие
временные затраты, трудность решения задач синтеза и т.д.
Значительно проще поставленная задача может быть решена путем
моделирования. Сущность моделирования заключается в замене исходных систем другими
системами, называемыми моделями. Под цифровым моделированием понимают
имитацию условий работы тех или иных реальных систем с помощью вычислительных
алгоритмов, которые реализуются в виде программ на ЭВМ или в виде
специализированных ЭВМ. Центральным при моделировании является понятие математической
модели.
Математическая модель системы отражает в той или иной мере свойства
реальной системы, в том числе ограничения, существующие в реальных условиях.
Математическая модель составляется в математических терминах и имеет
количественное описание. Очень часто математическая модель задается соответствующими
дифференциальными уравнениями.
Рассмотрим решение разобранной выше задачи методом моделирования,
предполагая, что известно ДУ системы и статистические характеристики входного сигнала
Yif).
На вход модели, которая реализуется на ЭВМ в виде соответствующей
программы решения дифференциального уравнения системы, подается конкретная
реализация yk(t) входного случайного сигнала Y(t)9 генерируемая с помощью программы
формирования воздействий. На выходе модели фиксируется соответствующая
реализация xk(t) выходного сигнала X(t) (решение дифференциального уравнения системы).
Описанная процедура повторяется п раз.
При этом каждый раз фиксируется попадание или непопадание выходного
процесса xk(t) при t = Т в заданную область. Тогда искомая величина, как и при натурных
испытаниях, принимается равной относительной частоте (6.88).
Структурная схема решения задачи на ЭВМ представлена на рис. 6.23.
Таким образом, математическое моделирование на ЭВМ при решении задач
исследования САУ позволяет заменить натурный эксперимент равнозначным в плане
ценности получаемой информации экспериментом на ЭВМ.
Преимущества последнего подхода очевидны. Метод статистических
испытаний предполагает, что с достаточной точностью известны математическая мо-
Глава 6. Методы исследования нелинейных САУ
385
dt ib как нелинейной нестационарной системы в форме, например,
дифференциальных уравнений, так и математические модели всех стохастических процессов,
действующих на САУ, включая и статистические характеристики случайных
параметров.
1
V(t)
^
2
Y(t)
—►
3
Y(i\
4
5
\
Ч
/
ЭВМ
6
—►
Рис. 6.23. Структурная схема решения задачи на ЭВМ:
/ - программа - генератор белого шума; 2 - программа, реализующая формирующий фильтр;
3 - программа решения ДУ системы; 4 - счетчик числа т;5- счетчик числа п;6- делитель т/п
При наличии такой информации можно на ЭВМ провести полное моделирование
работы системы. В случае, когда точно известны математические модели системы и
сигналов, результаты натурных испытаний и результаты моделирования должны
совпадать. По известным причинам, при вероятностном анализе сложных систем
управления такое совпадение практически недостижимо.
Часто применяют полунатурное моделирование., когда часть элементов системы
моделируется на ЭВМ (полагается, что их математические модели известны с
необходимой точностью), а в качестве второй части используются реальные элементы
(например, автопилот - при моделировании систем управления летательными
аппаратами).
Теперь можно сформулировать определение метода статистических испытаний:
метод статистических испытаний заключается в непосредственном
моделировании систем при действии на них случайных возмущений и обработке полученных
результатов с целью определения искомых величин рассматриваемой задачи.
Этот метод применяют и для оценки допустимости использования приближенных
методов анализа.
Изложим основные теоретические положения метода статистических испытаний.
Пусть нестационарная стохастическая нелинейная САУ описывается системой
дифференциальных уравнений
dt
= fi(t,Xl,X2,...,XnJl,Y2,...,Ym,vl,v2,...,vk),
(6.89)
(6.90)
*,-(0) = *,-(),
где Xi(t) - фазовые координаты,
*,(()) - случайные начальные условия,
Yi(t) - случайные процессы, действующие на САУ,
v, - случайные числа, от которых зависят параметры системы.
Таким образом, исследуемая система может иметь ненулевые начальные условия,
случайные параметры, рассматриваемые как случайные величины или как случайные
процессы, стохастические помехи, приложенные в различных точках системы.
Схема, реализующая метод статистических испытаний, включает следующие этапы:
386 Анализ и статистическая динамика САУ. Часть I
1). Генерирование случайных сигналов, действующих на САУ.
С помощью датчиков случайных чисел и генераторов случайных функций
генерируются случайные начальные условия, случайные параметры и все воздействия,
поступающие на систему. Будем полагать, что случайные функции К,(г) (/=1,2,...,
т) включают все случайные факторы (кроме случайных начальных условий).
Поскольку в МСИ в общем случае используется осреднение по множеству, то по
известным статистическим характеристикам процессов Yfj) строятся их реализации
У is (О С* = 1,2,... ,N; s - номер реализации).
2). Решение системы дифференциальных уравнений САУ.
При выбранных N реализациях случайных функций yis (t) (i = 1, 2 , ... , w;
s = 1, 2 , ... , N) выполняется интегрирование системы уравнений (6.89) на ЭВМ.
Другими словами, МСИ предполагает последовательное многократное
интегрирование уравнений, описывающих работу системы, при различных реализациях
случайных входных сигналов. При практической реализации МСИ на ЭВМ строится
дискретная модель системы, которую было бы удобно реализовать на
вычислительной машине [106]. Обычно исходная анализируемая система задается системой
дифференциальных уравнений (6.89). В этом случае переход к дискретной модели
осуществляется на основе использования численных методов решения систем
дифференциальных уравнений. Теория точности численного интегрирования систем
дифференциальных уравнений довольно хорошо разработана.
3). Обработка результатов эксперимента.
Пусть искомые величины задачи равны параметрам случайного процесса X{t).
Тогда приближенные значения искомых.величин на основании закона больших чисел
можно принять равными оценкам параметров процесса X(f), получаемым на
основании статистической обработки экспериментальных данных.
Центральным этапом применения МСИ является задача генерации случайных
параметров x&t), i = 1, 2,..., п и случайных функций yis(i) {i = 1, 2,..., п) [106].
Существует несколько принципиально различных подходов к генерации случайных функций в
МСИ. Один из них основан на применении специальных устройств - датчиков
случайных величин, в которых используются случайные физические явления
(радиоактивный распад, тепловые шумы и т.д.). Такие датчики дают последовательность
истинно случайных величин, которые не могут быть предсказаны или повторно
воспроизведены.
Во втором подходе используются программные методы получения реализаций
случайных чисел, с помощью которых происходит непосредственная генерация
случайных чисел в ЭВМ. Строго говоря, эти числа не являются истинно случайными,
т.к. всегда можно предсказать будущее случайное число и повторно воспроизвести
всю последовательность. Поэтому такие последовательности чисел называются
псевдослучайными.
Как показывает теория и эксперимент, к результатам моделирования при
использовании псевдослучайных чисел можно применять те же самые формулы оценок, что
и при использовании истинно случайных чисел. Причем возможность повторного
воспроизведения псевдослучайной последовательности упрощает процедуру
проверки используемых алгоритмов [106].
Обычно моделирование случайных или псевдослучайных функций разделяется на
две подзадачи. Сначала вырабатывается последрвательность независимых
равномерно распределенных на отрезке [0,1] чисел (белый шум). Затем с помощью
стационарного или нестационарного формирующего фильтра из последовательности
равномерно распределенных чисел генерируются случайные функции yis{t) с заданными
статистическими характеристиками.
Глава 6. Методы исследования нелинейных САУ
387
После генерации случайных функций yis(t) производится численное решение
дифференциальных уравнений исследуемой автоматической системы. В результате
получается N реализаций jc* (г) (i = 1, 2,..., п\ s = 1, 2,..., N).
На последнем этапе, как указывалось выше, производится статистическая
обработка полученных результатов, использующая осреднение по множеству полученных
решений ДУ (6.89).
Для одномерной системы структурная схема реализации МСИ имеет вид,
представленный на рис. 6.24.
1
1
3
L
y(t)
x(t)
Рис. 6.24. Структурная схема реализации метода статистических испытаний:
/ - генератор белого шума; 2 - стационарный или нестационарный формирующий фильтр; 3 - генератор
входного сигнала; 4 - ЭВМ, на которой решаются ДУ исследуемой автоматической системы;
5 - ЭВМ для обработки результатов эксперимента
Первый этап, содержание которого состоит в синтезе как стационарных, так и
нестационарных формирующих фильтров, подробно рассмотрен в параграфе t
Второй этап, содержание которого состоит в численном решении
дифференциальных уравнений анализируемой САУ, изучен достаточно хорошо и с основными
методами можно познакомиться в [8, 106, 126] и др.
Кратко изложим некоторые теоретические положения третьего этапа. Положим,
что в результате моделирования получены N значений векторов фазовых координат
системы при t = T (Г-заданный момент времени): jci/Г), х2£Г); ... , xnj(T),
(j =1,2,..., N).
Оценки моментов фазовых координат системы можно рассчитать по формулам [8]
;=i
Г 1 1 W
М Y*iY*2 Y*« ~ l Vrr \k4r № (г ^ -fY(*I+"'+kn)
(6.91)
где Ху - реализация фазовой координаты XtiN- общее число реализаций. При
вычислении вероятности того, что некоторая функция фазовых координат
%(Х1,Х2,... ,Хп) будет принимать значения в пределах а<%<Ь, расчеты ведутся
по формуле
* М
P[a<x(XlfX2,...,Xn)<b] = P[a<x<b] = — ,
N
(6.92)
где N - общее число реализаций случайных функций и величин, М - число этих
реализаций, при которых выполняется неравенство в формуле [8].'
Очевидно, что величина каждой из оценок сс^ и а(^+""+*и) зависит от числа /V,
т.е. является случайной величиной и, таким образом, степень отличия оценки от
истинного значения зависит от числа испытаний. В связи с этим естественной является
задача: определить такое число реализаций случайных величин N, чтобы оценка
заданного параметра отличалась от своего истинного значения на заданную величину
388
Анализ и статистическая динамика САУ. Часть I
с заданной вероятностью [8]. Или, что то же самое: определить число N для
заданных доверительного интервала EN и доверительной вероятности Р^.
Воспользовавшись законом больших чисел, в соответствии с которым среднее
значение большого числа слагаемых приближается к соответствующему
математическому ожиданию, и положением центральной предельной теоремы, из которого
следует, что это среднее есть случайная величина, распределенная по закону, близкому к
нормальному, можно записать [8]
8*
р[\хы-м[Хы]\<^ищ-
\ = Р,
ЛГ>
(6.93)
где eN - абсолютная погрешность:
если
5 _Щ-М[х„]
ТО
sN=&NjD[xn], (6.94)
Ф(г) - функция Лапласа.
Оценки математического ожидания и дисперсии случайной фазовой координаты
X(t) системы
mx(O = jYiXk(t), Dtxx(t) = -^^(xk(t)-m*x(t))2 ' (6.95)
с учетом факта, что если все реализации случайной величины X независимы, то
дисперсия суммы случайных величин равна сумме дисперсий слагаемых, могут быть
определены из зависимостей [8]
W[mi(01 = ^-Af £X*(O \ = M[Xk(f)] = mxp),
_*=i
N k-l ■ П
Щ«(01=']П^Щ'(')"т*(')]2=?н(0>
(6.96)
D[D»W]=FID"(O>
Откуда получаем формулы для вычисления относительных средних квадратических
отклонений оценок математического ожидания и дисперсии
jDxx(t) VF D
(6.97)
'XXV> Viv ^XXy
Полагая, что оценки т*х и D]^ распределены по нормальному закону, согласно
равенству (6.93) для заданных относительных доверительных интервалов vx, для
математического ожидания и v2 для дисперсии (соответствующие абсолютные доверительные
интервалы равны гх =V1A/Dxx(r), E2=v2Dxx(t)) и доверительной вероятности р,
можно построить табл. 6.3 и 6.4, показывающие, какое число опытов нужно выполнить,
Глава 6. Методь
чтобы для задан
и дисперсии coot
^^^ Р
0,6
0,7
0,8
0,9
0,6
0,7
0,8
0,9
[ исследовани
ной доверите
ветственно ос
0,2
18
27
41
68
0,2
37
. 55
83
137
я нелинейны?
льной вероят
гавались в зад
0,15
31
47
73
121 .
0,15
63
95
147
243 *
:САУ
ности оценки
анном доверил
0,10
70
108
164
272
0,10
141
217
239
545
математичес
гельном интер
0,05
281
431
651
1090
0,05
563
863
1300
2180
389
кого ожидания
вале.
Таблица 6.3
0,01
7000
10800
16400
27200
Таблица 6.4
0,01
14000
21600
32800
54400
Из приведенных рассуждений можно заключить, что для уменьшения
доверительных пределов в 10 раз {повышение точности метода на один порядок)
требуется увеличить число экспериментов в 100 раз, т.е. на два порядка. Можно считать,
что ошибка метода при заданной доверительной вероятности уменьшается обратно
пропорционально JN . С увеличением доверительной вероятности (повышение
надежности-достоверности метода) число опытов тоже возрастает. Поэтому при оценке
вероятностей с достаточно высокой точностью и достоверностью требуется большое
число экспериментов. Это существенный недостаток метода статистических
испытаний и его целесообразно применять, когда относительная точность в определении
статистических характеристик не превышает (15 - 20) % [8].
В [8] рассмотрен ряд способов, с помощью которых можно уменьшить требуемое
число испытаний для получения оценок с заданной точностью.
В заключение изложим алгоритм построения оценок математического ожидания и
автокорреляционной функции фазовых координат с использованием разложения по
ортонормированным базисам. Представим сигнал, оценки математического
ожидания и корреляционной функции которого необходимо найти, в виде разложения по
некоторому ОНБ
Ф(0 = (Ф1(О,Ф2(О,... ,ФДО)Т, (6.98)
*(0 = £с*фД0 = ФТ(0Сх,
(6.99)
i=i
где Сх = (с* ,с%,... ,cf )т - вектор коэффициентов разложения сигнала X(t) по ОНБ
Ф(0 или спектральная характеристика сигнала Х(г).Тогда его математическое
ожидание можно представить в виде
'тх(0 = А#{Х(0}=2^{^}фД0 = 2^хФ1.(0 = ФТ(0С^, (6Л0°)
i=i
i=i
где Ст* =\с™х ,с™х ,... , с™* ) -вектор математических ожиданий коэффициентов
разложения сигнала X(i). To есть для определения математического ожидания
сигнала X(t) необходимо знать математические ожидания его коэффициентов разложения.
390 Анализ и статистическая динамика САУ. Часть I
Корреляционная функция сигнала X(t) может быть представлена следующим
образом
Rxx(hh) = M{{X(tl)-mx(tl))-(x(t2)-mx(t2))}=
=м 11 («** -<** h ('■))( t(** -°т h ^
=£2>{(с* -ст* )-(cf -с-;* )}ф, (ОфД'2)= (6.Ю1)
/=1 7=1
= Фт(г,)Ся»Ф(г2),
где CRxx - квадратная матрица размерности £ х £ , элементами которой являются
корреляционные моменты cjjxx =Af{(c* -с™х j[cf -с'"х )} коэффициентов
разложения сигнала X(f). To есть для определения корреляционной функции Rxxih^h)
необходимо знать корреляционную матрицу коэффициентов разложения сигнала X(t).
Для расчета оценок математических ожиданий и корреляционных моментов
коэффициентов разложения сигнала X(t) воспользуемся формулами [8]
1 п
с,"»=-Ус£, i = l,2,.-J, (6.102)
Л *=Л д ^
где п - число реализаций сигнала X(t)\
cik - i-й коэффициент разложения /:-й реализации.
Алгоритм реализации метода статистических испытаний при изложенном
подходе к обработке результатов изменится следующим образом. На втором этапе после
получения каждой очередной реализации исследуемого сигнала производится ее
разложение по ОНБ и в дальнейшем хранится не сама реализация, а только
коэффициенты ее разложения. На этапе статистической обработки сначала вычисляются
оценки математических ожиданий и корреляционных моментов коэффициентов
разложения по формулам (6.102) и (6.103), а затем по формулам
"i(0 = j<f;<P/(O, (6.104)
1=1
i i
O'i>'2)=££^4('i)<p,('2) (6.Ю5)
i=l 7=1
рассчитываются оценки математического ожидания и корреляционной функции
исследуемого сигнала X(t).
Сокращение объема вычислений и промежуточных данных при таком подходе к
статистической обработке зависит от используемого ОНБ. Так, например, при
использовании ОНБ функций Уолша.и удержании £ = 32 членов разложения
потребуется хранить 32x1000 чисел (128 Кб памяти).. Для вычисления же оценок по
формулам (6.102) и (6.103) с учетом использования быстрого преобразования Уолша при
разложении реализаций по ОНБ на втором этапе потребуется выполнить
1,53 -106 операций умножения и 5,6-10 операций сложения (т.е. число операций по
сравнению с классической обработкой сокращается более чем на 2 порядка).
.Глава 7. Методы синтеза статистически оптимальных САУ 391
ГЛАВА 7. МЕТОДЫ СИНТЕЗА СТАТИСТИЧЕСКИ
ОПТИМАЛЬНЫХ СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Методы синтеза оптимальных линейных систем при случайных воздействиях
имеют необходимое теоретическое обоснование и широко используются при
решении инженерных задач. К таким методам можно отнести методы, использующие
параметрический синтез, основанные на решении уравнения Винера - Хопфа, Кал-
мана - Бьюси.
Основы статистической теории оптимальных систем, изучающей методы
получения наиболее вероятной, оптимальной, в известном смысле, оценки сигнала,
связанного с полезным сигналом некоторой заданной операцией, заложены в работах
А.Н. Колмогорова и Н. Винера. В русле развития этих работ построена теория
линейной фильтрации как для.скалярного случая, так и в пространстве состояний.
Получены одномерные и многомерные уравнения Винера - Хопфа, определяющие
импульсные переходные функции оптимальных линейных фильтров.
Наиболее общие результаты в теории линейных статистически оптимальных
систем получены B.C. Пугачевым [114].
Методы решения важных задач расчета оптимальных в статистическом смысле
динамических характеристик САУ (стационарных, нестационарных, дискретных и со
случайными параметрами) разработаны В.В. Солодовниковым и П.С. Матвеевым.
Ценный вклад в развитие теории фильтрации внес Р.Е. Калман. Построена общая
теория фильтров Калмана - Бьюси, включая фильтры Калмана - Бьюси для
несмещенной оценки. Результаты обобщены на дискретный вариант: разработана теория
дискретных фильтров. Наиболее существенным результатом теории является
описание оптимальных фильтров с помощью дифференциальных и разностных
уравнений. Это обстоятельство становится решающим в тех случаях, когда
формирующий фильтр имеет высокий порядок, ибо при этом решение интегральных уравнений
крайне усложняется.
Применение теории фильтров Калмана - Бьюси позволяет достаточно просто
построить структурные схемы оптимальных фильтров. Разработана теория
оптимальной фильтрации при небелых шумах.
Существенно более сложной как по постановкам задач, так и по методам их решения
и теоретического обоснования является проблема нелинейной фильтрации сигналов.
Эта теория недостаточно разработана и развивается по нескольким направлениям.
Приведем некоторые примеры задач, решение которых связано с проблемой
нелинейной фильтрации [114].
Важными являются задачи по обнаружению сигналов, когда их появлению
предшествует заранее неопределенный период ожидания, задачи по классификации
сигналов в условиях наличия мешающих факторов, а также оценивание параметров
сигналов в разной помеховой обстановке.
Задача обнаружения актуальна для станций обнаружения (радиолокация,
гидроакустика, сейсмология и др.), когда в зоне действия средств обнаружения спонтанно
возникают те или иные возмущения, вызванные самыми различными причинами, или
когда обнаружению подлежит начало работы какой-нибудь локационной станции.
392 Анализ и статистическая динамика САУ. Часть I
В этих условиях надо не пропустить, более того, как можно скорее обнаружить
появившийся сигнал.
Обнаружение сигнала, позволяет своевременно предпринять те или иные
неотложные действия, например, подать команду на изменение курса движения судна при
обнаружении другого судна, идущего встречным курсом.
Важной является задача классификации сигналов, под которой понимается
определение принадлежности параметров сигнала к одному из возможных
распределений. При решении практических задач это - распознавание объектов, поскольку
распознаваемым объектам свойственны разные распределения параметров сигнала. Сто-
хастичность сигнала и наличие помех требуют последовательной процедуры
классификации, при этом алгоритм классификации должен минимизировать ошибки
классификации.
Большую практическую ценность имеет задача оценивания параметров сигнала.
Например, в навигационных системах по параметрам сигналов вычисляются
координаты и элементы движения объектов. Байесовский подход позволяет наиболее полно
осуществить решение этой задачи.
Содержание каждого из направлений теории нелинейной фильтрации
определяется тем обстоятельством, что полезный сигнал и помеха имеют распределение,
отличное от нормального. Одно из направлений предполагает, что оцениваемый вектор
состояния представляет собой условный марковский процесс и находится
дифференциальное уравнение, определяющее первую условную функцию распределения
вектора состояния. Второе направление состоит в оценке вектора постоянных
случайных параметров, с помощью которых можно представить информацию, сообщение,
полезный сигнал или состояние объекта. Общий подход этого направления
основывается на байесовском критерии в оценке постоянных случайных параметров,
нелинейно связанных с наблюдаемым полезным сигналом, при наличии аддитивной
гауссовой коррелированной нестационарной помехи.
Наибольшее развитие получила теория нелинейной фильтрации при аддитивной
гауссовой помехе в наблюдаемом сигнале.
Цель настоящей главы - изложение некоторых подходов к синтезу статистически
оптимальных систем, знакомство с основными идеями и положениями проблемы.
Приведены некоторые положения, лежащие в основе теории фильтров
Колмогорова - Винера; рассмотрены скалярные и векторно-матричные уравнения Винера -
Хопфа и методы их решения.
Широкое применение в инженерной практике нашли фильтры Калмана - Бьюси.
Теория этих фильтров также изложена в настоящей главе.
Будут рассматриваться лишь простейшие задачи синтеза оптимальных систем при
случайных воздействиях в следующей постановке:
заданы вероятностные характеристики полезного сигнала и помехи, поступающие
на вход замкнутой нелинейной системы; часть элементов системы задана, в том
числе нелинейные элементы. Необходимо определить параметры или структуру и
параметры линейной или нелинейной корректирующей цепи из условия
воспроизведения полезного входного сигнала с минимальной среднеквадратичёской ошибкой.
Поскольку система нелинейна, то предварительно оценивается возможность
автоколебательного режима в ней без случайных возмущений. Далее используются
методы синтеза систем: если средний квадрат ошибки системы имеет единственный
минимум, то оптимальные параметры рь Р2> ••• »Ри минимизирующие величину
среднеквадратичёской ошибки, могут быть найдены методом нелинейного
программирования с введением условий абсолютной устойчивости нелинейной системы по
критерию В.М. Попова. Эти методы приводят к сокращению объема вычислений для
нелинейных систем высокого порядка; при этом облегчается поиск глобальных
экстремумов целевых функций.
Глава 7» Методы синтеза статистически оптимальных САУ
393
В-большинстве работ по оптимизации систем, описываемых рядами Вольтерра,
используется квадратичный критерий [84, 123]. Поэтому в этой главе основное
внимание уделяется получению системы интегральных уравнений, определяющих
оптимальную нелинейную систему и методы ее решения.
7.1. ФИЛЬТРЫ С ЗАДАННОЙ СТРУКТУРОЙ
(ПАРАМЕТРИЧЕСКАЯ ОПТИМИЗАЦИЯ)
Оптимальной среди систем данного класса называют систему, для которой
показатель ее качества имеет экстремальное значение (минимум или максимум в
зависимости от смысла показателя). Выбранный показатель качества называют, как
говорилось выше, критерием оптимальности.
Рассмотрим случай, когда заданы структура системы и статистические
характеристики входных сигналов. Требуется найти такие значения параметров системы (одного
или нескольких), при которых обеспечивается экстремум критерия оптимальности.
Эти значения параметров называют оптимальными параметрами системы [145].
Такая задача широко распространена на практике, т.к. структура системы часто
выбирается исходя из ее функционального назначения. Можно специально вводить
корректирующие звенья с изменяемыми параметрами [145].
Перейдем к рассмотрению задачи. Ясно, что ошибка системы состоит из двух
составляющих. Одна из них вызвана тем, что система не может абсолютно точно
воспроизводить полезный сигнал m(t), а другая - реакцией на помеху n(i). Стремление
уменьшить первую составляющую приводит к увеличению второй составляющей
ошибки и наоборот. Задача синтеза состоит в том, чтобы обеспечить минимально
возможную сумму обеих составляющих при заданной структуре системы (рис. 7.1).
£.(00),
nnv
А*№
О со .
Рис. 7.1. К задаче нахождения оптимальной ПФ системы
Наиболее простым является случай, когда полезный сигнал имеет более
низкочастотный спектр, чем помеха (рис. 7.2).
SJ№
• А»
Рис. 7.2. К иллюстрации задачи фильтрации'
394
Анализ и статистическая динамика САУ. Часть I
Тогда полоса пропускания системы должна быть выбрана достаточно широкой
для обеспечения необходимой точности воспроизведения m(i), но не такой ширины,
чтобы полностью отфильтровать помехи (рис. 7.3).
m{t)
Y(t) = m(t) + n(t)
I-*
Wycfop,,...,^
W0(s)
X(t)
Рис. 7.3. К постановке задачи фильтрации
Перейдем к рассмотрению общего случая, когда спектры 5,^(0)) и 5W/I(co)
перекрываются.
Пусть в структуре системы введена управляющая система (регулятор) с ПФ
Wvc(s,pk), причем параметры ри Рг,—, Рг могут меняться. Для простоты положим, -
что параметры остальной части системы фиксированы; эта часть имеет ПФ W0(s).
Тогда ПФ замкнутой системы имеет вид
щ5)= Уус('.й)УоС> .y(ltft),
l+Wyc(s,pk)W0(s)
Запишем выражение для СКО в предположении, что S^ (со) и Snn(co) - дробно-
рациональные функции частоты со и, следовательно, СП можно факторизовать:
Smm (со) = S^m (ja)S^, i№ = Smm(MSmm (-jco);
Snn(M = s;n( jco)5;n(jco) = 5пп(Усо)5„„(-усо).
Справедлива зависимость
oo oo
о2 = J \l-W(s,pk)\2\s=J(aSmm(a)d(o+ j |W(S,pt)|2|i=;lo5nn(co)dco =
—oo —oo
oo
= J (l-W(j(j>,pk))(l-W(-j<i>,pk))Smm(№Smm(-j(i»d0>+
—oo
oo
+ J W(Mpft)W(-Mpk)Snn(ju>)Snn(-jcoMco =
-2.
= 2пГп(рх,...,рг) + 2п1;(р{ p^) = a (P!,p2,...,pr). '
Таким образом, ст (P\,p2i—>Pr) является функцией параметров ри Ръ ..., рг (см.
Приложение 1).
Оптимальной системе соответствуют такие значенияр*, ..., р*, при которых a
достигает минимума.
Предположим, что минимум выпуклой функции о существует и единственен, а
ограничения на параметры отсутствуют. Тогда условие минимума находится прирав-
-2
ниваннем частных производных от a no pv нулю, т.е.
Глава 7. Методы синтеза статистически оптимальных САУ 395
Эа2(Р1,р2^,рг)=(); у = - (71)
Введем векторные обозначения:
Р= (Pi,...,'Pr)T - вектор-столбец параметров;
~-2 Л-2 Л-2
_—2,_ч ,"2,^4 ,ост ост da чт -
va (P) = graaa (P) = ( , ,..., ) - градиент - вектор-столбец частных про-
оРх ор2 дрг
изводных.
Тогда систему уравнений (7.1) можно записать в виде одного векторного
уравнения ,
Va2(P) = 0. . (7.2)
Решение этого уравнения и определяет оптимальный вектор параметров Р = Р =
= (Р\ ,Р2 ,...,Рг) •
Для решения системы (7.2) наиболее часто используют численные методы, а для
нахождения min a (P) можно применять методы оптимизации.
Если на параметры системы наложены ограничения, то для решения задачи опти-.
мизации необходимо использовать аппарат нелинейного программирования.
Пример 7.1. Рассмотрим задачу выбора параметров 4 и (0„ системы, которая описана в параграфе.
Необходимо найти ^и (0л, минимизирующие ошибку a . Коэффициент демпфирования £ должен
выбираться исходя из необходимости обеспечить достаточно быстрое затухание свободных колебаний
замкнутой системы (оптимальным значением является % = 0,7). Следовательно, единственным параметром
остается частота 0)й.
Выражение
«"2 2S
показывает, что с увеличением со„ составляющая от скоростной ошибки (первое слагаемое) уменьшается,
а составляющая от наличия помехи (второе слагаемое), наоборот, увеличивается. Оптимальное значение
со,, можно получить, исследовав выражение (7.3) на минимум. Имеем
Э?Ю_-2(ц,4$У я50
Эш„ а£ 2% ■
Решая полученное уравнение относительно 0)й , находим:
8I;V тц/5о
Отсюда получим
. nS0 У) nS0 ^ • TiS0 )
Найденная формула позволяет по известным /?ь So и заданному 4 вычислить оптимальное, с точки
зрения минимума СКО, значение параметра со,, замкнутой системы.
Пример 7.2. Рассмотрим систему, изображенную на рис. 7.4.
Y(t)=m(t)+n(t) +/Ov e(0
£
5(7^+1)
■щ
Рис. 7.4. Структурна схема системы
396 ' Анализ и статистическая динамика САУ. Часть I
На вход системы поступает аддитивная смесь полезного сигнала m(t) и помехи n{t), причем
Между помехой и полезным сигналом отсутствует корреляция.
Исходные данные: Т = 0,1 с; К =± 1/20 с"1; D^ = 100 град2; So = 0,01 град2/Гц.
Необходимо определить оптимальное значение коэффициента усиления К*, соответствующее
минимуму СКО.
Имеем зависимость, определяющую СКО через параметры системы (см. параграф 5.4):
К + а+а2Т2
Кроме того,
дЪ\к) _2D^aT{K + a + a2T2)-2Dmma{\ + aT + KT) , я/^_Q
дК К + а + а2Т2 V °
Отсюда находим
Ю^аПК + ос + а2Т2) - 2Dmma(l + ixT + КТ) = -nS0(K + a + a2r2)2;
2DmmaTK-2DmmaKT + nSo(K + a + a2T2)2 =
= -гп^аПа + а2Г2) + 2Dmma(l + 2Г).
Последняя зависимость определяет оптимальное значение К*.
7.2. ФИЛЬТРЫ КОЛМОГОРОВА - ВИНЕРА
Основополагающие результаты по теории фильтрации были получены
Н. Винером и А.Н. Колмогоровым (1941 г!). Ими рассматривались только
стационарные случайные процессы. В дальнейшем результаты были обобщены и на классы
нестационарных процессов.
IlejpeitaeM к изложению основных положений теории фильтров Колмогорова -
Винера.
Рассмотрим линейную систему, представленную на рис. 7.5.
Г(0=т(0+"«
-►
*(Лт)
Х(г)
Рис. 7.5. К постановке задачи фильтрации
Заданы взаимно не коррелированные центрированные случайные процессы в виде
функций времени m(t) и n(t) с корреляционными функциями
*mm('l.'2) = MHf,)/n(f2)],l '
" Rnn(tl,t2) = M[n(tl)n(t2)]. J
Требуется найти ИПФ k*(t,x) фильтра, оптимальным образом выделяющего
реализацию случайного процесса m{i) в виде некоторого процесса X(i) в условиях, когда
на вход поступает аддитивная смесь полезного сигнала m(t) и помехи n(t).
Критерием оптимальности является минимум среднеквадратической ошибки
(СКО)
м[ст2(0]' = т1п, (7.5)
где a(t) = m(t)-X(t).
Структурная схема, поясняющая постановку задачи фильтрации в классе
линейных систем, представлена на рис. 7.6.
Найдём уравнение, определяющее ИПФ оптимальной, в указанном выше смысле,
системы.
Глава 7. Методы синтеза статистически оптимальных САУ
397
m(t)
n(t)
it
Рис. 7.6. К постановке задачи фильтрации
Положим, что при t - О фильтр имеет нулевые начальные условия; тогда сигнал
ошибки а(0 определяется зависимостью
t
c(t) = m(t)-jk(tl,T)Y(x)dx. (7.6)
о
Для квадрата ошибки можно записать выражение
o2(0 = m2(0-2j*(r,T)F(T)m(0 dT+JJ*^) к^т2)Птх)¥(х2) dxxdx2. (7.7)
О 00
После осреднения по множеству получим
t гг.
M[a2(0]=D^(0-2j^(r^)/?J,m(T^MT + JJ^^T1)^^T2)/?^(T1,T2WT1JT2. (7.8)
О 00
Предположим, что ,
*(r,T) = **(f,T) + YM(f,T), (7.9)
т.е. ИПФ k(t,x) отличается от оптимальной ИПФ &*(г,т) на некоторую функцию
Тогда из (7.8) и (7.9) следует
Г ■ II
М [a2(r)] = Dmm{t)r-2\k\uT)RYm(r, t)dT+\\k\t,ix)k\ui2)RyY (тьт^х^х2 -
0 00
t t t
-2YjA^(r,T)/?Km(x,0^T+2YjJ/:*(r,T1)A/:(M2)/?jT &\**i)dxxd%2 +» (7.10)
о
11
00
где
• +y1^bk(tj\)bk(t,%2)RYY('Zx,'z2)d't\dtt1-
00
Или, что то же самое,
M[o2(0]=^h(0-2Y \\Ak(t,x)RYm(x,t)dx-
Lo
-jjk'it^Akit^RyyiT^dTfa \+y2E2(t),
00 J
t t
E2(t) = jJAk(t,xl)Ak(t,x2)RYY(xl,x2)dxldT2
(7.11)
(7.12)
00
398 Анализ и статистическая динамика САУ. Часть I
- существенно неотрицательная величина, являющаяся математическим ожиданием
Г/ ■*
квадрата интеграла М \bk(t,x)Y (x)dx
.о
Из (7.11) следует, что для того, чтобы М Гст2 (г) 1 = min, необходимо выполнение
условия
t t t
JAk(t,x)RYm(xj)dx-jjk*(tixx)Ak(tix2)RYY(xXix2)dxxdx2=0. (7.13)
0 00
Это условие легко получить, используя положение вариационного исчисления,
согласно которому необходимым условием экстремума функции м Гст2 (г)1 является
соотношение
ЭуГ"|_~ v/jjy=0
Подставляя (7.11) в (7.14), находим (7.13).
Можно показать, что уравнение (7.13) является также и достаточным условием
минимума среднеквадратической ошибки. Действительно, поскольку
M[a2(/)] = aL(0+Y2*2(')' (7Л5)
то т.к. у2Е2 (г) > 0, следовательно, М Гст2 (г)1 > ст^п (г) и, очевидно, функция k*(ttx)
действительно определяет фильтр, обеспечивающий минимальную СКО.
Перепишем (7.13) в виде
1>И')]} =°- (7-14)
}Д*(*,т) RrmM-!^(^i)Rrr(ti.t)rfT,
flfx=O, 0<т</. (7.16)
Поскольку J Д к (r,x)Z (т)dx = 0 тогда и только тогда, когда Z (т) = 0, то
о
ййи(т.0 = }**^т1)Я1Т(т1.т)Л1. (7.17)
о
Полученное интегральное уравнение 1-го рода (7.17) определяет оптимальную
ИПФ фильтра, обеспечивающего воспроизведение полезного сигнала m(t) с
минимальной СКО.
Уравнение (7.17) называется уравнением Винера - Хопфа, которое часто
записывается в виде
\k(uxx)RYY{xXix2)dxx=RmY{t,x2), 0<xXix2<u 'е[0,~). (7.18)
о
Подробно рассмотрим случай, когда m{t) и n{t) - стационарные стохастические
процессы.
Постановка задачи фильтрации по Колмогорову - Винеру для этого случая
такова [143].
1). Заданы взаимно не коррелированные СП в виде функций времени m{t) и n{t) с
КФ Rmm(x), /?яп(т), СПл 5ww(co) и 5nn(co); m{t) и n(t) - стационарные, эргодиче-
ские, центрированные случайные функции.
Глава 7. Методы синтеза статистически оптимальных САУ
399
2). Требуется найти ИПФ к*(т) фильтра, оптимальным образом выделяющего
реализацию СП m(t) в виде некоторого сигнала X(t) в условиях, когда на его вход
поступает аддитивная смесь m(t) + n(t).
3). Критерием оптимальности является минимум СКО c(t) = m(t) - X(t), т.е.
M[a2(r)] = a2 = min.
Для рассматриваемого случая уравнение Винера - Хопфа имеет вид
^ RYJ*) = \k*(u)RYY(T-u)du прит>0,
(7.19)
т.к. Яку© = Ryy(- £)> причем ЯгА?) - корреляционная функция сигнала Y(t) = m(t) + n(t),
определяемая по формуле
*ir(T) = iWx) + *«,(T);
^кт(т) - взаимная корреляционная функция сигнала на входе Y(t) и полезного
входного сигнала m(t).
Перепишем (7.19) в виде (после преобразования по Фурье)
SYm(s)\s=j*=W*(s)SMs)\s-j*>
откуда найдем
W*(jwi) = Ym - оптимальная ПФ;
SyyW)
к*(т) = — f W*(j(ti)ejmd(u - оптимальная ИПФ.
2п J
«-оо
Оптимальная ИПФ, определяемая этой формулой, будет отлична от нуля для
отрицательных значений т (рис. 7.7).
-т
-к
Рис. 7.7. График к*(г)
Такая система физически нереализуема. Однако приближенное построение
фильтра возможно (рис. 7.8).
**(т)а
Рис. 7.8. Приближенная ИПФ к*(т)
400
Анализ и статистическая динамика САУ. Частью!
Ясно, что результат обработки входного сигнала Y(t) = m(t) + n(t), поступившего в
момент времени t = 0, будет выдаваться фильтром с задержкой по времени на
величину т3ап- Качество обработки «покупается» ценой потери времени.
Рассмотрим теперь решение задачи о построении оптимального фильтра с учетом
условия его физической осуществимости.
Решение уравнения (7.19) наиболее просто осуществляется в частотной области.
Преобразуем уравнение (7.19) к виду
RYm{i) = ]k\u)R;Y{x-u)du = q{x\
(7.20)
где <?(т) - некоторая функция, равная нулю при т > 0. Условие <?(т) = 0 при т > 0
приводит к тому, что функция Q(j(u) <-> q(x) не может содержать полюсов в верхней
полуплоскости плоскости со (все полюсы находятся в нижней полуплоскости).
Необходимо помнить, что условие физической реализуемости состоит в
требовании равенства нулю ИПФ при т < 0 (рис. 7.9):
к(х) = 0 при т<0.
*(т) t
к (т)=0
к (т)*0
*=*—т
Рис. 7.9. ИПФ физически реализуемой системы
Но это может иметь место лишь тогда, когда соответствующая передаточная
функция W*(s) имеет все левые полюсы и, значит, все верхние полюсы частотной
характеристики W*(jco) (см. рис. 7.10 и 7.11).
со = -js
X
X
{
s
Рис. 7.10. Плоскость s
Рис. 7.11. Плоскость СО
(7.21)
Преобразуем обе части (7.20) по Фурье
5Ут(со) - W\j(u)SYY (со) = Q(jco).
Далее для простоты полагаем, что 5уу<со) имеет дребно-рациональный вид.
Представим
SYY (со) = SbU®)SnU(u) = ^(Л^гкС-ЛО), (7.22)
где SYY(j(ri) имеет все нули и полюсы в верхней полуплоскости (верхние нули и
полюсы;, a SYY(j(ti) имеет все нули и полюсы в нижней полуплоскости (нижние нули и
полюсы).
Глава 7. Методы синтеза статистически оптимальных САУ 401
Такая операция, как уже говорилось, называется факторизацией. Подставив
(7.22) в (7.21), получим
5Kw(©)-W*(y©)S^(y©)SJV0-©) = еО'о>). (7.23)
Произведя деление в (7.23) на SYY(j(ti), найдем
SYY(j(u) SYY(j(u)
Дробь B(j(u) = SYm((u)/SYY(j(u) можно представить в виде суммы
Я(7Ю) = Я+(7Ш) + Я'Оа)),
причем B+(j(u) имеет все нули и полюсы только в верхней полуплоскости, a B~(j(ti)
- только в нижней.
Эта операция, связанная с разложением на простейшие дроби и соответствующей
группировкой слагаемых, называется расщеплением.
Тогда
В+ (jco) + В~{./со) -W\jn)Sty(7(0) = Q(m . (7.24)
■SWO'co)
Поскольку по условию физической осуществимости необходимо выполнение
условия т > 0, решение уравнения ищется только в верхней полуплоскости со. В этом
случае полученное уравнение принимает вид
B+(j(u)-W*(j(u)S}Y(j(u) = O, (7.25)
т.е.
W-(jto)eJ^M; (7.26)
SyyiM
4-(т) = ±7«!Ш>е^са (7.27)
2nLSYY(J<*)
Замечание: Линейный фильтр является оптимальным для нормальных СП, если
сигнал отличен от нормального, оптимальный фильтр следует находить в классе
нелинейных систем.
Пример 7.3. Найти W*(s) и **(т), если
п р^ + со2
Приведем основные этапы решения задачи.
1-й этап: НахождениеСПл сигнала Y(t).
Поскольку 5ук(со) = 5mm(co) + 5лл(со), то
„л _ Р2 , 50 _ Р2 + (Р2 + со2)5о _ Р2 + Р25О + 0)250 _
5it(C0) = PW+7= р2+ш2 = р2+ш2 =
_ Р2(1 + 50) + 50со2 _ а2 + 50ш2
р2+ш2 " р2+со2 '
где д2=р2(1 + 50).
2-й этап: Факторизация СПл 5КУ((о):
где
3-й этап: Нахождение 5к,и(со). Ясно, что SYm(<u) = 5шт(со).
27 Зак. 232
402 Анализ и статистическая динамика САУ. Часть I
4-й этап: Расщепление
Я(;со) = ^
_ 5yw((o) _ 5mw((0)
Syy(j(a) SYY(ju>)
Имеем
вщщ р2/(О)2?2) -,»',»-*-
(а - усш) /(р - уш) р + а) л - усш
Р2 Р-уш_ Р2
(Р + уш)(Р - уш) а - усш (Р + уш)(а - jew)
Отсюда получим
B(ju>)=-—- + -
)+Уш a-jew
Методом неопределенных коэффициентов находим
«2 п2
г:-^
а + ф а + ф
Тогда
вЧМ=-
где
(д + ф)(Р+./(1))'
5-й этап:
*•(*»=.£<*»- Р2(Р**» --£ !-=—*—.
5?к(Усо) (а + сР)(Р + ;ш)(а + ;са)) а + фа + уеш Г(;ш) + 1
PVs^TT 1+50 + Сл/^й
Таким образом, оптимальный фильтр - инерционное (апериодическое) звено, у которого коэффициент
усиления всегда меньше единицы и зависит от 5о, а постоянная времени Т определяется как So, так и
спектром полезного сигнала.
Пример 7.4. Найти ПФ оптимального фильтра, если Rmm(i) = Dmme~^\ Rnn{i) = Dme~^t причем А™
= a2;Dnn = b\
Решение.
1-й этап: Найдем СПл сигналов m{t) и л(/); они равны
5mm(ш)= Dmm\ ; 5^,(0))= ^w|Ct? .
я(1 +со2) ™ я(а2 + ш2)
Найдем 5кк(ш):
где Р2 = 2а2ос2 + 2Ь2а2; у2 = 2а2 + 2Ь2ои
2-й этап: Факторизация СПл. Факторизуя, получим
<Лп (ш-j)(u>-ja) ^ ((0+j)(a>+ja)
Тгя (о-ухо-yoo'
5-r(yco) = -7l Y(0+^ .
Kr V27c(a)+y)((D+ya)
3-й этап: Найдем"5кот(со). Так как К(/) = w(/) + л(/), то /?Km(^) = #mm(x), и, следовательно,
1 2а2
5Km((D) = 5mm(0))=— 2".
2я 1 + о
4-й этап: НахождениеB(j(ti) и B+(j(u) (расщепление). Имеем
1 2а2
„2/... , ;\/,.> I ;/v\ I O/.2/
д (/-ш)= sYm«») 2я1 + о)2 J 2fl2((i)+y)((i)+ya)_ I 2^((o+ya)
5уу(/со) ^ Ytt>+JP 2я (w2 + l)(Y(i)+yp) 2я(а)-уКуа)+ур)"
72я (а)+У)(а)+уа)
Глава 7. Методы синтеза статистически оптимальных САУ 403
Найдем B+(j(u). Для этого можно воспользоваться разложением B(jwi) на слагаемые с
неопределенными коэффициентами и вычислением этих коэффициентов:
В( /о) = —*— + ^— (без -т=); А70) + А /р + Л2ш + Л2 / = 2а2(со + /ос).
со-у yw+fi yl2n
Умножением уравнения на j и выделением членов при равных степенях усо получим два
алгебраических уравнения:
Ду + ^2 = 2а2; -ДР - А2 = -2д2ос;
откуда
Y + P уГ2п Y + P со-у
5-й этап: Нахождение W*(j(a).
Оптимальная ПФ определяется выражением
w* _ B+(j<a) = 2a2q + ос) 1 (со- ;)(со- ja) _ 2а2{\ + а)[(;со) + а]
J Sfy(M) Y + P со-; YCO-yP (Y + P)[7(;co) + P] *
Далее легко найти ПФ разомкнутой системы или ПФ корректирующего устройства, если задана
неизменяемая часть системы.
Приведем векторно-матричное интегральное уравнение Винера - Хопфа.
Постановка задачи иллюстрируется на рис. 7.12. Постановка задачи идентична задаче для
скалярного случая; критерий качества имеет вид I = М{ [М(г) - X(r)]T x
x[M(0-X(f)]}->min.
К (f,T)
Ж*) к
1/
Рис. 7.12. К постановке задачи синтеза многомерных оптимальных фильтров
Решение задачи нахождения оптимальной- матрицы импульсных переходных
функций дается векторно-матричным интегральным уравнением Винера - Хопфа
t
bW'i^2) = jK4^Rr^i^2)^i> (7.28)
о
где RAfr(^i^2) = ^{M(r1)YT(r2)}; RYY{tbt2) = M{Y{tx)Y1{t2)}.
Как в скалярном, так и в векторном случаях применение оптимальных фильтров
требует решения двух сложных задач: решения уравнения Винера - Хопфа и
реализации структурной схемы системы.
7.3. ОПТИМАЛЬНОЕ ОЦЕНИВАНИЕ СОСТОЯНИЯ
Часто желательно иметь возможность оценивания состояния системы на основе
данных, которые имеют лишь статистическую связь с этим состоянием и,
следовательно, не обеспечивают его точного определения. Например, можно пытаться
определить положение или скорость находящегося в воздухе объекта по данным
слежения локатора, решить вопрос о виде принятого сигнала в линии связи, если известна
совокупность возможных передаваемых сигналов и т.д. и т.п. При этом, естественно,
встает вопрос об оптимальности (наилучшей точности) полученных оценок. Для
линейных систем в качестве критерия оптимальности выступает минимальная
среднеквадратичная ошибка оценивания (восстановления) вектора состояния. Обозначим
оценку вектора состояния X в некоторый момент времени tx > t0 на основе
измерений вектора Y(x) на интервале t0 < т < t через X(t{ \t). В зависимости от того, какая
задача оценивания решается, имеют место следующие задачи:
27*
404 Анализ и статистическая динамика САУ. Часть I
а) t\ > t, тогда задача называется прогнозированием, или предсказанием;
б) ц = г, задача фильтрации (получение текущей оценки);
в) t\ < г, задача сглаживания, или интерполяции.
В дальнейшем нас будет интересовать только задача фильтрации. Для вывода
уравнений оптимального фильтра нам нужны некоторые вспомогательные выкладки.
В первую очередь - это вывод так называемого дисперсионного уравнения.
7.3.1. Вывод дисперсионного уравнения
Теорема 7.1. Рассматривается следующая динамическая система
X(0 = A(0X(0 + G(0N1(r),
X(fo) = X°,
где Ni(0 - гауссовский белый шум с характеристиками
M[N1(O] = 0;M[N1(r1)N^(r2)] = S1(r1)5(r2-r1), . (7.30)
A(r),G(r) - матрицы размерности пхп, пхр соответственно, а Х° - случайный
вектор, независимый от Ni(r) со средним значением Х° = М |Х° 1 и матрицей дисперсий
Doo = m{ (хо-Х°)(хо-Х°)Т}: (7.31)
Тогда матрица дисперсий Dxx (t) = R^ (t,t) удовлетворяет следующему
матричному дифференциальному уравнению
D^ (г) = A(r)D^ (г) + Dxx (г) Ат (г) + GWS, (r)GT (r) (7.32)
с начальным условием
• ' Dxx(fo) = Doo. (7.33)
Доказательство. Известно, что решение системы дифференциальных
уравнений (7.29) имеет вид
X(r) = O(r,r0)X°JO(r,T)G(T)N1(T)JT, (7.34)
'о
где Ф(г,*0) ~ переходная матрица состояния для (7.29).
Найдем дифференциальное матричное уравнение для матрицы начальных
моментов второго порядка
Cxx(r1,r2) = M[x(r1)XT(r2)]. (7.35)
Известно, что корреляционная матрица Rxxth'h) и матрица начальных
моментов второго порядка связаны соотношением
Cxx(r1,r2) = Rxx(r1,r2) + X(r1)-XT(r2), (7.36)
где X(tt), (i = 1,2) - математическое ожидание случайного процесса Х(г) в момент
времени г,.
По определению (7.35) с учетом формулы (7.34) имеем
Cxxai^2) = ^{X(r1)XT(r2)} = O(r1,r0)M{X°.X°T}.OT(r2,r0) +
+м
[ф(г1,г0)Х°]
|ф(г2,т)С(т)^(т)</т
+
Глава 7. Методы синтеза статистически оптимальных САУ
• 405
+М\
j«K'i.
T)G(T)N,(x)dT
[ф(г2>г0)Х°]Т
+М
\ф{ц,х^{хх)Щ1,)^1 ]ф(12,т2)С(х2)Щг2)с1т2
L'o
(7.37)
Рассмотрим отдельно каждое из 4-х слагаемых в правой части выражения (7.37):
1) Ф(^0)М{Х0(Х°)г}Фт(12,10) = Ф(11,г0)(?Фт(12,10),
где Q0 - матрица вторых начальных моментов для г, = г2 = t0.
2)
М
[фа^о)Х°]
Ф(г2,т)С(т)Щт)с1т
h
= Ф(г1,г0)|м{Х°.^(х)}Ст(г)Фт(г2,тМт = 0
в силу некоррелированности случайного вектора Х° и белого шума Ni(r) и условия,
что ^{N,(0}= 0, т.е.
Аналогичный вывод получаем для третьего слагаемого выражения (7.37).
3)
М
\Ф(г19%)С(х)Щ%)с!т
Jo
[ф(г2,г0)Х°]Т =0.
Рассмотрим четвертое слагаемое:
4) М
\ф{1хл№{тхЩ{1х)<1тх JO(r2,T2)G(x2)N1(T2)JT2
= J Jo(r1,T1)G(T1)M{N1(x1)Ny(T2)} Ст(т2)Фт(г2,т2Мт^т2 .
Используя выражение (7.30) и воспользовавшись фильтрующим свойством
5-функции, окончательно получим для 4-го слагаемого:
min(/,,/2)
\ O(r1,T)G(T)S1(T)GT(T)OT(r2,x)rfx.
'о
Таким образом, имеем:
min(/,,f2)
Схх('1,'2) = Ф('1.'о)С>0ФТ('1>'о)+ J O(f,,T)G(T)S1(x)GT(T)OT(f2,T)dT. (7.38)
Найдем дифференциальное матричное уравнение для матрицы дисперсий
Ихх (t) = Rxx (t). Из формулы (7.36) для t{ = t2 = t получим
Cxx(t,t) = Q(t) = Rxx(t,t)+X(t)-XT(t) = Dxx(t) + X(t)-XT(t). (7.39)
Для нахождения производной Схх (t,t) = Q(f) продифференцируем (7.38) по t, где
406 Анализ и статистическая динамика САУ. Часть I
ot ot
+J^^G(T)S1(T)GT(T)OT0,x)dT.+
'О
+i
f f Ф(г, t)G(t)S, (x)GT (t) ЭФ (f'T) dx+
i dt (7.40)
+O(f,0G(0S1(0GT(f)OT(f,0.
Используя свойства переходной матрицы состояния
^^ = А(ОФ(^0), (7.41)
ot
^^ = Фта)?0)Ат(0, (7.42)
Ot
Ф(г,г) = Фт(г,г), (7.43)
и подставляя (7.41) - (7.43) в уравнение (7.40), получим
Cxx^0 = Q(0 = A(0O(r,r0)Q0OT(r,r0) + O(r,r0)Q°OT(r,r0)AT(r) +
t
+jA(r)O(r,T)G(T)S1(T)GT(T)OT(r,T)JT +
'о
+JO(M)G(T)S1(T)GT(T)OT(r,T)AT(r)JT + G(T)S1(T)GT(T). (7.44)
Сгруппируем в уравнении (7.44) первое и третье, второе и четвертое слагаемые.
Тогда, учитывая формулу (7.38) для t\ = t2 = t, получим
A(f )Ф(г, t0 )Q°OT (r, t0) + J А(г)Ф(г, 1)6(1)8! (x)GT (т)Фт (г, т) dx = A(r)Q(r)
И
. /
Ф(tJ0)Q0Фт(tJ0)Aт(t) + jф(t,x)G(т)S^(т)Gr(x)Фт(t,x)Aт(t)dx = Q(t)Aт(t)■,
'о '
окончательное дифференциальное уравнение для матрицы производных начальных
моментов имеет вид
Q(0 = A(0Q(f) + Q(f) Ат (г) + G(0S, (0GT (f). (7.45)
Чтобы получить уравнение для дисперсионной матрицы D^it), используем
формулу (7.45) и соотношение (7.39)
Q(0 = Dxx (0 + *(0Хт(0 + X(f)^T(O = i>xx (0 + A(f)XT(OX(f) +
+X(0XT(0AT (0 = A(0(Dxx (0 + Х(0Хт(0) + (7.46)
HD^ (0 + X(0XT (f)) АТ (f) + G(OS, (f)GT (0.
Из выражения (7.46) получим искомую формулу
Ьта (0 = МФХХ (t)+J>xx (t )AT(0 + G(0S! (0GT(0, (7.47)
Dxx('o) = I>oo(')., (7.48)
Глава 7. Методы синтеза статистически оптимальных САУ 407
Заметим, что дифференциальные уравнения для матрицы начальных моментов
второго порядка (7.45) и дисперсионной матрицы (7.48) с точностью до обозначений
совпадают, а при отсутствии регулярной составляющей на входе, т.е. когда
М {Х(г)} = Х(г) = 0, тождественны, т.е. Dxx (t) = Q(r).
7.3.2. Оптимальная линейная фильтрация по Калману
Для перехода к построению оптимального фильтра Калмана напомним
постановку и решение задачи оптимальной фильтрации в смысле Н. Винера.
Многомерная система определяется как система с /-входами и «-выходами,
которые связаны посредством матричной импульсной переходной функции (МИПФ)
К(г,т). Пусть Y(r) - /-мерный вектор входа фильтра, а Х(г) - и-мерный вектор
выхода. Тогда связь между векторами Х(г) и Y(r) определена интегралом
X(r) = JK(r,T)Y(T)JT, X(ro) = O. (7.49)
'о
Пусть Y(r) - действительный случайный процесс с нулевым математическим
ожиданием и корреляционной функцией Rrr(r,T). Обозначим норму произвольной
квадратной матрицы В через ||В|| и определим ее следующим образом:
|В| = >/tr(BBT), (7.50)
где tr(Z) - след, т.е. сумма диагональных элементов матрицы Z.
Пусть на вход многомерного фильтра поступает искаженный сигнал как сумма
полезного сигнала М(г) и помехи N(r), т.е.
Y(0 = M(0 + N(r), (7.51)
где М(г) и N(r) - /-мерные векторы с известными корреляционными функциями
КлшСт) и Raw(M:).
Предположим, что существует идеальный выход Х(г) некоторой системы,
который определяет желаемый выход и связан с полезным сигналом соотношением
t
Х(0 = /кид(г,т)М(т)^т, (7.52)
'о
где Кид(г,т) - МИПФ идеальной системы. Рассмотрим вектор ошибок
X'a(t) = X(t)-X(t). (7.53)
Задача состоит в том, чтобы выбрать такую физическую реализуемую матричную
ИПФ К*(г,т), чтобы математическое ожидание квадрата нормы ошибок было
минимальным
M{||Xa(r)|2}=min, (7.54)
К(/,т)
где К(г, т) = 0 для кт, а норма имеет вид (7.50).
В зависимости от того, какая задача стоит: прогнозирования, фильтрации или
сглаживания, определяется МИПФ идеальной системы. В задаче фильтрации
Х(г) = М(г), т.е. Кид(г,т) = 1-5(г - т). При такой постановке задачи минимум
среднеквадратичной ошибки (7.54) определяется МИПФ К*(г,т), получаемой из
обобщенного уравнения Винера - Хопфа для многомерных систем
KMY(t,T) = JK*(t,s)RYY(s,T)ds. (7-55)
408 Анализ и статистическая динамика САУ. Часть I
Известно, что если на вход системы поступает случайный сигнал Y(f),
являющийся стационарным,' в широком смысле, случайным процессом, оптимальную
матричную передаточную функцию W*(s) многомерного фильтра можно получить
факторизацией рациональной матрицы спектральных плотностей. В случае же
нестационарного случайного процесса решение интегрального уравнения Вольтерра 1-го рода
(7.55) даже для скалярного случая представляет серьезные трудности, не говоря уже
о векторном. Р. Калман в своих работах [193, 194] модифицировал постановку задачи
многомерной фильтрации Винера, придав ей форму проблемы пространства
состояния. В результате такой модификации был получен фильтр Калмана,
осуществляющий процедуру рекурсивного оценивания, когда подлежащий оцениванию сигнал
является выходным сигналом линейной нестационарной динамической системы.
7.3.3. Уравнение оптимального фильтра
В дальнейшем предполагается, что решается задача фильтрации, т.е. оценка
полезного сигнала X(fj|f) получена для t\ = г, поэтому обозначим ее Х(г).
Для вывода уравнений оптимального фильтра считаем, что полезный сигнал М(г)
является выходом формирующего фильтра, который описывается в пространстве
состояний линейным матричным дифференциальным уравнением с вектором
состояния Х(г). Отсюда замечаем, что полезным сигналом для оптимального фильтра будет
сигнал Х(г), т.е. Х(г) = М(г).
Пусть входной случайный процесс фильтра Y(r) является зашумленным выходом
формирующего фильтра, описываемого следующим уравнением:
Х(0 = А(0Х(г) + С(О^(г),
Х(г0) = Х° - случайный вектор начальных условий, (7.56)
где Ni(r) - гауссовский белый шум с статистическими характеристиками:
М{ВД} = 0 , RNiNi(r,T) = S1(O5(r-T), (7.57)
Si (г) - положительно определенная симметричная матрица интенсивности.
Предполагаем отсутствие корреляции между шумом Ni(r) и вектором Х°, т.е.
M{X°N[(r)} = 0. (7.58)
Известна дисперсия начального состояния вектора Х(г):
D00 = M{(X°-X0)(X0-X°)T}, (7.59)
где Х° = М{Х°} = 0.
Размерности матриц A(r), G(f) соответственно пхп и пхр . Здесь мы повторяем
постановку задачи, рассмотренную в 7.3.1. Дополним условия (7.56) - (7.59) матричным
алгебраическим уравнением выхода измерений:
Y(0 = C(f)X(0 + N2(f), (7.60)
где С(г) - матрица размерности 1хп, Х(г) - переменная состояния.формирующего
фильтра, N2(f) - гаусовский белый шум с характеристиками
M{N2(r)} = 0, R^2(r,T) = S2(r)8(r-x), (7.61)
S2(r) - положительно определенная матрица размерности 1x1. Причем предполагаем
некоррелированность шумов Ni(r) и N2(r), а также Х(г) и N2(r), т.е.
М{^ш1(т)} = 0, Vr,x>r0; M{X(f)N£(x)} = 0, Vr,x>ro. (7.62)
Теперь выясним, какова должна быть структура фильтра, чтобы получаемая
оценка была несмещенной и среднеквадратичная оценка фильтрации М{||Хо(г)|| }была
Глава 7. Методы синтеза статистически оптимальных САУ 409
минимальной, где XCT(r) = X(f)-X(r). Структуру фильтра выведем из уравнения
Винера - Хопфа (7.55). Для этого уравнение (7.55) представим в следующем виде
(с учетом того, что М(г) = Х(г)):
M{X(r)YT(T)} = Jk*(m)M{Y(5)Yt(t)} ds. (7.63)
'о
Дифференцируя уравнение (7.63) по t и учитывая соотношения (7.56), (7.57),
получим:
|-М{Х(0¥т(т)} = А(г)М{Х(0¥т(т)} + С(г)М{^(0¥т(т)}, to<z<t (7.64)
at
и
?-\K*(tis)M[Y(s)YT(T)]ds = \dK^s)M[Y(s)YT(x)} ds +
dti I dt (7.65)
+ K*(M)M{Y(r)YT(x)}, /0<x<r.
Учитывая некоррелированность Ni(r) с N2(t) (см. формулу (7.62)) и Х(т) для всех
г > т (условие причинности), а Х(г) некоррелирована с N2(t) для всех г, т > г0 (см.
формулу (7.62)), вторые слагаемые в правых частях выражений (7.64), (7.65) примут
вид:
М{^(г)¥т(т)} = М{^(О(С(т)Х(т) + ^(т))т} =
= М{^(г)Хт(т)}Ст(т) + М{^(г)^(т)} = 0, г>х>г0;
M{Y(r)YT(T)} = M{(C(r)X(r) + N2(r))YT(T.)}= ,__
т т т (7*67^
= C(r)M{X(0YT(T)} + M{N2(r)YT(T)} = C(0M{X(r)YT(T)}, t >x>r0.
Объединяя уравнения (7.64), (7.65), с учетом соотношений (7.66), (7.67) получим
/ -\Тг* /
или
A(r)M{X(0YT(T)}=f^^M{Y(5)YT(T)}^ +
+K*(r,r)C(r)M{X(r)YT(x)}, to<z<t,
(A(t)-K\tj)'C(t))M{X(t)YT(T)}=[^^M{Y(s)YT(T)}ds. (7.68)
J dt
'°
Подставляя в уравнение (7.68) вместо М{X(t)YT(т)} правую часть уравнения
Винера - Хопфа (7.63) и перенося все слагаемые влево, имеем:
j[A(t)K\tis)-^^-K\tj)C(t)K\t,s))M{Y(s)YT(x)}ds = O, to<x<t. (7.69)
h
Ясно, что уравнение (7.69) будет справедливо, если К*(г,т) будет решением
дифференциального уравнения:
ЭК,(Г>Т) = А(г)К*(г,т)-K*(u)C(f)K*(f,T), t0 < т < t, (7.70)
ot
т.к. M{Y(j)Yt(t)}*0 в общем случае.
С другой стороны, дифференцируя уравнение (7.49) по г, получим:
26 Зак. 232
410 Анализ и статистическая динамика САУ. Часть I
^ = j8K^Y(T)rfx+K.
dt J dt
h
Предположим, что оптимальный фильтр в пространстве состояний имеет матрицу
коэффициентов усиления, удовлетворяющую равенству:
к;(0 = К*(г,0. (7.72)
Тогда равенство (7.72) определяет структуру оптимального фильтра:
X(0 = F(0X(0 + K;(0Y(f),
решение которого
Х(г) = Ф(лго)Х(го) + }ф(г,т)К;(т)¥(т)^т = |ф(г,т)К;(т)¥(тМт,
'о 'о
т. к. Х(г0) = 0 дает матричную ИПФ
К*(г,т) = Ф(г,т)К*ф(т).
При t = т
к*(г,о = Ф(^,Ок;(О = Кф(О.
Найдем выражение для ¥(t). Подставляя в выражение (7.71) вместо — пра-
ot
вую часть (7.70), а также учитывая
t
Х(0 = JK*(r,T)Y(T)rfT, Х(го)=О (7.73)
'о
и соотношение (7.72), окончательно имеем
^Р = А(г)Х(О + к;(0( Y(r) - С(0Х(0) =
= (А(г) - К*ф(г)С(г))Х(г) + к;<0 Y(r).
Таким образом, мы видим, что F(r) = А(г)-Кф(г)С(г), а уравнение (7.74)
является дифференциальным уравнением оптимального фильтра, в котором требуется
найти оптимальную матричную функцию коэффициентов Кф (t).
7.3.4. Нахождение оптимальной матричной функции
коэффициентов фильтра
Определим ошибку восстановления (оценивая) Хст(г) полезного сигнала Х(г)
следующим соотношением:
Хо(0 = Х(0-Х(0. (7.75)
Тогда, учитывая уравнение формирующего фильтра (7.56) для полезного сигнала и
оптимального фильтра оценки (7.74), получим дифференциальное уравнение сигнала
ошибки:
^1 = [А(0 - К*ф(г)С(г)]Ха(г) + G(r)N1 (г) - K;(ON2(r). (7.76)
Кроме того, используя выражение (7.75), молено записать
M{X(r)YT(x)} = M{Xa(r)YT(T)} + M{X(r)YT(T)}. (7.77;
Глава 7, Методы синтеза статистически оптимальных САУ 411
Воспользовавшись уравнением Винера -Хопфа (7.63) и уравнением (7.73) для
оптимальной оценки Х(г), можно показать, что
M{Xa(f)YT(T)} = 0, r>T>to. (7.78)
Уравнение (US) - это одна из форм записи уравнения Винера -Хопфа. Из этого
уравнения покажем, что имеет место равенство
М{Ха(г)Хт(т)} = 0. (7.79)
Вначале заметим, что
t
M{Xa(r)XT(r)} = M{Xa(O[fK*(M)Y(TMT]T} =
'° f (7.80)
=M{[JXa(r)YT(T)K*T(r,TMT]} = jM{Xa(r)YT(T)}K*T(r,T)JT.
'о 'о
Тогда, учитывая выражение (7.78), получим формулу (7.79). Из уравнения (7.79)
можно сделать вывод, что оптимальная оценка не коррелирована с
соответствующей ошибкой оценки. Так как оба вектора являются гауссовскими, это означает, что
они независимы.
Рассмотрим две корреляционные функции M{X(r)YT(r)} и M{Y(s)Yt(t)} .
По определению:
M{X(r)YT(r)} = M{X(0XT(r)}CT(0+ /#7О1Ч
+M{X(f)Nj(r)} = M{X(r)XT(r)}CT(r),
где учтена некоррелированность выходного сигнала формирующего фильтра и шума
измерений. Аналогично для второй функции имеем:
M{Y(s)YT(t)} = M{Y(s)[C(t)X(t) + N2(t)]T} =
= M{Y(s)XT(t)}CT(t) + M{Y(s)NT2(t)} =
=M[Y(s)XT(t)}CT(t) + M{[C(s)X(s) + N2(s)]Nl(t)} =
=M{Y(s)XT(t)}CT(t) + C(s)M{X(s)Nl(t)} + S2(t)b(t-s).
С другой стороны, уравнение Винера - Хопфа (7.63) для т = t имеет вид:
M{X(r)YT(r)} = J K*(t,s)M{Y(s)YT(t)}ds. (7.83)
Подставляя выражения (7.81), (7.82) в уравнение (7.83), получим
M{X(0XT(r)}CT(r) = \K*(t,s)M{Y(s)XT(t)}CT(t)ds +
'о
(7.84)
+jK*(r,j)C(j)M{X(j)Nj(r)№+jK*(r,5)S2(05(r-j)dy.
'о 'о
В силу некоррелированности Х(г) и N2(0 второе слагаемое в правой части
уравнения (7.84) равно 0. Кроме того,
\K*(t,s)S2(t)8(t-s)ds = K*(r,0S2(0 = K;(r)S2(O, (7.85)
'о
где использовано фильтрующее свойство дельта-функции. Перенося влево первое
слагаемое соотношения (7.84), с учетом сделанных выводов получим:
26*
412 Анализ и статистическая динамика САУ. Часть I
M{X(t)XT(t)}CT(t)-JK\us)M{Y(s)XT(t)}CT(t)ds =
'о
t
=M{[XO)-JK\t,s)Y(s)ds]XT(t)}CT(t) = M{[XT(t)- (7.86)
'о
- X(t )]XT(t) }CT(O = M (Xo(f)(X(f) + Xc«) }TCT(O =
=M{Xa(t)XT(t)} + M{Xa(t)XTa(t))CT(t) = Kl(t)S2(t).
С учетом полученного выражения (7.79) о некоррелированности оптимальной
оценки и ошибки измерения и учитывая, что
M{Xo(t)XTa(t)} = Raa(t,t) = Doo(f),
где D00(f) - дисперсия ошибки фильтрации, окончательно получим:
D00(ocT(»=K;a)s2(o.
Откуда имеем оптимальную матрицу коэффициентов фильтра:
K;(0 = Doo(r)CT(r)S21(0. (7.87)
Для построения полной структуры фильтра необходимо найти дифференциальное
уравнение для дисперсии ошибки восстановления DCTCT(r).
7.3.5. Вывод дисперсионного уравнения для оптимального фильтра
Ранее (см. формулу (7.76)) было получено дифференциальное уравнение для
ошибки восстановления
Хо(0 = [А(0 - Кф(0С(г)]Хо(0 + G(r)N, (0 - К J(ON2(O (7.88)
с начальным условием
Xa(r0) = X^ = X(r0)-X(r0) = X(r0). (7.89)
По определению:
А#{Хо(г)} = Хо(0, (7.90)
M{[Xo(r)-Xa(r)][Xa(0-Xa(r)]T} = Daa(r). (7.91)
В постановке задачи оптимальной фильтрации по Винеру и Калману было
сказано, что оптимальная фильтрация обеспечивает минимум среднеквадратичной ошибки
восстановления. С учетом (7.90), (7.91) имеем:
minM{Xj(r)Xo(r)} = min{Xj(r)Xa(r) + tr[Daa(r)]}. (7.92)
Выражение (7.92) легко получается из известных соотношений
M{Z(r)ZT(r)} = Rzz(r,r) + Z(r)ZT(r) = Dzz(O + ZT(r)ZT(r)
и
tr(Z(f)ZT(f)) = ZT(r)Z(r), tr(A + B) = tr(A) + tr(B)
для случайных векторных процессов Z(r) и произвольных квадратных матриц А и В.
Из формулы (7.92) следует, что
Xj(r)Xo(0>0 (7.93)
для любого t>to, т.к. это положительно определенная квадратичная форма. С другой
стороны, применяя операцию математического ожидания к уравнению (7.88),
получим:
Хо(0 = [А(0-К*ф(г)С(г)]Хо(0. (7.94)
Глава 7. Методы синтеза статистически оптимальных САУ 413
Минимум выражения (7.93) достигается при Хст(г) = 0, t > г0, что обеспечивается
условием
Хо(г0) = 0 (7.95)
для уравнения (7.94).
Таким образом, если Х(ГО)^О, то выбор начальных условий с Х(го) = О
приводит к смещенной оценке вектора Х(г), т.к.
^ = М{Х(г)} = М{Х(0}-М{Хо} = Х(г)-Ха(г).
Выбор начальных условий для фильтра
X(fo) = X° (7.96)
обеспечивает несмещенность оценки и Xa(r) = 0.
Поэтому в дальнейшем мы можем считать что X Ф 0. В этом случае целевая
функция (7.92) примет вид:
minAf {Xj(0Xo(0} = min tr{Doa(f)}.
Кф(О
Теперь найдем матрицу Кф, такую, чтобы фильтр обеспечивал минимальную
среднеквадратичную ошибку
y(r) = tr{Daa(O} = M{||Xa(r)f}-> min . (7.97)
Кф(О
Представим дифференциальное уравнение (7.88) для ошибки восстановления в
следующем виде:
Xa(0 = [А(0 - к;(г)С(г)]Ха(0 + и(0 , (7.98)
где
u(0 = G(r)N1 {t) - К; (0N2 (t) (7.99)
- белый шум с нулевым математическим ожиданием M{u(t)} = 0 и моментами
второго порядка:
М{и(0ит(т)} = М{[С(0^(0-К;(0^(0][С(т)^(т)-
-K;(T)N2(x)]T} = [G(OS1(r)GT(O + K;(OS2(OK;T(O]5(r-T)
и
M[Xo(0uT(x)| = 0, Vx>r, (7.101)
т.к. и оценка Х(0 , и полезный сигнал Х(г) не коррелированы с шумами Ni(x) и N2(t)
для т > г.
Итак, рассматривая уравнение (7.98) как уравнение формирующего фильтра с
входным белым шумом u(f), корреляционной функцией (7.100) и M{u(r)} = 0, нам
необходимо найти, как изменяется дисперсия DCTCT(0 выхода этого фильтра. Но,
вспоминая постановку задачи в параграфе 7.3.1, мы видим, что если обозначить
А(0 = А(0-Кф*(0С(0,
G(0 = I,
Х(0 = Хо(0, N,(0 = и(0, ^(0 = С(г)81(0Сг(0 + Кф*(г)82(0Кф*т(0 ,
то будет полное совпадение задач (7.29) - (7.31) и (7.98) - (7.100).
414
Анализ и статистическая динамика САУ. Часть I
(7.103)
Таким образом, можно воспользоваться дисперсионным уравнением (7.47)
Daa(r) = A(r)Daa(r) + Daa(r)AT(r) + G(r)S1(r)GT(r) =
= (А(0 - Кф*(г )C(r ))Daa(r) + Daa(r)(A(r) - Кф*(г)С(г))т + (7.102)
+С(г)81(г)Ст(г) + Кф*(г)82(г)Кф*т(г)
с начальным условием
Daa(ro) = M{[X(ro)-X(ro)][X(ro)-X(ro)]T} =
= M{[X(ro)-X(ro)][X(ro)-X(ro)]T} = Doo,
где Dqq - дисперсия начального вектора состояния Х(г0), которая должна быть
известна.
Показатель качества (7.97) необходимо минимизировать в каждый текущий
момент времени путём соответствующего выбора матрицы Кф.
Оптимальная матрица коэффициентов Кф (7.87) была получена ранее из
уравнения Винера - Хопфа. Подставляя выражение (7.87) в уравнение (7.102), окончательно
получаем дифференциальное уравнение для дисперсионной матрицы минимальной
ошибки:
Daa(r) = A(ODaa(r) + Daa(r)AT(r) + G(r)S1(r)GT(r)-
-Daa(r)CT(r)S2-l(OC(r)Dao(r),
с начальным условием DCTCT(r) = Dqq .
Таким образом, структурная схема модели источника сообщений (формирующего
фильтра) и оптимального линейного фильтра, дающего несмещенную оценку с
минимальной среднеквадратичной ошибкой дисперсии min tr DCTO(r), имеет следующий
вид (см. рис. 7.13).
(7.104)
|Y(r)
\ Опти
■>
7
[малы
v
;кФ
ibm
Х(
Т
(0
фш
г)
\
4
1
—1
1Ы
1
т
ф
J
/^
Х(
—1
•_|
с
J
А /
А(
t) v
t)
г-*
IV
0
С(
[оде;
со
V/
1
t) -
1ЬИС
Общ?
ч
-Л
ГОЧ1
'НИ|
, 1
]In2(o|
К w!
&—h
х V*/ |
яика i
L J
1—>
Рис. 7.13
Рассмотренный оптимальный фильтр и его уравнение были впервые получены
Р Калманом и Р. Бьюси в 1961 году [194] и носит название фильтра Калмана - Бьюси
(ФКБ).
Полученные результаты можно суммировать следующем образом.
Глава 7. Методы синтеза статистически оптимальных САУ . 415
Теорема 7.2. Рассмотрим задачу оптимального фильтра (7.56) - (7.60).
Предполагаем по-прежнему, что шум Nt(r) модели источника сообщений и N2(0 шум
измерений являются белыми гауссовыми и не коррелированы. Тогда решение задачи
оптимального фильтра с несмещенной оценкой и минимальной среднеквадратичной
ошибкой получается путем выбора матрицы коэффициентов
K^(t) = DGG(t)CT(t)S2-\t\ f >f0, (7.105)
для дифференциального уравнения оптимального фильтра:
t(t) = [А(0 - Кф*(0С(0]х + Кф*(г )Y(r) (7.106)
с начальным условием
Х(го) = Х(го), (7.107)
a DCTCT(r) - решение матричного уравнения Риккати:
Dao(r) = A(r)Daa(r) + Daa(r)AT(r) + G(t)S{ (r)GT(r) -
( /.lUo)
-Doo(f)CT(f)S2-'(0C(0DTO(0
с начальным условием
Doo('o) = Doo-
Пример 7.5. Рассмотрим простой пример, когда требуется оценить значение постоянной величины.
Пусть модель сообщения (формирующий фильтр) для данной задачи описывается соотношениями
^ = 0,Л/{дг(0)} = 1,О00=10,
с уравнением наблюдения
у(0 = 2.г(0 + л2(0.Л#{л2(0)=0,
M{n2(t)n2(i)} = mt-T).
Задача состоит в том, чтобы найти наилучший фильтр для оценивания состояния x(t) по наблюдениям за
y(t), обеспечивающий минимальную среднеквадратичную ошибку (здесь дисперсию, т.к. рассматривается
скалярное уравнение).
Решение: Из постановки задачи следует, что A = G = 0,C = 2,52= hD^ = 10.
Решаем уравнение для дисперсии ошибки:
и получаем
DOT(f)~r+~40/
Таким образом, оптимальный коэффициент усиления фильтра
и уравнение для фильтра принимает вид
x(t) = j^(y(t)-2x(t)),x(0) = l. '
7.3.6. Обобщенный линейный фильтр Калмана - Бьюси
Рассмотрим обобщенную задачу аналитического построения линейного
оптимального фильтра для коррелированных гауссова белого шума измерения N2(0 и
полезного сигнала Х(г). Итак, постановка задачи следующая.
Полезный случайный процесс - выходной сигнал формирующего фильтра,
описываемого следующей системой дифференциальных уравнений:
Х(0 = A(0X(0 + G(0N,(0,X(r0) = Х°, (7.109)
где
416 Анализ и статистическая динамика САУ. Часть I
M{N,(O} = O,M{XO} = X0,
M{N1(f)N,(T)} = S1(f)5(f-T))Dxx(f0) = D00,
S{ - симметричная положительно определенная матрица интенсивности вектора
Nj(r). На интервале [r0,t]измеряется вектор Y(r)размерности 1<п, связанный с
вектором Х(г) линейным матричным уравнением
Y(O = C(OX(O + N2(r), (7.111)
где С(г) - матрица размерности /хи, N2(r) - гауссов векторный белый шум с
характеристиками
M{N2(r)} = 0,M{N2(ON2T(T)} = S2(05(r-T), (7.112)
где S2(r) - симметричная матрица интенсивности. Коррелированность N2(f) и Х(г)
определим следующим образом. Предполагается, что белые векторные шумы Nj(r) и
N2(0 коррелированы между собой со взаимно корреляционной матрицей
M{N1(ON2t(t)} = S3(O5(/-t). (7.113)
В этом случае имеем:
M{X(0N2T(T)} = M{O(r,r0)X(r0)N2T(t) +
t
+|Ф(Г,5)С(^1(5)^^2Т(Т)} = Ф(Г,ГО)М{Х(ГО)^Т(Т)} +
'о
/
'о
to<T<t,
где Ф(г,т) - переходная матрица состояния уравнения (7.109). В последнем
уравнении учтено ещё одно предположение: вектор начального состояния Х° и шумы
Nj(r) и N2(r) не коррелированы.
В формуле (7.113) S3(0 - симметричная матрица взаимных интенсивностей
белых шумов Nj(O и N2(r). Как и прежде, задача состоит в определение несмещенной
оценки вектора X(t) на основании измерения вектора Y(r) на интервале [to,t] при
минимальной среднеквадратичной ошибке оценки, min tr[DCTCT(r)].
Как и ранее, структуру и параметры оптимального фильтра можно получить из
уравнения Винера - Хопфа. Но мы, однако, применим здесь менее строгий способ
получения несмещенной оценки Х(г), но дающий возможность учесть начальные
условия.
Предположим, что искомый линейный последовательный фильтр описывается
уравнением:
£(0 = F(r)X(0 + Ko(0Y(0. (7.114)
Чтобы процесс на выходе фильтра можно было рассматривать как несмещенную
оценку, должно выполняться равенство:
А#{Х(О} = А#{Х(О} = Х(О. (7.115)
Вычислим безусловное математическое ожидание от обеих частей уравнения (7.114):
Af{^(0} = F(0Af{X(r)} + Ko(r)Af{Y(0}. (7.116)
fJO(r,i)G(i)M{Nl(i)N2T(x)}* = O(f,T)G(T)S3(x),
Глава 7. Методы синтеза статистически оптимальных САУ 417
Но из (7.115) следует, что
M{Y(r)} = M{C(r)X(r) + N2(r)} = C(r)X(r). (7.117)
Тогда дифференциальное уравнение (7.116) с учетом условия (7.115) примет вид
М{£} = (Р(г) + Кф(г)С(О)М{Х(О}. (7.118)
Вычисляя безусловное математическое ожидание от обеих частей уравнения
(7.109), с учетом (7.110) получаем еще одно уравнение:
Х(О = А(г)Х(О. (7.119)
Так как правые части выражений (7.119) и (7.118) должны совпадать, имеем:
F(r) = A(0-K+(0C(0, (7.120)
и структура фильтра имеет вид
*(0 = (А(0-Кф(0С(0)*(0 + Кф(0У(г), (7.121)
что полностью совпадает с ранее полученным из уравнения Винера - Хопфа
уравнением (7.74).
Второе условие получения несмещенной оценки (7.115) - это необходимость
интегрирования уравнений (7.118) и (7.119) с одними и теми же начальными условиями:
М{Х(го)} = М{Х(го)} = Х°. (7.122)
Это будет справедливо, если принять
Х(г0) = М{Х(г0)} = Х°. (7.123)
Можно показать, что эти два требования являются необходимыми, но не
достаточными для того, чтобы формируемая оценка была условно несмещенной, т.е.
чтобы
M{X(0|Y(0} = M{X(0|Y(f)}, (7.124)
где Y(/) означает всю реализацию Y(x) на интервале г0 < т < г. Если выполнить
требование безусловной несмещённости, то фильтр имеет вид (7.121) с начальными
условиями (7.123).
Найдем теперь матрицу Кф (О, такую, чтобы фильтр обеспечивал минимальную
среднеквадратичную ошибку
M{|Xo(0|2Mmin, (7.125)
где
Хо(0 = Х(0-Х(0, (7.126)
а
M{||Xa(r)||2} = tr[Daa(r)]. (7.127)
Дифференциальное уравнение для ошибки фильтрации Хо(г) легко получить,
вычитая (7.121) из (7.109). Имеем:
Хо (г) = А(г)Х(О + G(0N, (О - A(r)X(O + Кф (0( Y(0 - С(г)Х(О) =
(7.128)
= (А (0 - Кф(г)С(0)Хо(0 + и(0, Ха(/О) = Х(го) - Х°,
где
u(0 = G(0N,(0-K(i)(0N2(0, M{u(0} = 0. (7.129)
Найдем корреляционную матричную функцию для случайного процесса u(r) с
учетом выражений (7.110), (7.112) и (7.113):
418 Анализ и статистическая динамика САУ. Часть I
М{и(Оит(т)} = А/{(СШ,(О-Кф(О^(О)[С(т)^(т)-
-Кф(т)ГЧ2(т)]т} = tG(r)S1(»)GT'(O + K+(t)S2(r)KtT(O- (7.130)
-С(О83(г)Кфт(О-Кф(О83(ОСт(О]5(г-т).
Рассматривая уравнение (7.128) как дифференциальное уравнение формирующего
фильтра для выходной переменной Xo(f), входным белым шумом u(f) с
корреляционной функцией (7.130) и M{Xa(t)} = 0, для нахождения дисперсионного уравнения
для Хо(0 воспользуемся уравнением (7.47), аналогично тому, как оно было
использовано в параграфе 7.3.5. Имеем:
Doo(r) = (A(r) - Кф(0С(0)Воо(г) + DOT(f)(A(r) -Кф(г)С(О)т +
т т т т (7Л31>
+G(t)Sl(t)GT(t) + K^t)S2(t)K^(t)-G(t)S3(t)K^T(t)-K^t)SJ(t)Gr(t).
Согласно критерию (7.125), необходимо найти такую оптимальную матричную
функцию коэффициентов фильтра Кф(г), чтобы среднеквадратичная ошибка
tr[DCTCT(r)] была минимальной.
Применим способ, основанный на вариационном принципе при локальном
критерии качества в открытой области изменения матрицы Кф(г). Он состоит в том, что
минимуму положительно определенной квадратичной формы (7.127) по векторному
параметру (или векторной функции при фиксированном времени t) соответствует
максимум по тому же векторному параметру производной по времени этой
квадратичной формы с противоположным знаком, т.е.:
mintr{Dao(r)}^^(r), (7.132)
Кф(О
тах[-1г{Воо(0}]^Йф'(0, (7.133)
Кф(О
дают
Кф*(0 = Йф*(0.
Поэтому для нахождения оптимальной матрицы Кф (г) воспользуемся уравнением
(7.131) для DCTO(r). Условия экстремума для (7.127) запишем в виде:
—^—tr[Daa(r)] = O. (7.134)
<Жф(0
Для дифференцирования следа правой части уравнения (7.131) воспользуемся
следующими соотношениями, известными из матричной алгебры [48]. Пусть B,z -
некоторые матрицы. Тогда справедливы следующие соотношения:
3tr(zBzT)=z(B + BT);
3z
^^ = ВТ; (7.136)
dz
atr(ZB)=BT. (7137)
dz
3tr(BzT)
дг
8tr(zTB)
dz
= B; (7.138)
= B. (7.139)
Глава 7. Методы синтеза статистически оптимальных САУ
419
Дифференцируя правую часть следа уравнения (7.131) по Кф(г) с учетом
симметричности матриц DOT(O,S2(f).S3(O и формул (7.135) - (7.139), имеем:
atr[A(f)-K,,.(r)C(O] т
L Л =-Doo(0CT(0, (7.140)
Эк[Роо(;)(А(0-Кф(0С(0)т]_ Т
dtr[K,(t)S2(t)K,\t)]
— -2Кф(,)ЗД,
"К-ф(Г)
(7.141)
(7.142)
(7.143)
(7.144)
(7.146)
оКф(Г)
Подставляя полученные выражения в формулу (7.134) и разрешая относительно
Кф(г), получим оптимальную матрицу коэффициентов:
^*(r) = (Doa(r)CT(r) + G(r)S3(0)-S21(0. (7.145)
Если сравнить формулу (7.145) с (7.87) для оптимальной матрицы Кф*(г), то
видно, что соотношение (7.145) обобщает формулу (7.87) и совпадает с ней при
отсутствии корреляции между шумами Ni(r) и N2(0> т.е. копда S3(r) = 0.
Подставляя оптимальную матрицу коэффициентов (7.145) в уравнение для
дисперсии оценки (7.131), получим дифференциальное уравнение Риккати:
Dao(r) = [А(0 - G(t)S3(t)S-2\t)C(t)]DGG(t) + Daa(r)[A(r) - G(r)S3(r)S21(OC(r)]T-/
-Daa(OCT(r)S24OC(r)Daa(O + G(r)[S1(r)-S3(r)S2I(OSj(r)]GT(r),
где t > t0, а начальное условие DCTO(r0) = Dqq .
Как видно, оптимальный фильтр, доставляющий несмещенную оценку с
минимальной среднеквадратичной ошибкой, на основании наблюдения вектора Y(r) на
интервале (г0 < т < t), при коррелированном белом шуме измерений с полученным
сигналом имеет ту же структуру (см. рис. 7.13), что и при ее отсутствии (S3(f) = 0).
Однако оптимальная матрица коэффициентов Кф(г) и дисперсионное уравнение
различаются. Совпадение наблюдается при S3(r) = 0 для обобщенного фильтра.
Пример 7.6 [97]. Рассмотрим скалярную стационарную систему
x = x + n(t),
y(t) = x(t) + n(t)
для / > 0 при М{«(/)} = 0, M[n\t)) = a2 = const; M{x(0)} = 0; М{^(О)} = Doo = a2 = const и M[x(0)n(t)} = 0.
Структурная схема модели полезного сигнала (формирующего фильтра) с зашумленным выходом
приведена на рис. 7.14.
и(0"
№
Рис. 7.14. Структурная схема формирующего фильтра с зашумленным выходом
420 Анализ и статистическая динамика САУ. Часть I
Из постановки задачи видно, что
A(/) = G(0 = C(/) = l,
S,(/) = S2(/) = S3(O = a2,
так что
A(/)-G(/)S3(/)S;I(OC(0 = 0,
SI(/)-S3(OSiI(/)S3r(r) = O.
Следовательно, уравнение (7.146) для дисперсии ошибки принимает вид:
где Daa(t) - скалярная дисперсия ошибки фильтрации.
Решение данного дифференциального уравнения с От(0) = Gq имеет вид:
Dm(t)-
Оптимальный коэффициент фильтра:
2
K:(/) = (Dao(/)CT(/) + G(OS3(0)-S21(0=^-T- + l,
а уравнение фильтра будет иметь вид:
*(/) = *(/) + к;(0М/)-л(/)].
Заметим, что при / —»«> дисперсия Daa(t) —» 0, а /^ф(/) —> 1-
В установившемся состоянии дисперсия ошибки фильтрации достигает нулевого значения. Уравнение
фильтра в установившемся состоянии принимает вид х = v(/), т.е. действие фильтра сводится к
интегрированию.
Заметим, хотя система х = х + n(t) неустойчива, фильтр оказывается работоспособным и дисперсия
ошибки при достаточно большом времени фильтрации достигает нуля.
Предположим теперь, что для упрощения фильтра принято K^(t) =1 для всех />0 . Оценка (уже не
оптимальная) тогда будет иметь вид:
ч t
л-(0=ф(тКс.
о
Чтобы определить соответствующую дисперсию ошибки, положим в уравнении (7.131)
A(/) = G(O = C(/) = 1 и S1(/) = S2(/) = S3(/) = a2. Тогда получим Dao(0 = 0. Это значит, что Daa(t) = 6l
для всех t>0. Если дисперсия <з\ велика, то филыр будет приносить мало пользы, хотя его и
относительно просто реализовать, поскольку в нем нет переменного коэффициента передачи. С другой стороны,
если Cq является приемлемой дисперсией ошибки для любого / > 0, то такой субоптимальный фильтр
можно применять.
7.3.7. Оптимальная фильтрация при небелом (цветном) шуме
Теория оптимальных линейных фильтров, рассмотренных в предыдущих
параграфах, основывалась на том предположении, что шум измерений N2(0 был белым
гауссовым. В практических задачах шум измерений N2(0 может быть «окрашенным»,
поэтому важно рассмотреть следующую постановку задачи.
Пусть Х(г) - полезный случайный процесс, полученный на выходе
формирующего фильтра:
X(r) = A(f)X(0 + G(0N,(0, (7.147)
где по-прежнему:
M{N,(f)} = 0, M{N,(r)N[(T)) = S,(05(f-T),
X(fo) = X°, M{X°} = X°, M{X°X0T} = D00,
Глава 7. Методы синтеза статистически оптимальных САУ 421
а измерения характеризуются вектором Y(r) размерности /xl (/<«), связанным с
вектором Х(г) уравнением выхода (уравнением измерения):
Y(O = C(r)X(O + N2(O; (7.149)
С(г) - матрица Ixn, N2(0 - гауссов векторный марковский процесс, который связан
с помощью уравнения формирующего фильтра с вектором белого шума N3(f)
размерности /xl ,т.е.
N2(O = L(ON2(O + N3(O, (7.150)
N2(r) = N°, (7.151)
где
M{N°} = 0, M{N°N°T} = D°*, (7,152)
M{N3(r)} = 0, M{N3(r)Nj(T)} = S3(r)5(r-T), (7.153)
D^w, S3(r)-симметричные положительно определенные матрицы. Предполагаем
также, что выполнены следующие условия:
М{^(г)^(т)} = 0, Af{N3(0N§} = Af{N3(0-X°} = 0, (7.154)
т.е. отсутствует корреляция белых шумов N^r), N3(f) и белого шума N3(r) с
начальными условиями N2, Х°.
Как и прежде, необходимо определить структуру и найти параметры линейного
оптимального последовательного фильтра, дающего несмещенную оценку Х(г)
полезного случайного процесса Х(г) с минимальной среднеквадратичной ошибкой
фильтрации
^ = "}in tr{Doo(f)}. (7.155)
K4>'v
Так как по условию задачи шум измерения N2 (t) не является белым по
отношению к измерениям Y(r), для решения поставленной задачи воспользуемся
уравнением (7.150), для чего продифференцируем по г уравнение измерения (выхода) (7.149).
С учетом уравнений (7.147) и (7.150) получим:
Y(r)=c(0x(r)+c(0x(0+N2(0=(c(0+c(0A(0)x(0+ (?156)
+C(0G(0N1(/) + L(0N2(r)+N3(0.
Введем новую переменную (вектор-функцию):
Y(0 = Y(0-L(0Y(,) = (C(0+C(r)A(,))X(r)+
+C(0G(0NI(0 + L(0N2(0+N3(r)-L(f)(C(0X(0+N2(0)= (7.157)
= (C(t)+C(t)A(t)-L(t)C(t))X(t)+C(t)G(t)Nl(t)+-N3(t).
Это выражение можно рассматривать как уравнение выхода (измерения) Y(r) с
белым шумом измерения N2 (t):
Y(t) = C(t)X(t)+N2(t), (7.158)
где
C(r) = C(r)+C(r)A(O-L(r)C(r), (7-159>
a N 2 (t) = C(f)G(f)N, (f)+N3 (t) - белый шум с корреляционной функцией
422 Анализ и статистическая динамика САУ. Часть I
M{N2(0Nl(T)}=(c(0G(0S,(0(C(0G(r))T+S3(f))8(r-T) = S2(08(f-T) (7.160)
и нулевым математическим ожиданием М |N2 (0}= ^ •
Белый шум N2(f) уравнения (7.12) коррелирован с белым шумом Nj (r)
формирующего фильтра полезного сигнала. Их взаимная корреляционная функция имеет вид:
w{n1(0nIW}=^{n1(0(c(t)g(t)ni(t)+n3(t))t}=
1 J (7.161)
= S1(0GT(0C(r)5(r-x) = S3(05(r-T),
где
S3(r) = Sl(r)GT(r)CT(r) (7.162)
- симметричная матрица взаимной интенсивности шумов Nj(r) и N2(f).
Если теперь рассмотреть соотношения (7.147), (7.148) и уравнение измерения
(7.158) с матрицами (7.159), (7.160), (7.161), то получим постановку задачи
обобщенного фильтра Калмана - Бьюси, рассмотренную и решенную в предыдущем параграфе.
Таким образом, уравнение оптимального фильтра поставленной задачи имеет вид:
*(0-(а(»)-к;(0С(г))*(0+к;(0*(0. <7-163>
где C(r),Y(r) определены соотношениями (7.158), (7.159), а матрица Кф(г)
находится из формулы (7.145)
K;(0=(Doo(0cT(r)+G(0s3(0)s3'(0=
= [Doo(r)CT(0+G(0S1(r)GT(r)CT(0> (7.164)
x[c(OG(»)SI(r)(C(»)G(»))T+S3(r)j'.
Рассмотрим уравнение фильтра (7.163). В него входит переменная Y(f), которая,
согласно выражению (7.157), содержит производную Y(f) от измеряемого сигнала.
Однако эта операция нежелательна, т.к. дифференцирование повышает уровень
помех. Для того чтобы этого избежать, производим дальнейшие преобразования,
аналогичные тем, которые используются в наблюдателях пониженного порядка Люенбер-
гера. Введем дополнительную переменную (вектор-функцию) Q(f), которая связана
с оценкой X(f) формулой
*(r) = Q(0+K;(r)Y(0 (7-165)
или
Q(f) = £(r)-K;(/)Y(r). (7.166)
Дифференцируя (7.166) по г и используя уравнения (7.163), (7.157), (7.165),
получим
0(г)Л(о-к;(оу(о-к;(г)¥(о=(а(о-к;(ос(о)х(о+
+Kl(t)Y(t)-kl(t)Y(t)-Kl(t)(Y(t)+L(t)Y(t)) =
=(а(о-к;(ос(о)(о(0+к;(0¥(о)-(к;(о+к;(оь(о)¥(г)=
Глава 7. Методы синтеза статистически оптимальных САУ
423
(7.167)
-(А(»)-к;(оад)о(')+
+ (A(t)Kl(t)-Kl(t)C(t)Kl(t)-^(t)-Kl(t)L(t))Y(ty
Блок-схема оптимального фильтра в этом случае будет иметь вид (см. рис. 7.15).
А(/)К#)-К«(/)С№(0-
эд5
Х(0
А(0-К,(0С(0
к#)
(7.168)
Рис. 7.15
Для окончательного решения поставленной задачи найдем дисперсионное
уравнение. В соответствии с уравнением (7.131) имеем:
Dee(0-(A(o-K;(oc(o)Dee(»)+DOB(r)(A(0-K;(oe(o)T +
Подставляя в уравнение (7.168) выражение (7.164) для Кф(г), проводя
необходимые преобразования и учитывая симметричность матриц S2 (0»S3 (O'^aa (0»получим:
Doo(0 = A(r)Doo(r)+DTO(0AT(0-
-Dro(OCT(f)SiI(OC(ODaa(O-G(OS3(OSi'(OC(ODaa(O- (7169)
-С(0§з (OS;'S3 (r)GT (r)-Doo (r)CT (r)S;1 (r)S3 (r)GT (»)+G(OS, (r)GT (*).
Таким образом, оптимальный фильтр при коррелированном шуме измерений
определяется уравнениями (7.163) и (7.169). Остается только определить начальные
условия для уравнения (7.169) с учетом начальных условий X°,N2.
Для этого воспользуемся формулой Байеса, с помощью которой определим
условную плотность вероятности вектора Х° в начальный момент времени t0 при
наблюдении вектора Y (г0) = Y0 в тот же момент времени:
/x°lX |Y('o)-Y j- /o/Yo\ •
(7.170).
где fx (X°, Y°) - совместная плотность распределения случайных векторов (величин)
Х°, Y0, /уо (Y°) - плотность распределения случайного вектора Y0. Для
вычисления правой части (7.170) найдем совместную плотность распределения /ЛХ°,У°).
424 Анализ и статистическая динамика САУ. Часть I
Для чего используем совместную плотность распределения /2(X0,N2) случайных
величин X и N2.
Уравнение измерения (7.3) для t = t0:
Y(r0) = C(r0)X(r0) + N2(r0) = C(r0)X0 + N^ = Y0. (7.171)
Из теории вероятности известно [81], что в этом случае совместные плотности
распределения связаны соотношением
/1(X0,Y0) = /2(X°,N^)
3N
9YL
(7.172)
где
д№2
Э¥°
- якобиан преобразования (7.171). Из (7.171) видно, что якобиан равен 1,
поэтому совместные плотности распределения совпадают, т.е.
/2(XO,N5) = /1(XO,YO). (7.173)
Далее воспользуемся тем, что случайные величины (векторы) X°,N2 независимы
и нормально распределены. В этом случае
/2(Xo,N^) = /xo(X°)/No(N^), (7.174)
где /Xo(0»/No(0 - плотности распределения соответствующих случайных величин.
С учетом (7.148), (7.152) имеем
/хо(Х°) = [(2я)и det(Doo)]"X ехр[-1(Х° - Х°)т Щ}(Х° - Х°)т] (7.175)
и
/n? (NS) = [(27t)' det(D°CA/ )JK exp[-l(N° -N? f(D% )"l(N« -S°)T] =
= [(2n)'det(D^)]"Kexp[-l(Y0-Ca0)X0)T(D^)-1(Y0-C(f0)X0)T], (7.176)
где учтено M JN^ }= 0 и использована формула (7.149).
Обозначим для удобства в формулах (7.175), (7.176) константы через:
^[(гяГсВДоо)]^, (7.177)
/Y0(X°/Y(r0) = Y°). (7.178)
Из выражений (7.174), (7.170) получим
jOi
01 О /x»(X0)-/N»(N2)
/xo(X°|Y°)= Х ^ . (7.179)
При допущениях о нормальном распределении Х° и N2 вектор Y0 также
нормально распределен
/Yo(Yo) = [(2n)'det(DYOYO)]"Kexp[-l(Yo-Y5)TD;lovO(Yo-Y?)] =
= C3exp[-i(Y° - Y?)tD;1Oy<)(Y° - Y»)], (7.180)
где
Y° = M{Y0}=M{C(f0)X0 + N^}=C(f0)X°, (7.181)
Глава 7. Методы синтеза статистически оптимальных САУ 425
DYoYo = m{(Y° - Y°)(Y° - YV }= M Jc(fo)X° + N° -C(fo)X°],
[c(ro)X° + N^-C(ro)X^]Tj = C(ro)DooCT(ro) + D^. (7.182)
В формуле (7.182) учтена независимость N^ и Х°. Условная плотность
распределения (7.179) случайного вектора Х° при наблюдении вектора Y0 также является
нормальной и может быть записана в виде
/xo(X0|Y0) = C4exp[-l(X0-X°)T(D^r1(X0-X0)], (7.183)
где
D^ = M{(X0-X0)(X0-X0)T},
а константа С4 находится из выражения (7.179)
C4/Yo(Y°)exp{P} = C1C2exp{/?}, (7.184)
т.к. формула (7.183) определяет условную плотность распределения
/Yo(X°|Y(ro) = Y0). Константы Р и R будут найдены ниже. Приравнивая
показатели экспонент в формуле (7.179), с учетом соотношений (7.177), (7.178), (7.183),
(7.184) получим
C4/Yo(Y0)exp{-l(X0-X0)T(D°or1(X0-X0)}=
= С,С2ехр{-1(Х° -ХУЩ'СХ0 -Х°)-
-i[Y0-C(r0)X0]T(D^)-1(Y0-C(r0)X())}. (7.185)
Раскрывая скобки в левой и правой части выражения (7.185) и приравнивая
матричные коэффициенты при одинаковых «степенях» вектора X , получим:
а) квадратичная форма (Х°)т-Х°:
(D°o)-' =D^ + CT(f0XD^rlC(r0); (7.186)
б) вектор Х° слева, т.е. (Х°)т •:
(D^r'X0 =D^X" + CT(r0XD^r1Y0 ; (7.187)
в) вектор Х° справа, т.е. -(Х°):
(X°)TD^ = (X^)TD^ + (Y°)T(D^)-1C(r0); (7.188)
г) нулевая степень вектора Х°, т.е. константы слева и справа:
. C4/Y0(Y0)exP{(X0)T(D0oo)-1X0}=
= C1C2exp{(X0)TD^X0 + (Y0)T(D^)-IY0)}. (7.189)
Видно, что уравнения (7.187), (7.188) в силу симметричности матриц дисперсий
совпадают. Из уравнения (7.186) находим дисперсию начальной оценки для
уравнения (7.169)
D^fD^ + C^oXD^r'Ctfo)]'1, (7.190)
а из (7.187) - начальные условия для оценки, при которой фильтр (7.163) дает
несмещенную оценку
426 , Анализ и статистическая динамика САУ. Часть I
Х° =[D^ + CTa0)(D°A,)-|C(f0)J1[D^X" + CT(f0)(D°A,)-1Y°] (7.191)
при условии, что Y(r0) = Y°. Равенство (7.189) позволяет определить константу С4,
причем, сравнивая формулы (7.189) и (7.184), находим, что постоянные Р и R
имеют вид:
P = (X°)T(D^)-1X°, * (7.192)
R = (X^)TD^X^ + (Y°)T(D^)-1Y°. (7.193)
Пример 7.7. Полезный сигнал представляет собой случайную величину X(t) = Х°, т.е. постоянный
сигнал, амплитуда которого случайным образом зависит от начальных условий. Известно математическое
ожидание и дисперсия начального вектора М {х°}= Х°, Л/j(X° -X°)(X° -X°)T j= Dqq . Требуется найти
оптимальную в смысле среднеквадратической ошибки оценку Х(/) сигнала Х(/) по наблюдению на
отрезке [tQtt] суммы сигнала и помехи N2(0- Помеха N2(/) имеет равные нулю математическое ожидание
и корреляционную функцию
KN!N2(,,t) = D°cn-^H.
Формализуем задачу. Уравнения формирующего фильтра и измерения для полученного сигнала и помехи:
Х(/) = 0,Х(/0) = Х°,
Y(O = X(/) + N2(O.
N2(/) = -oN2(r) + N3(0, N2(/2) = N*;
причем М{Х°} = Х°; МГ(Х0-Х°)1 = Ооо; M{N^} = 0;
M{(N°)2} = D^; M{N3(ON3(t)) = 2cxD^5(/-t); M{N3(/)) = 0.
Матрицы уравнений: А(/) = 0; 8(0 = 0; C(f) = l; L(/) = -a. Уравнение оптимального фильтра для данной
задачи:
k{t) = -К° (/){С(/)Х(/) - Y(r)} = -K° (/)(-aX - Y(/) + aY) =
= Kj(/)(Y(0 + aX-aY).
Начальные условия для полученного фильтра найдем из (7.191):
*oBr^+1.j_.1yYiL+1.u_Yo>|eLO f^+^LY°l
[Doo D°CN ) [Dog Do^ J у Doc;vj у ^ J
yo=x° + n5.
Найдем необходимые в дальнейшем матрицы (здесь - это скаляры):
С(г) = С(0 + С(/)А(/) - L(/)C(/) = a,
S3=S1(OGT(r)CT(O = O,
S3(/) = 2aD^, •
S2(/) = C(OG(/)S1(/)(C(/)G(/))T +S3(O = 2aD^.
Если ввести новую переменную Q(/) согласно формуле (7.166), то уравнения фильтра будут (см. (7.167)):
Q(O = -Kj(/).a-Q(/) + (Kj(/).a-K;(/)-(K;(/))2.a)Y(r), (7.194)
X(/) = Q(/)+k;(/)Y(/).
Оптимальный коэффициент уравнения фильтра найдем из формулы (7.164)
Ki(f)=^^=i5^DOT(0- • (7л95)
2COJCN ZDCN
Дисперсионное уравнение (7.167) для данной задачи имеет вид:
£>от(о=-i&Wt*-=-тй-^w •
IV CN IDCN
Глава 7. Методы синтеза статистически оптимальных САУ
427
Начальные условия для этого уравнения найдем из выражения (7.190)
DSo = [ОЙ + СЧ) • (D°N )-1C(r0)J' = Роо-Ву .
Видно, что полученное выражение (7.195) для Кф(/) можно использовать для нахождения производной
Кф(/), которая требуется в уравнении фильтра (7.194):
1 ~ 1
к;<о=
<rD°°-
2D
к* (t \- gg -
eD-(r)—«к;»»».
(7.196)
Doo
2D"C/V ^D^+D^)
Подставляя соотношение (7.196) в (7.194), окончательно получим уравнение фильтра:
Q(/) = -Кф(0а«0 + (Кф(/)а + а(К;(/))2 - oc(K;(/))2)Y(/) =
= aKj(O(Y(O-Q(O).
Оптимальная оценка фильтра находится из выражения
X(o=qw+k;(oy(o. .
Структурная схема оптимального фильтра имеет вид (см. рис. 7.16.).
Х° • 1[/] полезный сигнал
N,(0
(7.197)
Рис. 7.16. Структурная схема оптимального фильтра
7.3.8. Оптимальный фильтр (наблюдатель) Калмана - Бьюси
В СИСТЕМАХ УПРАВЛЕНИЯ
Все рассмотренные выше оптимальные фильтры не касались напрямую задач
управления. А между тем фильтры Калмана - Бьюси нашли широкое применение в
системах автоматического управления, где они используются в качестве
оптимальных наблюдателей. В этих задачах фильтры выполняют ту же роль получения
несмещенной оценки Х(г) вектора состояния Х(г) при наличии помех, измерения и
шумов (возмущений) объекта управления. Роль случайных возмущений объекта,
например, могут играть порывы ветра, действующие на самодет; колебания момента
нагрузки на валу двигателя и т.д. и т.п.
Постановка задачи следующая. Рассматривается линейная система уравнений:
Х(0 = А(0Х(г) + В(0 Y(0 + G(r)N! (r), (7.198)
XB(0 = C(f)X(0 + N2(0, (7.199)
где X - n-мерный вектор состояния, Y - m-мерный вектор управления, Ni -р-мерный
вектор случайных возмущений (шум объекта), Хв - /-мерный вектор выхода
(измерений), N2 - /-мерный вектор помех измерений. Зная статистические
характеристики случайных процессов Ni(r) и N2(0 и управляющее воздействие Y(r), необходимо
428 Анализ и статистическая динамика САУ. Часть I
построить линейное последовательное устройство (фильтр), который давал бы
несмещенную оценку вектора Х(г) с минимальной среднеквадратичной ошибкой
фильтрации.
Если рассмотреть уравнения (7.198), (7.199), то с точностью до обозначений они
повторяют рассмотренные нами ранее постановки задач построения фильтров,
совпадают с этими уравнениями, за исключением слагаемого B(r)Y(r),
характеризующего целенаправленное неслучайное управляющее воздействие на систему. Так как
составляющая B(f)Y(r) является детерминированной составляющей, то для того, чтобы
получить те же структуры фильтров, которые были нами рассмотрены ранее,
необходимо только ввести составляющую B(f)Y(0 в уравнение фильтра, и все рассуждения
и выводы, полученные прежде, останутся в силе. Это легко проверить
непосредственными преобразованиями, которые нами использовались. Таким образом,
уравнение оптимального фильтра (наблюдателя) для системы (7.198), (7.199) будет:
2(0 = (A(r) - К;(0С(0)Х(1) + B(r)Y(O + к;(г)Хв(О, (7.200)
где входными воздействиями фильтра являются управление Y(f) и вектор выхода
системы (вектор измерений) Хв(?)<
Как и в рассмотренных ранее задачах синтеза оптимального фильтра, решение
задачи фильтрации зависит от многих дополнительных предположений, в частности, от
коррелированности или некоррелированности шумов Ni(r) и N2(r). Предполагается,
что шумы Ni(r) и N2(0 являются белыми гауссовыми и некоррелированными между
собой, с нулевыми математическими ожиданиями:
М{^(г)} = 0,М{^(г)} = 0,М{^(О^(т)} = 0,Уг,т; (7.201)
M{N1(r)N[(T)} = S1(r)5(r-T); M{N2(r)Nj(T)} = S2(r)5(r-T), (7.202)
где Si(r), S2(r) - положительно определенные симметричные матрицы интенсивно-
стей. Кроме того, начальное состояние Х(г0) = Х° не коррелировано с шумами Ni(f)
и N2(r), т.е.
M[X°Nj(t)} = M[X°Nl(t)}=0. (7.203)
Известны математические ожидания и дисперсия начального вектора Х°:
М{Х°} = Х°, M{(X0-X0)(X0-X°)T} = Doo. (7.204).
Тогда ставится задача определения матричной функции Кф(г), и начальные условия
Х(г0) задаются таким образом, чтобы получить несмещенную оценку вектора
состояния Х(г) с минимальной среднеквадратичной ошибкой фильтрации
. y = min tr[Daa(r)], (7.205)
Кф(0
где
Dao(r) = М {(Х(0 - Х(г))(Х(г) - Х(г))т} (7.206)
называется задачей оптимального наблюдения (задачей оптимального фильтра Кал-
мана - Бьюси для систем управления).
Решение поставленной задачи оптимального управления с учетом ранее
решенных задач оптимальной фильтрации и введенных обозначений сформулируем в виде
следующей теоремы.
Теорема 7.3. Рассматривается задача оптимального наблюдения (7.198) - (7.206).
Тогда решение данной задачи получается путем выбора матрицы коэффициентов
наблюдателя
К*ф(0 = Dao(r)CT(r)S21(0 , t > t0, (7.207)
Глава 7. Методы синтеза статистически оптимальных САУ 429
где
Doo(0 = A(r)Dao(0 + Daa(r)AT(r) + G(r)S1(0GT(r)-
-DGC(t)CT(t)S-2\t)C(t)Daa(t)j > t0
с начальными условиями
Doa('o) = Doo- (7.209)
Начальные условия для оптимального наблюдателя (7.200) должны быть выбраны
в виде
Х(го) = Х°. (7.210)
Выражения (7.207), (7.210) оптимального наблюдателя в точности повторяют
полученные ранее уравнения для оптимального фильтра (см. параграф 7.3.5).
Различаются только уравнения наблюдателя (7.200) и фильтра (7.74). Напомним, что здесь
вектор измерений обозначен через Хв(г), а Y(r) определяет вектор управлений.
Заметим, что в отличие от оптимального регулятора (задача АКОР), где требуется
решение уравнения Риккати в обратном времени, уравнение Риккати (7.208) для
оптимального наблюдателя можно реализовать в реальном масштабе времени, т.к.
уравнение (7.208) является дифференциальным уравнением с известными
начальными условиями (7.209).
7.3.9. Установившиеся свойства оптимального фильтра
Калмана-Бьюси
Когда начальное время г0 стремится к минус бесконечности, решение
DCTCT(r) матричного уравнения Риккати
Doo(f) = A(f)Daa(0 + Doa(r)AT(r) + G(r)S1(r)GT(r) -
(7.211)
-Daa(t)CT(t)S2-\t)C(t)Daa(t), t<t0
при некоторых нежестких ограничениях стремится к установившемуся решению
DCTCT(r), которое не зависит от Dqq, причем DCTO(r) является решением
алгебраического уравнения Риккати: '
O = A(r)Dca(O + Dca(OAT(r) + G(OS1(r)GT(r)-
-DGO(r)CT(r)S2-1(r)C(0DGCT(r), t0 -> -ос
Определим условия, при которых такое решение существует, которые
сформулируем в виде теоремы [61].
Теорема 7.7. Предположим, что матрица А (г) уравнения (7.198) является
непрерывной и ограниченной, а С(г), G(r), S{(t), S2(0 из соотношений (7.199)-(7.201)
- кусочно-непрерывные и ограниченные матрицы. Кроме того,
•ВД^сЛ, S2(r)>PI, Vf, (7.213)
где a, Р - положительные константы.
Тогда, если система
Х(г) = А(ОХ(г) + G(0N, (t), (7.214)
XB(0 = C(0X(0 + N2(0 (7.215)
является:
а) равномерно полностью наблюдаемой и равномерно полностью управляемой
или
б) экспоненциально устойчивой,
430 ; Анализ и статистическая динамика САУ. Часть I
то решение DOCT(r) уравнения Риккати (7.211) с начальным DCTO(r) = D00 сходится к
DCTCT(r) при t0 —»-©о для любого Dqq > 0.
Если Dqq = 0, то условие а) может быть ослаблено до условия полной
наблюдаемости.
Для систем с постоянными параметрами:
X(0 = AX(0 + GN!(0, (7.216)
XB(r) = CX(O + N2(O (7.217)
при некоррелированных шумах Nx(r) и N2(0> гДе Nj(f) и N2 (t) белые гауссовы
шумы постоянной интенсивности, соответственно S1(r) = S1, S2(^) = S2. Если пара
{A,G} является стабилизируемой, а {А, С}- обнаруживаемой, тогда алгебраическое
уравнение Риккати
0 = AD^ + D^AT +GS1GT -D^CVCD^ (7.218)
имеет единственное неотрицательно определенное решение DCTCT > 0, а если пара
{A,G} является полностью управляемой, то матрица DCTCT будет положительно
определенной и симметричной.
Заметим, что отсутствие управления Y(r) в уравнениях (7.214), (7.216) не влияет
на условия, накладываемые на получение установившегося решения уравнения
Риккати, т.к. оно учитывается в уравнении наблюдателя.
Пример 7.8 [61]. Система управления положением.
Представим объект, движущийся в плоскости. В центре плоскости располагается вращающаяся
антенна, которая, как предполагается, отмечает направление объекта во все моменты времени. Антенна
приводится в движение электродвигателем.
Задача управления заключается в таком воздействии на двигатель, при котором
<р(ООфь(О. '*'о. 0-219)
где ф(/) - означает угловое положение антенны, (ро(/) - угловое положение объекта. Предположим, что
угол фо(/) достижим для измерения с помощью визирного устройства.
Объект состоит из антенны и двигателя. Возмущением n{(t) (скаляр) является момент ветровой
нагрузки, приложенной к антенне. Наблюдаемой переменной является выходной сигнал потенциометра или
другого преобразователя на валу антенны, определяемый выражением
п1(/) = ф(0 + п2(/), (7.220) .
где /1г(0 ~ шум измерений.
Определяя переменные состояния как ^(0 = 9(0. *2(/) = Ф(0 ' ПОЛУЧИМ следующую систему диффе-.
ренциальных уравнений состояния:
*(')=(о -«^(к^РН ат)
в к \
Здесь а = —, К = —, у = — , В - коэффициент вязкого трения, J - момент инерции всех вращающихся
элементов конструкции, включая антенну, y(i) - напряжение, прикладываемое к двигателю, MB(t) = Ky(t) -
вращающий момент двигателя, ti\{t) - возмущающий момент, вызываемый ветром.
Наблюдаемой переменной является угол ф(/), который измеряется с помехой
*.(/) = (1 0)Х(/) + л2(г). (7.222)
Предполагаем, что интенсивность шума объекта - Si, интенсивность шума измерений - 5г.
Видим, что пара {A, G} является полностью управляемой, в том числе стабилизируемой, а пара
{А, С} - полностью наблюдаемой, в том числе обнаруживаемой:
rank{A,AG} = 2, rank{CT,(CA)T} = 2.
Поэтому можно определить установившийся, оптимальный наблюдатель для этой системы и Doo > 0 .
Глава 7. Методы синтеза статистически оптимальных САУ 431
Алгебраическое уравнение Риккати:
(7.223)
Используя свойство симметричности матрицы Daa , т.е. dn = ^21, получим алгебраические уравнения:
0 = 2</i2-—dn2,
0 = ^22-0^12 -—^11^12,
s2
0 = -2ad22+y2Sl-—di22.
S2 '
Из решения системы уравнений (7.224) получим
— _( -а+^+гр
Ia2 + p-a7c7+2p -a3-2aP + (a2'+P)Tc7+2P
(7.224)
R;=DaacV =
где Р = у
Отсюда следует, что матрица коэффициентов фильтра
[-a2 + p-aVa2+2pJ
Характеристический полином матрицы наблюдения А - КС определяем из выражения
det(А-КфС-5l) = s2 + s,JaF+2$ + Р .
Из этого следует, что полюса установившегося оптимального наблюдателя равны
-(-Va2+2P±Vct2-2p).
Примем следующие числовые значения параметров:
X =0,787 рад/(Вхс2),
ос = 4,6Оч,
у = 0,1 кг1м2.
Интенсивность Sl и 52 определим из следующих предположений. Величина S{ находится из условия
того, что среднеквадратичная величина возмущающего момента равна VlOOO = 31,6 Нм, спектральная
плотность постоянна в диапазоне от - 50 до 50 Гц и равна нулю вне этого диапазона. В этом случае
5!=10Н2хм2хс,
Аналогично, предполагая; что для шума наблюдений, который имеет среднеквадратичную величину
около 0,01 рад, функция спектральной плотности постоянна в диапазоне от - 500 до 500 Гц и равна нулю
вне этого диапазона. Тогда
S2 = 10"7 рад2хс .
к; =
При указанных численных значениях находим
("40,36^
= [814,3j'
Установившаяся матрица дисперсии ошибок оценки фильтрации определяется выражением
(0,000004036 0,00008143^
б„„ =
{ 0,00008143 0,003661 J'
432
Анализ и статистическая динамика САУ. Часть I
7.4. СТАТИСТИЧЕСКИЙ СИНТЕЗ ОПТИМАЛЬНЫХ НЕЛИНЕЙНЫХ
СИСТЕМ, ОПИСЫВАЕМЫХ ФУНКЦИОНАЛАМИ ВОЛЬТЕРРА
7.4.1. Интегральные уравнения, определяющие оптимальную систему
Постановка задачи. На вход нелинейной системы поступает аддитивная смесь
полезного входного сигнала m(t) и помехи n(t).
Необходимо:
1) по статистическим характеристикам сигналов m(t) и n{i) построить
оптимальную математическую модель замкнутой нелинейной системы в форме
ряда Вольтерра,
2) по известным рядам Вольтерра, описывающим динамику замкнутой
оптимальной САУ и объекта управления, построить ряд Вольтерра, являющийся
математической моделью корректирующего устройства.
Предполагается, что корректирующее устройство может быть как
последовательным (рис. 7.17), так и встречно-параллельным (рис. 7.18).
Y{t)=m{t)+n(t\*(f)
Нелинейное
последовательное
корректирующее
устройство
u(t)
>
Нелинейный
объект
управления
*(<L
Рис. 7.17. Структурная схема нелинейной САУ с последовательным корректирующим устройством
Теоретическая ценность аппарата рядов Вольтера, как указывалось в
параграфе 7.2, состоит в том, что многие положения линейной теории систем
автоматического управления обобщаются на класс нелинейных систем. Аппарат анализа и
синтеза линейных стационарных систем, основанный на применении преобразования
Лапласа, обобщается на указанный класс нелинейных систем с той лишь разницей,
что используется многомерное преобразование Лапласа [72, 123]. Введены понятия
амплитудно-фазовых соотношений. Получила решение проблема синтеза
корректирующих устройств в виде функциональных степенных рядов [72, 84, 123].
Обобщается на рассматриваемый класс нелинейных систем и изложенный выше аппарат
синтеза оптимальных фильтров (см. параграф 7.2).
Y(t)=m(t)+n(t)
е(')
Нелинейный
объект
управления
X(t)
Нелинейное
встречно-
параллельное
корректирующее
устройство
Рис. 7.18. Структурная схема нелинейной САУ с встречно-параллельным
корректирующим устройством
Глава 7. Методы синтеза статистически оптимальных САУ
433
При построении метода синтеза оптимальных нелинейных фильтров практически
используются все этапы, приведенные выше применительно к синтезу линейных
оптимальных фильтров.
Постановка задачи фильтрации заключается в следующем:
- заданы статистические моменты необходимого порядка случайных процессов
- требуется найти многомерные импульсные переходные функции нелинейного
фильтра k*(t,Tx) , k*2(t,тх,%2) » ^з (г>т1>т2'тз) » •••» оптимальным образом
выделяющего реализацию случайного процесса m(t) в виде некоторого процесса X{i) в
условиях, когда на его вход поступает аддитивная смесь случайных процессов m(i) и
л(0 (рис. 7.19).
m(t)
n(f)
) '
—*
—►
Ъ (t т \
*2(^ЬТ2)
£з('Дьт2,т3)
*р(Г,Ть...,Тр)
Рис. 7.19. К постановке задачи фильтрации в классе нелинейных систем
Часто используется несколько другая постановка задачи, позволяющая получить
вполне обозримые в практическом плане результаты с использованием современных
средств вычислительной техники. Сущность этого подхода состоит в том, что
сначала находится оптимальная ИПФ линейного фильтра /^(m^. Для ее нахождения
используется уравнение Винера-Хопфа (7.18). На следующем этапе
рассчитывается оптимальная ИПФ 1-го порядка ^2 (r» Ti»Т2) путем решения соответствующего
уравнения. Таким образом, последовательно находится необходимое число
оптимальных ИПФ [72, 84, 123].
Следует заметить, что каждая из кр (г,^,...,^) рассчитывается из условия
минимизации СКО вида
M[{m(t)-Xp(t))2] = M[cl(t)}
(7.225)
причем Xp.\(t) - выходной сигнал нелинейного фильтра, имеющего уже найденные
оптимальные ИПФ к*^,%х), k\(t,xx,x2),..., ^_i(r'Ti'T2»-»T/7-i) (рис. 7.20).
Рассмотрим задачу синтеза стационарного оптимального фильтра вида
оо оооо
X(r) = J*i(T)r(r-T)rfT+JJ*2(T1,T2)r(r-T1)r(r-T2)rfT1rfT2, (7.226)
0 00
предполагая при этом, что ИПФ к* (т) найдена с использованием формулы (7.18).
29 Зак. 232
434
Анализ и статистическая динамика САУ. Часть I
Y(t) = m(t)+n(t)
ki(t,x{)
х% w>
кг(итит2)
Х3(0
*з(^1.т2,т3)
wJi»-»v
Рис. 7.20. Структурная схема, поясняющая формирование составляющих Xi(t\ X2(t)> ОД')»*»» Xp(t)9...
Оценка X(f) отличается от оценки, определяемой формулой (7.18) наличием
нелинейного слагаемого. Таким образом, если получена оценка X(t) в классе линейных
систем, то к ней добавляется корректирующее слагаемое, являющееся выходом
квадратичного канала системы.
Пусть Gi(r) - ошибка фильтрации линейным каналом системы, т.е.
a,(0 = m(0-J*rW Y(t-x)dx.
(7.227)'
Ошибка ai(f) некоррелирована с входным сигналом Y(t), т.к.
M[r(f-T1)al(O] = A/[r(f-T1)w(r)]-M
]k;(x)Y(t-xl)Y(t-x)
Lo
dx =
(7.228)
= RmY^i)-]ktl(x)RYY(Tl-'c)dx = O.
Ошибка фильтрации нелинейным фильтром, включающим линейный и
квадратичный каналы, определяется зависимостью
ai = M[{m(t)-X(t))2] = M
m{t)-]k\{x)Y{t-x)dx-
-j]k2(xl,x2)Y(t-xi)Y(t-x2)dxldx2
о о
= М
ol{t)-]]k2{xl,x2)Y{t-xi)Y{t^2)dxldx2
00
(7.229)
= OaiO) -2j\k2(x{,x2)a™Y(xx,x2)dxxdx2 +
о о
оооо
+J J J J*2(Tl'r2)*2(rl'r2)air(Tl -T2'T1 -T1'T2 -X2)^TlrfT2rfV^2'
оооо оооо
0 0 0 0
Глава 7. Методы синтеза статистически оптимальных САУ 435
a$(xi,x2) = M[ol(t)Y(t-xl)Y(t-x2)] =
оо
= Щ(т(О-/*,*(т)Г(г-т)*)У(г-т1)1'(г-т2)] =
о
оо
= M[m(t)Y(t-xl)Y(t-x2)]-jk*l(x)M[Y(t-Tl)Y(t-T2)Y(t-r)]dx =
о
оо
= ай(Т|,х2)- /*Г(г)а1?(т, -т2>т, -тУт, (7.230)
о
44г)(т1-т2,т1-т1,т2-т2) = м[г(г-г1)>'('-т2)г(/-т1)г(г-т2)]. (7.231)
В (7.229) Dao - минимальная СКО, которая обеспечивается только линейным
каналом системы.
В отличие от линейного случая, при учете квадратичного канала системы СКО
зависит от смешанных статистических моментов третьего и четвертого порядков.
Для нахождения двумерной ИПФ kl(x{,T2), обеспечивающей наилучшую
линейную фильтрацию процесса m(t) из аддитивной смеси m(i) + n(t), можно
воспользоваться тем же приемом, который описан выше для линейного случая.
Результатом соответствующих аналитических рассуждений является
интегральное уравнение вида [31]
оо оо
^(TPT2)=JJ^(^^2)4t)(^-^2^1-^^2-^)^i^2 (7.232)
00
ДЛЯТ!>0, Т2>0.
Это уравнение является двумерным интегральным уравнением первого рода и
определяет неизвестную двумерную ИПФ через стохастические моменты: смешанный
момент третьего порядка между ошибкой Gi(f) и входным сигналом Y(t) и момент
четвертого порядка процесса Y(t). Это уравнение является прямым аналогом
уравнения Винера — Хопфа (7.18) для оптимального линейного фильтра. Однако между
ними есть большая разница. В то время как интеграл в уравнении Винера - Хопфа
представляет собой одномерный интеграл свертки, в двумерном уравнении (7.232)
правая часть не является сверткой по двум переменным, т.к. Щу зависит не только
от Ti - т2, но и от Ti -1\ [84]. Для доказательства факта, что минимальная СКО
достигается при &2(Т1>Т2) = ^2(Т1»Т2)' подставим (7.232) в (7.229). В результате
указанной подстановки имеем
оооооооо
<*2 = £>о,о, -2j J JJ*2(x,,x2)-*2(xi,-C2)-o4^)(Xi -x2>xx -т'„т2 -т2)^т^т2^х2 +
0000
оомоооо
+J J J 1*2(Т1Д2^2(Т1'Т2)аУт(Т1 -*2»T1 ~Tl'T2 ~ T2)dixdT2dT\dT2 =
00 0 0
оооооооо
= Dw -\\!№&1>Ъ)&ЪЪ)агу<?1 "T2^i -t!,t2 -x'2)JWVt2 +
0 0 0 0
436 Анализ и статистическая динамика САУ. Часть I
оооооооо
+ЛЛ[*2СС1.Т2)-*2^1Д2)][*2(^Д2)-*2(^Д2)]х
0 00 0
xaf$ (t\ - т2 • Tj - х\, т2 - т2 )dxxdx2dxxdx2. (7.233)
В полученном выражении последнее слагаемое содержит неизвестную функцию
&2СС1 ,Тг)» и это слагаемое неотрицательно, поскольку
оооооооо
////[*2(^^2)-*2^1Д2Ж*2(^^2)-*2(^Д2)]Х
0 0 0 0
= M[{jJ(^2(T1,T2)-/:2(T1,T2))r(r-T1)r(r-T2)JT1JT2)}2]>0.
о о
Очевидно, минимальное значение а2 будет соответствовать такому нелинейному
фильтру второго порядка, для которого указанное слагаемое обращается в нуль.
Это будет иметь место, если ядро &2(Tj,t2) = £2(Tj,t2). Используя это условие, из
(7.233) следует зависимость, определяющая минимальную СКО
оо оо оо оо
°2min = Авд -\\\\&*1.*2У£Ъ\*2><$<?1 ~Ь Д1 -Т1 ,Т2 -Т2)^Т^Т2^Т2. (7.234)
0000
Учитывая (7.232), получим
оооо
^min =^min " J J*2V Wa^l'T2 WT2, (7.235)
00
где c^imn =M[af(r)] = DOCT - минимальная СКО при использовании только линей-
ного канала. Величина
Я?-*, -^2min = J^1(т19т2)а^(т{9т2)dT{dT2 . (7.236)
00
количественно определяет тот эффект, который обеспечивается введением
квадратичного канала. Другими словами, использование квадратичного канала позволяет
дополнительно уменьшить СКО по сравнению с линейным фильтром на величину
(7.236) [84].
Пользуясь приведенными рассуждениями, но полагая, что найдены
**(Ti)»*2(Ti»T2)»—»*n-i(Ti»T2»—»T«-i)» построим интегральное уравнение,
определяющее *^(т1,т2,...,ти). Обозначим через Gn_{(t) ошибку, которая получается, еслр
для оценки m{i) используется нелинейный фильтр, имеющий линейный,
квадратичный и т.д. каналы до (и-1) включительно. Тогда
cVi(0 = m(0-£ J...J/:I.(T1,T2,...,T|.)y(r-T1)K(r-T2)...y(r-Tl.MT1rfT2...JT. (7.237
'=1 0 # 0
Отсюда находим
оо оо
^n=Ml(an.l(t)-j...jkn(xl,x2,...,xn)Y(t-xi)Y(t-T2)...Y(t-xn)dTl...dxa)2] =
о о
Глава 7. Методы синтеза статистически оптимальных САУ 437
оо оо
= DCniOni-2M[j...jkn(-cl,x2,...,Tn)Y(t-xl)Y(t-x2)...Y(t-xn)an.i(t)dx1...dxn] +
о о
+M[j...j kn(xl,x2,...,xn)kn(x\,x2,...,xn)Y(t-xl)...Y(t-xn)dxl...dx'n] =
о о
оо оо
= D<wv, -J-J *«<Т»'Х2 Tja^CT,,^,...,^)^,... dxa +
о о
оо оо
+f...fkn(Tl9x2,...,Tn)kn(T\^^ (7.238)
о о
В последнем выражении Da ст - минимальная СКО, которая Может быть
достигнута при использовании нелинейного фильтра, включающего (п - 1) канал.
Из (7.238) можно получить интегральное уравнение,' определяющее ИПФ и-го
канала [72, 84,123]:
оо оо
a£J(^2 г^=/:^*:(т;д2,...д^сх^)(т1,...дяд;,...д>т;..^. азд
о о
Очевидно [84]:
оо оо
<£irin=<U4)irin-f-J*»(*l.^^^ (7'24°)
О О
Рассмотрим задачу в общем виде, когда находятся ИПФ первого и второго
порядков из условия минимума СКО. Выражение, определяющее СКО, можно получить,
пользуясь следующими рассуждениями. Имеем
оо оооо
a(t) = m{t)-jkl(xl)Y(t-xl)dxl-jjk2(xl,x2)Y(t-xl)Y(t-x2)dxldx2. (7.241)
О 0 0
Отсюда находим
L2 +
o2(0 = m2(r)+JJ*i(T1)*1(T2)y(r-T1)r(/-T2)rfT1rfT:
00
оооо оооо
+jjjjk2(x1,x2)k2(x\,x2)Y(t-xl)Y(l-x2)Y(t-x\)Y(t-x2)dxldx2dx\dx2-
оооо
оо оооо
-2j*1(T1)y(r-T1)m(»)rfT1 -2Jlk2(xl,x2)Y(t-xl)Y(t-x2)m(t)dxldx2 +
0 0 0 ,-
оо оо оо
+2///^1(т^^(т1,т2)У(г-т;)У(г-т2)У(г--т1)^т2^т1.
000
Осреднение по множеству приводит к следующей зависимости:
оо оо оо
З2 = A™ -2jt, (т,)ЛиГ (т, )dx, -2Jjk2 (т„т2)а£} (т„т2)Л,Л:
0 0 0
оо оо
2 +
00
438 Анализ и статистическая динамика САУ. Часть I
оооооо
+2Ш*' (т>)*2 (x'ub)^YY (ti -t',,t, -x2)dx,<*xi«/x2 +
000 (7.243)
hJJJJ*2 (T1«T2)*2 (fi.^Jot^ (x, -T2,T, -Х„Х2 -T2)dWVT2.
О ОООООО
0 0 0 0
Тем же приемом, который применялся выше, можно показать, что минимум СКО
достигается при использовании такого нелинейного фильтра второго порядка, ИПФ
первого и второго порядков которого удовлетворяют следующей системе двух
интегральных уравнений [72, 84,123]:
оо оо оо
lJk*2(x2,x3)aY3}(xl-т2,х,-x3)dx2dx3 + jk;(x2)RYY(x,-x2)dx2 = RmY(т,), (7.244)
0 0 0
JJ*2 (*i.*i)aiT (Ti -*2.*i -f'l'^ -Хг)л;</х2 +
0 ° (7.245)
оо
о
Если полезный случайный сигнал m(t) и помеха //(/) независимы и имеют
симметричное распределение, а^(т1-т2,т1-т3) = 0 и записанная выше система
интегральных уравнений, определяющая оптимальные ИПФ к1(х),к\(хх,х2), распадается
на два уравнения, первое из которых переходит в одномерное уравнение Винера -
Хопфа, определяющее оптимальную ИПФ линейного канала, а второе - в уравнение
(7.232), определяющее ^С^Дг) квадратичного канала [72, 84, 123].
Для общего случая интегральные уравнения, определяющие оптимальную
нелинейную систему, имеют вид [72, 84, 123]
|;]..]^(трт2,...,тт)Г(г--т1)...У(г-<)Г(г-т1)...Г(г-тт>/т1... dxm =
m=0 о 0 (7.246)
= m(t)Y{t-xx)Y{t-T2)..Y(t-xn\ л = 0, 1, 2, ..., N,
или, что то же самое,
ДО оо оо
т=о о о (7.247)
= а^+1)(т1,т2,...Ди), n = 0,l,2,...fM
До сих пор не делалось никаких предположений о законах распределения
сигналов n{t) и т(г). Если предположить, что процессы n{t) и m{t) распределены по закону
Гаусса, то добавление квадратичного, кубичного и т.д. каналов к оптимальному
линейному фильтру не может уменьшить величины СКО. Другими словами, наилучшая
фильтрация стационарного или нестационарного нормального случайного процесса
m(t) из аддитивной смеси с нормальным случайным сигналом n(t) осуществляется
оптимальным линейным фильтром, ИПФ которого определяется интегральным
уравнением Винера - Хопфа (7.18).
Глава 7. Методы синтеза статистически оптимальных САУ
439
7.4.2. Синтез последовательного нелинейного корректирующего
устройства
Обозначим изображения многомерных импульсных переходных функций
корректирующего устройства так:
W^(sl9s29...9si) = ^k^(tlft2f...9ri)}9 1 = 1. 2, ... .
Аналогично:
WJ*(si,S29...,Sj) - многомерные ПФ объекта управления,
W*(si9s29...,$,-) ~ многомерные ПФ оптимальной (желаемой) системы (их
оригиналы определены уравнениями(7.247)).
Обозначив через G,- (.s^»—»^), i = h 2, ..., изображения ядер прямой цепи
системы, т.е. последовательного соединения корректирующего устройства и объекта
управления, получим следующие зависимости для изображения ядер замкнутой
системы (формулы, определяющие ПФ И^*^),^*^,^),... замкнутой оптимальной
(желаемой) системы получены выше, см. формулу (7.247)) [72,123]:
Ufa)- С'(''>
W2(Sl,s2) = -
Gijh'h)
[l + G,(*l+*2)] UH + Giis,)]
1
Г=1
(7.248)
Решая эту систему относительно Gl(sl)JG2(sl9s2)9... 9 получим формулы,
определяющие многомерные ПФ прямой цепи [72, 123]:
о,Ь)-*Ы
G2(j,,j2) —
1-^,(5,)
w;(sus2)
(7.249)
[l-Wfa+*2)] Щ1-^*^)]
1
С другой стороны, изображения ядер Gl(s{),G2(slis2),... соответствуют
последовательному соединению корректирующего устройства и объекта управления. Для
этого соединения известны зависимости (рис. 7.21) [72,123]:
8(0
W2K4sus2),
,s3),...
G,(ji),G2(j,,j
u/0/
3\si»^2»
k'l'A'2
*з)»
'2°(*.
\
...
Рис. 7.21. Структурная схема прямой цепи системы
440 Анализ и статистическая динамика САУ. Часть I
G,(*,) = W,Vi) И^,),
( г \ 2 (7 250)
G2(sl,s2) = Wl°\ ^sr \,W2K4slys2)+W2°(sl,s2)Y[WlKi'(sr),
{пЛ ) г=1
з > (г
G3(5,,52,53) = < ]\sr\ Wy(svs2,s3)+W2°\suZsr \W^(Sl) W?(s2,s3)+
+*?(5а.*з] Ъ"М W?(s3)+W°(svs2,Si)flwr(sr),
=1 J r=l
Учитывая (7.248) и (7.250), получим
-!£<£>-«*»(,,) ^(5,), (7.251)
1-W, (s,)
[l-Wl*(51 + J2)]n[l-Wl*(sr)]
Отсюда находим многомерные передаточные функции корректирующего
устройства, выраженные через ПФ оптимальной замкнутой системы и объекта управления
ИГ(*,) = -
Щ (*.)
W,°(s,)[ 1-<(*,)]
W2 (St,S2) -т-^ \ i
wn Ъг [ i-<(*>+*2)] n[ i-<(^)]
2
r^l
7.4.3. Синтез встречно-параллельного нелинейного
корректирующего устройства
Рассмотрим решение той же задачи, которая рассматривалась в предыдущем
подразделе, с той лишь разницей, что нелинейное корректирующее устройство имеет
место в цепи обратной связи, а оптимальная замкнутая система по классификации,
приведенной в [72], имеет глобальную структуру класса II.
Связь между входом и выходом оптимальной замкнутой системы определяется
рядом Вольтерра вида
X (0 = £ J...J*™ (т,.х2,...,т2,+1)Г(/-т1)х
1=0 0 О {1-ЯЭ)
xY(t-x2)... Y{t-x2M)dxv.. dx2M.
Глава 7. Методы синтеза статистически оптимальных САУ 441
Таким образом, многомерные импульсные переходные функции /:* (Xj,x2,...,xv) и
многомерные передаточные функции
<(j1,j2,...>jv) = Iv{*v*(t1t2,...,tv)}, v = 2i + 1 (7.254)
известны, причем импульсные ц передаточные функции содержат только нечетные
индексы.
Объект управления описывается рядом Вольтерра вида
X(t)=f]..]ko}(xl,x2,...,xj)e(t-x,)e(t-x2)...e(t-xJ)dTl...dxj =
И> о о
оо оо
= iJ-J/;;(T"'T2'-'T;)(r('-ri)-c/(/-T'))(r('-T2)-^(^T2))x...x (7.255)
j=o о о
x(Y(t-Xj)-U(t-Xj))dxl.^xJ.
И, наконец, связь между сигналами Y{t) и U(t) выражается рядом Вольтерра,
определяющим математическую модель корректирующего устройства:
U(t) = f,]Sjk:^Tl,x2,...,Tv)Y(t-Tl)Y(t-b)...Y(t-Tv)dTl...dTv. (7.256)
v=lO 0
В рассматриваемой задаче импульсные переходные функции и передаточные
функции оптимальной замкнутой системы
4+i(Ti,T2f...,x2i+1)oW2*+1(j1,52,...,J2/+1)> 1=0,1,2, ... 9NX (7.257)
и объекта управления
k0j(xl9x29...9Xj)<r>wf(sus29...9Sj)9 ; = 0,l,2, ... ,р (7.258)
известны; по этим динамическим характеристикам необходимо найти импульсные
переходные функции и передаточные функции корректирующего устройства
ife^(T1,T2,...,Tv)oWvKy(j1,j2,...,jv), v = 0, I, 2, ..., N. (7.259)
Подставим в (7.255) формулу, определяющую сигналы U{t-xx) ,
U(t-i2) , ... ,£/(г-Ту); имеем
^(0-iJ-J*"(Ti-x2.-.t>)[i'('-T1)-iJ...Jtv4'(T;,xj,...,i)x
у=о о о v=oo о
x¥(t-xl-x\)Y(t-xl-x2)...Y(t-xl-xv)dxl...dxv[Y(t-x2)-
-fl]Sjk^(x\,x2,...,x'v)Y(t-x2-x'l)Y(t-x2-x2)x...x
v=Oo 0
xy(f-T2-xv)rfTi...^x[r(f-x1)-
-%]•■№ (ъъ.»-.<)у (*-**-<)* (*-%-ъ)х
v=Oo 0
хУ (r-xv -Tv)rfti...rfXv. (7.260)
Таким образом, определены две зависимости, определяющие выходной сигнал
X(t): первая зависимость (7.253) связывает вход Y{t) и выход X{t) через оптимальные
28 Зак. 232
442 Анализ и статистическая динамика САУ. Часть I
многомерные ИПФ k2i+l (т{, т2,..., т2/+1 ); второе же выражение отражает ту же связь,
но через многомерные ИПФ объекта к® (T1,T2»—»T2i+i) и корректирующего
устройства £vy(Tl'T2>->Tv)-
Приравнивая соответствующие члены в зависимостях (7.253) и (7.260), находим
оо
f*;(t,) г(г-т,)л,=
о
оо оо оо
-JtfCc,) ^(r-TO-Jti^^JJ^^Jy^-Ti-Ti-TlJrfTlrfT; dxx. (7.261)
о L о о
Применяя к (7.261) одномерное преобразование Лапласа, легко найти выражение,
определяющее передаточную функцию Wj* {sx) линейного канала корректирующего
устройства [72]:
Или, что то же самое,
-[^•(..fl-'+fwi0 (,,)]"'•
Легко видеть, что передаточная функция линейного канала выражается через
передаточные функции линейных каналов объекта управления и оптимальной
замкнутой системы.
Наличие члена Г Wj° (sx) Wj* (s{) 1 говорит о том, что в рассматриваемом
подходе присутствует операция динамической компенсации [168].
Найдем зависимость, определяющую двумерную передаточную функцию
корректирующего устройства; имеем
о—К(х,)Я*,ч'(т;.^)Я*:(х;)*г(^)к(»-х1'-х1-т;)х
О 0 0 0 0
coco
xY(t-xl-x2-T2)dx\dx2dx"ldx"2 + jj^(x^i Y( r-x,)-
0 0
-/^(т;)/*,*^;) г(г-т1-т1-т;)л1,л;][к( г-т2)- (7.264)
о о
oo oo
-J*r ИК (^2) У (^-Ti -т2 -%2)dT2d%2 ]dxxdx2.
о о
Применение в последней зависимости двумерного преобразования Лапласа
приводит к формуле
0 = -W10(51+,2)W2lty(51)52K(.1K(^) + W2°(,1,52)x 7^5
Глава 7. Методы синтеза статистически оптимальных САУ 443
Отсюда находим передаточную функцию квадратичного канала корректирующего
устройства
*р(*.*)- '*"*/L ,„;, 'i::-!L,:w l Zi- o**>
_ W^sl,s2)[l-W1K4sl)Wl*(sl)][l-WlK:'(s2)Wl''(s2)]
W,° (*„ *2)W,*(*,)W£(*,)
Перейдем к нахождению передаточной функции кубического канала; имеем
/*з*(х„т2,т3)1',(г-х1)1'(г-т2)Г(г-Тз)Л1Л2</Тз =
=-К (т.) J...J *3ку (ti.^.x,) Jjj*r (х;к й*; (т"3)х
о оо ооо
xy^-Tj-Tj-xjV.. к(г-т1-Тз-Тз)^т'1'...^Тз^т11... dx3dxx-
-2jJ^0(t,.x2)i'(r-tI)JJ*?'(t;.x;)JJ*;(x;)*1*(x;)x
00 00 00
xY (t-i2- t'i - tAy (t - т2 - т2 ~ Т2) ^/Tj dx[ di1dfz>1d'Z'1 +
+/...^зО(х1,т2,Тз)[К(г-т|)-//:Г(т;)^;(т;)х
oo oo
хУ(г-х2-х1-х;)л1л;]...[К(г-х3)-/^(хз)/*1'(х3)х
о о
xY (r - т3 - Т3 - x3)dx3dx] ]dxxdx2dx3. (7.267)
В результате применения трехмерного преобразования Лапласа будем иметь [72]:
W;(sl,s2,s3) = -Wl°(sl+s2 + s3) W?(st,s2,s3) Wi(st) <(^2)x
x<(s3)-2 ^(j.^ + Js) W?(s2,s3) W*(s2) <(53)+ (7.268)
+<(,„,2,53) П[1-ИГ(*;)<(*,)]•
1=1
Теперь легко записать формулу, определяющую трехмерную передаточную
функцию:
Из°(*1.*2,*з) П[ l-^('lK('l)]-
W3'(j,,s2)s3) = -
1=1
Wi° (^1+^2 + ^3) (7.269)
-W3t(.1,.2>53)-2W2°(.1,52 + .3) W2K"(.2,.3) <(.2) <(.3)
<(5.) <(52) <(^3)
Аналогичным образом определяются Wfy (51,52,53>'у4) »••• •
Анализ полученных зависимостей показывает, что передаточные функции
корректирующего устройства с нечетными номерами 2v-l, v = l, 2, ... зависят от
2v -1 передаточных функций оптимальной системы, тогда как передаточные
функции корректирующего устройства с четными номерами 2v зависят только от
(2v -1 )-й передаточной функции оптимальной системы [72].
28*
444 . Анализ и статистическая динамика САУ. Часть I
7.4.4. Техническая реализация нелинейных
корректирующих устройств
В [117] подробно рассмотрено решение задачи технической реализации
корректирующих устройств в замкнутой системе. Здесь приведем решение задачи,
использующее разложение многомерных импульсных переходных функций
корректирующих устройств по аппаратно реализуемым ортогональным базисам. В качестве такого
базиса могут быть использованы функции Лягерра [54]
ф (о М *! H)v ff(-ov"'(*)vU (7270)
Фт() &(»-v)! (v!)2 |v^0(m-v)!(v!)2r ' (7>270)
где Ь = к t, к - масштабный множитель.
Запишем несколько функций Лягерра в развернутом виде [54]:
_kt
Фо(О=* 2>
ф,(0=0-*0«"2.
<p2(t)=(l-2kt+±k2t2)e~,
V-_LAM iix
(7.271)
Ф4(Г) =(l-4kt+-£-k2t2- J-jfcV+—*V] Л
V4W [ 2 ! 3 ! 4 ! J
9j(r)=fi-5Jfct+—*V-—*V+-^-*V—LjkV] Д
5W [ 2 ! ' 3 ! 4 ! 5 ! J
Представим п-ю ИПФ корректирующего устройства в виде
/,=0/2=0 /„=0
где
оооо оо
CSU = JJ-J*-4'(T"T2 Т»К <П)% (b)-% {\)dxv..dxn. (7.273)
00 0
Из предыдущего изложения ясно, что известными являются не ИПФ, а
передаточные функции всех каналов корректирующего устройства. Найдем зависимости,
определяющие коэффициенты с*£ л через W*y (sX9s2,:.,sn).
Имеем [54]
ooo h-o^i-v,)! (v,!) J
-t^^t^-^-
Глава 7. Методы синтеза статистически оптимальных САУ 445
-tt-t ; ~ —)..]КУ{хх,х2,...,тп)х ' 0.274)
v,=0v2=0 v,=0 Y[(ij-Vj)l(vj(f ° О
хт;Ч£...т> ~ге~... e~dxxdxv.. dxn =
п
= 2j 2j-2j"т; г ^v,v2...уя»
п-о^-о -°nO,-v,)'(v,!)2
где
^...v^J-J^^i.^.-tJt^?...!?^"^... e"^Vx2 ... dxn (7.275)
о о
- степенные моменты многомерной ИПФ.
Их легко найти через передаточную функцию W^ (sj,,^,...,^) по формуле
»,„.., -(-о—- sf^V^ *,)Ц. р^>
Поскольку ИПФ каждого канала корректирующего устройства представляется в
виде
*Р(т)=2ХЧ(т*
V|=Ov2=O
(7.277)
С(т1,...,т„)= I-X С2-„Фп (х.) - Ф„я (т„),
v,=0 уя=0
а многомерные ПФ записываются так
v=0
v,=0v2=0
(7.278)
w^(*,—*„)-2...2<^_W/M*) - ф¥.(^).
v,=0 vn=0
причем
446
Анализ и статистическая динамика САУ. Часть I
Ф,(О=«У*
(
к/У
(7.279)
и каждая из таких цепочек физически реализуема, очевидно, структура
корректирующего устройства будет иметь вид, представленный на рис. 7.22 [54, 84,117].
Рис. 7.22. Структурная схема нелинейного корректирующего устройства
Процедура вычисления коэффициентов cf? . значительно упрощается, если в
качестве базиса использовать ортогональные экспоненциальные функции,
определяемые формулой [54]
фЛО-Хчь.*"""-
(7.280)
m=l
Первые пять функций, ортонормированных на промежутке [0,°°), имеют вид:
Глава 7. Методы синтеза статистически оптимальных САУ
447
Ф2(г) = 7?(бе-2с'-4е-с'),
Фз (г) = Vfc(10<Г3с' - \2e~2ct + 3<ГС'),
Ф4(t) = ^(l0e~4ct -l20e~3ct + 60<Г2с' -Ъе~а), (7.281)
Ф5(О = у/Юс (126бГ5с' -280^"' + 210<Г3с/ -60бГ2с' + 5бГс'),
Каждая из приведенных функций физически реализуема в виде набора
апериодических звеньев, и, таким образом, может быть аппаратно реализовано нелинейное
корректирующее устройство.
Представляя многомерные ИПФ в виде (7.277), легко показать справедливость
формулы, определяющей коэффициенты cfj . [54]:
■&..<. - t £■••£ WW- ',лК'(',.!г s,
ii
v,=lv2=l vw=l
П ) 5,=V,C,
(7.282)
В качестве базиса можно выбрать ортогональные экспоненциальные функции,
порожденные полиномами Якоби или Лежандра (см. Приложение 3).
7.5. ОПТИМИЗАЦИЯ НЕЛИНЕЙНЫХ СИСТЕМ ПРИ СЛУЧАЙНЫХ
ВОЗДЕЙСТВИЯХ С ИСПОЛЬЗОВАНИЕМ СТАТИСТИЧЕСКОЙ
ЛИНЕАРИЗАЦИИ
Рассмотрим САУ, представленную на рис. 7.23.
^Ц
Wv(s,p)
ГА)
F&)
Xiit)
W0(s)
X(f)
Рис. 7.23. Структурная схема системы
В данной постановке, связанной с синтезом нелинейной системы по критерию
минимума среднеквадратической ошибки, полагаем, что часть элементов задана, в
том числе нелинейный элемент с характеристикой F и линейная часть с ПФ Wq(s);
необходимо определить передаточную функцию WKy(s) линейного корректирующего
устройства.
В рамках корреляционной теории приближенно поставленная задача может быть
решена с использованием метода статистической линеаризации [65].
Рассмотрим несколько подходов к решению задачи синтеза оптимальных систем.
Положим, что нелинейный элемент имеет однозначно непрерывную
характеристику. Варьируемые параметры р = (ри /?2,..., рг)Т имеют технические ограничения,
которые в векторной форме имеют вид
Рт^Р^Рм-
Для решения задачи воспользуемся статистической линеаризацией НЭ
448
Анализ и статистическая динамика САУ. Часть I
о
Xl(t) = K0(mYrGYi)mY]+K](mYrGY])Yl(t),
(7.283)
где mY - регулярная составляющая, математическое ожидание Y\{t)\ Y\(t) -
центрированный случайный процесс; Ко и К\ - соответственно первый и второй
коэффициенты статистической линеаризации, зависящие от математического ожидания и
дисперсии сигнала Yx (г).
В первом варианте в качестве критерия оптимальности принимается минимум
среднеквадратической случайной ошибки при предположении, что система работает
в установившемся режиме.
Для статистически линеаризованной системы целевая функция (среднеквадрати-
ческое значение ошибки системы) запишется в форме
ё = М [ е2 (г)] = е2 + G2nn -> min , (7.284)
где в предположении стационарности всех процессов выражения для е и апп имеют
вид
8 =
1
_l + WKy(s,p) K0(mYi,aYi) W0(s)
•m,
= e(p).
s = 0
Sim(oi)d(a = a2m(p).
(7.285)
(7.286)
Так как установившаяся ошибка (7.285) и дисперсия случайной ошибки,
порожденной помехой n(t) (7.286), зависят от коэффициентов статистической
линеаризации, для их определения в расчет должны быть введены математическое ожидание
mY и дисперсия су входной координаты нелинейного элемента; расчет
коэффициентов Ко (mY ,cY ) и Кх (mY ,ar ) производится по формулам
MmVa0=f р(у^уМ)^
K^m^G^^tl^JF^y^f^iy^-K^m^G^)
где
(7.287)
(7.288)
ехр
{Уг-тГгУ
2Д
Ух Yx
Так как оптимизация ошибки для статистически линеаризованной системы
проводится приближенно, необходимо ввести условия устойчивости, обеспечивающие
безусловную устойчивость при синтезированных параметрах, для чего используется
критерий абсолютной устойчивости процессов В.М. Попова [6].
В результате задача оптимизации системы по минимуму среднеквадратической
ошибки (7.284) может быть сформулирована как задача нелинейного
программирования: минимизируется по вектору параметров р целевая функция
Глава 7. Методы синтеза статистически оптимальных САУ 449
12(р)=е2(р)+аЦр)^гтп (7.289)
Р
с использованием соотношений (7.285) и (7.286) при ограничениях:
а) рт<р<рш
б) Ко (mY ,oY ) и K{(mY ,GY) - коэффициенты статистической линеаризации,
в) налагаемых требованием абсолютной устойчивости процессов.
Ввиду сложности ограничений при решении задачи нелинейного
программирования используется процедура численного направленного поиска - регулярного или
случайного. Имея в виду гибкость аппарата нелинейного программирования, та же
расчетная процедура может быть использована для оптимизации нелинейной
системы при случайных воздействиях по другим критериям.
При решении практических задач часто используется следующая постановка
задачи: на вход системы (рис. 7.23) подается полезный сигнал m(t) и помеха n(i)\ m(t) и
n(t) - стационарные случайные некоррелированные процессы, система работает
в установившемся режиме. Критерий оптимальности записывается в виде
&(Р\>Р2>->Рг) =
■j
l+WKy(>co ,pl,p2,...,Pr)Kl(myraYi)w0(j(ii)
5„и(со)Ло+ (7.290)
+
•к»
1
ч / \ , ч 5"-((°)</Сй
l + Wvy(j(O ,pl,p2,...,pr)Kl[mYroY{) W0(ja>)
Решается следующая задача с использованием аппарата нелинейного
программирования
а ( Pi>P2''**'Pr)~*niin,
р
при ограничениях:
а) рт<р<рш
б) Ко ( mY, Су ) и Кх (mY, о у) - коэффициенты статистической линеаризации,
в) налагаемых требованием абсолютной устойчивости процессов.
Может быть предложена также следующая приближенная процедура
оптимизации при стационарных и нестационарных случайных процессах. Пусть заданы
вероятностные моменты второго порядка случайного полезного сигнала и помехи,
имеющие нормальный закон распределения. В этом случае, как известно,
оптимальная система, в смысле минимума среднего квадрата ошибки, является линейной.
Динамические характеристики (передаточная функция для класса стационарных систем
и импульсная переходная функция для класса систем с переменными параметрами)
могут быть найдены известными методами: путем решения уравнения Винера -
Хопфа, методом Заде - Рогаззини (последний метод предполагает оптимизацию по
минимуму среднеквадратической ошибки при ограничениях на время переходного
процесса (система с конечной памятью) и коэффициенты ошибок).
Рассмотрим простейший случай, когда система стационарна (рис. 7.23), m(t) и n(t)
- стационарные некоррелированные сигналы, режим - установившийся.
Пользуясь методом статистической линеаризации, определяем коэффициент
усиления нелинейности по центрированной случайной составляющей Кх (mY ,gy ). По-
450
Анализ и статистическая динамика САУ. Часть I
ложим, что найдена передаточная функция оптимальной замкнутой системы W(s).
Тогда справедливо соотношение
W(s) =
W^K^my^Wpis)
l+W^W^my.OyWois)
(7.291)
(7.292)
из которого находится ПФ корректирующего устройства
W (J) - W^
v K^my^WoMll-Wis)]
Последняя зависимость может быть переписана в виде
W^(s) = Kl-\mY oY)W0-\s)-^- = K-1(mY ay)W0-\s)W:(s), (7.293)
\ — W{s) l
где W*(s) - оптимальная передаточная функция разомкнутой системы. Решение
задачи оптимизации параметров нелинейных многомерных систем при случайных
воздействиях с использованием аппарата нелинейного программирования приведено
в [6].
Пример 7.9 [65]. Рассмотрим следящую систему, структурная схема которой представлена на
рис. 7.24.
4&Щ
w (Л
WH \S)
W (s)
ку \ /
ЧЩ
f(y.)
\n(t)
X(f)
Рис. 7.24. Структурная схема следящей системы
ь\
На структурной схеме WQ(s) = передаточная функция неизменяемой части системы; пара-
5(7j5 + 1)
метры имеют следующие значения: Ь\ - 2,06-10'3 рал/с, Т\ = 0,2 с.
Нелинейный элемент представляет собой усилитель с насыщением с характеристикой
1406, Y{>\b,
40ylt -\b<Yx<\b,
-40 b, Y{<-\b.
Измеритель рассогласования имеет передаточную функцию
^^=20%ад-
На вход системы поступает сигнал Y(t) = m(/), а помеха n(t) поступает на вход неизменяемой части
(рис. 7.24)
5-.(cd) = —
а2 2Р
п Ш2+4Р2
а2 =0,5 рад2,
5ЯЯ((О) = So = 3,42 % Р = 0,84 Ра^/.
По статистическим характеристикам полезного сигнала и помехи легко найти передаточную функцию
оптимальной системы [65]
W(5):
0,45
■(, + 2)(5 + 3)"
Задача заключается в нахождении передаточной функции корректирующего устройства, при этом
полагается, что система работает в установившемся режиме.
Глава 7. Методы синтеза статистически оптимальных САУ
451
Для расчета коэффициента статистической линеаризации необходимо графически решить уравнение [65]
37
-№Ф
1
/Д
'У\У\ {V^Vi
где <P(z) - функция Крампа.
Графическое решение уравнения (7.294) приведено на рис. 7.25; из него следует, что К\ = 72.
*1А
(7.294)
12 3 4
Рис. 7.25. Графическое решение уравнения (7.294)
Из структурной схемы (рис. 7.24) следует
WKy(.t)fr0*|Vy0(s)
w(,)=
UW^boK^s)
Отсюда находим
W(s)[\ + WKi. {s)b0Kt W. (*)] = WK). (s)bt,K, Wo (*).
Последняя зависимость позволяет записать формулу, определяющую ПФ корректирующего устройства
(7.295)
»^(*) =
=b-0>K^w0-i(s)w;(s).
Как легко видеть из (7.295), при рассмотренном подходе реализуется принцип динамической
компенсации со всеми присущими ему недостатками [168]. Положение усложняется необходимостью
использовать в расчетах обратное звено линейного эквивалента нелинейного элемента.
Передаточная функция корректирующего звена имеет вид [65]
0,156,[0.2.^1]
^V ' s2 +55 + 5,55
452 Анализ и статистическая динамика САУ. Часть I
ГЛАВА 8. МЕТОД МАТРИЧНЫХ ОПЕРАТОРОВ
ЧИСЛЕННО-АНАЛИТИЧЕСКОГО РЕШЕНИЯ
ЗАДАЧ ДЕТЕРМИНИРОВАННОГО АНАЛИЗА
И СТАТИСТИЧЕСКОЙ ДИНАМИКИ СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Системы автоматического управления в общем случае представляют собой весьма
сложные устройства. Достаточно указать примеры управления ракетами различного
назначения, космическими аппаратами, ядерными реакторами, технологическими
процессами и др.
Математическая модель таких систем должна охватывать важнейшие физические
явления, связанные с ее функционированием. Наиболее сложная и ответственная
работа при постановке задачи построения математической модели заключается в
выборе связей и характеристик явления, существенных для данной задачи и подлежащих
формализации и включению в математическую модель.
При решении инженерных задач наиболее важным является этап математического
исследования модели. Для наиболее простых моделей зачастую удается получить
аналитические решения. Из-за грубости модели точность такого подхода часто не
удовлетворяет исследователя; нередко этот подход позволяет оценить лишь порядки
величин.
Для точных и сложных моделей (некоторые САУ описываются
дифференциальными уравнениями, имеющими порядок нескольких десятков) аналитические
решения удается получить в исключительных случаях.
Применение численных методов принципиально расширило класс
математических задач, допускающих исчерпывающий анализ. Теперь уже исследователю при
построении математической модели исследуемой САУ не нужно стремиться к
упрощениям, которые были необходимы раньше для получения ответа в явном виде. Его
внимание, прежде всего, должно быть направлено на то, чтобы правильно учесть все
наиболее существенные особенности изучаемого объекта и отразить их в
математической модели.
Таким образом, из сказанного следует: при построенной математической модели
САУ нахождение решения поставленной задачи в явной замкнутой форме возможно
только при определенном (часто весьма радикальном) упрощении проблемы. Такие
упрощения постановки задач могут оказаться полезными как контрольные варианты
для более общей исходной задачи.
Основным же инструментом для решения инженерных задач со сложными
математическими моделями являются численные методы, позволяющие свести
решение задачи к выполнению конечного числа арифметических действий над числами;
при этом результаты получаются в виде числовых значений. Эти методы позволяют
добиться решения поставленной задачи с высокой точностью.
Разработкой численных методов занимались такие крупнейшие ученые, как
К. Гаусс, И. Ньютон, О. Коши, Ш. Эрмит, Б.Г. Галеркин, А.Н. Крылов, Н.И.
Лобачевский, П.Л. Чебышев, Л. Эйлер.
В области аппроксимации, устойчивости и сходимости разностных схем
основополагающие работы были выполнены С.К. Самарским, А.Ф. Филипповым и др.
Большой вклад в развитие и практическое применение численных методов к
задачам математической физики внесли А.А. Дородницын, М.В. Келдыш, В.И. Крылов,
О.А. Ладыженский, Г.И. Марчук, А.А. Самарский, С.Л. Соболев и др.
Глава 8. Метод матричных операторов 453
Методы регуляризации разработаны А.Н. Тихоновым.
Численные методы в линейной алгебре получили значительное развитие
благодаря исследованиям В.В. Воеводина, Л.В. Канторовича, Д.К. Фаддеева, В.Н. Фаддеевой
и др.
В области оптимизации численных методов важные результаты получены
Н.С. Бахваловым, А.Н. Колмогоровым, С.Л. Соболевым и др.
С одной стороны, численные методы обладают чрезвычайно важным
достоинством: они являются универсальными и эффективными, т.к. позволяют находить
приближенное решение для широкого класса задач анализа и синтеза систем.
С другой стороны, они имеют существенный недостаток: они не позволяют
непосредственно, как аналитические методы, вскрыть причины того или иного
поведения системы, поскольку они позволяют лишь получить конкретный результат
(числовые значения) для конкретных исходных данных.
В связи с указанными выше обстоятельствами актуальной является проблема,
связанная с разработкой методов, сочетающих в известной мере достоинства
аналитических и численных методов. Поэтому возникла идея создания методов, сразу
ориентированных на применение вычислительной техники, но таких, которые позволяют
получать общие закономерности поведения исследуемых систем, что не характерно
для численных методов, лежащих в основе расчетов на ЭВМ. Этого можно
достигнуть, попытавшись, например, всю специфичность исследуемого объекта перевести в
какие-то его новые характеристики (они от этого могут стать очень сложными и
громоздкими, что не вызывает затруднений ввиду наличия ЭВМ) с таким расчетом,
чтобы этим характеристикам соответствовали наиболее простые алгоритмы их
использования при описании и исследовании систем, похожие, а еще лучше совпадающие с
хорошо известными в инженерной практике алгоритмами аналогичного
исследования линейных стационарных систем.
К числу таких методов относятся методы, использующие аппарат матричных
операторов и спектральную форму описания процессов.*
Эти методы, принадлежащие к численно-аналитическим, позволяют не только
получить количественные характеристики интересующих процессов в исследуемой
СЛУ с полной математической моделью, но и вскрыть факторы, влияющие на эти
характеристики, и целенаправленно менять их, т.е. дают возможность получить
общие закономерности функционирования СА У.
Сказанное отражает факт сочетания достоинств аналитических и численных
методов.
В основе идеологии проекционных и, в частности, спектральных методов лежит
матричное описание как элементов САУ, так и систем в целом. Теоретической же
основой послужил известный из функционального анализа факт матричного
представления операторов в ортогональных базисах. В монографии [9] Н.И. Ахиезера и
И.М. Глазмана этот факт отражается так: «Всякий ограниченный линейный
оператор, определенный во всем пространстве, допускает матричное представление в
любом ортонормированном базисе, и в этом состоит аналогия сепарабельного
пространства Гильберта с конечномерным пространством: ограниченные операторы
допускают матричное представление, которое вполне аналогично известному из
линейной алгебры матричному представлению операторов в конечномерных
пространствах».
Аппарат матричных операторов базируется на широком использовании теории
ортогональных функций. В теоретических и прикладных исследованиях для расчета
* Библиографию, посвященную аппарату матричных операторов и различным аспектам его
применения, можно найти в [83].
454 Анализ и статистическая динамика САУ. Часть I
и проектирования систем связи и управления широко используются спектральные
представления, в основе которых лежат интегральное преобразование Фурье и
разложения по ортогональным функциям.
В результате разложения сигналов по тригонометрической системе функций
сформировался аппарат гармонического анализа (классический спектральный
анализ). Основные положения этого аппарата изучались и применялись на практике с
1882 г., когда была опубликована работа Фурье по теории теплопроводности. Этот
аппарат получил распространение в физике, радиотехнике, автоматике, теории
информации и во многих других разделах науки и техники.
Большую роль в развитии классических спектральных представлений
применительно к решению задач теории связи и управления оказали работы
Л.И. Мандельштама, В.А. Котельникова, Г.С. Горелика, СМ. Рытова, Д. Габора,
А.А. Харкевича, Ф.М. Вудворда, В.В. Солодовникова, Е.П. Попова и др. К причинам,
обусловившим широкое распространение гармонических функций, относятся:
• инвариантность при прохождении через линейные системы с постоянными
параметрами (гармонический сигнал проходит через линейную стационарную
систему, не искажаясь по форме),
• синусоидальные функции являются собственными функциями систем,
описываемых линейными дифференциальными уравнениями с постоянными
коэффициентами,
• мультипликативность (при перемножении функций их аргументы
суммируются; на основе использования этого свойства оказались возможными
разработка операторного метода, введение понятия коэффициента передачи и т.д.).
Обобщение спектральных представлений на другие базисы порождено
следующими факторами:
• имеет место теоретически обоснованный математический факт, что в качестве
базисных функций при разложении сигналов можно использовать не только
тригонометрическую ортогональную систему, но и другие базисы: полиномы
Лежандра, Чебышева, функции Уолша, Лягерра и др. Более того, при
исследовании работы широко применяемых в цифровых устройствах элементов
«включено - выключено» трудно пользоваться гармоническими функциями
из-за наличия явления Гиббса и плохой точности приближения в точках
переключения;
• методы решения уравнений с переменными коэффициентами при помощи
синусоидальных функций, которые для этих уравнений не являются
собственными, оказываются чрезвычайно сложными;
• фильтры временных сигналов реализуются при помощи катушек
индуктивности, резисторов и конденсаторов; для построения фильтров
пространственных сигналов подобная аппаратура неприменима;
• существует много эффектов (например, различение отражающего объекта от
рассеивающего или проводящего рассеивателя от непроводящего), которые
трудно обнаружить при помощи синусоидальных электромагнитных волн.
Отмеченные, а также другие причины, тесно связанные с термином
«вычислительная технология», обусловили необходимость разработки обобщенной
спектральной теории, предполагающей использование других ортогональных базисов;
целесообразность же применения того или другого базиса диктуется особенностями
постановки конкретной задачи.
Глава 8. Метод матричных операторов 455
Метод матричных операторов и спектральные методы предполагают
разложение сигналов и временных динамических характеристик системы по ортогональным
базисам.
Пусть ф(г)=(ф ](г),ф2(г),...,ф/(г),...)т,где Т - знак транспонирования,
одностолбцовая матрица элементов ортонормированного базиса (ОНБ); С* = (c*,c£,...,c*,...j
- матрица-столбец коэффициентов Фурье разложения сигнала x(t) по ОНБ. Тогда
справедливо представление
*(0=|>>£)=фт(')с*.
В терминах спектральных методов под обобщенным спектром сигнала x{i)
понимают совокупность коэффициентов Фурье С* =(с*,с£,...,с*,...) этого сигнала
относительно выбранной ортонормированной системы функций Ф(г) (не
обязательно тригонометрической).
Таким образом, сложилось представление о совокупности коэффициентов Фурье
функции времени по некоторому базису как обобщенном спектре этой функции, в
котором номер коэффициента есть аналог значения частоты в частотной
характеристике функции времени.
Совокупности коэффициентов Фурье, описывающие временные характеристики
систем, сигналы или статистические характеристики сигналов рассматривают
как их дискретные спектральные характеристики, в отличие от непрерывных
частотных характеристик, основой которых является интеграл Фурье. Поэтому такая
форма описания систем и сигналов была названа спектральной. В последние годы
спектральные методы интенсивно развиваются как в плане использования различных
базисов, так и широты охвата современных задач теории систем, фильтрации,
передачи, обработки и сжатия информации, построения цифровых систем различного
назначения. Применение спектральной формы описания сигналов позволяет перейти
от исследования самих сигналов к рассмотрению координат (совокупности
коэффициентов разложения или спектральных характеристик) этих сигналов
относительно выбранного базиса. Операции над функциями заменяют действиями над числами;
последние легко реализуются на ЭВМ. Такой подход приводит к «алгебраизации»
методов решения задач расчета и проектирования.
Причина популярности техники матричных операторов в ее исключительной
простоте: сложные системы дифференциальных и интегральных уравнений, включая
некоторые классы нелинейных уравнений и уравнений в частных производных,
описывающие полные модели систем автоматического управления, почти механически
сводятся к системам алгебраических уравнений. Поскольку матричные операторы
строятся с использованием базисов, то можно сделать вывод, что их использование
основано на специфических свойствах некоторых базисов. Возможность применения
техники матричных операторов вытекает из самого определения базиса в
функциональном пространстве, и, следовательно, матричные операторы могут вводиться и
эффективно использоваться для любого базиса.
Как в настоящей главе, так и в последующих главах широко используются основы
матричного исчисления. Понятие вектора, матрицы, обратной матрицы и др.
являются рабочими. Применение матриц дает ряд преимуществ при изложении, т.к.,
пользуясь ими, легче удается выяснить закономерность многих расчетов.
Особенно выигрышным в этом смысле является проведение как доказательств,
так и расчетов, связанных со сходимостью различных численных процессов. И что
456 Анализ и статистическая динамика САУ. Часть I
особенно важно, современные ЭВМ легко осуществляют основные матричные
операции.
При сравнении с конечно-разностными методами преимущество предлагаемого
подхода проявляется не только в возможности существенно сократить размерности
аппроксимационных систем в случае, когда исходная непрерывная система и класс
рассматриваемых входных сигналов имеют высокую гладкость. Не менее важен и
другой факт: при проекционных аппроксимациях в явном виде сохраняется
зависимость того же типа, которая имела место в исходной системе, - аппроксимационная
система представляет собой линейный оператор, переводящий столбцы из
коэффициентов разложения входных векторов в столбцы из коэффициентов разложения
соответствующих векторов выхода. Для многих задач сохранение в явном виде такой
зависимости не только существенно облегчает понимание задачи и предотвращает от
ряда ошибок, но и позволяет применять более эффективные методы при
исследовании аппроксимационных систем.
Рассмотренный подход, как уже отмечалось, позволяет провести процесс
аппроксимации системы наиболее простым и наглядным способом, т.е. является наиболее
эффективным с алгоритмической точки зрения.
Таким образом, для инженерной практики метод проекционных аппроксимаций,
основанный на применении матричных операторов, наиболее прост, нагляден и не
уступает в точности другим численным методам.
Задачи детерминированного и статистического анализа можно успешно решать
численно с применением спектральных методов. Более того, спектральные методы
для такого класса задач существенно более эффективны многих других численных
методов, поскольку они позволяют сохранить в явном виде линейную зависимость
между набором коэффициентов разложения вектора входа и вектора состояния
системы.
Эта глава имеет ярко выраженную инженерную направленность, поэтому
изложение алгоритма решения конкретной задачи начинается с ее постановки,
рассматриваются основные этапы алгоритма и его структурная схема; изучение завершается
подробным анализом конкретной достаточно сложной задачи: решением ее на ЭВМ
с использованием пакета программ, наиболее эффективного применительно к
рассматриваемой задаче.
С методом матричных операторов (спектральными методами) можно
познакомиться в [9, 10, 42, 53, 56, 57, 58, 82, 83, 122, 127, 129, 131 - 136, 149, 152, 154, 155,
168 и др.].
8.1. ОПИСАНИЕ НЕСТАЦИОНАРНЫХ СИСТЕМ С ПОМОЩЬЮ
ОПЕРАТОРОВ ИНТЕГРИРОВАНИЯ, ДИФФЕРЕНЦИРОВАНИЯ
И УМНОЖЕНИЯ
Одномерная нестационарная линейная система описывается скалярным
дифференциальным уравнением вида
xW+fln(')^"')+-+«o(0^ = ^('))'(m)+Vl(03'('"4)+-^o(03'- (8-1)
Структурная схема, соответствующая последнему уравнению, имеет вид
(рис. 8.1).
Положим, что нестационарная система в пространстве состояний описывается
векторно-матричным дифференциальным уравнением вида [56]
X = A(f)X + B(f)Y, (8.2)
или, в развернутом виде,
Глава 8. Метод матричных операторов
457
xl=au(t)xl+...+aln(t)xn+bll(t)yl+... + blm(t)ym,
x2=a2l(t)xl+... + a2n(t)xn+b2l(t)y1+... + b2m(t)ym,
К = *„! (0*1 +- + а~. ('К +Ьп\ (О* +~ + *«и (<)Ут-
+ txW(0
из
an.\(t)
a\\t) 1
-rl
J
-^—
из
■2>(0
•*-
x(
T"|
1
V
1
1
1
Низ
ДЗ - дифференцирующее звено
ИЗ - интегрирующее звено
g(t)
ДО
«WO
множительное звено
(8.3)
Рис. 8.1. Структурная схема нестационарной системы
Воспользуемся обозначениями
Л, (f) = an (f)x, +al3(t)x3 +... + au (t)xn +bll (t)yi +... + b,m (t)ym,
Mt) = a2i(t)xi+a22(t)x2+a24(t)x4+...+a2n(t)xn+b21(t)yl+...+b2m(t)ym,
Д.-1 (0 = «(„-i)i (0*i+ -+>-iX«-i) (0x(n-i)+Vi)i (f) Л + -+fc(n-i>» (0 У™ •
A. (0 = fc»i (0 Л + fc«2 (0 Уг + -+*»» (0 Ут-
С учетом введенных обозначений (8.3) запишется в виде
x1=al2(t)x2 + Al(t),
x2=a23(t)x3 + A2(t),
(8.4)
Хп-1=У-1)п(1)Хп+\-Л*)'
К = апХ {t)xx+an2 (t)x2 +...+ann (1)х„ + А„(1).
По уравнениям (8.4) легко построить соответствующую структурную схему
(рис. 8.2).
458
Анализ и статистическая динамика САУ. Часть I
|
I
I
*
00
i
Глава 8. Метод матричных операторов 459
Из рассмотрения структурных схем, представленных на рис. 8.1 и 8.2, можно
заключить, что они содержат операторы интегрирования, дифференцирования и
умножения; соответствующие звенья имеют встречно-параллельное, параллельное и
последовательное соединения.
Аналогичные структурные схемы легко построить для класса нелинейных систем
с операциями умножения, систем с запаздыванием и др.
В методе матричных операторов каждый из указанных операторов
(интегрирования, дифференцирования, умножения и запаздывания) заменяется эквивалентным
матричным оператором, а для нахождения матричного оператора всей системы
используются соотношения, связывающие операторы соединения звеньев.
Введем в рассмотрение матричные операторы интегрирования,
дифференцирования и умножения скалярных функций, следуя [83].
8.2. МАТРИЧНЫЕ ОПЕРАТОРЫ ИНТЕГРИРОВАНИЯ,
ДИФФЕРЕНЦИРОВАНИЯ И УМНОЖЕНИЯ
8.2.1. Матричный оператор интегрирования
для произвольного базиса
Пусть В - некоторое банахово пространство функций с базисом, заданных на
отрезке [го»Г/],а
Ф/(0=[Фо«Фр""Фы]
- столбец из / базисных функций в пространстве В. Отметим, что для ряда
популярных базисов нумерация начинается не с нуля, а с единицы, но этот вопрос не
принципиален и при рассмотрении конкретных базисов будет использоваться принятая
для данного базиса нумерация. Здесь же, для единообразия изложения, будем
нумеровать элементы базиса, начиная с нуля.
Отметим также, что в дальнейшем чаще будем рассматривать или равномерную
метрику, т.е. будем полагать # = C|/0,fyJ , или среднеквадратичную метрику; пока
считаем В произвольным банаховым пространством, удовлетворяющим естествен-
ному требованию: если x(t)e В , то более гладкая функция r(t)= \x(x)dx также ле-
/о
жит в пространстве В.
Если x(t)e В , то ее можно приблизить с помощью разложения
*(0«*/(0=Ёс?Ф/(0=Ф/>(0сх. (8.5)
i=0
где Сх = [со, с\ > • • •, cf-iJ - столбец из коэффициентов разложения. Напомним, что
из того, что ф/(*) - базис, вытекает сходимость разложений xt(t) к x(t) в метрике
пространства В.
Способ вычисления коэффициентов разложения (8.5) определяется выбором
проекционного оператора. Далее будем считать, что некоторый оператор
проектирования фиксирован.
460 Анализ и статистическая динамика САУ. Часть I
Для задач, рассматриваемых в следующих параграфах, потребуется по разложе-
t
нию (8.5) находить разложения функций г, (t) = J xt (т) <h. Так как функции
to
являются более гладкими функциями, чем фД*), и, по крайней мере, тоже лежат в В
(по определению базиса фД$)е В, но для базисов из кусочно-постоянных функций
делается исключение - фД-Оё C|fo,f/J , но для них йД*)€ C[to,tf]), их также можно
разложить по базису ф/ (t). Обозначим коэффициенты этих разложений через щ\:
1-Х
h&)=^h№j{f\i = b...,l-\. (8.6)
Далее введем квадратную матрицу порядка / из коэффициентов разложений (8.6)
Аоо йю ••• йы,о
Aoi Аи ••• Амл
аи=р7'=
^Ао,м Ai,m ... Ам,/ч
Тогда в силу линейности оператора проектирования
(8.7)
'о 'о /=0 'о
=Е^(0=Е^ЁМу(0=^(0а„с^ ,
/=0 /=0 у=0
/
т.е., если обозначить столбец коэффициентов разложения элемента rt(t)= дсДт)^/т
/о
через СГ/ > справедлива формула
СГ'=А„С*. (8.8)
Матрица Аи = р7 называется матрицей оператора интегрирования в базисе
ф/(^). Этой матрице соответствует оператор, действующий в /-мерном
подпространстве с базисом ф/(0, называемый матричным оператором интегрирования.
8.2.2. Матричный оператор умножения на функцию
Для аппроксимации линейных нестационарных систем конечномерными
эквивалентами потребуется по разложению функции x(fy находить разложение
произведений t)(r)= *Д*)яД*), где дД*)- разложение некоторой фиксированной функции a(t).
Итак, пусть a(J) - некоторая фиксированная функция из пространства В, at(t) - ее
разложение по базису ф/ (t), а Са - столбец из коэффициентов разложения. Пусть
произведение г)(*)=аД*).*Дг)€ В , тогда v(t) также можно разложить по введенному
Глава 8. Метод матричных операторов
461
базису. Отметим, что для пространства L2[fo»f/J произведение двух функций из этих
пространств также лежит в [} [го»t/ J •
Тогда
^)-и/(0=в/(0*»(0=Ф?(г)си.
Установим формулы, связывающие элементы столбца С" с элементами
столбцов Са и С* • Ясно, что поскольку сомножители можно переставить, то столбец С"
можно выразить двумя способами. Нас интересует ситуация, когда одна из функций
- a(i) - фиксирована, а другая - x(t) - может меняться. В этом случае необходима
формула, выражающая столбец Сь через переменный столбец С* •
Так как в силу линейности оператора проектирования
м ы
/=0 у=0
то, разложив произведения базисных функций (всего будет l(l+l)/2 различных
разложений, но для удобства вводим как коэффициенты щк > так и совпадающие с ними
коэффициенты и^к )>
ы
Ф|(Офу(О=Е^ФЛ(О» U = 0,...,/-l,
Jt=O
Ы /-1 /Ч
получим
. 1=0 ;=0 Л=0
Определим квадратную матрицу и? порядка /
' /-1 /-1 /-1
Sw»oocf Хм/iocf ••• Sw'V-i,ocf
(8.9)
Ay(«) = U? =
1=0
Ъ
i=0
1=0
ы
1=0
/-1
jUmcf
Runlet .-. ^иц-i
1=0 i=0
i,icf
(8.10)
Ы /-1 /-1
^/=0 /=0 /=0
Матрица Ay(a(t))=\J? называется операторной матрицей умножения на
элемент a(t), а соответствующий ей оператор - матричным оператором умножения
на функцию a(t).
Функцию a(t) называют порождающей функцией1.
Тогда из формул (8.9) вытекает справедливость равенства
Cv = AyW0)cx = UeCx. (8.11)
Замечание 8.1. Изложенный метод позволяет формировать и матрицы умножения
на функции a(f). Естественно, в случае отказа от предварительного разложения
элемента a{t) по базису будут получаться более точные аппроксимации элементов вида
a(t)x(f). Этот факт можно использовать при решении некоторых конкретных задач,
Часто далее размерность / в обозначениях будем опускать, т.е.: р/=р, uf^u", <ц(г)=Ф(/) и т.д.
462 Анализ и статистическая динамика САУ. Часть I
однако идеология теории проекционных (спектральных) методов решения
технических задач состоит в разработке универсальных алгоритмов решения целого набора
разнообразных задач, включая и задачу оптимизации, а это наиболее просто
реализовать при аппроксимации всех функций, входящих в систему. В связи с этим в
качестве основного матричного оператора умножения рассматривается именно оператор
умножения на а{ (t) [83].
8.2.3. Матричный оператор дифференцирования
Для аппроксимации линейных нестационарных систем их дискретными
эквивалентами разложения по гладким базисам (полиномиальным или
тригонометрическим) используют также матричные операторы дифференцирования. Область
применения этих операторов существенно уже, т.к. оператор дифференцирования в
пространствах C|fo,f/J и L2|fo»f/J неограничен. Тем не менее в ряде случаев
использование матричного оператора дифференцирования корректно и удобно для
применения*.
Пусть x(t) - функция из пространства В, имеющая на отрезке [to,tf]
производную g(t)= x'(t)e В . Тогда эту производную также можно разложить по базису
пространства В. Обозначим столбец коэффициентов разложения функции g{t) по базису
ф/ (t) через С8 и установим связь между столбцами Сх и^. Предположим, что
элементы базиса Ф/(*) дифференцируемы на отрезке |fo,f/J и их производные
лежат в пространстве В. Если это условие не выполнено, то разложения xt(t) даже
сколь угодно гладких функций (бесконечно дифференцируемых или даже
аналитических) нельзя дифференцировать, следовательно, использование оператора
дифференцирования не может быть корректным. .
По принятому предположению функции ф.(г) также можно разложить по базису
фДг). Обозначим коэффициенты этих разложений через ^j:
Ф';(')=5А<РУ(4< = О,...,/-1. (8.12)
;=о
Введем в рассмотрение квадратную матрицу порядка / из коэффициентов
разложений (8.12)
doo d\o ••• di-w
do\ d\\ ••• d/-i,i
Afl = D = D/ =
(8.13)
^doj-i d\)-\ ••■ dt-ij-\j
Тогда в силу линейности оператора проектирования
1=0 /=0 ;=0 j=0\ i=0 )
или, в матричной форме,
С« = АДСХ = ОС*. (8.14)
Очевидно
Ад = АЙ •
Проблема нахождения матричных операторов дифференцирования связана с необходимостью
разложения по базисам дельта-функций и их производных, чем и порождаются указанные трудности.
Глава 8. Метод матричных операторов 463
8.3. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МЕТОДОВ РАСЧЕТА МАТРИЧНЫХ
ОПЕРАТОРОВ ИНТЕГРИРОВАНИЯ, УМНОЖЕНИЯ
НА ФУНКЦИЮ И ДИФФЕРЕНЦИРОВАНИЯ
В КОНКРЕТНЫХ ОРТОГОНАЛЬНЫХ БАЗИСАХ
8.3.1. Матричные операторы в базисе
ортогональных полиномов Лежандра
Ортогональные многочлены Лежандра, наряду с полиномами Якоби и Чебышева
1-го рода, представляют собой достаточно эффективный аппарат для приближения
функций. Многочлены Чебышева 1-го рода обладают экстремальными свойствами,
т.е. являются многочленами, наименее уклоняющимися от нуля. Однако для
вычисления их коэффициентов Фурье необходимо учитывать весовую функцию p(t). При
решении некоторых практических задач, например, при небольшом промежутке
[0,7], целесообразно использовать полиномы Лежандра, весовая функция которых
равна единице, т.е. p(f) = 1. Однако при численной реализации методов построения
матричных операторов в базисе полиномов Лежандра необходимо учитывать
следующее:
• При использовании ОНБ большой размерности (/ > 20) имеет место эффект
возрастания машинной погрешности, порожденный наличием слагаемых с
аргументом Г, имеющим высокую степень.
• При использовании большого промежутка [0,7] и / > 20 в вычислительном
процессе будет иметь место накопление ошибок, приводящее к ошибкам в
конечном результате.
Рассмотрим произвольный промежуток [r0, tj\. Смещенными на отрезок [fo, f/]
полиномами Лежандра называются многочлены*
P0(t) = l
1(0 = -
1
2('-0
'/-'о
-1 -1
, * = 1,2,...
к\ 2*
Многочлены Лежандра можно получить из рекуррентных формул
(t + l)Pft+1(O = (2t + lJ^L^o)_i \pk(t)-kPk^(t\k = 12
{'f-'o )
С помощью этих зависимостей можно найти и явные формулы для многочленов
Лежандра:
\п-2к
р„
1 [f] (-l)*(2n-2t)! (2(t-t0) Г
Многочлены Лежандра являются ортогональными на отрезке [г0, */] с весовой
функцией p(r) s 1. Для функций x(t) e L2[f0, tj\ коэффициенты Фурье определяются
соотношениями
ct=2^-jx(t)Pk(t)dt, к = 0,1,....
См. Приложение 3.
464
Анализ и статистическая динамика САУ. Часть I
Пример 8.1.
Пусть
t
y(t) = Ax(t) = lx(T)dx.
(8.15)
Последняя формула определяет операцию интегрирования. Задача расчета y(t) при x(t) = е'' является
бесконечномерной, поскольку x(t) e С(0,7) и y(t) e С(0,Г)-
Конечномерный эквивалент приведенного выше операторного соотношения имеет вид
C = AUC\ (8.16)
где Ац - матричный оператор интегрирования, С и С* - спектральные характеристики соответственно
сигналов y(f) и *(/).
Проведем расчеты по формулам (8.15) и (8.16) и сравним полученные результаты. Вычислим
коэффициенты Фурье функции x(t) = е*' на промежутке [0; 1], удерживая десять полиномов Лежандра.
Используя зависимость
1
4 = (2* + l)je-'Pk(t)dt, к = ОЛО,
С =
получим спектральную характеристику функции x(t) = e~'
(0,63212055883^
-0,3109149705
0,051453089
-0,00512502
0,0003652
-0,00002
0
0
0
0
Построим функцию */(0 по ее СХ С? ':
*,(/) = 0,9999-0,9999г + 0,4995г2 -0Д648Г3 + 0.03816/4 -0,00504г5.
Значения функций jt/(f) и x(t) в дискретных точках гк приведены в табл. 8.1.
Дискретные значения функций x(t) и */(г)
Таблица 8.1
tk
0
0,052632
0,10526
0,15790
0,21053
0,26316
0,31679
0,36842
0,42106
0,47369
0,52632
0,57895
0,63158
0,68422
0,73685
0,78948
0,84211
0,89474
0,94738
1,0000
Xl{h)
1,0000
0,94873
0,90009
0,85394
0,81015
0,76862
0,72922
0,69183
0,65635
0,62270
0,59079
0,56050
0,53174
0,50447
0,47864
0,45408
0,43081
0,40871
0,38776
0,36788
x(tk)
1
0,94873
0,90009
0,85394
0,81015
0,76862
0,72921
0,69183
0,65635
0,62270
0,59078
0,56049
0,53175
0,50448
0,47862
0,45408
0,43080
0,40871
0,38776
0,36788
Глава 8. Метод матричных операторов
465
Из рекуррентной формулы для полиномов Лежандра легко найти зависимость
П,Ю-т^
;(d(')-/£-,(O)l
2(2m + l)'
из которой можно рассчитать матрицу интегрирования в базисе многочленов Лежандра [83]
'/-'о
2
1
1
0
0
_±
3
0
i
0
о ...
1
5
о ...
1 ...
0
0
0
0
0
0
0
0
2т-3
О
2т-2
О
Для / * 10 и [Го, //] = [0,1] матрица интегрирования имеет вид:
0,50000 -0,16667 0 0 0 0 0 0 0 0'
0,50000 0 -0,10000 0 0 0 0 0 0 0
0 0,16667 0 0,071429 0 0 0 0 0 0
0 0 0,10000 0 -0,055556 0 0 0 0 0
0 0 0 0,071429 0 -0,045455 0 0 0 0
и" 0 0 0 0 0,055556 0 -0,038462 0 0 0
0 0 0 0 0 0,045455 0 0,033333 О О
0 0 0 0 0 0 0,038462 0 0,029412 О
0 0 0 0 0 0 0 0,033333 0 -0,026316
00000000 0,029412 О
Найдем приближение функции
пользуясь формулами
£TVr,re[O,l],
С>=АиС*иУ/(0=Х<^(0.
Приведем результаты расчета:
0,36787944117
0,31091497052
-0,051453088894
0,0051250200111
-0,00036516376624
0,000020288888889
-0,90909090910-10"6
О
О
О
Дискретные значения функций
y(t) = l-e- и у,(О = Ес/Р,(О
приведены в табл. 8.2.
Таким образом, с высокой точностью бесконечномерная задача заменена конечномерным эквивалентом.
31 Зак. 232
466
Анализ и статистическая динамика САУ. Часть I
Дискретные значения функций y(t) и yt(t)
Таблица 8.2
tk
0
0,052632
0,10526
0Д5790
0,21053
0,26316
0,31679
0,36842
0,42106
0,47369
0,52632
0,57895
0,63158
0,68422
0,73685
0,78948
0,84211
0,89474
0,94738
1,0000
yiih)
-0Д1011
0,051271
0,099909
0,14606
0,18984
0,23138
0,27078
0,30818
0,34365
0,37730
0,40923
0,43952
0,46825
0,49551
0,52139
0,54592
0,56920
0,59129
0,61224 ,
0,63211
y(h)
0
0,05127
0,09991
0,14606
0,18985
0,23138
0,27079 *
0,30817
0,34365
0,37730
0,40922
0,43951
0,46825
0,49552
0,52138
0,54592
0,56920
0,59129
0,61224
0,63212
Пример 8.2. Построим матричный оператор умножения в базисе полиномов Лежандра.
Рассмотрим операторное соотношение
y(t) = AxW^^-e'^fit) .e', (8.17]
где fit) = е"2* - порождающая функция.
Матрица оператора умножения в базисе полиномов Лежандра, порожденная функцией ДО,
вычисляется путем реализации следующих этапов:
- вычисляется спектральная характеристика функции fit) в базисе Ф(г), т.е. одностолбцовая матрица (У;
- вычисляются вспомогательные коэффициенты щ
«o = i; aw=[f^fK /=0-U;
- вычисляются вспомогательные коэффициенты uljk
а,ана{_л± 2к + 1 k=i-j + 2/,
'2/+2/+1' /=о,...у, />у,
**/-/+2/,
1 = 0,... j;
0,
при расчетах необходимо учесть, что ujik = «,# (коэффициенты щк заполняются после вычисления всех и#);
- вычисляется матрица оператора умножения а£ , порожденная функцией fit):
Ау(/(/)) =
;=о 1=0
т-\ т-\
i=0 i=0
m-\
1=0
m-\
1=0
i=0 i=0 1=0
Далее приведём результаты расчётов для следующих входных данных: /(О^е'2*, / = 10, [0,7] = [0,1]
-2»
Одностолбцовая матрица С = Се имеет вид:
Глава 8. Метод матричных операторов
467
Оператор ум ноже
Ау^е ; — Ay{j)-
ния и его Mi
< 0,43233
-0,40601
0Д3163
-0,025919
0,003666
-0,000404
С'=С'* =
прица запии
-0,13534
0,48499
-0,28178
0,080609
-0,014995
0,002053
0,43233235838'
-0,40600584972
0,1316325433
-0,025919180
0,00366596
-0,0004046
0,000036
-0,00001
-0,0002
п
и
цутся так (приведё
0,026327 -0,(
-0,16907 0,02
0,47099 -0,
-0,25064 0,4
0,068660 -0,:
-0,012449 0,06
н выре
Ю370*
14547
17903
6811
>3814
>3444
з 6x6):
0,000407
-0,004998
0,038145
-0,18522
0,46708
-0,23132
-0,000036
0,000559
-0,00566
0,040373
-0,18926
0,46663
(8.18)
Пользуясь матричнооператорным соотношением
Cy=Ay(f)Cx,
найдем Су . Спектральная характеристика сигнала y(t) представляет собой одностолбцовую матрицу
0,31673 '
-0,4163
0,1959
-0,0568
0,01190 '
-0,00195
0,00026025
-0,4969-10"5
-0,000125
0,0000327
Точные и приближённые дискретные значения сигнала y(t) представлены в табл. 8 3.
Операторное соотношение с оператором умножения (8.18) с помощью приведенных выше положений
заменено конечномерным эквивалентом - соотношением с матричным оператором
Су =
Таблица 3.3
Дискретные значения сигналов y(t) и yt(t)
tk
0
0,052632
0,10526
0,15790
0,21053
0,26316
0,31579
0,36842
0,421106
0,47369
0,52632
0,57895
0,63158
0,68422
0,73685
*Ы
0,99981
0,85402
0,72922
0,62266
0,53175
0,45411
0,38782
0,33107
0,28272
0,24146
0,20620
• 0,17606
0,1504
0,1284
0,1098
УМ
1
0,85394 -
0,72922
0,62269
0,53175
0,45408
0,38776
0,33111
0,28275
0,24145
0,20618
0,17607
0,15036
0,12839
0,10963
31*
468
Анализ и статистическая динамика САУ. Часть ]
Продолжение табл. 8.3
0,78948
0,84211
0,89474
0,94738
1,0000
0,0937
0,0800
0,0679
0,059
0,050
0,093630
0,079954
0,068276 •
0,058303
0,049787
8.3.2. Матричные операторы в базисе функций Уолша
Применение полиномов Лежандра, как уже указывалось выше, сопряжено с не
которыми трудностями. Чтобы избежать их, для решения некоторых задач теорш
управления целесообразно применять ортонормированные функции Уолша и блоч
но-импульсные функции. К классу таких задач следует отнести прежде всего те
которые требуют удержания в разложениях сигналов по базисам нескольких десят
ков членов разложения.
Функции Уолша - это полная ортонормированная система функций, замкнутая i
пространстве L2[0,l] (или, после линейного преобразования, в любом пространств!
L2[r0^yJ) и принимающая лишь два значения: ±1, что позволяет легко аппарат»
реализовывать функции этой системы. Кроме этого, существует несколько эффек
тивных способов вычисления коэффициентов разложения функций по базису функ
ций Уолша; имеются сравнительно простые алгоритмы построения матричных one
раторов интегрирования, дифференцирования и умножения. Кроме того, функци]
Уолша - эффективный аппарат для приближения кусочно-постоянных и релейны:
функций и поэтому ОНБ, порождённый функциями Уолша, является предпочтитель
ным для решения задач синтеза оптимальных систем: оптимального быстродействия
• задач с функционалом качества типа «минимум расхода топлива», а также- задач
терминальным функционалом качества.
Функции Уолша целесообразно рассматривать «пачками» по п = 2* первых функ
ций. Поэтому при необходимости повысить размерность базиса, например, с 64 д<
128, трудоемкость решения задач оптимизации резко возрастает, особенно для слож
ных нестационарных и нелинейных объектов.
Функции Уолша представляют собой множество прямоугольных волн, которо
строится по следующему принципу: частость следующей функции больше или рав
няется частости предыдущей функции и имеет ровно на одно пересечение нулевог
уровня больше в открытом интервале t G (0,1).
Поскольку функции Уолша принимают значения +1 и - 1, то дискретные функци
Уолша можно рассматривать как строки матрицы Адамара, элементы которой опре
деляют значения функций на множестве равноудалённых точек. Например, элемен
hij есть значение, которое принимает /-ая функция Уолша на интервале [0' - 1)*А,У-Д
где А - длина интервала,
П
Матрица Адамара используется в дальнейших расчетах, поэтому рассмотрим ос
новные этапы алгоритма ее формирования:
1) задаются размерностью базиса п = 2*;
2) рассматриваются все натуральные числа ij от 0 до п - 1 и находятся их двои1
ные представления:
* = *л-1*л-2"-*1*0»
где iv - двоичный знак,
j=jn-\jn-2--J]J0\
3) вычисляются вспомогательные коэффициенты gb(i), v = 0,..., п - 1 по правилу
Глава 8. Метод матричных операторов
469
4) вычисляются элементы матрицы Адамара по правилу
Для п = 8 матрица А
Н =
^а
"1
1
1
1
1
1
1
1
мара
1
1
1
1
-1
-1
-1
-1
име
1
1
-1
-1
-1
-1
1
1
(-D
2TBJ
1
1
-1
-1
1
1
-1
-1
1Д
1
-1
-1
1
1
-1
-1
1
)Л
1
-1
-1
1
-1
1
1
-1
1
-1
1
-1
-1
1
— 1
1
1
-1
1
-1
1
-1
1
-1
Построив матрицу Адамара Н, далее достаточно просто можно вычислить
коэффициенты разложения функции x(t) по системе функций Уолша
С*=-Н X,
(8.19)
где X - вектор размерности п, элемент X[i] которого представляет собой дискретное
значение функции x(t) в точке г = (1-0,5)А, т.е. в середине промежутка te[(i - \)h,
f "~ о
i-A], причем А = — длина промежутка.
Пример S3. Рассмотрим соотношение с оператором интегрирования
y(t) = jx(T)dx,
(8.20)
где re [0;l], *(/) = /.
Построим операторно-матричный эквивалент соотношения (8.20). Матрица оператора интегрирования
в базисе функций Уолша строится в соответствии со следующим алгоритмом:
- для я = 2 матрица интегрирования имеет вид К - \у q и
- если /I есть требуемое число функций Уолша, то алгоритм построения матрицы оператора
интегрирования закончен. В противном случае п увеличивается в 2 раза;
- к матрице интегрирования, полученной в последней итерации, «пристыковываются» матрицы,
построенные в соответствии с формулой
-где Аи/-/х«/\ " матрица, полученная на последней итерации размерности (^>х^>). ®(п/хп/\ -матрица,
АН(,
состоящая из нулей, размерности (/^х/^)» ^(п/хп/\ w матрица вида
"0
0
0
1
0
0
1
0
о ...
0 •••
0
1
0
0
1
0
0
0
размер-•
ности
№&
- осуществляется переход к шагу 2.
В результате реализации указанных этапов получим матрицу оператора интегрирования в базисе
функций Уолша на промежутке [0;1]. Для получения матрицы интегрирования на промежутке [0;7]
необходимо найденную матрицу умножить на Т.
470
Анализ и статистическая динамика САУ. Часть I
Воспользовавшись приведенным выше алгоритмом, построим матрицу оператора интегрирования,
полагая [0;7] = [0;1], п= 16.
Матрица оператора интегрирования имеет вид
0,5
-0,25
0
-0,125
0
0
0
-0,0625
Вычислим коэффициенты Фурье разложения функции x(t) ■
жутке [0;1]. Размерность базиса п = 16.
Построим вектор дискретных значений функции x(t) = / в соответствии с алгоритмом, изложенным
А =
0,25
0
-0,125
0
0
0
-0,0625
0
0
0,125
0
0
0
-0,0625
0
0
0,125
0
0
0
-0,0625
0
0 •
0
0
0
0
0,0625
0
0
0
0
0
0
0,0625
0
0
0
0
0
0
0,0625
0
0
0
0
0
0
0,0625N
0
0
0
0
0
0
0
■ t по системе функций Уолша на проме-
Хт = (0,03125;0,09375;0,15625;0,21&75;0,28125;0,34375;0,40625;0,46875;
0,53125;0,59375;0,65625;0,71875;0,78125;0,84375;0,90625;0,96875)т.
Используя зависимость (8.19), вычислим одностолбцовую матрицу С*, являющуюся спектральной
характеристикой функции x(t) = / в базисе функций Уолша
(Cx)T=(0,5;-0,25;0;-0,125;0;0;0;-0,0625;0;O;0;0;0;0;0;-0,O3125)T.
Далее легко найти вектор СУ
((7)т = (АИС*)Т = (0Д669921875;-0Д25;0,03125;-0,0625;0,0078125;0;0,015625;
-0,0312500;0,001953125;0;0;0;0,00390625;0;0,0078125;-0,015625)т.
Точным решением является функция y(t) = — . Найдем дискретные значения приближенного решение
y(t) по его спектру С у по следующей формуле
Y = H Су,
где Y - вектор дискретных значений функции у (О, причем дискретные значения функции У0) есть т<
значения, которые принимает кусочно-постоянная функция У (О на промежутке [h(i - 1), ih] (табл. 8.4).
Таблица 8.4
Дискретные значения функции y(tk) и y(tk)
h
0,03125
0,09375
0,15625
0,21875
0,28125
0,34375
0,40625
0,46875
0,53125
0,59375
0,65625
0,71875
0,78125
0,84375
0,90625
0,96875
0,00097656
0,0048828
0,012695
0,024414
0,040039
0,059570
0,083008
0,11035
0,14160
0,17676
0,21582
0,25879
0,30566
0,35645
0,41113
0,46973
yih)
0,00048828
0,0043946
0,012207
0,023926
0,039551
0,059080
0,082520
0,10987
0,14112
0,17627
0,21533
0,25830
0,30518
0,35596
0,41065
0,46924
Графики функции y(t) и точного решения y(t) приведены на рис. 8.3. Как видно из графиков, в сер<
дине промежутка значения y(t) и y(t) практически совпадают. Для увеличения степени приближения
точному решению рекомендуется увеличить размерность базиса. На рис. 8.4 приведено решение поста!
ленной задачи при п = 64.
Глава 8. Метод матричных операторов
471
У(Ф
у it)
0.5
0.4
0.3
0.2
0.1
0
0 0.2 0.4 0.6 0.8 1
Рис. 8.3. Графики функций y(t) и y(t) при п = 16
У(*)>\
У it)
0.5
0.4
0.3
0.2
0.1
0
0 0.2 0.4 0.6 0.8 1
Рис. 8.4. Графики функций y(i) и y(i) при п = 64
Матрица дифференцирования является обратной к матрице интегрирования
А, = (А.)-'. (8.21)
Воспользовавшись последней формулой, найдем дискретные значения функции
at at
Вычислим спектральную характеристику функции *(/) = 2/3 .
472
Анализ и статистическая динамика САУ. Часть I
(С*)т=(С2/3)т=(1,994;-1,499; 0,3749;-0,7499; 0,09375;-0,20-10"8; 0,1875;-0,375;
0,02343;0,6-1(Г8;-0,57.1(Г8; 0,6-КГ8; 0,0468; 0,9 10"8; 0,09375;-0,1875)т,
а по формуле
С'=АЛСГ
рассчитаем одностолбцовую матрицу Су - спектральную характеристику сигнала y{t).
Результаты расчетов приведены в табл. 8.5.
Дискретные значения сигналов y{t) и y(t)
Таблица 8.5
h
0,03125
0,09375
0,15625
0,21875
0,28125
0,34375
0,40625
0,46875
0,53125
0,59375
0,65625
0,71875
0,78125
0,84375
0,90625
0,96875
0,0019513
0,048828
0,14258
0,28320
0,47070
0,70508
0,98633
1,3145
1,6895
2,1113
2,5801
3,0957
3,6582
4,2676
4,9238
5,627
yih)
0,0058594
0,052735
0,14648
0,28711
0,47461
0,70896
0,99024
1,3184
1,6934
2,1152
2,5840
3,0996
3,6621
4,2715
4,9277
5,6309
Графики приближенного и точного решения при п = 16 и п = 64 приведены на рис. 8.5 и 8.6.
у('Х
о
О 0.2 . 0.4 0.6 0.8 1
Рис. 8.5 Графики функций y(t) и y(t) при и = 16
Глава 8. Метод матричных операторов
473
7(0.
y(t\
О
О 0.2 0.4 0.6 0.8 1 1.2
Рис. 8.6. Графики функций y(t) и y(t) при п = 64
Пример 8.4. Далее широко используется матричный оператор умножения. Проиллюстрируем его
применение, рассматривая операторное соотношение вида
>(0 =/(0 •*('). (8.22)
где /(/) = t - порождающая функция, x(t) = /.
Матрица оператора умножения в базисе функций Уолша, порожденная функцией /(г), строится в
соответствии со следующим алгоритмом:
1). Для п = 2 матрица умножения имеет вид
Ау(/) =
,/
(8.23)
2). Если п есть требуемое число функций Уолша, то используется матрица (8.23), в противном
случае п увеличивается в 2 раза. Новая матрица умножения получается путем «пристыковки» к матрице,
полученной на предыдущей итерации новых клеток, определяемых зависимостью
Ау(/) =
Ау/<Н» А'(Н'
If
<rh
(8.24)
где а£ ихф« - матрица умножения, полученная на предыдущей итерации, размерности (%х/4), Ay(VJ) -
матрица, построенная аналогично
А^>.
однако индексы у с.
А*Й4. =
^ >ТогдаА^, = к
увеличены на И. Например, если
2
3). Осуществляется переход к шагу 2.
Построим матричный эквивалент соотношения (8.22).
Матрица оператора умножения имеет вид (приводится вырез 8x8):
Ау(/) =
0.500
-Д250
0
-0,125
0
0
0
-Д0625
-0.250
Q500
-Д125
0
0
0
Ч), 0625
0
0
-а 125
Ц500
-Д 250
0
-0,0625
0
0
-Q125
0
-0,250
Ц500
-Д0625
0
0
0
0
0
0
-Д0625
Q500
-Д 250
0
-а 125
0
0
-0,0625
0
Ч), 250
Q500
-Д125
0
0
-U0625
0
0
0
-а 125
Q500
-Д 250
-Д0625
0
0
0
-0,125
0
-Д250
Ц500
30 Зак. 232
474
Анализ и статистическая динамика САУ. Часть I
Поскольку матрица Сх найдена в предыдущем примере, то, воспользовавшись матрично-
операторным соотношением
Cv = AV(/)C< = AV(/)C/,
получим спектральную характеристику сигнала y(t) = t2; она представляет собой вектор вида:
(СУ) = (С'2) = (О,ЗЗЗОО78125;-О,25ООО; 0,062500;-0,12500; 0,015625;0; 0,0312500;
-0,0625000; 0,000390625;0;0;0; 0,0078125;0; 0,015625;-0,03125)т.
Теперь легко получить дискретные значения решения y(t) = t-t и точного решения >>(/) =/2 (онр
приведены в табл. 8.6).
Таблица 8.6
Дискретные зн
'*
0,03125
0,09375
0,15625
0,21875
0,28125
0,34375
0,40625
0,46875
0,53125
0,59375
0,65625
0,71875
0,78125
0,84375
0,90625
0,96875
ачения функции
0,00097656
0,0087891
0,024414
0,047852
0,079102
0,11816
0,16504
0,21973
0,28223
0,35254
0,43066
0,51660
0,61035
0,71191
0,82129
0,93848
У it) И y(t)
УМ
0,00097656
0,0087891
0,024414
0,047852
0,079102
0,11816
0,16504
0,21973
0,28223
0,35254
0,43066
0,51660
0,61035
0,71191
0,82129
0,93848
Графики приближенного и точного решений, полученные при п = 16 и п = 64, приведены ь
рис. 8.7 и 8.8. . ...
Рис. 8.7. Графики функций >'(/) и y(t) при п = 16
Глава 8. Метод матричных операторов
475
0.4-
0.6
0.8
Рис. 8.8. Графики функций >'(/) и >'(/) при и = 64
8.3.3. Матричные операторы в базисе блочно-импульсных функций
Аппарат блочно-импульсных функций (БИФ) можно считать достаточно
перспективным для решения задач оптимального управления. Это определяется следующими
факторами:
• коэффициенты разложения функции по базису БИФ есть дискретные значения
функции, взятые в середине промежутка [(/ - 1)А, /А). Таким образом, можно
избежать промежуточной процедуры вычисления элементов спектральных
характеристик;
• т.к. БИФ принимают, как и функции Уолша, лишь 2 значения, они обладают
всеми преимуществами функций Уолша, связанными с областью
применимости функций Уолша в задачах оптимального управления;
• в отличие от функций Уолша, которые необходимо рассматривать по п = 2к
функций, размерностью базиса БИФ может служить любое N.
Рассмотрим некоторые положения, определяющие блочно-импульсные функции.
Фиксируем натуральное N и разобьем отрезок [t 0, t у ] на N равных отрезков
точками г,- =го+/А, А = (Гу -to)/N, /=1,...,N.
Блочно-импульсными функциями (БИФ) ранга N называются функции
fl, если re A,- =[r/_1,rl],
[О, в противном случае.
Функция ф#(0 доопределена в точке t = tf равенством ^N{tf)-\ (i-я БИФ
изображена на рис. 8.9). Из определения функций ф-(Г) видно, что они имеют
непересекающиеся носители и, следовательно, образуют ортогональную систему
функций на отрезке [t0, г у ]. Система БИФ, трактуемая как ортогональная система,
широко используется в приложениях.
ФДО =
476
Анализ и статистическая динамика САУ. Часть ]
/-1
Рис. 8.9. График БИФ x(t) = yi(t)
Система БИФ фиксированного ранга N, естественно, не полна. Однако, если ра<
сматривать суммы Фурье по БИФ возрастающих рангов, то разложения xN(t) cx<
дятся к функции x(t) при N —»«> равномерно на [fo,fy] [83]. В этом смысле сов<
купность систем БИФ разных рангов является замкнутой в пространстве С[го,Гу ].
К сожалению, добиться точности приближения выше O[l/N] нельзя даже ду
аналитических функций. Это означает, что алгоритм приближения суммами БИ
является насыщаемым с классом насыщения H{(S) [83]. Это известный дефект вс<
систем кусочно-постоянных функций, который требует использования сумм оче]
высоких порядков для приближения с высокой точностью сколь угодно гладк!
функций.
В технической литературе нашли применение и так называемые обобщенн]
блочно-импульсные функции (ОБИФ), или локальные сплайны нулевого порядка
неравномерным расположением узлов. Их определение отличается от определен
БИФ лишь тем, что точки разбиения {t (} выбираются произвольным образом. С*
тему БИФ удобно вводить при проекционном методе исследования разрывных с*
тем с известными неравномерно расположенными точками разрыва [83]. Различи
приложения системы ОБИФ к задачам аппроксимации и исследования систем ynpj
ления можно найти, например, в [83].
Коэффициентами Фурье по системе БИФ являются дискретные значения функц
/V
*(0« МО = £*/<&(').
1=1
Форма матричных операторов в базисе БИФ устанавливается чрезвычайно п
сто. Из определения БИФ ранга N следует, что коэффициенты {Ам„} при j > i о,
наковы и равны h, а при i = j равны /г/2. В результате получаем выражение для м
рицы оператора интегрирования в базисе БИФ
ГО.5/1 0 0 ... О О
h 0.5/г 0 ... О О
h h 0.5/г ... О О
Ам =
h
h
h
h
0.5Й О
h 0.5h
Глава 8. Метод матричных операторов
477
Матрица оператора дифференцирования для базиса, порожденного БИФ, не
определена, поскольку базисные функции разрывны. Однако в некоторых случаях
допускается использование матрицы дифференцирования как обратной к матрице
интегрирования.
Пример 8.5. Пусть
>(r) = Jjc(x)rfx = Je'Vx (8 25)
о о
и, кроме того, N = 20, [0,7] = [0,1]. Построим операторный эквивалент, используя матричный оператор
интегрирования.
Вычислим матрицу интегрирования, пользуясь приведенным выше алгоритмом Ниже представлен
вырез матрицы интегрирования размером 8 X 8:
Ам =
Спектральная характеристика функции *(/) = е~' в базисе БИФ представляет собой дискретные
значения указанной функции.
В табл. 8.7. и на рис. 8.10 и 8.11 приведены результаты расчетов.
0,0167
0,0333
0,0333
0,0333
0,0333
0,0333
0,0333
0,0333
0
0,0167
0,0333
0,0333
0,0333
0,0333
0,0333
0,0333
0
0
0,0167
0,0333
0,0333
0,0333
0,0333
0,0333
0
0
0
0,0167
0,0333
0,0333
0,0333
0,0333
0
0
0
0
0,0167
0,0333
0,0333
0,0333
0
0
0
0
0
0,0167
0,0333
0,0333
0
0
0
0
0
0
0,0167
0,0333
0
0
0
0
0
0
0
0,0167
Спектральные характеристики функций x(t) и
Таблица 8. 7
у(0
0,016666
0,049999
0,083332
0,11666
0,15000
0,18333
0,21666
0,24999
0,28333
0,31666
0,34999
0,38333
0,41666
0,44999
0,48333
0,51666
0,54999
0,58332
0,61666
0,64999
0,68332
0,71666
0,74999
0,78332
0,81666
0,84999
0,88332
0,91665
0,94999
0,98332
а"
0.98347
0,95123
0,92005
0,88989
0,86071
0,83249
0,80520
0,77881
0,75327
0,72858
0,70470
0,68159
0,65925
0,63763
0,61673
0,59651
0,57696
0,55804
0,53974
0,52205
0,50494
0,48838
0,47237
0,45689
0,44191
0,42742
0,41341
0,39986
0,38674
0,37407
с1""
0,016391
0,048636
0,079824
0,10999
0,13917
0,16739
0,19468
0,22108
0,24662
0,27131
0,29520
0,31830
0,34065
0,36227
0,38317
0,40339
0,42295
0,44187
0,46016
0,47786
0,49498
0,51153
0,52754
0,54303
0,55801
0,57250
0,58651
0,60007
0,61318
0,62586
0,01653
0,04877
0,07995
0,11011
0,13929
0,16751
0,19480
0,22119
0,24673
0,27142
0,29530
0,31841
0,34075
0,36237
0,38327
0,40349
0,42034
0,44196
0,46026
0,47795
0,49506
Q,51162
0,52763
0,54311
0,55809
0,57258
0,58659
0,60014
0,61326
0,62593
478
Анализ и статистическая динамика САУ. Часть I
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0 0.2 0.4 0.6 0.8 1
Рис. 8.10. Графики функций х(1) = е~' и x(t), полученные при N = 30
x(t)
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
О 0.2 0.4 0.6 0.8 1
Рис. 8.11. Графики функций x(t) = e~' и х((), полученные при N = 130
Графики функций у(') и y(t)= 1 - е~', вычисленные при Л^ = 30 и N = 130, приведены на рис. 8.
и 8.13.
Глава 8. Метод матричных операторов
479
у it)1
0.6
0.5
0.4
0.3
0.2
0.1
0
0 0.2 0.4 0.6 0.8 1
t
Рис. 8.12. Графики функций y{t)=\e~'dt и >'(/), полученные при N = 30
у ах
у а)
0.6
0.5
0.4
0.3
0.2
0.1
0 0.2 0.4 0.6 0.8 1
/
Рис. 8.13. Графики функций y(t) = ]e~'dt и у(/), полученные при N = 130
480
Анализ и статистическая динамика САУ. Часть I
8.4. МЕТОДЫ РАСЧЕТА МАТРИЧНЫХ ОПЕРАТОРОВ
(СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК) ЗАМКНУТЫХ
НЕСТАЦИОНАРНЫХ СКАЛЯРНЫХ ЛИНЕЙНЫХ СИСТЕМ
В предыдущей главе были введены в рассмотрение матричные операторы
(спектральные характеристики) элементарных звеньев: интегратора, дифференцирующего
звена и множительного элемента.
Структурные схемы одномерной нестационарной системы п-го порядка, а также
многомерной автоматической системы могут быть представлены в форме соединений
интеграторов, умножителей, дифференцирующих звеньев и сумматоров.
Если же сложная нестационарная система задана ее структурной схемой,
включающей звенья, описываемые линейными дифференциальными уравнениями с
переменными коэффициентами, то каждое из этих звеньев описывается эквивалентным
элементом, в состав которого входят интеграторы, дифференциаторы, умножители и
сумматоры.
Вывод состоит в том, что независимо от того, в какой форме задана
нестационарная линейная система (в форме скалярного дифференциального уравнения, век-
торно-матричного дифференциального уравнения или ее структурной схемы), всегда
можно построить ее эквивалентную структурную схему, включающую только
интеграторы, дифференцирующие элементы, умножители и сумматоры, а для
систем с запаздыванием - запаздывающие элементы.
Рассмотрим задачу нахождения матричного оператора всей системы в выбранном
ортогональном базисе, если задана ее структурная схема, состоящая из интеграторов,
дифференцирующих звеньев и умножителей.
Положим, для примера, что система задана ее структурной схемой (рис. 8.14).
У(0 e(f)
A *t/*S
1
r-n-JT
?w a, i/9w
A.
A,
A,
-^
Aa
< 1
\A 4
/\4 i
x(t)
Рис. 8.14. Структурная схема системы
Напомним, какую огромную пользу принесли теории и практике стационарных
систем автоматического управления понятия передаточной функции и структурной
схемы системы.
Простота, удобство и наглядность представления систем с помощью их
структурных схем позволили разработать методическую базу для описания и исследования
сложных взаимосвязанных систем, включая системы с местными обратными связями.
Структурные методы обобщены и на системы более сложной природы, в
частности для описания движения систем и объектов с распределенными параметрами,
поведение которых описывается дифференциальными и интегральными уравнениями,
интегро-дифференциальными уравнениями с частными производными, а также
системами уравнений подобного типа.
Построен общий формализм, охватывающий стационарные системы как с
распределенными, так и с сосредоточенными параметрами. Введение понятия матричных
Глава 8. Метод матричных операторов
481
операторов позволяет распространить структурные методы на системы с
переменными параметрами [155, 168].
Анализ конкретных структурных схем показывает, что все они состоят из
конечного набора отдельных элементов (интеграторов, дифференциаторов, умножителей и
сумматоров), соединенных последовательно, параллельно или с обратной связью.
Правила, позволяющие определять спектральные характеристики системы в целом
по. спектральным характеристикам отдельных элементов, составляют аппарат
структурных преобразований, или алгебру матричных операторов. Легко показать
справедливость следующих положений.
Параллельным соединением элементов называется такое соединение, при
котором входной сигнал один и тот же для всех элементов, а их выходные процессы
суммируются (рис. 8.15).
i ■»
Рис. 8.15. Параллельное соединение элементов
Матричный оператор параллельного соединения равен сумме матричных
операторов отдельных звеньев
A = Aj+A2. (8.26)
Последовательным соединением элементов называется такое соединение, при
котором выходная величина предшествующего элемента является входным
сигналом последующего (рис. 8.16). Матричный оператор последовательного соединения
элементов равен произведению матричных операторов отдельных элементов
А = A2Aj. (8.27)
1
1 *
1
А
Ai
А = А2 -А!
А
Аг
I
1С
Рис. 8.16. Последовательное соединение элементов
Соединением двух элементов с обратной связью называется такое соединение,
при котором выход каждого из элементов соединяется со входом другого элемента
(рис. 8.17).
Матричный оператор соединения с обратной связью равен произведению
матричных операторов, причем левым сомножителем является матричный оператор
прямой цепи А{,а правым - матричный оператор вида (I + A2At )ч, т. е.
А = А(1 + А2А1)~1
(8.28)
482
Анализ и статистическая динамика САУ. Часть I
г
1
с 1 **6
Г
С*'
А
А
А2
1
1 ^
А = А,
. (1 + А2А.)
Рис. 8.17. Соединение с обратной связью
Элемент, характеризуемый тождественным оператором I (единичная матрица),
называется единичным, поскольку он играет роль единицы.
Оператор А"1 называется обратным к оператору А , если
А"1А = АА"1=1.
Аппарат структурных преобразований, основанный на описании стационарных и
нестационарных звеньев с помощью матричных операторов в ортогональных
базисах, аналогичен аппарату структурных преобразований, основанному на описании
стационарных звеньев передаточными функциями.
Общая методика исследования замкнутых систем, заданных своими
структурными схемами, состоит в следующем:
• находят спектральные характеристики А, каждого звена системы;
•. преобразуют схемы так, чтобы образовались соединения: последовательное,
параллельное и с обратной связью;
• рассчитывают спектральную характеристику замкнутой системы, пользуясь
формулами (8.14), (8.15) и (8.17).
Пользуясь рассмотренными выше положениями, найдем матричный оператор
замкнутой системы (см. рис. 8.14), если А,- - матричные операторы элементарных
звеньев: интегратора, дифференциатора, умножителя.
Расчетная структурная схема системы представлена на рис. 8.18.
yit) + /Ov I I *W
Рис. 8.18. Расчетная структурная схема системы
Матричный оператор разомкнутой системы определяется зависимостью
Ар = А8А4А3 (I + А5А4А3 )"lA2[l + А7А6А4А3 (I + А5А4А3)"' А2 J' А,.
Матричный оператор замкнутой системы определяется выражением
А = А/Д1 + А/,Г1.
Вывод: структурная схема системы любой степени сложности может быть
представлена в виде соответствующего соединения элементарных звеньев:
интегратора, дифференциатора, умножителя и сумматора.
С помощью аппарата структурных преобразований легко найти матричный
оператор (спектральную характеристику) всей системы, используя при этом
только матричные операторы указанных выше элементарных звеньев.
Глава 8. Метод матричных операторов
483
Важным является тот факт, что матричные операторы элементарных звеньев
молено вычислить заранее и хранить в памяти ЭВМ.
Аппарат структурных преобразований матричных операторов может быть
использован для решения задач анализа и синтеза нестационарных систем при
детерминированных и случайных воздействиях [96, 155, 168].
Метод матричных операторов обобщается на нестационарные системы с
запаздыванием, поведение которых описывается дифференциальным уравнением вида
xn(t)+an.l(t)xn-l(t)+... + a0(t)x(t) + cm(t)xm(t-xm)+...+
+ci(t)x(t-xl)+co(t)x(t-xo)=y(t).
Структурная схема представлена на рис. 8.19.
x(n\t) x^'l)(t) x\t) x{t)
x{i)
Рис. 8.19. Структурная схема системы с запаздыванием, представленная в форме
соединения элементарных звеньев (элементов)
Описание нестационарных систем с запаздыванием с помощью матричных
операторов требует знания матричного оператора звена запаздывания. Формулы,
определяющие указанные матричные операторы, приведены в [96].
Матричный оператор системы можно построить, не переходя к структурным
схемам.
Этот подход подробно рассмотрен в [168]. Здесь приведем лишь основные
положения.
Положим, что линейная система с переменными параметрами описывается
дифференциальным уравнением вида
484 Анализ и статистическая динамика САУ. Часть I
*<"> + |>ДО*(У) = l>v (0/> = %('). (8-29)
v=l v=l
где y(t) - входной сигнал системы, x{i) - выходной процесс.
В (8.29) положим, что функции яо(О> «i(0»---, 0n-i(O> an(t) = I, yo(t) определены и
непрерывны на промежутке [0,7]. Тогда уравнение (8.29) имеет единственное
решение x(t), определенное на всем промежутке [0,7] для любого вектора начальных
условий
Обозначая
v=0 at v=0 at
- линейные дифференциальные операторы соответственно порядка пит,
зависимость (8.29) можно переписать в виде
Lxx = Lyy9 L°xx = y0.
Для корректной аппроксимации уравнения (8.29) необходимо сначала перейти от
дифференциальной формы описания системы к интегральной. Один из возможных
способов такого перехода состоит в предварительном переходе к нормальной
системе дифференциальных уравнений 1-го порядка (см. следующий параграф). Но
переход к интегральной форме описания можно произвести и иными способами. Укажем
здесь два наиболее естественных и популярных.
Первый способ состоит в следующем. Введем новую функцию z(t) = x{n\t).
Введем обозначения
и-1 n-\-v k-v
v=0 k=v \K V)'
Далее можно установить [168], что z(t) удовлетворяет уравнению
z(t)^\kz(tfx)z(x)dx = fz(t). (8.30)
о
Это уравнение относится к классу интегральных уравнений Вольтерра 2-го рода;
в нем функции кг (г,т) и/г(г) известны, a z(t) подлежит определению.
Решение уравнения может быть построено по формуле
fn-\ j t
При более жестких ограничениях, накладываемых на коэффициенты исходного
дифференциального уравнения системы (8.29), можно получить интегральное
уравнение относительно непосредственно решения x(t).
Будем полагать, что правая часть yo(t) непрерывна, а коэффициенты av(t)
dvav(t)
(v = 0,1,..., я -1; an{t) = 1) обладают непрерывными производными ^-,
dtv
(v = 0,l,..., и-1),при0<*<7\
Глава 8. Метод матричных операторов
485
Не уменьшая общности, допустим также, что решение имеет нулевые начальные
условия jc(O) = O,jc'(O) = O,..., *(иЧ)(0) = 0.
В результате интегрирования п раз равенства (8.29) и последующего
интегрирования по частям с учетом нулевых начальных условий найдем [168]
где
причем
x(t)+\kx(t,x)x(x)dx = f(t),
о
t
f(t) = jky(t,x)y(T)dx,
о
(8.31)
*=<U«-1)'
Итак, двумя способами получены интегральные уравнения Вольтерра 2-го рода.
Интегральные уравнения (8.30) и (8.31) имеют одинаковую форму записи, но между
ними есть существенная разница, которая особенно сильно может сказаться при
численном решении интегральных уравнений. Если точное решение исходного
дифференциального уравнения x(t) принадлежит некоторому классу W г[0,7] с г>и, то его
п-я производная z(t) = будет принадлежать лишь классу Wrn[09T], т.е. будет
dt
функцией существенно менее гладкой. Известно [83], что проекционные методы
решения интегрального уравнения (8.31) будут иметь существенно большую скорость
сходимости, чем для уравнения (8.30). Таким образом, если возможно применение и
первого и второго способов перехода к интегральному уравнению Вольтерра, то
следует избрать второй способ. Но, как отмечено выше, второй способ требует
дополнительных условий на гладкость коэффициентов, т.е. имеет более узкую область
применения. Возникают известные трудности и в случае, если коэффициенты av(t)
заданы приближенно.
В уравнениях (8.30) и (8.31) верхний предел является текущим. Если же ввести
в рассмотрение функции
кг{их) =
Гг(м),о<т<гдЛ^)=Г(''т)'°-Т-';
гК ' уК ' \ O,t<x<T;
„ , i \ \k.(t,x),O<x<t;
O,t<x<T;kJt,x) = \ хУ '
v ' [ O,t<x<T;
(8.32)
то можно перейти от уравнений Вольтерра 2-го порядка к уравнениям Фредгольма
2-го рода
Г
z(t) + jkz(tx)z(x)dx = f2(t)
°т \ (8.33)
c(t) + jkx(tx)x(x)dx = f(t)
486
Анализ и статистическая динамика САУ. Часть I
Все приведенные рассуждения имеют силу и для нестационарных систем с
запаздыванием, поведение которых описывается уравнением вида [149]
Ёву(/)*(>)(О+1бД0*(")('-в) = Уо(0. (8-34)
v=0 v=0
где .
yo(0=X'v(')y(v)(').
v=0
Второе уравнение в (8.33) можно переписать в форме
Ax = x + Axx = f.
Далее перейдем к построению матричного оператора А в выбранном ОНБ,
описывающего поведение системы, дифференциальное уравнение которой имеет вид
(8.29).
Поскольку ядро уравнения kx{t,x) в сиЛу условий, наложенных на коэффициенты
дифференциального уравнения системы (8.29), суммируемо с квадратом, т.е.
тт
IJk*(t,T)dtdT<B9
00
где В - постоянная, то оператор Ах ограничен, переводит L2[0,7] в себя.
Пусть Ф(г) = {<f>k (t): к = 1,2,...;te [О, t\) - ОНБ.
Воспользуемся следующим представлением:
*(г) = Фт(0-Сх,у(0 = ФТ(')-С"'
*,(*, т) = Фт(г)-А$.Ф(т),*,(»,т) = Фт(0-А>.Ф(т),
(8.35)
где
С* =
4
л
, cf =jx(t)(f>t(t)dt, / = 1,2,..., /...,
(8.36)
Су =
с2
,с[=)у(1)ъ(1)Л,1 = 1,2,...,1...,
Ахп =
Ау =
I
км
оо
(тт
//*Л^т)Ф/(г)Фу(т)АЛ .
оо 1/=.
(8.37)
Из (8.33) и (8.35) следует
т т
Фт (t)-Cx + /Фт (г) А5Ф(т)Фт (x)Cxdx = /Фт (г )А>Ф(т)Фт (т)С^т -
о о
Глава 8. Метод матричных операторов
487
Или, что то же самое,
i 1
Фт(г)-СЛ+Фт(г)А5|ф(т)Фт(т)^тСдг=Фт(0А^Ф(т)Фт(т)^тС);. (8.38)
о о
Поскольку J Ф(т)Фт (x)dx = I - единичная матрица, то из (8.38) находим
или
где
А* =
Сх+А£Сх=АуС>,
A*C*=A'C,
ax = i+a;,
аи+\ ап ... аи
а2\ «22+1 ••• а21
(8.39)
ап а12 ... Д/z+l^
тт __
аЧ = \\кх М<Р/ (Офу CO**", i,у = 1,/.
00
Из (8.39) находим
C^fA^^A^C^AC^.
Матрицу вида
A = (A*)"V =
а21 а22
а21
(8.40)
(8.41)
(8.42)
ап а12 ... %
будем называть матричным оператором или спектральной характеристикой
(СХ) системы относительно ортонормированного базиса ФхФ. Для процедуры
вычисления двойных коэффициентов Фурье во многих ОНБ (например, в
тригонометрическом базисе, базисе из косинусов, базисе из многочленов Чебышева, базисе
из функций Уолша) существуют эффективные «быстрые» алгоритмы [83]. Таким
образом, с алгоритмической точки зрения предварительный переход к уравнению
Фредгольма целесообразен.
Но переход от уравнения Вольтерра к уравнению Фредгольма имеет
существенный недостаток с точки зрения потери точности, если точность измеряется в
равномерной метрике. Действительно, при доопределении ядра в общем случае оно
становится разрывным. Исключение составляют, например, ядра вида k(t9 т) = £(м), где
4(0 - непрерывная функция, удовлетворяющая условию 4(0) = 0. Но, как известно
[83], разрывные функции нельзя гарантировано приближать в С[0,7] с порядком
выше, чем первый. Это означает, что погрешности в вычислении элементов матрицы АА
размерности / будут иметь порядок 0(1//). В этом случае и разность Ц*, -х|| между
решениями приближенного и точного уравнений не может быть лучше С/1. Таким
образом, если требуется аппроксимировать исходную систему в равномерной метри-
488 Анализ и статистическая динамика САУ. Часть I
ке, осуществляя переход к интегральному уравнению Фредгольма, мы теряем в
порядке точности. Таким образом, этот прием целесообразно применять или в случае
негладкого ядра, или при аппроксимации в пространстве L2[0,7]-
Итак, рассмотрены возможные способы аппроксимации системы (8.29),
основанные на переходе от дифференциального уравнения n-го порядка к скалярному
интегральному уравнению Вольтерра или Фредгольма. Как было отмечено, способ,
состоящий в переходе к уравнению Фредгольма, связан с потерей точности
аппроксимации в равномерной метрике. Но в то же время этот способ приводит к
одномерному интегральному уравнению, а при применении проекционной аппроксимации - к
системе линейных алгебраических уравнений порядка /.
Сделаем некоторые пояснения по поводу изложенных результатов. Функции, с
которыми приходится иметь дело инженеру, чаще всего являются решениями
функциональных уравнений, в данном случае - дифференциальных, и, следовательно, над
этими функциями должны производиться определенные операции, такие как
дифференцирование, интегрирование.
Подлинное значение спектральных представлений функций и аппарата
матричного представления интегральных операторов заключается в том, что они имеют
характер отображений, заменяющих функции из пространства L2[0,7] и
производимые над ними операции числовыми последовательностями и операциями с
матрицами (алгебраизация вычислений), причем выполняемые над ними операции
значительно проще и нагляднее исходных.
Это приводит к тому, что уравнения с интегральными, дифференциальными и
другими операторами заменяются системами линейных алгебраических уравнений,
которые являются более простыми, чем исходные, и решаются значительно проще.
Вопросы, связанные со сходимостью метода и оценкой погрешности,
рассмотрены в [96, 149].
Алгоритм, реализующий метод матричных операторов, обладает вычислительной
устойчивостью, поскольку матрично-операторное уравнение (8.41) эквивалентно
интегральным уравнениям 2-го рода (8.31) и (8.33), задача нахождения решения
которых принадлежит к числу корректно поставленных задач.
8.5. МЕТОД РАСЧЕТА МАТРИЧНЫХ ОПЕРАТОРОВ СИСТЕМ
В ПРОСТРАНСТВЕ СОСТОЯНИЙ С ИСПОЛЬЗОВАНИЕМ
МАТРИЧНЫХ ОПЕРАТОРОВ ДИФФЕРЕНЦИРОВАНИЯ
И УМНОЖЕНИЯ
Рассмотрим линейный объект, поведение которого описывается системой
дифференциальных уравнений вида
х2 =a2l(t)xl+a22(t)x2+... + a2n(t)xn+b2l(t)y{+... + b2m(t)ym*, (8.43)
i:n=awl(r)jc1+an2(O^2+--- + ^(O^+^i(Oyi+..- + ^m(Oym.
Введем обозначения
"en(0 an{t) ... а1и(0"
A(r),= *2l(0 a2l(t) "• U2n(t)
Глава 8. Метод матричных операторов
489
МО
МО
МО
МО
МО
*„2(0
- *km
- hm
- Km
(0
(0
(0
B(r) =
Х- (jC|,JC2»—»^n) '
Y= (Л,У2.-.Ут)Т.
Х0=(х1(0),х2(0)>...,хя(0))т.
Используя эти обозначения, система (8.43) может быть записана в виде одного
векторно-матричного уравнения
X = А(г)Х + В(г)Y, Х(0) = Х°. (8.44)
Если одномерный объект описывается дифференциальным уравнением
S*v(O*(v) = :v(O, KW^D, (8.45)
v=0
то этому уравнению эквивалентно уравнение (8.44).
Описание нестационарных систем с помощью векторно-матричного
дифференциального уравнения (8.44) будем называть дифференциальной формой описания.
К матричному оператору системы в пространстве состояний можно перейти,
воспользовавшись матричными операторами дифференцирования и умножения.
Каждое из уравнений системы (8.44) может быть представлено структурной
схемой, изображенной на рис. 8.20.
}
xn(t)r
г —Н
1 ч
1
1
X 1 |
уЛО
Уг «!
\bi2(t)
Рис. 8.20. Структурная схема, реализующая i-е уравнение системы (8.44)
Используя матричное представление операторов, входящих в эту структурную
схему, представим ее в виде, приведенном на рис. 8.21.
На структурной схеме, а также по тексту используются следующие обозначения:
• Ay(fly(r)) - матричный оператор умножения, причем матрица порождена
функцией Яу(г) (часто будем опускать аргумент t и пользоваться записью Ау(Яу)),
• Ад - матричный оператор дифференцирования.
Если Ф(г) - ОНБ, то имеют место зависимости
*;(0»Фт(г)АдС\ (8.46)
aa(t) */0«ФТ(')Ау(я/у(/)) СХ', (8.47)
где С*1 - спектральная характеристика сигнала л:,- (t).
490
Анализ и статистическая динамика САУ. Часть I
Ay(4i«)
АуЫ0)С*
Ау («,„('))
С*
' Ау(а,,(0)С»
А,(*И(О)
СЛ.
ау(ьп(<))с*
А,М'))
■Ay(U<))C"
Рис. 8.21. Структурная схема, реализующая 1-е уравнение системы (8.44)
в спектральной форме
Применяя (8.46) и (8.47) к (8.44), а также учитывая рис. 8.20 и рис. 8.21, получим
п '
Фт(0АдСх' =^Фт(г)Ау(а1у)Сд:^+У£фт(0Ау(Ьч)Су\
7=1 . 7=1.
ФТ(Г)АДС* = £фт(г)Ау(а2,.)С*' +§Фт(г)Ау(Ь2у.)С^,
7=1 7=1
(8.48)
ФТ(ОАДС*« =£фт(Г)АуКу)С^ +£фт(Г)Ау(^.)С^.
7=1 7=1
Из последних зависимостей находим
п тп
7=1 7=1
АДС^ -ХАу(а2у-)С^ =5Ау(^у.)С^,
7=1 7=1
КС" -2\(°ч)& = J,Ay(bnj)Cy'.
7=1 7=1
Отсюда следует
(Ад-Ау(ап))С* -АуСа^)^ -...-АуЦ^С"" =
m
, =£ау(^.)с^,
7=1
-Ау(а21)СХ| +(Ад-Ау(а22))СД(2 -...-Ay(a2n)Cx" =
(8.49)
= SAy(^.)C^,
7=1
Глава 8. Метод матричных операторов
491
-Ау(ая1)С«-Ау(£1я2)С
= ХАу(^.)С^.
Или, что то же самое,
((Ад-Ау(ап)) ' -Ау(л12)
-Ау(а21) (Ад-Ау(а22))
Х2 _ _
(Ад-Ау(аип))Сл;« =
-Ау(в1п)
-Ау(а2п)
,-Ау(ап1) -Ау(вв2) ... (Ад-Ау(а„и))1 <-.*,
съ
(Ау{Ьп) AyXfci2) - А/^)^
Ay(^,) Ау(Ь22) ... А/Ь^)
Ay(fcnl) Ay(bn2) ... Ау(Ьпш)
Последнее соотношение можно переписать в виде
С»
су»
сдг2
Сх"
Af, Af2 - А?„
A5i А?2 - Ал2п
Bf, Bf2 ... Bfm
ПД ПД ПД
ь21 в22 ••• а2т
В", BJ2 •- B«m
СЛ
Сх Ад Вд С"
Если ввести соответствующие обозначения, то окончательно получим
С*=АДВДСГ=АНС1\
где
Ан =
'А11 А12
А21 А22
х\т
*2т
Ы
vn2
Ап А12 ... Аи
А21 А22 — А2и
Ад Ад Ад '
Ап\ Аи2 — Апп t
пД пД рД
ьп в12 ... в1|Я
Г)Д пД пД
в21 в22 ... ь2т
пД пД пД
Вл1 Вл2 - **пт
(8.50)
(8.51)
(8.52)
- матричный оператор нестационарного линейного объекта, поведение которого
описывается нормальной системой дифференциальных уравнений.
Аналогичным образом можно получить матричный оператор объекта, поведение
которого описывается векторно-матричным дифференциальным уравнением с
запаздыванием. Для этого нербходимо воспользоваться матричным оператором
запаздывающего звена Апз, элементы которого вычисляются в соответствии со следующими
зависимостями.
Если в непрерывной форме имеет место соотношение
'у(О = х(г-т),
то матричный эквивалент запишется так
С' = АПЗС*,
где АПЗ=НТ.
Элементы матрицы Н вычисляются по формулам
492 Анализ и статистическая динамика САУ. Часть I
hi+l j = A,ty4 + hiJ+[ + 4т fy - Vij (Ддя ./ * 2)>
/г|у=0 при i = y,
т - постоянная запаздывания.
Векторно-матричное соотношение (8.52), с учетом того что компоненты вектора
управления уДО, i = l,m в спектральной форме .имеют описание вида
У|(О = Хсу'Фу(О = ФТ(ОСУ|, 1=1^,
v=l
а компоненты вектора состояний соответственно представляются формулой
*/*>=Ес*уф* о=фТ(ос^, у=п,
является конечномерным эквивалентом векторно-матричного дифференциального
уравнения (8.44), описывающего динамику линейного нестационарного объекта.
8.6. МЕТОД РАСЧЕТА МАТРИЧНЫХ ОПЕРАТОРОВ СИСТЕМ
С ПОМОЩЬЮ МАТРИЧНЫХ ОПЕРАТОРОВ
ИНТЕГРИРОВАНИЯ И УМНОЖЕНИЯ
Рассмотрим вопрос построения матричного оператора объекта, описываемого
дифференциальными уравнениями в пространстве состояний с использованием
матричных операторов интегрирования и умножения. ф
Поскольку оператор дифференцирования неограничен в пространстве с[о,г], при
наличии начальных условий стандартным является переход от дифференциальной
формы описания к интегральной. Для системы (8.44) такой переход очевиден: если
заданы начальные условия дсДО) = .*,•, / = 1,...,и, после интегрирования переходим
к векторно-матричному уравнению Вольтерра 2-го рода
Х(0 = J[A(x)X(x) + B(T)Y(T)]rfT+X°, (8.53)
о
где Х° =(xlt...,xn)T - столбец начальных условий.
Введем в рассмотрение структурные схемы, аналогичные тем, которые
представлены на рис. 8.20 и 8.21. Каждое из уравнений системы (8.53) может быть
представлено структурной схемой, приведенной на рис. 8.22.
Глава 8. Метод матричных операторов
493
>(<)
v
4
t
f 1 \Л>г
J wrfT
0
L
*„(')
X
4
t
f МЛг
J wrfT
0
*.(')
■** */(0
Рис. 8.22. Структурная схема системы, реализующая i-e уравнение системы (8.53)
Спектральная форма этой структурной схемы представлена на рис. 8.23.
АиАу(а,,)С"
+ JT
А„Ау(^)С*
А А
Л Л
АИА
«it
А„
у V" 1
lh
у 1^
Аи
ИЗ
>
[
У
ЛИ
л
А,
у
lh 1Л\
у\ьпКЧ)
(bim(t))
сл
Су-
сх>
Рис. 8.23. Структурная схема, реализующая i-e уравнение системы (8.53)
в спектральной области
Учитывая зависимости
*,« = ФТ(ОС\
jao(x)xj(j)dx = ФгАиАу(ау(1))Сх>,
494
Анализ и статистическая динамика САУ. Часть I
(Аи - оператор интегрирования), а также учитывая структурные схемы,
представленные на рис. 8.22 и 8.23, запишем уравнения (8.53) в спектральной форме,
используя матричные операторы интегрирования и умножения
ФТ(ОС* =|>т(г)АиАуЦ,.)Сд:' + fd<t>T(t)AllAy(blj)Cy> +Фт(Г)*1(0)Ф„,
У=1
У=1
ФТ(ОС*2 = j>>T(OAHAy(a2,)C*' +§Фт(г)АиАу(Ь2;)С^ + ФТ(О*2(О)Ф„,
7=1 ;=1 . къ.зч)
ФТ(ОС*" =£фт(0АиАу(ал;.)С^ +£фт(0АиАу(^.)С^ +ФТ(О*„(О)ФЛ„
где
Фд.=
t t t
|ф1(т)Л,|ф2(т)Л,...,|ф/(т)Л
Отсюда находим
1С* -ХАиАуК)с"У =2А"Ау^;)сУ' +*1(°)ф*>
у=1 у=1
(8.55)
1С* -£АиАу(ай7.)С^ =£АиАу(^.)СУ> +^„(0)0,,.
у=1 ;=i
Или, что то же самое,
(1-АиАу(ап))С* -АиАу(а12)Сх> -...-A(IAy(aln)CJt» =
= ХАиАу(61;)С>'+дс,(0)ФЛ„
-A.A/flj,)^ +(1-АиАу(а22))СДС2 -...-A,,Ay(a2n)Cx» =
= §АиАу(^)С^+д:2(0)Ф^,
7=1
(8.56)
-АиАу(ап1)С" -АиАу(й„2)С* -...+(I-A(IAy(ann))CJC" =
= ХАиАу(^.)С^+^(О)Ф^.
7=1
В матричной форме система (8.55) принимает вид
Глава 8. Метод матричных операторов
495
'(1-АиАу(аи)) -АиАу(а12)
(1-АиАу(а22))
-АиАу(а21)
~А„А (ап1) -А„А (ая2)
-АиАу(а,п)
-А„Ау(а2п)
(1-АиАу(аия))
Сдг,
Сх2
'АиАу(Ьп) АиАу(Ь12) ... АиАу(Ь,т)
АиАу(Ь21) АиАу(й22) — АиАу(Ь2т)
AHAy(fenl) AHAy(fen2) - АиАу(*пт)
ГсМ
С-
|Ч(0)ФИ
*2«»Ф*
Из последнего уравнения легко записать выражение
Схг
сх
Af, - AJ,
А|, - А£„
Вгу, - B|m
в„у, - bl
+
A5;
A*
Til
Hn
>Чп
А,ш
*г(О)Фд,
Если воспользоваться обозначением
AH=AXBY,
то окончательно получим
Сх = AXBYCY + АХФ°, = AHCY + АХФ°„,
А„ =
Af,
А|,
Af2
А^2
AJ,
^2п
4л1
^2
Bf, Bf2
в|, в>2
в?
\т
Ч.
Ах =
41
А12
l22
Вй Чг
... Af/
... А^Л
В?
L«i
А ^
Ал2
(8.57)
(8.58)
(8.59)
Поскольку при спектральном представлении уДг)» / = 1,/и и Xj(t), j = l,n
удерживается конечное число членов разложения, то (8.57) можно рассматривать
как конечномерный эквивалент векторно-матричной системы дифференциальных
уравнений (8.44). В [83] рассмотрены и другие подходы к решению
рассматриваемой задачи.
496 Анализ и статистическая динамика САУ. Часть I
8.7. ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЛИНЕЙНОЙ
НЕСТАЦИОНАРНОЙ СИСТЕМЫ УПРАВЛЕНИЯ МЕТОДОМ
МАТРИЧНОГО ПРЕДСТАВЛЕНИЯ ИНТЕГРАЛЬНОГО
ОПЕРАТОРА В ОРТОГОНАЛЬНОМ БАЗИСЕ (ОБЩИЙ ПОДХОД)
В предыдущих параграфах для решения задачи параметризации математической
модели объекта использовались матричные операторы интегрирования,
дифференцирования и умножения на функцию.
Матричный оператор системы Ан, описываемый векторно-матричным
уравнением (8.53),.можно получить и без использования операторов интегрирования и
умножения. Изложим соответствующие теоретические положения. Перепишем (8.53)
в виде
т т
Х(г) = |к^(г,т)Х(т)^т + /Ку(г,т)¥(т>/т+Х0, (8.60)
о о
где
fl(r)A(x), 0<т<г,
КЛ'>Т)=,
v ' [0, г<т<7\
Уравнение (8.60) - векторно-матричное интегральное уравнение Фредгольма 2-го
рода. В развернутой форме оно имеет вид
п т» m т»
*i (O-£JVv (*дК М^=£К Мл №+*1 (о),
v=l 0 v=l 0
*2 (0-ЁК ('ДК (x)rfx = fljk>v (t,x)yv (x)dx+x2 (0),
*n (')-EK (t,x)xv (x)dx = XjC (t,x)yv (x)rfx+xn (0),
v=lо v=lо
где
fKOa^CT), 0<т<г,
(8.61)
""l' j"[O,r<T<r.
Формулы (8.60) и (8.61) определяют интегральную форму описания линейных
систем. Перейдем к рассмотрению формы описания многомерных систем с помощью
матричных операторов.
Воспользуемся спектральным представлением всех функций, входящих в систему
уравнений (8.61):
y,(0-»C''=(c1'',c2'-,...,C/'')T, (v = l,«).
Глава 8. Метод матричных операторов
497
Тогда
уу-(0 = (СуОтФ(0 = Фт(0СУу,|
*ДО = (С«)ТФ(О = ФТ(ОС\ J
где Ф(г) = (ф,(г),ф2(О>...,ф/(г))Т•
Предполагая, что интегральные операторы в системе уравнений (8.61)
ограничены (задача рассматривается в сепарабельном гильбертовом пространстве L2[0,r|)>
получим эквивалентные уравнения с матричными операторами. Для этого в каждое
уравнение системы (8.61) подставим зависимости, определяющие спектральные
представления функций д:/(г) (i = l,n\ nyj(t) (j = l,m\, после чего обе части
полученного равенства умножим слева на матрицу-столбец Ф(г) и проинтегрируем на
промежутке [0,7]. В результате получим для /-го уравнения
)фк)ФтЬ)С*Л = )фЬ))%к]1Ьт)х
о
Т щ
0 7=1
хФт (т)Сх'*Л + /Ф(г) j^k? (г,т)Фт (x)Cyjdxdi
0У=1
I
+1ф(1)х1(0)с11у i = hn.
Сделаем некоторые пояснения, рассматривая отдельные слагаемые последнего
уравнения. Имеем
|<Pi(')| '-'
/ф(г)Фт(»)Сд»Л = }
Фг(О
Ф/(0
(<Pi(0.<P2(0--.<pi(0)<*
с?
i
Ф1Ф1 ... ФгФ1
Ф2.ф,
Ф2-Ф,
ФГФ, ... ФГФ,
dtCx'=lCx>,
поскольку система Ф(г) представляет собой ОНБ.
Аналогично можно записать
Фа (О
/ф(0-/а,у(т)Фт(х)^С^=/
Ф|(0
/а(/(т)(ф,(т),...,ф/(т)УтЛС^ =
г
0
ф.
ф2
•
(0
* •
(0
Je» (Т)Ф1 (t)rfT,..., Jaff (т)ф, (т)Л
d?Cx' =
33 Зак. 232
498
Анализ и статистическая динамика САУ. Часть I
i
J4 (Т)Ф1 (*)<1Щ (t)dt. . ]atj (т)ф, (т)Лф, (г)А
о о
/в</(х)ф,(т)^тф2(0Л. . .|в(,(т)ф,(т)</хф2(0А
J4 СОч>1 СО^/ (ОЛ- • -J4 (т)ф/ СО^Ф/ (Od
о о
t Т t
JJ^i/ (Т)Ф1 (ОФ1 (т)^^т. . .jjaij(x)(pl(t)(pl(x)dtdx
.0
L2 .
00
00
Т t
\\aij (Т)Ф/ (0Ф1 (х)ЛЛ. . .J jatj (т)ф, (г)ф/ (т)АЛ
00
00
= -А-С*>.
Теперь можно записать матричный эквивалент уравнений (8.61)
1С" +5ХС*> = 5Х.С' +*, (0)Ow,
IC^ +ХЧС'Гу =ЕВ2^У +^(О)Фдг.
;=1 у=1
ic^ +ХА^ =Ёв^чхЛо)ф^,
где
У=1
У=1
(8.62)
А1у=-|ф(г)|^(т)Фт(т)ЛА, /,у = 1,п;
о о
Г /
В^=-|ф(г)|^(т)Фт(т)^тА, / = 1,т,у = 1,л;
о о
г
ф^ = Гф(г)А.
Ах =
Матрицы
X
и
21 Л22
BY =
12 • • • А\п
кЪ+1 ... А^
^и1
уп2
... A1+I
- клеточная матрица размером (/ -п)х(/•«),
Ьп t512 ... Dlm
В|, В|2 ... В
2m
т\У т\У цу
Ьл1 Ьл2 • • • Ьлт
- клеточная матрица размером (/ • п) х (/ • п),
Глава 8. Метод матричных операторов 499
Сх =fc*l,C*2,. . .,СМ - клеточная матрица, размером (/-и)х1,
CY = (Cyi, СУ2,. . ., СМ - клеточная матрица, размером [/ • т] х 1,
"*i(0) Фдг"
хп(0) Ф„
(Т Т Т ЛТ т
где Ф„ = /ф,(г)Л. /ф2(0Л /<&(0Л = (фГ>Ф*>->Ф?) •
1° о о ) ,
Для расчета матриц C>v,Afy,B^ будем использовать алгоритмы быстрых
преобразований. С учетом введенных обозначений, систему уравнений (8.62) можно
переписать в виде
AXCX=BYCY+O>^. (8.63)
Соотношение (8.63) - система линейных неоднородных алгебраических уравнений
относительно Сх; решая ее, находим
Cx=(ax)'I(byCy+O0a,) = AxByCy+AxO0w=AhCy + AxO°a,. . (8.64)
Развернутая форма имеет вид (8.57).
Формулы (8.58) и (8.64) можно трактовать как простой способ алгебраизации
линейного интегрального уравнения Вольтерра 2-го рода. Однако значение формулы
(8.64) в теории автоматического управления далеко не исчерпывается простотой
сведения интегрального уравнения к алгебраическому. Более важен следующий факт.
Матрицу
AH=AXBY * (8.65)
в технической литературе называют спектральной характеристикой системы (8.53)
[83]. С математической точки зрения эту матрицу можно называть проекционной
характеристикой системы [83]. Этим определением подчеркивается факт
использования проекционных методов для решения уравнений, описывающих поведение
системы автоматического управления.
Значение формулы (8.64) заключается в том, что при решении различных задач
анализа систем управления, поиска оптимального управления, при проектировании
корректирующих устройств управляемых систем и т.п., приходится многократно
проверять реакцию модели на различные входные воздействия. При этом, если
варьируется только вектор управления, то после вычисления спектральной
характеристики исследуемой системы и записи ее в память компьютера поиск выходных сигналов
или компонент вектора состояний модели сводится к простому перемножению
матриц и добавлению к нему постоянного столбца.
Можно также подчеркнуть, что зависимости (8.52), (8.58) и (8.64) выражают в
явной форме связь между входом и вектором состояния, или выходом нестационарной
линейной системы.
Член АХФ^ отражает факт проекционного преобразования начального состояния
системы.
Спектральная характеристика А„ имеет блочную структуру
зз*
500 Анализ и статистическая динамика САУ. Часть I
(8.66)
Этот факт имеет двойное значение. Во-первых, становится более ясной структура
спектральной характеристики системы, поскольку каждый блок Ау указывает на
характер зависимости i-й компоненты вектора выхода оту-й компоненты входного
вектора. Во-вторых, реализовать формулу (8.64) проще, поскольку для стандартных
процедур перемножения матриц второй способ умножения требует меньше
компьютерной памяти.
В дальнейшем мы будем иметь ввиду указанную возможность разложения
спектральной характеристики системы (отметим, что аналогичное представление в виде
матриц блочной структуры может быть проведено и для матриц проекционного
преобразования начального состояния системы). В то же время для теоретических
вопросов более важным является использование спектральных характеристик в целом и
формулы типа (8.64).
8.8. АЛГОРИТМ РАСЧЕТА ВЫХОДНЫХ СИГНАЛОВ
ЛИНЕЙНЫХ НЕСТАЦИОНАРНЫХ СИСТЕМ
ПРИ ДЕТЕРМИНИРОВАННЫХ ВХОДНЫХ
ВОЗДЕЙСТВИЯХ (ДЕТЕРМИНИРОВАННЫЙ АНАЛИЗ)
Постановка задачи. Заданы структурная схема системы или ее
дифференциальное уравнение (скалярное или векторно-матричное) и входное воздействие y(t) или
Y(r). Задача заключается в том, чтобы построить выходной сигнал x(t) или Х(г).
Алгоритм решения задачи. Если проводится анализ скалярной системы
заданной или структурной схемой или ее дифференциальным уравнением (8.29), то с
помощью алгоритмов, изложенных в параграфе 8.6, можно найти матричный оператор
анализируемой системы А и по формуле (8.41) рассчитать спектральную
характеристику Сх выходного сигнала, а затем, используя выражение
*,(0 = Фт(г)С*,
можно построить выходной процесс x(t). Для решения той же задачи применительно
к одномерным и многомерным системам можно использовать метод, основанный на
переходе к нормальным системам дифференциальных уравнений.
В обоих случаях - когда исходная математическая модель системы описывается
системой линейных дифференциальных уравнений или линейным скалярным
.дифференциальным уравнением и-го порядка, - используя введенные выше матричные
операторы умножения, дифференцирования и интегрирования, можно
аппроксимировать систему, сохранив линейную зависимость между столбцами коэффициентов
разложения входного и выходного сигналов. Тогда при нулевом начальном
состоянии для нахождения приближенных выходных сигналов нужно разложить входное
сигнал по рассматриваемому базису и умножить его на спектральную
характеристику (матричный оператор), которая вычисляется заранее и хранится в памяти
компьютера. Затем остается только восстановить сигнал по набору его коэффициентов раз
ложения (см. приведенное выше последнее выражение).
Таким образом, задача вычисления выходных сигналов системы свелась к задачал
нахождения коэффициентов разложения входных сигналов, перемножению вычис
ленной заранее матрицы на столбец и восстановлению функции по ее разложению
Все эти процедуры просты, легко алгоритмизуемы, а этап выбора базиса позволяет)
Глава 8. Метод матричных операторов
501
при наличии априорной информации о степени гладкости входных сигналов и
элементов матриц А(г) и В(г) оптимизировать проекционный метод по точности
[83].Таким образом, проекционные методы дают простой и эффективный способ
вычисления выходных сигналов систем, поведение которых описывается
уравнениями высокого порядка.
( Начало j
±
Ввод исходных данных:
ду(0. v = 0ji\y(t)
Расчет матричного
оператора системы А
Расчет спектральной
характеристики Су
входного сигнала y(t)
Расчет спектральной
характеристики С*
выходного сигнала x(t)
Расчет выходного сигнала */(0
Печать результата */(0
( Конец j
Рис. 8.24. Структурная схема алгоритма детерминированного анализа нестационарных систем
Для аппроксимации систем, описываемых системами дифференциальных
уравнений первого порядка (нормальная форма), можно применять и матричные операторы
дифференцирования (при отсутствии помех). Структурная схема алгоритма
детерминированного анализа одномерных систем представлена на рис. 8.24.
8.9. АЛГОРИТМ РАСЧЕТА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ
И ДИСПЕРСИЙ ВЫХОДНЫХ СИГНАЛОВ ЛИНЕЙНЫХ
НЕСТАЦИОНАРНЫХ СИСТЕМ (СТАТИСТИЧЕСКИЙ АНАЛИЗ)
Постановка задачи. Известны структурная схема нестационарной одномерной
системы или ее дифференциальное уравнение (8.29). На вход системы поступает
нестационарный сигнал Y(t) с автокорреляционной функцией RyY(tl,t2)- Необходимо
502
Анализ и статистическая динамика САУ. Часть I
найти зависимость, определяющую автокорреляционную функцию Rxx^h^i) и Дис~
персию DXx(t) выходного сигнала X(t).
Алгоритм решения задачи. Положим, что найден матричный оператор системы
А с использованием или структурных преобразований, или с помощью матричного
представления дифференциального уравнения системы (см. параграф 8.4).
Для решения поставленной задачи рассмотрим формальное разложение
центрированного выходного сигнала X(t) по ОНБ
£(о=5>УЧ(о=Фт(')с*.
v=l
Известна зависимость, связывающая спектральные характеристики входного
о о
У (г) и выходного X (г) сигналов системы и ее матричный оператор А (параграф 8.4)
С* = ACV 48.67)
Из последней зависимости имеем
М
сх\ с
= м
АС АС
= м
АС С
= АМ
СЧС
Ат.
Более подробно рассмотрим формулы, определяющие
М
сх\ с
и М
счс
Имеем
М
сх\ с
= м
= м
о о
гх -гХ
с\ с\
о о
гХ гХ
с2 -с{
о о
гх -гх
С1 С\
тт
О
О
л
с2
О
с?
•с?
О
•с?
О
= м
о о
схсх
cl CJ
'/,;=1
= М
//х(г1)Х(г2)ф,(г1)фДг2)Л1Д
0 0
= \llRxx(ti>hfa(h)Vj(h)<bA
ij=
'т т
о о
_ Q^XX
«'.;=!
(8.68)
(8.69)
Глава 8. Метод матричных операторов
503
где CRxx - матрица коэффициентов Фурье разложения корреляционной функции
Rxx [txj2) • Таким образом, справедливы соотношения
М
Сх\ С
о о
( ~&хх ~Rxx
11 С12
Л\;=1
CR*
C\l
L21
U22
= cRxx
f.Rxx f.Rxx r^xi
C/l c/2 ... tu
- матрица коэффициентов разложения автокорреляционной функции RXx(h^ h)
в двойной ряд Фурье по ОНБ Ф(Г)хФ(Г). Матрицу CRxx будем называть
спектральной характеристикой функции Rxx (tlt t2) в ОНБ Ф(/)хФ(0-
Аналогично
М
сЧсу
_ qRyy
тт
Л/?ку(г1,/2)ф/(г1)ф;(г2)^г2
- спектральная характеристика автокорреляционной функции RYY(h^ h) в ^^^
Ф(г)хФ(г).
Из (8.68) с учетом приведенных выше рассуждений находим основную формулу
CRxx =АС/?УУАТ. , (8.70)
Сформулируем полученный результат: если известен матричный оператор
системы А, то по известной матрице С YY коэффициентов Фурье корреляционной
функции Ryyih* h) входа У(0 по формуле (8.70) можно рассчитать матрицу CRxx
коэффициентов Фурье автокорреляционной функции Rxx (tx, t2) выходного процесса
X(t)\ автокорреляционная функция выходного сигнала находится с помощью
зависимости
Rxx(h<h) = ^T(h)ACH-'A^(t2). (8.71)
Аналогичные формулы можно записать относительно математического ожидания
Стх =АС«к> (872)
Шх(г) = (с^)ТАтФ(г). (8.73)
Из (8.71) легко получить выражение, определяющее дисперсию выхода
Dxx (г) = Фт(г)АС^АтФ(г). (8.74)
Формулы (8.70), (8.71), (8.72), (8.73) и (8.74) являются основными,
составляющими содержание спектрального метода (метода матричных операторов)
вероятностного исследования линейных одномерных нестационарных систем
автоматического управления.
Укрупненная структурная схема алгоритма расчета математического ожидания
mx(t) и автокорреляционной функции Rxx(t{, t2) приведена на рис. 8.25.
504
Анализ и статистическая динамика САУ. Часть I
( Начало j
±
Ввод исходных данных:
А - оператор системы
±
Расчет спектральных характеристик
МОСШк и КОС*"
входного сигнала системы
i
Расчет спектральных характеристик
MOCWv иКФСЛхг
выходного сигнала системы
Т
Расчет МО m^t), КФ Rxxi^hh) и
дисперсии DXx(i)
i
Печать результатов расчета
±
( Конец j
Рис. 8.25. Структурная схема алгоритма статистического анализа
методом матричных операторов
Постановка задачи оценки точности САУ. Оценить точность системы - это
значит найти статистические характеристики сигнала ошибки c(t), под которым
понимается разность между-значениями действительного X(f) и требуемого m(t)
выходного сигналов (рис. 8.26).
Постановка задачи: на вход системы с матричным оператором А поступает
аддитивная смесь полезного сигнала m(t) и помехи n(i).
Предполагается, что сигналы m(t) и n(t) - взаимно не коррелированные случайные
процессы с корреляционными функциями Rmm(tu ti) и Rnn(h, ti).
Критерием, определяющим точность работы системы, выбрана средняя
квадратичная ошибка, т.е.
М [(т (?) - X (г))2 ] = £>от (*) = Яоо (г, ,г2)
Полагаем известными:
А - матричный оператор системы,
Глава 8. Метод матричных операторов
505
сй-=||/гтт(г1^)ф(ОФт('2)л1л2
о о
■ СХ автокорреляционной функции /?mm(fi, ^)»
тт
о о
- СХ автокорреляционной функции Rnn(ti, r2).
Система
со спектральной
характеристикой
А
_V
2&£(g)J*t
(8.77)
Рис. 8.26. Схема, поясняющая процесс формирования сигнала ошибки
Алгоритм решения задачи оценки точности САУ. На основе предыдущих
рассуждений можно записать
a(t) = m(t)-X{t).
В спектральной области последней зависимости соответствует соотношение
С°=Ст-С*, (8.75)
где Са, Ст и Сх - СХ соответствующих сигналов.
Для Сх справедлива зависимость
С* =ACy=A(cw+Cw). (8.76)
Подставив (8.76) в (8.75), получим
C°=Cw-A(cw+Crt) = Cw-ACw~ACn =
= (l-A)Cw-ACn=CXl-CX2.
Матричный оператор Аа = I - А назовем оператором системы относительно
сигнала ошибки.
Из (8.77) следует структурная схема системы для формирования СХ ошибки
системы Са (рис. 8.27).
Поскольку в спектральной области имеет место соотношение
С°=С*! -С*2,
то во временной области ему соответствует зависимость
o(t) = Xl{t)-X2{t).
Так как m(t) и n(t) - некоррелированы, то X\(t) и X2(t) - также-некоррелированы, и,
следовательно, формула, определяющая функцию корреляции сигнала а(г),
запишется так:
^('i.'2) = *ад {hh)+*x2x2 (h>h)-
Теперь, воспользовавшись зависимостью (8.71), сразу же находим основное
соотношение
32 Зак. 232
506
Анализ и статистическая динамика САУ. Часть I
откуда
М'.>'2) = ФТЫ(1-А)СК"™(1-А)ТФЫ+
+Фт(*,)АС*«АтФ(г2) = Яад (*„г2)+ЯХЛ (h,t2),
С*°° = (1-А)Сй-'(1-А)т + АС5"Ат.
(8.78)
Рис. 8.27. Структурная схема системы, формирующей спектральную характеристику
сигнала ошибки
Дисперсия сигнала ошибки определяется зависимостью
^(0 = ^(^2Ц^=Фт(0(1-А)С^(1-А)тФ(0+ (8?9)
+ФТ(*)АС*-АТФ(*).
Структурная схема алгоритма анализа точности нестационарной САУ совпадает
со схемой, представленной на рис. 8.25.
В заключение изучим законы преобразования СХ корреляционных функций
случайных сигналов многомерной системой. Пусть на вход многомерной системы
поступают сигналы У/(0, / = 1,/и , которые преобразуются в п выходных случайных
сигналов Х/0. J' = 1/л (рис. 8.28). Каждый входной сигнал Yk(t), к = \,т , преобразуется
в соответствующий выходной сигнал Хрк(0, p = l,n , и справедлива зависимость (см.
рис. 8.29)
к=\
С помощью матричных операторов динамика системы, представленной на
рис. 8.29, может быть описана соотношениями
С** = АМСГ< и С*' = JАМСУ<, р = пг,
*=i
где Арк - матричный оператор, осуществляющий преобразование СХ входного
сигнала Уkit) в СХ выходного сигнала Xpk(t).
Всего имеется- т-п каналов, осуществляющих преобразование т входных
сигналов в п выходных процессов. Поэтому динамические свойства многомерной системы
характеризуются матрицей матричных операторов
||A|| = ||ApJ, p = Un, к = 1,т.
Глава 8. Метод матричных операторов
507
1
1
Ym(t)
А„
А_1*_ — — -~~~
__> ilia ilia ilia ilia , „. ^Ь
—— «... **рт
*~" "**" Ih*
1
X,,(t)
^.
Рис. 8.28. Структурная схема многомерной системы
Задача статистического анализа формулируется так: заданы СХ статистических
характеристик входных сигналов: математических ожиданий С'"Ук , к = \,т и кор-
реляционных функций С YiYj JJ = l,m, а также матрица А. Требуется найти СХ
статистических характеристик (математических ожиданий и корреляционных
функций) выходных сигналов, а следовательно, и указанные функции в форме
разложения по ОНБ.
Yx(t)
*,(')(/> = !.*)
Рис. 8.29. Структурная схема подсистемы многомерной системы
Воспользовавшись рассуждениями, аналогичными скалярному случаю, получим
(8.80)
-xp(')=<E>T(0Evcm^
(mm \
^('„'з^ФЧ'.) £|>^АТрЛ Ф(,2).
*=1 Л=1
Поскольку
(8.81)
(8.82)
(8.83)
то сравнение (8.80) и (8.82), а также (8.81) и (8.83) приводит к следующему результату:
508
Анализ и статистическая динамика САУ. Часть I
т
(8.84)
*=i
С*"'*' =£ХАЛС^Атр;1) s,p = l,n. (8.85)
Зависимость (8.85) определяется СХ взаимной корреляционной функции
Rx%xp(h>h)-
Выражение для дисперсий выходных сигналов можно получить из формулы
(8.83), если принять t\ = t2 = t и s = р:
(mm \
Dx,Xp(t) = RXsXp(hJ2)\ =ФТ(<) ££АЛ(Л»А2к И»),
12 \к=\ Л=1 J
где 5 = 1,п.
Анализируя формулы (8.70), (8.72), (8.84), и (8.85), определяющие СХ
математических ожиданий и корреляционных функций на выходах одномерных и
многомерных систем, можно заключить: зная матричный оператор линейной одномерной
нестационарной системы А, СХ математического ожидания выходного сигнала
определяется как результат матричного преобразования (8.72) СХ входного сигнала, а
СХ корреляционной функции выходного сигнала - как результат матричного
преобразования вида (8.70) СХ корреляционной функции входного сигнала.
Для многомерных систем, зная совокупность матричных операторов линейной
многомерной нестационарной системы, СХ математического ожидания
рассматриваемого выходного сигнала определяют как сумму результатов матричного
преобразования вида (8.84) СХ математических ожиданий входных сигналов, а СХ
корреляционной функции рассматриваемой пары выходных сигналов определяют как
двойную сумму результатов матричного преобразования вида (8.85) СХ всех
автокорреляционных и взаимных корреляционных функций входных сигналов.
Приведенные выше результаты позволяют решить задачу оценки точности
многомерных систем.
Ошибка многомерной системы определяется как отклонение фактического
вектора выхода Х(г) от теоретического М(г) в текущий момент времени (рис. 8.30)
L(r) = X(0-M(r) = (a1(r),a2(r),...,ap(0)T-
mx(t)
Многомерная
система
Рис. 8.30. Схема, иллюстрирующая закон формирования вектора ошибки
в многомерной системе
Каждая из компонент вектора ошибки определяется зависимостью
M0 = m*(0-<M0'* = 1^'
Глава 8. Метод матричных операторов
509
где mk(t) - полезная составляющая входного сигнала; пк (f) - помеха.
В практических задачах в качестве показателя качества наиболее часто
применяют средний квадрат ошибки
Иногда используют обобщенный средний квадрат ошибки, определяемый
зависимостью
f(*)-M[f(0ra(0].
где R - матрица с неотрицательными элементами. Она вводится для того, чтобы
придать определенные веса составляющим ошибки. Если R = I, то обобщенный квадрат
ошибки совпадает с обычным.
Для вычисления ошибок многомерных систем необходимо воспользоваться
приведенными выше формулами.
8.10. АЛГОРИТМ ДЕТЕРМИНИРОВАННОГО И СТАТИСТИЧЕСКОГО
АНАЛИЗА САУ, ПОВЕДЕНИЕ КОТОРЫХ ОПИСЫВАЕТСЯ
ДИФФЕРЕНЦИАЛЬНЫМИ УРАВНЕНИЯМИ
С ПОЛИНОМИАЛЬНЫМИ КОЭФФИЦИЕНТАМИ
В этом параграфе рассматривается класс скалярных нестационарных систем
управления, поведение которых описывается дифференциальными уравнениями вида
Е^о^чо^мо/чо,
(8.86)
/=0
*=0
где я,(0= ^,а//; "полиномиальные коэффициенты.
Пример 8.6. Рассмотрим конкретный пример, что позволит проследить основные этапы решения
задачи детерминированного и статистического исследования.
Уравнение САУ имеет вид
2M0*(v)(0=y(0.
(8.87)
где
Пусть
«.(')
МО
«з(0
МО
«5(0
0,5596
0,7113
0,3717
0,1002
0,0140
0,0008
**(') =
1,8918
2,3843
1,2333
0,3278
0,0449
0,0025
2,5825
3,2220
1,6449
0,4300
0,0576
0,0031
(/ = 0,1,.
1,7855
2,1975
1,1038
0,2827
0,0369
0,0019
..,5).
0,6277
0,7588
0,3728
0,0930
0,0118
0,006
0,0909 "
0,1065
0,0507
0,0122
0,0015
0,00007
"Г
t
t2
t3
tA
t5
„-4r.
а) детерминированное воздействие имеет вид
;у(0=^5,7661 + 338,5984/ч+497,0437г2 +406,9496f3 +186,9354/4 +46,7809f5 +4,8258/6)<?~
б) случайный процесс имеет функцию корреляции
Требуется определить выходной детерминированный сигнал x(t) и корреляционную функцию
Rxx (/j t r2 ) выходного случайного процесса.
510 Анализ и статистическая динамика САУ. Часть I
В предыдущих параграфах были рассмотрены алгоритмы расчета матричных операторов систем
(параграфы 8.1, 8.2), а также изложены теоретические положения и построены структурные схемы
алгоритмов детерминированного и статистического анализа (рис 8.23 и 8.25).
Воспользуемся указанными результатами и построим сигнал *(/), автокорреляционную функцию
Rxx (r, yt2) и дисперсию Dxx (t) случайного процессаX(t).
Алгоритм включает следующие блоки.
Блок 1: иостроение матричного оператора нестационарной системы с использованием матричных
операторов интегрирования и умножения.
Уравнение (8.87) можно переписать в виде
^\0+*4(0*{4Ч0+М')П0+М')Ч0+М0Н')+М')*(<)=Ьо(')у(<)> <8-88>
где
*«■;» '*'-Ш •■<■•=$ w-Ш^Ш *"-*
Дифференциальному уравнению (8.88) соответствует структурная схема, представленная на рис. 8.31,
которой, в свою очередь, соответствует эквивалентная структурная схема, в которой в качестве
динамических характеристик используются матричные операторы интеграторов и множительных звеньев
(рис. 8.32).
Как и ранее, будем пользоваться обозначениями:
А - матричный оператор системы;
д (f(t\) = (с/^) ~ матричный оператор умножения, матрица которото порождена функцией f(t)\
Аи = Рт- матричный оператор интегрирования.
В качестве ОНБ воспользуемся функциями Уолша - Адамара. Обозначим структурные эквиваленты
соединений элементов системы через А,,А2,АзиА4 (Рис- 8.32). Тогда матричный оператор А можно
определить последовательным вычислением матричных операторов А,,А2,А3,А4, воспользовавшись
структурными преобразованиями
Al=PTfl + (c^)TPTV1,
A^P^I + ^Va,}"',
A3=PTA2(l + (c^)TPTA2]",
А4=РтАз(1 + (са-)ТРТАз]"\
A=PTfl + (c««)TPTA4T1(c^)T.
(8.89)
Процедура вычисления матричного оператора системы, как это следует из приведенных выше
зависимостей, свидетельствует о том, что применение подхода, основанного на использовании структурных
преобразований, обеспечивает высокую эффективность, поскольку он позволяет рассчитывать матричные
операторы линейных нестационарных систем (а по ним и требуемые характеристики выходного сигнала)
весьма высокого порядка без принципиальных усложнений порядка системы.
В результате расчетов по формулам (8.89) найдем матричный оператор А системы (приведем матрицу
оператора А размером 6x6 (первые 6x6 элементов матрицы 128x128)):
2,220<?-001 2,128е-001 1,504е-001 1,590е-001 7,122е-002 6,647е-002"
-7,229<?-002 -6,303е-002 -5,941е-003 -1,462*-002 2,552е-002 3,027е-002
-9,978е-002 -1,075е-001 -1,101е-001 -1,030е-001 -5,О83е-ОО2 -5,409е-002
-2,285<?-002 -1,515е-002 -7,177е-003 -1,429е-002 -1,968е-002 -1,642е-002
7,040е-003 5,264е-003 1,429е-002 1,552е-002 3,586е-ООЗ 4,458е-003
1,708<?-002 1,886е-002 4,924^-003 3,689е-ООЗ -9,989е-003 -1,086е-002
Блок 2: расчет спектральных характеристик (детерминированного) входного сигнала и
автокорреляционной функции RYY (г,, /2) в базисе функций Уолша - Адамара. Приведем первые шесть элементов
одностолбцовой матрицы Су:
Су =(2,935е + 001 2,297^ + 001 7,758^ + 000 1,163^ + 001 8,367^-001 -3,466e-00l)T.
Глава 8. Метод матричных операторов
513
Одностолбцовая матрица Су используется при решении задачи детерминированного анализа.
Статистический расчет требует знания матрицы CRrY . Приведем эту матрицу размером (6x6) (при расчетах
использовались матрицы размером (128x128) и (256x256 )).
3,196^-001 -8,999^-018 -3,727^-002 -8,999^-018
1,856е-001
1,090^-017
3,727^-002
1,301^-018
-3,597^-002
QRfY =
2,450е-017
-3,727^-002
-5,584^-018
-1,333^-002
1,512^-017
2,667е-017
1,111^-001
-2,114^-018
-6,299*-003
-2,534^-018
-1,333^-002
1,756^-017
-6,299^-003
-4,608^-018
4,296^-002
4,513^-018
-6,830е-018
-3,597^-002
6,017^-018
6,299^-003
-4,608^-019
3,913^-002
3,727^-002
4.39U-018
6,96^-002
-3,226^-018
6,299^-003
Спектральные характерисгики С} и CRyY соответственно детерминированного входного сигнала и
корреляционной функции случайного процесса на входе системы определяются как результат
соответственно одно- и двумерного БПФ.
Блок 3' расчет спектральных характеристик выходного сигнала Сх и автокорреляционной функции
CRxx . Соответствующие матрицы имеют вид:
СГ = АС' =
= (1,556^ + 001 -3,702е + 000 -8,197е + 000 -1,396е + 000 6,511^-001 9,640е-001)Т;
CRxx =АСЛ>ГАТ =
2,932^-002
-7,772^-003
-1,507^-002
-2,554^-003
1,224^-003
2,070^-003
-7,72^-003
2,90^-003
3,475^-003
6,336^-004
-2,446^-004
-1,507^-002
3,475е-003
8,139^-003
1,296^-003
-7,017^-004
-7,791е-004 -9,431^-004
-2,554<?-003
6,336^-004
1,296^-003
2,561е-004
-1,00^-004
-1,548^-004
1,224е-003 2,070^-003
-2,446^-004 -7,79к-004
-7,017^-004 -9,43^-004
-1,001^-004 -1,548^-004
7,230е-005 7,059^-005
7,059е-005 2,164^-004
Блок 4: расчет выходного сигнала x(t) и автокорреляционной функции случайного процесса X(t).
Анализ результатов.
Детерминированный выходной сигнал системы *(/) и корреляционная функция Rxx (r,,r2) случайного
процесса на выходе системы определяются как результат соответственно одно- и двумерного обратного
БПФ.
График выходного сигнала системы x(t) представлен на рис. 8.33, а дискретные значения с шагом 0,1с.
приведены в табл. 8.8.
1,5
2,5
Рис. 8.33. График детерминированного выходного сигнала системы x(t)
514
Анализ и статистическая динамика САУ. Часть I
Для сравнения приведены значения, полученные методом Рунге - Кутта 4-го порядка. На график
нанесены также значения, полученные спектральным методом при удержании 128 и 256 членов разложения
При удержании 256 членов разложения относительная погрешность расчета в точке достижения выходным
сигналом максимума составляет 1,41 %, максимальная же погрешность не превышает 2,8 %. При
ограничении 128 членами разложения относительная погрешность в точке экстремума составляет 2,85 %.
Графики корреляционной функции Rxx(tl,t2) выходного случайного процесса системы представлены
на рис. 8.34 и 8.35. Дискретные значения корреляционной функции Rxx (r,,r2) на № U Пх № 1, 1]
приведены в табл. 8.9.
График дисперсии dxx (t) выходного случайного процесса представлен на рис. 8.36, а дискретные
значения дисперсии приведены в табл. 8.10.
Таблица 8.8
/, с
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1Д
1,2
Дискреп
Метод
Рунге - Кутта
0
-0,0063
0,1425
0,7602
2,2436
4,7809
8,2821
12,4276
16,7749
20,8720
24,3410
26,9246
28,4980 .
рные значения
t)
Спектральный
метод
0
0,0064
0,1460
0,7775
2,3001
4,9465
8,5094
12,7096
17,1020
21,2342
24,7291
27,3284
28,9100
ВЫХОДИ
Л с
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2
2,1
2,2
2,3
2,4
2,5
ого сигнала х(
х(
Метод
Рунге - Кутта
29,0558
28,6854
27,5352
25,7846
23,6189
21,2114
18,7120
16,2408
13,8880
11,7149
9,7580
8,0336
6,5425
О
0
Спектральный
метод
29,4692
29,0940
27,9333
26,1659
23,9793
21,5475
19,0210
16,5212
14,1392
11,9371
9,9520
8,2010
6,6853
■ Rxx (f i ,ti)
t2
3 О
Рис. 8.34. График КФ Rxx (fi,fi) выходного случайного процесса системы
Глава 8. Метод матричных операторов
515
Дискретные значения корреляционной функции RXx
случайного процесса системы X(t)
Таблица 8.9
Ox.ti)
^S. Г|, С
/2, С ^\^
0
0,1
0,2
0,3
0,4
0,5
^\^^ /|,С
/2, С ^^х^
0,6
0,7
0,8
0,9
1
1Л
h, с ^\^
0
0,1
0,2
0,3
0,4
0,5
/2, С ^^^
0,6
0,7
0,8
0,9
1
1.1
0
0-
0
0
0
0
0 •
0,6
0
0
0,0001
0,0008
0,0024
0,0051
0
0
0
0
0
0
' 0
0,6
0,0088
0,0131
0,0174
0,0215
0,0248
0,0271
0,1
0
0
0
0
0
0
0,7
0
0
0,0002
0,0012
0,0036
0,0076
0,1
0
0
0
0
0
0
0,7
0,0131
0,0194
0,0261
0,0322
0,0372
0,0408
0,2
0
0
0
0.
0
0,0001
0,8
0
0
0,0003
0,0016
0,0048
0,0101
0,2
0,0001
0,0002
0,0003
0,0004
0,0004
0,0005
0,8
0,0174
0,0261
0,0350
0,0433
0,0503
0,0553
0,3
0
0
0
0
0,0002
0,0005
0,9
0
0
0,0004
0,0020
0,0058
0,0124
0,3
0,0008
0,00212
0,0016
0,0020
0,0023
0,0025
0,9
0,0215
0,0322
0,0433
0,0538
0,0625
0,0689
0,4
0
0
0
0,0002
0,0007
0,0014
1
0
0
0,0004
0,0023
0,0067
0,0143
0,4
0,0024
0,0036
0,0048
0,0058
0,0067
0,0073
1
0,0248
0,0372
0,0503
0,0625
0,0729
0,0805
0,5
0
0
0
0,0005
0,0073
0,0030
1,1
0
0
0,0005
0,0025
0,0073
0,0156
0,5
0,0051
0,0076
0,0101
0,0124
0,0143
0,0156
1,1
0,0271
0,0408
0,0553
0,0689
0,0805
0,0891
516
Анализ и статистическая динамика САУ. Часть I
1 Яхх('|.'2)
012
01
0 08
0 06
004
0 02
0
0
Рис. 1
1
0.12
0.1
0.08
О.ОЬ
0.04
0.02
i^
$.35. Графи
Dxx(t)
**
t2
кКФДхИ'
/
/
/
/
/
ш
ш
лХлу
3 25
l,fc) ВЫХ
/
1
V
%
2
одн
^^
-^
t1
ого случай!
\
юго процес
ч
)
са
t
0.5
1.5
2.5
Рис. 8.36. График дисперсии DXx (t) случайного выходного процесса системы X(tJ
Таблица 8.10
Дискретные значения дисперсии DXx (0 выходного
случайного процесса системы
Л с
Dxx (0
U с
Dxx (0
U с
Dxx(t)
г, с
Dxx (0
0
0
0,7
0,0194
1,4
0,1032
2,1
0,0289
0,1
0
0,8
0,0350
1,5
0,0963
2,2
0,0215
0,2
0
Р,9
0,0538
1.6
0,858
2,3
0,0157
0,3
0
1
0,729
1,7
0,735
2,4
0,0113
0,4
0,0007
1,1
0,891
1,8
0,0608
2,5
0,0081
0,5
0,0030
1,2
0,1002
1,9
0,0487
0,6
0,0088
1,3
0,1048
2
0,0380
Глава 8. Метод матричных операторов
517
Текст программы расчета в среде пакета MATLAB с использованием библиотеки SML (см.
параграф 8.15) приводится ниже. Продолжительность расчета по приведенной программе на ЭВМ типа
Pentium-120 при удержании 128 членов разложения составила 27 секунд. Структурная схема алгоритма
расчета представлена на рис. 8.37.
( Начало )
Ввод исходных данных:
у^в,(0(|- = ОД,...^%(г„/2)
I
Расчет коэффициентов ДУ
а|.(0(' = ОД)...,4)Ьо(0
I
Расчет матричных операторов
РТ>(С^)Т(/ = ОД,...)4Н)Г,А(,А
I
Расчет спектральных характеристик
С* и С*" с помощью БПФ
Расчет x(t) и Rxx (fь *г) с помощью обратных
одно- и двумерного.БПФ
соответственно, Dxx (t) = Rxx (t}, t2)
±
Печать результатов расчета
*(f\Rxx(fuh)>Dxx(f)
1
( Конец J
Рис. 8.37. Структурная схема детерминированного и статистического анализа
нестационарных систем
Программа расчета линейной нестационарной системы 5-го порядка
с полиномиальными коэффициентами
echo off
clear
format
clc
518
Анализ и статистическая динамика САУ. Часть I
setsize(256)
Т = 2.5;
settime(T)
global SML_SIZE SML_T
tic
DEL = SML_T/(SML_SIZE-1);
% Задание элементов матрицы А2*:
aOO
aO4
alO
al4
a20
a24
a30
a34
a40
a44
a50
a54
= 0
= 0
= 0
5596;
0.6277;
0.7113;
0.7588;
3717;
0.3728;
0.1002;
0930;
0.0140;
0.0118;
0008;
= 0
= 0.0006;
aOl
aO5
all
al5
a21
a25
a31
a35
a41
a45
a51
a55
= 1.
aO2 = 2.5825; aO3 = 1.7855;
= 0.
al2 = 3.2220; al3 = 2.1975;
a22 = 1.6449; a23 = 1.1038;
a32 = 0.4300; аЗЗ = 0.2827;
a42 = 0.0576; a43 = 0.0369;
a52 = 0.0031; a53 = 0.0019;
.8918;
0.0909;
2.3843;
0.1065;
1.2333;
0.0507;
0.3278;
0.0122;
0.0449;
0.0015;
.0025;
0.00007;
% Задание детерминированного входного сигнала и
% расчет коэффициентов дифференциального уравнения:
for J = 1:SML_SIZE
Tl = (J-l)*DEL;
% Задание детерминированного входного сигнала:
Y(J) = (85.7661+338.5984*Т1+497.0437*Т1*Т1+...
406.9496*Т1*Т1*Т1+186.9354*Т1*Т1*Т1*Т1 +...
46.7809*Т1*Т1*Т1*Т1*Т1+...
4.8258*Т1*Т1*Т1*Т1*Т1*Т1)*ехр(-4.0*Т1);
% Расчет коэффициентов дифференциального уравнения:
a0t(J) = а00 + а01*Т1 + аО2*Т1*Т1 + аОЗ*Т1*Т1*Т1 +.
аО4*Т1*Т1*Т1*Т1 + аО5*Т1*Т1*Т1*Т1*Т1;
alt(J) = alO + all*Tl + а12*Т1*Т1 + а13*Т1*Т1*Т1 +.
а14*Т1*Т1*Т1*Т1 + а15*Т1*Т1*Т1*Т1*Т1;
a2t(J) = a20 + a21*Tl + a22*Tl*Tl + a23*Tl*Tl*Tl +.
а24*Т1*Т1*Т1*Т1 + а25*Т1*Т1*Т1*Т?1*Т1;
a3t(J) = аЗО + а31*Т1 + а32*Т1*Т1 + аЗЗ*Т1*Т1*Т1 +.
+а34*Т1*Т1*Т1*Т1 + а35*Т1*Т1*Т1*Т1*Т1;
a4t(J) = а40 + а41*Т1 + а42*Т1*Т1 + а43*Т1*Т1*Т1 +.
а44*Т1*Т1*Т1*Т1 + а45*Т1*Т1*Т1*Т1*Т1;
a5t(J) = а50 + а51*Т1 + а52*Т1*Т1 + а53*Т1*Т1*Т1 +.
а54*Т1*Т1*Т1*Т1 + а55*Т1*Т1*Т1*Т1*Т1;
a0t(J)/a5t(J);
alt(J)/a5t(J);
a2t(J)/a5t(J);
a3t(J)/a5t(J);
a4t(J)/a5t(J);
l./a5t(J);
a0_t(J)
al_t(J)
a2_t(J)
a3_t(J)
a4_t(J)
bO_t(J)
end
% Задание корреляционной функции входного сигнала:
for Л = 1:SML_SIZE
for J2 = 1:SML SIZE
Глава 8. Метод матричных операторов 519
Т1 =
Т2 =
RYY(J
end
end
% Рас
СаО_Т
Cal_T
Са2_Т
СаЗ_Т
Са4_Т
(J1-1)*DEL;
(J2-1)*DEL;
1, J2) = exp(-2*abs(Tl-T2))
чет матриц умножения:
= mkmul (aO_f ) ;
= mkmul(al_t' ) ;
= mkmul (a2_f ) ;
= mkmul (a3_t' ) ;
= mkmul(a4_t' ) ;
B0_T = mkmul(bO_t');
% Формирование СХ входного сигнала системы:
CY = fwht(Y');
% Формирование единичной матрицы:
I = eye(SML_SIZE);
% Расчет матрицы оператора интегрирования:
РТ = mkint;
% Расчет матриц Ai:
Al = PT*inv(I+Ca4_T*PT) ;
А2 = PT*Al*inv(I+Ca3_T**PT*Al) ;
A3 = PT*A2*inv(I+Ca2_T*PT*A2);
A4 = PT*A3*inv(I+Cal_T*PT*A3) ;
% Расчет спектральной характеристики системы А:
А = PT*A4*inv(I+CaO_T*PT*A4)*B0_T;
% Расчет СХ выходного сигнала системы:
СХ = A*CY;
% Расчет СХ КФ входного сигнала системы:
CRYY = fwht2(RYY);
% Расчет СХ КФ выходного сигнала системы:
CRXX = A*CRYY*A';
% Расчет КФ выходного сигнала системы:
RXX = iwht2(CRXX);
DX = diag(RXX, 0); % Дисперсия выходного сигнала системы
% Расчет выходного сигнала системы:
X = iwht(CX);
toe
% Построение графиков:
shfun(X) % Выходного сигнала системы
shfun(DX) % Дисперсии выходного сигнала системы
shfun2(RXX) % Корреляционной функции
8.11. АЛГОРИТМ ДЕТЕРМИНИРОВАННОГО И СТАТИСТИЧЕСКОГО
АНАЛИЗА САУ, ПОВЕДЕНИЕ КОТОРЫХ ОПИСЫВАЕТСЯ
ДИФФЕРЕНЦИАЛЬНЫМИ УРАВНЕНИЯМИ
С ЭКСПОНЕНЦИАЛЬНЫМИ КОЭФФИЦИЕНТАМИ
Рассмотрим класс нестационарных систем, поведение которых описывается
дифференциальными уравнениями вида
Е«»(Ф(0=1**(Ф(). (8-9°)
/=0 *=0
520
Анализ и статистическая динамика САУ. Часть I
где
N
a/(0 = XV~7C'' C = const- (8.91)
Как и в предыдущем параграфе, построим алгоритм детерминированного и
статистического анализа нестационарных систем, поведение которых описывается диффе-'
ренциальными уравнениями с экспоненциональными коэффициентами вида (8.90).
Изложим основные этапы решения задачи, рассматривая конкретный пример.
Пример 8.7. Дифференциальное уравнение, описывающее поведение системы, имеет вид
5>(<)*(V) (<)=*(<)>
(8.92)
где
M0=IV";'(v=o,u,5).
Процессы изменения коэффициентов дифференциального уравнения определяются матрицей
"1,0000 3,5489 5,1523 3,8608 1,5192 0,2620"
1,1716 4,1050 5,8550
0,5579 1,9211 2,6761
А =
0,1349 0,4537 0,6125
4,2732
1,8881
0,4146
1,6091
0,6743
0,1405
0,0165
0,0008
0,0539 0,0699 0,0452 0,0146
0,2511
0,0973
0,0190
0,0018
0.0025 0,0031 0,0019 0,0006 0,00007
Воздействия, поступающие на вход системы:
а) детерминированное
у(г) = (2,1 + 1,3е-/)6е-4г,
б) случайное с автокорреляционной функцией
d Л , \_ -2|'2"'||
Требуется определить выходной детерминированный сигнал x(t) и корреляционную функцию
Rxx (Мг) ВЫХ°ДНОГО случайного процесса.
Блок 1: построение матричного оператора нестационарной системы с использованием матричных
операторов интегрирования и уменьшения.
Kajc и в предыдущем примере, разделим левую и правую части исходного ДУ (8.90) на коэффициент
a5(t) при старшей производной выходного сигнала системы. ДУ принимает вид (8.88); на основе
уравнения (8.88) строится структурная схема системы (см. рис. 8.31). От этой структурной схемы осуществляется
переход к эквивалентной структурной схеме относительно матричных операторов (см. рис. 8.32).
Далее в соответствии с алгоритмом (см. рис. 8.37) формируется матрица оператора интегрирования
Ан = Р(г) и рассчитываются матрицы операторов умножения
А,(го(«))= с ,a,(?,(,))= с \,\у{а2(,))=
-з,
-**
А, (%(/))= С
-*ЛТ
ММ'))=\с"
»а, (МОИ с
.^т
Приведем матрицы соответствующих операторов (первые 6x6 элементов матрицы размером 64x64), в
качестве базиса используются функции Уолша - Адамара:
1284е + 003 3382е + 001 3218е + 001 3222е + 001 2.318^ + 001 2.315e + 00l"
С =
3.382е + ОО1 1284е + 003 3222е+001 3.218^ + 001 2 315е + ОО1 2 318е + ОО1
3.218е + 001 3.222е + 001 1284е + 003 3382е + 001 2435е + 001 2438е + 001
3222е + 001 3218е + 001 3.382е + 001 1.284е + 003 2438е + 001 2.435е + 001
2318е + 001 2.315е+001 2.435е + 001 *2438е + 001 1284е + 003 3 382^ + 001
2.315^ + 001 2318е+001 2438е + 001 2.435е + 001 3382е + 001 1284е? + 003
Глава 8. Метод матричных операторов
521
с
~*2
С
~*3
с
"1499е + ООЗ 3457е + 001 3286е + 001 3290е + 001 2347е + 001 2344e + 00l"
3457е + 001 1499е + 003 3290е + 001 3286е + 001 2344е + 001 2347е + 001
3.286^ + 001 3290е + 001 1499е + 003 3457е + 001 2470е + 001 2473е + 001
3290е + 001 З.286е + О01 3457е + 001 1499е + 003 2473е + 001 2470е + 001
2 347е + 001 2.344е + 001 2 470е + 001 2 473е + 001 1499е + 003 3 457е + 001
2 344е + 001 2.347е + 001 2 473е + 001. 2 470е + 001 3457е + 001 1.499^ + 003
'7108е + 002 1342е + 001 1.274е + 001 1275е + 001 9002е + 000 8991е + 000"
1.342е + 001 7108е + 002 1275е + 001 1274е + 001 8991е + 000 9002е + 000
1274е + 001 1.275^ + 001 7108е + 002 1342е+001 9495е + 000 9.507е + 000
1275е + 001 1274е + 001 1.342^ + 001 7.108е + 002 9507е+000 9495е + 000
9002е + 000 8991е + 000 9.495е + 000 9507е + 000 7108е+002 1342е + 001
8 991е + 000 9002е + 000 9.507е + 000 9495е + 000 1.342^ + 001 7108е + 002
"1710е + 002 2.335е+ 000 2 211е + 000 2 214е + 000 1542е + 000 1540е + 000~
2.335е + 000 1710е + 002 2.214е + 000 2211е + 000 1540е + 000 1.542е + 000
2211е + 000 2.214е + 000 1.710е + 002 2.335е + ООО 1631е+000 1633е + 0О0
2 214е + 000 2.211е + 000 2.335е + ООО 1710е + 002 1633е + О0О 1.631е + 000
1542е + 000 1540^ + 000 1.631^ + 000 1633е+000 1710е + 002 2335е + ООО
1.540е + 000 1.542е + 000 1633е + 000 1631е + 000 2335е + 0ОО 1710е + 002
"2 078е + 001 1.582^-001 1.492е-001 1.494е-001 1015е-001 10l3e-00l"
1582е-001 2 078е + 001 1494е-001 1492е-001 1013е-001 1015е-001
1492е-001 1494е-001 2078е + 001 1582е-001 1079^-001 1081е-001
1494е-001 1492е-001 1582е-001 2 078е + 001 1081е-001 1079е-001
1015е-001 1013е-001 1079е-001 1081е-001 2 078е + 001 1582е-001
1.013е-001 1015е-001 1081е-001 1.079е-001 1582е-001 2 078е + 001
' Ш1е + 003 -1388е + ОО2 -1270е + 002 -1272е + 002 -6999е + 001 -6979е + 00Г
-1.388е + ОО2 ППе + 003 -1272е + 002 -1.270е + 002 -6979е + 001 -6999е + 001
-1270е + 002 -1272е + 002 ППе + 003 -1388е + ОО2 -7.843е + 001 -7864е + 001
-1.272е + 002 -1270е + 002 -1388е + ОО2 ППе + 003 -7.864е + 001 -7843е + 001
-6999е + 001 -6979е + 001 -7843е + 001 -7864е + 001 ППе + 003 -1388е + 002
-6979е + 001 -6999ё + 001 -7864е + 001 -7.843е + 001 -1.388^ + 002 ППе + 003
Используя аппарат структурных преобразований, легко получить формулы для расчета матричного
оператора системы:
~«4
С
~*0
С :
А.=РТ 1+ С
\-i
А,=Р!А, 1+ С
-«3
РТА,
А,=Р!А, 1+ С
.%^т
РТА2
A4=P'A3 I+ С
.ОТ
РТА3
522
Анализ и статистическая динамика САУ. Часть I
Приведем оператор системы А с матрицей размером (6x6) (в расчетах использовалась матрица
размером 128x128)
-3007е-002 -1.315е-001 1634е-002'
А =
8031е-001
-1959е-001
-1595е-001
-1604е-001
-4 209*-002
-4140е-002
-4 038е-002
6 477е-001
-3159е-001
-4 010е-003
1О55е-ОО1
-1 890^-001
-1860е-001
1254е-001
5173е-001
-1693е-001
-4158е-002
-3.376*-001
-3054е-002 -1307е-001 -2 786е-001
-1386е-002 -1 611е —001 2 816е-001
3618е-001 4287е-001 -1399е-002
-4 845е-001 2 856е-001 4 950е-002
1 053* - 001 -8 905е - 002 1 470е - 001
Блок 2. расчет спектральных характеристик детерминированного входного сигнала y(t) и
автокорреляционной функции Луу(/|,/2) в базисе функций Уолша- Адамара
Ниже приведены соответствующие матрицы.
Cv=(1046e + 002 1043е + 002 9859е + 001 9.882е + 001 7.242е + 001 7.227е + 001)Т,
"6.428^-002 -4.608^-018 -2.200^-003 3.198^-018 -2.100е-003 3.253^-018'
-2.900е-018 5.988^-002 -1.138е-018 2.200^-003 1.030^-018 -6.30^-003
-2.200^-003 4.147^-018 5.548^-002 9.405е-018 -2.098^-003 7.047е-019
-1.518^-018 2.200е-003 2.168е-019 5.108^-002 1.301^-018 2.098^-003
-2.100^-003 3.740^-018 -2.098^-003 2.711^-019 4.688^-002 3.253е-019
-1.328^-018 -6.301е-003 -5.421е-020 2.098^-003 -2.439^-019 4.287^-002
Для расчета С^и С >т использовались одномерное и двумерное быстрые преобразования Фурье -
Уолша.
Блок 3: расчет спектральных характеристик детерминированного выходного сигнала x(t) и
автокорреляционной функции случайного выходного процесса X(t).
Соответствующие матрицы имеют вид.
АСу=Сг=(981бе + 000 -4.983*-001 -5.805е + 000 -1.169е + 000 3243е-001 -4.619е-002)Т,
АСЛ|ТАт=СЛлп =
СЯп =
-1.001^-002 3.773е-002
-1.001в-002 -6.556е-003 -1.140е-002
-2.326е-003 9.079е-004
-1.001е-002 -2.326е-003 9246е-004*'
-6.556е-003 9.079е-004 -8 51 бе-003
-5262е-003 -2.230*-003
-2 215е-003 9165е-004
2.829е-002 -7.748е-003
4826е-002 -1.463е-002 -1.331е-002
-1.463е-002 4.150е-002 -1.001е-002
-1331е-002 -1.001^-002 3.773е-002 -1.140е-002
3.100е-002
-5.262е-003 -2.215е-003
9.246е-004 -8.516е-003 -2230е-003 9.165е-004 -7.748е-003 2.264е-002
Блок 4- расчет выходного сигнала x(t) и автокорреляционной функции случайного процесса X(t).
Анализ результатов Для расчета x(t)n Rxxi^'h) используются обратные одно- и двумерные обратные
быстрые преобразования Фурье - Уолша.
График детерминированного выходного сигнала x(t) представлен на рис. 8.38, а дискретные значения
с дискретностью 0,1 с приведены в табл. 8.11. Для сравнения приведены значения x(t), полученные
методом Рунге - Кутта 4-го порядка. На график нанесены также значения, полученные методом матричных
операторов при удержании 64 членов разложения При удержании 128 членов разложения относительная
погрешность расчета в точке экстремума составляет 1,7 %, максимальная же погрешность не превышает
3 % (левее точки экстремума). При удержании 64 членов разложения относительная погрешность в точке
экстремума составляет 3,49 %.
Графики корреляционной функции Rxxih'h) выходного случайного процесса системы представлены
на рис. 8.39 и рис 8 40. Дискретные значения корреляционной функции Rxxih^i) на [0; 5,5]х[0; 5,5]
приведены в табл. 8.12 (с шагом 0,5 с).
График дисперсии D^t) выходного случайного процесса представлен на рис. 8.41, а дискретные
значения дисперсии приведены в табл 8.13 (с шагом 0,5 с)
Глава 8. Метод матричных операторов
523
МО
0.5
1.5
2.5
Рис. 8.38. График детерминированного выходного сигнала системы х(1)
Таблица 8.11
Дискретные значения детерминированного выходного сигнала x(t)
/, с
0
ОД
0,2
0,3
0,4
' 0,5
0,6
0,7
0,8
0,9
1
1,1
1,2
*(
Метод
Рунге - Кутта
0
0,0092
0,1886
0,9217
2,5050
4,9400
7,9559
11,1439
14,0945
16,4891
18,1385
18,9813
19,0589
0
Метод
матричных
операторов
0
0,0094
0,1922
0,9425
2,6001
5,007
8,1890
11,4217
14,4012
16,8107
18,4701
19,3204
19,3809
Л с
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2
2,1
2,2
2,3
2,4
2,5
*(
Метод
Рунге - Кутта
18,4811
17,3939
15,9524
14,3021
12,5672
10,8462
9,2107
7,7080
6,3647
5,1915
4,1869
3,3416
2,6412
<)
Метод
матричных
операторов
18,7905
17,6932
16,2301
14,5509
12,7901
11,0504
9,3890
7,8630
6,4981
5,3050
4,2821
3,4210
2,7060
524
Анализ и статистическая динамика САУ. Часть I
Rxxih.h)
Рис. 8.39. График КФ Rxx (ti,h) выходного случайного процесса системы
10
12
n Rxx(ti9t2)
15 15
10
t1
Рис. 8.40. График КФ Я** (tht2) выходного случайного процесса системы
Глава 8. Метод матричных операторов
525
Таблица 8.12
Дискретные значения корреляционной функции Rxxih'h)
случайного выходного процесса
h. С ^^\
0
0,5
1
1,5
2
2,5
\Г|,С
'2. С ^^^
3
3,5
4
4,5
5
5,5
h, С ^^
0
0,5
1
1,5
2
2,5
'2. С ^\
3
3,5
4
4,5
5
5,5
0
0
0 •
0
0
0
0
3
0
0,0001
0,0020
0,0109
0,0397
0,0985
0
0
0
0
0
0
0
3
0,1565
0,1576
0,1102
0,0600
0,0278
0,0117
0,5
0
0
0,0002
0,0004
0,0004
0,0003
3,5
0
0
0,0010
0,0059
0,0241
0,0732
0,5
0,0001
0
0
0
0
0
3,5
0,1576
0,2269
0,2150
0,1441
0,0760
0,0344
1
0
0,0002
0,0019
0,0040
0,0043
0,0033
4
0
0
0,0005
0,0029
0,0122
0,0417
1
0,0002
0,0010
0,0005
0,0002
0 *
0
4
0,1102
0,2150
0,2896
0,2624
0,1709
0,0883
1,5
0
0,0004
0,0040
0,0121
0,0180
0,01631
4,5
0
0
0,0002
0,0012
0,0055
0,0201
1,5
0,0001
0,0059
0,0029
0,0012
0,0005
0,0002
4,5
0,0600
0,1441
0,2624
0,3375
0,2977
0,1904
2
0
0,0004
0,0043
0,0180
0,0395
0,0491
5
0
0
0
0,0005
0,0023
0,087
2
0,0397
0,0241
0,0122
0,0055
0,0023
0,0009
5
0,0278
0,0760
0,1709 •
0,2977
0,3723
0,3221
2,5
0
0,0003
0,0033
0,0163
0,0491
0,08935
5,5
0
0
0
0,0002
0,0009
0,0035
2,5
0,0985
0,0732
0,0417
0,0201
0,0087
0,0035
5,5
0,0117
0,0344
0,0883
0,1904
0,3221
0,3948
j
0.45
0.4
и.оэ
п о
U.O
П OR
г\ о
0.1О
П 1
Л ЛГ
О.Оэ
0
k Dxxit)
/
i
1
/
1
У
/
t, с
1 ►
0 5 10 15
Рис. 8.41. График дисперсии DXx if) случайного выходного процесса системы
526
Анализ и статистическая динамика САУ. Часть I
Диск
Л с
Dxx{t)
Г, С
Dxx(t)
Л с
Dxxit)
Л с
Dxx(t)
Л с
DxxO)
ретные з
0
0
3,5
0,2278
7
0,4253
10,5
0,4342
14
0,4345
начения
0,5
0
4
0,2896
7,5
0,4289
11
0,4343
14,5
0,4345
DxxU) ВЫ
1
0,0019
4,5
0,3379
8
0,4311
11,5
0,4344
15
0,4345
ходного
1,5
0,0121
5
0,3723
8,5
0,4324
12
0,4344
случайно
2
0,0395
5,5
0,3953
9
0,4332
12,5
0,4344
Tab Л
)го проце
2,5
0,0895
6
0,4101
9,5
0,4337
13
0,4345
ица 8.13
;сса
3
0,1565
6,5
0,4195
10
0,4340
13,5
0,4345
8.12. АЛГОРИТМЫ РЕШЕНИЯ ЗАДАЧИ ОПТИМАЛЬНОЙ
ФИЛЬТРАЦИИ НЕСТАЦИОНАРНЫХ СЛУЧАЙНЫХ
ПРОЦЕССОВ
8.12.1. Алгоритм построения оптимального фильтра,
основанный на решении уравнения винера- хопфа
Известно, что решение задачи оптимальной фильтрации сводится к решению
интегрального уравнения Вольтерра 1 рода
jk(t,s)RYY(s,i;)ds = Rmy(t,>z), 0<s, x<t, ге[0,оо],
(8.93)
в котором через RmY(t,T) обозначена взаимная корреляционная функция выходного
сигнала и его полезной составляющей. Это интегральное уравнение называется
уравнением Винера-Хопфа.
Если полезный сигнал m(t) и помеха n(t) некоррелированы, то имеет место
зависимость
RYY(t{,t2) = Rmm{tx,t2)^ Rnn{t{,t2)\ RmY(tbt2) = Rmm{txj2). t
Тогда уравнение (8,93) можно записать в виде
^k(t,s)[Rmm(s,z)^- Rnn(s,x)]ds= Rmm(t,x).
(8.94)
Решением уравнений (8.93) и (8.94) является импульсная переходная функция
к* (г, s) искомого оптимального фильтра. Нахождение решения уравнений (8.93)
или (8.94) при нестационарных сигналах представляет собой сложную задачу.
Не менее сложной является и задача построения дифференциального уравнения
оптимального фильтра по его импульсной переходной функции. Проекционное
представление функций и динамических характеристик фильтров, с вычислительной
точки зрения, часто приводит к более простым результатам и с постановки задачи
ориентирует проектировщика на использование ЭВМ.
Задача данного параграфа - изложить проекционный метод расчета оптимального
фильтра, который сводится к решению уравнения Винера - Хопфа. Случайные
процессы m(t) и n(t) будем считать некоррелированными.
Прежде всего, ограничим отрезок времени,.т.е. будем рассматривать уравнение
(8.94) при ге[О, Т\. Далее можно поступить следующим образом: выбрать на отрезке
[0, 7] некоторый базис {<p,(Oh i = 1 /. Этот базис порождает двумерный базис на
квадрате [0, Т]х[0, Т] из произведений базисных элементов
Глава 8. Метод матричных операторов
527
№)%<s)liJ = l,..J. (8.95)
Для решения уравнения Винера - Хопфа использовать матричные операторы
интегрирования, умножения и дифференцирования не удается. Действительно,
рассмотрим, например, произведение £(r,j)/?mm(s,T). В данном случае применять
оператор умножения на функцию k(t,s) нельзя, т.к.. перемножаемые функции имеют
различные аргументы. Поскольку перемножаемые функции имеют совпадающими
лишь один аргумент, по которому затем производится интегрирование, то можно
построить матричные операторы умножения и интегрирования, растянув матрицы в
столбцы и создав «разреженные» операторы умножения и интегрирования, которые
действуют аналогично одномерным, «выбирая» из длинных столбцов требуемые
элементы.
Здесь воспользуемся следующим подходом [83]. Сведем интегральное уравнение
Вольтерра к интегральному уравнению Фредгольма, доопределив входящие в
уравнение функции нулем вне треугольной области: полагаем
k(ts)= ИМ)> если0^Г'
• [0, если 0 < t < s < Г;
~ ( \ = lR™(t>s) ' если ^us^T,
Rmm[ ' 1.0, если 0<t<s<T;
КпЛ ' ' [0, если 0<
если 0<s<T,
0<t<s<T.
(8.96)
Тогда уравнение (8.94) можно записать в виде
т
о
При произведенном доопределении функций на квадрат они могут стать
разрывными, поэтому равномерная метрика далее неприменима. Но если базис был выбран
так, что разложения известных корреляционных функций сходились к функциям в
метрике L2{[0, 7]x[0, 7]}: при /-*а>
\R«un(t*s)-&)&(*'*)
||^^*)-^.*)||La =
/- i
/М^)-ЕЕ4'ИМФ/(')Ф;(*)
/=1 ;=1
/ /
м^)-Е5>Н(')ф,(*)
/=1 ;=1
->о,
->о,
то в среднеквадратичной метрике будут сходиться и разложения доопределенных
функций /?тш(г,*)и Rm(t,s).
Используя введенные выше обозначения столбцов из конечного числа базисных
функций Ф(0 и введя в рассмотрение квадратные матрицы 1-го порядка с^""" и C^'w ,
составленные из коэффициентов разложения доопределенных функций {cfj"1'"} и
{ cfjn"}, разложения доопределенных автокорреляционных функций можно записать в
матричной форме
л«(».*)-фт(0с*-ф(,),]11И(».,)=фТ(0с«-ф(*)- <8-97>
528 Анализ и статистическая динамика САУ. Часть I
Кроме того, воспользуемся обозначением
k(t,s) = <bT(t)A<b(s) , (8.98)
где А - матричный оператор, подлежащий определению (он соответствует
доопределенному ядру k(t,s)). •
Подставим (8.97) и (8.98) в (8.96)
т
|фт (г)АФ(*)Фт (,у)С*™Ф(т)& +
°т (8.99)
+}фт (г) АФ(^)ФТ ($)С*-Ф(т)Ж = Фт-(* )С*~Ф(т).
о
Из (8.99) находим
Фт (t) AI0 (С*"" + С*™ )Ф (т) = Фт (t) С*""» Ф (т),
где lo=j<J>(s)<pT(s)ds.<
о
Отсюда, учитывая линейную независимость базисных функций, получаем
А1О(С/?""И + С*»") = С*™. (8.100)
Поскольку матричное уравнение (8.100) получено путем аппроксимации
интегрального уравнения первого рода, оно плохо обусловлено и стандартные методы
решения могут привести к значительным ошибкам. Поэтому необходима
регуляризация уравнения, которая рассматривается в [165]. Здесь же в заключение отметим, что
если выбранный базис {ф,(0} является ортонормированным на отрезке [0, 7], то
матрица 1о = I (будет единичной) и уравнение (8.100) принимает вид
A(Cj^+C*") = C*~'.
В случае неортонормированного базиса (например, одного из базисов локальных
сплайнов), матрица 1о легко рассчитывается [83].
Часто в практических задачах входным сигналом считают белый шум с
корреляционной функцией Rnn (t,s) = 2nS<& (т2 ~ xi) (So - интенсивность белого шума). Такое
предположение позволяет существенно упростить теоретические выкладки, хотя и
требует определенных оговорок, поскольку белый шум является физически
нереализуемым сигналом. Как правило, ссылаются на то, что фактически в качестве входного
сигнала будет использоваться процесс типа белого шума с постоянной спектральной
плотностью в заданном диапазоне частот.
Решение уравнения Винера - Хопфа для произвольного входного сигнала требует
регуляризации, что ведет к существенному повышению трудоемкости решения.
Поэтому рассмотрим отдельно случай, когда помеха n(t) является белым шумом,
распределенным по нормальному закону и некоррелированным с полезным сигналом.
Для таких шумов интегральное уравнение (8.94) перепишется в виде
* т
J^^)[^mw(^x) + 27i5o5(x-5)№ = ^ww(r,x), (8.101)
о
или, что то же самое,
т
2nS(jc(ty х) + J k(t, s)Rmm(s, x)ds = Rmm(t, x).
0
Воспользовавшись разложением функций, входящих в (8.101), по ОНБ получим
Глава 8. Метод матричных операторов
529
2т15оФт(/)АФ(т) + J фт(/)АФ(5)фт(5)С^Ф(т)Л =
о
= Фт(г)С^-Ф(т).
Отсюда следует
A(2nS0l +С*"») = €*"*•
(8.102)
(8.103)
Y(t) =
m(t) + n(t)
N
\
\
А
т
х
1
i
Ф'(0
Ге
элем<
ф2
нерг
гнто
(0
1тор
в 01
<pi(r)
КБ
J ^Р
0
J ^
0
0
У2(Г)
м
0
пр
1—►
Ь(г)
гнкш
eo6f
>
i
лот
)азо]
<
i
MO
льнь
аател
\
/
/
1Й
ь
J'
Рис. 8.42. Структурная схема оптимального фильтра
Разница между матричными уравнениями (8.100) и (8.103) в том, что первое
является плохо обусловленным, в то время как второе, особенно при больших величинах
интенсивности шума, обусловлено очень хорошо. Это означает, что матричное
уравнение (8.103) можно решать любым способом и регуляризация его не нужна. Таким
образом, в случае, когда шум можно считать белым, процесс вычисления
оптимальной импульсной переходной функции существенно упрощается.
Наконец, предположим, что матричный оператор оптимального фильтра найден;
для его расчета используется формула
А = С*"'"'(2я5Л + С^'"')~1-
Тогда приближенная импульсная переходная функция оптимального фильтра
может быть построена по формуле
^Д) = ХХс£ф/1(ОФ/2(т) =
/,=i /2=i
2
'2=1
2<&фле>
/,=i
ф12(т)=5}ыоф*(т),
(8.104)
*=i
i
гдеЫ0 = Х^сР^*
35 Зак. 232
530
Анализ и статистическая динамика САУ. Часть I
Учитывая зависимость
*(') = ] k\t,T)Y(x)dx = £ЫОП(О,
гдег*(О = /ф,(т)Пт)</т,
легко построить структурную схему оптимального фильтра (рис. 8.42).
начало
Ввод исходных данных Ф(0»
Rmm{tutl\ Rnn{tutl), [0,7]
Расчет сг
Rmm
Решение
Расчет
V
ектральных х
системы алге
приближенно
к=
Печать р
арактеристик функций
браических уравнений
:*»")=с*"""
й оптимальной ИПФ
)а*(?)ф*(О
[
езультата ^*(г,т)
г
f конец )
Рис. 8.43. Структурная схема алгоритма расчета ИПФ оптимального фильтра
Глава 8. Метод матричных операторов
531
8.12.2. Алгоритм, основанный на минимизации зависимости,
определяющей среднеквадратичную ошибку
в спектральной области
Формула, определяющая корреляционную функцию сигнала ошибки а(0, имеет
вид
^ааа1^2)=ФТа1)[(1-А)С/?-(1-А)т + АС/?-Ат]ф(/2) =
(8.105)
(8.106)
t с
= фТа1)С/?-(А)Ф(Г2) = ^^С^'"(А)ф/(Г1)ф;(/2).
i=l 7=1
Формула для дисперсии выходного сигнала запишется так
t t
Daa(0 = XECf""'(A)(p'(r)(|)>(0-
i=l 7=1
Далее необходимо выбрать критерий минимизации, порожденный (8.105), и
построить процесс минимизации по элементам aps(p,s = 1,2,..., I) Матрицы А .
Такими критериями могут быть
Ы 7=1
/,«,„) = шах
(8.107)
t I
X£<£-(V>4>i«<P;<0
тт
о о
/=1 7=1
ЕЕ^^^)Ф/^)Ф;^2)
1=1 7=1
dU
dtxdt2.
(8.108)
(8.109)
Спектральная характеристика А* оптимального фильтра может быть найдена
путем минимизации одного из критериев (8.107) - (8.109):
/i(ap5)-»min,
a,>s
/2(a«,)->minf
'з (*,»)■
min.
а,»
8.13. ФОРМИРУЮЩИЕ ФИЛЬТРЫ
Важное значение при создании современных систем управления приобретает
вопрос практической реализации случайных процессов с заданными статистическими
характеристиками. Этот вопрос имеет большое значение при решении таких задач,
как задача статистического андлиза, оптимальной фильтрации, идентификации и т.д.
Эта проблема, рассматриваемая в рамках корреляционной теории, получила в
теории управления название задачи о формирующем фильтре. При этом
формирующий фильтр представляется как система, выходной сигнал которой X(t) имеет
заданную корреляционную функцию Rxxih'h) (ши> в стационарном случае,
заданную спектральную плотность 5^ (со)) при условии, что на ее вход поступает
белый шум Y(t). Предполагается также, что сигнал X(t) является непрерывным в средне-
35*
P^fW-. (8.111)
532 Анализ и статистическая динамика САУ. Часть I
квадратичном процессе. Отметим, что сформировать случайный процесс можно не
только из белого шума, но и из другого процесса, который имеет более широкий
спектр, чем тот, который требуется сформировать. Использование белого шума
существенно упрощает аналитические расчеты, хотя и создает проблемы в плане
практической реализации, поскольку белый шум является физически нереализуемым
процессом. Это означает, что на практике в качестве белого шума используются
процессы, имеющие равномерную спектральную плотность только в некоторой
ограниченной полосе частот.
При решении задачи о стационарном формирующем фильтре требуется показать,
что X(f) может быть представлен в виде
Х(О = /*фф('-т)1Чт)£/т, " . (8.110)
о
где £фф(т) - ИПФ формирующего фильтра, и дать конструктивный метод
нахождения &фф(т) или передаточной функции И^ф(^) фильтра.
Задача о формирующем фильтре получила решение для стационарных, в широком
смысле, процессов, спектральная плотность которых является абсолютно
непрерывной и удовлетворяет неравенству
_ 1 + со2
В частном случае дробно-рациональной спектральной плотности требуется,
чтобы передаточная функция W^(s) относилась бы к классу минимально-фазовых.
Рассмотрим вопрос определения передаточной функции формирующего фильтра.
Как известно, при прохождении случайного стационарного сигнала через линейную
устойчивую стационарную систему (в качестве которой в данном случае выступает
формирующий фильтр) имеет место следующее соотношение, определяющее
спектральную плотность установившегося случайного процесса на выходе системы
Sxx «о) = КФ(;со)|2 sw (©)• (8Л12)
где 5уу(со) - спектральная плотность входа, S^ (со) - спектральная плотность
выхода, МффО'оо) - передаточная функция системы.
Поскольку в качестве входного сигнала выступает белый шум, то Syy (w) =
= So = const.
Для простоты будем считать So = 1. Таким образом,
^(со) = |^фф(;а))|2, (8.113)
т.е. квадрат АЧХ формирующего фильтра должен совпадать (с точностью до
постоянного множителя) со спектральной плотностью сигнала, подлежащего
формированию.
Для дальнейших рассуждений важно отметить, что спектральная плотность
стационарного случайного процесса является действительной, четной,
неотрицательной функцией со при действительных значениях со.
Так как мы рассматриваем случай дробно-рациональной спектральной плотности,
то
S ((а)в!Ш, (8.114)
Глава 8. Метод матричных операторов 533
где А(со) и £(со) - многочлены с действительными коэффициентами, содержащие
только четные степени со (это следует из четности спектральной плотности).
Спектральная плотность 5^ (со) может быть представлена в виде
Sxx((0) = S+xx(j^)S-xx(j(0)i (8.115)
где S£x (yco) содержит нули и полюсы функции Sxx((u), расположенные в верхней
полуплоскости, и является ограниченной и аналитической функцией в нижней
полуплоскости; S^xijto) содержит нули и полюсы функции 5хх(со), расположенные в
нижней полуплоскости, и является ограниченной и аналитической функцией в
верхней полуплоскости.
Для действительных значений со
S-xx(M = S+xx(-ja>) (8.116)
и, следовательно,
Sxx'W = $xx (MSxx (-7©) = \Sxx (;co)|2 . (8.117)
Очевидно, функция 5^ O'co) обладает всеми свойствами, которыми должна обладать
передаточная функция устойчивой линейной стационарной минимально-фазовой
системы.
Имеем
Sxx (MS xx (-7©) = Кф(7©)|2 = ^фф(7СО)\Уфф(-усо). (8.118)
Отсюда следует
^(;co) = 5^(;co). (8.119)
Таким образом, разложив спектральную плотность формируемого сигнала на
комплексно-сопряженные множители, легко определить передаточную функцию
формирующего фильтра.
Пример 8.8. Пусть необходимо сформировать случайный сигнал, имеющий следующую
спектральную плотность
$хк«о) = -Г^Т (8-120)
а + со
(соответствующая корреляционная функция Rxx (x) = De~a™ ).
Разложим спектральную плотность на комплексно-сопряженные множители
5«(в)"тав^"^В5мг(^)5"("М (8Л2°
1 /а /а
Очевидно, что передаточная функция формирующего фильтра в этом случае будет иметь вид
Ts + \
При более высоких степенях полиномов разложение спектральной плотности на
сомножители может составить определенные трудности. Тогда можно
воспользоваться следующим приемом.
Пусть в общем случае
^W = ^m+^m:'+-+£)0=^, (8.123)
** ansn+an_lsn-x+... + a0 N(s)'
Sx*(со) = K(H2 = — = *< + *-^)+" + * . (8.124)
W»W-^-7. (8122)
534
Анализ и статистическая динамика САУ. Часть I
Тогда несложно получить следующие зависимости:
4o=flo,
Л, = а? -2аоа2,
А2=а\- 2ахаъ + 2а0а4,
Аъ=а\-2а2а4 + 2ахаъ -2а0а6,
А4=а4 - 2а3а5 + 2а2а6 - 2ахап + 2a0as,
(8.125)
в,
в2
в,
в4
-bl
=ь?
=ъ\
=ъ]
-2b0lh
-гьхьг
-2b2b4
-щь5
+ 2b0b4
+ 2bxb5
+ 2b2b6
-2b0b6,
-2^+2Ь0
(8.126)
Эти формулы позволяют вычислить коэффициенты в формуле, определяющей
спектральную плотность выходного сигнала системы по известным коэффициентам
передаточной функции системы. Но, с другой стороны, эти же соотношения можно
рассматривать как две несвязанные системы уравнений, которые позволяют по
известным коэффициентам полиномов в дробно-рациональной спектральной плотности
определить неизвестные коэффициенты передаточной функции формирующего
фильтра. При решении систем можно считать, что все коэффициенты а ,-> 0, что
вытекает из необходимого условия устойчивости фильтра, и все bj>Q, что
соответствует минимально-фазовой системе.
Решение указанных систем уравнений можно заменить решением одного
уравнения. Если разложить полином Л(со) в виде произведений двучленов
А(©) = ДДш2 +cl)*1(co2 +с2)*2 х...х(ш4 +е1оо2 + ^/'(а)4 +е2со2 +Л2)/2..., (8.127)
где kj и /, - кратности вещественных и комплексно-сопряженных нулей этого
полинома относительно со2, то полином N(s) в знаменателе передаточной функции
будет иметь вид
. .— . .— (8.128)
х(,у + у]е{ + 2y[d[s + y[I{)h(s2 + yje2 + 2^s + Jcb)'2....
Таким образом, основные вычисления сводятся к определению корней полинома
Л( со) относительно со2, т.е. к решению алгебраического уравнения
где z = со2.
Очевидно, что все приведенные рассуждения касаются и полиномов £(оо)
и Л*(.у).
Пример 8.9. Пусть спектральная плотность выходного сигнала имеет вид
5хх(о)) = -
2500
о8 - 9 о6 + 559 О)4 + 3069 со2 + 2500
Глава 8. Метод матричных операторов 535
Найдем корни знаменателя Решение уравнения четвертой степени
z4 -9г3 + 559г2 + 3069 г + 2500 = 0
дает следующие значения корней
г, = со? = -1, г2 = 0)2 = -4, г3,4 = <^з,4 = 7 ± У24-
Соответственно полином в знаменателе Sxx (со) может быть представлен в виде
Д(ш) = (О)2 + 1)(ш2 + 4)(ш2 - 7 - У24)(ш2 - 7 + ;24) =
= (со2 + 1)(со2 + 4)(со4 - 14со2 + 625).
Тогда полином N(s) будет иметь вид
N(s) = (s + \)(s + 2)(s2 +6s + 25).
В результате получим следующую передаточную функцию формирующего фильтра
w (,)Я 50
фф (j + 1)(j + 2)(52+ 6*+ 25)
Значительно более сложной является задача формирования нестационарных
случайных процессов.
В инженерных расчетах может быть использован следующий подход.
Корреляционная функция выходного сигнала нестационарного фильтра
определятся соотношением
Кхх('1.'2) = ФТ('1)АС*""АтФ(?2). (8.130)
Постановка задачи синтеза формирующего фильтра иллюстрируется рис. 8.44.
Y(t) I I X(t)
Rrr(h.h) RxxOvh)
Рис. 8.44. К постановке задачи формирующего фильтра
На рис. 8.44 автокорреляционные функции Ryyih^h) и ^xxih^h) известны
и корреляционная функция Ryyih^h) обладает известными свойствами,
порожденными необходимостью соблюдения условия: текущий спектр входного сигнала Y(t)
для всех re [0,7] должен быть «шире» текущего спектра выходного сигнала. Это
условие должно быть записано так
RYYdi^ZRxxdi'h) V/lfr26 [0,Г]х[0,Г].
Цель расчетов - определение элементов (а**),/,у = \Л спектральной
характеристики Афф.
Воспользуемся следующим критерием
тт
/(4Ф) = H[^xx(h,t2)-^TW^CRyyAl^(t2)] dtxdt2 . (8.131)
о о
Элементы (afj^Yi,j = IJ матрицы Афф могут быть найдены путем реализации
следующей процедуры оптимизации
/(4Ф)->гшп. (8.132)
аГ
536 Анализ и статистическая динамика САУ. Часть I
Функция / (яФ* ) является многрэкстремальной, поэтому нахождение глобального
минимума представляет собой сложную задачу.
8.14. РЕШЕНИЕ ОБРАТНЫХ ЗАДАЧ ДИНАМИКИ
МЕТОДАМИ КОНЕЧНОМЕРНОЙ ОПТИМИЗАЦИИ
Многие задачи аналитической механики (задачи определения сил, вызывающих
движение планет Солнечной системы; определение силовых функций по заданным
интегралам и др.), механики управляемого полета (определение закона изменения
массы материальной точки из условия, чтобы движение точки совершалось по
заданному закону и др.), теории автоматического управления относятся к классу задач,
получивших название «обратные задачи динамики» [75]. В [75] приведены примеры
обратных задач динамики, а также работы, в которых получены ценные результаты,
относящиеся к этому направлению.
Цель настоящего параграфа - изложение некоторых методов и построенных на их
основе алгоритмов решения обратных задач динамики, использующих
математическое программирование.
8.14.1. Содержание обратных задач динамики и примеры их решения
Приведем некоторые положения, составляющие содержание понятия «обратные
задачи динамики».
Рассмотрим линейную стационарную систему, описываемую уравнением вида
x + alx + aox = bou(t), Х° = (*(0), i(0)). (8.133)
Задача заключается в нахождении такого входного сигнала {управления) w*(r),
чтобы выходной процесс x{t) совпадал или был, в известном смысле, близок к
некоторой эталонной функции x3(t). Это - основное положение рассматриваемой
задачи; управление u*(t) будем называть оптимальным.
Такие задачи часто встречаются на практике. К ним можно отнести задачу
управления движением манипуляционных роботов по назначенным траекториям и задачу
управления посадкой спускаемого аппарата. Широкий спектр задач, относящихся к
классу обратных задач динамики, приведен в [75].
Рассматриваемый подход широко используется, например, при проектировании
систем нагружения для исследования и испытаний машин и механизмов. С помощью
систем нагружения должны быть созданы условия, которые соответствуют реальной
эксплуатации [44]. К таким системам следует отнести системы вибрационных
испытаний. В общем случае наиболее адекватным представлением вибрационных нагру-
жений являются случайные функции времени, например, нагружения, действующие
на изделия при их транспортировке автомобильным, железнодорожным или водным
транспортом. При проектировании этого класса систем имеет место обратная задача
статистической динамики: необходимо на вход системы вибрационных испытаний
подавать случайный сигнал с такими статистическими характеристиками, чтобы на
выходе этой системы сигнал, воздействующий на объект, имел заданные (эталонные)
статистические параметры. Под эталонными здесь понимаются статистические
характеристики сигнала, действующие на объект в реальных условиях эксплуатации.
На практике широко распространены системы вибрационных нагружений,
генерирующих детерминированные вибрации. Известно, что в возможности появления
резонансных колебаний состоит главная опасность воздействия вибраций на агрегаты и
приборы. Этим же частично объясняется и вредное влияние установившейся вибра-
Глава 8. Метод матричных операторов 537
ции на человеческий организм [44]. Внешние колебания в диапазоне частот (15-30)Гц
оказывают влияние на сосудистый тонус организма и на вестибулярный и
двигательный анализаторы [44].
Поэтому важное значение на практике имеют системы вибрационных испытаний
на гармонические и полугармонические вибрации [44]. Используются вибрации и
более сложной структуры. К примеру, для имитации обобщенной нормативной
функции внешнего нагружения по усталостной прочности планера самолета в
области низких частот, включающей режимы рулежки, взлета, заправки топливом в
полете, маневрирования и посадку, потребовалась установка 50 гидравлических силовоз-
будителей со специальной программой управления и диапазоном регулирования от 5
до 10000 кГс [44].
Во всех указанных выше задачах чрезвычайно важным является достижение
наибольшей степени адекватности параметров нагружения тем параметрам, которые
имеют место в реальных условиях эксплуатации. Во многих случаях этим
определяется степень безопасности проектируемого изделия при его эксплуатации [44].
В задачах испытаний на основе математической обработки исходной информации
получают эталонный процесс нагружения x3(t). Тогда в системе нагружения,
используемой для испытаний изделия, необходимо построить такое управление U*(f),
чтобы для физически реализуемого Х(г) и эталонного Хэ(г) процессов было
выполнено условие
|Хэ(0-Х(0||->тт
либо|Хэ(0-Х(0|<е,
где е - заданное значение оценки качества воспроизведения эталонного режима
нагружения [44].
А теперь вернемся к уравнению (8.133) и рассмотрим подходы к решению задачи
построения u*(t)'[15].
Положим, что x3(t) - осуществимая системой (8.133) траектория. Поскольку
x3(t) известна, то подставляя ее в уравнение (8.133), получим
u*(t)=bol\x3(t)+a{x3(t)+aoxM. (8.134)
Последняя формула определяет оптимальное программное управление u*(t).
Построим систему, работающую по принципу обратной связи.
Пусть
д:э(0=с1/1Чс2/2Г,Г>0, (8.135)
Х{ Д2 -известны.
Постоянные q и с2 находятся из условия
хэ(0)=х(0),;сэ(0)=4)).
Подставляя (8.135) в (8.134), найдем
и*(г)= Vk*i>i*V + A(X2)c2^], (8.136)
где
A^k)=\\+a{kk+a^ *=1,2.
На основе (8.136) можно построить систему, реализующую принцип обратной
связи, т.е. найти и*, зависящую от x(t) и x(t).
34 Зак. 232
538 Анализ и статистическая динамика САУ. Часть I
Имеем
с^ +с2ех* =jc(f> Vi*V +\2c2ex* = x(t). (8.137)
В формулу, определяющую u*(t), входят сомножители схеХх* и сгеХг*. Из
зависимостей (8.137), представляющих собой линейную систему алгебраических
уравнений относительно cxeXxt и с2е*2' при условии Хх фХ2 , легко найти соотношения
Подставляя полученные формулы в (8.136), получим искомое управление
и*(х,х), реализующее принцип обратной связи:
U*(x,x)=plX+p2X
где
Из рассмотренных положений ясно, что дифференциальное уравнение замкнутой
системы должно иметь частные решения вида е kt. Следовательно, реализовать
предписанные требования можно только в том случае, когда с помощью алгоритма
управления замкнутой системе придается соответствующая структура,
отвечающая виду назначенной траектории *э(0> причем замкнутая система
принадлежит к классу стационарных.
А теперь рассмотрим случай, когда [75]
Хэ(')=А£Г7 + ^7 'X = COnSt>0- (8.138)
Как и в предыдущем случае, сх и с2 определяются из условий
*э(0)=*(0),хэ(0)=л{0).
Задача построения u*(t) разрешима, поскольку
41(0 = 777' ^('^л ^Г
линейно независимы.
Используя приведенные выше рассуждения, получим зависимость,
определяющую оптимальное программное управление:
/ч а{ 2 / \ 2ах 6
где Yl(0-o -X77 + ^f ; Y2(')=a° -—t+l^f ■
Как и в предыдущем случае, найдем управление, реализующее принцип обратной
связи.
Поскольку справедлива следующая линейная система алгебраических уравнений
1 л . .vi . 2
X+t 1У ' X + t
то из последней находим
с& + 1У+-±-с2(к + 1Уг=-кк\
Глава 8. Метод матричных операторов 539
-E±- = 2x(t)+(X + t)x(t), ^ = -*(,)-(А + ф(?).
Теперь легко записать искомое оптимальное управление
2
м* (*,*) =
flo—;
^)+р"Х77]^^ (8Л39)
Процессы в рассматриваемой системе управления описываются
дифференциальным уравнением с переменными коэффициентами.
Из изложенного следует вывод: если для стационарного объекта x3(t)
выражается через функции eXkt (частные решения дифференциального уравнения с
постоянными коэффициентами), то замкнутая система является стационарной', в
противном случае - системой с переменными параметрами.
Закон управления (8.139) найден из условия, чтобы замкнутая система была
асимптотически устойчивой, а ее движение из точки (х(о), х(о)) осуществлялось в
начало координат. Существуют и другие постановки задач [75].
Часто вместо x3(t) можно задавать эталонную систему. Принципиальная
особенность этого направления заключается в том, что искомые законы управления
строятся из условия, чтобы замкнутая система была асимптотически устойчивой, а
траектория ее движения следовала бы за траекторией движения некоторой
системы сравнения [75]. При таком подходе задача синтеза решается по неполной
информации о математической модели объекта, а построенные законы управления
обеспечивают выполнение заданных требований при параметрических и
координатных возмущениях [75]. Это направление разработано СВ. Емельяновым и его
сотрудниками. Идея этого направления состоит в следующем.
Объект управления описывается векторно-матричным уравнением вида
X(r)=3(x(0u)+BU(;)l Х(0)=Х0, (8.140)
где X(t) и U(f) - n -мерные векторы координат состояния и управления. На
функцию 3 наложены известные ограничения: она непрерывна и по X удовлетворяет
условию Липшица.
Кроме модели объекта (8.140) задается модель системы сравнения
Хэ(0 = СХэ(г),Хэ(о)=ХэО, (8.141)
движение которой соответствует требованиям замкнутой синтезированной системы.
Задача заключается в построении закона управления U*(X,r), при котором
замкнутая система
х(0=з(х(0и)+ви(г), х(о)=хо
асимптотически устойчива в целом, а траектория x(f,X0) ее движения из точки Хо
в начало координат Х = 0 проходит в окрестности траектории Хэ(г,Х0) движения
системы (8.141) из точки Хэ0 = Хо.
8.14.2. Алгоритм построения программных управлений движением
одного класса нелинейных динамических систем
(ЗАДАЧА Е.А. БАРБАШИНА)
Рассмотрим объект, поведение которого описывается уравнением
X(t)=F(X,t)+V{t),te[O,T]. (8.142)
Или, в развернутой форме,
34*
540 Анализ и статистическая динамика САУ. Часть I
*\(f)= fi(xi(t\x2(t).--->xn(t\t)+u\(t)>
i|.(0=/nfe(4*2W-M^W0+«n(0-
Пусть Хэ(/)= 4*(t)= (\|/1(f)pv|/'2'(if)t---»V«(f))T " вектор-функция - заданная
траектория в фазовом пространстве (эталонный процесс).
Задача заключается в нахождении такого управления U*(/), которое
обеспечивало бы минимальное, в известном смысле, расстояние между вектор-функциями
Т(г) и Х*(г). Очевидно, эта задача относится к классу обратных задач динамики.
Для линейных стационарных и нестационарных объектов эта задача в терминах
математического программирования и матричного представления операторов
формулируется так:
itf =
/(сх,си)=|(х(О-ч'(О)т(х(О-ч'(ОМ=Н)-ч'
о
Ч п 1 п i , ы « i , v, (8-143)
0 L v=l J v=l r=l v=l r=l
при ограничениях
CX=AXBYCU+AX00 1
-/4Un ' (8Л44)
O(rJC e U - ограничения на управление]
Рассмотрим решение той же задачи для класса нелинейных объектов,
описываемых (8.142).
Поскольку Z(f)=X(f)-¥(/),
то
X(r)=Z(r)+'F(0,aZ(0=X(r)-«P(0
и, следовательно,
• x(0 = F(x(r)0=F(z(0+V(M+U(0;
для Z(t) имеем уравнение '
z(0=x(0-*(0=F(z(0+*(f)i0+u(0-*(0.
Прибавим к последнему равенству и вычтем из него функцию F(*P(f)lf);
результат имеет вид
z(r)=F(z(r)+^(r)r)+U(r)-4'(0+F(4'(r)l/)-F(v(40- (8-145)
Воспользуемся обозначениями
F,(z(0.r)=F(.z(0+4»(0.0-F(l|'(0.0.
a(0=u(0+f(*(0.0-*(0-
Тогда имеет место дифференциальное уравнение, определяющее меру близости
Х(/) к *(/),
Z(t)=Fz(Z(t\t)+\(t). (8.146)
Если объект описывается линейным векторно-матричным дифференциальным
уравнением
Глава 8. Метод матричных операторов
541
то
х(*)=А(0х(0+и(0.
Fz (Z(4r)= A(f Xz(f)+ T(f))- А(ф<(0= A(/)Z((),
A(r)=U(r)+A(r>l'(0-*(0.
или, в развернутом виде,
z2(t)
v2(0
*-С0
«и (0 - «и ('У
«21 (0 - «2л (О
«ni(0 - а™(0
(0
Z2
з.«
«21
«1
«2п
ft)
a«i(0 ••• ««(О
>i(0~
v2(0
vn(0
«2
(0
«»(0
(8.147)
Зависимость (8.146) является уравнением относительно Z(t), определяющей меру
близости эталонного ХЭ(?)=*Р(?) и реального Х(?) процессов на выходе объекта.
В (8.146) А(г) -управление, определяющее процесс изменения функции Z(/).
Положим
R(O = «P(O-F(44O,/) = X,(0-F(X,(f),0. (8.148)
В последнее выражение входит только известная функция Хэ(г)= *V(t), в связи с
чем функция R(r) является известной.
Отсюда можно записать
A(O = R(O-U(f). (8.149)
Поскольку, с одной стороны, z(t) определяет меру близости реальной траектории
Х(г) к эталонному процессу Т(г), с другой стороны, Z(r) - решение уравнения
(8.146), имеющего правую часть Д(г), очевидно, что для уменьшения
5г =
||Z(0| dt необходимо выбрать управление А(г) из некоторого класса
вектор-функций так, чтобы величина
8 = \j\\Mtfdt
1
\ —
V0
имела минимальное значение. Указанная задача минимизации может быть с учетом
(8.149) поставлена так
т
1)2
82 = [|R(0-U(0|| *-*min.
(8.150)
Последнюю зависимость молено рассматривать как задачу аппроксимации в
пространстве квадратично-интегрируемых вектор-функций. В самом деле, если
Ф(0 - ОНБ, то (8.150) можно переписать в виде
542 Анализ и статистическая динамика САУ. Часть I
/
£ U)-5>?94(o
dt -> min,
cV
/=1 V A:=l
Эта задача равносильна следующей: подобрать коэффициенты с]!', * = 1,/,
/ = 1, п так, чтобы величины
г( ' У —
sMUw-Z^H Л'/=1'л (8Л51>
(Л . М )
принимали наименьшее значение; такой подход используется в силу того, что выбор
с^ при одном значении / не влияет на выбор их при других значениях этого индекса.
Если на компоненты вектора управления не наложены ограничения, т.е. имеет
место задача безусловной минимизации, то ее решение определяется зависимостями
т
о
Если же на компоненты U(0 наложены ограничения, например
"/max-k(0|^0 У/€[0,Г],1 = п,
или в общем виде
Ф(0Сие1/л V/€[0,71,
то задача расчета с£ , к = 1,/; / = 1, л может быть сформулирована как задача
математического программирования
ы\L J с*
' I _ (8.152)
^с?ф4фоу/б[ОЛ/ = и
^=i г
В рассмотренном случае компоненты U*(0 определяются формулами
^0 = Хс*'Ф*(0,/ = 1,л. (8.153)
ы\
Структурная схема системы, управления U*(/) которой найдены изложенным
выше методом, представлена на рис. 8.45.
Напомним, что формулой (8.153) определено оптимальное управление U*(f), а на
структурной схеме (рис. 8.45) представлена система программного управления.
Безусловная задача минимизации может быть решена и при использовании
произвольного {не ортонормированного) базиса, выбранного таким образом, чтобы
учесть специфику конкретной задачи [160].
В этом случае компоненты вектора управления находятся в виде [160]
/
где
Глава 8. Метод матричных операторов
543
F(t)={fk{t):k = U-Jk(t)e L2[OJ]}
-полная в L2[0,r] система.
(8.154)
1 енератор
элеменов
ФИО
►
Ф 2 (0
■ -►
Ф/(0
-►
-*■
• у,
с Г
__
Cl
ия
С\
с"'
и k(t)
Нелинейный
объект
управления
*i(O
ХкО)
хАП
Рис. 8.45. Структурная схема системы
Числа с£* выбираются так, чтобы величина
«■j
/=i I к=\
Если г, (г) - заданный элемент, то числа
dt -> min .
г;1
(8.155)
c?=jn(f)fk(f)dt,k=ri
О
называют коэффициентами Фурье элемента r;(f) ло элементам системы (8.154), а
числа с^1, к = 1,1 у при которых линейная комбинация / первых элементов системы
i
(8.154) y^c^ifk(t) является наилучшим приближением к элементу rt(t) по норме
к=\
пространства I? [О,Г], - коэффициентами наилучшего приближения 1-го порядка.
Имеем
|U-i>*v*d| -ш-ф№+si>,-/*teic7i. (8.156)
544 Анализ и статистическая динамика САУ. Часть I
Последняя зависимость достигает минимума при тех значениях ее аргументов
с^ , к = 1,/, которые обращают в нуль ее первые производные по всем аргументам
qM\ к = \Л.
Продифференцировав функцию (8.156) по с£', к = 1,/, и приравняв результат
нулю, можно записать
I Т Т '
yZci;ilfj(t)fk№=jri(t)fk№ , *=п.
*=1 О О
Или, что тоже самое,
£/,,?;• =с7,* = п, (8.157)
к=\
где fjk={fjJk)-
Поскольку определитель ф = {/'д}/^_1 является определителем Грама линейно
независимой системы (8.154), то система алгебраических уравнений (8.157)
однозначно разрешима; ее решение имеет вид
^'=Z//*^, *=U, (8.158)
где //* , j\k = ltl - элементы матрицы, обратной к матрице Ф .
Г 1 1
Так как 8*- = ^^t-^^^f^c^c^1 , то квадрат ошибки определяется соотно-
о У=1 *=i
шением [160]
/ m T
I I \
VV fjkcncn -
;=1 k=\ j
i=l i=l о i=l
T m ( 1 I \ (8.159)
0 '=1 [ H k=l j
Чтобы коэффициенты с^ наилучшего приближения, определяемые формулами
(8.158), при / —><» стремились к определенным пределам для каждого /, необходимо
и достаточно, чтобы система функций /\(0. /г(0» ••• была минимальной в 1?[0,Г]
[160]. Если система функций /\(0, /г(0. ••• полна в 1?[0,Т], bcq величины
т( i \2
SS = J\n(t)-^cu'fk(t) U^O.
Рассмотренными выше методами эта задача может быть решена и с ограничением
на управление.
Решение рассматриваемой задачи можно получить, если воспользоваться
разложением вектора управления вида [160]
и(0 = Х^Л(0, *б[0,Г]. (8.160)
Глава 8. Метод матричных операторов 545
где fk(t), к = 1,2,... - система вектор-функций, cf -скалярные величины.
Числа с/ выбираются так, чтобы величина
S/2=J R(0-£?/V*(0 dt
oil *=i II
имела наименьшее значение.
Коэффициенты cf называются коэффициентами наилучшего линейного
приближения /-го порядка вектор-функции R(r) с помощью системы вектор-функций
F = {fk(t): к = 1, 2,...}. Указанные коэффициенты определяются формулой
?/=£//y?,R,;=u, (8.16D
7=1
где fj* - элементы матрицы, обратной к /-му вырезу матрицы Грама системы
вектор-функций fx (г), /2 (г),...,/, (О.
В формулу (8.161) входят коэффициенты с?, называемые коэффициентами
Фурье вектор-функции R(0 по элементам системы F и определяемые соотношением
т
с* =|(r(/),fj(t))dt, j = п. (8.162)
О
Зависимость, определяющая погрешность 8Z приближения (8.160), имеет вид
• 8/2=J||R(0|2*-Xt//*c~Rc«. (8Л63)
0 Ы\ к=\
Неравенство
JmSS/^W^jN)!2* (8.164)
/=1 /:=1 0
называют обобщенным неравенством Бесселя. Неравенство (8.164) при
использовании ОНБ переходит в известное неравенство Бесселя
£|c/f<f||R(<)|V
Ы о
Если обобщенное неравенство Бесселя переходит в равенство
JtaSS/i^W-jNf*. (8-165)
~* 1=1 /:=1 0
то говорят, что элемент R(0 принадлежит замыканию линейной оболочки системы
элементов F, а равенство (8.165) называют уравнением замкнутости.
Задачи с ограничениями на управление решаются методами математического
программирования.
Пример 8.10. Рассмотрим задачу синтеза управляющего сигнала изложенным выше методом на
примере электрогидравлического следящего вибратора (ЭГСВ) На рис. 8.46 представлена функциональная
схема ЭГСВ с электрогидравлическим усилителем (ЭГУ). На рис 8.47 представлена принципиальная
схема ЭГСВ. Здесь обозначены ЭМП - электромеханический преобразователь; Cl, C2 - сопла, Др1, Др2, ДрЗ
- дроссели, LI, L2 - катушки индуктивности датчика; Rl, R2 - сопротивление.
546
Анализ и статистическая динамика САУ. Часть I
Вибраторы такого типа работают следующим образом [12]. При подаче управляющего напряжения на
вход усилителя 1 возникает ток в обмотке катушки управления электромеханического преобразователя
(ЭМП) и якорь вместе с заслонкой 2 отклоняются от нейтрального положения, что приводит к повышению
управляющего давления на одном торце золотника 3 и понижению на противоположном. В результате
появившегося перепада давлений на торцах золотник 3 гидроусилителя смещается от нейтрального
положения, соединяя одну полость гидроцилиндра 4 с напорной линией, а другую - со сливной. Поршень 5 под
действием разности давлений в полостях гидроцилиндра перемещается до тех пор, пока управляющее
напряжение не будет скомпенсировано напряжением, подводимым к усилителю с выхода датчика 6
обратной связи. После этого ток в обмотке управления ЭМП становится равным нулю, якорь, заслонка
и золотник приходят в нейтральное положение, а поршень гидроцилиндра занимает новое
установившееся положение. Таким образом, при подаче на вход усилителя 1 синусоидального напряжения
заданной частоты, благодаря наличию электрической обратной связи, поршень 5 будет отслеживать
заданный закон управления.
1
Т
!_
O71V11 1
.
йог
ТГР J-I
ЗГР ^
1
^ И7Т
У
Рис. 8.46. Функциональная схема электрогидравлического вибратора:
УЭС -усилитель электрических сигналов; ЭМП - электромагнитный преобразователь;
ЗГР - золотниковый гидравлический распределитель; ЭГУ- электрогидравлический усилитель;
ИД - исполнительный двигатель; ДОС - датчик обратной связи
При аналитическом описании вибратора были сделаны следующие упрощающие допущения,
обоснованные опытом исследования электрогидравлических усилителей и поршневых следящих гидравлических
исполнительных механизмов [12]:
- внешние утечки, гидравлическое сопротивление трубопроводов, нулевое (начальное) перекрытие
рабочих окон золотника пренебрежимо малы;
- нагрузка на поршень вибратора состоит из сил инерции, позиционной нагрузки и сил вязкого трения;
- пренебрегаем волновыми процессами в трубопроводах;
- давление нагнетания постоянно;
- давление и скорость в живых сечениях потоков сопел ЭГУ распределены равномерно.
При сделанных допущениях динамические процессы в следящем электрогидравлическом вибраторе
описываются следующими уравнениями [12]*.
Уравнение электрической цепи ЭГУ:
dt Va dt
где (/-напряжение на входе ЭГУ, В; R- сопротивление обмотки ЭГУ, Я = 80 Ом; L - индуктивность
обмотки ЭГУ, L = 0.4 Гн; к^ - коэффициент ЭДС самоиндукции, KUa~0\ а-угол поворота якоря
ЭМП, рад.
Переходя к стандартной форме записи, получим
•KwUt (8.166)
у dt
где
= - = -1 = 0,005;^ =- = — = 0,0125.
80
R 80
Изложение ведется, следуя работам доц. Е.А. Мусатова и доц. Б.В. Добровольского.
Глава 8. Метод матричных операторов
547
в
ее
|
В
s
а
х
8.
00
548 Анализ и статистическая динамика САУ. Часть I
Дифференциальное уравнение движения якоря электромагнитного преобразователя:
. d2a „, da __ __ . ..
где jя - момент инерции якоря, Уя = 0,3 • 10~6, кг • м2; KfMoL - коэффициент демпфирования, К'Ма - 7 • 10~5;
КМа - жесткость, КМа = 0.1 Н/рад; Мн — момент нагрузки, Н • м.
MH=PrJ + P0Cl0C\ p = ^ст^ст ;
н гд ос ос г^ — . гст
где £ст - модуль Юнга стали, Па; /ст - момент инерции сечения, м4 ; х3 - перемещение золотника ЭГУ, м
^гд=Х<ЛРу'
где хс =1.03...1.06; Fc - площадь отверстия сопла, /?с =Z^£_, м2; ру - перепад давления на заслонке,
4
Ру = Ру\-Ру2 Па
Мн = Хс^ РУ + ЪЕ«'«1"а + 3£cT3CT/oc^;
'ст *ст
Л^н = ^Л/рРу + ^ста+ ^мос^з ,
где
^р=Хс^;.^=0;
Тогда
лмос з
Гя2^ + 2^яГя^ + а = /:я(/-<0С^), (8.167)
где
- = 0.1,
2^я(КМа + К„) 2д/о.З 10~6 (0.1 + 0.3)
Кя = ^ = ! = 2.5-
^а + ^ст 0.1 + 0.3
Сс=4^=т=1°-
^•'.^■v^-
Уравнение расходов ЭГУ.
где Vy - объем камеры управления, Vy=0, м3; Е-модуль упругости жидкости, £ = 109, Па;
F2 -площадь поперечного сечения золотника ЗГР, F, =0,785 10"4 м2;^^а=10 ; Kqp = 10 .
Ру=^уз(а-^аг^-), (8.168)
где
Глава 8. Метод матричных операторов 549
^Bff!L.i2l.1ooo.t(B-U-2^5^-a078S
yj кт, ю-6 " Kqp ю-6
Уравнение движения золотника
<1гх dx,
где ш3 - масса золотника, Wj=0.01 кг; кт i - коэффициент трения, к 3=0.5i Сгд - жесткость
гидравлической пружины, Сгд = 1.
Гз2^+2^Г3^ + л3 = ^ру, (8.169)
/Ил-ЗУ-+^3-^+20^3 = FjP> ;
где
/0.01 • г, ^трз 0.5
Г.-JJb-- JMI=0.071^ --рЬ—-Si—-1.7вв;
рСгя V 2-1 2^/т32Сгд 2V0.01 -2-1
_^_ = 0Л85^ = 0392510.4
2СГД 2-1
Линеаризованное уравнение расходов:
2Е Л G Gp Jr
где V - объем рабочей камеры гидроцилиндра в нейтральном положении, V = 647 -10"7 м3; Кп -
коэффициент перетечек между полостями гидроцилиндра, Кп = 0; F - рабочая площадь поршня,
F = 19.9.10"4 м2.
Кп= , ^>0 =10-'°.
Pn-Posign(^o)
2
KQx - KiV j ~
где К[ =\1упс1^1— ; хо> р0 - точки линеаризации расходно-перепадной характеристики ЗГР; рп -
давление питания, рп = ри - рсд ; ц - коэффициент расхода ЗГР; v - коэффициент использования щели ЗГР;
flf3 - диаметр золотника; р - плотность рабочей жидкости
Т !!Р-+р = К (х-т &А (8.170)
где
V 647-10"7
* 2E(KQp+Kn) 2109(10-10+0)~ *
*„=—^^ = -4^- = 4.3.1010;
^ % + а:п ючо+о
F 19.9-Ю"4
Уравнение нагрузки:
•" % 4.3
d'y^'iy
m^- + h^ + Cy = FP,
clt2 dt
где m - масса подвижных частей гидроцилиндра, m = 5000 кг; h - коэффициент демпфирования поршня,
А = 10; С- жесткость пружины, С = 2-106 Н/м.
T^^,Tt^y = KtP. (8.171)
550 Анализ и статистическая динамика САУ. Часть I
где
= 0.05;
=5-10"5;
2V5 103 -2 106
F = 19.9.10-^995>10-10
С 2106
Уравнение обратной связи:
где Кус - коэффициент усиления, Кус = 0.5 ; Кос - коэффициент ОС, Кос = 5.
U = Кусиъх - КусК0Су. (8.172)
Кроме того, индуктивный датчик обратной связи имеет существенную нелинейность в виде элемента с
насыщением
Уравнения (8.166) - (8.172) являются уравнениями математической модели электрогидравлического
следящего привода.
На основе полученных уравнений можно составить структурную схему (см. рис. 8.48).
Упростим полученную модель вибростенда. Не будем учитывать процессы, протекающие в ЭГУ.
Тогда электрогидравлический усилитель можно представить пропорциональным звеном с коэффициентом
усиления кэгу равным
^эгу - K(Ji '
VVJ
1+ Кя- /Туз • К.л • JfM0C
= 0.0125. 2.5.100Q.3.925-10-' =61909.ш-,
1 +2.5 1000-3.925-10"5 10
В этом случае получим структурную схему, представленную на рисунке 8.49, а, а после структурных
преобразований - структурную схему, изображенную на рисунке 8.49, б.
На рисунке 8.49, б введены следующие обозначения:
К - 1 -1-02.
Лос ->
= 0.5-5-6.190910"4-4.31010-9.9510"10=6.62410"2;
аъ =7^ -Гг2 =3.235 10"4 0.052 =8»08-10"7;
а2=Гг2 +27^7; =0.052 +2- 3.23510"4 -5-Ю"5- 0.05 = 2.5-10"3;
ах = К^К^^ + Т^ + 2^ГГГ = 4.3- 10ю • 9.95 • 10~10 • 4.628- Ю"4 +
+ 3.235-10-4 + 2-5 10-5-0.05 = 2.045-10-2 ;
ао=1.
Согласно рис. 8.49, бу можно записать дифференциальное уравнение, описывающее работу вибратора
где
-В, х<-Ь,
*(*(')) =
-л, -b<x<b,
Ь
В,х>Ь,
а коэффициенты нелинейной функции имеют следующие численные значения.
/7 = 0,005 м; 5 = 0,005 м.
В (8.173) обозначено x(t) = y(t) и u(t) = Uy(t).
Допустим, что на выходе системы необходимо получить гармонический закон
i|/(r)=A-sin(ow), (8.174)
где А - амплитуда выходного сигнала, А = 0.06; ш - его циклическая частота, со = 2 • п.
Необходимо определить входной сигнал u{t), при подаче которого на вход системы (8.173), на выходе
получили бы сигнал, максимально, в известном смысле, приближенный к эталонному (8.174).
Глава 8. Метод матричных операторов
551
+
8Н—'
^
t*
«и—'
оЧ
552
Анализ и статистическая динамика САУ. Часть I
|
К К
ЛусЛ
Кгу
ocj*
p.
—>
i
/
«г
/ >
7> + l
У
uv
K,
о >
i
a3s3
К
+ a2s4
l+a{s
У
где
Рис. 8.49. Упрощенные структурные схемы
Поставленную задачу будем решать методом, изложенным в данном параграфе.
Разделим обе части уравнения (8 173) на коэффициент av В результате получим*
x(t)+a23 •*(/)+fl13 •*(/)+дОз •*(')= ^oi3 -u(t)-Kl3'F(x(t)),
а2Ъ =-^- = 3094.06 ' в13 =-^- = 25309.41; я03 =^- = 8.08 107 ;
аъ аъ аъ
Км =-^-^- = 16396.04 ; Кп = ^- = 81980.2 .
voi3 ■
аъ
(8.175)
Введя в рассмотрение следующие две переменные *,(/) = x(t) и дс2(О = ^(0, дифференциальное
уравнение третьего порядка (8 175) можно записать в виде системы дифференциальных уравнений первого
порядка
-tl(')=*2(')>
*г (')= К<нз"(')-а23*2 (')" "b-'i (')-«оз4)- Ki3F(x(f)).
Обозначая
(8.176)
х(0=
• F(X,r)=
- а23х2 (/)- a,3x, (/)- amx(t)- Kl3F(x(t))
■ U(')=
0
.*0l3«W.
систему (8.176) можно записать в векторно-матричной форме
X(r) = F(X,/)+U(r).
Определим следующую вектор-функцию
Z(,)=X(r)-4<(,),
где
(8.177)
(8.178)
Глава 8. Метод матричных операторов
553
*(<)=
Гч>(<)1
v2(0
, v|/1(0 = vi/(/) = A-(D-cos(a)-0. v|/2(0 = 14/(0 = -^w2sin(a)0.
Произведем замену в уравнении <8.177) вектор-функции Х(0 вектор-функцией Z(0, после
несложных преобразований получим уравнение
Z(O = F,(Z(r),r) + A(O. (8Л79)
в котором
F, (Z(0,0 = F(Z(r) - 440,0 - F(V(0,0,
A(0=F(440,0-*(0 + U(0.
Решение Z(0 уравнения (8.179) представляет собой отклонение решения Х(0 уравнения (8.177) от
заданной вектор-функции ч*(0- Вектор-функция Z(0 B уравнении (8.179) определяется членом А(0-
Следовательно, управление и(0 необходимо подобрать таким, чтобы величина
)№*\
имела бы наименьшее значение. Если положить *р(0 -F(¥(0,0 = R(0» ТО получим следующую
постановку задачи: подобрать такое управление U(0 > ПРИ котором величина
82=J|R(r)-U(r)|2A
(8.180)
имеет минимальное значение.
Представим компоненты вектора управления U(r) в следующем виде
9
и*(0 = 2^^(0. i' = 1.23. /е[0,2],
где Р(г) = \рк (0 :^ = 0,9/ - система функций из первых десяти полиномов Лежандра.
Тогда вектор управления U(0 можно записать в виде
U(0 =
*oi3&"3P*(')
*=о
(8.181)
В этом случае (8.180) можно представить следующим образом
2 3 ( • 9 \2
S2 = \Ц П(0-Кт^рк(0 dt =
О '=1
■/
r,2(0 + r22(0+ г3(О-^о1з£^3РЛО I Л •
(8.182)
Следовательно, необходимо подобрать числа ски* такими, чтобы
*ч
П2(0 + г22(0+ г3(0-К0П^ск^рк(0
к=0
dt —> min.
Минимум функционала (8.182) будем искать с использованием алгоритма Нелдере - Мида-
алгоритма безусловной оптимизации функции многих переменных. В качестве начальных значений искомых
параметров ск*, к - 0,9, примем, например, единичные, т.е.
си7=[1 1 1 1 1 1 1 1 1 if.
При этих значениях искомых коэффициентов функционал (8.182) равен 52(сынач) = 4.3671 • 105 •
Минимум функционала (8.182) при точности расчета е = 0.0001 достигается в точке
с^ =[-0.0004 2.0858 0.2190 3.0213 0.9690 -8.0219 -0.8173 3.6015 0.2258 -0.719#,
554
Анализ и статистическая динамика САУ. Часть I
при этом значение функционала (8 182) 52(см* ) = 2.9493 103 •
Подставляя найденные оптимальные значения с* . к = 0^9 в (8.181), найдем компоненты вектора
управления и(г), первые два элемента которого - нулевые, а график третьего представлен на рис. 8.50.
Л «3 (О
1
о
-2
-3
-4
-5
/ \
/ \
\
"Л
1
\
\
\
\
\
/ \
/ \
/ \
' \
\
. 1
X 1
\ 1
0.5 1 1.5
Рис. 8.50. Сигнал управления
На рис 8.51 представлены эталонный сигнал выходной \|/(г) и оптимальный сигнал на выходе x\t)
^ " ' — х*=х\Л
\|/ = \|/(0
1.5
Рис. 8.51. Графики эталонного выходного сигнала \j/(r) и оптимального x*(t)
В некоторых случаях на выходе вибратора необходимо реализовать сигналы треугольной формы
(такие колебания часто используются в отсадочных машинах) Поэтому рассмотрим задачу синтеза входного
сигнала системы (8.173) при заданном эталонном выходном сигнале треугольной формы с амплитудой
А = 0 06 м и частотой v = 1 Гц
Глава 8. Метод матричных операторов
555
i|/(0 =
4Avt,
0<f<—;
4v
A(2-4vr),— <t<—;
4v 4v
A(4w-4),—<r<-.
4v v
В этом случае, решая задачу рассмотренным выше методом с использованием системы функций из
первых десяти полиномов Лежандра, при той же точности расчета и тех же начальных значениях искомых
коэффициентов с"3» к = 0^9 (значение функционала(8 182) в этом случае S2 (см"ач) = 4.0664 • Ю5), находим
следующие оптимальные значения с£3:
^=[-0.0046 1.8110 0.1575 2.5676 0.7987 -7.3447 -0.6946 3.2222 0.0676 -0.27987
и при этом 52 (см*з) = 4.5552 104.
На рисунках 8.52 и 8.53 представлены графики найденного компонента и3(0 вектора управления и (г)
и сигналов на выходе: эталонного \|/(0 и оптимального сигнала x*(t)
г"з(0
4
3
2
1
0
-1
-2
-3
-4
г, с
0.5 1 1.5
Рис. 8.52. Сигнал управления и3(О
0.06
0.04
0.02
0
-0.02
-0.04
x\t) \|/(0
I\
/ \
/ \
\ У
\ /
у 1 — v = v(0
f\\ г* - x*(t)
/1 \ х х V*
/ V ■
':.... \... /
i Л../
; У
0 0.5 1 1.5 2
Рис. 8.53. Графики эталонного выходного сигнала \|/(г) и оптимального **(')
556 Анализ и статистическая динамика САУ. Часть I
8.14.3. Алгоритм решения задачи слежения: воспроизведение
эталонной выходной вектор-функции
Одной из важных в теории управления является задача слежения [75].
Рассмотрим стационарную линейную систему
xGf)=AxG)+BuG),|
Хв(г)=СХ(0, J (8.183)
где X(f) - п-мерный вектор состояния системы,
U(/) - m-мерный вектор управления,
Хв(/) - р-мерный вектор выхода.
Предполагается, что система вполне наблюдаема.
Через Хд(/) обозначим р-мерный вектор, закон изменения которого во времени за-'
дается извне, представляющий собой желаемый (эталонный) выход системы. Вектор
E(r)=XB(r)-XB(r)
является рассогласованием или ошибкой системы.
Предписанный процесс может быть задан или в виде вектора Xl(t), или в форме
эталонной системы, описываемой уравнением вида
Хэ(г)= АэХэ(г), Х;(г)=СэХэ(0 , Х(0)=Хэ(0). (8.184)
Задача осуществления эталонной (назначенной) траектории X3B(t) сводится к
определению вектора управления U(f) из условия наилучшего приближения XB(t) к
Xj(f). В качестве меры близости принимается функционал
/ = |{[хв(г)-Х^(0Гу[хв(0-Х^(ф (8.185)
О
где V = VT > 0 - матрица, методика выбора которой изложена, например, в [75].
Постоянные матрицы А,В,С,АЭ,СЭ считаются заданными.
Положим, что с помощью измерителя измеряются сигналы Z\(t),z2(t),...,zr(t),
которые представляют собой или часть компонент вектора состояния или
компоненты вектора Z(t), функционально связанного с вектор-функцией Х(г).
Для вектор-функции Z(t) имеет место зависимость
Z(O = HX(r),
где
¥¥ _
(hn hi2 ••• hln
h2l h22 ••• h2n
- (rxn) - известная матрица.
hrl hr2 ••• hr
В общем случае полагается, что г < п .
Если имеется возможность измерить вектор Х(г), то
Н = I, где I - единичная матрица.
Закон управления строится в соответствии с зависимостью
U(0 = CZ(/) = CHX(/)f (8.186)
где С - неизвестная матрица.
Глава 8. Метод матричных операторов
557
Если воспользоваться обозначениями
CH = (C,,C2;...,Cr)-(i7,hJ,...,hj)=2c*hJ,
*=1
где
С,=
СП
Си
cmxj
.С2 =
c12N
с22
стг .
,....сг =
h,=
Ч,4
Л,2
*!„
. 1»2 =
.....hr =
4iN
Ar2
то в развернутой форме (8.186) запишется так:
V(x)=V(Xl(t),x2(t),...,xn(t)h
'All А12 ' •" .ftlnN
СИ С12 •" С1г
С21 С22 •" С2г
ст1 ст2 •" с»
^21 А22
йг1 йг2
Й2„
-2(0
- ЕсХ щ (8Л87>
и=1
Задача заключается в нахождении матрицы С , реализующей закон управления
и(Х(0)5 такой, которая обеспечила бы минимум функционала (8.185).
Другими словами, поскольку
Х.=Х.(г,С),
задача, в конечном итоге, сводится к отысканию минимума функционала
/(с)=/{[хв(^с)-х^(г)Гу[хв(г(с)-х^ф
по элементам матрицы С .
Если найдена оптимальная, в известном смысле, матрица С*, то структурная
схема системы слежения может быть представлена в виде (рис. 8.54).
U(X(r))
в
г'
^>с =>
Х.(О
<
Рис. 8.54. Структурная схема системы слежения по выходу
558 Анализ и статистическая динамика САУ. Часть I
Далее для упрощения рассуждений с целью изложения идеи подхода положим,
что u(t) и хв(г) - скалярные функции.
Тогда уравнения (8.183) принимают вид [75]
Х(0 = А-Х(0 + Ь.и(0, *B(O=qT-X(O = *(O, X(0) = X0, (8.188)
где, Х(0 = [х{ (г) х2 (0 ... хп (t)Y - вектор-функция состояния системы.
Здесь введены обозначения:
B=b, C = qT, xB(t) = x(t),
причем
qT=k Й2 - 9„1Ь = [Ь, Ъ2 ... bj.
Эталонная система в рассматриваемом случае имеет вид
X3(0 = F.X3(0, xl(t) = ql.X3(t) = y(t\
Хэ(О = к(О x\(t) ... x3n(t)J, Хэ(0) = Х(0) = Х0.
В случае скалярного выходного сигнала мера близости реального процесса x{t). к
эталонному выходному сигналу y(t) определяется функционалом
т
I=^[x(t)-y(t)fdt (8189)
о
Запишем уравнение измерителя при предположении, что измерения являются
идеальными
Z(O = bi(O z2{t) ... гг(г)]т=Н-Х(О,
где Н-(гхп) - заданная матрица.
Как уже отмечалось, с помощью измерителя измеряются или часть компонент
вектора состояния или некоторых сигналов, функционально связанных с
компонентами вектора Х(г), причем г < п .
Закон управления имеет вид
n(*1(0,*2(0,.-,^(0)=CT-Z(0 = CT.H.X(0, (8.190)
где, в связи с тем что и - скалярная функция, С - r-мерный вектор неизвестных
параметров. Элементы этой одностолбцовой матрицы cl,c2,...,cr подлежат
определению.
Учитывая, что x(t) - выходной сигнал - зависит от компонент вектора С, то
функционал (8.189) можно записать в виде
т
/(C) = J[^C)-y(0F*, (8.191)
о
а задача слежения формулируется как задача минимизации функционала (8.191), т.е.
/(С) -> min.
с
Сделаем важное замечание, связанное с вопросом точности решения
поставленной задачи [75]. В связи с предположением, что г <п , т.е. измеряется лишь часть
координат вектора состояния, выходная переменная x(t) может быть с какой-то
степенью точности приближаться к эталонному сигналу y(t). Точное совпадение
x(t) = y(t) возможно лишь тогда, когда для построения u(t) используются все ком-
Глава 8. Метод матричных операторов
559
поненты вектора состояния X(t), т.е. г = п . В частности, это достигается при
единичной матрице Н . В этом случае значение функционала (8.189) теоретически равно
нулю.
Следующим важным фактом является то, что в отличие от решения задачи
Е.А. Барбашина, в которой U*(0 - программное управление, в рассматриваемой
задаче система строится по принципу обратной связи (рис. 8.55).
j
х(о
z,(0
Измеритель
сматрицейН
x(t)
ЖР
!___1
Рис. 8.55. Структурная схема системы слежения
Таким образом, решение поставленной задачи слежения свелось к отысканию
минимума функционала (8.191) по параметрам ck, к = 1,г.
Для решения поставленной задачи воспользуемся аппаратом матричного
представления операторов и конечномерной оптимизацией.
Если задачу сформулировать так:
1
/(C) = Jkr,C)-y(0F*->mn
при ограничениях
Х(0 = (а + b • Ст • н)- Х(0, *(0 = qT • Х(г),
X,(0 = F-X3(0, y(t) = qT3'XD(t), Х(0) = Хэ(0),
то матричный эквивалент этой задачи имеет вид
Пс) = Efe)2 -2схксук +(с4у)2]-> min
при ограничениях
сх =(а+ь-ст-н)-аи-сх+ф^,
CXj =F-AH-CXj+O^, Cy=qJ-CXj,
где Аи - матричный оператор интегрирования.
Если накладываются ограничения на управление м(г), то к (8.192) следует
добавить ограничение w(f)e Ux.
Эта задача относится к классу задач математического программирования.
(8.192)
560
Анализ и статистическая динамика САУ. Часть I
Далее рассмотрим конкретные примеры, приведенные в [86], но решенные
методом, изложенным в настоящем параграфе.
Пример 8.11. Векторно-матричное уравнение системы имеет вид [75]
Х(г) = А • Х(0 + b • u(t), jc(f) = qT • X(f), X(0) = Xo, ' (8.193)
где X(0 = [^(O x2(t) Xs(t)Y - вектор координат состояния,
u(t) - управляющая функция,
x(t) - скалярная выходная функция,
А =
0 1 0
0 0 1
-1 -4 -2
.ь=
0
0
1
• q=
1
0
0
• хо =
1
0
0
Формула, определяющая закон управления, имеет вид
и(*) = ст.Н.Х(г),
где с = [с, с2 с3Г ~ вектор неизвестных параметров, которые подлежат определению;
(8.194)
1
0
0
0
1
0
0
0
1
Задано векторно-матричное дифференциальное уравнение, описывающее эталонный процесс
X,(0 = F-X9(0. y(O=qTX,(/). Хэ(0) = Х(0),
(8.195)
где
0"
1
-6
Т
0
0_
0 1
о о
-6 -11 -6
Необходимо определить искомые параметры с{, с2> с3» такие, при которых значение функционала
(Г« 12 с)
т
I=j[x(t)-y(t)fclt (8.196)
о
принимает минимальное значение, т.е. необходимо определить искомые параметры из условия, чтобы
выходная переменная x(t) максимально приближалась к эталонному процессу y(t) в смысле среднего
квадрата.
Поставленную задачу будем решать методом, рассмотренным в этом параграфе. В качестве базисных
функций Ф(/) = [ф|(/) ф2(0 ... ФДОГ выберем функции Уолша, упорядоченные по Уолшу, и будем
удерживать / = 32 члена разложения. Функционал (8.196) можно переписать следующим образом
/ = }к(0 + /(0-2^(0->'(0к = (С*)т-]>Ф(0-ФТ(0>Л-Сдг +
(8.197)
т т
+ (СУ)Т -|ф(/).фт(0Л-С' -2-(C*)T .|ф(/).фт(0Л-С =
о о
= (С^.С'+(С>)тХ^-2.(С')т.С^=|;[(^)2+к)2--2.^.с>],
где С* - спектральная характеристика скалярного сигнала x(t); Cv - спектральная характеристика
скалярного сигнала y(t).
Найдем спектральную характеристику Су выходного сигнала эталонной модели. Интегрируя
дифференциальное уравнение (8.195), получим
т
X,(/)=Fjx,(t)tft+X,(0),
или, в развернутом виде,
Глава 8. Метод матричных операторов
561
/=1 о
»=1
*?(<)= £/* }*?(Ф+*3э(о).
i=\ О
Используя понятие спектральных хараклеристик сигналов, последнюю систему уравнений можно
записать в виде
•Аи
сх'
+ cxi(0)f
+ С*0).
6
-3
0
-1.5
0
0
0
-0.75
3
0
-1.5
0
0
0
-0.75
0
0
1.5
0
0
0
-0.75
0
0
1.5
0
0
0
-0.75
0
0
0
0
0
0
0.75
0
0
0
0
0
0
0.75
0
0
0
0
0
0
0.75
0
0
0
0
0
0
0.75
0
0
0
0
0
0
0
Г1-/..-А., -/«-А. -/„-А.] С' С*™
-/21-А. 1-/и'А. -Л,-А. • С' = С*0» . (8.198)
.-/«•A» -/«-A. I-/M-Aj[c^J [С'-(О)
где I - единичная матрица размерностью 1x1; Аи - матрица оператора интегрирования в базисе функций
Уолша размерностью 1x1, клетка размерностью 8x8 которой будет выглядеть следующим образом
А =
СХ|(0) - вектор спектральной характеристики /-го (/='1,2,3) начального условия, первые элементы
которого будут соответственно равны элементам *?(()) вектора Хэ(0), а остальные элементы - нулевые
Из уравнения (8.198) с учетом числовых значений матрицы F находим
С*'
с*'
Теперь можно определить спектральную характеристику скалярного выходного сигнала y(t)
C>=£qrC*'.
Приведем первые восемь значений спектральной характеристики
С*= [0.1528 0.1516 0.1293 0.1303 0.0585 0.0579 0.0721 0.0728Г.
Полагая известным вектор Су , можно построить выходной сигнал эталонной модели y(t), который
представлен на рисунке 8.56.
Найдем спектральную характеристику скалярной выходной функции x(t) Подставляя (8 194) в
(8.193), получим
X(0 = (A + bcT-H)x(0 = D(c)X(r), (8.199)
где D(c) = A + bcTH.
37 Зак. 232
I
0
-6А..
-Ан
I
-ПА..
0
-Аи
1-6 А
С*'
(0)"
(0)
(0)
562
Анализ и статистическая динамика САУ. Часть I
Матричный эквивалент (8 199) имеет вид
(У1
С2
Сх>
1-</н(с)А„ -</12(с) А„ -</п(с) Аи
-J21(c).A,, 1-./22(с).А„ -</23(с) Аи
-</31(с)Аи -d,2(c) А„ 1-г/зз(с)Ам
-1
с
с
с
1) "
к|
0
*2
0
(8.200)
Отсюда находим спектральную характеристику скалярного сигнала x(t)
C<(c) = £q, С'(с).
/ = 1
С учетом последнего соотношения легко видеть, что функционал (8.197) будет зависеть от искомого
вектора с , т е
/(с) = (Сс(с))т .С*(с) + «У)Т •С> -2-(СЛ(с))' С\ (8.201)
Поскольку с помощью матричных операторов представилась возможность в явной форме найти
зависимости, определяющие спектральные характеристики сигналов x(t) и v(/), то это привело к упрощению
задачи - она формулируется как задача на безусловный экстремум.
Естественно, такое упрощение невозможно при наличии ограничений на управление u(t).
xit)x
09
П б
U.о
О 7
П f\
О S
О 4
О ^
п о
U.Z
Г^ 1
.. V • - -
" " \ "
\
. . . . \ .
\
\
i
\
\
л. v
= y(t)
= x'(t)
Г,С
О 2 4 6 8 10
Рис. 8.56. Графики скалярных сигналов v(/) и x*(t,c*)
12
Минимум функционала (8 201) будем искать с использованием алгоритма Нелдере - Мида -
алгоритма безусловной оптимизации функции многих переменных В качестве начальных значений искомых
параметров с,, съ с, примем нулевые, т.е с0 = [0 0 of В этом случае матрица D(c0) имеет вид
'0 1 0
D(co)= 0 0 1
-1 -4 -2
а спектральная характеристика Сд(с0) с удержанием первых восьми элементов запишется так
Сг(с0) = [0.3225 0.2246 0.0932 0.1327 0.0281 0.0199 0.0455 0.0660^;
функционал (8.201) имеет значение
/(с0) = 3.9567 -10~2.
Минимум функционала (8 201) при точности расчета е = 0.0001 достигается в точке
с* =[-5.0 -7.0 -4.0F-
При с* матрица D(c) принимает вид
Глава 8. Метод матричных операторов
563
D(c*) =
1.00
0
0
1.00
-6.00 -11.00 -6.00
причем
Сх(с*)= [0.1528 0.1516 0.1293 0.1303 0.0585 0.0579 0.0721 0.0728^.
Значение функционала (8.201) в точке с* У (с*) = 1.8319 10~15-
На рисунке 8.56 показаны выходные y(t) и x*(t,c*) Результаты совпали с результатами,
полученными в [75].
Структурная схема системы представлена на рис. 8.57.
В предыдущем примере эталонное движение задавалось с помощью
соответствующего дифференциального уравнения.
В следующем примере рассмотрим случай, когда эталонный процесс задается
аналитической зависимостью.
Пример 8.12. Рассмотрим систему, математическая модель которой приведена в предыдущем примере.
Пусть задан эталонный сигнал y(t), который необходимо получить на выходе системы (8.193); положим
y(r) = 0.5-sinr. (8.202)
График эталонного сигнала y(t) приведен на рисунке 8.58.
Зная эталонный сигнал (8.202), найдем вектор начальных условий
0
Хп =
Необходимо определить искомые параметры с,, с2« с3 такими, при которых функционал
принимает минимальное значение (Т = 16 с)
Функционал (8.203) можно переписать следующим образом
1 =(СК? -Сх +(СУ)Т -Су -2-(Сх)т -Су *
где
Cv=[0.0557 0.0124 0.1568 -0.0152 0.1732 0.0386 -0.1413 0.0137^
(удерживается восемь элементов спектральной характеристики).
Поскольку
(8.203)
(8.204)
X(0=D(c)-Jxfc)rfc+X(o)i
(8.205)
где D(c) = A + bcT H , то матричный эквивалент (8.205) имеет вид (8.200) (см. предыдущий пример), где
Аи- матрица оператора интегрирования в базисе функций Уолша размерностью 1x1, клетка
размерностью 8x8 которой имеет вид
А =
Сх> - спектральные характеристики начальных условий (/ = 1,2,3), первые элементы которых будут
соответственно равны элементам *.(0) вектора Х(0), а остальные элементы - нулевые.
Из предыдущих рассуждений имеем
C*(c) = ]£qrC*'(c).
8
-4
0
-2
0
0
0
-1
4
0
-2
0
0
0
-1
0
0
2
0
0
0
-1
0
0
2
0
0
0
-1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
0
37*
564
Анализ и статистическая динамика САУ. Часть I
XI
о о
4Z
О —I
*-* о
о о
I
"3-
II
<
II
а
о о —■
О -н О
*-* о о
-Лт-
6
OS
Глава 8. Метод матричных операторов
565
Далее приведем результаты расчетов Матрица D(c0) имеет вид
"0 1 0
D(co) =
0 0 1
_! _4 -2
Спектральная характеристика сигнала x(t) запишется так
Сг(с0) = [0.0619 0.0507 0.0266 0.0323 0.0119 00102 0.0176 0.0208^,
а функционал (8 204) примет значение
/(со) = 1.О8581О~1.
Минимум функционала (8 204) при точности расчета е = 0.0001 достигается в точке
с* = [- 3.9075 2.9894 - 2.6075]7 •
При найденных оптимальных значениях искомых параметров матрица D запишется в виде
0 1.0000 0
D(c*) = 0 0 1.0000
-4.9075 -1.0106 -4.6075
а для С* при с = с* справедлива формула
С*(с*) = [0.0582 0.014 0.1517 -0.032 0.1922 0.05 -0.1163 0.0208Г-
Значение функционала (8 204) в точке с* /(с*) = 2.149-10"3.
На рис 8.58 приведены сигналы y(t) - эталонный процесс и x*(t,c*) - реальный выходной сигнал
Структурная схема совпадает с той, которая представлена на рис 8.57.
у(0'
10
12
14
16
Рис. 8.58. Графики сигналов y(t) и л*(/)
8.14.4. Алгоритм решения задачи слежения:
воспроизведение эталонного вектора состояния
Приведенные выше положения, связанные с воспроизведением эталонного
выходного сигнала, можно обобщить на случай, когда ставится задача слежения за
эталонным вектором состояния Хэ(0 .
566 Анализ и статистическая динамика САУ. Часть I
Рассмотрим с целью упрощения изложения случай, когда система описывается
уравнением
X(t)= АХ(г)+Ьм(0, Х(0)=Х°. (8.206)
Необходимо построить асимптотически устойчивую систему, обладающую
требуемыми динамическими свойствами. Пусть этим свойствам системы (8.206)
соответствует эталонная система
X3(0 = F.X3(0, Хэ(0) = Х£, (8.207)
или желаемое движение (8.206) задано эталонной вектор-функцией Хэ(/) в виде
аналитической зависимости.
Мера близости реального движения Х(/) к эталонному Хэ(0 определяется
функционалом
т
/=J[x(O-X,(r)T -У-[Х(О-Х,(О]А. (8.208)
о
где V - заданная положительно-определенная матрица.
Закон управления примем в виде:
u(t) = Ст • Z(f), (8.209)
где Z(/) - г-мерный (г<п) измеряемый вектор, функционально связанный с
вектором состояния системы Х(/);
Z(0 = H-X(0, (8.210)
матрица Н -задана, C = [c|,c2,...,crJr - вектор неизвестных параметров, элементы
которого необходимо определить.
Учитывая (8.209) и (8.210), получим, что вектор состояния Х(г) системы (8.206)
зависит от искомого вектора С , следовательно, функционал (8.208) также будет
зависеть от С . Тогда можно записать
т
/(С) = |[х(г,С)-Хэ(0Г-У-[х(г,С)-Хэ(0^ (8.211)
о
и задача формулируется аналогично задаче, рассмотренной в параграфе 8.14.3, т.е.
/(С) -» min.
с
Отличие заключается в том, что в предыдущей задаче искомые параметры
cl,c2,...,cr определялись из условия наилучшего приближения скалярных выходных
переменных x(t) и y(t). В данной же задаче с{,с2,...,сг - из условия наилучшего
приближения вектора состояния синтезируемой системы X(t) и эталонного Хэ(г).
Кроме того, рассматриваемой задаче присущи некоторые особенности [75]. Эти
особенности обусловлены тем, что структура оптимизируемой системы должна быть
тождественна эталонной, т.е. уравнения движения управляемой и эталонной систем
должны быть записаны в какой-либо единой канонической форме, например, в форме
фазовых координат. Переход к описанию систем уравнениями в фазовых
координатах изложен в [75]. Предположим, что системы (8.206) и (8.207) описаны
уравнениями в фазовых координатах.
Отметим также, что полное совпадение траекторий движения синтезируемой
системы (8.206) и эталонной (8.207) достигается в том случае, когда для формирования
управляющей функции u(t) используется полный вектор состояния Х(/). В против-
Глава 8. Метод матричных операторов
567
ном случае движение системы (8.206) будет проходить в окрестности эталонной
траектории Хэ(г).
Таким образом, поставленная задача слежения, как и в предыдущем случае,
сводится к отысканию минимума функционала (8.211) по параметрам с,,с2,...,сг.
На рис. 8.59 представлена структурная схема синтезируемой системы.
j
Х(0
£>
Измеритель ^d
Измеритель
сматрицейН
Рис. 8.59. Структурная схема системы
Решать поставленную задачу будем с использованием аппарата матричного
представления операторов и конечномерной оптимизации. В этом случае функционал
(8.211) можно записать в следующем виде:
Т п п
/(С) = J X SV«(*<(С)" *> )ixi(C)" */ ^ =
о <=i /=1
= X2vj/[cl4C)-c*']T[cJt'(C)-cirJ] =
п и I
i=l /=1 Лг=1 L J
Задачу можно сформулировать следующим образом:
/=1 у=1 а=1 L J L
при ограничениях
сх =(а + ьстн)аисх+ф^
СХ> =FAHCX' +Ф^,
где Аи - матричный оператор интегрирования.
Рассмотрим конкретный пример.
Пример 8.13. Вектормо-матричное уравнение системы имеет вид
Х(г) = А • Х(/) + b • u(t), Х(0) = Хо,
где Х(г) = [лг,(/) л-2(0 x^(t)f - вектор координат состояния,
м(0 ~ управляющая функция,
• mm
с
(8.212)
(8.213)
(8.214)
568
Анализ и статистическая динамика САУ. Часть I
А =
О 1
О О
О'
1
-2
, ь =
"о"
О
1
"1"
О
О
-1 -4 -2
Закон управления определяется формулой
м(О = ст-Н-Х(О»
где с = [с, с2 c3Y - вектор неизвестных параметров, которые подлежат определению,
Н =
(8.215)
1
0
0
0
1
0
0'
0
1
Требуемым динамическим свойствам синтезируемой системы (8.214), (8 215) соответствует эталонная
система
X3(0 = F.X,(O.X,(0) = X(0). (8.216)
где
О 1 О
О 0 1
-1.04 -2.7 -3 25
Неизвестные параметры с,,с2,с'3 будем искать из условия достижения функционалом
F =
1
= J[x(o-x,(/)]r-v.[x(o-x,(ok
(8.217)
минимального значения (Т= 16 с)
Здесь V - положительно определенная матрица,
V =
Запишем векторно-матричные уравнения (8 214) и (8 216) в развернутом виде
л-,(г) = л2(О,
*2(О = л-3(О.
д:3(О = -л,(О-4 Jf2(O--v3(/) + «(O
1
0
0
0
1
0
0
0
5
(8.218)
i?(/) = -1.04 .vf(0-2.7-x?(/)-3.25-jcJ(/).
(8.219,
Нетрудно замегить, что системы уравнений (8 218), (8.219) записаны в одной форме - форме систем урав
нений в фазовых координатах
Задачу оптимизации по состоянию будем решать методом, рассмотренным в этом параграфе. В каче
стве базисных функций Ф(/) = [ф|(О,Ф2(О,....Ф/(ОГ выберем функции Уолша, упорядоченные по Уолшу
и будем удерживать / = 32 члена разложения Обозначив5(г,С) = Х(/,С)-Хэ(/), функционал (8 217
можно переписать следующим образом
/(О = }бт(/,С)- V .8(,,ф, = JX ]>>(,,C)5,.(,.CV = X X v j8,(r,C)5;(r,C>/, =
0 0 '=1 У=1 '=1 У=| 0
3 3 Т 3 3 (8220
= SSV jc5' (С)ф(')фт(0-с5' (ол=J£vtf -(с5' (о)т -с5' (с),
1=1 у=1 о '=1 У=>
где Cs< - спектральная характеристика /-го компонента вектора б(/,С) •
Рассмотрим эталонную модель Интегрируя дифференциальное уравнение (8 216), в развернутом вид
получим
Глава 8. Метод матричных операторов
569
4(')=Хл,}*?(Ф+*.э(о),
i=l О
^(')=^^|л-?(т)Л + ^(0),
|"=1 О
Используя понятие спектральных характеристик сигналов, последнюю систему запишем в виде
c*l'=X;fhA,-c*+cA'>(0)'
i=i
*-2ь
А -С* +С
х] (0),
~/21 Аи I-/22 ' Аи
С*0)
(8.221)
-Лз Аи] С"
-/23-Ан • С'
-/з! Аи -/зз-А,, I-/33-AHJ |СХ'
где I - единичная матрица размерностью 1x1;
А„ - матрица оператора интегрирования в базисе функций Уолша размерностью 1x1, клетка
размерностью 8x8 которой будет следующей
А =
С1(>(0) - вектор спектральной характеристики /-го (/ = 1,2,3) начального условия, первые элементы
которого будут соответственно равны элементам л?(0) век гора Хэ(0), а остальные элемешы - нулевые
Из уравнения (8 221) с учетом числовых значений матрицы F находим
8
-4
0
-2
0
0
0
-1
4
0
-2
0
0
0
-1
0
0
2
0
0
0
-1
0
0
2
0
0
0
-1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
0
с-
=
I
0
-6 А..
-Ан
I
-ПА.
I
0
-Аи
-6А..
-1
С'
ск
сх
(0)
(0)
(0)
Первые восемь элементов векторов спектральных характеристик фазовых координат эталонной модели
следующие
СГ|' = [0.1622 0.1686 0.1617 0.1545 0.0471 0.0511 0.0737 0.0695f;
Сxi =[-0.0625 -0.0665 -0.0402 -0.0365 0.022 0.0212 -0.0012 0.0002J1";
С?; =[-0.00002 0.0011 -0.0219 -0.0222 -0.0309 -0.032 -0.0201 -О.О^б]7.
На рисунке 8 60 представлены графики фазовых координат эталонной системы Найдем спектральные
характеристики фазовых координат системы (8 214) Подставляя (8 215) в (8.214), находим
Х(/) = (А + b • ст • II). Х(г) = D(c) • X(f), (8 222)
где D(c) = A + b cT-II.
Матричный эквивалент (8.222) следующий
36 Зак. 232
J/U
Анализ и статистическая динамика ^яу . часть 1
С*'
С*2
-1
С4
(8.223)
1-</„(с)-Аи -</12(с)Аи -^13(с)-Аи
-421(с)-Аи 1-</22(с)Аи -</23(с)-Аи
-</31(с)Аи -</32(с)Аи 1-</33(с)-Аи_
Отсюда легко найти спектральные характеристики фазовых координат.
Минимум функционала (8.220) будем искать с использованием алгоритма Нелдере - Мида -
алгоритма безусловной оптимизации функции многих переменных. В качестве начальных значений искомых
параметров Ci,c2,c3 примем нулевые,те. с0 = [0Д0]т.
В этом случае матрица D(c0) имеет вид
"0 1 0
*>(со) =
0
1
-1 -Л -2
первые восемь элементов векторов спектральных характеристик фазовых координат оптимизируемой
системы
C*l(c0) = [0.2474 0.2019 0.1046 0.1281 0.0379 0.0314 0.0589 0.0716f,
С*2(с0) = [-0.0618 -0.0488 -0.0218 -0.0285 0.0013 0.0032 -0.0036 -0.0072^,
C*4co) = [-0.0004 -0.0038 -0.0095 -0.0077 -0.0264 -0.0268 -0.0280 - 0.027 l]r,
а функционал (8.220) имеет значение/(с0) = 2.1528-Ю~2 •
Минимум функционала (8 220) при точности расчета е = 0.0001 достигается в точке
с* =[-0.04 1.3 -1.2501]7-
При с* матрица d(c) принимает вид
0 1.00 0
D(c*) = 0 0 1.00
-1.04 -2.7 -3.2501
а первые восемь элементов векторов спектральных характеристик фазовых координат
C*'(c*) = [0.2474 0 2019 0.1046 0.1281 0.0379 0.0314 0.0589 0.0716 J >
C*4c*) = [-0 06l8 -0 0488 -0.0218 -0.0285 0.0013 0.0032 -0.0036 -0.0072 J",
СХЧС) = [-0.0004 -0.0038 -0.0095 -0.0077 -0.0264 -0.0268 -0.0280 -0.0271 J •
Значение функционала (8 220) в точке с*
7(с*) = 2.47310"12.
На рисунке 8.60 показаны фазовые координаты д:*(г,с*) и xj(t), i = 1,2,3.
i
f\ О
0.8
U.о
0 4
П 9
0
-0 2
\
• • • •/
\ о
/(0
•
•
* • • 1 - • Ч^
+
т
0
—
x2{t)
хэ3(0
X3(t)
t, с
0 2 4 6 8 10 12 14 16
Рис. 8.60. Графики фазовых координат*?(г) и .г*(г,с*)
Глава 8. Метод матричных операторов
571
8.14.5. Алгоритм решения нестационарной задачи слежения
Рассмотрим объект, математическая модель которого представлена векторно-
матричным дифференциальным уравнением
Х(0 = А(0Х(0 + Ь(0и(0, Х(0) = ХО, (8.224)
где матрица А(г) и вектор b(r) зависят от времени.
Как и ранее, закон управления принимаем в виде
и(Х)=СтНХ(О, С = [с, с2 ... с,]7, (8.225)
причем искомые параметры ск также зависят от времени, т.е. ck =ck(t), к = 1,г .
По-прежнему будем рассматривать задачу определения оптимальных значений
параметров ck{t) из условия, чтобы траектория Х(г) замкнутой системы (8.224),
(8.225) в наибольшей степени приближалась к траектории Хэ (г) некоторой
эталонной системы
Хэ (Г) = F(r)X3 (Г), Хэ (0 = Хо . (8.226)
В качестве меры близости траекторий движения синтезируемой системы (8.224),
(8.225) и эталонной (8.226) принимаем функционал
7(С) = |[Х(г,С)-Хэ(0ГУ(г)[Х(/,С)-Хэ(0к
(8.227)
причем элементы положительно-определенной матрицы V(r) могут быть функциями
от времени.
Как нетрудно заметить, задача определения искомых параметров ck (t) сводится к
задаче безусловной минимизации функционала (8.227)
/(С)-
>min.
с
Представим искомые параметры ск (/) в виде
т
(8.228)
i=i
где dki - постоянные неизвестные коэффициенты, которые подлежат определению,
ф1(г)ф2(^...,фт(0 - система известных линейно-независимых функций.
В этом случае искомый вектор С(г) равен
с(0=
*2\
d22
l\m
Чт
>i(0"
ф2(0
ф*"(0
= ВФ(г).
'rl dr2 "• 4гт.
С учетом (8.229) закон управления (8.225) можно записать
tf(X) = OT(r)DTHX(0.
Тогда уравнение (8.224) примет вид
х(о = (а(о+фт(Фтн)х(о,
или
X(f,D)=G(f,D)-X(f,D),
где G(r,D)= А(г)+Фт(г>)тН.
36*
(8.229)
(8.230)
(8.231)
572 Анализ и статистическая динамика САУ. Часть I
Как видно из (8.231), траектория замкнутой синтезируемой системы (8.224),
(8.225) будет зависеть от постоянных параметров dki. Следовательно, и функционал
(8.227) будет зависеть от матрицы D.
Таким образом, можно записать
I(D) = j[X(t,D)-X3(t)Yv(tlX(t,D)-X3(t)]dt
о
И задача может быть сформулирована следующим образом
(8.232)
/(D) -» min
D
и
Воспользуемся аппаратом матричного представления операторов. В этом случае
функционал (8.232) примет вид
/a»=EE[cx'(D)-cJt?lTcVe[cx'(D)-cJtJl=
1=1 ;=1L J L J
;_| ;^t ,,^i „_i L J L J >
/=l /=1 ^=1 <7=1u
где CXi(D) - спектральная характеристика компонента вектора состояния X(f,D)
синтезируемой системы;
С*1 - спектральная характеристика компонента вектора Хэ(0 ;
С у - спектральная характеристика множительного элемента.
Рассмотрим эталонную систему (8.226). Проинтегрировав уравнение, в
развернутом виде получим
п Т
v=l о
п Т
xl(t) = ^]f2v(t)x3At)dt + xU0)
v=l о
« Т-
*2(O = SJ fnv(t)xU0dt + x3n(0).
v=I о
Матричный эквивалент (8.233) имеет вид
С*1
С4
А^Л' АИС^ ... АиС'"
А„СЛ' АиС/и ... А„С/2'
АХ'*1 АХ7»2 ... AuCf-
С
с
[с
*]
+
с
с
с
-г'(0)~
•v2'(0)
(8.233)
(8.234)
где Аи - матрица оператора интегрирования; С j - матрица множительного
элемента.
Уравнение (8.234) можно записать в свернутом виде
Сх> =АИСРСХ'+Ф^, (8.235)
здесь
Глава 8. Метод матричных операторов
573
СХз =
CF =
С'»' .
.. с'-"
.. с1-
с1'
(0)"
(0)
Аналогичным образом от уравнения (8.231) переходим к его матричному
эквиваленту
CX=AHCG(D)CX+OV (8.236)
Таким образом, можно сформулировать следующую задачу
п I I
;_1 :_1 „_1 I *- -• L. J
1=1 /=1 />=l q=\
—> min
D
при ограничениях
CX=AHCG(D)CX+O^,
Сх> =АИСРСХ'+Ф^.
(8.237)
Если накладываются дополнительные ограничения на управление u(t), то к
условиям (8.237) необходимо добавить ограничение u(t)eUl и поставленную задачу
решать методами математического программирования.
8.15. РЕАЛИЗАЦИЯ АЛГОРИТМОВ СПЕКТРАЛЬНЫХ МЕТОДОВ
В СРЕДЕ ПАКЕТА MATLAB
Удобным средством программной реализации рассмотренных в этой
книге.спектральных методов расчета и проектирования систем управления является известный
пакет MATLAB фирмы Math Works, Inc.
Пакет MATLAB ориентирован на решение широкого класса вычислительных
задач, предполагающих активное использование матричных операций. Взаимодействие
с пакетом осуществляется на естественном матричном языке в интерактивном
режиме. Имеется большой набор встроенных операций: арифметические действия над
матрицами, обращение матриц, решение систем линейных уравнений, вычисление
собственных векторов и собственных значений, быстрое преобразование Фурье,
расчет цифровых фильтров и др. Есть возможность работы с разреженными матрицами.
В пакете MATLAB имеются удобные средства графического представления
результатов вычислений: построение двух- и трехмерных графиков, графиков в
логарифмическом масштабе, различных диаграмм и др. Версия пакета для операционной
среды Windows дополнительно позволяет реализовать в программе на языке
MATLAB многооконный интерфейс пользователя со стандартными элементами
управления в стиле Windows.
Важным свойством пакета MATLAB является его открытость и способность к
расширению. Пользователи могут легко добавлять в MATLAB новые функции,
ориентируя пакет на использование в своих предметных областях. Имеется, например,
несколько САПР САУ, разработанных на базе пакета MATLAB [168].
Сказанное выше позволяет сделать вывод, что пакет MATLAB хорошо подходит
для программной реализации алгоритмов спектральных методов, опирающихся на
матричное представление данных и матричные операции. Дополнительным
преимуществом является наличие в пакете MATLAB мощной и гибкой системы управления
памятью (в том числе виртуальной памятью), которая позволяет практически забыть
о технических проблемах размещения больших матриц в программах, реализующих
спектральные методы. Это дает возможность использовать большее число членов
574 Анализ и статистическая динамика САУ. Часть I
разложения по ортогональному базису, что в конечном итоге повышает точность
расчетов.
В качестве примера рассмотрим библиотеку типовых вычислительных процедур,
написанных на языке пакета MATLAB, которые могут быть использованы при
реализации спектральных методов в базисе функций Уолша.
Процедуры библиотеки, условно названной SML, оформлены в виде функций
языка MATLAB. Каждая функция размещается в отдельном текстовом файле типа
«.т», имя которого совпадает с именем функции. Файлы с текстами функций
располагаются в одном подкаталоге, имеющем имя SML, который следует внести в список
подкаталогов пакета MATLAB.
Ниже приводятся исходные тексты функций библиотеки SML, реализованной в
среде MATLAB версии 5.0, с необходимыми пояснениями. Справочную информацию
по языку и встроенным функциям пакета MATLAB можно найти в документации,
входящей в комплект поставки пакета. Необходимую информацию также можно
получить, воспользовавшись развитой справочной системой пакета MATLAB.
Библиотека SML включает 16 основных функций (SETSIZE, SETTIME, FWHT,
IWHT, FWHT2, IWHT2, MKINT, MKDIF, MKMUL, SHFUN, SHFUN2, SHVEC,
SHMAT, PUTMAT, GETVEC, GETMAT) и 7 вспомогательных (MKHW, HW,
RGREY, BINXOR, D2B, B2D, МКМАТ), используемых основными функциями.
Функция SETSIZE. Задает число членов разложения по ортогональному базису.
SETSIZE(AO - задает N членов разложения, где N = 2*, к =0,1,2,.... Значение N
используется затем по умолчанию всеми остальными функциями библиотеки SML.
Функция SETSIZE инициализирует ряд глобальных переменных и обязательно
должна выполняться перед использованием любых функций библиотеки SML.
См. также SETTIME.
function SETSIZE(N)
ifN~ = 2Afix(log2(N))
error ('?SML-E-Heдoпycтимoe число членов разложения')
return
end
global SML_SIZE SML_Ww SMLJWw SML_MAT
SMLJSIZE = N;
HFNAME = sprintf('SML_W%03d.DAT',SML_SIZE);
ifexist(HFNAME) = = 2
FR = fopen(HFNAME, V);
[SML_Ww, CNT] = fread(FR, inf, 'real*4');
if CNT = = SML_SIZE*SML_SIZE
frewind(FR);
SMLJWw = fread(FR, [SML_SIZE,SML_SIZE], 'real*4');
fclose(FR);
SMLJWw = SMLJWw * SMLJSIZE;
else
fclose(FR);
[SMLJWw, SMLJWw] = MKHW;
PUTMAT(SML_Ww, HFNAME)
end
else
[SML_Ww, SMLJWw] = MKHW;
Глава 8. Метод матричных операторов 575
PUTMAT(SML_Ww, HFNAME)
end
% Формирование матрицы-шаблона оператора умножения
HFNAME = sprintf CSML_M%03d.DAT, SMLJSIZE);
ifexist(HFNAME) = = 2
FR = fopen(HFNAME, V);
[SML_MAT, CNT] = fread(FR, inf, теа1*4');
if CNT = = SML_SIZE*SML_SIZE
frewind(FR);
SML_MAT = fread(FR, [SML_SIZE, SML_SIZE], 'real*4');
fclose (FR);
else
fclose(FR);
SML_MAT = MKMAT;
PUTMAT(SML_Ww, HFNAME)
end
else
SML_MAT = MKMAT;
PUTMAT(SML_Ww, HFNAME)
end;
Функция SETTIME. Задает интервал исследования.
SETTIME(T) задает интервал исследования от 0 до Г секунд. Значение Т
используется затем по умолчанию всеми остальными функциями библиотеки SML.
Функция SETTIME обязательно должна выполняться перед использованием
любых функций библиотеки SML.
См. также SETSIZE.
v function SETTIME(T)
V global SML_T
SML_T = T;
Функция FWHT. Прямое преобразование Уолша.
Y = FWHT(X) возвращает в векторе Y результат прямого преобразования Уолша
вектора X, упорядоченный по Уолшу. Размер вектора X должен соответствовать
числу членов разложения, заданному в SETSIZE.
FWHT и другие функции библиотеки SML, выполняющие прямое и обратное
преобразования Уолша, нб используют алгоритмы быстрых преобразований,
поскольку реализация этих алгоритмов на языке интерпретирующего компилятора
пакета MATLAB не дает заметного преимущества в быстродействии.
См. также IWHT.
function Y = FWHT(X)
global SML_Ww
Y = SMLJWw * X;
Функция IWHT. Обратное преобразование Уолша.
Y = IWHT(X) возвращает в векторе Y результат обратного преобразования Уолша
вектора X, упорядоченного по Уолшу. Размер вектора .X должен соответствовать
числу членов разложения, заданному в SETSIZE.
576 Анализ и статистическая динамика САУ. Часть I
См. также FWHT.
function Y = IWHT(X)
global SMLJWw
Y = SMLJWw * X;
Функция FWHT2. Прямое двухмерное преобразование Уолша.
Y = FWHT2(X) возвращает результат прямого двухмерного преобразования
Уолша матрицы X в виде матрицы Y. При этом используется упорядочение по Уолшу.
Размеры матрицы X должны соответствовать числу членов разложения, заданному
в SETSIZE..
См. также IWHT2.
function Y = FWHT2(X)
global SML_Ww
Y = SML_Ww * X * SMLJWw;
Функция IWHT2. Обратное двухмерное преобразование Уолша.
Y = IWHT2(X) возвращает результат обратного двухмерного преобразования
Уолша матрицы X в виде матрицы Y. При этом используется упорядочение по
Уолшу. Размеры матрицы X должны соответствовать числу членов разложения,
заданному в SETSIZE.
См. также FWHT2.
function Y = IWHT2(X)
global SMLJWw
Y = SMLJWw * X * SMLJWw;
Функция MKINT. Формирование матрицы оператора интегрирования в базисе
функций Уолша, упорядоченных по Уолшу.
Р = MKINT возвращает в виде результата матрицу оператора интегрирования Р
размером NxN , где N задается через SETSIZE(N).
См. также MKDIF, MKMUL.
function AI = MKINT
global SML_SIZE SML_T
M = SMLJSIZE;
PN = [l/2];
if M = = 1, return, end
N = 2;
L2M = log2(M);
forI=l:L2M
N1 = N/2; N2 = (eye(Nl))/(2*N);
PN = [ PN -N2;
N2 zeros (N1)];
N = N*2;
end
PP = zeros(M);
forI=l:M
I1=RGREY(I-1,L2M)+1;
Глава 8. Метод матричных операторов 577
forJ=l:M
PP(I1,J) = PN(IJ);
end
end
forJ= 1:M
J1=RGREY(J-1,L2M)+1;
forI=l:M
PN(I,J1) = PP(I,J);
end
end
AI = SML_T * PN';
Функция MKDIF. Формирование матрицы оператора дифференцирования в
базисе функций Уолша, упорядоченных по Уолшу.
D = MKDIF возвращает в виде результата матрицу оператора дифференцирования
D размером N х N , где N задается через SETSIZE(N).
См. также MKINT, MKMUL.
function AD = MKDIF
AD = inv(MKINT);
Функция MKMUL. Формирование матрицы оператора умножения на функцию
x(t) в базисе функций Уолша, упорядоченных по Уолшу.
М = MKMUL возвращает в виде результата матрицу оператора умножения М
размером NxN , где N задается через SETSIZE(N). При этом вектор X размером N
должен содержать отсчеты функции x(t).
См. также MKINT, MKDIF.
function AM = MKMUL(X)
global SMLJSIZE SML.Ww SML_MAT
N = SMLJSIZE;
AM = zeros(N);
F = SML_Ww * X;
forI=l:N
forJ= 1:N
AM(I,J) = F(SML_MAT(I, J));
end
end
AM = AM';
Функция SHFUN. Построение графика функции.
SHFUN(X) рисует график функции, отсчеты которой заданы вектором X на
интервале от 0 до Т, где Т задается через SETTIME(T). Размер вектора X должен
соответствовать заданному в SETSIZE.
См. также SHFUN2, SHVEC, SHMAT.
function SHFUN(Y)
global SMLJSIZE SML_T
X = zeros(SML_SIZE,l);
DEL = SML_T/(SML_SIZE-1);
578 Анализ и статистическая динамика САУ. Часть I
forI=l:SML_SIZE
X(I) = (I-1)*DEL;
end
plot(X,Y)
grid
MINY = min(Y); MAXY = max(Y);
if MINY ~ = MAXY
axis([min(X) max(X) MINY MAXY])
end
xlabelCf), ylabel('f(t)')
titlefPress any key to continue...')
pause;
Функция SHFUN2. Построение трехмерного графика функции.
SHFUN2(X) рисует проекцию поверхности функции двух переменных, отсчеты
которой заданы матрицей X размером NxN на интервале (0,Г)х(0,Г), где N
задается через SETSIZE(N), Т- через SETTIME(T).
См. также SHFUN, SHVEC, SHMAT.
function SHFUN2(Z)
global SMLJSIZE SML_T
X = zeros(SML_SIZE,l);
DEL = SMLJT/(SML_SIZE-1);
forI=l:SML_SIZE
X(I) = (I-1)*DEL;
end
Y = X;
surf(X,Y,Z)
view(140,30)
MINZ = min(min(Z)); MAX2 = max(max(Z));
ifMINZ~ = MAXZ
axis([min(X) max(X) min(Y) max(Y) MINZ MAXZ])
end
xlabel('tl'), ylabel('t2'), zlabel('f(tl,t2)')
title('Press any key to continue...')
pause;
Функция SHVEC. Наглядное представление вектора.
SHVEC(X) рисует столбцовую диаграмму, в которой высоты столбцов
пропорциональны значениям элементов вектора X. Размер вектора X должен
соответствовать заданному в SETSIZE.
См. также SHMAT.
function SHVEC(Y)
global SMLiSIZE
bar(Y)
grid
MINY = min(Y); MAXY = max(Y);
if MINY ~ = MAXY
axis([l SMLJSIZE MINY MAXY])
Глава 8. Метод матричных операторов 579
end
xlabel('Number'), ylabel('Value')
title('Press any key to continue...')
pause;
Функция SHMAT. Наглядное представление матрицы.
SHMAT(X) рисует трехмерную столбцовую диаграмму, в которой высоты
столбцов пропорциональны значениям элементов матрицы X размером NxN , где N
задается через SETSIZE(N).
См. также SHVEC.
function SHMAT(Z)
global SML_SIZE
mesh(Z)
view(140,30)
MINZ = min(min(Z)); MAXZ = max(max(Z));
if MINZ ~ = MAXZ
axis([l SML_SIZE 1 SMLJSIZE MINZ MAXZ])
end
xlabel('X Number1), ylabel('Y Number'), zlabel('Value')
title('Press any key to continue...')
pause;
Функция PUTMAT. Запись вектора или матрицы в файл.
PUTMAT(X, FNAME) записывает матрицу X в файл с именем FNAME, например,
PUTMAT(M, 'c:\smldata\m.dat').
См. также GETMAT, GETVEC.
function PUTMAT(X, FNAME)
FW = fopen(FNAME, V);
fwrite(FW, X, 'real*4');
fclose(FW);
Функция GETVEC. Чтение вектора из файла.
X = GETVEC(FNAME) возвращает в виде результата вектор X, прочитанный из
файла с именем FNAME. Размер вектора X должен соответствовать заданному в
SETSIZE,
См. также GETMAT, PUTMAT.
function X = GETVEC(FNAME)
global SML_SIZE
FR = fopen(FNAME, V);
[X, CNT] = fread(FR, inf, 'real*4');
if CNT = = SMLJSIZE
frewind(FR);
X = fread(FR, SMLJSIZE, 'real*4');
fclose(FR);
else
fclose(FR);
disp('?SML-E-Heпpaвильный размер вектора')
end
580 Анализ и статистическая динамика САУ. Часть 1
Функция GETMAT. Чтение матрицы из файла.
X = GETMAT(FNAME) возвращает в виде результата матрицу X, прочитанную из
файла с именем FNAME. Размер матрицы X - NxN, где N задается через
SETSIZE(N).
См. также GETVEC, PUTMAT.
function X = GETMAT(FNAME)
global SMLJSIZE
FR = fopen(FNAME, V);
[X, CNT] = fread(FR, inf, 'real*4');
if CNT = = SML_SIZE*SML_SIZE
frewind(FR);
X = fread(FR, [SML_SIZE, SML_SIZE], 'real*4');
fclose(FR);
else
fclose(FR);
disp('?SML-E-HenpaBRiibHbm размер матрицы1)
end.
Ниже описаны вспомогательные функции библиотеки SML.
Функция MKHW. Формирование матрицы Адамара, упорядоченной по Уолшу.
[Ww,IWw] = MKHW возвращает в виде результата матрицу Адамара Ww
размером NxN и матрицу IWw, обратную Ww.
MKHW используется функцией SETSIZE.
function [Ww, IWw] = MKHW
global SML_SIZE
M = SMLJSIZE;
IWw = zeros(M);
N = log2(M);
forI=l:M
forJ=l:M
IWw(I,J) = HW(I-l,J-l,N);
end
end
Ww = IWw/M;
Функция HW. Вычисление элементов матрицы Адамара, упорядоченной по
Уолшу.
Вспомогательная функция, используемая MKHW.
function VHW = HW(I,J,N)
IBIN = D2B(I,N+1);
JBIN = D2B(J,N+1);
S = 0;
forI=l:N
S = S + (IBIN(I)+IBIN(I+1)) * JBIN(N+1-I);
end
VHW = (-1)AS;
Глава 8. Метод матричных операторов 581
Функция RGREY. Преобразование кода Грея в десятичное представление.
Вспомогательная функция, используемая MKHW.
function R = RGREY(NUM, NL)
NBIN = zeros(NL+l,l); NGREY = zeros(NL,l);
NBIN = D2B(NUM,NL+1);
forI = NL:-l:l
ISUM = 0;
forIl=(NL+l):-l:(I+l)
if NBIN(Il) - = 0, ISUM = ISUM+1; end
end
ISUM2 = fix(ISUM/2);
ifISUM = = ISUM2*2
NGREY(I) = NBIN(I);
elseifNBIN(I) = = 0
NGREY® =1;
else
NGREY(I) = 0;
end
end
R = B2D(NGREY);
Функция BINXOR. Поразрядное исключающее ИЛИ.
Вспомогательная функция, используемая МКМАТ.
function С = BINXOR(A, В, N)
BINA = D2B(A,N);
BINB = D2B(B,N);
BINC = zeros(N,l);
forI=l:N
ifBINA(I)~ = BINB(I)
BINC(I)=1;
end
end
С = B2D(BINC);
Функция D2B. Преобразование десятичного числа в двоичное представление.
Вспомогательная функция, используемая HW, RGREY, BINXOR.
function IPOWER = D2B(NUM,N)
IPOWER = zeros(N,l);
IB = NUM;IL=1;
while 1
IBD = fix(IB/2);
IPOWER(IL) = 1;
ifIB = = IBD*2
IPOWER(IL) = 0;
end
if IBD = = 0, break, end
IB = IBD;
IL = IL+1;
end;
582 Анализ и статистическая динамика САУ. Часть I
Функция B2D. Преобразование двоичного числа в десятичное представление.
Вспомогательная функция, используемая RGREY, BINXOR.
function NUM = B2D(IPOWER)
N = length(IPOWER);
NUM = O;IFAC=1;
forI=l:N
NUM = NUM + IFAC*IPOWER(I);
IFAC = IFAC + IFAC;
end.
Заметим, что хотя в версии 5 пакета MATLAB появились стандартные функции
DEC2BIN и BIN2DEC, выполняющие взаимные преобразования двоичного и
десятичного представления чисел, в данной версии библиотеки SML используются их
собственные реализации, поскольку к моменту ее написания текущая версия пакета
таких стандартных функций не имела.
Использование стандартных функций DEC2BIN и BIN2DEC вместо приведенных
выше D2B и B2D требует соответствующей модификации функций HW, RGREY и
BINXOR.
Функция МКМАТ. Формирование шаблона матрицы оператора умножения.
Вспомогательная функция, используемая MKMUL.
function MAT = МКМАТ
global SMLJSIZE
N = SML_SIZE
L2N = Iog2 (N);
MAT = zeros (N);
forI=l:N
forJ = l:N
AT (I, J) = BINXOR (1-1, J-l, L2N) + 1;
«nd
end.
8.16. АВТОМАТИЗИРОВАННОЕ ПРОЕКТИРОВАНИЕ САУ
Характерной чертой новых методов анализа и проектирования систем
управления, отличающей их от классических, является, наряду с большей
сложностью и формализованностью, необходимость выполнения большого объема
вычислений. По этой причине применение методов современной теории управления
для решения практических задач невозможно без использования средств
вычислительной техники.
Вместе с тем просто наличие ЭВМ с соответствующей библиотекой стандартных
подпрограмм еще не гарантирует того, что инженеры станут широко использовать
указанные методы на практике. Дело в том, что при таком подходе, принятом на
раннем этапе использования ЭВМ, от проектировщика, помимо его специфических
профессиональных знаний и навыков, требуется умение самому писать и отлаживать
программы, работать с операционной системой и вообще помнить массу технических
деталей, касающихся организации вычислительного процесса. Все это в конечном
итоге нарушает аналитическую связь между формулировкой задачи и ее решением.
Глава 8. Метод матричных операторов 583
Отсюда логически вытекает необходимость обеспечить для проектировщика
возможность формулировать свои задачи в привычных ему терминах на естественном
для данной профессиональной области языке, т.е. создать с помощью ЭВМ
некоторую среду, позволяющую непрофессионалу в области вычислительной техники
эффективно решать свои чисто профессиональные задачи.
Попытки создать такую среду привели к появлению первых систем
автоматизированного проектирования. В настоящее время под системой автоматизированного
проектирования (САПР) понимается сложный комплекс технических и программных
средств ЭВМ, а также других компонентов, из которых формируются отдельные
инструменты проектировщика.
Можно дать следующее определение САПР [168]: САПР - инструментарий
проектировщика, включающий в себя техническое, математическое, лингвистическое,
программное, информационное, методическое и организационное обеспечение и
предназначенный для автоматизации проектирования объектов на конкретном
предприятии на всех этапах - от выдачи технического задания до передачи проекта
заводу-изготовителю.
Следует обратить внимание на то, что понятие «автоматизированное
проектирование», в отличие от «автоматического проектирования», подразумевает
обязательное участие человека на основных этапах проектирования, т.е. САПР следует
рассматривать как человеко-машинную систему.
Применительно к проектированию систем управления САПР призвана
автоматизировать следующие этапы этого процесса:
• построение математических моделей САУ;
• моделирование САУ;
• анализ САУ;
• синтез САУ;
• конструкторскую разработку САУ;
• технологическое проектирование САУ;
• испытания САУ.
Выполнение каждого из этих этапов обычно возлагается на отдельную часть
САПР или подсистему. Рассмотрим кратко указанные подсистемы САПР САУ [168].
Подсистема автоматизированного построения математических моделей САУ
основана на сочетании аналитических и численных методов. При этом аналитические
методы используются для получения первоначальной и%по возможности наиболее
полной математической модели САУ, а численные методы служат для
количественной оценки параметров модели и ее уточнения в целях обеспечения наибольшей
адекватности реальной САУ. Процедура построения математической модели включает
следующие этапы:
1) вывод полной математической модели в аналитической форме на основе
классических принципов и формализмов динамики;
2) упрощение и преобразование математической модели в соответствии с
назначением и особенностями модели;
3) параметрическую идентификацию упрощенной математической модели по
результатам экспериментальных исследований и испытаний.
В идеальном случае подсистема построения математических моделей должна
автоматизировать каждый из этих этапов.
Подсистема моделирования С А У. служит для моделирования САУ на основе их
математических моделей с помощью ЭВМ в целях эффективной замены
макетирования на всех этапах проектирования САУ. Эта подсистема, в частности, позволяет:
• осуществлять анализ функционирования САУ, их устройств и элементов;
584 Анализ и статистическая динамика САУ. Часть 1
• исследовать влияние изменения параметров и возмущающих воздействий на
стабильность характеристик САУ, выбирать структурную схему САУ по
критериям, задаваемым проектировщиком;
• оценивать устойчивость, динамические и статические ошибки для различных
значений параметров выбранной структурной схемы и возмущающих
воздействий.
Подсистема автоматизации анализа в САПР САУ непосредственно-связана с
подсистемами синтеза и моделирования. В частности, задачи синтеза часто удается
свести к многократному решению соответствующих задач анализа. Подсистема
анализа строится на основе использования следующих методов:
• машинно-ориентированных традиционных методов анализа САУ
(алгебраических, частотных, спектральных и т.д.);
• чисто машинных методов, основанных на представлении процессов анализа
САУ последовательностью реализуемых на ЭВМ операций над исходными и
промежуточными числовыми данными;
• машинно-аналитических методов, необходимым условием применения
которых является ЭВМ, но промежуточные и конечные результаты исследования
могут быть получены не в числовой, а в аналитической форме.
Подсистема автоматизированного синтеза САУ предназначена для решения
наиболее сложной задачи - синтеза САУ на основе теоретических и инженерных
методов, ориентированных на применение ЭВМ. Некоторые из таких методов
рассмотрены в предшествующих главах. При этом определяющим условием является
формализация целей проектирования, а также критериев и ограничений, которые, в свою
очередь, часто многочисленны и противоречивы, существенно зависят от типа САУ
и условий их эксплуатации.
В случае, когда удается связать некоторые критерии со структурой и параметрами
САУ, задача синтеза САУ сводится обычно к задаче нелинейного (в частном случае -
линейного) программирования. Если при решении этой задачи приходится
интегрировать дифференциальные уравнения, то возникает задача вариационного
исчисления и ее развитие в виде принципа максимума Понтрягина, метода динамического
программирования Беллмана.
В САПР САУ могут применяться как традиционные методы синтеза, так и
машинные. При реализации традиционных методов к ним предъявляются следующие
специфические требования: устойчивость и скорость вычисления на ЭВМ;
методологические удобства применения методов в соответствии с общей идеологией САПР
САУ; достаточная близость или хотя бы непротиворечивость критериев синтеза по
отношению к критериям, применяемым разработчиками САУ.
Как показывает практика, вычислительные трудности, возникающие при
применении традиционных методов синтеза, не позволяют осуществить сквозной синтез
регуляторов САУ по единому функционалу качества с учетом возможностей
технической реализации и условий эксплуатации САУ. Поэтому синтез изменяемой части
САУ в рамках САПР САУ часто осуществляется в соответствии с итерационными
алгоритмами, в которых чередуются процедуры синтеза структуры регулятора,
моделирование, оптимизация параметров и творческие процедуры, связанные с
принятием решений о приемлемости полученных результатов.
В случаях, когда указанные алгоритмы оказываются неприемлемыми, например,
при синтезе многомерных САУ, применяются машинные методы, в частности,
методы пространства состояний. Эти методы разработаны для линейных САУ и
отличаются от других методов синтеза широкими возможностями по применению ЭВМ для
Глава 8. Метод матричных операторов 585
их реализации. В то же время применение методов пространства состояний для
«ручных» расчетов САУ неэффективно.
Следует отметить, что создание регулярных методов синтеза на основе
представления исходной модели в пространстве состояний еще далеко до завершения и на
сегодняшний день существует лишь ряд способов синтеза линейных управлений
линейными объектами [168].
Подсистема автоматизации конструкторской разработки САУ предназначена
для автоматизации процесса конструкторского проектирования, состоящего из
следующих логически связанных этапов:
• этапа функционального анализа, на котором анализируется техническое
задание и расчленяются общие функции конструируемого звена САУ на
единичные функции. Одновременно составляется функциональная схема
конструкции звена;
• этапа разработки принципиальных решений, на котором исходя из заданных
значений функций определяются принципы работы конструкции САУ и ее
устройств;
• этапа определения конфигурации и размеров устройств САУ, на котором в
соответствии с выбранной конструкцией устанавливается форма и габариты
элементов САУ;
• этапа деталировки, результатом которого являются законченные чертежи,
спецификации и другая конструкторская документация изделия.
Одной из центральных задач применения САПР в конструировании является
автоматизация разработки и изготовления конструкторской документации.
Подсистема автоматизации технологического проектирования САУ решает
задачу, состоящую в том, чтобы с помощью конструкторской документации на САУ
разработать технологическую производственную документацию, на основе которой
можно изготовить САУ. Результатом такого проектирования является информация,
определяющая, из чего, как, в какой последовательности, чем и в какое время
должны быть изготовлены элементы, устройства и «собрана» САУ. Подсистема
технологического проектирования позволяет автоматизировать такие рутинные операции
как: поиск необходимой информации о сортаменте, оборудовании, приспособлениях,
инструменте; разработка технологической документации; выполнение расчетов
припусков, размерных цепей, норм времени и т.д. Возможно также получение готовых
носителей информации для оборудования с ЧПУ.
Подсистема автоматизации испытаний САУ позволяет автоматизировать
совокупность проектных процедур, связанных с экспериментальной проверкой макетов,
опытных образцов САУ и ее устройств на соответствие требованиям технического
задания и с экспериментальной оценкой возможностей этих объектов
проектирования. Автоматизация испытаний преследует следующие цели:
• разработку инструментов САПР САУ проектировщика-испытателя на всех
этапах проектирования, например, инструментов для формирования
возмущающих воздействий, для обработки результатов испытаний и для управления
испытаниями;
• проведение испытаний в режимах, максимально приближенных к реальным
условиям эксплуатации САУ;
• сокращение расходов на испытания и сроков получения информации по
результатам испытаний;
• проведение идентификации проектируемых САУ и их устройств;
• повышение производительности и улучшение условий труда испытателей.
586 Анализ и статистическая динамика САУ. Часть I
Ключевой подсистемой САПР САУ является подсистема автоматизированного
синтеза.
Применительно к любому техническому объекту, в том числе и к САУ, понятие
«синтез», в широком смысле, близко по содержанию к понятию «проектирование».
Решение задачи синтеза предполагает получение проектного решения в виде
некоторого описания проектируемого объекта по заданному функциональному назначению
объекта или по закону его функционирования [168].
Синтез называется оптимизацией, если определяются наилучшие, в заданном
смысле, структуры и значения параметров. Когда рассчитываются оптимальные
значения параметров при заданной структуре, говорят о параметрической оптимизации.
Задачу выбора оптимальной структуры называют структурной оптимизацией.
На структуру и конструкцию любого проектируемого объекта всегда
накладывается множество различных ограничений, которые обусловлены, например,
требованиями технического задания на параметры проектируемого объекта, требованиями
стандартов и технологии изготовления узлов и различных элементов объекта и т.д.
При проектировании любого технического объекта также выбирается и задается
некоторый критерий оптимальности. В частности, для САУ в качестве критериев
оптимальности могут быть приняты качество, мощность, масса, габаритные размеры,
надежность, ремонтопригодность, стоимость.
Под оптимальным будем понимать такой результат решения задачи синтеза, при
котором получается вариант структуры и конструкции проектируемого объекта,
удовлетворяющий всем заданным ограничениям, а критерий оптимальности
принимает наилучшее (минимальное или максимальное) значение.
Получение оптимальных решений при проектировании стало возможным и
достижимым как по срокам, так и по стоимости реализации проектных процедур только
при автоматизированном проектировании, когда появляется возможность
синтезировать и исследовать множество вариантов структур и конструкций, а также проводить
количественное изучение проектируемых технических объектов, которые в прошлом
изучались лишь качественно. Отсюда видно, что идея оптимизации неразрывно
связана с понятием автоматизированного проектирования.
Для решения задачи синтеза технических объектов выделяют некоторую
совокупность независимых переменных, называемых переменными проектирования
X = (jc1,jc2,...,^w) , фиксация значений которых определяет один из вариантов
объекта и его качественные характеристики, в том числе значение критерия оптимальности
F(X), а также показателей, принятых в качестве ограничений.
В формальном виде задача синтеза технических объектов заключается в
определении значений независимых переменных X, при которых критерий оптимальности
проектируемого объекта
F(X) = F(xl9X2,...,xm) (2.238)
принимает экстремальное (минимальное или максимальное) значение при данных
ограничениях
е/(х,,х2,...,д:т)<0, i=u; (2.239)
cij^Xj^bj, j = hm.
Задача оптимального проектирования в приведенной выше форме представляет
собой задачу математического программирования. При этом если целевая функция
(2.238) и все ограничения (2.239) линейны, то задачу оптимизации называют задачей
линейного программирования, если же целевая функция или хотя бы одно
ограничение нелинейны, то задача оптимизации является задачей нелинейного программиро-
Глава 8. Метод матричных операторов 587
вания. В случае если некоторые переменные проектирования могут принимать лишь
определенные дискретные либо только целочисленные значения, задача оптимизации
называется задачей дискретного программирования.
Как показывает опыт, прямой синтез САУ, удовлетворяющей всем ограничениям,
указанным в техническом задании на проектирование, вряд ли возможен из-за
противоречивости требований и высокой размерности глобального критерия
оптимальности, а также из-за невозможности выразить в виде критериев опыт и интуицию
конструктора. Несмотря на появление значительного количества научных работ в
области теории алгоритмизации творчества и аналитических методов принятия решений
при проектировании, индивидуальные начала инженерного проектирования являются
в настоящее время основными.
Проблему большой размерности глобального критерия оптимальности,
включающего в себя множество частных критериев, можно решить, выполнив
декомпозицию общей задачи проектирования САУ на ряд последовательно решаемых подзадач
меньшей размерности. Например, если по условиям проектирования частные
критерии оптимальности САУ можно ранжировать по важности, то наиболее естественной
и простой, с точки зрения реализации в САПР, является стратегия оптимизации по
методу последовательных уступок [168]. Применение этой стратегии дополнительно
обеспечивает для проектировщика знание потерь качества по каждому из критериев
на каждом шаге оптимизации, в то время как оптимизация отдельно по каждому
критерию не дает такой информации.
Таким образом, выполняя декомпозицию общей задачи проектирования САУ,
можно получить последовательность частных или локальных подзадач меньшей
размерности, решаемых традиционными методами поиска экстремума функций п
переменных [168].
588 Анализ и статистическая динамика САУ. Часть I
ГЛАВА 9. ЛИНЕЙНЫЕ И НЕЛИНЕЙНЫЕ ОБЪЕКТЫ
УПРАВЛЕНИЯ: ДЕТЕРМИНИРОВАННАЯ
И СТАТИСТИЧЕСКАЯ ИДЕНТИФИКАЦИЯ
Проблема идентификации является в настоящее время одной из основных
проблем теории и практики управления. Без знания оператора объекта управления,
ставящего в соответствие входные и выходные сигналы, нельзя эффективно решать
задачи расчета и проектирования систем управления. Задачей идентификации является
построение математической модели объекта, под которой понимается оператор,
определяющий поведение объекта и описывающий все его информационные свойства.
В настоящей главе рассматриваемая проблема, которая при ее решении предполагает
экспериментальное изучение и сопоставление входных и выходных сигналов. В
качестве входного сигнала часто используется специальный сигнал, например, белый
шум с нормальным законом распределения или случайный сигнал, имеющий место в
реальных условиях эксплуатации (когда, например, подача специальных сигналов
недопустима, поскольку нарушает режим нормальной эксплуатации). Задача
идентификации состоит в подборе соответствующей модели: модель должна быть такой, что
ее реакция и реакция объекта на один и тот же сигнал должны быть, в известном
смысле, близкими.
В этой главе основное внимание уделено статистической идентификации, при
которой динамические характеристики объекта или его оператор определяются на
основе анализа статистических характеристик входного и выходного сигналов.
Использование статистических методов связано с проведением большого объема
вычислительной работы, но вместе с тем статистические методы дают возможность решать
задачи идентификации для широкого круга объектов, включая нелинейные, и
позволяют получить приемлемую точность решения поставленной задачи [179].
Результатом решения задачи идентификации является приближенное значение оператора, его
оценка, которая и используется в качестве характеристики истинного оператора [3].
Таким образом, результатом решения задачи идентификации являются
исходные данные для проектирования систем управления, не располагая которыми часто
нельзя выполнить ни оптимизации, ни синтеза регуляторов, ни анализа систем
управления.
В главе не ставилась задача изложить все методы и алгоритмы идентификации
динамических систем и провести общую классификацию. Цель состоит в том, чтобы
познакомить читателя с основным содержанием рассматриваемой проблемы и с
некоторыми подходами к ее решению.
9.1. ПРОБЛЕМА ИДЕНТИФИКАЦИИ
9.1.1. Общие понятия
Под идентификацией в широком смысле понимается получение или уточнение по
экспериментальным данным модели реального объекта, выраженной в тех или иных
терминах [156].
Глава 9. Линейные и нелинейные объекты управления
589
Идентификацией динамического объекта (процесса) называется определение
параметров и структуры математической модели, обеспечивающих наилучшее
совпадение выходных координат модели и объекта при одинаковых входных
воздействиях.
Задача статистической идентификации объекта управления формулируется как
задача определения его оператора при наблюдении за случайными входными и
выходными сигналами.
Приведём некоторые задачи, важным этапом решения которых является
построение математической модели.
Первым этапом решения проблемы синтеза регуляторов, синтеза оптимальных
систем, проектирования самонастраивающихся систем и др. является задача
идентификации (рис. 9.1 - 9.3).
Входные
данные
•Ой
-Т
1_
2-й этап
регул)
|
—i,
Регул
прямо
Регулято
ооратнс
г: синтез
*торов
ятор в
и цепи
\
р в цепи
)И СВЯЗИ
1
1-й этап: пострс
математической г
объекта управл
Объект
управления
>ение
лодел
ения
t
и
X
V)
Рис. 9.1. К постановке задачи синтеза регуляторов
Входные
данные
Алгорр
THMaj
ynpai
1ТМЫ ОП-
пьного
мления
U(t) -
оптимальная коман
1-йэ
мате
об
аа
тап: построение
матической моде.
ъекта управления
_J t_
Объект
управления
пи
1
хм
L
Рис. 9.2. Структурная схема оптимального управления объектом
Г(/) = 1я(0+и(0
Система,
руюшдя
полезной
m(t) и по
анализи-
свойства
о сигнала
мехи Mi)
t&~
Корректирующий фильтр
i
ЭВМ,
рассчитывающая
параметры
корректирующего фильтра
it
т
Объект
управления
Щ
Система идентификации,
определяющая
непрерывно изменяющиеся
параметры объекта
Рис. 9.3. Структурная схема самонастраивающейся САУ
590 Анализ и статистическая динамика САУ. Часть I
Решение проблемы идентификации связано с рассмотрением ряда важных
задач, которые в конечном счёте определяют степень эффективности используемого
подхода.
9.1.2. Критерии идентификации
При решении задачи идентификации важную роль играют критерии
идентификации, характеризующие степень близости выходного сигнала объекта X(t) и модели
ХМ
В большинстве работ, посвященных задаче идентификации, принято оценивать
степень близости параметров р объекта и рм модели по близости выходных
переменных X(t) и ХМ
Наиболее естественным является рассмотрение этого вопроса с использованием
понятия функции потерь (штрафа) fp(Ap),
где Ар = рм-р,
рм - параметры модели,
р - параметры объекта.
Формула для функции потерь записывается в форме fp(X(t\ XM(t,pM)).
Для функции^ справедливо:
- fp- скалярная функция,
-/,(0) = 0,
-fp(APx)>fp(Ap2\ еслир(ДЛ)*р(ДА), (9Л)
-fp(+Ap) = fp(-Ap).
Таким образом, из (9.1) следует: штраф - скаляр; при точной оценке параметров
объекта потери отсутствуют; чем ближе Ар к нулю, тем меньше потери; функция]^ -
симметрична. Если система функционирует на промежутке [0,7], вектор параметров
модели рм (этот вектор находится в результате решения задачи идентификации)
должен удовлетворять соотношению
т
min \fp[X(t\XM{t,pMj\ dt.
На практике в подавляющем большинстве случаев используется критерий
минимума СКО, являющийся частным случаем критерия минимума среднего риска, когда
функция потерь представляет собой квадрат разности между выходными сигналами
объекта и модели [3].
9.1.3. Классификация объектов, задач и методов идентификации
Поскольку задача идентификации сводится, как правило, к определению
структуры модели объекта и восстановлению её параметров, в качестве основы для
классификации объектов целесообразно выбрать степень предварительной изученности
объекта. При наличии априорной информации все объекты могут быть разделены на
следующие группы [3, 8, 50, 80, 116, 122, 141, 145, 163, 179, 180]:
1) объекты, для которых известны описывающие их динамику операторные
уравнения (например, дифференциальные уравнения) вплоть до
приблизительных значений коэффициентов,
2) объекты, для которых известны описывающие их динамику операторные
уравнения, а численные значения коэффициентов неизвестны,
3) объекты, для которых конкретный вид уравнения и численные значения
параметров неизвестны, но имеется некоторая априорная информация (объект
линеен, объект содержит нелинейность определенного вида и т.д.),
Глава 9. Линейные и нелинейные объекты управления 591
4) объекты, относительно которых отсутствуют какие-либо априорные сведения
(объекты типа «чёрный ящик»).
Провести чёткую границу между любой парой смежных групп в общем случае
затруднительно.
Методы идентификации разделяются и по следующим признакам:
1) по способу представления характеристик объекта:
• во временной области,
• в частотной области,
• в спектральной области относительно ОНБ;
2) по методу проведения эксперимента на объекте:
• активные-(предполагают подачу на вход объекта специальных пробных
сигналов),
• пассивные (используют реально действующие в системе сигналы и, таким
образом, нормальный режим эксплуатации не нарушается),
• смешанные (на объект подаются специальные пробные сигналы малой
интенсивности, не нарушающие его нормальной эксплуатации);
3) по принятому критерию идентификации;
4) по наличию сравнения полученного математического описания с объектом:
• разомкнутые,
• замкнутые.
9.1.4. Требования, предъявляемые к методам идентификации
К методам идентификации предъявляются следующие требования. Методы
идентификации должны:
• обладать достаточной точностью,
• обеспечивать возможность измерения в замкнутой и разомкнутой цепях,
• обладать помехозащищённостью,
• являться автоматическими или автоматизированными,
• быть независимыми от начальных условий, поскольку влияние последних
трудно исключается,
• обеспечивать построение математических моделей в режиме нормальной
эксплуатации (там, где необходимо),
• быть достаточно быстродействующими,
• реализовываться с помощью достаточно простой аппаратуры,
нечувствительной к внешним воздействиям.
9.1.5. ПОДХОДЫ К РЕШЕНИЮ ЗАДАЧИ ИДЕНТИФИКАЦИИ
1. Корреляционный подход. Этот подход является наиболее распространённым.
Рассмотрим линейный, в общем случае нестационарный, объект (рис. 9.4).
Y(i)
]
ко
Линейный
нестационарный объект
ДО
-►
Рис. 9.4. К постановке задачи идентификации линейного объекта
Как уже указывалось выше, часто при решении задачи идентификации в качестве
критерия, характеризующего степень близости объекта и модели, используется сред-
неквадратическая ошибка (СКО).
592 Анализ и статистическая динамика САУ. Часть I
Если для модели имеет место соотношение
XM(t) = AY(t), (9.2)
где А - оператор модели,
Y(t\ XJJ) - соответственно входной и выходной сигналы, то можно записать
следующую зависимость
м[{(Х(0-АУ(0У] = min. (9.3)
На основе (9.3) можно получить следующее выражение для оптимального
оператора
AY{x)=M\x{t)lY{4, (9.4)
т.е. (9.4) определяет регрессию выходной переменной X относительно входной У
(оператор условного математического ожидания) [116]. Этот оператор является
оптимальным в классе всех возможных операторов при использовании критерия
минимума СКО.
Для определения оптимального оператора в классе линейных систем умножим
правую и левую части зависимости (9.4) на Y(x\) и осредним по входному сигналу
м[А¥{х)У{^)\ = М[х(!)¥{^)\. (9.5)
Учитывая коммутативность операторов АиМ, получим
^Л/[у(х)У(т,)] = А/М/)у(т1)]. (9.6)
Последнее уравнение определяет оптимальную оценку оператора в классе линейных
операторов по критерию минимума СКО.
Если задачей идентификации является нахождение импульсной переходной
функции объекта управления, то (9.6) можно переписать в виде [116]
|М/,т)а(г2г)(т,т1)^т = а(^(г,т1), (9.7)
/-у
где Т - интервал наблюдения, а(^)(т,т,) = /ик(т)тк(т1) + /?}Т(т,х1); а$(г,т,) =
= %0K(Ti)+%(^.Ti)-
Если же рассматривается случай, когда X(t) и Y(t) - центрированные случайные
процессы, то уравнение (9.7) принимает вид
J k{Ui)RYY{^x)dx =RXY(t,Tx)- (9.8)
l-T
Оптимальный оператор в классе многомерных нестационарных линейных систем
представляет собой оператор условного математического ожидания при заданном
векторе входных сигналов, а оптимальные оценки операторов могут быть получены
из системы уравнений типа (9.8), содержащих корреляционные и взаимные
корреляционные функции рассматриваемых переменных.
Изложенный подход обобщается на класс нелинейных объектов, поведение
которых описывается функционалами Вольтерра.
Задача ставится так же, как и для линейного случая (рис. 9.5).
Связь между входом и выходом определяется нелинейным оператором А, т.е.
XM(t) = AY(t), (9.9)
а задача заключается в нахождении оператора А (ядер k\(t, ii), k2(t, ть т2), ..., *,{/, ть
т2,..., г,)), такого, что выполнено условие (9.3).
В отличие от линейного случая, когда решение задачи идентификации сводится к
решению одного уравнения (9.8), в нелинейном случае для входного сигнала Y(t) с
произвольным законом распределения нахождение ядер k{(t, ii), k2(t, ть т2), ...,
Глава 9. Линейные и нелинейные объекты управления
593
А:,-(/,Ti,х2 »••-,xf-)) сводится к решению системы многомерных интегральных
уравнений, являющейся обобщением интегрального уравнения Винера - Хопфа.*
Значительно более трудной является задача идентификации объектов,
содержащих существенные нелинейности.
Y(t)
Нелинейный
нестационарный
объект
Ни Ti)
ki(t, т,, т2)
kt(t9 Ti, т2,..., т,)
ДО
*-(')
Рис. 9.5. Структурная схема идентификации нелинейного объекта
2. Байесовский подход. Этот подход является общим к решению проблемы
идентификации. Здесь задача идентификации является конечной задачей принятия
решений, для которой точечные оценки параметров модели являются конечной целью.
После того как структура модели выбрана или задана, задача идентификации
объекта сводится к задаче оценивания параметров. С байесовских позиций, оценка - это
распределение вероятностей, зависящее от имеющихся данных, а любая точечная
оценка - это некоторое описание этого распределения. В байесовской статистике
неизвестные параметры не оцениваются, а для них вычисляется апостериорное
распределение вероятностей. Байесовский подход особенно плодотворен в тех случаях,
когда оценивание параметров составляет часть адаптивного управления и
выполняется в замкнутом контуре. С байесовской точки зрения можно рассмотреть понятие
модели объекта. Под моделью объекта понимается любая математическая модель,
которая определяет множество условных распределений вероятностей для
требуемого периода времени при помощи конечного множества параметров.
В процессе идентификации при использовании байесовского подхода выделяются
два этапа:
1) выбор структуры модели, определяющей условные распределения
вероятностей,
2) оценивание параметров модели. <
В рамках байесовского подхода к идентификации систем рассматриваются задачи
оценивания параметров и предсказания выхода и состояния, оценивания в замкнутом
контуре, устойчивого оценивания, оценивания и предсказания в реальном времени,
одноразового оценивания классификации систем. К вопросам, составляющим
содержание байесовского подхода, относятся:
• устойчивое оценивание и случаи наличия избыточных, неидентифицируемых
параметров,
Методы идентификации класса нелинейных систем, описываемых функционалами Вольтерра,
подробно рассмотрены в [72, 123], там же приведены алгоритмы и примеры решения конкретных задач
39 Зак. 232
594 Анализ и статистическая динамика САУ. Часть I
• оценивание и предсказание в реальном времени,
• случай обобщённой многомерной регрессионной модели,
• идентификация при изменяющихся во времени параметрах и адаптивность,
• байесовская точка зрения на адаптивность,
• анализ роли априорных распределений при классификации систем,
• применение к моделям со структурой регрессионного типа и др.
9.1.6. Оценивание параметров нелинейных систем.
Кроме байесовского подхода, нашёл применение метод получения оптимальных
оценок параметров нелинейного объекта по критерию минимума среднего квадрата
ошибки, при этом используется разложение в ряд Тейлора нелинейной вектор-функции
и матрицы коэффициентов, причём учитываются только линейные члены [141].
В специальной литературе подробно рассмотрены возможные подходы, методы и
алгоритмы решения задачи идентификации, в частности, рассмотрены:
• классические методы непараметрической идентификации линейных
динамических объектов,
• прямые методы параметрической идентификации,
• беспоисковые алгоритмы идентификации с адаптивной моделью,
• поисковые алгоритмы идентификации с адаптивной моделью,
• алгоритмы идентификации, основанные на теории оценивания процессов,
• рекуррентные алгоритмы идентификации при коррелированных шумах и др.
На практике нашли применение алгоритмы [141]:
• стохастической аппроксимации первого и второго порядков,
• стохастической аппроксимации с возмущением на входе,
• максимального правдоподобия,
• максимизирующий апостериорную вероятность,
• использующий расширенный фильтр Калмана - Бьюси,
• со случайным поиском,
• реализующий метод наименьших квадратов,
• основанный на использовании БПФ и др.
Более подробно с проблемой идентификации и методами её решения при
рассмотрении конкретных достаточно сложных задач можно познакомиться в [141].
9.2. ДЕТЕРМИНИРОВАННАЯ ИДЕНТИФИКАЦИЯ ЛИНЕЙНЫХ
СТАЦИОНАРНЫХ ОБЪЕКТОВ, ОСНОВАННАЯ НА РЕШЕНИИ
УРАВНЕНИЯ 1-ГО РОДА МЕТОДОМ МЕХАНИЧЕСКИХ
КВАДРАТУР
Для определения ИПФ необходима информация о системе. Для ее получения
проводят специальные эксперименты с измерением доступных параметров либо
снимают данные в процессе нормального функционирования системы. Отметим, что
указанное различие существенно: при проведении экспериментов можно выбирать
специальные наиболее информативные входные воздействия, тогда как при получении
данных в процессе нормального функционирования системы это обстоятельство не
учитывается.
Организацией специальных экспериментов с выбором наиболее информативных
входных воздействий в теории идентификации уделяется большое внимание. В
последние годы в данном направлении возникла новая научная дисциплина - теория
оптимального эксперимента [83]. Этот вопрос здесь не рассматривается; далее будем
Глава 9. Линейные и нелинейные объекты управления 595
использовать имеющуюся информацию с возможностью пополнять ее
количественно, например, увеличивая число точек измерения, повышая точность измерений,
проводя измерения реакции выходных параметров системы на новые входные сигналы,
но без возможности выбора наиболее информационных входных воздействий. Таким
образом, мы ориентируемся на результаты исследований объекта при подаче на него
набора стандартных входных воздействий.
Для выявления трудностей, имеющих место при решении задачи идентификации
нестационарных объектов, сначала рассмотрим класс объектов с постоянными
параметрами.
Рассмотрим линейный стационарный объект. Если при / = 0 объект имел нулевые
начальные условия (до подачи входа находился в состоянии покоя), то связь между
входом и выходом определяется интегралом свертки (интегральное уравнение Воль-
терра 1-го рода относительно £(т))
*(0 = }*(тМ*-т)£/т. (9.10)
о
В задаче идентификации можно измерить входной y(t) и выходной x(t) сигналы
и произвести обработку полученной информации в целях построения неизвестной
импульсной переходной функции к(т) .
Если же построена импульсная переходная функция, то можно считать известным
оператор А объекта (он определяется зависимостью (9.10)).
Как отмечалось, построение и обоснование метода идентификации предполагают
рассмотрение ряда очень сложных вопросов, таких, как:
• построение алгоритма идентификации;
• исследование точности полученных результатов;
• анализ ошибок, порожденных природой самого алгоритма (например,
алгоритма, предполагающего решение интегрального уравнения свертки, которое
представляет собой уравнение 1-го рода; последнее, как известно, поставлено
некорректно);
• анализ ошибок, связанных с наличием шумов, с квантованием входных и
выходных сигналов или с их разложением по базисной системе;
• исследование подходов, которые обеспечили бы ускорение сходимости
алгоритма, уменьшили бы влияние шумов и т.д.
Здесь не ставится цель построения и обоснования метода. Задача более простая -
рассмотрение лишь принципов идентификации, в основу которых положено решение
интегрального уравнения свертки.
Эти принципы можно распространить на нестационарные и некоторые классы
нелинейных систем, систем с распределенными параметрами.
В уравнении (9.10) k(i) - непрерывная функция; предполагается, что уравнение
свертки имеет единственное решение.
Изберем какую-нибудь формулу механических квадратур на промежутке [0,Г]
с п узлами /,(1</<я) (формулапрямоугольников):
г
J f№ = f(t0 )At + /(/, )Д/ +... + /(*„_, )А/ + 5(/) =
о
= Аг(/(го) + /Й) + ...+/(/я.1)) + 6(/),
где 5(/) - остаточный член.
39*
596
Анализ и статистическая динамика САУ. Часть I
Далее к (9.10) применим формулу прямоугольников, поясняя процедуру замены
графическим изображением свертки двух функций. Очевидно следующее равенство
(рис. 9.6, а):
х(*,)ч|*(тМ/-т)</т.
о
Цх)'
^тч
*(',)=*(Л)
t'o !'.
д |*(f,)=s(A)
К*У
W Л(2А)
'oj'i £■ ^2)=х(2А) х
Л(А) к(2А) к(ЗА)
х(А)
х(2Д)
х(ЗД)
tx t2
tQ tx t2 t3
Рис. 9.6. Свертка функций:
a - при t = tlt6- при t = t2 у в- при t - /3
Пользуясь рис. 9.6 запишем
'i
х(/1) = х(А) = |^(т)^1-тУт = /:(А)^(0)А + 51, (9.11)
о
где 5, - погрешность, возникающая при замене интеграла формулой
прямоугольников. Далее, заменим выражение
h
*(/2) = J*(tM/2-t)</t
Глава 9. Линейные и нелинейные объекты управления
597
формулой прямоугольников, для чего представим записанное выражение графически
(рис. 9.6, б). Имеем
x(t2) = x(2A) = jk(T)y(t2-T)dT = k(2A)y(0)A + k(A)y(A)A + 52, (9.12)
где 52 - погрешность.
И, наконец, заменим интеграл
'3
*(*з) = |*(тМ/з-т)Л
(9.13)
Или, что то >
А
ке
самое:
№
ЯД)
у(2А)
0
ЯО)
Д'(А)
0
0
уф)
... 0 '
... 0
... 0
^((«-1)А) Х(«-2)А) Я(«-3)Д) - уЩ
к(2А)
к(ЗА)
к(пА)у
+
[5'1
82
5з
Л,
=
Г х(А) ^
х(2Д)
х(ЗА)
х(«А),
(9.14)
квадратурной формулой (рис. 9.6). Пользуясь рис. 9.6, в, запишем квадратурную
формулу для (9.13)
h
x(t3) = x(3A) = ^k(T)y(t3-T)dx = k(3A)y(0)A =
о
= *(2A).y(A)A + *(A).y(2A)A + 53.
Введем следующие обозначения:
у(0) = уиу(А) = у2,у(2А) = у3,..., у((п-\)А) = у„;
k(A) = kb k(2A) = k2i /:(ЗА) = ^з— к(пА) = к„;
х(А) = хи х(2Д) = х2, х(ЗА) = х3,..., х(пА) = хп.
Сведем полученные выше зависимости в систему
^(А)^(0)А + 0 + 0 + ... + 0 = д:(А)-81;
/:(2А)^(0)А + ^(а)^(а)А + 0 + ... + 0 = д:(2А)-52;
^(ЗА)^(0)А + /:(2А)^(А)А + ^(А)^(2А)А + 0 + ... + 0 = ;с(ЗА)-5з;
к(пА)у(0) А + к((п- 1)А).у(А) А + к({п-2) а)^(2А)А + ... +
+^(А)>;((а7-1)а)а = х(а7А)-5,.
(9.15)
(9.16)
Воспользовавшись обозначениями (9.14), получим
598
Анализ и статистическая динамика САУ. Часть I
Уг
Уъ
\.Уп
0
У\
Уг
Уп-\
0
0
У\
Уп-г
° 1
0
0
Л,
(к 1
*2
*з
Л,
+
Г50
53
А,
=
/ ч
х2
(9.17)
Рассмотрим формальное решение задачи, предполагая, что квадратурная формула
достаточно точно аппроксимирует интеграл свертки и можно положить
81=0, 52=0, 83=0,..., 5„=0.
Обозначим
У\ О
Уг У\
Уъ Уг
О
О
У\
о
о
\Уп Уп-\ Уп-г ••' У\)
= А;
кг
к,
А,
= К;
хх
х2
х3
= х.
(9.18)
Тогда
АК = Х. (9.19)
Решая полученное уравнение, получим формальное решение задачи идентификации:
К = А"]Х. (9.20)
Далее проведем анализ ситуации, близкой к имеющей место на практике
(рис. 9.7).
1
яо
x(t) = xJt) + xn(t)
Рис. 9.7. К решению задачи идентификации
Выходной сигнал системы, как правило, состоит из двух составляющих: xy(t),
порожденной входом y{t); xn(t), порожденной неконтролируемой помехой n(t)\
(к помехам n(t) могут быть отнесены внутренние шумы объекта, шумы
измерительной аппаратуры, применяемые при идентификации, внешние помехи и др.).
Таким образом, в матричном уравнении (9.17) вместо матрицы-столбца
\Х\,Х2,...,Хп)
реально будет иметь место «возмущенный» вектор
(х1 +Ах1ух2 +Дх2,...,х„ +Лх„)Т, (9.21)
где
^^(Д), х2 =^(2А),..., хп=ху(пА);
Дх^хДд), Дх2=х„(2Д),..., Ахп=хп(пА).
Кроме того, предположим (что на практике также редко имеет место), что
дискретные значения входного сигнала У\,у2,..->уп измеряются точно. Тогда (9.17)
перепишем в виде (полагаем, что 5, * 0):
Глава 9. Линейные и нелинейные объекты управления
599
У\
Уг
Уъ
0
У\
Уг
0
0
У\
' к{ + Ак{ N
к2 + Ак2
к3+Ак3
=
'ъ+Ах^
х3 +Ахз
-
а,
(9.22)
Ui Уп-\ Уп-2 ••• л;
Поскольку правая часть задана с погрешностью, порожденной векторами
(AX],Ax2,...,Axw) и (51}52,...,5w) , то из-за этого к решению К = [к},к2,...,кп) Д°~
бавится вектор погрешности АК = (Ак1,Ак2,...,Акп) ; иными словами, (9.19) можно
переписать в виде
А(К + АК) = Х + АХ, (9.23)
где AX = (A*j -5,,Ах2 -52,...,Ах„ -5„) - погрешность, порожденная квадратурной
формулой и неконтролируемыми возмущениями.
Из (9.23) получим
К + АК=А"1(Х + АХ).
Из (9.24) имеем
АК = А"1(Х + АХ)-К = А"1(Х + АХ)-А"1Х.
Норма имеет вид:
|ак| = |а"1(х+ах)-а"1х|.
Для важного частного случая линейного оператора справедлива формула
||ак|| = ||а-'ах||<||а-Ч|||ах||.
После некоторых преобразований можно получить
AVll
(9.26)
(9.24)
(9.25)
||а-| 1|х|| - «к|| -|А||"А I |х« •
Последняя зависимость представляет собой относительную погрешность
исходных данных (погрешность, порожденную наличием члена АХ и решением задачи
идентификации АК).
Число К(А)= А -А"1 называется числом обусловленности оператора А.
Поскольку решение исходного уравнения свертки (уравнение Вольтерра 1-го
рода) поставлено некорректно, то эквивалентная уравнению свертки система
алгебраических уравнений (9.134) является неустойчивой (задача называется устойчивой,
если малые изменения исходных данных (в данном случае вектор АХ)'приводят
к малым изменениям решения, т.е. к малому вектору АК [5, 47].
Задачщ которые имеют единственное решение и являются устойчивыми,
называют корректно поставленными, или просто корректными. Если же говорят о
некорректной задаче, имеют ввиду ее неустойчивость. В рассматриваемом случае
решения проблемы идентификации задача поставлена некорректно (задачи решения
уравнений 1-го рода, в том числе уравнений свертки, т.е. уравнений Вольтерра 1-го
рода, поставлены некорректно), поэтому К(А) > 1.
Ясно, что в наиболее благоприятном случае, когда К(А) = 1, оценка
относительной погрешности решения задачи идентификации совпадает с оценкой относитель-
600 Анализ и статистическая динамика САУ. Часть I
ной погрешности исходных данных. Если же К(А) > 1 (имеет порядок сотен, тысяч и
более), то при малой погрешности исходных данных АХ возможна очень большая
погрешность решения АК. Именно такая ситуация имеет место в случае решения
задачи идентификации.
Задачи, когда К(А) > 1, часто называют плохо обусловленными [5, 47].
В оценке (9.26) участвуют нормы векторов; они определяются известными
формулами: если Z = (zj,z2,...,zw), то используют равномерную норму
или квадратичную (евклидову) норму
Вопрос определения нормы матриц (прямой и обратной) очень сложен. Чаще
всего используется спектральная норма матриц, согласованная с квадратичной
нормировкой векторов. В свою очередь, спектральная норма определяется через
собственные значения матриц.
Формула (9.26) в терминах собственных значений матрицы А может быть
записана так:
Th 1И < М < Т|ММ. (927)
max
\Ц \\X\\ \\K\\ min|^| |X|
Если правая часть в (9.23) задана точно, а элементы матрицы А содержат
погрешности, можно показать, что искажение элементов матрицы А по отношению к
погрешности равносильно определенному искажению правой части уравнения (9.23)
при сохранении неискаженной матрицы [5, 47].
Погрешности округления в ЭВМ воздействуют на результат как некоторые
эквивалентные вариации оператора А или правой части. Следовательно, о
чувствительности к погрешностям округлений можно судить по степени обусловленности
матрицы А - при большом числе обусловленности влияние округлений может быть
сильным.
Погрешность решения задачи идентификации, порожденная приближенным
характером исходных данных, носит название неустранимой погрешности', эта
погрешность часто называется трансформированной.
Ошибки, связанные с наличием внутренних шумов и внешних помех, ошибки,
связанные с квантованием входных и выходных сигналов объекта, учтены в
приведенных выше рассуждениях.
Вывод, который можно сделать из предыдущего изложения, состоит в
следующем: решение практических задач идентификации на основе уравнений 1-го рода
встречает принципиальные трудности, определяемые некорректностью
постановки задачи решения указанного класса уравнений [5, 47].
Для получения результатов, имеющих практический интерес, необходимо к
уравнениям (9.10) и (9.23) применить метод регуляризации, разработанный академиком
А.Н. Тихоновым [165].
Уравнение свертки можно решить другим методом, использующим разложение
входящих в него функций y(t),x(t) и k(i) в ряды по ортонормированным базисам.
Преимущество этого подхода состоит в том, что размерность системы
алгебраических уравнений во многих случаях уменьшается. Кроме того, система алгебраических
уравнений в этом случае будет треугольной и представляется возможность
непрерывно контролировать число обусловленности оператора А.
Глава 9. Линейные и нелинейные объекты управления 601
9.3. ДЕТЕРМИНИРОВАННАЯ ИДЕНТИФИКАЦИЯ ЛИНЕЙНЫХ
ОБЪЕКТОВ, ОСНОВАННАЯ НА РЕШЕНИИ УРАВНЕНИЯ
1-ГО РОДА СПЕКТРАЛЬНЫМ МЕТОДОМ
Пусть стационарный объект описывается интегральным соотношением
i
x(t) = jk(t-T)y(x)dx + n(t) + xc(t), (9.28)
о
где n(t) -помеха, xc(t) - свободные колебания.
Будем считать, что n(t) = 0, Х° = (х(0)х] (0)...л:""1 (0))т = 0, т.е. до подачи на вход
сигнала y(t) система находилась в состоянии покоя.
Положим, что в результате проведения одного эксперимента на промежутке [0,Г]
зафиксированы детерминированные сигналы y(t) и x(t). Воспользуемся аппаратом
матричных операторов. Представим все функции, входящие в (9.28), в виде
разложения по ОНБ (полагаем, что все они принадлежат А2[0,Г] ):
*(0 « Фт (ОС*, у{г)« Фт (0Сг, *(т) * Фт (т)А . (9.29)
Подставляя (9.29) в (9.28), найдем
С С ( '
Xc^r(o=XZ^c4^.(/-T)^(x)t/x- (930)
V=\ Г,=1Г2=1 о
Умножая (9.30) последовательно на ф|(/),ф2(О,--->Фг(О и интегрируя полученные
соотношения на [0,Г], получим следующую систему алгебраических уравнений
с с т t
Г,=1Г2=1 0 0
ее у
ее у
с*= И И % ск J j ф1/.(/" т)ф1/2 (т)^тф1 ^dL
1',-iKH oo
Или, что то же самое,
к,=1г2=1
где
т i
<r2 = J JqV, a - т)Лф„(0Л , л = U. (9.33)
о о
Числа с'у ^ характеризуют ОНБ и могут быть определены заранее: они хранятся в
памяти ЭВМ. С помощью формулы (9.32) можно получить решение задачи
идентификации - построить ИПФ стационарного объекта на промежутке [0, Т]. В самом деле,
поскольку спектральные характеристики Cr =(cjr,C2,...,c*)T и С^ =(с,>;,с^,...,с^)1
38 Зак. 232
602 Анализ и статистическая динамика САУ. Часть I
сигналов x(t) и y{t) известны (процессы x(t) и y(t) зафиксированы на промежутке
[0,Г]), то решая систему алгебраических уравнений, содержащую £ неизвестных
аьаг,...,а^ можно рассчитать спектральную характеристику ИПФ в ОНБ Ф(/)
A = (al9a2,...9ac)T.
Из предыдущих рассуждений можно сделать вывод, что для построения ИПФ
стационарной системы достаточно провести только один эксперимент, зафиксировав
входной и выходной сигналы на промежутке [0,Г]. Данные одного эксперимента
позволяют получить линейную систему алгебраических уравнений (9.32), решая которую,
можно рассчитать аь а2,..., ас и построить идентифицируемую ИПФ в форме
к{х)« Фт (т)А, т б [0,Г]. (9.34)
Вопросы, связанные с некорректностью рассматриваемой задачи, и трудности,
порожденные этим обстоятельством, рассмотрены в предыдущем параграфе.
Рассмотрим возможность применения этого подхода для идентификации ИПФ
нестационарной системы, предполагая сначала, что Х° = 0, n(t) = 0.
Имеем
x(t) = jk(t,T)y(T)dT. (9.35)
о
Представим, как и в предыдущем случае, все функции, входящие в (9.35), в виде
разложения по ОНБ, перейдя предварительно от уравнения с оператором Вольтерра
1-го рода к уравнению с оператором Фредгольма 1-го рода
т
x(t) = jk(t^)y(T)dT. (9.36)
о
Имеем
х,(0 = ФТ(ОС\ МО = Ф\0Су . (9.37)
Поскольку функция £(/,т) является функцией двух аргументов / и т (в отличие
от стационарного случая, когда ИПФ k{t) зависит от одного аргумента т), то ее
разложение по ОНБ имеет вид
с с
К С *)« Е S «к,к2 Фи, С)Фг2 (т), (9-38)
К,=0К2=0
г г
где a\Vi =||*(м)фК1(ОфГ2(т)ЛЛ, VX,V2 =U.
о о
Обозначим
/ ii J
Ак =
аи ап ... аи
а2\ ^22
- 4<
А\ аП ■■■ aU;
(9.39)
Глава 9. Линейные и нелинейные объекты управления
603
Поскольку £(/,т) неизвестна, то в результате решения задачи идентификации
должны быть найдены элементы ак, ij = \9C , матрицы Ак .
Из приведенных положений следует вывод: при идентификации стационарных
систем число неизвестных аьа2,...,ас равнялось £; в случае же решения задачи
идентификации нестационарного объекта число неизвестных а,у, ij = \/ , равно £2.
Поскольку (9.38) в матричной форме имеет вид
*(/,т) = Фт(0А*Ф(т),
то из (9.36) (9.37) и (9.40) находим
фт (t)Cx = [ Фт (0А*Ф(т)Фт (т)С^т.
Умножим (9.41) слева на Ф(/) и проинтегрируем на [0,Г])
г т г
[ Ф(/)ФТ {t)dtCx = [ Ф(/)ФТ (OdtAk [ Ф(т)Фт {i)dxCy.
0 0 0
Или, что то же самое,
СГ=А*С>'.
Запишем последнее соотношение в развернутой форме
(9.40)
(9.41)
(9.42)
=
и
4
л
4
... 41
... 4<
... в?о
Ус
(9.43)
Полученное соотношение не позволяет найти неизвестные элементы ак, ij = \,£,
поскольку имеет место информационная недостаточность в исходных данных.
Следствием этой информационной недостаточности является возможность
неоднозначного решения уравнения (9.36), что, естественно, не приводит к
детерминированному решению задачи идентификации. Поэтому необходимо пополнение
исходной информации [99-101].
На основе сказанного выше можно сделать вывод: для решения задачи
идентификации ИПФ нестационарной системы в приведенной выше постановке исходных
данных недостаточно. Поэтому постановку задачи следует скорректировать,
пополнив исходную информацию [99-101].
Из (9.36) легко заключить, что дополнительную информацию можно получить,
если провести £ экспериментов. Положим, что на промежутке [0,Г] в результате
проведения £ экспериментов зафиксированы сигналы yt{t) и *,(/)> / = 1,^,где y({t)
- входной сигнал, x^t) - соответствующий выходной процесс (реакция на yt{t)).
Тогда вместо (9.43) легко записать
=
и
Л
4
... 4
... 4<
... 4,
и-
, i = \,i
(9.44)
38*
604
Анализ и статистическая динамика САУ. Часть I
Перепишем (9.44) в виде
ср4]+с?42+...+с?4с=с?,
c{>ai'n+cpaii2+... + c>>ai:(C=cx(\
с>\'акп+4'а\2+... + с{'а$1=с*',
с{'4]+4<42+... + с>'4(=с-2\
c{'4l+c2v'ai:(2+... + c>('4t = cxc'.
Воспользуемся обозначениями
«11
«12
к =
«и
«21
«22
«2f
«П
V«fJ
(К
. А,=
о (с"')т ... о
о о ... (с*^
, А =
х =
сдг,
С*'
А2
vAf
(9.45)
(9.46)
Тогда система алгебраических уравнений (9.45) перепишется в виде
АК = X . (9.47)
При введении соответствующих обозначений система алгебраических уравнений
(9.32), определяющая одностолбцовую матрицу А = (ах,а2,...,ае)т, при решении
задачи идентификации стационарных объектов также может быть записана в форме
(9.47).
Таким образом, решение задачи идентификации стационарных и нестационарных
объектов сводится к решению уравнения (9.47) с матричным оператором А.
Глава 9. Линейные и нелинейные объекты управления 605
Из (9.47) получим формальное решение задачи идентификации
К = А~!Х; (9.48)
идентифицируемые ИПФ имеют вид:
1) для класса стационарных линейных объектов
*:(/)« ФТ(т)А; (9.49)
2) для класса нестационарных объектов
£(/,т)«Фт(0А*~Ф(т). (9.50)
При решении задачи идентификации стационарных объектов размерность (9.48)
для слабоколебательных объектов невелика (как правило, ^<(10-15)). В связи с
этим могут быть использованы известные методы решения линейных систем
алгебраических уравнений [5, 67].
Задача значительно усложняется, если (9.48) определяет решение задачи
идентификации нестационарных объектов. В этом случае число неизвестных достигает
нескольких сотен (например, если ^=10, то число неизвестных равно 100) и отыскание
решения (9.48) представляет собой трудную задачу. При практических расчетах
можно использовать факт разреженности матрицы А .
В этом случае достаточно эффективными являются итерационные методы
решения систем линейных алгебраических уравнений. Использование прямых методов
невозможно из-за необходимости выполнения чрезмерно большого числа
арифметических операций [5, 67]. Методы исключения для решения систем с разреженными
матрицами неудобны, поскольку при их использовании большое число нулевых
элементов превращается в ненулевые и матрица теряет свойство разряженности. В
противоположность им при использовании итерационных методов в ходе итерационного
процесса матрица не меняется (она остается разреженной).
Большая эффективность итерационных методов по сравнению с прямыми
методами тесно связана с возможностью существенного использования разреженности
матриц [5, 67]. Разработано большое число различных итерационных методов,
каждый из которых ориентирован на решение сравнительно узкого класса задач.
Для того чтобы воспользоваться методом простой итерации для решения системы
алгебраических уравнений (9.47), необходимо преобразовывать эту систему к виду
К = ВК + С. (9.51)
Необходимо отметить, что операция приведения системы (9.48) к виду (9.51),
удобному для итераций, не является простой и требует специальных знаний, а также
существенного использования специфики системы [5, 67].
Способы приведения системы (9.48) к виду, удобному для итераций, рассмотрены
в [5, 67].
Решение К итерационным методом рассчитывается по формуле
к(р+\) =вк(р) +с5 /? = 0,1,2,..., (9.52)
где К(л) - л-е приближение.
Изучена сходимость метода, получены формулы для оценки погрешности.
Например, показано [5], что если в (9.52) |в|| < 1, то решение К существует и
единственно, причем при произвольном начальном приближении К(0) итерационный
процесс (9.52) сходится и справедлива апостериорная оценка погрешности [5, 67]
|К<»> - К|| < -BLIkOO _ кОН) II. (9.53)
II II 1-в II II
606
Анализ и статистическая динамика САУ. Часть I
В связи с некорректностью уравнения (9.51) для решения системы алгебраических
уравнений (9.48) целесообразно применять метод регуляции А.Н. Тихонова. Задачу
идентификации можно решать с применением оптимизационных процедур, при этом
можно уменьшить влияние помех, вводя соответствующие функционалы.
Обозначим
(9.54)
(9.55)
(9.56)
(4)
с?'
-
и
4
Л
фт
(0СЕ'
...
...
ф
К=1
{А
А1,
-Р(4
=
)ф
4'
(4)
(4)
(4ь
где в общем случае L > £ .
Введем в рассмотрение функционал
/(4) = тахтахФт(0СБ'(4)
' 0<t<T0<i<L '
Задача идентификации сводится к задаче нахождения набора элементов
матричного оператора Ак =(a,*)f7=1, наиболее соответствующего экспериментальным
данным в равномерной метрике. Эта задача, в свою очередь, сводится к задаче
минимизации функционала (9.56), определенного на пространстве Re , т.е.
/(4)->inf. (9.57)
Задача может быть упрощена, если воспользоваться метрикой в £2[0,Г]; тогда
функционал может быть записан в форме
12
о <=i
/(4)={2>?('4)<*-
Отсюда имеем
7<4>=1 zd> ф^ (О)2*=£i>? Ф)г ■
(9.58)
-j Aarf ^щ^ ■ -J
'О /=1 V=\
Решение задачи идентификации сводится к минимизации функционала (9.58).
9.4. ПРИНЦИПЫ СТАТИСТИЧЕСКОЙ ИДЕНТИФИКАЦИИ
ЛИНЕЙНЫХ СТАЦИОНАРНЫХ ОБЪЕКТОВ, ОСНОВАННЫЕ
НА РЕШЕНИИ ИНТЕГРАЛЬНОГО УРАВНЕНИЯ ФРЕДГОЛЬМА
1-ГО РОДА
В основе статистических методов определения импульсных переходных функций
лежит интегральное уравнение [145]
оо
RXY ("О = f RYY (Т - А.ЖТ)<&, -00 < Т < 00 ,
(9.59)
Глава 9. Линейные и нелинейные объекты управления 607
позволяющее по корреляционной функции сигнала Y{t) на входе Ryy(t)
исследуемого объекта и взаимной корреляционной функции Ryy (т) между выходом
X(t) и входом Y{t) найти импульсную переходную функцию к(т).
Основным преимуществом статистических методов по сравнению с обычными,
требующими решения интегрального уравнения (9.10), является их
помехоустойчивость.
Предположим, что к объекту приложено не только воздействие Y(t), но и помеха
n{t). Тогда справедлива зависимость
00 00
X{t) = \Y{t-x)k(T)dx + \n{t-T)kn{x)d%. (9.60)
о о
Определить к(т) из последней формулы методами, описанными в предыдущем
параграфе, достаточно трудно, т.к. второй член в правой части является источником
погрешности.
Умножим обе части формулы (9.60) на Y(t + X) и произведем усреднение по
времени
00 00
X(t)Y(t + X) = \Y(t-T)Y(t + \)k(x)dT + \n(t-T)Y(t + X)kn(T)dT.
о о
В результате получаем уравнение (9.59), которое остается справедливым при
наличии помехи n{t), воздействующей на объект, при условии, что она не коррелиро-
вана с воздействием Y(t).
Статистические методы определения импульсной переходной функции
подразделяются на требующие и не требующие искусственных шумов. Первая группа методов
основана на том, что к реальному входному сигналу добавляется искусственный
вспомогательный сигнал m(t) с известной корреляционной функцией. Обычно
сигналом m{t) служит белый шум. При отсутствии корреляции между реальным
входным сигналом и m{t) имеем
00
RXm(T) = ^Rmm^-k)k(X)dX. (9.61)
О
Если m(t) - белый шум, то Rmm(r) является дельта-функцией, и выражение
(9.61) сводится к виду
ЛГш(т) = *(т).
Оно показывает, что определение импульсной переходной функции при этом не
требует решения интегрального уравнения. Однако в ряде случаев введение
искусственного шума в систему нежелательно и тогда приходится пользоваться
соотношением (9.59).
Отметим, что нахождение импульсной переходной функции из интегрального
уравнения (9.59) эквивалентно ее оценке по критерию минимума среднеквадратиче-
ской ошибки [180].
Действительно, пусть
00
е(0 = X{t) -1 k(x)Y{t - x)dx \ (9.62)
608 Анализ и статистическая динамика САУ. Часть I
E = iJs2(O<*. (9.63)
о
Если функция к(т) минимизирует критерии (9.63), то справедливо следующее
представление
*(х) = *(х) + а*и(х),
где ка(т) - произвольная функция, ки(т) = 0 при т < 0.
В соответствии с формулой (9.63) можно записать известное выражение
da
Поскольку
= 0.
а=0
Е '
у ( ~ ^2
= -:jU(O-J[*(T) + (xAa(T)]r(/-T)rfTl dt,
т
о I о J
то
j Г ( оо 1 Т оо
71 =71|^(0"1*(т)К(г"т^т|Я*а(т)К(/"т^тЛ = 0в
а'а=0 о [ о Jo о
Отсюда следует
-И A-(O-J*(T)K(/-x)rfx |ла(т)Г(/-тУти = О,
о
или, что то же самое,
7' оо 7" оо оо
0 0 0 0 О
Получаем
оо Г Г оо Г 1
о I о оо j
Далее находим
7 оо Г
-Jjf(/)K(/-x)d=J*WrfA.-Jr(/-x)K(/-x)A,
О 0 0
или
00
Rxr Ь> т) = \ ryy (х - *, ГЖ^Л. (9.64)
о
Условие эргодичности процессов при Т —> оо позволяет записать интегральное
уравнение (9.59), называемое уравнением Винера - Хопфа. Оно принадлежит к классу
уравнений Фредгольма 1-го рода.
Существуют формулы, позволяющие выбрать интервал наблюдений Т.
Например, если сигнал x{t) имеет автокорреляционную функцию вида [145]
Rxx (т) = D^e^ cos со0т,
то
Глава 9. Линейные и нелинейные объекты управления
609
Т>20\
ос
a2+G)o ocy
Если же Rxx (т) = еа|т|, то Т > — .
а
Получены формулы, при помощи которых можно, задаваясь корреляционной
функцией, полученной на основе опыта статистической обработки аналогичных
процессов, и исходя из заданной среднеквадратической ошибки, выбрать значение Т.
В соответствии с уравнением (9.59) для вычисления к(т) необходимо выполнить
два основных этапа (рис. 9.8) [145]:
1) определение корреляционных функций Ryy(t) и /^(т);
2) решение интегрального уравнения Винера - Хопфа.
к(т)
X(t)
Рис. 9.8. К выводу интегрального уравнения (9.59)
Корреляционные функции находятся с помощью корреляторов. Рассмотрим
решение уравнения (9.59), пользуясь заменой интеграла суммой. Представим уравнение
(9.59) в виде суммы [145]
N
/;=0
R^ (T) = ^k(nA)RYy (т-яД)Д .
Обозначим
А =
RYy(0)
Ryy(A)
RYy(A)
%(0)
{Ryy((N-\)A) RyydN-2)A)
K =
Ryy((N-\)A))
RYY((N-2)A)
%(0)
(9.65)
(9.66)
( *(A) )
k{2A)
k(3A)
^k(NA),
;Q =
<?i
<?2
Ъ
kQN;
(9.67)
где
_RXY(iA)
Тогда (9.65) перепишем в виде
АК = Q . (9.68)
В (9.68) А = (ау)^~}0 - квадратная симметричная матрица размером NxN
(см. (9.66)).
Как и в случае решения уравнения свертки, задача расчета импульсной
переходной функции свелась к решению системы линейных алгебраических уравнений.
Последняя является симметричной с доминирующей главной диагональю. Это свойство
610 Анализ и статистическая динамика САУ. Часть \
порождено свойствами корреляционных функций, входящих в исходное уравнение
Фредгольма 1-го рода (9.59).
Для уменьшения размерности операторного уравнения (9.68) с матричным
оператором можно воспользоваться разложением корреляционной функции и импульсной
переходной функции по ортонормированным базисам. В этом случае можно найти
систему алгебраических уравнений относительно коэффициентов Фурье
идентифицируемой ИПФ.
Кроме того, можно построить вычислительные устройства (аналоговое и
цифровое), позволяющие автоматически определять коэффициенты авто- и взаимнокорре-
ляционных функций, разложенных по ортонормированному базису [168].
9.5. ОПИСАНИЕ И ИДЕНТИФИКАЦИЯ НЕЛИНЕЙНЫХ СИСТЕМ
МЕТОДОМ ВИНЕРА
Рассмотрим основные теоретические положения метода Винера [31, 35, 72, 123,
163 и др.]. Этот метод позволяет построить математическую модель класса
нелинейных объектов, описываемых функциональными рядами Вольтерра.
Для определенности рассмотрим скалярный объект, описываемый нелинейным
ДУ вида
J^avx(vhF(x9X,..)=Y{t), (9.69)
v=0
где F\X,X,..J - аналитическая функция своих аргументов.
Функциональный ряд Вольтерра устанавливает явную связь между входом Y (/) и
выходом X[t) нелинейного объекта.
Определение ядер Мт^Тг,...,!,-) занимает большое место в теории Винера, где
ядра раскладываются в ряды по ортогональным функциям Лягерра
а)=
±exp(t)-^(tn exp(-f))Ы-0 (9.70)
« = 0,1,2,....
Если {Ln (t), n = 0,1,2,...} - последовательность функций Лягерра, то
v=0
MTi.T2)-£fXWT,WT2),
Lu L~l V1V2 "1 * " "2* <•" /4)714
v,=0v2=0 \7-'l)
v,=0v2=0 v,=0
В методе Винера определение коэффициентов \с„11, \с*\ |, •••, |c*'v ...v )
осуществляется измерением входного и выходного сигналов системы.
В качестве входного испытательного сигнала в рассматриваемом методе
используется нормальный белый шум с единичной интенсивностью. Винер показал, что
Глава 9. Линейные и нелинейные объекты управления 611
рассматриваемый класс нелинейных систем может быть представлен каскадом из
двух операций.
В первой операции используется система функций Лягерра, по которой
разлагается входной сигнал Y (t).
Спектральное представление Y (/) в базисе функций Лягерра запишется так
/
Г(/)«]Гс!Х(0, (9.72)
где
00
• cYv=^Y(t)Lv(t)dt, v = 0,l,2,.... (9.73)
о
Для спектральных характеристик С =[cQ ,q ,...,<?/ ) характерно следующее:
-элементы СХ CY статистически независимы [31, 35],
- дифференциальный закон распределения является законом Гаусса
Таким образом, если на вход нелинейного объекта подать множество реализаций
белого шума Y(t), для каждой реализации будет иметь место СХ, соответствующая
конкретной реализации ук (/); положим, что коэффициенты Фурье всех реализаций
распределены на оси (- оо, +оо), т.е.
-a)<c/K<+a),/=U,^={c^:A = l,2,...,/7},
где р - число элементов.
Выходной процесс X{t) нелинейной системы представляет собой функцию,
аргументами которой являются коэффициенты Фурье воздействия
X{t) = lim R(cY0 , с\ , с\,..., с] ), (9.75)
/—>00
где - оо < с] < +оо, / = 1, /.
В формуле (9.75) функция R неизвестна. Представим (9.75) в виде разложения по
многомерным полиномам Эрмита
оо оо оо
/г(4,сГ)с[,...)с/")=ХЕ-Ес'",..^'»(соКк)-^(с/0, (9.76)
/0 =0/, =0 //=0
где
00 00 00
<&...., = J f •••|^,сГ(...,с/)я„,(соОя/,(сГ)-Я„(с/'')х
(9.77)
— 00 —00 —00
хе 2У Jdcodc{ •••dcj .
Коэффициенты cj\ j (/0,/j,...,//=0,1,2,...) вычислить не представляется
возможным, поскольку неизвестна функция R\Cq ,с\,с\,...,с] j.
С учетом (9.76) зависимость (9.75) принимает вид
612 Анализ и статистическая динамика САУ. Часть I
/o=Gi,=0 //=0
Поскольку в (9.76) R\Cq ,c\,c\,...,<;/ J представляет собой функцию, зависящую
от системы случайных величин, статистические свойства которой известны, то для
нахождения зависимости, определяющей коэффициенты cf,%tmi , можно
воспользоваться операцией осреднения по множеству. Известно, что операцией математиче-
Cq,cx ,c29'..,Ci J системы из (/+1) случайных величин
Cq,c,k, c\,...,c] называется (/+1)-кратный интеграл от произведения указанной
функции на дифференциальный закон распределения системы случайных величин,
взятых по параметрам с\, с\, с\ ,...,с/ в бесконечных пределах.
При этом предполагается, что функция /^(со,^,^,...,^//обладает такими
свойствами, что (/+1)-кратный интеграл существует.
Согласно определению можно записать
00 00 00
m\r{cI,c\,c\,...,c]\=\ \-\r(cI,c\,c\,...,c]\
—00 —00 —00
х/с> {cl,c\,c\,...,c])dcldc\ ...dc].
Применяя операцию осреднения по множеству к обеим частям равенства (9.78),
получим
П^,(,)я,;(4Кк)..я;йИ':»'-("'' «•■>.
—00 —00 —00
*dcldc\...dc] -to^SI-S*-'. J н<Мк;М)*
V-КУ /0=0/,=0 //=0 -оо
хе-М'л*... J H^H^e-WdJ. (9.80)
-оо
Согласно принципу эргодичности осреднение по множеству может быть заменено
осреднением по времени, и, таким образом, имеет место равенство
о
{2п)2 /о=0/1=о //=о
-00
Вследствие ортогональности полиномов Эрмита, правая часть последнего
соотношения будет равна нулю, если /0 * /0,/'j ^/,,...,// фг1 ; если же
/0 =/o,/"i =/J,...,//=// , то все интегралы полиномов Эрмита будут равны единице.
Учитывая сказанное, соотношение (9.81) принимает вид
Глава 9. Линейные и нелинейные объекты управления
613
м)2 о
ЛйЧ4)г+~Ш)
dt, (9.82)
Ы-
где Г -достаточно большое время эксперимента.
Структурная схема вычислительного устройства, реализующего метод Винера,
представлена на рис. 9.9.
Приведенные на рис. 9.9 обозначения соответственно имеют вид:
fVmn=Hm(cYn)e~iicl)~,
ФП - функциональный преобразователь,
E(t) = EiQiiJi(clcl,...,c!),
U(t)= hm-\X(t)E, f ,■*,
z(0 = -
1 C'o'i '/ '
(2я)
БЛОК 1 - схема вычисления коэффициентов Фурье ^(/=0,1,...,/) по
функциям Лягерра,
БЛОК 2 - схема вычисления значений полиномов Эрмита.
до
h
—►
1—►
елиней
объек
А) (О
Т (т\
БЛОК1
ный
г
cl *
с0 1
1
1
1
Y •
1
1
'
'
1
1
1
•
1
1
1—►
—►
ч
—►
—►
i —►
1—^
i —►
—^
| БЛ
IX/
И оо
"10
■| иъ
ЮК2
. - -
1
— ч
-i
—i
1
-H
H
H
J
1
1
1
V
h
h
1
h
ФП
Щ
U(t)
Щ.
Рис. 9.9. Структурная схема вычислительного устройства, реализующего метод Винера
-iM Анализ и статистическая динамика САУ. Часть I
Воспользуемся обозначением
м U J (9.83)
Тогда (9.82) запишется в виде [31, 35, 123]
<', -., %!Ь^-Й'№4(/4(т)у(т)*]л. (9.84)
о *=о {о )
Обратимся к структурной схеме вычисления оценок cR. . . Нормальный белый
Vi '/
шум используется одновременно для получения выходного сигнала X{i) объекта
идентификации и значений системы Лягерра - Эрмита
%..j4^iv.^). (9.85)
Далее с помощью вычислительного устройства, реализующего операции
умножения и суммирования с весом, рассчитываются искомые коэффициенты.
Сделаем некоторые пояснения. Если объект стационарен, его математическая
модель может быть записана так
h =0 /,=0 /,=0 0
ьо U )
Среднеквадратическая сходимость последнего ряда имеет место, если
одновременно / —> оо и Т —> оо . Поэтому получаемая модель является приемлемым
приближением объекта идентификации лишь при достаточно большом времени наблюдения
и при использовании необходимого количества членов разложения.
Как указано в [123], особенность применения указанного подхода состоит в том,
что задача идентификации должна решаться для любого и Поэтому элементы
структурной схемы, представленной на рис. 9.9, должны обеспечивать непрерывное
определение соответствующих процессов. Например, для расчета спектральных
характеристик сигнала Y(t) в базисе функций Лягерра применяется вычислительное
устройство вида, представленного на рис. 9.10 [123].
Для каждого временного интервала [0, /] вычисления должны проводиться заново.
Это обстоятельство делает весьма неудобным применение подобных моделей в тех
случаях, когда идентифицируемый объект является частью сложной системы
физических объектов, работающих в реальном времени.
Поэтому для реализации алгоритма идентификации целесообразно пользоваться
цифровыми ЭВМ; соответствующие формулы имеют вид
^>-й-2&..л4}'.м*)4 <9-8"
причем
Глава 9. Линейные и нелинейные объекты управления
615
%
,4%!-^-ип4К(т)у(т)*]*
\L T
У \^^^^^1Г I Ш У * У * I
(9.88)
о ьо Vo
Рассматриваемый метод идентификации целесообразно применять в задачах со
случайными входными сигналами, когда представляет интерес задача
идентификации в среднеквадратическом.
по
1
5-1
i
7*
s-\
Т
-1
т
т2
л. Т
1
г
ч
i
+
J' Св'
Рис. 9.10. Структурная схема аналогового вычислительного устройства для расчета спектральной
характеристики сигнала Y(t) иа промежутке 10,7] в базисе функций Лягерра
Подробное обоснование метода Винера, а также примеры его применения для
решения конкретных задач можно найти в [123].
В [31] показана эквивалентность характеризации нелинейных систем методом
Винера и функциональным разложением Вольтерра.
Метод Винера радикально отличается от существующих методов описания и
исследования нелинейных систем, но в нем даются только основы новой теории. По
известным работам трудно оценить его практическое значение. Однако
теоретическая ценность этого метода очевидна.
Остановимся на некоторых фактах, затрудняющих применение метода Винера.
Принципиально важным является обстоятельство, связанное со сходимостью
разложений процессов по ортогональным базисам Лягерра и Эрмита. В [123] для
решения конкретной задачи использовались полиномы Лягерра и Эрмита третьего и
четвертого порядков соответственно, что потребовало определения 64 коэффициентов
ряда Лягерра - Эрмита. При исследовании достаточно сложных объектов для
достижения заданной точности часто используется большое число элементов спектральной
характеристики сигнала Y(t) в базисе функций Лягерра (часто оно достигает
нескольких десятков даже для решения задач исследования линейных систем). Это
порождает весьма серьезные трудности, связанные с реализацией метода даже с
помощью современных средств вычислительной техники и с проблемой достижения
приемлемой точности.
По коэффициентам, определяемым формулами (9.82) и (9.88), трудно оценить
структуру и свойства системы, которую они представляют.
При применении ряда методов имеется возможность воспользоваться какой-либо
априорной информацией относительно идентифицируемого объекта с целью
сокращения времени вычислений и достижения большей точности решения поставленной
задачи. В методе Винера такая возможность практически отсутствует.
616 Анализ и статистическая динамика САУ. Часть I
Модели Винера чрезвычайно громоздки и их использование для решения
последующих задач, например, построения корректирующих устройств при решении
проблемы фильтрации, вызывает значительные трудности.
В методе Винера важным является обеспечение качества зондирующего сигнала,
определяющего степень адекватности объекта и его модели. Отличие свойств
пробного сигнала от белого шума в соответствующей полосе частот приводит к ошибкам
в решении поставленной задачи (ограниченность частотного диапазона пробного
процесса тесно связана с точностью решения задачи). На точность оцениваемых
параметров также оказывает влияние время проведения эксперимента.
Перечисленные недостатки данного подхода явились основными причинами, из-
за которых метод Н. Винера и его модифицированный вариант, предложенный
А. Боузом, до сих по не нашли широкого применения для решения конкретных,
достаточно сложных инженерных задач.*
9.6. ОЦЕНКА ПАРАМЕТРОВ НЕЛИНЕЙНЫХ СИСТЕМ
МЕТОДАМИ ФИЛЬТРАЦИИ
Положим, что [161]:
задано дифференциальное уравнение объекта идентификации
X = f(X,/M) + B(/M)Y(f), (9.89)
где Х(/) - л-мерная вектор-функция фазовых координат, f(X,/?,/) - нелинейная
вектор-функция размерности л, р - вектор случайных параметров, причем р = рн+Ар,
где рн = тр - вектор номинальных значений параметров (эти значения заданы) и
А/? - вектор случайных малых отклонений, в(/?,/) - матрица коэффициентов; Y(/)
- вектор-функция входного сигнала;
Известны необходимые статистические характеристики случайных параметров.
Требуется определить оценку параметров р по наблюдению на интервале [о,г]
сигнала
Z(/)=HAX(f)+N(f) (9.90)
по критерию минимума среднеквадратической ошибки; в формуле (9.90) N(/) -
помеха, АХ(/) = Х(/)-Хн(/) , где Хн(/) - сигнал на выходе модели объекта,
имеющей номинальные значения параметров, Н - известная матрица.
Структурная схема объекта может быть представлена в виде, показанном на
рис. 9.11.
Для решения задачи идентификации проведем некоторые преобразования. Введем
в рассмотрение нелинейную модель объекта, имеющую номинальные значения
параметров (полагаем, что номинальные параметры системы равны своим
математическим ожиданиям); уравнение такой модели имеет вид
XH=f(XH,A,/) + B( pH9t)Y{t). (9.91)
В последнем уравнении \(t) - входной сигнал, Хн (/) - вектор фазовых
координат модели.
Некоторые применения приведены в книге С.Н. Музыкина иЮ.М Радионова. «Моделирование
динамических систем». Ярославль: Верхне-Волжское издательство, 1984.
Глава 9. Линейные и нелинейные объекты управления
617
v(/)
f(x,/v)
+}
d
Ui/)
1
S
Идентифицируемый
объект управления
xW
Рис. 9.11. Структурная схема объекта управления
Структурная схема для формирования сигнала Хн (/) представлена на рис. 9.12.
v(<)
и
f(xH
в(
>р»
р»
.<)
.0
Модель объекта при
номинальных значениях
параметров
Рис. 9.12. Структурная схема модели объекта с номинальными значениями параметров
Линеаризуем нелинейную вектор-функцию f(X,p,t) (воспользуемся рядом
Тейлора), полагая при этом:
1) f(X,/?,/) и B(p,t) - дифференцируемы по фазовым координатам и
параметрам;
2) линеаризация проводится относительно опорного движения, определяемого
уравнением (9.91);
3) отклонения параметров р от номинальных значений параметров рн
незначительны;
4) отклонения фазовых координат системы (9.89) от фазовых координат системы
(9.91) малы.
Результат имеет вид [116]
f(X,p,0 = f(XH+AX,/7H+Ap,0 =
= f(XH,/7H,/) + D1(XH,pH,0AX + D2(XH,pH,0Ap, (9.92)
где D{(XH,pH9t) =
#(X,p,Q|
axt
- матрица производных векторной функции f по
компонентам вектора Х(/) при X = Хн, р = /?н,
D2(XH,/?H,0 =
df,(X,P>t)
дрк
- матрица производных векторной функции f по
компонентам вектора/? при X = Хн, р = рн,
618
Анализ и статистическая динамика САУ. Часть I
AX(f) = X(f)-XH(f), Ap = p-pH, /,у = 1,и, k = \J.
Аналогичйо получим
B(p,t) = B(pU9t) +D3(a,,0Aa
(9.93)
где
^з(/7н>0= —^—"— ~ матрица производных от матрицы коэффициентов
дРк
В(/?,/) по компонентам векторар, при р = рн, /, j = 1, л, к = 1, /.
Найдем линейное дифференциальное уравнение относительно ДХ(/) [116]
AX = /(XH,pH,0 + D1(XH,pH,0AX + D2(XH,pH,r)Ap +
+B(pH9t)Y(t) + D3(pH,t)ApY(t)-f(XH,pH,t)-B(PH9t)Y(t)= (9.94)
= В1(Хн,Лэ/)ДХ + В2(Хн,рнэ/)Ар + В3(Л,0АрУ(0-
Перепишем последнее уравнение в виде
AX-D]{Xt,,ptt,t)A\ = (D2(Xtt,pH,t) + D3(pH,t)Y{t))Ap. (9.95)
Введем в рассмотрение матричную импульсную переходную функцию,
определяемую уравнением
dK(t,,,xu,Pu) = j)^^t) к(,)Т)Хн)/0) (996)
при К(т,т,Хн,/?н) = 1, I - единичная матрица.
Решение векторно-матричного дифференциального уравнения (9.95), выраженное
в форме интеграла Коши, запишется в виде
АХ(г) = }к(/,т,Хн,/7н) (D2(XH,pH,i) + D3(p,,,T)Y(T))dT-AP. (9.97)
Воспользуемся обозначением
Ф(/) = }к(/,т,Хн,Л) (D2(XH,pH,T) + D3(/7H,T)Y(T)).fT.
(9.98)
Структурная схема вспомогательной системы, выходом которой является процесс
ф(/), представлена на рис. 9.13.
Хн(0
D2(XH,pH>0
+®-^
Пз(д,.О
Звено с ИПФ
К(/,т,Х„,Л)
Модель вспомогательной
системы
Ф(/)
Рис. 9.13. Структурная схема вспомогательной системы
Формулу, определяющую ДХ(/), можно переписать так
дх(*)=ф(04р-
(9.99)
Глава 9. Линейные и нелинейные объекты управления 619
Наблюдению подвергается вектор-функция Z(t), определяемая соотношением
Z(/) = HAX(/)+N(/)=HO(/)A/? + N(/), (9.100)
где Н - матрица, характеризующая измеритель,
1Ч(/) - вектор-функция помех измерителя.
Воспользовавшись обозначением
S(/)=HO>(/), (9.101)
соотношение (9.100) перепишем в виде
Z(/) = S(f)A/? + N(/). (9.102)
Таким образом, получена формула (9.102), в которой Z(t) линейно зависит от
вектора случайных параметров системы Ар.
Поскольку имеет место случай наблюдения аддитивной помехи и полезного
сигнала, линейно зависящего от вектора параметров, то оптимальная оценка параметров
может быть получена в соответствии с формулой [116]
р =(rppC + \)-1RppQ9 (9.103)
где Rpp - априорная корреляционная матрица вектора параметров,
I - единичная матрица,
т т
C = JkJ(t)s(t)</t, Q = JkJ(t)z(t)*, (9.104)
о о
причем
т
JkJ(t)R^(/,t)^t = St(/); (9.105)
о
из (9.105) следует, что для нахождения матрицы Ко(/), входящей в зависимости,
определяющие матрицы С и Q, необходимо решить интегральное уравнение.
Алгоритм значительно упрощается, если n(/) - белый шум.
Тогда
*m(t»'2) = SoB(h-'i) (9-106>
и
т т
KT0{t) = ST{t)S-0\ C = |st(t)So1S(t)^t, Q = Jst(t)So1Z(t)^t. (9.107)
о о
Апостериорная корреляционная матрица, характеризующая точность получения
компонент вектора оценки Ар, имеет вид
К*рр=м(кррС + 1Укрр, (9.108)
где М- оператор математического ожидания.
Структурная схема системы, позволяющей получить оценку вектора параметров
Ар* нелинейной системы, представлена на рис. 9.14.
Для получения алгоритма оценки вектора случайных параметров нелинейной
системы можно использовать подход, содержание которого состоит в том, что
параметры системы принимаются за дополнительные фазовые координаты расширенной
нелинейной системы [116].
Положим, что нелинейный объект описывается векторно-матричным нелинейным
дифференциальным уравнением вида
620 Анализ и статистическая динамика САУ. Часть I
X = f(X,/>,/)+Y(f)+M(0, (9.Ю9)
где Y(/) - детерминированный входной сигнал,
М(/) - случайная вектор-функция (зондирующий сигнал) с корреляционной
матрицей
*W'i>'2) = M'i)5('2-'i)-
Наблюдаемым является сигнал Z(t), определяемый формулой
Z(f)=HX(f)+N(f), (9.110)
где Н - заданная матрица, характеризующая измеритель,
1Ч(/) - ошибка измерителя (центрированный векторный случайный процесс),
причем
Требуется определить параметры нелинейного объекта по наблюдениям вектор-
функции Z(t) при известных статистических характеристиках соответствующих
процессов.
Математическое ожидание ^-мерного вектора фазовых координат определяется
уравнением
mXii=f(mx,pH,0 + Y(0, тХн(0) = 0. (9.111)
При принятых предположениях в результате линеаризации функции f(X,/?,/)
относительного номинального режима, можно получить соотношение вида
(используется ряд Маклорена)
f(X,/7,0 = f(mXH,/7H,/)+D1(mXH,pH,/)x + D2(mXH,pH,/)/7, (9.112)
где Dx( mx ,/?„,/) - матрица производных векторной функции f по компонентам
вектора шх,
D2( mx ,pH,t) - матрица производных векторной функции f по компонентам
вектора р.
Линеаризованное уравнение имеет вид
X = D1X + D2/7 + f(mXH,/7H,/)+Y(/) + M(/) , X(0) = 0. (9.113)
Основная идея подхода состоит в том, что фазовое пространство объекта
расширяется - в него включается вектор параметров/?; уравнения (9.113) дополняются
векторным уравнением
р = рн, /?(0) = /?0. (9.114)
Для расширенной вЬкторно-матричной системы с целью оценки параметров р
применяется теория обобщенного линейного фильтра в пространстве состояний [116].
Уравнения для оценок имеют вид
X = D,X + D2p + f( mXH,/?H,/)+Y(/) + B,v(Z-HX), (9.115)
х(о) = о,
^ = A+Bp(z-HX),p(0) = A(0). (9.116)
Матрицы Вх и В^ определяются из матрицы
B = RHTSo1, (9.117)
где R - симметричная корреляционная матрица расширенного вектора ошибки
оценок Х-Х и р-р\ Н- известная матрица.
Y(/)
Объект
X(0
Л ДХ(/)
Y(0
Модель объекта
при номинальных
значениях
параметров
Н
х„(0
Y(0
7
| N(0
+ 1 Z(o
Расчет
матрицы Q
Модель
вспомогательной системы
Ф(0
Расчет
матрицы С
Крр
i
Ар'
|\nn
рр
RPPc
Расчет
матрицы
(R^C+I)"1
(RppC+iyl
М( RPPC+I )-'R™
R
рр
Рнс. 9.14. Структурная схема системы для оценки вектора параметров Др* нелинейной системы
622 Анализ и статистическая динамика САУ. Часть I
Если известна матрица В, то Вх - прямоугольная матрица, состоящая из первых п
строк, а В^ - прямоугольная матрица, состоящая из последующих п строк, т.е.
в =
в,
(9.118)
р )
Уравнения (9.115) и (9.116) определяют структуру и параметры системы, с
помощью которой можно определить оценки вектора состояния и параметров объекта при
наблюдении на интервале (О,/) вектор-функции Z(/), связанного с вектором
состояния х(/).
Рассмотренный подход предполагает, что функция f(x,p,t) может быть
разложена в ряд Маклорена; если же нелинейная функция не является аналитической, то
можно воспользоваться статистической линеаризацией. Алгоритм получения оценок
остается прежним.
9.7. ОЦЕНКА ПАРАМЕТРОВ НЕЛИНЕЙНЫХ ОБЪЕКТОВ МЕТОДОМ
НАИМЕНЬШИХ КВАДРАТОВ С ИСПОЛЬЗОВАНИЕМ
ТЕОРИИ ЧУВСТВИТЕЛЬНОСТИ
Положим, что объект идентификации описывается системой нелинейных
дифференциальных уравнений вида
Х\ = f\{X\>X2,...,Xn; YxJ2i...Jm\ рьр2,...,р{; t),
*г = fi\X\,X2,...,Xn\ Yl9Y2,...,Ym\ P\,p2,...,Pi\ t)9 ^
Xn=fn{X\,X29...,Xn'9 Y]9Y2,...9Ym; Р\9р2,-,РГ> 0>
где Y = (Y^, Y2,..., Ym)T - /w-мерный векторный случайный входной сигнал,
X = (ХьХ2,...9Хп)т - «-мерный случайный вектор фазовых координат,
P~{p\^Pi>•••>Pi)T - вектор идентифицируемых параметров,
Рн =(/71н>/72н>-->/7/н) -вектор номинальных значений параметров,
Ар = (АриАр2,...,Арп) - вектор отклонений фактических значений
идентифицируемых параметров от номинальных, т.е.
*Pi=Pi-PiH> / = U.
Задача идентификации состоит в определении Api9 /=1,/, при наблюдении
одной или нескольких координат объекта.
Перепишем (9.119) в векторной форме
X = f(X,Y,/7,/), X(0)=0. (9.120)
Очевидно, режим функционирования объекта при номинальных значениях
параметров можно определить как номинальный; он определяется векторным уравнением
XH=f(XH,Y,/7H,0, XH(0) = 0, (9.121)
или в скалярной форме
Глава 9. Линейные и нелинейные объекты управления
623
Х\и -/1(^1н»^2н>--->^Г/?/<>^1>^2>--->^/и>Ан»/72н>--->/7/н»0 >
(9.122)
Введем в рассмотрение функцию чувствительности, которая определяется
уравнением [116]
ir Up,) *Wy Л)
(9.123)
/ = 1,2,..., л, r = l,2,...,/,
где звездочка (*) означает, что производные и переменные вычисляются при
номинальных значениях параметров.
В развернутом виде (9.123) можно записать так
W,
(9.124)
11 [dxj " [дх2) 2I [a^J "' Ы
21 [dXj " {dX2j 21 [dxj "' {dPl)'
"' [dXj " {dX2j v [dXj "' {dp,)
Системы дифференциальных уравнений (9.121) и (9.123) определяют модели,
позволяющие получить Хн (/) - вектор состояния в номинальном режиме и функции
чувствительности Wir{t) (рис. 9.15).
Y(0
1 .
Y(/)
1 '
п/
■N
Модель объекта
С* ЦЛМ1И1Я ПLULI\>f if
параметрами
\
Модель,определяю-
щая функции
чувствительности
XJf)
Рис. 9.15. Структурная схема вспомогательной системы
Взаимосвязанную систему двух моделей можно рассматривать как некоторую
вспомогательную систему.
Учитывая следующее:
- процессы XiH(t) и Wir{t) могут быть определены путем интегрирования
дифференциальных уравнений вспомогательной системы,
- отклонения параметров /?, от их номинальных значений полагаются малыми,
624 Анализ и статистическая динамика САУ. Часть I
можно записать соотношение, определяющее Xt(t) в виде
*,-(0 = *ж(0 + 2Х(')4Рг> / = 1Я (9.125)
г=\
Положим, что проведено необходимое число экспериментов и измерено N
значений одной фазовой координаты Xt{t), а также процессов XiH[t), Wir{t) в точках
t\9t29-.9tqi т.е. известны величины
*,(v)(O. хф)М> K{v)(h), *=п; v=uv. (9.126)
Считаем, что ошибки измерения указанных выше величин независимы и имеют
нормальный закон распределения.
Составим квадратичную форму вида
/(A/?,,...,Ap/) =
= Тг£ £p*U(v)('*) -^„(v)(^) -£^<v)('*)4p,1 > (9-127)
'v v=l [*=1 L r=\ J J
где p^ - весовые коэффициенты; их можно выбрать, исходя из условия
P*=[tf,2U)]~\
причем а,2 (**) - дисперсии ошибок измерений.
С целью упрощения расчетов коэффициенты веса можно положить равными
между собой.
Оценки параметров идентифицируемого объекта находятся из условия
/(Д/^А/^.^А/^-мпт. (9.128)
А/7
В соответствии с условием (9.128), можно получить систему алгебраических
уравнений относительно вектора А/?, для чего, исходя из необходимого условия
оптимальности, надо от (9.127) взять частные производные по каждому из параметров и
полученные соотношения приравнять к нулю
aaPs /v a=i [k=\ L f=i J (9.129)
x^is(v)('*)) = 0.5 = l,/.
Последнюю зависимость целесообразно записать в более удобном для
практического использования виде, сгруппировав члены относительно идентифицируемых
величин,
(9.130)
zfzp^iw'*) woV=zp*^*
r=lV*=l " v=l J *=1 n
xl[^(v)('»)-^(v)('*)] ^(v)('*). S = U.
> обозначениями
v=l
Воспользовавшись обозначениями
k=\ 1У v=l
Глава 9. Линейные и нелинейные объекты управления
625
£р* тг£|Ч(у) в) -^h(v) &)] ^(v) [h )=ь89
к=\ п v=l
из (9.130) получим систему алгебраических уравнений.
-auAp]+anAp2+... + allApl=bl,
a2lApl + а22Ар2 +... + a2iApt = b2,
(9.132)
(9.133)
апАрх + а12Ар2 +... + а^Ар/ = Ъ{.
Или, что то же самое,
ААр = В. (9.134)
Отсюда для вектора идентифицируемых параметров можно записать соотношение
Ap = A-!B. (9.135)
Приведенные рассуждения показывают, что оценки являются линейными
функциями результатов наблюдений; последние являются несмещенными и имеют
наименьшую дисперсию среди всех линейных несмещенных оценок.
Число измерений определяется заданной точностью статистической обработки.
Метод обобщается на нестационарные нелинейные объекты.
Структурная схема системы идентификации представлена на рис. 9.16.
г(,)
г^>
^>
Объект
идентификации
Модель объекта с
номинальными
параметрами
Модель,
определяющая функции
чувствительности
Т
xff)
+ '
d
XM(t)
Измеритель
A*4v)('*)
Формирование и
решение
системы
алгебраических
уравнений
Ар
Рис. 9.16. Структурная схема системы идентификации
41 Зак. 232
626 Анализ и статистическая динамика САУ. Часть I
ГЛАВА 10. ОПИСАНИЕ НЕПРЕРЫВНО-ДИСКРЕТНЫХ
СИСТЕМ С ПОМОЩЬЮ ИНТЕГРАЛЬНЫХ
ПРЕОБРАЗОВАНИЙ
Наличие микропроцессора в контуре управления приводит к необходимости
квантования непрерывных сигналов по времени и по уровню, что сразу переводит
исходную систему в класс непрерывно-дискретных систем, который требует новых
методов описания, исследования и проектирования. Эти методы хотя и в
значительной мере опираются на привычные для непрерывных систем понятия, далеко не
исчерпываются ими, что заставляет выделять системы с ЭВМ в контуре управления в
особый класс.
Если в качестве регулятора динамической системы используется
микропроцессор, то в описании системы присутствуют дифференциальные и разностные
уравнения, функциональные зависимости, отражающие преобразования сигналов из
непрерывной формы в дискретную и обратно, а также алгебраические выражения связи
между звеньями. Такое описание приводит к серьезным затруднениям уже на этапе
характерлзации систем и последующем решении задач управления.
Традиционный путь предполагает замену дифференциальных уравнений
разностными моделями, так что система в целом описывается лишь разностными
уравнениями. Несколько реже применяется прямо противоположный подход, когда с
учетом малости периода квантования система рассматривается как непрерывная. Анализ
и синтез системы ведется известными методами теории непрерывных систем, и лишь
синтезированный непрерывный регулятор реализуется в разностной форме. Каждый
из указанных подходов приводит к методическим погрешностям, т.к. связан с
заменой непрерывно-дискретной системы либо непрерывной, либо дискретной моделью,
каждая из которых в той или иной степени отличается от исходной. В частности,
можно показать, что при переходе к разностным моделям могут происходить
качественные изменения, например, система из управляемой может стать неуправляемой.
С другой стороны, даже ограничиваясь лишь разностными уравнениями, можно
заметить, что используемый формальный аппарат описания динамики существенно
усложняется при любой попытке расширить класс исследуемых систем. Простые
связи вход-выход на основе передаточных функций приходится заменять на
существенно более сложные, в которых исчезают алгебраические правила, хорошо
знакомые инженеру из теории стационарных непрерывных систем. В частности, это
обстоятельство проявляется уже при попытках описать связи вход-выход простейших
преобразующих устройств, таких как ключ и экстраполятор, при любых
предположениях о математических моделях и способах их реализации.
Опыт анализа и синтеза непрерывных систем широко используется при
проектировании микропроцессорных систем. Однако при этом приходится искать ответ
на целый ряд новых вопросов, таких как выбор требуемой разрядности, периода
квантования, рационального программирования алгоритма, соответствующего
масштабирования всех переменных и коэффициентов, преобразователей аналог-код
и код-аналог.
Глава 10. Описание непрерывно-дискретных систем 627
В полной мере теория цифровых систем к настоящему времени еще не сложилась,
чему есть много причин, которые частично обсуждаются ниже. Очевидная сложность
процессов управления, обусловленных эффектами квантования, наличием
непрерывных и дискретных элементов, приводит к качественно новым явлениям в поведении
систем, для глубокого исследования которых требуются весьма тонкие методы
анализа. Тем не менее ответы на многие из поставленных выше вопросов могут быть
получены без привлечения сложных математических конструкций качественной
теории нелинейных систем, оставаясь в рамках привычных инженеру понятий теории
регулирования.
В настоящей главе обсуждаются проблемы описания линейных динамических
объектов, и делается попытка с единых позиций решить задачу характеризации
динамических систем различных классов.
Хорошо известны и повсеместно используются понятия передаточных функций
стационарных линейных систем (непрерывных W{s) и дискретных W{z)).
Своей популярностью передаточные функции обязаны простому и красивому
соотношению, связывающему вход и выход системы. При этом формально простая
процедура, характеризующая действие линейного оператора, оказывается фактически
простой операцией умножения двух комплексных выражений.
К сожалению, эта простота сохраняется лишь для линейных стационарных систем
с однородной структурой сигналов и исчезает при любых попытках расширить эти
рамки. В частности, уже при описании непрерывно-дискретных систем появляется
ряд методических, трудностей (физически нереальные ключи второго рода [23],
невозможность определить передаточные функции при некоторых соединениях
звеньев, определение статистических характеристик импульсных сигналов и др.).
Похожие препятствия приходится преодолевать с параметрической передаточной
функцией в нестационарных системах. Формально простую связь вход-выход не
удается применить даже для простейшей задачи вычисления передаточной функции
последовательного соединения двух нестационарных звеньев.
Источники указанных затруднений ясны и связаны с попытками расширить
область применения привычной передаточной функции за рамки непрерывных
стационарных систем, что чаще всего не приводит к успеху.
Исходное описание системы обычно задается уравнениями (дифференциальными,
разностными, в частных производных). Системы с цифровыми регуляторами, в силу
универсального характера и гибкости последних получившие большое
распространение, приходится описывать смешанными (дифференциальными и разностными)
уравнениями. Поскольку уравнениями системы связь вход-выход задаётся в неявной
форме, для целей характеризации динамических звеньев используются системные
характеристики, для которых указанная связь оказывается явной.
Ограничимся рассмотрением двух основных характеристик для внешнего
описания системы: весовой функции, связывающей вход и выход во временной области, и
передаточной функции, выполняющей ту же функцию для изображений.
Соотношения для других характеристик, в частности, для внутреннего описания системы,
очевидным образом следуют из рассмотренных выше.
Используя интегральные преобразования весовых функций (одномерные й
двумерные), удается определить передаточные функции и с их помощью установить
соотношения вход-выход для разных классов линейных, в общем случае,
нестационарных систем: непрерывных, дискретных, дискретно-непрерывных и непрерывно-
дискретных. Получающиеся при этом выражения по форме и по существу являются
одинаковыми для разных типов линейных звеньев, что обеспечивает общность
описания в переменных вход-выход для основных классов линейных систем. В частном
41*
628 Анализ и статистическая динамика САУ. Часть I
случае, когда звенья являются стационарными, из общих соотношений как следствие
получаются известные формулы. Для таких систем приведенный материал носит
скорее методический характер, отражающий одну из возможных точек зрения на
способы описания линейных систем.
10.1. СИСТЕМНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ
ДИНАМИЧЕСКИХ ЗВЕНЬЕВ
Исходное описание динамических звеньев в виде обыкновенных
дифференциальных и разностных уравнений представляет собой неявную форму записи
соотношений вход-выход. Поэтому в практике решения задач регулирования и управления
получили распространение характеристики, позволяющие получить явные
соотношения, определяющие зависимость реакций системы от входных воздействий.
Во временной области такими характеристиками являются весовые функции,
определяемые как реакции системы на импульсные воздействия. Интегральные
преобразования весовых функций приводят к определению соответствующих
передаточных функций и связанных с ними частотных характеристик.
Понятие передаточной функции линейной стационарной системы было обобщено
сначала на непрерывные нестационарные [30], а затем и на дискретные
нестационарные системы [127]. По-видимому, впервые систематическое описание всего класса
линейных нестационарных систем удалось осуществить в рамках спектрального
метода.
Примерно тогда же стало ясно, что известные понятия передаточных функций
стационарных непрерывных W{s) и дискретных W(z) систем могут быть
распространены на весь класс линейных динамических систем (нестационарных,
непрерывных и дискретных, описываемых смешанной системой непрерывных
дифференциальных и разностных уравнений) [135].
10.1.1. Непрерывные системы
Весовая функция линейной непрерывной в общем случае нестационарной
системы А(/,т) определяется как реакция системы на импульсное воздействие
5(/-т)Л"'' = Т> ' (10.1)
(0, t*x,
со
J5(t)Jt = 1. (10.2)
-00
Если вход и выход системы являются вектор-функциями, то импульсное
воздействие записывается как произведение единичной матрицы I, соответствующей
размерности входного вектора, и дельта-функции 5(/-т). При этом весовая функция
будет прямоугольной матрицей тхп, соответственно входному т-вектору и
выходному «-вектору.
Весовая функция определяет явную связь вход-выход в виде интегрального
соотношения
X(0 = fK(M)Y(T)rfx, (10.3)
'о
где размер матрицы весовых функций К(/,т) согласован с размерностями векторов
входных воздействий Y(/) и реакцией Х(/). Не ограничивая общности, выберем
Глава 10. Описание непрерывно-дискретных систем 629
начальный момент t0 = 0. Поскольку дальнейшее изложение в данной главе не
зависит от того, является ли весовая функция матричной или скалярной', мы не будем
каждый раз останавливаться на размерностях матриц весовых функций, предполагая,
что их размеры согласованы с векторами входных воздействий Y(/) и реакций X(t),
X(0 = fK(M)Y(x)rfx. (10.4)
о
Передаточные функции определяются как интегральные преобразования весовой
функции. Поскольку последняя является функцией двух переменных, могут быть
определены три передаточные функции по каждой из переменных т и / и по тем же
двум переменным одновременно. Соответствующие передаточные функции были
определены сначала Л. Заде, а затем И.Н. Бриккером [30].
Подчеркнем, что для нестационарной системы целесообразно определить именно
три передаточные функции, поскольку для различных задач удобно пользоваться
разными функциям, тогда как попытки использовать одну передаточную функцию
Заде заведомо обречены на неудачу.
Обобщенную передаточную функцию V(s9t) определим как преобразование
Лапласа по переменной /:
00
V(.s,T) = \k(t,T)e~*l'-z)dt. (10.5)
Нижний предел интегрирования выбран с учетом известного свойства весовой
функции
*(/,т) = О, /<т. (10.6)
Вводя новую переменную 6 = / - т, обобщенную передаточную функцию можно
записать также в виде
00
к(5,т) = |*(е+т,т>гл0б/е. (ю.7)
о
Если система является стационарной, то весовая функция k(t,x) зависит от
разности переменных / и т, т.е. £(/-т), и тогда из последнего, соотношения получим
известное выражение для определения передаточной функции стационарной системы
W(s):
00
V(s9t) = W{s) = J k(Q)e~^dQ. (10.8)
о
Чтобы получить выражение для связи вход-выход на основе V(s,x), преобразуем
по Лапласу обе части соотношения (10.4)
со /
X(s) = \e~stdt^k{t,x)y{x)dx.
0 т
Меняя порядок интегрирования, с учетом определения (10.5) будем иметь
00 00
X(s) = J dx J **(/, x)g-J(/-T) j/(T)e~AT.
0 x
И окончательно:
00
X{s) = \dt-V(sj)y(r)e-S\ (10.9)
630 Анализ и статистическая динамика САУ. Часть I
Для стационарной системы передаточная функция F(s,x) не зависит от времени
V(s,i) = W(s). Из (10.9) получим широко известное выражение для связи вход-выход
X(s) = W(s)Y(s). (10.10)
Завершая обсуждение обобщенной передаточной функции, сделаем одно
замечание относительно смысла V(s9t) . Из основного определения (10.5) следует, что
V{s,x)e-" = \k{t,x)e-s'dt.
-St
То есть, если рассматривать е s в качестве входного воздействия, то интеграл
справа представляет собой интеграл свертки системы, сопряженной с исходной.
Иначе говоря, если на вход системы, сопряженной с исходной, подать сигнал e~st,
то на выходе получим обобщенную передаточную функцию, умноженную на тот
же сигнал.
Сопряженная передаточная функция определяется как интегральное
преобразование по переменной т
#(/, s) = J *(/, т)<Г5('-х)б/т. • (10.11)
о
Для установления связи вход-выход на основе сопряженной передаточной
функции выразим в (10.3) воздействие y{t) через его изображение с помощью обратного
преобразования Лапласа
x(t) = \k(t,T)~ J e"-Y{s).ds.dT.
2nj J.
0 J c-jco
Или, с учетом определения (10.11),
C+jco
jc(O = — f ds-~estH(t,s)-Y(s). (10.12)
2nj J.
J c-jco
Последний интеграл отвечает формуле обратного преобразования Лапласа,
отсюда следует, что
H{t,s)Y(s) = X(s,t). (10.13)
Вместе с тем смысл изображений Y{s) и X(s,t) разный. Изображение Y(s) есть
обычное преобразование Лапласа воздействия y(t), тогда как параметр / в левой
части выражения (10.13) свидетельствует о существенной разнице соотношения
вход-выход для стационарных систем (10.10) и соблазнительно похожего на него
выражения (10.13).
Хотелось бы иметь конструкцию, связывающую обычные изображения
воздействия и вызываемой им реакции. Для нестационарных систем такая конструкция
существует и задается бичастотной передаточной функцией, которая определяется как
двумерное интегральное преобразование
ОО ОО 00 /
T(s,p) = \d%.\dt-k(t,%)e-stepx=\dt'\dTk(t,x)e-step\ (10.14)
От 0 0
ЕсЛи звено стационарное и аргументом весовой функции будет разность / - т, то
непосредственным вычислением из (10.14) получим
Г(з9р)=¥&9 (10.15)
s-p
Глава 10. Описание непрерывно-дискретных систем 631
где W(s) - известная передаточная функция стационарного звена.
Связь вход-выход на основе бичастотной передаточной функции найдем,
преобразовав по Лапласу (10.4) и выразив воздействие y(t) через его изображение Y(s)
00 t . C+JOO
X{s) = \dte-st'\dx-k{t^)^ j eptY(p)dp.
0 0 2llJ c-joo
Меняя порядок интегрирования, с учетом определения (10.14) получим искомое
соотношение
ВД = — J Г(з9р)Г(р)ф. (10.16)
2 я/ .
c~jco
В стационарной системе эта формула преобразуется в известную, поскольку,
подставляя T(s,p) вида (10.15), запишем сначала
2nj J s-p
Ось интегрирования с абсциссой «с» разделяет особенности Y(p) и 1 /(s - р).
Интегрируя вычетами в правой полуплоскости, приходим к известному
соотношению (10.10).
Подчеркнем, что для нестационарных динамических систем не существует
простого алгебраического соотношения вида (10.10), связывающего изображения
входного воздействия и реакции, и интегральное представление связи вход-выход (10.16)
'является типовым характерным представлением для всех классов линейных
нестационарных систем.
Найдем соотношения, связывающие введенные передаточные функции.
Переписав определение (10.14) для бичастотной передаточной функции в виде
ОО /00
о U J
получим с учетом (10.5) выражение, связывающее обобщенную и бичастотную
передаточные функции
00
Г(5, р) = J dx • V(s9 T)e~(s~p)x. (10.17)
о
Откуда очевидно, что Г(^, р) есть преобразование Лапласа по переменной т от
обобщенной передаточной функции. В качестве комплексной переменной выступает
s-p. ш
Обратный переход от T(s,p) к V(s,t) получим как обратное преобразование из
(10.17)
1 с+уоо
V(s,x) = — \ Y{s,s-p)epxdx. (10.18)
2nj J
Если звено стационарное, то
r(M-P).J0£L=m, (10.|9)
s-s+p р
1 c+rw(s)
и из (10.18) V(s,t) = ——epxdp = W(s), что и следовало ожидать.
2nj J. р
J c-jco г
632 Анализ и статистическая динамика САУ. Часть I
Выделив в определении (10.14) составляющую (10.11), найдем соотношение,
связывающее бичастотную и сопряженную передаточные функции:
Г(з,р) = ]л
t
-*'-т) L-v",
откуда
00
Г(5, р) = J Л • Я (/, р)^"^'. (10.20)
о
Другими словами, T(s,p) есть преобразование Лапласа для сопряженной
передаточной функции по переменной /. При этом комплексная переменная - (s- р).
Переход от T(s,p) к H(t,s) выполняется при помощи обратного преобразования
Лапласа. Переписав последнее соотношение в виде
ОО
r(s + pyp) = ldt-H(.t,p)e-\
о
найдем искомую зависимость
H(t,p)~ | r(s + p,p)es'ds. (10.21)
C-JOO
Исходные весовые функции получим как обратные преобразования от
соответствующих функций:
*(',т) = — J V(s,T)es{t-x)ds, (10.22)
с+уоо
£(/,т) = _ f H(t,s)es{l-X)ds, (10.23)
2тс/ J.
^ с-/оо
с, + /сос2+уоо
*(/,т) = —Ц- J J r(s9p)exte-pzdsdp. (10.24)
(27У) c.-yoo^-yoo
Непосредственно проверяется, что для стационарных звеньев весовая функция
зависит от разности /-т,т.е. k(t,T) = k(t-T).
10.1.2. Дискретные системы
Рассмотрим чисто дискретную систему, входным воздействием которой является
последовательность (скалярная или векторная) у{п) (п - целочисленная
переменная), а выходом - последовательность х(п).
Весовую функцию дискретной системы к(-п,т) определим как реакцию на
импульсное воздействие Д(л - т)
А(п-т) = \]'П = т' (10.25)
[О, п Ф т.
Считая, что воздействие подается на систему в момент п0 = 0, связь вход-выход
описывается соотношением
х(п)=^к(п,т)у(т). (10.26)
ш=0
Глава 10. Описание непрерывно-дискретных систем 633 .
Передаточные функции дискретных систем определим как дискретные аналоги
соответствующих интегральных преобразований. Таковыми для временных
последовательностей являются дискретные преобразования Лапласа и Z-преобразования.
С методической точки зрения целесообразно было бы начать с дискретного
преобразования Лапласа, поскольку соответствующие динамические характеристики
допускают ясную физическую интерпретацию [23, 63].
Вместе с тем на этапе определения системных характеристик достаточно
ограничиться Z-преобразованием, имея в виду, что связь последнего с дискретным
преобразованием Лапласа известна [63] и в случае необходимости соответствующие
соотношения получаются простой подстановкой.
Обобщенную передаточную функцию дискретной, в общем случае,
нестационарной системы определим как Z-преобразование весовой функции к(п,т) по
переменной п:
V(z,m) = X k(n,m)Z-{"-m\ (10.27)
п=т
которое можно также записать как
00
V(z9m) = Y,k(P + m>m>>Z~P' (10.28)
/7=0
Для получения соотношения, связывающего вход и выход системы, преобразуем
по Z обе части выражения (10.26)
X{z)=ftftk(n,m)y(m)z-'>zmz-m.
п=0т=0
Меняя порядок суммирования и учитывая определение (10.27), получим искомую
зависимость
X{z) = § X k(n,m)z-in-m)y(m)z-n = £ V(z9m)y(m)z'n. (10.29)
т=0п=т /н=0
У стационарной системы, весовая функция которой зависит от разности
аргументов
к(п,т)=--к(п-т), (10.30)
обобщенная передаточная функция не зависит от временного параметра т,
У(2,т)=^к(п-т)1-("-т) = f^k(p)z-p =W(z\ (10.31)
а выражение для связи вход-выход (10.29) превращается в известное алгебраическое
соотношение
X(z) = ]Г W{z)y(m)z-m = W(z)Y{z). (10.32)
m=Q
Таким образом, в общем случае обобщенная передаточная функция связывает
изображение реакции X(z) с оригиналом воздействия у(п), и только если система
стационарна, удается записать алгебраическую связь между изображениями (10.32).
Сопряженную передаточную функцию дискретной системы определим как
преобразование весовой функции к(п,т) по второму аргументу т
И(п,г)=^к(п,т)г-(п-т). (10.33)
/и=0
40 Зак. 232
634 Анализ и статистическая динамика САУ. Часть I
Как и для непрерывных систем, сопряженная передаточная функция позволяет
установить любопытное соотношение для изображений входа и выхода системы.
Заменим в (10.26) оригинал у(т) его изображением У(z), используя обратное Z-npe-
образование
т=0
2nj
В последнем выражении поменяем местами операции интегрирования и
суммирования. Тогда, принимая во внимание определение (10.33), получим
x(n) = —($zn-lH(n,z)Y(z)dz. (10.34)
2nj J
Интеграл (10.34), представляющий собой обратное Z-преобразование, позволяет
предположить, что стоящее под знаком интеграла выражение можно
интерпретировать как изображение реакции
X(z,n) = k(n9z)Y(z). (10.35)
К сожалению, произведение (10.35) не есть изображение нормальной реакции
х(п), о чем свидетельствует «застрявший» параметр п, а связь между обычными
изображениями в общем случае нестационарных систем оказывается сложнее и
устанавливается другой системной характеристикой.
Наиболее общей характеристикой нестационарных динамических систем в
области изображений будет бичастотная передаточная функция, которую определим как
двумерное Z-преобразование:
Ц:^,)^^^*^"1 = SZ^^V1. (Ю.36)
л=0т=0 /w=0w=m
Если звено стационарное и весовая функция зависит от разности аргументов
п - т, то непосредственными вычислениями получим
r(z2,z,)= jr ^к{п-т)2-2"г^ = £ %к(р)#'z?'г,"1"''.
т=0п=т т=0 р=0
Принимая во внимание, что передаточная функция стационарной системы есть Z-
преобразование весовой функции
»Ч*2)=2>2'*(/>)> О°-37)
/7=0
и полагая | zx \<\ z21, передаточную функцию стационарной системы запишем в
следующем виде
Г(^) = -^--^-. (10.38)
*1 Z2~z\
Заметим, что тождественное преобразование характеризуется передаточной
функцией
T(z2,zx)= /2 . (10.39)
zx{z2-zx)
Найдем теперь связь между Z-преобразованием входа и выхода дискретной
системы, для чего преобразуем обе части соотношения (10.26), выразив предварительно
у(т) через изображение Y(z)
X(z2) = fjz^nfdk<<n9m)^-:j<<z]r-lY<<zl)dz].
„=0 m=0 2.TIJ
Глава 10. Описание непрерывно-дискретных систем 635
Меняя порядок интегрирования и суммирования, приведем последнее выражение
к виду:
*(*2)=™<f Z %,к(п,т)г?гГ1У(гх)(ЬХ9
из которого с учетом определения (10.36) получим искомую связь
X(z2) = ^-:jr(z29z])Y(zl)dz]. (10.40)
Итак, для нестационарных дискретных систем связь между изображениями входа
и выхода устанавливается на основе бичастотной, а не сопряженной передаточной
функции. Причем эта связь является не алгебраической, а интегральной. Только если
звено является стационарным (10.38), из последней формулы прямыми
вычислениями легко получить знакомую алгебраическую зависимость
X(z2) = W(z2)±№—!—Y(zxykx=W(z2)Y(z2). (10.41)
2nj J z, z2-zx
В последнем случае для вычисления интеграла используется вычет в полюсе
zx = z2 вне контура интегрирования.
Для установления связи между бичастотной и обобщенной передаточными
функциями в определении (10.36) выделим составляющую, отвечающую обобщенной
передаточной функции:
„-да да-1
откуда
r(z2)z,)= £[f>(«,«)2j-<-">]zrzf
1 «о /Vя
Г(22,2,) = ~Х^2^)' - , -(Ю.42)
Zl,=0 \Zl)
и, следовательно, с точностью до множителя \/zx, T(z2,zx) может рассматриваться
как Z-преобразование V{z2,m) по переменной т, а в качестве комплексной
переменной выступает отношение z2/ zx.
Обратный переход от Y(z2,zx) к V(z2im) должен»отвечать некоторому
обратному Z-преобразованию. Перепишем последнее соотношение, обозначая для
наглядности z2fz},
S S /я=0
Выражение справа в точности отвечает Z-преобразованию функции V(z2,m).
Вычисляя обратное Z-преобразование, получим искомую зависимость
V(z29rn) = ^-:jz2r(z2^m-2d^ (10.43)
Воспользуемся последним соотношением для стационарного звена, у которого
r(*2,^) = »4*2)i—V-
z2-
V W4..i
Тогда из (10.43) найдем
1 с/я
F(Z2,W) = ^(Z^ — Cf^-^ = »F(Z2),
2я/ ^-1
40*
636 Анализ и статистическая динамика САУ. Часть I
что и следовало ожидать.
Сходным образом, выделив в определении (10.36) часть, отвечающую
соотношению (10.33), получим
п=0\_т=0 J
Откуда найдем выражение, связывающее бичастотную и сопряженную
передаточные функции,
r(z2,z0 = -Z"(">*i)(-| > (10-44>
и бичастотная передаточная функция с1 точностью до множителя \lzx может
рассматриваться как преобразование сопряженной передаточной функции по
переменной /?, где в качестве комплексной переменной используется отношение
С помощью замены z2 /z, = rj перепишем последнее соотношение в виде
00
z,r(z,i1)z1) = X//("'zi)Tl"">
/7=0
которое показывает, что H(n,zx) является обратным преобразованием:
Я(/7,21) = ^т^1Г(21л,21)л/7"1^Л. (10.45)
В заключение приведем сводку формул, связывающих передаточные функции с
оригиналом к(п,т), которые получаются очевидным образом как обратные
Z-преобразования соответствующих определений (10.27), (10.33) и (10.36):
к(п,т) = — 6v(z,m)zn-m-ldz, (10.46)
к(п,т) = —6 H(n,z)zn-m~]clz, (10.47)
2ту J
k(n,m) = —^jjjr(z2,zl)zn-'z-m. (10.48)
Если звено стационарное, то V{z,m)-W{z) и из (10.46) очевидным образом
следует, что к(п,т) = к(п-т), а из (10.48) прямыми вычислениями находим
(2ту)
1 j* f _m_» 1
= -i-^ dz.zr' тЦ^ dz2W(z2)-^- =
2я/ J 2я/ J Z2 ~ zi
1
2nj J
что и следовало ожидать.
10.1.3. Непрерывно-дискретные системы
Будем рассматривать системные характеристики непрерывно-дискретных
объектов, у которых при непрерывных входных воздействиях реакция представлена
квантованными по времени сигналами. Примером таких звеньев является ключ.
Глава 10. Описание непрерывно-дискретных систем 637
В данном случае для связей вход-выход не следует ожидать простых
соотношений даже для стационарных систем, поскольку воздействия и реакции являются
разными по математическому описанию и физической природе сигналов.
Весовая функция к(пТ,т) определяет систему, которая является дискретной по
аргументу t = nT (T - период квантования) и непрерывной по аргументу т. Во
временной области весовая функция устанавливает связь вход-выход в виде известного
интеграла
пТ
х(пТ) = J А(л7\т).у(т)Л . (10.49)
о
Обозначим через а = [т/Т] - минимальное целое, удовлетворяющее условию
а>х1Т.
Обобщенную передаточную функцию непрерывно-дискретной системы
определим соотношением
* -№11
V(z,t)= У к(пТ,т)г ^ 1П). (10.50)
4-1
[г]
Для стационарной системы, в общем случае, существенных упрощений получить
не удается
z,x)= £ к(Т(п-?-))2~{"и\\
У(2, _
"И
и только в тактовые моменты времени х-пТ
V(z,x) = V(z), (10.51)
тогда как при тч±пТ
F(z,t)*F(z).
Воспользуемся Z-преобразованием для обеих частей равенства (10.49)
A-(2) = f>-"J*(ii7\TMT)rfT,
л=0 о
и после очевидных преобразований соотношение, связывающее изображение
реакции с оригиналом воздействия, запишем в следующем виде:
ill
X(z) = \V(z^)y(T)z^TW (10.52)
о
Сопряженн'ая передаточная функция непрерывно-дискретной системы
определяется интегральным преобразованием весовой функции к(пТ,т) попеременной т
пТ
H(nT,s) = J k(nT,T)e's{nT~x)clx. (10.53)
о
Как и в случае непрерывных систем, связь вход-выход получим, представив
оригинал у(т) в (10.49) через обратное преобразование Лапласа. После чего, меняя
порядок интегрирования, найдем
C+JCO
х(пТ) = f H{nT,s)Y{s)e~snTds. (10.54)
2тс/ J.
638 Анализ и статистическая динамика САУ. Часть I
Откуда следует интересное по форме соотношение
X(s,nT) = H(nT,s)Y(s), (10.55)
относительно которого справедливы все оговорки, упомянутые для непрерывных
систем.
Наиболее полной характеристикой, описывающей непрерывно-дискретную
систему в области изображений, является бичастотная передаточная функция,
определяемая совместным интегральным и Z-преобразованием
r(z9s) = X f k(nT,x)z-"esxdT. (10.56)
и=0 о
Проиллюстрируем последнюю характеристику на примере ключа, для которого
к(пТ,х) = Ь(пТ-т). (10.57)
Непосредственным вычислением по формуле (10.56)
r(z,*) = f>-Vy\
w=0
Полагая | z |> esl , передаточную функцию ключа T(z,s) получим в виде
Г(*,*)= \ чТ. (10.58)
\-z e
Бичастотная передаточная функция определяет характерное соотношение,
связывающее изображения воздействия и реакции, которые нетрудно получить, используя
Z-преобразования для (10.49) и обратное преобразование Лапласа для у{х)
«г пТ « с +/оо
*(z)=Zz-"[*(/j7\t)— f Y(s)e"dsdv.
to I ЗяуД,
Откуда, меняя порядок интегрирования, с учетом определения (10.56) получим
искомую зависимость
c+jx
X(z) = — f r(z,s)Y(s)ds. (10.59)
2nJc-j«,
В частности, для ключа:
•"(7)=^Хт^л- (|0-60)
Как и следовало ожидать, последняя формула воспроизводит знакомую запись,
связывающую преобразование Лапласа непрерывного сигнала Y(s) с его
Z-преобразованием Y(z). Другими словами, ядро интегрального преобразования,
связывающего изображения по Лапласу непрерывного сигнала с его же
Z-преобразованием является динамической характеристикой соответствующего
непрерывно-дискретного звена (ключа).
Если в определении (10.56) выделить составляющую (10.50), получим
соотношение, связывающее бичастотную и обобщенную передаточные функции
-\L]
r(z,s) = jV(z,i)exxz LrJ</T. (10.61)
о
Точно так же, выделяя в (10.56) составляющую (10.53), найдем связь между бича-
стотной и сопряженной передаточными функциями
Глава 10. Описание непрерывно-дискретных систем 639
T(z9s) = %Н(пТ,5У"т2-" =^Г(пТ95)\-^г] , (10.62)
т.е. T(z9s) есть Z-преобразование сопряженной передаточной функции по
переменной п. В качестве переменной преобразования выступает со = (z/e~sl).
В этом случае z = сое~л/ и последнюю формулу можно переписать как
T((oe-Sl\s)= JTH(nT,s)<o-", (10.63)
что позволяет рассматривать сопряженную передаточную функцию как обратное
преобразование от Г(сое~л7 ,s)
Н(пТ9 s) = —<$ Г(ае-яТ, j)<d"-i da. (10.64)
2я/ J
Вычисление, весовой функции к(пТ,т) по известным передаточным функциям
выполняется по очевидным формулам соответствующих обратных интегральных
преобразований
1 л "-tel"1
*(лГ,т) = —Cmz,T)z L J *, (10.65)
2я/ J
с+уоо
*(лГ,т) = — f H(nT9s)esinT-x)ds, (10.66)
2я/ J
с+уоо
*(лГ,т) = —Ц-cfA f dsr(z9s)znAe'". (10.67)
10.1.4. Дискретно-непрерывные системы
Дискретно-непрерывные звенья, представителями которых являются, например,
экстраполяторы, преобразуют дискретную последовательность у(пТ) в
непрерывный сигнал x(t) и потому характеризуются весовой функцией k(t,nT). Обозначая
через (tIT) целую часть числа tIT, так что
запишем связь вход-выход во временной области
х(0=^к(1,пТ)у(пТ). (10.69)
По уже привычной схеме определим обобщенную передаточную функцию
V(s,nT) как интегральное преобразование по непрерывной переменной /
00
V(s,nT) = J k(f9nT)e-*~nT)dt. (10.70)
пТ
В стационарных звеньях весовая функция зависит от разности аргументов t-nT ,
тогда
ОО 00
V(s,nT) = J k{t-nT)e-s(t-"T)dt = jA(e)e"*</e = W(s).
nT 0
640 Анализ и статистическая динамика САУ. Часть I
То есть обобщенная передаточная функция совпадает с обычной передаточной
функцией непрерывного звена
V(s,nT) = lV(s). (10.71)
Преобразуем по Лапласу обе части выражения (10.69)
X(s) = J Ае* X Kt,nT)y{nT). (10.72)
0 "=0
Меняя местами операции интегрирования и суммирования, выделим
составляющую V(s,nT) в соответствии с определением (10.70)
X(s) = X f k(t,nT)e-s(t-"T)dte-snTy(nT). (10.73)
/i=0 и'/'
Тогда связь вход-выход на основе обобщенной передаточной функции запишется
как сумма
со
X(s)=Y,y(s,nT)y(nT)e'snT. (10.74)
/7=0
В стационарных звеньях, с учетом (10.71), в последнем соотношении V(s,nT) не
зависит от а? и ее можно вынести за знак суммы
Х(з) = 1¥(5)%у(пТ)е-тТ.
/i=0
Здесь суммирование определяет известное дискретное преобразование Лапласа
У\з) = -£у(пТ)е-тГ.
/7=0
Поэтому, как и следовало ожидать,
X(s) = W(s)Y\s).
Если ограничиться дискретными значениями х(пТ) непрерывного сигнала *(/),
что соответствует сигналу на выходе фиктивного ключа, и воспользоваться
Z-преобразованием, то для стационарных звеньев из (10.61) получим более простое
соотношение
X(z) = § z-n X КпТ - mT)y(mT) = £ £ к(пТ - mT)z^n~m)y{mT)z-m,
/7=0 /w=0 m=0n=m
ИЛИ
X(z) = W(z)Y(zl (10.75)
где вход и выход звена заданы их Z-преобразованиями.
Сопряженную передаточную функцию дискретно-непрерывного звена определим
преобразованием по дискретному аргументу
W -(1)+я
H{t,z)=Y,k^^T)z Т ' (10-76)
/7=0
Ждать упрощений для стационарных звеньев здесь не приходится. Поэтому сразу .
переходим к определению связи вход-выход. Представляя воздействие у(пТ) через
его Z-преобразование, можно записать
Глава 10. Описание непрерывно-дискретных систем 641
Выделяя в последнем выражении составляющую с определением (10.76)
х(0 = —<PfifeYA(f,w7> w Y(z)zK-T) ,
получим искомое соотношение
jc(O = —^(/,2)r(z)z^7^ flb. (10.77)
2ту J
Интеграл обратного Z-преобразования (10.77) позволяет получить формально
красивую формулу для связи вход-выход
X(z) = H(t9z)Y(z)9 (10.78)
к сожалению, с теми же оговорками, что и выше. Иными словами, если Y(z)
является Z-преобразованием воздействия у(пТ), то этого нельзя сказать о реакции *(/)
и даже о ее дискретной последовательности х(пТ).
Поэтому для того, чтобы получить явную связь вход-выход для изображений,
потребуется бичастотная передаточная функция дискретно-непрерывного звена,
определяемая соотношением:
T(s9z) = X J k(t,nT)e-stz"-ldt. (10.79)
n=QnT
В стационарных звеньях эта конструкция конкретизируется. В самом деле,
прямыми преобразованиями (10.79), учитывая, что в стационарных звеньях
k(t,nT) = k(t-nT),
найдем
Г(*,*) = £ J k(t-nT)e-stzn-xdt = Y,zn-x J k{t-nT)e-s{t-nT)dt-e-snT.
n=0nr п=0 пт
Принимая во внимание определение передаточной функции как преобразования
Лапласа от весовой функции (10.8), будем иметь
r(5,z) = ^)fy-V*"r.
/7=0
Выберем значение абсциссы сходимости (с = Re 5 ) так, чтобы выполнялось условие
|z<Tv7'|<l. (10.80)
По формуле геометрической прогрессии получим искомую передаточную
функцию дискретно-непрерывной стационарной системы
1 (5,2)- ^тг. (10.81)
z \-ze '
В структуре последней формулы выделены явно два множителя, каждый из
которых имеет отличительное функциональное назначение. Изменяемая часть,
множитель W{s), будучи непрерывной системой, выполняет роль формирующего фильтра,
тогда как оставшаяся часть, одинаковая для всех стационарных звеньев, является
некоторым преобразователем код-аналог. Свойства последнего будут рассмотрены
ниже при изучении экстраполятора.
642 Анализ и статистическая динамика САУ. Часть I
Связь вход-выход будем искать по традиционной схеме. Преобразуем по Лапласу
обе части выражения (10.69), выразив при этом воздействие у{пТ) через его
преобразование Y(z)
X(s) = [ А • е~" У k(t, иГ)—(j> Y{z)zn~xdz.
о £о 2nJ J
Меняя порядок интегрирования и учитывая определение (10.79), получим
искомое соотношение
ВД = т-:$ ns,z)Y(z)dz, (10.82)
по существу и по форме повторяющее аналогичные соотношения для других
комбинаций сигналов входа и выхода.
Выделив в определении (10.79) интегральную составляющую выражения (10.70)
T(s9z) = J J k{t9nT)e'^'nT)dt'e'snTzn'1 , (10.83)
п=0„т
найдем связь между обобщенной и бичастотной передаточными функциями
Г(5,2) = -£У(5,пТ)е-я'тг"-\
Переписывая последнее выражение в виде
оо (psTX"
zrfrz) = £v{s9nT)\Z-\ ,
заметим, что с точностью до множителя z бичастотная передаточная функция может
интерпретироваться как ^-преобразование обобщенной передаточной функции по
дискретной переменной пТ с комплексной переменной
esT
w = ,
z
esTr(s,—) oo
V-^V&nT)*".
w «=o
Поскольку сумма справа представляет собой прямое Z-преобразование (z = w),
обобщенную характеристику найдем, выполняя обратное преобразование
1 psT
V(s9nT) = —(f e^ris,— )w"-2dw. (10.84)
2 ту J w
Сходным образом выделим в определении (10.79) сумму, определяющую
согласно (10.76) сопряженную передаточную функцию
Г(5,2) = J X КЬпГ)АтУ*1т>\-*А,
0 и=0
что позволит получить соотношение, выражающее V(s9z) через H(t,z)
- fiVi
T{s,z) = \H(t,z)z^T) e^dt. (10.85)
Глава 10. Описание непрерывно-дискретных систем 643
Для установления связи между H(t,z) и T(s9z) воспользуемся дискретным
преобразованием Лапласа (z = epl)
Y(s9p) = epT\H(t9p)e<'-p)<b,
откуда
H(f%p) = — \ r(s + p9p)e-pTeslds. (10.86)
J c-jco
Исходная весовая функция дискретно-непрерывного звена определяется по
передаточным функциям соответствующими обратными интегральными
преобразованиями
C+JCO
k(t9nT) = — f V(s,nTy{l-nT)ds9 (10.87)
2 я/ v
c-700
k(t9nT) = —iH(t9z)z^T^n dz, (10.88)
2nj J
c+jm
k(t9nT) = — { idsdz-Y{s,z)estz-\ (10.89)
2nj 3 J
c-yoo
* * *
Подведем некоторые промежуточные итоги. Итак, для линейных
нестационарных, в общем случае, систем вводятся не одна, а три различные передаточные
функции. Попытка ограничиться одной (например, параметрической передаточной
функцией Л. Заде) заведомо обречена на неудачу.
Каждая из передаточных функций по-своему важна. Для разных задач управления
удобно использовать разные передаточные функции. Таким образом, создается
единая методологическая основа для описания и исследования линейных систем,
оперирующих с сигналами разной физической природы.
Причем наиболее общей и естественной для описания нестационарных систем
разных типов являются бичастотные характеристики, связывающие изображения
воздействий и реакций.
10.2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ЭЛЕМЕНТАРНЫХ
И ТИПОВЫХ ЗВЕНЬЕВ
В качестве элементарных для непрерывно-дискретных систем будем
рассматривать следующие звенья: квантователи сигналов, экстраполяторы, усилительные,
суммирующие разности, интегрирующие, дифференцирующие, понижения такта и
сдвига тактовых точек. Типовые, равно как и любые другие звенья, являются результатом
соединений элементарных звеньев.
Квантователь (ключ) является непрерывно-дискретным элементом с бесконечно
малым временем замыкания и описывается уравнением
у{пТ) = у{1)\1=пТ, (10.90)
которому соответствует весовая функция
к(пТ-х) = Ь(пТ-г). (10.91)
Если тактовые точки определены произвольной временной последовательностью
/„ (п = 0,1,...), то
644 Анализ и статистическая динамика САУ. Часть I
*('и-т) = 8(/и-т). (10.92)
Сопряженная передаточная функция вычисляется согласно (10.53):
#(/„,*) = 1. (10.93)
Бичастотную передаточную функцию ключа
r(z,s) = fV4-" (10.94)
/7=0
для постоянного периода квантования Т записываем в виде
Г(*,*)= \ <г. (10.95)
1-z ё
Легко видно, что последняя является ядром интегрального преобразования,
связывающего Z-преобразование Y(z) функции y{t) с преобразованием Лапласа Y(s)
той же функции, что и следовало ожидать.
Экстраполятор нулевого порядка, преобразующий дискретную
последовательность у(пТ) в непрерывный сигнал, описывается уравнением
x(t) = у{пТ\пТ <t<{n +1)7\ (10.96)
которому отвечает весовая функция
k(t,nT) = \(t-nT)-\(t-(n + \)T). (10.97)
Согласно определению (10.70) обобщенная передаточная функция V(s,nT)
отвечает стационарной системе
\-e-sT
V(s9nT) = W{s) = , (10.98)
s
связывая дискретное изображение Лапласа Y*(s) с изображением непрерывной
реакции X(s)
X(s) = W(s)Y\s). (10.99)
Вычисляя бичастотную передаточную функцию по определению (10.79),
соответствующую весовой функции (10.97), найдем
\-е-*т 1
Г(*,2) = -. (10.100)
sz \-ze~sl
В последнем выражении присутствует в качестве множителя хорошо знакомая
передаточная функция экстраполятора нулевого порядка. Такая структура
передаточной функции не случайна и имеет ясную физическую интерпретацию. Второй
множитель в последнем выражении выполняет функцию преобразователя
решетчатой функции у(пТ) в импульсную последовательность дельта-функций с весами
у{пТ), чему отвечает бичастотная передаточная функция
Гэ(5'2)=^1^у (10101)
Таким образом, операцию экстраполирования дискретной последовательности
можно представить как последовательное выполнение двух шагов. Сначала
дискретная последовательность превращается в последовательность дельта-функций
линейным преобразованием с весовой функцией
k(t,nT) = &(t-nT). (10.102)
На втором шаге формируется искомый непрерывный сигнал посредством чисто
непрерывного устройства - формирователя сигнала в пределах шага квантования.
Этот формирователь в зависимости от способа преобразования может быть разных
Глава 10. Описание непрерывно-дискретных систем 645
порядков [63], но в любом случае это будет некоторое непрерывное устройство,
реагирующее на импульсные сигналы.
Такая интерпретация носит в основном методический характер, объясняя
математические модели преобразования сигналов. Ясно, что в реальных устройствах
упомянутого разделения на физическом уровне не существует.
Дискретное усилительное звено описывается уравнением
х(п) = а(п)у(п), (10.103)
которому отвечает весовая функция
к(п9т) = а(пЩп-т). (10.104)
Обобщенная и сопряженная передаточные функции, вычисленные по формулам
(10.27) и (10.33), соответствуют коэффициенту передачи, в общем случае зависящему
от дискретного параметра
V(z9m) = a(m), (10.105)
,H(n,z) = a(n). (10.106)
Для бичастотной передаточной функции по формуле (10.36) найдем
r(z2,z,) = -UW, (10.107)
z\ \z\)
т.е. с точностью до множителя — это - Z-преобразование функции а(п), когда
z\
в качестве комплексной переменной выступает отношение —.
z\
Как и следовало ожидать, связь вход-выход
X(z2) = ^j-J^ )Y(z])dz] ' (10.108)
2nj J z, {zj
повторяет известную формулу для изображения произведения а{п)у{п).
Непрерывное усилительное звено описывается уравнением
*(0 = *('М0 (Ю.109)
с весовой функцией
*(/,т) = а(05(/-т), (10.110)
для которой обобщенная и сопряженная передаточные функции записываются в виде
V(s,T) = a(T), (10.111)
H(t9s) = a(t)9 (10.112)
а бичастотная характеристика согласно (10.14)
r(s,y) = a(s-p) (10.113)
есть преобразование Лапласа коэффициента передачи a(t) относительно
комплексной переменной s-р .
Непрерывные и дискретные звенья чистого сдвига описываются соотношениями
x(t) = y(t-Q\ (10.114)
х(пТ) = у(пТ-1Т), (10.115)
где 6 и IT - величины сдвига соответственно в непрерывных и дискретных цепях.
У дискретного звена тактовые моменты на входе и выходе совпадают.
Весовым функциям, описывающим указанные процессы сдвига,
*(/,т) = 8(/-т-в), (10.116)
k(nT,mT) = A(n-m-lJ), (10.117)
646 Анализ и статистическая динамика САУ. Часть I
отвечают передаточные функции
V(s9x) = e-sQ, V(z,m) = z~l, (10.118)
H(n9s) = e"*, H(n,z) = z~l, (10.119)
Г(з,р) = е-*—, r(z2,z,) = -^ (Ю.120)
При 6 > 0 и / > 0 сдвиг приводит к звеньям чистого запаздывания, а при 0 < 0 и
/ < 0 получим звенья чистого упреждения. Если первые являются физическими
выражениями, то вторые оказываются физически неосуществимыми. При 0 = 0 и / = 0
звенья чистого сдвига превращаются в усилительное звено с коэффициентом
передачи равным единице.
Звено сдвига тактовых частот является дискретным звеном, которое сдвигает
тактовые моменты на выходе относительно тактовых моментов на входе на величину
0<АТ<Т. В отличие от дискретного звена чистого сдвига, в котором величина
сдвига является кратной числу тактов, здесь тактовые моменты на входе и выходе не
совпадают. Весовая функция, реализующая сдвиг тактовой точки,
х(пТ) = у(пТ-АТ\ (10.121)
задается А-функцией вида
к(пТ,тТ) = А(пТ-тТ-АТ). (10.122)
Физически ясно, что временная последовательность дискретных сигналов на
выходе привязана к моментам времени пТ-AT. Поэтому при определении бичастот-
ной передаточной функции (применяя для наглядности дискретное преобразование
Лапласа) следует пользоваться соотношением
T(s9p)= j^^A(nT-mT-AT)e-s(nr-AT)epT. (10.123)
m=0n=m
При этом соответствующая характеристика r(z2,zx) отвечает тождественному
преобразованию
r(z2,z,) = —А—. (10.124)
Ф2~г\)
Звено понижения такта относится к дискретным звеньям. Тактовые моменты на
входе и выходе звена совпадают, но число их различно. Поскольку звенья этого типа
встречаются лишь в особом классе систем с многократным синхронным
прерыванием, подробно они рассматриваются ниже в разделе, относящемся к анализу
указанных систем.
Элементарные непрерывные звенья - дифференцирующие и интегрирующие,
являются стационарными звеньями. При использовании системных характеристик,
принятых при описании нестационарных процессов, передаточные функции
элементарных звеньев, подобно другим стационарным звеньям, входят в конструкции бича-
стотных передаточных функций в качестве множителей
Г(5,р) = -2— (10.125)
s-p
- для дифференцирующего звена и
T(s,p)=—!— (10.126)
s(s-p)
- для интегрирующего звена.
Глава 10. Описание непрерывно-дискретных систем
647
Сходным образом, если возникает необходимость оперировать с бичастотными
передаточными функциями для элементарных дискретных звеньев - разностными и
суммирующими, то в соответствии с общим правилом вычисления бичастотных
передаточных функций дискретных стационарных звеньев будем иметь:
r(z2,z,) = -^±-
2,(22-2,)
- для разностного звена и
Г(22,2,) =
4
(22-1)2,(22-2,)
(10.127)
(10.128)
- для суммирующего.
10.3. ХАРАКТЕРИСТИКИ СОЕДИНЕНИЙ
НЕПРЕРЫВНО-ДИСКРЕТНЫХ ЗВЕНЬЕВ
В этом разделе описываются способы вычисления передаточных функций
соединений непрерывно-дискретных, в общем случае, нестационарных звеньев. Эти
способы определяются типом соединения и выбранными характеристиками звеньев.
Заметим, что для одного и того же соединения вычисления могут быть проще или
сложнее, в зависимости от того, какие характеристики выбираются для описания
исходных звеньев.
Опишем сначала характеристики последовательного соединения двух
непрерывных звеньев (рис. 10.1).
КО
Y(s)
G(s)
Tifep)
*(0
X(s)
Рис. 10.1. Последовательное соединение звеньев НН-НН
Записывая связь вход- выход для изображений, в соответствии с рис. 10.1 найдем
j с+уоо - с+уоо с+уоо
ЛГ(*)--Ц J </|Г|(*,Ш§)=тт J dpfaQ-J-: J Г2(Ц,рЖр)Ф-
2w v 2nj J. 2tlj j
J C-JOO J C-JOO J C-JOO
Меняя порядок интегрирования, выразим бичастотную передаточную функцию
последовательного соединения через аналогичные характеристики звеньев:
Г(з,р)~ t Гх(з9$Г2&р)ф. • (Ю.129)
9тп J
2nj
C-J<X
Если изображение G(s) в промежуточной точке определить как функцию от
X{S)=2T I rf5r,(*,$)JrfTF2(iT)<f«\
J c-jco 0
(10.130)
то, записывая реакцию X(s) как результат интегрирования обобщенной передаточной
функции соединения
00 - C+JQQ
Ь27Ус->
648 Анализ и статистическая динамика САУ. Часть I
выразим последнюю через T\(s,p) и V2(s, т):
V(s,t)~ [ Tx(s£)V2&i)e(s-®xd\. (10.131)
2nj J
c-yoo
Перейдем к определению сопряженной характеристики соединения. В
соответствии с рис. 10.1,
x(t) = j- J Hx(t9i\)g(i\)e*d4 =
1
i
с+уоо с+уоо
2nj
C-JCO
= -^ J di\Hx(t9T\)e* ± J V2(r],s)Y(s)ds =
2nj J 2nj J
J c-jco J c-jco
= 7t| dsesl^- f й(т1Я10)т1)Г2(л,^(11-^}'(5) =
Z71/ J 2nj J.
J c-joo J c-jco
= -^- J ds<?H{t,s)Y(s).
c-700
Откуда сопряженная передаточная функция #(/, s) соединения выражается через
#,(/,*) и Г2(*,р)
с+уоо
H(t9s)~ j ^(/,n)r2(^^(n"J)l^. (Ю.132)
Попытаемся теперь найти* сопряженную передаточную функцию по сопряженным
же характеристикам звеньев. Для этого в (10.132) вместо ГгСп, s) запишем ее
представление через #2(/, s)
00
r2(i\9s) = \dtH2(t9s)e<^^9
о
и тогда перепишем (10.132) несколько иначе
. с+уоо оо
#(М) = Т- ^(^лЯЯз^^-^-^^^^т^л- (10.133)
2^'с-7оо 0
Очевидно, что попытка вычислить сопряженную передаточную функцию
соединения через сопряженные же характеристики звеньев приводит к существенно более
сложным выражениям, чем записанные ранее (10.132). Другими словами,
неправильный выбор исходных характеристик может заметно осложнить задачу вычисления
характеристик соединений.
Бичастотная передаточная функция в (10.129) получена интегрированием в
комплексной области. Отталкиваясь от обобщенной характеристики, удается получить
иное представление:
X{s) = \dTVx{s^)gW =
1
C+JCO
= |ЛК,(5,т)е-"^- j H2(T,p)Y(p)e'"dp.
0 J c-jco
Откуда, меняя порядок интегрирования, найдем
Глава 10. Описание непрерывно-дискретных систем
649
C+JCO 00
X(S) = 2T I dPJd*vi(s'^H2^P)eHs~P)ZY(P)-
' C-jao 0
Последнее выражение связывает изображения входа Y(s) и выхода X(s), откуда
следует, что бичастотная передаточная функция соединения может быть получена
как результат интегрирования по времени обобщенной У\(\,т) и сопряженной #2(т, s)
характеристик исходных звеньев
Г(5,р) = /ЛК1(5,ту/2(т,р)в-('"р)т.
(10.134)
Если звено 1 стационарное, то
V](s,t) = W](s),
и из (10.134) для последовательного соединения получается более простое
соотношение
Г(*, р) = W, (*) J dxH2 (т, p)e-(s-p)x.
Вспоминая зависимость между Н(х, s) и Г(з, p), вместо последнего можно
записать алгебраическое выражение
r(s,p) = Wl(s)r2(s,p), (10.135)
которое также является очевидным следствием (10.129).
Точно так же, если второе звено - стационарное, то алгебраическое выражение
для бичастотной передаточной функции соединения выглядит следующим образом
r(s,p) = rl(s,PW2(p). (10.136)
Найдем соответствующие зависимости для соединений дискретных звеньев
(рис. 10.2).
у(п)
*-
Y(z)
Vi(z, m)
UJyj 7\
r2(zbz2)
gin)
G(z)
V&, m)
Н\\П> z)
ri(zbz2)
*(«)
X(z)
Рис. 10.2. Последовательное соединение звеньев ДД-ДД
Последовательно записывая связь вход-выход для изображений, легко получить
соотношения для бичастотной передаточной функции соединения
1
r(z2,z,) = — JTx{z2,T\)T2{r\,zx)dT\.
(10.137)
Если одно из звеньев является стационарным, тем же путем легко получить
алгебраические выражения
Y{z2,zx) = Wl(z2)V2(z2,z]), (10.138)
r(z2,z1) = rl(z2,z1)^2(z1). (10.139)
Найдем обобщенную передаточную функцию соединения, вычисляя изображение
X{z) как отклик на воздействие у(п)\
X(z) = -iT(|rl(z^)g^yn =
650 Анализ и статистическая динамика САУ. Часть I
=™<f Г,(2,Л)Е У2(ят)у{тУ(\-т<1у\ =
т=027У ЧЛУ
Тогда искомая обобщенная передаточная функция F(z, m) выражается через
Fi(zb ^2) и V2(z9 m) следующим образом
1 ( У1
V(z,m) = —jrx(z,vi)V2{rbm)\-\ dr\. ' (10.140)
2nj J {r]J
Для сопряженной передаточной функции соответствующую связь получим,
последовательно вычисляя реакцию х(п):
2nj J
= ^-jzn-]Hl(n,z)dz^-jr2(z,4)y(4)dr] =
Znj J 2nj J
1 1 ( Y"1
= —^ЛЛ""1— $dzHx{n9z)T2{z9y\)\ - y(y\).
2nj J 2nj J {r\J
Принимая во внимание связь вход-выход на основе сопряженной характеристики,
выразим последнюю через Нх(п, z) и Г2(г, ц)
H(n,VL) = ^jdzHx{n9z)r2{z,ri)(-] . (10.141)
2nj J {г})
Для дискретных систем найдем аналог формулы (10.134), вычисляя связь между
изображениями Y(z) иХ(г):
X(z2)=f,Vl(z29m)z2-my(m) =
/w=0
= I) Vx (z2, m)z-2m J-;j zf"1 Щ (m, z, )У(г, )*, =
m=0
2nj
II00 (z \m
= —:jdzl-YJVdz2,m)H2(miz])\^\ Y(zx).
Сравнивая последнее соотношение с формулой связи вход-выход на основе
Ffe, Zi), выразим бичастнотную характеристику соединения через обобщенную и
сопряженную характеристики звеньев
Г(22,21)=^К1(22,т)Я2(т,21)Ы -. (10.142)
m=0 \Z\) Z\
Сходным образом получаются характеристики соединений звеньев с различными
формами входных и выходных сигналов. На рис. 10.3 показано соединение, в
котором внутренний сигнал является непрерывным, а сигналы на входе и выходе
соединения - дискретные.
Бичастотная передаточная функция соединения записывается очевидным образом
r(z29zx)~ \ rx(z29s)r2(s,zx)ds. (10.143)
c-700
Глава 10. Описание непрерывно-дискретных систем
651
у(п)
Vi(s, m)
UJf 7\
"2l/> z)
T2(5,i)
Vfc, t)
II (m <Л
Щуп, s)
x(«)
Рис. 103. Последовательное соединение звеньев ДН-НД
Для вычисления обобщенной передаточной функции соединения в соотношении,
связывающем изображения X(z) и G(s),
*(*)=" f Tx(z9s)G(s)dz9
c-700
выразим G(s) как функцию V2(s, ri) ny(ri)
, C+70O a,
X(z) = — f rl(z9s)dzYtV2(s9n)y{n)e'snT.
2nJc-J« "=0
Меняя порядок интегрирования и суммирования, изображение X(z) представим
как функцию у(п)
00 ( Ч C+JCO ' \
ад = Л^ J rx{z9s)V2(s9n)e-aTz»dsUn)z-n.
Вспоминая связь вход-выход на основе обобщенной характеристики (10.29),
получаем искомую зависимость для V(z, n)
1
C+JCO
V(z9n) = ^- Tx(z,s)V2{s,n)e-snTznds.
2nJc-j«>
(10.144)
Сопряженную характеристику соединения найдем, записав цепочку соотношений
вход-выход:
Ф) = ^-т f Hx^s)G{s)esnTds^
2nj J
с-уоо
C+JCO
= г^т J Hl(n,s)esnTds^-jr2(s,z)Y(z)dz =
2nJ c-j* 2%J
C+JOO
= —<$dzz"-1 \ Hl(n,s)r2(s,z)esnTz-{"-l)dsY(z).
2nj J J
c-700
Учитывая выражение (10.34), связывающее х(п) и Y(z), для сопряженной
передаточной функции соединения получим соотношение
с+уоо
Я(л,2) = -1Т J Hx{ri9s)T2{s9z)^Tz<n^ds. (10.145)
2nj
C-700
Пусть теперь вход и выход соединения представлены непрерывными функциями,
а промежуточная координата - дискретным сигналом (рис. 10.4).
Бичастотная характеристика соединения записывается в традиционной форме
T(s9p)~<iTx{s9z)r2(z9p)dz. (Ю.146)
2я/ J
652
Анализ и статистическая динамика САУ. Часть I
КО
v&, 0
r2(Z;S)
si»)
4s, n)
И At т\
Г,(*,2)
x(t)
Рис. 10.4. Последовательное соединение звеньев НД-ДН
Она же может быть выражена через обобщенную и сопряженную характеристики
составляющих соединение звеньев. Для этого воспользуемся следующей цепочкой
соотношений
Х(з)^Ух(з9п)8(п)е'мТ =^Ух(з9п)е'аТ^ \ H2(n,p)epnTY(p)dp =
C-joo
п=0
/7=0
1
с+уоо да
= TL J с*р%У^п)Н2(п,р)е-^р)"тУ(р).
Изображения X(s) и Y(s) связываются друг с другом бичастотной передаточной
функцией, для которой справедливо выражение
(10.147)
r(s9p)^Vx(s9n)H2{n9p)e-<s'pynT.
А?=0
Сходным образом можно записать сопряженную и обобщенную передаточные
функции соединения, которые оставим для самостоятельных упражнений.
Пусть теперь соединение представлено дискретно-непрерывным звеном на входе
(звено 2) и непрерывным звеном на выходе (рис. 10.5).
А")
V2(s, ri)
Hy(t Z)
r2(s,z)
Vx{s, t)
Г,(*,р)
*(')
Рис. 10.5. Последовательное соединение звеньев ДН-НН
Бичастотная передаточная функция выражается через аналогичные
характеристики звеньев уже знакомым соотношением
с+уоо
(10.148)
T(s,z) = — f Гх(з9р)Г2(р92)ф.
2iV c-yoo
Соотношение для обобщенной передаточной функции найдем после следующих
преобразований
C+j СО
X(s) = ^- ( Г,(5,р)ОДф™ J r](s,P)dpftV2{p,n)y(n)e-'"ir =
?1Г; J 2%J J -
2nj
c-j<x
c-jco
w=0
= Т,е-»т±Тгх(з9рШр9п)е^р)яТАп).
Вспоминая связь между X(s) иу(п) (10.74), для обобщенной передаточной
функции получим выражение
С+уоо
V(s,n) = — | r,(s,p)V2(p,n)e(x-p)nr.
c-yoo
(10.149)
Глава 10. Описание непрерывно-дискретных систем
653
Х0
F,(z, m)
П\{П, Z)
х(п)
Рис. 10.6. Последовательное соединение звеньев НД-ДД
Если непрерывно-дискретное звено на входе соединения сопрягается с
дискретным звеном на выходе (звено 1), то бичастотную передаточную функцию соединения
находят по формуле
Г(г9з)~$Гх(г9г\)Г2(т\9з)<1т\. (Ю.150)
2 71/ J
Сопряженную характеристику соединения найдем, последовательно записывая
связь оригинала х{п) с изображением {G(z)}, которое является преобразованием
воздействия Y(s) функцией Г2(г, s). В результате будем иметь
H(n,s) = — §HAn,z)T2{z,s)zn-xs-stdz. (10.151)
2nj J
Отличное от (10.150) выражение для бичастотной характеристики соединения
получим, если в качестве исходных описаний звеньев выбрать обобщенную и
сопряженные характеристики
X{z) = jr V{(z,m)g(m)z-m = JT У^т)2~т^-iH2{m,s)Y{s)esmTds .
m=0 /w=0 ZnJ
Или, изменяя порядок суммирования и интегрирования,
1
*(Ю = —j ds £ Vy{z,m)H2{m,s){ze-sTymY(s).
m=0
Откуда
Г(2, J) = X К1(2,т)Я2(т,5)(2^Г)-Ш ,
(10.152)
m=0
что, как и следовало ожидать, является вариантом Z-преобразования
соответствующей временной функции.
у(п)
V&, п)
И (П 7\
П2{П, Z)
r2fe, zi)
g(n)
U (t т\
п\\ч z)
Tifcz)
x(t)
Рис. 10.7. Последовательное соединение звеньев ДД-ДН
Для показанного на рис. 10.7 соединения бичастотная характеристика есть
результат свертки аналогичных характеристик звеньев по дискретной переменной
r(s9z)~jrx(s9r\)r2(r\9z)di\.
2nj /
(10.153)
Обобщенную передаточную функцию удобно искать через обобщенную же
входного звена и бичастотную - выходного
V(s,n) = ^-jrl(s,z)V2(z,n)esnTz-"dz. (10.154)
271/ J
654
Анализ и статистическая динамика САУ. Часть I
Повторив вывод (10.152), для бичастотной характеристики заданного соединения
получим
r(s,z) = -YdVl(s,n)H2(n,z)(z-ieiTrn.
(10.155)
' и=0
Наконец, рассмотрим соединение непрерывного и непрерывно-дискретного звена
(рис. 10.8).
КО
Vi{s, т)
U (л \
пг(1, s)
. T2(s,p)
g(.t)
LJ Ум «Л
П\[П, S)
Tife s)
x(n)
Рис. 10.8. Последовательное соединение звеньев НН-НД
Последовательно связывая изображение входа и выхода, для бичастотной
характеристики найдем
1 с+уоо
r(z,s) = — f Tx(z,p)T2(p,s)dp. (10.156)
Повторяя вывод (10.132) для сопряженной передаточной функции, получим
соотношение, почти совпадающее с (10.132),
Я(и,Л)=™ f ".(«.л)^,*)^-^. (Ю.157)
znj J.
J c-joo
Итак, хотя разные системные характеристики связаны друг с другом известными
соотношениями, для вычислекия характеристик соединений не все они равноценны.
Так, бичастотную передаточную функцию удобнее вычислять либо через бичастот-
ные же характеристики звеньев, либо через сопряженную и обобщенную
характеристики звеньев. Для вычисления обобщенной передаточной функции следует брать
аналогичную характеристику входного звена, связывая ее с бичастотной
характеристикой звена на выходе, тогда как для сопряженной характеристики,- напротив,
удобно воспользоваться той же характеристикой выходного звена, сопрягая ее с
бичастотной характеристикой звена на входе соединения.
Любые другие комбинации передаточных функций приводят к лишним
неоправданным затруднениям, что, в частности, не позволяет ограничиться использованием
одной сопряженной характеристики.
В качестве полезного упражнения рассмотрим соединения ключа и экстраполятора.
х(п)
Рис. 10.9. Последовательное соединение экстраполятор-ключ
Из физических соображений ясно, что результатом последовательного
соединения (рис. 10.9) будет тождественное преобразование, т.е. х(п) = у(п). Характеристикой
соединения должна быть, в частности, передаточная функция (10.39), отвечающая
этому преобразованию.
Подставляя в (10.143) характеристики ключа Vx(z, s) и экстраполятора T2(s, z),
будем иметь
Глава 10. Описание непрерывно-дискретных систем 655
с+уоо sT
1 i-TJ* SI л
r(Z2)Zl)=-L ^ _ е -1 <& =
Как следует из определения передаточных функций,
H<W"K1>I4
Для вычисления интеграла 3 удобно перейти к дискретному преобразованию
Лапласа
Ось интегрирования разделяет особенности, состоящие из счетных множеств
простых полюсов
s = s\+j—£> к-0, ±1,... и
s = s2+j—т9 т = 09 ±1,....
Будем интегрировать вычетами, для вычисления которых воспользуемся
известной формулой
.RJm] =j£i
iQWLs' 4Ш
ds
Интегрируя по контуру, охватывающую левую полуплоскость, имеем
5Ф=5,+Уу-Л, * = 0, ±1,...
P(S) =
esT-\
s(es>T-esT)'
О1*) = е"-е#иЩ =Те*Т.
ds U/
~S\T i +oo i i
e ^e e )k=_coi Sl+jyk
Принимая во внимание, что бесконечная сумма в последнем выражении
допускает представление
+оо j es{T
Л +00
Т~ .2я. e*iT _l'
^=-°°5i + j — к е 1
Т
для интеграла 3(eSlT\eS{T) получим
азг ^.Гч !
Возвращаясь к Z-преобразованию, для передаточной функции соединения будем
иметь:
656 Анализ и статистическая динамика САУ. Часть I
1
r(z2,z,) = ^-
*\ Z2~z\
что, как и следовало ожидать, отвечает тождественному преобразованию.
Поменяем местами ключ и экстраполятор (рис. 10.10).
хЦ
Рис. 10.10. Последовательное соединение ключ-экстраполятор
При любом типе экстраполятора, как это очевидно из физических соображений,
такое соединение не приведет к тождественному преобразованию. Поэтому
ограничимся экстраполятором, который дискретную последовательность g(ri) на входе
экстраполятора преобразует в последовательность дельта-функций с весами g(ri) на
выходе. Другими словами, исключим формирующий элемент экстраполятора.
Вычислим бичастотную передаточную функцию соединения по формуле (10.146)
'" 2nj> z(\-ze-sT)z-epT
При этом \esT\ > \z\ > \epT\.
Контур интегрирования разделяет особенности
z = epT и: = /.
Интегрирование с помощью вычета в полюсе внутри контура дает
Запишем связь между изображениями входа и выхода для такого соединения
C+JOO
™-±)J&*-
2nj J.
c-joc
Откуда видно, что T(s, р) совпадает с ядром интегрального оператора,
определяющего дискретное преобразование Лапласа по преобразованию Лапласа
непрерывного сигнала, что и следовало ожидать.
10.4. УРАВНЕНИЯ ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
. Для нестационарных систем, непрерывных и дискретных, в общем случае не
существует простых алгебраических соотношений для определения передаточных
функций. Для получения любой из передаточных функций приходится решать
соответствующие дифференциальные или интегральные уравнения. Другими словами, по
сложности задачи определения любой из системных характеристик близки. Принято
считать, что такая ситуация является типичной для любых попыток поиска
«удобных» для анализа интегральных преобразований.
Вместе с тем системные характеристики, временные и частотные, слишком важны
и информативны, чтобы отказаться от их определения, ограничиваясь рассмотрением
лишь стационарных систем. Непрерывно-дискретные системы по самой своей
природе меняются в пределах такта квантования и в этом смысле будут
нестационарными, даже если составляющие их непрерывные и дискретные звенья описываются
стационарными выражениями. Напомним, что последнее обстоятельство приводит
Глава 10. Описание непрерывно-дискретных систем 657
к невозможности определения привычных дискретных передаточных функций для
некоторых соединений стационарных звеньев.
Уравнения для передаточных функций могут быть получены либо из исходных
дифференциальных и разностных уравнений, либо непосредственно из их
определения. Запишем сначала искомые уравнения для непрерывных звеньев. Ограничимся
рассмотрением матрицы перехода и связанных с ней передаточных функций,
поскольку весовые функции очевидным образом получаются из матрицы перехода.
Для уравнений состояния
X = A(r)X + U(0 (10.158)
матрица перехода К(/,т) является решением уравнения
— К(/, т) = А(/)К(/, т) +15(/, т) (10.159)
А
при нулевых начальных условиях.
Умножим (10.159) на е~л(/~х) и проинтегрируем полученное выражение по т.
Предварительно учтем, что
4(К(/,т)е-) = -^^в-*-Ж(/,т)в-1'.
at at
Принимая во внимание определение сопряженной передаточной функции H(t,s)
(10.11), получим искомое дифференциальное уравнение
М^9^ = [ А(0 - sl]H(t, s) +1. (10.160)
dt
Это уравнение можно получить непосредственно из исходного определения
(10.11), дифференцируя последнее как интеграл с переменным верхним пределом
dt J dt J
Учитывая определение (10.11) и уравнение для матрицы перехода (10.159), из
последнего приходим к записанному выше уравнению (10.160).
Чтобы получить уравнение для обобщенной характеристики, удобно
воспользоваться выражением, определяющим матрицу перехода как решение уравнения при
дифференцировании по второму аргументу т
^-К(/,т)А(т),
А
с начальным условием К(/,т) = I.
Как и выше, матрицу перехода можно рассматривать как решение неоднородного
уравнения с нулевыми начальными условиями
^^ = -К(М)А(т)-15(/-т). (10.161)
d\
Умножая последнее выражение на e~v(/~x) и интегрируя по / от т до оо,
получим
— J К(/, т)е-'(|"т)А - s] K(f, х)е'*-х)Л = -J К(/,т)в-т(|"т)Л - J I8(r - т)*"*"^А.
XX XX
Вспоминая определение (10.5), из последнего соотношения получим искомое
уравнение для обобщенной передаточной функции
dV(s9x)
di
43 Зак. 232
•=V(5,T)[5l-A(T)]-I. (10.162)
658 Анализ и статистическая динамика САУ. Часть I
Заметим, что, как и выше, для сопряженной характеристики последнее уравнение
может быть получено непосредственно из определения (10.5) дифференцированием
по т.
В стационарных системах А(т) = А = const, V(s,t) = XV(s) и из уравнения
(10.162) как следствие получается известная передаточная функция системы по
вектору состояния
W(s) = [sl-A]-\
что и следовало ожидать.
Уравнение для бичастотной передаточной функции будем определять, используя
известную связь H(/,s) и T(s,p) (10.20). Полученное выше выражение (10.160)
умножим на е~^~р^ и проинтегрируем от 0 до оо
1 e~{s-p)t ^^- Л = ? <Г<*-'>' [(А(0 - pI)H(/, p) +1] dt.
о Л о
Из определения Н(/, р) следует, что Н(0, р) = 0, и тогда левая часть последнего
выражения будет равна (s - p)T(s, p).
Правую часть преобразуем одним из следующих способов:
оо оо . С+у'оо
[e-(s-p)'A(t)H(t,p)dt={dteHs-p)'— f A(\)ex'd\H(t,p) =
■* •* 27П ^
0 0 AllJ с-уоо
C+JCO 00 - С+7<»
= _!_ [ ^А(Х)ГЛе-(^-'')'Н(?)р)=— f A(X.)T(*-X,p)rfA.
2 л/ J i 2 л/ •".
' c-J<*> 0 ' c-7«>
ИЛИ
1 dte-(s-p)'A(t)H(t, p) = l dte^-p)'A(t)— f d\e{%-p)lY{\, p) =
I 0 2nJc-j«
. C + 700 00 - f+700
= — f £/х[Лв"(д"Х)|А(0Щ,р) = — [ A(s-X)T(X,p)dX.
2nj J. i 2nj 3
J c-yoo 0 J C-/00
Таким образом, для бичастотной передаточной функции имеем два равносильны:
уравнения:
л C+JCO -
лГ(5,р) = — f A(A.)r(j-X,p)dA, + 1 (10.163
2я/ J. j-p
И
dT(j,p) = — A(j-A.)r(A.,p)rfA. + 1. (10.164
Для стационарной системы с постоянной матрицей состояния A(s) = -А . Учиты
s
вая, что ось интегрирования разделяет особенности A(s) и F(s,p), будем интегри
ровать с помощью вычетов в точке Х = 0 для (10.163) и Х = р для (10.164). Как
следовало ожидать, в каждом случае будем иметь
r(s,p) = [sl-AT
1-1 *
s-p
Глава 10. Описание непрерывно-дискретных систем 659
Уравнение (10.163) может быть получено непосредственно из уравнений
состояния (10.159). Домножая обе части уравнения (10.159) на e~ste~px и интегрируя
дважды, будем иметь
л dt а
От 6
Для интеграла в левой части получим
00 00 „ j. / v 00
е-йК(Г,т)|%4е"Л'К(Г,т^
Л
что с учетом начальных условий (10.163) приводит к выражению sT(s,p).
' В правой части, используя обратное преобразование Лапласа, матрицу А(/)
выразим через соответствующее изображение А(Х), что с учетом определения V(s,p)
дает
оо 00 . С+у'оо -
[dx\dtepxe-st[A(t)K(t,x) + l8(t-T)] = — f A(X)r{s-X9p}dX + -^—l.
От J c-joo r
Результат очевидно совпадает с записанным выше уравнением (10.164).
Рассмотрим теперь уравнения состояния для систем с дискретным временем
х(л +1) = А(л)х(л) + В(л)и(л) . (10.165)
Матрица перехода К(л,т) является решением однородного уравнения
х(л + 1) = А(л)х(л) • (10.166)
с начальным условием \(т) = I либо решением неоднородного уравнения
х(л + 1) = А(л)х(л) + 1Д(л + 1-/и) (10.167)
с нулевыми начальными условиями \{т -1) = 0 .
Уравнение для сопряженной передаточной функции будем искать, отталкиваясь
от определения (10.33). Поскольку
К(л + 1,/и) = А(л)К(л,/и), К(т,т) = 1, (10.168)
то, вспоминая определение (10.33), домножим последнее соотношение на z~(w~w) и
просуммируем
X K(/i + l,*i)z-("-m) = X A(n)K(n,m)z-{n-m\
/и=0 ш=0
Левую часть последнего выражения перепишем в виде
£ К(и + 1,m)z-<"-> = z["f К(л +1, W)Z-("+1-"l) - il
т=0 [_т=0 J
Тогда в соответствии с определением Н(л,г) получим искомое уравнение
Н(л + 1,2) = 2"1А(л)Н(л,2) + 1. (10.169)
Чтобы получить уравнение для обобщенной передаточной функции, удобно
воспользоваться уравнением, сопряженным исходному (10.166),
х(л + 1) = [а"1(л)]Тх(л),
которому, как известно [60], матрица перехода удовлетворяет по второму аргументу,
следствием чего является следующее соотношение
К(л, т +1) А(/и) = К(л, аи). (10.170)
43*
660 Анализ и статистическая динамика САУ. Часть I
По привычной схеме домножим обе части последнего уравнения на z~(w~w) и
просуммируем от п = т до оо:
00 00
£ K(«,w + 1)A(aw)z"(w~/w) = £ K(n9m)z~in-m).
п=т п=т
Правая часть определяет, согласно (10.27), обобщенную характеристику. Чтобы
воспользоваться этим определением для матрицы перехода, левую часть последнего
уравнения перепишем сначала в виде
]Г К(л, т + l)A(w)z'("~m) =
= z~l
£ К(л, т +1)A(m)z'{n~m~l) + K(/w, w +1)A(m)z =
=m+l J
=/я+1 J
В соответствии с определением (10.27) получим искомое уравнение для
обобщенной передаточной функции
z'1V(z,w + l)A(/w) + I = V(z,m). (10.171)
Заметим, что для стационарной системы А(т) = А = const, V(z,w) = W(z), и из
последнего уравнения найдем изображение матрицы перехода
W(z) = z[zI-A]-\
Уравнение для бичастотной характеристики можно искать, используя известные
связи между передаточными функциями (10.44), (10.42), отталкиваясь от полученных
выше уравнений (10.169) или (10.171), но можно также в соответствии с
определением применить двумерное Z-преобразование непосредственно к исходному
соотношению (10.166) для матрицы перехода
JT ХК(л + 1,m)z-2nzrX =X X А(п)К(п,т)2-2"2Г1.
Выражая матрицу А(я) через её изображение А(Х) посредством обратного
Z-преобразования, правую часть последнего выражения запишем в виде
интегрального соотношения
n=0n=mZnJ ZnJ K K
В левой части соотношения, выполняя последовательно преобразования,
позволяющие применить определение (10.36) для r(z2,Zj), найдем
JT X K(« + l)WJ)z2-"Zr' = Z Ъ t K(n + l>m)z-2^zrl =
n=0n=m /w=0 n-tn
=^ZzT"1 E K(/,m)rj'=z2|;2r-1||;K(/,«)4-K(«,«)r2-"l.
m=0 /=m+l m=0 L/=w J
Принимая во внимание, что К(т,т) = 1 и | z2 |>| zx \, объединяя снова обе части, с
учетом определения (10.36) для бичастотной передаточной функции получаем
следующее интегральное уравнение в комплексной области
Глава 10. Описание непрерывно-дискретных систем 661
z2r(z2,z0-—^Ц—^^ГА,^)^. (10.172)
2,(22-^) 2ilJ J X X
Применим последнее уравнение для частного случая А(т) = А = const. Тогда
А(Х) = -^-А.
А, — 1
Контур интегрирования разделяет особенности А(Х) и Г(— ,z). Интегрируя вы-
« X
четами в полюсах А(Х), получим
r(z2>z1) = z2[z2I-A]-1 Z2
z\\zi"z\)
что и следовало ожидать для стационарной системы.
662 Анализ и статистическая динамика САУ. Часть I
ГЛАВА 11. АНАЛИЗ НЕПРЕРЫВНО-ДИСКРЕТНЫХ
СИСТЕМ
В настоящей главе рассматривается решение типовых задач анализа непрерывно-
дискретных, в общем случае, нестационарных динамических систем. На единой
методической основе, использующей аппарат двумерных интегральных
преобразований, устанавливаются соотношения вход-выход для анализа систем при
детерминированных и случайных воздействиях. В последнем случае обеспечивается
возможность оценивать не только установившиеся ошибки, но и соответствующие
переходные процессы.
Наряду с простыми непрерывно-дискретными системами исследуются достаточно
трудные для анализа системы с несколькими ключами и разными периодами
квантования, а также существенно нестационарные классы систем управления конечным
значением и с конечным временем замыкания ключа.
Известны многочисленные попытки изучать указанные классы систем, не выходя
за привычные определения. Вместе с тем заметим, что попытки на основе известного
аппарата анализа стационарных систем описать более сложные классы; например,
системы с конечным временем замыкания ключа, не приводят к эффективным
результатам. При этом не удается получить аналитических выражений для
динамических характеристик, а соотношения, с которыми приходится оперировать,
оказываются намного сложнее привычных формул (см., например, метод Р-преобразования
для систем с конечным временем съема данных). Это обстоятельство привело, в
частности, к рекомендации [169] применять для анализа методы пространства
состояний (по существу - метод припасовывания).
Указанные затруднения обусловлены не столько сложностью самих систем,
сколько непригодностью исходных характеристик для новых классов систем.
Напротив, переход к более общим характеристикам, принятым при описании
нестационарных систем, позволяет получить единообразные, относительно простые
соотношения для различных, в том числе и для упомянутых классов линейных
нестационарных систем.
11.1. АНАЛИЗ НЕПРЕРЫВНО-ДИСКРЕТНЫХ СИСТЕМ
ПРИ ДЕТЕРМИНИРОВАННЫХ ВОЗДЕЙСТВИЯХ
Непрерывно-дискретные системы описываются смешанной системой уравнений и
содержат дифференциальные и разностные составляющие для описания
непрерывных и дискретных звеньев. Соответственно решением этих уравнений являются
непрерывные и дискретные выражения для описания соответствующих сигналов.
Хотелось бы, чтобы не терять информацию, вычислять реакции в таких системах, не
прибегая к квантованию непрерывных сигналов. В рамках теории нестационарных
систем такая задача может быть решена. Вместе с тем получение аналитически* рг-
шений в нестационарных системах является скорее исключением, чем правилом.
Поэтому ждать аналитических решений для общего случая нестационарных объектов
не приходится.
Глава 11. Анализ непрерывно-дискретных систем 663
Ограничимся рассмотрением достаточно общего описания непрерывно-
дискретных систем, которые заданы дифференциальными и разностными
уравнениями с постоянными коэффициентами.
Итак, будем считать, что система представлена уравнениями состояния
*i(0
= апх1(О + а12Э[х2(л)] + Ь1ин(О, (U.1)
Л
х2(л + 1) = а12О[х1(0]+а22Х2(я)+Ь2ид(л), (11.2)
с начальными условиями Xj(O) и х2(0),где
Xj(O - вектор состояния непрерывной части системы,
х2(и) - вектор состояния дискретной части системы,
ин (/) - непрерывный вектор управления,
ид(и) - дискретный вектор управления,
a/bb, - числовые матрицы соответствующих размерностей.
Через Э[х2(п)] и О[х^)] обозначены соответственно операции экстраполяции
дискретного сигнала х2(л) и квантования по времени непрерывного сигнала Xj(/).
Эти операции удобно для дальнейшего рассмотрения записать при помощи
импульсных переходных функций экстраполятора нулевого порядка и ключа
Г\Т<А
Э[х2(/1)]= X №-пТУЩ-пТ-Т)Ып\ (11.3) •
пТ
Dlx^lSinT-x^Wdx. (11.4)
о
Поскольку рассматриваемая система не является чисто непрерывной или чисто
дискретной, простых алгебраических выражений, связывающих воздействия и
соответствующие им реакции, получить не удается. Поэтому ожидаемым результатом
будет установление связей вход-выход в комплексной области на основе матрицы
бичастотных передаточных функций, связывающей входные воздействия и реакции
интегральным соотношением
C+jco
J *,ГИ(52, *,) jdz{Tn(s2,zA)
C-JOO
X1O2)
x2(z2)
ij 2nj
C+700
Гин(*1)1 Гф,(х,(0))"|
J dsxT2l(z2,st)jdzxT22(z2,z,)
C-JOO
Уравнения состояния (11.1) и (11.2) можно записать в более общей форме,
добавив в правую часть дополнительные воздействия (дискретные в (11.1) и непрерывные
в (11.2)) с соответствующими преобразователями, а также дополнить уравнения
состояния алгебраическими выражениями для вектора выходных координат.
Получающиеся при этом соотношения очевидным образом следуют из приведенных здесь
результатов и не приводятся только по причине упрощения записи.
Чтобы определить явные выражения для матрицы передаточных функций через
коэффициенты уравнений состояния, преобразуем уравнения (11.1) и (11.2) с
помощью преобразования Лапласа и Z-преобразования соответственно. Кроме того,
получающиеся при этом изображения сигналов, подвергающихся экстраполяции и
квантованию, выразим через соответствующие изображения сигналов на входах
экстраполятора и ключа. После очевидных преобразований найдем
664 Анализ и статистическая динамика САУ. Часть I
sxi(s)-x](0) = auxi(s) + an^-jr3(s,z)x2(z)dz+biuH(s), (11.5)
27TJ J
z(x2(r)-x2(0)) = a21-iT f Гк(2,*)х,(5)Л + а22х2(г) + Ь2ид(2). (11.6)
111] .
C-700
Здесь через T3(s,z) и FK(z,s) обозначены передаточные функции экстраполято-
ра и ключа
Гэ(*,*)= ,1"е-,уч. (Н.7)
sz(l-ze )
Гк(г,5) = ^г. (11.8)
z-e'
Перепишем уравнения (11.5) и (11.6) для последующего матричного
представления неявной зависимости вход-выход, обозначив для сокращения записи
b,uH(0 = 11,(0, Ь2ид(л) = и2(л)
[sl]-uu]x](s)-u]2-^jr3(s,z)x2(z)ck = x](0) + u](s), (11.9)
-a2i— J rK(z,5)x1(5)^ + [zI2-a22]x2(z) = zx2(0) + u2(z). (11.10)
с-уоо
Или в матричной форме
d.-a,, -а12Э ]Гх,(5)1=Гх,(0)1 Ги,(«)1
-а2)£> zI2-a22JLx2(z)J [zx2(0)J Lu2(z)J'
где через Э и D обозначены операции экстраполирования и квантования сигналов,
смысл которых раскрывается в исходных уравнениях (11.9) и (11.10). Разрешив
последние уравнения относительно искомых переменных, формально запишем
_x2(z)J [-а21Д zI2-a22J [Lu2(z)J Lzx2(0)JJ
Из последнего соотношения следует, что успех в решении исходной задачи
вычисления явной связи вход-выход зависит от того, можно ли получить явное
выражение для обратного оператора, представленного блочной матрицей. Этот вопрос
решается положительно, и в рамках двумерных интегральных преобразований
удается получить требуемые выражения для искомого оператора.
Для сокращения промежуточных выкладок воспользуемся известной формулой
Фробениуса для обращения блочных матриц [89]. Блочная матрица
Чс 1\
у которой А - неособенная матрица, имеет обратную
(11.14)
, А"1 + А^ВН^СА"1 -А^ВН"1
М =
-1
-НСА1 Н
где H = D-CA"1B.
Смысл последующих преобразований сводится к тому, чтобы каждый из
операторов блочной матрицы МП1 выразить через простые соединения известных операторов.
Глава 11. Анализ непрерывно-дискретных систем 665
Очевидно, что для искомого оператора выражение М"1 представляет собой
изображение матрицы перехода непрерывной части
WH(5) = [5I1-aI1rI. (11.15)
Оценим оператор Н"1. Обозначив
Wa(z) = [2I2-a22r1, (11.16)
по формуле Фробениуса для оператора Н~' имеем
ИГ1 =[\VH-I(z)-a21DWH(5)al23]"1,
ИЛИ
И4 =[I2 - WH(z)a21DWH(5)a123]-1 WH(z). (11.17)
Оператор DWH (s)3, у которого вход и выход являются дискретными сигналами,
для стационарной системы описывается соответствующей передаточной функцией,
вычисляемой по известной передаточной функции непрерывной части системы. Тот
же результат получается непосредственным вычислением оператора
последовательного соединения звеньев D , WH и Э, или, что то же самое, последовательным
соединением двух интегральных операторов, отвечающих операциям экстраполяции и
квантования. Принимая во внимание передаточные функции ключа (11.8) и экстра-
полятора (11.7) для бичастотной передаточной функции соединения, сначала
получим
1 C+JC° 7. 1 - P~ST
r(z2,z1) = -ir j —^WHW ; ds. (11.18)
Для вычисления интеграла удобно воспользоваться дискретным преобразованием
Лапласа. Ось интегрирования разделяет особенности подынтегральной функции,
отвечающие полюсам выражения WH(s), которые неизвестны, поскольку линейная
непрерывная часть системы задана в общем виде, и счетному множеству простых
полюсов ключа
sk=s2+j?y-9k=09±\9 ±2,.... (11.19)
Интегрируя с помощью вычетов в полюсах sk , найдем
rv>T,Zl)=-f; ^луйп , (п.20)
к=-оо
где
P(s) = WH(*)b£-L, Q(s) = es>T - esT.
s
Подставляя P(s) и Q(s) в (11.20) и производя вычисления, получим
Пе ■Zl)-rz,(1-e-'z,),i 2Лк ■ ("-21)
2 J T
42 Зак. 232
666 Анализ и статистическая динамика САУ. Часть I
Выражение вида — ]Г W(s + j—к) является дискретным преобразованием Лап-
ласа, которое соответствует непрерывной функции с изображением W(s). Снова
возвращаясь к Z-преобразованию, т.е. при z2 = thT, получим
viz ^-z20-V1)z fw.wl
* U2 > z\) - —: rz2 i r • U1-22)
^ife-^) I * J
Здесь через Z2{W(s)} обозначено Z-преобразование функции с изображением
W(s) по переменной z2 .
В частном случае, когда WH (s) = I,
(l-z^^zJi^I. (11.23)
При этом, как и следовало ожидать, соединение DWH3 приводит к оператору
тождественного преобразования
Т{2Ъ2Х)= /2 I (11.24)
Таким образом, искомый оператор Н"1 задается бичастотной передаточной
функцией Г22(z2,Z!)
r22(z2^i)= , Zl Jli-Wfl(z2)a21(l-z2-1)Z2(^^}a121 W,(z2). (11.25)
Передаточная функция Г^^,^) описывает стационарную дискретную систему.
Это легко заключить из рассмотрения структуры функции r22(z2,z1), составленной
из матричной функции переменной z2 и скалярного множителя тождественного
преобразования . Выполняя интегрирование по переменной zx, указанное в
zx(z2-zx)
(11.5), получают известное алгебраическое выражение, связывающее изображение
входа и выхода стационарной дискретной системы. По этой причине всюду ниже для
обозначения оператора Н"1 целесообразно использовать естественное обозначение в
виде Фд(г), отвечающее обычной матричной передаточной функции одной
переменной для замкнутой дискретной системы с выходом x2(z) и входом u2(z).
Сходным образом находятся передаточные функции для операторов -Н~1СА~1 и
r12(V) = WH(j)a12Ofl(z) )'**, (И.26)
sz(\-ze )
Г21(^) = Oa(z)a21WH(*)—V- С1 L27)
z-e
Для вычисления передаточной функции ^,(^,5^ в соответствии с формулой
(11.14) нужно выполнить следующие преобразования
А-'а + ВЫ'СА^ WH(s)[lx +a123Ofl(z)a21DWH(j)]. ' (11.28)
Глава 11. Анализ непрерывно-дискретных систем 667
Из формального операторного выражения (11.28) следует, что искомый оператор
включает в себя последовательное соединение экстраполятора, дискретного
стационарного звена и ключа. Найдем характеристику такого соединения по известным
характеристикам каждого звена
l^W.M-^,,.^* (П.29)
Ф (z)
Контур интегрирования здесь разделяет особенности функций —^у и
z-e'
О-яГ*7")-1.
Удобно вычислять интеграл с помощью вычета в точке z - eSlT . Тогда для инте-
И**.)- ' %^т- (11-30)
грала (11.29) будем иметь
1-<Гд»7' Фл(е*т)
s2 1-е
Заметим, что множитель (1-е~(л'2~~Л|)7 у1 представляет собой ядро интегрального
преобразования для вычисления дискретного преобразования Лапласа по
изображению непрерывной функции.
С учетом последней формулы, искомую бичастотную передаточную функцию,
связывающую непрерывные составляющие входа и выхода, запишем в виде
rnCWi) = WhC*2)
1 1 — p~s^
-1 + а12Фд(^)а21\Ун(5,)
(11.31)
_*2V " "VI%2(l-e^-">7").
Итак, определены все четыре матрицы бичастотных передаточных функций,
связывающих непрерывную и дискретную составляющие вектора состояния с векторами
входных воздействий и соответствующими начальными условиями. Как показывает
вышеприведенный анализ, относительно просто удается определить поведение
системы в дискретные моменты времени для дискретного воздействия, что согласуется с
известными физическими представлениями о поведении дискретной системы. Для
описания движения системы по всей совокупности фазовых координат потребовался
переход к двумерным интегральным преобразованиям, которые позволяют получить
явную зависимость полного вектора состояния от входных воздействий и начальных
условий.
По блочной матрице бичастотных передаточных функций можно получить
матрицу перехода непрерывно-дискретной системы, для чего следует определить
двумерные оригиналы соответствующих передаточных функций.
Пример 11.1. Для иллюстрации предложенного выше подхода рассмотрим простой пример
непрерывно-дискретной системы, описывающейся следующими уравнениями
^1 = -х^)-Эх2(п) + щ(0,
x2(n + \) = Dx}(t) + x2(n) + u2(n).
Непрерывная часть системы описывается передаточной функцией
ф+1)
которой отвечает Z-преобразование
W(z) = ^jr.
z-e
Соответственно для стационарной передаточной функции замкнутой системы имеем
Г22(22^,) = Фд(72)-7 -,
Z\\Z2~Z\)
42*
668 Анализ и статистическая динамика САУ. Часть 1
Оставшиеся три бичастотных передаточных функции найдем соответственно по формулам (11.26),
(11.27) и (11.31)
Г12(^) = -Фд(г) 1"е>Г
sz(s + \)(\-ze )
Г21(2,5) = ФД(7) Z
^'(s + Diz-e^y
Г"(^^(^-Ф*(е%
Найдем реакции системы на непрерывное воздействие м,(/) = 1(/) С учетом найденных выражений
Г,,(.s2,.$!) и Г2|(z,s), найдем
*iW =
ф+1)(1-(1-е-7>~'7'+е-ът)
, ч (1-^)2
х2йг —
(z-\)(z2-(\+e-r)z + \)'
11.2. МЕТОД РАСЧЁТА НЕПРЕРЫВНО-ДИСКРЕТНЫХ СИСТЕМ
ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
Распространённые способы расчёта случайных ошибок в динамических системах
частотным методом связаны, как известно, с интегрированием спектральных
плотностей. Получающиеся при этом соотношения позволяют определять лишь
установившиеся значения характеристик случайных функций, оставляя открытым вопрос о
поведении системы в переходном режиме. Применение многомерных интегральных
преобразований позволяет снять это ограничение. Причём для стационарных
линейных систем возможность анализа переходных процессов при случайных
воздействиях не сопровождается сколько-нибудь заметным усложнением расчётных
соотношений.
Что касается оценок математического ожидания, то очевидно, что для линейных
систем расчётные формулы не отличаются от соответствующих соотношений для
детерминированных сигналов, и мы не будем на них останавливаться, переходя сразу
к оценкам вторых моментов.
Начнём с рассмотрения непрерывных систем.
Определим спектральную плотность Sjf{s,p) случайного сигнала, заданного на
(0,оо) и отвечающего корреляционной функции /fy-(/,x), которая описывает в
общем случае нестационарный процесс, соотношением:
00 00
Sjf (s, р) = J dt\ Rff (M)<f Wt. (11.32)
о о
Другими словами, спектральная плотность определяется как двумерное
интегральное преобразование корреляционной функции. Применение многомерных
преобразований позволяет распространить частотный метод, широко используемый для
описания стационарных систем и сигналов, на нестационарные процессы [132].
Если случайный сигнал является стационарным, корреляционная функция зависит
от разности переменных /ит:
%(/,t) = /^(/-t).
Глава 11. Анализ непрерывно-дискретных систем 669
Для автокорреляционной функции, симметричной относительно своих
аргументов, по формуле (11.32) найдём:
Sff(s,p) = ]dt]dTRff(t-T)e-sle-p' =
о о
00 00 СО СО
= \di\dtRjf{t-i:)e-ste-pT +\dt\RfJ{t-x)e-sie'pTdx.
От 0 /
Обозначив
00
Sff(p) = lRjff(T)e-sTdT9 (11.33)
о
для спектральной плотности стационарного процесса получим соотношение:
м s + р
Как и следовало ожидать, это выражение является симметричным по аргументам
s и /?, поскольку соответствует автокорреляционной функции с аналогичными
свойствами. Взаимная спектральная плотность, определяемая тем же соотношением
(11.32), этим свойством обладать не будет в силу известных свойств
соответствующей корреляционной функции.
Для белого шума с корреляционной функцией
Rff(tJ) = N28(t-T),
учитывая известные свойства 5-функции, спектральную плотность запишем в виде
Sy/(5,/7) = —. (11.35)
JJ s + р
Спектральные плотности случайных сигналов используются для расчета
случайных ошибок, характеризуемых дисперсиями или соответствующими среднеквадрати-
ческими отклонениями.
Процедуры вычисления изображения дисперсии по спектральной плотности
носит название ассоциации переменных [132] и отвечает операции отождествления
переменных / и т в корреляционной функции
DJf(t)=Rff(t9t).
Отталкиваясь от обратного преобразования для вычисления корреляционной
функции по спектральной плотности
Rff{t*T)=^b i dseSli^ У dPePZsJi^p^ (lL36>
•* c-jco J c-jco
отождествляя / и т, найдем
*#('.')— J e"*T~ J dpSff(s-p,p).
. 2nj J znj J.
J c-jco J c-j<x>
Откуда видно, что изображение дисперсии получается ассоциацией переменных
s и р по формуле
с+уоо
Dff(t) = DfJ(s)=— j SJf{s-p,p)-dp. (П.37)
с-700
670 Анализ и статистическая динамика САУ. Часть I
Заметим, что последнее выражение можно также вывести из известного свойства
преобразования Лапласа, которое операцию умножения во временной области
связывает со свёрткой в области комплексной переменной.
Для установления связи вход-выход между спектральными плотностями будем
исходить из известного [132] соотношения между автокорреляционными функциями
входа RYY(t9t) и выхода Rxx(t,T):
^(^'2) = Л*(^1э^Ж^Л)%(т,л)Л£/л.
о о
Применяя к последнему соотношению в соответствии с (11.32) двумерное
преобразование Лапласа и выражая корреляционную функцию RYY(t,T) с помощью
обратного преобразования через SYY (s, p), будем иметь:
00 00 /| *2
(271У) оо оо
c+jw c+jw
х J j dp]dp2SYY(pbp2)e^ep^.
c-jw с- fw
Меняя порядок интегрирования и учитывая определение бичастотной
передаточной функции, получим искомую зависимость:
- C+JCO C+JCO
SYy(sus{) = —~-2 j j dp\dp1T{sbpx)T(<s2,p1)SYY(pbp2). (11.38)
\^Ц/) C-j<x>c-J<X>
Для стационарных систем интегральное выражение заменяется алгебраическим. В
самом деле, вспомним, что T(s9p) и W{s) связаны соотношением
r(s9p) = W(s)- l
s-p
перепишем сначала (11.38) в виде
Tc+r_s
J J Глг, -
i 7 7 Syy(PiPi)
(2*/) c_% с_% (s\ - Pi )(^2 - Pi)
Интегрируя вычетами в полюсах рх = sx и p2=s2i приходим к простому
алгебраическому выражению:
S)Oc(s19s2)^IV(s])W(s2)SYy(sus2). (11.39)
Напомним, что Sxx(s,p) характеризуют нестационарный случайный процесс и,
в частности, позволяют оценивать переходные процессы по дисперсии.
Проиллюстрируем это простым примером.
Пример 11.2. Будем рассматривать прохождение белого шума через динамическое звено с
передаточной функцией
Спектральная плотность сигнала на выходе звена
с / ч * К N2
^ F) Tas + \ Тар + \ s + p
Ассоциируя переменные (11.37), найдём изображение дисперсии:
D 1 С7°° К К N2 d K2N2
Xx{S) = 2njJjxTa(s-p) + \Tap + \sp + pP = 2TA]]Ls + {)
Глава 11. Анализ непрерывно-дискретных систем 671
Откуда, переходя к оригиналу, найдем дисперсию как функцию времени:
Традиционный путь, базирующийся на одномерном преобразовании Фурье, позволяет выявлять лишь
K2N2
установившиеся значения дисперсии (в нашем случае D& = ).
Найдём теперь связи вход-выход для взаимной спектральной плотности. Во
временной области для корреляционных функций имеем:
о
Преобразуем последнее выражение в соответствии с определением (11.32)
00 00 /
SXY{s,p) = \dt\d™-ste-^\k(tiy\)RYY(y\,>i)dT\.
0 0 О
Корреляционную функцию входного воздействия RYY(j\,i) выразим через
спектральную плотность
с+уоо с+уоо
(27у) 4„ с.%
Учитывая, что
о P-V-
J_T_L
7ni J п-i
271/ J p-ii
J c-700 ^ ^
и меняя порядок интегрирования, получим искомое соотношение
Sxr^P)~ ( r(s9v)SYY(v9p)dv. (11.40)
2Ч с-уоо
Для стационарных динамических звеньев, у которых бичастотная передаточная
функция представлена зависимостью
r(s,v) = W(s)—9
s-v
интегральное соотношение заменяется простым алгебраическим
SXY(s,p) = W(s)SYY(s,p). (11.41)
Снова подчеркнём, что фигурирующие в (11.41) спектральные плотности
описывают нестационарные случайные процессы.
Обратимся теперь к описанию дискретных сигналов. Случайная
последовательность х(п)9 л = 0,1,»., которой во временной области отвечает корреляционная
функция Rxx(n9m), в комплексной области характеризуется спектральной
плотностью Sxx(z2,z2):
Sxx(***\) = Z Z Rxx(">*")*in*\m- (П-42)
rt=Om=O
672 Анализ и статистическая динамика САУ. Часть I
Изображение дисперсии Dxx(n) = Rxx(n,n) найдём, ассоциируя переменные zx и
z2. Для этого в формуле обратного преобразования
Rxx(nim)=—^jdz2jcizlzn2-lzrlSxx(z2iz]) (11.43)
отождествим переменные пиши заменим сначала выражение для оригинала:
^Ax(0 = ^(r)0 = ^-f^2-zrI^T<|^l-zrI5AX(|-)z1),
откуда видно, что изображение дисперсии определяется формулой
Dxx{z2) = ^dzx>z?Sxx(^zx). (11.44)
Найдём спектральную плотность белого шума, для которого корреляционная
функция
Яхх(п9т) = М2А(п-т) = Г2>П = т. (11.45)
[0,пФт
Прямыми вычислениями из (11.42) получим
Sxx(z2,zx) = N2-^-. (11.46)
Для стационарных последовательностей Rxx(n9m)- Rxx(n-m). Для
спектральной плотности стационарного сигнала сначала запишем
Sxx(^x)=Z Z ади-»)*гЧ"+Z Z ад* -п)г-гп2-хт.
m=0n=m n=0m=n
Обозначив
^(^) = ЕЛах(^Л (Н.47)
w=0
для стационарного сигнала получим соотношение
5^(z2,z1) = [SJO,(z2) + 5A3r(zI)]-S£L. (11.48)
Z2Z1 ~ A
При установлении связей вход-выход между спектральными плотностями будем
исходить из соотношения (10.26), которому отвечает известная зависимость между
корреляционными функциями входа и выхода:
п т
Rxx(n9m) = ^Hk(n^(mJ)RYY(U\
/=о /=о
Воспользуемся определением (11.42) для спектральной плотности Sxx(z2,zx),
выразив RYY(iJ) с помощью обратного преобразования через Syy(z2izx):
ад*2.*,)=Z Z z2-^rmZZA(w'/)A('».o--L3-<|<|5KK(v,M)v'-vM^M.
w=0m=0 /=0/=0 {2П1)
Вспоминая определения передаточных функций, из последнего получим искомое
соотношение:
^л'(^2^1) = Т^^П^2^)Г(21,ц)5кП^ц)^^ (11.49)
Взаимную спектральную плотность будем искать, преобразуя по формуле (11.42)
связь вход-выход для корреляционных функций:
Глава 11, Анализ непрерывно-дискретных систем 673
п
RXY(n,m) = Yjk(n,l)RYY(l,m),
/=о
где, как и выше, вместо RYY(l,m) используем соответствующие проставления через
SYY(.z2,zx):
w=0m=0/=0 (27У)
Учитывая тождество
-Ц У rrV'^Cv.MVM =SYY(y,zx),
получим искомую зависимость
SXY(z2,zu) = ^-jn^^)SYY(v,zl)dv. • (11.50)
2lt/ J
Если динамические звенья являются стационарными, то интегральные
соотношения (11.49) и (11.50) упрощаются. Поскольку для стационарных систем
r(z2,z,) = 04z2)-
z{(z2-z2)
то, интегрируя, получим выражения:
5^(z2,z1) = fF(z2)-fF(z1)-5rK(22,z1), • (11.51)
SXY(z2,z]) = W(z2)-SYY(z2,zl). (11.52)
Пример 11.3. Будем оценивать дисперсию сигнала в дискретные моменты времени на выходе
динамической системы, состоящей из экстраполятора нулевого порядка и непрерывного апериодического звена с
постоянной времени, равной 1с при белом шуме на выходе. Передаточная функция динамического звена
(Г - период квантования)
Поэтому для спектральной плотности реакции системы на белый шум будем иметь:
с (z , N\\-e-T)z2zx
(z2-e-')(zl-e-i)(z2z^\)
Ассоциируя переменные z2 и z,, изображение реакции запишем в виде:
<2\
Интегрируя с помощью вычета в точке z, = е'т , найдём изображение дисперсии:
(z2-\)(z2-e Zl)
Вычисляя оригинал, получим дисперсию реакции, как функцию дискретного времени.
Dxx(n) = N2l-^r(\-e-2nr).
\ + е
Заметим, что традиционный путь, связанный с использованием одномерных спектральных плоскостей,
позволяет оценить лишь установившееся значение дисперсии:
** \ + е~т
Перейдём к описанию случайных сигналов в непрерывно-дискретных звеньях.
Корреляционную функцию определим, естественным образом, как математическое
ожидание центрированных сигналов:
/^(иГ,0 = Лф(иГ)Я0], (И.53)
674 Анализ и статистическая динамика САУ. Часть I
RxrfonT) = M[x(t)y(nT)l (11.54)
Спектральная плотность вводится как двумерное преобразование корреляционной
функции вида:
SXY(z9s) = ftz-n]Rxr(nT9t)e"ldt9 (11.55)
и=0 о
Sxyis,!) = \Y4RXY(t,nT)z-"e-stdt. (11.56)
О w=0
Связи вход-выход между спектральными плотностями найдём, отталкиваясь от
соответствующих зависимостей для корреляционных функций, которые для звеньев с
непрерывным сигналом на входе и дискретным на выходе могут быть записаны в
виде:
пТ
Rxy(nT,t)= \ RyyinTrfRyyfrOdT, (11.57)
о
пТтТ
Rxx(nT,mT) = J J k(nT,t)k(mT,x)RYY(t9x)dtdx. (11.58)
о .о
Применив к обеим частям последних равенств двумерное преобразование (11.53)
и (11.42), получим требуемые соотношения:
SM*>s)~ t T(z9p)SYY(Pis)dp9 (11.59)
Sxx(z29zx) = —L_ t j r(z2,s)r(zup)SYY(s9p)dsdp. (11.60)
При выводе (11.59) учтено тождественное преобразование
t . C+jco
\e~stdt— f estX(s)dt = X(s).
{ 271/ J.
0 J c-jco
Пример 11.4. Проиллюстрируем применение связей вход-выход на простом примере непрерывно-
дискретного звена, составленного из последовательного соединения интегрирующего звена и ключа.
Найдём дисперсию как функцию времени на выходе ключа при белом шуме на входе интегратора.
Такое соединение описывается передаточной функцией
rv \ Z \
z-esl s
Спектральную плотность реакции найдем согласно (11.60)
- c+jco c+j<x> - ..2
5 (2 2) = _> f ds dp-- 2г - *' - .
Изображение дисперсии получим, ассоциируя переменные z2 и г,:
Dxx(z2)=^jz;lsJ^ziyi =
N2 г _, 1 С7°° С+Г
= -—<bdzxzx г ds dp-
a**-1 erf ' " ' ", fa..„V. -•" »<»-»
■(t-"r):
Результатом ассоциации будет выражение
^2 с+/» <уо
(2*)2^ ,.% sp(s + p)z1-e^T'
Глава 11. Анализ непрерывно-дискретных систем 675
интегрируя которое, получим изображение дисперсии:
п , ч N2z2T
Как и следовало ожидать, дисперсия реакции линейно возрастает:
Dxx(nT) = N2nT.
Для звеньев с дискретным сигналом на входе и непрерывным на выходе
соотношение вход-выход для корреляционных функций записывается в следующем виде:
Rxr^n)^k(t9m)Ryy(m9n)9 (11.61)
w=0
пТ<1тТ£т
Ялх('>-О=Е Z Kt,n)k(i,m)Ryy(n,m). (11.62)
и=0 /и=0
Связи вход-выход между спектральными плотностями найдём, применив к
последним соотношениям преобразования (11.56) и (11.32) соответственно. В
результате с учётом определения бичастотной передаточной функции (10.79) и соотношения
(11.42) получим искомые соотношения:
SXY(s,z) = ^jr(s,v)Syy(viz)dvi (11.63)
Znj J
Sxx (s, p) = —Lj-lJ j Г(«, у)Г(р, v)Syy (v, ц)А</ц. (11.64)
При выводе (11.63) учтено очевидное тождество
Пример 11.5. Проиллюстрируем полученные связи вход-выход на методическом примере. Дискретно-
непрерывное звено представлено экстраполятором нулевого порядка, на вход которого поступает
дискретный белый шум. Найдём спектральную плотность на выходе. В соответствии с (11.64) имеем*
где Гэо(.у,у) = — zpfr-
sv(\-ve 5/)
Непосредственным вычислением получаем:
W{s)W(p)
Sxx(s>P)={_eHs+p)T>
где W(s) = ——.
11.3. НЕПРЕРЫВНО-ДИСКРЕТНЫЕ СИСТЕМЫ С МНОГОКРАТНЫМ
СИНХРОННЫМ ПРЕРЫВАНИЕМ
Рассмотрим класс непрерывно-дискретных систем с несколькими
квантователями, которые замыкаются синхронно, но с разными периодами квантования. Такие
системы относятся к числу достаточно сложных для анализа [169].
Если требуется определить детерминированные реакции системы в дискретные
моменты времени, то такая задача может быть решена известными методами [63],
хотя расчетные формулы при этом существенно отличаются от известных
соотношений для дискретных систем с одним квантующим элементом. Более того, как будет
показано ниже, аппарат анализа названного класса систем приводит к зависимостям,
676 Анализ и статистическая динамика САУ. Часть I
принятым при расчете нестационарных систем, что является следствием уже
упоминавшегося факта нестационарной природы непрерывно-дискретных систем.
Введенные выше описания непрерывно-дискретных звеньев используются здесь
для получения явных аналитических соотношений, определяющих динамические
характеристики - бичастотные передаточные функции и связи «вход-выход» в
линейных системах с двумя и более синхронными прерываниями.
Строго говоря, требование синхронности прерывания не является обязательным.
В самом деле, рассмотрим соединение линейного непрерывного звена с ключами на
входе и выходе, замыкающимися с периодами Тх и Т2 (рис. 11.1).
У{пТх)
/
4s, zx)
х(пТ2)
Рис. 11 Л. Система с разными периодами квантования
Обозначив через Гк (z2,s4) передаточную функцию ключа на выходе звена, в
соответствии с общими правилами вычисления характеристик последовательного
соединения найдем бичастотную передаточную функцию, связывающую сигналы
у{пТх) и х(пТ2),
Г\(*2>*х)~ I rk(z2,s)T(s^)ds.
2л/ J
J с- /оо
Здесь Z-преобразование по переменной z\ определено относительно периода 7], а
по переменной z2 - относительно Т2. Для разомкнутых систем удается получить
явные соотношения всегда, если известны соответствующие описания динамических
звеньев рассматриваемых соединений. Трудности возникают при вычислениях
характеристик замкнутых систем, для чего в общем случае приходится решать
интегральные уравнения, которые для нестационарных звеньев общего вида не имеют
явных аналитических решений.
Ограничимся рассмотрением систем с синхронными кратными прерываниями, с
тем чтобы сопоставить рассматриваемый подход к описанию непрерывно-
дискретных систем с известными результатами [63, 173].
Типовыми для данного класса систем являются звенья изменения тактовой
частоты, которые можно рассматривать как линейные объекты с соответствующими
передаточными функциями.
Звено понижения такта представляет собой ключ, который замыкается с частотой
в к раз меньшей частоты входного сигнала и описывается весовой функцией
Mkn-m)-\\ k" = m' (11.65)
[О, кп Ф т.
Вычисляя по определению (10.36) бичастотную передаточную функцию,
непосредственными вычислениями найдем
Г(22,z,) = - jr X z-2nz^{nk-т\
z\ л=0т=0
ИЛИ
r(z2,2t) = ^—Ц-- (П.66)
z\ z2-zx
W) = TrA~—Y<n)dr\-
Глава 11. Анализ непрерывно-дискретных систем 677
Эта передаточная функция является ядром известной интегральной зависимости
вход-выход (см. например формулу (24) на стр. 552 в [63]). Заметим, что в данном
случае проявляется общее правило, когда для описания цепей более сложной
природы, чем простейшие стационарные дискретные системы, не удается ограничиться
простыми алгебраическими формулами Z-преобразования. Попытки преодолеть
возникающие затруднения приводят к соотношениям, типичным для описания
нестационарных линейных систем с помощью аппарата бичастотных передаточных
функций.
Соотношение вход-выход записывается в виде
Ф ь
2nJ7J\z-rf
Здесь У(г|) - изображение сигнала входа звена. Контур интегрирования разделяет
особенности функций {У(г|)/г|} и (г-У]к)~1. Поскольку для произвольного
воздействия полюсы У (г|) неизвестны, будем интегрировать с помощью вычетов в полюсах
г|от известной функции (z-r\ky]
I 1е
цт = zke к ,/и = 0,1,...,*-1.
Кратность каждого из полюсов равна единице, поэтому для вычетов можно вос-
льзоваться известной формулой
можно искать следующим образом
пользоваться известной формулой [63]. EomG(r|) = , то вычет в полюсе цт
б(л)
П=П,п
Re,G(n)= ^
Л Jr
В нашем случае Q(r\) = z-r\k, Р(ц) = zY(r\)/r\.
Суммируя вычеты и принимая во внимание направление обхода контура
интегрирования, получим известную формулу [63], которая выводится проще:
к-\ 1 -2яда
ад = 7ХНг*вУ*и). (н.67)
Применение последней формулы при к > 3 требует громоздких вычислений.
В практике расчета конкретных задач для нахождения изображения реакции проще
при известном выражении Y(r\) интегрировать с помощью вычетов в полюсах
У(Т1)/Л.
Звену с весовой функцией Д(л - km) отвечает ключ, который замыкается
синхронно с тактовыми моментами, по частоте в к раз большей. Ему соответствует
передаточная функция
1 zk
Г(22,2,) = j-2—. (11.68)
zm\-zx
Если на вход такого звена поступает сигнал с изображением Y (z), то для
изображения реакции справедливо соотношение
•Х(22) = -Ц-~^— r(z,)&, =Y(zk2). (11.69)
2nj J zx z\-zx
678 Анализ и статистическая динамика САУ. Часть I
Для анализа замкнутых систем потребуются характеристики соединений
непрерывно-дискретных звеньев и ключей, изменяющих частоту квантования. Вычислим
передаточную функцию типового последовательного соединения, состоящего из
ключа, замыкающегося с периодом Т2, и дискретно-непрерывной части. Последняя
состоит из экстраполятора, на вход которого поступает дискретный сигнал с
периодом квантования Th и стационарного непрерывного звена.
Соответствующие бичастотные передаточные функции упомянутых звеньев
описываются соотношениями
rK(z2,s) =—LJhr>
z2 - ё L 2
2,(1-V'r')
Через Wx (s) обозначена обычная передаточная функция стационарной
непрерывной части, включающей формирующее устройство экстраполятора и
непрерывное звено. Для последовательного соединения упомянутых звеньев имеем
2*jJj«Z\-eT* zx(\-zxesT>)
Чтобы упростить интегрирование, воспользуемся дискретным преобразованием
Лапласа, заменив z2 на eSlTl , и будем интегрировать с помощью вычетов в простых
полюсах
s = s2+j—т, т = 0,±1,±2,... .
Т2
Суммируя вычеты, для искомой передаточной функции соединения получим
следующие соотношение
r,(*2,*i)=-=r Z h~ ■ (1L7°)
\-z^e
В частности, при Т\ =Т2 = Т
\-zxe 2 zxl m=_w i2
Заметим, что сумма в правой части выражения с коэффициентом \/Т описывает
дискретное преобразование Лапласа W|(z2)| =^т, отвечающее непрерывной
функции с изображением Wx(s2)
^i(*) = 7 I Щ^+j^m), z2=es>r. (11.71)
' /И=-00 '
Возвращаясь к Z-преобразованию по переменной eSl1 , найдем
zx(z2-zx)
Из последнего, в частности, следует очевидное из физических соображений
заключение, что соединение экстраполятора и ключа дают в итоге тождественное со-
Глава 11. Анализ непрерывно-дискретных систем
679
единение. А именно, поскольку для запоминающего элемента экстраполятора
^(z) = 1,to
ri(*2,*,)= /2 .■
z{(z2-zx)
Что отвечает тождественному преобразованию.
Пусть теперь Т\ = кТъ т.е. ключ на выходе замыкается с частотой в к раз большей
частоты квантования входного воздействия. Тогда
1 °°
ri(52,z,) = —- Y,
„. , . 271 ч
Принимая во внимание (11.71), найдем
T(Z -л-1 W^
Несколько большие затруднения вызывает рассмотрение случая, когда Т2 = Л71!.
г-
(11.72)
Рис. 11.2. Система с разными периодами квантования
При этом (рис. 11.2) из (11.70) имеем
Г2(*2,*1)=— Ё
h
-Wi+./-T-«)
1-Z^ *
(11.73)
Воспользуемся формулой для изменения порядка суммирования
0 А:—1 оо
/и=-оо /=0 /=-оо
и перепишем выражение (11.73) в виде
Г2(*2,г,)~11
Zi/Cii
*71
21Л^ /=0/=-оо -isiTi+J^i+H))
\-zxe k
Принимая во внимание связь между непрерывным и дискретным
преобразованием Лапласа, найдем
k_xW2(es* + A)
г2(^) = -^Х к—.
\-zxe k
680
Анализ и статистическая динамика САУ. Часть I
Возвращаясь к Z-преобразованию по переменной z2 = eSlTl, получим искомую
передаточную функцию
!;¥<
l2V2>z\)-—L j 5Г-
\-z}z2ke k
(11.74)
При вычислении передаточных функций замкнутых систем приходится сначала
определять характеристики разомкнутых систем, составленных из звеньев,
определяемых формулами (11.72) и (11.74). Передаточную функцию последовательного
соединения таких звеньев запишем сначала в виде
Щ z\k ,-0. -т 7Т/ zl 1-V
\-zz2 e K
Интегрируя с помощью вычетов в простых полюсах
найдем явное выражение для Г p(z2i z{)
k-\ I Zil/ I ^
rp(z2iZ])= /2 jJ^W^zbeb'w^eb'). (11.75)
z,(z2 -zx) К /=0
Для получения передаточных функций замкнутых систем необходимо найти
явное выражение для обратного оператора [l + r/7(z2,z1)l . Непосредственно
проверяется, что бичастотная передаточная функция указанного обратного оператора
записывается в следующей форме
r(z2,z,) =
z\(?i-z\)
k-\
.2л.
J~r'
1 .2*.
7 J"7~l
1+tZ»2(^ " W\(?2* ' >
' /=0
-1
(11.76)
Найденные соотношения в совокупности с исходными описаниями звеньев
системы позволяют получить явные аналитические зависимости вход-выход между
любыми точками системы как для дискретных, так и непрерывных систем и как
следствие вычислять реакции при детерминированных и случайных воздействиях.
Пример 11.6. Проиллюстрируем применение методики на примере расчета системы, изображенной на
рис. 11.3.
*0=1(/) е(')ЗГ
У
{
1
S
\Jf\
и
0,5
лгч-1
x(t)
Рис 11.3. Система с двумя различными периодами квантования
В [169] эта система анализировалась методами пространства состояний. Используемые при этом
методы припасовывания не позволяют получить решения в аналитической форме и весьма громоздки.
Глава 11. Анализ непрерывно-дискретных систем
681
В принятых выше обозначениях элементы системы описываются соотношениями
Щ{*) =
Щ') =
1-е
-ЗлТ
-,ад =
1-е"
s2
,2
-,Щ*) =
2-Х
(l-rf)(z2+Z + l)
d = e~
25(5 + 1) > — 2z\z-d)
Передаточную функцию разомкнутой системы для указанных составляющих сначала запишем в виде
1 л Г(1-с/)(л2+л + 1)
Г„(*2.*|) = -
тМ
13^-
z{(z2 - z,) 2тг/ * 2Л3(Л " 0(Л " d){z2 - л3)"
Как отмечалось выше, эту передаточную функцию удобно вычислять не по явной формуле (11.75),
а интегрируя с помощью вычетов. Определяя вычеты в простых полюсах л = 1, Л = ^ и в полюсе л = О
кратности 3, найдем характеристику разомкнутой системы (Т = 1/3 с)
z2 0.129z2 +0.188
P{Z2'Zi)~ Zl(Z2 _Z|) z| -1.366z2 +0.366
и передаточную функцию замкнутой системы по ошибке Ге(г2>г1)
re(z2,zl)= *» ^-1.366z2+0.366
еКЪ V z2(r2-z,)z22-1.237z2 +0.554
Используя передаточную функцию, связывающую ошибку e(t) с координатой x(t),
r2iZ2'Zl) = 2s(s + mi*e-')
и найденную выше re(zz,z(), по формуле вычисления характеристик последовательного соединения
найдем искомую передаточную функцию, связывающую изображения X(s) и Y(z).
= l-g~v l-1.366g"v+0.366g"2t
5'Z 25(5 + l)z(l-zg-s)l-1.237e-v+0.554g-2v '
По формулам связи вход-выход найдем изображение непрерывной реакции системы x(s) на
единичное ступенчатое воздействие
1 l-1.366g-*+0.366e-2j
~ 25(5 + 1)1-1.237g"v + 0.554g"2i" '
Соответствующая этому изображению реакция системы показана на рис. 11.4.
*«
ю
4?
Рис. 11.4. Реакция системы на ступенчатое воздействие
Сравнения объемов вычислений для этого примера частных методов и методов пространства
состояний оказывается не в пользу последних.
682
Анализ и статистическая динамика САУ. Часть I
11.4. АНАЛИЗ НЕПРЕРЫВНО-ДИСКРЕТНЫХ СИСТЕМ
С ОСОБОЙ ТОЧКОЙ
Системы с особой точкой [148], в которых коэффициент при старшей
производной обращается в нуль, относятся к трудным для анализа существенно
нестационарным системам. Вместе с тем такими уравнениями описывается ряд прикладных
задач, в частности, линеаризованные модели систем самонаведения, что обусловило
пристальный интерес проектировщиков к исследованию таких моделей. Поскольку
нестационарный характер системы проявляется больше по мере сближения
движущихся объектов, применение стационарных моделей для исследования наиболее
интересных заключительных этапов движения оказывается недопустимым.
На рис. 11.5 показана типовая структурная схема систем указанного класса, где
через Wx(z) и W2(z) обозначены соответственно стационарные передаточные функции
дискретного фильтра и непрерывной части системы, Э - экстраполятор нулевого
порядка; N-п - переменный коэффициент (0 <п <N) дискретного типа, N = const,
характеризующая временной интервал конечного этапа движения.
е(0 Т
\
1
N-n
W\\Z)
W2(s)
x(t)
Рис. 11.5. Система с особой точкой
Процедура динамического расчета систем с особой точкой базируется на
возможности представления замкнутых нестационарных систем с переменным
коэффициентом, неограниченно возрастающим на конечном интервале времени, в виде
последовательного соединения стационарных звеньев, разделенных переменным
коэффициентом.
Изначально возможность такого представления была сформулирована для
непрерывных систем. Можно показать, что процедура приведения замкнутой
нестационарной системы к разомкнутой справедлива и для непрерывно-дискретных систем.
Более того, если объект управления задан системой линейных дифференциальных и
разностных уравнений, то все характеристики указанного представления
определяются в явной форме.
Рассмотрим сначала характеристики соединения двух дискретных звеньев,
составленного из переменного коэффициента (N - п) и стационарного динамического
звена с передаточной функцией W(z) в комплексной области.
N-n
W(z)
Рис. 11.6. Соединение звеньев
Переменный коэффициент Да?) описывается веровой функцией Д(л - m)f{ri),
которой в комплексной области отвечает передаточная функция
r/(z2,z1) = ~F(Z2
(11.77)
Глава 11. Анализ непрерывно-дискретных систем
683
Здесь через F(z) обозначено Z-преобразование дискретной функции J[n). Для
нашего случая Дл) = Nn, которому отвечает преобразование
F(z) = -
z-\ (z-1)2'
Вычисляя бичастотную передаточную функцию соединения, найдем
Г(22,21) = ^(22)[
Nz2 z2
■].
(11.78)
Воспользуемся теперь соотношением, связывающим сопряженную #(л, z) и
бичастотную F(z2, zx) передаточные функции,
271/ J
которое для рассматриваемого случая записывается в виде
H{n9z) = ±&W{T\z)[—-—{-^}r\ndy\.
2я/7 -Л —1 (л-1)2
Интегрируя вычетами в кратном полюсе г| = 1, перепишем соотношение в форме
дифференциального уравнения
dz
(11.79)
Полученному выражению отвечает структурная схема (рис. 11.7), которую можно
интерполировать как результат структурных преобразований, а именно, как
результат переноса переменного коэффициента через динамическое звено по ходу
движения сигнала.
0-^
Рис. 11.7. Эквивалентное соединение
Для каждого из соединений на рис. 11.6 и 11.7 найдем обратные, структурные
схемы которых показаны соответственно на рис. 11.8 и 11.9.
1
W(z)
1 ^
1
N-n '
Рис 11.8. Соединение, обратное 11.6
—Hg>
г
-z a
W(z)
1
N-n
ЩО
dz
1
W(z)
Рис. 11.9. Соединение, обратное 11.7
684
Анализ и статистическая динамика САУ. Часть I
На рис. 11.8 и 11.9 показаны разные представления одной и той же системы.
Откуда легко заключить, что система с обратной связью (рис. 11.9) эквивалентна
последовательному соединению стационарного дискретного звена и переменного коэффи-
1
циента .
N-n
Вернемся теперь к исходной системе и выполним очевидные преобразования
с тем, чтобы привести исходную структуру к рассмотренной выше (рис. 11.9).
Результат преобразования приведен на рис. 11.10.
1
N-n
Рис 11.10. Эквивалентное преобразование структурной схемы 11.5
Через W0(z) здесь обозначена дискретная передаточная функция стационарной
части разомкнутой системы
^0(z) = ^(z)Z
11-е"
г*Т
-W2(s)\.
Принимая во внимание установленную выше эквивалентность структур, для
исходной системы получим искомое представление в виде разомкнутой системы,
показанное на рис. 11.11.
1
W{z)
1
N-n
W{z) \-*VHz)
Рис 11.11. Разомкнутое представление замкнутой системы 11.5
Передаточные функции W(z) и W0(z) связаны дифференциальным уравнением в
области комплексной переменной z
^o(z) = ___L_^(£).
0V ' W{z) dz
Если объект управления задан системой дифференциальных и разностных
уравнений с постоянными коэффициентами, то W0(z) является дробно-рациональной
функцией, которую можно представить в виде
Дифференциальное уравнение при этом легко интегрируется и для искомой
передаточной функции W(z) после очевидных преобразований находится явное
представление
/=1
Глава 11. Анализ непрерывно-дискретных систем 685
Произвольная постоянная интегрирования, которая, строго говоря, должна
выбираться из краевых условий для функции W{z), без ущерба для расчета реакций в
системе может быть выбрана произвольно (например, равной 1), поскольку она входит
множителем в выражение для W(z), а разомкнутая структура наряду с функцией W(z)
содержит также и обратную 1/ W(z).
В заключение заметим, что если передаточная функция Wq{z) не содержит
неустойчивых и неминимально-фазовых звеньев, а непрерывная часть исходной системы
устойчива, то из найденного представления следует, что исходная замкнутая система
будет устойчива в смысле определения: ограниченный вход - ограниченный выход
на конечном интервале времени.
Пример 11.7. В качестве простого иллюстрирующего примера рассчитаем непрерывную реакцию
системы, изображенной на рис. 11.5, на единичное ступенчатое воздействие.
Пусть Wx(z) = 1, W2(s) = — .
Z 2-1 Z
Отсюда следует, что решение для W{z) записывается в виде
тУ ■
Принимая КТ = 1, непосредственными вычислениями по структурной схеме найдем сигнал на входе
экстраполятора G(z)
Учитывая связь вход-выход для сигналов G(z) и X(s\ для изображения непрерывной реакции X(s) имеем
w ч х Дх~е~*Т { z л *
X(S) = ^ s> z(l-ze-)(z-lH = ^ *
Другим словами, на интервале 0< = / < «Греакция x(t) является линейно возрастающей функцией.
11.5. СИСТЕМЫ С ПЕРИОДИЧЕСКОЙ
КОММУТАЦИЕЙ ПАРАМЕТРОВ
Рассмотрим класс линейных систем, параметры которых периодически
изменяются, оставаясь постоянными на интервалах между коммутацией параметров. К
такому классу относятся, в частности, импульсные системы с конечным временем
замыкания ключа. Известно достаточно большое количество работ, в которых
рассматривались такие системы. Во всех случаях, однако, анализ их предполагал громоздкие
вычисления. Поэтому не случайно в [169] отмечалось, что наиболее простым
способом анализа таких систем является непосредственное вычисление реакций путем
припасовывания с использованием матрицы перехода. К сожалению, и этот путь не
является исчерпывающим. С его помощью, равно как и другими известными
способами, не удается решать такие задачи, как определение реакций систем при
случайных воздействиях, для которых более предпочтительным является использование
системных характеристик типа передаточной функции.
Отмеченные трудности являются показательным примером дополнительных
проблем при попытках распространить методы описания стационарных систем на
объекты, которые по своей природе являются нестационарными.
Периодическая коммутация параметров объекта очевидно переводит эти объекты
в класс нестационарных, в рамках которого и целесообразно выполнять их анализ.
Вместе с тем частный характер нестационарности позволяет для данного класса
получить явное аналитическое выражение для системных характеристик, что для
нестационарных систем является скорее исключением, чем правилом.
686 Анализ и статистическая динамика САУ. Часть
Будем считать, что динамическая система, параметры которой могут изменяться
скачком, описывается уравнениями состояния
^ = A(r)X + U, Х(0) = Х0, (11.80
at
где матрица состояния А(/) в промежутках между коммутацией параметро]
принимает постоянные значения
А(/) = А,, kT + T^utKkT + T; (11.81
(* = 0, 1, 2, ... ; 1 = 1, 2, ... ,m-l).
Ясно, что при таком описании матрица А(/) удовлетворяет условию
А(*) = А(* + Г) (11.82
и динамическая система (11.80) является периодической. Известно [49], что дл:
невозмущенной системы
-~А(/)Х, Х(0) = Х0 (11.83
аХ
состояния системы в моменты времени, кратные интервалам периодичности, связань
соотношением
Х((к + 1)Т) = СХ(кГ)9 (11.84
где С - некоторая постоянная матрица, которую обычно называют дискретши
матрицей перехода [49]. Этот результат является следствием теории Флоке [49] дл:
периодических систем. Поскольку в промежутках между коммутацией параметрь
системы остаются постоянными, матрица С легко определяется припасовываниеь
решений на смежных отрезках интервала периодичности
X(T) = eAm(T~Tm-l)... eAl(T2~Tl)eAlTlX0. (11.85
Здесь через eA>t обозначены матрицы перехода стационарных систем с матрицам]
состояния А,.
Сравнивая (11.84) и (11.85) при X = 0, искомую матрицу С выразим через произ
ведение матриц перехода, вычисленных для моментов времени, в течение которы:
параметры системы остаются постоянными
С = вА«(г-г-Ч.. eA^-7i)eA'r'-. (11.86
Не ограничивая общности, лишь для упрощения изложения примем m = 2 . Инач!
говоря, изменение параметров на интервале периодичности происходит один раз
При этом матрица С определена произведением
С = A^W1 = eAlTleA^. (11.87
Заметим, что устойчивость системы (11.80) определяется характеристическим)
числами X, матрицы С, и если
|Х,|<1, / = 1, 2, ... ,л, (11.88
где л- размерность вектора состояния, то система является асимптотичесю
устойчивой [11].
Соотношения (11.84) и (11.87) устанавливают поведение системы (11.83) в мо
менты времени 0, Г, 27\ .... Для других моментов времени соответствующая мат
рица С в общем случае будет иной.
Глава 11. Анализ непрерывно-дискретных систем 687
В частности, свободное движения системы для моментов времени 7], 7J + Т,
7] + 2Т, .... определяется выражением
Х(кТ + Т + Т1) = С1Х(кТ + Т1)9
где С^е^е^2.
А Т AT* AT* AT*
В общем случае е ххе 2 2 *е 22е "и С^ * С. Поэтому при устойчивом
характере некоторой последовательности наблюдаемых значений можно было бы ожидать
скрытое раскачивание системы. Однако нетрудно показать [89], что
характеристические уравнения матриц Сх и С совпадают, вследствие чего условие (11.88) является
необходимым и достаточным для устойчивости системы (11.80) при любой
последовательности дискретных значений.
Дискретная матрица перехода С позволяет построить решение однородной
системы (11.83) для любого момента времени
ГеА,(/-*г)с*х kT<t<kT + Tx
X(/) = i ° . (Н.89)
[eA*t-kT-T*)eAiTiCkX0, kT + T}<t<kT + T
Из последнего видно, что фундаментальная матрица решений Ф(/) системы
(11.83) определяется выражениями:
\е
(t-kT)ck^ kT<t<kT + Tx
Ф(/)= ' ! . (И.90)
W l^'-^W'C*, kT + Tx<t<kT + T
По фундаментальной матрице найдем системную характеристику £(/,т)
^(/,т) = Ф(/)Ф-1(т), (11.91)
которую можно использовать для вычисления реакций системы при нулевых
и отличных от нуля начальных условиях. Реакции системы, получаемые при этом,
отвечают известной процедуре припасовывания решений и являются весьма
громоздкими. Более компактные выражения можно получить, если решать задачу
в комплексной области. При этом в качестве основной динамической характеристики
выступает бичастотная передаточная функция, определяемая соотношением (10.14).
При вычислении передаточных функций интегрирование по каждой переменной
/ и т выполняется по областям, указанным в (11.90), после чего производится
суммирование по целочисленным переменным. Выполняя указанные действия с учетом
(11.90) и (11.91), по формулам (10.14) получим явное выражение для искомой
передаточной функции
+[\V, (А,) We^C + W, (А2) e~sTi eAiT> w] W2 (A,) +
+W, (А,)ер7"'е-:гГ\УеАЛ\У2(А2)},
где
w = [i-e-src]'\.
688
Анализ и статистическая динамика САУ. Часть I
Щ(Ак) = [р1-Ак]-*[ерТ'е-^-1]>
I-W,(A4)
*>М-Ъ*-а>Г{^*-1
p-s
* = 1, 2.
Бичастотная передаточная функция позволяет вычислять изображения реакций
системы (11.80) при детерминированных и случайных воздействиях при нулевых и
отличных от нуля начальных условиях.
Пример 11.8. Проиллюстрируем применение предполагаемого подхода на простейшем примере
системы первого порядка (рис. 11.12), чтобы показать особенности выражений, определяющих истинные
реакции в системах указанного класса.
a(f)
1
Г
ait)
Г, Т
дл
2Г
Рис. 11.12. Система с конечным временем замыкания ключа
Однородная система с уравнением
dx _{-х, кТ<1<кТ + Ть
"^={ 0, kT + Tx<t<kT + T,
имеет решение х(кТ) = Скх0, где С = е~Тх.
Бичастотная передаточная функция, отвечающая весовой функции Л:(/,т)я(т),
п*> p)=-^w
-г.(е<'+'№_,)
1-e-V"
,-*•(,_,-<»■№)
(* + 1)(р + 1)
*(р+1) J+(,+l)(*-p)" (*+1)(р+1) [•
Реакцию на единичное ступенчатое воздействие найдем, интегрируя выражение
Результатом интегрирования является изображение реакции X(s)
U (\-e-T^T)(l-e-.'T)\s(s + l)
Глава 11. Анализ непрерывно-дискретных систем 689
11.6. ЗАМЕЧАНИЯ ОБ УСТОЙЧИВОСТИ
НЕПРЕРЫВНО-ДИСКРЕТНЫХ СИСТЕМ
Последовательное применение частотного метода для описания и анализа
непрерывно-дискретных в общем случае нестационарных систем предполагает
определение и использование бичастотных передаточных функций, которые в отличие от
привычных передаточных функций Лапласа для стационарных линейных систем к
настоящему моменту еще не получили широкого распространения в инженерной
практике. Сама конструкция передаточных функций, зависящих от двух комплексных
переменных, достаточно сложна, что, очевидно, является платой за возможность
описания достаточно сложных классов динамических систем.
Задачей данного раздела не является формулировка критериев устойчивости.
Здесь обсуждается несравненно более скромная задача. Целью последующего
изложения будет интерпретация классических понятий устойчивости по Ляпунову, когда
в качестве объекта исследования выступает бичастотная передаточная функция.
Рассмотрим сначала непрерывные объекты. Для скалярной весовой
функции к (/, т) воспользуемся оценкой
\k(t,x)\<Me^-x)e^\ ;>т.
Система является асимптотически устойчивой, если при любом т выполняется
условие
Упомянутое условие заведомо выполняется, если гх < О.
Определим двумерное преобразование Лапласа соотношением
^(j,p)=frfxJrfrt(M)e"j(l"VpT.
О т
Нетрудно заметить, что определенная здесь функция W(s,p) очевидным образом
связана с бичастотной передаточной функцией T(s,p):
]dx)dtk(t,T)e-ste{s-p)x =r(s,s-p).
О т
Другими словами, указанная связь определяется соотношением
W(s9p) = r(s9s-p).
Интеграл сходится, если Res>Ai, Re p > г2. Тогда функция W(s,p) является
заведомо аналитической всюду, где выполняются эти неравенства Re s > rx, Rep > r2.
На плоскости (Res, Rep) неравенства выделяют область, где функция W[s,p)
является заведомо аналитической (заштрихованная область на рис. 11.13).
Rep A
П Res
Рис. 11.13. Область аналитичности W(s,p)
45 Зак. 232
690 Анализ и статистическая динамика САУ. Часть I
Истинный вид области сходимости, расположенной в правом верхнем углу,
определяется особенностями функции W(s,p).
Нанося на плоскость (Res, Rep) все нарушения аналитичности W(s,p),
получим монотонно невозрастающую характеристику сходимости (рис. 11.14).
Res
V
X
V
\ —»- Rep
Рис. 11.14. Характеристика сходимости
Если она такова, что включает в себя точки, где Res <0, то выполняется
неравенство \k(t, т)| <A//l('~xV2X, где гх <0, что гарантирует асимптотическую
устойчивость.
Учитывая связь между W[s,p) и T(s,p), для оценки устойчивости
динамической системы, описываемой бичастотной передаточной функцией r(s,/?), следует
формально положить p = s-p и для полученной функции T(s,s-p) строить
характеристику сходимости.
/ ч W(s)
В стационарных системах T{s,p) = —^-^, и
s-p
T(s, s-P) = T(Si p)\p___p=W(s)±-.
Ясно, что особенности W[s) не зависят от Р , и, таким образом, приходим к хо
рошо известному результату: стационарная система, описываемая передаточно
функцией Лапласа W(s), устойчива, если все полюсы W(s) расположены в лево
полуплоскости.
Для весовой функции дискретной системы к(п, т) рассмотрим оценку
\к{щ m)\<Ma"-mbm, n>m, a>0, b>0.
Динамическая система с весовой функцией к(п, т) асимптотически устойчив
если для любого т а<\.
Определим двумерное Z-преобразование функции к(п9т) соотношением
W(z2,Z])=±±k(n, m)z}n-mVr.
т=0п=т
Глава 11. Анализ непрерывно-дискретных систем
691
Двумерная функция W(z2,zx) является аналитической всюду, где
|z2|>a, l^l>fc. Последние неравенства на плоскости (|z2|, |^|) выделяют правый
верхний угол (заштрихованная область на рис. 11.15).
Ь-
-► \z7
Рис. 11.15. Область аналитичности JPfojZi)
Система будет асимптотически устойчивой, если этот угол заходит в область, где
Ы<1-
Как и выше, вычисляя нарушение аналитичности для функции W(z2iz{), можно
построить характеристику сходимости, которая является невозрастающей функцией
(рис. 11.16). Если эта характеристика заходит в область, где |z2| < 1, то система
асимптотически устойчива.
hi
^
+
ч-Ы
1
Рис. 11.16. Характеристика сходимости
Переписав определение W[z2,zx) в виде
m=0n=m \Z\J
и сравнивая его с определением бичастотной передаточной функции дискретной
системы
т=0п=т
легко видеть, что W^^^ и r(z2,z1) связаны соотношением
W(z2,Zl) = zr(z2,z)\2t^
45*
692
Анализ и статистическая динамика САУ. Часть I
Для стационарной дискретной системы бичастотная передаточная функция
записывается в виде
Z2
T(z2,z1) = -
(*2-*l)
W(z2).
Тогда
W{z2,z^zT{z2,z%_±=W{z2)^-
У функции W(z2,zl) особенности W(z2) не зависят от z,, и, как следствие,
получаем привычное условие устойчивости: все корни характеристического уравнения
zk передаточной функции W(z) должны удовлетворять условию |^|<1.
Обратимся к рассмотрению дискретно-непрерывных систем. Пусть весовая
функция системы k{t,nT), которая является непрерывной по первому аргументу / и
дискретной по второму пТ , удовлетворяет неравенству
\k(t,nT)\<Mer(t~nT)a\ t>nT, a>0.
Система с такой весовой функцией будет асимптотически устойчива, если для
любого п
lim k(t,nT) = Q,
/->О0
что, очевидно, будет иметь место при г < 0.
Определим двумерное преобразование функции k{t,nT) соотношением
W{s,z) = j^\k{unT)e-s{t-nT)z-ndt.
п=0„т
Интеграл и сумма сходятся, если Res>r, |z|>a. Другими словами, функция
l¥(s,z) является асимптотической всюду, где -выполняются неравенства
Re s > r, \z\ > а . На плоскости (Res, |z|) эти условия выделяют область
(заштрихованную на рис. 11.17), где функция W[s,z) является аналитической. Более того
область сходимости определяется особенностями функции W[s,z). Невозрастающа*
характеристика сходимости может быть получена при нанесении на плоскость
нарушений аналитичности.
Re s
Рис. 11.17. Область аналитичности W{s, z)
Если область сходимости включает в себя точки, где Res < 0 , где г < 0, то сие
тема является асимптотически устойчивой.
Глава 11. Анализ непрерывно-дискретных систем 693
Сравнивая определения W(s,z) и r(s,z), установим связь между ними
W(s,z) = ± ]dtk{t,nT)e-« (esTz-*J=r(s, e'V1).
п=0пТ
Откуда искомая зависимость устанавливается соотношением
Итак, если известна бичастотная передаточная функция дискретно-непрерывной
в общем случае нестационарной системы T(s9z), то для оценки устойчивости
следует вместо z в выражении для T(s9z) положить esTz~l и по полученной функции
оценивать устойчивость.
В качестве принципиального примера рассмотрим устойчивость типовой
стационарной дискретно-непрерывной системы (рис. 11.18).
т
-*\iv(sj
*l
(')
П*)
r(s,z)
X(s)
Рис. 11Л8. Дискретно-непрерывная система
Здесь непрерывная часть системы, описываемая передаточной функцией Лапласа
W(s), включает в себя и формирующее устройство экстраполятора.
Бичастотная передаточная функция замкнутой системы определяется выражением
Переходя к W(s,z), найдем
/ ч W(s)0e(esT\
Таким образом, особенности W(s,z) no s и z независимы. Особенности по s
совпадают с особенностями функций W(s) и Фе (esl j, или, что то же, с
особенностями непрерывной разомкнутой системы W[s) и замкнутой дискретной системы
•.К).
Отсюда следует, что замкнутая дискретно-непрерывная система будет устойчива,
если:
• полюсы разомкнутой непрерывной системы лежат в левой полуплоскости (т.е.
Re^ <0);
• полюсы замкнутой системы удовлетворяют условию \eSfl < 1, т.е. Z -
характеристическое уравнение замкнутой системы имеет корни, по модулю не
превосходящие единицы |z,| < 1.
694
Анализ и статистическая динамика САУ. Часть I
ПРИЛОЖЕНИЕ!.
МНОГОМЕРНЫЕ ПЕРЕДАТОЧНЫЕ
ФУНКЦИИ И ЧАСТОТНЫЕ
ХАРАКТЕРИСТИКИ НЕЛИНЕЙНЫХ
СИСТЕМ, ОПИСЫВАЕМЫХ
ФУНКЦИОНАЛАМИ ВОЛЬТЕРРА
Центральными понятиями теории линейных САУ является передаточная функция
и соотношение, связывающее входной и выходной сигналы системы через
передаточную функцию (рис. П1.1)
X(s) = W(s)Y(s). (П1.1)
Y(s)
W(s)
x(t)
X(s)
Рис. П1.1. К иллюстрации понятия ПФ САУ
Понятие передаточной функции и соотношение (П1.1) можно обобщить на класс
нелинейных САУ, описываемых рядами Вольтерра.
Для рассмотрения задачи обобщения введем в рассмотрение многомерное
преобразование Лапласа [72, 123].
Пусть
/(М2>-Л) = 0 ПРИ '!>'2>-Л<0,
\f{tut2^tn)\<Me^^\
где М,<зх,...,<зп - некоторые константы.
Многомерное преобразование Лапласа функции /(*1,*2 >"•••> О определяется
выражением
^...jf(tl,...,tn)e-s>l>e-^...e-s-'-dt]dt2...dtn =
0 0 0
= Ln {/(/„...,tn)} = F(sus2i...,sn)9
(П1.2)
где s} =a + j(ul,...>sn =an +y'cow - комплексные числа, такие, что Rest >а/5 / = 1,и.
При этом условии интеграл равномерно сходится, в связи с чем изображение (П1.2)
имеет смысл.
Числа ouo2>->Gn называют абсциссами сходимости интеграла (П 1.2).
Обратное многомерное преобразование Лапласа имеет следующий вид
/('„■••>'„)=—Ч^ f - f F(sis2,..;Sn)e*...es"<"dsl...dsn. (Ш.З;
Приложение \. Многомерные ПФ и ЧХ нелинейных систем 695
Приведем свойства многомерного преобразования Лапласа.
Линейность. Рассмотрим выражение
/
/(М2>-"Л) = Х^И'1>'2>-..Л)> (П1.4)
v=\
где Xv - некоторые коэффициенты.'Применяя к обеим частям равенства (П1.4) п-
мерное преобразование Лапласа, получим
/
v=\
Смещение аргументов в области изображений. Рассмотрим изображение
F(s, la,,...,,. ±aj4-]/('>'-"''»K(A±ai)''-" ^"^Ч- <*„ =
О О
= }...}/(/„/2,..,/„) е^... е*а*'*е-*>... e^'dh... *„;
О О
отсюда следует
А,{/('|,'2,-.'л) етаЛ- e*a"''} = F(Sl±au...,sn±an).
Дифференцирование в области оригиналов. Это свойство выражается
зависимостью вида
&
'"К
^f(tb...,tn)\ = s?...s?F(Sl,...,sn),
где к - количество разных индексов /}; т\,тъ...,тк- количество одинаковых
индексов /*!,...,ik соответственно.
Интегрирование в области оригиналов. Для этого свойства можно записать
f'l *п 1
AiU-J/(Tiv"*T«)rfTi-rfT«r = F{sx,sl9...9sn).
[О 0 J 1 2 и
Дифференцирование в области изображений. Для этого свойства справедлива
зависимость
^l^LF(Si,s2,...,sn) = (-\y+ +'" ].'Ш... ^f(t,,...,tn)^... е-'-1* х...х
х Л,...ЛЯ =£„{ (-1)^"+'-/?...^/(/„...,/я)}.
Перемножение двух функций в области оригиналов. Положим, что
M^('|.".,*B)} = /;i(*i,*2.-,*B),
"М/г ('i»-»'n)} = F2 (s,,s2 ,...,*„)
и функции /j (5,,...,5„) и F2(su...,sn) имеют полюсы - точки. Тогда имеет место
соотношение (многомерная свертка в комплексной области)
Мл('1»~л)/2('1.~л)} =
(2^Г
С1-У°° ся-уоо
696 Анализ и статистическая динамика САУ. Часть I
Свертка во временной области. Это свойство играет важнейшую роль при
построении аппарата анализа и синтеза рассматриваемого класса нелинейных систем.
Сверткой двух функций f\(t\>—->tn) и fiifu—^n) называется функция
/(*!,...,/„), определяемая зависимостью вида
t\ i,
'I ln
/(^1э».,^0 = |.-|у;(т1^..,т^/2(/1-т1,...,/я-т/1)Л1...Ля. (П1.5)
о о
Справедлива формула
р. <* 1
[о о J
В [72, 123] рассмотрены особенности, возникающие при определении
изображения свертки двух функций с различными размерностями аргументов.
В [72, 123] подробно анализируются методы определения оригиналов по
изображениям.
Применим многомерное преобразование Лапласа к зависимости, определяющей
выходной сигнал «-го канала
хл(/) = |...|*и(т1,...,ти)^(/-т1)...^(/-ти)Л„Л2,...,Л||, (П1.6)
о о
записав (П1.6) в форме
^Л/1^2--^)=|4^Лт1--т«)>;(/1-"т1)--->;(^-т«)б/т1---^- (ш-7)
О О
Очевидно, справедливо соотношение
ио=*лм2>-..>'41=/2= =,я=/.
Воспользовавшись теоремой свертки, получим
Xn(s],...,sn) = fVn{sl,...,sn)Y(si)Y(s2)...Y{sn)>
где
00 00
О О
Отсюда, по аналогии с линейными системами, назовем отношение
Y(S])...Y(sn)
п-мерной передаточной функцией п-го канала системы.
Поскольку нелинейная система, описываемая функционалами Вольтерра, имеет
вид параллельного соединения подсистем 1-го, 2-го,..., п-ro порядков, то,
следовательно, ее можно характеризовать последовательностью передаточных функций
(рис. П 1.2)
Wx(sx),W2(sus2),^Wn{sus2^snY
где
Wx (s{) = Ц j/ч (ij)} - ПФ первого (линейного) канала,
Щ (51>52) = Ч. {^2 (Ti>T2)} ~ ПФ второго (квадратичного) канала,
;(*„...,*„) = J...J^(xt тя)е"-"х-... е-1-1-*/!, ... dxn =Цк(тХ9...,%И)}. (П1.8)
истемами, назовем отношение
= Wn(sx,...,sn) (П1.9)
Приложение 1. Многомерные ПФ и ЧХ нелинейных систем
697
Wn(sus2,,..,sn) = L{kn(T],...iTn)) - ПФ п-го канала.
Если в линейных системах изображение выхода имеет вид
X(s) = fV(s)Y(s),
то в нелинейных системах изображение выхода определяется формулой
X(si,s2,...,si) = fVl(sl)Y(si) + W2(s],s2)Y(si)Y(s2) + ...+
+Wi{su...,si)Y(sl)...Y(si).
(П1.10)
(шло
Цз)
W,(Si)
W2(su s2)
И^зОь s2, si)
Wi(SuS2,...,S,)
X(Sl,S2,--;S,)
Рис. П1.2. Структурная схема нелинейной системы
Если применить к (П 1.11) формулу обращения, то для выходного сигнала можно
записать зависимость
Если в классе линейных систем в задачах синтеза находится импульсная переходная
функция k{i) или передаточная функция W{s\ то в нелинейных системах искомыми
характеристиками являются многомерные импульсные переходные функции и
передаточные функции.
К указанным задачам можно отнести:
• задачу синтеза корректирующих устройств;
• задачу фильтрации по критерию минимума среднеквадратической ошибки
(получены системы многомерных интегральных уравнений, эквивалентные
уравнениям Винера - Хопфа для линейных систем);
• задачу идентификации и др.
Перейдем к определению частотных характеристик нелинейной системы. Полагая
в (П1.9) st = j(o j (|' = 1,л), получим частотную характеристику канала нелинейной
системы
^.(усо1,...,усо/)=^(51,...^/)|дч=7Ш|>> лш,в| . (П1.12)
Частотная характеристика представляет собой многомерную комплексную
функцию, которая при изменении частот со; от нуля до бесконечности описывает в
комплексном пространстве размерности 2/ некоторую поверхность. При / = 1 это
пространство переходит в хорошо известную комплексную плоскость, в которой
^(ycoj) характеризуется некоторой кривой [123]. Для этого случая имеют место
КЧХ, АЧХ, ФЧХ, ДЧХ и МЧХ.
44 Зак. 232
/-vncuiFi^ и ciaiHciичс^кал динамика \^>f\y . "lacib 1
Но уже при / = 2 приходится рассматривать характеристику Й^О'^^У^г) в
четырехмерном пространстве [123]. На рис. П1.3 показан качественный вид этой
частотной характеристики.
IlTlj, I1TI2
W2(0,jo>2)
Рис. П1.3. Частотная характеристика квадратичного канала системы
В таблице П1.1 приведены передаточные функции различных соединений звеньев
[123].
Таблица П1.1
п/п
1
2
3
У(
УК
0
А
Ч
/
Соед»
к
' И
—►
мнение н
^)
лг V1/
■
■
■
кг(т)
Wr{sh..
и
елин
и
w
.иных
и
)
—1
Т
X
к
т
систем
г
—
V
X
к
t
КАТ)
Х(Л
4.0 w
Передаточные функции соединений
it/ ( \
= fVl.(sl)fVr(s2)...Wr(sr)
=^(S])..w;(sr)
Г/f/ (а с \ Г/f/ /р_1_о _L. I p \v
l¥r(sl,...,sr)-Wl{sl+s2+... + sr)x
Приложение 1. Многомерные ПФ и ЧХ нелинейных систем
699
Продолжение табл. П1.1
АО
^ if—— — \
WASy Sr)
ki(i) -
x(t)
Wr{s,,...,sr) =
= Wx(sx +s2 +... + sr)x
xWr(sr)
m
и
\
-
vJ
z
40
x[^(^+1)-^(%,)]-.x
xh(^,-.b)-^(v2)]
y(0
*'(t)
w
w''
»ts,,...,sr)
^(5,,...,Jr) =
+ж,2(5,)...»;2(5,)
W{su...,sr+i) =
= l¥4(si+s2+... + sr+i)-
W2(s]+... + s2)iV](s])x
y(t\
(ti
(t,
t,:)
^..-.^)
40
w(*,,...,vr2)=
•W,. [sri+],...,s,.+,.2)
44*
/ии Анализ и статистическая динамика l,aу . часть i
ПРИЛОЖЕНИЕ 2. ЭЛЕМЕНТЫ ФУНКЦИОНАЛЬНОГО
АНАЛИЗА [83]
ЛИНЕЙНЫЕ НОРМИРОВАННЫЕ ПРОСТРАНСТВА
В курсе линейной алгебры введено понятие линейного пространства Линейным
пространством называется множество X элементов произвольной природы, на
котором введены две операции - умножения элементов х е X на действительные
числа ос, обозначаемая our, и сложения элементов х,уеХ, обозначаемаях+у,
причем эти операции удовлетворяют восьми условиям (аксиомам линейного
пространства):
1) для любых элементов х,уеХ справедливо равенствох+у = у+х;
2) для любых трех элементов x,y,ze X имеет место равенствоx+(y+z)=(x+y)+z;
3) в пространстве X существует нулевой элемент 0, для которого х+ О =х для
любого элемента хеХ;
4) для любого элемента хеХ в пространствеX существует противоположный
элемент - х, такой, что х+(- х) = 0 ;
5) для любого элемента хеХ и для любых а,$ eR имеет место равенство
а(рх) = (ар)*;
6) 1 • х = х для любого элемента х е Х\
7) для любого элемента хеХ и для любых а,$ eR справедливо равенство
(oc+P)jc= ocjc+Pjc;
8) для любых элементов х,уеХ и для любого ае R а(х + >>) = ах + ау.
Линейное пространство X называется нормированным, если каждому элементу
x€iX поставлено в соответствие некоторое неотрицательное число ЦхЦ,
называемое нормой элементах иудовлетворяющееусловиям:
1) ||jc|| = 0 тогда и только тогда, когда х = 0 ;
2) для любого х е X и для любого aeR
||<хх|| = |<х|||х||; (П2.1)
3) для любых элементов :с, у е X справедливо неравенство
M*IMI + lbi - , (П2-2>
Условие (П2.1) называется однородностью нормы, а неравенство'(П2.2) -
неравенством треугольника
Таким образом, нормированное пространство — это линейное пространство с
определенной на нем нормой. В одном и том же линейном пространстве норма может
быть введена различными способами. В этом случае все нормированные
пространства считаются различными, хотя как множества они совпадают.
Приведем примеры нормированных пространств, которые будут использоваться в
последующих параграфах.
Пространство R" упорядоченных групп из п действительных чисел
Приложение 2. Элементы функционального анализа 701
Линейность этого пространства очевидна. Что касается нормы, то на пространстве
R" она может быть введена различными способами. Наиболее естественными
являются следующие три
1Ы1о=тахЫ, (П2.3)
п
14=24 (П2.4)
Ы2= Xх' I • (П2'5)
Для всех трех формул (П2.3) - (П2.5) первые два условия определения нормы
очевидны, неравенство треугольника для первых двух норм вытекает из известного
свойства действительных чисел: модуль суммы двух чисел не превосходит суммы их
модулей. Для нормы (П2.5) это неравенство менее очевидно - оно вытекает из
неравенства Коши - Буняковского, известного из курса линейной алгебры.
Пространство R" с любой из трех введенных норм будем называть «-мерным
координатным пространством, а обозначать его, в зависимости от выбора нормы, будем
символами R£ , R" и R" . Отметим: хотя в трехмерном случае наиболее популярной
является норма (П2.5), называемая евклидовой метрикой, в «-мерных координатных
пространствах зачастую существенно удобнее рассматривать другие нормы,
например норму (П2.3).
Пространства R? , / = 0,1,2, будем трактовать так же, как пространства «-мерных
столбцов.
Пространство матриц фиксированного размера (тхп). Линейность этого
пространства известна из курса линейной алгебры. Норму в этом пространстве также
можно ввести различными способами. Наиболее естественно согласовывать ее с
выбранной нормой в пространстве R". Это связано с тем, что каждую матрицу размера
(тхп) можно рассматривать как линейный оператор из R" в Rm и норму матрицы
естественно определить таким образом, чтобы она совпадала с нормой
определяемого ей оператора
Если в пространствах R" в Л'" и в качестве норм выбрать одну из норм,
определенных в примере 1 (естественно, для пространства Rm суммирование или выбор
наибольшего элемента должны производиться от 1 до т), то для матрицы А с
элементами {ау} норму следует определить соответственно формулами
п
||A|lo = maxYL|, (П2.6)
т
|A||,=maxYL, , (П2.7)
( V/2
||а||2= max 5. , (П2.8)
\}*j*n )
где Sj - сингулярное число матрицы А, т.е. собственное значение матрицы В = АТА.
Доказательство справедливости всех условий определения нормы и согласования
введенных норм с соответствующими нормами (П2.3) - (П2.5) можно найти,
например, в [37].
702 Анализ и статистическая динамика САУ. Часть I
Множество всех функций *(/), непрерывных на отрезке [а,Ь]. Наиболее
естественной нормой на этом множестве является норма
||jc|| = max|jc(O|. (П2.9)
Условия 1) и 2) для этой метрики очевидны, условие 3) также легко проверяется.
Пространство непрерывных на отрезке [а,Ь] функций с нормой (П2.9) обозначается
символом С[а,Ь].
Пространство С2[а,Ь] функций, непрерывных на отрезке [я,6], но
рассматриваемое с квадратичной нормой
1Ы|= }*2(/)А . (П2.10)
Условия 1) и 2) очевидны, а справедливость неравенства треугольника выводится из
интегрального неравенства Коши - Буняковского.
Пространство L2[a,b] функций, интегрируемых с квадратом на отрезке [а,Ь]
в смысле Лебега. Норма в этом пространстве определяется той же формулой
(П2.10), но вместо изучаемого в курсе математического анализа интеграла Римана
(называемого обычно определенным интегралом) берется интеграл Лебега, а
элементами этого пространства считаются не отдельные функции, а совокупность
эквивалентных по Лебегу функций.
Подробное изложение меры Лебега и интеграла Лебега можно найти в [68]; здесь
лишь кратко укажем некоторые отличия интеграла Лебега от интеграла Римана.
Если интегрируемая функция непрерывна, то ее интегралы Римана и Лебега
совпадают. Если функция имеет конечное число точек разрыва первого рода или
бесконечное число отделимых друг от друга точек разрыва первого рода, то ее интеграл
Лебега совпадает с несобственным интегралом Римана. Поскольку встречающиеся
в настоящем учебном пособии функции исчерпываются указанными классами
функций, под интегралом Лебега можно понимать интеграл Римана, дополненный
понятием несобственного интеграла.
Более важно описать элементы пространства Лебега L2[a,b]. Две функции jc(/) и
y(t), определенные на отрезке [а, Ь], называются эквивалентными по Лебегу, если
множество точек отрезка, на которых они отличаются, имеет нулевую меру Лебега,
т.е. множество точек
M = {te[a,b]:x(t)*y(t)}
можно покрыть объединением интервалов сколь угодно малой суммарной длины.
Преимущество интеграла Лебега состоит в том, что существенно расширяется класс
интегрируемых функций.
Условия 2) и 3) определения нормы в пространствах Лебега устанавливаются тем
же способом, что и для пространства С2[а, Ь]. Условие 1) выполняется именно в силу
того, что под элементами пространства Лебега понимается класс эквивалентных
функций.
Весовые пространства Лебега 1р[я,б]. Функция р(/), определенная на отрезке
[а,Ь], называется весовой функцией, или весом, если она неотрицательна,
интегрируема по Лебегу на отрезке [а, Ь] и ее интеграл конечен и положителен.
Приложение 2. Элементы функционального анализа 703
ь
jp(t)dt>0.
а
Пространством Лебега /£[#,6] называется множество функций jc(/), определенных
на [а,Ь], для которых конечен интеграл
р(/)р(/)А
а
Норма в весовом пространстве Лебега 1р[я,б] определяется формулой [68]
1Ы|= J*2(/)p(f)A . (П2.11)
Отметим, что нормированные пространства, определенные в примерах 1 и 2,
являются конечномерными (их размерность соответственно п и тп), в то время как
пространства, рассмотренные в примерах 3-6, бесконечномерны.
В нормированных пространствах естественно вводится понятие расстояния
(метрики) между элементами: расстоянием между элементами jc, уеХ называется
величина
Р(*,;О=Ф-;И|. (П2-12)
Понятие расстояния позволяет перенести на нормированные пространства
основные понятия математического анализа, такие, как предел, сходимость, непрерывность
и т.п. Отметим, что эти понятия можно ввести и для более общих метрических
пространств [68].
Пусть X - некоторое нормированное пространство, Ь-окрестностью точки
х$еХ называется множество
иь(х0) = {хеХ:\\х-х0\\<д}.
Пусть {хп} - последовательность точек нормированного пространства X.
Точка х е X называется пределом бесконечной последовательности {хп}, если для
любого г >0 найдется N = УУ(е), такое, что для всех номеров п> N элементы хп
будут лежать в окрестности £/e(jc), т.е. будет выполняться неравенство
\хп -jc||<8.
Используя обозначение предела, сходимость последовательности {jcw} к точке хеХ
будем обозначать так:
\\тр(х,хп) = 0.
Л-»ОО
Если последовательность {хп} имеет некоторый предел хеХ, то она называется
сходящейся
Поскольку приведенное определение предела аналогично его определению из
курса математического анализа, все свойства предела в произвольных
математических пространствах устанавливаются аналогичным образом.
Выясним конкретный смысл сходимости в некоторых из метрических
пространств, введенных выше.
п-мерные координатные пространства R" ,/ = 0,1,2 . В этих пространствах
сходимость по метрике совпадает со сходимостью по координатам [68], т.е. хт->х тогда
и только тогда, когда для каждого / = 1,2,..., п будет
704 Анализ и статистическая динамика САУ. Часть I
Х,т->Х, При AW-»OO,
где через х? и jc, обозначены соответственно / -е координаты элементов хт и jc.
Пространство матриц фиксированного размера (т х п). В этих пространствах с
любой из введенных норм (П2.6) - (П2.8) сходимость по метрике совпадает со
сходимостью по соответствующим элементам [68].
Сходимость в пространствах С[а,Ь]. В этих пространствах сходимость
совпадает с равномерной сходимостью. Действительно, пусть некоторая последовательность
{xn(t)} элементов из С[а,Ь] сходится к элементу jc(/). Это означает, что для любого
s>0 найдется N = N(e), такое, что при n>N справедливо неравенство
max x(t)-xn(t)\ <s.
a<t<b W "W|
Однако последнее неравенство равносильно тому, что неравенство |лг(О - xn(f)\ < £
выполняется одновременно для всех точек te[a,b]. Но это означает, что
последовательность {*„(/)} сходится к x(t) равномерно.
Из приведенного рассуждения вытекает и обратное: если последовательность
{*„(/)} сходится к x(t) равномерно, то она сходится к x(f) и по метрике С[а,Ь].
Таким образом, сходимость в пространстве С[а,Ь] равносильна равномерной
сходимости. Поэтому часто метрика пространства С[а,Ь] называется равномерной.
Сходимость в пространствах С2[а,Ь] и L2[a,b]. Эта сходимость называется
среднеквадратичной сходимостью, или сходимостью в смысле среднеквадратичного
отклонения Она существенно слабее равномерной сходимости в следующем смысле:
если последовательность функций {xn(t)} из С[а,Ь] сходится в метрике этого
пространства (т.е. равномерно), то она будет сходиться и в смысле
среднеквадратичной метрики. Обратное же неверно.
Таким образом, сходящиеся в смысле среднеквадратичного отклонения
последовательности функций могут в некоторых точках отличаться очень сильно, вплоть до
бесконечно больших отклонений. В этом смысле для инженерной практики
равномерная сходимость существенно важнее и, при возможности, необходимо
оценивать сходимость именно в метрике пространства С[а,Ь]. Ввод же пространства
Лебега L2[a, b] связан с тем, что в этом пространстве многие результаты и
соотношения существенно упрощаются и устанавливать теоремы и получать оценки
скорости сходимости значительно проще.
В теории последовательностей действительных чисел важную роль играет
критерий Коти, состоящий в том, что последовательность сходится тогда и только
тогда, когда она фундаментальна Этот критерий верен и во многих других
пространствах, например в «-мерных координатных пространствах С[а,Ь], пространстве
Лебега L2[a,b]. Однако в произвольном нормированном пространстве критерий Коши
может не выполняться.
Последовательность точек {х„} метрического пространствах называется
фундаментальной, если она удовлетворяет критерию Коши: для любого s > 0 найдется
N = yV(s), такое, что для всех элементов последовательности с номерами п, m>N
справедливо неравенство р(хп,хт) <г. Легко видеть, что если последовательность
сходится, то она фундаментальна Но как уже отмечено, в некоторых метрических
пространствах можно указать фундаментальные последовательности, которые не
сходятся ни к одному элементу этого пространства Примером такого пространства
является пространство С*[а,Ь] [68].
Приложение 2. Элементы функционального анализа 705
Нормированное пространство X называется полным, если в нем любая
фундаментальная последовательность сходится к некоторому элементу X. Полные
нормированные пространства называются банаховыми пространствами В
дальнейшем все изложение будем вести для банаховых пространств.
Точка хеХ называется предельной точкой множества MczX, если любая ее
окрестность содержит бесконечное число точек множества М. Предельная точка
множества может не принадлежать ему. Операция присоединения к множеству М
всех его предельных точек называется операцией замыкания, а множество,
полученное в результате присоединения к множеству всех его предельных точек,
называется замыканием множества М и обозначается [М\.
Множество МеХ называется замкнутым, если оно содержит все свои
предельные точки, т.е. если [М] = М.
Пусть М- подмножество нормированного пространствах Множество М
называется всюду плотным в X, если его замыкание [М\ совпадает со всем
пространством X. Например, множество рациональных чисел плотно на числовой прямой.
Пространства, в которых имеется счетное всюду плотное множество,
называются сепарабельными. Отметим, что все введенные примеры нормированных
пространств являются сепарабельными [68]. Например, в С[а,Ь] в качестве счетного
всюду плотного множества можно взять совокупность всех алгебраических
многочленов с рациональными коэффициентами.
Пусть X - бесконечномерное банахово пространство. Последовательность
элементов {фьф2,...,Ф/7} •••} пространства^ называется базисом этого пространства, если
любой элемент хеХ можно представить, и притом единственным образом, в виде
суммы сходящегося в метрике X ряда
* = |>*Ф*. (П2.13)
Ы\
Сходимость ряда в пространстве X означает, что для любого е > 0 найдется N = yV(s),
такое, что при всех n>N будет
<г,
II *=i
Единственность представления (П2.13) означает, что
00
^c^=0«c,=0,/=l,2,....
ы\
Примеры конкретных базисов в пространствах С[а,Ь] и L2[a,b] рассматриваются
ниже. Здесь же отметим, что если бесконечномерное банахово пространство X
имеет базис, то оно сепарабельно. Действительно, как нетрудно видеть, счетным всюду
п
плотным множеством в X будет множество линейных комбинаций вида У^ф/ с ра-
ы
циональными коэффициентами rt. Таким образом, несепарабельные банаховы
пространства (например, пространство бесконечных ограниченных числовых
последовательностей т или пространство М ограниченных всюду на отрезке [а,Ь], за
исключением множества нулевой меры Лебега- см., например, [68]) не могут иметь базиса.
В последующих параграфах будут рассматриваться банаховы пространства, в
которых имеется и фиксирован некоторый базис. Такие пространства будем называть
банаховыми пространствами с базисом.
706 Анализ и статистическая динамика САУ. Часть I
Напомним, что если пространство конечномерно и размерность его равна п, то
базис в этом пространстве состоит ровно из п элементов. В бесконечномерных
банаховых пространствах базисы состоят из бесконечного (счетного) числа
элементов.
Множество LtzX называется линейным многообразием нормированного
пространствах, если линейные операции, применяемые к элементам L, не выводят за
пределыЬ, т.е. для любой пары элементов x,yeL их суммах+ yeL, а для любого xeL
и любого aeR будет axeL.
Линейное многообразие L называется линейным подпространством
нормированного пространствах, если оно замкнуто в метрикеX.
В дальнейшем будут рассматриваться конечномерные линейные многообразия и
подпространства Они будут обозначаться Ln, где индекс п - размерность
многообразия или подпространства
Компактные множества в нормированных пространствах. Множество М
нормированного пространствах называется предкомпактньщ если любая
последовательность элементов {хп} этого множества содержит подпоследовательность
{х„к}, сходящуюся к некоторому элементу xGlX. Очевидно, что если множество М не
ограничено, то оно не может быть предкомпактным. В конечномерных
пространствах понятия ограниченности и предкомпактности равносильны, но в
бесконечномерных пространствах далеко не каждое ограниченное множество является предком-
пактным.
Множество М нормированного пространства X называется компактным, или
компактом, если любая последовательность элементов {хп} этого множества
содержит подпоследовательность {*„*}, сходящуюся к некоторому элементу х, при-,
надлежащему множеству М.
Непосредственно из определений вытекает, что если множество М предкомпакг-
но, то его замыкание [М] является компактом, а для замкнутых множеств введенные
понятия совпадают.
Множество SczX называется г-сетью множества МаХ , если для любого хеМ
найдется точкаseeS, такая, что
р(х,хе) = \\х-хе\\<г.
Множество М называется вполне ограниченным в нормированном пространстве
X, если для любого 8 >0 в пространстве X найдется конечная г-сеть, т.е. г-сеть,
состоящая из конечного числа элементов. Таким образом, множество называется
вполне ограниченным, если все его элементы можно приблизить с любой
фиксированной точностью элементами из некоторого конечного множества.
Если нормированное пространство конечномерно, то понятие полной
ограниченности совпадает с обычным понятием ограниченности. Для бесконечномерных
пространств понятие полной ограниченности является существенно более сильным.
Хорошо известен следующий критерий предкомпактности в полных пространствах:
множество М банахова пространствах предкомпактно тогда и только тогда,
когда оно вполне ограничено.
В банаховых пространствах с базисом удобен следующий критерий предкомпакг-
ности [68]: множество М банахова пространства с базисом X предкомпактно
тогда и только тогда, когда множество М ограничено, и для любого s > 0 существует
номер N = УУ(е), такой, что для любого элемента хеМ остаток его разложения по
базису порядка п> N будет меньше е:
Приложение 2. Элементы функционального анализа 707
к=п+\ II
Для конкретных бесконечномерных метрических пространств известны удобные
критерии компактности. Приведем здесь критерий компактности в пространстве С[а,Ь]
- известную теорему Лрцела. Ее доказательство можно найти, например, в [68].
Для формулировки теоремы необходимо дать два определения.
Множество функций М, определенных на отрезке [а, Ь], называется равномерно
ограниченным, если существует число М> 0, такое, что \x{t)\ < М при tG [a,b] для
ecexx(t)eM.
Множество функций М, определенных на отрезке [а, Ь], называется
равностепенно непрерывным, если для любого s>0 существует число 5 = 5(s)>0, такое, что
|*('i)-*('2)<e|
для всех t\, (2^[а, b], таких, что \t} -t2\ ^ 5 и для ecexx(t)eM.
Теперь можно сформулировать теорему Арцела: множество функций MczC[a,b]
предкомпактно тогда и только тогда, когда оно равномерно ограничено и
равностепенно непрерывно.
Используя приведенный результат, легко установить, что компактным в
пространстве С[а,Ь] будет, например, множество М= {x(t)eC[a,b]: существует
xf (t)eC[a,b], и существуют постоянные Q >0,С2>0, такие, что |х(/, )| :£ Q,
\хЩ<С2, te[a,b]}.
Понятие компактности является очень важным, поскольку компактные множества
являются аналогами замкнутых ограниченных множеств в конечномерных
пространствах. Из курса математического анализа известно, что, например, функция,
непрерывная на замкнутом ограниченном множестве, ограничена, принимает свои наименьшее и
наибольшее значения, принимает все промежуточные значения между наименьшим и
наибольшим и т.п. Аналогичным свойством обладают и непрерывные операторы на
компактных множествах в бесконечномерных банаховых пространствах.
ЛИНЕЙНЫЕ ОПЕРАТОРЫ В НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
Пусть X и Y - два нормированных пространства Линейным оператором,
действующим из X в Y, называется отображениеу - Ах, х€.Х, yS У, удовлетворяющее
условиям
А(ах)=аАхппявсеххеХ,аеЯ, (П2.14)
А(х+у) =Ах+Аудля всехх^еХ (П2.15)
Из свойств (П2.14) и (П2.15) вытекает, что линейный оператор переводит любую
линейную комбинацию элементов пространства X в линейную комбинацию с
соответствующими коэффициентами их образов.
Множество всех элементов О[Л) с X, на которых определен оператор А,
называется областью определения оператора А. Для линейных операторов D(A)
область должна быть линейным многообразием, т.е. линейная комбинация любых
элементов из D(A) также должна лежать в D(A). В дальнейшем, если не будет
оговариваться особо, будем считать D(A) = X. Через R(A) будем обозначать множество
образов>>G Y при отображении А. Это множество называется множеством
значений оператора А.
708 Анализ и статистическая динамика САУ. Часть I
Если X -Y ,то говорят, что линейный оператор действует в пространстве X.
Линейный оператор А называется непрерывным в точке jc0 eD(/l), если для
каждого s >0 существует такое 5 = 8(е) > 0, что для всех х е D{A)r\Ub (х0)
выполнено неравенство
р(Ах,Ахо)=\\Ах-Ахо\\<г.
Заметим, что в последнем неравенстве используется метрика пространства Y, в то
время как окрестность точки jc берется в метрике пространствах Если оператор А
непрерывен во всех точках области определения D(A), то он называется
непрерывным.
Линейный оператор А, действующий из X в Y, называется ограниченным, если он
определен на всем X и каждое ограниченное множество пространствах переводит
в ограниченное множество пространства Y. Хорошо известно, что для линейных
операторов в банаховых пространствах (вообще говоря, необходимо предположить
еще выполнение первой аксиомы счетности, но останавливаться на этом не будем)
понятия непрерывности и ограниченности равносильны - линейный оператор А,
действующий из X в Y и определенный на всем пространстве X, непрерывен тогда и
только тогда, когда он ограничен.
Таким образом, в дальнейшем для линейных операторов будем предполагать
наличие одного из свойств (например, ограниченности), а второе свойство
(непрерывность) будет выполняться автоматически.
Определение ограниченности линейного оператора можно сформулировать и
иначе: линейный оператор А, действующий из X в Y, называется ограниченным, если
он определен на всем X и существует постоянная С > 0, такая, что для всех jceX
И|<С||4 ' (П2.16)
Наименьшее из неотрицательных чисел С, для которых неравенство (П2.16)
выполнено для всех хеХ, называется нормой оператора А и обозначается \\A\\. Заметим,
что обычно используется один и тот же символ |.|| как для норм в пространствахX и
Y, так и для нормы операторов, отображающих одно из этих пространств в другое.
Обычно к недоразумениям это не приводит и в книге также будет использоваться
этот единый символ.
Известно [68], что норма ограниченного линейного оператора может быть
вычислена по формуле
IUH = supl^. (П2.17)
Приведем примеры линейных ограниченных операторов в пространствах R" ,
С[а,Ь]. Здесь мы ограничимся несколькими простыми примерами операторов,
которые будут использоваться ниже.
1). Оказывается, что любой линейный оператор, действующий из пространства
R" с любой из норм (П2.3) - (П2.5) в пространство Rm, в котором также
можно выбрать любую из норм, можно представить в виде матрицы размера
(тхп). Все эти операторы при любом сочетании норм в координатных
пространствах будут ограниченными. Если же .в обоих пространствах Rn и Rm
выбрать однотипную норму, то норма оператора совпадет с соответствующей
(согласованной с нормами в пространствах столбцов) нормой матрицы из
(П2.6)-(П2.8).
Приложение 2. Элементы функционального анализа 709
2). Рассмотрим в пространстве С[а,Ь] оператор умножения на непрерывную
функцию a(t) eC[a,b] :U(a)x(t) = a(t)x(t). Этот оператор действует в
пространстве С[а,Ь] и ограничен. Очевидно, что
1Ж1=здИ')|=114 (П2-18)
3). Рассмотрим в пространстве С[а,Ь] оператор интегрирования
t
Px(t)=\x(x)dx.
а
Так как
Px(t)<j\x(xpx<(t-a)\\4,
а
то ЦрЦ < (6 —а). На функции, тождественно равной единице, неравенство
переходит в равенство. Следовательно,
И = (*>-*). (П2.19)
4). Рассмотрим теперь в пространстве С[а,Ь] оператор дифференцирования
Dx(t) = xr (/). Прежде всего отметим, что в отличие от операторов из
предыдущих примеров, этот оператор определен не на всем пространстве С[а,Ь]: его
областью определения является класс непрерывно дифференцируемых
функций С^]'[а9Ь]. Отсюда уже вытекает неограниченность оператора
дифференцирования в пространстве непрерывных функций. Неограниченность
оператора D можно показать и с помощью следующего простого примера Для
функций хп (/) = sin (л/) их нормы ограничены в совокупности: |дсЛ| < 1. Но для их
производных Dxn (t) = x'(/) = ncos{nt), начиная с некоторого ЛГ, период
колебаний будет меньше длины отрезка [а,Ь], следовательно, для n>N будет
||/)хп|| = п -» оо при п -» оо . Таким образом, оператор дифференцирования
является примером линейного, но неограниченного оператора в пространстве
С[а,Ь].
5). Пусть Хп - некоторое я-мерное подпространство пространства С[а,Ь].
Например, это может быть подпространство с базисом из степенных функций
{I,/,...,/""1}, из многочленов Чебышева {Г0(0, Tx(t\...Jn.\(i)} и т.п. Любой
линейный (не обязательно ограниченный) оператор Qn, отображающий
пространство С[а,Ь] на подпространство Хп , будем называть оператором
проектирования С[а,Ь] на Хп.
Пусть А и В - линейные операторы, отображающие нормированное пространство
X в нормированное пространство Y. Суммой операторов называется оператор
С - А+В, определенный на области О^А^глО^В) и действующий по правилу
Сх = Ах + Вх.
Легко видеть, что если операторы А и В линейны и ограничены, то и оператор
С =А+В также является линейным и ограниченным. Легко проверяется
справедливость следующего неравенства [68]
|Л + 4Ф||+И- (П2.20).
710 Анализ и статистическая динамика САУ. Часть I
Далее, для любого линейного оператора А и любого действительного числа X
можно определить оператор С = ХА, область определения которого совпадает с
областью определения оператора/* и для которого Сх = ХАх для всех xeD(A). Очевидно,
что если оператор Л линеен и ограничен, то теми же свойствами обладает и оператор
С = ХА, причем
II Ml = 1 * МИН.
Нетрудно видеть, что множество линейных ограниченных операторов, действующих
из нормированного пространствах в нормированное пространство Y, само
является линейным пространством Это пространство обозначается символом C(X,Y).
Менее очевидным является то, что линейное пространство C(X,Y) является
нормированным с нормой, равной норме оператора [68]. Более того, если пространство Y
является полным, то полным будет и C(X,Y), т.е.-пространство всех линейных
ограниченных операторов из нормированного пространства X в банахово
пространство Y само является банаховым пространством [68].
Пусть А - линейный оператор, отображающий нормированное пространство X в
нормированное пространство У, а В- линейный оператор, отображающий Yв
нормированное пространство Z. Произведением или композицией операторов А и В
называется оператор С = Во А , ставящий в соответствие элементу х из области D(A)czX
элемент
z = В(Ах)
из пространства Z Ясно, что при этом множество значений оператора/1 должно
принадлежать области определения оператора В: R(A)aD(B). Если Аи В - линейные
ограниченные операторы, то оператор. С = ВоА = ВА также линеен и ограничен в
соответствии с [68]
|5о4<||5|И|- (П2.21)
Оператор А, действующий из нормированного пространствах в нормированное
пространство Y, называется обратимым, если для любого у eR(A) уравнение
Ах = у
имеет единственное решение.
Если оператор А обратим, то каждому yeR(A) можно поставить в
соответствие единственный элемент xeD(A), являющийся его прообразом. Оператор,
осуществляющий это соответствие, называется обратным к оператору А и
обозначается А'1.
Приведем несколько важных теорем об обратных операторах [68].
1). Оператор А~х, обратный к линейному оператору А, таксисе линеен.
2). Если оператор А взаимно однозначно отображает банахово пространство X
на все банахово пространство Y, то обратный оператор А~] ограничен.
Этот результат называется теоремой Банаха об обратном операторе и имеет
большую область применения в инженерной практике.
3). Если оператор А является линейным и ограниченным оператором из банахова
пространствах на все банахово пространство Y и имеет ограниченный
обратный оператор А~1, то для любого оператора АА е С(Х, Y),
удовлетворяющего условию
1И1<|Лр (П2-22)
Приложение 2. Элементы функционального анализа 711
оператор В = А+АА также непрерывно обратим, и
П
HMiluil
\В-Х\\< ,' „," ,„■ (П2.23)
Этот результат, доказательство которого можно найти в [68], будем называть
теоремой об обратимости возмущенного оператора
Линейный оператор А, действующий из нормированного пространствах в
нормированное пространство Y, называется компактным, если он определен на всем X
и каждое ограниченное множество пространства X переводит в предкомпактное
множество пространства Y.
Так как предкомпактные множества всегда ограничены, то любой компактный
оператор ограничен. Обратное в бесконечномерных пространствах неверно.
Простейшим примером ограниченного, но некомпактного оператора в любом
бесконечномерном нормированном пространстве является тождественный оператор I: Ix = x
для всех хеХ. Это вытекает из известного результата о некомпактности единичного
шара В = {jcgX:||jc||<1} в бесконечномерных нормированных пространствах [68].
Таким образом, класс компактных операторов, отображающихX в Y, существенно
уже класса C(X,Y). Но выделение класса компактных операторов играет
исключительно важную роль, особенно в прикладных вопросах, поскольку компактные
операторы обладают рядом важных и удобных свойств, которых лишены произвольные
ограниченные операторы.
Отметим следующие свойства компактных операторов.
1). Если А - компактный оператор, а В - ограниченный оператор, действующие
в банаховом пространстве X, то операторы А° В и Во А компактны [68].
2). Если {Ап} - последовательность компактных операторов в банаховом
пространстве X, сходящаяся по норме к некоторому оператору А, т.е.
lim \А - АА - О, то оператор А также компактен [68].
Линейный ограниченный оператор, отображающий бесконечномерное
нормированное пространство X в конечномерное нормированное пространство Yn,
называется конечномерным. Так как в конечномерном пространстве любое ограниченное
множество предкомпактно, конечномерные операторы являются компактными.
Конечномерные операторы являются исключительно удобными, поскольку к
уравнениям в конечномерных пространствах можно эффективно применять
численные методы с использованием вычислительной техники. Таким образом,
конечномерные операторы образуют важный подкласс в множестве компактных
операторов.
Важным свойством компактных операторов в банаховых пространствах с базисом
является их близость к конечномерным, которую можно выразить следующей теоремой.
Пусть А - компактный оператор, отобраоюающий банахово пространство с
базисом X в себя. Тогда для любого s > О оператор А можно представить в виде
суммы операторов А = А^ + А2, где операторА\ конечномерен, а оператор А2 имеет
малую норму. 1\А2\1 < s.
Иначе говоря, компактные операторы в банаховых пространствах с базисом
«почти» конечномерны.
Линейные ограниченные операторы, отображающие произвольное
нормированное пространство X на действительную ось R, называются линейными
функционалами. Естественно, на линейные функционалы переносятся, причем с упрощением,
все свойства, изложенные для ограниченных линейных и компактных операторов.
712 Анализ и статистическая динамика САУ. Часть I
ГИЛЬБЕРТОВО ПРОСТРАНСТВО И ОРТОГОНАЛЬНЫЕ БАЗИСЫ
Линейное пространство X называется евклидовым, если на этом пространстве
определено скалярное произведение - на каждой паре элементов хуеХ определена
действительная функция (лг^у), удовлетворяющая следующим свойствам:
1). для любого элемента хеХ справедливо неравенство (jc, jc)>0, причем (х, х)=0
только при jc = 0 ;
2). для любой пары элементов (х,у) = (у,jc);
3). для любых трех элементов x,y,z e X справедливо равенство
(x + y9z) = (x,z)+(y,z);
4). для любой пары элементов хуеХ и любого действительного числа а имеет
место равенство (ах,у) = oc(jcj>).
Любое евклидово пространство является нормированным пространством с
нормой
\\4=уК^)' (П2-24)
Норма (П2.24) называется согласованной со скалярным произведением Таким
образом, евклидовы пространства образуют подмножество во множестве всех
нормированных пространств.
В любом евклидовом пространстве выполняется уже упомянутое неравенство
Коши - Буняковского
1МФ1ИМ1- (П2-25)
Далее, в евклидовых пространствах вводится понятие угла между элементами. Если
через у обозначить угол между элементами jc и у евклидова пространства X, то
полагают
М
C0SY=ihnnr
ИИ
Элементы jc и у называются ортогональными, если (jc,j>) = О- Система элементов
{хп} евклидова пространствах называется ортогональной, если ортогональны
любые пары элементов этой системы. Ортогональная система элементов {хп}
евклидова пространства X называется ортонормированноц или, сокращенно, ОНС, если
нормы всех ее элементов равны единице. Таким образом, для элементов ОНС {ф„}
справедливы соотношения
/ ч f 1, если / = у,
(Ф''ФЛ = 1<),если;*у.
Хорошо известен процесс ортогонализациц который с помощью линейных
преобразований элементов произвольной счетной системы превращает ее в ОНС [68].
Полное бесконечномерное сепарабельное евклидово пространство называется
гильбертовым пространством и обозначается обычно символом Я. В гильбертовом
пространстве всегда имеется базис [68], причем, используя процесс ортогонализации,
этот базис можно превратить в ортонормированный
Заметим, что любой ортонормщюванный базис является и ОНС, но не всякая
ОНС образует базис в пространстве Я- для этого нужна еще и замкнутость системы.
Пусть Н- гильбертово пространство, а {ф„} - ортонормированный базис (в
дальнейшем будем обозначать его аббревиатурой ОНБ). Разлагать элементы пространства
Н по ОНБ можно различными способами. Наиболее популярный метод - разложение
Приложение 2. Элементы функционального анализа 713
в ряды Фурье. Коэффициентами Фурье элемента хеН по ОНС {ф„} называются
коэффициенты
с*=(*,ф,),*=1,2,..., (П2.26)
а рядом Фурье - выражение
|>*Ф*. (П2.27)
ОНС {ф„} называется полной в пространстве Н, если в Н отсутствуют
элементы, за исключением нулевого, ортогональные всем элементам ОНС. Если ОНС
полна, то различные элементы Н имеют различные ряды Фурье.
ОНС {фя} называется замкнутой в пространстве Н, если любой элемент хеН
можно с любой точностью приблизить частичными суммами его ряда Фурье. Это
условие равносильно тому, что для любого элемента хеН для коэффициентов
ск = (х,ук) выполняется равенство Ларсеваля
2>НМ|- (П2.28)
Аг=1
Известно [68], что в гильбертовых пространствах понятия полноты и замкнутости
равносильны.
Если ОНС полна (замкнута) в пространстве Н, то она образует ОНБ в этом
пространстве, причем коэффициентами разложения можно брать коэффициенты Фурье.
Среди приведенных выше примеров нормированных пространств евклидовыми
являются пространства Щ со скалярным произведением
и пространства С2[а, Ь] со скалярным произведением
ъ
(x,y) = jx(t)y(t)dt. (П2.29)
а
Они не гильбертовы, поскольку первое из них конечномерно, а второе неполно.
Примером гильбертова пространства является пространство L2[a, b]. Скалярное
произведение в нем вводится по той же формуле (П2.29), но интеграл понимается в
смысле Лебега. Гильбертовыми являются и весовые пространства Лебега I?p [a, b].
В гильбертовом пространстве L2[a, b] можно рассмотреть те же операторы,
которые были введены в пространстве С[а, Ь].
1). Операторумножения на функцию a(t)eI?[a,b]:U(a)x(t)= a(t)x(t). U(a)
будем обозначать также через Ау(а). Этот оператор действует в пространстве
L2[a,b] и ограничен. Ограниченность оператора и оценка его нормы легко
получается с помощью неравенства Коши - Буняковского. В результате
устанавливается равенство, аналогичное (П2.18):
кжмнИ'Н =»4 (П2.30)
714 Анализ и статистическая динамика САУ. Часть I
2). В пространстве L2[a,b] можно рассматривать и оператор интегрирования,
поскольку каждая его функция, интегрируемая по Лебегу с квадратом, является
интегрируемой [68]
Для этого оператора легко устанавливается аналог формулы (П2.19)
KN*-«)1/2- (П2-31)
3). Оператор дифференцирования Adx(t) = Dx(t) = xr(t) также можно
рассматривать как оператор, действующий в пространстве L2[a,b]. В этом случае он
будет определен на классе дифференцируемых функций, производные которых
лежат в L2[a,b] (при определенном выборе норм это так называемые
пространства Соболева). Как и в пространстве С[а,Ь], в пространстве Лебега оператор
дифференцирования неограничен.
4). Пусть Х„ - некоторое «-мерное подпространство гильбертова пространства
L2[a,b]. В этом случае пространство Лебега можно разложить в сумму
L2[a,b] = Xn uJfj", где подпространство ^ортогонально (т.е. каждый
элемент Х^ ортогонален каждому элементу Хп). Оператор, отображающий
гильбертово пространство на его подпространство, называется оператором
ортогонального проектирования, или ортопроектором Существенное
отличие между операторами проектирования Qn в банаховых пространствах и
операторами ортогонального проектирования Р„ в гильбертовых пространствах
состоит в том, что ортопроекторыЛ, всегда ограничены и их нормы равны 1.
НЕКОТОРЫЕ ПОНЯТИЯ ТЕОРИИ ПРИБЛИЖЕНИЙ
Пусть Х- некоторое банахово пространство, М - некоторое его подмножество.
Элемент х е М называется элементом наилучшего приближения элемента хеХ,
если
£(*,M) = |jc-jc1= inf |U-5|.
v ' II II хеМ" "
Величина Е(х,М) называется наилучшим приближением элемента jc множеством М
Естественно, возникает вопрос о существовании элемента наилучшего
приближения. Оказывается [83], если множество М компактно, то элемент наилучшего
приближения существует (но может быть не единственным).
В дальнейшем в качестве аппроксимирующего множества будут рассматриваться
конечномерные подпространства U пространства X. Если такое подпространство
фиксировано, то величину наилучшего приближения элемента обозначают символом
Ei(x). Так как конечномерные подпространства нормированного пространства
являются компактными множествами, элементы наилучшего приближения в этом
случае всегда существуют.
Пусть Х- нормированное пространство, К - его компактное подмножество.
Поперечником Колмогорова компакта К в пространствеX называется величина
d{ (К, X) = inf sup Е(х, Ц), (П2.32)
Li xeK
где внешняя нижняя грань берется по всевозможным линейным подпространствам
размерности п. Смысл поперечника Колмогорова в том, что он указывает
наименьшую из возможных величин наилучших приближений компакта К линейными под-
Приложение 2. Элементы функционального анализа 715
пространствами фиксированной размерности п, т.е. является оценкой снизу точности
аппроксимации класса К линейным подпространством данной размерности.
Функция
Г(г;К,Х) = inf {Ык(К,Х) < е} (П2.33)
указывает минимально возможную размерность линейного подпространства,
позволяющую приблизить любой элемент компакта К с точностью не ниже е, т.е.
минимально возможное количество числовых параметров^ с помощью которого можно
приблизить любой элемент компакта с точностью s.
Пусть d^K^X), I - 1,2,... - поперечники Колмогорова класса К. Теоретически для
каждого натурального / существует метод аппроксимации, реализующий наилучшую
точность приближения dtfCJC). Такие алгоритмы называются алгоритмами
наилучшего приближения класса К. Однако доказательства существования элемента
наилучшего приближения часто неконструктивны и для многих широко используемых
компактных классов функций алгоритмы наилучшего приближения неизвестны.
Кроме того, оператор наилучшего приближения обычно нелинеен, что существенно
затрудняет его использование. Таким образом, необходим поиск удобных в
применении конструктивных алгоритмов приближения, близких к оптимальным.
Обычно поступают следующим образом: выбирают некоторый оператор
проектирования Qi на подпространство Ц, такой, что приближения элементами jc/ = Qpc
элементов хеК близки к наилучшим приближениям.
Проекционным алгоритмом приближения класса К называется совокупность
проекционных алгоритмов приближения размерности /: X={Qi}, согласованных либо
по вложению (например, при приближении суммами Фурье), либо по типу (при
приближении локальными сплайнами или интерполяционными многочленами). Грубо
говоря, для каждого / выбор соответствующего алгоритма QieX должен
осуществляться по одному и тому же правилу.
Класс всех проекционных алгоритмов приближения компакта КаХ будем
обозначать через Л = А(К, X). Для каждого алгоритма ^еЛ определим функцию
l(z\X) = M{k\s\iv\x-Qkx\x <s},
хеК
где {Qk}~ множество линейных операторов из алгоритма аппроксимации X. Величина
1(г;Х) указывает минимально возможную размерность линейного подпространства,
позволяющую приблизить любой элемент компакта К с точностью не ниже s с
помощью данного проекционного алгоритма
Если при s->0 будет 1(г;Х) = / (г;КуХ), проекционный алгоритм X аппроксимации
класса К называется оптимальным по размерности. Иначе говоря, оптимальным по
размерности является тот алгоритм, который для каждого s позволяет построить
приближение требуемой точности при использовании информации наименьшей
размерности.
Из отмеченной выше нереализуемости поперечников некоторых классов К следует
нереализуемость оптимальных по размерности алгоритмов приближения этих классов.
Это приводит к необходимости ввода понятий алгоритмов^ близких к оптимальным.
Проекционный алгоритм X называется оптимальным по порядку размерности, если
lim sup ,/(8;X>) < М < оо. (П2.34)
<~о / (г;К,Х)
В ряде работ используется понятие оптимальности по точности. Если Qn -
некоторый проекционный алгоритм, величина
e(Ql,K) = suv\x-Qlx\
хеК
716 Анализ и статистическая динамика САУ. Часть I
называется погрешностью алгоритма Qn на классе К. Минимизируя величину
e{QiJC) на множестве всевозможных алгоритмов фиксированной размерности /,
приходим к понятию алгоритма, оптимального по точности. Оптимальность по порядку
точности определяется аналогичным оптимальности по порядку размерности образом.
Из приведенных определений легко видеть, что любой оптимальный по порядку
точности алгоритм аппроксимации является оптимальным по порядку
размерности, и наоборот. Таким образом, можно использовать лишь одно из этих понятий.
В дальнейшем будут использоваться следующие принятые в теории приближений
обозначения. Будем писать
Л0 = 0(8(0),
если существует постоянная С > 0, такая, что
/(/)<Cg(/),/-»o>.
Если же найдутся две положительные постоянные С\ и С2, для которых
Clg(/)</(/)<C2g(/),/-+«>,
то говорят, что последовательности (Дл)} и {g(n)} имеют один порядок возрастания
(если они стремятся к бесконечности при /->оо) или убывания (если они стремятся к
нулю при /->0), и обозначают этот факт символом
Введем классы функций, определенных на отрезке S = [to,tj], которые будут
рассматриваться в последующих параграфах. В качестве основного функционального
пространства рассмотрим сначала пространство непрерывных функций C[t0 ,tj ].
Обозначим через Wr(M,S) класс функций, имеющих на отрезке [to,tf]
непрерывные производные до (г - \)-го порядка включительно и r-ю производную,
ограниченную постоянной М > О: /(r)(0 ^ M,te [/0 ,/у].
Классы W(M,S) являются компактами в пространстве C[to,tj] в силу теоремы
Арцела. Наряду с этими классами будут рассматриваться и неограниченные
(следовательно, и некомпактные) классы Wr(S). Классом W(S) называется объединение
классов Wr (M, S) при фиксированном г и всевозможных положительных А/.
Через H](M,S) будет обозначаться класс функций x(t) e C[t0,tj],
удовлетворяющих на отрезке [tOytf] условию Липшица с постоянной М > О
\х«х)-х«2)\*М\ь-ь\
для любых точек t\ и t2 из отрезка [tQ,tj]. В частности, классу Hl(M,S)
принадлежат функции, имеющие во всех точках отрезка [to,ty], за исключением некоторого
конечного множества точек, производные, ограниченные по модулю постоянной М
Через H{(S) будем обозначать соответствующий некомпактный класс функций.
Для г>1 вместо классов Wr(M,S) и W(S) также можно вводить классы
функций, имеющих непрерывные на [to,tj ] производные (г - 1)-го порядка, которые
принадлежат классу W]HM(S) или Нх (S). Эти классы будут обозначаться
Wr-]H\M,S) и W'-xH\S) соответственно.
Очевидно, что при всех г > 1
Приложение 2. Элементы функционального анализа 717
W(M,S) с Wr~xH\M,S), W(S) с Wr~xH\S).
Если рассматривать некомпактные классы Wr (S), то очевидны вложения
Wp(S)czWq(S), при p>q.
В этом случае будем говорить, что класс WP{S) имеет большую гладкость, чем
класс Wq(S). Если же p-q-\-\, будем говорить, что степень гладкости класса
WP(S) на единицу выше, чем класса Wq{S).
Наряду с классами Wr(M,S) будут рассматриваться классы 2тг-периодических
функций W{K(M) и соответствующие им некомпактные классы Щ%-
Через W2K(M) обозначается класс 2%-периодических функций, имеющих
производные до r-го порядка, причем производная x^r\t) ограничена постоянной М >0
на отрезке [-7с,тг] (следовательно, в силу периодичности функции, на всей числовой
прямой).
В ряде монографий проекционные методы изучались на существенно более
тонкой шкале пространств, но в данном учебнике (см. главу 8) упор сделан на
алгоритмическую реализацию проекционных методов, в связи с чем в вопросах
оценок точности и скорости сходимости было решено ограничиться наиболее
простыми пространствами.
718
Анализ и статистическая динамика САУ. Часть I
ПРИЛОЖЕНИЕ 3. ОРТОНОРМИРОВАННЫЕ БАЗИСЫ
Наименование
группы
1
2
3
4
5
6
Ортогональные
полиномы
Полиномы
Якоби
Полиномы
Лежандра
Полиномы
Чебышева
1-го рода
Полиномы
Чебышева
Н-го рода
Смещенные
ПО ПИ НОМЫ
Якоби
Смещенные
полиномы
Лежандра
Промежуток
определения
(-i;+i)
•
(-1;+1)
го п
1и> 1)
(0;1)
Весовая функция
Р(2) = 0-2)ах
х(1 + г)р,а>-1;
Р>-1
p(z) = l (а = р = 0)
VI -z1
(а = Р = ~)
1
p(z) = (l-z2)2
(а = Р = ~) t
a>-l;P>-l;5 = £Ji
Явное выражение,
определяющее
ортогональные полиномы
/и=0
хГИ + Р}(г-1)»-.(* + 1)"
я/2
/>n(r) = 2-"^(-l)mX
/и=0
х (2w-2iif)! -Л_2да
т\{п-т)\(п-2т)\
п/2
ТМ-" V(w"W"1)!x
r"U) 2 2-(я-2т)!т!
х(-1)ш-(2г)""2т,л = 1,2,...
Un(') Lj (n-2m)\m\ '
/и=0
x(2z)(w-OT)
TW^ + a + P + l)^
Z-rf^J(a + l)(a + 2)
■%^*'-i)l
/?i(o=5](-i)*4*x
,( (n + *)l
"(*')2(n-*)!
Приложение 3. Ортонормированные базисы
719
Рекуррентная формула
2(л + 1Хл + а + р + 1)(2л + а +
+P)-^iP)W = (2« + a + p+l)x
х[(2л + а + р)(2л + а + р + 2)г +
+а2 - р2 ]/>ia'p) (z) - 2(л + а) х
х(я + р)(2л + а + р + 2)Pw(aiP)(z)
(/i + l)/}f+1(z) = (2/i + l)r./}I(r)-
rw+1(z)-2z7;(z) + rw_1(z) = 0
t/n+1(z) = 2zt/w(z)-t/n_1(z)
(я+1)/5,+1Й)-(2я + 1)(25-1)х
*/>„(« +л-/},-lK) = 0
(
+1
-1
-1
r/7
+1
/■
+1
-1
+1
!«.
-1
+ 1
0
0
Соотношение орто
^«Л)(х)^«4»)(г)
гЛ, при w = w
0, при п*гп
2а+Р+1Г(« + ач
«!(2w + a + p + l)
Pn(z)Pm(z)dz = \ 2r
(z)Tm(z)p(z)dz =
1(z)Um(z)p(z)dz =
р^\урЬа3)&)
, Г(л + а + 1)Г(
«!(2« + а + р + 1)Г
при п = т,
0, при пФт
1зи
гональности
p(z)dz =
ie
■1)Г(я + р + 1)
Г(« + а + р + 1)
—, при п-т
+ 1
0 , при /1 ± т
0, при « Ф т
71 _
—, при п = тФ0
л, при п = т = 0
0, при л * т
— ,ПрИА?=Ш^0
0, при п = т = 0
Р1(ВД =
л + Р + 1)
(w + a + p + 1)'
, при w^w
+1 F
Формула для
коэффициентов Фурье
/(г) = ]Г <„/>„("%),
/7=0
+ 1
'я J
-1
с»
/(г) = 2]сяРя(г);
/7=0
+ 1
cn=^-jf(z)Pn(z)dz
-1
ОО
/(г) = 2]сяГя(г),
/7=0
+1
ся=—f/M^MpWA
оо
/7=0
+1
ся=—f/(z)^(z)p(z)A
/Ю = 2]ся/>я^)й);
п=0
1
rn J
0
ОО
/К) = ][/л/>я«);
п=0
1
ся=(2л + 1)|/(6У>я®^
0
720
Анализ и статистическая динамика САУ. Часть I
Наименование группы
7
8
Ортогональные
полиномы
Смещенные
полиномы
Чебышева
1-го рода
Смещенные
ПППМНПМК1
Чебышева
И-го рода
Промежуток
определения
(0;1)
(0;1)
Весовая функция
1 1
Р1© = £ 20-5) 2 >
2 + 1
1 1
Явное выражение,
определяющее
ортогональные полиномы
Т„£) = (-\)ппх
.у(-1)*2*(и + *-1)! кк
' £*1{п-к)\(2к-\)\\к\ **
к=0
ип£) = (-\)"х
V4-l)*2*(w + * + l)!
X2^i (2к + \/2)(п-к)\ 'С
ПОЛИНОМЫ ЛЕЖАНДРА, ЧЕБЫШЕВА 1-ГО РОДА
И ЧЕБЫШЕВА 11-ГО РОДА, ИСПОЛЬЗУЮЩИЕ ЗАМЕНУ
ПЕРЕМЕННОЙ % = е"", а>0; а - МАСШТАБНЫЙ
КОЭФФИЦИЕНТ
Наименование группы
9
10
11
Ортогональные
полиномы
Полиномы
Лежандра
Полиномы
Чебышева
1-го рода
Полиномы
Чебышева
П-го рода
Промежуток
определения
[О;*)
[0;оо)
[0;«)
Весовая функция
р(0=е-<"
at 1
p(t)=e~2(i-e-<")~2
iat 1
р(0 = е"~(1-е-°')2
Явное выражение,
определяющее
ортогональные полиномы
п
*=0
.с 0i + *)!
"(к\)2(п-к)\
п
Tn(t) = n^e-katx
Аг=О
(-\)к+п2к(п + к-\)\
{п-к)\{2к-\)\\к\
и(л-У Н)*+Я2* ..
U"{t)-2^(2k + \)(n-k)\
к=0
jc (и + * + 1)! -to
*!(2*-1)!!
Приложение 3. Ортонормированные базисы
721
Рекуррентная формула
Г„+1К) = 2(2£-1)Г„К)-
-Г„_,©,л = 1,2,....
t/w+1K) = 2(24-l)t/wK)-
-£/„-,©,« = 1,2,... •
Соотношение орто
+ 1
0
1
0
тональности
—, при п = т*0
я, при п = т = 0
0, при п*т
(я
—, при /i = m
[0, при п±т
Формула для
коэффициентов Фурье
оо
/й)=т+ЕсЛй);
1
0
оо
1
Л J
0
Рекуррентная формула
(n + \)Pn+](t)-(2n + \)x
x(\-2e'at)x
xP/1(0 + /iPw_1(0 = 0
Гл+1(/) = 2(2е-о/-1)Гл(0-
-^-1(0
t/w+1(0 = 2(2e-a/-l)t/w(/)-
-t//i-i(0
Соотнс
00
J'
0
QO
JTH(t)TM{
0
00
0
шение ортогональности
»n(t)Pm(t)e-atdt =
7~,при « = m
(2л + 1)а
0, при n^m
ч , ч , —э при п = т
t)p(t)dt = l2ay V
[о, при п*т
[0, при n^m
Формула для
коэффициентов Фурье
00
Д0=]Гс,Л(0;
/1=0
00
ся=в(2л + 1)|/(О/5,(/)в"вГЛ
0
оо
/i=l
оо
сл=^|/(О^(Ор(О^
0
оо
/1=0
00
Сп=т1/(оап(Ор(')Л
0
47 Зак. 232
722
Анализ и статистическая динамика САУ. Часть I
ПРИЛОЖЕНИЕ 4.
Стандартный интеграл имеет вид
1
ВЫЧИСЛЕНИЕ СТАНДАРТНОГО
ИНТЕГРАЛА
'••tJ
КО®)
-d(o.
(114.1)
2nig,(y©)g,(-ya>)
Полагается, что все корни многочлена gn(s) расположены в левой полуплоскости s.
Значение интеграла (П4.1) вычисляется по формуле
(-1ГЧ
/.-
2а0Мп
где Мп - определитель Гурвица для многочлена gn(s) ; при п = 6 он равен
0 0 0 0
Мб =
а. ап
а, я,
а. ал а, а.
0 ал
0
0
а5
0
0
**4
о
о
я,
5,
а5 а,
0 Z
а определитель Nn равен определителю Мл, в котором первый столбец заменен
коэффициентами многочлена hn(s); при п = 6 имеет место равенство
^
ЛЬ
«о
"5,
0 0
Si «о
0
0
5;
*3 ^б- а$
ь4 о о
65 О О
О 0 а.
Пусть w = 1, тогда g, (усо) = а0 (усо) + а,; Л, (усо) = 60;
/,=
(-1)2*с
2а,ах
JL-.
|2аоа,|'
для п = 2 можно записать
Тогда
йг (усо) = Ьо (усо)2 + 6,; g2 (усо) = а0 (усо)2 + а, (усо) + а2.
2ao(Sia2-5oa3)
/
У2
(-D3
2а0
*°
а.
«0
Приложение 4. Вычисление стандартного интеграла 723
Jl <h_
Л1
поскольку а3 = 0.
Аналогично
7 ^-а2Ьо+аоЬх-аоахЬ2/а3^
2aQ(a&-axa2)
_ bo(axaA +fl2a3)-aoflf3fc) + flog|62 + ао6з(аоа3 -a^la^
У4 ~ Л_ , 2.-2- --u. — ч >
где
2ао(аоа32+^2«4-^^2^з)
5 2а0М5'
M5 = а02а52 -2aQaxaAas -аоа2а3а5 +
+аоа32а4 + я,2а42 +а,а22а5 -а,а2а3а4; ,
N5=bo(-aoa4a5 +ахалг +а2гаъ -а2агаА) +
+афх(-а2аь+агаА) + аф2{аоа5-ахаА) +
+афг{-аоаг +ala2) + a0b4(-a0a]a5 +а0аг2 +ах2аА -аха2аъ)1ау
46 Зак. 232
724
Анализ и статистическая динамика САУ. Часть I
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
И А
Абсолютный минимум 570
Автокорреляционная функция 312
Автоматизированная система управления. .18
Автоматический регулятор 18
Автоматическая система
(см система автоматического управления)... 18
Автопилот 18
Алгебра структурных преобразований 32
- вариант описания систем импульсными
переходными функциями 55
- вариант описания систем передаточными
функциями 32
- вариант описания систем
спектрами 459
- вариант описания систем уравнениями
вынужденных колебаний 50
Алгоритм 572
Алгоритм наилучшего приближения 717
Алгоритмическое обеспечение 572
Амплитудно-частотная характеристика 63
Анализ качества управления 504
Астатическая система 108
Базовая система 717
Банахово пространство с базисом 701
Белый шум 318
- генератор 382
БИФ - блочно-импульсные функции 471
БПФ - быстрое преобразование Фурье 463
■ в »
Вектор ортогональный 699
Вектор состояния 168
Вероятностные характеристики
- белого шума 391
- полезного сигнала 391
- помехи 391
Весовая функция
-дискретной системы 626
- дискретно-непрерывной системы 634
- непрерывной системы 54
- непрерывно-дискретной системы 634
Вещественная частотная характеристика
замкнутой системы 61
Взаимная корреляционная функция
- нестационарных случайных функций 282
-нормированная 282
- случайных процессов 289
--в нестационарной системе 289
-- в стационарной системе 289
- стационарных случайных функций 289
-- нормированная 289
Взаимно простая факторизация матрицы
-правая 401
Воздействия 18
-возмущающие 18
-задающие 18
- единичное ступенчатое 49
-типовые 49
Возмущения случайные 335
Вольтерра интегральное уравнение .. . 473
Вольтерра интегральный оператор 473
Время запаздывания 85
Вход системы 18
Входной сигнал системы 18
Вынужденные колебания 49
Выход системы 18
Галеркина метод 450
Генерирование случайных сигналов . ...282, 381
Гильбертово пространство 699
Гипотеза эргодичности 282,312
Датчики случайных чисел 381
Двойные ряды Чебышева 462
Декада 61
Дельта-функция (см. единичная
импульсная функция) 54
Децибел 61
Динамика статистическая 271
Динамическая точность 105
Динамические характеристики
(см также уравнение динамики) 32
Динамические модели реальных систем 586
Дисперсия выходного сигнала 320
- при стационарном входном сигнале 318
Дисперсия 282
- нестационарной случайной функции .. 282
- случайного процесса 282
-- в нестационарной системе 292
-- в стационарной системе 292
аналитический способ вычисления .... 300
- стационарной случайной функции 292
- дискретного случайного сигнала 300
--непрерывного случайного сигнала 300
Дифференциальный закон распределения .. 292
-системы случайных величин 292
- случайной величины 294
- функций 292
Дифференциальные уравнения
- объекта регулирования 32
Дифференциатор 66
Доверительная вероятность 381
Доверительные пределы 381
Предметный указатель
■ е '
Единичная импульсная функция 54
■ з '
Задача
-анализа 93
-Винера 394
- идентификации системы 586
- об оптимальной системе 537
- оценки характеристик выходных
сигналов 312
- постановка задачи о корректирующих
фильтрах 437
-расчета 437
- синтеза систем 437
- слежения 554
- соответствия модели 587
- фильтрации по Колмогорову - Винеру 394
Задающее устройство 18
Закон больших чисел 381
Звено апериодическое (инерционное) 65
- второго порядка 65
- дифференцирующее (форсирующее) 65
-запаздывающее 66
-интегрирующее 67
- колебательное 68
- неустойчивое апериодическое 69
- первого порядка 65
-усилительное 65
-эквивалентное 65
Значение среднее квадратическое 312
Идеальная следящая система 18
Идентификация в узком смысле 586
Идентификация гарантированная 586
Идентифицируемость 586
Изображение 32
Изображение функции
- по Лапласу 32
Импульс мгновенный 54
Импульсная переходная матрица 171
Импульсная переходная функция
- непрерывной системы 54, 123
- параллельного соединения 54, 123
- последовательного соединения 54, 123
- системы с интегрирующей частью 123
- системы с сосредоточенными
параметрами 54
- способы вычисления 54
Интегральный закон распределения 282
Интегратор 65
Интервал частот 61
Информация о системе 18
Исполнительное устройство 18
■ « »
Качество САУ 105
Классификация динамических звеньев 65
46*
725_
Компактное множество, компакт 698
Компактный оператор 698
Конечномерный оператор 698
Корректирующее устройство
-параллельное 18
-последовательное 18
Коррелятор 282
Корреляционная функция выходного
сигнала 305
Корреляционная функция 300
- дискретного случайного сигнала 300
- непрерывного случайного сигнала 304
- нестационарных случайных функций 300
- нормированная 303
- случайных процессов 303
- в нестационарной системе 303
- - в стационарной системе 304
-свойства 305
- связь со спектральной плотностью 305
Корреляционные моменты 304
Косинусов система 698
Коэффициент демпфирования 65
Коэффициент статистической
линеаризации 352
- по случайной составляющей 352
- по средней составляющей 352
Коэффициенты Фурье 716
Критерий
- Раусса - Гурвица 98
- устойчивости 98
Критерий оптимальности
- байесов 587
- вероятностной эквивалентности функций. 587
-квадратичный 394
- минимума среднего квадрата ошибки 394
-Сильвестра 176
КУ - корректирующее устройство 18
Лежандра многочлены 459
Линеаризация статистическая 350
Линейное ортогональное преобразование... 698
Линейное подпространство 698
Линейный оператор 698
Логарифмическая амплитудно-частотная
характеристика (ЛАЧХ) 60
Логарифмические частотные
характеристики (ЛЧХ) 60
- анализ устойчивости 60
- динамических звеньев 60
- метод построения 60
-САУ 60
Локальные сплайны 698
м ^^
Математическая модель системы 585
Математическое ожидание входного
сигнала 312
Математическое ожидание выходного
сигнала 312
Математическое ожидание 312
- нестационарной случайной функции 313
726
Анализ и статистическая динамика САУ. Часть I
- случайного процесса
- в нестационарной системе
-- в стационарной системе
Матричная передаточная функция
Матрица состояния
- нестационарной системы
- стационарной системы
Матричный метод расчета свободных
колебаний
Матричный оператор
-дифференцирования
- интегрирования
- умножения
Метод уравнивающих операторов
Метод
- анализа точности нелинейных систем
- вычисления переходной матрицы
- ортогональных разложений
- переменных состояний
- переходных процессов
- статистической линеаризации
- статистических испытаний
(Монте-Карло)
- устойчивости
Метрика равномерная
Метрика среднеквадратичная
Мнимая частотная характеристика
МНК - метод наименьших квадратов
Модель динамической системы
Моделирование системы управления
.313
.313
.312
.145
.155
.156
.155
.171
.450
.457
.458
.110
.339
. 163
.479
. 163
.164
.351
.381
...98
.698
.698
...65
.698
.585
на ЭВМ
— полное
-частичное
Модель
- детерминированная
-статистическая ,
381
381
383
585
585
СВ.
Наилучшего приближения величина..
Некорректно поставленная задача
Нелинейность
.698
.592
- безынерционная
— многомерная
Неустойчивость процесса
Норма
Норма оператора
Нормированное пространство
НЭ - нелинейный элемент
1_0
184
184
95
698
698
698
185
1
Область устойчивости
- построение 98
-САУ 98
Обратная связь: 18
-в САУ 18
-отрицательная 18
Объект управления 18
Октава 60
ОНБ - ортонормированный базис 716
ОНС - ортонормированная система
элементов 716
Оператор 698
- аппроксимирующий 698
- дифференцирования 698
- интегрирования.
-компактный
-обратимый
-обратный
-ограниченный....
- проектирования.
-Теплица
- умножения
-уравнивающий
Оператор системы
-нестационарной
-обратный
-стационарной
Операторное уравнение 2-го рода
Операционная матрица
-дифференцирования
- интегрирования
- умножения
Определитель Гурвица
Оригинал
Ортогональная проекция
Отклонение регулируемой величины.
Отклонение среднее квадратическое..
Оценка точности
Оценка
-дисперсии
- математического ожидания
Ошибка идентификации
.698
.698
.695
.710
.711
.711
.705
.706
.708
.110
.698
...31
.700
.457
.458
.459
.460
...99
...31
.700
...18
.312
.105
.312
.313
- системы
-средняя квадратическая
II п
Параллельное соединение элементов
Параметры
— детерминированные
— системы
— случайные ...
Передаточная матрица
Передаточная функция
— методы вычисления ...
— нестационарной системы
-обобщенная непрерывной системы
— определение.
— ошибки ....
- параллельного соединения
- последовательного соединения
- системы с периодически
изменяющимися параметрами
- сопряженная непрерывной системы
— дискретной системы
— дискретно-непрерывной системы
— непрерывно-дискретной системы
— стационарной системы
— дискретной
— дискретно-непрерывной системы
— непрерывно-дискретной системы
— непрерывной
Переменные состояния
Перерегулирование
Переходная характеристика системы
Переходная функция
Переходные процессы . .
Плоскость фазовая
Показатели качества регулирования
Полезный сигнал
587
588
1|
31
18
18
31
645
П8
653
645
645
139
140
141
653
654
655
656
31
6?4
636
.642
31
155
49
..49
49
49
185
49
393
Предметный указатель -_
Помеха 393
Поперечник Колмогорова 710
Последовательное соединение элементов 32
Постоянная времени 65
Преобразование
-Лапласа 32
- двумерное 692
--формула обращения 693
-Фурье 694
--двумерное 696
--формула обращения 696
Преобразования структурные 31
Привод 18
Проблема динамической точности 105
Проблема формирующего фильтра 381
Проектирование САУ 580
Проекционная аппроксимация системы 451
Проекционная характеристика системы 485
Пространство 700
-Лебега 700
- Харди 701
Пространство непрерывных функций
ф,Т] 706
Пространство нормированное 708
- функциональное 710
Пространство функций £2[0,Т] 702
Процесс
- абсолютно устойчивый 191
- математическое описание 31
- неустойчивый 95
- неустановившийся 49
-расчет 448
- установившийся 49
- устойчивый 95
Распределенные системы управления 85
Расчет САУ (см. проектирование САУ) 580
Регулируемая величина 28
Регулятор 28
Риккати матричное уравнение 402
Ряд Фурье 702
Свободные колебания 49
Связь обратная 18
Сигнал 18
- входной 19
-выходной 19
- главной обратной связи 20
-детерминированный 21
- дискретный 22
- непрерывный 23
- ошибки 24
- полезный 25
-случайный 26
- сосредоточенный 24
-стохастический 25
Синтез корректирующего устройства
- параллельного 437
-последовательного 437
727_
- постановка задачи 437
Синтез САР при входных случайных
воздействиях 392
Система
- автоматического управления.. 18
-астатическая 107
-детерминированная 18
-динамическая 18
-дискретная 630
-линейная 18
- многомерная 21
-многоконтурная 22
-нелинейная 185
- дискретная стационарная 631
- непрерывная нестационарная 31
-нестационарная 110
-одномерная 110
- с отрицательной обратной связью 18
- с случайными параметрами 375
- сопряженная 110
-статистическая 107
- хорошо обусловленная 592
Система линейная
-детерминированная 26
- линейных дифференциальных уравнений 155
- непрерывная 155
--обратная 535
-многосвязная 26
- многосвязная с двумя или более входами... 26
-непрерывная 26
-нестационарная НО
- с сосредоточенными параметрами 535
-стационарная 26
Случайная функция 282
- множество возможных реализаций 282
- плотность распределения одномерная 282
- распределения одномерная 292
-реализация 282
-сечение 292
- стационарная 300
- стационарная в узком смысле 300
- стационарная в широком смысле 300
- эргодическая 300
Случайные воздействия 282
Случайные начальные условия 283
Случайные процессы 283
- в нестационарной системе 284
- в нестационарной системе - при одном
воздействии в виде белого шума 284
- в стационарной системе 285
--при нестационарных воздействиях 285
- при стационарных воздействиях 300
неустановившиеся 298
установившиеся 288
Случайные функции 282
- коррелированные (связанные) 282
- некоррелированные (несвязанные) 283
-нестационарные 283
- нормированные 285
- центрированные 285
Соединение
- параллельное 31
- последовательное 31
Соединение элементов с отрицательной
обратной связью 32
728
Анализ и статистическая динамика САУ. Часть I
Состояние системы 155
Спектр сигнала 305
Спектр сигнала комплексный 305
Спектральная плотность 306
- двумерная дискретного сигнала 308
- двумерная непрерывного сигнала 308
-дискретного стационарного сигнала 308
- непрерывного стационарного сигнала 307
- нормированная 306
- случайного процесса 307
- случайной функции 309
Сравнивающее устройство 18
Среднее квадратическое отклонение
(см. дисперсия) 292
Статическая характеристика 18
Статистическая динамика нелинейных
систем 336
Статистические характеристики белого
шума 305
Стационарность случайного процесса 305
Стационарный случайный процесс 305
Сумматор 27
Сходимость 698
Теория
- автоматического управления 18
- линейной фильтрации 391
- нелинейной фильтрации 428
Точность идентификации 589
Точность работы системы 105
Точность систем
-линейных 107,312
-нелинейных 339
Тригонометрическая система функций 716
Тригонометрический ряд Фурье 716
Уолша функции 467
Управляющий сигнал 34
Уравнение Вольтерра 1-го рода 478
Уравнение Винера- Хопфа 394
Уравнение вынужденных колебаний 49
Уравнение свободных колебаний 49
Уравнение сопряженное 110
Уравнение Фредгольма 1-го рода 475,698
Уравнение характеристическое 31
Уравнение
-динамики 18
-линеаризации 257
-Ляпунова 187
- объекта регулирования 18
-ошибки 105
Уравнения
- дифференциальные в форме Коши .. .155
Условие
- минимума среднего квадрата ошибки 394
-физической возможности 394
Условие физической осуществимости
системы 53
Установившийся режим в нелинейной
системе 204
Устойчивость вычислительная 592
II ф
Фазовая частотная характеристика
системы
Фазовая плоскость
Фильтр корректирующий
Фильтр корректирующий физически
реализуемый....
Фильтр Винера
Фильтр формирующий
Формирующее устройство
- нестационарное
— стационарное
Формула
-Байеса
1|
60
186
437
342
394
300
300
300
300
592
- минимального среднего квадрата ошибки 592
Фредгольма интегральное уравнение 698
Фредгольма оператор 698
Функциональная схема САУ 18
Функция
- автокорреляционная 292
- весовая . 53
-корреляционная 292
--белого шума 292
--взаимная 292
Z-преобразование 630
-двумерное 630
Характеристика многосвязных систем 64
Характеристика многосвязных систем 64
-частотная 65
Характеристика частотная амплитудная 60
Характеристика частотная амплитудно-
фазовая 60
Характеристика частотная вещественная 61
Характеристика частотная комплексная 61
Характеристика частотная мнимая 62
Характеристика частотная фазовая 63
Частота
-сопрягающая
-среза
Чебышбва многочлены (1-го) рода ....
Чувствительный элемент
ш
Шум белый
э
Экспериментальное определение
корреляционной функции
-спектральной плотности
— частотных характеристик
Элемент наилучшего приближения
Эргодичность
. ... 60
.. ..60
478
.. .18
1|
305
1|
301
302
302
.300
304
Список литературы к 1-й части 729
СПИСОК ЛИТЕРАТУРЫ К 1-Й ЧАСТИ
1. Автоматизированное проектирование систем автоматического управления /
Под ред. В.В. Солодовникова. - М.: Машиностроение, 1989. - 546 с.
2. Лйзерман МЛ., Гантмахер Ф.Р. Абсолютная устойчивость регулируемых
систем. - М.: АН СССР, 1963. - 450 с.
3. Александровский ИМ., Дейч AM. Методы определения динамических
характеристик нелинейных объектов (обзор) // Автоматика и телемеханика. 1968.
№ 1.-С. 167-188.
4. Амербаев ВМ. Некоторые применения ортогональных многочленов к
численному обращению интеграла Лапласа // Труды 2-й Республиканской конф.
по математике и механике. 1959. Алма-Ата: АН Каз ССР. - С. 26 - 38.
5. Амосов АЛ., Дубинский ЮЛ., Копченова А.Н. Вычислительные методы для
инженеров. - М.: Высш. школа, 1994. - 544 с.
6. Анализ и оптимальный синтез на ЭВМ систем управления / Под ред.
А.А. Воронова и И.А. Орурка. - М.: Наука, 1984. - 344 с.
7. Андреев Ю.Н. Управление конечномерными линейными объектами. - М.:
Наука, 1976.-424 с.
8. Астапов Ю.М., Медведев B.C. Статистическяя теория систем автоматического
регулирования и управления. - М.: Наука, 1982. - 304 с.
9. Ахиезер Н.И., Глазман ИМ. Теория линейных операторов в гильбертовом
пространстве. - М.: Наука, 1966. - 544 с.
10. Ахмед И., Рао К. Ортогональные преобразования при обработке цифровых
сигналов / Пер. с англ. - М.: Связь, 1980. - 248 с.
11. Банди Б. Методы оптимизации. Вводный курс. - М.: Радио и связь, 1988. -
352 с.
12. Баранов В.Н. Электрогидравлические следящие приводы вибрационных
машин. - М.: Машиностроение, 1988. - 264 с.
13. Баранов В.Н., Захаров Ю.Е. Электрические и гидравлические вибрационные
механизмы. Теория, расчет и конструкции. 2-е изд., перераб. и доп. - М.:
Машиностроение, 1977. - 328 с.
14. Барботин ЕЛ. Введение в теорию устойчивости. - М.: Наука, 1967. - 312 с.
15. Барбашин ЕЛ., Красовский Н.Н. Об устойчивости движения в целом // ДАН
СССР. 1952. Т.86. № 3. - С. 453 - 458.
16. Баркин А.И., Зеленцовский АЛ. Критерий абсолютной устойчивости
нелинейных систем управления // Автоматика и телемеханика. 1981. № 7. - С. 5 - 10.
17. Баркин А.И., Зеленцовский А.Л. Абсолютная устойчивость систем
регулирования с единственным нелинейным элементом // ДАН СССР. 1984. Т.276. №. 4. -
С. 809-812.
18. Баркин А.И., Зеленцовский АЛ., Пакшин П.В. Абсолютная устойчивость
детерминированных и стохастических систем управления. - М.: МАИ, 1992. -
425 с.
730 Анализ и статистическая динамика САУ. Часть I
19. Барковский В.К., Захаров В.Н., Шаталов А.С. Синтез линейных систем
автоматического управления с применением вычислительных машин. - М:
Машиностроение, 1967. -320 с.
20. Батков A.M. Обобщение метода формирующего фильтра на нестационарные
случайные процессы // Автоматика и телемеханика 1959. Т.20. № 8. - С. 1081
- 1094.
21. Березин И.С, Жидков НЛ. Методы вычислений. Т. I, II. - М.: Физматгиз, 1959.
T.I-464cT.il-620 с.
22. Бесекерский В.А., Ванюрихин Г.И., Герасимов А.Н. Расчет нестационарных
систем автоматического регулирования методом замороженных реакций //
Техническая кибернетика. 1966. № 2. - С. 27 - 38.
23. Бесекерский В А. Цифровые автоматические системы. - М.: Наука, 1976. -
576 с.
24. Бесекерский В А., Попов ЕЛ. Теория систем автоматического регулирования -
М.: Наука, 1975.-320 с.
25. Бесекерский В А., Попов ЕЛ. Теория систем автоматического регулирования. -
М.: Наука, 1975.-768 с.
26. Бирюков В.Ф., Реутов В.Ф. Метод построения решений уравнения Бутона для
класса исходных данных // Труды МВТУ. 1975. № 190. - С. 50 - 54.
27. Бицадзе А.В. Уравнения математической физики. - М.: Наука, 1976. - 296 с.
28. Большаков НА., Рахошщ B.C. Приложения ортогональных систем. 4.1 Изд.
АН СССР // Техническая кибернетика. 1977. № 5. - С. 143 - 147.
29. Бородин Ю.И., Ионнисиан А.Б. Частотный метод проектирования одного класса
систем с переменными параметрами // Электричество. 1967. № 1. - С. 43 - 54.
30. Бриккер И.Н. О частотном анализе линейных систем с переменными
параметрами // Автоматика и телемеханика. 1966. № 8. - С. 43 - 54.
31. Ван-Tpuc Г. Синтез оптимальных нелинейных систем управления. - М: Мир,
1964.-168 с.
32. Васильев Д.В., Чуич ВТ. Системы автоматического управления. - М.: Высш.
школа, 1967.-368 с.
33. Венгеров А.А., Щаренский В.А. Прикладные вопросы оптимальной линейной
фильтрации. - М.: Энергоиздат, 1982. - 192 с.
34. Вилепкин НЯ. О приближенном вычислении кратных интегралов / Сб.
«Вычислительная математика». - М.: Изд-во АН СССР, 1959. № 5. - С. 43 - 49.
35. Винер Н. Нелинейные задачи в теории случайных процессов: Пер. с англ. / Под
ред. Ю.Л. Климантовича. - М.: ИЛ, 1961. - 160 с.
36. Воеводин В.В. Вычислительные основы линейной алгебры. - М.: Наука, 1977.
- 304 с.
37. Воеводин В.В., Кузнецов ЮД. Матрицы и вычисления. - М.: Наука, 1984. -
320 с.
38. Волков И.К. Условия идентифицируемости математических моделей
эволюционных процессов по результатам дискретных косвенных измерений вектора
состояния // Известия РАН. Техническая кибернетика. 1994. № 6. - С. 65 - 72.
39. Воронов АА. Основы теории автоматического управления. Ч. 1, 2. - М.:
Энергия, 1965, 1966.-472 с, 336 с.
40. Вулих Б.З. Введение в функциональный анализ. - М.: Наука, 1967. - 415 с.
41. Ганпгмахер Ф.Р. Теория матриц. - М.: Наука, 1966. - 576 с.
Список литературы к 1-й части 731
42. Гайский В.А., Егупов НД., Корнюшин ЮЛ. Применение функций Уолша в
системах автоматизации научных исследований. - Киев: Наукова думка, 1993.
-212 с.
43. Гелиг АХ., Леонов ГА., Якубович В А. Устойчивость нелинейных систем с
неединственным состоянием равновесия. - М: Наука, 1978. - С. 45 - 53.
44. Гладкий В.Ф. Прочность, вибрация и надежность конструкции летательного
аппарата. - М: Наука, 1975. - 454 с.
45. Гноенский Л.С., Каменский ГА., Эльсголъц Л.Э. Математические основы
теории управляемых систем. - М.: Наука, 1969. - 512 с.
46. Голубое Б.И., Ефимов А.В., Скворцов В А. Ряды и преобразования Уолша. - М:
Наука, 1987.-344 с.
47. Горинштейн A.M. Численное решение задач радиотехники и техники связи на
ЭЦВМ. - М.: Связь, 1972. - 200 с.
48. ГронД. Методы идентификации систем.: Пер. с англ. / Под ред. Е.П. Кринец-
кого. - М.: Мир, 1979. - 302 с.
49. Д' Анжело Г. Линейные системы с переменными параметрами. Анализ и
синтез: Пер с англ. / Под ред. Н.Т. Кузовкова. - М.: Машиностроение, 1974. -
288 с.
50. Дейч AM. Методы идентификации динамических объектов / Пер. с англ. - М.:
Энергия, 1979. - 240 с.
51. Докури Э., Цыпкин ЯЗ. Теория дискретных автоматических систем (обзор). //
Автоматика и телемеханика. 1970. № 6. - С. 6 - 24.
52. Диткин В А., Прудников АЛ. Операционное исчисление. - М.: Высш. школа,
1966.-406 с.
53. Дмитриев АЛ., Егупов ИД., Шершеналиев Ж.Ш. Спектральные методы
анализа, синтеза и идентификации систем управления. - Фрунзе: Илим, 1986. -
,234 с.
54. Дмитриев АЛ., Егупов НД. Анализ и синтез нелинейных систем
автоматического регулирования при помощи рядов Вольтерра и ортогональных спектров.
- В кн.: Техническая кибернетика / Под ред. В.В. Солодовникова. Кн.З. 4.2. -
М.: Машиностроение, 1969. - С. 223 - 254.
55. Доступов Б.Г. Метод эквивалентных возмущений. - В кн.: Статистические
методы в проектировании нелинейных САУ / Под общ. ред. Е.П. Попова. - М.:
Машиностроение, 1970. - С. 97 - 123.
56. Егупов НД., Лапин СВ. Численный метод решения систем нелинейных диф- '
ференциальных уравнений с помощью разложения в ряды по системе Уолша //
Конструирование алгоритмов и решение задач математической физики. - М.:
ИПМ АН СССР. 1989. - С. 174 - 178.
57. Егупов НД., Лапин СВ. Анализ непрерывных нестационарных систем с
помощью разложений по блочно-импульсным функциям // Труды МГТУ. 1992.
№560.-С. 53-72.
58. Егупов НД., Лапин СВ. Идентификация нестационарных систем управления с
помощью разложений по блочно-импульсным функциям // Труды МГТУ.
1992. №558. -С. 55 -73.
59. Иванов В А., Медведев B.C., Чемоданов Б.К. Математические основы теории
автоматического регулирования: В 2-х т. - М.: Высш. школа, 1977. Т.1. - 518 с.
60. Иванов В.А., Ющенко А.С Теория дискретных систем автоматического
управления. - М.: Наука, 1983. - 336 с.
732 Анализ и статистическая динамика САУ. Часть I
61. Квакернаак X., Сиван Р. Линейные оптимальные системы управления. - М.:
Мир, 1977. -324 с.
62. Корн Г., Корн Т. Справочник по математике. - М: Наука, 1968. - 720 с.
63. Кузин Л.Т. Расчет и проектирование дискретных систем управления. - М.:
Машгиз, 1962.-684 с.
64. Казаков И.Е. Статистическая теория систем управления в пространстве
состояний. - М.: Наука, 1975. - 432 с.
65. Казаков И.Е. Статистические методы проектирования систем управления. -
М.: Машиностроение, 1969.-270 с.
вв. Казаков И.Е., Доступов Б.Г. Статистическая динамика нелинейных
автоматических систем. - М.: Физматгиз, 1962. - 332 с.
67. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. - 512 с.
68. Канторович Л.В., Акилов Г.П. Функциональный анализ. - М.: Наука, 1977. -
742 с.
69. Канторович Л.В., Крылов В.И. Приближенные методы высшего анализа. -
М.- Л.: ГИФМЛ, 1962. - 708 с.
70. Караванов В А. О некоторых возможностях применения частотного метода к
анализу линейных динамических систем с переменными параметрами //
Некоторые вопросы теории систем автоматического управления / Под ред. В.В. Со-
лодовникова. - М.: Оборонгиз, 1955. - С. 42 - 54.
71. Караванов В.А., Севрюков AT. Структурные преобразования линейных САР,
основанные на использовании обратных динамических систем // Известия
ВУЗов. - Приборостроение. 1979. T.XY. № 2. - С. 13 - 26.
72. Киселев О.Н., Попков Ю.С., Шмулъян Б.Л. Идентификация и оптимизация
нелинейных стохастических систем. - М.: Энергия, 1976. - 440 с.
73. Киселев О.Н., Попков Ю.С. Синтез нелинейных систем по статистическим
критериям. // Труды I симпозиума по статистическим методам в технической
кибернетике. Нелинейные и оптимальные системы. - М.: Наука, 1970. - С. 64 - 74.
74. Кочетков В.Т., Половко A.M., Пономарев В.М. Теория систем управления
и самонаведения ракет. - М.: Наука, 1964. - 536 с.
75. Крутько ПД. Обратные задачи динамики управляемых систем. Линейные
модели. - М.: Наука, 1987. - 304 с.
76. Крылов В.И. Приближенное вычисление интегралов. - М.: Наука, 1967. -
410 с.
77. • Крылов В.И., Сковля Н.С. Методы приближенного преобразования Фурье
и обращения преобразования Лапласа. - М.: Наука, 1974. - 224 с.
78. Кузовков Н.Т. Модальное управление и наблюдающие устройства. - М.:
Машиностроение, 1976. -184 с.
79. Кузовков Н.Т. Динамика систем автоматического управления. - М.:
Машиностроение, 1968. - 386 с.
80. Кузовков Н.Т., Караванов В.А., Салычев О.С. Непрерывные и дискретные
системы управления и методы идентификации. - М.: Машиностроение, 1978. -
222 с.
81. Купер Дж., Мангиллем К. Вероятностные методы анализа сигналов и систем.:
Пер. с англ. / Под ред. В.Т. Горячнова. - М.: Мир, 1989. - 376 с.
82. Лапин СВ. Оптимизация по емкости проекционных методов аппроксимации
систем. - М.: Изд-во МГТУ им. Н.Э. Баумана, 1995. - 224 с.
Список литературы к 1-й части 733_
83. Лапин СВ., Егупов НД. Теория матричных операторов и ее приложение к
задачам автоматического управления. - М: Изд-во МГТУ им. Н.Э. Баумана,
1996.-496 с.
84. Левин Б.Р. Теоретические основы статистической радиотехники. Кн. 2. - М.:
Сов. радио, 1968. - 504 с.
85. Левин Б.Р., Шварц В. Вероятностные модели и методы в системах связи и
управления. - М: Радио и связь, 1985. Вып. 24. - 312 с.
86. Лесин В.В., Лисовец ЮЛ. Основы методов оптимизации. - М: МАИ, 1995. -
340 с.
87. Лившиц НА., Пугачев В.Н. Вероятностный анализ систем автоматического
управления. Т.1 и 2. - М.: Сов. радио, 1963. Т.1 - 896. Т.2 - 484 с.
88. Мамонтова Л А., Пономарев ВА.У Попечителев ЕЛ. Матричные операторы
связи дискретных спектров Фурье и Уолша // Автометрия. 1977. № 1. С. 41 - 53.
89. Маркус М., Минк X. Обзор по теории матриц и матричных неравенств. - М.:
Наука, 1972.-176 с.
90. Мита Ц., Хара С, Кондо Р. Введение в цифровое управление. - М.: Мир, 1994.
-250 с.
91. Марчук Г.И., Агошков В.И. Введение в проекционно-сеточные методы. - М.:
Наука, 1981.-416 с.
92. Матвеев П.С., Синщин А.С. Определение динамических характеристик систем
из неидеальных элементов // Аналитические самонастраивающиеся системы
автоматического управления / Под ред. В.В. Солодовникова. - М.:
Машиностроение, 1965. - С. 43 - 57.
93. Матвеев П.С, Синщин А.С. Глебачев Ю.М. Оптимизация систем
автоматического управления с учетом нелинейностей, случайных параметров и помех //
Автоматическое управление и вычислительная техника / Под ред. В.В.
Солодовникова. - М.: Машиностроение, 1968. Вып 8. - С. 29 - 41.
94. Математические основы теории автоматического регулирования. Т.1 / Под
ред. Б.К. Чемоданова. - М.: Высш. школа, 1977. - 366 с.
95. Математические основы теории автоматического регулирования. Т.2. /Под
ред. Б.К. Чемоданова. - М.: Высш. школа, 1977. - 456 с.
96. Машинные методы расчета и проектирования систем электросвязи и
управления / Дмитриев А.Н., Егупов Н.Д., Шестопалов A.M., Моисеев Ю.Г. - М.:
Радио и связь, 1990. - 272 с.
97. МедичДж. Статистически оптимальные линейные оценки и управление.: Пер.
с англ. / Под ред. А.С. Шаталова. - М: Энергия, 1973. - 440 с.
98. Микеладзе Ш.Е. Приближенные формулы для кратных интегралов //
Сообщения Грузинской АН. 1952.Т.13.№4.-С. 18-26.
99. Михайлов ФА. Динамика нестационарных линейных систем. - М.: Наука,
1976.-368 с.
100. Михайлов Ф.А., Теряев ЕД., Булеков ВЛ. Динамика нестационарных линейных
систем. - М.: Наука, 1967. - 344 с.
101. Михайлов Ф.А., Теряев ЕД., Булеков ВЛ. Динамика непрерывных линейных
систем с детерминированными и случайными параметрами. - М: Наука, 1971.
-286 с.
102. Моисеев Н.Н., Иванилов ЮЛ., Столярова ЕМ. Методы оптимизации. - М.:
Наука, 1978.-420 с.
48 Зак. 232
734 Анализ и статистическая динамика САУ. Часть I
103. Мороз А.И. Курс теории систем. - М.: Высш. школа, 1987. - 380 с.
104. Наумов Б.Н., Цыпкин ЯЗ. Частотный критерий абсолютной устойчивости
процессов в нелинейных системах автоматического управления // Автоматика и
телемеханика. 1964. № 6. - С. 852 - 867.
105. Нелинейная оптимизация систем автоматического управления / Под общ. ред.
Е.П. Попова. - М: Машиностроение, 1970. - 308 с.
106. Основы автоматического управления. 3-е изд. / Под ред. B.C. Пугачева. - М:
Наука, 1974.-720 с.
107. Основы теории автоматического управления / Под ред. Н.Б. Судзиловского. -
М.: Машиностроение, 1985. - 512 с.
108. Первозванский Л.А. Курс теории автоматического управления. - М.: Наука,
1986. -616 с.
109. Первозванский Л.Л. Случайные процессы в нелинейных автоматических
системах. - М.: ГИФМЛ, 1962. - 352 с.
НО. Попков Ю.С. Достаточные характеристики нелинейных систем // Автоматика
и телемеханика. 1970. № 3. - С. 55 - 64.
111. Попов В.М. Об абсолютной устойчивости нелинейных систем автоматического
регулирования // Автоматика и телемеханика. 1961. № 8. - С. 961 - 979.
112. Попов Е.П. Теория линейных систем автоматического регулирования и
управления. - М.: Наука, 1978. - 720 с.
113. Попов Е.П. Теория нелинейных систем автоматического регулирования и
управления. - М.: Наука, 1979. - 256 с.
114. Пугачев B.C. Теория случайных функций и их применение в задачах
автоматического управления. - М.: Физматгиз, 1962. - 884 с.
115. Пугачев B.C. Лекции по функциональному анализу. - М.: Изд-во МАИ, 1996. -
744 с.
116. Пугачев B.C., Казаков И.Е., Евланов Л.Г. Основы статистической теории
автоматических систем. - М.: Машиностроение, 1974. - 560 с.
117. Пупков К А. Метод исследования точности существенно нелинейных систем
автоматического управления при помощи эквивалентной передаточной
функции // Автоматика и телемеханика. 1960. Т.21. № 2. - С. 31 - 38.
118. Пупков К А. Об устойчивости нелинейных систем с ограничением при
случайных воздействиях // Изв. АН СССР. Техническая кибернетика. 1966. № 4. -
С. 161-166.
119. Пупков К А. Основы кибернетики. Математические основы кибернетики. - М.:
Высш. школа, 1974. - 416 с.
120. Пупков К.А. Статистический расчет нелинейных систем автоматического
управления. - М.: Машиностроение, 1965.-404 с.
121. Пупков К А., Егупов ЯД., Коньков ВТ. Методы анализа, синтеза и
оптимизации нестационарных систем автоматического управления / Под ред.
Н.Д. Егупова. - М.: Изд-во МГТУ им. Н.Э. Баумана, 1999. - 684 с.
122. Пупков К.А., Егупов НД., Трофимов А.И. Статистические методы анализа,
синтеза и идентификации систем автоматического управления / Под ред.
Н.Д. Егупова. - М.: Изд-во МГТУ им. Н.Э. Баумана, 1998. - 560 с.
123. Пупков К А., Капалин В.И., Ющенко А.С. Функциональные ряды в теории
нелинейных систем. - М.: Наука, 1976. - 448 с.
Список литературы к 1-й части 735
124. Пупков К.А., Коньков В.Г. Мировоззрение управленца. - М.: Биоинформ, 1997.
-С. 80.
125. Рей УХ. Методы управления технологическими процессами. - М.: Мир, 1983.
-386 с.
126. РосинМ.Ф. Статистическая динамика и теория эффективности систем
управления. - М.: Машиностроение, 1970. - 336 с.
127. Рыбин В.В., Семенов В.В. Алгоритмическое и программное обеспечение
расчета нестационарных непрерывно-дискретных систем управления ЛА
спектральным методом: Учебное пособие. - М.: МАИ, 1984. - 84 с.
128. Санковский Е.Л. Вопросы теории автоматического управления. - М.: Высшая
школа, 1971.-232 с.
129. Семенов В.В. Спектральный анализ линейных систем с переменными
параметрами на конечных нестационарных интервалах времени // Вычислительная
техника для управления производством / Под ред. В.В. Солодовникова. - М.:
Машиностроение, 1969. - 344 с.
130. Семенов В.В. Методические указания к курсовым работам по теории
управления. - М.: Изд-во МАИ, 1992. - 60 с.
131. Семенов В.В., Сивцов В.И. Обобщение спектрального метода анализа
нестационарных систем на конечных интервалах времени на нелинейные системы с
переменными параметрами // Изв. вузов. Приборостроение. 1969. №12.-
С.64-68.
132. Семенов В.В., Сивцов В.И. Статистический анализ одного класса нелинейных
систем в частотной области // Изв. вузов. Приборостроение. 1976. №8. -
С. 29-33.
133. Семенов В.В., Солодовников В.В. Спектральная теория нестационарных систем
управления. - М.: Наука, 1974. - 336 с.
134. Семенов В.В., Панин ЕД. Обобщение спектрального метода анализа линейных
систем с переменными параметрами на многомерные системы // Изв.
вузов. Приборостроение. 1970. № 1. - С. 44 - 58.
135. Семенов В.В., Сивцов В.И. К определению передаточных функций
непрерывно-дискретных систем // Труды МВТУ. Системы автоматического управления.
1978. Вып. 5. № 265. - С. 27 - 39.
136. Семенов В.В., Солодовников В.В. Спектральный анализ линейных систем с
переменными параметрами на конечных нестационарных интервалах времени //
Автоматика и телемеханика. 1968. Т.29. № 11. - С. 14 - 27.
137. Сивцов В.И. Анализ линейных систем с периодической коммутацией
параметров // Изв. вузов. Приборостроение. 1980. № 10. - С. 27 - 30.
138. Сивцов В.И. Анализ линейных непрерывно-дискретных систем частотным
методом. - В кн. Спектральные методы обработки информации в научных
исследованиях. - Пущино, 1980. - С. 70-^78.
139. Сивцов В.И. Организация среды обучения в задачах управления // Вестник
МГТУ. Серия приборостроение. - 1993. № 3. - С. 65 - 75.
140. Сивцов В.И., Чулин НА. Автоматизированный синтез систем регулирования на
основе частотного метода теории автоматического управления. - М.:
Машиностроение, 1982.-236 с.
141. Современные методы идентификации систем / Под ред. П. Эйхкоффа. - М.:
Мир, 1983.-440 с.
48*
736 Анализ и статистическая динамика САУ. Часть I
142. Солодов А.В. Линейные системы автоматического управления с переменными
параметрами. - М: Физматгиз, 1962. - 264 с.
143. Солодов А.В. Методы теории систем в задаче непрерывной линейной
фильтрации. - М.: Наука, 1976. - 264 с.
144. Солодов А.В., Петров Ф.С. Линейные автоматические системы с переменными
параметрами. - М.: Наука, 1971. - 324 с.
145. Солодовников В.В. Статистическая динамика линейных систем
автоматического управления. - М: Физматгиз, 1960. - 656 с.
146. Солодовников В.В. Об одном применении операторного исчисления к
динамическим системам с переменными параметрами // Изв. АН СССР. ОТН. 1945.
№12.-С. 17-40.
147. Солодовников В.В. Частотный метод в теории автоматического регулирования
// Автоматическое управление и вычислительная техника / Под ред.
В.В. Солодовникова. - М: Машиностроение, 1968. Вып. 8. - С. 44 - 59.
148. Солодовников В.В., Бородин Ю.//., Ионисян А.Б. Частотные методы анализа и
синтеза нестационарных линейных систем. - М.: Советское радио, 1972. - 168 с.
149. Солодовников В.В., Дмитриев А.Н., Егупов ИД. Спектральные методы расчета
и проектирования систем управления. - М.: Машиностроение, 1986. - 440 с.
150. Солодовников В.В., Коньков В.Г., Суханов В.А. Микропроцессорные
автоматические системы регулирования / Основы теории и элементы. - М.: Высш.
школа, 1991.-324 с.
151. Солодовников В.В., Матвеев П.С. Расчет оптимальных систем
автоматического управления при наличии помех. - М.: Машиностроение, 1973. - 240 с.
152. Солодовников В.В., Милое Л.Т. Спектральное представление линейных
нестационарных систем в пространстве состояния // Техническая кибернетика. 1979.
№5.-С. 47-60.
153. Солодовников В.В., Плотников В.Н., Яковлев А.В. Теория автоматического
управления техническими системами. - М.: Изд-во МГТУ им. Н.Э. Баумана,
1993.-492 с.
154. Солодовников В.В., Семенов В.В. Спектральная теория нестационарных систем
управления. - М.: Наука, 1974. - 336 с.
155. Солодовников В.В., Семенов В.В. Спектральный метод расчета
нестационарных систем управления летательными аппаратами. - М.: Машиностроение,
1975.-272 с.
156. Справочник по теории автоматического управления / Под ред.
А.А. Красовского. - М.: Наука, 1987. - 712 с.
157. Статистические методы в проектировании нелинейных систем
автоматического управления / Под ред. Б.Г. Доступова. - М.: Машиностроение, 1970. -
408 с.
158. СуетинП.К. Классические ортогональные многочлены. - М.: Наука, 1979. -
412 с.
159. СуетинП.К. Ортогональные многочлены по двум переменным. - М.: Наука,
1988.-384 с.
160. Талдыкин А.Т. Элементы прикладного функционального анализа: Учеб.
пособие. - М.: Высш. школа, 1982. - 384 с.
161. Теория автоматического управления / Под ред. А.А. Воронова ч.1, ч.2. - М.:
Высш. школа, 1986. - 362, 382 с.
Список литературы к 1-й части 737
162. Теория автоматического управления. Изд. 2. / Под ред. А.В. Нетушила. - М.:
Высш. школа, 1983.-432 с.
163. Техническая кибернетика / Под ред. В.В. Солодовникова. Кн.1. Кн.2. Кн.З. 4.1.
- М.: Машиностроение, 1967. Кн.1 - 768 с, 1967. Кн.2 - 679 с, 1969. Кн.З -
608 с, 1969.
164. Техническая кибернетика за рубежом / Под ред. В.В. Солодовникова. - М.:
Машиностроение, 1968.-280 с.
165. Тихонов Л.Н., Арсенин ВЯ. Методы решения некорректных задач. - М.: Наука,
1974.-342 с.
166. ТицА.В. Приближенное вычисление «-кратных интегралов // Изв. АН СССР.
Серия математическая. 1940. № 4. - С. 8 - 14.
167. Топчеее Ю.И., ЦыпляковА.П. Задачник по теории автоматического
регулирования. - М.: Машиностроение, 1977. - 720 с.
168. Трофимов А.И., Егупов НД., Дмитриев А.Н. Методы теории автоматического
управления, ориентированные на применение ЭВМ. - М.: Энергоатомиздат,
1997.-654 с.
169. Ту Ю. Современная теория управления: Пер. с англ. / Под ред. В.В.
Солодовникова. - М.: Машиностроение, 1971. - 474 с.
170. Уваев А.И. Теория автоматического управления. Задания и методические
указания к курсовой работе. - Рязань, 1985. - 20 с.
171. Федосов Е.А., Себряков Г.Г. Спектральный анализ систем управления со
случайно изменяющимися параметрами // Автоматическое управление и
вычислительная техника. Частотные методы. - М.: Машиностроение, 1968. Вып. 8. -
С. 207-238.
172. ЦыпкинЯЗ. Основы теории автоматических систем. - М.: Наука, 1977. -
650 с.
173. Цыпкин ЯЗ. Теория импульсных систем. - М.: Физматгиз, 1963. - 724 с.
174. Чернецкий В.И. Анализ точности нелинейных систем управления. - М.:
Машиностроение, 1968.-246 с.
175. Шаталов А.С. Отображение процессов управления в пространстве состояний.
- М.: Энергоатомиздат, 1986.-256 с.
176. Шаталов А.С. Преобразование сигналов автоматического управления. - М. - Л.:
Энергия, 1965.-344 с.
177. Шахназаров Г.А. Программное обеспечение расчета систем автоматического
регулирования: Учебное пособие. - М.: Изд-во МГТУ им. Н.Э. Баумана, 1985.
-50 с.
178. Шахт арии Б.И. Оптимальная фильтрация и прогнозирование случайных
процессов. - М.: Изд-во МГТУ им. Н.Э. Баумана, 1991.-210 с.
179. Эпкхофф П. Основы идентификации систем управления: Пер. с англ. - М.:
Мир, 1979.-464 с.
180. Эпкхофф П. Основы идентификации систем управления: оценивание
параметров и состояния: Пер. с англ. - М.: Мир, 1975. - 684 с.
181. Якубович В.А. Метод матричных неравенств в теории устойчивости нелинейных
регулируемых систем. Абсолютная устойчивость вынужденных движений //
Автоматика и телемеханика. 1964. № 7. - С. 577 - 590.
182. Якубович В.А. Методы теории абсолютной устойчивости // Методы
исследования нелинейных систем автоматического управления. - М.: Наука, 1975. -
С. 177-182.
738 Анализ и статистическая динамика САУ. Часть I
183. Belanger P.R. Control Engineering. A Model Approach. - Orlando, Florida, 1995. -
472 p:
184. Bernsterein D.S., Haddad W.M. LQG control with an H-performance bound: A Ric-
cati equation approach. IEEE Transactions on automatic control. 1989. Vol. 34. N3.
185. Desoer C.A., Vidyasagar M. Feedback Systems. Input-Output Properties. Academic
Press. NY. 1975.-406 p.
186. Francis B.A. Course in H-Control Theory. Lecture Notes in Control and Information
Sciences. Berlin, Heidelberg: Springer-Verlag, 1987. Vol 88. 156 p.
187. Franklin G.F., Powell J.D., Workman ML. Digital Control of Dynamic Systems.-
California, 1994. - 842 p.
188. Glover K. All optimal Hankel-norm approximations of linear multivariable systems
and their L°°-error bounds // Int. J. Control. 1984. Vol. 39. N6.
189. Gu D.W., Tsai M.C., Oyoung S.D. Postlethwaite I.. State-Spase formulae for
discrete-time H optimization // Int. J. Control. 1989. Vol. 49. N5.
190. Hung Y.S. Optimal control. Part 1. Model matching // Int. J. Control, 1989.
Vol. 49. N4.
191. Hung Y.S. Optimal control. Part 2. Solution for controllers // Int. J. Control. 1989.
Vol. 49. N4.
192. Iglesias P.A., Glover K. State-Space approach to disrete-time H-control // Int. J.
Control. 1991. Vol. 54. N5.
193. Kalman R.E., Busy R.S. New results in linear filtering and prediction theory // Trans.
ASME. Y., Basic Eng. Vol. 83. N1. PP. 95 - 108.
194. Kalman R.E. New methods in Wiener filtering theory // Proced. of the first
symposium on Engineering applications of random function theory and probability:
Jonh Wiley, 1983. PP. 270 - 388.
195. MacFarlane £>., Glover K. Robust controller design using normalised coprime factor
plant description // Lecture Notes in control and Information Sciences. New-York:
Springer-Verlag 1989. Vol. 138.
196. Zadeh LA., Deser C.A. Linear Systems Theory. McGr. H.B.C.NY, 1963. - 564 p.
Содержание 739
СОДЕРЖАНИЕ
ОБЩЕЕ ПРЕДИСЛОВИЕ К УЧЕБНИКУ 5
ПРЕДИСЛОВИЕ К 1-МУ ТОМУ 11
СПИСОК ИСПОЛЬЗУЕМЫХ АББРЕВИАТУР 13
СПИСОК ИСПОЛЬЗУЕМЫХ ОБОЗНАЧЕНИЙ 16
ГЛАВА 1. ЛИНЕЙНЫЕ ОДНОМЕРНЫЕ НЕПРЕРЫВНЫЕ СТАЦИОНАРНЫЕ
СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ:
МАТЕМАТИЧЕСКИЕ МОДЕЛИ, ДИНАМИЧЕСКИЕ
ХАРАКТЕРИСТИКИ, УСТОЙЧИВОСТЬ,
ТОЧНОСТЬ ОТРАБОТКИ СИГНАЛОВ 20
1.1. Системы автоматического управления: основные понятия,
цели и принципы управления, оператор системы 20
1.1.1. Примеры систем автоматического управления 20
1.1.2. Цели и принципы управления 30
1.1.3. Типовая функциональная схема САУ.
Классификация систем 30
1.1.4. Математические модели систем; оператор системы 32
1.2. Математическое описание линейных стационарных систем:
передаточная функция системы 34
1.3. Переходный (динамический) и установившийся (статический)
режимы работы системы; переходная характеристика системы 51
1.4. Математическое описание линейных стационарных систем:
импульсная переходная функция системы 56
1.5. Математическое описание линейных стационарных систем:
частотные характеристики системы 62
1.6. Элементарные звенья стационарных систем
и их динамические характеристики 67
1.7. Некоторые выводы, основанные на анализе частотной
и временной форм описания систем 82
1.8. Передаточные функции, импульсные переходные функции,
частотные характеристики систем с распределенными параметрами
и с запаздыванием 87
1.9. Исследование линейных стационарных систем
автоматического управления: постановка задачи 92
1.10. Устойчивость линейных стационарных одномерных систем.
Необходимые и достаточные условия 95
1.11. Алгебраические критерии устойчивости 100
1.11.1. Критерий Рауса 100
1.11.2. Критерий Гурвица 101
1.11.3. Критерий Льенара -Шипара 104
1.12. Методы исследования точности работы систем
в установившемся режиме 107
1.12.1. Оценка точности работы системы для класса воздействий 107
1.12.2. Приближенное исследование точности работы системы
в установившемся режиме 109
740 Анализ и статистическая динамика САУ. Часть I
ГЛАВА 2. ЛИНЕЙНЫЕ ОДНОМЕРНЫЕ НЕПРЕРЫВНЫЕ
НЕСТАЦИОНАРНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ: МАТЕМАТИЧЕСКИЕ МОДЕЛИ,
ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ, УСТОЙЧИВОСТЬ 112
2.1. Математическое описание одномерных линейных нестационарных
систем с помощью импульсных переходных функций 112
2.1.1. Дифференциальные уравнения систем 112
2.1.2. Понятие ИПФЛНС и ее основные свойства 115
2.2. ИПФ ПРОСТЕЙШИХ ЗВЕНЬЕВ И ИХ СОЕДИНЕНИЙ 125
2.2.1. ИПФ некоторых элементарных звеньев 126
2.2.2. ИПФ основных соединений 128
2.3. Описание и исследование ЛНС с помощью преобразования
Лапласа и Фурье 132
2.3.1. Общее интегральное уравнение ЛНС 133
2.3.2. Понятие параметрической передаточной функции (ППФ) 135
2.3.3. Понятие параметрической частотной характеристики (ПЧХ) 137
2.3.4. Понятие нормальной и бичастотной
передаточных функций 140
2.4. Описание линейных стационарных и нестационарных систем
с помощью преобразования Лапласа (сравнительный анализ) 142
2.5. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ НЕСТАЦИОНАРНЫХ СИСТЕМ
(ОСНОВНЫЕ ПОНЯТИЯ) 146
2.5.1. Устойчивость ЛНС относительно начальных условий 147
2.5.2. Устойчивость ЛНС относительно управления 149
2.5.3. Устойчивость ЛНС на конечном интервале 150
2.5.4. Устойчивость на конечном интервале
по отношению к начальным условиям 152
2.5.5. Устойчивость на конечном интервале
по отношению к управлению 155
ГЛАВА 3. МЕТОД ПРОСТРАНСТВА СОСТОЯНИЙ: МАТЕМАТИЧЕСКИЕ
МОДЕЛИ И ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ
СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ 157
3.1. Описание линейных систем автоматического управления
в нормальной форме 157
3.2. Фундаментальная система. Свободные колебания
в стационарных и нестационарных системах 166
3.3 Фундаментальная матрица. Вынужденные колебания
В СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ СИСТЕМАХ;
ВЕКТОРНО-МАТРИЧНЫЙ ИНТЕГРАЛ КОШИ » 173
3.4. Применение преобразования Лапласа к описанию многомерных
стационарных систем.
Передаточные функции 178
ГЛАВА 4. НЕЛИНЕЙНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ: МОДЕЛИ,
УСТОЙЧИВОСТЬ, ПЕРИОДИЧЕСКИЕ КОЛЕБАНИЯ,
РАСЧЕТ ВЫХОДНЫХ ПРОЦЕССОВ 187
4.1. Описание основных моделей 187
4.2. Устойчивость и функции Ляпунова 189
4.3. устойчивость линеаризованных систем 191
4.4. Задача об абсолютной устойчивости 193
4.5. Метод априорных интегральных оценок и частотные критерии 198
4.6. Обобщение задачи об абсолютной устойчивости 201
4.7. Связь метода Ляпунова с частотными методами 202
4.8. Интегральные оценки 204
4.9. Периодические движения и автоколебания 206
4.10. Метод гармонического баланса 211
Содержание 741
4.11. Метод степенных преобразований 215
4.11.1. Степенное преобразование координат 216
4.11.2. Алгебра степенных преобразований 218
4.11.3. Иерархия моделей нелинейной системы управления 223
4.11.4. Анализ устойчивости нестационарных моделей 227
4.11.5. Сравнение с круговым критерием 230
4.11.6. Устойчивость неавтономных систем 232
4.11.7. Устойчивость дискретных систем 236
4.11.8. Квадратичные связи в стационарных системах 238
4.11.9. Критерий устойчивости стационарных систем 241
4.11.10. Сравнение с критерием Попова 244
4.11.11. Оценки качества 245
4.12. Метод функциональных рядов математического описания
и исследования класса нелинейных систем 247
4.12.1. Общие положения 247
4.12.2. Описание нелинейных систем функциональными рядами
Вольтерра 248
4.13. Методы линеаризации математических моделей систем
автоматического управления 257
4.13.1. Линеаризация вблизи опорной траектории 259
4.13.2. Линеаризация функциональных преобразователей 259
4.13.3. Линеаризация нелинейных дифференциальных уравнений 262
4.13.4. Линеаризация систем нелинейных
дифференциальных уравнений 264
4.13.5. Линеаризация Ньютона -Канторовича 265
ГЛАВА 5. ЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ:
СТАТИСТИЧЕСКИЙ АНАЛИЗ
И ОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ 271
5.1. Примеры систем, работающих при случайных воздействиях 271
5.2. Случайная функция и ее вероятностное описание 284
5.2.1. Одномерные законы распределения, математическое
ожидание и дисперсия случайной функции X(t) 284
5.2.2. Двумерные законы распределения и корреляционная функция
случайного процесса X(i) 294
5.2.3. Стационарные и эргодические случайные сигналы 302
5.2.4. Спектральная плотность стационарного
случайного сигнала 307
5.3. Статистический анализ одномерных линейных систем
с использованием импульсных переходных функций
(анализ во временной области) 314
5.4. Статистический анализ одномерных линейных систем
с использованием передаточных функций
(анализ в частотной области) 320
5.5. Алгоритмы анализа динамической точности линейных
автоматических систем 326
5.6. Статистический анализ линейных систем, основанный
НА ОПИСАНИИ В ПРОСТРАНСТВЕ СОСТОЯНИЙ 333
ГЛАВА 6. МЕТОДЫ ИССЛЕДОВАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ 340
6.1. Особенности преобразования случайных процессов нелинейными
элементами и системами 341
6.2. Статистический анализ нелинейных систем, описываемых
ФУНКЦИОНАЛЬНЫМИ РЯДАМИ ВОЛЬТЕРРА 344
742 Анализ и статистическая динамика САУ. Часть I
6.3. Метод статистической линеаризации вероятностного анализа
нелинейных систем 354
6.4. Численно-спектральный метод статистического анализа
нелинейных нестационарных автоматических систем..! 378
6.5. Вероятностное исследование нелинейных нестационарных систем
методом статистических испытаний 383
ГЛАВА 7. МЕТОДЫ СИНТЕЗА СТАТИСТИЧЕСКИ ОПТИМАЛЬНЫХ
СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ 391
7.1. Фильтры с заданной структурой (параметрическая оптимизация) 393
7.2. Фильтры Колмогорова - Винера 396
7.3. Оптимальное оценивание состояния 403
7.3.1. Вывод дисперсионного уравнения 404
7.3.2. Оптимальная линейная фильтрация по Калману 407
7.3.3. Уравнение оптимального фильтра 408
7.3.4. Нахождение оптимальной матричной функции
коэффициентов фильтра 410
7.3.5. Вывод дисперсионного уравнения для оптимального
фильтра 412
7.3.6. Обобщенный линейный фильтр Калмана -Бьюси 415
7.3.7. Оптимальная фильтрация при небелом (цветном) шуме 420
7.3.8. Оптимальный фильтр (наблюдатель) Калмана -Бьюси
в системах управления 427
7.3.9. Установившиеся свойства оптимального фильтра
Калмана -Бьюси 429
7.4. Статистический синтез оптимальных нелинейных систем,
ОПИСЫВАЕМЫХ ФУНКЦИОНАЛАМИ ВОЛЬТЕРРА л 432
7.4.1. Интегральные уравнения, определяющие оптимальную
систему 432
7.4.2. Синтез последовательного нелинейного
корректирующего устройства 439
7.4.3. Синтез встречно-параллельного нелинейного
корректирующего устройства 440
7.4.4. Техническая реализация нелинейных
корректирующих устройств 444
7.5. Оптимизация нелинейных систем при случайных воздействиях
с использованием статистической линеаризации 447
ГЛАВА 8. МЕТОД МАТРИЧНЫХ ОПЕРАТОРОВ ЧИСЛЕННО-
АНАЛИТИЧЕСКОГО РЕШЕНИЯ ЗАДАЧ
ДЕТЕРМИНИРОВАННОГО АНАЛИЗА
И СТАТИСТИЧЕСКОЙ ДИНАМИКИ СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ 452
8.1. Описание нестационарных систем с помощью операторов
интегрирования, дифференцирования и умножения 456
8.2. Матричные операторы интегрирования, дифференцирования
и умножения 459
8.2.1. Матричный оператор интегрирования
для произвольного базиса 459
8.2.2. Матричный оператор умножения на функцию 460
8.2.3. Матричный оператор дифференцирования 462
8.3. Численная реализация методов расчета матричных операторов
интегрирования, умножения на функцию
и дифференцирования в конкретных ортогональных базисах 463
8.3.1. Матричные операторы в базисе ортогональных полиномов
Лежандра 463
Содержание 743
8.3.2. Матричные операторы в базисе функций Уолша 468
8.3.3. Матричные операторы в базисе блочно-импульсных
функций 475
8.4. Методы расчета матричных операторов
(спектральных характеристик) замкнутых
нестационарных скалярных линейных систем 480
8.5. Метод расчета матричных операторов систем
в пространстве состояний с использованием матричных
операторов дифференцирования и умножения 488
8.6. Метод расчета матричных операторов систем с помощью
матричных операторов интегрирования и умножения 492
8.7. Построение математической модели линейной нестационарной
системы управления методом матричного представления
интегрального оператора в ортогональном базисе (общий подход) 496
8.8. Алгоритм расчета выходных сигналов линейных нестационарных
систем при детерминированных входных воздействиях
(детерминированный анализ) 500
8.9. Алгоритм расчета корреляционных функций и дисперсий
выходных сигналов линейных нестационарных систем
(статистический анализ) 501
8.10. Алгоритм детерминированного и статистического анализа САУ,
ПОВЕДЕНИЕ КОТОРЫХ ОПИСЫВАЕТСЯ ДИФФЕРЕНЦИАЛЬНЫМИ УРАВНЕНИЯМИ
С ПОЛИНОМИАЛЬНЫМИ КОЭФФИЦИЕНТАМИ 509
8.11. Алгоритм детерминированного и статистического анализа САУ,
ПОВЕДЕНИЕ КОТОРЫХ ОПИСЫВАЕТСЯ ДИФФЕРЕНЦИАЛЬНЫМИ УРАВНЕНИЯМИ
с экспоненциальными коэффициентами 519
8.12. Алгоритмы решения задачи оптимальной фильтрации
нестационарных случайных процессов 526
8.12.1. Алгоритм построения оптимального фильтра, основанный
на решении уравнения Винера -Хопфа 526
8.12.2. Алгоритм, основанный на минимизации зависимости,
определяющей среднеквадратичную ошибку
в спектральной области 531
8.13. Формирующие фильтры 531
8.14. Решение обратных задач динамики методами
конечномерной оптимизации 536
8.14.1. Содержание обратных задач динамики
и примеры их решения 536
8.14.2. Алгоритм построения программных управлений движением
одного класса нелинейных динамических систем
(задача Е.А. Барбашина) 539
8.14.3. Алгоритм решения задачи слежения: воспроизведение
эталонной выходной вектор-функции 556
8.14.4. Алгоритм решения задачи слежения: воспроизведение
эталонного вектора состояния 565
8.14.5. Алгоритм решения нестационарной задачи слежения 571
8.15. Реализация алгоритмов спектральных методов
в среде пакета MATLAB 573
8.16. Автоматизированное проектирование САУ 582
ГЛАВА 9. ЛИНЕЙНЫЕ И НЕЛИНЕЙНЫЕ ОБЪЕКТЫ УПРАВЛЕНИЯ:
ДЕТЕРМИНИРОВАННАЯ И СТАТИСТИЧЕСКАЯ
ИДЕНТИФИКАЦИЯ 588
9.1. Проблема идентификации 588
9.1.1. Общие понятия 588
744 ' Анализ и статистическая динамика САУ. Часть I
9.1.2. Критерии идентификации 590
9.1.3. Классификация объектов, задач и методов идентификации 590
9.1.4. Требования, предъявляемые к методам идентификации 591
9.1.5. Подходы к решению задачи идентификации 591
9.1.6. Оценивание параметров нелинейных систем 594
9.2. Детерминированная идентификация линейных стационарных
объектов, основанная на решении уравнения 1-го рода
методом механических квадратур 594
9.3. Детерминированная идентификация линейных объектов,
основанная на решении уравнения 1-го рода
спектральным методом 601
9.4. Принципы статистической идентификации линейных стационарных
объектов, основанные на решении интегрального уравнения
фредгольма1-города '. 606
9.5. Описание и идентификация нелинейных систем
методом Винера 610
9.6. Оценка параметров нелинейных систем методами фильтрации 616
9.7. Оценка параметров нелинейных объектов
методом наименьших квадратов с использованием
теории чувствительности 622
ГЛАВА 10. ОПИСАНИЕ НЕПРЕРЫВНО-ДИСКРЕТНЫХ СИСТЕМ
С ПОМОЩЬЮ ИНТЕГРАЛЬНЫХ ПРЕОБРАЗОВАНИЙ 626
10.1. Системные характеристики линейных динамических звеньев 628
10.1.1. Непрерывные системы 628
10.1.2. Дискретные системы 632
10.1.3. Непрерывно-дискретные системы 636
10.1.4.' Дискретно-непрерывные системы 639
10.2. Передаточные функции элементарных и типовых звеньев 643
10.3. Характеристики соединений непрерывно-дискретных звеньев 647
10.4. Уравнения для определения передаточных функций 656
ГЛАВА 11. АНАЛИЗ НЕПРЕРЫВНО-ДИСКРЕТНЫХ СИСТЕМ 662
11.1. Анализ непрерывно-дискретных систем при детерминированных
воздействиях 662
11.2. Метод расчёта непрерывно-дискретных систем
при случайных воздействиях 668
11.3. Непрерывно-дискретные системы с многократным синхронным
прерыванием 675
11.4. Анализ непрерывно-дискретных систем с особой точкой 682
11.5. Системы с периодической коммутацией параметров 685
11.6. Замечания об устойчивости непрерывно-дискретных систем 689
ПРИЛОЖЕНИЕ 1. МНОГОМЕРНЫЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ НЕЛИНЕЙНЫХ
СИСТЕМ, ОПИСЫВАЕМЫХ ФУНКЦИОНАЛАМИ
ВОЛЬТЕРРА 694
ПРИЛОЖЕНИЕ 2. ЭЛЕМЕНТЫ ФУНКЦИОНАЛЬНОГО АНАЛИЗА 700
ПРИЛОЖЕНИЕ 3. ОРТОНОРМИРОВАННЫЕ БАЗИСЫ 718
ПРИЛОЖЕНИЕ 4. ВЫЧИСЛЕНИЕ СТАНДАРТНОГО ИНТЕГРАЛА 722
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ 724
СПИСОК ЛИТЕРАТУРЫ 729
745
ANNOTATION TO THE TEXTBOOK
"Classical and state-of-the-art control theory methods".
This textbook is published in three volumes.
I volume: "Analysis and automatic control systems statistic dynamics".
II volume: "Regulator synthesis and automatic control systems optimization theory".
HI volume: "State-of-the-art control theory methods".
I. Characteristic properties of the textbook.
1. This textbook is addressed to the broad reading public.
a). Students who begin to obtain knowledge in the field of control theory. It should be
mentioned that this subject may be both an obligatory one evaluating the level of
engineer's proficiency and an optional one.
b). Students and specialists who have to resume studies in the field of control theory
because of expanding tasks of process automation for different purposes.
c). Students and specialists who want to refresh their knowledge studying the part of the
textbook, which has not been included into engineering specialities curricula.
The readers have to choose the material according to the particular tasks a), b), c) and to
general curriculum opportunities. Taking into consideration the purpose of this textbook it
should be noted that it presents sufficient material for the choice to be made.
2. Material introduction methods.
This textbook attempts to provide the readers with knowledge of control theory methods
from initial concepts of control theory (control aims and concepts, control systems analysis,
systems classification, analysis and synthesis of the main tasks and others) to its state-of-
the-art issues.
In other words, this textbook presents both fundamental concepts of classical control
theory and concepts determining the subject-matter of some state-of-the-art trends.
Thorough understanding of control theory is impossible within the limits of up-to-date
investigation programmes, that is why the subject-matter of some trends has not been included
into this textbook.
3. The level of readers mathematical background.
The authors of this textbook set out the material in easy and readily available way.
A scope of knowledge of higher mathematics required for the textbook contents
understanding is restricted to the programme for junior students at higher technical educational
institutions.
Concepts of functional analysis are implemented in this textbook. The necessary
information is given in a due corresponding section of the textbook. Owing to language applica^
tion and the results of functional analysis the subject-matter of each method is better
revealed, the opportunity of obtaining in - depth theoretical information is developed, the
connection between methods that seem to be different at first sight is clarified.
4. Technical character of the textbook.
The subject matter of the textbook is presented from the engineering point of view.
The author stresses the main ideas forming the bases of the methods but does not always
adduce strict methodological proofs. The subject-matter of the textbook is supposed to
form the base.
It is supposed that the material of the textbook will be the base for finding more easily
the ways of solving practical tasks. Besides, the material is presented in such a way that the
reader can imagine the ways of practical use of the methods under consideration.
746
In most cases the methods are reduced to the calculated algorithms, the tables and other
additional material, facilitating their application are given in the textbook.
The main merit of the textbook is the consideration of the particular control systems
being used in the atomic industry with the aim of regulating the thermotechnical processes:
• It presents principal, functional and structural circuits of the system.
• It illustrates the calculations using particular algorithms.
• It gives the analysis of the results, etc.
It is impossible to study control theory without mastering the engineering aspect. That is
why the engineering aspect of formulating and solving practical tasks is accentuated during
the whole course.
5. "Computing colouring" of the material.
The contents of the book is characterized by a certain "computing colouring" because
the present-day computers give the possibility of reducing the term of the automatic control
systems design and thus make an imprint on numerical methods of the automatic control
theory.
Successful solving of problems of computing and design with the use of computer
depends on many factors:
• The degree of the adequacy of the system mathematical model.
• The degree of the numerical methods efficiency being used in the algorithmic
provision.
• The presence of high-quality software.
• To what degree the creativeness of a researcher-designer is used.
The author of the textbook tried to take into consideration all these factors.
II. The contents.
1. Mathematical models of the automatic control systems.
The problems of the mathematical description of the singular and nonsingular linear and
non linear control systems, the systems with the distributed parameters, the continuous
discrete systems are considered in the textbook in detail. Considerable attention is paid to the
method of the state space in the linear system which gives basically new possibilities of the
system analysis and control laws synthesis. The description by the Volterra series is
considered in the non-linear system class.
2. Determinated analysis of the automatic control systems.
The system theory methods were studied for solving the following problems:
a). The investigation of the steady-state singular, non-stationary and доп-linear systems:
- the criteria of stability are considered in detail;
- considerable attention is paid to non-linear system class;
(The original material concerning the problems of stability is given in a due chapter).
b). The study of the system performance in unstable mode and creation of output
processes,
c). The investigation of performance accuracy in the stable mode.
3. Statistic analysis of the automatic control systems.
The technical methods of the broad class ACS statistic research, including non-linear
and stochastic system are considered in the textbook.
4. Filtration and control systems statistical synthesis.
This chapter includes the following methods:
a). Synthesis of optimal filters, using Kolmogorov - Wienner's theory as well as
R. Caiman and R. Busy,
b). Synthesis of optimal observers,
c). Synthesis of optimal analytical and non-linear filters, described by Volterra series
and so on.
747
5. Numerical methods of complex control system analysis under determined and
random action.
Matrix operator method forms the bases of computerized control system investigation
useful for algorithmisation and programming.
6. Control objects identification.
Formulation of the problem of linear and non-linear objects class identification, main
problems, engineering approach to its solution are outlined in this textbook.
7. Control system synthesis based on quality (regulators synthesis).
Alongside with traditional methods of regulator synthesis (frequency, modal control,
dynamic compensation methods and other) great attention is devoted to mathematics
programming process application due to the fact, that the latter one determines general
approach to optimization problems solution and is computer oriented.
8. Synthesis of optimal automatic control systems.
The following problems were depicted:
a). Basis principles of calculus of variations;
b). Pontryagin's principle of the maximum including the problem of phase variables;
c). Dynamic programming;
d). Linear-quadratic problems;
e). Moments method;
f). Mathematic programming process as applied to optimal programmed controls
development.
9. Method of up-to-date CAD theory.
Method including the process of rough control systems synthesis, H - control theory
and robust methods as well as, the problems of multi-object and multi-criteria systems
optimization together with the application of effective compromises, calculation tasks and
design of adaptive and intellectual control systems, differential geometry methods
application in control theory and others.
Учебное издание
Константин Александрович Пупков
Александр Иванович Баркин
Евгений Михайлович Воронов
Николай Дмитриевич Егупов
Виктор Григорьевич Коньков
Владимир Николаевич Пилишкин
Вячеслав Иванович Сивцов
Адольф Иванович Трофимов
Николай Васильевич Фалдин
МЕТОДЫ КЛАССИЧЕСКОЙ
И СОВРЕМЕННОЙ ТЕОРИИ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
В трех томах
Том 1
АНАЛИЗ И СТАТИСТИЧЕСКАЯ ДИНАМИКА
СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Редактор С.Н Капранов
Корректор КЮ. Савинченко
Компьютерная верстка М.П. Трубачев
Изд. лиц. №020523 от 25.04.97. Подписано в печать 29.06.2000.
Формат 70 х 100 1/16. Печ. л. 46,75. Усл. печ. л. 60,8. Уч.-изд. л. 59,3.
Бумага офсетная. Печать офсетная. Тираж 2000 экз. Заказ № 232
Издательство МГТУ им. Н.Э. Баумана
107005, Москва, 2-я Бауманская, 5
Оригинал-макет подготовлен редакционно-издательским отделом
филиала МГТУ им. Н.Э. Баумана в г. Калуге
Отпечатано с готового оригинал-макета в ГУП «Облиздат»
248640, г. Калуга, пл. Старый торг, 5
ISBN 5-7038-1578-9
81
78