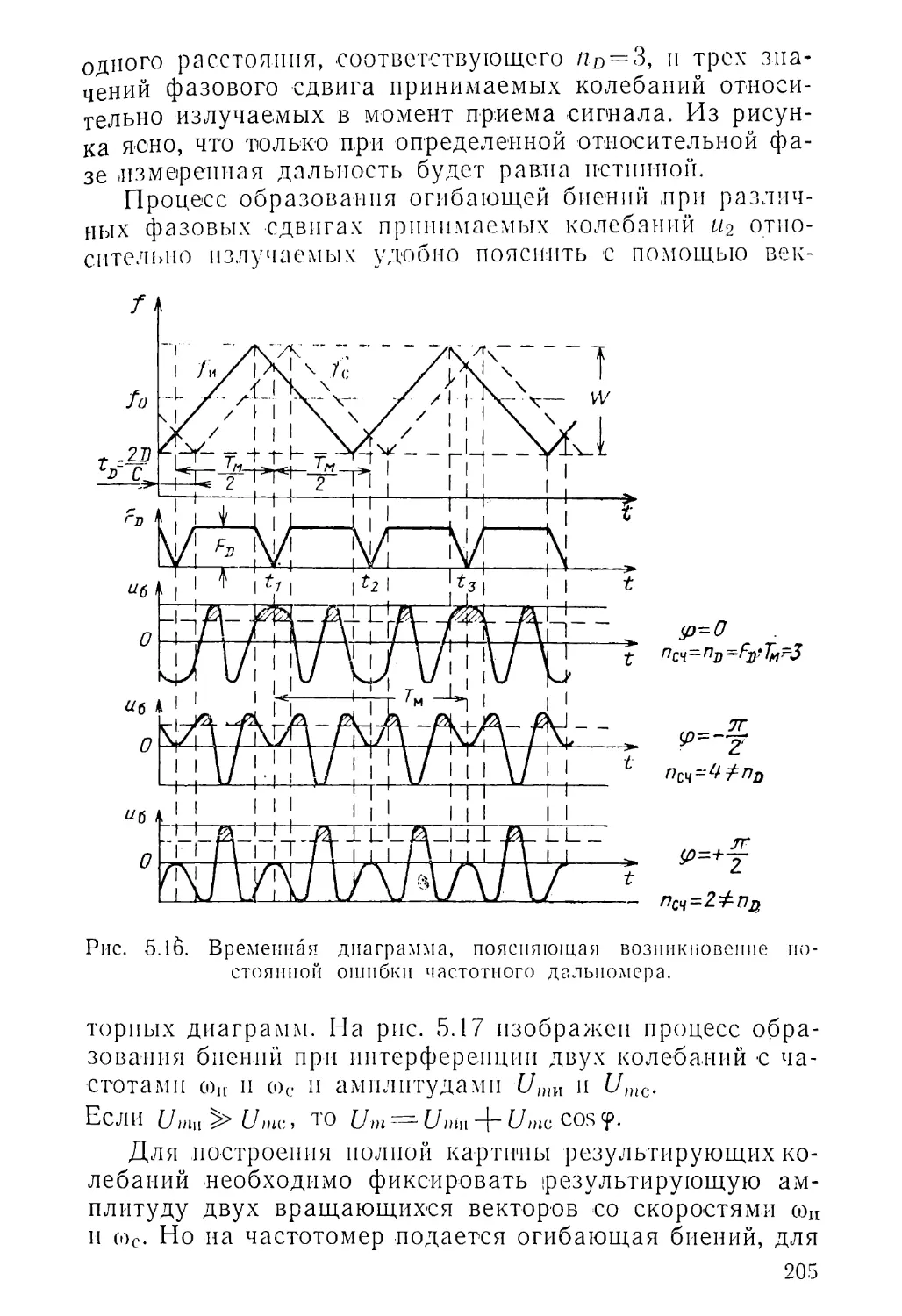
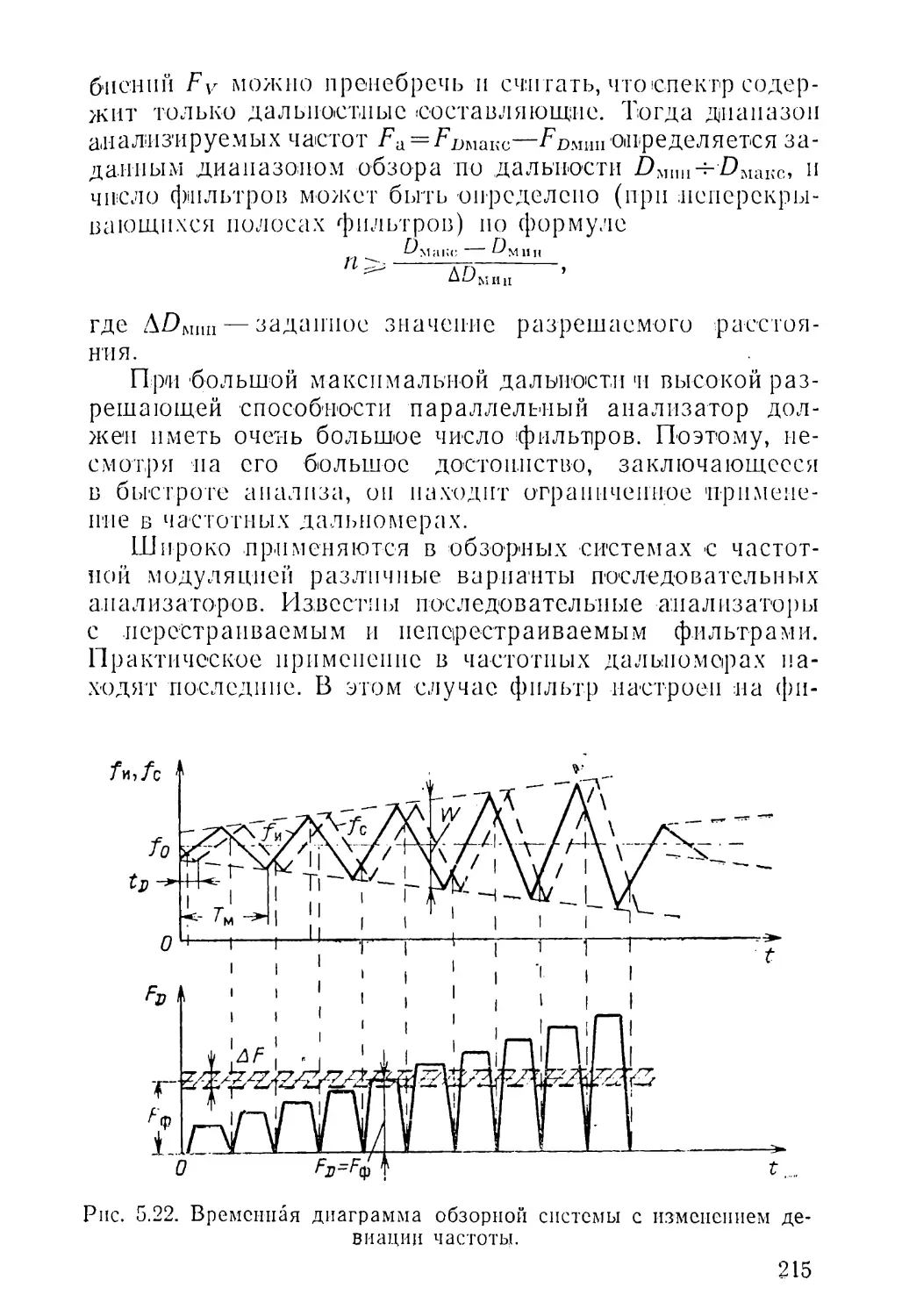
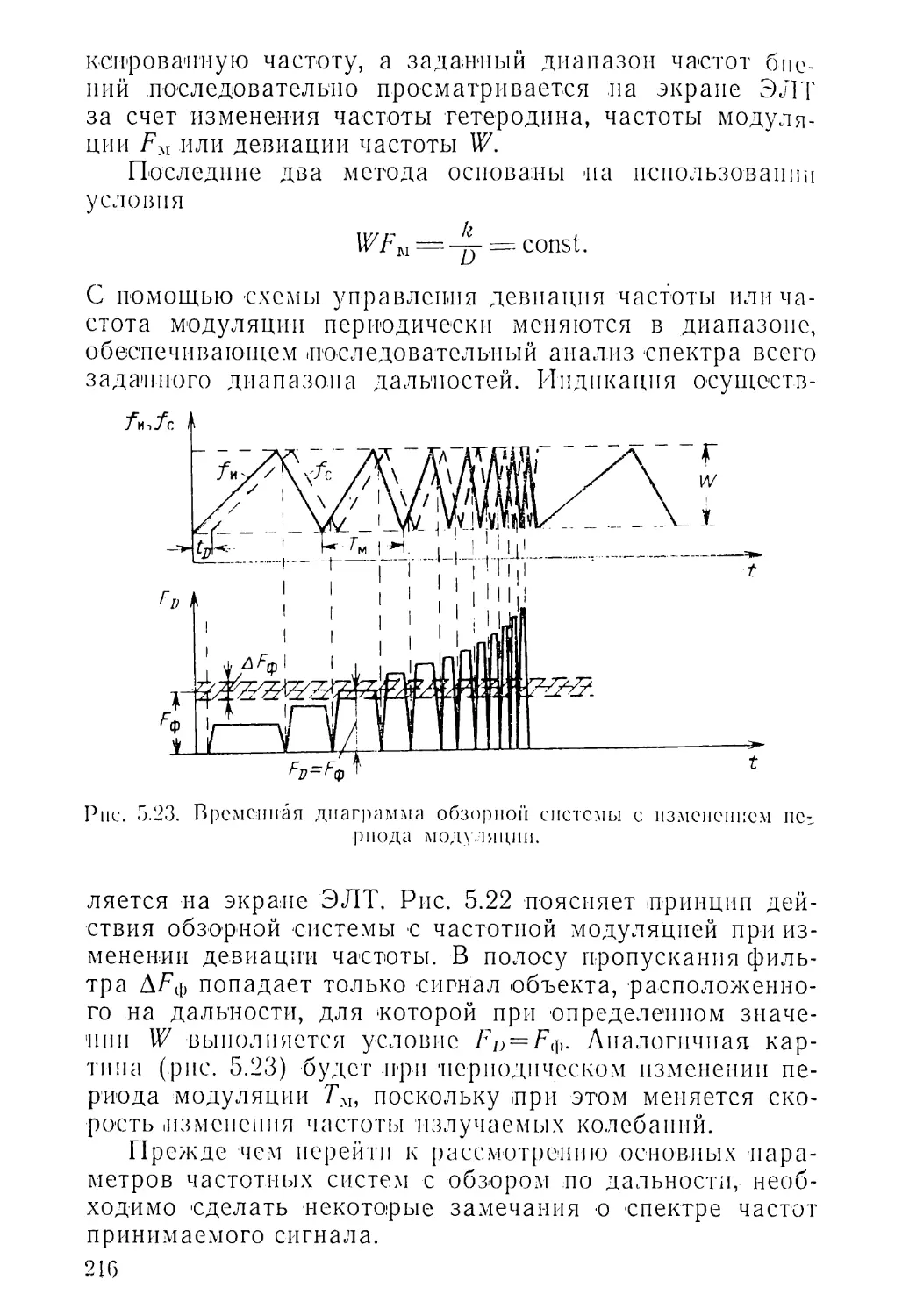
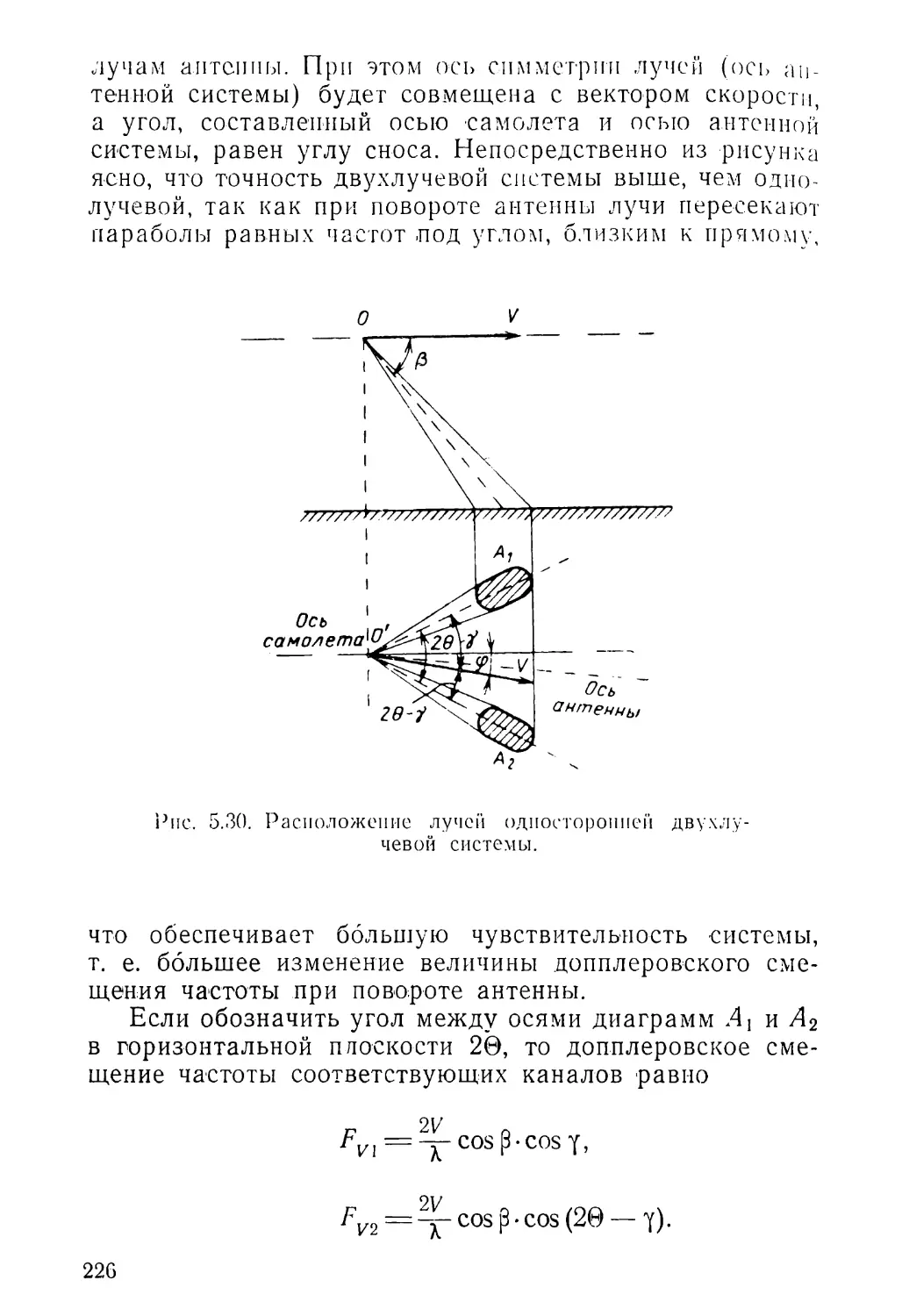
Текст
РАДИО•
ТЕХНИЧЕСКИЕ
СИСТЕМЫ
РАДИОТЕХНИЧЕСКИЕ
СИСТЕМЫ
IO. М. Казаринов,
Ю- А. Коломенский,
Ю. К- Пестов,
С. В- Толоконников,
В. И. Шломин
Под редакцией Ю. М. Казаринова
Допущено Министерством высшего
и среднего специального образования РСФСР
в качестве учебника для радиотехнических
вузов и факультетов
«СОВЕТСКОЕ РАДИО» МОСКВА 1968
УДК 621.396.9(075)
Коллектив авторов, под ред. Ю. М. Казаринова.
Радиотехнические системы. Учебник для вузов. М., Изд-во
«Советское радио», 1968, стр. 496.
В книге изложены теоретические основы и прин¬
ципы построения систем радиолокации, радионавига¬
ции и радиоуправления, которые связаны общностью
решаемых задач и используемых методов получения
и обработки информации.
Книга написана в соответствии с программой кур¬
са «Радиотехнические системы» на основе открытых оте¬
чественных и зарубежных источников и предназначена
служить учебником для студентов специальности «Ра¬
диотехника» радиотехнических вузов и факультетов.
3-4-1
57-68
РАДИОТЕХНИЧЕСКИЕ СИСТЕМЫ
Под редакцией Ю. М. Казаринова
Редактор И. К. Ганин
Художественный редактор В. Т. Сидоренко
Технический редактор Г. 3. Шалимова
Корректоры Л. И. Кирилъченко, Л. С. Глаголева
Сдано в набор 27/Ш 1968 г. Подписано к печати 14/VIII 1968 г.
Т-08482 Формат 84хЮ8/1в Бумага типографская № 2
Объем 26,04 ус г. п. л. Уч.-изд. л. 25,373 Тираж 65 000 экз.
Цена 1 р.
Издательство „Советское радио" Москва, Главпочтамт п/я 693 Зак. 1173
Московская типография № 10 Главполиграфпрома
Комитета по печати при Совете Министров СССР.
Шлюзовая наб., 10.
Предисловие 7
Глава 1
КРАТКАЯ ХАРАКТЕРИСТИКА МЕТОДОВ 4И СИСТЕМ РАДИО¬
ЛОКАЦИИ И РАДИОНАВИГАЦИИ 9
§ 1.1. Основные понятия и определения 9
§ 1.2. Физические основы радиолокации 12
§ 1.3. Основные методы определения местоположения . . 17
§ 1.4. Основные тактические и технические характеристики
радиолокационных и радионавигационных систем . 24
§ 4.5. Основное уравнение дальности радиообнаружения . 28
§ 1.6. Методы измерения дальности 30
§ 1.7. Методы измерения угловых координат .... 38
§ 1.8. Определение траекторий объектов 45
§ 1.9. Измерение скорости и ускорения объектов ... 46
§ 1.10. Распознавание радиолокационных объектов . 47
§ 1.11. Радиолокационные системы опознавания . 50
Глава 2
РАССЕИВАЮЩИЕ СВОЙСТВА ОБЪЕКТОВ . 51
§ 2.1. Рассеяние радиоволн объектами наблюдения и их эф¬
фективная площадь рассеяния 51
§ 2.2. Вычисление эффективной площади рассеяния некоторых
объектов 52
§ 2.3. Эффективная площадь рассеяния множества объектов 63
§ 2.4. Эффективная площадь рассеяния некоторых реальных
радиолокационных объектов ... ... 65
Глава 3
ЗОНДИРУЮЩИЕ радиолокационные СИГНАЛЫ 67
§ 3.1. Зондирующий радиолокационный сигнал и его совме¬
стная автокорреляционная функция 67
§ 3.2. Использование автокорреляционной функции для
опенки разрешающей способности, точности и одно¬
значности при измерении дальности и скорости цели 68
§ 3.3. Принцип неопределенности в радиолокации и диаграм¬
мы неопределенности радиолокационных сигналов . . 72
§ 3.4. Сложные (широкополосные) сигналы и сжатие импуль¬
сов о 80
3
Глава 4
ОБНАРУЖЕНИЕ СИГНАЛОВ 87
§ 4.1. Введение 87
§ 4.2. Прием сигналов как статистическая задача ... 88
§ 4.3. Функция правдоподобия 90
§ 4.4. Отношение правдоподобия 95
§ 4.5. Понятие среднего риска. Статистические критерии обна¬
ружения 97
§ 4.6. Структура и качественные показатели устройств опти¬
мальной обработки одиночого радиоимпульса . . 101
§ 4.7. Качественные показатели устройств оптимальной обра¬
ботки пачек когерентных радиоимпульсов . . . 124
§ 4.8. Структура устройств оптимальной обработки пачек ко¬
герентных радиоимпульсов 126
§ 4.9. Структура устройств оптимальной обработки широко¬
полосных сигналов 137
§ 4.10. Структура устройств оптимальной обработки пачек
некогерентных радиоимпульсов . 139
§ 4. Н. Качественные показатели устройств оптимальной обра¬
ботки пачек некогерентных радиоимпульсов . . . 143
§ 4.12. Накопительные устройства видеоимпульсов . . . 146
§ 4.13. Накопительные устройства квантованных видеоим¬
пульсов и их эффективность 147
Глава 5
ИЗМЕРЕНИЕ ДАЛЬНОСТИ И СКОРОСТИ ... 152
§ 5.1. Потенциальная точность измерения дальности . . 152?
§ 5.2. Импульсные дальномеры с визуальной индикацией . 159
§ 5.3. Автоматическое сопровождение по дальности в непре¬
рывном режиме ' ... 172
§ 5.4. Автоматическое сопровождение по дальности в режиме
обзора 178
§ 5.5. Цифровой метод автоматического измерения дальности 182
§ 5.6. Импульсные разностно-дальномерные радионавигацион¬
ные системы 186
§ 5.7. Фазовый метод далыюметрии .... . . 195
§ 5.8. Фазовые разностно-дальномерные системы . . . 200
§ 5.9. Частотный метод дальнометрии 203
§ 5.10. Допплеровские системы измерения скорости и угла
сноса самолета 220
Глава 6
ИЗМЕРЕНИЕ УГЛОВЫХ КООРДИНАТ .... 234
§6.1. Виды обзора пространства и их характеристика . . 234
§ 6.2. Потенциальная точность и разрешающая способность
систем при измерении угловых координат . . . 248
§ 6.3. Амплитудные методы пеленгования 252
§ 6.4. Автоматическое сопровождение по направлению при
круговом обзоре 266
§ 6.5. Угловая разрешающая способность и метод бокового
обзора земной поверхности с помощью синтезированных
антенн 277
4
§ 6.6. Принцип построения систем автоматического сопро¬
вождения по направлению при коническом сканировании 286
§ 6.7. Фазовый метод измерения угловых координат и угло¬
вой скорости 291
§ 6.8. Моноимпульсный метод автоматического измерения
угловых координат . >. . . . ... 296
Глава 7
СЕЛЕКЦИЯ СИГНАЛОВ ДВИЖУЩИХСЯ ЦЕЛЕЙ (СДЦ) НА
ФОНЕ ПАССИВНЫХ ПОМЕХ . . . 307
§7.1. Введение . 307
§ 7.2. Принцип действия и построение систем СДЦ с вну¬
тренней когерентностью . . . ..... 309
§ 7.3. Требования к отдельным узлам системы СДЦ с вну¬
тренней когерентностью 314
§ 7.4. Принцип действия когерентно-импульсных систем СДЦ
с внешней когерентностью 321
§ 7.5. Эффективность систем СДЦ с череспериодной компен¬
сацией . . 323
Глава 8
ПАССИВНАЯ РАДИОЛОКАЦИЯ . 325
§8.1. Физические основы пассивной радиолокации . . . 325
§ 8.2. Характеристики теплового радиоизлучения физических
объектов 326
§ 8.3. Обнаружение радиотепловых сигналов. Дальность дей¬
ствия радиотеплолокатора (РТЛ) 328
§ 8.4. Приемные устройства радиотеплолокаторов . . . 335
§ 8.5. Методы пассивной радиолокации: радиотеплопеленга-
ция, измерение дальности и измерение скорости . . 338
Глава 9
ФАКТОРЫ, ОПРЕДЕЛЯЮЩИЕ ДАЛЬНОСТЬ РАДИООБНАРУЖЕ¬
НИЯ II ТОЧНОСТЬ МЕСТООПРЕДЕЛЕНИЯ ... -341
§ 9.1. Обобщенное уравнение радиолокации 341
§ 9.2. Влияние режима работы и отдельных факторов на
дальность действия систем 344
§ 9.3. Дальность действия РЛС с учетом отражения от земной
поверхности и зона обнаружения (видимости) станции 346
§ 9.4. Влияние преломления, поглощения и рассеяния радио¬
волн на дальность действия РТС 351
§ 9.5. Эффект Кабанова и его использование в радиолокации 354
§ 9.6. Уравнение дальности радиолинии с активным ответом 356
§ 9.7. Точность определения линий положения .... 358
§ 9.8. Точность местоопределения на плоскости .... 364
§ 9.9. Точность местоопределения в пространстве t • 371
5
Глава 10
РАДИОРАЗВЕДКА, РАДИОПРОТИВОДЕЙСТВИЕ И БОРЬБА
С ОРГАНИЗОВАННЫМИ ПОМЕХАМИ (КОНТРРАДИОПРОТИВО¬
ДЕЙСТВИЕ) . . 377
§ 10.1. Радиоразведка . 377
§ 10.2. Радиопротиводействие 384
§ 10.3. Борьба с организованными помехами (контррадио¬
противодействие) . . 389
Глава 11
ОБЩИЕ СВЕДЕНИЯ ОБ УПРАВЛЯЕМЫХ ОБЪЕКТАХ
И СПОСОБАХ УПРАВЛЕНИЯ 392
§ 41.1. Основные типы управляемых объектов .... 392
§ 11.2. Органы управления реактивных снарядов . . . 395
§ 14.3. Процесс управления, системы координат и уравне¬
ние движения объекта 397
§ 14.4. Методы наведения.' Траектории движения . . . 405
§ 11.5. Динамические и флюктуационные ошибки наведения.
Промах 411
Глава 12
СИСТЕМЫ УПРАВЛЕНИЯ И ИХ ХАРАКТЕРИСТИКИ 416
§ 42.1. Введение 416
§ 42.2. Системы стабилизации и автономного управления . 416
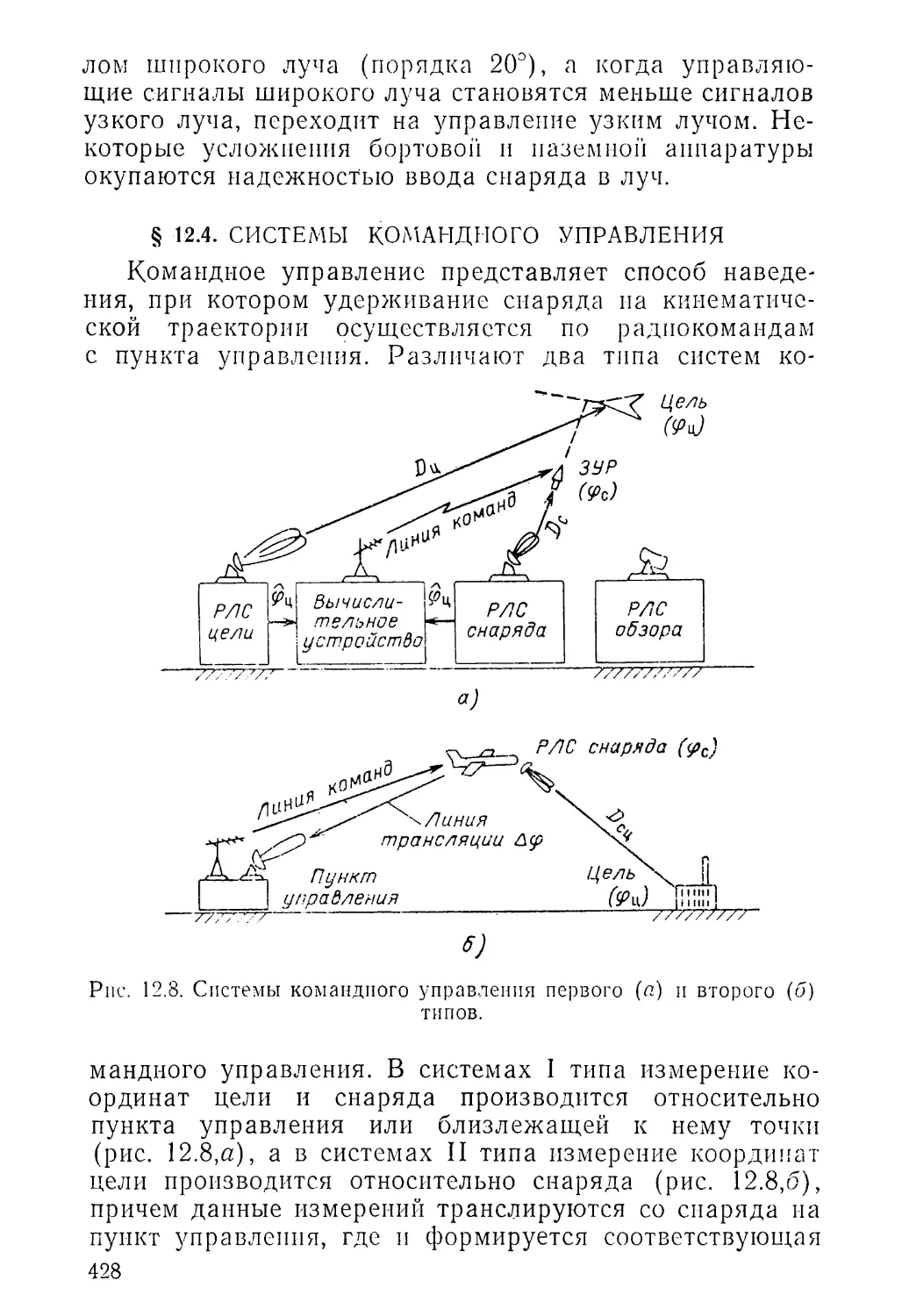
§ 12.3. Системы радиотеленаведения . 421
§ 12.4. Системы командного управления 428
§ 12.5. Линии передачи информации систем радиотелеуправ¬
ления 432
§ 42.6. Системы самонаведения . . . 442
§ 12.7. Радиовзрыватели . 449
Глава 13
РАДИОТЕХНИЧЕСКИЕ СИСТЕМЫ КОНТРОЛЯ ТРАЕКТОРИЙ
БАЛЛИСТИЧЕСКИХ РАКЕТ, ИСКУССТВЕННЫХ СПУТНИКОВ
ЗЕМЛИ И КОСМИЧЕСКИХ АППАРАТОВ .... 452
§ 13.1. Общие сведения о траекториях баллистических ракет
и искусственных спутников Земли . .... 452
§ 13.2. Принципы радиоуправления движением БР на пуско¬
вом активном участке траектории 456
§ 43.3. Определение параметров орбиты ИСЗ по данным ра¬
диолокационных наблюдений 460
§ 13.4. Фазовые пеленгаторы систем контроля траекторий ИСЗ 465
§ 13.5. Суммарно-разностные радиопеленгаторы ИСЗ . . 469
§ 13.6. Допплеровские системы контроля траекторий ИСЗ 476
§ 13.7. Радионавигационные системы с использованием ИСЗ 484
Литература 492
Предметный указатель , . . 493
6
ПРЕДИСЛОВИЕ
Настоящая книга предназначена служить учебником
по курсу «Радиотехнические системы». В соответствии
с программой, утвержденной Министерством высшего и
среднего специального образования СССР в 1965 г. для
специальности «Радиотехника», в курсе ’изучаются тео¬
ретические основы 1И ’принципы построения систем радио¬
локации, радионавигации и 'радиоуправления, которые
связаны общностью решаемых задач и используемых ме¬
тодов получения и обработки информации. Таким обра¬
зом, содержанием книги является рассмотрение радио¬
технических методов и систем определения местоположе¬
ния и параметров движения объектов.
При построении курса имелось в виду наличие в учеб¬
но м пл ан е сп е ци ал ьности «Ра ди отех ни ка » отдел ын ы х
курсов «Телевидение» и «Системы передачи информа¬
ции», в которых изучаются соответствующие системы,
а также курсов «Импульсная техника», «Основы автома¬
тики» и «Основы вычислительной техники», предшеству¬
ющих курсу «Радиотехнические системы».
Учебник подготовлен коллективом преподавателей
кафедры радиосистем Ленинградского ордена Ленина
электротехнического института им. В. И. Ульянова
(Ленина).
Главы 1, 2, 3, 5, 6 и 7 написаны Ю. М. Казариновым;
глава 4 — Ю. А. Коломенским; главы 8 и 10 —
В. И. Шломиным; главы 11 и 12 — Ю. К. Пестовым
(§ 12.5 написан В. П. Васильевой); глава 13 — С. В. То¬
локонниковым; глава 9 написана совместно Ю. М. Ка¬
зариновым и С. В. Толоконниковым.
Т
Авторы весьма признательны коллективу преподава¬
телей кафедры радиосистем Рязанского радиотехниче¬
ского института и проф., д. т. и. IO. С. Лезину за крити¬
ческие замечания и советы, высказанные при рецензи¬
ровании рукописи.
Глава 1
КРАТКАЯ ХАРАКТЕРИСТИКА МЕТОДОВ
И СИСТЕМ РАДИОЛОКАЦИИ И
РАДИОНАВИГАЦИИ
§ 1.1. ОСНОВНЫЕ ПОНЯТИЯ и ОПРЕДЕЛЕНИЯ
Как указано в предисловии, содержанием книги явля¬
ется (Изучение радиотехнических методов и систем опре¬
деления местоположения и параметров движения объек¬
тов. Под объектами понимаются летательные аппараты,
ракеты, корабли или любые другие неподвижные или
движущиеся объекты, параметры движения которых из¬
меряются радиотехническими средствами, т. е. с помо¬
щью электромагнитных воли.
В общем случае мгновенное положение объекта в про¬
странстве характеризуется тремя координатами х, (7 =
= 1, 2, 3) в той или другой системе координат. Для ха¬
рактеристики движения объекта необходимы также про¬
изводные координат х\п), число которых зависит от
сложности траектории движения объекта. В абсолютном
большинстве случаев практики используют производные
порядка не выше второго, т. е. скорость объекта Vi = Xi и
ускорение ai = xi. При этом имеют в виду координаты и
их производные для центра тяжести объекта. В боль¬
шинстве радиотехнических систем непосредственно из¬
меряются собственно координаты, a их производные по¬
лучаются последующим дифференцированием с помощью
специальных устройств. Применяются также системы,
позволяющие непосредственно измерить составляющую
о гное и тел ь но й с кор ости объекта, 11 е р 11 ен ди куля р и у ю
фронту электромагнитной волны. Скорость измеряется
в таких системах допплеровским смещением частоты
сигнала, поэтому их принято называть допплеровскими.
Интегрированием скорости можно получить координату
объекта, а дифференцированием — его ускорение. Из чи-
9
ела систем, обеспечивающих получение 'информации
о движении объектов, важнейшее значение имеют радио¬
локационные и радионавигационные системы.
Радиолокацией называют отрасль техники, охватыва¬
ющую радиотехнические методы и средства обнару¬
жения, определения координат и параметров движения
различных объектов * с помощью отражения, переизлу-
чения или излучения ими радиоволн.
Процесс обнаружения объектов, измерения 'их коор¬
динат и параметров движения называют обычно радио¬
локационным наблюдением (иногда просто радиолока¬
цией), а устройства, используемые для этой цели,—ра¬
диолокационными станциями (РЛС) или радиолокато¬
рами **.
Радионавигация — наука о вождении кораблей, само¬
летов и других объектов с помощью радиосредств.
Таким образом, радиолокация и радионавигация тес¬
но связаны общностью основной решаемой ими задачи—
определением координат объекта. Во многих случаях
РЛС используются для решения чисто навигационных
задач.
Тесно связано с радионавигацией также и радиоуп¬
равление — отрасль техники, охватывающая радиотехни¬
ческие методы и средства управления движением бес¬
пилотных объектов. Совокупность устройств, осуществ¬
ляющих наведение беспилотного объекта в заданную
точку пространства с использованием радиосредств, на¬
зывается системой радиоуправления. В радиоуправлении
широко используются радиолокационные методы.
В зависимости от природы возникновения электро¬
магнитного излучения, доставляющего информацию об
объекте радиолокационното наблюдения и -называемого
радиолокационным сигналом, различают активную, .по¬
лу активную, активную с активным ответом и пассивную
радиолокацию.
В случае активной радиолокации сигнал, принимае¬
мый приемником РЛС, создается в результате отраже-
* В радиолокации обнаруживаемые объекты часто называют
целями.
** В американской и английской литературе для радиолока¬
ции и радиолокационных станций принято название Radar (Radio
detection and ranging) — радиообнаружение и определение расстоя¬
ния.
Ю
ния объектом электромагнитных колебаний, излучаемых
антенной РЛС. Сигнал, излучаемый РЛС, называется
прямым или зондирующим, а принимаемый приемником
станции — отраженным. Таким образом, активную ра¬
диолокацию отличает наличие передатчика в составе
РЛС и использование отраженного сигнала (рис. 1.1,а).
При полуактивной радиолокации носителем информа¬
ции является также сигнал, отраженный объектом, но
I
РАС
Прямой согнал
Отраженный
сигнал
/ Отра- \
у жающий ;
объект J
I
РЛС
РАС
Прямой (запросный)
сигнал
Переизлучаю-
щий объект
Переизлученный
(отдетный)
сигнал
Рис. 1.1. Методы радиолокации:
« — активный; б — активный с активным ответом; в — пассивный.
п)
источник электромагнитных колебаний, облучающих
объект, вынесен относительно приемного устройства РЛС
и может быть с ним вообще не связан. Передающее
устройство, облучающее цель, может быть расположено,
например, на земле или корабле, а приемное, обнаружи¬
вающее отраженный сигнал,—на ракете, направляемой
на цель.
Возможность обнаруживать объекты, не являющиеся
источниками радиоизлучения, — большое достоинство ак¬
тивного и полуактивного методов радиолокации.
В случае активной радиолокации с активным ответом
используется сигнал, ретранслируемый специальным
приемопередатчиком (ответчиком), установленным на
объекте (рис. 1.1,6). Приемник ответчика принимает сиг¬
нал РЛС, который вызывает излучение ответного сигна¬
11
ла, генерируемого передатчиком ответчика. Ответный
сигнал может иметь мощность, значительно большую,
чем отраженный, поэтому применение активного ответа
позволяет существенно повысить дальность действия си¬
стемы. Кроме того, ответный сигнал может быть исполь¬
зован для передачи дополнительной информации с объ¬
екта. С помощью ответчика решается, например, задача
опознавания объекта, т. е. отличия «своих» самолетов
или кораблей от «чужих». Принцип активного ответа
широко используется в радионавигации и радиоуправле¬
нии.
В пассивной радиолокации сигналом является есте¬
ственное излучение объектов в радиодиапазоне преиму¬
щественно теплового происхождения, поэтому пассивная
радиолокация иногда называется радиотеплолокацией.
Таким образом, в пассивной радиолокации, так же как и
в активной, для обнаружения объектов и определения
их координат используется радиосигнал. Но специфика
сигнала не позволяет использовать в пассивной радио¬
локации опорный сигнал, что исключает возможность
определения дальности объекта одноканальной пассив¬
ной РЛС. В этом случае возможно определить лишь
направление (пеленг) на объект, т. е. осуществить ра-
диопелентование. Поэтому пассивная радиолокация тес¬
но смыкается с радиопеленгацией — отраслью радиона¬
вигации, изучающей вопросы, связанные с определением
направления на объекты, имеющие источники радиоиз¬
лучения.
§ 1.2. ФИЗИЧЕСКИЕ ОСНОВЫ РАДИОЛОКАЦИИ
Основой радиолокационного обнаружения объекта,
определения координат и их производных, а возможно,
и некоторых других характеристик (размеров, формы,
физических свойств) объекта является радиосигнал, от¬
ражаемый, переизлучаемый или излучаемый объектом
наблюдения.
В активной радиолокации источником электромагнит¬
ных колебаний является передающее устройство РЛС.
Но электромагнитные колебания становятся носителем
информации об объекте, т. е. радиолокационным сигна¬
лом лишь после их отражения объектом наблюдения.
Электромагнитные колебания зондирующего сигнала
кроме облучения объекта для создания отраженного или
12
ответного сигналов используются также в качестве опор¬
ных при измерении параметров, характеризующих обна¬
руженный объект. При этом используется свойство ра¬
диоволн распространяться в однородной среде прямоли¬
нейно и с постоянной скоростью. Скорость распростра¬
нения радиоволн зависит от электрических свойств среды
и составляет в свободном пространстве (вакууме) с =
= 299 793 км!сек. Там, где это не вызывает существенных
ошибок, обычно используют приближенное значение ско¬
рости с = 3 • 105 км!сек.
Посто янство скор ости и п р я молнией ноет ь р асп рост-
ранения радиоволн позволяют определить дальность D
от РЛС до объекта измерением времени прохождения
сигнала tD от РЛС до объекта и обратно:
Свойство п р я моли ней ности р асп ростр анен и я р а ди о -
волн является основой радиометодов непосредственного
определения угловых координат по направлению прихо¬
да сигнала от объекта. При этом в том или ином виде
используются направленные свойства антенн.
От вида и параметров зондирующего сигнала зависят
основные характеристики РЛС: дальность действия, точ¬
ность определения координат и скорости объектов, раз¬
решающая способность станции, т. е. в конечном счете
объем информации, который может быть извлечен при
обработке радиолокационного сигнала.
В зависимости от предъявляемых к системе требова¬
ний может быть использована амплитудная, частотная
или фазовая модуляция излучаемого сигнала, а иногда
и их комбинация. В общем случае напряжение модули¬
рованного сигнала можно записать в комплексной форме
« (0 = а (0>*Р {/ [«>0^ + <Р (0 + ?о]}, (1 -2)
где функция описывает закон амплитудной моду¬
ляции;
Ф (/) —закон фазовой модуляции;
dm (t)
~ =Ы —закон частотной модуляции;
<оо—несущая частота колебаний;
фо — начальная фаза излучаемых колебаний.
13
Под зондирующим обычно понимают сигнал после из¬
лучении а 11 т ей 11 о й, и о э то м у м о д у л я ш i я с 11 г 11 а ла оказы¬
вается связанной также -с параметрами антенной систе¬
мы. Например, при перемещении диаграммы направлен¬
ности антенны относительно направления на объект
амплитуда сигнала изменяется, т. е. появляется допол¬
нительная амплитудная модуляция, определяемая шири¬
ной и формой диаграммы направленности, а также ско¬
ростью ее перемещения относительно направления на
объект.
Антенная система определяет также поляризацию
зондирующего сигнала. В современных РЛС применяет¬
ся излучение линейно-поляризованных (горизонтально и
вертикально) сигналов и сигналов с круговой поляриза¬
цией.
Если объект попадает в зону облучения РЛС, соз¬
дается отраженный 'или переизлученный (при наличии
ответчика) сигнал, несущий информацию об объекте.
Прием сигнала свидетельствует об обнаружении объек¬
та, а амплитуда, фаза, частота, вид поляризации и на¬
правление прихода сигнала позволяют определить коор¬
динаты и параметры движения объекта; при наличии
нескольких объектов—разделить их, выделить объект
с определенными свойствами и т. д.
Так, амплитуда сигнала и ее изменения во времени
содержат информацию о размерах и некоторых физиче¬
ских свойствах обнаруженного объекта (например, ко¬
эффициенте отражения), о его движении и дальности.
Практическое значение имеет статистический анализ
флюктуаций амплитуды отраженного сигнала, позволя¬
ющий в ряде случаев установить вид, размеры и харак¬
тер движения объекта. Анализ флюктуаций дает возмож¬
ность выделить сигнал одного объекта среди сигналов
других объектов, в частности ложных, используемых
противником для маскировки таких объектов, как кораб¬
ли, самолеты, ракеты.
Для определения дальности амплитудная информа¬
ция не используется, так как амплитуда отраженного
сигнала в сильной степени зависит от размеров и фор¬
мы объекта, направления облучения и условий распро¬
странения.
При использовании активного ответа ответный сиг¬
14
нал может быть промодулнрован но амплитуде для пере¬
дачи необходимой информации с объекта на РЛС.
В пассивной радиолокации амплитуда принимаемого
сигнала дает возможность судить о некоторых свойст¬
вах объекта, (излучающего сигнал. В частности, на экра¬
не самолетной пассивной РЛС можно получить своеоб¬
разное изображение земной поверхности благодаря раз¬
личию интенсивности радиоизлучения ее отдельных уча¬
стков в зависимости от их физических свойств.
Как указывалось выше, определение дальности объ¬
екта основано на измерении пропорционального ей вре¬
мени между излучением зондирующего сигнала и прие¬
мом отраженного или переизлученного. Для оценки это¬
го времени может быть использовано сравнение фазы,
частоты или непосредственно временного положения
(в зависимости от вида, модуляции) принимаемого и зон¬
дирующего сигналов.
При относительном перемещении РЛС ;н объекта ча¬
стота отраженного (или ответного) сигнала изменяется
в силу эффекта Допплера на величину Fv, пропорцио¬
нальную радиальной составляющей относительной ско¬
рости Vr. С учетом двустороннего распространения сиг¬
нала в случае активной радиолокации допплеровское
смещение частоты равно
где Zo — длина волны излучаемых РЛС колебаний.
Измерение допплеровского смещения позволяет непо¬
средственно определить радиальную составляющую ско¬
рости объекта относительно РЛС
2
Таким образом, скорость объекта может быть опре¬
делена при излучении немодулированного сигнала.
Анализ поляризации отраженного сигнала также по¬
зволяет извлечь некоторую информацию об объекте, по¬
скольку изменение поляризации при отражении сигнала
связано с формой и размерами объекта.
Полезная информация, которую доставляет прини¬
маемый сигнал, выделяется при его обработке в прием¬
ном и оконечном устройствах радиолокационной или дру-
15
гой радиотехнической системы. Эта задача усложняется
наличием естественных или искусственно создаваемых
противником помех. Помехи могут вызвать искажение
сигнала, его пропуск или образование ложного сигнала,
т. е. ведут к потере полезной информации, несомой сиг¬
налом. В процессе обработки сигнала стремятся пода¬
вить помехи и сохранить полезную информацию. Проце¬
дура обработки должна быть согласована не только с ти¬
пом сигнала, но и с видом помех.
Рис. 1.2. Радиолокационный канал.
С учетом помех взаимодействие блоков РЛС, объек¬
та наблюдения и источников помех может быть пред¬
ставлено в виде блок-схемы на рис. 1.2.
Си i н х ро ни з а тор об ес п еч ив а е т зада и 11 у ю л оследо в а-
тельность работы блоков РЛС. В частности, в наиболее
распространенных РЛС с импульсной модуляцией см.и-
х р они з а тор оп р ед ел я ет м о м ент ф о р мир о в ани я мо дули -
рующих импульсов модулятором и излучения зондирую¬
щих импульсов антенной (в импульсных РЛС обычно ис¬
пользуется одна антенна, которая антенным переклю¬
чателем автоматически подключается к передатчику на
время излучения импульса). Синхронизатор управляет
работой оконечного устройства, может открывать (стро¬
бировать) приемный канал в определенный момент и на
заданный интервал времени.
Приемное устройство осуществляет усиление, преоб¬
разование, фильтрацию и детектирование сигнала.
Дальнейшая обработка сигнала с целью извлечения по¬
лезной информации из смеси сигнала и помех осуществ-
16
л я етс я о к ом е иным у стр о йст в о м. О ko i i с ч и о с у с т р о йс тво
решает также задачу определения координат и парамет¬
ров движения объекта на основе анализа выделенного
сигнала.
Тип и построение оконечного устройства зависят как
от .вида сигнала и извлекаемой информации, так и от
получателя информации. Если получателем информации
является оператор, то в качестве оконечного устройства
обычно применяется индикатор с электроннолучевой
трубкой (ЭЛТ). При непосредственном вводе информа¬
ции в вычислительное устройство аналогового или ци¬
фрового типа оконечным устройством является соответ¬
ственно аналоговая или цифровая система автоматиче¬
ского съема координат.
Построение радиолокационной или радионавигацио.н-
ной системы и выбор их характеристик зависит от ис¬
пользуемых методов определения местоположения, ко¬
торые рассматриваются в следующем параграфе.
§ 1.3. ОСНОВНЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ
МЕСТОПОЛОЖЕНИЯ
Для определения местоположения объекта в прост¬
ранстве необходимы дри координаты. В навигации для
характеристики местоположения используется понятие
о поверхностях и линиях положения. Под поверхностью
положения понимают геометрическое место точек, имею¬
щих постоянную координату * относительно опорного
пункта. Так, если сохраняется постоянной дальность D
до опорного пункта, то поверхностью положения будет
сфера с радиусом, равным D. Пересечение двух поверх¬
ностей положения дает линию положения. Таким обра¬
зом, для определения липин положения объекта необхо¬
димы две координаты. Точка определяется пересечением
трех поверхностей положения пли линии положения и
поверхности положения. Форма поверхности положения
определяется видом измеряемой координаты. Непосред¬
ственно измерены радиотехническими методами могут
быть дальность до опорного пункта D, разность дальне-
* Точнее — постоянный навигационный параметр, т. е. пара¬
метр, непосредственно измеряемый радионавигационной системой.
2-1173
17
стей (D{—D2) до двух опорных пунктов и угловые коор¬
динаты объекта в горизонтальной (а) и вертикальной
(р) плоскостях.
В соответствии с видом измеряемых координат раз¬
личают три основных метода определения местоположе¬
ния объекта: угломерный, дальномерный и разностно¬
дальномерный. Широко используется, особенно в радио¬
локации, комбинированный угломерно-дальномерный ме¬
тод.
Рассмотрим кратко эти методы определения место¬
положения объекта.
Рис. 1.3. Угломерный метод определения местоположения.
РП — радиопеленгатор; РМ — радиомаяк.
Угломерный метод. Для определения направления ис¬
пользуются направленные свойства антенны при приеме
или при передаче. В связи с этим применяются два вари¬
анта построения угломерных систем. В первом — приме¬
няемый радиоканал состоит из направленного приемни¬
ка (радиопеленгатора) и передатчика (радиомаяка)
с ненаправленной антенной. При расположениях пелен¬
гатора и маяка на поверхности земли (рис. 1.3,а) на¬
правление на маяк определяется пеленгом а. Если пе¬
ленг отсчитывается от географического меридиана (на¬
правления север — юг), то он называется истинным пе¬
ленгом или азимутом. Часто азимутом называют угол
в горизонтальной плоскости, отсчитанный от любого на¬
правления, принятого за нулевое. Определение направ¬
ления производится в точке расположения приемника,
18
который может быть как па земле, так и на борту объ¬
екта. В первом случае производится пеленгование объ¬
екта 'С земли, и при 'необходимости измеренное значение
передается на объект по каналу -связи. При расположе¬
нии радиопеленгатора на объекте пеленг на радиомаяк
/измеряется непосредственно на борту.
Во втором варианте угломерной системы (рис. 1.3,6)
используется ненаправленный приемник и радиомаяк
с направленной антенной. В этом случае в месте распо¬
ложения приемника измеряется так называемый обрат¬
ный пеленг а' относительно нулевого направления, при¬
вязанного к радиомаяку. Может быть использован, на¬
пример, радиомаяк с вращающейся характеристикой на¬
правленности антенны. В момент совпадения оси
диаграммы направленности с нулевым направлением
(например, северным) вторая — ненаправленная — ан¬
тенна радиомаяка излучает специальный нулевой сигнал,
который принимается приемником системы и является
началом отсчета. Фиксируя момент совпадения оси вра¬
щающейся диаграммы маяка с направлением на прием¬
ник (по максимуму сигнала), можно определить обрат¬
ный пеленг, который при равномерном вращении диа¬
граммы маяка будет пропорционален промежутку
времени между приемом нулевого сигнала и сигнала
в момент пеленга. В этом варианте системы приемник
упрощается, что является существенным преимуществом
при его расположении на борту.
Радиопеленгатор и маяк, расположенные в горизон¬
тальной плоскости, позволяют определить направление,
т. е. прямую линию, проходящую через точки располо¬
жения пеленгатора и маяка и являющуюся линией поло¬
жения. Для определения местоположения радиопеленга¬
тора необходим второй радиомаяк (рис. 1.3,в). Опреде¬
ляя два пеленга си и а2, можно найти местоположение
радиопеленгатора как точку пересечения двух линий по¬
ложения. Если система расположена в пространстве, то
для определения местоположения приемника необходим
третий радиомаяк. Каждая пара (пеленгатор — маяк)
позволяет определить лишь поверхность положения, ко¬
торая является в данном случае плоскостью. При опре¬
делении местоположения приемника предполагается, что
координаты радиомаяков известны.
2*
19
Дальномерный метод. Для измерения дальности
в дальномерной -системе (рис. 1.4) используются два
приемопередатчика — запросчик 3 и ответчик О. Пере¬
датчик запросчика излучает сигнал запроса, который
принимается через время, равное t^Djc, приемником
ответчика. Передатчик ответчика излучает ответный сиг¬
нал, который принимается приемником запросчика так¬
же через время, равное tQ=Dlc. Таким образом, если за-
Рис. 1.4. Дальномерный метод определения местоположения:
а — линия связи; б — определение положения с помощью запросчика и двух
ответчиков.
держка сигнала в цепях ответчика равна 0, то измеряе¬
мая запросчиком дальность определяется по формуле
где / = /3+Аь
Поверхностью положения дальномерной системы яв¬
ляется поверхность шара, радиус которого равен D. Ли¬
ниями положения в фиксированной плоскости будут
окружности, поэтому иногда дальномерные системы на¬
зываются круговыми. Для определения местоположения
объекта на плоскости необходимы запросчик на борту и
20
два 'Ответчика с известными координатами (рис. 1.4,6).
Положение объекта может быть определено также с по¬
мощью двух запросчиков на земле и ответчика на борту.
Местоположение объекта определяется при этом как
точка пересечения двух линий положения. Так как пере¬
сечение окружностей дает две точки пересечения, то для
ио к л ю ч ени я д в у з,н а чности дол ион ы ис по л ь зов а т ьс я до -
пол ни те л ьн ы е спосо б ы ориентиров а и и я, точно сть кото¬
рых может быть невысокой, но достаточной для выбора
одной из точек пересечения линий положения. В частном
случае запросчиком может быть РЛС, а в качестве от¬
ветного используется отраженный сигнал.
П ос кольку 11 з м ер ei in е времени рад и о т е х i iti ч ес к и мп
средствами может производиться с весьма малыми
о ши б к а м и, д а л ы ю м ер 11 ы е ci 1 с те м ы о б cci i е чч1 в а ю г высо¬
кую точность определения местоположения.
В самолетовождении ’иногда используется полет по
окружности с ответчиком в центре, которая носит на¬
звание линии равных расстояний. При нанесении на кар¬
ту окружностей разных радиусов D2, ..., Dn с общим
центром в точке расположения ответчика получается сет¬
ка линий положения, позволяющая легко определять ме¬
стоположение объекта непосредственно на географиче¬
ской карте.
Исторически радио дальномерные методы определе¬
ния местоположения начали применяться позже угло¬
мерных. Первые образцы радиодальномеров, основанные
на фазовых измерениях, разработаны в СССР под руко¬
водством Л. И. Мандельштама, Н. Д. Папалекси и
Е. Я. Щеголева в 1935—1937 гг. Импульсные радиодаль¬
номеры появились к началу второй мировой войны.
Разностно-дальномерный метод. В разностно-дально¬
мерной системе с помощью приеме индикатор а, располо¬
женного на борту объекта, определяется разность вре¬
мени приема сигналов от передатчиков двух опорных
станций А и В. Станция А называется ведущей, так как
ее сигналами осуществляется синхронизация работы ве¬
домой станции В. Измерение разности расстояний AD
позволяет определить лишь то, что объект расположен на
соответствующей поверхности положения, которая для
разностно-далытомерной системы имеет форму гипербо¬
лоида. Обычно можно считать, что приемом иди к а тор и
станции расположены в плоскости земли. В этом слу-
21
час измерение AD дает линию положения, являющуюся
гиперболой &D = Da—DB = const. Для данной нары стан¬
ций можно построить семейство гипербол с общими фо¬
кусами, в которых расположены станции А и В. Рас¬
стояние между станциями .называется базой d. Для за¬
данной базы сетка гипербол наносится на карту заранее
и оцифровывается.
Рис. 1.5. Определение местоположения объекта разностно-дально¬
мерным методом с помощью ведущей А и двух ведомых стан¬
ций Bi и В2.
Однако одна пара станций позволяет определить
только линию положения. Для определения местополо¬
жения необходима вторая пара станций, база которых
d2 должна быть расположена под углом к базе d\. Обыч¬
но ведущая станция является общей и синхронизирует
работу обеих ведомых станций В{ и В2. Сетка линий по¬
ложения такой системы (рис. 1.5) состоит из двух се¬
мейств пересекающихся гипербол. Точность разностно¬
дальномерной системы выше точности угломерной систе-
м ы. Но гл а-вн ы м пр ей м у ществ ом раз постно -дал ьн о м ер -
ной системы является ее неограниченная пропускная спо¬
собность, так как наземные станции могут обслуживать
любое число приемоиндикаторов, находящихся в преде¬
лах дальности действия системы.
Следует заметить, что асимптотами гипербол явля¬
ются прямые линии, проходящие через центр базы каж¬
дой пары станций системы. Таким образом, на расстоя-
22
ниях, в несколько раз превышающих длину базы, линии
положения вырождаются в прямые, и разностно-дально¬
мерная система может быть .использована как угломер¬
ная. В этом случае длина базы обычно выбирается рав¬
ной половине длины волны станций, и уже на небольших
расстояниях от базы гиперболы достаточно точно аппро¬
ксимируются прямыми.
Рис. 1.6. Определение местоположения объекта в пространстве угло¬
мерно-дальномерным методом.
Принцип ‘импульсной разностно-дальномерной систе¬
мы впервые был предложен советским инженером
Э. М. Рубчинским в 1938 г., но широкое распростране¬
ние такие системы получили в качестве средства даль¬
ней радионавигации лишь к концу второй мировой вой¬
ны, когда были разработаны методы точного измерения
временного положения импульсов. Первая разностно¬
дальномерная система, основанная на измерении разно¬
сти фаз (фазовый зонд), была разработана в СССР
в 1938 г. В дальнейшем этот принцип использован в ря¬
де систем.
Комбинированный угломерно-дальномерный метод.
Этот метод позволяет определить местоположение объ¬
екта из одной точки. Действительно, измерение дально¬
сти D определяет шаровую поверхность положения с ра¬
диусом, равным Z), а измерение углового направления
определяет местоположение объекта. Комбинированный
метод обычно используется в радиолокационных систе¬
мах, которые в общем случае определяют наклонную
дальность D, азимут а и угол места 0 (рис. 1.6). Углом
места называется угол между направлением на объект
23
и горизонтальной плоскостью Г. Азимут отсчитывается
от направления север — юг или другого -направления,
принятого за тачальное. Кроме основных координат D,
се и р иногда определяются также высота /г, горизон¬
тальная дальность Dr и ее проекции на направление се¬
вер— юг и восток — запад. Осуществляется это путем
пересчета основных координат.
Возможность определения местоположения из одной
точки и с помощью одной станции является большим
преимуществом комбинированного метода.
§ 1.4. ОСНОВНЫЕ ТАКТИЧЕСКИЕ И ТЕХНИЧЕСКИЕ
ХАРАКТЕРИСТИКИ РАДИОЛОКАЦИОННЫХ
И РАДИОНАВИГАЦИОННЫХ СИСТЕМ
Любая радиотехническая система характеризуется
большим числом тактических, технических и эксплуата¬
ционных параметров. Число и вид параметров системы,
которые включаются в тактико-техническую характери¬
стику, зависят от назначения системы. Среди них можно
выделить ряд основных, которые в той пли иной степени
могут быть отнесены к любой из систем.
Т актическим и называют х ар а ктер нети к и си сте м ы,
определяющие ее возможности при практическом (в ча¬
стности, боевом) мспользо'ва'ПИ1И.
К числу основных тактических характеристик РЛ и
PH систем относятся:
— зона действия (рабочая область) системы, опре¬
деляемая сектором обзора (поиска) по угловым коор¬
динатам и дальностью действия системы;
— время обзора (поиска);
— определяемые координаты и точность их измере¬
ния;
— разрешающая способность;
— пропускная способность;
— п о м е хо з а щ п щ е ш гос т ь;
— надежность;
— экономичность.
Поскольку эти параметры широко используются для
оценки различных систем, целесообразно рассмотреть их
общие определения, которые в дальнейшем могут быть
уточнены применительно к конкретным типам систем.
24
Зоной действия называется область пространства,
в которой система надежно выполняет функции, опре¬
деляемые ее назначением. Так, для РЛС обнаружения
зоной действия является область пространства, в кото¬
рой объекты обнаруживаются с заданной надежностью.
Для РЛС точного измерения координат и PH систем
границы зоны действия обычно определяются допусти¬
мыми ошибками местооп'ределения при заданном уров¬
не помех. Таким образом, определение зоны действия
3aiB.noит от назначения системы. Одним из параметров,
определяющих зону действия, является дальность дейст¬
вия системы.
Под дальностью действия обычно понимают макси¬
мальное расстояние, на котором еще обеспечивается по¬
лучение заданных показателей системы. Чаще всего ма¬
кси м а л ь н а я да л ьност ь действи я си сте м ы о пр ед ел я етс я
допустимой величиной ошибок при измерении парамет¬
ров движения объекта 'или управлении его движением.
Под дальностью действия РЛС обнаружения имеют в ви¬
ду максимальную дальность, на которой сигнал требуе¬
мой интенсивности обнаруживается на фоне шумов с за¬
данной вероятностью.
Иногда дальность действия системы ограничена и со
стороны минимума. В этом случае система характеризу¬
ется двумя параметрами: минимальной £>мии и макси¬
мальной Рмакс дальностью действия.
Временем обзора (поиска) называют время, необхо¬
димое для однократного обзора заданной зоны действия
системы. Выбор времени обзора связан с маневренно¬
стью наблюдаемых или управляемых объектов, объемом
пространства поиска, а также с рядом других тактиче¬
ских и технических характеристик системы.
Число измеряемых координат, так же как и точность
их измерения, определяют возможности системы при ее
пр а кти ч ее ко м ис пользован ни.
Точность характеризуется величиной ошибок при из¬
влечении информации, несомой сигналом. Причинами
ошибок являются несовершенство применяемого метода
и аппаратуры, влияние внешних условий и радиопомех,
субъективные качества оператора, если процессы полу¬
чения и реализации информации не автоматизированы.
Требования к точности определяются назначением си¬
стемы. Неоправданно завышенные требования к точно-
25
•сти приводят к усложнению системы, что отрицательно
сказывается на показателях экономичности и надежно¬
сти системы и, следовательно, нецелесообразно.
Разрешающей способностью системы называют спо¬
собность раздельного измерения параметров двух близ¬
ко расположенных в пространстве объектов или раз¬
дельного управления их движением. Соответственно раз¬
личают разрешающую способность по дальности и угло¬
вым координатам, а также по соответствующим состав¬
ляющим скорости и ускорения объектов.
Разрешающую способность принято оценивать непо¬
средственно минимальной разностью измеряемых пара¬
метров двух объектов, при которой они разрешаются си¬
стемой. Для многих случаев практического использова¬
ния систем разрешающая способность является харак¬
теристикой первостепенной важности.
Пропускная способность системы определяется ма¬
ксимальным числом объектов, обслуживаемых системой.
Пропускная способность зависит как от назначения и по¬
строения системы, так и от ее основных параметров:
точности, разрешающей способности и дальности дейст¬
вия, а также уровня помех.
Помехозащищенностью радиотехнических систем на¬
зывается способность надежно работать в условиях есте¬
ственных и организованных помех. Помехозащищенность
определяется помехоустойчивостью системы и скрытно¬
стью ее работы. Помехоустойчивостью называется спо¬
собность системы сохранять основные параметры в за¬
данных пределах при воздействии помех определенного
т ипа. По м ехоусто й чи в ость опр ед ел я етс я р а цион а л ьн ы м
выбором технических параметров и построением си¬
стемы.
Под скрытностью системы понимают качественный
показатель, характеризующий трудность обнаружения ее
работы и определения основных характеристик сигнала,
а следовательно, и создания специально организованных
(прицельных) помех. Скрытность обеспечивается приме¬
нением остронаправленного излучения, сокращением вре¬
мени работы и полосы частот сигнала, изменением основ¬
ных параметров сигнала во времени.
Под надежностью, в широком смысле, понимают спо¬
собность системы сохранять рабочие характеристики
в заданных пределах при определеных условиях эксплуа-
26
тации. В этом смысле помехозащищенность также вхо¬
дит в определение надежности. В последнее время поня¬
тие надежности стало более определенным и получило
количественную оценку в виде вероятности исправной
(безотказной) работы.
Надежность определяется выбранным методом реше¬
ния задачи, построением системы, принципиальной схе¬
мой устройств, входящих в нее, количеством и качеством
узлов и деталей, конструкцией устройства, качеством из¬
готовления, сборки и регулировки, наличием резервного
обо р удо в ан и я, в ыпо л не н и е м тр еб о в аний эксплуатации
и т. д.
Экономичность радиотехнического оборудования оце¬
нивается стоимостью затрат на его производство и экс¬
плуатацию. При такой оценке должны учитываться мно¬
гочисленные факторы, влияющие на стоимость решения
поставленной задачи. Так, применительно к бортовому
радионавигационному оборудованию самолета, оценива¬
ется стоимость всего навигационного комплекса с уче¬
том эксплуатационных расходов. Учитывается также
стой мост ь тр ан сп орти ров ки каждого килограмма в еса
аппаратуры и обслуживающего персонала, потери аэро¬
динамических качеств самолета из-за выступающих ча¬
стей системы (антенны, обтекатели), потери возможности
перевозки полезного груза, эквивалентного весу аппара¬
туры, и обслуживающего персонала и др.
Таким образом, оценка экономичности системы пред¬
ставляет трудную задачу. Однако в связи со все расши¬
ряющимся применением радиотехнических систем, уве¬
личением их относительной стоимости экономические со¬
ображения приобретают все большее значение и долж¬
ны всесторонне взвешиваться при проектировании радио¬
технических систем с учетом их взаимодействия с дру¬
гими системами, обеспечивающими выполнение общей
задачи.
К основным техническим характеристикам системы
относятся параметры, непосредственно определяющие ее
основные тактические характеристики.
К числу основных технических характеристик РЛ и
PH систем относятся:
— метод измерения дальности и радиальной скоро¬
сти движения объектов;
27
— метод обзора пространства л метод измерении
у гл о в ы z\ коо'рдатн а т;
— тип о конечно го устройства;
— длина волны или несущая частота излучаемых ко¬
лебаний;
— мощность излучаемых колебаний;
— вид модуляции излучаемых колебаний;
— форма и ширина диаграммы 'направленности ан-
т ei 111 ы в .в ер т.п калы го й 11 гo>p i 1 зон гт а л ы io й ’ плоскостях,
а также се коэффициент нап<ра1вленпости;
— чувствительность и полоса пропускания, а также
форма частотной и амплитудной характеристик прием¬
ного устройства;
— габариты и вес устройств, составляющих систему,
а также мощность, потребляемая от источника питания.
В последующих параграфах более подробно рассма¬
триваются основные технические характеристики РЛС,
их взаимосвязь между собой и с основными тактически¬
ми характеристиками станции. Наиболее наглядно такую
связь можно показать на примере зависимости дально¬
сти действия активной РЛС от ее технических парамет¬
ров.
§ 1.5. ОСНОВНОЕ УРАВНЕНИЕ ДАЛЬНОСТИ
РАДИООБНАРУЖЕНИЯ
Основным уравнением дальности радиообнаружения
(основным уравнением радиолокации) называют урав¬
нение, связывающее максимальную дальность действия
активной РЛС с ее основными параметрами и отражаю¬
щей способностью объекта, при условии, что станция и
объект расположены в так называемом свободном про¬
странстве, т. с. когда в зоне действия станции нет дру¬
гих отражающих объектов и источников излучения, кро¬
ме обнаруживаемого объекта и передатчика РЛС.
Если в точке О расположена антенна РЛС, а в точке
М на расстоянии D от станции находится отражающий
объект (рис. 1.7), то плотность потока мощности в месте
расположения объекта (который в радиолокации назы¬
вается целью) будет равна
г-Т РИ б II
28
где Рп — мощность ’излучения станции;
Gu — коэффициент направленности передающей ан¬
тенны в направлении цели.
При облучении цель становится вторичным излуча¬
телем и часть рассеянной ею энергии принимается при¬
емником станции в виде сигнала, позволяющего обнару¬
жить цель и определить се координаты. Свойства цели
как вторичного излучателя характеризуют параметром
сгэ, называемым эффективной площадью рассеяния цели.
Рис. 1.7. К определению даль¬
ности действия РЛС.
Эффективной площадью рассеяния цели называют
площадь поперечного сечения такой воображаемой це¬
ли, ’которая рассеивает всю падающую на нее энергию
изотропно, т. е. равномерно во всех направлениях, и при
этом создает в приемнике такой же сигнал, как и реаль¬
ная цель.
При эффективной площади рассеяния ап мощность
отраженного сигнала будет сьП\, а .плотность потока
мощности, создаваемая им в месте расположения антен¬
ны РЛС:
Т-Т
(4л)2/л’’
При эффективной площади приемной антенны А мощ¬
ность отраженного сигнала на входе приемника будет
О Л ГТ РцСкА^о
ГС—/Н12— (471)2£)4 .
Если решить это уравнение относительно D, то полу¬
чается выражение
°=Г^Г с-3)
которое носит название уравнения радиолокатора в сво¬
бодном пространстве или основного уравнения радиоло¬
кации.
29
Наибольший интерес представляет уравнение для ма¬
ксимальной дальности, на которой еще возможно обна¬
ружение цели с эффективной площадью рассеяния ст:)
при заданных параметрах станции:
Мощность .порогового сигнала РСмип зависит от ряда
факторов, и в частности от выбранного критерия обна¬
ружения. Этот вопрос будет рассмотрен несколько позже.
§ 1.6. МЕТОДЫ ИЗМЕРЕНИЯ ДАЛЬНОСТИ
Определение дальности в дальномерных системах сво¬
дится к измерению временного запаздывания tD, пропор¬
ционального дальности D, в соответствии с формулой
tD=D!c при непосредственном приеме излученного сиг¬
нала или соотношением tD = 2DIс при приеме излученно¬
го сигнала после его отражения или переизлучения объ¬
ектом.
В зависимости от вида используемого сигнала оцен¬
ка временной задержки tD производится измерением фа¬
зового, частотного или непосредственно временного сдви¬
га принимаемого сигнала относительно опорного. Соот¬
ветственно различают фазовый, частотный и импульс¬
ный (временной) методы измерения расстояний. Воз¬
можно также комбинированное применение импульсно¬
го и фазового методов или 'импульсного и частотного.
Те же методы применяются в разностно-дальномер¬
ных системах для измерения временного смещения сиг¬
налов ведомых станций относительно сигнала ведущей.
Рассмотрим коротко фазовый, частотный и импульс¬
ный методы измерения временных интервалов.
Фазовый метод. Для пояснения фазового метода из¬
мерения дальности используем упрощенную блок-схему
фазового дальномера (рис. 1.8).
Мерой дальности здесь является фазовый сдвиг ср^ =
= (0m*/d колебаний принимаемого сигнала относительно
колебаний генератора масштабной частоты (ом,
«2 У,П2 SIH JoM (/ — tj <j>M — ?д — ?от].
где срм — начальная фаза масштабных колебаний;
<Рд — фазовый сдвиг в цепях дальномера;
30
Фот — фазовый 'Сдвиг масштабных колебаний в цепях
ответчика или при отражении объектом.
Разность фаз напряжения и2 и равна
фр ='(Md + фд + ф'от,
отсюда
_ ур _ у., _ уот _2Р
D С
и, следовательно,
п_ с (fp — Уд —‘Рот)
2<ом
(1.5)
Если фазовые сдвиги фд и фът известны или могут быть
измерены, то 'расстояние D может быть определено по
формуле (1.5) при измерении разностной фазы фр фазо¬
метром.
Рис. 1.8. Блок-схема фазового дальномера.
Масштабный генератор может быть как задающим
генератором несущей частоты, так и модулятором. Соот¬
ветственно различают системы, измерения дальности на
высокой частоте и на частоте модуляции. Кроме того,
применяются разновидности дальномерных систем с из¬
мерением фазы на частоте биений колебаний вспомога¬
тельных частот.
Простейшая фазовая система с измерением дально¬
сти непосредственно на несущей частоте обеспечивает
однозначное измерение дальности лишь до половины
длины волны излучаемых колебаний Вмакс^^/2, когда
выполняется условие однозначного измерения фазового
сдвига фр^2л. Даже на сверхдлинных волнах, иногда
используемых в радионавигации, это условие о грани чм-
* 31
вает пределы однозначного измерения расстояния такой
системой несколькими километрами.
В фазовых системах с измерением разности фаз на
частоте модуляции выполнение условия однозначности
обеспечивается применением низкочастотных модулиру¬
ющих колебаний, а в системах с измерением разности
фаз на частоте биений—использованием двух вспомога¬
тельных частот <01 и (02 и измерением разности фаз на
разностной частоте (op = (Oi—(02, которая выбирается до¬
статочно низкой для удовлетворения условия однознач¬
ности на максимальной дальности
С
2D
макс
ИЛИ
гамаке
Следует заметить, что при понижении масштабной ча¬
стоты точность измерения дальности (при сохранении
той же погрешности фазометра) понижается. Поэтому
в фазовых системах используется обычно несколько
масштабных частот, т. е. применяется многошкальный
метод, хорошо поясняемый :на примере часов, имеющих
шкалы: часовую, минутную и секундную. Применитель¬
но к системе измерения дальности на частоте биений
этот метод сводится к использованию нескольких вспо¬
могательных частот (01, (о2, (Оз, • • •, позволяющих полу¬
чить ряд разностных частот (opi, (оР2, ..на которых и
производятся последовательно все более точные измере¬
ния дальности.
Фазовые системы с непрерывным излучением не об¬
ладают разрешающей способностью по дальности. Кро¬
ме того, при работе по отраженному сигналу разделение
прямого и отраженного сигналов возможно лишь в слу¬
чае движущегося объекта, когда частота принимаемого
сигнала отличается от частоты излучаемого на величину
допплеровского смещения, пропорционального радиаль¬
ной скорости объекта, что и используется для разделения
сигналов. Допплеровский эффект может быть использо¬
ван также для разрешения двух объектов, если они име¬
ют различные радиальные скорости, а следовательно, и
различные допплеровские смещения, которые разделя¬
ются фильтрами.
Для разделения прямого и отраженного сигналов и
для устранения неоднозначности в фазовых дальномерах
иногда прибегают к периодической манипуляции часто-
32
ты, фазы пли амплитуды излучаемых колебаний. Такие
системы позволяют измерять дальность до неподвижных
объектов, но сохраняют основной недостаток фазовых
систем: отсутствие разрешения ио дальности, так как
/отраженные сигналы двух или большего числа объектов,
налагаюсь, образуют на входе приемника дальномера
сложный результирующий сигнал, из которого невозмож¬
но выделить сигналы, соответствующие отдельным объ¬
ектам, за исключением случая, когда амплитуда сигнала
какого-либо из объектов значительно превышает все дру¬
гие. Разрешение по дальности обеспечивается примене¬
нием импульсного и частотного методов измерения даль¬
ности.
Частотный метод. Применение частотной модуляции
(ЧМ) излучаемого сигнала позволяет осуществить даль¬
номер с непрерывным излучением, обладающий разре¬
шающей способностью по дальности. При этом сохраня¬
ется возможность измерения скорости движения объек¬
тов.
Определение дальности ЧМ радиодальномером сво¬
дится к измерению изменения частоты излучаемых коле¬
баний за время распространения сигнала до объекта и
обратно.
Бели частота излучаемых колебаний /и изменяется
dfn
непрерывно по линейному закону со скоростью у =
то приращение частоты излучаемых колебаний зг1 время
распространения сигнала tD=Wlc будет равно
Измеряя разность частот излучаемых и принимаемых
колебаний Fd=--M^ определим дальность объекта:
о-6)
Однако 1пепрерывное изменение частоты по линейному
закону практически не осуществимо, поэтому приходит¬
ся применять периодическую модуляцию частоты, что
вносит существенные особенности в работу системы.
Практически находят применение два вида модуляции:
пилообразная и синусоидальная.
Рассмотрим работу частотного дальномера в случае
симметричной пилообразной модуляции. Блок-схема
3—1173 33
дальномера включает элементы, изображенные па
рис. 1.9. Работу дальномера при неподвижном объекте,
расположенном на расстоянии £>, поясняет временная
диаграмма на рис. 1.10. Верхний график диаграммы изо¬
бражает изменение частоты излучаемых и принимаемых
(пунктирная линия) колебаний, имеющих среднюю ча¬
стоту /0, период модуляции Гм и девиацию частоты W.
Частот¬
ный
модулятор
Г еиератир
высокой
Частоты
1
1
1
i
Объект
Индика¬
Усилитель
Усилитель
/
тор даль¬
Часто¬
напряжения
высокой
ности
томер
биений
частоты и
гтг
детектор
Рис. 1.9. Блок-схема частотного радиодальномера.
Ниже изображен закон изменения разностной частоты
биений Fd. При выполнении условия FD^>F^=\/T^ мож¬
но записать:
/и = /о-Ь V— /оН Л
1 м
fc=-h + i(t — tD)=f0+^-(t —
Р » с w г>
— fc~TKcD'
Выражение для FD не учитывает уменьшения часто¬
ты биений до 0 (провалы кривой FD) при равенстве ча¬
стот излучаемых и принимаемых колебаний. Фактиче¬
ски частотомер фиксирует среднюю частоту биений за
период модуляции
TKcD\ Тм )'
Обычно выполняется условие В этом случае
FDw~FD и, следовательно,
1 4WTM 4U7
Напряжение биений, полученное на выходе детекто¬
ра, после усиления подается на частотомер, который гра¬
дуируется непосредственно в единицах дальности.
84
В качестве частотомера применяются счетчики им¬
пульсов, а также анализ а торы спектра последовательно¬
го и параллельного типа.
Рис. 1.10. Временная диаграмма частотного радиодаль¬
номера.
Импульсный метод измерения дальности. Идея им¬
пульсного метода чрезвычайно проста и наглядна. При
передаче дальномер излучает кратковременный импульс
высокочастотных колебаний, которые, распространяясь,
достигают объекта и отражаются или переизлучаются
им. Отраженный или переизлученный сигнал принима¬
ется приемным устройством дальномера и после усиле¬
ния и детектирования подается на оконечное устройство,
позволяющее измерить запаздывание принятого сигнала
относительно излученного.
Рис. 1.11. Измерение дальности импульсным методом.
3
35
Если задержки сигнала в ответчике и приемном трак¬
те дальномера пренебрежимо малы или точно известны и
могут быть учтены, измерение времени запаздывания tD
позволяет непосредственно определить дальность:
Кратковременность излучаемых импульсов позволяет
воспроизводить раздельно сигналы и измерять дальность
объектов, расположенных на одном направлении, но на
различных дальностях, т. е. импульсный метод обеспечи¬
вает разрешение по дальности, причем разрешающая
способность тем выше, чем короче импульс, что непо¬
средственно очевидно из рис. 1.11.
Повышение разрешающей способности по дальности
при укорочении импульса легко связать с шириной спек^
гра сигнала. ЧехМ короче импульс, тем шире занимаемый
им спектр. Следовательно, разрешающая способность по
дальности растет с расширением спектра. Это объясняет
возможность получения высокой разрешающей способ¬
ности при ЧМ и отсутствие разрешения по дальности при
фазовом методе, при котором используются .незатухаю¬
щие колебания, теоретически имеющие нулевую ширину
спектра.
Импульсный метод позволяет просто решить пробле¬
му разделения прямого и отраженного сигналов, так как
они разнесены во времени (если дальность объекта не
очень мала).
Просто и естественно решается также задача собст¬
венно измерения дальности путем регистрации момента
приема сигнала и измерения его запаздывания относи¬
тельно зондирующего импульса. В качестве оконечного
устройства чаще всего используется индикатор с элек¬
тронно-лучевой трубкой (ЭЛТ) или система автоматиче¬
ского съема дальности, позволяющая автоматически и
непрерывно измерять дальность одного или нескольких
объектов. Находят применение как аналоговые, так и
цифровые системы автосьема.
Импульсному методу измерения дальности свойствен¬
ны и некоторые недостатки, Прежде всего необходимо
отметить, что для получения большой дальности дейст¬
вия системы необходима и большая энергия излучаемых
импульсов. Увеличение энергии может быть достигнуто
увеличением длительности импульсов тп или повышением
импульсной мощности Ри, а если при обработке исполь-
зуется накопление принимаемых сигналов— увеличением
частоты -повторения импуль-сов Fn. Простое увеличение
длительности импульсов связано с ухудшением разре¬
шающей способности, а повышение частоты повторения
может привести к появлению неоднозначности при изме¬
рении больших дальностей. Поэтому -в импульсных си¬
стемах большой дальности действия иногда приходится
применять импульсные мощности, достигающие десят¬
ков мегаватт, что вызывает ряд трудностей пр'и практи¬
ческом осуществлении систем.
В некоторых случаях важной является возможность
измерения весьма малых расстояний, что при использо¬
вании импульсного метода представляет известные труд¬
ности, связанные с инерционностью устройств переклю¬
чения антенны импульсной системы с передачи на прием.
Проблемой является также обеспечение однозначно¬
сти при одновременном измерении дальности и скорости
объектов, если они могут изменяться в широком диа¬
пазоне.
Однако отмеченные недостатки импульсного метода
в значительной степени преодолимы тем или иным спо¬
собом в зависимости от конкретных требований, и им¬
пульсный метод имеет самое широкое применение в даль¬
номерных и разностно-дальномерных системах.
В последние годы в дальномерных и разностно-даль¬
номерных системах все шире применяется комбинация
импульсного и фазового методов измерения временных
интервалов. При этом точное измерение обеспечивается
измерением фазы несущей сигнала, а многозначность
фазовых измерений устраняется более грубым определе¬
нием дальности (или разности дальностей) по огибаю¬
щей сигнала, т. е. импульсным методом. Все большее
применение находит также частотная модуляция и фа¬
зовая манипуляция высокочастотных колебаний излучае¬
мых импульсов, что позволяет увеличить их энергию за
счет увеличения длительности, сохранив или даже повы¬
сив при этом разрешающую способность и точность
дальномера применением методов обработки принятого
сигнала, обеспечивающих так называемое «сжатие им¬
пульсов». Эти методы будут рассмотрены в последующих
главах.
37
§ 1.7. МЕТОДЫ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ
Определение .направления радиотехническими сред¬
ствами основано ла прямолинейном распространении ра¬
диоволн в однородной среде и сводится, таким образом,
к определению направления прихода радиоволн, излу¬
чаемых или отражаемых от объектов,, путем 'сравнения
амплитуды, фазы или частоты колебаний, возбуждаемых
в антенной системе. Следовательно, принципиально .воз¬
можны амплитудный, фазовый и частотный методы ра-
Рис. 1.12. Фазовый метод пеленгования.
диопслепговапия. Практически в радиолокации и радио¬
навигации применяются амплитудные, фазовые и ком¬
бинированные амплитудно-фазовые методы измерения
угловых координат. Частотный метод самостоятельного
значения пока не имеет и иногда .используется в комби¬
нации с амплитудным для повышения точности и угловой
разрешающей способности системы.
Фазовые методы основаны на измерении разности фаз
колебаний, принимаемых двумя антеннами, разнесенны¬
ми в пространстве (радиопеленгатор). Прием может осу¬
ществляться и на одну антенну, ио тогда излучение при¬
нимаемого сигнала должно осуществляться разнесенны¬
ми антеннами (фазовый радиомаяк).
Рассмотрим пеленгование объекта в одной плоскости
фазовым методом при 'использовании двух ненаправ¬
ленных приемных антенн А{ и Л2 (рис. 1.12). Пусть рас¬
стояние между антеннами, которое называется базой,
равно d и пеленгуемый объект удален от центра базы
на расстояние D, во много раз превышающее d. В этом
случае направления прихода сигналов от объекта к ан-
38
теинам Ai -и /Ь можно считать параллельными и запи¬
сать разность расстояний в виде
\D-=D2—Dx=^d sin а,
где а — угол между направлением на объект и .нор¬
малью к базе, проходящей через ее центр.
Зная величину базы и измеряя тем пли иным спосо¬
бом разность расстояний АО, можно определить направ¬
ление на пеленгуемый объект а.
При фазовом методе измеряется разность фаз <р. ко¬
лебаний, возбуждаемых сигналом в антеннах и Л2.
Если длина волны принимаемых колебаний равна 2i, то
= 2тс sin а.
При применении в качестве фазочувствительного эле¬
мента фазового детектора напряжение на его выходе
будет
/7фД = КфЛи cos <р = cos (2л sin а), (1.8)
где U — амплитуда сигнала на входе детектора.
Д л я и ск л ючени я в ли ян и я неизвестно й а м п литуды
применяют эффективную АРУ или ограничение сигнала,
благодаря чему напряжение на входе фазового детекто¬
ра можно считать постоянным и записать выражение
(1.8) ,в виде
Uфд = Uq cos ^2-п sin а
где Uo = const.
Поскольку косинус — функция четная, то знак напря¬
жения на выходе фазового детектора не зависит от сто¬
роны уклонения антенны от направления на объект. Для
устранения этого недостатка в один из приемных кана¬
лов вводят цепь сдвига фазы на л/2, благодаря чему за¬
висимость от угла ip несогласован и я а приобретает вид
дискри мп и а торной хар актеристики
t/(l>H = C/oSin (2*sin а). (1.9)
При малых а зависимость (7фД(а) имеет приближенно
линейный характер
(1.10)
39
и позволяет непосредственно ио напряжению на выходе
фазового детектора определить величину и знак угла
рассогласования а. Зависимость относительного значе¬
ния напряжения рассогласования U$R/Uo от угла рассо¬
гласования а называется пеленгационной характеристи¬
кой угломера:
= (1.11)
а ее производная при а = 0 носит название крутизны пе¬
ленгационной характеристики или чувствительности пе¬
ленгования
dF (а)
da.
(1-12)
Таким образом, чувствительность, а следовательно, и
точность пеленгования растут с увеличением отношения
d/X. Однако при d/X>il2 появляется неоднозначность из¬
мерения угла а, что видно из выражения (1.9). Длт ис¬
ключения неоднозначности с повышением точности при¬
бегают (так же как и в фазовых дальномерных систе¬
мах) к применению нескольких шкал, т. е. проводят из¬
мерения при различных отношениях d/k
Следует подчеркнуть, что рассмотренный фазовый
угломер с ненаправленными антеннами не обладает раз¬
решающей способностью по углу, так как два или не¬
сколько объектов, расположенных на различных направ¬
лениях, создадут в антеннах единый результирующий
сигнал (соответствующий какому-то ложному направле¬
нию), что исключает возможность раздельного наблю¬
дения объектов и измерения их пеленгов. Для разреше¬
ния объектов по углу должны использоваться антенны
с достаточно узкой амплитудной характеристикой на¬
правленности.
При использовании остронаправленных антенн ам¬
плитудные методы могут обеспечить также высокую
точность пеленгования.
Амплитудные методы пеленгования. При пеленгова¬
нии с помощью двух разнесенных ненаправленных ан¬
тенн могут быть использованы не только фазовые, но и
амплитудные соотношения. При отсчете фазы сигналов,
приходящих к антеннам и Л2 (рис. 1.12) относитель-
40
но центра базы, можно записать их выражения на вхо¬
де приемных каналов в виде
U^Uq^12 и U2 — Ua~i'fl2.
Суммарный сигнал
и С = Ui + и» = и (е/<₽/2+ е_7<₽/2) = 2(7 cos sin а)
(1-13)
позволяет производить пеленгование но максимуму его
амплитуды.
Определение направления по максимуму амплитуды
сигнала .называется методом максимума.
Из выражения (1.13) очевидны существенные недо¬
статки метода максимума: низкая пеленгационная чув¬
ствительность, поскольку пеленгование ведется в обла¬
сти максимума косинусоидальной функции, где ее кру¬
тизна весьма мала; непосредственно не определяется сто¬
рона уклонения антенной системы от направления на
объект; амплитуда суммарного сигнала зависит не толь¬
ко от величины отклонения а, но и от неизвестной ампли¬
туды принимаемых сигналов.
Чувствительность пеленгования существенно повыша¬
ется при использовании разностного сигнала
Uv = Ut _ и2 = и (e7W2 - ~'М2)
= 2[J sin (к sin .
Момент пеленга соответствует минимальной ампли¬
туде сигнала (в данном случае равной 0), поэтому такой
метод пеленгования называется методом минимума.
Метод минимума обладает существенным недостат¬
ком, заключающимся в том, что в момент пеленга ре¬
зультирующий сигнал t7p равен 0, что исключает воз¬
можность его наблюдения и тем более использования
для измерения дальности объекта. Поэтому применение
метода минимума в основном ограничивается радиопе¬
ленгаторами с рамочными антеннами, противоположные
стороны которых (играющие роль антенн /Ц и А2) вклю¬
чены встречно, благодаря чему на выходе рамки обра¬
зуется разностный сигнал.
41
Отпошешие разностного 'сигнала к 'Суммарному соз¬
даст /пеленгационную характеристику вида
F(a)=^-=tg^4sina)’ О-14)
позволяющую '.исключить влияние меняющейся амплиту¬
ды входных сигналов, определить сторону уклонения
(тангенс — функция нечетная) и обеспечить высокую
точность пеленгования, так как крутизна пеленгационной
характеристики в рабочей области (а —0) может быть
сделана высокой:
dF (a) d
Кроме того, наличие суммарного сигнала позволяет
наблюдать объектна экране индикатора в момент пелен¬
гования п измерять его дальность.
Рассмотренный вариант амплитудного метода пелен¬
гования называется суммарно-разностным. Достоинства
суммарно-разностного метода обеспечили его широкое
применение в моноимпульсных РЛС.
Амплитудным и фазовым методам пеленгования с по¬
мощью двух ненаправленных антенн свойственны, по
существу, одни и те же 'основные недостатки: отсутствие
разрешающей способности по углу и появление неодно¬
значности при увеличении базы сверх Z/2, что необходи¬
мо для повышения точности.
Для обеспечения высокой угловой разрешающей спо¬
собности необходимо использовать остронаправленные
антенны. Ширина диаграммы направленности антенны
на уровне половинной мощности аа, выраженная в радиа¬
нах, при равномерном распределении облучающего поля
по раскрыву антенны примерно равна обратной величи¬
не относительного раскрыва:
Л
В радиолокационных системах, использующих весь¬
ма малые длины волн, можно получить большие величи¬
ны относительного раскрыва dA/K и, следовательно, вы¬
сокую направленность антенн, поэтому в радиолокации
амплитудные методы пеленгования могут обеспечить
42
большую точность в сочетапиш с высокой разрешающей
способностью и однозначностью отсчета.
Метод м а к си м у м а при м ей я ет-с я п р ей м у щест.в енн о
в обзорных РЛС, диаграмма направленности которых,
перемещаясь в пространстве, проходит направление на
объект. Если объект имеет малую протяженность, срав¬
нительно с шириной диаграммы (объект точечного типа),
а создаваемый им сигнал не флюктуирует, то амплитуда
сигнала на входе приемника изменяется в соответствии
с формой диаграммы направленности антенны /(а)
Рис. 1.13. ^Максимальный метод пеленгования.
(рис. 1.13). Анализ огибающей принимаемого сигнала
позволяет зафиксировать максимум амплитуды сигнала
и определить соответствующее ему направление на объ¬
ект. В связи с этим метод максимума иногда называется
методом анализа огибающей.
Следует заметить, что при работе по отраженному
сигналу и применении одной антенны диаграмма направ¬
ленности участвует в формировании огибающей дважды:
и при излучении и при приеме сигнала, поэтому в каче¬
стве Е(а) должна быть принята результирующая диа¬
грамма /р(а), равная произведению диаграмм передаю¬
щей и приемной антенн. В РЛС чаще всего используется
одна и та же антенна (и при передаче и при приеме),
поэтому
Г(а)=/р(а)=Г(«).
Ошибки пеленгования методом максимума составля¬
ют порядка Vs ширины диаграммы, и для получения вы¬
сокой точности необходимы очень узкие диаграммы, при¬
менение которых не всегда приемлемо как вследствие
43
трудностей обеспечения необходимой величины относи,
тельного раскрыва антенны, так -и в связи с возрастанием
времени обзора заданного
Равносигнальная О
Рис. 1.14. Равносигнальный
пеленгования.
сектора пространства.
Значительно более вы¬
сокую точность при той
же ширине диаграммы на¬
правленности дает метод
сравнения, который чаще
называется равносигналь¬
ным методом. При равно¬
сигнальном методе произ-
,водится сравнение ампли-
' ' гуд сигналов, принимае¬
мых от объекта в двух по¬
ложениях диаграмм на¬
правленности антенны
(рис. 1.14). Если направ¬
ление на объект совпада¬
ет с линией, проходящей
,д через точку пересечения
диаграмм (равносигналь¬
ное направление), то ам¬
плитуды сигналов, соответствующих первой и второй
диаграммам, равны, и разностный сигнал
будет равен 0.
При наличии рассогласования Да между направле¬
нием на объект и равносигнальным направлением появ¬
ляется разностный сигнал £7р(Да), величина и знак ко¬
торого определяются углом рассогласования Да.
Выбирая угол смещения диаграмм у таким, чтобы
диаграммы пересекались в области высокой крутизны,
можно получить высокую точность пеленгования.
Сравнение сигналов может осуществляться последо¬
вательно для двух положений одной и той же диаграммы
(одноканальная схема с последовательным сравнени¬
ем) или для двух одновременно существующих пересе¬
кающихся диаграмм (многоканальная схема одновре¬
менного сравнения). Многоканальная схема имеет ряд
преимуществ и, в частности, благодаря одновременности
сравнения позволяет исключить дополнительные ошибки,
44
связанные с ф л ю к ту а ц и я м и а м п л 11 т уды и р i г н и маемых
сигналов, по сложнее одноканальной.
Равносигпальпый метод пеленгования широко приме¬
няется в радиолокации, радионавигации и радиоуправ¬
лении.
§ 1.8. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ ОБЪЕКТОВ
Во многих случаях конечной целью радиолокацион¬
ных измерений является определение траектории движе¬
ния объекта. Траекторию, представляющую собой зави¬
симость координат центра тяжести движущегося объекта
во времени, принято задавать в прямоугольной систе¬
ме координат. По каждой из осей координат х, у и z дви¬
жение точечного объекта с массой т под воздействием
силы F можно описать в соответствии с законом Ньюто¬
на дифференциальным уравнением второго порядка
2х р { dx
(1.15)
Аналогичные уравнения можно записать для коорди¬
нат у и г. Для решения каждого из трех уравнений не¬
обходимо в общем случае две произвольные постоянные.
Таким образом, для опреде¬
ления траектории объекта,
движущегося в безвоздуш¬
ном пространстве под воз¬
действием приложенных к
нему внешних сил и сил
инерции, необходимо по дан¬
ным радиолокационных из¬
мерений вычислить шесть
параметров. Так, для опре¬
деления траектории балли¬
стического снаряда от точки
запуска до точки падения
достаточно знать время t и
5/
У<
[ у
и
1
“ 1
/ /1
i
и .
1 // !
I
i
/1 i
! 1 1
1 i !
i
i
1
i
0
.Г/ Д ?
I
Рис. 1.15. К определению
траектории объекта.
пять других параметров, характеризующих эллиптиче¬
скую траекторию.
Другие объекты, например самолеты, могут иметь бо¬
лее сложные и разнообразные траектории. Сложность
траектории связана с маневренностью объекта, ограни¬
ченной максимальным допустимым ускорением, которое
45
определяет минимальный возможный радиус кривизны
траектории.
Траектория объекта может быть определена как при
непрерывном, так и при дискретном измерении его коор¬
динат. Определяя последовательно координаты объекта
в точках /, 2, 3 и фиксируя соответствующие моменты
времени, можно по результатам измерений вычислить со¬
ставляющие скорости и ускорения объекта и, следова¬
тельно, не только найти его положение в промежутках
между измерениями (интерполяция), т. е. определить
траекторию движения, но и предсказать будущее поло¬
жение объекта (экстраполяция), если предположить, что
закон движения сохранится неизменным. Рис. 1.15 иллю¬
стрирует определение траектории объекта, движущегося
на плоскости х, у.
§ 1.9. ИЗМЕРЕНИЕ СКОРОСТИ И УСКОРЕНИЯ
ОБЪЕКТОВ
Для управления движением в большинстве случаев
наряду с местоположением необходимо знать скорость,,
а часто и ускорение объектов управления. При непрерыв¬
ном и достаточно точном определении местоположения
составляющие скорости и ускорения могут быть опреде¬
лены путем однократного и двукратного дифференциро¬
вания текущих координат. Такой метод определения ско¬
рости и ускорения требует предварительного измерения
самой координаты. Кроме того, дифференцирование ве¬
дет к потере точности измерения. В связи с этим боль¬
шое значение имеют методы непосредственного измере¬
ния скорости и ускорения объектов, тем более что такие
измерения могут быть сделаны на борту объекта авто¬
номно, т. е. вне связи с какой-либо наземной радиотех¬
нической системой. Интегрированием скорости и ускоре¬
ния можно определить пройденный путь и, следователь¬
но, найти координаты объекта. Особое значение
автономные системы имеют при управлении ракетами и
летательными аппаратами.
Важнейшей характеристикой движения летательного
аппарата является его скорость относительно поверхно¬
сти земли, которая носит название путевой скорости.
Путевая скорость может быть определена по радиоло¬
кационному или телевизионному изображению земной
46
поверхности. Измеряя время, за которое самолет прохо¬
дит расстояние между двумя известными ориентирами,
легко вычислить путевую -скорость. Однако более пред¬
почтителен метод непосредственного измерения путевой
скорости радиолокационными устройствами, в которых
определение скорости основано на эффекте Допплера.
Допплеровское смещение частоты Fv пропорциональ¬
но скорости изменения расстояния Vr (т. е. радиальной
скорости) между приемником и 'излучателем и с доста¬
точно высокой точностью может бьггьнайдено по формуле
<1Л6)
если принимается отраженный сигнал, а приемник и пе¬
редатчик имеют длину волны % и расположены в одной
точке.
Скорость объекта и пройденный им путь могут быть
определены также интегрированием ускорения. Ускоре¬
ние не может быть измерено непосредственно радиотех¬
ническими средствами, и для его определения использу¬
ются инерциальные методы.
Инерциальные методы полностью автономны и абсо¬
лютно помехоустойчивы, 'вследствие чего их применение
особенно целесообразно для управления беспилотными
объектами. Однако инерциальным методам свойственно
накопление ошибок во времени, т. е. по мере удаления от
точки вылета объекта. В связи с этим инерциальные ме¬
тоды используются обычно совместно с радиотехнически¬
ми средствами, которые позволяют получить высокую
точность, но подвержены воздействию помех.
§ 1.10. РАСПОЗНАВАНИЕ РАДИОЛОКАЦИОННЫХ
ОБЪЕКТОВ
Под распознаванием в радиолокации имеют в виду
выделение сигналов, соответствующих определенным
объектам, среди всей совокупности сигналов, поступаю¬
щих на .вход приемного устройства РЛС. Проблема рас-
по з н а в ани я об ычно р асе м а три в а етс я пр и м е ни тел ьн о
к РЛС, использующим отраженные сигналы, так как
в случае РЛС с активным ответом выделение нужного
объекта обеспечивается кодированием ответного сигна¬
ла. Кодирование используется также в PH системах и
системах РУ. В настоящем параграфе кратко рассма-
47
триваются .возможные методы распознавания сигнала,
отраженного определенным объектом, среди мешающих
отражений, создаваемых отражающим фоном и другими
отражающими объектами, .находящимися в зоне наблю¬
дения РЛС.
Для выделения определенного объекта используются
отличия отраженных им сигналов от мешающих отра¬
жений по амплитуде, статистическим характеристикам
флюктуаций амплитуды, характеру поляризации. Для
распознавания движущихся объектов используется раз¬
личие в скоростях и траекториях движения.
В РЛС с визуальной индикацией, не имеющих спе¬
циальных устройств для выделения сигналов определен¬
ного типа, распознавание объектов производится опера¬
тором по характеру отметок цели на экране индикатора.
При применении индикатора с модуляцией отклонением
используется различие амплитуд выбросов на экране
и характера их флюктуаций. В случае индикатора с яр¬
костной модуляцией распознавание объектов может осу¬
ществляться по яркости отметок, по следам, которые они
оставляют .при перемещении по экрану. В последнем
случае оператор, наблюдая за перемещением опреде¬
ленной отметки, ожидает ее появления при очередном
обзоре в определенной точке экрана, т. е. использует ви¬
зуальную корреляцию. При наблюдении протяженных
объектов для их распознавания может быть использова¬
но также различие конфигурации отметок .на экране.
Эффективность распознавания увеличивается с повыше¬
нием разрешающей способности РЛС, а также при ис¬
пользовании специальных устройств, обеспечивающих
селекцию определенных сигналов перед их поступлени¬
ем на индикатор. Это позволяет не воспроизводить на
экране целый ряд мешающих отметок, затрудняющих
распознавание и увеличивающих время, необходимое опе¬
ратору для надежного распознавания. Такие устройства
совершенно необходимы, если распознавание объекта
должно быть осуществлено без участия оператора.
В радиолокации и радиоуправлении, как правило,
приходится иметь дело с движущимися объектами, для
выделения которых на фоне неподвижных окружающих
объектов применяются системы селекции движущихся
целей (СДЦ). Селекция основана на отличии частоты
сигнала, отраженного движущимся объектом (в силу
48
эффекта Допплера), от частоты сигналов, отраженных
н еподвижными объектами.
Различие допплеровских -смещений частоты сигналов
используется также для распознавания объектов, дви¬
жущихся с различными -скоростями, например самолета
на фоне облака металлизированных лент, сброшенных
для его радиомаскировки.
Различие поляризационных характеристик отражен¬
ных сигналов достаточно эффективно используется для
распознавания объектов ла фоне отражения от поверх¬
ности моря, дождя, града и т. п.
Широкие возможности для повышения эффективности
р аспо зн а в а ни я о бъ е кто в откр ы в а ю те я п ри пр и м ен ении
вычислительных машин, которые могут выполнять за¬
данные логические операции, позволяющие выделить
сигнал с определенными свойствами. Так, в одной из си¬
стем обнаружения и распознавания баллистических ра¬
кет, состоящей из РЛС дальнего обнаружения и вычис¬
лительных устройств обработки данных, выполняются
следующие логические операции. Прежде всего опреде¬
ляется скорость обнаруженного объекта в направлении
РЛС. Для этого используется анализатор частоты в ви¬
де набора фильтров, позволяющих определить доппле¬
ровское смещение частоты по максимуму сигнала на вы¬
ходе того или иного фильтра. Выбор фильтра с макси¬
мальным сигналом осуществляется специальной систе¬
мой съема данных, которая позволяет также определить
текущую дальность цели, ее азимут и наличие корреля¬
ции между отраженными импульсами за один обзор. При
наличии корреляции по дальности, скорости и азимуту
на выходе системы съема появляется кодированный сиг¬
нал цели, поступающий для дальнейшей обработки на
вычислительную машину. Для распознавания целей вы¬
числительная машина выполняет ряд операций, позволя¬
ющих распознать сигналы, отраженные ракетой, среди
других отражений. Эти операции сводятся к вычисле¬
нию траекторий обнаруженных целей и определению ме¬
ста запуска и вероятного района падения.
Сопоставление вычисленных данных с параметрами,
заложенными в память машины, дает возможность рас¬
познать сигналы ракет. Сигналы выделенных целей в ви¬
де кодов передаются для дальнейшей проверки и при¬
нятия решений.
4—1173
49
Рассмотренный пример иллюстрирует важность и
сложность проблемы распознавания объектов.
§ 1.11. РАДИОЛОКАЦИОННЫЕ СИСТЕМЫ
ОПОЗНАВАНИЯ
В отличие от распознавания обнаруженных РЛС объ¬
ектов по характеру отраженных ими сигналов, системы
опознавания позволяют выделить определённый объект
при наличии на нем ответчика, излучающего кодирован¬
ный ответный сигнал при приеме сигнала запроса опре¬
деленного типа.
Первоначально подобные системы применялись для
опознавания своих самолетов и кораблей среди объек¬
тов, обнаруженных РЛС. Затем область применения от¬
ветчиков значительно расширилась, и в настоящее время
они находят самое разнообразное применение. Здесь мы
остановимся лишь па использовании ответчиков для опо¬
знавания объектов.
Возможны два вида систем опознавания — совмещен¬
ная и автономная.
В совмещенной системе функции запросчика выпол-’
няет сама РЛС и ответные сигналы воспроизводятся не¬
посредственно на экране ее индикатора. Несмотря на
простоту и экономичность, совмещенная система для це¬
лей опознавания почти не применяется, так как ответчик
в такой системе может работать лишь с РЛС определен¬
ного типа.
В автономных системах опознавания сигнал запроса
излучается специальным запросчиком после обнаруже¬
ния объекта РЛС. Таким образом, в этом случае для
опознавания используется самостоятельная линия радио¬
связи «запросчик — ответчик — запросчик», которая мо¬
жет работать совместно с РЛС любого типа.
В автономных системах применяется кодирование
не только ответного, но и запросного сигнала, что повы¬
шает помехозащищенность системы, так как исключает
срабатывание ответчиков от сигналов РЛС и уменьшает
количество срабатываний из-за различных помех. В ча¬
стности, кодирование запроса уменьшает вероятность от¬
вета на имитацию сигналов запроса противником.
£0
Глава 2
РАССЕИВАЮЩИЕ СВОЙСТВА ОБЪЕКТОВ
§ 2.1. РАССЕЯНИЕ РАДИОВОЛН ОБЪЕКТАМИ
НАБЛЮДЕНИЯ И ИХ ЭФФЕКТИВНАЯ ПЛОЩАДЬ
РАССЕЯНИЯ
Физически всякий отражающий (рассеивающий) объ¬
ект, называемый в радиолокации целью, представляет
собой источник вторичного излучения. Если проводи-
димость, диэлектрическая постоянная или магнитная
проницаемость среды изменяются достаточно резко, то
при облучении поверхности раздела сред часть падаю¬
щей энергии рассеивается, т. е. поверхность становится
источником вторичного излучения.
Явления вторичного излучения принято разделять на
зеркальное отражение, диффузное рассеяние и резонанс¬
ное излучение.
Отражение наблюдается при облучении больших по¬
верхностей, размеры которых много больше длины вол¬
ны, а поверхность достаточно гладкая (размеры шерохо¬
ватостей не превосходят Х/16). В этом случае соблюдает¬
ся закон зеркального отражения: угол падения равен
углу отражения.
Свойством диффузного рассеяния обладают поверх¬
ности с размерами шероховатостей порядка X. В радио¬
локационном диапазоне диффузное рассеяние наблюда¬
ется при облучении поверхностей, покрытых раститель¬
ностью.
Резонансное вторичное излучение имеют объекты, раз¬
меры которых равны или кратны Х/2.
Независимо от вида объекта его отражающие, свой¬
ства характеризуются при вычислении дальности дейст¬
вия РЛС и в некоторых других случаях эффективной
площадью рассеяния сгп, которая может быть найдена из
равенства (1.3):
аэ(а, = (2.1)
4*
51
где П2— плотность потока мощности, создаваемая от¬
раженным сигналом в месте расположения ан¬
тенны РЛС;
П1 — плотность потока мощности, облучающего цель;
D — дальность цели.
Эффективная площадь рассеяния зависит от направ¬
ления облучения, что подчеркнуто наличием переменных
а и р, характеризующих взаимное положение цели и
РЛС. Зависимость оэ(а, Р) может быть представлена
пр остр а.нствеин о й ди а гр а м м о й, а н а л о ги ч н о й д11 а пр а м м е
направленности излучателя и называемой диаграммой
рассеяния цели. Диаграмма рассеяния практически изо¬
бражается отдельно в плоскости азимута стэ(а) и угла
места сГэ(Р) -
§ 2.2. ВЫЧИСЛЕНИЕ ЭФФЕКТИВНОЙ ПЛОЩАДИ
РАССЕЯНИЯ НЕКОТОРЫХ ОБЪЕКТОВ
Эффективная площадь рассеяния может быть вычис¬
лена аналитически лишь для объектов простейшей фор¬
мы; во всех остальных случаях она определяется экспе¬
риментально. Рассмотрим некоторые примеры аналити¬
ческого определения эффективной площади рассеяния.
Эффективную площадь рассеяния можно представить
через напряженность ноля в месте расположения цели£1
и антенны РЛС Е2 в виде
(2-2)
Отношение Е2!ЕХ, входящее в это выражение, можно
найти на основании принципа Гюйгенса, полагая, что
каждая элементарная площадка поверхности облучае¬
мого объекта становится источником элементарной сфе¬
рической волны. Суммируя действие вторичных сфериче¬
ских волн, можно найти напряженность результирующе¬
го поля вторичного излучения в месте расположения ан¬
тенны РЛС по формуле
^2=="Т* [ 7Г ехР ЛГ cos (2-3)
s
где dS— элемент поверхности S (рис. 2.1);
0 — угол между направлением на РЛС и нормалью
к поверхности в данной точке;
52
£) = + — расстояние между антенной РЛС и
рассматриваемым элементом поверхности.
В большинстве практических случаев D -и Е\ в преде¬
лах размеров цели изменяются мало, поэтому
F^^-exp [— рхР[—/’“Г d] cos QdS-
Рис. 2.L К вычислению сгэ криволинейной
поверхности.
Тогда
так как
cos QdS,
s
а
Воспользуемся полученным выражением для вычис¬
ления эффективной площади рассеяния некоторых про¬
стейших объектов.
Эффективная площадь рассеяния плоского металли¬
ческого листа. Если металлический лист, размеры кото¬
рого во много раз превышают длину волны, расположен
перпендикулярно направлению распространения радио-
53
Волл и па расстоянии D, во много раз превышающем
его размеры, то
<5
cos QdS
4nS2
№ ’
так как cos0=l и exp —j 4^- d J = 1, поскольку для
плоского листа, расположенного Перпендикулярно направле¬
нию облучения, d — О для всех точек листа.
Рис. 2.2. К вычислению cra плоского листа.
При лер мал ь'н ом о б л у ч ел тип э ф ф е кти вн ая площадь
рассеяния листа благодаря зеркальному отражению
в сторону РЛС имеет очень большую величину. Так, на¬
пример, для листа площадью S=1 м2 и длины волны %=
= 10 см эффективная площадь рассеяния равна
4?rS2 4л
От = —ГТ А ■ -х-г
э № 0,01
1256 м\
Однако даже при небольшом отклонении направления
облучения от нормали оэ листа резко уменьшается.
Приведем без вывода формулу для сгэ листа длиной а
и высотой Ь, расположенного под углом а между направ¬
лением облучения и нормалью к листу (рис. 2.2) в пло¬
скости стороны а
cos2
(2.6)
где
sin’a
S = ab.
54
Из формулы (2.6) видно, что диаграмма рассеяния
листа аналогична диаграмме направленности синфазной
антенны и описывается функцией
Е (х) = Ет
sin х
х
Таким образом, при некоторых углах облучения а эф¬
фективная площадь рассеяния падает до 0, а для дру¬
гих— значительно меньше аэ при а = 0.
В некоторых случаях желательно получить большое
значение стэ в широком секторе. Это позволяет осущест¬
вить уголковый отражатель.
Эффективная площадь рассеяния уголкового отража¬
теля. Простейший уголковый отражатель состоит из трех
взаимно перпендикулярных пластин, обладающих свой¬
ствами отражения по направлению падения облучающе¬
го луча. Это свойство объясняется трехкратным отра¬
жением от стенок отражателя (рис. 2.3), которое испы¬
тывает полна, если направление облучения находится
вблизи оси симметрии уголкового отражателя.
д
А
Рис. 2.3. К вычислению сгэ уголкового отражателя.
Уголковый отражатель сохраняет свойство зеркаль¬
ного отражения в сторону РЛС при облучении в преде¬
лах телесного угла 45°, что обеспечивает сохранение
большой эффективной площади рассеяния цели в преде¬
лах этого угла. Из рис. 2.3 нетрудно видеть, что трех¬
кратное отражение происходит, если падающий луч про¬
ходит в пределах шестиугольника, вписанного во внеш¬
ний контур отражателя, и, следовательно, эффективная
площадь (рассеяния уголкового отражателя приближен¬
но равна сгэ такого вписанного шестиугольника, облучае¬
мого по нормали. Подставляя площадь вписанного ше¬
стиугольника S = a2h/'3 в выражение (2.5), получаем
формулу для эффективной площади рассеяния уголково¬
го отражателя
47Ш4
(2.7)
в направлениях, близких к его оси симметрии.
Вычислим, например, огэ уголкового отражателя с раз¬
мером ребра а— \ м при длине волны РЛС А,= 10 см:
Таким образом, сгэ уголкового отражателя несколько
меньше оэ плоской пластины с размерами а=Ь= 1 м, но
уголковый отражатель сохраняет большое значение сгэ
в достаточно широком секторе, тогда как сгэ плоской пла¬
стины резко уменьшается при незначительных отклоне¬
ниях направления облучения от нормали. Следует за¬
метить, что большая (Уэ получается лишь при высокой
точности изготовления уголкового отражателя. Для рас¬
ширения действующего сектора изготавливаются угол¬
ковые отражатели, состоящие из четырех и даже вось¬
ми уголков. Уголковые отражатели используются в каче¬
стве пассивных радиомаяков, искусственных целей, для
увеличения сгэ некоторых объектов, например спасатель¬
ных лодок для облегчения их поиска.
Аналогичное применение находит биконический отра¬
жатель, составленный из двух конусов вершинами друг
к другу. Если между образующими конусов угол равен
90°, то падающий луч после двукратного отражения от
поверхности конусов направляется в сторону РЛС, что
и обеспечивает большую величину сгэ. Достоинством би-
конического отражателя является равномерная диаграм¬
ма рассеяния в плоскости, перпендикулярной его оси.
Эффективная площадь рассеяния шара. Для опреде¬
ления оэ большого хорошо проводящего шара можно
использовать общую формулу (2.4). Обозначим через R
радиус шара и введем сферические координаты с нача-
56
лом в центре'сферы (рис. 2.4). В качестве элементарной
площадки выберем сферическое кольцо радиусом г =
=R s»in @ и шириной RdQ.
Рис. 2.4. К вычислению сгэ шара.
Площадь элементарного кольца будет
dS —2nR2 sin QdQ.
Обозначив Dq дальность до центра сферы, представим
выражение (2.4) в виде
<*э=уг | j р с°—j 2тг/?2 sin 0 cos QdQ .
о
Введем новую переменную z=cos0 и обозначим ш =
= 4л/?/Х, тогда
16л3/?1
°э—
В случае большого шара, т. е. при выполнении условия
ш>1,
1 _J Л
w
Таким образом, для большого идеального проводящего
шара независимо от длины волны и направления облу¬
чения
(2.8)
57
<7В = Я/?2.
Благодаря этому большой шар с хорошо проводящей
поверхностью очень удобен в качестве эталона при
экспериментальном определении аэ реальных объектов.
Если при неизменных размерах шара увеличивать
длину волны X до значений -порядка диаметра шара, то
появляется ряд резонансных максимумов сгэ- Для малого
шара, который имеет определяется форму¬
лой Рэлея
<уэ —4,4* 104W4 (2.9)
и характеризуется резкой зависимостью от длины волны
облучающих колебаний. Этот случай имеет место, на-
пример, при рассмотрении отражений от капелек дождя
и тумана.
Рис. 2.5. К вычислению сгэ диффузно-рассеивающеи по¬
верхности.
Для любой выпуклой поверхности эффективная пло¬
щадь рассеяния может быть вычислена по формуле оэ =
= л7?17?2, если главные радиусы кривизны в блестящей
точке и значительно больше длины волны Под
блестящей точкой понимают точку на отражающей по¬
верхности, в которой нормаль совпадает с направлением
на РЛС, т. е. происходит зеркальное отражение в сто¬
рону РЛС.
Эффективная площадь рассеяния диффузно-рассеи-
вающей поверхности. При диффузном рассеянии плот¬
ность потока мощности отраженной! волны равна
n2 = n2mCOS 0,
58
где 0 — угол между рассматриваемым направлением
и нормалью к поверхности;
Пгт—плотность потока в направлении нормали
(0 = 0).
Если плотность потока мощности, облучающей по¬
верхность по направлению нормали, равна Пь то вся
мощность, отраженная площадью So, будет
= П iSo/Л
где р— коэффициент отражения поверхности.
Для определения эффективной площади рассеяния
найдем Р2, вычислив полный поток мощности отражен¬
ной волны. Вообразим полусферу радиуса Z), которая
перехватывает всю отраженную мощность (рис. 2.5). От¬
раженная мощность, проходящая через элемент поверх¬
ности dS, равна
dP2 = /72nicos QdS,
где
dS = DdQ • D sin Qdy = D2 sin 0 dQd<f.
Вся мощность, проходящая через полусферу,
2тс
/72Ш cosOdS — H2mD2 f d<p X
о
u/2
Xj sin0 cosOdO = т!)2П2т.
о
(2.Ю)
Приравнивая выражения (2.9) и (2.10), найдем
П^о/^тг^Пз™,
отсюда
Но, по определению,
и, следовательно,
аа = 4itD2 ^y=4S0/2 (2.11)
является эффективной площадью рассеяния диффузно-
рассеивающей поверхности при облучении по нормали.
59
Если РЛС расположена иод углом 0 к нормали, то
Зэ (O) = 4So/?cos20.
(2-12)
Таким образом, сгэ диффузно-рассеивающей поверх¬
ности не зависит от Формула (2.12) используется, на¬
пример, для вычисления сигнала, отраженного поверх¬
ностью земли, при определении дальности действия са¬
молетных панорамных РЛС, радиовысотомеров, доппле-
ности.
ровских измерителен путевой скорости и угла сноса са¬
молета. Во всех этих случаях для вычисления сгэ необхо¬
димо найти площадь So участка поверхности земли, ко¬
торый создает отраженный сигнал. Этот участок назы¬
вается отражающей или разрешаемой площадью и име¬
ет площадь, отраженные сигналы от всех точек которой
достигают приемной антенны и, суммируясь, создают
результирующий сигнал. Показательным является случай
импульсной панорамной РЛС. Предположим, что ширина
диаграммы направленности станции в горизонтальной
плоскости равна а, длительность импульса, излучаемого
станцией, равна тп. В вертикальной плоскости диаграм¬
ма направленности широкая, так что отражающая пло¬
щадь определяется только а и ги, а также дальностью
отражающего участка D.
С помощью рис. 2.6 легко найти
a = aD, seep.
Тогда отражающая площадь будет равна
S0 = a& = aD^secp. (2.13)
Нетрудно вычислить отражающую площадь и в других
случаях.
Что касается коэффициента отражения р, то его вели¬
чина зависит от свойств облучаемой поверхности.
Уместно подчеркнуть, что отраженный сигнал на вхо¬
де приемника панорамной РЛС является суммой вторич¬
ного излучения всех отражателей в пределах So. Поэтому
для наблюдения малоразмерных целей на фоне отра¬
жающей поверхности необходимо стремиться уменьшить
величину отражающей площади, т. е. повысить разре¬
шающую способность РЛС.
Эффективная площадь рассеяния полуволнового пас¬
сивного вибратора. Пассивным называется вибратор, ко¬
лебания в котором возбуждаются облучающим элек¬
тромагнитным полем. Найдем <тэ такого вибратора при
условии, что он расположен параллельно электрическо¬
му вектору поля с напряженностью его длина точно
равна Х/2, а сопротивление в центре активно и равно
сопротивлению излучения 7?,. =73 ом. В этом случае по¬
ле будет индуктировать в вибраторе ток, находящийся
! ‘l \ р ___ j?
'"'Г j Р/1С
L
/
Рис. 2.7. К вычислению полуволнового
вибратора.
61
в фазе с Е{. Допустим, что ток, возбуждаемый в центре
вибратора, равен / и его распределение по длине вибра¬
тора (рис. 2.7) синусоидально i =/cos 2лх/%.
Мощность, извлекаемая вибратором из поля, будет
равна
Х/4
Pt= Ejcos'fdx,
—Х/4
где <р — фазовый сдвиг между Е{ и i. В нашем случае
Ф = 0, поэтому
>-/4
Л = J E^idx.
-ip
Считая, что вибратор потерь не имеет и вся погло¬
щенная им мощность излучается в пространство, можем
записать
Х/4
pi = pR^ j E1Icos^-xdx=^E.
-X/4
Исключив отсюда / = E^/nR^ получим рассеиваемую
вибратором мощность
Плотность потока мощности отраженной волны
в месте расположения антенны РЛС найдем из выра¬
жения
П —Р
2—4л£2 ’
где G= 1,64 — коэффициент направленности вибратора
в направлении нормали. Следовательно,
п E^G 1,64£2;Х2
2=4лО2л2/?Е = 4л’£)2-73 ’
(2.14)
Учитывая связь плотности потока мощности с напря¬
женностью поля Е2 =120лП], получим формулу для эф¬
фективной площади рассеяния полуволнового вибратора
аэ = 4'пО2-щ-=0,86Л.2. (2.15)
62
Если угол между вибратором и вектором электриче¬
ского поля равен 0, то
o3(0) = O,86Pcos40. (2.16)
Если вибратор расстроен, т. е. условие не вы¬
полняется, то в его полном сопротивлении появляется ре¬
активная составляющая и эффективная площадь рассея¬
ния уменьшается.
Резонансное вторичное излучение позволяет получить
большую эффективную площадь рассеяния при неболь¬
ших размерах отражающего объекта. Это используется,
например, для создания помех РЛС противника. С са¬
молета сбрасывается большое количество станиолевых
лент или металлизированных нитей. Так как их длина
выбирается близкой к половине длины волны РЛС про¬
тивника, то облако лент создает сильные мешающие от¬
ражения, затрудняющие обнаружение объекта и опреде¬
ление его координат.
§ 2.3. ЭФФЕКТИВНАЯ ПЛОЩАДЬ РАССЕЯНИЯ
МНОЖЕСТВА ОБЪЕКТОВ
Во многих случаях в зону облучения РЛС одновре¬
менно попадает большое количество объектов, и отра¬
женный сигнал представляет собой совокупность вторич¬
ных излучений всех этих объектов. Типичным примером
является отражение от облака металлизированных лент.
В таких случаях для расчета отраженного сигнала необ¬
ходимо уметь вычислять эффективную площадь рассея¬
ния совокупности п целей.
Если вибраторы ориентированы в пространстве слу¬
чайно, то согласно [16] среднее значение составляет
оэ = 0,1 U2. (2.17)
Таким образом, зная число отражателей в единице
объема п, можно найти эффективную площадь рассея¬
ния единицы объема, заполненного отражателями =
= ОЭ'П.
Однако для вычисления результирующего сигнала на
входе приемника необходимо знать отражающий (разре¬
шаемый) объем станции, в пределах которого элемен¬
тарные отраженные сигналы суммируются, достигая
приемной антенны РЛС.
63
Для импульсной РЛС отражающий объем опреде¬
ляется шириной диаграммы направленности антенны
в горизонтальной аа и вертикальной ра плоскостях, дли¬
тельностью импульса Ты, а также дальностью D до рас¬
сматриваемого участка пространства. Полагая сечение
диаграммы направленности антенны эллиптическим
(рис. 2.8), запишем
(2.18)
Тогда эффективная площадь рассеяния всего отра¬
жающего объема Vo, заполненного лентами с плотностью
п на единицу объема, будет равна
«э. = ОэпУ0 = 0,11 Гп «а₽а.
(2.19)
Аналогичным образом может быть найдена эффек¬
тивная площадь рассеяния других распределенных це¬
лей, таких, как дождь, снег, град. В этом случае отра¬
Рис. 2.8. К вычислению отражающего объема им¬
пульсной РЛС.
женные сигналы в большинстве случаев являются ме¬
шающими, так как маскируют сигнал полезной цели и
уменьшают дальность ее обнаружения.
Для уменьшения влияния мешающих отражений па¬
раметры РЛС необходимо выбирать таким образом, что¬
бы по возможности уменьшить отражающий объем, т. е.
необходимо повышать разрешающую способность РЛС,
64
§ 2.4. ЭФФЕКТИВНАЯ ПЛОЩАДЬ РАССЕЯНИЯ
НЕКОТОРЫХ РЕАЛЬНЫХ РАДИОЛОКАЦИОННЫХ
ОБЪЕКТОВ
Реальные радиолокационные объекты типа кораблей,
самолетов, ракет и т. п. имеют весьма сложную конфигу¬
рацию, поэтому их эффективная площадь рассеяния
сильно зависит от направления облучения. При движе¬
нии цели относительно РЛС направление облучения не¬
прерывно меняется, а вместе с ним меняется и величи¬
на эффективной площади рассеяния. Кроме того, при
движении отдельные части объекта могут вибрировать и
перемещаться друг относительно друга. Это также при¬
водит к изменению сгэ (рис. 2.9).
Рис. 2.9. Диаграмма рассеяния, двухмотор¬
ного самолета в горизонтальной плоскости
(Х=10 см).
Таким образом, эффективная площадь рассеяния
цели меняется случайным образом (флюктуирует), и для
определения параметров отраженного сигнала необходи¬
мо знать распределение вероятности гуэ и временные или
спектральные характеристики флюктуаций (функцию
корреляции или спектральную плотность) эффективной
площади рассеяния. Знание закона распределения веро¬
ятностей важно для расчета дальности обнаружения це-
5—1173 65
ли. Характер изменения сь во времени влияет также на
точность определения координат цели и обязательно дол¬
жен учитываться при выборе параметров РЛС, особенно
при автоматическом съеме координат.
ТАБЛИЦА 2.1
Отражающий объект
°Э’ м?
С амоле ты -истребители
5—15
Средние бомбардировщики
40—70
Тяжелые бомбардировщики
100—150
Подводные лодки (в надводном положении) . . .
30—150
Малые суда (водоизмещением 50—200 //?) . . . .
50—250
Средние корабли (1000—10000 т)
3000—10 000
Большие корабли (более 10000 пг)
Более 10 000
При расчете дальности действия РЛС используются
срединные (вероятные) значения эффективной площади
рассеяния. В табл. 2.1 приводятся ориентировочные зна¬
чения о*э для наиболее распространенных радиолокацион¬
ных объектов [17].
Глава 3
ЗОНДИРУЮЩИЕ РАДИОЛОКАЦИОННЫЕ
СИГНАЛЫ
§ 3.1. ЗОНДИРУЮЩИЙ РАДИОЛОКАЦИОННЫЙ СИГНАЛ
И ЕГО СОВМЕСТНАЯ АВТОКОРРЕЛЯЦИОННАЯ
ФУНКЦИЯ
От параметров зондирующего сигнала зависят основ¬
ные характеристики РЛС: максимальная дальность дей¬
ствия, точность определения координат и скорости объ¬
ектов, разрешающая способность по дальности и скоро¬
сти. В зависимости от предъявляемых требований выби¬
рают тот или другой вид модуляции сигнала.
В радиолокационных системах наиболее распростра¬
нена импульсная модуляция, являющаяся частным слу¬
чаем амплитудной. В некоторых системах импульсная
модуляция сочетается с фазовой или частотной модуля¬
цией колебаний несущей частоты.
Для измерения скорости движения объекта импульс¬
ной системой по допплеровскому смещению частоты вы¬
сокочастотные колебания соседних импульсов должны
быть когерентными, причем под когерентностью здесь по¬
нимают отсутствие случайных изменений фазы от одного
импульса к другому. Известные изменения фазы колеба¬
ний могут быть устранены методами когерентного прие¬
ма, при котором колебания гетеродина приемника фази¬
руются колебаниями каждого зондирующего импульса.
При таком определении когерентности непрерывное из¬
лучение колебаний всегда когерентно в течение времени,
за которое фазовые сдвиги, вызываемые нестабильностя¬
ми передатчика, еще пренебрежимо малы.
В связи с развитием статистических методов анализа и
синтеза устройств обработки сигнала первостепенное
значение для характеристики зондирующего сигнала при¬
обрела функция автокорреляции, поскольку оптимальная
обработка сигнала включает операцию умножения при-
5* 67
пятого сигнала на ожидаемый с последующим усредне¬
нием результата для уменьшения влияния помех.
Если обозначить через т разность между истинным и
ожидаемым временем задержки сигнала, обусловленным
дальностью цели x = tD—tDo, а через F — соответственно
разность истинного и ожидаемого допплеровского сме¬
щения частоты, вызванного движением цели F = Fy—Fvo,
то нормированную двумерную автокорреляционную
функцию сигнала (1.2) можно записать в виде
(3.1)
Функцию 4J’(t, F) часто называют совместной авто¬
корреляционной функцией или корреляционной функцией
модуляции, а также функцией неопределенности. В даль¬
нейшем для сокращения функция ^(т, F) обычно назы¬
вается просто автокорреляционной функцией.
§ 3.2. ИСПОЛЬЗОВАНИЕ АВТОКОРРЕЛЯЦИОННОЙ
ФУНКЦИИ ДЛЯ ОЦЕНКИ РАЗРЕШАЮЩЕЙ
СПОСОБНОСТИ, ТОЧНОСТИ И ОДНОЗНАЧНОСТИ
ПРИ ИЗМЕРЕНИИ ДАЛЬНОСТИ И СКОРОСТИ
ЦЕЛИ
Автокорреляционная функция является весьма удоб¬
ной характеристикой, позволяющей оцепить потенциаль¬
ные возможности сигнала и наиболее целесообразно вы¬
брать его параметры и методы обработки. Принято изо¬
бражать автокорреляционную функцию в виде сечений
фигуры, поверхность которой изображает функцию Ч7(т,
F) (рис. 3.1), спроектированных на плоскость (т, F).
Для решения большинства задач достаточно изображе¬
ние сечений на двух уровнях: Чг^0,1, соответствующем
области низкой (или отсутствия) корреляции; и —С
(С = 0,5 или С = 1/1/е =0,607), ограничивающем область
высокой корреляции на плоскости (т, F). Уровень С =
= 0,607 оказывается достаточным для разрешения двух
откликов на выходе согласованного фильтра, если об-
68
ласти высокой корреляции этих откликов по осям т и г
не перекрываются.
Конфигурация области высокой корреляции характе¬
ризует основные показатели радиолокационной системы:
разрешающую способность по времени (дальности) и по
частоте допплеровского сме¬
шения (скорости); точность
измерения дальности и ско¬
рости объекта; неоднознач¬
ность обнаружения.
Рассмотрим вначале наи¬
более простой случай обна¬
ружения неподвижной цели
на фиксированном направ¬
лении. В этом случае един¬
ственным полезным парамет¬
ром является временной
сдвиг т и совместная корре¬
ляционная функция сводится
к Чг(т). Для автокорреляци¬
онных функций с одним рез¬
А
Рис. 3.1. Пространственное изо¬
бражение совместной автокор¬
реляционной функции.
ко выраженным максимумом
на интервалы 1т1^тт (рис. 3.2) можно воспользоваться
аппроксимацией графика автокорреляционной функции
прямоугольником равной площади, т. е.
Ф(х) =
1°
при
при
Рис. 3.2. Автокорреляционная функция сигнала при неподвижном
объекте.
69
QO
где тк — |ЧГ (т)|2 йл — время корреляции.
В рассматриваемом случае
?/1
J |Ч*(т)|Мт.
(3-2)
ЛАожно считать, что разрешение по дальности практиче¬
ски возможно, если временной сдвиг между двумя сигна¬
лами лежит вне области сильной корреляции. Таким об¬
разом, тк может служить качественной оценкой потен¬
циальной разрешающей способности по дальности. Вре¬
мя корреляции характеризует и точность системы, так как
в некотором масштабе представляет область возможных
ошибок при измерении временного сдвига.
Для однозначного измерения дальности автокорре¬
ляционная функция в диапазоне измерения должна
иметь один резко выраженный максимум. При наличии
дополнительных максимумов их величина должна быть
существенно меньше основного по абсолютному значе¬
нию. Если корреляционная функция имеет несколько
изолированных выбросов и значение максимума, напри¬
мер, при т—:т0 мало отличается от основного при т = 0, то
практически нельзя установить, какое время запаздыва¬
ния имет обнаруженный сигнал.
Таким образом, для осуществления радиолокацион¬
ного наблюдения неподвижных целей зондирующие си¬
гналы должны выбираться так, чтобы функция г1г(т) име¬
ла вид кратковременного импульса. Соответственно ши¬
рина частотного спектра сигналов должна быть порядка
А/=1/тг:. Этим требованиям удовлетворяет широкий
класс функций, что позволяет использовать в радиоло¬
кации импульсные сигналы, непрерывные сигналы с ши¬
рокополосной угловой модуляцией, сигналы шумового ти¬
па, кодированные последовательности импульсов.
При радиолокационном наблюдении движущихся объ¬
ектов принимаемый сигнал будет иметь не только вре-
меннбй сдвиг tD, но и частотный сдвиг Fv, определяемый
радиальной скоростью объекта. На рис. 3.3,а изображена
область высокой корреляции сигнала при временном
сдвиге tDQ и частотном FVq. Вид диаграммы позволяет не
только оценить потенциальные возможности данного си¬
то
гнала, но и предопределить схему оптимальной обработ¬
ки. Если, например, требуется производить поиск по
скорости, то может быть использована многоканальная
схема (рис. 3.3,6), содержащая ряд линейных фильтров
МЛ осуществляющих операцию свертки принимаемого
сигнала //(/) с ожидаемым ME),
x(tD, { у (/) u(t — tu-., kkFjdt,
—00
и безынерционных детекторов. Решающее устройство
определяет по выходному напряжению детекторов, ка¬
кому из каналов соответствует обнаруженный объект.
;1 1 г
. г- / )'■
—
Г
к-— ..С',
:■ дл
F I/O
н
1 i
1
1
i
2 л г
...
1
t]JO t'nm t])
а)
Н*
/7 /ЗЛ
I—
о
Рис. 3.3. Область высокой корреляции (с) при наблюдении движу¬
щегося объекта и возможная схема обработки (б) сигнала.
Полезная составляющая выходного эффекта хк(6ъ ME)
в произвольном &-м канале определяется значением
функции xV(tD—tDo, khF—Fvq) вдоль соответствующей
горизонтальной линии на диаграмме. Для получения вы¬
броса корреляционной функции хотя бы в одном из ка¬
налов частотный сдвиг между каналами не должен пре¬
восходить протяженности области высокой корреляции
по оси частот. Обычно принимают АЕ равным протяжен¬
ности области высокой корреляции. Исходя из возмож¬
ного диапазона изменения скорости движения объектов,
можно найти максимальное допплеровское смещение
±ЕУт и необходимое число каналов N ==2FVnJ/sF анали¬
затора.
71
Таким образом, диаграмма совместной автокорреля¬
ционной функции позволяет определить требования к ра¬
диолокационному сигналу при наблюдении движущихся
объектов. Сигналы, область высокой корреляции которых
на рабочем участке плоскости (т, F) сосредоточена вбли¬
зи оси F, обеспечивают высокую разрешающую способ¬
ность по дальности, а для получения хорошего разреше¬
ния по скорости эта область должна быть, сосредоточена
вблизи оси т. Для разрешения временного интервала по¬
рядка Дт необходим сигнал с шириной спектра порядка
1/Дт. Аналогично разрешающая способность по частоте
порядка Д/ обеспечивается сигналом с длительностью по¬
рядка 1/ДД
Изучение функции ЧДт, F) с целью выяснения потен¬
циальных возможностей разрешения сигналов по време¬
ни и частоте привело к формулировке принципа неопре¬
деленности в радиолокации.
§ 3.3. ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ
В РАДИОЛОКАЦИИ И ДИАГРАММЫ
НЕОПРЕДЕЛЕННОСТИ РАДИОЛОКАЦИОННЫХ
СИГНАЛОВ
Наряду с автокорреляционной функцией ЧДт, F) для
оценки свойств радиолокационного сигнала может быть
использована также функция хР2(т, F). Функция ^(т, F)
обладает весьма интересным свойством: независимо ог
длительности, вида модуляции амплитуды или фазы си¬
гнала объем Иф.г тела, ограниченного поверхностью, изо¬
бражающей функцию ^(т, F), и плоскостью т, F, остает¬
ся постоянным и равным 1.
Это утверждение носит название принципа неопре¬
деленности в радиолокации и может быть доказано не¬
посредственным вычислением объема Таким обра¬
зом,
JJ |Т(т, F)\*d-tdF = 1. (3.3)
—00
Постоянство объема тела неопределенности означает,
что любое изменение параметров сигнала, ведущее
к сжатию тела неопределенности по оси т, вызывает со¬
ответствующее расширение его по оси F. Иными слова-
72
ми, повышение точности и разрешающей способности но
дальности приводит к снижению точности и разрешаю¬
щей способности по скорости, и, наоборот, улучшение
точности и разрешающей способности по скорости про¬
исходит за счет их ухудшения по дальности. В этом мож¬
но усмотреть некоторую аналогию с принципом неопре¬
деленности в физике, который заключается в невозмож¬
ности определить одновременно с любой наперед
заданной точностью положение и скорость элементарной
частицы. Видимо, эта аналогия и послужила поводом
применения названий: «принцип неопределенности' в ра¬
диолокации» и, как следствие, «тело неопределенности»,
«диаграмма неопределенности», «функция неопределен¬
ности».
Анализ функции неопределенности Чг2(г, F) позволя¬
ет выявить потенциальные возможности радиолокацион¬
ного сигнала в отношении точности, разрешающей спо¬
собности и однозначности при измерении дальности и
скорости цели. При этом используется как ее объемное
представление в виде тела неопределенности, так и про¬
екция сечения тела неопределенности на некотором уров¬
не на плоскость т, F. Уровень сечения выбирается так,
чтобы произведение площади сечения на единичную вы¬
соту дало объем тела неопределенности Уф2, также рав¬
ный 1. Таким образом, тело неопределенности заменяет¬
ся эквивалентным цилиндром или несколькими цилинд¬
рами (если тело неопределенности имеет несколько
пиков, превышающих уровень сечения), суммарная пло¬
щадь оснований которых равна 1. Изображение основа¬
ний цилиндров на плоскости т, F называется диаграм¬
мой неопределенности.
На практике при анализе свойств сигнала чаще ис¬
пользуют непосредственно совместную автокорреляцион¬
ную функцию Т(т, Z7) и проекцию сечения се об|емиого
изображения на плоскость т, F. Такая плоскостная диа¬
грамма также называется диаграммой неопределенности.
Ниже рассматриваются диаграммы неопределенное!п
некоторых наиболее распространенных радиолокацион¬
ных сигналов.
Синусоидальный сигнал с прямоугольной огибающей.
Рассмотрим случай весьма длительного и короткого сигна¬
лов. Первый случай соответствует непрерывному излуче¬
нию, когда длительность пакета синусоидальных колсба-
73
нин тп значительно превышает максимально возможное
время задержки
В силу большой длительности сигнала ти выполняет¬
ся также условие
1 - 2Ут
ти 1 X ’
где Vm— максимально возможное значение скорости
цели, а
Z — длина волны излучаемых колебаний.
Второй случай соответствует кратковременному им¬
пульсному СИГНалу, ПрИ КОТОРОМ Xn<^tDm И l/TyF^>FVrn.
Автокорреляционная функция для прямоугольною
импульса может быть записана в виде
F)\ =
sin nF (ти — |т|)
(3-4)
Если записать корреляционную
оси т и Д, получим
функцию отдельно по
|'Ю 0)| =
1'6(0, F)| =
Ти
sin тгГти
7гГтн
при F = 0, (3.5)
при т = 0.
(3.6)
Для выяснения конфигурации пространственной ди¬
аграммы функции |V(r, F) | положим |т|=ти, а затем
|тр=ти/2. Заметим, что при |т| =тя значение |W(r, F) | =0;
при |т.|=тп/2 автокорреляционная функция принимает
вид
Отсюда следует, что по мере роста г центральный пик
(рис. 3.4) не только уменьшается по величине пропор¬
ционально т, но и расширяется по оси F. Так, при 1т| =
= ти/2 ширина центрального максимума по оси F стано¬
вится равной 4/ти вместо 2/ти при т = 0. Заметим также,
что ширина центрального пика по осям т и F тесно взаи¬
мосвязана. Расширение импульса ти ведет к сужению
спектра, т. е. уменьшению протяженности пика по оси F.
Это наглядно представлено диаграммами на рис. 3.5,
74
изображающими сечения автокорреляционной функции
на уровне С — 0,5 для длительного и короткого импуль¬
сов. Из рассмотрения диаграмм неопределенности можно
сделать вывод о том, что нет необходимости осуществ¬
лять поиск отраженного сигнала по дальности при Ти^>
и поиск по скорости, если l/x^>FVm. Диаграмма
неопределенности позволяет также определить нужное
Рис. 3.4. Совместная автокорреляционная функция одиночного пря¬
моугольного импульса.
Рис. 3.5. Диаграммы неопределенности длительного (с) и кратковре¬
менного (б) импульсов.
число каналов системы поиска по дальности и скорости,
если они оказываются необходимыми.
Диаграмма наглядно показывает, что система непре¬
рывного излучения несущей (при ти^>1/рт) не обладает
разрешением по дальности, но имеет высокую точность и
разрешающую способность при измерении скорости. При
кратковременных импульсных сигналах (ти<С/гт) даль¬
ность и скорость ^меняются местами. Таким образом, для
одновременного измерения дальности и скорости сигнал
должен иметь диаграмму неопределенности с малой про¬
тяженностью по осям т и F одновременно. Такие сигналы
будут рассмотрены несколько дальше, а сейчас рассмот¬
рим сигнал с огибающей колоколообразной формы,
который широко используется в теоретических исследо¬
ваниях и находит применение в реальных системах.
Импульсный сигнал с колоколообразной огибающей.
Для одиночного сигнала с огибающей
Uа (0 =- Uи СХр Г — Д.
и длительностью ти на уровне 0,67 выражение для сов¬
местной автокорреляционной функции имеет вид
(3-7)
Таким образом, для рассматриваемого сигнала проекция
сечений функции 1Т(т, F) на плоскость (т, F) представ¬
ляет семейство эллипсов с общим центром, главные оси
которых совпадают с осями т и F. Длину полуосей эллип¬
са можно найти из выражения (3.7), приравнивая |Чг(т,
0)| и |гР(0, F) | выбранному уровню С. Полуось х = а при
F^O из условия рТ(я, 0)| — -ехр[—“ С равна
а = 2,„ /2р.
Аналогично для полуоси F = b из уравнения
|Ф(0, 6)| = ехр [
пандем
Ь——^ -1- (— 1пС>
тп F п v 7
76
Принимая уровень 'отсчета С—у -у-~ 0,607, получим
о = 0,8т:и, й = 0,4/ти.
На рис. 3.6 изображена диаграмма неопределенности
для рассмотренного одиночного сигнала колокольной
формы в виде эллипса с осями 2а и 2Ь, вычисленными на
уровне С = 0,607.
Рис. 3.6. Диаграмма неопределен¬
ности одиночного импульса коло¬
колообразной формы.
Периодическая последовательность импульсов. Среди
импульсных синусоидальных сигналов независимо от
формы огибающей основное применение находят крат¬
ковременные (xn<^tDm и TnFy?n<;l), обеспечивающие вы¬
сокую разрешающую способность и точность при изме¬
рении дальности, но не обладающие разрешающей спо¬
собностью по скорости. Достоинство импульсных сигна¬
лов заключается в максимальной простоте осуществле¬
ния оптимальной обработки сигнала, а также развязки
приемника и передатчика РЛС. Недостатком является
трудность получения высокой энергии импульса, необхо¬
димой для увеличения дальности действия системы, и
отсутствие разрешения по скорости. Эти недостатки мо¬
гут быть в значительной степени устранены использова¬
нием периодически повторяющихся импульсов.
Обычно принимается пачка отраженных импульсов,
огибающая которой определяется диаграммой направ¬
ленности антенны. При аппроксимации огибающей пачки
колоколообразпой функцией (так же как и излучаемых
импульсов) диаграмма неопределенности имеет вид, изо-
77
пульсов) диаграмма неопределенности имеет вид, изо¬
браженный на рис. 3.7. Диаграмма показывает, что Не¬
определенность по частоте распадается на узкие полосы,
а неопределенность по времени становится повторяющей¬
ся. Однако суммарная неопределенность, определяемая
суммарной площадью диаграммы, сохраняется примерно
такой же, как и для одиночного сигнала (рис. 3.6) с те¬
ми же параметрами, ио разделяется на ряд областей.
Такое разделение приводит к неоднозначности в опреде¬
лении т и F.
Рис. 3.7. Диаграмма неопределенности периоди¬
ческой последовательности импульсов.
Разумным выбором частоты повторения импульсов
Fn неопределенность может быть вытеснена за пределы
рабочего диапазона станции. Для этого необходимо вы¬
брать Tu^tDm и Fn= -^-^FVm, но совмещение этих
J п
требований не всегда возможно, и в большинстве случа¬
ев стремятся выполнить первое условие. При этом систе¬
ма обеспечивает точное измерение дальности, ио имеет
неоднозначность измерения скорости. Так, например,
в системах с селекцией движущихся целей периодиче¬
ская структура диаграммы неопределенности по оси F
приводит к появлению слепых скоростей при Fv = nFn и
неоднозначности определения скорости.
Частотно-модулированный сигнал. Анализ диаграмм
неопределенности импульсного сигнала показывает его
ограниченные возможности. Поскольку ширина спектра
импульса с ^смодулированной несущей обратна длитель-
78
ности сигнала ти, невозможно найти такое значение, при
котором одновременно обеспечивается высокая точность
и разрешающая способность по дальности и скорости.
Вызывает трудности также совмещение требований уве¬
личения дальности действия РЛС с сохранением и тем
более повышением ее точности и разрешающей способ¬
ности.
Для решения поставленной задачи необходимо вы¬
брать такой сигнал, ширина спектра которого во много
раз превышает величину, обратную длительности, сигна¬
ла ти. Наиболее очевидным путем расширения спектра
импульсного сигнала без уменьшения его длительности
Рис. 3.8. Диаграмма неопределенности ча¬
ст отно - м одул и р ов а и 11 о го сигнала.
является применение линейной частотной модуляции не¬
сущей.
Для прямоугольного импульса длительностью ти с ли¬
нейной модуляцией частоты колебаний с девиацией U7
автокорреляционная функция имеет вид
sin [(ли/гДи |т|)
I (nW'i/tji + nF) ти
(3-8)
»
а соответствующая ей диаграмма неопределенности
(рис. 3.8) представляет эллипс, который в силу ЧМ вы-
79
тягивастся вдоль оси F и сжимается по осп т, а также
поворачивается пропорционально девиации U7, опреде¬
ляющей ширину спектра сигнала.
Из рассмотрения диаграммы ясно, что при этом точ¬
ность и разрешающая способность при измерении даль¬
ности могут быть повышены. Так, если для импульса без
ЧМ разрешаемое расстояние пропорционально тп, то при
ЧМ пропорционально \/W, следовательно, выигрыш со¬
ставляет TnV7.
§ 3.4. СЛОЖНЫЕ (ШИРОКОПОЛОСНЫЕ) СИГНАЛЫ
И СЖАТИЕ ИМПУЛЬСОВ
Из изложенного ясно, что для получения высокой
разрешающей способности, точности и однозначности при
измерении дальности и скорости необходим сигнал, авто¬
корреляционная функция которого имеет единственный
пик в начале координат. Остаточный фон (значение
Ч^т, F) в области низкой корреляции) должен быть по
F
Рис. 3.9. Диаграмма неопределен¬
ности сигнала шумоиодобной
формы.
возможности малым и
равномерно распределен¬
ным на участке плоскости
(т, Z7), ограниченном
(рис. 3.9) длительностью
сигнала Т и шириной
спектра А/. Площадь не¬
определенности уменьша¬
ется пропорционально
TAf, и с этой точки зре¬
ния «идеальным» сигна¬
лом является белый шум
с бесконечной полосой и
длительностью. Функция
корреляции такого сигна¬
ла обращается в 6-функ¬
цию, и неопределенность сокращается до потенциально¬
го минимума.
Однако сигнал с бесконечно широким спектром и бес¬
конечной длительностью практически не реализуем, и
можно лишь в большей или меньшей степени к нему при¬
ближаться. Практический вывод из рассмотрения идеаль¬
ного сигнала заключается в том, что сигнал должен
иметь шумоподобную форму, опнсываслмую многими па¬
80
раметрами, а не двумя-тремя, как в рассмотренных выше
примерах (длительность, частота повторения, девиация
частоты). Но применять обычную выборку гауссова шу¬
ма. ограниченную временем Т и в полосе Af, имеет смысл
только при очень больших значениях TAf>104, при кото¬
рых вероятность побочных всплесков функции Чг(т, F)
достаточно мала. При ТД/<103 шумовой сигнал должен
выбираться с осторожностью, так как вероятность появ¬
ления в рабочей области плоскости т, F побочных пиков,
соизмеримых с основным, становится достаточно боль¬
шой, что приводит к неоднозначности при определении
параметров движения цели.
Наиболее удовлетворяет сформулированным требова¬
ниям сигнал в виде кодированной по фазе последова¬
тельности из большого числа импульсов. Такая последо¬
вательность может быть образована путем деления паке¬
та синусоидальных колебаний длительностью Т на N~
= TAf интервалов длительностью 1/Af. Начальные фазы
колебаний в интервалах имеют значения 0°( + ) и
180°(—), чередующиеся в соответствии с выбранным ко¬
дом. Наиболее интересны кодовые последовательности,
минимизирующие значения функции хР(т, Т7) везде, кро¬
ме центрального пика, расположенного в начале коорди¬
нат (т = 0, F = 0). Для 7V<:13 Баркером путем подбора
найдены кодовые последовательности (называемые ко¬
дами Баркера), автокорреляционная функция которых
имеет уровень остатков, равный \/N, если амплитуду
центрального пика принять за 1. Наиболее эффективно
применение ФМ сигналов при больших N. К сожалению,
для ЛЛ> 13 кодовые последовательности дают автокорре¬
ляционные функции с уровнем остатков больше 1/ЛЗ
Одним из лучших кодов является код, представляющий
последовательность длиной N = TAf = 2n—1, где п—осно¬
вание кода. W является периодом кода, так как даль¬
нейшее увеличение числа импульсов приводит к повто¬
рению кода. Такой код, называемый кодом пулевой по¬
следовательности максимальной длительности, позволяет
получить функцию V(t, 5), центральный пик которой
превышает уровень фона в }FN — \STAf раз.
Чем больше длина кодированной последовательности,
тем больше превышение основного пика над. уровнем
([.юна и, следовательно, тем меньше неопределенность
G—1173
81
при измерении дальности и скорости и тем выше точ¬
ность и разрешающая способность системы. Конечно,
схема оптимальной обработки с возрастанием N услож¬
няется. Оптимальная обработка обеспечивается согласо¬
ванным фильтром, в качестве которого может быть ис¬
пользована линия задержки с отводами и сумматором.
Отводы линии выбираются таким образом, что в сум¬
маторе элементарные импульсы последовательности
складываются в фазе. При этом амплитуда сигнального
импульса на выходе фильтра возрастает в N = Tkf раз,
а длительность уменьшается в T&f раз по сравнению
с входнЫлМ сигналом. Таким образом, происходит сжатие
импульса во времени с соответствующим увеличением
амплитуды.
Для измерения дальности может быть использован
также корреляционный метод, заключающийся в созда¬
нии опорной последовательности, аналогичной модули¬
рующему сигналу, но задержанной относительно него.
При совпадении времени задержки опорной последова¬
тельности с временем задержки сигнала, обусловленной
дальностью объекта, получается всплеск функции авто¬
корреляции. Фиксация времени задержки опорного сиг¬
нала позволяет определить дальность объекта. При этом
точность и разрешающая способность по дальности опре¬
деляются протяженностью функции автокорреляции
вдоль оси т.
Для создания кодовой последовательности модули¬
рующего и опорного сигналов могут быть использованы
регистры сдвига с обратной связью. Рис. 3.10 поясняет
создание кода длиной М = 2П—1=23—1=7 с помощью
трехкаскадного регистра сдвига. В цепи обратной связи
производится перемножение выходных напряжений двух
последних триггеров регистра с последующей подачей ре¬
зультата на вход первого триггера. С приходом каждого
тактового импульса состояние регистра последовательно
меняется, повторяясь через каждые N=7 импульсов.
Напряжение кодовой последовательности снимается
с выхода одного из триггеров регистра. Если, например,
снимать напряжение с выхода первого триггера, то кодо¬
вая последовательность будет —+Ч 1 .
Таким образом, основание кода и, так же как и его
период Л/, определяется числом разрядов регистра. Так,
для получения кодовой последовательности длиной N=
8:?
= 511 необходим регистр с п=^9 каскадами. Повышение
точности и разрешающей способности при измерении
дальности достигается повышением частоты повторения
тактовых импульсов 1/Гт, поскольку период их повторе¬
ния Тт определяет длину элементарного участка даль¬
ности (на которые разбивается весь диапазон измере¬
ния) и протяженность автокорреляционной функции си¬
гнала ио оси дальности. Увеличение п и соответственно
JV обеспечивает повышение дальности действия дально¬
мера и однозначность отсчета дальности.
о
—Ч - 1 •+-
4-
-М -Т -
-
Y
г ±
V
Рис. 3.10. Формирование кода нулевой последо¬
вательности.
Кодовая манипуляция фазы излучаемого сигнала на¬
ходит все более широкое применение не только в радио¬
локационных, но и в радионавигационных системах.
Другим способОхМ сжатия импульса является частот¬
ная модуляция излучаемого импульса. Предположим, что
излучается импульс длительностью п (рис. 3,1 Г), несу¬
щая частота которого модулирована по линейному зако¬
ну в пределах длительности co = 2nf = со0 + а/ при |/|^Ti/2.
При приеме отраженный сигнал подается на согла¬
сованный фильтр. Найдем форму импульса на выходе
фильтра и связь его длительности Т2 с девиацией часто¬
ты W — ат\/2л.
6*
83
Рис. 3.11. Сжатие частотно-модулироваииого импульса.
Напряжение сигнала на входе фильтра при амплиту¬
де Ua=l можно записать в виде
w1(0 = exp[7 (3-9)
а его спектр представить выражением
gi(U))= J "ИО ехР [—/«•'/] Л =
—00
-с,/2
= J ехр/[(со0 — со) tЦ- cit2^] dt.
--Ч/2
84
Если время задержки фильтра /3(/) является линейной
функцией частоты, но с наклоном, обратным наклону
изменения частоты, коэффициент передачи фильтра ра¬
вен
Дф (О = ехр [/ (®0 — ш)2/2а]
и спектр сигнала на выходе фильтра будет
#2 (“)/=.Яф»-
Тогда напряжение сигнала на выходе фильтра можно
представить выражением
со
<(0=17 J £* (■«) exp [/«/] d<>,
—оо
которое после подстановки £2(0)) и преобразований при¬
водится к виду
М2 (0 = j/TjF СХ-Р I'M
= у/^^ТСехр[/ЧД (3.10)
Таким образом, импульс на выходе фильтра имеет ча¬
стоту «о, форму огибающей, описываемую функцией
sinx/x, а его длительность на уровне половинной мощ¬
ности Т2 — 1/W. Следовательно, коэффициент укорочения
(сжатия) импульса в результате фильтрации равен
T1/T2—T1U/. Амплитуда импульса па выходе фильтра
будет [у2 = )/т:11Г, т. е. возрастает в раз.
Сжатие импульса позволяет радикально улучшить
тактические характеристики РЛС и достигнуть очень
больших дальностей действия при высокой точности и
разрешающей способности по дальности. Это покупается
ценой увеличения энергии излучаемого импульса пропор¬
ционально длительности Ti и расширения его спектра
пропорционально W.
В заключение следует отметить, что для ряда совре¬
менных РЛС характерна тенденция повышения не только
точности и разрешающей способности по дальности и
скорости (временным характеристикам), по и по угло¬
вым координатам и их производным (пространственньш
характеристикам). Для выполнения этих требований при¬
меняются сигналы с весьма широким спектром и антен-
85
иы с очень большим относительным раскрывом. При этом
становится существенной взаимосвязь временных и про¬
странственных характеристик РЛС, для учета которой
может быть использована обобщенная функция неопре¬
деленности, охватывающая как временные, так и про¬
странственные характеристики. РЛС рассматривается
в этом случае как пространственно-временнбй фильтр,
анализирующий пространственно-временное поле сигна¬
лов.
Разработке методов анализа и синтеза миогопара-
метричсских РЛС на основе обобщенной функции не¬
определенности уделяется сейчас значительное внимание.
Глава 4
ОБНАРУЖЕНИЕ СИГНАЛОВ
§ 4.1. ВВЕДЕНИЕ
Первая задача, возникающая поп приеме сигналов
радиотехнических систем, заключается в установлении
факта наличия сигнала в принятом колебании. Эта за¬
дача носит название задачи обнаружения.
Задача обнаружения теоретически сводится к отыска¬
нию определенной системы правил, позволяющих наблю¬
дателю решить, содержит ли принятое колебание полез¬
ный сигнал или нет. Необходимость установления такой
системы правил объясняется следующим. Принятое ко¬
лебание— в зависимости от того, присутствует или от¬
сутствует полезный сигнал — представляет собой либо
смесь полезного сигнала с различного рода помехами,
всегда присутствующими в месте приема, либо одни по¬
мехи. Поэтому наличие некоторого сигнала в месте прие¬
ма еще не означает, что этот сигнал именно тот, который
необходимо обнаружить. В связи с этим, прежде чем
принять решение, наблюдатель должен провести анализ
принятого колебания, который по совокупности призна¬
ков дал бы возможность отличить смесь полезного сигна¬
ла с помехой от чистой помехи. Анализ принятого ко¬
лебания позволяет уменьшить число ошибочных решений,
но не исключает их полностью. Система правил анализа
принятого колебания может быть названа оптимальной,
если эти правила в наиболее полной мере удовлетворя¬
ют требованиям, предъявляемым к качеству обнаруже¬
ния.
Для успешного решения задачи обнаружения наблю¬
датель должен заранее располагать некоторыми сведе¬
ниями о полезном сигнале и помехах и по возможности
полнее использовать эти сведения при анализе принятого
колебания. Именно эти априорные данные и дают воз¬
можность по совокупности различий между сигналом и
87
помехой установить факт наличия или отсутствия полез¬
ного сигнала в принятом колебании. Поэтому оптималь¬
ная система правил может быть установлена для сигна¬
ла и помех, структура которых в topi или иной мере опре¬
делена заранее.
Таким образом, располагая некоторыми априорными
сведениями о полезном сигнале и помехах, возможно
найти правила обработки принятого колебания, опти¬
мальные с точки зрения требований, предъявляемых
к качеству обнаружения. Располагая последними, можно
синтезировать структуру устройства оптимальной обра¬
ботки сигнала.
Установление структуры и потенциальных возможно¬
стей устройства оптимальной обработки сигнала являет¬
ся лишь первой частью решения задачи обнаружения.
Вторая часть — практическая реализация таких уст¬
ройств— часто наталкивается на серьезные технические
трудности. В связи с этим представляет большой инте¬
рес отыскание более простых в реализации способов ква-
зиоптимальной обработки сигналов и сравнение их ка¬
чественных показателей с оптимальными.
Указанный подход к теоретическому и практическому
решению задачи обнаружения развивается в настоящей
главе применительно к различным видам сигналов, ис¬
пользуемых в радиотехнических системах. В качестве по¬
мехи, действующей на входе приемника, рассматривается
нормальный шум с равномерным в широкой полосе час¬
тот спектром. Шум представляет собой наиболее опасный
вид помехи, с которой чаще всего приходится встречать¬
ся на практике. Использованию нормального шума в ка¬
честве основной модели помехи способствует также и
простота его математического описания, что существен¬
но упрощает исследование устройств обработки сигналов.
§ 4.2. ПРИЕМ СИГНАЛОВ КАК СТАТИСТИЧЕСКАЯ
ЗАДАЧА
Если не ограничиваться рассмотрением только случая
простого обнаружения, когда число возможных сообще¬
ний равно двум, то задачу приема можно определить как
воспроизведение одного сообщения из множества всех
возможных сообщений. Именно такой подход к задаче
приема оказывается наиболее плодотворным, так как по-
88
зволяет получить оощие закономерности, применимые не
только к задаче обнаружения, но и к ряду других задач,
возникающих после обнаружения полезного сигнала, и
прежде всего к задаче измерения параметров принятого
сигнала.
С точки зрения получателя посланное сообщение но¬
сит случайный характер, так как получателю неизвестно,
какое именно из множества всех возможных сообщений
выбрано для передачи.
Поэтому до приема сообщения получатель • может
в лучшем случае лишь приписать каждому из возмож¬
ных сообщений ожидаемую пли априорную вероятность
его появления.
Сообщение передается в точку приема посредством
сигнала, который, так же как и несомое им сообщение,
носит случайный характер, проявляющийся во флюктуа¬
циях его параметров: амплитуды, фазы и т. д. Наличие
всякого рода помех, поступающих наряду с сигналом на
вход приемника, а также возникающих в элементах са¬
мого приемника, еще более подчеркивает случайный ха¬
рактер принимаемого колебания. В связи с этим приня¬
тый сигнал лишь с некоторой вероятностью может быть
поставлен в соответствие с одним из возможных сооб¬
щений. Эта вероятность, называемая апостериорной, бу¬
дет распределена между несколькими из возможных со¬
общений или даже между всеми сообщениями. С умень¬
шением мешающего действия перечисленных ранее фак¬
торов степень концентрации апостериорной вероятности
на одном сообщении будет возрастать. В пределе, при
полном отсутствии помех, апостериорная вероятность
сконцентрируется на одном (переданном) сообщении.
Если задачу приема ограничить воспроизведением
апостериорного распределения вероятностей, остается не¬
решенным вопрос о том, какое же из сообщений было
передано. Поэтому следующим этапом является приня¬
тие решения на основе анализа апостериорного распре¬
деления вероятностей.
Таким образом, прием сигналов представляет собой
статистическую задачу, решение которой разбивается на
два последовательных этапа: вычисление апостериорно¬
го распределения вероятностей и принятие решения на
основе анализа этого распределения.
89
ё 4.3. ФУНКЦИЯ Ги’АВДОГЮДОБИЯ
В общем случае па вход приемника поступает смесь
.;(/) сигнала и помехи
!/(0=ф[«х(0> «п(0Г (4.1)
• je их(1) —сигнал, несущий сообщение х;
ип(0 — помеха.
Задачей приема является воспроизведение сообщения
л на основе анализа колебания y(t). На первом этапе
обработки принятого колебания у(1) должно быть выра¬
ботано апостериорное распределение вероятностей ^(х)
для каждого из возможных сообщений х. Если множест¬
во сообщений х дискретно, то Wv(x) —распределение ве¬
роятностей; если же множество сообщений х непрерыв¬
но, то ИдДх)—плотность распределения вероятностей.
Взаимное соответствие между переданным сигналом
их(1) и принятым колебанием y(t) определяется их сов¬
местным распределением вероятностей W(xt у), которое
согласно теореме умножения вероятностей равно
1У(х, y)=W(x)V7x(y) = W(y)Wv(x)t (4.2)
где 1Г(х)—распределение вероятностей сообщения х
(априорное);
Wx(y)—условное распределение вероятностей зна¬
чений у при известном х;
П7(у) —распределение вероятностей значений у
(безусловное);
U7^(x) —условное распределение вероятностей со¬
общения х при известном у (апостериор¬
ное) .
Из выражения (4.2) следует:
= WW (4.3)
Поскольку реализация y(t) задана, т. е. в выражении
(4.3) у является известной величиной, W (у) представляет
собой некоторую постоянную величину, следовательно,
1^(х)--Ж(х)1Г/х(//), (4.4)
Таким образом, для определения апостериорного рас¬
пределения л,остаточно найти функцию Wx(y), так как
90
априорное распределение W(х) предполагается задан¬
ным. Wx(y) представляет собой распределение вероятно¬
стей значений у при заданном х. Но в рассматриваем >й
нами задаче значение у задано и необходимо пайтм
№Х(У) как функцию от х. В такой постановке Wx(y) бу¬
дет не распределением вероятностей, а некоторой функ¬
цией величины х для заданной реализации у, получив¬
шей название функции правдоподобия.
Итак, при заданном априорном распределении ве¬
роятностей вычисление апостериорного распределения
вероятностей сводится к нахождению функции правдопо¬
добия Wx(y). Если априорное распределение равиомер
но в интервале всех возможных сообщений х, апосте¬
риорное распределение совпадает с точностью до по¬
стоянного множителя с функцией правдоподобия.
В качестве примера найдем функцию правдоподобия
для аддитивной смеси сигнала uxj(t), несущего нскою^ле
сообщение х>, и стационарного нормального шума :
(4.5)
существующей в течение времени Т.
Предположим, что сообщение х,- принадлежит мно¬
жеству сообщений Xi, хд, ..х/;!, которому соответствует
множество сигналов ux[(t), ux2(t), ..., все пара¬
метры которых заранее известны. Будем также считать,
что спектральная плотность шума равномерна в интер¬
вале частот Оя-Гп и равна нулю вне этого интервала.
Воспользовавшись теоремой Котельникова, разло¬
жим шум пш(7) на интервале времени Т в ряд по орто-
г о н а л ь н ы м ф у 11 к ц и я м:
2К пг
иш. (0^
Л=1
sip Зтт/Д (/ — ДД/)
(4.6)
где
ВИЯ
_1_
2тгД1В ’
a выбрана так,
что выполняются
усло-
(4.7)
Ы=
где п — число точек отсчета в интервале 7;
— ширина спектра сигнала ux(i>.
91
В каждой f-й точке отсчета значение y(ti) может бьиь
представлено в виде суммы
У (М = i) ^ш(М • (4.8)
При заданном х функция ux(t) известна точно, и вероят¬
ность того, что у примет значение y(ti) равна вероятно¬
сти того, что шум в рассматриваемой точке отсчета при¬
мет значение т. е.
WHM1 = к (Ml = «М [у (М - (ML (4.9)
где 1^ш[иш(/г)]—распределение вероятностей мгновенных
значений шума в i-й точке отсчета.
Так как шум цш(/) стационарен и нормален, то для
любой точки отсчета
9
“п,
(Ищ) — ехр ( 2а2 } ’
где о2 — дисперсия шума.
Поэтому
_ 1 [Ш)-МАЛ2 1
Р[ ’ 2°2 Г
(4.Ю)
(4.И)
Как известно, корреляционная функция шума, спектраль¬
ная плотность которого No равномерна и ограничена ча¬
стотой FB, равна
/ \ 1 Г Л Г J А Т Г'' S1Г1 2тс Г J] Т
/?(т)=-^- No cos сот d(0 — N0FB—
о
^2
sin 2пГгр,т
2кЛ)Вт
(4.12)
График функции /?(т), изображенный на рис. 4.1, пока¬
зывает, что значения шума в точках отсчета, отстоящих
друг от друга на интервал At= -^г-, не коррелированы
между собой, следовательно, при вычислении функции
правдоподобия можно рассматривать отсчеты как неза¬
висимые между собой случайные величины. В таком
случае условная вероятность Wx(y) реализации y(t) рав-
92
на произведению условных вероятностей для
всех рассматриваемых точек отсчета, т. е.
п
(f/)=Г1 [У (W)]=[тУ" X
п
~Х. ехр{—Ху- у} [у (/еД/) — Их (^Д/)]аJ• (4-13)
k=\
Интеграл в показателе степени принимает минимальное
воспользуемся известным следствием теоремы Котель¬
никова:
п Т
27-^ \y(kM)-ux(kM)]^ (4.14)
k=\ о
Тогда выражение (4.13) для функции правдоподобия
приводится к виду
т
(У) = |уУ" ехР {-J \у (0 - «X (OP dt}. (4.15)
О
Интеграл в показателе степени принимает минимальное
значение при таком которое наилучшим образом
совпадает с рассматриваемой реализацией y(t) на всем
93
интервале наблюдения Т. Именно при этом значении
полезного сигнала функция правдоподобия имеет мак¬
симум. Указанное значение ux(t) является наиболее ве¬
роятным из всех возможных для данной реализации y(t).
Таким образом, Wx(y) характеризует степень соответст¬
вия между y(t) и всеми возможными ux(t), а ее макси¬
мальное значение соответствует наиболее правдоподоб¬
ной оценке принятого сообщения. Для иллюстрации на
рис. 4.2,в приведен график функции правдоподобия для
реализации у(/) (рис. 4.2,6). Здесь все возможные сооб¬
щения принадлежат множеству х0, хь х2, Хз, а соответ¬
ствующие им сигналы представлены на рис. 4.2,а.
Приведенные соображения легко распространить и на
случай непрерывного в заданном интервале хмип-^Хмакс
сообщения. При этом Wx(y) будет непрерывной функ¬
цией X.
Проанализируем несколько подробнее выражение
(4.15), предварительно представив его в виде
г*<М7НифЬН‘',<'),я+
6
т т
+дУ f у (О «х (0 dt-± j Z? (/) dt;. (4.16)
6 6
Первый интеграл не интересен для получателя сообще¬
ния, поскольку он представляет собой операцию над
y(t) безотносительно к ux{t) и численно равен энергии
принятого колебания. Последний, третий, интеграл во¬
обще не представляет собой операции над принятой реа¬
лизацией и может быть вычислен без обращения к ней.
Поэтому единственной операцией над принятой реализа¬
цией y(t), отражающей связь ее с сигналом ux(t), яв¬
ляется вычисление интеграла
т
z = J у (/) их (/) dt (4.17)
о
для всех значений х. Интеграл z называют корреляцион¬
ным интегралом, так как он является мерой взаимной
корреляции между реализацией y(t) и всеми возможны¬
ми сигналами ux(t). Если последние имеют одинаковую
энергию, го наибольшее значение z будет соответство-
94
вать сигналу, взаимная корреляция которого с принятой
реализацией максимальна. При равномерном априорном
распределении W (х) наибольшее значение г соответству¬
ет сообщению, имеющему максимальную апостериор¬
ную вероятность.
а)
Рис. 4.2. Сигналы, соответствующие сообщениям хо, Xj, Х2, х3 (а)\
принятая реализация (б); функция правдоподобия (в).
^х(У)
Х0 Х1 X? Ху
Располагая значениями корреляционного интеграла
для всех возможных сообщений х, можно построить
функцию правдоподобия без повторного обращения
к реализации y(t). Поэтому единственное преобразова¬
ние, которому должна быть подвергнута в приемнике
реализация y(t), заключается в образовании корреля¬
ционного интеграла (4.17). Все остальные операции не
связаны с действиями над принятой реализацией z/(Z) и
вводятся лишь в тех случаях, когда возникает необхо¬
димость представления функции правдоподобия в явном
виде.
§ 4.4. ОТНОШЕНИЕ ПРАВДОПОДОБИЯ
При обнаружении сигнала, когда число возможных
сообщений равно двум («сигнал есть» и «сигнала нет»),
апостериорная вероятность распределена между этими
95
двумя сообщениями. Поэтому операция принятия реше¬
ния должна быть основана на сравнении апостериорной
вероятности наличия сигнала с апостериорной вероятно¬
стью отсутствия сигнала. Для сравнения используется
отношение вероятностей В(х), которое с учетом (4.3)
равно
D (х0) ~ (*о) (У) (*о) . k
(4.18)
где Xi — сообщение «сигнал есть»;
х0— сообщение «сигнала нет»;
Л(х) =
^■У1 (И
-UZvo (У) ‘
Операция принятия решения сводится к сравнению
значения В(х) с некоторым порогом В, что соответству¬
ет правилу:
сигнал есть, если
д /и Д •
сигнала нет, если
(4.19)
Величина Л(х) показывает, во сколько раз условная
вероятность приема реализации y(f) при наличии полез¬
ного сигнала отличается от условной вероятности приема
той же реализации при отсутствии сигнала. Эта вели¬
чина может быть определена еще и как отношение зна¬
чений функции правдоподобия в точках х{ и х0 и носит
название отношения правдоподобия.
Устройство, вычисляющее отношение правдоподобия
Л(х) и вырабатывающее решение на основании сравне¬
ния отношения правдоподобия с порогом Ло, называют
оптимальным приемником обнаружения.
При испытании отношения правдоподобия на порог
возникают ошибочные решения двух видов: «пропуск це¬
ли» и «ложная тревога». «Пропуск цели» имеет место
в том случае, когда при наличии сигнала отношение
правдоподобия Л(х) оказывается ниже порога Ао. Услов¬
ная вероятность пропуска цели D связана с вероятностью
правильного обнаружения D равенством
D = 1—0, (4.20)
96
поскольку при наличии полезного сигнала решения
«сигнал есть» и «сигнала нет» образуют полную группу
событий. Ошибочное решение — «ложная тревога» —
возникает, когда при отсутствии полезного сигнала про¬
исходит превышение порога До. Условная вероятность
ложной тревоги равна
F — \ — F, (4.21)
где F — вероятность пепревышепия порога До при усло¬
вии отсутствия полезного сигнала (вероятность правиль¬
ного необнаружепия).
Условные вероятности правильного обнаружения и
ложной тревоги являются основными качественными по¬
казателями приемников обнаружения. Эти вероятности
зависят от величины порога Ло. С уменьшением порога
вероятность правильного обнаружения и вероятность
ложной тревоги возрастают.
§ 4.5. ПОНЯТИЕ СРЕДНЕГО РИСКА. СТАТИСТИЧЕСКИЕ
К Р ИТЕ Р И И 015 НА Р У ЖЕ IIИ Я
В общем случае требования, предъявляемые к опти¬
мальному приемнику обнаружения, должны быть выра¬
ботаны с учетом относительной опасности каждого из
возможных ошибочных решений. В таких случаях целе¬
сообразно использовать понятие среднего риска, которое
позволяет единообразно подойти к решению задачи об¬
наружения и сформулировать с общих позиций единый
статистический критерий обнаружения.
Введем понятие среднего риска на примере радио¬
локационного обнаружения цели.
При обнаружении цели в заданной точке пространст¬
ва возможны четыре ситуации:
1. Правильное обнаружение с вероятностью Р[ =
=AV(xi)b.
2. Правильное необнаружение с вероятностью Л> =
= W(x0)F.
3. Пропуск цели с вероятностью Ps=W(xi)D.
4. Ложная тревога с вероятностью P4=lF(x0)/?.
7— 1173
97
Перечисленные ситуации представляют собой полную
группу случайных событий, поэтому сумма их вероят¬
ностей
4
£ Рг=1. (4.22)
i 1
Каждой из ситуаций может быть приписана опреде¬
ленная плата за ошибку в зависимости от стоимости или
опасности последней. Очевидно, правильным решениям
целесообразно приписать пулевую плату, а ошибочным—
тем большую, чем опаснее их последствия. Так как каж¬
дая из ситуаций имеет случайный характер, вводится
понятие средней платы в виде математического ожида¬
ния
(4.23)
i = \
где Ri — плата за f-ю ситуацию.
Подставляя в (4.23) плату RF за ошибку ложной
тревоги и плату R~ за ошибку пропуска цели, а также
нулевую плату за правильное обнаружение и правильное
необнаружеиие, получим
RpFW (xQ) + R3DW « (4.24)
Величина R называется средним риском, а система
обработки принятого колебания //(/), минимизирующая
средний риск, — устройством оптимальной обработки
сигнала. Критерий минимума среднего риска является
наиболее общим из всех статистических критериев обна¬
ружения. Большинство известных статистических крите¬
риев обнаружения представляют частные случаи мини¬
мума среднего риска.
При Rf=R^= \ средний риск
Й = ^(хо) + Ж(А) (4.25)
дает значение суммарной вероятности ошибок обнаруже¬
ния. Условие минимума суммарной вероятности ошибок
обнаружения носит название критерия идеального на¬
блюдателя. Критерий идеального наблюдателя не учи¬
тывает относительной стоимости ошибок ложной тревоги
и пропуска цели и является менее общим. При U7(xi)==
= W(х0) критерий идеального наблюдателя сводится к ус-
98
ловию минимизации условной вероятности ошибочного
решения
рош — F О = min, (4.26)
которое называется критерием максимального правдопо¬
добия. Из выражения (4.19) следует правило принятия
решения, удовлетворяющее критерию максимального
правдоподобия:
сигнал есть, если А(х)^1, (4 27)
сигнала нет, если Л(%)<1.
Критерий максимального правдоподобия удобен, так как
не требует знания априорных вероятностей наличия и
отсутствия цели. Недостатком этого критерия, как и кри¬
терия идеального наблюдателя, является равная стои¬
мость ошибок ложной тревоги и пропуска цели.
Часто вероятность ложной тревоги не должна превос¬
ходить некоторого заранее заданного значения, а апри¬
орные вероятности наличия и отсутствия цели неизвест¬
ны. В таких случаях желательно иметь приемник обна¬
ружения, обеспечивающий наибольшую вероятность пра¬
вильного обнаружения при фиксированном значении F.
Указанное условие носит название критерия Неймана —
Пирсона и также вытекает из критерия минимума сред¬
него риска как частный случай. Выбор критерия опреде¬
ляется тактическими задачами, решаемыми той или иной
радиотехнической системой. Так, критерий Неймана —
Пирсона находит широкое применение при решении за¬
дачи радиолокационного обнаружения. Действительно,
в данном случае, как правило, отсутствуют априорные
сведения о наличии или отсутствии цели в рассматривае¬
мой точке пространства, а ложная тревога крайне неже¬
лательна и ее вероятность может быть ограничена неко¬
торым наперед заданным числом. Критерий идеального
наблюдателя соответствует задачам, возникающим в си¬
стемах связи. Критерий максимального правдоподобия
находит применение, когда априорные вероятности не
могут быть заданы, а ложная тревога и пропуск цели
одинаково опасны.
Реализация любого из критериев основана на образо¬
вании отношения правдоподобия, а различная трактовка
условий оптимальности выливается в выбор определен¬
ного значения порога Ло.
99
В изложенном подходе к проблеме обнаружения пред¬
полагалось, что в распоряжении наблюдателя имеется
совокупность п выборочных значении (отсчетов) у (/;•),
полностью определяющих реализацию у(/) в заданном
интервале времени Т. Для образования отношения прав¬
доподобия использовались все п статистически независи¬
мых отсчетов и, следовательно, время наблюдения было
фиксированным и равным Т. Возможен иной подход
к решению задачи, когда последовательно, на каждом
f-м шаге наблюдения составляется отношение правдопо¬
добия Л/(х) на основании всех отсчетов от первого до
/-го. Отношение правдоподобия Л,(х) на каждом шаге
наблюдения сравнивается с двумя порогами — верхним
D
(4.28)
и нижним
(4.29)
Решение о наличии цели принимается немедленно по
превышении верхнего порога, а об отсутствии цели — ес¬
ли отношение правдоподобия пересекает нижний порог.
Если значение отношения правдоподобия оказывается
в зоне неопределенности, между нижним и верхним по¬
рогами, испытание продолжается. Такая процедура но¬
сит название последовательного анализа. Время наблю¬
дения при последовательном анализе является случай¬
ной величиной. Среднее время наблюдения зависит от
величины порогов Ав и Ан и в конечном счете определя¬
ется вероятностями D и F. Последовательный анализ яв¬
ляется оптимальной процедурой обнаружения, так как
позволяет минимизировать среднее время наблюдения
при фиксированных значениях D и F. Указанное условие
получило название критерия последовательного наблю¬
дателя, который находит широкое применение в импульс¬
ных радиолокационных и радионавигационных системах,
когда сигнал представляет собой последовательность им¬
пульсов, что облегчает практическую реализацию крите¬
рия.
Использование последовательного анализа вместо
классического, имеющего фиксированный объем выбор¬
ки y(/i), //(/2), • • У(б), • . У(Л?)> доет возможность су¬
щественно сократить среднее время наблюдения при тех
100
>ке значениях D и F. Однако в отдельных опытах время
наблюдения может заметно превосходить среднее зна¬
чение и превышать время наблюдения при классической
процедуре анализа.
§ 4.6. СТРУКТУРА И КАЧЕСТВЕННЫЕ ПОКАЗАТЕЛИ
УСТРОЙСТВ ОПТИМАЛЬНОЙ ОБРАБОТКИ
ОДИНОЧНОГО РАДИОИМПУЛЬСА
1. Сигнал с полностью известными параметрами. Функ¬
ция правдоподобия для сигнала ux(t), параметры кото¬
рого полностью известны, была определена ранее (4.16)
как
о
т т
+л7рС) ux(t)dt~ ± Jz? (о
о о
Применительно к задаче обнаружения
Цзс (0
ил (/ — т0) при наличии цели,
О при отсутствии цели,
где to — время запаздывания.
Отношение правдоподобия в соответствии с выраже¬
нием (4.18) равно
т
Л (х)=^Ж=ехр{лТ f у ® Uc ~То) dt ~
О
т т
“~/7Г f “с У — т») f Uc У ~
О 6
(4.30)
где Е — энергия полезного сигнала.
Процедура обнаружения, заключающаяся в сравне¬
нии отношения правдоподобия Л (х) с порогом Ло, мо¬
жет быть заменена испытанием любой монотонной функ¬
ции этого отношения па соответствующий порог. Сущест¬
101
венное упрощение обработки сигнала в процессе опти¬
мального обнаружения может быть достигнуто логариф¬
мированием отношения правдоподобия. Тогда правило
принятия решения будет:
сигнал есть, если
т
y(t)uc(t-x0)dt — ^-^lnAa, (4.31)
О
сигнала нет, если
т
О
Вводя сокращенную запись
W-a^111A° <4-32)
т
(где z — J у (/) ис (t — т0) dt — корреляционный интеграл) и
oJ
переписывая (4.32) в виде
z^-Ц- (1п Ло+^-)= za, (4.33)
замечаем, что в оптимальном приемнике обнаружения
должно производиться вычисление корреляционного ин¬
теграла z и сравнение его с порогом г0.
Выражение (4.33) определяет структуру оптимально¬
го приемника обнаружения сигнала с полностью извест¬
ными параметрами. В зависимости от того, рассматри¬
вать ли корреляционный интеграл как функцию взаим¬
ной корреляции или как интеграл свертки функций £/(/)
7
2
3
y(t)
и 1
Умножи- |
Интегратор
Пороговое
О—
г——з*
устройство
*0
1— -. . J
* (t-'C.jje t
Решение
Рис. 4.3. Структурная схема корреляционного прием¬
ника.
102
й Uc(^l to), возможны два метода реализации оптималь¬
ного приемника обнаружения: корреляционный и согла¬
сованной фильтрации.
Корреляционный прием. На рис. 4.3 приведе¬
на структура устройства оптимальной обработки оди¬
ночного радиоимпульса согласно выражению (4,33).
Временные диаграммы, приведенные на рис. 4.4, пояс¬
няют работу схемы.
Рис. 4.4. Временные диаграммы, поясняющие работу
корреляционного приемника.
На один вход умножителя поступает реализация y(t),
а на другой — образец сигнала uc(t—т0). Результат ум¬
ножения интегрируется и сравнивается с порогом г0. Та¬
кое устройство называется корреляционным приемником
обнаружения. Корреляционные приемники обнаружения
одиночных радиоимпульсов практически не находят при¬
менения из-за сложности реализации. Значительно боль¬
103
шее распространение получили устройства обнаружения,
в которых операции вычисления корреляционного инте¬
грала осуществляется линейным фильтром.
Оптимальная фильтрация. Корреляционный
интеграл
т
z—\y Uc ~
о
может рассматриваться как интеграл свертки двух функ¬
ций. Как известно из теории линейных цепей, интеграл
свертки выражает с точностью до постоянного множите¬
ля напряжение па выходе линейного фильтра, отклик
которого па единичный б-импульс определенным образом
согласован с функцией uc(t—ю).
Пусть на вход фильтра, имеющего отклик на единич¬
ный б-импульс т](/), действует напряжение y(t). Тогда
напряжение на выходе фильтра может быть представ¬
лено как
4-оэ
(4.34)
— 00
Потребуем, чтобы напряжение на выходе фильтра
в некоторый фиксированный момент времени То + ^о рав¬
нялось значению корреляционного интеграла, т. е.
т
«вых (t0 +t0) = С J у (/) uc (t — т0) dt, (4.35)
О
где С — постоянный множитель.
Используя выражение (4.34) и приводя к одной и той
же переменной интегрирования, получим
Т
00
J У (П Ч (% + <о -1') dt' = С (t') wc - to) dt'.
—oo
(4.36)
Равенство (4.36) выполняется, если
Т] (*0 + tQ - V) = Си. (t' - ТО). (4.37)
Различие в пределах интегрирования не должно сму¬
щать, так как реализация y(t) ограничена интервалом
времени от 0 до Т.
Вводя новую независимую переменную /=То + /о—
найдем
Tj (/) Си. (t. — /).
104
Таким образом, фильтр с импульсной характеристи¬
кой (4.38) дает в заданный момент времени то + /о зна¬
чение корреляционного интеграла г. Такой фильтр на¬
зывают оптимальным или согласованным фильтром. Им¬
пульсная характеристика согласованного фильтра, или
отклик на единичный б-пмпульс, полностью определяет¬
ся формой сигнала ис (/) и представляет собой его зер¬
кальное отображение относительно прямой
Заметим, что согласованный фильтр не может быть
реализован при произвольном значении интервала вре¬
мени /о- Так, если /о = О, то отклик фильтра должен был
бы иметь вид т](/) = Сис(—/), т. е. возникать раньше, чем
воздействующий на вход фильтра 6-пмиульс. Ясно, что
такой фильтр не реализуем. Поэтому величина /о должна
выбираться так, чтобы отличные от нуля значения от¬
клика располагались в области />0. Последнее условие
выполняется, если интервал времени /0 равен или пре¬
восходит протяженность сигнала.
Перейдем к частотному представлению структуры со¬
гласованного фильтра. Для этого найдем его частотную
характеристику k(со)0Пт как преобразование Фурье от
импульсной характеристики:
k (")опт — J Т1 (0 ехР dt =
— 00
Производя замену переменных /0—x = t, получим
со
k (")опт = Сехр {—/<■>/„} «с (0 exp{jW} dt. (4.39)
— со
Интеграл в выражении (4.39) представляет собой
комплексно-сопряженную спектральную плотность сиг¬
нала
оо
£* (<,>) = J цс (/) exp {/«>/} dt,
—co
поэтому
k С)оПТ = Cg* (co) exp {—№„}.
(4.40)
105
Следовательно, частотная характеристика согласован¬
ного фильтра с точностью до постоянного множителя С
и множителя запаздывания ехр {—/co/о} совпадает с ком¬
плексно-сопряженной спектральной плотностью сигнала.
Модуль частотной характеристики совпадает с ампли¬
тудно-частотным спектром сигнала. Поэтому при форми¬
ровании сигнала на выходе фильтра большую роль иг¬
рают те спектральные составляющие сигнала, которые
находятся в лучших условиях с точки зрения отношения
сигнал/помеха. Комплексная сопряженность частотной
характеристики приводит к компенсации взаимных фазо¬
вых сдвигов между спектральными составляющими сиг¬
нала, так что в момент То+^о все составляющие спектра
сигнала суммируются в фазе и сигнал достигает макси¬
мального значения, равного
т
«гых^о+^о) — С j «е (t — *0) dt = С£\ (4.4 1)
о
что следует непосредственно из формулы (4.35).
Таким образом, максимальное значение сигнала на
выходе согласованного фильтра определяется только
энергией сигнала и не зависит от его формы, что объяс¬
няется зависимостью напряжения на выходе согласован¬
ного фильтра в момент времени то + ^о только от ампли¬
тудно-частотного спектра сигнала.
Найдем дисперсию шума на выходе согласованного
фильтра. Частотные компоненты шума не коррелировали
между собой, следовательно, изменение их взаимных фа¬
зовых сдвигов за счет фазо-частотной характеристики
фильтра не влияет на дисперсию шума. Поэтому диспер¬
сия шума на выходе согласованного фильтра определя¬
ется лишь его спектральной плотностью на входе и ам¬
плитудно-частотной характеристикой фильтра и равна
00
(“) 1/г *■>, (4.42)
— 00
где Sm(o)) —спектральная плотность шума на входе,
представленная в области частот от —оо до +оо.
Если спектральная плотность шума постоянна в ин¬
тервале частот —Ев-^-Ев и равна нулю вне этого интер¬
вала, то
106
5Ш (to) — 2F^
(4-43)
где о2— дисперсия шума на входе фильтра.
Подставляя (4.43) и (4.40) в выражение (4.42), най¬
дем
1
2 2 тс
О
.вых
00
—00
(4.44)
2
Отношение сигиал/помеха но напряжению на выходе
согласованного фильтра может быть найдено с помощью
выражений (4.41) и (4.44):
«■ВЫХ (*0 + *о)
® В Ы х
Таким образом, отношение сигнал/помеха на выходе
согласованного фильтра зависит только от спектральной
плотности шума и энергии полезного сигнала и никак не
зависит от его формы.
Покажем, что ни один из фильтров не может дать
отношение сигнал/шум большее, чем согласованный
фильтр. Для этого воспользуемся известным неравенст¬
вом Буняковского — Шварца:
—00
j I# И!2
—со
где А (со) и В (оз) — некоторые функции со.
Положим
А (Ш) = k (ш) N-^- exp {/to (т0 + /0)},
где k (w) — частотная характеристика некоторого фильтра.
107
Подставляя значения Л (со) и В (со) в неравенство, при.
ведем его к виду
со
2Г
—РО
k (со) ехр {/со (т0 + to)} du
00
2^Г j ЛГ Iй (")12 а<*
— 00
(4.46)
2
Левая часть неравенства представляет собой квадрат от¬
ношения сигнал/шум на выходе фильтра с частотной ха¬
рактеристикой k (со). Поскольку
dt^E,
то в правой части неравенства будет
2Е
9
следовательно,
отношение сигпал/шум на выходе фильтра
(4-47)
Отсюда следует, что отношение сигнал/шум на вы¬
ходе любого фильтра не может быть большим, чем на
выходе согласованного фильтра.
у (t) Согласован¬
ную ■ о** ный
фильтр
Временной
селектор
Пороговое
устройство
Селекторный
импульс
'CQ^tQ
Рис. 4.5. Структурная схема оптимального приемника
обнаружения с согласованным фильтром.
Итак, операция образования корреляционного инте¬
грала z может быть заменена эквивалентной операцией
согласованной или оптимальной фильтрации.
Структура оптимального приемника обнаружения
с согласованным фильтром приведена на рис. 4.5. Здесь
напряжение с выхода согласованного фильтра поступает
на временной селектор, на который также подается уз-
108
кий селекторный импульс, соответствующий моменту
времени то + бь Отсслектированное напряжение, пропор¬
циональное значению корреляционного интеграла, срав¬
нивается с порогом г0. На рис. 4.6 приведены времен¬
ные диаграммы, поясняющие работу схемы.
Качественные показатели оптимально¬
го приемника обнаружения. Перейдем к рас¬
смотрению качественных показателей устройства опти¬
мальной обработки сигнала с полностью известными па¬
раметрами.
I I
Селекпю.ршй | ?
iiMnU/ibc t;
+ -и t
Рис. 4.6. Временные диаграммы, поясняющие работу
схемы рис. 4.5.
Вне зависимости от способа реализации оптималь¬
ного приемника процедура принятия решения заключает¬
ся в сравнении корреляционного интеграла с пороговым
уровнем. В отсутствие шумов корреляционный интеграл
может принимать лишь два значения:
109
7
% j^(Z— ^)dt~E при наличии сигнала,
oJ
. О при отсутствии сигнала,
и вероятность правильного обнаружения будет равна
единице, а вероятность ложной тревоги — нулю. При на¬
личии шума корреляционный интеграл становится слу¬
чайной величиной. Поэтому вероятности пропуска цели
и ложной тревоги принимают некоторое конечное значе¬
ние, определяемое отношением энергии сигнала к спек¬
тральной плотности шума. Для подсчета этих вероятно¬
стей необходимо знать закон распределения корреляци¬
онного интеграла.
Корреляционный интеграл подчиняется нормальному
закону распределения, так как представляет собой ли¬
нейное преобразование нормального случайного процес¬
са. Поэтому определению подлежат лишь математиче-
— 2
ское ожидание г и дисперсия корреляционного ин¬
теграла. При наличии сигнала
___ т т
г — y(t)uc(t — To)'Z^ ~
о о
T
= J t? (Z — %)dt=E,
О
так как
j 1/(0 "с (t — т0) dt~
У (0 = — To) + (0 = wc (t — t0).
Когда сигнал отсутствует, z = 0.
Дисперсия корреляционного интеграла с точностью до
постоянного множителя равна дисперсии флюктуаций на
выходе согласованного фильтра (4.44), поэтому
а2 = 2^£. (4.48)
Заметим, что а2 всегда определяется выражением (4.48)
вне зависимости от того, присутствует или отсутствует
полезный сигнал.
Плотность вероятности нормальной случайной вели¬
чины z при наличии сигнала равна
lt7cnW==-J_exp{-<^F),
(4.49)
а при отсутствии сигнала
ПО
(4.50)
Плотности вероятности 117сп(г) и ITn(z) представле¬
ны на рис. 4.7 для некоторого значения Е и <тг. Там же
указан пороговый уровень Zq.
Рис. 4.7. Условные плотности вероятности при наличии
сигнала lFcn(^) и при отсутствии сигнала 1Гп(г).
Вероятность ложной тревоги равна вероятности пре¬
вышения порогового уровня 2о при условии отсутствия
сигнала, т. е.
F = JU7n(z)rfz. (4.51)
Вероятность правильного обнаружения
P = Jrcn(z)</z. (4.52)
го
Подставляя значения U7Cn(z) и lFn(z), найдем
Г = 0,5[1-ф(-|^], (4.53)
П = 0,5[1+Ф(^=^-у], (4.54)
где Ф(у)—интеграл вероятности.
Таким образом, вероятность ложной тревоги опреде¬
ляется отношением порогового уровня z0 к эффективно-
111
му значению флюктуаций корреляционного интеграла
oz. Вероятность же правильного обнаружения зависит
еще и от отношения энергии ожидаемого сигнала Е к ве¬
личине oz:
которое совпадает с отношением спгнал/помеха на вы¬
ходе согласованного фильтра. Величину q называют
параметром обнаружения.
Вводя обозначение qQ=—, приведем формулы (4.53) и
(4.54) к окончательному виду:
(4.56)
0-0,5[1+Ф(7-7о)].
(4.57)
Зависимость D = q(q) при /? = const (7o = const) носит
название характеристики обнаружения. Семейство ха¬
рактеристик обнаружения для нескольких F представле¬
но па рис. 4.8.
Характеристики обнаружения позволяют найти ми¬
нимальную энергию сигнала, необходимую для дости¬
жения заданного значения D при фиксированной вели-
112
чине F. Определив по кривым рис. 4.8 значение 7МИН,
соответствующее заданным D и Е, можно найти мини¬
мальную энергию сигнала
щ
N ПН 9 »
обеспечивающую заданную надежность обнаружения.
При длительности сигнального импульса тс минималь¬
ная или пороговая мощность сигнала, необходимая для
обеспечения заданных D и F, равна
п ^М1ТИ
'смшг— _ ~ •
Итак, качественные показатели оптимального при¬
емника обнаружения могут быть найдены из характе¬
ристик обнаружения и для сигнала с известными пара¬
метрами определяются только энергией сигнала и нс
зависят от его формы.
2. Сигнал со случайной начальной фазой. Если все
параметры сигнального радиоимпульса, в том числе и
его начальная фаза 0, заранее известны, отношение
правдоподобия в соответствии с выражением (4.30),
имеет вид
т
Л (х/0) = ехр (Д- J у (/) ис е —хо) dt—(4.58)
О
где Л(х/0) означает, что отношение правдоподобия вы¬
числено для определенного значения начальной фазы
радиоимпульса.
Ниже рассматривается сигнал с неизвестной началь¬
ной фазой
(t — ^о) и G — ^о) COS («</ 4- 6), (4.59)
где !/(/- То) —огибающая сигнала;
со о— несущая частота;
0 — начальная фаза несущей частоты, зна¬
чение которой может быть любым в ин¬
тервале 0 4-2я.
Так как при обнаружении определению подлежит
сам факт наличия или отсутствия сигнала вне зависи¬
мости от значения его начальной фазы, отношение прав-
8—1173 ИЗ
доподобия может быть найдено как среднее по всем
возможным значениям 0:
2тс
Л(х, 9) = f Р(9)Л(х/9)б/9, (4.60)
б
где Р(0)—априорное распределение начальной фазы.
Обычно фаза распределена равномерно в интервале
2л, поэтому
2тс
Л(х, 0)= 2^ j Л(х/0)</9.
о
Воспользовавшись соотношениями (4.58) и (4.59), най¬
дем
2п Т
а (*, е)=i j* ехР {at fу (i)U V—х
о о
Xcos(<o0f + 6)<ft—^-J.tf9. (4.61)
Корреляционный интеграл
т
г~\у —т°)cos +0) =
о
т
= [и (t — то) C°S cos 0 —
о
т
— U(t — sin woz sin 0| di = J у (/) (/) cos belt +
о
т
+ у (/) м2 (О sin Qdt — z, cos 9 z2 sin 9,
б
где ul (/) — и (t — т0) cos wot;
т
zi=y(t)ut(t) dt;
Q
Вводя обозначения
(0 = — U G — т0) sin соо/;
(4.62)
т
г2 = (О МО
о
z = V z | 4- ?2 , cos -|4, sin ф = ,
114
представим корреляционный интеграл в виде
z — Z j^~cos 9 + -у-sin О] cos(f — 9). (4.63)
Так как энергия сигналов, используемых в радиотехни¬
ческих системах, практически не зависит от начальной
фазы
f(9)= U2 (t — То) cos2 (<%/ 9) dt Е,
—00
отношение правдоподобия (4.61) с учетом (4.63) может
быть переписано как
Л(х, 9)=-exp^~^j>X
х [ 2Г j ехР cos ('l' -0)}м ] •
О
Интеграл в квадратных скобках представляет собой мо¬
дифицированную функцию Бесселя первого рода нуле¬
вого порядка с аргументом 2ZIN^ поэтому
ли. О) = ехР)-А}Ц^). (4.64)
Корреляционный прием с двумя квад¬
ратурными каналами. Отношение правдоподо¬
бия (4.64) является монотонной функцией величины Z,
поэтому операция испытания Л(х, 0) на порог Ло может
быть заменена более простой операцией сравнения с не¬
которым порогом Zo. Не затрагивая пока вопросов, свя¬
занных с выбором значения Zo, рассмотрим один из спо¬
собов образования величины Z.
Структурная схема устройства, реализующего опе¬
рацию
2 = =
(4.65)
8*
115
(где U(i—То)—полностью известная огибающая сигна¬
ла), приведена на рис. 4.9. Здесь принятая реализация
y(t) поступает на два параллельных канала — синусный
и косинусный, — каждый из которых содержит умножи¬
тель и интегратор. В качестве опорных напряжений
умножителей использованы сдвинутые на 90° относи¬
тельно друг друга радиоимпульсы, огибающая каждого
из которых идентична огибающей ожидаемого сигнала.
После интегрирования результатов перемножения обра-
г
А
y(t)
1
*
Интегратор?—'
I U (t-Vo) cos
о
Рис. 4.9. Структурная схема корреляционного приемни¬
ка с двумя квадратурными каналами.
зуются величины и z2. Вычислительное устройство,
осуществляющее операции: возведение в квадрат, сум¬
мирование и извлечение квадратного корня, завершает
образование величины Z.
Рассмотренный способ обработки сигнала называет¬
ся корреляционным приемом с двумя квадратурными
каналами. Наличие двух квадратурных каналов позво¬
ляет исключить возможность пропуска сигнала за счет
незнания его начальной фазы. Действительно, если фаза
принятого сигнала такова, что на выходе синусного
канала приращение напряжения, обусловленное подклю¬
чением сигнала, равно нулю, то на выходе косинусного
канала приращение напряжения будет максимально, и
наоборот.
Оптимальная фильтрация. Оптимальный
приемник обнаружения для сигнала со случайной на¬
чальной фазой (распределенной равномерно в интер¬
вале 2л) может быть построен и с помощью согласован¬
ного фильтра. Так как при равномерном распределении
116
фазы информация о наличии сигнала содержится только
в амплитуде сигнала, то после согласованной фильтра¬
ции необходимо продетектировать сигнал, т. е. выде¬
лить его огибающую. Можно показать, что результат
детектирования в момент времени (то + /о) совпадает
с точностью до постоянного множителя С с величиной Z,
определяемой выражением (4.65). Поэтому после детек¬
тирования напряжение должно испытываться на порог
[jQr=CZoy причем Zo— пороговый уровень в схеме кор-
y(t) Согласован-
ный
фильтр
Детектор
Временной
селектор
Пороговое
устройство
Uo=cZ.o
Решешл-
Селекторный
импульс
] -Д—
^0 * *0
Рис. 4.10. Структурная схема онгимa.iиного приемника обнаружения
для сигнала со случайной начальной фазой.
с согласованным фильтром может быть
в виде последовательного соединения со-
фильтра, детектора огибающей, временпо-
и порогового устройства (рис. 4.10, 4.11).
согласованного фильтра позволяет обой-
реляционного приемника с двумя квадратурными ка¬
налами.
Таким образом, структура оптимального приемника
обнаружения
представлена
гласованного
го селектора
Применение
тись одноканальной схемой обработки сигнала и исклю¬
чить трудно реализуемую операцию перемножения.
Качественные показатели оптималь¬
ного приемника обнаружения. Напряжение
на выходе согласованного фильтра представляет собой
аддитивную смесь полезного сигнала и шума. Огибаю¬
щая этого напряжения в момент времени (то + /о) подчи¬
няется обобщенному закону распределения Рэлея:
(« = exp [ J /. (««)
°вых ( 2обых j у °вых J
где U — значение огибающей в рассматриваемый мо¬
мент времени;
Umc — амплитуда сигнала на выходе согласованного
фильтра (в момент (То + ^о));
°вых — дисперсия шума на выходе согласованного
фильтра.
117
При отсутствии сигнала
Г„(и)=^ехр/--^Ц. (4.67)
°вых ( ®вых J
Вводя обозначение s — , а также учитывая, что
0 вых
отношение сигнал/помеха на выходе согласованного фильтра
равно
Овых Г Wo Ч’
Пороговый
уровень
t
Рис. 4.11. Временные диаграммы, поясняющие работу
схемы рис. 4.10.
представим (4.66) и (4.67) в виде
Гсп (s) = s ехр { /0 (<?«),
I7n(s) = sexp J—
(4.68)
(4.69)
118
Тогда вероятность правильного обнаружения и вероят¬
ность ложной тревоги можно представить в виде
оо
D = j sexp/— I0(qs) ds, (4.70)
s0
00 9
F = J sexpШ cfs = exp { —(4.71)
So
UQ— пороговый уровень.
Выражение (4.71) дает возможность для заданного
значения F найти величину s0 и далее с помощью соот¬
ношения (4.70) рассчитать зависимость вероятности пра¬
вильного обнаружения от параметра обнаружения q.
Рис. 4.12. Характеристики обнаружения для сигнала со
случайной начальной фазой (сплошные линии) и для
сигнала с полностью известными параметрами (пунк¬
тирные линии).
На рис. 4.12 представлено семейство характеристик
обнаружения jD = cp(<7) для нескольких значений F. Для
сравнения приведены также характеристики обнаруже¬
ния для сигнала с полностью известными параметрами.
Сравнение кривых показывает, что незнание начальной
фазы сигнала приводит к ухудшению качественных по¬
119
казателей приемника обнаружения. Так, например, при
У7 = 104 и ^ = 5 вероятность правильного обнаружения
сигнала с неизвестной начальной фазой равна 0,8, тогда
как для сигнала с полностью известными параметрами
она составляет 0,9. Это различие усиливается с умень¬
шением отношения энергии сигнала к спектральной
плотности шума. В случае сильных сигналов, когда q>
>10, качественные показатели рассмотренных приемни¬
ков обнаружения практически совпадают.
3. Сигнал со случайными амплитудой и начальной
фазой. Сигнал, амплитуда и начальная фаза которого
случайны, может быть представлен в виде
«с (Z — т0) — AU (t — т0) cos (о0/ +> (4.72)
где А — случайный безразмерный коэффициент.
Применительно к радиолокационному сигналу, отра¬
женному от движущейся цели, коэффициент А можно
считать распределенным по закону Рэлея со средним
квадратом, равным единице, т. е.
IF (Л) = 2Аехр [—/?],
/Г2 = j 2А3 ехр {— Д2} dA = 1.
о
(4-73)
Начальную фазу 0 будем полагать независимой от А
и равновероятной в интервале 2л.
На основании выражения (4.61) запишем отношение
правдоподобия для фиксированного значения А в виде
A(х, 8) = -)- j«P +
->) “<>■ (4-74)
Усредняя отношение правдоподобия (4.74) по всем
возможным значениям А, получим
00 2л:
А (х, 0, Д) = 2 J А ехр {— Д2} j ехР|^Х
О о
т
</0]<7Д.
О
X j у (О и (t - г0) cos Ы + 0) clt
(4-75)
120
Здесь £(0, Л) — энергия радиоимпульса, начальная фа¬
за которого равна 0, а огибающая имеет вид AU(t—ту).
Так как энергия радиоимпульса практически не за¬
висит от 0, то
£ (О, А) = J A2U2 (/ — т0) di - А2Е. (4.76)
— 00
Если коэффициент А подчиняется закону распределения
Рэлея, то средняя энергия сигнала
ЕС]. 2 J Л“ ехр {— /V} Ed Л = Е. (4.77)
О
Подставляя значение £(0, /1) из (4.76) в (4.75), по¬
лучим
00
Л (х, О, Д) = 2 j А ехр •{- А2 (1 + '» X
О
J ехр(Х7 j -г/ U 'о)cos ОоН-в)^j- j<M.
0 0
Выражение в квадратных скобках, как было показано
, поэтому
00
Л(х, О, Д) = 2 j^exp|—A2(l + ^-)j./0
(4-78)
Интеграл (4.78)—табличный. Он равен
Л(л-, 8, Д)==——-ехр ( (£, + л,») j• (4-79)
Л(%, О, А) определяет отношение правдоподобия для
сигнала со случайными амплитудой и начальной фазой.
Сравнивая Л(х, О, Л) с отношением правдоподобия для
сигнала со случайной начальной фазой (4.64), замечаем,
что и то и другое являются монотонными функциями
одной и той же величины Z. Поэтому способы реализа¬
ции оптимального приемника обнаружения сигнала со
121
случайными амплитудой и начальной фазой остаются
теми же, что и рассмотренные в п. 2. Отличие заключа¬
ется лишь в качественных показателях этих приемников.
Качественные показатели о п т и м а л ь н о-
го приемника обнаружения. Если приемник
обнаружения выполнен на принципе согласованной
фильтрации, то на вход порогового устройства
(рис. 4.10) поступает напряжение, равное значению оги¬
бающей па выходе согласованного фильтра в момент
(То + /о)- Плотность вероятности огибающей аддитивной
смеси сигнала и шума в случае, когда амплитуда сигна¬
ла случайна и подчиняется рэлеевскому закону распре¬
деления, равна
№сЯ (U)^W(A)Wca(u/A)dA,
о
(4.80)
где
^сп (U/ А)
митси\
’вых J
— плотность вероятности огибающей на выходе со¬
гласованного фильтра при фиксированной амплитуде
сигнала, равной AUm0.
По аналогии с (4.78) после интегрирования по¬
лучим
вых ~ me
ехр {
(4-81)
или
J м
I 2 + ^р
где s
^сп (S) = 2Т? 6ХР
и
®вых
При условии отсутствия сигнала
wa (s) = s ехр | —4") •
(4.82)
(4.83)
122
Вероятность правильного обнаружения и вероятность
ложной тревоги будут
50
2^-^s-exp
(4.84)
00
77 = ^sexp { — -f}ds = exp{—-у-|. (4.85)
So
Исключая из выражения (4.84) с помощью соотно¬
шения (4.85) параметр s0, получим
£> = F~l+f'2/2 . (4.86)
Зависимость Д = ср(7) представлена на рис. 4.13
семейством характеристик обнаружения. Там же для
Рис. 4.Щ Характеристики обнаружения для сигнала со
случайной амплитудой и начальной фазой (сплошные
линии) и для сигнала со случайной начальной фазой
(пунктирные линии).
сравнения приведены характеристики обнаружения для
сигнала с фиксированной амплитудой. Интересно, что
для сигнала со случайной амплитудой даже при очень
больших отношениях сигнал/шум вероятность правиль¬
ного обнаружения существенно отличается от единицы.
123
Это связано с тем, что при флюктуации амплитуды
полезного сигнала приводят к увеличению вероятности
пропуска сигнала. При малых значениях отношения сиг-
нал/шум вероятность правильного обнаружения оказы¬
вается больше, чем в случае сигнала с постоянной
амплитудой. Дело в том, что сравнение качественных
показателей рассматриваемых приемников обнаружения
производится при равных средних энергиях сигналов.
В случае же флюктуирующего сигнала амплитуда по¬
лезного сигнала на выходе согласованного фильтра ча¬
сто превосходит значение, соответствующее средней
энергии сигнала. При больших уровнях шума эти вы¬
бросы сигнала имеют существенное значение, так как
облегчают условия превышения порога С70, который
в данном случае должен быть достаточно велик, чтобы
вероятность ложной тревоги не превосходила заданную.
Здесь уместно заметить, что значение порога t/0 при
Л = const и одном и том же уровне шума одинаково для
сравниваемых приемников обнаружения.
§ 4.7. КАЧЕСТВЕННЫЕ ПОКАЗАТЕЛИ УСТРОЙСТВ
ОПТИМАЛЬНОЙ ОБРАБОТКИ ПАЧЕК
КОГЕРЕНТНЫХ РАДИОИМПУЛЬСОВ
1. Общая характеристика пачек когерентных радио¬
импульсов. Пусть полезный сигнал представляет собой
последовательность (пачку) из п радиоимпульсов. На
Рис. 4.14. Пачка когерентных радиоимпульсов.
рис. 4.14 представлена одна из возможных последова¬
тельностей при /?^3. Каждый импульс пачки характе¬
ризуется амплитудой Umi, формой огибающей
несущей частотой fa, моментом возникновения и началь-
124
ной фазой 0/. Если зависимость между перечисленными
параметрами импульсов пачки известна точно, то такие
импульсы называются когерентными. Отсюда следует,
чт0 если в месте приема известны параметры одного из
импульсов пачки, то тем самым определена и вся пачка
U с ’
2. Сигнал в виде нефлюктуирующей пачки когерент¬
ных радиоимпульсов. Сигнал в виде пачки нефлюктуи¬
рующих когерентных радиоимпульсов может быть от¬
несен к группе сигналов, известных точно, или к группе
сигналов со случайной начальной фазой в зависимости
от того, известна или нет в месте приема начальная
фаза. Если начальная фаза хотя бы одного из импульсов
пачки известна, то тем самым определена и фаза осталь¬
ных импульсов пачки, что вытекает из приведенного
выше определения пачки когерентных радиоимпульсов.
А так как все остальные параметры рассматриваемого
вида сигнала предполагаются неизменными и извест¬
ными точно, то он может рассматриваться как сигнал
с полностью известными параметрами. При этом каче¬
ственные показатели оптимального приемника обнару¬
жения определяются полученными ранее формулами
(4.56), (4.57). Входящий в эти формулы параметр об¬
наружения
должен быть вычислен для энергии всей пачки, т. е.
Е (4.87)
где Ei — энергия /-го импульса пачки.
Если начальная фаза пачки когерентных радиоим¬
пульсов неизвестна и распределена равномерно в интер¬
вале 2л, а все остальные, параметры импульсов заданы,
то такой сигнал может быть отнесен к группе сигналов
со случайной начальной фазой. Поэтому качественные
показатели оптимального приемника обнаружения пач¬
ки импульсов с неизвестной начальной фазой опреде¬
ляются формулами (4.70) и (4.71), если под энергией Е
подразумевать энергию всей пачки импульсов, как и
в предыдущем случае.
125
Отсюда следует, что разбиение сигнала, известного
точно, или сигнала со случайной начальной фазой на
ряд импульсов не изменяет качественных показателей
оптимального приемника обнаружения, если, конечно,
суммарная энергия сигнала остается неизменной.
3. Сигнал в виде флюктуирующей пачки когерентных
радиоимпульсов. Пачка радиоимпульсов называется
флюктуирующей, если амплитуды Umi и фазы 0/ от одно¬
го опыта к другому изменяются как непрерывные слу¬
чайные величины. Применительно к пачке когерентных
радиоимпульсов, для которой амплитуда и фаза перво¬
го импульса пачки полностью определяют амплитуды и
фазы всех остальных импульсов, такой сигнал может
быть отнесен к группе сигналов со случайными ампли¬
тудой и фазой, рассмотренной в § 4.6, п. 3.
Если все импульсы пачки имеют одинаковые ампли¬
туды, изменяющиеся от опыта к опыту в соответствии
с законом Рэлея, а начальная фаза импульсов распре¬
делена равномерно в интервале 2л, качественные пока¬
затели оптимального приемника обнаружения определя¬
ются полученными ранее формулами (4.84) и (4.85).
При этом
п
E=^Et,
i = l
где Et — средняя энергия f-ro импульса пачки.
Если форма и длительность импульсов пачки одина¬
ковы, то
Е = пЕ\, (4.88)
где Ei — средняя энергия одного импульса пачки.
§ 4.8. СТРУКТУРА УСТРОЙСТВ ОПТИМАЛЬНОЙ
ОБРАБОТКИ ПАЧЕК КОГЕРЕНТНЫХ
РАДИОИМПУЛЬСОВ
1. Структура оптимального фильтра. При приеме па¬
чек когерентных радиоимпульсов устройство оптимально¬
го обнаружения может быть выполнено как на принципе
корреляционного приема, так и на принципе оптималь¬
ной или согласованной фильтрации *. Для корреляцион-
* Возможна также и смешанная корреляционно-фильтрационная
обработка, см. [21 ].
126
пого метода структура оптимального приемника в рас¬
сматриваемом случае сохраняется такой же, как и для
сигнала в виде одиночного радиоимпульса. Разница за¬
ключается лишь в том, что образец сигнала, поступаю¬
щий на умножитель (рис. 4.3, 4.9), должен иметь вид
ожидаемой пачки импульсов. Иначе обстоит дело при
использовании принципа оптимальной фильтрации.
Здесь структура согласованного фильтра в сильной сте¬
пени зависит от вида ожидаемого сигнала. Поэтому не¬
обходимо более подробно остановиться на вопросах, свя¬
занных с построением согласованных фильтров для
сигналов, имеющих вид пачек радиоимпульсов.
Будем считать, что временной интервал между
импульсами в пачке равен Т и все импульсы имеют оди¬
наковые параметры. Если спектральную плотность пер¬
вого импульса пачки обозначить через g((o), то спек¬
тральная плотность пачки, состоящей из п импульсов
gt (“) = g И £ exp {— /<о (г — 1 )Т}. (4.89)
i=l
Частотная характеристика фильтра, согласованного
с рассматриваемым сигналом, в соответствии с выраже¬
ниями (4.40) и (4.89), будет
/г (со)оит = Cg\ (<■>) ехр {— =
= Cg* О) £ ехР (»~ Ч Т} ехр {— /Wo}. (4.90)
i = l
Напомним, что (то + ^о) — момент времени, соответст¬
вующий максимальному значению полезного сигнала
на выходе согласованного фильтра, который для физи¬
чески реализуемого фильтра должен удовлетворять
условию
(то 4“ to) % -Ид — то 4" 4" (п 1) (4-9^)
где тп— длительность пачки;
тс — длительность импульса.
Пусть для определенности пачка радиоимпульсов
имеет вид, представленный на рис. 4.15,а, причем время
запаздывания пачки То = 0, а
^ = тс+(/г-1)Г (4.92)
127
Рис. 4.15. Временные диаграммы, иллюстрирующие работу фильтра,
согласованного с пачкой прямоугольных когерентных радиоимпуль¬
сов.
Подставляя (4.92) в (4.90), получим
/е (®)оят = ]Cg* (<•>) охр {— £ ехр {— /<о (/i — z) Т}.
(4.93)
Множитель, заключенный в квадратные скобки, пред¬
ставляет собой частотную характеристику фильтра, со¬
гласованного с одиночным импульсом, а сумма
п
(4.94)
1=1
является частотной характеристикой сумматора на ли¬
нии задержки с отводами (рис. 4.16).
Таким образом, фильтр, согласованный с пачкой ко¬
герентных радиоимпульсов, может быть представлен
в виде последовательного соединения фильтра, согласо¬
ванного с одиночным импульсом, и сумматора, осущест-
12S
вляющего линейное, суммирование всех импульсов пач¬
ки. Остановимся подробнее на функциях, выполняемых
указанными звеньями.
Спектральная плотность прямоугольного радиоим¬
пульса может быть представлена в виде
g (О = До 1 со?) г1 — ехР<~ /(■« —0,о) ''с}!, (4.95)
где то — несущая частота.
Рис. 4.16. Сумматор на линии задержки с отводами.
Полагая для простоты, что импульс содержит целое
число периодов несущей частоты, а Z0 = rc, получим вы¬
ражение для частотной характеристики согласованного
с одиночным импульсом фильтра
Жоип = — ехр{— /"-с}!- (4-96)
Можно показать, что —- представляет собой
частотную характеристику высокодобротного контура,
настроенного на частоту со0; exp {—является ча¬
стотной характеристикой линии задержки на время /3==
=тс. Поэтому фильтр, представленный на рис. 4.17,а,
реализует частотную характеристику (4.96). Здесь за¬
держанный на время /3 = тс сигнал суммируется в про¬
тивофазе с входным сигналом, в результате чего обра¬
зуется прямоугольный импульс удвоенной длитель¬
ности, фаза несущей частоты которого изменяется на л
в момент времени /=тс (рис. 4.17,6). Этот импульс воз¬
действует на узкополосный резонансный контур, что
приводит к появлению на нем линейно растущего си¬
нусоидального напряжения. В момент времени /=тс
фаза напряжения, воздействующего на контур, изменя¬
ется на обратную, и амплитуда колебаний на его выхо-
9-1173 129
де начинает линейно падать. В результате на выходе
фильтра образуется ромбовидный радиоимпульс, дли¬
тельность которого равна удвоенной длительности вход¬
ного сигнала.
На рис. 4.15,6 приведены временные диаграммы, по¬
ясняющие работу рассмотренного фильтра при воздей¬
ствии на его вход пачки радиоимпульсов. Рис. 4.15,в по¬
ясняет механизм суммирования импульсов в схеме, изо¬
браженной на рис. 4.16.
Рис. 4.17. Структурная схема фильтра, согласованного с прямоуголь¬
ным радиоимпульсом (а); временные диаграммы (б), соответствую¬
щие точкам 1, 2, 3 и 4.
Таким образом, механизм оптимальной фильтрации
пачки радиоимпульсов сводится к согласованной филь¬
трации одиночных импульсов и когерентному суммиро¬
ванию всех импульсов пачки. Когерентное суммирование
ведет к улучшению отношения сигнал/помеха в ]/ п
130
раз, так как все импульсы пачки складываются в фазе,
а помехи — со случайными фазами.
Механизм оптимальной фильтрации пачки когерент¬
ных радиоимпульсов может быть пояснен также и с по¬
мощью частотной характеристики согласованного
фильтра.
Рис. 4.18. Спектр прямоугольной пачки прямоугольных радиоимпуль¬
сов (а); амплитудно-частотные характеристики фильтра, согласован¬
ного с одиночным импульсом (б), и сумматора (в).
Амплитудно-частотная характеристика фильтра, со¬
гласованного с одиночным прямоугольным радиоимпуль¬
сом, имеет вид
| I — С
(<д — (Ое)
9*
Амплитудно-частотная характеристика
может быть найдена из выражения
сумматора
(4.94) как
Т
sin
“ _ Т~
sin со ~2~
,(4.98)
отсюда
тс
sin (со — со0) -у
Т
sin C0/2-Q-
(со — <о0)
Т
sin со -у
(4.99)
На рис. 4.18 представлен спектр пачки прямоуголь¬
ных радиоимпульсов и амплитудно-частотные характе¬
ристики (4.97), (4.98). Гребенчатая структура амплитуд¬
но-частотной характеристики сумматора позволяет
пропустить на выход оптимального фильтра только те
составляющие частоты, которые содержатся в спектре
сигнала. Чем большее число импульсов содержит пачка,
тем уже отдельные «зубцы» частотной характеристики
сумматора и, следовательно, тем лучше сигнал будет от¬
фильтрован от помех.
Итак, переход от одиночного сигнала к сигналу
в виде пачки когерентных радиоимпульсов приводит
к изменению структуры оптимального приемника обна¬
ружения только в части, касающейся построения согла¬
сованного фильтра, который дополняется линейным сум¬
матором, осуществляющим когерентное накопление всех
импульсов пачки. Остальная часть схемы оптимального
приемника обнаружения выполняется так же, как п для
одиночного сигнала. Если пачка известна полностью, то
на пороговое устройство поступает напряжение, отсе-
лектированное в момент времени то + /о- Если начальная
фаза пачки случайна или пачка флюктуирует еще и по
амплитуде, то временному селектору предшествует де¬
тектор огибающей (рис. 4.10).
2. Структура квазиоптимальных фильтров. Практи¬
ческая реализация устройств оптимальной обработки си¬
гналов часто наталкивается па большие трудности, свя¬
занные как с построением фильтров, согласованных
с одиночным сигналом, так и с построением линейных
сумматоров. Поэтому получили большое распространен
132
ние устройства квазиоптимальной обработки сигналов,
отличающиеся простотой реализации при близких к по¬
тенциальным качественных показателях.
Роль квазиоптимального фильтра часто выполняет
усилитель промежуточной частоты, полоса пропускания
которого согласована с шириной спектра сигнала.
В данном случае отклонение от оптимальных условий
заключается в несовпадении формы спектральной плот¬
ности сигнала с частотной характеристикой усилителя.
Рис. 4.19. Структурная схема экспоненциального сумматора на ли¬
нии задержки с положительной обратной связью.
Однако если полоса пропускания усилителя согласо¬
вана с шириной спектра сигнала, то отношение сиг-
нал/помеха на его выходе лишь незначительно отли¬
чается от максимально достижимого. Так, например, для
прямоугольного сигнала и прямоугольной частотной ха¬
рактеристики оптимальное соотношение между длитель¬
ностью импульса и полосой пропускания имеет вид
Д/тс=1,37. При этом отношение сигнал/помеха по на¬
пряжению оказывается лишь на 10% меньше, чем
в случае согласованной фильтрации.
Основным препятствием, затрудняющим реализацию
линейных сумматоров, является создание неискажающих
линий задержки. Так как время задержки равно
(п—1)Т, трудность реализации подобных устройств воз¬
растает с увеличением числа импульсов в пачке и периода
повторения импульсов. В таких случаях находят приме¬
нение экспоненциальные сумматоры, которые при вы¬
полнении определенных условий дают практически тот
же эффект, что и линейные.
На рис. 4.19 приведена схема экспоненциального сум¬
матора на линии задержки с положительной обратной
связью.
Пусть на вход схемы поступает пачка из п когерент¬
ных радиоимпульсов, период повторения кртррых равен
13^
времени задержки в линии, а несущая частота кратна
частоте повторения. Если коэффициент усиления широ¬
кополосного усилителя k=l, а коэффициент усиления по
петле обратной связи р<1, то первый импульс пачки
без изменения передается на выход схемы, второй
импульс суммируется с ослабленным в петле обратной
связи первым импульсом, третий импульс суммируется
с ослабленным в р раз вторым выходным импульсом и
так далее. В результате амплитуда n-го импульса пачки
на выходе оказывается равной
«—1
Um,, Um J] = Um • (4-100)
k=()
Применяя подобные рассуждения к дисперсии шума,
получим следующее выражение для дисперсии шума на
выходе схемы:
Vi1 1 В2"
k = Q
где N — число циклов суммирования, начиная с момен¬
та включения схемы.
В случае, когда схема включена задолго до момента
прихода пачки, дисперсия успевает достигнуть устано¬
вившегося значения
(4.Ю2)
Тогда отношение сигнал/шум на выходе схемы
к моменту времени То + ^о, соответствующему вершине
n-го импульса пачки, достигает значения
<4'103>
Когда временное положение ожидаемой пачки известно,
имеется возможность включать схему в момент прихода
первого импульса пачки. Тогда n = N и дисперсия к мо¬
менту времени То+/о не успевает достигнуть установив¬
шегося значения, поэтому
Urnn Um yf (1 ftW) (1 “h Р)
• Г (l+pn)(1_p)-
(4 Л 04)
134
Сравнивая выражения (4.103) и (4.104), замечаем,
что в последнем случае отношение сигнал/помеха на вы¬
ходе схемы больше, чем в первом. Поэтому при обнару¬
жении пачек импульсов имеет смысл производить вре¬
менную селекцию перед накоплением и выбирать (3 как
можно ближе к 1. Действительно, преобразуя (4.104)
к виду
и полагая р.= 1, получаем
(4.105)
что соответствует линейному суммированию п импуль¬
сов. Следовательно, при (3=1 сумматор на линии за¬
держки с положительной обратной связью позволяет
получить те же качественные показатели обнаружения,
что и оптимальный линейный сумматор. Однако этот
случай не может быть реализован практически, так как
схема с положительной обратной связью при 0— 1 воз¬
буждается. В реальных схемах получение 0 даже по¬
рядка 0,9—0,95 представляет большую трудность из-за
неравномерной частотной характеристики линии за¬
держки и широкополосного усилителя, вследствие чего
на некоторых частотах 0 будет превосходить единицу,
и схема возбудится. Если же на всех частотах 0 мень¬
ше единицы, то среднее значение 0 заметно отличается
от единицы. Не менее существенной трудностью явля¬
ется обеспечение высокой стабильности задержки в ли¬
нии для выполнения условий когерентного накопления.
Требования к стабильности задержки возрастают с уве¬
личением несущей частоты импульсов, периода повто¬
рения и числа накапливаемых импульсов. Поэтому ре¬
шение о возможности применения рассмотренной схемы
сумматора в каждом отдельном случае может быть при¬
нято лишь после анализа ее эффективности с учетом
всех вышеперечисленных факторов.
В некоторых радиотехнических системах, в частно¬
сти в импульсно-фазовых радионавигационных системах,
находят применение сигналы в виде пачек низкочастот-
135
пых когерентных радиоимпульсов. В таких случаях при
обработке сигнала находят применение схемы экспонен¬
циальных сумматоров на накопительных конденсаторах.
На рис. 4.20 приведена схема квазиоптимальной обра¬
ботки пачки радиоимпульсов с известной начальной фа¬
зой, в основу которой положен такой сумматор. Сигнал
поступает на фильтр, согласованный с одиночным им¬
пульсом, и далее на ключевую схему, осуществляющую
селектирован не сигнала узкими селекторными импуль¬
к
Вход
Согласован¬
ный фильтр
В Выход
<нЬп
Сигнал после согласованного
фильтра
Рис. 4.20. Структурная схема квазиоитимального фильтра для пачки
когерентных радиоимпульсов с известной начальной фазой (а); вре¬
менные диаграммы (б).
сами. Отселектированные значения накапливаются с по¬
мощью интегрирующей цепи RC. Напряжение на кон¬
денсаторе С в момент времени То + /о оказывается
пропорциональным сумме всех п отселектированных зна¬
чений и, следовательно, пропорционально корреляцион¬
ному интегралу
т
J У (t) Чс (t — to) di,
О
136
гчс —то) ожидаемый сигнал в виде пачки п ко¬
герентных радиоимпульсов с известной начальной фа¬
зой.
На принципе суммирования отселектированиых на¬
пряжений может быть построена и схема обработки пач¬
ки когерентных импульсов с неизвестной начальной фа¬
зой. Для этого необходимо сигнал после фильтра, со¬
гласованного с одиночным импульсом, подать на две
ключевые схемы, работающие со сдвигом во времени,
Рис. 4.21. Структурная схема квазиоптимальноги фильтра для пачки
когерентных радиоимпульсов с неизвестной начальной фазой.
равным четверти периода несущей частоты (рис. 4.21).
Тогда напряжения, накопленные на конденсаторах С>
и С2, будут пропорциональны величинам х\ и г2, вы¬
численным по формуле (4.62) в предположении, что
zzc(Z—т0)—сигнал в виде пачки п когерентных радио¬
импульсов с неизвестной начальной фазой. Дальнейшие
операции, как и в схеме обработки одиночного сигнала
со случайной начальной фазой, сводятся к возведению
накопленных напряжений в квадрат, суммированию и
сравнению полученной величины с пороговым уровнем.
§ 4,9. СТРУКТУРА УСТРОЙСТВ ОПТИМАЛЬНОЙ
ОБРАБОТКИ ШИРОКОПОЛОСНЫХ СИГНАЛОВ
Рассмотрим сигнал в виде пачки фазоманипулиро-
ванных когерентных радиоимпульсов, примыкающих
друг к другу и имеющих одинаковую амплитуду и не¬
сущую частоту. Примером такого сигнала может слу¬
жить пачка из трех импульсов, представленная на
рис. 4.22,а. Здесь закон фазовой модуляции представлен
условно в виде последовательности знаков «Ч-» и «—»,
соответствующих значениям начальной фазы элементар-
137
Рис. 4.22. Временные диаграм¬
мы, поясняющие работу филь¬
тра, согласованного с пачкой
фазоманипулированных коге¬
рентных радиоимпульсов.
ных импульсов 0 и л. На рис. 4.23,г приведен импульс¬
ный отклик фильтра, согласованного с рассматривае¬
мым сигналом. Указанный отклик может быть получен
с помощью схемы, изображенной на рис. 4.23,а. Напря¬
жения, снимаемые с отводов
линии задержки, расстояние
между которыми соответст¬
вует временному интервалу
между элем ента р ны м и и м -
пульсами, поступают на фа-
зоинверсные каскады и за¬
тем на сумматор. Закон ин¬
версии, как видно из рисун¬
ка, соответствует закону фа¬
зовой модуляции импульс¬
ного отклика, поэтому при
воздействии на вход схемы
единичного импульса (рис.
4.23,6) на выходе суммато¬
ра образуется последова¬
тельность кратковременных
знакопеременных импульсов
(рис. 4.23,в).
Эти импульсы, воздей¬
ствуя на оконечное устрой¬
ство — фильтр, согласован¬
ный с одиночным импуль¬
сом, — завершают процесс
формирования оптимального
отклика.
Прохождение сигнала че¬
рез рассмотренную схему
иллюстрируется временны-
и в пояснениях не нуждается.
ми диаграммами рис. 4.22
При решении задачи обнаружения, когда временное
положение сигнала известно, устройство оптимальной
обработки фазоманипулированного сигнала может быть
реализовано и более простыми техническими средства¬
ми. Так, например, если несущая частота сигнала доста¬
точно низка, может быть использован экспоненциаль¬
ный сумматор (рис. 4.20). Необходимо только напря¬
жение, снимаемое с фильтра, согласованного с одиноч-
138
яым импульсом, инвсрсировать во времени в соответ¬
ствии с законом фазовой модуляции сигнала.
1
г~
Рис. 4.23. Структурная схема фильтра, согласованного с пачкой фа-
зоманипулированных когерентных радиоимпульсов (а)\ временные
диаграммы (о, в, г).
§ 4.10. СТРУКТУРА УСТРОЙСТВ ОПТИМАЛЬНОЙ
ОБРАБОТКИ ПАЧЕК НЕКОГЕРЕНТПЫХ
РАДИОИМПУЛЬСОВ
Во многих радиотехнических системах сигнал пред¬
ставляет собой периодическую последовательность п ра¬
диоимпульсов, начальные фазы которых случайны и не¬
зависимы между собой. Такие последовательности но¬
сят название пачек некогерентных радиоимпульсов.
Рассмотрим особенности оптимальной обработки пачек
некогерентных радиоимпульсов в предположении, что
огибающая пачки прямоугольна, а импульсы имеют оди¬
наковую форму.
1. Нефлюктуирующая пачка. Если амплитуда всех
п импульсов пачки заранее известна, т. е. пачка явля¬
ется нефлюктунрующей, отношение правдопобия мо¬
жет быть получено с помощью выражения (4.61) путем
139
подстановки в него вместо одиночного сигнала образца
рассматриваемой пачки радиоимпульсов:
— Toft)cos(%;-)-еh), (4.106)
k^{
где Тоь — время запаздывания й-го импульса пачки;
— начальная фаза ^-го импульса пачки, распре¬
деленная равномерно в интервале 2л.
При этом отношение правдоподобия принимает вид
(4.107)
Сравнивая (4.107) с (4.64), замечаем, что отношение
правдоподобия для нефлюктуирующей пачки, состоя¬
щей из п некогерентных радиоимпульсов, представляет
собой произведение п отношений правдоподобия для
одиночных радиоимпульсов со случайной начальной фа¬
зой. К такому же выводу нетрудно прийти, рассматри¬
вая процедуру обработки пачки как последовательность
п независимых испытаний при неизменном значении пе¬
редаваемого сообщения, когда вероятность совместного
осуществления независимых событий равна произведе¬
нию их вероятностей.
Логарифмируя выражение (4.107), получим
1пЛ(х, 1п/0 (4.108)
При этом операция умножения заменяется более про¬
стой в реализации операцией суммирования, и операции
оптимального приемника обнаружения, связанные с об¬
работкой принятого сигнала, сводятся к вычислению
суммы
140
Ранее отмечалось, что вычисление величины Zk может
быть заменено согласованной фильтрацией одиночного
импульса с последующим выделением огибающей. По¬
этому для пачки, состоящей из одинаковых по амплиту¬
де импульсов, операция (4.109) может быть реализова¬
на устройством, представленным на рис. 4.24.
Заметим, что при оптимальной обработке одиночного
импульса со случайной начальной фазой форма харак¬
теристики детектора не имеет принципиального значе¬
ния, лишь бы она была монотонной функцией входного
напряжения. Действительно, в данном случае изменение
формы характеристики детектора может быть учтено
соответствующей корректировкой порога Zo. То же са¬
мое можно сказать и об обработке пачки когерентных
радиоимпульсов, когда детектирование производится
после суммирования реализаций. Совсем иначе обстоит
дело при оптимальной обработке пачек некогерентных
радиоимпульсов. Так как начальные фазы импульсов
случайны, то детектирование производится до суммиро¬
вания реализаций. Поэтому отклонение формы харак¬
теристики от оптимальной может привести к невозвра¬
тимым потерям. Однако анализ показывает, что
качественные показатели устройства обнаружения прак¬
тически не изменяются, если оптимальный детектор заме¬
нить обычным линейным детектором. Это объясняется,
тем, что характеристика вида ln/0(w) достаточно хоро¬
шо совпадает с реальной характеристикой линейного де¬
тектора, который для больших отношений сигнал/поме-
ха имеет линейную зависимость между приращением
среднего значения сигнала на выходе и амплитудой
входного сигнала, а при малых отношениях сигнал/по-
меха — квадратичную.
2. Флюктуирующая пачка. Будем полагать, что ампли¬
туды импульсов пачки флюктуируют независимо друг
от друга в соответствии с законом распределения Рэлея
(4.73), а начальные фазы импульсов случайны и неза¬
висимы.
Здесь, так же как и в случае нефлюктуирующей пач¬
ки, отношение правдоподобия может рассматриваться
как произведение п отношений правдоподобия одиноч¬
ных радиоимпульсов. Поэтому в соответствии с выра¬
жением (4.79) можно написать
А (х, 6, Л) — Г|. ^л,в-ехру .vo(£ft + vo) }•
где Ek — средняя энергия fe-ro импульса пачки.
Для импульсов одинаковой интенсивности
А (х, 9, Л) — П -/7 + уо ехР {дГДТГV- NJ } ‘ И-IЮ)
/г = 1 1
После логарифмирования получим
In А (х, 0, Л) = л? In F-/Vo (£4_/у0) J] Zk • (4-111)
Отсюда следует, что единственной операцией, связанной
с действиями над принятым сигналом, является образо-
72
вание суммы Z~. Поэтому структура устройства
k~ 1
оптимальной обработки флюктуирующей пачки импуль¬
сов отличается от представленной на рис. 4.24 лишь
квадратичной характеристикой детектора.
Рис. 4.24. Структурная схема оптимального приемника обнаружения
для пачки некогерентных радиоимпульсов.
Таким образом, оптимальная обработка сигналов
в виде пачек нефлюктуирующих и независимо флюктуи¬
рующих радиоимпульсов со случайными начальными
фазами сводится к пропусканию принятого сигнала че¬
рез фильтр, согласованный с одиночным радиоимпуль¬
сом, детектированию и суммированию всех п продетек-
тированных реализаций. Процедура оптимального обна¬
ружения завершается сравнением накопленного в сум¬
маторе напряжения с некоторым пороговым уровнем.
112
§ 4.11. КАЧЕСТВЕННЫЕ ПОКАЗАТЕЛИ УСТРОЙСТВ
ОПТИМАЛЬНОЙ ОБРАБОТКИ ПАЧЕК
НЕКОГЕРЕНТНЫХ РАДИОИМПУЛЬСОВ
Методика вычисления вероятностей правильного об¬
наружения и ложной тревоги при оптимальной обработ¬
ке пачек некогерентных радиоимпульсов сводится к сле¬
дующему. Производится вычисление закона распреде¬
ления вероятностей амплитуды одиночного импульса на
выходе детектора в присутствии шума. Если сигнал
представляет собой нефлюктуирующую пачку, в каче-
мых импульсов п при £> = 0,9; Д=10~7 для некогерептного суммиро¬
вания (сплошная кривая I) и когерентного суммирования (пунктир¬
ная кривая II).
стве оптимального детектора может быть принят линей¬
ный детектор. Тогда распределение напряжения на вы¬
ходе детектора совпадает с распределением огибающей
смеси сигнала с шумом на выходе согласованного филь¬
тра и подчиняется обобщенному распределению Рэлея.
Если же пачка флюктуирует и, следовательно, опти¬
мальным является квадратичный детектор, необходимо
найти закон распределения квадрата огибающей. Сле¬
дующий шаг заключается в нахождении плотности ве¬
143
роятности напряжения на выходе сумматора. Зная за¬
кон распределения каждого из п слагаемых, можно най¬
ти плотность вероятности их суммы при условии, что
полезный сигнал присутствует Wxi(U) и при условии
наличия лишь одного шума №хо(^). Интегрируя услов¬
ные плотности вероятности Wxi(U) и WxQ(U) в преде¬
лах от порогового уровня iUq до оо, можно вычислить
вероятности правильного обнаружения D и ложной тре¬
воги F.
На рис. 4.25 приведены результаты * подобных вы¬
числений (кривая I) применительно к оптимальной об¬
работке нефлюктуирующей пачки некогерентных радио¬
импульсов для случая, когда Z) = 0,9 и /7=10-7. По оси
абсцисс отложено число суммируемых импульсов, а по
оси ординат — необходимое превышение энергии оди¬
ночного импульса Е над спектральной плотностью шума
Nq. Там же для сравнения приведена аналогичная за¬
висимость для пачки когерентных радиоимпульсов (кри¬
вая II).
Интересно провести сравнение выигрыша в величине
порогового сигнала при когерентном и некогерентном
накоплении в зависимости от числа импульсов в пачке.
Сравнивая кривые I и II, замечаем, что пороговый сиг¬
нал при когерентном накоплении с увеличением п па¬
дает быстрее, чем при некогерентном. Кривая III, пред¬
ставляющая собой разность зависимостей I и II, харак¬
теризует потери в помехоустойчивости некогерентного
обнаружения по сравнению с когерентным. При п=\
пороговые сигналы в обоих случаях одинаковы. Это и
■понятно, так как процедура обработки одиночного им¬
пульса в сравниваемых случаях одинакова. Разница
появляется лишь при п>1, когда оптимальная обработ¬
ка сигнала включает операцию суммирования импуль¬
сов. Суммирование когерентных импульсов производится
до детектирования в линейной части приемника. Отно¬
шение епгпал/шум па выходе когерентного сумматора
возрастает с увеличением числа накопленных импуль¬
сов, и поэтому детектированию подвергается сигнал,
имеющий заметное превышение над шумом. При обра¬
ботке же некогерентных импульсов сигнал должен де¬
тектироваться до накопления, т. е. при тем меньшем от-
* Результаты вычислений заимствованы из [21].
144
ношении сигнал/помеха, чем больше п. При детектиро¬
вании имеет место эффект подавления слабого сиг¬
нала помехой, что эквивалентно уменьшению отноше¬
ния сигнал/помеха. Поэтому и после суммирования
отношение сигнал/помеха оказывается меньше, чем
в случае когерентного накопления, что приводит к ухуд¬
шению качественных показателей приемника обнару¬
жения. Для сохранения заданных значений D и F не¬
обходимо увеличивать энергию некогерентной пачки.
Последнее может быть достигнуто либо увеличением
энергии каждого импульса пачки, либо увеличением
числа импульсов в пачке. Например, для пачки из п =
= 100 когерентных радиоимпульсов значения £> = 0,9 и
£
/г=10~7 достигаются (кривая II) при ^- =—6 дб. Те
же значения D и F для пачки из /1=100 некогерентных
импульсов могут быть получены (кривая I), если
£
jj- =—0,5 дб. Таким образом, переход от когерентного
суммирования к некогерентному при сохранении тех же
качественных показателей влечет за собой увеличение
энергии каждого импульса пачки на 5,5 дб. Эти же
качественные показатели могут быть получены и при не¬
изменной энергии каждого импульса пачки. Для этого
потребуется увеличение п от 100 до 1 000, что равно¬
сильно десятикратному увеличению энергии пачки.
Как следует из рассмотренного примера, увеличение
энергии пачки некогерентных импульсов путем измене¬
ния энергии каждого импульса и путем изменения чис¬
ла импульсов не эквивалентно. Это объясняется неоди¬
наковыми условиями детектирования сигналов в рас¬
сматриваемых случаях. При увеличении энергии каж¬
дого импульса пачки возрастает отношение сигнал/по¬
меха после согласованного фильтра, а следовательно,
и на входе детектора. Во втором же случае это отноше¬
ние остается прежним, и, следовательно, детектирование
происходит при меньшем отношении сигнал/помеха и
приводит к большему подавлению сигнала помехой.
Потери, вызванные переходом от когерентного сум¬
мирования к некогерептному, уменьшаются с уменьше¬
нием пив пределе при п=1 отсутствуют. Поэтому дроб¬
ление одиночного импульса на ряд некогерентных им¬
пульсов в энергетическом отношении невыгодно.
Ю-1173 145
§ 4.12. НАКОПИТЕЛЬНЫЕ УСТРОЙСТВА
ВИДЕОИМПУЛЬСОВ
Основные трудности технической реализации
устройств оптимальной обработки пачек некогерентных
радиоимпульсов связаны с суммированием продетекти-
рованных импульсов. Суммирование видеоимпульсов
или некогерентное накопление может быть выполнено
с помощью тех же устройств, что и для когерентных
сигналов (рис. 4.19, 4.20). Кроме того, здесь может быть
использована запись сигналов на потенциалоскопе, маг¬
нитная запись и т. д.
В тех случаях, когда временное положение сигнала
заранее известно, наиболее простыми в реализации ока¬
зываются сумматоры на накопительных Конденсаторах.
Однако в большинстве случаев временное положение
ожидаемой пачки импульсов известно лишь приближен¬
но с точностью до временного интервала между им¬
пульсами пачки. Поэтому не представляется возможным
осуществить временную селекцию с точностью до дли¬
тельности импульсов, а, следовательно, накопитель,-
представленный на рис. 4.20, не может быть использо¬
ван. В таких случаях находят применение сумматоры,
осуществляющие накопление импульсов вне зависимо¬
сти от временного положения ожидаемого сигнала.
К этой категории может быть отнесен и сумматор на
накопительных конденсаторах, если временной интер¬
вал, соответствующий расстоянию между импульсами
пачки, разбить на элементарные участки длительностью
тс и в каждом из них призводить накопление с помо¬
щью цепи RC подобно тому, как это делается в схеме
рис. 4.20. Такие устройства получили название синхрон¬
ных фильтров на накопительных конденсаторах. Исполь¬
зованию таких фильтров препятствует большая скваж¬
ность сигнальных импульсов, так как при этом число
накопительных ячеек становится чрезмерно большим.
Указанного недостатка лишены накопители видеоим¬
пульсов на линии задержки с положительной обратной
связью (рис. 4.19). Здесь в качестве линии задержки
могут быть использованы различные варианты ультра¬
звуковых линий задержки, с помощью которых оказы¬
вается возможным получить задержку импульсов до не¬
скольких миллисекунд при полосе пропускания порядка
146
единиц мегагерц. Для этой же цели могут быть исполь¬
зованы и потенциалоскопы — электроннолучевые трубки,
в которых электрические колебания записываются в ви¬
де потенциального рельефа на диэлектрической мишени.
Потенциалоскоп может быть использован не только
в качестве задерживающего устройства, но и как син¬
хронный фильтр, осуществляющий накопление зарядов
на элементах мишени.
Для накопления видеоимпульсов находит примене¬
ние и магнитная запись электрических колебаний. При
этом электрические сигналы воспроизводятся в виде
магнитного рельефа па магнитной ленте, диске или ба¬
рабане. Достоинством магнитной записи является по
существу неограниченное время хранения информации.
§ 4.13. НАКОПИТЕЛЬНЫЕ УСТРОЙСТВА
КВАНТОВАННЫХ ВИДЕОИМПУЛЬСОВ И ИХ
ЭФФЕКТИВНОСТЬ
До сих пор нами рассматривались накопительные
устройства, которые в том или другом виде осуществля¬
ли суммирование поступающих на вход сигналов. Прин¬
ципиально подобные накопительные устройства осущест¬
вляют оптимальную операцию обработки повторяю¬
щихся сигналов, но не всегда могут быть практически
реализованы из-за технического несовершенства
устройств памяти и других элементов. В этом отноше¬
нии значительно более перспективны накопительные
устройства квантованных видеоимпульсов.
В рассматриваемых здесь накопительных устройст¬
вах суммируемые импульсы подвергаются временной
селекции с помощью узких селекторных импульсов
(рис. 4.26,я), а затехМ квантуются по уровню.
Квантование по уровню заключается в разбиении
всего амплитудного диапазона на ряд уровней, как это
показано на рис. 4.26,а. Каждому импульсу приписы¬
вается определенное число, соответствующее с точно¬
стью до шага квантования Ли его амплитуде. Это число
в виде цифрового кода поступает на запоминающее
устройство, где хранится до момента прихода очеред¬
ного импульса. С приходом очередного импульса опе¬
рация временной селекции и квантования повторяется и
10* 147
соответствующий цифровой код поступает на цифровой
сумматор, куда с другой стороны вводится ранее запом¬
ненное число. Результат суммирования отсылается в за¬
поминающее устройство, где хранится до прихода оче¬
редного импульса и т. д. После п циклов работы в запо¬
минающем устройстве накапливается сумма п
квантованных видеоимпульсов, представленная в. виде
<дантодания
вход .
г Цифровой
| сумматор
I
Заломи- Выход
нающее °
устройств^
Рис. 4.26. Временные диаграммы, поясняющие процесс квантова¬
ния (а); структурная схема цифрового суммирующего устройст¬
ва (б).
цифрового кода. Поэтому рассматриваемый накопитель
квантованных видеоимпульсов может -быть назван циф¬
ровым накопительным устройством или цифровым нако¬
пителем.
При двоичном кодировании чисел результат кванто¬
вания и накопления представляется в виде последова¬
тельности нулей и единиц, что позволяет сравнительно
просто реализовать цифровой накопитель. Запоминание
одноразрядного двоичного числа (0 или 1) осуществля¬
ется одной двоичной ячейкой памяти. Для хранения
многоразрядного двоичного числа используется несколь¬
ко ячеек памяти, которые совместно со вспомогательны¬
ми элементами и образуют запоминающее устройство.
В качестве запоминающих устройств находят примене¬
ние триггерные схемы, магнитные устройства памяти,
линии задержки, потенциалоскопы и т. д. Часто запоми¬
нающее устройство выполняет одновременно и функции
сумматора. Так, например, запоминающее устройство
в виде нескольких последовательно включенных триггер-
148
ftbix ячеек будет не только хранить записанное число,
но и с приходом на счетный вход первого триггера оче¬
редного слагаемого в виде i импульсов произведет опе¬
рацию суммирования так, что состояние триггерных
ячеек будет соответствовать сумме, выраженной в дво¬
ичном коде.
Существенно, что при двоичном кодировании чисел
достаточно различать только два состояния (0 и 1),
а поэтому не предъявляется жестких требований
к амплитудному диапазону запоминающего устройства.
Здесь амплитудный диапазон входных видеоимпульсов
и их суммы оказывается трансформированным в необ¬
ходимое число двоичных ячеек памяти. При этом увели¬
чение числа суммируемых видеоимпульсов в два раза
требует добавления лишь одной ячейки памяти. Поэтому
не возникает трудностей при накоплении даже очень
большого числа импульсов.
Число уровней квантования определяет точность
аппроксимации амплитуд накапливаемых импульсов
числами. Поэтому с уменьшением числа уровней кван¬
тования качественные показатели цифровых накопите¬
лей должны ухудшаться. Однако, как показывает ана¬
лиз, даже при простейшем бинарном квантовании (число
уровней квантования минимально и равно двум) качест¬
венные показатели цифрового накопителя незначительно
отличаются от оптимального. Если к тому же учесть,
что бинарное квантование дает возможность до предела
упростить квантователь и свести к минимуму число
ячеек памяти в запоминающем устройстве, станет ясно,
почему именно этот вид квантования нашел широкое
распространение в цифровых устройствах накопления.
Остановимся подробнее на оценке качественных по¬
казателей цифровых устройств накопления.
Обозначим вероятность превышения порога кванто¬
вания произвольным импульсОхМ пачки через Do, а веро¬
ятность превышения этого же порога выбросом помехи
при отсутствии сигнала — через Fo. Будем считать, что
обнаружитель вырабатывает решение о наличии сигна¬
ла, если т или более импульсов из числа п импульсов
пачки превышают порог квантования. Таким образом,
число т может быть названо порогом счета. Вероят¬
ность превышения порога квантования k импульсами
равна , а вероятность превышения того же порога k
149
выбросами помехи равна F*. Соответствующие вероят¬
ности непревышения порога остальными (n—k) импуль¬
сами будут
(]_РО)П-Ь и
Поэтому вероятность появления одной комбинации k
импульсов из п равна
Dka(\-Day-*
при наличии сигнала, и
если присутствует лишь помеха. Число комбинаций k из
п равно числу сочетаний С*, а вероятность образова¬
ния любой из этих комбинаций будет
CkDkQ(\-D^~\
если сигнал присутствует, и
в отсутствие сигнала. Поэтому условная вероятность
правильного обнаружения равна
D V CkD'[} (1 — Do)" - к (4.112)
k=m
и условная вероятность ложной тревоги
F = V CknFk0 (1 — F9)n (4.113)
k=tn
Формулы (4.112), (4.113) определяют качественные
показатели устройств обнаружения пачек импульсов при
цифровом накоплении бинарно-квантованных видеоим¬
пульсов. Вероятности Do и FQ могут быть найдены по
формулам или кривым обнаружения для одиночного сиг¬
нала со случайной начальной фазой.
Проиллюстрируем полученные результаты простей¬
шим примером.
Пусть п = 2 и т = 2. Тогда в соответствии с выраже¬
ниями (4.112), (4.113)
п F = F„.
150
Если F= 10~8 и £ = 0,8, то Го и Do должны быть 10~1 и
0,895 соответственно. С помощью кривых рис. 4.12 нахо¬
дим /7 = 5,5, что соответствует энергии одного импульса
пачкщ В пересчете же на энергию всей пачки qu =
=- j/2g = 7,75. Те же значения £=10~8 и £> = 0,8 при
оптимальном когерентном накоплении достигаются, если
711К = 6,3. Сопоставление и дает различие на 25%
пли на 1 дб. Так как потери за счет некогерентностп им¬
пульсов при п = 2 очень малы (рис. 4.25), то практически
все потери обусловлены бинарным квантованием и со¬
ставляют всего 1 дб.
Если провести аналогичный расчет для порога счета
т= \ при том же /г=2, то результаты окажутся несколь¬
ко худшими. Вообще, для каждого п существует свой
оптимальный порог счета, при котором потери за счет
бинарного квантования оказываются наименьшими. Бо¬
лее подробный анализ показывает, что оптимальный по¬
рог счета
~ 1,5 V п.
При этом потери за счет бинарного квантования не пре¬
вышают 3 дб при любых /г.
Когда временное положение пачки импульсов извест¬
но лишь приближенно, используются многоканальные
цифровые обнаружители. Каждый канал такого обнару¬
жителя «настроен» на определенное временное положе¬
ние ожидаемой пачки, так что несколько каналов пере¬
крывают весь временной интервал, в котором может ока¬
заться ожидаемая пачка импульсов. В таких случаях
одновременно с установлением факта наличия сигнала
может быть зафиксировано и временное положение об¬
наруженной пачки.
Глава 5
ИЗМЕРЕНИЕ ДАЛЬНОСТИ И СКОРОСТИ
§ 5.1. ПОТЕНЦИАЛЬНАЯ ТОЧНОСТЬ ИЗМЕРЕНИЯ
ДАЛЬНОСТИ
Любое измерение связано с оценкой измеряемой ве¬
личины. Если х— истинное значение измеряемой вели¬
чины, а х— оценка, т. с. результат измерения, то Ах==
= х—х является ошибкой измерения.
Вероятность того, что произойдет ошибка Дх, равна
вероятности совместного осуществления событий х и х:
dP = W(x, x)dxdx.
Чем больше опасность ошибки, тем большее значение
ей придается, т. е. тем больше ее стоимость (риск), оце¬
ниваемая функцией стоимости (риска) R(x, х). Для по¬
лучения оптимальной оценки нужно минимизировать
величину
Л = R (х, х) dx dx,
- со
называемую средним риском.
Рассмотрим измерение величины х (сигнала) в при¬
сутствии помехи п. Наличие сигнала считается уже уста¬
новленным, и задача сводится к оценке х на основе ее
априорного распределения IF(x) и измеренного значе¬
ния у = х + п. При этом оценка х должна быть оптималь¬
ной, г. е. удовлетворять критерию минимума среднего
риска. Так как каждому у соответствует оценка х=
-x(z/), то
W (х, х) dx dx —
= W (х, //) dx dy = \V(y) (x)
152
и, следовательно,
Л
■ dy j R (x, x) W (y) Wy (x) dx =
— QO — ОС
= \ Ru(x) W (y)dy, (5.1)
— GO
где
co
Ru (x) = J R (x, x) Wу (x) dx
—CO
— условный средний риск, рассчитанный для фиксиро¬
ванного значения у.
Так как W (у)—заданная величина, то условие Л =
= min соответствует условию
Ry (х) = \ R(x, х) W у (х) dx =
— ос
= J R (х, х) /г117 (х) (if) dx — in in,
— 00
где
, _ 1 _ 1
J W(x^Wx (y)dx
—00
— нормирующий множитель, определяющий масштаб
кривой апостериорного распределения Wy(x) по оси х
так, что площадь, ограниченная этой кривой и осью х,
равна 1. Найдем теперь оптимальную оценку хОпт, обес¬
печивающую минимум условного среднего риска Ry(x)
при квадратичной функции стоимости ошибки 7?(х, х) =
= (х—х)2, что соответствует минимальной среднеквадра-
153
тичной ошибке измерения аыпн. Значение хопт найдем из
условия
э
R(x, х) Wy (х) dx —
(•'■ - *опт)г tt7, (X) dx =
— 00
J 2 (x0I„ — x) Wy (x) dx = 0.
—00
Отсюда
00
Xom== j xWy(x)dx. (5.2)
—00
Таким образом, оптимальной является оценка по
«центру тяжести» апостериорного распределения Wy(x)
измеряемой величины.
Определение центра тяжести Wy(x) достаточно
сложно, поэтому практически применяются квазиопти-
мальные оценки. При 1Г(х) =const, Wy(x) =^\Wx(y),
т. е. апостериорное распределение Wy(x) с точностью до
постоянного множителя совпадает с функцией прав¬
доподобия Wx(y), и оценка по центру тяжести сводится
к максимально правдоподобной.
Рассмотрим этот способ применительно к определе¬
нию временного положения видеоимпульса при наличии
шума, к которому обычно сводится задача измерения
дальности в импульсных дальномерах. Предположим,
что на вход приемника (схемы обработки) поступает
аддитивная смесь видеосигнала пс(/—То), временное по¬
ложение которого характеризуется параметром т0 (при
измерении дальности РЛС To = /d=2D/c), и помехи в ви¬
де нормального белого шума иш(/) с нулевым средним
значением, т. е.
y(t) = Uc(t—То) + Щп(0-
При равномерном априорном распределении №(т)
в пределах возможных значений Тмин-^т-макс (соответст¬
вующих диапазону измеряемых дальностей 2)Мин-^
-Омакс) и малом уровне помех, что имеет место при вы-
154
сокой точности измерений, апостериорное распределение
UZv(t) практически определяется функцией правдоподо¬
бия
т
= \ exp^- f у (0 «с (t — z)dt,
6
которая в этом случае представляет собой одногорбую
кривую, симметричную относительно координаты макси¬
мума. В связи с этим оптимальной оценкой измеряемого
временного положения будет значение т, при котором
функция правдоподобия максимальна. Поскольку
Wz (у) является монотонной функцией корреляционного
интеграла
т
б
максимум W (у) совпадает с максимумом z(t) и дис¬
персии оценок по максимуму функций (у) и г(т)
также совпадают.
Корреляционный интеграл г(т) равен сумме авто¬
корреляционной функции сигнала
т
гс W = J ttc (I — т0) ис (/ — z)dt (5.3)
б
и шумовой функции
т
гш W J (О (/ — *) dt. (5.4)
oJ
Так как сигнальная и шумовая функции неразделимы,
то при измерении временного запаздывания т может
быть зафиксирован лишь момент прохождения через ма¬
ксимум суммарного сигнала г(т), являющийся оцен¬
кой т. Из-за наличия шумов оценка т отличается от
истинного значения временного запаздывания То на слу¬
чайную величину Дт=т—То, что вызывает ошибку в из*
мерении дальности М)=Лтс/2.
При достаточно большом отношении сигнала к шуму
случайные ошибки невелики, а для оценки точности из¬
мерения дальности можно воспользоваться разложением
155
производной функции г(т) в ряд Тейлора в окрестно¬
сти то, ограничившись первыми двумя членами:
z (т) « zc (х0) + Дтгс (х0) + гш (т),
где гс (т0) и zc (t0) — первая и вторая производные сиг-
нальной функции при т = т0.
В момент отсчета т = т функция z (т) проходит через
максимум, следовательно, ее первая производная
г (т) гс (т0) 4- Дтгс (т0) Ц- гП1 (т) = 0.
Отсюда случайная ошибка Дт равна
Дт ' Т То
поскольку при т = т0 функция гс (т) проходит через ма¬
ксимум и £с(т;о) = О.
Дисперсия ошибки в окрестности т = то будет
(?- V)2 -= (5.5)
Как видно из этой формулы, среднеквадратичная ошиб¬
ка измерения времени запаздывания уменьшается
с уменьшением производной шумовой функции гш(т) и
увеличением гс(т), т. е. с увеличением крутизны сигналь¬
ной функции.
Имея в виду, что функция 2с(т) определяется вре¬
менным сдвигом т—То подынтегральных функций выра¬
жения (5.3), для вычисления 2с(т) можно применить
поочередное дифференцирование функций uc(t—то) и
ис-(/—т) под знаком интеграла:
Zc(-c) = Juc(Z — Elicit — X)dt. (5,6)
о
Функция гр (т0) достигает максимума при т = т0:
г„(т)==| file (t — т0)]М(.
156
Таким образом, минимальное значение дисперсии ошиб¬
ки при измерении т будет
Здесь числитель представляет собой дисперсию шумовой
функции и может быть записан с помощью дискретных
представлений, использованных в предыдущей главе,
и
т {^т
= х‘!'1
О i = l
в виде
(5-8)
157
Подставляя вместо числителя выражения (5.7) его
эквивалент (5.8), получим
2 1
о.МВи= т (5-9)
[ “с (* — хо) dt
о
Умножив и разделив знаменатель формулы (5.9) на интеграл
т
С и2 (t — т0) dt, представляющий собой энергию сигнала
получим выражение для минимального значения дисперсии
ошибки в более удобном виде
х мин
1 _1
2Е I «с U — то) dt bft
Tj~ 'V°
° j «С (t — xo) dt
Тогда минимальное значение среднеквадратичной
измерения будет
1 1
(5.10)
ошибки
(5.11)
где
а
1 мин
имеет размерность частоты и называется эффективной
шириной спектра сигнала.
Таким образом, минимальная среднеквадратичная
ошибка а , определяющая потенциальную точ-
II л
ность измерения дальности, обратно пропорциональна
отношению сигнал/помеха и эффективной ширине спек¬
тра сигнала.
Если производится когерентное суммирование п оди¬
наковых сигнальных импульсов, то q увеличивается,
азмии уменьшается соответственно в У п раз. При
некогерентпом суммировании выигрыш меньше п из-
за эффекта подавления слабого сигнала помехой при
детектировании, о чем подробно говорилось в предыду¬
щей главе.
158
§ 5.2. ИМПУЛЬСНЫЕ ДАЛЬНОМЕРЫ С ВИЗУАЛЬНОЙ
ИНДИКАЦИЕЙ
Определение дальности в импульсных дальномерах
сводится к измерению пропорционального ей временно¬
го интервала tD между начальным импульсом, соответ¬
ствующим моменту излучения импульса антенной пере¬
датчика, и приемом сигнального импульса приемником
радиодальномера. Для измерения временных интерва¬
лов применяется несколько методов, отличающихся ти¬
пом индикатора и способом отсчета дальности.
Наиболее распространенным типом индикатора, при
неавтоматических измерениях является электроннолуче¬
вая трубка. Сигнальный импульс после усиления и де¬
тектирования в приемнике подается на модулирующий
электрод трубки. Применяется модуляция луча отклоне¬
нием или по яркости. Для измерения дальности преду¬
сматривается отсчетное устройство того или другого
типа, позволяющее по положению отметки сигнала непо¬
средственно отсчитывать дальность.
По характеру применяемой развертки индикаторы
имеют несколько разновидностей. Наибольшее приме¬
нение в РЛС точного измерения дальности находят ин¬
дикаторы с линейной разверткой (типа Л) и круговой
разверткой (типа 7).
В тех случаях, когда производится измерение даль¬
ности одного объекта и от дальномера не требуется раз¬
решения по дальности, возможно применение стрелоч¬
ной индикации.
На рис. 5.1 представлены блок-схема индикаторного
устройства с линейной разверткой и ее временная диа¬
грамма.
Линия развертки на экране ЭЛТ, являющаяся осью
времени, образуется при отклонении луча трубки слева
направо пилообразным напряжением генератора раз¬
вертки. После окончания прямого хода развертки на¬
пряжение на отклоняющих пластинах уменьшается и
пятно на экране возвращается в исходное положение.
Обратный ход должен закончиться до прихода следую¬
щего пускового импульса на генератор развертки. На
время обратного хода луч трубки гасится большим отри¬
цательным смещением на ее сетке. На время прямого
хода трубка открывается импульсом подсвета. Сигнал
с выхода приемника после усиления его до необходимо-
159
"ГГускобой
импульс
«к-
-чк--
к
t
- г' —
3
Излучаемые
импульсы
Пусковые
импульсы
Прямоугольные
импульсы
Пилообразное
напряжение
¥
I
1р?рям. ход у* ~ | Обрати, ход г
L-L-LJ. L 1 1 L I
Импульс
подсвета
Сигнальные
импульсы
Импульсы
масштаба
Рис. 5.1. Блок-схема индикатора типа А и соответствующая e’i вре¬
менная диаграмма.
Импульсы
масиагшиа
Начальный импульс
Сигнальные отметки
— Шумы
Экран трубки
160
re, уровня видеоусилителем подается на вертикально
отклоняющие пластины трубки, вызывая появление на
развертке сигнального выброса.
Измерение времени задержки сигнального импульса
может осуществляться с помощью «механической» или
«электрической» шкалы дальности непосредственно на
экране трубки. Используются также специальные изме¬
рительные импульсы. Изменяя временную задержку из¬
мерительного импульса, оператор совмещает его с сиг¬
нальным. При этом время задержки измерительного им¬
пульса является мерой дальности, которая может быть
отсчитана по шкале устройства задержки.
В рассматриваемом индикаторном устройстве шкала
дальности создается с помощью импульсов масштаба.
Кроме измерения дальности индикатор с линейной
разверткой дает возможность фиксировать совмещение
оси антенны с направлением па источник сигнала. Инди¬
катор обладает хорошей различимостью сигналов на
фоне шумов (коэффициент различимости /77р близок
к единице). Эти качества обеспечили широкое примене¬
ние индикатора с линейной разверткой для измерения
дальности.
Индикатор типа J, имеющий круговую развертку,
может обеспечить более высокую точность измерения
дальности, так как при той же шкале дальности и оди¬
наковом диаметре экрана трубки длины линии разверт¬
ки индикатора типа J в 2л-2,5 больше, чем у индикато¬
ра типа А. Однако основная причина высокой точности
индикатора типа J заключается в возможности созда¬
ния генераторов развертки очень высокой стабиль¬
ности.
Круговая развертка образуется при подаче па гори¬
зонтальные и вертикальные отклоняющие пластины
трубки синусоидальных напряжений, сдвинутых по фазе
на 90°. Скорость движения пятна по окружности будет
постоянной, т. е. развертка линейной во времени, при
условии строго синусоидальной формы напряжений раз¬
вертки, фазовом сдвиге, равном точно 90°, и обратной
пропорциональности амплитуды напряжения развертки
чувствительности горизонтального и вертикального от¬
клонений трубки.
На рис. 5.2 представлены блок-схема простейшего
индикатора типа J и вид изображения на экране трубки
11-1173 1б1
индикатора. Начало развертки определяется началом
импульса подсвета трубки, который совпадает с момен¬
том излучения импульса антенной передатчика дально¬
мера.
Сигнал от приемника подается на центральный элек¬
трод трубки индикатора и отклоняет луч от центра, ес¬
ли полярность сигнала отрицательна. При этом па ли¬
пни развертки появляется выброс, положение которого
относительно начала развертки определяется дально¬
стью источника сигнала.
Сигнальные
Начальный
Рис. 5.2. Блок-схема индикатора типа J и вид изображения на экра¬
не трубки.
К числу основных характеристик радиодальномера
относятся точность, разрешающая способность, мини¬
мальная и максимальная дальность измерения. Ниже
кратко рассматривается зависимость этих характеристик
от технических параметров импульсных дальномеров
с электроннолучевыми индикаторами.
Точность измерения дальности. Полагая, что среднее
значение скорости с учетом условий распространения
известно достаточно точно, рассмотрим ошибки измере¬
ния временного положения сигнальных импульсов, опре¬
деляющих точность радиодальномера с индикатором на
ЭЛТ. В этом случае процесс отсчета сводится к совме¬
щению оператором сигнального выброса или пятна па
экране трубки с визирной линией или электронной мет¬
кой. При этом обычно точность измерения дальности
в основном определяется инструментальной ошибкой
измерения, существенно превышающей минимальное
значение среднеквадратичной ошибки, представленное
выражением (5.11).
162
Основными причинами, вызывающими инструмен¬
тальные ошибки, являются:
1) Неодиовремеиность запуска модулятора передаю¬
щего устройства и генератора развертки индикатора.
2) Задержка сигнала в приемном тракте радиодаль¬
номера.
3) Неточность отсчетного устройства индикатора.
4) Нелинейность развертки и несоответствие скоро¬
сти развертки шкале индикатора.
Первые две причины вызывают ошибку измерения
дальности, если временная задержка сигнального им¬
пульса отсчитывается относительно начала развертки.
При отсчете непосредственно относительно положения
излучаемого импульса влияние этих причин может быть
практически исключено. Заметим также, что отклонение
скорости развертки от номинала вызывает ошибки лишь
при использовании механической шкалы дальности. При
применении для отсчета подвижной метки или масштаб¬
ных меток изменение скорости развертки не приводит
к ошибкам, так как положение меток на экране опреде¬
ляется соответственно временной задержкой измери¬
тельного импульса или периодом повторения масштаб¬
ных импульсов. Однако в этом случае возможны систе¬
матические ошибки из-за отклонения времени задержки
или периода повторения импульсов от номинала. К со¬
жалению, ошибки, вызванные упомянутыми причинами,
не сохраняются строго постоянными и поэтому не могут
быть полностью устранены при калибровке системы. Со
временем и в связи с изменением условий работы вели¬
чина ошибок несколько изменяется. Периодическая ка¬
либровка системы позволяет уменьшить влияние таких
отклонений, но полностью они неустранимы и поэтому
составляют часть случайной ошибки системы.
К числу других причин, вызывающих случайные
ошибки, относятся причины, связанные с процессом от¬
счета дальности:
1) Неточность совмещения визира или измеритель¬
ного импульса с отметкой сигнала вследствие ошибки
в определении уровня совмещения, конечных размеров
пятна на экране индикатора и влияния шумов.
2) Неточность интерполяции при отсчете по шкале.
3) Параллакс при снятии отсчета.
11*
163
Две последние причины свойственны любому измери¬
тельному прибору со шкальным устройством и не тре¬
буют пояснений. Ошибки совмещения, особенно при на¬
личии шумов, следует рассмотреть подробнее.
Обычно отсчет производится по переднему фронту
сигнального импульса (рис. 5.3), что обеспечивает более
высокую точность совмещения, чем по максимуму. Для
исключения влияния задержки в приемном, тракте от-
Рис. Ь.З. 1\ оценке ошибки совмещения при отсутствии (а) и нали¬
чии (б) шумов.
счет производится относительно точки переднего фрон¬
та излучаемого импульса (зондирующего или запрос¬
ного), заданной на каком-либо уровне h совмещением
визирной линии с передним фронтом сигнального им¬
пульса на том же уровне.
Рассмотрим влияние па точность совмещения конеч¬
ных размеров пятна на экране трубки и шумов прием¬
ника, на фоне которых обычно воспроизводится сигнал
на экране. Рис. 5.3,а иллюстрирует процесс совмещения
визира с сигналом при конечных размерах пятна. Если
размер пятна равен d=BC, а амплитуду выброса на
экране трубки /ги представить через напряжение сигнала
Uс, и чувствительность вертикального отклонения труб¬
ки Sy, найдем
*ф:
164
Ошибку совмещения можно записать так:
Переходя к масштабу дальности, получим выражение
ошибки совмещения в единицах дальности
2v,
где М — коэффициент масштаба индикатора.
Следовательно, для уменьшения ошибки совмещения
необходимо увеличивать скорость развертки и ампли¬
туду напряжения сигнала и уменьшать длительность
фронта импульса. Очевидна также выгодность исполь¬
зования трубок с высокой чувствительностью и разре¬
шающей способностью.
Предположим, что вместе с сигналом амплитудой Uc
поступает шум с действующим значением напряжения
Um. Так как шум вместе с сигналом проходит приемный
тракт с полосой пропускания Af, шумовые выбросы име¬
ют длительность порядка 1/АД т. е. приблизительно рав¬
ную длительности сигнала, и их влияние сказывается
в хаотическом изменении амплитуды и формы сигнала
на экране. Благодаря инерционности глаза и экрана
трубки колебания сигнала сливаются и воспринимаются
оператором как размытие очертаний сигнального выбро¬
са. Ориентировочную оценку ошибки отсчета в завп-
мости от отношения епгпал/шум можно найти с по¬
мощью рис. 5.3,6.
Ширину линии развертки у основания импульса
с учетом размытости из-за воздействия шума можно
записать
t/p ~ d+SyUш*
Аналогично ширина линии на фронте импульса будет
о!ф — СВ = d -ф- SyUm cos а.
165
Имея в виду, что tg a = S/;[/сДутф, представим вели¬
чину ошибки отсчета на экране выражением
Д/ =
2“ 1 +ctg2a -|-
А13 с1ф d
2 2 sin а 2 sin а
I SyUш
*2 tg «
д/
Отсюда
/л
с
7
С(1 /" 1 I / гДтФ \2 |
4-jp у ' \^SyUc J "Г’ 4^/Л
(5.13)
Таким образом, в этом случае ошибка совмещения
имеет две составляющие: ADd и АРШ, вызванные конеч¬
ными размерами пятна и воздействием шума. Шумовая
составляющая ошибки растет с увеличением длительно¬
сти фронта сигнального импульса и отношения помехи
к сигналу.
Конечно, проведенный анализ является весьма гру¬
бым приближением, однако упрощенная трактовка на¬
глядна и позволяет сделать ряд конкретных рекоменда¬
ций, реализация которых при построении дальномеров
позволяет повысить точность измерения дальности.
Учитывая простоту формирования импульса и сохра¬
нения стабильной частоты колебаний в течение его дли¬
тельности, в РЛС используются импульсы прямоуголь¬
ной формы. При согласованной фильтрации сигнальный
импульс на выходе приемника становится треуголь¬
ным. При использовании оптимальных автоматических
методов временное положение такого импульса может
быть зафиксировано по вершине столь же точно, как и
исходного прямоугольного по фронту. Однако при визу¬
альном методе измерения оператором более высокую
точность дает фиксация по переднему фронту, причем
ошибка отсчета падает с увеличением крутизны фронта
и отношения сигнал/шум.
Если отношение сигнал/помеха достаточно велико, то
выигрыш в точности при расширении полосы, связанный
166
с увеличением кр\тпзпы фронта, превалирует над проиг¬
рышем из-за уменьшения отношения сигнала к шуму, по¬
этому полоса пропускания приемников дальномерных
РЛС с индикаторами на ЭЛТ обычно выбирается в 2—
3 раза шире согласованной.
Составляющая ошибки за счет конечных размеров
пятна снижается при увеличении скорости развертки.
Однако при этом соответственно снижается и участок
дальности, воспроизводимый на экране трубки. Для
того чтобы иметь возможность просмотреть всю' задан¬
ную дальность, можно изменением задержки начала
развертки перемещать развертку по оси дальности. Не¬
достатком этого способа является невозможность одно¬
временного наблюдения всего заданного диапазона
дальности.
Частичное решение противоречия между необходи¬
мостью повысить скорость развертки и возможностью
сохранить достаточно большую шкалу дальности дает
применение индикатора с участком ускоренной развертки,
который часто называется лупой времени. Перемещение
растянутого участка развертки происходит путем изме¬
нения задержки импульса, запускающего генератор
быстрой развертки. Сигнальный импульс изменением
задержки располагают на экране в пределах участка
быстрой развертки, где точность отсчета и разрешающая
способность возрастают. Однако такой индикатор имеет
и недостатки. Во-первых, здесь нельзя получить значи¬
тельного увеличения скорости, так как для ускоренного
участка используется сравнительно небольшая часть
экрана трубки, и, во-вторых, участок развертки, распо¬
ложенный за растянутым, дает уже искаженное пред¬
ставление о дальности.
Радикальное решение задачи получения высокой ско¬
рости развертки при одновременном наблюдении всего
заданного диапазона дальности дает применение, много¬
шкальных методов измерения, из которых широкое рас¬
пространение получили двушкальпыс методы измерения
дальности. Поясним принцип двушкального метода из¬
мерения на примере индикатора с линейной разверткой,
имеющего две трубки (рис. 5.4). Вся заданная шкала
дальности Dr в таком индикаторе воспроизводится труб¬
кой грубого измерения дальности (ТГД). Небольшая
часть всей дальности Лт развертывается на весь экран
1G7
трубки точного измерения дальности (ТТД). Если отно¬
сительная ошибка измерения дальности на ТГД состав¬
ляет A/Jf/Dr, а на ТТД — соответственно ^T = A/lr/DTt
то результирующая ошибка индикатора относительно
всей шкалы дальности Dv равна
6
7Гг ‘
Если выбрать шкалу дальности ТТД из условия Рт —
= ADr, то
j. AZ\ ADTDT AZ)rADT
— ТД” DvDr ~ l)v[)y~ ~ ‘
При одинаковых трубках и условиях наблюдения
£г = $т=Ч и, следовательно, £р-=£2.
Рис. 5.4. Двушкальный метод измерения дальности.
Если требуется еще более высокая точность, необхо¬
димо использовать многошкальные системы. Но при их
построении возникает ряд трудностей, не позволяющих
использовать возможности повышения точности, поэтому
даже трехшкальные системы применяются сравнительно
редко.
Разрешающая способность по дальности характери¬
зует систему с точки зрения возможности раздельного
наблюдения сигналов двух близко расположенных
объектов и измерения дальности каждого из них.
Разрешающую способность РЛС по дальности при¬
нято оценивать непосредственно тем минимальным рас¬
стоянием между двумя точечными объектами, располо¬
женными на одном угловом направлении (в створе
с РЛС), при котором возможно их раздельное наблю¬
дение.
168
Как показано в гл. 3 при отсутствии впутрппмпульс-
иой модуляции зондирующего сигнала для разрешения
двух неподвижных или медленно движущихся объектов
необходимо, чтобы временной сдвиг между соответст¬
вующими сигналами превышал время корреляции ти.
При прямоугольной форме сигнала и широкой полосе
приемника время корреляции практически равно дли¬
тельности импульса ти, и минимальное значение разре¬
шаемого расстояния равно протяженности импульса
Ти<72. Однако приемное и индикаторное устрой¬
ства снижают разрешающую способность.
Рис. 5.5. К определению разрешающей способности ио
дальности.
На рис. 5.5 представлено расположение РЛС и двух
точечных целей, соответствующее расположение отра¬
женных сигналов и увеличенное изображение сигналь¬
ных выбросов на линии развертки индикатора типа А.
Минимальное расстояние на экране, при котором выбро¬
сы можно разделить, равно
Д^мин ~ ^рТи 4"
где t’p — скорость развертки.
Переходя к единицам дальности, получим
д^:Ин=т==:¥+^-’ (5Л4>
где М = —масштаб индикатора.
Часто задают не диаметр пятна, а разрешающую
способность трубки, измеряемую отиощениехМ рабочего
169
диаметра экрана трубки D-> к диаметру пятна d, т. е.
Для индикатора типа /1 длина линии развертки
— Рэ, следовательно:
ДО.. —,221е—|—22L-I—Д__
-- 2 Т Л11) 2 ~
Но L/Vy
а х[с1(2—-■ D[ , поэтому
т
ДД
где Dl — шкала дальности индикатора.
Чтобы индикатор не ухудшал существенно разре¬
шающей способности системы, необходимо выбирать
шкалу дальности из условия
Приведенная упрощенная трактовка разрешающей
способности по дальности показывает, что предельное
значение разрешаемого расстояния определяется дли¬
тельностью импульса и, следовательно, повышение раз¬
решающей способности импульсной системы при про¬
стом сигнале может быть достигнуто лишь уменьшением
длительности сигнальных импульсов.
В гл. 3 показано, что применение частотной или фа¬
зовой модуляции несущей частоты сигнальных импуль¬
сов с соответствующей обработкой при приеме позволяет
радикально повысить разрешающую способность по
дальности без уменьшения длительности излучаемого
импульса, а следовательно, и энергии сигнала, что весь¬
ма важно для обеспечения большой дальности действия.
Минимальная дальность действия. Минимальной даль¬
ностью действия, или мертвой зоной импульсной систе¬
мы, называется минимальное расстояние, па котором
сигнальный импульс может быть отделен от излучаемо¬
го, и его временное положение измерено с заданной
точностью. Очевидно, минимальное время распростране¬
ния, при котором сигнальный импульс будет наблюдать¬
ся на экране раздельно от излучаемого, должно удов¬
летворять условию /рмтш>Тц.
На время излучения мощного зондирующего или за¬
просного импульса приемный тракт дальномера запи¬
рается, и его чувствительность после окончания излуче-
170
пия импульса восстанавливается не сразу. Если время
восстановления чувствительности приемного тракта со¬
ставляет тв, то
Отсюда минимальная дальность действия импульсно¬
го дальномера будет
Дм„н^(ти+Д)с. (5.15)
Максимальная дальность однозначного отсчета. Боль¬
шинство импульсных дальномерных систем излучает
импульсы периодически с частотой повторения 7ЛП. Если
энергия излучаемого сигнала достаточна для создания
ответного или отраженного сигнала с энергией, превы¬
шающей пороговую на расстоянии 7)макс, то при наличии
объекта такой сигнальный импульс будет принят в сле¬
дующем периоде повторения. При этом отсчет дально¬
сти будет неоднозначным. Конечно, могут быть
использованы различные методы для исключения неод¬
нозначности, однако все они в той или иной степени
усложняют систему, поэтому, если это допустимо усло¬
виями работы, целесообразно выбрать ее параметры
так, чтобы удовлетворялось условие однозначного отсче¬
та дальности
п с7 п £
Ь'макс “2“ 2ЛП *
Непрерывное определение координат объекта, или, как
принято говорить в радиолокации, сопровождение цели
оператором на экране индикатора, не может обеспечить
высокой точности измерения координат и их производ¬
ных, особенно при сопровождении объектов, имеющих
высокие скорости и ускорения. Это относится как к со¬
провождению по угловым координатам, так и по даль¬
ности.
Использование полуавтоматического сопровождения
по дальности несколько облегчает работу оператора, но
не решает задачи получения высокой точности. В связи
с этим в настоящее время широко применяются авто-
дальномеры, позволяющие автоматически сопровождать
объект, а часто осуществлять также его автоматический
поиск и ввод системы в режим автосопровождеиия.
171
§ 5.3. АВТОМАТИЧЕСКОЕ СОПРОВОЖДЕНИЕ
ПО ДАЛЬНОСТИ В НЕПРЕРЫВНОМ РЕЖИМЕ
Подробное изучение систем автосопровождения
является предметом специального курса, поэтому здесь
рассматриваются лишь основные принципы построения
систем автоматического измерения дальности, взаимо¬
действие элементов системы и некоторые требования
к ним с точки зрения точности и надежности автомати¬
ческого сопровождения.
Принцип автоматического измерения дальности сво¬
дится к изменению времени задержки селекторных
импульсов с помощью управляющего напряжения, про¬
порционального временному рассогласованию положе-
Рис. 5.6. Блок-схем.'! автоматического радиодальномера.
ний сигнального и селекторного импульсов. Напряжение
рассогласован!!я вырабатывается временным дискрими¬
натором и обычно называется сигналом ошибки, так -как
пропорционально временному рассогласованию (ошиб¬
ке) в совмещении сигнального и селекторных импуль¬
сов.
Па рис. 5.6 изображена блок-схема автоматического
радиодальномера, в котором используется дискримина¬
тор с двумя селекторными импульсами, и временная
диаграмма, поясняющая его работу. Пусковые импуль¬
сы от синхронизатора одновременно с запуском моду¬
лятора передатчика подаются на схему управления
задержки. На выходе схемы задержки формируются
два селекторных импульса, задержка которых tDc опре¬
деляется управляющим напряжением, пропорциона л ь-
172
ным сигналу ошибки. На дискриминатор подаегсй сиг¬
нальный импульс от приемника и селекторные импульсы
со схемы задержки. Если линия раздела раннего и позд¬
него селекторных импульсов смещена относительно сере¬
дины сигнала, на выходе дискриминатора появится
напряжение сигнала ошибки, величина и полярность
которого определяются временным рассогласованием
Д/е. Эго напряжение после усиления и преобразования
схемой управления воздействует па схему задержки та¬
ким образом, чтобы свести рассогласование к нулю.
Следовательно, время задержки селекторных импульсов
автоматически поддерживается равным tJh а соответст¬
вующая этому времени дальность D может быть отсчи¬
тана по шкале или непосредственно введена в вычисли¬
тельное устройство в виде пропорционального угла пово¬
рота вала, напряжения или числа импульсов. В послед¬
нем случае целесообразно использовать цифровую схему
задержки.
Итак, временной дискриминатор позволяет выявить
отклонение сигнального импульса относительно селек¬
торных, вырабатывая сигнал ошибки в виде тока i (или
напряжения), пропорционального временному рассогла¬
сованию:
г- = /г1А/в = /г. /Пс).
Коэффицпенг пропорциональности /г1? связывающий
входную величину Л/е с выходной /, называется коэф¬
фициентом передачи временного дискриминатора.
Коэффициент передачи схемы управления /г2 выби¬
рается таким, чтобы получить управляющее напряже¬
ние //, необходимое для воздействия на временной моду¬
лятор. В качестве временного модулятора используется
одношкальная пли двушкальпая схемы задержки. Вели¬
чина задержки селекторных импульсов изменяется под
действием управляющего напряжения таким образом,
чтобы свести к пулю временное рассогласование Д/е.
Функция передачи u = схемы управления зависит от
заданной точности воспроизведения уравнения измене¬
ния дальности сопровождаемого объекта во времени.
Если объект неподвижен, то уравнение дальности будет
£>(/) = Dq = const.
173
Условие отсутствия ошибки при сопровождении —
= D(t)—Dc(t)=DQ—Dc(t), т. е. Dc(t)=D0, где Dc(t)—
дальность, соответствующая задержке селекторных
импульсов.
Звено, обеспечивающее постоянную выходную вели¬
чину lD0 при входной ев = 0, является интегрирующим.
Действительно, подбирая коэффициент усиления систе¬
мы /(, всегда можно выполнить условие
Do = J S/)dt = /< J О Л = КС.
Таким образом, требование отсутствия статической
ошибки (ошибки в установившемся состоянии) по поло¬
жению выполняется при наличии в схеме управления
одного интегратора, т. е. при использовании схемы
с астатизмом первого порядка. Схема с одним интегра¬
тором запоминает значение дальности в момент пропа¬
дания сигнала или, как говорят, обладает памятью по
положению. Действительно, при пропадании сигнала ток t
на выходе дискриминатора будет равен 0, что равно¬
сильно ер = 0, а в этом случае система останавливается
в положении, соответствующем дальности объекта в мо¬
мент пропадания сигнала.
Если объект удаляется с постоянной скоростью Vo,
то уравнение дальности имеет вид
D(t)=DQ + Vot. (5.16)
Сопровождение без ошибки в этом случае возможно
при наличии в схеме управления двух интеграторов,
которые при соответствующем выборе коэффициентов
передачи &И1 и /г112 обеспечивают при любом t выполне¬
ние условия
Dc (/) = /ги1 J idtY + ^112 J J idtxdt2 = D(t\
что равносильно
sd=Z)(/)-Dc (0 = 0.
Система с астатизмом второго порядка обладает
памятью по скорости, запоминая значение скорости
объекта в момент пропадания сигнала.
Для точного воспроизведения системой изменения
дальности при наличии ускорения схема управления,
очевидно, должна иметь три интегратора.
174
(5.17)
В общем случае уравнение движения объекта может
содержать производные более высоких порядков и мо¬
жет быть записано в виде бесконечного степенного ряда
А (^) = Ао AJ -|- А212 Аь _ Е
Осуществляя преобразование Лапласа, получим изобра¬
жение входной функции
QO
А (Р) -- f д (0 e-r ‘di = A-h . +
О
I (/г—1)!Л/<_1
’ р*
Но i/р есть оператор интегрирования. Таким обра¬
зом, непосредственно из преобразованного уравнения
движения видно, что для его точного воспроизведения
системой, она должна содержать число интегрирующих
звеньев, на единицу превышающее число производных
измеряемой координаты. Если число интеграторов мень¬
ше необходимого, то появляется ошибка сопровождения,
которую можно найти, зная функцию передачи системы
и уравнение изменения координаты сопровождаемого
объекта.
Так, для объекта, удаляющегося с постоянным уско¬
рением а, уравнение изменения дальности во времени
можно записать
D(t) =Do-\-Vot
а его изображение
где Dq и Vo — начальные значения дальности и скорости.
В этом случае система будет сопровождать объект
без ошибки при наличии трех интегрирующих звеньев.
Однако на практике в радиодальномерах очень редко
используют больше двух интегрирующих звеньев, по¬
скольку введение каждого интегрирующего звена услож¬
няет систему и затрудняет обеспечение ее устойчивой
работы.
175
При na/Hiuiiii двух интеграторов ошибка сопровож¬
дения объекта, движущегося равноускоренно, имеет по¬
стоя !1нос значение, пропорциональное ускорению объек¬
та. При одном интеграторе ошибка системы растет про¬
порционально Vq [-at, и если сигнал пропадает па
длительное время, то ошибка может превысить ширину
зоны захватывания дискриминатора, и после появления
сигнала сопровождение объекта не восстанавливается.
То же самое происходит, если ширина селекторных
импульсов не согласована с дискретностью поступления
информации о движении объекта.
Итак, выбор функции управления -системы
определяется уравнением движения объекта .и дспусти-
м ы м значение м ди 11 а м и ч е с к о й о ш-i i б к и со пр о в о ж де и ня.
Заметим, что управляющий сигнал не обязательно яв¬
ляется напряжением, а может быть, например, углом по¬
ворота вала.
Системы автоматического измерения дальности могут
обеспечить высокую точность измерения дальности, если
их параметры выбраны не только в соответствии с урав¬
нением движения сопровождаемого объекта, но и с уче¬
том воздействия помех. Точность системы принято оце¬
нивать среднеквадратичной ошибкой сопровождения,
которая слагается из динамической составляющей ошиб¬
ки Д/д, вызванной движением объекта, и флюктуацион¬
ной составляющей А/(ь, вызванной воздействием помех.
Таким образом, средний квадрат ошибки равен
Др^_Д?4_д7Д (5.18)
До енх пор рассматривался установившийся режим
автоматического сопровождения, при котором сигнал на¬
ходится в пределах рабочей золы временного дискрими¬
натора. Очевидно, режиму автоматического сопровожде¬
ния должен предшествовать режим поиска и ввода систе¬
мы в сопровождение, иногда называемый <в радиолока¬
ции «захватом».
При визуальном поиске по экрану индикатора опера¬
тор вручную совмещает сигнальный и селекторные им¬
пульсы и включает систему автоматического сопрожде-
ння. Таким образом, осуществляется так называемый
ручной ввод системы в режим сопрожденпя.
176
При автоматическом поиске задержка селекторных
импульсов периодически изменяется от /рСм1Ш до /рсмакс,
перекрывая заданный диапазон дальности от /)мШ1 до
£)Л1а1;с. Скорость перемещения селекторных импульсов по
должна быть очень высокой, так как .при этом затруд¬
няется надежный ввод системы в режим сопровождения.
В связи с этим период изменения задержки значительно
превышает период повторения импульсов.
Для обеспечения непрерывного перекрытия заданного
диапазона поиска нужно выполнить условие
/ /
1 ) Опа а - Л с макс i) с мин
I п тс. и
где Тс и -- длительность селекторного импульса.
Р ас с мо гр е и и ы й вариант а в то п о ис к а и а з ы в а е т с я по¬
следовательным, а система автопоиска — одноканальной.
Ее недостатком является значительное время поиска,
увеличивающееся пропорционально диапазону поиска и
разрешающей способности по дальности.
Используется также параллельный поиск, при кото¬
ром применяется много к ан а льна я система, причем каж¬
дый канал осуществляет поиск сигнала на небольшом
участке дальности; при этом в-ремя поиска уменьшается
пропорционально числу каналов, но сложность оборудо¬
вания возрастает, поэтому для реализации таких систем
выгодно использовать цифровые методы и схемы.
В настоящем параграфе рассматривались системы
автоматического измерения дальности, инерционность
которых значительно превышает период поступления ин¬
формации о движении сопровождаемого объекта, что по-
з в о л я ет р а сс м а три в а т ь и м п ул ьс и ы й а вто д а л ьн о м е р к а к
непрерывную следящую систему. Это условие обычно
выполняется, если антенна автодальномера в процессе
сопровождения поддерживается направленной на источ¬
ник сигнала и, следовательно, информация о движении
объекта поступает с частотой повторения сигнальных
импульсов. Для решения некоторых задач необходимо
обеспечить автоматическое определение (съем) коорди¬
нат, сохраняя обзор заданного сектора пространства.
В этом случае дискретность поступления информации
о движении объекта определяется периодичностью обзо¬
ра и обычно значительно превышает инерционность си¬
стемы. Большая дискретность поступления информации
12-1173 177
определяет 'специфику выбора параметров и построения
с I гсте м а в т осъ е м а, ко то рая кратко р а с с м а гр 11 в а е т с я
в следующем параграфе применительно к автоматиче¬
скому .измерению дальности.
§ 5.4. АВТОМАТИЧЕСКОЕ СОПРОВОЖДЕНИЕ
ПО ДАЛЬНОСТИ В РЕЖИМЕ ОБЗОРА
В настоящее время широко применяется'автоматиче¬
ское определение (автосъем) координат объектов РЛС
кругового или секторного обзора сопряженное с си¬
стемой автос'ьема аналогового или цифрового типа.
Основным достоинством обзорных систем с автосъемом
является возможность автоматического сопровождения
одновременно многих, объектов при сохранении обзора
всего заданного сектора пространства.
Информация о (Положении объекта на систему авто¬
съема поступает в виде пачек видеоимпульсов с выхода
приемника станции, следующих с 'периодом обзора То,
равным периоду вращения пли качания диаграммы на¬
правленности антенны. Если угловая скорость отклонения
диаграммы направленности постоянна, временное поло¬
жение пачки импульсов относительно положения, приня¬
того за начальное, будет характеризовать азимут объекта.
Дальность определяется временной задержкой каждого
импульса пачки относительно соответствующего ему им¬
пульса запроса (или зондирующего). В результате об¬
работки пачек система автосъема позволяет определить
параметры движения объекта не только во время суще¬
ствования пачки, но и экстраполировать их на осталь¬
ную часть периода обзора.
Рассмотрим случай применения системы автосъема
аналогового типа, в которой экстраполяция по каждой
из координат осуществляется отдельными каналами
автосъема. При этом на выходе канала дальности непре¬
рывно выдается текущая дальность объекта, а на выходе
азимутального канала —азимут объекта. К приходу оче¬
редной пачки в каждом из каналов системы вырабаты¬
вается селекторный импульс, положение которого харак¬
теризует ожидаемое положение сигнала. Чем больше
возможные ошибки системы, тем больше должна быть
длительность селекторных импульсов для того, чтобы
приходящий сигнал оказался в пределах селекторного
178
импульса н сопровождение не было нарушено. В связи
с большой дискретностью поступления информации об
объекте и воздействием шумов ошибки таких систем до¬
статочно велики, и надежное сопровождение обеспечи¬
вается (особенно в системах кругового обзора с боль¬
шим периодом обзора) при длительности селекторных
импульсов, значите, тыю превышающей длительность
об
Рис. 5.7. Функциональная схема канала сопровождения по дально¬
сти и его временная диаграмма.
сигнальных. Вследствие этого разрешающая способность
обзорной РЛС в режиме автоматического сопровожде¬
ния практически определяется длительностью селектор¬
ных импульсов. От длительности селекторных импульсов
12* 179
зависит также и лальность действия системы, так как
с увеличением длительности селекторных импульсов воз¬
растает вероятность появления ложных шумовых выбро¬
сов, вызывающих срабатывание системы, и, следователь¬
но, увеличивается м и и и м а л ь ное отн о ш ей и е с и г и а л а
к шуму, необходимое для сопровождения объекта с за-
д а нно й н а д еж н о с т ь ю.
На рис. 5.7 изображена функциональная' схема кана¬
ла сопровождения по дальности и временная диаграм¬
ма, поясняющая его работу. На входе системы включен
каскад, селектирующий пачку сигнальных импульсов,
отраженных пли псреизлучеиных сопровождаемым объ¬
ектом, пока он находится -в пределах вращающейся диа¬
граммы направленности антенны. Селекторный импульс
выделения пачки поступает от азимутального канала и
характеризует азимут объекта.
Каждый из импульсов пачки далее селектируется по
дальности селекторным импульсом длительностью xD.
При большой дискретности поступления пачек времен¬
ное рассогласование между сигнальным и серединой се¬
лекторного импульсов может во много раз превышать
длительность сигнального импульса, поэтому временной
дискриминатор должен иметь широкую рабочую зону,
соответствующую длительности селекторного импульса.
Временной дискриминатор с широкой рабочей зоной
обычно содержит пороговое устройство, позволяющее
выделить сигнал на фойе шума. Далее выделенный сиг¬
нал формируется в импульс определенной амплитуды и
длительности, который подается на схему преобразова¬
ния временного рассогласования Д/е в напряжение
сигнала ошибки величина и знак которого соот¬
ветствует временному рассогласованию Д/е. Затем, как
и в обычной схеме автосопровождеипя, сигнал ошибки
подается па схему управления, которая управляет схе¬
мой задержки селекторных импульсов. При движении
объекта задержка селекторного импульса соответствен¬
но изменяется, и он следит за перемещением сигнально¬
го импульса во времени. Таким об разом, временное по¬
ложение середины селекторного импульса дальности бу¬
дет характеризовать дальность сопровождаемого объекта.
В зависимости от порядка астатизма системы и траек¬
тории движения (маневра) объекта предсказываемое си-
180
стемой к моменту приема очередной пачки положение
объекта отличается от действительного на величину
ошибки сопровождения. Так, если -сопровождение ведет¬
ся в горизонтальной плоскости (по дальности и азиму¬
ту) и объект выполняет круговой разворот (рис. 5.8), то
для системы с астатизмом I порядка ошибка измеряется
отрезком ДО, для системы с астатизмом II порядка —
отрезком BD и для системы с астатизмом III порядка. —
отрезком CD.
При воздействии помех или собственных шумов, при¬
емника при приеме слабых сигналов па больших даль¬
ностях возникает дополнитель¬
ная ошибка из-за ложного сра¬
батывания системы сопровож¬
дения и подавления сигналь¬
ных импульсов помехой. Пер¬
вое — эквивалентно ошибочно¬
му предсказанию параметров
движения объекта, второе —
пропуску очередной пачки и
увеличению дискретности по¬
ступления информации об объ¬
екте. Ошибка сопровождения
является, таким образом, слу¬
чайной величиной и слагает¬
ся из ошибки дискретности,
Рис. 5.8. Ошибки при дви¬
жении объекта по круговой
траектории.
обусловленной маневром объекта и подавлением сигна¬
ла помехой, п ошибки, вызванной ложным срабатыва¬
нием системы. Наиболее специфичной и .-весомой особен¬
но для систем с большим периодом обзора является
ошибка дискретности. Приближенно можно оценить
ошибку, обусловленную дискретностью поступления ин¬
формации, математическим ожиданием ее абсолютного
значения
СО
z-I
(5.19)
где в/ — ошибка за счет маневра объекта к /-му обзору;
Р[ = Р(1—P)il— вероятность превышения сигна¬
лом на фоне шума порогового уровня (уровня
срабатывания дискриминатора системы) за /-й
обзор;
181
Р— вероятность превышения порогового уровня им¬
пульсами пачки за один обзор;
i — число обзоров между предыдущей и последую¬
щей успешной фиксацией пачки системой.
Наиболее часто для автосъема используются систе¬
мы с астатизмом I порядка, когда наиболее неблагопри¬
ятным является прямолинейное перемещение объекта
с максимальной скоростью. Если объект движется ради¬
ально со скоростью V, ошибку по дальности, вызванную
дискретностью, можно записать в виде
si=VToi,
где То — период обзора.
И з м е и eiii I е па р а м стр о в д в и ж е и и я с о п р о в о ж д а с ого
объекта, а также режим ввода системы в сопровожде¬
ние значительно усложняют задачу выбора параметров
системы. Эти вопросы рассматриваются в работах, по¬
священных импульсным следящим системам.
В случае одновременного сопровождения нескольких
объектов аналоговая система автосъема должна иметь
число каналов сопровождения по каждой координате,
равное числу сопровождаемых объектов. При большом-
числе объектов многоканальная система аналогового ти¬
па получается сложной, поэтому для сопровождения
одновременно большого числа объектов целесообразнее
применять системы автосъема цифрового типа. Приме¬
нение таких систем облегчает также их сопряжение с ци¬
фровыми вычислительными машииа.ми, которые все бо¬
лее широко используются для обработки информации,
доставляемой радиотехническими системами и в част¬
ности текущих координат объекта на выходе системы
автосъема.
§ 5.5. ЦИФРОВОЙ МЕТОД АВТОМАТИЧЕСКОГО
ИЗМЕРЕНИЯ ДАЛЬНОСТИ
П pi 111 ци и д е й стви я щ1ф р о в о го (ди скр ети о го) а в то -
дальномера сводится к преобразованию временного ин¬
тервала, пропорционального дальности, в число. Про-
■стейшая схема измерения временного интервала состоит
из генератора измерительных (счетных) импульсов, сле¬
дующих с весьма стабильным периодом Т. Генератор
запускается в момент излучения импульса запроса и
182
останавливается в момент прихода ответного сигнала.
Число импульсов 'серии, регистрируемое счетчиком, и
является мерой дальности. Точность 'измерения времени
определяется величиной дискрета Т.
Эта схема позволяет за .период повторения запрос¬
ных (зондирующих) импульсов дальномерной системы
измерять дальность только одного объекта, так как в мо¬
мент прихода сигнального импульса поступление счет-
Яускобой
В блок памяти вычислительной машини
1 Ш I 1 1 1 L! I 1 I 1 I 1 I U L1J1-LU
__1 L- J
7 Я 3 5 S 7 S 9 10 11 1213 1'^15 1617131920
i 1 1 1 1 1 1 1 1 1 i 1 1 Ml 1 1 1 1 1
t
i
l~ >
I t
н———>
1 1 1 p г
t
. J ~пт
Д
11 "
t
1 i
L .
t
Рис. 5.9. Блок-схема преобразователя дальности в цифровой код и
временная диаграмма, поясняющая его работу.
ных импульсов на пчетчик прекращается. Опрокидыва¬
ние триггера схемы и прекращение счета может быть
вызвано также импульсом помехи, поступившим перед
приходом сигнального импульса.
Для исключения этих недостатков применяются более
сложные схемы преобразования дальности в цифровой
код. Одна из возможных схем вместе с поясняющей ее
183
работу временной диаграммой изображена на рис. 5.9.
В этой гхсмс-счет импульсов происходит все время, пока
от генератора строба на вентиль совпадений ВС подаст¬
ся положительный импульс строба. Начало строба опре¬
деляется моментом излучения импульса системой, а его
длительность определяет время работы счетчика, а так¬
же время, в течение которого открыт приемник системы.
Счет прекращается, и счетчик (регистр дальности) воз¬
вращается в исходное состояние .импульсом сброса, по-
л у ч е 1 ги ы м Д: 11 ф ф ер ей ц; i ро в а 1 и i е м за Д11 е го фр о 11 т а ст р о б -
импульса. После этого [регистр дальности готов к новому
циклу счета в следующем периоде повторения. Таким об¬
разом, в каждый момент рабочего цикла счета импуль¬
сов состояние триггеров регистра дальности соответст¬
вует времени, прошедшему от момента излучения им¬
пульса системой, а следовательно, в любой момент с ре¬
гистра дальности может быть считано число в двоичном
коде, характеризующее текущую дальность объекта.
Такое считывание происходит в момент поступления
сигнального импульса с выхода преселектора, который
•производит предварительную очистку сигнала на выходе
приемника от помех. Сигнальный импульс от преселек¬
тора подается на генератор импульсов считывания, со¬
гласующий момент считывания с тактом работы реги¬
стра дальности, исключая поступление импульсов счи¬
тывания во время переходных процессов в триггерах
регистра дальности. Поскольку начало переходного про¬
цесса определяется счетными импульсами, работа гене¬
ратора импульсов считывания синхронизируется именно
счетными импульсами. Вентили считывания открываются
импульсами считывания, и число, соответствующее даль¬
ности объекта, выдается в двоичном коде в блок памяти,
цифровой вычислительной машины. При этом процесс
счета импульсов не прекращается, и с приходом сиг¬
нального импульса другого объекта в цифровую вычис¬
лительную машину может быть введено число, характе¬
ризующее и его дальность. Таким образом, такая схема
позволяет измерять дальность многих объектов. Для рас¬
пределения данных об отдельных объекта?; по соответ¬
ствующим ячейкам памяти машины предусмотрена схе¬
ма распределителя-сдвигателя. С каждым последующим
импульсом считывания распрсделптель-сдвигатель под¬
ключает соответствующую ячейку памяти машины,
Если через преселектор пройдет импульс помехи, То
он может быть опознан и отброшен в процессе вторич¬
ной обработки данных в цифровой вычислительной ма¬
шине. Вторичная обработка заключается в сопоставле¬
нии данных, поступающих в данный цикл, с данными,
полученными за предыдущие циклы работы 'Системы. На
основании предыдущих циклов машина вычисляет пред¬
полагаемую координату (в рассматриваемом случае —
дальность) к последующему циклу, т. с. производит экс¬
траполяцию координат. С приходом сигнального импуль¬
са с регистра дальности считывается дальность, которая
сопоставляется с вычисленной машиной ожидаемой или
упрежденной даль нос т ь ю. При это м уст а и а в ли в а е тс я,
принадлежит ли считанная дальность уже сопровождае¬
мому объекту, для которого вычислена дальность, или
нет. Этот процесс носит 'Название идентификации целей.
Число разрядов регистра дальности определяется за¬
данным диапазоном и точностью измерения дальности.
Ес ли, например, м а кс и м а л ь пая и з м е р я с м а я да л ь 11 ос т ь
£>?п=100 км, а дискретность измерения, определяемая
допустимой ошибкой, составляет ДО=Ю м, то число раз¬
рядов и из соотн ош сип я
2" S’ -ЙН-'О'
должно быть выбрано равным /г= 14. Для упрощения па
рис. 5.9 представлено в регистре всего пять разрядов.
Каждый счетный импульс опрокидывает триггер то
в .прямом, то в обратном направлении. При этом число
импульсов на выходе будет вдвое меньше числа импуль¬
сов на входе. Таким образом, единица каждого триггера
имеет цену своего разряда: первого 2°= 1, второго 21 = 2,
третьего 22 = 4 и т. д.
К моменту /7) после начала счета, который показан на
временной диаграмме пунктиром, состояние триггеров
регистра соответствует числу 01111(15). Если в этот мо¬
мент на вентили считывания поступит импульс, то на
выходе вентилей, находящихся под высоким потенциа¬
лом (соответствующим 1), появятся импульсы и в па¬
мять цифровой машины будет введено число 01111, ха¬
рактеризующее дальность соответствующего объекта.
Реальные схемы имеют значительно большее число
разрядов и каналов. Однако использование транзисто-
185
ров, НОЛупроВОДИИГОВЫХ ДИОДОВ II фсррИЮВЫХ КО.Щц
(в качестве вентилей совпадений) позволяет выполнить
схему измерения дальности .малогабаритной и надежной,
поэтому цифровые методы и схемы получают все более
широкое применение в радиотехнических системах.
§ 5.6. ИМПУЛЬСНЫЕ РАЗНОСТНО-ДАЛЬНОМЕРНЫЕ
РАДИО 11А В И Г АЦИО Н Н Ы Е С ИСТЕМЫ
Принцип определения местоположения объекта раз¬
ностно-дальномерной системой изложен в гл. 1 и заклю¬
чается в измерении разности времени прихода сигналов
от двух станций к антенне ирпемоиидпкатора, располо¬
женного на борту объекта.
Каждому временному сдвигу соответствует своя ли¬
ния положения. Поскольку приемоиндикатор измеряет
непосредственно временное смещение импульсных сиг¬
налов, то оцифровка линий положения производится
в единицах времени (микросекундах) без перевода в раз¬
ность расстояний.
Если станции /1 и В излучают .импульсные сигналы,
одновременно, то пулевому сдвигу т = 0 соответствует
нулевая линия положения (рис. 1.6), являющаяся пря¬
мой, пересекающей базу .в середине под прямым углом.
При расположении приемоиндикатора слева от нулевой
линии импульсы от станции А будут приходить раньше
импульсов В и задержка т считается положительной.
При перемещении приемоиндикатора правее нулевой ли¬
нии знак задержки меняется. Задержка т достигает ма¬
ксимального значения TMai;c = tiB при расположении при¬
емоиндикатора на линии, являющейся продолжением ба¬
зы. Диапазон изменения задержки, следовательно, будет
±tAB. Зиакоперемеиность задержки (вносит неоднознач¬
ность при определении местоположения.
Для устранения неоднозначности импульсы станции В
задерживаются на интервал времени т3^/дв- При этом
измеряемый временной сдвиг т будет всегда положи¬
тельным. Синхронизация работы системы осуществляет¬
ся от 'ведущей станции А. Всдо-мая станция В излучает
импульс после приема сигнала ведущей станции через
некоторое фиксированное время /0 + ^. Таким образом,
общее время задержки т3 сигнала В относительно сиг¬
нала станции А составляет t3 = Cib + ^o+Av Задержка /0,
186
называемая постоянной, вводится для опознавания им¬
пульсов станций. Задержка Д называется кодовой и
вводится для изменения оцифровки линий положения по
определенной программе с целью затруднения возмож¬
ности использования системы противником.
С учетом фиксированных задержек измеряемый при-
емоиндикатором временной сдвиг равен Ti=T-h/o--l-/H,
.причем x=(DB—D^lc изменяется в пределах oi 0 до
Тмакс ='2/дд.
Система, состоящая из одной пары станций, позво¬
ляет определить лишь одну линию положения и может
быть использована для движения по определенным на¬
правлениям. Для определения местоположения объекта
необходима еще одна пара станций, расположенных так,
чтобы сетки линий положения обеих пар станций пере¬
секались. Две пары станций и Л2В2 могут работать
независимо или синхронно. В первом случае каждая па¬
ра станций может иметь свою несущую частоту и часто¬
ту повторения импульсов. При независимой работе пар
станций ориентировка баз может быть относительно про¬
извольной. Базы могут быть разнесенными, пересекаю¬
щимися или совмещенными. Для получения одинаковой
точности длины баз выбираются примерно одинаковыми.
При независимой работе оператор определяет линии по¬
ложения последовательно для каждой пары станций. Это
требует значительного времени.
При синхронизированной работе станции и А2объ¬
единяются в одну ведущую станцию Л, управляющую
работой двух ведомых станций и В2, а часто также и
третьей ведомой станцией В3. Все станции работают на
одной несущей частоте.
Рассмотрим наиболее распространенный случай ра¬
боты системы, когда станция А синхронизирует работу
двух станций В{ и В2. Ведомая станция Bj синхронизи¬
руется нечетными импульсами станции /1, а станция В2—
четными. Таким образом, частота повторения импульсов
ведущей станции вдвое выше частоты повторения ведо¬
мых. Для опознавания четные импульсы излучаются
двойными.
На рис. 5.10 изображена временная диаграмма одно¬
го цикла работы системы и юответствующее изображе¬
ние на экране ЭЛТ. Ведущая станция излучает импульс
Ль который через время 1Ав\ принимается ведомой стан-
187
цией п через время 1А\ приемоинднкатором С. Спустя
время задержки /01 'Станция В{ также излучает импульс,
-принимаемый приемоиндикатором с временной задерж¬
кой tB\. Временной сдвиг импульсов /ц и ВА измеряемый
и p i I е м о I гн ди к а тор о м, р а в ев
Т1 “ дв\ ^01 4“ В\ Л\ ВЛ C11) “Н L ЛВ\ 4“ ^01'
В течение второго полупериода ведущей станции лри-
смоиидикатор принимает импульсы /12 и В2 и измеряет
временной интервал
Т2 = Сй2 + Д _ С12 = + 1АВ2 + Д-
Задержки ZOi и t02 обычно одинаковы: /01 = to2 — /о~Нк.
Рис. 5.10. Временная диаграмма одного цикла работы системы.
Задержка /о при синхронизированной работе вводит¬
ся для того, чтобы при /к = 0 импульсы /С и Bi (или А2
и В2) нигде не приходили к приемоипдикатору одновре¬
менно. При этом исключается необходимость в сравни¬
тельно сложных измерениях малых временных интер¬
валов.
Измерение временных интервалов в неавтоматических
индикаторах производится с помощью ЭЛТ, развертка
188
которой состоит из двух .строк. На нижней строке вос¬
производятся импульсы /12, а импульсы /11—точно над
ними па верхней строке. Импульсы ведомых станций В{
и В2 воспроизводя тс я соответственно па верхней и ниж¬
ней развертках со сдвигом вправо относительно импуль¬
сов /11 и Л2 на временные интервалы Ti и т2, измерение
которых позволяет найти соответствующие линии поло¬
жения и определить местоположение объекта.
Точность определения местоположения объекта. Вы¬
сокие требования к точности отсчета (порядка 0,5 мксек)
при большой длительности импульсов (40 мксек и боль¬
ше) и форме, близкой к колоколообразной, практически
могут быть удовлетворены при визуальном отсчете толь¬
ко при совмещении переходных фронтов сигнальных им¬
пульсов Л и В. При этом амплитуды импульсов предва¬
рительно уравниваются для обеспечения возможности
точного совмещения передних фронтов импульсов. Отсчет
производится отдельно для каждого из трех масштабов
развертки с помощью меток, следующих соответственно
через 10, 50 и 500 мксек.
Полученный отсчет позволяет зафиксировать линию
положения из семейства одной пары станций. Затем все
операции повторяются для второй пары станций. Опозна¬
вание нужных пар импульсов производится по частотам
повторения, которые несколько отличаются.
Отсчет временного интервала по .масштабным меткам
последовательно для трех шкал требует значительного
времени, что вносит ошибки, особенно существенные при
больших скоростях объектов, на борту которых установ¬
лен приемоппдикатор. Этот недостаток устранен в нрие-
моиндикаторах с прямым отсчетом, в которых отсчет
производится в момент совмещения сигнальных импуль¬
сов непосредственно по шкале устройства задержки ве¬
домо го селе кто рч го го и м п ул ьс а, н а з ы в а е м о го пьедеста¬
лом. Необходимая точность обеспечивается применением
трехшкальной схемы задержки с фазовращателями и
автоматического совмещения сигнальных импульсов, что
исключает субъективные ошибки оператора.
В приемоиндикаторах может быть осуществлена как
полная, так и частичная автоматизация процессов опре¬
деления местоположения. В первом случае индикаторы
называются автоматическими и обеспечивают автомати¬
ческий поиск сигналов станций, ввод в режим слежения
189
\ Сигнальный
V" импульс
Пьедестал
Рис. 5.11. Определение временного
положения сигнального импульса
по переднему фронту.
пульса ведомой станции так,
за сигналами выбранной пары и непрерывное слежение
с выдачей временного интервала в навигационное вычис¬
лительное устройство.
Полуавтоматические индикаторы осуществляют авто¬
матическое слежение за сигналами после того, как опе¬
ратор произвел настройку приемника и тачальную син¬
хронизацию индикатора, т. е. осуществил ввод в режим
слежения. Последующие
операции производятся
автоматически.
Различают два режи¬
ма слежения. При слеже¬
нии за импульсом веду¬
щей станции автоматиче¬
ской регулировкой фазы
задающего генератора ин¬
дикатора обеспечивается
сохранение определенного
положения сигнального
импульса А на ведущем
пьедестале. При слежении
за импульсом ведомой
станции с л ед я i ц а я .с и сте -
ма перемещает пьедестал
В в соответствии с изме¬
нениями положения им-
чтобы импульс В занимал
на пьедестале положение, совпадающее с импульсом А.
Одновременно в схеме производится автоматическая
б а л а и с и р о в к а а м 11 л и гуд 11 р и и и м а е м ы х си гн а л о в стан¬
ций А и В.
Для автоматического управления положением пьеде¬
сталов 'используется сигнал ошибки, вырабатываемый
врем е н н ы м ди с к р им и и а т о р о м при р а с со гл a-со в а и i ти в о
времени сигнального импульса и специального селектор¬
ного импульса, временное положение которого относи¬
тельно пьедестала постоянно (время т0 на рис. 5.11).
В связи с тем, что па основной сигнальный импульс
часто накладываются импульсы, пришедшие после одно¬
кратного или многократного отражения ионосферой
с соответствующей временной задержкой, форма сигна¬
ла искажается, а его амплитуда флюктуирует. Свобод¬
ной от ионосферных искажений остается только часть
190
191
Переднего фронта в пределах примерно 30 мксек от его
начала. В связи с этим для ■слежения используется имею
но эта часть.
Максимальная точность определения временного по¬
ложения импульса обеспечивается, если слежение про¬
изводится за точкой максимальной крутизны переднего
фронта, которой соответствует вершина импульса, по¬
лученного однократным дшфферсшщровацием сигналь¬
ного импульса (рис, 5.11,6), пли точка .перехода через
* /А ~
1
Г t
2
и
и t
Тш
t
-1500 мксек
2
ч
—I
к
I
t
I
o'3—1 КПП мхпрх
t
I
——Ч
I
Ж 1Г
Л
ЧЯ-
— <?= ДО
t
t
t
А к/
в к/
t ’
Рис. 5.13. Временная диаграмма приемоиидикатора.
5
5
ь
7
8
9
нуль огибающей, сформированной двукратным диффе¬
ренцированием сигнального импульса (рис. 5.11,в). По¬
следний случай 'наиболее часто применяется практиче¬
ски. Огибающая дважды продифференцированного им¬
пульса имеет форму дискриминаторной характеристики
и может быть непосредственно -использована для .выде¬
ления сигнала ошибки, пропорционального временному
р а осотл асо в a 11 и ю.
На рис. 5.12 представлена упрощенная блок-схема по¬
луавтоматического приемоиидикатора, а на рис. 5.13 —
временная диаграмма, поясняющая его работу. Синхро¬
низация всех цепей индикатора производится задающим
генератором с кварцевой стабилизацией. Частота коле-
192
банпй кварцевого генератора /=100 кгц понижается де¬
лителем частоты до частоты повторения импульсов ве¬
дущей станции Fa = 50 гц. Импульсы после делителя ча¬
стоты предварительно задерживаются схемой общей за¬
держки на время т3о = 5ОО мксек, что исключает влияние
переходных процессов в делителе на последующие цепи.
Импульс на выходе схемы общей задержки запускает
генератор пьедестала А и триггер, являющийся генера¬
тором прямоугольного напряжения с периодом Тв^=
= 40 000 мксек, равным периоду повторения ведомых
■станций. Прямоугольное напряжение используется для
поо ч ер е д 11 ого з а и ус к а с х с м тот го й з а де р ж кч i капа л о в
слежения за сигналами ведомых станций и В2. Для
точной задержки селекторных импульсов слежения за
с и гн а л о м в е до мой ст а и ц и и п р-и м е н я етс я т р е х ш к а л ь н а я
схема с двумя фазовращателями и фантастроном ,в каче¬
стве схемы грубой задержки. На фазовращатели пода-1
юте я синусоидальные напряжения с частотами 1 кгц и
5 кгц, которые выделяются после соответствующих кас¬
кадов делителя частоты. Оба фазовращателя (грубый и
точный) через редукторы связаны между собой и с по¬
тенциометром фантастрона и могут вращаться как вруч¬
ную, так и двигателем в режиме автоматического поиска
и сопровождения сигнала.
Импульс с выхода схемы точной задержки запускает
задержанный мультивибратор, являющийся генератором
пьедестала В длительностью 1 500 мксек. Генератор пье¬
дестала А запускается одновременно с запуском генера¬
тора прямоугольных импульсов.
Генератор селекторных импульсов запускается с за¬
держкой То = 500 мксек относительно передних фронтов
импульсов пьедесталов и вырабатывает селекторные им¬
пульсы длительностью 20 мксек, которые подаются на
дискриминаторы каналов А и В. Общий генератор селек¬
торных импульсов применяется для того, чтобы избе¬
жать ошибок из-за относительных временных сдвигов
ф Oip мм р у е м ы х импульсов, и ей з б е ж 11 ы х пр и пр и м ei i е и и и
отдельных генераторов. Для разделения селекторных им¬
пульсов А, В{ и В2 применяются каскады совпадения
в каждом канале, которые открываются и пропускают
на дискриминаторы селекторный импульс только при его
совпадении с соответствующим пьедесталом. На дискри¬
минаторы поступают также сигнальные импульсы, полу-
13-1173 193
чинные в результате двукратного дифференцирования
видеосигналов на выходе приемника.
При совпадении середины 'Селекторного импульса
с точкой перехода продифференцированного ‘сигнала че¬
рез нулевой уровень напряжение рассогласования равно
нулю. При .наличии временного рассогласования на на¬
копительном конденсаторе дискриминатора появится на¬
пряжение сигнала ошибки, величина и знак которого
определяются величиной и знаком временного рассогла¬
сования.
Сигнал ошибки канала А используется для автома¬
тической подстройки частоты задающего генератора при-
смоиидикатора, чем обеспечивается непрерывная син¬
хронизация приемоиндикатора импульсами ведущей
станции. Автоматическая подстройка осуществляется ре¬
активной лампой и подстроечным конденсатором, управ¬
ляемым двигателем. Применение реактивной лампы
обеспечивает ‘малую инерционность, а электромеханиче¬
ская схема автолодстройки исключает остаточное вре¬
менное рассогласование сигнального и селекторного .им¬
пульсов, соответствующее напряжению на реактивной
лампе в момент компенсации расстройки задающего ге¬
нератора. При совместной работе подстроечный конден¬
сатор компенсирует эквивалентную емкость реактивной
лампы и сводит временное рассогласование импульсов
к нулю.
Слежение за сигналом ведомой станции осуществля¬
ется несколько иначе. Сигнал ошибки с -времениого дис¬
криминатора канала В после усиления магнитным уси¬
лителем подается на двигатель, управляющий положе¬
нием фазовращателей и потенциометра схемы точной за¬
держки. Двигатель вращается до тех пор, пока селек¬
торный импульс не совместится точно с сигнальным, и
сигнал ошибки становится равным пулю. Точный фазо¬
вращатель связан со счетчиком, показывающим в ми¬
кросекундах величину задержки т между импульсами
ведущей и ведомой станций.
Приемоипдикатор содержит, кроме того, систему
автоматического выравнивания амплитуд сигналов,
электроннолучевую трубку ,и цепи сигнализации, позво¬
ляющие производить контроль работы каналов автома¬
тического сопровождения.
194
Для повышения точности и пороговой помехоустойчи¬
вое т 11 при с. м 01111 д 11 к а то р а .пред ус м о т репа во з м о ж.ы о с т ь
автоматического слежения за сигнальными импульсами
по высокочастотной наполняющей. При этом каналы сле¬
жения за огибающей служат для iii-сключе'ння многознач¬
ности, возникающеьт при слежении за фазой колебаний.
Для слежения за фазой предусмотрен специальный блок
фазового отсчета, который содержит фазовый дискрими¬
натор с вспомогательными цепями. Сигнал ошибки фа¬
зового дискриминатора подается на магнитные усилите¬
ли соответствующих каналов и попользуется для управ¬
ления двигателями так же, как л в рассмотренном слу¬
чае слежения по огибающей.
Электромеханические следящие системы имеют боль¬
шую инерционность, не позволяющую получить высокой
точности .при больших скоростях и ускорениях объектов.
Кроме того, приемоипдикатор с электромеханической си¬
стемой не может быть выполнен легким и малогабарит¬
ным, а главное, надежным.
От этих недостатков в значительной степени свобод¬
ны цифровые системы автоматического измерения вре¬
менных интервалов, поэтому в последнее время уделяет¬
ся большое внимание разработке автоматических прие-
моиндикаторов, построенных на основе цифровой техни¬
ки. Данные от приемоиндикатора получаются в виде ци¬
фрового кода, который без каких-либо промежуточных
преобразователей может быть введен в навигационное
вычислительное устройство объекта. Эти преимущества
дают основания полагать, что в ближайшие годы цифро¬
вые приемоиндикаторы станут основным типом приемо-
индикаторов импульсных и импульсно-фазовых разност¬
ью -д а л ьы о м ер ы ы х систе м.
§ 5.7. ФАЗОВЫЙ МЕТОД ДАЛЬНОМЕТРИИ
Фазовый метод в основном применяется в радионави¬
гации для точных измерений дальности. В таких случаях
всегда используется ответчик, который в радионавига¬
ции принято называть отражающей станцией. В ответчи¬
ке обычно предусматривается преобразование принимае¬
мого запросного сигнала, позволяющее легко селектиро¬
вать ответный сигнал в радиодальномере и сравнить его
фазу с фазой опорных колебаний.
13®
19S
Из формулы (1.5)
jj _ S (?р —Уд —УЛо»)
2со м
следует, что ошибка в измерении дальности AD может
быть следствием ошибки в знании масштабной частоты
Дюэм «и ошибок в измерении фазовых сдвигов Дф*.
Точность измерения дальности повышается при уве¬
личении масштабной частоты. Однако при увеличении
частоты следует помнить о возможности появления не¬
однозначности отсчета, если фазовый сдвиг превысит
значение 2л. Для обеспечения однозначности измерения
должно быть выполнено неравенство
П < 2т
из которого следует условие
(520)
совпадающее с аналогичным условием в импульсном
методе.
Для совмещения требований точности и однозначно¬
сти приходится измерять фазовый сдвиг на двух или
даже на трех масштабных частотах, т. е. применять мно¬
го ш к а л ьн ы й метод измерения дал ы-юсти. Со о т и о ш ей и е
частот определяется возможными ошибками в отсчете
фазы и заданным диапазоном измерения дальности,
определяющим выбор самой низкой частоты из условия
однозначности измерения. В параграфе 1.6 упоминалась
возможность измерения разности фаз па несущей часто¬
те, на частоте модуляции и на частоте биений. Рассмот¬
рим эти разновидности фазового метода.
Измерение разности фаз на несущей частоте. В даль¬
номерах этого типа применяют два метода измерения
расстояний: метод изменения частоты и метод переме¬
щения дальномера.
Определение дальности методом меняющейся частоты
производится путем подсчета изменения разности фаз
при плавном изменении частоты излучаемых колебаний.
Этот метод позволяет производить абсолютное измере¬
ние дальности и поэтому получил название метода ра¬
диодальномера,
196
Измерение расстояния производится следующим об¬
разом. Задающая станция (запросчик) излучает коле¬
бания, частота которых может плавно изменяться между
двумя значениями, соответствующими длинам волн М и
%2. В схему станции входит прибор, называемый девио-
метром, с помощью которого можно произвести провер¬
ку фазового сдвига в цепях станции, а при необходимо¬
сти изменить установку начальной фазы. Предположим,
что па дальности '2D укладывается некоторое целое чи¬
сло длин волн, т. е. k{n = 2D. В .процессе изменения ча¬
стоты до высшего фиксированного значения ^ = с1м из¬
менение фазы пройдет некоторое число циклов z. При
достижении верхней граничной частоты f2 замеряется
значение остаточной фазы ср, и уравнение дальности при¬
нимает вид
9~) = 20-
Отсюда
АЛ
2 (Л. — Л2)
(5.21)
Таким образом, радиодальномер позволяет опреде¬
лить расстояние однозначно, если известны граничные
значения рабочих воли и л2 и измерены значения чи¬
сла полных циклов z и остаточной фазы ср. Процедура
измерения расстояния занимает значительное время, что
является существенным недостатком метода.
В другой разновидности фазовой системы, называе¬
мой радиолагом (разработан под руководством Ман¬
дельштама, Папалекси и Щёголева), измерение дально¬
сти производится в процессе перемещения задающей
станции, расположенной на борту подвижного объекта.
С целью разделения прямого и ответного сигналов зада¬
ющая и отражающая станции работают па различны.х
частотах coi и со2, находящихся в целочисленном отноше¬
нии
со, т
со2
Если была произведена начальная привязка станции,
т. е. определено каким-либо способом начальное рассто¬
яние Dq от задающей до ответной станции, то радиолаг
197
позволит непрерывно измерять расстояние при движении
объекта: £) = О0 + ДО.
Действительно, если после исходной привязки и пер¬
вого отсчета базы (соответствующего дальности Dj)
с т ал I ц и 11 з ар с п i с т рч i р о в а т i о
л/
11 p:i i и ер е м е ще1 гни зада ю щс й
Генератор
масштабной
частоты Я
>.
Передатчик
О), + Я
Г Q
| 5?
Приемник
ДаРьис-мер ь'ц объекте
J
Приемник
ш } 3 5?
J V
я
L. .
Передатчик
ш2± Я
На ре мнан от дети ан
станции
Рис. 5.14. Блок-схема фазовой дальномерной системы с измерением
разности фаз па частого модуляции.
изменение разности фаз па z полных циклов и новому
расстоянию О2 соответствует .показаише фазометра ср2,
то
(г2г. + ?£)-'Р1-2^(С --
Отсюда
др = Р2_О1 = 2-^(г21С + <Р2-?1) = 4(г + ^)’
где Дер — ср2—ф1 — разность двух отсчетов фазометра.
Естественно, что, зная время между отсчетами А/,
можно определить радиальную скорость движения объ¬
екта относительно отражающей станции
1'-=т=я(г+5). <5-и>
Собственно, это и послужило поводом назвать систему
радиолагом но аналогии с лагом, используемым в море¬
ходной практике для измерения скорости корабля.
Измерение разности фаз на частоте модуляции. Раз¬
деление прямого и ответного сигналов может быть осу¬
ществлено разносом их несущих частот с измерением
19^
разности фаз на модулирующей частоте. Передающая
антенна дальномера (рис. 5.14) излучает сигнал на несу¬
щей частоте сщ, модулированной (низкой частотой Q, яв¬
ляющейся масштабной. Понятые приемником ответчика
колебания детектируются, и выделенные колебания ча¬
стоты Q модулируют несущую частоту (о2, на которой
происходит ответное излучение. При детектировании
принятых колебаний в приемнике дальномера колебания
частоты Q выделяются и подаются на фазометр, изме¬
ряющий фазовый сдвиг огибающей принятых колебаний
относительно опорного напряжения частоты. Q. Так как
фазовый сдвиг пропорционален дальности, то фазометр
может быть непосредственно проградуирован в едини¬
цах дальности.
Однозначность измерения 'расстояния обеспечивается
при выполнении условия
Омаке (5.23)
где с—скорость .распространения радиоволн;
F — частота модуляции.
Однако выполнение условия (5.23) при увеличении
дальности ведет к снижению точности се измерения при
той же точности измерения фазы. Это противоречие тре¬
бований может быть удовлетворено использованием дву¬
шкального метода отсчета.
Измерение разности фаз на частоте биений. Принцип
действия таких систем основан на измерении фазовых
сдвигов двух гстеродипиро'ваи.пых колебаний. При этом
используется известное свойство сохранения 'неизменным
фазового сдвига двух колебаний при трансформации их
частот путем гетеродинирования. Этот метод широко
■применяется в фазовых разпостпо-далыюмерных систе¬
мах и будет рассмотрен в следующем параграфе.
Система с хранением опорной фазы на борту. Все
рассмотренные фазовые системы имеют двусторонний об¬
мен информацией, т. е. на борту объекта обязательно
д о л жен быть и ер е д а т ч и к, что о гр a 1111 ч 11 в a e т д а л ь и о с т ь
действия систем и демаскирует движущийся объект.
Создание высокостабильных генераторов позволяет
осуществить длительное храпение опорной фазы на бор¬
ту объекта. В такой системе станции па объекте и на
земле имеют высокостабильиые генераторы, колебания
199
которых фазируются в исходный момент и затем началь¬
ная разность фаз ср0 сохраняется неизменной.
При движении объекта фаза принимаемых колебаний
сравнивается с фазой эталонного генератора. Их раз¬
ность равна ср=фо + «£)/с. Отсюда
Такое построение позволяет резко увеличить даль¬
ность действия системы и обеспечивает радиомаскировку
объекта. Особенно перспективны подобные системы для
самолетов, ракет и подводных лодок. Однако в случае
длительной работы требуется чрезвычайно высокая ста¬
бильность частоты эталонного генератора и дополни¬
тельных устройств, обеспечивающих хранение опорной
фазы. Так, в американской системе «Наваро», исполь¬
зующей принцип хранения фазы на борту, частота бор¬
тового генератора .поддерживается с точностью 10 9
в течение 8 час.
Достижения в создании молекулярных и квантовых .
генераторов позволяют в настоящее время получить еще
более высокую стабильность частоты. Следовательно,
системы с хранением опорной фазы на борту объекта
весьма перспективны, тем более что одна наземная стан¬
ция может обслуживать неограниченное число объектов,
находящихся в зоне ее действия.
§ 5.8. ФАЗОВЫЕ РАЗНОСТНО-ДАЛЬНОМЕРНЫЕ
СИСТЕМЫ
Высокая точность фазовых разностно-дальномерных
систем в сочетании с большой дальностью действия и
неограниченной пропускной способностью обеспечила им
широкое применение в радионавигации. Ниже кратко
рассматриваются некоторые вопросы точности.
Применение комбинационных частот позволяет полу¬
чить о дн о вр е м е нн о 11 ес ко л ь к о масштабов и з м е р ей и й,
обеспечивая совмещение требований высокой точности
и однозначности определения местоположения.
Рис. 5.15 поясняет построение системы с заданием
фазовой сетки на комбинационных частотах. Каждая из
наземных станций А и В излучает колебания на двух
фиксированных, частотах ((oM, (о2л) и (оив, со2В), причем
200
частоты 41 начальные фазы колебаний поддерживаются
в следующих соотношениях:
“1.4 — “1й = “2/>- — 0,2.i = (5-24)
Сигналы обеих станций достигают антенны прнсмоиндп-
катора с фазовыми сдвигами,. определяемыми пройден¬
ными расстояниями
7 I D.
4’1.4^ “l.l Z + ai.l “И|.1Д’ 4>2.1 -=<->20+ а21 — «2.4—>
, | . DB
—“1B Z + «1B — «IB <?■>„ =«>27! Z + a2B ~ “2B~'
Рис. 5.15. Фазовая разностно-дальномерная система с заданием фа¬
зовой сетки на комбинационных частотах.
В результате попарного смешения колебаний частот ома,
o)ib и со2а, <т>2в на выходах первого и второго каналов
приемоинд.икатора выделяются колебания разностной
частоты Q с фазами
Ф1 = ~ + “>1в'
^2 — ?2В ^2.1 — °2/3 Н°2.1 “7“’
201
Разность фаз этих колебаний, измеряемая фазомет¬
ром прнемоиндикатора, равна
, . . wih+C02h п + п
Ф=Ф1 - ф3 = -с Ов -— рл=
“|.1 + ®2.1 zn n . ®с ,n n ,
с
где юс— суммарная частота, равная тю условию
“с = «|Д <о„л-=ыи, 4- о>2Д .
Таким образом, разность фаз измеряется в системе
на низкой разностной частоте Q, а сетка линий положе¬
ния задается на высокой суммарной частоте о)с:
Если каждая из станций будет излучать колебания
еще на одной фиксированной частоте (о3д и со3в соответ¬
ственно, причем
то при выделении разностной частоты Й в
каторе получаются колебания с фазами
Фх = — (,Тл "7" Н~<01 в ~Y~ ’ Фз —■ ~ °3д ■
присмонпдп- •
Разность фаз этих низкочастотных колебаний, изме¬
ряемая фазометром, равна
. . . ■(«!/; -<^зв)
Фх = Фх — ф2 = -
(Db-Da) =
с
с
где сор = со1В — co3s = о>1Л — созд — разностйая частота.
Следовательно, в этом случае сетка линий положения
задается на разностной частоте
ДГ> = £)„ —£>. = —■ ф.
ь А top
Таким образом, используя различное согласование
излучаемых колебаний, можно изменять масштаб сетки
линий положения, не меняя частоты, на которой измеря¬
ется (разность фаз. Для4 получения двух масштабов не¬
обходимы три пары частот, три сетки получаются при
202
четырех парах. Фиксированные частоты стабилизируют¬
ся кварцами; кроме того, для точного согласования ко¬
лебаний станций Л и В по частоте и фазе применяется
специальный контрольный приемник.
Ф а з о в ы с р а зл1 о с ri i о - да л ы i о м epi 1 ы е с 11 с те м ы м о гу т
быть использованы не только для определения местопо¬
ложения подвижных объектов приемоиндикаторамп на
борту, по и для определения пх местоположения с зем¬
ли и, следовательно, для управления движением объек¬
тов. Такая задача может быть решена применением бор¬
тового передатчика и наземных приемных пунктов, свя¬
занных между собой линией связи. Сравнение фаз коле¬
баний, принимаемых в трех наземных пунктах, позволяет
определить местоположение объекта.
Подобная система может быть использована при кон¬
троле траектории при запуске искусственных спутников
Земли и космических ракет.
§ 5.9. ЧАСТОТНЫЙ МЕТОД ДАЛЫЮМЕТРИН
Основные характеристики частотных дальномеров.
Принцип действия частотного дальномера рассматривал¬
ся в гл. 1. Там была получена формула (1.7)
41Г
связывающая дальность объекта D с частотой биений
F/>, девиацией частоты W и частотой модуляции Гм.
Рассмотрим основные характеристики частотных
дальномеров. Прежде всего остановимся на факторах,
определяющих точность измерения расстояния до един¬
ственного неподвижного или медленно движущегося объ¬
екта, когда допплеровское приращение частоты биений
Fv мало сравнительно с FD.
В этом случае точность в основном определяется чув¬
ствительностью и постоянной ошибкой системы.
Под чувствительностью системы по дальности kD по¬
нимают приращение частоты биений FD на единицу из¬
менения расстояния до объекта:
, FD 4Г г ,
— Фм-
Постоянная ошибка частотного дальномера является
следствием периодичности изменения частоты и опреде-
203
ляется параметрами модуляции. Рассмотрим этот вопрос
подробнее. При измерении дальности определяется число
периодов биений FD за период модуляции Тм:
т. е. измеряемая частотомером частота биений может
иметь дискретные значения, кратные частоте -модуляции
FD = nFM.
Расчетное значение частоты биений
совпадает с измеряемым FD = nFM только для дальностей
D
с
кратных величине называемой постоянной ошиб¬
кой системы.
Иногда величину c/W называют модуляционной дли¬
ной волны и обозначают k]V. Тогда постоянная ошибка
системы может быть записана в виде
Этот же результат можно получить и несколько иначе.
Обычно в частотных системах измерения дальности одно¬
го объекта в качестве частотомера используется счетчик
импульсов, который фиксирует число биений за период
модуляции
Дискретность отсчета AD, соответствующая изменению
числа биений п» па единицу, может быть найдена из со¬
отношения
Отсюда
■4“’
(5.25)
Этот вывод наглядно иллюстрирует рис. 5.16, на кото¬
ром изображена форма напряжений биений Иб = [(1) для
204
одного расстояния, соответствующего /7г> = 3, п трех зна¬
чений фазового сдвига принимаемых колебаний относи¬
тельно излучаемых в момент приема сигнала. Из рисун¬
ка ясно, что только при определенной относительной фа¬
зе .измеренная дальность будет равна истинной.
Процесс образования огибающей биений при различ¬
ных фазовых сдвигах принимаемых колебаний и2 отно¬
сительно излучаемых удобно пояснить с помощью век¬
7
Рис. 5.16. Временная диаграмма, поясняющая возникновение по¬
стоянной ошибки частотного дальномера.
пСЧ - nD
JT
2
торных диаграмм. На рис. 5.17 изображен процесс обра¬
зования биений при интерференции двух колебаний с ча¬
стотами соц и о)с и амплитудами (7ШИ и Umc.
ЕСЛИ ТО COS?.
Для построения полной картины результирующих ко¬
лебаний необходимо фиксировать результирующую ам¬
плитуду двух вращающихся векторов со скоростями соц
и о)с. Но на частотомер подается огибающая биений, для
205
построения которой вектор Umn принимается неподвиж¬
ным, а вектор — вращающимся относительно конца
(7ти с разностной частотой биений сои—<ос-
Пр ос л ед и м п ос л е до в а т е л ьн о форм и р о в ан не о ги б а ю -
щей биений при Ло = 3, фазовом сдвиге -ср — —л/2
(рис. 5.18). В момент 1\ — равенства частот принимае¬
мых и излучаемых колебаний— вектор :l/mc имеет отно¬
сительную фазу ф=<р«и—фс = —л/2. Так как после 1\ ча¬
стота принимаемого сигнала превышает частоту излу¬
чаемого, то вектор t/wc вращается против часовой стрел¬
ки, совершая за время Тм/2 число оборотов, равное
/гг>Тм/2 = 3/2. В момент /2 частоты снова становятся рав¬
ными и вектор останавливается в положении + л/2
и затем 'начинает вращаться :в противоположном •направ¬
лении, так как частота принимаемых колебаний стано¬
вится меньше частоты излучаемых. Во второй полуперп-
од частоты модуляции вектор UpWr также совершит 3/2
оборота и к концу периода (момент времени /3) займет
исходное положение. График наглядно показывает, что
при относительной фазе <р=—л/2 счетчик зафиксирует
Псч = 4, хотя истинная дальность соответствует пп = 3. Ана¬
логично можно построить трафики напряжения биений
и для других значений относительной фазы.
Относительная фаза принимаемых колебаний резко
изменяется при очень небольших изменениях расстояния,
например, за счет флюктуаций центра отражения объек¬
та. Так, при работе частотного дальномера в трехсапти-
метровом диапазоне изменение расстояния па 0,37 см,
соответствующее 7/8, вызывает изменение относительной
206
фазы на л/2, что приводит к изменению .показаний даль¬
номера 'на достаточно большую величину, равную посто¬
янной ошибке системы
При измерении малых дальностей, соизмеримых с AZ),
простейший частотный дальномер имеет очень большие
Рис. 5.18. Формирование огибающей биений.
относительные ошибки. Так, при девиации частоты W=
= 1 Мгц постоянная ошибка имеет величину ДО = 75 м.
Одним из очевидных путей уменьшения постоянной
ошибки является увеличение девиации частоты. Однако
в силу ряда причин возможности увеличения девиации
частоты ограничены, поэтому в случае .необходимости
устранения или радикального уменьшения постоянной
ошибки применяют усложненные системы, например,
с двойной частотной модуляцией.
При определении дальности движущегося объекта ча¬
стота биений в счетчике усредняется, и его .показания
207
будут меняться плавно, достаточно точно отражая теку¬
щее значение дальности.
Однако движение объекта вызывает также осложне¬
ния, связанные с допплеровским пли скоростным смеще¬
нием частоты Fv.
а)
Рис. 5.19. Временная диаграмма частотного дальномера
при a) Fd>Fv и б) Fd<Fv.
208
Рассмотрим два возможных случая работы системы.
В первом случае FD>/7v, т. е. дальностное прираще¬
ние частоты превышает скоростное (рис. 5.19,а) и резуль¬
тирующая частота биений равна
4W
сТ м
1U7
Т
°F
V
с
где V — радиальная составляющая относительной ско¬
рости.
Если не у ч иты в ать относ и тел ьно кр атков р е.м е н.п ы е
провалы частоты биений, то среднее значение измеряе¬
мой системой частоты будет
Д’ _ ^б.»л ^бп д’
1 б С' ~~ Q С и ,
Измерение среднего значения частоты биений за каждый
иолупериод модуляции Fqb и Еон позволяет определить
раздельно дальность D, пропорциональную
/7 Fб в + Fбн
1 I) 9 ’
и скорость V, пропорциональную
Г? FС) D ^бц
“ 2 *
Для измерения необходимы два счетчика, фиксирующих
дальность и скорость объекта.
При превышении так называемой критической скоро¬
сти Viq), соответствующей условию У7 vi,-p = Z7/.,, картина
меняется (рис. 5.19,6), и, следовательно, справедливы
равенства
р у FaB — Fch f р
2 V F ’ 2 1 d
Возможность раздельного измерения дальности и скоро¬
сти при симметричной частотной модуляции наглядно
иллюстрируется диаграммой неопределенности. В этом
случае диаграмма неопределенности представляет собой
два эллипса (рис. 5.20), оси которых пересекаются в на¬
чале координат. Углы наклона у и —у определяются де¬
виацией частоты и периодом модуляции и соответствуют
полупериодам возрастания и уменьшения частоты излу¬
чаемых дальномером колебаний. Диаграмма неопреде¬
ленности ясно указывает на возможность получения при
14—1173 209
симметричной модуляции не только достаточно точного
измерения дальности и скорости одного объекта, по и
разрешения двух или нескольких объектов но дальности
лсшюсти сигнала с симметричной
ч а с т о т 11 о й модуляцией.
и скорости, что будет об¬
суждаться при рассмо¬
трении обзорных РЛС
с ч а стог 11 о й м одул я ц11 с ii.
Для обеспечения одно¬
значности измерения
дальности и скорости объ¬
екта во всем заданном
диапазоне дальностей и
скоростей необходимо вы¬
брать соответствующие
значения f0 и W. В даль-
11 о мс р а х стр с м я тс я обе -
спечить высокую чувстви¬
тельность по дальности и
поэтому обычно выбирают
параметры с и с т е м ы так,
чтобы выполнить условие
F D>] и 11 >F Умакс-
Поскольку
то 'необходимо обеспечить
2U7
7\f0
(5.2G)
Отсюда следует, что при заданной средней частоте излу¬
чения для получения однозначного измерения дальности
и скорости приходится увеличивать девиацию частоты W
и частоту модуляции FM, чтобы вывести критическую
скорость за пределы измеряемого диапазона.
Если необходимо обеспечить высокую чувствитель¬
ность системы но скорости
‘Д
то для получения однозначного отсчета параметры выби¬
рают так, чтобы выполнить условие FDM3il{C<FVKp во всем
заданном диапазоне измерений.
210
Постоянная ошибка дискретности не единственная
причина, ограничивающая точность измерения дально¬
сти частотным дальномером. Из формулы (1.7) для опре¬
деления дальности следует, что ошибка в измерении ча¬
стоты биений Д/д), а также отклонения величин девиации
частоты ДЛГ и частоты модуляции AiFM от их номиналь¬
ных значений вызывают соответствующие ошибки в из¬
мерении дальности:
ДО _ Г ДО ш гдгм
D — FD t D ~ w ’ D Гы '
Точность частотного дальномера зависит также от
ошибок отсчета, которые определяются типом отсчетно¬
го устройства и используемым масштабом измерения,
как и для любой измерительной системы.
До сих пор рассматривался случай применения сим¬
метричной пилообразной модуляции частоты. Возникает
вопрос, каково влияние нелинейности модуляции на ра¬
боту частотного дальномера, возможно ли применение
нелинейной модуляции, и в частности синусоидальной?
Исследования показывают, что при измерении даль¬
ности и скорости одного объекта основные соотношения,
полученные для линейной модуляции, справедливы при
всех периодических законах изменения частоты, при ко¬
14*
Рис. 5.21. К вычислению средней частоты биений при
синусоидальной модуляции.
211
торых кривые изменения частоты /и и /с имеют не более
одного пересечения «на каждый полупериод модуляции.
Проверим справедливость этого утверждения на приме¬
ре синусоидального закона модуляции, который получил
широкое распространение в частотных дальномерах бла¬
годаря простоте технической реализации.
Форма кривых изменения частоты излучаемых /и и
принимаемых fc колебаний, а также частоты биений
изображена на рис. 5.21. Аналитически изменение часто-
т ы и з л у ч а е м ы х и и р ш i и м а е м ы х колебаний запишем
в виде
fc (0 = Г+-у- sin 2zF„ (t — tD),
отсюда частота биений равна
/?б (0 — /и — f С — -у- [sin 2тгЛ\7 — sin 2r.FM (I — / J] =
= IF cos 2jtFV1
sin 2nFu
c
Найдем среднюю частоту биений за период модуля¬
ции Тм
D/C + TJ4 ,
ГбсП=А ( F6(f)dt =
D/c
D/c + 7\./l
= f IF cos 2^м sin -£-<//==
D/c
4W
sin 2^1
-Г—
с [2лЛм
sin 2kFM (t — D/c
D/c-\-TJ4
D/c
Отсюда
sin 2nFM
4W
2rc
При выполнении условия tD=2Djc <
4U7
сТ м
D
4W Fn •
(5.27)
212
Таким образом, при выполнении условия форму¬
лы для дальности при линейной и 'синусоидальной моду¬
ляции совпадают, если подставляется средняя частота
биений Focp- Поскольку реально частотомер дальномера
и измеряет среднюю частоту биений, то, следовательно,
все основные выводы и соотношения, полученные для
линейной модуляции частоты, справедливы и для сину¬
соидальной модуляции при определении дальности оди¬
ночного объекта.
Следует заметить, что частотная модуляция обычно
сопровождается паразитной амплитудной модуляцией,
которая приводит к искажению огибающей биений. При
искажении огибающей в спектре биений появляются па¬
разитные составляющие, которые могут вызвать допол¬
нительные ошибки и даже вообще нарушить работу
дальномера особенно на 'больших расстояниях, когда
отраженный сигнал весьма мал. Для уменьшения пара¬
зитной амплитудной модуляции стремятся обеспечить
равномерную частогпую характеристику высокочастотно¬
го тракта в заданной полосе. Решение этой задачи об¬
легчается при уменьшении отношения W/'o-
В некоторых случаях (в частности, при измерении
дальности многих объектов), когда требуется высокая
линейность изменения частоты в широких пределах, при¬
ходится применять сложные схемы 1передатчнков.
В более совершенных системах с ЧМ и допплеров¬
ских применяют отдельный следящий гетеродин и основ¬
ное усиление сигнала осуществляют на промежуточной
частоте. В этом случае спектр полезного сигнала пере¬
носится в область более высоких частот и .низкочастот¬
ные помехи могут быть легко отфильтрованы. Частота
гетеродина должна быть жестко связана с частотой пе¬
редатчика. Это обеспечивается применением автоподст¬
ройки или гетеродинирования боковой составляющей.
Автоматическое сопровождение одиночного объекта
по дальности и скорости. В системах с частотной моду¬
ляцией автоматическое сопровождение по дальности и
скорости сводится к автоматическому удержанию часто¬
ты биений в полосе пропускания узкополосного фильтра.
Автоматическое сопровождение позволяет сделать систе¬
му узкополосной и тем снизить влияние шумов по срав¬
нению с неперестраиваемым усилителем с полосой про¬
пускания, охватывающей весь диапазон возможных ча-
213
■стот биений, тогда как в каждый момент времени сигнал
занимает лишь очень небольшую часть полосы.
Одна из распространенных схем автоматического со¬
провожден ия по дальности применяется при сравнитель¬
но медленном изменении расстояния, например, в высо¬
томерах, когда выполняется условие FD>FV. В обычную
схему частотного дальномера .вводится блок управле¬
ния, изменяющий частоту модуляции или девиацию ча¬
стоты так, чтобы частота биений поддерживалась по¬
стоянной и равной частоте .настройки усилителя биений
Ffjo при изменении дальности D в заданном диапазоне:
F6 = d = = const. (5.28)
При этом напряжение, пропорциональное дальности, сни¬
мается с блока управления.
Находят применение и другие варианты схем автосо-
провождеиия. В одном из них осуществляется автоподст¬
ройка гетеродина, т. е. система регулирования охваты¬
вает лишь приемную часть системы. Эта схема имеет не¬
которые преимущества особенно применительно к доппле¬
ровским измерителям путевой скорости и угла сноса, по¬
строение которых рассматривается несколько позже.
Измерение дальности многих объектов. При наличии
в зоне облучения антенны нескольких объектов, находя¬
щихся .на различных дальностях и движущихся с раз¬
личными скоростями, на вход приемника одновременно
поступает целый спектр частот, составляющие которого
будут определяться дальностями и скоростями объектов.
Для обнаружения и определения параметров движения
объектов необходимо произвести обзор по дальности,
т. е. проанализировать спектр частот принимаемого сиг¬
нала. Для анализа могут быть использованы анализато¬
ры спектра как параллельного, так и последовательного
типа.
Анализатор с параллельным или одновременным ана¬
лизом имеет набор фильтров, частоты настройки которых
установлены с шагом порядка полосы пропускания
фильтра Л/7, а число фильтров п выбирается в соответ¬
ствии с заданным диапазоном анализируемых частот би¬
ений F‘(\ = F(j мане Fб мин*
В случае неподвижных пли сравнительно медленно
движущихся объектов скоростной составляющей частоты
214
биений Fv можно пренебречь и считать, что спектр содер¬
жит только далыгостныс составляющие. Тогда диапазон
анализируемых частот Fd = FDMdi{C—/Ткшпопределяется за¬
данным диапазоном обзора по дальности £>мш1н-£)макс, и
число фильтров может быть определено (при псперскры-
вающихся полосах фильтров) ио формуле
^Millie ^МПЛ
где ДРмип — заданное значение разрешаемого расстоя¬
ния.
При большой максимальной дальности «и высокой раз¬
решаю щ е й спо со 6'1 юс т и п а р а л л е л ь ■ н ы й а н а л и затор дол¬
жен иметь очень большое число фильтров. Поэтому, не¬
смотря на его большое достоинство, заключающееся
в быстроте анализа, он находит ограниченное 'примене¬
ние в частотных дальномерах.
Широко применяются в обзорных системах с частот¬
ной модуляцией различные варианты последовательных
анализаторов. Известны последовательные анализаторы
с и ер ест р a 11 в а е м ы м и не и ер ест раиваемым фи л ьтр а м и.
Практическое применение в частотных дальномерах на¬
ходят последние. В этом случае фильтр настроен на фи-
Рис. 5.22. Временная диаграмма обзорной системы с изменением де¬
виации частоты.
215
ксированиую частоту, а заданный диапазон частот бие¬
ний последовательно просматривается па экране ЭЛТ
за счет изменения частоты гетеродина, частоты модуля¬
ции Fyl или девиации частоты W.
Последние два метода основаны на использовании
условия
WFM = const.
С помощью схемы управления девиация частоты или ча¬
стота модуляции периодически меняются в диапазоне,
обеспечивающем последовательный анализ спектра всего
заданного диапазона дальностей. Индикация осущсств-
Рпс. 5.23. Временная диаграмма обзорной системы е изменением пс-^
риода модуляции.
ляется на экране ЭЛТ. Рис. 5.22 поясняет принцип дей¬
ствия обзорной системы с частотной модуляцией при из¬
менении девиации частоты. В полосу пропускания филь¬
тра Д^ф попадает только сигнал объекта, расположенно¬
го на дальности, для ‘которой при определенном значе¬
нии W выполняется условие FI} = F^. Диалогичная, кар¬
тина (рис. 5.23) будет при периодическом изменении пе¬
риода модуляции 7\г, поскольку при этом меняется ско¬
рость изменения частоты излучаемых колебаний.
Прежде чем перейти к рассмотрению основных пара¬
метров частотных систем с обзором по дальности, необ¬
ходимо сделать некоторые замечания о спектре частот
принимаемого сигнала.
216
Если время наблюдения 7П значительно превышает
период модуляции частотный спектр биений имеет
дискретный характер, частоты составляющих спект-ра
кратны частоте модуляции Ем, а их амплитуды изменя¬
ются по закону огибающей спектра одиночного пакета
колебаний длительностью 7Д/2 при симметричной пило¬
образной модуляции (рис. 5.24,а) и Тм при пилообраз¬
ной модуляции с мгновенным обратным ходом
(рис. 5.24,6).
Рис. 5.24. Спектр биений при симметричной модуляции (а) и моду¬
ляции с мгновенным обратным ходом (б).
Для заданной частоты модуляции частота повторе¬
ния .пакетов Еп при симметричной модуляции вдвое вы¬
ше, и соответственно вдвое шире спектр сигнала. Одна¬
ко по отношению к частоте отсчетов дальности, равной
частоте повторения пакетов, ширина основного лепестка
огибающей спектра в обоих случаях равна 2Fn. Интер¬
вал между соседними линиями спектра равен Еп, после¬
довательно, погрешность определения FD, вызванная ди¬
скретностью спектра, имеет величину порядка половины
интервала (АЕв~Ёи/2).
Таким образом, для повышения точности и разре¬
шающей способности системы нужно стремиться снизить
дискретность уменьшением Frr. При увеличении дально¬
сти D зоны обращения (провалы FD) расширяются, а зо-
217
цы постоянной частоты биений соответственно сокраща¬
ются, что приводит к дополнительному расширению оги¬
бающей спектра и снижению точности и .разрешающей
способности системы. Отсюда становится очевидной не¬
пригодность нелинейной модуляции частоты в системах
с обзором по дальности, так -как при этом частота бие¬
ний Fd меняется при неизменной дальности объекта, что
исключает возможность ее однозначного отсчета. Тре¬
бования, предъявляемые к линейности модуляции, до¬
статочно высоки. Так, если диапазон анализа равен Fn =
= Лэмакс—^рмпн, а число дискретных значений частот
FDi которое необходимо разрешать, равно N, то для
однозначности отсчета каждая из частот должна фикси¬
роваться с ошибкой, не превышающей ±Fa/2N, т. е.
относительная ошибка не должна превышать величины
Fa/2NFD. Например, при N=100 и FJ2FD = 0,5 нелиней¬
ность модуляции не должна превышать 0,5%* что явля¬
ется весьма жестким требованием.
Для частотных систем измерения дальности многих
о б ъ с кто в большое значение пр ио б р о т а е т р а зр с ш а ю i ц а я
способность по дальности.
Разрешающая способность по частоте определяется
динамической полосой фильтра анализатора 6Fn и в ко¬
нечном счете ограничивается дискретностью спектра
6FD = 2FU. Таким образом, так же как и постоянная
ошибка системы, предельное значение разрешающей спо¬
собности по дальности определяется параметрами моду¬
ляции
до — —
Для симметричной пилообразной модуляции F,n=2FM, и,
следовательно,
ДП
Мин
С 4/?м с г
4Г W
(5.29)
т. с. разрешающая способность ограничена выбранным
значением девиации частоты системы. Этот вывод может
быть сделан и непосредственно из рассмотрения диа¬
граммы 'неопределенности для ЧМ сигнала.
Анализатор спектра и индикатор могут существенно
снизить разрешающую способность. Так, разрешающая
способность по дальности снижается при чрезмерном
расширении полосы фильтра. С другой стороны, суже-
218
ние полосы фильтра приводит к увеличению числа филь¬
тров параллельного анализатора и увеличению времени
анализа последовательного анализатора.
При параллельном анализе все составляющие спектра
воздействуют на фильтры одновременно, поэтому при
выборе оптимальной полосы пропускания каждого филь¬
тра время анализа 7\ = Ти= l/FIf, поскольку время уста¬
новления колебаний в фильтре не может превышать дли¬
тельности каждого пакета! анализируемых колебаний:
При последовательном анализе для просмотра каж¬
дой составляющей спектра необходимо время Тп. Пол¬
ное время обзора пропорционально числу разрешаемых
участков дальности N при условии, что полоса пропуска¬
ния фильтра и шаг настройки фильтров выбраны таки¬
ми же, как и .в параллельном анализаторе, равно
С поел - ц-1] тп. (5.30)
Следовательпо, при прочих равных условиях после¬
довательный метод анализа требует время обзора, в N
раз большее, чем параллельный. Для ускорения обзора
частотных систем с последовательным анализом в более
узком диапазоне дальностей, а также для повышения их
точности и разрешающей способности в этом узком диа¬
пазоне применяется стробирование по частоте, анало¬
гичное стробированию по времени в импульсных систе¬
мах.
Сокращение диапазона анализа до Fc позволяет
уменьшить время обзора до Tc = TaFc/F^ сохранив точ¬
ность и разрешающую способность неизменными, так как
скорость перестройки частоты анализатора и, следова¬
тельно, его динамическая полоса пропускания при этом
•не изменяются (рис. 5.25,а).
При желании повысить точность и разрешающую спо¬
собность системы также сокращают диапазон анализа
с до Fc, но время анализа сохраняют неизменным
(рис. 5.25,6), что приводит к уменьшению скорости пере¬
стройки анализатора в Fa/Fc раз и позволяет сократить
полосу пропускания фильтра анализатора и соответст¬
венно повысить точность и разрешающую способность
системы. Конечно, это возможно лишь до предела, опре-
5И9
деляемог'О дискретностью спектра сигнала. Заметим, что
стробированный участок в этом случае аналогичен точ¬
кой шкале индикатора при двушкальном методе измере¬
ния дальности в импульсных дальномерных системах.
а) Ы
Рис. 5.25. Стробирование ио частоте для уменьшения времени ана¬
лиза (а) и повышения точности и разрешающей способности систе¬
мы (б).
Как мы видели, периодичность частотной модуляции
приводит к появлению постоянной ошибки, снижающей
точность и ограничивающей минимальное значение из¬
меряемой дальности ЧМ системы. Одним из путей устра¬
нения этого недостатка является применение шумовой
модуляции сигнала по частоте в сочетании с корреля¬
ционным методом приема. Однако при шумовом законе
ЧМ однозначность 'измерения расстояния обеспечивается
лишь при весьма широком спектре излучаемого сигнала,
что обсуждалось при рассмотрении автокорреляционной
функции шумового сигнала.
Значительно лучшие результаты при ограниченной
полосе частот дает применение псевдослучайной моду¬
ляции, при которой частота излучаемого сигнала изме¬
няется в соответствии с кодом, обеспечивающим получе¬
ние автокорреляционной функции модуляции с большим
центральным пиком и низким уровнем боковых выбро¬
сов. В качестве такого кода может быть использован код
нулевой последовательности, который рассматривался
в гл. 3 применительно к ФМ.
§ 5.10. ДОППЛЕРОВСКИЕ СИСТЕМЫ ИЗМЕРЕНИЯ
СКОРОСТИ И УГЛА СНОСА САМОЛЕТА
В настоящее время все большее применение для уп¬
равления самолетами, вертолетами и беспилотными
220
объектами получают автономные средства 'навигации.
К -их числу относятся н допплеровские .измерители век¬
тора скорости. Наиболее распространено применение
допплеровских 'систем для измерения путевой скорости
Рис. 5.26. Навигационный треугольник.
и угла сноса самолета, поэтому целесообразно прежде
всего рассмотреть принцип действия и основные харак¬
теристики таких систем.
Рис. 5.27. К образованию допплеровского спектра при
наклонном облучении земной поверхности.
Измерение путевой скорости и угла сноса однолучс-
вой системой. Напомним, что путевой скоростью назы¬
вается горизонтальная проекция скорости объекта_отно-
сительно земной поверхности. Путевая скорость V свя-
221
зана с воздушной скоростью VB, скоростью ветра U н
вызываемым им углом сноса <р навигационным треуголь¬
ником (рис. 5.26). Допплеровская система позволяет не¬
посредственно определить путевую скорость по спектру
частот сигнала, отраженного земной поверхностью.
При горизонтальном полете самолета применяется
наклонное облучение земной поверхности (рис. 5.27),
чтобы обеспечить достаточно большую проекцию векто-
Р_
Рт,
0,5
Fкмйн ^vo Рvt Fимис Ру
Рис. 5.28. Огибающая спектра при
наклонном облучении.
ра скорости па направление облучения и в то же время
сохранить достаточно сильное отражение в направлении
на станцию. Для определения спектра частот сигнала
вырежем из облучаемой площади элементарную поло¬
ску, все точки которой расположены на направлениях,
составляющих угол рг с вектором скорости V. При на¬
клонном облучении эти полоски имеют форму параболы.
Все точки такой элементарной полоски создадут отра¬
женный сигнал с частотой fCi = fw+fvi- Имея в виду, что
каждой из N элементарных полосок соответствует дон-
плеровскии сдвиг частоты cosp^, можно для
всей облучаемой площади представить спектр отраженного
сигнала последовательностью частот
.V
(5.31)
/=1
Максимальную мощность Рт в этом случае имеет сиг¬
нал па средней частоте спектра FVq (рис. 5.28). Огибаю¬
щая спектра будет примерно симметрична относительно
222
частоты Fro, соответствующей направлению максималь¬
ного излучения антенны, а ширина спектра на уровне
половинной мощности равна
Д/70,5= ^cos — C0s^o + "1F^ =
4V . Q . аа
= -j- SHI р0 Sin -2",
где аа — ширина диаграммы ’'направленности па уровне
половинной мощности.
Рис. 5.29. Пояснение .принципа действия однолучевой
системы.
При достаточно узких диаграммах, которые исполь¬
зуются в реальных 'Системах, можно принять sina/2«
~a/2, и, следовательно,
^0,5= -у aa SHI ро.
Для измерения путевой скорости объекта необходимо
определить среднюю частоту допплеровского спектра
Fvo. Если вектор путевой скорости V горизонтален
(рис. 5.29) и составляет с осью диаграммы направлен¬
ности антенны угол у в горизонтальной и Ро в верти¬
кальной плоскостях, то
7^=-^ cos ft,-cosy.
223
При повороте диаграммы 'направленности в горизон¬
тальной .плоскости до совмещения «с направлением век¬
тора путевой скорости (у = 0) приращение частоты до¬
стигает максимального значения
yV„I = -x-cos₽e- (5-32)
При известных К и >р0 путевую скорость V можно оп¬
ределить непосредственно измерением FVm. Угол сноса р
равен углу, составленному осью самолета и осью антен¬
ны в момент ее совмещения с направлением вектора пу¬
тевой скорости.
Однолучевая система не находит практического при¬
менения, так как имеет низкую точность измерения. Для
выяснения влияния ошибки в определении максималь¬
ного значения частоты допплеровского смещения пред¬
положим, что в момент измерения частоты FVm диаграм¬
ма направленности фактически не совмещена с вектором
путевой скорости, т. с. у=т^0. При этом допплеровское
смещение отличается от максимального .па величину
Д/*у Fytn Fy ~ cos Ро ■ cos (30 * Y
9V
=^cosp0(l — cosy) =
=^cosp02sin2-K ^FVm
Отсюда определим ошибку измерения угла сноса ср,
вызванную неточностью определения максимальной ча¬
стоты допплеровского смещения:
/2Д/?1/
~Г- (5.33)
При относительной ошибке определения FVm, равной
1%, ошибка в измерении угла сноса составляет Аср=-
= 0,14 рад (~8°). Такие большие ошибки однолучевых
систем при определении угла сноса являются следствием
низкой чувствительности системы к изменению угла у
при его малых значениях. Ошибка в определении часто¬
ты вызывает также соответствующую ошибку измерения
путевой скорости, величина которой может быть иайде-
224
на непосредственно из выражения (5.32):
ду Му
Второй причиной ошибок однолучевых систем яв¬
ляется крен самолета. Предположим, что из-за крена
истинное значение угла р отличается от расчетного на
величину Др. Дифференцируя выражение (5.32) для
FV)n но параметру р, получим
dFVm 2V .
~аГ=—
При конечных приращениях запишем
= —?Ksinp.Ap. (5.34)
Следовательно,
FVm
Др = др-tg p.
sin ₽
COS 0
В реальных системах угол облучения р выбирается по¬
рядка 70°. В этом случае относительная ошибка опреде¬
ления путевой скорости составляет 4,7% на каждый гра¬
дус погрешности Др в значении истинного угла облуче¬
ния р.
Уменьшение ошибки, вызываемой креном, дости¬
гается стабилизацией антенны в горизонтальной плоско¬
сти или введением поправок на крен (стабилизация дан¬
ных) в вычислительном устройстве. Это приводит к су¬
щественным усложнениям системы, но не устраняет ор¬
ганических недостатков однолучевого метода, к кото¬
рым следует также отнести высокие требования к ста¬
бильности частоты излучаемых колебаний.
Наиболее радикальным путем повышения точности
измерения угла сноса и путевой скорости является при¬
менение многолучевых систем, т. е. систем с излучением
в двух, трех или четырех направлениях.
Измерение путевой скорости и угла сноса многолуче¬
выми системами. На рис. 5.30 представлено расположе¬
ние лучей односторонней двухлучевой системы. При
измерении путевой скорости и угла сноса антенная си¬
стема поворачивается до совмещения спектров сигналов
на выходе каналов приемника, соответствующих двум
15 — 1173 225
лучам антенны. При этом ось симметрии лучей (ось ан¬
тенной системы) будет совмещена с вектором скорости,
а угол, составленный осью самолета и осью антенной
системы, равен углу сноса. Непосредственно из рисунка
ясно, что точность двухлучевой системы выше, чем одио-
лучевой, так как при повороте антенны лучи пересекают
параболы равных частот под углом, близким к прямому,
Рис. 5.30. Расположение лучей односторонней дву.хлу-
чевой системы.
что обеспечивает большую чувствительность системы,
т. е. большее изменение величины допплеровского сме¬
щения частоты при повороте антенны.
Если обозначить угол между осями диаграмм и Л2
в горизонтальной плоскости 20, то допплеровское сме¬
щение частоты соответствующих каналов равно
cos р-cos у,
FV2 = -у cos р • cos (20 — у).
226
Разностная частота будет
FvP = Fv\ — Fv-> = V cos i> • lcos I - - cos (2e — Y)1 =
— cos p [— 2 sin 0 • sin (y — 0) ] =
= — ~p~ cos [3• sin 0-sin (y — 0).
(5.35)
Если равенство частот 77vi и FV2 установлено неточ¬
но и их разность составляет NFV = FV^ то это вызывает
ошибку в определении угла сноса Дф=у — Так как
величина ошибки незначительна, можно принять
(5.36)
При относительной ошибке измерения частоты, равной
1%, ошибка определения угла сноса составляет Дср =
= 0,005 рад (0,28°), т. е. примерно в 30 раз ниже, чем
у однолучевой системы. Однако ошибка в измерении пу¬
тевой скорости при неточном знании угла облучения (3
(из-за крена) остается примерно такой же, как и у одно¬
лучевой системы.
Точность определения путевой скорости значительно
повышается при применении двусторонних систем, имею¬
щих лучи, направленные вперед и назад (рис. 5.31).
В этом случае частоты Допплера на выходе первого и
второго каналов равны
г 2V Q
FV\ =-г COS р-cosy,
FV2 = cos р • cos y,
а их разность
“ ^v\ Fyz= Д7 cos P ’cos Y-
Предположим, что угол облучения р определен с ошибкой
Др. Тогда
fvp=Тcos 1 tcos д р)+cos $+=
4V О Л А
=-у- cos Y • cos р • cos Др.
15*
227
Отклонение разностной частоты от ее максимального зна¬
чения составляет
Д/^р = cos у cos (1 — cos Д(5).
Поскольку путевая скорость I/ связана с максимальной
разностной частотой выражением
у = .,
4 cos J cos у
то ошибка в определении максимума разностной частоты
Рис. 5.31. Расположение лучей двусторонней двухлу¬
чевой системы.
Д^Ур приводит к соответствующей ошибке измерения
путевой скорости
v -cosAB) ~ V 4^- (5.37)
4 cos р cos y 2
Относительная ошибка измерения путевой скорости состав-
ляет
др _ др
-у~ ~
Таким образом, каждый градус ошибки в установке
угла облучения приводит к относительной ошибке изме-
228
рения путевой скорости порядка 0,015%. Видим, что дву-
с т ор'отгн я я система обеспечивает з и а чи тельное повыше¬
ние точности определения путевой скорости, снижая
влияние крена самолета. Однако ошибки в определении
угла сноса остаются практически такими же, как и у од¬
нолучевой системы.
Рис. 5.32. Четырехлучевая система.
Одновременное повышение точности измерения путе¬
вой скорости и угла сноса достигается .при использова¬
нии в системе трех и четырех лучей.
Если накрест лежащие лучи (Дь Д3 и Д2, А) четы¬
рехлучевой системы (рис. 5.32) расположены в одной
вертикальной плоскости, то, например, для пары /lj и А3
Д, =-TC0S ?C0SY.. FV3 = ^cospcosYj.
На выходе приемника выделяется сигнал разностной
частоты
Ы1..3 = Fvi ■ - Fv?, = %cos₽cos Ъ~2/и’
так как по условию yi = уз-
229
Аналитично для второй пары антенн /42 н /Ь
Fv>.\ =^2 ■ ■■ rvI ='■ 4r cos ? cos Y22Fvz-
При совмещении осн антенной системы с вектором пу¬
тевой скорости Yj = Y2 и з = Л/‘\1 •
Таким образом, добившись равенства разностных ча¬
стот, можно определить угол сноса непосредственно по
положению оси антенной системы относительно оси са¬
молета, а путевую скорость — по измеренной величине
разностной частоты.
Четырехлучевая система сочетает преимущества од¬
носторонней и двусторонней двухлучевых систем, за¬
ключающиеся в уменьшении ошибок из-за продольного
и поперечного кренов, поскольку они практически ком¬
пенсируются при вычитании допплеровских смещений.
Удвоение частоты смещения при вычитании повышает
чувствительность системы, а следовательно, и ее точ¬
ность. Большим достоинством системы является также
снижение требований к кратковременной стабильности
частоты, поскольку взаимодействующие сигналы кана¬
лов приходят примерно с одинаковых расстояний (£>i и
£>з для пары лучей и А3) и их временной сдвиг Л/].з =
= 2(Z>!—Dz)/c, определяющий требования к стабильно¬
сти частоты, весьма мал. Примерно такие же результа¬
ты могут быть получены и при использовании трехлуче¬
вых систем .
При анализе точности систем допплеровское смеще¬
ние предполагалось представленным единственной часто¬
той, тогда как фактически приходится иметь дело с це¬
лым спектром частот, что было показано ранее. Это
вносит дополнительные ошибки, а также некоторые осо¬
бенности в работу и построение систем.
О построении допплеровских систем. Построение доп¬
плеровских систем в значительней степени определяется
выбранным режимом излучения. Применяются системы
непрерывного излучения без модуляции и с частотной
модуляцией, а также системы с импульсным излучением.
Основным достоинством системы непрерывного излу¬
чения без модуляции является сосредоточенность спектра
отраженного сигнала в пределах одной полосы частот,
что обеспечивает наиболее полное использование эпер-
230
гии сигнала, а также сравнительно простое устройство
передатчика, приемника и индикатора. Существенным
недостатком таких систем является сильное влияние по¬
мех, вызванных отражениями от вибрирующих частей
самолета, обтекателя антенной системы и турбулентных
потоков, созданных работой двигателей. Значительное
влияние на работу системы оказывают также вибрации
антенно-фидерного устройства. Благодаря низкочастот¬
ной модуляции мешающие сигналы содержат составляю¬
щие, лежащие в полосе спектра полезного сигнала, ко¬
торые приводят к ошибкам в определении средней ча¬
стоты допплеровского спектра.
В связи с этим чаще используются системы с частот¬
ной или импульсной модуляцией.
Допплеровские четырехлучевые или трехлучевые си¬
стемы с ЧМ являются наиболее подходящими для одно¬
временного измерения высоты и трех составляющих век¬
тора скорости объекта. Создание такого комбинирован¬
ного измерителя особенно необходимо для вертолетов,
самолетов с вертикальным взлетом, а также космиче¬
ских кораблей с мягкой посадкой.
При использовании трехлучевой антенны (рис. 5.33),
стабилизированной по продольному и поперечному кре¬
ну, ортогональные составляющие скорости — продольная
Vnp, поперечная Vc (скорость сноса) и вертикальная
— могут быть определены из выражений:
F.. -- Flz = cos 3 cos 0,
V 1 и3 Л 1
— FVi = —cos Р sin 0, (5.38)
?vt + Fv, ~ Т“sin
Следует заметить, что приращения частоты FV{ и Fy3
в первом уравнении и FV\ и FV2 во втором имеют проти¬
воположные знаки, зависящие соответственно от знака
продольной и поперечной составляющих скорости.
Использование импульсного излучения позволяет лег¬
ко устранить помехи, вызванные мешающими отраже¬
ниями и вибрациями, путем запирания приемника на
•время излучения импульса и на некоторое время после
излучения. Это также обеспечивает развязку приемного
231
Рис. 5.33. Трехлучевая си¬
стема для измерения высо¬
ты и вектора скорости.
и передающего трактов при применении одной антенны
для передачи и приема.
Применяются когерентные (с внутренней когеренн
ностью) и некогерентные (с внешней когерентностью)
допплеровские системы с импульсным излучением. В ко¬
герентных системах отра¬
женный сигнал смешивается
с колебаниями, высокоста¬
бильного гетеродина, коле¬
бания которого жестко фа¬
зируются с излучаемыми ко¬
лебаниями. Допплеровский
сигнал образуется в резуль¬
тате детектирования обоих
колебаний. Когерентный ме¬
тод широко используется в
импульсных РЛС с селек¬
цией сигналов движущихся
целей (СДЦ) и будет по¬
дробно рассмотрен в гл. 7.
В некогеретных системах
допплеровский сигнал вы¬
деляется при детектировании отраженных сигналов от
двух антенн, направленных вперед и назад. Поскольку
при этом допплеровские -сдвиги имеют разные знаки, то
при детектировании двух сигналов выделяется удвоенная
допплеровская частота 2FV, которая и используется для
определения путевой скорости и угла сноса в индика¬
торном устройстве.
Параметры допплеровских измерителей с импульс¬
ным излучением варьируются в довольно широких пре¬
делах в зависимости от поставленной задачи.
Для измерения средней частоты допплеровского спек¬
тра Fvo, пропорциональной путевой скорости V, исполь¬
зуются частотомеры с прямым отсчетом типа счетчиков,
частотомеры следящего типа и корреляторы.
В частотомерах с прямым отсчетом измерение осно¬
вано па счете числа пересечений нулевого уровня доп¬
плеровским напряжением за 1 сек. Число, фиксируемое
счетчиком, равно среднеквадратичной частоте доппле¬
ровского спектра, и путевая скорость непосредственно
отсчитывается на индикаторе, а также вводится в счи-
■слитель пути.
232
Индикаторы с прямым отсчетом имеют сравнительно
низкую помехоустойчивость, так как полоса пропускания
тракта должна быть широкой, рассчитанной на весь диа¬
пазон изменения частоты допплеровского сдвига. Этот
недостаток устраняется в частотомерах следящего типа,
имеющих узкую полосу пропускания, рассчитанную па
пропускание небольшой части текущего допплеровско¬
го спектра. В зависимости от формы спектра выделяется
его средняя плп крайняя частота. При изменении теку¬
щего спектра осуществляется непрерывное автоматиче¬
ское слежение за выделяемой составляющей спектра.
В заключение коснемся вопроса о месте допплеров¬
ской системы в составе навигационного комплекса. Ав¬
тономный навигационный комплекс самолета или раке¬
ты кроме допплеровского измерителя может содержать
пр ибо р ы ги рос коп и че с ко й и и н ер ци а л ы i о й н а в и га ц и и,
а также астронавигации. В основе работы комплекса ле¬
жит непрерывное счисление пути, пройденного объектом
от заданного пункта, путем интегрирования скорости
или ускорения. По данным о путевой скорости и угле
сноса, получаемым от допплеровской системы, а также
о курсе, даваемом компасом, навигационный вычисли¬
тель определяет пройденный путь и текущие координа¬
ты объекта. Путем непрерывного сравнения с коорди¬
натами пункта назначения вычислитель определяет рас¬
стояние до пункта назначения п необходимый курс
объекта. Дублирование и сопоставление данных от раз¬
личных систем комплекса позволяет повысить точность
счисления и практически исключить влияние помех. Дан¬
ные радиотехнических навигационных устройств в таких
системах используются для уточнения координат в усло¬
виях, когда их применение допускается уровнем помех.
Глава 6
ИЗМЕРЕНИЕ УГЛОВЫХ КООРДИНАТ
§ 6.1. ВИДЫ ОБЗОРА ПРОСТРАНСТВА И’ИХ
ХАРАКТЕРИСТИКА
При рассмотрении методов измерения угловых коор¬
динат в § 1.7 предполагалось, что источник сигнала на¬
ходится в пределах диаграммы направленности систе¬
мы, т. е. режим поиска закончен и осуществляется точное
измерение координат объекта. В большинстве случаев
поиск должен производиться в секторе, значительно пре¬
вышающем ширину диаграммы направленности, путем
последовательного перемещения диаграммы в пределах
заданного сектора пространства. Такое перемещение
(сканирование) диаграммы называется пространствен¬
ным обзором. Во многих радиолокационных системах
определение координат осуществляется непосредственно
в процессе обзора, поэтому выбор способа и параметров
обзора оказывается связанным с основными тактически¬
ми и техническими характеристиками системы.
Время обзора заданного сектора, являющееся основ¬
ным параметром в режиме поиска, тесно связано с не¬
обходимыми дальностью действия, точностью и разре¬
шающей способностью системы. В самом деле, обеспе¬
чение большой дальности действия при ограничении от¬
ношения энергий излучаемого и принимаемого сигналов
возможно лишь за счет сужения диаграммы направлен¬
ности антенны. Повышение угловой разрешающей спо¬
собности и точности системы также связано с примене¬
нием узких диаграмм. Сужение диаграммы приводит
к увеличению времени, необходимого для обзора задан¬
ного объема пространства.
Определим время обзора объема пространства, за¬
данного максимальной дальностью системы и
сектором обзора импульсной РЛС с диаграммой на¬
правленности, охватывающей телесный угол 14 (рис. 6.1).
234
Минимальное время, необходимое для того, чтобы
объект, 'находящийся на расстоянии £>макс от РЛС, облу¬
чался хотя бы одним импульсом, равно /Dm = 2D5iaK(./c.
Для надежного обнаружения, а также для определения
координат объекта в процессе обзора необходимо вы¬
брать скорость обзора такой, чтобы за время нахожде¬
ния объекта в пределах диаграммы направленности на
Рис. 6.1. Обзор заданного сектора 0О диаграммой на¬
правленности с телесным углом ft.
вход пр и е м н и к а пос ту и а л о 11 ес к о л ь к о с. 11 n i а л ы i ы x
импульсов. Если необходимое число импульсов равно 7V,
то минимальное время обзора То заданного сектора об¬
зора @о диаграммой с телесным углом О будет равно
2/Лу.ак<
С
/V.
(6.1)
При этом предполагается, что диаграмма перемещается
равномерно и каждая точка сектора обзора находится
в равных условиях. Применяя программированный об¬
зор или обзор с последовательным анализом, можно
уменьшить необходимое время обзора, сохранив задан¬
ную надежность поиска.
Рассмотрим вначале способы равномерного обзора,
получившего наибольшее распространение. Находят при¬
менение круговой, винтовой, спиральный, конический,
спирально-конический и спирально-поступательный, пи¬
лообразный и другие методы обзора. Наиболее часто
используются круговой, винтовой и конический методы
обзора.
235
При круговом обзоре антенна вращается равномерно
в горизонтальной плоскости. Для характеристики кру¬
гового обзора достаточно знать максимально допусти¬
мую скорость вращения антенны со*. Если ширина ди¬
аграммы направленности антенны в горизонтальной пло¬
скости равна аа, а число импульсов, принимаемых за
время поворота диаграммы на угол аа, должно быть
то
Имея в виду выполнение условия однозначного измере¬
ния дальности tDm^Tn, найдем
При круговом обзоре сектор обзора в горизонтальной пло¬
скости 0a = 2n, а в вертикальной плоскости равен
ширине диаграммы направленности 0 = [3. Следовательно,
время, необходимое для обзора, равно
2тс
2kN
aaCi
(6-4)
В случае секторного обзора диаграмма направленно¬
сти качается в азимутальной плоскости в некотором сек¬
торе 0а. Необходимое время обзора будет
«а’Ci
(6.5)
Полученные формулы показывают, что уменьшение
времени обзора возможно за счет увеличения аа и Fu-
Однако эти параметры определяются требованиями раз¬
решающей способности, точности и однозначности изме¬
рения дальности, поэтому их выбор должен учитывать
все основные, зачастую противоречивые требования.
Круговой и секторный обзоры при использовании од¬
ной диаграммы (одноканальные или однолучевые систе¬
мы) позволяют определить две координаты — дальность
и азимут. В связи с этим в иностранной литературе.стан-
236
ции с таким обзором часто называются РЛС типа 2D,
т. е. станциями двух измерений *, в отличие от РЛС ти¬
па 3£>, измеряющих три координаты. Для обнаружения
объектов и определения их координат в двухкоординат¬
ных системах используются индикаторы кругового обзо¬
ра, секторные индикаторы и индикаторы типа В, имею¬
щие яркостную модуляцию луча трубки. При этом сиг¬
нальная отметка на экране образуется в результате воз¬
действия па управляющий электрод трубки последова¬
От синхро¬
низатора
Схема J
развертки
дальности
=Fp
подсвета Г
Г0/77 антенны
Связь
с антенной
Схема П \
развертки Ъ
к т
по азимуту |
г
—
Усилитель
сигнала
Сигнал от
приемника
Сигнальная
изображения на
Рис. 6.2. Блок-схема индикатора типа В и вид
экране ЭЛТ.
тель.ности импульсов, образующих пачку, огибающая ко¬
торой определяется формой диаграммы направленности
антенны.
В индикаторе типа В развертка осуществляется
в прямоугольных координатах: вертикальная—по даль¬
ности и горизонтальная — по азимуту (рис. 6.2). Раз¬
вертка по дальности создается так же, как и в индика¬
торе типа А, но пятно на экране отклоняется снизу
вверх. Развертка по азимуту осуществляется отклоне¬
нием луча трубки по горизонтали в соответствии с откло¬
нением антенны.
Если антенна периодически качается относительно
среднего положения, то луч трубки также отклоняется
синхронно с антенной. Так как отклонение по азимуту
совершается значительно медленнее, чем по дальности,
то за время полного отклонения по горизонтали обра¬
зуется большое число вертикальных линий развертки,
т. е. на экране создается прямоугольный растр. Положе-
Di mension — п.дм open не.
237
нис каждой линии растра соответствует определенному
азимуту, а расстояние от начала развертки дальности
пропорционально дальности. Шкала наносится на проз-
зрачном светофильтре перед экраном или создается -с по¬
мощью электронной схемы в виде меток дальности и ази¬
мута непосредственно на экране трубки.
Связь
Рис. 6.3. Блок-схема ИКО и вид изображения на экране ЭЛТ.
Иногда отсчет дальности производится совмещением
специального измерительного импульса с сигнальным.
В этом случае индикатор включает схему точной задерж¬
ки и формирования измерительного импульса.
Рис. 6.4. Винтовой обзор.
В ИКО используется радиально-круговая развертка,
при которой отклонение пятна по радиусу пропорцио¬
нально дальности, а азимут определяется положением
радиальной линии развертки, вращающейся синхронно
с антенной. Сигнальный импульс подается на управляю¬
щий электрод трубки и воспроизводится в виде яркой
238
метки, расстояние которой от центра трубки определяет
дальность, а ее угловое положение на экране (рис. 6.3) —
азимут. Шкала дальности в ИКО представляет ряд кон¬
центрических окружностей, нанесенных на светофильтре
перед экраном •ил.и создаваемых электрически шепосред-
ствен-HiO на экране в виде ярких колец. Расстояние меж¬
ду окружностями соответствует определенной дально¬
сти. Шкала азимута в градусах наносится на том же
светофильтре или на кольце, обрамляющем экран труб¬
ки. Иногда для отсчета дальности используется метка
в виде окружности переменного радиуса, которая соз¬
дается с помощью специального измерительного им¬
пульса.
При винтовом обзоре каждая точка диаграммы на¬
правленности (точка а ;на рис. 6.4) описывает линию,
близкую к винтовой.
Движение диаграммы представляет собой комбина¬
цию кругового вращения по азимуту со скоростью
и постепенного подъема по углу места со 'скоростью су
Обратный ход по углу места производится значительно
быстрее.
При винтовом обзоре важно нс только согласование
скорости вращения соа с частотой повторения Fu и ши¬
риной диаграммы аа, но и обеспечение перекрытия смеж¬
ных витков при отклонении по углу места. Для исключе¬
ния возможности пропуска целей практически обеспечи¬
вается двойное перекрытие. Таким образом, при ширине
диаграммы в вертикальной плоскости ра за один
оборот антенны по азимуту диаграмма должна сме¬
щаться по углу места па угол ра/2. Так как один оборот
диаграммы по азимуту совершается в течение времени
/1=2л/о)а, то скорость отклонения по углу места с уче¬
том двойного перекрытия будет
Ра
Если по углу места задан сектор обзора 03, то время
обзора
т _ __ 4те0з
239
Подставляя значение wa — aaA1I(//V, найдем
ð МаЛ,
Так, например, если аа—4Э; ₽а = 5°; 0^ = 60°; N---5;
Fn^= 1 000 гц, то Гов^ Ю сек.
При более узкой диаграмме время обзора соответст¬
венно возрастает. Таким образом, при узких диаграм¬
мах и достаточно большом секторе обзора информация
о цели будет поступать с большой дискретностью, что
приводит к ряду недостатков, и в первую очередь к сни¬
жению точности определения параметров движения
объекта.
Винтовой обзор применяется в ряде станций, и в част¬
ности в наземных и корабельных станциях управления
огнем зенитных орудий. Для обнаружения целей, опре¬
деления их дальности и азимута используется ИКО.
Спиральный метод обзора, так же как и винтовой,
представляет комбинацию вращения диаграммы с одно¬
временным изменением угла между осью вращения и
осью диаграммы (рис. 6.5). Различие заключается в ве¬
личине угла у: при винтовом обзоре у>45°, при спи¬
ральном у <45°.
Пусть 0а—--:0 — сектор обзора в горизонтальной и
вертикальной плоскостях; (»а- угловая скорость вращения
вдоль витка спирали; о—-угловая скорость отклонения от
240
оси вращения. Принимая по-прежнему двойное перекрытие
витков спирали, запишем
_ 2ti0
Скорость вращения соа находится так же, как и при
круговом обзоре, по для диаграммы, спроектированной
на плоскость вращения:
Тогда
2л0 JV sin у
Рааа-^ и
Для обычно применяемых симметричных диаграмм аа=ра и
2?10У sin у /г*
/ ос 9— • (и./)
При спиральном обзоре для определения угловых
координат целесообразно использовать индикатор со
спиральной разверткой, в котором луч трубки повторяет
движение диаграммы направленности антенны.
Конический обзор является частным случаем спи¬
рального. Угол у при коническом обзоре постоянен и
обычно не превышает сы, а сектор обзора оказывается
равным 0 = аа + 2у. Для расчета времени обзора исполь¬
зуется формула (6.7). Коническое сканирование чаще
всего используется в режиме точного и автоматического
измерения азимута и угла места равпосигнальиым ме¬
тодом.
В некоторых типах РЛС находят применение методы
обзора с более сложными траекториями движения диа¬
грамм, и в частности поступательно-конический и спи¬
рально-конический методы обзора, являющиеся комби¬
нациями секторного с коническим и спирального с ко¬
ническим обзором.
Управление движением диаграммы при больших
углах сканирования чаще всего осуществляется механи¬
ческим качанием или вращением всей антенной системы
в горизонтальной и вертикальной плоскостях. Скапиро-
16—1173 241
ванне в небольших пределах производится качанием или
вращением облучателя пли рефлектора антенной систе¬
мы. При механических методах сканирования большие
моменты инерции антенных систем часто являются фак¬
торами, ограничивающими возможную скорость обзора,
поэтому в последнее время все большее распростране¬
ние получают электрические методы сканирования и их
комбинации с механическими.
Однако при любом из рассмотренных методов обзо¬
ра время обзора определяется общей формулой (6.1).
Радикальное повышение скорости обзора можно по¬
лучить при использовании многоканальных методов об¬
зора.
Принцип многоканального обзора легко пояснить на
примере использования нескольких РЛС, каждая из ко¬
торых производит обзор отведенного ей узкого сектора
в пределах заданного широкого сектора обзора. Умень¬
шая сектор обзора ©/t каждой из станций, можно полу¬
чить любое заданное время обзора за счет увеличения
числа используемых станций (каналов). Информация,
получаемая каждой из РЛС, поступает на центральный
пункт сбора информации.
Конечно, система из нескольких станций сложна и
не всегда применима.
Многоканальная работа может быть обеспечена и
одной РЛС с несколькими лучами (лепестками диаграм¬
мы направленности) и возможностью разделения инфор¬
мации, принимаемой каждым из лучей.
Пр имером такой системы является РЛС с двухка¬
нальным К-обзором. Антенна РЛС (рис. 6.6,а) создает
две диаграммы (рис. 6.6,6), оси сечений которых верти¬
кальной плоскостью расположены иод углом 45° и об¬
разуют буквы V. Ширина диаграммы в вертикальной
плоскости должна быть достаточной для перекрытия за¬
данного сектора обзора Антенна станции вращает¬
ся или качается в заданном секторе в горизонтальной
плоскости. При вращении антенны цель попадает сна¬
чала в зону действия вертикального луча, а затем в зону
действия наклонного луча. Угол Ап, на который повора¬
чивается антенна от момента облучения цели верти¬
кальным лучом до момента облучения наклонным, опре¬
деляет высоту цели 1т и угол места цели р.
212
вид антенной системы станции: б - определ.
243
Из Л АО В и ЬВОС имеем h — D sin р — 2D cos
X sin—, отсюда tgp = 2sin —.
При h, малых сравнительно с D, углы [3 и Ла малы,
и с достаточной точностью можно считать р —Ла. Таким
образом, угол места может быть непосредственно опре¬
делен измерением разности азимутов Ла двух отметок
цели. При круговом вращении антенны в такой РЛС
применяется ИКО, при качании антенны в секторе ис¬
пользуются различные разновидности секторных индика¬
торов азимут — дальность.
Радиолокационная станция с V-обзором обеспечива¬
ет высокую скорость обзора, так как диаграммы пере¬
крывают сразу весь заданный сектор по вертикали, при
этом применение второго луча дает возможность опре¬
делять угол места и высоту. Однако при большом числе
целей определение координат становится затруднитель¬
ным из-за низкой разрешающей способности системы по
углу места и удвоения числа сигнальных отметок на
экране индикатора.
Находят применение многоканальные системы с ис-’
пользованием парциальных лучей (лепестков), качаю¬
щихся или неподвижных в вертикальной плоскости. Ле¬
пестки формируются отдельными излучателями, причем
каждый из излучателей подключен к своему каналу
приема и обработки сигнала. Иногда используются и
отдельные передающие каналы. В последнем случае
многоканальная РЛС по существу аналогична упомя¬
нутой системе из нескольких станций.
Для формирования многолучевой диаграммы разра¬
ботаны антенные системы различных типов. Одной из
первых и наиболее распространенных является парабо¬
лическая антенна с числом излучателей, равным числу
лучей. Каждый из излучателей создает независимый
луч, положение которого в пространстве определяется
смещением излучателя относительно фокуса параболи¬
ческого зеркала. Число лучей такой антенны ограничено
допустимыми искажениями формы лучей, которые
растут с увеличением расстояния излучателя от фокуса.
Широко используется для формирования многолуче¬
вых диаграмм линза Люнеберга, выполненная в виде
сферы из диэлектрика с диэлектрической постоянной,
244
изменяющейся обратно пропорционально расстоянию от
центра сферы. Такая линза обладает свойством фокуси¬
ровать излучение точечного излучателя в параллельный
пучок. Располагая излучатели по периферии линзы, мож¬
но получить заданное число и распределение лучей. При
перемещении излучателя по поверхности сферы форми¬
руемый луч отклоняется.
Находят применение антенные системы в виде ре¬
шетки, излучатели которой подключены к отдельным ка¬
налам. Качание диаграмм в этом случае можно осу¬
ществить электрически, изменяя частоту излучаемых ко¬
лебаний или управляя фазой колебаний в отдельных
каналах с помощью фазовращателей. При достаточно
высокой направленности антенны число элементов ре¬
шетки велико, и для управления лучом изменением фазы
излучаемых колебаний требуется большое число фазо¬
вращателей и управляющих сигналов, т. е. система по¬
лучается весьма сложной.
Наиболее интересна многоканальная система с вза¬
имно неподвижными лучами, одновременно перекрываю¬
щими весь заданный сектор по углу места, при этом по
азимуту может производиться круговой или секторный
обзор, и время обзора определяется соответственно по
формулам (6.4) и (6.5). Поскольку соседние лепестки
антенной системы частично перекрываются, принимае¬
мый сигнал появляется сразу на выходе двух соседних
каналов и угол места определяется номерами каналов
и соотношением амплитуды сигналов на их выходах.
Азимут измеряется так же, как и в одноканальной си¬
стеме. Точность измерения угловых координат, так же
как и угловая разрешающая способность системы, зави¬
сит от ширины парциальных лучей в азимутальной и
угломестной плоскостях.
При фазовом методе пеленгования многоканальная
система отличается лишь способом обработки сигнала.
Если в многолучевой системе использовать один канал
обработки, на который поочередно подаются сигналы
от отдельных излучателей, то такая система окажется
эквивалентной системе с качанием одиночной диаграммы
направленности.
До сих пор рассматривались одноканальные и мно¬
гоканальные системы, в которых ширина диаграмм на¬
правленности, частота повторения и энергия импульсов
245
в процессе обзора сохранялись неизменными. Для уве¬
личения скорости обзора возможно ввести программи¬
рованное изменение этих параметров.
При программированном обзоре предполагается, что
максимальная дальность действия является функцией
направления /)Макс (а, Р). В оптимальной (с энергети¬
ческой точки зрения) системе необходимое отношение
сигнала к шуму при обнаружении стандартной цели на
расстоянии />макс должно сохраняться постоянным и ми¬
нимально достаточным для обеспечения заданных ве¬
роятностей обнаружения D и ложной тревоги F. Если
максимальная дальность является известной функцией
направления £>макс («, ₽), то с помощью основного урав¬
нения радиолокации и характеристик обнаружения мож¬
но найти закон изменения ширины диаграммы направ¬
ленности и энергии импульса для сохранения постоян¬
ства отношения сигнала к шуму.
Как следует из формулы (6.1), время обзора Го при
заданном секторе обзора (% можно представить соотно¬
шением
О
Следовательно, минимальное время обзора может быть
обеспечено изменением частоты повторения Еп обратно
пропорционально дальности. Если средняя мощность пе¬
редатчика Pop = Лт • ти • Еп ограничена, то программиро¬
ванное изменение Fn должно сочетаться с соответствую¬
щим изменением мощности передатчика или длительно¬
сти импульса и полосы пропускания приемника.
При программированном изменении ширины диа¬
граммы направленности О с сохранением постоянства
импульсной мощности Рп максимальная скорость обзора
обеспечивается при соблюдении условия
При этом следует учитывать, что изменение ширины
диаграммы связано с изменением точности и угловой
разрешающей способности системы в различных направ¬
лениях.
Программированное изменение параметров системы
реализуемо лишь при заранее известных законе измепе-
246
ния дальности, величине эффективной площади рассея¬
ния цели и уровне помех. Эти данные известны, напри¬
мер, в случае систем слежения за ракетами и спутника¬
ми с заранее рассчитанными траекториями. В случаях,
когда данные, необходимые для создания программи¬
рованного обзора, отсутствуют, повышение скорости об¬
зора может быть получено использованием последова¬
тельного анализа ситуаций в различных точках задан¬
ного сектора обзора.
При использовании метода последовательного анали¬
за диаграмма направленности антенны производит скач¬
кообразное зондирование пространства обзора. Для
управления временем каждого пробного шага применя¬
ется двухпороговое решающее устройство, которое с по¬
мощью блока управления перемещает диаграмму на¬
правленности антенны в соседнее положение по оконча¬
нии цикла анализа. РЛС включает также многоканаль¬
ный накопитель, в ячейках которого производится на¬
копление сигнала в каждом из элементов разрешения
по дальности. Двухпороговое решающее устройство при¬
нимает решение об отсутствии цели на данном направ¬
лении, если сигнал на выходе накопителя не превышает
нижнего порога. Если сигнал превысит верхний порог,
то принимается решение о наличии цели. В том и дру¬
гом случае диаграмма переводится в следующую пози¬
цию. Если сигнал, полученный в результате накопления,
оказывается в промежуточной области, анализ продол¬
жается и диаграмма остается в том же положении до
принятия решения.
Приведем соображения, позволяющие оценить воз¬
можное сокращение времени обзора при использовании
последовательного анализа. Среднее время обзора п
элементов разрешения ио дальности па данном направ¬
лении при отсутствии сигнала равно
С ш /? • Д / щ (D, /’),
где ДГШ — средняя длительноегь пробного шага при на¬
личии только шума;
D — требуемая надежность обнаружения сигнала;
F — допустимая вероятность ложных срабатыва¬
ний.
247
При наличии сигнала в одном из элементов разре¬
шения среднее время обзора будет
Геш = (п -- 1) А?ш (D, F) + Д7CI11 (D, F),
где АГсш — средняя длительность пробного шага при на¬
личии сигнала.
Так как число элементов п обычно весьма велико и
Д 7/
выполняется условие А-Сш , то 7’сш —Ли и выигрыш
во времени обзора составляет
я То Д/о
С'т~" Тш А Пи ’
где А/о— длительность пробного шага при равномерном
зондировании.
Анализ показывает, что для различных значений D
и Г применение последовательного анализа позволяет
за счет усложнения схемы обработки получить выигрыш
во времени обзора до 4. При сохранении времени обзора
неизменным использование последовательного анализа
дает возможность повысить надежность обнаружения
или уменьшить энергию сигнала при сохранении надеж¬
ности.
§ 6.2. ПОТЕНЦИАЛЬНАЯ ТОЧНОСТЬ И РАЗРЕШАЮЩАЯ
СПОСОБНОСТЬ СИСТЕМ ПРИ ИЗМЕРЕНИИ
УГЛОВЫХ КООРДИНАТ
Методы оценки потенциальных возможностей РЛС
при измерении дальности и скорости могут быть рас¬
пространены и на случай определения азимута и угла
места.
Рассмотрим измерение угловой координаты а в про¬
цессе равномерного отклонения (обзора) диаграммы на¬
правленности с угловой скоростью Если ширину ди¬
аграммы направленности в плоскости измеряемой коор¬
динаты на уровне половинной мощности обозначить аа,
то время нахождения точечного объекта в зоне облуче¬
ния будет равно
та=а°К-
При непрерывном излучении отраженный точечным
объектом сигнал будет представлять импульс длитель-
248
ностью 7\, форма которого определяется формой ди¬
аграммы направленности антенны. Измерение угловой
координаты сводится к фиксации временного положения
этого импульса (который может быть назван угловым
сигнальным импульсом) тем или иным способом. Как и
при измерении дальности, точность и разрешающая спо¬
собность определяются длительностью углового сигналь¬
ного импульса, пропорциональной ширине диаграммы
направленности антенны.
Продолжая аналогию, можно ввести спектр углово¬
го сигнального импульса, причем при сужении диаграм¬
мы ширина спектра Afa (рис. 6.7) увеличивается и со¬
ответственно повышаются угловая разрешающая спо¬
собность и точность системы.
Это обстоятельство используется в антеннах с синте¬
зированным раскрывом,
с частотной модуля¬
цией или манипуляцией
фазы в раскрыве ан¬
тенны, т. е. по суще¬
ству используется
принцип, аналогичный
сжатию импульса.
Таким образом, для
о цен к и п отен ци а л ы i ы х
возможностей РЛС при
измерении угловой ко¬
ординаты а и угловой
скорости сс можно так¬
же использовать корре¬
ляционную функцию
Ч^а, а), которая в об¬
щем случае взаимоза¬
висима с функцией
^(т, J7). При этом
а также в антенных системах
Рис. 6.7. К понятию углового сигналь¬
ного импульса и углового спектра.
должна рассматривать¬
ся совместная корреля¬
ционная функция Чт(т,
F, а, а). Однако необходимость учета взаимозависи¬
мости возникает лишь при весьма широкополосных
сигналах и больших относительных раскрывах антенн.
Для большинства современных РЛС пренебрежение
249
взаимным влиянием не вносит существенных ошибок и
в то же время сильно упрощает анализ.
Рассмотрим наиболее простой и распространенный
случай, когда кроме дальности и радиальной скорости
производится измерение азимута а, а взаимным влия¬
нием временных и пространственных характеристик
можно пренебречь. В этом случае совместная корреля¬
ционная функция может быть представлена произведе¬
нием двух функций:
|Т(т, F, а)| = |Т(т, F) I • ЦР(а)|, (6.8)
причем функция Ф‘(а) зависит только от ширины и фор¬
мы диаграммы направленности антенны, а функция
Чг(т, F)—только от параметров излучаемого сигнала.
Протяженность области высокой корреляции Да, кото¬
рая является мерой угловой разрешающей способности,
можно оценить углом корреляции ак, равным
е/2
Да^ак = | ЧГ (а) ] 2 б/а,
-0/2
где ±0/2 — рабочая область изменения угловой коорди¬
наты (сектор обзора).
При колоколообразной аппроксимации диаграммы на¬
правленности корреляционная функция по оси а имеет
вид
Ч' (а) = ехр Л-- 2 1п 2 —а- —\
\ “a J
где аа — ширина результирующей диаграммы при пере¬
даче и приеме на уровне половинной мощности.
Протяженность области высокой корреляции по оси
а в этом случае будет
Да ак = аа 1,5аа.
Потенциальная точность измерения угловых коорди¬
нат определяется дисперсией оценки которая так же,
как и при измерении дальности [выражение (5.10)], мо¬
жет быть представлена формулой
1
(6-9)
250
Здесь ра—параметр, связанный с шириной спектра Д/а и
скоростью обзора *>а формулой
При колоколообразпой аппроксимации диаграммы
направленности, а следовательно, и формы углового сиг¬
нального импульса ширина спектра равна
где ал — ширина диаграммы направленности, измеряемая
на том же уровне d, что и Д/а.
Но ширина диаграммы связана с протяженностью
раскрыва антенны dA в рассматриваемой плоскости об¬
ратной пропорциональностью:
следовательно, дисперсия может быть представлена фор¬
мулой
а минимальная среднеквадратичная ошибка
амип" £|Аг^д/Х’
(6.И)
Таким образом, относительный раскрыв антенны
dA/X при измерении углов аналогичен ширине спектра
сигнала при измерении дальности.
При импульсном излучении угловая разрешающая
способность и точность остаются такими же, как и при
непрерывном излучении синусоидальных колебаний, при
условии, что период повторения импульсов Ти достаточ¬
но мал и угловая дискретность поступления сигналов
(т. е. угловой сдвиг диаграммы за время Тп) значитель¬
но меньше ошибки фиксации углового сигнального им¬
пульса. Это требование определяется тем, что при им¬
пульсной работе угловое положение цели может быть
отсчитано с погрешностью порядка угла дискретности
°а Ты если угловое положение объекта определяется по
251
временному положению импульсов начни или ее оги¬
бающей.
Для реализации потенциальных возможностей в от¬
ношении точности измерения угловой координаты при
одпоканалы-юй обработке необходимо иметь не менее
двух импульсов на протяжении области высокой корре¬
ляции, что равносильно условию
7а^2Гп. (6.12)
При левыполпении условия (6.12) потенциальная
точность может быть достигнута использованием мно¬
гоканальной схемы обработки.
В зависимости от построения схемы обработки потен¬
циальная точность измерения угла а изменяется.
При применении суммарно-разностной схемы обра¬
ботки непосредственно на выходе антенны образуется
сумма и разность двух сигналов, которые затем усили¬
ваются и преобразуются суммарным и разностным при¬
емными каналами. В окрестности направления точного
пеленга амплитуды и фазы сигналов на выходе антенны
примерно одинаковы, поэтому при суммировании ампли¬
туда результирующего сигнала удваивается. Поскольку
собственные шумы суммарного и разностного приемных
каналов независимы, удвоение амплитуды суммарного
сигнала приводит к снижению потенциальной дисперсии
отсчета угла а в два раза. Таким образом, суммарно¬
разностная обработка дает более высокую потенциаль¬
ную точность. Имея в виду также другие преимущества
суммарно-разностного метода обработки, становится
ясным, почему этот метод получил наибольшее распро¬
странение в моноимпульсных системах, рассматривае¬
мых в § 6.8.
§ 6.3. АМПЛИТУДНЫЕ МЕТОДЫ ПЕЛЕНГОВАНИЯ
Принцип амплитудных методов пеленгования изло¬
жен в § 1.7. Здесь рассматриваются некоторые причины
ошибок определения направления амплитудными мето¬
дами в РЛС и угломерных РНС с индикацией на ЭЛТ.
Метод максимума. Пеленгование осуществляется сов-
м е ще н нем максимума п е л е 11 г а ц и о 11 и о и х а р а кте. р и е т и к i т
с направлением на пеленгуемый объект (рис. 6.8щ). Пе¬
ленг отсчитывается в момент совмещения, когда сигнал
252
на выходе приемника достигает максимальной величи¬
ны. В качестве индикатора принципиально можно ис¬
пользовать любой прибор, позволяющий регистрировать
изменение амплитуды сигнала при повороте антенной
системы. Наиболее часто для индикации используется
Рис. 6. В. Метод пеленгования по максимуму.
ЭЛТ с модуляцией луча отклонением. Если пеленгова¬
ние производится в режиме обзора, т. е. без прекраще¬
ния вращения или качания диаграммы направленности
антенны, то определение направления производится по
положению яркостной сигнальной отметки на экране
трубки индикатора кругового обзора, индикатора типа
В или другого индикатора с яркостной модуляцией луча
ЭЛТ. При этом пеленгование производится по середине
яркостной от?летки, соответствующей максимуму диа¬
граммы направленности.
Основными достоинствами метода является простота
пеленгования, особенно в обзорных системах, и исполь¬
зование при пеленговании максимального отношения
сигнала к помехе, что обеспечивает высокую пороговую
помехоустойчивость систем. Однако по точности опреде¬
ления направления метод максимума уступает методу
минимума и равносигнальному.
Рассмотрим основные причины ошибок измерения
азимута методом максимума при применении индикато¬
ра типа А, на экране которого оператор фиксирует мак-
253
спмальную высоту сигнального выброса h (рис. 6.8,6)
в момент совмещения максимума пеленгационной ха¬
рактеристики с направлением на пеленгуемый объект.
Применительно к импульсной радиолокационной
станции, в которой для приема и передачи используется
одна и та же антенна, пеленгационная характеристика
Е(а) определяется квадратом функции /Е(а), описы¬
вающей диаграмму направленности по напряженности
поля. В этом случае относительное изменение амплиту¬
ды сигнала па входе приемника в зависимости от угла
отклонения максимума диаграммы от направления на
объект Да можно записать в виде
&U и (0) — и (Да) (0) — (A°0
WT — Щб) — ~kf^} •
Сокращая коэффициент пропорциональности k и под¬
ставляя fE (Да) = I (0) — Д^ получим
Д(/ _ f г (0) - [fE Ф) - Д _ 24 (°) ^Е~^Е <2^'е
(;(°) ~ Г^(О) " ’ 4(0) НЖ
Если приемный тракт имеет линейную амплитудную
характеристику, то
Д/С/? 1 Г Д// 11 Д/г
4Т°Т^“ГР(°) I 2 ~h~'
При небольших отклонениях Да, соответствующих
ошибке пеленгования, справедливо соотношение
Д/\ ~
отсюда
Аа_ Д^'(О)
2/£(Да)//£(0) ’
где f (Да) — средняя крутизна fE (а) в пределах Да.
Формула ясно показывает, что причиной сравнитель¬
но низкой точности пеленгования методом максимума
является низкая крутизна пеленгационной характеристи¬
ки [малая величина /Е(Д-а)] в рабочей области или,
иначе говоря, низкая пеленгационная чувствительность
угломерных устройств, работающих но максимуму сиг-
254
нала. Величина составляющей ошибки пеленгования,
вызванной неточностью определения максимума сигна¬
ла, составляет примерно 1/-1 1/5 ширины диаграммы
направленности антенны на уровне половинной мощно¬
сти.
Одной из основных причин случайных ошибок пелен¬
гования являются внешние помехи шумового типа и соб¬
ственные шумы приемника. Среднеквадратичное значе¬
ние угловой ошибки отсчета аа прямо пропорционально
среднеквадратичному значению флюктуаций выходного
напряжения пеленгатора
ut .
Воздействие шумов понижает угловую чувствитель¬
ность системы, т. с. зона нечувствительности, измеряемая
углом нечувствительности системы фп, расширяется.
При амплитудных методах пеленгования изменение
углового положения объекта приводит к изменению ам¬
плитуды выходного сигнала. Наименьшее различимое
изменение напряжения сигнала <\U0 при воздействии шу¬
мов пропорционально среднеквадратичному значению
выходных флюктуаций
= (6.14)
В зависимости от метода отсчета и времени усреднения
величина коэффициента различимости /ир колеблется
в пределах 0,5—1. С учетом соотношения (6.14) угол
нечувствительности
'К =--- 2^рРа-
При отклонении оси диаграммы от направления на
объект на некоторый угол Да0, соответствующий наи¬
меньшему различимому изменению сигнала At7o, спра¬
ведливо равенство
~ F (Да0) ^aoUc макс»
где t/смакс — максимальное напряжение сигнала,
F(Дао) —средняя крутизна пеленгационной харак¬
теристики в пределах Аа0.
Выражая среднеквадратичное значение флюктуаций
(7ф через спектральную плотность флюктуаций 7V0 и по¬
лосу пропускания измерительного устройства AF]b полу¬
чим
255
AUQ"—(A^o) AaQUc Макс :^рС/ф
= /Л^од? н.
Так как фн = 2Да0, то
2//?1, ]ЛУ0ДЛу.
Л (Да) (J,. маис
Отсюда среднеквадратичное значение ошибки пелен¬
гования, вызванной воздействием шумов, равно
з ЖЖ — ! .
“ F (Д«о) Uc макс (Д“о) ,Ус маке/
Таким образом, ошибка уменьшается с увеличением
отношения сигнала к шуму и крутизны диаграммы на¬
правленности, что согласуется с выводами предыдущего
параграфа.
Получение достаточно высокой точности пеленгова¬
ния методом максимума возможно лишь при узких диа¬
граммах направленности.
Метод минимума. При пеленговании по минимуму
сигнала используются диаграммы направленности с рез¬
ким провалом, позволяющим получить высокую чувст¬
вительность пеленгования. Наиболее часто в радиопелен¬
гаторах используются диаграммы направленности в ви¬
де восьмерки и кардиоиды. Диаграмма в форме кар¬
диоиды получается при взаимодействии направленной
рамочной антенны, имеющей диаграмму направленности
в виде восьмерки, и ненаправленного излучателя. Кар¬
диоида позволяет исключить двузначность отсчета, не¬
избежную при диаграмме типа восьмерки, но имеет ме¬
нее резкий провал и, следовательно, позволяет получить
несколько меньшую точность пеленгования.
Рассмотрим некоторые причины ошибок пеленгова¬
ния по минимуму. На рис. 6.9 изображен участок пелен¬
гационной характеристики в рабочей области. Остаточ¬
ное напряжение £70ст, сглаживающее провал пеленга¬
ционной характеристики, является следствием воздейст¬
вия отражений от местных предметов и ионосферы, при¬
ходящих с боковых направлений, внутриприемных шу-
256
мов, а также недостаточного экранирования высокоча¬
стотных цепей пеленгатора, что делает возможным ирисам
сигнала непосредственно этими цепями помимо антенны.
Остаточное напряжение можно разложить на две
составляющие (рис. 6.9,в): синфазную £/Сф== t/0CT cos ср
Рис. 6.9. Пеленгование по минимуму:
а — притупление минимума из-за осииочюл и напряжения ^ост; б - вектор¬
ная диаграмма, поясняющая компенсацию (/кп.
и квадратурную Ul<B=77ОТ с sin ср. Синфазная составляю¬
щая снижает чувствительность пеленгования и, следо¬
вательно, отрицательно сказывается на точности. Одна¬
ко более опасна квадратурная составляющая, которая
дает непосредственный вклад в ошибку пеленгования.
Поэтому в радиопеленгаторах обычно предусматривает¬
ся возможность компенсации квадратурной составляю¬
щей введением компенсирующего напряжения t/K.
Влияние собственных шумов приемника и флюктуа¬
ционных помех зависит от типа пеленгатора. Применя¬
ются две разновидности пеленгаторов, работающих по
минимуму. В первом из них направление на пеленгуе¬
мый радиомаяк определяется непосредственно по мини¬
муму амплитуды принимаемого сигнала. Пеленгаторы
такого типа относятся к амплитудным устройствам
типа Е, в отличие от амплитудных устройств типа М,
в которых используется зависимость глубины модуля¬
ции колебаний от пеленга при постоянной напряженно¬
сти поля сигнала.
Рассмотрим влияние шумов только для случая пе¬
ленгатора типа М, поскольку для пеленгатора типа Е
метод анализа и выводы аналогичны рассмотренным
выше для максимального метода пеленгования.
В пеленгаторах типа М используется зависимость
17—1173 257
коэффициента модуляции принимаемого сигнала от на¬
правления на радиомаяк:
т(а) =MF(a), (6.15)
где М— максимальное значение коэффициента модуля¬
ции;
/?(а) —пеленгационная характеристика, имеющая ми¬
нимум при a^cio-
Зависимость (6.15) получается в результате сложе¬
ния сигнала ti\ = U[m cos cof, принимаемого ненаправлен¬
ной антенной пелангатора, с сигналом а2 =
= (72шЕ(а) cos со/, принимаемым направленной антенной
с характеристикой ^(а). Напряжение и2 с помощью ба¬
лансного модулятора предварительно преобразуется
к виду
ur2 — U2mF (a) cos Qt cos of
и затем складывается с и\. В результате получается
и = ^14- 1 -ф- F (a) cos O/j cos со/ ==
= Uim [ 1 + ш (а) COS Ш] COS со/.
Таким образом,
щ (а) = F (а) = MF (а).
01 т
Если средняя крутизна пеленгационной характери¬
стики в окрестности минимума равна Е(Да), то при не¬
больших отклонениях от направления минимума Да
можно использовать приближенное выражение
т(Да) ~МЕ(Да)Да.
При некотором отклонении от направления минимума
Да0 будет выполняться условие различимости сигнала
на фоне шумов
MUc.-pF (Да0) Да0 = ni^N^F.,, (6.16)
где С7сд— напряжение сигнала на выходе детектора.
Вследствие подавления сигнала шумом при детекти¬
ровании напряжение на выходе детектора связано с на¬
пряжением на его входе известным соотношением
г г ^Ср
258
где р = отношение сигнала к
шуму по действующим
значениям напряжения.
Полагая пеленгационную характеристику
минимума симметричной, найдем из условия
нечувствительности пеленгатора типа М:
фн — 2Да0
= 2/n„ /;УОДГИ ]/?+ 1 .
MUeF (Да0) Р
в области
(6.16) угол
(6-17)
При сильных сигналах р > 1 и, следовательно,
V" MUCF (Д«о)
При слабых сигналах р<1> Кр2~Н/р~1/р> и> сле'
довательно,
'' (Д«о)
Коэффициент модуляции сигнала определяется отно¬
шением напряжения направленной и ненаправленной
антенн М = U2m/Uim-
Таким образом, при слабом сигнале угловая чувст¬
вительность пеленгатора типа М повышается при уве¬
личении напряжения ненаправленной антенны.
Приведенные формулы в равной мере пригодны и
для определения угловой чувствительности радиомаячных
устройств типа М в которых направление задается ми¬
нимумом коэффициента модуляции сигнала. В этом слу¬
чае величины М и F(Да) характеризуют собственно ра¬
диомаяк, а остальные величины, входящие в формулы,
относятся к приемному устройству угломерной системы.
Получили применение, например, радиомаяки, в ко¬
торых используется минимум излучения боковых частот
модуляции для задания определенного направления а0.
В этом направлении /п;(ао)=О, а при отклонении от это¬
го направления коэффициент модуляции возрастает, при
этом фаза огибающей модулированного колебания опре¬
деляется знаком отклонения. Оценивая амплитуду и фа¬
зу огибающей модулированного сигнала в точке приема
на подвижном объекте, можно определить положение
объекта относительно заданного маяком направления
(курса). Подобные маяки называются курсовыми.
17*
259
Метод пеленгования по минимуму применяется также
в пеленговых всенаправленных радиомаяках. В таких
маяках направление минимума сигнала плавно или
скачкообразно изменяется последовательно во времени
в пределах 360°. Приемоиндикатор на объекте имеет не¬
направленную антенну и фиксирует момент приема сиг¬
нала минимальной величины. При этом обратный пеленг
может быть определен измерением времени от момента
оперного сигнала до момента прохождения направления
Рис. 6.10. Равносигнальный ме¬
тод пеленгования.
минимума при плавном вра¬
щении диаграммы направ¬
ленности антенны маяка.
При скачкообразном переме¬
щении направления мини¬
мума каждому его положе¬
нию соответствует опреде¬
ленный код сигнала. Это по¬
зволяет определить обрат¬
ный пеленг непосредственно
в момент прохождения на¬
правления минимума по ко¬
ду принимаемого сигнала,
что, безусловно, удобнее и
обеспечивает более высокую
точность определения место¬
положения.
Метод пеленгования по
минимуму обладает сущест¬
венным недостатком, заклю¬
чающимся в малой величине
сигнала в момент пеленгова¬
ния, что приводит к низкой
помехоустойчивости систем. В некоторых системах в мо¬
мент точного пеленга сигнал вообще остсутствует, что
неудобно и затрудняет контроль исправности системы.
Вследствие этих причин метод минимума используется
лишь в условиях, когда может быть обеспечено доста¬
точно большое отношение сигнала к шуму. Эти условия
выполняются в радионавигационных системах, в кото¬
рых принимаются прямые сигналы радиомаяков. В РЛС
этот метод практически не применяется.
Равносигнальный метод. Равносигнальный метод пе¬
ленгования сводится к сравнению амплитуд сигналов,-
260
соответствующих двум положениям диаграммы направ¬
ленности антенны. Равенство амплитуд принимаемых
сигналов означает, что направление от приемника на
источник сигнала совпадает с равносигнальным направ¬
лением (рис. 6.10), которое часто называют равносиг¬
нальной осью. Равносигнальная ось (S) может быть
создана как при излучении, так и при приеме сигналов.
В импульсных РЛС, в которых для передачи и приема
используется одна антенна, равносигнальная ось созда¬
ется обычно и при передаче, и при приеме сигналов.
Рис. 6.11. Блок-схема приемной части РЛС с поочеред¬
ной работой двух антенн.
При применении двух антенн они могут работать
одновременно или поочередно. Диаграммы направлен¬
ности антенн смещены на некоторый угол ус, который
называется углом смещения и выбирается в зависимо¬
сти от ширины используемых диаграмм и заданной точ¬
ности пеленгования.
На рис. 6.11 изображена упрощенная схема приемной
части импульсной РЛС, в которой используется равно¬
сигнальный метод пеленгования при поочередной рабо¬
те двух антенн. Переключатель Пх поочередно подклю¬
чает антенны Л1 и Л2 ко входу приемника. С помощью
переключателя П2, работающего синхронно с /7Ь на го¬
ризонтально отклоняющие пластины подается напряже¬
ние (Усдв, сдвигающее линию развертки по горизонтали
вправо при подключении антенны Благодаря этому
261
сигнальные выбросы на экране индикатора оказываются
расположенными рядом, причем левой диаграмме соот¬
ветствует левый выброс, а правой — правый. Поворотом
антенной системы оператор уравнивает амплитуды им¬
пульсов, при этом направление прихода сигнала совпа¬
дает с равносигнальной осью. Пеленг определяется по
положению антенной системы в момент равенства ам¬
плитуд выбросов.
двух антенн.
Коммутация антенн осуществляется с частотой, пре¬
вышающей 15 гц, что устраняет мерцание сигналов по
яркости, и оператор видит два устойчивых сигнальных
выброса. Поскольку частота повторения импульса РЛС
обычно составляет сотни герц, каждый из выбросов
представляет результат накопления экраном нескольких
десятков импульсных сигналов.
Для образования равносигнального направления ис¬
пользуются различные способы в зависимости от назна¬
чения угломерной системы и диапазона, в котором она
работает. В радиолокационных системах наибольшее
распространение получили методы двух антенн, методы
дефазирования и дефокусировки.
Метод двух антенн применяется в основном в систе¬
мах метрового и дециметрового диапазонов. Часто равно¬
сигнальное направление образуется только при приеме.
При передаче обе антенны (рис. 6.12) работают синфаз-
по, и ось антенной системы совпадает с осью диаграммы
направленности. При приеме точки подключения прием¬
ника смещены относительно середины системы на рас-
262
стояние, при котором равенство фаз в точках подключе¬
ния КК\ получается при приходе волны с направления
ОТ, а равенство фаз в точках LL{ — при приходе волны
по направлению OR. Направление OS будет равносиг-
нальиым. Таким образом, для смещения диаграммы и
образования равносигнального направления здесь ис¬
пользуется метод дефазирования.
Рис. 6.13. Образование равносигнальной оси в пространстве с по¬
мощью изменения фазы питания четырех антенн:
а — схема включения антенн и фазирующего кольца; б — вращение диаграм¬
мы (сечение) вокруг равносигнальной оси (точка О) в зависимости от поло¬
жения /( переключателя 77.
Управление фазой питания антенн широко исполь¬
зуется для вращения или скачкообразного перемещения
диаграммы направленности вокруг равносигнальной оси.
Рис. 6.13 поясняет принцип вращения диаграммы на¬
правленности в пространстве. Две пары антенн, распо¬
ложенных соответственно в азимутальной и угломестной
плоскостях, подключены к так называемому фазирующе¬
му кольцу. Если точка подключения приемника будет
плавно перемещаться по фазовому кольцу, результирую¬
щая диаграмма будет поворачиваться в пространстве,
образуя равносигнальную ось. Однако реализация плав¬
ного перемещения точки подключения приемника на
сверхвысоких частотах затруднительна, поэтому практи¬
чески используется скачкообразное перемещение точки
подключения (/, 2, 3, 4). При этом диаграмма направ¬
ленности последовательно отклоняется вверх, вправо,
вниз и влево, также образуя в пространстве равносиг¬
нальную ось. Этот метод часто используется в РЛС ме-
263
трового и дециметрового диапазонов для пеленгования
объектов в пространстве.
В РЛС сантиметрового диапазона для образования
равносигнальной оси в пространстве используется метод
дефокусировки, при котором излучатель параболиче¬
ской антенны смещается относительно фокуса зеркала
(рис. 6.14). Благодаря этому диаграмма направленности
оказывается смещенной относительно оси антенны. При
Рис. 6.14. Образование равносигнальной оси в пространстве при вра¬
щении дефокусированного излучателя параболической антенны.
вращении излучателя диаграмма также вращается, об¬
разуя равносигнальное направление, совпадающее с осью
антенны. Такое вращение диаграммы носит название ко¬
нического сканирования. Коническое сканирование по¬
лучило широкое распространение в радиолокационных
системах с автоматическим сопровождением цели по
угловым координатам, а также в радиоастрономических
пеленгаторах космических источников излучения.
Широкое распространение равносигнального метода
пеленгования обусловлено возможностью получения вы¬
сокой точности определения направления при достаточ¬
но высокой помехоустойчивости систем.
Ошибка пеленгования равносигнальным методом при
использовании индикатора с ЭЛТ в основном определя¬
ется неточностью уравнивания амплитуд сигнальных вы¬
бросов в момент взятия пеленга. Приближенное выра¬
жение для оценки ошибки, вызванной этой причиной,
в отсутствие помех можно получить так же, как это бы¬
ло сделано в случае максимального метода пеленгова¬
ния. Обращаясь к рис. 6.10, запишем выражение для
разности амплитуды напряжения сигналов в двух поло-
264
(6.18)
жениях диаграммы направленности в виде
w _ 41’, («.) + if,.,]' - |f„ (а.) - Л/к|-) =
=Ч2/е ы ■ +w;, - if«)|,
где k — коэффициент пропорциональности.
Поскольку при малых отклонениях Ла можно счи¬
тать
Д/El е2> ТО А/ А/ 0» а А/£1 “Н А/ р2 ~ 2&fр и,
следовательно, Д/7 4kfE (а0) Д/£ 4kfE (аэ) • f Е (а0) Да.
Переходя к относительным величинам, получим
MJ . л .
— Д а 4 -т Да,
U (ао): /е/ е (ао) £ (%)
откуда
Да= Д W (%)
4/£ (%)/^ (%)
Точка пеленгования при равносигнальном методе
расположена на крутом спаде диаграммы направленно¬
сти, где ее крутизна /^(ао) значительно больше, чем
вблизи вершины. Это позволяет получить точность пе¬
ленгования значительно выше, чем при максимальном
методе. При ширине диаграммы направленности по точ¬
кам половинной мощности аа в отсутствие помех равно¬
сигнальный метод позволяет получить ошибку при ис¬
пользовании индикатора с ЭЛТ порядка (1/404-1/50) аа,
т. е. почти на порядок выше, чем при применении мето¬
да максимума. Еще лучший результат может быть по¬
лучен сочетанием равносигнального метода с автомати¬
ческим съемом угловых координат.
Из условия (6.18) следует, что для получения мини¬
мальной ошибки угол смещения диаграмм ус целесооб¬
разно выбирать так, чтобы диаграммы пересекались
в точке максимальной крутизны. При расчетах часто ис¬
пользуют аппроксимацию диаграммы направленности
кривой Гаусса:
/к(а) —exp (—1,39~).
265
В этом случае угол сдвига диаграмм утс, соответст¬
вующий пересечению диаграмм в точках максимальной
крутизны и, следовательно, максимальной чувствитель¬
ности пеленгования, равен Y?7}c = 0,85aa, что соответствует
пересечению диаграмм на уровне 0,606. Таким образом,
выбор ус=/у?пс ведет к большой потере мощности (63%)
и существенному сокращению дальности действия стан¬
ции (22%)- Поэтому с учетом наличия помех и жела¬
тельности лучшего использования мощности сигнала
уровень пересечения диаграмм обычно выбирается выше
и составляет (0,74-0,85) fE(0). Таким образом, в отличие
от метода минимума, равносигнальный метод обеспечи¬
вает лучшее использование энергии сигнала и, следова¬
тельно, более высокую помехоустойчивость системы.
§ 6.4. АВТОМАТИЧЕСКОЕ СОПРОВОЖДЕНИЕ
ПО НАПРАВЛЕНИЮ ПРИ КРУГОВОМ ОВЗОРЕ
Во многих случаях требуется автоматическое опре¬
деление угловых координат нескольких целей с сохра¬
нением обзора заданного сектора пространства. В та¬
ких случаях используются системы сопровождения в ре¬
жиме обзора, особенности которых уже рассматрива¬
лись применительно к определению дальности. При
автоматическом сопровождении в режиме кругового или
секторного обзора кроме дальности обычно определяется
только азимут, поэтому ниже обсуждаются особенности
построения азимутального канала системы автосъема и
его сопряжение с каналом дальности и лишь кратко
затрагивается определение угла места или высоты
объекта.
Рис. 6.15 поясняет принцип действия системы авто¬
матического сопровождения одной цели в режиме сек¬
торного обзора. Диаграмма направленности антенны ка¬
чается в горизонтальной плоскости в пределах сектора
обзора 0а с периодом 7%, причем обратный ход диа¬
граммы осуществляется обычно значительно быстрее,
а излучение на время обратного хода прекращается.
В этом случае объект попадает в зону облучения один
раз за период обзора TQ. При этом на выходе приемника
станции образуется пачка сигнальных импульсов, дли¬
тельность которой Тпач определяется шириной диаграм-
266
А1Ы направленности, сектором и периодом обзора: Г1гач =
= ааЛ)/На- Число импульсов в пачке определяется ча¬
стотой повторения импульсов /г = ГПач*/7п, а форма оги¬
бающей пачки зависит от формы диаграммы направлен¬
ности антенны.
В момент прохождения диаграммой середины секто¬
ра обзора формируется азимутальный селекторный им¬
пульс, который подается на азимутальный дискримина¬
тор, вырабатывающий напряжение сигнала ошибки,
Рис. 6.15. Блок-схема РЛС с автоматическим сопровождением
в режиме секторного обзора.
пропорциональное рассогласованию временного положе¬
ния вершины огибающей пачки относительно середины
азимутального селекторного импульса. Напряжение сиг¬
нала ошибки усиливается и управляет электродвигате-
267
лем, поворачивающим антенную систему в положение,
при котором сопровождаемый объект оказывается на оси
антенны, т. е. в середине сектора обзора.
Таким образом осуществляется непрерывное автома¬
тическое слежение за перемещением объекта. Величина
азимута определяется по положению антенны и может
непрерывно передаваться в вычислительное устройство
с помощью сельсина-датчика или потенциометра, меха¬
нически связанных с антенной.
Селекторный
„ импульс
Личка X дальности
сигнальных *
импульсов
от приемники
Селектор
1
Инерцион¬
ный
детектор
со сбросом
2
Фильтр
Азимутальный
селекторный
‘ импульс
3
Генератор
пилообраз-
кого
напряжения |
5
Схема
выделения
сигнала
ошибки
4
=
Ограничи¬
тель и
формиро¬
ватель
J7
Сигнал
ошибки
Рис. 6.18. Функциональная схема азимутального дискримина¬
тора.
На рис. 6.16 изображена функциональная схема одно¬
го из возможных вариантов построения азимутального
дискриминатора, а временные диаграммы на рис. 6.17
поясняют роль отдельных элементов дискриминатора.
Продетектированные и усиленные сигнальные импульсы
на выходе приемника селектируются по дальности и ази¬
муту селекторными импульсами, которые формируются
специальными схемами дальностного и азимутального
каналов системы. Отселектированные импульсы пачки
подаются на инерционный детектор со сбросом, который
вместе с последующим сглаживающим фильтром служит
для выделения огибающей пачки сигнальных импульсов.
Через каскад ограничения снизу проходит вершина оги¬
бающей, которая далее формируется в прямоугольный
импульс и подается на схему выделения сигнала ошиб-
268
пилообразного напряжения
антенны,
интегри-
ки. На эту схему поступает также пилообразное напря¬
жение с пулевой точкой, соответствующей середине ази¬
мутального селекторного импульса. В момент поступле¬
ния импульса, полученного формированием вершины оги¬
бающей пачки, нарастание
прекращается. В ре¬
зультате напряжение
сигнала ошибки на вы¬
ходе схемы оказывает¬
ся пропорциональны м
временному рассогла¬
сованию вершины оги¬
бающей относительно
середины азимутально¬
го селекторного им¬
пульса. Усиленный сиг¬
нал ошибки подается
на двигатель
являющийся
рующим звеном. Таким
образом, система со¬
провождения имеет
астатизм первого по¬
рядка, т. е. запоминает
положение.
Рассмотренное пост¬
роение системы авто¬
съема связано с пово¬
ротом всей антенной
системы и поэтому при¬
годно лишь при сопровождении
необходимости сопровождения одновременно нескольких
объектов или при желании исключить электромеханиче¬
ское управление положением антенны может быть при¬
менен другой вариант построения системы автоматиче¬
ского определения азимута в режиме кругового или сек¬
торного обзора.
На рис. 6.18 изображена упрощенная блок-схема
РЛС кругового обзора с автоматическим съемом коорди¬
нат. Антенна РЛС равномерно вращается двигателем
вращения антенны. Оператор с помощью ИКО и спе¬
циального устройства ввода системы в режим автома¬
тического сопровождения может произвести начальную
269
Рис. 6.17.
пеняющая
Временная д
работу азимутального ди¬
скриминатора.
одного объекта. При
установку диска с контактом В в положение, при кото¬
ром контакты А и В замыкаются в момент, когда антен¬
на направлена на интересующий оператора объект. При
замыкании контактов вырабатывается импульс запуска
генератора азимутальных селекторных импульсов. Сфор¬
мированный генератором азимутальный селекторный им¬
пульс подается на азимутальный дискриминатор, кото¬
рый вырабатывает напряжение сигнала ошибки, про-
Рис. 6.18. Блок-схема РЛС кругового обзора с автоматическим
съемом координат.
порциональное рассогласование временных положений
пачки сигнальных импульсов и азимутального селектор¬
ного импульса. Схема дискриминатора может быть по¬
строена аналогично рассмотренной выше.
Усиленное напряжение сигнала ошибки управляет
двигателем слежения, который стремится повернуть
диск с контактом В в положение, при котором сигналь¬
ная пачка совпадает во времени с азимутальным селек¬
торным импульсом. Таким образом, азимутальный се¬
лекторный импульс автоматически совмещается с пачкой.
При этом положение контакта относительной нулевой
отметки (обычно направление север — юг) соответствует
азимуту сопровождаемого объекта. Связав контактный
диск с датчиком синхронной связи, можно непрерывно
передавать значение азимута в вычислительное устрой¬
ство.
270
Рассмотренный вариант построения системы авто¬
съема принципиально позволяет осуществить одновре¬
менно сопровождение нескольких объектов. Для этого
необходимо иметь число контактных дисков и число ка¬
налов азимута и дальности, равное числу одновременно
сопровождаемых объектов.
При большом числе сопровождаемых объектов мно¬
гоканальная система становится громоздкой, особенно
Рис. 6.19. Сопряжение РЛС с ЦВМ.
при применении электромеханических устройств. В та¬
ких случаях предпочтительнее применение автосъема
координат с помощью ЦВМ, которые все шире исполь¬
зуются в сопряжении с РЛС.
Раньше уже рассматривался принцип измерения даль¬
ности с помощью устройств дискретного счета, поэтому
здесь затрагиваются лишь характерные особенности циф¬
рового метода при определении угловых координат.
Рис. 6.19 поясняет сопряжение РЛС с ЦВМ. Для
ввода текущих дальности, азимута и угла места сопро¬
вождаемого объекта они должны быть представлены
в двоичном коде. Задача преобразования времени за¬
держки сигнального импульса, характеризующего даль¬
ность, и углового положения антенны в момент приема
сигнала от сопровождаемого объекта в двоичный код
выполняется устройством инструментального съема дан¬
ных.
Сигнал с выхода приемника РЛС поступает на пре¬
селектор, который производит выделение полезного сиг¬
нала из помех, пли, как принято говорить, первичную
271
обработку сигнала. Как известно, воздействие помех мо¬
жет привести к подавлению сигнала и, следовательно,
к его пропуску или, наоборот, к появлению ложного вы¬
броса, который может быть принят за сигнал. При изме¬
рении азимута по центру пачки пропуск импульсов в на¬
чале пачки или появление ложных выбросов в конце пач¬
ки ведет к смещению центра пачки в сторону увеличения
азимута и вызывает ошибку измерения положительного
знака. Противоположное воздействие выбросов шумов
приводит к ошибке отрицательного знака.
t
2
и У У и
t
3
и и и
t
4
Ш ...
5
ПУП
t
6
11
t
7
п
' t
6)
t
Рис. 6.20. Блок-схема пресе¬
лектора на линиях задержки
с фиксацией азимута (а) и
временная диаграмма (6),
поясняющая работу схемы.
При первичной обработке сигнала обычно использу¬
ются различные методы накопления периодически по¬
вторяющегося полезного сигнала. Здесь мы остановимся
только на одном примере дискретной обработки пачки,
позволяющей выделить из шумов импульсы пачки и
фпксировагь азимутальное положение пачки по второму
импульсу пачки или по началу и концу пачки.
272
Применяется много способов дискретной обработки.
Ниже рассматривается простейший способ обработки по
методу совпадений I импульсов подряд из пачки с чи¬
слом импульсов, равным п. Блок-схема преселектора на
линиях задержки с фиксацией азимута для 1 = 2 приве¬
дена на рис. 6.20,а. Пачка сигнальных импульсов преоб¬
разуется генератором стандартных импульсов в после¬
довательность прямоугольных импульсов постоянной
амплитуды и длительности. Эти импульсы подаются на
схему совпадений, состоящую из линии задержки Л3\
с временем задержки т3, равным периоду повторения им¬
пульсов Т^, и вентиля совпадения ВС. При 1 = 2 вентиль
имеет два входа и пропускает импульс на выход только
при совпадении импульсов на входах. Таким образом,
для получения выходного импульса необходимы по край¬
ней мере два стандартных импульса, следующих с пе¬
риодом Тп. При этом первый, задержанный на период
Тп, и второй, незадержанный, совпадают, и на выходе
появляется импульс цели. Случайные выбросы помех
проходят сравнительно редко, так как интервалы между
ними случайны и, как правило, отличаются от Тп.
Для фиксации азимута по второму импульсу пачки
используется вторая линия задержки Л32 и вентиль не¬
совпадений ВН[, пропускающий импульс на выход при
отсутствии импульса на втором входе. Из временной
диаграммы на рис. 6.20,6 ясно, что на выход схемы про¬
ходит импульс (6), соответствующий второму импульсу
пачки. При этом точка фиксации пачки будет смещена
относительно ее центра. Точность отсчета азимута можно
повысить при фиксации азимута по началу и концу пач¬
ки. В этом случае измеряемый азимут будет средним
значением двух отсчетов
„ gH + «к
При построении рассматриваемой схемы за конец
пачки принят первый пропуск, который фиксируется вто¬
рым вентилем несовпадения ВН2. Из временной диа¬
граммы видно, что первый пропуск соответствует в дан¬
ном случае последнему импульсу пачки. Таким образом,
на выходе преселектора выдается импульс (или два им¬
пульса) цели, позволяющий измерить азимут и даль¬
ность цели.
] 8—11.73 27.3
Если импульс па выходе преселектора получился
в результате комбинации шумовых выбросов, то он на¬
зывается ложным. Этому импульсу также соответствуют
определенные дальность и азимут, которые являются
координатами ложной цели. Ложные цели могут быть
исключены в результате обработки данных вычислитель¬
ной машиной, которая называется вторичной обработ¬
кой.
В блок памяти ЦВМ
Рис. 6.21. Схема простейшего электронно-оптического
преобразователя угла поворота в двоичный код.
Для ввода в ЦВМ координаты должны быть пред¬
ставлены в двоичном коде. Преобразование дальности
в число было рассмотрено при измерении дальности. Для
измерения азимута или угла места необходимо осуще¬
ствить преобразование угла поворота в число.
При постоянной скорости вращения антенны оа угол
поворота антенны пропорционален времени <\t, и изме¬
рение азимута сводится к рассмотренному ранее преоб¬
разованию временного интервала в цифровой код.
Однако в большинстве случаев невозможно обеспечить
достаточную стабильность скорости вращения антенны,
особенно при переменных ветровых нагрузках. Поэтому
косвенный способ преобразования используется редко.
Обычно применяются различные способы непосредствен¬
ного преобразования угла поворота в число.
Простейший электронно-оптический преобразователь
изображен на рис. 6.21. Непрозрачный диск с прорезя¬
ми, число которых определяется дискретностью отсчета
274
угла, располагается между источником света и фотоэле¬
ментом. При вращении диска синхронно с антенной фо¬
тоэлемент периодически освещается через прорези, пре¬
образуя световые импульсы в электрические, которые
считаются двоичным счетчиком.
В момент поступления импульсов цели от преселек¬
тора генератор импульсов считывания вырабатывает им¬
пульс, который подается па вентили совпадения. При
этом со счетчика считывается число в двоичном коде,
соответствующее азимуту цели. Это число через.распрс-
делитель-сдвигатель вводится в блок памяти ЦВМ, ко¬
торая производит дальнейшую обработку информации.
При плавном отклонении диаграммы направленности
антенны в угломестной плоскости измерение угла места
может производиться так же, как азимута, т. е. с по¬
мощью преобразования угла отклонения диаграммы
в числовой код. Однако во многих случаях диаграмма
направленности антенны перемещается по углу места
не плавно, а скачками со строки на строку. Следова¬
тельно, при использовании одноканальных систем можно
указать лишь номер строки или двух смежных строк, на
которых зафиксировано наличие сигнала, а для много¬
канальных систем — номер канала.
При моноимпульсном методе возможен отсчет и
в промежутке между строками. В подобных случаях воз¬
никает необходимость преобразования напряжения в чи¬
сло, которое может быть осуществлено различными спо¬
собами. Обычно номер строки или канала дает старшие
разряды кода, а уточнение выражается младшими раз¬
рядами.
Таким образом, за каждый цикл обзора с устройства
инструментального съема в блок памяти ЦВМ вводятся
координаты целей. ЦВМ производит вторичную обработ¬
ку сигналов, которая сводится к идентификации и экстра¬
поляции траекторий движения целей.
Идентификация заключается в установлении при¬
надлежности получаемых от устройства инструменталь¬
ного съема координат определенной цели, известной по
предыдущим циклам обзора или обнаруженной впервые.
Эта задача решается сопоставлением данных об ожи¬
даемых координатах сопровождаемой цели, вычислен¬
ных по предыдущим циклам обзора (экстраполяция
18* 275
Данных), с координатами, получаемыми от устройства
инструментального съема.
Вторичная обработка радиолокационных сигналов
позволяет не только определить параметры движения
объектов, но также сохранить сопровождение при крат¬
ковременном пропадании сигналов, опознать и отбросить
ложные цели.
Рис. 6.22. Экстраполяция и идентифи¬
кация траектории движения цели.
Рассмотрим операции вторичной обработки сигналов
обзорной РЛС, причем предположим, что используется
прямоугольная система координат х, у, которая имеет
ряд преимуществ сравнительно с полярной и находит
все более широкое применение как в цифровых, так и
аналоговых системах автоматического съема координат.
Допустим, что по данным трех предыдущих циклов
обзора (k—2, k—1 и k) необходимо определить, в ка¬
кой точке плоскости х, у будет находиться цель
к (&+1)-му циклу обзора. При экстраполяции (рис. 6.22)
естественно считать, что цель продолжает перемещаться
по той же траектории и с той же скоростью. Ожидаемое
положение цели с упрежденными координатами х\+г и
z/\+b вычисляемыми машиной, изображено на рисунке
точкой Ау. ЦВМ рассчитывает также возможное уклоне¬
ние (Дх и Ду) цели от упрежденного положения, пред¬
сказываемого машиной. Причинами таких уклонений
являются ошибки РЛС, а также отличие маневра цели
от принятого при экстраполяции траектории машиной.
Сравнение фактических координат цели в (й+1)-м цик¬
ле обзора с предсказанными ЦВМ позволяет произвести
276
идентификацию целей. Фактические координаты ад-н и
признаются принадлежащими уже сопровождаемой
цели, если выполняются неравенства
|х\+1—xk+i I Ах, It/'fc+i—г/fe+i I sCАг/,
проверка которых производится машиной. Если неравен¬
ства удовлетворяются, машина приступает к вычисле¬
нию упрежденных координат для (£ + 2)-го цикла обзо¬
ра на основе (k—1)-го, А-го и (7г+1)-го циклов.
При невыполнении неравенств для данной цели ма¬
шина производит последовательное сопоставление изме¬
ренных координат с вычисленными машиной для всех
других сопровождаемых целей. При невыполнении не¬
равенств для всех целей измеренные координаты призна¬
ются принадлежащими новой цели и записываются
в свободную ячейку памяти. Выполняя экстраполяцию
и сравнение в последующих циклах обзора, можно уста¬
новить принадлежность записанных данных реальному
объекту или ложной цели, вызванной помехами. В по¬
следнем случае данные отбрасываются и соответствую¬
щие ячейки памяти машины освобождаются.
Благодаря непрерывному вычислению упрежденных
координат и сопоставлению их с измеряемыми ЦВМ
осуществляет непрерывное сопровождение каждой цели
в отдельности. При этом сопровождение не нарушается
даже при пересекающихся траекториях, а также при
пропадании сигнала в каком-либо из циклов обзора.
Большой объем памяти и высокая скорость счета ЦВМ
позволяют одновременно сопровождать большое число
объектов, и в этом большое преимущество сопровожде¬
ния с помощью ЦВМ по сравнению с многоканальной
системой автосъема аналогового типа.
§ 6.5. УГЛОВАЯ РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ
И МЕТОД БОКОВОГО ОБЗОРА ЗЕМНОЙ
ПОВЕРХНОСТИ С ПОМОЩЬЮ
СИНТЕЗИРОВАННЫХ АНТЕНН
Напомним, что под угловой разрешающей способ¬
ностью (УРС) понимают способность системы воспроиз¬
водить раздельно однотипные сигналы двух точечных
источников, находящихся на одинаковом расстоянии от
приемника системы, на близких, но отличающихся угло-
277
вых направлениях. Количественно УРС принято измерят!
непосредственно минимальным углом между направле-
пнями на точечные источники, при котором их сигналы
еще фиксируются системой раздельно.
Особенно важное значение УРС имеет для панорам¬
ных РЛС, так как практически определяет четкость по¬
лучаемого радиолокационного изображения местности
Рис. 6.23. К определению угловой разрешающей способности пано¬
рамной РЛС:
а — вращающаяся диаграмма и две точечные цели; б — отметки целей на
экране ИДО; в — распределение яркости отметок в зависимости от углового
направления.
в секторе обзора станции, поэтому дальше УРС рассма¬
тривается применительно к таким станциям.
Предположим, что два точечных радиолокационных
объекта расположены иа одной дальности и облучаются
вращающейся антенной с диаграммой направленности,
имеющей в плоскости вращения ширину сса (рис. 6.23,а).
При вращении антенны амплитуда отраженных сигна¬
лов меняется по закону, описывающему диаграмму на¬
правленности антенны. Если в станции используется ин¬
дикатор с яркостной модуляцией луча трубки, как это
имеет место в панорамных РЛС, то объекты на экране
воспроизводятся в виде ярких пятен. Два объекта мож-
278
но видеть раздельно, если между пятнами будет замет¬
ный провал яркости. На рис. 6.23,6 изображено распре¬
деление яркости двух близко расположенных отметок
в функции угла поворота антенны. Если размер пятна
трубки мал сравнительно с шириной диаграммы в мас¬
штабе индикатора, то распределение яркости отметки
будет определяться формой диаграммы направленности.
Минимальный разрешаемый угол ДаМШг соответствует
провалу яркости между отметками ДВ«0,ЗВпг, еще раз¬
личимому глазом оператора. Разрешаемый угол в общем
случае превышает ширину диаграммы а.а, так как при
Да = аа провал яркости отсутствует. Расчет показывает,
что разрешаемый угол приближенно равен
Дс&мпп~ l>2ct'a« (6.19)
Таким образом, предельное значение УРС опреде¬
ляется диаграммой направленности антенны и практи¬
чески обычно принимается равной ее ширине аа в точках
половинной мощности. Этот вывод совпадает с получен¬
ным в § 6.2, где потенциальное значение УРС оценива¬
лось протяженностью области высокой корреляции авто¬
корреляционной функции углового импульса.
Если угловой размер пятна трубки индикатора кру¬
гового обзора, равный ап= -р соизмерим с шириной
диаграммы направленности антенны, то УРС ухудшает¬
ся. С учетом конечных размеров пятна трубки разре¬
шаемый угол приближенно можно принять равным
.Дар~аа + ап. При расположении отметок целей на не¬
больших расстояниях г от центра экрана трубки угло¬
вой размер пятна ап может значительно превышать ши¬
рину диаграммы направленности. В этом случае УРС
далека от потенциальной и определяется в основном ин¬
дикатором:
где clu— диаметр пятна трубки.
Для полного использования возможностей РЛС мас¬
штаб индикатора следует выбирать так, чтобы отметки
целей располагались дальше от центра экрана для вы¬
полнения условия агг<^аа, обеспечивающего приближе¬
ние к предельному значению УРС.
279
Для сопоставления разрешающей способности по
дальности и по углу последнюю удобно характеризовать
расстоянием, разрешаемым в направлении, перпендику¬
лярном линии пеленга. Очевидно, в рассматриваемом
случае разрешаемое расстояние по углу зависит от
дальности D и приближенно равно
Абанин = АаМии * В аа * D. (6.20)
Для антенн с поперечным излучением (рупорные, па¬
раболические и линзовые антенны) и размером раскры¬
ва dA можно принять
(6.21)
Для антенных систем с осевым излучением (провод)
длиной /д ширина диаграммы приближенно равна
~ (6.22)
Таким образом, для заданной дальности разрешающая
способность систем с обычными антеннами может быть
повышена лишь путем увеличения размеров антенны или
укорочения длины волны.
Насколько актуальна проблема повышения УРС, по¬
казывает простое сопоставление разрешаемых расстоя¬
ний по углу и по дальности. Предположим, что импульс¬
ная РЛС, имеющая длительность импульса ти = 0,2 мксек
и ширину диаграммы направленности аа = 3°, производит
обзор местности на расстоянии D = 20 км. Тогда раз¬
решаемые системой расстояния составляют
А£иин~--у- = 30 м, по дальности и
Д0а>1ин^аа0=1050 М П0 УГЛУ’
При увеличении D разрешение по углу будет еще
хуже.
Расстояния Д-Омип и ДРами„ определяют размеры
элемента, разрешаемого системой, который часто назы¬
вают разрешаемой или отражающей площадью. При
воспроизведении изображения участка местности на
экране индикатора станции разрешаемая площадь игра¬
ет роль элемента разложения, величина которого, так
же как и в телевидении, определяет четкость изображе-
280
НИЯ на экране. Таким образом, решение проблемы раз¬
решающей способности систем, и в частности повыше¬
ния четкости радиолокационного изображения, заключа¬
ется в основном в сужении диаграмм направленности
антенных систем. Прямые методы повышения направ¬
ленности путем увеличения размеров антенн или укоро¬
чения длины волны не всегда реализуемы, поэтому
в последнее время большое внимание уделяется разра¬
ботке сверхнаправлепных и синтезированных антенн.
Цель
I
I
V у
ТГ~,~7 И Г~
Р ез у ль т up у нищий
сигнал
'"Х . X
Рис. 6.24. К принципу синтезированной антенны:
а — воображаемые диполи синтезированной решетки; б — последовательные
положения реальной антенны самолетной панорамной РЛС.
Теоретически возможно создать антенны с шириной
диаграммы направленности, значительно меньшей, чем
это следует из формул (6.21) и (6.22), путем специаль¬
ного подбора распределения поля в раскрыве антенны
с поперечным излучением или распределения тока вдоль
провода линейной антенны. Такие антенны называются
сверхнаправленными. В настоящее время такие антенны
представляют интерес для применения в системах
ионосферной связи в дециметровом диапазоне, а также
для связи с космическими объектами на дециметровых
волнах, т. е. в тех случаях, когда необходимая направ¬
ленность не может быть достигнута обычным путем из-
за большой стоимости и громоздкости антенных систем.
281
В частном, но очень важном случае самолетных па¬
норамных РЛС обзора земной поверхности большие воз¬
можности улучшения четкости радиолокационных изо¬
бражений местности открывает применение так называ¬
емых синтезированных антенн, позволяющих радикально
повысить УРС.
При поступательном движении самолета, несущего
радиолокационную антенн
Рис. 6.25. К определению дли¬
ны фокусированной синтезиро¬
ванной антенны.
, диаграмма направленности
которой перпендикулярна
продольной оси самолета
(производится так называе¬
мый боковой обзор), после¬
довательные положения ан¬
тенны в пространстве могут
рассматриваться как эле¬
менты некоторой линейной
антенной решетки (рис.
6.24). Запоминая с помощью
специального устройства ин¬
формацию о фазе принимае¬
мых сигналов в этих поло¬
жениях антенны и суммируя
эти сигналы, можно синте¬
зировать воображаемую ан¬
тенну большой длины Lc, по¬
зволяющую получить очень
высокую направленность. В
синтезированной антенне ди¬
поли одновременно не существуют, и крестики на
рис. 6.24 соответствуют последовательным положениям
реальной антенны, размер которой по направлению дви¬
жения самолета равен dA,
Если запоминаются и обрабатываются все сигналы,
поступающие за время прохождения зоны, облучаемой
реальной антенной и равной ааО, длина синтезирован¬
ной антенны будет равна (рис. 6.25)
Lc=a*D. (6.23)
Фазовый сдвиг сигнала для каждого элемента синте¬
зированной антенны определяется прохождением удвоен¬
ного расстояния D, поэтому ширина диаграммы направ-
282
ценности
синтезированной антенны будет примерно
Л Л
2ЛС — 2ааО ‘
(6.24)
Имея в виду выражение (6.21) для ширины диаграм¬
мы реальной антенны станции аа, найдем расстояние,
разрешаемое синтезированной антенной в азимутальном
направлении:
(6.25)
Таким образом, при использовании всей информации
о сигналах, поступающих за время прохождения само¬
летом линейной ширины луча реальной антенны, синте¬
зированная антенна позволяет разрешать объекты на
расстоянии, равном половине размера антенны станции.
Следует подчеркнуть, что реализация предельных зна¬
чений длины синтезированной антенны (6.23) и разре¬
шающей способности (6.25) возможна лишь при строго
синфазном сложении сигналов, принимаемых всеми эле¬
ментами воображаемой решетки.
Для выполнения условия синфазности при суммиро¬
вании вводятся фазовые поправки на разность расстоя¬
ний, проходимых сигналом до различных элементов син¬
тезированной решетки. Такая антенна называется фоку¬
сированной.
В некоторых случаях не требуется реализации пре¬
дельной разрешающей способности (6.25). При этом
длина синтезированной антенны может быть уменьшена
до значения
Л”—-
X W
2<хс —2-ADa’
(6.26)
определяемого заданными значениями дальности систе¬
мы D и разрешаемого в угловом направлении расстоя¬
ния ДОа.
При некоторых значениях D и ADa может оказаться
ненужной дополнительная фазовая обработка сигналов,
так как при небольшой длине L синтезированной антен¬
ны фазовые сдвиги, вызванные разницей расстояний,
становятся несущественными. При отсутствии дополни¬
тельной фазовой обработки синтезированная антенна
называется нефокусированной.
283
мируются оез введения
>4—X---X X * У. -Яг
r< L зф
Рис. 6.26. К определению
эффективной длины £Эф не¬
фокусированной синтезиро¬
ванной антенны.
Несфокусированную антенну создать значительно про¬
ще, так как когерентные сигналы непосредственно сум-
дополнительных фазовых сдви¬
гов перед суммированием. От¬
сутствие фазовой обработки
ограничивает возможную дли¬
ну синтезированной антенны.
Эффективную предельную дли¬
ну нефокусированной антенны
легко найти, исходя из допу¬
стимой разности фаз сигналов,
принимаемых крайними эле¬
ментами синтезированной ре¬
шетки, равной л/2 (что соот¬
ветствует разности хода в од¬
ном направлении Z/8). Непо¬
средственно из рис. 6.26 это
условие можно выразить урав¬
нением
(° + т)!=(ЦгУ + с’.
решение которого в предположении, что D^>Х/16, позво¬
ляет определить эффективную длину нефокусированной
синтезированной антенны:
Дэф — V Ю,
где D — расстояние от середины синтезированного рас¬
крыва до цели.
С учетом зависимости относительных фаз принимае¬
мых сигналов от удвоенного расстояния от антенны до
цели ширина диаграммы нефокусированной антенны
равна
__ *
Ян* -- 2£эф — V 4D ’
Отсюда найдем разрешаемое расстояние по углу при
нефокусированной антенне:
AO..:-2-?’ (6J7>
Видим, что в нефокусированных антенных системах
разрешаемое расстояние в направлении, перпендикуляр-
.28.1
ном линии самолет — цель, не зависит от раскрыва ре¬
альной антенны и определяется только дальностью и
длиной волны. При этом УРС улучшается обратно про¬
порционально J/"X, в то время как для систем с реаль¬
ными антеннами — обратно пропорционально %.
Из изложенного ясно, что по мере повышения требо¬
ваний к УРС панорамных РЛС следует переходить по¬
следовательно к использованию несфокусированных и фо¬
кусированных антенн с синтезированным раскрывом.
Повышение разрешающей способности системы, и
в частности УРС, ведет к повышению информационных
возможностей системы. В связи с этим остановимся ко¬
ротко на информационной оценке радиолокационных си¬
стем, которая в ряде случаев является весьма удобной,
так как позволяет оценить систему по совокупности
основных параметров и получить рекомендации к их
рациональному выбору. Поясним это на примере РЛС
кругового обзора.
Найдем количество информации, доставляемое стан¬
цией за один обзор при длительности импульса ти, ши¬
рине диаграммы направленности антенны аа и макси¬
мальной дальности надежного обнаружения DMauc. При
круговом обзоре сектор обзора РЛС составляет 2л.
В этом случае число разрешаемых станций в пределах
сектора обзора элементарных площадок составляет
2тс ^макс 2л 2DMaKC //? 0q\
/г — . (b.zo)
Дамии АОмип аа тиС
Количество информации связано с числом элемен¬
тов п формулой
/ = lg2S-, (6.29)
где S — число различимых градаций в пределах каждо¬
го элемента.
В рассматриваемом случае станции обнаружения
S = 2, так как в пределах элементарной площадки цель
может быть обнаружена или не обнаружена. В связи
с этим количество информации, доставляемое системой
за один обзор, равно числу разрешаемых элементов за
время обзора 7У, т. е.
(б.зо)
285
Более удобно использовать количество информации,
доставляемое системой в единицу времени:
/
7 о С7ати7о
(6.31)
Параметр Нс характеризует скорость сбора информа¬
ции системой или пропускную способность и иногда для
сокращения называется информативностью системы.
Если в формулу (6.31) подставить выражение для РМакс,
получается уравнение, связывающее основные техниче¬
ские характеристики РЛС и позволяющее дать рекомен¬
дации к их рациональному выбору. Особенно удобна ин¬
формационная оценка при рассмотрении обзорных ра¬
диолокационных систем с автоматическим съемом коор¬
динат, так как облегчает выбор оптимальных техниче¬
ских параметров по совокупности заданных тактических
характеристик системы — дальности действия, точности
и разрешающей способности.
§ 6.6. ПРИНЦИП ПОСТРОЕНИЯ СИСТЕМ
АВТОМАТИЧЕСКОГО СОПРОВОЖДЕНИЯ
ПО НАПРАВЛЕНИЮ ПРИ КОНИЧЕСКОМ
СКАНИРОВАНИИ
Системы автоматического сопровождения при кони¬
ческом сканировании широко применяются в РЛС со¬
провождения воздушных и космических объектов, в си¬
стемах самонаведения ракет, в радиоастрономических
пеленгаторах.
Принцип автоматического сопровождения по направ¬
лению поясним на примере импульсной РЛС орудийной
наводки, который стал классическим. Жак и при кони¬
ческом обзоре, антенна РЛС формирует луч, отклонен¬
ный от оси антенной системы на угол у. При вращении
луча образуется равносигнальная ось, совпадающая
с осью антенны. При отклонении оси антенны от направ¬
ления на объект амплитуда принимаемого сигнала будет
изменяться в зависимости от мгновенного положения
диаграммы направленности антенны (рис. 6.27) прибли¬
зительно по синусоидальному закону с частотой враще¬
ния диаграммы Qr. Глубина модуляции амплитуды сиг¬
нальных импульсов в пределах небольших отклонений
пропорциональна величине рассогласования равиосиг-
286
пального направления и направления на объект, а фаза
модуляции зависит от направления отклопе-
модуляции однозначно определяет ве-
отклонения объекта от равносиг-
оги бающей
ния. Огибающая
личину и направление
налы-юй оси и поэтому но¬
сит название сигнала ошиб¬
ки. Таким образом, роль ди¬
скриминатора, выделяющего
сигнал ошибки, здесь играет
антенна (рис. 6.28).
Напряжение сигнала оши¬
бки формируется путем де¬
тектирования сигнальных
импульсов пиковым детекто¬
ром сигнала ошибки, кото¬
рый включен после видео¬
усилителя приемника, от¬
крывающегося селекторны¬
ми импульсами дальности
только для сигнала сопро¬
вождаемого объекта. Далее
с помощью фазовых дискри¬
минаторов азимутального и
угломестного каналов выде¬
ляются азимутальная и уг¬
ломестная составляющие
сигнала ошибки. Эти состав¬
ляющие подаются на входы
азимутальной и угломестной
следящих систем, непрерыв¬
Рис. 6.27. Изменение ампли¬
туды сигнальных импульсов
при различных положениях
цели.
но совмещающих равносигнальную ось с направлением
на объект.
Данные о положениях антенны по азимуту и углу ме¬
ста могут быть переданы на управляемые станцией ору¬
дия с помощью сельсин-датчиков или потенциометров.
При применении подобной системы для самонаведения
ракет сигнал ошибки, пропорциональный рассогласова¬
нию осей ракеты и направления на цель, используется
в следящих системах управления рулями ракеты. При
автоматическом определении угловых координат в ра¬
диолокационном прицеле на истребителе данные об
угловом положении объекта выводятся на специальный
287
индикатор, позволяющий осуществлять прицельный
огонь в отсутствие оптической видимости.
Следящие системы азимутального и угломестного ка¬
налов принципиально одинаковы, поэтому достаточно
рассмотреть более подробно, например, азимутальный
канал. Сигнал ошибки после детектора усиливается уси¬
лителем, коэффициент усиления которого автоматически
изменяется обратно пропорционально средней амплиту-
Кана/i азимута
Рнс. 6.28. Функциональная схема РЛС с автоматическим определе¬
нием угловых координат [17].
де сигнальных импульсов. Благодаря этому амплитуда
сигнальных импульсов не зависит от силы принимаемого
сигнала и сохраняется пропорциональной только глуби¬
не модуляции. После усиления сигнал ошибки подается
на фазовый дискриминатор, на который подается также
напряжение от генератора опорных напряжений. По¬
следний связан с двигателем вращения излучателя, бла¬
годаря чему частота опорного напряжения равна часто¬
те ©ращения диаграммы, а его фаза строго соответствует
мгновенным положениям диаграммы. Обычно угловая
скорость вращения диаграммы выбирается в пределах
1 500—3 000 об/мин, что соответствует частоте сигнала
288
ошибки и опорного напряжения, равной 25—50 Двух¬
фазный генератор опорных напряжений 'вырабатывает
две составляющие опорного напряжения, сдвинутых по
фазе на 90°. Эти составляющие подаются соответствен¬
но на азимутальный и угломестный фазовые дискрими¬
наторы, преобразующие сигнал ошибки в постоянные
напряжения, величины которых пропорциональны соот¬
ветственно рассогласованиям в азимутальной и угло¬
местной плоскостях.
После сглаживания специальным фильтром напряже¬
ние сигнала ошибки усиливается двухтактным усилите¬
лем постоянного тока и подается на две управляющие
обмотки электромашинного усилителя (ЭМУ). Разность
намагничивающих ампервитков этих обмоток, пропор¬
циональная величине сигнала ошибки, создает на выход¬
ных щетках ЭМУ усиленное напряжение, которое по¬
дается на исполнительный двигатель поворота антенны.
Если ось антенны совпадает с направлением на объект,
то напряжение сигнала ошибки равно нулю и двигатель
остается неподвижным, так как система имеет только
один интегратор (двигатель) и запоминает положение.
При наличии рассогласования появляется сигнал ошиб¬
ки, пропорциональный рассогласованию, и двигатель по¬
ворачивает антенну, ликвидируя рассогласование. Для
получения высокой точности сопровождения следящие
системы имеют 'высокую чувствительность и начинают
отработку при рассогласованиях порядка долей угловой
минуты. Такая высокая чувствительность обеспечивает¬
ся большим коэффициентом усиления, при котором си¬
стема оказывается неустойчивой. Для придания системе
достаточной устойчивости вводятся корректирующие це¬
пи. В рассматриваемой системе коррекция осущест¬
вляется цепью обратной связи.
При переходе системы от ручного сопровождения
к автоматическому или, как принято говорить, при вво¬
де системы в режим сопровождения возможны большие
рассогласования. Для быстрого уменьшения рассогласо¬
вания система должна иметь достаточное быстродей¬
ствие, определяемое длительностью переходного процес¬
са Тпер. Длительность переходного процесса связана об¬
ратной пропорциональностью с полосой пропускания
следящей системы, ограниченной частотой среза соСр.
В связи с этим полоса пропускания, так же как и коэф-
19—1173 289
фицпепт усиления системы, является одним из основных
параметров системы. При выборе полосы пропускании
учитываются не только заданная динамическая точность
и быстродействие системы, но и необходимость обеспе¬
чить помехоустойчивость системы. Для уменьшения воз¬
действия флюктуационных ошибок полоса пропускания
системы должна быть по возможности уже. Таким обра¬
зом, так же как и в системе сопровождения по даль¬
ности, полоса пропускания выбирается для получения
минимальной результирующей ошибки системы.
В рассматриваемой системе сопровождения по на¬
правлению с использованием конического сканирования
луча применяется резонансный фильтр, настроенный на
частоту сканирования, который позволяет уменьшить ис¬
кажения синусоидального напряжения сигнала ошибки,
вызванные флюктуациями амплитуды сигнальных им¬
пульсов из-за флюктуаций эффективной площади рас¬
сеяния цели и воздействия помех. Такие искажения мо¬
гут быть вызваны также умышленными помехами. Зная
частоту сканирования, легко создать помеху с большой
спектральной плотностью вблизи частоты сканирования.
Такая помеха окажется в полосе пропускания системы
и может привести к большим ошибкам сопровождения и
даже сделать сопровождение невозможным. В связи
с этим применяются системы со скрытой частотой скани¬
рования (в которых диаграмма сканирует только при
приеме), обладающие более высокой помехоустойчи¬
востью, так как противник не имеет возможности изме¬
рить частоту сканирования РЛС и, следовательно, со¬
здать эффективную прицельную помеху. При этом обыч¬
но используют не вращающиеся диаграммы, а откло¬
няющиеся последовательно вверх — вправо — вниз —
влево путем переключения соответствующих излучателей
антенной системы. При передаче все излучатели рабо¬
тают синфазно и формируют результирующую диаграм¬
му, ось которой совпадает с осью антенной системы.
Метод конического сканирования в сочетании с авто¬
матическим совмещением равносигнальной оси с направ¬
лением на источник сигнала широко используется в ра¬
диоастрономических пеленгаторах [3]. Благодаря скани¬
рованию одновременно обеспечивается модуляция (моду¬
ляционный метод приема) сигналов пеленгуемого косми¬
ческого источника излучения, необходимая для отделе-
290
ния принимаемых сигналов шумового типа от собствен¬
ных шумов приемника. Действительно, при вращении
диаграммы шумовой сигнал источника, смещенного от¬
носительно равносигнальной оси, оказывается модулиро¬
ванным по амплитуде с частотой вращения диаграммы.
Это позволяет выделить полезную составляющую сигна¬
ла ошибки, которая используется для управления поло¬
жением антенны с помощью следящих систем, аналогич¬
ных применяемым в рассмотренной РЛС сопровождения
воздушных целей. Конечно, характеристики системы от¬
личаются, так как угловые скорости и ускорения при со¬
провождении космических источников излучения, как
правило, значительно меньше, чем при сопровождении
самолетов или ракет. Однако в связи с применением
рефлекторов очень больших размеров моменты сопро¬
тивления антенных систем радиоастрономических пелен¬
гаторов весьма велики, что вызывает специфические
трудности при создании следящих систем.
Рассмотренная система автоматического сопровожде¬
ния ио направлению может обеспечить высокую точ¬
ность сопровождения, но подвержена влиянию специфи¬
ческих помех. В частности, точность сопровождения рез¬
ко снижается при наличии спектральных составляющих
флюктуаций амплитуды сигнала, близких по частоте
к частоте сканирования диаграммы. От этого недостатка
свободны моиоимпульсныс системы автоматического со¬
провождения, рассматриваемые в § 6.8.
§ 6.7. ФАЗОВЫЙ МЕТОД ИЗМЕРЕНИЯ УГЛОВЫХ
КООРДИНАТ И УГЛОВОЙ СКОРОСТИ
В § 1.7 указывалось, что при чисто фазовых методах
пеленгования направление определяется разностью фаз
напряжений сигналов пеленгуемого обьекта, принимае¬
мых двумя разнесенными в пространстве антеннами:
= (6.32)
где AD = Da—DB — разность расстояний пеленгуемого
объекта от антенн А и В;
d --- база антенной системы.
Фазовые угломерные системы позволяют не только
определить направление на объект, но п измерить его
угловую скорость относительно центра базы. В самом
19* 291
деле, дифференцируя выражение (6.32) но времени,
ПО-
лучим
dt
Отсюда
можно найти угловую скорость
-у COS а
Л. и13
Но -у- и у- представляют допплеровские приращения ча¬
стоты Fva и Fvb, пропорциональные радиальной скорости
объекта Ьл и Ьв относительно антенн А и В. Измерение
разностной частоты допплеровских приращений Fa = FyA —
da db
— FVB = у у позволяет непосредственно определить
Рис. 6.29. К определению направления на плоскости (а) и в про¬
странстве (б).
Если пеленгуемый объект находится над земной по¬
верхностью (рис. 6.29,6), разность фаз колебаний, прини¬
маемых антеннами А и В, будет зависеть дополнитель¬
но от угла места [3:
<рх = sin a cos (6.33)
Для раздельного определения азимута и угла места
необходима вторая пара антенн Л и С, которые могут
292
быть расположены в той же плоскости, но с базой
перпендикулярной базе первой пары. Тогда фазовый
сдвиг для второй пары антенн будет
27С^2 п
?2 = —COS a cos р. (6.34)
позволяет
типа с когерентным из-
Схема расположения
антенн и рабочих секторов радио¬
маяка,
Совместное решение уравнений (6.33) и (6.34)
найти азимут а и угол места (3.
Фазовые системы с разнесенными антеннами приме¬
няются в основном в радионавигации и называются там
фазовыми угломерными системами интерференционного
типа. На это^м принципе выполняются как радиомаяки,
так и радиопеленгаторы.
Широкое распространение получил всенаправленный
радиомаяк интерференционного
лучением антенн. Радио¬
маяк имеет три антенны
(рис. 6.30), расположен¬
ные в вершинах равно¬
стороннего треугольника.
Разность фаз сигналов,
приходящих от любых
двух антенн, определяет¬
ся положением точки
приема относительно ба¬
зы. Линии постоянной
разности фаз являются
гиперболами, которые на
удалениях, превышающих
пятикратный размер ба¬
зы, практически сливают¬
ся с прямыми, направлен¬
ными к центру базы и
являющимися аспмптота-
ми гипербол.
В рассматриваемом радиомаяке длина базы выбрана
равной А/2. При этом имеется двузначность отсчета угла
и точность сильно зависит от величины угла а. Приме¬
нение трех баз позволяет устранить двузначность отсче¬
та и использовать каждую из трех сеток линий положе¬
ния и узком секторе zb30° от нормали к каждой из баз.
В секторе ±30° липни расположены равномерно, и, сле¬
довательно, равномерной будет и шкала азимута.
293
На границах сектора при а =30°
ср° 360° sin а = 90°.
Таким образом, шкала азимутов а связана со шкалой
разности фаз соотношением а=ф/3.
В системе все три антенны работают на одной часто¬
те f = 300 кгц, поэтому для разделения сигналов приме¬
няется поочередное подключение антенн Л, В и С. Син¬
хронно с той же частотой переключаются каналы при-
емоиндикатора, в которых прерывистые колебания при¬
нятого сигнала превращаются в непрерывные. Измере-
Рис. 6.31. Блок-схема фазового радиопелен¬
гатора.
ние фазометром разности фаз колебаний соседних кана¬
лов позволяет определить азимут.
Работа всех каналов на одной несущей частоте по¬
зволяет использовать узкую полосу пропускания прием¬
ника и, следовательно, обеспечить большую дальность
действия и сравнительно высокую помехоустойчивость и
точность.
Следует заметить, что любая фазовая разностно¬
дальномерная система может быть использована в каче¬
стве фазового радиомаяка на удалениях, значительно
превышающих длину базы.
Ввиду малой протяженности требуемой базы прин¬
цип интерференции особенно удобен для применения
в радиопеленгаторах, как наземных, так и бортовых. На
рис. 6.31 изображена блок-схема двухканального фазо-
294
вого радиопеленгатора. Разность фаз измеряется в при-
емоиндикаторе фазометром на промежуточной частоте.
Ранее уже отмечалось, что гетеродирование не изменяет
фазовых соотношений, но для исключения ошибок из-за
разных фазовых сдвигов в приемных каналах необходи¬
мо обеспечить их идентичность.
Рассмотрим вопрос об источниках ошибок и точности
фазовой угломерной системы более подробно.
Поскольку величины X и d известны с большой точ¬
ностью, источником ошибок в определении пеленга явля¬
ется неточность измерения разности фаз двух сигналов.
Дифференцируя выражение (6.32) и переходя к ко¬
нечным приращениям, получим
Да = , (6.35)
2л -у cos а
где Лер — ошибка при измерении разности фаз.
Таким образом, точность увеличивается при увеличе¬
нии отношения d/h и уменьшении а. Но при d^X/2 появ¬
ляется неоднозначность пеленгования. Неоднозначность
может быть устранена использованием направленных
антенн с шириной диаграммы направленности, не пре¬
вышающей ширину зоны однозначности. Для исключе¬
ния многозначности отсчета может быть использовано
также пеленгование при разной длине базы. Длина баз
должна выбираться так, чтобы ошибки пеленгования при
малой базе не превышали ширину зоны однозначности
при большой базе, т. е. требования аналогичны требова¬
ниям, предъявляемым при выборе параметров двух¬
шкальных систем измерения дальности.
Для уменьшения ошибок рабочий сектор пеленгова¬
ния не должен превышать ±30° относительно нормали
к базе. Для расширения рабочей зоны применяются си¬
стемы с позоротной базой или с двумя и тремя базами,
расположенными под определенными углами друг к дру¬
гу. При применении трех баз, как это показано на при¬
мере фазового радиомаяка, обеспечивается практически
одинаковая точность в пределах 360°.
Ошибки измерения разности фаз зависят также от
стабильности и идентичности фазовых характеристик
приемных каналов и точности фазометра.
295
При воздействии помехи шумового типа с нормаль
иым распределением среднеквадратичная ошибка изме¬
рения фазы равна
где — дисперсия ошибки, вызванной воздействием шу¬
ма; Um и Uc— действующие значения напряжений шума
и сигнала.
На основе (6.35) и (G.36) среднеквадратичная ошибка
измерения азимута при воздействии шума будет
v=—— <6-37)
2тт -д- cos а
Фазовые угломерные системы обеспечивают высокую
точность пеленгования. Предельная точность измерения
зависит от метода обработки.
Применяются две различные схемы обработки сиг¬
нала в фазовых угломерных системах. В первой из них
сигналы, принятые каждой из двух антенн, усиливаются
и преобразуются двумя идентичными приемными кана¬
лами и затем на частоте сравнения подаются на фазо¬
метрический индикатор, регистрирующий разность фаз
сигналов на выходе каналов. Во второй схеме обработки
сигналы, принятые двумя антеннами, подаются на сум¬
мирующее и вычитающее устройства. Далее суммарный
и разностный сигналы усиливаются и преобразуются дву¬
мя приемными каналами с идентичными фазовыми ха¬
рактеристиками. Затем производится измерение разно¬
сти фаз выходных сигналов. Как уже отмечалось в § 6.2,
суммарно-разностный вариант обработки позволяет
уменьшить влияние собственных шумов приемных кана¬
лов па точность измерения фазы, поскольку шумы двух
независимых каналов некоррелированны, и при суммиро¬
вании складываются в квадратуре. Суммарно-разностная
обработка широко применяется в моноимпульсных РЛС.
§ 6.8. МОНОИМПУЛЬСНЫЙ МЕТОД АВТОМАТИЧЕСКОГО
ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ
В рассмотренных выше однолучевых системах с ко¬
ническим сканированием сигнал ошибки выделяется
в результате сравнения амплитуд сигналов, прииимае-
296
мых в разнос время. При таком последовательном срав¬
нении амплитуд большое влияние на точность сопровож¬
дения оказывают флюктуации амплитуды принимаемых
сигналов, вызванные флюктуациями эффективной пло¬
щади рассеяния сопровождаемой цели и воздействием
помех. Составляющие этих флюктуаций, находящиеся
в полосе пропускания системы автосъема, искажают сиг¬
нал ошибки, что приводит к случайным отклонениям оси
антенны от направления на цель, т. е. к ошибкам сопро¬
вождения. Уменьшить воздействие флюктуаций можно
в такой системе лишь уменьшением ее полосы пропуска¬
ния, но это вызывает повышение инерционности системы
и, следовательно, увеличение динамических ошибок со¬
провождения движущихся объектов.
Принципиальное устранение ошибок из-за флюктуа¬
ций амплитуды сигнала возможно при одновременном
сравнении амплитуды или фазы сигналов, принятых по
двум или нескольким каналам, т. с. при использовании
многолучевых (многоканальных) систем. При использо¬
вании импульсного сигнала метод одновременного срав¬
нения амплитуд или фаз сигнала называется моноим-
пульсным, а РЛС и системы управления, в которых при¬
меняется этот метод, носят название моиоимпульсиых.
Моноимпульсные системы, разработанные первоначально
как средство устранения ошибок при автоматическом со¬
провождении цели из-за флюктуаций амплитуды сигна¬
лов, обнаружили впоследствии ряд ценных особенностей,
позволивших расширить область их применения. Оказа¬
лось, например, возможным использование моноимпульс-
пой системы для одновременного определения координат
нескольких объектов, находящихся в пределах диаграм¬
мы направленности антенны. В мопоимпульсиой системе
возможно также применение компенсационных методов
подавления помех, приходящих к антенне с определенно¬
го направления.
При определении направления в одной плоскости мо-
ноимпульсная система должна иметь две пересекающие¬
ся и существующие одновременно диаграммы направ¬
ленности антенны. Каждой из диаграмм соответствует
свой прнемио-усилитсльный канал. Сравнение фазы или
амплитуды сигналов на выходе каналов позволяет опре¬
делить направление на источник сигнала. Возможно так¬
же использование суммы и разности сигналов, образо¬
297
ванных непосредственно после антенной системы н обра¬
ботанных далее двумя самостоятельными приемными ка¬
налами— суммарным и разностным. В зависимости от
используемого метода сравнения сигналов и выделения
сигнала ошибки моноимпульсные системы имеют три
разновидности: фазовые, амплитудные и суммарно-раз¬
ностные.
f(^i)
Рис. 6.32. Блок-схема моноимпульсиой системы с фазовой пеленга
цией.
Система с фазовой пеленгацией (рис. 6.32) имеет ан¬
тенну с двумя разнесенными на некоторое расстояние
фазовыми центрами. Практически два фазовых центра
могут быть получены, например, с помощью двух разне¬
сенных на расстояние d антенн. При этом оси диаграмм
направленности параллельны. Если пеленгование произ¬
водится в азимутальной плоскости, а диаграммы направ¬
ленности антенн одинаковы и описываются функциями
f(ai) и f(«2), то напряжения на выходе антенн первого
и второго каналов будут
«1 =[/im sin (of + у) = kf (04) sin (mt 4- ,
«2 =U2mSin (<о/ |-) = kf (a2) sin — у),
где U\m = kf(ai) и ^2m = kf(a2)—амплитуды сигналов;
k — коэффициент пропорциональности, определяе¬
мый направленностью антенны и мощностью
сигнала;
Ф — разность фаз сигналов в фазовых центрах А[
и Д2.
298
При большом расстоянии до источника сигнала D~^>d
МОЖНО принять 01 = 02 = а и
<р = -у dsma.
Для получения пеленгационной характеристики с цен¬
тральной симметрией типа характеристики дискримина¬
тора во втором канале осуществляется дополнительный
фазовый сдвиг на угол л/2, с учетом которого напряже¬
ния на входах приемников каналов будут
kf (a) sin sin a
u2 = kf (a) sin ~ sin a
Фазы сигналов на выходе обоих каналов сравнива¬
ются с помощью фазового дискриминатора. Для исклю¬
чения влияния неодинаковости и нестабильности коэффи¬
циентов усиления каналов сигналы ограничиваются на
уровне U, и напряжение на выходе фазового дискрими¬
натора можно записать
ифц — КфЛис05 (<р — -у) = /СфдС/sin ^-^-sina
При автоматическом сопровождении угол рассогла¬
сования а достаточно мал, следовательно, sinu^a и
Uфд Д^фдГ/sin а^*
Полученная зависимость сигнала ошибки от углового
рассогласования имеет вид дискриминаториой характе¬
ристики. Разиосигиалыюму направлению, проходящему
через точку А перпендикулярно базе антенной системы,
соответствует нулевое рассогласование а = 0.
При неидентичных и нестабильных фазовых характе¬
ристиках каналов равносигпальное направление будет
определяться с ошибкой, что является существенным не¬
достатком фазового метода.
Сигнал ошибки с выхода фазового дискриминатора
подается на следящую систему, которая непрерывно сов¬
мещает равносигнальную ось с направлением на сопро¬
вождаемый объект. Следящая система может быть по¬
строена аналогично системе, рассмотренной ранее при¬
менительно к коническому сканированию луча. При отно-
299
сительно небольших изменениях направления па объект
совмещение равпоспгпалыюго направления можно осу¬
ществить изменением фазового сдвига в одном из кана¬
лов с помощью фазовращателя. При этом антенная си¬
стема остается неподвижной, что позволяет снизить инер¬
ционность всей системы и обеспечить ее высокое быстро¬
действие, точность и устойчивость. С помощью феррито¬
вого фазовращателя можно управлять фазовым сдвигом
путем изменения магнитного поля, в котором находится
феррит фазовращателя. В этом случае возможно исклю-
Рис. 6.33. Блок-схема мопоимпульсной системы с амплитудной пелен¬
гацией.
чить из следящей системы двигатели, что способствует
повышению ее быстродействия и позволяет сделать си¬
стему компактной, легкой, экономичной, надежной и со¬
вершенно бесшумной.
Моноимпульсная система с амплитудной пеленгацией
(рис. 6.33) имеет диаграмму направленности антенны
с двумя пересекающимися лепестками, каждому из кото¬
рых соответствует свой приемный канал. Такая диаграм¬
ма может быть сформирована параболической антенной
с двумя облучателями, смещенными симметрично отно¬
сительно фокуса зеркала на расстояние -А/. При фокус¬
ном расстоянии параболоида /ф и сравнительной неболь¬
шой величине смещения Д7 диаграмма отклоняется от
оси параболического зеркала приблизительно на угол
Уо —А///ф, при этом фазовую диаграмму можно считать
неизменной.
При симметричном смещении облучателей лепестки
диаграммы образуют равносигналыюе направление, сов¬
падающее с осью антенны. Если направление на источ-
300
ник сигнала лежит в азимутальной плоскости и откло¬
нено от равносигпальпой оси на угол а, то напряжения
на выходе облучателей и Д2 будут
Щ. =- Urm sin (cnZ Д- <р0) = kf (Yo — a) sin («7 <f>0),
= t/2m sin (g7 4- <P0) = kf (Yo 4- a) sin W ?o),
где фо — начальная фаза принимаемого сигнала.
При небольших смещениях облучателей отклонение
от равносигпальпой оси вызывает только изменение
амплитуды сигнала на входе приемных каналов, в то
время как фазы сигналов практически одинаковы. При
(Z = 0 амплитуды сигналов равны, что свидетельствует
о нахождении пеленгуемого объекта на равиосигпаль-
ной оси. Разность амплитуд сигналов на выходе каналов
является мерой угла рассогласования а. Для исключе¬
ния влияния интенсивности принимаемого сигнала и ко¬
эффициента усиления каналов па величину измеряемого
угла применяется вычитание сигналов, усиленных УПЧ
с логарифмической характеристикой и продетектирован-
иых линейным детектором. В этом случае мерой углового
рассогласования является отношение амплитуд сигналов
на выходе приемных каналов. Действительно, при ис¬
пользовании приемных каналов с логарифмической ам¬
плитудной характеристикой напряжение на выходе вычи¬
тающего устройства, являющееся сигналом ошибки, мож¬
но записать в виде
Uby==7(Byt/oln^=Z<,lyt/oln <6-38)
где КВу — коэффициент усиления вычитающего устрой¬
ства;
Uo — начальное напряжение на выходе логарифми¬
ческого усилителя.
Выражение (6.38), описывающее пеленгационную ха¬
рактеристику системы, показывает, что ее крутизна зави¬
сит от крутизны диаграммы направленности в окрестно¬
сти равносигпального направления, коэффициента пере¬
дачи вычитающего устройства и характеристики логариф¬
мического усилителя. Таким образом, зависимость изме¬
ряемого угла от силы принимаемого сигнала при исполь¬
зовании логарифмических усилителей исключается.
Однако неравенство коэффициентов усиления каналов и
их нестабильность приводят к ошибкам в определении
301
равносигнального направления, на что указывает зависи¬
мость сигнала ошибки от начального напряжения на вы¬
ходе логарифмических усилителей.
При автоматическом сопровождении объекта совме¬
щение равиосигналыюй оси с направлением на объект
обычно производится поворотом антенной системы с по¬
мощью следящей системы. Для управления положением
равиосигналыюй оси в небольших пределах можно ис¬
пользовать также изменение коэффициента усиления
одного из каналов обратно пропорционально величине
сигнала ошибки на выходе вычитающего устройства.
Суммарно-разностный вариант моноимпульспой си¬
стемы является наиболее совершенным, так как позво¬
ляет исключить влияние амплитуды и фазы сигнала на
стабильность равиосигнального направления и пеленга¬
ционной характеристики и тем самым обеспечить наи¬
большую точность определения направления. При сум¬
марно-разностной обработке обычно сравниваются
амплитуды сигналов, но для исключения влияния нера¬
венства и нестабильности коэффициентов усиления кана¬
лов сравнение амплитуд производится до приемных кана¬
лов непосредственно после облучателей антенны. Для
этого используются высокочастотные мостовые схемы,
выполняемые на волноводах или коаксиальных линиях
в зависимости от рабочего диапазона системы.
* См. С к о л л и к М. Введение в технику радиолокационных
систем. Изд-во «Мир», 1965.
302
Принцип действия суммарно-разностной системы по¬
ясняет функциональная схема на рис. 6.34. Излучате¬
ли Л1 и А2, симметрично смещенные относительно фо¬
куса зеркала, как и в амплитудном варианте системы,
подсоединены к точкам и а2 суммарно-разностного
моста. Расстояния ахс и а2с между отводами одинаковы
и равны 274, поэтому при излучении импульса энергия
высокочастотных колебаний от передатчика распрсделит-
Рис. 6.35. Диаграммы направленности антенны (в полярной и прямо¬
угольной системах координат) при суммарно-разностной обработке
сигналов:
а — раздельно для излучателей и /12; б —суммарная и разностная диа¬
граммы.
ся поровну между излучателями А\ и Л2, и они работают
синфазно, образуя суммарную диаграмму направленно¬
сти антенны fc(a) (рис. 6.35). В режиме приема сигна¬
лы, принятые облучателями А{ и Л2, приходят в точку с
моста с сохранением фаз и суммируются, при этом зави¬
симость суммарного напряжения ис от угла, составлен¬
ного направлением на объект и осью антенны, аналогич¬
на суммарной диаграмме при излучении. В точке р
моста, отстоящей от отвода на 272 дальше, чем от отво¬
303
да (7-2, образуется разностное напряжение ир, так как сиг¬
налы приходят сюда со сдвигом на 180°. Суммарный и
разностный сигналы поступают на вход суммарного и
разностного приемных каналов.
Зависимость разностного напряжения от угла рас¬
согласования представляет разностную диаграмму fp(a),
также изображенную на рис. 6.35 в полярной и прямо¬
угольной системах координат. Если объект отклонен от
равносигнального направления в сторону излучателя Дь
фаза разностного сигнала противоположна фазе суммар¬
ного; а при отклонении в сторону излучателя Л2 фазы
суммарного и разностного сигналов совпадают. При рас¬
положении объекта на равносигнальной оси амплитуда
разностного сигнала равна нулю. Таким образом, раз¬
ностная диаграмма аналогична дискриминаторной ха¬
рактеристике и показывает величину и знак рассогласо¬
вания.
Для выявления величины и знака рассогласования
в разностном канале используется фазовый дискримина¬
тор, причем в качестве опорного напряжения использует¬
ся сигнал на выходе УПЧ суммарного канала. После де¬
тектирования суммарный сигнал подается на индикатор¬
ное устройство и используется для обнаружения объекта
и измерения его дальности.
Для исключения влияния изменения амплитуды сиг¬
нала на крутизну пеленгационной характеристики систе¬
мы применяется быстродействующая автоматическая
регулировка усиления (БАРУ), которая работает по сум¬
марному сигналу и изменяет коэффициент усиления ка¬
налов обратно пропорционально входному напряжению
суммарного канала. При этом напряжение па выходе
суммарного канала остается постоянным, а выходное
напряжение разностного канала изменяется обратно про¬
порционально напряжению на входе суммарного кана¬
ла ис. Поскольку выходное напряжение фазового дискри¬
минатора пропорционально среднему значению произве¬
дения выходных напряжений суммарного и разностного
каналов, при эффективной работе БАРУ напряжение сиг¬
нала ошибки на выходе фазового дискриминатора ока¬
зывается пропорциональным отношению разностного и
суммарного напряжений:
7 7 11 Р
(7фл ~
f (to Ci о + tt)
f (to— “) + /■' (YoT°) ’
(6.39)
304
Таким образом, пеленгационная характеристика сум¬
марно-разностной системы определяется отношением
разности сигналов к их сумме, вследствие чего неиден-
тичиость амплитудных характеристик влияет на крутизну
пеленгационной характеристики, по нс сказывается на
положении равносигнальной оси. Тем самым устраняется
влияние флюктуаций амплитуды принимаемых сигналов.
Фазовые нестабильности также не влияют на точность,
так как в системе используется сравнение амплитуд сиг¬
налов.
Независимость положения равносигнальной .оси от
изменений амплитуды сигналов и коэффициента усиле¬
ния каналов очевидна, поскольку при суммарно-разност¬
ной обработке равпосигнальное направление определяет¬
ся не равенством напряжений па выходе двух каналов
(как в чисто амплитудной системе), а нулевой амплиту¬
дой в разностном канале. Положение же нуля не зави¬
сит ни от амплитудных, ни от фазовых характеристик
углового дискриминатора. Большая стабильность равно-
сигпалыюго направления и связанная с этим высокая
точность сопровождения является существенным достоин¬
ством суммарно-разностного метода, благодаря чему
этот метод получил наибольшее применение в моиоим-
пульсных системах.
До сих пор рассматривалось использование моно-
импульсной системы в режиме автоматического сопро¬
вождения цели, когда направление прихода сигнала
практически совпадает с равноепгнальпым. Моиоимпульс-
ная система может быть использована также для поиска
цели и для одновременного измерения угловых координат
многих целей. В этих случаях сигнал на выходе угло¬
вого дискриминатора является мерой угла отклонения
направления па цель от равносигнальной оси. Для изме¬
рения угловых отклонений производится предваритель¬
ная калибровка системы. Полученные табличные дан¬
ные могут быть введены в память ЦВМ при автомати¬
ческих измерениях или использованы оператором при
измерении углов с помощью индикатора.
При поиске целей и измерении координат многих це¬
лей возникает задача их разрешения в пределах диа¬
граммы направленности антенны. В моноимпульсной си¬
стеме такое разрешение возможно осуществить селекти¬
рованном сигнальных импульсов но дальности, если, ко-
20—1173 305
вечно, объекты расположены на разных дальностях. При
этом можно одновременно измерять угловые координаты
многих объектов, находящихся в зоне облучения станции,
по выходному напряжению углового дискриминатора,
пропорциональному углу отклонения направления на
объект от равносигнального. Возможно также осуще¬
ствить электрическое сканирование равноенгналы-юй оси
в некотором секторе, определяемом шириной диаграммы
направленности. При амплитудной пеленгации управле¬
ние положением равносигнальной оси осуществляется из¬
менением коэффициента усиления одного из каналов; при
фазовом методе — введением фазового сдвига, регулируе¬
мого с помощью фазовращателя.
Глава 7
СЕЛЕКЦИЯ СИГНАЛОВ ДВИЖУЩИХСЯ
ЦЕЛЕЙ (СДЦ) НА ФОНЕ ПАССИВНЫХ ПОМЕХ
§ 7.1. ВВЕДЕНИЕ
Отражения от местных предметов земной или водной
поверхности, гидрометеоров (облака, дождь, туман, снег),
облака металлизированных лент или сосредоточенных
отражателей могут затруднить или сделать невозможным
радиолокационное обнаружение и определение коорди¬
нат целей, так как уровень мешающих отражений может
значительно превышать полезный сигнал. В связи
с этим задача выделения полезного сигнала на фоне
пассивных помех весьма актуальна.
Для выделения полезного сигнала из помех исполь¬
зуется в основном отличие скоростей реальных целей от
скорости мешающих отражателей, которые обычно не¬
подвижны или имеют сравнительно небольшие скорости.
Могут быть использованы также различия статистиче¬
ских свойств сигнала и помех. Источники помех в связи
с этим делятся па два типа. К первому относят совокуп¬
ность большого числа случайно распределенных в про¬
странстве отражателей (гидрометеоры, поверхность мо¬
ря, облако лент), создающих сильно флюктуирующий
сигнал с широким спектром флюктуаций. Второй тип ме¬
шающих отражателей дает достаточно устойчивый сиг¬
нал с относительно узким спектром флюктуаций.
Полезные и мешающие отражатели часто отличаются
также пространственной протяженностью.
В зависимости от типа цели и мешающих отражате¬
лей для выделения полезного сигнала используются раз¬
личные методы. Поскольку свойства мешающих отраже¬
ний в значительной степени определяются видом и пара¬
метрами облучающего сигнала, для эффективной борьбы
с пассивной помехой необходимо прежде всего рацио¬
нально выбрать зондирующий сигнал.
20*
307
Наибольшее практическое применение находят перио¬
дические зондирующие сигналы, которые могут обеспе¬
чить высокую разрешающую способность по дальности
и скорости. Эффективная селекция сигналов движущихся
целей может быть осуществлена в импульсных системах
с периодическим излучением импульсов с нсмодулиро-
ванной несущей, а также с фазокодовой или частотной
модуляцией несущей. Применение периодических сигна¬
лов в системах СДЦ приводит к появлению слепых ско¬
ростей, т. е. таких радиальных скоростей цели, при кото¬
рых полезный сигнал подавляется системой и цель нс
может быть обнаружена. Для устранения слепых скоро¬
стей используются различные средства, и в частности
вобуляцня (изменение) частоты повторения импульсов
или работа па двух несущих частотах.
Колебания, отраженные неподвижными обьектамн,
отличаются от колебаний, излучаемых антенной РЛС,
амплитудой и фазовым сдвигом (р=соп• 2D/с, который
остается постоянным, если частота излучаемых колеба¬
ний соп и дальность объекта D постоянны. При облуче¬
нии объекта, движущегося с радиальной скоростью V,
фазовый сдвиг отраженных колебаний изменяется во вре¬
мени соответственно изменению дальности D(l), а часто¬
та колебаний отличается на величину допплеровского
смещения Fv = fu2V/c. При импульсной работе станции
изменяется также длительность и частота повторения
импульсов.
Принципиально для СДЦ могут быть использованы
все изменения отраженного сигнала, однако практиче¬
ски используется изменение частоты и фазы высокоча¬
стотного заполнения, так как другие изменения ввиду их
малости зафиксировать трудно. Когерентно-импульсные
системы СДЦ действуют аналогично допплеровским си¬
стемам с импульсным излучением, но в системах СДЦ
скорость цепей обычно не измеряется и допплеровское
смещение используется лишь в качестве признака, позво¬
ляющего выделить сигналы движущихся целей. Сигналы
неподвижных объектов, по имеющие допплеровского сме¬
щения, подавляются специальным компенсирующим
устройством, а сигналы движущихся целей проходят на
индикаторное устройство и систему автосъема станции.
Различают системы СДЦ с внутренней и внешней ко¬
герентностью. В системах с внутренней когерентностью
308
эталонные колебания (когерентные с излучаемыми),
с которыми производится сравнение фазы колебаний при¬
нимаемого сигнала, вырабатываются специальным коге¬
рентным гетеродином. В системах с внешней когерент¬
ностью в качестве когерентных используются колебания,
отраженные неподвижными объектами, расположенными
на одной дальности с движущейся целью.
§ 7.2. ПРИНЦИП ДЕЙСТВИЯ И ПОСТРОЕНИЕ СИСТЕМ
СДЦ С ВНУТРЕННЕЙ КОГЕРЕНТНОСТЬЮ
Рассмотрим систему с внутренней когерентностью
(рис. 7.1). Во время излучения импульса колебания ко¬
герентного гетеродина фазируются колебаниями высоко¬
частотного генератора. Когерентность колебаний должна
сохраняться на время, соответствующее максимальной
дальности действия системы.
Рис. 7.1. Блок-схема системы СДЦ с внутрен¬
ней когерентностью.
Принимаемый сигнал Uc и напряжение когерентного
гетеродина подаются на вход детектора. При разно-
сти фаз когерентных колебаний и сигнала
рующее напряжение биений будет
ср результи-
и б = К С + С +2^к(/с COS
(7.1)
При условии Ui;^>Uc
Пб = Пк(1 +^cos<p),
(7.£)
Uc
где m =
309
Фазовый сдвиг ср в основном определяется дальностью
<р=(Ои^п = (ои*2D/c, так как в системах высокой скваж¬
ности длительность импульса ти мала, и набегом фазы за
время длительности импульса можно пренебречь. При
движении цели ср- изменяется, вызывая изменение от
периода к периоду, в то время как при неподвижном объ¬
екте оно остается неизменным.
В компенсирующем устройстве происходит череспе-
риодная компенсация, т. е. вычитание сигналов в двух
соседних периодах повторения. При этом сигналы непо¬
движных объектов, имеющие одинаковые амплитуды,
будут скомпенсированы. Фазовый сдвиг колебаний, отра¬
женных движущейся целью, изменяется, что приводит
к изменению напряжения биений Uq, При чересперпод-
ном вычитании появляется разностный сигнал, который
подастся па выходное устройство системы и фиксирует¬
ся им.
Амплитуда сигналов при движении цели будет изме¬
няться с частотой Допплера Fv. Если частота Допплера
равна или кратна частоте повторения импульсов
Pv = nF^ (7.3)
то фазовый сдвиг ф за время Гп равен 2лп, и напряжение
биений [7б остается постоянным, несмотря на движение
цели, и сигнал при череспериодиом вычитании будет
скомпенсирован.
Радиальная скорость цели, соответствующая условию
(7.3), равна
Усл-
2FT
(7-4)
и называется «слепой скоростью», так как цель, движу¬
щаяся со скоростью Есд, не обнаруживается системой
(если, конечно, отраженный сигнал не имеет флюктуаций
амплитуды).
При условии
(7-5)
разность амплитуд импульсов соседних периодов будет
максимальной, так как набег фазы за равен нечетно¬
му числу л. Максимальным будет и результирующий сиг¬
нал на выходе компенсирующего устройства. Поэтому
310
скорость движения цели, соответствующая условию (7.5),
называется оптимальной
(7-6)
Как указывалось раньше, появление слепых скоростей
представляет существенный недостаток, являющийся
Индикатор 1 [ компенси - i
яркостной —* рующее
отметкой J \рстройстдо\
Ю
Индикатор с
амплитудной
отметкой
а)
Рис. 7.2. Функциональная схема (п) и временная диаграмма (6) си¬
стемы СДЦ с фазированием когерентного гетеродина и сравнением
фаз на промежуточной частоте.
L
311
следствием периодичности сигнала. В режиме автомати¬
ческого сопровождения цели и в других случаях, когда
скорость движения цели известна, изменением частоты
повторения импульсов или частоты излучаемых колеба¬
ний можно обеспечить выполнение условия (7.6) опти¬
мального обнаружения движущейся цели и наилучшего
подавления помехи.
Построение систем СДЦ с внутренней когерентностью
определяется в основном методом получения когерент¬
ного напряжения и типом компенсирующего устройства.
Когерентное напряжение может быть получено на высо¬
кой или промежуточной частоте, а фазирование может
осуществляться от передатчика или, наоборот, от коге¬
рентного гетеродина. Наибольшее распространение по¬
лучила схема (рис. 7.2), в которой фазирование когерент¬
ного гетеродина и сравнение фаз когерентных и прини¬
маемых колебаний производится па промежуточной
частоте.
Пусковые импульсы синхронизатора запускают моду¬
лятор, управляющий работой высокочастотного генера¬
тора. Высокочастотные импульсы поступают через антен¬
ный переключатель в антенну, а также на смеситель
фазирования. Колебания промежуточной частоты на вы¬
ходе смесителя используются для фазирования когерент¬
ного гетеродина в течение каждого импульса передат¬
чика.
Частота колебаний принимаемого сигнала понижает¬
ся смесителем сигнала до той же промежуточной часто¬
ты. Поскольку на оба смесителя подаются колебания от
одного стабильного местного гетеродина, операция пре¬
образования не вносит относительных фазовых сдвигов
сигнальных и когерентных колебаний. Сигнальные им¬
пульсы после усиления на промежуточной частоте и огра¬
ничения подаются на фазовый детектор. В качестве
опорных колебаний при детектировании используются
колебания когерентного гетеродина. Ограничитель слу¬
жит для сжатия динамического диапазона сигнала и
устранения изменений амплитуды сигнала из-за флюк¬
туаций эффективной площади рассеяния цели и враще¬
ния диаграммы направленности антенны.
Напряжение па выходе фазового детектора зависит от
фазового сдвига ср сигнальных и когерентных колебаний.
312
При использовании индикатора с амплитудной отмет¬
кой выходные импульсы фазового детектора после уси¬
ления могут быть непосредственно поданы на вертикаль¬
ные отклоняющие пластины трубки. Амплитуда сигналь¬
ных импульсов, соответствующих движущейся цели, бу¬
дет изменяться с частотой Допплера, поэтому отметки
движущихся целей двуполярны и имеют характерную
штриховку, что позволяет выделить их среди отметок не¬
подвижных целей, имеющих обычный вид.
Um приемники
_J .
Модули | I
руемый гг*’
усилитель I
i Генератор^
i частоты I
i i
Прямой канал
! Аттё\ I УСиЛи
’'нюатор\J mt ''ь
| Диффе- Н
\ренциаль-\
Iная АРУ 1
j а держа н н ь7й ~
ЭЗ/О ^усилитель^
1
инди-
гатору
И
: Схема-1 \Двухполу-\
дычи- ^периодныи\
\ танин ; |детектор»
- ' 1
; Детек- t |
]_'77<7£ |
! Генератор 1
1 ударного
! бозбужде-
I кия |
Фильтр 1
Л i
t
4
1 Блокине-
генератор
Детек-
■*1 тор
1
3
Синхронизирующие
импульсы с периодом
1
п
I
-т:^~
Рис. 7.3. Блок-схема компенсирующего устройства с УЗЛЗ.
При яркостной модуляции луча сигнальные импульсы
движущихся и неподвижных объектов, поданные на мо¬
дулирующий электрод трубки непосредственно с фазо¬
вого детектора, дают примерно одинаковые яркостные
отметки. Для выделения сигналов движущихся целей
в этом случае необходимо компенсирующее устройство,
подавляющее сигналы неподвижных объектов.
Схема череспериодной компенсации с использованием
ультразвуковой линии задержки (УЗЛЗ) изображена
на рис. 7.3. Для осуществления череспериодиого вычита¬
ния сигналы от фазового детектора проходят по двум
каналам — прямому («незадержанному») и «задержан¬
ному», в котором включена УЗЛЗ с задержкой, равной
периоду повторения сигнальных импульсов. Для эффек-
313
тнвпой компенсации сигналов неподвижных объектов не¬
обходимо обеспечить идентичность характеристик обоих
каналов. Чтобы получить полосу пропускания УЗЛЗ, до¬
статочную для неискаженной передачи импульсов, они
передаются на высокой частоте /Y Выбор значения
определяется требуемой полосой пропускания и типом
возбудителя ультразвуковых колебаний в линии. Наи¬
более часто применяют частоты от 10 до 30 Мгц.
Видеосигнал с выхода фазового детектора приемника
модулирует колебания частоты fi, которые в виде высо¬
кочастотного импульса подаются на вход прямого и «за¬
держанного» каналов. Линия задержки сильно ослабляет
сигнал (до 80—90 дб), поэтому в «задержанном» канале
используется резонансный усилитель с большим коэффи¬
циентом усиления и достаточной полосой пропускания.
Для идентичности каналов точно такой же усилитель
включается в прямой канал, а для уменьшения напряже¬
ния на входе усилителя применяется делитель напряже¬
ния с ослаблением, равным затуханию УЗЛЗ. Точное
уравнивание коэффициентов усиления обоих каналов
обеспечивается дифференциальной АРУ.
После детектирования сигнальные видеоимпульсы ка¬
налов сравниваются в схеме вычитания, при этом мешаю¬
щие сигналы неподвижных объектов, имеющие одинако¬
вую амплитуду, компенсируются. Сигналы движущихся
целей, выделяющиеся при вычитании смежных периодов,
могут иметь как положительную, так и отрицательную
полярность. Поэтому перед подачей сигналов на индика¬
тор с яркостной отметкой или на систему автосъема они
предварительно преобразуются двухполупериодным де¬
тектором в однополярные.
§ 7.3. ТРЕБОВАНИЯ К ОТДЕЛЬНЫМ УЗЛАМ СИСТЕМЫ
СДЦ С ВНУТРЕННЕЙ КОГЕРЕНТНОСТЬЮ
Хорошая компенсация мешающих сигналов неподвиж¬
ных объектов достигается лишь при выполнении опреде¬
ленных требований к точности начальной установки ряда
параметров и их стабильности в процессе работы си¬
стемы.
Одним из важнейших условий хорошей компенсации
является равенство времени задержки линиит3и периода
повторения зондирующих импульсов станции Тп. В рас-
314
сматриваемой системе равенство обеспечивается тем, что
период синхронизирующих импульсов задается той же
УЗЛЗ, которая используется в задержанном канале. При
этом автоматически поддерживается выполнение усло¬
вия Тз=Лт. Для разделения сигнальных и синхронизи¬
рующих импульсов последние передаются через УЗЛЗ
на другой несущей частоте f2, колебания которой выра¬
батываются генератором ударного возбуждения при воз¬
действии импульсов задающего блокинг-генератора. Бло-
кинг-генератор синхронизируется импульсами, прошед¬
шими линию задержки, при этом период повторения
синхронизирующих импульсов Тп устанавливается рав¬
ным времени задержки линии т3.
Рассмотрим требования к другим элементам систе¬
мы СДЦ.
Стабильность частоты гетеродинов и генератора вы¬
сокой частоты оказывает существенное влияние на эф¬
фективность СДЦ. Разность фаз колебаний сигнала и
когерентного гетеродина зависит от частот местного и ко¬
герентного гетеродинов (сом и сок), а также времени рас¬
пространения сигнального импульса до цели и обратно:
? = = (“м ± <■>„) tD,
где сои — угловая частота излучаемых колебаний.
Здесь положительный знак соответствует случаю
(Ом<(оп, отрицательный — случаю сом>(оп.
Если частота одного из гетеродинов за период повто¬
рения импульсов Тп изменится на Аси, то это вызовет до¬
полнительный фазовый сдвиг Аф=А(о/р. При условии по¬
стоянства скорости ухода частоты гетеродина
dm п df .
-т- = 2it —const,
dt dt
(7.7)
dU6 _
d<f
Дифференцируя выражения (7.2) по <р, получим
— sin = £/бо sin <р. При малых значениях Д<? < 0,06
можно принять
315
В точках максимальной чувствительности системы к изме¬
нению фазы
sin <р 1 и « Д<р.
Следовательно, изменение фазы на Дер- радиан численно
равно относительному изменению амплитуды биений.
Если при черсспериодной компенсации уход частоты при¬
водит к изменению фазы за период Тп на Дф радиан, то
появляются нескомпенсированные остатки мешающих
сигналов неподвижных объектов (остаточный фон).
Считая допустимым остаточный фон Дф^0,06, опре¬
делим допустимую скорость ухода частоты гетеродинов
0,06 _ 1 _ Fn (7Q
Idt Люи c ~~ 1 oorY.tD 100^ • <'
2D
Так, например,*”для Fn=1000 гц и tD= —=500 мксек
(D 80 км)
<20 кгц)сек.
ДОП
При череспериодной компенсации имеет значение уход
частоты за период повторения Тп- В рассматриваемом
примере
Мдопп 20 гц.
Допустимая скорость ухода частоты может быть сравни¬
тельно легко достигнута в когерентном гетеродине, рабо¬
тающем на сравнительно низкой промежуточной частоте
(десятки мегагерц), и с большими трудностями — в мест¬
ном гетеродине, работающем на высокой частоте (тысячи
мегагерц). Так, для обеспечения ухода частоты, не пре¬
вышающего Д/= 20 гц, при работе местного гетеродина
на частоте = 101 Мгц (Х = 3 см) необходима относитель¬
ная стабильность частоты = 10-9. Несмотря на то
что это значение кратковременной стабильности, обеспе¬
чить ее можно лишь применением специальных мер ста¬
билизации частоты местного гетеродина. Стабилизация
осуществляется высокодобротиыми резонаторами, приме¬
нением схем АПЧ или использованием стабильного квар¬
цевого генератора с последующим умножением частоты
до заданного значения.
316
Когерентный гетеродин также должен иметь доста¬
точную стабильность, а его частота точно равна проме¬
жуточной. При неточной настройке видеосигнал будет
содержать несколько периодов биений п = (fk—/Пч)тп. Для
нормальной работы системы расстройка не должна пре¬
вышать значения /к—/пч^1/4ти, при котором в пределах
длительности импульса ти укладывается не более чет¬
верти периода биений.
Требования к стабильности частоты генератора вы¬
сокой частоты значительно ниже, чем к местному, гете¬
родину, так как для генератора существенным является
уход частоты только за время длительности импульса ти,
значительно меньшей периода повторения. Допустимая
скорость ухода частоты определится из условия
«<; —— -—
' ЮОТпТи Ю0ти
(7.9)
Дополнительно накладывается требование максимально
допустимого ухода частоты за время длительности им¬
пульса (Л/п)доп^ 1/4тц. При выполнении этого условия
практически исключаются нежелательные изменения ам¬
плитуды сигналов неподвижных объектов, вызванные
биениями из-за различия частот в пределах импульса.
Л4одулятор системы СДЦ должен обеспечить задан¬
ную форму и амплитуду модулирующих импульсов, ста¬
бильную длительность и равенство периода повторения
импульсов на выходе модулятора периоду синхронизи¬
рующих импульсов. Обычно стремятся получить прямо¬
угольную форму модулирующих импульсов, так как при
этом легче выполнить условие неизменности частоты ко¬
лебаний генератора высокой частоты на протяжении
импульса, особенно при использовании генератора на
магнетроне.
При изменении длительности импульса за период по¬
вторения па величину Дти после вычитающего устройства
остается иескомпенспровапиый фон, допустимый уровень
которого определяет наибольшее допустимое изменение
длительности импульса (Дтц/тп) за период повторения Тп.
Влияние флюктуаций амплитуды сигналов. Сигналы
неподвижных объектов обычно не имеют строго постоян¬
ной амплитуды из-за флюктуаций эффективной площади
рассеяния объектов. Кроме того, большинство мешаю¬
щих объектов нс являются строго неподвижными (де-
317
ревья, кусты), и отраженный ими сигнал имеет некото¬
рое смещение частоты. В связи с этим, даже при идеаль¬
ном выполнении всех узлов системы СДЦ, не удается
полностью избавиться от фона местных предметов. Кро¬
ме случайных флюктуаций амплитуды сигнала при рабо¬
те системы в режиме обзора сказывается также измене¬
ние амплитуды сигнальных импульсов по закону, опре¬
деляемому формой диаграммы направленности антенны
При аппроксимации диаграммы колоколообразной функ¬
цией относительное изменение амплитуды соседних им¬
пульсов пачки в области максимальной крутизны диа¬
граммы составляет
Д[/ 1,4
где пп — число импульсов пачки на уровне половинной
мощности;
UQ — амплитуда импульсов, соответствующих макси¬
муму диаграммы.
Влияние модуляции амплитуды сигналов, отражен¬
ных от неподвижных объектов, может быть уменьшено
рациональным выбором амплитудной характеристики
приемника. В рассматриваемой схеме используется ам¬
плитудное ограничение напряжения сигналов. Хорошие
результаты дает также применение усилителей с лога¬
рифмической амплитудной характеристикой и быстродей¬
ствующей регулировки усиления (БАРУ).
Важное значение имеет также выбор величины коге¬
рентного напряжения UK и типа детектора.
Чувствительность системы к изменению разности фаз
при U1{^>UC определяется выражением
|^б
= тик | sin <р | = /7б0 | sin |.
(7.Ю)
При применении обычного амплитудного детектора чув¬
ствительность системы падает до 0 при ф=/7Л. В случае
выражение (7.1) приводится к виду (7б =
1 dU о
= 2{/с cos<p/2, и чувствительность системы будет
= и с sin .
318
Таким образом, провалы чувствительности будут при
Ф = 2/1л, т. о. в два раза реже. Самые лучшие результаты
дает применение балансного (фазового) детектора. При
условии Uc = Uix напряжение биений на нагрузке детек¬
тора будет
Uq — ZUc ("cos-| sin-y-^ при 0<«p<7t,
при it <? <С 2тг.
Чувствительность системы определяется в этом случае
выражением
cos sin 4" • (7-Н)
Следовательно, при использовании фазового детектора
полные провалы чувствительности системы отсутствуют.
Нестабильности параметров системы СДЦ и флюк¬
туации амплитуды сигналов неподвижных объектов су¬
щественно снижают эффективность их подавления. Осо¬
бое внимание при проектировании системы СДЦ с вну¬
тренней когерентностью уделяется стабильности гетеро¬
динов и сохранению равенства задержки сигнала перио¬
ду повторения. Последняя задача усложняется при ис¬
пользовании переменного периода для исключения сле¬
пых скоростей, так как вместе с периодом должна соот¬
ветственно изменяться задержка сигнала в задержанном
канале. Выполнение равенства т3=Гп автоматически
обеспечивается при использовании в качестве запоми¬
нающего устройства потенциалоскопа.
Компенсирующее устройство на потенциалоскопе
с барьерной сеткой представлено упрощенной схемой на
рис. 7.4. Сигнал от приемника через усилитель записи
подается на сигнальную пластину. При этом потенциал
поверхности мишени изменится в соответствии с ампли¬
тудой сигнала. За цикл развертки все точки мишени, обе¬
гаемые электронным лучом, приобретут потенциал, соот¬
ветствующий входному напряжению.
В следующий период повторения луч обегает те же
точки мишени. При этом потенциальный рельеф изме¬
нится в соответствии с новым распределением напряже¬
ния во времени. При перезаписи происходит перезаряд
в каждой точке развертки с предыдущего напряжения на
повое. При этом на нагрузочном сопротивлении ./?п в цепи
319
коллектора выделяется разностное напряжение, которое
через усилитель считывания подается на индикатор. Та¬
ким образом, потенциалоскоп выполняет также и роль
вычитающего устройства.
Компенсирующее устройство с потенциалоскопом ра¬
ботает хорошо при условии весьма стабильной развертки.
Обычно применяют круговую или спиральную разверт¬
ки, которые обеспечивают стабильность и хорошее ис-
Тормозящая Сигнальная
Схема
развертки
Синхрони¬
зирующие
импульсы
Рис. 7.4. Блок-схема компенсирующего устройства иа потенциало-
скопе.
пользование площади мишени, что позволяет получить
достаточную разрешающую способность по дальности.
Возможно также применение -растровой развертки, но
в этом случае трудно получить необходимую стабиль¬
ность. Совмещение в потенциалоскопе функций задержки
и вычитания сигналов, легкость обеспечения равенства
= при переменном периоде являются причиной все
более широкого применения потенциалоскопа в системах
СДЦ. К недостаткам потенциалоскопа относятся сравни¬
тельно высокий уровень собственных шумов и недоста¬
точная надежность.
Компенсация собственной скорости РЛС. Когерентно¬
импульсные системы СДЦ с внутренней когерент¬
ностью нашли широкое применение в стационарных усло¬
виях, когда система неподвижна. При установке системы
на движущемся объекте, например самолете, для подав¬
ления сигналов, отраженных фоном, иа котором движет¬
ся цель, необходима компенсация собственной скорости
системы. Компенсация осуществляется путем изменения
320
частоты когерентного гетеродина на величину допплеров¬
ского смещения частоты
01/
^Vc^~rC°S^C0S^ (7.12)
вызванного собственной скоростью системы Vc. Таким
образом, для точной компенсации частота когерентного
напряжения должна изменяться соответственно с изме¬
нением Ус, у и [3, что связано с большими трудностями,
особенно в режиме обзора.
Более просто решается задача СДЦ при собственном
движении системы на основе использования принципа
внешней когерентности.
§ 7.4. ПРИНЦИП ДЕЙСТВИЯ
КОГЕРЕНТНО-ИМПУЛЬСНЫХ СИСТЕМ СДЦ
С ВНЕШНЕЙ КОГЕРЕНТНОСТЬЮ
В системах СДЦ с внешней когерентностью в каче¬
стве эталонных (когерентных) колебаний используются
сигналы, отраженные от неподвижных объектов, находя¬
щихся в пределах разрешаемой площади (или разрешае¬
мого объема) РЛС. Такой сигнал можно представить
как сумму сигналов, отраженных от элементарных от¬
ражателей, заключенных в пределах разрешаемого
объема
п
u(t) = ^ Uim sin — <p0i), (7.13)
Z=1
где Uim, и фог — амплитуда, частота и начальная фа¬
за сигнала, отраженного от f-го отражателя.
Если относительное положение элементарных отража¬
телей неизменно, суммарный сигнал является регулярной
функцией времени. Реально элементарные отражатели
взаимно смещаются из-за ветра (волны, растительность)
и в силу собственного движения системы, поэтому сум¬
марный сигнал имеет существенную случайную состав¬
ляющую, снижающую эффективность подавления пассив¬
ных помех.
Средняя частота спектра флюктуаций помехи fCp>
определяемая радиальной скоростью Vn движения мно¬
жественного отражателя в целом, равна
f cp — fn — Pv ср,
21—1173
321
где Fv ср — допплеровское смещение средней частоты
спектра помехи.
Чем уже спектр флюктуаций по сравнению с частотой
повторения импульсов Fn, тем лучше выделяются сигна¬
лы движущихся целей на фоне пассивных помех.
Сигнал на входе приемника является результатом
биений сигналов, отраженных движущейся целью и не¬
подвижным фоном. Поэтому после детектирования ам¬
плитуда видеоимпульсов, соответствующих движущейся
цели, будет изменяться с частотой, равной разности доп¬
плеровского смещения частоты сигнала движущейся цели
и допплеровского смещения средней частоты спектра по¬
мехи. Отсюда ясно, что разность допплеровских смеще¬
ний частот сигналов, отраженных движущейся целью и
неподвижным фоном, определяется радиальной состав¬
ляющей скорости цели относительно фона независимо от
собственной скорости РЛС. Следовательно, компенсация
собственной скорости в системах с внешней когерент¬
ностью получается автоматически.
В простейшем случае выделение сигнала движущейся
цели осуществляется на экране индикатора с амплитуд¬
ной отметкой. Отметка цели, движущейся на фоне отно¬
сительно неподвижных отражателей, имеет характерную
размытость или штриховку, поскольку амплитуда видео¬
сигнала цели меняется. При использовании индикатора
с яркостной отметкой или системы автосъема для подав¬
ления отражений от фона применяется компенсирующее
устройство, как и в системах с внутренней когерент¬
ностью.
В системах СДЦ с внешней когерентностью применя¬
ются приемники с логарифмической амплитудной харак¬
теристикой. Логарифмическая характеристика, сжимая
динамический диапазон флюктуаций входных сигналов,
в то же время позволяет сохранить различие амплитуд
сигналов на выходе приемника, что необходимо для вы¬
деления сигналов движущихся целей в системах с внеш¬
ней когерентностью.
Системы с внешней когерентностью при использова¬
нии компенсирующего устройства имеют существенный
недостаток, заключающийся в том, что сигнал движу¬
щейся цели не может быть обнаружен при отсутствии
отражений от фона или при малой интенсивности этих
отражений. В этих случаях биения отсутствуют, ампли-
322
туда сигнального импульса не меняется и сигнал движу¬
щейся цели подавляется компенсирующим устройством.
§ 7.5. ЭФФЕКТИВНОСТЬ СИСТЕМ СДЦ
С ЧЕРЕСПЕРИОДНОЙ КОМПЕНСАЦИЕЙ
Эффективность систем СДЦ характеризуется коэф¬
фициентом подавления помехи и вероятностью обнару¬
жения сигнала движущейся цели при заданном отноше¬
нии сигнала к помехе.
Под коэффициентом подавления помехи понимают
отношение мощности помехи на входе и выходе схемы
череспериодного вычитания
00
gu (u>)da>
= i, (7.14)
О
где £п(со)—энергетический спектр флюктуаций помехи;
Кку — коэффициент передачи компенсирующего
устройства.
Коэффициент подавления тем меньше, чем больше
нескомпенсированные остатки на выходе схемы вычита¬
ния
вызванные изменением амплитуды сигналов неподвиж¬
ных объектов из-за флюктуаций элементарных отража¬
телей (Af/ф), вращения антенны (ДСЦ), движения РЛС
(ДЦС) и нестабильностей параметров системы (Д(/Нст)-
Коэффициент подавления уменьшается при расширении
спектра флюктуаций. Так, отражения от дождевых ка¬
пель, имеющие достаточно широкополосный спектр
флюктуаций, почти не подавляются. Коэффициент по¬
давления помех при наличии флюктуаций, вызываемых
движением элементарных отражателей и вращением
антенны, не превышает 30 дб. При движении РЛС
(и отсутствии его компенсации) коэффициент подавле¬
ния резко снижается. Практика показывает, что хоро¬
шая наблюдаемость отметок движущихся целей на экра¬
не обеспечивается при Кп = 254-30 дб, что соответствует
21* 323
остаточному фону 6—3%. Из этого условия обычно и
исходят при определении требований к стабильности
параметров системы СДЦ. Коэффициет подавления ха¬
рактеризует лишь ослабление помехи, но не показывает
воздействия системы на полезный сигнал. Для характе¬
ристики прохождения сигнала движущейся цели через
систему используют рабочие характеристики систем
СДЦ, представляющие графики зависимости порогового
сигнала (вероятности обнаружения сигнала D) от от¬
ношения мощности полезного сигнала к мощности по¬
мехи. Рабочие характеристики сильно меняются в зави¬
симости от скорости движения цели и спектра флюктуа¬
ций помехи. С расширением спектра флюктуаций по¬
мехи вероятность обнаружения сигнала уменьшается.
Вероятность обнаружения полезного сигнала уменьшает¬
ся также при слепой скорости, но не падает до нуля,
так как полезный сигнал обычно также флюктуирует.
При слепой скорости величина порогового сигнала воз¬
растает в десятки и сотни раз по сравнению со слу¬
чаем оптимальной скорости.
Таким образом, метод череспериодной компенсации
мало эффективен при широкополосных пассивных по¬
мехах и особенно при движении цели со слепой ско¬
ростью. Более эффективны методы многократной ком¬
пенсации помех, при которых производится т-кратная
компенсация сигналов неподвижных объектов. Напри¬
мер, при двукратной компенсации (т = 2) последова¬
тельно выделяются первая и вторая разности
Ui — u - Ги),
U2 (t) = Ur (/) -Ur(t- 7л) = u (t)—2U(t -Та) -и Ю~27’п),
где Ти — период повторения импульсов РЛС.
Эффективность повышения кратности вычитания за¬
висит от быстроты спадания и ширины спектра флюк¬
туаций помехи. Для каждой ситуации существует неко¬
торая предельная кратность, начиная с которой повыше¬
ние кратности мало эффективно и даже вредно, так
как уменьшает диапазонность системы по скорости.
В заключение заметим, что в связи со случайным
характером когерентного напряжения в системах СДЦ
с внешней когерентностью их эффективность ниже
сравнительно с системами с внутренней когерентностью.
324
Глава 8
ПАССИВНАЯ РАДИОЛОКАЦИЯ
§ 8.1. ФИЗИЧЕСКИЕ ОСНОВЫ ПАССИВНОЙ
РАДИОЛОКАЦИИ
Область радиоэлектроники, в которой используются
методы и средства определения местонахождения физи¬
ческих объектов по их собственным (пассивным) радио¬
излучениям, получила название пассивной радиолока¬
ции. Все естественные радиоизлучения можно в первом
приближении разбить на два класса: тепловые радиоиз¬
лучения, обусловленные электродинамическими процес¬
сами в атомах и молекулах вещества, из которого со¬
стоит физический объект, и радиоизлучения, обуслов¬
ленные естественными или искусственными электроди¬
намическими процессами не теплового происхождения.
Тепловое радиоизлучение физических объектов проис¬
ходит за счет преобразования внутренней тепловой
энергии микроскопических частиц вещества излучаю¬
щего тела в энергию электромагнитного поля, распро¬
страняющегося за пределы излучающего тела. Радио¬
излучения за счет естественных или искусственных
электродинамических процессов не теплового происхож¬
дения, используемые в пассивной радиолокации, харак¬
теризуются большой мощностью и сравнительно низко¬
частотным спектром (ниже 30—40 кгц). К таким
излучениям относятся излучение столба ионизированных
газов при запуске ракет, радиоизлучения при ядерных
взрывах, грозовых разрядах и т. д.
Все виды естественных излучений физических объек¬
тов как теплового, так и не теплового происхождений
представляют собой случайные процессы, так как яв¬
ляются результатом возбуждения очень большого числа
осцилляторов, причем момент и интенсивность возбуж¬
дения каждого осциллятора зависят от многих слу¬
чайных факторов. Поэтому, в отличие от активной ра¬
325
диолокации, основанной на обнаружении на фоне шу¬
мов детерминированного сигнала, в пассивной радио¬
локации производится обнаружение шумоподобного
сигнала на фоне шумов. В одноканальных пассивных
радиолокаторах принципиально невозможно измерение
дальности и допплеровского сдвига частоты из-за от¬
сутствия опорных сигналов, в качестве которых в актив¬
ных радиолокаторах используются излучаемые сигналы.
Преимуществом пассивных радиолокаторов является
скрытность их работы в силу отсутствия излучаемого
сигнала. Наибольшее распространение получила пассив¬
ная радиолокация, использующая собственные тепловые
радиоизлучения в сантиметровом и миллиметровом
диапазонах и поэтому называемая радиотеплолокацией.
Радиотеплолокация имеет много общего как с активной
радиолокацией, так и с ИК техникой, использующей
тепловое излучение в инфракрасном диапазоне волн
(0,1—0,001 мм), смежном с радиодиапазоном.
§ 8.2. ХАРАКТЕРИСТИКИ ТЕПЛОВОГО
РАДИОИЗЛУЧЕНИЯ ФИЗИЧЕСКИХ ОБЪЕКТОВ
Излучение реальных излучателей зависит от коэф¬
фициента отражения поверхности излучателя, от кон¬
фигурации поверхности и других факторов, учесть кото¬
рые в большинстве случаев для реальных излучателей
практически невозможно. Поэтому основные расчетные
соотношения для пассивной радиолокации выводятся
применительно к некоторому идеальному излучателю —
абсолютно черному телу (АЧТ). В сантиметровом и мил¬
лиметровом диапазонах характеристиками, близкими
к характеристикам АЧТ, обладают противорадиолока-
циопные покрытия, участки местности, поросшие лесом,
и в некоторых участках диапазона — земная атмосфера.
Важнейшим законом теплового излучения АЧТ яв¬
ляется закон, описываемый формулой Планка и выра¬
жающий связь спектральной плотности излучения с тем¬
пературой тела:
/г hf г вт я
S4> J ) — ~г 7hf~\ ■]' ’
|exP(jfJ-4
где g(f, Т)—спектральная плотность излучения при
данной температуре;
326
h = 6,624 • 10-34 дж • сек — постоянная Планка;
k = 1,38 • 10~23 дж/град • гц—постоянная Больц-
мана;
с = 3 • 108 м/сек — скорость распространения
электромагнитных волн;
Т — абсолютная температура АЧТ, °К,
f — частота, гц.
Спектральной плотностью излучения называется от¬
ношение мощности, излучаемой в полосе, равной 1 гц,
элементарной площадкой, выделенной на поверхности
Рис. 8.1. Зависимость кажущейся температуры от угла
визирования для травяного покрова ( ) и асфаль¬
та ( ).
-
' 1
———-
/Г"орялзоят аль чая
поляризация
/
/
Вертикальная
поляризация
/
~ 1
г
/
/
1 X
\
X
%= 3,2 см
/
/
/
/
к
, град
излучателя, в пространство, ограниченное полусферой,
описанной вокруг этой площадки, к площади элемен¬
тарной площадки. Для расчета спектральной плотности
излучения АЧТ в диапазоне частот и температур пас¬
сивной радиолокации пользуются упрошенным видом
формулы Планка, получившим название формулы
Рэлея — Джинса:
g(h о
2nf2 f гр 2nkT
=—4- kT = —,
с2 X2
[ги,-лг J
Свойства реальных излучателей, излучение которых
отлично от излучения АЧТ, могут быть описаны при из¬
вестной яркостной температуре реальных излучателей.
Яркостная температура Тя численно равна температуре
327
АЧТ, помещенного на место реального излучателя при
определенных направлениях, частоте и поляризации. 11а
рисунке 8.1 приведены зависимости яркостных темпера¬
тур травяного покрова и асфальта от угла визирования
для к = 3,2 см. Из этого рисунка видно, что асфальт на
фоне травяного покрова при вертикальной поляризации
волн выглядит достаточно контрастно.
§ 8.3. ОБНАРУЖЕНИЕ РАДИОТЕПЛОВЫХ СИГНАЛОВ.
ДАЛЬНОСТЬ ДЕЙСТВИЯ РАДИОТЕПЛОЛОКАТОРА
(РТЛ)
Радпотепловое излучение представляет собой случай¬
ный процесс, у которого отсутствует регулярная состав¬
ляющая, а спектральная плотность в пределах полосы
пропускания применяемых в пассивной радиолокации
приемных устройств, как правило, мала и равномерна.
Закон распределения амплитуд радиотеплового про¬
цесса при весьма общих допущениях можно считать
нормальным
где о2 — дисперсия радиотеплового сигнала.
Основными характеристиками радиотеплового сигна¬
ла являются его длительность, определяющая энергию
сигнала, и форма, задающая требования к расчету ха¬
рактеристик НЧ фильтров. Форма и длительность радио-
тепловых сигналов определяются формой диаграммы
направленности, параметрами движения диаграммы,
а также видом и параметрами движения источника
радиотепловых сигналов. Для обзорных РТЛ форма
сигнала повторяет форму диаграммы направленности
антенны, а длительность сигнала — на уровне 0,5:
/ аа
с — 2С + 2Ц ’
где аа — ширина диаграммы направленности на уров¬
не 0,5;
Qu — угловая скорость относительного движения
цели в направлении сканирования;
йс — угловая скорость сканирования при обзоре.
Для РТЛ, работающих в режиме автоматического
сопровождения цели, длительность и форма сигнала
328
зависят от параметров движения цели и параметров
следящей системы. Для удобства рассмотрения работы
РТЛ вместо сигнала вводят так называемую сигналь¬
ную функцию, представляющую собой относительное
изменение спектральной плотности сигнала во времени
/И(г‘)==_ДО.<11
J а маге
где 7д(/) —температуры антенны РТЛ, зависящая от
кажущейся температуры и размеров цели,
эффективности антенного устройства и
взаимного расположения антенны и цели;
Т'а макс — максимальное значение температуры антен¬
ны РТЛ.
Задача обнаружения радиотеплового сигнала в об¬
щем аналогична по постановке задаче обнаружения
сигнала в радиолокации: на входе обнаружителя дейст¬
вует аддитивная смесь сигнала и мешающего шума
u(f) =и0(/)+иш(7), из которой оптимальным образом
необходимо выделить сигнал ис(1). Отличие же состоит
в том, что радиотепловым сигналом является шумовой
сигнал с нормальным распределением амплитуд и со
спектральной плотностью, равномерной в пределах по¬
лосы пропускания приемного устройства РТЛ. Решение
задачи обнаружения, так же как и в радиолокации,
сводится к нахождению оптимальной структуры обнару¬
жителя, выбору его параметров и расчету характери¬
стик обнаружения. Оптимальная структура обнаружи¬
теля находится через отношение правдоподобия
А (и)
^СШ О)
— (U) ’
где WUi(u) и 1^сш(и)—плотности вероятностей шума
и смеси сигнала и шума.
Если сигнальная функция М(1) и частотная харак¬
теристика высокочастотного тракта обнаружителя пря¬
моугольны, а спектральные плотности сигнала =
п шума = равномерны в пределах полосы про¬
пускания Д/, то плотности вероятностей будут равны
соответственно
п
2
1
2л(’с + Вш)
•ехр
1
gc +
'с
$ u2(t)dt ,
0 J
329
а отношение правдоподобия представлено выражением
4<“)=ЫтМ! f “!(')Л •
о
где — Рс — kTJtf, а^--Р ш — — дисперсии сигна¬
ла и шума, а /г—~2Д/7С— минимальное число дискретных
значений, достаточное для восстановления сигнала (по тео¬
реме Котельникова).
Выходной эффект оптимального обнаружителя дол¬
жен быть пропорционален отношению правдоподобия
или любой монотонной функции этого отношения, т. е.
в конечном счете члену
Таким образом, оптимальное обнаружение радиотепло-
вого сигнала состоит из квадратичного детектирования
и последующего интегрирования в течение времени, рав¬
ного длительности сигнала. Зная плотности вероятно¬
стей и найдя отношение правдоподобия, можно затем
рассчитать рабочие характеристики обнаружителя: ве¬
роятность обнаружения, вероятность ложной тревоги и
вероятность пропуска сигнала. Однако эти расчеты со¬
пряжены обычно с большими вычислительными трудно¬
стями, и поэтому на практике часто пользуются другим
критерием качества работы обнаружителя — отноше¬
нием сигнал/шум на выходе фильтра низкой частоты
обнаружителя, состоящего из фильтра высокой частоты
с частотной характеристикой feB(co) и шириной полосы
пропускания Д/, квадратичного детектора с характери¬
стикой ^Двых = ^2вх, фильтра низкой частоты (ФНЧ)
с частотной характеристикой Ai(Q) и шириной полосы
пропускания AF, и решающего устройства. Отношение
сигнал/помеха на выходе ФНЧ равно отношению мощ¬
ности сигнала к мощности шума:
2 Рс -вы х
в ы х в Ь1 х
330
Отношение сигнал/помеха на входе обнаружителя
2 Рсвх = gcW
Dx Рш вх gm (f) А/ ш
Отношение сигнал/помеха на выходе высокочастотного
фильтра (ФВЧ)
00
I g< (to)^ (to) d<o
2 _ j5_ =1\_
1 Р1П1 ш
J g<" («) % (w)
о
Для нахождения спектров сигнала и шума на выходе
детектора необходимо найти корреляционную функцию
напряжения ^двых, которая для квадратичного детекто¬
ра вычисляется по известному соотношению [14]
7?д(т) =/?2(0)+27?2(т),
где /?д(т)—корреляционная функция выходного напря¬
жения;
/?(т)—корреляционная функция входного напря¬
жения.
Корреляционная функция входного напряжения де¬
тектора равна сумме автокорреляционных функций сиг¬
нала и собственных шумов обнаружителя:
00
Rc (*) — j gcv (°) COS сот d(n —
6
= kTa C k2* (co) cos (dt du = kTa/?B (t),
0
oo
Rni (T) = J £шв W COS du =
0
= kTm C k\ (co) COS (ОТ du — kTmRb (t) ,
0
где Ra (t) — автокорреляционная функция ФВЧ.
Автокорреляционная функция выходного напряжения
квадратичного детектора
R*«=сс+ <+2 К +2v;+ <1 р;
331
где
Рв (*) =
/?в(т)
Я.в(О)
ан1в 11 %— дисперсии шума и сигнала на выходе ФВЧ.
Зная корреляционные функции полезной составляю¬
щей на выходе детектора
и шумовой составляющей
(т) = % + 2 [% + +ас1 Рв (Т)
можно рассчитать мощности сигнала и шума на выходе
ФНЧ. Мощность сигнала равна квадрату обратного
преобразования Фурье спектра сигнала на выходе ФНЧ:
со
Рс = °C [i J SM (Q) k« (Q) eXP (№) d€1 j2«
—co
00
где SM (£2) = J M (/) exp (— j£lt) dt — амплитудный спектр
—00
сигнальной функции М (t).
При согласованном ФНЧ [kn (£2) = S*M (£2)] мощность
сигнала на его выходе
00
—со
се
где kM =-j- J М2 (Z) dt—коэффициент формы сигнала.
—оэ
Спектральная плотность шума на выходе ФНЧ
со
(Q) = ± j {? 4- 02] р2в (t)} cos £h dt.
О
При прямоугольной форме частотной характеристики ФВЧ
спектральная плотность на входе ФНЧ на частоте £2 = 0
(0) = 4 [°- +т3ш+т ] •
332
Обычно ширина полосы пропускания ФНЧ Д/7 << Д/, по¬
этому мощность шума на его выходе
РШ ВЫЛ (0)
1 2А/?
.1 •
Отношение сигнал/помеха на выходе ФНЧ для прямоу¬
гольной сигнальной функции (/гм=1)
РС ВЫX
дг
РIII вых
[°ш + “с’п! + ~ °C
24F-
__ Рвх ДГ
Г, , 2 1 4 I
Рвх "Ь 2 Рвх J
При согласованном по ширине полосы ФНЧ^Д/? = 2р^
р4
v вх
р2
Г вых
’ Д/^С-
При малых значениях р^ (рвх <<1)
2
Р вых'
(8.1)
Выражение (8.1) показывает, что так же как и в актив¬
ной радиолокации, выходное отношение сигнал/шум за¬
висит от входного отношения и от энергии сигнала,
пропорциональной произведению ширины полосы ФВЧ
Af на время наблюдения сигнала
Одним из важнейших параметров РТЛ является его
чувствительность, т. е. значение антенной температуры,
при котором выходное отношение сигнал/помеха равно
единице. Потенциальная чувствительность, т. е. чувст¬
вительность оптимального обнаружителя радиотепловых
сигналов,
'7’’ Т ш
По аналогии с РЛС можно определить и дальность дей¬
ствия РТЛ. При этом необходимо учитывать следующие
обстоятельства.
333
Радиотепловое излучение цели изотропно в про¬
странстве.
Мощность излучения пропорциональна кажущейся
температуре цели и площади цели S4.
Наряду с целью излучает и фон, на котором видна
цель. Фон заменяется однородной плоскостью, имеющей
кажущуюся температуру Тф.
Пространство между целью и антенной РТЛ (среда
распространения) также является излучателем радио-
тепловой энергии. Интенсивность излучения среды рас¬
пространения характеризуется ее кажущейся темпера¬
турой Тс, а поглощение средой электромагнитных коле¬
баний определяется коэффициентом поглощения сре¬
ды %.
Антенная температура РТЛ
7"а = ^ац-(“^ас“Ь^аф,
где
ц = 47-£)2 ТnSuCn\ exp [ /О],
т& с = 7Vq[l —exp (—//))], Гаф = Гфть
г] — к. п. д. антенно-фидерного тракта РТЛ;
Тац, Т& с, Таф— приращения антенной температуры за
счет излучений цели, среды и фона;
D — дальность до цели;
G — коэффициент усиления антенны РТЛ.
Отношение сигнал/помеха на выходе РТЛ для
Рвх^С 1
S^TlG^fic 2
(4п)2 D4 (Г'ш)2 ‘ х’
(8-2)
где Т'ш = Тш + Тас + Таф — приведенная шумовая темпе¬
ратура;
&z = exp [—■/£)].
Для получения заданной вероятности обнаружения
или заданной точности сопровождения выходное зна¬
чение отношения сигнал/помеха должно быть не менее
некоторого порогового значения рвыхмин- Подставив это
334
значение в (8.2) и решив относительно D, получим даль¬
ность действия РТЛ в режиме автосопровождения
‘ вых мин
При работе РТЛ в режиме обзора эффективное время
наблюдения малоразмерной цели tc зависит от ско¬
рости обзора Qc и ширины диаграммы направлен¬
ности аа
'«=^“-67 /Ч"- <М
где —коэффициент, зависящий от формы диа¬
граммы направленности (при прямоугольной форме
£с=1).
Подставив (8.4) в (8.3), получим выражение, опре¬
деляющее дальность действия радиотеплолокатора в ре¬
жиме обзора.
Для случая работы РТЛ по протяженным целям,
угловые размеры которых Д(рц>аа, уравнение дальности
действия несколько отличается, но может быть выведено
аналогичным образом.
Из выражений (8.3) и (8.4) видно, что на дальность
действия РТЛ сильнее всего влияют кажущаяся темпе¬
ратура и площадь цели. В меньшей степени дальность
действия зависит от скорости сканирования и эффектив¬
ной длительности сигнала. Коэффициент усиления ан¬
тенны существенно влияет на дальность действия только
в следящих РТЛ, так как в обзорных РТЛ одновременно
с увеличением коэффициента усиления антенны умень¬
шается ширина диаграммы направленности, а следова¬
тельно, и длительность сигнала.
§ 8.4. ПРИЕМНЫЕ УСТРОЙСТВА
РАДИОТЕПЛОЛОКАТОРОВ
Радиотеплолокатор состоит, как правило, из антен¬
ного устройства, приемного устройства и решающего
устройства (индикатора). Наиболее важным звеном, от
которого зависит качество работы РТЛ и которое наи¬
более сильно отличается от аналогичного звена актив¬
ного радиолокатора, является приемник радиотеплового
излучения. Наибольшее распространение получили три
335
типа приемников: компенсационный, модуляционный и
корреляционный.
Компенсационный приемник радиотеплового излуче¬
ния имеет блок-схему, полностью совпадающую с блок-
схемой, изображенной на рис. 8.2, и является простей¬
шим из всех видов приемников радиотеплового излу¬
чения. Решающее устройство такого приемника пред¬
ставляет собой вычитающую схему, компенсирующую
постоянную составляющую выходного напряжения от
Антенна
\ ВЧ
фильтр
J feu)
Квадратич¬
ный
детектор [
Д. !5bi:
j
L
Рис. 8.2. Блок-схема простейшего радиотеплолокатора
(радиометра).
собственных шумов приемника, и пороговый индикатор.
Преимущество компенсационного приемника перед
другими состоит в его простоте и высоком коэффи¬
циенте использования энергии входного сигнала. Круп¬
ным недостатком является наличие так называемых
аномальных флюктуаций выходного сигнала за счет
флюктуаций коэффициентов усиления УВЧ и УНЧ, что
приводит к значительной потере реальной чувствитель¬
ности. Так как спектр аномальных флюктуаций лежит
в области инфранизких частот, то ослабление влияния
этих флюктуаций в модуляционном приемнике (рис. 8.3)
производится переносом спектра сигнала в область бо¬
лее высоких частот путем амплитудной модуляции вход¬
ного сигнала ФВЧ. Амплитудная модуляция осущест¬
вляется до источников аномальных флюктуаций (ВЧ и
НЧ фильтры), поэтому спектр флюктуаций не изме¬
няется и остается по-прежнему в области инфрапиз-
ких частот, вследствие чего спектры сигнала и аномаль¬
ных флюктуаций оказываются разделенными. Избира¬
тельный усилитель, синхронный детектор и НЧ фильтр
служат для выделения напряжения сигнала из промо-
дулированного входного напряжения приемника. Ре¬
шающая схема представляет собой пороговый индика¬
тор. Модуляционный приемник значительно ослабляет
влияние аномальных флюктуаций по сравнению с ком-
336
пенсационным, однако коэффициент использования мощ¬
ности сигнала у него в среднем в два раза меньше.
С целью увеличения коэффициента использования мощ¬
ности сигнала на практике обычно используются двух¬
тактные модуляционные приемники радиотепловых
сигналов (рис. 8.4), в которых модулятор заменяется
Рис. 8.3. Модуляционный приемник радиотепловых излучений.
высокочастотным коммутатором, попеременно подклю¬
чающим антенну ко входам двух высокочастотных ка¬
налов. Если потери в ВЧ коммутаторе отсутствуют,
энергия входного сигнала используется полностью.
Мощность собственных шумов в двухтактном прием¬
нике в два раза больше, чем в однотактном. Большим
преимуществом двухтактного приемника является его
Рис. 8.4. Двухтактный модуляционный приемник.
22—1173
337
повышенная надежность по сравнению с остальными
типами приемников, так как при выходе из строя одного
из каналов приемник продолжает работать на исправ¬
ном канале, при этом лишь в два раза уменьшается
выходное отношение сигнал/шум.
Корреляционный приемник (рис. 8.5) состоит из двух
ВЧ фильтров, перемножающего устройства, НЧ филь¬
тра и решающей схемы, представляющей собой порого-
'Антенна
I L
] фильтр I
Г Пег,
H Ч фильтр p
J ) Pom
P ..
'ющсе
■jjcmdo
-Г’-
!
Э7/
i
'lpuilCirit-G
Рис. 8.5. Корреляционный приемник радиотепловых излучений.
вый индикатор. Напряжение на выходе перемножаю¬
щего устройства такого приемника при условии, что оба
ВЧ фильтра идентичны, а собственные шумы каналов
(включая и аномальные флюктуации) независимы,
будет
(0 = [^1Д1 (О (01 ’ [^Ш2 (0 4“ (0J ~
— Uc (ty Uc W (0 ^ш2 (0-
Члены и2ш(0, дающие дополнительную постоянную со¬
ставляющую выходного напряжения за счет аномаль¬
ных флюктуаций и характерные для компенсационного
и частично модуляционного приемников, в корреляцион¬
ном приемнике отсутствуют.
§ 8.5. МЕТОДЫ ПАССИВНОЙ РАДИОЛОКАЦИИ:
РАДИОТЕПЛОПЕЛЕНГАЦИЯ, ИЗМЕРЕНИЕ
ДАЛЬНОСТИ И ИЗМЕРЕНИЕ СКОРОСТИ
В пассивной радиолокации, так же как и в активной,
конечной задачей является получение информации о це¬
ли: угловых координат, дальности и скорости движения
цели относительно пассивного радиолокатора. Ввиду
принципиальной невозможности использования в ПРЛ
опорных сигналов прямым путем могут быть определе-
338
пы только угловые координаты цели. 1
росгь перем ощеним цели определяются
тодами. Поэтому основной метод пассивной
ции — это радиотеплопелепгация.
Радиотеплопелепгация основана
направленности антенны РТЛ, при
применение нашли два метода
пеленгации: метод максимума,
•кругового обзора, и метод
(альпость и ско-
косвенными ме-
радиолока-
н а использовании
этом наибольшее
амплитудной радиотепло-
применяемый в РТЛ
сравнения амплитуд, при¬
меняемый в следящих
РТЛ. В активной радио¬
локации предпочтение от¬
дают более сложному, но
зато более точному па¬
раллельному способу
сравнения, так как при
этом устраняется влия¬
ние флюктуаций центра
отражения на точность
определения угловых ко¬
ординат. В пассивной ра-
Рис. 8.6. Угломерно-базовый метод
определения дальности в пассив¬
ной радиолокации.
диолокации положение
центра излучения относи¬
тельно самой цели прак¬
тически постоянно вслед¬
ствие большого количе¬
ства излучателей. Поэто¬
му в РТЛ широко приме¬
няется способ последовательного сравнения амплитуд,
осуществляемый чаще всего с помощью конического ска¬
нирования диаграммы направленности антенны. Работа
амплитудных пассивных пеленгаторов, их характеристики
и расчет практически тождественны аналогичным актив¬
ным радиолокационным пеленгаторам.
Простейшим косвенным методом измерения даль¬
ности в пассивной радиолокации является угломерно¬
базовый (рис. 8.6), основанный на решении треуголь¬
ника по известным стороне (база d) и двум углам (<pi
и ф2). Ввиду невозможности использования опорных
сигналов, относительно которых можно было бы опре¬
делить допплеровский сдвиг частоты, в пассивной ра¬
22*
339
диолокации используются специфические методы изме¬
рения скорости:
1. Методы, основанные на окраске спектров некото¬
рых естественных радиоизлучений, которые исполь¬
зуются, например, в радиоастрономии для определения
скорости движения облаков межзвездного водорода.
2. Методы, использующие один из каналов базового
дальномера в качестве генератора опорного сигнала.
Эти методы основаны на том, что относительно ПРЛ1 и
ПРЛц (рис. 8.6) движущаяся цель имеет различные
радиальные скорости, вследствие чего средние частоты
сигналов от этих целей на входах ПРЛ также раз¬
личны. Измерив разность частот и зная расстояние от
опорной точки до цели, можно расчетным путем опреде¬
лить и скорость движения цели относительно опорной
точки.
В заключение следует подчеркнуть, что пассивная
радиолокация — это очень молодая и бурно развиваю¬
щаяся отрасль техники, главные области применения
которой:
1) Обнаружение и определение координат назем¬
ных, надводных, подводных, воздушных и космических
объектов.
2) Решение навигационных задач.
3) Самонаведение средств поражения на источники
радиоизлучения.
4) Всепогодная астронавигация (радиосекстанты).
5) Всепогодное обнаружение источников тепловой
энергии.
6) Неконтактное измерение распределения темпера¬
тур объектов.
Весьма важными достоинствами пассивной радио¬
локации является сочетание абсолютной скрытности со
всепогодностью, а также относительная дешевизна и
надежность аппаратуры.
Глава 9
ФАКТОРЫ, ОПРЕДЕЛЯЮЩИЕ ДАЛЬНОСТЬ
РАДИООБНАРУЖЕНИЯ И ТОЧНОСТЬ
МЕСТООПРЕДЕЛЕНИЯ
§ 9.1. ОБОБЩЕННОЕ УРАВНЕНИЕ РАДИОЛОКАЦИИ
В § 1.5 приведена простейшая форма уравнения ра¬
диолокации
Тумаке
РиСиАоэ
(4л)2 Рс мин
устанавливающего связь дальности действия РЛС с ее
параметрами (излучаемой мощностью Ри, коэффициен¬
том направленности передающей антенны GH, эффек¬
тивной площадью приемной антенны Л), пороговой
мощностью сигнала Ромни и эффективной площадью
рассеяния наблюдаемого объекта <уэ. Это уравнение
может быть использовано во всех случаях работы РЛС
в свободном пространстве при расположении передаю¬
щей и приемной антенн в одном месте. Однако разнооб¬
разие реальных условий работы РЛС приводит к необ¬
ходимости применения для расчета более универсальных
форм уравнения дальности, позволяющих учесть влия¬
ние многочисленных факторов. В частности, целесо¬
образно использовать в уравнении не мощность, а энер¬
гию сигнала. Это наиболее очевидно при рассмотрении
случая импульсного излучения.
Из уравнения (1.4) можно сделать заключение, что
увеличением мощности в импульсе за счет сокращения
его длительности можно повысить дальность действия
без увеличения энергии станции. Ошибочность такого
заключения становится ясной при введении в уравне¬
ние дальности длительности сигнала ти в явном виде.
Это нетрудно сделать при более детальном рассмотре¬
нии порогового сигнала РСмпи.
341
Для работы оконечного устройства станции с задан¬
ной надежностью необходимо, чтобы отношение сиг-
нал/шум превышало некоторую величину тр, которая
применительно к визуальной индикации сигнала на
экране ЭЛТ называется коэффициентом различимости.
Тогда мощность порогового сигнала можно записать
в виде
где Рш— мощность шумов приемника, приведенных
к его входу;
N — коэффициент шума приемника.
Пороговый сигнал становится минимальным при
полосе Af, согласованной с длительностью сигнала,
= (9.2)
где g — некоторый коэффициент (близкий к 1), завися¬
щий от формы сигнала.
С учетом соотношений (9.1) и (9.2) уравнение даль¬
ности (1.4) приводится к виду
Г) ■и/' Ри'Еиби^Р'Э ZQ П\
ь'макс— у (4п)2
Уравнение (9.3) ясно показывает, что дальность
действия импульсной РЛС определяется энергией излу¬
чаемого сигнала ЕИ = РптИ, а не его импульсной мощ¬
ностью.
Для сравнительной оценки дальности действия раз¬
личных РЛС и выявления значения отдельных пара¬
метров системы необходима еще более общая форма
уравнения дальности.
Если передатчик и приемник системы размещены
в разных точках на расстоянии и О2 от объекта, то
мощность сигнала на входе приемника можно записать
в виде
Рс
(9.4)
где Лаф и Лр — коэффициенты, учитывающие потери
энергии сигнала в антенно-фидерном устройстве и из-за
поглощения при распространении.
342
Размещение передатчика и приемника РЛС в раз¬
ных местах имеет место при полуактивпом обнаружении,
которое находит применение в системах радиоуправ¬
ления.
Подставляя в (9.4) вместо эффективной площади
приемной антенны Ап ее эквивалент Лп= GnX2/4n, по¬
лучим
р Р
° _ (4Л)’О2^£а„Лр ’
Введем в уравнение отношение энергии принимаемого
сигнала Е = Р^ к спектральной плотности шума Nq.
Введенное в гл. 4 отношение 2E/-NQ может быть исполь¬
зовано для характеристики практически любой РТС и
придает уравнению (9.5) обобщенный характер:
2Е 2РiiG 1А2ав^н /д
— (4л)3 1 ’
где NQ = kTm— спектральная плотность шума, приведен¬
ного ко входу приемника;
тп — время накопления, которое зависит от
типа и режима работы РЛС.
Так, для РЛС с непрерывным автоматическим со¬
провождением цели тп зависит от постоянной времени
системы, а для обзорных РЛС — от скорости обзора и
ширины диаграммы направленности антенн.
Эквивалентная шумовая температура Тш слагается
из шумовой температуры антенны 1\ и приемного
тракта
7 ш = 7\ + 7дТ = 7\ + (А^ - 1) 290°, (9.7)
где Л7ф — коэффициент шума линии передачи антенна—
приемник.
Система обнаружения с оптимальным согласован¬
ным фильтром обеспечивает обнаружение сигнала при
минимальном значении 2£7Л70. В § 4.6 для такой систе¬
мы был введен параметр обнаружения q=V 2EINq и
приведены характеристики обнаружения, позволяющие
найти его величину по заданным значениям вероятно¬
стей правильного обнаружения D и ложной тревоги F.
В связи с этим целесообразно для сравнительной оцен¬
ки систем представить отношение 2EINq, необходимое
для пор ма л ь 11 ого ф у 11 к ц и о ни р о вапня расс м а тр и в а е м о й
343
системы, в виде произведения q'1 на коэффициент С,
учитывающий специфику системы и отклонения ее па¬
раметров от оптимальных. Тогда получим обобщенное
уравнение
G 2 = g
пригодное для расчета дальности действия и сравни¬
тельной оценки различных систем. Имея в виду обыч¬
ный для активных РЛС случай размещения приемной и
передающей антенн в одном месте (D1 = D2 = -D) и
решая уравнение (9.8) относительно D при ^=^мип, по¬
лучим обобщенное уравнение для максимальной даль¬
ности РЛС
(4л;)3 kTmL^LvCq2wwl
(9-9)
удобство которого заключается в возможности исполь¬
зования имеющихся характеристик обнаружения при
вычислении порогового сигнала Сд2мип различных си¬
стем.
§ 9.2. ВЛИЯНИЕ РЕЖИМА РАБОТЫ И ОТДЕЛЬНЫХ
ФАКТОРОВ НА ДАЛЬНОСТЬ ДЕЙСТВИЯ СИСТЕМ
Расчет дальности действия конкретной РЛС с за¬
данной технической характеристикой представляет да¬
леко не простую задачу, так как предварительно долж¬
ны быть найдены значения коэффициента С и учтены
условия распространения сигнала. Еще более сложным
является выбор параметров системы по заданной даль¬
ности действия, поскольку при этом должны учитывать¬
ся и другие тактические характеристики системы.
В настоящем параграфе кратко рассматриваются
факторы, определяющие величину коэффициента С,
выражающего увеличение отношения сигнала к шуму,
требуемого для обеспечения заданных D и F реальной
системы, по сравнению с идеально согласованной си¬
стемой, для которой С=1. Иначе говоря, коэффициент С
отражает проигрыш (потери) в отношении сигнала
к шуму из-за пеоптимальпости характеристик системы.
В зависимости от вида системы причины потерь несколь¬
ко видоизменяются.
344
Рассмотрим определение коэффициента С на при¬
мере импульсных РЛС. В импульсных РЛС обзора -при¬
нимаемый сигнал представляет пачку из п импульсов,
следовательно, Тц = пги.. При применении когерентного
интегрирования и при условии одинаковой амплитуды
импульсов пачки это равносильно увеличению дальности
в ц' п по сравнению со случаем одиночного импульса
длительностью тп. Однако в большинстве импульсных
РЛС применяется некогерентпое последетекториос на¬
копление, при котором выигрыш в дальности' мень¬
ше у//г, что связано с эффектом подавления сигнала
шумом при детектировании, подробно обсуждавшимся
в § 4.11.
Потери последетекторного интегрирования можно
представить коэффициентом Си, являющимся одной из
составляющих коэффициента С в формуле (9.9). Кроме
того, в системе возможны потери из-за отклонения по¬
лосы пропускания УПЧ от оптимальной—Сд/; потери,
связанные с наложением сигналов — С1Ь и потери при
визуальном наблюдении отметок целей на экране инди¬
катора оператором—Со. Таким образом, С = СИСД/СНСО, а
если составляющие определены в децибелах, то
С — (Си + £Д/Н“Сн + С0) дб.
Для определения потерь последетекторного интегри¬
рования Си можно воспользоваться имеющимися в ли¬
тературе * графиками Си = /(п). Такой график для зна¬
чений £> = 0,9 и £=10-7 приведен на рис. 4.27 (кри¬
вая III).
В реальных системах, как уже указывалось, в силу
различных причин полоса пропускания УПЧ (Д/Пч)
обычно превышает согласованную полосу Д/с, что ведет
к проигрышу в отношении сигнала к шуму на выходе
УПЧ. Для определения потерь на несогласованность
полосы CLf можно использовать тот же график Си = Дп)
Если определить Си для п импульсов пачки и СИ1 для
= /г импульсов, то Сд/^ СИ1/СИ.
* Например: К. В. Голев «Расчет дальности действия РЛС».
Изд-во «Советское радио», 1962.
345
Аналогично можно найти потери из-за наложения
сигналов, возникающие при скорости развертки инди¬
катора или полосе пропускания видеоусилителя AF,
значительно меньших их оптимальных значений. При
этом отметка в рассматриваемой точке экрана представ¬
ляет результат наложения суммарных импульсов сигна¬
ла с шумом и только шумовых выбросов. Если число
импульсов сигнала с шумом по-прежнему равно п (опре¬
деляется числом импульсов пачки), а число только шу¬
мовых выбросов, появляющихся в том же месте экрана,
равно пш, то коэффициент потерь наложения Сп может
быть вычислен также с помощью графика Cn = f(n).
Определив Си для п импульсов и Си2 для /г2 = ^ + ^ш им¬
пульсов, найдем Сн = Си2/Си.
Значение п2 можно вычислить, зная длительность
сигнальных импульсов ти, скорость развертки и диа¬
метр пятна на экране трубки dn, по формуле
п =nrfn + t,PT-.
Ур'Си
Коэффициент Со зависит от типа индикатора и субъек¬
тивных качеств оператора. При применении ИКО
Со^2 дб.
При расчете дальности действия РЛС в режиме об¬
зора должны быть учтены также потери энергии, вы¬
званные модуляцией сигнальных импульсов пачки по
закону диаграммы направленности антенны.
§ 9.3. ДАЛЬНОСТЬ ДЕЙСТВИЯ РЛС С УЧЕТОМ
ОТРАЖЕНИЯ ОТ ЗЕМНОЙ ПОВЕРХНОСТИ
И ЗОНА ОБНАРУЖЕНИЯ (ВИДИМОСТИ) СТАНЦИИ
Во многих случаях сигнал в силу отражения радио¬
волн от земной поверхности, ионосферы или другой но-
верхности раздела достигает приемного устройства не
одним, а двумя или даже несколькими путями. При
этом возникает интерференция сигналов, которая в за¬
висимости от относительной фазы приходящих колеба¬
ний может привести как к усилению, так и к ослабле¬
нию принимаемых колебаний. Это непосредственно
сказывается на дальности действия систем. Кроме того,
интерференция основного и отраженного сигналов вы¬
зывает их искажения, которые могут привести к сииже-
346
нию точности и разрешающей способности радиотехни¬
ческих систем.
При отражении от земной поверхности на расстоя¬
ниях, много больших А, результирующий сигнал Ер
является результатом интерференции прямого Еп и от¬
раженного £0 сигналов. Разность фаз сигналов опреде-
деляется разностью хода двух лучей и скачком . фазы
при отражении. Если передающая антенна поднята на
высоту Л1>л/2, то в вертикальной плоскости диаграмма
излучения имеет лепестковую структуру, причем, при
равенстве амплитуд прямого и отраженного сигналов
Еп = Е0 результирующий сигнал на направлениях ма¬
ксимумов лепестков достигает £Р = 2ЕП, а в провалах
между лепестками падает до 0. Соответственно распо¬
ложению лепестков изменяется и дальность действия
системы. Распределение напряженности результирую¬
щего поля непосредственно связано с понятием зоны
обнаружения РЛС — области пространства, в пределах
которой РЛС обеспечивает обнаружение объектов
с определенной площадью рассеяния о0 и с вероят¬
ностью не менее заданной.
Таким образом, зона обнаружения РЛС ограничи¬
вается поверхностью равных напряженностей отражен¬
ного поля, минимально достаточных для обнаружения
цели. С помощью коэффициента распространения при
отражении Е0 = Ер/Еп нетрудно получить выражение для
зоны обнаружения станции с учетом отражения от зем¬
ной поверхности, поскольку влияние отражения ска¬
зывается в увеличении или уменьшении напряженности
поля в определенных направлениях.
Рассмотрим случай, когда максимальная дальность
действия существенно меньше дальности горизонта и
земную поверхность можно считать плоской. Кроме того,
предположим, что поверхность гладкая, т. е. отраже¬
ние зеркальное, и сигнал при отражении претерпевает
изменение фазы на ф радиан и уменьшение амплитуды
в р раз. Допустим, что ненаправленный излучатель
и цель расположены на высотах h\ и h2 (рис. 9.1),
а расстояние между ними равно D.
Прямой луч имеет напряженность поля в месте
расположения цели Еп, а отраженный — Е0 = рЕп и от¬
стает по фазе на у = ф + ц> радиан (ср — фазовый сдвиг
347
за счет разности путей прямой и отраженной волн).
Результирующая напряженность поля у цели будет
Fn -|- рЕп е 77.
Отсюда коэффициент распространения при отражении
равен
Fo = -1^-= I 1 4“ Ре~П I = I 1 + Р (cos Y “ 1 sin Y)| =
— ]/(l -j—/7 cos Y)2 + (/?sin у)2 —
— К1 Ц- 2p cos у + /А (9.10)
Коэффициент Fq часто называют интерференцион¬
ным множителем. Таким образом, при наличии отра¬
жения от земли характеристика направленности в вер-
Рис. 9.1. Ход прямого и отраженного лучен.
тикальной плоскости определяется произведением диа¬
граммы направленности антенны /(р) и интереферен-
ционного множителя Fo. Произведение f(P)*F0 и опре¬
деляет форму зоны обнаружения РЛС в вертикальной
плоскости.
Определим интерференционный коэффициент для
случая гладкой и хорошо проводящей поверхности (на¬
пример морской воды) и горизонтальной поляризации
поля. В этом случае р~ 1, ф = л и
F. = /2 + 2 cos (тс + <р). (9.11)
Значение Fo изменяется от 0 при ф=2лЛ до 2 при
Ф= {2k + 1) л.
Таким образом, зона обнаружения РЛС сильно ме-
348
пяется в зависимости от характера отражения от зем¬
ной поверхности.
Из простых геометрических построений нетрудно
найти, что разность хода AD при условии и h2
равна
а соответствующий фазовый сдвиг
<Р
2тс д п 4тс/ц/г2
Тогда
f.= j/ 2 + 2с«(я+4^.
Так как
1 4- cos а = 2 cos2
то
Fo = 2cos(^-\-2-^^ = 2sm^^. (9.12)
Таким образом, для принятых условий интерферен¬
ционный коэффициент изменяется в зависимости от hi,
h2 и D по синусоидальному закону от 0 до 2. Графиче¬
ски обычно представляют зависимость Fo в координа¬
тах /?2, D при фиксированной высоте излучателя hi.
т—г ^7ihihn
Полагая последовательно величину аргумента —д- -
тс Зтс (2/гД-1)тс
равной у, -у—2 " > можно наити направление
„ , 2nh1h2
максимальной напряженности поля, а принимая —по¬
следовательно равным 0, тс, 2«, . . ., 2&тс, найдем положение
минимумов напряженности поля. Число лепестков опреде¬
ляется отношением hjh и равно
На рис. 9.2 представлен график зависимости резуль¬
тирующего коэффициента распространения Fp = f(|3)F0,
определяющей зону обнаружения РЛС в вертикальной
плоскости с учетом формы диаграммы направленности
антенны f (,р).
349
Если используемые дальности велики и приближа¬
ются к дальности горизонта, то при построении зоны
обнаружения приходится вводить поправку на кривизну
Земли. При выполнении условия hi<^h2 учет сферично¬
сти Земли сводится к замене истинной высоты цели при¬
веденной высотой:
Л 2 11 2 Д/i ' Il 2 >
где — радиус Земли.
Рис. 9.2. Диаграмма видимости РЛС.
При этом вид зоны обнаружения остается таким же,
как и для «плоской» Земли, а поверхность Земли будет
изображаться параболой (пунктир на рис. 9.2), уравне¬
ние которой A/z = —D2I2R3. Линии равных высот будут
также параболами, параллельными параболе, изобра¬
жающей поверхность Земли.
В случае отражения от слабо проводящей или не¬
ровной поверхности использованные предположения
относительно р и ф уже неприемлемы и вычисление Го
необходимо производить по исходной формуле (9.10).
Так как р всегда меньше 1, то пределы изменения Fo
обычно меньше, чем для идеальной отражающей поверх¬
ности, но общий характер изменений сохраняется.
В реальных условиях работы РЛС приходится учи¬
тывать влияние рельефа местности на зоны обнаруже¬
ния станции. Строгий учет влияния рельефа представ¬
ляет весьма сложную задачу, поэтому приведем лишь
некоторые общие сооображения и рекомендации. Если
местность имеет на значительном протяжении неболь¬
шой уклон б, то диаграмма видимости поворачивается
на угол б. Это обстоятельство следует учитывать при
350
выборе позиции РЛС. Так, если необходимо получить
возможно большую дальность обнаружения низколетя¬
щих самолетов, целесообразно установить станцию так,
чтобы был уклон местности в сторону ожидаемого по¬
явления самолетов. При этом первый лепесток диа¬
граммы видимости займет положение, близкое к гори¬
зонтальному, и в этом направлении дальность обнару¬
жения будет максимальной. Напротив, подъем местно¬
сти в сторону цели поворачивает диаграмму обнаруже¬
ния вверх, при этом увеличивается дальность действия
при больших углах места цели.
Таким образом, условия распространения сильно
влияют на дальность действия РЛС, так же как и дру¬
гих радиотехнических систем, и должны обязательно
учитываться при выборе основных технических характе¬
ристик системы.
§ 9.4. ВЛИЯНИЕ ПРЕЛОМЛЕНИЯ, ПОГЛОЩЕНИЯ
И РАССЕЯНИЯ РАДИОВОЛН НА ДАЛЬНОСТЬ
ДЕЙСТВИЯ РТС
Преломлением (рефракцией) называется отклонение
распространения радиоволны от прямолинейного при
прохождении через границу двух сред или среды с из¬
меняющимися электрическими параметрами. Прелом¬
ляющие свойства среды характеризуются коэффициен¬
том преломления^ п, определяемым диэлектрической по¬
стоянной п=У е.
Коэффициент преломления обычно уменьшается
с высотой, что приводит к искривлению траектории ра¬
диоволн в сторону земной поверхности (огибанию). При
этом дальность радиогоризонта увеличивается так же,
как и возможная дальность действия РТС. В связи
с этим при расчетах эквивалентный радиус Земли
искусственно увеличивают с тем, чтобы при спрямлен¬
ной траектории получить дальность радиогоризонта Орг,
равную реальной. При нормальном состоянии атмо¬
сферы коэффициент кажущегося увеличения радиуса
Земли равен /(=4/3 и дальность радиогоризонта увели¬
чивается до
(9.13)
351
Орг — 4,1 (p^ilZ/Zj) км,
по сравнению с дальностью горизонта при отсутствии
преломления
Dr = 3,57 ([Z/z! ]/^2) (9.14)
В формулах hi и h2 — высоты передающей и прием¬
ной (или отражающего объекта) антенн — в метрах.
При определенных состояниях атмосферы, в частно¬
сти при высокой влажности слоев вблизи поверхности
Земли, могут наступить условия равенства величины
градиента коэффициента преломления dnldh и кривизны
Земли:
dn 1
яг*
В этом случае радиус кривизны траектории волнырп
равен радиусу Земли:
(9.15)
dh
и волна, направленная горизонтально, будет огибать по¬
верхность Земли. Это явление называется сверхрефрак¬
цией и приводит к аномальному увеличению дальности
действия систем, работающих в метровом, дециметровом
и сантиметровом диапазонах.
Остановимся на потерях поглощения энергии радио¬
волн при распространении и связанным с этим сокраще¬
нием дальности действия РТС.
В зависимости от длины волны и условий распро¬
странения оказывают преимущественное влияние те или
иные причины потерь энергии. Потери энергии вызыва¬
ются проводимостью земли, в которой радиоволны воз¬
буждают вихревые токи. Из-за потерь в земле диаграм¬
ма излучения в вертикальной плоскости изменяется с рас¬
стоянием D. Напряженность поля вблизи земли убывает
пропорционально I/O2 (вместо 1//)). Чем больше D, тем
относительно больше ослабляется поле вблизи земли.
Поэтому для направлений касательных к земной поверх¬
ности на больших расстояниях остается только поле,
обусловленное дифракцией. При горизонтальной поля¬
ризации влияние поглощения в земной поверхности
больше, чем при вертикальной.
Второй причиной потерь энергии при распростране¬
нии является молекулярное поглощение в атмосфере на
352
частотах, близких к резонансным. Резонансные линии
всех газов атмосферы, за исключением кислорода и во¬
дяного пара, расположены вне диапазона радиоволн, по¬
этому существенным с точки зрения дальности действия
радиотехнических систем является поглощение только
молекулами кислорода и водяного пара. Поглощение мо¬
лекулами кислорода имеет максимумы на волнах л =
— 5 мм и /, = 2,5 мм, а молекулы водяного пара дают
максимум поглощения при л=13,5 мм, при повы¬
шении частоты наблюдается небольшой провал и затем
снова увеличение поглощения. Таким образом, молеку¬
лярное поглощение существенно в сантиметровом и осо¬
бенно в миллиметровом диапазонах, где оно является
фактором, сильно ограничивающим дальность действия
систем, особенно радиолокационных, использующих
отраженные сигналы.
Еще одной причиной, вызывающей потери энергии
при распространении, является рассеяние и прежде
всего дождевыми каплями и туманом. Чем больше отно¬
шение радиуса капли г к длине волны Л, тем больше по¬
тери энергии за счет рассеяния ее во всех направлениях.
Это рассеяние возрастает пропорционально четвертой
степени частоты. Эффективная площадь рассеяния капли
при определяется по формуле
где е — диэлектрическая постоянная рассеивающей
среды.
Если известны диаметр капель и их число на еди¬
ницу объема, можно определить величину коэффициента
затухания %. Величина % обычно указывается для дождя
в зависимости от длины волны и интенсивности дождя.
Интенсивность дождя J измеряется количеством осадков
в миллиметрах, выпадающих в течение часа. Коэффи¬
циент затухания зависит также от частоты колебаний.
В сантиметровом диапазоне коэффициент затухания
изменяется приблизительно пропорционально f2. Напри¬
мер, при /=1 мм!час /=0,002 дб!км при f —3000 Мгц\
и х~0,18 дб!км при / = 30000 Мгц. Ослабление градом и
снегом значительно меньше, чем дождем, и его влиянием
обычно можно пренебречь. Ослабление в тумане прямо
пропорционально величине концентрации воды в тумане.
23—1173 353
Максимальная дальность действия РЛС в свободном
пространстве с учетом затухания может быть найдена
по формуле
D'MaKC=DM(1KclO“W'Ma'I<> (9.17)
где Омаке — дальность действия в свободном простран¬
стве при отсутствии ослабления, км.
Уравнение (9.17) является трансцендентным и мо¬
жет быть решено графически или методом последова¬
тельных приближений. Принимая за нулевое приближе¬
ние Оо=0Макс, находят первое приближение D{~ -
— Do 10~0’05/-°о, а затем второе 02 = DolCTo’O:,z/\ Если при
п-м приближении с достаточной точностью выполняется
условие
то уравнение решено, и максимальная дальность с уче¬
том ослабления равна D\un{C^Dn.
Для некоторых случаев применения РТС существен¬
ное значение имеет поглощение в ионизированных сре¬
дах (например, факел, образующийся при работе дви¬
гателя ракеты, представляет собой облако ионизирован¬
ных газов).
Рассматривая влияние условий распространения ра¬
диоволн на дальность действия радиотехнических си¬
стем, нельзя не упомянуть влияния внешних помех, ко¬
торые в ряде случаев являются основным фактором,
ограничивающим дальность действия системы.
§ 9.5. ЭФФЕКТ КАБАНОВА И ЕГО ИСПОЛЬЗОВАНИЕ
В РАДИОЛОКАЦИИ
В 1947 г. советским ученым Н. И. Кабановым было
открыто явление дальнего рассеянного отражения ра¬
диоволн от земной поверхности, которое получило на¬
звание эффекта Кабанова. В силу этого эффекта в диа¬
пазоне коротких волн сигнал может быть принят в месте
передачи после нескольких последовательных отраже¬
ний (скачков) от ионосферы и земли. Таким образом,
появилась возможность создания коротковолновых РЛС
сверхдальнего обнаружения межконтинентальных бал¬
листических ракет (МБР), мест пуска раке г и взрывов
354
атомных бомб. Такие станции получили название стан¬
ций ионосферной радиолокации (ИРЛ) или загоризонт¬
ных РЛС.* Как и в обычных РЛС, дальность до цели
в станциях ИРЛ определяется по времени запаздывания
отраженного сигнала, а направление фиксируется с по¬
мощью направленной антенны. В то же время станции
ИРЛ имеют специфические особенности и, в частности,
при формировании зоны обнаружения. При обнаруже¬
нии цели на сравнительно малых дальностях и больших
высотах обнаружение и измерение координат объекта
происходит так же, как и обычной РЛС. При обпаруже-
Рис. 9.3. Формирование зоны обнаружения целей станцией ИРЛ:
а — в вертикальной плоскости; б — в плоскости земли;
(Апс — высота ионосферного слоя).
нии целей, находящихся за горизонтом, по в пределах
первого скачка, зондирующий и отраженный сигналы
испытывают однократное отражение от ионосферы, и их
траектория представляет ломаную линию, что исключает
возможность достаточно точного измерения угла места.
При еще больших расстояниях до цели зондирующий
и отраженный сигналы испытывают несколько отраже¬
ний от земли и ионосферы. Вид зоны обнаружения
(рис. 9.3) изменяется при этом в зависимости от высоты
* См. Мищенко Ю. А. Зоны обнаружения. Воеииздат, 1963.
23* 355
ионизированного слоя, формы диаграммы, направленно¬
сти антенны и ее наклона по отношению к земле. Так
как высота ионизированного слоя меняется в зависимо¬
сти от сезона, времени суток и солнечной активности, то
соответственно изменяется вид зоны обнаружения, что
необходимо учитывать при измерении дальности и вы¬
соты обнаруженного объекта. На вид зоны обнаружения
оказывает влияние также неоднородность рассеивающих
свойств земной поверхности вдоль трассы.
Недостатком станций ИРЛ, особенно, существенном
при обнаружении МБР, является ограничение зоны
обнаружения — высотой отражающего слоя ионосферы,
которая в среднем составляет 300 км. Расчет дальности
действия станции ИРЛ представляет сложную задачу,
так как при этом должны учитываться потери из-за рас¬
сеяния и поглощения на пути распространения, а также
при отражении от земли и ионосферы. Имеют место так¬
же потери из-за изменения плоскости поляризации сиг¬
нала.
§ 9.6. УРАВНЕНИЕ ДАЛЬНОСТИ РАДИОЛИНИИ
С АКТИВНЫМ ОТВЕТОМ
Радиолинии с активным ответом используются в ра¬
дионавигационных дальномерных системах, в радио¬
локационных системах с активным ответом, в системах
опознавания и телеизмерения.
Одной из основных особенностей радиолиний с актив¬
ным ответом является независимость каналов запроса
и ответа. В связи с этим дальность действия каналов
может быть различной, и дальность действия системы
в целом, а следовательно, и ее тактические возможности
определяются каналом с меньшей дальностью действия.
Очевидно, целесообразно выбирать параметры радиоли¬
нии такими, чтобы дальность действия каналов запроса
и ответа была одинаковой. Если обозначить мощность
передатчика запросчика Рпз, коэффициент направлен¬
ности антенн передатчика и приемника капала запроса
соответственно GI13 и G1I3, то уравнение дальности капала
запроса запишем в виде
Р IT 3 G и 3 G | 3 7 ~
356
При мин дальность действия канала запроса
равна максимально н
/} и з G ц з G j.: Д
(4 те)"/\ з Vi ии
(9.18)
Совершенно аналогично для канала ответа можно полу¬
чить уравнение
РhoGhqG, о^о
^со = (4тг)2 D2
И
PwoGuoGI 0^0
(Чл)2/5(о МИ11
(9.19)
где Лю — мощность, излучаемая передающей антенной
ответчика, имеющей коэффициент направлен¬
ности би0;
Gno — коэффициент направленности приемника от¬
ветного капала (приемника запросчика);
Zo — длина волны ответного канала;
Рсо мпн — минимальная мощность ответного сигнала, до¬
статочная для срабатывания приемного
устройства запросчика с заданной надеж¬
ностью.
Для получения равенства дальности действия кана¬
лов запроса и ответа необходимо обеспечить выполне¬
ние условия
Р из£? ИзОпЗ^з Р Во£?иоЛ.о\;
5 = р~ > (9.20)
1 СЗ МИН 1 (О МИН ' 7
которое легко получить, приравнивая выражения (9.18)
и (9.19).
Часто в запросчике и ответчике для передачи и
приема используется одна антенна. В этом случае
^изСцз = GIIOGno
и выражение (9.20) упрощается:
_ —. * (9.21)
1 СЗ м !■! н J ( О мин * '
357
Если каналы запроса и ответа работают на одной
пли близких частотах, то —Хо и условие (9.21) сводит¬
ся к виду
^ИЗ^СО М1П1~ Р сз .мин- (9.22)
Формулы (9.20), (9.21) и (9.22) являются разновид¬
ностями уравнения сбалансированной системы с актив¬
ным ответом, которая энергетически наиболее выгодна
при равенстве мощностей, излучаемых передатчиками
запросчика и ответчика.
§ 9.7. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ ЛИНИИ
ПОЛОЖЕНИЯ
В зависимости от принципа работы РТС определение
линий положения объекта производится путем измере¬
ния времени запаздывания, амплитуды, фазы или часто¬
ты принимаемых электрических сигналов. На практике
измерение любого из указанных параметров сигнала
происходит с ошибкой, в результате чего найденная ли¬
ния положения не соответствует действительному рас¬
положению объекта в пространстве. Ошибки измерения
можно условно классифицировать по причинам их воз¬
никновения.
а) Инструментальные ошибки. Основной причиной
возникновения инструментальных погрешностей являют¬
ся процессы, протекающие внутри узлов бортовой и на¬
земной аппаратуры РТС местоопределения. Такими про¬
цессами являются: изменение элементов, параметров и
режимов работы схем при изменении окружающей тем¬
пературы, влажности, давления, питающих напряжений;
старение элементов схемы; воздействие внутренних шу¬
мов. В инструментальную ошибку входят также погреш¬
ности измерения, вызванные неточностью и нестабиль¬
ностью градуировки шкал и несовершенством систем
индикации и отсчета показаний.
б) Ошибки распространения. Источником ошибок
распространения являются нестабильность условий рас¬
пространения радиоволн (скорости распространения,
рефракции, затухания в атмосфере Земли) и воздей¬
ствие на систему паразитных сигналов, отраженных от
местных предметов, земной поверхности, гидрометеоров
и ионосферных слоев. Иа характер процессов распро¬
странения и отражения радиоволн оказывает влияние
358
состояние солнечной активности, суточное и годовое вра¬
щение Земли, метеорологическая обстановка, располо¬
жение местных предметов в момент излучения и приема
сигналов.
в) Ошибки, обусловленные действием внешних помех.
Характер и величина погрешностей измерения, вызван¬
ных действием внешних источников помех, зависят от
вида помех, их интенсивности и расположения источни¬
ков помех относительно станций системы.
aft)
Яср
Со
-а
4t,
А
а2
At%
Оз
At3
д-
- 4х*
Л
Gi
Att
4
A
_ _bc
0
i
7 t
Рис.. 9.4. Вид записи результатов непрерывного и дискретного изме¬
рений параметра а\
«о — iiciникое значение измеряемого параметра; аср — среднее арифметическое
результатов измерения; Дбг— случайная и Дас — систематическая составляю¬
щие ошибок отдельных замеров.
г) Картографические ошибки и ошибки каналов пере¬
дачи и обработки данных измерения. Для данного класса
ошибок характерны такие причины возникновения, как
неточности картографического изображения линий поло¬
жения, погрешности при интерполяции дискретных дан¬
ных измерения, ошибки кодирующих и декодирующих
устройств, субъективные ошибки операторов при отсче¬
тах и вычислениях и др.
Действие чрезвычайно большого числа независимо
действующих факторов приводит к тому, что. ошибки
определения линий положения носят случайный харак¬
тер, и оценку точности местоопределения можно произ¬
водить только на основе статистических данных, полу¬
ченных в результате большого числа измерений. Воз¬
можно также производить вероятностную оценку
точности аналитическим путем, изучая характер воздей¬
359
ствия различных факторов и задаваясь предполагаемы¬
ми условиями реальной работы системы.
Рассмотрим основные статистические показатели, ха¬
рактеризующие точность определения линий положения.
Пусть а0 — истинное значение параметра (угла, дально¬
сти или разности расстояний), определяющего линию
положения неподвижного объекта; а(1) —автоматиче¬
ская запись на ленте самописца выходных показаний
системы при непрерывном характере измерений пара¬
метра; <21, а2, ..ап— результаты п независимых отсче¬
тов или замеров при дискретном характере измерений;
Д/г— интервалы времени между отдельными замерами;
Т — общее время, затраченное на весь цикл измерений
(рис. 9.4). Тогда среднее арифметическое значение ре¬
зультатов измерения может быть рассчитано по одной
из двух формул, пригодных соответственно для непре¬
рывного и дискретного процессов измерения в условиях
стационарного действия внешних и внутренних дестаби¬
лизирующих факторов:
т
и
или
I—п
«ср = « = • (9.23)
Разность между средним арифметическим и истинным
значением измеряемой величины является систематиче¬
ской составляющей ошибки или просто систематической
ошибкой измерения:
Дас = «ср—«о. (9.24)
Определение систематической ошибки играет очень
важную роль в оценке точности измерения. Однако
сама по себе величина Л<2С еще не является исчерпываю¬
щим критерием точности. Полную ошибку измерения
в пределах цикла Т в любой момент времени следует
рассматривать как сумму двух составляющих — систе¬
матической определенной по формуле (9.24), и
случайной >\а\
оа а — а0 hac -|- ha. (9.25)
360
Случайную составляющую ошибки характеризует
дисперсия о2, которая является средним квадратом от¬
клонения результатов измерения от среднего значения:
■= Да'- (а —
ИЛИ
i~n
У (««— «<■>)■’
У = =--- . (9.26)
В тех случаях, когда систематическая ошибка не
равна нулю, следует различать среднеквадратичное зна¬
чение случайной составляющей ошибки А«ср.кв = па и
Рис. 9.5. Плотность вероятности случайной величины а и отклонения
от среднего (случайной составляющей ошибки)
среднеквадратичное значение полной ошибки измерения,
которое равно
ср нв = *|/Г(а е/о)2 — ]/ (9.27)
Таким образом, численными статистическими показа¬
телями точности измерения параметра являются систе¬
матическая ошибка Дас и среднеквадратичное значение
случайной составляющей ошибки оу. Однако для полной
оценки точности необходимо еще знать, какова вероят¬
ность появления ошибки той или иной величины.
Если случайная величина а принимает дискретный
ряд значений, то найденная при достаточно большом
числе п независимых замеров относительная частота по¬
вторения отдельных результатов измерения позволяет
определить вероятность данного дискретного значения
361
ошибки. Если же случайная величина а непрерывна, для
расчета вероятности должна быть задана плотность ве¬
роятности U/(a) или W(Аа) *.
Обычно нот необходимости в экспериментальном
определении как относительной частоты повторения ре¬
зультатов измерения, гак и W(a), так как известно, что
закон распределения W(Aci) в большинстве случаев
является нормальным и полностью определяется вели¬
чиной дисперсии случайной составляющей ошибки ста
(рис. 9.5):
—L— exp f (9.28)
V2^a >. аа ]
Тогда вероятность того, что случайная составляющая
ошибки не
личину 'АаР,
Р (I Да | <
превысит некоторую наперед заданную ве¬
бу дет равна
Д<7р
Ч>) = j W (Дп)б/(Дй) = ф(^-\ (9.29)
-Дар '• Д//
,т / Artр \ 2 р
ГДе 4 \ ~ ’ Ф " FT 1 СХР (— с’х ~~ табулирован-
4 б
Аяр
ный интеграл вероятности; z = .
Полагая, например, AaP = ort, найдем, что Р(1А|=С
^art) ==Ф(0,707) =0,68. Следовательно, в 68% замеров
или в течение времени 0,68 Т случайная составляющая
ошибки Аа не будет превышать свое среднеквадратич¬
ное значение ва- По формуле (9.29) можно решить и
обратную задачу: найти такое значение АаР, которое не
будет превышено случайной ошибкой с заданной ве¬
роятностью Р. Полагая вероятность Р соответственно
равной 0,9; 0,95 или 0,997, найдем, что Да0,9 = 1,65сга;
Aao;95“2(7n; Даод97 = 3ста. Последнюю величину обычно
называют «максимальным» значением случайной
ошибки.
* Обе зависимости 1Г(л) и 1Г(Дя) отличаются лишь выбором
начала координат на оси абсцисс (рис. 9.5).
362
При оценке точности следует учитывать, что система¬
тическая составляющая ошибки отсчета является также
случайной функцией времени. Однако, в отличие от слу¬
чайной составляющей Да, систематическая ошибка изме¬
няется медленно, что позволяет считать Дас в пределах,
по крайней мере, одного цикла измерения Т постоянной
величиной. Это создает условия для своевременного вы¬
явления и устранения систематических ошибок измере¬
ния.
Если в системе проведена надлежащая калибровка
шкал отсчета, то систематическая ошибка Дас = 0. Тогда
ошибки измерения определяются только случайной со¬
ставляющей: 6а=Да; 6аСркв = Па, а среднее значение ре¬
зультатов измерения должно соответствовать истинному
значению параметра aQ. Однако среднее значение асрп
при конечном числе замеров п отличается от математи¬
ческого ожидания aC5C0 = limaC!: п случайной величины при
«->00
бесконечном числе замеров на величину случайной ошибки
ДаМн. Поэтому измерение а0 происходит с ошибкой
ДЯМн = Яс1, 7? <^cnco=:^’ci п~ ^0' (9.30)
В отличие от случайной ошибки Да однократного за¬
мера величина Дами является случайной ошибкой много¬
кратных измерений одной и топ же величины. Пусть,
например, произведено п замеров ах, а2, ..., ап величи¬
ны а0 с ошибками Даг-, каждая из которых подчинена
одному и тому же закону распределения вероятно¬
сти W(Да) (9.28). Тогда в соответствии с (9.23)
1
и, если события —а* независимы, можно воспользоваться
правилом: дисперсия суммы независимых случайных ве¬
личин равна сумме дисперсий слагаемых. А так как дис¬
персии слагаемых одинаковы, то среднеквадратичное
значение ошибки многократных измерений будет равно
Число независимых замеров п за ограниченный
интервал времени Т не может быть бесконечно большим.
363
Согласно теореме Котельникова случайный процесс а(0
полностью характеризуется независимыми значения¬
ми Gi, взятыми через интервалы времени = где
2/в
/в — наивысшая частота спектра a(t). Поэтому число заме¬
ров п определяется из условия
(9.33)
Из изложенного следует и порядок обработки ре¬
зультатов измерения. Все время наблюдения Т разби¬
вают на интервалы Д/; и производят фиксацию результа¬
тов измерения. Далее производят расчет аСр (9.23),
(9.26) и находят среднеквадратичную ва и максималь¬
ную 3(ТО ошибки однократного замера. При многократ¬
ных измерениях точность характеризуется соответствен¬
но значениями сгами и Заамп.
§ 9.8. ТОЧНОСТЬ МЕСТООПРЕДЕЛЕНИЯ
НА ПЛОСКОСТИ
При местоопредслении на плоскости истинному поло¬
жению объекта О соответствует точка пересечения линий
положения с параметрами и Ьо. Пусть систематиче¬
ские ошибки измерения указанных параметров равны
нулю: Дас = 0 и Д&с = 0. Тогда, если каждый из пара¬
метров определен с ошибкой, то за местоположение объ¬
екта будет ошибочно принята точка пересечения О' ли¬
ний положения, соответствующих значениям а0 + Да и
Так как на практике необходимо знать ве
только величину, но и направление отклонения от истин¬
ного положения О, то ошибку местоопределения 00' це¬
лесообразно представлять в виде радиус-вектора г.
Вследствие относительной малости ошибок \а и Д&
можно принять линии положения в окрестности точки О
прямыми и параллельными в каждом семействе линий а
или Ь. При этих допущениях истинные и ошибочные ли¬
нии положения образуют параллелограмм (рис. 9ХДj,
диагональ которого г =00' является суммой векторов
линейных ошибок Д/(/ и \б, -сторон параллелограмма.
364
Определим величину линейных ошибок. Из чертежа
на рис. 9.6,а следует, что
COS(/2a, /и)
Д/га Д/га
cos ‘(90° —у) sin у ’
(9.34)
где у — угол между линиями положения aQ и bQ. Для на¬
хождения Дпа — расстояния по нормали между линия¬
ми и Яо + Аа — воспользуемся понятием о градиенте
поля. Если область вокруг точки О рассматривать как
поле скалярной величины а, то градиент этого ноля
grad а есть вектор, который показывает величину и на¬
правление максимальной скорости изменения параме¬
тра а. Так как величина а наиболее быстро изменяется
а — ошибки угломерной системы: б — ошибки дальномерной системы: в —
ошибки разностно-дальномерной системы; г - параллелограмм ошибок.
365
по нормали к линиям постоянного значения а, то, следо¬
вательно,
_ . -'да . Да
grad а = п1а—т--=п1а lim -д-,
011 Ьп->Ь
где п1а— единичный вектор нормали па. Заменяя частную
производную конечными приращениями, найдем Дла:
<9'36)
Таким образом, окончательно для расчета Д/а получим
Д/О=- . (9.37)
а | grad а | sin у ' '
В угломерной системе измеряемый параметр а — угло¬
вая координата объекта а«. Тогда Дл = Даа, &па —
= DaAaa (Da = OA на рис. 9.6,а) и, следовательно,
|grad а| = 1/D. Для дальномерной системы (рис. 9.6,6)
соответственно a = Da, Aa = &JDa, &па = Ы)а |grad D| =
= 1. В разностно-дальномерной
где Di = OAi и D2=OA2 (рис.
уравнение гиперболы, найдем,
где ср= ЛА\ОА2. На больших
d=AxA2 расстояниях D гипербола вырождается в пря¬
мую линию, образующую с базой угол 1]. Тогда
. < г-ч I d sin т.
| grad £р |s
Перейдем теперь к расчету статистических характе¬
ристик ошибки местоопределения г. Так как ошибки \а
и ДЬ независимы и случайны, то согласно (9.37) незави¬
симы и случайны линейные ошибки Д/а и Д/ь,
дули также подчинены нормальному закону и
ризуются дисперсиями
„2
2 °а 2
la | grad a |2 sin2y ’ ib | grad b |2 sin2y
Из (9.28) следует равновероятность положительных и
отрицательных значений ошибок. Однако изменение на¬
правления одного из векторов Д/п, или Д/л изменяет не
только направление, по и величину ошибки г. Поэтому
разные по величине ошибки местоопределения г оказы-
366
(9.35)
системе a=Dv = Dx—D2,
9.6,в). Дифференцируя
что |grad Dp| =2 sin -g,
по сравнению с базой
а их мо-
характе-
О
°ь
(9.38)
ваются равновероятными, и о взаимозависимости вели¬
чины и направления г можно судить в псрвОлМ прибли¬
жении по форме параллелограмм^! рассеяния. Для по¬
строения параллелограмма рассеивания по обе стороны
от истинных линий положения проводят линии, соответ¬
ствующие среднеквадратичным ошибкам ±аа и ±сгь
или откладывают линейные ошибки с модулями ±ща и
±db (рис. 9.7).
Рис. 9.7. Параллелограмм, круг и эллипс рассеивания:
а — при произвольном пересечении линий положения; б — при пересечении
линий положения под прямым углом.
В качестве численной меры точности местоопределе-
иия в геодезии и картографии используют среднеквадра¬
тичную круговую ошибку
(9.39)
Найдем средиеквадратичпую круговую ошибку для угло-
мерных (УМ), дальномерных (ДМ) и разностно-дальномер¬
ных систем (РДМ) при =
1/"2 а э
sin у
367
дм —'
У2 sin у
2
2
°1
sin2 7(1
I
D2
2
sin2
(9.40)
Использование круговой ошибки предполагает, что
большинство ошибок местоопределения г не выходит за
пределы круга с радиусом. оу Действительно, расчет по¬
казывает, что в круге радиусом заключено (бЗ-е-68) %.
а в круге с радиусом 2(уг— (95л-98)% всех ошибок ме¬
стоопределения. Однако сравнение круга ошибок хотя
бы с параллелограммом рассеяния (рис. 9.7) показы¬
вает, что численная мера точности носит условный и
приближенный характер, так как при этом не учиты¬
вается, что вероятность ошибок по отдельным направле¬
ниям различна. Вероятностная оценка точности связана
с построением так называемого эллипса рассеивания
ошибок.
Вероятность того, что О' будет принята за ме¬
стоположение объекта, соответствует вероятности со¬
вместного осуществления двух случайных независимых
событий — измерения aG с ошибкой Да и Ьо с ошиб¬
кой Ab— и, следовательно, равна произведению вероят¬
ности каждого из событий в отдельности. Поэтому с уче¬
том формул (9.28) и (9.38) плотность вероятности ошиб¬
ки г будет равна
W[A - W (ДО • W (Д/6) == ^-1—- X
Хехр
(9-41)
Условию IF (г)—const соответствует бесконечное
множество точек О', образующих замкнутую вокруг точ¬
ки О линию равных вероятностей вектора г = 00'. А так
как плотность вероятности постоянна при
. А/?
—- —--- ра _ eonsf (9.42)
°1а К ?
то (9.42) есть уравнение линии равных вероятностей
в косоугольной системе координат (А/п, ArtJ). В частно-
368
сти, при у---90° система координат (Д/и, Д/ф) ортого¬
нальна, и (9.42) представляет собой в канонической
форме уравнение эллипса с размерами полуосей qa =
-—Via-V и qb = Qib-V (рис. 9.7,6). При у^90° (рис. 9.7/z)
линия равных вероятностей является также эллипсом,
однако размеры его полуосей и их положение в про¬
странстве могут быть найдены только при преобразова¬
нии косоугольных координат (Д/а, Д/&) в прямоугольные
(X У)-
Пусть направление оси у отличается от биссектрисы
угла у на угол ср (рис. 9.7,а). Тогда координаты точ¬
ки О' будут равны
х = — sill ( ? V'r ±lb sin + и
у —- A/a cos i 4 7! "4 cos • (9.43)
Так как средние значения линейных ошибок; приняты
равными нулю, то дисперсии случайных величин х и у
определятся выражениями
'Зх =C7aSltl ? ^"2~ +?4
% — COS2 7^4" 4" ? Y (9.44)
Случайные величины х и у взаимозависимы. Однако,
если коэффициент корреляции этих величин ----- • ху- ра-
ал°у
вей нулю, вероятность совместного осуществления событий
х и у также равна произведению вероятностей этих событий.
Следовательно, при рх/у=-0 плотность вероятности ошибки
равна
w (7)=w ь,
//)---=иДх).Ц7(у)= ■
1 \/
271а л а у
X ехг>
1 < х2 1 у2 \1
9 .2 т 2
" ’.V ’// !
(9.45)
а уравнение линии равных вероятностей ошибки
иметь вид эллипса:
будет
>2 . ;
- уг, — Г2 —const-
’.V
(9.46)
24—1173
369
Ориентация осей Ох и Оу в пространстве должна при
этом соответствовать условию рЛ?7 = 0 или ху — 0. Пере¬
множая правые части выражения (9.43) и приравнивая
среднее значение произведения нулю, получим
2 2
= -tgY. (9.47)
°la + °U>
Формулы (9.47) и (9.44) позволяют найти полуоси
эллипса по координатам х и у. ^Л. = сх-Г и qy — crv • Г.
Величина Г, определяющая размеры полуосей эллип¬
сов рассеивания в выражениях (9.42) и (9.46), связана
с вероятностью ошибки местоопределения следующими
соотношениями. Если Ps(E)—вероятность того, что точ¬
ка О' не выйдет за пределы эллипса рассеивания, пло¬
щадь которого равна S, то
ps (Г)---- [ jiv (X, у) dxdy = 1 - ехр(—J). (9.48)
Отсюда следует, что
Г = |/^2Т1?[1 - Д.(Г)] . (9.49)
Эллипс, заключающий 68% ошибок местоопределе-
ння, называется среднеквадратичным по аналогии со
среднеквадратичной ошибкой одномерного измерения.
Полагая ps = 0,68, найдем Г= 1,51. На рис. 9.7 показа¬
ны среднеквадратичные эллипсы рассеивания для двух
значений угла у. Принимая /%- = 0,99 (Г = 3,04), получим
«максимальный» эллипс рассеивания.
Если в качестве численной меры точности взять сред¬
неквадратичную величину из полуосей среднеквадратич¬
ного эллипса рассеивания, то согласно формулам (9.44),
(9.46) и (9.49) получим
- К - 1П (1 -0,68) Ц <•+ 4, = 1,07 У < (9.50)
Как видно из сравнения формул (9.50) и (9.39), числен¬
ные меры стгэ и стг практически совпадают, что подтверж¬
дает применимость среднеквадратичной круговой ошиб¬
ки в качестве меры точности местоопределения на пло¬
скости.
730
§ 9.9. ТОЧНОСТЬ МЕСТООПРЕДЕЛЕГШЯ
В ПРОСТРАНСТВЕ
Рассмотрим местоопределеиие с помощью РЛС, опре¬
деляющей дальность объекта £)0, азимут а0 и угол ме¬
ста ро (рис. 9.8). Пересечение поверхностей const
(сфера), ao = const (вертикальная полуплоскость) и (30 —
= const (коническая поверхность) определяет истинное
положение объекта — точку О.
Рис. 9.8. Форма поверхностей положения и параллелепипед ошибок
в угломерно-дальномерной РЛС.
Местоопределение объекта может быть произведено
также с помощью трех дальномеров или трех пар раз¬
ностно-дальномерных станций. В первом случае место¬
положение объекта находится как точка пересечения
трех сферических поверхностей, а во втором — как точка
пересечения гиперболических поверхностей. Последние
образуются вращением каждой из линий положения раз¬
ностно-дальномерной системы вокруг прямой, соединяю¬
щей данную пару станций (например, Лр42на рис. 9.6,б?).
На больших по сравнению с ЛИ? дальностях поверх¬
ность гиперболоида можно рассматривать как круглую
24* 371
коническую поверхность с вершиной в середине пря¬
мой ДИг и углом между образующей конуса и осью вра¬
щения, равным тр
Методы статистической оценки точности местоопре-
деления. в пространстве во многом аналогичны уже рас¬
смотренным методам оценки точности местоопределе-
пия на плоскости. Ошибки в измерении угла, дальности
или разности расстояний вызывают смещение поверхно¬
стей положения. Величина смещения по нормали к по¬
верхности в точке О зависит от градиента поля данного
параметра в точке О и рассчитывается по формуле
(9.36).' Значения модулей градиентов поля дальномер¬
ных и разностно-дальномерных систем сохраняют при
этом свои ранее рассчитанные значения. Что же касает¬
ся угломерных систем, то при расчете смещения поверх¬
ностей положения 0 = const и a = const (рис. 9.8) полу-
чим, что I gradp |=Л_, I grad а'
Вследствие относительной малости ошибок участки
истинной и смещенной поверхностей положения могут
быть приняты плоскими и параллельными друг другу.
Поэтому, задаваясь ошибками Дя, Ай и Ad трех изме¬
ряемых параметров а, b и d и смещая поверхности поло¬
жения по нормалям на величины Д//Л, кпъ и А/?^, полу¬
чим параллелепипед ошибок OKLMNPO'Q (рис. 9.8 и
9.9), ребрами которого являются линейные ошибки Д/а,
Д/&, AZrf, а диагональ 00' — ошибкой местоопределе-
ния г, причем
г Д/а д_|-Дld = -z_> Н
| grad а | cos(/?a Za)
Н Г (9.51)
| grad b | cos(/z6 /г.) |grM Д | cos (ndld)
где 1-аи Ibi, Idx — единичные векторы линейных ошибок.
Направления нормалей к поверхностям положения
определяются сравнительно просто в каждом из кон¬
кретных методов местоопределения. Поэтому для иа-
372
хождения г необходимо рассчитать направление векто¬
ров линейных ошибок относительно этих нормалей. Рас¬
смотрим, например, положение в пространстве Д/ь
(рис. 9.9). Вектор направлен по линии пересечения
плоскостей d—const и tt~const и принадлежит этим
плоскостям. Следовательно, Д/& перпендикулярен пбрма-
-> -> ->
лям п(] и па, а это означает, что 1ъу равен единичному
вектору векторного произведения этих нормалей
ТЛ- (9.52)
Аналогичным образом могут быть определены lai и /ы.
Рис. 9.9. Параллелепипед ошибок при произвольном пересечении по¬
верхностей положения.
Численная приближенная оценка точности место-
определения в каждой точке пространства производится
по величине так называемой сферической среднеквадра¬
тичной ошибки, равной корню квадратному из суммы
дисперсий линейных ошибок измерения:
373
асф— V Ъа + °1Ь + °ld —
| grad b\2 cos2 (nb I ь)
а
2
а
| grad а\2 cos2 (па 1(1)
jgrad J|2 cos2 (nd ld)
(9.53)
Однако такая оценка не позволяет рассчитать вероят¬
ность появления ошибок той или иной величины по раз¬
личным направлениям и является грубой мерой точ¬
ности. Наиболее полную характеристику точности
местоопределения в данной точке пространства дает по¬
строение поверхностей равной вероятности ошибок ме¬
стоопределения.
Поскольку плотность распределения вероятности осу¬
ществления трех независимых событий Д/а, Д/ь и Д/л
равна
W (7) = W . W (Д/ь). W (A/d)
1
exp
(9.54)
то поверхность равной вероятности ошибки г в системе
координат (А/а, A/d, A/d) описывается уравнением эллип¬
соида
G2-
(9.55)
В общем случае система координат (Д/а, Д/^, Д/л) косо¬
угольна, поэтому для нахождения направления и вели¬
чины главных полуосей эллипсоида необходимо предва¬
рительно ввести новую ортогональную систему коорди¬
нат (х, у, г) и расположить ее в пространстве таким
образом, чтобы координаты точки О7(хг, уг и гг) были
корреляционно-независимыми, т. е. чтобы выполнялись
условия:
х,.?,. = 0, yrz,.—-0.
(9.56)
374
Тогда направления главных осей эллипсоида совпадут
с направлениями осей ортогональной системы коорди¬
нат и размеры эллипсоида будут определены.
Для рассмотренного выше примера местоопределе-
пня с помощью РЛС необходимости в столь сложном
преобразовании нет, так как векторы линейных ошибок
в этом случае взаимно перпендикулярны и совпадают
к тому же с нормалями к поверхностям положения
(рис. 9.8). Поэтому выберем направления осей ортого¬
нальной системы координат так, чтобы они совпали
с нормалями /7а , /?? и пп. Тогда Д/а = Д/а ='Дпа---л:,
Д/д= Д/?~-Д/?р—Д/(Г= Д/^ - - Д/?,}-—- z и, следователь¬
но,
Д2 I У2 _| z2
1
(9.57)
Данное выражение есть уравнение эллипсоида в канони¬
ческой форме. Размеры эллипсоида (главные его полуоси)
= G<5a£)0 cos рэ, qy = Gs^Dq, qz = GaDопределяют равнове-
роятные ошибки по направлениям па, и nD.
Определим вероятность того, что ошибка местоопре-
—>
деления г не выйдет за пределы пространства, ограни¬
ченного поверхностью (9.55). Интегрируя W(г) по за¬
данной области пространства, получим
Pv (G) = Ф (G) _ ехр ( - , (9.58)
где Ф(6)—интеграл вероятности. Задаваясь значения¬
ми G, найдем Ру(1) = 0,2; Ру(2)=0,74; Ру(3)=0,97.
«Среднеквадратичный» эллипсоид рассеивания, в преде¬
лах которого заключено 0,68% всех ошибок местоопре-
деления, соответствует значению G = 1,8.
Рассмотренные выше методы статистической оценки
точности мсстоопределенпя объектов на плоскости и
в пространстве позволяют рассчитать вероятные ошибки
местоопределения в различных точках рабочей зоны ра¬
диотехнической системы в зависимости от типа системы,
взаимного расположения станций системы и точности
375
измерений параметров. Но данным этого расчета опре¬
деляется наивыгоднейшее расположение станций систе¬
мы для решения конкретной тактической задачи либо
находятся зоны, в которых местоонределение осуще¬
ствляется с одинаковой, а также с наиболее высокой
или недопустимо низкой точностью. Итогом расчета
является составление специальных географических карт
с изображением в различных точках пространства
эллипсов рассеяния или сечений эллипсоидов по направ¬
лениям главных осей. Такне карты дают полную кар¬
тину точности местоопределения объектов.
Глава 10
РАДИОРАЗВЕДКА,
РАДИОПРОТИВОДЕЙСТВИЕ И БОРЬБА
С ОРГАНИЗОВАННЫМИ ПОМЕХАМИ
(КОНТРРАДИОПРОТИВОДЕЙСТВИЕ) *
§ 10.1. РАДИОРАЗВЕДКА
Для борьбы с радиоэлектронными средствами про¬
тивника необходимо прежде всего иметь сведения об
основных характеристиках этих средств. Тактико-техни¬
ческие характеристики радиоэлектронных средств про¬
тивника добываются всеми известными видами развед¬
ки: радиоразведкой, агентурной разведкой, фотографи¬
рованием, визуальным наблюдением и т. д. Получаемая
средствами радиоразведки информация может быть
разделена на два больших класса: оперативную и тех¬
ническую.
Составными частями оперативной информации явля¬
ются: типы используемых противником радиотехниче¬
ских систем и их количество, что позволяет судить
о плотности насыщения тем или другим родом войск
разведываемого района; тактика и стратегия, выявляе¬
мые путем непрерывно ведущейся в течение достаточно
длительного времени радиоразведки и анализа получен¬
ных сведений.
К технической информации, получаемой с помощью
радиоразведки, относятся: уровень технического разви¬
тия боевых средств противника, оснащенных радиоэлек¬
тронными системами; техника и тактика радиопротиво¬
действия и контррадиопротиводействия, используемые
противником, определив которые, можно определить и
наиболее эффективные меры защиты.
Обнаружение и анализ сигналов радиоэлектронных
систем противника. Конечными целями радиоразведки
Эта н последующие главы написаны по материалам открытой
отечественной и зарубежной печати.
377
являются: оопаружеиие и перехват излучаемых против¬
ником сигналов, определение координат источников из¬
лучений и расшифровка перехваченных сигналов. Для
выполнения этих задач в состав радиоразведывательной
станции входят: антенна со специальными характери¬
стиками, разведывательный приемник, индикатор обна¬
ружения н перехвата, регистрирующее устройство и
анализатор сигналов. В некоторых случаях функции ре¬
гистрации (записи) и анализа (расшифровки) бывают
разделены, и тогда в задачу разведывательной станции
Рис. 10.1. Двухканальный автоматический радиопеленгатор с непо¬
движными рамочными антеннами.
входит только запись перехваченных сигналов. Такие раз¬
ведывательные станции устанавливаются иа самолетах
или других подвижных объектах, где невозможно раз¬
местить аппаратуру большого веса и габарита. Еще бо¬
лее простой модификацией является радиоразведыва-
тельная станция, состоящая из антенны, приемника и
индикатора, устанавливаемая на самолетах, подводных
лодках и других объектах и служащая для предупрежде¬
ния экипажей этих объектов об облучении вражескими
РЛС или другими радиоэлектронными средствами.
Эффективность работы радиоразведывательной стан¬
ции определяется вероятностью обнаружения работаю¬
щего источника излучения и точностью определения ко-
378
ординат источника излучения. Местоположение источ¬
ника излучения определяется пеленгационно-базовым
методом. На рис. 10.1 приведена блок-схема двухканаль¬
ного автоматического радиопеленгатора, использующего
две взаимно перпендикулярные рамочные антенны. При
идентичности каналов I и II, а также одинаковой чув¬
ствительности горизонтальных и вертикальных пластин
ЭЛТ индикатора SA- = Sy = S, угол между линией раз¬
вертки на экране ЭЛТ и вертикалью
В УКВ, дециметровом и сантиметровом диапазонах
пеленгация источников излучения осложняется тем, что
в этих диапазонах источники излучения имеют узкие диа¬
граммы направленности, и поэтому скорость поиска на¬
правления на источник излучения (скорость вращения
диаграммы направленности станции радиоразведки)
должна быть согласована с предполагаемой скоростью
вращения и шириной диаграммы направленности антен¬
ны источника излучения. Особенно затруднительно опре¬
деление пеленга работающей в режиме кругового обзора
РЛС. Если приемник радиоразведывательной станции
уже настроен на частоту РЛС и требуется определить
только пеленг РЛС, то для этого нужно, чтобы в течение
времени, не меньшего, чем период повторения импульсов
РЛС ('Гп), диаграммы направленности антенн РЛС и
пеленгатора были направлены навстречу друг другу.
При этом в принципе возможны два режима работы пе¬
ленгатора: режим быстрого вращения диаграммы на¬
правленности (антенна пеленгатора должна сделать не
менее одного оборота за время, в течение которого ось
антенны РЛС повернется на угол, равный ширине ее
диаграммы направленности) и режим медленного вра¬
щения, при котором за время одного оборота антенны
РЛС диаграмма направленности пеленгатора должна
повернуться на угол, не превышающий ее ширину.
Определение частоты излучения перехваченных сиг¬
налов и выделение этих сигналов па фоне помех и
других сигналов производятся с помощью разведыватель¬
ных приемников, основным отличием которых от прием¬
ников других радиотехнических систем является чрезвы¬
чайно широкий частотный диапазон. В радиоразведке
379
используются как приемники прямого усиления, так и
приемники супергетеродинного типа. Применяемые в ра¬
диоразведке многоканальные приемники прямого уси¬
ления (рис. 10.2,а) просты по конструкции, не требуют
перестройки, а выходной сигнал таких приемников появ-
Апг
-.у
I
Канал Ш
Канал IV
Лиг
Кана/J I
Широкополое
Детек-
тор
Узкополос-
ный УПЧ Г"
Гетеро-
дин К
-<
I
Команда „ Остановка
перестройки ”
1
“Г
.I
Детектор]
±1
Индикатор
И
Канал И
Смеси - ■
тель I Г
I
I
I
I
I
I
I
Г увч in | 1
| УЗЧ IV 1
1 Г УЗЧ V |
;zo
'7
1
IДетектор] 1
Детектор
1 Детектор
1 /я 1
IV
! 7
1 ; | |
| унч ш\ |
| УНЧ IV
1 | унч у |
1 ! 1 1 1
Индикатор] |
Индикатор
1 Индикатор
ЛГ | 1
IV
! *
Канал V
Смеси -
тель И
Электронный
или механиче¬
ский привод
перестройки
гетероди¬
нов
смесителей
и УВЧ
Гетеро-] i
Гетерсдин II
I Генес а тор
дин I ;
L 1 1
(частотно -
модулированный)
пилообразного
напряжена»
Реактивна» 1 J | Парафа оный
лампа j j усилитель
/9
к регистрирующему
—i усп-ртиствц
унч L—
—Г |
й Команда
I s—г-i „ Запись "
I Индикатор I——
обнаружения |
0)
Система панопамной развертки
т
Рис. 10.2. Разведывательные приемники [17]:
амногоканальный прямого усиления: б — супергетеродинный с двойным
преобразованием; в — панорамный приемник.
380
ляется практически одновременно со входным. Недостат¬
ками приемников прямого усиления являются их малая
чувствительность и очень широкая полоса пропускания,
вследствие чего оказывается невозможным определение
частоты перехваченного сигнала (определяется только
диапазон, равный по ширине полосе пропускания одного
канала многоканального приемника прямого усиления).
Наиболее типичной областью применения приемников
прямого усиления являются радиоразведывательные
станции предупреждения экипажей кораблей, самолетов,
подводных лодок об облучении РЛС противника.
Приемники супергетеродинного типа с двойным пре¬
образованием частоты (рис. 10.2,6) имеют чувствитель¬
ность на несколько порядков лучшую, чем приемники
прямого усиления; имеют высокую разрешающую спо¬
собность по частоте, определяемую шириной полосы
пропускания УПЧ, и допускают перестройку в широком
диапазоне частот. Недостатками таких приемников
являются сложность в устройстве и эксплуатации; зна¬
чительное время поиска по частоте (перестройки), вслед¬
ствие чего в некоторых случаях значительно уменьшает¬
ся по сравнению с приемниками прямого усиления ве¬
роятность обнаружения кратковременно работающих
РТС противника. Для того чтобы сигнал РТС противника
был перехвачен разведывательным приемником, необхо¬
димо одновременное выполнение двух условий: 1) диа¬
грамма направленности РТС должна быть направлена
в сторону антенны разведывательного приемника и
2) разведывательный приемник должен в это время быть
настроенным на несущую частоту РТС.
Одной из наиболее сложных в радиоразведке задач
поиска считается обнаружение (поиск по частоте) сигна¬
лов РЛС, работающих в режиме кругового обзора. Воз¬
можны два режима поиска по частоте: быстрый и мед¬
ленный (рис. 10.3). При быстром поиске и всенаправ¬
ленной приемной антенне разведывательный приемник
просматривает весь диапазон поиска по частоте А/поиека
за время, не большее, чем время облучения антенны раз¬
ведывательного приемника импульсами РЛС:
а'* (п
гр _ p.lC 'р
7 обл —’ "ЗбО3” ‘0 ’заг
381
где a‘\c -ширина диаграммы направленности антен¬
ных РЛС;
— период повторения пачек импульсов РЛС;
/1а— скорость вращения антенны РЛС, обIмин.
При медленном поиске за время, равное предпола¬
гаемому периоду повторения пачек импульсов РЛС 7о,
ZThUX Crj
Рис. 10.3. Поиск ио чистоте сигналов РЛС, работающей в режиме
кругового обзора.
частота настройки гетеродина II изменяется на величину,
не превышающую ширину полосы пропускания УПЧ II
разведывательного приемника А/уПчп, определяющую
точность измерения несущей частоты разведываемой
РЛС. Максимальное время обнаружения при быстром и
медленном поиске равно соответственно
Д/ ] Oik ьа
Д^упчТ1
•л.
Для сокращения времени поиска в разведывательных
приемниках чаще всего перестраиваются оба гетеро¬
дина: гетеродин I — медленно, а гетеродин II — быстро.
Такой метод перестройки называется комбинированным.
С выхода разведывательного приемника сигнал по¬
ступает на индикатор обнаружения (перехвата) и реги¬
382
стрирующую аппаратуру, с помощью которой сигнал
может быть записан с целью дальнейшего его анализа
и расшифровки. Находят применение световые, звуковые
и осциллографические индикаторы. Световая и звуковая
индикация используется в тех случаях, когда не тре¬
буется определения технических характеристик приня¬
того сигнала, а нужно установить только сам факт
приема. Приемники с осциллографическими индикатора¬
ми получили название панорамных разведывательных
приемников (рис. 10.2,а). В таких приемниках горизон¬
тальная развертка луча ЭЛТ индикатора и управление
перестройкой гетеродина осуществляются одним и тем
же пилообразным напряжением, вследствие чего гори¬
зонтальная развертка экрана ЭЛТ оказывается програ¬
дуированной по частоте.
Аппаратура анализа в станциях радиоразведки мо¬
жет определять следующие характеристики сигналов: не¬
сущую частоту; длительность, форму и период повторе¬
ния импульсов; вид и скорость обзора; ширину и форму
диаграммы направленности антенны; поляризацию излу¬
чений и их интенсивность. В некоторых случаях задачи
анализа могут быть ограничены лишь определением не¬
сущей частоты, длительности и периода повторения
импульсов; в других случаях задачи анализа могут быть
расширены, например, определением характера цели по
спектру флюктуаций амплитуд или допплеровскому
сдвигу частот.
Параллельные анализаторы спектра, несмотря на то,
что время анализа у них значительно меньше, чем
у последовательных, в радиоразведке применяются срав¬
нительно редко ввиду их громоздкости и сложности на¬
стройки и эксплуатации. В последнее время за рубежом
в радиоразведке получили распространение ускоренные
по сравнению с последовательными методы анализа,
основанные на предварительном сжатии сигнала и по¬
следовательном анализе сжатой копии сигнала.. При
сжатии сигнала в N раз его длительность уменьшается,
а ширина спектра увеличивается также в N раз. При
анализе с одинаковым числом градаций спектров сжа¬
того и несжатого сигналов время последовательного ана¬
лиза сжатой в N раз копии сигнала оказывается в /V раз
меньше, чем время анализа спектра несжатого сигнала.
383
Дальность радиоразведки. Дальность радиоразведки
зависит от условий распространения радиоволн и пара¬
метров радиоразведывательной аппаратуры и разведы¬
ваемых РТС. Средства радиосвязи и радионавигации,
работающие в КВ, СВ и ДВ диапазонах, могут быть
разведаны па расстояниях, примерно равных дальностям
их действия. Дальность радиоразведки в метровом и бо¬
лее коротковолновом диапазонах с учетом рефракции и
дифракции радиоволн ограничена дальностью радиого¬
ризонта.
Дальность действия радиоразведки по обнаружению
работы РЛС превышает в 1,5—2 раза их максимальную
дальность действия и определяется как
где Рпрлс — импульсная мощность передатчика РЛС;
Орле и Gp — коэффициенты усиления антенн РЛС и
станции радиоразведки соответственно;
1 — коэффициент, учитывающий несовпадение
поляризаций антенн РЛС и разведыватель¬
ной станции;
л--длина волны;
Рс, мни—минимальная мощность сигнала на входе
разведывательного приемника, необходи¬
мая для обнаружения с заданной вероят¬
ностью сигнала на фоне помех.
§ 10.2. РАДИОПРОТИВОДЕЙСТВИЕ
Радиопротиводействием называются организационно¬
технические мероприятия по нарушению работы радио¬
электронных средств противника или уменьшению их
эффективности. К таким мероприятиям относятся: по¬
мехи радиоэлектронным средствам противника (актив¬
ные и пассивные), противорадиолокацнонная маски¬
ровка, радиодезинформация и меры по уничтожению ра¬
диоэлектронных средств противника.
Активные помехи, т. е. помехи за счет активного излу^
чения, классифицируются: 1) по виду модуляции — не-
модулированная помеха, несущая с синусоидальной мо¬
дуляцией, несущая с шумовой модуляцией (НМШ), пря-
384
мошумовая помеха, регулярная импульсная помеха
(РИН), хаотично-импульсная помеха (ХИП), мерцаю¬
щая помеха (шумовая или несущая с низкочастотной
модуляцией); 2) по ширине спектра излучаемых ча¬
стот— заградительная (ширина спектра помехи значи¬
тельно больше ширины спектра подавляемой РТС) и
прицельная (спектры РТС и помехи имеют ширину
одного иорядка).
Шумовые помехи по своей структуре наиболее близки
к структуре собственных флюктуационных шумов при¬
емников РТС. {-Смодулированная или модулированная
низкочастотным напряжеииехМ несущая может применять¬
ся в качестве помех системам связи и РЛС с автосопро¬
вождением цели. Импульсные помехи (ХИП и РИП)
применяются для подавления РЛС, а также РТС, рабо¬
тающих с импульсной или импульсно-кодовой модуля¬
цией. В некоторых случаях воздействие импульснькх по¬
мех может быть более эффективным, чем воздействие
непрерывных (например, шумовых) помех. Одними из
наиболее эффективных импульсных помех считаются так
называемые имитационные ответные импульсные по¬
мехи. Ответными импульсными помехами называ¬
ются импульсные помехи, излучаемые с частотой повто¬
рения, равной или кратной частоте повторения
импульсов подавляемой РЛС. На экране индикатора
РЛС под воздействием ответных импульсных помех воз¬
никает большое количество ложных целей, среди кото¬
рых трудно, а иногда и невозможно найти отметку
реальной цели. Высокоэффективными помехами против
радиоэлектронных средств управления оружием (напри¬
мер, головок самонаведения) считаются ответные им¬
пульсные уводящие помехи, нарушающие работу схем
автосопровождения по дальности, скорости или угловым
координатам. Передатчик ответной уводящей по даль¬
ности помехи, установленный на защищаемой цели, по¬
сылает в ответ на каждый зондирующий импульс РЛС
головки самонаведения импульс ответной помехи с по¬
степенно нарастающей по отношению к зондирующему
импульсу задержкой. Такой режим работы ответной по¬
мехи будет имитировать постепенное удаление от реаль¬
ной цели некоей фиктивной цели, имитируемой импуль¬
сами ответной помехи. Если мощность импульса ответ¬
ной помехи достаточно велика, строб системы автосо-
25--1173 385
провождения по дальности будет следить за импульсом
ответной помехи, а не за импульсом, отраженным от за¬
щищаемой ответной помехой цели.
Дальность активного радиопротиводействия. Эффек¬
тивность воздействия помехи на подавляемую РТС оце¬
нивается отношением мощности помехи к мощности
полезного сигнала на входе приемника РТС. Минималь¬
ная величина этого отношения, при которой еще обеспе¬
чивается требуемая степень подавления РТС, называет¬
ся коэффициентом подавления РТС и обозначается kn.
Если коэффициент подавления РТС известен, можно
определить зоны расположения передатчика помех и
приемника подавляемой РТС, в пределах которых воз¬
действие помехи на РТС будет эффективным. При актив¬
ном радиопротиводействии РЛС для совмещенного
с целью передатчика помех (рис. 10.4,а) минимальная
дальность радиопротиводействия равна
ту И ]УЛсбрле0-Э^Л1
где РПп — мощность передатчика помехи,
Д/рлс — ширина полосы пропускания приемника РЛС,
Afn — ширина спектра помехи (для обычно выпол¬
няемого условия Afn>Afpnc).
Рис. 10.4. Активное радиопротиводействие РЛС:
а— передатчик помех совмещен с целью; б — передатчик помех не совмещен
с целью.
Если передатчик помех не совмещен с защищаемом
целью (рис. 10.4,6), то при удалении передатчика по¬
мехи на расстояние Оп от РЛС максимальная дальность
обнаружения цели на фоне активной помехи (т. е. ми-
386
нимальная дальность радиопротиводействия) может
быть рассчитана по формуле
k. Pvi рлсСр.1с/?“а£)Д/:п
(®п) Д/рЛС
где ©п — угол между направлениями на цель и источник
помехи.
Пассивные помехи. Пассивные помехи основаны на
использовании вторичного радиоизлучения и могут
создаваться только РТС, работающим по принципу
приема отраженных сигналов, т. е. только радиолока¬
ционным станциям. Пассивные помехи, представляющие
собой отражения от различного рода искусственных,
а в некоторых случаях и естественных отражателей, за¬
трудняют наблюдение на экранах радиолокаторов отме¬
ток от истинных целей или нарушают работу автомати¬
ческих систем управления, получающих информацию от
РЛС. Одним из средств создания пассивных помех
является рассеяние в воздухе большого количества тон¬
ких металлических полосок, длина которых равна поло¬
вине длины волны забиваемой РЛС (полуволновых ди¬
полей). При произвольной ориентации оси диполя сред¬
нее значение его площади рассеяния сгэ=0,112v2. Радио¬
локационная цель, находящаяся в облаке полуволновых
диполей будет не видна на фоне этого облака на экране
РЛС, если
где Рп и Рс — мощности пассивной помехи и сигнала
на входе приемника РЛС;
сгэо и стЭц — эффективные площади рассеяния отра¬
жающего объема облака диполей и це¬
ли соответственно.
Минимально необходимое количество диполей в отра¬
жающем объеме для подавления пассивной помехой
РЛС с коэффициентом подавления /гп будет
ДГ
Vwhh — ~
Радиомаскировка. Для маскировки от радиолока¬
ционного обнаружения широко используются пассивные
отражатели: уголковые, биконические, дипольные ре-
25* 887
шетки и т. д., дающие возможность имитировать на
экранах РЛС различные цели там, где их в действи¬
тельности нет, скрыть боевую технику и наземные со¬
оружения от радиолокационного обнаружения, затруд¬
нить возможность применения радиолокационных
бомбоприцелов, а также заставить наводиться радио¬
локационные головки самонаведения на ложные цели
(радиолокационные ловушки).
Скрыть от радиолокационного обнаружения боевую
технику и сооружения можно также применением спе¬
циальных защитных противорадиолокациоиных покры¬
тий, в значительной степени ослабляющих отражение
радиоволн от защищаемых объектов. Поглощающие за¬
щитные покрытия не должны отражать падающую на
внешнюю поверхность покрытия электромагнитную
энергию и должны полностью поглощать радиоволну,
распространяющуюся внутри самого покрытия. Ослаб¬
ление отраженных волн в интерференционных покры¬
тиях происходит за счет интерференции волн, отражен¬
ных от внешней поверхности покрытия и защищаемой
поверхности и имеющих фазовый сдвиг, близкий к 180°.
Защитные покрытия позволяют значительно снизить
эффективную площадь рассеяния защищаемой цели.’
Радиодезинформация 16. Раднодезинформация, задачей
которой является введение в заблуждение противника,
заключается в передаче по радио ложных сообщений,
подделке радиоизлучений, искажении действительной
картины работы радиоэлектронных средств, переизлуче-
нии сигналов радиоэлектронных средств противника,
особенно его радионавигационных систем, и т. д. Радио¬
дезинформация, как правило, проводится в сочетании
с другими мероприятиями по введению противника
в заблуждение.
Борьба методов радиопротиводействия и контррадио¬
противодействия составляет две стороны конфликтной
ситуации, которую иногда называют радиовойной. Ха¬
рактерной особенностью радиовойны является ее высо¬
кая динамичность, обусловленная сильной зависимостью
методов радиопротиводействия и контррадиопротиво¬
действия от контрмер противника. Успех в радиовойне
достигается превосходством над противником в количе¬
стве и качестве радиоэлектронной техники и умением ее
боевого применения.
388
Таким образом, на современном этапе развития ме¬
тодов вооруженной борьбы радиоэлектронные средства
стали оружием в буквальном смысле этого слова — ору¬
жием радиовойны.
§ 10.3. БОРЬБА С ОРГАНИЗОВАННЫМИ ПОМЕХАМИ
(КОНТРРАДИОПРОТИВОДЕЙСТВИЕ)
Одной из основных задач при проектировании РТС
является обеспечение помехозащищенности этих систем
в условиях радиопротиводействия противника. Методы
и средства борьбы с организованными помехами могут
базироваться па следующих основных принципах.
1. Форма сигнала РТС должна выбираться с учетом
необходимости затруднять его анализ противником и
создание помех средствами радиопротиводействия.
2. Обработка сигнала в приемном устройстве должна
обеспечивать максимальное использование известных
характеристик полезного сигнала, организованных по¬
мех и шумов.
3. Обнаружение полезного сигнала на фоне органи¬
зованных помех можно в некоторых случаях осуще¬
ствлять сравнением информации, получаемой двумя или
более разнесенными приемными системами, использую¬
щими различные принципы выделения сигнала или хотя
бы различные способы обработки сигнала.
Технические методы и устройства защиты от актив¬
ных помех основаны на использовании частотных,
амплитудных и поляризационных различий сигналов и
помех, а также различий отражающих свойств целей и
амплитудных и спектральных характеристик имитирую¬
щих цели сигналов. Большинство технических методов
защиты основано на различных способах селекции: про¬
странственной, временной, частотной, амплитудной и по¬
ляризационной, а также на способах выделения разли¬
чий в амплитудных и спектральных характеристиках
сигналов и помех.
Пространственная селекция, уменьшающая вероят¬
ность приема помех и затрудняющая противнику веде¬
ние радиоразведки, достигается применением передаю¬
щих и приемных антенн с узкими диаграммами направ¬
ленности и минимальными уровнями боковых лепестков.
Амплитудная селекция, предохраняющая приемный
389
тракт от перегрузок под воздействием сильных сигналов
и помех, обеспечивается применением амплитудных
ограничителей и различного типа автоматических регу¬
лировок: МАРУ, ВАРУ, ШАРУ и т. д. Хорошую ампли¬
тудную селекцию дают приемники с линейно-логариф¬
мическими амплитудными характеристиками.
Временная селекция достигается открыванием прием¬
ника с помощью стробирующих схем и регулировкой
чувствительности во времени только на время действия
Рис. 10.5. Определение истинных и фиктивных целей методом засечек
с двух разнесенных РЛС:
1 — место расположения фиктивной цели для РЛС!; 2 — место расположения
фиктивной цели для РЛСП; 3 — постановщик ответной переизлучепной с за¬
держкой /зач помехи.
полезного сигнала. Методы частотной селекции, приме¬
няемые для защиты от активных помех, являются одни¬
ми из наиболее эффективных и распространенных. Сре¬
ди этих методов наиболее часто используется пере¬
стройка по частоте или одновременная работа на
нескольких несущих частотах, разнесенных по диапа¬
зону.
Защита РТС от организованных помех методом по¬
ляризационной селекции состоит в использовании разли¬
чия поляризаций полезного сигнала и помех. Эффектив¬
ным средством борьбы с несинхронными с рабочим сиг¬
налом помехами (шумовыми, ХИП и т. д.) является
накопление периодически повторяющихся сигналов.
Для борьбы с различного рода имитационными по¬
мехами могут использоваться либо логические методы,
390
либо методы, основанные на спектральных различиях
сигналов, отраженных от истинных целен и имитирующих
цели сигналов. Примером логического метода борьбы
с ответными перензлученными с задержкой импульсами
РЛС является определение истинных и фиктивных целей
с помощью двух или более разнесенных РЛС (рис. 10.5).
Реальная цель будет па всех РЛС давать отметки, со¬
ответствующие одним и тем же координатам — коорди¬
натам реальной цели. Отметки же за счет переизлучен-
ных с задержкой сигналов РЛС будут для каждой РЛС
имитировать свою ложную цель, расположенную на ли¬
нии, соединяющей РЛС и передатчик помех. Проанали¬
зировав показания индикаторов нескольких разнесенных
РЛС, можно отделить реальные цели от фиктивных.
Глава 11
ОБЩИЕ СВЕДЕНИЯ ОБ УПРАВЛЯЕМЫХ
ОБЪЕКТАХ И СПОСОБАХ УПРАВЛЕНИЯ [19]
§ 11.1. ОСНОВНЫЕ ТИПЫ УПРАВЛЯЕМЫХ ОБЪЕКТОВ
Управляемым объектом называется снаряд, ракета,
летательный аппарат (ЛА) или космический аппарат
(КА), снабженный органами управления, с помощью ко¬
торых объект изменяет траекторию полета в процессе
своего движения. Под системой управления понимается
вся совокупность технических средств, обеспечивающих
движение объекта по заданной траектории с необходи¬
мой точностью.
Управляемые объекты могут различаться по кон¬
структивному исполнению, месту старта, тактическому
назначению и способу управления.
Все типы управляемых снарядов (кроме авиабомб)
снабжены реактивными двигателями, предназначенными
либо для разгона снаряда до определенной скорости,
либо для поддержания заданной скорости в течение
всего времени полета. Применение реактивных двигате¬
лей обеспечивает большие скорости полета и возмож¬
ность работы на больших высотах за пределами атмо¬
сферы. Большие скорости полета, особенно сверхзвуко¬
вые, обусловливают аэродинамическую форму снарядов
в виде тела вращения с острой головной частью и раз¬
мещением двигателей в хвосте.
В конструктивном отношении снаряды делятся на
плоскокрылые, крестокрылые, с кольцевым крылом и
бескрылые. Первые при повороте вокруг продольной оси
обладают аэродинамической несимметрией. Для трех
последующих видов характерна осевая аэродинамиче¬
ская симметрия.
В соответствии с местом старта снаряда и располо¬
жением цели управляемые объекты делятся на классы:
392
«земля — земля», «земля — воздух», «воздух — земля»,
«воздух — воздух». Следует отметить, что термин «зем¬
ля» относится и к водной поверхности.
По тактическому назначению различают: балли¬
стические ракеты и самолеты — снаряды дальнего дей¬
ствия, управляемые авиационные бомбы и торпеды,
управляемые реактивные снаряды воздушного и назем¬
ного боя.
Кроме указанных типов управляемых снарядов,
траектория которых проходит в атмосфере Земли, имеет¬
J
Рис. 11.1. Траектории движения и зоны управления снарядов.
ся несколько типов управляемых снарядов, движущихся
к цели в воде. Техника управляемых снарядов разви¬
вается очень быстро. К наиболее известным из перечис¬
ленных выше типов зарубежных снарядов [19] относятся:
баллистическая ракета «Атлас», самолет — снаряд
«Снарк», управляемая авиационная бомба «Тарзои»,
управляемый снаряд противовоздушной обороны «Найк
Геркулес», управляемый снаряд воздушного боя «Сайд-
випдер» и противотанковый управляемый снаряд
«Норд 5200».
Основные данные этих снарядов приведены в [19].
Ниже приводится лишь определение названия каждого
из этих типов снарядов и дается их общая характе¬
ристика.
Баллистическими ракетами (БР) называются снаряды,
траектория полета которых (рис. 11.1,а, а также 13.1,а),
за исключением активного участка AG, когда работает
ракетный двигатель, представляет траекторию движе¬
ния свободно брошенного тела. Для точного попадания
393
в цель Е вектор скорости БР VG в точке выключения
двигателей G должен иметь заданную величину и на¬
правление, что контролируется и обеспечивается сред¬
ствами управления. Дальность L полета БР колеблется
от нескольких десятков километров (тактические БР) до
нескольких тысяч километров (стратегические БР).
Баллистические ракеты могут запускаться с наземных
стартовых установок, с кораблей и подводных лодок.
Баллистические ракеты большую часть времени движут¬
ся по траекториям, форма которых определяется закона¬
ми свободного движения тел в поле сил тяготения Зем¬
ли, Солнца и планет солнечной системы.
Самолетом-снарядом или крылатой ракетой (КР) на¬
зывается снаряд, полет которого в основном обеспечи¬
вается подъемной силой крыла. КР имеют такую же
аэродинамическую схему, как и пилотируемые семолеты.
Как правило, на всей траектории полета КР (рис. 11.1,а)
работает двигатель, который принято называть марше¬
вым. Обычно полет к цели происходит иа постоянной
высоте Лкр, определяемой потолком данной КР. Даль¬
ность действия некоторых КР сравнима с дальностью
действия БР. Управление КР с небольшим радиусом
действия осуществляется радиотехническими сред¬
ствами, а КР с большим радиусом действия — инер¬
циальными и астроинерциальными системами.
Управляемыми авиационными бомбами называются
свободно падающие снаряды, снабженные небольшими
крыльями, которые позволяют в некоторых пределах
изменять траекторию падения. Управление осуще¬
ствляется с самолета-носителя при помощи радиотехни¬
ческих или оптических средств. К этой группе управляе¬
мых снарядов могут быть также отнесены планирующие
авиационные торпеды.
Зенитными управляемыми ракетами (ЗУР) называ¬
ются ракеты противовоздушной обороны, наведение ко¬
торых на цель осуществляется радиотехническими сред¬
ствами. На начальном и среднем участках траекто¬
рии (рис. 11.16) ракета управляется радиосистемой
командного телеуправления, а при сближении с целью
система управления ракетой переходит в режим само¬
наведения. Как правило, ЗУР оснащаются неконтакт¬
ными радиовзрывателями.
Управляемые ракеты воздушного боя представляют
394
сравнительно небольшие ракеты, располагаемые на са¬
молетах-носителях и действующие по воздушным целям.
При большой скорости движения они обладают высокой
маневренностью. Наведение на цель может осуще¬
ствляться радиотехническими и оптическими системами,
а также устройствами, реагирующими на тепловое излу¬
чение самолета-цели.
Управляемые снаряды наземного боя также пред¬
ставляют собой небольшие управляемые ракеты, предна¬
значенные для борьбы с тапками, пехотой и т. п.
Для управления такими снарядами .иногда исполь¬
зуется проводная связь. Провода намотаны на катуш¬
ках, расположенных в снаряде, и в полете разматы¬
ваются.
Перечисленные снаряды и ЛА не исчерпывают всего
многообразия управляемых объектов. Следует также
учитывать чрезвычайно большой класс самолетов граж¬
данской авиации и ВВС, надводных кораблей, подвод¬
ных лодок ВМФ и судов торгового флота, для управле¬
ния движением которых также используются радиотех¬
нические системы управления.
§ 11.2. ОРГАНЫ УПРАВЛЕНИЯ РЕАКТИВНЫХ
СНАРЯДОВ
Траектории управляемых снарядов определяются на¬
чальными условиями запуска и силами, действующими
в процессе движения: силой тяги двигателя Р, силой
тяжести Fg, подъемной силой фюзеляжа и крыльев У,
подъемной силой руля Ур, силой лобового сопротивле¬
ния X. На рис. 11.2,а эти силы представлены приме¬
нительно к прямолинейному полету плоскокрылого
снаряда в горизонтальной плоскости. Для изменения
траектории полета снаряда нужно изменить величину
или направление действия этих сил. Эту задачу
выполняют аэродинамические или газовые рули, соз¬
дающие в соответствующей плоскости силы, перпен¬
дикулярные траектории полета. Если отклонить руль
высоты снаряда на некоторый угол Дб по часовой стрел¬
ке, то отрицательная подъемная сила руля увеличится
на ДУР (рис. 11.2,6). Снаряд начнет поворачиваться во¬
круг центра тяжести, увеличивая угол атаки до значе-
395
ния Uc+Aac. При этом произойдет приращение подъем¬
ной силы крыла и фюзеляжа ДУ. Поскольку прираще¬
ние ДУ значительно больше ЛУР, новая сила ДУ—ДУР
совместно с тягой Р и силой сопротивления X вызовет
поворот вектора скорости полета V на угол 0, называе¬
мый углом наклона траектории. Аналогичный результат
можно получить, увеличивая силу тяги двигателя Р или
Рис. 11.2. Способы создания управляющих сил ЛЛ.
прерывая интерцепторами (пластинками, выдвигаемыми
из крыла) поток, обтекающий профиль крыла.
Управляющая сила в горизонтальной плоскости
у плоскокрылых снарядов может создаваться путем по¬
ворота рулей направления (плоский поворот) или путем
поворота совместно с рулем направления элеронов, вы¬
зывающих накренение ЛА (координированный раз¬
ворот). При угле крена у подъемная сила снаряда У
(рис. 11.2, в) имеет горизонтальную составляющую
У sin у, которая и является управляющей. Такое управ¬
ление называется полярным и используется для управ¬
ления плоскокрылыми снарядами.
У снарядов с аэродинамической симметрией способы
создания управляющих сил одинаковы в горизонтальной
и вертикальной плоскостях. Для управления ими
используется декартовая система управления («вверх —
вниз», «влево — вправо») при автономной стабилизации
снаряда по крену.
396
У бескрылы,х снарядов тяга двигателей значительно
превосходит силу тяжести и силу сопротивления воз¬
духа, вследствие чего управляющая сила, перпендику¬
лярная к траектории полета, образуется как проекция
силы тяги на это направление, когда корпус снаряда по¬
вернут в пространстве газовыми или аэродинамическими
рулями. По мере увеличения высоты полета эффектив¬
ность аэродинамических рулен снижается, и в безвоз¬
душном пространстве снаряд управляется при по¬
мощи поворота основного двигателя (рис. 11.2,г) или
вспомогательными реактивными устройствами.
Преобразование электрических сигналов (команд)
управления в механические перемещения рулевых орга¬
нов на снарядах выполняют рулевые приводы (рулевые
машинки) электрического, гидравлического или пневма¬
тического типов.
Эффективность действия рулевых органов определяет
маневренность ЛА. Последняя характеризуется или ми¬
нимально допустимым радиусом разворота гмин, или ма¬
ксимально допустимым поперечным ускорением &’Пмакс,
или перегрузкой /г, которые при постоянной скорости по¬
лета связаны зависимостями
макс
где g— ускорение силы тяжести.
§ 11.3. ПРОЦЕСС УПРАВЛЕНИЯ, СИСТЕМЫ
КООРДИНАТ И УРАВНЕНИЕ ДВИЖЕНИЯ
ОБЪЕКТА
Процессом управления летательным аппаратом ЛА
называется удерживание его центра массы на заданной
или вырабатываемой в процессе управления траектории.
Как правило, процессу управления предшествует про¬
цесс стабилизации ЛА. Процессом стабилизации ЛА на¬
зывается сохранение определенного углового положения
ЛА относительно траектории полета. Устройство, стаби¬
лизирующее угловое положение ЛА, называется автопи-
397
лотом. На рис. 11.3 представлены структурные схемы
стабилизации и управления ЛА. В отсутствие крена
сильно оперенный ЛА может совершать прямолинейный
горизонтальный полет без автопилота (рис. 11.3,а),
однако движение такого ЛА сильно зависит от внешних
условий, и управление им затруднено. В сочетании с авто¬
пилотом (рис. 11.3,5) ЛА может совершать устойчивый
полет в заданном направлении
Рис. 11.3. Упрощенные схемы стабилизации и управления ЛА.
или выполнять отдельные
f^3bixj
0)
маневры (разворот, снижение, набор высоты и т. п.).
Схема управления ЛА, представленная на рис. 11.3,0,
отличается от предыдущих тем, что она предусматривает
возможность изменения текущих координат ЛА по
командам, вырабатываемым в пункте управления.
Положение центра тяжести ЛА на заданной траек¬
тории полета в земной, прямоугольной системе коорди¬
нат (х3, z/3, г3) определяется высотой /1, боковым от¬
клонением Z и пройденным расстоянием L (рис. 11.4,а),
а в полярной — азимутом а, углом места [3 и наклонной
дальностью D. Рассмотрим взаимосвязь «подвижной»
системы координат (хс, Ус, £с), начало которой располо¬
жено в центре тяжести ЛА, с неподвижной земной си¬
стемой (х3, у3, г3). На рис. 11.4,5 показаны проекции
осей хс, ус и zc на плоскости Х3ОУ3, У3023, X3OZ3, кото¬
рые образуют с осями х3, у3, z3 три угла: угол тангажа й,
угол крена у и курсовой угол ф. Проекции вектора ско¬
рости V, определяющего траекторию движения ЛА,
образуют с осями земной системы координат в вер¬
398
тикальной плоскости угол наклона траектории 0 и в го¬
ризонтальной плоскости — путевой угол Ф. Углы между
проекциями V и проекциями осей ЛА на те же плоско¬
сти определяют угол атаки czc = ^—0 и угол скольже¬
ния Рс=ф—Ф.
В отсутствие автопилота движение ЛА описывается
системой дифференциальных уравнений, которые в век¬
торной (сокращенной) форме имеют вид
(11Л)
где V(x, у, г) —вектор скорости движения центра масс;
R(x, у, z) —вектор внешних сил;
М(х, у, z) —главный момент внешних сил;
/<(х, у, z)—кинематический момент системы;
со — вектор угловой скорости ЛА.
399
Решение системы уравнений (11.1), в общем случае
нелинейных, для нахождения зависимостей выходных
координат /г, Z, 0, Ф, <6', ij?, и L от отклонений рулевых
органов связано со значительными трудностями. Однако
сложное движение ЛА можно представить в виде ряда
простых: плоского продольного движения (полет на за¬
данной высоте, набор высоты, снижение); бокового дви¬
жения (чистое рысканье, плоский и координированный
развороты),— что значительно упрощает математиче¬
ское описание движения и процесса управления.
Уравнения движения ЛА в связанной системе коор¬
динат при плоском продольном движении в отсутствие
возмущающих сил имеют вид:
//г cos — X — Fg sin 0,
mV — P sin ac У — Fg cos 0,
(П-2)
& = 0-{-ac,
где Д, ЛД —момент инерции и момент сил сопротивле¬
ния ЛА;
Д, 7ИВ— момент инерции и момент сил сопротивле¬
ния руля высоты;
Р—сила тяги двигателей.
При решении задачи движения ЛА в координатах
(х3, r/з, Дз) уравнения (11.2) должны быть дополнены за¬
висимостями
(11.3)
Уравнения (11.2) и (11.3) нелинейны, однако при не¬
больших отклонениях параметров движения от устано¬
вившихся значений, характеризующих заданное движе¬
ние, они могут быть линеаризированы. Полагая в (11.2)
и (11.3) V= Vo + AV, h = h&+ Xh, 0~Go + A0, cic =
= aco+,Acic и вычитая из них уравнения установившегося
400
режима полета, находят уравнения для малых отклоне¬
ний (вариаций) ДУ, Д/г, Д©, Дас и т. д. Применяя к си¬
стеме уравнений в вариациях преобразование Лапласа,
можно представить искомые зависимости в форме функ¬
ций передач. Например, для продольного движения ЛА
функция передачи от 6В к ДО может быть представлена
в виде
ДО (/?) В (/?) Р3 + В2 + Р + В4 /11 м
А (Р) ~ Р* + А1 РТ+ А2 Р2 + Л3 Р +А4 ’ ‘
где коэффициенты Bi и определяются конструкцией
ЛА и параметрами среды, в которой происходит движе¬
ние.
Полиномы В(р) и А(р) для продольного движения
любого ЛуХ с достаточной степенью точности могут быть
разложены па множители в виде трехчленов и двучле¬
нов. Например, А(р) разлагается на два трехчлена
Л О) « A4(a, р2 + ь1 р4- 1) (а2 р2-\-Ь2 р Д 1),
корни которых значительно отличаются друг от друга.
Первому трехчлену соответствует пара больших корней,
а второму — пара малых корней. Трехчлену с большими
корнями соответствует быстрое периодическое движение,
а трехчлену с малыми корнями — медленное периодиче¬
ское движение (фугоидиое). Фугоидное движение вы¬
звано медленным изменением скорости полета при из¬
менении угла атаки. Для некоторых систем управления
время полета снаряда до цели мало, в связи с чем мед¬
ленные процессы движения могут не учитываться.
Тогда функциональная зависимость между углом тан¬
гажа и отклонением руля высоты для плоского продоль¬
ного движения в пренебрежении силой тяжести и из¬
менением скорости полета приводится к виду
(р) -MW+1) (1 j 5)
®«(Р) ~ 70рГ2а/ + 2е\р+1) ’
где — безразмерный коэффициент передачи;
Г9 —постоянная обратная скорости нарастания на¬
клона траектории;
7 —постоянная времени устано'вленпя угла атаки;
t — коэффициент демпфирования.
26-1173
401
Функциональная связь между углом наклона траек¬
тории Д© и отклонением руля высоты 6В записывается
в виде
№ (р)__ — (116)
М/>) Тв р + 2f/-Oc р + 1)
Выражения (11-5) и (11.6), а также зависимость
приращения высоты Д/г от угла наклона траектории
Рис. 11.5. Структурная схема ЛА при управлении рулем высоты
(продольное движение).
Д0 = ДД—Дас, ДЛ=1/Д0/р, отображающая движение ЛА
относительно земной поверхности, представлены на
рис. 11.5 в виде функционально-структурной схемы.
В соответствии с функциями передачи данная струк¬
турная схема содержит колебательное звено и два
идеальных интегратора. Управление высотой полета по
данной схеме при пропорциональном отклонении рулей
высоты бв = МА обладает неустойчивостью, так как
в контур управления входят два идеальных интегратора.
Устойчивость управления может быть достигнута, если
в закон отклонения рулями ввести производную от вы¬
соты или фазовое опережение, т. е. dB = ^(Tp +1), или,
охватив жесткой обратной связью один из интеграторов,
понизить порядок астатизма контура управления.
В случае плоского бокового движения функции пере¬
дачи, описывающие связь курсового ф и путевого Ф уг¬
лов с отклонениями руля направления бп, имеют вид,
402
аналогичный выражениям (11.5) и (11.6):
Дф (р) ^гн (Т'ц, Р + 1)
МЛ=Гф + 25Г?с ЯЛ)
ДФ (р) —^п
Т^р^ + Т^р + Х)'
(11-8)
Рис. 1'1.6. Структурная схема ЛА при управлении рулем направления
(боковое движение).
вого угла, а —постоянная времени установления угла
скольжения рс-
Учитывая зависимость бокового отклонения AZ от
путевого угла в виде AZ = I/ДФ/р, построим структурную
схему ЛА, отображающую его движение в горизонталь¬
ной плоскости (рис. 11.6). Так же как и в предыдущем
случае, структурная схема содержит два интегратора и
колебательное звено. Управление боковым движением
при пропорциональном отклонении руля направления от
бокового отклонения 6i-I = /ez\Z' связано с теми же трудно¬
стями, что и управление по высоте. В отсутствие авто¬
пилота, нейтрализующего, как правило, действие одного
из интеграторов или придающего устойчивость ЛА дру¬
гими способами, управление по данной схеме может осу¬
ществлять лишь опытный оператор (пилот), учитываю¬
щий производную от бокового отклонения и действую¬
щий в соответствии с законом
бп = k (Тр + 1) AZ.
26*
403
Наряду с функциями передачи ЛА по угловым коор¬
динатам (11.4) — (Н.8) можно составить функции пере¬
дачи и по линейным координатам. На рис. 11.7 приведе¬
на структурная схема ЛА, учитывающая поперечное
ускорение гип или перегрузку. Пунктиром показана
структура по угловым координатам. При управлении
ЛА в декартовой системе координат схема, учитываю-
in, ая перегрузки, более выгодна. Измерение последних
осуществляется датчиками перегрузок. Управление ЛА
при этом может производиться путем задания необхо¬
димой перегрузки, а не угловой координаты.
Движения ЛА вокруг продольной оси ,гс, т. е. движе¬
ния крена для разных аэродинамических схем, отлича-
Рис. 11.7. Структурная схема ЛА с учетом перегрузок.
ются друг от друга. Для ЛА с аэродинамической сим¬
метрией (крестокрылый снаряд), у которого площадь
крыльев мала, движение крена можно считать незави¬
симым от продольного и бокового движения. В этом слу¬
чае зависимость крена от поворота элеронов характери¬
зуется функцией передачи
^(р) Р(7т^ + 1) ’
(И-9)
где Г—постоянная времени ЛА при повороте его во¬
круг продольной оси.
Движение крепа у таких снарядов приводит к пере¬
крестным связям между каналами продольного и боко¬
вого управления, а увеличение крена до 90° нарушает
правильное управление, так как руль направления начи-
404
нает выполнять функции руля высоты и наоборот. В свя¬
зи с этим все снаряды снабжаются жесткими стабилиза¬
торами крена или устройствами, сохраняющими правиль¬
ное управление в вертикальной и горизонтальной плоско¬
стях.
ЛА с аэродинамической несимметрией. (плоскостная,
самолетная схема) обладают способностью восстанавли¬
вать свое горизонтальное положение за счет момента,
возникающего при скольжении, которое сопутствует кре¬
ну. В этом случае зависимость крена Ду от §э может
носить или апериодический, или затухающий колебатель¬
ный характер. Для обеспечения правильного коорди¬
нированного разворота (боковое движение без скольже¬
ния) в таких ЛА также применяются стабилизаторы
крена. Они согласуют повороты элеронов и руля направ¬
ления.
§ 11.4. МЕТОДЫ НАВЕДЕНИЯ. ТРАЕКТОРИИ
ДВИЖЕНИЯ
Автоматическое наведение снаряда или ЛА на цель
неразрывно связано с измерением текущих координат
цели <рц(х, у, г) и снаряда фс(х, У, z). Согласно упрощен¬
ному представлению системы наведения как системы
автоматического регулирования (рис. 11.3 и 11.8) мгно¬
венная разница координат цели и снаряда Д<р(/) =
= Т'п-(0—Фпых(0 образует сигнал рассогласования, ко¬
торый используется для управления движением снаряда
таким образом, чтобы уменьшать эту разницу до пуля
и тем самым обеспечивать наибольшую вероятность по¬
падания в цель. Закон образования сигнала рассогласо¬
вания зависит от метода наведения или способа задания
опорной (кинематической) траектории, по которой про¬
исходит сближение снаряда с целью.
Кинематической траекторией (КТ) снаряда назы¬
вается путь его движения до встречи с целью, при кото¬
ром снаряд, цель и пункт управления представляются
в виде геометрических точек, размещенных в их центрах
масс. Реальное движение снаряда происходит по дина¬
мической (ДТ) и фактической (ФТ) траекториям, учи¬
тывающим соответственно инерционность снаряда, свой¬
ства системы управления и действие внешних возмуще¬
ний и помех (рис. 11.8).
405
В общем случае вся траектория движения снаряда и
процесс наведения могут быть разбиты на отдельные
этапы: выведение снаряда на траекторию наведения
(старт), движение снаряда по траектории наведения
(сближение) и движение снаряда непосредственно к цели
после прекращения работы системы управления (попа¬
дание в цель). Применительно к процессу сближения тра¬
ектории наведения подразделяются на фиксированные
(жесткие) и подвижные (гибкие). Жесткая траектория
задается в виде линии положения, курса, маршрута, со¬
здаваемых системой управления или программой полета,
и используется при наведении на неподвижную цель.
Если наведение снаряда производится с подвижного
пункта управления по движущейся цели, то траектория
движения снаряда становится подвижной в пространстве,
гибкой.
Один из способов создания подвижной траектории
состоит в том, что система управления в течение всего
времени полета снаряда удерживает его на линии, сое¬
диняющей пункт управления и цель. Такой метод наве¬
дения называется трехточечным. Трехточечный метод
может также обеспечивать наведение снарядов в упреж¬
денную точку. В случае, когда траектория наведения не
может быть задана извне, т. е. с пункта управления,
задание траектории заменяется заданием направления
устройствами самонаведения, обеспечивающими выход
406
снаряда на цель (самонаведение, полет на маяк, посадка
и т. п.). Метод наведения, в котором участвует лишь сна¬
ряд и цель, называется двухточечным методом. Двухто¬
чечный метод наведения в упрежденную точку имеет не¬
сколько разновидностей: метод постоянного упреждения,
методы параллельного и пропорционального сближения.
Метод постоянного упреждения состоит в . том, что
в процессе движения снаряда угол между линией, сое¬
диняющей снаряд и цель (линия визирования), и век¬
тором путевой скорости снаряда должен оставаться по¬
стоянным (имеется в виду движение в одной плоскости).
Рис. 1'1.9. Траектории движения ЛА при наведении по кривой пого¬
ни (а) и параллельном сближении (б).
В частном случае этот угол, называемый углом упреж¬
дения, может быть равен нулю. Наведение при нуле¬
вом угле упреждения называется наведением по кривой
погони или чистым преследованием. На рис. 11.9,а пока¬
зана траектория кривой погони при наведении навстречу.
Траектория построена приближенно, графическим спосо¬
бом, на основании равенства Ac/Vc=An/VrTi = const. Из
рисунка видно, что траектория движения снаряда сильно
искривлена. Наведение на быстро движущуюся цель ме¬
тодом кривой погони затруднительно, особенно при
стрельбе навстречу, когда радиус кривизны траектории
по мере приближения снаряда к цели стремится к нулю
(гтр—>0). В этом случае снаряд, обладающий мннималь-
407
ным радиусом разворота (гс мин>^тр), сходит с кинема¬
тической траектории.
Метод параллельного сближения заключается в том,
что в процессе движения снаряда (рис. 11.9,6) линия ви¬
зирования перемещается параллельно самой себе, т. е.
угловая скорость липки визирования равна нулю. При
этом методе наведения радиусы разворотов снаряда и
связанные с ним перегрузки минимальны.
Наиболее общим методом наведения является метод
пропорционального сближения (пропорциональной нави¬
гации), отличающийся тем, что в процессе наведения от¬
ношение угловой скорости снаряда к угловой скорости
линии визирования остается постоянным. Математиче¬
ски метод пропорционального сближения описывается
уравнением
<и-10)
которое после интегрирования приводится к выражению
вида
Ф=Ап+'По, (11.11)
где Ф, г) — соответственно путевой угол снаряда и угол'
визирован ия относительно неподвижной
оси х3;
А— постоянная, a rjo— начальный угол визиро¬
вания.
Уравнение (11.10) может быть использовано и для
описания других методов наведения. Наведению с посто¬
янным углом упреждения соответствуют условия: А =
= 1, цо^О; наведению по кривой погони: /1=1, ц = 0;
наведению по методу параллельного сближения: т] = 0
или Л = оо. Метод параллельного сближения, так же как
и метод пропорциональной навигации, требует измере¬
ния угловой скорости линии визирования т], что значи¬
тельно сложнее, чем непосредственное измерение угла ви¬
зирования при наведении по кривой погони.
Математическое описание кинематической траектории
для различных методов наведения связано с решением
ряда дифференциальных и тригонометрических уравне¬
ний. При решении этих уравнений желательно получить
управляющую функцию срвх(О или закон отклонения ки¬
нематической траектории от прямой линии, соединяющий
408
снаряд и цель в момент старта. Эта управляющая функ¬
ция определяет те маневры снаряда, которые он должен
выполнить в процессе наведения. Управляющая функция
Фвх(0 может быть рассчитана пли в угловых, или в ли¬
нейных величинах в зависимости от метода, принятого
для управления снарядом. Например, для трехточечных
методов (управление в луче и по командам) предпочти¬
тельно рассчитывать функцию фвх(0 в виде линейного
перемещения снаряда относительно линии, соединяющей
пункт управления и цель (рис. И.Ю.л). При прямолиней¬
ном движении цели и постоянной величине скорости
Рис. 11.10. Геометрические соотношения при трехточечном и двух¬
точечном наведении.
409
цели и снаряда управляющая функция имеет вид
Твз] лип (0 = dt = ^DcQdt,
О б
(11.12)
где VH — нормальная к лучу составляющая скорости
снаряда;
Dc— текущая дальность снаряда, a Q— угловая
скорость движения луча, следящего за целью.
Для нахождения срвх(О необходимо учесть уравнение
(11.13)
Решение для Vn(t) при Dc~ Vc имеет вид
Ун = рсО = Уц
Ро (0,, + К/)
О20 "Ь хо— 2х0Уц/ + (Рц£)2
(И.14)
>
где обозначения ясны из рисунка *.
Значение ср-вх(/) в угловых величинах соответственно
равно
t
ТвХ) У гл == ^Qdt.
о
Для двухточечных методов управляющая функция
обычно имеет еще* более сложную форму. Так, при чи¬
стом преследовании (рис. 11.10,6) решение уравнений
погони
^- = -Го+УцСО8-гь 1
(11.15)
имеет неявную форму
(Sin
и (1 + COS 7))» ’
(11.16)
где
Рс
■ Гц
(1 + ^)»
(sin io)’-1
* Числовые примеры см. Щукин А. Н. Динамические и флюк¬
туационные ошибки управляемых объектов. Изд-во «Советское ра¬
дио», 1961.
410
Текущее время t и угол т] связаны зависимостью
Do (COS 7)о + 5) — D (COS 7) + s)
s-Vc — Vc
(И.17)
Для представления управляющей функции ф'пХ = ,п(0
в удобной для последующих расчетов форме приходится
выражать зависимость т](/), вычисленную по точкам,
приближенно в виде степенного ряда в ограниченном ин¬
тервале времени.
Для методов параллельного и пропорционального
сближения (рис. 11.10,0) управляющие функции фвх(/)
находятся численным интегрированием соответствующих
уравнений
Vc-sin(714-11o) = Vusin(i94 + ₽o)) (11.18)
d^ , д d (Ецо 4~ рц) 10)
Зависимости фъх(0 представляют в виде таблиц или
графиков. Для последующих расчетов фвх(/) также ап¬
проксимируют в виде степенных рядов.
Одним из важнейших вопросов при разработке систе¬
мы наведения является выбор наилучшей траектории
движения снаряда. При выборе траектории следует стре¬
миться к снижению ее протяженности и кривизны, по¬
скольку при этом сокращается время полета снаряда,
снижаются требования к двигателю, может быть увели¬
чен боевой заряд снаряда и менее жесткими становят¬
ся требования к перегрузкам и маневренности снаряда.
§ 11.5. ДИНАМИЧЕСКИЕ И ФЛЮКТУАЦИОННЫЕ
ОШИБКИ НАВЕДЕНИЯ. ПРОМАХ
Расчет динамических ошибок наведения с учетом все¬
го процесса наведения и многочисленных параметров
контура, а также выбор оптимальных методов управле¬
ния (перекладки рулей, регулирования тяги, самонаст¬
ройки автопилота и т. п.) относятся к области техниче¬
ской кибернетики. Определение ошибок конкретной
системы наведения производится обычно на аналоговых
моделях или цифровых вычислительных машинах, при¬
чем такие элементы контура, как автопилот и оператор
пункта управления, также учитываются при моделиро-
411
вании. Однако моделирование, несмотря на высокую точ¬
ность решения, часто не позволяет выявить общих зако¬
номерностей, на основании которых можно проектиро¬
вать лучшие системы наведения. В этой связи представ¬
ляет интерес упрощенный анализ ошибок наведения объ¬
екта на цель.
Функция передачи разомкнутого контура управления
движением в одной плоскости при линейном представ¬
лении ЛА в общем случае имеет вид
KW(p)
(Гр +!)■■■ е-^ , , J J О0)
р\т№ + ^7\р+\)...(Т1р+\)
где k(t) —коэффициент передачи всего контура; е~'*р—
звено, отражающее запаздывание в линиях передачи ин¬
формации, а число и вид других сомножителей в числи¬
теле и знаменателе определяется числом и характером
звеньев контура управления.
Учет всех элементов контура делает выражение
(11.20) сложным даже в том случае, если все элементы
линейны.
Точное знание всей функции передачи является необ¬
ходимым при исследовании устойчивости системы, одна¬
ко при определении и оценке ошибок наведения нет не¬
обходимости учитывать характеристики всех звеньев кон¬
тура. В первом приближении можно «заморозить» сред¬
нее значение коэффициента k(t), считая его постоянным
на определенной дистанции, а также не учитывать ха¬
рактеристики рулевой машинки и радиотехннчеких
устройстс вследствие их малой инерционности по
сравнению с инерционностью ЛА.
Дополнительные упрощения функции передачи могут
быть сделаны, если частота собственных угловых коле¬
баний корпуса ЛА соо относительно вектора скорости V
значительно выше граничной частоты общего контура
управления <ок. В этом случае в выражении (11.20) со¬
множитель вида 1/(Т2ор2 + 2£7”с/Н-1) может быть опущен.
Тогда функцию передачи упрощенной системы KW(p)
можно представить одним из двух эквивалентов:
»
Р (Ле1Р +.1)
(11.21)
412
или
. (11.22)
Первым необходимым условием при замене
реальной функции передачи KW (р) одним из
эквивалентов должно быть соблюдение равен¬
ства установившихся значений ошибок, т. е. сохранение
порядка астатизма системы. Вторым желательным усло¬
вием является соразмерность собственного периода коле¬
баний и времени затухания переходного процесса в ре¬
альной и эквивалентной системах.
Основное уравнение системы наведения как системы
автоматического регулирования можно записать в виде
Дф(0 фвых(0, (11.23)
где Аф(/) —ошибка управления, равная разности между
текущей координатой кинематической траектории <рВх(0
и текущей координатой динамической или фактической
траекторий фВЫх(0 (рис. 11.8).
В процессе движения объекта его кинематическая
траектория изменяется и должна в каждый новый мо¬
мент времени вычисляться от соответствующей точки на
динамической траектории. Однако, если управление по
кинематической траектории просходит достаточно точно,
эту особенность можно не учитывать и при расчетах оши¬
бок пользоваться выражением (11.23) как равенством.
Как указывалось ранее (§ 11.4), функцию управления
Фвх(^), описывающую кинематическую траекторию
в угловых или в линейных координатах, в большинстве
случаев представляют в виде ряда по степеням
(0 = А + Att + + ... + + ... (11.24)
Тогда ошибка наведения
Д? (Р) — J Тад 0°) (11 -25)
может быть представлена в виде ряда
д?:(о=(о с.+Кх (о с,+(о сг+..., (и .26)
413
где
бок.
— коэффициенты оши-
р=о
Как известно, для систем, обладающих астатизмом
первого порядка, Со = О и ошибка по положению равна
нулю. Для системы, обладающей астатизмом второго
порядка, Co = Ci = O, т. е. отсутствуют ошибки по положе¬
нию и скорости.
При выбранной управляющей функции для заданной
траектории наведения и предполагаемого маневра цели
число п учитываемых членов ряда (11.26) определяется
из условия
с.л.С-с-»с,+л„,С!. (и-27)
где /макс — предварительно вычисленное максимальное
значение времени движения ЛА до цели по кинематиче¬
ской траектории.
При известных /мйкс и п ошибка наведения опреде¬
ляется по формуле
А? (*макс) — ?вх макс ) С0-ф- (/ макс )С + ... (11.28)
Кроме динамической ошибки Аср в процессе наведе¬
ния могут образоваться ошибки за счет воздействия вет¬
ра или воздушных течений. В тех случаях, когда скорость
и направление ветра U известны и могут быть приняты
постоянными, ошибки (в одной из плоскостей движения)
рассчитываются по известным методам учета возмущаю¬
щих воздействий в виде
_U_ W.B (Р)
р • 1+ОМ/0’
(11.29)
где KWB(p)—функция передачи части общего контура
с функцией передачи KWd(p) от точки приложения век¬
тора U до выхода всей системы.
Ошибки управления, вызванные случайными стацио¬
нарными возмущениями и помехами Асрш могут быть вы¬
числены по формуле
00
—Об
I2
(11.30)
KW„ (/со)
1 4- KW» (/«)
414
где S’n(co) —спектральная плотность эквивалентных
флюктуаций координаты системы управления в точке
приложения, вызванных возмущениями или помехами,
а —функция передачи от этой точки до выход¬
ной измеряемой координаты.
Работа системы управления в конечном итоге харак¬
теризуется суммарной ошибкой наведения и вероятно¬
стью поражения цели. Для упрощения связи между
ошибкой наведения и вероятностью поражения цели ис¬
пользуется понятие промаха. Промах определяется как
минимальное расстояние между целью и снарядом в мо¬
мент пролета снаряда вблизи цели Дгпр.
Понятие промаха как линейной ошибки при наведе¬
нии по направлению может быть представлено в виде
функциональной связи
А?ЛИН пр ~ Д?угл^мз рь/мз? (11.31)
где гмз — расстояние между целью и снарядом в момент
выключения управления (расстояние мертвой зоны),
а рн — угол между вектором скорости снаряда и линией
визирования в тот же момент времени.
В зависимости от размеров цели, эффективности дей¬
ствия заряда и закона распределения ошибок может
быть подсчитана вероятность поражения цели.
Глава 12
СИСТЕМЫ УПРАВЛЕНИЯ И ИХ
ХАРАКТЕРИСТИКИ
§ 12.1. ВВЕДЕНИЕ
В системах управления для определения текущих ко¬
ординат и параметров движения объекта и цели исполь¬
зуются радиотехнические, оптические, гироскопические и
инерциальные измерители. В сочетании с функциональ¬
ными преобразователями и вычислительными устройст¬
вами измерители образуют так называемые координа¬
торы, выходные сигналы которых используются в каче¬
стве команд для управления объектами.
В зависимости от места установки координаторов (на
управляемом объекте или в пункте управления) и взаи¬
мосвязей между объектом и пунктом управления системы
управления делятся на четыре основных типа: автоном¬
ного управления, радиотеленаведения, радиотелеупраз-
ления и самонаведения.
§ 12.2. СИСТЕМЫ СТАБИЛИЗАЦИИ И АВТОНОМНОГО
УПРАВЛЕНИЯ
Автономное управление представляет способ наведе¬
ния подвижного объекта или летательного аппарата
по программе, задающей траекторию в виде фик¬
сированного направления движения или маршрута. От¬
клонения от направления или маршрута определяются
бортовыми координаторами, не имеющими какого-либо
контакта с пунктом управления и целью. К числу таких
координаторов относятся гироскопические и инерциаль¬
ные. При автономном управлении координатор, как пра¬
вило, воздействует на автопилот ЛА. На рис. 12.1 в ка¬
честве примера приведена упрощенная функциональная
схема системы автономного управления по заданному
направлению (курсу или тангажу). Система управления
416
содержит три основных контура: контур рулевого управ¬
ления, контур стабилизации угловых движений ЛА отно¬
сительно центра масс и контур управления движением
центра масс в заданном направлении. Первые два кон¬
тура составляют автопилотный контур или автопилот и
обеспечивают необходимые характеристики работы ру¬
левого привода п угловой стабилизации при исполнении
«команд» координатора, входящего в контур управления
движениелМ центра масс.
Координатор
А вгпз1Ш71?гпный контур
аппарат (ЛА)
Летательной
Рис. 12.1. Упрощенная функциональная схема автономного управ¬
ления.
Задание и измерение угловых координат ЛА коорди¬
натором осуществляется с помощью позиционных гиро¬
скопов. Принцип действия позиционного гироскопа (об¬
ладающего тремя степенями свободы и называемого так¬
же свободным гироскопом) сводится к следующему.
В отсутствие внешних сил главная ось свободного гиро¬
скопа сохраняет в мировом пространстве заданное на¬
правление. Поворот основания гироскопа относительно
осей, не совпадающих с главной осью, приводит к угло¬
вому перемещению внутренней и внешней рамок гиро¬
скопа относительно друг друга и корпуса ЛА.
Эти перемещения с помощью соответствующих дат¬
чиков преобразуются в сигналы, пропорциональные угло¬
вым поворотам ЛА. Гироскоп в зависимости от способа
установки на ЛА позволяет попарно измерять угол тан¬
гажа и курса, угол тангажа и крена, угол курса и
крена.
27—1173 417
С помощью двухстепенных гироскопов, называемых
также прецессионными, или скоростными, можно изме¬
рять скорости вращения ЛА вокруг его осей. С помощью
гироскопов других типов можно формировать сигналы,
пропорциональные угловым ускорениям (демпфирован¬
ный гироскоп), и получать сигналы, пропорциональные
интегралу от угловых отклонений (интегрирующие гиро¬
скопы) .
В реальных гироскопах всегда существуют возмущаю¬
щие силы и моменты (трение в опорах, несовпадение
центра тяжести гироскопа с центром тяжести подвеса
и т. п.), вызывающие медленный уход его главной оси
от первоначального, заданного направления (прецессия
гироскопа). В силу указанных причин в процессе по¬
лета необходимо корректировать положение главной оси
гироскопа. Кроме того, в условиях полета вокруг Земли
необходимо, чтобы главная ось гироскопа была перпен¬
дикулярна плоскости горизонта. Это обеспечивается раз¬
личного рода искусственными вертикалями и горизонта¬
лями.
Для ЛА и снарядов дальнего действия, использую¬
щих автономную систему управления, коррекция гиро¬
скопов обязательна. Для ЛА ближнего действия уходы
гироскопов за время полета незначительны и коррекция
может не производиться.
Весьма часто управление по заданному курсу соче¬
тается с управлением по заданному маршруту, когда си¬
стема управления контролирует движение ЛА по линей¬
ным отклонениям от заданной линии наведения. В ка¬
честве примера на рис. 12.2 представлена подробная
структурная схема автономного управления ЛА при по¬
лете на заданной высоте, что условно соответствует дви¬
жению по заданному маршруту в вертикальной плоско¬
сти. Контур управления состоит из координатора, авто¬
пилота и кинематического звена. Координатор включает
в себя задатчики высоты Ло и измеритель высоты h ра¬
диотехнического или барометрического типов. Автопилот
предполагается линейным и состоящим из усилителя йу,
рулевой машинки с функцией передачи /’рм/р ( ТрмР + 1) ,
скоростного и позиционного гироскопов, измеряющих
скорость изменения тангажа й и сам тангаж Ф, и уст¬
ройств в цепях дополнительных обратных связей W\(p),
1^2 (р), ^з(р), 1^4 (р), ^б(р), обеспечивающих устойчи-
418
вость !и требуемые переходные характеристики управле¬
ния ЛА. Обратная связь через элемент (тахо¬
метрическая обратная связь) обеспечивает высокую про¬
порциональность скорости работы рулевой машинки
входному сигналу усилителя. Через элемент IF2(p)=£2
осуществляется жесткая обратная связь по отклонениям
руля высоты, которая исключает интегрирующий эффект
Задат¬
чик
/
//.(Зл;
С'Пи/ют -
Летательный аппарат
Кинематиче¬
ское звено
Рис. 12.2. Структурная схема системы управления ЛА с автопилотом
по тангажу и высоте [13].
рулевого привода, придавая контуру, охваченному этой
связью, свойства апериодического звена с малой постоян¬
ной времени. Обратная связь через скоростной гироскоп
и элементы №3(р) и W±(p) обеспечивает быстроту и не¬
обходимые качества переходного процесса управления по
тангажу.
В качестве других стабилизирующих дополнительных
обратных связей используются связи через датчики пе¬
регрузок Ws(p'), которые охватывают часть контура ЛА
не только по угловым координатам, но и по линейным
поперечным перемещениям, так как сС’п = А/г.
Как видно из рисунка, общий контур управления по
высоте, без учета обратной связи по тангажу, содержит
два интегратора (1/Гдр и V/p) и неустойчив. Жесткая
обратная связь по тангажу, действующая при полете с за¬
данным тангажом устраняет интегрирующие свойства
ЛА по наклону траектории \ГГ$р и придает контуру
27е 419
управления по высоте устойчивость. Устойчивость общего
контура может быть также получена, как это указыва¬
лось ранее в гл. 11, за счет формирования сигнала рас¬
согласования в виде u=k(Tp+ 1) АЛ. Однако это связано
с дифференцированием сигналов измерителя высоты, что
приводит к увеличению уровня его собственных и внеш¬
них шумов.
Рис. 12.3. Структурная схема стабилизации крена и использование
его при управлении боковым движением ЛА.
Структурная схема автономного управления полетом
ЛА по заданному маршруту при так называемом поляр¬
ном управлении в горизонтальной плоскости (соответст¬
вует условию Z0 = const и AZ—>0) приведена на рис. 12.3.
При декартовом управлении структурная схема повторя¬
ет рис. 12.2. Измерение бокового отклонения AZ может
производиться интегрирующими гироскопами, инерциаль¬
ными устройствами или допплеровскими системами,
определяющими боковой снос ЛА. Большой интерес при
управлении подвижными объектами представляет ис¬
пользование инерциальных измерителей, определяю¬
щих как боковое уклонение, так и весь пройденный путь
двукратным интегрированием соответствующих состав¬
ляющих вектора ускорения юп(^) или перегрузок п:
т
Lx~- ^wx(t)dtdt^-LXo. (12.1)
б
Контур управления в этом случае замыкается через
акселерометры, которые измеряют составляющие векто¬
ра ускорения, и вычислительное устройство, содержащее
420
два интегратора. При измерении составляющих перегру¬
зок датчики ускорении (акселерометры) должны уста¬
навливаться на гиростабилизироваииых платформах, со¬
храняющих вполне определенное положение в простран¬
стве независимо от положения осей ЛА. Сигналы аксе¬
лерометров могут сами использоваться для стабилизации
таких платформ.
Системы управления, использующие гироскопические
и инерциальные координаторы, составляют группу
полностью автономных систем, не требующих не только
какого-либо контакта с пунктом управления, но также
и с внешней средой и внешними ориентирами — Землей,
Солнцем, звездами. Контакт с последними необходим
для работы астронавигационных или допплеровских си¬
стем, также относящихся к группе автономных, посколь¬
ку для них не требуется связь с пунктом управления.
Достоинством автономных систем является практиче¬
ски неограниченная дальность действия и невозможность
создания организованных помех. Недостатком систем
с гироскопическими и инерциальными измерителями яв¬
ляется нарастание ошибки определения координат во
времени. Поэтому они обычно используются в комплексе
с другими системами управления, позволяющими перио¬
дически определять точное местонахождение подвижного
объекта или ЛА.
В комплексных системах управления использование
измерителей различных типов может осуществляться как
последовательно, в соответствии с этапами наведения,
так и параллельно. Примерами комплексных систем
управления являются все последующие системы радио¬
управления, так как в той или иной степени они преду¬
сматривают сочетание автономных систем стабилизации
и управления с радиотехническими устройствами.
§ 12.3. СИСТЕМЫ РАДИОТЕЛЕНАВЕДЕНИЯ
Управление в радиозоне. Радиотеленаведение является
одним из способов радиоуправления с наземного пункта,
когда боковое отклонение ЛА от создаваемых радионави¬
гационными системами линий положения (радиозон) из¬
меряется непосредственно на борту ЛА. При радиотеле¬
наведении ЛА наводится на неподвижную цель по фик¬
сированным траекториям, которые соответствуют
линиям положения радионавигационных систем.
421
В тех случаях, когда линия положения является пря¬
мой линией, исходящей из 'пункта управления, структур¬
ная ехема бортовой системы теленаведения близка
к структурным схемам автономного управления по за¬
данному курсу или маршруту (рис. 12.1 —12.3). Разница
заключается в том, что в системе радиотеленаведения бо¬
ковое отклонение ЛА от линии положения контролирует¬
ся радиотехническими координаторами и что масштаб¬
ный коэффициент между измеренным координатором от¬
клонением AZ и необходимым значением команды zzAZ
изменяется с дальностью. Последнее вызывает необходи-
Рис. 12.4. Схема использования AByzX источников инфор¬
мации для лучшей фильтрации помех.
мость корректировать коэффициент передачи системы
управления по мере удаления ЛА от пункта управления.'
В тех случаях, когда линии положения, образуемые
той или иной радионавигационной системой, представля¬
ют окружности или гиперболы, координатор должен вы¬
рабатывать сигналы управления, учитывающие геомет¬
рию линий положения.
Координатор системы теленаведения в общем
случае является комплексным устройством, в кото¬
рое, кроме радиотехнической части, входят вычисли¬
тельные устройства и автономные средства управ¬
ления. Комплексное устройство управления обычно
предполагает использование двух или нескольких
источников информации о положении ЛА для определе¬
ния истинного значения его координат, что повышает
точность и надежность наведения. Упрощенным приме¬
ром системы с двумя источниками информации может
служить схема совместного использования гироскопа и
радиотехнического угломерного устройства, определяю¬
щих направление (рис. 12.4). Гироскоп вырабатывает
сигнал курса ф с медленно меняющейся ошибкой F(/)
(возникающей вследствие ухода гироскопа), а радио-
422
угломер определяет значение курса ар с высокочастотной
помехой f (/). В простейшем случае оба сигнала поступа¬
ют на следящую систему с одним интегрирующим зве¬
ном, замкнутую, когда имеется радиотехнический источ¬
ник. Выходной сигнал гироскопа может быть записан
уравнением Aj Тр (ip + f)/T/J + 1, а радиоугломера урав¬
нением х2= (\\)-\-f)/Tp~\-1. Общий выходной сигнал х =
= Xi + x2 определяется выражением
Г/'р
* = Н
(12.2)
из которого видно, что уход гироскопа подавляется
фильтром высоких частот, а высокочастотная помеха —
фильтрОхМ низких частот, в результате чего истинный
сигнал оказывается в значительной степени очищенным
от помех и возмущений. В более сложном комплексе
«очищенный» сигнал может быть использован для взаим¬
ной коррекции как гироскопа, так и угломера.
Управление в луче. Системы теленаведения, в которых
в качестве радиозоны используется равносигнальная
ось, называются системами управления в радиолуче.
Управление в луче позволяет осуществлять наведение
по гибкой траектории на быстродвижущуюся цель.
Система управления в радиолуче состоит из двух ра¬
диоустройств: РЛС пункта управления, которая создает
равносигнальиую ось, направленную па движущуюся
цель, и бортового координатора, измеряющего отклоне¬
ние снаряда от этой равносигнальной оси (рис. 12.5).
Если равносигнальная ось РЛС поддерживается совме¬
щенной с направлением на цель, а управляющий сигнал,
вызванный отклонением снаряда от этой оси, устраняет
эти отклонения, то в конечном счете обеспечивается
встреча снаряда с целью. При таком способе наведения
необходима лишь одна РЛС. Как правило, кривизна тра¬
ектории наведения при работе с одной РЛС велика,
вследствие чего управляемый снаряд должен обладать
высокой маневренностью. Для снижения кривизны траек¬
тории и соответствующего снижения требований в манев¬
ренности снаряда может быть использован упрежденный
метод наведения. В этом случае пункт управления дол¬
жен содержать: РЛС определения координат (визирова¬
ния) .цели, РЛС управления снарядом и счетно-вычисли¬
тельное устройство, определяющее направление и вели-
423
чину упреждения. В этом случае усложняется лишь на¬
земное оборудование, а бортовое остается по-прежнему
простым. Работа бортовой приемно-усилительной части
координатора подобна работе аналогичной части авто¬
угломера с коническим сканированием. Сформированные
составляющие сигнала рассогласования по тангажу и
курсу или высоте и боковому отклонению с выхода бор¬
тового устройства поступают в автопилот, который с по¬
мощью рулевых органов возвращает снаряд на равно¬
сигнальную ось. Для правильного выделения указанных
Рис. 12.5. Система управления в луче при одной РЛС.
составляющих в бортовое устройство вводятся опорные
сигналы, определяющие начало отсчета координат х и у,
которые передаются с пункта управления путем дополни¬
тельной модуляции излучаемых импульсов или другими
методами. Сам снаряд для сохранения правильного
управления по азимуту (курсу) и углу места (тангажу)
стабилизируется по крену.
Особенность управления снарядом в радиолуче
(рис. 12.5) заключается в том, что его траектория за¬
дается изменением направления равносигнальной оси по
азимуту Да и углу места Д|3, так как РЛС визирования
измеряет не линейные перемещения цели АЛ и AZ, а уг¬
ловые приращения
(12.3)
где £)ц — дальность до цели.
424
Эти приращения углов Дссц и А[3Ц задают новое на¬
правление луча. Новое положение луча в районе снаряда
оказывается смещенным на величины
Дгс^.ДацОс и ДЛС^ДРЦОС, (12.4)
где Dc— дальность до снаряда от пункта управления.
Снаряд, двигаясь в сторону нового положения луча
согласно (12.4), при больших значениях Dc должен про¬
ходить большие расстояния AZC и Д/гс. Это равносильно
Кинематическое Пункт
звено цели управления
л /ouvi Кинематиче-
Снаряд (ЗУг) ское здено ЗУР
Рис. 12.6. Структурная схема контура управления в луче при стаби¬
лизации снаряда только по крену.
тому, что в процессе удаления снаряда от пункта управ¬
ления интенсивность управления должна возрастать про¬
порционально дальности Dc(t). На рис. 12.6 представле¬
на упрощенная структурная схема управления снарядом,
стабилизированного только по крену с учетом изменяю¬
щейся дальности до цели и снаряда. Система состоит из
двух контуров, включенных последовательно: контура
автоматического определения координат цели и контура
управления снарядом. Последний обладает переменным
коэффициентом передачи и содержит два интегратора.
Для придания контуру управления устойчивости и по¬
стоянства коэффициента передачи необходимо ввести фа¬
зоопережающее звено и устройство, увеличивающее зна¬
чение коэффициента передачи пропорционально дально¬
сти. Увеличение коэффициента передачи может осуще¬
ствляться с помощью функционального преобразователя
или программного механизма, определяющего дальность
по средней скорости полета Dc = Vcp-/.
Значительное увеличение устойчивости контура наве¬
дения может быть достигнуто введением в него дополни¬
тельных обратных связей, например, через позиционные
425
гироскопы с начальными (стартовыми) значениями кур¬
са и тангажа (рис. 12.7). В этом случае, контур бу¬
дет содержать одно интегрирующее звено. Управление
по такой схеме при больших угловых ускорениях входно¬
го сигнала срц(О может привести к значительным ошиб¬
кам. Однако такая схема может применяться в системе
управления в двумя РЛС по упрежденной траектории,
при которой вторые производные углового перемещения
управляющего луча малы.
Кинематин^
Цель ПУ Память Снаряд — автопилот ское звена
Рис. 12.7. Структурная схема контура управления в луче при стаби¬
лизации снаряда по курсу и тангажу.
В тех случаях, когда все же используется одна РЛС
и необходимо повысить порядок астатизма, в автопилот
наряду с позиционным гироскопом может быть введено
устройство, запоминающее текущие значения курса ф (/)
и тангажа t)(Q. На рис. 12.7 такое устройство названо
«памятью». Запоминание осуществляется электронными
или электромеханическими интеграторами, действие ко¬
торых эквивалентно повороту основания (базы) гиро¬
скопа на углы ф(/)—тро и -&(/)—-&о. В такую систему обя¬
зательно должно быть также введено фазоопережающее
звено.
Применение той или иной структурной схемы зависит
от конкретных условий наведения. В качестве таких
условий может быть задана точность и помехоустойчи¬
вость. Системы управления с двумя РЛС обладают тем
преимуществом, что случайные колебания луча, сопро¬
вождающего цель, вызванные флюктуациями отражен¬
ных сигналов и помехами, могут быть в значительной
мере отфильтрованы, прежде чем они будут использова¬
ны для задания направления управляющему лучу. В си¬
стеме с одной РЛС угловые флюктуации сопровождаю-
426
щего луча полностью передаются в контур управления.
Во всех случаях повышение точности наведения может
достигаться не только путем увеличения астатизма кон¬
тура сопровождения и управления, но и переводом вбли¬
зи цели бортовой аппаратуры в режим полуакГивного
или пассивного самонаведения.
Работа бортовой аппаратуры при управлении в луче
отличается некоторыми специфическими особенностями.
Эти особенности, в частности, заключаются в том, что
антенна приемного устройства располагается в хвостовой
части снаряда, в зоне действия ионизированных газов,
выбрасываемых реактивным двигателем, что приводит
к ослаблению и паразитной модуляции принимаемых
сигналов. Кроме того, если коническое сканирование
РЛС пункта управления осуществляется вращением об¬
лучателя, а не отражателя, то плоскость поляризации
принимаемых сигналов вращается с частотой ска¬
нирования. Последнее заставляет применять антенны
с круговой поляризацией.
К числу других особенностей работы радиоаппарату¬
ры в радиолуче относится работа на стартовом участке.
После пуска снаряда, когда действует автономная систе¬
ма управления, устойчивый переход на радиоуправляе¬
мый полет в узком радиолуче возможен лишь при опре¬
деленных углах подхода снаряда к лучу. При больших
углах возможен «проскок» снаряда через луч, при ма¬
лых— длительное пребывание в зоне действия боковых
лепестков. Последние могут образовывать ложные равно¬
сигнальные направления, препятствующие сближению
снаряда с главным равносигнальным направлением. На¬
рушение нормальной работы бортовой аппаратуры при
вхождении в луч может происходить и при отсутствии
или весьма низком уровне боковых лепестков за счет
прерывистого облучения снаряда вблизи конуса сканиро¬
вания. В этом случае принимаемые сигналы имеют вид
пачек, повторяющихся с частотой сканирования. Потеря
чувствительности приемника после прохождения сильной
пачки приводит к прерывистой работе канала формиро¬
вания сигнала ошибки и искажает работу органов управ¬
ления снарядом.
Процесс ввода снаряда в луч облегчается, если пункт
управления имеет добавочную, широкую диаграмму на¬
правленности. Снаряд первоначально управляется сигна-
427
лом широкого луча (порядка 20°), а когда управляю¬
щие сигналы широкого луча становятся меньше сигналов
узкого луча, переходит на управление узким лучом. Не¬
которые усложнения бортовой и наземной аппаратуры
окупаются надежностью ввода снаряда в луч.
§ 12.4. СИСТЕМЫ КОМАНДНОГО УПРАВЛЕНИЯ
Командное управление представляет способ наведе¬
ния, при котором удерживание снаряда па кинематиче¬
ской траектории осуществляется по радиокомандам
с пункта управления. Различают два типа систем ко¬
'ТТ/Т^ТТ" 77777777777
РЛС
вычисли¬
0ц
РЛС
РЛС
цели
тельное
устройство
снаряда
обзора
<*)
Рис. 12.8. Системы командного управления первого (я) и второго (б)
типов.
мандного управления. В системах I типа измерение ко¬
ординат цели и снаряда производится относительно
пункта управления или близлежащей к нему точки
(рис. 12.8,6?), а в системах II типа измерение координат
цели производится относительно снаряда (рис. 12.8,6),
причем данные измерений транслируются со снаряда на
пункт управления, где и формируется соответствующая
428
команда управления. Формирование команд (сигналов)
управления может осуществляться автоматически с по¬
мощью вычислительных устройств или вручную — опера¬
тором. Отличительной особенностью систем командного
управления является возможность наблюдения (визиро¬
вания) процесса наведения снаряда на цель в некотором
достаточно широком угловом секторе пространства,
окружающем цель, что создает удобство и наглядность
контроля за работой системы.
Система ручного управления [19]. Одним из возможных
способов управления снарядом при наведении его на
цель на относительно небольших расстояниях является
ручное управление при визуальном наблюдении за целью
и снарядом в оптический или радиолокационный прицел.
При ручном управлении оператор выполняет функции
слежения за целью и управления снарядом путем пере¬
дачи на него команд. В этом случае наиболее подходя¬
щим является трехточечиый метод наведения по так на¬
зываемому нулевому методу, когда отметка цели удер¬
живается в центре оптического или радиолокационного
индикатора, а отметка снаряда в процессе управления
совмещается с отметкой цели (рис. 12.9). Для создания
контрастной отметки снаряда па экране индикатора
Оптический
индикатор
Ручное управление Кинематиче-
ьнаряо ское 3qgh0
Рис. 12.9. Система ручного управления и ее упрощенная структурная
схема.
429
снаряд снабжается пиротехническим трассером или ра¬
диоответчиком.
Динамика управления снарядом по нулевому методу
полностью повторяет динамику управления в луче. При
управлении оператор должен учитывать изменение даль¬
ности до снаряда и при одном и том же угловом несов¬
падении отметок при большей дальности увеличивать
степень отклонения ручки управления или рулевых орга¬
нов снаряда. При управлении снарядом, имеющим стаби¬
лизацию только по крену, общий контур содержит два
интегратора и сигналы управления (команды) должны
содержать производную по отклонению. Для облегчения
управления применяются устройства полуавтоматиче¬
ского формирования команд, учитывающие дальность и
производную угла отклонения. Так как при указанном
управлении оператор входит в общую замкнутую цепь
системы, то необходимо учитывать и его «функцию пере¬
дачи». На основании статистических исследований реак¬
ция оператора на зрительное восприятие может быть
описана зависимостью
= (12.5)
отображающей инерционность 1/Тр+\ и задержку во
времени е“/зр его действий. Высоко натренированный
оператор может действовать с опережением, осуществляя
также функциональную зависимость Тр+1, необходимую
для устойчивого управления процессом наведения.
Система командного управления I типа. В эту систему
(рис. 12.8,а) входят: обзорная РЛС, РЛС точного (авто¬
матического) определения координат цели, РЛС точного
определения координат снаряда, счетно-решающее уст¬
ройство и передатчик команд. При автоматическом опре¬
делении координат цели могут применяться РЛС с сек¬
торным и коническим сканированием. РЛС автоматиче¬
ского сопровождения снаряда работает, как правило,
в режиме конического сканирования с активным отве¬
том со снаряда, что повышает точность и помехоустой¬
чивость определения координат снаряда. Счетно-вычис¬
лительное устройство пункта управления, определяющее
по текущим значениям координат цели и снаряда кине¬
матическую траекторию, в общем случае упрежденную,
вырабатывает сигналы управления в аналоговом пли
430
цифровом виде. Эти сигналы кодируются и ио радиоли¬
нии передачи команд поступают на снаряд.
Структурные схемы управления по командам с уче¬
том автогшлотных контуров повторяют структурные схе¬
мы управления в луче (рис. 12.6 и рис. 12.7) с той раз¬
ницей, что сигнал команды (рассогласования) форми¬
руется не на борту снаряда, а в пункте управления и
поступает в автопилот с некоторым запаздыванием, при¬
сущим линии передачи команды. На конечном этапе на¬
ведения система командного управления также допускает
переход в режим самонаведения.
Система командного управления II типа. Бортовое
устройство системы командного управления II типа
(рис. 12.8,6) может выполняться в виде РЛС визирова¬
ния с секторным сканированием или телевизионной пере¬
дающей камеры с разложением изображения по строкам.
Информация о положении цели относительно снаряда,
соответствующая радиолокационному или телевизионно¬
му изображению, на. борту снаряда преобразуется
в удобную последовательность кодированных импульсов
и по радиолинии трансляции передается в пункт управле¬
ния. Приемная аппаратура пункта управления восстанав¬
ливает соответствующие изображения цели в координат¬
ных осях снаряда и позволяет оператору контролировать
угловые рассогласования, возникающие в процессе наве¬
дения. Об оставшейся дальности оператор может судить
по задержке отраженных сигналов радиолокационного
визира снаряда или по размерам цели и местных пред¬
метов при телевизионном визировании. В последнем слу¬
чае система управления обладает высокой разрешающей
способностью независимо от дальности до пункта управ¬
ления и применяется при наведении снарядов класса
«воздух—земля». При использовании системы управле¬
ния снарядами класса «земля—земля» дальность дейст¬
вия системы может значительно превышать дальность
прямой видимости.
Структурная особенность системы управления заклю¬
чается в том, что по мере сближения с целью трансфор¬
мация линейных перемещений цели AZ или ДА в угло¬
вые а, р возрастает обратно пропорционально расстоя¬
нию между снарядом и целью:
Да
j £ZL
(12.6)
431
Вследствие этого структурная схема системы соответст¬
вует структурной схеме системы самонаведения
(рис. 12.6) и отличается от последней лишь тем, что сиг¬
нал управления (команда) вырабатывается на пункте
управления, а не на борту. Помехоустойчивость системы
управления второго типа несколько ниже, чем системы
первого типа в силу того, что она имеет дополнительную
линию трансляции, открытую со стороны цели. В систе¬
мах управления по гибким траекториям, особенно в си¬
стеме командного управления, следует учитывать относи¬
тельные расположения осей трех систем координат: из¬
мерительной системы, например РЛС визирования сна¬
ряда, исполнительной системы, связанной с мгновенным
положением осей снаряда, и командной системы, опреде¬
ляемой вычислительным устройством пункта управления.
В процессе наведения исполнительная и измерительная
системы координат вращаются и скручиваются друг от¬
носительно друга, создавая искаженное изображение от¬
носительных перемещений цели и снаряда. Эти искаже¬
ния могут приводить к неправильной выработке команд
и перекрестному управлению. Явление скручивания про¬
является весьма сильно и при управлении в луче. При
самонаведении оно сказывается меньше, так как в этом
случае измерительная система координат практически
совпадает с исполнительной. Скручивание координат уст¬
раняется, если координаторы пункта управления и сна¬
ряда гиростабилизированы в пространстве. Скручивание
может быть устранено также введением соответствую¬
щих поправок в команды управления.
§ 12.5. ЛИНИИ ПЕРЕДАЧИ ИНФОРМАЦИИ СИСТЕМ
РАДИОТЕЛЕУПРАВЛЕНИЯ
В состав любой системы радиотелеуправления вхо¬
дят линии передачи информации, которые подразделяют¬
ся на радиолинии командного управления и радиоли¬
нии контроля (рис. 12.8).
Радиолинию передачи информации можно рассматри¬
вать как линейное радиотехническое звено системы
управления с функцией передачи:
KW (р) = ЛГ, л (р) е-^.
432
где и (р) и (/?) — преобразованные по Лапласу
vbx ~пых j
входной и выходной сигналы линии передачи;
/г])л — коэффициент передачи радиолинии;
^рл(р) —нормированная функция передачи;
/3 — время задержки сигнала в линии.
По радиолиниям командного управления передаются
сигналы на управляемый объект, вырабатываемые в пунк¬
те управления.
Назначением линии контроля является измерение и
передача на командный пункт различных данных, харак¬
теризующих состояние управляемого объекта или окру¬
жающей среды. Такими данными являются: скорость и
направление движения объекта, текущее или прогнози¬
рованное положение объекта или цели и другие.
Для одновременной передачи нескольких независи¬
мых сообщений применяются многоканальные системы
связи, использующие устройства для уплотнения и раз¬
деления каналов передачи информации. Такие радио¬
линии строятся по принципу частотного, временного
или логического разделения каналов.
В системах с частотным разделением каналов переда¬
ча отдельных независимых сообщений осуществляется па¬
раллельно во времени с помощью частотного преобразова¬
ния спектров сообщений и разделения их на приемной
стороне полосовыми фильтрами. Для частотного преоб¬
разования спектров вводятся вспомогательные колеба¬
ния, которые называются поднесущими частотами, их
число соответствует количеству передаваемых сообще¬
ний.
В системах с временным разделением каналов вход¬
ные независимые сообщения передаются последователь¬
но во времени. При этом передача непрерывных сообще¬
ний заменяется передачей мгновенных значений функций
через определенные промежутки времени. В качестве
переносчика информации используются периодические
последовательности импульсов, называемые импульсны¬
ми поднесущими. Последовательность передачи отдель¬
ных сообщений осуществляется распределительными уст¬
ройствами как на передающей, так и на приемной сторо¬
нах.
В системах с логическим разделением каналов все
независимые входные сигналы передаются параллельно
28—1173 433
во времени. Уплотнение и разделение каналов осуществ¬
ляется логическими устройствами. Функциональная схе¬
ма такой радиолинии представлена на рис. 12.10.
Передаваемая информация от источника данных или
соответствующего преобразователя поступает в виде по¬
следовательности двоичных символов 0 и 1, каждый про¬
должительностью Го-
Рис. 12.10. Функциональная схема радиолинии с логическим разделе¬
нием каналов.
Кодирующее устройство состоит из сумматора и гене¬
ратора кодового слова длиной L символов. Каждое
кодовое слово представляет собой одну из ортогональных
кусочно-постоянных функций и состоит из нулей и единиц.
Длительность кодового слова равна продолжительности
нуля или единицы, появляющихся на выходе источника
данных. Суммирование происходит по модулю два. Та¬
ким образом, при появлении на выходе источника данных
Гго канала 0 или 1 в логическую схему подается или
кодовое слово А\ или его дополнение.
434
Значения последовательностей на выходе каждой схе¬
мы сложения представлены в виде матрицы
-(1)
I ’
я(!)
•. 4°
(0
1 •
а^,...
■ • 4*
1 ’
а{п)
’ •'
•• - 4Л)
В момент времени k на вход логического устройства пода¬
ется столбец матрицы А^{а(^\а^\ ... ,а^\ ...
Каждому вектору Ak приписывается значение логиче¬
ской функции flAb), равное +1 или —1, в зависимости
от числа единиц, содержащихся в столбце Ah. Число век¬
торов Ah за время действия элементарного двоичного им¬
пульса Го равно L. Длина кодового слова определяется
примененным кодом из условия наименьших перекрест¬
ных искажений. Следовательно, передача всех каналов
информации осуществляется кусочно-постоянной логиче¬
ской функцией /"(Л), принимающей значения +1 и —1.
Для приема используются п корреляционных уст¬
ройств. На вход каждого устройства подается входная
последовательность f(A) п соответствующее кодовое
слово А&. Так как отдельные кодовые слова являются
ортогональными функциями, то они легко разделяются.
При передаче сигналов в многоканальных линиях
связи применяются сложные виды модуляции. Сначала
входными сигналами модулируются непрерывные или
импульсные поднесущие, а затем суммарным спектром
модулируется высокочастотная несущая передатчика.
Для сложных видов модуляции приняты сокращенные
обозначения. Применительно к радиолинии эти обозначе¬
ния указывают последовательность формирования сигна¬
ла в передающем тракте в направлении от источника со¬
общений к передающей антенне.
Выбор методов модуляции, кодирования и приема
в системах радиотелеуправления должен производиться
с учетом назначения радиозвена, технических характе¬
ристик контура управления, возможных видов помех и
других конкретных условий тактической задачи.
Линии командного управления. Линии командной ин¬
формации используются при управлении движением объ-
28* 435
окта и для передачи па движущийся снаряд отдельных
разовых команд, таких как «выключение двигателя», «са¬
моликвидация снаряда» и др.
Источником команд в радиолиниях при ручном управ¬
лении является оператор, а при автоматическом — управ¬
ляющий счетно-решающий прибор (УСРП).
Рис. 12.11. Радиолиния командного управления.
По радиолинии могут передаваться как плавные, так
и фиксированные команды управления движением. При
передаче плавных команд сигнал команды внутри пре¬
делов ограничения может рассматриваться как непре¬
рывная величина. При этом используются методы моду¬
ляции как с непрерывным излучением сигнала, так и им¬
пульсные. При фиксированных командах передается
ограниченное число дискретных значений сигнала и при¬
меняются кодовые методы модуляции.
Типичной для управления движением снаряда являет¬
ся двухканальная радиолиния с плавной передачей
команд курса ф и тангажа Ф (рис. 12.11).
Напряжения входных сигналов и могут прини¬
мать значения от нуля до ±//макс в зависимости от ве-
436
личин i|- и г*}. Канальные модуляторы преобразуют вход¬
ные напряжения к виду, удобному для передачи по ли¬
нии связи. В кодирующих устройствах отдельные посыл¬
ки сигнала приобретают структуру, наиболее отличаю¬
щуюся от ожидаемой помехи. Для кодирования сигналов
наиболее часто применяются импульс.по-времеппые коды
(ИВК) и импульсно-частотные коды (КЧМ).
* й'маь.с
“Л
ид 1
‘и макс
Рис. 12.12. Формирование плавных команд.
Формирование плавных команд в радиолинии
ВИМ — ИВК — AM иллюстрируется временной диа¬
граммой на рис. 12.12.
Входные сигналы w и преобразуются в соотношения
временных интервалов Г1ф и Г2ф и и Т2^У В зависимос¬
ти от величины входных сигналов рабочие импульсы перво¬
го канала РИф перемещаются между тактовыми импуль¬
сами ТИ в пределах первой половины периода Гп, а ра¬
бочие импульсы второго канала РИ& занимают вторую по¬
ловину периода Тп. В кодирующих устройствах тактовые
и рабочие импульсы обоих каналов кодируются импульсно¬
временными кодами, в которых временные интервалы между
импульсами различны для последовательностей ТИ, РИ^
437
и РИЬ. После суммирования последовательности ИВК по¬
ступают на модулятор передатчика. Декодирующие устрой¬
ства и канальные демодуляторы преобразуют кодовые груп¬
пы в управляющие напряжения w. и
Радиоканалы для передачи отдельных разовых
команд обычно совмещаются с радиолинией управления
движением в виде дополнительных каналов.
В системах командного управления большое значение
с точки зрения организации помех противником играет
скрытность излучения радиолинии связи. Скрытность мо¬
жет быть обеспечена применением целого ряда мер.
К ним относятся смена рабочих волн, применение узко¬
направленных передающих антенн, снижение излучаемой
мощности полезного сигнала до минимально необходи¬
мой, смена кодов и другие.
Радиолинии контроля. Радиолинии контроля, пред¬
назначенные для передачи данных координат цели или
снаряда, измеренных с помощью РЛС, носят название
линий трансляции радиолокационных данных (ЛТРД).
Г1о способу передачи данных системы трансляции де¬
лятся па телевизионные, системы с непосредственной пе¬
редачей данных и системы, использующие преобразова¬
ние спектра сигнала.
В современных ЛТРД обычно используется преобра¬
зование спектра сигнала с целью уменьшения полосы ка¬
пала радиолинии для повышения надежности ее работы
и использования имеющихся узкополосных телефонных
линий связи.
Для преобразования широкополосной радиолокаци¬
онной информации в узкополосную применяется метод
накопления. Системы, работающие по методу накопле¬
ния, должны располагать устройствами запоминания ин¬
формации на время, соответствующее повороту диаграм¬
мы направленности антенны на угол, равный ее ширине,
с целью последующей обработки радиолокационных
сигналов для устранения избыточной информации. Из¬
быточность информации обусловлена в основном много¬
кратностью облучения цели. Сжатие полосы возможно
благодаря тому, что несколько следующих друг за дру¬
гом импульсов пачки несут мало отличающуюся инфор¬
мацию о цели и в результате обработки могут быть за¬
менены одним импульсом, растянутым во времени. При
438
этом наибольший коэффициент сжатия полосы частот Z?i
ограничен числом импульсов в пачке //п (Ац = /zIT).
Дальнейшее сжатие полосы возможно за счет неис¬
пользуемой части периода повторения импульса гк = 7п—
—to мыс, где Тп— период повторения зондирующих им¬
пульсов, a tD макс — время задержки сигнала наиболее
удаленного объекта. Время передачи сигнала в этом
случае может быть увеличено в k2 раз, где k2 = T?JtD манс.
В таком же отношении можно уменьшить полосу ча¬
стот без потери информации. Результирующий коэффи¬
циент сжатия полосы будет k=k{k2.
При применении РЛС с круговым обзором распреде¬
ление во времени импульсов, полученных после обработ¬
ки радиолокационных сигналов, носит случайный харак¬
тер, определяемый пространственным расположением це¬
лей в зоне действия станции, а также методом и ско¬
ростью обзора. Поэтому необходимо перед входом ра¬
диолинии связи применять буферное запоминающее уст¬
ройство (БЗУ). Выходные импульсы БЗУ растягиваются
во времени и поступают в радиолинию связи с постоян¬
ной скоростью, выбранной так, чтобы вся информация
передавалась за период обзора станции.
Для увеличения помехоустойчивости радиолинии
связи и более рационального построения БЗУ и непо¬
средственного ввода информации на приемном конце
в ЦВМ применяется метод кодирования координат. При
этом координаты цели, измеряемые в полярной системе
или преобразованные в декартовую, кодируются двоич¬
ным кодом. Импульсы двоичного кода, отображающие
два числа, определяющих положение цели, пере¬
даются по линии связи на приемный пункт. Ширина по¬
лосы частот канала связи определяется необходимой
точностью и скоростью передачи радиолокационной ин¬
формации. Заданная точность определения координат
обеспечивается количеством разрядов кода. Скорость пе¬
редачи информации зависит от скорости перемещения
диаграммы направленности антенны. При этом ширина
полосы частот может быть сделана в сотни раз меньше,
чем при непосредственной передаче радиолокационных
сигналов.
Функциональная схема ЛТРД, обеспечивающая авто¬
матическое обнаружение целей и обработку радиолока-
439
циоиных сигналов с целью сужения необходимой полосы,
приведена на рис. 12.13.
В рассматриваемой системе сигналы РЛС поступают
на автоматическое устройство обнаружения целей, в ка¬
честве которого могут применяться различные запо¬
минающие устройства, как, например, аналоговый нако¬
питель с пороговым детектором или специальная ЦВМ.
При работе РЛС в неблагоприятных условиях (наличие
активных и пассивных помех) более выгодно применять
ЦВМ, которая при рациональном выборе логики обеспе¬
чивает более высокие разрешающую способность, точ¬
ность измерения и эффективность обнаружения цели.
P/JC
Автоматиче-\
ское устрой.-'
ство оонару-Y*
ж ено я цели |
1 1
Устройство
преобразо¬
вания
координат
Буферное
запоми¬
нающее
устройство
Радио¬
линия
связи
Ц ифровая
вычисли¬
тельная
машина
Рис. 12.13. Функциональная схема ЛТРД.
Выделенный устройством обнаружения целей сигнал
поступает на преобразователь координат, на выходе ко¬
торого образуются кодовые группы импульсов, соответ¬
ствующие положению цели в декартовых координатах.
Один из методов преобразования полярных коорди¬
нат в декартовые применительно к РЛС с круговым об¬
зором поясняется функциональной схемой, изображен¬
ной на рис. 12.14. Преобразование координат произво¬
дится путем создания отметок времени, следующих через
интервалы, обратно пропорциональные синусу и коси¬
нусу угла поворота антенны РЛС по азимуту а. Отмет¬
ки формируются напряжениями двух генераторов на
биениях, которые синхронизованы по фазе с разверт¬
кой дальности РЛС. Частоты колебаний каждого гене¬
ратора на биениях изменяются при помощи переменных
конденсаторов, роторы которых вращаются синхронно
с антенной РЛС. Генераторы включаются импульсом,
запускающим развертку дальности, и создают колеба¬
ния в течение всей развертки. Из синусоидальных коле¬
баний генераторов, частоты которых пропорциональны
sin а и cos ос, вырабатываются прямоугольные импульсы,
поступающие на пересчетные схемы по X и Y. Длитель¬
ности импульсов обратно пропорциональны sin а и cos а.
Число таких импульсов за отрезок времени между за¬
440
пуском развертки дальности и приходом отраженного
сигнала будет пропорционально X = Dcosa и /=Dsin ос.
В результате на выходе устройства получаются группы
импульсов двоичного кода, соответствующие координатам
цели X и Y. Генератор опорньнх напряжений служит для
устранения неоднозначности в определении координат.
^Антенна
i
РЛС
Опорное напряжение
ПО X
• Импульс
цели
| гон
Пересчет-
ная схема
по X
—>.
Устройство
кодирования
по X
—*•
£
н
Г~ Г Генератор бие- ~~±2 171
Оэ
к
| Ген ера тор ний канала х
| fx=k cos об
I
Смеситель
-Синхро-1
импульс 1
i
_J
1
Генератор
Иоператор
постоянной
строба
частоты f
.„zpz
—
i
“1
i
Г-Д-”
1 Ъ'ГГТГ11 ^меситмь
| |Д' ■< ~1П ; Генератор бие- [ _
I ” -- - ни- канс/ш у
’Пересчет-—=
\ная схема
по у —i
Опорное напряжение по у
Устройство —
* кодирования^^
по у р—
| Импульс
цели
^5 о
£
|!
*
Рис. 12.14. Функциональная схема преобразования координат.
БЗУ предназначено для приема, хранения и равно¬
мерной выдачи кодов координат цели, поступающих
с выхода преобразователя координат. Координаты цели
из БЗУ поступают в линию связи с постоянной ско¬
ростью. Передача сигналов по радиолинии может произ¬
водиться как параллельным, так и последовательным
кодами.
На приемной стороне кодированный сигнал поступает
в ЦВМ или в управляющий счетно-решающий прибор
для выработки команд управления.
441
Радиолинии контроля, предназначенные для передачи
непрерывно измеряемых параметров с движущегося
объекта на наземные контрольные пункты, носят назва¬
ние радиотелеметрнческих линий. Радиотелеметрпческие
линии входят в состав замкнутого контура управления
как измерительные радиотехнические звенья. Однако,
наиболее часто они используются в самостоятельных ра-
днотелеметрических системах (РТМ), обеспечивающих
измерение интересующих параметров и их передачу на
пункты приема с последующей дешифрацией и обработ¬
кой.
В настоящее время РТМ нашли широкое применение
па космических объектах для научного исследования
межпланетных космических пространств, а также для
изучения поведения и жизнедеятельности живых организ¬
мов в космосе.
Особенностями передачи информации с космических
объектов являются в первую очередь большие дальности
связи, достигающие десятков миллионов километров, и
ограниченность энергетических ресурсов бортовых
устройств. В связи с этим особенно остро стоит вопрос
создания высокоэффективных систем связи, т. е. выбор
оптимальных способов обработки сигналов как на прием¬
ной, так и па передающей сторонах линии.
Для РТМ могут применяться цифровые систе¬
мы передачи информации, которые дают возможность
использовать наиболее совершенные методы передачи,
приема и обработки сигналов.
§ 12.6. СИСТЕМЫ САМОНАВЕДЕНИЯ
Самонаведение представляет собой способ наведения
снаряда на цель с помощью координатора, устанавливае¬
мого на снаряде (рис. 12.15). Основная задача определе¬
ния направления па цель и выявление углового отклоне¬
ния управляемого объекта от этого направления решает¬
ся в системах самонаведения с помощью радиотех¬
нического, теплового или оптического угломеров,
использующих соответственно радиотехнический, инфра¬
красный или оптический диапазоны радиоизлучения.
В зависимости от расположения первичного источника
излучения различают системы активного (передатчик на
снаряде), полуактивного (передатчик вне снаряда) и
442
пассивного (источник излучения сама цель) самонаведе¬
ния.
В системах самонаведения бортовая аппаратура
определяет направление на источник излучения одним из
равносигнальных методов. При отклонении оси снаряда
и связанной с ней равносигнальной оси диаграммы прие¬
ма бортового устройства от направления на цель обра¬
зуется управляющий сигнал, воздействующий на. снаряд
таким образом, что он движется по траектории, обеспе¬
чивающей встречу с целью. При самонаведении могут
применяться методы погони, параллельного и пропор¬
ционального сближения.
б)
Рис. 12-15. Система самонаведения (я) и схема образования угла
наведения ц (б).
При определении направления на цель обычно ис¬
пользуются автоугломеры с узкой диаграммой направ¬
ленности, обеспечивающие высокую угловую селекцию
цели. При активном и полуактивном самонаведении уг¬
ломер может осуществлять селекцию и по дальности,
повышая помехоустойчивость системы. В зависимости от
установки угломера на снаряде различают: неследящий
угломер, антенна которого жестко закреплена на корпусе
снаряда; следящий и гиростабилизированный угломеры,
равпосигнальные осн которых имеют возможность от¬
клоняться от оси снаряда. Использование того пли иного
вида угломера обусловлено рядом причин, главная из
которых заключается в величине угловой скорости отно¬
сительного движения цели. При наведении на неподвиж¬
ную или медленно движущуюся цель часто используется
443
неследящий угломер, а при наведении па быстродвнжу-
щуюся—следящий или гиростабилизнроваппый угломер.
Самонаведение на неподвижную цель. При самонаве¬
дении на неподвижную цель, например, методом чистой
погони не требуется больших углов упреждения и полу¬
чения производной от углового вращения линии визиро¬
вания (т]о = О и г] = 0). Использование неследящего угло¬
мера при наведении по кривой погони образует так
называемый прямой метод самонаведения. При этом
методе выходной сигнал угломера в пределах линейной
Рис. 12.16. Схема образования командного сигнала при прямом
самонаведении на неподвижную цель.
зоны пеленгационной характеристики пропорционален
угловому положению
рования (рис. 12.16)
снаряда относительно линии визп-
не = /гг, (12.7)
где е=Рс + Рп — сумма угла скольжения и угла наведе¬
ния (в горизонтальной плоскости). Углом наведения рп
называется угол между линией визирования и вектором
скорости снаряда V. В случае движения по кинематиче¬
ской траектории — кривой погони — должно выполнять¬
ся условие Рп = 0. Прямой метод наведения в лучшем
случае обеспечивает лишь е—>0. Для обеспечения усло¬
вия е = рн из сигнала управления иг должен вычитаться
сигнал, пропорциональный углу скольжения ^с=/фе,
который может быть измерен флюгером.
ААалый угол скольжения при управлении плоскокры¬
лым снарядом может достигаться использованием коор¬
динированного разворота, однако при этом угломер сле¬
дует стабилизировать по крену или вводить поправки
в его выходные сигналы.
444
Структурная схема прямого самонаведения в гори¬
зонтальной плоскости представлена на рис. 12.17. При
наведении в вертикальной плоскости структурная схема
идентична и в ней следует лишь заменить угол Ф на 0,
ф па О и рс на ас. К особенностям структурной схемы
самонаведения следует отнести цепь дополнительной
кинематической обратной связи, охватывающей угломер
и весь автопилотиый контур по курсовому углу Дф
(вследствие того, что угломер отслеживает и угол Дф),
Рис. 12.17. Структурная схема контура прямого самонаведения.
ние которого увеличивается по мере сближения снаряда
с целью. Охват жесткой кинематической связью ЛА
приводит к понижению порядка астатизма системы и
к повышению устойчивости управления, но одновременно
увеличивает влияние рысканья Дф или Дй (быстрых ко¬
лебаний оси снаряда вокруг центра масс) на процесс
слежения. При значительной амплитуде рысканья или
случайном повороте корпуса снаряда сравнительно узкая
диаграмма приема может оказаться в стороне от направ¬
ления на цель, что приведет к срыву нормальной работы
контура. Таким образом, при прямом самонаведении
диаграмма направленности должна быть достаточно ши¬
рокой, чтобы цель не была потеряна. Особенно важно
учитывать это обстоятельство вдали от цели. При под¬
лете к цели, когда £>сц^0, управление выключается. Вы¬
ключение управления необходимо при использовании
радиолокационных головок самонаведения в тот мо¬
мент, когда начинает сказываться явление блуждания
центра отражения и угловые размеры цели начинают
превышать ширину диаграммы направленности приема.
Коэффициент передачи общего контура во время управ¬
ляемого движения желательно поддерживать постоян¬
ным. Стабилизация коэффициента передачи может осу¬
445
ществляться по данным дальномера или программного
устройства, вычисляющего дальность по средней скоро¬
сти снаряда.
Самонаведение на быстродвижущуюся цель. При само¬
наведении на быстродвижущуюся цель, когда линия ви¬
зирования снаряд — цель сравнительно быстро изменяет
свое направление и в закон управления необходимо
вводить производные от угла поворота линии визирова¬
ния, применяются следящие угломеры. На рис. 12.18
представлен угломер следящего типа и его взаимодей-
Рнс. 12.18. Схема образования командного сигнала при самонаве¬
дении с упреждением на быстродвижущуюся цель.
ствие со снарядом при образовании сигнала рассогласо¬
вания. Сигнал рассогласования и команды формируются
в виде
(12.8)
где Де — ошибка слежения автоугломера, а е— ошибка,
как и при прямом наведении, равная сумме рс и рп.
Однако с и [Зн могут перекрывать угол, значительно
больший, чем раствор диаграммы направленности. Сле¬
дящий угломер может обеспечить большие углы упреж¬
дения ру и вырабатывать сигнал, пропорциональный ско¬
рости изменения угла визирования. Если инерционность
следящего угломера невелика, он может работать при
узкой диаграмме приема, так как рысканье оси снаряда
быстро выбирается следящей системой и не приводит
к значительным колебаниям диаграммы направленности
и потере цели.
446
Структурная схема системы самонаведения со следя¬
щим угломером (рис. 12.19) остается по существу такой
же, как и при прямом самонаведении. Она содержит
один интегратор, определяемый кинематическим звеном.
Повысить порядок астатизма можно, устранив связь по
углу рысканья Дф или ДО-, установкой следящего угло¬
мера на гиростабилизироваипой платформе (стабиплате)
или введением в привод угломера сигналов от скорост¬
ных гироскопов, измеряющих Дф и ДО. Устранение связи
по углу Дф показано на рис. 12.19 пунктирными линиями.
Дд имение цели
, Координатор и адтопилот
Г pf Г L
У—^—Гстабиплвта
-Дф -1
Дбимение снаряд-:
Рис. 12.19. Структурная схема системы самонаведения на быстро-
движущуюс.я цель (обобщенный вариант с одним и двумя интегра¬
тор ами).
Контур связи через стабиплату нейтрализует контур
связи по рысканыо. Схема содержит два интегратора,
обеспечивает высокую точность наведения и позволяет
применять инерционный угломер с узкой диаграммой
приема.
Кинематическая траектория при наведении на бы-
стродвижущуюся цель в значительной степени опреде¬
ляется движением цели, которое отображено на схеме
в виде соответствующих звеньев, устанавливающих связь
между ее линейными перемещениями и изменением вход¬
ной угловой координаты фВх(0- Если автопилотный кон¬
тур снаряда содержит связи не только через скоростные
гироскопы, но и через позиционные, то сохранение вто¬
рого порядка астатизма контура может быть достигнуто
введением в автопилот интегратора, запоминающего сиг¬
налы управления или команды, как это показано на
рис. 12.19 пунктиром. При наличии двух интеграторов
для обеспечения устойчивости в контур необходимо вво¬
дить корректирующие звенья фазоопережающего типа.
447
Наряду со следящим угломером в структурную схему
управления в зависимости от назначения снаряда могут
входить: блок автономного поиска и захвата цели, блок
селекции цели по скорости, блок программного управле¬
ния антенной при специальных маневрах снаряда, блок
выключения управления и подготовки радиовзрывателя
к действию и т. п.
Сравнительные характеристики координаторов самона¬
ведения. Наряду с радиолокационными координаторами,
иногда называемыми радиолокационными головками
Рис. 12.20. Упрощенная блок-схема теплового координатора [14, 19].
самонаведения (РЛГС), в системах самонаведения,
а также в системах командного наведения II типа нахо¬
дят применение тепловые и оптические координаторы.
Упрощенная блок-схема теплового (инфракрасного) ко¬
ординатора (ИКГС) показана на рис. 12.20. Тепловая
энергия, излучаемая целью (в основном ее двигателями),
попадает в линзовую.или зеркальную оптическую систе¬
му, которая фокусирует лучистый поток и направляет
его па чувствительный элемент. Между оптической си¬
стемой и чувствительным элементом помещается подвиж¬
ная шторка или вращающийся диск со сложным растром
(штриховкой), который модулирует лучистый поток по
интенсивности в соответствии с угловым рассогласова¬
нием направления на источник излучения и осью коор¬
динатора. При этом ток или напряжение на выходе чув¬
ствительного элемента оказываются функционально
связанными с угловым рассогласованием. Этот ток (на¬
пряжение) подается на блок разделения (коммутатор)
сигнала ошибки на азимутальную и угломестную состав¬
ляющие, которые далее используются как команды
управления по курсу и тангажу. В качестве чувствитель¬
ных элементов в тепловых координаторах используются
448
болометры и фотосопротивления. Дальность действия
тепловых координаторов определяется интенсивностью
теплового излучения цели, затуханием при распростране¬
нии и параметрами чувствительного элемента.
Важными достоинствами тепловых координаторов
являются: высокая угловая разрешающая способность,
трудность создания искусственных помех, возможность
пассивного, скрытного наведения, а также малые габа¬
риты, вес и потребление электроэнергии. Однако работа
ИКГС в пределах атмосферы Земли существенно зависит
от времени суток, метеорологических условий и мешаю¬
щих излучений, создаваемых Солнцем, отражениями от
облаков, земной и водной поверхностей.
Все неравномерности излучения фона, окружающего
цель, вызывают ложные сигналы, трудно отличимые от
полезного. Оптические координаторы отличаются от теп¬
ловых но существу лишь типом чувствительного эле¬
мента. Как тепловые, так и оптические координаторы мо¬
гут входить в комплекс автономных и астроинерцпаль-
ных систем управления.
Радиотехнические координаторы лишены ряда недо¬
статков тепловых и оптических координаторов: работа
их не зависит от метеорологических условий, они могут
обеспечивать очень большую дальность действия, а так¬
же высокую разрешающую способность по дальности,
что исключительно важно для управления большинством
объектов. Радиокоординаторы сравнительно легко соче¬
таются в комплекс с координаторами других типов, что
расширяет возможности их применения в системах
управления.
§ 12.7. РАДИОВЗРЫВАТЕЛИ [13]
Вероятность прямого попадания снаряда в малораз¬
мерную быстродвижущуюся цель очень мала. Вследст¬
вие этого подрыв боевого заряда вблизи цели произво¬
дится при помощи радиовзрывателя — радиотелеметри-
ческой системы разового действия. Тип радиовзрывателя
и предъявляемые к нему требования определяются осо¬
бенностями цели, характером взрыва и углами встречи
снаряда с целью. Последнее означает, что аппаратура
29—1173 449
радиовзрывателя должна обеспечить подрыв боевого за¬
ряда в тот момент, когда цели может быть нанесен наи¬
больший ущерб.
Различают две основные группы радиовзрывателей:
радиовзрыватели, работающие по сигналам самой бор-
Рис. 12.21. Условия эффективной работы радиовзрыва¬
теля.
товой аппаратуры и работающие по командам с пункта
управления. Радиовзрыватели первой группы могут быть
пассивными, полуактивными и активными. Наибольшее
распространение получили радиовзрыватели активного
действия.
Согласование области эффективного поражения цели
осколками боевой части снаряда с моментом срабатыва¬
ния активного радиовзрывателя в упрощенном представ¬
лении сводится к тому, что направление максимума из¬
лучения и приема радиовзрывателя, при котором осу¬
ществляется подрыв заряда, должно совпадать с на¬
правлением вектора относительной скорости движения
наибольшего количества осколков. На рис. 12.21 эти ус*
ловия представлены графически для случая подрыва
заряда направленного (анизотропного) действия.
Оптимальное значение угла |30, при котором должен
срабатывать радиовзрыватель, может быть найдено из
450
уравнения
fo; 3 — Vo. ь-sill уо,.1; + Vu sin p,lt
° V Осн ’ COS (foci; “I” V с + V ц COS Рщ
где обозначения ясны из рисунка.
При Уоск^Уц и цц(04-360°) угол ро составляет 50 —
80°. При поражении наземных и надводных целей, когда
Уц<^Ус, условия определения р0 значительно упрощают¬
ся. На эффективность поражения цели влияет также
дальность £>сц, па которой осуществляется подрыв за¬
ряда. Определение дальности радиовзрывателем осу¬
ществляется частотным и так называемым амплитудным
методом. Амплитудный метод заключается в том, что
отраженный сигнал цОтр должен превысить заранее вы¬
ставляемый порог zznop. Этот метод имеет недостатки,
связанные с тем, что дальность при взрыве будет зави¬
сеть от эффективной отражающей поверхности цели.
В отсутствие флюктуаций отраженного сигнала большей
точностью определения дальности обладает метод срав¬
нения с порогом производных отраженного сигнала ц0Тр
и цОтр- Определение минимальной дальности £>сц весьма
просто осуществляется допплеровской системой, изме¬
ряющей нулевую частоту биений. Использование послед¬
него метода целесообразно для подрыва заряда нена¬
правленного (изотропного) действия.
Глава 13
РАДИОТЕХНИЧЕСКИЕ СИСТЕМЫ КОНТРОЛЯ
ТРАЕКТОРИИ БАЛЛИСТИЧЕСКИХ РАКЕТ,
ИСКУССТВЕННЫХ СПУТНИКОВ ЗЕМЛИ
И КОСМИЧЕСКИХ АППАРАТОВ
§ 13.1. ОБЩИЕ СВЕДЕНИЯ О ТРАЕКТОРИЯХ
БАЛЛИСТИЧЕСКИХ РАКЕТ И ИСКУССТВЕННЫХ
СПУТНИКОВ ЗЕМЛИ
Траектории баллистических ракет (БР), искусствен¬
ных спутников Земли (ИСЗ) и космических аппаратов
(КА) состоят из активных и пассивных участков. На
активных участках траектории (отрезки ABCG и B'C'Gf
на рис. 13.1,а) ракета приводится в движение силой
тяги своих двигателей. В граничных точках G и G' про¬
исходит выключение двигателей, и дальнейшие участки
траектории (GB'E или GB' и G'E') называются пас¬
сивными, поскольку на этих участках головная часть ра¬
кеты движется по инерции под влиянием только сил
тяготения Земли, Солнца и планет солнечной системы.
Активный участок ABCG является пусковым. В процессе
движения по инерции возможно кратковременное вклю¬
чение специальной двигательной установки (участок
BfC'Gf) для необходимой коррекции пассивной траекто¬
рии движения.
Пусковой активный участок траектории, в свою оче¬
редь, делится на три характерных отрезка. Вертикальный
стартовый участок АВ необходим для придания ракете
такой скорости движения, которая достаточна для удов¬
летворительного управления ее движением. Кроме этого,
вертикальный запуск значительно упрощает конструк¬
цию стартовой участановки и снижает тербования к по¬
перечной жесткости ракеты. На участке выведения ВС
ракете сообщается заданное направление движения
в вертикальной и горизонтальной плоскостях. На участ-
452
кс выключения CG раксга летит прямолинейно и в про¬
цессе ускоренного движения приобретает требуемую на¬
чальную скорость движения VG.
Как правило, протяженность активных участков
траектории баллистических объектов весьма мала по
сравнению с протяженностью пассивных участков. Если
учитывать только силу земного притяжения (что в до¬
статочной мере справедливо для БР и ИСЗ) и пренсб-
Рис. 13.1. Траектории БР и ИСЗ:
а —активные и пассивные участки траектории ЬР; б — формы траектории
ЬР, ИСЗ и 1\Л при различных скоростях запуска.
речь влиянием атмосферы, то каждый из пассивных
участков траектории (например, GB'E) однозначно опре¬
деляется, во-первых, координатами граничной точки G
и, во-вторых, вектором скорости ракеты VG в этой точке.
Азимутальный угол aVG проекции вектора скорости опре¬
деляет наклон плоскости орбиты к плоскости экватора,
а величина скорости VG, угол запуска @G и высота точки
G над поверхностью Земли hG — форму траектории
в этой плоскости.
Движение баллистического объекта совершается
в плоскости, проходящей через вектор скорости V и
центр Земли. Это объясняется тем, что все силы, дейст¬
вующие па объект, лежат в этой плоскости и, следова-
453
тслыю, нс способны вывести из псе объект, двигающий¬
ся по инерции. Сила земного притяжения Fgi направлен¬
ная к центру Земли (рис. 13.1,а), способна лишь изменить
направление вектора V в этой плоскости и его величину.
Вследствие этого движение объекта становится криволи¬
нейным и появляется центробежная сила Тщ. Соотноше¬
ние между силами и Fg и определяет характер даль¬
нейшего движения. Можно показать, что кривизна
траектории в точке Р, а следовательно, и форма траек¬
тории зависят от параметра и, представляющего собой
удвоенное отношение кинетической и потенциальной
энергий объекта в точке Р.
Пусть в результате запуска ракеты и последующего
пассивного движения в поле сил Fg объект с массой т
приобрел в точке Р скорость V и его кинетическая эиер-
т\/2
гия в этой точке равна Ev-=—^~. Согласно закону все¬
мирного тяготения Ньютона сила Fg земного притяже¬
ния убывает обратно пропорционально квадрату рас¬
стояния R\
F<f
ь
(13.1)
где gR --- ускорение силы тяжести на расстоянии R
от центра Земли; f — гравитационная постоянная; М —
масса Земли; /\ = fzzz = 3,986• 1014 м3]сек2.
Следовательно, потенциальная энергия объекта
равна
Ea^FsR = mgRR=^, (13.2)
а удвоенное отношение кинетической и потенциальной
энергий определится выражением
V2/?
К *
(13.3)
Пассивную траекторию можно найти, интегрируя
уравнения движения материальной точки с массой т
в поле сил Fg земного притяжения. Уравнение пассив¬
ного участка траектории в полярных координатах
454
((/?, t/), за начало которых принят центр Земли и поло¬
жение радиуса-вектора RG граничной точки G
(рис. 13.1,я), имеет вид
FG UG cqs2QG
1 — cos о' + uG cos (o' + 0G) cos ©G ’
(13.4)
где RG=R3+hG, a R3— радиус Земли.
В зависимости от начальных условий движения пас¬
сивный участок траектории может представлять собой
эллипс, параболу или гиперболу.
Рассмотрим случай, когда угол запуска в граничной
точке G равен нулю (рис. 13.1,6). Тогда уравнение
траектории (13.4) примет вид
%G UG
1 + (uG — 1) cos о
(13.5)
Анализ уравнения (13.5) показывает, что при uG—l,
т. е.
при начальной скорости
называ¬
емой первой космической скоростью, пассивная траектория
представляет собой окружность с радиусом RG = R3-\-hG
(орбита 2 на рис. 13. 1, 6). В этом случае силы и Fg
равны и противоположны друг другу, а линейная скорость
движения по орбите постоянна. В частности, если hG — 0
и точка G находится на поверхности Земли, то RG — R3
и максимальное значение первой космической скорости
равно У1макс = 7 910 м]сек.
При uG<l и 1<ug<2 баллистический объект имеет
эллиптические траектории (траектории 1 и 3 на
рис. 13.1,6). Однако в первом случае (uG<l) точка G
является апогеем (точкой наибольшего удаления от
центра Земли), а во втором случае — перигеем (точкой
наименьшего удаления от центра Земли). Если коорди¬
нату ъ отсчитывать в обоих случаях от радиуса-вектора
в перигее, то уравнение эллипса можно записать в сле¬
дующей форме:
а (1 — е2)
1 + е cos о ’
(13.6)
455
где а и Ь — большая и малая полуоси эллипса;
— эксцентриситет эллипса;
г = /(/—/п) - истинная аномалия движения; /н --вре¬
мя прохождения ИСЗ через перигей.
Из уравнения (13.5) следует, что при Ug = 2, т. е.
в случае, когда начальная скорость движения VG равна
второй космической скорости Vn = |/ 2 Ур расстояние R
от объекта до центра Земли непрерывно возрастает и
при н = я становится бесконечно большим. Эта предель¬
ная траектория является параболой (траектория 4 на
рис. 13.1,6). Максимальное значение второй космической
скорости равно Упмакс=Н,2 км!сек.
При nG>2 траектория также не замкнута и соответ¬
ствует гиперболе (траектория 5 на рис. 13.1,6). При лю¬
бом угле запуска превышение второй космической ско¬
рости уводит объект в космическое пространство.
Форма записи уравнения траектории в виде соотно¬
шения (13.4) удобна для прогнозирования движения по
начальным условиям запуска. При расчетах траектории
ИСЗ по данным последующих радиолокационных изме¬
рений чаще используется вторая форма записи уравне¬
ния траектории (13.6).
§ 13.2. ПРИНЦИПЫ РАДИОУПРАВЛЕНИЯ ДВИЖЕНИЕМ
БР НА ПУСКОВОМ АКТИВНОМ УЧАСТКЕ
ТРАЕКТОРИИ
Задачей управления на пусковом участке является
вывод БР в расчетную точку G с заданной скоростью
lzG- Следовательно, для попадания БР в цель (точка Е
на рис. 13.1,а и 13.2) в общем случае должны быть зада¬
ны 6 параметров: три пространственные координаты
точки G и три величины, характеризующие вектор VG
(V'g, avG и ©g).
Контролирование программы запуска и управление
движением БР значительно упрощаются при размеще¬
нии РТС контроля в точке О, где пересекаются горизон¬
тальная плоскость (ГП) и расчетные плоскости выведе¬
ния— вертикальная (ВРП) и наклонная (НРП)
456
(рис. 13.2). Тогда координатами точки G являются
«vg, и дальность DCr — OG, а общее число контроли¬
руемых параметров сокращается до четырех (ccrG, 0G,
Dg, Vg).
Рассмотрим основные принципы контроля и управ¬
ления движением БР. Угломерная часть РТС контроля
представляет равносигнальный радиомаяк, сигналы ко¬
торого излучаются из точки О по двум взаимно перпеп-
дикулярньнм парам лепестков диаграммы направленно¬
сти антенны. Равносигнальная ось всех четырех лепест¬
ков совпадает с направлением OCG, причем одна пара
веерных лепестков создает равносигнальную зону в вер¬
тикальной плоскости, а другая пара контролирует дви¬
жение БР в наклонной расчетной плоскости. Отклонения
от ВРП и НРП индицируются приемным устройством на
борту БР, и сигналы ошибок, пропорциональные этим
отклонениям, подаются на систему управления верти¬
кальными и горизонтальными рулями БР.
Вместе с угломерной системой в точке О располага¬
ются дальномерная и допплеровская РТС. Данные о те¬
кущей дальности до БР и скорости ее движения посту¬
пают в наземный пункт управления, где формируются
командные сигналы для регулировки тяги двигате¬
лей БР.
457
Отклонения от заданных параметров запуска вызывают
ошибки попадания БР в цель. Радиус-вектор ошибки пред¬
ставляет сумму векторов АЛ и Z, один из которых пред¬
ставляет ошибку по дальности и направлен вдоль следа
траектории GrE, а другой — вектор бокового отклонения
Z — перпендикулярен AL. Размеры полуосей среднеквадра¬
тичного эллипса рассеивания определяются величинами
qL— 1,51 и 7Z—1,51 az (см. § 9.8), где- и oz —
соответственно среднеквадратичные ошибки по дальности
и боковому отклонению.
Боковое отклонение точки падения БР является
функцией двух погрешностей запуска: поворота плоско¬
сти траектории (вектора скорости VG) относительно
ВРП на угол Дауо и начального бокового отклонения
точки отсечки двигателей G на величину NZg=GF
(рис. 13.2).
Из решения сферических треугольников G[EP, КРМ
и KG\FX найдем
% ~ dZ^ = C0S Е + S*n U E'
(13.7)
где v'e— угол между радиусами-векторами RG и Re
(рис. 13.1,а). Полагая погрешности запуска независи¬
мыми и случайными, найдем
°Z — ]f°ZG COs2 , (13-8)
где crZG и oa vg — среднеквадратичные ошибки запуска
по начальному отклонению и азимутальному углу ско¬
рости.
При боковом смещении точки О на AZGc и повороте
антенны на угол Ааус возникает систематическая ошиб¬
ка Zc. По формуле (13.7) найдем
Zc = AZGc cos ’jfE (Dg cos 0g cos У e /?3 sin э'£) AalZc.
(13.9)
Формулы (13.8) и (13.9) определяют требования
к точности РТС контроля и управления движением по
боковому отклонению. Заметим, что при i/e = jt:/2 (т. е.
при G\E= 10 000 км) главную роль играют ошибки Да^,
458
а при = л (0^ = 20 000 км) —ошибки начального от¬
клонения AZg.
Рассмотрим особенности контроля и управления
дальностью полета БР. Если отрезок ОА обозначить ве¬
личиной /о, то дальность полета (дуга АЕ на рис. 13.1,а и
13.2) определится выражением
L=Dgcos0g + Z?3o'£-/o. (13.10)
Центральный угол х>'Е может быть найден по формуле
(13.4), где следует положить R=RE = R3 и 7?g=i7?3 +
+BGsin0G. Таким образом, L является функцией трех
параметров: DG, VG и 0G, и, следовательно,
dD^ ^Dg + dV^ =
= ^GA£>G-|-/elzAVG-|-^e Д0С. (13.11)
Отсюда среднеквадратичная ошибка дальности равна
= + , О3-12)
где kD,kv и kQ — коэффициенты ошибок, и o0G—
среднеквадратичные ошибки параметров запуска.
dL
d&G
Из условия
0 может быть найден оптимальный
угол запуска 0GO = 45°
при котором для достиже¬
ния требуемой дальности L необходима минимальная
скорость VG. Режим запуска при % = 0GO не только эко¬
номичен, но и выгоден с точки зрения точности попадания,
так как в этом режиме kQ — 0.
При оптимальных углах запуска необходимо изме¬
рять в точке О лишь текущую дальность и скорость БР,
а для нахождения скорости в упрежденной точке — про¬
изводить расчет величины ускорения по результам не¬
прерывного слежения. Этих данных достаточно, чтобы
определить такой момент времени выключения двигате¬
лей БР, при котором систематическая ошибка ALC будет
равна нулю. Условие компенсации систематической
ошибки определится из (13.11):
(13.13)
459
Обычно команда па уменьшение тяги двигателей по¬
дается в два приема. В начальной части участка вы¬
ключения ракета движется с ускорением 60 —80 м!сск2.
После достижения скорости, близкой к расчетной, дает¬
ся команда на резкое уменьшение тяги двигателей, и
дальнейшее движение происходит с небольшим ускоре¬
нием, что повышает точность определения момента пол¬
ной отсечки двигателей. В ряде образцов ракет, данные
о которых опубликованы в открытой печати, допустимая
относительная погрешность измерения дальности долж¬
на быть не более 10~4, а скорости — не более 10“5.
При запуске глобальных БР и ИСЗ точка располо¬
жения РТС контроля не может находиться на продол¬
жении линии CG. В этом случае РТС контроля в режиме
непрерывного слежения измеряет три пространственные
координаты ракеты и три производные этих координат.
В расчетной точке выключения двигателей все шесть
параметров запуска должны быть равны номинальным
значениям, и отклонения от заданных параметров вызо¬
вут траекторные ошибки. С помощью уравнений оши¬
бок, аналогичных формулам (13.7) и (13.11), может
быть найдена методика коррекции траектории путем по-,
сылки предварительных команд и упреждения или за¬
паздывания момента полной отсечки двигателей ракеты.
§ 13.3. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ОРБИТЫ ИСЗ
ПО ДАННЫМ РАДИОЛОКАЦИОННЫХ
НАБЛЮДЕНИЙ
Назначением РТС контроля траекторий ИСЗ и КА
является определение орбитальных параметров, которые
могут отличаться от расчетных из-за ошибок, допущен¬
ных при запуске, а также в результате действия атмо¬
сферы и других случайных факторов, изменяющих
траекторию полета.
Эллиптическую орбиту ИСЗ полностью характери¬
зуют шесть параметров. Большая полуось эллипса а и
эксцентриситет е определяют форму и размеры эллипти¬
ческой орбиты. Положение ИСЗ на орбите в любой мо¬
мент времени определяется углом и, который, в свою
очередь, зависит от момента времени /п прохождения
ИСЗ через перигей. Далее должны быть заданы: поло¬
жение перигея на плоскости орбиты и положение самой
460
плоскости орбиты в пространстве. Так как иовозмущен*
пая орбита занимает неизменное положение в простран¬
стве, то указанные параметры должны определяться
в инерциальной системе координат, оси который непод¬
вижны относительно точек космического пространства
на небесной сфере.
Такой системой является, в частности, инерциаль¬
ная экваториальная система координат ц, £ (рис. 13.3).
В этой системе за начало координат выбран центр Зем¬
ли. Координатная ось проходит через Северный'полюс,
а ось £ совпадает с линией пересечения плоскостей эква¬
тора и эклиптики и направлена в неподвижную точку у
Рис. 13.3. Инерциальные геоцентрические системы координат для
определения положения ИСЗ и БР.
небесной сферы (точку весеннего равноденствия), нахо¬
дящуюся в созвездии Овен.
Последовательным поворотом осей (рис. 13.3) на
углы Л (вокруг оси £), i (вокруг оси У) и Y (вокруг
оси г) можно получить новую инерциальную систему
координат х, у, z, у которой оси х и у лежат в плоскости
орбиты и ось х проходит через перигей. В этом случае
полярные координаты R и и ИСЗ из уравнения (13.6)
будут связаны простыми соотношениями с х и //, а по¬
следние могут быть пересчитаны в инерциальные коор-
461
дипаты §, £ и ц, если известны углы Л, i и Y. Угол i опре¬
деляет наклон плоскости орбиты к плоскости экватора,
Л — положение линии пересечения к' плоскостей орбиты
и экватора относительно оси g и называется углом вос¬
ходящего узла орбиты. Угол Г определяет положение
перигея относительно восходящего узла орбиты.
Рассмотрим принципы определения параметров орби¬
ты ИСЗ. Точка наблюдения О (рис. 13.3 и 13.4) нахо¬
дится на земной поверхности и не лежит, в общем слу-
Рис. 113.4. Расположение орбиты ИСЗ относительно точки наблюде¬
ния О при радиолокации ИСЗ.
чае, в плоскости орбиты ИСЗ. Если заданы географиче¬
ские координаты точки О — широта <р0 и долгота Ло,—
то с учетом вращения Земли с угловой скоростью со3 =
= 7,3 • 10-5 1/сск, координаты точки О в инерциальной
экваториальной системе будут равны
= #з COS <р0 cos 2 = cos <f>0 cos (20 — 2^ -ф- соз/),
Р-0 = COS <р0 sin 2 = яз cos <Ро sin (20 — 2^ -ф- (»3t),
(13.14)
Со = #з sin <р0,
где 2^—долгота оси | (относительно гринвичского ме¬
ридиана) в начальный момент времени / = 0.
462
Предположим, что РЛС измеряет в точке О азимута,
угол места |3 и наклонную дальность D ИСЗ, располо¬
женного в точке Р (рис. 13.4). Проекция точки Р на
земной поверхности обозначена точкой а след орби¬
ты— линия пересечения плоскости орбиты с поверх¬
ностью Земли — линией Р{М.
Проведем через точку О — центр Земли — и ось z
плоскость, перпендикулярную плоскости орбиты ИСЗ.
След этой плоскости — линия ОМХ — образует со следом
Рис. 13.5. Геометрические соотношения при расчете орбитальных
параметров ИСЗ:
а — сферический треугольник на поверхности Земли; б — расположение точки
наблюдения О и ракеты Р в плоскости, проходящей через центр Земли.
орбиты прямой угол в точке Тогда очевидно, что
положение плоскости орбиты в пространстве однозначно
характеризуется координатами (13.14) точки О, азиму¬
том а0 дуги ОМ\ и размером этой дуги, т. е. централь¬
ным углом vo. По этим данным несложно найти в даль¬
нейшем углы А и i.
Произведем расчет искомых величин а0 и vo- Из
АРЦВ и LOPF (рис. 13.5,6) получим
tg v
D cos р
R3 + О sin 0
(13.15)
По формулам Непера, справедливым для сферического
прямоугольного треугольника ОР{М} (рис. 13.5,а),
найдем
tg v0 = tg v COS (<х0 — a) = cos (a0 — a).
(13.16)
4C3
Для расчета v0 и а0 по формуле (13.16) необходимо из¬
мерять координаты ИСЗ по крайней мере в двух точках
орбиты. Эти измерения разнесены во времени, и необхо¬
димо учитывать изменение координат (13.14) точки О.
Однако, если интервал времени между измерениями до¬
статочно мал, вращением Земли можно пренебречь.
Следующим этапом расчета является нахождение
полярных координат ИСЗ R и и в момент времени /,
соответствующий измерению а, р и Z), а также т>о —
истинной аномалии точки М. Из АРЦВ (рис. 13.5,6) по¬
лучим
R = j/D4os2p + (/?3 + £sin₽)2 —
= |/^4-D2 + 2/?3Dsmp (13.17)
а из сферического треугольника ОР[МУ (рис. 13.5,а)
найдем
Ди = d0 —• и,
tg (% -- u) = tg = tg (а — ао) sin v0. (13.18)
Найденные по формулам (13.17) .и (13.18) значе¬
ния R и Av необходимо подставить в уравнения эллипса
(13.6), которое примет вид
1 + е cos (о0 — До)
В данном уравнении три неизвестные величины: а, е и
•ио. По результатам измерения а, р и D по крайней мере
в трех точках орбиты можно рассчитать параметры
эллипса и положение перигея (угол v0), а следователь¬
но, п орбитальный параметр Т.
Для определения последнего параметра — времени
/п прохождения ИСЗ через перигей — воспользуемся
формулой для расчета истинной аномалии движения, ко¬
торая имеет вид
О = £)С(Л + (2е У е3'') sin Осо^ +
+(4" е3 — В- е1) sin 2QC0^ -f-е3 sin 30С(Л,
(13.19)
где ti — t — tn; Qco = j/"-^—средняя угловая скорость
обращения ИСЗ; /< = 3,986-IO5 км* [сек*.
464
Поскольку измерение координат ИСЗ всегда проис¬
ходит с ошибкой, то для повышения точности расчета
параметров траектории целесообразно увеличивать чис¬
ло измерений, производя вычисления по многим точкам
орбиты. При наличии избыточной информации расчет
параметров производится по методу наименьших квад¬
ратов, который сводится к решению системы линейных
уравнений путем последовательных приближений. Тем
самым достигается выигрыш в точности, аналогичный
выигрышу при многократных измерениях одной и той
же величины (§ 9.7).
Наибольшему числу измеряемых точек отвечает не¬
прерывное слежение за положением . ИСЗ, которое
к тому же позволяет найти нс только сами координа¬
ты— а(/), •₽(/), Щ1), — но и функциональную за¬
висимость от времени производных координат: a(Z),
|3(0, Измерение последних является допол¬
нительным, а часто и самостоятельным источником
информации о траектории ИСЗ или КА. Можно
показать, что все орбитальные параметры могут быть
найдены и в том случае, если измерению подвергается
только одна координата ИСЗ или ее производная. Для
этого необходимо только, чтобы число точек измерения
было достаточно большим. Однако одновременное изме¬
рение нескольких координат упрощает расчеты и повы¬
шает точность траекторных измерений, так как количе¬
ство информации о движении ИСЗ возрастает.
В системах контроля траекторий! ИСЗ и КА для из¬
мерения угловых координат используются фазовые и
суммарно-разностные радиопеленгаторы. При этом
вместе с измерением азимута a(t) и угла места р(/)
ИСЗ обычно измеряется и величина допплеровского
смещения частоты принимаемых сигналов, которая про¬
порциональна D (/). Существуют также и чисто доппле¬
ровские системы контроля, в которых расчет орбиталь¬
ных параметров производится по графику D(t).
§ 13.4. ФАЗОВЫЕ ПЕЛЕНГАТОРЫ СИСТЕМ КОНТРОЛЯ
ТРАЕКТОРИЙ ИСЗ
Рассмотрим основные показатели работы фазовых
пеленгаторов ИСЗ.
30—1173
465
В системе, состоящей из двух пар разнесенных
антенн Ai—Л2 и Л3— Л4, базы которых d\ и d% перпен¬
дикулярны друг другу (рис. 13.6), разности фаз коле¬
баний, принимаемых от источника Р, следующим обра¬
зом связаны с азимутом а и углом места р точки Р:
?21 = sin a cos р,
(13.20)
ЗгсЩ п
= -у1 COS а COS р.
Рис. 13.6. Расположение ИСЗ (точка Р) относительно антенн А\—А2
(запад—восток) и Лз—А4 (север—юг) фазового пеленгатора ИСЗ.
Обычно базы обеих пар антенн выбираются равными:
dx = d2 = d. Поэтому, измерив разность фаз ф21 и <р34,
найдем а и р из соотношений
а = arctg р -= arccos ( Щ- /.
(13.21)
Рассмотрим точность определения угловых коорди¬
нат. В соответствии с формулой полного дифференциала
измеряемых величин <p2i и <рз4 получим для конечных
приращений
— -у- (c°s a cos рДа — sin а sin рДр).
Д<рм = — (sin а cos Р Да -ф- cos а sin р Др).
(13.22)
466
Отсюда могут быть найдены ошибки в определении ази¬
мута и угла места
Да = 2^Дгг С03 а —
(13.23)
Ар = ~ 2nd sin р (Д?21 S‘n а + Д?31 C0S •
Ошибки в измерении разности фаз могут быть вызва¬
ны как неточностью показаний фазометров, так и ошиб¬
ками в определении размеров d\ и d2. Обычно случай¬
ные ошибки фазометров независимы, а их среднеквадра¬
тичные значения одинаковы: о = з = о . Поэтому сред-
<?21 Ч>31 <₽ J 1
и р
неквадратичные значения ошибок
найти по формулам
| COS р | ’
измерения а
можно
(13.24)
Неточности в определении размеров баз &d\ и Ad2
вызывают систематические ошибки отсчета
Д?21С =^^-sinacosp, Дф31С — —^--cosacosP; (13.25)
и, следовательно,
(13.26)
Для того чтобы систематические ошибки не вносили
заметных погрешностей в измерения, максимальные значе¬
ния Д?21С и Д<р31С должны быть много меньше, чем. средне¬
квадратичная ошибка о . Например, при о =0,36° необ¬
ходимо измерять базы и обеспечивать стабильность размеров
базы с точностью -10"3, что при длине волны 2 =
~3 мЦ—ЮОМгц) соответствуют ошибке Arf<3 мм.
Для уменьшения случайных составляющих ошибок
отсчета необходимо увеличивать размеры базы по срав-
30* 467
пению с длиной волны. Однако уже при г/>0,5л отсчет
разности фаз становится неоднозначным. Разрешение
неоднозначности отсчета при d^>K осуществляется пе¬
ленгационными системами грубого отсчета. В качестве
первых ступеней грубого отсчета используются ампли¬
тудные пеленгаторы с направленными антеннами или
фазовые пеленгаторы с базой Д[^О,5Л,. Для того чтобы
максимальная ошибка Звп предыдущей, более грубей
ступени с базой dn не превышала -180° показа¬
ний фазометра последующей ступени с базой dn-^>dn,
необходимо выполнить условие
11 11
По формуле (13.27) можно найти размеры баз всех гру¬
бых ступеней отсчета миогошкальиой системы.
При действии шумовых помех среднеквадратичная
ошибка измерения разности фаз в основном определяет¬
ся помехой и в первом приближении равна — рад. По¬
этому применение направленных антенн целесообразно
также для улучшения соотношения сигнал/помеха р па
входе детектора. Это позволяет повысить точность от¬
счета разности фаз. Однако использование направлен¬
ных антенн в фазовых системах уменьшает рабочую
зону пеленгатора, так как в целях обеспечения высокой
точности измерений и уменьшения ошибок, вызванных
погрешностями Adi и АД?, антенны пеленгатора делают¬
ся неподвижными, а их диаграммы направленности за¬
нимают фиксированное положение в пространстве.
Прием сигналов от ИСЗ, расположенных под более
низкими, чем [3 = 45° л-50° углами наклона к горизонту,
нецелесообразен из-за больших ошибок, возникающих
при рефракции радиоволн в атмосфере Земли. Поэтому
в системе точного отсчета применяются антенны с веер¬
ными диаграммами направлен пости (ширина диаграм¬
мы 10° в одной плоскости и 60°—75° в другой), оси сим¬
метрии которых направлены вертикально вверх. Веер¬
ные диаграммы всех антенн вытянуты вдоль одного и
того же направления, которое выбирается с учетом за¬
данного наклона плоскости орбиты ИСЗ к плоскости
экватора Земли.
46»
§ 13.5. СУЛШЛРНО-РАЗНОСТИЫЕ РАДИОПЕЛЕНГАТОРЫ
исз
Во многих современных системах контроля траекто¬
рий используется упрощенный метод фиксации дискрет¬
ных положений ИСЗ по данным амплитудных измерений
суммарного и разностного сигналов двух разнесенных
антенн.
Рассмотрим систему из дву,х приемных антенн и
Л2 с базовым расстоянием (рис. 13.6 и рис. 13.7,а).
Складывая и вычитая сигналы антенн (рис. 13:7,6), по¬
лучим
мс = «1 + «2 = («, Р) cos -Д cos (<Л — (
и, ~ut — и2—~[7ШДО (a, p)sin -^i-sin • Д-\
'(13.28)
где р) —диаграмма направленности каждой из
антенн в отдельности.
Определив ср21 по формуле (13.20), найдем суммар¬
ную и разностную диаграммы направленности:
Цс Ц Р) = До («> ₽) cos ГCOS ₽] =
= До (а> ₽)cos р-с°м].
Др е- и До (*> P)>in [Га c°s р] =-:
cos 7] , (13.
где т] - -угол между базовой линией d и направлением
прихода волны, а
cos Г| = sin сс • cos р. (13.30)
Примем для простоты, что /ео(сх, р) = fEo (₽), т. е. что
диаграммы антенн симметричны и направлены верти¬
кально вверх (рис. 13.7,(2), и рассмотрим форму сум¬
марной и разностной диаграмм.
Из (13.29) следует, что диаграммы fEc(a, Р) и
/ер (а, Р) имеют сложную многолепестковую структуру.
Па рис. 13.7,62 показана форма сечений /Ес(а, р) и
/ер(а, Р) в вертикальной плоскости, проходящей через
базовую линию d. Нулевым значениям амплитуд сум-
469
маркого и разностного сигналов соответствуют углы
прихода волны трп (при wc = 0) и т]п (при ир = 0), а рав¬
носигнальным направлениям (uc = up)—углы т|г, значе¬
ния которых могут быть найдены из соотношений:
(13.31)
X , 2r + 1 X
COS 11 , COS /Д f/ *
где т, п и г — целые числа.
Зоны нулевого приема и равносигнальные зоны об¬
разуют в пространстве конические поверхности поло¬
жения п = const (рис. 13.7,6?) с .вершинами конусов, ле¬
жащими в середине базовой линии d. Разность углов
между двумя соседними равносигнальными направле-
Рис. 13.7. Принцип действия суммарно-разностных пеленгато¬
ров ИСЗ [22]:
а — форма суммарной и разностной диаграмм направленности в вертикальной
плоскости; б —упрощенная блок-схема пеленгатора: в — равносигнальные по¬
верхности положения; г — вид записи напряжения суммарного и разностного
каналов; д — вид записи напряжения равносигнального канала.
470
пнями Атм- зависит от отношения —и вдвое меньше
* d
углов Дт]т и Ат]п между двумя соседними направления¬
ми пулевьгх амплитуд суммарного и разностного сиг¬
налов:
Д'<|г=^г“
~ 2
X
2d sin т]г
(13.32)
В частности, при ~ =50 и г|Г = 90° интервал между
равносигнальными направлениями составляет величину
АПг = 0,01 =34z.
Используя указанные зависимости амплитуд сум¬
марного и разностного сигналов от угла прихода волны
т], можно индицировать дискретные положения ИСЗ
в моменты времени, когда координаты спутника а и р
удовлетворяют значениям т]/п и т]п (пеленгование по
минимуму сигнала) или значениям тц (пеленгование по
равносигнальным направлениям). Для этого необходи¬
мо регистрировать либо нулевые значения, либо равен¬
ства амплитуд напряжений ис и ир.
По упрощенной блок-схеме суммарно-разностного
пеленгатора (рис. 13.7,6) можно проследить последова¬
тельность операций при измерении угловых координат.
Для получения напряжений (13.28) используется сум¬
марно-разностный кольцевой мост или гибридное волно¬
водное сочленение, где происходит сложение и вычита¬
ние сигналов антенн щ и и^. Усиленные и отфильтрован¬
ные в приемниках сигналы детектируются. Напряжения
^свых и ^рвых, пропорциональные амплитудам напряже¬
ний ис и цр, сравнительно медленно изменяются во вре¬
мени, и поэтому они могут быть поданы прямо на за¬
писывающие устройства, куда поступают и масштабные
отметки сигналов точного времени. Вид записи интер¬
ференционного сигнала суммарного (сплошная линия)
и разностного (пунктирная линия) каналов показан на
рис. 13.7,г.
Для пеленгования ИСЗ по равносигнальным направ¬
лениям целесообразно производить предварительное вы-
471
• Ф 9 1
sm
2
читаппе напряжений wCBUX и //рвых и записывать раз¬
ностное напряжение прсйЫх
^гс ВЫХ —;^сеых 7ЙНЫХ” fEQ (а> Ю
(13.33)
На рис. 13.7, д показан примерный вид записи
пРсвых(0- Нулевым точкам записи соответствуют момен¬
ты времени, когда ИСЗ находится на равносигнальных
направлениях щ. Линейный вид зависимости црсВых (Ф21)
в окрестностях точек црСвых = 0 позволяет производить
интерполяцию данных измерения для моментов времени,
не совпадающих с нулевыми точками записи.
Рис. 13.8. Блок-схема суммарно-разностного радиопеленгатора
ФИАН [3].
Наибольшее число точек пересечения орбиты ИСЗ
с поверхностями положения т]т, т]п и т]г образуется
в том случае, если наблюдаемый отрезок орбиты парал¬
лелен базовой линии, а рабочая зона пеленгатора нахо¬
дится в области перпендикуляра к середине базы d. По¬
этому следует выбирать направление базовой линии
с учетом ожидаемого угла i наклона плоскости орбиты
к плоскости экватора.
Неоднозначность показаний устраняется либо при¬
менением малобазных систем грубого отсчета, либо
использованием антенн с малой шириной диаграммы
472
направленности н плоскости, проходящей через базовую
линию. В последнем случае число нулей интерферен¬
ционной записи в пределах ширины диаграммы не мо¬
жет быть большим, а ширина диаграммы не должна
превышать (84-10) Дт]г.
Практические схемы суммарно-разностных пеленга¬
торов ИСЗ отличаются от упрощенной . схемы
(рис. 13.7,6) рядом конструктивных особенностей. В ка¬
честве примера практической реализации рассмотрим
суммарно-разностный радиопеленгатор Физического
института Академии наук СССР, блок-схема которого
показана па рис. 13.8 [3].
В радиопеленгаторе ФИАН для усиления суммарно¬
го и разностного сигналов двух разнесенных антенн
используется один и тот же приемный канал, что сокра¬
щает объем аппаратуры и существенно повышает точ¬
ность отсчета за счет устранения ошибки из-за неиден-
тичности коэффициентов усиления каналов при раз¬
дельном усилении ис и ир.
Усиленные в УВЧ сигналы антенн преобразуются
по частоте в смесителях 1 и 2. Напряжение гетеродина,
поступающее на смеситель /, периодически изменяется
по фазе на 180° с помощью фазового модулятора. Рабо¬
той фазового модулятора управляет генератор опорного
напряжения частоты F = 72 гц, а сам фазовый модуля¬
тор представляет собой гибридный переключатель, из¬
меняющий электрическую длину кабеля питания на по¬
ловину длины волны. Преобразованные по частоте
сигналы антенн усиливаются в широкополосном пред¬
варительном УПЧ и по кабельной линии передачи по¬
ступают в точку В, где происходит сложение сигналов.
Широкополосные УВЧ и УПЧ не вносят существен¬
ных фазовых искажений в принимаемые сигналы. Поэто¬
му в точке В, отстоящей от середины линии передачи на
1/8 длины волны колебаний промежуточной частоты,
преобразованные сигналы двух антенн имеют вид
Z/I[ ; «,2 -- Unif£() (?-, c) COS ^<011, ?2+ "4~j »
где T= —период колебаний опорного напряжения.
Суммарный сигнал, получаемый в точке В, имеет вид
^nfE0 («, И cos COS («>„,. t + ■ j/2 )
при 0</< -Г-,
WB = I
2^с0(а, iS)sin^+^ sin(<W +
при -T-< t < T.
(13.35)
Сравнивая (13.35) и (13.28), найдем, что зависи¬
мость амплитуд напряжения ив от разности фаз q?2i
в различные полупериоды колебаний опорного напря¬
жения аналогична законам изменения амплитуд суммар¬
ного ис и разностного ир сигналов двух антенн с тем
лишь отличием, что в выражения (13.35) входит по¬
стоянный сдвиг фазы на угол Этот сдвиг вызывает
смещение в пространстве нулевых и равносигнальпых
направлений, определяемых формулами (13.31), на угол,
О
равный
В дальнейшем суммарное напряжение детектируется
и поступает на УНЧ. В отличие от упрощенной схемы
пеленгатора (рис. 13.7,6), здесь возможно применение
УНЧ после детектора, так как напряжение на его выхо¬
де носит переменный характер. Вид напряжения на вхо¬
де и выходе детектора при движении ИСЗ в пределах
рабочей зоны пеленгатора показан на рис. 13.9,а и
13.9,6.
Напряжение на выходе УНЧ (^БВЬ1Х) можно рассма¬
тривать как сумму двух составляющих: иВс и ивр
(рис. 13.9,в и 13.9,г). Опорное напряжение мОц
(рис. 13.9,6)) будет в фазе с одной из составляющих
напряжения uBiiblx и в противофазе с другой. Поэтому
474
при подаче на вход синхронного (фазового) детектора
напряжений иВВых и иоп на его нагрузке будет выделять¬
ся медленно изменяющееся во времени напряжение
и ^рСВых, равное разности амплитуд иВс и wSp (рис.
13.9,е). Напряжение ^рсВых поступает на записывающее
устройство. Нулевым точкам записи соответствуют мо¬
менты времени, когда ИСЗ проходит равносигнальные
направления щ.
7
Рис. 13.9. Диаграммы напряжений в различных точках схемы радио¬
пеленгатора ФИЛИ.
Радиопеленгатор ФИАН был впервые использован
для наблюдения за советскими космическими ракетами,
запущенными 2 января, 12 сентября и 4 октября 1959 г.
Несущая частота принимаемых сигналов равнялась
186,3 Мгц (Х=1,63 м), а базовое расстояние антенн
было выбрано равным d=176 м. Радиопеленгатор
ФИАН регистрировал сигналы от космической ракеты,
находящейся около Луны, с точностью угловых измере¬
ний 1'—27 (0,017°—0,033°), при мощности бортового ра¬
диопередатчика 0,03 вт '[3].
475
§ 13.6. ДОППЛЕРОВСКИЕ СИСТЕМЫ КОНТРОЛЯ
ТРАЕКТОРИЙ ИСЗ
Определение расстояния от пункта наблюдения до
ИСЗ может осуществляться либо по принципу радио¬
локации с активным ответом, либо на основе исполь¬
зования эффекта Допплера. В системах контроля траек¬
торий ИСЗ и в навигационных системах ИСЗ более
простому конструктивному решению отвечает примене¬
ние допплеровских систем.
Допплеровские системы хорошо согласуются с други¬
ми радиотехническими системами ИСЗ. Они не нужда¬
ются в установке на борту ИСЗ какой-либо дополни¬
тельной аппаратуры, так как для измерения допплеров¬
ской частоты могут быть использованы сигналы любой
линии передачи ИСЗ — Земля, в том числе линии пере¬
дачи телеинформации и эфемерид*. В свою очередь
использование в точке наблюдения узкополосных при¬
емных устройств для пеленгования ИСЗ и приема теле¬
метрической информации нуждается в измерении доп¬
плеровского смещения частоты. Чтобы принимаемые
сигналы попадали в полосу пропускания УПЧ, частота
местных гетеродинов должна следовать за изменяющей¬
ся вследствие эффекта Допплера частотой приходящих
колебаний.
Рассмотрим принципы расчета расстояний по резуль¬
татам измерений допплеровской частоты. В основе этого
расчета лежит закономерность орбитального движения
ИСЗ. Согласно второму закону Кепплера радиус-вектор
спутника R (рис. 13.1,6) в равные промежутки времени
описывает равные площади. Следовательно, определен¬
ным участкам орбиты соответствует также вполне опре¬
деленное значение скорости движения, зависящее от ве¬
личины R. В частном случае движения ИСЗ по круговой
орбите линейная скорость движения V постоянна и рав¬
на первой космической скорости.
Примем для простоты, что в пределах зоны радио¬
наблюдения траектория ИСЗ прямолинейна и движение
происходит с постоянной скоростью V. Тогда величину
допплеровского смещения частоты Fv можно рассчитать
* Эфемериды — прогнозированные данные о положении Г1СЗ
в инерциальной системе координат.
476
на основе геометрических соотношений, очевидных из
рис. 13.10,^:
Fv^=-
f*_oD_
с dt
V2(t-h)
V^t - toy + Dl
где f0 — частота колебаний бортового передатчика;
D — наклонная дальность до ИСЗ;
/о — момент времени, когда ИСЗ находится на ми¬
нимальном расстоянии Do от точки наблюде¬
ния О.
Рис. 13.10. К расчету дальности по графику изменения допплеров¬
ского смещения частоты:
а — геометрические соотношения при прямолинейном движении источника из¬
лучения; о — график изменения допплеровского смещения частоты; в — вспо¬
могательное построение зависимости у =f(x).
На рис. 13.10,6 показан график зависимости частоты
принимаемых колебаний fc(t) = fo + Fv(t) от времени
для различных значений Do при одном и том же значении
у
Из (13.36) следует, что при удалении в обе стороны
от t~t0 абсолютное значение допплеровской частоты стре-
г V
мится к максимальной величине а крутизна
477
кривой Fy (/) в точке /0 обратно пропорциональна минималь¬
ному расстоянию и определяется выражением
dfc
dFv
V2
dt
t=t0
dt
t=f. — ЛР.
(13.37)
Пользуясь построенным по результатам, измерений
графиком зависимости fc(0> можно найти неизвестные
величины /0, Dq и V, которые необходимы для расчета
дальности D и траекторных параметров ИСЗ.
Если частота излучаемых колебаний /о известна и
достаточно стабильна, то момент времени /0 определяет¬
ся по совпадению частот /0 местного гетеродина и fc(t)
приходящих колебаний. Нестабильность частоты борто¬
вого передатчика Д/ может вызвать ошибку в определе¬
нии tQ, величина которой в соответствии с (13.37) равна
= (13.38)
В тех случаях, когда f0 заранее неизвестна или ее неста¬
бильность -~^10“7—Ю 8, строят график зависимости
F'v(t) —fr для произвольного уровня частоты [г
местного гетеродина. На этом графике проводят секу¬
щую АС таким образом, чтобы отрезки АВ и ВС были
равны (рис. 13.10,6). Точка пересечения В с кривой
F'v (/) определяет момент времени /0 и значение часто¬
ты fo излучаемых колебаний.
Наиболее простым способом нахождения DQ и V
является графический метод расчета. Для этого по не¬
скольким точкам кривой Fv(t) строят вспомогательный
график y=f(x), рис. 13.10,0, где
x — (t — /0)2, а у= ——9^—. Из (13.36) найдем
Fv
У =
7 V
Л2
V2
— А>)’ + yrj
И
V- '
(13.39)
478
График представляет собой прямую линию, про¬
должение которой отсекает на осях х и у отрезки а и Ь\
а —
V2'
1 _
~b~
(13.40)
Определив а и &, найдем
o. = v^ = ^=4ft- <13Л1>
Приведенные соотношения справедливы для прямо¬
линейного и равномерного движения ИСЗ в зоне радио¬
видимости. Практически движение является криволиней¬
Рпс. 13.11. Блок-схемы наземного и бортового устройств допплеров¬
ской системы с активным ответом.
ным, ускоренным или замедленным. Для эллиптических
и круговых орбит ИСЗ может быть предложена анало¬
гичная методика расчета с учетом тех изменений, кото¬
рые вносят в ход зависимости />(■/) криволинейность
траектории и неравномерность движения. Такая мето¬
дика была разработана в ИРЭ АН СССР под руковод¬
ством акедемика В. А. Котельникова и использовалась
при расчете орбитальных параметров ИСЗ.
479
В системах контроля траекторий иногда целесооб¬
разно использовать допплеровские сислемы с ретрансля¬
цией сигналов, что обеспечивает высокую точность и по¬
мехоустойчивость радиолиний измерения. Упрощенная
блок-схема такой системы показана на рис. 13.11.
Передатчик наземной станции излучает непрерывный
сигнал со стабильной 'частотой колебаний На борту
ИСЗ частота принятого сигнала умножается на дробное
число р и сигнал ретранслируется на частоте f2 = pfi, что
необходимо для развязки приемного и передающего
каналов бортовой и наземной аппаратуры.
Принимаемый в наземной станции сигнал имеет доп¬
плеровское смещение частоты Fv. Принятый сигнал
дважды преобразуется по частоте с помощью смесите¬
лей 1 и 2 и вспомогательных напряжений с частотой
колебаний ,fi и —1)+FV. Благодаря этому часто¬
та преобразованного напряжения па выходе смесителя
2 постоянна и равна f, что позволяет применить узкопо¬
лосный УПЧ для фильтрации принимаемого сигнала от
помех. Усиленный и отфильтрованный сигнал поступает
в систему фазовой автоподстройки генератора /, частота
колебаний которого —1)+Fy изменяется в соот¬
ветствии с изменением Fv.
Допплеровская частота Fv выделяется с помощью
смесителей 3 и 4, на вход которых поступают напряже¬
ния генератора /, эталонного генератора стабильной ча¬
стоты / и умноженное по частоте в р—1 раз напряжение
излучаемого сигнала. Полученное напряжение с частотой
колебаний Fv поступает в цифровой блок измерения
допплеровского смещения частоты.
Блок-схема другого варианта допплеровской системы
с цифровым отсчетом разностной частоты приведена на
рис. 13.12. В приемном устройстве производится сравне¬
ние частоты принимаемых сигналов со стабильной
частотой местного гетеродина fr. На выходе смесителя
вырабатывается напряжение разностной частоты
—fr, которое после усиления формируется
в импульсы, следующие с частотой повторения Fzv(/)
(точка Ь на схеме рис. 13.12). Эти импульсы поступают
на блок измерения и записи данных.
Работой блока измерения управляет эталонный гене¬
ратор, включающий делители частоты и схему синхрони¬
зации фазы колебаний с сигналами точного времени.
480
Синхроимпульсы с периодом следования Тт = 2 сек от¬
крывают вентиль 1 с помощью триггера 1, Импульсы F'v
проходят через вентиль 1 и первый из них открывает
вентиль 2 с помощью триггера 2. В счетчике 1 через п
периодов частоты F'v вырабатывается импульс, закры¬
вающий вентили 1 и 2. Этот процесс иллюстрируется диа¬
граммами рис. 13.12,6 и 13.12,г, па которых показаны
напряжения триггеров 1 п 2. Импульсы эталонного гене¬
ратора, следующие с частотой [э=1 Мгц, проходят на
а
б
г
Гт—Н
Рис 13 12. Блок-схема допплеровской системы с цифровым отсчетом,
в —приемное устройство; б — временные диаграммы напряжений в различных
точках схемьь
счетчик 2 в течение интервала времени Д/ =
когда вентиль 2 открыт. Подсчет импульсов эталонного
генератора в счетчике 2 позволяет найти число тк— дли¬
тельность интервала времени Ы в мксек. Таким образом,
среднее за интервал № значение разностной частоты
в момент времени tk=kTT будет равно —
Показания счетчика 2 в. конце интервала Д/ записы¬
ваются с помощью печатающего устройства или нано¬
сятся на перфоленту в виде 11-разрядного двоичного
кода. Момент считывания определяется синхроимпульса¬
ми эталонного генератора. Первые пять разрядов обо¬
значают время в секундах, а последующие шесть — чис¬
ло тк.
Примером устройства, в котором согласованно ис¬
пользуются допплеровская система, пеленгатор и канал
482
приема телеметрических данных, является приемник си¬
стемы «Микролок» (рис. 13.13).
В состав амплитудного пеленгатора системы «Микро¬
лок» входят антенны и Л2, приемный канал с двойньш
преобразованием частоты и схема записи напряжения
суммарного канала.
Для приема телеметрической информации и измере¬
ния допплеровской частоты используется отдельный ка¬
нал с направленной и автоматически следящей антенной
Л3 и приемником, который аналогичен приемнику пелен¬
гатора.
Принимаемые сигналы имеют частоту /с(/) =
= 108 Мгц + Fv^t). Так как общий для обоих каналов
приемника гетеродин 1 входит в систему фазовой авто¬
подстройки частоты по сигналам /с (О, частота гетеро¬
дина переменна и равна /Г1 = ЮЗ Мгц+Fy (t). Благодаря
этому на выходе смесителей 1 и 2 сигналы всегда по¬
стоянны по частоте, которая равна 5 Мгц. Второе преоб¬
разование частоты с помощью гетеродина 2 и смесителей
3 и 4 позволяет применять на промежуточной частоте
узкополосные УПЧ с шириной полосы 3 кгц. Выходное
напряжение второго канала со сдвигом на 90° по фазе
поступает на фазовый детектор, куда также подается
стабильное по частоте /гз = 455 кгц напряжение кварце¬
вого генератора 3. Если сигнал на выходе УПЧ будет
отличаться по фазе и частоте от напряжения гетероди¬
на 3, то на выходе фазового детектора возникнет управ¬
ляющее напряжение, которое изменит частоту гетеродина
1. В равновесном состоянии частоты обоих напряжений
равны, а фазы отличаются на небольшой угол ф, величи¬
на которого обратно пропорциональна коэффициенту
усиления петли обратной связи системы автоподстройки
частоты.
Так как при достаточно большом коэффициенте уси¬
ления регулятора фазы напряжений гетеродина 3 и сиг¬
нала примерно равны, напряжение гетеродина исполь¬
зуется для синхронного детектирования сигналов
в детекторах 1 и 2. Благодаря этому существенно повы¬
шается отношение сигнал/помеха на выходе детектора.
Напряжения, пропорциональные амплитуде суммарного
сигнала антенн At и А2 и амплитуде сигналов, приходя¬
щих на вход антенны Л3, поступают на схемы записи.
31* 483
Для выделения допплеровской частоты в смесителе
5 сравниваются частоты управляемого гетеродина 1 и
стабильного кварцевого генератора 4, вырабатывающего
напряжение частоты fr4= ЮЗ Мгц. Разностная частота
fri—fr4, равная допплеровскому смещению частоты Fv(t),
поступает на схему измерения и записи данных наблю¬
дения.
Сигналы телеметрической информации, передаваемые
с помощью частотной модуляции несущей, выделяются
на выходе фазового детектора и также поступают на
блок обработки и записи информации.
§ 13.7. РАДИОНАВИГАЦИОННЫЕ СИСТЕМЫ (РИС)
С ИСПОЛЬЗОВАНИЕМ ИСЗ
Использование ИСЗ открывает большие возможности
для создания РИС дальнего действия. Существующие
наземные радиосистемы дальней навигации работают
в перегруженном диапазоне средних и длинных волн и
обладают конечным радиусом действия. Радиосистемы,
применяющие ИСЗ, могут работать в метровом, децимет¬
ровом и сантиметровом диапазонах УКВ, позволяют
определять местоположение объектов в любой точке зем¬
ного шара и обеспечивают более высокую точность мес-
тоопределения.
В состав РИС, использующей ИСЗ, входят: несколько
ИСЗ, снабженных радиоаппаратурой для приема и пере¬
дачи сигналов и движущихся по заданным орбитам
вокруг Земли; сеть станций контроля траекторий ИСЗ
с вычислительным центром для определения эфемерид
ИСЗ; аппаратура и средства связи для передачи эфеме¬
рид ИСЗ на борт объекта; комплекс навигационной ап¬
паратуры на каждом из объектов для приема сигналов
и расчета координат.
Ранее было показано, что станции контроля, располо¬
женные в известных точках на земной поверхности, спо¬
собны определять орбитальные параметры по сигналам
ИСЗ, принятым в пределах зоны наблюдения.
В РИС с применением ИСЗ решается обратная зада¬
ча: по сигналам ИСЗ, положение которого в каждый
момент времени известно, находится местоположение
точки наблюдения. По сравнению с первой вторая задача
усложняется тем, что объект имеет собственную скорость
484
движения и может находиться как на поверхности Зем¬
ли (надводные корабли, подводные лодки), так и над
ней (самолеты и другие летательные аппараты).
Местоопределение объектов с помощью РНС с ИСЗ
предусматривает выполнение ряда последовательных
операций (рис. 13.14). Станции контроля траектории
ИСЗ (СК на рис. 13.14) в моменты времени, когда ИСЗ
находится в зоне радпопаблюдсния этих станций, произ¬
водят прием сигналов, измерение допплеровской частоты
Рис. 13.14. Прппг.ип действия РНС с использованием ИСЗ:
СК — станции контроля траектории ИСЗ; ВЦ — координационно-вычислитель¬
ный центр; СПД— станция передачи данных; t^ts — положения ИСЗ в раз¬
личные моменты времени.
и угловых координат, обработку и запись результатов
измерения. В цифровой кодированной форме результаты
измерений СК передаются по обычным линиям провод¬
ной или радиосвязи в вычислительный центр (ВЦ).
В координационно-вычислительном центре производится
расчет эфемерид ИСЗ не более чем на один день вперед.
Эфемериды ИСЗ поступают на станцию передачи дан¬
ных (СПД).
Для передачи эфемерид на борт объекта местоопре-
делепия можно использовать различные каналы связи.
Ио проще всего эта задача решается с помощью аппа¬
ратуры, установленной на самом ИСЗ. Дважды в сутки,
когда ИСЗ появляется в зоне действия СПД, на его борт
передается таблица эфемерид. В блоке памяти ИСЗ сти¬
485
рается старая информация и записывается новая.
Одновременно с этим осуществляется коррекция борто¬
вого генератора сигналов точного времени.
Таблица эфемерид должна содержать сведения о по¬
ложении ИСЗ в инерциальной геоцентрической системе
координат для каждой 1—2 мин единого времени на про¬
тяжении первых 12—14 час. Аппаратура спутника регу¬
лярно с интервалом 1—2 мин транслирует полученные от
СПД эфемериды. При этом нет необходимости переда¬
вать полный объем информации, так как наблюдателю
нужно знать только текущие координаты ИСЗ. Поэтому
передается строка таблицы, соответствующая данному
моменту времени, три предыдущие и четыре последую¬
щие строки/ Так как время сеанса связи с ИСЗ длится
несколько минут, то на объекте одни и те же строки
таблицы принимаются несколько раз, что повышает на¬
дежность приема. Для фиксации момента времени, кото¬
рому соответствует первая передаваемая строка, каждое
сообщение начинается с передачи сигнала точного вре¬
мени.
Па объекте принимаются сигналы точного времени и
эфемериды. Одновременно с этим измеряется допплеров¬
ская частота принимаемых сигналов. По результатам
измерений и данным о положении ИСЗ производится
расчет координат подвижного объекта.
Если не учитывать рефракцию радиоволн в атмосфе¬
ре Земли, то прием сигналов ИСЗ возможен лишь при
нахождении ИСЗ в пределах прямой видимости с по¬
движного объекта. Продолжительность сеансов связи
с ИСЗ зависит от периода обращения ИСЗ вокруг Зем¬
ли, высоты полета и положения точки наблюдения отно¬
сительно плоскости орбиты. Так, например, при высоте
полета 1 000 км и периоде обращения ИСЗ НО мин ма¬
ксимальная продолжительность сеанса связи составляет
20 мин. Практически время наблюдения значительно
меньше и колеблется в пределах 8—12 мин.
Интервалы между сеансами связи зависят от числа
навигационных ИСЗ, взаимного положения их орбит,
расположения ИСЗ на орбитах, высоты полета и периода
обращения вокруг Земли. Расчеты показывают, что че¬
тыре спутника, циркулирующие на полярных орбитах,
могут обеспечить измерение координат в любой точке
земного шара с интервалом 0,5— 1 час [22].
486
Кратковременность сеансов связи и невозможность
непрерывного измерения координат объекта является не¬
достатком допплеровских РНС и ИСЗ и вынуждает
сочетать эти системы с другими средствами и системами
навигации. Одним из возможных вариантов комплекса
является параллельное использование на объекте инер¬
циальной системы навигации, непрерывные показания
которой периодически корректируются более точной РНС
с использованием ИСЗ. При комплексировании систем
местоположение, курс и скорость движения объекта пе¬
ред сеансом связи с ИСЗ приблизительно известны, что
упрощает методику точного расчета координат объекта
и уменьшает ошибки измерения.
Форма орбиты оказывает существенное влияние на
показатели РНС и ИСЗ. Наиболее стабильна и удобна
для целей навигации круговая орбита, которая облег¬
чает расчет эфемерид и учет влияния гравитационных и
аэродинамических сил на движение ИСЗ. Однако вывод
ИСЗ на круговую орбиту сложен и требует больших
энергетических затрат. Поэтому реальные орбиты будут
эллиптическими, но достаточно близкими к круговой.
Высота полета при этом выбирается как из условий обе¬
спечения достаточно широкой зоны прямой видимости
в окрестности следа орбиты на земной поверхности, так
и с точки зрения устойчивого приема сигналов ИСЗ при
заданной мощности бортового передатчика. Проектируе¬
мая высота полета 800—1 000 км обеспечивает нахожде¬
ние навигационного ИСЗ на орбите в течение 5 лет.
Радионавигационные системы с использованием ИСЗ
находятся с-ще в стадии разработки. Поэтому в настоя¬
щее время известны лишь общие принципы построения
схем наземного и бортового оборудования системы. Па
рис. 13.15 приведены составленные по данным зарубеж¬
ной литературы возможные варианты упрощенных блок-
схем бортового оборудования ИСЗ (рис. 13.15,а) и при¬
емно-вычислительного навигационного комплекса на по¬
движном объекте (рис. 13.15,6), которые отражают основ¬
ные функциональные связи звеньев аппаратуры [3].
В состав бортового оборудования ИСЗ входят: хрони-
затор, приемное устройство с блоком памяти и двухча¬
стотный передатчик. По разовым командам, передавае¬
мым с наземной станции передачи . данных, стирается
в блоке памяти старая информация и производится за¬
487
пись новой таблицы эфемерид. Кодовые числа 2 таблицы
эфемерид и разовые команды 1 выделяются на выходе
приемного устройства с помощью дешифратора сигналов
(рис. 13.15,62).
При заданной точности фиксации положения ИСЗ на
орбите (1 000—1 800 м) таблица эфемерид должна со¬
держать большой объем информации. Так как каждой
из трех инерциальных координат соответствует пять де¬
сятичных чисел, то каждому двухминутному интервалу
(строке таблицы) соответствует пятнадцать чисел,
a 14-адс периоду — 6 300 десятичных чисел. Для запоми¬
нания таблицы таким образом понадобился бы объем
блока памяти в 25 200 единиц двоичного кода, что превы¬
шает возможности существующих устройств.
Поскольку реальная орбита достаточно близка к эл¬
липтической вида (13.6) и параметры эллипса сравни¬
тельно медленно изменяются во времени, то для расчета
положения ИСЗ на такой переменной (оскулирующей)
орбите требуется значительно меньше чисел. Данные,
вводимые в блок памяти, разделяются на две группы.
Группа постоянных величин состоит из десятичных чисел,
которые определяют средние и неизменные в течение
12 час параметры эллипса, аппроксимирующего реаль¬
ную оскулирующую орбиту. К ним относятся: большая
полуось и эксцентриситет эллипса; углы Эйлера
а)
Рис. 13.15. Плох схемы бортового устройства МСЗ и наземного
488
в момент времени /п* io, Ао и Yo; средние угловые скоро¬
сти: обращении ИСЗ вокруг Земли Псо, прецессии пери¬
гея 42п и прецессии восходящего узла орбиты Од; сред¬
ние значения измейения истинной аномалии о за 1 час Да
и за 2 мин 8о, а также значение времени /п — первого
прохождения ИСЗ через перигей после 0 или 12 часов
единого времени.
Группа эфемерид содержит поправки к средним па¬
раметрам, относящиеся к текущему моменту времени th.
По постоянным и переменным данным таблицы, переда¬
ваемым в момент времени 4 с борта ИСЗ, в пункте мес-
тоопределсиия предварительно вычисляются истинные
значения r/t, аь, А/<, 1\. Далее с помощью формулы
(13.6), куда подставляются ah, с0 и находят Rtl и рас¬
считывают инерциальные координаты хк и ук- Последним
этапом расчета является нахождение с учетом углов ы,
и Tk экваториальных инерциальных координат рл
и
Выбор строк таблицы эфемерид 3 из блока памяти
происходит по сигналам точного времени 4, вырабаты¬
ваемым хронизатором ИСЗ (рис. 13.15,я). Сигналы точ¬
ного времени, постоянные и переменные данные табли¬
цы эфемерид поступают па шифратор сигналов, который
преобразует их в форму 6, удобную для передачи сооб-
б)
приемно-вычислительного комплекса РЫС с использованием ИСЗ.
489
щепий по каналу связи. Передача данных осуществляет¬
ся на несущей частоте лежащей в пределах от
50 до 500 Мгц.
Для формирования сигналов точного времени и обра¬
зования несущих частот передатчика fi = mfQ и /2 =/До
используется кварцевый высокостабильный задающий ге¬
нератор, работающий на частоте /о- В хронизаторе про¬
исходит деление частоты f0, а в передатчике — умноже¬
ние этой частоты в т и п раз. С помощью сигналов кор¬
рекции 5 (рис. 13.15,а), передаваемых наземной СПД,
периодически происходит синхронизация сигналов 4
с сигналами точного единого времени.
При рефракции радиоволн в атмосфере Земли
допплеровское смещение частоты сигналов, принимаемых
от движущегося ИСЗ, происходит с ошибкой А/7, вели¬
чина которой обратно пропорциональна несущей частоте
сигналов. При излучении двух колебаний с частотами /1
и f2 в точке приема имеем
/.ПР + l!t F —
(13.42)
где A — коэффициент, который изменяется при движении
ИСЗ, по не зависит от частоты.
Если в точке приема умножить частоту принимаемых
колебаний f2np на отношение и вычесть из получен¬
ного значения частоту принимаемых колебаний flnp, то
в результате получим
f J4 f У — 1 clD\ _
/прД— т 12Щ1 /inp— ~ /о^
= Л + Щ (13.43)
где точное значение допплеровского смещения частоты
е п2—т2 с
490
равно
„ ft_dD_
'Ъ с dt
п2 — m2 f0 dD
пг c dt
(13.44)
Таким образом, благодаря применению двухчастотно¬
го передатчика ИСЗ (рис. 13.15,а) в точке приема можно
устранить ошибки измерения допплеровской частоты,
вызванные рефракцией радиоволн. В частности, при
т 1
— = ~тг имеем
п 2
(13.45)
Для нахождения координат подвижного объекта па
нем устанавливается двухканальное приемное устройство
с блоками поправки на рефракцию радиоволн, измере¬
ния допплеровской частоты FVh, выделения орбиталь¬
ных данных и сигналов точного времени, а также вычи¬
слитель— специальная ЦВМ с блоком ввода расчетных
данных (рис. 13.15,6).
Принятые и усиленные сигналы ИСЗ подвергаются
в блоке поправки преобразованию (13.43). Данные изме¬
нения в цифровой форме и кодовые числа таблицы
эфемерид поступают на блок ввода расчетных данных.
В этом блоке входные числа наносятся на перфоленту и
регистрируются иа обычной ленте с помощью печатаю¬
щего устройства для последующего контроля. Перфо¬
лента поступает в вычислительную машину, где произво¬
дится расчет координат подвижного объекта.
Экспериментальные исследования показали, что сред¬
неквадратичные ошибки в местоопределении объектов
при использовании указанной методики расчетов не
должны превышать 900 м. Дальнейшее повышение точ¬
ности местоопределении связано с повышением точности
работы станций контроля траекторий ИСЗ, а также с не¬
обходимостью учета реальной формы Земли. Выполнение
этих условий позволит значительно повысить точность
м естоо ир одел е и и я.
Л И Т Е Р А Т У Р Л
1. Астафьев Г. П., Шебшаевпч В. С., Юрков 10. Л.
Радиотехнические средства навигации летательных аппаратов.
Изд-во «Советское радио», 1962.
2. В а ш а р и и о в Л. Е., Ф л е и ш м а и В. С. /Методы статистиче¬
ского последовательного анализа и их приложения. Изд-вэ
«Советское радио», 1962.
3. Б е л а в и и О. В., 3 е р о в а М. В. Современные средства ра¬
дионавигации. Изд-во «Советское радио», 1965.
4. Богомолов А. Ф. Основы радиолокации. Изд-во «Советское
радио», 1954.
5. В и и и ц к и й А. С. Очерк основ радиолокации ври непрерывном
излучении радиоволн. Изд-во «Советское радио», 1961.
6. Вудворд Ф. М. Теория вероятностей и теория информации
с применениями в радиолокации. Изд-во «Советское радио»,
1955.
7. Г утки и Л. С. Теория оптимальных методов радиоприема при
флюктуационных помехах. Госэнергоиздат, 1961.
8. Дудко Г. К., Р е з и и к о в Г. Б. Допплеровские измерители
•скорости и угла сноса самолета. Изд-во «Советское радио»,
1964.
9. Дул ев и ч В. Е. (ред.). Теоретические основы радиолокации.
Изд-во «Советское радио», 1964.
10. Жаков А. М., Пигулевский Ф. А. Управление балли¬
стическими ракетами. Воениздат, 1965.
11. Казаринов Ю. М. (ред.). _Расчет элементов импульсных
радиотехнических устройств. Госэнергоиздат, 1963.
12. Котельников В. А. Теория потенциальной помехоус¬
тойчивости. Госэнергоиздат, 1956.
13. Максимов М. В., Г о р г о и о в Г. И. Радиоуправление ра¬
кетами. Изд-во «Советское радио», 1964.
14. Николаев А. Г., Перцов С. В. Радиотеплолокация.
Изд-во «Советское радио», 1964.
15. Раков В. И. Индикаторные устройства радиолокационных
станций. Судпромгиз, 1962.
16. В а к и и С. А., Шустов Л. И. Основы радиопротиводействия
и радиотехнической разведки. Изд-во «Советское радио», 1968.
17. Сиверс А. П., Суслов И. А:, Метельский В. И. Осно¬
вы радиолокации. Судпромгиз, 1959.
18. Т а р т а к о в с к и й Г. П. (ред.). Вопросы статистической тео¬
рии радиолокации, т. 1. Изд-во «Советское радио», 1963.
19. Д о б р о л е и с к .и й Ю. П. и др. Автоматика управляемых сна¬
рядов. Оборонгпз, 1963.
20. Фалькович С. Е. Прием радиолокационных сигналов на
фоне флюктуационных помех. Изд-во «Советское радио», 1961.
21. Ширм ан Я. Д., Голиков В. И. Основы теории обнаруже¬
ния радиолокационных сигналов и измерения их параметров.
Изд-во «Советское радио», 1963.
22. Бычков С. И. и др. Космические радиотехнические комплексы.
Изд-во «Советское радио*, 1967.
492
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автономная и совмещенная систе¬
мы опознавания 50
Автономное управление 416—421
Автопилот 397
Автосопрово/кденне по дальности
в непрерывном режиме 172—178
— в режиме обзора 178—182
и скорости одиночного объ¬
екта 213, 214
— по направлению при коническом
сканировании 286 —29i
— по направлению при круговом
обзоре 266—277
Азимут 18
Азимутальный дискриминатор 268,
269
Активная радиолокация 10
Активные помехи 384—387
Амплитудные методы пеленгования
40-15, 252-266
, метод максимума 41—43,
252
, метод минимума 41, /56
— . равносигнальный метод 44,
260—266
Антенная температура РТЛ 334
Апостериорная вероятность сообще¬
ния 89
База 22
Баллистические ракеты (БР) 39S
Бпконнческий отражатель 56
Блестящая точка 58
Борьба с организованными помеха¬
ми 389—391
Виды обзора 234—248, 282
, боковой 277, 282
, винтовой 238. 239
, конический 241
, круговой 236. 266. 269. 270
, секторный 236, 266, 267
. спиральный 240, 241
Время обзора (поиска) 25, 234
Всенаправленный радиомаяк интер¬
ференционного типа 293
Вторая космическая скорость 456
Дальномер автоматический 172
— импульсный 35. 159—171
— фазовый 31. 195
частотный 33, 34
Дальномерный метод 20, 21
Дальность активного радиопротиво¬
действия 386. 387
Дальность действия 25. 344—357
радиолокатора 328, 333—335
— радиоразведки 384
Двухточечный метод наведения 407
Двушкальпый метод измерения
дальности 167, 168
Диаграмма видимости РЛС 350
Диаграмма неопределенности 73
импульсного сигнала с коло-
колообразной огибающей 76, 77
— — периодической последователь¬
ности импульсов 77, 78
— — сигнала с симметричной ча¬
стотной модуляцией 210
синусоидального сигнала с пря¬
моугольной огибающей 73—76
ЧМ сигнала 78, 79, 218
Динамическая траектория (ДТ) 405
Динамические ошибки наведения
411—414
Диффузное рассеяние 51
Длина синтезированной антенны 282
Допплеровские системы измерения
скорости и угла сноса- самолета
220-233
, многолучевые 225—230
— , однолучсвая 221—225
, построение 230—233
контроля траекторий ИСЗ
476-481
Допплеровское смешение частоты 1о
Загоризонтная РЛС 355
Заградительная помеха 385
Закон излучения АЧТ (формула
Планка) 326
Зенитные управляемые снаряды
(ЗУР) 394
Зона действия 24. 25
— обнаружения
ции 346, 347
— обнаружения
ИРЛ 355
Зондирующие ...
сигналы 11. 67—86, 306
Зоны управления снарядов 393
(видимости) стад-
целей станцией
радиол ока циопн ые
Идентификация целей 185, 276, 277
Измерение дальности и скорости
152
автоматическим цифровым ме¬
тодом 182—186
— — двушкальпым методом J67
импульсным методом 35—37
фазовым методом 30—32
— — частотным методом 33—35
в пассивной радиолока¬
ции 338
и ускорения объектов 46,
47
— угловых координат 234, 291—296
Имитационные ответные импульс¬
ные помехи 385, 390
Импульсные дальномеры с визуаль¬
ной индикацией 159—171
, дальность действия 171
, разрешающая способность
168—170
, точность измерения 162—168
Импульсные разностно-дальномер¬
ные системы 186—195
Индикатор кпугового обзора 238
— типа А 159, 160
— типа В 237
— типа J 159, 162. 169
Инерциальные экваториальные си¬
стемы координат 461, 462
Инструментальная ошибка 162, 163,
358
Интеграл вероятности 362, 375
— свертки 104
Информативность системы 286
Истинная аномалия 464
493
Кинематическая траектория (КТ) 405
Когерентно-импульсные системы
СДЦ 321—323
Когерентные радиоимпульсы 125
Коды Баркера 81
Командное управление 428—432
Комбинированный угломерно-даль¬
номерный метод 23—24
Компенсационный приемник радио-
тепловых излучений 336
Компенсирующее устройство на по-
тенциалоскопе 319, 320
с УЗЛЗ 313
Контрраднопротпводействие 389—391
Корреляционная функция шума 92
Корреляционный интеграл 9J
— прием 103, 115— lift
— приемник радиотепловых излуче¬
ний 338
Коэффициент подавления помехи
323. 324
» РТС 386, 387
— преломления 351
— различимости сигналов 161, 255
342
— распространения при отражении
348
Критерий идеального наблюдателя
98
— максимального правдоподобия 99
— минимума среднего риска 98, 152
— Неймана — Пирсона 99
— последовательного наблюдателя
100
Крутизна пеленгационной характе¬
ристики 40
Крылатые ракеты 394
Линза Люнеберга 244
Линия визирования 407, 443, 444, 446
— положения 17
точность определения 358—364
, в пространстве 371—376
‘ , на плоскости 364—370
Ложная цель 274
Мертвая зона 170
Мерцающая помеха 385
Методы измерения дальности 30—37
, импульсный 35—37, 159—
171, 186—195
, фазовый 30—33. 195—200
. частотный 33—35, 203—220
Методы измерения угловых коорди¬
нат 38—45
амплитудные 40—45, 252—
266. 339
, моноимпульсный авто¬
матический 296. 306
фазовые 38—40, 291—296
частотные 38
Методы наведения 405—411, 423
, параллельное и пропорцио¬
нальное сближение 407—410
, постоянное упреждения 407
, самонаведение 442—450
Методы определения местоположе¬
ния 17—24
= , дальномерный 20, 21
, комбинированный угломер¬
но-дальномерный 23, 24
— , разностно-дальномерный
21-23
, угломерный 18, 19
Методы пассивной радиолокации
338-340
Многоканальный обзор 242
Модуляционная длина волны 204
Модуляционный приемник радио¬
тепловых излучений 337
Моноимпульсная система с ампли¬
тудной пеленгацией 300
— — с суммарно-разностной обра¬
боткой сигналов 302
Наведение по кривой погони 407,
409
Навигационный треугольник 221,222
Надежность радиосистемы 26
Наклонная дальность 23, 398
Накопительные устройства видеоим¬
пульсов 146—151
Неравенство Буняковского — Швар¬
ца 107
Обнаружение сигналов 87
радиосредств противника 377—383
— радиотепловых сигналов 328—335
Обобщенное уравнение радиолока¬
ции 341—344
Определение параметров орбиты
ИСЗ 460-465
Оптимальная фильтрация 104. 116
Оптимальный приемник обнаруже¬
ния 96
для пачки когерентных ра¬
диоимпульсов 132
для пачки некогерентных
радиоимпульсов 142
для сигнала со случайной
амплитудой и начальной фазой
122
—- «-ч для сигнала со случайной
начальной фазой 116
, качественные показатели
109—113. 117—120, 122—126
Оптические координаторы 448, 449
Органы управления реактивных сна¬
рядов 395—397
Оскулирующая орбита ИСЗ 489
Основное уравнение радиолокации
28-30. 341—344
Отношение правдоподобия 95—97,
101. 113. 139. 141. 331
Отражающая (разрешаемая) пло¬
щадь 60. 280
Ошибки инструментальные и ошиб¬
ки распространения 358. 359
— местоопределення па плоскости
365
— наведения динамические и флюк¬
туационные 411—415
систематическая и случайная 360
Параллелепипед ошибок 371—373
Параллелограм, круг и эллипс оши¬
бок 367, 368
Параметр обнаружения 112
Пассивная радиолокация 12, 325—
340
Пассивные помехи 387
Пачка когерентных радиоимпульсов
124, 126, 136
494
— пекся еренткых радиоимпульсов
139, 141, 143—146
Пеленгационная характеристика
угломера 40
Первая космическая скорость 455
Плата за ошибку 98
Поверхность положения 17, 371
Поглощение в атмосфере 352, 353
Полуавтоматический приемоиндика-
тор 191, 192
Полуактивная радиолокация 11
Помехозащищенность и помехо¬
устойчивость радиоспстемы 26
Порог счета 149, 151
Последовательный и параллельный
автопоиск 177
Постоянная Больцмана 327
— Планка 327
Потенциальная точность измерения
дальности 152—158
угловых координат 248—252,
279
Преломление (рефракция) радио¬
волн 351
Преобразование координат 440, 441
Преселектор на линиях задержки
272
Приемные устройства радиолокато¬
ра 335—338
Принцип неопределенности в ра¬
диолокации 72
Прицельная помеха 385
Промах 411, 415
Пропускная способность системы 26,
286
Путевая скорость 46, 47, 221, 225
Прямошумовая помеха 384
Равносигнальный метод пеленгова¬
ния 44, 260
Радиовзрыватели 449—451
Радиодезинформация 384, 388
Радиолаг 197, 198
Радиолинии командного управления
432, 433, 435-439
— контроля 438—442
с активным ответом 356—358
Радиолокация 10, 11, 12, 26
Радионавигация 10
Радиомаскировка 384, 387, 388
Радионавигационные системы с
использованием ИСЗ 384—491
Радиолепенгатор ФИАН 472, 473
Радиопеленгация 12
Радиопротиводействие 384—389
Радиоразведка 377—384
Радиотеленаведение 421—428
Радиотелеуправление 432—443
Радиотеплолокация 12
Радиотеплопеленгация 339
Радиоуправление 10
Разрешающая способность системы
26, 68, 168—170, 248—252, 277—286
Распознавание радиолокационных
объектов 47—50
Регулярная импульсная помеха
(РИП) 384, 385
Сверхнаправленная антенна 281
Сверхрефракция 352
Селекция сигналов движущихся це¬
лей 48, 307-324
Сигнальная функция 329
Синтезированные антенны 281, 282
Система «Микро.юк» 482
Системы координат 397—399, 461, 462
— опознавания 50
— СДЦ с внутренней когерентно¬
стью 309—321
Системы управления 391, 416—452
командного 428—432
, радиотеленаведение 421—428
, радиотелеуправление 432—442
— ручного управления 429, 430
■ , самонаведение 442—450
, стабилизация и автономное
управление 416—421
Сканирование 234, 264, 286, 290
Скручивание координат 432
Скрытность радиосистемы 26
Следящий угломер 446—448
Совместная автокорреляционная
функция 67—85, 249, 250
Согласованный (оптимальный)
фильтр 105, 126, 130, 141
Способы создания управляющих сил
ЛА 396
Среднеквадратичная круговая ошиб¬
ка 367
■— сферическая ошибка 373, 374
Среднеквадратичный эллипс рассеи¬
вания ошибок 370
— эллипсоид рассеивания ошибок
375
Средний риск 97, 98. 152, 153
Статистические критерии обнаруже¬
ния 97—101
Структура квазиоптпмальных филь¬
тров 132, 136, 137
Структурные схемы ЛА 402—406
Суммарно-разностные радиопеленга¬
торы ИСЗ 469—475
Суммарно-разностный вариант мо-
ноимпульсиой системы 302, 303
— — метод пеленгования 42, 302
Сумматор на линии задержки 129
— — накопительных конденсаторах
146
— цифровой 148
Схемы стабилизации и управления
ЛА 398
Теорема Котельникова 91, 94, 330,
364
Тепловой (инфракрасный) коорди¬
натор 448, 449
Типы управляемых объектов 393—
395
Точка весеннего равноденствия 461
Точность местоопределения 341—376
в пространстве 371—376
— на плоскости 364—371
— определения линии положения
358-364
— радиосистемы 25, 68
Траектории БР, ИСЗ и КА 452—456,
475—484
— ЛА и управляемых снарядов 393,
405-407
Трехточечный метод наведения 406,
429, 430
Угловая разрешающая способность
277
495
Уг.ЮВоЙ С И ГН ЙЛ Ь Н ЫЙ НМИуЛЬС И
угловой спектр 24')
Угломерно базовый метод в ПРЛ
339
Угломерный метод определения ме¬
стоположения J8. 19
Угол атаки 395, 396, 398
— запуска БР 453, 459
— крена 396, 398
— курсовой 398, 402
— места 23, 398
— наведения 443, 444
— путевей 398, 402
— рассогласования 40
— рысканья 447
— скольжения 398
— смещения 261
— тангажа 398, 401
— упреждения 407
Уголковый отражатель 55
Управление в луче 423--428
— в радиозояс 421—423
Управляемые объекты 392—395
Управляющая функция 409
Упрежденный метод наведения 423
Уравнение радиолокации 28—30
обобщенное 341—344
Устройства оптимальной обработки
сигнала 98, 143, 146
со случайной амплитудой
и начальной фазой 120—124
со случайной начальной
фазой 113-120
с полностью известными
параметрами 101 — 113
— пачек когерентных радио¬
импульсов 124, 126
пачек некогерентных радио¬
импульсов 139—142
— широкополосных сигналов
137-139
Фазовые методы пеленгования 38—40
— пеленгаторы систем контроля
ИСЗ 465-468
— разностно-дальномерные системы
200—203
Фазовый метод измерения дально-
сти
30—33, 195-
-200
,
измерение
на
несущей
часто-
те
196
— — ,
измерение
на
частоте
биений
199
,
измерение
на
частоте
моду-
ляции 198
— — измерения угловых координат
38—40, 291—296
Фактическая траектория (ФТ) 405
Флюктуационные ошибки наведения
411, 414
Фокусированная антенна 283
Формула Планка 326
— Рэлея 58
— Рэлея -- Джинса 327
Формулы Непера 463
Фугоидпис движение 401
Функция Бесселя 115
— неопределенности 68, 73. 86
— правдоподобия 90—95, 100, 152,
155
Хаотично-импульсная помеха (ХИП)
385, 390
Характеристика обнаружения 112,
119, 123
Характерно!пки радиосистемы так¬
тические 24—27
— — технические 27, 28
— теплового излучения физических
объектов 326—328
Цифровой метод автоматического
измерения дальности 182—186
— — при определении угловых ко¬
ординат 271
Частотный метод измерения даль¬
ности 33—35, 203—220
Череспериодпая компенсация 310,
313, 323
Чувствительность пеленгования 40
— системы по дальности 203
ио скорости 210
Эквивалентная шумовая температу¬
ра 343
Эклиптика 461
Экономичность радиосистем 27
Экстраполяция координат 185, 275—
277
Эллипсоид рассеивания ошибок 375
Эллипс рассеивания ошибок 367—370
Эфемериды 475
Эффект Допплера 15
— Кабанова 354
Эффективная площадь рассеяния
цели 29, 51
диффузно-рассеивающей по¬
верхности 58, 61
капли 353
множества объектов 63, 64
— плоского металлического
листа 53—55
полуволнового пассивного
вибратора 61—63
реальных объектов 65, 66
уголкового отражателя 55—
56
шара 56—58
— ширина спектра сигнала 158
Эффективность систем СДЦ 323
Яркостная температура 327, 328
Цена<!_₽^б.