Лекции об аналитических множествах и их приложениях - Лузин Н.Н.

Автор: Лузин Н.Н.

Теги: математика теория множеств

Год: 1953

Похожие

Собрание сочинений Т.2 Дескриптивная теория множеств

Справочная книга по математической логике. Часть 2

Математика в СССР за тридцать лет. 1917-1947

Современная теория множеств. Начала дескриптивной динамики.

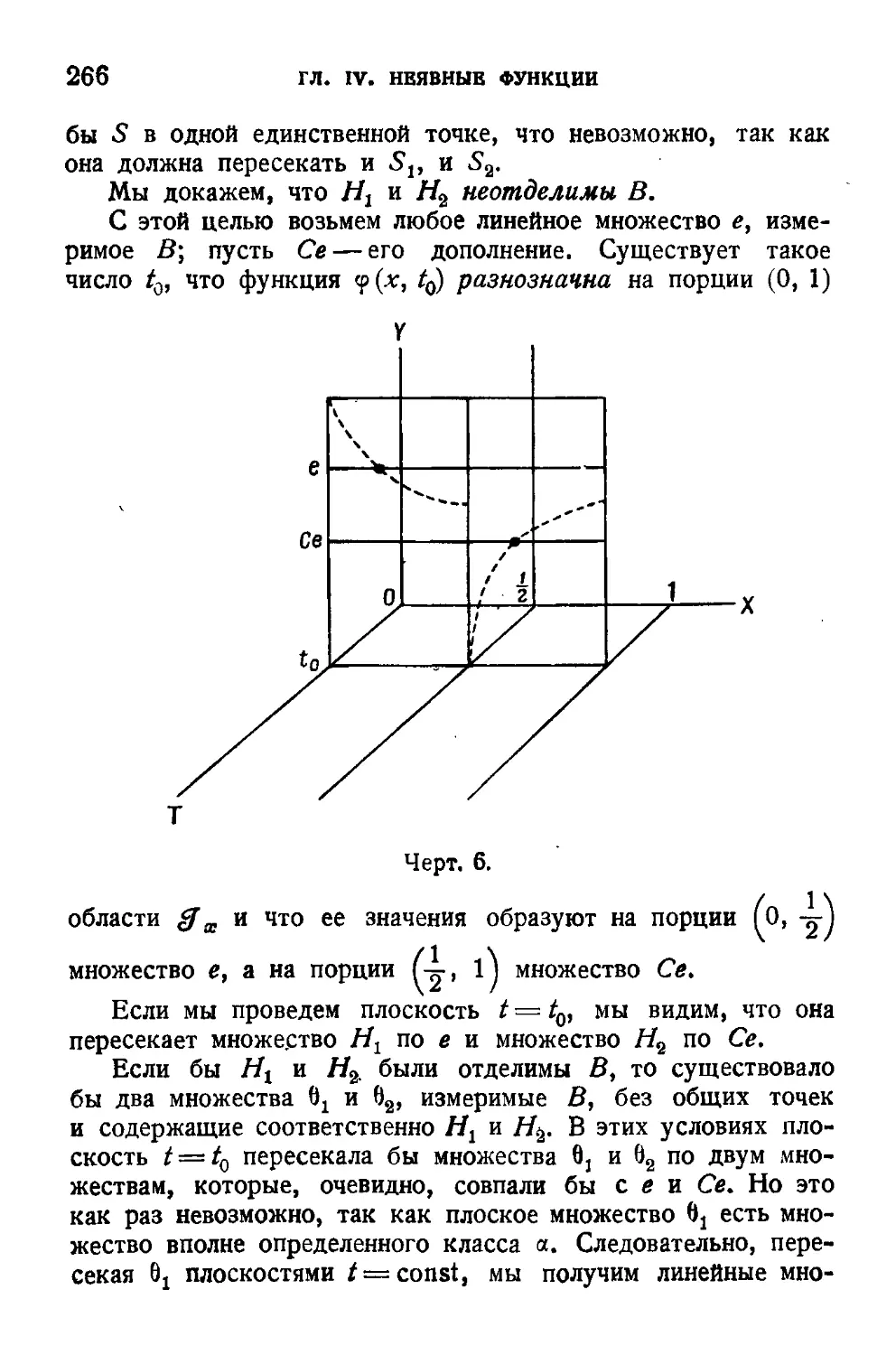
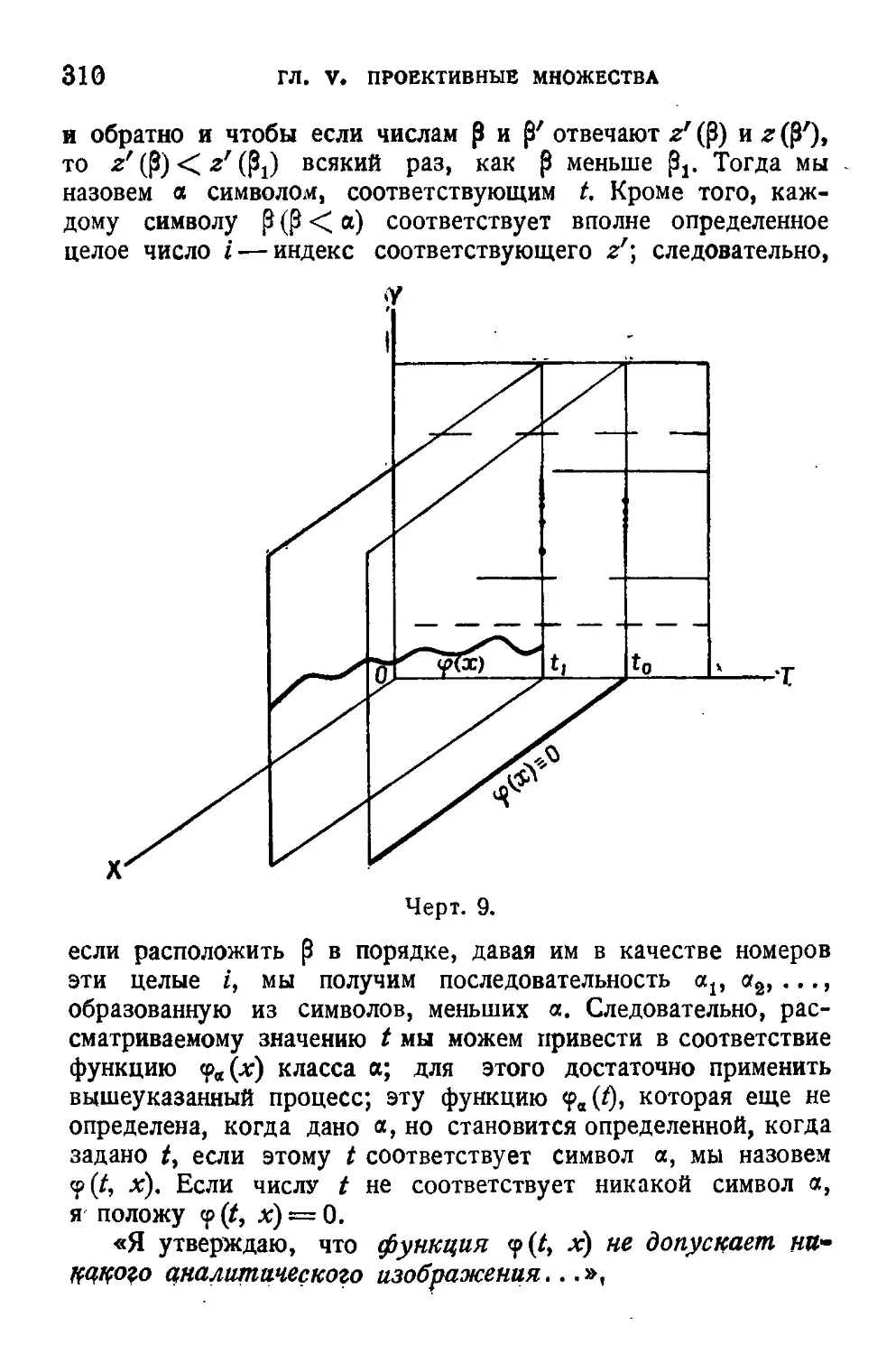
Текст

БИБЛИОТЕКА
РУССКОЙ
НАУКИ

БИБЛИОТЕКА РУССКОЙ НАУКИ
е х cmti к ее
Си с тЪ о н о-м ил
МИНИСТЕРСТВО КУЛЬТУРЫ СССР-ГЛАВИЗДАТ
Государственное издательство
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
JHock&cz - 1Q53

Н.Н.ЛУЗИН
-ОС-
ЛЕКЦИИ
ОБ АНАЛИТИЧЕСКИХ
МНОЖЕСТВАХ
И ИХ ПРИЛОЖЕНИЯХ
, преЪисловие
и примечания
Л В. КЕЛДЫШИ П.С НОВИКОВА
МИНИСТЕРСТВО КУЛЬТУРЫ СССР- ГЛАВИЗДАТ
Государственное издательство
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
JHock<?cz -

ПРЕДИСЛОВИЕ РЕДАКТОРОВ
Дескриптивная теория множеств возникла в связи с про-
проблемой об измеримости множеств. В различных разделах ма-
математики, особенно в анализе, постоянно возникает вопрос
об измеримости того или иного множества или измеримости
некоторой функции. Поэтому очень важно иметь средства
для доказательства измеримости множеств и функций.
Практически все известные до сих пор доказательства
измеримости некоторого множества связаны с указанием про-
процесса, с помощью которого это множество может быть по-
построено, т. е. его дескриптивной структуры. Вопрос же об
измеримости некоторой функции / (дг) сводится к вопросу об
измеримости ее лебеговских множеств, т. е. множеств [/(*)>а].
Одно из первых определений меры было дано Борелем. Мно-
Множества, измеримые по Борелю, получившие впоследствии
название множеств, измеримых В или В-множеств, это — мно-
множества, которые могут быть получены, отправляясь от интер-
интервалов, с помощью счетно-кратного применения операций сум-
суммирования и пересечения счетного числа множеств. Впослед-
Впоследствии, когда Лебег ввел свое определение меры множества,—
класс измеримых множеств оказался значительно шире класса
множеств, измеримых В. В связи с этим возник вопрос об
отыскании насколько возможно более широких классов изме-
измеримых множеств и функций.
Простейшие разрывные функции были изучены Бэром.
Он указал трансфинитную классификацию разрывных функ-
функций, которые могут быть получены счетно-кратным примене-
применением операции перехода к пределу, отправляясь от непрерыв-
непрерывных функций, и построил примеры функций первых трех
классов. Лебег доказал, что множества, измеримые В, являются

б ПРЕДИСЛОВИЕ РЕДАКТОРОВ
лебеговскими множествами для функций классификации Бэра
и классифицируются по классам, соответствующим классам
функций классификации Бэра. Он доказал непустоту всех
классов Ка, где а — натуральное число или трансфинитное
число второго класса, и построил без применения аксиомы
Цермело пример функции, не входящей в классификацию
Бэра, или, что то же — пример множества, неизмеримого В.
К этому времени обнаружились, с одной стороны, большие
трудности, связанные с континуум-проблемой, а с другой сто-
стороны, возможность, с использованием аксиомы Цермело, строить
множества, далеко выходящие за пределы множеств, изме-
измеримых В, в частности множества, неизмеримые по Лебегу.
Благодаря этим обстоятельствам возникла необходимость по-
подробно изучить природу арифметического континуума и его
подмножеств, указать процессы построения измеримых мно-
множеств и проанализировать способы задания неизмеримых мно-
множеств. Эта работа и была предпринята Н. Н. Лузиным.
Исключительное умение Н. Н. Лузина выбрать плодотвор-
плодотворное направление, способность правильно поставить задачу и
найти нужное определение привели к тому, что вокруг него
объединилась большая группа талантливой молодежи, рабо-
работавшей над поставленными им проблемами. Благодаря тому,
что Н. Н. Лузин не только сам интенсивно работал, но и
направил большой коллектив молодых ученых на решение
наиболее актуальных и трудных задач дескриптивной теории
множеств, целый ряд этих задач был решен в течение сравни-
сравнительно короткого времени.
Основное направление в области дескриптивной теории
множеств, которым занимался Н. Н. Лузин и его школа, —
это изучение эффективных множеств, т. е. тех множеств,
которые можно построить без применения аксиомы Цермело.
Настоящая книга является переводом книги Н. Н. Лузина,
впервые изданной в 193Э г. в Париже в серии монографий
по теории функций, издававшейся под редакцией Э. Бореля,
и содержит изложение основных результатов, полученных
в этом направлении Н. Н. Лузиным и рядом его учеников
за период 1915—1929 гг.
Первый вопрос, поставленный Лузиным, — это вопрос, не
решенный Лебегом, который исследовал множества, измери-
измеримые В: содержит ли каждое несчетное множество, измери-

ПРЕДИСЛОВИЕ РЕДАКТОРОВ 7
мое В, совершенное подмножество? Иными словами — имеет
ли оно мощность континуума? Этот вопрос был решен в по-
положительном смысле П. С. Александровым, построившим для
его решения новую операцию получения множеств, измери-
измеримых В, — операцию, получившую название Л-операции.
П. С. Александров показал, что с помощью Л-операции,
отправляясь от интервалов, можно получить любое множество,
измеримое В, и что всякое множество, полученное таким об-
образом, содержит совершенное подмножество. Тогда Н. Н. Лу-
Лузин поставил вопрос: можно ли с помощью Л-операции над
системой интервалов получить множество, неизмеримое В?
Этот вопрос был решен М. Я. Суслиным, показавшим, что
существует множество, которое получается с помощью Л-опе-
рации над системой интервалов и неизмеримо В. Множества,
получаемые с помощью Л-операции над системой интерва-
интервалов, получили название Л-множеств. В тексте книги Н. Н. Лу-
Лузин называет Л-множества «аналитическими множествами».
Однако такое название не привилось. В литературе они из-
известны под названием Л-множеств или суслинских множеств.
Дальнейшее развитие дескриптивной теории множеств было
посвящено подробному изучению множеств измеримых В,
Л-множеств и отысканию эффективных множеств, выхо-
выходящих за пределы Л-множеств.
Первая и вторая главы книги Н. Н. Лузина посвящены
теории множеств, измеримых В. В первой главе, которая
носит вводный характер, изложены различные операции, с по-
помощью которых могут быть получены множества, измеримые В,
и установлены связи между ними. Глава II содержит подроб-
подробное изложение теории множеств, измеримых В. Здесь изло-
изложены все основные . результаты, касающиеся этих множеств,
которые были известны к моменту написания книги.
Н. Н. Лузин рассматривает множества, лежащие в про-
пространстве Бэра &х — множестве всех иррациональных точек
отрезка (или множестве Зхх...х всех иррациональных
точек я-мерного евклидова пространства). При таком изло-
изложении формулировки теорем дескриптивной теории множеств
получают особую простоту благодаря тому, что рассматри-
рассматриваемое пространство имеет размерность нуль. Н. Н. Лузин
принимает классификацию множеств, измеримых В, Бэра —
Балле-Пуссена., В этой классификации к нулевому классу Ко

8 ПРЕДИСЛОВИЕ РЕДАКТОРОВ
принадлежат все открыто-замкнутые множества простран-
пространства 0д.. Множество Е принадлежит к классу а, если оно
является пределом последовательности множеств классов < а
и не принадлежит ни к какому классу <а. Множества
класса а разбиваются на элементы или множества, дости-
достижимые сверху, которые являются пересечениями множеств
классов < а, множества, достижимые снизу, которые
являются суммами множеств класса < а, и недостижимые,
которые не являются ни пересечениями, ни суммами множеств
классов < а. Если а — число второго рода, то в классе КЛ
есть еще множества, двусторонне достижимые, которые
являются одновременно и пересечениями и суммами множеств
классов < а. Такие множества составляют базу Ва. Н. Н. Лу-
Лузин показывает, что каждое множество класса а является
суммой элементов классов <;<*. В главе II изучается вопрос
о том, каким образом множество класса а строится из эле-
элементов классов <^а.
Н. Н. Лузиным введено понятие отделимости множеств,
которое играет очень важную роль в дескриптивной теории
множеств: два непересекающихся множества Ех и ?2 назы-
называются отделимыми при помощи множеств класса L,
если существуют два непересекающихся множества Нх и Н2
класса L, одно из которых содержит 2?„ а другое — Е2
EtczHv E2cH.2) tfjtf^O.
Лузин показал, что два непересекающихся элемента класса а
всегда отделимы при помощи множеств классов < а или
аз базы Ва (если а второго рода). На основании этой тео-
теоремы находится критерий неповышения класса, т. е. крите-
критерий для • того, чтобы счетная сумма элементов класса <; а
была множеством класса ^ а. .
Так как множества, измеримые В, строятся из элементов,
то Н. Н. Лузин поставил задачу об исследовании структуры
элементов класса а, а также о конструктивном построении
элементов низших классов. Он излагает здесь пример Бэра
элемента класса 3 и пример Л. В. Келдыш — элемента клас-
класса 4. Изучение структуры элементов класса а было сделано
позднее Л. В. Келдыш (см. Примечания). Наконец, в конце
главы Н. Н. Лузин излагает работу М. А. Лаврентьева о разг

ПРЕДИСЛОВИЕ РЕДАКТОРОВ 9
биении множеств класса а на подклассы в зависимости от
того, как эти множества строятся из элементов.
Исследуя вопрос о способах задания множеств, измери-
измеримых В, Лузин доказывает важную теорему о регулярном па-
параметрическом изображении множеств, измеримых В. Именно,
он показывает, что всякое множество, измеримое В, если
исключить из него не более, чем счетное множество,
есть непрерывный и взаимно однозначный образ простран-
пространства 0 х.
Эта теорема имеет большое значение в теории. Л-мно-
жеств, так как регулярность изображения множества Е, как
непрерывного образа 0х, т. е. его взаимная однозначность,
является, как показал Лузин (гл. III), достаточной для того,
чтобы множество Е было измеримо В.
Глава III содержит теорию Л-множеств. Л-множества— это
множества, которые могут быть получены, исходя из системы
интервалов пространства 0х (или параллелепипедов простран-
пространства ??х,х. ...х ) с помощью Л-операции, открытой П. С. Алек-
сандровым при решении вопроса о мощности множеств, изме-
измеримых В. Из теоремы П. С. Александрова непосредственно
следует, что всякое несчетное Л-множество содержит совер-
совершенное подмножество, следовательно, имеет мощность кон-
континуума. Н. Н. Лузин показал, что всякое Л-множество
измеримо и обладает свойством Бэра1).
Лузин поставил вопрос об отыскании критерия для того,
чтобы Л-мкожество было неизмеримо В. Такой критерий был
найден М. Я. Суслиным, который показал, что для того,
чтобы А-множество Е было неизмеримо В, необходимо и
достаточно, чтобы его дополнение СЕ не было А-множе-
ством. С этой теоремой был открыт новый класс множеств, —
так называемых <?Л-множеств, которые являются дополнениями
к Л-множествам, неизмеримым В. Изучение СЛ-множеств
сыграло большую роль в развитии дальнейших работ Н. Н. Лу-
Лузина в области дескриптивной теории множеств. Первоначально
доказательство теоремы Суслина было очень громоздко и ис-
использовало совокупность всех трансфинитных чисел второго
а) Множество Е обладает свойством Бэра, если на каждом со-
совершенном множестве найдется порция, на которой либо Е, либо
его дополнение СЕ есть множество первой категории.

10 ПРЕДИСЛОВИЕ РЕДАКТОРОВ
класса. Н. Н. Лузин затратил мйого усилий на то, чтобы
исключить трансфиниты из доказательства теоремы Суслина.
Для этой цели им было найдено оказавшееся чрезвычайно
плодотворным понятие об отделимости множеств, о ко-
котором мы уже говорили выше, и доказана замечательная тео-
теорема, носящая название первого принципа отдели-
отделимости: всякие два непересекающиеся А-множества отде-
отделимы В, т. е. отделимы при помощи множеств, измеримых В.
Из этой теоремы немедленно вытекает как следствие теорема
Суслина.
Вопрос об отделимости В — для СЛ-множеств был ис-
исследован П. С. Новиковым, который доказал, что суще-
существуют два СА-множества, неотделимые В. Тем самым
было выяснено, что отделимость при помощи С4-множеств
не сводится к отделимости В, как это имеет место для отде-
отделимости при помощи Л-множеств, в силу первого принципа
отделимости. Тогда Лузин сформулировал и доказал вто-
второй принцип отделимости: если из двух А-мно-
жеств ?j и ?а выбросить их общую часть, то оставшиеся
множества Et— ?а и ?2—Е1 отделимы при помощи СА-
множеств.
Стремясь сделать теорию Л-множеств и СЛ-множеств
наиболее геометрически ясной и облегчить задачу их иссле-
исследования, Н. Н. Лузин много занимался изучением различных
способов задания Л-множеств. В связи с этим изложение
теории Л-множеств в книге носит несколько особый характер.
Н. Н. Лузин совсем не излагает здесь Л-операции, той опе-
операции, с помощью которой Л-множества были открыты, но
зато находит и подробно исследует другие, более геометри-
геометрические способы задания Л-множеств. Первым из таких спо-
способов является параметрическое изображение, иначе го-
говоря,— получение Л-множества Е как непрерывного образа
пространства 0х. При этом, как мы уже указывали, Н. Н. Лу-
Лузин установил, что если непрерывное отображение взаимно
однозначно, то Е измеримо В. Затем П. С. Новиков показал,,
что если параметрическое изображение счетно-кратно (т. е.
прообраз каждой точки не более, чем счетен), то множе-
множество Е также измеримо В. Другой способ задания Л-мно-
Л-множества, лежащего в пространстве,^хх ,.,х , есть проекти-
проектирование множества, измеримого В, лежащего в простран-

ПРЕДИСЛОВИЕ РЕДАКТОРОВ 11
стве 0'хх ...х у Этот способ основан на теореме Суслина
о том, что всякое А-множество в пространстве 0х....х
есть проекция множества типа G8, лежащего в простран-
пространстве ?Jx....xy И, наконец, очень важный способ задания
Л-множества, введенный Н. Н. Лузиным, есть задание с по-
помощью элементарного решета (см. гл. III).
Все эти три способа задания множества эквивалентны
Л-операции над системой интервалов. Отметим, что в примене-
применении к более сложным множествам, в частности — уже к СА-
множествам операции проектирования и непрерывного отобра-
отображения являются более сильными, чем Л-операция и операция
решета. Если задано элементарное решето С, определяющее
Л-множество Е, то в каждой точке х дополнительного мно-
множества СЕ это решето определяет некоторый трансфинитный
индекс а. Для того чтобы множество Е было неизме-
неизмеримо В, необходимо и достаточно, чтобы его трансфи-
трансфинитные индексы были неограниченны. Множество §а тех
точек х множества СЕ, в которых трансфинитный индекс
равен определенному числу а, называется конституантой
с индексом а решета С. Все конституанты $а измеримы В.
Поэтому если множество Е неизмеримо В, то решето С
определяет разбиение СЛ-множества СЕ на tfj множеств,
измеримых В. Это обстоятельство оказалось теснейшим об-
образом связано с проблемой о мощности СЛ-множеств.
Если СЛ-множество содержит совершенное подмножество,
то среди его. конституант существует по крайней мере одна
несчетная. Если же все конституанты неизмеримого В СА-
множества не более чем счетны, то это множество состоит
из N j точек и не содержит совершенного подмножества.
Н. Н. Лузин много занимался исследованием трудностей,
связанных с проблемой о мощности СЛ-множеств. В связи
с этим он изучал структуру разбиения СЛ-множества на
конституанты. Целый ряд его работ, вышедших после пер-
первого издания рассматриваемой книги, посвящен этому во-
вопросу. На страницах своей книги Лузин высказывает мысль,
что трудности, связанные с проблемой о мощности СЛ-мно-
СЛ-множеств, носят принципиальный характер и что она не может
быть решена, исходя из принципов классической теории
множеств. В настоящее время П. С. Новиков построил

12 ПРЕДИСЛОВИЕ РЕДАКТОРОВ
С4-множество, относительно которого непротиворечиво пред-
предположение, что оно не содержит совершенного подмножества
(Труды ин-та им. Стеклова, т. XXXVIII, 1951 г.). Тем са-
самым показано, что невозможно доказать утверждение, что
всякое счетное СЛ-множество содержит совершенное под-
подмножество.
Четвертая глава посвящена теории неявных функций. За-
Задача ставится следующим образом: дана система уравнений
хп;
хт;
Fq(xit ..., хт; ylt ... , у) = О,
A)
где все F{ — функции классификации Бэра. Требуется найти
функции
Л=/«(*1. •••> **). B)
удовлетворяющие этой системе уравнений, и изучить дескрип-
дескриптивную структуру этих функций. Точнее, вопрос ставится
следующим образом: можно ли в случае, когда Fj принад-
принадлежат к классификации Бэра, удовлетворить систе-
системе A) с помощью функций B), входящих в классифика-
классификацию Бэра?
Лебег рассмотрел частный случай, когда каждой точке
пространства 0х а ... х соответствует не более одной точки
M(xit ... , хт, уи ... , ур) пространства gXi... Хтух •••vp,
координаты которой удовлетворяют системе A), т. е. когда
неявные функции определены однозначно. В этом случае
система A) имеет однозначное решение и все функции си-
системы B) принадлежат к классификации Бэра. В общем слу-
случае, когда точке пространства 0х ... х может соответ-
соответствовать более, чем одна точка пространства 0х ... х у • • -у
координаты которой удовлетворяют системе A), задача ста-
становится значительно сложнее. Легко видеть, что, вообще
говоря, система A) может иметь решения сколь угодно слож-
сложной природы. Вопрос заключается в выяснении, существует
ли решение системы' A) вида B), где все функции /< при-
принадлежат к классификации Бэра? Н. Н. Лузин придал

ПРЕДИСЛОВИЕ РЕДАКТОРОВ 13
проблеме о неявных функциях чрезвычайно ясную геометри-
геометрическую форму. Он заметил, что так как все функции Ft
принадлежат к классификации Бэра, то множество Е всех
точек пространства Ях.-'-х у • • • у , координаты которых
удовлетворяют системе A), измеримо В. Область существо-
существования неявных функций $ есть проекция множества Е в про-
пространстве Ях •••х , т. е., вообще говоря, есть Л-множе-
ство. Проблема об отыскании решения системы A) сводится
к проблеме о выделении из множества Е однозначной поверх-
поверхности, т. е. такого множества Е', которое с каждой гипер-
гиперплоскостью хх = х°, лга = лг°, ... , хт = х°т, где точка
М {х\, х\, ... ,х°п) принадлежит к $, пересекается в точно-
точности в одной точке. Эту проблему Н. Н. Лузин называет
проблемой об униформизации множества Е. Тогда задача
о неявных функциях сводится к задаче: можно ли произ-
произвести унаформизацию измеримого В множества Е при
помощи множества, измеримого В?
П. С. Новиков показал, что в том случае, когда каждая
гиперплоскость хх =¦ х\, ... , хт = х? пересекает множе-
множество Е не более, чем в счетном множестве точек, задача ре-
решается положительно, т. е.. в Е содержится однозначное
измеримое В множество Е, проекция которого в 0 х ... w
совпадает с $. Отсюда следует, что в этом случае область
существования неявных функций $ есть множество, измери-
измеримое В, и что система AJ может быть удовлетворена при
помощи функций классификации Бэра. Н. Н. Лузин доказал,
что если Е есть измеримое В множество, лежащее в про-
пространстве д х ... а, у и пересекающееся с каждой пря-
прямой, параллельной оси OY не более, чем по счетному
множеству точек, то все точки множества Е лежат
на сумме счетного множества попарно непересекающихся
однозначных поверхностей Sn измеримых В, причем, ка-
каковы бы ни были две из них St и Sj, одна из них распо-
расположена под другой.
В том случае, когда точке М{хи дг2, ... , хт) простран-
пространства Я х • • • х может соответствовать несчетное множество
1 т
значений какого-либо yit П. С. Новиков показал, что реше,-

14 ¦ПРЕДИСЛОВИЕ РЕДАКТ<М>бв
"кия B) системы A), у которого все функции ft принад-
принадлежат к .классификации Бэра, может не .существовать.
Именно, он построил такую функцию F(x, у), непрерывную
в пространстве 0ху, что уравнению
•не удовлетворяет никакая функция у==/(х), принадлежащая
к классификации Бэра, хотя областью существования неявной
функции является все пространство gj х.
Проблема неявных функций, как мы уже указывали,
тесно связана с проблемой об униформизаций множеств.
Легко видеть, что в случае, когда проекция плоского мно-
множества Е, измеримого В, на ось ОХ есть Л-множество, не-
неизмеримое В, то множество Е нельзя униформизировать при
помощи множества, измеримого В, потому что, как показал
Лузин, проекция однозначного множества, измеримого В,
есть множество, измеримое В. Из результата П. С. Нови-
Новикова о неявных функциях следует, что существует плоское
множество В, измеримое В, проекция которого в $ х совпа-
совпадает с 0 а и которое все же нельзя униформизировать при
помощи множества, измеримого В. Несколько позже Н. Н. Лу-
Лузин и независимо от него польский математик В. Серпинский
показали, что всякое множество, измеримое В, можно уни-
униформизировать при помощи СЛ-множества. Проблема об
униформизаций множеств оказалась очень важной для изу-
изучения множеств более сложной структуры, именно проектив-
проективных множеств.
Проективные множества, которым посвящена пятая и по-
последняя глава книги, были открыты Н. Н. Лузиным в связи
с исследованием трудностей, связанных с проблемой о в мощ-
мощности СД-множеств. Проективным называется множество,
которое может быть получено, отправлясь от некото'
рого множества Е, измеримого В, лежащего в простран-
пространстве gх ... х с помощью последовательного применения
конечного числа раз двух операций: проектирования в про'
странство gx ....» множества, лежащего $ простран-
пространстве 0'а ... д. ... д. (р < q ^ я) и взятия дополнения
к множеству, лежащему в пространстве ?Гх • • .ж отно-
относительно этого пространства. Н. Н. Лузин высказал

ПРЕДИСЛОВИЕ РЕДАКТО1ЮВ 15
утверждение, что для проективных множеств невозможно ни
доказать, ни опровергнуть, исходя из принципов теории мно-
множеств, утверждения, что они все- измеримы, обладают свой-
свойством Бэра и имеют мощность континуума. Утверждение
Лузина о неразрешимости в теории множеств указанных
проблем полностью не доказано до настоящего времени.
В 1950 г. П. С. Новиков построил проективное множество,
относительно которого непротиворечиво предположение, что
оно неизмеримо, и С4-множество, относительно которого
непротиворечиво предположение, что оно не содержит совер-
совершенного подмножества. Отсюда следует, что ¦ невозможно
доказать измеримость всех проективных множеств и су-
существование у них совершенного подмножества. Однако
еще не опровергнута возможность доказать теоретико-множе-
теоретико-множественными средствами существование неизмеримого проектив-
проективного множества и множества, не содержащего совершенного
подмножества.
В пятой главе книги Н. Н. Лузин ставит целый ряд
проблем о проективных множествах, в частности проблему
отделимости и проблему униформизации. Некоторые из этих
проблем были впоследствии решены (см. гл. V и примечания
к ней), некоторые остались нерешенными до настоящего
времени, причем многие из них, повидимому, также связаны
с принципиальными трудностями. Для проективных множеств
второго класса J) проблема отделимости решена П. С. Нови-
Новиковым.
Н. Н. Лузин применил проективные множества к построе-
построению резольвент для некоторых трудных проблем теории мно-
множеств. Он говорит, что проблема (Р) поставлена в резоль-
резольвенту, если построено множество Е такое, что указание
в нем точки влечет за собой решение проблемы (Р) в по-
положительном смысле, а доказательство пустоты множе-
множества Е влечет за собой решение проблемы (Р) в отрица-
отрицательном смысле. Н. Н. Лузин строит резольвенты для
некоторых проблем теории множеств. Эти резольвенты яв-
являются проективными множествами, которые построены,
') А- и С-Д-множества являются проективными множествами
первого класса. Проективными множествами второго класса яв-
являются проекции С/4-множеств и дополнения к этим проекциям.

16 ПРЕДИСЛОВИЕ РЕДАКТОРОВ
отправляясь от вполне определенных множеств, измеримых В.
В частности, Н. Н. Лузин строит резольвенту Е для проблемы
о мощности &4-множеств. Из результата П. С. Новикова
о непротиворечивости предположения, что существует СА-
множество, не содержащее совершенного подмножества, сле-
следует, что невозможно доказать пустоту резольвенты Е.
Вопрос же о возможности указать точку в Е остается нере-
нерешенным.
В конце пятой главы Н. Н. Лузин проводит подробный
анализ мемуара Лебега «Sur les fonctlons representables ana-
Jytiquement». Основной вопрос, который его интересует,—
это вопрос о дескриптивной структуре универсальной поверх-
поверхности Лебега, которую тот построил для доказательства
существования функции, не входящей в классификацию Бэра.
Н. Н. Лузин излагает здесь построение этой "Поверхности,
освободив его от целого ряда сложных деталей и придав ему
очень ясную геометрическую форму, которой не было у Лебега.
Основываясь на том, что построение поверхности Лебега
носит особый характер использования совокупности всех
трансфинитных чисел второго класса, так как здесь приме-
применяется трансфинитная индукция, идущая по всем трансфинит-
трансфинитным числам второго класса, Н. Н. Лузин предполагал, что
поверхность Лебега может оказаться множеством, выходящим
за пределы проективных множеств. Лузин считал очень важ-
важным выяснение дескриптивной структуры поверхности Лебега,
так как предполагал, что здесь можно получить новые классы
множеств, выходящие за пределы проективных множеств.
Однако впоследствии Нейман и Куратовский показали, что
поверхность Лебега представляет собой проективное множе-
множество второго класса.
Настоящая книга содержит изложение основных резуль-
результатов дескриптивной теории множеств, полученных до 1929 г..
В последней главе поставлен целый ряд новых актуальных
проблем теории множеств, направленных на изучение струкг
туры арифметического континуума. Благодаря этому эта книга
в значительной степени определила дальнейшее развитие не
только дескриптивной теории множеств, но и раздела мате-
математической логики, направленного на изучение трудностей,
связанных с некоторыми основными'проблемами теории мно-
множеств.

ПРЕДИСЛОВИЕ РЕДАКТОРОВ 1?
Перевод этой книги выполнен Н. К. Барй. Ой был сделан
еще при жизни Н. Н. Лузина. Однако Лузин не успел про-
произвести окончательное редактирование книги, и это пришлось
сделать после его смерти.
В русском переводе книги, согласно указаниям Н. Н. Лу-
Лузина, сделаны некоторые сокращения по сравнению с фран-
французским текстом.
В главе ИГ перед доказательством теоремы о сравнении
решет нам пришлось вставить новый параграф о простран-
пространственном множестве подобия для исправления неточности,
вкравшейся в доказательство теоремы о сравнении решет.
Отдельные мелкие неточности исправлены непосредственно
в тексте. Кроме того, в русское издание не включено добав-
добавление В. Серпинского, имеющееся во французском издании.
Вместо этого в русское издание включены в качестве добав-
добавлений две статьи Н. Н. Лузина, содержание которых есте-
естественно дополняет содержание книги.
2 Зж. 284. Н. Н. Луэии

Н.Н.ЛУЗИН
ЛЕКЦИИ
ОБ АНАЛИТИЧЕСКИХ
МНОЖЕСТВАХ
И ИХ ПРИЛОЖЕНИЯХ

ГЛАВА I
ОБЩИЕ ПОНЯТИЯ О МНОЖЕСТВАХ, ИЗМЕРИМЫХ В
Протяженность. Рассмотрим линейную протяженность Е.
В этой протяженности Е мы прежде всего различаем рацио-
рациональные точки; это те точки, расстояние которых от начала
координат О есть рациональное число.
Но в протяженности Е есть много других точек. Непосред-
с 1 венный пример такой точки дается нам диагональю квадрата со
стороной 1: это точка, которую мы получаем непосредствен-
непосредственным построением, не употребляя никакого арифметического
приближения.
Но протяженность Е содержит еще другие точки, кроме
рациональных и конструктивных точек. Классическим при-
примером служит неперова база е\ все эти точки даются нам
при помощи арифметических приближений ]).
Итак, протяженность Е далеко не исчерпана одними
рациональными точками, и было бы желательно иметь одно-
однородный процесс, который позволил бы определить каждую
иррациональную точку: в этом конкретный смысл теории Де-
декинда.
Цель теории множеств. Повидимому, при современном
состоянии науки является преждевременным нападать на де-
декиндовскую теорию иррациональных чисел, если только,
J) Первая трудность, которая нам представляется, относится
к существованию конструктивных точек, не имеющих никакого
арифметического приближения, а также существованию арифмети-
арифметических точек, не допускающих никакой конструкции. Не входя
в тяжелые дискуссии, я ограничился указанием на то, что суще-
существуют точки, для которых сначала дается конструкция, и суще-
существуют точки, для которых сначала дается приближение.

22 ГЛ. I. ОБЩИЕ ПОНЯТИЯ О МНОЖЕСТВАХ, ИЗМЕРИМЫХ В
желать, чтобы это нападение оказалось плодотворным, а имен-
именно дало новые положительные результаты, ускользающие от
нас в области этой теории.
Таким образом, мы ограничимся тем, что примем ее и
будем рассматривать как промежуточный инструмент, считая
возможным в дальнейшем указывать на некоторые трудности
этой теории.
Но если мы примем однородное определение иррациональ-
иррационального числа из теории Дедекинда, где иррациональное число
рассматривается как сечение, произведенное в области рацио-
рациональных чисел, независимо от его происхождения, мы по-
получаем возможность (хотя, быть может, лишь иллюзорную)
рассматривать континуум как множество, образованное из
рациональных и иррациональных точек. Таков был взгляд на
континуум, принятый a priori Г. Кантором.
Целью теории множеств является вопрос чрезвычайной
важности: можно или нет рассматривать линейную протяжен-
протяженность атомистическим образом как множество точек; вопрос
этот, кстати, уже не нов и восходит к эллинам.
Область. Порции. Начальный класс
Основная область. Для того чтобы в дальнейшем иметь
формулировки логических законов в наиболее простой форме,
мы исключили из наших рассмотрений все рациональные
точки.
, М
х *-
Черт. 1.
Следовательно, мы примем за базу рассуждений и в каче-
качестве основных элементов иррациональные числа х
— со < х < -f- оо,
рассматриваемые a priori; мы примем для "этих элементов гео-
геометрическое изображение при помощи точек М прямой }?Х.
Множество всех иррациональных точек будет называться
основной областью и обозначаться через 0 или g ж, ffy,

ОБЛАСТЬ. ПОРЦИИ. НАЧАЛЬНЫЙ КЛАСС 23
01 и т. д., если рассматривать множество иррациональных
точек, принадлежащих, соответственно, осям OX, OY, ОТ и
и т. Д.1) I1]-
В дальнейших теориях мы будем изучать множества ирра-
иррациональных точек, и относительно этих множеств мы примем
те же классические обозначения, которые принимаются для
произвольных точечных множеств.
Когда даны множества из иррациональных точек Еи Ег,
?8, ... в конечном или счетном числе, мы будем обозначать
через ?j -J- Е2 + Еъ -\- ..., Et • Е2 • Еъ ... соответственно
множество, образованное соединением Еи ?3, ?8, ..., и мно-
множество, составленное из общих точек для Еи ?2, Ег, ...
Формулы
выражают соответственно, что Et тождественно с ?2, что Е1
есть часть ?2, что Е не содержит ни одной точки.
Точно так же обозначают через Е2 — Ех множество точек,
содержащихся в ?2 и не содержащихся в Ег, причем вовсе
не предполагается, что Е1 есть часть ?2.
Наконец, мы обозначим через СЕ дополнение к Е, т. е.
множество иррациональных точек, не входящих в Е. Мы
имеем очевидное тождество
2 1 2 1*
J) Одна из основных идей, которой мы обязаны Рснэ Бэру, это
вполне ясное указание на тот факт, что все логические формули-
формулировки становятся очень простыми, если рассматривать одни только
иррациональные числа. Это он первый ввел основную область cj t
названную им пространством нулевого измерения [В a i r e, Sur
la representation des fonctions ' discontinues. ' Acta Mathem. т. 32,
1909, стр. 134.
Причина этой простоты станет ясной, если мы заметим, что
в теории Дедекинда рациональные числа даются нам непосред-
непосредственно, тогда как происхождение иррационального числа в некото-
некотором смысле вторичное.
Поэтому естественно, что получаются сложные логические за-
законы, если» рассматривать континуум как составленный из разно-
разнородных элементов: рациональных точек и иррациональных точек [2J.

24 ГЛ. I. ОБЩИЕ ПОНЯТИЯ О МНОЖЕСТВАХ, ИЗМЕРИМЫХ В
Порции. Мы назовем порцией основной области g вся-
всякое множество иррациональных точек, либо содержащихся
в интервале (а, Ь) с рациональными концами а и Ь, либо
соответственно превосходящих или меньших некоторого рацио-
рационального числа с.
В первом случае соответствующая порция области g
будет обозначена через (а, Ь), во втором и третьем случае
мы употребляем, соответственно, обозначения {с, -\- оо) и
( — со, с).
Точно так же мы будем рассматривать как порцию и
самую основную область g и обозначим ее в этом случае
через (— оо, • -j-°°)-
Вообще мы назовем порцией любого множества Е, обра-
образованного из иррациональных точек, множество тех точек из
Е, которые содержатся в некоторой порции основной области g.
Начальный класс. По определению, всякое множество Ё
из иррациональных точек входит в начальный класс или
в класс Ко, если оно является суммой конечного или беско-
бесконечного множества порций основной области g, так оке
как и его дополнение СЕ.
Преобразуем это определение.
¦ Пусть х есть любая иррациональная точка прямой Х'Х.
Только что формулированное олределение говорит нам, что х
содержится в некоторой порции (а, Ь) основной области g,
полностью принадлежащей либо к Е, либо к СЁ.
Но если мы удалим из прямой Х'Х все интервалы (а, Ь)
с рациональными концами, не содержащие одновременно
точек обоих множеств Е и СЕ, мы получим на прямой Х'Х
замкнутое множество F, образованное из рациональных точек,
и, следовательно, счетное. Ясно, что всякая порция основной
области 0, определяемая некоторым интервалом (а, Ь), смеж-
смежным к F, содержится полностью либо в Е, либо в СЕ, и
что ни один из смежных к F интервалов нельзя расширить
без тою, чтобы он нг потерял этого свойства.
Окончательно, всякое множество Е начального класса Ко
и его дополнение СЕ можно рассматривать как образо-
образованные из порций основной области g, смежных к неко-
некоторому замкнутому множеству F, составленному из
рациональных точек, причем две соседние смежные порции
принадлежат двум различным множествам^

ОПЕРАЦИИ НАД МНОЖЕСТВАМИ 26
Операции над множествами
Мы рассмотрим пять элементарных операций, при помощи
которых можно строить множества, отправляясь от уже опре-
определенных множеств.
Эти пять операций состоят в том, чтобы: совершать пере-
переход к пределу Ит над множествами Еи ?2, ...; брать
сумму + и общую часть • ; брать верхний предел Ш
и нижний предел Нт множеств Eit ?2, ...
Указанные пять операций, строго говоря, не являются не-
независимыми друг от друга, но одновременное их употребление
представляет большие преимущества.
Основная операция. Основной операцией, которая по-
послужит нам в этом исследовании, является операция перехода
к прзделу.
Назовем сходящейся последовательностью всякую беско-
бесконечную последовательность множеств из иррациональных точек
такую, что каждая иррациональная точка х прямой Х'Х или
принадлежит, или не принадлежит всем Е, кроме ограниченного
числа этих множеств, зависящего от х.
Дадим теперь основное определение: Множество Е на-
называется пределом сходящейся последовательности Еи
?2, . .., Еп, ..., если Е есть множество всех иррацио-
иррациональных точек х прямой Х'Х, которые - принадлежат
всем Еп, начиная с некоторого номера п, зависящего от х.
В этом случае мы скажем, что множество Е получено из
сходящейся последовательности Ev Е2, ..., Еп, ... при
помощи операции перехода к пределу, и это предельное
множество Е мы будем обозначать через
Ит Еп
П-> 00
или просто через
lim ?„.
„.
Из этого определения следует, что последовательность
множеств Ev ?2, ..., Еп, ... не перестает сходиться и
иметь то* же самог предельное множество Е, если мы отбро-
отбросим ограниченное число ее членов, •

26 ГЛ. I. ОБЩИЕ ПОНЯТИЯ О МНОЖЕСТВАХ, ИЗМЕРИМЫХ В
Точно так же ясно, что если данная последовательность
множеств Ev ?2, ..., Еп, ... сходится и имеет пределом мно-
множество Е, то последовательность дополнений СЕЛ, CEV ...
..., СЕп, ... тоже сходится и имеет пределом СЕ.
Наконец, заметим, что множество Е можно рассматривать
как предел множества Еп, изменяющегося вместе с п. Это
позволяет, нам применять к переходам к пределу над множе-
множествами классический принцип анализа: сумма фиксирован-
фиксированного числа k переменных множеств, имеющих пределы,
также имеет предел, равный сумме пределов составляю-
составляющих множеств:
Точно так же общая часть фиксированного числа перемен-
переменных множеств, имеющих пределы, имеет предел, равный
общей части пределов составляющих множеств:
Нш (En-El... El) = Нш Еп • lim Е\ ... lim ?*.
В заключение мы укажем одно свойство перехода к пре-
пределу, которым придется пользоваться:
Если переменное множество Еп содержится в предель-
предельном множестве Е, Еп с Е, то это предельное множество
Е тождественно с соединением всех Еп, Е = Е1-\-Е^-{-
4- ... -f- En -f- .. . Обратно, если переменное множество
Еп содержит предельное множество Е, Еп з Е, то это
предельное множество Е тождественно с общей частью
всех Е„, Е = Et • ?2 • • •
Монотонцые последовательности множеств. Последова-
Последовательность множеств Е1У Е%, ... называется возрастающей,
если каждый из ее членов содержится в следующем:
?:, с ?2 с ... Возрастающая последовательность всегда схо-
сходится и имеет пределом Е сумму всех Еп, ? = Ej-j-f^ -\-...
Последовательность множеств Ev Е%, ... называется убы-
убывающей, если каждый из ее членов содержит следующий:
El ^ Es =э ... Убывающая последовательность множеств также
сходится и имеет пределом Е общую часть всех Еп,
Е = Е1-Е%...
Убывающие и возрастающие последовательности множеств
называются- монотонными.

ОПЕРАЦИИ НАД МНОЖЕСТВАМИ 27
В. Юнг первый употребил монотонные последовательности
множеств, как инструмент для построгния множеств все более
и более сложных.
Другие операции. Рассмотрим бесконечную последова-
последовательность множеств
?ц -^2> • • • >
образованных из иррациональных точек основной области 0х.
Мы будем производить над этими множествами следующие
четыре операции:
I. Сумма. Эта операция ставит в соответствие всякой
бесконечной последовательности множеств Et, Е2, ... их
соединение Ег-\-Е2-\- ..., т. е. множество, образованное из
точек, принадлежащих по крайней мере одному из множеств Еп.
Так полученное множество Е1 -j- Е% -\~ ... называется суммой
данных множеств. '
Чтобы выразить тот факт, что множества Ех, Е^, ... не
имеют попарно общих точек, мы скажем, что множество
5 = ?, -f- Е2 4" • • • есть сумма а узком смысле и что 5
получено из Еи ?2> • • • ПРИ помощи сложения в узком
смысле.
Если множества Et могут иметь общие точки, множество
5 будет называться суммой в широком смысле; в этом слу-
случае мы скажем, что S получено из Еу, Е%, ... при помощи
сложения в широком смысле.
Ясно, что множество-сумма Е = Ех -j- ?2 -\- ... не зави-
зависит от порядка слагаемых множеств Et.
Сложение счетного числа множеств сводится опять
к переходу к пределу.
В самом деле, когда дана бесконечная последовательность
Еи ?, ..., Еп, ..., мы можем получить, из нее другую по-
последовательность множеств Sj, 52, ..., Sn, ..., полагая
Так как последовательность 5,, S2, ..., Sn, ... есть возра-
возрастающая, то она сходится к некоторому предельному множе-
множеству S, и мы, очевидно, имеем
И. «Общая часть. Эта операция дает множество,
образованное из общих точек всех множеств данной беско-

28 ГЛ. I. ОБЩИЕ ПОНЯТИЯ О МНОЖЕСТВАХ, ИЗМЕРИМЫХ В
нечной последовательности Еи Е2, ..., Еп, ... Так получен-
полученное множество Е называется общей частью данных мно-
множеств Elt E%, ...; мы обозначим эту операцию символом
Е — Е • Е или Е Е
Общая часть Е также не зависит от порядка составляю-
составляющих множеств Еп.
Общая часть счетного числа множеств также сво-
сводится к переходу к пределу.
В самом деле, если мы положим
р р р р р п р р р
то последовательность множеств Р, з Р2 г>, ..., э^э...
есть, очевидно, убывающая, а потому она сходится к неко-
некоторому определенному предельному множеству Р. Ясно, что
р — р , р р
III. Верхний предел последовательности мно-
множеств. Пусть дана бесконечная последовательность мно-
множеств Еи ?2> ..., Ёп, ... Мы называем верхним пределом
последовательности множеств ?,, Е2, ..., Еп, ... множе-
множество Е, образованное из точек, каждая из которых принадле-
принадлежит бесконечному множеству из множеств Еп.
Мы будем обозначать верхний предел последовательности
множеств через
lim En или \imEn.
Из определения вытекает, что всякая последовательность
множеств Еи Е%, ... имеет верхний предел и что можно пре-
пренебрегать порядком членов последовательности и ограничен-
ограниченным числом их без того, чтобы изменить верхний предел.
Операция III, состоящая в том, чтобы взять верхний пре-
предел, сводится к операциям сложения и взятия общей части
по формуле:
Отсюда мы немедленно заключаем, что операция Hm?n
сводится к выполнению двух последовательных простых

бпЗДАЦИЙ НАД МНОЖЕСТВАМИ 2?)
Переходов к пределу с двумя различными индексами, так как
если Епт обозначает общую часть конечных сумм
• • • \^п ~Г • • • "Г" ^i»)»
то мы, очевидно, имеем
lim..En= lim lim Enm.
и->со т-*со
Тем не менее интересно заметить, что операция Tim вовсе
не эквивалентна совокупности двух последовательных
простых переходов к пределу с различными индексами
lim lim. Мы увидим, что среди множеств, получающихся
двойным применением простого перехода к пределу, боль-
большинство не может быть получено при помощи операции lim,
произведенной только один раз.
С другой стороны, операция limfn охватывает, как част-
частный случай, основную операцию lim, так как если данная
последовательность множеств Elt Е2, ..., Еп, ... сходится,
то верхний предел lim?n, очевидно, совпадает с пределом
)imEn этой последовательности.
В дальнейшем мы уточним границы применимости опера-
операции lim?n (стр. 77 этой книги).
IV. Нижний предел. Пусть-дана бесконечная после-
последовательность множеств Еи ?2> • • •» мы назовем нижним
пределом для Еи ?2> • • • множество Е, образованное из ирра-
иррациональных точек х, для каждой из которых можно опреде-
определить такое я, что эта точка принадлежит Еп, Еп+1, En+i, ...
Нижний предел Е мы будем обозначать через lim En или
|»->0О
Ит?я.
Ясно, что нижний предел Е тоже не зависит ни от порядка
членов последовательности Еи Е2> •. •, ни от конечного числа
этих членов.
Операция IV, limEn, также сводится к операциям сложе-
сложения и взятия общей части по формуле
и, следовательно, сводится к двум простым переходам к пре-

30 ГЛ. I. ОБЩИЕ ЛОНЯТЙЯ 6 МНОЖЕСТВА*, ИЗМЕРИМЫХ В
делу lim lim. Но эта операция опять-таки не эквивалентна
П->ОО «1-Х»
последовательному двукратному переходу к пределу. Мы уви-
увидим в дальнейшем, какова область применимости этой опера-
операции (стр. 77 этой книги).
Сравнение введенных операций. Чтобы сравнить опе-
операции над множествами Еи ?а, ..., мы заметим, что общая
часть этих множеств есть часть нижнего предела lim En,
которШ содержится в верхнем пределе НтЕп. С другой сто-
стороны, верхний предел есть часть суммы множеств Ех-\-Е%-{-.¦.
и, таким образом, мы имеем одновременно выполненные не-
неравенства
Р с. lim Е„ с пт Еп с S.
Важно заметить, что в общем случае нижний предел lim En,
составляя часть верхнего предела lim?n, вовсе с ним не со-
совпадает. Множества ИтЕп и lim?n совпадают в том и
только в том случае, когда последовательность множеств
Еи ?2> • • • сходится: в этом случае оба предельных множе-
множества совпадают с единственным пределом lim?n этой после-
последовательности.
Наконец, можно заметить, что верхний предел Нт Еп мно-
множеств ?j, ?2, ... есть дополнение к нижнему пределу допол-
дополнений СЕи СЕ%, ...; то же справедливо, если переставить
слова верхний и нижний:
Характеристические функции. Мы теперь определим
характеристическую функцию множества, введенную Валле-
Пуссеном J). Введение этого понятия очень полезно для обыч-
обычной интерпретации предельных операций над множествами.
Назовем характеристической функцией множества Е
функцию f(x), определенную в основной области 0', равную 1
для точек Е и равную 0 всюду вне Е.
Обратно, всякая функция f(x), определенная «а 0 и
принимающая лишь значения 0 и 1, есть характеристи-
х) Ch. de la Vallee-Potissin, Sur 1'integrale de Lebesgue
(Trans. Araer. Maih. Soc, ,1915).

нАд множествами . Si
веская функция для множества Е точек X, для которых
Рассмотрим бесконечную последовательность множеств
р р р
и их характеристические функции
Из определения сходимости последовательности множеств
вытекает, что для того, чтобы последовательность характери-
характеристических функций !?j,-<рз» ••• была сходящейся в класси-
классическом смысле математического анализа, необходимо и
достаточно, чтобы последовательность соответствующих мно-
множеств Ej, Е$, ... была сходящейся в ранее определенном
смысле. В этом случае предельная функция <p = lkn<pn есть
характеристическая функция для предельного множества
Е = Нт Еп.
Если последовательность множеств Еи ?2> • • • не есть
сходящаяся, то последовательность соответствующих характе-
характеристических функций <pj, <р2,... расходится фактически
в каждой точке X множества-разности
\imEn—Hm?n
и только в этих точках.
В этом случае, если принять обычные обозначения Нт <рп
п-*оо
и Нт <рп для верхнего предела и нижнего предела последо-
п->оо
вательности функций <р1} <р2, ..., то ясно, что Нт <рп есть
п-»оо
характеристическая функция для верхнего предела lim?n
последовательности множеств Еи Я2, ... и, соответственно,
Нт <рп есть характеристическая функция для нижнего пре-
П-+ОО
дела Нт Еп.
Можно ааметйть, что характеристическая функция в отно-
отношении других операций обладает следующими свойствами *):
Если <р есть характеристическая функция множества Е,
то 1 — ? есть характеристическая функция дополнения СЕ
х) Gh. de la Vallee-PoussJn, Integrales de. Lebesgue, ion-
Ctiotis d'ensetnble, classes de Baire, ctp. 7.

§2 ГЛ. I. ОБЩИЙ ПбНЯТИЯ О МНОЖЕСТВАХ, ИЗМЕРИМЫХ В
к множеству Е; если «pi» ?2» • • • СУТЬ характеристические
функции для Е1г ?2, ..., то их бесконечное произведение
<Pi ¦ ?2 • • • есть характеристическая функция для общей ча-
части ?t-?^...
Так как дополнение к бесконечной сумме Et -j- ?2 -f- ...
есть общая часть дополнений: СЕХ- СЕ2..., то мы заклю-
заключаем, что характеристическая функция для бесконечной суммы
Ег -\- ?2 -\- ¦. • моЖет быть представлена в форме сходяще-
сходящегося аналитического выражения 1 — A — <pj) A — <р2)...; если
множества Е1г ?2, -.. попарно без общих точек, то харак-
характеристическая функция для их суммы Et -|- ?2 -j- • • • сводится
к сходящемуся ряду <pj (х) -\- <р2 (д:) + ...
Наконец, множество-разность ?2—Ег имеет характери-
характеристическую функцию <р2 — <Pi<p2> так как эт0 множество может
быть представлено в виде ?2 • CEV
Алгебраическое обозначение
Полиномы, образованные из множеств. Это понятие
часто бывает удобно для доказательств. Его введение осно-
основывается на следующем замечании.
Знаки алгебраической логики естественно вводятся в опе-
операции над множествами, так как они обладают свойствами,
аналогичными арифметическим операциям.
Мы уже видели, что для того, чтобы выразить, что мно-
множество Ei содержится во множестве ?, уславливаются писать
Еу с ?2 или ?2 гэ Ех.
Сложение Ех~\-Е^-\- ... и вычитание Е$ — Е1 множеств
соответственно аналогичны сложению и вычитанию конечных
величин. Общая часть Е1- ??2... аналогична произведению
чисел; по этой причине часто называют умножением опера-
операцию, состоящую в том, чтобы взять общую часть заданных
множеств ?j, Es, .. i Образование дополнения СЕ некоторого
множества Е есть частный случай вычитания.
Умножение и вычитание сводятся к сложению при помощи
дополнений; это замечание часто бывает ценным при доказа-
доказательствах. В самом деле, имеем

АЛГЕБРАИЧЕСКОЕ ОБОЗНАЧЕНИЕ 33
Сложение и умножение коммутативны, ассоциативны, ди-
дистрибутивны, как соответствующие операции арифметики.
Например, мы имеем
?-1 ' ?-2 == ^2 ' ¦*'1> (~ " / * ^З === **1 ' ("а ' А$)»
Все правила алгебраических вычислений над полиномами
с положительными членами могут, следовательно, применяться
к полиномам, образованным из множеств.
Установив это, рассмотрим любой полином
Р (х1г лг2, ..., хп)
относительно лгп х2, ..., хп) все члены которого имеют коэф-
коэффициенты, равные 1. Если заменить буквы хи лг2, ..., хп
соответственно любыми точечными множествами Еи ?2) ..., Еп
и рассматривать знаки операций -j- и • как сумму и общую
часть в области множеств, то полином Р становится вполне
определенным множеством точек, которое мы обозначим
через
Р(Еи ?2, ...
Смысл Р(Еи ..., Еп) нисколько не зависит от порядка
членов полинома Р.
Указанные правила уже неприменимы, если имеются отри-
отрицательные члены, так как вычитание множеств не обладает
ни ассоциативностью, ни коммутативностью. Лишь дистрибу-
дистрибутивный закон сохраняется:
Тем не менее, если полином
Р(хи х2, ..., хп)
имеет коэффициенты, равные -f-1 или —1, и если первый
член полинома Р положителен, то можно сохранить интер-
интерпретацию для
Р(Еи ?2, .... Еп)
в области множеств, если условиться полагать
3 Зак. 284. Н. Н. Лузин

34 ГЛ. I. ОБЩИЕ ПОНЯТИЯ О МНОЖЕСТВАХ, ИЗМЕРИМЫХ В
где буквы U, V, W—любые множества точек. Но в этом
.случае смысл выражения Р(Еи Е2, ..., Еп), разумеется,
зависит, от порядка членов полинома P{xv л:2, ..., хп).
Ряды .множеств. Для дальнейшего мы введем понятие
ряда множеств г).
Назовем рядом множеств бесконечный символ
где буквы ип обозначают множество точек, которому пред-
предшествует знак -j- или —.
Множество точек, которое получается, если отбросить знак
члена ип, будет называться абсолютной величиной ип; это
множество мы обозначим через
Мы скажем, что некоторый ряд множеств
сходится, если сходится последовательность множеств
"И > " - '» "»i • ¦ ¦ >
где Sn есть сумма п первых членов ряда. В этом случае
предельное множество S для этой последовательности будет
называться суммой ряда их -\- н2 -(-..., и мы будем писать
равенство
В дальнейшем,мы рассматриваем только сходящиеся ряды;
у этих рядов первый член и1 есть множество точек, пред-
предшествуемое знаком -J-, так как в противном' случае сумма Sn
первых п членов предложенного ряда не имела бы никакого
смысла.
Знакочередующиеся ряды множеств. Займемся убываю-
убывающими знакочередующимися рядами множеств: это ряды вида
!) Мы вводим понятие ряда множеств, чтобы облегчить формаль-
формальный ход рассуждений. " - - ' - ¦ -

АЛГЕБРАИЧЕСКОЕ ОБОЗНАЧЕНИЕ 35
где множества Еи ?2> • • • образуют убывающую последо-
последовательность
Для этих рядов множеств мы имеем предложение, вполне
аналогичное предложению классического анализа о числовых
знакочередующихся рядах:
Теорема. Для того чтобы убывающий знакочере-
знакочередующийся ряд множеств Ех—Е^-\-Еь—Ei-)-... был
сходящимся, необходимо и достаточно, чтобы общий член
этого ряда стремился к нулю, когда я неограниченно
возрастает, т. е, чтобы ми имели
Ига Еп = 0.
п
Условие необходимо. В самом деле, так как последова-
последовательность множеств Еи Е2, ... есть убывающая, множе-
множество Еп стремится к вполне определенному пределу Е,
когда я неограниченно возрастает, Е = Ит Еп. Кроме того,
известно, что этот предел Е должен совпадать с общей
частью множеств Elt Е%, ..., и, таким образом, мы имеем
Если переменное множество Еп не стремится к нулю,
когда я неограниченно возрастает, то предельное множество Е
эффективно содержит точки. Но если некоторая точка при-
принадлежит к Е, то она принадлежит ко всем членам ряда—¦
множествам Еп. Отсюда следует, что точка х принадлежит
ко всем множествам Sn для нечетного п и не принадлежит
ни одному из множеств Sn с четным я, где Sn есть сумма я
первых членов предложенного знакочередующегося ряда
Е1 — Е2-\-Е3 — Ei-\-... Отсюда мы заключаем, что после-
последовательность Su 52, ..., Sn, ... расходится, а, значит, и
знакочередующийся ряд также.
Условие достаточно. В самом деле, какова бы ни была
иррациональная точка х основной области g, принадлежа-
принадлежащая множеству Ех, можно найти целое положительное я
такое, что х принадлежит к Еп, но не принадлежит к En+t.
Отсюда мы заключаем, что если я нечетно, то х принадлежит
всем множествам Sn, Sn+1, Sn+2> • • • и что х не
3*

36 ГЛ. I. ОБЩИЕ ПОНЯТИЯ О МНОЖЕСТВАХ, ИЗМЕРИМЫХ В
принадлежит ни одному из множеств Sn, Sn+1, Sn+2, ..., если
п четное. Если же х не принадлежит Elt то она не принад-
принадлежит ни одному из множеств Slt S2, ... Значит, последо-
последовательность множеств Slt S2, ..., Sn, ... сходится, а это
и доказывает сходимость предложенного знакочередующегося
ряда. Ч. т. д.
Важно заметить, что сумма S знакочередующегося схо-
сходящегося ряда множеств
может, быть представлена в следующих двух «идах:
S = El — (?2 — ?8)-(Е4 — Еь)— ...,
где все множества-разности, написанные в скобках, не
имеют попарно общих точек.
Из первой формулы следует, что множество S есть пре-
предел возрастающей последовательности множеств, но вторая
формула показывает, что 5 есть в то же время и предел
убывающей последовательности множеств.
Понятие множества, измеримого В
Одним из понятий наибольшей важности в математическом
анализе является концепция множества, измеримого В х). Это
множества, которые получаются из порций основной
области 3 с помощью следующих двух элементарных
операций, повторяемых бесконечное множество раз:
1° Взятие разности двух множеств Et и Е2 уже
определенных и таких, что каждая точка Ех принад-
принадлежит к Е2
Еъ — Ev (D)
2° Взятие суммы бесконечного числа множеству Еи
Е2, ..., Еп, ... уже определенных и попарно без общих
точек:
.. E)
1) Эти множества рассмотрены впервые Э. Борелем в его книге
«Lecons sur la theorte des fonctlons», 1898, гл. III.

ПОНЯТИЕ МНОЖЕСТВА, ИЗМЕРИМОГО В 37
Это определение множества, измеримого Bi тесно связано
с самим возникновением этих множеств ]). Можно дать опре-
определению следующую форму:
Мы скажем, что множество точек Е измеримо В,
если мы умеем получить счетную вполне упорядоченную
последовательность множеств, имеющую множество Е
своим последним членом, и каждый член которой, не
являющийся порцией области 0', есть результат опера-
операции вычитания (D) или операции сложения (S) в узком
смысле, произведенной над предыдущими членами
?р р р \ р
Это определение, к которому мы естественно пришли,
без сомнения, покажется более ясным, если мы отметим, что
множества ?р, предшествующие ? и не являющиеся порциями
области 3, оказываются предварительными множествами,
которые нужно приготовить заранее, чтобы получить резуль-
результирующее множество Е.
Если мы будем стараться сделать это определение более
«экономным», т. е. избегающим тех предварительных мно-
множеств, которые не являются строго необходимыми для оп-
определения результирующего множества Е, то нужно ввести
следующее дополнительное условие: невозможно удалить из
этой вполне упорядоченной последовательности Ео, Еи ...
..., Ер, ... | ? ни одного члена, кроме Е, без того, чтобы
эта последовательность утратила свое основное свой-
свойство : каждый из ее членов определим при помощи предыду-
предыдущих членов.
Это дополнительное условие исключает множества, пол-
полностью инородные по отношению к множеству Е, т. е. те,
знание которых нисколько не необходимо при окончательном
образовании множества Е.
Но здесь речь не идет о классе множества Е, измери-
измеримого В, т. е. не о таком новом условии: вполне упорядочен-
упорядоченная последовательность Ео, Еи ..., Е$, ... \Е, предна-
предназначенная для определения множества Е, должна быть
наиболее короткой, т. е. соответствующей наименьшему
трансфинитному числу.
*) См. о проблеме меры Бореля, стр. 47. (Прим. ред.)

38 ГЛ. I. ОБЩИЕ ПОНЯТИЯ О МНОЖЕСТВАХ, ИЗМЕРИМЫХ В
Преобразования определения множества,
измеримого В
Характер основных операций. Операция (S), состоящая
в том, чтобы взять сумму счетного множества уже опреде-
определенных множеств, имеет положительный характер, так как
точки, из которых образована сумма f:j-j-E2-J- ..., даны
положительным образом :).
Точно так же мы можем рассматривать как положитель-
положительную операцию (Р), состоящую в том, чтобы взять общую
часть счетного множества уже определенных множеств.
Напротив, операция (D), состоящая в том, чтобы взять
разность двух множеств, при помощи которой строятся мно-
множества, измеримые В, есть, безусловно, отрицательная, так
как мы образуем разность Е2 — Ev беря точки ?2, кото-
которые не принадлежат данному множеству Ег 2).
Но если указывают некоторое множество точек, то почти
всегда указывают все точки, ему принадлежащие, без того,
чтобы дать критерий, позволяющий узнать, принадлежит ли
произвольно взятая точка этому множеству или нет. В самом
деле, мы увидим в дальнейшем примеры, где для того, чтобы
узнать, принадлежит ли данная точка рассматриваемому мно-
множеству, надо совершить несчетное множество не зависящих
друг от друга операций, или же, где даже нет никакого
регулярного процесса8). То, что мы сказали, достаточно,
1) Мы, естественно, предполагаем, что точки каждого члена Еп
названы при помощи положительною свойства.
. 2) Если Ег есть множество конкретных предметов, то ясно, что,
вычитая из Е% некоторую часть, мы получим остаток вполне реаль-
реальный. 'Но' если Е2 есть бесконечное множество, то нисколько не
очевидно, что, вычитая из Е% бесконечное множество его элементов,
мы получим остаточную часть, имеющую некоторое определение
(положительное свойство). Это некоторого рода постулат, который,
на мой взгляд, очень мало вероятен. •
8) Если некоторая функция /(дг) рассматривается как заданная,
то естественно считать заданным и множество Е значений f(x).
Но ничто, на мой взгляд, не оправдывает распространение этого
взгляда на дополнения к «данным» множествам, если мы не можем
преобразовать отрицательное определение такого множества в по-
положительное определение. В то время как мы получаем все эле-
элементы Е, производя операцию/над веема действительными числами,
мы не имеем никакого, регулярного процесса, чтобы узнать, при-

ПРЕОБРАЗОВАНИЯ ОПРЕДЕЛЕНИЯ 5-МНОЖЕСТВА . 39
чтобы предвидеть большие трудности, связанные с. операм
цией (?>).•
Как частный случай операции вычитания (D) -мы рассма-
рассматриваем операцию (С) перехода от данного множества Е
к его дополнению СЕ, так как для получения дополнения СЕ
достаточно взять множество-разность 0—Е, где д есть:
основная область. ¦ . . : .:
Таким образом, мы естественно приходим к тому, .чтобы
поставить следующий вопрос: узнать, можно ли получить,
всякое множество, измеримое В, . при помощи положи-
положительных операций и, в частности, при помощи операций:
суммы (S) и общей части (Р).
Речь, следовательно, . идет о преобразовании определения
множества, измеримого В.
Образование множеств, измеримых В, при помощи
операций (S) и (Р). Мы сначала покажем, что любое дан-
данное-измеримое В-множество можно получить, отправляясь
от порций основной области Ц', при помощи двух опе-
операций: суммы в узком смысле (S) и общей части (Я),
неограниченно повторенных.
Чтобы доказать это предложение, мы заметим следующее:
сказать, что некоторое множество Е получено из порций
области 3 при помощи операций (S) и (Р), неограниченно
повторенных, это значит сказать,, что Е есть последний член
счетной вполне упорядоченной последовательности $0, §>и
?2, ..., $-, ... | Е, каждый член которой, не являющийся
порцией области g, получается из предыдущих членов, или.
при помощи операции (S), или же при помощи операции (Р)..
Установив это, мы можем во вполне упорядоченной послет
довательности Ео, Ev Е2, ..., Е$, ... \ Et служащей для
определения данного множества Е, измеримого В, поставить
непосредственно перед каждым членом Е$ его дополнение СЕ$;
надлежит ли данное действительное число _у<> к дополнению к ? или
нет, и можнохильно сомневаться, чтобы удалось дать общее решение
этой проблемы. Если функция / (дг) есть проективная, то надо про-
произвести множество операций, мощность которого континуальна,-и
много шансов за то, что эти попытки будут независимы друг от
друга, хотя / и определена при помощи перечислимого множества
условий. См. N. L u sfn, Remarques 8ur les ensembles projecttfs,Comp-
tes Renjlus, стр. 835—837, 192'T, ... . , ; :

40 ГЛ. I. ОБЩИЕ ПОНЯТИЯ О МНОЖЕСТВАХ, ИЗМЕРИМЫХ В
если Ер есть порция области 0', то дополнительное множе-
множество СЕр, вообще говоря, состоит из двух порций обла-
области 0 и, в этом случае, мы перед СЕр поставим эти две
порции.
Ясно, что этим способом мы получим вполне упорядочен-
упорядоченную счетную последовательность $0, &1( Ё2, ..., &v .. . \ Е,
имеющую Е своим последним членом.
Я теперь утверждаю, что последовательность $0, 8,,'. ..
...,$-,... | Е, полученная таким способом, служит для опреде-
определения множества Е, отправляясь от порций области 0, при
помощи операций (S) и (Р), неограниченно повторенных.
В самом деле, если & не есть порция области 0', мы
имеем либо $т = Е$, либо &т = СЕ$. Следует различать два
случая. В первом случае мы имеем Ер = Ер ~\- Е$ -j- ...,
где {^ < р. Отсюда следует, что СЕр = СЕ$ • СЕ$ ... Из
этого мы заключаем, что & определимо при помощи опера-
операции (S) или операции (Р), примененной к счетному числу
множеств &,-, предшествующих §r, Y < f. Во втором слу-
случае мы имеем Ер = Е$ —Ер, где f^ и C2 меньше р. В этом
случае мы можем написать Ер = Ер • СЕр и СЕр = CEpj -\- Ер .
Из этого мы заключаем, что &. получается применением
одной из двух операций (S) и (f1) к предшествующим мно-
множествам iT', ^<т- Ч. т. д.
Более важным является следующее предложение: всякое
множество Е, получаемое, отправляясь от порций об-
области 0', при помощи двух операций: суммы в широком
смысле (S) и общей части (Р), повторенных неограниченно,
измеримо В.
Чтобы доказать это, возьмем вполне упорядоченную счет-
счетную последовательность множеств «
''О» ^1> ^*9> •••» Е$, ...\Е, A)
служащую для определения множества Е при помощи опера-
операций (S) и (Р), отправляясь от порций области 0.
Назовем нормальным всякий член этой последователь-
последовательности такой, что общая часть этого члена (или его дополне-
дополнения) и некоторых предшествующих множеств (или их допол-
дополнений), взятых в конечном числе, может быть определена,
отправляясь от порций области 0, при помощи операций:

ПРЕОБРАЗОВАНИЯ ОПРЕДЕЛЕНИЯ В-МНОЖЕСТВА 41
E) в узком смысле и операции (С), позволяющей переходить
от множества к его дополнению.
Ясно, что нормальные члены существуют: таковым является
каждый член Еп последовательности A) с конечным индек-
индексом я потому, что в этом случае Еп и все предшествующие
члены состоят из конечного числа порций области $,
Я теперь утверждаю, что каждый член последователь-
последовательности A) нормален.
Чтобы доказать это предположим, что существуют анор-
анормальные члены. Пусть Е$ — первый из них. Так как каждый
член последовательности A) может быть получен при помощи
операций (S) и (Р), примененных к предыдущим членам,
нужно различать два случая.
В первом случае мы имеем ?? = Е$ -f- E$ -j- ..., где
Pj < [32 < ... все меньше |3.
Так как Е§ — анормальный член, то среди множеств
[Шр- • ПСЕу. • Е9 и "ПЕр- • TLCEr • СЕ?,
где два первых сомножителя обозначают, соответственно, об-
общие части множеств Ер и дополнений к множествам Е$»,
предшествующим ?э, §' < J3 и [3" < |3, найдется по крайней
мере одно множество, которое нельзя получить, отправляясь
от порций области 3 при помощи операций (S) в узком
смысле и (С).
Но мы можем написать
и, следовательно,
= 2 ПЕ9- • ПСЕ», • СЕ« -СЕ? ... СЕ* - Еп.
П=1 1 2 n-1¦
Так как все члены последовательности A), предшествующие Е9,
нормальны, мы заключаем, что множество ILEp/ • ПС?р» • Е$
получается из порций области 0 при помощи операций (S)
в узком смысле и (С).
Остается лишь рассмотреть множество ЕШр- • ПС?р» »СЕ$+
Но мы можем записать это множество в виде
С[С(ПЕг-ЛСЕг)-\-Е9]

42 ГЛ. I. ОБЩИЕ ПОНЯТИЯ О МНОЖЕСТВАХ, ИЗМЕРИМЫХ В
и, следовательно, представить его в виде
оо
С [С(ПЕ?> • ПСЯр.) + 2 1Щ}' • ПСЕ9' • СЕ?1.,. СЕ^ - E9J.
Так как все члены последоватзльности A)? предшествую-
предшествующие Е$, нормальны, то написанное множество может быть
задано, отправляясь от порций области 0 при помощи опе-
операций: (S) в узком смысле и (С).
Во втором случае мы имеем Ер = Ел • Е$ ..., что дает
нам
и, следовательно,
• ЛСЕГ
| ^ • ??2 ... ?Pn_t • СЕК].
Отсюда легко заключить, как и в предыдущем случае,
что множества НЕу . ЦСЕ$<г • СЕ$ и ПЕу • ПСЁр» • Ер опре-
определимы, отправляясь от порций области g при помощи опе-
операций: (S) в узком смысле и (С).
Таким образом, мы пришли к противоречию, а это пока-
показывает, что каждый член последовательности A) нормален.
Установив это, возьмем множество Е. Если мы имеем
Е ~ Ел .-J- ?р -\- ..., то можно писать '
Так как член Е$ последовательности A) нормален, то каждый
член этого ряда определяется при помощи (S) в узком смысле
и'(С), отправляясь от порций области д. Значит, это спра-
справедливо и для самого множества Е и, следовательно, оно
измеримо В, ¦¦¦.'..._...

ПРЕОБРАЗОВАНИЯ ОПРЕДЕЛЕНИЯ ^-МНОЖЕСТВА , 43
Если мы имеем Е = Е$ • Е$ ... Ер ...., то можно Писать
l
а так как член Ер последовательности A) нормален, то мы
вынуждены заключить, что множество СЕ, а значит, и' само
множество Е определимо при помощи операций E) в узком
смысле и (С), отправляясь от порций области 0. Итак,
Е измеримо В *), ч. т. д.
Одним из следствий этого является то, что всякое мно-
множество, измеримое В, может бить получено, отправляясь
от порций основной области 0, при помощи следующих
двух операций, неограниченно повторенных:
1° Составление суммы бесконечного числа уже опреде-
определенных множеству Еи Е2, ..,, Еп, ... без общих частей
+ ...; E)
2° Взятые дополнения к данному множеству Е
СЕ. ¦ (С)
Образование множеств, измеримых В, при помощи
переходов к пределу. Мы хотим теперь изучить связь между
понятием множества, измеримого В, и другими операциями.
Прежде всего мы имеем следующее важное предложение,
которое позволяет получать множества, измеримые В, рас-
рассматривая лишь монотонные последовательности множеств:
Множество, которое можно получить, отправляясь
от множеств начального класса Ко при помощи переходов
к пределу, применяемых каждый раз к монотонной
]) Эта теорема чрезвычайно важна, так как она показывает
нам, что в определении множества, измеримого В, можно одни
операции заменять другими. Самая важность теоремы, мне кажется,
заставляет отметить один пункт в данном доказательстве: мы непо-
непосредственно образовали вполне упорядоченную последовательность,
которая служит для определения множества, измеримого В при по-
помощи операций E) и (Я); но, когда такая последовательность дана,
мы не умеем непосредственно получить вполне упорядоченную
последовательность, которая служит для определения рассматривает
мого множества при помощи операций E) и (С). Ход рассуждения
в этом случае очень косвенный.

44 ГЛ. I. ОБЩИЕ ПОНЯТИЯ О МНОЖЕСТВАХ, ИЗМЕРИМЫХ В
последовательности множеств и неограниченно повторен-
повторенных, есть множество, измеримое В; обратно, всякое множе-
множество, измеримое В, может быть получено этим способом.
Первая часть этого предложения вполне очевидна, так
как предел монотонной последовательности множеств Ev
Ez, ... есть либо сумма этих множеств, либо их общая
часть. Следовательно, если множество Е может быть полу-
получено при помощи пределов монотонных последовательностей,
отправляясь от множеств начального класса Ко, то множе-
множество Е может быть получено и при помощи двух операций
(S) и (Р), отправляясь от порций области 0. Поэтому
в силу предыдущей теоремы Е измеримо В.
Чтобы доказать вторую часть предложения, возьмем
вполне упорядоченную счетную последовательность
¦^0' ^1» ^2 Щ-> • • •> | Е, A)
служащую для определения заранее данного множества Е,
измеримого В при помощи операций (S) и (Р), неограниченно
повторенных, отправляясь от порций области 0'.
Назовем нормальным всякий член Еа последовательности A)
такой, что каждое множество-полином Р(Е^, Е§«, ..., Е§),
образованное из конечного числа членов последовательности A)
с индексами, не превосходящими |3, может быть получено,
отправляясь от множеств начального класса Ко при помощи
переходов к пределу, примененных к монотонным последо-
последовательностям множеств. Ясно, что существуют нормальные
члены, так как таковым является начальный член Ео.
Я теперь утверждаю, что каждый член последователь-
последовательности A) нормален. В ?амом деле, в противном случае суще-
существуют анормальные члены; пусть Е$ — первый из них. Сле-
Следует различать два случая.
В первом случае мы имеем
где pj < j?2 < ... предшествуют р. Обозначим через Sn
сумму п первых членов этого ряда. Бесконечная последова-
последовательность 5„ S2, ..., Sn, ... очевидно, возрастающая, и
мы имеем
5П.

ПРЕОБРАЗОВАНИЯ ОПРЕДЕЛЕНИЯ В-МНОЖЕСТВА 45
Пусть Р(Ер, Е$»,..., ??) — любое множество-полином,
образованное из конечного числа множеств последователь-
последовательности A) с индексами, не превосходящими р. Мы, очевидно,
имеем
• Р(ЕУ, Ег Ef)= lim P{EV, Еу SJ,
n->oo
причем важно заметить, что множества Р(Еу, Е$», ..., Sn)
образуют при неограниченно возрастающем п возрастающую
последовательность множеств, так как Sn растет. Следова-
Следовательно, операция lim здесь применена к случаю монотонной
последовательности.
С другой стороны, множество-полином Р(Ер, Е$«, ..., Sn)
может быть» записано в форме
Мы видим, что это множество-полином образовано из
множеств с индексами строго меньшими, чем р. Отсюда сле-
следует, что множество Q может быть определено, отправляясь
от множеств класса Ко, при помощи монотонных переходов
к пределу и, следовательно, то же справедливо и для мно-
множества-полинома Р{Еу, Еу, ..., Е$). Значит, ?? есть нор-
нормальный член последовательности A), что противоречит нашей
гипотезе.
Во втором случае мы имеем
Е9 — E?i-E9i...,
где j3j < j32 < ... предшествуют р. Обозначим через яи
общую часть п первых членов последовательности Ел, Е§, ...
Бесконечная последовательность izu it2, ..., itn, ..., очевидно,
убывающая, и мы имеем
?р= lim яя.
Как и в предыдущем случае, мы можем написать
Р(ЕГ, Е9; .... ?р)= Ит Р{Еу, Ег, .... irn).

46 ГЛ. I. ОБЩИЕ ПОНЯТИЯ О МНОЖЕСТВАХ, ИЗМЕРИМЫХ В
Мы видим, что переменное множество Р(Ер, Еу/, ..., яп)
убывает, когда п неограниченно возрастает. Следовательно,
множество Р(Еу, Еу/, ..., Е$) получается при помощи мо-
монотонного перехода к пределу.
С другой стороны.'переменное множество Р(Еу, Еу/,..., ип)
может быть записано в виде полинома:
= Q(E9; Еу/, ..., Eh,..., Е?п),
образованного из множеств с индексами, строго меньшими,
чем р. Значит, множество Q можно определить, отправляясь
от множеств начального класса Ко, при помощи монотонных
переходов к пределу. Отсюда следует, что Е$ — нормальный
член последовательности A), что противоречит нашей ги-
гипотезе.
Итак, все члены последовательности A) нормальны.
¦Перейдем теперь к рассмотрению данного множества Е.
Мы имеем:
Е = \m^ (E
или
где все ?s являются множествами, предшествующими Е; так
как все Е$, нормальны, мы отсюда заключаем, что множе-
множество Е может быть определено, отправляясь от начального
класса Ко, при помощи неограниченно повторенных моно-
монотонных переходов к пределу.: Ч. т. д.
Это предложение чрезвычайно важно, так как оно пока-
показывает, что при изучении множеств, измеримых В, можно
ограничиваться изучением начального класса Ко и рас-
рассмотрением монотонных переходов к пределу, неограни-
ченно повторенных и, разумеется, чередующихся *).
Остается рассмотреть лишь общий (не монотонный) пере-
переход к пределу lim, а также операции взятия верхнего пре-
предела lim и нижнего предела lim. Эти рассмотрения не пред-
представляют никакого затруднения.
J) Это основной результат теории Юнга.

ПРЕОБРАЗОВАНИЯ ОПРЕДЕЛЕНИЯ В-МНОЖЕСГВА 47
Прежде всего, так как нахождение предела монотонной
последовательности множеств есть частный случай опера-
операций lim, lim и lim, всякое множество, измеримое В, может
быть получено, отправляясь от начального класса Ко, при
помощи каждой из трех операций lim, lim и lim, неограни-
неограниченно повторенных.
С другой стороны, так как каждая из этих операций мо-
может быть приведена к сложению и взятию общей части
(стр. 28 и 29), то множества, которые могут быть- получены,
отправляясь от начального класса Ко, при помощи операции
lim, lim и lim, неограниченно повторенных, будут все изме-
измеримы В.. •
Проблема меры Бореля. Вышеуказанный процесс обра-
образования множеств (стр. 36) Борель ввел с целью уметь «из-
«измерять» множества.
Пусть
Е0,ЕиЕа,..'.,Е9,...\Е A)
— счетная вполне упорядоченная последовательность мно-
множеств, служащая для определения множества Е, измеримого В,
отправляясь от порций области 0, при помощи операций:
(S)—составления суммы счетного числа множеств без общих
частей и (D) — взятия разности двух множеств, из которых
одно содержит другое. Мы предполагаем, что все множества
последовательности A) расположены на @,1).
Следуя идеям Бореля, каждому члену последовательно-
последовательности A), являющемуся порцией области 0, приписывают его
длину. Этим способом некоторым членам последовательности A)
будут поставлены в соответствие числа-, которые мы будем
называть мерами этих множеств.
Допустим, чт процесс определения меры дошел до чле-
члена Е9. В этом случае, если Е$ = Ер +?p -f- ... -\-Е$ -\-...
то Борель приписывает Е$ меру тЕ$, равную сумме ряда:
где Е$ , в силу сделанной гипотезы, уже получило меру тЕ$ ,
так как Р» < р. Если же Е$ = Е^ — Е^, то Борель

48 ГЛ. I. ОБЩИЕ ПОНЯТИЯ О МНОЖЕСТВАХ, ИЗМЕРИМЫХ В
приписывает Е$ меру тЕ$, равную разности
mEh — mEh'
причем множества Е$ и Е$ уже имеют меру, так как они
предшествуют Е?, C, < |3 и Р2 < р.
Таким образом, в принципе процесс продолжается, не
останавливаясь, и пробегает последовательность A) до тех
пор, пока мы не дойдем до последнего члена Е, который,
таким образом, получает некоторую меру тЕ. Так получен-
полученное число тЕ называется мерой Бореля.
Это определение меры так естественно, как только можно,
и, однако, мы наталкиваемся на следующие три затруднения:
1° Мы можем встретить расходящиеся ряды.
2° Мы можем придти к отрицательной мере.
3° Получая некоторое множество Е двумя различными
способами, мы можем гфиписать ему две разные меры.
Все эти трудности отпадают, если принять концепцию
меры Лебега, так как, по самому ее определению, мера Ле-
Лебега есть всегда неотрицательное число и единственное для
каждого измеримого множества. И так как легко доказать,
что число тЕ Бореля совпадает с мерой Лебега, то все труд-
трудности устранены.
Тем не менее, если рассматривать теорию меры Бореля
независимо от лебеговской, очевидно^ что надо внутренним
образом преодолеть эти три затруднения. В этом проблема
меры Бореля.
Не входя в рассмотрение вопроса о возможности разре-
разрешить эту проблему *), мы заметим, что все три затруднения
сводятся ко второму, т. е. к невозможности получить от-
отрицательную меру.
Прежде всего, если бы мы встретили расходящийся ряд
2
п=1
!) На мой взгляд, эта проблема представляет лишь техниче-
технические трудности, ее решение не требует непременно бесконечного
множества операций, имеющего мощность континуума.

преобразования Определения В-множёства . 49
где множества Е^, Е^, ... попарно без общих точек, мы
могли бы взять столь большое число N его членов, что их
сумма превосходит 1. Останавливая последовательность A)
после того, как написаны члены Е$ , Е$ , ..., E$N и при-
прибавляя затем два новых члена, из которых один есть сумма
Е$ -\- ?? -f- ... -J- E$N, а другой — дополнение к этой сумме по
отношению к порции @,1), мы видим, что последний член
получает отрицательную меру.
Чтобы доказать, что трудность 3° также сводится к труд-
трудности 2°, допустим, что некоторое множество Ё было опре-
определено двумя различными погледовательностями A). Заставляя
все члены одной последовательности следовать за членами
другой и прибавляя к так полученной последовательности
мнвжество &, не содержащее ни одной точки, мы видим, что $
получает отрицательную меру, если его рассматривать как
разность двух множеств Е геометрически тождественных, но
построенных разными способами.
Итак, все сводится к тому, чтобы доказать, что невоз-
невозможно получить отрицательную меру J).
Множество многих измерений. Для определенности мы
ограничимся случаем множеств в пространстве двух измерений.
Возьмем евклидово пространство $ двух измерений. Пусть
в этом про;транстве дана какая-нибудь система прямоуголь-
прямоугольных осей, которую мы обозначим через XOY.
Назовем основной областью двух измерений множество
всех точек М(х, у) плоскости XOY, у которых обе коор-
координаты х и у иррациональны. Эту основную область мы обо-
обозначим через 0ху.
Назовем порцией области 0 ху множество тех точек М (х, у)
этой области, координаты х и у которых принадлежат пор-
порциям (а, Ь) и (с, d), лежащим, соответственно, в линейных
основных областях g т и 0у [3J.
Мы скажем, что множество Е точек области 0ху есть
множество начального класса Ко, если как Е, так и его
дополнение СЕ (по отношению к 0 xy) является суммой ко-
конечного или бесконечного множества порций области 0 ху.
1) В главе II мы укажем элемзнты, позволяющие, на наш взгляд
найти решение проблемы меры Бореля.
4 Зак. 384. Н. Н. Лузин

?>0 ГЛ. I. ОБЩИЕ ПОНЯТИЯ 6 МНОЖЕСТВАХ, ИЗМЕРИМЫХ В
Если мы захотим проанализировать все определения и рас-
рассмотрения, которые были даны выше и касались линейных
множеств, то мы убедимся, что они применяются без всяких
изменений к многомерным областям.
В частности, множества, измеримые В, это множества,
которые могут быть получены из множеств начального класса Ко
при помощи операций (S), (P), lim, lim, lim или же при по-
помощи только монотонных переходов к пределу, неограниченно
повторяемых.

ГЛАВА Ii
ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ,
ИЗМЕРИМЫХ В
Классификация множеств, измеримых В
Классы Валле-Пуссена. Отправляясь от начального
класса Ко при помощи основной операции lim, мы формально
определяем шаг за шагом последовательные классы Валле-
Пуссена J)
Класс Ka здесь определяется логически (т. е. формально),
как множество всех точечных множеств Е, которые являются
пределами множеств Еп предыдущих классов Е = lim En, но
сами не принадлежат к предыдущим классам.
1) Бэр дал лишь классификацию функций [4].
С тех пор было дано много классификаций множеств; среди
них первая была дана Лебегом («Sur les fonctions representables
analytiquement», стр. 156). Вот принципы этой классификации: неко-
некоторое множество точек, измеримое В, называется множеством
класса а, если его можно рассматривать как множество тех точек,
где некоторая функция класса а обращается в нуль, и если это
невозможно для функции класса меньше, чем а.
Классификация множеств, которую мы здесь принимаем, при-
принадлежит Валле-Пуссену (см. его книгу «Integrates de Lebesgue,
fonctions d'ensetnble, classes de Baire», стр. 371). Повидимому,
Валле-Пуссен более верен идее Бэра, чем Лебег, так как классифи-
классификация Валле-Пуссена есть, в сущности, не что иное, как непосред-
непосредственное применение принципов Бэра к классификации функции,
принимающих лишь два значения 0 и 1.
Мы вводим лишь легкое изменение в эту классификацию! устра-
устраняя рациональные точки, что позволяет нам формулировать резуль-
результаты в более простом виде и избегать исключительных случаев.
4*

S2 ГЛ. il. ИССЛЕДбвАНИЯ 6 СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ Ё
Из этого определения следует, что каждый класс может
содержать только множества, измеримые В; обратное также
справедливо: всякое множество точек Е, измеримое В, при-
принадлежит к некоторому определенному классу КЛ, так как Е
получается из начального класса Ко при помощи операции lim,
неограниченно повторенной, и каждоэ промежуточноз множе-
множество Ер счетной вполне упорядоченной последовательности
Ео, ?j, ?2> •••• Am •••> Ер, ...|?, A)
Служащей для определения множества Е, очевидно, принад-
принадлежит к классификации Валлэ-Пуссена. Таким образом, мы
видим* что совокупность множеств, измеримых В, совпадает
С совокупностью множеств, входящих в классы Валле-Пус-
Сена.
Ясно, что все классы классификации Валле-Пуссена не
имеют попарно общих элементов.
Для удобства речи мы в дальнейшем не будем делать сло-
словесного различия между классом* к которому принадлежит
данное множество точек Е, и рангом, соответствующим этому
Классу. В- этом смысле класс некоторого множества Е есть
просто . конечное число или трансфинитноэ число второго
класса.
Класс, множества Е будет обозначаться символом
cl Е.
Таким образом, мы будем для множества Е, принадлежащего
.классу КЛ классификации Валле-Пуссена, писать равенство
. с\Е = а.
Раньше мы указывали, что классы Валле-Пуссена опреде-
определены лишь формальным образом, т. е. логически; чтобы.убе-
чтобы.убедиться в этом, достаточно заметить, что если один из этих
¦Классов, например /С?, пуст (лишен элементоз), то весь оста-
остаток классификации
по необходимости также пуст, и последовательность логически
Определенных классов становится иллюзорной.
Итак, для того чтобы иметь концепцию вполне определен-
,ного класеа Kt, надо доказать, что он не пуст, т. е. что он

КЛАССИФИКАЦИЯ МНОЖЕСТВ, ИЗМЕРИМЫХ В ¦ ' 53
содержит эффективно множества. Мы видим, что речь идет
о некотором рассуждении, при помодци которого.можно уста-
установить существование множеств Е, принадлежащих к этому
классу Кл.
Способы, при помощи которых в настоящее время уста-
устанавливают существования в математическом анализе, могут*
быть разделены на четыре категории.
1° Доказательство существования с использованием
аксиомы Цермело, полученное применением принципа про-
произвольного выбора. В дальнейшем мы устраним этот способ
рассуждения по причине тех затруднений, которые возникают
при желании хорошо понять его сущность. Кроме того, этот
способ рассуждения никогда не дает индивидуальных объектов,
но всегда приводит нас к классам, быть может, лишенным
элементов, которые можно индивидуально различить.
2° Доказательство существования с использованием сово-
совокупности трансфинитных чисел второго класса. Этот спо-
способ действий был впервые употреблен Лебегом в его исследо-
исследованиях о .функциях, не допускающих никакого аналитического
изображения г).
3° Доказательство существования, установленное при
помощи диагонали Кантора. Этот способ оказал науке
серьезные услуги: им в теории . функций доказаны важные
теоремы существования.
4° Конструктивное доказательство существования. Бэр
первый дал конструктивные примеры функций классов 0, 1,
2 и 3 в его классификации2). Было бы чрезвычайно жела-
желательно, чтобы исследования Бэра о конструктивном существо-
существовании множеств высших классов были продолжены и распро-
распространены, несмотря на всю их трудность. В дальнейшем мы
даем лишь" конструктивное доказательство существования мно-
множества (или функции) класса 4, принадлежащее Л. В. Келдыш.
Трудности быстро возрастают с повышением класса множеств.
Если мы хотим проанализировать процессы, при помощи
которых устанавливается существование математических объек-
J) «Sur les fonctions representative analytiquement» (Journ. de
Math., 1905, стр. 214).
2) R. В a i r e, Sur la representation des fonctions d.jscontjnue§,
Acta Afatti., т. 30, 1905. «-....

54 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
тов, то вот что мы практически констатируем: методы дока-
доказательства существований бывают весьма различной природы
и теоретически не сводимы друг к другу; таким образом,
нельзя говорить о существовании в общем смысле или в абсолют-
абсолютном смысле. Понятие существования математического объекта
в абсолютном смысле кажется при современном состоянии
науки слишком неясным, чтобы приписать ему смысл. Все,
что можно сделать, это просто говорить о существовании,
установленном тем или другим методом, т. е. об относитель-
относительном существовании.
По этой-то причине, говоря о существовании, мы всегда
будем указывать метод, в смысле которого установлено рас-
рассматриваемое существование. Так мы будем говорить q суще-
существовании в смысле совокупности Q, о существовании в смысле
диагонали и о существовании конструктивном [б].
В данный момент мы не останавливаемся на доказательствах
существования множеств всех классов классификации Валле-
Пуссена: мы предпочитаем принять это существование как
постулат и извлечь из него все полезные следствия.
Простейшие свойства классов Валле-Пуссена. Мы сначала
укажем свойства классов в некотором роде формальные,
а именно те, которые являются немедленным следствием логи-
логического определения класса.
Теорема 1. Если множество точек Е принадлежит
к К%, то и его дополнение СЕ также принадлежит к Ка.
По самому определению, начальный класс Ко обладает
указанным свойством.
Допустим, что существуют классы анормальные, г. е.
лишенные этого свойства, и обозначим через К$ первый анор-
анормальный класс. Пусть Е есть множество, принадлежащее к К§
без того, чтобы его дополнение принадлежало к К$.
Мы тогда имеем равенство
Е= Нш Еп,
где Еп есть множество класса Крп, предшествующего К$,
Р„ < р. Так как класс К$п нормален, то дополнение СЕп при-
принадлежит к К$п. В силу очевидного равенства, СЕ = Игл СЕп;
отсюда следует, что СЕ не может принадлежать к классу

достижимость .55
выше, чем р. С другой стороны, СЕ не может быть класса
ниже |3, так как АГр есть первый анормальный класс, и мы имели
бы cl?<p. Итак, мы имеем cl,C? = j3, и мы пришли к про-
противоречию.
Итак, все классы классификации Валле-Пуссена нормальны,
что и доказывает наше предложение. Ч. т. д.
Теорема II. Сумма конечного числа множеств и общая
часть конечного числа множеств принадлежит к классу,
не превосходящему наибольший из классов составляющих
множеств.
Теорема III. Сумма счетного множества множеств
и общая часть счетного множества множеств принадлежит
к классу, не превосходящему класс, непосредственно сле-
следующий за классами всех составляющих множеств.
Теорема IV. Операции lim Еп и Нт Еп приводят
к множествам класса, не более, чем на единицу превосхо-
превосходящего тот, который непосредственно следует за классами
всех множеств Еп. '
Метод доказательства этих трех теорем тот же,- как и для
случая теоремы 1. Мы убеждаемся, что класс 0 обладает
формулированным свойством и, предполагая, что сушествуют
«анормальные» классы, приходим к противоречию. Это есть
рассуждение методом трансфинитной индукции. Чтобы не
утомлять читателя повторением одних и тех же слов, мы
опускаем доказательства.
Теорема V. Множество-разность ?2 — Е1 принадле-
принадлежит к классу, не превосходящему наибольший из двух
классов cl?j и cl?2.
В самом деле, если Е = Ей— Ег, то мы можем написать
E = EZ-CEU и теорема сводится к теореме II,
Достижимость,
Определения. Чтобы изучить структуру каждого класса
классификации Валле-Пуссена, нам нужны следующие важные
определения.
Мы скажем, что множество Е, принадлежащее к классу Ка,
достижимо сверху, если Е есть общая часть счетного мно-
множества множеств классов, меньших а.

56 ГЛ. II. ИССЛЕДОВАНИЯ О С1РУК1УРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
' Точно так же мы скажем, что множество Е, принадлежащее
к классу Кл, достижимо снизу, если Е есть сумма счетного
множества множеств классов, меньших а.
Из определения следует, что если множество Е класса Ка
достижимо сверху, то его дополнение СЕ достижимо снизу
и обратно.
В самом деле, из равенства E = Et • ?2... следует равен-
равенство
Ясно, что необходимым условием для того, чтобы множе-
множество Е было достижимо сверху или снизу, является равенство
E = \imEn, где множество Е класса ниже, чем, класс Е, и
где. Ёп^Е или же Епс^Е при всяком п.
Установив эти основные определения, дадим еще некоторые
весьма полезные определения.
Назовем двусторонним всякое множество класса АГ„, дости-
достижимое одновременно сверху и снизу. Множество Е класса АГ„
называется односторонним, если оно достижимо сверху или
снизу, не не есть двустороннее.
Наконец, мы скажем, что множество Е класса Кл недости-
недостижимо с обеих сторон, если оно не является достижимым ни
сверху, ни снизу.
Несуществование двусторонних множеств в классах
первого рода. Класс Кл классификации Валле-Пуссена будет
называться классом первого рода, если существует класс КЛ*,
непосредственно ему предшествующий; <х = а*-|-1. В гро-
тивном случае К* будет второго рода.
Начальный класс Ко мы будем считать классом вто-
второго рода. ¦
Все классы первого рода обладают важным свойством:
Теорема. Классы первого рода не могут содержать
двусторонних множеств,
В самом деле, пусть Е есть множество, принадлежащее
к классу /Г«+1. Если Е двустороннее, то мы имеем

ДОСТИЖИМОСТЬ 5?
где все еп и ч\п — множества классов ^ а попарно без общих
точек.
Следовательно, мы можем писать
еи= Нт е™ и 7jn== Ит $\
где множества с двумя индексами е<*) и tjM все класса ниже а.
Установив это, возьмем множество Еп, определенное сле-
следующим равенством:
Еп = 2 4Ч) • c*iin) • С74И)- • • <*№¦
Ясно, что cl Еп < с.
Мы докажем, что множество Еп имеет своим пределом
множество Е, когда я неограниченно возрастает.
Если точка х принадлежат к Е, то существует соста-
составляющее множество для Е, пусть е^ которое содержит х.
Значит, точка х принадлежит к каждому из множеств е(") для
достаточно большого я. С другой стороны, эта точка не при-
принадлежит к СЕ; значит, она не принадлежит ни одному из i
множеств YJ,, ?i2, ...,%. Так как i есть постоянное число,
то х не входит ни в одно из i множеств i\W, т^"), ..., г\^
для достаточно большого я. Отсюда мы заключаем, что х
принадлежит каждому из i дополнительных множеств Ст^"),
С-г$\ ..., Сч\ф и, следовательно, принадлежит к Еп при до-
достаточно большом п.
Если точка х принадлежит к СЕ, то существует такое
число /, что х принадлежит к г\{. Следовательно, х не при-
принадлежит ни к одному из i множеств в,, г2, . . ., е{_, и С%.
Так как индекс i постоянен, мы отсюда заключаем, что х не
принадлежит ни одному из множеств sW, e(n), ..., &^t и
Crfp, если только число п достаточно велико. Из определе-
определения множества Еп следует, что х не принадлежит к Еп при
достаточно .большом п.
Таким образом, мы вынуждены заключить, что бесконеч-
бесконечная последовательность множеств Еи Eit ..., Еп, ... сходится
и имеет Е своим пределом. А так как с1?и< а, то класс Е
не может превосходить а, что противоречиво, ибо cl? = а -|- 1,

58 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
Итак, множество класса /С,,., не может быть двусторон-
двусторонним. Ч. т. д.
Теорема о знакочередующихся рядах. Мы теперь дока-
докажем одну теорему, которая будет очень полезна в дальнейшем.
Теорема. Если множество точек Е есть сумма убы-
убывающего знакочередующегося ряда множеств классов, мень-
меньших а, то множество Е либо класса ниже а, либо дву-
стщюннее класса а.
В самом деле, пусть
где
Е^Е^Е^ ... =э?и=з. .. и
Так как мы можем писать (стр. 36)
и
мы заключаем, что или cl Е < а или Е есть двустороннее
класса а, что возможно только в том случае, когда а вто-
второго рода, т. е. является предельным классом. Ч. т. д.
Мы дополним этот результат следующими замечаниями:
Замечание I. Если Е есть сумма убывающего знакоче-
знакочередующегося ряда множеств классов О, то класс Е также О.
В самом деле, класс Ка+1 не может содержать двусторон-
двусторонних множеств.
Замечание II. Если Е есть сумма убывающего знако-
знакочередующегося ряда множеств либо класса < а, либо дву-
двусторонних класса Ка, то множество Е также либо класса
< а, либо двустороннее класса К%.
В самом деле, формулы
и
СЕ = СЕ, + (?2 — Л8) + (?4 — Еъ
показывают, что Е и СЕ являются суммами множеств класса
< а. Значит^ либо cl Е <, а, либо Е есть двустороннее
класса а..

СТРУКТУРА КЛАССОВ 59
Структура классов
Чтобы изучить структуру классов классификации Валле-
Пуссена, мы постулируем существование множеств Е всякого
класса.
Значит, мы предполагаем, что каков бы ни был класс Ки
классификации Валле-Пуссена, существуют множества Е, при-
принадлежащие к АГ„.
Из этого постулата мы теперь извлечем важные следствия,
касающиеся структуры каждого класса К, классификации
Валле-Пуссена.
Лемма 1. Если классы, предшествующие некоторому
классу второго рода Кх, не лишены элементов, то
в классе Ка содержатся двусторонние множества.
В самом деле, пусть К,, — предельный класс (т, е. второго
рода) и пусть
а1 < «2 <•••<«»<•••
есть бесконечная последовательность возрастающих трансфи-
трансфинитных чисел, имеющих а своим пределом.
Раз класс Kt не лишен элементов, то существуют мно-
множества этого класса; пусть Еп и есть множество, принадле-
принадлежащее к Ка . Мы можем предположить, что это множество Еп
содержится в порции (я — 1, п) основной области 0, так
как можно преобразовать всю область 0 = (—оо, ~\- сю)
в порцию (я — 1, л) при помощи непрерывной возрастающей
функции так, чтобы всякая порция области 0 преобразова-
преобразовалась в некоторую порцию из (л—1, л) и обратно: это пре-
преобразование *) приведет в соответствие всякому множеству Е,
измеримому В и лежащему в области 0, множество Е', также
измеримое В и того же класса, лежащее в (я — 1, я).
*) Чтобы увидеть возможность подобного преобразования, за-
X
метим сначала, что преобразование х' = -т—г— преобразует указан-
1 -f- х
ным способом бесконечную порцию @, +оо) в конечную порцию
(О, +1). Отсюда следует, что можно преобразовать указанным об-
образом всю область g в порцию (— 1, +1). С другой стороны,
всякую конечную порцию можно преобразовать в любую конечную
порцию при помощи линейного преобразования с рациональными,
коэффициентами.

60 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
Установив это, рассмотрим множество Е, определенное
равенством
Ясно, что с1?<! а. Но мы не можем иметь cl?<<*.
В самом деле, если cl?<a, то существует такое число ап,
что мы имеем неравенство cl E < ап < а, ибо а. есть предел
чисел <хп. А так как класс общей части Е и любой порции
области 0 никогда не превзойдет класса Е, то мы приходим
к противоречию, так как общая часть Е и (я — 1, я) есть
множество Еп, класс которого ап превосходит с\Е.
Итак, множество Е есть в точности класса ,сг.
Обозначим через $п дополнение к Еп относительно пор-
порции (я —1,'я). Ясно, что cl $п — cl Еп =s= ап. Мы, очевидно,
имеем: . . ¦ - '
C? = (-oo,0) + e, + fa+...+*»+.•• B)
Равенства A) и B) показывают нам, что Е и СЕ дости-
достижимы снизу. Значит, Е есть двустороннее множество класса а.
Ч. т. д.
Лемма 2. Если класс Ка первого рода не лишен эле-
элементов, то в этом классе есть множества односторон-
односторонние и множества, недостижимые с обеих сторон.
В самом деле, в классе Ка не может существовать дву-
двусторонних множеств. Значит, если Е есть множество класса от,
то возможны только два случая:
В первом случае множество Е достижимо только с одной
определенной стороны; в этом случае его дополнение СЕ есть
тоже одностороннее множество, но уже достижимое с другой
стороны. Так jcaK область 0 может быть преобразована
в порцию при помощи непрерывной возрастающей функции,
то существуют в каждой порции {а, Ь) области 0 односто-
односторонние множества класса а, достижимые сверху и достижи-
достижимые снизу.
Установив это, возьмем на @, -|-оо) множество Е% класса а,
достижимое сверху, и в (— со, 0) множество ?2 класса а,
достижимое снизу. Ясно, что сумма Ех ~\- ?2 есть множество
класса а, недостижимое с обеих сторон.
Во втором слуцае множество Е недостижимо с обеих
сторон, . ¦

классов 61
Возьмём равенство
Е = lim Еп,
П->оо
где Еп есть множество класса < а. Так как операция lim
есть частный случай операции lim, мы можем написать
Я теперь утверждаю, что среди скобок имеется не более
конечного числа таких, классы которых < а. В самом деле,
в противном случае Е было бы достижимо сверху, так как
мы могли бы стереть все скобки класса < а без того, что-
чтобы общая часть оставшихся скобок изменилась.
Итак, существуют скобки, класс которых в точности
равен а. Ясно, что это будут множества, достижимые снизу,
так как с\Еп<С.а. Итак, второй случай сводится к первому.
Ч. т. д.
Лемма 3. Если класс КЛ второго рода содержит мно-
множество, которое не является двусторонним, то он содерг
жит множества односторонние и недостижимые с обеих
сторон.
Доказательство этой леммы тождественно с предыдущим,
так как гипотеза, что а первого рода, была введена лишь
для того, чтобы получить множество, которое не будет дву-
двусторонним.
Чтобы закончить изучение структуры классов, нам потре-
потребуется одно важное предложение, показывающее, какую осо-
особую роль играют двусторонние множества в классификации
Валле-Пуссена.
Теорема. Предел последовательности двусторонних
множеств класса а. есть всегда множество класса ^<х.
Чтобы доказать эту теорему, возьмем такое множество,
что
Е= lim En,
П-*оо
где все ^ — двусторонние множества класса а.
Мы имеем следующие равенства:

62 ГЛ. tl. ИССЛЕДбвАнИЯ 6 СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
Так как каждое Е4 есть двустороннее класса а, то все
скобки в обоих разложениях Е оказываются множествами
класса ^ а. Значит, если бы множество Е было класса a -j- 1,
оно было бы двусторонним в Ка+1. Но это невозможно, так
как класс Ка+1 первого рода. Ч. т. д.
Итак, операция предела двусторонних множеств класса а
не повышает класса.
Теперь мы можем формулировать основное предложение:
Основная теорема о структуре классов. Вся-
Всякий класс Ка+1 первого рода образован из Множеств одно-
односторонних и недостижимых с обеих сторон; всякий класс
Ка второго рода содержит, кроме того, двусторонние
множества.
Эта теорема есть синтез трех предыдущих лемм.
В самом деле, если КЛ первого рода, то достаточно пред-
предположить, что в Ка есть множества: в силу леммы 2 суще-
существование множества в Ка влечет за собой существование
в классе /Q множеств всех возможных видов.
Если Ка второго рода, достаточно предположить, что есть
множества в следующем классе КЛ+1; в силу леммы 3 суще-
существование множества в Ка+1 влечет существование в КЛ мно-
множеств всех видов.
Интересно заметить, что если а второго рода, недостаточно
существования в Ка одного множества, так как оно может
оказаться двусторонним. Напротив, существование множества
в следующем клаосе Ка+1 влечет существование в КЛ множеств,
которые не будут двусторонними, так как нельзя получить
множество класса а —(— 1 переходом к пределу, отправляясь
от двусторонних множеств. В этих условиях лемма 3 при-
применима.
С другой стороны, всякое множество Е класса а второго
рода, очевидно, может быть получено как предел двусторон-
двусторонних множеств класса а.
Окончательно мы приходим к следующему заключению
о структуре классов второго рода в классификации Валле-
Пуссена: двусторонние множества образуют очень важную со-
составную, часть каждого класса второго рода. В образовании
множеств, измеримых В, можно сравнить роль двусторонних
множеств с ролью множеств начального класса Ко: порции
начального класса Ко играют ту же -роль, как множества

ОТДЕЛИМОСТЬ 63
классов, меньших а, а другие множества из Ко играют ту
же роль, как множества двусторонние, тогда как односторон-
односторонние множества и множества, недостижимые с обеих сторон
класса Кл второго рода, играют ту же роль, как множества
класса Кх 1).
В силу особых свойств двусторонних множеств мы назо-
назовем базой каждого предельного класса Кл множество всех
двусторонних множеств и обозначим ее через Ва.
Отделимость
Мы теперь введем одно очень важное определение, кото-
которое в дальнейшем будет играть самую существенную роль.
Мы скажем, что два множества Et и Е2 класса а первого
рода отделимы, если можно построить два множества.Я!
и #2 классов ниже а без общей части, которые содержат
соответственно множества Е1 и ?2; множества Нх и Я2 будем
называть отделяющими. Точно так же назовем отделимыми
два множества Ех и Е% класса КЛ второго рода, не принад-
принадлежащие к базе Ва, если отделяющие множества Нх и Н2
принадлежат к этой базе. Наконец, два множества ?j и Е2
базы Ва называются отделимыми, если классы отделяющих
множеств Н1 и #2 меньше а.
Эти определения имеют качественный характер, так как
они дают нам лишь идею отдаленности двух множеств, без
того, чтобы эта отдаленность могла быть точно измерена.
В дальнейшем мы дадим дескриптивную меру «расстояния»
двух множеств, измеримых В.
Пока же мы ограничимся указанием на то, что два мно-
множества ?j и Е2, лежащие в двух непересекающихся порциях
(аи Ьг) и (а2, Ь%) основной области 0', должны быть рас-
рассматриваемы как чрезвычайно отдаленные. Взаимное отдале-
отдаление множеств ?j и ?2, измеримых В, становится тем меньше,
чем выше класс отделяющих их множеств Ht и //2.
Элементы класса К%. Мы рассмотрели структуру классов
классификации Валле-Пуссена. Чтобы анализировать структуру
х) Представляется естественным объединить классы0и1 в один
и рассматривать его как предельный класс. Быть может, в этом и
заключается причина, по которой теорема Бэра относится к функ-
функциям класса ¦< 1, а не только класса 1.

64 ГЛ. П. ЙССЛЗДбвАЧИЯ б СТРУКТУРА МНОЖЕбГВ, ИЗМЗРЙИЫХ В
самих, множеств данного класса Kt, мы примем за инстру-
инструмент множества, достижимые сверху.
Назовем элементом всякое множество класса КЛ, дости-
достижимое сверху, но не принадлежащее к базе 5„, когда класс КЛ
второго рода.
Введение понятия элемента класса а очень естественно по
причине многочисленных и глубоких аналогий между элемен-
элементами любого класса и обыкновенными точками.
х,Ь,
х2 Ъг
Черт. 2.
Отдельно взятая точка есть элемент класса 1. Если хх
и х2 — две различные точки, они отделимы при помощи пор-
порций (aj, b^ и (а2, Ь2) основной области 0.
Мы имеем глубокую и полную аналогию между этим свой-
свойством точек и следующим свойством элементов класса КЛ:
два любых элемента класса КЛ без общей части всегда отде-
отделимы при помощи множеств низших классов или множеств,
принадлежащих базе ВЛ.
Эго мы изображаем на следующем схематическом чертеже,
где символические границы элементов Ех и ?2 должны быть
тем более иззилисты, чем выше класс а.
Черт. 3.
Мы теперь переходим к доказательству основной теоремы
об отделимости элементов, не имеющих общей части.

ОГДЕЛИМОСГЬ
65
Основная теорема. Два элемента любого класса КЛ
без общей части всегда отделимы.
Пусть Е и $ — два элемента класса КЛ без общей части.
Так как Е и $ суть множества, достижимые сверху, то
мы можем образовать две убывающие последовательности мно-
множеств класса < а
такие, что предел первой из них есть элемент Е, а предел
второй — элемент $.
Установив это, напишем две вертикальные схемы:
и возьмем все произведения двух букв, лежащих на одной и
той же Наклонной прямой со знаком -(-, а произведения двух
букв, стоящих на одной и той же горизонтальной прямой со
знаком —. Мы получим, таким образом, два убывающих знако-
знакочередующихся ряда множеств классов < а
х — $1El -j- Е]$2 — ?2
Эти ряды множеств, очевидно, сходятся, так как элементы
Е и $ не имеют общей части и, следовательно, общий член
обоих рядов имеет пределом пустое множество. :
Пусть Нг есть сумма первого иЯ2:— сумма второго ряда.
5 Зак. 284. Н. Н. Лузин

66 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
Возьмем теперь любую точку х области 0 и предполо-
жим^ что она принадлежит к k членам левой колонны и к?
членам правой колонны предыдущей вертикальной схемы. Так
как первым членом в обеих колоннах стоит ff, то k^l
и />Ь
Надо различать три случая:
Первый случай: ?</. В этом случае точка х не принад-
принадлежит к Ht, но принадлежит к Н2.
Второй случай: & = /. В этом случае точка х не при-
принадлежит ни к Я), ни к Я2.
. Третий случай: k > /. В этом случае точка х принадле-
принадлежит к Нх, но не принадлежит к Я2.
Отсюда следует, что множества Н1 и #2 не имеют общей
точки.
Так как общий член обоих рядов есть множество класса
< а, то множества Я, и Я2 либо класса < а, либо принад-
принадлежат к базе ВЛ (стр. 58).
Наконец, ясно, что EczH1 и §>сН2. Значит, множества
Нх иЯ, — отделяющие для данных элементов Е и Ь. Ч. т. д.
Итак, мы имеем полную аналогию между отделимостью
двух различных точек и двух элементов без общей части.
То же справедливо и для аналогии между одновременной отде-
отделимостью конечного числа различных точек при помощи
отделяющих порций области 0, не перекрывающихся между
собой, и одновременной отделимостью конечного числа эле-
элементов без общих частей при помощи отделяющих множеств,
также попарно не перекрывающихся. В самом деле, мы можем
дополнить доказанную теорему следующим следствием:
Элементы класса КЛ в конечном числе, не имеющие
попарно общих частей, одновременно отделимы, т. ,е. могут
быть соответственно заключены в отделяющие множества
либо класса < а, либо базы ВЛ, попарно без общих точек 1).
') Эту теорему можно рассматривать, как первый шаг на пути
к автономной теории меры Бореля. В самом деле, лишь только все
множества классов, меньших а, получили меру Бореля, элементы
класса Ка ею также обладают. И предложение текста показывает
нам, что мы никогда не встретим расходящихся рядов мер Бореля
элементов класса Ка, так как в противном случае в силу одно-
одновременной отделимости элементов мы имели бы отрицательные меры
Бореля в классах, предшествующих а. С другой стороны, каждое
множество Е класса а состоит из элементов (стр. 71).

ОТДЕЛИМОСТЬ 67
В самом деле, пусть Ev Е%, ..., Ет—элементы класса Кв)
не имеющие попарно общих точек; число т конечно.
Возьмем два любых элемента ?^ и Ej, i Ф). Так как эти
элементы отделимы, мы можем обозначить через Нц и Ны
отделяющие множества Е{czНц и EjCzH^; множества Нц и Hjf
не имеют общей точки и будут либо класса < а, либо из
базы Вя.
Установив это, возьмем общую часть всех множеств Нф
где первый индекс фиксирован, а второй принимает все зна-
значения 1, 2, ..., т, кроме значения /. Эту общую часть мы
обозначим через /f^.
Ясно, что множество /ff содержит множество Et и что
оно либо класса < а, либо из базы Вл. Кроме того, так как
два множества Ну и Н1{ не имеют общей точки, то мы заклю-
заключаем, что и два множества Ht и Н$ также не имеют ни одной
общей точки.
Значит, одновременное отделение элементов Еи Е2, ...
..., Ет при помощи множеств Hv H2, ..., Нт реализовано,
Ч. т. д.
Очень естественно теперь поставить следующий вопрос:
будет ли эта одновременная отделимость опять иметь
место, если речь зайдет о счетном множестве элементов
попарно без общей частив
Мы видим немедленно, что ответ отрицателен, даже когда
дело касается точек области g: достаточно взять любое счет-
счетное множество точек, всюду плотное на 0. Хотя любые две
точки этого множества заведомо отделимы при помощи пор-
порций, но нельзя отделить одновременно все точки этого мно-
множества.
Тем не менее и здесь имеется полная аналогия между точ'
ками и элементами. Чтобы выявить эту аналогию, полезно
ввести понятие изолированного элемента.
Изолированные множества. Известно, что точка х мно-
множества Е называется изолированной во множестве Е, если
можно найти порцию (а, Ь) области $', содержащую х и не
содержащую никакой другой точки из Е. Для того чтобы
точка х из Е была одновременно отделима от всех остальных
точек Е, необходимо и достаточно, чтобы х была изолирован-
изолированной в Е. Именно по этой причине мы будем изучать множе-
множества точек, называемые изолированными.
5*

68 ГЛ. И. ИССЛЕДОВАНИЯ 6 СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ ft
. "По определению, -множество точек ? .есть изолированное,
если каждая его точка изолирована. Изолированное множество
точек Е непременно счетно
' ' Д?ц -^j) ¦ • • > хп> ' ' ' v )
и нетрудно доказать, что точки изолированного множества
всегда одновременно (т. е. равномерно) отделимы: достаточно
заключить его точки в ряд порций области g, причем каждая
из порций имеет диаметр, не превосходящий половину нижней
грани расстояний между рассматриваемой точкой и другими
точками множества. • «
Возьмем теперь в качестве путеводной нити указанную
аналогию между точками и элементами.
¦ Пусть дана бесконечная последовательность элементов
класса КЛ попарно без общих частей
мы назовем изолированным в этой последовательности всякий.
элемент et такой, что можно определить множество //4 либо
класса < а, Либо из базы Ва, которое содержит е{ и не
имеет общей части ни с одним из остальных элементов после-
последовательности.
Последовательность элементов класса
мы назовем изолированной в том случае, когда каждый из ее
элементов изолирован в этой последовательности.
Следующее предложение, вполне аналогичное тому, кото-
которое касается изолированных последовательностей точек:
Теорема. Все элементы изолированной последователь-
последовательности класса Kt могут быть одновременно (равномерно)
отделены.
Пусть еи е2, ..., еп, ... —бесконечная изолированная по-
последовательность элементов' класса АГ„. Для заданного целого
положительного числа п обозначим через Нп множество, отде-
отделяющее еп от остальных элементов последовательности; зна-
значит, Нп либо множество класса < а, либо из- базы ВЛ и
содержит элемент еп, не имея общей части ни с каким дру-
другим элементом последовательности.

ОТДЕЛИМОСТЬ 69
Установив это, возьмем множество Ьп, определенное равен-
равенством
каково бы ни было п.
Ясно, что Ьп либо класса < а, либо из базы ВЛ и что
оно содержит элемент еп.
Так как множества
очевидно, попгрно без общих частей, то одновременное отде-
отделение элементов еи г2, ..., еп, ... осуществлено. Ч. т. д.
Мы теперь возвратимся с несколько более общей точки
зрения к вопросам, касающимся изолированных семейств, рас-
рассматривая случай любых множеств.
Пусть F есть семейство, образованное из любых множеств.
Мы скажем, что множество Е, принадлежащее к F, изо-
изолировано в F относительно класса КЛ, если существует мно-
множество Н либо класса < а, либо из базы Ва, которое содер-
содержит ? и не имеет общей части ни с одним из остальных
множеств семейства F.
Семейство F, каждое из множеств которого изолировано
относительно Ка, само называется изолированным относи-
относительно Ка.
Доказательство предыдущей теоремы снова -применимо, и
мы можем формулировать несколько более общее предложение:
Всякое счетное семейство F, изолированное относи-
относительно класса Ка, равномерно изолировано, т. е. все мно-
множества Е из F можно одновременно заключить в ряд мно-
множеств И попарно без общих частей и класса < а или из
базы ВЛ.
Важно знать природу множеств, которые можно получить,
составляя сумму членов изолированного семейства. Вот общее
предложение:
Теорема. Сумма членов счетного семейства, изоли-
изолированного относительно Кя и образованного из множеств
класса <[а, есть множество класса О. " '.
Пусть F.есть семейство, образованное из множеств Et, Z?2,-....
класса О- Так как F изолировано относительно Kat суще-
существует последовательность Нр.:Н2, .-,.. .множеств либо,

70 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
< а, либо из базы Ва попарно без общих частей и таких,
что fjCHj.
Возьмем равенства
Et = Hm
где
Множество Sn, определенное равенством
• я2+... +е™ • нп
будет либо класса < а, jiu6o из базы В„.
Пусть дг — произвольная точка области 0. Следует раз-
различать два случая:
В первом случае точка х принадлежит к сумме Et-\-E2-\-...
Значит, существует целое положительное число i такое, что
х принадлежит к Е{ и, следовательно, к Е^ при достаточно
большом п. Так как мы имеем Е{аН{, то х принадлежит
к Sn при достаточно большом п.
Во втором случае точка х не принадлежит к сумме
Ех -\- Е% -\- . ¦. Если х не принадлежит ни одному из мно-
множеств Hi, оно не принадлежит и к Sn, каково бы ни было и.
Если х принадлежит к некоторому Нь то х не принадлежит
ни к какому другому из множеств Нр j ф i, так как мно-
множества Hv H2, ... не имеют общих частей. Отсюда следует,
что точка х перестает принадлежать к Sn, как только ?<
перестает содержать х,' что произойдет при достаточно боль-
большом п.
Отсюда мы заключаем, что сумма /?, -|- Е2 -\- ... есть пре-
предел сходящейся последовательности Sv 52, ..., а так как
Sn либо класса < а, либо из базы Ва, то мы имеем:
. cl(?1+?2+...)<a. Ч. т. д.
Мы дополним этот результат следующими замечаниями:
Замечание I, Для того чтобы сумма членов счет-
счетного семейства множеств класса ^ot, изолированного от-
относительно Кл, была множеством класса АГ,, недостижи-
недостижимым снизу, необходимо и достаточно, чтобы по крайней
мере один из членов семейства.был недостижимым снизу.

ПЕРВЫЕ СВЕДЕНИЯ О СТРУКТУРЕ МНОЖЕСТВА ТОЧЕК 71
Условие необходимо, так как в противном случае каждый
член Et рассматриваемого семейства достижим снизу, и, сле-
следовательно, и сумма Е1-\-Е2-{- . .. тоже.
Условие достаточно, так как если сумма E1~\-E<i-\- ...
достижима снизу, то это же справедливо для ее общей части
с Ht; но эта общая часть есть как раз Е{.
Замечание II. Если члены Et счетного семейства,
изолированного относительно АГ«, суть элементы класса Кя
и если сумма Нt -f- /f2 -f-... отделяющих множеств будет
либо класса < «¦, либо из базы Ва, то сумма Е1 -\- Е2 -(- ...
есть элемент класса КЛ.
В самом деле, в силу предыдущего случая сумма Ei-\-E%-\-. ..
недостижима снизу и класса КЛ. С другой стороны, возьмем
убывающую последовательность множеств класса < а
определяющую элемент Еь где / — любое целое положитель-
положительное число. Пусть Rn есть сумма Нп+1-\-Нп+^-\- ... В этих
условиях множество Sn> определенное равенством
s
n
есть, очевидно, либо класса < а, либо из базы ВЛ.
Но последовательность множеств Su S2, ... убывающая
и имеет пределом сумму Ех-\-Е%-\- ... Значит, Е1-\-Е^-\-..¦.
непременно будет элементом класса КЛ. Ч. т. д.
Первые сведения о структуре множества точек
данного класса
Произвольное множество данного класса. Если мы хотим
проанализировать структуру множества данного класса КЛ,
то вполне естественно попробовать разложить это множество
на счетное множество элементов класса Kt по причине пол-
полной аналогии между элементами и обыкновенными точками, .
Прежде всего мы имеем следующее важное предложение:
Теорема. Всякое множество класса КЛ есть сумма
счетного множества элементов класса ^ а, не имеющих
попарно общих частей, .

72 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
Чтобы доказать это, предположим, что теорема верна для
всех классов |3, меньших, чем а, и покажем, что она тогда
верна я для класса а. .
. . . Пусть Е— любое множество класса К9. Мы имеем равен-
равенство
Е = Нш Еп,
И->оо
где cl?n< а.
Так как операция lim есть частный случай операции Нт,
мы можем написать
Е = (Е, .Е9.ЕЛ...) + (СЕ, • Е2 ¦ Ел...) + (С?2 • ?„...)+..'.
Ясно, что скобки «редставляют собой множества, не имею-
имеющие попарно общих частей, и что класс каждой из скобок -^ а.
Если класс некоторой скобки меньше а, то эта скобка,
по сделанной гипотезе, есть сумма счетного множества эле-
элементов класса ¦< а без общих частей. Если скобка есть дву-
двустороннее множество класса АГа, то она является суммой счет-
.ного числа множеств класса < а и, следовательно, суммой
счетного множества элементов класса < а.
Но если скобка есть множество класса а и притом не
двустороннее в этом классе, то она должна быть элементом
класса Ка. Итак, Е есть сумма счетного множества элементов
класса <^ а без общих частей.
Так как каждое множество Е класса Ко есть сумма счет-
счетного множества порций области g, то теорема верна для
а = 0 и, следовательно, верна для любого а. Ч. т. д.
Таким образом, каждое множество Е класса К* может
бить написано в форме
^ а, причем все еп попарно
без общих частей. . .
:':. Обратное . заключение неверно, так как сумма счетного
множества элементов класса -^ а без общей части может ока-
оказаться эффективно .класса.выше а: это, очевидно, тот случай,
когда Е есть множество класса КЛ+и. достижимое снизу,
:: По этой причине очень естественно искать необходимые
V достаточные условия для того, чтобы сумма счетного
чщажесщт. SMjieHmoQ. класса К„.не давала повышения
класса, . . .:...г ' - ... ¦ .-.

. ПЕРВЫЕ СВЕДЕНИЯ О СТРУКТУРЕ МНОЖЕСТВА ТОЧЕК 73
Легко отдать себе отчет в чрезвычайной важности этой
проблемы. В самом деле, если нам удастся найти достаточ-
достаточные условия для того, чтобы класс повышался, мы в то'же
время получим эффективный процесс для реального построе-
построения множеств все более и более высоких классов, а этого
нам в данный момент нехватает.
¦ Мы дадим несколько предварительных результатов по этому
вопросу.
Теорема. Если основная область 0 полностью раз-
разбита на счетное множество неперекрывающихся элемен-
элементов Еп класса < а, то сумма бесконечного множества
элементов Еп, выбранных произвольно, будет всегда класса
< а или принадлежать к базе ВЛ. Обратно, если сумма
счгтного множества неперекрывающихся элементов класса
< а есть множество класса < а. или из базы Ва, то эти
элементы образуют часть полного разбиения всей обла-
области 0 на счетное множество элементов класса < а.
В самом деле, если мы имеем разбиение
где Sj и т\{ суть элементы класса < а, то множества S а Т,
определенные равенствами
будут либо класса < а, либо достижимые снизу класса КЛ.
А так как S и Т взаимно дополнительны, они достижимы
сверху и, следовательно, они двусторонние множества класса КЛ.
Обратно, если ? есть множество либо класса < а, либо
из базы Ва, то таким же будет и его дополнение СЕ. Сле-
Следовательно, в силу предыдущей теоремы мы имеем два раз-
разложения, для Е и для СЕ, в ряды элементов класса <-а
СЕ = 71,'+-48+...^-tin +';.'• ' '
Если эти разложения' сложить, почленно, то очевидно по-
поручится. раз0ие.1ще*.'всейрблас^иЖ.&^Ш^$ТШФ& множество

74 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
ментов класса < а попарно без общих частей:
что и доказывает формулированную теорему. Ч. т. д.
• Мы дополним этот результат следующим предложением,
которое может играть роль критерия, позволяющего убедиться
в том, что класс суммы бесконечного множества элементов
не повысился:
Т е о»р е м а. Необходимое и достаточное условие для
того, чтобы сумма счетного множества элементов класса
^ а. без общих частей была класса <[ а, состоит в том,
чтобы она была частью полного разбиения всей области 0
на счетное множество элементов класса <[ а без общих
частей.
Условие необходимо. Если множество-сумма 5 = &t -f-
—|— еа —J— .. _ будет класса -^а, то его дополнение CS также
класса ^ а. Значит, мы можем разложить CS на сумму эле-
элементов класса -С а и написать CS — т^ -\- т]2 -\- . ., Складывая
эти разложения почленно, мы получим искомое разбиение 0
Условие достаточно. Если мы имеем разбиение обла-
области 0 на счетное множество элементов класса -^ а
то сумма
не может быть класса КЛ+1, так как, в противном случае,
множество S и его дополнение
были бы множествами, достижимыми снизу класса a -j-l, сле-
следовательно, двусторонними, что невозможно, так как класс
К+1 первого рода1).
х) Вот немедленное обобщение этой теоремы: если множество Е
класса ^ а разложено на счетное множество множеств класса
<; а попарно без общих точек, то каждая часть Р этого раз-
разложения есть множество класса ^ а,
Чтобы доказать это, достаточно заметить, что каждое из соста-
составляющих множеств есть сумма счетного множества элементов класса

ПЕРВЫЕ СВЕДЕНИЯ О СТРУКТУРЕ МНОЖЕСТВА ТОЧЕК 75
Критерий неповышения класса. Мы дадим критерий
того, чтобы сумма элементов класса -^а была класса <;а
в такой форме, которая нам будет полезна при более углу-
углубленном анализе структуры множеств точек данного класса.
Вот этот критерий.
Теорема. Необходимое и достаточное условие для
того, чтобы сумма Et -j- Е2 ~\- ... -j- Еп ~\- ... счетного
множества элементов класса -^ а попарно без общих
частей была класса ^ а, состоит в том, чтобы можно
было заключить каждый элемент Еп во множество Ип
либо класса < а, либо из базы ВЛ так, что lim Нп = 0.
Условие необходимо. В самом деле, если Е ==Е1-\-Е2-\-
~\- ... -j- Еп + ... будет класса -^ а, то и его дополнение СЕ
также класса -^а. Следовательно, мы имеем разложение
множества СЕ в счетный ряд элементов §>п класса -^ а по-
попарно без общих частей.
Установив это, рассмотрим 2и—1 элементов класса <;<х:
Еи Е%, ..., En_t; $,, f2, ..., gn_i и $п. Ясно, что сумма
Ьп этих элементов есть также элемент класса -^а.
Так как два элемента 6„ и Еп не имеют общей части, то
мы можем определить отделяющее множество Нп либо класса
< а, либо из базы Ва, которое содержит Еп и не имеет
общей точки с Ьп.
Легко видеть, что lim Нп — 0. В самом деле, в противном
П->оо
случае существует точка ? основной области 0, которая при-
принадлежит бесконечному числу множеств Ни Н%, ... Но так
как мы имеем полное разложение
то эта точка \ принадлежит к некоторому вполне определен-
определенному множеству Et или §{ и не принадлежит ни к какому дру-
<а-)-1, и это же верно для дополнения СЕ. Следовательно, мы
имеем полное разбиение области 0 на счетное множество элементов
класса < а -\> 1 и Р есть часть этого разбиения. Отсюда следует,
что класс Р должен быть ^а, так как класс K«+i не содержит
двусторонних множеств,

76 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
гому из составляющих множеств. Значит, как только п пре-
превзойдет i, множество Нп уже больше не содержит точки \,
. что противоречит сделанной гипотезе. Отсюда следует, что'
НтЯ„==0.
п-±ао
Условие достаточно. В самом деле, допустим, что
EnczHn и что lim Hn = Q, где множество Нп либо класса
п->оо .
< а, либо из базы ВЛ.
Так как Еп есть элемент класса <[а, мы можем написать
равенство
?n= lim
где множество Е^ с двумя индексами будет класса < а.
Тогда множество 5П, определенное равенством
будет либо класса < а, либо из базы В„. Мы докажем, что
последовательность множеств
"Ij ^2' ¦ • •> "»> • • • '
сходится и имеет своим пределом сумму Е = Е1 -\- Е% -\- ...
Чтобы убедиться в этом, возьмем любую точку х обла-
области 0. Мы будем различать два случая, смотря по тому,
принадлежит ли х или нет ко множеству Е.
Первый случай. Точка х принадлежит к вполне опреде-
определенному элементу Е{; следовательно, она принадлежит к Н4.
Ясно,,что она принадлежит к Ei , как только п превзойдет
какое-то значение. Отсюда следует, что точка х принадле-
принадлежит к Sn при достаточно большом п.
Вторрй случай. -Точка -х не. принадлежит к Е. Так как
мы имеем lim Ип = 0, то точка х принадлежит ограничен-
-. -. i»->-oo .' ".'.-.:. . ... . '.
лому числу множеств Н1г Hs, ... Пусть /и есть целое поло-
положительное число такое, что х не принадлежит .ни_ одному. _из
множеств Нт+{, Я^+3 ... С -другой- стороны, х не прина^г
лежит ни одному из . т множеств Еи ?2, ..., Ет. Так как
.число: т постоянно, .то хочка.д; не принадлежит н,и одному

ПЕРВЫЕ СВЕДЕНИЯ О СТРУКТУРЕ МНОЖЕСТВА ТОЧЕК 77
лико. Отсюда следует, что точка х не принадлежит к Sn
при достаточно большом п.
Таким образом, последовательность множеств Sv S%, ...
сходится и имеет своим пределом Е, Е = lim Sn. Так как
га->оо
Sn либо класса < ос,, либо из базы В„, то множество Е
будет класса -^ а. Ч. т. д.
Границы применимости операций lim и lim. Возьмем
любой класс Кл классификации Валле-Пуссена и рассмотрим
бесконечную последовательность каких-нибудь множеств
класса < а
?-1> *-8> • • •» Ер, ... A)
Если мы произведем над этой последовательностью опе-
операцию lim, мы получим вполне определенное множество, кото-
которое мы обозначим через iim En и которое совпадает с пре-
и->оо
дельным множеством lim En, когда последовательность мно-
»->со
жеств A) сходится.
Таким образом, всякое множество Е класса К*, может
быть получено при помощи операции lim , произведенной
один раз над множествами предшествующих классов.
- Если мы спросим себя, каковы множества Е класса > а,
которые #огут быть получены таким способом, мы немедлен-
немедленно заметим, что только элементы класса ATa+i могут бить
получены при помощи операции lim, произведенной над по-
последовательностью множеств класса < а.
В самом деле, мы знаем, что верхний предел lim En
я -> оо
может быть написан в форме (стр. 28)
Каждая скобка есть множество класса <^а. Следовательно,
если множество lim En принадлежит к классу Еа+и то оно
П + оо
есть элемент этого класса.
Более важным предложением является следующее: каж-
каждый элемент класса Ka+i можно получить этим способом.

t8 ГЛ. II. ИССЛЕДОВАНИЯ б СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ Ё
Чтобы доказать это, возьмем элемент Е класса K«+i.
Дополнение СЕ есть сумма элементов класса <! а попарно
без общих частей в счетном множестве
Так как Еп есть элемент класса <[а, то его дополнение
СЕп есть сумма счетного множества элементов класса < а
без общих' частей
На основании очевидной формулы
Е = СЕ j • СЕ%... СЕп...
мы можем написать
Но общая часть конечного числа элементов класса < а
есть множество класса < а и, следовательно, сумма счетного
множества элементов класса ¦< а. Отсюда следует, что мы
можем считать каждый элемент е^> из я-й скобки содержа-
содержащимся в некотором элементе е*"-1) предыдущей скобки без
того, чтобы множество Е изменилось.
В этих условиях каждая точка дг из ? принадлежит беско-
бесконечному множеству элементов е(") с двумя индексами. С дру-
другой стороны, каждая точка х, не принадлежащая к Е, содер-
содержится в ограниченном числе элементов с двумя индек-
индексами е&>.
Следовательно, если мы перенумеруем все элементы е(")
с двумя индексами при помощи целых положительных чисел
е1) е2> • • •» S»> • • "I
то данное множество Е будет верхним пределом этой
последовательности, образованной из элементов класса <а.
Чтобы изучить границы применимости другой операции,
lim, достаточно заметить, что равенство Е = lim Еп может
быть записано в виде
Е = С Tim CEn.

МНОЖЕСТВА КЛАССА О И 1. ИССЛЕДОВАНИЯ БЭРА 7§
Следовательно, при помощи операции lim можно полу-
получить в классе K*+i лишь множества, достижимые снизу,
и каждое множество класса Кх+i, достижимое снизу,
может быть получено этим способом, отправляясь от
множеств класса < а, достижимых снизу.
Окончательно, операции lim и lim, примененные ко мно-
множествам класса < а, позволяют получить все множества
класса -^а и среди множеств класса Яа+i первая — все эле-
элементы этого класса, а вторая — все множества этого класса,
достижимые снизу.
Мы видим, что операции lim и lim являются более общими,
чем операция lim (простой переход к пределу), но менее
общими, чем двойной переход к пределу lim lim, который,
очевидно, позволяет получить все множества класса AT«+i.
Множества класса 0 и 1. Исследования Бэра
Предварительные замечания. Бэр создал свои методы и
свою классификацию для изучения функций, а не собственно
множеств. Тем не менее, все идеи Бэра применимы в обла-
области множеств, так как принятая нами классификация мно-
множеств есть не что иное, как классификация функций f(x),
определенных на основной области 0 и принимающих только
два значения 0 и 1.
Если такая функция f(x) непрерывна в каждой точке х0
области 0 относительно 0, то она является характеристи-
характеристической функцией некоторого множества Е класса 0, согласно
принятой классификации функций, и обратно. С другой сто-
стороны, предел ф (если он существует) характеристических
функций »!, «2, ... для множеств Ev Е2, ... есть характе-
характеристическая функция для множества Е, служащего пределом
множеств Et, Е2, -.., ? = Нт?и.
Отсюда следует, что классы характеристических функ-
функций /, определенных на 0 и классифицированных по прин-
принципам Бэра'), совпадают с классами множеств, измеримых В
!) a priori нисколько не очевидно, что функция f(x), допускаю-
допускающая лишь значения 0 н 1 и класса а в полной классификации Бэра
должна быть того же класса в классификации, которую мы полу-
получаем, распределяя по классам, согласно принципам Бэра, функции,
которые могут принимать лишь одно из двух значений 0 и 1.

80 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
в принятой классификации. В этих условиях каждой тео-
теореме из классификации функций соответствует теорема
о множествах.
: Бэру принадлежит результат чрезвычайной важности
в области функций; его можно формулировать так: для
того чтобы функция f(x) была класса 1, необходимо и
достаточно, чтобы она имела по крайней мере одну
точку непрерывности на всяком совершенном множе-
множестве. ¦ .
: На основании сказанного выше, мы получим соответствую-
соответствующее предложение о множествах, если возьмем характеристи-
характеристические функции класса <1, определенные на основной
области 0. \\ этом случае, по определению, совершенным
на 0 будет такое множество точек 0, которое не имеет
ни одной изолированной точки и содержит каждую точку из
0, в соседстве с которой имеется бесконечное множество
точек этого множества. :
Другой общий результат Бэра, относящийся ко всем
функциям его классификации, следующий: для того чтобы
некоторая функция принадлежала к классификации, н е-
о б х од им о, чтобы на каждом совершенном множестве
Р она отличалась от некоторой функции класса <] 1,
определенной на Р лишь в точках некоторого множества
первой категории на Р.
Чтобы получить соответствующее свойство множеств,
т. е. свойство, которое принадлежало бы всем множествам,
измеримым В, достаточно перенести понятие множества пер-
первой категории на Р, заменяя совершенные множества на
евклидовой прямой совершенными множествами на 0. К тому
же это обобщение понятия категории мгновенно: не надо
ничего менять в обычных определениях ]).
Что же касается функций высших классов, то Бэр
ограничился классом 3: он дал простое построение функции
класса 3. Пример Бэра следующий: если разложить в не-
непрерывную дробь иррациональное число х, заключенное
*) Это обобщение было сделано самим Бэром. См. его мемуар
«Sur la representation des fonctlons discontinues», часть вторая
(Acta Math., т. 32, стр. 116).

МНОЖЕСТВА КЛАССА О И 1. ИССЛЕДОВАНИЯ БЭРА 81
между 0 и 1
¦1+-
'as+ •
то функция f(x), равная 1, если неполные частные
oij, a2, ... неограниченно возрастают, и 0 в противном
случае, есть в точности функция класса 3.
Множество Е точек х, для которых ап неограниченно
возрастает, есть как раз множество класса 3.
Таковы результаты исследований Бэра. Если мы поста-
постараемся проанализировать характер этих исследований, то одна
вещь не может не поразить нас: Бэр никогда не доказывает
существование функции того или иного класса методом диа-
диагонали (наложением на континуум). Он всегда старается до-
доказать существование функций некоторого класса непосред-
непосредственным построением. А так как этот метод требует чрез-
чрезвычайных усилий, отсутствие конструктивных примеров функций
высших классов вполне естественно.
Напротив, пользование методом диагонали (наложение на
континуум) очень легко и приводит к немедленным результа-
результатам. Тем не менее, так как в этом методе употребляют на-
наложение на континуум всех функций (или множеств) классов,
предшествующих рассматриваемому классу, то нужно еще
хорошо изучить природу примеров, получаемых этим методом,
и сравнить их с результатами конструктивного метода Бэра*).
Важно заметить, что теорема Бэра о функциях класса 1
отличается такой красотой и настолько удобна для приложе-
приложений, что ее можно считать за идеал для предложений теории
функций. Поэтому нет недостатка в попытках получить
обобщение этой теоремы для высших классов. Среди этих,
попыток мы должны цитировать две главные, которыми мы'
обязаны Лебегу2) и Валле-Пуссену3).
*) См. мою статью «Les analogies entre les ensembles mesurab-
les В et les ensembles analytlques» Fund. Math. т. XVI, 1930.
2) «Sur les fonctions representables analytlquement», стр. 191. Мы
слегка изменили формулировку определения Лебега, введя понятие
ЭЛ6М6НТЭ
3) Ch. de la Vallee-Poussin «Integrate de Lebesgue, foncttons d'en-
semble, classes de Balre, гл. VIII, стр. 144.
6 Зак. 284. H. Н. Лузин

82 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
Лебег вводит понятие непрерывности (а).
Функция / называется непрерывной (а) на совершенном
множестве Р в точке х из Р, если для каждого положи-
положительного числа е можно найти такую порцию Р, содержа-
содержащую л:, котсрая является суммой счетного множества элементов
класса <!<х, на каждом из которых / постоянна с точностью
до е, причем все эти элементы, кроме одного, содержа-
содержащего х, нигде не плотны на Р.
Установив это определение, можно, согласно Лебегу, вы-
выразить следующим образом необходимое и достаточное усло-
условие для того, чтобы функция f(x) была класса ^ а: необ-
необходимо а достаточно, чтобы f(x) была непрерывна (а) по
крайней мере в одной точке на каждом совершенном
множестве.
С другой стороны, Валле-Пуссен ввел следующие понятия,
при помощи которых он приходит к искомому обобщению
теоремы Бэра:
Бесконечная последовательность функций /„ называется
сходящейся к / с точностью до е на множестве Е, если
в каждой точке Е верхний и нижний пределы /п для и —>• со
Um/n и lim/n равны / с точностью до е.
Функция / есть функция класса а на Е с точностью
до е, если существует последовательность функций /„ класса
< а, сходящаяся к / на Е с точностью до е. / есть функ-
функция класса а с точностью до г на Е в некоторой точке х,
если существует псрция Е, содержащая х, на которой х
класса а с точностью до е.
Вот какова формулировка Валле-Пуссена: Необходимое
и достаточное условие для того, чтобы функция f была
класса <! а, состоит в том, чтобы для всякого положи-
положительного числа е и для всякого совершенного множества Р
Можно было найти точку из Р, в которой f на Р класса а
с точностью до е.
- В дальнейшем мы внимательно изучим теорему Бэра
о .множествах класса 1, чтобы найти аналогичное предложе-
предложение для множеств высших классов, возможно более близкое
к теореме Бэра.
- ^Множество класса 0. Сначала мы рассмотрим множества
начального класса АГ0.

МНОЖЕСТВА КЛАССА О И 1. ИССЛЕДОВАНИЯ БЭРА . 83
По самому определению, в класс 0 входит всякое множе-
множество точек Е такое, что само Е и его дополнение СЕ являются
суммами счетного множества порций области 0 попарно без
общих точек.
Мы видели (стр. 24), что для получения заранее за-
заданного множества Е класса 0 достаточно взять на прямой
Х'Х1) замкнутое множество F, составленное из рациональ-
рациональных точек, и заставить войти в Е порции основной области 0,
смежные к F так, чтобы оставшиеся порции 0, смежные
к Е, вошли в дополнение СЕ, причем две соседние порции
принадлежат двум разным множествам.
Ясно, что замкнутое множество F, обладающее этим свой-
свойством, единственно.
Пусть
р р' р" е-М тМ
— последовательные производные множества от F.
Так как F счетно, то существует вполне определенное
число а, конечное или трансфинит второго класса такое, что
производное множество /^7> пусто, тогда как каждое пред-
предшествующее производное множество F®\ j3 < а эффективно
содержит точки.
Таким образом, каждому множеству Е класса О соот-
соответствует вполне определенное число а конечное или
трансфинит второго класса.
Мы видим, что это число а может быть как угодно
«большим» 2).
Было бы чрезвычайно интересно уметь аналогичным спо-
способом привести в соответствие каждому двустороннему мно-
множеству Е класса К„ второго рода некоторое конечное или
трансфинитное число j3.
Теорема Бэра в приложении к множествам класса 1.
Мы теперь изучим структуру общего множества точек клас-
класса 1. Прежде всего мы применим теорему Бэра о функциях
J) Прямая Х'Х здесь евклидова. (Прим. ред.)
2) Это значит, что какова бы ни была счетная вполне улорядо-
ченная последовательность, можно эффективно образовать множе-
множество Е класса 0 такое, чтобы соответствующая последовательность
производных множества F, эффективно содержащих точки, была бы
подобна данной вполне упорядоченной последовательности.

84 ГЛ. Н. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
класса 1 к случаю характеристической функции, определен-
определенной на 0 \ вот что мы получим:
Для того чтобы множество точек Е было класса <! 1,
необходимо и достаточно, чтобы, каково бы ни было мно-
множество Р, совершенное относительно 0', существовала
порция Р, целиком содержащаяся или в Е, или в его до-
дополнении СЕ.
Важно заметить, что это характеристическое свойство
множеств класса <! 1 выведено из теоремы Бэра о функциях
класса 1, но не из определения множества класса 1.
Мы выведем это характеристическое свойство непосред-
непосредственно из определения множества класса 1.
Условие Бэра необходимо. В самом деле, пусть Е — мно-
множество класса < 1, лежащее в основной области 0.
Пусть Р есть произвольное совершенное (относительно 0)
множество, лежащее в 0.
На основании общего предложения о структуре множества
класса а (стр. 71), Е и его дополнение СЕ являются оба
суммами счетного множества элементов класса <! а попарно
непересекающихся. С другой стороны, элемент класса 1 есть
не что иное, как множество замкнутое (относительно 0), так
как дополнение к элементу класса 1 есть сумма счетного
множества порций 0.
Таким образом, мы имеем разложение
где гп и ч\п суть замкнутые множества.
Хотя бы одно из гп или ч\п должно быть плотным на Р;
следовательно, оно содержит порцию Р. Но это и есть свой-
свойство Бэра.
Условие достаточно. Пусть Е есть множество точек,
обладающее указанным свойством.
В силу этого свойства, какова бы ни была порция (а, Ь)
области 0, найдется другая порция (а', Ь'), содержащаяся
в (а, Ь) и заключенная целиком либо в Е, либо в СЕ.
Отсюда следует, что существует замкнутое неплотное
множество Fv каждая смежная порция к которому принад-
принадлежит целиком либо к Е, либо к СЕ J).
1) Мы прибавим, если это нужно, некоторые рациональные
точки к F, чтобы эта формулировка оправдалась.

МНОЖЕСТВА КЛАССА О И 1. ИССЛЕДОВАНИЯ БЭРА 86
Заметив это, обозначим через Р, наибольшее совершенное
множество, содержащееся в F,. Предыдущее рассуждение,
произведенное над основной областью ?f, прекрасно приме-
применяется к случаю совершенного множества Р, и, таким обра-
образом, мы имеем новое замкнутое множество F%, содержащееся
в Р]; неплотное на Р, и такое, что каждая порция Pv смеж-
смежная к Fa, принадлежит либо к Е, либо к СЕ.
Продолжая таким же образом, мы получим вполне упо-
упорядоченную последовательность
^з^эРр ... э Рш =э ... э Рр э ...
совершенных множеств таких, что из любых двух множеств
следующее содержится в предыдущем и неплотно на нем 1).
Отсюда вытекает, что эта последовательность должна быть
счетной. Значит, мы придем к пустому множеству.
С другой стороны, из построения совершенных множеств Рр
следует, что каждое Рр есть наибольшее совершенное мно-
множество, содержащееся в замкнутом множестве F$, и что
если j3 первого рода |3 = |3*-}-1, то каждая порция Рр,
смежная к Fq, заключена полностью либо в Е, либо в СЕ.
Отсюда мы заключаем, что оба множества Е и СЕ являются
суммами конечного или счетного числа отдельных точек и
порций' совершенных множеств, попарно неперекрывающихся.
Но каждая отдельно взятая точка и каждая порция совершен-
совершенного множества есть элемент класса 1 (или порция if). Сле-
Следовательно, мы получаем полное разбиение, основной об-
области 0 на конечное или счетное число элементов класса 1
и множество Е есть часть этого разбиения.
На основании общей теоремы о структуре множества
класса а (стр. 74), множество Е будет класса <[1. Ч. т. д.
Свойство Бэра для всех множеств, измеримых В. Мы
видели, что каждое множество Е класса 1, так же как и
его дополнение СЕ, есть сумма счетного множества отдель-
отдельных точек и совершенных множеств.
Так как общая часть двух совершенных множеств есть
замкнутое множество и так как всякое замкнутое множество
1) Совершенное множество Ра содержится в замкнутом множе-
множеFp. Если индекс {5 второго рода, то Fp определяется как общая
часть для всех fp/ (или для всех Р^,), предшествующих Р, ?'<?•
стве

86 ГЛ. П. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
есть сумма совершенного множества и счетного числа отдель-
отдельных точек, мы заключаем, что тонки множества Е класса 1,
содержащиеся в совершенном множестве Р, а также точки
дополнения СЕ образуют на Р сумму счетного числа от-
отдельных точек и совершенных множеств.
Свойство Бэра теперь может быть формулировано следую-
следующим образом:
Всякое множество, измеримое В, а также и его до-
дополнение являются на каждом совершенном множестве Р
суммами счетного числа порций Р, если пренебрегать
множеством первой категории по отношению к Р.
Другими словами, каковы бы ни были множество Е, изме-
измеримое В, и совершенное множество Р, можно определить на Р
замкнутое множество F, неплотное на Р и такое, что каждая
порция Р, смежная к F, содержится либо в Е, либо в СЕ,
если пренебрегать точками множества первой категории по
отношению к Р.
Сравнивая эту форму свойства Бэра с указанным свой-
свойством множеств класса 1, мы придадим свойству Бэра сле-
следующую форму: всякое множество Е, измеримое В, на всяком
совершенном множестве Р отличается от множества Ех пер-
первого класса, лежащего на Р, лишь в точках некоторого мно-
множества первой категории по отношению к Р.
В этой форме рассматриваемое свойство есть не что иное,
как свойство Бэра для функций f (х), определенных на g и
допускающих лишь два значения 0 и 1. Следовательно, можно
вывести свойство Бэра, касающееся множеств, из того, ко-
которое касается функций.
Чтобы доказать его непосредственно, достаточно заме-
заметить, что если каждое из множеств Еи Е2, ..., Еп, ...
обладает свойством Бэра на совершенном множестве Р,
то их сумма и общая часть также обладают свойством
Бэра на Р.
В самом деле, обозначим через Sn сумму порций Р, от-
отличающуюся от Еп лишь в точках некоторого множества еп
первой категории по отношению к Р; множество еп образо-
образовано из точек Е„, не принадлежащих к Sn, и из точек Sn,
не принадлежащих к Еп.
Обозначим через 5 сумму множеств Sn. Очевидно, что 5
есть множество класса <! 1, отличающееся от суммы

КОНСТРУКТИВНОЕ СУЩЕСТВОВАНИЕ КЛАССОВ 1, 2, 3 И 4 87
Е1~\-Е2 -\~ ... лишь в точках множества е1 -\- е2 -(- ... пер-
первой категории по отношению к Р.
Следовательно, свойство Бэра инвариантно по отношению
к операции (S): составления суммы.
Но, по самому определению, свойство Бэра инвариантно
относительно операции (С): взятия дополнения.
Так как всякое множество, измеримое В, может быть
образовано при помощи этих двух операций, отправляясь от
порций ?f (стр. 43), то свойство Бэра принадлежит всякому
множеству, измеримому В 1).
Конструктивное существование множеств
1, 2, 3 и 4-го классов
Канонические элементы класса 1. Мы назовем канони-
каноническими элементы данного класса КаУ которые обладают
некоторым достаточно простым свойством и такие, что
каждое множество класса КЛ можно получить, образуя сумму
счетного множества канонических элементов 2).
Мы рассмотрим канонические элементы первых классов
классификации Бэра—Валле-Пуссена.
Порция фундаментальной области 0 может быть рассмат-
рассматриваема как канонический элемент класса 0.
В первом классе каноническими элементами являются:
точка и совершенное множество, нигде не плотное на 0'.
Для того чтобы убедиться в этом, достаточно заметить,
что элемент класса Кх совпадает с замкнутым множеством
(относительно ?f). Действительно, если?— элемент класса АГ],
то его дополнение СЕ достижимо снизу, следовательно, есть
сумма порций $', отсюда мы заключаем, что Е — замкнуто.
Обратно, каждое замкнутое множество F есть, очевидно,
элемент класса Kv
1) См. также Сообщение Польской ^Академии Nikodym «Sur
la condition de Baire», Bull. Ac. Pol., 1929, стр. 591.
2) Данное определение канонического элемента неопределенно,
так как мы не указали, в чем заключается это достаточно простое
свойство. Мы не умеем этого сделать в общем случае. Было бы
желательно иметь в каждом классе конечное число родов канони-
канонических элементов так, чтобы элементы одного рода были между
собой гомеоморфны [6].

88 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
Так • как каждое несчетное замкнутое множество есть
сумма счетного множества точек и совершенного множества,
то ясно, что каждый элемент класса К^ состоит из порций
области g отдельных точек в счетном числе и совершенного
множества нигде не плотного на 0. Следовательно, канони-
каноническими элементами класса К^ являются точки и совершен-
совершенные, нигде не плотные множества.
Канонические элементы класса 2. В классе К2 есть
канонические элементы двух родов:
1° Можно получать канонический элемент класса 2,
выбрасывая из совершенного множества Р счетное мно-
множество точек, всюду плотное на Р.
2° Можно получить канонический элемент класса 2,
выбрасывая из совершенного множества Р счетное мно-
множество нигде не плотных на Р совершенных множеств
попарно без общих точек, сумма которых всюду плотна
на Р.
Чтобы в этом убедиться, достаточно показать, что каж-
каждое множество Е класса 2 есть сумма счетного множества
элементов этих двух родов и множеств класса <; 1. Так как
каждое множество класса 2 есть сумма счетного множества
элементов класса /С2, то достаточно ограничиться рассмотре-
рассмотрением элементов ['].
Пусть Е— элемент класса 2. Выбросим из в все пор-
¦ ции, на которых Е класса <[ 1. Мы получим совершенное
множество Ри каждая порция которого содержит часть мно-
множества Е, образующую элемент класса 2.
Я утверждаю теперь, что между порциями Рг найдется
хотя бы одна такая, что часть Е, ей принадлежащая, есть
канонический элемент.
В самом деле, дополнение СЕ состоит из порций, отдель-
отдельных точек и совершенных множеств в счетном числе. Но СЕ
всюду плотно на Ри так как иначе существовала бы порция
области 0, содержащая точки Pj и определяющая часть Ё
класса -<! 1, что противоречит определению Р.
С другой стороны, СЕ очевидно первой категории на Pv
так как в противном случае существовала бы порция Р„ не
содержащая точек Е, что также противоречит условию. Сле-
Следовательно, среди порций Pi есть порции, которые опреде-
определяют канонические части Е. Ясно, что эти порции образуют

КОНСТРУКТИВНОЕ СУЩЕСТВОВАНИЕ КЛАССОВ 1, 2, 3 И 4 89
множество, всюду плотное на Р1г так что, выбрасывая эти
порции из Plt мы получим замкнутое множество F2, нигде
не плотное на Pv
Обозначим через Р2 наибольшее совершенное множество,
содержащееся в F2.
Легко видеть, что, поступая так же с множеством Р2, мы
получим новое совершенное множество Р3, содержащееся
в Р2 и нигде не плотное на нем, а так далее.
Мы построим последовательность совершенных множеств
с/ > » "а» • • •'» "ш> • • •> Р> • • •>
каждое следующее множество содержится в предыдущем и
нигде не плотно на нем. Следовательно, существует число а
конечное, или трансфинитное второго класса, такое, что мно-
множество Ра пусто.
Отсюдахмы заключаем, что данное множество Е разла-
разлагается на счетную сумму множеств класса <[ 1 и элементов
класса а обоих указанных родов. Ч. т. д.
До сих пор мы предполагали установленным существова-
существование множеств класса 2. Нам остается восполнить этот пробел.
Пусть Е — множество одного из двух рассмотренных
родов. В силу самой конструкции Е множество Е, так же
как и его дополнение СЕ, всюду плотно на совершенном мно-
множестве Р.
Я утверждаю теперь, что Е есть множество класса 2.
В самом деле, если бы класс Е был меньше, чем 2, то мно-
множество Е обладало бы свойством множеств класса ^ 1. Зна-
Значит, существовала бы порция Р, принадлежащая целиком
либо к Е, либо к СЕ; но это противоречит тому, что Е и СЕ
оба всюду плотны на Р.
Итак, множество Е строго класса 2.
Заметим, наконец, что каждое совершенное нигде не плот-
плотное множество строго класса 1. Действительно, такое мно-
множество не может быть класса 0, так. как не содержит никакой
порции g.
Конструктивное доказательство Бэра существования
элементов класса 3. Основной целью двух мемуаров Бэра
«Sur ]a representation des fonctions discontinues» (первый
мемуар в Acta. Math., т. 30, 19Q5; второй мемуар там же,
т. 32, 1909) является строгое построение элемента класса 3.

90 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
Наиболее важная часть первого мемуара посвящена этому
вопросу. И во втором мемуарг Бэр возвращается к этому
построению с более общей точки зрения.
Принципы, изложенные нами выше, позволяют нам без
затруднения изучить результаты Бэра о конструктивном суще-
существовании элементов класса 3.
Прежде всего уточним условия существования элемента
класса 3. Предположим, что существует элемент Е класса 3.
Мы видели (стр. 78), что Е может быть написано в виде:
? = 0f>+41)+41)+ • • •) • (<f+42)+42)+ • • •)• • •> О)
где е№— элементы класса ^1. При этом мы можем пред-
предположить, что элементы, стоящие в одной скобке, не имеют
попарно общих точек и что каждый элемент е№ k-ft скобки
содержится в некотором элементе е^-1) предшествующей
скобки.
В силу того, что мы говорили о канонических элементах
класса 0 и 1, мы "можем предположить, что элементы «W
являются: либо порциями фундаментальной области g, либо
отдельными точками, либо совершенными нигде не плотными
множествами.
Каждый элемент класса 3, если он существует, может
быть получен таким образом. Таков вывод из предшествую-
предшествующего текста.
Открытие Бэра заключается в том, что он дал до-
достаточное условие для того, чтобы множество Е, опре-
определенное равенством A), было в точности класса 3.
Вот условия Бэра:
1° Множества е'М совершенные (относительно 0).
2° Каждое множество е№, содержащееся в s'^~^, нигде
не плотно на в^'.
3° Множества е&\ содержащиеся в фиксированном мно-
множестве ej*', образуют множество, всюду плотное на ^~1}.
В этих условиях Бэр доказывает, что Е есть множество
строго класса 3.
Для доказательства этого результата Бэра удобно изме-
изменить обозначения.

КОНСТРУКТИВНОЕ СУЩЕСТВОВАНИЕ КЛАССОВ 1, 2, 3 И 4 91
Обозначим через р<1(/1=1, 2, 3, ...) все множества е{„
первой скобки равенства A). Пусть элементы (k— 1)-й скобки
обозначены через /-*< ... *ft—i; обозначим через Pi ...<fc_ ¦«.,
где индекс ik принимает значения 1, 2, 3, ..., все элементы
k-ft скобки, содержащиеся в ^j...<ft_j.
При таких обозначениях все элементы &-й скобки суть
множества Р» . i с & индексами, и каждое множество /V ... i
с к индексами есть элемент k-Vi скобки. Чтобы получить все
элементы (k-\-\)-Vi скобки, содержащиеся в Pi ..,< , доста-
достаточно добавить новый индекс /д.,., так, чтобы получился
символ с k-\-l индексами, и заставить 1к+1 пробегать значе-
значения 1, 2, 3, ...
После этого обозначим через Q{ ... { сумму всех мно-
множеств Р^...1к_^к, ik=l, 2, 3, ..., у которых ft — 1 пер-
первых индексов фиксированы, и через Qk — сумму всех мно-
множеств Pi1%..ik с k индексами.
Вот формулировка Бэра: если 1° множества Р{ ,,,'j со-
совершенные относительно g и, при фиксированном k, не
имеют попарно общих точек; 2° множество Pi, ...иг,х,
содержится в Pi .,. < и нигде не плотно на этом мно-
множестве; 3° множество Qt,... i, всюду плотно на Pit ... г- ,
1 К 1 К
то общая часть .
E = Q1-Qt...Qk...
есть множество в точности класса 3.
Чтобы это доказать, обозначим через Ro множество точек
области ff, не принадлежащих ни одному из множеств
Pi, t = l, 2, 3, ..., и через Ri < ...< множество-разность
Р< ...к — Q* ...!,,• Легко видеть, что Ro и Ri,...i. являются
1 К 1 ft 1 ft
каноническими элементами класса 2 !) и что
J) Мы предполагаем, что сумма Qt множеств Р{, ir= 1,2,3
всюду плотна на В'. При этих условиях Ro есть в точности кано-
канонический элемент класса 2.

92 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
где индексы i1, /2, ..., /д. и само k принимают значения
1, 2, 3, ... независимо один от другого.
Так как канонические элементы Ro и Ri ...< не имеют
попарно общих точек, то мы можем применить критерий
неповышения класса, ранее нами полученный (стр. 75). Мы
заключаем, что если множество Е есть множество
класса <; 2, то можно заключить каждый элемент Rs ... i.
1 ft
в множестве Н{ ... <, класса <! 1 так, что lim Яг- ... *ь = О,
lft lft
когда один из индексов it, ..., ib или k бесконечно растет.
Покажем, что при этих условиях мы придем к противо-
противоречию. Прежде всего, так как множестг-о Яо, содержащее Ro,
есть множество класса ^1 и всюду плотно на ff, то суще-
существует наверняка порция 80 фундаментальной области <*7,
содержащаяся целиком в Но.
Заметив это, перенумеруем все рациональные точки при
помощи целых положительных чисел. Пусть г5, г2, г8, ...—
полученная последовательность. Так как порция 80 фиксиро-
фиксирована и так как множество Qj всюду плотно на g, то суще-
существует множество Р.о, имеющее точки в 80. С другой сто-
стороны, множество Я о всюду плотно на Р .о, так как содержит
канонический элемент R о> всюду плотный на Р. о- Так
как Я\о класса <[1, то можно определить порцию 8] об-
области 0, содержащуюся в 80 и не имеющую точки г1 в ка-
качестве своей предельной точки такую, что порция Р 0, кото-
h
рую она определяет, содержится целиком в Я.о.
h
Предположим вообще, что мы нашли порцию 8fc_t об-
области 0, для которой точки rj, г2, ..., rfc_j не являются
предельными точками, и множество Р 0 .о такое, что его
порция, которую определяет 8ft_lJ целиком содержится
в Я о .о .о • Так как множество Q о .о .о всюду плотно
на Р.оо ,о » го существует множество Я о о .о о,
имеющее точки в 8fc_j. С другой стороны, множество Я.о .о

КОНСТРУКТИВНОЕ СУЩЕСТВОВАНИЕ КЛАССОВ 1, 2, 3 И 4 93
всюду плотно на Р о ,о, так как содержит канонический
элемент, всюду плотный на Р.о .о- Так как Н.о.о о
класса -^1, то можно найти порцию Ък области g, содер-
содержащуюся в 8ft_i, для которой точка гк не является предель-
предельной, такую, что порция Р о.о .о, которую определяет 8Ь
hl2 ••• 1к
содержится целиком в Н л о ,о.
Легко видеть, что, продолжая таким образом, мы построим
последовательность порций области g:
такую, что каждая последующая содержится в предыдущей
и для порции 8fc рациональные точки ги г2, ..., гк не
являются предельными точками.
Отсюда следует, что длины 8ft стремятся к нулю, когда к
бесконечно возрастает. Следовательно, существует одна и
только одна точка $, общая всем порциям Ъи. Эта точка |
заведомо иррациональная в силу свойства порций 8fc.
Так как множество Р о о о содержится в множестве
Р .о .о о, где h < к, то, если к достаточно велико, пор-
Ч\ • ¦ ¦ ih
ция 8ft области g содержит точки множества Р .0 о, где v
гх ... <v
фиксировано. Но множества Р.о .о совершенные. Отсюда
\ ¦- гк
следует, что точка % принадлежит всем множествам
Р,0, Р.0,0, ...,Р.0,0 ...О--.
и, следовательно, всем множествам
что невозможно, так как, по предположению, мы имеем:
lim H о .о ,о = О.
ЧН-~*к
Итак, мы пришли к противоречию и, следовательно, мно-
множество Е есть элемент класса 3. Ч. т. д.

94 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
Назовем элементами Бэра элементы класса 3, которые по*
строены по приведенному выше правилу. Мы не касаемся
вопроса, являются ли элементы Бэра единственными в классе 3,
которые заслуживают названия канонических элементов.
. В силу крайней простоты применения правила Бэра можно
дать арифметический пример элемента 3. Бэр сам нашел
такой пример *).
Положим, вместе с Бэром,
1
«2 +
где каждое ап — целое положительное число.
Обозначим через p№(av a2, ..., ah) множество всех ир-
иррациональных точек сегмента [0,1|, которые изображаются
непрерывными дробями, начинающимися с (аи я2, ..., ah) и
у которых остальные неполные частные все больше, чем га.
Легко доказывается, что рМ(а1, а2, ..., ah) — совершен-
совершенное множество (относительно g), нигде не плотное на 0'.
Множество рМ называется нормальным, если й = л или
если А>я и если ай^л.
При фиксированном я все нормальные множества попарно
не имеют общих точек. Легко видеть, что их сумма Qn
есть множество всех иррациональных точек сегмента
[0,1], у которых все неполные частные, начиная с неко-
некоторого ранга, больше, чем п.
Заметив это, обозначим через Pi (г=1, 2, ...) все нор-
нормальные множества pW, перенумеровав их некоторым обра-
образом. Так как два нормальных множества р(п~^) и рМ либо не
имеют общих точек, либо р^ содержится в pfa-1), то мы
!) См. R. В a ire, «Sur la representation des functions disconti-
discontinues» (Acta Math., т. 30, 1905, стр. 34—47).

КОНСТРУКТИВНОЕ СУЩЕСТВОВАНИЕ КЛАССОВ 1, 2, 3 И 4 95
можем обозначить через Р^...^_^к все нормальные множе-
множества, содержащиеся в Ргх..лк_х (ik=l, 2, 3, ...).
Легко показать, что Pi ..л, «.нигде не плотно на Pi ,.л и
что сумма Qiv.Ak_t множеств Piv..ik_sk (**=1, 2, 3, . . .)
всюду плотна на Pi .,.< J).
Итак, множества А„..«. удовлетворяют всем условиям
правила Бэра. Так как это правило здесь применимо, мы за-
заключаем, что общая часть
есть элемент класса 3.
Можно немедленно указать очень изящное характеристи-
характеристическое свойство точек Е.
Множество Е есть множество всех иррациональных
точек сегмента [0,1], у которых неполные частные но-
номера п бесконечно возрастают вместе с п.
Это свойство точек Е можно получить, рассматривая ха-
характеристическое свойство множеств Qn.
Итак, можно назвать элемент класса 3, указав неко-
некоторое его прифметическое свойство.
Исследования Л. В. Келдыш о конструктивном суще-
существовании элемента класса 4. Можно ли продолжить изы-
изыскания Бэра за пределы класса 3? Мы приведем здесь кон-
конструктивное доказательство существования элемента класса 4,
принадлежащее Л. В. Келдыш. Этот результат является наи-
наиболее естественным в направлении, открытом Бэром.
Вот ход рассуждений Л. В. Келдыш: строится сначала
счетная последовательность элементов Бэра (класса 3) ev е^,...
... еп, ... попарно без общих точек, выбранных соответствую-
соответствующим образом, и доказывается затем, что сумма ei~\-e2 -f-...
.-.. -f- en -j- ... не может быть класса меньше, чем 4. Этот
важный факт устанавливается применением критерия неповыше-
неповышения класса (стр. 75): элемент еп заключается в множество Нп
класса -^ 2 и доказывается, что никогда не имеет места
lim Нп = 0, каков бы ни был выбор Нп.
!).Подробности см. в цитированном мемуаре Бэра (Acta Math.,
т. 30, 1905, стр. 39).

96 ГЛ. И. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
Все сводится к выбору элементов Бэра еи г2, ...,en, ...
Существенная роль в этой конструкции принадлежит элемен-
элементам класса 2, и мы начнем с доказательства следующей
леммы:
Лемма I. Если элемент Бэра Е, заданный опреде-
определяющей системой Pi л , содержится в счетной сумме ка-
канонических элементов класса ^2, ftj, 62 .,., 0п, ..., ото
существует такое Нт и такая порция тс некоторого об-
образующего множества Рдо .о, что Ьт — второй катего-
категории на каждой порции тс, так же как на каждой порции
любого определяющего множества, содержащегося в тс.
Предположим, наоборот, что такого Ьт не существует.
Это значит, что существует порция Uj определяющего мно-
множества Р о о о такая, что 0. не содержит точек тс.. Так
щ2..лк
как 02 не удовлетворяет условиям леммы, то существует
в тс, порция тс„ определяющего множества Р 0 о о такая,
«i-VS
что 92 не содержит точек тс2. Существует также в тс2 пор-
порция тс3 определяющего множества Р 0 о о о такая, что 03
не содержит точек тс3. Продолжая таким образом до беско-
бесконечности, мы получим неограниченную последовательность
порций Ttj, тс2, ..., tcv, .. . каждая из которых содержится
в предшествующей и такую, что множество те, не содержит
точек v множеств 0j, 92, ..., 6,. Пусть $ — точка, принадле-
принадлежащая всем tcj, тс2, ..., itv, ... Эта точка принадлежит, оче-
очевидно, элементу Бэра Е и, так как она не принадлежит ни
одному из множеств 6j, 02, ..., то мы пришли к противо-
противоречию. Ч. т. д.
Введем теперь следующее определение. Пусть 0 — кано-
канонический элемент класса 2, который получается выбрасыва-
выбрасыванием из совершенного множества Р счетного множества со-
совершенных множеств Ри Р2, . . ., Рп, ... попарно без об-
общих точек, каждое из которых нигде не плотно на Р и
сумма которых всюду плотна на Р. Пусть Е — элемент Бэра
класса 3, содержащийся в 0 и всюду плотный на Р, задан-
заданный определяющей системой Рц ...{ .
Определение. Мы будем говорить, что Е есть эле-
элемент Бэра, плотный на 9, если каждая порция произвольного

КОНСТРУКТИВНОЕ СУЩЕСТВОВАНИЕ КЛАССОВ 1, 2, 3 И 4 97
определяющего множества Рц лк содержит порцию какого-
либо совершенного множества Рп.
Установив это определение, мы докажем следующее пред-
предложение:
Лемма И. Каждый канонический элемент 6 класса 2
содержит элемент Бэра класса 3, плотный на 0.
Прежде всего мы заметим, что лемма будет доказана, если
мы сумеем построить совершенное множество я, содержа-
содержащееся в Р, нигде не плотное на Р и такое, что каждая пор-
порция it содержит порцию некоторого множества Рп, причем
эта порция нигде не плотна на тт.
В самом деле, предположим, что мы построили такое мно-
множество я; обозначим его Wj и в смежных интервалах к че1
возьмем совершенные множества гс2, яв, ....каждое из кото-
которых обладает тем же свойством. Сумму i:1 -J- я2 -J- ... -f-
-4- nn -)-... можно выбрать всюду плотной на Р и первой
категории на Р.
Эти множества irf будут определяющими множествами
с одним индексом элемента Бэра ?, который мы получим.
Поступая таким же образом для множеств nif осущест-
осуществляя для каждого из них те же операции, которые мы про-
производили над множеством Р, мы построим определяющие мно-
множества iti 1, it{2> • • •» Ъгл » • ¦ • с двумя индексами для
элемента Е, и так далее. Можно, очевидно, предположить,
что множества щ < с двумя индексами не содержат точек Pt,
так как Pt нигде не плотно на каждом ir< . Таким же об-
образом можно предположить, что множества кц ,.л. с k ин-
индексами не содержат точек множества Ял_3. Легко видеть,
что элемент Бэра Е, заданный определяющей системой "Кц ...{ ,
содержится в 0, так как он не может содержать точек мно-
множеств Pv Я2, ..., РпУ ... Следовательно, элемент Бэра Ef
таким образом определенный, плотен на 0.
Все сводится к построению совершенного множества «,'
обладающего указанным свойством.
Для этого возьмем в множестве Р точки lit Eg, ..., &„,...,
не принадлежащие ни одному Рк и образующие счетное,
всюду плотное на Р множество. Рассмотрим множество Pt и
выбросим из Р порцию Oj, смежную к Я, и содержащую
точку Sj.
7 3«к. 284. Н. Н. Лузин

9& гл. и. иссладовАчйя о структуре множеств, измеримых В
Пробегая последовательность Р2, Р3, ..., Р„, ..., мы
найдем множество, некоторая порция которого принадлежит
к Р— 0^ пусть Рч —первое такое множество. Выбросим
из Р порцию о2 множества Р, смежную к Pj-j-P, и со-
содержащую точку ?2. Пробегая последовательность P»1+i,
Ру,+2. • ••» Рп> •••> мы найдем множество, некоторая пор-
порция которого принадлежит к Р — Oj — о2; пусть Р, — первое
из.таких множеств. Выбросим из Р порцию о3 множества Р,
смежную к Р1-\- Р, -\- Р, и содержащую точку ?8 и так
далее.
Продолжая таким образом до бесконечности, мы построим
бесконечную последовательность порций <it, о2, ..., оп, ...
множества Р. Множество тс точек Р, которое получается
выбрасыванием из Р всех о^, есть совершенное множество, и
легко видеть, что тг обладает требуемыми свойствами. Ч. т. д.
Перейдем теперь к конструкции элемента класса 4.
Возьмем сначала в порции @,1) области g элемент
Бэра Ео, всюду плотный на этой порции; пусть Р°пп п •—>
определяющие множества для Ео. Если мы выбросим из пор-
порции @,1) элемент Ео, то оставшаяся часть разбивается на
счетное, множество канониче;ких элементов класса 2, кото-
которые мы обозначим через 6 , v1 = l, 2, ...
Напомним, что каждоз 6<Vl) есть не что иное, как раз-
разность
00
Применяя лемму II, мы построим в каждом 6^ элемент
Бэра E^'V плотный на 6(''\ Если мы выбросим из 6(ll) эле-
элемент ?^'*-, то оставшаяся часть разбивается на счетное мно-
множество канонических элементов класса 2, которые мы обо-
обозначим; через. frV*.
« Каждое 6*V|r* есть не что иное, как" разность

КОНСТРУКТИВНОЕ СУЩЕСТВОВАНИЕ КЛАССОЗ 1, 2, 3 И 4 99
и мы можем, очевидно, предположить, что элементы Ео и
?(<l) всюду плотны на каждом Р^1]..^-
Вообще, когда определен элемент 6(V2"-V) класса 2, мы,
применяя лемму II, строим в 0(Y"W элемент Бэра f^'iV'-V^
плотный на 0("i""v»»\ Если мы выбросим из 8*Va" ¦ •'да) эле-
элемент Е<''\2'"ч'>п\ то оставшаяся часть разбивается на счетное
множество канонических элементов класса 2, которое мы
обозначим через fi^fW+i'. Каждое 6(Y"VWi) есть не что
иное, как разность
и мы можем, очевидно, предположить, что элементы Бэра Ео,
E'"i\ E^iV /*'i—V всюду плотны на каждом Р^'"*™1.
Пусть 5 — сумма всех элементов Бэра, таким образом
построенных:
2e{v
o
-1 Va
Мы покажем, что множество S, таким образом по-
построенное, есть множество в точности класса 4.
Действительно, как мы заметили выше, если бы это было
не так, то можно было бы заключить каждое ZTY"V' в мно-
множество //(vi""m> класса 2 таким образом, что каждая точка
области 0 принадлежит не более, чем к конечному числу
множеств H^iV-'V),
Предположим, наоборот, что такие множества //^viV"t»»)
существуют и рассмотрим элемент Бэра Ео. Так как Но есть
сумма счетного множества канонических элементов класса 2,
то мы находимся в условиях леммы I. Пусть 0о — канониче-
канонический элемент класса 2 и тг0 — порция некоторого определяю-
определяющего множества для Ео такая, что 60 —второй категории на
каждой порции тга, так же как и на каждой содержащейся
в я0 порции произвольного определяющего множества для Ео.
В этих условиях мы можем написать:
7*

100 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
где Foft есть замкнутое множество, нигде не плотное на те0
и на каждом определяющем множестве для Ео.
Следует заметить, что каждое множество F^ нигде
не плотно на любом определяющем множестве. Докажем
это по индукции. Предположим, что Fok нигде не плотно на
каждом определяющем множестве для множеств ir i, Er'fv, ...,
.,., ?(V2 ••• V и покажем, что это имеет место и для ?*'i"" Vx+i>.
Предположим, что это не так и, следовательно, множество Foll
плотно на некоторой порции о некоторого определяоццего
множества для ?V" V*+i. в силу леммы II о содержит пор-
О О
цию определяющего множества для ?Vl""\ что не имеет
места. Ч. т. д.
Пусть 1Г* — плотный элемент Бэра, всюду плотный на it0.
Этот элемент заключен в множество FT1 класса 2. Применяя
лемму I, мы можем определить канонический элемент 0^ и
порцию irj некоторого определяющего множества для Е 1
такую, что 6^ второй категории на nv так же как на каждой
содержащейся в пг порции любого определяющего множества
для Е -1 . В этих условиях можно написать:
где F11e есть замкнутое множество нигде не плотное на itj
и на каждой лежащей в itj порции определяющего множества
для Е^д. Повторяя предыдущее рассуждение, мы покажем,
что каждое множество Flk нигде не плотно на содержащейся
в «J порции любого определяющего множества. Мы выберем
порцию itj так, чтобы она не содержала ни одной точки Fol>
что всегда возможно, так как Fol нигде не плотно на ir0.
Вообще, после того, как получены равенства:
4- •••,

КОНСТРУКТИВНОЕ СУЩЕСТВОВАНИЕ КЛАССОВ 1, 2, 3 И 4 101
(ч°чв v° )
мы берем в порции кт плотный элемент Бэра f1Г" *ж„
всюду плотный на vm. Этот элемент заключен в множество
И 1 а'" к класса 2. Применяя лемму II, мы можем опреде-
определить канонический элемент 6. и порцию irm+] неко-
некого уо vo .
торого определяющего множества для Е 1'" » »+*' такую,
что 6^ _ _и. ^ второй категории на каждой порции тгт+1
и на каждой содержащейся в irm+.j порции произвольного
,0 0.0 *
определяющего множества для ZT*1'" чтчт+1> > в этих усло-
условиях мы можем написать:
Н~ Fm+l, а ~Г • • • ~Ь Fm+i, k~T~ • • • i
где Fm+^ /с есть замкнутое множество, нигде не плотное
на itm+1 и на всякой содержащейся в 5tm+1 порции любого
определяющего множества для Е 1'" m+1 . Повторяя приве-
приведенное выше рассуждение, можно показать, что Fm+it j нигде
не плотно на содержащейся в пт+1 порции произвольного
определяющего множества. Мы выбираем порцию ят+1 таким
образом, чтобы она не содержала точек т -\- 1 первых мно-
множеств F каждой строки, что всегда возможно, так как каждое
из этих множеств F нигде не плотно на ят.
Установив это, обозначим через ? точку, общую всем пор-
порциям тг0, я,, 1г2, ..., 7tm, ... Такая точка обязательно суще-
существует, так как порции жт суть совершенные множества,
включенные одно в другое [8]. Из построения следует, что
точка ? не может принадлежать ни одному из замкнутых
множеств Fpll. Следовательно, точка S принадлежит всем мно-
множествам 0о, 6^, 0w ..., G^...^... и, следовательно,
бесконечному числу множеств Н^1'^, что противоречит
предположению.
Итак, класс S есть в точности класс 4, и его дополне-
дополнение CS есть элемент класса 4. Ч. т. д.
Арифметический пример элемента класса 4. Мы видели,
что Бэр, после того как он нашел регулярный процесс

102 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
построения элемента класса 3, построил арифметический при-
пример элемента класса 3. Следуя этому пути Бэра, Л. В. Келдыш
приходит к интерпретации своего регулярного процесса для
построения элемента класса 4 с помощью арифметического
примера элемента класса 4.
Так как полное изучение этого примера содержит много
элементарных кропотливых деталей, мы ограничимся описанием
хода конструкции этого элемента.
Мы начинаем с того, что берем в качестве Ео в точности
арифметический элемент Бэра класса 3. Итак, элемент Ео
есть множество всех иррациональных точек, заключенных
между 0 и 1, у которых неполные частные ранга п бес-
бесконечно возрастают вместе с п.
Каждое определяющее множество Рйпп ...w/? элемента Ео
может быть характеризовано следующим образом: это множе-
множество иррациональных точек (а1( &2, ..., av, ...) интервала @,1)
таких, что среди неполных частных а, есть в точности пх,
равных 1, я2, равных 2, ..., пк, равных k. Отсюда следует,
что каждый канонический элемент Ь^ класса 2, который
Явялется разностью
У Р°
может быть характеризован следующим образом: это множе-
множество точек Pi ...» , у которых среди неполных частных суще-
существует бесконечное множество равных k-\-l.
В этих условиях можно немедленно доказать, что плотный
на 6**i* элемент JS^V может быть характеризован следующим
образом: это множество тех иррациональных точек из 8(vi\
у которых все целые положительные числа, исключая k-\- 1,
повторяются среди неполных частных лишь конечное
число раз.
* - - СО
Отсюда следует, что сумма 2 ^"^ может быть характе-
ризована как множество тех точек, у которых среди непол-
неполных частных, одно и только одно целое положительное число
повторяется бесконечное число раз.

: понятие рассеянного множества (по, данжуа) .: 103
Таким образом, следуя шаг за шагом приведенной выше
общей конструкции множества 5,
можно показать без труда, с помощью простых рассуждений,
что двойная сумма 2 ? ' а может быть охарактеризована
v,- ¦ ".¦¦:¦¦
как множество тех иррациональных точек, у которых среди
неполных частных av два и только два целых положитель-
положительных числа повторяются бесконечное множество раз. И во-
вообще, /в-кратная сумма 2 ?Di""Vm) может быть характе-
ризована как множество всех тех иррациональных точек,
у которых среди неполных частных а, /и и только т це-
целых положительных чисел повторяются, бесконечное множе-
множество раз.
Отсюда следует, что дополнение к множеству-сумме S,
т. е. элемент класса 4есть множество тех иррациональ-
иррациональных точек («j, а2, ..., а.,, ...), содержащихся между 0 и 1,
у которых среди неполных частных а, есть бесконечное
множество различных, каждое из которых повторяется
бесконечное множество раз.
Понятие рассеянного множества, (по Данжуа)
Данжуа ввел в теорию множеств важное понятие рассеян-
рассеянного множества и показал его фундаментальную роль в теории
счетных множеств; это понятие в дальнейшем обобщалось и
углублялось в работах по топологии1).
Мы перенесем эти идеи Данжуа в теорию множеств высших
классов. Используя их, можно постигнуть сущность теоремы
Бэра, касающейся класса 1, и искать аналогии ей в теории
высших классов.
J) См. F г е с h e t, Quelques proprletes des ensembles abslralts,
Fundaraenta Matb.,.T. X, стр. 28. См. также «Espaces abstrails», Paris,
1928, стр. 174 и 267.

104 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
Рассеянные множества точек. Данжуа называет рассеян-
рассеянным всякое счетное множество, которое не содержит ника-
никакой части, плотной на себе *).
Другими словами,- рассматриваемое множество Е должно
обладать следующим свойством: какова бы ни была его часть
Еи в ней существует точка д^, изолированная в ??1#
Всякое счетное рассеянное множество может быть вполне
упорядочено
таким образом, что каждая точка Ц изолирована в множестве
всех точек ?т, ^1>Р, т. е. можно найти порцию ор фунда-
фундаментальной области if, которая содержит точку L и не
содержит ни одной из последующих точек Ц, -у > C.
Чтобы в этом убедиться, перенумеруем все точки х дан-
данного рассеянного множества Е с помощью целых положитель-
положительных чисел
•*li Х2> • • • > Xni • • • \Е)
Так как множество Е рассеянное, то существуют точки,
изолированные в Е; выберем из этих точек первую в после-
последовательности (Е) и обозначим ее Ео.
Удалим из последовательности (?) эту точку ?0. Так как
множество Е рассеянное, то среди оставшихся точек после-
последовательности (Е) существуют изолированные точки; первую
лз них обозначим 51#
Вообще, определив вполне упорядоченное множество ?0,
?j, E2, ..., ?р, ...|т> состоящее из точек Е, снабженных
индексами, меньшими числа "(, конечного или второго класса,
мы удалим из последовательности Е все эти точки. Если
в последовательности (Е) остались точки, то мы выберем
среди них первую изолированную точку и обозначим ее через (L.
Так как Е счетно, то этот процесс обязательно кончится.
Итак, всякое счетное рассеянное множество может быть
представлено во вполне упорядоченной форме
') Множество называется плотним на себе, если каждая его
точка является для него предельной точкой (Б э р, Теория разрыв-
разрывных функций, ГТТИ, М.—Л., 1932, стр. 60). .

ПОНЯТИЕ РАССЕЯННОГО МНОЖЕСТВА (ПО ДАНЖУА) 105
таким образом, что каждая точка ?р может быть отде-
отделена от последующих точек с помощью порции о? обла-
области ?j', которая содержит ^ и не содержит ни одной
последующей точки Ет, где -у больше, чем р.
Обратно, всякое счетное множество точек Е, которое
можно представить в форме (S) таким образом, что каждая
точка ?р изолирована в множестве последующих точек L,
Y ^ Р> обязательно рассеяно.
Чтобы в этом убедиться, достаточно заметить, что, так
как (S) вполне упорядочено, что каждая часть Et множества Е
содержит первый элемент Ц, и так как Ц изолирована в мно-
множестве всех последующих точек Ц, f ^ C, то она тем более,
изолирована в Ех, чем наше утверждение доказано.
Итак, счетные рассеянные множества идентичны с мно-
множествами, которые могут быть представлены в приведенной
выше вполне упорядоченной форме.
Установив это, мы докажем фундаментальное предложение
относительно счетных множеств класса 1.
Теорема. Для того чтобы счетное множество точек
было класса 1-, необходимо и достаточно, чтобы оно было
рассеяно.
Условие необходимо. Действительно, по самому опреде-
определению, если счетное множество Е не является рассеянным,
то оно содержит часть Еи плотную на самой себе. В этих
условиях множество Р точек фундаментальной области 0,
которые являются предельными точками для Еи есть множе-
множество совершенное (относительно g), содержащее Е}. Так
как Еи очевидно, всюду плотно на Р, то это имеет место
и для общей части ?2 множеств Е и Р. Предположим, что Е2
есть множество класса <^1. Тогда, в силу теоремы Бэра
о множествах класса <^1, существует порция тг множества Р,
которая содержится целиком или в Е2, или же в его допол-
дополнении СЕ2, что, очевидно, невозможно.
Мы заключаем, что всякое нерассеянное счетное множество
точек есть в точности множество класса 2 (достижимое снизу).
Условие достаточно [9]. Пусть Е — рассеянное множество
точек. Это значит, что Е может быть представлено во вполне
упорядоченной форме

106 ГЛ. П. ИССЛЕДОВАНИЯ О СТРУК ТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
где каждая Ц отделима с помощью порции о^ области 0,
содержащей Ц и не содержащей ни одной из последующих
точек Sf, где -( больше, чем C.
Пусть F$ -г- замкнутое множество, которое получается
выбрасыванием из g всех порций ар-, где J3' меньше, чем [3.
В силу свойства порций ар- ясно, что F9 содержит точку Ц.
Тогда, если обозначить через irp порцию F$, определенную ор,
то замкнутое множество тг? содержит точку Ц.
Установив это, обозначим через Н множество тех точек 0,
которые не принадлежат ни одной из порций в^, 0<^C<а;
множество Н, очевидно, замкнуто. В этих условиях вполне
упорядоченная последовательность
#» V ffi» •••» "и» •••> к?> •••1а A)
состоит из счетного множества замкнутых множеств попарно
без общих точек, сумма которых совпадает с 0. Значит,
последовательность A) представляет собой разложение всей
области g на счетное множество замкнутых множеств без
общих точек.
Легко видеть, что каждый член последовательности A),
кроме первого члена И, содержит одну и только одну точку
множества Е; для члена тер это точка ?р.
Если мы выбросим из iup точку Ц, то оставшееся множе-
множество будет, очевидно, множеством класса 1; обозначим его
через /?р.
Итак, вся область g разложена на счетное множество
множеств класса <^ 1: это множества Н, 1$ и R?, где 0<[ fJ < a.
Так как эти множества попарно не имеют общих точек, то
мы заключаем (стр. 74), что сумма счетного числа этих мно-
множеств, произвольным образом выбранных, есть множество
класса ^ 1.
В частности, это имеет место для множества Е, состоящего
из точек ??. Ч. т. д.
Анализ оперативного процесса теоремы Бэра для мно-
множеств класса 1. Для того чтобы найти отправную точку для
наиболее естественного обобщения предшествующей теоремы,
мы рассмотрим оперативный процесс, который послужил Бэру
при доказательстве его теоремы.
Пусть Е — точечное множество, обладающее необходимым
свойством множеств класса ^ 1. Это значит, что, каково бы

понятие рассеянного множбства (по данжуа) 107
ни было совершенное множество Р, существует его порция it,
которая содержится целиком: либо в Е, либо в его дополне-
дополнении СЕ.
Назовем нормальной всякую порцию it множества Р,
которая обладает этим свойством. Так как каждая порция
точечного множества определяется некоторой порцией обла-
области g, концы которой рациональны, то нормальных порций
может быть счетное множество.
Опишем теперь оперативный процесс Бэра. Мы начинаем
с того, что выбрасываем из области 0 все нормальные пор-
порции этой области. Множество всех оставшихся точек замкнуто;
мы его обозначим через Рх. Ясно, что все порции 0', смеж-
смежные к Flt нормальны*); обозначим их через it?>, я = 1, 2, 3,...
Пусть Р — наибольшее совершенное множество, содержа-
содержащееся в Fj. Поступим таким же образом с Рх, т. е. выбро-
выбросим из Pj все его нормальные порции; множество оставшихся
точек есть замкнутое множество, которое мы обозначим
через F2. Ясно, что части Ри смежные к Р2, разбиваются
на нормальные порции2); мы их обозначим через it?>, п = 1,
2, 3, ...
Вообще, если определено замкнутое множество F$ (если
Р — второго рода, то F^, по определению, есть общая часть
всех замкнутых множеств, ранее определенных), то мы обо-
обозначим через Р$ наибольшее содержащееся в F$ совершенное
множество. Выбросим из Рр все его нормальные порции.
Множество оставшихся точек Рр есть замкнутое множество,
которое мы обозначим через F^+1. Ясно, что части Р$, смеж-
смежные к F9+1, разбиваются на нормальные порции; мы их обо-
обозначим через тс(М, я = 1, 2, 3, ...
Продолжая таким же образом, мы построим вполне упоря-
упорядоченную последовательность совершенных множеств
с/, Aj, P2, •••, "ш> •••» Рр1»1)
J) Можно включить, если это необходимо, в Е\ рациональные
точки.
2) Если замкнутое множество F содержится в совершенном мно-
множестве Р, то мы называем частью Р, смежней к F, множе-
множество всех точек Р, принадлежащих некоторому смежному интер-
интервалу к F.

108 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
где каждое последующее множество содержится в предше-
предшествующем и нигде не плотно на нем.
Отсюда следует, что эта последовательность заведомо
счетна и что, следовательно, применение процесса Бэра
закончится остановкой на некотором члене с индексом а ко-
конечным или второго класса, таким, что множество Р„ пусто
Р« = 0.
Таков процесс Бэра.
Если мы захотим анализировать этот процесс, то вот что
мы констатируем; его конечной целью является осуществле-
осуществление полного разбиения области g на счетное множество
отдельных точек и нормальных порций совершенных мно-
множеств попарно без общих точек.
Действительно, так как множество Рр наибольшее в F$
совершенное множество, то множество-разность F$ — Р$ счетно
(теорема Кантора-Бендиксона); значит, всех точек, принадле-
принадлежащих к сумме множеств F8 — Рр— счетное множество.
С другой стороны, всех порций и№) (о <; C < а, п = 1, 2, 3,...)
также счетное множество. Но фундаментальная область 0
есть, очевидно, сумма счетных множеств Е§ — Рр и нормаль-
нормальных порций я(М.
Так как всякая нормальная порция целиком содержится
или в Е, или же в его дополнении СЕ, то мы заключаем,
что рассматриваемое множество Е есть часть полного раз-
разбиения фундаментальной области 0 на счетное множество
элементов класса <1 и, следовательно, есть само множество
класса ^ 1 (стр. 74).
Мы приходим, таким образом, к заключению: с принятой
нами точки зрения процесс Бэра есть не что иное, как кон-
констатация для класса 1 того общего факта, что всякое мно-
множество Е класса а есть часть полного разбиения фундамен-
фундаментальной области 0 на счетное множество попарно непересе-
непересекающихся элементов класса <] ос.
Значит, с принятой точки зрения, теорема Бэра о мно-
множествах класса 1 есть частный случай общей- теоремы
о структуре множеств, измеримых В (см. стр. 74).
Однако эта точка зрения несколько поверхностна, так как
процесс Бэра не вполне адэкватен указанной теореме о струк-
структуре множеств, измеримых В, но содержит нечто большее.

понятие рассеянного множества (по данжуа) 109
Прежде всего, упомянутая теорема о структуре имеет
неопределенный характер, так как все элементы, составляющие
множества Е и СЕ, перенумерованы при помощи целых
положительных чисел. Процесс же Бэра существенно транс-
трансфинитен и это трансфинитное не может быть исключено
никоим образом: мы докажем в дальнейшем, что существуют
эффективно множества Е класса 1, для которых процесс
Бэра не остановится никогда раньше трансфинитного числа б
и это, каково бы ни было 3, заранее фиксированное. Благо-
Благодаря этому важному факту можно классифицировать мно-
множества класса 1 по длине разложения Бэра, и подклассы,
так полученные, представляют последовательность, подобную
той, которую дает сама классификация Бэра — Валле-Пуссена.
Аналогия между теоремой стр. 74 и процессом Бэра
неполна, так как замкнутые множества it(W, которые соста-
составляют множество Е, не являются произвольными замкнутыми
множествами попарно без общих точек, но обладают вполне
определенным свойством, которого лишено, вообще говоря,
произвольное разложение области 0 на замкнутые множе-
множества. Это свойство и составляет самое существо доказа-
доказательства Бэра его теоремы о функциях (или множествах)
класса 1.
Чтобы увидеть, в чем состоит это свойство, вернемся
к аналогии, которая существует между обычными точками и
элементами какого-либо класса.
Если $ — счетное множество элементов е класса 1, то мы
назовем это множество рассеянным, если каждая его часть Ьх
обладает изолированнымJ) элементом. Это — естественное
обобщение понятия Данжуа для точек.
Если мы вернемся теперь к рассмотренному выше мно-
множеству Е, то мы констатируем без труда, что элементы яР>
класса 1, которые образуют множество Е и которые нам
дает процесс Бэра, образуют рассеянное множество
в смысле введенного обобщения.
*) Общее понятие изолированного элемента дано выше (стр. 68).
В рассматриваемом случае элемент е класса 1 изолирован в мно-
множестве $ элементов е класса 1, если можно заключить е в мно-
множество Н начального класса Ко таким образом, что N не пересе-
пересекается ни с одним другим элементом из $.

ПО ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
В самом деле, обозначим через $ множество отдельных
точек и нормальных порций «W, которые принадлежат к Е.
Чтобы убедиться, что множество $ рассеянное, достаточно
показать, что каждая его часть Sj содержит изолированный
элемент. Но множество $t состоит из точек множеств-раз-
множеств-разностей Fp — P? и из порций icjp. Среди индексов ft этих
множеств есть наименьший; пусть это |30. Если множество Sj
содержит эффективно точки F9— Рр, то среди этих точек
есть наверняка изолированная точка, так как множество
F9— Рр рассеянное. Если $j не содержит ни одной точки
F$ — Рр, то оно содержит эффективно порции и*). Я утвер-
утверждаю теперь, что каждая из этих порций изолирована в f>j.
Чтобы в этом убедиться, достаточно заметить, что порция я^
Нормальна, следовательно, определена порцией области g? f
которая не содержит ни одной точки ни множества F~, — Р»,,
ни порций к®">, если р' превосходит |3, |3' > {5. Следовательно,
рассматриваемая порция njjj) изолирована в Zv Ч. т. д.
Аналогичным образом, точки F$ — Рр и порции «(?), из
которых состоит дополнение СЕ, образуют также рассеянное
множество.
Обратно, если Е и СЕ оба являются рассеянными после-
последовательностями элементов класса 1, то существует процесс
Бэра, который дает Е и СЕ.
Значит, имеется тождество между процессом Бэра и
процессом, который позволяет представить множество
класса 1 в форме рассеянной последовательности счетного
множества элементов класса 1 (замкнутых множеств).
Итак, мы естественно пришли к тому, чтобы рассматривать
как обобщение процесса Бэра некоторый процесс разложения
всякого множества класса а в рассеянную последовательность
элементов класса а с условием, чтобы было доказано эффек-
эффективное существование всех подклассов класса а, которые
получатся, если классифицировать множества класса а по
трансфинитной длине этого разложения.
Этот процесс будет предметом наших последующих рас-
Смотрений.

ПРОЦЕСС БЭРА В ВЫСШИХ КЛАССАХ 111
Процесс Бэра в высших классах
Рассеянная последовательность элементов класса < а.
Предшествующее изучение множеств точек было необходимо
для того, чтобы изучить роль элементов класса -^ а в обра-
образовании множеств. Сейчас своевременно по образцу идей Дан-
жуа ввести новые понятия относительно последовательностей
элементов класса О, понятия, которые позволят, как мы
увидим, установить необходимые и достаточные условия для
того, чтобы множество было класса -s^a, и распределить
множества класса а в трансфинитную последовательность
подклассов по длине разложения Бэра.
Прежде всего мы установим следующее фундаментальное
определение: Множество $, образованное из счетного мно-
множества непересекающихся элементов класса ос, называется
рассеянным, если каждая часть $ содержит изолиро-
изолированный элемент1).
Повторяя те же рассуждения, которые мы делали в слу-
случае рассеянных точечных множеств, мы заключаем, что S
можно представить во вполне упорядоченной форме
е0> eV е2' •••» ev>i •••> ер» •••IT (•)
таким образом, что каждый элемент е^ может быть отделен
от последующих элементов с помощью множества Н$, содер-
содержащего ер и не содержащего никакой части элемента е~,, где
индекс $' превосходит |3, причем Щ либо множество класса
меньшего, чем вр, либо же принадлежит к базе класса е$.
С другой стороны, ясно, что каждое множество элемен-
элементов $, которое можно представить в форме ($) таким обра-
образом, что каждый элемент е$ изолирован в множестве всех
последующих элементов е.,, ф'^-$,—обязательно рассеянно.
Мы можем теперь приступить к изучению условий, кото-
которым удовлетворяют множества класса а. Достаточное усло-
условие для того, чтобы множество было класса -^ а, выра-
выражается следующим образом:
1) Мы говорим вообще,.что элемент е класса о, принадлежащий
семейству множеств F, изолирован в этом семействе, если суще-
существует отделяющее множество Н или класса ¦< о, "или из базы Ва,
которое содержит е и не содержит точек ни одного из других
множеств семейства F.

112 ГЛ. II. ИССЛЕДОВАНИЕ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
Теорема 1. Всякое рассеянное множество элементов
класса <^а есть множество класса ^а.
Пусть
рассеянное множество класса ^а. Член е$ содержится в отде-
отделяющем множестве Н$, которое не имеет общей части ни
с одним из последующих множеств е„,, C' > р. Множество Н$
либо класса меньшего, чем е^ либо же принадлежит к базе
класса е$.
Пусть F$ — множество, которое получается выбрасыванием
из g всех отделяющих множеств //„,, где $' меньше, чем Р;
легко видеть, что F9 или класса < ос, или принадлежит
к базе ВЛ1 или же есть элемент класса а. В силу свойства
множеств И,, ясно, что F. содержит элемент е.. Следова-
Следовательно, если мы обозначим через тг^ общую часть Ия * F$, то
множество 7Гр содержит е$. Установив это, обозначим через Q
множество точек 0, которые не принадлежат ни одному из
отделяющих множеств Н$, 0 <; р < •j. Вполне упорядоченная
последовательность
состоит, очевидно, из счетного множества множеств: или
класса < а, или из базы Ва, или же элементов класса а.
Легко видеть, что эти множества не имеют попарно общей
части и что их сумма совпадает с областью g. Следова-
Следовательно, последовательность A) есть разбиение всей области 0
на счетное множество множеств класса <^ а.
После этого обозначим через Е сумму членов рассеянной
последовательности ($). Ясно, что множество Q не содержит
ни одной точки Е, и что точки Е, принадлежащие к тгр,
образуют элемент е^. Следовательно, если мы вычтем из тер
элемент е$, то множество-разность Щ есть множество
класса <]« и не содержит точек Е.
Отсюда следует, что вся область g разложена на счетное
множество множеств класса <[ос: это множества Q, <?p, R$,
где 0 <! j3 < y« Так как эти множества попарно без общих
точек, то мы заключаем (стр. 74, примечание), что сумма
бесконечного множества этих множеств, произвольно выбран-

ПРОЦЕСС БЭРА В ВЫСШИХ КЛАССАХ 113
ных, есть множество класса <] ос. В частности, это так; для
множества Е, составленного из е$.
Следует заметить, что доказательство этой теоремы тожде-
тождественно (кроме обозначений) с доказательством соответствую-
соответствующей теоремы для точечных рассеянных множеств (стр. 105).
Регулярное параметрическое изображение множеств.
Мы пришли к вопросу, является ли это найденное нами
достаточное условие, для того чтобы точечное множество
было класса <[ а, необходимым. Чтобы решить этот вопрос
в положительном смысле, нужно сначала изучить некоторые
предварительные вопросы.
Мы установим сначала новое определение.
Назовем регулярной всякую функцию f{t), определенную
в фундаментальной области 0t, которая никогда не прини-
принимает двух равных значений; каждая регулярная функция есть
разнозначная функция: если fi=f, то
Мы говорим теперь, что какое-либо множество Е точек
фундаментальной области 0 х обладает регулярным пара-
параметрическим изображением, если Е есть множество значений
функции x=f(t), определенной на порции @,1) фундамен-
фундаментальной области 0t, непрерывной и регулярной на этой порции.
Ясно, что каждое множество Е, которое обладает
регулярным параметрическим изображением, имеет мощ->
ность континуума и содержит совершенное множество.
Чтобы в этом убедиться, возьмем в порции @,1) области 0't
множество Р, совершенное в абсолютном смысле. Так как
функция x=f(f) непрерывна и регулярна, то множество Q
значений, которые f(t) принимает на Р, есть совершенное
множество; легко видеть, что Q содержится в Е.
Можно заметить, что каждое множество Е, обладающее
регулярным параметрическим изображением, не может иметь
изолированных точек.
Установив это, введем следующее определение. Пусть
Е — множество класса Ка, состоящее из точек 0х; мы пред-
предположим, что Е обладает регулярным параметрическим изо-
изображением x=f(t). Назовем это изображение нормальным,
если множество значений, которые f{f) принимает на произ-
произвольной порции, есть множество класса <]ос.
8 Зак. 284. Н. Н. Лузин

114 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
Установив это определение, мы можем доказать следующую
теорему:
Теорема. Всякое несчетное измеримое В множество
обладает нормальным параметрическим изображением, если
исключить из него счетное множество точек.
Утверждение очевидно в случае, если Е принадлежит
начальному классу /Со, так как в этом случае Е есть сумма
счетного множества порций области & a.:E = iz1-\-ici-\- .. .
и можно построить подобное отображение интервала Бэра (я)
порядка 1 области ?f t на vn, что и определяет нормальное
изображение Е*).
Установив это, предположим, что предложение верно для
всех классов, предшествующих Ка, и докажем, что оно верно
и для класса а.
Заметим сначала, что все сводится к доказательству
утверждения для элементов класса Ка. Действительно, всякое
множество Е класса Ка есть сумма счетного множества эле-
элементов класса ^а попарно без общих точек: E=v1-\-v2-\- .. .
Достаточно, очевидно, изобразить нормально itra на интервале
Бэра (я) порядка 1, чтобы иметь нормальное изображение Е.
Предположим же, что Е есть элемент (несчетный, если
ос = 1) класса ос. Мы имеем:
F — F . F F
где все множества Еп класса < а, и последовательность их
убывающая
Пусть x=fn(f) — нормальное изображение Еп на порции
фундаментальной области g t ; в этом изображении исклю-
исключена, быть может, счетная часть Еп..
Установив это, рассмотрим новую область 01 и возьмем
порцию @,1)'этой области. Мы установим взаимно однознач-
однозначное соответствие между точкой t порции @,1) области 01
*) Вообще, если дана система целых положительных чисел,
расположенных в определенном порядке: аь а2,..., щ, то интер-
интервалом Бэра (аь а2,..., а^) называется множество всех иррацио-
иррациональных точек, у которых представление в виде непрерывной дроби
начинается с а^, а2,..., а^; этот интервал называется интервалом
порядка k.

ПРОЦЕСС БЭРА В BblCUHX КЛАССАХ 115
и системой, состоящей из счетного множества точек tt, t%t,..
..., tn, ..., где каждая точка tn взята в порции @,1) соответ-
соответствующей области 01 . Процесс, который позволит нам
установить это соответствие, заключается в следующем:
Каждому интервалу Бэра порядка 1 области 01 мы поста-
поставили в соответствие интервал Бэра порядка 1 области 01 и
наоборот.
Всякому интервалу Бэра 8 порядка 2 области 01 мы
поставим в соответствие группу Г2> состоящую из двух интер-
интервалов Бэра порядка 2 — 8j и 82, соответственно содержащихся
в 31. и 01 таким образом, что интервал порядка 1, содер-
содержащий 8, соответствует интервалу порядка 1, содержащему 8Х;
и обратно, каждой аналогичной группе Г2 соответствует
интервал Бэра порядка 2 из области 0t.
Вообще, каждому интервалу Бэра 8 ранга и из области 01
соответствует группа Гп, состоящая из п интервалов Бэра
8j, 82 8П порядка п, содержащихся соответственно
в 0t, 011 • • •, 0t таким образом, что интервал Бэра
порядка п — 1, содержащий 8, соответствует группе Гп_1,
состоящей из интервалов Бэра порядка п — 1, содержащих
соответственно 81( 82, ..., 8га_1; и обратно, всякой анало-
аналогичной группе Гп соответствует интервал Бэра порядка п
области 01.
Так как каждая иррациональная точка, заключенная между 0
и 1, есть общая часть последовательности интервалов Бэра
порядка 1, 2, ..., и, ..., заключенных один в другой, то
указанный процесс нам дает уравнения:
срп(/) непрерывна на 01. Каждой последовательности точек
tt, /2, ..., *„,..., расположенных соответственно в пор-
порциях @,1) областей 0t^ 0t%, ..., 0tn, •••, соответствует
одна и только одна точка области 01. Если t'ф(\ то суще-
существует число i такое, что «р<@ Ф ?<•/')) т^к как Двум раз-
различным интервалам Бэра о' и 8" порядка п, содержащим
точки f и t", соответствуют две различные группы Г„ и Гп,
состоящие каждая из п интервалов Бэра порядка п,
8*

116 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
расположенных в gt, g t^ •••» 6tn- Суперпозиции:
дают функции, непрерывные на gt. Отсюда следует, что
совместные равенства
^@ = ^@ = . ..=Fn(f)=...
определяют в gt множество точек, замкнутое в gt, мы его
обозначим через Г.
Когда t пробегает @,1), то точка tt пробегает бесконечно
много раз порцию @,1) области gt . Следовательно, х — Fi(t)
пробегает бесконечно много раз множество Et> и никогда из
него не выходит. Отсюда следует, если обозначить через
F{i) общее значение функций
что уравнение
дает нам точку общей части E1--Ei ... Еп ... и что всякая
точка х этой общей части может быть получена таким об-
образом. ¦ ;
Функция x = F(f) непрерывна на Г. Важно заметить, что
она регулярна на Т, так как если f Ф f, то существует
функция ср4 такая, что
значит, так как /<(^) регулярна на gt , то имеем
и, следовательно,
Мы предположим, что множество Е несчетно. Тогда и
множество Г несчетно; при этом оно замкнуто в gt.

ПРОЦЕСС БЭРА В ВЫСШИХ КЛАССАХ 117
Так как 7* несчетно, то существует полное разложение
порции @,1) области g t на интервалы Бэра 8 такое, что су-
существует бесконечно много интервалов 8, каждый из которых
содержит несчетное множество точек Г. Установим взаимно-
взаимнооднозначное соответствие между этими 8 и интервалами Бэра Д
порядка 1 новой фундаментальной области g ^.
Каждый из этих 8 может быть разложен полностью на
интервалы Бэра 87 так, что найдется бесконечно много 8',
каждый из которых содержит несчетную часть Т. Установим
взаимно однозначное соответствие между этими 8/, содержа-
содержащимися в 8, и интервалами Бэра Д' порядка 2, принадлежа-
принадлежащими соответствующему Д,
Вообще, если 8*"* и Д(л-1)— два соответственных ин-
интервала Бэра, первый из которых содержит несчетную часть Т,
а второй есть интервал Бэра порядка (я — 1) области 0\,
мы разобьем полностью 8(л-1) на интервалы Бэра 8(п) таким
образом, чтобы существовало бесконечное множество 8^п),
каждый из которых содержит несчетную часть Т. Установим
взаимно однозначное соответствие между этими 8(п) и интер-
интервалами Бэра Д(п* порядка л, принадлежащими Д*™'-
Мы определили в порции @,1) новой области g z функцию
непрерывную и регулярную на @,1). Если т пробегает пор-
порцию @,1) области gz, то точка t пробегает множество Т
кроме, быть может, счетного множества точек Т. Когда т
пробегает интервал Бэра Д области gт, то точка t пробегает,
очевидно, часть Т, содержащуюся в интервале Бэра 8, соот-
соответствующем Д (с точностью до счетного множества точек
этой части). Пусть v — порядок 8. Когда t пробегает 8, то точки
пробегают каждая интервал Бэра порядка v, и эти интервалы
содержатся соответственно в gt, gt, •«., 0t, тогда как
другие точки ?v+, = cpv+1 (t), /v+2 = <pv+2 (/), .-.. пробегают каж-
каждая порцию @,1) соответственных областей g ^ , g\+2> ...
Но каждая функция х=/{(^) дает нам нормальное изо-
изображение Ei на порции @,1) области g*. Это значит» что

118 ГЛ. И. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
когда tt пробегает порцию области 0t^ то точка х пробе-
пробегает часть Et класса < а. Отсюда следует, что когда t про-,
бегает 8, то сложная функция ft [ср< (f)\ пробегает часть Е{
класса < а, если / ^ v, и пробегает все множество Е<, если
/ > v. Отсюда можно заключить, что когда х пробегает ин-
интервал Бэра Д в Ц'т, то сложная функция
пробегает общую часть бесконечного множества множеств
класса < а, т. е. или множество класса < а, или множество
базы Ва, или же элемент класса otllOl. С другой стороны,
легко видеть, что Ф(х) непрерывна и регулярна на порции
@,1) области ?JX, и что множество значений на @,1) совпа-
совпадает с множеством Е = Et • Е.2 ..., кроме счетного множества
точек. Следовательно, уравнение д; = ф(т) дает нам регуляр-
регулярное параметрическое изображение Е.
Нам остается только доказать, что это изображение нор-
нормальное. Для этого мы докажем, что множество значений Ф (т)
на каждом множестве И класса О, расположенного в порции
@,1) области &т, есть множество класса <ос. Но так как
Н и его дополнение СН являются оба суммами счетного мно-
множества порций 0'т, то они являются очевидно суммами ин-
интервалов Бэра. Отсюда следует, что множество значений Ф (г)
на И, которое мы обозначим Ф(//), так же как и множество
Ф(СН) значений Ф(т).на СН, являются оба суммами счетного
множества множеств класса <! а без общих точек. Так как
полная сумма этих множеств есть, очевидно, Е, то мы за-
заключаем, что Ф(Я) есть часть полного разбиения множества
класса <^ а на счетную сумму множеств класса <] а без об-
общих точек. Следовательно1), класса Ф(Н) не превосходит а
и параметрическое изображение Е, дг = Ф(т) нормаль-
нормально. Ч. т. д.
Мы дополним этот результат следующими замеча-
замечаниями:
Замечание I, Из доказательства следует, что если Е—•
элемент класса а, то нормальное параметрическое изображе-
изображение лг = Ф(т), которое мы сейчас получили, ставит в соот-
соответствие каждому интервалу Бэра 8 из 0Х множество Ф(8)
1) Си. примечание на стр. 74.

ПРОЦЕСС БЭРА В ВЫСШИХ КЛАССАХ Ц9
значений Ф (т) на 8, которое либо класса < <х% либо из базы 5„,
либо же элемент класса ос. •
Замечание II. Если ?;—двустороннее множество класса а,'
то для Е существует нормальное изображение х = Ф (т) такое.
Что каждому, множеству Н класса О соответствует или мно-
множество класса < а, или множество из базы Вл,
Действительно, достаточно разложить Е на счетную сумму
элементов класса < а и осуществить нормальное изображение
этих элементов соответственно на интервалах Бэра ранга 1
области 0\. Ясно, что полное изображение х — Ф (т) мно-
множества Е, таким образом полученное, есть нормальное изо-
изображение, обладающее высказанным свойством.
Изображение произвольного множества класса я
в форме рассеянной последовательности элементов. Мы
предпримем сейчас общее изучение произвольного множества
класса Ка. Пусть Е — какое-то множество класса ос. Мы имеем
Е = Нш Еп,
»->оо
где множества Еп класса <а. '¦'
Прежде всего мы устраним случай, когда одно из допол-
дополнительных множеств CEi счетно (или конечно). Действительно,
если множества СЕ{, которые счетны (конечны), имеются
в ограниченном числе, то мы можем исключить соответствую-
соответствующие множества Et из последовательности*^, ?2, ...
Если этих множеств СЕ{ бесконечно много, то само мно-
множество СЕ, очевидно, счетно (конечно). Тогда, ила Е есть
элемент класса 2, или же Е класса 1 и, следовательно,
СЕ—рассеянное множество точек (стр. 105).
Итак, все сводится к изучению случая, когда каждое из
множеств Еп и СЕп несчетно, каково бы ни было целое
положительное я. ,
В этих условиях мы можем написать последовательность
уравнений
х =/i ft), х=/2&), ..., х =fn(tn\ .... г
которые дают, каково бы ни было п, нормальное изображе-
изображение Еп на порции (о, у) и СЕп на {—:, \\ области 0'* f
исключая счетное множество точек.'

120 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
Возьмем новую фундаментальную область 01 и рассмотрим
уравнения
и сложные функции
которые мы изучали при доказательстве предыдущей тео-
теоремы (стр. 115—116).
Так же как в этом доказательстве, совместные равенства
определяют на 01 множество точек Т, замкнутое в этой об-
области.
Пусть F (f) — общее значение этих функций на Т. Это
функция, определенная на Т, непрерывная и регулярная на
этом множестве и такая, что уравнение
х = F(t) ¦
преобразует множество Т во всю область 0 х, кроме счетного
множества ее точек.
Так же как в доказательстве предыдущей теоремы, мы
преобразуем с помощью функции
порцию @,1) области 0\ в множество Т, кроме, быть может,
счетного множества точек из Т.
Сложная функция
, _дг = /?№(т)] = Ф(т)
непрерывна и регулярна в @,1) и преобразует эту порцию,
во всю область 0х,'с точностью до счетного множества точек.
Нужно изучить свойства функции Ф(х).
¦ Прежде всего, функция x—fn(tn) дает нам нормальное
изображение Еп и СЕп на (о, yj и (-j, 1J области &t.,
это значит, что функция fn (tn) ставит в соответствие каждому

ПРОЦЕСС БЭРА В ВЫСШИХ КЛАССАХ . . 121
интервалу Бэра 8 области 01 множество /п (8).значений /я (/„)
на 8, которое есть множество класса < а. Отсюда вытекает,
с помощью такого же рассуждения, как то, которое мы про-
проводили для. доказательства предыдущей теоремы, что рассма-
рассматриваемая функция х = Ф (т) ставит в . соответствие каждому
интервалу Бэра 8 области ^т множество Ф(8) класса строго
меньшего а, лежащее в &х1)-
Установив это, обозначим через еп прообраз множества Еп
при отображении с помощью функции х = Ф (т); е„ есть мно-
множество, лежащее в ^т, такое, что Ф (еп) совпадает с Еп,
Легко видеть, что множество еп есть класса О.
Действительно, необходимое и достаточное условие для
того чтобы точка х = Ф (т) принадлежала к Еп, состоит в том,
что значение <э„ [ф(т)] принадлежит порции @, -к-J области 0t >
что в силу непрерывности «„['К'1)] возможно только в слу-
случае, когда еп есть множество начального класса Ко.
Очевидно, что последовательность множеств класса О
сходится и имеет пределом множество е, которое есть про-
прообраз Е для дг = Ф(т); множество Е, очевидно, класса -^1.
Возможны два случая.
Первый случай: множество е класса О. В этом случае
е и его дополнение Се являются оба суммами счетного мно-
множества интервалов Бэра. Отсюда следует, что Е и СЕ являются
оба суммами счетного множества множеств класса < а. Зна-
Значит, Е есть множество из базы ВЛ.
Второй случай: класс е равен 1. В этом случае процесс
Бэра, примененный к е, дает нам вполне определенное раз-
разложение е в рассеянную последовательность элементов класса 1
(замкнутых множеств):
где t\n с конечным индексом п есть интервал Бэра и
*) Мы обозначаем здесь через Ф (8) множество значений функ-
функции Ф (т) на интервале В. Вообще, если дана некоторая функция/(л:),
определенная в области 0 х, и множество Е, лежащее в этой обла-
области, то мы обозначаем через f(E) множество значений, которые
принимает f (х) на Е, . . .

122 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
где индекс р второго класса и меньше f, есть нигде не плот-
плотное совершенное множество и изолировано от всех после-
последующих \п Р' > Р с помощью интервала Бэра К.
• Это разложение е осуществлено в области ?f ^ В области
&х ему соответствует следующее разложение множества Е:
? = ео + е1 + е2+---+гш+...+ер+...|т, A)
где sp есть образ т^ для х = Ф (т). Интервал Бэра Ар пре-
преобразуется в множество Н$ класса, строго меньшего ос. Легко
видеть, что ер содержится в Н$, так как т\$ содержится в Ар.
Из того, что Ар не имеет общих точек ни с одним из после-
последующих множеств ту, C' > р, следует, что Яр не имеет
общих точек ни с одним из последующих множеств е.,, |3' > р.
Остается только изучить природу множеств вр. Так как
¦ни — совершенное нигде не плотное множество, то его допол-
дополнение Сч\а есть сумма интервалов Бэра. Тогда образ Оги есть
или множество класса < а, или же множество класса а,
достижимое снизу. В этих условиях множество ер есть либо
множество класса < а, либо из базы Ва, либо элемент класса а.
Установив это, удалим из разложения A) множества В
все е, которые либо суть множества класса < а, либо из
базы ВЛ и составим их сумму S. Остаются только элементы s»
строго класса а, заключенные в соответствующие множества Щ
класса < а, которые их отделяют от множеств е„, за ними
следующих. Множество R оставшихся элементов есть рассеян*
кое множество.
Мы пришли, таким образом, к следующему результату:
Всякое множество Е класса а может быть разложено
на множество S класса а, достижимое снизу, и рассеян-
рассеянное множество R, образованное из элементов класса а
Подклассы, их существование
Распространение результатов на случай множества
точек в пространстве нескольких измерений. Мы теперь
рассмотрим с общей точки зрения вопросы, изученные в пред-
предшествующих номерах, и для этого остановимся на случае

ПОДКЛАССЫ, ИХ СУЩЕСТВОВАНИЕ 123
множества точек в пространстве нескольких измерений. Для
определенности мы ограничимся случаем пространства двух
измерений.
Прежде всего, рассматривая определения главы I (стр. 49),
относящиеся к множествам в пространстве нескольких изме-
измерений, мы заметим немедленно, что все понятия и все рас-
рассуждения, сделанные для линейных точечных множеств, сохра-
сохраняются для евклидова пространства нескольких измерений,
Таким же образом мы можем классифицировать измеримые В
множества, лежащие в пространстве нескольких измерений
в трансфинитную последовательность классов Бэра — Валле-
Пуссена, и в каждом классе этой классификации мы будем
иметь элементы множества, достижимые снизу, и множества,
недостижимые с обеих сторон; если класс Ка второго рода,
то в нем есть двусторонние множества, которые образуют
базу ВЛ этого класса.
Остается уяснить понятие параметрического изображения
в случае множества точек нескольких измерений.
Мы говорим, что точечное множество Е, лежащее в фун-
фундаментальной области 0хх ...я т измерений, обладает пара-
метрическим изображением, если множество Е есть сово-
совокупность последовательных положений подвижной точки
M{xv лг2, ..., хт), координаты которой суть функции пере-
переменного параметра t, определенного в порции @,1) фунда-
фундаментальной области 0t
Параметрическое изображение множества Е называет-
называется регулярным, если двум различным значениям f и f
параметра t соответствуют две различные точки множе-
множества Е.
Пусть Е — измеримое В множество какого-то класса Ка.
Мы говорим, что регулярное параметрическое изображение
множества
нормально, если функции ft непрерывны в порции @,1) обла-
области 01 и если каждой порции этой области соответствует
часть Е, класс которой не превосходит а.

124 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
Все рассуждения предыдущих параграфов остаются вер-
верными, и мы имеем следующую теорему:
Всякое несчетное измеримое В множество обладает
нормальным изображением, если исключить точки этого
множества в конечном или счетном числе.
С помощью этой теоремы, не делая никаких измеяений
в предшествующих рассуждениях, мы приходим к следующему
фундаментальному результату:
Всякая рассеянная последовательность, образованная из
счетного множества элементов класса <! а, есть множе*
етво класса ^. а. Обратно, каждое множество Е класса КЛ
может быть разложено на множество S класса а, дости-
достижимое снизу, и на рассеянное множество R, образованное
элементами класса а:
E = S + R.
Для а = 1 мы получаем теорему Бэра о множествах
класса 1, так как эффективный процесс Бэра есть не что
иное, как разложение множества класса 1 в рассеянную по-
последовательность элементов класса 1.
Возникает вопрос — может ли трансфинитная рассеянная
последовательность элементов класса КЛ всегда быть сведена
к некоторому, относительно малому, трансфинитному числу -у
своих членов? Другими словами, можно ли всегда разложить
данное множество Е класса К* таким образом, что рассеянной
вполне упорядоченной последовательности R элементов класса а
соответствует трансфинитное число -у, всегда меньшее некото-
некоторого фиксированного числа второго класса?
Мы увидим, что ответ отрицателен и что существуют
эффективно множества Е класса Ка, для которых рассеянному
множеству R соответствует сколь угодно большое трансфи-
трансфинитное число второго класса f, причем это число не может
быть понижено. В. порядке этих идей удобно ввести новое
понятие подкласса классификации Бэра — Валле-Пуссена.
Пусть дано множество Е класса Ка\ мы говорим, что Е
есть множество подкласса [3, если при каждом разложении Е
на множество 5 класса а* достижимое снизу, и на счетную
вполне упорядоченную рассеянную последовательность R,
образованную из элементов класса а

ПОДКЛАССЫ, ИХ СУЩЕСТВОВАНИЕ 125
соответствующее R число f не меньше, чем [3, и если оно
эффективно равно р при некотором определенном разложе-
разложении Е.
Из этого определения следует, что каждое множество Е
класса а, достижимое снизу, есть множество подкласса О
и каждый элемент класса а есть множество подкласса 1.
Возникает вопрос: существуют ли множества класса а
и всякого подкласса?
Мы изложим теперь исследования по этому вопросу
М. А. Лаврентьева, важные результаты которого опублико-
опубликованы им в статье «Sur les sous-classes de la classification de
M. Baire»1).
Универсальный элемент двух измерений. Возьмем
в области 0„.у двух измерений множество Е класса Ка. Если
мы его пересечем прямой х = хф параллельной оси OY, то
получим вполне определенное линейное множество е. Рассмот-
Рассмотрим природу этого линейного множества.
Прежде всего, если Е класса О, то таково же и линейное
множество Е, так как в этом случае Е и его дополнение
СЕ — оба являются суммами порций двух измерений; но каждая
такая порция пересекается прямой х = х0 по линейной порции.
Методом трансфинитной индукции легко доказать для мно-
множеств высших классов: всякое множество Е двух измерений
класса а пересекается каждой прямой х = х0 по линейному
множеству класса <^а, рассмотренному не как часть пло-
плоскости, но как линейное множество, измеримое В, лежащее
в области 0. Эта теорема верна для а = 0 и легко видеть,
что она верна для а (первого или второго рода) при условии,
что она верна для всех трансфинитных чисел < а.
Так как каждое множество класса а, достижимое сверху,
есть общая часть счетного числа множеств классов < а, то
мы имеем следующее следствие: всякий элемент Е двух изме-
измерений класса а пересекается каждой прямой х = х0 по
множеству е, которое либо класса < а, либо из базы ВЛ,
либо же элемент класса а.
Установив это, мы введем следующее определение: мы го-
говорим, что элемент Е двух измерений класса а универсален,
если всевозможные линейные элементы класса а можно
С. R. Acad. Sc, 12 января 1925.

126 ГЛ. И. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
получить, пересекая множество Е прямыми х = Хо, параллель-
параллельными оси OY,
. Существуют универсальные элементы класса 1. Чтобы
в этом убедиться, возьмем последовательность
образованную из всех порций линейной фундаментальной
области 0у.
Пусть Ь = (а1г Og, ..., ak) — произвольный интервал Бэра
ранга k, лежащий в фундаментальной области 0х. Поставим 8
в соответствие множеству Es тех точек области двух измере-
измерений 0ау, абсциссы которых принадлежат к 8, а ординаты у
принадлежат к сумме k порций ir0 -j- тса + ... + пак- Ясно,
что Еь есть сумма конечного числа порций двух измерений.
Затем возьмем сумму 5 всех множеств ?$ таким образом
определенных. Легко видеть, что 5 есть множество класса 1,
достижимое снизу. Я утверждаю теперь, что его дополнение
E*=CS есть универсальный эл'емент класса 1.
Чтобы в этом убедиться, возьмем произвольное линейное
множество класса 1, достижимое снизу; пусть е это множество.
По определению, е есть сумма жа -j-ir0 + .. • ~1ton+ • •'
счетного множества различных порций линейной области 0 у.
Если мы возьмем иррациональную точку х0, определенную
бесконечной непрерывной дробью
то легко видеть, что прямая х = х0 пересекает 5 в точности
по е. Следовательно, можно получить всевозможные линейные
элементы класса 1, пересекая Е прямыми х*=х0. Ч. т. д.
Установив это, мы докажем существование в каждом
классе Ка универсальных элементов двух измерений. В наших
доказательствах мы воспользуемся следующей леммой:
Лемма. Если § есть плоское множество, лежащее
в области 0^х, и если мы преобразуем область
в новую область 0^ х с помощью уравнений
где функция <? непрерывна в 0Z, то прообраз $' множе-
множества $ есть множество, класс которого не превосходит
класса $.

ПОДКЛАССЫ, ИХ СУЩЕСТВОВАНИЕ 127
Эта лемма доказывается трансфинитной индукцией.
Утверждение очевидно, если $ класса О, так как прообраз
порции области 0 ^т есть множество класса О, лежащее в 0'ьх.
С другой стороны, каждая последовательность множеств
$!, $2, ..., $п, ..., имеющая пределом множество $, преобра-
преобразуется, очевидно, в сходящуюся последовательность множеств
gj, $2 &п, имеющую пределом прообраз $ множества §.
Это замечание завершает доказательство. Ч. т. д.
После того как это доказано, вернемся к существованию
универсальных элементов двух измерений. Мы предположим,
что это существование уже доказано для всех классов, мень-
меньших а, и мы докажем, что оно имеет место и для самого
класса Ка.
Пусть
— последовательность универсальных элементов всех предше-
предшествующих классов (кроме Ко), причем каждый из этих геоме-
геометрических элементов повторяется в последовательности A)
счетное множество раз. Мы предположим, что универсальный
элемент $п лежит в области 01 x.
Положив это, возьмем последовательность функций
непрерывных на области 0Х и таких, что, какова бы ни была
последовательность иррациональных чисел tl, $,, ..., $, су-
существует иррациональное число г° такое, что имеют место
равенства:
Обозначим через %>п прообраз $„ при отображении с по-
помощью уравнения tn = <р„ (х), х = х. В силу предшествующей
леммы, класс множества $'п не превосходит класса $п. Тогда
сумма 5 множеств $„ есть множество либо класса < а, либо
же достижимое снизу класса а. Мы докажем, что 5 обла-
обладает следующим свойством: каково бы ни было линейное
J) Здесь идет речь, очевидно, о непрерывной кривой Пеано,
заполняющей все пространство счетного числа измерений.

128 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ 5
множество е, являющееся либо множеством класса < а, либо
достижимым снизу класса а, существует такое иррациональное
число х0, что прямая х=т0, параллельная оси ОХ в области 0Z> x,
пересекает S в точности по множеству е.
Действительно, мы имеем е = ех -J- <?2 -|- ... -J- eh + ...,
где ек есть элемент класса < а. В силу самого определения
последовательности &v §2, ..., $п, ... существует иррацио-
иррациональное число 4L такое, что прямая tn = /JL, параллельная
оси ОХ в области 0tn tX, пересекает множество §„ в точ-
точности по ек. Так как в последовательности универсальных
элементов $1( &2, ..., $п, ... каждый член, рассматриваемый
как геометрическое множество, повторяется бесчисленное мно-
множество раз, то мы можем предположить, что последователь-
последовательность целых положительных чисел nv п%; ..., пк, ... возра-
возрастающая, и значит, в ней нет одинаковых чисел. При этих
условиях в силу предположенного свойства функций <р1} <р2, ...
существует иррациональное число т0 такое, что 4L — ?». (у°)>
каково бы ни было k, и что другие 4. определенные равен-
равенствами ^ = <?п (х )» таковы, что прямые tn = ^, параллельные
оси ОХ в области 01 , не пересекают соответствующих уни-
универсальных элементов &п. Если иррациональное число х° опре-
определено таким образом, то легко видеть, что прямая т = х°,
параллельная оси ОХ в области 07 х, пересекает 5 в точ-
точности по множеству е.
Отсюда следует, что множество S, так определенное,
строго класса а, так как существуют прямые т = х0, которые
пересекают 5 в точности по линейным множествам класса а,
достижимым снизу; при этом, естественно, предполагается,
что такие линейные множества класса Кх существуют.
Легко видеть, что 5—универсальное множество класса а,
достижимое снизу, так как, пересекая 5 прямыми параллель-
параллельными оси ОХ, можно получить все линейные множества
класса < а и все линейные множества класса Ка, достижи-
достижимые снизу.
Значит, дополнение Е к множеству 5 есть универсальный
элемент класса а, и утверждение доказано- Ч. т.» д.
Мы дополним этот результат следующим замечанием: если
универсальный элемент Е класса а, лежащий в 0tiX, npe-

ПОДКЛАССЫ, ИХ СУЩЕСТВОВАНИЕ
129
образован с помощью уравнений / = ?(т), х — х, где функ-
функция о непрерывна на ffr, то прообраз $ множества Е есть
также универсальный элемент класса а, лежащий в обла-
области g^x.
Прежде всего, так как прообраз множества класса а есть
множество класса <[а, то прообраз § множества Е есть или
множество класса < а, или множество класса Ка, достижимое
снизу. С другой стороны, очевидно, что, пересекая %> прямыми
т = т0, параллельными оси ОХ в области У^^, можно полу-
получить всевозможные линейные множества класса < а и все
достижимые сверху линейные множества класса Ка. Значит,
$ — универсальный элемент класса /Q.
Существования. Фундаментальная теорема М. А. Лав-
Лаврентьева. Мы построили универсальный элемент класса 1
прямым методом, не делая никаких дополнительных гипотез.
Черт. 4.
Далее мы определили множество Е, и мы доказали, что оно
есть универсальный элемент класса а, если эффективно су-
существуют линейные множества класса КЛ. Сейчас мы исклю-
исключим эту гипотезу и докажем непосредственно, что плоское
множество Е, выше определенное, есть эффективно элемент
класса Ка и, следовательно, что существуют множества
всех классов.
9 Зак. 284. Н. Н. Лузин

130 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
Чтобы в этом убедиться, мы проведем в области &ty!e
диагональ x = t и обозначим через tj множество точек этой
¦диагонали, не принадлежащих к Е.
Пусть е — проекция i\ на ось ОХ. Мы начнем с доказа-
доказательства того факта, что е не может быть получено в резуль-
результате пересечения Е какой-либо прямой х = х0, параллельной
оси ОХ.
В самом деле, пусть t0 — точка области gt такая, что
прямая t = t0 пересекает Е по е. Рассмотрим точку М диаго-
диагонали, лежащую на прямой t — t0. Возможны два случая.
В первом случае точка М принадлежит к Е. Так как пря-
прямая t = tQ пересекает Е по е, то проекция N точки М при-
принадлежит к е. С другой стороны, е есть проекция множества ч\,
состоящего из точек дополнения СЕ, принадлежащих диаго-
диагонали. Значит, М принадлежит к СЕ, что противоречит пред-
предположению.
Во втором случае точка М принадлежит к СЕ. В этом
случае проекция N точки М принадлежит к е. Но мно-
множество е есть проекция точек Е, лежащих на прямой
t = t0. Значит, М принадлежит к Е, и мы опять получили про-
противоречие.
Установив это, покажем, что определенное нами множе-
множество Е принадлежит классу Ка. В силу самого определения Е
всякое линейное множество класса < а может быть получено
в результате пересечения Е прямой t = t0, параллельной оси ОХ.
Если бы множество Е было само класса < а, то это имело
бы место и для пересечения Е с диагональю х = t. При этих
условиях множество ч\ было бы класса < а, так же как и
его проекция е на ось ОХ. Тогда множество е можно было
бы получить, пересекая Е некоторой прямой t = t0, что за-
заведомо невозможно.
Итак, множество Е — строго класса а и, следовательно,
существуют множества всех классов.
Читатель заметил, что в этом доказательстве мы исходили
из некоторого частного (однако, произвольного) пересчета всех
трансфинитных чисел, меньших а при помощи целых положи-
положительных чисел. Этот пересчет вошел в последовательность A):
61г ?2, ..., $п, ..., A)
состоящую из универсальных элементов всех классов, пред-

ПОДКЛАССЫ, ИХ СУЩЕСТВОВАНИЕ 131
шествующих а. Итак, мы можем доказать существование эле-
элемента Е каждого данного класса я, так как мы умеем полу-
получить конструкцию Е из пересчета всех чисел, .меньших а,
с помощью целых положительных чисел.
Но мы не умеем назвать семейства элементов всех клас-
классов, в котором содержался бы один и только один элемент
каждого класса, так как это предполагало бы (если ограни-
ограничиваться предшествующим методом) возможность назвать
единственный пересчет трансфинитных чисел, предше-
предшествующих каждому трансфинитному числу а.
Мы думаем, что такой пересчет невозможен I11;.
Перейдем теперь к доказательству фундаментальной тео-
теоремы М. А. Лаврентьева о существовании множеств всех под-
подклассов.
Вот метод М. А. Лаврентьева.
Мы берем формально класс а и один из его подклассов 8.
Каждое линейное множество е, принадлежащее этому под-
подклассу, может быть представлено в форме
где S есть сумма счетного множества элементов класса < а,
a R — рассеянное счетное множество элементов класса а; это
последнее множество вполне упорядочено и имеет р соответ-
соответствующим трансфинитным числом.
Таким образом, мы можем написать:
и поставить в соответствие этому разложению трансфинитную
последовательность
где каждое ew класса < а и i\^ — элемент класса а; от-
отделяющее множество Н^ класса < а содержит ?]„ и не со-
содержит ни одной точки из элементов т\^, следующих
за т)г f > ?.
Всякое множество е класса а и подкласса р может
быть представлено в форме A), и обратно: каждое линейное
9*

132 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
точечное множество е, представленное в форме A), есть
очевидно: или класса < а, или же класса а и под-
подкласса ^ р.
Удобно написать разложение A) в следующей форме:
где тг)т — или элемент класса < а, или же элемент в точности
класса се.
Мы запишем также соответствующую трансфинитную по-
последовательность отделяющих множеств в форме
HQ, Hv ..., Нш, ..., Hv ... J Р,
где #т совпадает с t\v если класс tl меньше, чем а, если же
т]г есть элемент класса а, то множество Н^ класса < а, со-
содержит т|т и не содержит ни одной точки из элементов r\f,
которые следуют за ти, yf >> f.
Легко видеть, что обратное также имеет место: если ка-
какое-нибудь линейное множество е представлено в форме B),
то это множество либо класса < а, либо класса а и под-
подкласса <; |3.
Доказав это, мы поставим в соответствие каждой простой
бесконечной последовательности элементов класса < а,
и каждому трансфинитному -числу |3 линейное множество е.
Для этого пересчитаем все конечные и трансфинитные числа •{,
меньшие ^, при помощи целых нечетных чисел 1, 3, 5, ...
..., 2и — 1,... и запишем соответствующие ev e3, еъ,...
•••> e2n-i-' • в трансфинитную последовательность
где каждое Н., есть то множество ein_u номер которого
2и—1 соответствует трансфинитному числу f.
Определим теперь множество е следующим трансфинитным
разложением:

ПОДКЛАССЫ, ИХ СУЩЕСТВОВАНИЕ 133
где ¦»]„ есть множество, определенное формулой
Очевидно, что множество ?]Y, таким образом определенное,
есть или класса < а или из базы ВЛ, или же элемент
класса а. С другой стороны, т]т содержится в Hv a #Y — мно-
множество класса < а, не имеющее общих точек ст),-, где "у' > ?.
СледоЕательно, множество е, таким образом определенное, есть
или класса < а, или же класса а и подкласса <! C.
Нужно заметить, что каждое линейное множество е, кото-
которое есть или класса < а, или же класса а и подкласса ¦< J3,
может быть получено таким способом при надлежащем выборе
множеств е1г ?2, . .., еп, ... В самом деле, так как еп — про-
произвольные элементы класса < а, то множитель
П2Bс1)
к=1
есть произвольный элемент класса а или произвольное множе-
множество из базы Ва, или же произвольное множество класса < а.
С другой стороны, в определении рассеянного множества
каждое множество Н( класса < а, отделяющее т\^ от после-
последующих элементов, может всегда быть разложено на элементы
классов, не превосходящих класса Н.{. Следовательно, мы
можем всегда считать, что отделяющие множества суть эле-
элементы класса < а.
Отсюда следует, что множество е, определенное равен-
равенством C), может совпадать с каждым множеством класса а
и подкласса <[ C,
Предположим теперь, что последовательность
еи е2, . .., еп, ...
состоит из универсальных элементов всех классов < а, при-
причем каждый элемент повторяется в этой последовательности
бесчисленное множество раз. Очевидно, что множество е, опре-
определенное с помощью этой последовательности и данного транс-
трансфинитного числа р, есть множество или класса < а, или же
класса а и подкласса -^ р. Но класс множества е не может
быть меньше а, так как, пересекая е прямыми параллельными

134 ГЛ. II. ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
оси ординат, можно получить всевозможные линейные множег
ства класса а и подкласса ^р и, в частности, все элементы
класса а ]).
Следовательно, класс е равен а.
Установив это, пересечем множество е диагональю х = /.
Так как класс е равен а, то множество точек диагонали, не
принадлежащих к е, есть множество класса ^ се. Отсюда
следует, что и его проекция на ось ОХ есть множество
класса -^[а. Нужно заметить, что это линейное множество не
может быть класса < а, так как в противном случае его
можно было бы получить, пересекая е какой-то прямой t = ^0,
что невозможно.
Следовательно, это линейное множество есть множество
класса а.
Оно не может также быть подкласса -<[ [3, потому что
в этом случае его можно было бы получить, пересекая е ка-
какой-то прямой t = t0.
Отсюда следует, что е есть множество класса а и под-
подкласса > C, что доказывает существование сколь угодно вы-
высоких подклассов [12].
х) Для этого достаточно, чтобы, какова бы ни была последова-
последовательность $it $2 &п> '•• линейных элементов классов <а, на-
нашлась прямая х = х0, которая пересекает каждый универсальный
элемент еп по множеству %п, т. е. чтобы последовательность еи
e*L е„, ... совпадала с последовательностью универсальных эле-
элементов. (Прим. ред.)

ГЛАВА III
АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
Определения и простейшие свойства
Линейные аналитические множества. Мы видели
(стр. 114), что всякое несчетное множество Е, измеримое В,
расположенное в области gx, допускает регулярное пара-
параметрическое изображение
при помощи функции /, непрерывной на gt, если прене-
пренебрегать счетным множеством точек множества Е.
Это значит, что множество Е (с точностью до счетного
множества точек) можно рассматривать как множество зна-
значений, принимаемых на порции @,1) функцией f(t), непре-
непрерывной на gt, причем условие регулярности / заключается
именно в том, что функция f(t) никогда не принимает двух
равных значений; следовательно, если if ф t", то
В этой главе мы изучим свойство множеств, которые
получаются устранением условия регулярности, наложенного
на изображающую функцию /(/).
Определение. Мы назовем аналитическим всякое
множество, которое допускает параметрическое изобра-
изображение x=f{t) при помощи функции, непрерывной на gt1).
*) Это определение тождественно с теоремой I моей заметки.
Касающейся аналитических множеств и опубликованной в Comptes
Rendus Acad, Sc> 8 января 1917 г.

133 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
Смысл этого названия совершенно ясен: так как всякая
функция
x=f(f),
непрерывная на 01 (по отношению к этой области), есть
функция 1-го класса по классификации Бэра, то существует
ряд многочленов относительно t с рациональными коэф-
коэффициентами !)
сходящийся для всех значений t на @,1) и имеющий суммой
функцию f(t). Следовательно, всякое линейное аналитическое
множество есть множество значений, принимаемых на @,1)
суммой ряда многочленов с рациональными коэффициентами,
а потому оно определено при помощи аналитического равен-
равенства [13].
Мы хотим обратить внимание на тот важный факт, что
в определении аналитического множества изображающая
функция f(f) может принимать равные значения. Мы скоро
увидим, что этот факт дает определению аналитического
множества очень большую широту.
Рассмотрим теперь несколько простых примеров множеств,
которые являются аналитическими в вышеуказанном смысле.
Прежде всего, точка области g х, отдельно взятая,
есть аналитическое множество: достаточно при::ять постоян-
постоянную величину за изображающую функцию f{t).
Отсюда следует, что всякое счетное множество точек
есть аналитическое множество: достаточно принять за f{t)
функцию, равную соответствующим образом выбранной
!) И даже с целыми коэффициентами, так как всякая функция
первого класса, определенная на @<лт<1), исключая концы
этого интервала, разлагается в ряд многочленов с целыми
коэффициентами. Это теорема И. Н. Хлодовского. См. его за-
заметку в Матем. Сборнике, т. 32, 1925 г.
Кроме того, мы можем предположить, что ряд многочленов
Рх (t) -(- P2(t) + •.. абсолютно сходится, причем этого можно
•достигнуть, не уменьшая общности данного определения аналити-
аналитического множества. См. мой Memoire sur les ensembles analyfiques
et projectjfs в Матем. Сборя., т. 33, 1926 г., стр. 266. См. также
работу Серпинского «JLeg ensembles analyHques et les fonctioiM semi-
contjnues», CracovJe, 1927,

ОПРЕДЕЛЕНИЯ И ПРОСТЕЙШИЕ СВОЙСТВА 137
постоянной величине в каждом интервале Бэра 1-го ранга
области 0 х.
Пусть теперь Е есть линейное множество, измеримое В.
Если Е счетно (или конечно), мы уже видели, что Е — ана-
аналитическое. Если Е несчетно, то, по доказанному на стр. 114,
множество Е может быть разложено следующим образом:
где ?j допускает нормальное изображение, a D счетно, (или
конечно). Сделав непрерывное параметрическое изображение Ех
на порции Го, y) и Z) на порции (-„¦, 1], мы, очевидно,
придем к непрерывному параметрическому изображению всего
множества Е на @, 1).
Итак, всякое линейное множество, измеримое В, есть
аналитическое множество.
Следовательно,' семейство аналитических множеств содер-
содержит семейство множеств, измеримых ВJ).
Аналитические множества нескольких измерений. Ана-
Аналогичным образом мы назовем аналитическим всякое мно-
множество точек Е, расположенное в от-мерной области 0 х Xi>...х
и допускающее непрерывное параметрическое изображение:
это значит, что множество Е есть геометрическое место после-
последовательных положений движущейся точки М (хи х%, ..., хп),
координаты которой являются функциями некоторого пере-
переменного параметра t, причем эти функции определены и
непрерывны на порции @,1) области 01
*i =fi @. -*2 =/а (')' • • •. *»»=/« О-
Мы видим, что это определение есть вполне естественное
обобщение понятия линейного аналитического множества2).
Все замечания, которые мы сделали по поводу линей-
линейных аналитических множеств, немедленно применяются и
!) Суслин вывел это предложение из того факта, что семейство
аналитических множеств инвариантно относительно двух операций:
суммирования в широком смысле и взятия общей части. См. тео-.
рему 1 его заметки в Comptes Rendus, т. 164 A917).
2) См. мою заметку в Compte9 Rendus Acad. Sc. в мае 1925 г.
и мой мемуар «Sur les ensembles analytiques», Fund. Math. 1926,
т. X, стр. 20.

138 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
к аналитическим множествам многих измерений. В частности,
всякое множество, измеримое В, в многомерном простран-
пространстве есть аналитическое множество.
Простейшие свойства аналитических множеств: сумма
и общая часть. Мы докажем первое основное свойство ана-
аналитических множеств:
Теорема. Сумма счетного множества аналитиче-
аналитических множеств есть аналитическое множество1).
Пусть Еи Я2, ...,Еп, ...—бесконечная последователь-
последовательность аналитических множеств. Разделим @,1) области fft на
интервалы Бэра 1-го ранга: A), B), C), ..., (л),... и
изобразим параметрически Еп на интервале Бэра (я). Ясно,
что таким образом мы получим непрерывное параметрическое
изображение суммы Е1~\~Е^-\- ... -\-Еп-\- ... на @,1).
Итак, эта сумма есть аналитическое множество. Ч. т. д.
Здесь надлежит сделать следующее замечание: можно
формально изобразить множество точек в пространстве мно-
многих измерений при помощи одной и только одной функции,
если ввести комплексные числа с т мнимыми единицами
a\h Л~ а2г2 Н~ ¦ • • ~\~ ат1т и УСЛОВИТЬСЯ ПИСЭТЬ
когда имеем в отдельности а± — Ьх, а% = Ь%, ..., ат = Ьт,
так что одно уравнение между комплексными числами сво-
сводится к т уравнениям с действительными числами. В этих
условиях всякое аналитическое множество Е в пространстве т
измерений изображается при помощи одной и только одной
комплексной функции
1 @ =/i @ h +/2 W h + • • • +/* С) *»
действительного параметра t, причем эта функция опреде-
определена и непрерывна на порции @,1) области gft.
Это замечание будет нам часто полезно, так как боль-
большинство рассуждений, касающихся линейных аналитических
множеств, сохранится в силе для многомерных аналитических
множеств, если ввести комплексные функции.
J) Эта теорема принадлежит Суслину. См. его лемму II в ци-
цитированной заметке (Comptes Rendus Acad. Sc, 8 января 1917 г.).

ОПРЕДЕЛЕНИЯ И ПРОСТЕЙШИЕ СВОЙСТВА 139
Теорема. Общая часть счетного множества анали-
аналитических множеств есть аналитическое множество*).
Пусть Е есть общая часть аналитических множеств
Еи Я2, ...,Еп, ... и пусть
— непрерывные параметрические изображения этих множеств
на порциях @,1) соответствующих областей g , gt, ...
СГ П 2
• ••. »v-
Определим новую область <sf t и возьмем уравнения
которыми мы пользовались' при доказательстве теоремы
о существовании нормального изображения для всякого не-
несчетного множества, неизмеримого В (стр. 115).
Эти функции »„(/) непрерывны на @,1) области gt и
принимают иррациональные значения, заключенные между 0 и 1.
Кроме того, какова бы ни была последовательность fj, t%, ...
..., /®, ... иррациональных чисел, заключенных между 0 и 1,
существует одно и только одно иррациональное число t0
такое, что значения функций <pi, ?2> • • •» ?п> • • • в ^о соот~
ветственно равны t°, t°, ..., Рп, ...
Установив это, образуем сложные функции
Pi (О =Л [?i @1, ^ =/21ъ W], • •.. ^» @ =/» [?»@1, •: •
Ясно, что эти функции непрерывны на @,1). Следова-
Следовательно, совместные уравнения
F1(f) = Ft(f)=... = Fn(f)=...
определяют замкнутое на gt множество Т.
*) Эта теорема принадлежит Суслину. См. лемму III в его за-
заметке (Comptes Rendus Acad. Sc. 8 января 1917 г.). Метод Суслина,
основанный на употреблении кортежей индексов (см. стр. 303 этой
книги), существенно отличается от того, который мы даем в тексте.
Я указал метод, даваемый в тексте, в своем мемуаре «Sur les en-
вещЫез analytiques», Fund. Math., т. Х, 1926, стр. 40), он полезен
во многих случаях и, в частности, применяется к проективным мно-
множествам. См. стр. 279 этой книги и работу Серпинского «Sur les
produits des imagee continues».

140 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
Из определения сложных функций Ft следует, что когда
переменное t пробегает множество Т, то общая величина
функций Ff(t), которую мы обозначим просто через F(f),
пробегает в точности общую часть Ег • Е2.... Еп... заданных
множеств.
Но замкнутое множество Т измеримо В. Следовательно, Т
есть аналитическое множество, а потому существует непре-
непрерывное параметрическое изображение
множества Г на порции @,1) новой области 0Z, причем
функция ty(x) определена и непрерывна на @,1) области 0\.
Отсюда следует, что сложная функция
дает искомое непрерывное параметрическое изображение
множества ? = Е1 ¦• Е% ... Еп ... Значит, это множество есть
аналитическое. Ч. т. д.
Важно заметить, что данное доказательство, проведенное
для линейных аналитических множеств, остается без измене-
изменений для множеств многих измерений, если предположить,
что изображающие функции x=fn комплексные и что
буква х обозначает точку множества Еп. Остальные функ-
функции ¦»„ и ty должны оставаться действительными.
Проекции
Элементарные множества. Рассмотрим основную область m
измерений ffx x ш_.х . Разделим каждую линейную область
0х на порции при помощи целых чисел; каждая из полу-
полученных порций имеет длину, равную 1, и мы их назовем
интервалами Бэпа порядка 0. В каждом из них мы опреде-
определим интервалы Бэра порядков 1, 2, 3, ..., в точности так,
как это обычно делается для порции @,1).
Установив это, мы назовем параллелепипедом Бэра
порядка k в тге-мерной области 0ХХ ...х "множество тех
точек этой области, координаты которых принадлежат каким-
нибудь интервалам Бэра порядка k, например bv 82, ..., 8„,,
расположенным соответственно в 9Х), 0Xi, •••, 8'хт-

ПРОЕКЦИИ 141
Мы теперь введем очень полезное понятие, а именно
понятие элементарного множества.
С этой целью возьмем в области gх.х ...х определен-
определенную счетную или конечную последовательность параллелепи-
параллелепипедов Бэра порядка 0 попарно без общих точек: эти парал-
параллелепипеды Бэра назовем параллелепипедами рата 0.
В каждом параллелепипеде ранга 0 возьмем вполне опре-
определенную, счетную или конечную, последовательность парал-
параллелепипедов Бэра порядка 1 и попарно без общих точек:
эти параллелепипеды назовем параллелепипедами ранга 1.
Вообще, каково бы ни было я, п > 1, возьмем в каж-
каждом из параллелепипедов Бэра ранга л — 1 вполне определен-
определенную, конечную или счетную, последовательность параллеле-
параллелепипедов Бэра порядка л попарно без общих точек; мы их
назовем параллелепипедами ранга п.
Так как всех параллелепипедов Бэра лишь счетное мно-
множество (или конечное число), то их сумма есть множество,
измеримое В; обозначим его через Sn. Следовательно, общая
часть $ всех сумм Sn
S
n
есть опять множество, измеримое В.
О п р е д е л,е н и е. Мы назовем элементарным множе-
множеством так определенное множество &.
Легко видеть, что всякое элементарное множество есть
множество не очень сложной природы, но, строго говоря, это
лишь очень относительно1).
Установив это определение, мы докажем следующую тео-
теорему:
Теорема. Всякое аналитическое множество, распо-
расположенное в области т измерений, есть ортогональная
проекция некоторого элементарного множества, располо-
расположенного в области т -j- 1 измерений.
1) «Простота» элементарных множеств нам кажется весьма ил-
иллюзорной. Перевод определения элементарного множества на язык
арифметики наталкивается на все препятствия, связанные с тео-
теорией роста. Повидимому, все трудности теории проективных мно-
множеств содержатся, как в зародыше, в теории элементарных мно-
множеств.

142 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
Чтобы доказать это, возьмем аналитическое множество Е,
содержащееся в области. &х.х2...х • Пусть
*1 =/l @. *Я =Л С) Xm=fm{t) A)
есть непрерывное параметрическое изображение Е.
Рассмотрим данную область &хх ,,.х как часть новой
области т-{-\ измерений 0ХХ ...а, ж . Обозначим через S
множество точек N(xv лг2, ...,лгт, /) этой области, коор-
координаты которых удовлетворяют уравнениям A). Ясно, что
ортогональная проекция $ на область &Хх ...се есть данное
множество Е.
Итак, все сводится к доказательству того, что $ есть
элементарное множество.
С этой целью рассмотрим интервал Бэра 8 порядка k,
расположенный в 01. Пусть f5 есть множество тех точек
из %, у которых координата t принадлежит 8. Обозначим
через S<?) сумму тех параллелепипедов Бэра порядка k в об-
области &хх ...х t, которые содержат точки из §s. Сумма
1 2 W
всех Sf>, соответствующих интервалам Бэра порядка k,
будет обозначена через S^.
Легко видеть, что общая часть &' = Sx • S2 ... Sk .. .
есть элементарное множество, содержащее множество $.
Остается лишь доказать что $' содержится в §.
Чтобы убедиться в этом, возьмем точку N (#J, л^, . .., х°т, t0)
из $'. Пусть uv есть параллелепипед Бэра порядка v, содер-
содержащий точку N. Если мы буде.,1 изменять v, мы получим
бесконечную последовательность и0, я,, ..., и„ ... парал-
параллелепипедов Бэра порядков 0, 1, 2, ..., v, ..., содержащих
точку N, каждый из которых содержится в предыдущем.
Если мы обозначим через 8V проекцию тгу на ось ОТ, то
последовательность 80, 8j, 82, ...,8„ ... образована из
интервалов Бэра порядков 0, 1, 2, ...,v,..., содержащих
точку tQ, каждый из которых содержится в предыдущем.
Так как параллелепипед тс., есть часть суммы S<'), то он
. содержит точки множества §8. Значит, интервал Бэра 8„
обязательно содержит точку tv такую, что точка N^ с коор-

ПРОЕКЦИИ 143
динатами х^\ л?> jcW, t4, удовлетворяющими уравне-
уравнениям
'«i4)=/,W, 4V)=/,W •*??=/«(*,). ¦ B)
принадлежит к и,.
Если мы будем неограниченно увеличивать v, то t, будет
стремиться к t0. С другой стороны, каждое л?*> стремится
к х^, так как диаметр параллелепипеда тс„ содержащего
постоянную точку N и переменную точку /V,, стремится
к нулю с возрастанием v.
Так как функции ft(f) непрерывны, то уравнения B) нам
дают
„* f (j. \ „О f /j. \ 0 f /j\
xl—J l\lQh X2—/2vJo'» •••» •*я»—Jm\lQJ>
откуда и следует, что точка N принадлежит к $. Итак,
множество $' тождественно с § и, следовательно, $ есть
элементарное множество. Ч. т. д.
Обратная теорема также имеет место: ортогональная
проекция всякого аналитического множества есть также
аналитическое множествоJ).
Чтобы доказать эту теорему, возьмем в /га-мерной области
9хх ...х аналитическое множество Е, заданное непрерыв-
непрерывным параметрическим изображением
Чтобы получить ортогональную проекцию Е на /га'-мер-
ную область Sfxx ...а, л т' </га, очевидно, достаточно от-
отбросить уравнения, которые следуют за xm/=fm/(t); это
дает
*i =/i @» -^2 =/а W' • • •. -«W =/«/ (О-
Итак, проекция ? есть аналитическое множество. Ч. т. д.
Эта теорема имеет большое значение, так как она пока-
показывает, что операция взятия ортогональной проекции уже
определенною множества не выводит из класса аналитических
х) См. теорему VI заметки Суслина (Comptes Rendus Acad. Sc,
8 января 1917 г.).

144 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
множеств. В частности, взяв ортогональную проекцию мно-
множества, измеримого В, мы получаем аналитическое мно-
множество. А так как каждое аналитическое множество есть
проекция некоторого элементарного множества, т. е. мно-
множества, измеримого В (элемента класса 2), то мы заключаем
отсюда, что аналитические множества тождественны,
проекциям множеств, измеримых В.
Параметрическое изображение при помощи функций,
входящих в классификацию Бэра. Мы определили анали-
аналитическое множество как множество, которое допускает
непрерывное параметрическое изображение
Xl =/l @. *2 =Л (')> ¦•¦ •, Хт =fm(f).
Но непрерывные на 01 функции суть функции класса О
по классификации Бэра2). Поэтому вполне естественно теперь
изучить природу тех множеств, которые допускают непре-
непрерывное параметрическое изображение при помощи любых
функций классификации Бэра.
В наших рассуждениях мы будем пользоваться следующей
теоремой, принадлежащей Лебегу: Множество тех точек
области 0' хх ...х , в которых функция /(х^х^, . .., хт),
вкодящая в классификацию Бэра, равна нулю, есть всегда
множество, измеримое В'1).
Другое свойство функций классификации Бэра, которым
мы будем пользоваться, состоит в следующем: суммы, раз-
!) Согласно условию рассматривать всегда лишь иррациональ-
иррациональные точки, мы назовем функциями класса 0 функции, непрерыв-
непрерывные на области 01 относительно этой области. Ясно, что
функция класса 0 в смысле этого определения будет класса <J 1
в обычной классификации Бэра, где рациональные точки не ис-
исключаются. Заметим, что такие переходы могут происходить лишь
в классах 0 и 1, высшие же классы ;> 2 остаются неизменными.
2) Это частный случай общей теоремы Лебега: для того чтобы
функция /, всюду определенная, была класса не выше а, необ-
необходимо и достаточно, чтобы, каковы бы ни были рациональ-
рациональные числа Г) и г2, множество точен, где г^ <!/<! гг, было класса
не выше a. (Sur les fonctions represcntables analytiquenent, стр. 168,
теорема V.)
Доказательство- этой теоремы построено на трансфинитной
индукции. В случае текста мы имеем г^ = г2 = 0.

проекции 145
поста и произведения функций классификации Бэра вхо-
входят в ту же классификацию!).
Эти теоремы можно доказать методом индукции', тео-
теорема очевидна для класса 0; затем доказывают, что если она
верна для классов < <х, то верна и для класса а.
Мы не будем больше останавливаться на этом пункте.
Установив это, вернемся к изучению множества Е, опре-
определенного параметрическим изображением A), в котором функ-
функции ft входят в классификацию Бэра.
Рассмотрим функцию F(xlt х2 хт) t) от т-\-\
действительных переменных, определенную равенством
хт -/м №
Так как функции /,, /2, ..., fm входят в классификацию
Бэра, то и функция г также в нее входит. Следовательно,
множество $ точек N(xv дг2, ..., хт, t) m-\-1 -мерной об-
области ZfxiXi...xmt, где функция F(xu лг2, ..., хт, t) обра-
обращается в нуль, измеримо В. Но множество $ есть как раз
множество тех точек N, координаты которых удовлетворяют
уравнениям A). В этих условиях ясно, что ортогональная
проекция $ на область ?fx.a;a...x есть множествоЕ. Значит,
Е есть аналитическое множество.
Таким образом, мы приходим к следующему заклю-
заключению:
Понятие аналитического множества нисколько нельзя
расширить, рассматривая геометрическое место последо-
последовательных положений подвижной точки М (хи хъ ..., хт),
координаты которой суть произвольные функции пара-
параметра t, входящие в классификацию Бэра а)
*i =Л @. *я = Л О. • • • > хт ==/„, @.
Универсальное аналитическое множество. Мы видели,
что семейство аналитических множеств содержит семейство
множеств, измеримых В. Чтобы решить вопрос о том,
!) См. Lebesgue, там же, стр. 153.
2) Э III й
) См. Lg, , р
2) Это теорема III моей заметки в Comptes Rendus Acad. Sc.
8 января 1917 г.
10 Зак. 284. Н. Н. Лузин

146 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
выходят ли аналитические множества за пределы множеств, из-
измеримых В, мы введем следующее определение *):
Аналитическое множество Е точек двумерной обла-
области 0т мы назовем универсальным, если, пересекая его
прямыми х = х0, параллельными оси OY, мы получим
всевозможные линейные аналитические множества.
Легко доказать существование универсальных аналитиче-
аналитических множеств.
С этой целью замети^, прежде всего, что всякое элементар-
элементарное множество будет или класса <2 или же элементом класса 2.
Это вытекает из самого определения элементарного множе-
множества (стр. 140), так как если Е — элементарное множество,
то оно является общей частью E = S1-Si... Sn ... сумм Sn,
каждая из которых образована из счетного множества парал-
параллелепипедов Бэра [м].
Но мы видели (стр. 126), что существуют универсальные
элементы каждого класса а классификации Валле-Пуссена' и
притом в пространстве любого числа измерений. Возьмем же
в трехмерной области gxye универсальный элемент класса 2.
В силу свойства универсальных элементов, пересекая $ пло-
плоскостями у = const, параллельными плоскости X0Z, мы по-
получим всевозможные плоские элементы класса 2. В частности,
получаются всевозможные элементарные множества.
Пусть теперь Е есть ортогональная проекция универсаль-
универсального элемента § на плоскость YOZ. Так как $ измеримо В,
то его проекция Е есть плоское аналитическое множество.
Я утверждаю, что Е есть универсальное анилитическое
множество. В самом деле, каково бы ни было линейное ана-
аналитическое множество е, оно является ортогональной проек-
проекцией некоторого плоского элементарного множества. И так
') Я ввел понятие универсального аналитического множества
в своей заметке «Sur les ensembles поп mesurables В et l'emploi de
la diagonale de Cantor» (Coraptes Rendus Acad. Sc. 20 июля 1925 г.),
но идея плоского множества, универсального по отношению к дан-
данному семейству множеств, была у Лебега (Sur les fonctions гёр-
resentables analytiquement», стр. 207). Относительно других прило-
приложений понятия универсального множества см. извлечение из моего
письма к Серпинскому, «Sur l'accessibilite des points» (Fund. Math,
m. XI) и интересные работы Серпинского «Sur l'exlstance des dl-
verses classes d'ens>embles» (Fund. Math. т. XIV) и Никодима «Sur
les diverses chasses d'cnsembles» (Fund. Math. т. IV).

проекций 14?
как мы можем получить это элементарное плоское множество,
пересекая элемент $ подходяще выбранной плоскостью у = у0,
то мы получим линейное аналитическое множество е, пере-
пересекая Е прямой у=у0, параллельной оси OZ и лежащей
в плоскости YOZ. Это показывает нам, что Е есть плоское
универсальное аналитическое множество.
Принимая во внимание всю важность существования уни-
универсальных аналитических множеств, мы дадим другое дока-
доказательство, с некоторых точек зрения более простое, чем пре-
предыдущее :).
Метод, который мы сейчас изложим, основан на пользо-
пользовании функцией 9 (л:, t), обладающей следующими двумя
свойствами: 1° она определена для всех х и t, принадлежа-
принадлежащих интервалу @, 1), и входит в классификацию Бэра; 2"
всякая функция f(x) переменного х и класса <^ 1 может
быть получена, если дать переменному t некоторое частное
числовое значение t0.
В самом деле, возьмем функцию <р(лг, f), обладающую
указанными двумя свойствами, и рассмотрим в трехмерном
пространстве OXTY поверхность S, определенную уравне-
уравнением
.У = ?(*. *)•
Если эту поверхность 5 рассматривать как множество
точек в пространстве OXTY, то это множество, очевидно,
измеримо В.
Следовательно, ортогональная проекция 5 на плоскость
TOY есть аналитическое множество; обозначим эту проек-
проекцию через Е. Я теперь утверждаю, что Е есть универсаль-
универсальное аналитическое множество.
Чтобы убедиться в этом, достаточно заметить, что всякая
функция f(x), непрерывная во всех иррациональных точках,
необходимо будет класса -^ 1 по классификации Бэра. По-
Поэтому, по самому определению линейного аналитического
множества, мы получим все линейные аналитические множе-
множества, пересекая Е прямыми, параллельными оси OY. Отсюда
следует, что Е есть универсальное аналитическое множество.
Итак, все сводится к построению такой функции <р (лг, t).
Пусть Pj (лг), Р% (х), ..., Рп (лг), ... есть последовательность,
*) См. мою заметку в Comptes Rendus Acad. S& 20 июля 1925 г.
10*

14$ ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
образованная из всех многочленов относительно х с рацио-
рациональными коэффициентами, и пусть <pj @» ?а @> • • •» 9п $> • • •
есть последовательность функций, непрерывных между 0 и 1
и обладающих следующим свойством: какова бы ни была
последовательность действительных чисел в], Sj в,
существует такое число t0, что
i?i(U «?«&) npn(g,)
Установив это, обозначим через Sn(x, t) сумму я первых
членов бесконечного ряда
Ясно, что Sn(x, t) есть непрерывная функция по сово-
совокупности своих аргументов. Следовательно, функция <р(лг, /),
определенная как верхний предел
<р(лг, *) = msn(x, t),
есть функция класса 2 по классификации Бэра. А так как.
каждая функция класса -^ 1 может быть представлена в виде
суммы ряда многочленов с рациональными коэффициентами,
то мы видим, что так определенная функция <р(*, t) обла-
обладает двумя вышеуказанными свойствами 2). Ч. т. д.
Установив этот результат, возьмем плоское универсаль-
универсальное аналитическое множество Е, расположенное в плоско-
плоскости XOY. Так как Е универсально, то мы получим все ли-
линейные аналитические множества и среди них все линейные
множества, измеримые В, пересекая Е прямыми * = лг0,
параллельными оси ОК. Рассмотрим диагональ у = х и обо-
обозначим через е общую часть универсального аналитического
множества Е и этой диагонали. Ясно, что е есть линейное
аналитическое множество.
Но если мы обратимся к рассуждению по поводу диаго-
диагонали, сделанному выше (стр. 130), мы немедленно заметим,
*) Речь идет о кривой Пеано, заполняющей целую область в про-
пространстве счетного числа измерений.
2) Отметим интересную работу В. Серпинского «Sur un ensemble
analytlque universel pour les ensembles mesurables B» (Fund. Mathem.
т. XII, стр. 75), где Серпинский строит плоское аналитическое мно-
множество, которое параллелями к оси OY пересекается только по
множествам, измеримым В, и каждое линейное множество, изме-
измеримое В, может быть получено таким способом.

СВОЙСТВА АНАЛИТИЧЕСКИХ МНОЖЕСТВ 149
что ортогональная проекция на ось OY дополнения Се к мно-
множеству е относительно диагонали у = х не может принад-
принадлежать к семейству тех множеств, которые получаются при
пересечении Е прямыми х = х0.
Следовательно, проекция множества Се на ось OY не есть
аналитическое множество. Это показывает, что линейное мно-
множество е не измеримо В, так как в противном случае его
дополнение Се было бы также измеримым В и, следова-
следовательно, его проекция на ось OY была бы в этом случае
аналитическим множеством.
Итак, линейное множество е есть линейное аналитическое
множество, неизмеримое В, и, следовательно, плоское универ-
универсальное множество Е само является аналитическим множе-
множеством, неизмеримым В.
Это рассуждение можно дополнить следующим простым
замечанием: универсальное аналитическое множество Е не
может быть измеримым В, так как в противном случае Е
должно было бы принадлежать к определенному классу Кл
классификации Валле-Пуссена. Отсюда следует, что никогда
нельзя получить линейное множество, измеримое В, и класса
выше а, если пересекать Е прямыми х — х0. Но так как Е
универсально, мы заведомо будем получать множества
класса >¦ а, если только подходящим образом выберем
точку х0. Таким образом, мы приходим к притиворечию.
Но это последнее рассуждение, каким бы оно ни казалось
простым, вводит трансфинитные числа и пользуется сущест-
существованием множеств всех классов. С этой точки зрения первое
рассуждение предпочтительнее.
Таким образом, мы доказали, что понятие аналитического
множества есть более общее, чем понятие множества изме-
измеримого В. Это заставляет нас изучить для этих множеств
основные свойства точечных множеств, каковыми являются
мощность, мера а категория.
Свойства аналитических множеств
Когда дано какое-либо точечное множество, тотчас же
возникают три основных вопроса: если это множество не-
несчетно— имеет ли оно мощность континуума? Измеримо ли
это множество? Обладает ли оно свойством Бэра? Мы теперь

150 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
исследуем свойства аналитических множеств по отношению
к этим вопросам.
Мощность. Пусть Е есть несчетное аналитическое мно-
множество, расположенное в /га-мерной области. Пусть § есть
элементарное множество в т -j-1 -мерном пространстве, при-
причем его ортогональная проекция есть данное множество Е.
Так как диаметр параллелепипеда Бэра порядка к стре-
стремится к нулю, когда я неограниченно возрастает, то суще-
существует целое положительное число п, достаточно большое
для того, чтобы среди параллелепипедов ранга п (стр. 141)
нашлось два параллелепипеда it и тг', обладающих следую-
следующими двумя свойствами: 1° проекции тг и тг' не имеют общих
точек; 2° проекции частей §, содержащихся в it и в it',
являются обе несчетными множествами.
Раз так, то мы находимся в тех же условиях, как и
раньше, и мы можем определить в каждом из двух парал-
параллелепипедов тс и тт' два новых параллелепипеда ранга выше
л, обладающих теми же свойствами; мы получаем, таким
образом, четыре вполне определенных параллелепипеда. Мы
продолжаем оперировать также над каждым из них и полу-
получаем восемь определенных параллелепипедов, обладающих
теми же свойствами, и так далее безгранично.
Ясно, что множество точек, каждая из которых принад-
принадлежит бесконечному множеству параллелепипедов Бэра, так
определенных, есть совершенное множество в классическом
смысле, и притом содержащееся в данном элементарном мно-
множестве $. К тому же проекции двух различных точек этого
совершенного множества всегда различны.
Отсюда следует, что проекция этого совершенного мно-
множества есть опять совершенное множество в классическом
смысле. А так как это последнее, очевидно, содержится в дан-
данном аналитическом множестве Е, то мы получаем теорему:
Всякое несчетное аналитическое множество необхо*
димо содержит совершенное множество и, следовательно,
имеет мощность континуума*).
Мера. Пусть Е — произвольное аналитическое множество,
о котором известно только, что оно имеет внешнюю меру,
не равную нулю, теЕ > 0.
1)?Теорема Суслина. См. Comptes Rendus, ^января 1918 г.

СВОЙСТВА АНАЛИТИЧЕСКИХ МНОЖЕСТВ 151
Сделаем прежде всего одно весьма банальное замечание:
чтобы доказать, что некоторое точечное множество Е с не
равной нулю внешней мерой измеримо, необходимо и доста-
достаточно установить, что оно содержит замкнутое множество F,
мера которого превосходит mji — в, где е — как угодно
малое положительное число.
В самом деле, с одной стороны, можно заключить точки Е
в ряд параллелепипедов (прямоугольников, интервалов), общая
протяженность которых (объем, площадь, длина) меньше, чем
теЕ~\~е. С другой стороны, все точки, не принадлежащие
к Е, очевидно, заключаются в ряде параллелепипедов, внешних
к замкнутому множеству F; их общая протяженность меньше,
чем 1 — mF ~\- а. Значит, общая протяженность этих двух
рядов параллелепипедов меньше, чем
теЕ-\-a-j-l — mF-\-e <1 +3з
и, следовательно, Е измеримо. Несмотря на свою банальность,
это замечание будет нам очень полезно.
Сделаем еще одно замечание: если мы имеем последова-
последовательность Elt ?2, ... любых множеств, не подчиненных ни-
никакому закону, то внешняя мера множества-суммы я пер-
первых членов этой последовательности стремится к внешней
мере суммы всех членов этой последовательности, когда л
неограниченно возрастает.
Отсюда следует, что можно выбрать достаточно большое
число пх параллелепипедов ранга 1, для того чтобы часть
элементарного множества $, содержащаяся в этих п1 парал-
параллелепипедах, имела проекцию, внешняя мера которой пре-
превосходит meE — Sj.
Будем оперировать также над параллелепипедами ранга 2,
содержащимися в выбранных параллелепипедах ранга 1: мы
можем взять число л2 настолько большим, чтобы часть §,
Содержащаяся в них, имела проекцию, мера которой превос-
превосходит теЕ — Sj — е2, и так далее.
Мы образуем таким образом суммы S[, Sr2, S'a, ... парал-
параллелепипедов рангов 1, 2, 3... соответственно, каждая из S^
состоит из конечного числа параллелепипедов множества Sn
(стр. 141) и содержится внутри предыдущей S'n_v а проек-
проекция части элементарного множества $, содержащейся

152 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
в параллелепипедах из S'n, имеет внешнюю меру, превосходящую
mJE — st — s2— .. ,гп; здесь ряд с положительными членами
8j -j- eg -f- ... -j- гп + ... сходится и имеет как угодно малую
сумму в.
Отсюда следует, что проекция Sn имеет протяженность,
превосходящую теЕ—s. Но так как проекция множества^,
очевидно, состоит из конечного числа параллелепипедов Бэра
и содержится в проекции множества S»_i, то общая часть
проекций всех Sn есть замкнутое множество F, мера кото-
которого превосходит mji — е.
С другой стороны, общая часть сумм Si, S2, ..., Sn, .. .
есть, очевидно, замкнутое множество, содержащееся в эле-
элементарном множестве §; это замкнутое множество мы обо-
обозначим через Н.
Легко видеть, что множество Н имеет своей проекцией
множество F. Значит, F содержится в данном аналитическом
множестве Е.
В силу предыдущего замечания множество Е есть изме-
измеримое, и, следовательно, мы получили теорему:
Всякое аналитическое множество измеримо J).
Категория. Мы теперь докажем, что всякое аналитиче-
аналитическое множество обладает свойством Бэра, принадлежащим
всем множествам, измеримым В 2).
Обратимся к стр. 86: все сводится к тому; чтобы дока-
доказать, что если данное аналитическое множество Е не есть
множество 1-й категории ни на какой порции некоторого
совершенного множества Р, то его дополнение СЕ есть мно-
множество 1-й категории на Р.
Начнем с того, что выбросим из т ~\- 1-мерной области,
где помещается элементарное множество $, все параллелепи-
параллелепипеды, каков бы ни был их порядок, такие, что содержащаяся
в них часть $ имеет проекцию первой категории на Р. Ясно,
что сохранятся при этом параллелепипеды всех порядков.
Установив это, мы будем оперировать с каждым из со-
сохраненных параллелепипедов, каков бы ни был его порядок,
*) См, теорему V моей заметки в Comptes Rendus Acad. Sc.
8 января 1917 г.
2) См. теорему VI моей заметки в Copiptes Rendus Acad. 5c,
8 января 1917 г,

СВОЙСТВА АНАЛИТИЧЕСКИХ МНОЖЕСТВ 153
следующим образом: пусть тс— рассматриваемый параллеле-
параллелепипед; мы возьмем часть $, содержащуюся в ж. Так как тс
сохранен, эта часть $ имеет проекцию уже не первой кате-
категории на Р. Следовательно, на Р существует замкнутое мно-
множество F, обладающее следующими двумя свойствами:
1° если о есть порция Р, содержащаяся в F, то проек-
проекция части $, содержащаяся в тс, будет первой категории
на о;
2° если о есть порция Р, содержащая точку, которая
не принадлежит к F, то указанная проекция не будет первой
категории на о.
Установив этот первый пункт, мы определяем для каждого
сохраненного параллелепипеда тс', содержащегося в тс, и по-
порядка, непосредственно следующего за порядком тс, соответ-
соответствующее замкнутое множество F'.
Ясно, что общая часть всех замкнутых множеств F' есть
множество нигде не плотное на всякой порции Р, не содер-
содержащей точек F. Это значит, что множество точек, принадле-
принадлежащих всем F' и не принадлежащих F, есть множество не
плотное на Р; мы его обозначим через Я„.
Таким образом, всякому сохраненному параллелепипеду
Бэра тс, каков бы ни был его порядок, соответствует вполне
определенное множество Нк, не плотное на Р. Отсюда сле-
следует, что сумма всех множеств Нк, соответствующих различ-
различным тт, есть множество первой категории на Р. Обозначим
его через Н.
Мы сейчас докажем, что каждая точка М множества Р,
не принадлежащая к Н, есть точка данного аналитиче-
аналитического множества Е.
В самом деле, так как М не принадлежит к //, то суще-
существует сохраненный параллелепипед Бэра тс0 порядка 0 такой,
что М не входит в замкнутое множество Fo, соответствую-
соответствующее тг0; так как М не принадлежит к //« , то существует
в тс0 сохраненный параллелепипед Бэра itj порядка 1 такой,
что М не входит в замкнутое множество Fu соответствую-
соответствующее tcjJ так как М не принадлежит к //„ , то в tcj суще-
существует сохраненный параллелепипед Бэра тг2 порядка 2 такой,
что М не входит в замкнутое множество, F^, соответствую-»
щее itj и так далее,

154 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
Таким образом, мы получим последовательность сохранен-
сохраненных параллелепипедов тг0, те,, гса, ... порядков, соответственно
равных 0, 1, 2, 3 ..., каждый из которйх содержится в пре-
предыдущем, причем точка М не принадлежит ни одному из
замкнутых множеств Fn, я = 0, 1, 2, 3, ... Следовательно,
точка М непременно принадлежит к проекции каждого из
параллелепипедов it0, itj, тс2, ...
Отсюда мы заключаем, что М есть проекция некоторой
точки N, принадлежащей всем параллелепипедам ir0, izu ir2, ...
и, следовательно, являющейся точкой элементарного множе-
множества $. Итак, М принадлежит к Е.
Таким образом, каждая точка Р, не принадлежащая к Е,
должна принадлежать к Н. Но так как Н первой категории
на Р, то и СЕ также. Ч. т. д.
Мы дополним этот результат следующими замечаниями:
Замечание I. Пусть Е есть линейное аналитическое
множество, неизмеримое В и пусть f(x) есть характеристи-
характеристическая функция для Е, т. е. f(x) равна 1 на ? и 0 на его
дополнении. Так как Е неизмеримо В, то f(x) не входит
в классы Бэра. Но, согласно доказанной теореме, множество Е
обладает свойством Бэра и, следовательно, функция f(x)
точечно разрывна на всяком совершенном множестве, если
пренебречь множеством первой категории на этом совер-
совершенном множестве.
Мы видим, что свойство, открытое Бэром и принадлежащее
всем функциям его классификации, не является достаточным.
Замечание .II. Если некоторое множество точек изме-
измеримо, то и его дополнение тоже. Та же взаимность имеет
место для свойства Бэра. Следовательно:
Дополнение к аналитическому множеству измеримо и
обладает свойством Бэра.
В дальнейшем мы будем называть кратко те множества,
которые являются дополнениями к аналитическим множествам,
аналитическими дополнениями.
Первый принцип аналитических множеств.
Отделимость В
Общие идеи. В данном нами определении аналитических
множеств понятие трансфинитного явно не входит. Тем не
менее, детальное изучение этих множеств показывает, что

ПЕРВЫЙ ПРИНЦИП ОТДЕЛИМОСТИ 155
совокупность всех трансфинитных чисел второго класса по
Кантору глубоко спрятана в аналитических множествах, неиз-
неизмеримых В.
Полученные в теории аналитических множеств результаты
наилучшим образом показывают, что необходимо рассматри-
рассматривать аналитические множества, неизмеримые В, как в неко-
некотором роде продолжение классификации Валле-Пуссена за
классы К*, перенумерованные при помощи всех трансфинит-
трансфинитных чисел второго класса по Кантору. Точнее говоря, на эти
аналитические множества надо смотреть, как на элементы
класса Q, где Q — первое трансфинитное число «третьего
класса» по Кантору. Среди многочисленных, бьющих в глаза
аналогий, мы укажем ту, которая связана с отделимостью
множеств.
В теории множеств, измеримых В, мы видели, что два
элемента класса КЛ без общих точек всегда отделимы при
помощи множеств или класса < <х или базы ВЛ.
Вполне аналогичное предложение имеет место и для ана-
аналитических множеств'). Чтобы убедиться в этом, введем
новое понятие* а именно понятие об отделимости В.
Мы скажем, что два множества Е и Е' без общих точек
отделимы В, если существуют два множества Н и //', изме-
измеримые В, без общей точки и содержащие соответственно
множества Е и Е'.
Множества Н и //', обладающие этим свойством, мы на-
назовем отделяющими множествами.
Установив это определение, мы формулируем основное
предложение теории аналитических множеств, называемое
первым принципом этой теории 2).
Принцип I. Два аналитических множества без общих
точек всегда отделимы В.
Мы дадим два различных доказательства принципа I. Для
того чтобы лучше оценить существенную разницу между
этими двумя доказательствами, напомним две классические
J) Читатели, желающие получить более детальные разъяснения
по поводу этой аналогии, могут обратиться к моему мемуару: «Ana-
«Analogies entre les ensemble» mesurables В et les ensembles analytiques»
(Fund. Math., XVI, 1930).
' *) Я высказал в явной-форме и доказал этот принцип в'своем
мемуаре «Sur lee ensembles analytiques», Fund. Math., т. Xt стр. 52.

156 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
теоремы: всякое замкнутое множество, не содержащее
никакого совершенного множества, счетно (Кантор — Бенди-
ксон) и теорему Бэра о функциях класса 1.
Каждое из этих предложений имеет два доказательства.
Одно из них дает не только доказательство теоремы, но и
регулярный процесс, который, в первом случае, дает нам
вполне определенное перенумерование точек рассматриваемого
замкнутого множества при помощи целых чисел, а во втором
случае эффективное построение ряда многочленов, сходяще-
сходящегося к рассматриваемой функции класса 1. Это доказатель-
доказательство можно рассматривать как положительное и известно, что
оно дано для замкнутых множеств Бендиксоном и Серпин-
ским, а для функций класса 1 самим Бэром.
Но есть другой вид доказательств для этих теорем. Дока-
Доказательства этого рода не дают ни процесса перенумерования
точек замкнутого множества, ни построения ряда полиномов,
имеющего суммой функцию класса 1, но доказывают лишь
существование такого перенумерования и такого ряда поли-
полиномов. Вот механизм доказательств; каждый раз вводят неко-
некоторое общее, но чисто отрицательное понятие: в случае
замкнутых множеств это понятие точки сгущения, которым
мы обязаны Линделефу, а в случае функций класса 1 это по-
понятие точки, где функция не есть класса 1; этим понятием
мы обязаны Лебегу. Эти доказательства можно рассматривать
как отрицательные.
Аналогичным образом мы дадим два доказательства прин-
принципа 1: одно из них чисто отрицательное и очень короткое
(как, впрочем, и доказательства Линделефа и Лебега), дру-
другое— положительное и достаточно трудное; его преимуще-
преимуществом является то, что оно дает эффективное построение
множеств Н и Н', которые осуществляют отделение данных
аналитических множеств Е и Е', тогда как в первом дока-
доказательстве дается лишь существование этих множеств.
Отделимость В для аналитических множеств. Перей-
Перейдем теперь к доказательству принципа I.
Первое доказательство (отрицательное). Пусть x=f(t)
есть непрерывное параметрическое изображение аналитиче-
аналитического множества Е и х = <р (f) такое же изображение для
аналитического множества Е'. Мы предполагаем, что Е и Ег
не имеют общих точек.

Первый принцип отделимости 157
Возьмем на порции @,1) области 01 интервал Бэра 8
порядка k и аналогично интервал Бэра 8' того же порядка к
на @,1) в области 0 р. Обозначим через Еь и Еь части
Е и Е', которые мы получим, если заставим t ъ f пробегать
соответственно 8 и 8'. Ясно, что Еь и Еу не имеют общей
точки.
Установив это, назовем пару (8, 8') интервалов Бэра 8 и
8' особой, если соответствующие множества Еь и Еу неот-
неотделимы В.
Очевидно, что если пара (8, 8') особая, то существует
пара (8j, 8]), образованная из интервалов Бэра 8, и 8i порядка
k-\-l, содержащихся соответственно в 8 и 8', причем эта
пара будет опять особой. В самом деле, если множества Еь,
и Ev отделимы В, каковы бы ни были 81 и b'v взятые соот-
соответственно в 8 и 8', то множество Еь отделимо В от Ev, так
как достаточно взять общую часть множеств, отделяющих Е^
от множеств Егь', где 8^ пробегает все интервалы Бэра по-
порядка k-j-1, содержащиеся в 8': эта общая часть, будучи
измеримой В, очевидно, отделяет Еь от Еу. Но лишь только
ЁЪ1 отделимо В от Еь , каково бы ни было Ь1 в 8, предыду-
предыдущее рассуждение снова применимо, и отсюда мы заключаем,
что Ev отделимо В от Еь, что невозможно, так как пара
(8, 8') особая.
Таким образом, каждая особая пара (8, 8') необходимо
содержит пару (Ъи о[) интервалов Бэра следующего порядка,
являющуюся опять особой.
Установив это, допустим, что данные множества Е и Е'
неотделимы В. В этих условиях существует бесконечная
последовательность особых пар
(8Х, Ь% (82, 8J) (8П, 8;),...
порядков, соответственно равных 1, 2, ..., и, ... причем
каждая из этих пар содержится в предыдущей. Отсюда сле-
следует, что интервалы Бэра 8П стремятся к иррациональной
точке t0, a 8^ к иррациональной точке /0.
Так как множества Е и Е' не имеют общей точки, то
?= <Р (*о). С другой стороны, функции /(/) и

158 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
непрерывны. Это значит, что значения функций / и © в Ьп и Ьп
как угодно близки соответственно к двум фиксированным
точкам f(t0) и <p(*o)i когда п неограниченно возрастает. Отсюда
следует, что множества Еъ и Е'ь^ расположены в двух раз-
различных порциях а и о' области 0х; эти порции при доста-
достаточно большом п не имеют общей точки. Следовательно,
?в и Е'ь'п отделены друг от друга при помощи порций, и мы
пришли к противоречию. Ч. т. д.
Сделаем следующее замечание: для определенности мы
ограничились линейными аналитическими множествами. Но,
принимая за / и 9 комплексные функции, мы, очевидно,
получим доказательство принципа I для аналитических функ-
функций любого числа измерений.
Второе доказательство (положительное). Это доказа-
доказательство основано на следующей геометрической лемме:
Если порция @ < /< 1, 0< ^ < 1) двумерной области
0t,v разделена на прямоугольники Бэра, то множество R
тех прямоугольников Бэра, которые не содержатся в узком
смысле ни в одном из прямоугольников этого разбиения,
может быть эффективно представлено в виде вполне
упорядоченной последовательности р0, Гц р2» •••> p»i •••
...,ра, ...,{•( так, что из двух любых прямоугольниковр„
и рз этой последовательности или последующий содержит
предыдущий, или они не имеют ни одной общей точки.
Чтобы убедиться в этом, расположим прямоугольники из R
в простую бесконечную последовательность
rlt г» ..., гп, ... A)
Мы скажем, что вполне упорядоченная последователь-
последовательность Е прямоугольников из R образует цепь, если: 1° первый
член р0 из Е есть первый из членов последовательности A),
который встречается в разбиении порции @ < ?< 1, 0 < ^<1)
на частные интервалы Бэра; 2° каков бы ни был член р из Е,
он является первым прямоугольником последовательности A),
не совпадающим ни с одним из предшествующих членов р
в Е, и притом он либо является частичным прямоугольником
рассматриваемого разбиения, либо все прямоугольники Бэра
порядка, непосредственно следующего за порядком р, являются
членами последовательности Е, предшествующими р.

ПЕРВЫЙ ПРИНЦИП ОТДЕЛИМОСТИ 159
Ясно, что цепи существуют, так как первый из членов
последовательности A), входящих в рассматриваемое разбие-
разбиение, является цепью; ясно., что если рассмотреть две какие-
либо цепи Е и Е', то одна из них есть сегмент другой, так
как каждый член одной цепи единственным образом опреде-
определяется предшествующими членами и знанием последователь-
последовательности A). Отсюда следует, что каждой цепи Е, не являю-
являющейся самой большой, т. е. служащей сегментом другой
более длинной цепи, соответствует один и только один член
простой бесконечной последовательности A), и значит одно
вполне определенное целое число п. Из этого мы заключаем,
что множество всех возможных цепей счетно, так как оно
уже перенумеровано при помощи целых чисел.
Установив это, обозначим через С соединение всех воз-
возможных цепей. Так как каждая цепь есть всегда сегмент
другой цепи, то С есть опять цепь. Ясно, что это самая
большая цепь, т. е. такая, что каждая другая цепь есть
сегмент С.
Я теперь утверждаю, что цепь С состоит из всех прямо-
прямоугольников R и что сама порция @<?< 1, 0 < ^ < 1) есть
последний член С.
В самом деле, обозначим через R' множество прямоуголь-
прямоугольников из R, которые входят в С. Если в R есть члены, ко-
которые не входят в R', то каждый из них содержит прямо-
прямоугольники Бэра непосредственно следующего порядка и также
не содержащиеся в R', а следовательно, и в R. В самом деле,
в противном случае среди прямоугольников разности R—R'
в последовательности A) найдется первый, пусть гт, в кото-
котором все прямоугольники непосредственно следующего порядка
принадлежат к С. Тогда, прибавляя гт к цепи С, мы полу-
получим новую цепь (С, гт), более длинную, чем С, что невозможно.
Итак, каков бы ни был прямоугольник разности R — R'
(если эта разность существует), он содержит прямоугольники
непосредственно следующего порядка, также принадлежащие
к R — R'. Следовательно, мы имеем бесконечную последова-
последовательность прямоугольников Бэра
порядков, соответственно равных 0, 1, 2, ..., k, ..., каждый
из которых лежит внутри предыдущего, причем все они

160 Гл. ut. Аналитические множества
принадлежат к R— R' и, разумеется, стремятся к некоторой
точке M(t0, to) области ?ftr, расположенной внутри них.
С другой стороны, порция @ < / < 1, 0 < ^ < 1) пол-
полностью была разделена на частичные прямоугольники Бэра;
следовательно, точка М принадлежит к некоторому вполне
определенному прямоугольнику этого разбиения; пусть это
прямоугольник /% в последовательности A). Так как последо-
последовательность B) содержит все прямоугольники Бэра, содержа-
содержащие точку М, то гч должен фигурировать в последователь-
последовательности B), а это невозможно, так как гч заведомо принадлежит
к С, а значит, и к R'.
Итак, R/ совпадает с R.
Отсюда следует, что наибольшая цепь С состоит из всех
прямоугольников R. Но среди этих прямоугольников имеется
и сама порция @<tf< 1, 0<^< 1). Так как она содержит
все остальные члены из R, то из самого определения цепи
вытекает, что эта порция есть последний член цепи С. Ч. т. д.
Установив эту важную лемму, возвратимся теперь к дока-
доказательству принципа I.
Пусть
Х1 —/l @> Х2 =Л @ xm—fm{t)
непрерывные параметрические изображения аналитических мно-
множеств Е и ?', не имеющих общих точек.
Рассмотрим порцию @ < ?< 1, 0< ^ < 1) области gfw.
Каждой точке Ро (t0, /0) этой порции соответствуют две точки
Мо и Мо, принадлежащие соответственно Е и Е' и располо-
расположенные в m-мерной области Зхх ... х •
Так как множества Е и Е' без общих точек, то точки
Мо и Мо всегда различны. Отсюда следует в силу непре-
непрерывности fi и <ot, что на @<?<1, 0<//<1) существует
прямоугольник Бэра г, содержащий точку Ро и такой, что
если точка Р ((, f) движется в г, соответствующие точки М
и М описывают две соответственные части множеств Е и Ег,
расположенные в двух порциях области 0ХХ ... х , не имею-
имеющих общих точек. Среди таких прямоугольников Бэра г мы

ПЕРВЫЙ ПРИНЦИП ОТДЕЛИМОСТИ Х61
выберем тот, порядок которого наименьший, т, е, самый,
большой. ;. . :
Таким образом, каждой точке P(t, t1) мы приводим в Со-
Соответствие содержащий ее прямоугольник Бэра. Отсюда сле-
следует, что порция @ < rf < 1, 0 < ?' < 1) полностью разделена
на прямоугольники Бэра попарно без общих точек и, вообще
говоря, различных порядков. В самом деле, если бы два таких
прямоугольника имели общую точку, один из них должен
был бы содержать другой, что невозможно, так как среди
прямоугольников Бэра, содержащих некоторую точку Р, мы
каждый раз берем наибольший, соответствующий частям Е
и Е', отделимым друг от друга при помощи порций. Обо-
Обозначим через 91 множество прямоугольников этого разбиения.
Установив это, применим предыдущую лемму и рассмотрим
цепь С ;
Ро> Pl> Р2 Рш. •••> Рос) ••• lPv. (Q
образованную из всех прямоугольников Бэра, не содержа-
содержащихся в узком смысле ни в одном из частичных прямоуголь-
прямоугольников ранее определенного разбиения.
Из определения цени С следует, что каков бы ни был'
член ра цепи Са, он или является прямоугольником из ffi, или
все прямоугольники непосредственно следующего порядка, со-
содержащиеся в рв, принадлежат к сегменту цепи С, опреде-
определяемому членом р„. Наконец, известно, что последний член р„
цепи С есть порция @ < t<. 1, 0 < f < 1) области 0' tv •
Каждому члену ра цепи С соответствуют две части мно-
множеств Е и Е', которые получаются, когда точка P(t, if) про-
пробегает прямоугольник ра. Эти части мы обозначим через Ef
и ?р .
Так как р0 есть прямоугольник из 9t, то отделимость В
множеств Ef и Е? осуществлена при помощи двух вполне
определенных порций области 0„ ...а, , не имеющих общей
точки. Допустим теперь, что мы имеем вполне определенную
отделимость В для двух множеств ?р и Щ , соответствую-
а л'
щих члену ра, цепи С, предшествующему данному члену ра^
а' < а, каково бы ни было а', меньшее, чем а..Из этого" мы
П Зак. 284. Н. Н. Лузин

162 гЛ. Hi. Аналитические множества
.выведем вполне определенную отделимость В для множеств
Ef и Ef . Мы естественно предполагаем, что р, не есть прямо-
прямоугольник из ift, так как в этом случае отделимость В мно-
множеств Е и ?ра была бы уже осуществлена при помощи
порций области Вх^ ... ат-
Пусть 8 и 8' — проекции ра на оси ОТ и ОТ'. Ясно, что
8 и 8' суть интервалы Бэра того же порядка, как и р„; пусть
k — этот порядок. Пусть 8, и 8i — интервалы Бэра порядка
А-j-l, содержащиеся соответственно в 8 и Ь'. Прямоуголь-
Прямоугольник р, проекциями которого на оси ОТ и ОТ служат 8, и bv
есть, очевидно, прямоугольник Бэра порядка k -f-1, содер-
содержащийся в р0; по определению цепи С, прямоугольник р за-
заведомо входит в цепь С и предшествует р„. Следовательно,
на основании сделанной гипотезы, множества Е?(=Ек) и
Е}{=ЕЬ') отделены, и мы'умеем получить отделяющие мно-
множества Нь и //5», измеримые В.
Установив это, рассмотрим два новых множества Нц и H't,,
определенные формулами
где для получения //s берется сначала общая часть всех /А,
когда 8^ пробегает все интервалы Бэра порядка k -\-1, со-
содержащиеся в 8', а затем берется сумма так полученных общих
частей, когда 8t пробегает все интервалы Бэра порядка k~\- 1,
содержащиеся в 8; аналогичным образом получается Hv
Вполне очевидно, что так определенные множества Нь
и Нь> не имеют общих точек и что они соответственно со-
содержат Ef (=?5) и Ер (=Е'ъ<). А так как Я$ и н[>, оче-
очевидно, измеримы В, то отсюда следует, что множества Ее
и ?р отделимы В, причем это отделение осуществлено един-
единственным образом.

РЕГУЛЯРНЫЕ Й ПОЛУРЕГУЛЯРНЫЕ ИЗОБРАЖЕНИЯ 16$
Установив это, вернемся к доказательству принципа I.
Так как ра есть произвольный член цепи С, мы можем при-
принять за ра последний член из С. Отделяющие множества Н
и Н' построенные для этого члена, дают нам искомое отде-
отделение данных аналитических множеств Е и Е'. Ч. т. д.
Изучение регулярных и полурегулярных изображений
аналитических множеств
Регулярное изображение
Измеримость В аналитических множеств, допускаю-
допускающих регулярное параметрическое изображение. Мы видели
(стр. 114), что всякое несчетное множество, измеримое В,
допускает непрерывное (и даже нормальное) параметрическое
изображение, если пренебречь счетным множеством его точек.
Обратное предложение также имеет место:
Всякое аналитическое множество Е, допускающее не-
непрерывное регулярное изображение, обязательно изме-
измеримо В, и из его изображения можно вывести эффектив-
эффективное построение Е, отправляясь от порций основной об-
области, при помощи двух операций', сложения и взятия
общей части, неограниченно повторяемых J).
Пусть Е есть аналитическое множество и
xl —J 1 \ch X2 —/2W» • • • > xm —-Jm\l)
— его непрерывное регулярное параметрическое изображение.
Пусть k — любое целое положительное число, &!>1. Раз-
Разделим порцию @,1) области 01 на интервалы Бэра порядка k\
') Это теорема IV моей заметки в Comptes Rendus Acad. Sc.
8 января 1917 г. Если какое-либо множество Е допускает регуляр-
регулярное параметрическое непрерывное изображение, то оно непременно
измеримо б и мы видим, что каждая точка Е есть точка сгуще-
сгущения в смысле Линделефа.
В. Серпянский доказал, что всякое множество, измеримое В,
каждая точка которого есть точка сгущения в смысле Линделефа,
допускает непрерывное регулярное параметрическое изображение
без того, чтобы было необходимо пренебрегать хоть одной точкой
этого множества. См. его работу «Sur les images continues et biuni-
voques de l'ensemble de tons les nombres irrationales», Mathematica,
т. 2, 1928, Cluj, стр. 18.
11*

164 ГЛ. Ш. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
пусть 8i , bf\ ..., 8^, ... эти интервалы. Заставляя t про-
пробегать SJ, , мы получаем часть Е, которую обозначим через Е^ ¦
Ясно, что при фиксированном k, множества Еп суть анали-
аналитические множества попарно без общих точек. Обозначим
через Д„ параллелепипед Бэра области 0ХХ ... х t наивыс-
наивысшего порядка содержащий Е^\ такой параллелепипед заве-
заведомо существует, так как множество ?„ не может свестись
к одной единственной точке.
Установив это, вернемся к множествам Е%\ где число k
все еще фиксировано. Так как аналитическое множество Е„
не имеет ни одной общей точки с суммой остальных анали-
аналитических множеств Е%) при п', отличном от п, и так как эта
сумма есть аналитическое множество, непрерывное параметри-
параметрическое изображение которого известно, то мы можем найти
множество Нп\ измеримое В и покрывающее Е%\ которое
с этой суммой не имеет ни одной общей точки. Если мы
построим Н%? для всякого Е„\ мы получим бесконечную по-
последовательность множеств, измеримых В
каждое из которых содержит один и только один член по-
последовательности Ef\ ?2, ..., En , ... и не имеет ни одной
общей точки с другими членами этой последовательности.
В этих условиях общая часть
параллелепипеда Бэра Д^, множества Н„^ и дополнений к мно-
множествам Н%) для всякого пг, неравного п, есть множество,
измеримое В, содержащееся в Д^ и содержащее Е$; мы
обозначим эту общую часть через 0^« Важно заметить, что
когда число k фиксировано, то множества Ч<*), 0W, .. ., 9№, ...
не имеют попарно общих точек и, следовательно, осущест-
осуществляют одновременную отделимость множеств

РЕГУЛЯРНЫЕ И ПОЛУРЕГУЛЯРНЫЕ ИЗОБРАЖЕНИЯ 165
Установив это, обозначим через Sk сумму отделяющих
•множеств Ь%\ п = 1, 2, 3, ... и через ? общую часть сумм Sk,
g = S1 • S2 ... Sk .... Так как каждое Ь^ измеримо В, то
и множество $ также измеримо В.
Рассматриваемое аналитическое множество Е есть, оче-
очевидно, сумма множеств Еп' при k фиксированном и
п = 1, 2, 3; ... Отсюда следует, что Е содержится в каждой
сумме 5ft, а следовательно, и во множестве §.
Мы докажем, что каждая точка М из $ принадлежит к Е.
В самом деле, если точка Ма области 0'хх ...ж содер-
1 2 т
.жится в Е, то в каждой сумме S^ имеется один и только
один член Ь%\ содержащий Мо; пусть <4*? этот член. Обо-
Обозначим через 8^ интервал Бэра, соответствующий множе-
множеству ?«
Ясно, что интервалы Бэра последовательности 8^, 8^\...
..., 8^, ... имеют соответственно порядок, равный 1,2,...
..., k, ... и заключены друг в друге. Следовательно, су-
существует одна и только одна иррациональная точка t0, кото-
которая принадлежит всем этим интервалам.
Установив это, рассмотрим точку Ро (д;°, х\, ..., х°т) об-
области 0хх ...я> , определенную уравнениями:
1 2 WI
Легко видеть, что Ро есть точка Е, Докажем, что она
совпадает с Мо.
В самом деле, так как t0 принадлежит к 8^, каково бы
ни было число k, то точка Ро принадлежит к (jj?*. С другой
стороны, точка Мо принадлежит тому же множеству Ь$. Сле-
Следовательно, две постоянные точки Ма и Рп принадлежат
одному и тому же параллелепипеду Бэра Д}Л содержащему
множество щ . Но когда k стремится к бесконечности, диа-
диаметр Д„*' необходимо стремится к нулю в силу непрерывности
функций fi{t), Отсюда следует, что Я» совпадает с М*.

166 ГЛ. HI. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
Таким образом, мы доказали, что данное аналитическое
множество Е совпадает с множеством ?, измеримым В. Ч. т. д.
Приложение к проекциям множеств, измеримых В.
Мы видели (стр. 143), что ортогональная проекция аналити-
аналитического множества есть опять аналитическое множество.
В частности, ортогональная проекция всякого множества, из-
измеримого В, есть аналитическое множество. С другой сто-
стороны, мы видели, что всякое аналитическое множество есть
ортогональная проекция множества, измеримого В, некоторого
частного вида; такое множество мы назвали элементарным
множеством; оно является элементом класса 2.
Отсюда следует, что в общем случае ортогональная проек-
проекция множества, измеримого В, неизмерима В.
Но есть один случай, когда можно утверждать измери-
измеримость проекции множества измеримого В.
Теорема. Ортогональная проекция множества Е, из-
измеримого В и расположенного в т-мерной области на
т'-мерную область, т' < т, непременно измерима В, если
проекции двух различных точек множества Е различны.
Чтобы доказать это, возьмем множество Е, измеримое В;
пусть
*l =h if), *. =Л @- • • •, *т =/* (О
есть его непрерывное регулярное изображение.
Ясно, что проекция Е на m'-мерную область 0' х^х ... Хт,
дается непрерывным регулярным изображением
*1 = /l @. *« = /я (Of • • •» *т- == /ж' @.
где т' < т.
Но, согласно сделанной гипотезе, проекции на 0'хх ... х ,
двух различных точек Е также различны. Так как рассматри-
рассматриваемое непрерывное изображение Е регулярно, то двум раз-
различным значениям t отвечают две различные точки из Е,
а стало быть, и две различные точки его проекции.
Отсюда мы заключаем, что непрерывно? парамзтрическое
изображение этой проекции регулярно, а следовательно, сама
эта проекция измерима В. Ч. т. д.
Регулярное параметрическое изображение с помощью
произвольных функций классификации Бэра, Мы видели,

РЕГУЛЯРНЫЕ И ПОЛУРЕГУЛЯРНЫЕ ИЗОБРАЖЕНИЯ 167
что,нельзя расширить определения аналитического множества,
взяв параметрическое изображение
осуществленное при помощи произвольных функций класси-
классификации Бэра. ':
Важное аналогичное предложение существует также для
случая регулярного параметрического изображения. Действи-
Действительно, мы имеем следующую важную теорему:
«• Теорема. Всякое аналитическое множество, обладаю-
обладающее регулярным параметрическим изображением с помощью
произвольных функций из классификации Бэра, измеримо В.
В саадм деле, пусть *,=/, (t), Jfe=/a(*), ..., *m =/«,(*)—
такое регулярноз изображение множества Е. Рассмотрим функ-
функцию F(xv x2, ..., хт, f), определенную следующим равен-
равенством :
Г (ATj, Х2, . . ., Хт, I) —
= [*1 -А (ОJ2 + 1Ь - fm (OP + • • • + \*щ -fm Ш.
Легко видеть, что эта функция, определенная на области
т-\~1 измерений 0Хх ... х t, входит в классификацию Бэра.
Тогда в силу теоремы Лебега (стр. 144) множество § то-
точек области 0хх ...х t, для которых эта функция обра-
обращается в нуль, измеримо В. Очевидно, что координаты точек
N{xvxv ..., хт, t) множества § удовлетворяют совмест-
совместным равенствам
*1 = /l @. *2 = /« @. • • •. Xm=fm (t).
Следовательно, ортогональная проекция § на область 0х w . х
1 з m
совпадает с множеством Е.
Но из регулярности системы функций /4 следует, что
проекции на область g'хх ...д. двух различных точек &
различны. Следовательно, в силу предшествующей теоремы
множество Е измеримо В. Ч. т. д.
Обобщение предыдущего результата. Очень легко зна-
значительно обобщить предыдущие теоремы, распространив их
на тот случай, когда за область определения функции /{ при-
принимают или аналитическое множество, или произврльнре мно-
множество, измеримое В,

168 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
. В самом деле, мы имеем следующее предложение:
Теорема. Если x1=f1(f), *2 = Д (*), ..., *m =/m (/)
есть система каких-либо. функций . классификации
Бэра, то множестЬо Е, которое пробегает точка
М(хи х^, ..., хт, t), когда t пробегает аналитическое
множество е, есть также аналитическое множество.
Кроме того, если е измеримо В и если параметрическое
изображение, осуществленное при помощи функций fit
регулярно на е, то множество Е измеримо В.
В самом деле, так как е есть аналитическое множество,
то мы имеем непрерывное параметрическое изображение
этого множества на порции @,1) области',*7Т, причем <$> не-
непрерывна на этой порции.
В этих условиях сложные функции
xi =/i I? COL Ч =Л I? @1. • • •. хт=/т[<о (т)]
осуществляют параметрическое изображение Е на порции @,1)
области В\. Легко видеть, что эти функции входят в клас-
классификацию Бэра. Следовательно, множество Е аналитическое.
Если е несчетно и измеримо В, то, пренебрегая счетным мно-
множеством точек е, функцию в можно предположить регулярной.
Отсюда следует, что если предложенная система функций ft
регулярна на е, то такой же будет исистема функций/j [в (т)].
Значит, множество Е измеримо В. Ч. т. д.
Полурегулярное изображение
Мы скажем, что параметрическое изображение некоторого
множества точек Е, расположенного в области 0ХХ ,.х
12' Ш
Х1 = /l if), Х2 =/а №» • • •. xm=fm if)t
полурегулярно, если каждой точке М множества Е соответ-
соответствует самое большее счетное множество значений t1).
В. частности, функция f{t), определенная на @,1), назы-
называется полурегулярной, если уравнение х° =f(t) имеет не
: J) См. мою заметку в Camptes Rendus Acad. Sc. 29 июля 1929 г.:
«Sur la representation parametricjue semi-reguliere de? ensepil^les»,

РЕГУЛЯРНЫЕ И ПОЛУРЕГУЛЯРНЫЕ ИЗОБРАЖЕНИЯ 169
более, чем счетное число корней для всякого действитель-
действительного х°.
Мы будем изучать природу англитических множеств,
допускающих полурегулярное изображение, осуществляемое
при помощи непрерывных функций или функций классифика-
классификации Бэра.
Для изучения этих вопросов нам понадобится следующая
теорема из геометрии:
Если &— аналитическое множество, расположенное
в т~\~ 1-мерной области 0ХХ ...х у, то множество Е тех
точек М т-мерной области 0 х х ^ в которых прове-
проведенная через М параллель к оси OY пересекает & по край-
крайней мере в двух точках, есть аналитическое множество.
Чтобы доказать это, расположим все рациональные точки
оси OY в бесконечную последовательность rv г%, ..., гп,.. .
и возьмем точку гп. Пусть Ъ'п и %"п — части $, для точек
¦которых мы имеем соответственно у < гп и у > гп. Обозна-
Обозначим через Е'п и е"п проекции множеств $'п и $'^ на область
??*.*,...* и через ?„ — общую часть е'„-Е'п.
Легко видеть, что Е есть множество тех точек М из Е,
в которых параллель к оси OY, проведенная через М, пере-
пересекает Е по крайней мере в двух точках, для которых у < гя
и у~>гп> Следовательно, сумма Ех-{-?2-(- ... -f-En-(-...
совпадает с множеством Е.
Но так как §п и §„ — аналитические множества, то такими
же будут е'п и Еп- Следовательно, Еп аналитическое, а потому
и Е аналитическое.
Преобразование многомерной области в линейную
область. Начнем с доказательства того, что изучение мно-
множеств точек в многомерной области можно свести к изучению
линейных множеств. С .этой целью мы преобразуем т-мерную
область ^хх ...х в линейную область g'Л при помощи
взаимно однозначного и взаимно непрерывного преобразования.
Рассмотрим в области &Х]х2...хт. все параллелепипеды
Бэра порядка 1 и осуществим взаимно однозначное соответ-
соответствие между этими параллелепипедами it/ и интервалами Бэра
1-го порядка 8' на порции @,1) области g х. Установив
соответствие между i/ и 8', приведем во взаимно однозначное

170 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
соответствие все параллелепипеды Бэра и" порядка 2, лежа-
лежащие в чс7, и все интервалы Бэра 8" порядка 2, лежа-
лежащие в 8'. Вообще, установив соответствие между некоторым
параллелепипедом Бэра я*** порядка k — 1 области 0х х,...хт
и интервалом Бэра S^ на порции @,1) области 0x, при-
приведем во взаимно однозначное соответствие все параллелепи-
параллелепипеды Бэра tv порядка k, лежащие в тг ~ , и все интервалы
Бэра 8<fc) порядка k, лежащие в й'**.
Ясно, что мы получаем таким образом взаимно однознач-
однозначное соответствие между точками всей области 0ХХ ...х
и точками порции @,1) линейной области 0 х. Легко видеть,
.что это соответствие взаимно непрерывно и что если точка х
пробегает интервал Бэра порядка k на @,1) в 0 х, то
.соответствующая точка М(х11 лг2 хт) пробегает
параллелепипед Бэра порядка k в 0Хх....х .
Следовательно, это соответствие между 0Хх. ...х и пор-
порцией @,1) области gx можно написать в двух формах
х = О(хи х2, ..., хт), j
где функции ?*(.*;) непрерывны на @,1) в 0х и функция
О^,, х2, ..., хт) непрерывна на ffxx x .
Установленное соответствие, очевидно, ставит в соответ-
соответствие каждому множеству е класса 0 на 0х некоторое
множество Е класса 0 на 0Хх ...х и Обратно. С другой
стороны, каждая последовательность множеств ev ea, ...
..., еп, ..., расположенных в 0 х и стремящихся к некоторому
пределу е, преобразуется в некоторую последовательность
множеств Ev Е2, ..., Еп, ..., расположенных в 0х^...хт
и стремящихся к пределу Е, являющемуся образом е. Отсюда
следует, что всякое множество е, измеримое В, в линейной
области 0 х преобразуется в некоторое множество Е /и-мер-
ной области 0х%х^...х i также измеримое В и того же
класса и подкласса, и обратно.
Установ.ий это, рассмотрим аналитическое множество Е,
расположенное в 0Х^ ...а> и допускающее полу регулярное

РЕГУЛЯРНЫЕ И ПОЛУРЕГУЛЯРНЫЕ ИЗОБРАЖЕНИЯ 171
параметрическое изображение
Если мы подставим эти функции /4 в функцию
G(xlt х2, ..., хт), ранее определенную, то мы получим
непрерывную функцию f(t), определенную равенством
*=/(/) = о :/,(*),/„(*), ...,/ш(*ц.
Если' мы заставим t пробегать порцию @,1} области §ь
то точка х, очевидно, будет пробегать некоторое линейное
множество е на 0ХУ и легко видеть, чго е есть образ Е,
получающийся при преобразовании A) области ??хк....х
Если система функций xi = fi{i) полурегулярна, то такой
же будет и функция f(t). Следовательно, и учение множества Е
из if х х ...х ) допускающзго полурэгулярно? изображение,
сводится к изучению линейного множества е, допускающего
полурегулярное изображение. Таким образом, если нам удастся
доказать, что е измеримо В, то это же будет иметь место
и для Е.
Изучение непрерывных полурегулярных изображений.
Мы сейчас докажем теорему, относящуюся к полурегулярным
изображениям и во всех отношениях аналогичную предыдущей
теореме, касающейся регулярных изображений (стр. 163).
Теорема. Всякое аналитическое множество Е, допу-
допускающее полурегулярное параметрическое изображение,
обязательно измеримо В.
Так как общий случай аналитического множества несколь-
нескольких измерений сводится к случаю линейного аналитического
множества, то мы ограничимся (этим последним.
Возьмем непрерывную полурегулярную функцию
X =/(/),
определенную на @,1) в области 01, и обозначим через Е
множество значений /(/) на @,1). Так как f(f) полурегулярна,
то каждой точке х из Е соответствует не более, чем счетное
множество значений t.
Все сводится к тому, чтобы доказать, что Е измеримо В,
Допустим обратное, т. е. что Е неизмеримо В,

172 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
Я утверждаю, что в этих условиях существует два раз-
различных интервала Бэра Ь1 и 82, расположенные в 01 и
такие, что если е, и е2 множества значений f(f) соответ-
соответственно на 8j и 82, то общая часть е1 ¦ е2 неотделима В от
дополнения СЕ к данному множеству Е.
В самом деле, если бы это было не так, то каждая общая
часть ?j • е2 была бы отделима В от СЕ. Пусть h — мно-
множество измеримое В, содержащее СЕ и не содержащее ни
одной точки ех • ev Так как этих общих частей е1 • е2 лишь
счетное множество, то столько же будет и соответствующих
множеств h. Обозначим через И общую часть всех множеств А;
ясно, что Н измеримо В и содержит СЕ. Кроме того, Н не
содержит ни одной точки общих частей ег • е.2. Следовательно,
каково бы ни было х из Н, существует самое большее одно
значение t, удовлетворяющее уравнению x=f(t). Обозначим
через 6 множество точек t, для которых соответствующие
точки х принадлежат к Н. В силу обобщения теоремы
Лебега1) множество 0 измеримо В. А так как функция f(t)
регулярна на 0 (т. е. имеет в разных точках 6 различные
значения), то отсюда следует, что множество значений /F)
на f) измеримо В (стр. 168). Обозначим это множество
через НЛ\ множество Ht расположено в 0х. Так как мно-
множество СЕ есть, очевидно, разность между Н и Ни то мы
видим, что СЕ измеримо В, что невозможно, так как мы
предположили, что Е не измеримо В.
Установив это, допустим, что существует k различных
интервалов Бэра 81( 82, ..., 8fc, расположенных в &t и таких,
что если мы обозначим через е{ множество значений f{t)
на bit то общая часть ег • е2 ... ек неотделима В от мно-
множества СЕ. Я утверждаю, что в этих условиях мы можем
выбрать в каждом ^ два новых интервала Бэра 8г- и 8<
без общих точек и таких, что если е'{ и е'{ — множества
значений f{t) соответственно на 8^ и 8^', то общая часть
х) Речь идет о следующем предложении: какова бы ни была
функция f классификации Бэра и каково бы ни было множество $,
измеримое В, множество Е тех точек, для которых значение f
принадлежит к $, измеримо В. Это предложение доказывается
трансфинитной индукцией, отправляясь от ранее цитированной
теоремы Лебега (стр. 144 этой книги) AВ|,

РЕГУЛЯРНЫЕ Й ПОЛУРЕГУЛЯРНЫЕ ИЗОБРАЖЕНИЯ 173
(е' • ej) X («2 • «?') • • • (е'к' ej) таКже неотделима В от СЕ.
В самом деле, допустим противное. Это значит, что каков
бы ни был выбор интервалов Бэра 8* и 8< в 84, i= 1, 2,..., k,
соответствующая общая часть {е\ • е") • (е[ • ер ... (е'к • е'к)
отделима В от СЕ. Пусть h — множество, измеримое В,
содержащее СЕ и не содержащее никакой точки этой общей
части. Так как этих общих частей лишь счетное множество,
то столько же будет и множеств h. Следовательно, общая
часть Н этих множеств h есть множество, измеримое В, и
легко видеть, что Н содержит СЕ, но не содержит точек
общей части (е[ • е") ¦ (^ • е*') ... (е^ • е'?). Отсюда следует,
что если точка х принадлежит к Н, то уравнение x=f(f)
имеет хотя бы в одном из интервалов Ь( самое большее один
корень.
Установив это, обозначим через t\t множество точек х,
для которых уравнение x=f(t) имеет по крайней мере два
корня в 84. Ясно, что ч]г содержится в et. Легко видеть,
что ^ — аналитическое множество. Чтобы убедиться в этом,
обратимся к ранее доказанной (стр. 169) теореме из геомет-
геометрии и рассмотрим в плоскости ТОХ часть кривой x = f(f),
которая получается, когда t пробегает интервал Бэра Ьг. Так
как функция / непрерывна на 01, то кривая x=f(t) есть
плоское множество, измеримое В. Такою же будет и часть
этой кривой, соответствующая интервалу 8f. В силу указан-
указанной теоремы из геометрии множество kjj точек х0, для кото-
которых прямая х = х0 пересекает эту часть кривой x=f(t) по
крайней мере в двух точках, есть аналитическое множество.
Установив, это, докажем, что множество tj4 обладает сле-
следующим замечательным свойством: каждое множество Q,
измеримое В, лежащее на 0х и не содержащее ни одной
точки Vjj,. таково, что общая часть Q • а непременно изме-
измерима В.
Чтобы убедиться в этом, обозначим через Т множество
тех точек t из 84, для которых точки x=f(f) принадлежат
К Q. В силу теоремы Лебега [см. примечание 1) на стр. 144
(см. также [1Б] — Ред.)', Т измеримо В. Легко видеть, что /
регулярна на Т (имеет различные значения). Следовательно,
множество значений f(f) на Т измеримо В (стр. 168). Но это
множество и есть как раз общая часть Q • et.

174 ГЛ. III. АНАЛИТИЧВСКИВ МНОЖЕСТВА .
. Установив это, вернемся к множеству Н, измеримому В.
Мы видели, что если х принадлежит к Н, то уравнение
x = f(t) имеет хоть в одном из интервалов 8{ не более одного
корня. Отсюда следует, что общая часть t/j • т;2 . .. t\k не
имеет общих точек с Н. Значит, всякая точка Н может при-
принадлежать не более чем к k — 1 множествам т]4 одновременно.
Обозначим через Oj какую-либо из общих частей k — 1
множеств v> существует k множеств 0г Общая часть Н и 6j
есть аналитическое множество, не имеющее общей точки
с некоторым аналитическим множеством И • у]{. Следовательно,
6j • Н можно заключить во множество ftv измеримое Л и не
содержащее ни одной точки множества •»),•. Значит, общая
часть fJj и соответствующего множества е^ измерима В. Отсюда
следует, что точки общей части е = et • е2 ... ек, лежащие
в ttj, образуют множество, отделимое В от СЕ.
Установив это, удалим из Н точки, принадлежащие со-
соединению множеств Ь1 и обозначим через Ц\ множество остаю-
остающихся точек. Легко видеть, что Ht измеримо В и что каждая
точка х из Нх принадлежит самое большее k — 2 множест-
множествам Kji одновременно. Кроме того, часть е, содержащаяся
в Н—Hv отделима В от СЕ.
Обозначим через Ь2 какую-либо из общих частей для
группы из k—2 множеств -г\{. Существует самое большее -^-д—-
множеств 92. Общая часть Н1 и 0.2 есть аналитическое мно-
множество, не имеющее ни одной общей точки с каким-либо кв
аналитических множеств Н • т){. Следовательно, каждое мно-
множество И ¦ 62 можно заключить во множество fJ2, измеримое В
и не содержащее ни одной точки множества f\t. Следовательно,
общая часть 62 и соответствующего множества е{ измерима В.
Отсюда следует, что точки общей части е = е1-е2 ... et,
находящиеся в Й2, образуют множество, отделимое В от СЕ.
Установив это, удалим из Н^ точки, принадлежащие
соединению множеств Ь.2, и обозначим через Я2 множество
остающихся точек. Легко видеть, что Н2 измеримо В и что
каждая точка х из //2 принадлежит самое большее k —-3
множествам vjf одновременно. Кроме того, часть е, принадле-
принадлежащая //] — Н2, отделима В от СЕ.

Регулярные и полурегулярные изображения 176
Продолжая таким же образом, мы получим конечную
последовательность множеств Н, Нх, Hv ..., Нк_2, Hk_v
Эти множества обладают следующими свойствами: каждое
множество Н^ измеримо В и содержится в предыдущем Hj_t;
каждая точка х из Hj принадлежит самое большее к k—j — 1
множествам у\{; но наиболее важное свойство состоит в том,
что часть множества е, содержащаяся в Hj__t — Hj, отде-
отделима- В от СЕ.
Так как часть множества е, содержащаяся в Н, неотде-
неотделима В от СЕ, то мы заключаем, что часть множества е,
содержащаяся в Hk_i, также неотделима В от СЕ. Но Нк_1
не содержит точек ч\? следовательно, часть множества е,
содержащаяся в Нк_1г измерима В, а потому отделима В
от СЕ, что приводит нас к противоречию. Ч. т. д.
Установив это, вернемся к доказательству предложенной
теоремы. Прежде всего мы доказали, что если Е неизме-
неизмеримо В, то существуют в gt два интервала Бэра 8j и 82 без
общих точек и такие, что если е, н «2 — множества значе-
значений f(t) соответственно на 8j и 82, то общая часть ех • е2
неотделима В от СЕ. С другой стороны, мы доказали, что
если мы имеем k различных интервалов Бэра 8j, 82, ..., Ьк,
расположенных' в 01 и попарно без общих точек, причем
общая часть ег • е2 .... ек (где ек — множество значений / (/)
на Ьк), неотделима В от СЕ, то можно в каждом 8f най-
найти два интервала Бэра 8* и 8$ без общих точек и такие,
что общая часть {е'х • е") • (е'2 • е'^) ... (е'к - e'Q также неотдели-
неотделима В от СЕ.
Сравнивая эти два результата, мы видим, что в д t суще-
существует совершенное множество Р такое, что каково бы ни
было п совершенное множество Р заключено в 2п интерва-
интервалах Бэра попарно без общих точек 8Х, 82, ..., 83» таких,
что общая часть соответствующих множеств е = е1 • е2 ... е2п
неотделима В от СЕ. Кроме того, мы можем предполагать
порядок интервалов Бэра 8$ как угодно высоким.
Отсюда следует, что рассматриваемая функция f{f)
постоянна на Р. В самом деле, если существуют две точки tt
и t.2 из Р, в которых /(^)?=/(^а)« т0 в СИЛУ непрерывности f (f)
на 3t среди интервалов Бэра 8j, 82, ..., 88п найдутся два
интервала, пусть 8,- и 8^-, содержащие соответственно точки ^

176 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
и /2 и такие, что соответствующие множества е^ и е2 не
имеют общей точки. Но это невозможно, так как общая
часть е == ех • е2 ... ек неотделима В от СЕ, а следовательно,
она фактически содержит точки.
Итак, функция / (f) постоянна на Р; обозначим ее значе-
значение на Р через х0. Так как уравнение
имеет несчетное множество корней, то f(t) не есть полурегу-
полурегулярная функция, что противоречит гипотезе. Ч. т. д.
Полурегулярное параметрическое изображение при
помощи произвольных функций классификации Бэра. Мы
теперь обобщим предыдущий результат и докажем следующее
предложение:
Теорема. Всякое аналитическое множество, допускаю-
допускающее полурегулярное изображение при помощи любых функ-
функций классификации Бэра, измеримо ВJ).
Чтобы установить это, возьмем в /и-мерной области
if х х ...х аналитическое множество Е, допускающее полу-
регулярное изображение
*\ =/l @. Х2 = /2 @» • • •. хт =/» (')>
осуществляемое при помощи функций ftt входящих в класси-
классификацию Бэра.
Рассмотрим функцию F (xlt x2, ..., xm,t) от т-\-\ дей-
действительных переменных, определенную в (/я-j-l) мерной
области 0х я ...х t формулой
/*(*„ Jf9, . . ., Хт, f) = [X, —/, @12 +
+ [*,—ft @12 +... + [*•-/« @1е-
Так как эта функция, очевидно, входит в классификацию
Бэра, то множество § точек M(xv xv ..., хт, t) области
ffx1xi...xmu в которых F обращается в нуль, измеримо В.
Ясно, что координаты точек М из § удовлетворяют урав-
уравнениям
*l =/l @. *2 =Л W» • • •. *т =fm @-
i) См. мою заметку в Comptes Rendus Acad. Sc. 29 июля 1929 г.

РЕГУЛЯРНЫЕ^ ПОЛУРЕГУЛЯРНЫЕ ИЗОБРАЖЕНИЯ 177
Отсюда следует, что рассматриваемое аналитическое мно-
множество Е есть проекция &.
Так как $ измеримо В, то (с точностью до счетного мно-
множества его точек) оно допускает непрерывное регулярное
изображение на порции @,1) области 0\
Х1 = ?1 COi Х2 = Ъ СО. • • •» Хт — ?т (*)• '
Ясно, что т первых уравнений
дают нам непрерывное изображение рассматриваемого анали-
аналитического множества.
Я теперь утверждаю, что это изображение полурегулярно.
В самом деле, если Мо (х°и х\, ..., х°т) есть точка Е, то
существует не более чем счетное множество значений t4, удо-
удовлетворяющих уравнениям
х\ =Л (t), х\ =/, @, .... х°т =/ж (О,
так как изображение (xi^fi(t), 1=1, 2, 3,.,.,/п) полу-
полурегулярное. Но каждой системе чисел х\, х\, ..., х^, t,
удовлетворяющей этим уравнениям, соответствует одна точка S
и, следовательно, одно и только одно значение х0 перемен-
переменного т. Отсюда следует, что каждой точке Мо из Е соответ-
соответствует самое большее счетное множество значений х, удовле-
удовлетворяющих уравнениям
;ti = ?i('c). ¦*¦ •= Та Wi • • •. *»» = <?». СО-
Значит, это непрерывное изображение множества Е полу-
полурегулярно, откуда и следует измеримость В множества Е.
Ч. т. д.
В качестве обобщения этого результата мы имеем;
Если параметрическое изображение
*! =Д @, *2 =/¦ @- • • •. ¦*• =/« Wi
осуществляемое при помощи любых функций классифи-
классификации Бэра, полурегулярно на множестве е, измеримом В
и лежащем в ?ft, то множество Е тех точек, которые
получаются, когда t пробегает множество е, измеримо В.
12 Зак. 284. Н. Н. Лузин

178 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
В самом деле, так как е измеримо В, существует непре-
непрерывное регулярное изображение е:
если пренебречь счетным множеством точек е. В этих усло-
условиях сложные функции
*i =/i 1<Р С01. *2=/« I? СОК • • • I *•=/»[? С01
дают нам, очевидно, полурегулярное изображение Е, осуще-
осуществляемое функциями классификации Бэра. Следовательно, Е
измеримо В.
Приложение к проекциям множеств, измеримых В.
Мы видели (стр. 166), что ортогональная проекция Е изме-
измеримого В множества §>, расположенного в /я-мерной области
на m'-мерную область, где т' < т, измерима В, если проек-
проекции двух различных точек $ различны.
Как обобщение этой теоремы мы имеем:
Теорема, Ортогональная, проекция Е множества &,
измеримого В и расположенного в т-мерной области на
т!-мерную область т! < т, измерима В, если каждая
точка Е есть проекция не более чем счетного числа точек
множества S1).
Чтобы убедиться в этом, достаточно взять непрерывное
и регулярное изображение I, xi=f1(f), x2=f2{t), .. .,хт=
=fm(f). Первые т' уравнений дают непрерывное параметри-
параметрическое изображение Е, и легко видеть, что оно полурегу-
полурегулярно в силу гипотезы, сделанной относительно точек Е.
Следовательно, Е измеримо В. Ч. т. д.
Решета
Общее определение решета2). Предыдущие исследова-
исследования об аналитических множествах устанавливали свойства
1) См. мою заметку «Sur la representation parametrique seml-
regullere des ensemble»» (Comptes Rendus Acad. Sc. 29 июля 1929 г.).
Ср. с результатами П. С. Новикова, касающимися неявных функ-
функций [«].
2) Я ввел в явном виде общее понятие решета в своем мемуаре
«Sur les ensembles analytlques», Fund. Math., т. X, 1926, стр. 20.
См. также работу Серпинского: «Le crlble de M. Lusin et l'operation
A dans les espaces abstraits», Fund. Math., т. XI, стр. 16.

РЕШЕТА 179
этих множеств, не зависящие от понятия трансфинитного. Но
теперь пора ввести одно понятие, которое, как мы увидим,
позволит установить прямую связь между аналитическими
множествами, неизмеримыми В и трансфинитным.
Возьмем /и-)-1-мерную область Зх.т....х у, рассмот-
рассмотрим в этой области любое множество точек С. Пусть
М{хх, лг2, ..., хт) есть точка области 3 ххх2...хт и
DM — прямая, параллельная оси OY и проведенная через
точку М.
Обозначим через Rm множество точек С, которые принад-
принадлежат к Dm- Возможны только два случая.
Первый случай. Линейное множество Rm вполне упоря-
упорядочено в положительном направлении оси Y.
Второй случай. Линейное множество Dm не есть вполне
упорядоченное, если таким же образом устанавливать порядок.
Обозначим через g совокупность точек М области
cfx1x2...x , для которых имеет место первый случай, и
через Е множество точек М этой области, для которых
наблюдается второй случай.
Множество Е есть дополнение к множеству $, и мы видим,
что это множество $ названо положительным образом,
тогда как определение множества Е отрицательно.
Однако в дальнейшем мы увидим, что если С—аналити-
С—аналитическое множество, то имеет место как раз обратное: мы
докажем, что Е — аналитическое множество и, следовательно,
допускает положительное определение (параметрическое изо-
изображение, проекция множества, измеримого В). Что же ка-
касается до множества ?>, то мы не имеем для него другого
положительного определения, кроме того, которое только что
было дано.
Чтобы сократить изложение, мы введем следующую тер-
терминологию. Принимая во внимание роль /и-j~l-мерного мно-
множества С, заключающуюся в том, что оно автоматически
просеивает точки /я-мерной области ifx.x...x , пропуская
точки совокупности $ и задерживая те, которые входят в Е,
мы это множество С назовем т-\- 1-мерным решетом.
Согласно этому наименованию мы назовем просеянным при
помощи решета С именно это множество Е (но не множе-
множество I).
12*

180 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
Среди различных решет С мы можем различать следую-
следующие:
in -|- 1-мерное решето С называется счетным, если каж-
каждая прямая D, параллельная оси OY, пересекает С самое
большее в счетном числе точек. Решето С мы назовем несчет-
несчетным в противном случае; в этом случае существует такая
точка М области 0 х ...х , что прямая Dm, параллельная
оси OY и проведенная через М, пересекает решето С по
несчетному линейному множеству RM.
Изучение аналитических решет. Так как каждое мно-
множество С, расположенное в области 0Х х ...х у, может быть
принято за решето, то изучение просеянных множеств Е
представляет значительные трудности. Поэтому сколько-нибудь
значительные результаты получаются лишь если ограничи-
ограничиваться частными семействами решет. Мы изучим случай ана-
аналитического решета.
Теорема. Всякое множество, просеянное при помощи
аналитического решета, есть аналитическое множество1).
Для определенности мы рассмотрим только плоские решета,
так как изучение решета, расположенного в области любого числа
измерений, сводится к изучению плоских решет: для этого доста-
достаточно преобразовать область 0 х х,...х в линейную область 0х
при помощи взаимно однозначного и взаимно непрерывного
преобразования; если мы прибавим к уравнениям, определяю-
определяющим это преобразование (стр. 170), тождество у=у, то мы
получим аналогичное преобразование области 0Х х...х у
в плоскую область 0ху. Легко видеть, что таким образом мы
преобразуем каждое /и-)-1-мерное решето в плоское решето
и что если рассматриваемое т-\-\ -мерное решето есть изме-
измеримое В или аналитическое, то таким же будет и преобразо-
преобразованное.
1) Это обобщение одной теоремы о решетах весьма специаль-
специального вида, которую я дал в мемуаре «Sur les ensembles analyti-
ques» (Fund, Math., 1926, стр. 21). Другое обобщение в области
проективных множеств было опубликовано Серпинским в его
заметке «Sur quelques proprletes des ensembles projectifs» (Comptes
Rendus Acad. Sc, 24 октября 1927, теорема VI).
Аналогичное обобщение было мною рассмотрено в моих лек-
лекциях по теории проективных множеств (см. стр. 270 и 289 этой
кннги).

РЕШЕТА 181
Установив это, возьмем в плоской области g любое
решето С. В данный момент мы относительно природы С не
делаем никаких гипотез.
Пусть
* = ?(*), -у
t=F(x,y)
— формулы, определяющие преобразование области gxv в пор-
порцию @,1) линейной области gt; функции «, ф и F — непре-
непрерывны.
Рассмотрим в то же время бесконечную последовательность
функций
'i=/iW. ^=/a(t),..., tn=fn{x),...t
непрерывных яа порции @,1) области gx и обладающих сле-
следующим свойством: какова бы ни была последовательность
иррациональных чисел tl, f2, • ¦ ¦, 4»> • • • > заключенных между
0 и 1, существует иррациональное число х0, 0<х0<1,
такое, что
Г»Ы = & (« = 1,2,3,...).
Обозначим через Ttn точку области g xy, координаты
хп, уп которой определяются формулами
*« = ?[/,.COL yn = *t\f»®\-
Если мы заставим х пробегать область g%, то каждая точка
Шп пробегает всю область g ^ независимо от движения
остальных точек, таким образом, что, какова бы ни была
последовательность фиксированных точек Ш°и Зй", • • •, 2К^> • • • >
существует иррациональное число х0 такое, что при х = х0
подвижные точки 2КП совпадают соответственно с фиксиро-
фиксированными точками Зйи-
Давая п некоторое фиксированное значение, изучим при-
природу множества Нп точек х, для которых соответствующая
точка Шп принадлежит решету С.
Так как функции <е [/„ (х)] и ф[/и(т)] непрерывны на g'¦,,
то легко видеть, что рассматриваемое множество Нп есть
прообраз решета С при непрерывном преобразовании

182 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
Следовательно, если решето С измеримо В или аналити-
аналитическое, то таким же будет и множество Нп.
Для того чтобы все точки Шг, 2К2, ..., Шп, ... при-
принадлежали решету С, необходимо и достаточно, чтобы т
принадлежало к общей части
Из предшествующего следует, что Н измеримо В или ана-
аналитическое, смотря по тому, будет ли С измеримым В или
аналитическим.
Установив это, исследуем природу множества 6 тех то-
точек т, для которых мы имеем одновременно следующие равен-
равенства или неравенства:
i СО! = ?IU СО! = • • • =?[/« СО! = • ¦ -,
О1 ><И/а W1 > • • •
Мы видим немедленно, что Й измеримо В, так как все эти
сложные функции непрерывны на g\.
Если т принадежит к общей части б • Н, то соответствую-
соответствующие точки ЯК,, 3R2, ..., 2К„, ... принадлежат решету С,
расположены на одной и той же прямой, параллельной
оси OY, и образуют нисходящую последовательность точек.
Следовательно, точка х, определенная формулой лг = ф[/](х)],
принадлежит множеству Е, просеянному при помощи данного
решета С, когда т принадлежит к Й • Й. И так как мы,
очевидно, можем получить указанным способом все нисходя-
нисходящие последовательности точек решета С, то отсюда заклю-
заключаем, что просеянное множество Е есть множество значе-
значений функции <p[/i(i:)], непрерывной на 6 • Н.
На основании сказанного относительно природы мно-
множеств Н и 6 и в силу непрерывности «[/jfV)] на 0т, мы
окончательно заключаем, что просеянное множество Е анали-
аналитическое. Ч. т. д.
Таким образом, мы не выходим из границ семейства ана-
аналитических множеств, производя операцию, состоящую во
взятии просеянного множества, если только решето аналити-
аналитическое. В дальнейшем мы дадим этой теореме значительное
расширение, распространив ее на семейство проективных
множеств (стр. 289).

РЕШЕТА 183
Мы дополним этот результат следующим замечанием: если
мы расклассифицируем точки М области g' х^ х ...х в зави-
зависимости не от вполне упорядоченности, но от рассеянности
линейного множества RM, по которому прямая Dm, параллель-
параллельная оси ОУ и проходящая через М, пересекает данное мно-
множество С, лежащее в g x х ...х у, то мы придем к тому
же результату:
Множество точек М области g'х х ...х , в которых
прямая Dm, проведенная через М параллельно OY,
пересекает данное аналитическое множество С, располо-
расположенное в &х^хг...хту, по линейному множеству Rm не
рассеянному, есть также аналитическое множество.
Чтобы притти к этому результату, достаточно повторить
слово в слово предыдущее рассуждение, но заставить множе-
множество чисел <H/i(t)], <НЛ(*)]. •••> <МЛ»(Х)]> ••• быть плот-
плотным на себе *). В этих условиях множество 9 также изме-
измеримо В и все заключения остаются в силе. Ч. т. д.
Прежде чем продвинуть дальше изучение аналитических
решет, следует ввести одно важное предварительное понятие.
Пусть С—любое решето, лежащее в gXlx...w у,
и Е— множество на ifx,x...x , просеянное при помощи С.
Возьмем любую точку М в 0'х х ...х . Если М не принад-
принадлежит к Е, то прямая ?)#, проведенная через М параллельно
оси OY, пересекает решето по вполне упорядоченному мно-
множеству, следуя положительному направлению оси OY; пусть
Rm это множество. Так как Rm вполне упорядочено, то Rm,
а следовательно, и самой точке М соответствует некоторое
вполне определенное трансфинитное число второго класса
(или конечное); мы его обозначим через адо. Таким образом,
каждой точке М из g^ ava;m' не пРинадлежаш-ей к ^»
отвечает вполне определенное трансфинитное (или конечное)
ЧИСЛО ОСдг.
Установив это, рассмотрим любое множество 9, располо-
расположенное в gх х ...х и не содержащее ни одной точки Е.
Каждой точке М из 8 соответствует вполне определенное
*) Множество называется плотным на себе, если каждая из
его точек есть предельная для этого множества. См. Р. Бэр, Тео-
Теория разрывных функций, ГТТИ, М. — Л., 1932, стр. 60.

184 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
трансфинитное (или конечное) число aw; если М пробегает
множество в, то ам меняется.
В этих условиях мы скажем, что решето С ограни-
ограничено на 9, если существует трансфинитное число {3
второго класса, фиксированное и превосходящее все транс-
трансфинитные числа ам, соответствующие точкам М из 9.
Решето С называется не ограниченным на Ь в про-
противном случае1).
Если решето С ограничено на 0, то существует некоторое
постоянное множество W, счетное и вполне упорядоченное,
образованное из любых элементов и более протяженное,
чем каждое из вполне упорядоченных множеств Rm, какова
бы ни была точка М на 6; это значит, что Rm подобно
сегменту W, когда М принадлежит к в.
Установив это понятие, мы воспользуемся следующей
важной теоремой:
Теорема. Всякое аналитическое решето С ограни-
ограничено на каждом аналитическом множестве 9, не имею-
имеющем общих точек с множеством Е, просеянным при по-
помощи С2).
Чтобы убедиться в этом, мы докажем, что придем к про-
противоречию, если допустим существование аналитического мно-
множества в без общих точек с ? и такого, что С неограни-
чено на в.
С этой целью обозначим через Н множество точек С, про-
проекции которых на 0х.хг..!ст принадлежат к 9. Так как мно-
множества Сив аналитические, то и Я будет таким же.
Так как каждая прямая D, параллельная оси OY, пере-
пересекает Н самое большее в счетном числе точек, то мы мо-
можем применить теорему следующей главы, касающуюся струк-
структуры аналитических множеств, обладающих этим свойством
(стр. 245 и 253). Следовательно, множество Я составлено из
счетного множества аналитических множеств Н1г Н2, • • •
..., Нп, ..., расположенных соответственно на однозначных
*) Я ввел понятия «ограниченного» и «неограниченного решета»
в мемуаре «Sur les ensembles analytiques» (Fund. Math., т. X, 1926,
стр. 70).
2) Эта теорема есть обобщение аналогичной теоремы, касаю-
касающейся решет специального вида и доказанной в цитированном ме-
мемуаре.

РЕШЕТА 185
поверхностях Sly 52, ..., Sn, ..., измеримых В, из которых
каждая полностью лежит под или над другой.
Установив это, возьмем непрерывное параметрическое изо-
изображение 8
*\ = 9lC0» Х2 = «foCO. • • •. хт =
и пусть
— параметрическое изображение множества//Л на порции @,1)
области 0f, k = l, 2, 3, ...
Будем теперь поступать следующим образом. Возьмем по-
поверхность Sk и обозначим через Ск часть С, лежащую под Sk.
Мы выбираем целое число kx таким образом, чтобы Ск было
неограничено на проекции множества Ну Выбрав kx таким
образом, мы берем на порциях @,1) соответствующих обла-
областей 0Х и &tk Два интервала бэра порядка 1, пусть \ и
8(*i), такие, что если т и ^ пробегают соответственно Sj и
Ь^1> в первых т уравнениях соответствующих параметриче-
параметрических изображений и если мы берем общую часть Ь1 двух
полученных при этом аналитических множеств, то Ск не-
неограничено на &j.
Будем поступать таким же образом на ftj. Мы берем це-
целое положительное /г2 такое, что поверхность Sk находится
под Sk и в то же время Ск неограничено на общей части Ь1
и проекции множества Ни • Мы берем на порциях @,1) об-
ластей 0' 0t. , 0t. соответственно три интервала Бэра по-
1 2
рядка 2: 82, 8^, 8^, из которых два первых содержатся
соответственно в 8: и 8$V и такие, что если т, tk и 4 про-
пробегают соответственно 82, 8^ и 8^ в т первых уравнениях
соответствующих параметрических изображений и если мы
берем общую часть &2 трех полученных при этом аналитиче-
аналитических множеств, то Cki неограничено на ^2.
Будем поступать таким же образом на fv2; найдется по-
поверхность Sk и часть Си решета С, неограниченная на К.
3 3
Здесь &3 есть общая часть четырех аналитических множеств,

186 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
полученных, если заставить т, 4, 4 и ty пробегать соот-
соответственно интервалы Бэра порядка 3: 88, bfi\ 8(8*У и 833» из
которых первые три содержатся соответственно в 82, ffi', b{ у
ранее определенных, и так далее.
Мы получим таким образом аналитические множества &1(
ft2, ft8, ..., каждое из которых содержится в предшествую-
предшествующем, причем все они имеют общую точку М, принадлежа-
принадлежащую множеству 9. В самом деле, мы, очевидно, получим эту
точку М, полагая т = т0 в параметрическом изображении в,
где т„ есть иррациональное число, принадлежащее всем ин-
интервалам Бэра 8,, 82, 83, ...
С другой стороны, эта точка М, очевидно, принадлежит
к ортогональной проекции на Вхх...х множества Ни, ка-
1 2 т v
ково бы ни было v *). Следовательно, прямая Dm, параллель-
параллельная О К и проведенная через М, непременно пересекает мно-
множества Hjr, Hjc, .. ., Ну , ... Но эти множества расположены
соответственно на поверхностях S* , Sj,, ..., Su , ..., каж-
каждая из которых лежит под предыдущей. Следовательно, пря-
прямая /)лг пересекает решето С по нисходящей последователь-
последовательности точек, что невозможно, так как точка М не принадлежит
к просеянному множеству Е. Ч. т. д.
Мы дополним этот результат следующими замечаниями:
Замечание I. Доказанная теорема может быть пере-
перенесена на случай определения аналитического множества по
признаку рассеянности. Чтобы убедиться в этом, следует
начать с общих рассмотрений.
Если дано некоторое множество точек Е, то мы обозначим
через ?(') результат произведенной над Е операции, состоя-
состоящей в том, что из Е удаляют все его изолированные точки.
Если произвести такую же операцию над ?('), мы получим
множество, которое обозначим через Е®. Если произвести
ее над ?<2), то получим множество Е<® и т. д.
*) В самом деле, так как функции <р и Л непрерывны, мы, оче-
очевидно, получим ту же точку М, полагая tk = t\ в т первых урав-
уравнениях параметрического изображения Нь , где tl есть иррацно-
1 V
нальное число, принадлежащее всем интервалам Бэра'
5,^2,..., каково бы ни было фиксированнее число у..

РЕШЕТА 187
Мы образуем таким образом множества
Е, #'>, ?«-, ..., ?<<¦>), ?(«),'. ..|Q,
каждое из которых содержится в предшествующем, полагая
по определению, что если а второго рода, то ?М будет об-
общей частью предшествующих множеств.
Установив это, мы мгновенно докажем, что, каково бы
ни было начальное множество Е, существует некоторое число В,
начиная с которого все рассматриваемые множества тожде-
тождественны, т. е.
) ) ,,.| Q.
Если, данное множество Е — рассеянное, то множества
будут пустыми. В этом случае наименьшее число |3, обла-
обладающее этим свойством, называется порядком рассеянного
множества Е. Напротив, если множество Е не есть рассеян-
рассеянное, то множество ?№) = ?№+]) = .., есть наибольшая часть Е,
плотная в себе.
Установив это, рассмотрим в Вхх...х у аналитическое
множество С и обозначим через Е множество точек М из
0xw...x таких, что проведенная через М параллельно
оси OY прямая Dm пересекает Е по линейному множеству Rm,
которое не есть рассеянное. Ранее мы видели, что Е есть
аналитическое множество.
Если точка М не принадлежит к Е, то ей отвечает транс-
трансфинитное (или конечное) число ам, которое служит порядком
рассеянного множества Rm- Пусть в есть множество точек,
расположенное в 0'хх ,,.х и не имеющее общих точек с Е.
1 2 W
Если числа ам, соответствующие точкам М из 9, все меньше
некоторого трансфинитного числа |3 второго класса, то множе-
множество С называется ограниченным на 6 в смысле рассеянности.
С этими определениями теорема, вполне аналогичная только
что доказанной, звучит так:
Аналитическое множество С ограничено в смысле рас-
рассеянности на каждом аналитическом множестве Ь, не
имеющем общих точек с Е.
Доказательство вполне аналогично предыдущему и со-
состоит в построении аналитических множеств Oj, 02, ...,&„...,-

188 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
у которых имеется общая точка М, принадлежащая к 0, и
однако же таких, что соответствующее множество RM не
есть рассеянное.
Замечание II. Вернемся теперь к случаю полной упо-
упорядоченности. Назовем ограниченным решетом всякое ре-
решето С, которое ограничено на дополнении к множеству Е,
просеянному при помощи С. Ранее мы видели, что каждое
аналитическое решето С непременно ограничено на всяком
аналитическом множестве 6, не имеющем общих точек с Е.
Следовательно, если просеянное множество Е измеримо В,
то аналитическое решето С непременно будет ограниченным
решетом.
Итак, мы пришли к заключению, что для каждого не-
неограниченного аналитического решета просеянное им мно-
множество неизмеримо В.
К сожалению, эта теорема необратима, так как аналити-
аналитическое решето может быть ограниченным и тогда, когда про-
просеянное им множество неизмеримо В. Тем не менее, суще-
существует семейство решет, для которых обратное предложение
все же имеет место: это семейство решет счетных и изме-
измеримых В.
Изучение счетных решет, измеримых В. Для изучения
важных свойств этих решет полезным инструментом является
понятие конституанты просеянного множества Е и его
дополнения S.
Рассмотрим в области ?Jxx...x у решето С любой при-
природы и обозначим соответственно через Е и & множество,
просеянное при помощи решета С, и его дополнение; мно-
множества Е и $ расположены в области 0Хх...х •
Возьмем в области 0хх...х какую-нибудь точку Ж и
обозначим через Dm параллель к оси OY, проведенную через М;
эта прямая пересекает решето С по линейному множеству
точек, которое мы обозначим через ifo.
Если точка М принадлежит к §, то множество Rm
вполне упорядочено в положительном направлении оси OY;
в этом случае точке М соответствует вполне определенное
трансфинитное число второго класса (или конечное); мы его
обозначим через ам.

РЕШЕТА 189
Если точка М принадлежит к Е, множество Rm уже
не будет вполне упорядоченным, если порядок понимать в том
же смысле. Но в этом случае на прямой DM непременно
найдется такой сегмент (—оо<^_у-^/V), что часть Rm, ле-
лежащая на нем, есть вполне упорядоченное множество при
тех же предположениях относительно порядка, тогда как сег-
сегмент большей длины (—оо^у <]iV-(-e), где е — как угодно
малое положительное число, уже этим свойством не обладает.
Так как такая точка N на прямой Dm только одна 1), то
единственной будет и вполне упорядоченная часть Rm, заклю-
заключенная в (—оо <;_у <^Л/). Следовательно, точке М соответ-
соответствует вполне определенное трансфинитное число второго класса
(или конечное), которое мы также обозначим через аМш
Установив это, примем следующие определения:
Назовем конституантой (а) просеянного множества Е
или просто конституантой Еа множество тех точек М
из Е, которые соответствуют данному числу а, аш = а.
Назовем также конституантой (а) дополнения $ к про-
просеянному множеству Е или просто конституантой &„ мно-
множество тех точек М из $, для которых мы снова имеем
ос^ —<х, где а — фиксированное число конечное или транс-
трансфинитное второго класса.
Легко видеть, что конституанты ЕЛ и §, попарно не
имеют общих точек и, следовательно, множества Я и § пол-
полностью разлагаются на свои конституанты:
Складывая эти равенства, мы получим разложение всей
области 0 в последовательность множеств, перенумерованных
при помощи конечных чисел и трансфинитов второго класса
Установив это, мы докажем следующую важную теорему:
1) Число N может быть, в частности, равным отрицательной бес-
бесконечности.

190 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
Теорема. Если данное решето С счетно и изме-
измеримо В, то все конституанты Еа и $„ измеримы В.
Покажем сначала, что начальные конституанты Ео и So
измеримы В. Это очевидно для &0, так как если решето С счетно
и измеримо В, то проекция С на область 0' хх ...х из-
измерима В (стр. 178), но очевидно, что конституанта $0 есть
дополнение к этой проекции.
Чтобы изучить природу конституанты ?0, нам понадобится
теорема о структуре множеств, измеримых В и пересекаемых
каждой параллелью D к оси OY самое большее по счетному
множеству (стр. 245). В силу этой теоремы точки решета С
распределяются на счетном множестве однозначных поверх-
поверхностей Sv 52, ..., ^п, ..., измеримых В, определенных
всюду на Зхх.:.х и таких, что про любые две из этих
поверхностей можно сказать, что одна из них лежит целиком
над или целиком под другой. Установив это, обозначим
через Нп множество точек решета С, расположенных на по-
поверхности Sn; множество Нп измеримо В и однозначно по
отношению к 0ХХ...Х • Обозначим через Гп множество то-
точек решета С, расположенных под поверхностью Sn; легко
видеть, что проекция Г„ на область 0'х х ...х измерима В.
Отсюда мы заключаем, что множество точек из Нп, про-
проекции которых на 0хх...х не принадлежат к проек-
проекции Г„, также измеримо В; мы обозначим это множество
через Ьп. Так как однозначных множеств bv 62, ... лишь
счетное множество, то соединение 5 их проекций на 0х х ,..х
измеримо В. Но точки М множества S, очевидно, обладают
тем характеристическим свойством, что прямая Г>м, прове-
проведенная через М параллельно оси OY, пересекает решето С
по линейному множеству RM> имеющему начальную точку,
т. е. такую точку, у которой координата у меньше, чем
у всех остальных точек из R^. Отсюда мы заключаем, что
если из 0хх...х удалить точки $О и S, то множество
оставшихся точек совпадает с Ео. Следовательно, Ео из-
измеримо В.
Чтобы установить измеримость В конституант Еа и &„, мы
введем понятие производного решета С: это решето, кото-

РЕШЕТА 191
рое получается из данного решета С удалением из каждого
множества Я„ всех точек множества йп(я = 1, 2, ...).
Легко видеть, что производное решето С' есть вполне
определенное счетное решето, измеримое В, имеющее то же
просеянное множество Е, и что если С рассматривать как
множество точек в 0хх ,,.х у, то оно содержится в решете С.
Но наиболее важным свойством производного решета С яв-
является следующее: чтобы перейти от С к С, надо удалить
на каждой прямой D, параллельной оси OY, начальную
точку решета С (если такая точка существует). Из этого
следует, что начальные конституанты множеств Е и $, опре-
определенные производным решетом С, совпадают соответственно
с ?o + ?i и &o + gi-
Установив это, мы образуем трансфинитную последова-
последовательность производных решет
С, С, С, ..., СМ, ..., СИ, .... CM, ...\Q.
Если а первого рода, а — а.*-\-1, то решето СМ опреде-
определяется как производное от решета №*'; если а второго рода,
то решето С<а> есть общая часть всех ранее определенных
решет. Легко видеть, что все решета С*") имеют одно и то
же просеянное множество Е и что начальные конституанты
множеств Е и $, определенные решетом С»', совпадают соот-
соответственно с суммами
образованными из конституант ?р и $$, предшествующих
соответственно Еа и §„.
Так как начальные конституанты всегда измеримы В, то
и написанные выше суммы также. Отсюда следует, что и
конституанты Еа и $а также измеримы В, что и доказывает
предложенную теорему. Ч. т. д.
Одно из наиболее важных приложений предшествующих
рассмотрений относится к самим аналитическим множествам.
В самом деле, мы теперь имеем возможность доказать сле-
следующее предложение:
Теорема. Для того чтобы аналитическое множество Е,
просеянное при помощи счетного решета С, измеримого В,

192 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
было само измеримым В, необходимо и достаточно, чтобы
решето С было ограниченным.
Условие необходимо, так как каждое аналитическое ре-
решето С ограничено на всяком аналитическом множестве Ь, не
имеющем общих точек с множеством Е, просеянным при
помощи С. Следовательно, если Е измеримо В, то и его до-
дополнение $ тоже измеримо В, а потому решето С ограничено.
Условие достаточно. В самом деле, если решето С огра-
ограничено, то множество $ есть сумма счетного множества
конституант $„, так как все остальные конституанты $ пусты.
А так как каждая конституанта %>а измерима В, то мно-
множество & также измеримо В. Следовательно, просеянное мно-
множество Е измеримо В. Ч. т. д.
Можно было бы спросить себя, нельзя ли рассматривать
всякое аналитическое множество как просеянное при помощи
счетного решета, измеримого В. Если это так, то практиче-
практическая польза, если уже не говорить о теоретическом значении
изучения счетных решет, измеримых В, значительно возра-
возрастает. Мы увидим, что действительно, каково бы ни было
аналитическое множество Е, можно эффективно опреде-
определить решето С счетное, измеримое В и некоторой чрез-
чрезвычайно элементарной природы так, чтобы Е было про-
просеяно при помощи решета С.
Чтобы убедиться в этом, введем следующее определение.
Рассмотрим бесконечную последовательность замкнутых сег-
сегментов
с иррациональными концами, расположенных на оси OY; мы
предполагаем, что эти сегменты попарно не имеют общих то-
точек и общих концов. Эта последовательность а1г о2, .. .,о„ ...
называется восходящей, если индекс сегмента возрастает
в положительном направлении оси OY; это значит, что каж-
каждый из этих сегментов лежит выше предшествующего.
Установив это, возьмем в области ^,, ...х какое-либо
аналитическое множество Е. Пусть Я есть элементарное мно-
множество, расположенное в т-f-1 -мерной области 0х.х%...х у,
ортогональной проекцией которого на область 0х.х„...х
является Е.

РЕШЕТА ' 193
По самому определению элементарное множество Н есть
общая часть И = St • S2 ... Sn .... где каждое множество Sn
есть сумма счетного множества параллелепипедов Бэра я(я),
/=1, 2, 3, ..., расположенных в т-^- 1-мерной области
9х^у.х^ и не имеющих попарно общих точек. Эти парал-
параллелепипеды Бэра itj"), i = l,2,3, ... называются параллеле-
параллелепипедами ранга и; порядок каждого параллелепипеда ранга п
равен и. Кроме того, известно, что всякий из параллелепи-
параллелепипедов и^) ранга я содержится во вполне определенном парал-
параллелепипеде гс^-1) предшествующего ранга п — 1 и содержит
счетное множество параллелепипедов следующего, я-j-'1-го
ранга (стр. 141).
Преобразуем теперь элементарное множество Н. -Так как
ортогональная проекция на область 0Хх....х некоторого
т -J- 1 -мерного параллелепипеда и, ориентированного по осям
ОХи ОХ%, ..., ОХШ OY, очевидно, не изменится, если пе-
переместить или сжать параллелепипед в направлении оси OY,
то мы можем предположить, что ортогональные проекции
параллелепипедов uW ранга 1 на ось OY образуют восходя-
восходящую последовательность сегментов о^1* с иррациональными
концами; мы их назовем сегментами ранга I. Вообще, ка-
каков бы ни был параллелепипед и^*-1) ранга я-^-1, мы можем
предполагать, что ортогональные проекции на ось OY содер-
содержащихся в нем параллелепипедов itj") ранга п образуют вос-
восходящую последовательность соответствующих сегментов о<п>
с иррациональными концами; мы называем эти сегменты о<п>
сегментами ранга я.
Таким образом, каково бы ни было я, сегменты о|")
ранга п не имеют попарно общих точек, а сегменты o<n+1)
ранга п -\~ 1, содержащиеся в некотором оДО ранга и, всегда
образуют восходящую последовательность.
Наконец, сделаем следующее замечание. Расположим ра-
рациональные точки оси OY в простую бесконечную последо-
последовательность ги г2 ...,/•„,..., Я теперь утверждаю, что,
каково бы ни было целое положительное я, можно предпо-
предположить рациональную точку гп не принадлежащей ни одному
из сегментов а(") ранга я. В самом деле, когда сегмент о^-1)
13 Зак. 384. Н. Н. Лузин

194 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
ранга я — 1 определен, мы можем образовать в о^-1) восхо-
восходящую последовательность сегментов о(™> ранга я, содержа-
содержащихся в oj*-1) так, чтобы ни один из них не содержал ра-
рациональную точку гп.
Во всем дальнейшем мы предположим, что выбор парал-
параллелепипедов всех рангов и, следовательно, элементарного
множества Н сделан указанным образом. Данное аналитиче-
аналитическое множество Е есть ортогональная проекция на об-
область 0хх,...х так построенного элементарного множества Я
(стр. 141). ¦
Установив это, обозначим через С множество точек об-
области gXlxg...xmy, расположенных на верхних гранях веек
построенных таким образом параллелепипедов тсФ> (я = 1,
2, 3, .. .)• Легко видеть, что С есть соединение счетного
множества однозначных множеств, измеримых В и весьма
простых, и что каждая прямая D, параллельная оси О К,
пересекает С самое большее по счетному множеству точек.
Следовательно, множество С есть счетное решето, измери-
измеримое В и весьма элементарной структуры. В дальнейшем так
построенное решето С мы будем называть элементарным
решетом.
Мы теперь докажем следующую теорему:
Теорема. Всякое аналитическое множество может
быть просеяно при помощи элементарного решета.
Чтобы убедиться в этом, достаточно доказать, что ранее
рассмотренное нами аналитическое множество Е можно счи-
считать просеянным при помощи построенного элементарного
решета С.
Пусть М — любая точка области Вхх.,...^ • Обозначим
через Dm прямую, параллельную оси OY и проведенную
через М; пусть Rm— множество точек С, принадлежащих ?>jf.
Я теперь утверждаю, что необходимое я достаточное
условие для того, чтобы линейное множество Rm не было
вполне упорядоченным в положительном направлении оси
ординат, состоит в том, чтобы прямая DM содержала точку
элементарного множества Н.
Условие необходимо. В самом деле, если Rm не есть
'вполне упорядоченное в условленном смысле, то можно опре-

Решета , 195
делить неограниченную нисходящую последовательность точек
из Rm- Pv P%, ¦•-, Рч, ••¦, каждая из которых ниже пре-
предыдущей. Так как ортогональные проекции на ось OY всех
параллелепипедов rcW фиксированного ранга л образуют счет-
счетное множество сегментов о<и), попарно без общих точек и
вполне упорядоченное в положительном направлении оси OY,
то все точки Рг, Р2, .. ., Рч, . .., начиная с некоторого
индекса v,, принадлежат одному и тому же параллелепипеду и|")
ранга я; пусть тгп этот параллелепипед ранга п.
Неограниченная последовательность ¦к1, л2, .. ., лп, ,. .,
очевидно, образована из параллелепипедов всех рангов, вло-
вложенных друг в друга, причем каждый из них содержит все
точки Pv P2, ..., Р,„ ,.., кроме конечного числа их. Сле-
Следовательно, точка Л/о, общая всем параллелепипедам жи -к2г...
..., it.,, ..., наверное, принадлежит прямой D^, Кроме того?
все координаты х^, х\, ..., х°т, у точки ЛГ0—-иррациональ-
ЛГ0—-иррациональные числа. Это очевидно для координат х*\, так как ортого-
ортогональная проекция %п на область iJXx....x есть параллеле-
параллелепипед Бэра порядка п. Но ортогональная проекция яя на
ось OY есть сегмент ранга п и, следовательно, не содержит
ни одной из я первых рациональных точек бесконечной по-
последовательности /-j, г2, ...,/•„,..., в которую мы распо-
расположили все рациональные точки оси OY (стр. 193). Итак,
число у0 иррационально.
Отсюда следует, что точка No области ?7х.х....х у при-
принадлежит к элементарному множеству Я.
Условие достаточно. В самом деле, если прямая Dm
содержит точку N элементарного множества Н, то, очевидно,
эта точка N есть предел нисходящей последовательности
точек множества /?jj, значит, /?да не является вполне упоря-
упорядоченным в положительном направлении оси OY.
Таким образом, множество, просеянное при помощи эле-
элементарного решета С, совпадает с проекцией элементарного
множества Н и, следовательно, тождественно с Е. Ч. т. д,_
Предыдущие рассмотрения чрезвычайно важны, так как
они показывают нам, что есть три строго эквивалентных
метода для определения аналитических множеств:
1° Писать параметрические уравнения Xi—fi(f).
13*

196 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
2° Проектировать элементарные множества, измери-
измеримые В. ¦
3° Просеивать при помощи счетных решет, измери-
измеримых В[14].
Трансфинитный критерий измеримости В аналитиче-
аналитических множеств. Выше мы доказали существование аналити-
аналитического множества, неизмеримого В, следующим образом
(см. стр. 149): мы нашли линейное аналитическое множе-
множество е, дополнение к которому Се заведомо не есть ана-
аналитическое множество. Вот рассуждение, позволившее нам
констатировать неизмеримость В множества е, обладающего
этим свойством: если бы множество е было измеримо В, то
и его дополнение Се было бы таким. Значит, оно было бы
аналитическим, тогда как это не так.
Мы теперь докажем весьма простым рассуждением,
что рассмотренный случай не представляет ничего исключитель-
исключительного, так как „каково бы ни было аналитическое множе-
множество Е, неизмеримое В, его дополнение СЕ не может
быть аналитическим1). Таким образом, неаналитичность
дополнения к какому-либо аналитическому множеству Е есть
не только достаточное, но в то же время и необходимое
условие для того, чтобы аналитическое множество Е было
неизмеримым В.
Чтобы убедиться в этом, допустим, что СЕ есть анали-
аналитическое множество. Так как Е тоже аналитическое и не
имеет общих точек с СЕ, то множества Е и СЕ отделимы В.
Ясно, что, отделяющие множества, измеримые В, обязательно
совпадают с ? и СЕ. Ч. т. д.
Это простое рассуждение дает нам, таким образом, необ-
необходимый и достаточный критерий для неизмеримости В ана^
литического множества, и легко видеть, что это критерий
чисто отрицательного характера: надо констатировать, что
дополнительное множество СЕ не есть аналитическое. Но
предыдущие рассмотрения, касающиеся счетных решет, изме-
измеримых В, показывают нам, что существует критерий другой
') Эта теорема III заметки Суслина (Comptes Renius Acad. Sc.
8 января 1917 г.). Теорема II о существовании аналитических мно-
множеств, неизмеримых В, была им доказана при помощи рассужде-
рассуждения, основанного'на специальных свойствах кортежей индексов [И].

РЕШЕТА ... 197
природы, тесно связанный с совокупностью трансфинитных
чисел второго класса, критерий положительного характера,
позволяющий констатировать неизмеримость В некоторого
аналитического множества. Этот критерий возникает из воз-
возможности рассматривать всякое аналитическое множе-
множество Е, как просеянное при помощи счетного решета, изме-
измеримого В.
В самом деле,' с одной стороны, мы показали, что можно
эффективно построить для каждого аналитического множе-
множества Е элементарное решето С, которое, следовательно, счетно
и Измеримо В, причем Е просеяно при помощи этого решета.
С другой стороны, мы ввели важное различие между реше-
решетами. По самому определению, мы называем решето С огра-
ограниченным, если существует эффективно перечислимое фикси-
фиксированное множество W, более протяженное, чем всякое
вполне упорядоченное множество Rm, какова бы ни была
точка М, не принадлежащая множеству Е, просеянному при
помощи С. В случае, если такого фиксированного множе-
множества W не существует, решето С называется неограниченным.
Чрезвычайная важность этого различия проистекает из
выше доказанной теоремы (см. 191), формулируемой так: для
того чтобы аналитическое множество Е было изме-
измеримо В, необходимо и достаточно, чтобы оно могло быть
определено при помощи счетного решета С, измеримого В
и ограниченного. Ясно, что этот критерий имеет в некото-
некотором роде положительный характер.
Итак, все сводится к тому, чтобы решить следующую
проблему:
Узнать, будет ли данное счетное решето С, измери-
измеримое В, ограниченным или нет.
К сожалению, эту проблему, повидимому, легко решить
лишь в том случае, когда решето a priori задается ограни-
ограниченным; следовательно, общего решения проблемы мы не
имеем даже для элементарных решет.
Мы сильно сомневаемся в том, чтобы можно было дать
общее решение этой проблемы, по крайней мере, если, со-
согласно Лебегу, условиться считать, что определить решето С
это значит назвать некотогое свойство Р, характеризую-
характеризующее С; из него надо вывести ограниченность или неограничен-
неограниченность решета С. Мы сильно сомневаемся, чтобы можно былр

198 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
во всех случаях вывести из этого свойства Р констатиро-
констатирование границы для решета С.
В этих условиях возникает вопрос, является ли сделанное
различие достаточно серьезным, чтобы придавать ему смысл.
Понятие ограниченного решета, очевидно, законно, так как
речь идет о вполне упорядоченном множестве W, эффективно
перечислимом: надо сравнивать переменное вполне, упорядо-
упорядоченное множество 7?лг с этим фиксированным множеством W.
Напротив, понятие неограниченного решета чисто отри-
отрицательно, так как для того, чтобы эффективно констатиро-
констатировать, что некоторое элементарное решето С неограничено,
очевидно, необходимо взять все счетные вполне упорядоченные
множества и сравнить их с переменным вполне упорядочен-
упорядоченным множеством Rm, а это приводит к совокупности всех
трансфинитных чисел второго класса.
Таким образом, кажется более предпочтительным вер-
вернуться к первому критерию. Я хотел бы указать кратко и
не входя в дискуссию по поводу природы этого; критерия,
что характер его отрицательный; так как второй критерий
строго эквивалентен первому, мы вынуждены заключить, что
положительное определение, осуществленное при помощи
трансфинитного, может быть эквивалентно отрицатель-
отрицательному определению, не вводящему трансфинитное в яв-
явном виде.
Итак, трансфинитное может быть глубоко
спрятано под видом отрицательного опреде-
определения или понятия.
Пример аналитического множества, неизмеримого В,
Однако, несмотря на предыдущие критические замечания,
есть один частный случай, когда мы можем немедленно кон-
констатировать, что рассматриваемое решето С неограничено,
а следовательно, множество Е, просеянное при помощи С,
неизмеримо В.
Это случай счетного решета измеримого В и универсаль-
универсального, т. е. такого, что всевозможные линейные счетные мно-
множества получаются, если пересекать С прямыми D, парал-
параллельными оси OF. В самом деле, в силу исследований
Г. Кантора, каково бы ни было вполне упорядоченное счетное
множество U?, составленное из любых элементов, можно эф-
эффективно построить линейное множество точек R, которое

РЕШЕТА 199
подобно W. Так как всевозможные линейные счетные мно-
множества получаются, если пересекать С прямыми D, парал-
параллельными оси OY, то a priori видно, что рассматриваемое
решето С не может быть ограниченным1).
Итак, все сводится к построению счетного решета, изме-
измеримого В и универсального. Но это построение может быть
сделано мгновенно.
В самом деле, возь лем неограниченную последовательность
функций
У\ = ?i (*)> Л = ?2 (*)> • • •. Уп = ?»(*)>
непрерывных на интервале @<дг<1) и обладающих сле-
следующим свойством: какова бы ни была последовательность
действительных чисел у\, у\, ..., уйп, ..., существует дей-
действительное число х0 между 0 и 1, для которого _у° = оп (дг0),
каково бы ни было я.
Установив это, обозначим через Сп непрерывную между О
и 1 кривую, начерченную в плоскости XOY и определенную
уравнением у = <?п(х); соединение С кривых С,, С2, ...
... ,Сп, ... есть, очевидно, плоское множество, измеримое В,
и легко видеть, что С есть универсальное счетное решето.
Ч. т. д.
Свойства конституант. Свойства конституант Е„ самого
аналитического множества Е неизвестны: мы знаем только,
что все ЕЛ измеримы В, когда порождающее решето С счетно
и измеримо В. Мы имеем больше сведений о свойствах кон-
конституант |, дополнительного множества %:
Прежде всего мы укажем одно интересное свойство кон-
конституант Sa: каково бы ни было аналитическое множе-
множество Е', содержащееся в $, оно всегда принадлежит счет-
счетному множеству конституант §„.
Чтобы убедиться в этом, достаточно заметить, что порож-
порождающее решето С ограничено на Е'. Это значит, что суще-
существует фиксированное трансфинитное число C второго класса,
*) Очень важно было бы знать, является ли этот случай един-
ствейным, если, разумеется, не считать очевидных видоизменений,
когда из определения С удается вывести, что С есть нгограннчен»
ное решето. Мы думаем, что эта проблема неразрешима.

200 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
которое превосходит все трансфинитные числа ajf, соответ-
соответствующие точкам Ж из Е' (см. стр. 184). Отсюда следует,
что каждая точка М из Е' принадлежит к некоторой консти-
конституанте ?¦„, у которой индекс а меньше, чем [3. ' Следова-;
тельно, множество Е' содержится в сумме счетного множе-
множества конституант Ь^. Ч. т. д.
Мы дополним этот результат следующим замечанием: до-
доказанное свойство конституант ?а дает нам немедленно новое
доказательство важной теоремы о том, что всякие два анали-
аналитические множества Е и Е'- без общих точек отделимы В.
В самом деле, возьмем все конституанты §„ множества СЕ,
содержащие точки Е'. Этих конституант счетное множество
и они измеримы В. Значит, их сумма Н' есть множество,
измеримое В, содержащее Е' и без общей точки с Е. Если
мы обозначим через Н дополнение к Я', то множество Н
измеримо В и содержит Е. Следовательно, Е и Е' отделимы
при помощи двух множеств Н и Н', измеримых В. Ч. т. д.
Мы думаем, что на это замечание не нужно смотреть
лишь как на курьез, так как, по нашему мнению, здесь со-
содержится нечто большее. В самом деле, мы знаем, что
в классификации Валле-Пуссена два любых элемента Е
и Е' класса а всегда отделимы при помощи двух множеств Н
и Н' низших классов. С другой стороны, дополнение СЕ
каждого элемента Е класса а может быть разложено на счетное
множество множеств класса ниже а. Для аналитических мно-
множеств неизмеримых В мы имеем два совершенно анало-
аналогичных предложения: два аналитических множества Е и Е' без
общей точки всегда отделимы при помощи двух мно-
множеств Н и Н', измеримых В. С другой стороны, дополне-
дополнение СЕ к некоторому аналитическому множеству Е, неизме-
неизмеримому В, всегда разлагается в трансфинитную сумму мно-
множеств, измеримых В.
Так как в научных исследованиях аналогия часто служит
весьма ценным и даже необходимым инструментом для даль-
дальнейшего продвижения этих исследований, то мы, естественно,
приходим к тому, чтобы рассматривать аналитические
множества, неизмеримые В, как элементы класса 2 про-
продолженной классификации Бэра — Валле-Пуссена. Эта
бьющая в глаза аналогия между аналитическими множествами,
неизмеримыми В, и элементами гипотетического класса Q

РЕШЕТА 201
может оказать ценные услуги, направляя нас на открытие
новых феноменов, которые затем останется доказать.
Мы увидим, например, что существуют два аналитических
дополнения I и $' без общей точки и неотделимых В (стр. 221,
262 и 265). Это предложение можно вывести по принципу
двойственности из теоремы.
В каждом классе Ка классификции Бэра — Валле-Лус-
сена существуют два множества § и $', достижимые
снизу, без общих точек и неотделимые при помощи мно-
множеств класса ниже а.
Доказательство этой теоремы не представляет никаких
затруднений 1).
Вернемся теперь к установленному свойству конституант §„:
Мы знаем, что все эти конституанты измеримы В. Следо-
Следовательно, каков бы ни был индекс а, множество §„ или
счетно (конечно), или содержит совершенное множество Р2),
И в этом последнем случае множество S, очевидно, имеет
мощность континуума8).
С другой стороны, если § содержит совершенное множе-
множество Pj, то по крайней мере одна из его конституант должна
быть несчетной и, следовательно, должна содержать совершен-
совершенное ядро. В самом деле, если $ содержит совершенное мно-
множество Pv то это множество, будучи измеримо В, должно
содержаться в сумме счетного множества конституант |„
в силу указанного свойства. Следовательно, хоть одна из этих
конституант должна быть несчетной.
Итак, для того чтобы аналитическое дополнение $
содержало совершенное множество, необходимо и доста-
достаточно, чтобы хоть одна из его конституант §„ была
несчетной *).
J) См. мою работу «Analogies entre les ensembles mesurables В
et les ensembles analytiques» (Fund. Math. т. XVI, 1930).
2) Теорема Александрова «Sur la puissance des ensembles mesu-
mesurables B» (C. R. Acad. Sc. 1916, стр. 323).
8) Теорема Кантора — Бернштейна.
4) Точно так же легко видеть, что если аналитическое дополне-
дополнение имеет положительную меру, или есть множество второй кате-
категории на некотором совершенном множестве Р, то до крайней мере
одна из его конституант имеет положительную меру ид» есть мно-

302 ГЛ. HI. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
Следовательно, если аналитическое дополнение § неизме-
неизмеримо В и не содержит совершенного множества, то это. ана-
аналитическое дополнение ? есть соединение счетных {конеч-
{конечных) множеств, перенумерованных при помощи трансфи-
трансфинитных чисел второго класса по Кантору.
С другой стороны, всякое аналитическое множество Е,
очевидно, определено счетным множеством условий.
Именно по этой причине математики, которые допускают
рассуждения с трансфинитами и допускают одновременное
разбиение аналитического дополнения, неизмеримого В, на
трансфинитную бесконечность конституант, перенумерованных
при помощи всех трансфинитных чисел второго класса по
Кантору, — эти математики стремятся определить такое исклю-
исключительное аналитическое дополнение. В самом деле, если
такое" аналитическое дополнение, логически возможное, к тому
же практически реально, то можно будет утверждать, что
существование всех грансфинитных чисел второго класса есть
как бы экспериментальный факт.
Узкая проблема континуума и узкая проблема Лебега.
Чтобы объяснить наилучшим образом, в чем заключаются эти
проблемы, мы сначала возьмем какое-нибудь аналитическое
множество Е, неизмеримое В. Пусть С—счетное решето, из-
измеримое В, при помощи которого просеяно множество Е.
В этих условиях мы имеем разложения
0 + g, -(- gt + ... + $ш + ...+«, + ... | 2
множества Е и его дополнения $ на бесконечное множество
конституант Еа и &„, каждая из которых измерима В.
Так как данное аналитическое множество Е предположено
неизмеримым В, то второе разложение заведомо имеет транс-
трансфинитную бесконечность непустых членов. Следовательно,
экество второй категории на Р. Кроме того, если мы умеем выбрать
одну и только одну точку во всякой конституанте ga множества Р,
то множество выбранных точек есть множество первой кате-
категории на каждом совершенном множестве Р. См. заметку Лузина
и Серпинского «Sur un ensemble поп denombrable, qul est de pre-
premiere categorte sur tout ensemble parfalt» (Rendicontt dei Lincei,
Roma, февраль 1928 г.).

РЕШЕТА • 203
если мы обозначим через б„ сумму Еа~\-$а и если мы сложим
почленно предыдущие разложения,, мы получим формулу
| Q,
которая дает нам полное разложение всей области 0
на трансфинитную бесконечность множеств 9„ измери-
измеримых В, непустых и перенумерованных при помощи всех
трансфинитных чисел второго класса по Кантору*).
Известно, что знаменитая проблема континуума состоит
в том, чтобы узнать, можно ли перенумеровать все точки
некоторого сегмента при помощи всех трансфинитных чисел
второго класса по Кантору. Ясно, что эту проблему можно
рассматривать как некоторого рода полное разложение обла-
области 0 на трансфинитную бесконечность множеств 6а, изме-
измеримых В, перенумерованных при помощи всех трансфинитных
чисел второго класса по Кантору, каждое из которых сво-
сводится к одной и только одной точке.
Но взятая отдельно точка есть множество, измеримое В,
класса 1. Следовательно, на основании предыдущего, было
бы очень желательно получить некоторые общие результаты,
касающиеся разложения континуума на трансфинитную беско-
бесконечность множеств Й„, измеримых В ограниченных классов.
Это в некотором роде ослабленная проблема континуума, мы
ее назовем узкой проблемой континуума.
С другой стороны, Лебег поставил проблему: узнать,
можно ли назвать множество различных точек, перену-
перенумерованных при помощи всех трансфинитных чисел вто-
второго класса по Кантору2). Лишь после того, как будет
') Возможность подобного разложения всей области 0 впервые
была констатирована Серпинским и мною. См. нашу заметку в Сотр-
tes Rendus Acad. Sc, т. 175, p. 357, «Sur une decomposition du con-
tinu».
г) Цитируем текстуально соответствующее место у Лебега в его
письме к Борелю (Cinq letlres sur la theorie des ensembles, Bull, de
la Soc. mathem. de France, декабрь 1904 г.).
«... Когда я слышу, как говорят о законе, определяющем
трансфинитную бесконечность выборов, я всегда отношусь с недо-
недоверием, так как я еще никогда не видел подобных законов, тогда
как я знаю законы, определяющие счетное множество выборов. Но
это лишь вопрос рутины и, после некоторого размышления, я часто
вижу трудности, на мой взгляд, столь же серьезные в рассужде-

204 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
найдено положительное решение этой проблемы, можно счи-
считать установленным, что мощность континуума сравнима
с мощностью множества всех трансфинитных чисел второ-
второго класса по Кантору. Поэтому было бы вполне естест-
естественно стараться назвать трансфинитную бесконечность мно-
множеств $а не пустых, измеримых В и ограниченных классов.
Это тоже ослабленная проблема; мы ее назовем узкой про-
проблемой Лебега.
Таким образом, мы естественно приходим к тому, чтобы
поставить следующий важный вопрос: Каковы классы кон-
конституант ?„ аналитического дополнения ?•? И можно
ли назвать такое неизмеримое В аналитическое дополне-
дополнение, у которого конституанты ?•„ будут ограниченных
классов?
Мы здесь ограничимся просто доказательством существо-
существования аналитических дополнений ?, у которых классы
конституант ?„ неограничены').
Чтобы убедиться в этом, возьмем в плоскости X0Y уни-
универсальное аналитическое множество U: это значит, что
всевозможные линейные аналитические множества можно полу-
получить, пересекая U прямыми х — х0, параллельными оси OY.
Мы теперь утверждаем, что дополнение CU обладает ука-
указанным свойством,
В самом деле, допустим, что в разложении
конституанты ?„ имеют ограниченные классы, т. е. их классы
ниях, где входит лишь счетное множество выборов, как и в тех,
где их трансфинитное число.. Например, если я не считаю устано-
установленным классическим рассуждением, что каждое множество мощ-
мощности выше счетной содержит множество той же мощности, как
и множество всех трансфинитных чисел класса II по Кантору, то
я также мало значения придаю методу, при помощи которого дока-
доказывают, что не конечное множество содержит счетное множест-
множество. Хотя я сильно сомневаюсь, чтобы когда-нибудь было названо
множество, которое не будет ни конечным, ни бесконечным,
однако невозможность такого множества не кажется мне до-
доказанной...».
1) Серпинский и я констатировали существование таких анали-
аналитических дополиеннй в нашей заметке в Comptes Rendus 12 ноября
1929 г. «Stir les classes des constituantes й'ип complementaire ana-
lytiqae». . ...

. второй принцип отделимости 205
меньше некоторого фиксированного трансфинитного числа
Р < 2. Отсюда мы заключаем, что сумма
счетного множества конституант есть множество, измеримое В
и класса «^ р -J-1. Следовательно, каково бы ни было транс-
финитное число а, параллели лг = лг0 к оси OF пересекают 5„
по множеству, измеримому В, класса <[ J3 -f- 1.
¦ Но, с другой стороны, так как множество U есть уни-
универсальное, то существуют параллели к оси OY, пусть лг = дг0,
которые пересекают О по множеству Н, измеримому В и
заранее заданному. А так как Н должно принадлежать
к счетному множеству конституант !„, то существует трансфи-
трансфинитное число а, достаточно большое и такое, что Н есть
пересечение 5в с прямой х = х^. Следовательно, Н всегда
Класса ^Р-)-1> что невозможно, так как //есть произволь-
произвольное множество, измеримое В.
Второй принцип аналитических множеств.
Отделимость (СА)
Отделимость при помощи аналитических дополнений.
Мы теперь обобщим понятие отделимости В двух мно-
множеств и введем понятие отделимости при помощи множеств
из других семейств.
Точнее, мы введем понятие отделимости при помощи
двух аналитических дополнений без общих точек.
Пусть ?j и Е2—-два любых множества точек, лежащих
в области ir^a, ...а, . Мы предполагаем, что Е1 и ?2 не
имеют общих точек.
Определение. Мы скажем, что два множества Ег
и Е2 отделимы при помощи двух аналитических дополне-
дополнений, если существуют два множества Ht и /У2 без общих
точек, содержащие соответственно Е1 и ?2, каждое из
которых есть аналитическое дополнение.
Это важное понятие будет играть существенную роль
в дальнейших рассмотрениях.
Сделаем теперь одно замечание: было бы бесполезно вво-
вводить понятие одновременной отделимости при помощи двух
аналитических множеств. В самом деле, если бы множества Н1

206 ГЛ. III. АНАЛИТИЧВ.СКЙЕ МНОЖЕСТВА
и //2, содержащие соответственно Et и ?2, были аналити-
аналитическими множествами, то Ht и #2 были бы отделимы В, н
мы бы не получили ничего нового. Напротив, понятие одно-
одновременной отделимости при помощи аналитических дополне-
дополнений имеет чрезвычайно важное значение, так как мы увидим, что
существуют два аналитических дополнения, неотдели-
неотделимые В.
Кроме того, можно рассматривать отделимость в некотором
роде одностороннюю, осуществляемую при помощи аналитиче-
аналитических множеств или аналитических дополнений. Вот в чем
состоит первая из них.
Пусть ?j и ?2— два любых множества без общей точки.
Мы скажем, что Et и ?2 отделимы друг от друга при
помощи аналитических множеств, если существуют два
аналитических множества И1 и Я2, содержащие соответ-
соответственно Ej и Е% и такие, что Ht не содержит ни одной
точки из Е2, а Н% ни одной точки из Ev
Мы получим совершенно аналогичное определение, отно-
относящееся, к отделимости множеств Ег и ?2 друг от друга при
помощи аналитических дополнений, если просто заменим
в предыдущем определении слова аналитическое множество
Через аналитическое дополнение.
Однако, мы сейчас же увидим, что введение этих двух
понятий иллюзорно, так как каждый из этих двух видов
отделимости полностью совпадает с одновременной отдели-
отделимостью при помощи двух аналитических дополнений, определе-
определение которой было дано в начале этой страницы.
Формулировка второго принципа теории аналитических
множеств. Теперь пора ввести один общий принцип, от
которого зависит решение многочисленных вопросов теории
аналитических множеств и их дополнений; в частности, этот
принцип позволяет полностью решить вопросы об односто-
односторонней отделимости при помощи двух аналитических множеств
или аналитических дополнений; с другой стороны, именно
этот принцип позволяет установить природу проекции мно-
множества единственности (стр. 257).
Принцип 1Т. Если удалить из двух аналитических
множеств их общую часть, то оставшиеся части всегда
одновременно отделимы при помощи двух аналитических
дополнений.

Второй принцип отдгёлймоСгй ; 207
Прежде чем приступить к доказательству этого принципа,
мы покажем, что он позволяет свести понятия односторонней
отделимости, определенные выше, к понятию одновременной от-
отделимости при помощи аналитических дополнений.
В самом деле, пусть Ех и ?2—два любых множества,
образованные из точек и отделимые друг от друга при помощи
двух аналитических множеств Н1 и #2. Это значит, что //,
содержит Ег и не имеет общей точки с Е& и .обратно,
#2 содержит Е2 и не имеет общей точки с Ev :
Пусть Н есть общая часть Hi и //2. На оснований вто-
второго принципа остающиеся множества И1 — Н и W2 — Н одно-
одновременно отделимы при помощи двух аналитических до-
дополнений (Jj и 02. без общих точек. А так как (Jj содер-
содержит Е1 и Ч2 содержит Е2, то множества Ег и Б2. одновременно
отделимы при помощи двух аналитических дополнений;
Ч. т. д.
Обратно, мы немедленно замечаем, что если два мно-
множества Е1 и ?2 одновременно отделимы при помощи двух
аналитических дополнений Ь1 и 02, то они отделимы друг
от друга при помощи двух аналитических множеств. Доста-
Достаточно обозначить через Нх дополнение к 02 и через /У2 — до-
дополнение к Ojj множества ¦Н1 и //2 — аналитические и осу-
осуществляют одностороннюю отделимость.
Точно так же легко видеть, что если Е^ и Я2 отделимы
друг от друга при помощи двух аналитических дополнений Ьг
и 62, то они одновременно отделимы при помощи двух ана-
аналитических дополнений. Достаточно заметить, что, обозначая
через Н1 и #2 дополнения ко множествам 6, и %, мы получим два
аналитических множества, осуществляющие одностороннюю
отделимость данных множеств Е1 и ?2. Итак, эти последние
рассмотрения приводятся к предыдущему случаю. Ч. т. д.
¦ Заметим, что второй принцип справедлив для аналитиче-
аналитических множеств, расположенных в области любого числа изме-
измерений. Но достаточно доказать его для двух линейных ана-
аналитических ' множеств, расположенных на порции @,1), так
как мы видели, что можно совершить взаимно однозначное
и взаимно непрерывное преобразование области любого числа
измерений в порцию @,1) линейной области, причем это
преобразование сохраняет аналитические множества и их
дополнения. . - - . . ...

208 Гл. in. Аналитические множества
Универсальное множество подобия. Рассмотрим на пло-
плоскости YOZ квадрат, стороны которого определяются урав-
уравнениями
V = 0, y = l, z = 0, z = l.
Мы ставим себе целью построить внутри этого квадрата
последовательности кривых Lu L2, ..., Ln, ... непрерывных
на порции @,1) области 0у и обладающих следующими
свойствами: .
1° Если pv pg, .,., рп, ... есть вполне определенная
последовательность, образованная из всех рациональных точек
оси OZ, заключенных между 0 и 1, то кривая Lt целиком
лежит под кривой Lj, 1ф), если р< < Pj и Lt лежит пол-
полностью над Lj, если Pi~>pf, здесь индексы i и j — любые
целые положительные числа.
2° Каково бы ни было множество е, составленное из ра-
рациональных точек, расположенных между 0 и 1, и подобное
множеству всех рациональных точек между 0 в 1, суще-
существует иррациональное число у0 такое, что прямая у = _у0
пересекает последовательность кривых Lu L^, ..., Ln, ...
в точности по е.
Мы назовем универсальным множеством подобия соеди-
соединение кривых Lit Z.2, ..., Ln, ..., обладающих указанными
свойствами.
Перейдем теперь к построению последовательности кри-
кривых Z.j, Ц, ..., Ln, ... Пусть z=fn(y) есть уравнение,
определяющее кривую 1Я.
Мы определяем первую функцию Д (у) следующим обра-
образом: пусть 8,, 82, ..., 8ft, ... есть последовательность, обра-
образованная из всех интервалов Бэра порядка 1; мы положим
/i (У) = Р* на h) здесь k = 1, 2, 3, ...
Допустим, что мы уже определили функции /,, /а, ...
...,/„_! и что функция ft постоянна на каждом интервале
Бэра порядка i; кроме того, мы предполагаем, что взаимное
положение уже определенных кривых Lu L2, ..., Ln_1 такое
же, как и соответствующих рациональных точек ри. р.2, . ..
• • •• P»-i на оси OZ.
Чтобы определить функцию /п, мы разделим каждый инт
тервал Бэра Д порядка л — 1 на интервалы Бэра порядка »;
пусть А1г Д2, . •., Дк, ... эти интервалы. Очевидно, что

ВТОРОЙ ПРИНЦИП ОТДЕЛИМОСТИ 209
функции Д, /2, ..., /„_, постоянны на Д; пусть г]5 г2, ...
• • •> гп-\ — эти постоянные. Согласно сделанной гипотезе, мно-
множество ги г2, ..., rn-i подобно множеству точек р4, р2, ...
• • •»Pn-i- Пусть ги г2, ..., ги,... —все рациональные числа,
каждое из которых занимает по отношению к числам rlt
г2, ..., гп_и то же положение, как и р„ по отношению
к точкам pj, p2, ..., pn_j. Мы положим fn{y) — rk на Дл
(*=1, 2, 3, ...)•
Мы видим, что функция fn(y) полностью определена и
что соответствующая кривая Ln имеет по отношению к уже
определенным кривым Lv L%, ..., Ln_v ..., то же положе-
положение, как точка рп по отношению к точкам ~ри p2, ..., рм_!.
Следовательно, последовательность так определенных кри-
кривых Lv L2, ..., Ln, ..., очевидно, обладает свойством 1°.
Чтобы доказать, что она обладает свойством 2°, возьмем мно-
множество е, образованное из рациональных точек и подобное
множеству рациональных точек, заключенных между 0 и 1.
Пусть ?„ есть точка из е, соответствующая точке р„, при-
причем это соответствие есть соответствие подобия. Найдем
интервал Бэра 8j порядка 1, в котором /i(^) = ^', затем
найдем в 8j интервал Бэра 82 порядка 2, где /2 (у) = Сд и
так далее.
Ясно, что иррациональная точка у0, которая принадлежит
всем этим 8j, 82, ..., 8Л, ..., такова, что прямая у=у0
пересекает кривые Lv Ь%, ..., Ln, ... в точности по е.
Итак, мы построили искомую последовательность кривых
Lv L2, ..., Ln, ... Ч. т. д.
Пространственное универсальное множество подо-
подобия* [19j. Рассмотрим в области g^ ^ я куб, стороны которого
определяются уравнениями:
$ = 0, 5 = 1, ^ = 0, у=\, г = 0, г = 1.
Мы построим внутри этого куба последовательность по-
поверхностей Q], Q2, ..., Qn, . ., каждая из которых опре-
определена и непрерывна на некотором множестве, состоящем из
конечного числа полос, лежащих в квадрате @<$<1;
0<^<1) области Зцъ параллельных оси OY. Последо-
Последовательность Qv Q2, ..., Qn, ... обладает следующими свой-
свойствами:
14 Зак. 284. Н. Н. Лузин

210 АНАЛИТИЧЕСКИЕ МНОЖЕСТВА [ГЛ. Ill
1° Пусть plf р2, • • •) рм, •. • — вполне определенная по-
последовательность, состоящая из всех рациональных точек
оси OZ, лежащих в интервале @,1). Пусть Ец 1ф} — мно-
множество всех точек области 0iy, в которых определены обе
поверхности Qi и Qj (различные поверхности определены на
различных множествах области c?tv)- Тогда, если р< < рр то
часть Qj( проектирующаяся в Ец, лежит под частью Qj,
проектирующейся в Ещ, а если p{>Pj, то часть Qu проекти-
проектирующаяся в Еф лежит над соответствующей частью Qj.
2° Какова бы ни была подпоследовательность p4l, р,-2, ...
..., pt ,... (конечная или бесконечная) нашей последовательности
рациональных чисел, найдется такое ?0, что плоскость ? = ?0
пересекается со всеми поверхностями Qh, QJ2, ..., Q<m, ...
3° Поверхности Qiv Qi2, ..., Q(ni ... пересекаются
с плоскостью S = Чо по системе кривых LjJ, b\o, ..., L|o,...,
образующих множество подобия для последовательности piu
?О> •••> Р<„> • • • Эт0 значит, что кривые Цо, l\ 1н%,...
(определенные для всех значений у плоскости S = !0) распо-
расположены подобно соответствующим точкам piv piv ..., pf ,...
и каково бы ни было множество рациональных точек rlt
г2, ..., г„, ..., подобное множеству ph, ph, ..., pin, ...,—
найдется такое у0, что прямая Р^0Уи> проходящая через точку
A0, у0) области 3\у и параллельная оси OZ, пересекает
каждую кривую Л<о в точке г = гп.
Перейдем к построению поверхностей Qv Q2, ..., Qn>...
Разделим сторону у = 0 квадрата @<$<1, 0<^<1),
лежащего в области 0\у> на счетное множество интервалов
Бэра первого порядка 81( 82, ..., 8И, ... и рассмотрим по-
полосу /j нашего квадрата, две стороны которой параллельны
оси OY и которая опирается на интервал 82 оси О?. Поверх-
Поверхность Q1 мы определим с помощью функции ft (?, у), задан-
дой в точках полосы /:. Для определения f1 (k, у) мы разде-
разделим полосу /j на счетное множество параллелепипедов Бэра
¦Kj,. 1т2, ..., 1г„, ... первого порядка так, чтобы параллеле-
параллелепипед пп проектировался на ось OF в интервал Бэра пер-

второй принцип отделимости 211
вого порядка Ам . Во всех точках (?, у) параллелепипеда wi
мы положим:
Л (&> .У) = P»v
Очевидно, что/j (S, у) — непрерывная функция, определенная
во всех точках полосы /,.
Пусть теперь построены поверхности Qu Q2, ..., Qn_t,
причем так, что для них удовлетворяется условие 1°. Каждая
поверхность Qit i^.n — 1 определена с помощью непрерыв-
непрерывной функции fi(l, у), заданной на конечном числе полос,
параллельных оси OY и опирающихся на интервалы Бэра по-
порядка <^i области &$. При этом в полосе, опирающейся на
интервал Бэра 8 порядка к, функция постоянна на параллеле-
параллелепипедах Бэра порядка k, проектирующихся на 8.
Для построения функции /„($, у) нужно прежде всего
указать те полосы, на которых эта функция будет опреде-
определена. Для этого достаточно указать те интервалы Бэра
области #$, на которые эти полосы опираются.
В числе этих интервалов находится интервал 8п+1 первого
порядка. Для указания остальных интервалов поступим сле-
следующим образом. Пусть на интервал Бэра 8j * . * порядка
й<« опирается полоса 1\%2..лк, где Л —'i + *> Jr==ir~~
—tr_j-)-l> во всех точках которой определены функции
fi > Л, fiu
и только они. Тогда выберем в bj л ...j интервал Бэра по-
порядка k-\-l с номером я— *"й+1: ^...^(n-^+iy (Если
ik — n — 1, то это — второй интервал Бэра порядка k -f- I,
подчиненный ^j1...jk' Если /fc<«—1, то это первый, кроме
&j ...j и из интервалов Бэра порядка k-\-l, подчиненных
fy —J » такой, что в опирающейся на него полосе не опре-
определены функции с номерами > ih, в полосе, опирающейся
на интервалы 8у ...j.и функции с номерами > 1к не опреде-
определяются.) Совокупность всех -выбранных таким образом интер-
интервалов Бэра вместе с интервалом 8п+1 и составляет множество
всех интервалов Бэра, на которые опираются полосы, в кото-
которых определяется функция /п ($, у).
14*

212 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
Чтобы определить функцию/„ в полосе /* ...«, опираю-
опирающейся на 8^ *,(»-ik+i), заметим, что все функции f{,r4^.k
постоянны на каждом прямоугольнике Бэра ранга k, содер-
содержащемся в полосе k ...< и проектирующемся на ось OY
в интервал Бэра ранга k. Пусть г< , /v , ..., /•< — соответ-
соответственные значения этих функций на некотором прямоуголь-
прямоугольнике it порядка k. Это множество, по условию, подобно мно-
множеству р<, pi, ..., pi Разделив интервал Бэра порядка k
12 it
области 0у, в которой проектируется i: на интервалы Бэра
порядка ft-f-1, мы разобъем пересечение тс/f ...< „ прямо-
прямоугольника тс с полосой U ...in Ha счетное множество прямо-
прямоугольников Бэра порядка k^\-\ tcj, tc2, ..., пр, ... Пусть
r'v г'г, ..., г', ... — множество всех рациональных чисел,
расположенных относительно чисел rv rv ..., гп_^ так же,
как точка рм расположена относительно точек pv p2, ...
•••iPn-l- /
Положим fn ($, у) = гр на тс^,. Тем самым функция fn (?, у)
определена. Легко видеть, что в полосе /< „.< ,„ опирающейся
на интервал Бэра 8,- ... ib(W-<.) ранга k-\- 1 определено в точ-
ности ft -J- 1 функций
Соответствующая поверхность Qn имеет на полосе Цt...tkn
то же расположение относительно поверхностей Qt , Qi , ...
. ..,Qib как точка р„ относительно точек р<, рг , . .., pf
Заметим, что каждая плоскость \ = ;0, пересекающая по-
полосу Li ,..in, пересекает поверхность Qn по одной и той
же кривой, которую мы обозначим Lnl'"n. Плоскости 1 = Ь0,
пересекающие различные полосы, на которых определена
функция /„, пересекают поверхность Qn> вообще говоря, по
различным кривым.
Покажем, что построенная система поверхностей удовле-
удовлетворяет условиям 1°, 2°, 3°. Условие 1° удовлетворяется по
построению. Чтобы доказать, что выполняется условие 2°,
. выберем произвольную подпоследовательность р<, р , ...
..., pi , ... (конечную или бесконечную) последовательности

ВТОРОЙ ПРИНЦИП ОТДЕЛИМОСТИ 213
р1( р2, ..., ри, ... На интервал Бэра 8< +iобласти g$опирает-
g$опирается полоса 1{, на которой определена функция /г- и не опре-
определена никакая функция fj, ] < /г
На интервал Бэра 8у j порядка 2 опирается полоса U * y
на которой определены функции /^ и /<2 и не определена
никакая функция /}, / ф it и / < i2 и так далее.
Точка ?0, принадлежащая всем интервалам Бэра 8j , 8у j , ...
..., bj j ,... такова, что плоскость 5 = S-q пересекает поверх-
поверхности Q< , Q< , ..., Q{ , ... и только их. Заметим, что если
i a n
последовательность р< , ..., р< конечна, то с0 есть любая
точка интервала Бэра Ъ$ j ,..j t.
Покажем, что выполняется условие 3°. Очевидно, что
плоскость % = So пересекает поверхности Qi , Qi Qi , ...
соответственно по кривым Lfо, 1^°, ..., L^J>, ..., располо-
расположенным одна относительно другой так же, как соответствен-
соответственные рациональные точки р< , р{>, ..., р» , ... Пусть е — про-
произвольное множество рациональных точек г,, г2, ..., гп, ...,
подобное множеству р<, Р<» •--» Р< » •-- В полосе /i, опи-
1 2 W 1
рающейся на интервал Бэра Ь{ +1, найдется прямоугольник
Бэра первого порядка irp , в точках которого /*, —/V В по-
полосе IlU4 найдется прямоугольник Бэра второго порядка ¦кр^> )
содержащийся в -kp , в точках которого / = г2 и т. д.
Точка М, принадлежащая всем прямоугольникам
itp р > • ¦ • лежит в плоскости ? = ?0, так как принадлежит
всем полосам 1{, Ци , ... Прямая Рш, проходящая через
точку М параллельно оси OZ, пересекает кривые Li, /.*„, • • •
..., Ц , ... в точности по множеству е.
Сравнение решет. Чтобы доказать второй принцип тео-
теории аналитических множеств, мы должны научиться сравни-
сравнивать решета.
Возьмем в пространстве OXYZ куб с ребрами, равными
единице, расположенными на осях координат. Пусть С есть
решето, лежащее на грани у = 0 этого куба, и С — другое
решето, лежащее на грани у = 1 того же куба. Мы предпо-
предполагаем, что каждое из этих решет образовано из прямолиней-
t

214
ГЛ. Ш. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
ных сегментов, параллельных оси ОХ с рациональными коор-
координатами г.
Установив это, проведем через точку х0, лежащую на
оси ОХ, плоскость х = х0. Эта плоскость пересекает решета
/
Z
S^ у'
уЯ-'Ъ
/
1
у ;
/
/
/
с'
7
/,-
^ _
у
/
'L
i
/
х0 С
1
У У^~
Черт. 5.
С и С по двум счетным множествам, которые мы обозначим
через Ra.Q и R'Xq.
Возможны только два случая:
Первый случай. Множество RXq подобно части R^, при-
причем эта часть может совпасть с самим Rx^.
Второй случай. Множество RX{t не подобно никакой
части R'x , включая и само это множество.
Мы докажем, что множество точек х0, для которых имеет
место первый случай, есть аналитическое множество.
* Пусть х0 — любая точка интервала @,1) оси ОХ. Точки
множества Rx имеют рациональные координаты z. Следо-
Следовательно, множество RXq есть подпоследовательность после-
последовательности pi, р2, ..., рп, ..., рассмотренной в предыду-

ВТОРОЙ ПРИНЦИП ОТДЕЛИМОСТИ 215
щем параграфе. Тогда ему соответствует последовательность
кривых l\, Z.|o, ..., l)pn, ..., расположенных подобно точ-
точкам множества Rx . Проведем в квадрате, который получается
от пересечения куба плоскостью х = х0, все эти кривые.
Заставляя изменяться точку х0, мы получим внутри куба
множество точек Л, образованное из всех проведенных кри-
кривых. Изучим природу этого множества Л.
¦ С этой целью напомним, что решето С состоит из счет-
счетного множества прямолинейных отрезков, параллельных оси ОХ.
Обозначим через оге проекцию на ось ОХ суммы всех тех
отрезков, у которых координата г равна р„. Множество о„
может быть представлено в следующем виде:
п-1
°п = ап 2 2 «v* ... щ
Каждое множество Н? ...i — о„с< ... о^ ЦСо^, очевидно,
измеримо В. Для каждой точки х0 множества Щ ...i соот-
соответствующее множество Rx содержит точки с координатами
z = p{i, р{^ ..., pik, ... и не содержит точек с координа-
координатами z = pj, /<n и / Ф ij, г2, ..., 1к. Следовательно, кри-
кривая Ln°, проведенная в плоскости х — х0, совпадает с кри-
кривой Z^tV" fcn. Значит, всем точкам множества Я"...< соот-
2 1 1 Я
ветствует одна и та же кривая L,%x'" *и. Так как //"...*
и i,,i""*fcn — множества, измеримые В, то и сумма кривых
lJn\ ••• hn) соответствующих всем точкам х0 множества Я™., j »
есть множество, измеримое В. Так как множество ом есть
сумма конечного числа попарно не пересекающихся множеств
H?.,.i , то соединение всех кривых Щ, соответствующих
всем точкам множества оя, есть множество, измеримое В,
однозначное по отношению к плоскости X0Y. Если мы про-
проделаем это построение для всех множеств оп, соответствую-
соответствующих рациональным числам рге, то получим, очевидно, рассма-
рассматриваемое множество А. Следовательно, множество А состоит
из счетного множества однозначных множеств, измеримых В*.

216 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
Проведем теперь через каждую точку решета С прямую,
параллельную оси OY. Пусть 5 — множество точек куба,
расположенных на этих прямых. Ясно, что 5 измеримо В,
Следовательно, дополнение к 5 относительно куба также
измеримо В; мы его обозначим через ?. Общая часть А и ?
также измерима В.
Природа этой общей части AS такова: множество А есть
соединение счетного числа однозначных множеств, измери-
измеримых В. Но общая часть каждого из этих однозначных мно-
множеств и 2 есть, очевидно, также однозначное множество,
измеримое В. Следовательно, множество AS образовано из
счетного числа однозначных множеств, измеримых В.
Отсюда мы заключаем, что проекция множества AS на
плоскость XOY непременно измерима В.
Пусть S эта проекция и 9 — ее дополнение относительно
грани куба z = 0. Множество 9 измеримо В.
Пусть М — любая точка из 9 и Рш — перпендикуляр
к плоскости z — 0, проведенный через М. Так как точка М
принадлежит к 9, то ясно, что Рм не пересекает множе-
множества AS.
Отсюда следует, что все точки А, лежащие на Рм, при-
принадлежат к 5. Но в силу свойства кривых L точки Р, при-
принадлежащие к А, образуют множество, подобное множеству RXq%
По самому определению 5 мы заключаем, что точка х0 удо-
удовлетворяет первому из указанных выше случаев.
Итак, взяв проекцию 9 на ось ОХ, мы получим только
точки лг0, удовлетворяющие первому условию. Но легко видеть,
что и обратное также справедливо.
В самом деле, пусть л:0 удовлетворяет первому условию.
Это значит, что множество Rx подобно части (в широком
смысле) множества Rx , пусть е эта часть. Точки А, лежа-
лежащие в плоскости х = х0, образуют множество кривых Lfo,
которое соответствует множеству Rx. Но в силу универсаль-
универсального свойства этого множества кривых на прямой z = Q,
лг = лг0 существует точка М такая, что перпендикуляр Рм
пересекает А как раз по множеству, тождественному е. Сле-
Следовательно, все точки А, лежащие на Рм, принадлежат к 5.
Отсюда следует, что множества А и ? не имеют общей точки
на Рм. Следовательно, точка М принадлежит множеству 9.

ВТОРОЙ ПРИНЦИП ОТДЕЛИМОСТИ 217
Итак, ортогональная проекция множества 6 на ось ОХ
в точности совпадает со множеством точек х0, удовлетворяю-
удовлетворяющих первому условию. Но мы видели, что 0 измеримо В,
значит, его проекция есть аналитическое множество. Ч. т. д.
Резюмируем все, что было изложено в этой последней
части. Пусть С и С — два решета, расположенных в пло-
плоскости XOY, х — любая точка на оси ОХ, Р^ — перпенди-
перпендикуляр в точке х к оси ОХ, лежащий в плоскости XOY.
Пусть Rx и Rx— множества точек С и С, лежащих на Рх.
Мы предполагаем, что решета С к С образованы каждое
из счетного числа прямолинейных сегментов, параллельных
оси ОХ и имеющих рациональные координаты у. Мы знаем
(стр. 194), что всякое линейное аналитическое множество Е
можно считать просеянным при помощи решета такой при-
природы.
Обозначим через Н множество всех тех точек х, для
которых Rg, подобно части (в широком смысле) Rx. Точно
так же обозначим через Н' множество всех точек х, для ко-
которых R'x подобно части Rx (в широком смысле).
Результат, который мы только что получили, состоит
в том, что так определенные множества Н и Н' суть анали-
аналитические множества.
Доказательство второго принципа. Возьмем в пло-
плоскости XOY квадрат, стороны которого имеют уравнения
х = 0, х = 1, у = 0, .У —!•
Пусть Et и Е2— два любых аналитических множества,
расположенных в интервале @ < х < 1).
Проведем прямую у = -у и рассмотрим два решета Ct и С2,
из которых первое расположено ниже, а второе выше этой
прямой; мы предполагаем, что эти решета определяют соот-
соответственно множества Е1 и ?2 и природа их такая, как мы
рассматривали выше.
Пусть Е есть общая часть Ех и ?2, Е^. Обозначим
через Rt множество точек Е1г которые не входят в ?2, и
соответственно через /?2 множество точек ?2, которые не
входят в ?а:
/\j === -Cj ^2' ^2 '—' ^2 1"

218 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
Надо доказать, что #, и /?2 одновременно отделимы при
помощи двух аналитических дополнений.
Пусть х — любая точка на @,1) и Рх — перпендикуляр
в этой точке к оси ОХ; обозначим через R'x и R'^ соответ-
соответственно части решет Cj и С2, лежащие на Рх.
Пусть Нх — множество всех тех х, для которых R^ не
подобно никакой части (в широком смысле) R'?, и соответ-
соответственно, //2— множество всех тех х, для которых R^ не
подобно никакой части Р'х (в широком смысле). В силу пред-
предшествующего, множества Нх и #2 суть аналитические до-
дополнения.
Обозначим через Г, общую часть Нх и С?2 и через Г2
общую часть #2 и СЕХ'.
Yl = H1-CEi, Ti = Hi-CE1.
Ясно, что 1\ и Г2 также аналитические дополнения.
Легко видеть, что 1\ содержит множество Rx. В самом
деле, если х принадлежит к Rv то множество Rx не будет
вполне упорядоченным в положительном направлении оси OY,
тогда как Rx, наверное, вполне упорядочено при том же усло-
условии относительно порядка точек, так как х принадлежит к Е1
и к С?2. Точно так же доказывается, что Г2 содержит /?2.
Остается доказать, что 1\ и Г2 не имеют общих точек.
В самом деле, если бы точка х принадлежала и к Г], и
к Г2, то она принадлежала бы к С?, и к СЕ2. Значит, мно-
множества Ra, и Rx были бы вполне упорядочены. Но так как
х принадлежит к Нх и к //2, то Ra, не подобно никакой
части Rx, и обратно, Rx не подобно никакой части Rx. Но
это как раз невозможно, ибо Rx и R,. вполне упорядочены,
а следовательно, одно из них подобно сегменту другого. Ч. т. д.
Итак, формулированный принцип доказан.
Как немедленное следствие этого принципа мы имеем:
Если §, и §2 — два аналитических дополнения и если
мы устраним из &, и |-2 их общую часть, то остающиеся
множества всегда одновременно отделимы при помощи
двух аналитических дополнений.
В самом деле, обозначим через $ общую часть S, и &2,
через Rt — разность $t — g и через R2 — разность f-2—$.

ВТОРОЙ ПРИНЦИП ОТДЕЛИМОСТИ 219
Надо доказать, что Rt и R2 одновременно отделимы при
помощи двух аналитических дополнений.
Обозначим через //, дополнение к ?2 и через /У2 допол-
дополнение к S,; множества Нх и #2— аналитические. Ясно, что
Нх содержит Rx и не имеет общих точек с /?2; точно так же
#2 содержит /?2 и не имеет общих точек с Rv Мы можем
сказать, что Rx и /?2 отделимы d/гуг от друга при помощи
двух аналитических множеств. Но мы видели (стр. 207), что
в этом случае Rr и /?2 одновременно отделимы при помощи
двух аналитических дополнений. Ч. т. д.
Обращение второго принципа. Множества Rt и i?2,
о которых говорится во втором принципе, являются каждое
разностью двух аналитических множеств, но эти раз-
разности некоторой особой природы. В самом деле, нельзя утвер-
утверждать, что два любых множества, каждое из которых есть
разность двух аналитических, всегда одновременно отделимы
при помощи двух аналитических дополнений, если только у них
нет общей точки: для этого достаточно принять за Ri анали-
аналитическое множество, неизмеримое В, а за R2 — его дополнение.
Чтобы узнать природу множеств, каждое из которых есть
разность двух аналитических, и которые допускают одновре-
одновременную отделимость при помощи двух аналитических допол-
дополнений, мы докажем теорему, являющуюся обращением второго
принципа.
Обращение второго принципа. Если Ех и ?2—
два множества без общих точек, причем каждое из них
есть разность двух аналитических множеств, и если Ег
и Е9 отделимы при помощи двух аналитических дополнений,
тогда Е^ и Е2 получаются из двух аналитических мно-
множеств путем удаления их общей части 1).
Чтобы доказать это, положим
Е\ = Е\ — Ei и ?2 = E<i — Еъ,
где множества Е с двумя индексами аналитические. Мы можем
написать
Ei = е'х ¦ СЕ'[ и Е.2=-Е'2- CE'i
1) После опубликования в Compfes Rendus Ac. Sc. формулировки
этого предложения Хаусдорф и Серпинский независимо пожелали
сообщить мне свои доказательства его; эти доказательства, с точ-
точностью до обозначений, тождественны с данным в тексте.

220 ГЛ. III. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
Допустим, что Е1 и ?2 одновременно отделимы при по-
помощи двух аналитических дополнений Я1 и Я2
Так как Et принадлежит к Я] и не имеет общей точки
с На, то можно написать
и точно так же
?, = (??. ОД (СЕ?-ЯО.
Для сокращения мы обозначим через Кх и К% первые
скобки в каждом из этих равенств
Очевидно, множества Кх и /С2 — аналитические. Вторые
скобки каждого из равенств — аналитические дополнения; мы
их обозначим через CTt и СГ2, предполагая Т1 и Г2 аналити-
аналитическими.
Итак, мы имеем
CTi = СЕ\ • Hi, СГ2 == СЕ% • Я2
и, следовательно,
Et = /fj • CFj, ?2 = /Q • СГ2.
Положим, наконец,
6Я + ^ и 62 =
Ясно, что Я — аналитическое множество; значит, это же
имеет место для bt и 62.
Мы теперь докажем, что, удаляя из 6j и 62 их общую
часть 6, мы получим в точности данные множества Ei и Ev
С этой целью мы заметим, что множества 6: и 62 могут
быть написаны в виде
СЯ = Я-Н^я (СГ, + СГ2)=Я+/<-2 • СГ2=Я-1-?2,
так как /fj и СГ2, очевидно, не имеют общих точек, так же
как и К2 и CTV

ВТОРОЙ ПРИНЦИП ОТДЕЛИМОСТИ 221
Так как множества Е1 и ?2, по предположению, не имеют
общих точек, отсюда следует, что
6 = в, . Й2 == Н.
Кроме того, ?:, и И, очевидно, не имеют общих точек,
так же как ?2 и И. Следовательно,
6j — 6 == ?¦, и 62 — 0=?2.
Итак, ?j и ?2 получаются удалением из двух аналитиче-
аналитических множеств 6j и 02 их общей части 6. Ч. т. д.
Существование двух аналитических дополнений неот-
неотделимых В. Это существование очень важно, так как именно
благодаря ему теория отделимости при помощи аналитических
дополнений приобретает самостоятельный интерес. Если бы
два аналитических дополнения были всегда отделимы В, если
только у них нет общей точки, то все свелось бы к изуче-
изучению отделимости В.
В силу чрезвычайной важности этого факта, мы дадим три
доказательства существования двух аналитических дополнений
неотделимых В.
Первое доказательство1). Пара {Еи ?2) аналитических
множеств Е1 и ?2, расположенных в плоскости XOY, назы-
называется дважды универсальной, если, каковы бы ни были
линейные аналитические множества ег и е2, существует пря-
прямая, параллельная оси OY и пересекающая Е1 по еи а ?2
по е2.
Существуют дважды универсальные пары. Чтобы дока-
доказать это, рассмотрим в плоскости TOY универсальное анали-
аналитическое множество U, т. е. такое, что, пересекая его пря-
прямыми, параллельными оси OY, мы получим всевозможные
линейные аналитические множества.
Пусть tt = '¦? (t), t% = ф (х) — кривая Пеано, заполняющая
всю плоскость TjOTj, причем функции ф и <}» непрерывны
на @,1).
Рассмотрим преобразование плоскости TOY в плоскость
XOY, полагая t = y(x), y=y\ пусть f71 есть прообраз U.
') Другие доказательства находятся на стр. 262 и 265 этой
книги. См. также исследования П. С. Новикова по теории неявных
функций ро].

222 ГЛ. Ш. АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
Аналогично, полагая t = ty {х), у =у, преобразуем TOY в XOY;
пусть ?/2 есть прообраз U. Ясно, что ?/j и U2— аналити'
ческие множества. Легко видеть, что пара (Ult U2) дважды
универсальна. В самом деле, всегда существует такое х0,
что прямая х = х0 пересекает Ux и ?/2 по двум заранее задан-
заданным аналитическим множествам ех и ev
Установив это, применим второй принцип к аналитическим
множествам U1 и ?/2. Пусть R1 и R2— множества, которые
получаются, если из U1 и ?/2 удалить их общую часть. В силу
второго принципа существует два аналитических дополнения
Нх и Н2 без общей точки, содержащие соответственно Rt и R2.
Я теперь утверждаю, что аналитические дополнения Нх
и Н2 неотделимы В.
В самом деле, если бы существовали два множества О,
и 62, измеримые В, без общей точки и содержащие соот-
соответственно Я] и //2, то каждая параллель к оси OY пересекала
бы 6j и 82 по линейным множествам, измеримым В, и классов
всегда низших, чем некоторое фиксированное трансфинитное
число а. Но пара (f/j, ?/2) дважды универсальна. Следова-
Следовательно, существует прямая х — х0, которая пересекает ?/х
и С/2 по двум множествам ех и е2, измеримым В, класса a -j- 1
и взаимно дополнительным. Так как множества Ь1 и 62 соот-
соответственно содержат Rx и /?2, ясно, что прямая х = х0 пере-
пересекает 6j и 62 как раз по ег и е2, что невозможно, так как
класс ех превосходит а. Ч. т. д.

Г Л А В А IV
НЕЯВНЫЕ ФУНКЦИИ
Общие замечания о неявных функциях
Проблема неявных функций. Целью этой главы является
изучение функций, определенных неявно при помощи ана-
аналитических изображений, т. е. при помощи функций класси-
классификации Бэра1).
Рассмотрим аналитические соотношения
/i \xii X4i • • •» хт; yv у2, ..., Ур) = О,
Л 0*1» -*2> • • •» Хт> Уи У2> • • • у Ур) = °> /j\
где функции /4 определены всюду в m-j-jp-мерной области
3ялс ...а у,уг..у и входят в классификацию Бэра.
Легко видеть, что изучение общего случая сводится к изу-
изучению системы (I), так как, если какая-либо из функций ft
этой системы не была бы повсюду определена, мы могли бы
дополнить ее до функции, определенной во всей области без
того, чтобы она перестала принадлежать к классификации
Бэра и без изменения величин неявных функций; с другой
стороны, если один из аргументов лг< или у$ не фигурирует
в одном из уравнений, мы тем не менее можем его считать
х) Эта глава есть подробное изучение проблемы, поставленной
Лебегом и решенной им для частного случая. См. Lebesgue «Sur
les fonctions representablee analytlquement» (Journ. de Math., 1905,
стр. 192).

224 ГЛ. IV. НЕЯВНЫЕ ФУНКЦИИ
зависящим от этого аргумента, подобно тому как постоянное
число можно рассматривать, как зависящее от любого пере-
переменного.
Раз так, то проблема при заданной системе уравнений (I)
состоит в изучении:
1° Области Е существования неявных функций ylt
Л» •••' УР-
2° Природы этих неявных функцийг).
Геометрическая постановка проблемы. Чтобы сделать
это изучение возможно более ясным и простым, мы возьмем
т -\~ р-мерную область <?х х у у и рассмотрим в этой
области функцию F переменных xt, у^ определенную равенством
Так как функции /,- входят в классификацию Бэра, то это
справедливо и для F. Следовательно, множество S точек
N{xv л:2, ..., хт; yv ..., ур)
этой области, в которых функция F обращается в нуль, необ-
необходимо измеримо В. Поэтому его ортогональная проекция Е
на m-мерную область 0'х ...» есть аналитическое множество.
Мы покажем, что это аналитическое множество Е есть
область существования неявных функций у{.
В самом деле, если точка Мо (xi, xl, ..., лгда) принадлежит
к Е, то найдется точка Мо (xl, ..., х°т, yl, ..., уар) в обла-
области g'xv..xmvy..y , имеющая Мо своей проекцией. Так как
функция F обращается в нуль в точке No, то это же верно
и для каждой из /<; следовательно, система уравнений (I)
удовлетворена. Таким образом, в этом случае числа _yj,
Уг • • •' Ур СУТЪ значения неявных функций yv yv ..., ур.
Обратно, если точка Мо не принадлежит к Е, то функция F
не обращается в нуль ни в какой из точек N(x°i, xl, ..., х°т,
_У], ..., ур), каковы бы ни были числа yv у2, ..., ур. Сле-
') В классическом анализе (см. Hadamard, Sur les transform,
portct. Bull, de la Soc. math. France, т. 34, 1906, стр. 71) проблему
можно рассматривать двумя различными способами, а именно,
с точки зрения локальной или с точки зрения всей протяженности.
Этого различия не будет в вопросе, который мы изучаем,

ОБЩИЕ ЗАМЕЧАНИЯ О НЕЯВНЫХ ФУНКЦИЯХ 225
довательно, для .каждой из, этих точек N по крайней мере
одна из функций ft не равна нулю; таким образом, если мы
положим
о о о
Xi = Xit Х% = Х%, . • . j Хт = Хт,
то не существует чисел у{, удовлетворяющих всем уравне-
уравнениям системы (I).
Итак, аналитическое множество Е есть область существо-
существования неявных функций.
Мы дополним этот результат следующими замечаниями:
Замечание I. Изучение системы уравнений (I) сводится
к изучению единственного уравнения F = О, где F есть функ-
функция классификации Бэра. Следовательно, с геометрической
точки зрения все сводится к изучению произвольного мно-
множества S, измеримого В, расположенного в m-j-p-мерной
области g'я xmyv..y > и взаимоотношений, которые суще-
существуют между этим множеством §> и его ортогональной проек-
проекцией Е на от-}-/>-мерную область $х ...х •
Замечание II. Областью Е существования неявных
функций у{ может быть любое аналитическое множество.
В самом деле, если в области Ях х дано любое аналити-
1 и»
ческое множество Е, мы можем его рассматривать как орто-
ортогональную проекцию множества §>, измеримого В и распо-
расположенного в m-j- 1-мерной области Ях...хт<ц- Функция
F(xv лг2, ..., хт, у), которая равна нулю на $ и 1 вне $,
очевидно, входит в классификацию Бэра. Но уравнение
F{xv x2, ..., хт, у) = 0
определяет у как неявную функцию от переменных xit причем
область существования этой функции в точности совпадает с Е.
Итак, мы видим, что проблема об области существова-
существования неявных функций сводится к вопросу о том, будет ли
эта область измерима В в каждом рассматриваемом
случае.
Однозначные и многозначные неявные функции. Мы
теперь обратим наше внимание на самые неявные функции yt.
Пусть М(хи лг2, ..., хт)—любая точка области gx±... хт>
Если точка М не принадлежит к аналитическому множеству Е,
то не существует никакой системы чисел yv y%, ..., ур,
15 Зак. 284. Н. Н. Лузин

226 ГЛ. IV. НЕЯВНЫЕ ФУНКЦИИ
удовлетворяющих уравнениям (I). Если М принадлежит к Е,
то существуют системы чисел yv у2, ..., ур, удовлетворяю-
удовлетворяющие уравнениям (I) и в общем случае их существует беско-
бесконечное множество.
Следовательно, если М принадлежит к Е, то при задан-
заданном i, 1<^г<Ср, неявная функция yt имеет вполне определен-
определенное множество значений в точке М; это множество мы обозначим
через Н\м\ Очевидно, это множество //|Ж) фактически со-
содержит точки и, вообще говоря, меняется вместе с изменением
точки М множества Е.
Легко видеть, какова природа множества Н^\ В самом
деле, так как множество S измеримо В, то множество точек,
принадлежащих §>, ортогональные проекции которых на
область 0х ... я, совпадают с М, очевидно, измеримо В;
обозначим его через g^. Но ясно, что tif^ есть ортогональ-
ортогональная проекция §(М) на прямую Df\ проведенную через М
параллельно оси OY{.
Следовательно, Н\ ' есть линейное аналитическое мно-
множество.
~ Если проделать это построение для всех точек М из Е,
то ясно, что получается вполне определенное множество Н{,
расположенное в т-j-1 -мерной области 0Х ... Хту. Это мно-
множество Н( есть изображающее множество для неявной функ-
функции y{(xv дг2, ..., хр), так как для получения всех значений,
принимаемых у^ в точке М, достаточно пересечь множество Hi
перпендикуляром D^ к области 0х ... х , проведенным
через М в области ga ... „тУ.
Изображающее множество Hi есть, очевидно, ортогональ-
ортогональная проекция $ на т-\~ 1-мерную область 0хх ... х у.- Сле-
Следовательно, //,• есть аналитическое множество. А так как мно-
множество $ есть произвольное множество, измеримое В, то ясно,
что Hi есть, вообще говоря, аналитическое множество, неизме-
неизмеримое В.
¦ Из предшествующего следует, что неявная функция у{
в общем случае многозначна, так как, вообще говоря, пер-
перпендикуляр D^ пересекает множество Я4 в нескольких точ-
точках. В самом деле, аналитическое множество Н(, очевидно,

ОБЩИЕ ЗАМЕЧАНИЯ О НЕЯВНЫХ ФУНКЦИЯХ 227
может быть произвольным аналитическим множеством, так
как всегда можно найти множество $, измеримое В, располо-
расположенное в д'х ... Хту ... у , проекция которого на 0' х ... щ,
совпадает с Ht.
Таким образом, мы приходим к следующему результату:
Неявная функция yit вообще говоря, имеет область
существования Е, аналитическую и неизмеримую В, и для
каждой точки М из Е множество значений ^ есть линей-
линейное аналитическое множество Н\ \ которое, вообще говоря,
неизмеримо В и, следовательно, имеет мощность конти-
континуума.
Следовательно, для каждой неявной функции yt в каждой
точке М области Е может представиться только три случая:
1° Функция у{ имеет единственное значение в точке М;
2° Функция у{ имеет в точке 'М счетное (или конечное)
множество значений;
3° Множество значений yt в точке М содержит совер-
совершенное множество и, значит, имеет мощность континуума.
Мы увидим, что в первых двух случаях имеют место те
самые законы, которые впервые были указаны Лебегом, тогда
как третий случай совершенно неожиданно от них отличается.
Эффективное существование однозначного решения во
всех случаях. Мы докажем, что во всех случаях можно на-
назвать однозначное решение данной системы (I) уравнений.
Чтобы убедиться в этом, возьмем непрерывное параметри-
параметрическое изображение множества S, измеримого В
xi =/i (Oi Х2 =/я @. • • •. хщ =/« @.
Пусть MQ (л:°, х°, ..., х°т) — любая точка множества Е.
Совместные уравнения
*!=Л@, *2=/,Ю *!,=/.«>
определяют на порции @,1) области 01 замкнутое множество,
так как функции ft непрерывны. Обозначим это множество
через FUq.
Ясно, что если точка Мо отличается от точки Mv лежа-
лежащей в Е, то замкнутые множества Fjr и Fm не имеют общих
15*

228 ГЛ. IV. НЕЯВНЫЕ ФУНКЦИИ
точек. С другой стороны, очевидно, что каждая точка t0 пор-
порции @,1) области 0t принадлежит замкнутому множеству Fu,
соответствующему некоторой точке М из Е: координаты этой
точки М получаются, если положить t = t0 в уравнениях
xi=fi(t), i = l, 2, ..., т. Отсюда следует, что вся пор-
порция @,1) области 01 разложена на замкнутые множества Ядг,
соответствующие точкам М из Е.
Установив это, допустим, что мы- можем назвать одну и
только одну точку в каждом множестве F^. Пусть L — мно-
множество так выбранных точек t. Я теперь утверждаю, что мно-
множество L позволяет нам назвать однозначное решение
Л. У» •••» Ур
данной системы (I).
В самом деле, заставим /0 пробегать множество L. Соот-
Соответствующая точка Mg (х®, х%, ..., jcJj) пробегает всю область
существования Е, причем двум различным значениям t соот-
соответствуют две различные точки М из Е. С другой стороны,
уравнения
у\=g, (У. у°2=sa ('„)> ¦•-..)$=*„ (О.
где t0 есть точка из L, определяют вполне определенное ре-
решение
„0 у.0 v-0 . v0 v0 v0
xv x%, ..., xm, y±, y2, ..., yp
заданной системы (I). Итак, мы умеем назвать однозначное
решение уи _у2, .. ., ур системы (I).
Итак, все сводится к тому, чтобы назвать одну и только
одну точку t в каждом замкнутом множестве F. Эта
проблема не представляет никакой трудности, когда речь идет
о замкнутых множествах в классическом смысле, т. е. когда
не исключают из рассмотрений рациональных точек. Но в рас-
рассматриваемом нами случае речь идеть о множестве, замкнутом
относительно области 0и и, следовательно, рациональными
точками пренебрегают.
Чтобы преодолеть это небольшое затруднение, перенуме-
перенумеруем все интервалы Бэра, расположенные на порции @,1)
области 0' t, при помощи целых положительных чисел

ОБЩИЕ ЗАМЕЧАНИЯ О НЕЯВНЫХ ФУНКЦИЯХ 229
Среди этих интервалов мы берем первый, пусть 8„ , кото-
который содержит точки из F. Пусть 8п_ — первый интервал пре-
предыдущей последовательности, содержащийся в 8„ и содержащий
точки F. Вообще, 8„ есть первый интервал предшествую-
ft
щей последовательности, содержащийся в 8„ и содержащий
п —1
точки F. Убывающая последовательность 8„ , 8„ , ... опре-
определяет иррациональную точку t, принадлежащую всем интер-
интервалам 8П . Так как 8„ непременно содержит точки F и так
К ft
как г замкнуто, точка t должна принадлежать к F. Итак,
мы назвали точку во множестве F.
Таким образом, мы во всех случах назвали однозначное
решение yv у%, ..., ур, определенное во всей области суще-
существования Е, но мы не знаем, какова природа этого решения.
В дальнейшем мы увидим, что решение уи у2, ..., ур, так
названное, составлено из проективных функций у{, что и
уточняет их природу.
Мы дополним полученный результат следующим замеча-
замечанием: если область существования Е есть множество,
неизмеримое В, то не существует ни одного решения
Ук Уъ> •••) УР, составленного из р однозначных функций,
берущих свои значения от р функций классификации Бэра.
Чтобы убедиться в этом, допустим, что мы имеем р функций
ух = Ф(хи xv ..., хт), у2 = Ф2, ..., ур = Фр (II)
классификации Бэра, определенных во всей области 0'хх ... х
и удовлетворяющих уравнениям (I), когда точка M(xv ..., хт)
принадлежит к Е.
Возьмем область 0'х ... ХтУ ... у и рассмотрим в этой
области множество точек M(xv ..., хт; yv ..., ур), коор-
координаты которого удовлетворяют уравнениям (II); пусть %>' это
множество. Легко видеть, что §' измеримо В. В самом деле,
функция
(>i - $i)a+Си. - ф2J + • • • + (ур - %)*
от т-\-р действительных переменных л:^, yj, очевидно, входит
в классификацию Бэра. Следовательно, множество N точек,
для которых эта функция равна нулю, измеримо В, Но это
множество, очевидно, как раз совпадает с $'.

230 ГЛ. IV. НЕЯВНЫЕ ФУНКЦИИ
Установив это, обозначим через Н общую часть $ и $г;
множество Н измеримо В. Так как Н есть часть §, то проек-
проекция Н на g'.„j ... хт принадлежит к Е. С другой стороны,
какова бы ни была точка M(xv ..., хт) из Е, точка из S'
удовлетворяет уравнениям системы (I); следовательно, эта точка
принадлежит к S, а значит, и к Я. Отсюда следует, что
проекция Н на 0'х ... х совпадает с Е.
Из самого определения множества Н следует, что двум
различным точкам из Н соответствуют две различные точки
его проекции Е. Отсюда мы заключаем (стр. 166), что Е
измеримо В, что противоречит гипотезе. Ч. т. д.
Таким образом, мы убедились, что в случае, когда область
существования Е неизмерима В, невозможно выбрать одно-
однозначное решение yv y%, ..., ур, составленное из функций
классификации Бэра. Это, однако, нисколько не препятствует
тому, чтобы в однозначном решении какая-либо одна из неявных
функций yi была функцией классификации Бэра.
Исследования Лебега. Мы обязаны Лебегу первыми иссле-
исследованиями о тождестве двух семейств функций: функций, опре-
определенных аналитически явным образом (у = аналитическому
выражению от х1г лг2, ..., хт) и функций, определенных ана-
аналитически неявным образом (аналитическое выражение от
х1г л:2, ..., хт, у равно нулю). Обычно эти две категории
функций не различают, так как на практике тот самый про-
процесс, который доказывает существование неявной функции, дает
и ее разложение; но тождество двух семейств не очевидно.
Лебег рассмотрел случай, где каждой системе чисел,
xlt л:2, ..., хт соответствует не более одной системы
чисел yt, у$, ...» ур, удовлетворяющих предложенным урав-
уравнениям (I), и указал следующие два закона, имеющие место
в этом случае:
(Z-j) Область существования Е неявных функций yvyv ...
..., ур есть множество, измеримое В;
(Lg) Каждая неявная функция yi совпадает на ? с некото-
некоторой однозначной функцией «<(#,, дг2, ..., дгт), входящей
в классификацию Бэра и всюду определенной.

ИЗУЧЕНИЕ ОДНОЗНАЧНЫХ НЕЯВНЫХ ФУНКЦИЙ 231
Естественно стараться узнать, сохраняются ли эти два
закона Лебега во всех случаях, которые могут представиться.
Среди других случаев, кроме рассмотренного, наиболее инте-
интересными являются следующие:
I. одна из неявных функций, пусть у{, однозначна, а о дру-
других неявных функциях ничего неизвестно;
II. все неявные функции yv y%, ..., ур допускают не
более счетного множества значений в каждой точке области
существования Е\
III. одна из неявных функций, пусть yj допускает не более
счетного множества значений в каждой точке области суще-
существования Е, а об остальных неявных функциях ничего не
известно;
IV. общий случай, где не делается никаких гипотез о неявт
ных функциях.
Мы увидим, что случай II во всех отношениях аналогичен
основному случаю Лебега, так как его законы (?,) и (Z,2)
сохраняются в этом случае. Точно так же случай III анало-
аналогичен случаю I, так как в обоих этих случаях закон (Lt) не
сохраняется, тогда как закон (Zg) частично сохраняется. Нако-
Наконец, в общем случае IV ни закон (Lj), ни закон (Z,2) не сохра-
сохраняются.
Изучение однозначных неявных функций.
Исследования Лебега
Основной случай Лебега, где решение однозначно и
единственно. Мы начнем с изучения основного случая, рас-
рассмотренного самим Лебегом; это тот случай, когда система (I)
допускает единственное решение для каждой точки М {xv х2,...
..., хт) области существования Е.
Область существования. Из предшествующего немедленно
следует, что в основном случае Лебега область существования Е
измерима В. В самом деле, достаточно заметить, что Е есть
ортогональная проекция на &Хт ...х множества $, измери-
измеримого В, и что проекции двух различных точек $ всегда
различны. Отсюда мы заключаем (стр. 166), что Е изме-
измеримо В.
Таким образом, мы приходим к первому закону (Z,j) Лебега:

232 ГЛ. IV. НЕЯВНЫЕ ФУНКЦИИ
Теорема I. Если система уравнений допускает един-
единственное решение для каждой точки области существова-
существования, то эта область существобания необходимо измерима В.
Природа неявных функций. Мы докажем, что в рас-
рассматриваемом случае единственное решение yv y2, ..., ур
предложенной системы (I) образовано из функций классифи-
классификации Бэра.
В самом деле, рассмотрим какую-нибудь неявную функцию
¦Л ¦=*<(¦*!. **•••! *«)•
В силу известной теоремы Лебега (стр. 144), для того
чтобы некоторая функция у = Ф(х1, лг2, ..., хт) входила
в классификацию Бэра, необходимо и достаточно, чтобы,
какова бы ни была порция (а, Ь) области 0Р, множество
точек M{xv xv ..., хт), для которых мы имеем неравенство
а < у < Ь, было измеримо В.
Применим этот критерий к неявной функции yt. Пусть
есть регулярное параметрическое изображение множества S;
мы предполагаем, что все функции /< и gt непрерывны и
определены на порции @,1) области gt.
Так как функция g{ (t) непрерывна, множество значений,
для которых а < gt (t) < b, измеримо В; обозначим это мно-
множество буквой е. Если мы заставим t пробегать е, то множество
соответствующих точек М(Xj, лг2, . •., хт) из Е необходимо
измеримо В, так как двум различным точкам е отвечают две
различные точки Е (стр. 167). Но это множество точек М
есть как раз то, для которого мы имеем неравенства
а<Ф{(х1, х2, ...,xj<b.
Следовательно, неявная функция у = Ф4 входит в классифи-
классификацию Бэра. Ч. т. д.
Остается лишь сделать одно замечание, касающееся не-
неявной функции Ф*. В настоящий момент эта функция опре-
определена лишь на области существования Е. Но мы можем
закончить ее определение, полагая ее равной любому постоян-
постоянному С вне Е. Так как Е измеримо В, то функция Ф4,
дополненная таким образом, заведомо входит в классификацию

ИЗУЧЕНИЕ ОДНОЗНАЧНЫХ НЕЯВНЫХ ФУНКЦИЙ 233
Бэра. Следовательно, мы можем рассматривать неявную функ-
функцию yt как часть явной функции классификации Бэра, всюду
определенной, но рассматриваемой только на множестве Е,
измеримом В. Таким образом, мы приходим ко второму
закону (Lg) Лебега:
Теорема И. Если система уравнений допускает един-
единственное решение для каждой точки области существо-
существования, то это решение состоит из функций уи входящих
в классификацию Бэра.
Случай I, когда одна из неявных функций однозначна1).
В общем случае система уравнений (I) не допускает един-
единственного однозначного решения и, следовательно, существуют
точки М (хи дг2,..., хт) из Е, которым соответствует несколько
систем значений yvys, ...,ур. В этом случае по крайней
мере одна из неявных функций уи yit ..., ур многозначна.
Мы изучим тот интересный случай, когда одна из неявных
функций, например у{, остается однозначной.
Область существования. В противоположность тому, что
мы нашли в предыдущем случае, эта область может быть про-
произвольным аналитическим множеством, значит неизмеримым В.
Чтобы убедиться в этом, возьмем в области 0'w произ-
произвольное аналитическое множество Е. Пусть f(x)—произволь-
f(x)—произвольная функция классификации Бэра. Возьмем в области 0т
множество Н точек Р(х, у), для которых ордината у имеет
значение, определенное уравнением y=f(x), а абсцисса
пробегает данное аналитическое множество Е.
Легко видеть, что множество Н есть аналитическое. В самом
деле, если х =о(f) есть непрерывное параметрическое изо-
изображение Е, то уравнения
x = ?(t), у =/[?(*)]
дают параметрическое изображение Н при помощи функций
• классификации Бэра. Следовательно (стр. 145), Я есть ана-
аналитическое множество.
Установив это, возьмем в трехмерной области 0' ауг мно-
множество $, измеримое В, ортогональная проекция которого на
*) Этот случай был рассмотрен в моей заметке Sut le ргр-
bleme des fonctlons implicites в Comptes Rendus 8 июля 1929 г.

234 ГЛ. IV. НЕЯВНЫЕ ФУНКЦИИ
плоскость XOY совпадает с //; Пусть F(x, у, г) есть
функция, равная 0 на § и 1 вне S. Так как §> измеримо В,
то функция F(x, у, г) входит в классификацию Бэра. Но
если мы рассмотрим уравнение
F(x,y, г) = 0,
то область существования неявных функций у и z, очевидно,
совпадает с Е, причем неявная функция у однозначна, так
как она равна f(x) на ? и не существует вне Е.
Таким образом, мы констатируем, что если одна из нер-
неравных функций (но не все) однозначна, то область суще-
существования может быть неизмерима В.
Следовательно, закон (Z.j) Лебега не сохраняется.
Природа однозначной неявной функции. Пусть
есть неявная функция, однозначная всюду в области суще-
существования Е. Если мы геометрически изобразим эту функцию
в /»-]-1-мерной области 0Х,Х х у., мы получим анали-
аналитическое множество (стр. 226) Н, ортогональная проекция
которого на область 0ХХ ...х совпадает с Е. Так как не-
неявная функцияyt однозначна, то каждая параллель Dm к оси OY{,
проведенная через точку М из Е, пересекает аналитическое
множество Н в одной и только одной точке. Отсюда следует,
что две различные точки Н имеют различные проекции. Из
этого вытекает (стр. 166), что аналитическое множество Я
измеримо В в том и только в том случае, когда область
существования Е измерима В, что является частным случаем.
Значит, вообще говоря, изображающее множество И не-
неизмеримо В. Тем не менее, мы констатируем тот неожиданный
факт, что в области 0хх ...я, можно провести однозначную
поверхность S, измеримую В,
которая проходит; через все точки Н.
Другими словами, однозначная неявная функция, опре-
определенная на области существования Е, совпадает с неко-
некоторой функцией классификации Бэра, определенной всюду
на 0х ха...х •

ИЗУЧЕНИЕ ОДНОЗНАЧНЫХ НЕЯВНЫХ ФУНКЦИЙ 235
Мы видим, что это и есть второй закон A^) Лебега.
Этот факт есть прямое следствие одного общего пред-
предложения из геометрии.
Теорема. Если $ есть аналитическое множество,
расположенное в т~\~ 1-мерной области 0'х ,,.х у, такое,
что каждая параллель к оси OY пересекает $ не более
чем в одной точке, то существует функция <?(х1, х2,..., хт),
входящая в классификацию Бэра, всюду определенная
и такая, что множество $ лежит на поверхности S,
определенной уравнением у = <о(х1,х2,..., хт).
Чтобы доказать это, возьмем непрерывное параметрическое
изображение $
Обозначим через $t множество точек области &х ...х у,
расположенных под S. Ясно, что координаты всех точек §>t
можно записать в виде
где т— любое отрицательное число.
Аналогично, обозначим через ?-2 множество точек, лежащих
над &; все точки $2 можно получить, приняв в предыдущих
формулах за z любое положительное число.
Очень легко доказать, что множества $1 и §2—аналити-
§2—аналитические; достаточно заполнить кривой Пеано t = g(u), t = A()
область @<?< 1, — оо<т<0). Уравнения
*i = ?i[?(«)!> Ч
очевидно, дают параметрическое изображение $]а Точно так же
доказывается аналитичность множества f2.
Так как аналитические множества S-f-^i и ^2 не имеют
общей точки, то они отделимы В. Пусть И есть множество,
измеримое В, содержащее ё-j-Sj и не имеющее общей точки
с ё2- Точно так же пусть Н2 — множество, измеримое В,
содержащее § -\- ?2 и не имеющее общей точки с Sj. Пусть Н—
общая часть Нх и //2. Ясно, что Н есть множество, изме-
измеримое В, содержащее S и такое, что всякая параллель к оси OY,

236 ГЛ. IV. НЕЯВНЫЕ ФУНКЦИИ
проведенная через точку Е, пересекает Н в одной и только
т)дной точке.
Установив это, обозначим через Q множество точек об-
области 0'х ...^ у, расположенных на всех параллелях к оси OY,
каждая из которых пересекает Н по крайней мере в двух
различных точках. Так как ортогональная проекция Q на
область 0х...х есть аналитическое множество (стр. 169), то
и само Q есть аналитическое множество.
Отсюда следует, что общая часть V множеств Q и Н есть
аналитическое множество. Но мы заметили, что каждая
прямая, параллельная оси OY и проведенная через точку из Е,
пересекает Н в одной и только одной точке. Значит, анали-
аналитические множества V и $ не имеют ни одной общей точки.
Отсюда следует, что существует множество 5', измеримое В,
содержащее § и не имеющее общей точки с V. Обозначим
через S общую часть S' и Н. Так как множества S' и Н
измеримы В, то и S будет таковым.
Легко видеть, что не существует ни одной параллели
к оси OY, которая пересекает 5 в двух различных точках.
В самом деле, если прямая D, параллельная оси OY, пере-
пересекает 5 в двух различных точках, то прямая D пересекает Н
в двух различных точках, а значит, D принадлежит к Q.
Следовательно, все точки Н, расположенные на ?>, принад-
принадлежат к V, что невозможно, так как среди этих точек есть
точки S, а множества 5 и V не имеют общей точки.
Отсюда следует, что множество 5 есть множество, изме-
измеримое В, содержащее S и такое, что каждая параллель
к оси OY пересекает S не более, чем в одной точке. Поэтому
проекция 5 на 0'х ...х есть множество, измеримое В; обо-
обозначим его через о.
Очевидно, что функция <о (хи х2, ..., хт), равная любой
постоянной вне о и равная координатам у точек S на о, есть
функция классификации Бэра. С другой стороны, однозначная
поверхность у = ю (хи х2, ..., хт), очевидно, проходит через
все точки множества S. Ч. т. д.
Природа множества точек, в которых неявная функция
ииеет единственное значение. Рассмотрим какую-нибудь не-
неявную функциюу{(хj, х2,..., хт) и возьмем в области 0Xlsn2...xmy
представляющее ее множество //». Все значения, которые

ИЗУЧЕНИЕ ОДНОЗНАЧНЫХ НЕЯВНЫХ ФУНКЦИЙ 237
принимает у{ в какой-либо точке М области существования Е,
можно получить, пересекая множество Н{ параллелью Dm
к оси OY^ проведенной через М.
Отсюда следует, что функция yt имеет единственное
значение в точке М, когда прямая DM пересекает Ht в одной
и только одной точке.
Так как множество Я4 есть проекция S на область 0Х ...х у ,
то Ht есть произвольное аналитическое множество.
Итак, все сводится к определению природы множества Е'
тех точек области 0'х ...а, , в которых параллели к оси 0Y
пересекают данное аналитическое множество Н, лежащее
в д х ...х у, в одной и только одной точке.
Мы докажем, что Е' есть разность двух аналитических
множеств.
Чтобы убедиться в этом, обозначим через Е проекцию Н
на область 3 х ...х и через Е" — множество точек этой
области, в которых параллели к оси 0Y пересекают мно-
множество И не менее чем в двух различных точках. Так как
множество Н аналитическое, то и множества Е и Е" будут
аналитическими (стр. 169). Но рассматриваемое множество Е'
есть, очевидно, разность Е — Е", что и доказывает наше
предложение. Ч. т. д.
С другой стороны, обратное предложение, очевидно, также
справедливо: каждое множество точек, являющееся разностью
двух аналитических, может быть рассматриваемо как мно-
множество точек, в которых параллели к оси 0Y пересекают
некоторое аналитическое множество в одной и только одной
точке.
В общем случае разность двух аналитических множеств
не есть ни аналитическое множество, ни аналитическое допол-
дополнение; это множество новой природы.
Легко видеть, какова природа множества, представляющего
единственные значения неявной функции. Достаточно рассмо-
рассмотреть множество тех точек Н, проекции которых принад-
принадлежат к Е'. Так как множество Н аналитическое, и так как
множество точек Н, проекции которых принадлежат к Е",
тоже аналитическое, то рассматриваемое изображающее мно-
множество есть разность двух аналитических множеств.

238 ГЛ. IV. НЕЯВНЫЕ ФУНКЦИИ
Таким образом, мы заключаем, что множество точек
области 0Ху..х у, изображающих единственные значения
неявной функции. у{, есть разность двух аналитических
множеств, равно как и ортогональная проекция этого
изображающего множества на 3х ...хт1)-
Теперь легко узнать природу множества, образованного
из точек области существования Е, в которых уравнения (I)
допускают единственное решение. Это множество есть, оче-
очевидно, общая часть множеств E'v i=\, 2,...,р, каждое из
которых есть разность двух аналитических: Е^ = Е— Е'!. Так
как эту разность можно представить в виде Е • СЁ1 и так
как общая часть конечного числа аналитических дополнений
есть опять аналитическое дополнение, мы заключаем, что
множество точек области существования Е, в которых
уравнения (I) допускают единственное решение, есть раз-
разность двух аналитических множеств.
Изучение многозначных неявных функций со счетным
множеством значений
Случай II, когда все неявные функции многозначны
и имеют не более счетного множества значений2). Этот
случай аналогичен случаю Лебега.
Область существования. Легко видеть, что эта область
измерима В и, следовательно, первый закон (Z,,) Лебега
сохраняется. В самом деле, множество §>, измеримое В, имеет
своей проекцией область существования Е, и притом каждая
точка Е есть проекция не более чем счетного множества
точек S. Известно (стр. 178), что в этих условиях множество Е
измеримо В.
*) Мы увидим в конце этой главы, что если изображающее
множество N для неявной функции у измеримо В (а не произ-
произвольное аналитическое множество), то множество, которое изображает
единственные значения yit а также и проекция этого множества
на &Ху..хт, оказываются оба аналитическими дополнениями. Это
очень важный факт, доказательство которого представляет значи-
значительные трудности.
2) См. П. С. Н о в и к о в, Sur les fonctions impHcltes mesurables В,
Fund. Math., т. XVII, 1931.

ИЗУЧЕНИЕ СЧЕТНОЗНАЧНЫХ НЕЯВНЫХ ФУНКЦИЙ 239
Природа неявных функций. Гораздо труднее установить
природу неявных функций. Для того чтобы ее изучить, мы
вынуждены рассмотреть структуру непрерывной полурегуляр-
полурегулярной функции.
' Пусть y=f(x) есть непрерывная и полурегулярная функ-
функция, определенная на порции @,1) области 0Х; это значит,
что каково бы ни было действительное число у0, уравне-
уравнение yo — f(x) имеет не более счетного множества корней.
Итак, возьмем любое у на оси OY. Пусть Fy есть
множество корней уравнения _уо=/(лг). Так как f {х) не-
непрерывна и полурегулярна, то множество Fy счетно (или
конечно) и замкнуто в 0х. Отсюда следует, что если мы
возьмем последовательные производные от этого множества,
мы придем к некоторому производному множеству, которое
будет пустым (лишенным точек). Пусть а.у есть наименьшее
трансфинитное число второго класса (или конечное), такое,
что производное множество от Fy порядка ау лишено точек.
Это число ау мы назовем индексом остановки, соответ-
соответствующим точке у0.
Установив это, мы докажем, что индексы остановки огра-
ограничены для каждой непрерывной полурегулярной функ-
функции f(x). Это значит, что существует трансфинитное число
второго класса (или конечное) C, которое превосходит всякий
индекс остановки ау , какова бы ни была точка у на оси ОК.
Допустим обратное; это значит, что каково бы ни было
трансфинитное число f второго класса, найдется точка у,
для которой ау > у.
Я теперь утверждаю, что на ?f x существует два интервала
Бэра, Ьх и 82, без общих точек и такие, что, как бы велико
Ни было f, производное порядка f от Fy эффективно содержит
точки в Sj и 82, если только у выбрано надлежащим образом.
В самом деле, мы можем выбрать точку у так, чтобы
производное порядка f от Fy содержало не менее двух раз-
различных точек. Пусть Ьг и 82 — два интервала Бэра без общих
точек, причем каждый из них эффективно содержит точки
производного Fy. Так как существует лишь счетное множество
пар интервалов Бэра, тогда как трансфинитных чисел ^ не-
несчетное множество, то пара Ь1 и 82 с указанным свойством
должна существовать.

240 ГЛ. IV. НЕЯВНЫЕ ФУНКЦИИ
Установив это, допустим, что существует k интервалов
Бэра 8j, 8g, . ..,8ft попарно без общих точек и таких, что,
как бы велико ни было -(, производное порядка f от Fy
эффективно содержит точки в каждом из этих интервалов,
если только у выбрано надлежащим образом. Мы докажем,
что в этих условиях существует в каждом 8^ два интервала
Бэра 8< и hi без общих точек и таких, что система из 2k
интервалов 8Ь 8lf ..., 8*, 8* обладает тем же свойством.
В самом деле, на основании свойства интервалов 81( .. . ,8Й,
как бы велико ни было •(, можно найти точку у такую, что
производное множество порядка •( от Fy содержит по крайней
мере две различные точки Х{ и Х{ в каждом 84. Заключим
эти точки х{ и x'i в два интервала Бэра 8* и 8< без общих
точек и содержащихся в 8^. Так как существует лишь счетное
множество систем интервалов 8$ и 8»-, /== 1, 2, ...,&, и так
как трансфинитных чисел f несчетное множество, мы заключаем,
что существует система из Ik интервалов Бэра 8i, 8">• • •» ^> &%,
обладающая указанным свойством.
Из предшествующего мы заключаем, что на 0'х суще-
существует такое совершенное множество Р, что каково бы ни
было п, совершенное множество Р содержится в 2й интер-
интервалах Бэра попарно без общих точек 81, 82, ..., 82п таких,
что каждый из этих интервалов эффективно содержит точки
замкнутого множества Fy при надлежаще выбранном у. Кроме
того, порядок интервалов Бэра 8^ 82,..., 82„ можно пред-
предполагать как угодно высоким.
Так как/(дг) непрерывна на 0^ отсюда следует, что/(дг)
постоянна на Р. В самом деле, в противном случае мы
имели бы две точки Р, xt и х2, такие, что f{xx) ?=f(x2).
Эти две точки заключены в двух различных интервалах 8^
и bj системы 8±, 8а, ..., 8а». Так как длина этих интервалов
стремится к нулю, когда п неограниченно возрастает, то
отсюда следует, что множества значений f(x) на 84 и 8^- не
имеют общей точки. Но это невозможно, так как множество Fy
для некоторого у имеет точки в bt и 8^ одновременно.
Таким образом мы приходим к заключению: если индексы
остановки ау неограничены, то существует точка у, для
которой множество ,Fy несчетно, а следовательно, функция / (дг)

ИЗУЧЕНИЕ СЧЕТНОЗНАЧНЫХ НЕЯВНЫХ ФУНКЦИЙ 241
не будет полурегулярной. Итак, в рассматриваемом нами
случае индексы остановки ограничены. Ч. т. д.
Прежде чем приступить к изучению природы множества
измеримого В, пересекаемого каждой параллелью к некоторому
данному направлению не более чем в счетном множестве
точек, мы докажем следующую лемму: если $ есть множе-
множество, измеримое В, лежащее в ifXlxy..xmy и. такое, что
всякая параллель к оси OY пересекает §> не более чем
в счетном множестве точек, то множество Е тех точек
области ?Jxx...x , для которых параллели к оси OY
пересекают § в одной и только одной точке, измеримо В.
Чтобы доказать это, возьмем на оси О Y все рациональные
точки г,, г2, ••-,/¦„, ... Пусть &'п и Ь"п — части Ь, для
которых координата у соответственно меньше или больше /•„.
Эти множества §„ и Ьп измеримы В и таковы, что каждая
параллель к оси OY пересекает их не более счетного числа
раз. В силу предшествующего (стр. 178) проекции е'п и е"п
множеств ?>„ и §п на область 0'х ...д, измеримы В. Это же
имеет место для общей части Еп ¦ Е'п и для суммы S всех
этих общих частей, где я = 1,2, 3,... Но множество S
есть, очевидно, множество всех точек области 0Хх ...х > для
которых параллель к оси OY пересекает S по крайней мере
в двух точках. С другой стороны, проекция Е множества S
на 8х~...хт также измерима В; поэтому то же справедливо
и для разности Е — 5. Но эта разность, очевидно, совпадает
с рассматриваемым множеством Е'. Ч. т. д.
Установив это предварительное предложение, возвратимся
к изучению структуры непрерывной полурегулярной функ-
функции /(¦*). Мы хотим доказать следующее предложение:
если функция f (x) непрерывна и полурегулярна, то кри-
вую y=f{x) можно разложить на счетное множество
множеств, измеримых В и однозначных по отношению
к оси OY. Это значит, что всякая параллель к оси ОХ пере-
пересекает каждое из этих множеств не более чем в одной
точке.
Чтобы доказать это важное предложение, рассмотрим
в области 0„.у все прямоугольники Бэра Rlt R2, ..., Rn,...
Обозначим через Qn множество точек кривой у =/ (лг), лежащих
16 Зах. 284. Н. Н. Лумш

g42 'ГЛ. IV. НЕЯВНЫЕ ФУНКЦИЙ
в Rn. Рассмотрим множество всех параллелей к оси ОХ,
пересекающих Qn в одной и только одной точке. Пусть d%\
есть множество точек Qn> лежащих на этих прямых. В силу
предыдущих рассмотрений, 1^' есть множество, измеримое В.
Удалив из кривой y—f{x) все точки, принадлежащие мно-
множествам ij?', мы получим в области 0' ау множество $0, изме-
измеримое В; это множество получается непосредственно, если
провести все параллели к оси ОХ и удалить из каждой из
этих параллелей изолированные точки тех линейных замкнутых
множеств, по которым эта параллель пересекает кривую.
Мы можем повторить эту операцию и удалить из $0 все
изолированные точки, лежащие на параллелях к оси ОХ, что
дает нам счетное множество новых множеств Lj1', lip, . . .
..., L%\ ..., измеримых В и однозначных по отношению к оси О К,
Легко видеть, что эту операцию можно повторять и что мы
не встретимся ни с каким препятствием до тех пор, пока все
точки кривой y=f(x) не будут удалены. Но это, несомненно,
случится после счетного множества указанных операций, так
как индексы остановки а ограничены.
Итак, мы можем рассматривать кривую у =/(л:) как
соединение счетного множества множеств, измеримых В:
Z.j, 12, ...,?„, ...» однозначных по отношению к оси OY.
Этими рассуждениями наше предложение доказано, но мы
хотим еще уточнить выбор однозначных множеств Ln.
Прежде всего мы можем предполагать, что множества Ln
попарно без общих точек. Чтобы убедиться в этом, доста-
достаточно сохранить в Ln точки, которые не принадлежат ни
одному из предыдущих множеств L,, Z^, ..., /.„_,, что не
уничтожает измеримости В множества сохраненных точек.
Установив это, преобразуем множества Ln следующим об-
образом: возьмем Lx и прибавим к Lt все точки Ln, проекции
которых на ось OF не принадлежат ни к одной из проекций
предшествующих множеств Lt, i < я. Если мы произведем эту
операцию для каждого п, мы получим множество, измеримое В,
однозначное по отношению к оси OY, проекция которого
на OY совпадает с проекцией кривой y*=f(x). Обозначим
это однозначное множество через Aj; ясно, что точки А, при-
принадлежат к кривой y*=f(x) и.что Aj содержит Lv

ИЗУЧЕНИЕ СЧЕТНОЗНАЧНЫХ НЕЯВНЫХ ФУНКЦИЙ 243
Удалим из каждого из членов последовательности Ьг, 1^,...
. .., Ln, ... все точки, принадлежащие к Ах; первый член будет
полностью удален. Но с остающимися частями множеств Ln,
п > 1 мы можем повторить ту же операцию, и таким образом
мы получим множество А2, однозначное и измеримое В, без
общей точки с Z.,. Ясно, что сумма At-\-A2 содержит Lj-j-Lg
и что проекция А2 на QY в точности совпадает с множеством
тех точек Е, в которых параллели к оси ОХ пересекают
кривую y=f{x) по крайней мере в двух точках1).
Ясно, что если мы возобновим эту операцию и будем ее
повторять неограниченно, мы получим конечную или беско-
бесконечную последовательность множеств, измеримых В,
попарно без общих точек, однозначных по отношению к оси OY,
причем их соединение совпадает в точности с самой кривой
у = f(x). Важно заметить, что проекция Ап+1 на OF содер-
содержится в проекции Ап. Но разность этих двух проекций есть
множество тех точек оси OY, в которых параллели
к оси ОХ пересекают кривую y=f(x) равно в п точках.
Значит, это множество также измеримо В.
Произведем другое преобразование множеств LJt L%, ...
..., Ln, ... Прежде всего прибавим к Lx точки всех тех Ln,
п > 1, проекции которых на О К не принадлежат ни к одной
из проекций предшествующих множеств Lv L^, ..., Ln_x.
Этим способом мы получим множество, измеримое В, одно-
однозначное и проекция которого на О К совпадает с Е\ пусть Ха
это множество. На плоскости XOY мы можем провести
однозначную кривую Jg'^ которая содержит множество kt
и задана уравнением х = фг (у), где tyi есть однозначная
функция классификации Бэра, всюду определенная на об-
области оГу.
Установив это, обозначим через L' и L" части множе-
множества Ln, расположенные соответственно ниже и выше одно-
однозначной и всюду определенной кривой ^v Очевидно, мы
можем возобновить указанную операцию над последователь-
последовательностями однозначных множеств L'^ L'3, ... и L^, V^ ..., что
J) Напомним, что Е есть проекция кривой у =/(аг) на ось ОК.
16*

244 ГЛ. IV. НЕЯВНЫЕ ФУНКЦИИ
дает нам две новые кривые, однозначные и определенные всюду
на OY, пусть _2V н J?b, из которых первая целиком лежит
ниже Jj?v а вторая целиком, выше ??у Важно заметить, что
соединение кривых J?x, ^2 и J3?b содержит Lt и 1^. По-
Построенные кривые .2*2 и S'b задаются уравнениями х — ^(у)
и х, = 4*з (у), где ф2 и фз суть однозначные функции класси-
классификации Бэра, определенные всюду на ОК.
¦ Три построенные таким образом кривые ^»х, ^2 й •З'з
делят плоскость XOY на четыре части, и мы можем возобно-
возобновить указанную операцию над частями множеств Lg, L4, ...,
содержащимися а этих частях плоскости; таким образом, мы
получим четыре новые кривые ^4, jg>6, jg'g, J?4, однознач-
однозначных и всюду определенных на OY.
Важно заметить,'что соединение предыдущих кривых и
этих кривых содержит кривые Lj, L2, L%.
Продолжая таким же образом, мы получим неограниченную
(или конечную) последовательность кривых .J2?v J?v • • •
¦ • •, .2V •¦ •»однозначных относительно оси ОУи всюду опреде-
определенных, соединение которых непременно содержит все точки
рассматриваемой кривой у =/(лг); каковы бы ни были
две кривые _2»4 и .2^ из этой последовательности, одна
из них расположена ниже другой. Кроме того, всякая кри-
кривая J3?n задается уравнением х = tyn (у), где ф„ есть одно-
однозначная функция классификации Бэра, определенная всюду
на OY.
В итоге, точки кривой у =/(лг), где f есть непрерывная
и полурегулярная функция, распределяются на не более
чем счетном множестве однозначных относительно OY
кривых; каждая из этих- кривых задается уравнением
x'=ty(y), где <у есть однозначная функция классификации
Бэра, всюду определенная на OY; наконец, каждая из этих
кривых лежит либо ниже, либо выше другой.
После того как этот важный частный случай изучен
подробно, мы рассмотрим несколько более общий случай.
Требуется доказать, что всякое множество &, измеримое В,
расположенное в плоской области §ху и такое, что каж-
каждая параллель к оси OY пересекает & не более, чем в счет-
счетном-множестве точек, есть соединение счетного множества
множеств, измеримых В, и однозначных относительно
оси ОХ.

ИЗУЧЕНИЕ СЧЕТНОЗНАЧНЫХ НЕЯВНЫХ ФУНКЦИЙ 245
Чтобы убедиться в этом, достаточно взять непрерывное
регулярное изображение множества §
где, если это нужно, мы пренебрегаем счетным множеством
точек $.
Так как всякая прямая х = const пересекает § не более
чем в счетном множестве точек, то функция g(f) полурегу-
полурегулярна. Следовательно, уравнение х = g (f) определяет t как
обратную функцию аргумента х, и легко видеть в силу
полученного результата, что эта обратная функция есть соеди-
соединение счетного множества явных однозначных функций
входящих в классификацию Бэра; кроме того, каждая из этих
функций со„ рассматривается лишь на некотором множестве еп,
измеримом В, расположенном на 0 х.
Подставляя t в уравнение
мы получаем счетное множество явных однозначных функций
входящих в классификацию Бэра. Заставляя х в уравнении
у = h [сои (х)] пробегать множество еп, мы получим в плоско-
плоскости XOY множество Ln, однозначное относительно оси ОХ
и измеримое В. Ясно, что данное множество $ есть соедине-
соединение этих множеств Ln. Ч. т. д.
Перейдем теперь к общему случаю. Мы докажем следую-
следующую общую теорему J):
Теорема. Если $ есть множество точек, лежащцх
в т-\- 1-мерной области 0х ...х у, измеримое В и такое,
что каждая параллель к оса OY пересекает $ не более
чем в счетном множестве точек, то точки $ распреде-
распределяются на счетном множестве однозначных поверх-
поверхностей Sn, измеримых В, определенных уравнениями
y=fn(xu x2, ..., хп), где каждая fn есть однозначная
*) См. мою заметку «Sui la representation pararaetrique seraire-
gullere des ensembles» (C. R. Acad. Sc, 29 июля 1929).

246 ГЛ. IV. НЕЯВНЫЕ ФУНКЦИИ
функция классификации Бэра, определенная всюду в обла-
области &хх ...х ', кроме того, про любые две поверхности
Sf и Sj можно утверждать, что одна из них лежит
под другой.
Чтобы доказать это, преобразуем тя-мерную область $ х ,%%х
в линейную область g m при помощи взаимно однозначного и
взаимно непрерывного преобразования (стр. 170).
Пусть
И A)
x=Q(xlt лг2, ..., хт) )
— уравнения, определяющие это преобразование; функции g{
и О непрерывны.
Если мы прибавим к этим уравнениям тождество
У=У>
то получим взаимно однозначное и взаимно непрерывное пре-
преобразование /и-f-1-мерной области &хх х у в плоскую об-
область tfny. Известно (стр. 170), что множество, получаемое
при таком преобразовании из множества, измеримого В, само
измеримо В и того же класса и подкласса; кроме то-
того, ясно, что множество, однозначное по отношению к оси
ОХ в области 0ху, преобразуется во множество, также од-
однозначное относительно области $ х. шХ в Я х х „
X п 1 т*
и обратно.
Установив это, обозначим через $' результат преобразо-
преобразования $. Очевидно, что $' есть плоское множество, измери-
измеримое В, и что каждая параллель к оси OY пересекает t/ не
более чем в счетном множестве точек. Следовательно, мно-
множество &' есть соединение счетного множества множеств Z-i,
Lz, ..., измеримых В, однозначных относительно оси ОХ.
Следовательно, данное множество S, будучи прообразом $',
есть соединение множеств Lx, Lv ..., Ln. ..; здесь мы
через Ln обозначаем прообраз Ln. Все эти множества одно-
однозначны относительно области 3Xt...x и измеримы В.
Если над полученными однозначными множествами L^L^, ...
мы будем оперировать так, как мы это делали раньше в случае

ИЗУЧЕНИЕ СЧЕТНОЗНАЧНЫХ НЕЯВНЫХ ФУНКЦИЙ 247
полурегулярной функции y=f(x), мы придем к последова-
последовательности поверхностей Su S2 Sw ..., содержащих
точки данного множества $ и удовлетворяющих формулировке
предложенной теоремы. Ч. т. д.
Установив это, вернемся к исследованию данной системы
уравнений (I):
•, xm\ yu y%, ..., yp) = 0,
/а (•*!» *2> • • •. *»»"» .Ун Л» • • • > Ур) — °
(I)
Мы предполагаем, что каждой системе чисел Arlt лг2, ..., хт
соответствует не более чем счетное множество систем чи-
чисел у у, у2, ..., ур, удовлетворяющих этим уравнениям.
Возьмем две области 3х ...х и 8'у .. „ и преобразуем
их соответственно в две линейные области ?f x и 0у при
помощи двух взаимно однозначных » взаимно непрерывных
преобразований. Пусть
x=Q(xv лг2, ..., хт) ]
и
Л = Л1W. Л = К (У), •¦-, Ут = Ьт (У),
—уравнения, устанавливающие эти два преобразования.
Легко видеть, что уравнения A) и B), взятые вместе,
устанавливают взаимно однозначное и взаимно непрерывное
преобразование m-j-p-мерной области &х...х у ...у в пло-
плоскую область 0 ху. Отсюда следует, что множество S', являю-
являющееся результатом преобразования §, есть множество, изме-
измеримое В, расположенное на плоскости XOY и такое, что
всякая параллель к оси OY пересекает g' не более чем
в счетном множестве точек.
Пусть Lv Ig, ..., Lit . . . суть множества, измеримые В,
однозначные по отношению к оси ОХ и такие, что их со-
соединение совпадает с $'. Мы предполагаем, что Lt располо-
расположено на однозначной кривой у = щ (х), где функция <о{ (лг)
всюду определена и входит в классификацию Бэра.

248 ГЛ. IV. НЕЯВНЫЕ ФУНКЦИИ
Если мы подставим найденное значение у '= <ot (x) в урав-
уравнения B) и затем возьмем значение х из уравнений A), то
мы придем к решению предложенной системы (I), выражен-
выраженному при помощи функций, входящих в классификацию Бэра,
от аргументов xlt лг2, ..., хт:
1, лг2, ..., хт)]},
¦ Ур = К Ы°(*i> *2. • • •' *»»)]}•
Ясно, что написанные здесь сложные функции входят
в классификацию Бэра и что полное решение предложенной
системы (I) мы получим, полагая t=l, 2, 3, ...
Итак, мы приходим к следующему заключению: полное
решение предложенной системы уравнений образовано из
счетного множества систем из р функций <р№, <$(»), .., f (p(*>}
входящих в классификацию Бэра; каждая из этих систем
удовлетворяет предложенным уравнениям на некоторой
части Ejc области существования Е, причем эта часть
измерима В.
Итак, закон (Z.2) Лебега в этом случае сохраняется.
Случай III, где одна из неявных функций многозначна
и имеет не более счетного множества значений. Этот
случай аналогичен случаю I, где одна из неявных функций
однозначна.
Область существования. Эта область, вообще говоря,
неизмерима В, так как рассматриваемый случай содержит, как
частный случай, случай I, а в случае I область существо-
существования может быть неизмерима В.
Итак, первый закон (А,) Лебега уже не применим здесь.
Природа рассматриваемой неявной функции. Напротив,
второй закон (?2) Лебега остается в силе. В самом деле, мы
увидим, что рассматриваемая неявная функция принимает зна-
значения со счетного множества однозначных неявных функций,
входящих в классификацию Бэра.
С этой целью мы докажем следующую теорему из гео-
геометрии:
Теорема. Если $ есть аналитическое множество,
лежащее -в т-\- 1-мерном пространстве 0'х ... х у и такое,

ИЗУЧЕНИЕ СЧЕТНОЗНАЧНЫХ НЕЯВНЫХ ФУНКЦИЙ 249
что каждая параллель к оси OY пересекает $ не более
чем в счетном множестве точек, или не пересекает его
совсем, то множество S можно рассматривать как часть
некоторого множества Н, измеримого В и обладающего
тем же свойством.
Прежде всего для упрощения доказательства этой теоремы
мы сведем общий случай т -j- 1 -мерной области ?}х ... х у
к случаю плоской области g xy.
С этой целью преобразуем m-мерную область $х ... а,
в линейную область ?}х при помощи взаимно однозначного и
взаимно непрерывного преобразования. Пусть
х\ = g\(*)» x2 = g2(x), ..., xm = gm(x), \ j.
х = О(х1, х2, ..., хт) }
—уравнения, устанавливающие это преобразование; функции gt
и G непрерывны.
Если мы прибавим к этим уравнениям A) тождество
то мы получим взаимно однозначное и взаимно непрерывное
преобразование т -\- 1 -мерной области 0Х ...х у в плоскую
область 0ху. Если §> есть аналитическое множество, распо-
расположенное в gfx ...а, у и такое, что каждая параллель к оси OY
пересекает § не более чем в счетном множестве точек, то
образ $' множества $ есть аналитическое множество, обла-
обладающее тем же свойством.
Допустим, что рассматриваемая теорема справедлива для
плоской области и, следовательно, существует плоское мно-
множество Нг, измеримое В, содержащее аналитическое множе-
множество $' и такое, что каждая прямая, параллельная оси OY,
пересекает И' не более чем в счетном множестве точек. Ясно,
что прообраз Н множества Н' измерим В, содержит § и обла-
обладает опять тем же свойством.
Итак, все сводится к доказательству теоремы для пло-
плоского аналитического множества $.
Мы начнем с того, что рассмотрим в трехмерной обла-
области & xyz элементарное множество (стр. 141), проекция

250 ГЛ. IV. НЕЯВНЫЕ ФУНКЦИИ
которого на плоскость X0Y совпадает с данным аналитическим
множеством S. Мы предполагаем (стр. 193), что элементар-
элементарное множество Q есть общая часть сумм параллелепипедов
рангов 1, 2, 3, ..., таких, что каждый параллелепипед ранга п
содержит счетное множество параллелепипедов следующего
(я-]-1)-го ранга, причем их проекции на ось OZ образуют
возрастающую последовательность сегментов. Верхние грани
этих параллелепипедов образуют решето (стр. 194) С, назы-
называемое элементарным и определяющее аналитическое мно-
множество $.
Пусть it — один из этих параллелепипедов. Обозначим
через QK часть Q, содержащуюся в тг, через Ск — часть С,
содержащуюся в и, и через §л — проекцию QK на плос-
плоскость XOY. Легко видеть, что Ск есть решето, определяющее
аналитическое множество $ж.
Пусть х — любая точка линейной области g х и пусть
Рх— перпендикуляр из точки х к оси ОХ, лежащий в пло-
плоскости X0Y. Так как множество § пересекается каждым Рх
не более чем в счетном множестве точек, то дополнение С@к
измеримо В на Рх.
Отсюда следует, что общая часть СЬК и Рх содер-
содержится в счетном множестве конституант, измеримых В,
на которые разлагается дополнение С&к. Отсюда мы
заключаем, что для каждого Рх существует конечное или
трансфинитное число второго класса а?\ такое, что сумма
конституант с индексами, превосходящими или равными а$,
содержит лишь счетное множество точек на Рх, причем это
число <х?? нельзя уменьшить, не теряя этого свойства.
Если мы рассмотрим все решето С, а не его часть, ле-
лежащую в некотором параллелепипеде я, то мы обозначим про-
просто через ах трансфинитное число, которое мы только что
определили.
Установив это, мы докажем, что числа лх ограниче-
ограничены, т. е. что существует трансфинитное число р второго
класса, превосходящее каждое ах, каково бы ни было х в
области 0 х.
С этой целью допустим обратное, т. е. что числа ах не
ограничены. В этих условиях мы рассматриваем систему из k
параллелепипедов itlt it2, ..., ил, проекции которых на пло-

ИЗУЧЕНИЕ СЧЕТНОЗНАЧНЫХ НЕЯВНЫХ ФУНКЦИЙ 251
скость XOY не имеют попарно общих точек, и которые обла-
обладают следующим свойством: каково бы ни было трансфинитное
число -(, существует точка х такая, что у каждого множе-
множества с?« (i = l, 2, ..., k) по крайней мере одна конститу-
конституанта с индексом, превосходящим f, имеет несчетное
множество точек на Рх. Такие системы itj, it2, ..., -кк
существуют, так как вся область 3 xyz является такой
системой (k = 1).
Мы докажем, что каждый параллелепипед щ (i = 1, 2,..., k)
содержит пару параллелепипедов чц и щ такую, что система
из 2k параллелепипедов чси itu ..., щ, 7rft обладает тем же
свойством.
Чтобы доказать это, возьмем любое трансфинитное число f.
Пусть "[' есть трансфинитное число, превосходящее произве-
произведение f > а>ш. В силу гипотезы о параллелепипедах itlf u2, ...
. .., uft существует точка х, обладающая следующим свойством:
каждое аналитическое дополнение CJL (/ = 1,2, ..., к) имеет
конституанту bt индекса, превосходящего f', и содержащую
несчетное множество точек на Рх. Так как общая часть bt ¦ Рх
несчетна, то на Рх найдется такой сегмент Af, что часть 8^ • Рх,
содержащаяся в А{, несчетна, тогда как часть д4 • Яд,, лежа-
лежащая вне &it счетна, причем Д^ есть наименьший сегмент, обла-
обладающий этим свойством.
Установив это, возьмем целое положительное п, настолько
большое, чтобы все параллелепипеды ранга п, содержащиеся
в параллелепипеде it{, имели ребра меньше, чем -^ длины Д4,
каково бы ни было j = l, 2, ..., k.
Разделим каждый сегмент Д{ на три равные части и уда-
удалим центральную часть. Каждый из двух остающихся сегмен-
сегментов содержит несчетное множество точек Ьг • Рх. Выберем
произвольно точку множества Ьг • Рх в каждом из этих сег-
сегментов; пусть Mi и Mi — эти точки. Легко видеть, что суще-
существует несчетное множество таких пар точек М» и Мi. Про-
Проведем через точки Mi и Mi прямые, параллельные оси OZ;
пусть Di и D" — эти параллели. Так как точки Mi и м\
принадлежат к конституанте ftit отсюда следует, что пря-
прямые Di и Di пересекают решето С„ по двум вполне

252 ГЛ. IV. НЕЯВНЫЕ ФУНКЦИИ
упорядоченным множествам R • и R », каждому из которых
i 4.
соответствует трансфинитное число, превосходящее •(. Но про-
проекции параллелепипедов ранга я на ось OZ образуют вполне
упорядоченное множество сегментов, которому соответствует
трансфинитное число <оп. Отсюда следует, что существует по
крайней мере два параллелепипеда ранга п таких, что частям
R*r' и Кц,"» содержащимся соответственно в этих параллеле-
i i
пипедах, соответствуют два трансфинитных числа, превосходя-
превосходящих -(. Очевидно, что проекции этих двух параллелепипедов
ранга я на плоскость XOY не имеют общей точки, так как
эти проекции содержат соответственно точки Ж< и Mi и
имеют стороны, длина которых меньше, чем -к- длины Д4.
Так как существует лишь счетное множество пар парал-
параллелепипедов ранга я и так как, с другой стороны, существует
несчетное множество пар точек М{ и М{, мы заключаем, что
в каждом параллелепипеде irt существует два параллелепи-
параллелепипеда щ и и< ранга я такие, что прямые D{ и D{> проведен-
проведенные через точки М{ и Miy пересекают решета С/ и Cn"t
по вполне упорядоченным множествам, которым соответствуют
трансфинитные числа, превосходящие -f, причем таких точек
М{ и Mi несчетное множество.
Другими словами, мы доказали, что каково бы ни было
трансфинитное число Y» перпендикуляр Рх содержит несчетное
множество точек двух конституант с индексами, превосходя-
превосходящими y, Ь г и Ь и. аналитических дополнений С$ • и С§> » :
здесь аналитические множества § • и % и суть проекции эле-
ментарных множеств Q < и Q и, содержащихся в параллеле-
*i *i
пипедах щ и щ.
Из предшествующего следует, что система из 2k паралле-
параллелепипедов it!, щ, ..., uft, Ufc обладает тем же свойством,
как и начальная система k параллелепипедов [21].
Установив это, вернемся к доказательству формулирован-
формулированной теоремы. Выше мы определили для каждого перпендику-
перпендикуляра Рх трансфинитное число <Хд, и предположили, что числа ав

ИЗУЧЕНИЕ СЧЕТНОЗНАЧНЫХ НЕЯВНЫХ ФУНКЦИЙ 253
неограничены, когда х пробегает область §х. При этой ги-
гипотезе мы доказали, что каждая система из k параллелепи-
параллелепипедов itj, it2, ..., тсь обладающая специальным свойством,
содержит систему из 2k параллелепипедов ъ'х, к", ..., тс^,
обладающую тем же свойством. Так как проекций Параллеле-
Параллелепипедов itj, it2,..., itj. на плоскость XOY попарно не имеют
общих точек и все имеют точки на одной и той же параллели
к оси ОY, то, повторяя этот процесс неограниченно, мы по-
получим совершенное множество, содержащееся в элементарном
множестве Q, проекция которого на плоскость XOY есть
совершенное множество, лежащее на прямой, параллельной
оси OY. Но это невозможно, так как проекция Q на пло-
плоскость XOY есть аналитическое множество §, а мы знаем,
что каждая параллель к оси OY пересекает % не более чем
по счетному множеству точек.
Итак, трансфинитные числа ах ограничены.
Установив это, возьмем трансфинитное число |3 второго
класса, превосходящее все аа. Рассмотрим все конституанты
аналитического дополнения С!, индексы которых меньше fJ.
Пусть S есть соединение этих конституант; множество 5, оче-
очевидно, измеримо В. Обозначим через Н дополнение ко мно-
множеству S; множество Н также измеримо В. Ясно, что Н
содержит данное аналитическое множество &.
Я теперь утверждаю, что множество Н пересекается каж-
каждой параллелью к оси OF не более чем в счетном множестве
точек. В самом деле, в противном случае мы бы имели пер-
перпендикуляр Яд,, содержащий несчетное множество точек из И.
Эти точки образуют множество, измеримое В. Значит, это
множество содержится в счетном множестве конституант Сё,
причем эти конституанты имеют индексы, превосходящие р. От-
Отсюда следует, что существует конституанта индекса, превосхо-
превосходящего |3, и имеющая несчетное множество точек на перпенди-
перпендикуляре Рх. Но это невозможно, так как |3 превосходит а^.
Итак, мы определили множество Н, измеримое В, содер-
содержащее данное аналитическое множество $ и такое, что каждая
параллель к оси OY пересекает Н не более, чем в счетном
множестве точек, а это и доказывает высказанную теорему.
Ч. т. д.
Из доказанной теоремы следует, что всякое аналитиче-
аналитическое множество $, лежащее в т~\-\-мерной области

254 ГЛ. IV. НЕЯВНЫЕ ФУНКЦИИ
$х ... х у и такое, что каждая параллель к оси 0Y пере-
пересекает $ не более чем в счетном множестве точек, есть
соединение счетного множества аналитических множеств
§j, $а, ..., $к, ..., расположенных соответственно на
однозначных поверхностях у = (рк(х1, аг2, ..., хк), где <pfc
суть явные функции классификации Бэра, определенные
всюду на§Х1...Ят.
Чтобы применить этот результат к изучению неявных мно-
многозначных функций с не более чем счетным множеством зна-
значений, достаточно заметить, что многозначная неявная функ-
функция у{ имеет в качестве геометрического образа аналитическое
множество $У\ лежащее в области §х ... а Vi и получаемое
проектированием множества $ на эту область. Если мы пред-
предположим, что неявная функция yt имеет не более счетного
множества значений, то аналитическое множество §A) удовле-
удовлетворяет условиям предыдущего результата.
Итак, счетнозначная неявная функция yt разлагается на
счетное множество однозначных функций, входящих
в классификацию Бэра, а это показывает, что второй закон
A2) Лебега частично сохраняет силу.
Изучение общего случая в проблеме • неявных функций
Общие замечания. После того как были изучены есте-
естественно представлявшиеся частные случаи, мы переходим
к общему случаю.
Изучение этих частных случаев показало нам, что область
существования неявных функций бывает, в зависимости от
того или иного случая, измерима или неизмерима В. Итак,
первый закон Лебега иногда сохраняется, а иногда не сохра-
сохраняется в этих частных случаях.
Напротив, второй закон (L2) Лебега в этих частных слу-
случаях всегда сохраняется хотя бы частично. Точнее говоря,
предполагая одну из неявных функций, например, jv», имеющей
не более счетного множества значений, мы видели, что можно
каждой точке M(xv *2, ..., хт) области существования Е
привести в соответствие единственное число ср, выбранное среди
значений этой неявной функции у{ в точке М так, что опре-

ОБЩИЙ СЛУЧАЙ В ПРОБЛЕМЕ НЕЯВНЫХ ФУНКЦИЙ 255
деленная этим способом однозначная функция ср (xv х2, ..., хт)
совпадает с некоторой функцией классификации Бэра.
Но мы увидим, что в общем случае, где относительно не-
неявных функций ничего не предполагается, определение такой
однозначной функции ср 0*11 -*а> • • • > хт) становится невоз-
невозможным. Это значит, что хотя мы всегда можем образо-
образовать однозначную функцию o(xit х%, ..., хт), выбирая
соответствующим образом ее значения среди значений
рассматриваемой неявной функции (стр. 227), но эта функ-
функция ср не совпадает на области существования Е ни с ка-
какой функцией классификации Бэра.
Эта невозможность становится почти банальной, если
область существования Е неизмерима В. Чтобы убедиться
в этом, возьмем уравнение
такое, что область Е существования неявной функции у не-
неизмерима В. Так как F входит в классификацию Бэра, то
множество $ точек плоскости XOY, в которых F обращается
в нуль, измеримо В. Область существования Е есть ортого-
ортогональная проекция $ на ось ОХ. Если существует однозначная
функция <p(Jf), определенная на Е, удовлетворяющая уравне-
уравнению F = 0 и совпадающая на Я с функцией, входящей в клас-
классификацию Бэра, то общая часть Н множества $ и кривой
у = ср (х) есть однозначное множество, измеримое В. Следо-
Следовательно, проекция Н на ось ОХ должна быть измерима В,
что невозможно, так как эта проекция совпадает с областью Е.
Ч. т. д.
Итак, изучение случая, когда область существования не-
неизмерима В, не представляет никаких затруднений. Но не так
обстоит дело, когда область существования измерима В. Однако
мы увидим, что есть случаи, когда область существования
измерима В (и даже совпадает с основной областью 0Х ... х у)
и где тем не менее невозможно определить однозначную
функцию ср (atj, аг2, ..., хт), входящую в классификацию
Бэра, значения которой выбираются из значений много-
многозначной неявной функции.
Эти случаи очень важны, но, чтобы доказать, что такие
случаи эффективно существуют, мы нуждаемся в некоторых
предварительных рассмотрениях.

256 ГЛ. IV. НЕЯВНЫЕ ФУНКЦИИ
Прежде, чем перейти к доказательству, мы заметим, что
речь идет о решении следующей проблемы из геометрии:
Найти множество S, измеримое В, расположенное в т-\-1-
мерной области ?[х.я> ... х у > проекция которого на
cfxi...x совпадает со всей этой областью и которое
обладает следующим свойством: не существует никакой
поверхности S, определенной уравнением
y = o(xv х2, ..., хт),
где <? входит в классификацию Бэра, и каждая точка 3
принадлежит к Ь.
6 самом деле, пусть /7(аг1, лг2, ..., хт,у) есть характе-
характеристическая функция для множества $. Так как & измеримо В,
то F входит в классификацию Бэра. Так как каждая точка
M(xv х2, ..., хт) области $х ... х есть проекция точек $,
то уравнение F(xu ..., хт, у) = 0 допускает по крайней
мере одно решение у для каждой системы чисел xv ..., хт.
Но в силу предполагаемого свойства множества $ ясно, что
не существует никакого однозначного решения у = <о(х1,
лг2, ..., хт), где <р входит в классификацию Бэра. Ч. т. д.
Итак, все сводится к решению только что поставленной
геометрической проблемы.
Точки единственности:). Для решения предложенной про-
проблемы из геометрии нам понадобится одно важное понятие,
а именно понятие о точках единственности.
Пусть $ — любое множество точек, расположенное в обла-
области 0Х ... х у Мы скажем, что точка N(xv .-.., Хф у)
из $ есть точка единственности относительно оси OY, если
параллель к этой оси, проведенная через N, не пересекает $
ни в какой точке, Отличной от N. Множество всех точек
единственности называется множеством единственности
для $ и будет обозначаться через 8Х.
Пусть Е — проекция $ на область g х Хп, Пусть
?Oi> х2 хт)
х) В качестве метода для анализирования общего случая неяв-
неявных функций я взял изучение точек единственности. См. мою за-
заметку в Comptes Rendus Acad. Sc. 16 сентября 1929 г. Sur les
points d'unicite d'un ensemble mesurable B.

ОБЩИЙ СЛУЧАЙ В ПРОБЛЕМЕ НЕЯВНЫХ ФУНКЦИЙ 257
есть однозначная функция, определенная на Е, и 5 — поверх-
поверхность, определенная уравнением у = у(хи ..., *„,).
Ясно, что если каждая точка из S принадлежит к §>, то
эта поверхность непременно должна пройти через всякую точку
единственности для S; это значит, что множество $t должно
принадлежать к поверхности S.
Метод для разрешения поставленной проблемы из геометрии
состоит в том, чтобы построить множество &, измеримое В,
у которого множество единственности $г таково, что a priori
невозможно провести через $, однозначную поверхность 5,
определяемую при помощи функции классификации Бэра.
Заметим, что легко установить природу множества един-
единственности $, для множества $, измеримого В: это — анали-
аналитическое дополнение.
В самом деле, мы видели (стр. 169), что точки М(х1 ... хт)
области 3xx...xmi в которых параллель к оси О К пересе-
пересекает Ъ по крайней мере в двух точках, образуют аналитиче-
аналитическое множество. Пусть ?2 — это множество. Так как § изме-
измеримо В, то все точки $, проекции которых принадлежат
к Е2, образуют множество S2, которое должно быть аналити-
аналитическим. Следовательно, точки $, не принадлежащие к §2,
образуют аналитическое дополнение. Но ясно, что это мно-
множество совпадает с $,. Ч. т. д.
Проекция множества единственности. Проблема о при-
приводе этой проекции и ее редукция. Мы видели, что очень
легко установить природу самого множества единственности Sj.
Напротив, очень трудно узнать природу проекции ?, множе-
множества единственности &t. Следующие страницы имеют целью
констатировать тот замечательный факт, что множество Е1
есть также аналитическое дополнение.
Чтобы избежать второстепенных осложнений в наших рас-
рассуждениях, мы начнем с редукции проблемы, упрощая при-
природу множества Ev
Пусть $ — множество, измеримое В, расположенное в т -\~ 1-
мерной области $х ...Хп^ и Sj — множество единственности
Е
для $. Пусть Е и Е1 — соответственно проекции $ и $х на
область 8хх...а>т.
Мы уже видели, что можно установить взаимно однознач-
однозначное и взаимно непрерывное соответствие между точками
17 Зм. 284. Н. Н. Луша

258 ГЛ. IV. НЕЯВНЫЕ ФУНКЦИИ
области 8хх...хт и точками новой линейной области gя,
причем это соответствие устанавливается формулами
*l = /iD *Я =/я (*).•¦••*» = /¦,(*), J
где все функции /< и Z7 непрерывны.
Мы видели, что в этом соответствии двух областей
хт и ^Гд, каждому множеству, измеримому Б, соот-
соотх
... хт
ветствует множество, измеримое В того же класса и что каж-
каждое аналитическое множество преобразуется в аналитическое.
Прибавляя к предыдущим уравнениям A) тождество
У=У,
мы получаем преобразование т~\- 1-мерной области $х ... х у
в плоскую область &„#. Пусть е, slt e и ех — образы мно-
множеств ё, 6lf Е и Ev
Ясно, что е измеримо В, ех — множество единственности
для е, е и <?! — проекции е и ех на ОХ Для того чтобы Е1
было аналитическим дополнением, необходимо и достаточно,
чтобы «! было аналитическим дополнением.
Итак, все дело сводится к плоской проблеме. Но мы уви-
увидим, что возможно ее еще упростить.
С этой целью рассмотрим регулярное и непрерывное пара-
параметрическое изображение множества е (пренебрегая, быть
может, счетным числом его точек). Пусть
это изображение; функции <р и ф непрерывны на 0t.
Рассмотрим на плоскости ХОТ кривую х = <а (t). Множе-
Множество значений <p(Y), очевидно, совпадает с е, тогда как ех
есть множество всех тех точек х, в которых прямая, парал-
параллельная оси ОТ, пересекает кривую один и только один раз.
Итак, все сводится к выяснению природы множества ех
тех точек д;, в которых параллель к оси ОТ пересекает кри-
кривую л; = <р (t) один и только один раз, причем функция ©
непрерывна на Ч t. Это и есть редукция проблемы.
Природа проекции множества единственности. Итак,
надо изучить природу множества Е тех точек у, для которых

ОБЩИЙ СЛУЧАЙ В ПРОБЛЕМЕ НЕЯВНЫХ ФУНКЦИЙ 259
уравнение .у—/(х) имеет единственный корень, причем/(л:)
непрерывна на &х.
Пусть 8lf 82, ..., 8П, ... — все интервалы Бэра порядка 1
в интервале @ < х < 1). Пусть еп — множество значений / (х)
на 8П и пусть Дп — наименьший сегмент, содержащий еп\ Д„
расположен на оси OY. Так как множества еп аналитические,
то к любым двум из них, например, к et и ej, можно при-
применить второй принцип. Обозначим через e{j общую часть et
и е^ через Ry и Rjt разности et — etj и ej—ejt. В силу
второго принципа можно найти два аналитических дополне-
дополнения Hij и Hji без общих точек, содержащие соответственно Ry
и Rjt. Очевидно, можно предположить, что Ну содержится
в Д4, a Hji в Д^.
Установив это, фиксируем индекс i и заставим ] пробе-
пробегать все целые положительные числа, исключая i. Пусть Hi —
общая часть всех этих Яу
Щ = Н{1 • Hi2 ... Hi, i-t • Hit t+i ...
Ясно, что Н{ есть аналитическое дополнение, содержащееся
в А{. Легко видеть, что все эти Нг{1=\, 2, 3, ...) не
имеют попарно общих точек.
Главное свойство Ht состоит в том, что это множество
заведомо содержит все те точки у, для которых уравнение
y=if(x) имеет один и только один корень, причем этот
корень лежит в §j.
В самом деле, каждая точка у, удовлетворяющая этому
условию, принадлежит всем R{j, значит, всем Нц и, следо-
следовательно, множеству Н{.
Кроме того, для всякого у, принадлежащего к Нь все
корни уравнения ^=/(лт) принадлежат к bi%
Таким образом, мы получили счетную последовательность
#i, #2, ..., Нп ... аналитических дополнений попарно без
общих точек; их соединение содержит множество Ех. Мы
назовем эти множества Н„ аналитическими дополнениями
порядка 1.
Чтобы определить аналитические дополнения порядка 2, мы
берем любое множество Н{ и соответствующий интервал
Бэра &t. Мы делим 84 на все интервалы Бэра порядка 2;
пусть &[, Sg, ..., 8fc, ... эти интервалы. Обозначим через е^
17*

260 ГЛ. IV. НЕЯВНЫЕ ФУНКЦИИ
множество значений /(лг) на Ьк и через Д*—наименьший сег-
сегмент оси OY, содержащий е^.
Мы можем оперировать с множествами е'ь таким же обра-
образом, как с ранее определенными множествами et и мы таким
образом получим счетную последовательность аналитических
дополнений Н]с попарно без общих точек, содержащихся в соот-
соответствующих Ля и в Н{.
Важно заметить, что Ни содержит все точки у, для кото-
которых уравнение y=f(x) имеет один и только один корень,
причем этот корень принадлежит к 8».
Кроме того, для каждого у, принадлежащего к Hi, все
корни уравнения y=f(x) принадлежат к 8*.
Все так определенные для каждого Ht множества Нк мы
назовем аналитическими дополнениями порядка 2.
Описанный нами процесс неограниченно продолжается и
дает нам аналитические дополнения всех порядков.
Обозначим через Sn сумму всех аналитических дополнений
порядка п; множество Sn есть аналитическое дополнение.
Пусть, наконец, Н есть общая часть всех Sn; множество Н
есть, очевидно, аналитическое дополнение.
Я теперь утверждаю, что Н в точности совпадает
с множеством Е1г природу которого мы хотим определить.
Прежде всего, Н содержит Ех, так как каждое Sn, оче-
очевидно, содержит Ev
С другой стороны, пусть у0 есть точка Н\ так как Sn
есть сумма аналитических дополнений попарно без общих
точек, то у0 принадлежит одному и только одному из них.
Пусть hn — это аналитическое дополнение, оп — наименьший
сегмент, содержащий hn и Ъп — интервал Бэра порядка я,
соответствующий hn. В силу свойства аналитических до-
дополнений порядка п все корни уравнения yo=f(x) ^содер-
жатся в Ьп.
Заставляя изменяться п, мы получаем неограниченную
последовательность интервалов Бэра dlt 02 ftn, ... по-
порядков соответственно 1, 2, 3, ..., содержащихся друг
в друге. Следовательно, существует иррациональная точка х0,
принадлежащая всем $м.

ОБЩИЙ СЛУЧАЙ В ПРОБЛЕМЕ НЕЯВНЫХ ФУНКЦИЙ 261
Я теперь утверждаю, что _у0 =/(#). В самом деле, обе
точки у0 и f(x0) принадлежат к Ъп, каково бы ни было я,
а так как длина **п стремится к нулю, когда « неограниченно
возрастает, то постоянные точки у0 и /(лт0") должны совпасть.
С другой стороны, дг0 есть единственный корень уравнения
yo=f(xo). В самом деле, все корни этого уравнения содер-
содержатся в Ьп, каково бы ни было я, а длина Ьп стремится
к нулю.
Значит, множества //и Е, тождественны и, следовательно, Ег
есть аналитическое дополнение. Ч. т. д.
Таким образом, мы приходим к следующему результату:
Теорема. Каково бы ни было множество $, измери-
измеримое В, множество Sj его точек единственности и проек-
проекция ?, этого множества единственности являются оба
аналитическими дополнениями.
Важно заметить, что проекция Е множества точек един-
единственности §1 есть произвольное аналитическое дополнение.
Чтобы убедиться в этом, ограничимся случаем множества $,
измеримого В и лежащего на плоскости.
Пусть ЕЛ — совершенно произвольное линейное аналитиче-
аналитическое дополнение, лежащее на оси ОХ. Множество CEt есть
аналитическое множество. Значит, существует плоское мно-
множество Н, измеримое В, проекция которого на ось ОХ сов-
совпадает с CEt. Обозначим через $ соединение Н и параллели
к оси ОХ, не пересекающей Н. Такие параллели всегда суще-
существуют, так как мы можем предположить, что множество Н
лежит между прямыми у = 0 и у = 1. Легко видеть, что $
измеримо В и имеет Et проекцией своего множества един-
единственности.
К Однако нельзя утверждать, что всякое плоское аналити-
аналитическое дополнение 8, пересекаемое не более чем в одной
точке каждой параллелью к оси OY, служит множеством
единственности^для некоторого плоского множества §, изме-
измеримого В.
В самом деле, если бы это было так, то проекция 8 на
ось ОХ была бы непременно аналитическим дополнением. Но
в силу исследований Мазуркевича, которое мы изложили
в главе V, проекция однозначного аналитического дополнения
может, в некоторых случаях, быть произвольным анали-
аналитическим множеством.

262 ГЛ. TV. НЕЯВНЫЕ ФУНКЦИИ
Второе доказательство существования двух аналитиче-
аналитических дополнений, неотделимых В. Доказательство преды-
предыдущей теоремы о природе проекции множества единственности
и пример, который мы только что привели, дают нам вполне
ясное указание на существование таких аналитических допол-
дополнений.
В самом деле, допустим противное, т. е. что всякие два
аналитических дополнения Н' и Н" без общих точек отде-
отделимы В. В этих условиях любые два множества, взаимно
отделимые при помощи аналитических дополнений, просто
отделимы В. Отсюда следует, что в предыдущем доказатель-
доказательстве мы можем предполагать все отделяющие множества Нц
просто измеримыми В. Из этого вытекает, что множества Hi
всех порядков, а следовательно, и суммы Sv 52, ..., Sn, ...
также измеримы В. Но множество Н есть общая часть всех
5П(« = 1, 2, 3, ...). Поэтому Н измеримо В и мы отсюда
заключаем, что проекция множества единственности всегда
измерима В.
Но это невозможно, так как мы показали, что проекция
множества единственности может быть произвольным анали-
аналитическим дополнением, а следовательно, неизмеримым В. Ч. т. д.
Общий случай неявных функций. Отступление в сторону
проекций множеств единственности было сделано с целью
разрешения ранее поставленной проблемы из геометрии: найти
в пространстве OXYZ множество %>, измеримое В, проекция
которого на плоскость XOY совпадает с этой плоскостью и
которое обладает следующим свойством: не существует ника-
никакой поверхности S, определенной уравнением z = F (лг, у),
где F входит в классификацию Бэра, причем каждая точка S
принадлежит к $.
Мы теперь дадим решение этой'проблемы.
С этой целью возьмем функцию ер (лг, f), которую мы
определили выше (стр. 147). Эта функция обладает следую-
следующими свойствами: 1° она определена для всех х и t, принад-
принадлежащих интервалу @,1), и входит в класс 2 классификации
Бэра; 2° какова бы ни была функция /(лг), определенная на
@ < х < 1) и непрерывная для всякого иррационального х,
существует такое иррациональное t0, что мы тождественно
имеем

ОБЩИЙ СЛУЧАЙ В ПРОБЛЕМЕ НЕЯВНЫХ ФУНКЦИЙ 263
Установив это, возьмем в пространстве OXYZ множество
точек М (х, у, г), координаты которых удовлетворяют урав-
уравнению
л: = <р (г, у).
Это множество, очевидно, измеримо В; мы его обозначим
через Н. Легко видеть, что Н расположено ниже плоскости
г = 1. Важно заметить, что множество И пересекается пло-
плоскостью у = у0 по любой кривой, непрерывной для каждой
иррациональной точки г.
Возьмем теперь на оси ОХ произвольное множество е,
измеримое В. Мы можем определить функцию /(г), непре-
непрерывную для всякого иррационального г и такую, что урав-
уравнение х=/(г) дает регулярное параметрическое изображе-
изображение множества е (с точностью до счетного множества точек е),
когда г пробегает иррациональные точки от 0 до -^ , и дает
в то же время регулярное параметрическое изображение (с точ-
точностью до счетного множества точек) дополнения Се, когда г
пробегает иррациональные точки от -д- до 1. Но так как суще-
существует всегда число у0 такое, что мы тождественно имеем
то мы отсюда заключаем, что плоскость у = у0 пересекает
множество И по однозначной кривой
где g есть функция, обратная для f{z). Следовательно, эта
функция g(x) входит в классификацию Бэра.
Я теперь утверждаю, что эта функция g(x) может
быть как угодно высокого класса.
В самом деле, рассмотрим множество тех х, для которых
мы имеем неравенство
О < g{x) < у.
Очевидно, что это множество в точности совпадает с мно-
множеством е. А так как множество' е может быть выбрано из

264 ГЛ. IV. НЕЯВНЫЕ ФУНКЦИИ
любого класса классификации Бэра, то мы заключаем1), что
класс функции g (x) может быть предположен как угодно
высоким, если только е выбрано надлежащим образом.
Следовательно, множество Н пересекается некоторыми
плоскостями у =у0 по однозначным кривым, входящим
в классификацию Бэра и как угодно высоких классов.
Отсюда немедленно вытекает, что невозможно провести
через точки единственности множества Н однозначную поверх-
поверхность г = F(x, у), где F входит в классификацию Бэра, так
как, если бы это было возможно, то класс этой поверхности
был бы вполне определенным числом а, и все плоскости
у = const пересекали бы эту поверхность по кривым классов,
не превосходящих а. Но мы видели, что классы этих кривых
могут быть как угодно высоки.
Нам остается дополнить множество Н, прибавляя к нему
новое множество /if, измеримое В, так, чтобы сумма Н-\-Н'
имела те же точки единственности, как и Н, и чтобы в то
же время проекция Н на XOY совпадала со всей этой пло-
плоскостью.
Но это возможно в силу теоремы о природе проекции
множества единственности. В самом деле, обозначим через $1
множество точек единственности для Н и через /?, '¦— его
проекцию на плоскость XOY. Мы знаем, что /?, есть анали-
аналитическое дополнение. Значит, его дополнение С?, есть ана-
аналитическое множество. Поэтому существует множество 9,,
измеримое В, лежащее под плоскостью г=1, проекция ко-
которого на XOY совпадает с СЕ. Обозначим через 62 множе-
множество, симметричное с 6} по отношению к плоскости 2 = 1.
Установив это, обозначим через Н' сумму 6, -f- V Мно-
Множество Ъ = Н-\-Нг, очевидно, измеримо В и имеет своей
проекцией на XOY всю эту плоскость. А так как множество
единственности для $, очевидно, совпадает с можеством един-
х) Речь идет о следующем предложении Лебега: для того
чтобы всюду определенная функция f была класса а, необходимо
и достаточно, чтобы, каковы бы ни была а и Ь, множество
точек, где мы имеем а <!/¦< Ь, было класса •<! а а чтобы оно
было эффективно класса а для некоторых значений а и b («Sur
les fonctlona repres. analyt.», стр. 167, теорема IV).
Это предложение доказывается трансфинитной индукцией.. См.
также стр. 144 этой книги.

ОБЩИЙ СЛУЧАЙ В ПРОБЛЕМЕ НЕЯВНЫХ ФУНКЦИЙ 265
ственности для Н, то мы получили решение поставленной
проблемы. Ч. т. д.
Третье доказательство существования двух аналити-
аналитических дополнений, неотделимых В. Мы теперь непосред-
непосредственно укажем два аналитических дополнения без общих
точек, неотделимые В.
Возьмем снова функцию
У = ?(***)>
указанную выше. Свойства этой функции, которые нам будут
нужны, таковы: 1° функция <р(х, f) входит в классификацию
Бэра; 2° какова бы ни была функция f(x), непрерывная
в каждой иррациональной точке, существует такое число tQ,
что мы имеем тождество
?(*> 'о)— /(*)•
Эта функция у = <р (х, f) геометрически изображается
в виде однозначной поверхности, расположенной в простран-
пространстве OXTY) мы обозначим эту поверхность через 5.
Установив это, проведем плоскость х = -к. Эта плоскость
делит нашу поверхность на две части, S, и 52.
Обозначим через $ множество всех точек поверхности S,
в которых прямая, параллельная оси ОХ, пересекает 5 в одной
и только одной точке. Легко видеть, что множество В есть
множество единственности для поверхности 5 по отноше-
отношению к оси ОХ.
Пусть ?>' и V — аналогичные множества единственности
соответственно для поверхностей 5, и 5?. Обозначим через Е,
Е' и Е" соответственно проекции f, V и %" на плоскость TOY.
В силу теоремы о природе проекции множества единствен-
единственности, множества Е, Е' и Е" суть аналитические дополнения.
Пусть Н, есть общая часть Е и Е', а Я2 — общая часть Е
и Е":
Эти множества Я, и Я2 являются также аналитическими
дополнениями. Легко видеть, что Ht и //2 не имеют общей
точки. В самом деле, если бы М принадлежало к Нх и //2,
то параллель к оси ОХ, проходящая через М, пересекала

266
ГЛ. IV. НЕЯВНЫЕ ФУНКЦИИ
бы 5 в одной единственной точке, что невозможно, так как
она должна пересекать и 5„ н ^,
Мы докажем, что Нх и //2 неотделимы В.
С этой целью возьмем любое линейное множество е, изме-
измеримое В; пусть Се— его дополнение. Существует такое
число tu, что функция <р(лг, t0) разнозначна на порции @, 1)
Се
\
ч
\
\
ч
0
p-
Г i
у
1
/
Черт. 6.
области 0х и что ее значения образуют на порции К), -к-
множество е, а на порции (-^, 1) множество Се.
Если мы проведем плоскость t = t0, мы видим, что она
пересекает множество Ht no e и множество Я2 по Се.
Если бы Ht и //2. были отделимы В, то существовало
бы два множества Ь1 и 62, измеримые В, без общих точек
и содержащие соответственно Н1 и Н%. В этих условиях пло-
плоскость t = t0 пересекала бы множества 9j и 92 по двум мно-
множествам, которые, очевидно, совпали бы с е и Се. Но это
как раз невозможно, так как плоское множество bt есть мно-
множество вполне определенного класса а. Следовательно, пере-
пересекая 6j плоскостями t = const, мы получим линейные мно-

ОБЩИЙ СЛУЧАЙ В ПРОБЛЕМЕ НЕЯВНЫХ ФУНКЦИЙ 267
жества классов, не превосходящих а. Но множество е выбрано
произвольно, значит, можно предполагать, что его класс
выше а. Ч. т. д.
Метод П. С. Новикова. Выше мы доказали (стр. 255
и 262), что в общем случае неявных функций второй закон (Х2)
Лебега больше неприменим. Это значит, что не существует
никакой явной однозначной функции, входящей в классифика-
классификацию Бэра и принимающей значения среди значений рассматри-
рассматриваемой многозначной неявной функции. Мы знаем (стр. 256),
что этот вопрос сводится к построению множества $, изме-
измеримого В, лежащего в пространстве OXYZ, проекция кото-
которого на плоскость XOY совпадает со всей этой плоскостью,
и такого, что не существует ни одной однозначной поверх-
поверхности S, входящей в классификацию Бэра, каждая точка
которой принадлежит к ?•. Мы построили такое множество,
пользуясь свойствами множества единственности и его про-
проекции.
П. С. Новиков решил эту проблему, опираясь на суще-
существование двух аналитических дополнений, неотделимых В!).
Щ Вот метод П. С. Новикова:
Рассмотрим в плоскости XOY два аналитических дополне-
дополнения Ех и ?2 без общих точек и неотделимые В,
Возьмем в пространстве OXYZ два множества, измери-
измеримых В, пусть Н1 и //2, из которых первое лежит ниже пло-
плоскости г = 0 и имеет проекцией дополнение CEt к множе-
множеству Е,, а второе лежит выше плоскости г = 0 и имеет про-
проекцией дополнение СЕ% к множеству Ev
Соединение Н^Н^-^-Н^ есть множество, измеримое В,
которое дает решение поставленной проблемы.
Вот доказательство П. С. Новикова:
Допустим, что существует однозначная поверхность 5,
заданная уравнением z = F(x, у), где F входит в классифи-
классификацию Бэра, причем каждая точка 5 принадлежит к Н.
Части 5, расположенные соответственно ниже и выше пло-
плоскости z = 0, обозначаются через 5] и S2. Множества Sj
и S2, очевидно, однозначны и измеримы В.
J) Построение которых было дано им самим. См. его исследо-
исследования о неявных функциях «Sur les fonctions implicites mesurables В»
(Fund. Math., т. XVII, 1931).

268 ГЛ. IV. НЕЯВНЫЕ ФУНКЦИИ
Отсюда следует, что проекция ot множества 5, на пло-
плоскость XOY измерима В, так же как и аналогичная проек-
проекция о2 для 52. Пусть о — общая часть Oj и о2, о = о, • о2;
множество о, очевидно, измеримо В.
Пусть 9j есть разность о,—ои соответственно 62 — раз-
разность о2— о. Ясно, что 9Х и б2 измеримы и не имеют общих
точек.
Мы докажем, следуя методу П. С. Новикова, что 6t и 62
отделяют множества Ех и ?2.
В самом деле, пусть М есть точка ?и Параллель к оси OZ,
проведенная через Ж, не пересекает поверхности Slf но пере-
пересекает поверхность 52; следовательно, М принадлежит к о2.
А так как М не принадлежит к о]} то она принадлежит к \.
Итак, множество Ег содержится в 62. Так же доказы-
доказывается, что Е2 принадлежит к bv Следовательно, множества Ь1
и 92 измеримы В и отделяют множества ?2 n_Elt что про-
противоречит сделанной гипотезе. Ч. т. д.

ГЛАВА V
ПРОЕКТИВНЫЕ МНОЖЕСТВА
Определение проективного множества, его преобразование
Введение. В этой главе мы рассмотрим новое семейство
точечных множеств, называемых проективными; их геометри-
геометрическое происхождение очень ясно. Это важное семейство
множеств содержит, как частный случай, все аналитические
множества и их дополнения.
В математической литературе можно найти лишь очень
немногие сведения о проективных множествах. Тем не менее,
те минимальные результаты, которые мы имеем, показывают,
что мы имеем дело с чрезвычайно важным семейством мно-
множеств, имеющих почти парадоксальные свойства.
Операция проектирования является одной из наиболее про-
простых и в то же время наиболее важных операций в геомет-
геометрии; эта операция позволяет образовывать новые множества,
которые можно получить, отправляясь от уже известных
множеств.
Рассматривая проектирование (Р) как операцию и комби-
комбинируя ее с операцией (С), позволяющей переходить от мно-
множества к его дополнению, мы получаем, отправляясь от мно-
множеств, измеримых В, сначала все аналитические множества Е,
потом, отправляясь от их дополнений СЕ, новый класс мно-
множеств РСЕ совершенно неизвестной природы; потом, отправля-
отправляясь от их дополнений СРСЕ, новые множества РСРСЕ, и так
далее. Это и будут проективные множества.
Это общее определение проективного множества я дал
в своих первых заметках по проективным множествамJ). В этих
*) «Surles ensembles projecffis...» (Comptes Rendus Acad. Sc. 25 мая
1925 г.). См. также мои заметки в Comptes Rendus Acad. Sc. «Sur un

270 ГЛ. V. ПРОЕКТИВНЫЕ МНОЖЕСТВА
заметках я указал те принципиальные трудности, которые
вызываются теорией этих множеств, а также сомнения, касаю-
касающиеся законности их определения. Я опустил в этих замет-
заметках и в своем мемуаре «Sur les ensembles analytiques»J)
формулировки и доказательства положительных результатов
об этих множествах, так как изложение их, казалось, должно
было быть длинным и представлять лишь копию теории ана-
аналитических множеств2).
С другой стороны, Серпинский опубликовал в Fund. Ma-
them.3) статью «Sur une classe d'ensembles», где он очень
ясно указал на трудности, возникающие при изучении даже
весьма простых точечных множеств: неизвестно ничего ни об
измеримости в смысле Лебега, ни о категории проекций
плоских аналитических дополнений. Позднее Серпинский
в заметке «Sur quelques proprietes des ensembles projectifs»4)
формулировал первые теоремы из этой теории и дал их
доказательства в ряде статей, появившихся в Fund. Ma-
them. 6).
В этой главе я изложу некоторые положительные резуль-
результаты из теории проективных множеств. При этом в форму-
формулировках и доказательствах я буду выдерживать возможно
более полную аналогию с теорией аналитических множеств.
Метод, которому я буду следовать, — геометрический; именно
probleme de M. Emile Borel et les ensembles projectHs...»D мая 1925 г.);
«Les proprietes des ensembles projectifs.» A5 июня 1925 r); «Sur les en-
ensembles поп-mcsurables В et l'emploi de la diagonale...»B0июля 1925г.);
«Sur un probleme de M. Borel et la methode des resolvantes»
A7 августа 1925 г.). «Remarques sur les ensembles projectifs»
B4 октября 1927 г.).
!) Fund. Mathematicae, т. X, 1926.
г) Теория проективных множеств была предметом моих лекций,
прочитанных в 1924—1925 гг. в Московском университете. Я сохранил
в своих заметках и своем мемуаре лишь следы предложений, кото-
которые, однако, предполагают теорию проективных множеств достаточно
разработанной. Таковы предложения о существовании, а также
о сумме и о произведении проективных множеств.
3) 4W 7, 1925, стр. 237—243.
*) Comptes Rendus Acad. Sc, 24 октября 1927.
Б) Том XI.I, стр. 228 «Sur les families Inductives et projec-
tives d'ensembles». См. также т. XI, стр. 117, «Sur les projec-
projections des ensembles complementaires aux ensembles (А)» и
т. XI, стр. 123, «Sur les prodults des images continues des en-
ensembles (CA)».

ОПРЕДЕЛЕНИЕ ПРОЕКТИВНОГО МНОЖЕСТВА 271
этим методом я, несколько лет тому назад, дал техническое
изложение теории проективных множеств').
Определение проективных множеств. Мы называем про-
проективным всякое множество точек, которое можно получить,
отправляясь от множества, измеримого В, при помощи двух
основных геометрических операций, повторенных конечное
число раз:
1° Взятие ортогональной проекции уже определенного
множества Е на область меньшего числа измерений
РЕ. (Р)
2° Взятие дополнения уже определенного множества Е
СЕ. (С)
Это определение проективного множества естественно при-
приводит к определению класса проективного множества.
Мы скажем, что некоторое множество точек есть
проективное множество класса п, если его можно пред-
представить в виде
РСР... РЕ
или
СРС... РЕ,
где Е есть множество, измеримое В, лежащее в области
любого числа измерений, и где буква Р, чередуясь с бук-
буквой С, написана ровно п раз, причем такое изображение
уже невозможно, если число п заменить меньшим числом.
Чтобы иметь возможно более полную аналогию с теорией
аналитических множеств, их дополнений и множеств, измери-
измеримых В, мы будем различать в каждом классе проективных
множеств три различных рода множеств:
I. Проективное множество $ класса и мы назовем мно-
множеством первого рода, если его можно представить в виде
РСР ...РЕ
*) Я намеревался дать полное изложение лекций о проективных
множествах, прочитанных мною в 1924—1925 гг. в Московском универ-
университете, в работе «Memoire sur les ensembles analytiques et projectifs»,
первая часть которого появилась в Математическом Сборнике, т. 33,
1926, стр. 327.

272 ГЛ. V. ПРОЕКТИВНЫЕ МНОЖЕСТВА
и если его невозможно представить в виде СРС... РЕ, где
буква Р в обоих случаях написана ровно к раз. Для сокраще-
сокращения мы будем говорить в этом случае, что проективное мно-
множество $ есть аналитическое множество порядка п и при-
примем для него обозначение (Ап).
Эти множества во всех отношениях аналогичны обыкно-
обыкновенным аналитическим множествам, неизмеримым В.
II. Проективное множество $ класса к мы назовем мно-
множеством второго рода, если его можно представить в виде
СРС ...РЕ
и если его нельзя представить в виде РСР ... РЕ, где буква Р
в обоих случаях написана ровно я раз. Для сокращения мы
скажем, в этом случае, что проективное множество $ есть
аналитическое дополнение порядка п и примем для него
обозначение (СЛ,,)!22].
Эти множества во всех отношениях аналогичны обыкно-
обыкновенным аналитическим дополнениям, неизмеримым В.
Ш. Проективное множество S класса я называется множе-
множеством третьего рода, если его возможно представить одно-
одновременно в обоих видах
РСР...РЕ' и СРС... РЕ",
где буква Р в обоих случаях написана ровно я раз, а мно-
множества Е' и Е" измеримы В. Для сокращения мы будем
говорить, в этом случае, что проективное множество % есть
двустороннее порядка я или измеримое В порядка я; мы
будем его обозначать через (?п).
Эти множества аналогичны множествам, измеримым В в обыч-
обычном смысле.
После того как эти определения установлены, легко видеть,
что всякое аналитическое множество, неизмеримое В, есть
множество (i4i), что его дополнение есть (СА^, а каждое
множество, измеримое В, есть (В^ и обратно. Итак, теория
аналитических множеств содержится в теории проективных
множеств. Это замечание показывает, что понятие проектив-
проективного множества является совершенно естественным.
Преобразование определения проективного множества.
Прежде чем перейти к доказательству эффективного сущест-
существования проективных множеств каждого класса и, в частно-

ОПРЕДЕЛЕНИЕ ПРОЕКТИВНОГО МНОЖЕСТВА 273
сти, множеств (Лп), (СЛП) и (Лп) в отдельности, мы преобра-
преобразуем предложенное определение проективных множеств.
Вот каково это преобразование. Мы ввели операцию (/>),
которая состоит в том, чтобы брать ортогональную проекцию
множества точек, лежащего в /я-мерной области, на область
меньшего числа, например т', измерений. Это число т' не
обязательно равно т—1.
Тем не менее, мы покажем, что, не уменьшая общности
определения проективного множества класса и, можно пред-
предполагать, что каждая операция (Р), фигурирующая в этом
определении, уменьшает число измерений в точности на
одну единицу, в результате чего, если $> есть проективное
множество класса и, лежащее в /я-мерной основной области,
то множество § можно рассматривать, как получившееся из
множества Е, измеримого В и лежащего в области m-j-n
измерений.
Мы начнем со следующего замечания: если Мо (х\, х\,..., л?)
есть точка [А-мерной области 0хх...х » то ее проекция
^oi^v ¦*& • • •>¦?!!) на ^-мерную область 0Xlx%..,x4, где v < [»,
получается сохранением v первых координат точки М и от-
отбрасыванием всех остальных.
Установив это, возьмем проективное множество $ класса я,
расположенное в /и-мерной области ffXlx2...xm- Мы предпо-
предполагаем, что $> получается из некоторого множества Е, изме-
измеримого В, лежащего в р-мерной области 0'х ,,.х . Пусть
M(xlt x2, ..., хр) есть переменная точка, пробегающая об-
область 0х^...хр-
Так как каждая операция Р уменьшает число координат
на несколько единиц, то координаты точки М мы можем
разделить на несколько групп: '
где число групп равно я-{-1.
Рассмотрим любую из этих групп, следующую за первой;
пусть это будет группа хЧ/с_1+1... х^. Мы можем устано-
установить взаимно однозначное и взаимно непрерывное преобра-
преобразование области 0хч +1*--о! на область 0у . Мы, таким
18 Зак. 284. Н. Н. Луз

274 " гл. V. ПРОЕКТИВНОЙ множества "
образом, получаем взаимно однозначное и взаимно непрерывное
соответствие между областью gх х ,.х и некоторой новой обла-
областью ^ х а, ...а, у ...у . Это преобразование областей ставит в со-
соответствие множеству Е, измеримому В и лежащему в области
3'х^...х ...х , множество Ег, также измеримое В и лежащее
в области gXl...Xmvv..yn.
Если мы будем применять поочередно к множеству Е,
измеримому В, операции (Р) и (С), для того чтобы в конце
концов получить из него данное проективное множество §>,
то мы последовательно уничтожим все скобки, начиная с по-
последней, и мы придем к первой скобке (xt ... хт), содержа-
содержащей координаты точек множества §.
Так как каждой из исчезнувших скобок соответствует
одно" и только одно число у, то ясно, что, применяя к мно-
множеству Е', измеримому В, те же операции (Р) и (С), мы,
в итоге,,, придем к тому же проективному множеству $.
Итак, мы приходим к следующему результату: можно
предполагать, что в определении проективного множе-
Ътва классй п каждая операция (Р) уменьшает число из-
измерений только на одну единицу.
В частности, каждое линейное проективное множество
класса п получается из я -j- 1-мерного множества Е, изме-
измеримого В. ¦•¦¦¦¦-¦
Мы дополним этот; результат следующим замечанием:
изучение проективных множеств, лежащих в многомер-
многомерной области, сводится к изучению линейных проективных
множеств.
В самом деле, пусть Ь есть проективное множество, ле-
лежащее в области 0х,...х • Соответствие
, . хт), •{.._--
где gi и G непрерывны, установленное между точками рас-
рассматриваемой области $х....х и новой линейной области 0х,
преобразует данное проективное, множество .§ в линейное
множество %>'. В сийу предшествующего очевидно, что пре-
образованиое нножество t' есть проективное множество того
же класса и .того же рода, как и '$.-.

ПРОСТЕЙШИЕ СВОЙСТВА ПРОЕКТИВНЫХ МНОЖЕСТВ 275
Простейшие свойства проективных множеств
Проекции. Из результатов предыдущего параграфа сле-
следует, что проекция множества (Ап) есть либо проектив-
проективное множество класса ниже п, либо множество (Вп), либо
множество (Ап). Точно так же проекция множества (В^)
либо класса ниже п, либо (Вп), либо (Ап). Только проек-
проекции множеств (САп) могут дать проективные множества
высшего класса, именно: (Ап+1) или (Вп+1).
В самом деле, если $> есть (Ап) или (Вп), то его можно
представить в виде
РСР ...РЕ,
где буква Р фигурирует п раз. Если мы проектируем $, то
получаем множество вида
РРСР ...РЕ.
Но двойная операция (РР), очевидно, тождественна с прод-
продетой операцией (Р), уменьшающей число измерений по край>-
ней мере на две единицы. Следовательно, результирующее
множество можно записать, повторяя букву Р не более, чем
я раз (предыдущий параграф); значит, это множество либо
класса < п, либо (Вп), либо (Ап). Ч. т. д.
Легко видеть, что установленное предложение аналогичго
теореме из теории аналитических множеств: проекция анали-
аналитического множества или множества, измеримого В, есть
множество либо аналитическое, либо измеримое В; каждое
аналитическое множество есть проекция множества, измери-
измеримого В.
В силу полной аналогии между множествами (Ап), (CAJ,
(Вп), с одной стороны, и множествами аналитическими, их
дополнениями и множествами, измеримыми В, с другой сто-
стороны, естественно возникает большое число важных проблем.
Чтобы поставить некоторые из этих проблем, удобно
предварительно ввести следующую терминологию: мы скажем,
что множество L, лежащее в плоской области 0 щ, есть
однозначная кривая, если каждая параллель к оси OY пере-
пересекает L. в одной и только одной точке. Точно так же мы
скажем, что $ есть однозначное множество относительно
18*

276 ГЛ. V. ПРОЕКТИВНЫЕ МНОЖЕСТВА
оси ОХ, если всякая параллель к оси OY пересекает § не
более, чем в одной точке.
Установив эти определения, мы немедленно встречаемся
со следующими вопросами:
Если $ есть плоское множество (Вп), однозначное отно-
относительно оси ОХ, должна ли проекция Е множества & на
эту ось быть непременно множеством (Вп) или класса < я?
Имеет ли однозначное плоское множество класса п — 1
своей проекцией множество (Вп) или класса < и? [аз].
Можно идти дальше. Мы видели, что каждое однознач-
однозначное аналитическое множество содержится в однозначной кри-
кривой, измеримой В (стр. 235), и что каждое множество Е,
измеримое В, пересекаемое всякой параллелью к оси О Г не
более чем в счетном множестве точек, составлено из счет-
счетного множества однозначных множеств, измеримых В (стр. 253).
Вполне естественно поставить аналогичные вопросы отно-
относительно проективных множеств (Ап) и (Вп).
Точно так же вполне естественно спросить себя, будет
ли всякое плоское множество (Ап), пересекаемое каждой
параллелью к оси OY не более чем по счетному множе-
множеству, содержаться во множестве EW), обладающем тем же
свойством.
И аналогично, было бы чрезвычайно интересно доказать,
что всякое плоское множество {САп), пересекаемое каждой
параллелью к оси OY не более чем по счетному множе-
множеству, является соединением счетного множества однозначных
Проективное множество, как множество значений не-
некоторой функции. Мы видели, что всякое линейное анали-
аналитическое множество можно рассматривать, как множество
значений, принимаемых на 01 некоторой непрерывной на 01
функцией /(/).
Аналогично, мы докажем, что всякое линейное множе-
множество (Ап) или (Вп) можно рассматривать, как множество
значений, принимаемых на некотором проективном множе-
множестве Н низшего класса функцией f(t), непрерывной на 01.
В самом деле, линейное множество Е вида (Ап) или (?„)
можно рассматривать как проекцию плоского множества $
вида (САп_1). Мы предполагаем, что $ расположено в об-
области 0 ху и что Е есть проекция $> на ось ОХ.

ПРОСТЕЙШИЕ СВОЙСТВА ПРОЕКТИВНЫХ МНОЖЕСТВ 277
Преобразуем 0ху в новую линейную область 01 при
помощи взаимно однозначного и взаимно непрерывного пре-
преобразования
t=F{x, у),
где », ty и F непрерывны.
Известно, что в этом преобразовании каждому проектив-
проективному множеству соответствует проективное множество того
же класса и того же рода. В частности, множество $ пре-
преобразуется в линейное множество Н вида (САп_1), лежащее
в области 01.
Легко видеть что непрерывная функция х = о {f) пробе-
пробегает данное проективное множество Е, когда t пробегает
проективное множество Н. Ч. т. д.
Если Е есть проективное множество (Ап), лежащее
в /я-мерной области 0ХХ ...х , то мы преобразуем эту об-
область в линейную область 0 х при помощи формул
х\ == &\ \х)г Х2 == §2 \Х)> • • ') Хт == &т \х)> 1 ....
X = U{X1, Х%, . • ., Хт), )
где gt и О непрерывны.
Образ Е' множества Е есть линейное множество (Ап).
Следовательно, Е' есть множество значений, принимаемых
непрерывной функцией jc = ср (/) на некотором множестве Н
вида (САп_1). Если мы в функции gt(x) вместо х подставим
о(/), то мы придем к следующему результату:
Всякое проективное множество (Ап) или (Вп), лежащее
в т-мерной области 0Х ,..х , можно рассматривать как
геометрическое место последовательных положений по-
подвижной точки M(xv xv ..., хт), координаты которой
являются функциями переменного параметра t, непре-
непрерывными на 01,
причем t пробегает проективное множество (САп_1).
Таким образом, мы получили параметрическое изобра-
изображение множеств (Ап) и (Вп); легко видеть, что оно

278 ГЛ. V. ПРОЕКТИВНЫЕ МНОЖЕСТВА
аналогично параметрическому изображению аналитических мно-
множеств.
Но, как только эта аналогия констатирована, естественно
поставить следующие вопросы: можно ли для каждого мно-
множества Вп найти регулярное параметрическое изображение?
С другой стороны, если $> есть множество (Ап), допу-
допускающее регулярное или полурегулярное параметрическое
изображение, должно ли оно непременно быть множеством
)?26
Множества параллелей. Для дальнейшего нам понадо-
понадобится узнать природу множеств, образованных из точек, ле-
лежащих на прямых, перпендикулярных некоторой области и
проходящих через точки некоторого проективного множества,
лежащего в этой области.
Пусть Е есть проективное множество класса я, лежащее
в области 0'х х ...-,, . Будем рассматривать эту область, как
часть области 0'хх ,,.х у, и проведем через каждую точку Е
прямую, параллельную оси OY. Пусть § есть множество
точек, лежащих на всех этих прямых. Надо узнать при-
природу g.
Так как множество Е есть проективное множество, то мы
можем его получить, отправляясь от множества 6, измери-
измеримого В, и лежащего в области 0ХХ ...х Р измерений:
Е = ... РСРЬ.
Мы можем предполагать, что здесь каждая операция (Р)
уменьшает число измерений на одну единицу.
Пусть М (xltxit..., хт) есть любая точка области 0х^...хт-
Точки N, лежащие на прямой, проходящей через М и парал-
параллельной оси OY, имеют координаты у, х1г лг.2, ..., хт, где
у есть любое число.
Если точка М' (xv ..., хт, ..., хр) пробегает множе-
множество 9, измеримое В, то множество точек N' {у, xv ..., хр),
где число у произвольно, пробегает множество Й', также из-
измеримое В. Если мы применим ко множеству 9 последова-
последовательные операции (Р) и (С), то мы в конце концов придем
к данному проективному множеству Е. Те же операции, при-
примененные ко множеству 6', дают нам, очевидно, множество $,
природу которого мы стремились узнать.

ПРОСТЕЙШИЕ .СВОЙСТВА ПРОЕКТИВНЫХ МНОЖЕСТВ 279
Итак, множество ?, образованное из точек, лежащих
на параллелях, есть проективное множество того же
класса и того же рода, как Е.
Сумма и произведение проективных множеств. Мы
знаем, что сумма счетного множества аналитических мно-
множеств и общая часть счетного множества аналитических мно-
множеств суть опять аналитические множества. Аналогичный
результат имеет место и для аналитических дополнений.
Именно, мы имеем в виду доказать следующую теорему:
Сумма и произведение конечного или счетного числа
множеств (Ап), или (Вп) или класса < я есть (А^), или
(Вп), или класса < п. Аналогичный результат имеет Место
для (САп) и (Вп). .
Мы начнем с доказательства этой теоремы для суммы.
Пусть S = Et -J- ?a -f- ... -j- Ek + • • • есть сумма счет-
счетного множества множеств ~(Ап) или (Вп). Мы предполагаем,
что Ек есть линейное множество и -является проекцией пло-
плоского проективного множества $к класса < п. Пусть 2 есть
сумма множеств §>к. ' ч-
Предложенная теорема верна дляя = 1. Допустим, что
она верна для всех классов <я и докажем, что она тогда
верна и Дли я. ¦ • •
В силу сделанной гипотезы множество 2 есть проектив-
проективное • множество класса ниже я. •
С другой стороны, множество 5, очевидно, есть проек-
проекция S- Следовательно, S есть либо (Ап), либо (Вп), либо
класса < я. Ч. т. д.
Рассмотрим теперь общую часть
счетного, числа множеств (Ап) или (Вп). .
Прежде всего мы можем предположить, что множества Ек
линейные, так как мы видели, что каждое проективное мно-
множество можно преобразовать в линейное проективное мно-
множество того же класса и рода при помощи преобразования
многомерной области в линейную, причем это преобразование
областей не зависит, от операций, с помощью которых полу-
получены проективные множества. Итак, предположим, что все
Ек лежат в линейной области 09. , ,.i;, ...

280 ГЛ. V. ПРОЕКТИВНЫЕ МНОЖЕСТВА
В силу предшествующего мы можем рассматривать Ек
как множество значений функции Д(лгк), где Д непрерывна
на gXk, а переменная точка хк пробегает проективное мно-
множество Ну, вида (САп_1).
Установив это, возьмем неограниченную последовательность
непрерывных на 01 функций
таких, что какова бы ни была последовательность чисел
x°i, лга, •.., х\, ... в 0я, существует иррациональное t0, за-
заключенное между 0 и 1, для которого мы имеем
- у0, (ь 1 2 4 *i
Сложные функции Д[»й(/)] непрерывны на @, 1) об-
области 0 р Следовательно, множество точек t, для которых
удовлетворяются одновременно равенства
Л [?i @1 =Л 1% @1 = • • • = ЛI?» (Я = • • •
есть замкнутое на 01 множество. Обозначим его через 7.
Обозначим через Ьк множество всех точек t, для которых
<рй(О принадлежит к Нк. Установим природу Ьк.
С этой целью рассмотрим кривую xk—<ok{t) в области 0tx1l.
Линейное множество Нк расположено на оси ОХк. На осно-
основании предыдущего параграфа множество точек, лежащих на
всех прямых, параллельных оси ОТ и проведенных через
точки Нъ, есть плоское множество (САп_1). Обозначим это
множество через Qk. Рассмотрим дополнение CQk к множе-
множеству Qk; это множество (Ап_1).
Мы предполагаем, что теорема верна для всех классов
ниже п. Отсюда следует, что общая часть CQ^ и кривой
¦** = ?(') есть множество G4W-1) или (Вп_1), или класса ниже
< п. Значит, проекция этого множества на ось ОТ есть
(Лп_,) или (Bn_j), или класса <я—1. Но множество Ьк
есть, очевидно, дополнение к этой проекции. Значит, 6fc есть
{САп_1) или (Вп_1), или класса <я — 1.

ПРОСТЕЙШИЕ СВОЙСТВА ПРОЕКТИВНЫХ МНОЖЕСТВ 281
Установив это, вернемся к доказательству предложенной
теоремы. Так как мы предположили теорему верной для всех
классов ниже я, то общая часть
есть (САп^1) или (Bn_t), или класса < п—1.
Если точка t пробегает Ьк, то %(/) принадлежит к Нк,
значит, Д [<fk (t)] принадлежит к Ек. И так как t принадлежит
к Т, то все значения Д [?*(/)] равны между собой. Значит,
любая из этих функций Д [<sk (t)], например первая, f1 \<o1 (f)],
принимает на 9 значения, принадлежащие Р.
С другой стороны, множество Р содержится во множестве
значений Д [cpj (/)] на 6. В самом деле, пусть Мо — некоторая
точка из Р. Так как Мо принадлежит к Ек, то существует
число х^, принадлежащее к Hh и такое, что точка fk(x^)
совпадает с Мо.
Но в силу свойства функций <sk(f) существует иррацио-
иррациональное tQ такое, что »fc (/0) = хйк для всякого k. Эта точка t0
непременно принадлежит к Т, так как все значения Д \<?к (/0)]
равны между собой. Кроме того, t0 принадлежит каждому
из 6Д, так как ?fcD)) принадлежит к Нк.
Отсюда следует, что t0 принадлежит к 9, значит, множе-
множество Р тождественно со множеством значений /: [<ог (t)] на 6.
Так как Ь есть проективное множество {САп_1) или (Вп_1),
или класса <я—1, то это же справедливо для множества
точек, расположенных на параллелях к оси ОХ и проведенных
через точки 8. Отсюда следует, что точки кривойлг=/х [^(f)],
расположенные на этих параллелях, образуют плоское мно-
множество А вида (САп_1), или {Вп_1), или класса <я—1.
А так как рассматриваемое множество Р есть, очевидно,
проекция А на ось ОХ, то мы видим, что Р есть (Ап), или
{Вп), или класса < л — 1.
Итак, мы установили ту часть формулированной теоремы,
которая касается множеств (^4„).
Так как каждое (САп) есть дополнение к некоторому (Ап),
и так как мы имеем очевидные формулы

282 ГЛ. V. ПРОЕКТИВНЫЕ МНОЖЕСТВА
то мы видим, что и часть теоремы, относящаяся ко множе-
множествам (САп), доказана.
Остается рассмотреть лишь множества (Вп). Но по самому
определению, каждое множество (Вп) может быть предста-
представлено одновременно в двух видах
РС...СРЕ и СР...СРЕ.
Из предыдущих рассуждений следует, что сумма и общая
часть счетного множества множеств (Вп) может быть
представлена в этих двух формах, а потому она либо (Вп),
либо класса < я. Ч. т. д.
Мы дополним этот результат следующим замечанием:
мы доказали, что сумма и общая часть множеств (Вп) (или
класса < п) есть также (Вп) (или класса < я). Но легко
видеть, что даже сумма двух множеств класса п — 1 мо-
может быть эффективно множеством (Вп).
Чтобы убедиться в этом, возьмем множество (Ап_1), лежа-
лежащее на @, -к-) в области ^ж; пусть Е1 это множество.
Пусть ?2 — множество.{САп_^), лежащее на f-^-, l) в gx.
Обозначим через Е сумму Е%~\-Е^.
Я теперь утверждаю, что Е есть эффективно множе-
множество (Вп), но не класса ниже п. В самом деле, если Е класса
<л, то Я есть либо (^4w_i), либо (САп_г). Пусть, например,
Е рсгъ (Ап_1). Но часть Е, лежащая на порции (у, 1J,
есть (САп_1), что противоречит условию. Значит, Е в точ-
точности проективное множество класса л [26]. Значит, Е в точ-
точности (Вп). Ч. т. д.
Итак, существуют эффективно множества (Вп), кото-
которые можно получить при помощи операций суммирования и
взятия общей части, отправляясь от проективных мно-
множеств класса ниже л.
Возникает теперь вопрос, можно ли получить всякое (Вп),
отправляясь от проективных множеств классов ниже я, при
помощи операций суммы и общей -части, повторенных счет-
счетное множество,раз? I27].

ТЕОРЕМА МАЗУРКЕВИЧА. ОБОБЩЕНИЕ СЕРПИНСКОГО 283
Теорема С. Мазуркевича. Обобщение В. Серпинского
Исследования С. Мазуркевича. Мы обязаны С. Мазурке-
вичу результатом чрезвычайной важности J), непосредственно
связанным с предыдущими рассмотрениями и касающимся
теории аналитических множеств и их дополнений.
Для определенности мы, излагая результат Мазуркевича,
ограничимся рассмотрением плоской области ?[ху.
Пусть Я есть множество, измеримое В, лежащее в 0ху.
Мы скажем, что точка Мо (х0, у0) есть нижняя точка мно-
множества Н, если Мо принадлежит к Н и если не существует
никакой точки М (х0, у) из Н с ординатой у, меньшей чем у0.
Установив это определение, легко узнать, какова природа
множества всех нижних точек некоторого множества Н, изме-
измеримого В.
Обозначим через //(г) множество всех нижних точек мно-
множества Н. Очевидно, это множество Я(г> можно получить
следующим образом. Возьмем прямую у — р, где р—рацио-
р—рациональное число. Обозначим через Нр множество всех точек Н,
лежащих ниже этой прямой. Пусть Ар есть множество парал-
параллелей к оси OY, проходящих через все точки Н?. Множество
всех точек 0ху, принадлежащих к Ар, есть, очевидно, анали-
аналитическое множество. Следовательно, то же имеет место и
для множества 6р всех точек Н, лежащих выше прямой у = р
и принадлежащих к Лр. ,
Установив это, заставим р пробегать все рациональные
числа; сумма б всех множеств 6р есть, очевидно, аналитиче-
аналитическое множество, принадлежащее к Н. Отсюда следует, что
разность Н—в есть аналитическое дополнение, которое,
в частных случаях, может оказаться измеримым В. Но это
множество, очевидно, совпадает с рассматриваемым множе-
множеством Я( . А так как всякая параллель к оси OY пересекает
H(i> не более, чем в одной точке, то мы приходим к сле-
следующему результату Мазуркевича:,
Множество Н^ всех нижних точек множества Н,
измеримого В, есть аналитическое дополнение, однознач-
однозначное относительно оси ОХ.
') См. MazurkJewlcz, Sur une proprlete des ensembles CA,
Fund. Math., т. X (стр. 172—174).J' ¦

284 ГЛ. V. ПРОЕКТИВНЫЕ МНОЖЕСТВА
Прежде чем идти дальше, полезно доказать следующие
две леммы, принадлежащие Серпинскому:
Лемма 1. Сумма Ег ~\- ?2 -)-...-)- Еп + .. . счетно-
?о множества линейных множеств попарно без общих
точек, каждое из которых есть проекция однозначного
аналитического дополнения, обладает тем же самым
свойством.
В самом деле, если Еп есть проекция однозначного анали-
аналитического дополнения А„, то сумма Aj -j-А2-]-••• + А„~\-...
есть, очевидно, однозначное аналитическое дополнение, имею-
имеющее проекцией заданное множество-сумму ?j+?2-)-...-| En-\-...
Ч. т. д.
Лемма 2. Общая часть ?, • ?2.. .Еп... счетного множе-
множества линейных множеств, каждое из которых есть проек-
проекция однозначного аналитического дополнения, также обла-
обладает этим свойством.
Пусть Ап есть аналитическое дополнение, однознач-
однозначное относительно оси ОХ, проекция которого на эту ось
есть Еп.
Если мы преобразуем область gху в порцию @,1) линей-
линейной области 01 при помощи взаимно однозначного и взаимно
непрерывного соответствия
* = ?(/),
A)
то образ Хп множества Ап есть аналитическое дополнение.
Легко видеть, что функция cs (f) разнозначна на Хп и что Еп
есть множество ее значений на Хп.
Установив это, рассмотрим бесконечную последователь-
последовательность непрерывных на 0\ функций ,
обладающих следующим свойством: какова бы ни была по-
последовательность иррациональных чисел fv Р2, ..., Q, заклю-
заключенных между 0 и 1, существует одно и только одно ирра-
иррациональное -с0, заключенное между 0 и 1, для которого
/W i( 1 2 3)

ТЕОРЕМА МАЗУРКЕВИЧА. ОБОБЩЕНИЕ СЕРПИНСКОГО 285
Так как функции /п непрерывны на &т, множество ftn
точек т, для которых /„ (т) принадлежит к Х„, есть аналити-
аналитическое дополнение. Отсюда следует, что общая часть & всех &„
есть также аналитическое дополнение.
Рассмотрим теперь множество Т точек т, для которых
удовлетворены равенства
?1Л (*)] ==?[/« W1 = ¦ ¦ • =?I/nWl = • • •
Так как функции ?[/ra(t)] непрерывны на ^т, то легко
видеть, что Т замкнуто на д\.
Множество Т • Ь есть, следовательно, аналитическое допол-
дополнение. Повторяя рассуждение (стр. 281), мы видим, что Е
есть множество значений © \fk (t)\ на & • Т.
С другой стороны, очевидно, что функция у [Д (т)] разно-
разнозначна на Т • Ь.
Обозначим через Л множество точек области gx^, при-
принадлежащих кривой x = <p[f1 (т)], причем х принадлежит
к Г • ft. Это множество есть, очевидно, плоское аналитиче-
аналитическое дополнение. Но функция <p[/i(V)] разнозначна на Г- ft.
Следовательно, множество А однозначно относительно оси ОХ,
что и доказывает лемму. Ч. т. д.
Перейдем теперь к доказательству основного результата
Мазуркевича.
Теорема (Мазуркевич). Всякое аналитическое множе-
множество есть проекция однозначного аналитического допол-
дополнения.
Так как область 0'х ...х у может быть преобразована
в плоскую область gxy, мы ограничимся рассмотрением линей-
линейных аналитических множеств.
Пусть Е — линейное аналитическое множество, лежащее
в области 0х. Мы можем рассматривать Е как проекцию
элементарного множества §, построенного следующим обра-
образом (стр. 193): $ есть общая часть S1- S2.. .Sn..., где Sn
есть сумма прямоугольников Бэра ранга п, попарно без общих
точек; проекции прямоугольников Бэра ранга л на ось-О К
попарно не имеют общих точек и образуют на этой оси
вполне упорядоченное множество интервалов, причем поря-
порядок соответствует положительному направлению оси OY.
Кроме того, каждый прямоугольник ранга л содержится

286 ГЛ. V. ПРОЕКТИВНЫЕ МНОЖЕСТВА
в одном и только одном прямоугольнике ранга я — Г 'и содер-
содержит счетное множество прямоугольников ранга п -J- 1-.'
Так определенное элементарное множество Ь есть множе-
множество, измеримое В, и легко видеть, что Е есть проекция его
нижних точек, что и доказывает теорему Мазуркевича. Ч. т. д.
Сам Мазуркевич ограничился тем, что вывел из своей
теоремы лишь следующий результат:, всякое множество Е,
являющееся разностью двух аналитических множеств,
есть проекция однозначного аналитического дополнения.
Серпинский указал '), что применение двух предыду-
предыдущих лемм позволяет получить следующий более общий ре-
результат:
Всякое множество, которое можно получить, отпра-
отправляясь от аналитических множеств и их дополнений и
Повторяя счетное множество раз операцию взятия суммы
или общей части, есть проекция однозначного аналити-
аналитического дополнения.
Так как каждое линейное аналитическое дополнение можно
рассматривать как проекцию тождественного с ним множе-
множества, то можно было бы думать, что рассматриваемое пред-
предложение уже доказано. Но следует принять во внимание, что
здесь идет речь о сумме в широком смысле, следовательно,
ее члены могут иметь попарно общие точки. Между тем,
лемма 1 Серпинского доказана лишь для суммы в узком
смысле.
Чтобы устранить эту трудность, немедленно доказывают,
что можно получить те же самые множества, если взять за
две основные операции суммирование в узком смысле и
взятие общей части. Это замечание заканчивает доказатель-
доказательство теоремы. Ч. т. д.
Сделаем еще следующее замечание: каждое множество Е,
которое можно получить таким способом, отправляясь от ана-
аналитических множеств и их дополнений, есть, очевидно, множе-
множество E2). Возникает вопрос, будет ли всякое множество (В2)
проекцией однозначного аналитического дополнения и можно ли
распространить теорему Мазуркевича на проективные множе-
множества высших классов? I28].
2) См. Slerplnsky, Sur les images сопНпиез et biunlvoqties
des complementalres analytiques, Fund. Math., т. XII, стр. 211—213.

ТЕОРЕМА МАЗУРКЕВИЧА. ОБОБЩЕНИЕ СЕРПИНСКОГО 287
Обобщение теоремы о параметрическом изображении
проективных множеств. Мы видели, что всякое проектив-
проективное множество (Ап) можно рассматривать как геометриче-
геометрическое место последовательных положений подвижной точки
M(xit лг9, ..., хт), координаты которой являются функциями
переменного параметра t
непрерывными на области gt, причем t пробегает проектив-
проективное множество (САп_1).
Мы докажем, что семейство множеств (Ап) не расши-
расширится, если за функции ft принять произвольные функции
классификации Бэра и если заставить t пробегать любое
проективное множество класса < п, лежащее в 01.
В самом деле, пусть ft (t = l, 2, ..., т) — любые функ-
функции классификации Бэра, определенные на gt, и Н—любое
проективное множество класса < и, лежащее в gt.
Рассмотрим в т-\- 1-мерной области 0Ху..х t множество ?
точек N(xu . .., хт, t), удовлетворяющих уравнениям
*i =/i @, *« = /а @. • • •» хт =fm (f).
Это множество $ необходимо измеримо В.
Установив это, отметим на оси ОТ данное множество Н
и рассмотрим в области 0х....х t множество всех тех точек,
для которых координата t принадлежит к Н. Пусть V это
множество. Выше мы доказали (стр. 278), что V есть про-
проективное множество того же класса и того же рода, как И.
Следовательно, общая часть множеств V и $ есть проек-
проективное множество класса <^ и и, следовательно, его проекция
в область gx .Хт есть проективное множество (Ап) или EП),
или класса < п.. Ч. т. д.
Заметим, что мы придем к тому же результату, если мно-
множество Н есть (Ап) или (Вп).
Вспомнив аналогию между множествами (Вп) и множе-
множествами, измеримыми В, естественно поставить вопрос:
Если дано параметрическое изображение
*i =/i @i Х2 =?/вD • • •» хш —/» W • - ¦

288 ГЛ. V. ПРОЕКТИВНЫЕ МНОЖЕСТВА
из функций классификации Бэра, причем оно регулярно или
полурёгулярно на Н, где Н есть (Вп), будет ли множество,
допускающее это параметрическое изображение, непременно
(Вп)' или класса < «? (См. прим. [аб].)
Проективные функции. Для определенности, мы ограни-
ограничимся рассмотрением функций одного независимого пере-
переменного.
Введем следующее определение:
Мы скажем, что однозначная, всюду определенная функ-
функция f(x) есть проективная функция, если множество точек
области gxy, лежащих на изображающей кривой y—f(x),
есть проективное множество.
Проективные функции f (х) можно классифицировать по
классам и родам проективных множеств.
Как только понятие проективной функции введено, воз-
возникают важные вопросы относительно параметрического изо-
изображения множеств при помощи проективных функций.
Среди этих многочисленных проблем мы ограничимся ука-
указанием некоторых: если дана проективная функция f(x),
являющаяся плоским аналитическим дополнением, каково мно-
множество ее значений на ?ГХ? Известно, что это множество
есть (А^), или (В2), или проективное множество класса 1,
но мы не знаем, можно ли всякое (Л2) представить таким
образом.
Больше того, мы не знаем, можно ли всякое аналитиче-
аналитическое дополнение, неизмеримое В, представить в этой форме.
Ответ положителен и до некоторой степени банален, если
это аналитическое дополнение содержит совершенное множе-
множество: этот результат можно получить, отправляясь от преды-
предыдущей теоремы Мазуркевича. Но если не делать никакой
гипотезы, то ничего не известно.
В заключение мы хотим привлечь внимание математиков
к одной проблеме первостепенной важности.
Дана проективная функция f (х) однозначная, всюду
определенная и такая, что изображающая ее кривая L
есть аналитическое дополнение; узнать, содержит ли не-
непременно L совершенное множество"} I89].
Чрезвычайная важность этой проблемы вызвана тем, что
если ее решение отрицательно, то знаменитая проблема кон-
континуума решается положительно.

ТЕОРЕМА МЛЗУРКВВИЧА. ОБОБЩЕНИЕ СЕРПИНСКОГО 289
В самом деле, множество L есть сумма несчетного мно-
множества конституант, измеримых В и. перенумерованных при
помощи конечных и трансфинитных чисел второго класса по
Кантору
Так как L не содержит никакого совершенного множе-
множества, то каждая его конституанта Е есть счетное множество
и такова же будет ее проекция Е% на ось ОХ. Но проекция
кривой L на ось ОХ в точности совпадает с этой осью. Сле-
Следовательно, мы имеем
что и доказывает, что мощность континуума есть Kj.
Проективные решета. Мы теперь обобщим результаты,
относящиеся к аналитическим решетам (стр. 180).
Легко показать, что мы не выходим за пределы проек-
проективных множеств, производя операцию, которая состоит
в том, чтобы брать множество, просеянное при помощи про-
проективного решета.
Теорема. Всякое множество, просеянное при помощи
проективного решета класса п, есть проективное множе-
множество Ип+t) иЛи класса <[л.
Чтобы убедиться в этом, достаточно следовать доказа-
доказательству, относящемуся к аналитическим решетам (стр. 180).
В самом деле, если дано проективное решето С класса и, то
множество Е, просеянное при помощи С, есть множество
значений непрерывной функции <р[/, (x)j на 0 • Н. Но множе-
множество Ь измеримо В. С другой стороны, мы имеем
Н = //j • //2... Hjc...
Так как Нк есть результат непрерывного преобразования
С, то Ик есть проективное множество класса -^л, каково
бы ни было k. Следовательно, 9 • Н есть также проективное
множество класса <^& и, следовательно, Е есть (^4я+1) или
проективное множество класса <[«. Ч. т. д.
Обратно, всякое множество Hn+i) можно рассматривать
как просеянное при помощи решета (САп). Это замечание
19 Зшс 284. Н. Н. Лузин

290 ГЛ. V. ПРОЕКТИВНЫЕ МНОЖЕСТВА
весьма банально, так как каждое множество Е вида (Ап+1)
есть проекция множества Н вида (САп). Если мы обозначим
через Нк множество (САп), лежащее между прямыми у = . . .
и у = т-| проекция которого на ось ОХ совпадает с Е, то
ясно, что Е просеяно при помощи суммы Н1-\-Н2-\-
-|- ... -J- Hjc -)-..., а эта сумма есть множество (САп).
Ч. т. д.
Среди проективных решет наиболее интересны счетные:
это такие проективные решета С, что каждая прямая, парал-
параллельная вертикальной оси, пересекает С не более, чем по
счетному множеству точек. К сожалению, по этому вопросу
известно очень мало.
Известно, что каждое аналитическое множество можно
рассматривать как просеянное при помощи счетного решета,
измеримого В. Но неизвестно, можно ли каждое множество
(Л2) рассматривать как просеянное при помощи счетного ре-
решета (В2). Неизвестно даже, можно ли каждое счетное решето
(В2) разложить на счетное множество однозначных мно-
множеств (в2).
С этими рассмотрениями, можно связать понятие прямоли-
прямолинейного решета. Счетное решето С называется прямолиней-
прямолинейным, если оно составлено из счетного множества множеств,
лежащих на параллелях к оси ОХ. Было бы чрезвычайно
интересно узнать, каковы линейные множества (Л2), кото-
которые могут быть получены при помощи прямолинейных ре-
решет (Bjj).
Я должен отметить одну работу Е. А. Селивановского,
относящуюся к этому вопросу. Этот молодой автор рассмат-
рассматривал семейство множеств, которое можно получить, отправ-
отправляясь от множеств, измеримых В, при помощи двух опе-
операций: прямолинекного решета и взятия дополнения
повторенных неограниченно. Эти множества носят название
множеств (С) и разбиваются на бесконечное множество
классов, перенумерованных при помощи всех конечных
чисел и всех трансфинитных чисел второго класса по Кан-
Кантору I80].
Селивановский доказал, что все эти множества измеримы
и имеют определенную категорию, но связь этого семейства

НЕПУСТОТА ВСЕХ КЛАССОВ. УНИВЕРСАЛЬНЫЕ МНОЖЕСТВА 291
множеств с семейством проективных множеств остается не-
неизвестной *).
Отделимость. Одна из наиболее важных проблем теории
проективных множеств, ожидающая еще своего решения, есть
проблема их отделимости.
Известно, что любые два аналитических множества без
общих точек всегда отделимы В. Было бы очень важно до-
доказать, что любые два множества (Ап) без общей точки
всегда отделимы (Вп).
Точно так же мы знаем, что если удалить их общую
часть из двух аналитических множеств, то оставшиеся части
отделимы при помощи двух аналитических дополнений. Есте-
Естественно возникает вопрос, сохранится ли этот принцип, если
заменить аналитические множества через (Ап), а их дополне-
дополнения через {САп). Эта проблема, несмотря на свою трудность,
заслуживает того, чтобы привлечь внимание математиков.
Кроме того, важно было бы узнать, существуют ли два
множества (САп), которые неотделимы (Вп) I82].
Существование проективных множеств всякого класса
и всякого рода. Универсальные множества
Теперь пора восполнить пробел, доказав существование
проективных множеств всякого класса и рода. Мы отложили
это доказательство к концу теории проективных множеств
для того, чтобы некоторые предварительные очень полезные
предложения были уже доказаны2).
*) См. заметку Е. А. Селивановского, Sur une classe
d'ensembleb definis par une infinite denombrable de conditions
(Comptes Rendus Acad. Sc., 30 мая 1927 г.).
Исправляя корректуры, я добавлю, что исследования, относя-
относящиеся к этой проблеме, были предприняты недавно двумя учени-
учениками Г. М. Фихтенгольца Канторовичем и Ливенсоном; они пока-
показали, что множества (С) суть проективные множества второго
класса. См. их заметки в Comptes Rendus Acad. Sc. Канторо-
Канторович и Ливенсон, Sur lesensembles projectifs de deuxiemeclasse,
30 декабря 1929г.; Kantorovitch et Livenson, Sur les
BB-fonctions de M. Hausdorli A0 февраля 1930 г.); Sur les ensembles
projectifs de M. Lusin A2 мая 1930 г.) [31J.
*) См. также мою заметку «Les proprletes des ensembles pro-
projectifs» (Comptes Rendus Acad. Sc. 15 июня 1925 г.).
19*

292 ГЛ. V. ПРОЕКТИВНЫЕ МНОЖЕСТВА
Сделаем сначала одно очень простое замечание: чтобы
доказать существование множеств (Вп), достаточно доказать
существование множеств (/!„-]) и (САп_1). В самом деле,
мы видели (стр. 2»2), что сумма двух множеств, из которых
одно (/!„_!), а другое (САп_1), расположенных в двух непе-
неперекрывающихся порциях области g х, необходимо имеет вид
(Вй). С другой стороны, если Е есть {Ап), то его дополне-
дополнение СЕ есть (САп). Итак, все сводится к доказательству
существования проективных множеств (Ап).
Метод, позволяющий нам доказать это существование,
опирается на построение универсальных плоских множеств
различных типов.
Мы называем универсальным множеством типа (Ап)
всякое плоское проективное множество U вида (Ап) или (В^
или класса < я, обладающее следующим свойством: всякое
линейное множество (Ап) или {Bj, или класса < и можно
получить, пересекая U подходяще выбранной параллелью
к оси О У.
Легко видеть, что каждое универсальное множество U
типа (Ап) само является эффективным примером множества (Ап).
В самом деле, пересечем U диагональю у = х. Пусть е есть
множество точек U, лежащих на этой диагонали, и пусть е'
есть проекция е на ось О У.
Прежде всего дополнение Се' заведомо не может быть
получено, если пересекать U параллелями к оси О У. Этот
важный факт мы уже видели на стр. 130.
Отсюда следует, что линейное множество е есть эффек-
эффективно множество (Ап). В самом деле, в противном случае это
множество есть либо (Вп), либо класса < п. Следовательно,
линейные множества е' и Се' одной и той же природы, что
невозможно, так как в этом случае Се' можно было бы по-
получить, пересекая U параллелью к оси ОУ.
Итак, мы уже имеем пример линейного множества (Ап):
это множество е. Но можно утверждать нечто ббльшее:
само множество U есть множество (Ап). В самом деле, если
бы U было (Вп) или класса < п, то его часть е, лежащая
на диагонали у = х, была бы той же природы.
Итак, все сводится к построению универсальных мно-
множеств типа (Ап), каково бы ни было целое положитель-
положительное п.

НЕПУСТОТА ВСЕХ КЛАССОВ. УНИВЕРСАЛЬНЫЕ МНОЖЕСТВА 293
Прежде всего на стр. 146 мы построили универсальное
аналитическое множество U. Его дополнение CU есть, оче-
очевидно, универсальное аналитическое дополнение, так как
каждое линейное аналитическое дополнение (и, в частности,
каждое множество, измеримое В) можно получить, пересекая
CU параллелью к оси OY.
Установив это, применим метод простой индукции. Итак,
допустим, что мы построили множество ?/„_,, лежащее в пло-
плоскости ХОТ и являющееся универсальным множеством типа
(Л„_,). Его дополнение CUn_t есть, очевидно, универсальное
множество типа (САп_1).
Возьмем функцию
г = <р(лг, т)
класса 2 по классификации Бэра, определенную всюду на
0 я„ и такую, что всевозможные функции f(x) класса 1
классификации Бэра можно получить, выбирая подходящим
образом значение т0 параметра т
Такие функции <р мы строили на стр. 147.
Установив это, преобразуем множество ?/„_, и функцию ф
во множество Vn_, и функцию <|» таким образом, чтобы по-
получить новую пару (Vn_j, ф), в некотором роде дважды
универсальную.
С этой целью возьмем две функции
непрерывные яа ^9 и обладающие следующим свойством:
каковы бы ни были два иррациональных числа t0 и т0, най-
найдется такое иррациональное у0, что tQ = g(yJ и то = А(_уо).
Чтобы получить множество Vn_t, возьмем преобразование
области gtm в новую область g ут, данное формулами
Множество Vn_j есть, по определению, образ множества
n-i' Ясно, что Уп^ есть плоское проективное (A)

294 ГЛ. V. ПРОЕКТИВНЫЕ МНОЖЕСТВА
С другой стороны, преобразуем функцию <р(х, т) в новую
функцию «|)(лг, у) при помощи подстановки т = А(У):
<К*> У) = <?[х, h(y)\.
Множество Vn_i и функция <|* образуют дважды универ-
универсальную пару, так как, выбирая подходящим образом число
у0, мы получаем одновременно произвольное линейное мно-
множество (Ап_)), или (Sw-i), или класса <« — 1, как резуль-
результат пересечения Vn_t прямой у=у0, и любую функцию/(х)
класса 1 при помощи равенства f(x) = ty(x, у0).
Установив это, рассмотрим трехмерную область 0'xyz.
Пусть S есть поверхность, определенная уравнением
z = f(x, у).
Возьмем на горизонтальной плоскости XOY множество
CVn_, и обозначим через % множество тех точек S, проек-
проекции которых на плоскость XOY принадлежат к CVn_v
Ясно, что $ есть (САп_)), или (Bn_j), или класса <и—1.
Следовательно, проекция ? на плоскость ZOY есть проек-
проективное множество (Ап), или (Вп), или класса < п.
Я теперь утверждаю, что так определенное множество
Е есть универсальное множество типа (Ап).
В самом деле, мы знаем, что всякое линейное множество е
вида (Ап), или (Вп), или класса < и можно рассматривать,
как множество значений некоторой функции f(x), непрерыв-
непрерывной на 0х, когда х пробегает линейное множество Н вида
(C4n_j), или (#„_]), или класса <л — 1.
Но, выбирая соответствующим образом у0, мы получим
множество Н, пересекая CVn_i прямой у=у0, и функцию
/(ж), подставляя у=у0 в ^{х, у).
Отсюда можно заключить, что наперед заданное множе-
множество е рода (Л„) или (Вп) или класса < п можно получить,
пересекая Е прямой у — у0, а это и доказывает, что Е есть
универсальное множество типа (Ап). Ч. т. д.
Резольвенты
Резольвенты. Мы скажем, что некоторая проблема Р
теории функции поставлена в резольвенту, если мы можем
назвать множество точек Е такое, что проблема Р решается
положительно, каждый раз как можно назвать точку.из Е,

РЕЗОЛЬВЕНТЫ . 295
и решается отрицательно, если можно доказать, что Е пусто*).
Само множество точек Е, от которого зависит окончательное
решение предложенной проблемы Р, называется резольвентой
проблемы Р.
Среди проблем теории функций, решение которых, пови-
димому, представляет трансцендентные трудности, большин-
большинство может быть поставлено в резольвенту, причем важно
заметить, что все эти резольвенты оказываются проектив-
проективными множествами. Среди этих проблем наиболее интересны
следующие: эффективное вполне упорядочивание контину-
континуума и отыскание аналитического обозначения, лишенного дву-
двусмысленности, для всех трансфинитных чисел второго класса
по Кантору. Этой последней проблемой мы обязаны Борелю;
мы сейчас объясним, в чем ее смысл.
Известно, что среди трансфинитных чисел второго класса
по Кантору «маленькие» трансфинитные числа могут быть
написаны при помощи буквы со. Это значит, что существует
много трансфинитных чисел, в некотором смысле близких
к «о, которые могут быть написаны в виде многочленов или
показательных функций от со. Все эти трансфинитные числа
вполне определены. Но таким способом нельзя определить
все трансфинитные числа второго класса. В самом деле,
какие бы определения мы ни дали (определения, содержащие
конечное число символов), найдутся трансфинитные числа,
которые не подпадут под эти определения, но могут быть
определены другими символами в конечном числе и так до
бесконечности а).
Итак, в настоящем состоянии науки мы не имеем никакого
алгорифма, позволяющего написать все трансфинитные числа
второго класса. Тем не менее существует алгорифм, позво-
позволяющий написать все действительные числа: достаточно на-
напомнить разложение в бесконечную десятичную дробь.
Вышеуказанная проблема Бореля состоит именно в том,
чтобы найти алгорифм, составленный из счетного множества
х) О методе резольвент см. мою заметку «Sur le probleme de
М. Emile Borel et la methode des resolvantes» (Comptes Rendus
Acad. Sc, 17 августа 1925 г.) и цитированный мемуар «Sur les ensem-
ensembles analytlques» (Fund. Math., т. Х, стр. 91).
2) См. Bore I, La philosophic tnath6matique et e'iafihi, Revue
du Mois, aoflt, 1912 r. •¦¦-.¦

296 ГЛ. V. ПРОЕКТИВНЫЕ МНОЖЕСТВА
символов и позволяющий написать все трансфинитные числа
второго класса.
Проблема Э. Бореля была бы решена, если бы мы умели
перенумеровать все действительные числа при помощи сово-
совокупности трансфинитных чисел второго класса или, по край-
крайней мере, назвать часть континуума, перенумерованную этим
способом. Но в первом случае сама проблема континуума
была бы полностью решена, а во втором случае мы бы имели
решение проблемы о сравнении двух мощностей: мощности
континуума и мощности к, *)•
Вернемся теперь к резольвентам. Самое введение понятия
резольвенты тесно связано с идеями Э. Бореля. В своем
сообщении IV Математическому конгрессу (Рим, апрель 1908 г.)
Борель говорит: «Чтобы дать понять мою точку зрения,
я укажу проблему, кажущуюся мне одной из наиболее важ-
важных в арифметической теории континуума: Можно ли опре-
определить множество Е такое, что нельзя назвать ни одного
индивидуального элемента этого множества Е, т. е. без дву-
двусмысленности отличить его от всех остальных элементов Е» 2).
Цель дальнейших рассмотрений состоит в том, чтобы
указать проективные множества, образованные из точек сег-
сегмента @, 1) и которые я рассматриваю как решение только
что цитированной проблемы Бореля.
Эти проективные множества являются резольвентами неко-
некоторых проблем, решение которых в абсолютном смысле, по
моему мнению, выходит за пределы классической теории
множеств.
Среди многочисленных проблем теории функций я огра-
ограничусь рассмотрением только двух и построю резольвенты
этих проблем.
Проблема I. Узнать, не будут ли все аналитиче-
аналитические дополнения либо счетны, либо иметь мощность кон~
тинуума.
Интерес этой проблемы вызывается тем, что если до-
допускать существование всех трансфинитных чисел второго
1) См. письмо Лебега; «Cinq lettres sur la thiorie des ensem-
ensembles» (Bulletin de la Soc. Math, de France, decembre 1904 г.).
. . a.).Cu..B.oijel, Lecons sui la theorie des fonctions, 3 ed. 1928,
стр. 162, ' ,.

РЕЗОЛЬВЕНТЫ 297
класса, то можно безукоризненно доказать, что всякое не-
несчетное аналитическое дополнение, не содержащее совер-
совершенного множества, необходимо является соединением не-
несчетного множества счетных множеств попарно без общих
точек, перенумерованных вполне точно, при помощи всех
трансфинитных чисел второго класса. Следовательно, если
этот логически возможный случай практически реален, то
можно будет утверждать, что существование всех трансфи-
трансфинитных чисел второго класса есть факт как бы эксперимен-
экспериментального характера.
Резольвента Е этой проблемы есть проективное мно-
множество класса не выше 3. Если можно назвать точку из Е,
то такое необыкновенное аналитическое дополнение суще-
существует, и обратно.
Перейдем теперь к построению этой резольвенты.
Возьмем трехмерную область Й xvt и рассмотрим в пло-
плоскости XOZ универсальное аналитическое множество U,
т. е. такое, что всевозможные линейные аналитические мно-
множества можно получить, пересекая U параллелями к оси OZ.
С другой стороны, возьмем в плоскости YOZ множе-
множество U' такое, что всевозможные линейные совершенные
множества и только их можно получить, пересекая U'
параллелями к оси OZ. Такое множество U' построить очень
легко [88].
Обозначим через S множество точек области 3 xyz^ ГР°~
екции которых на плоскость YOZ принадлежат к U. Анало-
Аналогично, пусть V есть множество точек &xyz, проекции кото-
которых на плоскость YOZ принадлежат U''.
Ясно, что 8 есть аналитическое множество и что $'
есть либо (Ая), либо (В2), либо класса 1. Значит, общая
часть % • Ъ' есть либо множество (А%), либо (в2), либо
класс 1.
Произведем над S • §' операции, указанные в следующей
формуле: Е, = РСР (g ¦ $0.
где мы проектируем $ • $' на XOY, затем берем дополнение
к этой проекции, и, наконец, проектируем это дополнение
на ОХ.
Ясно, что так полученное проективное множество Ei
есть либо (As), либо (Вд), либо класса <]2.

298 ГЛ. V. ПРОЕКТИВНЫЕ МНОЖЕСТВА
Установив это, возьмем в плоскости YOZ множество U",
измеримое В, такое, что всевозможные счетные линейные
множества можно получить, пересекая U" параллелями
к оси OZ. Чтобы получить такое U", достаточно взять
бесконечную последовательность непрерывных функций
/i Су)» /aOO» •••>fn(y\ ••• таких, что, какова бы ни была
система иррационных чисел г°, z°, ..., z°n, ..., существует
число у0, для которого при всяком и имеем Zn=fn(yQ).
Если мы проведем в плоскости YOZ все эти кривые
z=fn(y), « = 1, 2, 3, ..., то их соединение и есть, оче-
очевидно, искомое множество О".
Заметив это, обозначим через &" множество точек 0' „
проекции которых на плоскость YOZ принадлежат к и".
Ясно, что &" измеримо В и что сумма Ь-\-%" есть анали-
аналитическое множество.
Произведем над §-j-g" операции, указанные формулой
где дополнение берется в области gxyz, затем мы проек-
проектируем на XOY, затем берем дополнение и, наконец, проек-
проектируем на ОХ.
Легко видеть, что так полученное проективное мно-
множество Е2 есть либо (Л3), либо (В3), либо класса <] 2.
Отсюда следует, что множество-сумма Ех -J- Е2 есть
проективное множество класса <] 3. Значит, если мы обо-
обозначим через Е дополнение к этой сумме, то множество Е
есть также проективное и класса ^ 3.
Я теперь утверждаю, что множество Е есть резольвента
поставленной проблемы. Это значит, что если бы мы
умели указать точку во множестве Е, то мы бы полу-
получили несчетное аналитическое дополнение, без совершен-
совершенной части; а если бы удалось доказать, что Е пусто, то
было бы доказано, что таких аналитических дополнений
не существует.
В самом деле, если мы расшифруем смысл несколько
сложных построений двух линейных проективных множеств Et
и ?2, то мы найдем, что Е1 есть множество тех точек х,
в которых параллели к оси OZ пересекают универсальное
аналитическое множество U по обыкновенным аналитическим

РЕЗОЛЬВЕНТЫ 299
множествам, дополнения к которым содержат, каждое, по
совершенному множеству; точно так же ?2 есть множество
тех точек х, для которых соответствующие аналитические
множества имеют счетные (или конечные) дополнения: это
также обыкновенные дополнения.
Если мы удалим из оси ОХ все точки множеств Ех и
?2, мы, разумеется, получим точки х, которые соответствуют
необыкновенным аналитическим дополнениям.
Итак, в конечном итоге мы здесь имеем лишь чисто
логическую трудность, хорошо запрятанную под квазигео-
квазигеометрической внешностью.
Проблема II. Узнать, существует ли функция f (x),
всюду определенная и такая, что изображающая ее кри-
кривая y—f(x) есть аналитическое дополнение без совер-
совершенной части.
Важность этой проблемы объясняется тем, что в случае
положительного ответа мощность континуума окажется рав-
равной К] (стр. 288).
Кроме того, эта кривая y=f(x) не может быть
измерима в смысле Лебега. В самом деле, если бы эта
кривая была измерима в смысле Лебега, то на оси ОХ
существовало бы совершенное множество Р, на котором
f(x) была бы непрерывна. Это значит, что рассматриваемая
кривая y=f(x) содержит совершенное множество, что про-
противоречит сделанной гипотезе.
Чтобы не утомлять читателя, повторяя одни и те же
операции, мы просто укажем путь построения резольвенты
предложенной проблемы.
Прежде всего мы возьмем в области gxyz аналити-
аналитическое универсальное множество U трех измерений,
такое, что всевозможные плоские аналитические множества
получаются при пересечении U плоскостями, параллель-
параллельными XOY.
Обозначим через Н1 множество точек прямых, парал-
параллельных оси OY и не пересекающих дополнение CU к U.
Точно так же пусть //2 есть множество точек прямых,
параллельных оси OY, каждая из которых пересекает CU не
менее двух раз. Пусть ?, и ?2 соответственно проекции Я,
и //2 на ось OZ'. Так как Нх есть либо (СЛ2), либо (?2),
либо класса < 2, а Я2 либо (А%), либо (S2), либо класса < 2,

300 ГЛ. V. ПРОЕКТИВНЫЕ МНОЖЕСТВА
то Е есть проективное множество класса <!3, Е2 — про-
проективное множество класса <]2.
Обозначим через Еъ множество таких точек С оси OZ,
что каждая плоскость z — С пересекает U по аналитическому
множеству, дополнение к которому либо счетно (или конечно),
либо имеет мощность континуума. Чтобы получить мно-
множество Е%, достаточно преобразовать взаимно однозначно и
взаимно непрерывно область & ху в область gf д. при помощи
уравнений
0
г = z.
Образ U' множества U при этом преобразовании есть пло-
плоское аналитическое множество и плоскости, параллельные XOY,
преобразуются в прямые, параллельные оси ОТ.
Отсюда следует, что дополнение к множеству Е3 то-
тождественно с резольвентой предшествующей проблемы. Значит,
Es есть проективное множество класса ^ 3.
Если удалить из оси OZ множества Еи Е2 и Еъ, то
множество Е оставшихся точек есть, очевидно, проективное
множество класса <С 3. Это проективное множество Е и
есть резольвента поставленной проблемы.
Мы видим, что лицо, которое сумело бы назвать точку
во множестве Е, сумело бы перенумеровать все точки оси ОХ
при помощи всех трансфинитных чисел второго класса.
Анализ мемуара Лебега «Sur les fonctlons representables
analytiquement»
На следующих страницах мы укажем некоторые пункты
этого мемуара1), тесно связанные с предметом наших рас-
рассмотрений. В то же время мы хотели бы привлечь внимание
аналистов к одному методу, употребленному Лебегом для
построения точечных множеств.
Природа этого метода очень сложна и. несколько зага-
загадочна. С одной стороны, он совершенно избегает рассужде-
рассуждения Цермело. С другой стороны, базируется на совокупности
Journal de Mathdmatique, 1905, стр. 139—216,

АНАЛИЗ МЕМУАРА ЛЕБЕГА 301
всех трансфинитных чисел второго класса. Важно заметить,
что самый способ пользования этой совокупностью суще-
существенно отличается от способов, употребляемых во всех
известных рассуждениях.
В самом деле, есть много точечных множеств, которые
могут быть определены при помощи совокупности трансфи-
трансфинитных чисел второго класса: таков, например, случай ана-
аналитических дополнений (стр. 197), а также проективных
множеств. Но мы видели, что каждый раз, как эта сово-
совокупность появляется, ее можно исключить при помощи от-
отрицательных определений. Например, любое решето С опре-
определяет аналитическое дополнение положительным образом:
это множество точек, где перпендикуляры пересекают решето С
по вполне упорядоченным множествам, которым, вообще
говоря, соответствуют все более и более высокие трансфи-
трансфинитные числа. Итак, все трансфинитные числа второго класса
эффективно вошли в это определение. Тем не менее, если
мы хотим избежать понятия трансфинитного, достаточно
определить аналитическое дополнение, как множество точек,
которые не принадлежат данному аналитическому множеству.
Ясно, что здесь совокупность трансфинитных чисел заменена
отрицательной операцией: взятием дополнения к уже опре-
определенному множеству.
Но употребление совокупности трансфинитных чисел
в методе Лебега совершенно другое. Лебег пользуется транс-
трансфинитной последовательностью действительных чисел, опре-
определенных не одновременно, а последовательно, таким об-
образом, что определение каждого из этих чисел суще-
существенно зависит от предыдущих численных опреде-
определений.
Этот способ пользоваться совокупностью трансфинитных
чисел делает чрезвычайно затруднительным исключение этой
совокупности при помощи отрицательных определений. Мо-
Может случиться, что такое исключение является даже абсолютно
невозможным.
Дескриптивный метод Лебега для определения мно-
множеств конечных классов. Важным пунктом мемуара
Лебега является способ эффективно получить все функции
конечных классов классификации Бэра при помощи функций
многих переменных непрерывных по каждому из них.

302 ГЛ. V. ПРОЕКТИВНЫЕ МНОЖЕСТВА
, Лебег доказывает следующую теорему, касающуюся этих
функций (стр. 201, строка 10):
«XX. Функция от п переменных,, непрерывная по каж-
каждому из них, будет класса не выше п—1».
Из этой теоремы следует, что если'/^, лг2, ...,лгп)
есть такая функция, то функция f(x, x, ...,х), которую
мы получим, полагая
ЛГ| = Х% = . . . = Хп = X,
есть функция класса не выше и — 1.
Установив это, цитируем один отрывок из Лебега
(стр. 202, строка 1):
«Правда, можно спросить себя, возможно ли, чтобы най-
найденный для класса верхний предел был фактически достигнут.
Ответ положителен; в самом деле, мы докажем, что
«XXI. Если f(t) есть функция класса п, то существует
функция <?(xv лг2, ...,хп+г), непрерывная по каждому из
своих п-г\-1 переменных и такая, что f (t) тождественна
с <o{t, t, ..., t)».
Рассмотрения Лебега относятся к функциям. Если мы
применим их ко множествам, то вот что мы получим:
Если % есть множество точек, лежащее в и -|-1 -мерной
области g'as.x ...xx и такое, что, какова бы ни была
точка М этой области, существует фигура, составленная из
«-|-1 прямолинейных интервалов, параллельных осям ОХи
ОХ2, ..., ОХп+1 и проходящих через точку Ж1), причем
эта фигура либо целиком принадлежит к S, либо не имеет
с $ ни одной общей точки, — тогда линейное множество _Е,
которое получается при разрезании § прямой лг,=л:2=... = хп,
есть множество класса не выше п и каждое множество
конечного класса п может быть получено этим способом.
Итак, метод Лебега позволяет получить все множества
конечных классов дескриптивным путем, не употребляя
никакого оперативного процесса.
Было бы желательно распространить метод Лебега на
множества трансфинитных классов. Но следует заметить, что
невозможно непосредственно обобщить метод Лебега. В са-
') Точка М есть внутренняя в узком смысле для каждого из
этих интервалов.

АНАЛИЗ МЕМУАРА ЛЕВЕГА 303
мом деле, для этого пришлось бы рассматривать функции
счетного множества переменных хи лг2, ..., хп, ..., непре-
непрерывных по каждому из них. Но если определять функцию
f(xlt лг2, ...,хп, ...) от счетного множества переменных,
как соответствие между числом у и бесконечной последо-
последовательностью х1г лг2, ..., хп, ..., то можно тотчас же придти
к следующему отрицательному результату: можно опреде-
определить функцию /(*!, лг2, ..., хп, ...), непрерывную по каж-
каждому из переменных и такую, что, полагая х = ху =
= х2 = ... = хп = ..., мы получим совершенно произ-
произвольную функцию f(x) переменного х.
Этот факт показывает нам, что для обобщения резуль-
результата Лебега надо идти другим путем.
Метод Лебега для доказательства существования
функций всех классов. Перейдем теперь к той части мему-
ара Лебега, где он доказывает существование функций всех
классов и функции, которая не допускает никакого аналити-
аналитического изображения.
Пусть а — любое число, конечное или трансфинитное
второго класса. Требуется определить функцию fa(t, x)
двух действительных переменных t и х, входящую в класси-
классификацию Бэра и такую, что каждую заранее данную функ-
функцию F (х) класса а можно заведомо получить, выбрав под-
подходящим образом значение t0 параметра t:
fm(t0, x)^F(x).
Чтобы получить такую функцию fa(t, x), делаются сле-
следующие рассмотренияJ):
Каждая функция / (х) класса <] 1 классификации Бэра
есть предел последовательности полиномов
/(*)= ШРп(х),
где можно предполагать, что полином Рп(х) имеет степень
О. Обозначим через afj? коэффициенты полинома Рп{х),
k = 0, 1, 2 и.
J) Я позволяю себе слегка изменить метод Лебега в его техни-
технической части, чтобы осветить основные принципы.

304 ГЛ. V. ПРОЕКТИВНЫЕ МНОЖЕСТВА
С другой стороны, рассмотрим счетное множество функ-
функций $\1); определенных на порции @,1) области gt, не-,
прерывных в каждой точке -этой порции и обладающих сле-
следующим свойством: какова бы ни была система чисел а^>
найдется такое иррациональное tQ между 0 и 1, что <$? (t0) = а%\
каковы бы ни были п и к.
Эти функции <f^{t) определяют то, что Лебег называет
«кривой, заполняющей целую область в пространстве счетного
числа измерений» (стр. 211, примечание).
Если мы в полиномах Р„(х) заменим коэффициенты а&"*
соответствующими функциями <р^№» мы получим функцию
tyn(t, х) двух переменных tax, непрерывную по совокуп-
совокупности этих переменных и совпадающую, очевидно, с заранее
заданным полиномом относительно х степени п, когда зна-
значение tQ параметра / выбрано надлежащим образом.
Установив это, вернемся к данному трансфинитному
числу а. Чрезвычайно важно заметить, что Лебег предпола-
предполагает это число а не только названным, но данным в неко-
некотором смысле эффективно, именно так, чтобы вместе с ним
задан был пересчет я1( <х2, ... всех трансфинитных чисел,
которые предшествуют а. Известно, что в теории трансфи-
трансфинитных чисел смысл символа
о",
где а и р два трансфинитных числа, определяется по индук-
индукции. Лебег выводит из простой бесконечной последова-
последовательности ах, а2 образованной из всех трансфинит-
трансфинитных чисел, предшествующих а, новую вполне определен-
определенную последовательность, также простую бесконечную,
Pii ?2» • • •» составленную из всех трансфинитных чисел, пред-
предшествующих О)*.
В этом заключается основной пункт, так как этот факт
позволяет построить множество точек F, линейное, замкну-
замкнутое и вполне упорядоченное в положительном направлении
прямой, содержащей F, причем ему соответствует трансфи-
трансфинитное число со".

АНАЛИЗ МВМУАРД ЛЕБЕГА 305
Главное свойство числа <о« заключается в том, что если
мы рассмотрим последовательность производных мно-
множеств для F
F, F', F", ...,Л«>, ...,FW |Я->,
то производное множество Я") состоит из одной и только
одной точки х, следовательно, дальнейшие производные
будут пусты.
Заметив это, установим взаимно однозначное соответ-
соответствие между изолированными точками F и всеми непрерыв-
непрерывными функциями- tyn (t, x). Так как мы умеем перенумеровать
все точки F при помощи целых чисел, то мы можем эф-
эффективно получить это соответствие.
Установив это, будем действовать следующим образом:
прежде всего каждой изолированной точке I первого произ-
производного множества F' мы приведем в соответствие вполне
определенную функцию переменных t и х класса •< 1, полу-
получаемую, если взять предел последовательности функций
ф„(/, х), соответствующих изолированным точкам \х, ^,..., S,
из F, стремящимся к рассматриваемой точке \ из F.
Допустим, что каждой изолированной точке каждого из
производных множеств F®\ предшествующих множеству FW,
приведена в соответствие вполне определенная функция пере-
переменных tax класса <[ fJ и установим аналогичное соответ-
соответствие для изолированных точек самого множества F^\
Следует различать два случая.
В первом случае число f первого рода ^ = ^*-|-1.
В этом случае мы приводим в соответствие каждой изолиро-
изолированной точке I из Fb) вполне определенную функцию пере-
Г'
Черт. 7.
менных t и х класса <f, получаемую, если взять предел
последовательности функций, соответствующих изолирован-
изолированным точкам ?!, ?2, ...,Е„ ... из Я**>, стремящихся к рас-
рассматриваемой точке \ из Я*)
20 Зак. 284. Н. Н. Лузин

30(> ГЛ. V. ПРОЕКТИВНЫЕ МНОЖЕСТВА
Во втором случае число f второго рода. В этом случае
мы" начнем с того, что заключим все изолированные точки \
из /*<!> в последовательность интервалов 8 неперекрывающихся
и таких, что каждый интервал 8 содержит одну и только
одну изолированную точку 5 из /*W.
Так как мы имеем вполне определенную нумерацию для
точек множества F при помощи целых чисел, то мы можем
определить для каждой изолированной точки \ из FW после-
последовательность точек |j, 52, ..., ?„ ..., лежащих в соответ-
соответствующем интервале 8, и таких, что точка \п есть изолиро-
в' 6" <tm 6in
Черт. 8.
ванная точка производного множества F($n), где последова-
последовательность C] < р2 < ... < р„ < ... стремится к if. Точке Е
мы приведем в соответствие вполне определенную функцию
переменных tux, являющуюся пределом функций, соответ-
соответствующих точкам Ej, Е2> • • • > ?»>
Очевидно, что, действуя дальше таким же образом, мы
в конце концов придем к единственной точке из /"М и мы
приведем ей в соответствие вполне определенную функцию
класса О; это и будет искомая функция fa(t, x).
Чтобы увидеть это, достаточно доказать, что, выбирая
надлежащим образом значение t0 параметра t, мы получим
для изолированных точек производного множества F® про-
произвольно данные функции класса -^^ переменного х,
каково бы ни было ?.
С &той целью заметим, что это верно для f = l, так как
функции tyn(t, x) представляют собой произвольные полиномы
относительно х степени п, если только удачно выбрать
параметр t.
Случай, когда -у первого рода, ^ = -J* -J-1 не предста-
представляет никаких трудностей. В самом деле, по гипотезе, можно
выбрать параметр t так, чтобы функции, соответствующие
изолированным точкам производного Fb*\ обратились в про-

Анализ йёмуара лёбёгА ЗО1?
Извольные функции переменного х класса <!f*. В этих усло-
условиях рассматриваемый случай тождественен со случаем
Случай, когда ? второго рода, несколько более сложен.
Чтобы устранить трудности, мы определим в каждом интер-
интервале 8, содержащем изолированную точку \ из FW, после-
последовательность интервалов 8', 8", ..., 8М, ... попарно без
общих точек и содержащих, соответственно, внутри (в узком
смысле) точки \v Е2, ...,?„,... В этих условиях мы, оче-
очевидно, можем выбрать значение t так, чтобы точкам
?1( $2> •••> ?„... отвечали заранее данные функции класса
соответственно р2, р2> ..., |Зга, , и так для всех изолиро-
изолированных точек % из FW. Из этого немедленно следует, что изо-
изолированным точкам ? из FW соответствуют заранее данные
функции класса <^f.
Итак, процесс Лебега приводит нас к единственной
функции, которую мы обозначим через /e (t, x) и которая
отвечает единственной точке производного множества Л").
Предыдущее рассуждение показывает, что, выбирая над-
надлежащим образом значение параметра t, мы получаем
произвольно данную функцию класса ^ а.
Представляется еще одна трудность, которую важно устра-
устранить. Функция/а (t, x) не всюду определена, ибо для некоторых
значений ? пределы, которыми мы пользовались, могут не суще-
существовать. Чтобы преодолеть эту трудность, мы просто заменим
операцию lim (переход к пределу) через операцию lim (верхний
предел). Так как операция lim есть частный случаи опера-
операции lim, мы заключаем, что ни один из случаев перехода
к пределу (когда он возможен) не будет потерян. Но в слу-
случае, когда переход к пределу невозможен по причине нали-
наличия расходящихся последовательностей функций, операция lim,
заключающаяся во взятии верхнего предела, дает нам всегда
вполне определенный результат. Мы видим, что таким обра-
образом мы приходим к функции Д (t, x), всюду определенной на
( *)
( + )
Покажем, что функция /e (t, x) входит в классифика-
классификацию Бэра. Это очевидно для функций tyn(t, лг), .так как они
непрерывны по совокупности переменных. А так как опера-
операция lim, произведенная над функциями классификации Бэра,
20*

368 гл. V. проективные мнбжйствА
всегда приводит к функциям этой классификации, то мы
заключаем, что функции, соответствующие изолированным
точкам производных множеств FM, все принадлежат класси-
классификации Бэра. В частности, и /„ (t, х) входит в эту класси-
классификацию.
Отсюда мы заключаем, что функция переменного х
/«С*, х)
входит в классификацию Бэра и ее класс меньше или равен
классу /e (t, x)!).
Мы докажем, что класс функции /„ (дг, х) не может
быть меньше а.
В самом деле, допустим, что класс /в(дг, х) будет < а;
пусть C этот класс. Функция да„(дг), определенная равенством
будет класса меньшего или равного J3a). Следовательно, пре-
предельная функция
да(дг) = Шпфп(лг)
будет класса не выше а, так как p-J-l-^a> Но это невоз-
невозможно, так как, если класс <р(лг) не превосходит а, мы мо-
можем выбрать значение t0 для t так, чтобы /„ (^0, х) = да (дг)
при всяком х. Полагая в этом тождестве x = t0, мы прихо-
приходим к невозможному равенству /в (^0, ^0) = да (^0), так как
каждый раз, как /в (^, ^0) отлично от нуля, мы имеем да (?0) = О
и обратно.
Итак, нам удалось назвать функцию, класс которой
заведомо не ниже а; это функция /„ (лг, х).
Отсюда следует, что существуют функции класса, в точ-
точности равного а, так как, если бы таких функций не было,
функция /„ (дг, дг) не могла бы существовать.
]) В самом деле, не представляет никаких затруднений дока-
доказать при помощи трансфинитной индукции, что если Ф (х, у) есть
функция класса < а, то это же имеет место для Ф (дг, х).
а) Речь идет о теореме Лебега: если функция tp(^, t» ..., tp)
будет класса 0, а функции /и /2,.... fp — класса не выше а, то
Ф = <р(/1( /г,...,/р) будет класса не выше a (Sur les fonctions
reprfesentablcs analytiquement, стр. 153, строка 17). Доказательство
, такое же: методом трансфинитной индукции.

АНАЛИЗ МЕМУАРА ЛЕБЕГА 309
Прежде чем идти дальше, сделаем следующее важное
замечание: функция /„(лг, х) построена при помощи счетного
.множества переходов к пределу. Эти переходы расположены
во вполне упорядоченную последовательность, которой со-
соответствует данное трансфинитное число а, и они налагаются
друг на друга, т. е. они проделаны последовательно один за
другим, но так, что знание численного результата одного
из переходов к пределу существенно предполагает знание
численных результатов всех предшествующих переходов
к пределу.
А так как трансфинитное число а может быть как угодно
большим, то очень вероятно, что нельзя назвать функцию
fi(x, x) без того, чтобы знать все численные результаты
предшествующих переходов к пределу, т. е. без того, чтобы
построить само это трансфинитное число <х.
Метод Лебега для построения функции, ие допускающей
никакого аналитического изображения. Перейдем теперь
к последнему пункту мемуара Лебега, а именно к тому, где
он указывает функцию-индивидуум, неизобразимую аналити-
аналитически.
Прежде всего цитируем текстуально несколько отрывков
из Лебега (стр. 213, строка 25):
«... Я предполагаю, что рациональные числа, заключен-
заключенные между 0 и 1, расположены в некотором порядке,
который я не уточняю, но предполагаю вполне определенным;
пусть zv z%, . . .—рассматриваемая последовательность. Я
беру некоторое значение t, заключенное между 0 и 1, и за-
записываю его по двоичной системе счисления, употребляя,
если это возможно, цифру 1 только конечное число раз;
выражение для t вполне определено, как только t известно
«Вычеркнем из последовательности ги zv ... веете г,-, ко-
которые соответствуют индексам i цифр 64, равных нулю; пусть
г'и z'z,... — оставшиеся г. Возможно, и так всегда будет,
если чисел г1 лишь конечное число, что можно найти символ
класса а, обладающий следующим свойством: можно устано-
установить соответствие между числами г' и всеми символами f},
меньшими а, так, чтобы одному z' отвечало, только одно J3

310
ГЛ. V. ПРОЕКТИВНЫЕ МНОЖЕСТВА
и обратно и чтобы если числам р и Р' отвечают z1 (Р) и z (Р7),
то У (р)< г'(Cj) всякий раз, как Р меньше pj. Тогда мы
назовем а символом, соответствующим t. Кроме того, каж-
каждому символу р (Р < а) соответствует вполне определенное
целое число {— индекс соответствующего г1; следовательно,
Черт. 9.
если расположить р в порядке, давая им в качестве номеров
эти целые i, мы получим последовательность av а2, ...,
образованную из символов, меньших а. Следовательно, рас-
рассматриваемому значению t мы можем привести в соответствие
функцию <р«(лг) класса а; для этого достаточно применить
вышеуказанный процесс; эту функцию ф„@> которая еще не
определена, когда дано а, но становится определенной, когда
задано t, если этому t соответствует символ а, мы назовем
<f(t, x). Если числу t не соответствует никакой символ а,
я положу ф (t, х) = 0.
«Я утверждаю, что функция <?(t, х) не допускает нп-
аналитического изображения...»,

АНАЛИЗ МЕМУАРА ЛЕБЕГА 311
Если построение Лебега мы переведем на геометрический
язык, то получим следующее: в пространстве трех измерений
берется система прямоугольных осей координат OXTY и рас-
рассматривается на плоскости OTY прямолинейное решето Г.
Прямые, на которых лежат отрезки решета, перенумерованы. •
Далее рассматриваются на оси ОТ те точки t, в которых
прямая, параллельная оси OY, пересекает решето Г по вполне
упорядоченному множеству. Пусть $ — это множество и Е его
дополнение.
Установив это, заставляем t пробегать ось ОТ, Если
точка t0 принадлежит множеству Е, то полагаем
9 Со. *)^0-
Если tx принадлежит к $, то прямая t=ti пересекает ре-
решето Г по вполне упорядоченному множеству и таким об-
образом ему соответствует трансфинитное число а.
Важно заметить, что во втором случае знание tt влечет
за собой знание последовательности av a2, ..., образованной
из трансфинитных чисел, предшествующих а. В самом деле,
решето Г образовано из счетного множества прямолинейных
отрезков, параллельных оси ОТ и расположенных в простую
бесконечную последовательность. А так как каждому транс-
трансфинитному числу, меньшему а, отвечает один и только один
составляющий отрезок решета Г и, следовательно, одно целое
число, то эти трансфинитные числа уже перенумерованы. Но
это нам позволяет применить построение Лебега для функции
Д (лг, лг) и положить
9 ft. *)¦*/«(*. ¦*)•
Таким образом, получается поверхность
y = <?(t, х),
всюду определенная и дающая пример функции, аналитически
неизобразимой.
В самом деле, пересекая эту поверхность плоскостями
t= const, мы получаем кривые, измеримые В, как угодно
высоких классов, что было бы невозможно, если бы ? (t, x)
была функцией классификации Бэра и, следовательно, входила
в„ некоторый вполне определенный класс этой классификации.

312 ГЛ. V. ПРОЕКТИВНЫЕ МНОЖЕСТВА
Анализ функции, построенной Лебегом. Если мы будем
пытаться анализировать процесс, при помощи которого Лебег
построил свою функцию <?(t, х), не допускающую никакого
аналитического изображения, то вот что мы найдем: построе-
• ние этой функции разбито на две части, а именно: 1° опре-
определение ф (t, х) для точек t0; 2° определение © (t, x) для
точек fj.
В первом случае Лебег полагает « (t0, лг) =з 0. Но точки t0
образуют линейное множество Е, лежащее на оси. О Г и опре-
определенное при помощи решета Г. Следовательно, это множе-
множество Е, которое, кстати, во всем построении Лебега играет
вспомогательную роль, являясь лишь промежуточным инстру-
инструментом при поисках функции <<o(t, x), есть аналитическое
множество, неизмеримое В.
Во втором случае Лебег полагает cp(tf,, лг) ^/„ (лг, лг).
Так как точки tt образуют дополнение к Е, то построение
функции ф (if, лг) полностью закончено. Поверхность у = © (t, лг)
таким образом определена при помощи совокупности транс-
трансфинитных чисел второго класса по Кантору.
Но употребление совокупности трансфинитных чисел здесь
совершенно отлично от того, которое имеет место в теории ана-
аналитических и проективных множеств. В самом деле, мы видели,
что в области проективных множеств трансфинитное всегда
может быть исключено и заменено эквивалентным отрица-
отрицательным определением. Здесь же не видно, как можно было
бы исключить трансфинитное из определения Лебега для функ-
функции <p(t, лг). Трудность состоит именно в том, что числен-
численные значения /„ (лг, лг) получаются в результате бесконечного
множества переходов к пределу, наложенных друг на друга
и расположенных в трансфинитную последовательность; не-
неизвестно, как можно было бы получить численные значения
/„(лг, лг) непосредственно, не переходя через эти предвари-
предварительные переходы к пределу.
Итак, метод Лебега основан на употреблении трансфинит-
трансфинитных последовательностей действительных чисел, каждое из
которых имеет численное определение, существенно зависящее
от численных определений предыдущих членов.
По этой же причине чрезвычайно вероятно, что поверх-
поверхность <?(t, лг) Лебега не может быть определена без привле-
привлечения трансфинитного, Едли это так, то природа этой поверх^

АНАЛИЗ МЕМУАРА ЛЕБЕГА
313
яости совершенно новая, более интересная, чем у проективных
множеств, и, без сомнения, она скоро привлечет внимание
математиков. Изучение точечных множеств, которые можно
. назвать без рассуждения Цермело, но при помощи бесконеч-
бесконечного множества последовательных численных определений,
зависящих друг от друга, может нас привести к совершенно
неожиданным результатам [84].
И тем не менее, хотя кривую <о (t, х) нельзя задать не-
непосредственно, не пользуясь предварительными переходами
к пределу, но совокупность этих кривых может быть пред-
представлена сразу и без привлечения трансфинитного.
Точнее говоря, хотя координаты у поверхности Лебега
y = <t(t, х)
не могут быть численно определены без того, чтобы осуще-
осуществить все переходы к пределу, приводящие к численному
значению <?(t, x), так как этих переходов к пределу транс-
трансфинитное число, зависящее от t и от лг, тем не менее можно
сразу, без малейших затруднений и без привлечения транс-
финитов, назвать проективную поверхность
которая пересекается плоскостями t= const по всем возмож-
возможным кривым y = f(x), измеримым В и, в частности, повеем
кривым y—ftt(x, x) Лебега.
Чтобы получить эту проективную поверхность, мы отпра-
отправляемся от универсального аналитического множества Е, лежа-
лежащего в трехмерном пространстве OXTY и пересекаемого
плоскостями t*= const по всем возможным плоским аналити-
аналитическим множествам.
Пусть РЕ есть проекция множества Е на плоскость ХОТ;
рассмотрим дополнение СРЕ этой проекции и спроектируем
его на ось ОТ. Множество 60
Ь0 = РСРЕ,
полученное таким образом, есть линейное проективное мно-
множество класса не выше 2. Если t0 есть точка оси ОТ, при-
принадлежащая 60, то ясно, что плоскость t=t0 заведомо содер-
содержит прямую, параллельную оси OY ш не пересекающую
универсальное множество Е,

314
ГЛ. V. ПРОЕКТИВНЫЕ МНОЖЕСТВА
С другой стороны, обозначим через Н множество точек
М (t, х) плоскости ХОТ таких, что параллель к оси О Y,
проведенная через М, пересекает универсальное множество Е
Черт. 10.
по крайней мере в двух различных точках. Известно (стр. 169),
что Н есть аналитическое множество. Значит, проекция 62
множества Я на ось ОТ
есть линейное аналитическое множество. Если ?2 есть точка
оси ОТ, принадлежащая 62, то ясно, что плоскость t = t%
заведомо содержит прямую, параллельную оси OY и пересе-
пересекающую универсальное множество Е по крайней мере в двух
различных точках.
Отсюда следует, что множество 6j тех точек, которые
мы получим, удаляя из оси ОТ точки множества 90 и 62,
есть проективное множество класса 2. Если tx есть точка
из 6Д, то ясно, что плоскость * = ?а пересекает универсальное.

АНАЛИЗ МЕМУАРА ЛЕБЕГА 315
множество Е по однозначной кривой у =/(¦*), определенной
для каждого значения х. Так как точки этой однозначной
кривой образуют аналитическое множество, то это множество
по необходимости измеримо В и, следовательно, функция
y=f(x) входит в классификацию Бэра (см. дополнение II,
стр. 327. — Ред.).
С другой стороны, так как аналитическое множество Е
универсально, то мы, очевидно, можем получить всякую кри-
кривую y=f(x), измеримую В, выбирая подходящим образом
точку tt множества Ь1 и пересекая Е плоскостью t*=tv
Установив это, мы возвратимся к предыдущему методу
Лебега (стр. 311). Мы определим однозначную поверхность
y=*t(t, х)
следующим образом:
1° Если точка ? принадлежит множеству-сумме 60 —|— 92,
мы просто положим
2° Если точка f принадлежит множеству 61? мы полагаем
где однозначная функция f(x) определяется однозначной кри-
кривой y = f(x), измеримой В, которую мы получим, пересекая
множество Е плоскостью t = f.
Ясно, »то так построенная однозначная поверхность
y=.ty(t, x) всюду определена. Я теперь утверждаю, что эта
поверхность проективга, Это значит, что множеэтво точек
трехмерного пространства OXTY, принадлежащих этой по-
поверхности, есть проективное множество.
Чтобы убедиться в этом, заметим, прежде всего, что рас-
рассматриваемая поверхность y = ty(t, x) составлена из следую-
следующих двух частей: 1° первую часть мы получим, если возьмем
общую часть плоскости ХОТ к множества плоскостей, парал-
параллельных плоскости XOY и проведенных через точки множе-
множества 90-j- 62. Так как множество 60 -\- 02 проективное, класса^ 2,
то такою же будет и рассматриваемая часть поверхности
y = ty(t, x); 2° вторую часть мы получим, если возьмем общую
часть аналитического множества Е и множества плоскостей,
параллельных плоскости XOY, проведенных через точки.

316 ГЛ. V. ПРОЕКТИВНЫЕ МНОЖЕСТВА
множества Ь1. Так как это последнее множество проективное
Класса «С 2, то такою же будет и рассматриваемая часть по-
поверхности у = ty (t, х).
Таким образом, мы приходим к следующему заключению:
однозначная поверхность у = <J* {t, х), построенная таким
способом, есть проективное множество класса <12. Пере-
Ъекая эту поверхность плоскостями t = const, мы получим
только однозначные кривые у =/(лг), измеримые В, и каж-
каждая однозначная кривая, измеримая В, может быть по-
получена таким образом.
Наличие парадокса не подлежит сомнению. И объяснение
его не легкое, оно, повидимому, глубоко скрыто. Вот что
я могу придумать. Кривые y—fa(x, x), определенные Лебе-
Лебегом и получаемые при пересечении поверхности Лебега
y = <p(t, x) плоскостями t= const, разумеется, находятся среди
разрезов проективной поверхности у = ty (t, x) плоскостями
t — const. Но они там сдвинуты в направлении, парал-
параллельном оси ОТ так, что разрез поверхности у = <» (t, x)
Лебега плоскостью t = f становится разрезом проективной
поверхности y = ty(t, x) при помощи плоскости t=f, где
Но в этих условиях трудность получить кривую
_у=Д(лг, х), соответствующую данному трансфинитному
числу <х, сколь угодно большому, преобразуется в труд-
трудность получить точку f. Чем больше нам нужно совершить
предварительных переходов к пределу, чтобы определить
функцию <р(/, х)=/Л(х, х), тем труднее нам будет вы-
вычислить численное значение соответствующего f', так как
функция fy(t, x) относительно проста.
. Понятие континуума приобретено геометрической интуи-
интуицией. При изучении континуума не встречается никаких труд-
трудностей до тех пор, пока мы стоим на чисто геометрической
.точке зрения; все точки прямой тождественны, так как они
все имеют одни и те же свойства; трудности появляются лишь
с арифметическими определениями, так как узнавание этих
общих свойств становится менее легким. Полное арифмети-
арифметическое понятие континуума требует того, чтобы геометриче-
геометрический континуум рассматривался как множество точек и, следо-
следовательно, арифметический континуум как множество чисел,
причем каждой точке континуума соответствует некоторое

Анализ мёмУара Лебега
действительное число. Но геометрический континуум суще-
существенно однороден, тогда как арифметический континуум не
имеет никакой однородности. Правда, каждое действительное
число, заключенное между 0 и 1, может быть представлено
в виде бесконечной десятичной дроби
О, ata^ ... ап ...,
но было бы иллюзорно думать, что эта дробь есть опреде-
определение действительного числа. Действительные числа, которые
могут' быть определены таким способом, очень немногочис-
немногочисленны. Всех их таким способом получить нельзя. Мы убеди-
убедились в том, что истинное определение числа t" требует
трансфинитного числа предварительных переходов к пре-
пределу и, следовательно, эффективное определение каждого
десятичного знака числа f не может быть достигнуто прежде,
чем будет проделано трансфинитное число предварительных
операций. Мы видим, что в этих условиях десятичное разло-
разложение ни на что негодно.
Но как только мы констатировали, что арифметический
континуум совершенно разнороден и что существуют действи-
действительные числа F, определение которых требует трансфинитной
бесконечности предварительных операций, соответствующих
как угодно большому трансфинитному числу, становится
вероятным, что в геометрическом континууме имеются
точки, которые не допускают никакого арифметического
или аналитического изображения.
Из таких точек можно образовать множество. Но нельзя
назвать ни одной индивидуальной точки в таком множестве.
Мы даже не будем знать, «существуют» ли точки в таком
множестве. Таков случай множеств-резольвент (стр. 294) .и
таков, на мой взгляд, случай большинства проективных мно-
множеств. Определение этих множеств, хотя оно и конечно, за-
зависит от отрицательных операций и строго эквивалентно
трансфинитному.
Аналитическое выражение. Являются ли функции клас-
классификации Бэра единственными, которые допускают аналити-
аналитическое изображение? Этот вопрос, на мой взгляд, не имеет
никакого абсолютного смысла, так как, очевидно, надо уточ-
уточнить, какие "операции мы допускаем.

318 ГЛ. V. ПРОЕКТИВНЫЕ МНбЖЁСТвА
Чтобы убедиться в этом, мы докажем, что если допу-
допустить в качестве аналитического выражения классическую
операцию, состоящую во взятии верхнего предела неко-
некоторой функции lim Ф, то можно изобразить аналитически,
отправляясь от полиномов, однозначную функцию f{x), не
входящую в классификацию Бэра.
С этой целью возьмем плоскость XOY и рассмотрим на
оси ОХ линейное аналитическое множество Е, неизмеримое В.
Характеристическая функция f(x) множества Е, равная 1 на ?
и 0 вне Е, очевидно, не входит в классификацию Бэра.
Установив это, обозначим через $п элементарное множе-
множество, лежащее в плоскости XOY между прямыми у = п и
у = п -\-1 и такое, что его ортогональная проекция на ось ОХ
совпадает с данным аналитическим множеством Е. Известно
(стр. 146), что $„ измеримо В и класса^ 2. Значит, сумма
// = $! + &2 + • • • +^п-(- • • • тоже измерима В и класса <[ 2.
Отсюда следует, что характеристическая функция Ф(х, у)
множества Н есть функция класса-^2 классификации Бэра.
Значит, мы можем изобразить функцию Ф (лг, у) в виде двой-
двойного предела полинома от х и у
Ф (лг, у) = lim lim Pm „ (лг, у).
С Другой стороны, возьмем любую точку лг0 оси ОХ.
Следует различать два случая:
Первый случай. Точка лг0 не принадлежит к Е. В этом
случае прямая, параллельная оси OY и проведенная через д:0, не
встречает множества Н. Значит, функция Ф(лг0> у) перемен-
переменного у тождественно равна нулю, Ф (лг0, у) == 0.
Второй случай. Точка х0 принадлежит к Е. В этом слу-
случае прямая x = xQ пересекает множество Н в бесконечном
множестве точек, ординаты которых неограниченно возрастают.
Следовательно, верхний предел функции Ф (лг0, у) переменного
у заведомо равен 1, когда у стремится к -j-oo.
Итак, мы можем написать
и, следовательно, окончательно
/() Й lim lim Рт,п(х, у),

Анализ мёмуаН лёёегА 319
где буква Р обозначает полином относительно х а у а
где f(x) не входит в классификацию Бэра.
Следовательно, при помощи классических операций Нт
и Нт, употребленных конечное число раз, можно записать
функцию, не входящую в классификацию Бэра.
Кроме того, можно доказать, что этим способом можно
записать все проективные функции и только проективные
функции. Но если повторить эти две операции счетное мно-
множество раз, то мы заведомо выйдем из семейства проективных
функций. Но мы не будем останавливаться на этом пункте,
так как в данном случае тот факт, что функция допускает
аналитическое изображение, есть, в некотором роде, побочное
обстоятельство, не прибавляющее ничего к ее первоначаль-
первоначальному логическому определению.
Замечание
Некоторые интересные исследования, касающиеся проек-
проективных множеств, были предприняты недавно Канторовичем
и Ливенсоном. Полученные результаты формулированы в Сотр-
tes Rendus Acad. Sc, 30 декабря 1929 г., 10 февраля, 12 мая
и 2 июня 1930 г. Подробный мемуар опубликован в Funda-
menta Math., тт. XVIII, XX.

ЗАКЛЮЧЕНИЕ
Чтобы не покидать области математики, я избегал глубоко
входить в те философские дискуссии, которые могли быть
вызваны многими из встреченных вопросов; да будет мне
позволено в этом кратком резюме сказать все же настолько
ясно, насколько я смогу это сделать, каковы, на мой взгляд,
наиболее важные проблемы, которые сейчас можно поставить
более четко, чем несколько лет тому назад.
На предыдущих страницах были изложены многие теории,
касавшиеся различных семейств точечных множеств. В двух
первых главах я старался продолжить и распространить ра-
работы Бэра, остановленные на изучении множеств класса 3.
Была дана общая теория множеств, измеримых В; она привела
к арифметическому результату о множествах класса 4, вполне
аналогичному результату Бэра. В других главах целью явля-
являлось изучение семейств точечных множеств, выходящих из
классификации Бэра.
Интерес исследований такого рода заключается главным
образом в том,, что с точки зрения принципов математическо-
математического анализа можно сравнивать роль множеств, измеримых В,
с ролью рациональных чисел, уподобляя множества, неизмери-
неизмеримые В, числам иррациональным. Хотя идея наиболее общего
иррационального числа содержит в зародыше наиболее слож-
сложные аналитические трудности, однако неоспоримо, что суще-
существуют иррациональные числа, представляющиеся естественно.
Непосредственным примером такого числа служит диагональ
квадрата со стороной 1.
Мы изучали, далее, множества, неизмеримые В. Чтобы
найти множество точек вне классификации Бэра и предста-
представляющееся так же естественно, как квадратичное иррацио-
иррациональное число, мы образовали довольно многочленные примеры
множеств вне классификации Бэра, названных при помощи

ЗАКЛЮЧЕНИЕ 321
простых логических законов, где трансфинитное явным обра-
образом не входит. Тем не менее автор вовсе не считает, что он
приблизился к решению этой важной проблемы. Различные
средства, которые он мог придумать, чтобы определить такое
множество, все сводятся к тому, чтобы предполагать данной
совокупность иррациональных чисел (актуальная бесконеч-
бесконечность, имеющая мощность континуума) или употреблять
отрицательные определения, аналогичные понятию точки сгу-
сгущения. Но если мы будем стремиться изгнать эти отрицатель-
отрицательные определения, мы неизбежно наткнемся на совокупность
чисел второго класса по Кантору (трансфинитное). Таким
образом, отрицательное понятие может стать эквивалентным
трансфинитному.
Автор этой книги склонен рассматривать проективные
множества как объекты, определение которых не может быть
вполне закончено: это чисто отрицательные понятия, которые
ускользают от всякого вида положительного определения.
И много шансов за то, что эти понятия попарно неприво-
димы. Например, автор рассматривает как неразрешимый
вопрос о том, все ли проективные множества измеримы или
нет, так как, на его взгляд, самые процессы определения
проективных множеств и меры в смысле Лебега являются
несравнимыми понятиями и, следовательно, они лишены ло-
логических взаимоотношений [86]. Короче говоря, область проек-
проективных множеств есть область, где принцип исключенного
третьего уже неприменим, хотя всякое проективное множество
формально определимо при помощи счетного множества условий.
Но если допускать все множества, измеримые В, то необ-
необходимо допустить проективные множества. Следовательно,
если желать ограничивать математический анализ лишь изу-
изучением вполне законченных объектов и вполне определенных
взаимоотношений, то нужно пожертвовать некоторыми мно-
множествами, измеримыми В, и даже некоторыми иррациональ-
иррациональными числами. В конечном итоге вполне определимых ирра-
иррациональных чисел имеется лишь счетное множество, хотя их
перенумерование и не может быть осуществлено при помоши
математического закона. Таким образом, арифметический
континуум заведомо содержит неопределимые точки. Эти точки,
каждая из которых имеет бесконечное определение, являются
паразитными во всяком рассуждении, которое можно сделать
21 Зак. 284. Н. Н. Лузин

322 ЗАКЛЮЧЕНИЕ
эффективно, и таком, что оно устанавливает вполнэ опреде-
определенную связь между ужг опргдэленными объектами. Можно
было бы отметить, что в истории математической науки вве-
введение идеальных элементов оказало важные услуги, чего никто
не станет отрицать. Но на это легко возразить, чго истинно
полезные идеальные элементы индивидуально различимы, чего
нет в данном случае. Исключение этих точек создало бы
большое упрощение в методах математического анализа. Однако
в данный момент из таких неопределимых точек можнэ обра-
образовать множества, но нельзя ни назвать индивидуальную точку
такого множества, ни узнать, «существуют» ли точки в таком
множестве, ни узнать его свойства. По мнению автора, таков
случай большинства проективных множеств. В самом деле,
повидимому, в этом и заключается единственное естественное
объяснение трудностей теории про активных множеств.
В конечном счете вопрос будет разрешен определенно лишь
усилиями научной мысли, т. е. наблюдением математических
фактов. Философские рассмотрения служат лишь для того,
чтобы отличить истинно плодотворное направление от беско-
бесконечного множества других. Только два случая возможны:
Или дальнейшие исследования приведут когда-нибудь к точ-
точным соотношениям между проективными множествами, а также
к полному решению вопросов относительно меры, категории
и мощности этих множеств. С этого момента проективные
множества приобретут в математике право гражданства наравне
е наиболее классическими из множеств, измеримых В.
Или указанные проблемы из теории проективных множеств
останутся навсегда нерешенными и к ним добавится множе-
множество новых проблем, столь же естественных и столь же не-
недоступных. В этом случае ясно, что пришло время произвести
реформу в наших идеях об арифметическом континууме.

ДОПОЛНЕНИЕ I
АРИФМЕТИЧЕСКИЙ ПРИМЕР ФУНКЦИИ,
НЕ ВХОДЯЩЕЙ В КЛАССИФИКАЦИЮ БЭРА ')
1. Известно, что Бэр дал чисто арифметический пример
функции 3-го класса его классификации.
Вот этот пример.
Рассмотрим основной интервал (О, 1) и в нем какое-нибудь
иррациональное число лг, изображенное в виде непрерывной
дроби
=(«1, а2, ...', а„, ...),
где Oj, а2, «8, ..., ап, ... — натуральные числа. Каждому
иррациональному числу х однозначно соответствует опреде-
определенная последовательность натуральных чисел av а2, ...
..., а„, ... и, обратно, каждая такая последовательность
определяет единственное иррациональное х.
Достаточно положить теперь, согласно Бэру, / (х) = 1,
если эта последовательность натуральных a.v a2, ..., ап,...
стремится к бесконечности, и положить / (л:) = 0 в против-
противном случае.
Так определенная функция f(x), согласно исследованиям
Бэра (см. Acta Math., т. 30), является функцией в точности
3-го класса.
») Comptes Rendns Acad. Sc, 1926 г., т. 182, стр. 1521—1522.
(Перевод А. Л. Лунц.)
21*

324 ДОПОЛНЕНИЕ I
2. Для построения арифметическим путем аналогичной
функции f(x), не содержащейся в классах Бэра, введем сле-
следующее определение:
Будем говорить, что последовательность натуральных
чисел <х:, а2, ..., ап, ... является составной, если
среди ее членов имеется бесконечное множество чисел а,
делящихся одно на другое: ... а„^: ап : ап ; в против-
противном случае скажем, что данная последовательность
etj, а2, ..., ап, ... является простой.
Определяемая таким образом функция f(x) не входит
в классификацию Бэра [8в|.
3. Переходя к доказательству этого, назовем решетом
всякую счетную совокупность С замкнутых отрезков о,
параллельных оси ОХ, расположенных внутри основного
квадрата К, уравнения сторон которого суть
Обозначим через & совокупность всех точек х интервала
@ < х < 1) таких, что перпендикуляр Ря, восставленный
к оси ОХ из точки х, пересекает решето С по вполне
упорядоченному множеству Rx, если считать, что Rx упоря-
упорядочено в положительном направлении оси OY.
Множество точек интервала @ < х < 1), не принадле-
принадлежащих совокупности S, обозначим Е. Именно это множество
Е (а не $) мы будем называть множеством, определяемым
решетом С.
Введем важное понятие, позволяющее различать решета:
Говорят, что С есть ограниченное решето, если
существует счетное вполне упорядоченное множество W,
порядковый, тип которого больше порядкового типа мно-
множества Ra при любом х, не принадлежащем к опреде-
определяемому решетом С множеству Е.
Будем говорить, что решето С имеет лебегов-
ский тип, если, каково бы ни было подмножество Y1
счетного множества Y, составленного из ординат сегмен-
сегментов о решета С, найдется точка х, для которой мно-
множество Rx совпадает с Yt.
Для того чтобы решето С было ограничено, необходимо
и достаточно, чтобы множество Е было измеримо В. Никакое

АРИФМЕТИЧЕСКИЙ ПРИМЕР НЕ 5-ФУНКЦИИ .325
множество, определенное с помощью решета лебеговского
типа, не может быть измеримым В множеством.
4. Множество Е точек, для которых /(лг) = 1,
является множеством, определенным с помощью решета
лебеговского типа. Чтобы убедиться в этом, достаточно поста-
поставить в соответствие каждому интервалу Бэра 0 (а,, а8,..., ап)
сегмент о(ар а8, ..., ап), следующим образом определенный:
1. Проекция о на ось ОХ совпадает с 0.
2. Ордината отрезка o(all...,am) есть рациональное
число вида
2 ""•"2 ' '" * ' 2»-1 ' 2я'
где 9П = 1, а для t<n имеем Ь{ = 0, если af есть делитель
«„ и в( = 1 в противном случае.
Совокупность всех таких сегментов о составляет решето С
лебеговского типа, определяющее множество \f(x)—.\].
' Таким образом, среди законов арифметики можно найти
такие, которые приводят к множествам, не измеримым В.

ДОПОЛНЕНИЕ It
НЕКОТОРЫЕ ЗАМЕЧАНИЯ О КРИВЫХ,
ЯВЛЯЮЩИХСЯ АНАЛИТИЧЕСКИМИ ДОПОЛНЕНИЯМИ ')
1. Назовем униформной кривой в плоскости XOY всякое
точечное множество С, которое пересекается каждой прямой,
параллельной оси OY в одной и только одной точке. Если
Ж —какая-либо точка множества С, определенная коорди-
координатами х и у, то ордината у является, очевидно, величиной,
зависящей от х, и является, таким образом, однозначной
функцией действительного переменного f{x), определенной
для всех значений х бесконечного интервала (— оо<дг< -|- оо).
В этом случае равенство
>=/(¦*)
называется уравнением кривой С.
Обозначим через J и S два множества точек плоско-
плоскости XOY, определенные кривой С и расположенные соответ-
соответственно ниже и выше этой кривой. По точному определению
J есть множество точек М(х, у) плоскости, координаты ко-
которых удовлетворяют неравенству у < f(x). Точно так же 5 есть
множество точек М(х, у), для которых у >/(#). В результате
плоскость XOY разбита на три множества J, С и 5, не
имеющие попарно общих точек. Совершенно очевидно, что
среди трех множеств J, С я S одно вполне определяет два
других.
*) Mathematica, Cluj, 1934 г., т. 10, стр. 70—80. (Перевод
Р. Ю. Мацкиной.)

некоторые Замечания о &4-кривых
Установив это, приведем теперь основные факты, кото-
которые следуют из работ Бэра, Бореля, Лебега и Валле-Пус-
сена:
I. Если функция f(x) входит в классификацию Бэра$
то три множества J, С и S измеримы В.
II. Если одно из двух множеств J и S измеримо Bt
то функция f(x) входит в классификацию Бэра.
Мы дополним эти основные результаты следующим свой-
свойством :
III. Если множество С аналитическое, в частности из-
измеримое В, то функция f(x) обязательно входит в клас-
классификацию Бэра *).
Доказательство получается немедленно, если применить
теорию аналитических множеств. В самом деле, известно, что
необходимое и достаточное условие для того, чтобы функция
действительного переменного f(x) входила в классификацию
Бэра, состоит в том, что одно из четырех множеств
?(/>Л), ?(/<Л), E(f>A), ?(/<Л)
было измеримо В, каково бы ни было Л (см. Ch. de la Val-
1 ё е-Р о u s s i n, Integrates, Fonctions, Classes de Baire, стр. 32).
Проведем в плоскости XOY прямую у = А, параллельйую
оси ОХ, и обозначим через С часть данной кривой С, ко-
которая расположена ниже этой параллели; пусть С" — множе-
множество остальных точек С. Так как множество С, по предпо-
предположению, аналитическое, то множество С — тоже аналити-
аналитическое, потому что общая часть двух аналитических мно-
множеств (С и открытой полуплоскости, определенной параллелью
у = А) является также аналитическим множеством2). Точно
так же множество С" — аналитическое, будучи общей частью
множества С и замкнутой полуплоскости, определенной пря-
прямой у = А.
Установив это, спроектируем два множества С и С" на
ось ОХ и обозначим через е' и е" соответствующие проек-
проекции множеств С и С". Так как кривая С униформна, мно-
множества е' и е" не имеют общих точек и их сумма е' -\-е"
!) W. Sierpinskl, Fundamenta Math., т. II A921), стр.78
и 79.
1) См. мои лекции об аналитических множествах, стр. 1оУ
(в настоящем издании стр. 139. — Ред.).

Дополнение it
совпадает с осью ОХ. Но множества С и С" — аналитиче-
аналитические; из этого следует, что их.проекции е' и е" на ось ОХ
являются аналитическими множествами 1).
С другой стороны, множества е' и е", будучи аналити-
аналитическими и не имея общих точек, отделимы В8). Это озна-
означает, что существуют два множества Н' и Н", измеримые В,
не имеющие общих точек и такие, что Н' содержит «' и со-
соответственно Н" содержит е". Так как множества е' и е"
являются взаимными дополнениями, они необходимо совпадают
с соответствующими отделяющими множествами Н' и Н".
Мы заключаем отсюда, что два рассматриваемых множества,
е' и е", измеримы В.
Но из самого определения множества е* мы имеем тож-
тождество
*'=?(/< A),
и так как е' измеримо В, мы заключаем, что рассматриваемая
функция f(x) входит в классификацию Бэра. Ч. т. Д.
Важно заметить, что если и ввести ограничительное предполо-
предположение относительно измеримости В рассматриваемой кривой С,
все же нет другого доказательства, не привлекающего теорию
аналитических множеств. Было бы очень интересно суметь
дать другое доказательство, позволяющее вывести без помощи
теории аналитических множеств, непосредственно из измери-
измеримости В кривой С, тот важный факт, что соответствующая
функция f(x) входит в классификацию Бэра8).
Предположения I, II и III можно рассматривать как поло-
положительные предложения, т. е. такие, которые дают положи-
положительный ответ на поставленный вопрос, и было бы очень
желательно, чтобы последующие исследования всегда продол-
продолжались и распространялись в таком же направлении. Но на
этом пути мы сталкиваемся с определенно отрицательными
результатами.
Прежде всего, мы видели, что из аналитичности множе-
множества С следует, что функция f(x) входит в классификацию
1) См. мои лекции об аналитических множествах, стр. 144 (в на-
настоящем издании стр. 143. — Ред.).
*) Там же, стр. 156 (в настоящем издании стр. 155.—'¦ Ред.).
8) По мнению Серпинского, эта проблема трудна, даже если
предположить, что С является множеством типа а5.

НЕКОТОРЫЕ ЗАМЕЧАНИЯ О СЛ-КРИВЫХ 329
Бэра. Но мы не можем получить аналогичного результата из
предположения аналитичности множества / или S:
Аналитичность одного из двух множеств J и S не вле-
влечет за собой измеримость В кривой С, а функция f (x)
может не быть функцией классификации Бэра.
Чтобы это увидеть, достаточно рассмотреть следующий
пример. Пусть Е — какое-либо аналитическое множество, не-
неизмеримое В, расположенное на оси ОХ. Пусть / (х) — харак-
характеристическая функция множества Е, т. е. равная 1 в точках
множества Е и равная 0 в остальных точках. Обозначим че-
через С кривую, определенную уравнением y=f(x). Я утвер-
утверждаю теперь, что плоское множество J является множе-
множеством аналитическим. Действительно, множество J является,
очевидно, объединением двух частей Jt и У2, имеющих общие
точки: первая часть Jt представляет собой множество точек
М (х, у) плоскости, у которых отрицательна ордината, следо-
следовательно, множество /j есть открытая полуплоскость, а зна-
значит, измеримо В и, таким образом, есть аналитическое мно-
множество. Вторая часть J2 является множеством точек М {х, у)
плоскости, абсцисса которых входит в данное аналитическое
множество Е, а ордината у меньше 1, у < 1. Легко доказать,
что множество /2 — аналитическое.
Чтобы увидеть это, возьмем параметрическое представле-
представление
О)
данного аналитического множества Е; здесь <р@ — функция,
определенная для всех иррациональных значений t интервала
@</< 1) и непрерывная в каждой точке1). Если мы напи-
напишем одновременно два уравнения
=\-и\ J
мы получим, очевидно, параметрическое представление мно-
множества У2, осуществленное с помощью двух функций ф (f)
и 1 — и2 двух действительных переменных / и и, которые
явно входят в классификацию Бэра. Мы заключаем отсюда2),
J) См. мои лекции об аналитических множествах, стр. 135 (в на-
настоящем издании стр. 135. — Ред.).
а) Там же, стр. 146 (в настоящем издании стр. 145,—Ред.),

<330 ДОПОЛНЕНИЕ II
что рассматриваемое множество У2 является аналитическим
множеством.
Отсюда следует, что- само множество J — множество
аналитическое, так как мы имеем J=^J1-\-J91).
С другой стороны, так как данное аналитическое множе-
множество Е неизмеримо В, характеристическая функция f(x)
множества Е не может входить в классификацию Бэра. Ч. т. д.
3. Итак, множество J, определенное какой-либо кривой С,
может быть аналитическим без того, чтобы соответствующая
функция f(x) входила в классификацию Бэра. Точно так же
аналитичность множества 5 не влечет за собой измеримость В
соответствующей кривой С, так как множество /, опреде-
определенное для кривой
у=П*),
является, очевидно, множеством 5 для кривой
Но важно заметить, что одновременная аналитичность мно-
множеств У и 5 влечет положительное утверждение, которое гла-
гласит:
IV. Если оба множества J и S аналитические, то
функция f(x) входит обязательно в классификацию Бэра.
Чтобы показать это, предположим сначала, что только
множество J аналитическое, и рассмотрим новую кривую, ко-
которую мы обозначим через С(е), определенную уравнением
.?=/(¦*) + •,
где функция f(x) соответствует данной кривой С, as — про-
произвольное положительное число. Пусть J^ и 5(s) — множества,
определенные кривой С и расположенные соответственно ниже
и выше этой кривой. Ясно, что множество У(е)—не что иное,
как множество J, перемещенное в положительном направлении
оси OY на положительную величину. Отсюда следует, что
оба множества 7 и 7(<) одной природы. Так как множество /,
по предположению, аналитическое, то множество /(•) также
аналитическое.
Будем теперь придавать е бесконечную убывающую после-
последовательность значений ги е2, ... , еп ... , стремящуюся
*) См. мои лекции об аналитических множествах, стр. 138 (в на-
настоящем издании стр. 138. — /Vd)

НЕКОТОРЫЕ ЗАМЕЧАНИЯ О С4-КРИВЫХ 331
к нулю. Так как множество /•«> аналитическое, каково бы
ни было натуральное число п, пересечение аналитических
множеств УМ, /<•>), ..., J<-*n ^ ... является снова множеством
аналитическим !). Но это пересечение, очевидно, есть не что
иное, как сумма двух множеств J и С. Таким образом, если
мы предполагаем множество J аналитическим, то сумма J-\-C
является обязательно аналитическим множеством и, следова-
следовательно, множество 5 является аналитическим дополнением.
До сих пор мы делали единственное допущение, что мно-
множество J аналитическое. Мы вывели из этого, что множе-
множество 5 является аналитическим дополнением. Из этого сле-
следует, что если мы сделаем второе допущение и предположим
множество 5 аналитическим, мы придем к выводу, что мно-
множество S заведомо измеримо В и, следовательно, функция
f(x) входит в классификацию Бэра. Ч. т. д.
Из самого доказательства предыдущей теоремы мы ви-
видели, что аналитичность множества J влечет за собой анали-
аналитичность суммы 7-j-C. Но и обратное предложение опять-
таки имеет место:
Аналитичность суммы J -\-С влечет за собой обяза-
обязательно аналитичность множества J.
Чтобы убедиться в этом, достаточно рассмотреть кри-
кривую С„ определенную с помощью
где е — произвольное положительное число, и функция /(л:)
соответствует данной кривой С. Обозначим через Л и 5, два
"множества, расположенные соответственно ниже и выше кри-
кривой С,. Ясно, что множество J, и кривая Св являются не чем
иным, как множеством J и данной кривой С, перемещенными
в отрицательном направлении оси О К на положительную ве-
величину е. Отсюда следует, что оба множества-суммы ),-\~С»
и J-\-C являются множествами одной природы, и, следова-
следовательно, если множество J~\-C аналитическое, то и множе-
множество Jt-\-Ct также аналитическое.
Будем придавать теперь е бесконечную убывающую после-
последовательность значений е1з е2, ... , еп, ... , стремящуюся
1) См. мои лекции об аналитических множествах, стр. 139 (в на-
настоящем издании стр. 139.—- Ред.). .,

332 ДОПОЛНЕНИЕ II
к нулю. Так как множество J*n-\-Ctn аналитическое, ка-
каково бы ни было натуральное число «, сумма множеств
J^-{-Cn(« = 1, 2, 3 ...) является также аналитическим
множеством1). Но это множество-сумма совпадает, оче-
очевидно, с исследуемым множеством /, что и доказывает ана-
аналитичность /. Ч. т. д.
Точно так же аналитичность С -\- S влечет аналитич-
аналитичность S.
4. Желая изучать различнее кривые С с точки зрения
чисто геометрической, следует начать с различения наиболее
простых кривых. Очевидно, что среди кривых С наибо-
наиболее простыми являются кривые, измеримые В, и что тем
более простой является кривая С, чем меньше класс множе-
множества С.
Казалось бы, что наиболее простыми кривыми С, .идущими
вслед за кривыми, измеримыми В, являются аналитические
кривые, неизмеримые В. Но изучение таких кривых было бы
ложным шагом, потому что, как мы видели, не существует
таких кривых: каждая аналитическая кривая обязательно
измерима В.
Следовательно, здесь имеется нечто вроде разрыва, скачка,
и наиболее простыми кривыми, идущими за кривыми, изме-
измеримыми В, повидимому, являются аналитические допол-
дополнения.
Следует заметить, что точка зрения чисто геометриче-
геометрическая очень заметно отличается от точки зрения аналитиче-
аналитической. С точки зрения анализа характеристическая функция
f(x) аналитического множества Е, неизмеримого В, является
функцией довольно простой, и может рассматриваться как
немедленно следующая за функциями классификации Бэра.
В противоположность этому, геометрия рассматривает кри-
кривую С, соответствующую^функции
как кривую очень сложную, потому что ее геометрическая
природа представляет собой объединение, части которого
имеют между собой отношения сложные и трудно уловимые:
!) См. мои лекции об аналитических множествах, стр. 138 (в на-
настоящем издании стр. 138, — Ред.),,

НЕКОТОРЫЕ ЗАМЕЧАНИЯ О СЛ-КРИВЫХ 333
действительно, эта кривая С не является ни аналитическим
множеством, ни аналитическим дополнением, будучи суммой
двух множеств, одно из которых аналитическое, а другое
аналитическое дополнение.
Исходя из этого, ставится вопрос, узнать, существуют
ли в действительности кривые С, которые являются ана-
аналитическими дополнениями, неизмеримыми В. Этот вопрос
является тем более естественным, что не имеется аналитиче-
аналитических кривых, неизмеримых В.
И очень важная теорема Мазуркевича]) дает нам от-
ответ определенно положительный. Вот формулировка этой тео-
теоремы: каково бы ни было аналитическое множество Е,
расположенное на оси ОХ, существует униформное ана-
аналитическое дополнение Н, расположенное в плоскости XOY,
ортогональная проекция которого на ось ОХ совпадает с Е.
Чтобы хорошо понять смысл этой теоремы, следует от-
отметить, что униформным называют всякое множество точек
плоскости XOY, которое пересекается каждой прямой, парал-
параллельно оси OY, не более чем в одной точке. В первую ми-
минуту этот важный результат С. Мазуркевича кажется весьма
парадоксальным, потому что всякое аналитическое дополне-
дополнение, расположенное на измеримой В кривой С, имеет проек-
проекцией аналитическое дополнение, и потому что имеется очень
обширное семейство униформных аналитических дополнений,
которые не могут быть помещены на измеримой В кривой С
и тем не менее имеют в качестве проекций на ось ОХ ана-
аналитические дополнения: а именно, таким является множество
точек единственности плоского измеримого В множества §,
т. е. множество точек I, лежащих на параллелях оси OY,
пересекающих $ в одной и только одной точке8).
Теорема Мазуркевича доставляет нам средство для оты-
отыскания униформной кривой С, являющейся аналитическим до-
дополнением, неизмеримым В. В самом деле, возьмем на оси ОХ
какое-нибудь аналитическое множество, неизмеримое В. Пусть
И—униформное аналитическое дополнение, расположенное
!) См. S. Mazurkiewicz, Sur une propriety des ensembles
С (A), Fundamenta Matheraaticae, т. Х, стр. 172—174. Лекции об
аналитических множествах, стр. 284 (в настоящ. изд. стр. 285.—Ред.).
2) См. мои лекции об аналитических множества*, стр. §55 (в на-
настоящем издании стр. 257. — Ред.),

334 ДОПОЛНЕНИЕ II
над осью ОХ, проекция которого на эту ось совпадает с дан-
данным аналитическим множеством Е,
Возьмем в качестве униформной кривой С множество, со-
состоящее из точек Я и из точек оси ОХ, которые не входят
в Е. Ясно, что С является суммой двух аналитических до-
дополнений: Н и СЕ. Таким образом, С является аналитическим
дополнением. С другой стороны, очевидно, что С неизмеримо В,
потому что часть Я кривой С, расположенная над осью ОХ,
была бы в противном случае множеством, измеримым В, что
невозможно, ибо проекция Е множества И— заведомо неиз-
неизмеримое В множество J).
Итак, существуют неизмеримые В кривые С, которые
являются тем не менее аналитическими дополнениями.
Из этого предложения следует, что аналитичность суммы
J-\-S не влечет за собой измеримости В кривой С, и
функция f(x) может не быть функцией классификации
Бэра.
5. Так как можно рассматривать кривые С, являющиеся
аналитическими дополнениями, как наиболее простые вслед за
измеримыми В кривыми, было бы очень желательно, чтобы
имелись какие-либо общие результаты относительно соответ-
соответствующих функций f{x). Первая из проблем, которые ста-
ставятся в связи с функциями / (х), — проблема о природе мно-
множеств / и 5. Являются ли эти множества всегда проектив-
проективными множествами? Положительный ответ нетруден и почти
очевиден. Но строгие исследования относительно точной
природы множеств J и S кажутся представляющими большие
трудности.
Пусть С — кривая, являющаяся аналитическим дополнением,
af{x) — соответствующая функция. Возьмем последователь-
последовательность Г], гв> ..., гп, ... всех рациональных чисел и прове-
проведем в плоскости XOY прямую у = гп, параллельную оси ОХ.
Пусть Сп — часть С, расположенная над этой параллелью;
ясно, что Сп — аналитическое дополнение, измеримое В или
неизмеримое В. Обозначим через еп проекцию Сп на ось ОХ;
ясно, что еп—проективное множество, которое может быть
представлено в форме РСРЕ, где Е — измеримое В множе-
1) Проекция униформного измеримого В множества всегда из-
измерима В. Там же, стр. 166 (в настоящем издании стр. 166. — Ред.).

НЕКОТОРЫЕ ЗАМЕЧАНИЯ О СЛ-КРИВЫХ 335
ство, так как множество С„, являющееся аналитическим до-
дополнением, может быть записано как СРЕ ]). Таким образом,
множество еп является множеством (/42). Отсюда следует, что
линейное дополнение множества еп, которое мы обозначим
через Yjn, является проективным множеством (СЛ2). Согласно
теореме о множествах параллелей 2), мы заключаем, что мно-
множество Нп точек М(х, у) плоскости, абсциссы которых х
принадлежат iqn и ординаты у < гп, является плоским проек-
проективным множеством (СЛ2). Теперь, если мы будем изменять на-
оо
туральное число я, я = 1, 2, 3, ..., и возьмем сумму 2 Нп,
мы будем иметь плоское проективное множество, которое снова
является множеством (СА2), так как сумма счетного числа мно-
множеств (САп) является проективным множеством и самое боль-
оо
шее (САп) 3). Но, очевидно, что множество-сумма 2 Нп со"
п=1
впадает с множеством /, определенным для данной кри-
кривой С. Таким образом, множество J проективно и самое боль-
большее (СА%).
Так как множество S, определенное для кривой y=f(x),
является множеством J для кривой у = —f{x), мы заключаем,
что множество 5 также проективно и самое большее (Су42).
Так как данная кривая С является аналитическим дополнением,
а значит (СА^, то отсюда следует, что множество-сумма C-\-S
является самое большее (СА2), и значит, дополнительное мно-
множество J не более чем (Л2). Так как множество J является
одновременно (СА^) и (Л^), мы заключаем, что множество J
не более чем (?2). То же заключение имеет место и для
множества 5.
Итак: если кривая С является аналитическим допол-
дополнением, то два соответствующих множества J и S
являются проективными множествами не более чем (Б2).
Между тем вероятно, что это — грубое определение при-
природы / и S и что дальнейшие исследования будут проведены
со всей точностью.
) Там же, стр. 269 (в настоящем издании стр. 271. — Ред.).
2) Там же, стр. 276 (в настоящем издании стр. 278. — Ред.).
3) Там же, стр. 277 (в настоящем издании стр. 279. — Ред.).

336 ДОПОЛНЕНИЕ II
В случае кривой Мазуркевича природа множеств J и 5
может быть уточнена. В самом деле, если дано какое-либо
аналитическое множество Е на оси ОХ, Мазуркевич строит
в плоскости XOY множество $, измеримое В, проекцией
которого на ось ОХ является данное аналитическое множе-
множество Е. Следует отметить, что каждая прямая, параллельная
оси OY, проведенная через какую-либо точку х множества Е,
пересекает множество $ по множеству $х точек, нижняя
грань которого р является обязательно точкой множе-
множества $я. Мазуркевич доказал, что множество Я точек [Хд,,
соответствующих точкам множества Е, является аналитическим
дополнением, которое, очевидно, униформно. И легко доказать,
что множество 6 точек М (х, у) плоскости, расположенных
над точками [ie, является множеством аналитическим.
Действительно, множество 1 обладает параметрическим
представлением с двумя переменными
'
где уравнения х = <р (/), у = ty (f) дают параметрическое пред-
представление плоского измеримого В множества S, а и — произ-
произвольный параметр.
С другой стороны, ясно, что множество всех точек М {х, у)
плоскости XOY, абсциссы которых х принадлежат Е, является
плоским аналитическим множеством; пусть/) — это множество.
Наконец, обозначим через О множество точек М (х, у) пло-
плоскости, абсциссы которых х не принадлежат Е и ординаты у
отрицательны. Ясно, что О является плоским аналитическим
дополнением.
Далее очевидно, что исследуемое множество J предста-
представляется следующей формулой:
/= G + (D — 6}= G + ?> • Св.
Из этого следует, что J есть сумма аналитического дополне-
дополнения и общей части аналитического множества и аналитического
дополнения. Таким образом, множество J является множе-
множеством E?) очень частного вида, будучи составлено из анали-

нйк6то4>ыё замечания о <2Д-кривых
тических множеств и их дополнений с помощью двух опе-
операций: суммы и пересечения, повторенных конечное число
оаз J).
6. Теперь ставится интересный вопрос: обязательно ли
отделимы В две кривые, являющиеся аналитическими допол-
дополнениями, одна из которых находится под другой? Ответ, оче-
очевидно, зависит от самого определения отделимости В-кривых.
Здесь можно дать следующие три определения отделимости
Б-кривых:
Первое определение. Две произвольные.кривые С1
и С2, одна из которых расположена над другой, называются
отделимыми В с помощью кривой, если можно провести
в плоскости промежуточную кривую С 2), измеримую В, кото-
которая расположена под одной и над другой из данных двух
кривых Ct и С2.
Это определение не может представлять, очевидно, ника-
никакого интереса, потому что, какова бы ни была кривая y = f(x),
проведенная в плоскости XOY и неизмеримая В, можно ука-
указать такую положительную величину е, чтобы две кривые
y=zf(x) и у =f(x)-\-e были неотделимы В в смысле пер-
первого определения. Действительно, в противном случае легко
видеть, что если придавать е убывающую последовательность
значений еи е2, ...> вп, ..., стремящуюся к нулю, то функ-
функция /(л?) является пределом последовательности промежуточ-
промежуточных функций ДО*), Уч(х), ..., fn(x), ..., входящих в клас-
классификацию Бэра, равномерно сходящейся к/(лг). Таким обра-
образом, функция f(x) и сама входит в классификацию Бэра.
Второе определение. Две произвольные кривые Ct
и С2 называются отделимыми В с помощью двух множеств,
если можно найти два множества Hi и //2, измеримые В, не
имеющие общих точек и такие, что С1 содержится в Ht и
соответственно С2 содержится в Я2.
В связи с этим определением можно указать без труда,
что существуют две кривые Сг и С2, являющиеся аналити-
аналитическими дополнениями и неотделимые В в смысле второго
определения.
*) Там же, стр. 281 и 285 (в настоящем издании стр. 282 и 286. —
Ред.).
2) Ср. Ch. de la V а 11 ё е - Р о u s s i n, Integrates, Fonctions, ClaS>
ses de Baife, стр. 128.
22 Зак. 284. H. H. Лузин

§38 д6полненЙв ii
Чтобы убедиться в этом, возьмем в интервале @ < х < 1)
оси ОХ два аналитических дополнения ей и е^ которые не-
неотделимы В с точки зрения отделимости В точечных мно-
множеств. Известно, что такие аналитические дополнения суще-
существуют *).
Пусть Н1 — униформное аналитическое дополнение, рас-
расположенное под осью ОХ, проекция которого на эту ось
совпадает с линейным аналитическим множеством С$х. Точно
так же, пусть /78 — униформное аналитическое дополне-
дополнение, расположенное над осью ОХ, проекция которого на
ось ОХ совпадает с линейным аналитическим множест-
множеством С§2.
Исходя из этого, мы определим две функции действитель-
действительного переменного ft(x) и /2(х) следующим образом:
/i (x) равна нулю на §>1 и ординатам точек униформного
множества Нх вне Ъх\
/8(х) равна нулю на ?2 и ординатам точек униформного
множества Н2 вне §2.
Совершенно очевидно, что /i (¦*)< Д (¦*), каково бы ни
было х, что кривые Ct и С8, определенные соответственно
уравнениями y=fi(x) и y=f$(x), являются аналитическими
дополнениями и что С1 и С2 неотделимы В в смысле второго
определения.
Третье определеннге. Две произвольные кривые Gt
и С2, одна из которых расположена под другой, называются
отделимыми В с помощью множества, если существует
в плоскости ХО Y измеримое В множество Е, расположенное
между двумя данными кривыми Cj и С2, которое пересекается
обязательно каждой прямой, параллельной оси OY, по край-
крайней мере в одной точке.
С точки зрения этого определения ничего не известно
об отделимости кривых, которые являются аналитиче-
аналитическими дополнениями. Можно только заметить, что каждое
плоское измеримое В множество содержит униформизирую-
щее множество И, которое является аналитическим дополне-
I) См. мои лекции об аналитических множествах, стр. 220, 260,
263 (в настоящем издания стр. 221, 262, 265. — Ред.). См. чакже
П. С. Новиков, Sur les fonctions ifflplicites mesurables В (Funda-
menta Matheraaticae, т. XVII, «p. 8).

НЕКОТОРЫЕ ЗАМЕЧАНИЯ О СЛ-КРИВЫХ
нием *) и что униформизирующая кривая С множества Е
должна быть расположена между двумя данными кривыми Сх
и С2, равно как и отделяющее множество Е.
Замечу, что вопросы, очень блийкие к тем> которые рас-
рассматривались в настоящей статье, излагаются в работе:
W. Sierpinski; Sur certains ensembles plans (Mathematica,
f. IV, стр. 178, Gluj, 1931).
i) См. работы по униформизации множеств В. Серпинского,
«Sur certains ensembles plans» и Н. Лузина, «Sur le piobleme de
M. Jacques Had mard d'uniformisatJon des ensembles» (Mathematica,
т. IV, Cluj, 1930, стр. 62 и 178).

ПРИМЕЧАНИЯ

ПРИМЕЧАНИЯ К ГЛАВЕ I
[*| (стр. 23). Пространством Бэра R называется топологическое
пространство, элементами которого являются всевозможные после-
последовательности целых положительных чисел:
Окрестностью в /? является множество тех точек R, у которых
первые k знаков фиксированы. Это множество—'Обозначим его
ЬП1... П]с—называется интервалом Бэра порядка к. Пространство-^?
взаимно однозначно и взаимно непрерывно отображается на множе-
множество всех иррациональных точек, заключенных в отрезке [0, 1],
а следовательно, и на множество &х всех иррациональных точек
оси ОХ. Для доказательства достаточно заметить, что каждое ирра-
иррациональное число, заключенное между 0 и 1, может быть предста-
представлено в виде непрерывной дроби:
х =х
«н
"8 +
В пространстве Бэра вводится расстояние между двумя точками
(х, у) следующим образом: если первые к знаков пь п2, ..., я»
у элементов х и у одинаковы, a (k + l)-e знаки различны, то
Определенное таким образом пространство /? является пол-
полным метрическим пространством, в отличие от пространства
иррациональных точек с евклидовским расстоянием между двумя
точками. Н. Н. Лузин рассматривает основную область 3х как мно-
множество всех иррациональных точек оси ОХ, не касаясь ее тополо-
топологической структуры. Однако он фактически неоднократно на нее

344 ПРИМЕЧАНИЯ
опирается, используя тот факт, что бесконечная убывающая после-
последовательность интервалов Бэра всегда содержит точку.
[2] (стр. 23). Нельзя согласиться с утверждением автора о при-
причине простоты изложения дескриптивной теории множеств в про-
пространстве &х. Эта простота связана не с тем обстоятельством, что
пространство Эх более однородно, тогда как классическая числовая
прямая содержит разнородные элементы, а с тем, что пространство
ffx нульмерно (не содержит никакой связной части). Выбросив из
оси ОХ произвольное всюду плотное счетное множество Е, мы по-
получим пространство R, на котором построение дескриптивной теории
множеств будет в точности таким же, как в пространстве 9Х, неза-
независимо от арифметической структуры элементов множества Е.
[3] (стр. 49). Область 9^ является топологическим произведе-
произведением SxY,STy областей STX и &у, а порция области &ху— тополо-
топологическим произведением (а, Ь) X (с. d) двух порций соответственно
областей Эх и ffy. Интервалом Бэра порядка ДП].. ,и> области &ху
называется топологическое произведение двух интервалов Бэра по-
порядка k областей &х и ffy. Заметим, что все области &ху, &Хуе
и т. д. гомеоморфны области &х. Для доказательства достаточно
сначала установить взаимно однозначное соответствие между интер-
интервалами Бэра порядка 1 области STX и интервалами Бэра порядка 1
области 9ху. После того как установлено соответствие между ин-
интервалами порядка k — 1, установить взаимно однозначное соответ-
соответствие между всеми интервалами Бэра порядка к области &х; со-
содержащимися в интервале Ъ® , и всеми интервалами Бэра
порядка k области &ху> содержащимися в интервале Бэра
Аху «, . соответствующем S* ' „
Важно заметить, что области ffx, &Ху Эя^ ^хт имеют
размерность 0. Как мы уже'указывали (прим. 2), этим и объясняется
то обстоятельство, что дескриптивная теория множеств в этом про-
пространстве становится особенно простой и стройней. Употребляемый
Н. Н. Лузиным термин «область т измерений» &xlX^ • ¦• хт отно-
относится только к расположению области &XJ ... Хт в евклидовом
пространстве, а не к размерности этой области. Следует отметить,
что, используя области 9Х. ... Хт, лежащие в евклидовых про-
пространствах нескольких измерений, Н. Н. Лузин достигает чрезвы-
чрезвычайно большой геометрической ясности при исследовании очень
сложных Ьопросов теории множеств.
ПРИМЕЧАНИЯ К ГЛАВЕ II
[4] (стр. SI).1" Бэр дал первоначально классификацию функций,
определенных на евклидовой прямей. И. Н. Лузин рассматривает
здесь функции, определенные на ??т. Классы Бэра для таких функ-<
ций определяются следующим образом. Функции, непрерывные на &х,
принадлежат к классу 0. Функция принадлежит к классу а, если она

ПРИМЕЧАНИЯ 345
йе принадлежит ни к какому классу а' < о, и является пределом
Сходящейся на &х последовательности функций классов < о:,
Ит/П(ж); d/n(#)<a.-
П->со
Изучая функции, определенные на области ffx, естественно потре-
потребовать, чтобы эти функции принимали только иррациональные зна-
значения, т. е. рассматривать отображения области дх в область &и.
Тогда кривая, изображающая функцию .у =/(дг), содержится в обла-.
сти &Ху- Лебеговскими множествами для функции f(x) называются
множества \f(x)>r] и [/(*)</•] тех точек оси ОХ, где выпол-
выполняются неравенства соответственно /(-*¦)> г или f{x)<^r, причем
г — рациональное число.. Если функция f(x) принадлежит
к классу а классификации Бэра, то ее лебеговские множества
являются измеримыми В множествами класса а и обратно (см.
Ляпунов, fi-функции, Успехи матем. наук, т. V, вып. 5 C9),
1950, стр. ПО). .
[8] (стр. 54). Понятия математики в силу своей абстрактной при-
природы, вообще говоря, являются законными и осмысленными в опре-
определенном круге вопросов, при соблюдении определенных предпосы-
предпосылок. Вне этих условий эти понятия могут становиться фиктивными
и терять смысл. Это относится, в частности, к понятию существова-
существования математического объекта. Н. Н. Лузин относится критически
к утверждению существования тех объектов, которые порождаются
принципом произвольного выбора и также к тем, в основе которых
лежит утверждение о существовании всех трансфинитиых чисел вто-
второго и тем более высших классов.
По существу мы здесь .имеем дело с гносеологическими труд-
трудностями, которые порождает идея актуальной бесконечности, вы-
выраженная в теоретико-множественной форме. Трудности эти наибо-
наиболее ярко выражаются в вопросах, связанных с принципом выбора и со-
совокупностью всех трансфииитных чисел хотя бы только второго класса.
В своих трудах Н. Н. Лузин постоянно вскрывал и анализиро-
анализировал указанные трудности. В этой книге он также неоднократно
возвращается к этому анализу.
[в] (еТрр 87). Элементы класса 2 были" изучены П. С. Урысоном
и П. С. Александровым, Mathem. Annaleri, H. 1, 1927. Бэр указал
конструкцию элемента класса 3 (Acta Math,, т. 30, 1950 г.). Л. В. Кел-
Келдыш показала, что элементы, построенные Бэром, являются канони-
каноническими («О гомеоморфности канонических элементов третьего
класса», Матем. сборник, т. 41, 2, 1934 г.). Канонические элементы
класса Кл найдены Л. В. Келдыш. Оказалось, что в каждом классе
Ка, <х>2 есть один род канонических элементов. Они между со-
собой гомеоморфны, топологически инвариантны, и каждый эле-
элемент класса Ка есть сумма одного канонического элемента класса К*
и не более чем счетного множества элементов классов <а (см.
Л. В. Келдыш, Структура fl-множеств, Труды Матем. ин-та им.
В. А. Стеклова, т. XVII, 1944 .г).
П (стр. 88). Канонические элементы класса 2 рода Р гомео-
гомеоморфны каноническим элементам рода 2°, как показали

§46 ПРИМЕЧАНИЯ
П. С. Александров и П. С. Урысон (Mathem. Annalen, H. 1, 1927 г.).
Поэтому топологически эти два рода эквивалентны. Заметим, что
канонические элементы класса 2 гомеоморфны области 3 и, следо-
следовательно» гомеоморфны некоторым множествам класса 0 и некото-
некоторым множествам класса 1. Это происходит в силу того, что сама фун-
фундаментальная область S есть абсолютное Gj, которое не есть Fe.
Для а>.3 элементы класса К* топологически инвариантны, как
пбказал М. А. Лаврентьев (Fundamenta Math., 6, 1924 г.).
Если Объединить в один род канонические элементы рода 1° и
рода 2° и назвать каноническим элементом класса 2 элемент класса 2,
который получается выбрасыванием из совершенного множества Р
всюду плотной на Р суммы счетного множества нигде, не плотных
на Р замкнутых множеств, то имеет место следующее: каждый эле-
элемент класса 2 является суммой одного канонического элемента
класса 2 и одного множества класса а<;1.
Заметим, что для случая а>2 в настоящее время доказано
более слабое утверждение. Именно: каждый элемент класса а,
а > 2 является суммой одного канонического элемента класса а
и не более чем счетного множества множеств классов <<*
(Л. В. Келдыш, Структура 5-множеств, Труды Матем. ин-та им.
В. А. Стсклова, т. XVII, 1944 г.). Вопрос о возможности предста-
представления произвольного элемента класса а в виде суммы одного кано-
канонического элемента класса а и одного множества класса < а остается
открытым до настоящего времени.
[8] (стр. 101). Для того чтобы существовала иррациональная
точка ?, общая всем пт, достаточно, чтобы каждая порция «т была
высечена из соответствующего определяющего множества с помощью
интервала Бэра, что, очевидно, всегда возможно.
[9] (стр. 105). Доказательство достаточности можно провести
значительно проще: часть Е, принадлежащая произвольному совер-
совершенному множеству Р, содержит первый элемент Ц. Пусть гср —
порция Р, отделяющая ?р от всех остальных точек множества Е-Р%
В порции ка найдется порция я^ множества Р, не содержащая точки ?а
и, следовательно, целиком принадлежащая к СЕ. Следовательно,
Е есть множество класса-^ 1.
[10] (стр. 118). Когда г пробегает интервал Бэра А, то t пробе-
пробегает часть Т, заключенную в соответствующем интервале Бэра В,
Но эта часть Т получается выбрасыванием из S счетного множества
интервалов Бэра V. Когда t пробегает V, то функция Ft (t) пробе-
пробегает часть ?,• класса < а-. Так как функция Ft регулярна, то часть Е{,
которую пробегает F,- (<), когда t пробегает Т, получается выбра-
выбрасыванием из части Е(, которую пробегает Ft (<), когда t пробегает Ь,
всех частей ?$, которые пробегает Ft (t), когда t пробегает все V.
Отсюда следует, что когда t пробегает множество Т, то каждое Ft (/),
а значит и F(t), пробегает либо множество класса <а, либо мно-
множество базы ВЛ, либо элемент класса а.
[U] (стр. 131). Речь идет о построении трансфинитной функции,
которая каждому трансфинитному числу а. ставила бы в соответствие
пересчет всех трансфинитных чисел, меньших а. Автор говорит

ПРИМЕЧАНИЙ 347
6 невозможности построения такой функции без аксиомы Цермело.
Термин «данное число а» употребляется автором в том смысле, что
число а задано каким-то законом, так что вместе с ним дан пере-
пересчет всех чисел, меньших а.
[12] (стр# 134). Заметим, что здесь доказано существование сколь
угодно высоких подклассов, но не доказано существование всех
подклассов. На самом деле, не все подклассы существуют. Легко
видеть, что если трансфинитное число {3 имеет вид Р' + и, где
л— конечное число, большее 1, и>1, то подкласса р не существует,
так как множество, которому при некотором разложении в рассеян-
рассеянную последовательность элементов класса а соответствует число [3,
можно представить в виде рассеянной последовательности, которой
соответствует число р' +1- Для этого достаточно объединить сумму
элементов ^'+1 + 1)?'+2+ ... +Уу+п в один элемент ^,+1.
ПРИМЕЧАНИЯ К ГЛАВЕ III
[13] (стр. 136). Употребляемое автором название «аналитическое
множество» не является общеупотребительным. В литературе эти
множества известны под названием А-множеств или суслинских
множеств. /4-множествами называются множества, которые могут
быть получены, исходя из интервалов с помощью некоторой теоре-
теоретико-множественной операции, носящей название /4-операции. Впо-
Впоследствии было выяснено, что -4-операция над интервалами про-
пространства &х эквивалентна операции непрерывного отображения
пространства &„.. /4-операция была введена П. С. Александровым
(Comptes Rendus, 1916, стр. 323). П. С. Александров показал, что
всякое 5-множество, лежащее в ffx, может быть получено с по-
помощью Л-операции над интервалами, и использовал это для доказа-
доказательства теоремы о мощности Д-множеств. Затем Н. Н. Лузиным был
поставлен вопрос: можно ли с помощью /4-операции над интервалами
получить множества, которые не являются 5-множествами? Суслин
дал утвердительный ответ на этот вопрос, показав, что существуют
А-множества, которые не являются В-множествами.
[Щ (стр. 146). Легко заметить, что элементарное множество Е
есть замкнутое множество в пространстве &ху, так как каждая
сумма Sn состоит из параллелепипедов Бэра одного порядка, и,
следовательно, дополнение к Sn есть сумма параллелепипедов Бэра
того же порядка, т. е. Sn есть множество класса 0. Следовательно,
Е есть самое большее — элемент класса 1 в пространстве &ху,
1. е. замкнутое в &Ху множество.
[15] (стр. 172). Это легко доказать по индукции. Если $•— мно-
множество класса 0, то это непосредственно следует из теоремы Лебега.
Пусть теперь утверждение верно для всех a'<a и $ — множество
класса а. Тогда g= lim %п, причем %п—множество класса <а.

348 ПРИМЕЧАНИЯ
Тогда, по условию, прообраз множества $„ • Q, где 0 — множество
значений функции /, измерим В. Но прообраз множества $ • Q есть
предел прообразов §„•?
f-i ($. Q) =/-i [ Um $n • Q] = Urn /-»(gn ¦ (?)
и, следовательно, есть также множество, измеримое В.
[и] (стр. 178). См. П. С. Новиков, Stir les fonctions implicltes
mesurables В, Fundamenta Math., т. XVII, 1931 г.
[17] (стр. 196). Первоначально аналитические множества, или,
иначе, /4-множества были определены при помощи введенной
П. С. Александровым /4-операции над системой множеств, когда эти
ножества являются порциями пространства &а _-а, . Л-операция
может быть произведена над счетной системой множеств произволь-
произвольной структуры и определяется следующим образом. Пусть дана
счетная система множеств, занумерованных при помощи конечных
кортежей индексов:
iE}
где k = 1, 2,... до бесконечности и для каждого к, щ=\, 2..
до бесконечности. Система {Еп ..,„ } называется А-системой.
Множества Ёп с одним индексом называются элементами
А'системы первого ранга, и вообще множества Е„ „ _ с k индек-
сами называются элементами ранга к. пели кортеж множества
Еп „ #я_ получается присоединением одного индекса пк+1 к кор-
кортежу множества Еп ¦ то элемент ?„ __ называется под-
чиненным элементу ?„„,,.„• Последовательность элементов А
системы
каждый последующий из которых подчинен предыдущему, называется
цепью. Множество называется результатом А-операции над систе-
системой {Епп .,.,.}, если оно определяется равенством:
где сумма 2 берется по всевозможным цепям A). Таких цепей,
очевидно, континуум. В том случае, когда все множества Епп _„
являются параллелепипедами Бэра пространства &хх х , мно-
1 8"' т
жество Е, которое является результатом операции над системой A),
Называется А-множеством. Покажем, что А-множества тожде-
тождественны с аналитическими множествами. Для этого мы покажем

ПРИМЕЧАНИЯ
349
что Л-операция над системой параллелепипедов Бэра"8яп--.п
в области &хх...х эквивалентна операции проектирования
в область &хх ,--а, .лежащего в пространстве области 9гсеа _ х у
элемента класса 2 классификации Бэра. Действительно, пусть дана
система параллелепипедов Бэра области 3 х х
и множество Е является результатом Л-операции над этой системой.
Каждому элементу первого ранга Вп мы поставим в соответствие
т 4- 1-мерный параллелепипед itM в области ?Г„ _ _ „ так, чтобы
проекции гс„ в область &хх ж совпадали с Вп, а проекции
параллелепипедов кп на ось OY были интервалами Бэра обла-
области &у и не пересекались между собой. Параллелепипеды пп на-
называются параллелепипедами первого ранга. После того как
построены т + 1-мерные параллелепипеды гсй п # п ранга k, соот-
соответствующие параллелепипедам Ьпп 1>п ранга k, m + 1-мерные
параллелепипеды кп <й п ранга k + 1 строятся следующим обра-
образом: 1) все параллелепипеды яп ..га „ , соответствующие паралле-
лепипедам о„ ' подчиненным о„ „ , содержатся в парал-
t ** и. rfc
лелепипеде теп _ _п , соответствующем Вп , 2) проекции на ось
ОК параллелепипедов
являются интервалами Бэра в области Ву и попарно не пересе-
пересекаются. Лежащее в области &хх шш%х у множество $, определен-
определенное равенством
s, it , \^)
является, очевидно, элементом класса 2 классификации Бэра.
Легко видеть, что проекция множества $ в области &х х ,,-а,
совпадает с множеством Е, которое является результатом Л-опера-
ции над системой {Ьпп >#%я }. Действительно, каждой цепи
12 к'
\ \П2 ЧП2 ''' "ft" Ч"» • • • Vft+l'
соответствует убывающая последовательность параллелепипедов:

350 ПРИМЕЧАНИЯ
и обратно, причем Ьп _ „ есть, проекция в область ffx т х
1 ft 12*'' WI
параллелепипеда кп _„ . Следовательно, множество Я есть проек-
проекция множества § и, значит,— результат ^-операции над системой
{Вп п ..,„ } тождественен с результатом проектирования множества,
12 ft
измеримого В, следовательно, Е—аналитическое множество.
Обратно, если Е есть аналитическое множество, определенное
как проекция множества $, заданного равенством C), то мы немед-
немедленно построим /4-операцию, определяющую Е. Для этого достаточно
каждому параллелепипеду *„„...„ в области &тз> „щ1В у поста-
вить в соответствие его проекцию Ь„ _ „в область S- „ _
И считать, что элемент В подчинен В если
П1П"'ИЛ+1 "Л'"ЙЙ
\n2...nknk+i содержится в «„^...„^ Очевидно, что Л-система
{Ъп п тчП } определяет множество Е, которое является проекцией g.
I 2 ft
Геометрическая форма определения Л-множества, введенная
Н. Н. Лузиным, оказалась чрезвычайно плодотворной при изучении
множеств, лежащих в евклидовом пространстве, так как она позво-
позволяет пользоваться геометрическими образами. Следует, однако, от-
отметить, что первоначальная форма определения -4-множества при
помощи Л-операции, данная П. С. Александровым и определенная
формулой B), дает возможность изучать не только множества,
лежащие в пространствах Евклида, но также и множества, лежащие
в абстрактных пространствах.
[18] (стр. 196). М. Я. Суслин для определения /4-множества поль-
пользовался /4-операцией. Другие способы задания /4-множества были
найдены позже.
Суслин непосредственно доказал сформулированную теорему.
Данное в тексте доказательство принадлежит Н. Н. Лузину и дано
значительно позже, когда им было введено понятие об отделимо-
отделимости и доказан первый принцип отделимости В для /1-множеств.
[19] (стр. 209). Доказательство Н. Н. Лузина теоремы о сравне-
сравнении решет, изложенное в следующем параграфе оригинала книги,
содержит неточность. В самом конце доказательства автор, исполь-
используя построенную им в предыдущем параграфе систему кривых L{,
приписывает ей более сильное, чем ей присуще, свойство универ-
универсальности, которым она не обладает. С целью исправления этого
доказательства мы вводим в текст этот параграф, отмеченный звез-
звездочкой. Полностью сохраняя идею автора, изложенную в предыду-
предыдущем номере, и лишь вводя необходимые технические усложнения,
мы строим систему кривых L?'" *", удовлетворяющих требуемому
условию. После этого доказательство следующего 'параграфа со-
сохраняется почти полностью. Небольшие изменения, введенные нами
В текст следующего параграфа в связи с заменой кривых автора Ln

ПРИМЕЧАНИЯ 351
на кривые L?'" к > отмечены в тексте звездочками в начале и в конце.
Весь остальной текст следующего параграфа является точным пере-
переводом с оригинала книги.
Р>] (стр. 221). См. П. С. Новиков, Sur les fonctions ImpHcfteS
mesurables В, Fundamenta Math., т. XVII, 1931 г.
ПРИМЕЧАНИЕ К ГЛАВЕ IV
[м] (стр. 252). Здесь доказательство содержит небольшую не-
неточность. Построенная система параллелепипедов «J, «",..., п'к, %'к
еще не удовлетворяет требуемым свойствам. Пока доказано только,
что, каково бы ни было трансфинитное число у, существует такая
точка х и такая система параллелепипедов n'v icj,..., ж'к, пк, что
прямая Р~ содержит несчетное множество точек на каждой из кон-
конституант « ,, Ь ,/, I = 1, 2, ..., к, причем индексы всех этих консти-
туант превосходят f. Точка х и система параллелепипедов nv я", ..,
••¦• пк> *к зависят от числа •(. Для того чтобы выбрать требуемую
систему параллелепипедов, достаточно заметить, что различных чисел
Y — несчетное множество, тогда как различных систем параллеле-
параллелепипедов n'v к", ..., п'к, к'к существует лишь счетное множество.
Поэтому среди этих систем параллелепипедов найдется такая, кото-
которая соответствует несчетному множеству различных чисел ~(. Эта
система, очевидно, уже обладает требуемым свойством.
ПРИМЕЧАНИЕ К ГЛАВЕ V
[22] (стр. 272). Термины «аналитическое множество» порядка п
и «аналитическое дополнение» порядка п не привились. В литера-
литературе употребительны термины проективное множество класса (А„)
и проективное множество класса (СД,).
[!3] (стр. 276). Оба эти вопроса решены отрицательно для п = 2
в работе: Коп do, L'uniformisation des complementalies analytiques,
Proc. Imp. Acad. Tohoku, 1937, т. XIII. Кондо доказал следующую
теорему: всякое проективное множество класса (А%) или (&г)
есть проекция однозначного аналитического дополнения. Эта
теорема получена как следствие следующей теоремы: Каково бы
ни было плоское СА-множество В, в нем содержится такое
однозначное СА-множество $
что проекция g на ось ОХ совпадает с проекцией ?.
[24] (стр. 276). Вопрос о покрытии однозначного плоского мно-
множества класса (/12) однозначным плоским множеством класса E2)
решается отрицательно, Это непосредственно следует из теоремы

352 ПРИМЕЧАНИЯ
П. С. Новикова о существовании двух непересекающихся множеств
"класса А* неотделимых посредством множеств класса 52. (П. С. Н о-
в и к о в, Snr ta separabilite des ensembles projectifs de scconde classe,
Fundamenta Math., т. XXV, 1935, стр. 459—466). В самом деле,
пусть Ех и ?2 — Два непересекающихся множества класса (Л2),
неотделимых посредством множеств класса (В2). Пусть, далее,
% — плоское множество класса (/42), лежащее в области &ху и
состоящее из множества Ех, положенного на прямой у = rjt, и
множества ?2, положенного на прямой у = ¦»),, г\х < тJ> и к|г и тJ ир-
-рациональны. Очевидно, что % — однозначное относительно оси ОХ
плоское множество класса (Аг). Покажем, что $ нельзя покрыть
однозначным множеством класса (В2). Действительно, если бы это
было возможно, то " существовало бы плоское множество Н
класса (В2), однозначное относительно оси ОХ и содержащее $.
Пусть //]—пересечение Н с прямой у = щ, а Н2— пересечение И
с прямой у s= iJ. Очевидно, что
и ¦ оба множества Нх и Я2 являются множествами класса (Д2)-
А так как множества ?t и ?2 неотделимы посредством (Дг), то
найдется прямая РХ(), параллельная оси OY, пересекающая как Н\,
так и Я2. Но Нх и Н2 принадлежат к Я, следовательно, прямая PXq
пересекает Я в двух точках, и значит, множество Я не однозначно
.относительно оси ОХ, вопреки предположению. Итак, мы показали,
что существует однозначное плоское множество класса (А2),
которое нельзя покрыть однозначным плоская множеством
класса (В2).
Совершенно так же можно показать, что существует плоское
СА-множество, однозначное относительно оси ОХ, которое
нельзя покрыть множеством, измеримым В, однозначным отно-
относительно оси ОХ.
Для я>2 вопрос не решен в классическом смысле.
Исследование проективных множеств более высоких классов
связано, как указывал Н. Н. Лузин (см. заключение), с трудностями,
повидимому, не преодолимыми методами теории множеств. Боль-
Большинство проблем здесь нельзя решить в классическом смысле, т. е.
дать положительный или отрицательный ответ на поставленный
вопрос. Но тогда можно ставить вопрос о непротиворечивости того
или иного утверждения теории множеств (см. предисловие). Такая
задача может решаться методами математической логики. П. С. Но-
-виков показал, что непротиворечиво предположение, что суще-
существует число АГ:> 2 такое, что для всякого //>¦ N существуют два
множества класса (Ап), неотделимые посредством множеств
класса (Вп). Отсюда, рассуждая так же, как для я »= 2, заключаем,
что непротиворечиво предположение, что для всякого и > N
Существует однозначное плоское множество класса (Ап), которое
нельзя покрыть однозначным плоским множеством класса (В„).
, - Всё "остальные поставленные "вопросы остаются открытыми
¦даже' для'случая п ±*2, ¦ ¦ ¦ :

ПРИМЕЧАНИЯ 353
С6] (стр. 278). Для я = 2 отрицательный ответ на этот вопрос
-непосредственно следует из теоремы Кондо (см. примеч. 23). Именно
Каждое множество класса (А^) допускает регулярное параме-
параметрическое изображение. Действительно, пусть Е есть линейное (Л2),
лежащее в области &х. В силу теоремы Кондо Е есть проекция
однозначного СА — множества g, лежащего в области &ан. Пусть
теперь функции
осуществляют гомеоморфное отображение области &ху на об-
область fff. Образ g' множества g при этом отображении есть линей-
линейное СЛ-множество, лежащее в области &t. При этом в силу одно-
однозначности g разным значениям t из множества %' соответствуют
разные значения х, и х пробегает множество Е, когда t пробегает
множество g'. Следовательно, функция х = ср (/) осуществляет
регулярное параметрическое изображение множества ?.
Для я>2 вопрос остается открытым.
[-6J (стр. 282). Это рассуждение предполагает, что существуют
множества (СЛ„_г) и (>!„_!). Доказательство этого факта изло-
изложено в одном из последующих параграфов текста. Множества же {В-)
являются по определению одновременно РС...РЬ и СР...РЪ',
где операция Р употреблена ровно я раз.
Чтобы показать, что Е есть (Вп), покажем, что оно есть одно-
одновременно проекция (C/4n_j) и дополнение к проекции (САп-{).
Выберем в области Sxy проективное множество g' класса п—2,
проекция которого в ffx совпадает с Е\. Множество $' + Е2 есть,
очевидно, плоское (CAn-t), и проекция его в &х совпадает с Е.
Следовательно, Е есть проекция (C<4ra_j). Теперь покажем, что Е
есть также дополнение к проекции (С/Ц-а). Для этого достаточно
показать, что СЕ есть проекция (CAn-i). Выберем плоское проек-
проективное множество g" класса я — 2, проекция которого в ^совпа-
^совпадает с разностью
(т- О-*
и рассмотрим множество (О, -^-J— ?i + g". Это, очевидно, пло-
плоское (C/4«_j). Проекция его в ffx, очевидно, совпадает с дополне-
дополнением к Е относительно @, 1). Следовательно, Е есть дополнение
к проекции (САп-!). Итак, Е есть одновременно проекция (САп-{)
и дополнение к проекции (C4n_t), следовательно, Е есть (Вп).
[27J (стр. 282). Этот вопрос решается отрицательно: в каждом
классе я проективных множеств существуют множества класса В„,
которые нельзя получить, исходя из множества класса п — 1 счет-
нократным применением операций суммы и пересечения. (См.
Л. В. Канторович и Е. М. Ливенсон, «Memoir on the analytical
operations and protective sets», Fund. Math., тт.XVUI A932) иХХ A933))
23 За». 284. H. H. Лузин
•С)

354 примечания
Не только применением операции пересечения и суммы, но и
счетнократным применением Л-операции и операции взятия допол-
дополнения, исходя из множеств класса я — 1 нельзя исчерпать всех
множеств класса Вп. А. Н. Колмогоровым были определены
новые более сложные операции над множествами: /?-операции,
частным случаем которых является /1-операция. Эти операции
изучены Ливенсоном и Канторовичем в упомянутой статье и
А. А. Ляпуновым в статье «/?-множества» (Труды Математич. ин-та
им. В. А. Стеклова, т. 40, 1953 г.). Множества, которые могут быть
получены, исходя из множеств, измеримых В с помощью ^-операции,
повторенной счетное множество раз, носят название /?-множеств.
A. А. Ляпунов показал, что 7?-множества разбиваются на Hi классов.
Все С-множества (получаемые из множеств, измеримых В счетно-
кратным применением -4-операции и операции взятия дополнения)
входят в первый класс /?-множеств. А. Н. Колмогоров и А. А. Ля-
Ляпунов показали, что все У?-множества измеримы и входят в класс (fij)-
П. С. Новиков показал, что предположение о существовании
в классе (В2) неизмеримого множества не может привести к про-
противоречию («О непротиворечивости некоторых положений дескрип-
дескриптивной теории множеств», Труды Матем. ин-та им. В. А. Стеклова,
1951 г., т. XXXVII, стр. 315, теорема 4). Отсюда следует, что
невозможно доказать, что 7?-множества исчерпывают класс (B.z).
Точнее: непротиворечиво предположение, что в классе (fi2) содер-
содержится множество, не входящее в класс ^-множеств.
[28] (СТр. 286). Положительный ответ на первый из поставленных
вопросов следует из теоремы Кондо (см. прим. 23). Что же касается
до распространения теоремы Мазуркевича на проективные мно-
множества высших классов, то для случая я = 2, как уже указано,
имеется более сильная теорема — теорема Коидо. Для случая же
я>2 вопрос сводится к проблеме о структуре однозначного мно-
множества, которое можно выделить из плоского множества класса
(CAn-i) так, чтобы проекция его в &х совпадала с проекцией
данного (C.4n_i). Однако едва ли можно надеяться на решение
этой задачи в классическом смысле.
Р9] (стр. 288). В классическом смысле эта проблема не решена.
Как указывает Н. Н. Лузин (стр. 296), эта проблема, повидимому,
принадлежит к числу тех проблем, решение которых в рамках
теории множеств невозможно. Привлекая методы математической
логики, можно ставить вопрос о ее непротиворечивости. П. С. Но-
Новиков доказал непротиворечивость утверждения, что существует
проективная функция f(x) однозначная, всюду определенная и такая,
что изображающая ее кривая L есть СА-множество, не содержащее
Совершенного множества. (П. С. Новиков, О непротиворечивости
некоторых положений теории множеств, Труды Матем. ин-та им.
B. А. Стеклова, т. XXXVIII, 195 1г., теорема 2.) Заметим, что кривая
f = ¦») (у) П. С. Новикова есть проективная кривая класса (А2).
Однако из нее немедленно извлекается и (М-кривая L. Для этого

ПРИМЕЧАНИЯ 355
лространственную кривую, которая является С4-множеством и
определена для всех значений у области &у. Чтобы получить
плоскую кривую L, достаточно гомеоморфно отобразить простран-
пространство Styis на пространство Sty с помощью преобразования.
у**у, t =
Кривая П. С. Новикова t = г) (у) строится средствами классической
теории множеств. Но для доказательства непротиворечивости пред-
предположения, что эта кривая не содержит совершенного множества,
он опирается на результат Гёделя — о непротиворечивости конти-
континуум-гипотезы (см. Гёдель, Совместимость аксиомы выбора и
обобщенной коитинуум-гипотезы с аксиомами теории множеств,
перев. В. А. Маркова, Успехи матем. наук, 1948 г., т. III, вып. 1 B3)).
Поэтому дальнейшие заключения Н. Н. Лузина о выводимости
континуум-гипотезы из отрицательного решения указанной проблемы
здесь теряют Смысл.
[во] (стр. 290). Из теоремы Кондо (см. примечание 23) непосред-
непосредственно следует, что каждое множество % класса (А2) можно рас-
рассматривать как просеянное при помощи счетного решета (СА).
Для этого достаточно в каждой полосе (—< j/<——r J области &ху
поместить однозначное СЛ-множество Еп, проекция которого в об-
область ifg. совпадает с $. Множество $ просеяно с помощью пло-
плоского решета (СА)
Что же касается до просеивания с помощью прямолинейного
решета С, составленного из (В2) множеств или, что то же — л-опе-
рации над множествами класса (Вг), то, как показали Канторович
и Ливенсон, она всегда приводит к множествам класса (В2). (См.
Kantorovltch and TJvenson, Fundementa Math., тт. XVIII, XX.) Мно-
Множества, которые получаются из А- и СЛ-множеств с помощью
счетнократного применения /4-операции и операции взятия допол-
дополнения, носящие название С-множеств, были введены А. Н. Колмо-
Колмогоровым. Им же, независимо от Е. А. Селивановского, была дока-
доказана их измеримость и наличие свойства Бэра. Однако работа
А. Н. Колмогорова осталась неопубликованной. Она будет опубли-
опубликована в журнале «Успехи матем. наук».
[si] (стр. 291). Результаты Канторовича и Ливенсоиа опубли-
опубликованы в статье «Memoir on the analytical operations and projective
sets» (Fundamenta Math., тт. XVIII A932), XX A933)).
[32] (стр. 291). Проблема об отделимости проективных множеств
второго класса была решена П. С. Новиковым «Sur la separabMte
des ensembles projectifs de seconde classe» (Fundamenta Math.,
т. XXV A935 r.) 459—466). Законы отделимости здесь оказались
обращенными, т. е. они получаются из законов отделимости для
/1-множеств, если заменить /4-множества через СЛ^-миожества
23*

356 ПРИМЕЧАНИЯ
а СЛ-множества через /42-миожество. Основные принципы отдели-
отделимости во втором классе проективных множеств формулируются так:
Теорема I. Два множества класса (СА2) без общих точек
всегда отделимы с помощью двух множеств класса (В2).
Теорема II. Если удалить из двух множеств (СА%) их
общую часть, то оставшиеся части отделимы с помощью А%~мно-
жеств.
Теорема III. Если удалить из двух множеств (At) их об-
общую часть, то оставшиеся множества отделимы с помощью
множеств (А2).
Теорема IV. Существуют два множества (А2) без общих
точек, неотделимые при помощи множеств (?2).
Для случая «>2в классическом смысле ничего не доказано.
Однако П. С. Новиков показал, что непротиворечиво предположение,
что для всех п, ббльших некоторого N, в я-м классе проективных мно-
множеств принципы отделимости такие же, как и во втором классе
(т. е. обращенные по отношению к классу /4-множеств). (См. Нови-
Новиков, О непротиворечивости некоторых положений дескриптивной
теории множеств, Труды Матем. ин-та им. В. А. Стеклова, т. XXXVIII,
1951 г.)
[зз] (СТр. 297). Для построения W рассмотрим в плоскости YOZ
построенный выше универсальный элемент Е класса 1, т. е. плоский
элемент класса 1, который пересекается с прямыми, параллельными
оси OZ, по всевозможным линейным замкнутым множествам (см.
стр. 126). Обозначим через Ег часть множества Е, заключенную
в полосе (rj < г < г2), а через er r множество тех точек М об-
области &у, для которых прямая Р*> проходящая через М параллельно
оси OZ, пересекает Er r не более чем в одной точке. Все множе-
множества er r являются аналитическими дополнениями (стр. 261). Рас-
Рассмотрим множество
Легко видеть, что Н есть множество всех тех точек М области &у,
в которых прямая Р* либо вовсе не пересекает множества Е, либо же
пересекает его по множеству, содержащему хотя бы одну изо-
изолированную точку, т. е. несовершенному. Так как все множе-
множества PEr r аналитические, a«ff — аналитические дополнения, то
множество Н есть либо множество класса (Ла), либо (В2), либо
проективного класса 1. Пусть теперь Н' — множество всех точек
области &уг, проекция которых в &у принадлежит к Н. Очевидно,
что Н' есть либо (А%), либо (В2), либо проективного класса 1. Поло-
Положим теперь
?/' = ? + Я'.
Очевидно, что всякая прямая, параллельная оси OZ, пересекает U

примечаний 357
ПО совершенному (в &z) множеству, и что U' универсально для
всех линейных совершенных множест Так как Е— элемент класса 1,
а Н' либо множество класса (А2), либо (Яа), либо класса 1, то и U'
есть множество либо класса (А2), либо (АЛ, либо класса 1.
[Щ (стр. 313). Природа поверхности Лебега была изучена Ней-
Нейманом и КуратОвским. Оказалось, что эта поверхность представляет
собой проективное множество второго класса, точнее — пересечение
Л-множества и дополнения к /1-множеству.
ПРИМЕЧАНИЯ К ЗАКЛЮЧЕНИЮ
[35] (к стр. 321). Предположение Н. Н. Лузина о невозмож-
невозможности доказать измеримость проективных множеств в настоящее
время полностью оправдалось., Именно, Л. С. Новиков построил
проективное множество класса (В.2), относительно которого непро-
непротиворечиво утверждение, что оно неизмеримо (П. С. Новиков,
О непротиворечивости некоторых положений дескриптивной теории
множеств, Труды Матем. ии-та им. В. А. Стеклова, 1951 г., т, XXXVIII,
стр. 315, теорема 4). Отсюда следует, что невозможно доказать
измеримость проективных множеств. Однако вопрос о возможности
доказательства методами теории множеств существования неизмери-
неизмеримого проективного множества в настоящее время еще остается
открытым, так как пока не доказана непротиворечивость утвержде-
утверждения об измеримости проективных множеств.
ПРИМЕЧАНИЯ К ДОПОЛНЕНИЮ I
[Зв] (к стр. 324). Предполагается, что / (х) есть функция, харак-
характеристическая для множества всех точек, которые изображаются
непрерывными дробями, у которых совокупность неполных частных
at, <x2 ап,... образует составную последовательность нату-
натуральных чисел.

СОДЕРЖАНИЕ
Предисловие редакторов ¦ 5
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
И ИХ ПРИЛОЖЕНИЯХ
Глава I. Общие понятия о множествах, измеримых В . . . 21.
Область. Порции. Начальный класс 22
Операция над множествами 25
Алгебраическое обозначение 32
Понятие множества, измеримого В 36
Преобразования определенна множества, измеримого В . . . . 38
Глава II. Исследования о структуре множеств, измеримых В . 51
Классификация множеств, измеримых В 51
Достижимость ¦ 55
Структура классов • 69
Отделимость . 63
Первые сведения о структуре множества точек данного класса. 71
Множества класса 0 и 1. Исследования Бэра . . 79
Конструктивное существование множеств 1, 2, 3 и 4 класса 87
Понятие рассеянного множества (по Данжуа) 103
Процесс Бэра в высших классах . • 111
Подклассы, их существование 122
Глава III. Аналитические множества 135
Определения и простейшие свойства 135
Проекции 140
Свойства аналитических множеств 149
Первый принцип аналитических множеств. Отделимость В . . . 154
Изучение регулярных и полурегулярных изображении аналити-
аналитических множеств 163
Решета . 178
Второй принцип аналитических множеств. Отделимость (СА). . 205
Глава IV. Неявные функции 223
Общие замечания о неявных функциях . . 223
Ичучение однозначных неявных функций. Исследования Лебега 231
Изучение мьогозначных неявных функций со счетным множе-
множеством значений 238
Изучение общего случая в проблеме неявных функций 25

Содержание 359
Глава V. Проективные множества 269
Определение проективного множества. Его преобразование . 269
Простейшие свойства проективных множеств 275
Теорема Мазуркевича. Обобщение В. Серпинского . . 283
Существование проективных множеств всякого класса и всякого
рода. Универсальные множества . . 291
Резольвенты 294
Анализ мемуара Лебега «Sur les fonctions representables analy-
tiquement» 308
Заключение 320
Дополнение I. Арифметический пример функции, ие входящей
в классификацию Бэра 323
Дополнение II. Некоторые замечания о кривых, являющихся
аналитическими дополнениями 326
Примечания 343

Редактор В. М. Ландае
Техн. редактор Л. А, Голубко$а
Корректор Л. О. Сечейко
*
Подписано к печати 13/VI 19S3 г.
Бумага 84ХШ8/31. 5,63 бум. л. 18,45 печ. л.
18,9 уч.-изд. л. 40 970 тип. зи. в net. л.
Тираж 6000 экз. Т-02897.
Цена книги 9 руб. 45 коп. Переплет 2 р
Заказ № 2S4.
4-я типография им. Евг. Соколовой
Союзполиграфпрома Главиздата
Министерства культуры СССР.
Ленинград, Измайловский пр., 29.