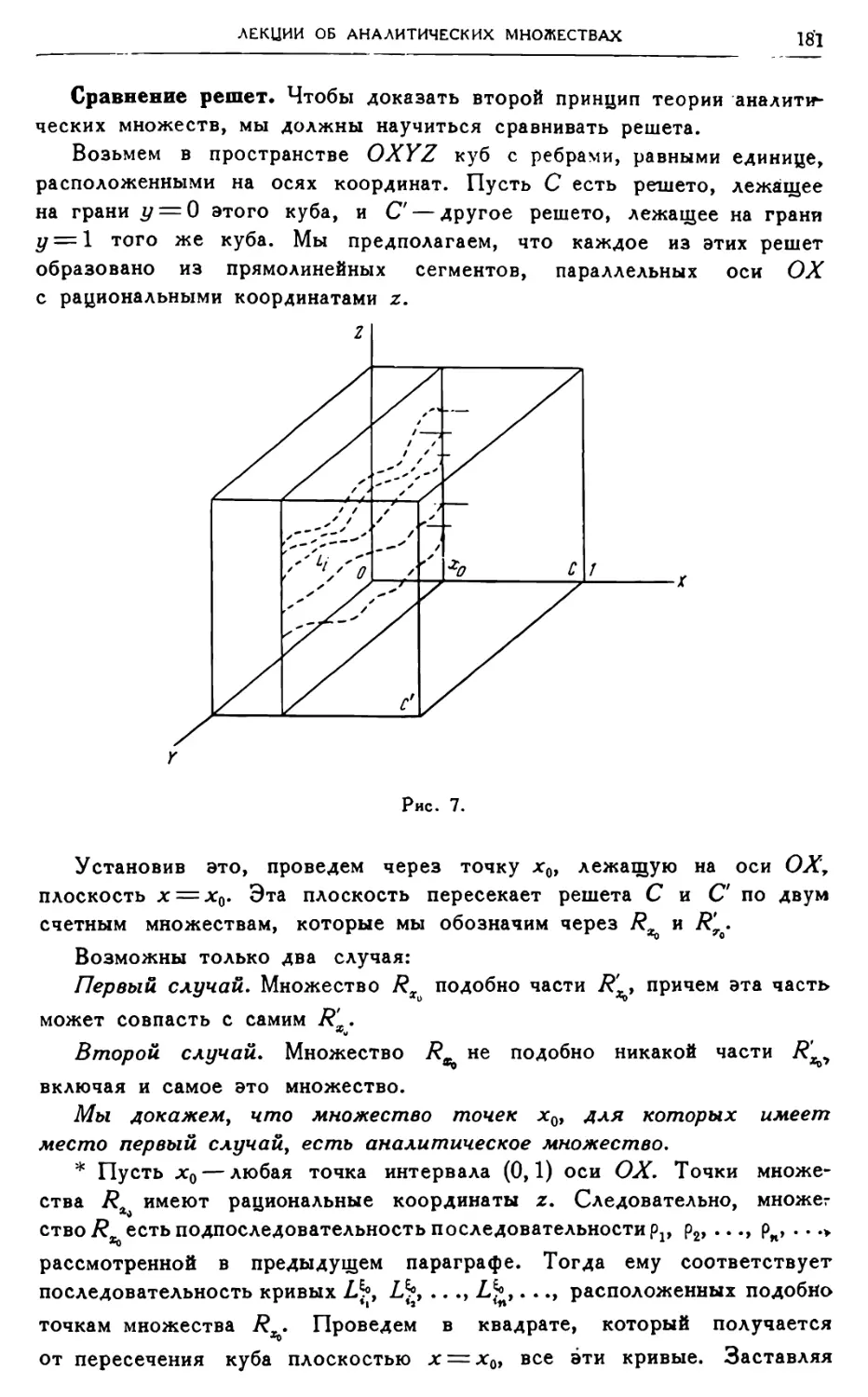
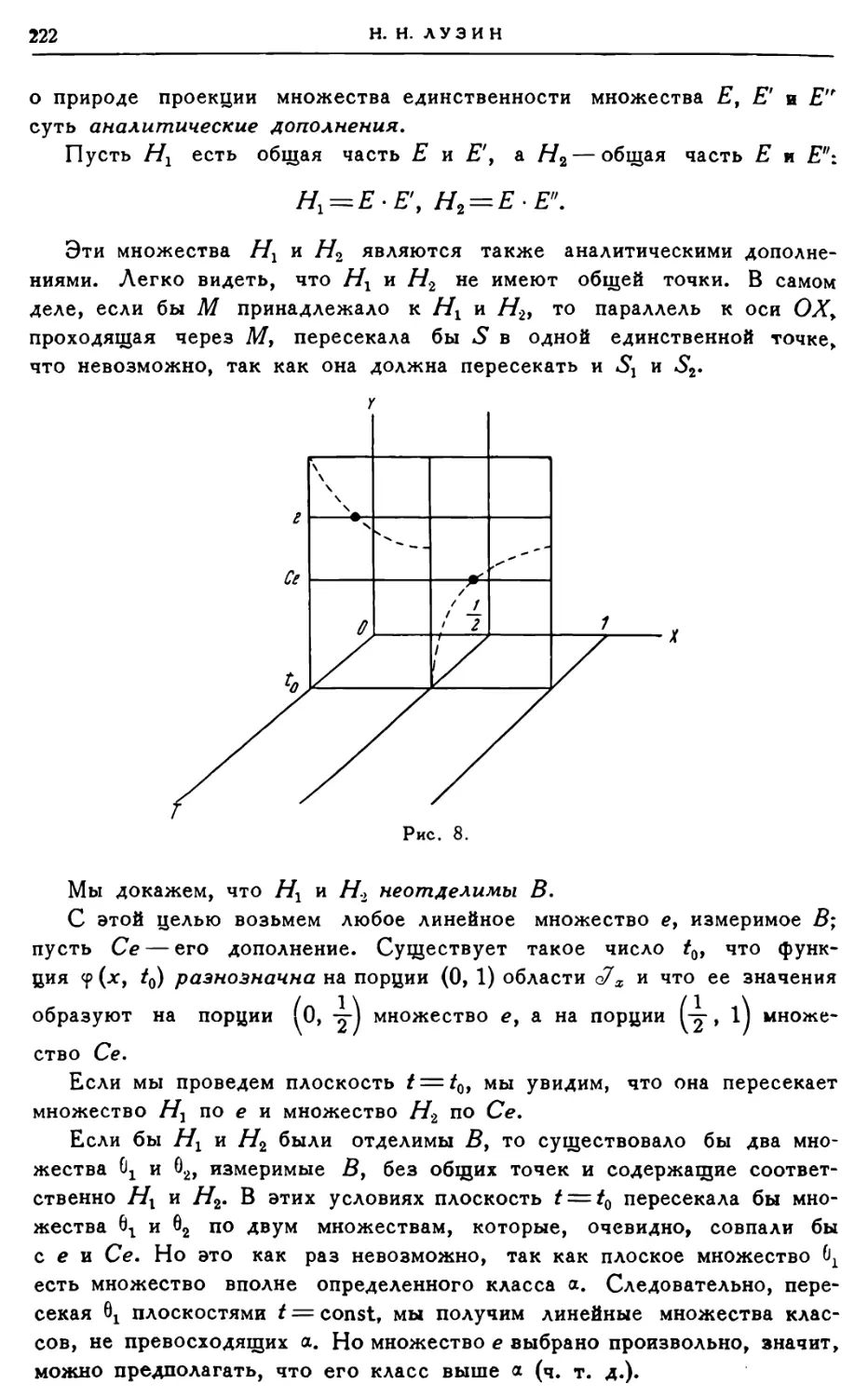
Автор: Лузин Н.Н.
Теги: математика ан ссср дескриптивная теория множеств эффективные множества измеримость и мощность
Год: 1958
Текст
АКАДЕМИЯ НАУК СССР
Н.Н.ЛУЗИН
СОБРАНИЕ
СОЧИНЕНИЙ
ТОМ
II
ДЕСКРИПТИВНАЯ ТЕОРИЯ
МНОЖЕСТВ
ИЗДАТЕЛЬСТВО АКАДЕМИИ НАУК СССР
МОСКВА
J 9 5 6
КОМИССИЯ ПО ИЗДАНИЮ ТРУДОВ
АКАДЕМИКА Н. Н.ЛУЗИНА
академик М. А. Лаврентьев (председатель), академик А. И. Некрасов
члены-корреспонденты АН СССР
Л. Н. Сретенский, Д. Е. Меньшое, 77. С. Новиков.
доктора фиэ.-мат, наук
Н.К.Бари, А. В. Келдыш
ОТВЕТСТВЕННЫЕ РЕДАКТОРЫ 2-го ТОМА
член-корреспондент АН СССР 77. С. Новиков
и доктор фиэ.-мат. наук Л, В. Келдыш
ОТ РЕДАКТОРОВ ТОМА
Второй том трудов Н. Н. Лузина охватывает его работы в области
дескриптивной теории множеств. К моменту вступления Н. Н. 'Лузина
в эту область уже были известны понятие множества измеримого В
и классификация этих множеств по трансфинитам первого и второго
класса. Лебегом был построен без принципа выбора, но с использованием
совокупности всех трансфинитных чисел второго класса пример
множества неизмеримого «В. Было известно мероопределение Лебега в
доказана измеримость (в смысле Лебега) всех множеств измеримых В*
В то же время с помощью принципа выбора были построены примеры
неизмеримых множеств. Возник вопрос об изучении измеримых множеств.
Эта задача представляет собой основную задачу дескриптивной теории
множеств. Использование принципа выбора наряду с примерами
неизмеримых множеств дало ряд других важных, но подчас парадоксальных,
фактов. Обозначились также трудности, связанные с идеей
трансфинитного числа и с континуум-проблемой. С использованием принципа
выбора можно лишь доказать неравенство tfi ^ с, но не удалось точно
указать места мощности континуума с в шкале алефов. Все эти
трудности, в своей сущности связанные с теоретико-множественной идеей
бесконечности, породили критическое направление в теории множеств.
Критика началась с анализа идеи трансфинитного и вопроса об
использовании принципа выбора. Начало этой критики и связанная с ней
полемика содержатся в ряде статей Бореля, Лебега и в переписке
между Адамаром, Борелем, Бэром и Лебегом (см. Е. В о г е 1. Lemons sur
la theorie des fonctions. Paris, 1914, note IV).
Одни математики (Адамар) не усматривали ничего сомнительного
в теоретико-множественной идее бесконечности и считали законным
неограниченное употребление принципа выбора. Другие (Борель, Бэр,
Лебег) считали, что необходим пересмотр основных
теоретико-множественных понятий и принципов. Они утверждали, что неограниченное
употребление в математике понятия бесконечного и, в частности,
принципа выбора часто приводит к заключениям, лишенным всякого
гносеологического смысла. Первых Борель называет „ идеалистами*4,
вторых „реалистами". Термин „реалист" иногда заменяется терминами
„эмпирист" или „натуралист". Отметим, что эта терминология никак не
связана с классификацией философских школ и выражает лишь отно-
4
ОТ РЕДАКТОРОВ ТОМА
шение к идее бесконечности в математике и к вопросу о принципе
выбора. Представители критического направления отмечали, что
построение, сделанное с использованием принципа выбора, не может дать
индивидуального объекта, а определяет всегда лишь класс объектов,
удовлетворяющих некоторым требованиям. Лебег ввел понятие
„эффективного" или „называемого" множества. По существу, это множество, которое
может быть задано без применения принципа выбора. Весьма важным
Аля приложения к анализу и теории функций является вопрос об
измеримости множества. Все известные до настоящего времени
доказательства измеримости некоторого множества связаны с его структурными,
т. е. дескриптивными, свойствами.
Вместе с тем, при изучении структурных свойств множества всегда
возникает вопрос о его мощности и о свойстве Бэра.
Основная задача, которая составляет предмет исследований
Н. Н. Лузина и руководимой им школы в области дескриптивной
теории множеств, — это проблема изучения эффективных множеств,
в особенности вопрос об их измеримости и мощности.
Благодаря своей огромной интуиции и богатству идей Н. Н. Лузин
создал новое направление в математической науке — изучение
эффективных множеств. Им самим и его учениками был решен ряд важнейших
задач в этом направлении.
После того как М. Я. Суслиным были открыты Л-множества и
был затем решен вопрос об их измеримости и мощности, вскоре
обнаружилось, что для СЛ-множеств (дополнений к Л-множествам) вопрос
об их мощности представляет значительные трудности, которые не
удалось преодолеть. Глубокий анализ этой задачи привел Н. Н. Лузина
к мысли, что эти трудности носят принципиальный характер и что
проблема мощности СЛ-множеств не может быть разрешена теоретико-
множественными средствами. В связи с этим Н. Н. Лузин поставил
вопрос об исследовании границ теоретико-множественных методов и
об отыскании таких эффективных множеств, для которых оказалась бы
неразрешимой и проблема их измеримости* После открытия Л-множеств
рядом ученых (Колмогоров, Хаусдорф) были построены различные
теоретико-множественные операции, приводящие к эффективным
множествам (С-множества, ^-множества и др.), которые все оказались
измеримыми. В то же время критический анализ трудностей, которые
лежат на пути проблемы о мощности СЛ-множеств, привел Н. Н.
Лузина к идее проективных множеств, которые получаются, отправляясь
от множеств измеримых В, применением в конечном числе операций
проектирования и взятия дополнения. Н. Н. Лузин высказал
утверждение, что невозможно доказать измеримость произвольного
проективного множества. Это утверждение было доказано 25 лет спустя
методами математической логики. Именно, П. С. Новиков построил такое
проективное множество, относительно которого непротиворечиво
предположение, что оно неизмеримо.
ОТ РЕДАКТОРОВ ТОМА
S
Основной цикл работ Н. Н. Лузина в области дескриптивной
теории множеств есть цикл, направленный на изучение эффективных
множеств, который завершается постановкой ряда проблем, относительно
которых он высказал утверждение об их неразрешимости в теории
множеств. Большинство результатов этого цикла содержится в его
книге „Лекции об аналитических множествах* (стр. 9).
Второй цикл исследований Н. Н. Лузина представляет собой
изучение задач, лежащих на пути к центральным проблемам теории множеств:
континуум-проблеме и проблеме о мощности СЛ-множеств. Он
стремился выяснить, что можно сделать на этом пути
теоретико-множественными средствами.
С этой целью он изучал разбиение отрезка (или СЛ-множеств а) на
Si 5-множеств, которое определяется решетом (Л-системой), задающим
Л-множество. Сюда относится исследование классов конституант С А-
множества (стр. 624 и стр. 627), пример СЛ-множества, классы
конституант которого растут ао 2. К этому же кругу вопросов примыкает
и статья „О стационарных последовательностях44 (схр. 642). Следует
отметить, что в последней работе дается распространение известной
теоремы Бэра о стационарных последовательностях на случай некоторых
последовательностей множеств типа F0 - Это расширение представляет
собой полезное доказательное средство.
Наконец, третий цикл работ Н. Н. Лузина в области дескриптивной
теории множеств содержит результаты, полученные с использованием
принципа выбора. Относясь к нему критически, Н. Н. Лузин не
отказывался, однако, от возможности в тех случаях, когда не удается
решить задачу эффективными средствами, посмотреть, что дает принцип
выбора. Отметим, что при состоянии теории множеств в то время
использование принципа выбора в некоторых случаях было неизбежно,
так как иначе некоторые важные проблемы, как, например, вопрос
о существовании неизмеримого множества, оставались бы без ответа.
В настоящее время известно, что принцип выбора непротиворечив, и
следовательно утверждение, доказанное при его помощи, не может
быть опровергнуто в теории множеств. К кругу работ, связанных
с принципом выбора, относятся работы, относящиеся к построению и
изучению несчетного множества первой категории на всяком
совершенном множестве (стр.692), разбиение интервала на несчетное
множество неизмеримых множеств (стр. 686) и др. Сюда же примыкают
исследования последних лет жизни Н. Н. Лузина „О частях
натурального ряда" (стр. 714). Эти работы вызваны результатом Хаусдорфа,
показавшим с использованием принципа выбора, что отрезок есть сумма
St непересекающихся ^-множеств второго класса (Fund. Math., t. XXVI,
Hausdorff. Summen von Si Mengen, 1936).
Проблеме разбиения отрезка на ^ 5-множеств ограниченного класса
Н. Н. Лузин придавал большое значение: он рассматривал ее как
задачу, .представляющую собой ослабление континуум-проблемы. Работа
6
ОТ РЕДАКТОРОВ ТОМА
Н. Н. Лузина „О частях натурального ряда" (часть натурального
ряда соответствует здесь изображению точки в виде непрерывной
дроби) посвящена постановке проблем, решение которых дало бы
усиление результата Хаусдорфа. Относительно них, однако, можно сказать,
что возможность решения их теоретико-множественными средствами мало
вероятна.
В целом, направление работ Н. Н. Лузина и возглавляемой им
школы в области дескриптивной теории множеств имело целью критику
основ теории множеств и отыскание границ ее методов. Отправляясь
от позиций французских математиков (Борель, Лебег), связанных
с критикой понятия бесконечности и принципа выбора, Н. Н. Лузин
пошел значительно дальше. Он провел глубокий анализ способов
задания эффективных множеств и тех причин, которые для некоторых из
них приводят к принципиальным трудностям при решении ряда задач,
в частности проблемы мощности и проблемы измеримости. Этот анализ,
как мы уже указывали, привел его к понятию проективных множеств,
относительно которых он высказал утверждение о неразрешимости
в теории множеств вопросов об их измеримости, мощности и свойстве
Бэра. Доказательство этого утверждения выходит за пределы теории
множеств. В настоящее время еще не существует полного доказательства
неразрешимости ни для одной теоретико-множественной проблемы. Имеются
лишь сделанные методами оснований математики доказательства
невозможности решения их в определенном смысле. Так, из работы Геделя
[„Совместимость аксиомы выбора и обобщенной континуум-гипотезы
с аксиомами теории множеств". Пер. Маркова, УМН, 1948, т. III,
вып. 1 (23)] следует невозможность опровержения аксиомы Цермело
и континуум-гипотезы, а из работы П. С. Новикова (Труды Мат. ин-та
им. В. А. Стеклова АН СССР, ХХХУШ, 1951) следует невозможность
доказать существование совершенного подмножества в каждом
несчетном СЛ-множестве и невозможность доказать измеримость
проективных множеств. В настоящее время можно уже утверждать, что
дальнейшее исследование проблемы дескриптивной теории множеств должно
быть тесно связано с современными идеями и методами оснований
математики.
Работы Н. Н. Лузина, направленные на критику основ теории
множеств, сами лежат внутри методов теории множеств. Но он всегда
интересовался развивавшимися в то время течениями в области оснований
математики и их связью с теорией множеств. В ряде своих докладов
он касался этих вопросов и анализировал их. В частности, большое
внимание уделено теории Гильберта и теории Брауэра в докладах
„О путях развития теории множеств" (стр.464) и „Современное
состояние теории функций действительного переменного" (стр.494). Теорию
Брауэра в ее полном виде он считал неприемлемой ввиду ее
разрушительного действия в математике. С теорией Гильберта он также
не соглашался. Прежде всего, он не считал удовлетворительным
ОТ РЕДАКТОРОВ ТОМА 1
решение теоретико-множественных проблем только в смысле
непротиворечивости и делал разницу между понятиями непротиворечивости и
истинности. Н. Н- Лузин считал, что из двух противоположных
непротиворечивых утверждений теории множеств наука должна либо
отобрать то, которое истинно, либо установить, что самая постановка
вопроса теряет смысл. Что же касается до самого существа теории
Гильберта, то Н. Н. Лузин определенно считал, что невозможно
формализовать всю математику. Эта мысль была полностью
подтверждена дальнейшим развитием науки: Гёдель доказал, что во всякой
достаточно сильной формальной системе в смысле Гильберта есть
неразрешимая в ней проблема. Точнее, существует утверждение такое,
что ни оно, ни его отрицание недоказуемо в данной системе. Тем не
менее, вопрос об истинности или ложности этого утверждения
однозначно решается вне системы.
Огромная интуитивная сила позволила Н. Н. Лузину выбрать
важное направление в развитии дескриптивной теории множеств. Им
и рядом его учеников был решен ряд важных задач в этом
направлении. Н. Н. Лузин поставил ряд проблем, решение которых не
поддавалось методам теории множеств, и предсказал факты,
доказательство которых выходит за пределы теории множеств и оказалось
возможным лишь значительно позднее.
Настоящий том избранных произведений Н. Н. Лузина в области
дескриптивной теории множеств составлен так, что в него вошли все
его результаты в этой области, а также статьи, содержащие
высказывания, касающиеся вопросов основания математики и перспектив
развития теории множеств.
Исключены из издания лишь некоторые статьи, содержащие
сообщения о результатах без доказательств, и некоторые статьи, содержание
которых покрывается работами, включенными в настоящее издание.
/7. С. Новиков и Л. В, Келдыш
I цикл
ЛЕКЦИИ
ОБ АНАЛИТИЧЕСКИХ
МНОЖЕСТВАХ
И ИХ ПРИЛОЖЕНИЯХ
ГЛАВА I
ОБЩИЕ ПОНЯТИЯ О МНОЖЕСТВАХ, ИЗМЕРИМЫХ В
Протяженность* Рассмотрим линейную протяженность Е. В этой
протяженности Е мы прежде всего различаем рациональные точки;
это те точки, расстояние которых от начала координат О есть
рациональное число.
Но в протяженности Е есть много других точек. Непосредственный
пример такой точки дается нам диагональю квадрата со стороной 1:
это точка, которую мы получаем непосредственным построением, не
употребляя никакого арифметического приближения.
Но протяженность Е содержит еще другие точки, кроме
рациональных и конструктивных точек. Классическим примером служит непе-
рова база е; все эти точки даются нам при помощи арифметических
приближений1.
Итак, протяженность Е далеко не исчерпана одними рациональными
точками, и было бы желательно иметь однородный процесс, который
позволил бы определить каждую иррациональную точку: в этом
конкретный смысл теории Дедекинда.
Цель теории множеств* По-видимому, при современном состоянии
науки является преждевременным нападать на дедекиндовскую теорию
иррациональных чисел^ если только желать, чтобы это нападение
оказалось плодотворным, а именно, дало новые положительные результаты,
ускользающие от нас в области этой теории.
Таким образом, мы ограничимся тем, что примем ее и будем
рассматривать как промежуточный инструмент, считая возможным в
дальнейшем указывать на некоторые трудности этой теории.
Но если мы примем однородное определение иррационального числа
из теории Дедекинда, где иррациональное число рассматривается как
«сечение, произведенное в области рациональных чисел, независимо от
его происхождения, мы получаем возможность (хотя, быть может, лишь
1 Первая трудность, которая нам представляется, относится к существованию
конструктивных точек, ее имеющих никакого арифметического приближения, а также
<уществованию арифметических точек, не допускающих никакой конструкции. Не
входя в тяжелые дискуссии, я ограничился указанием на то, что существуют точке,
для которых сначала дается конструкция, и существуют точки, для которых сначала
лается приближение.
12
Н. Н. ЛУЗИН
иллюзорную) рассматривать континуум как множество, образованное
из рациональных и иррациональных точек. Таков был взгляд на
континуум, принятый a priori Г. Кантором.
Целью теории множеств является вопрос чрезвычайной важности:
можно или нет рассматривать линейную протяженность атомистическим
образом как множество точек; вопрос этот, кстати, уже не нов и
восходит к эллинам.
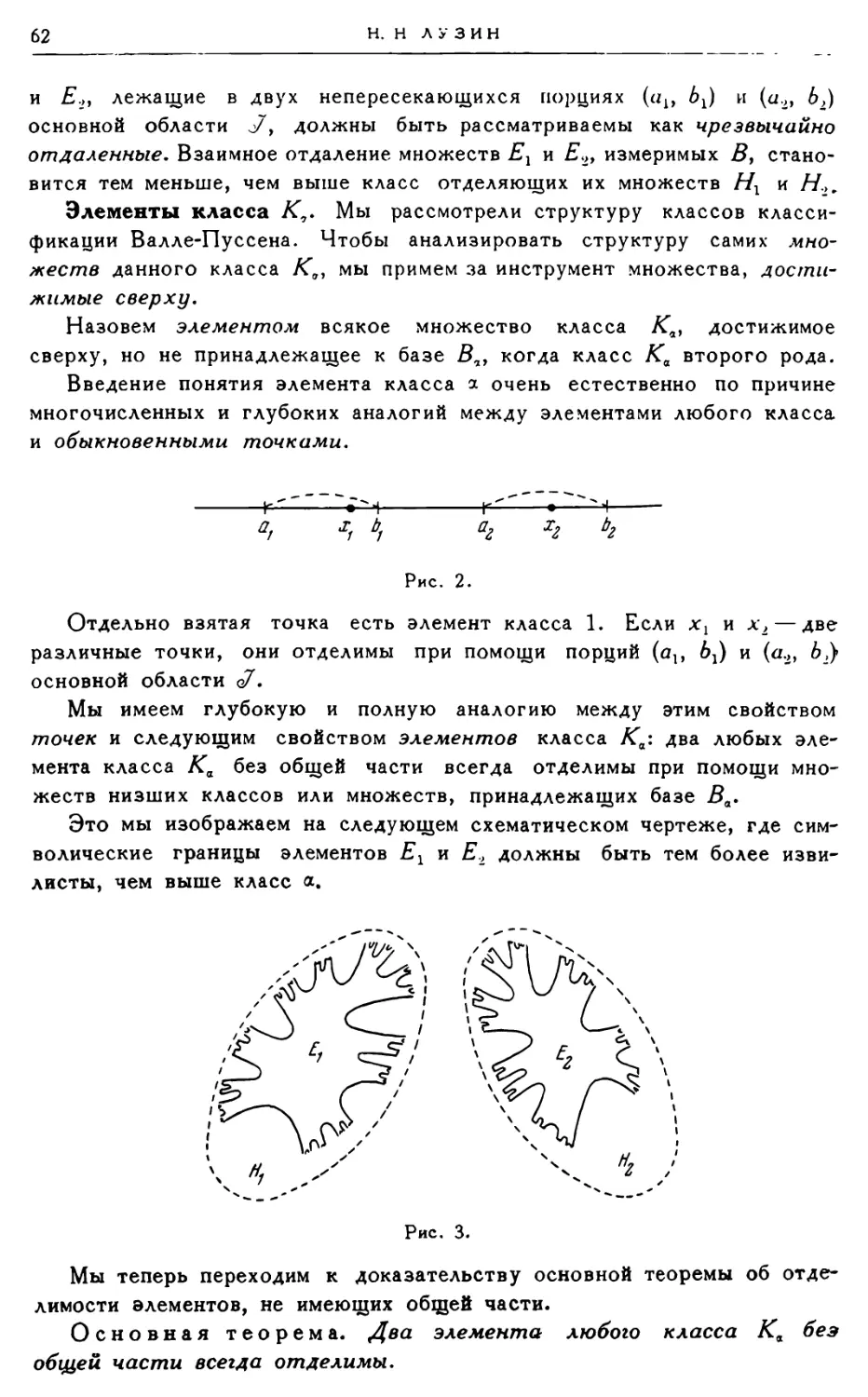
Область* Порции. Начальный класс
Основная область* Лая того чтобы в дальнейшем иметь
формулировки логических законов в наиболее простой форме, мы исключили
из наших рассмотрений все рациональные точки.
Рис. 1.
Следовательно, мы примем за базу рассуждений и в качестве
основных элементов иррациональные числа х
— 00 < JC <-Ъ 00,
рассматриваемые a priori; мы примем для этих элементов
геометрическое изображение при помощи точек М прямой XX*
Множество всех иррациональных точек будет называться основной
областью и обозначаться через о7 или о/ху с/уу oft и т. д., если
рассматривать множество иррациональных точек, принадлежащих
соответственно осям OX, 0Yy ОТ и т. д.1 [1].
В дальнейших теориях мы будем изучать множества иррациональных
точек, и относительно этих множеств мы примем те же классические
обозначения, которые принимаются для произвольных точечных
множеств.
Когда даны множества из иррациональных точек Е±, Е2, Ez,,...
в конечном или счетном числе, мы будем обозначать через Ех-*-Е2-+-
н-£3"*- • • •> Еу • Е2- Ez ... соответственно множество, образованное
1 Одна из основных идей, которой мы обязаны Рене Бэру, это вполне ясное
указание на тот факт, что все логические формулировки становятся очень простыми;
если рассматривать одни только иррациональные числа. Это он первый ввел
основную область с7, названную им пространством нулевого измерения (Baire. Sur
la representation des fonctions discontinues. Acta Math., 32, стр. 134, 1909).
Причина этой простоты станет ясной, если мы jaMeTHM, что в теории Дедекинда
рациональные числа даются нам непосредственно, тогда как происхождение
иррационального числа в некотором смысле вторичное.
Поэтому естественно, что получаются сложные логические законы, если
рассматривать континуум как составленный из разнородных элементов: рациональных
точек и иррациональных точек [2].
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
13
соединением Elt Ег, Е2, ..., и множество, составленное из общих точек
для Ех, Еъ Ez, • • •> формулы
выражают соответственно, что £х тождественно с Е2> что £j есть
часть Ег, что £ не содержит ни одной точки.
Точно так же обозначают через Е2 — Ех множество точек,
содержащихся в Ег и не содержащихся в ЕХУ причем вовсе не предполагается,
что Е1 есть часть Ег.
Наконец, мы обозначим через СЕ дополнение к Е, т. е. множество
иррациональных точек, не входящих в Е. Мы имеем очевидное
тождество
П> 2 " Е*\ — а->2 * wxSj.
Порции. Мы назовем порцией основной области <Sf всякое
множество иррациональных точек, либо содержащихся в интервале (а, Ь)
с рациональными концами а и Ь, либо соответственно превосходящих
или меньших некоторого рационального числа с.
В первом случае соответствующая порция области с7 будет
обозначена через (а, Ь), во втором и третьем случаях мы употребляем
соответственно обозначения (с, -+- оо) и (— оо, с).
Точно так же мы будем рассматривать как порцию и самую основную
область о/ и обозначим ее в этом случае через (— оо, н- оо).
Вообще мы назовем порцией любого множества Е, образованного
яз иррациональных точек, множество тех точек из Я, которые
содержатся в некоторой порции основной области с7.
Начальный класс. По определению, всякое множество Е из
иррациональных точек входит в начальный класс или в класс К0, если оно
является суммой конечного или бесконечного множества порций
основной области с7, так же как и его дополнение СЕ.
Преобразуем это определение.
Пусть х есть любая иррациональная точка прямой XX. Только что
«формулированное определение говорит нам, что х содержится в
некоторой порции (а, Ь) основной области о7, полностью принадлежащей
либо к Е, либо к СЕ.
Но если мы удалим из прямой XX все интервалы (а, Ь) с
рациональными концами, не содержащие одновременно точек обоих
множеств Е и СЕ, мы получим на прямой XX замкнутое множество F,
•образованное из рациональных точек, и, следовательно, счетное. Ясно,
что всякая порция основной области о?, определяемая некоторым
интервалом (а, Ь), смежным к F, содержится полностью либо в Е, либо в СЕ,
и что ни один из смежных к F интервалов нельзя расширить без того,
чтобы он не потерял этого свойства.
Окончательно, всякое множество Е начального класса К$ и его
.дополнение СЕ можно рассматривать как образованные из порций
14 Н. Н. ЛУЗИН
основной области Ы, смежных к некоторому замкнутому множеству Fy
составленному из рациональных точеку причем две соседние смежные
порции принадлежат двум различным множествам.
Операции над множествами
Мы рассмотрим пять элементарных операций, при помощи которых
можно строить множества, отправляясь от уже определенных множеств.
Эти пять операций состоят в том, чтобы: совершать переход к
пределу lim над множествами Ev Е2, ...; брать сумму-*-и общую часть;
брать верхний предел lim и нижний предел lim множеств ЕХУ Е2> . ..
Указанные пять операций, строго говоря, не являются независимыми
друг от друга, но одновременное их употребление представляет
большие преимущества.
Основная операция* Основной операцией, которая послужит нам
в этом исследовании, является операция перехода к пределу.
Назовем сходящейся последовательностью всякую бесконечную
последовательность множеств из иррациональных точек
^1> ^-2» • • •» ^п> • • •
такую, что каждая иррациональная точка х прямой XX или
принадлежит, или не принадлежит всем Еу кроме ограниченного числа этих
множеств, зависящего от х.
Дадим теперь основное определение: Множество Е называется
пределом сходящейся последовательности Егу Е2,..., Епу ..., если
Е есть множество всех иррациональных точек х прямой ХХУ
которые принадлежат всем Епу начиная с некоторого номера пу
зависящего от х.
В этом случае мы скажем, что множество Е получено из сходя^
щейся последовательности Elf Е2У .. ♦, Епу — при помощи операции
перехода к пределу, и это предельное множество Е мы будем обозначать через
lim Ev
я-*оо
или просто через
lim Eu.
Из этого определения следует, что последовательность множеств
Е1У Е2у ..., Еп, ... не перестает сходиться и иметь то же самое
предельное множество Е, если мы отбросим ограниченное число ее членов.
Точно так же ясно, что если данная последовательность множеств
Егу Е2, ..., Епу ... сходится и имеет пределом множество Еу то
последовательность дополнений СЕ1У СЕ2У ..., СЕпу... тоже сходится и
имеет пределом СЕ.
Наконец, заметим, что множество Е можно рассматривать как
предел множества Епу изменяющегося вместе с л. Это позволяет нам
применять к переходам к пределу над множествами классический прин-
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
IS
цип анализа: сумма фиксированного числа к переменных множеств,
имеющих пределы, также имеет предел, равный сумме пределов
составляющих множеств:
lim(£;^£^...H-£J) = lim£/nH-lim£^...-Hl5m£J.
Точно так же общая часть фиксированного числа переменных
множеств, имеющих пределы, имеет предел, равный общей части
пределов составляющих множеств:
lim(£'„ • E2n .. .Екя) = \\тЕ'я • lim £*... lim Е\.
В заключение мы укажем одно свойство перехода к пределу,
которым придется пользоваться:
Если переменное множество Еп содержится в предельном
множестве Е, ЕП^Е, то это предельное множество Е тождественно
с соединением всех £я, £ = £1н-£2-н...-н£я + ... Обратно, если
переменное множество Еп содержит предельное множество Е, £„э£г
то это предельное множество Е тождественно с общей частью
всех £я, Е = Ег- £2
Монотонные последовательности множеств* Последовательность
множеств Е19 Е2,... называется возрастающей, если каждый из ее
членов содержится в следующем: £ас £2 С . • • Возрастающая
последовательность всегда сходится и имеет пределом £ сумму всех £„,
ZS — Е*\ ~т~ /1л ""• • • •
Последовательность множеств Ех, £2,... называется убывающей,
если каждый из ее членов содержит следующий: £х 3 £2 D #..
Убывающая последовательность множеств также сходится и имеет пределом
£ общую часть всех fcn, t» —2s ^ • 2s2 ...
Убывающие и возрастающие последовательности множеств
называются монотонными.
В. Юнг первый употребил монотонные последовательности множеств
как инструмент дкя построения множеств все более и более сложных.
Другие операции. Рассмотрим бесконечную последовательность
множеств
Е\* 2S2, • • • >
образованных из иррациональных точек основной области с7*.
Мы будем производить над этими множествами следующие четыре
операции:
I. Сумма. Эта операция ставит в соответствие всякой бесконечной
последовательности множеств Ег, £2,... их соединение Е1-*-Е2-*-* • •>
т. е. множество, образованное из точек, принадлежащих по крайней
мере одному из множеств £„. Так полученное множество Ег -+• £2 -+-...
называется суммой данных множеств.
Чтобы выразить тот факт, что множества Е1У £2>... не имеют
попарно общих точек, мы скажем, что множество *£=£1-*-£2н-
16
Н. Н. ЛУЗИН
-есть сумма в узком смысле и что S получено из Elf Е2,... при помощи
^сложения в узком смысле.
Если множества Ei могут иметь общие точки, множество S будет
называться суммой в широком смысле; в этом случае мы скажем,
что S получено из Ех, Е2,... при помощи сложения в широком смысле.
Ясно, что множество-сумма Е = Ех -+- Е2 ■+-... не зависит от порядка
слагаемых множеств Е{.
Сложение счетного числа множеств сводится опять к переходу
к пределу.
В самом деле, когда дана бесконечная последовательность
Elt Е2, •.., Епу..., мы можем получить из нее другую последовательность
множеств Si, S2,..., Sn,..., полагая
*^1 ^= £ц *^2 == *-*\ "*" **2> • • •> *^и == **1 ~"*~ ^2 ~~*"~ • • • ~~*~~ ^п> • • •
Так как последовательность Si9 S2,..., Sn,... есть возрастающая,
то она сходится к некоторому предельному множеству S, и мы,
очевидно, имеем
*J —■— И*1 "~1~" Л>2 ""#~~ . . . ш~ Ёщ "+- • х •
II. Общая часть* Эта операция дает множество, образованное
из общих точек всех множеств данной бесконечной последовательности
ЕХ9 Е2,..., Ея,..* Так полученное множество Е называется общей
частью данных множеств Ех, Е2,...; мы обозначим эту операцию
символом
Ct — *-*\ ' -"2 • • • ИЛИ Il»iE*2. • •
Общая часть Е также не зависит от порядка составляющих
множеств Еп.
Общая часть счетного числа множеств также сводится к пере*
ходу к пределу.
В самом деле, если мы положим
М ^— <£i> * 2 == ^1 * ^2> • • • *и ~= **1~2 ♦ ♦ • *-я> • • •>
то последовательность множеств PlZD P2ZD ,..., ZD PnZD ... есть,
очевидно, убывающая, а потому она сходится к некоторому определенному
предельному множеству Р. Ясно, что
* Е*\ * *^2 • • • *^ш • • •
Ш. Верхний предел последовательности множеств.
Пусть дана бесконечная последовательность множеств ЕХ9 Е2,..., Еп,...
Мы называем верхним пределом последовательности множеств
Ei, Е2,..., Е,„... множество Е, образованное из точек, каждая из
которых принадлежит бесконечному множеству из множеств Ен.
Мы будем обозначать верхний предел последовательности множеств
через
lim En или lim En.
н-*оо
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
17
Из определения вытекает, что всякая последовательность множеств
Е1У £2,... имеет верхний предел и что можно пренебрегать порядком
членов последовательности и ограниченным числом их без того, чтобы
изменить верхний предел.
Операция III, состоящая в том, чтобы взять верхний предел,
сводится к операциям сложения и взятия общей части по формуле
lim Еп = (£х -+- £2 -+■ £3 -»-...) (Е2 -+■ Ez -н...) (£3 -ь ...)...
Отсюда мы немедленно заключаем, что операция lim En сводится
к выполнению двух последовательных простых переходов к пределу
с двумя различными индексами, так как если Е,^ обозначает общую
часть конечных сумм
Еят = {Е1 + Егч-... + ЕЛ(Е1 + ... + Ем)...(Еп-*-... + Ет),
то мы, очевидно, имеем
lim Еп = lim lim £ят.
«-►со т-*ао
Тем не менее, интересно заметить, что операция Ьт вовсе не
эквивалентна совокупности двух последовательных простых переходов
к пределу с различными индексами lim lim. Мы увидим, что среди
множеств, получающихся двойным применением простого перехода
к пределу, большинство не может быть получено при помощи операции
lim, произведенной только один раз.
С другой стороны, операция \\тЕя охватывает как частный случай
основную операцию lim, так как если данная последовательность
множеств Elf £2, •. •> £»,. • • сходится, то верхний предел lim £„, очевидно,
совпадает с пределом lim£„ этой последовательности.
В дальнейшем мы уточним границы применимости операции lim£,
(стр. 72 атой книги).
IV. Нижний предел. Пусть дана бесконечная последовательность
множеств £х, £2,...; мы назовем нижним пределом для £х, £2,. ..
множество £, образованное из иррациональных точек х, для каждой
из которых можно определить такое л, что эта точка принадлежит
Нижний предел £ мы будем обозначать через lim£„ или lim£„.
к-* со
Ясно, что нижний предел £ тоже не зависит ни от порядка членов
последовательности Е19 £2,..., ни от конечного числа этих членов.
Операция IV, lim £„, также сводится к операциям сложения и
взятия общей части по формуле
lim Еп = (Ех • £2 • £3...)-»- (Е2 • Е* • • •) ~+- (£3 ...)-•-•• •
и, следовательно, сводится к двум простым переходам к пределу
lim lim. Но эта операция опять-таки не эквивалентна последовательному
п-гсо т-*со
18
Н. Н. ЛУЗИН
двукратному переходу к пределу. Мы увидим в дальнейшем, какова
область применимости этой операции (стр. 72 этой книги).
Сравнение введенных операций. Чтобы сравнить операции над
множествами Е1У Е2,..., мы заметим, что общая часть этих множеств
есть часть нижнего предела \imEn, который содержится в верхнем
пределе lim En. С другой стороны, верхний предел есть часть суммы
множеств Ег-*-Е2-*~* • •> и, таким образом, мы имеем одновременно
выполненные неравенства
Р С lim Еп С Ип7Еп С S.
Важно заметить, что в общем случае нижний предел lim Еп>
составляя часть верхнего предела lim ЕпУ вовсе с ним не совпадает.
Множества lim En и lim En совпадают в том и только в том случае, когда
последовательность множеств Е1У Е2,... сходится: в этом случае оба
предельных множества совпадают с единственным пределом lim^
этой последовательности.
Наконец, можно заметить, что верхний предел lim En множеств
Ev Е2У •.. есть дополнение к нижнему пределу дополнений СЕ1У СЕ2У...;
то же справедливо, если переставить слова верхний и нижний:
С lim En = lim CEn; C lim En = \imCEn.
Характеристические функции. Мы теперь определим
характеристическую функцию множества, введенную Валле-Пуссеном1. Введение
этого понятия очень полезно дая обычной интерпретации предельных
операций над множествами.
Назовем характеристической функцией множества Е функцию
/(л:), определенную в основной области с7, равную 1 для точек Е и
равную 0 всюду вне Е.
Обратно, всякая функция /(х), определенная на о/ и принимающая
лишь значения 0 и 1, есть характеристическая функция дая
множества Е точек х, дая которых /(х) = 1.
Рассмотрим бесконечную последовательность множеств
и их характеристические функции
Из определения сходимости последовательности множеств вытекает,
что дая того, чтобы последовательность характеристических функций
9и ?2> • • • была сходящейся в классическом смысле математического
анализа, необходимо и достаточно, чтобы последовательность
соответствующих множеств Elf Е29... была сходящейся в ранее определен-
х Gh.de la Vallee-Poussin. Sur Tintegrale de Lebesgue (Trans. Amcr.
Matb. Soc, 1915).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
19
иол* смысле. В этом случае предельная функция <р = lim <рш есть
характеристическая функция для предельного множества Е = ИтЕя.
Если последовательность множеств Е19 Е2У... не есть сходящаяся,
то последовательность соответствующих характеристических функций
?i> ?2> • • • расходится фактически в каждой точке х множества-
разности
\\тЕи—lim Ея
и только в этих точках.
В этом случае, если принять обычные обозначения lim <p* и lim <ря
лая верхнего предела и нижнего предела последовательности функций
?и Тг» • • •> то ясно> что lim <p« есть характеристическая функция для
л-*со
верхнего предела lim£„ последовательности множеств Еи Е*,... и,
соответственно, lim <р* есть характеристическая функция для нижнего
И-* 00
предела lim En.
Можно заметить, что характеристическая функция в отношении
других операций обладает следующими свойствами1:
Если <р есть характеристическая функция множества Е, то 1 — <р
есть характеристическая функция дополнения СЕ к множеству Е; если
?i> ?2> • • • СУТЬ характеристические функции для Еи Е2У •.., то их
бесконечное произведение <рг • <Рг • • • есть характеристическая функция
для общей части Ег • Е2...
Так как дополнение к бесконечной сумме Ег -+- Е2 -+-... есть общая
часть дополнений: СЕ1- СЕ2..., то мы заключаем, что
характеристическая функция для бесконечной суммы Ех -+- Е2 -+- ... может быть
представлена в форме сходящегося аналитического выражения 1 — (1 — <pj X
X (1 — <р2)» • м если множества Е1У Е2У... попарно без общих точек, то
характеристическая функция для их суммы Ех -+■ Е2 -+-... сводится
к сходящемуся ряду <pj (лс) -+- <р2 (■*) "•-•••
Наконец, множество-разность Е2 — Ех имеет характеристическую
функцию <р2— ?i?2> так как это множество может быть представлено
в виде Е2 • CEY.
Алгебраическое обозначение
Полиномы, образованные из множеств. Это понятие часто бывает
удобно для доказательств. Его введение основывается на следующем
замечании.
Знаки алгебраической логики естественно вводятся в операции над
множествами, так как они обладают свойствами, аналогичными
арифметическим операциям.
1 Ch. de la Vallee-Poussin. Integrates de Lebesgue, fonctlons d'ensemble,
classes de Baire. Paris, 1916, стр. 7.
20
Н. Н. ЛУЗИН
Мы уже видели, что для того, чтобы выразить, что множество Ег
содержится во множестве Е2, уславливаются писать
Ег С Е2 или E2Z) Ех.
Сложение Ег -+- Е2 -+- •«• и вычитание Е2 — Ех множеств
соответственно аналогичны сложению и вычитанию конечных величин. Общая
часть E<i • Е2... аналогична произведению чисел; по этой причине
часто называют умножением операцию, состоящую в том, чтобы взять
общую часть заданных множеств Elf Е2у... Образование дополнения СЕ
некоторого множества Е есть частный случай вычитания.
Умножение и вычитание сводятся к сложению при помощи
дополнений; это замечание часто бывает ценным при доказательствах. В самом
деле, имеем
С(Ег. £2) = СЕХ ч- СЕ2; С(Е2 — £J = CE2 -+- Ег.
Сложение и умножение коммутативны, ассоциативны, дистрибутивны,
как соответствующие операции арифметики. Например, мы имеем
Ьг • Ь<ь=^Ь2 • Ь1У (Ьг • Ь2) • Ь$=^Ь1 • \Ь2 • /s3)>
"1 * v^2 ~*~ ^3/ == ^1 * ^2 "*" Е*\ ' ^Ъ*
Все правила алгебраических вычислений над полиномами с
положительными членами могут, следовательно, применяться к полиномам,
образованным из множеств.
Установив это, рассмотрим любой полином
х \Х\у Х2у • • ., Хп)
относительно х1У х2У...ухпу все члены которого имеют коэффициенты,
равные 1. Если заменить буквы х1У х2>...ухп соответственно любыми
точечными множествами Е19 Е2У..., Еп и рассматривать знаки
операций н- и • как сумму и общую часть в области множеств, то полином Р
становится вполне определенным множеством точеку которое мы
обозначим через
r\Pii fc2f..., /sw).
Смысл P(Elf •.., Еп) нисколько не зависит от порядка членов
полинома Р.
Указанные правила уже неприменимы, если имеются отрицательные
члены, так как вычитание множеств не обладает ни ассоциативностью,
ни коммутативностью. Лишь дистрибутивный закон сохраняется:
Тем не менее, если полином
У (xlf лг2,..., хп)
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
21
имеет коэффициенты, равные н-1 или —1, и если первый член
полинома Р положителен, то можно сохранить интерпретацию для
P(EV Et,..., Ея)
в области множеству если условиться полагать
U— V— W= (U— V)—Wy
где буквы U, Vy W—любые множества точек. Но в этом случае
смысл выражения Р(Е1У Е2У..., Ея)у разумеетсяу зависит от порядка
членов полинома Р{х1У дс2,..., хн).
Ряды множеств. Для дальнейшего мы введем понятие ряда
множеств х.
Назовем рядом множеств бесконечный символ
Ul "*" и2 "*" • • • "+■ ип ■+■ • • м
где буквы им обозначают множество точек, которому предшествует
знак -+- или —.
Множество точек, которое получается, если отбросить знак члена и„,
будет называться абсолютной величиной ип; это множество мы
обозначим через
|о.|.
Мы скажем, что некоторый ряд множеств
Ui + Hj + .^ + ^H-,..
сходится у если сходится последовательность множеств
*^1> *^2> • • •> *^я> • • •>
где Su есть сумма л первых членов ряда. В этом случае предельное
множество S для этой последовательности будет называться суммой ряда
иг -+- ц2 -+- ..., и мы будем писать равенство
В дальнейшем мы рассматриваем только сходящиеся ряды; у этих
рядов первый член иг есть множество точек, предшествуемое знаком -ь,
так как в противном случае сумма Sn первых п членов предложенного
ряда не имела бы никакого смысла.
Знакочередующиеся ряды множеств. Займемся убывающими
знакочередующимися рядами множеств: это ряды вида
Ех—£2-ь £3—£* -ь...-t- (—1)я+1£» -н...,
где множества £lt Е1У... образуют убывающую последовательность
xl»i _J Е*^ —J • • • —J *-*% —^ • • •
1 Мы вводим понятие ряда множеств, чтобы облегчить формальный ход
рассуждений.
22
Н. Н. ЛУЗИН
Для этих рядов множеств мы имеем предложение, вполне
аналогичное предложению классического анализа о числовых
знакочередующихся рядах:
Теорема. Для того чтобы убывающий знакочередующийся ряд
множеств Ег — Е2-+-Е3 — £4 н- ... был сходящимся, необходимо и
достаточно, чтобы общий член этого ряда стремился к нулю,
когда п неограниченно возрастает, т. е. чтобы мы имели
lim En = 0.
п-*оо
Условие необходимо. В самом деле, так как последовательность
множеств Е1У Е2У... есть убывающая, множество Еп стремится к вполне
определенному пределу Еу когда п неограниченно возрастает, £ = lim En.
Кроме того, известно, что этот пределе должен совпадать с общей частью
множеств Е1У Е2У . . •> и, таким образом, мы имеем
Если переменное множество Еп не стремится к нулю, когда п
неограниченно возрастает, то предельное множество Е эффективно
содержит точки. Но если некоторая точка принадлежит к Е, то она
принадлежит ко всем членам ряда — множествам Еп. Отсюда следует,
что точка х принадлежит ко всем множествам Sn для нечетного п и
не принадлежит ни одному из множеств Sn с четным я, где Sn есть
сумма п первых членов предложенного знакочередующегося ряда
Ех— Е2-\-Еъ— £4-§-... Отсюда мы заключаем, что последовательность
Sly S2y ..., Sny расходится, а, значит, и знакочередующийся ряд
также.
Условие достаточно. В самом деле, какова бы ни была
иррациональная точка х основной области с7, принадлежащая множеству Е1У
можно найти целое положительное п такое, что х принадлежит к Епу
но не принадлежит к Еп+Х. Отсюда мы заключаем, что если п нечетно,
то х принадлежит всем множествам Sn, Sn+l9 Sn+2y... и что х не
принадлежит ни одному из множеств Snf Sn+l9 Sn+2, ..., если п четное.
Если же х не принадлежит Е1У то она не принадлежит ни одному
из множеств Sly S29... Значит, последовательность множеств Sly S2,...
..., Sny... сходится, а это и доказывает сходимость предложенного
знакочередующегося ряда (ч. т. д.).
Важно заметить, что сумма S знакочередующегося сходящегося
ряда множеств
£*1 fc2-t- fc$ b,±-f-...
может быть представлена в следующих двух видах:
S= (Ех - Ег) -+- (£3 - Et) -н (£5 - £„) ч- ...
S=Et—(£2 — Е3) — (£* — ^б) — •••>
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
23
где все множества-разности, написанные в скобках, не имеют
попарно общих точек.
Из первой формулы следует, что множество S есть предел
возрастающей последовательности множеств, но вторая формула показывает,
что 5 есть в то же время и предел убывающей последовательности
множеств.
Понятие множества, измеримого В
Идеи Э. Бореля. Две концепции математического анализа*
Современное состояние математического анализа убедительно доказывает,
насколько важно установить точное разграничение между
математическими сущностями, которые рассматриваются как существующие, и
другими, реальность которых лишь кажущаяся.
С одной стороны, логическое направление в современной теории
множеств есть источник неисчислимого количества математических
сущностей, существование которых, в действительности, лишь чисто
словесно.
С другой стороны, в последние годы, становясь на почву
непротиворечивости, по методу Гильберта, пытаются легализировать эти
сущности, отождествляя то, что не противоречиво в себе, с тем, что имеет
неоспоримую реальность.
Именно это разграничение и было содержанием знаменитых Пяти
писем по теории множеств1 Адамара, Бэра, Лебега и Бореля, и на
необходимости этого разграничения Э. Борель настаивал с крайней
точностью в своих дальнейших трудах2.
Это разграничение между математическими сущностями, которые
в самом деле реальны, и теми, которые кажутся реальными, но на деле
не имеют никакого substratum и которым ничего интуитивно не
соответствует, в данное время очень необходимо; но близкое
осуществление такого разграничения кажется мало правдоподобным при
современном состоянии науки.
Тем не менее, если считать необходимым сохранить классические
части математики, размышление указывает нам одну естественную
попытку такой реализации.
С одной стороны, если постулировать множество с7 всевозможных
иррациональных точек, то невозможно отрицать право рассматривать
порции (а, Ь) основной области о7 как законные множества точек. Средн
1 Bull, de la Soc. Math, de France, декабрь 1904; см. также Е. В о г е 1. Lemons
sur la theorie des fonctions, 3* ed., 1928, стр. ISO.
2 Cm. E. В о г е 1. La philosophie mathematique et Tinfini (Revue du Mois, август
1912 г.); его же. L'infini mathematique et la realite (Revue du Mois, 10 июля 1914г.);
его же. La theorie de la mesure et la theorie de Integration (Lemons sur la
theorie des fonctions. 2* ed, 1914, Note VI, стр. 217—225); его же. Methodes et problemes
de la treorie des fonctions. Paris, 1922, стр. 146.
24
Н. Н. ЛУЗИН
множеств точек области о/ именно эти множества являются наиболее
простыми и представляются наиболее естественно 1.
С другой стороны, если признать эту законность, то кажется
необходимым рассматривать как законные все множества, которые
получаются, отправляясь от порций, при помощи следующих двух
элементарных операций, повторенных бесконечное множество раз:
1°. Составить разности двух множеств EY и Е2 уже
определенных и таких, что Ег содержится в Е2:
Еа-Ег. (D)
2°. Составить сумму бесконечного множества уже определенных
множеств:
Е1-+-Е2+ . . . -+-£„-*- . . . (S)
Представляется, что отрицание законности множеств, которые
получаются при помощи этих элементарных операций, равносильно
исключению полностью самого классического анализа.
Одна из наиболее важных идей в математическом анализе, идея,
которой мы обязаны Э. Борелю, это идея концепции этих множеств.
Он дал им сначала название измеримых множеств2, потом вполне
определенных множеств3 и рассматривал их как наиболее простые и
наиболее важные после порций.
С тех пор Анри Лебег подверг эти множества углубленному
изучению во всей их общности4. Это он первый понял тот важный факт,
что в классическом анализе речь идет прежде всего о множествах,
полученных в точности этим способом5, и что обратное предложение
также имеет место: классический анализ никогда не сможет выйти из.
1 Мы ни в коем случае не рассматриваем множество, составленное из одной
точки, как простое, так как эта точка может быть получена в результате
чрезвычайно сложной конструкции, образованной из бесконечного множества предварительно*
проделанных промежуточных операций, и эта конструкция в общем случае не может
быть сведена к более короткой конструкции.
2 См. Е. В о г е 1. Lecons sur la theorie des fonctions. Iе ed., 1898, гл. III.
3 См. там же, 2е ed., 1914, стр. 226. В этом издании Борель дал название
измеримых множеств множествам Е, заключенным между двумя вполне определенными
множествами Е\ и Е2, EiCZ E <^Е2, имеющими одну и ту же меру. Идея таких
множеств впервые была введена Борелем в первом издании (см. стр. 48 и 67).
Дальнейшие изыскания по поводу меры Лебега показали, что семейство этих множеств
Е совпадает с семейством множеств, которые Лебег назвал измеримыми
множествами. То, что отличает меру Лебега от меры Бореля, это, быть может, не
протяженность той категории множеств, к которым применяются определения меры,.
но употребление понятий, в некотором смысле трансцендентных, зависящих от
несчетного множества предварительных операций. Тем не менее, ограниченное
множество точек, не имеющее внешней меры при современном состоянии науки, по-ви-
димюму, не может быть ясно осознано. См. также Н. Lebesgue. Lecons sur Tinte"-
gration 2* ed., 1928, стр. 117, сноска1.
*rwSur les fonctions representables analytiquement" (Jonrn. de Math., 1905, стр. 165)»
ь Там же, стр. 165, сноска1.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
25
области этих множеств, которым Лебег дал название множеств,
измеримых В1.
Таким образом, 'кажется неоспоримым, что нет никаких оснований
ставить под сомнение реальность множеств, измеримых В> по крайней
мере тех из них, которые получаются с помощью первых шагов в
применении указанных операций2. Именно множества (и функции),
измеримые Bf являются постоянными объектами классического математического
анализа, по крайней мере те из этих множеств, которые получаются из
порций при помощи относительно небольшого числа указанных
операций.
Можно ли распространить область математического анализа вне поля
множеств, измеримых В, с той же уверенностью и не внося какой-либо
вызывающий сомнение элемент?
Известно, что этот вопрос двадцать пять лет тому назад был
предметом замечательного мемуара Лебега „Sur les fonctions representables
analytiquement" 3. Лебег старался решить этот вопрос в положительном
смысле с помощью созданного им нового понятия — понятия,
кажущегося логически неопределимым, но выражаемого только одним глаголом
назвать.
Мы не пытаемся дать определение слова назвать; нам кажется, что
это понятие настолько примитивное, что определение для него по
меньшей мере бесполезно; можно только поставить себе целью пояснить
примерами смысл этого слова. Назвать функцию, множество это
значит указать эту функцию индивидуально без какой бы то ни было
расплывчатости, единственным образом.
Одна из основных идей, которой мы обязаны Лебегу, — это точное
разграничение между понятиями множества называемого и множества
неназываемого*
1 Loc. cit.« стр. 166, сноска2.
2 „Простота** множеств, измеримых В даже класса 2, нам кажется весьма
иллюзорной. Перевод определения множества, измеримого В класса 2, на язык арифметики
наталкивается на все возражения, связанные с теорией роста. По-видимому, все
трудности теории проективных множеств содержатся как в зародыше во множествах,
измеримых В класса 2.
Интересно отметить, что дате с точки зрения идеалистов есть большая
разница между множествами, измеримыми В класса 0 и 1, с одной стороны, и
множествами, измеримыми В класса 2, с другой стороны: мы не знаем, какова мощность всей,
совокупности множеств, измеримых В класса 2.
В самом деле, на основании исследований Бэра о функциях класса 0 и 1, строго
доказывается, что совокупность множеств, измеримых В классов 0 и 1, имеет
мощность континуума. Но, не прибегая к рассуждению Цермело (аксиома произвольного
выбора), нельзя доказать аналогичное предложение для множеств, измеримых В и.
класса 2. Серпинский доказал, что человек, который сумел бы эффективно
расположить эту совокупность в простую упорядоченную последовательность, мог бы на
основании этого эффективно построить множество точек, не измеримое в смысле
Лебега, т. е. назвать такое множество.
3 Journ. de Math., 1905.
26
Н. Н. ЛУЗИН
Мы уже знаем, что, следуя Лебегу, надо понимать под называемым
множеством: это множество точек, которое можно назвать, т. е. можно
охарактеризовать при помощи подходящего определения без какой бы
то ни было неясности. По мнению Лебега, называемые множества
это как раз те, которые являются необходимым объектом
математического анализа. Что касается слов неназываемое множество, то они
в самом общем своем смысле обозначают всякое множество, которое
не может быть названо. Впрочем, известно, что при современном
состоянии науки неназываемые множества это те, которые получаются
применением рассуждения Цермело или пользуясь каким-либо
аналогичным рассуждением.
Эти-то неназываемые множества Лебег рассматривал как
сомнительные: их нельзя вводить в науку иначе, как при обязательном условии,
что они покажут свой интерес, свою пользу, свою действительность
тем, что решат какую-либо классическую проблему. Но вообще главным
образом область называемых объектов является областью
математического анализа. Такова концепция математического анализа, которая
была предложена Лебегом.
В частности, примеры сущностей называемых, но не измеримых В
были даны Лебегом в цитированном мемуаре. Но все они были
названы знаменитым автором при помощи совокупности всех
трансфинитных чисел класса 2. Лебег заканчивает свой мемуар приглашением
изучать общие свойства, принадлежащие всем математическим
сущностям, которые можно назвать1. Этот призыв автора так же
необходим ввиду его концепции математического анализа, как естественен,
так как, изучив множества, измеримые В, настолько полным образом,
насколько это было возможно в ту эпоху, Лебег был практически
приведен к постановке проблемы изучения всех сущностей, которые можно
назвать, — по крайней мере тех, которые следуют „непосредственно"
за сущностями, измеримыми В, как, например, те, которые называют,
употребляя совокупность всех трансфинитных чисел второго класса; эта
совокупность представляется уже названной2.
Известно, что Эмиль Борель, следуя своей идее иллюзорности
трансфинитного, был вынужден адресовать упреки примерам называемых
сущностей, неизмеримых В, которые были даны Лебегом. Здесь не
место входить в дискуссию по поводу всех высказанных аргументов.
Поэтому мы ограничимся тем, что процитируем текстуально один отры-
1 „Таким образом, можно назвать функции, не представимые аналитически; но не
•следует смешивать исследование, только что предпринятое, с исследованием функций,
которые можно назвать, исследование, которое интересно было бы начать" („Sur les
fonctions representables analytiquement", стр. 21S).
2 He приходится удивляться глубокому впечатлению, которое было произведено
этим философским открытием Лебега, так как его важность можно сравнить лишь
с важностью открытия иррационального числа: в области философии можно сравнить
роль множеств, измеримых В% с ролью рациональных чисел.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
27
вок из статьи Бореля „Le calcul des integrates definies" (Journ. de Math.,
1912, стр. 208):
„Я оставляю в стороне возражения, которые можно сделать по
поводу существования функции, „названной* Лебегом, который,
впрочем, сам настаивал на различии между назвать и определить функцию;
я охотно буду более категорически высказываться, чем он: всюду, где
должны были бы эффективно входить все трансфинитные числа
второго класса (а не только те, которые меньше какого-нибудь одного из
них, заранее фиксированного), мне кажется выходят из области матема-
тики".
Таким образом, концепция математического анализа Эмиля Бореля
состоит в том, что надо ограничить поле математики изучением
сущностей действительно определимых, без того, чтобы надо было вводить
совокупность всех трансфинитных чисел второго класса, так как мы не
можем эффективно достигнуть, коснуться трансфинитной
бесконечности1. Эта концепция математического анализа ощутимо совпадает
с концепцией классического анализа: по преимуществу ограничиваются
изучением множеств, измеримых В> и, быть может, даже некоторыми
из них, чтобы не рассматривать всю их совокупность.
И так как многие ученые не рассматривают совокупность всех
трансфинитных чисел второго класса как истинную математическую
концепцию, потому что невозможно полностью описать содержание
этой концепции, то примеры Лебега далеко не были единодушно
приняты всеми математиками. Основной вопрос: „Можно ли продолжить
математический анализ за область множеств, измеримых В?а оставался
открытым.
В 1916—1918 гг. Суслин, В. Серпинский и я, стремясь
выполнить предложенную Лебегом программу изучения наиболее общих
множеств, которые можно назвать, пришли к изучению нового класса
точечных множеств, заведомо выходящего за границы класса множеств,
измеримых В, и, однако, образованного из множеств, которые можно
определить без всяких трансфинитных чисел. Ввиду тесной связи между
этими множествами и рядами полиномов они получили название
аналитических множеств согласно предложению Лебега [4].
1 Это выражение принадлежит Борелю („Methodes et problemes de la theorie des
functions", 1922, стр. 14S—146): WB ^теории функций трудность, которая мне кажется
существенной и на которой я часто настаивал, это различие между возможным и
действительным. Возможных сущностей существует трансфинитное множество; без
сомнения, можно формулировать некоторые очень общие теоремы и создать
некоторые методы, которые применимы ко всем, т. е. к каждому из них; но их детальное
исследование и их полная классификация запутаны, так как мы не можем эффективно
достигнуть, коснуться трансфинитной бесконечности. Потому приходятся решиться
действовать систематически, но бе* определенной системы, т. е. ограничиться
изучением функций, которые представляются естественным образом*. Отсюда видно, что
Борель стоит на почве натуралиста, а не логика.
28
Н. Н. ЛУЗИН
Первые шаги теории аналитических множеств, казалось,
подтверждали независимость этих множеств от совокупности трансфинитных чисел
второго класса. Тем не менее, дальнейшие исследования показали, что
идея этой совокупности проникла в теорию, будучи глубоко скрытой
в форме отрицательных определений.
К тому же изучение аналитических множеств естественно привело
к изучению проективных множеству свойства которых столь
парадоксальны, что, по-моему мнению, мы вынуждены ставить вопрос о самой
законности этих множеств.
Я ограничусь здесь этими краткими указаниями, не желая выбирать
между двумя концепциями математического анализа. Цель моей книги
изложить основные результаты теории аналитических и проективных
множеств, оставляя читателю выбор точки зрения.
Идеи Адамара. Мы изложили ранее реалистические концепции
математического анализа Бореля и Лебега. Мы укажем теперь точку
зрения в некотором смысле противоположную, принадлежащую Адамару.
Это идеалистическая точка зрения, близкая идеям самого Г. Кантора
и, может быть, Цермело1.
Согласно идеям Адамара, математический анализ нисколько не
обязан делать различие между разными существованиями в зависимости
от того, как они были доказаны: дкя Адамара существования, о
которых говорит математический анализ, являются фактами, как всякие
другие2.
Не надо различать между множествами называемыми и неназывае-
мыми: это различие в некотором смысле обязано случайности или
структуре наших мозгов. В самом деле, вещь, не названная сегодня,
может сделаться названной завтра, если выдумают соответствующую
конструкцию; и наоборот, вещь, названная сегодня, может стать не
названной завтра, если данное построение уже забыто. Следовательно,
не надо ставить вопрос, является ли множество называемым, со страха,
что придется уточнить, что это значит: этот вопрос ведет к
психологии и вводит в рассмотрение свойства нашего мозга3.
В частности, соответствия, о которых нам говорит рассуждение
Цермело {принцип произвольного выбора), и существования, которые
из него возникают, абсолютно законны. Тот факт, что мы не умеем
описать подобное соответствие и назвать сущность, которая его-
определяет, — это обстоятельство второстепенного порядка. Есть много
вещей, которых мы никогда не сможем узнать4 и которые, однако*
1 Если я не ошибаюсь, точка зрения Хаусдорфа близка к идеям Адамара.
2 См. второе письмо Адамара к Борелю в „Cing lettres sur la theorie des
ensembles" (Bull, de la Soc. Math, de France, декабрь 1904 г.).
3 Там же.
* См. третье письмо Адамара к Борелю по поводу теория-, множеств, напечатан,-
вое в статье Бореля JL!inf ini matbematique et la, realite" (Revue du Mois, 10 июля
1914 г. или „Lecons sur la theorie des functions4*, 3« edM 1928, стр. 174).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
29
существуют в себе независимо от способности человека их описать,
независимо от активности нашего ума и независимо от самого
существования человека на земле. Цель палеонтологии описать процессы,
которые имели место на нашем земном шаре до появления человека, и
элементарная геометрия дает нам прекрасную теорию треугольников,
не останавливаясь на вопросе о том, являются ли вершины этих
треугольников называемыми точками или нет.
При каждом состоянии науки необходима известная идеализация,
потому что таков ход развития науки. Гидродинамика говорит нам
об идеальных средах, современная физика дает нам множество
идеальных понятий: такова структура нашего мозга. И, в частности, таково
понятие функции / (х), значения которой появляются от произвольного
выбора одного числа х в переменном множестве Ехг.
Только логическое противоречие может остановить нашу способность
создавать идеальные понятия и, вместе с ней, развитие науки в том
направлении, в котором мы пошли2.
Таковы идеи Адамара. Ясно видна глубокая разница между его
точкой зрения и точкой зрения реалистов, каковы Борель и Лебег.
Нельзя заставить принять ту или иную из этих двух точек зрения:
принять одну из них или ее изгнать — это вопрос личного убеждения
или вкуса. Не &\я того, чтобы вступать в полемику, но только а\я
того, чтобы осветить позицию реалистов, я позволяю себе цитировать
следующие строки Бореля („Methodes et ploblemes de la theorie
des fonctions", 1922, стр. 92): „Я не понимаю точку зрения
аналитиков, которые считают возможным рассуждать об индивидууме, который
•определен, но не задан; здесь есть противоречие в терминах, на
котором я много раз настаивал".
1 См. конец первою письма Адамара, письмо Лебега и второе письмо Адамара по
поводу теории множеств (Е. В о г е I. Lecons sur la theorie des f о actions, 3* ed., 1928,
стр. 151—152, 155^156 и 159).
Здесь речь идет об одной очень важной проблеме Адамара:
Дано плоское множество точек <£, имеющее точки на каждой параллели к оси
-OY; найти однозначную функцию /(*), всюду определенную и такую, что все
точки кривой y=f(x) принадлежат £.
Для Адамара существование такой функции f(x) не вызывает сомнений, даже
если мы никэгда не сможем извлечь из определения S получения такой функции fix).
Рассуждение Цермело позволяет идеалистам верить в это существование: эту
функцию получают, выбирая произвольно одну и только одну точку ii3 $ на каждой
параллели к оси OY. См. мою статью Sur le probleme de M. J. Hadamard d'uaiior-
misation des ensembles (Matematica, IV, 1930, Cluj).
2 Вот очень важный пункт, касающийся взаимоотношения между идеями Адамара
и исходной точкой логических исследования Гильберта. Для Гильберта слово
существование применимо ко всякой вещи, про которую мы можем доказать, что она
непротиворечива. А для Адамара это условие необходимо, но может не быть
достаточным, так как Адамар, по-видимому, верит, что существование вещи,
непротиворечивой в себе, должно, в конечном счете, быть предписано интуицией самой науки.
30
Н. Н. ЛУЗИН
Я хочу указать здесь на один специальный пункт, в котором, как
мне кажется, слишком легко принимали точку зрения идеалистов.
Представляется, что наша способность создавать идеальные
понятия не имеет границ, даже если стремиться избегать логических
противоречий, и в результате, если мы не остановимся, наука наверное
сделается слишком фантастической. Гипотеза астронома о существовании
млечного пути, удаленного на счетное множество километров от нашей
солнечной системы, или гипотеза физика, что реальное пространство
есть неархимедовское, не являются логически противоречивыми, однако
они бесполезны д\я науки, так как в обоих случаях речь идет об
элементах материи, которые не могут оказать никакого влияния на
наблюдаемые феномены.
Таким образом, мы видим, что необходимо ограничить нашу
способность идеализации, и, по-моему, эти границы не могут быть поставлены
интуицией. Обычно думают, что есть много вещей, логически
возможных, но ускользающих от нашей интуиции. Но, по-видимому,
обратное тоже верно: есть случаи, когда наша интуиция дает (или думает,
что дает) совершенно ясную картину понятия, логически
противоречивого в себе. Таков, по-моему, случай совокупности всех
трансфинитных чисел.
В самом деле, если мы имеем (или думаем, что имеем) совершенно
ясное представление о совокупности всех трансфинитных чисел
второго класса
0, 1, 2, ..., о), (D-+-1, ..., а,...,
мы видим с той же ясностью совокупность всех трансфинитных
чисел, и однако рассуждение Бурали-Форти нас учит, что эта
совокупность логически противоречива в себе1. Этот парадокс обычно
разрешают так: мы не имеем права рассматривать совокупность всех
трансфинитных чисел, а только совокупность трансфинитных чисел,
обладающих некоторым свойством Р (буква Р может означать,
например, быть второго класса или другое свойство, все равно какое).
Парадокс исчезает в этом случае, потому что рассуждение Бурали-Форти
утверждает, что есть заведомо трансфинитные числа, которые не
обладают свойством Р (и, в частности, те, которые принадлежат
третьему классу).
Но так как свойство Р может быть абсолютно произвольным, такое
решение парадокса кажется мне слишком легким для того, чтобы быть
математическим. Я рассматриваю интуитивное представление
совокупности трансфинитных чисел как дефектное^ и я думаю, что есть
некоторая доля иллюзии в ясности, которую вносит в наше интуитивное
1 См* второе письмо Адамара о теории множеств (Е. В or el. Lemons sur
la theorie des fonctions, 3e ed.f 1928, стр. 158).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
31
представление об этой совокупности обычай обозначения „малых*
трансфинитных чисел.
Таким образом, мы приходим к неточным интуитивным
представлениям, и этот факт, как и другие аналогичные, должен сделать нас
очень осторожными при введении трансфинитных чисел второго класса
логическим путем.
Анализ данного определения множеств,
измеримых В. Мы теперь проанализируем данное ранее определение
множеств, измеримых В (стр. 24). Согласно этому определению,
измеримым В называется всякое множество точек, которое может быть
получено повторным применением двух основных операций
(вычитание двух уже определенных множеств и сложение счетного множества,
уже определенных множеств без общих частей), отправляясь от
порций основной области <Р'.
Это определение, несомненно, кажется особенно ясным, когда речь
идет о множествах, уже реализованных; но оно не имеет еще
достаточной ясности, аля того чтобы фигурировать в математическом
доказательстве, где рассуждают о множестве, измеримом Ву реализация
которого лишь виртуальна.
Необходимость вести подобные рассуждения немедленно возникает,
если поставить себе целью изучать общие свойства множеств,
измеримых В. И тогда стремятся уточнить это определение при помощи
дополнительных фраз.
С этой целью, после того как рассматриваемое определение
сформулировано, обычно поясняют, что две основные операции, при помощи
которых строятся множества, измеримые В> отправляясь от порций
основной области, могут быть взаимно скомбинированы очень сложным
способом, так как для получения желаемого множества, измеримого В,
часто приходится предварительно приготовить бесконечное множество
других множеств, также измеримых Ву комбинация которых при
помощи основных операций в конце концов приводит нас к получению
результирующего множества Е.
Эти объяснения, кстати необходимые, если мы хотим изучать
множества, измеримые Ву во всей их общности, делают ясной всю
сложность общего понятия множества, измеримого В. Но сами эти
объяснения заставляют понять, что предыдущее определение множества,
измеримого Ву если взять только егоу не имеет ясного смысла; в самом
деле, что без них означают слова: повторное применение двух
основных операций? Таким образом, эти объяснения неотделимы от
предыдущего определения; или, пожалуй, эти объяснения и являются
самим определением множеств, измеримых В.
Если мы постараемся проанализировать эти объяснения, то вот что
мы констатируем: мы отправлялись от порций основной области о7,
которые рассматривали как заданные; потом мы должны были строить
бесконечное множество промежуточных множеств, которые заведомо
32
HI Н...ЛУЗИН
зависели друг от друга. В каком порядке надо их брать, чтобы быть
уверенным, что они получены все, чтобы не заблудиться в их
безграничном многообразии и чтобы не попасть в порочный круг?
С этим вопросом впервые встречаются в элементах, когда
начинают изучение функций, и обычно принимают следующее определение:
функция f(x) называется элементарной, если ее можно получить
повторным применением основных операций (сложение, вычитание,
умножение, деление, |/~ log, sin и т. д.), отправляясь от
действительного переменного х и от констант. Невозможно не поражаться
аналогией между этим определением и предыдущим определением множества,
измеримого В. Но эта аналогия чисто формальная.
В случае понятия элементарной функции каждая из основных
операций применима самое большее к двум функциям, определенным
ранее; таким образом, множество промежуточных функций заведомо
конечно. Именно по этой причине можно эти промежуточные
функции расположить в определеленном порядке таким образом, чтобы
можно было определить при помощи основных операций все
промежуточные функции друг за другом, без того чтобы исключить
какую-либо из них и без того чтобы повторить хоть одну из них
несколько раз, и в конце концов придти к желаемой функции. Именно
в силу этого порядка невозможно впасть в порочный круг, и,
следовательно, данное определение элементарной функции есть истинное
определение1.
Совсем иначе обстоит дело в случае понятия множества,
измеримого В. В этом случае промежуточных множеств бесконечно много,
и порядок, в котором эти множества располагаются, гораздо важнее,
чем самое понятие множества, измеримого В. Не зная этого порядка, мы
постоянно будем находиться в положении математика, который
претендует на то, что умеет получить все натуральные числа, и, однако, не
знает принципа полной индукции. Именно этот порядок промежуточных
1 Обычно понятие элементарной функции рассматривают как совершенно ясное,
и в большинстве Курсов математического анализа вовсе не настаивают, и вполне
правильно, на атом понятии: в атом случае рекурренция не может войти бесконечное
множество раз.
Но все становится значительно сложнее, когда речь идет о математических
определениях, которые могут быть выражены при помощи конечного числа уже принятых
понятий. Бесконечная реккуренция входит по существу, как показывают последние работы
школы Д. Гильберта о логических основаниях математического анализа, и важное
понятие высоты числа, введенное Борелем, или ранга функционала, введенного
Аккерманом, становится необходимым. Следуя его идее, ранг функционала есть не
что иное, как высота числа, но перенесенная и уточненная в области математической
логики. По поводу понятия высоты числа см. E..Borel. Lecons sur la theorie
de la croissance. 1910, последняя глава; его же. Lecons sur la theorie des fonctions,
2« ed., 1914, Note VI, стр. 220—221. О понятии ранга функционала см. W. Acker-
man п. Begriindun? des „tertium поп datur" mitt els der Hilbertschen Theorie der
Wieder.spruch freihcit (Math, Ann. 93,15,192S).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
33
множеств есть истиинный нерв всех конструктивных определений
множества, измеримого В. Теоретическая необходимость
конструктивных определений множества, измеримого Ву таким образом
преобразуется на почве общих рассуждений в математическую необходимость
строгого определения порядка промежуточных множеств.
Известно, что все процессы для эффективного установления этого
порядка могут быть подвергнуты общему изучению, которое впервые
было сделано Г. Кантором для последовательных производных
данного множества и которое привело к понятию трансфинитных чисел
второго класса.
Самое трансфинитное число есть не что иное, как сокращенное
обозначение для указания порядка, в котором должно быть
произведено счетное множество операций, содержащих счетное
множество последовательных или суперпозированных переходов к
пределу г.
Если не ограничивать поле математики изучением лишь одной
категории множеств, измеримых В> например, проистекающих из
функций классификации Бэра конечного класса, то приходится вводить
в определение множества, измеримого В, как угодно большие
трансфинитные числа.
1 Это важное определение трансфинитного числа принадлежит Борелю (см. его
„Lecons sur la theorie des fonctions*. 1914, Note VI, стр. 231).
Важно заметить, что существует несколько теорий трансфинитных чисел, среди
которых мы прежде всего должны цитировать m?opuv Г. Кантора эманации типов,
где трансфинитное число рассматривается как тип, происходящий от каждого
данного вполне упорядоченного множества; номиналистские теории Бэра и Лебега,
которые рассматривают трансфинитное число либо как ранг некоторого элемента в
заданном вполне упорядоченном множестве, либо как производное множество, либо
как класс в классификации Бэра (см. R. В a i г е. Lemons sur les fonctions
discontinues. 1905, стр. 42; H. Lebesgue. Lemons sur Integration, 2e 6d.t Note,
стр. 314); логические теории Рёсселя, Серпинского и Фреше, которые стремятся
определить трансфинитное число как класс вполне упорядоченных множеств, попарно
подобных и образованных из элементов некоторого более или менее специального
семейства (см. также мой мемуар „Sur les ensembles analytiques". Fund. Math., X,
#5, 1926, стр. 380 настоящего тома—Ред.).
Мне представляется, что все эти теории приводят к замене концепции
трансфинитного числа рассмотрением вполне упорядоченного счетного множества.
Но вот какая, по-моему, здесь возникает трудность: чтобы констатировать
для нас самих, что рассматриваемое вполне упорядоченное множество скетно,
необходимо уже иметь представление о трансфинитном числе, соответствующем
этому множеству: без этого, по-моему, это невозможно. В природе нет конкретных
вполне упорядоченных множеств, которые соответствуют трансфинитным числам,
превосходящим со; такое множество есть всегда вторичный результат активности
человеческого ума. Таким образом, всякое усилие, сделанное лля того, чтобы подставить
вместо трансфинитного числа вполне упорядоченное счетное множество, предполагая
его счетность констатированной s располагает вещи в порядке, противоположном
тому, которому нужно было бы следовать, и является в некотором смысле petitio
principu. Вот почему мы принимаем ранее данное определение Бореля.
34
Н. Н. ЛУЗИН
Вот заключение, к которому мы пришли в результате этой долгой
дискуссии. Его можно сформулировать так:
Если принять то определение множества, измеримого В, которое
было ранее предложено, то. совокупность множеств, измеримых Bf
есть веш,ь, безусловно адекватная совокупности всех
трансфинитных чисел второго класса.
Концепции открытого и замкнутого тела Бореля. Именно
в силу этой близости понятий множества, измеримого В, и
трансфинитного числа Борель предложил при изучении множеств,
измеримых В, всегда ограничиваться рассмотрением некоторого открытого
тела множеств, измеримых В; знаменитый автор назвал этим именем
коллекцию множеств, измеримых В, которые отвечают трансфинитным
числам, меньшим, чем некоторое заранее фиксированное число,
следовательно такую, что она заведомо может быть расширена при
повторении основных операций.
Этой концепции Борель противопоставляет концепцию замкнутого
тела, т. е. такого, которое нельзя расширить повторением тех же
операций, причем эту последнюю концепцию он считает неясной
и незаконной1.
Борель считает, что трудность приобретения концепции замкнутого
тела заключается в том, что можно формулировать эффективно лишь
конечное число условий, и как бы далеко эти условия не позволили
пойти, сущности (трансфинитные числа, множества, измеримые В)г
до которых они позволяют добраться, суть ничто сравнительно с теми,
которые от них ускользают, но которые можно определить при
помощи других условий в конечном числе, без того чтобы когда-нибудь-
дойти до конца2.
Концепция конструктивной совокупности множеств, измеримых Ву
хотя она и непротиворечива в себе, не есть истинная математическая
концепция, так как нельзя описать точно при помощи конечного числа
условий конструкцию такой совокупности: необходимо было бы иметь
бесконечное множество условий, абсолютно независимых друг от
друга, для того чтобы фиксировать ее обозначение способом,
лишенным двусмысленности3.
Тем не менее, математическая необходимость иметь общие
свойства всех множеств, iизмеримых В, возникает мгновенно, как только-
получена концепция этих множеств. Но если дано конечное
определение для совокупности любых сущностей, то общие свойства всех этих
сущностей получается прямым анализом самого определения
(предполагаемого конечным) предложенной совокупности. Блестящий пример-
1 См. Е. В о г с 1. Lecons sur la theorie des fonctions» 2* ed.^ Note VI*
стр. 235—236.
2 См. Е. В or el. La philosophie mathematique et Tinfini (Revue du Mois-
август 1912 г.).
8 Там же.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИ МНОЖЕСТВАХ
$5
этого метода действий представляется в случае совокупности всех
функций класса 1 по классификации Бэра. Но ;как надо действовать
в случае совокупности, лишенной всякого конечного определения,
т. е. в случае несовершенной совокупности, которая представляет
собой непрекращающееся образование новых элементов без того, чтобы
когда бы то ни было дойти до конца1? И прежде всего как вообще
возможны такие свойства?
В случае совокупности множеств, измеримых В, метод для
получения общих свойств, присущих всем множествам, измеримым В, связан
с концепцией открытого тела и всегда заключается в том, чтобы
получать новые множества из множеств уже определенных; только
вместо того, чтобы отправляться от порций основной области <7 и
следовать конструкции шаг за шагом, предполагают, что конструкция
до некоторого места уже сделана и обладает некоторыми свойствами,
и доказывают, что эти свойства сохраняются, если сделать новый
шаг.
Этот способ действия непогрешим с точки зрения логики, и, что
еще важнее, он безупречен и с точки зрения математической
реальности. Кроме того, он плодотворен: большая часть ценных свойств
(мера, категория), присущих всем множествам, измеримым В, обязаны
этому методу2. Таким образом, позиция этого метода теоретически
очень сильна.
Практически она, конечно, гораздо менее сильна. Достаточно
указать, что этот способ действий один раз привел даже к потере одного
свойства, общего для всех несчетных множеств, измеримых В, и столь
же важного, как свойство: иметь моиуностъ континуума. Так как это
обстоятельство, может быть, мало известно, то нам кажется, что
представляет интерес остановиться на этом пункте.
В замечательной работе Лебега („Sur les fonctions representables
analytiquement*) находится много основных свойств, присущих всем
несчетным множествам, измеримым В. Знаменитый автор получил все
эти свойства, постоянно применяя указанный метод: их проверяют
для порций и потом доказывают, что эти свойства инвариантны
относительно двух основных операций (сложение и взятие общей части)3.
Но среди этих свойств не встречается важное свойство, которое
устанавливает существование совершенного множества во всяком
несчетном множестве, измеримом В. Это свойство было открыто впервые
1 Е. В о г е 1. La philosophic mathematique et rinfini (Revue du Mois,
август 1912 г.).
2 См. H. Lebesgue. Sur les fonctions representables analytlquement (Joum.
de Math., 166—174 и 187, 1905); см. также R. Baire. Sur la representation des
fonctions continues (Acta Math., SO, 21—30,1905).
3 Лебег, определяя множества, измеримые £, не употребляет вычитания; он
рассматривает операции суммы и общей части („Sur les fonctions representables
analytiquement", стр. 165).
36
Н. Н. ЛУЗИН
Хаусдорфом и П. С. Александровым десять лет спустя после мему-
ара Лебега. *
Здесь основной пункт: все свойства, выведенные Лебегом,
индуктивны^ т. е. сохраняются в обеих фундаментальных операциях; но
свойство, найденное Хаусдорфом и Александровым, не является
таковым: повторяя рассуждения идеалистов, доказывают, что это свойство
неинвариантно относительно Ьторой фундаментальной операции
и, следовательно, не может быть получено предыдущим методом2.
Таким образом, отсутствие этого свойства в мемуаре Лебега было
неизбежным.
Здесь мы имеем очень важный факт: существуют свойства
неиндуктивные и принадлежащие всем множествам, измеримым В. Но как
могут существовать такие свойства?
Ответ, мне кажется, напрашивается: существует другое
определение замкнутого телау которое опирается лишь на понятия,
заимствованные из классических ветвей математики, и которое, следовательно,
выражено в конечной форме. Именно благодаря этому конечному
определению несовершенная совокупность множеств, измеримых В,
становится в известном смысле законной. Этому конечному
определению и обязано существование неиндуктивных свойств множеств,
измеримых В. Знание этого определения достаточно для того, чтобы
получить все свойства множеств, измеримых В, — как индуктивные, так
и неиндуктивные.
Другие определения замкнутого тела* Мы укажем кратко два
других определения замкнутого тела. Первое из них принадлежит
Серпинскому и имеет базой принцип минимума.
Первое определение замкнутого тела. Чтобы увидеть насколько
возможно ясно, в чем заключается это определение, мы будем
руководствоваться высшей арифметикой.
Известно, что одной из самых прекрасных концепций теории чисел,
восходящей к Галуа, является понятие тела чисел.
Мы называем в общем случае „телом чисел1 всякую систему
чисел, такую, что, совершая над любыми числами системы четыре
основные операции: сложение, вычитание, умножение и деление
(деление на нуль исключается), получаем числа, принадлежащие той же
системе. Тело чисел дано, если множество его элементов есть
множество с конечным определением; такое тело тогда называется
эффективным телом.
Первый пример эффективного тела дается множеством всех
рациональных чисел; его называют областью рациональности. Другой
пример эффективного тела, гораздо более достойный интереса, это
1 См. Felix Hausdorff. Die Machtigkeit derBoirelschen Mengen (Math. Ann.,
77, 430,1916) и P. Alexandroff. Surla puissance des ensembles mesurables В
(Compos Riendus. 323, 1916).
2 Матем. сборник, 277, 1926.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
тело, полученное из области рациональности присоединением
заданного иррационального числа. Вот что под этим понимают.
Пусть R — область рациональности; прибавим к ней некоторое вполне
определенное несоизмеримое число а (например е); мы получим, таким
образом, новую систему чисел
которая не образует тела; она становится телом лишь после того, как
к ней присоединят все числа, которые рождаются, когда а
комбинируется с элементами из R при помощи основных операций. Таким
образом, получается тело более протяженное, содержащее R и а и
полностью определенное при помощи R и а; мы его назовем телом /?(а)
и скажем, что R (а) получается из R присоединением а.
В этих разъяснениях мы узнаем „определение", вполне аналогичное
определению совокупности множеств, измеримых В. Как и в этом
последнем случае, это определение по всей строгости незаконное. Но вот
корректное определение.
Тело R (а) есть множество всех рациональных функций от &
с целыми коэффициентами.
Благодаря этому конечному определению тело R(<*) вполне
эффективно.
Что делает законной нашу концепцию тела /?(а) во втором
определении? Не изучая углубленным образом этот затруднительный вопрос,
мы хотим указать, что это в конечном счете факт существования
совершенно ясного представления о натуральном ряде целых чисел1
1, 2, 3, 4, ...
Напротив, если нет четкого и ясного представления неограниченной
последовательности целых чисел (что в данный момент есть чистое
предположение, так как если совершенно ясное представление
бесконечного отсутствует, то и классические ветви математики уже не
существуют), то остается только дать третье определение тела /?(<*),
а именно:
Тело /?(&) есть наименьшее телоу содержащее данное число а.
Закончив это введение, мы теперь можем ввести a priori следующие
определения:
Мы назовем в общем случае телом множеств систему линейных
точечных множеств такую, что обе фундаментальные операции
(сложение, вычитание), произведенные над любыми множествами системы,
приводят всегда ко множеству, принадлежащему той же системе.
Вот теперь определение замкнутого телау принадлежащее В. Сер-
пинскому 2:
1 См. Е. В о г е 1. L'infini mathematique et la realite (Revue du Mois, 10 жюля
1914 г.).
2 См. статью В. И. Сероинского „Sur les definitions axiomatiques des ensembles
mesarables B11 (Ball, de TAcademie des Sciences de Cracovie, январь—март 1918 г.).
38
Н. Н. ЛУЗИН
Мы назовем „замкнутым телом" наименьшее из тел множеству
содержащих все порции фундаментальной области о/. Линейное
множество Е называется измеримым Ву если оно принадлежит
замкнутому телу.
Это определение В. Серпинский назвал аксиоматическим
определением множеств, измеримых В.
Это определение, к которому мы естественно пришли по аналогии
с предыдущим, без сомнения покажется совершенно ясным читателю,
слишком привыкшему к идее актуальной бесконечности; но если мы
проанализируем это определение ближе, то мы не можем прежде всего
не поразиться существенными различиями между ним и тем
определением, которое мы приняли в случае арифметического тела. Отметим
фактически лишь одно из этих различий: наименьшее из арифметических
тел, содержащих а, несомненно существует, потому что существует
множество рациональных функций от а с рациональными
коэффициентами; таким образом, третье определение тела /?(<*) узаконивается
благодаря законности второго определения этого тела; в случае тела
множеств это совсем не так: мы не имеем для замкнутого тела определения,
аналогичного второму определению тела /?(а).
Таким образом, мы приходим к постановке следующего вопроса.
Какими средствами можно узаконить предложенное определение
замкнутого тела? И, прежде всегоу как можно доказать существование
этого тела? Не приходится обсуждать истинность этого определения;
надо искать источник реального существования той сущности, которую
это определение описывает.
Попытка такого рода, которая кажется наиболее естественной и
имеет то преимущество, что она чрезвычайно проста и элементарна,
дается следующим рассуждением: ясно, что существуют тела множеств,
содержащие все порции области с7, так как множество всех линейных
точечных множеств является таковым; очевидно, что если рассмотреть
множество F всех тел, содержащих порции g7, to множество-делитель
для F (делителем конечного или бесконечного множества множеств Е
называется множество элементов, общих всем Е) есть тело той же
природы; это наименьшее тело. Существование замкнутого итела таким
образом доказано.
Эти аргументы не новы: их можно прочесть с незначительным
изменением в первых строчках известного рассуждения Цермело,
относящегося к вполне упорядоченным множествам1.
1 См. Е. В 6* г е 1. Le continu bien ordonne d'apres M. Zermelo („Lemons sur la
theorie des fonctions", 2е ed.% 1914, стр. 48).
Я однажды, уже давно, употребил это рассуждение, начиная изучать теорию
аналитических множеств; на этой манере рассуждения я основал доказательство теоремы:
всякое множество, измеримое #, есть множество аналитическое; см., например*
Су с лин. Sar ane definition des ensemoles mesurables B sans nombres transfinls
(Comptes Rendus de I'Acatb Sci., 8 января 1917 г.). В то время я сильно колебался
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
39
Вот трудность, которая в этом рассуждении останавливает реалистов.
Чтобы подтвердить точность предыдущего рассуждения, необходимо
прежде всего строго доказать существование тел множеств,
содержащих порции области 3'. Но приведенный пример всех точечных
множеств есть плохо выбранный пример: для реалистов не существует
никакой реальной сущности, которая соответствует этому понятию. Когда
говорят об этом множестве, то не указывают ни закона этой
бесконечности, ни способа ее назвать. Мы в настоящее время не знаем
никакого способа, чтобы определить множество всех точечных множеств:
когда мы говорим о нем, мы по сути дела лишь воображаем
различные приемы, которые можно изобрести, чтобы получить очень сложные
множества, за отсутствием регулярного процесса, который позволил бы
охватить их все одним взглядом. Но как только дело касается
человеческой способности создавать процессы определения и системы условий,
так мы находимся в области субъективного. Таким образом, для
реалистов множество всех точечных множеств, будучи меняющимся от
математика к математику, не имеет в любой момент другого существования,
кроме чисто словесного.
Другой пункт в этом рассуждении, подлежащий критике, — это
употребление множества всех тел множеств; это множество также
незаконно для реалистов.
Все, что можно надеяться извлечь из этого рассуждения, это
единственность замкнутого тела: так как общая часть двух любых тел
есть опять тело, то замкнутое тело, если оно существует, есть тело,
определенное единственным образом без всякой расплывчатости.
Несмотря на эти трудности, стоит принять провизорно
существование минимального тела как в некотором роде постулат; мы его назовем
принципом минимума1.
Правда, для этого принципа представляется следующая трудность:
мы имеем право образовывать множества лишь из объектов, заранее
существующих; но легко видеть, что определение замкнутого тела
предполагает обратное; таким образом, это определение ставит вещи
в порядке, обратном тому, которому надо было бы следовать: здесь
уже не образуется совокупность при помощи элементов, но элементы
определяются при помощи совокупности, которая предполагается
существующей еще до этого.
между точкой зрения идеалистов и реалистов. Теперь я уже не рассматриваю это
рассуждение как убедительное.
1 Можно было бы также принять за основные другие операции вместо сложения
и вычитания. Можно, например, рассматривать сложение и умножение (состоящее
в образовании общей части) или операции перехода к пределу, или любую другую
операцию, которая приводит в соответствие бесконечной последовательности
множеств Е\% Efr ..., Еп% ... некоторое вполне определенное множество, выбирая
соответствующим образом основные операции; можно, применяя принцип минимума,
получить другие тела вместо ранее определенного замкнутого тела Бореля.
40
Н. Н. ЛУЗИН
Тем не менее, нет затруднения в том, чтобы принять провизорно
этот принцип как промежуточный инструмент, действительной
полезностью которого не следует пренебрегать, но который нужно
рассматривать лишь как средство для того, чтобы преобразовывать ложные
совокупности в совокупности с конечным определением; эти последние
представляют единственную реальность, которой мы можем достигнуть.
Кроме того, и это важно, рассмотрение этого принципа не может
привести к трудностям вириационного исчисления.
Второе определение замкнутого тела*. Чтобы придти к этому
определению, сделаем прежде всего следующее замечание:
Среди точечных множеств, мощность которых бесконечна, наиболее
простыми являются множества, элементы которых могут быть за-
нумерованы целыми положительными числами.
Это счетные множества.
Также среди несчетных множеств естественно рассматривать как
самые простые множества, элементы которых могут быть
занумерованы при помощи иррациональных чисел, или условиться
употреблять только непрерывные соответствия.
Углубленное изучение этих множеств доказывает, что их семейство
совпадает с семейством несчетных множеств, измеримых В. Это
показывает нам, что эти последние должны рассматриваться как
непосредственно следующие за множествами конечными и счетными.
Вот теперь определение замкнутого тела:
Назовем регулярной функцией2 всякую функцию f(x),
определенную на фундаментальной области о7, и такую, что двум различным
точкам из g7 соответствует два существенно различных значения f{x).
Фундаментальная теорема3, которая связывает это понятие с
понятием замкнутого тела, следующая:
Для того чтобы несчетное множество Е было измеримо В,
необходимо и достаточно, чтобы Е было с точностью до счетного
множества множеством значений регулярной функции, непрерывной на о/.
Эта теорема позволяет нам дать следующее определение замкнутого
тела:
Можно получить все множества, измеримые В, если взять все
конечные множества, все счетные множества и все те, которые
с точностью до счетного множества являются множествами
значений функций f{x), регулярных и непрерывных на о?'.
1 См. мой мемуар „Sur les ensembles analytiques" (Fund. Math. X, 59).
2 Монтель говорит однозначная функция. Эта терминология и очень точна и
совершенна, и если мы принимаем расплывчатое название регулярная функция, то это
для того» чтобы дать имя полу регулярных функций тем функциям/, которые не могут
принимать никакое значение несчетное множество раз (стр. 144 настоящего тома. —
Ред.). Выражение полу однозначная было бы неприемлемым, а выражение почти
однозначная — неточным.
3 Я формулировал эту теорему в своей заметке от 8 января 1917 г. „Sur la
classification de M. Baire" (Comptes Rendus, 164).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
41
Кажется, нельзя сделать возражений против этого определения
замкнутого тела, так как понятия функции непрерывной и функции
регулярной фигурируют в классических ветвях математики*
Остается только одна трудность: так как всякое несчетное
множество, измеримое В, может быть представлено бесконечным множеством
способов как множество значений непрерывной регулярной функции, то
предложенное определение замкнутого тела дает нам скорее
множество непрерывных регулярных функций, чем множество множеств,
измеримых В» Но такая же трудность имеется и для счетных множеств,
так как мы никогда не обладали совокупностью счетных множеству
но лишь совокупностью бесконечных последовательностей 1.
Уточнение обычного определения множества, измеримого В.
Закончив это философское введение, вернемся к первому
определению множества, измеримого В, а именно к тому, которое тесно связано
с самим происхождением этих множеств 2. Если мы попробуем исключить
из этого определения психологические элементы и избежать, по
крайней мере формально, понятия трансфинитного3, мы будем приведены
к тому, чтобы дать этому определению следующую форму:
Мы скажем, что множество точек Е измеримо В, если мы умеем
получить счетную вполне упорядоченную последовательность
множеств, имеющую множество Е своим последним членом, и каждый
член которой, не являющийся порцией области <3, есть результат
операции вычитания (D) или операции сложения (S) в узком смысле,
произведенной над предыдущими членами
Ео, Е\, £2, .. .1 Е$, .. .| Е.
Это определение, к которому мы естественно пришли, без сомнения
покажется более ясным, если мы отметим, что множества Ер>
предшествующие Е и не являющиеся порциями области <9\ оказываются
предварительными множествами, которые нужно приготовить заранее, чтобы
получить результирующее множество Е.
Если мы будем стараться сделать это определение более
„экономным", т. е. избегающим тех предварительных множеств, которые не
являются строго необходимыми для определения результирующего
множества Е, то нужно ввести следующее дополнительное условие:
невозможно удалить из этой вполне упорядоченной последовательности
Еоу Ei, ..., Е?, ...\Е ни одного члена, кроме Е, без того чтобы эта
последовательность утратила свое основное свойство: каждый из ее
членов определим при помощи предыдущих членов.
1 Напомним, что в силу исследований В. Серпинского, если бы мы умели
доказать (без аксиомы Цермело.—Ред.)% что множество всех счетных точечных
множеств имеет мощность континуума, то мы могли бы отсюда построить множество,
неизмеримое по Лебегу (см. сноску на стр. 25.— Ред.).
2 См. о проблеме меры Бореля, стр. 49. — Ред»
3 По поводу определения трансфияитного числа см. сноску на стр. 33 — Ред.
42
Н. Н. ЛУЗИН
Это дополнительное условие исключает множества, полностью
инородные по отношению к множеству Е> т. е. те, знание которых
нисколько не необходимо при окончательном образовании множества Е.
Но здесь речь не идет о классе множества Е, измеримого Ву т. е.
не о таком новом условии: вполне упорядоченная последовательность
Еоу Ely ..., £3, ... | Еу предназначенная для определения множества Е,
должна быть наиболее короткойу т. е. соответствующей
наименьшему трансфинитному числу.
Преобразования определения множества» измеримого В
Характер основных операций. Операция (S)y состоящая в том,
чтобы взять сумму счетного множества уже определенных множеств,
имеет положительный характер, так как точки, из которых образована
сумма £хн-Е2-+- ♦ ••> даны положительным образом1.
Точно так же мы можем рассматривать как положительную
операцию (Р)у состоящую в том, чтобы взять общую часть счетного
множества уже определенных множеств.
Напротив, операция (Z)), состоящая в том, чтобы взять разность
двух множеств, при помощи которой строятся множества,
измеримые By есть, безусловно, отрицательная, так как мы образуем
разность^— ^1> беря точки Егу которые не принадлежат данному
множеству Ех2.
Но если указывают некоторое множество точек, то почти всегда
указывают все точки, ему принадлежащие, без того чтобы дать
критерий, позволяющий узнать, принадлежит ли произвольно взятая точка
этому множеству или нет. В самом деле, мы увидим в дальнейшем
примеры, где для того, чтобы узнать, принадлежит ли данная точка
рассматриваемому множеству, надо совершить несчетное множество не
зависящих друг от друга операций или же где даже нет никакого регу-
1 Мы естественно предполагаем, что точки каждого члена Еп названы при помощи
положительного свойства.
2 Если Е2 есть множество конкретных предметов, то ясно, что, вычитая из Е%
аекоторую часть, мы получим остаток вполне реальный. Но если £2 есть бесконечное
множество, то нисколько не очевидно, что, вычнтая из Е% бесконечное множество его
•элементов, мы получим остаточную часть, имеющую некоторое определение
(положительное свойство). Это некоторого рода постулат, который, на мой взгляд, очень мало
вероятен.
Приведем место из Бэра (письмо Бэра Адамару „Cinq Uttres sur la theorie
«des ensembles". Bull, de la Soc. Math, de France, декабрь 1904 г.)? „Когда говорят
о бесконечности (даже счетной; и в этом я склонен быть более радикальным, чем
Борель), то сознательное или бессознательное сравнение с мешком шаров, которые
передают из рук в руки, должно, на мой взгляд, полностью исчезнуть и мы находимся
в области виртуального.
Думать, что мы пошли дальше, мне не кажется законным. В частности, если
дано множество, ошибочно, с моей точки зрения, рассматривать как данные
части этого множества". Это точка зрения реализма.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
43
лярного процесса1. То, что мы сказали, достаточно, чтобы предвидеть
большие трудности, связанные с операцией (D).
Как частный случай операции вычитания (D) мы рассматриваем
операцию (С) перехода от данного множества Е к его дополнению С£,
так как для получения дополнения СЕ достаточно взять множество-
разность g7 — £, где с7 есть основная область.
Таким образом, мы, естественно, приходим к тому, чтобы поставить
следующий вопрос: узнать, можно ли получить всякое множество,
измеримое В, при помощи положительных операций и в частности
при помощи операций: суммы (S) и общей части (Р).
Речь, следовательно, идет о преобразовании определения множества,
измеримого В.
Образование множеств, измеримых В, при помощи операций (5)
и (Р). Мы сначала покажем, что любое данное измеримое В-множество
можно получить, отправляясь от порций основной области <Р\ при
помощи двух операций: суммы в узком смысле (S) и общей части (Р),
неограниченно повторенных.
Чтобы доказать это предложение, мы заметим следующее: сказать,
что некоторое множество Е получено из порций области J при помощи
операций (S) и (Р), неограниченно повторенных, ато значит сказать,
что Е есть последний член счетной вполне упорядоченной
последовательности So, S\y £2, ..., £7, . ..|£, каждый член которой, не
являющийся порцией области <з7\ получается из предыдущих членов или при
помощи операции (£), или же при помощи операции (Р).
Установив это, мы можем во вполне упорядоченной
последовательности £о, Eiy Еъ, ..., £р, .. *|£, служащей для определения данного
множества Е, измеримого В9 поставить непосредственно перед каждым
членом Е$ его дополнение С£р; если Е$ есть порция области о7, то
дополнительное множество СЕ$, вообще говоря, состоит из двух порций
области с/ и в этом случае мы перед СЕ$ поставим эти две порции.
Ясно, что этим способом мы получим вполне упорядоченную счетную
последовательность £0> &и &*> • • •> #т> •••l^t имеющую Е своим
последним членом.
1 Если некоторая функция /(*)' рассматривается как заданная, то естественно
считать заданным и множество Е значений f{x). Но ничто, на мой взгляд, не
оправдывает распространение этого взгляда на дополнения к „данным*4 множествам, если
мы не можем преобразовать отрицательное определение такого множества в поло-
жителънсе определение. В то время как мы получаем все элементы Е% производя
операцию / над всеми действительными числами, мы не имеем никакого регулярного
процесса, чтобы узнать, принадлежит ли данное действительное число ^о к
дополнению к Е нли нет, и можно сильно сомневаться, чтобы удалось дать общее решение
«той проблемы. Если функция f(x) есть проективная, то надо произвести множество
операций, мощность которого континуальна, и много шансов за то, что вти попытки
будут независимы друг от друга, хотя / и определена при помощи перечислимого
множества условий. См. N. Lusin. Remarques surles ensembles projectifs (Comptes
Rondos, 835—837, 1927). (Стр.,460 настоящего тома — Ред.)
44
Н. Н. ЛУЗИН
Я теперь утверждаю, что последовательность <§Qy <§i> ..., &и . ..|£,
полученная таким способом, служит для определения множества £,
отправляясь от порций области Jy при помощи операций (S) и (Р),
неограниченно повторенных.
В самом деле, если <5Г не есть порция области о/, мы имеем либо-
<£т = £з, либо <5т=С£р. Следует различать два случая. В первом
случае мы имеем £(в = £?1 + £р, + ..., где Р»<р. Отсюда следует, что
СЕ$ = С£р, • С£р, ... Из этого мы заключаем, что £г определимо при
помощи операции (S) или операции (Р), примененной к счетному числу
множеств <§f, предшествующих <£т, т'^Т- Во втором случае мы имеем
Ер^Е^—Е$1У где pi и рг меньше (3. В этом случае мы можем написать
£p = £Pi. С£р, и СЕ$=СЕ$х-\-Еъ* Из этого мы заключаем, что £т
получается применением одной из двух операций (S) и (Р) к
предшествующим множествам &у> т'<С Т (ч- т- Д-)«
Более важным является следующее предложение: всякое множество £,
получаемое, отправляясь от порций области с/, при помощи двух
операций: суммы в широком смысле (S) и общей части (Р),
повторенных неограниченно, измеримо В,
Чтобы доказать это, возьмем вполне упорядоченную счетную
последовательность множеств
£о, Е\, £2, . •., Ефш..\Е, (1)
служащую для определения множества Е при помощи операций (S) и (Р),
отправляясь от порций области <з7.
Назовем нормальным всякий член этой последовательности такой,
что общая часть этого члена (или его дополнения) и некоторых
предшествующих множеств (или их дополнений), взятых в конечном числе,
может быть определена, отправляясь от порций области (7У при помощи
операций: (S) в узком смысле и операции (С), позволяющей переходить
от множества к его дополнению.
Ясно, что нормальные члены существуют: таковым является каждый
член Еп последовательности (1) с конечным индексом п потому, что
в этом случае Еп и все предшествующие члены состоят из конечного
числа порций области о/.
Я теперь утверждаю, что каждый член последовательности (1)
нормален.
Чтобы доказать это, предположим, что существуют анормальные
члены. Пусть £р— первый из них. Так как каждый член
последовательности (1) может быть получен при помощи операций (S) и (Р),
примененных к предыдущим членам, нужно различать два случая.
В первом случае мы имеем £р = £р, + £р, + ..., где Pi<CP2<C •••
все меньше р.
Так как Е$ — анормальный член, то среди множеств
П£3,. ПС£Г • Е% и П£р, . ПС£р» • CEh
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
45
где два первых сомножителя обозначают соответственно общие части
множеств Ер и дополнений к множествам Еу, предшествующим Е$,
?'<СР и Р"<Р, найдется по крайней мере одно множество, которое
нельзя получить, отправляясь от порций области с7 при помощи
операций (S) в узком смысле и (С).
Но мы можем написать
E, = Eh + CE9, -£з,+ ... +С£.ч,-С£,, ... С£?1%_, •£>„+ ...
и, следовательно,
Ц£?- -ПС£?".£з =
= 2 П£Э1 • ПС£з- • С£3, • С£,ч ... С£>_, • £„.
я=1
Так как все члены последовательности (1), предшествующие Е^
нормальны, мы заключаем, что множество ШГ^ • UCEy> • £•> получается из
порций области о/ при помощи операций (S) в узком смысле и (С).
Остается лишь рассмотреть множество П£^ • ПСЕ у • СЕ$. Но мы
можем записать это множество в виде
С[С(П£?, .ПС£р") + £?1
и, следовательно, представить его в виде
С[С(П£Р, . ПС£Р")+ 2 п^' • пС£р- • С£?1 ... СЕ^п_х • £3п].
Так как все члены последовательности (1), предшествующие £р,
нормальны, то написанное множество может быть задано, отправляясь от
порций области <з7 при помощи операций: (S) в узком смысле и (С).
Во втором случае мы имеем £3 = £р, • £& ..., что дает нам
С£р = С£р, -+- £р, • С£р, -+- ... -+- £3, • £?, ... £?*_, * СЕ^ -н ...
и, следовательно,
П£р, . ПС£з« • С£? = 2 п£?' • п^£з- • £?, • £* ... £*,_, • С£:%
я=1
И
П£р, • ПС£р» • £э = С[С(П£р, . ПС£р-) -+-
-н 2 П£р, . ПСЕ? ■£*•£* ... £*>_, • C£U.
♦/=1
Отсюда легко заключить, как и в предыдущем случае, что
множества П£р/ . ПС£р» • С£р и П£р/ . ПС£р" • £р определимы, отправляясь от
порций области <з7 при помощи операций (5) в узком смысле и (С).
Таким образом, мы пришли к противоречию, а это показывает, что
каждый член последовательности (1) нормален.
46
Н. Н. ЛУЗИН
Установив это, возьмем множество Е. Если мы имеем Е = Е^ -+-
■+- Е& -н . .., то можно писать
£ = |]С£з, -С£р, ...СЕ9м_,-Е9п.
Так как член Е$ последовательности (1) нормален, то каждый член этого
ряда определяется при помощи (5) в узком смысле и (С), отправляясь
от порций области о7. [Значит, это справедливо и для самого
множества Е и, следовательно, оно измеримо В.
Если мы имеем Е = Е$1 • Е^ ... Е$п ..., то можно писать
СЕ = 2 £р. " £ь • • • ^Зп-t * СЕ$Н,
n=l
а так как член Ер последовательности (1) нормален, то мы вынуждены
заключить, что множество С£, а, значит, и самое множество £
определимо при помощи операций (S) в узком смысле и (С), отправляясь
от порций области <Э'. Итак, Е измеримо В1 (ч. т. д.).
Одним из следствий этого является то, что всякое множество,
измеримое Ву может быть получено, отправляясь от порций основной
области <Э', при помощи следующих двух операций, неограниченно
повторенных:
1°. Составление суммы бесконечного числа уже определенных
множеств Е1У Е2, ..., Еп, ... без общих частей
Ех -+• £2 -+- ... -ь Еп ■+- (S)
2°. Взятие дополнения к данному множеству Е
СЕ. (О
Образование множеств» измеримых В, при помощи переходов
к пределу» Мы хотим теперь изучить связь между понятием
множества, измеримого В, и другими операциями.
Прежде всего мы имеем следующее важное предложение, которое
позволяет получать множества, измеримые В, рассматривая лишь
монотонные последовательности множеств.
Множество, которое можно получить, отправляясь от множеств
начального класса К0, при помощи переходов к пределу, применяемых
1 Эта теорема чрезвычайно важна, так как она показывает нам, что в
определении множества, измеримого В% можно одни операции заменять другими. Самая
важность теоремы, мне кажется, заставляет отметить один пункт в данном
доказательстве: мы непосредственно образовали вполне упорядоченную последовательность,
которая служит для определения множества, измеримого 2?, при помощи операций (S\
и (Р); во когда такая последовательность дана, мы не умеем непосредственно
получить вполне упорядоченную последовательность, которая служит для определения
рассматриваемого множества при помощи операций (S) и (С). Ход рассуждения
в этом случае очень косвенный.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
47
каждый раз к монотонной последовательности множеств и
неограниченно повторенных, есть множество^ измеримое В; обратно,
всякое множество, измеримое В, может быть получено этим способом.
Первая часть этого предложения вполне очевидна, так как предел
монотонной последовательности множеств El9 Е*,, ... есть либо сумма
этих множеств, либо их общая часть. Следовательно, если множество Е
может быть получено при помощи пределов монотонных
последовательностей, отправляясь от множеств начального класса К0, то множество Е
может быть получено и при помощи двух операций (S) и (Р),
отправляясь от порций области g7. Поэтому в силу предыдущей теоремы
Е измеримо В.
Чтобы доказать вторую часть предложения, возьмем вполне
упорядоченную счетную последовательность
Ео, El, Ег, ..., Ер, ..., | Е, (1)
служащую для определения заранее данного множества Е, измеримого В,
при помощи операций (S) и (Р), неограниченно повторенных,
отправляясь от порций области с7.
Назовем нормальным всякий член Ер последовательности (1) такой,
что каждое множество-полином Р(Ер>, Еу, ..., Ер), образованное иа
конечного числа членов последовательности (1) с индексами, не
превосходящими Р, может быть получено, отправляясь от множеств
начального класса К0, при помощи переходов к пределу, примененных к
монотонным последовательностям множеств. Ясно, что существуют
нормальные члены, так как таковым является начальный член Е0.
Я теперь утверждаю, что каждый член последовательности (1)
нормален. В самом деле, в противном случае существуют анормальные
члены; пусть Ер — первый из них. Следует различать два случая.
В первом случае мы имеем
Ер = Ерх -+- Ept -+- ... -t-Ерщ-*- ...,
где р! < Р2 <! • • • предшествуют р. Обозначим через SH сумму п первых
членов этого ряда. Бесконечная последовательность Sl9 S2, ..., S„, ♦..
очевидно, возрастающая, и мы имеем
Ep = \imSn.
«-►00
Пусть Р{Еу, Ер», ..., Ер) — любое множество-полином, образованное
из конечного числа множеств последовательности (1) с индексами, не
превосходящими р. Мы, очевидно, имеем
Р(Ер>, Ер-, ..., Ер) = \\тР{Ер>, Ер», ..., Sn),
Н->00
причем важно заметить, что множества Р(Ер», Ерп9 ..., S„) образуют
при неограниченно возрастающем п возрастающую последовательность
48
Н. Н. ЛУЗИН
множеств, так как SH растет. Следовательно, операция lim здесь
применена к случаю монотонной последовательности.
С другой стороны, множество-полином Р(Еу, Е$», ..., Sn) может
быть записано в форме
Р(£>, £3", ..., Е&-*-Е& ч- ... -+-E?u) = Q(Ep, Ey, ..-,£?,, -.., Е?п).
Мы видим, что это множество-полином образовано из множеств
с индексами, строго меньшими, чем (3. Отсюда следует, что множество Q
может быть определено, отправляясь от множеств класса К0, при
помощи монотонных переходов к пределу и, следовательно, то же
справедливо и для множества-полинома Р(Ер, Ер»> ..., Е$). Значит, £р есть
нормальный член последовательности (1), что противоречит нашей
гипотезе.
Во втором случае мы имеем
Е? = Е& • Е& •• •»
где Рх <СГ Рг <С • • • предшествуют (3. Обозначим через ъп общую часть п
первых членов последовательности £?„ £&, Бесконечная
последовательность ъ19 ^2) • • •> ^п, • • •> очевидно, убывающая, и мы имеем
£р = lim^n.
и-* со
Как и в предыдущем случае, мы можем написать
Р{Е?У Ер», ..., £e) = lim Р(Е$>9 Еу, ..., wM).
Я->СО
Мы видим, что переменное множество Р(Е$> Е$»., ..., ъп) убывает, когда
л неограниченно возрастает. Следовательно, множество Р(£р', £р«, ...
..., Е$) получается при помощи монотонного перехода к пределу.
С другой стороны, переменное множество Р(£р', Еу, ..., тс„) может
быть записано в виде полинома
Р(£р>, £>, ..., £(э, •£&, ..., £р„) = Q (£|3', £(*", ..., £р,, ..., £pw),
образованного из множеств с индексами, строго меньшими, чем р.
Значит, множество Q можно определить, отправляясь от множеств
начального класса К0, при помощи монотонных переходов к пределу. Отсюда
следует, что £р— нормальный член последовательности (1), что
противоречит нашей гипотезе.
Итак, все члены последовательности (1) нормальны.
Перейдем теперь к рассмотрению данного множества Е.
Мы имеем
Е = lim (£<з, -+- £& -ь ... -+- £(зм)
П-*СО
ИЛИ
Е = lim (£Pl • £р2 ... £рп),
♦|-*СО
где все E$t являются множествами, предшествующими £; так как все £^
нормальны, то мы отсюда заключаем, что множество £ может быть
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
49
определено, отправляясь от начального класса К0> при помощи
неограниченно повторенных монотонных переходов к пределу. Ч. т. д.
Это предложение чрезвычайно важно, так как оно показывает, что
при изучении множеству измеримых Ву можно ограничиваться
изучением начального класса К0 и рассмотрением монотонных переходов
к* пределу у неограниченно повторенных м, разумеетсяу чередующихся1.
Остается рассмотреть лишь общий (немонотонный) переход к
пределу lim, а также операции взятия верхнего предела lim и нижнего
предела lim. Эти рассмотрения не представляют никакого затруднения.
Прежде всего, так как нахождение предела монотонной
последовательности множеств есть частный случай операций lim, lim и lim,
всякое множество, измеримое 5, может быть получено, отправляясь от
начального класса К0> при помощи каждой из трех операций lim, lim
и lim, неограниченно повторенных.
С другой стороны, так как каждая из этих операций может быть
приведена к сложению и взятию общей части (стр. 17), то
множества, которые могут быть получены, отправляясь от начального
класса ЛГ0, при помощи операций lim, lim и lim, неограниченно
повторенных, будут все измеримы В.
Проблема меры Бореля. Вышеуказанный процесс образования
множеств (стр. 24) Борель ввел с целью уметь „измерять" множества.
Пусть
Еоу Е\у E<iy —, Е$у ... | £ (1)
— счетная вполне упорядоченная последовательность множеств,
служащая дая определения множества Еу измеримого Ву отправляясь от
порций области <Э\ при помощи операций: (S) — составления суммы
счетного числа множеств без общих частей и (D) — взятия разности двух
множеств, из которых одно содержит другое. Мы предполагаем, что
все множества последовательности (1) расположены на (0, 1).
Следуя идеям Бореля, каждому члену последовательности (1),
являющемуся порцией области g7, приписывают его длину. Этим способом
некоторым членам последовательности (1) будут поставлены в
соответствие числа, которые мы будем называть мерами этих множеств.
Допустим, что процесс определения меры дошел до члена £р.
В этом случае, если Е$ = Е^ -+-Е& -+- •.. -н£рп-н ..., то Борель
приписывает £р меру тя£р, равную сумме ряда:
тЕь ■+- тЕъ -+- ... -+- тЕ^ -+- ...,
где Е$п в силу сделанной гипотезы уже получило меру rnEfa так как
Зп<р. Если же Е? = Еь—Е$и, то Борель приписывает £? меру тЕ$,
равную разности
тЕрг — тЕ$х у
1 Это основной результат теории Юнга.
50
Н. Н. ЛУЗИН
причем множества Е\ и Е\ уже имеют меру, так как они предшествуют
Е?, ?iO и %<$.
Таким образом, в принципе процесс продолжается, не останавливаясь,
и пробегает последовательность (1) до тех пор, пока мы не дойдем до
последнего члена £, который, таким образом, получает некоторую меру тЕ.
Так полученное число тЕ называется мерой Бореля.
Это определение меры так естественно, как только можно, и однако
мы наталкиваемся на следующие три затруднения:
1°. Мы можем встретить расходящиеся ряды.
2°. Мы можем придти к отрицательной мере.
3°. Получая некоторое множество Е двумя различными способами,
мы можем приписать ему две разные меры.
Все эти трудности отпадают, если принять концепцию меры Лебега,
так как по самому ее определению мера Лебега есть всегда
неотрицательное число и единственное для каждого измеримого множества.
И так как легко доказать, что число тЕ Бореля совпадает с мерой
Лебега, то все трудности устранены.
Тем не менее, если рассматривать теорию меры Бореля независимо
от лебеговской, очевидно, что надо внутренним образом преодолеть эти
три затруднения. В этом проблема меры Бореля.
Не входя в рассмотрение вопроса о возможности разрешить эту
проблему1, мы заметим, что все три затруднения сводятся ко второму,
т. е. к невозможности получить отрицательную меру.
Прежде всего, если бы мы встретили расходящийся ряд
где множества £&,, £^,... попарно без общих точек, мы могли бы
взять столь большое число N его членов, что их сумма превосходит 1.
Останавливая последовательность (1) после того, как написаны члены
Ен , Е^ ,..., Е«у9 и прибавляя затем два новых члена, из которых один
есть сумма Е^ ■+- Е^ -*-... -+- Е^х, а другой — дополнение к этой сумме
по отношению к порции (0,1), мы видим, что последний член получает
отрицательную меру.
Чтобы доказать, что трудность 3° также сводится к трудности 2°,
допустим, что некоторое множество Е было определено двумя
различными последовательностями (1). Заставляя все члены одной
последовательности следовать за членами другой и прибавляя к так полученной
последовательности множество <§, не содержащее ни одной точки, мы
видим, что S получает отрицательную меру, если его рассматривать
как разность двух множеств £, геометрически тождественных, но
построенных разными способами.
1 На мой взгляд, эта проблема представляет лишь технические трудности» ее
решение не требует непременно бесконечного множества операций, имеющего
мощность континуума.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
51
Итак, все сводится к тому, чтобы доказать, что невозможно получить
отрицательную меру1.
Множество многих измерений. Для определенности мы
ограничимся случаем множеств в пространстве двух измерений.
Возьмем евклидово пространство S двух измерений. Пусть в этом
пространстве дана какая-нибудь система прямоугольных осей, которую
мы обозначим через XOY.
Назовем основной областью двух измерений множество всех точек
М(х> у) плоскости XOY, у которых обе координаты х и у
иррациональны. Эту основную область мы обозначим через 7АУ.
Назовем порцией У'ху множество тех точек М(х, у) этой области,
координаты z и у которых принадлежат порциям (а, Ь) и (с, d)>
лежащим, соответственно, в линейных основных областях -7х и -7Ь [4].
Мы скажем, что множество Е точек области 7ху есть множество
начального класса К0, если как Е, так и его дополнение СЕ (по
отношению к 72у) является суммой конечного или бесконечного множества
порций области 7ху.
Если мы захотим проанализировать все определения и рассмотрения,
которые были даны выше и касались линейных множеств, то мы
убедимся, что они применяются без всяких изменений к многомерным
областям.
В частности, множества, измеримые 5, это множества, которые
могут быть получены из множеств начального класса К$ при помощи
операций (S), (P), lim, lim, lim или же при помощи только монотонных
переходов к пределу, неограниченно повторяемых.
1 В главе II мы укажем элементы, позволяющие, на ьаш вэгакл, вайти решение
проблемы меры Бореля.
ГЛАВА II
ИССЛЕДОВАНИЯ О СТРУКТУРЕ МНОЖЕСТВ, ИЗМЕРИМЫХ В
Классификация множеств, измеримых В
Классы Валле-Пуссена. Отправляясь от начального класса ЛГ0, при
помощи основной операции Нт мы формально определяем шаг за шагом
последовательные классы Валле-Пуссена 2
^М)> ^М> ^29 • - •» К-пу • • •> Л,,-,» • • •» Ла, . . . I У.
Класс Ка здесь определяется логически (т. е. формально), как
множество всех точечных множеств Е, которые являются пределами
множеств Еп предыдущих классов E = \imEn, но сами не принадлежат
к предыдущим классам.
Из этого определения следует, что каждый класс может содержать
только множества, измеримые В; обратное также справедливо: всякое
множество точек Е, измеримое В, принадлежит к некоторому
определенному классу Ка, так как Е получается из начального класса К0
при помощи операции lim, неограниченно повторенной, и каждое
промежуточное множество Ез счетной вполне упорядоченной
последовательности
^о» £\1 *^ъ • • •» **<л» • • •» ^З» • • • I ^ч \ч
1 Бэр дал лишь классификацию функций [5].
С тех пор было дано много классификаций множеств; среди них первая была дана
Лебегом (»Sur les fonctions representables analytiquement", стр. 156). Вот принципы
этой классификации: некоторое множество точек, измеримое В% называется
множеством класса а, если его можно рассматривать как множество тех точек, где
некоторая функция класса а обращается в нуль, и если это невозможно л^я функции
класса меньше, чем а.
Классификация множеств, которую мы здесь принимаем, принадлежит Валле-
Пуссену (см. его книгу „Tntegrales de Lebesgue, fontions d'ensemble, classes de Baire",
стр. 371). По-видимому, Валле-Пуссен более верен идее Бэра, чем Лебег, так как
классификация Валле-Пуссена есть в сущности не что иное, как непосредственное
применение принципов Бэра к классификации функций, принимающих лишь два
значения 0 и 1.
Мы вводим лишь легкое изменение в эту классификацию, устраняя рациональные
точки, что позволяет нам формулировать результаты в более простом виде и избегать
исключительных случаев.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
53
служащей для определения множества £, очевидно, принадлежит к
классификации Валле-Пуссена. Таким образом, мы видим, что совокупность
множеств, измеримых Ву совпадает с совокупностью множеств,
входящих в классы Валле-Пуссена.
Ясно, что все классы классификации Валле-Пуссена не имеют
попарно общих элементов.
Для удобства речи мы в дальнейшем не будем делать словесного
различия между классом, к которому принадлежит данное множество
точек Еу и рангом, соответствующим этому классу. В этом смысле
класс некоторого множества Е есть просто конечное число или
трансфинитное число второго класса.
Класс множества Е будет обозначаться символом
cl£.
Таким образом, мы будем для множества Е> принадлежащего классу Кл
классификации Валле-Пуссена, писать равенство
с1£=ос.
Раньше мы указывали, что классы Валле-Пуссена определены лишь
формальным образом, т. е. логически; чтобы убедиться в этом,
достаточно заметить, что если один из этих классов, например Кр пуст
(лишен элементов), то весь остаток классификации
^p+i» ^р+2> • • •> АГа, ... | 2
по необходимости также пуст, и последовательность логически
определенных классов становится иллюзорной.
Итак, дая того чтобы иметь концепцию вполне определенного
класса Ка, надо доказать, что он не пуст, т. е. что он содержит
эффективно множества. Мы видим, что речь идет о некотором рассуждении,
при помощи которого можно установить существование множеств Е>
принадлежащих к этому классу АГв.
Способы, при помощи которых в настоящее время устанавливают
существования в математическом анализе, могут быть разделены на
четыре категории.
1°. Доказательство существования с использованием аксиомы
ЦермелОу полученное применением принципа произвольного выбора.
В дальнейшем мы устраним этот способ рассуждения по причине тех
затруднений, которые возникают при желании хорошо понять его
сущность. Кроме того, этот способ рассуждения никогда не дает
индивидуальных объектов, но всегда приводит нас к классам, быть может,
лишенным элементов, которые можно индивидуально различить.
2°. Доказательство существования с использованием совокупности
трансфинитных чисел второго класса. Этот способ действий был
.54 н. н. л у з и н
впервые употреблен Лебегом в его исследованиях о функциях, не
допускающих никакого аналитического изображения1.
3°. Доказательство существования, установленное при помощи
диагонали Кантора. Этот способ действия был употреблен Борелем и
Лебегом2 и оказал науке серьезные услуги: им в теории функций
доказаны важные теоремы существования.
4°. Конструктивное доказательство существования. Бэр первый
дал конструктивные примеры функций классов 0, 1, 2 и 3 в его
классификации^. Было бы чрезвычайно желательно, чтобы исследования
Бэра о конструктивном существовании множеств высших классов были
продолжены и распространены, несмотря на всю их трудность. В
дальнейшем мы даем лишь конструктивное доказательство существования
множества (или функции) класса 4, принадлежащее Л. В. Келдыш.
Трудности быстро возрастают с повышением класса множеств.
Если мы хотим проанализировать процессы, при помощи которых
устанавливается существование математических объектов, то вот что
мы практически констатируем: методы доказательства существований
бывают весьма различной природы и теоретически не сводимы друг
к другу; таким образом, нельзя говорить о существовании в общем
смысле или в абсолютном смысле. Понятие существования
математического объекта в абсолютном смысле кажется при современном
состоянии науки слишком неясным, чтобы приписать ему смысл. Все, что
можно сделать, это просто говорить о существовании, установленном
тем или другим методом, т. е. об относительном существовании.
По этой-то причине, говоря о существовании, мы всегда будем
указывать метод, в смысле которого установлено рассматриваемое
существование. Так мы будем говорить о существовании в смысле
совокупности 2, о существовании в смысле диагонали и о существовании
конструктивном [6].
В данный момент мы не останавливаемся на доказательствах
существования множеств всех классов классификации Валле-Пуссена: мы
лредпочитаем принять это существование как постулат и извлечь из
него все полезные следствия.
Простейшие свойства классов Валле-Пуссена. Мы сначала укажем
свойства классов в некотором роде формальные, а именно те, которые
являются немедленным следствием логического определения класса.
Теорема I. Если множество точек Е принадлежит к КаУ то и
его дополнение СЕ также принадлежит к Ка.
1 „Sur les fonctions representables analytiquement" (Journ. de math., 214» 190S).
2 E. В о г е 1. Lemons sur les fonctions de variables reeles, Iе ed.t 1905, стр. 156,
Note III: Sur Texistence des fonctions de classes quelconque; H. Lebesgue. Sur
les fonctions representables analitiquement, стр. 207.
3 R. В aire. Sur la representation des fonctions discontinues (Acta Math., 30,
1905).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
55
По самому определению, начальный класс Ки обладает указанным
свойством.
Допустим, что существуют классы анормальные, т. е. лишенные
этого свойства, и обозначим через К^ первый анормальный класс.
Пусть Е есть множество, принадлежащее к К^ без того, чтобы его
дополнение принадлежало к К^
Мы тогда имеем равенство
Е = lim £„,
где Еп есть множество класса К^ предшествующего К^, ^м<£. Так
как класс ЛГ^ нормален, то дополнение СЕп принадлежит к К^ В силу
очевидного равенства СЕ = lim CEH; отсюда следует, что СЕ не может
принадлежать к классу выше, чем гр. С другой стороны, СЕ не может
быть класса ниже (3, так как К^ есть первый анормальный класс, и мы
имели бы cl£<p. Итак, мы имеем с1С£ = Р, и мы пришли к
противоречию.
Итак, все классы классификации Валле-Пуссена нормальны, что и
доказывает наше предложение (ч. т. д.).
Теорема II. Сумма конечного числа множеств и общая часть
конечного числа множеств принадлежит к классу, не превосходящему
наибольший из классов составляющих множеств.
Теорема III. Сумма счетного множества и общая часть
счетного множества множеств принадлежит к классу, не превосходящему
класс, непосредственно следующий за классами всех составляющих
множеств.
Теорема IV. Операции lim En и lim En приводят к множествам
класса не более чем на единицу превосходящего тот, который
непосредственно следует за классами всех множеств Е%.
Метод доказательства этих трех теорем тот же, как и для случая
теоремы I. Мы убеждаемся, что класс 0 обладает формулированным
свойством, и, предполагая, что существуют „анормальные*4 классы,
приходим к противоречию. Это есть рассуждение методом трансфинитной
индукции. Чтобы не утомлять читателя повторением одних и тех же
слов, мы опускаем доказательства.
Теорема V. Множество-разность Е%—Ех принадлежит к классу,
не превосходящему наибольший из двух классов о\Ех и cl£2*
В самом деле, если Е = Е2 — Ev то мы можем написать Е = Е2- СЕ1У
и теорема сводится к теореме II.
Достижимость
Определения. Чтобы изучить структуру каждого класса
классификации Валле-Пуссена, нам нужны следующие важные определения.
Мы скажем, что множество Е, принадлежащее к классу Ка,
достижимо сверху, если Е есть общая часть счетного множества множеств
классов, меньших а.
56
Н. Н. ЛУЗИН
Точно так же мы скажем, что множество Е, принадлежащее
к классу Ка, достижимо снизу, если Е есть сумма счетного множества
множеств классов, меньших а.
Из определения следует, что если множество Е класса Ка
достижимо сверху, то его дополнение СЕ достижимо снизу, и обратно.
В самом деле, из равенства £"= Ег- Е2- -. следует равенство
СЕ = СЕ1-+-СЕ2 + ...
Ясно, что необходимым условием для того, чтобы множество Е
было достижимо сверху или снизу, является равенство E = limEn, где
множество Еп класса ниже, чем класс Е, и где Enz^E или же EnczE
при всяком п.
Установив эти основные определения, дадим еще некоторые весьма
полезные определения.
Назовем двусторонним всякое множество класса Ка, достижимое
одновременно сверху и снизу. Множество Е класса Ка называется
односторонним, если оно достижимо сверху или снизу, но не есть
двустороннее.
Наконец, мы скажем, что множество Е класса Ка недостижимо
с обеих сторон, если оно не является достижимым ни сверху, ни снизу.
Несуществование двусторонних множеств в классах первого
рода» Класс Ка классификации Валле-Пуссена будет называться
классом первого рода, если существует класс Ка*у непосредственно ему
предшествующий; а = а*ч-1. В противном случае Ка будет второго
рода.
Начальный класс К0 мы будем считать классом второго рода.
Все классы первого рода обладают важным свойством:
Теорема. Классы первого рода не могут содержать
двусторонних множеств.
В самом деле, пусть Е есть множество, принадлежащее к классу К<1^.1.
Если Е двустороннее, то мы имеем
£ = е1-не2-н...-|-ея-|-.. .
и
СЕ = \Ч- 7)2 Н-. . .-«- 7]Я-Н . . .,
где все ея и ?)„ — множества классов ^а попарно без^общих точек.
Следовательно, мы можем писать
где множества с двумя индексами е^ и i)W все класса ниже а.
Установив это, возьмем множество ЕПу определенное следующим
равенством:
Еп = 2 ф • О* • C-r\f... Ст)И.
Ясно, что cl£„<a.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ 57
Мы докажем, что множество Еп имеет своим пределом множество Е,
когда п неограниченно возрастает.
Если точка х принадлежит к Е, то существует составляющее
множество для Е> пусть е<, которое содержит х. Значит, точка х
принадлежит к каждому из множеств г<и> дая достаточно большого л.
С другой стороны, эта точка не принадлежит к СЕ; значит она не
принадлежит ни одному из / множеств \, г\2, ..., rti. Так как / есть
постоянное число, то х не входит ни в одно из / множеств r^\ yf»\ .. ., т^>
для достаточно большого п. Отсюда мы заключаем, что х принадлежит
каждому из / дополнительных множеств О//1), Ctf£\ ..., Сг{р и,
следовательно, принадлежит к Еп при достаточно большом я.
Если точка х принадлежит к СЕ, то существует такое число /,
что х принадлежит к v Следовательно, х не принадлежит ни к одному
из / множеств elt е2, ..., е4_х и Ст)». Так как индекс / постоянен, мы
отсюда заключаем, что л: не принадлежит ни одному из множеств
E<i\ e2W)> • • •» £{i-i и Ст$\ если только число п достаточно велико. Из
определения множества Еп следует, что х не принадлежит к Ея при
достаточно большом п.
Таким образом, мы вынуждены заключить, что бесконечная
последовательность множеств Ех> Е2, • •., Ем ... сходится и имеет Е своим
пределом. А так как cl £„<<*, то класс Е не может превосходить аг
что противоречиво, ибо cl £ = <*-*-1.
Итак, множество класса Ка+1 не может быть двусторонним (ч. т. д.).
Теорема о знакочередующихся рядах* Мы теперь докажем одну
теорему, которая будет очень полезна в дальнейшем.
Теорема. Если множество точек Е есть сумма убывающего-
знакочередующегося ряда множеств классов, меньших а, то
множество Е либо класса ниже а, либо двустороннее класса а.
В самом деле, пусть
h ^=-1,^ h2 ~*-<Ьз ^4 "**"• • • >
где
fjD^DjpjD ...Э£„Э... и с1£я<а.
Так как мы можем писать (стр. 22)
£=(£1_£2) ч-(£3-£4)-ь(£6-£в)-1-...
и
СЕ=СЕ1 + (Е2-Е3)-*-(Е<-Еь)ч-...у
мы заключаем, что или cl Е < а или Е есть двустороннее класса а, что'
возможно только в том случае, когда а второго родау т. е. является
предельным классом (ч. т. д.).
Мы дополним этот результат следующими замечаниями:
Замечание I. Если Е есть сумма убывающего
знакочередующегося ряда множеств классов ^а, то класс Е также ^а.
58
Н. Н. ЛУЗИН
В самом деле, класс К х не может содержать двусторонних
множеств.
Замечание II. Если Е есть сумма убывающего знакочередующегося
ряда множеств либо класса <а, либо двусторонних класса КаУ то
множество Е также либо класса <[ а, либо двустороннее класса КЛ.
В самом деле, формулы
£ = (£,-£8)-ь (£,-£,)-и...
С£ = С£, -ь (£, - £3) ■+• (£* - £8) ■+- • • •
показывают, что Е и СЕ являются суммами множеств класса <[а.
Значит, либо cl£<Ca, либо Е есть двустороннее класса а.
Структура классов
Чтобы изучить структуру классов классификации Валле-Пуссена,
мы постулируем существование множеств Е всякого класса.
Значит, мы предполагаем, что каков бы ни был класс Ка
классификации Валле-Пуссена, существуют множества Е, принадлежащие к Ка.
Из этого постулата мы теперь извлечем важные следствия,
касающиеся структуры каждого класса ЛГа классификации Валле-Пуссена.
Лемма 1. Если классы, предшествующие некоторому классу
второго рода Ка> не лишены элементов, то в классе Ка содержатся
двусторонние множества.
В самом деле, пусть Ка — предельный класс (т. е. второго рода)
и пусть
есть бесконечная последовательность возрастающих трансфинитных
чисел, имеющих а своим пределом.
Раз класс Кап не лишен элементов, то существуют множества этого
класса; пусть Еп и есть множество, принадлежащее к АГ3и. Мы можем
предположить, что это множество Еп содержится в порции (п — 1, п)
•основной области о7, так как можно преобразовать всю область
<>7 = (—со, н-оо) в порцию (п — 1, п) при помощи непрерывной
возрастающей функции так, чтобы всякая порция области 3f
преобразовалась в некоторую порцию из (л — 1, п) и обратно: это преобразование1
приведет в соответствие всякому множеству Е9 измеримому В и
лежащему в области о/\ множество Е\ также измеримое В и того же класса,
лежащее в (п — 1, п).
1 Чтобы увидеть возможность подобного преобразования, заметим сначала, что
преобразование х = , _^_ преобразует указанным способом бесконечную порцию
(О, ч-оо) в конечную порцию (О, -4-1). Отсюда следует, что можно преобразовать
указанным образом всю область с? в порцию (—1, -+-1). С другой стороны, всякую
конечную порцию можно преобразовать в любую конечную порцию при помощи
линейного преобразования с рациональными коэффициентами.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
59
Установив это, рассмотрим множество £, определенное равенством
£ = £,-«-.£, »-.. .н-£я-ь...
Ясно, что cl£^a. Но мы не можем иметь с1£<д. В самом деле,
^сли cl£<a, то существует такое число *„, что мы имеем неравенство
cl£<an<a, ибо а есть предел чисел aw. А так как класс общей
части £ и любой порции области J никогда не превзойдет класса £,
то мы приходим к противоречию, так как общая часть Е и (п—1, п)
•есть множество £„, класс которого ая превосходит cl£.
Итак, множество Е есть в точности класса а.
Обозначим через 6п дополнение к Еп относительно порции (п — 1, л).
Ясно, что cl Sn = cl En = ая. Мы, очевидно, имеем
СЕ = {—оо, 0)н-6\-ь^ь...-ь6>... (2)
Равенства (1) и (2) показывают нам, что £ и СЕ достижимы снизу.
Значит £ есть двустороннее множество класса а (ч. т. д.).
Лемма 2. Если класс Ка первого рода не лишен элементов, то
в этом классе есть множества односторонние и множества,
недостижимые с обеих сторон.
В самом деле, в классе Ка не может существовать двусторонних
множеств. Значит, если £ есть множество класса а, то возможны
только два случая.
В первом случае множество £ достижимо только с одной
определенной стороны; в этом случае его дополнение СЕ есть тоже
одностороннее множество, но уже достижимое с другой стороны. Так как
область J может быть преобразована в порцию при помощи
непрерывной возрастающей функции, то существуют в каждой порции (а, Ь)
области с7 односторонние множества класса а, достижимые сверху и
достижимые снизу.
Установив это, возьмем на (0, -ноо) множество Ег класса а,
достижимое сверху, и в (—оо, 0) множество £2 класса а, достижимое снизу.
Ясно, что сумма Ех ■+■ £2 есть множество класса а, недостижимое с обеих
•сторон.
Во втором случае множество Е недостижимо с обеих сторон.
Возьмем равенство
£ = lim£„,
и -►оо
где £я есть множество класса <Са- Так как операция lim есть частный
случай операции lim, мы можем написать
£ = (£1-»--£2-н£зН-...)(£о-н£зЧ-...)(£зЧ-...)...
Я теперь утверждаю, что среди скобок имеется не более конечного
числа таких, классы которых <а. В самом деле, в противном случае
60
Н. Н. ЛУЗИН
Е было бы достижимо сверху, так как мы могли бы стереть все скобки
класса <С а без того, чтобы общая часть оставшихся скобок изменилась.
Итак, существуют скобки, класс которых в точности равен а. Ясно,,
что это будут множества, достижимые снизу, так как cl £„<!<*. Итак,
второй случай сводится к первому (ч. т. д.).
Лемма 3. Если класс Ка второго рода содержит множество,
которое не является двусторонним, то он содержит множества
односторонние и недостижимые с обеих сторон.
Доказательство этой леммы тождественно с предыдущим, так как
гипотеза, что а первого рода, была введена лишь для того, чтобы
получить множество, которое не будет двусторонним.
Чтобы закончить изучение структуры классов, нам потребуется одно
важное предложение, показывающее, какую особую роль играют
двусторонние множества в классификации Валле-Пуссена.
Теорема. Предел последовательности двусторонних множеств
класса а есть всегда множество класса ^а.
Чтобы доказать эту теорему, возьмем такое множество, что
Е = lim ЕПУ
где все Е„ — двусторонние множества класса а.
Мы имеем следующие равенства:
Е = (£x4-£2-b £3-*-•••)• (£2 -«"£3 -*-..-) -(£3 -+-.>)• ••
и
Е = (Ег • Е2 • £3- • •) -+- (£2 * £з- • •) -+- (Ез- -О-1"--
Так как каждое Е4 есть двустороннее класса а, то все скобки в обоих:
разложениях Е оказываются множествами класса ^а. Значит если бы;
множество Е было класса а-+-1, оно было бы двусторонним в ЛТа+1,
Но это невозможно, так как класс Ка+1 первого рода (ч. т. д.).
Итак, операция предела двусторонних множеств класса а не пег
вытает класса.
Теперь мы можем формулировать основное предложение:
Основная, теорема о структуре классов. Всякий класс
Ка+1 первого рода образован из множеств односторонних и
недостижимых с обеих сторон; всякий класс Ка второго рода содержитТ
кроме того, двусторонние множества.
Эта теорема есть синтез трех предыдущих лемм.
В самом деле, если Ка первого рода, то достаточно предположить,
что в Ка есть множества; в силу леммы 2 существование множества
в Ка влечет за собой существование в классе Ка множеств всех
возможных видов.
Если Ка второго рода, достаточно предположить, что есть
множества в следующем классе /Гв+1; в силу леммы 3 существование
множества в АГа+1 влечет существование в Кл множеств всех видов.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
61
Интересно заметить, что если а второго рода, недостаточно
существования в Ка одного множества, так как оно может оказаться
двусторонним. Напротив, существование множества в следующем классе К%+г
влечет существование в Ка множеств, которые не будут двусторонними,
так как нельзя получить множество класса а -+-1 переходом к пределу,
отправляясь от двусторонних множеств. В этих условиях лемма 3
применима.
С другой стороны, всякое множество Е класса а второго рода,
очевидно, может быть получено как предел двусторонних множеств
класса а.
Окончательно мы приходим к следующему заключению о структуре
классов второго рода в классификации Валле-Пуссена: двусторонние
множества образуют очень важную составную часть каждого класса
второго рода. В образовании множеств, измеримых В, можно сравнить
роль двусторонних множеств с ролью множеств начального класса Ки:
порции начального класса К0 играют ту же роль, как множества
классов, меньших а, а другие множества из К0 играют ту же роль, как
множества двусторонние, тогда как односторонние множества и
множества, недостижимые с обеих сторон класса Ка второго рода, играют
ту же роль, как множества класса Кг!.
В силу особых свойств двусторонних множеств мы назовем базой
каждого предельного класса Ка множество всех двусторонних множеств
и обозначим ее через Ва.
Отделимость
Мы теперь введем одно очень важное определение, которое в
дальнейшем будет играть самую существенную роль.
Мы скажем, что два множества Ег и Е2 класса а первого рода
отделимы, если можно построить два множества Нх и Н2 классов
ниже а без общей части, которые содержат соответственно множества Ех
и Е2; множества Нх и Н2 будем называть отделяющими. Точно так же
назовем отделимыми два множества Ег и Е2 класса Ка второго рода,
не принадлежащие к базе 2?а, если отделяющие множества Нх и Н2
принадлежат к этой базе. Наконец, два множества Ех и Е2 базы BQ
называются отделимыми, если классы отделяющих множеств Нх и Нг
меньше а.
Эти определения имеют качественный характер, так как они дают
нам лишь идею отдаленности двух множеств, без того чтобы эта
отдаленность могла быть точно измерена. В дальнейшем мы дадим
дескриптивную меру „расстояния" двух множеств, измеримых В.
Пока же мы ограничимся указанием на то, что два множества Ег
1 Представляется естественным объединить классы 0 и 1 в один и рассматривать
«го как предельный класс. Быть может» в этом и заключается причина, по которой
теорема Бэра относится к функциям класса < 1, а не только класса 1.
62 н. н л у з и н
и £.,, лежащие в двух непересекающихся порциях (aiy bx) и (а2, Ь>)
основной области У, должны быть рассматриваемы как чрезвычайно
отдаленные. Взаимное отдаление множеств Ег и Е2, измеримых В,
становится тем меньше, чем выше класс отделяющих их множеств Нг и //.,„
Элементы класса К0. Мы рассмотрели структуру классов
классификации Валле-Пуссена. Чтобы анализировать структуру самих
множеств данного класса К0, мы примем за инструмент множества,
достижимые сверху.
Назовем элементом всякое множество класса К^ достижимое
сверху, но не принадлежащее к базе 57, когда класс Ка второго рода.
Введение понятия элемента класса а очень естественно по причине
многочисленных и глубоких аналогий между элементами любого класса
и обыкновенными точками.
}^— ^Н \^— •——Ч
at x1 bt аг х2 Ьг
Рис. 2.
Отдельно взятая точка есть элемент класса 1. Если хх и х,— две
различные точки, они отделимы при помощи порций (ат, Ьх) и (а.,, Ь,)
основной области g7.
Мы имеем глубокую и полную аналогию между этим свойством
точек и следующим свойством элементов класса Ка: два любых
элемента класса Ка без общей части всегда отделимы при помощи
множеств низших классов или множеств, принадлежащих базе Ва.
Это мы изображаем на следующем схематическом чертеже, где
символические границы элементов Е1 и Е., должны быть тем более
извилисты, чем выше класс а.
Рис. 3.
Мы теперь переходим к доказательству основной теоремы об
отделимости элементов, не имеющих общей части.
Основная теорема. Два элемента любого класса КЛ без
общей части всегда отделимы.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
63
Пусть £ и о—два элемента класса К7 без общей части.
Так как £ и S суть множества, достижимые сверху, то мы можем
образовать две убывающие последовательности множеств класса <С*
£^£,1)...=)£„::...
О ~ -> С —\ —^ с*
такие, что предел первой из них есть элемент £, а предел второй
элемент &.
Установив это, напишем две вертикальные схемы:
Рис. 4.
и возьмем все произведения двух букв, лежащих на одной и той же
наклонной прямой, со знаком н-, а произведения двух букв, стоящих
на одной и той же горизонтальной прямой, со знаком —. Мы получим,,
таким образом, два убывающих знакочередующихся ряда множеств
классов <Са
з/Е1 — Ег£г "+■ SiE* — £>62 "+■ &>Е$ —...
и
?7б\ &\Ех-*~ Ех§2 62^2 "*" &2^3
Эти ряды множеств, очевидно, сходятся, так как элементы £ и о
не имеют общей части и, следовательно, общий член обоих рядов имеет
пределом пустое множество.
Пусть Их есть сумма первого и Нг — сумма второго ряда.
Возьмем теперь любую точку х области с/ и предположим, что она
принадлежит к к членам левой колонны и V членам правой колонны
предыдущей вертикальной схемы. Так как первым членом в обеих
колоннах стоит g7, to к^ 1 и /^1.
Надо различать три случая:
Первый случат к </. В этом случае точка х не принадлежит к Нх,-
но принадлежит к //2.
Второй случай: * = /. В этом случае точка х не принадлежит ни*
к Hlf ни к Нг.
Третий случай: Jt>/. В этом случае точка х принадлежит к Н1У.
но не принадлежит к Нг.
■64
Н. Н. ЛУЗИН
Отсюда следует, что множества Нх и Н2 не имеют общей точки.
Так как общий член обоих рядов есть множество класса <Са, то
множества Н1 и Н2 либо класса <Са, либо принадлежат к базе Ва
<стр. 58).
Наконец, ясно, что Е^НХ и <§С//2# Значит, множества Нх и Н2—
отделяющие для данных элементов Е и <§ (ч. т. д).
Итак, мы имеем полную аналогию между отделимостью двух
различных точек и двух элементов без общей части. То же справедливо
и дая аналогии между одновременной отделимостью конечного числа
различных точек при помощи отделяющих порций области с7, не
перекрывающихся между собой, и одновременной отделимостью
конечного числа элементов без общих частей при помощи отделяющих
множеств, также попарно не перекрывающихся. В самом деле, мы можем
дополнить доказанную теорему следующим следствием:
Элементы класса Ка в конечном числеу не имеющие попарно общих
частей, одновременно отделимы, т. е. могут быть соответственно
заключены в отделяющие множества либо класса <Са» либо базы Ва>
попарно без общих точек1.
В самом деле, пусть Е19 Е2>• ♦•> Ет — элементы класса КаУ не
имеющие попарно общих точек; число т конечно.
Возьмем два любых элемента Ei и Ej, i=^=j. Так как эти элементы
отделимы, мы можем обозначить через Ну и Hji отделяющие
множества Ei^Hij и Ej^Hji) множества Я,-у и Ни не имеют общей точки
1Л будут либо класса < а, либо из базы Ва.
Установив это, возьмем общую часть всех множеств Нуу где
первый индекс фиксирован, а второй принимает все значения 1, 2, —, ту
кроме значения /. Эту общую часть мы обозначим через //,-.
Ясно, что множество Hi содержит множество Е4 и что оно либо
класса <С а> либо из базы Ва. Кроме того, так как два множества Ну
и Ни не имеют общей точки, то мы заключаем, что и два множества
Hi и Hj также не имеют ни одной общей точки.
Значит, одновременное отделение элементов Е1У Е1У. .., Ет при
помощи множеств Hv Н2У...уНт реализовано (ч. т. д.).
Очень естественно теперь поставить следующий вопрос: будет ли
эта одновременная отделимость опять иметь местоу если речь
зайдет о счетном множестве элементов попарно без общей части?
Мы видим немедленно, что ответ отрицателен, даже когда дело
касается точек области о7: достаточно взять любое счетное множество
1 Эту теорему можно рассматривать как первый шаг на пути к автономной теории
меры Бореля. В самом деле, лишь только все множества классов, меньших а,
получили меру Бореля, элементы класса Ка ею также обладают. И предложение текста
показывает нам, что мы никогда не встретим расходящихся рядов мер Бореля
элементов класса КаУ так как в противном случае в силу одновременной отделимости
элементов мы имели бы отрицательные меры Бореля в классах, предшествующих а.
С другой стороны, каждое множество Е класса а состоит из элементов (стр. 68).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
65
точек, всюду плотное на <з7. Хотя любые две точки этого множества
заведомо отделимы при помощи порций, но нельзя отделить
одновременно все точки этого множества.
Тем не менее и здесь имеется полная аналогия между точками и
элементами. Чтобы выявить эту аналогию, полезно ввести понятие
изолированного элемента.
Изолированные множества* Известно, что точка х множества Е
называется изолированной во множестве Е, если можно найти порцию
(а, Ь) области о/, содержащую х и не содержащую никакой другой
точки из Е. Для того чтобы точка х из Е была одновременно
отделима от всех остальных точек £, необходимо и достаточно, чтобы х
была изолированной в Е. Именно по этой причине мы будем изучать
множества точек, называемые изолированными.
По определению, множество точек Е есть изолированное, если
каждая его точка изолирована. Изолированное множество точек Е
непременно счетно
и нетрудно доказать, что точки изолированного множества всегда
одновременно (т. е. равномерно) отделимы: достаточно заключить его
точки в ряд порций области <Э\ причем каждая из порций имеет
диаметр, не превосходящий половину нижней грани расстояний между
рассматриваемой точкой и другими точками множества.
Возьмем теперь в качестве путеводной нити указанную аналогию
между точками и элементами.
Пусть дана бесконечная последовательность элементов класса К€
попарно без общих частей
€li ^2> • • * у €*i • • • >
мы назовем изолированным в этой последовательности всякий элемент
ei такой, что можно определить множество Hi либо класса <Са, либо
из базы Ва, которое содержит е4 и не имеет общей части ни с одним
из остальных элементов последовательности.
Последовательность элементов класса
^1> ^2> * * * у €п> • » •
мы назовем изолированной в том случае, когда каждый из ее
элементов изолирован в этой последовательности.
Следующее предложение, вполне аналогичное тому, которое касается
изолированных последовательностей точек:
Теорема. Все элементы изолированной последовательности
класса Ка могут быть одновременно (равномерно) отделены.
Пусть еи е2,••., епу...— бесконечная изолированная
последовательность элементов класса Ка. Для заданного целого положительного
числа п обозначим через Нп множество, отделяющее ея от остальных
элементов последовательности; значит Ня либо множество класса <Са>
либо из базы Вл и содержит элемент ея> не имея общей части
ни с каким другим элементом последовательности.
66 Н. Н. Л У 3 И H
Установив это, возьмем множество 6Я, определенное равенством
0М = Нп • СНг • СН2 • ... • С//П_р
каково бы ни было /г.
Ясно, что 0Я либо класса <Са> либо из базы Ва и что оно
содержит элемент еп.
Так как множества
ei> 02>.. ., &„,...,
очевидно, попарно без общих частей, то одновременное отделение
элементов elf e2t •••> ея> • • • осуществлено (ч. т. д.).
Мы теперь возвратимся с несколько более общей точки зрения
к вопросам, касающимся изолированных семейств, рассматривая случай
любых множеств.
Пусть F есть семейство, образованное из любых множеств.
Мы скажем, что множество Е, принадлежащее к F, изолировано
в F относительно класса ЛТв, если существует множество Н либо
класса <Са> либо из базы Ва, которое содержит £ и не имеет общей
части ни с одним из остальных множеств семейства F.
Семейство F, каждое из множеств которого изолировано
относительно Ка, само называется изолированным относительно Ка.
Доказательство предыдущей теоремы снова применимо, и мы можем
формулировать несколько более общее предложение:
Всякое счетное семейство F, изолированное относительно класса
Ка> равномерно изолировано, т. е. все множества Е из F можно
одновременно заключить в ряд множеств Н попарно без общих частей
и класса <Са или из базы 2?а.
Важно знать природу множеств, которые можно получить,
составляя сумму членов изолированного семейства. Вот общее предложение:
Теорема, Сумма членов счетного семейства, изолированного
относительно Ка и образованного из множеств класса ^а, есть
множество класса ^а.
Пусть F есть семейство, образованное из множеств Е19 Е2У -. •
класса ^<х# Так как F изолировано относительно Ка> существует
последовательность Hv //2,... множеств либо класса <С а> либо из
базы Ва попарно без общих частей и таких, что Е{^Н4.
Возьмем равенства
к -*■ оо
где cl £f><«.
Множество S„, определенное равенством
^ = £Н.Я1-+-Д«).Я2-ь...н-£<Г).Яп1
будет либо класса <Са> либо из базы Вв.
Пусть х — произвольная точка области <з7. Следует различать два
случая:
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
67
В первом случае точка х принадлежит к сумме Ех-*-Е.> -+-...
Значит, существует целое положительное число / такое, что х
принадлежит к Е{ и, следовательно, к Е[м) при достаточно большом л. Так как
мы имеем £<С//^ то х принадлежит к Sn при достаточно большом л.
Во втором случае точка х не принадлежит к сумме Ех -+- Et -+ ...
Если х не принадлежит ни одному из множеств //*, оно не
принадлежит и к Sn> каково бы ни было л. Если х принадлежит к некоторому
Н{9 то х не принадлежит ни к какому другому из множеств //>, У^='\
так как множества //1Э //2,... не имеют общих частей. Отсюда
следует, что точка х перестает принадлежать к Sn9 как только Е*"}
перестает содержать х, что произойдет при достаточно большом л.
Отсюда мы заключаем, что сумма /^-+-£t-н ... есть предел
сходящейся последовательности *Slf «?2»°**> а так как *S» либо класса <Са>
либо из базы ВаУ то мы имеем
cl(£,-+-£2-+- .. )<* (ч- т. д.).
Мы дополним этот результат следующими замечаниями.
Замечание L Для того чтобы сумма членов счетного семейства
множеств класса ^<х, изолированного относительно Ка9 была
множеством класса КаУ недостижимым снизу, необходимо и достаточно,
чтобы у по крайней мереу один из членов семейства был
недостижимым снизу.
Условие необходимо, так как в противном случае каждый член £<
рассматриваемого семейства достижим снизу и, следовательно, и сумма
Z?! -+- Е2 -+-... тоже.
Условие достаточноу так как если сумма Е1 -+- Е2 -+- ... достижима
снизу, то это же справедливо а^я ее общей части с //<; но эта общая
часть есть как раз Et.
Замечание П. Если члены Et счетного семейства,
изолированного относительно Кау суть элементы класса К9 и если сумма
//х-|-//2-*- ... отделяющих множеств будет либо класса <Са> либо
из базы ВаУ то сумма Е1-*-Е2-+- ... есть элемент класса Кл.
В самом деле, в силу предыдущего случая сумма Ег ■+■ Е2 -ь ...
недостижима снизу и класса АГв. С другой стороны, возьмем
убывающую последовательность множеств класса <Са
£(0=)£(0Э...З£(0Э...,
определяющую элемент Eiy где / — любое целое положительное число.
Пусть Rn есть сумма Hw¥1 -+- Нп+ъ -§-... В этих условиях множество
«$,, определенное равенством
есть очевидно, либо класса <Са> либо из базы /?«.
Но последовательность множеств Slf S^ ... убывающая и имеет
пределом сумму £х-н£2"*--•• Значит Я,-ь£2-*-. .. непременно будет
элементом класса Кй (ч. т. д*).
68 Н. Н. ЛУЗИН
Первые сведения о структуре множества точек данного класса
Произвольное множество данного класса. Если мы хотим
проанализировать структуру множества данного класса Ка> то вполне
естественно попробовать разложить это множество на счетное множество
элементов класса Ка по причине полной аналогии между элементами
и обыкновенными точками.
Прежде всего мы имеем следующее важное предложение:
Теорема. Всякое множество класса Ка есть сумма счетного
множества элементов класса ^а, не имеющих попарно общих
частей.
Чтобы доказать это, предположим, что теорема верна для всех
классов р, меньших, чем а, и покажем, что она тогда верна и для
класса а.
Пусть Е — любое множество класса Ка, Мы имеем равенство
Е = \\тЕп,
где с!£я<а.
Так как операция lim есть частный случай операции lim, мы можем
написать
Е = (Е1- Е2- £3 • • •) ■+■ (СЕг • Е2 • Ez...) -+- {СЕ2 • £3*..) "■"• • •
Ясно, что скобки представляют собой множества, не имеющие
попарно общих частей, и что класс каждой из скобок^а.
Если класс некоторой скобки меньше а, то эта скобка по
сделанной гипотезе есть сумма счетного множества элементов класса <Са без
общих частей. Если скобка есть двустороннее множество класса Ка,
ТО она является суммой счетного числа множеств класса <^а и,
следовательно, суммой счетного множества элементов класса <а.
Но если скобка есть множество класса а и притом не
двустороннее в этом классе, то она должна быть элементом класса Ка. Итак, Е
есть сумма счетного множества элементов класса ^а без общих частей.
Так как каждое множество Е класса К0 есть сумма счетного
множества порций области <7, то теорема верна для а = 0 и,
следовательно, верна для любого а (ч. т. д.).
Таким образом, каждое множество Е класса Ка может быть
написано в форме
где еп есть элемент класса ^а, причем все еп попарно без общих
частей.
Обратное заключение неверно, так как сумма счетного множества
элементов класса <^а без общей части может оказаться эффективно
"Класса выше а: это, очевидно, тот случай, когда Е есть множество
класса АГв+1, достижимое снизу.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
09
По этой причине очень естественно искать необходимые и
достаточные условия для motOy чтобы сумма счетного множества
элементов класса Ка не давала повышения класса.
Легко отдать себе отчет в чрезвычайной важности этой проблемы.
В самом деле, если нам удастся найти достаточные условия для того,
чтобы класс повышался* мы в то же время получим эффективны!
процесс для реального построения множеств все более и более высоких
классов, а этого нам в данный момент не хватает.
Мы дадим несколько предварительных результатов по этому
вопросу.
Теорема. Если основная область 7 полностью разбита на
счетное множество неперекрывающихся элементов Еп класса <Са»
то сумма бесконечного множества элементов Епу выбранных про-
извольноу будет всегда класса <<* или принадлежать к базе В±.
ОбратнОу если сумма счетного множества неперекрывающихся
элементов класса <Са есть множество класса <Са или из базы Вл> то
эти элементы образуют часть полного разбиения всей области 7
на счетное множество элементов класса <Са-
В самом деле, если мы имеем разбиение
7 = *х ■+- t)i -ь h -+- Ъ ■+■ • • •-*- е» "*■ У* ■+■ • • м
где е< и y\i суть элементы класса <[<*, то множества S и 7\
определенные равенствами
S= гг -+- е2 -»- ... -ь £я -*- ...
и
будут либо класса <а, либо достижимые снизу класса Кш. А так как
S и Т взаимно дополнительны, они достижимы сверху и, следовательно,
они — двусторонние множества класса Ка.
ОбратнОу если Е есть множество либо класса <С&, либо из базы
Вау то таким же будет и его дополнение СЕ. Следовательно, в силу
предыдущей теоремы мы имеем два разложения, для Е и для СЕУ
в ряды элементов класса <Са
и
С£ = ъ ■+■ *)2 -+■... -+- ъ -+-...
Если эти разложения сложить почленно, то очевидно получится
разбиение всей области 7 на счетное множество элементов класса
<а попарно без общих частей:
</ =£-ьС£ = е1-Н7|1 Ч-е2ч-у\2ч- ... +е, н-ти -ь .. .,
что и доказывает формулированную теорему (ч. т. д.).
70 н. н лузин
Мы дополним этот результат следующим предложением, которое
может играть роль критерия, позволяющего убедиться в том, что класс
суммы бесконечного множества элементов не повысился:
Теорема. Необходимое и достаточное условие для того, чтобы
сумма счетного множества элементов класса ^ а без общих частей
была класса ^а, состоит в том, чтобы она была частью полного
разбиения всей области о7 на счетное множество элементов класса
^а без общих частей.
Условие необходимо. Если множество-сумма £=s1-+-s2 -+-— будет
класса ^ а, то его дополнение CS также класса ^ а. Значит мы можем
разложить CS на сумму элементов класса ^а и написать CS=t]1h-
-*-у\2-*-.. . Складывая эти разложения почленно, мы получим искомое
разбиение <J\
J = ei -+" \ -+- е2 ■+" ^2 -*- • • •
Условие достаточно. Если мы имеем разбиение области <з7 на
счетное множество элементов класса ^а
то сумма
5 = е1н-£2н- . . .-*-e„-f . . .
не может быть класса /Га+1, так как в противном случае множество
S и его дополнение
Т= T)1 + 7]2-*-... + 7]B-h...
были бы множествами, достижимыми снизу класса ан-1, следовательно,
двусторонними, что невозможно, так как класс Ка+1 первого рода1.
Критерий неповышения класса* Мы дадим критерий того, чтобы
сумма элементов класса ^а была класса <.. а в такой форме, которая
нам будет полезна при более углубленное глизе структуры множеств
точек данного класса.
Вот этот критерий.
Теорема. Необходимое и достаточное условие для того, чтобы
сумма Ег -+- Е2 -+-... -+- Еп -+-... счетного множества элементов класса
^а попарно без общих частей была класса ^а, состоит в том,
чтобы можно было заключить каждый элемент Еп во множество
Нп либо класса <С а, либо из базы Ва так, что lim//n = 0.
н->со
1 Вот немедленное обобщение этой теоремы: если множество Е класса ^ а
разложено на счетно** множество множеств класса < о. попарно без общих точек,
то каждая часть Р этого разложения есть множество класса < а.
Чтобы доказать это, достаточно заметить, что каждое из составляющих
множеств есть Сумма счетного множества элементов класса <а-+-1, и это же верно для
дополнения Сс.. Следовательно, мы имеем полное разбиение области <& на счетное
множество элементов класса < а н-1, и Р есть часть этого разбиения. Отсюда следует,
что класс Р должевг быть < а, так как класс АГа41 не содержит двусторонних
множеств.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ 71
Условие необходимо. В самом деле, если Е = Ег -ь Et -+-„.. ~ь £я -+-...
будет класса ^а, то и его дополнение СЕ также класса ^а.
Следовательно, мы имеем разложение
СЕ = &!-*- &г ч- ... -+- gn -н...
множества СЕ в счетный ряд элементов <£„ класса ^а попарно
без общих частей.
Установив это, рассмотрим In — 1 элементов класса ^а: Е1У Е2, ,
-£я—х; S\9 S2y • • м <?»—1 и £„. Ясно, что сумма 0. этих элементов есть
также элемент класса <^а.
Так как два элемента Ья и Ея не имеют общей части, то мы можем
определить отделяющее множество Нп либо класса <а, либо из базы
Ва, которое содержит Еп и не имеет общей точки с 6„.
Легко видеть, что lim//ll = 0. В самом деле, в противном случае
и-* со
существует точка S основной области <з7, которая принадлежит
бесконечному числу множеств НХ9 Нг>... Но так как мы имеем полное
разложение
<У = Ег -+- Si -Н ^2 ~"*~~ <?2 ~*~ • • • ~*~ ^» "^ ^» "•"...,
то эта точка £ принадлежит к некоторому вполне определенному
множеству Ei или £< и не принадлежит ни к какому другому из
составляющих множеств. Значит, как только п превзойдет /, множество Н9
уже больше не содержит точки £, что противоречит сделанной
гипотезе. Отсюда следует, что lim//„ = 0.
«-►00
Условие достаточно. В самом деле, допустим, что ЕпСИя и что
lim//M = 0, где множество Нм либо класса <а, либо из базы ВЛ.
Так как Еп есть элемент класса ^&, мы можем написать равенство
£„ = lim£»
где множество ££} с двумя индексами будет класса <<*. Тогда
множество Snt определенное равенством
5„=£<«> • Н, -*-£<«> • Я, н-... ч- £<••>•#„.
будет либо класса <а, либо из базы Ва. Мы докажем, что
последовательность множеств
«сходится и имеет своим пределом сумму Е = Е1ч-Еъ~*-...
Чтобы убедиться в этом, возьмем любую точку х области о7. Мы
будем различать два случая, смотря по тому, принадлежит ли х или
нет ко множеству £.
Первый случай. Точка х принадлежит к вполне определенному
элементу £<; следовательно, она принадлежит к //<. Ясно, что она при-
72
Н. Н. ЛУЗИН
надлежит к Ef\ как только п превзойдет какое-то значение. Отсюда
следует, что точка х принадлежит к Sn при достаточно большом п.
Второй случай. Точка х не принадлежит к Е. Так как мы имеем
Нт//я = 0, то точка х принадлежит ограниченному числу множеств
п-*оо
Ни H2t ... Пусть т есть целое положительное число такое, что х
не принадлежит ни одному из множеств //т+1, Нт+2... С другой
стороны, х не принадлежит ни одному из т множеств Е19 Е2, ..., Ет.
Так как число т постоянно, то точка х не принадлежит ни одному из
т множеств Е{^\ Е2и\ ..., Е%\ когда п достаточно велико. Отсюда
следует, что точка х не принадлежит к Sn при достаточно большом п.
Таким образом, последовательность множеств Sl9 S29 ... сходится
и имеет своим пределом Е, Е = lim*Sn. Так как Sn либо класса <Са>
п->со
либо из базы Вау то множество Е будет класса ^а (ч. т. д.).
Границы применимости операций lim и lim. Возьмем любой класс
Ка классификации Валле-Пуссена и рассмотрим бесконечную
последовательность каких-нибудь множеств класса <Са
Если мы произведем над этой последовательностью операцию lim,
мы получим вполне определенное множество, которое мы обозначим
через \\тЕп и которое совпадает с предельным множеством \хтЕпУ
когда последовательность множеств (1) сходится.
Таким образом, всякое множество Е класса Ка может быть по-
лучено при помощи операции lim, произведенной один раз над
множествами предшествующих классов.
Если мы спросим себя, каковы множества Е класса ^>а, которые
могут быть получены таким способом, мы немедленно заметим, что
только элементы класса /Га+1 могут быть получены при помощи
операции lim, произведенной над последовательностью множеств
класса <а.
В самом деле, мы знаем, что верхний предел lim£„ может быть
и-*оо
написан в форме (стр. 17)
(Ех н- Е2 -ь £3 -*-...)• (£2 ■+■ £з -»-...)• (£з -+-...)•• •
Каждая скобка есть множество класса ^а. Следовательно, если
множество limEn принадлежит к классу Еа+1> то оно есть элемент
к-* со
этого класса.
Более важным предложением является следующее: каждый элемент
класса АГв+1 можно получить этим способом.
Чтобы доказать это, возьмем элемент Е класса Ка+г. Дополнение
СЕ есть сумма элементов класса ^а попарно 6es общих частей
в счетном множестве
СЕ = Ег -ь Е2 -+-... -•- Еп -+-...
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
73
Так как Еп есть элемент класса <а, то его дополнение СЕЯ есть
сумма счетного множества элементов класса <а без общих частей:
СЕя = е™ -ь е<2»)-+ . .. -+ *<«) ч- ...
На основании очевидной формулы
Е = СЕ1-СЕ2...СЕЯ...
мы можем написать
Но общая часть конечного числа элементов класса <<* есть
множество класса <Са и, следовательно, сумма счетного множества
элементов класса <а. Отсюда следует, что мы можем считать каждый
элемент е{^ из л-й скобки содержащимся в некотором элементе е**_1>
предыдущей скобки без того, чтобы множество Е изменилось.
В этих условиях каждая точка х из Е принадлежит бесконечному
множеству элементов е^ с двумя индексами. С другой стороны, каждая
точка х, не принадлежащая к Е, содержится в ограниченном числе
элементов с двумя индексами е^'К
Следовательно, если мы перенумеруем все элементы е^ с двумя
индексами при помощи целых положительных чисел
то данное множество Е будет верхним пределом этой
последовательности, образованной из элементов класса <а.
Чтобы изучить границы применимости другой операции, lim,
достаточно заметить, что равенство £ = Нт£„ может быть записано в виде
£ = СНт~С£я.
П-+СО
Следовательно, при помощи операции lim можно получить в классе
АГв+1 лишь множества, достижимые снизу, и каждое множество
класса Ка+1, достижимое снизу, может быть получено этим способом,
отправляясь от множеств класса <а, достижимых снизу.
Окончательно, операции lim и lim, примененные ко множествам
класса <а, позволяют получить все множества класса <^а, и среди
множеств класса АГв+1 первая — все элементы этого класса, а вторая —
все множества этого класса, достижимые снизу.
Мы видим, что операции lim и lim являются более общими, чем
операция lim (простой переход к пределу), но менее общими, чем двойной
аереход к пределу Km lim, который, очевидно, позволяет получить
все множества класса £«-ц.
74
Н. Н. ЛУЗИН
Множества класса 0 и 1. Исследования Бэра
Предварительные замечания* Бэр создал свои методы и свою
классификацию для изучения функций, а не собственно множеств.
Тем не менее все идеи Бэра применимы в области множеств, так как
принятая нами классификация множеств есть не что иное, как
классификация функций f {х)у определенных на основной области о7 и
принимающих только два значения 0 и 1.
Если такая функция f(x) непрерывна в каждой точке jc0 области
с/ относительно с/, то она является характеристической функцией
некоторого множества Е класса 0 согласно принятой классификации
функций, и обратно. С другой стороны, предел <р (если он существует)
характеристических функций <р1э ср2, ... для множеств Ev Е2, ... есть
характеристическая функция для множества Е> служащего пределом
множеств Е19 Е2, .... E = \im Еп.
Отсюда следует, что классы характеристических функций /,
определенных на g7 и классифицированных по принципам Бэра1, совпадают
с классами множеств, измеримых В в принятой классификации. В этих
условиях каждой теореме из классификации функций соответствует
теорема о множествах.
Бэру принадлежит результат чрезвычайной важности в области
функций; его можно формулировать так: для того чтобы функция
/(х) была класса 1, необходимо и достаточно, чтобы она имела по
крайней мере одну точку непрерывности на всяком совершенном
множестве.
На основании сказанного выше мы получим соответствующее
предложение о множествах, если возьмем характеристические функции
класса ^1, определенные на основной области <7. В этом случае по
определению совершенным на о/ будет такое множество точек с7,
которое не имеет ни одной изолированной точки и содержит каждую
точку из с7, в соседстве с которой имеется бесконечное множество
точек этого множества.
Другой общий результат Бэра, относящийся ко всем функциям его
классификации, следующий: для того чтобы некоторая функция
принадлежала к классификации, не о бхо димоу чтобы на каждом
совершенном множестве Р она отличалась от некоторой функции
класса ^1, определенной на Р, лишь в точках некоторого множества
первой категории на Р.
Чтобы получить соответствующее свойство множеств, т. е. свойство,
которое принадлежало бы всем множествам, измеримым В, достаточно
1 A priori нисколько не очевидно* что функция f(x), допускающая лишь
значения 0 и 1 и класса а в полной классификации Бэра, должна быть того же классе
в* классификации, которую мы получаем, распределяя по классам согласно принципам
Бэра функции, которые могут принимать лишь одно из двух значений 0 и L.
ЛЕКЦИЙ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ 75
перенести понятие множества первой категории на Р, заменяя
совершенные множества на евклидовой прямой совершенными множествами на с7.
К тому же это обобщение понятия категории мгновенно: не надо ничего
менять в обычных определениях *.
Что же касается функций высших классов, то Бэр ограничился
классом 3: он дал простое построение функции класса 3. Пример Бэра
следующий: если разложить в непрерывную дробь иррациональное
число дс, заключенное между Owl
то функция f (х)9 равная 1, если неполные частные а,, <зц, ...
неограниченно возрастаюту и 0 в противном случаеу есть в точности
функция класса 3.
Множество Е точек х, для которых д„ неограниченно возрастает,
есть как раз множество класса 3.
Таковы результаты исследований Бэра. Если мы постараемся
проанализировать характер этих исследований, то одна вещь не может не
поразить нас: Бэр никогда не доказывает существование функции того
или иного класса методом диагонали (наложением на континуум). Он
всегда старается доказать существование функций некоторого класса
непосредственным построением. А так как этот метод требует
чрезвычайных усилий, отсутствие конструктивных примеров функций высших
классов вполне естественно.
Напротив, пользование методом диагонали (наложение на континуум)
очень легко и приводит к немедленным результатам. Тем не менее, так
как в этом методе употребляют наложение на континуум всех функций
(или множеств) классов, предшествующих рассматриваемому классу, то
нужно еще хорошо изучить природу примеров, получаемых этим методом,
и сравнить их с результатами конструктивного метода Бэра2.
Важно заметить, что теорема Бэра о функциях класса 1 отличается такой
красотой и настолько удобна д\я приложений, что ее можно считать
за идеал для предложений теории функций. Поэтому нет недостатка
в попытках получить обобщение этой теоремы для высших классов.
Среди этих попыток мы должны цитировать две главные, которыми мы
обязаны Лебегу3 и Валле-Пуссену4.
1 Это обобщение было сделано самим Бэром; см. его мемуар „Sur la
representation des fonctions", часть вторая (Acta Math., 32, 116).
2 См. мою статью „Les analogies entre les ensembles mesurables В et les
ensembles analytiques", Fund. Math., XVI, 1930 [стр. 470 настоящего тома] —Ред.).
3 „Sur les fonctions representables analytiquement", стр. 191. Мы слегка
изменили формулировку определения Лебега, введя понятие элемента.
4Ch. dela Vallee-Poussin. Integrale de Lebesgue, fonctions d'ensemble;
classes de Baire, гл. VIII, стр. 144.
76
Н. Н. ЛУЗИН
Лебег вводит понятие непрерывности (а).
Функция / называется непрерывной (а) на совершенном множестве
Р в точке х из Р, если для каждого положительного числа е можно
найти такую порцию Р, содержащую х, которая является суммой
счетного множества элементов класса ^а, на каждом из которых /постоянна
с точностью до е, причем все эти элементы, кроме одного, содержащего
х, нигде не плотны на Р.
Установив это определение, можно, согласно Лебегу, выразить
следующим образом необходимое и достаточное условие для того, чтобы
функция / (х) была класса ^а: необходимо и достаточно, чтобы
/(х) была непрерывна (а) по крайней мере в одной точке на каждом
совершенном множестве»
С другой стороны, Валле-Пуссен ввел следующие понятия, при
помощи которых он приходит к искомому обобщению теоремы Бэра:
Бесконечная последовательность функций /„ называется сходящейся
к / с точностью до е на множестве Е, если в каждой точке Е верхний
и нижний пределы/я д\я л->оо lim/n и "Щ/п равны/с точностью до е.
Функция / есть функция класса а на Е с точностью до е, если
существует последовательность функций /м класса < а, сходящаяся
к/ на £ с точностью до е. / есть функция класса а с точностью до
е на Е в некоторой точке х, если существует порция Е, содержащая
х, на которой х класса а с точностью до е.
Вот какова формулировка Валле-Пуссена: Необходимое и
достаточное условие для того, чтобы функция f была класса <^ а, состоит
в том, чтобы для всякого положительного числа е и для всякого
совершенного множества Р можно было найти точку из Р, в которой / на
Р класса а с точностью до *.
В дальнейшем мы внимательно изучим теорему Бэра о множествах
класса 1, чтобы найти аналогичное предложение дая. множеств высших
классов, возможно более близкое к теореме Бэра.
Множество класса 0* Сначала мы рассмотрим множества
начального класса /С0.
По самому определению, в класс 0 входит всякое множество точек
Е такое, что само Е и его дополнение СЕ являются суммами счетного
множества порций области о/ попарно без общих точек.
Мы видели (стр. 13), что для получения заранее заданного
множества Е класса 0 достаточно взять на прямой XX1 замкнутое
множество F, составленное из рациональных точек, и заставить войти
в Е порции основной области о?', смежные к F так, чтобы оставшиеся
порции о/, смежные к Е, вошли в дополнение СЕ, причем две
соседние порции принадлежат двум разным множествам.
Ясно, что замкнутое множество F, обладающее этим свойством,
единственно.
1 Прямая XX здесь евклидова — Ред,
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
П
Пусть
F F F" F«> F'
— последовательные производные множества от F.
Так как F счетно, то существует вполне определенное число а,
конечное или трасфинит второго класса такое, что производное
множество F(a) пусто, тогда как каждое предшествующее производное
множество F(p), P<Ca эффективно содержит точки.
Таким образом, каждому множеству Е класса 0 соответствует
вполне определенное число а конечное или трансфинит второго
класса.
Мы видим, что это число а может быть как угодно „большим* *.
Было бы чрезвычайно интересно уметь аналогичным способом
привести в соответствие каждому двустороннему множеству Е класса
Ка второго рода некоторое конечное или трансфинитное число р.
Теорема Бэра в приложении к множествам класса 1. Мы теперь
изучим структуру общего множества точек класса 1. Прежде всего
мы применим теорему Бэра о функциях класса 1 к случаю
характеристической функции, определенной на <з7; вот что мы получим:
Для того чтобы множество точек Е было класса ^1, необходимо
и достаточно, чтобы, каково бы ни было множество Р, совершенное
относительно о/, существовала порция Р, целиком содержащаяся
или в Еу или в его дополнении СЕ.
Важно заметить, что это характеристическое свойство множеств
класса ^ 1 выведено из теоремы Бэра о функциях класса 1, но не
иэ определения множества класса 1.
Мы выведем это характеристическое свойство непосредственно из
определения множества класса 1.
Условие Бэра необходимо. В самом деле, пусть Е—множество
класса ^ 1, лежащее в основной области g7.
Пусть Р есть произвольное совершенное (относительно о/)
множество, лежащее в о/.
На основании общего предложения о структуре множества класса
а (стр 68), Е и его дополнение СЕ являются оба суммами счетного
множества элементов класса ^ а, попарно не пересекающихся. С другой
стороны, элемент класса 1 есть не что иное, как множество замкнутое
(относительно о7), так как дополнение к элементу класса 1 есть сумма
счетного множества порций <7.
Таким образом, мы имеем разложение
о7 =е1~нт)1-4-£2-1- т]2. ..-1-ея-Ы|я-|- ... ,
где ея и у\п суть замкнутые множества.
1 Это значит* что какова бы ни была счетная вполне упорядоченная
последовательность, можно эффективно образовать множество Е класса 0 такое, чтобы
соответствующая последовательность производных множества F% эффективно
содержащих точки, была подобна данной вполне упорядоченной последовательности.
78 н. н. лузин
Хотя бы одно из £я или г\п должно быть плотным на Р;
следовательно, оно содержит порцию Р. Но это и есть свойство Бэра.
Условие достаточно. Пусть Е есть множество точек, обладающее
указанным свойством.
В силу этого свойства какова бы ни была порция (а, Ь) области о7г
найдется другая порция (a', b'), содержащаяся в (а, Ь) и заключенная
целиком либо в Е9 либо в СЕ.
Отсюда следует, что существует замкнутое неплотное множество Fiy
каждая смежная порция к которому принадлежит целиком либо к Еу
либо к СЕ1.
Заметив это, обозначим через Рх наибольшее совершенное
множество, содержащееся в FL. Предыдущее рассуждение, произведенное
над основной областью g7, прекрасно применяется к случаю
совершенного множества Plt и, т'ким образом, мы имеем новое замкнутое
множество F2> содержащ еся в Р1У не плотное на Рх и такое, что
каждая порция Р19 смежная к Р2> принадлежит либо к £, либо к СЕ+
Продолжая таким же образом, мы получим вполне упорядоченную
последовательность
JZ>PXZ>P2Z> ... ЗРШ3... Z)PpD...
совершенных множеств таких, что из любых двух множеств следующее
содержится в предыдущем и не плотно на нем2.
Отсюда вытекает, что эта последовательность должна быть счетной*
Значит мы придем к пустому множеству.
С другой стороны, из построения совершенных множеств Рр следует,,
что каждое Рр есть наибольшее совершенное множество, содержащееся
в замкнутом множестве Рр, и что если (3 первого рода р = р*-н1, то
каждая порция Рр, смежная к Рр, заключена полностью либо в Еу
либо в СЕ.
Отсюда мы заключаем, что оба множества Е и СЕ являются
суммами конечного или счетного числа отдельных точек и порций
совершенных множеств, попарно не перекрывающихся. Но каждая отдельно
взятая точка и каждая порция совершенного множества есть элемент
класса 1 (или порция g7). Следовательно, мы получаем полное
разбиение основной области о/ на конечное или счетное число
элементов класса 1, и множество Е есть часть этого разбиения.
На основании общей теоремы о структуре множества класса а (стр. 70)
множество Е будет класса ^1 (ч. т. д.).
Свойство Бара для всех множеств, измеримых В. Мы видели,
что каждое множество Е класса 1, так же как и его дополнение СЕУ
1 Ц.Ы прибавим* если это нужно, некоторые рациональные точки к /\ чтобы эта
формулировка оправдалась,
2 Совершенное множество Pfi содержится в замкнутом множестве Fq. Если индекс
р второго рода, то F» определяется как общая часть лля всех Fa' (или для всех Ра').
предшествующих (I, р <?.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
79
есть сумма счетного множества отдельных точек и совершенных
множеств.
Так как общая часть двух совершенных множеств есть замкнутое
множество и так как всякое замкнутое множество есть сумма
совершенного множества и счетного числа отдельных точек, мы
заключаем, что точки множества Е класса 1, содержащиеся в совершенном
множестве Р, а также точки дополнения СЕ образуют на Р сумму
счетного числа отдельных точек и совершенных множеств.
Свойство Бэра теперь может быть формулировано следующим
образом:
Всякое множество^ измеримое В, а также и его дополнение
являются на каждом совершенном множестве Р суммами счетного
числа порций Р, если пренебрегать множеством первой категории
по отношению к Р.
Другими словами, каковы бы ни были множество Еу измеримое В,
и совершенное множество Р, можно определить на Р замкнутое
множество Fy не плотное на Р и такое, что каждая порция Р, смежная к Р:
содержится либо в Е, либо в СЕ9 если пренебрегать точками
множества первой категории по отношению к Р.
Сравнивая эту форму свойства Бэра с указанным свойством
множеств класса 1, мы придадим свойству Бэра следующую форму,
всякое множество Еу измеримое 5, на всяком совершенном
множестве Р отличается от множества Е1 первого класса, лежащего
на Р, лишь в точках некоторого множества первой категории по
отношению к Р.
В этой форме рассматриваемое свойство есть не что иное, как
свойство Бэра м^ функций f(x)> определенных на о7 и допускающих
лишь два значения 0 и 1. Следовательно, можно вывести свойство
Бэра, касающееся множеству из того, которое касается функций.
Чтобы доказать его непосредственно, достаточно заметить, что
если каждое из множеств Е1У Е2> • • •, Еп, ... обладает свойством Бэра
на совершенном множестве Р, то их сумма и общая часть также обладают
свойством Бэра на Р.
В самом деле, обозначим через Sn сумму порций Р, отличающуюся
от Еп лишь в точках некоторого множества ея первой категории по
отношению к Р; множество ел образовано из точек Епу не
принадлежащих к 5Я, и из точек Sm не принадлежащих к Ея.
Обозначим через S сумму множеств *S*. Очевидно, что S есть
множество класса ^1, отличающееся от суммы Ех-*-Ег-*-... лишь
в точках множества ех -+- е2 ■+■... первой категории по отношению
к Р.
Следовательно, свойство Бэра инвариантно по отношению к операции
(S): составления суммы.
Но, по самому определению, свойство Бэра инвариантно
относительно операции (С): взятия дополнения.
80
Н. Н. ЛУЗИН
Так как всякое множество, измеримое В, может быть образовано
при помощи этих двух операций, отправляясь от порций о/ (стр. 70),
то свойство Бэра принадлежит всякому множеству, измеримому В1.
Конструктивное существование множеств 1, 2, 3 и 4 классов
Канонические элементы класса 1. Мы назовем каноническими
элементы данного класса Ка, которые обладают некоторым
достаточно простым свойством и такие, что каждое множество класса
Ка можно получить, образуя сумму счетного множества канонических
элементов2.
Мы рассмотрим канонические элементы первых классов
классификации Бэра — Валле-Пуссена.
Порция фундаментальной области о/ может быть рассматриваема
как канонический элемент класса 0.
В первом классе каноническими элементами являются: точка и
совершенное множество, нигде не плотное на <з7.
Для того чтобы убедиться в этом, достаточно заметить, что элемент
класса Кх совпадает с замкнутым множеством (относительно о7).
Действительно, если Е — элемент класса Ки то его дополнение
СЕ достижимо снизу, следовательно, есть сумма порций с7; отсюда мы
заключаем, что Е замкнуто.
Обратно, каждое замкнутое множество F есть, очевидно, элемент
класса АГг.
Так как каждое несчетное замкнутое множество есть сумма
счетного множества точек и совершенного множества, то ясно, что каждый
элемент класса Кх состоит из порций области о/, отдельных точек
в счетном числе и совершенного множества нигде не плотного на g7.
Следовательно, каноническими элементами класса Кх являются точки
и совершенные, нигде не плотные множества.
Канонические элементы класса 2* В классе К2 есть канонические
элементы двух родов:
1°. Можно получить канонический элемент класса 2, выбрасывая
из совершенного множества Р счетное множество точек, всюду
плотное на Р.
2°* Можно получить канонический элемент класса 2, выбрасывая
из совершенного множества Р счетное множество нигде не плотных
на Р совершенных множеств попарно без общих точек, сумма
которых всюду плотна на Р.
1 См. также Сообщение Польской академии: N i k о d у m. Sur la condition de
Baire (Bull. Ac. Pol., 1929, стр. 591).
2 Данное определение канонического элемента неопределенно, так как мы не
указали, в чем заключается это достаточно простое свойство. Мы не умеем этого
сделать в общем случае. Было бы желательно иметь в каждом классе конечное число
родов канонических элементов так, чтобы элементы одного рода были между собой
гомеоморфны [7].
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
Чтобы в этом убедиться, достаточно показать, что каждое
множество Е класса 2 есть сумма счетного множества элементов этих двух
родов и множеств класса ^ 1. Так как каждое множество класса 2 есть
сумма счетного множества элементов класса Kt> то достаточно
ограничиться рассмотрением элементов [8].
Пусть Е — элемент класса 2. Выбросим из / все порции, на
которых Е класса <11. Мы получим совершенное множество Р1У каждая
порция которого содержит часть множества £, образующую элемент
класса 2.
Я утверждаю теперь, что между порциями Рг найдется хотя бы
одна такая, что часть Еу ей принадлежащая, есть канонический элемент.
В самом деле, дополнение СЕ состоит из порций, отдельных точек
и совершенных множеств в счетном числе. Но СЕ всюду плотно на Р1У
так как иначе существовала бы порция области <У, содержащая точки
Рх и определяющая часть Е класса ^1, что противоречит
определению Р.
С другой стороны, СЕ очевидно первой категории на Р1У так как
в противном случае существовала бы порция Р1У не содержащая точек
Еу что также противоречит условию. Следовательно, среди порций
Pj есть порции, которые определяют канонические части Е. Ясно, что
эти порции образуют множество, всюду плотное на Р1У так что,
выбрасывая эти порции из Рр мы получим замкнутое множество Р2, нигде
не плотное на Рх.
Обозначим через Р2 наибольшее совершенное множество,
содержащееся в Р2.
Легко видеть, что, поступая так же с множеством Р2, мы получим
новое совершенное множество Р3> содержащееся в Р2 и нигде не
плотное на нем; и так далее.
Мы построим последовательность совершенных множеств
О/ у /р Г^2> • • • » *ш> • • • > * р> • • • >
каждое следующее множество содержится в предыдущем и нигде не
плотно на нем. Следовательно, существует число а конечное, или
трансфинитное второго класса, такое, что множество Рв пусто.
Отсюда мы заключаем, что данное множество Е разлагается
на счетную сумму множеств класса ^1 и элементов класса а обоих
указанных родов (ч. т. д.).
До сих пор мы предполагали установленным существование
множеств класса 2. Нам остается восполнить этот пробел.
Пусть Е — множество одного из двух рассмотренных родов. В силу
самой конструкции Е множество Еу так же как и его дополнение СЕ.
всюду плотно на совершенном множестве Р.
Я утверждаю теперь, что Е есть множество класса 2. В самом
деле, если бы класс Е был меньше, чем 2, то множество Е обладало
бы свойством множеств класса <^1. Значит существовала бы порция
82
Н. Н. ЛУЗИН
Р, принадлежащая целиком либо к Е> либо к СЕ; но это противоречит
тому, что Е и СЕ оба всюду плотны на Р.
Итак, множество Е строго класса 2.
Заметим наконец, что каждое совершенное нигде не плотное
множество строго класса 1. Действительно, такое множество не может быть
класса 0, так как не содержит никакой порции ?7.
Конструктивное доказательство Бэра существования элементов
класса 3. Основной целью двух мемуаров Бэра „Sur la representation
des fonctions discontinues" (первый мемуар в Acta. Math., 30, 1905;
второй мемуар там же, 32, 1909) является строгое построение элемента
класса 3.
Наиболее важная часть первого мемуара посвящена этому вопросу.
И во втором мемуаре Бэр возвращается к этому построению с более
общей точки зрения.
Принципы, изложенные нами выше, позволяют нам без затруднения
изучить результаты Бэра о конструктивном существовании элементов
класса 3.
Прежде всего уточним условия существования элемента класса 3.
Предположим, что существует элемент Е класса 3. Мы видели (стр. 73),
что Е может быть написано в виде
£ = (*а) + е£>н-*£>-!-...) .(е^ч-е^ч-е^ч-...)..., (1)
где е{**— элементы класса ^ 1. При этом мы можем предположить,
что элементы, стоящие в одной скобке, не имеют попарно общих точек
и что каждый элемент е^ k-й скобки содержится в некотором
элементе e|f_1) предшествующей скобки.
В силу того, что мы говорили о канонических элементах класса 0
и 1, мы можем предположить, что элементы е^ являются: либо
порциями фундаментальной области <3', либо отдельными точками, либо
совершенными нигде не плотными множествами.
Каждый элемент класса 3, если он существует, может быть
получен таким образом. Таков вывод из предшествующего текста.
Открытие Бэра заключается в том, что он дал достаточное
условие для того, чтобы множество Е, определенное равенством (1),
было в точности класса 3*
Вот условия Бэра:
1°. Множества е[р совершенные (относительно <з7).
2°. Каждое множество е\*\ содержащееся в е^"1\ нигде не плотно
на е£~Ч
3°. Множества е^\ содержащиеся в фиксированном множестве
eJJ"""1), образуют множество, всюду плотное на е^~1\
В этих условиях Бэр доказывает, что Е есть множество строго
класеа 3.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
Лая доказательства этого результата Бара удобно изменить
обозначения.
Обозначим через Р<|(/1 = 1, 2, 3,...) все множества ^ первой
скобки равенства (1). Пусть элементы (к—1)-й скобки обозначены
через Р^...,^,; обозначим через Р<,...,Wjk> где индекс it принимает
значения 1, 2, 3,..., все элементы к~й скобки, содержащиеся в Р{
При таких обозначениях все элементы £-й скобки суть множества
Р^ ik с к индексами, и каждое множество Р^...^ с к индексами есть
элемент к-& скобки. Чтобы получить все элементы (£-§-1)-й скобки,
содержащиеся в Р^ iV достаточно добавить новый индекс ik x так,
чтобы получился символ с к-+-\ индексами, и заставить ik+l пробегать
значения 1, 2, 3,...
После этого обозначим через Q{ 4 сумму всех множеств
Pt яяш4к ikf 4=1> 2, 3,..., у которых к — 1 первых индексов
фиксированы, и через Qk — сумму всех множеств Р^..^ с к индексами.
Вот формулировка Бэра: если 1° множества Рiik совершенные
относительно о/ и при фиксированном к не имеют попарно общих
точек; 2° множество Р. .. содержится в Pfi„tik и нигде не
плотно на этом множестве; 3° множество Q4 ik всюду плотно на
P. ik, то общая часть
E=QX-Q2...Q*...
есть множество в точности класса 3.
Чтобы это доказать, обозначим через /?0 множество точек области о?',
не принадлежащих ни одному из множеств Р{> /=1, 2, 3,..., и через
/?t.^ ib множество-разность P. ik — Qt .. ^- Легко видеть, что Р0 и
/?. ., являются каноническими элементами класса 2х и что
С£=/?о-ь2/?....<4,
где индексы г\, /2»**м z* и само к принимают значения 1, 2, 3,...
независимо один от другого.
Так как канонические элементы Р0 и /?»-... <ik не имеют попарно общих
точек, то мы можем применить критерий неповышения класса, ранее
нами полученный (стр. 70). Мы заключаем, что если множество Е
есть множество класса ^ 2, то можно заключить каждый элемент
R. .в множестве //. .. класса <Г1 таку что\\тН. /. = 0, когда
один из индексов i}, —, ik или к бесконечно растет.
Покажем, что при этих условиях мы придем к противоречию.
Прежде всего, так как множество //0, содержащее Р0, есть множество
класса ^1 и всюду плотно на о7> то существует наверняка порция Ь9
фундаментальной области о7, содержащаяся целиком в //0.
1 Мы предполагаем, что сумма Qi множеств Р^% г1 = 1, 2» 3>. . .» всюду влотна
на <?. При этих условиях #ф есть в точности канонический элемент класса 2.
S4
Н. Н. ЛУЗИН
Заметив это, перенумеруем все рациональные точки при помощи
целых положительных чисел. Пусть г19 г2, г3,... — полученная
последовательность. Так как порция Ъ0 фиксирована и так как множество Qx
всюду плотно на <7, то существует множество Р{о, имеющее точки в Ъ0.
С другой стороны, множество Н,о всюду плотно на Р о, так как
содержит канонический элемент R .о, всюду плотный на Р .о. Так как
*i *i
Н л класса ^ 1, то можно определить порцию &х области g7, содержа-
щуюся в 80 и не имеющую точки гг в качестве своей предельной точки
такую, что порция Р.о, которую она определяет, содержится цели-
*i
ком в //.о.
*1
Предположим вообще, что мы нашли порцию Ьк_г области о7, а^я
которой точки г19 г2,..., />_! не являются предельными точками, и
множество Р.о .о такое, что его порция, которую определяет 8^_,,
целиком содержится в Н о о о . Так как множество Q .о .о .о всюду
*i V4-i *iV--*jfc—1
плотно на Р.о.о .о , то существует множество Р.о.о .о .о, имеющее
«1*2 •••**—1 *1*2~лк-1%к
точки в Sjt х- С Другой стороны, множество Но .о всюду плотно на
V**
Р о .о, так как содержит канонический элемент, всюду плотный на
Рп ,о. Так как Н.ол .о класса ^1, то можно найти порцию Ьк об-
*1-~4к •i*2-eei*
ласти о/, содержащуюся в Ьк_и Ам которой точка гк не является
предельной, такую, что порция Р 0 о ,о, которую определяет &*, содержится
целиком в Но .о .о.
•l*2*"*fc
Легко видеть, что, продолжая таким образом, мы построим
последовательность порций области с7
К 51> 82>---> 8Ь--«
такую, что каждая последующая содержится в предыдущей и а^я
порции Ьк рациональные точки г19 г2, ..., г* не являются предельными
точками.
Отсюда следует, что длины Ьк стремятся к нулю, когда к
бесконечно возрастает. Следовательно, существует одна и только одна
точка S, общая всем порциям Ьк. Эта точка £ заведомо иррациональная
в силу свойства порций Ькщ
Так как множество Рлл л содержится в множестве Р о о о. где
•1*2—Ъ V2--V
Л<£, то, если £ достаточно эелико, порция 8Л области J содержит
точки множества Рл .о, где v фиксировано. Но множества! Р я о
V-S *i|—<*
совершенные. Отсюда следует, что точка 5 принадлежит всем
множествам
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
85
и, следовательно, всем множествам
Н о, #.о,о, .. ., //.о.о .о . • ->
что невозможно, так как, по предположению, мы имеем
lim//.o.o ,o = 0.
Итак, мы пришли к противоречию и, следовательно, множество Е
есть элемент класса 3 (ч. т. д.).
Назовем элементами Бэра элементы класса 3, которые построены
по приведенному выше правилу. Мы не касаемся вопроса, являются ли
элементы Бэра единственными в классе 3, которые заслуживают
названия канонических элементов.
В силу крайней простоты применения правила Бэра можно дать
арифметический пример элемента 3. Бэр сам нашел такой пример1.
Положим вместе с Бэром,
1_
1
ах-+
<*2 +
— (<*\> &>> • • •> а„,...),
где каждое ап— целое положительное число.
Обозначим через />(M)(ai> a2...., аА) множество всех иррациональных
точек сегмента [0, 1], которые изображаются непрерывными дробями,
начинающимися с (а1У а2, ..., а*) и у которых остальные неполные
частные все больше, чем л.
Легко доказывается, что pin)(au a2, ..., аь) — совершенное
множество (относительно </), нигде не плотное на </.
Множество /?(п) называется нормальныму если h = п или если А > п
и если а^ ^ л.
При фиксированном л все нормальные множества попарно не имеют
общих точек. Легко видеть, что их сумма Qn
есть множество всех иррациональных точек сегмента [0, 1], у
которых все неполные частныеу начиная с некоторого рангау больше,
чем л.
Заметив это, обозначим через Р, (i1 = l, 2, ...) все нормальные
множества /7(1), перенумеровав их некоторым образом. Так как два нор-
1 См. R. В air e. Sur la representation des fonctions discontinues (Acta Math.,
30, 34—47, 1905).
86
Н. Н. ЛУЗИН
мальных множества />(,,_1) и pln) либо не имеют общих точек, либо р№
содержится в /?(w~'1), то мы можем обозначить через Р{ ik_ ik все
нормальные множества, содержащиеся в Р<...^_|('* = 1> 2, 3,...).
Легко показать, что Р^...^^ нигде не плотно на Piv,tik и что сумма
^ .*-, множеств *V-w* ('*=1> 2> 3,...) всюду плотна на Р,,...^1.
Итак, множества Р^ ^ удовлетворяют всем условиям правила Бэра.
Так как это правило здесь применимо, мы заключаем, что общая часть
£=<?!• Q....Q....
есть элемент класса 3.
Можно немедленно указать очень изящное характеристическое
свойство течек Е.
Множество Е есть множество всех иррациональных точек
сегмента [0, 1], у которых неполные частные номера п бесконечно
возрастают вместе с л.
Это свойство точек Е можно получить, рассматривая
характеристическое свойство множеств Qn.
Итак, можно назвать элемент класса 3, указав некоторое его
арифметическое свойство.
Исследования Л. В* Келдыш о конструктивном существовании
элемента класса 4. Можно ли продолжить изыскания Бэра за
пределы класса 3? Мы приведем здесь конструктивное доказательство
существования элемента класса 4, принадлежащее Л. В. Келдыш. Этот
результат является наиболее естественным в направлении, открытом
Бэром.
Вот ход рассуждений Л. В. Келдыш: строится сначала счетная
последовательность элементов Бэра (класса 3) elf е2,... епу... попарно
без общих точек, выбранных соответствующим образом, и
доказывается затем, что сумма е1н-е2+...-ьеп + ... не может быть класса
меньше, чем 4. Этот важный факт устанавливается применением
критерия неповышения класса (стр. 70): элемент еп заключается в
множество Нп класса ^2, и доказывается, что никогда не имеет места
Нт//я=0, каков бы ни был выбор Нп.
Все сводится к выбору элементов Бэра е1У е2> ..., еп, ...
Существенная роль в этой конструкции принадлежит элементам класса 2, и мы
начнем с доказательства следующей леммы:
Лемма I. Если элемент Бэра Еу заданный определяющей
системой Pt 4 у содержится в счетной сумме канонических элементов
класса ^2, Ь17 82, ...,8П, ..., то существует такое Ьт и такая
порция тг некоторого образующего множества Р.о .о ,о, что Ьт — вто-
рой категории на каждой порции я, так же как на каждой порции
любого определяющего множества, содержащегося в тс.
1 Подробности см. в оптированном м ему аре Бэра (Acta Math., 30, 39, 1905).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ 87
Предположим, наоборот, что такого 0„ не существует. Это значит,
что существует порция тсх определяющего множества Р о о о такая,
что 0Х не содержит точек тс1# Так как 62 не удовлетворяет условиям
леммы, то существует в тсх порция тс2 определяющего множества
Р .о .о о такая, что 62 не содержит точек тс0. Существует также в тс2
порция тс3 определяющегося множества Род о л такая, что % не
содержит точек тс3. Продолжая таким образом до бесконечности, мы
получим неограниченную последовательность порций ^, тс2> • • •> *»> • • •>
каждая из которых содержится в предшествующей и такую, что
множество tcv не содержит точек v множеств 6lf 62,..., Ьч. Пусть \ — точка,
принадлежащая всем тсг, тс2,..., тс„,... Эта точка принадлежит,
очевидно, элементу Бэра Е и, так как она не принадлежит ни одному из
множеств 8lf 62,..., то мы пришли к противоречию (ч. т. д.).
Введем теперь следующее определение. Пусть 6 — канонический
элемент класса 2, который получается выбрасыванием из совершенного
множества Р счетного множества совершенных множеств Р19 Р2,...
, Р„,... попарно без общих точек, каждое из которых нигде не
плотно на Р и сумма которых всюду плотна на Р. Пусть Е — элемент
Бэра класса 3, содержащийся в В и всюду плотный на Р, заданный
определяющей системой Piit..,in-
Определение. Мы будем говорить, что Е есть элемент Бэра,
густой на 8, если каждая порция произвольного определяющего
множества Pi. t. содержит порцию какого-либо совершенного
множества Ря.
Установив это определение, мы докажем следующее предложение:
Лемма II. Каждый канонический элемент & класса 2 содержит
элемент Бэра класса 3, плотный на 6.
Прежде всего мы заметим, что лемма будет доказана, если мы
сумеем построить совершенное множество тс, содержащееся в Р, нигде
не плотное на Р и такое, что каждая порция тс содержит порцию
некоторого множества Ря, причем эта порция нигде не плотна на тс.
В самом деле, предположим, что мы построили такое множество тс;
обозначим его тсх и в смежных интервалах к тсх возьмем совершенные
множества тс2, тс3,..., каждое из которых обладает тем же свойством.
Сумму тс2 -ь тс2 -+-.,. -I- тся ч- ... можно выбрать всюду плотной на Р и
первой категории на Р.
Эти множества тс, будут определяющими множествами с одним
индексом элемента Бэра Е> который мы получим.
Поступая таким же образом для множеств тс0 осуществляя для
каждого из них те же операции, которые мы производили над
множеством Р, мы построим определяющие множества тс^р ъ.2> ..., nw...
с двумя индексами для элемента Е, и так далее. Можно, очевидно,
88
Н. Н. ЛУЗИН
предположить, что множества к{ с двумя индексами не содержат
точек Р19 так как Рг нигде не плотно на каждом те^. Таким же обра-
зом можно предположить, что множества т*ц ik с к индексами ^не
содержат точек множества Р*^. Легко видеть, что элемент Бэра Е>
заданный определяющей системой ^ t.„. -, содержится в 6, так как он
не может содержать точек множеств Р1У Р2,..., Р„,... Следовательно,
элемент Бэра Е, таким образом определенный, плотен на 6.
Все сводится к построению совершенного множества те,
обладающего указанным свойством.
Для этого возьмем в множестве Р точки ?т, £2, •••»£*>•• •> не
принадлежащие ни одному Pic и образующие счетное, всюду плотное на Р
множество. Рассмотрим множество Рх и выбросим из Р порцию ах>
смежную к Рх и содержащую точку £1#
Пробегая последовательность Р2, Р3,..., Рп> • • •> мы найдем
множество, некоторая порция которого принадлежит к Р — ох\ пусть Pv,—
первое такое множество. Выбросим из Р порцию о2 множества Р,
смежную к Р1-^-Р^3 и содержащую точку £2. Пробегая последовательность
PVa+i, Pv,-i-2,..., Р„,..., мы найдем множество, некоторая порция
которого принадлежит к Р — ох— о2; пусть PVj — первое из таких множеств»
Выбросим из Р порцию <з3 множества Р, смежную к Рх -+- Pv, -+- Pv, и
содержащую точку £3 и так Далее.
Продолжая таким образом до бесконечности, мы построим
бесконечную последовательность порций а19 о2, ..., ап> ... множества Р.
Множество те точек Р, которое получается выбрасыванием из Р всех с<>
есть совершенное множество, и, легко видеть, что те обладает
требуемыми свойствами (ч. т. д).
Перейдем теперь к конструкции элемента класса 4.
Возьмем сначала в порции (0, 1) области о/ элемент Бэра Е0> всюду
плотный на этой порции; пусть P°iWj...,< —определяющие множества
для Е0. Если мы выбросим из порции (0, 1) элемент £0, то оставшаяся
часть разбивается на счетное множество канонических элементов
класса 2, которые мы обозначим через 6 , v1 = l,2, ...
Напомним, что каждое 6 есть не что иное, как разность
ро _ у р
Применяя лемму И, мы построим в каждом 6(Vl) элемент Бэра Е? j
плотный на 8V|. Если мы выбросим из 6(Vl) элемент Е , то оставшаяся
часть разбивается на счетное множество канонических элементов
класса 2, которые мы обозначим через 6 *)•
Каждое Ь(^ есть не что иное, как разность
ры _ ^ РЫ
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
и мы можем, очевидно, предположить, что элементы Е0 и £*V|) всюду
плотны на каждом Р[**\
Вообще, когда определен элемент 6(v,Vl"v,,,J класса 2, мы, применяя
лемму И, строим в 0Cv"Vm) элемент Бэра ЕЬхЪ"**т), плотный на Ь{''1"'*т).
Если мы выбросим из 6с*л'"'т) элемент Е{^3'"*т\ то оставшаяся часть
разбивается на счетное множество канонических элементов класса 2,
которое мы обозначим через 0(v"VmVm+,). Каждое 0(У|'"*т1'яи") есть не что
иное, как разность
p(»....»m> — V P(V..vm)
и мы можем, очевидно, предположить, что элементы Бэра £0, &"1\
£V|V|),..M £v«—v«) ВСЮду плотны на каждом Р!////.***-
Пусть »S—сумма всех элементов Бэра, таким образом построенных:
Мы покажем, что множество S, таким образом построенное, есть
множество в точности класса 4.
Действительно, как мы заметили выше, если бы это было не так,
то можно было бы заключить каждое £(v'—Vm) B множество /fv"*m>
класса 2 таким образом, что каждая точка области о7 принадлежит
не более, чем к конечному числу множеств
Предположим, наоборот, что такие множества //v,v,*Vm существуют,
и рассмотрим элемент Бэра Е0. Так как Н0 есть сумма счетного
множества канонических элементов класса 2, то мы находимся в
условиях леммы I. Пусть 60 — канонический элемент класса 2 и ^ — порция
некоторого определяющего множества для Е0 такая, что &0 — второй
категории на каждой порции ^0, так же как и на каждой
содержащейся в тг0 порции произвольного определяющего множества для Е0*
В этих условиях мы можем написать
где Fqic есть замкнутое множество, нигде не плотное на тс0 и на каждом
определяющем множестве для Е0.
Следует заметить, что каждое множество F^ нигде не плотно на
любом определяющем множестве. Докажем это по индукции.
Предположим, что F& нигде не плотно на каждом определяющем множестве
для множеств £*v,), ^1Ъ\ ..., £(v,*,evx), и покажем, что это имеет место
и для £*v»*"vxvx+,). Предположим, что это не так и, следовательно,
множество F& плотно на некоторой порции о некоторого определяющего
0 0 0
множества для E*v""x*x+l. В силу леммы П о содержит порцию опре-
о о
деляющего множества для Е г" х, что не имеет места (ч. т. д.).
90
Н. Н. ЛУЗИН
/ 0\
Пусть Е"1' — густой элемент Бэра, всюду плотный на тг0. Этот
элемент заключен в множество 1~г *' класса 2. Применяя лемму I, мы
можем определить канонический элемент 0^ и порцию ^ некоторого
определяющего множества для Е^ 1' такую, что 6^, второй категории
на nlf так же как на каждой содержащейся в кх порции любого
определяющего множества для Е . В этих условиях можно написать
где Ftf есть замкнутое множество, нигде не плотное на кг и на каждой
лежащей в тгх порции определяющего множества для ЕV|. Повторяя
предыдущее рассуждение, мы покажем, что каждое множество Fxi
нигде не плотно на содержащейся в тсх порции любого определяющего
множества. Мы выберем порцию тсг так, чтобы она не содержала ни
одной точки F0l, что всегда возможно, так как F0l нигде не плотно
на ^0.
Вообще, после того как получены равенства:
~0 = ^0 * fy) -+- F0l -+- FQ2 -+- . . . Н- Fofc -4- . . .,
■Fn ■+■ F1%-*-... -*-Flk-ь...,
мы берем в порции тст густой элемент Бэра Ек 1 , всюду плот-
ный на гсда. Этот элемент заключен в множество /Т^1*2"**' класса 2.
Применяя лемму II, мы можем определить канонический элемент
^1...н4пШи+1 и порцию TCm+i некоторого определяющего множества для
(v°...v° v° )
£\ 1— m m+v такуЮ> что 6(4..44nlJLflH_1 второй категории на каждой
порции тст+1 и на каждой содержащейся в кт+1 порции произвольного
определяющего множества для Ех l m т+1\ В этих условиях мы можем
написать
где Fm+i,k есть замкнутое множество, нигде не плотное на ^V^ и на
всякой содержащейся в тст+1 порции любого определяющего множества
для Er r" m+1'. Повторяя приведенное выше рассуждение, можно
показать, что /sn+i, fc нигде не плотно на содержащейся в тст+1 порции
произвольного определяющего множества. Мы выбираем порцию iw*-i таким
образом^ чтобы она не содержала точек т -+-1 первых множеств F
каждой строки, что всегда возможно, так как каждое из этих
множеств F нигде не плотно на тст.
ЛЕКЦИЙ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
91
Установив это, обозначим через ; точку, общую всем порциям ~0, ки
~2, ..., ^т, — Такая точка обязательно существует, так как порции ~ш
суть совершенные множества, включенные одно в другое [9]. Из
построения следует, что точка ; не может принадлежать ни одному из
замкнутых множеств Fpq. Следовательно, точка ; принадлежит всем
множествам 60, 8^, б^^, . . #> 6^iJ4.,t[Lmf.m и, следовательно, бесконечному
числу множеств f-p*1—"" f что противоречит предположению.
Итак, класс S есть в точности класс 4, и его дополнение CS
есть элемент класса 4 (ч. т. д).
Арифметический пример элемента класса 4. Мы видели, что Бэр,
после того как он нашел регулярный процесс построения элемента
класса 3, построил арифметический пример элемента класса 3.
Следуя этому пути Бэра, Л. В. Келдыш приходит к интерпретации своего
регулярного процесса для построения элемента класса 4 при помощи
арифметического примера элемента класса 4.
Так как полное изучение этого примера содержит много
элементарных кропотливых деталей, мы ограничимся описанием хода
конструкции этого элемента.
Мы начинаем с того, что берем в качестве Е0 в точности
арифметический элемент Бэра класса 3. Итак, элемент Е0 есть множество
всех иррациональных точек, заключенных между 0 и 1, у которых
неполные частные ранга п бесконечно возрастают вместе с п.
Каждое определяющее множество ^ *,...** элемента Е0 может быть
характеризовано следующим образом: это множество иррациональных
точек («J, а2> •••»*»»•••) интервала (0,1) таких, что среди неполных
частных cl, есть в точности^, равных 1, л2, равных 2, ..., л*, равных к.
Отсюда следует, что каждый канонический элемент 6^ класса 2,
который является разностью
00
DO У DO
может быть характеризован следующим образом: это множество точек
Р% , у которых среди неполных частных существует бесконечное
множество равных £-н1.
В этих условиях можно немедленно доказать, что плотный на 6*
элемент Е^ может быть характеризован следующим образом: это
множество тех иррациональных точек из 6 , у которых все целые
положительные числа, исключая кч-1у повторяются среди неполных частных
лишь конечное число раз.
со
Отсюда следует, что сумма 2 & может быть характеризована как
множество тех точек, у которых среди неполных частных одно и только
одно целое положительное число повторяется бесконечное число раз.
92
Н. Н. ЛУЗИН
Таким образом, следуя шаг за шагом приведенной выше общей
конструкции множества S,
5=£0 + 2£м + Е£ы + ...+ 2 £( Vm)-*-...,
v, vtv2 V--Vm
можно показать без труда при помощи простых рассуждений, что
двойная сумма zjE V|V* может быть охарактеризована как множество тех
иррациональных точек, у которых среди неполных частных а., два и
только два целых положительных числа повторяются бесконечное
множество раз. И вообще m-кратная сумма 2 i^1" может быть харак-
vt...vm
теризована как множество всех тех иррациональных точек, у которых
среди неполных частных av m и только т целых положительных чисел
повторяются бесконечное множество раз.
Отсюда следует, что дополнение к множеству-сумме *S, т. е.
элемент класса 4, есть множество тех иррациональных точек
(ai> аоу •> а*> • • •)» содержащихся между О и 1, у которых среди
неполных частных av есть бесконечное множество различных, каждое
и$ которых повторяется бесконечное множество раз.
Понятие рассеянного множества (по Данжуа)
Данжуа ввел в теорию множеств важное понятие рассеянного
множества и показал его фундаментальную роль в теории счетных
множеств; это понятие в дальнейшем обобщалось и углублялось в работах
по топологии1.
Мы перенесем эти идеи Данжуа в теорию множеств высших классов.
Используя их, можно постигнуть сущность теоремы Бэра, касающейся
класса 1, и искать аналогии ей в теории высших классов.
Рассеянные множества точек, Данжуа называет рассеянным
всякое счетное множество, которое не содержит никакой части, плотной
на себе2.
Другими словами, рассматриваемое множество Е должно обладать
следующим свойством: какова бы ни была его часть Е19 в ней
существует точка х19 изолированная в Ег.
Всякое счетное рассеянное множество может быть вполне
упорядочено
£0> £ц ^2> • • •> £ш> • • •» ^ . .. I « (s)
таким образом, что каждая точка fy изолирована в множестве всех
точек tj, 1^$, т. е. можно найти порцию а фундаментальной области о/,
1 См. Freeh et. Quelques propriety des ensembles abstraits (Fund. Math., X, 28).
См. также „Espaces abstraits1*, Paris, 1923, стр. 174 и 267.
2 Множество называется плотным на себе, если каждая его точка является для
него предельной точкой (Бв р. Теория разрывных функций. М,—Л., ГТТИ, 1932,
стр. 60).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ 93
которая содержит точку Е? и не содержит ни одной из последующих
точек £т, Т>Р»
Чтобы в этом убедиться, перенумеруем все точки х данного
рассеянного множества £ при помощи целых положительных чисел
Так как множество Е рассеянное, то существуют точки,
изолированные в Е; выберем из этих точек первую в последовательности (Е)
-я обозначим ее Е0.
Удалим из последовательности (£) эту точку Е0. Так как множество
(Е) рассеянное, то среди оставшихся точек последовательности {Е)
существуют изолированные точки; первую из них обозначим ^.
Вообще, определив вполне упорядоченное множество £0, ?1Э Е2, ...
..., £р, • •. | Т» состоящее из точек Еу снабженных индексами, меньшими
числа 7» конечного или второго класса, мы удалим из
последовательности Е все эти точки. Если в последовательности (£) остались точки,
то мы выберем среди них первую изолированную точку и обозначим
«е через £г
Так как Е счетно, то этот процесс обязательно кончится. Итак,
всякое счетное рассеянное множество может быть представлено
во вполне упорядоченной форме
Ч)> П> Ч> • • • > ?л> • • • > ^у • • • I a (а)
таким образом, что каждая точка Ер может быть отделена от
последующих точек с помощью порции о области с/у которая
содержит Ер и не содержит ни одной последующей точки Ет, где 7
больше у чем р.
Обратно, всякое счетное множество точек £, которое можно
представить в форме (Э) таким образом, что каждая точка Ер изолирована
в множестве последующих точек Ц, 7 ^ Р> обязательно рассеяно.
Чтобы в этом убедиться, достаточно заметить, что, так как (Е)
вполне упорядочено, каждая часть £j множества Е содержит первый
элемент Ер, и так как Ер изолирована в множестве всех последующих
точек ^, 7 ^ Р> т0 она тем более изолирована в £1Э чем наше
утверждение доказано.
Итак, счетные рассеянные множества идентичны с множествами,
которые могут быть представлены в приведенной выше вполне
упорядоченной форме.
Установив это, мы докажем фундаментальное предложение
относительно счетных множеств класса 1.
Теорема. Для того чтобы счетное множество точек было
класса 1, необходимо и достаточно, чтобы оно было рассеяно.
Условие необходимо. Действительно, по самому определению, если
счетное множество £ не является рассеянным, то оно содержит часть Еи
плотную на самой себе. В этих условиях множество Р точек фунда-
94
Н. Н. ЛУЗИН
ментальной области g7, которые являются предельными точками аля Ev
есть множество совершенное (относительно g7), содержащее Ех. Так
как Е1У очевидно, всюду плотно на Р, то это имеет место и для общей
части Е2 множеств Е и Р. Предположим, что Е2 есть множество
класса ^1. Тогда в силу теоремы Бэра о множествах класса ^1
существует порция те множества Р, которая содержится целиком или
в Е2, или же в его дополнении СЕ2, что, очевидно, невозможно.
Мы заключаем, что всякое нерассеянное счетное множество точек
есть в точности множество класса 2 (достижимое снизу).
Условие достаточно [10]. Пусть Е — рассеянное множество точек.
Это значит, что Е может быть представлено во вполне упорядоченной
форме
Чу *1> ^2> • • • У ^ii,> • • • У Ер ... | Ot, (&)
где каждая 5р отделима с помощью порции с области g7,
содержащей ;р и не содержащей ни одной из последующих точек 5Т, где ?
больше, чем (3.
Пусть /р— замкнутое множество, которое получается
выбрасыванием из о/ всех порций ар/, где Р' меньше, чем р. В силу свойства
порций ар* ясно, что /р содержит точку Ер. Тогда, если обозначить
через те^ порцию /*р, определенную ар, то замкнутое множество тер
содержит точку 5р.
Установив это, обозначим через Н множество тех точек о/, которые
не принадлежат ни одной из порций ар, 0 ^ Р <Са; множество //,
очевидно, замкнуто. В этих условиях вполне упорядоченная
последовательность
Ну те0, те1э . . . , теш, . .., тер, . . . | а (1)
состоит из счетного множества замкнутых множеств попарно без общих
точек, сумма которых совпадает с g7. Значит, последовательность (1)
представляет собой разложение всей области 3 на счетное множество
замкнутых множеств без общих точек.
Легко видеть, что каждый член последовательности (1), кроме
первого члена Ну содержит одну и только одну точку множества Е; для
члена те^ это точка 5р.
Если мы выбросим из тер точку 5р, то оставшееся множество будет,
очевидно, множеством класса 1; обозначим его через /?р.
Итак, вся область g7 разложена на счетное множество множеств
класса ^1: это множества //, 5р и /?р, где 0^Р<Са« Так как эти
множества попарно не имеют общих точек, то мы заключаем (стр. 70), что
сумма счетного числа этих множеств, произвольным образом
выбранных, есть множество класса ^1.
В частности это имеет место для множества /?, состоящего из
точек 5р (ч. т. д.).
Акали» оперативного процесса теоремы Бэра для множеств
класса !• Д\я *гбго чтобы найтв: отправную точку &кя наиболее ест^ст-
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
95
венного обобщения предшествующей теоремы, мы рассмотрим
оперативный процесс, который послужил Бэру при доказательстве его
теоремы*
Пусть Е — точечное множество, обладающее необходимым
свойством множеств класса ^1. Это значит, что, каково бы ни было
совершенное множество Р, существует его порция тс, которая содержится
целиком либо в Еу либо в его дополнении СЕ.
Назовем нормальной всякую порцию ~ множества Р, которая
обладает этим свойством. Так как каждая порция точечного множества
определяется некоторой порцией области 7У концы которой
рациональны, то нормальных порций может быть счетное множество.
Опишем теперь оперативный процесс Бэра. Мы начинаем с того,
что выбрасываем из области J все нормальные порции этой области.
Множество всех оставшихся точек замкнуто; мы его обозначим
через Fi* Ясно, что все порции с7, смежные к Fv нормальны1;
обозначим их через ъ@\ л = 1, 2, 3, ...
Пусть Рг — наибольшее совершенное множество, содержащееся в Fv
Поступим таким же образом с Р19 т. е. выбросим из Рх все его
нормальные порции; множество оставшихся точек есть замкнутое
множество, которое мы обозначим через Ft. Ясно, что части Р19 смежные к Р2,
разбиваются на нормальные порции2; мы их обозначим через я£), л=1,
2, 3, ...
Вообще, если определено замкнутое множество F? (если р —
второго рода, то F$ по определению есть общая часть всех замкнутых
множеств, ранее определенных), то мы обозначим через Р? наибольшее
содержащееся в F$ совершенное множество. Выбросим из Р все его
нормальные порции. Множество оставшихся точек Р? есть замкнутое
множество, которое мы обозначим через Рр+ь Ясно, что части Ря,
смежные к />и, разбиваются на нормальные порции; мы их обозначим
через *Jf>, п = 1, 2, 3, ...
Продолжая таким же образом, мы построим вполне упорядоченную
последовательность совершенных множеств
О/ у 1 1> I 2> * • • > * ш> • • • » *р • • • >
где каждое последующее множество содержится в предшествующем и
нигде не плотно на нем.
Отсюда следует, что эта последовательность заведомо счетна и
что, следовательно, применение процесса Бэра закончится остановкой
на некотором члене с индексом а конечным или второго класса, таким,
что множество Ра пусто:
Таков процесс Бэра.
1 Можно включить, если это необходимо, в Е\ рациональные точки.
2 Если замкнутое множество F содержится в совершенном множестве Рл то мы
называем частью Р* смежной к Л множество всех точек Р% принадлежащих
некоторому смежному интервалу к F.
"96
Н. Н. ЛУЗИН
Если мы захотим анализировать этот процесс, то вот что мы
констатируем: его конечной целью является осуществление полного
разбиения области о/ на счетное множество отдельных точек и
нормальных порций совершенных множеств попарно без общих точек.
Действительно, так как множество Рр наибольшее в Рр совершенное
множество, то множество-разность Рр— Рр счетно (теорема Кантора-
Бендиксона); значит всех точек, принадлежащих к сумме множеств
рр— Рр— счетное множество. С другой стороны, всех порций тг^Э>
^0<^(3<Са> л=1, 2, 3,...) также счетное множество. Но
фундаментальная область о/ есть, очевидно, сумма счетных множеств Ер — Рр и
нормальных порций n\fh
Так как всякая нормальная порция целиком содержится или в Еу
или же в его дополнении СЕ, то мы заключаем, что рассматриваемое
множество Е есть часть полного разбиения фундаментальной области с7
на счетное множество элементов класса ^1 и, следовательно, есть
само множество класса ^ 1 (стр. 70).
Мы приходим таким образом к заключению: с принятой нами точки
зрения процесс Бэра есть не что иное, как констатация для класса 1
того общего факта, что всякое множество Е класса а есть часть
полного разбиения фундаментальной области о/ на счетное множество
попарно не пересекающихся элементов класса <^а.
Значит, с принятой точки зрении теорема Бэра о множествах
класса 1 есть частный случай общей теоремы о структуре множеств,
измеримых В (см. стр. 70).
Однако эта точка зрения несколько поверхностна, так как процесс
Бэра не вполне адекватен указанной теореме о структуре множеств,
измеримых В, но содержит нечто большее.
Прежде всего упомянутая теорема о структуре имеет неопределенный
характер, так как все элементы, составляющие множества Е и СЕ,
перенумерованы при помощи целых положительных чисел. Процесс же
Бэра существенно трансфинитену и это трансфинитное не может быть
исключено никоим образом: мы докажем в дальнейшем, что существуют
эффективно множества Е класса 1, дая которых процесс Бэра не
остановится никогда раньше трансфинитного числа {3, и это, каково бы ни
было Р, заранее фиксированное. Благодаря этому важному факту можно
классифицировать множества класса 1 по длине разложения Бэра,
и подклассы, так полученные, представляют последовательность,
подобную той, которую дает сама классификация Бэра — Валле-Пуссена.
Аналогия между теоремой стр. 70 и процессом Бэра неполна, так
как замкнутые множества ^\ которые составляют множество Ef
не являются произвольными замкнутыми множествами попарно без
общих точек, но обладают вполне определенным свойством, которого
лишено, вообще говоря, произвольное разложение области с7 на
замкнутые множества. Это свойство и составляет самое существо
доказательства Бэра его теоремы о функциях (или множествах) класса 1.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
97
Чтобы увидеть, в чем состоит это свойство, вернемся к аналогии,
которая существует между обычными точками и элементами какого-
либо класса.
Если £— счетное множество элементов е класса 1, то мы назовем
это множество рассеянным, если каждая его часть £х обладает
изолированным х элементом. Это — естественное обобщение понятия Данжуа
для точек*
Если мы вернемся теперь к рассмотренному выше множеству Е}
то мы констатируем без труда, что элементы *№ класса 1, которые
образуют множество Е и которые нам дает процесс Бэрау образуют
рассеянное множество в смысле введенного обобщения.
В самом деле, обозначим через £ множество отдельных точек и
нормальных порций ^, которые принадлежат к Е. Чтобы убедиться,
что множество £ рассеянное, достаточно показать, что каждая его
часть £1 содержит изолированный элемент. Но множество £г состоит
из точек множеств-разностей /р—Рр и из порций i^fK Среди
индексов Р этих множеств есть наименьший; пусть это р0. Если множество £1
содержит эффективно точки /р— Рр, то среди этих точек есть
наверняка изолированная точка, так как множество /р — Рр рассеянное»
Если £г не содержит ни одной точки F$— Рр, то оно содержит
эффективно порции т№л Я утверждаю теперь* что каждая из этих порций
изолирована в £^ Чтобы в этом убедиться, достаточно заметить, что
порция rcJW нормальна, следовательно, определена порцией области е7,
которая не содержит ни одной точки ни множества Fp — Рр', ни
порций т№\ если Р' превосходит Р, Р' > р. Следовательно, рассматриваемая
порция т№ изолирована в £г (ч. т. д.).
Аналогичным образом, точки F$ — Рр и порции ъ$\ из которых
состоит дополнение С£, образуют также рассеянное множество.
Обратно, если Е и СЕ оба являются рассеянными
последовательностями элементов класса 1, то существует процесс Бэра, который
дает Е и СЕ.
Значит, имеется тождество между процессом Бэра и процессом,
который позволяет представить множество класса 1 в форме рас
сеянной последовательности счетного множества элементов класса 1
(замкнутых множеств).
Итак, мы естественно пришли к тому, чтобы рассматривать как
обобщение процесса Бэра некоторый процесс разложения всякого
множества класса а в рассеянную последовательность элементов класса а
с условием, чтобы было доказано эффективное существование всех
подклассов класса а, которые получатся, если классифицировать мно"
жества класса а по трансфинитной длине этого разложения»
Этот процесс будет предметом наших последующих рассмотрений.
1 Общее понятие изолированного элемента дано выше (стр. 65). В
рассматриваемом случае элемент е класса 1 изолирован в множестве & элементов е класса 1,
если можно заключить е в множество Н начального класса Kq таким образом, что Н
не пересекается ни с одним другим элементом из £.
98
Н. Н. ЛУЗИН
Процесс Бэра в высших классах
Рассеянная последовательность элементов класса <^а.
Предшествующее изучение множеств точек было необходимо для того, чтобы
изучить роль элементов класса <^а в образовании множеств. Сейчас
своевременно по образцу идей Данжуа ввести новые понятия
относительно последовательностей элементов класса <^&, понятия, которые
позволят, как мы увидим, установить необходимые и достаточные
условия для того, чтобы [множество было класса ^а, и распределить
множества класса а в трансфинитную последовательность подклассов
по длине разложения Бэра.
Прежде [всего мы установим следующее фундаментальное
определение: Множество £, образованное из счетного множества
непересекающихся элементов класса а, называется рассеянны му если
каждая часть & содержит изолированный элемент 1.
Повторяя те же рассуждения, которые мы делали в случае
рассеянных точечных множеств, мы заключаем, что S можно представить во
вполне упорядоченной форме
^0> ^1> ^2> • • • » ^ч>> • • • у &/$> • • • I T (6)
таким образом, что каждый элемент е может быть отделен от
последующих элементов при помощи множества Н$у содержащего е\ и не
содержащего никакой части элемента е^, где индекс Р' превосходит Р,
причем Н$ либо множество класса меньшего, чем класс е.у либо же
принадлежит к базе класса е..
С другой стороны, ясно, что каждое множество элементов £>
которое можно представить в форме (<§) таким образом, что каждый
элемент е. изолирован в множестве всех последующих элементов е>у
р' ^ р, обязательно рассеянно.
Мы можем теперь приступить к изучению условий, которым удовле*
творяют множества класса а. Достаточное условие для того, чтобы
множество было класса ^а, выражается следующим образом:
Теорема. Всякое рассеянное множество элементов класса ^а
есть множество класса ^а.
Пусть
*0> в1> е2> • • • у в<»У • • • > ец> • • • I T (<§)
рассеянное множество класса ^а. Член е^ содержится в отделяющем
множестве Н$у которое не имеет общей части ни с одним из
последующих множеств ер9 Р' ^> р. Множество //р либо класса меньшего, чем
класс еЛ% либо же принадлежит к базе класса еа.
р р
1 Мы говорим вообще, что элемент е класса а, принадлежащий семейству
множеств F, изолирован в этом семействе, если существует отделяющее множество И
или класса <а, или из базы Ва% которое содержит еиве содержит точек ни одного
из других множеств семейства F.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
99
Пусть F$ — множество, которое получается выбрасыванием из <£f
всех отделяющих множеств Ну, где Р' меньше, чем р; легко видеть,
что /р или класса <Са> или принадлежит к базе ВаУ или же есть
элемент класса а. В силу свойства множеств Ну ясно, что F^ содержит
элемент е . Следовательно, если мы обозначим через ^ общую часть
Щ • Fp, то множество ^з содержит е^. Установив это, обозначим
через Q множество точек <з7, которые не принадлежат ни одному^из
отделяющих множеств //з, 0-^Р<Л* Вполне упорядоченная
последовательность
Q, К0, -р ^2, . . . , 7С<о, , . . , *р, • • • | 7 (1)
состоит, очевидно, из счетного множества множеств: или класса <С а,
или из базы ВаУ или же элементов класса а. Легко видеть, что эти
множества не имеют попарно общей части и что их сумма совпадает
с областью о/. Следовательно, последовательность (1) есть разбиение
всей области с7 на счетное множество множеств класса ^а.
После этого обозначим через Е сумму членов рассеянной
последовательности (<§). Ясно, что множество Q не содержит ни одной точки Е>
и что точки Еу принадлежащие к тер, образуют элемент е .
Следовательно, если мы вычтем из яр элемент г., то множество-разность R4
есть множество класса ^аине содержит точек £.
Отсюда следует, что вся область о/ разложена на счетное множество
множеств класса ^ а: это множества Q, e, R , где 0 ^ Р <С Т- Так как
эти множества попарно без общих точек, то мы заключаем (стр. 70,
примечание), что сумма бесконечного множества этих множеств,
произвольно выбранных, есть множество класса ^а. В частности, это так для
множества Еу составленного из е..
Следует заметить, что доказательство этой теоремы тождественно
(кроме обозначений) с доказательством соответствующей теоремы для
точечных рассеянных множеств (стр. 9*3).
Регулярное параметрическое изображение множеств. Мы пришли
к вопросу, является ли это найденное нами достаточное условие, для
того чтобы точечное множество было класса ^а, необходимым. Чтобы
решить этот вопрос в положительном смысле, нужно сначала изучить
некоторые предварительные вопросы.
Мы установим сначала новое определение.
Назовем регулярной всякую функцию /(/), определенную в
фундаментальной области о/и которая никогда не принимает двух равных
значений; каждая регулярная функция есть разнозначная функция:
если t'^t\ то
Мы говорим теперь, что какое-либо множество Е точек
фундаментальной области о/х обладает регулярным параметрическим изобра-
жениеМу если Е есть множество значений функции х =/(/),
определенной на порции (0, 1) фундаментальной области o7iy непрерывной и
100
Н. Н. ЛУЗИН
регулярной на этой порции. Ясно, что каждое множество Е, которое
обладает регулярным параметрическим изображением, имеет
мощность континуума и содержит совершенное множество. Чтобы
в этом убедиться, возьмем в порции (0, 1) области Ы\ множество Р,
совершенное в абсолютном смысле. Так как функция x=/(t)
непрерывна и регулярна, то множество Q значений, которые f{t) принимает
на Ру есть совершенное множество; легко видеть, что Q содержится
в Е.
Можно заметить, что каждое множество Е, обладающее регулярным
параметрическим изображением, не может иметь изолированных точек.
Установив это, введем следующее определение. Пусть Е —
множество класса Ка9 состоящее из точек <?7Х; мы предположим, что Е
обладает регулярным параметрическим изображением x=f(t). Назовем
это изображение нормальным, если множество значений, которые /(f)
принимает на произвольной порции, есть множество класса <Га.
Установив это определение, мы можем доказать следующую теорему:
Теорема. Всякое несчетное измеримое В множество обладает
нормальным параметрическим изображением, если исключить из
него счетное множество точек.
Утверждение очевидно в случае, если Е принадлежит начальному
классу К0, так как в этом случае Е есть сумма счетного множества
порций области о/х: Е = кх -+- гс2 "^ • • • и можно построить подобное
отображение интервала Бэра (л) порядка 1 области o/t на тг„, что и
определяет нормальное изображение Е1.
Установив это, предположим, что предложение верно для всех
классов, предшествующих Ка, и докажем, что оно верно и для класса а.
Заметим сначала, что все сводится к доказательству утверждения
для элементов класса Ка. Действительно, всякое множество Е класса К9
есть сумма счетного множества элементов класса <^а попарно без
общих точек: Е = тсх -+- тс2 -i- ... Достаточно, очевидно, изобразить
нормально т:п на интервале Бэра (л) порядка 1, чтобы иметь нормальное
изображение Е.
Предположим же, что Е есть элемент (несчетный, если а= 1) класса а.
Мы имеем
Ь = hi • b2 •. . Ьп .. .,
где все множества Еп класса <Са, и последовательность их убывающая
fpfp...z>Enz>...
Пусть x]=/n(t) — нормальное изображение Еп на порции
фундаментальной области о7/я; в этом изображении исключена, быть может,
счетная часть Еп.
1 Вообще,, если дана система целых положительных чисел, расположенных в
определенном порядке: qlt a2» •••» ak% то интервалом Бэра (alf а2, ...» я*) называется
множество всех иррациональных точек, у которых представление в виде непрерывной
дроби начинается с alt a2, ..., ОД этот интервал называется интервалом порядка к.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
101
Установив это, рассмотрим новую область o/t и возьмем порцию
(О, 1) этой области. Мы установим взаимно однозначное соответствие
между точками / порции (0, 1) области o7t и системой, состоящей из
счетного множества точек tl9 t2, ..., tn .-., где каждая точка tn взята
в порции (0, 1) соответствующей области <з7*я. Процесс, который
позволит нам установить это соответствие, заключается в следующем:
Каждому интервалу Бэра порядка 1 области g7* мы поставим в
соответствие интервал Бэра порядка 1 области з7/р и наоборот.
Всякому интервалу Бэра 8 порядка 2 области >7t мы поставим в
соответствие группу Г2, состоящую из двух интервалов Бэра порядка
2 — \ и о2, соответственно содержащихся в с7^ и g7/2 таким образом,
что интервал порядка 1, содержащий 8, соответствует интервалу
порядка 1, содержащему \; и обратно9 каждой аналогичной группе Г2
соответствует интервал Бэра порядка 2 из области g7*.
Вообще каждому интервалу Бэра 8 ранга л из области o7t
соответствует группа Гя, состоящая из л интервалов Бэра Ь19 82> ..., 8Я
порядка л, содержащихся соответственно в ЗьхУ o7t39 -.., o/tn таким
образом, что интервал Бэра порядка л—1, содержащий 8, соответствует
группе Гя_х, состоящей из интервалов Бэра порядка п — 1, содержащих
соответственно Ьи 82, ..., Ьп_г; и обратно, всякой аналогичной группе
Г„ соответствует интервал Бэра порядка п области е7*.
Так как каждая иррациональная точка, заключенная между 0 и 1,
есть общая часть последовательности интервалов Бэра порядка
1, 2, ..., л, ..., заключенных один в другой, то указанный процесс нам
дает уравнения:
<ря (t) непрерывны на g7*. Каждой последовательности точек tlf tv ...,
tn, ..., расположенных соответственно в порциях (0,1) областей o7tiy
~o?t2, ..., o7tn, ..., соответствует одна и только одна точка области o?t. Если
ИфГу то существует число i такое, что <р» (О ^ ¥< (О» так как двум
различным интервалам Бэра 8' и 8" порядка л, содержащим точки {
и t"$ соответствуют две различные группы Гп и Г^г, состоящие каждая
из л интервалов Бэра порядка л, расположенных в o7tl, <Э\2> ..., ?7*п.
Суперпозиции:
*=/«[?« (01 = Л С).
х =/.[<?. (t)\=F. V)
дают функции, непрерывные на 3\. Отсюда следует, что совместные
равенства
102
H.H. ЛУЗИН
определяют в c/t множество точек, замкнутое в o/t; мы его обозначим
через Т.
Когда t пробегает (0, 1), то точка U пробегает бесконечно много раз
порцию (0, 1) области о/ц* Следовательно, x = Fi (t) пробегает
бесконечно много раз множество £, и никогда из него не выходит. Отсюда
следует, если обозначить через F(t) общее значение функций
Fl(t) = Fi{t)=...=F.(t)=...,
что уравнение
x = F(t)
дает нам точку общей части Ех • Et . •. Еп ... и что всякая точка х
этой общей части может быть получена таким образом.
Функция х = F(t) непрерывна на 7\ Важно заметить, что она
регулярна на Ту так как если f=£t", то существует функция <р< такая,
что
?«<0¥=<Р«(О;
значит, так как /*(£*) регулярна на o7/t., то имеем
Fiifi + Ftif)
и, следовательно,
F(t')^F(f).
Мы предположим, что множество Е несчетно. Тогда и множество Т
несчетно; при этом оно замкнуто в o7f
Так как Т несчетно, то существует полное разложение порции (0,1)
области o/t на интервалы Бэра 8 такое, что существует бесконечно
много интервалов 8, каждый из которых содержит несчетное множество
точек 7*. Установим взаимно однозначное соответствие между этими 8
и интервалами Бэра А порядка 1 новой фундаментальной области g7t.
Каждый из этих 8 может быть разложен полностью на интервалы
Бэра 8' так, что найдется бесконечно много 8', каждый из которых со
держит несчетную часть 7\ Установим взаимно однозначное
соответствие между этими 8', содержащимися в 8, и интервалами Бэра А'
порядка 2, принадлежащими соответствующему А.
Вообще, если 8(n—1) и Д(п~1>— два соответственных интервала Бэра,
первый из которых содержит несчетную часть Т, а второй есть
интервал Бэра порядка (п — 1) области с7т, мы разобъем полностью S^"-"1)
на интервалы Бэра 8<я) таким образом, чтобы существовало бесконечное
множество &(W), каждый из которых содержит несчетную часть Т.
Установим взаимно однозначное соответствие между этими 8(я) и
интервалами Бэра А(п) порядка л, принадлежащими Д(и-1>.
Мы определили в порции (0, 1) новой области о7т функцию
непрерывную и регулярную на (0, 1). Если х пробегает порцию (0, 1)
области g7t, to точка t пробегает множество Т9 кроме, быть может,
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
103
счетного множества точек Т. Когда т пробегает интервал Бэра Д
области о/ъ то точка t пробегает, очевидно, часть Г, содержащуюся
в интервале Бэра £, соответствующем А (с точностью до счетного
множества точек этой части). Пусть v — порядок &. Когда t пробегает 8,
то точки
пробегают каждая интервал Бэра порядка v, и эти интервалы
содержатся соответственно в <7il9 с7*2> • • • > с7/ > тогда как другие точки
Iv+l = <?v+i(t)y *v+2 = Ту+г (0> ••• пробегают каждая порцию (0,1)
соответственных областей g7/v+1, c7*v+2, ...
Но каждая функция x=f4(tj) дает нам нормальное изображение Ei
на порции (0, 1) области с7^. Это значит, что когда tt пробегает
порцию области о/ц% то точка х пробегает часть Ei класса <jx. Отсюда
следует, что когда t пробегает Ъ, то сложная функция /, [ср< (/)]
пробегает часть Е{ класса <Са, если z^v, и пробегает все множество Eiy
если />^ Отсюда можно заключить, что когда х пробегает интервал
Бэра А в o/zf то сложная функция
пробегает общую часть бесконечного множества множеств класса <С&,
т. е« или множество класса <^а, или множество базы ВаУ или же
элемент класса л [11]. С другой стороны, легко видеть, что Ф(~)
непрерывна и регулярна на порции (0, 1) области с7_, и что множество ее
значений на (0,1) совпадает с множеством Е = Ех- Е2 • •., кроме счетного
множества точек. Следовательно, уравнение х = Ф(т) дает нам
регулярное параметрическое изображение Е.
Нам остается только доказать, что это изображение нормальное.
Для этого мы докажем, что множество значений Ф(^) на каждом
множестве Н класса О, расположенного в порции (0, 1) области g7t, есть
множество класса ^а. Но так как Н и его дополнение СН являются
оба суммами счетного множества порций <з7т, то они являются, очевидно,
суммами интервалов Бэра. Отсюда следует, что множество значений
Ф(~) на Ну которое мы обозначим Ф(//), так же как и множество
Ф(С//) значений Ф(т) на СН, являются оба суммами счетного
множества множеств класса ^а без общих точек. Так как полная сумма этих
множеств есть, очевидно, Еу то мы заключаем, что Ф(//) есть часть
полного разбиения множества класса ^а на счетную сумму множеств
класса <^а без общих точек. Следовательно1, класс Ф(//) не
превосходит а и параметрическое изображение Е, лг = Ф(х), нормально (ч. т.д.).
Мы дополним этот результат следующими замечаниями:
Замечание L Из доказательства следует, что если Е—элемент
класса а, то нормальное параметрическое изображение х = Ф(т), которое
1 См. примечание на стр. 70.
104
Н. Н. ЛУЗИН
мы сейчас получили, ставит в соответствие каждому интервалу Бэра о
из г7т множество Ф($) значений Ф(^) на &, которое либо класса <jxy
либо из базы ВаУ либо же элемент класса а.
Замечание II. Если Е—двустороннее множество класса а, то
для Е существует нормальное изображение х = Ф (т) такое, что каждому
множеству Н класса О соответствует или множество класса <а, или
множество из базы Ва.
Действительно, достаточно разложить Е на счетную сумму
элементов класса <а и осуществить нормальное изображение этих элементов
соответственно на интервалах Бэра ранга 1 области <з7т. Ясно, что
полное изображение х = Ф(~) множества Е, таким образом полученное,
есть нормальное изображение, обладающее высказанным свойством*
Изображение произвольного множества класса а в форме
рассеянной последовательности элементов. Мы предпримем сейчас
общее изучение произвольного множества класса ЛГв» Пусть Е — какое-то
множество класса а. Мы имеем
Е = lim £„,
«-►00
где множества Еп класса <jx.
Прежде всего мы устраним случай, когда одно из дополнительных
множеств CEi счетно (или конечно). Действительно, если множества CEiy
которые счетны (конечны), имеются в ограниченном числе, то мы можем
исключить соответствующие множества Ei из последовательности Е1У
-Сто, • • •
Если этих множеств CEi бесконечно много, то самое множество СЕ,
очевидно, счетно (конечно). Тогда или Е есть элемент класса 2, или же
Е класса 1 и, следовательно, СЕ — рассеянное множество точек
(стр. 93).
Итак, все сводится к изучению случая, когда каждое из множеств
Еп и СЕп несчетно, каково бы ни было целое положительное л.
В этих условиях мы можем написать последовательность
уравнений
*=/i(*i)» x=/2{t2)9 •••> x=fn{tn), .♦.,
которые дают, каково бы ни было я, нормальное изображение Еп на
порции (О, -у] и СЕп на (у, 1) области о7*п, исключая счетное
множество точек.
Возьмем новую фундаментальную область g7* и рассмотрим
уравнения
'i = <Pi(0. 'i=TiWt •••» <• = ?»(')» •••
и сложные функции
*=ЛЫ')]=Л(0,
*=f.b.(t)\ = F.ifi,
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
105
которые мы изучали при доказательстве предыдущей теоремы
(стр. 100—101).
Так же как в этом доказательстве, совместные равенства
Л(о=/;(/)=...=я,(*)=...
определяют на Jt множество точек Г, замкнутое в этой области.
Пусть F(t) — общее значение этих функций на Г. Это функция,
определенная на 7*, непрерывная и регулярная на этом множестве и
такая, что уравнение
x = F{t)
преобразует множество Т во всю область 3ху кроме счетного
множества ее точек.
Так же как в доказательстве предыдущей теоремы, мы преобразуем
при помощи функции
* = ф(т)
порцию (0, 1) области о7т в множество Т> кроме, быть может, счетного-
множества точек из 7*.
Сложная функция
* = /г[<1Ф)]=Ф^
непрерывна и регулярна в (0,1) и преобразует эту порцию во всю
область о/я с точностью до счетного множества точек. Нужно изучить
свойства функции Ф(^).
Прежде всего, функция x=fn(tn) дает нам нормальное изображение
Ея и СЕп на (О, "о") и (т> l) области Jtn\ это значит, что функция
fn{tn) ставит в соответствие каждому интервалу Бэра о области с7*л
множество /„ (Ь) значений /«(tn) на 8, которое есть множество класса <j*.
Отсюда вытекает при помощи такого же рассуждения, как то, которое
мы проводили аля доказательства предыдущей теоремы, что
рассматриваемая функция х = Ф(т) ставит в соответствие каждому интервалу
Бэра 8 области о7т множество Ф (8) класса, строго меньшего а,
лежащее в Jxl.
Установив это, обозначим через еп прообраз множества Еп при
отображении при помощи функции дг = Ф(х); еп есть множество, лежащее
в g7t, такое, что Ф (еп) совпадает с Еп. Легко видеть, что множество еп
есть класса О.
Действительно, необходимое и достаточное условие для того чтобы
точка х = Ф (т) принадлежала к £п, состоит в том, что вначение <ря [ф (t)\
принадлежит порции (0, -Л области с7*п, что в силу непрерывности
1 Мы обозначаем здесь через Ф (о) множество значений функции Ф (х) на
интервале Ь. Вообще, если дань некоторая функция /(*), определенная в области &х+
и множество Еу лежащее в этой области, то мы обозначаем черев /(£) множество-
значений, которые принимает f (х) на Е*
106
Н. Н. ЛУЗИН
(ря[ф(т)] возможно только в случае, когда еп есть множество начального
класса К0.
Очевидно, что последовательность множеств класса О
ё\у &2> ' * • у &пу • • •
сходится и имеет пределом множество е, которое есть прообраз Е для
х = Ф(т); множество Еу очевидно, класса <Л.
Возможны два случая.
Первый случай: множество е класса О. В этом случае е и его
дополнение Се являются оба суммами счетного множества интервалов
Бэра. Отсюда следует, что Е и СЕ являются оба суммами счетного
множества множеств класса <jx. Значит, Е есть множество из базы Ва.
Второй случай: класс е равен 1. В этом случае процесс Бэра,
примененный к е, дает нам вполне определенное разложение е в
рассеянную последовательность элементов класса 1 (замкнутых множеств):
е = -Ц0-+-\-+- ... -ьт]ш-1- ... -ьт)р ■+-... | Т»
где т)„ с конечным индексом п есть интервал Бэра и тцз, где индекс р
второго класса и меньше ?> есть нигде не плотное совершенное
множество и изолировано от всех последующих т^,, (У > Р, при помощи
интервала Бэра А .
Это разложение е осуществлено в области с7т. В области <Эfx ему
соответствует следующее разложение множества Е:
£ = е0ч-е1ч-еач-...-неюн-...-*-ер-|-...|т, (1)
где е есть образ ttl для х = Ф (х). Интервал Бэра А преобразуется в
множество //р класса, строго меньшего а. Легко видеть, что е содержится
в //, так как *»] содержится в h . Из того, что Л3 не имеет общих
точек ни с одним из последующих множеств !)«,, Р'^>(3, следует, что
Н~ не имеет общих точек ни с одним из последующих множеств е.,,
р'>р.
Остается только изучить природу множеств ер. Так как t\ —
совершенное нигде не плотное множество, то его дополнение Сщ есть сумма
интервалов Бэра. Тогда образ С^э есть или множество класса <j*>
или же множество класса а, достижимое снизу. В этих условиях
множество £з есть либо множество класса <аэ либо из базы ВаУ либо
элемент класса а.
Установив это, удалим из разложения (1) множества Е все е,
которые либо суть множества класса <jx, либо из базы Ва, и составим
их сумму S. Остаются только элементы ер строго класса а, заключенные
в соответствующие множества //р класса <а, которые их отделяют от
множеств ер/ за ними следующих. Множество R оставшихся элементов
-есть рассеянное множества.
Мы пришли, таким образом, к следующему результату:
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
107
Всякое множество Е класса а может быть разложено на
множество S класса а, достижимое снизу, и рассеянное множество R,
образованное из элементов класса а:
E = S+R.
Подклассы, их существование
Распространение результатов на случай множества точек в
пространстве нескольких измерений* Мы теперь рассмотрим с общей
точки зрения вопросы, изученные в предшествующих номерах, и для
этого остановимся на случае множества точек в пространстве
нескольких измерений. Для определенности мы ограничимся случаем
пространства двух измерений.
Прежде всего, рассматривая определения главы I (стр. 51),
относящиеся к множествам в пространстве нескольких измерений, мы заметим
немедленно, что все понятия и все рассуждения, сделанные для
линейных точечных множеств, сохраняются для евклидова пространства
нескольких измерений. Таким же образом мы можем классифицировать
измеримые В множества, лежащие в пространстве нескольких измерений,
в трансфинитную последовательность классов Бэра—Валле-Пуссена,
и в каждом классе этой классификации мы будем иметь элементы
множества, достижимые снизу, и множества, недостижимые с обеих сторон;
если класс Ка второго рода, то в нем есть двусторонние множества,
которые образуют базу Ва этого класса.
Остается уяснить понятие параметрического изображения в случае
множества точек нескольких измерений.
Мы говорим, что точечное множество Е, лежащее в
фундаментальной области о/а^-хт772 измерений, обладает параметрическим
изображением, если множество Е есть совокупность последовательных
положений подвижной точки М{хх, х2, ..., хт), координаты которой суть
функции переменного параметра t, определенного в порции (0,1)
фундаментальной области g7<:
*l=/l(0» *1=Л(0» •-•» Xn=fn(t).
Параметрическое изображение множества Е называется регулярным,
если двум различным значениям t' и /" параметра t соответствуют две
различные точки множества Е.
Пусть Е — измеримое В множество какого-то класса Ка. Мы
говорим, что регулярное параметрическое изображение множества
-*1=Л(0> *2=Л(0> •••> X»=fn(t)
нормально, если функции /< непрерывны в порции (0,1) области <Э't
и если каждой порции этой области соответствует часть Е, класс
которой не превосходит а.
108
Н. Н. ЛУЗИН
Все рассуждения предыдущих параграфов остаются верными, и мы
имеем следующую теорему:
Всякое несчетное измеримое В множество обладает нормальным
изображением, если исключить точки этого множества в конечном
или счетном числе.
При помощи этой теоремы, не делая никаких изменений в
предшествующих рассуждениях, мы приходим к следующему
фундаментальному результату:
Всякая рассеянная последовательность, образованная из
счетного множества элементов класса ^а, есть множество класса ^а^
Обратно, каждое множество Е класса Ка может быть разложено
на множество S класса а, достижимое снизу, и на рассеянное
множество R, образованное элементами класса а;
E = S+R.
Дхя а=1 мы получаем теорему Бэра о множествах класса 1, так
как эффективный процесс Бэра есть не что иное, как разложение
множества класса 1 в рассеянную последовательность элементов класса 1.
Возникает вопрос: может ли трансфинитная рассеянная
последовательность элементов класса Ка всегда быть сведена к некоторому,
относительно малому, трансфинитному числу т своих членов? Другими
словами, можно ли всегда разложить данное множество Е класса Ка таким
образом, что рассеянной вполне упорядоченной последовательности R
элементов класса а соответствует трансфинитное число f, всегда
меньшее некоторого фиксированного числа второго класса?
Мы увидим, что ответ отрицателен и что существуют эффективна
множества Е класса Ка, для которых рассеянному множеству R
соответствует сколь угодно большое трансфинитное число второго класса ?>
причем это число не может быть понижено. В круге этих идей удобна
ввести новое понятие подкласса классификации Бэра—Валле-Пус-
сена.
Пусть дано множество Е класса Ка; мы говорим, что Е есть
множество подкласса (3, если при каждом разложении Е на множество S
класса а, достижимое снизу, и на счетную вполне упорядоченную
рассеянную последовательность R, образованную из элементов класса а;
E = S+R,
соответствующее R число у не меньше, чем (3, и если оно эффективна
равно р при некотором определенном разложении Е.
Из этого определения следует, что каждое множество Е класса а,
достижимое снизу, есть множество подкласса О и каждый элемент
класса а есть множество подкласса 1.
Возникает вопрос; существуют ли множества класса а и всякого
подкласса?
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
109
Мы изложим теперь исследования по этому вопросу М. А.
Лаврентьева, важные результаты которого опубликованы им в статье
„Sur les sous-classes de la classification de M. Baire" l.
Универсальный элемент двух измерений. Возьмем в области £ ху
двух измерений множество Е класса Ка. Если мы его пересечем
прямой х = х09 параллельной оси О К, то получим вполне определенное
линейное множество е. Рассмотрим природу этого линейного множества.
Прежде всего, если Е класса О, то таково же и линейное
множество Е, так как в этом случае Е и его дополнение СЕ оба являются
суммами порций двух измерений; но каждая такая порция пересекается
прямой jc = JCo по линейной порции.
Методом трансфинитной индукции легко доказать для множеств
высших классов: всякое множество Е двух измерений класса а
пересекается каждой прямой х = х0 по линейному множеству класса ^ а,
рассмотренному не как часть плоскости, но как линейное множество,
измеримое Ву лежащее в области о7. Эта теорема верна дая а = 0, и
легко видеть* что она верна для а (первого или второго рода) при
условии, что она верна для всех трансфинитных чисел <а.
Так как каждое множество класса а, достижимое сверху, есть общая
часть счетного числа множеств классов <Са> то мы имеем следующее
следствие: всякий элемент Е двух измерений класса а пересекается
каждой прямой jc = jc6 по множеству еу которое либо класса <Са,
либо из базы Яа, либо же элемент класса а.
Установив это, мы введем следующее определение: мы говорим, что
элемент Е двух измерений класса а универсален, если всевозможные
линейные элементы класса а можно получить, пересекая множество Е
.прямыми x = Xq>, параллельными оси OY.
Существуют универсальные элементы класса 1. Чтобы в этом
убедиться» возьмем последовательность
образованную из всех порций линейной фундаментальной области 3у*
Пусть 8 = (а19 а2У..., at) — произвольный интервал Бэра ранга к9
лежащий в фундаментальной области о/х. Поставим 8 в соответствие
множеству Еь тех точек области двух измерений c/xffy абсциссы
которых принадлежат к 8, а ординаты у принадлежат к сумме k порций
^Ч -+■ Яа,-*- . •. -ь ^а^ Ясно, что Еь есть сумма конечного числа порций
двух измерений.
Затем возьмем сумму S всех множеств Я8, таким образом
определенных. Легко видеть, что S есть множество класса 1, достижимое
снизу. Я утверждаю теперь, что его дополнение E = CS есть
универсальный элемент класса 1.
1 C«mptes Rendus, 12 января 1925 г.
110
Н. Н. ЛУЗИН
Чтобы в этом убедиться, возьмем произвольное линейное множество-
класса 1, достижимое снизу; пусть е это множество. По определению,.
е есть сумма тса, -+- ^а, -+■... -+■ ^ап "*-••• счетного множества различных
порций линейной области о7у. Если мы возьмем иррациональную точку
х09 определенную бесконечной непрерывной дробью
Xq ^= \#1> ^2» • • •» апу • • •/>
то легко видеть, что прямая х = л:0 пересекает S в точности по е.
Следовательно, можно получить всевозможные линейные элементы,
класса 1, пересекая Е прямыми д: = л:0 (ч. т. д.).
Установив это, мы докажем существование в каждом классе Ка
универсальных элементов двух измерений. В наших доказательствах мы
воспользуемся следующей леммой:
Лемма. Если S есть плоское множество, лежащее в области <7^ х>
и если мы преобразуем область Jt,x в новую область 3^х при
помощи уравнений
/=ср(т), х = ху
где функция <р непрерывна в с7т, то прообраз §' множества & есть-
множество, класс которого не превосходит класса &.
Эта лемма доказывается трансфинитной индукцией. Утверждение-
очевидно, если £ класса О, так как прообраз порции области oft,*
есть множество класса О, лежащее в g7t,*.
С другой стороны, каждая последовательность множеств Sl9 <§2> • • -
..., Sn>..., имеющая пределом множество £, преобразуется, очевидно,,
в сходящуюся последовательность множеств &'19 <§'2,..., &'п> имеющую-
пределом прообраз &' множества &. Это замечание завершает
доказательство (ч. т. д.).
После того как это доказано, вернемся- к существованию универ-
сальних элементов двух измерений. Мы предположим, что это
существование уже доказано для всех классов, меньших а, и мы докажем,,
что оно имеет место и д\я самого класса Ка.
Пусть
£\> &2> • • •> <Sn9... (1}
— последовательность универсальных элементов всех предшествующих
классов (кроме /Q, причем каждый из этих геометрических элементов-
повторяется в последовательности (1) счетное множество раз. Мы
предположим, что универсальный элемент &п лежит в области o?tn,x.
Положив это, возьмем последовательность функций
'l=CPl(T)> *2=CP2(X)> • • •» 'я = <Р*(Х)> • . •>
непрерывных на области о7т и таких, что, какова бы ни была
последовательность иррациональных чисел fv t\y..., /£, существует
иррациональное число t° такое, что имеют место равенства
<1 = <?ЛЛ $ = ?, (А--1.
1 Здесь идет речь, очевидно, о непрерывной кривой Пеано, заполняющей все
пространство счетного числа измерений.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
ш
Обозначим через &'п прообраз &п при отображении при помощи
уравнения tn = yu(z), x = x. В силу предшествующей леммы класс
множества &'п не превосходит класса <?я. Тогда сумма S множеств £'п
есть множество либо класса <а, либо же достижимое снизу класса а.
Мы докажем, что S обладает следующим свойством: каково бы ни было
линейное множество е> являющееся либо множеством класса <а, либо
достижимым снизу класса а, существует такое иррациональное число тог
что прямая ^ = ^0» параллельная оси ОХ в области е7т, т, пересекает S
в точности по множеству е.
Действительно, мы имеем е = ег -+- е2 -*-... -+- ек -+-..., где ек есть
элемент класса <а. В силу самого определения последовательности
Sit S2y • • • <Sny • • • существует иррациональное число t* такое, что
прямая tnk = *Pk9 паРаллельная оси ОХ в области ^ , пересекает
множество &*к в точности по eic. Так как в последовательности
универсальных элементов £19 <£2, •... <§пУ... каждый член, рассматриваемый
как геометрическое множество, повторяется бесчисленное множество
раз, то мы можем предположить, что последовательность целых
положительных чисел п19 л2,... Щу... возрастающая, и значит в ней нет
одинаковых чисел. При этих условиях в силу предположенного свойства
функций <р!, <р2,... существует иррациональное число ~0 такое, что
t* = <рп (х°)> каково бы ни было ку и что другие £°, определенные
равенствами £J| = cpn(T0), таковы, что прямые tn=t^, параллельные оси ОХ
в области o7ttt не пересекают соответствующих универсальных
элементов &п. Если иррациональное число х° определено таким образом, то
легко видеть, что прямая т = т°, параллельная оси ОХ в области g7t,*,
пересекает S в точности по множеству е.
Отсюда следует, что множество S> так определенное, строго класса а,
так как существуют прямые т = т0, которые пересекают S в точности
по линейным множествам класса а, достижимым снизу; при этом>
естественно, предполагается, что такие линейные множества
класса КЛ существуют. Легко видеть, что S—универсальное
множество класса а, достижимое снизу, так как, пересекая S прямыми
параллельными оси ОХу можно получить все линейные множества
класса <а и все линейные множества класса Ка, достижимые снизу.
Значит, дополнение Е к множеству S есть универсальный элемент
класса а, и утверждение доказано (ч. т. д.).
Мы дополним этот результат следующим замечанием: если
универсальный элемент Е класса а, лежащий в g7*,«, преобразован при
помощи уравнений * = ср(т), х = х, где функция ср непрерывна на о7т,
то прообраз & множества Е есть также универсальный элемент
класса а, лежащий в области <3\,х.
Прежде всего, так как лрообраз множества класса а есть
множество класса ^а, то прообраз S множества Е есть или множеству
112
Н. Н. ЛУЗИН
класса < а, или множество класса /fef достижимое снизу. С другой
стороны, очевидно, что, пересекая S прямыми 1 = хОУ параллельными
оси ОХ в области о7т, *, можно получить всевозможные линейные
множества класса <Са и все достижимые сверху линейные множества
класса Ка. Значит £ — универсальный элемент класса Ка.
Существование подклассов. Фундаментальная теорема М. А.
Лаврентьева. Мы построили универсальный элемент класса 1 прямым методом,
не делая никаких дополнительных
гипотез. Далее мы определили
множество Еу и мы доказали, что оно
есть универсальный элемент класса а,
если эффективно существуют
линейные множества класса Ка.
Сейчас мы исключим эту гипотезу и
докажем непосредственно, что
плоское множество Еу выше
определенное, есть эффективно элемент
Т класса Ка и, следовательно,
существуют множества всех классов.
Рис. 5 Чтобы в этом убедиться, мы
проведем в области g? ^ диагональ
эс=* в обозначим через т] множество точек этой диагонали, не
принадлежащих к Е.
Пусть е — проекция т\ на ось ОХ. Мы начнем с доказательства того
-факта, что е не может быть получено в результате пересечения Е
какой-либо прямой х = х$> параллельной оси ОХ.
В самом деле, пусть t0 — точка области с7/ такая, что прямая t = t0
пересекает Е по е. Рассмотрим точку М диагонали, лежащую на
прямой t=t0. Возможны два случая.
В первом случае точка М принадлежит к Е. Так как прямая *=£0
пересекает Е по е> то проекция N точки М принадлежит к е. С дру-
той стороны, е есть проекция множества т|, состоящего из точек
дополнения СЕу принадлежащих диагонали. Значит М принадлежит к СЕ,
что противоречит предположению.
Во втором случае точка М принадлежит к СЕ. В этом случае
проекция N точки М принадлежит к е. Но множество е есть проекция
точек Еу лежащих на прямой t = t0. Значит М принадлежит к Еу и мы
-опять получили противоречие.
Установив это, покажем, что определенное нами множество Е
принадлежит классу Ка. В силу самого определения Е всякое линейное
множество класса <а может быть получено в результате пересечения
Е прямой t = t0y параллельной оси ОХ. Если бы множество Е было
само класса < а, то это имело бы место и для пересечения Е с
диагональю х = г. При этих условиях множество ?| было бы класса <<*,
так же как и его проекция е на ось ОХ. Тогда множество е можно
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
113
было бы получить, пересекая Е некоторой прямой t = t0, что заведомо
невозможно.
Итак, множество Е строго класса а, и, следовательно, существуют
множества всех классов.
Читатель заметил, что в этом доказательстве мы исходили из
некоторого частного (однако произвольного) пересчета всех трансфинитных
чисел, меньших а, при помощи целых положительных чисел. Этот
пересчет вошел в последовательность (1):
<§l> <S2y > <§п> . • •> (1)
состоящую из универсальных элементов всех классов,
предшествующих а. Итак, мы можем доказать существование элемента Е каждого
данного класса а, так как мы умеем получить конструкцию Е из
пересчета всех чисел, меньших а, при помощи целых положительных чисел.
Но мы не умеем назвать семейства элементов всех классов, в
котором содержался бы один и только один элемент каждого класса, так
как это предполагало бы (если ограничиваться предшествующим
методом) возможность назвать единственный пересчет трансфинитных
чисел, предшествующих каждому трансфинитному числу а.
Мы думаем, что такой пересчет невозможен [12].
Перейдем теперь к доказательству фундаментальной теоремы
М. А. Лаврентьева о существовании множеств всех подклассов.
Вот метод М. А. Лаврентьева.
Мы берем формально класс а и один из его подклассов р. Каждое
линейное множество е, принадлежащее этому подклассу, может быть
представлено в форме
где S есть сумма счетного множества элементов класса <Са, a R —
рассеянное счетное множество элементов класса а; это последнее
множество вполне упорядочено и имеет р соответствующим
трансфинитным числом.
Таким образом, мы можем написать
е = (ег н- £2 -+- ... -н еп -н .. .) -+-
+ К н-Ъ + .-. + ^н-...-*-^-■-...) IP <2)
и поставить в соответствие этому разложению трансфинитную
последовательность
Д)> Нц • • •> Дь> • • •> Hv ..., | Р,
где каждое ея класса <а и ?]т— элемент класса а; отделяющее
множество Ну класса < а содержит ?]у и не содержит ни одной точки
из элементов у\уу следующих за т]т, т'>т.
Всякое множество е класса а и подкласса {3 может быть
представлено в форме (2), и обратно: каждое линейное точечное множество е.
114
Н. Н. ЛУЗИН
представленное в форме (2), есть очевидно: или класса <С а> или же
класса а и подкласса ^ (3.
Удобно написать разложение (2) в следующей форме:
е = т\о + г11ч-г12ч-...-+-г1ю-1-...ч-'Г}у + ...\$у (3)
где т}г — или элемент класса <<*, или же элемент в точности класса а.
Мы запишем также соответствующую трансфинитную
последовательность отделяющих множеств в форме
Н0, Н19..., Hw>..., Hv ... | р,
где //г совпадает с f[v если класс т]у меньше, чем а, если же г\у есть
элемент класса а, то множество Ну класса < а содержит т)т и не
содержит ни одной точки из элементов iqTs которые следуют за г\1У т'^>7»
Легко видеть, что обратное также имеет место: если какое-нибудь
линейное множество е представлено в форме (3), то это множество
либо класса <<*, либо класса а и подкласса ^р.
Доказав это, мы поставим в соответствие каждой простой
бесконечной последовательности элементов класса <Са>
С\> &2> • • •» еп> • • •
и каждому трансфинитному числу р линейное множество е. Д\я этого
пересчитаем все конечные и трансфинитные числа ?> меньшие р, при
помощи целых нечетных чисел 1, 3, 5,..., 2л — 1,... и запишем
соответствующие е19 е3, еъ,..., е2п-1... в трансфинитную
последовательность
Н0, Н1У Н2У..., //ш,..., Hv ... | Р,
где каждое Н( есть то множество e2n-i» номер которого 2л—1
соответствует трансфинитному числу "f.
Определим теперь множество е следующим трансфинитным
разложением:
где f)T есть множество, определенное формулой
00
т) = # . С 2 #х П Ce2U (2fc_1}.
Очевидно, что множество ?]т, таким образом определенное, есть
или класса <Са> или из базы Вау или же элемент класса а. С другой
стороны, т]г содержится в Н(У а //т — множество класса <Са, не
имеющее общих точек с ?)Т', где т'^7* Следовательно, множество еу таким
образом определенное, есть или класса <Са, или же класса а и
подкласса ^ р.
Нужно заметить, что каждое линейное множество еу которое есть
или класса <а, или же класса а и подкласса ^р, может быть
получено таким способом при надлежащем выборе множеств е1у еъ ..., епу...
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
115
В самом деле, так как еп— произвольные элементы класса <а, то
множитель
00
есть произвольный элемент класса а, или произвольное множество
из базы Ва, или же произвольное множество класса <С&. С другой
стороны, в определении рассеянного множества каждое множество Н7
класса <Са> отделяющее т)г от последующих элементов, может всегда
быть разложено на элементы классов, не превосходящих класса Hv
Следовательно, мы можем всегда считать, что отделяющие множества
суть элементы класса <Са.
Отсюда следует, что множество е, определенное равенством (4),
может совпадать с каждым множеством класса а и подкласса ^р.
Предположим теперь, что последовательность
е\у е2> • • •> епу • • •
состоит из универсальных элементов всех классов <Са, причем каждый
элемент повторяется в этой последовательности бесчисленное
множество раз. Очевидно, что множество е, определенное при помощи этой
последовательности и данного трансфинитного числа р, есть множество
или класса <а, или же класса а и подкласса <^р. Но класс
множества е не может быть меньше а, так как, пересекая е прямыми,
параллельными оси ординат, можно получить всевозможные линейные
множества класса а и подкласса ^р и в частности все элементы
класса а1.
Следовательно, класс е равен а.
Установив это, пересечем множество е диагональю x = t. Так как
класс е равен а, то множество точек диагонали, не принадлежащих к е>
есть множество класса ^а. Отсюда следует, что и его проекция
на ось ОХ есть множество класса ^ос. Нужно заметить, что это
линейное множество не может быть класса <С а> так как в противном случае
его можно было бы получить, пересекая е какой-то прямой t=tQy что
невозможно.
Следовательно, это линейное множество есть множество класса а.
Оно не может также быть подкласса ^Р, потому что в этом
случае его можно было бы получить, пересекая е какой-то прямой t = t0.
Отсюда следует, что е есть множество класса а и подкласса 2> Р,
что доказывает существование сколь-угодно высоких подклассов (13].
1 Для этого достаточно, чтобы, какова бы ви была последовательность
&1% ^2» • • •» <^n» • • • линейных элементов классов < а, нашлась прямая х = х^
которая пересекает каждый универсальный элемент еп по множеству £п, т. е. чтобы
последовательность е1э е2, . .., гя, .. . совпадала с последовательностью
универсальных элементов.—Ред*
ГЛАВА III
АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
Определения и простейшие свойства
Линейные аналитические множества. Мы видели (стр. 100), что
всякое несчетное множество Е9 измеримое 5, расположенное в
области <РгХу допускает регулярное параметрическое изображение
при помощи функции /, непрерывной на о/и если пренебрегать счетным
множеством точек множества Е.
Это значит, что множество Е (с точностью до счетного множества
точек) можно рассматривать как множество значений, принимаемых на
порции (0,1) функцией /(/), непрерывной на <3и причем условие
регулярности f заключается именно в том, что функция f(t) никогда не
принимает двух равных значений; следовательно, если Иф1!\ то
/(О ¥■/(*").
В этой главе мы изучим свойство множеств, которые получаются
устранением условия регулярности, наложенного на изображающую
функцию /(f).
Определение. Мы назовем аналитическим всякое множество^
которое допускает параметрическое изображение x = f(t) при помощи
функции у непрерывной на <з7Д
Смысл этого названия совершенно ясен: так как всякая функция
непрерывная на oft (по отношению к этой области), есть функция
первого класса по классификации Бэра, то существует ряд многочленов
относительно t с рациональными коэффициентами2
1 Это определение тождественно с теоремой I моей заметки, касающейся
аналитических множеств н опубликованной в Comptes Rendus 8 января 1917 г. (стр. 270
настоящего* тома. — Ред.).
2 И даже с целыми коэффициентами, • так как всякая функция первого класса,
определенная на (0<.г<1), исключая концы этого интервала, разлагается в ряД
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
117
сходящийся для всех значений t на (0,1) и имеющий суммой функцию
/(/). Следовательно, всякое линейное аналитическое множество есть
множество значений, принимаемых на (0,1) суммой ряда многочленов
с рациональными коэффициентами, а потому оно определено при помощи
аналитического равенства [14] *.
многочленов с целыми коэффициентами. Это теорема И. Н. Хлодовского; см. его
заметку в Мат. сборнике, 32, 1925.
Кроме того, мы можем предположить, что ряд многочленов Р} (f) -+- Р2 М "*-• ♦ •
абсолютно сходится, причем этого можно достигнуть, не уменьшая общности данного
определения аналитического множества. См. мой „Memoire sur les ensembles analyti-
ques et projectifs" в Матем. сборнике, 33, 266, 1926; см. также работу Серпинского
„Les ensembles analytiques et les fonctions semicontinues", Cracovie, 1927.
1 Название аналитическое множество дано согласно предложению Лебега
называть аналитическими множествами все множества, которые могут быть определены
при помощи аналитических равенств вли неравенств.
„Из того, что будет доказано в дальнейшем, следует, что множествами,
измеримыми /?, являются те, которые могут быть определены при помощи аналитических
равенств или неравенств; по этой причине они заслуживали бы названия
аналитических множеств" (Н. Lebesgue. Sur les fonctions representables analytiquement,
стр. 165, примечание1).
Обратное предложение (т. е. что всякое множество, определенное при помощи
аналитических равенств или неравенств, есть множество, измеримое В) никогда им
не было высказано. Лебег не написал ни одной фразы, не сделал и простого
намека на возможность этого обращения. По этой причине Суслин и я, стремясь
осуществить программу Лебега—изучение наиболее общих функций, которые можно
назвать, и встретив при этом новый класс множеств, тесно связанных с рядами
многочленов,—мы нашли для них уже готовую терминологию самого Лебега. Но
в то же время мы позаботились о том, чтобы воздержаться от применения названия
аналитических множеств к дополнениям к этим множествам; эти последние, будучи
определены чисто отрицательным способом как собрания точек, которые не . . ., не
нуждались в специальном доказательстве их аналитичности в смысле Лебега. Но
специальный пример аналитического дополнения, полученный мимоходом самим Лебегом
(см. стр. 165 этой книги), выяснил невозможность получения положительного и
конечного определения дхя аналитических дополнений; это и было доказано впоследствии,
когда теория оказалась достаточно продвинутой: всякое положительное определение
аналитического дополнения неизбежно приводит к пользованию всеми трансфинитными
числами второго класса (а не только теми, которые меньше некоторого заданного
числа) или же к чему-нибудь заведомо эквивалентному этой незаконной
совокупности. Значение этого факта станет особенно ясным, когда мы приступим к
изучению множеств, которые я называю проективными; первая мысль о них принадлежит
Лебегу (см. мои пять заметок в Comptes Rendus, относящиеся к аналитическим и
проективным множествам: 4 мая, 25 мая, 15 июня, 13 июля и 25 августа 1925 г.)
(стр. 304, 307, 309, 312, 315 настоящего тома. — Ред.)
В узких рамках наших заметок в Comptes Rendus de TAcademie des Sciences
[Sou si in. Sar une definition des ensembles mesurables В sans nombres transfinis;
N. Lusin. Sur la classification de M. Baire Comptes Rendus, 8 января 1917 г.,
стр. 88 и 91 (стр. 270 настоящего тома.—Ред.)]ч где можно найти все главные
результаты об аналитических множествах, но формулированные без доказательств,
мы назвали аналитические множества сокращенным названием А-множеств. Но
так как в самых различных случаях употреблялось то же самое название [например
термин Л-мвожества Борель применял ко множествам, вполне определенным (Ыеп
definis), а они все измеримы В—см. Е. Во г el. Le calcul des integrales definies.
118
Н. Н. ЛУЗИН
Мы хотим обратить внимание на тот важный факт, что в
определении аналитического множества изображающая функция f(t) может
принимать равные значения. Мы скоро увидим, что этот факт дает
определению аналитического множества очень большую широту.
Рассмотрим теперь несколько простых примеров множеств, которые
являются аналитическими в вышеуказанном смысле.
Прежде всего точка области о/ХУ отдельно взятая, есть
аналитическое множество: достаточно принять постоянную величину за
изображающую функцию /(/).
Отсюда следует, что всякое счетное множество точек есть
аналитическое множество: достаточно принять за f(t) функцию, равную
соответствующим образом выбранной постоянной величине в каждом интервале
Бэра 1-го ранга области <з7х.
Пусть теперь Е есть линейное множество, измеримое В. Если Е
счетно (или конечно), мы уже видели, что Е — аналитическое. Если
Е несчетно, то по доказанному на стр. 100 множество Е может быть
разложено следующим образом:
E = E1-i-Dy
где Еу допускает нормальное изображение, a D счетно (или конечно).
Сделав непрерывное параметрическое изображение Ех на порции
(О, j) и Д на порции (у, 11, мы, очевидно, придем к непрерывному
параметрическому изображению всего множества Е на (0, 1).
Итак, всякое линейное множество, измеримое В, есть
аналитическое множество.
Следовательно, семейство аналитических множеств содержит
семейство множеств, измеримых В1.
Аналитические множества нескольких измерений* Аналогичным
образом мы назовем аналитическим всякое множество точек £,
расположенное в m-мерной области о7 # # и допускающее непрерывное
параметрическое изображение: это значит, что множество Е есть
геометрическое место последовательных положений движущейся
точки М(х1У х2у..., хп)9 координаты которой являются функциями
некоторого переменного параметра /, причем эти функции определены
и непрерывны на порции (0, 1) области <//:
*Х=Л(')| *2=Л('). •••» Xm=fm{t).
Journ. de Math., 84, 1912; см. также множества A (ambigus) у Вале-Пуссена:
Ch. dela Vallee-Poussin. Integrales de Lebesgue, fonctions densembles, classes
de Baire, стр. 135], то я хотел бы от сокращенного названия Л-множества
возвратиться к первоначальному смыслу: аналитическое множество (см. [3]).
1 Суслин вывел это предложение иа того факта, что семейство аналитических
множеств инвариантно относительно двух операций: суммирования в широком смысле
и взятия общей части; см. теорему I его заметки в Comptes Rendus, 164, 1917.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
119
Мы видим, что это определение есть вполне естественное
обобщение понятия линейного аналитического множества 1.
Все замечания, которые мы сделали по поводу линейных
аналитических множеств, немедленно применяются и к аналитическим
множествам многих измерений.
В частности всякое множество, измеримое В, в многомерном
пространстве есть аналитическое множество.
Простейшие свойства аналитических множеств: сумма и общая
часть. Мы докажем первое основное свойство аналитических множеств:
Теорема. Сумма счетного множества аналитических множеств
есть аналитическое множество2.
Пусть Ех, Е2, ..., Еп, ...— бесконечная последовательность
аналитических множеств. Разделим (0, 1) области g7/ на интервалы Бэра
1-го ранга: (1), (2), (3), ..., (п), ... и изобразим параметрически Ея на
интервале Бэра (п). Ясно, что таким образом мы получим непрерывное
параметрическое изображение суммы Е1-\-Е2-\-» • . + £„ + ... на (0,1).
Итак, эта сумма есть аналитическое множество (ч. т. д.).
Здесь надлежит сделать следующее замечание: можно формально
изобразить множество точек в пространстве многих измерений при
помощи одной и только одной функции, если ввести комплексные
числа с т мнимыми единицами fli^-j-a^-f--• .+«mim и условиться
писать
яЛ + aih + • • • + aJm = Mi + hh + • • • +bmimy
когда имеем в отдельности al:=bl, a2 = 62, ..., am = bm, так что одно
уравнение между комплексными числами сводится к т уравнениям
с действительными числами. В этих условиях всякое аналитическое
множество Е в пространстве т измерений изображается при помощи
одной и только одной комплексной функции
действительного параметра t, причем эта функция определена и
непрерывна на порции (0, 1) области <7*.
Это замечание будет нам часто полезно, так как большинство
рассуждений, касающихся линейных аналитических множеств, сохранится
в силе для многомерных аналитических множеств, если ^ввести
комплексные функции.
1 См. мою заметку в Comptes Rendus Acad. Sci. в мае 1925 г. и мой мемуар
„Sur les ensembles analytiques". Fund. Math., X, 20, 1926 (стр. 380 настоящего
тома. —Ред.).
2 Эта теорема принадлежит Су ели ну; см. его лемму II в цитированной заметке
(Comptes Rendus, 8 января 1917 т.).
120
Н. Н. ЛУЗИН
Теорема. Общая часть счетного множества аналитических
множеств есть аналитическое множество1»
Пусть Е есть общая часть аналитических множеств Е1У Е29 ..., Епу ...
и пусть
х =Л (0> х =/2 (*,), ..., х =/„ (О, ...
— непрерывные параметрические изображения этих множеств на
порциях (0, 1) соответствующих областей с7^, 31, ..., о/1 , ...
Определим новую область <7/ и возьмем уравнения
'l = ?1 W, U = <г2 (0. ...,tn=?n (0. • • .,
которыми мы пользовались при доказательстве теоремы о
существовании нормального изображения д\я всякого несчетного множества,
неизмеримого В (стр. 101).
Эти функции <ри(0 непрерывны на (0,1) области <9\ и принимают
иррациональные значения, заключенные между 0 и 1. Кроме того, какова бы
ни была последовательность t\y t\, ..., /°, ... иррациональных чисел,
заключенных между 0 и 1, существует одно и только одно иррациональное
число t0 такое, что значения функций срг, <р2, ..., <ря,... в t0
соответственно равны *J, t\, ..., t^y ...
Установив это, образуем сложные функции
Л С) =Л [?i(')l, Г-1=АШ*),.--1 Fn(t)=M<?n(t)l...
Ясно, что эти функции непрерывны на (0,1). Следовательно,
совместные уравнения
FAt) = FAt)=... = Fn(t)=-..
определяют замкнутое на <Sft множество 7*.
Из определения сложных функций Ft следует, что когда
переменное t пробегает множество Т, то общая величина функций Ft (t),
которую мы обозначим просто через F{t)y пробегает в точности общую
часть Ех * 2?.2 • • • £п- • • заданных множеств.
Но замкнутое множество Т измеримо 5. Следовательно, Т есть
аналитическое множество, а потому существует непрерывное
параметрическое изображение
множества Т на порции (0,1) новой области g7t, причем функция ф(х)
определена и непрерывна на (0,1) области g7t.
1 Эта теорема принадлежит гСуслииу; см. лемму Ш в его заметке (Comptes Ren-
dus Acad. Sci., 8 января 1917. г.). Метод Суслина, основанный на употреблении
кортежей индексов (см. стр. 303 этой книги), существенно отличается от того, который
мы даем в тексте. Я указал метод, даваемый в тексте, в своем мемуаре „Sur les
ensembles analytiques" (Fund. Math., X, 40, 1926), он полезен во многих случаях
и в частности применяется к проективным множествам; см. стр. 303 этой книги в работу
Серпинского „Sur les produits des images continues".
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
121
Отсюда следует, что сложная функция
x = f[*(t)] = 0(-)
дает искомое непрерывное параметрическое изображение множества
Е = Ег- Е2*. *Еп... Значит, это множество есть аналитическое (ч. т. д).
Важно заметить, что данное доказательство, проведенное для
линейных аналитических множеств, остается без изменений для множеств
многих измерений, если предположить, что изображающие функции л:=/я
комплексные и что буква х обозначает точку множества £„. Остальные
функции <ря и ф должны оставаться действительными.
Проекции
Элементарные множества. Рассмотрим основную область т
измерений с7У7з # . Разделим каждую линейную область </ на порции при
помощи целых чисел; каждая из полученных порций имеет длину,
равную 1, и мы их назовем интервалами Бэра порядка 0. В каждом из
них мы определим интервалы Бэра порядков 1, 2, 3, ... в точности
так, как это обычно делается для порции (0,1).
Установив это, мы назовем параллелепипедом Бэра порядка к
в /n-мерной области о/ множество тех точек этой области,
координаты которых принадлежат каким-нибудь интервалам Бэра порядка к,
например Ь1У 82э ..., 8да> расположенным соответственно в с7г,, с7^,..., с/у^
Мы теперь введем очень полезное понятие, а именно понятие эле-
ментарного множества.
С этой целью возьмем в области <7 # определенную счетную
или конечную последовательность параллелепипедов Бэра порядка 0
попарно без общих точек: эти параллелепипеды Бэра назовем
параллелепипедами ранга 0.
В каждом параллелепипеде ранга 0 возьмем вполне определенную,
счетную или конечную, последовательность параллелепипедов Бэра
порядка 1 и попарно без общих точек: эти параллелепипеды назовем
параллелепипедами ранга 1.
Вообще, каково бы ни было л, л>1, возьмем в каждом из
параллелепипедов Бэра ранга п — 1 вполне определенную, конечную или
счетную, последовательность параллелепипедов Бэра порядка п попарно
без общих точек; мы их назовем параллелепипедами ранга п.
Так как всех параллелепипедов Бэра лишь счетное множество (или
конечное число), то их сумма есть множество, измеримое В; обозначим
его через Sn. Следовательно, общая часть & всех сумм Sn
есть опять множество, измеримое В.
Определение. Мы назовем элементарным множеством так
определенное множество &.
122
Н. Н. ЛУЗИН
Легко видеть, что всякое элементарное множество есть множество
не очень сложной природы, но, строго говоря, это лишь очень
относительно Ч
Установив это определение, мы докажем следующую теорему:
Теорема, Всякое аналитическое множество, расположенное в
области т измерений, есть ортогональная проекция некоторого
элементарного множества, расположенного в области т -\-1 измерений.
Чтобы доказать это, возьмем аналитическое множество Е,
содержащееся в области qJь^тятХт* Пусть
*1 =/l О. *2 = Л (')> . . ., Хт =/ж (0 (1)
«сть непрерывное параметрическое изображение Е.
Рассмотрим данную область g/#>#ж как часть новой области /л + 1
измерений q7.XCh tJC r Обозначим через <§ множество точек N(xlf х2, ...
..,, хт, t) этой ' области, координаты которых удовлетворяют
уравнениям (1). Ясно, что ортогональная проекция & на область о/ХЖи 9 есть
данное множество Е.
Итак, все сводится к доказательству того, что <§ есть элементарное
множество.
С этой целью рассмотрим интервал Бэра о порядка к,
расположенный в g7*. Пусть <£8 есть множество тех точек из &, у которых
координата t принадлежит 8. Обозначим через Sb сумму тех
параллелепипедов Бэра порядка к в области е7...xmv которые содержат точки
из <§8, Сумма всех Sb , соответствующих интервалам Бэра порядка к,
будет обозначена через S*.
Легко видеть, что общая часть £f = Sx • S2 ,.« S^... есть
элементарное множество, содержащее множество &. Остается лишь доказать,
что &' содержится в &.
Чтобы убедиться в этом, возьмем точку N(x^, х%, ..., х^, t0) из <£'.
Пусть т^ есть параллелепипед Бэра порядка v, содержащий точку N.
Если мы будем изменять v, мы получим бесконечную
последовательность тс0, iCj, ..., 7iv, .. параллелепипедов Бэра порядков 0, 1, 2,..., v,...,
содержащих точку N, каждый из которых содержится в предыдущем.
Если мы обозначим через 8v проекцию ъу на ось ОТ, то
последовательность 80, Ь19 82, .. #> 8v, .. #> образована из интервалов Бэрап порядков
О, 1, 2, ..., v, .. #> содержащих точку /0, каждый из которых содержится
в предыдущем. Так как параллелепипед ~v есть часть суммы SI , то он
содержит точки множества <§а , Значит, интервал Бэра 8v обязательно
1 „Простота" элементарных множеств нам кажется весьма иллюзорной. Перевод
определения элементарного множества на язык арифметики {наталкивается на все
препятствия, связанные с теорией роста. По-видимому, все трудности теории проективных
множеств содержатся, как в зародыше, в теории элементарных множеств.
ЛЕКЦИИ СБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
123
содержит точку *v, такую, что точка iVv с координатами х^\ х%\ ..., ^
/v, удовлетворяющими уравнениям
<=Л(0- 4"=ЛЮ,--.. *м=/ж(0, (2)
принадлежит к ~v.
Если мы будем неограниченно увеличивать v, то /v будет стремиться к *0.
С другой стороны, каждое х^ стремится к jcJ, так как диаметр
параллелепипеда tcv, содержащего постоянную точку N и переменную точку /Vv,
стремится к нулю с возрастанием v.
Так как функции /,"(*) непрерывны, то уравнения (2) нам дают
*?=/,('о>. *5=/«(<о).--м *2, =/*>('<>)>
•откуда и следует, что точка N принадлежит к &. Итак, множество £*
тождественно с & и, следовательно, & есть элементарное множество
(ч. т. д.).
Обратная теорема также имеет место: ортогональная проекция
всякого аналитического множества есть также аналитическое
множество 1.
Чтобы доказать эту теорему, возьмем в m-мерной области а7
аналитическое множество Е, заданное непрерывным параметрическим
изображением:
*l=/l(*)i X2=ft{t), . . .,
*«'=/«'(')» •••» Xm=fm(t).
Чтобы получить ортогональную проекцию £ на m'-мерную область
<?xp2...tm» m<Cm> очевидно, достаточно отбросить уравнения, которые
следуют за xin,-=^fm,{i)\ это дает:
*i=/iWt *2=Л(0> • •> xmP=fm,(i).
Итак, проекция £ есть аналитическое множество (ч. т. д.).
Эта теорема имеет большое значение, так как она показывает, что
•операция взятия ортогональной проекции уже определенного множества
не выводит из класса аналитических множеств. В частности, взяв
ортогональную проекцию множества, измеримого В, мы получаем
аналитическое множество. А так как каждое аналитическое множество есть
проекция некоторого элементарного множества, т. е. множества,
измеримого В (элемента класса 2), то мы заключаем отсюда, что
аналитические множества тождественны проекциям множеств, измеримых В.
Параметрическое изображение при помощи функций, входящих
в классификацию Бэра. Мы определили аналитическое множество как
множество, которое допускает непрерывное параметрическое
изображение:
*i = Л (*)» х2 =Л (*), • • •» хт =/» (*)•
1 См. теорему VI заметки Суслина (Comptes Rendus Acad. Sci., 8 января 1917 г,).
124
Н. Н. ЛУЗИН
Но непрерывные на qJt функции суть функции класса 0 по
классификации Бэра*. Поэтому вполне естественно теперь изучить природу
тех множеств, которые допускают непрерывное параметрическое
изображение при помощи любых функций классификации Бэра.
В наших рассуждениях мы будем пользоваться следующей теоремой,
принадлежащей Лебегу: Множество тех точек области <з7кх % ^
в которых функция f(xv х2, ..., х,п), входящая в классификацию
Бэра, равна нулю, есть всегда множество, измеримое В2.
Другое свойство функций классификации Бэра, которым мы будем
пользоваться, состоит в следующем: суммы, разности и произведения
функций классификации Бэра входят в ту же классификацию3.
Эти теоремы можно доказать методом индукции: теорема очевидна
для класса 0; затем доказывают, что если она верна для классов <<*>
то верна и для класса а.
Мы не будем больше останавливаться на этом пункте.
Установив это, вернемся к изучению множества Е, определенного
параметрическим изображением (1), в котором функции /< входят в
классификацию Бэра.
Рассмотрим функцию F(xx, х2, . .., хт, t) от m-j-l действительных
переменных, определенную равенством
F= [*i -Л W18 +1*2 - /, ЮР+...+[*« -Л, (01*.
Так как функции /19 /2, ..., /т входят в классификацию Бэра, то
и функция F также в нее входит. Следовательно, множество S точек N (х^>
*2> •••• xmt t)m + 1-мерной области е?^*,...^, где функция F (х19 х2,...
..., xm, t) обращается в нуль, измеримо 5. Но множество & есть как
раз множество тех точек N, координаты которых удовлетворяют
уравнениям (1). В этих условиях ясно, что ортогональная проекция & на
область q7„ r _ есть множество Е. Значит Е есть аналитическое мно-
жество.
Таким образом, мы приходим к следующему заключению:
1 Согласно условию рассматривать всегда лишь иррациональные точки, мы
назовем функциями класса 0 функции, непрерывные на области q7\ относительно этой
области. Ясно, ято функция класса 0 в смысле втого определения будет класса < 1
в обычной классификации Бэра, где рациональные точки не исключаются. Заметим,
что такие переходы могут происходить лишь в классах 0 и 1, высшие же классы > 2
остаются неизменными.
2 Это частный случай общей теоремы Лебега: для того чтобы функция /,
всюду определенная, была класса не выше а, необходимо и достаточно, чтобы,
каковы бы ни были рациональные числа гх и г2, множество точек, где гх < / ^ г%,
было класса не выше a (Sur Its fonotions representables analytiquenent, стр. 168,
теорема V).
Доказательство этой теоремы построено на трансфинитной индукции. В случае
текста мы имеем ri = г2 = 0.
3 См. Lebesgue, там же, стр. 153,
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
125
Понятие аналитического множества нисколько нельзя расширить,
рассматривая геометрическое место последовательных положений
подвижной точки М{х1У х2, ..., хт), координаты которой суть
произвольные функции параметра t, входящие в классификацию Бэра1:
*i=/i(0> x2 = f2{t)9 ..., xm=fM(t).
Универсальное аналитическое множество. Мы видели, что
семейство аналитических множеств содержит семейство множеств,
измеримых В. Чтобы решить вопрос о том, выходят ли аналитические
множества за пределы множеств, измеримых В, мы введем следующее
определение 2:
Аналитическое множество Е точек двумерной области <5fху мы
назовем универсальным, если, пересекая его прямыми х = х0,
параллельными оси OY, мы получим всевозможные линейные
аналитические множества.
Легко доказать существование универсальных аналитических
множеств.
С этой целью заметим прежде всего, что всякое элементарное
множество будет или класса <2 или же элементом класса 2. Это
вытекает из самого определения элементарного множества (стр. 121),
так как если Е — элементарное множество, то оно является общей
частью E = Si • S2 . . . Sn . . . сумм Sn9 каждая из которых
образована из счетного множества параллелепипедов Бэра [15].
Но мы видели (стр. 111), что существуют универсальные элементы
каждого класса а классификации Валле-Пуссена и притом в пространстве
любого числа измерений. Возьмем же в трехмерной области £хщв
универсальный элемент класса 2. В силу свойства универсальных
элементов, пересекая S плоскостями у = const, параллельными
плоскости XOZj мы получим всевозможные плоские элементы класса 2.
В частности получаются всевозможные элементарные множества.
Пусть теперь Е есть ортогональная проекция универсального
элемента S на плоскость YOZ. Так как S измеримо В, то его проекция Е
есть плоское аналитическое множество.
Я утверждаю, что Е есть универсальное аналитическое множество.
В самом деле, каково бы ни было линейное аналитическое множество е,
1 Это теорема III моей заметки в Comptes Rendus, 8 января 1917 г. (стр. 270
настоящего тома. — Ред.).
2 Я ввел понятие универсального аналитического множества в своей заметке
„Sur les ensembles non mesurables В et l'emploi de la diagonale de Cantor" (Comptes
Rendus, 20 июля 1925 г.), но идея плоского множества, универсального по отношению
к данному семейству множеств, была у Лебега („Sur les fonctions representables
analytiquement", стр. 207). Относительно других приложений понятия универсального
множества см. извлечение из моего письма к Серпинскому: „Sur l'accessibilite
des points" (Fund. Math., XI) и интересные работы Серпинского „Sur resistance
des diverses classes d'ensembles" (Fund. Math., XIV) и Никодима „Sur les diverses
classes d'ensembles* (Fund. Math., IV).
126 н. н. лузин
Г)но является ортогональной проекцией некоторого плоского элементарного*
множества. И так как мы можем получить это элементарное плоское
множество, пересекая элемент & подходяще выбранной плоскостью у = уОУ
то мы получим линейное аналитическое множество е, пересекая Е
прямой */ = #<)> параллельной оси OZ и лежащей в плоскости YOZ.
Это показывает нам, что Е есть плоское универсальное аналитическое
множество.
Принимая во внимание всю важность существования универсальных
аналитических множеств, мы дадим другое доказательство, с
некоторых точек зрения более простое, чем предыдущее1.
Метод, который мы сейчас изложим, основан на пользовании
функцией <р(л:, Ot обладающей следующими двумя свойствами: 1° она
определена аля всех х и t, принадлежащих интервалу (0, 1), и входит
в классификацию Бэра; 2° всякая функция f(x) переменного х и
класса ^ 1 может быть получена, если дать переменному t некоторое
частное числовое значение /0.
В самом деле, возьмем функцию <р(лг, 0> обладающую указанными
двумя свойствами, и рассмотрим в трехмерном пространстве OXTY
поверхность S, определенную уравнением
у = <?(х, О-
Если эту поверхность S рассматривать как множество точек в
пространстве OXTY, то это множество, очевидно, измеримо В.
Следовательно, ортогональная проекция S на плоскость TOY есть
аналитическое множество; обозначим эту проекцию через Е. Я теперь
утверждаю, что Е есть универсальное аналитическое множество.
Чтобы убедиться в этом, достаточно заметить, что всякая
функция /{х)у непрерывная во всех иррациональных точках, нообходимо
будет класса ^1 по классификации Бэра. Поэтому по самому
определению линейного аналитического множества мы получим все
линейные аналитические множества, пересекая Е прямыми, параллельными
оси OY. Отсюда следует, что Е есть универсальное аналитическое
множество.
Итак, все сводится к построению такой функции <р (х, 0- Пусть
РЛ{х), Р2(*), • • •> Рп(*)> • • • есть последовательность, образованная
из всех многочленов относительно х с рациональными коэффициентами,
и пусть срх (0, <р2 (0> • • • > Уп (0> • • • есть последовательность функций,
непрерывных между 0 и 1 и обладающих следующим свойством: какова
бы ни была последовательность действительных чисел а1э а2, . . . , ая, . .. ,
существует такое число £0, что
al = ?1(t0)9 я2=<р2(/0), . . ., ап = срп(/0), . . . 2
1 См. мою заметку в Comptes Rendus, 20 июля 1925 г. (стр. 309 настоящего
тома. —Ред.).
2 Речь идет о кривой Пеано, заполняющей целую область в пространстве
счетного числа измерений.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
127
Установив это, обозначим через Sn(x, t) сумму п первых членов
бесконечного ряда
PiWTiW+^WTiW-b. • .+-Р.(*)?Л0-*-. . .
Ясно, что Sn(x9 t) есть непрерывная функция по совокупности своих
аргументов. Следовательно, функция <?(ху t), определенная как верхний
предел
<?(*, t) = l\mSn{x, t),
есть функция класса 2 по классификации Бэра. Атак как каждая функция
класса <Z 1 может быть представлена в виде суммы ряда многочленов
с рациональными коэффициентами, то мы видим, что так определенная
функция <р (х, t) обладает двумя вышеуказанными свойствами 1 (ч. т. д.).
Установив этот результат, возьмем плоское универсальное
аналитическое множество £, расположенное в плоскости XOY. Так как £
универсально, то мы получим все линейные аналитические множества
и среди них все линейные множества, измеримые 5, пересекая Е
прямыми х = х0, параллельными оси OY. Рассмотрим диагональ у = х
и обозначим через е общую часть универсального аналитического
множества Е и этой диагонали. Ясно, что е есть линейное
аналитическое множество.
Но если мы обратимся к рассуждению по поводу диагонали,
сделанному выше (стр. 112), мы немедленно заметим, что ортогональная
проекция на ось OY дополнения Се к множеству е относительно
диагонали у=х не может принадлежать к семейству тех множеств,
которые получаются при пересечении Е прямыми х = х0.
Следовательно, проекция множества Се на ось О У не есть
аналитическое множество. Это показывает, что линейное множество е не
измеримо В> так как в противном случае его дополнение Се было бы
также измеримым В и, следовательно, его проекция на ось OY была бы
в этом случае аналитическим множеством.
Итак, линейное множество е есть линейное аналитическое
множество, неизмеримое В> и, следовательно, плоское универсальное
множество Е само является аналитическим множеством, неизмеримым В.
Это рассуждение можно дополнить следующим простым
замечанием; универсальное аналитическое множество Е не может быть
измеримым В, так как в противном случае Е должно было бы принадлежать
к определенному классу Ка классификации Валле-Пуссена. Отсюда
следует, что никогда нельзя получить линейное множество, измеримое
1 Отметим интересную работу В. Серпинского „Sur un ensemble analytique
universel pour les ensembles mesurables B" (Fund Math., ХП, 75), где Серпинский
строит плоское аналитическое множество, которое параллелями к оси OY пересекается
только по множествам, измеримым В, и каждое линейное множество, измеримое Ву
может быть получено таким способом.
128
Н. Н. ЛУЗИН
By и класса выше а, если пересекать Е прямыми х = х0. Но так как £
универсальноу мы заведомо будем получать множества класса >• а,
если только подходящим образом выберем точку л:0. Таким обра-
зом, мы приходим к противоречию.
Но это последнее рассуждение, каким бы оно ни казалось простым,
вводит трансфинитные числа и пользуется существованием множеств
всех классов. С этой точки зрения первое рассуждение
предпочтительнее.
Таким образом, мы доказали, что понятие аналитического
множества есть более общее, чем понятие множества, измеримого В. Это заставляет
нас изучить для этих множеств основные свойства точечных множеств,
каковыми являются мощностъу мера и категория.
Свойства аналитических множеств
Когда дано какое-либо точечное множество, тотчас же возникают
три основных вопроса: если это множество несчетно, имеет ли оно
мощность континуума? Измеримо ли это множество? Обладает ли оно
свойством Бэра? Мы теперь исследуем свойства аналитических
множеств по отношению к этим вопросам.
Мощность. Пусть Е есть несчетное аналитическое множество,
расположенное в m-мерной области. Пусть & есть элементарное множество
в т -+- 1-мерном пространстве, причем его ортогональная проекция есть
данное множество Е.
Так как диаметр параллелепипеда Бэра порядка п стремится к нулю,
когда п неограниченно возрастает, то существует целое положительное
число л, достаточно большое д\я того, чтобы среди параллелепипедов
ранга п (стр. 121) нашлось два параллелепипеда тс и тс', обладающих
следующими двумя свойствами: 1° проекции тс и тс' не имеют общих
точек; 2° проекции частей &, содержащихся в тс и в тс', являются обе
несчетными множествами.
Раз так, то мы находимся в тех же условиях, как и раньше, и мы
можем определить в каждом из двух параллелепипедов тс и тс' два
новых параллелепипеда ранга выше л, обладающих теми же свойствами;
мы получаем таким образом четыре вполне определенных
параллелепипеда. Мы продолжаем оперировать так же над каждым из них и
получаем восемь определенных параллелепипедов, обладающих теми же
свойствами, и так далее безгранично.
Ясно, что множество точек, каждая из которых принадлежит
бесконечному множеству параллелепипедов Бэра, так определенных, есть
совершенное множество в классическом смысле, и притом содержащееся
в данном элементарном множестве &. К тому же проекции двух
различных точек этого совершенного множества всегда различны.
Отсюда следует, что проекция этого совершенного множества есть
опять совершенное множество в классическом смысле. А так как это
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
129
последнее, очевидно, содержится в данном аналитическом множестве Еу
то мы получаем теорему:
Всякое несчетное аналитическое множество необходимо содержит
совершенное множество и> следовательно^ имеет мощность
континуума Ч
Мера. Пусть Е—произвольное аналитическое множество, о котором
известно только, что оно имеет внешнюю меру, не равную нулю,
т,£>0.
Сделаем прежде всего одно весьма банальное замечание: чтобы
доказать, что некоторое точечное множество Е с не равной нулю
внешней мерой измеримо, необходимо и достаточно установить, что оно
содержит замкнутое множество F, мера которого превосходит твЕ — е,
где е — как угодно малое положительное число.
В самом деле, с одной стороны, можно заключить точки Е в ряд
параллелепипедов (прямоугольников, интервалов), общая протяженность
которых (объем, площадь, длина) меньше, чем mJE-*-e. С другой
стороны, все точки, не принадлежащие к Е, очевидно, заключаются
в ряде параллелепипедов, внешних к замкнутому множеству F; их
общая протяженность меньше, чем 1 — mF-he. Значит, общая
протяженность этих двух рядов параллелепипедов меньше, чем
теЕн-е + 1 — mF-t- е < 1 -+-3s,
и, следовательно, Е измеримо. Несмотря на свою банальность, это
замечание будет нам очень полезно.
Сделаем еще одно замечание: если мы имеем последовательность
Ev E2f • . • любых множеств, не подчиненных никакому закону, то
внешняя мера множества-суммы п первых членов этой
последовательности стремится к внешней мере суммы всех членов этой
последовательности, когда п неограниченно возрастает.
Отсюда следует, что можно выбрать достаточно большое число /^
параллелепипедов ранга 1, для того чтобы часть элементарного
множества &, содержащаяся в этих пг параллелепипедах, имела проекцию,
внешняя мера которой превосходит т,Е — е1#
Будем оперировать также над параллелепипедами ранга 2,
содержащимися в выбранных параллелепипедах ранга 1: мы можем взять число /ij
настолько большим, чтобы часть &, содержащаяся в них, имела
проекцию, мера которой превосходит тД — ех — 52, и так далее.
Мы образуем таким образом суммы S'19 *S"2» *S's» • • •
параллелепипедов рангов 1, 2, 3 . . . соответственно, каждая из Sn' состоит
из конечного числа параллелепипедов множества S„ (стр. 121) и
содержится внутри предыдущей S'n—l9 а проекция части элементарного
множества <?, содержащейся в параллелепипедах из Sn\ имеет внешнюю
меру, превосходящую твЕ — ^ — е2 —. . . гп; здесь ряд с положитель-
1 Теорема Суслина; см. Comptes Rendas, 8 января 1918 г.
130
н. н. лузин
ными членами ^-нг,-ь. . ,-ьг„+-. . . сходится и имеет как угодно
малую сумму е.
Отсюда следует, что проекция S'n имеет протяженность,
превосходящую т,Е — е. Но так как проекция множества S'n, очевидно, состоит из
конечного числа параллелепипедов Бэра и содержится в проекции
множества S'n—U то общая часть проекций всех S'n есть замкнутое
множество F, мера которого превосходит теЕ — £.
С другой стороны, общая часть сумм S\y S'2, . . . *S'„, . . . есть,
очевидно, замкнутое множество, содержащееся в элементарном
множестве &; это замкнутое множество мы обозначим через Н.
Легко видеть, что множество Н имеет своей проекцией
множество F. Значит F содержится в данном аналитическом множестве Е.
В силу предыдущего замечания множество Е есть измеримое, и,
следовательно, мы получили теорему:
Всякое аналитическое множество измеримо1.
Категория. Мы теперь докажем, что всякое аналитическое
множество обладает свойством Бэра, принадлежащим всем множествам,
измеримым В2.
Обратимся к стр. 79: все сводится к тому, чтобы доказать, что
если данное аналитическое множество Е не есть множество первой категории
ни на какой порции некоторого совершенного множества Р, то его
дополнение СЕ есть множество первой категории на Р.
Начнем с того, что выбросим из т -j- 1-мерной области, где
помещается элементарное множество &, все параллелепипеды, каков бы
ни был их порядок, такие, что содержащаяся в них часть & имеет
проекцию первой категории на Р. Ясно, что сохранятся при этом
параллелепипеды всех порядков.
Установив это, мы будем оперировать с каждым из сохраненных
параллелепипедов, каков бы ни был его порядок, следующим образом:
пусть тс — рассматриваемый параллелепипед; мы возьмем часть &9
содержащуюся в тс. Так как тс сохранен, эта часть & имеет проекцию уже
не первой категории на Р. Следовательно, на Р существует замкнутое
множество F, обладающее следующими двумя свойствами:
1° если а есть порция Р, содержащаяся в F> то проекция части £,
содержащаяся в тс, будет первой категории на а;
2° если о есть порция Р, содержащая точку, которая не
принадлежит к F, то указанная проекция не будет первой категории на а.
Установив этот первый пункт, мы определяем д\я каждого
сохраненного параллелепипеда тс', содержащегося в тс, и порядка,
непосредственно следующего за порядком тс, соответствующее замкнутое
множество F'.
1 См. теорему V моей заметки в Comptes Rendus, 8 января 1917 г. (стр. 270
настоящего тома. —Ред.).
2 См. теорему VI моей заметки в Comptes Rendus, 8 января 1917 г. (стр. 270
настоящего тома. — Ред.).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
Ясно, что общая часть всех замкнутых множеств F есть множество,
нигде не плотное на всякой порции Р, не содержащей точек F. Это
значит, что множество точек, принадлежащих всем Г и не
принадлежащих Р, есть множество, не плотное на Р; мы его обозначим
через Нг.
Таким образом, всякому сохраненному параллелепипеду Бэра -, каков
бы ни был его порядок, соответствует вполне определенное
множество ИкУ не плотное на Р. Отсюда следует, что сумма всех множеств НЖУ
соответствующих различным к, есть множество первой категории на Р.
Обозначим его через //.
Мы сейчас докажем, что каждая точка М множества Р, не
принадлежащая к Ну есть точка данного аналитического множества Е.
В самом деле, так как М не принадлежит к //, то существует
сохраненный параллелепипед Бэра тг0 порядка 0 такой, что М не входит
в замкнутое множество Р0, соответствующее ~0; так как М не
принадлежит к /До, то существует в ^0 сохраненный параллелепипед Бэра ъх
порядка 1 такой, что М не входит в замкнутое множество Fly
соответствующее TCj; так как М не принадлежит к Нх1У то в ^ существует
сохраненный параллелепипед Бэра тг2 порядка 2 такой, что М не входит
в замкнутое множество Р2> соответствующее *2, и так далее.
Таким образом, мы получим последовательность сохраненных
параллелепипедов ^0, ~х, ^2> • • • порядков, соответственно равных
0, 1, 2, 3 . . ., каждый из которых содержится в предыдущем,
причем точка М не принадлежит ни одному из замкнутых множеств Fnt
л=0, 1, 2, 3, . . . Следовательно, точка М непременно принадлежит
к проекции каждого из параллелепипедов тг0, кХ9 тс2, . . .
Отсюда мы заключаем, что М есть проекция некоторой точки Л/,
принадлежащей всем параллелепипедам ^0, к.19 ~2, . . . и, следовательно,
являющейся точкой элементарного множества &. Итак, М
принадлежит к Е.
Таким образом, каждая точка Р, не принадлежащая к £, должна
принадлежать к //. Но так как Н первой категории на Р, то и СЕ
также (ч. т. д.).
Мы дополним этот результат следующими замечаниями:
Замечание I. Пусть Е есть линейное аналитическое множество,
неизмеримое By и пусть f(x) есть характеристическая функция для £,
т. е. f(x) равна 1 на Е и 0 на его дополнении. Так как Е
неизмеримо By то f(x) не входит в классы Бэра. Но согласно доказанной
теореме множество Е обладает свойством Бэра и, следовательно,
функция /(х) точечно разрывна на всяком совершенном множестве,
если пренебречь множеством первой категории на этом совершенном
множестве.
Мы видим, что свойство, открытое Бэром и принадлежащее всем
функциям его классификации, не является достаточным.
132
Н. Н. ЛУЗИН
Замечание II. Если некоторое множество точек измеримо, то и
его дополнение тоже. Та же взаимность имеет место дая свойства
Бэра. Следовательно:
Дополнение к аналитическому множеству измеримо и обладает
свойством Бэра.
В дальнейшем мы будем называть кратко те множества, которые
являются дополнениями к аналитическим множествам, аналитическими
дополнениями.
Первый принцип аналитических множеств.
Отделимость В
Общие идеи. В данном нами определении аналитических множеств
понятие трансфинитного явно не входит. Тем не менее детальное
изучение этих множеств показывает, 4tq, совокупность всех
трансфинитных чисел второго класса по Кантору глубоко спрятана в
аналитических множествах, неизмеримых В.
Полученные в теории аналитических множеств результаты
наилучшим образом показывают, что необходимо рассматривать аналитические
множества, неизмеримые В9 как в некотором роде продолжение
классификации Валле-Пуссена за классы Ка, перенумерованные при помощи
всех трансфинитных чисел второго класса по Кантору, Точнее говоря,
на эти аналитические множества надо смотреть, как на элементы
класса 2, где 2 — первое трансфинитное число „третьего класса" по
Кантору» Среди [многочисленных бросающихся в глаза аналогий мы
укажем ту, которая связана с отделимостью множеств.
В теории множеств, измеримых В9 мы видели, что два элемента
класса К% без общих точек всегда отделимы при помощи множеств
или класса <Са мли базы Ва.
Вполне аналогичное предложение имеет место и для аналитических
множеств1. Чтобы убедиться в этом, введем новое понятие, а именно
понятие об отделимости В*
Мы скажем, что два множества Е и Е' без общих точек
отделимы Ву если существуют два множества Н и //', измеримые Bt без
общей точки и содержащие соответственно множества Е и Е'.
Множества Н и Н', обладающие этим свойством, мы назовем
отделяющими множествами.
Установив это определение, мы формулируем основное
предложение теории аналитических множеств, называемое первым принципом
этой теории2.
1 Читатели, желающие получить более детальные разъяснения по поводу втой
аналогии, могут обратиться к моему мемуару: „Analogies entre les ensembles mesur-
ables В et les ensembles analytiques" (Fund. Math., XVI, 1930) (стр. 470 настоящего
тома. —Ред.).
2 Я высказал в явной форме и доказал этот принцип в своем мемуаре „Stir les
ensembles anlytiques". Fund. Math., X, 52 (стр, 380 настоящего тома. — Редщ).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
Принцип I. Два аналитических множества без общих точек
всегда отделимы В.
Мы дадим два различных доказательства принципа I. Для того чтобы
лучше оценить существенную разницу между этими двумя
доказательствами, напомним две классические теоремы: всякое замкнутое
множество, не содержащее никакого совершенного множества, счетно
(Кантор — Бендиксон) и теорему Бэра о функциях класса 1.
Каждое из этих предложений имеет два доказательства. Одно из
них дает не только доказательство теоремы, но и регулярный
процесс, который в первом случае дает нам вполне определенное
перенумерование точек рассматриваемого замкнутого множества при помощи
целых чисел, а во втором случае эффективное построение ряда
многочленов, сходящегося к рассматриваемой функции класса 1. Это
доказательство можно рассматривать как положительное, и известно, что
оно дано д\я замкнутых множеств Бендиксоном и Серпинским, а для
функций класса 1 самим Бэром.
Но есть другой вид доказательств д\я этих теорем. Доказательства
этого рода не дают ни процесса перенумерования точек замкнутого
множества, ни построения ряда полиномов, имеющего суммой функцию
класса 1, но доказывают лишь существование такого перенумерования
и такого ряда полиномов. Вот механизм доказательств: каждый раз
вводят некоторое общее, но чисто отрицательное понятие: в случае
замкнутых множеств это понятие точки сгущения, которым мы
обязаны Линделефу, а в случае функций класса 1 это понятие точки>
где функция не есть класса 1; этим понятием мы обязаны Лебегу.
Эти доказательства можно рассматривать как отрицательные.
Аналогичным образом мы дадим два доказательства принципа 1:
одно из них чисто отрицательное и очень короткое (как, впрочем, и
доказательства Линделефа и Лебега), другое — положительное и
достаточно трудное; его преимуществом является то, что оно дает
эффективное построение множеств Н и Н\ которые осуществляют отделение
данных аналитических множеств Е и Е\ тогда как в первом
доказательстве дается лишь существование этих множеств.
Отделимость В для аналитических множеств. Перейдем теперь
к доказательству принципа I.
Первое доказательство (отрицательное). Пусть x=f(t) есть
непрерывное параметрическое изображение аналитического множества Е
и x = y(t) такое же изображение дая аналитического множества Е.
Мы предполагаем, что Е и Е не имеют общих точек.
Возьмем на порции (0, 1) области с7/ интервал Бэра В порядка к
и аналогично интервал Бэра Ъ' того же порядка к на (0, 1) в области .Уг.
Обозначим через £5 и Е\ части Е я Е, которые мы получим, если
заставим t я f пробегать соответственно о и &'. Ясно, что Еь и Еь>, не
имеют общей точки.
Установив это, назовем пару (&, Ь') интервалов Бэра S и S' особой>
если соответствующие множества Еь и Е\> неотделимы В.
134
Н Н. Л У 3 ИН
Очевидно, что если пара (8, 8') особая, то существует пара (о19 Ь'г)г
образованная из интервалов Бэра 6Х и Ь\ порядка &ч-1, содержащихся
соответственно в 8 и 8', причем эта пара будет опять особой. В самом
деле, если множества Е$ и £'§' отделимы В, каковы бы ни были
oL и Ъ'19 взятые соответственно в 8 и 8', то множество Еь отделимо В
от Е'ь,у так как достаточно взять общую часть множеств, отделяющих Eh
от множеств 2Г „ где 8'L пробегает все интервалы Бэра порядка &н-1,
содержащиеся в 8': эта общая часть, будучи измеримой В, очевидно,
отделяет Еь от Е'ь,. Но лишь только Е\, отделимо В от Е% , каково бы ни
было ох в 8, предыдущее рассуждение снова применимо, и отсюда мы
заключаем, что E'h, отделимо В от £$, что невозможно, так как пара (8, V)
особая.
Таким образом, каждая особая пара (о, 8') необходимо содержит
пару (8р 8'г) интервалов Бэра следующего порядка, являющуюся опять
особой.
Установив это, допустим, что данные множества Е и Е'
неотделимы В. В этих условиях существует бесконечная последовательность
особых пар
(\,*;), (К, ц> (*„, &;,)—
порядков, соответственно равных 1, 2, . . . , п, ..., причем каждая из этих
пар содержится в предыдущей. Отсюда следует, что интервалы Бэра 8Я
стремятся к иррациональной точке £0, а 8^ к иррациональной точке t'0.
Так как множества Е и Е не имеют общей точки, то /(*0) 7^ ?(*'<))•
С другой стороны, функции /(/) и ср (f) непрерывны. Это значит, что
значения функций /и ср в 8м и 8^ как угодно близки соответственно
к двум фиксированным точкам /(*0) и у{?0), когда п неограниченно
возрастает. Отсюда следует, что множества Е$ и Е\' расположены
в двух различных порциях о и о' области о7х; эти порции при
достаточно большом л не имеют общей точки. Следовательно, £3м и Еь^
отделены друг от друга при помощи порций, и мы пришли к
противоречию (ч. т. д.).
Сделаем следующее замечание: для определенности мы ограничились
линейными аналитическими множествами. Но, принимая за / и <р
комплексные функции, мы, очевидно, получим доказательство
принципа I для аналитических функций любого числа измерений.
Второе доказательство (положительное). Это доказательство
основано на следующей геометрической лемме:
Если порция (0<О<1, 0<С'<1) двумерной области <?7w
разделена на прямоугольники Бэра, то множество R тех
прямоугольников Бэра, которые не содержатся в узком смысле ни в одном из
прямоугольников этого разбиения, может быть эффективно представлено
в виде вполне упорядоченной последовательности р0, р19 р2,. . . , рш,. . .
• • • > Ра> • • • I T так, что из двух любых прямоугольников р„ и р^ этой
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ 135
последовательности или последующий содержит предыдущий^ или
они не имеют ни одной общей точки.
Чтобы убедиться в этом, расположим прямоугольники из R в простую
бесконечную последовательность
г„ г2> . . . , г,п . . . (1)
Мы скажем, что вполне упорядоченная последовательность Е
прямоугольников из R образует цепь, если: 1° первый член р0 из Е есть
первый из членов последовательности (1), который встречается в
разбиении порции (0<Zt<Zl9 0<C^<C1) на частные интервалы Бэра;
2° каков бы ни был член р из £, он является первым прямоугольником
последовательности (1), не совпадающим ни с одним из
предшествующих членов р в £, и притом он либо является частичным
прямоугольником рассматриваемого разбиения, либо все прямоугольники Бэра
порядка, непосредственно следующего за порядком р, являются членами
последовательности Е, предшествующими р.
Ясно, что цепи существуют, так как первый из членов
последовательности (1), входящих в рассматриваемое разбиение, является цепью;
ясно, что если рассмотреть две какие-либо цепи Е и Е\ то одна из
них есть сегмент другой, так как каждый член одной цепи единственным
образом определяется предшествующими членами и знанием
последовательности (1). Отсюда следует, что каждой цепи Е, не являющейся
самой большой, т. е. служащей сегментом другой более длинной цепи,
соответствует один и только один член простой бесконечной
последовательности (1) и значит одно вполне определенное целое число п. Из
этого мы заключаем, что множество всех возможных цепей счетно,
так как оно уже перенумеровано при помощи целых чисел.
Установив это, обозначим через С соединение всех возможных
цепей. Так как каждая цепь есть всегда сегмент другой цепи, то С
есть опять цепь. Ясно, что это самая большая цепъу т. е. такая, что
каждая другая цепь есть сегмент С.
Я теперь утверждаю, что цепь С состоит из всех
прямоугольников R и что сама порция (0<£<С1> 0<О'<1) есть последний член С.
В самом деле, обозначим через Rf множество прямоугольников из Ry
которые входят в С. Если в R есть члены, которые не входят в Rf9
то каждый из них содержит прямоугольники Бэра непосредственно
следующего порядка и также не содержащиеся в R', а следовательно,
и в /?. В самом деле, в противном случае среди прямоугольников
разности R — R' в последовательности (1) найдется первый, пусть rw,
в котором все прямоугольники непосредственно следующего порядка
принадлежат к С. Тогда, прибавляя гт к цепи С, мы получим новую
цепь (С, rm), более длинную, чем С, что невозможно.
Итак, каков бы ни был прямоугольник разности R — R (если эта
разность существует), он содержит прямоугольники непосредственно
136
Н. Н. ЛУЗИН
следующего порядка, также принадлежащие к R— R1. Следовательно >
мы имеем бесконечную последовательность прямоугольников Бэра
*"п0> **Я]> Г*29 * * * » Гпку * * * '^)
порядков, соответственно равных 0, 1, 2, ...,£,..• , каждый из
которых лежит внутри предыдущего, причем все они принадлежат
к R— R' и, разумеется, стремятся к некоторой точке M{t0, t'0}
области q/w, расположенной внутри них.
С другой стороны, порция (0<С^<С1> 0<*'<С1) полностью была
разделена на частичные прямоугольники Бэра; следовательно, точка М
принадлежит к некоторому вполне определенному прямоугольнику этого
разбиения; пусть это прямоугольник г, в последовательности (1). Так
как последовательность (2) содержит все прямоугольники Бэра,
содержащие точку Му то rv должен фигурировать в последовательности (2),
а это невозможно, так как г, заведомо принадлежит к С, а значит, и
к R'.
Итак, R' совпадает с /?.
Отсюда следует, что наибольшая цепь С состоит из всех
прямоугольников R, Но среди этих прямоугольников имеется и сама порция
(0<С*<Г1, 0<С*'<С1). Так как она содержит все остальные члены из R*
то из самого определения цепи вытекает, что эта порция есть
последний член цепи С (ч. т. д.).
Установив эту важную лемму, возвратимся теперь к доказательству
принципа I.
Пусть
и
непрерывные параметрические изображения аналитических множеств Е
и Е\ не имеющих общих точек.
Рассмотрим порцию (0 < t <[ 1, 0 < t' <C 1) области q/w. Каждой
точке Р0 (t0f to) этой порции соответствуют две точки М0 и iWo,
принадлежащие соответственно Е и Я' и расположенные в m-мерной области
Так как множества Е л Е' без общих точек, то точки М0 и Л/0 всегда
различны. Отсюда следует в силу непрерывности /^ и <р<, что на
(0<*<С1, 0<У<С1) существует прямоугольник Бэра г, содержащий
точку Р0 и такой, что если точка P(t, t) движется в г,
соответствующие точки М и М описывают две ^соответственные части множеств Е
и £', расположенные в двух порциях области <9^х,...*»», не имеющих
общих точек. Среди таких прямоугольников Бэра г мы выберем тот,,
порядок которого наименьший, т. е. самый большой.
Таким образом, каждой точке P(t> £) мы приводим в соответствие:
содержащий ее прямоугольник Бэра. Отсюда следует, что порция
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
137
(0<*<1, 0<У<С1) полностью разделена на прямоугольники Бэра
попарно без общих точек и, вообще говоря, различных порядков. В самом
деле, если бы два таких прямоугольника имели общую точку, один из^
них должен был бы содержать другой, что невозможно, так как среди
прямоугольников Бэра, содержащих некоторую точку Р, мы каждый
раз берем наибольший, соответствующий частям Е и £", отделимым
друг от друга при помощи порций. Обозначим через 9? множество
прямоугольников этого разбиения.
Установив это, применим предыдущую лемму и рассмотрим цепь С:
Р0> Pi» Р2>---» Рш»---> Pa,"- |Pv» (СУ
образованную из всех прямоугольников Бэра, не содержащихся в узком
смысле ни в одном из частичных прямоугольников ранее определенного
разбиения.
Из определения цепи С следует, что каков бы ни был член рв цепи
Св, он или является прямоугольником из 9?, или все прямоугольники
непосредственно следующего порядка, содержащиеся в рв, принадлежат
к сегменту цепи С, определяемому членом ра. Наконец, известно, что-
последний член р¥ цепи С есть порция (О <С * <С 1> 0 < /' <С 1)
области c7V.
Каждому члену ра цепи С соответствуют две части множеств Е и
Е'у которые получаются, когда точка P(t, t') пробегает прямоугольник рв.
Эти части мы обозначим через Е?а и Е'
Так как р0 есть прямоугольник из 9?, то отделимость В множеств
Е и Е осуществлена при помощи двух вполне определенных порций
области o/х^...хту не имеющих общей точки. Допустим теперь, что мы
имеем вполне определенную отделимость В для двух множеств £Рв, и
£Рв„ соответствующих члену р«' цепи С, предшествующему данному члену
рв, а! < а, каково бы ни было а', меньшее, чем а. Из этого мы выведем
вполне определенную отделимость В для множеств Е и Е' . Мы
естественно предполагаем, что р' не есть прямоугольник из Я, так как
в этом случае отделимость В множеств £рв и £рв была бы уже
осуществлена при помощи порций области gT^a,...^.
Пусть 5 и 8'— проекции рв на оси ОТ и ОТ. Ясно, что В и 8' суть
интервалы Бэра того же порядка, как и ра; пусть к — этот порядок.
Пусть \ и Ь[— интервалы Бэра порядка &+1, содержащиеся
соответственно в 8 и 8'. Прямоугольник р, проекциями которого на оси ОТ и
ОТ служат 8xjh Ъ'19 есть, очевидно, прямоугольник Бэра порядка к-\-\у
содержащийся в рв; по определению цепи С прямоугольник р заведомо
входит в цепь С и предшествует рв. Следовательно, на основании
сделанной гипотезы множества £р(=£$) и ЕЧ=ЕА отделены, и мы умеем
получить отделяющие множества //г и //а', измеримые В.
138
Н. Н. ЛУЗИН
Установив это, рассмотрим два новых множества Нъ и Hv,
определенные формулами
я5=2Ця5,
h h
и
где для получения Нь берется сначала общая часть всех /У8], когда
о'х пробегает все интервалы Бэра порядка &+1, содержащиеся в &',
а затем берется сумма так полученных общих частей, когда \
пробегает все интервалы Бэра порядка к-\-1, содержащиеся в о;
аналогичным образом получается H'v.
Вполне очевидно, что так определенные множества Нь и Нь, не
имеют общих точек и что они соответственно содержат Е9а(=Еь) и
£pe(=£j,). А так как Нь и Нь,, очевидно, измеримы В, то отсюда
следует, что множества Е. и Е' отделимы В, причем это отделение осу-
Ра Ра
ществлено единственным образом.
Установив это, вернемся к доказательству принципа I. Так как р
есть произвольный член цепи С, мы можем принять за ра последний
член из С. Отделяющие множества Н и Н, построенные аая этого
члена, дают нам искомое отделение данных аналитических множеств Е
и Е (ч. т. д.).
Изучение регулярных и полурегулярных изображений
аналитических множеств
Регулярное изображение
Измеримость В аналитических множеств, допускающих
регулярное параметрическое изображение. Мы видели (стр. 108), что
всякое несчетное множество, измеримое В, допускает непрерывное
(и даже нормальное) параметрическое изображение, если пренебречь
счетным множеством его точек.
Обратное предложение также имеет место:
Всякое аналитическое множество Е, допускающее непрерывное
регулярное изображение, обязательно измеримо В, и из его
изображения можно вывести эффективное построение Е, отправляясь от
порций основной области, при помощи двух операций: сложения и
взятия общей части, неограниченно повторяемых 1.
1 Это теорема IV моей заметки в Comptes Rendus, 8 января 1917 г. Если какое;
либо множество Е допускает регулярное параметрическое непрерывное изображение,
то оно непременно измеримо 2?, и мы видим, что каждая точка Е есть точка
сгущения в смысле Линделефа.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ 139
Пусть Е есть аналитическое множество и
— его непрерывное регулярное параметрическое изображение.
Пусть к—любое целое положительное число, к^\. Разделим
порцию (0, 1) области о7/ на интервалы Бэра порядка к; пусть Ъ{*\
о?),..., 8J),.. . эти интервалы. Заставляя t пробегать о[*>, мы получаем
часть £, которую обозначим через Е%\ Ясно, что при фиксированном
к, множества Е^ суть аналитические множества попарно без общих
точек. Обозначим через Д^ параллелепипед Бэра области о7х
наивысшего порядка, содержащий Е^\ такой параллелепипед заведомо
существует, так как множество Е^ не может свестись к одной
единственной точке.
Установив это, вернемся к множествам Е£\ где число к все еще
-фиксировано. Так как аналитическое множество Е& не имеет ни одной
общей точки с суммой остальных аналитических множеств Е$ при п,
отличном от /I, и так как эта сумма есть аналитическое множество,
непрерывное параметрическое изображение которого известно, то мы
можем найти множество Н%\ измеримое В и покрывающее Е£\ которое
с этой суммой не имеет ни одной общей точки. Если мы построим Н&
аля всякого Е%\ мы получим бесконечную последовательность множеств,
измеримых В:
каждое из которых содержит один и только один член
последовательности Ef\ Е£\. .., Е&\. .. и не имеет ни одной общей точки с другими
членами этой последовательности. В этих условиях общая часть
п'фч
параллелепипеда Бэра Д£\ множества Н\? и дополнений к множествам
Н$ для всякого л', неравного л, есть множество, измеримое В,
содержащееся в ДФ и содержащее Е^; мы обозначим эту общую часть через
6^. Важно заметить, что когда число к фиксировано, то множества
в(*), 8W,..., Ъ&\... не имеют попарно общих точек и, следовательно,
осуществляют одновременную отделимость множеств
£(*) £(« £(*)
В. Серпинский доказал, что всякое множество, измеримое В, каждая точка
которого есть точка сгущения в смысле Линделефа, допускает непрерывное регулярное
параметрическое изображение без того, чтобы было необходимо пренебрегать хоть
•одной точкой этого множества; см. его работу „Sur les images continues et biunivo-
ques de I'ensemble de tous les nombres irrationales", Mathematics, 2, Cluj, 18, 1928.
140
Н. Н. ЛУЗИН
Установив это, обозначим через Sk сумму отделяющих множеств №
л = 1, 2, 3,... и через <§ общую часть сумм Sk, & = SX • S2.. .Sk....
Так как каждое СМ измеримо 5, то и множество £ также измеримо В.
Рассматриваемое аналитическое множество Е есть, [очевидно, сумма
множеств Е$ при к фиксированном и /г = 1, 2, 3,... Отсюда следует,
что Е содержится в каждой сумме Sk, а следовательно, и во
множестве &.
Мы докажем, что каждая точка М из & принадлежит к Е.
В самом деле, если точка М0 области o/Ztzi...zm содержится в £, то
в каждой сумме Sk имеется один и только один член 8М, содержащий
М0; пусть СМ— этот член. Обозначим через 8W интервал Бэра,
соответствующий множеству Е&\
Ясно, что интервалы Бэра последовательности о$\ Ъ№9..,, 8(A),.. #
имеют соответственно порядок, равный 1, 2, ..., к,..., и заключены
друг в друге. Следовательно, существует одна и только одна
иррациональная точка /0, которая принадлежит всем этим интервалам.
Установив это, рассмотрим точку Р0 (jcJ, х\,..., л:^) области
(/«а...**», определенную уравнениями
А=Л ('•)• А=Л Со). • • •> <=/»('в)-
Легко видеть, что Р0 есть точка Е. Докажем, что она совпадает с М0.
В самом деле, так как tQ принадлежит к §^, каково бы ни было
число ку то точка Р0 принадлежит к 8W. С другой стороны, точка М0
принадлежит тому же множеству 6J*>, Следовательно, две постоянные
точки М0 и Р0 принадлежат одному и тому же параллелепипеду Бэра
А^, содержащему множество Ь£\ Но когда к стремится к
бесконечности, диаметр ДЮ необходимо стремится к нулю в силу непрерывности
функций fi (/). Отсюда следует, что Р0 совпадает с М0.
Таким образом, мы доказали, что данное аналитическое множество Е
совпадает с множеством §, измеримым В (ч. т. д.).
Приложение к проекциям множеств, измеримых В. Мы видели
(стр. 123), что ортогональная проекция аналитического множества есть
опять аналитическое множество. В частности, ортогональная проекция
всякого множества, измеримого В, есть аналитическое множество.
С другой стороны, мы видели, что всякое аналитическое множество
есть ортогональная проекция множества, измеримого В, некоторого
частного вида; такое множество мы назвали элементарным множеством;
оно является элементом класса 2.
Отсюда следует, что в общем случае ортогональная проекция
множества, измеримого В, неизмерима В.
Но есть один случай, когда можно утверждать измеримость
проекции множества измеримого В.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
141
Теорема. Ортогональная проекция множества Е, измеримого В
и расположенного в т-мерной области, на т-мерную область, т < т,
непременно измерима В, если проекции двух различных точек
множества Е различны1.
Чтобы доказать это, возьмем множество Е, измеримое В; пусть
*l=/l(')i *2 = Л('),-..э Xm = fm{t)
есть его непрерывное регулярное изображение.
Ясно, что проекция Е на m'-мерную область ^х^...^ дается
непрерывным регулярным изображением
v*l =/l (')> *2 = Л (0» • • • , Хт* =fm, {t),
где т <С /п.
Но согласно сделанной гипотезе проекции на с/*^...^ двух
различных точек Е также различны. Так как рассматриваемое непрерывное
изображение Е регулярно, то двум различным значениям t отвечают
две различные точки из Е, а стало быть, и две различные точки его
проекции.
Отсюда мы заключаем, что непрерывное параметрическое
изображение этой проекции регулярно, а следовательно, сама эта проекция
измерима В (ч. т. д.).
Регулярное параметрическое изображение при помощи
произвольных функций классификации Бэра. Мы видели, что нельзя
расширить определения аналитического множества, взяв параметрическое
изображение
*i=/i(')i x2 = f2(t),...y xm = /m(*)>
осуществленное при помощи произвольных функций классификации
Бэра.
Важное аналогичное предложение существует также для случая
регулярного параметрического изображения. Действительно, мы имеем
следующую важную теорему:
Теорема. Всякое аналитическое множество, обладающее
регулярным параметрическим изображением при помощи произвольных
функций из классификации Бэра, измеримо В.
В самом деле, пусть xl=fl{t), x2=f2(t)y..., xm = fm(t) — такое
регулярное изображение множества Е. Рассмотрим функцию F(xl9 х2,...
..., хт, t), определенную следующим равенством:
F(xl9 x2,..., xm, t) = [xl-f1(t)Y^[x2-fm(tW^...^[xn-fm(^f.
Легко видеть, что эта функция, определенная на области т -\- 1
измерений о/%&...* ти входит в классификацию Бэра. Тогда в силу теоремы
Лебега (стр. 124) множество S точек области Зг^...*^ для которых
эта функция обращается в нуль, измеримо В. Очевидно, что коорди-
1 Ср. Н. Lebesgne. Remarques sur les theories de la mesnre et de rintSgra-
tion [Ann. de i'Ecole Norm. Super. Серия 3, XXXV, 242 (1918), Note 3].
142
Н. Н. ЛУЗИН
наты точек N(xx, jc2, ..., хт, t) множества & удовлетворяют
совместным равенствам
*i=/i(0» Xz = f2(t),..., xm=fm{t).
Следовательно, ортогональная проекция £ на область з7«л...хт
совпадает с множеством Е.
Но из регулярности системы функций /< следует, что проекции на
область c7xlxt...xm двух различных точек <S различны. Следовательно,
в силу предшествующей теоремы множество Е измеримо В (ч. т. д.).
Обобщение предыдущего результата. Очень легко значительна
обобщить предыдущие теоремы, распространив их на тот случай, когда
за область определения функции fi принимают или аналитическое
множество, или произвольное множество, измеримое В.
В самом деле, мы имеем следующее предложение:
Теорема. Если xl = fl{t), x2=/2(f),..., xm=fm(t) есть система
каких-либо функций классификации Бэра, то множество Е, которое
пробегает точка М(х19 х2,.. ., хт, t), когда t пробегает
аналитическое множество е, есть также аналитическое множество. Кроме
того, если е измеримо В и если параметрическое изображение,
осуществленное при помощи функций fi, регулярно на е, то множество
Е измеримо В.
В самом деле, так как е есть аналитическое множество, то мы имеем
непрерывное параметрическое изображение
этого множества на порции (0, 1) области /т, причем <р непрерывна на.
этой порции.
В этих условиях сложные функции
*1=Л1<Р(Х)Ь ^2 = Л[СР(Х)]»--., *т = /Л?(Х)]
осуществляют параметрическое изображение Е на порции (0, 1)
области с7т. Легко видеть, что эти функции входят в классификацию
Бэра. Следовательно, множество Е аналитическое. Если е несчетно
и измеримо В, то, пренебрегая счетным множеством точек е, функцию <р
можно предположить регулярной. Отсюда следует, что если
предложенная система функций jit регулярна на е, то такой же будет и система
функций /{[ср (х)]. Значит, множество Е измеримо В (ч. т. д.).
Полу регулярное изображение
Мы скажем, что параметрическое изображение некоторого множества-
точек Е, расположенного в области c7xiz2...xm:
*i=/i(*)» x2=f2(t\,...f xn = fm{t),
полурегулярно, если каждой точке М множества Е соответствует самое-
большее счетное множество значений t1.
1 См. мою заметку в Comptes Rendus, 29 июля 1929 г.: „Sur la representation pa—
rametrique semi-reguliere des ensembles".
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ 143"
В частности, функция f(t), определенная на (0, 1), называется
полурегулярной, если уравнение x°=/(t) имеет не более, чем счетное число
корней дая всякого действительного х°.
Мы будем изучать природу аналитических множеств, допускающих
полурегулярное изображение, осуществляемое при помощи непрерывных
функций или функций классификации Бэра.
Для изучения этих вопросов нам понадобится следующая теорема
из геометрии:
Если & — аналитическое множество, расположенное в
т-*-1-мерной области Л^...*„#» гпо множество Е тех точек М т-мерной
области a/x1...zm, в которых проведенная через М параллель к оси OY
пересекает & по крайней мере в двух точках, есть аналитическое
множество.
Чтобы доказать это, расположим все рациональные точки оси OY
в бесконечную последовательность rl9 r2,.. •, гя,... и возьмем точку г„.
Пусть &'п и $"п — части &, дая точек которых мы имеем соответственно
у <[ гя и у^>гп. Обозначим через Е'н и £п' проекции множеств &'п и ё^
на область о/ххлг..лт и через Еп — общую часть Е'п-Е'^.
Легко видеть, что Е есть множество тех точек М из £, в которых
параллель к оси О У, проведенная через М, пересекает Е по крайней
мере в двух точках, дая которых у<^гп и у^>гя. Следовательно, сумма
Ег ■+- Е2 -+■... -+* Еп -+- ... совпадает с множеством Е.
Но так как &'п и £w' — аналитические множества, то такими же будут
Е'п и Е"п. Следовательно, Еп аналитическое, а потому и Е аналитическое.
Преобразование многомерной области в линейную область.
Начнем с доказательства того, что изучение множеств точек в
многомерной области можно свести к изучению линейных множеств, С этой
целью мы преобразуем /п-мерную область <7х1хг...хт в линейную область-
о/х при помощи взаимно однозначного и взаимно непрерывного
преобразования.
Рассмотрим в области Зхлхг...хт все параллелепипеды Бэра порядка 1
и осуществим взаимно однозначное соответствие между этими
параллелепипедами тс' и интервалами Бэра 1-го порядка 8' на порции (0, 1)
области 3fх* Установив соответствие между тс' и о', приведем во
взаимнооднозначное соответствие все параллелепипеды Бэра тс" порядка 2,
лежащие в тс', и все интервалы Бэра о" порядка 2, лежащие в &'. Вообще,
установив соответствие между некоторым параллелепипедом Бэра тс<*—*)
порядка к—1 области о/%1%г...гт и интервалом Бэра В*-1) на порции
(О, 1) области с7*, приведем во взаимно однозначное соответствие все
параллелепипеды Бэра тсМ порядка к, лежащие в т№~1\ и все интервалы
Бэра 81*) порядка к, лежащие в 8(fc_1).
Ясно, что мы получаем таким образом взаимно однозначное
соответствие между точками всей области о7х1хъ...хт и точками порции (0, 1)
144
Н. Н. ЛУЗИН
линейной области о7х. Легко видеть, что это соответствие взаимно
непрерывно и что если точка х пробегает интервал Бэра порядка к
на (0, 1) в о7х9 то соответствующая точка М(х19 х2,---> хт)
пробегает параллелепипед Бэра порядка k в о/г]г2...хт.
Следовательно, это соответствие между о7х1х2...хт и порцией (0, 1)
области о7х можно написать в двух формах:
xi = gi (x)f x2 = g2(x)9...f xm = gm(x)
x ^= О \xl9 x29..., xm)9
где функции gi (x) непрерывны на (0, 1) в о7х и функция G(xl9 x29. .., хт)
непрерывна на о/Х1х2...хт-
Установленное соответствие, очевидно, ставит в соответствие
каждому множеству е класса 0 на о7х некоторое множество Е класса 0 на
Vгл1Я2...хт и обратно. С другой стороны, каждая последовательность
множеств е19 е29...9 еп9...9 расположенных в о7х и стремящихся к
некоторому пределу е9 преобразуется в некоторую последовательность
множеств ЕХ9 Е29...9 ЕП9...9 расположенных в ^х1хг...хт и стремящихся
к пределу Е9 являющемуся образом е. Отсюда следует, что всякое
множество е9 измеримое В9 в линейной области о7х преобразуется в
некоторое множество Е m-мерной области <з7х1х2...хт9 также измеримое В
и того же класса и подкласса, и обратно.
Установив это, рассмотрим аналитическое множество Е9
расположенное в Q/rxlx2...z и допускающее полурегулярное параметрическое
изображение
*i=/i(0» x2 = f2(t),...t xM = fm{t).
Если мы подставим эти функции /^ в функцию G(xl9 х29..., хт)9
ранее определенную, то мы получим непрерывную функцию /(£),
определенную равенством
*=/(/)=с[л(*),/.(<),...,/.(0].
Если мы заставим t пробегать порцию (0, 1) области <з7*, то точка х9
очевидно, будет пробегать некоторое линейное множество е на <РfХ9 и
легко видеть, что е есть образ Е9 получающийся при преобразоваг
нии (1) области о7х1х2^.хт в о7я.
Если система функций xi=fi{t) полурегулярна, то такой же будет
т функция f(t). Следовательно, изучение множества Е из 3%\жг...%т
допускающего полурегулярное изображение, сводится к изучению
линейного множества е9 допускающего полурегулярное изображение. Таким
образом, если нам удастся доказать, что е измеримо В9 то это же будет
иметь место и а^я Е*
Изучение непрерывных полурегулярных изображений. Мы сейчас
.докажем теорему, относящуюся к полурегулярным изображениям и во
(1)
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
14S
всех отношениях аналогичную предыдущей теореме, касающейся
регулярных изображений (стр. 138).
Теорема. Всякое аналитическое множество Е, допускающее полу-
регулярное параметрическое изображение, обязательно измеримо В.
Так как общий случай аналитического множества нескольких
измерений сводится к случаю линейного аналитического множества, то
мы ограничимся этим последним.
Возьмем непрерывную полурегулярную функцию
определенную на (0, 1) в области с7*, и обозначим через Е множество
значений f{t) на (0, 1). Так как f(t) полурегулярна, то каждой точке х
из Е соответствует не более, чем счетное множество значений /.
Все сводится к тому, чтобы доказать, что Е измеримо В. Допустим
обратное, т. е. что Е неизмеримо В.
Я утверждаю, что в этих условиях существуют два различных
интервала Бэра Ьх и В2, расположенные в oft и такие, что если ех и ег
множества значений /(/) соответственно на \ и &2, то общая часть
ех • е.г неотделима В от дополнения СЕ к данному множеству Е.
В самом деле, если бы это было не так, то каждая общая часть
ех • е2 была бы отделима В от СЕ. Пусть h — множество, измеримое В%
содержащее СЕ и не содержащее ни одной точки ех • е2. Так как этих
общих частей ех • е2 лишь счетное множество, то столько же будет и
соответствующих множеств А. Обозначим через Н общую часть всех
множеств А; ясно, что Н измеримо В и содержит СЕ. Кроме того, Н
не содержит ни одной точки общих частей ех • е2. Следовательно, каково
бы ни было х из Н, существует самое большее одно значение /,
удовлетворяющее уравнению л: =/(£). Обозначим через 6 множество точек t,
для которых соответствующие точки х принадлежат к И. В силу
обобщения теоремы Лебега1 множество 6 измеримо В. А так как функция
/(/) регулярна на 6 (т. е. имеет в разных точках 6 различные
значения), то отсюда следует, что множество значений /(6) на 9 измеримо В
(стр. 143), Обозначим это множество через Нх; множество Нх
расположено в о7х. Так как множество СЕ есть, очевидно, разность между
Н и //р то мы видим, что СЕ измеримо В9 что невозможно, так как
мы предположили, что Е неизмеримо В.
Установив это, допустим, что существует к различных интервалов
Бэра Sp 82>--м 8fc, расположенных в g7/ и таких, что если мы обозначим
через е4 множество значений f(t) на bi9 то общая часть ех -в2...е*
неотделима В от множества СЕ, Я утверждаю, что в этих условиях мы
1 Речь идет о следующем предложении: какова бы ни была функция /
классификации Бэра и каково бы ни было множество &, измеримое В% множество Е
тех точек% для которых значение f принадлежит к S, измеримо В. Это
предложение доказывается трансфинитной индукцией, отправляясь от ранее цитированной
teopeMbi Лебега (стр. 124 этой книги.—Ред.) [15].
146 н. н. лу зин
можем выбрать в каждом о{ два новых интервала Бэра о', и &'! без
общих точек и таких, что если е. и е! — множества значений f(t)
соответственно на &'. и о^', то общая часть (е[ • е[) X (е'2 • е2').. .(е^ • ек)
также неотделима В от СЕ.
В самом деле, допустим противное. Это значит, что каков бы ни
был выбор интервалов Бэра о', и о^ в о^, i = l, 2,..., k>
соответствующая общая часть (е\ - е[) • (е'2 • е'%).. .(е'к • е^) отделима В от С£. Пусть
А — множество, измеримое В, содержащее С£ и не содержащее
никакой точки этой общей части. Так как этих общих частей лишь счетное
множество, то столько же будет и множеств А. Следовательно, общая
часть Н этих множеств h есть множество, измеримое В, и легко видеть,
что Н содержит СЕ, но не содержит точек общей части (е[ • е\) - (е^ • е^)...
• • -{е'к ' е'к)- Отсюда следует, что если точка х принадлежит к Н, то
уравнение х =f(t) имеет хотя бы в одном из интервалов о^ самое
большее один корень.
Установив это, обозначим через \ множество точек х, для которых
уравнение x=f(t) имеет по крайней мере два корня в &,-. Ясно, что т^.
содержится в е<. Легко видеть, что \ — аналитическое множество.
Чтобы убедиться в этом, обратимся к ранее доказанной (стр. 143)
теореме из геометрии и рассмотрим в плоскости ТОК часть кривой
л: =/(£), которая получается, когда t пробегает интервал Бэра Ь{. Так
как функция/ непрерывна на с7/, то кривая x=f(t) есть плоское
множество, измеримое В* Такой же будет и часть этой кривой,
соответствующая интервалу о,.. В силу указанной теоремы из геометрии
множество y\i точек jc0, для которых прямая х = х0 пересекает эту часть
кривой x=f(t) по крайней мере в двух точках, есть аналитическое
множество.
Установив это, докажем, что множество "*и обладает следующим
замечательным свойством: каждое множество Q, измеримое В, лежащее
на о/х и не содержащее ни одной точки rli9 таково, что общая часть
Q • ei непременно измерима В.
Чтобы убедиться в этом, обозначим через Т множество тех точек t
из Зй для которых точки *=/(/) принадлежат к Q. В силу теоремы
Лебега (см. примечание1 на стр. 124) (см. также [15] — Ред.) Г
измеримо В. Легко видеть, что / регулярна на Т (имеет различные
значения). Следовательно, множество значений /(f) на 7* измеримо В (стр. 142).
Но это множество и есть как раз общая часть Q • е%.
Установив это, вернемся к множеству /У, измеримому В. Мы видели,
что если х принадлежит к //, то уравнение x = f(t) имеет хоть в одном
из интервалов Ъ- не более одного корня. Отсюда следует, что общая
часть у\х • т]2... т)* не имеет общих точек с Н. Значит всякая точка Н
может принадлежать не более чем к к — 1 множествам т\4 одновременно.
Обозначим через 8Х какую-либо из общих частей к — 1 множеств ty;
существует к множеств 81в Общая часть И и 6Х есть аналитическое
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
147
множество, не имеющее общей точки с некоторым аналитическим
множеством И • T\i. Следовательно, ^ • И можно заключить во множество 0^
измеримое В и не содержащее ни одной точки множества у\(. Значит общая
часть bv и соответствующего множества е{ измерима В. Отсюда
следует, что точки общей части е = е{ • е2 ... еку лежащие в 0,, образуют
множество, отделимое В от СЕ.
Установив это, удалим из И точки, принадлежащие соединению
множеств 61, и обозначим через Нх множество остающихся точек. Легко
видеть, что Нх измеримо В и что каждая точка х из Нх принадлежит
самое большее к— 2 множествам ^ одновременно. Кроме того, часть е>
содержащаяся в Н—Н19 отделима В от СЕ.
Обозначим через 62 какую-либо из общих частей а^я группы из к—2
множеств ?),. Существует самое большее ~ множеств 62. Общая
часть Нх и 62 есть аналитическое множество, не имеющее ни одной
общей точки с каким-либо из аналитических множеств Н'• ?)».
Следовательно, каждое множество Н • 62 можно заключить во множество 8.2,
измеримое В и не содержащее ни одной точки множества \.
Следовательно, общая часть 02 и соответствующего множества et измерима В,
Отсюда следует, что точки общей части е = ех - е.> . . . ек, находящиеся
в Q2, образуют множество, отделимое В от СЕ.
Установив это, удалим из Нх точки, принадлежащие соединению
множеств б2, и обозначим через Н2 множество остающихся точек.
Легко видеть, что Нг измеримо В и что каждая точка х из Нг
принадлежит самое большее к — 3 множествам ги одновременно. Кроме
того, часть е9 принадлежащая Нх — Нъ отделима В от СЕ.
Продолжая таким же образом, мы получим конечную
последовательность множеств //, Ни //,,...,/Л-2, //*—!- Эти множества обладают
следующими свойствами: каждое множество Hj измеримо В и
содержится в предыдущем Hj-Y\ каждая точка х из Hj принадлежит самое
большее к к—j—1 множествам ^$; но наиболее важное свойство
состоит в том, что часть множества е, содержащаяся в ///_,—Hj,
отделима В от СЕ.
Так как часть множества е, содержащаяся в Н, неотделима В
от СЕ, то мы заключаем, что часть множества е, содержащаяся в //*_г>
также неотделима В от СЕ. Но M-i не содержит точек т),;
следовательно, часть множества е, содержащаяся в H*—ly измерима В, а
потому отделима В от СЕ, что приводит нас к противоречию (ч. т. д.)*
Установив это, вернемся к доказательству предложенной теоремы.
Прежде всего мы доказали, что если Е неизмеримо 5, то существуют
в off два интервала Бэра \ и Ъ2 без общих точек и такие, что если
е^ и е2 — множества значений f(t) соответственно на \ и &2, то общая
часть ех • е2 неотделима В от СЕ. С другой стороны, мы доказали, что
если мы имеем к различных интервалов Бэра Ь19 В2, ..., Ък, расположен-
ных в о7* и попарно без общих точек, причем общая часть ех • ег ... е*
148
Н. Н. ЛУЗИН
[где eic — множество значений f(t) на &*], неотделима В от СЕ, то можно
в каждом bi найти два интервала Бэра Ь'{ и Ъ'! без общих точек и такие,
что общая часть (е\ • е[) • (е2 • е2) •.• (е'к • ^') также неотделима В от С£.
Сравнивая эти два результата, мы видим, что в <Э\ существует
совершенное множество Р такое, что каково бы ни было л, совершенное
множество Р заключено в 2я интервалах Бэра попарно без общих точек
^i> 82, ...,82л таких, что общая часть соответствующих множеств
е = е± • е2 ... е2п неотделима В от СЕ. Кроме того, мы можем
предполагать порядок интервалов Бэра ^ как угодно высоким.
Отсюда следует, что рассматриваемая функция /(/) постоянна
на Р. В самом деле, если существуют две точки tx и t2 из Р, в
которых f(t^)^f(t2), то в силу непрерывности f(t) на o/t среди интервалов
Бэра Ь19 82, ...,8гл найдутся два интервала, пусть bi и bj9 содержащие
соответственно точки tl и U и такие, что соответствующие множества
ех и е.г не имеют общей точки. Но это невозможно, так как общая часть
е = е1 • е2 ... еь неотделима В от СЕ, а следовательно, она фактически
содержит точки.
Итак, функция f(t) постоянна на Р; обозначим ее значение на Р
через х0. Так как уравнение
*0=/С)
имеет несчетное множество корней, то f(t) не есть полурегулярная
функция, что противоречит гипотезе (ч. т. д.).
Полурегулярное параметрическое изображение при помощи
произвольных функций классификации Бэра. Мы теперь обобщим
предыдущий результат и докажем следующее предложение:
Теорема. Всякое аналитическое множество, допускающее
полурегулярное изображение при помощи любых функций классификации
Бэра, измеримо В1.
Чтобы установить это, возьмем в т-мерной области g7V* ••.*«•
аналитическое множество Е, допускающее полу регулярное изображение:
Xi=A(t)t x2=f2{t), ..., xm=fm{t),
осуществляемое при помощи функций fi9 входящих в классификацию
Бэра.
Рассмотрим функцию F(xl9 Х2, • • •» хшу
t) от т ■+■ 1 действительных
переменных, определенную в (то-+- 1)-мерной области Ji,xt...*mt формулой
F{xlt х, хт, t) = ta —Л {t)]r -ь
н- [*, -Л (01* -ь . • • -ь [х« -U ЮР-
Так как эта функция, очевидно, входит в классификацию Бэра, то
множество S точек
хи xi> • • • xmt 0 области о?^*,...*^*, в которых F
обращается в нуль, измеримо В.
1 См. мою заметку в Comptes Rendus, 29 июля 1929 г.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
149
Ясно, что координаты точек М из § удовлетворяют уравнениям
'1 =Л (0, *2 =Л ('), • • ., Хт =fm (t).
Отсюда следует, что рассматриваемое аналитическое множество Е
есть проекция &.
Так как & измеримо В, то (с точностью до счетного множества его
точек) оно допускает непрерывное регулярное] изображение на порции
(О, 1) области g7t:
*1 = тЧ(Х)э *2=<Р2(Т)> •••>*•* = ¥*• 00, t = <fm+l (*).
Ясно, что т первых уравнений
-*l = ?l(')> ^2=?2(0, ••', Xm = <?m(t)
дают нам непрерывное изображение рассматриваемого аналитического
множества.
Я теперь утверждаю, что это изображение полурегулярно. В самом
деле, если М^(х\, -*2» • • •»**) есть точка £, то существует не более
чем счетное множество значений tfv, ^удовлетворяющих уравнениям
*?=/i('),*S=/,(0, ••-,<=/„(О,
так как изображение [*<=/<(£), /= 1, 2, 3, ..., m] полурегулярное. Но
каждой системе чисел xj, *2> • • •»*St» *> удовлетворяющей этим
уравнениям, соответствует одна точка & и, следовательно, одно и только одно
значение t0 переменного ~. Отсюда следует, что каждой точке Л/0 из Е
соответствует самое большее счетное множество значений т,
удовлетворяющих уравнениям
*i = <Pi(T), *2 = <b(')> •••, **. = ?« СО-
Значит, это непрерывное изображение множества Е полурегулярно,
откуда и следует измеримость В множества Е (ч. т. д.).
В качестве обобщения этого результата мы имеем:
Если параметрическое изображение
Х\=А (')> *2=Л(0| • • •> Xm=fm(t),
осуществляемое при помощи любых функций классификации Бэра,
полурегулярно на множестве е, измеримом В и лежащем в q/v то
множество Е тех точек, которые получаются, когда t пробегает
множество е, измеримо 5.
В самом деле, так как е измеримо В, существует непрерывное
регулярное изображение е:
' = ?(*),
150
Н Н. Л У 3 И Н
если пренебречь счетным множеством точек е. В этих условиях
сложные функции
*i=/iI<pWK **=/*l?Wl,---. *«=/«[?W]
дают нам, очевидно, полурегулярное изображение Е, осуществляемое
функциями классификации Бэра. Следовательно, Е измеримо В.
Приложение к проекциям множеств, измеримых /?. Мы видели
(стр. 141), что ортогональная проекция Е измеримого В множества £,
расположенного в m-мерной области, на m'-мерную область, где т <С т,
измерима В> если проекции двух различных точек § различны.
Как обобщение этой теоремы мы имеем:
Теорема. Ортогональная проекция Е множества £, измеримого В
и расположенного в т-мерной области, на т-мерную область т <^т>
измерима В, если каждая точка Е есть проекция не более чем
счетного числа точек множества 6м.
Чтобы убедиться в этом, достаточно взять непрерывное и
регулярное изображение &, ^i —/i (0» «*2=Л(0> • • •> Xm = fm(t)- Первые т
уравнений дают непрерывное параметрическое изображение Е, и легко
видеть, что оно полурегулярно в силу гипотезы, сделанной
относительно точек Е. Следовательно, Е измеримо В (ч. т. д.).
Решета* Бинарное решето Лебега
Общее определение решета2. Предыдущие исследования об
аналитических множествах устанавливали свойства этих множеств, не
зависящие от понятия трансфинитного. Но теперь пора ввести одно
понятие, которое, как мы увидим, позволит установить прямую связь между
аналитическими множествами, неизмеримыми В9 и идеей трансфинитного.
Возьмем /п-ь-1-мерную область ^«....х,^, рассмотрим в этой области
любое множество точек С. Пусть М(х19 х2, ••., х,п) есть точка области
о/%хх7...гт и Dm— прямая, параллельная оси OY и проведенная через
точку М.
Обозначим через Rm множество точек С, которые принадлежат к Dm.
Возможны только два случая.
Первый случай. Линейное множество Rm вполне упорядочено в
положительном направлении оси OY.
Второй случай. Линейное множество Dm не есть вполне
упорядоченное, если таким же образом устанавливать порядок.
1 См. мою заметку „Sur la representation parametrique semiregultere des
ensembles" (Comptes Rendus, 29 июля 1929 г.). Ср. с результатами П. С. Новикова,
касающимися неявных функций [17].
2 Я ввел в явном виде общее понятие решета в своем мемуаре „Sur les ensembles
analytiques", Fund. Math., X 1926. (стр. 383 настоящего тома. —Ред.), См. также работу
Серпинского: „Le crible de M. Lusin et l*operation A dans les espaces abstraits"»
Fund. Math., XI, 16.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ 151
Обозначим через о совокупность точек М области <7x&...*my для
которых имеет место первый случай, и через Е множество точек М
этой области, для которых наблюдается второй случай.
Множество Е есть дополнение к множеству <?, и мы видим, что ато
множество & названо положительным образом, тогда как определение
множества Е отрицательно.
Однако в дальнейшем мы увидим, что если С—аналитическое
множество, то имеет место как раз обратное; мы докажем, что
Е—аналитическое множество и, следовательно, допускает положительное
определение (параметрическое изображение, проекция множества,
измеримого В). Что же касается до множества S, то мы не имеем для него
другого положительного определения, кроме того, которое только что
было дано.
Чтобы сократить изложение, мы введем следующую терминологию.
Принимая во внимание роль т -+- 1-мерного множества С,
заключающуюся в том, что оно автоматически просеивает точки /п-мерной
области о/ху^^.хт, пропуская точки совокупности S и задерживая те,
которые входят в Е, мы это множество С назовем т -+- \-мерным
решетом.
Согласно этому наименованию мы назовем просеянным при помощи
решета С именно это множество Е (но не множество S).
Среди различных решет С мы можем различать следующие:
m-t- 1-мерное решето С называется счетным, если каждая прямая Dy
параллельная оси OY, пересекает С самое большее в счетном числе
точек. Решето С мы назовем несчетным в противном случае; в этом
случае существует такая точка М области с/^х,...*,*, что прямая Dm,
параллельная оси OY и проведенная через М, пересекает решето С по
несчетному линейному множеству Rm.
Изучение аналитических решет* Так как каждое множество С,
расположенное в области Л,*,...*,,,*, может быть принято за решето, то
изучение просеянных множеств Е представляет значительные трудности.
Поэтому сколько-нибудь значительные результаты получаются лишь
если ограничиваться частными семействами решет. Мы изучим случай
аналитического решета.
Теорема. Всякое множество, просеянное при помощи
аналитического решета, есть аналитическое множество1.
Для определенности мы рассмотрим только плоские решета, так
как изучение решета, расположенного в области любого числа
измерений, сводится к изучению плоских решет: для этого достаточно преобра-
1 Это обобщение одной теоремы о решетах весьма спедиального вида, которую
я дал в мемуаре „Sur les ensembles analytiques" (Fund. Math., X, 21, 1926). Другое
обобщение в области проективных множеств было опубликовано Серпинским в его
заметке „Sur quelques proprietes des ensembles projectifs" (Comptes Rendus, 24 октября
1927, теорема VI).
Аналогичное обобщение было мною рассмотрено в моих лекциях по теории
проективных множеств (см. стр. 240 и 241 втой книги).
152
Н. Н. ЛУЗИН
зовать область g7Xi*,...*w в линейную область о/х при помощи взаимно
однозначного и взаимно непрерывного преобразования; если мы
прибавим к уравнениям, определяющим это преобразование (стр. 144),
тождество у = у, то мы получим аналогичное преобразование области о/ад...*^
в плоскую область о/ху. Легко видеть, что таким образом мы
преобразуем каждое т -ь 1-мерное решето в плоское решето, и что если
рассматриваемое т н- 1-мерное решето есть измеримое В или
аналитическое, то таким же будет и преобразованное.
Установив это, возьмем в плоской области <3ху любое решето С.
В данный момент мы относительно природы С не делаем никаких
гипотез.
Пусть
t = F(x, у)
— формулы, определяющие преобразование области <Э ху в порцию (0,1)
линейной области <з7<; функции <р, ф и F—непрерывны.
Рассмотрим в то же время бесконечную последовательность функций
*i=/iW> *2=ЛМ, .-•, *п=Ш,...,
непрерывных на порции (0,1) области о/х и обладающих следующим
свойством: какова бы ни была последовательность иррациональных
чисел fj, f£, ...,^, ..., заключенных между 0 и 1, существует
иррациональное число t0, O^^o^l* такое, что
/„W = '° (« = 1, 2, 3,...).
Обозначим через Т1п точку области 3гху, координаты хп> уп которой
определяются формулами
Если мы заставим т пробегать область g7t» to каждая точка Tin
пробегает всю область <Sfху независимо от движения остальных точек
таким образом, что, какова бы ни была последовательность
фиксированных точек ЗЙ?, 2J?2> • •., <Ш°, ..., существует иррациональное числом такое,
что при ^ = ^о подвижные точки Т1п совпадают соответственно с
фиксированными точками ЭД°.
Давая п некоторое фиксированное значение, изучим природу
множества Нп точек t, дая которых соответствующая точка Tin
принадлежит решету С.
Так как функции <р [/я (х)] и ф (/„ (т)] непрерывны на с7т, то легко
видеть, что рассматриваемое множество Нп есть прообраз решета С
при непрерывном преобразовании
* = <рГ/„(х)Ь у = Ф1/«(*)].
11>
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
153
Следовательно, если решето С измеримо В или аналитическое, то
таким же будет и множество Ня.
Для того чтобы все точки Я1Э ЗЯ2, ..., ая«, .. - принадлежали
решету С, необходимо и достаточно, чтобы т принадлежало к общей
части
//= Нх • Нг... Нп...
Из предшествующего следует, что Н измеримо В или аналитическое,
смотря по тому, будет ли С измеримым В или аналитическим.
Установив это, исследуем природу множества 0 тех точек ~, для
которых мы имеем одновременно следующие равенства или неравенства:
?[Л W1 = ?IA(-)1 = ... = ?[/. С0] = ...,
Мы видим немедленно, что 6 измеримо В> так как все эти сложные
функции непрерывны на с7т.
Если х принадлежит к общей части б • //, то соответствующие точки
ЗИ1Э Ш?2> • • •> ЭД*> • • • принадлежат решету С, расположены на одной и
той же прямой, параллельной оси ОУ, и образуют нисходящую
последовательность точек. Следовательно, точка х9 определенная формулой
х = <Р [/г 0е)], принадлежит множеству £, просеянному при помощи
данного решета С, когда т принадлежит к 6 • //. И так как мы, очевидно,
можем получить указанным способом все нисходящие
последовательности точек решета С, то отсюда заключаем, что просеянное
множество Е есть множество значений функции <р [Д (~)], непрерывной
наЪ-Н.
На основании сказанного относительно природы множеств И и 6 и
в силу непрерывности <р \fx (х)] на о7т мы окончательно заключаем, что
просеянное множество Е аналитическое (ч. т. д.).
Таким образом, мы не выходим из границ семейства аналитических
множеств, производя операцию, состоящую во взятии просеянного
множества, если только решето аналитическое. В дальнейшем мы дадим
этой теореме значительное расширение, распространив ее на семейство
проективных множеств (стр. 240).
Мы дополним этот результат следующим замечанием: если мы
расклассифицируем точки М области с/х,*, ...**» в зависимости не от вполне
упорядоченности, но от рассеянности линейного множества Rm, по
которому прямая Dx, параллельная оси OY и проходящая через М,
пересекает данное множество С, лежащее в j^z,...»,^, то мы придем
к тому же результату:
Множество точек М области с7«,^...»т, в которых прямая Dm*
проведенная через М параллельно OY, пересекает данное
аналитическое множество С, расположенное в С27ад...*ту, по линейному
множеству Rm не рассеянномуу есть также аналитическое
множество.
154
Н. Н. ЛУЗИН
Чтобы придти к этому результату, достаточно повторить слово
в слово предыдущее рассуждение, но заставить множество чисел
Ф 1Л(Т)]> Ф (ЛС1)]» • • •> Ф [Л(х)]> • • • быть плотным на себе1. В этих
условиях множество 0 также измеримо В и все заключения остаются в силе,
(ч. т. д.).
Прежде чем продвинуть дальше изучение аналитических решет,
следует ввести одно важное предварительное понятие.
Пусть С — любое решето, лежащее в Лл...Яоту, и Е — множество
на <7Xlxt...xmy просеянное при помощи С. Возьмем любую точку М
в с7*,*,...ат. Если М не принадлежит к Е, то прямая Dm, проведенная
через М параллельно оси OY, пересекает решето по вполне
упорядоченному множеству, следуя положительному направлению оси OY;
пусть Rm — это множество. Так как Rm вполне упорядочено, то Rxy
а следовательно, и самой точке М соответствует некоторое вполне
определенное трансфинитное число второго класса (или конечное); мы
его обозначим через ам. Таким образом, каждой точке М из о7а1х,...^,
не принадлежащей к Е, отвечает вполне определенное трансфинитное
(или конечное) число ам.
Установив это, рассмотрим любое множество 6, расположенное
в о7хххг...гт и не содержащее ни одной точки Е. Каждой точке М из 6
соответствует вполне определенное трансфинитное (или конечное)
число а^; если М пробегает множество в, то <х>м меняется.
В этих условиях мы скажем, что решето С ограничено на 6,
если существует трансфинитное число р второго класса,
фиксированное и превосходящее все трансфинитные числа а>м,
соответствующие точкам М из в. Решето С называется не
ограниченным на 0 а противном случае2.
Если решето С ограничено на 6, то существует некоторое
постоянное множество IV, счетное и вполне упорядоченное, образованное из
любых элементов и более протяженное, чем каждое из вполне
упорядоченных множеств /?j/, какова бы ни была точка М на 6; это значит,
что Rm подобно сегменту W, когда М принадлежит к 6.
Установив это понятие, мы воспользуемся следующей важной
теоремой:
Теорема. Всякое аналитическое решето С ограничено на каждом
аналитическом множестве б, не имеющем общих точек с
множеством Е, просеянным при помощи С3.
1* Множество называется плотным на себе, если каждая из его точек есть
предельная аля этого множества; см. Р. Бэр. Теория разрывных функций. М.—Л.,
ГТТИ, 1932, стр. 60.
2 Я ввел понятия „ограниченного" и „неограниченного решета* в мемуаре „Sor
les ensembles analytiquesa (Fund. Math., X, стр. 70, 1926).
3 Эта теорема есть обобщение аналогичной теоремы, касающейся решет
специального вида и доказанной в цитированном мемуаре.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ 155
Чтобы убедиться в этом, мы докажем, что придем к противоречию,
«ели допустим существование аналитического множества 0 без общих
точек с £ и такого, что С неограничено на Ь.
С этой целью обозначим через Н множество точек С, проекции
которых на 7«|Х,...Х|1| принадлежат к 0. Так как множества С и Ь
аналитические, то и Н будет таким же.
Так как каждая прямая D, параллельная оси ОУ, пересекает Н
самое большее в счетном числе точек, то мы можем применить теорему
следующей главы, касающуюся структуры аналитических множеств,
обладающих этим свойством (стр. 209 и 212). Следовательно,
множество Н составлено из счетного множества аналитических множеств
Нх, Н2,..., Н„9 ..., расположенных соответственно на однозначных
поверхностях Slf S>, ..., Sny ..., измеримых В, из которых каждая полностью
лежит под или над другой.
Установив это, возьмем непрерывное параметрическое изображение 6
*1 = ?1 (Т)> X* = ?2 (Т)> • • •» Хт = ?т (')
и пусть
*1=/Г(М. *=/**'(<»).•••.*. =/2.*'(<*). у=*М<*)
— параметрическое изображение множества //* на порции (ОД) области
/v * = 1, 2, 3,...
Будем теперь поступать следующим образом. Возьмем поверхность 5*
и обозначим через С* часть С, лежащую яод 5*. Мы выбираем целое
число кх таким образом, чтобы C*t было не ограничено на проекции
множества Нкх. Выбрав 1сх таким образом, мы берем на порциях (0,1)
соответствующих областей с7т и <?. два интеграла Бэра порядка 1, пусть 8Х
и Ъ&*\ такие, что если хи /t пробегают соответственно \ и 8J») в
первых т уравнениях соответствующих параметрических изображений и
если мы берем общую часть Ь1 двух полученных при этом
аналитических множеств, то Скх не ограничено на *%.
Будем поступать таким же образом на &1# Мы берем целое
положительное kL такое, что поверхность Stt находится под Skt и в то же
время С*, не ограничено на общей части Ъг и проекции множества /&,.
Мы берем на порциях (0,1) областей <з7т> 31 , о/1 соответственно
*i и
три интервала Бэра порядка 2: о2, о^\ Ъ{**\ из которых два первых
содержатся соответственно в Ьг и 8^ и такие, что если ?, /*г и /*,
пробегают соответственно 82, 82*l) и 8<*«) в т первых уравнениях
соответствующих параметрических изображений и если мы берем общую часть Ь%
трех полученных при этом аналитических множеств, то С*, не
ограничено на fr2.
Будем поступать таким же образом на Ъг; найдется поверхность *St, и
часть Скл решета С, не ограниченная на &3* Здесь &3 есть общая часть
четырех аналитических множеств, полученных, если заставить т, tk%9 fc,
156
Н. Н. ЛУЗИН
и tks пробегать соответственно интервалы Бэра порядка 3: 83> 4*l)> ^
и Ъ£**9 из которых первые три содержатся соответственно в 82, Ъ%*\ Ь^
ранее определенных, и так далее.
Мы получим таким образом аналитические множества &г, $2, ft3> • • -у
каждое из которых содержится в предшествующем, причем все они
имеют общую точку М, принадлежащую множеству 6. В самом деле,
мы, очевидно, получим эту точку М, полагая х = т0 в параметрическом
изображении б, где х0 есть иррациональное число, принадлежащее всем
интервалам Бэра Ь19 &2, 83...
С другой стороны, эта точка Му очевидно, принадлежит к
ортогональной проекции на с7щхг...хт множества //ц, каково бы ни было v1.
Следовательно, прямая Djf, параллельная О К и проведенная через Мг
непременно пересекает множества Нк1У //*,,..., //*„, ... Но эти
множества расположены соответственно на поверхностях Skl9 &„...,&„...,
каждая из которых лежит под предыдущей. Следовательно, прямая Dm
пересекает решето С по нисходящей последовательности точек, что
невозможно, так как точка М не принадлежит к просеянному
множеству £ (ч. т. д.).
Мы дополним этот результат следующими замечаниями:
Замечание I. Доказанная теорема может быть перенесена на
случай определения аналитического множества по признаку
рассеянности. Чтобы убедиться в этом, следует начать с общих рассмотрений.
Если дано некоторое множество точек £, то мы обозначим через £(1>
результат произведенной над Е операции, состоящей в том, что из Е
удаляют все его изолированные точки. Если произвести такую же
операцию над £(1), мы получим множество, которое обозначим через £(2>.
Если произвести ее над £(2), то получим множество £(3> и т. д.
Мы образуем таким образом*множества
£, Е*\ £<2), ..., £<">, £<*>, ...\Q,
каждое из которых содержится в предшествующем, полагая по
определению, что если а второго рода, то £(а) будет Общей частью
предшествующих множеств.
Установив это, мы мгновенно докажем, что, каково бы ни было
начальное множество £, существует некоторое число (3, начиная с
которого все рассматриваемые множества тождественны, т. е.
£<Р> = £(N-i) = £(N-2) = ... | S.
Если данное множество £ рассеянное, то множества
£(Р)_£(Р+1)_###
1 В самом деле, так как функции f и /♦ непрерывны, мы, очевидно, получим
ту же точку М, . полагая t^ = fy в т первых уравнениях параметрического
изображения Нъ. , где f2 есть иррациональное число, принадлежащее всем интервалам
*v v
Бэра Ь^*\ &5ЗД, &v+2» •••» каково бы ни было фиксированное число N.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ 157
будут пустыми. В этом случае наименьшее число ?, обладающее этим
свойством, называется порядком рассеянного множества Е. Напротив,
если множество Е не есть рассеянное, то множество £('1) =£(>И) = ...
есть наибольшая часть £, плотная в себе.
Установив это, рассмотрим в о?\%l...%wSi аналитическое множество С
и обозначим через Е множество точек М из о/х^...хщ, таких, что
проведенная через М параллельно оси OY прямая Dm пересекает Е по
линейному множеству /?*, которое не есть рассеянное. Ранее мы
видели, что Е есть аналитическое множество.
Если точка М не принадлежит к Е> то ей отвечает трансфинитное
(или конечное) число а-х, которое служит порядком рассеянного
множества Rjf. Пусть б есть множество точек, расположенное в Js,z7...xm
и не имеющее общих точек с Е. Если числа ам, соответствующие
точкам М из в, все меньше некоторого трансфинитного числа Р второго
класса, то множество С называется ограниченным на Ъ в смысле рас
сеянное ти.
С этими определениями теорема, вполне аналогичная только что
доказанной, звучит так:
Аналитическое множество С ограничено в смысле рассеянности
на каждом аналитическом множестве В, не имеющем общих точек с Е.
Доказательство вполне аналогично предыдущему и состоит в
построении аналитических множеств Ъ19 &2, ...,&*,..., у которых имеется общая
точка М, принадлежащая к в, и однако же таких, что соответствующее
множество R^ не есть рассеянное.
Замечание II. Вернемся теперь к случаю полной упорядоченности.
Назовем ограниченным решетом всякое решето С, которое ограничено
на дополнении к множеству £, просеянному при помощи С. Ранее мы
видели, что каждое аналитическое решето С непременно ограничено
на всяком аналитическом множестве 6, не имеющем общих точек с Е.
Следовательно, если просеянное множество Е измеримо Ву то
аналитическое решето С непременно будет ограниченным решетом.
Итак, мы пришли к заключению, что для каждого неограниченного
аналитического решета просеянное им множество неизмеримо В.
К сожалению, эта теорема необратима, так как аналитическое решето
может быть ограниченным и тогда, когда просеянное им множество
неизмеримо В. Тем не менее существует семейство решет, для которых
обратное предложение все же имеет место: это семейство решет
счетных и измеримых В.
Изучение счетных решет, измеримых В. Для изучения важных
свойств этих решет полезным инструментом является понятие
конституанты просеянного множества Е и его дополнения S.
Рассмотрим в Области c?Vt ♦•♦*»** решето С любой природы и
обозначим соответственно через Е и & множество, просеянное при помощи
решета С, и его дополнение; множества Е и & расположены в области
158 н. н. лузин
Возьмем в области o7*}Jh...zm какую-нибудь точку М и обозначим
через Dm параллель к оси О К, проведенную через М; эта прямая
пересекает решето С по линейному множеству точек, которое мы
обозначим через RM.
Если точка М принадлежит к S, то множество Rm вполне
упорядочено в положительном направлении оси О У; в этом случае точке М
соответствует вполне определенное трансфинитное число второго класса
(или конечное); мы его обозначим через а^.
Если точка М принадлежит к Е, множество Rm уже не будет
вполне упорядоченным, если порядок понимать в том же смысле. Но
в этом случае на прямой Dm непременно найдется такой сегмент
(—oo^i/^TV), что часть Rm, лежащая на нем, есть вполне
упорядоченное множество при тех же предположениях относительно порядка,
тогда как сегмент большей длины (—оо ^i/^7V-{-e), где е — как угодно-
малое положительное число, уже этим свойством не обладает. Так как
такая точка N на прямой Dm только одна1, то единственной будет
и вполне упорядоченная часть Rm, заключенная в (—°°^1/^Л^).
Следовательно, точке М соответствует вполне определенное трансфинитное
число второго класса (или конечное), которое мы также обозначим
через ос^.
Установив это, примем следующие определения:
Назовем конституантой (а) просеянного множества Е или проста
конституантой Еа множество тех точек М из Е, которые соответствуют
данному числу а, ам = а.
Назовем также конституантой (а) дополнения S к просеянному
множеству Е или просто конституантой &а множество тех точек М
из S, для которых мы снова имеем <*^ = а, где а — фиксированное число
конечное или трансфинитное второго класса.
Легко видеть, что конституанты Еа и Sa попарно не имеют общих
точек и, следовательно, множества Е и S полностью разлагаются на
свои конституанты:
Е=Е0+Ег-*-Е%-*- .. .-н Еюч- .. .-ь£вн- ... | Q
и
<£ = <£0 н-<?! н-<£2-ь ... h-cS^h-... -+-<?ан- ... \Q.
Складывая эти равенства, мы получим разложение всей области
<г/ в последовательность множеств, перенумерованных при помощи
конечных чисел и трансфинитов второго класса
j = Е0ч- £0-+- Ех-+- £г-*- ... -ь£ш-+-£ш-1- ... н-£в-+-£в-ь ... \Q.
Установив это, мы докажем следующую важную т.еорему:
Теорема. Если данное решето С счетно и измеримо В> то все
конституанты Еа и ёа измеримы В.
Число N может быть, в частности, равным отрицательной бесконечности.
ЛЕКЦИИ ОЬ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ 159
Покажем сначала, что начальные конституанты Е0 и £0 измеримы В.
Это очевидно лая. <л0, так как если решено С счетно и измеримо В, то
проекция С на область Vx.z,...** измерима В (стр. 150), но очевидно,
что конституанта &0 есть дополнение к этой проекции.
Чтобы изучить природу конституанты £0, нам понадобится теорема
о структуре множеств, измеримых В и пересекаемых каждой параллелью/)
к оси OY самое большее по счетному множеству (стр. 206). В силу
этой теоремы точки решета С распределяются на счетном множестве
однозначных поверхностей Sly S>y ..., SMi..., измеримых Ву определенных
всюду на o/х^...хт и таких, что про любые две из этих поверхностей
можно сказать, что одна из них лежит целиком над или целиком под
другой. Установив это, обозначим через Нп множество точек решета С,
расположенных на поверхности Sh\ множество Нн измеримо В и однозначно
по отношению к g/*^,...*». Обозначим через Гя множество точек
решета С, расположенных под поверхностью SM; легко видеть, что
проекция Гя на область c7Xl^...xm измерима 5. Отсюда мы заключаем,
что множество точек из Нм, проекции которых на Jst*t...%M не
принадлежат к проекции Гя, также измеримо В; мы обозначим это
множество через 6„. Так как однозначных множеств Ь19 02, ... лишь
счетное множество, то соединение S их проекций на о?^*,...*»
измеримо В. Но точки М множества S, очевидно, обладают тем
характеристическим свойством, что прямая Z)*, проведенная через М
параллельно оси OY, пересекает решето С по линейному множеству Rm>
имеющему начальную точку, т. е. такую точку, у которой координата
у меньше, чем у всех остальных точек из R*. Отсюда мы заключаем,
что если из <7х%х^...хт удалить точки &0 и S, то множество оставшихся
точек совпадает с Е0. Следовательно, Е0 измеримо В.
Чтобы установить измеримость В конституант Еа и £а, мы введем
понятие производного решета С: это решето, которое получается
из данного решета С удалением из каждого множества Нп всех точек
множества 6и(/г = 1, 2,—).
Легко видеть, что производное решето С есть вполне
определенное счетное решето, измеримое В> имеющее то же просеянное
множество Е, к что если С рассматривать как множество точек в <7хг%г...хт9>
то оно содержится в решете С. Но наиболее важным свойством
производного решета С является следующее: чтобы перейти от С к С\
надо удалить на каждой прямой D, параллельной оси OY, начальную
точку решета С (если такая точка cyxujecmeyem). Из этого следует,
что начальные конституанты множеств Е и £, определенные
производным решетом С, совпадают соответственно с Е0-*-Е1я S0-^-^i.
Установив это* мы образуем трансфинитную последовательность
производных решет
С, С, С", ..., СЧ .. .,CW,.. .,С<«>, ...\Q.
Если а первого рода, а = а*+1, то решето С*а) определяется как
160
Н. Н. ЛУЗИН
производное от решета С^; если а второго рода, то решето С^ есть
общая часть всех ранее определенных решет. Легко видеть, что все
решета С(а) имеют одно и то же просеянное множество Е, и что
начальные конституанты множеств Е и &, определенные решетом С^\
совпадают соответственно с суммами
£0н-Ех + .. .н-£шч- .. .-ь£в
и
образованными из конституант Ер и <5р, предшествующих соответственно
£« и ёа.
Так как начальные конституанты всегда измеримы В, то и
написанные выше суммы также. Отсюда следует, что и конституанты Еа и £а
также измеримы В, что и доказывает предложенную теорему (ч. т. д.).
Одно из наиболее важных приложений предшествующих
рассмотрений относится к самим аналитическим множествам. В самом деле, мы
теперь имеем возможность доказать следующее предложение:
Теорема. Для того чтобы аналитическое множество Е,
просеянное при помощи счетного решета С, измеримого В, было само
измеримым В, необходимо и достаточно, чтобы решето С было
ограниченным.
Условие необходимо, так как каждое аналитическое решето С
ограничено на всяком аналитическом множестве б, не имеющем общих
точек с множеством Е, просеянным при помощи С. Следовательно,
если Е измеримо В, то и его дополнение S тоже измеримо В, а потому
решето С ограничено.
Условие достаточно. В самом деле, если решето С ограничено,
то множество S есть сумма, счетного Множества конституант &а, так
как все остальные конституанты & пусты. А так как каждая
конституанта £а измерима В, то множество S также измеримо В.
Следовательно, просеянное множество Е измеримо В (ч. т. д.).
Можно было бы спросить себя, нельзя ли рассматривать всякое
аналитическое множество как просеянное при помощи счетного решета,
измеримого В. Если это так, то практическая польза, если уже не
говорить о теоретическом значении изучения счетных решет, измеримых В,
значительно возрастает. Мы увидим, что действительно, каково бы ни
было аналитическое множество Е, можно эффективно определить
решето С счетное, измеримое В и некоторой чрезвычайно
элементарной природы так, чтобы Е было просеяно при помощи решета С*
Чтобы убедиться в этом, введем следующее определение. Рассмотрим
бесконечную последовательность замкнутых сегментов
с иррациональными концами, расположенных на оси OY; мы
предполагаем, что эти сегменты попарно не имеют общих точек и общих
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
161
концов. Эта последовательность з19 з2, ..., 3v, ... называется восходящей,
если индекс сегмента возрастает в положительном направлении оси О К;
это значит, что каждый из этих сегментов лежит выше предшествующего.
Установив это, возьмем в области >7х*ь...* какое-либо
аналитическое множество Е. Пусть И есть элементарное множество,
расположенное в т-t- 1-мерной области Jмх...г^, ортогональной
проекцией которого на область с/гхъ...хт является Е.
По самому определению элементарное множество Н есть общая
часть H=Sl- S2... Sn..., где каждое множество Su есть сумма счетного
множества параллелепипедов Бэра тс}"), / = 1, 2, 3, , расположенных
в тн-1-мерной области о7*,*,...тт* и не имеющих попарно общих
точек. Эти параллелепипеды Бэра тсН, / = 1, 2, 3,... называются
параллелепипедами ранга л; порядок каждого параллелепипеда ранга л равен л.
Кроме того, известно, что всякий из параллелепипедов тс}") ранга л
содержится во вполне определенном параллелепипеде 7Г^'*"1) предшествующего
ранга л — 1 и содержит счетное множество параллелепипедов следующего,
л-ь 1-го ранга (стр. 131).
Преобразуем теперь элементарное множество //. Так как
ортогональная проекция на область <7*,,,...7т некоторого т-+■ 1-мерного
параллелепипеда тс, ориентированного по осям ОХ1У ОХг,..., ОХт, OY,
очевидно, не изменится, если переместить или сжать параллелепипед
в направлении оси О К, то мы можем предположить, что ортогональные
проекции параллелепипедов тс}1) ранга 1 на ось OY образуют восходящую
последовательность сегментов о}1) с иррациональными концами; мы их
назовем сегментами ранга 1. Вообще, каков бы ни был
параллелепипед тс(./<—1) ранга л — 1, мы можем предполагать, что ортогональные
проекции на ось OY содержащихся в нем параллелепипедов тсН ранга л
образуют восходящую последовательность соответствующих сегментов <Л'>
с иррациональными концами; мы называем эти сегменты о*»1* сегментами
ранга л.
Таким образом, каково бы ни было л, сегменты оМ ранга л не имеют
попарно общих точек, а сегменты о^'+:) ранга лн-1, содержащиеся
в некотором dp ранга л, всегда образуют восходящую
последовательность.
Наконец, сделаем следующее замечание. Расположим рациональные
точки оси О У в простую бесконечную последовательность ги гг..., г„....
Я теперь утверждаю, что, каково бы ни было целое положительное л,
можно предположить рациональную точку ги не принадлежащей нн
одному из сегментов dp ранга л. В самом деле, когда сегмент of-**
ранга л — 1 определен, мы можем образовать в <&-1) восходящую
последовательность сегментов dp ранга л, содержащихся в о<к-^ так, чтобы нн
один на них не содержал рациональную точку гм.
162
Н. Н. ЛУЗИН
Во всем дальнейшем мы предположим, что выбор параллелепипедов
всех рангов и, следовательно, элементарного множества Н сделан
указанным образом. Данное аналитическое множество Е есть
ортогональная проекция на область o7xxxt.„xm так построенного элементарного
множества Н (стр. 131).
Установив это, обозначим через С множество точек области
G7Vl.,.ym//, расположенных на верхних гранях всех построенных
таким образом параллелепипедов к№ (п = 19 2, 3,...). Легко видеть,
что С есть соединение счетного множества однозначных множеств,
измеримых В и весьма простых, и что каждая прямая Z), параллельная оси О Yy
пересекает С самое большее по счетному множеству точек.
Следовательно, множество С есть счетное решето, измеримое В и весьма
элементарной структуры, В дальнейшем так построенное решето С мы будем
называть элементарным решетом.
Мы теперь докажем следующую теорему:
Теорема. Всякое аналитическое множество может быть
просеяно при помощи элементарного решета.
Чтобы убедиться в этом, достаточно доказать, что ранее
рассмотренное нами аналитическое множество Е можно считать просеянным при
помощи построенного элементарного решета С.
Пусть М—любая точка области о7хххг.<.хт. Обозначим через D^
прямую, параллельную оси OY и проведенную через М; пусть RM—
множество точек С, принадлежащих Dm»
Я теперь утверждаю, что необходимое и достаточное условие для
того, чтобы линейное множество Rm не было вполне упорядоченным
в положительном направлении оси О К, состоит в том, чтобы
прямая Dm содержала точку элементарного множества Н.
Условие необходимо. В самом деле, если RM не есть вполне
упорядоченное в условленном смысле, то можно определить неограниченную
нисходящую последовательность точек из R^: Р1У Р2,..., Pv,..., каждая
из которых ниже предыдущей. Так как ортогональные проекции на
ось OY всех параллелепипедов тсМ фиксированного ранга п образуют
счетное множество сегментов а%'\ попарно без общих точек и вполне
упорядоченное в положительном направлении оси ОК, то все точки
Ри Р*> • • •»Р^ • • м начиная с некоторого индекса v, принадлежат одному
и тому же параллелепипеду ^"} ранга п; пусть тся — этот
параллелепипед ранга п.
Неограниченная последовательность ^, тс2,..., тгя,..., очевидно,
образована из параллелепипедов всех рангов, вложенных друг в друга,
причем каждый из них содержит все точки Рг, Р2> • • •> Pv> • • •, кроме
конечного числа их. Следовательно, точка NQi общая всем
параллелепипедам тс1э тг2,..., tcv, ..., наверное, принадлежит прямой Dm. Кроме того,
все координаты xj, х\,..., х°т, y° точки N0 — иррациональные числа. Это
очевидно для координат jcJ, так как ортогональная проекция кп на область
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
163
с7*,т,...гт есть параллелепипед Бэра порядка п. Но ортогональная
проекция тгя на ось 0Y есть сегмент ранга п и, следовательно, не
содержит ни одной из п первых рациональных точек бесконечной
последовательности г1У г2, ..., г„, ..., в которую мы расположили все
рациональные точки оси OY (стр. 161). Итак, число г/° иррационально.
Отсюда следует, что точка 7V0 области с/»,*,...*^/ принадлежит
элементарному множеству //.
Условие достаточно. В самом деле, если прямая Dm содержит
точку TV элементарного множества //, то, очевидно, эта точка N есть
предел нисходящей последовательности точек множества /?*, значит R*
не является вполне упорядоченным в положительном направлении оси О К
Таким образом, множество, просеянное при помощи элементарного
решета С, совпадает с проекцией элементарного множества Н и,
следовательно, тождественно с Е (ч. т. д.).
Предыдущие рассмотрения чрезвычайно важны, так как они
показывают нам, что есть три строго эквивалентных метода для определения
аналитических множеств:
1°. Писать параметрические уравнения х{ = /{^).
2°. Проектировать элементарные множества, измеримые В.
3°. Просеивать при помощи счетных решет, измеримых В [17].
Трансфинитный критерий измеримости В аналитических
множеств. Выше мы доказали существование аналитического множества,
неизмеримого В, следующим образом (см. стр. 125): мы нашли линейное
аналитическое множествое,дополнение к которому Се заведомо не естьанаг
литическое множество. Вот рассуждение, позволившее нам
констатировать неизмеримость В множества е, обладающего этим свойством:
если бы множество е было измеримо В, то и его дополнение Се было бы
таким. Значит, оно было бы аналитическим, тогда как это не так.
Мы теперь докажем весьма простым рассуждением, что
рассмотренный случай не представляет ничего исключительного, так как, каково бы
ни было аналитическое множество Е, неизмеримое В, его
дополнение СЕ не может быть аналитическим1. Таким образом,
неаналитичность дополнения к какому-либо аналитическому множеству Е есть не
только достаточное, но в то же время и необходимое условие для того,
чтобы аналитическое множество Е было неизмеримым В.
Чтобы убедиться в этом, допустим, что СЕ есть аналитическое
множество. Так как Е тоже аналитическое и не имеет общих точек
с СЕ, то множества Е и СЕ отделимы В. Ясно, что отделяющие
множества, измеримые В, обязательно совпадают с Е и СЕ (ч. т. д-).
Это простое рассуждение дает нам, таким образом, необходимый и
достаточный критерий для неизмеримости В аналитического множества, и
1 Эта теорема III заметки Суслина (Comptes Rendus, 8 января 1917г.). Теорема II
о существования аналитических множеств, неизмеримых В, была им доказана при
помощи рассуждения, основанного на специальных свойствах кортежей индексов |19|.
164
Н. Н. ЛУЗИН
легко видеть, что это критерий чисто отрицательного характера: надо
констатировать, что дополнительное множество СЕ не есть
аналитическое. Но предыдущие рассмотрения, касающиеся счетных решет,
измеримых Ву показывают нам, что существует критерий другой
природы, тесно связанный с совокупностью трансфинитных чисел второго
класса, критерий положительного характера, позволяющий
констатировать неизмеримость В некоторого аналитического множества. Этот
критерий возникает из возможности рассматривать всякое
аналитическое множество Е как просеянное при помощи счетного решета,
измеримого В,
В самом деле, с одной стороны, мы показали, что можно эффективно
построить а^я каждого аналитического множества Е элементарное
решето С, которое, следовательно, счетно и измеримо В, причем Е
просеяно при помощи этого решета. С другой стороны, мы ввели важное
различие между решетами. По самому определению, мы называем решето
С ограниченным, если существует эффективно перечислимое
фиксированное множество Wy более протяженное, чем всякое вполне
упорядоченное множество /?jf, какова бы ни была точка М, не принадлежащая
множеству £", просеянному при помощи С. В случае, если такого
фиксированного множества W не существует, решето С называется
неограниченным.
Чрезвычайная важность этого различия проистекает из выше
доказанной теоремы (стр. 191), формулируемой так: для того чтобы
аналитическое множество Е было измеримо By необходимо и достаточно
чтобы оно могло быть определено при помощи счетного решета С,
измеримого В и ограниченного. Ясно, что этот критерий имеет в
некотором роде положительный характер.
Итак, все сводится к тому, чтобы решить следующую проблему:
Узнать, будет ли данное счетное решето С, измеримое В,
ограниченным или нет.
К сожалению, эту проблему, по-видимому, легко решить лишь в том
случае, когда решето a priori задается ограниченным; следовательно,
общего решения проблемы мы не имеем даже для элементарных
решет.
Мы сильно сомневаемся в том, чтобы можно было дать общее
решение этой проблемы, по крайней мере, если, согласно Лебегу,
условиться считать, что определить решето С это значит назвать некоторое
свойство Р, характеризующее С; из него надо вывести ограниченность
или неограниченность решета С. Мы сильно сомневаемся, чтобы можно
было во всех случаях вывести из этого свойства Р констатирование
границы Аля решета С.
В этих условиях возникает вопрос, является ли сделанное различие
достаточно серьезным, чтобы придавать ему смысл. Пэнятие
ограниченного решета^ очевидно, законно, так как речь идет о вполне упорядо*
ченном множестве Wf эффективно перечислимом: надо сравнивать пере-
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
165
менное вполне упорядоченное множество Rx с этим фиксированным
множеством W.
Напротив, понятие неограниченного решета чисто отрицательно,
так как для того, чтобы эффективно констатировать, что некоторое
элементарное решето С неограничено, очевидно, необходимо взять все
счетные вполне упорядоченные множества и сравнить их с переменным
вполне упорядоченным множеством Rjr, а это приводит к совокупности
всех трансфинитных чисел второго класса.
Таким образом, кажется более предпочтительным вернуться к
первому критерию. Я хотел бы указать кратко и не входя в дискуссию по
поводу природы этого критерия, что характер его отрицательный;
так как второй критерий строго эквивалентен первому, мы вынуждены
заключить, что положительное определение, осуществленное при помощи
трансфинитного у может быть эквивалентно отрицательному
определению, не вводящему трансфинитное в явном виде.
Итак, трансфинитное может быть глубоко спрятано
под видом отрицательного определения или понятия.
Пример аналитического множества, неизмеримого В,
принадлежащий Лебегу* Бинарное решето Лебега* Однако, несмотря на
предыдущие критические замечания, есть один частный случай, когда мы
можем немедленно констатировать, что рассматриваемое решето С
неограничено, а следовательно, множество Е, просеянное при помощи С,
неизмеримо В.
Это случай счетного решета, измеримого В и универсального,
т. е. такого, что всевозможные линейные счетные множества получаются,
если пересекать С прямыми D, параллельными оси ОК. В самом деле,
в силу исследований Г. Кантора, каково бы ни было вполне
упорядоченное счетное множество W, составленное из любых элементов, можно
эффективно построить линейное множество точек R, которое
подобно W. Так как всевозможные линейные счетные множества получаются, если
пересекать С прямыми D, параллельными оси О К, то a priori видно,
что рассматриваемое решето С не может быть ограниченным 1.
Итак, все сводится к построению счетного решета, измеримого В и
универсального. Но это построение может быть сделано мгновенно.
В самом деле, возьмем неограниченную последовательность функций
ifl = ?l(4 У2 = ?S (A •••ilfr = ?»(*)» •••
непрерывных на интервале (0 < х < 1) и обладающих следующим
свойством: какова бы ни была последовательность действительных чисел
1 Очень важно было бы знать, является ля этот случай единственным, если»
разумеется, не считать очевидных видоизменений, когда из определения С удается
вывести, что С есть неограниченное решето. Мы думаем, что эта проблема
неразрешима, так как понятие неограниченного решета лишено смысла (по крайней мере
кронекеровского).
166
Н. Н. ЛУЗИН
УЬ У» • • '>у1> • ■ •> существует действительное число х0 между 0 и 1,
А\я которого у% = срп (х\ каково бы ни было л.
Установив это, обозначим через Сп непрерывную между 0 и 1
кривую, начерченную в плоскости XOY и определенную уравнением
у = <ря(лс); соединение С кривых Си С2,..., Спу... есть, очевидно,
плоское множество, измеримое 5, и легко видеть, что С есть
универсальное счетное решето (ч. т. д.).
Так определенное универсальное счетное решето С есть лишь
видоизменение другого счетного решета Г, также неограниченного,
открытого в 1905 г. Лебегом; мы его назовем бинарным решетом1.
Чтобы определить бинарное решето Г, мы будем следовать тексту
Лебега (Journ. de Math., 1905, стр. 213, строка 25):
„Я предполагаю, что рациональные числа, заключенные между 0 и 1,
расположены в некотором порядке, который я не указываю, но
предполагаю установленным; пусть zu z2,... есть рассматриваемая
последовательность. Я беру некоторое число t, расположенное между 0 и 1,
и записываю его по двоичной системе счисления, употребляя, когда это
возможно, число 1 лишь конечное число раз; выражение для t вполне
определено, лишь только / задано:
Вычеркнем из последовательности zlf z2,..., zn,... все те ziy которым
соответствуют такие индексы /, что величина 6, равна нулю; пусть
zv zv . . . будут сохраненные z.
Вот что мы получим, если шаг за шагом интерпретируем
геометрически аналитическую конструкцию Лебега: знаменитый автор берет
плоскость TOZ и на этой плоскости квадрат (0^£<^1, O^z^l).
На стороне
* = 0
этого квадрата Лебег берет все рациональные точки и нумерует их
в определенном (безразлично каком) порядке при помощи целых чисел
^1 ^2» • • •» ^я> • • •
Далее, Лебег проводит через точку zn параллель к горизонтальной
оси ОТ и, разделив часть этой параллели, заключенную в квадрате,
на 2я равных сегментов, он сохраняет лишь те сегменты, индексы
которых (считая в направлении возрастания абсцисс) оказываются четными.
Далее, Лебег заставляет п меняться (л = 1, 2, 3,...) и отмечает в
рассматриваемом квадрате все сохраненные сегменты.
Полученная таким образом фигура очевидно образована из
счетного множества сегментов, параллельных оси ОТ; следовательно, это —
1 См. его мемуар „Sur les fonctions representables analytiquement" (Journ. de
Math., 1905).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
167
счетное решето, измеримое В. Это решето Лебега мы назовем
бинарным решетом и будем обозначать через Г.
Легко видеть, что эта геометрическая конструкция есть лишь
пространственная интерпретация аналитической конструкции Лебега. В
самом деле, если
i — 2 2i
есть двоичное разложение иррационального числа t, заключенного
между 0 и 1, то необходимое и достаточное условие для того, чтобы
мы имели 9„ = 1, заключается в том, что параллель Dt к оси OZ,
проведенная через точку /,
пересекает прямую z = zn в
какой-нибудь точке одного
из сохраненных сегментов.
Отсюда следует, что если мы
„вычеркнем из
последовательности zlf z2,... все те
ziy которым соответствуют
такие индексы i, что
величина 6* равна нулю", то
остающиеся z являются
просто координатами z тех
точек, в которых прямая
Dt пересекает бинарное
решето Г.
Итак, аналитический процесс Лебега есть лишь описание бинарного
решета Г, если стоять на чисто геометрической точке зрения.
Вот как употребляет Лебег свою аналитическую конструкцию (там же,
стр. 214, строка 2):
„Возможно, и так всегда будет, если всех z будет лишь конечное
число, что можно найти символ класса а, обладающий следующим
свойством: можно установить соответствие между числами z и всеми
символами р, меньшими а, так, чтобы каждому z отвечало лишь одно (3,
в наоборот; и притом, если числам (3 и \ отвечают z($) и z($x)f то
для (3, меньшего чем рх, мы имели бы z ф) < z фх). Тогда мы назовем а
символом, соответствующим / ...
„Следовательно, рассматриваемому значению t мы можем привести
з соответствие функцию <ра (х) класса а...; эту функцию, не являющуюся
определенной, когда а дано, но являющуюся определенной, как только
.дано t, если числу t соответствует символ а, я назову <р (/, х). Если же
числу t не соответствует никакой символ а, я положу <р(£, дг) = 0*.
Если мы интерпретируем геометрически аналитические операции Лебега,
то мы констатируем, что знаменитый автор разделяет (—со<£<н-со)
на два взаимно дополнительных множества S и Е такие, что если /
лринадлежит к <§> то прямая Di пересекает бинарное решето Г по вполне
6.
168
Н. Н. ЛУЗИН
упорядоченному множеству так, что числу t соответствует вполне
определенное трансфинитное число а, а если i принадлежит к £, то прямая/)/
не пересекает Г по вполне упорядоченному множеству, если брать
порядок в смысле возрастания z. В первом случае Лебег полагает
<р (/, х) = <рл (х), где <ра (х) есть вполне определенная функция класса а;
во втором случае Лебег полагает ср(/, х) = 0.
Итак мы видим, что Лебег просеивает множество Е при помощи
бинарного решета Г и определяет функцию <р (t, x) при помощи так
полученных взаимно дополнительных множеств Е и £.
Мы хорошо знаем, что множество Е есть аналитическое, и так как
его решето Г есть счетное и измеримое В, то дкя того, чтобы Е
было неизмеримо 5, необходимо и достаточно, чтобы решето Г былб
неограниченным.
Приведем теперь метод, при помощи которого сам Лебег доказал
неограниченность своего решета Г. Мы цитируем текстуально соответ^
ствующий отрывок у Лебега (там же, стр. 214, строчка 18):
„Я теперь утверждаю, что функция <?(t,x) ускользает от всякого
аналитического изображения; это, очевидно, будет доказано, если
будет обнаружено, что каждый символ а соответствует некоторому зна»
чению /, и таким образом, что каково бы ни было а, существует такое
значение t, при котором <р (t, jc), как функция от х, будет класса а.. „
„Пусть а — некоторый символ и а19 а2>..., меньшие а; каждый из
них взят один раз, и они расположены в простую бесконечную после*
довательность. Я беру произвольный сходящийся ряд с положительными
членами elf е2,... и суммой, меньшей чем 0,5. Пусть (3 есть символу
меньший а; он имеет некоторый ранг / в последовательности а1э а2,...;
числу Р я заставляю отвечать е<в Пусть S? есть сумма всех е,
соответствующих символам, меньшим р; тогда Sp меньше 0,5 — е,-; положим
Ц =2Sp -+- ef., Zjj = 2^ -+- 2е<; пусть, наконец, у^ есть то рациональное
число, заключенное между /^ и /^, которое, будучи написано в виде
несократимой дроби, дает дкя суммы своих двух членов наименьший
возможный результат. Последовательность чисел у* есть
последовательность вида z'v 2Г2,... В последовательности z число у^ занимает /-е место;
в последовательности z оно занимает у-е место (у ^ /).
Я полагаю
г — 2 "*^ о ^^ * * * ^^ 2W ^^ * * "'
условившись считать 6* = 1, если к есть одно из чисел у,
соответствующих величинам Р<Са, и 6^ = 0 в противном случае. Тогда очевидно,
что этому значению t соответствует а; впрочем, остается доказать, что
выбранное выражение дкя t не есть одно из недопустимых, т. е. что
все б с достаточно большим индексом не могут быть равны 1. Если бы
это было так, то множество из ув отличалось бы от множества из гр
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
169
лишь устранением конечного числа членов, что невозможно, так как
все рациональные числа, заключенные между ух и у.,} не являются
числами i pu.
Впрочем, к тому же результату можно придти следующим путем.
Прежде всего замечаем, что какова бы ни была бесконечная часть Р
последовательности zx, z2,..., z„ ..., существует одна и только одна
такая точка /0, что прямая Dt, пересекает бинарное решето Г как раз
в точках, координаты z которых образуют множество Р. Чтобы убе-
0, 0.,
диться в этом, достаточно взять двоичное разложение -£ ■+- -£ -+- ...
п„
... н—- -ь ... и положить 6Я = 1, если zn принадлежит к Р, и Ья = О
в противном случае. Число /0 = -у -+- -р -+- ..., определенное таким
образом, очевидно, обладает указанным свойством.
Итак, пересекая бинарное решето Г прямыми D, параллельными
оси OZ, мы получаем всевозможные части бесконечной
последовательности Zj, Z2, . . ., ZH, . . .
Но множество zu z2,... образовано из всех рациональных чисел,
заключенных между 0 и 1; следовательно, это множество всюду плотно.
В этих условиях опять применима теорема Г. Кантора (стр. 165), и>
следовательно, каково бы ни было вполне упорядоченное счетное
множество W, состоящее из любых элементов, можно определить часть Р
последовательности zv zt,..., которая, будучи расположена в порядке
возрастания z, подобна W. Отсюда мы заключаем,что бинарноерешетоГ
не может быть ограниченным.
Вот заключение, к которому мы приходим; Лебег построил счетное
решето Г, измеримое В; затем он определил множество Е, просеянное
при помощи Г, и рассмотрел его дополнение &; далее он доказал, что
решето Г неограничен^; наконец, он употребил так определенные
множества Е и <£, как инструмент для построения функции ср (t7 х),
ускользающей от всякого способа аналитического изображения. В итоге
оставалось лишь доказать неизмеримость В множества §, но это как
раз требовало того, чтобы теория аналитических множеств была
достаточно продвинута.
Просеянное множество Е, определенное Лебегом, является первым
примером аналитического множества, неизмеримого В, который су
шествует в математической библиографии. Именно изучение этого
примера и послужило началом исследований Суслина и моих 1 по теории
аналитических множеств через 10лет после появления мемуара Лебега [20J.
1 См. ваши заметки в Comptes Rendus, 8 января 1917 г.; см. также мою более
.позднюю заметку в Comptes Rendus, 4 мая 1925 г. Символика, которой мы пользовались
в этих исследованиях („кортежи индексов*, согласно выражению Лебега), была нами
заимствована из его мемуара „Sur les fonctions representables analyti4uement*\
стр. 209.
170
Н. Н. Л У 3 И Н
Природа лебеговской функции <р (t, x) не известна. Если эта функция
не есть проективная, то она, несомненно, послужит началом ряда
важных работ, которые приведут к новым понятиям [21].
Свойства констатуант. Свойства конституант Еа самого
аналитического множества Е не известны: мы знаем только, что все Ел
измеримы 5, когда порождающее решето С счетно и измеримо В. Мы имеем
больше сведений о свойствах конституант £а дополнительного
множества &:
<§ — £0 -к gx н- £2 -ь... н- <gw -+-... -+- <Sa ч-... |2.
Прежде всего мы укажем одно интересное свойство конституант &а:
каково бы ни было аналитическое множество Е у содержащееся в &>
оно всегда принадлежит счетному множеству конституант &а.
Чтобы убедиться в этом, достаточно заметить, что порождающее
решето С ограничено на Е\ Это значит, что существует
фиксированное трансфинитное число р второго класса, которое превосходит все
трансфинитные числа а^, соответствующие точкам М из Е (см. стр. 154).
Отсюда следует, что каждая точка М из Е принадлежит к некоторой
конституанте £а, у которой индекс а меньше, чем р. Следовательно,
множество Е содержится в сумме счетного множества конституант &а
(ч. т. д.).
Мы дополним этот результат следующим замечанием: доказанное
свойство конституант £а дает нам немедленно новое доказательство
важной теоремы о том, что всякие два аналитические множества Е и Е'
без общих точек отделимы В.
В самом деле, возьмем все конституанты §й множества СЕУ
содержащие точки Е\ Этих конституант счетное множество, и они
измеримы В. Значит, их сумма Н есть множество, измеримое Ву
содержащее Е и без общей точки с Е. Если мы обозначим через Н
дополнение к //, то множество Н измеримо В и содержит Е. Следовательно,
Е и Е отделимы при помощи двух множеств Н и //, измеримых В
(ч. т. д.).
Мы думаем, что на это замечание не нужно смотреть лишь как на
курьез, так как, по нашему мнению, здесь содержится нечто большее.
В самом деле, мы знаем, что в классификации Валле-Пуссена два
любых элемента Е и Е класса а всегда отделимы при помощи двух
множеств Н и Н низших классов. С другой стороны, дополнение СЕ
каждого элемента Е класса а может быть разложено на счетное
множество множеств класса ниже а. Для аналитических множеств,
неизмеримых В9 мы имеем два совершенно аналогичных предложения: два
аналитических множества Е и Е без общей точки всегда отделимы при
помощи двух множеств Н и /Г, измеримых В. С другой стороны,
дополнение СЕ к некоторому аналитическому множеству £,
неизмеримому Ву всегда разлагается в трансфинитную сумму множеств,
измеримых В.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
171
Так как в научных исследованиях аналогия часто служит весьма
ценным и даже необходимым инструментом для дальнейшего продвижения
этих исследований, то мы, естественно, приходим к тому, чтобы
рассматривать аналитические множества, неизмеримые В, как элементы
класса 2 продолженной классификации Бэра—Валле-Пуссена. Эта
•бросающаяся в глаза аналогия между аналитическими множествами,
неизмеримыми Ву и элементами гипотетического класса 2 может оказать
ценные услуги, направляя нас на открытие новых феноменов, которые
затем останется доказать.
Мы увидим, например, что существуют два аналитических
дополнения £ и £' без общей точки и неотделимых 5 (стр. 187, 219 и 221). Это
нредложение можно вывести по принципу двойственности из теоремы.
В каждом классе Ка классификации Бэра—Валле-Пуссена
существуют два множества £ и £\ достижимые снизу, без общих точек
и неотделимые при помощи множеств класса ниже а.
Доказательство этой теоремы не представляет никаких затруднений1.
Вернемся теперь к установленному свойству конституант £а:
£ = <?о ■+■ £ 1 -+■ £2 -*- •••-*- £<» -+■ ...-•- £* -*--.. I 2 •
Мы знаем, что все эти конституанты измеримы В.
Следовательно, каков бы ни был индекс а, множество £а или счетно (конечно),
или содержит совершенное множество Р". И в этом последнем случае
•множество £, очевидно, имеет мощность континуума3.
С другой стороны, если £ содержит совершенное множество Рр то,
по крайней мере, одна из его конституант должна быть несчетной и,
•следовательно, должна содержать совершенное ядро. В самом деле,
«если £ содержит совершенное множество Рх, то это множество, будучи
измеримо Ву должно содержаться в сумме счетного множества
конституант <§а в силу указанного свойства. Следовательно, хоть одна из этих
лсонституант должна быть несчетной.
Итак, для того чтобы аналитическое дополнение £ содержало
совершенное множество, необходимо и достаточно, чтобы хоть одна
из его конституант £а была несчетной*.
1 См. мою работу „Analogies entre les ensembles mesurables В et les ensembles
«analytiques* (Fund. Math.f XVI, 1930) (стр. 470 настоящего тома.— Ред.).
2 Теорема Александрова „Sur la puissance des ensembles mesurables B" (Comptes
Rendus, 323, 1916).
3 Теорема Кантора—Бернштейна.
* Точно так же легко видеть, что если аналитическое дополненне имеет
положительную меру или есть множество второй категории на некотором совершенном
множестве Р, то, по крайней мере, одна из его конституант имеет положительную меру
ели есть множество второй категории на Р. Кроме того, если мы умеем выбрать
•одну и только одну точку во всякой конституанте £в множества Я, то множество
выбранных точек есть множество первой категории на каждом совершенном мно*
жестве Я. См. заметку Лузина и Серпинского „Sur un ensemble non denombrable,
qui est de premiere categoric sur toot ensemble parfait" (Rendiconti dei Lincei, Roma,
февраль 1928 г.).
172
Н. Н. ЛУЗИН
Следовательно, если аналитическое дополнение & неизмеримо В и
не содержит совершенного множества, то это аналитическое дополнение <§
есть соединение счетных (конечных) множеству перенумерованных при
помощи трансфинитных чисел второго класса по Кантору.
С другой стороны, всякое аналитическое множество Еу очевидно,.
определено счетным множеством условий.
Именно по этой причине математики, которые допускают
рассуждения с трансфинитами и допускают одновременное разбиение
аналитического дополнения, неизмеримого В, на трансфинитную бесконечность
конституант, перенумерованных при помощи всех трансфинитных чисел
второго класса по Кантору, — эти математики стремятся определить
такое исключительное аналитическое дополнение. В самом деле, если
такое аналитическое дополнение, логически возможное, к тому же
практически реально, то можно будет утверждать, что существование всех
трансфинитных чисел второго класса есть как бы экспериментальный
факт.
Узкая проблема континуума и узкая проблема Лебега* Чтобы
объяснить наилучшим образом, в чем заключаются эти проблемы, мы
сначала возьмем какое-нибудь аналитическое множество Е>
неизмеримое В. Пусть С—счетное решето, измеримое В, при помощи которого
просеяно множество £.
В этих условиях мы имеем разложения
Е = Е0-*-Е1-+-Е2ч-. ..-*-£ш-*-.. .-ь£в-ь...|2
и
S = ё0 -ь ёг -+- £2 н-... -+- £ш -+-.. .ч- £а -к... | 2
множества Е и его дополнения & на бесконечное множество
конституант Еа и &а> каждая из которых измерима В.
Так как данное аналитическое множество Е предположено
неизмеримым Ву то второе разложение заведомо имеет трансфинитную
бесконечность непустых членов. Следовательно, если мы обозначим через 6^
сумму Еа-*-&а и если мы сложим почленно предыдущие разложения^
мы получим формулу
<7 = в0-ьв1ч-...н-вшч-...-ьВвн-...|2>
которая дает нам полное разложение всей области с/ на
трансфинитную бесконечность множеств 6а, измеримых В, непустых и
перенумерованных при помощи всех трансфинитных чисел второго класса
по Кантору1.
Известно, что знаменитая проблема континуума состоит в том, чтобы
1 Возможность подобного разложения всей области <& впервые была ковстатвро-
вьна Серпинским и «гной; см. нашу заметку в Comptes Rendus, 175,1922, 3S7, „Smr Yrafe.
decomposition du continu" (стр. 621 настоящего тома. —Ред.),
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
173
узнать, можно ли перенумеровать все точки некоторого сегмента при
помощи всех трансфинитных чисел второго класса по Кантору. Ясно,
что эту проблему можно рассматривать как некоторого рода полное
разложение области с7 на трансфинитную бесконечность множеств 0в,
измеримых Ву перенумерованных при помощи всех трансфинитных чисел
второго класса по Кантору, каждое из которых сводится к одной
и только одной точке.
Но взятая отдельно точка есть множество, измеримое В, класса 1.
Следовательно, на основании предыдущего, было бы очень желательно
получить некоторые общие результаты, касающиеся разложения
континуума на трансфинитную бесконечность множеств &в, измеримых В
ограниченных классов. Это в некотором роде ослабленная проблема
континуума, мы ее назовем узкой проблемой континуума.
С другой стороны, Лебег поставил проблему: узнать, можно ли
назвать множество различных точек, перенумерованных при помощи
всех трансфинитных чисел второго класса по Кантору1. Лишь после
того, как будет найдено положительное решение этой проблемы, можно
считать установленным, что мощность континуума сравнима с мощностью
множества всех трансфинитных чисел второго класса по Кантору.
Поэтому было бы вполне естественно стараться назвать
трансфинитную бесконечность множеств Sa не пустых, измеримых В и 01раничен-
ных классов. Это тоже ослабленная проблема; мы ее назовем узкой
проблемой Лебега.
Таким образом, мы, естественно, приходим к тому, чтобы поставить
следующий важный вопрос: Каковы классы конституант £а
аналитического дополнения £? И можно ли назвать такое неизмеримое В
аналитическое дополнениеу у которого конституанты &а будут
ограниченных классов?
1 Цитируем текстуально соответствующее место у Лебега в его письме к Борелю
4„Cinq lettres sur la theorie des ensembles". Bull, de la Soc. Math, de France,
декабрь 1904 г.);
„Когда я слышу, как говорят о законе, определяющем трансфинитную
бесконечность выборов, я всегда отношусь с недовернем, так как я еще никогда не видел
подобных законов, тогда как я знаю законы, определяющие счетное множество
выборов. Но это лишь вопрос рутины, и после некоторого размышления я часто вижу
трудности, на мой взгляд столь же серьезные в рассуждениях, где входят лишь
счетное множество выборов, как я в тех, где их трансфинитное число. Например,
•если я не считаю установленным классическим рассуждением, что каждое множество
мощности выше счетной содержит множество той же мощности, как и множество всех
трансфинитных чисел класса II по Кантору, то я также мало значения придаю
методу, при помощи которого доказывают, что неконечное множество содержит счетное
.множество,. Хотя я сильно сомневаюсь, чтобы когда-нибудь было названо множество,
которое не будет ни конечным, ни бесконечным; однако невозможность такого
множества не кажется мне доказанной. ..".
Таковы направления, по которым можно приблизиться к атаке против принципа
исключенного третьего, поднятой в работах Брауара я Вейля; см. Н. Lebesgue*
iLecons sur rinte^ration. 2е M.t 1928, стр.32&
174
Н. Н. ЛУЗИН
Мы здесь ограничимся просто доказательством существования
аналитических дополнений <?, у которых классы конституант &а не
ограничены 1.
Чтобы убедиться в этом, возьмем в плоскости XOY универсальное-
аналитическое множество U: это значит, что всевозможные линейные-
аналитические множества можно получить, пересекая U прямыми х = х09
параллельными оси OY. Мы теперь утверждаем, что дополнение CU
обладает указанным свойством.
В самом деле, допустим, что в разложении
С£/=50-ь51-н5,-н...-ь5ш-ь...ч-5в-|-...|2
конституанты £а имеют ограниченные классы, т. е. их классы меньше-
некоторого фиксированного трансфинитного числа Р<С^. Отсюда мы
заключаем, что сумма
S* = <§о -+- £i -+■ • • • -+■ £o>-*- • • • Ia
счетного множества конституант есть множество, измеримое В и класса:
<^.р-+-1. Следовательно, каково бы ни было трансфинитное число ьу
параллели jc = x0 к оси OY пересекают Sa по множеству, измеримому В*
класса ^(3-н 1.
Но, с другой стороны, так как множество U есть
универсальное, то существуют параллели к оси OY> пусть х = х0, которые
пересекают U по множеству //, измеримому В и заранее заданному. А так:
как Н должно принадлежать к счетному множеству конституант &а> та
существует трансфинитное число а, достаточно большое и такое, что Н
есть пересечение Sa с прямой л: = л:0. Следовательно, Н всегда класса
^Р~*~Л> что невозможно, так как Н есть произвольное множество*
измеримое В.
Второй принцип аналитических множеств. Отделимость (СА)
Отделимость при помощи аналитических дополнений. Мы теперь
обобщим понятие отделимости В двух множеств и введем понятие
отделимости при помощи множеств из других семейств2.
Точнее, мы введем понятие отделимости при помощи двух
аналитических дополнений без общих точек.
Пусть Е1 и Е2 — два любых множества точек, лежащих в
области о7*,х,... «я,. Мы предполагаем, что Е^т Е2 не имеют общих точек►
1 В действительности, если употреблять терминологию идеалистов, классы &9
„стремятся равномерно к Q". Серпинский и я констатировали существование таких
аналитических дополнений в нашей заметке в Comptes Rendus, 12 ноября 1929 г*
„Sur les classes des constituantes d'un coznplementaire analitique" (стр. 622 настоящего*
тома. Метод принадлежит Серпинскому — Ред.).
2 Определения и предложения этой части были сформулированы в моей заметке
„Sur un principe general de la theorie des ensembles analitique*4 (Comptes Rendus,.
2 сентября 1929 г.) (стр. 622 настоящего тома.—Ред.).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
17S
Определение. Мы скажем, что два множества Ех и Е2
отделимы при помощи двух аналитических дополнений, если существуют
два множества Нх и Н2 без общих точек, содержащие
соответственно Ег и Е2, каждое из которых есть аналитическое
дополнение.
Это важное понятие будет играть существенную роль в дальнейших
рассмотрениях.
Сделаем теперь одно замечание. Было бы бесполезно вводить
понятие одновременной отделимости при помощи двух аналитических
множеств. В самом деле, если бы множества Нх и //.>, содержащие
соответственно^ и£2, были аналитическими множествами, чоНх и Н, были бы
отделимы В, и мы бы не получили ничего нового. Напротив, понятие
одновременной отделимости при помощи аналитических дополнений
имеет чрезвычайно важное значение, так как мы увидим, что
существуют два аналитических дополнения, неотделимые В.
Кроме того, можно рассматривать отделимость в некотором роде
одностороннюю, осуществляемую при помощи аналитических множеств
или аналитических дополнений. Вот в чем состоит первая из них.
Пусть Е^ и Е2— два любых множества без общей точки. Мы
скажем, что Ех и Е2 отделимы друг от друга при помощи
аналитических множеств, если существуют два аналитических множества Нх
и Н2, содержащие соответственно Е} и Е» и такие, что Нг не
содержит ни одной точки из Е2, а Нг ни одной точки из £,.
Мы получим совершенно аналогичное определение, относящееся к
отделимости множеств Ег и Е2 друг от друга при помощи аналитических
дополнений, если просто заменим в предыдущем определении слова
аналитическое множество через аналитическое дополнение.
Однако мы сейчас же увидим, что введение этих двух понятий
иллюзорно, так как каждый из этих двух видов отделимости полностью
совпадает с одновременной отделимостью при помощи двух
аналитических дополнений, определение которой было дано в начале этой
страницы.
Формулировка второго принципа теории аналитических
множеств* Теперь пора ввести один общий принцип, от которого зависит
решение многочисленных вопросов теории аналитических множеств и их
дополнений; в частности, этот принцип позволяет полностью решить
вопросы об односторонней отделимости при помощи двух аналитических
множеств или аналитических дополнений; с другой стороны, именно
этот принцип позволяет установить природу проекции множества
единственности (стр. 216).
Принцип. Если удалить из двух аналитических множеств их
общую часть, то оставшиеся части всегда одновременно отделимы
при помощи Двух аналитических дополнений.
Прежде чем приступить к доказательству этого принципа, мы
покажем, что он позволяет свести понятия односторонней отделимости,
176
Н. Н. ЛУЗИН
определенные выше, к понятию одновременной отделимости при помощи
аналитических дополнений.
В самом деле, пусть Ех и Е.> — два любых множества, образованные
из точек и отделимые друг от друга при помощи двух аналитических
множеств Н{ и //2. Это значит, что Н{ содержит Ev и не имеет
общей точки с Е2> и обратно, Н2 содержит £2 и не имеет общей
точки сЕ{.
Пусть Н есть общая часть Нх и //>• На основании второго принципа
остающиеся множества Нх — Н и Н> — Н одновременно отделимы при
помощи двух аналитических дополнений Ьу и 02 без общих точек. А так
как 01 содержит Е{ и б2 содержит Е>, то множества Е1 и £2
одновременно отделимы при помощи двух аналитических дополнений (ч. т. д.).
Обратно, мы немедленно замечаем, что если два множества Е} и Ег
одновременно отделимы при помощи двух аналитических дополнений 6Х
и 62, то они отделимы друг от друга при помощи двух аналитических
множеств. Достаточно обозначить через Нх дополнение к 02 и через Н2
дополнение к Ь}; множества HY и Н2 аналитические и осуществляют
одностороннюю отделимость.
Точно так же легко видеть, что если Ех и Е2 отделимы друг от друга
при помощи двух аналитических дополнений Ь1 и б2> то они
одновременно отделимы при помощи двух аналитических дополнений.
Достаточно заметить, что, обозначая через Н1 и Н.2 дополнение ко
множествам Ьг и Ь2У мы получим два аналитических множества,
осуществляющие одностороннюю отделимость данных множеств Е1 и Е2. Итак, эти
последние рассмотрения приводятся к предыдущему случаю (ч. т. д.).
Заметим, что второй принцип справедлив для аналитических
множеств, расположенных в области любого числа измерений. Но
достаточно доказать его для двух линейных аналитических множеств,
расположенных на порции (0, 1), так как мы видели, что можно совершить
взаимно однозначное и взаимно непрерывное преобразование области
любого числа измерений в порцию (0, 1) линейной области, причем это
преобразование сохраняет аналитические множества и их дополнения.
Универсальное множество подобия. Рассмотрим на плоскости YOZ
квадрат, стороны которого определяются уравнениями
17 = 0, у = 1, z = 0, * = 1.
Мы ставим себе целью построить внутри этого квадрата
последовательность кривых ЬХУ L29..., L„f... непрерывных на порции (0, 1)
области о/у и обладающих следующими свойствами:
1°. Если Pi, р2,..., р„,... есть вполне определенная
последовательность, образованная из всех рациональных точек оси OZ9 заключенных
между 0 и 1, то кривая L{ целиком лежит под кривой Lj, 1ф}> если
9i<C?J и L{ лежит полностью над L/, если р< >р/; здесь индексы /и/ —
любые целые положительные числа.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
177
2\ Каково бы ни было множество е, составленное из
рациональных точек, расположенных между 0 и 1, и подобное множеству всех
рациональных точек между О и 1, существует иррациональное число у0
такое, что прямая у = у0 пересекает последовательность кривых LX9
L2,.. -, Ln,... в точности по е.
Мы назовем универсальным множеством подобия соединение
кривых Lt\y J-ку) . . ., Ltny . . ., обладающих указанными свойствами.
Перейдем теперь к построению последовательности кривых L{f
L.2f..., Ln>... Пусть z =/„ {у) есть уравнение, определяющее
кривую Ln.
Мы определяем первую функцию /, (у) следующим образом: пусть
Oj, о2, —, оК9... есть последовательность, образованная из всех
интервалов Бэра порядка 1; мы положим /х (г/) = р*на ьк; здесь к=\9
2, 3,...
Допустим, что мы уже определили функции /19 /2,..., /„_! и что
функция fi постоянна на каждом интервале Бэра порядка /; кроме того,
мы предполагаем, что взаимное положение уже определенных ^кривых
Lu L2,.. ♦, Ln—X такое же, как и соответствующих рациональных точек
Pi» Р-2> • • •» Ря-1 На ОСИ OZ.
Чтобы определить функцию /я, мы разделим каждый интервал
Бэра А порядка п — 1 на интервалы Бэра порядка л; пусть Д1Э А2,...
• •., Д*> • • • эти интервалы. Очевидно, что функции /19 /2,..., /п—1
постоянны на А; пусть г1У г2,..., гп-х — эти постоянные. Согласно
сделанной гипотезе, множество г19 г2,..., гя—х подобно множеству точек р1э
Р2,..., ря_г. Пусть г[9 г2. •.., г'к9... — все рациональные числа, каждое
из которых занимает по отношению к числам г19 г2,..., г„_1 то же
положение, как и ря по отношению к точкам рр р2,..., ря_1в Мы положим
Ш = гк на Afc (k= 1,2,3,...).
Мы видим, что функция /я (у) полностью определена и что
соответствующая кривая Ln имеет по отношению к уже определенным кривым
L19 L2y..., ^n-i>..- то же положение, как точка ря по отношению к
точкам р!, р2, . . ., рп-х-
Следовательно, последовательность так определенных кривых Ll9
L2,.. ♦, Ln9..., очевидно, обладает свойством 1°. Чтобы доказать, что
она обладает свойством 2°, возьмем множество е9 образованное из
рациональных точек и подобное множеству рациональных точек,
заключенных между 0 и 1. Пусть Сл есть точка из е, соответствующая
точке ря, причем это соответствие есть соответствие подобия. Найдем
интервал Бэра Ьх порядка 1, в котором /1(у) = С1; затем найдем в 8Х
интервал Бэра &2 порядка 2, где Л(#) = С2> и так далее.
Ясно, что иррациональная точка у0, которая принадлежит всем этим
&i> <>2>**-> ^,..., такова, что прямая у = Уо пересекает кривые Ll9
L2, • •., Ln9... в точности по е.
Итак, мы построили искомую последовательность кривых Ll9L29..<
• • •> i**n9... \ч» т. д.^.
178
Н. Н. ЛУЗИН
Пространственное универсальное множество подобия* [22].
Рассмотрим в области o7i,yfs куб, стороны которого определяются
уравнениями:
5 = 0, S = l, y = 0, y = lf z = 0, z = \.
Мы построим внутри этого куба последовательность поверхностей
Q\y Q>y • • •> Qny • • •> каждая из которых определена и непрерывна на
некотором множестве, состоящем из конечного числа полос, лежащих
в квадрате (0 <Г ?<Г 1; 0<!у<С1) области -7^ и параллельных оси OY.
Последовательность QXf Q2,..., Q„,... обладает следующими
свойствами:
1°. Пусть рр р.,,..., рл, ... — вполне определенная
последовательность, состоящая из всех рациональных точек оси OZ> лежащих в
интервале (0, 1). Пусть Е j i=f^j — множество всех точек области с7^9
в которых определены обе поверхности Q, и Qj (различные
поверхности определены на различных множествах области о7&). Тогда, если
р^ <С 9j9 то часть Q<, проектирующая в Ej, лежит под частью Qy,
проектирующейся в E.jy а если р»0> Р>> т° часть Q,, проектирующаяся в Еи>
лежит над соответствующей частью Q/.
2°. Какова бы ни была подпоследовательность p., pf,..., р^,...
(конечная или бесконечная) нашей последовательности рациональных чисел,
найдется такое $0, что плоскость Е = ;0 пересекается со всеми
поверхностями Q.y QtV..., Qin,...
3°. Поверхности Q{, Q.j..., Qt. ,... пересекаются с плоскостью
$ = ^ по системе кривых Z^°, /Л0,..., Lj°,..., образующих множество
подобия для последовательности р{, р.,..., р. ,. .. Это значит, что
кривые Lj°, L\°9..., L;°,... (определенные дкя всех значений у плоскости
£ = %о) расположены подобно соответствующим точкам pf., ptj,..., р,я,. *.,
и каково бы ни было множество рациональных точек rv r2,..., r,„. •.,
подобное множеству р^, р.,..., р^,..., найдется такое у0> что прямая Р* 7
проходящая через точку (Е0, у0) области о/г и параллельная оси OZy
пересекает кривую Ь^п в точке z = rn (n=l, 2, 3...)«
Перейдем к построению поверхностей QL, Q2»*.«> Qn • • • Разделим
сторону i/ = 0 квадрата (O^S^l» 0 <С 1/ <С 1)> лежащего в области с/^г
на счетное множество интервалов Бэра первого порядка 81э о2,..., Вя,...
и рассмотрим полосу /х нашего квадрата, две стороны которой
параллельны оси OY и которая опирается на интервал о2 оси ОЪ.
Поверхность Qx мы определим при помощи функции /х(£, у)> заданной в
точках полосы /х. Для определения/^, у) мы разделим полосу 1Х на
счетное множество параллелепипедов Бэра ~х, ^2,..., ^„,, ♦.. первого порядка
так, чтобы параллелепипед rcWl проектировался на ось OY ъ интервал
Бэра первого порядка A,v Во всех точках (Е, у) параллелепипеда тся, мы
положим:
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ 17V
Очевидно, что /t (E, у) — непрерывная функция, определенная во всех
точках полосы /1#
Пусть теперь построены поверхности Q,, Q2,..., QH-i} причем такг
что дая них удовлетворяется условие 1°. Каждая поверхность Q,, / <С п — 1,
определена при помощи непрерывной функции/<(;, у)у заданной на
конечном числе полос, параллельных оси OY и опирающихся на
интервалы Бэра порядка ^/ области <?7^ При этом в полосе, опирающейся
на интервал Бэра о порядка к, функция постоянна на параллелепипедах
Бэра порядка к, проектирующихся на о.
Для построения функции fn (;, у) нужно прежде всего указать те
полосы, на которых эта функция будет определена. Для этого
достаточно указать те интервалы Бэра области >Л, на которые эти полосы
опираются.
В числе этих интервалов находится интервал оя+1 первого порядка.
Для указания остальных интервалов поступим следующим образом.
Пусть на интервал Бэра bjjt...jk порядка £<я опирается полоса
Лу,... »*. гДе j\ = zi"+" 1» jr = 'V — Л—1 -*- 1, во всех точках которой
определены функции
fill fi*. • • •> Jik
и только они. Тогда выберем в ^,л-.-Л интервал Бэра порядка кч-1
с номером п — zjt —■— 1: о,х... jk(„_,- +i). Если i\ = п — 1, то это второй
интервал Бэра порядка £-н1, ьодчиненный ^j\...jk. Если/*<я— 1, то
это первый, кроме ^jx...jk\ из интервалов Бэра порядка £н-1,
подчиненных bjt...jk> такой, что в опирающейся на него полосе не
определены функции с номерами > /* (в полосе, опирающейся на
интервалы ^j\...j^, функции с номерами > U не определяются). Совокупность
всех выбранных таким образом интервалов Бэра вместе с интервалом
ожЧ_: и составляет множество всех интервалов Бэра, на которые
опираются полосы, в которых определяется функция /я (;, у).
Чтобы определить функцию /я в полосе /,-,...t-k> опирающейся на
оj ...; /и_4 +1\, заметим, что все функции /<г, г^к постоянны на каждом
прямоугольнике Бэра ранга ку содержащемся в полосе ^...^ и
проектирующемся на ось OY в интервал Бэра ранга к. Пусть г., г.,.. .,rt.fc —
соответственные значения этих функций на некотором прямоугольнике тс
порядка к. Это множество, по условию, подобно множеству pt., р^,..., pt>.
Разделив интервал Бэра порядка к области о7у> в которой
проектируется тс на интервалы Бэра порядка £-ь1, мы разобьем пересечение
тсЛ прямоугольника тс с полосой lix%mmiJtn на счетное множество
прямоугольников Бэра порядка к -+-1, тса, тс2,..., izpt... Пусть г\, r'v .„.
...,/,... —множество всех рациональных чисел, расположенных
относительно чисел rlf r2,..., гп^1 так же, как точка р„ расположена
относительно точек р1э р2,..., Ря—!•
Щ) Н. Н. ЛУЗИН
Положим /я(£, у) = г? на кр. Тем самым функция/я (?, г/) определена.
Легко видеть, что в полосе lit„tiin, опирающейся на интервал Бэра
<V••«*("-*'*) Ранга £-t-l, определено в точности k-t-1 функций
*<\9 f*i*• • •> Л*» ?"'
Соответствующая поверхность Qn имеет на полосе ^...^ то же
расположение относительно поверхностей Q.9 Q^,..., Qt. , как точка ря
относительно точек р., р.,..., рл.
Заметим, что каждая плоскость £ = £0, пересекающая полосу I..
пересекает поверхность Qn по одной и той же кривой, которую мы
обозначим L*«"'M. Плоскости ? = £0, пересекающие различные полосы,
на которых определена функция fny пересекают поверхность Qn, вообще
говоря, по различным кривым.
Покажем, что построенная система поверхностей удовлетворяет
условиям 1°, 2°, 3°. Условие 1° удовлетворяется по построению.
Чтобы доказать, что выполняется условие 2°, выберем произвольную
подпоследовательность р^, р^, ..., р. ,. .. (конечную или бесконечную)
последовательности р19 р2,..., рп,... На интервал Бэра о,1+1 области с^
опирается полоса I., на которой определена функция f. и не
определена никакая функция fj, j <C *\-
На интервал Бэра bjjt порядка 2 опирается полоса Z,-lia, на которой
определены функции f. и f. и не определена никакая функция fp]^\
j <C h и так Далее.
Точка ?0 принадлежащая всем интервалам Бэра о ., о .,..., о . ,,...,
такова, что плоскость \ = EQ пересекает поверхности Qf., Q<,..., Qtn,...
и только их. Заметим, что если последовательность Р,,..., Р<п конечна,
то £0 есть любая точка интервала Бэра &/,/,...ywi.
Покажем, что выполняется условие 3°. Очевидно, что плоскость
$ = $0 пересекает поверхности Qi9 Q^, ..., Q^, ... соответственно по
кривым L'°, L£,..., Z,£j,. .., расположенным одна относительно другой
так же, как соответственные рациональные точки pif p.,..., р.,...
Пусть е — произвольное множество рациональных точек rl9 г2,..., гя,...,
подобное множеству р,, р^, ..., р^, ... В полосе 1{, опирающейся на
интервал Бэра &»,-и, найдется прямоугольник Бэра первого порядка Ърх,
в точках которого Д = г1в В полосе 1{1^ найдется прямоугольник Бэра
второго порядка ^j?t, содержащийся в кРх9 в точках которого
/2 = г2 и т. д.
Точка Му принадлежащая всем прямоугольникам ^Pl, ~PiPiy ...,
лежит в плоскости £ = £<), так как принадлежит всем полосам I., Z„,...
Прямая Рю проходящая через точку М параллельно оси OZ,
пересекает кривые Li9 L^ ..., L^y... в точности по множеству е.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
181
Сравнение решет* Чтобы доказать второй принцип теории
аналитических множеств, мы должны научиться сравнивать решета.
Возьмем в пространстве OXYZ куб с ребрами, равными единице,
расположенными на осях координат. Пусть С есть решето, лежащее
на грани у = 0 этого куба, и С — другое решето, лежащее на грани
z/ = l того же куба. Мы предполагаем, что каждое из этих решет
образовано из прямолинейных сегментов, параллельных оси ОХ
с рациональными координатами z.
2\
Рис. 7.
Установив это, проведем через точку х0, лежащую на оси ОХу
плоскость х = х0. Эта плоскость пересекает решета Си С по двум
счетным множествам, которые мы обозначим через R^ и /?^.
Возможны только два случая:
Первый случай. Множество Rx^ подобно части R'^, причем эта часть
может совпасть с самим R'x.
Второй случай. Множество R^ не подобно никакой части R'^
включая и самое это множество.
Мы докажем, что множество точек х0> для которых имеет
место первый случащ есть аналитическое множество.
* Пусть х0 — любая точка интервала (0,1) оси ОХ. Точки
множества Rx имеют рациональные координаты г. Следовательно, множег
ствоЯ есть подпоследовательность последовательности pv р2, ..., Ря> • • •>
рассмотренной в предыдущем параграфе. Тогда ему соответствует
последовательность кривых Z^, Ц*, ..., Щ,. .., расположенных подобно
точкам множества R^. Проведем в квадрате, который получается
от пересечения куба плоскостью х = х0, все эти кривые. Заставляя
182
Н. Н. ЛУЗИН
изменяться точку лг0, мы получим внутри куба множество точек Л,
образованное из всех проведенных кривых. Изучим природу этого
множества Л.
С этой целью напомним, что решето С состоит из счетного
множества прямолинейных отрезков, параллельных оси ОХ. Обозначим
через оп проекцию на ось ОХ суммы всех тех отрезков, у которых
координата z равна ря. Множество зя может быть представлено в
следующем виде:
з« = 5п2 2 °.-,з<, • • •з»* П c°j-
Каждое множество Hlx...ik = з^оч ... oik \\ Сзу, очевидно, измеримо В.
Для каждой точки л:о множества //,"...,-л соответствующее множество/?^
содержит точки с координатами z = р^, р^,..., pt.fc,... и не содержит
точек с координатами z = py, j<in и j ^= i\9 /2, • •., 4« Следовательно,
кривая L^y проведенная в плоскости л: = х0, совпадает с кривой
Ln4'"tk>l. Значит, всем точкам множества /Л',...«4 соответствует одна и
та же кривая Ц\'лЛьн. Так как //»"...»А. и Lu"'ikn—множества,
измеримые Ву то и сумма кривых Ll,!'"ik"9 соответствующих всем точкам л:0
множества Hil • ••*>, есть множество, измеримое В. Так как множество ои
есть сумма конечного числа попарно не пересекающихся множеств
Hlx-~ik> то соединение всех кривых Lny соответствующих всем точкам
множества оя, есть множество, измеримое Ву однозначное по
отношению к плоскости XOY. Если мы проделаем это построение для всех
множеств оя, соответствующих рациональным числам р„, то получим,
очевидно, рассматриваемое множество Л. Следовательно, множество Л
состоит из счетного множества однозначных множеств, измеримых 5*.
Проведем теперь через каждую точку решета С прямую,
параллельную оси OY. Пусть S— множество точек куба, расположенных
на этих прямых. Ясно, что *S измеримо В. Следовательно, дополнение
к S относительно куба также измеримо В; мы его обозначим через Е.
Обшая часть Л и Е также измерима В.
Природа этой общей части ЛЕ такова. Множество Л есть
соединение счетного числа однозначных множеств, измеримых В. Но общая
часть каждого из этих однозначных множеств и Е есть, очевидно,
также однозначное множество, измеримое В. Следовательно,
множество ЛЕ образовано из счетного числа однозначных множеству
измеримых В*
Отсюда мы заключаем, что проекция множества ЛЕ на плоскость
XOY непременно измерима 5.
Пусть S — эта проекция и Ь — ее дополнение относительно грани
куба z = 0. Множество 8 измеримо В.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ 183
Пусть М—любая точка из 0 и Рм— перпендикуляр к плоскости
х = О, проведенный через М. Так как точка М принадлежит к 0, то
ясно, что Рм не пересекает множества АЕ.
Отсюда следует, что все точки Л, лежащие на Рм> принадлежат к S.
Но в силу свойства кривых L точки Р, принадлежащие к Л, образуют
множество, подобное множеству Rx. По самому определению 5 мы
заключаем, что точка .^'удовлетворяет первому из указанных выше случаев.
Итак, взяв проекцию 6 на ось ОХ> мы получим только точки дс0,
удовлетворяющие первому условию- Но легко видеть, что и обратное
также справедливо.
В самом деле, пусть х0 удовлетворяет первому условию. Это
значит, что множество R подобно части (в широком смысле)
множества Rx , пусть е — эта часть. Точки А, лежащие в плоскости х = х0,
образуют множество кривых L*?, которое соответствует множеству /?v
Но в силу универсального свойства этого множества кривых на
прямой z=0, х = х0 существует точка М такая, что перпендикуляр Рм
пересекает А как раз по множеству, тождественному е. Следовательно,
все точки А, лежащие на Рм> принадлежат к S. Отсюда следует, что
множества А и £ не имеют общей точки на PF. Следовательно, точка М
принадлежит множеству 6.
Итак, ортогональная проекция множества 0 на ось ОХ в точности
совпадает со множеством точек х0, удовлетворяющих первому условию.
Но мы видели, что Ь измеримо В; значит, его проекция есть
аналитическое множество (ч. т. д.).
Резюмируем все, что было изложено в этой последней части.
Пусть С и С" — два решета, расположенных в плоскости XOY,
х — любая точка на оси ОХу Рх — перпендикуляр в точке х к оси ОХ,
лежащий в плоскости XOY. Пусть Rx и R'x—множества точек С и С,
лежащих на Рх,
Мы предполагаем, что решета С и С образованы каждое из
счетного числа прямолинейных сегментов, параллельных оси ОХ и имеющих
рациональные координаты у. Мы знаем (стр. 162), что всякое линейное
аналитическое множество Е можно считать просеянным при помощи
решета такой природы.
Обозначим через Н множество всех тех точек х, для которых Rx
подобно части (в широком смысле) R[. Точно так же обозначим через Н
множество всех точек х, дая которых R'x подобно части Rx (в
широком смысле).
Результат, который мы только что получили, состоит в том, что
так определенные множества Н и Н суть аналитические множества.
Доказательство второго принципа. Возьмем в плоскости XOY
квадрат, стороны которого имеют уравнения
х = 0, х = 1, # = 0, у=1.
184
Н. Н. ЛУЗИН
Пусть Е1 и Е2— два любых аналитических множества,
расположенных в интервале (0<^х<^1).
Проведем прямую У=~о и рассмотрим два решета Сг и С2, из
которых первое расположено ниже, а второе выше этой прямой; мы
предполагаем, что эти решета определяют соответственно множества
Е1 и Е2 и природа их такая, как мы рассматривали выше.
Пусть Е есть общая часть Ег и Е2, ЕХЕ2. Обозначим через /?х
множество точек Elf которые не входят в Е2, и соответственно через R2
множество точек Е2, которые не входят в Ех:
Надо доказать, что R1 и R2 одновременно отделимы при помощи
двух аналитических дополнений.
Пусть х — любая точка на (0,1) и Рх — перпендикуляр в этой точке
к оси ОХ; обозначим через R'x и R'x' соответственно части решет
Сх и С2, лежащие на Рх.
Пусть Н1 — множество всех тех дс, для которых R'z не подобно
никакой части (в широком смысле) R'x> и соответственно,
Н2—множество всех тех х, для которых R'x не подобно никакой части Р'т
в широком смысле). В силу предшествующего, множества Нх и Н2
суть аналитические дополнения.
Обозначим через 1\ общую часть Нх и СЕ2 и через Г2 общую
часть Н2 и СЕХ:
1\ = //г . СЕ2, Т2 = Н2 • СЕЛ.
Ясно, что 1\ и Г2 также аналитические дополнения.
Легко видеть, что Г1 содержит множество Rx. В самом деле,
если х принадлежит к Rv то множество R'x не будет вполне
упорядоченным в положительном направлении оси OY, тогда как R"£y наверное,
вполне упорядочено при том же условии относительно порядка точек,
так как х принадлежит к Ех и к СЕ2. Точно так же доказывается,
что Г2 содержит R2.
Остается доказать, что 1\ и Г2 не имеют общих точек.
В самом деле, если бы точка х принадлежала и к 1\, и к Г2, то
она принадлежала бы к СЕХ и к С£2. Значит, множества R'x и R'x' были бы
вполне упорядочены. Но так как х принадлежит к Нг и к Н2> то R'x
не подобно никакой части Rx, и обратно, R'x' не подобно никакой
части Rx. Но это как раз невозможно, ибо R'x и R'z' вполне
упорядочены, а следовательно, одно из них подобно сегмену другого (ч. т. д.)-
Итак, формулированный принцип доказан.
Как немедленное следствие этого принципа мы имеем:
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
185
Если Si и S2 — Два аналитических дополнения и если мы
устраним из S1 и S2 ux общую часть, то остающиеся множества всегда
одновременно отделимы при помощи двух аналитических
дополнений.
В самом деле, обозначим через S общую часть <§\ и <§.,, через
/^ — разность ^-(S и через R2 — разность £., — £.
Надо доказать, что Rx и R2 одновременно отделимы при помощи
двух аналитических дополнений.
Обозначим через Нх дополнение к е., и через Н2 дополнение к б\;
множества Нх и Н2— аналитические. Ясно, что Нх содержит Rx и
не имеет общих точек с R2; точно так же Н2 содержит R2 и не имеет
общих точек с Rv Мы можем сказать, что Rx и R2 отделимы друг
от друга при помощи двух аналитических множеств. Но мы видели
(стр. 176), что в этом случае Rx и R2 одновременно отделимы при
помощи двух аналитических дополнений (ч. т. д.).
Обращение второго принципа. Множества Rx и R2, о которых
говорится во втором принципе, являются каждое разностью двух
аналитических множеству но кэти разности некоторой особой природы.
В самом деле, нельзя утверждать, что два любых множества, каждое из
которых есть разность двух аналитических множеств, всегда одновременно
отделимы при помощи двух аналитических дополнений, если только
у них нет общей точки: для этого достаточно принять за Rx
аналитическое множество, неизмеримое В, а за R2 — его дополнение.
Чтобы узнать природу множеств, каждое из которых есть разность
двух аналитических множеств и которые допускают одновременную
отделимость при помощи двух аналитических дополнений, мы докажем
теорему, являющуюся обращением второго принципа.
Обращение второго принципа. Если Е} и \Е2 — два
множества без общих точек, причем каждое из них есть разность
двух аналитических множеств, и если Ех и Е2 отделимы при помощи
двух аналитических дополнений, тогда Ег и Е2 получаются из
двух аналитических множеств путем удаления их общей части1.
xli И>л С»х И iL2 — /1о & >
где множества Е с двумя индексами аналитические. Мы можем
написать
ЕХ = Е\-СЕ"Х и Et=Ex.CE"v
Допустим, что Ех и Е2 одновременно отделимы при помощи двух
аналитических дополнений Нх и Н2
Ех d Нх, Е2 (Z. Н2\ Нх • Н2 = 0.
1 После опубликования в Comptes Rendus формулировки этого предложения
Хаусдорф и Серпинский независимо пожелали сообщить мне свои доказательства
его; эти доказательства с точностью до обозначений тождественны с данным
в тексте-
186
Н. Н. ЛУЗИН
Так как Ех принадлежит к Нх и не имеет общей точки с Н2, то
можно написать
Е1=(Е['СЮ(СЕ^Н1)
и точно так же
£2 = (£;C^)(C£2'^2).
Для сокращения мы обозначим через Кх и К2 первые скобки в
каждом из этих равенств:
Кх= Е'х • СНЪ К2= Е2- CH[t
Очевидно, множества Кг и К2— аналитические. Вторые скобки
каждого из равенств — аналитические дополнения; мы их обозначим через
•CTj и СГ2, предполагая 1\ и Г2 аналитическими.
Итак, мы имеем
ci\=ce;h^ сг,= се;н2
и, следовательно,
Е1 = К1 • С1\, Е2 =: К2 - СТ2.
Положим, наконец,
Ясно, что Н— аналитическое множество; значит, это же имеет место
.для 0Х и 02.
Мы теперь докажем, что, удаляя из Oj и О., их общую часть 0, мы
получим в точности данные множества Ех и Е2.
С этой целью мы заметим, что множества 02 и 02 могут быть
написаны в виде
bl = H + Kl-CH = H + ^(С^ *-СГ2) = Н-*-К1-СТ1 = Нч-Е1
и
ъ,=н+к2-сн=н+к.лсг1-*-сг2)=н+кл-сг2=н-*-е»
так как /^ и СГ2, очевидно, не имеют общих точек, так же как
и ЛГ2 и С1\.
Так как множества £\ и £"2, по предположению, не имеют общих
точек, отсюда следует, что
о = е1.о2=я.
Кроме того, Е1 и Н, очевидно, не имеют общих точек, так же как
Е2 и Н. Следовательно,
Ь1 — Ь = Е1 и 62 — 6 = £2.
Итак, Ех и Е2 получаются удалением из двух аналитических множеств
^ и 62 их общей части 0 (ч. т. д.).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
187
Существование двух аналитических дополнений, неотделимых В.
Это существование очень важно, так как именно благодаря ему теория
отделимости при помощи аналитических дополнений приобретает
самостоятельный интерес. Если бы два аналитических дополнения были
всегда отделимы В, если только у них нет общей точки, то все
свелось бы к изучению отделимости 5.
В силу чрезвычайной важности этого факта мы дадим три
доказательства существования двух аналитических дополнений, неотделимых В.
Первое доказательство1. Пара (Е1У Е>) аналитических множеств
Е\ и Ео, расположенных в плоскости XOY> называется дважды
универсальной, если, каковы бы ни были линейные аналитические
множества ег и е2, существует прямая, параллельная оси OY и пересекающая
Е1 по еи а Е2 по е2.
Существуют дважды универсальные пары. Чтобы доказать это,
рассмотрим в плоскости TOY универсальное аналитическое множество С/,
т. е. такое, что, пересекая его прямыми, параллельными оси OY, мы
получим всевозможные линейные аналитические множества.
Пусть /1 = ср(/)> /2 = ф(х) — кривая Пеано, заполняющая всю
плоскость Т1ОТ2, причем функции f и f непрерывны на (0,1).
Рассмотрим преобразование плоскости TOY в плоскость XOYy
полагая / = ср (л:), y=zy; пусть Ux есть прообраз СЛ Аналогично, полагая
t = b (л:), у = у, преобразуем TOY в XOY; пусть С/2 есть прообраз СЛ
Ясно, что Ux и U2 — аналитические множества. Легко видеть, что
пара (СД, СЛ) дважды универсальна. В самом деле, всегда существует
такое х0> что прямая х=х() пересекает СД и СЛ по двум заранее
заданным аналитическим множествам ех и е2.
Установив это, применим второй принцип к аналитическим
множествам Ux и С/2. Пусть Rx и #2 — множества, которые получаются, если
из С/т и С/2 удалить их общую часть. В силу второго принципа
существуют два аналитических дополнения Нх и Н± без общей точки,
содержащие соответственно Rx и /?2.
Я теперь утверждаю, что аналитические дополнения Нх и Н,
неотделимы 5.
В самом деле, если бы существовали два множества Ьг и 02,
измеримые В} без общей точки и содержащие соответственно Н} и Н2,
то каждая параллель к оси OY пересекала бы 0а и 02 по линейным
множествам, измеримым By и классов всегда низших, чем некоторое
фиксированное трансфинитное число а. Но пара (СД, U2) дважды универсальна.
Следовательно, существует прямая х = х09 которая пересекает СЛ и СЛ
по двум множествам ех и е2, измеримым Ву класса ач-1 и взаимно
дополнительным. Так как множества 0Х и 02 соответственно содержат Rx
и #2, ясно, что прямая х = х0 пересекает Ьг и 02 как раз по ех и е2,
что невозможно, так как класс ет превосходит а (ч. т. д.).
1 Другие доказательства находятся на стр. 219 и 221 этой книги. См. также
исследования П. С. Новикова по теории неявных функций [23].
188
Н. Н. ЛУЗИН
Замечание
Я отмечу, что, кроме уже цитированных исследований Серпинского
и его школы, работами, связанными с вопросами, изученными в
настоящей главе, являются следующие фундаментальные трактаты:
F. Hausdorff. Grundlagen der Mengenlehre, zweite Auflage;
A. Frank el. Einleitung in die Mengenlehre, letzte Auflage;
и чрезвычайно интересный мемуар:
W. Hurewicz. Zur Theorie der analitischen Mengen (Fund. Math.r
XV, 4).
ГЛАВА IV
НЕЯВНЫЕ ФУНКЦИИ
Общие замечания о неявных функциях
Проблема неявных функций* Целью этой главы является изучение
функций, определенных неявно при помощи аналитических изображений,
т. е. при помощи функций классификации Бэра1.
Рассмотрим аналитические соотношения
Л(*1> Х2> •••> Хт> У\> У*, ..., Ур) = 0,
Л(*1> х2> • •> хт\ ylt у29 . .., УР) = 0,
Jq\X\> х2' • • •> Хту У\> Учу •••» Ур) == 0>
где функции fi определены всюду в m-i-p-мерной области (7Х1Х ...^ у ...у
и входят в классификацию Бэра.
Легко видеть, что изучение общего случая сводится к изучению
системы (I), так как, если какая-либо из функций /< этой системы
не была бы повсюду определена, мы могли бы дополнить ее до
функции, определенной во всей области, без того чтобы она перестала
принадлежать к классификации Бэра и без изменения величин неявных
функций; с другой стороны, если один из аргументов х{ или у< не
фигурирует в одном из уравнений, мы тем не менее можем его считать
зависящим от этого аргумента, подобно тому как постоянное число
можно рассматривать как зависящее от любого переменного.
Раз так, то проблема при заданной системе уравнений (I) состоит
в изучении:
1°. Области Е существования неявных функций уи у>, .. ., ур.
2°. Природы этих неявных функций2.
Геометрическая постановка проблемы. Чтобы сделать это
изучение возможно более ясным и простым, мы возьмем т -+- р-мерную об-
1 Эта глава есть подробное изучение проблемы, поставленной Лебегом и
решенной им для частного случая; см. Lebesgue. Sur les fonctions representables analy-
tiquement (Jonrn. de Math., стр. 192, 1905).
2 В классическом анализе (см. Hadamard. Sur les transform, ponct. Bull, de
la Soc. Math, de France, Э4, 71, 1906), проблему можно рассматривать двумя
различными способами, а именно, с точки эрения локальной или с точки зрения всей
протяженности. Этого различия не будет в вопросе, который мы изучаем.
(D
190 н. н. лузин
ласть g7>Cj ..Xfny,...y и рассмотрим в этой области функцию F перемен-
ных xit yj, определенную равенством
г=Л+А* ■■■+/;,■
Так как функции /< входят в классификацию Бэра, то это
справедливо и для F. Следовательно, множество S точек
N(xlf х,у .. ., хт; у1У . .., ур)
этой области, в которых функция F обращается в нуль, необходимо
измеримо В. Поэтому его ортогональная проекция Е на /п-мерную об*
ласть 7х щ,.х есть аналитическое множество.
Мы покажем, что это аналитическое множество Е есть область
существования неявных функций yit
В самом деле, если точка M0(x°v xu)f ..., х°т) принадлежит к Еу
то найдется точка N0(x°v ..., х°тУ y°v . . ., у°р) в области ^xr,tmyr^p,
имеющая М0 своей проекцией. Так как функция F обращается в нуль
в точке Л/о, то это же верно и для каждой из/»; следовательно, система
уравнений (I) удовлетворена. Таким образом, в этом случае числа z/Jt
У% • • •» У1 сУть значения неявных функций у1У у.1У ..., ур. Обратно,
если точка М0 не принадлежит к £, то функция F не обращается
в нуль ни в какой из точек N(x°}> х\, ..., х°т, \yv . .., ур), каковы бы
ни были числа уи у2, ..., ур. Следовательно, аая каждой из этих
точек N по крайней мере одна из функций /{ не равна нулю; таким
образом, если мы положим
x1 = xv дс2 = л*о, . . ., -Х",п = *„0
то не существует чисел yi9 удовлетворяющих всем уравнениям
системы (I).
Итак, аналитическое множество Е есть область существования
неявных функций.
Мы дополним этот результат следующими замечаниями:
Замечание I. Изучение системы уравнений (I) сводится к
изучению единственного уравнения F= О, где F есть функция
классификации Бэра. Следовательно, с геометрической точки зрения все сводится
к изучению произвольного множества £, измеримого 5, расположенного
в m-1-р-мерной области с?^...*^..^ , и взаимоотношений, которые
существуют между этим множеством S и его ортогональной проекцией Е
на т -+-/7-мерную область о7Хх..,Хт.
Замечание II. Областью Е существования неявных функций yt
может быть любое аналитическое множество. В самом деле, если
в области 3х ...хт дано любое аналитическое множество Е, мы можем
его рассматривать как ортогональную проекцию множества <?, измери-
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ 19Г
мого В и расположенного в т-ь- 1-мерной области V* ЖшУ. Функция
F(xu х2У ..., хт, у)> которая равна нулю на $ и 1 вне £, очевидно,,
входит в классификацию Бэра. Но уравнение
F{xv х,, ..., хт, у) = 0
определяет у как неявную функцию от переменных xi9 причем область
существования этой функции в точности совпадает с Е.
Итак, мы видим, что проблема об области существования неявных
функций сводится к вопросу о тому будет ли эта область измерима
В в каждом рассматриваемом случае.
Однозначные и многозначные неявные функции. Мы теперь
обратим наше внимание на самые неявные функции у+.
Пусть М(х1У х2, ..., хт) — любая точка области п/Хг.Хт. Если точка М
не (принадлежит к аналитическому множеству Е> то не существует
никакой системы чисел у1У у2, -.., уР> удовлетворяющих уравнениям (I).
Если М принадлежит к £, то существуют системы чисел yl9 z/2, .. ., yFr
удовлетворяющие уравнениям (I), и в общем случае их существует
бесконечное множество.
Следовательно, если М принадлежит к £, то при заданном /,
1^/^р, неявная функция у{ имеет вполне определенное множество'
значений в точке М; это множество мы обозначим через Н[МК Очевидно,
это множество Н^ фактически содержит точки и, вообще говоря,
меняется вместе с изменением точки М множества £".
Легко видеть, какова природа множества HfK В самом деле, так
как множество <§ измеримо 5, то множество точек, принадлежащих <£,
ортогональные проекции которых на область ofx Хт совпадают с М,
очевидно, измеримо В; обозначим его через &МК Но ясно, что Iff'
есть ортогональная проекция £{Я) на прямую D[M\ проведенную через М
параллельно оси OYit
Следовательно, Н^ есть линейное аналитическое множество.
Если проделать это построение дая всех точек М из Е, то ясно,,
что получается вполне определенное множество Hiy расположенное
в m-ь 1-мерной области о7х...хту Это множество Н. есть
изображающее множество для неявной функции yi{xl9 х.1У ..., хр)> так как д\я
получения всех значений, принимаемых у{ в точке М, достаточно
пересечь множество Н{ перпендикуляром D[:V) к области <7Х1...ХтУ
проведенным через М в области Jrx ..Xmy
Изображающее множество //, есть, очевидно, ортогональная
проекция ё на тн- 1-мерную область </*А..Лдау»- Следовательно, Hi есть
аналитическое множество. А так как множество & есть произвольное
множество, измеримое Ву то ясно, что //< есть, вообще говоря,
аналитическое множество, неизмеримое В.
192
Н. Н. ЛУЗИН
Из предшествующего следует, что неявная функция у{ в общем
случае многозначна, так как, вообще говоря, перпендикуляр D^
пересекает множество Н{ в нескольких точках. В самом деле,
аналитическое множество Hiy очевидно, может быть произвольным аналитическим
множеством, так как всегда можно найти множество &, измеримое В}
расположенное в с7' хг.хтуг.ур> проекция которого на о/Х1...ху{ совпадает
С Hi.
Таким образом, мы приходим к следующему результату:
Неявная функция yiy вообще говоря, имеет область
существования Е, аналитическую и неизмеримую В, и для каждой точки М
из Е множество значений yi есть линейное аналитическое
множество Н^\ которое, вообще говоря, неизмеримо В и, следовательно
имеет мощность континуума.
Следовательно, для каждой неявной функции */, в каждой точке М
области Е могут представиться только три случая:
1°. Функция yt имеет единственное значение в точке М.
2°. Функция у4 имеет в точке М счетное (или конечное) множество
значений.
3°. Множество значений z/t в точке М содержит совершенное
множество и, значит, имеет мощность континуума.
Мы увидим, что в первых двух случаях имеют место те самые законы,
которые впервые были указаны Лебегом, тогда как третий случай
совершенно неожиданно от них отличается.
Эффективное существование однозначного решения во всех
^случаях. Мы докажем, что во всех случаях можно назвать
однозначное решение данной системы (I) уравнений.
Чтобы убедиться в этом, возьмем непрерывное параметрическое
изображение множества &, измеримого В:
*l=/l(')> *2=Л(')| •••> *т =/«.(')>
Л = &(')> •••> Ур = 2р(*)-
Пусть Мь{х\, х\, ..., х^) — любая точка множества Е. Совместные
уравнения
А=Л (/), х\ =/2 (*), ..., x°n ==/„ (t)
определяют на порции (0,1) области с7/ замкнутое множество, так как
♦функции fi непрерывны. Обозначим это множество через Fm0.
Ясно, что если точка М0 отличается от точки М19 лежащей в Е,
то замкнутые множества FM и FM не имеют общих точек. С другой
стороны, очевидно, что каждая точка /0 порции (0,1) области о/t
принадлежит замкнутому множеству FM, соответствующему некоторой
точке М из Е: координаты этой точки М получаются, если положить
/ = /0 в уравнениях лг*=/<(*)> / = 1, 2, ..., т. Отсюда следует, что
вся порция (0,1) области o/t разложена на замкнутые множества FUy
♦соответствующие точкам М из Е.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
193
Установив это, допустим, что мы можем назвать одну и только одну
точку в каждом множестве FM. Пусть L — множество так выбранных
точек /. Я теперь утверждаю, что множество L позволяет нам назвать
однозначное решение
У\> У2> • •., Ур
данной системы (I).
В самом деле, заставим t0 пробегать множество L. Соответствующая
точка М0(х[у х\у ..., х°т) пробегает всю область существования £,
причем двум различным значениям t соответствуют две различные точки М
из Е. С другой стороны, уравнения
У\ = 8х Со), У\ = §2 Со). • • -, y°f = gP ('„),
где t0 есть точка из L, определяют вполне определенное решение
заданной системы (I). Итак, мы умеем назвать однозначное решение ylf
у2У ..., ур системы (I).
Итак, все сводится к тому, чтобы назвать одну и только одну точку t
в каждом замкнутом множестве F. Эта проблема не представляет
никакой трудности, когда речь идет о замкнутых множествах в
классическом смысле, т. е. когда не исключают из рассмотрений
рациональных точек. Но в рассматриваемом нами случае речь идет о множестве,
замкнутом относительно области J iy и, следовательно, рациональными
точками пренебрегают.
Чтобы преодолеть это небольшое затруднение, перенумеруем все
интервалы Бэра, расположенные на порции (0,1) области /,, при помощи
целых положительных чисел
°1> Ь2> • • •> °п>
Среди этих интервалов мы берем первый, пусть о}<1, который
содержит точки из F. Пусть 8Ма — первый интервал предыдущей
последовательности, содержащийся в bUx и содержащий точки F. Вообще,
Кк есть первый интервал предшествующей последовательности,
содержащийся в ЪПк_! и содержащий точки F. Убывающая
последовательность 8Ml, о„а, ... определяет иррациональную точку ty
принадлежащую всем интервалам Ъпк. Так как опк непременно содержит
точки F и так как F замкнуто, точка t должна принадлежать к F.
Итак, мы назвали точку во множестве F.
Таким образом, мы во всех случаях назвали однозначное решение
Ух* Уъ> " м Уру определенное во всей области существования Еу но мы
не знаем, какова природа этого решения. В дальнейшем мы увидим,
что решение у19 г/2, ..., у^ так названное, составлено из проективных
функций yiy что и уточняет их природу.
194
Н. Н. ЛУЗИН
Мы дополним полученный результат следующим замечанием: если
область существования Е есть множество, неизмеримое Ву то не
существует ни одного решения у1У у2$ ..., уру составленного из р
однозначных функций, берущих свои значения от р функций
классификации Бэра.
Чтобы убедиться в этом, допустим, что мы имеем р функций
у1 = Ф{х1У х2, ..., хт)у у2 = Ф2, ..., Ур = ®р (II)
классификации Бэра, определенных во всей области Л,*,...*,, и
удовлетворяющих уравнениям (I), когда точка М{х1У ..., хт)
принадлежит к Е.
Возьмем область <Эf %х..^^ух...Ур и рассмотрим в этой области множество
точек N(xly ..., хт; у1У ..., ур)у координаты которого удовлетворяют
уравнениям [(И); пусть &' — это множество. Легко видеть что &'
измеримо В. В самом деле, функция
Gfc - *i)* + G/2 - Ф2)2 -ь • • • -ь (Ур ~ Ф/
от m-t-р действительных переменных xiy yjy очевидно, входит в
классификацию Бэра. Следовательно, множество N точек, для которых эта
функция равна нулю, измеримо В. Но это множество, очевидно, как
раз совпадает с §'.
Установив это, обозначим через Н общую часть S и <§'; множество Н
измеримо В. Так как Н есть часть <£, то проекция Н на <РгХх...хт
принадлежит к Е* С другой стороны, какова бы ни была точка М(х1У ..., хт)
из £, точка из &'
Х\У Х%у • . ., Хту
УГ=Ф1> У2 = Ф2> ..м Ур = ФР
удовлетворяет уравнениям системы (I); следовательно, эта точка
принадлежит к &у а значит, и к Н. Отсюда следует, что проекция Н на
о7*,...*т совпадает с Е.
Из самого определения множества И следует, что двум различным
точкам из И соответствуют две различные точки его проекции ЕЛ
Отсюда мы заключаем (стр. 141), что Е измеримо Ву что противоречит
гипотезе (ч. т. д.).
Таким образом, мы убедились, что в случае, когда область
существования Е неизмерима Ву невозможно выбрать однозначное решение
Ух> Учу • • •> Ур> составленное из функций классификации Бэра. Это,
однако, нисколько не препятствует тому, чтобы в однозначном решении
какая-либо одна из неявных функций у4 была функцией классификации
Бэра.
Исследования Лебега. Мы обязаны Лебегу первыми исследованиями
о тождестве двух семейств функций: функций, определенных аналити-
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
195
чески явным образом (у = аналитическому выражению от х1У х2> ..., хт),
и функций, определенных аналитически неявным образом
(аналитическое выражение от х1У х2У ..., хту у равно нулю). Обычно эти две
категории функций не различают, так как на практике тот самый
процесс, который доказывает существование неявной функции, дает и ее
разложение; но тождество двух семейств не очевидно.
Лебег рассмотрел случай, где каждой системе чисел, xi9 х1У ..., хту
соответствует не более одной системы чисел у19 у2$ ..., уру удов-
летворяющих предложенным уравнениям (I), и указал следующие два
закона, имеющие место в этом случае:
(Ьх) Область существования Е неявных функций у1У у2У ..., ур есть
множество, измеримое В.
(L2) Каждая неявная функция у{ совпадает на £ с некоторой
однозначной функцией 4i{xv х2У ..., хт)у входящей в классификацию Бэра
и всюду определенной.
Естественно стараться узнать, сохраняются ли эти два закона
Лебега во всех случаях, которые могут представиться. Среди других
случаев, кроме рассмотренного, наиболее интересными являются
следующие:
I. Одна из неявных функций, пусть yiy однозначна, а о других
неявных функциях ничего неизвестно.
II. Все неявные функции у1У у2У ..., ур допускают не более счетного
множества значений в каждой точке области существования Е.
III. Одна из неявных функций, пусть yjy допускает не более
счетного множества значений в каждой точке области существования Е,
а об остальных неявных функциях ничего не известно.
IV. Общий случай, где не делается никаких гипотез о неявных
функциях.
Мы увидим, что случай II во всех отношениях аналогичен основному
случаю Лебега, так как его законы (Lx) и (L2) сохраняются в этом
случае. Точно также случай III аналогичен случаю I, так как в обоих этих
случаях закон (La) не сохраняется, тогда как закон (L2) частично
сохраняется. Наконец, в общем случае IV ни закон (I^), ни закон (L2) не
сохраняются.
Изучение однозначных неявных функций*
Исследования Лебега
Основной случай Лебега» где решение однозначно и единственно*
Мы начнем с изучения основного случая, рассмотренного самим
Лебегом; это тот случай, когда система (1) допускает единственное решение
для каждой точки М(х1У х2, ..., хт) области существования Е.
Область существования. Из предшествующего немедленно следует,
что в основном случае Лебега область существования Е измерима В.
В самом деле, достаточно заметить, что Е есть ортогональная проек-
196
Н. Н. ЛУЗИН
ция Ha^7a,z,_aw множества <£, измеримого В, и что проекции двух
различных точек с? всегда различны. Отсюда мы заключаем (стр. 141), что
Е измеримо В.
Таким образом, мы приходим к первому закону (Ьг) Лебега:
Теорема I. Если система уравнении допускает единственное
решение для каждой точки области существования, то эта область
существования необходимо измерима В.
Природа неявных функций. Мы докажем, что в рассматриваемом
случае единственное решение уи у±, . .., ур предложенной системы (I)
образовано из функций классификации Бэра.
В еамом деле, рассмотрим какую-нибудь неявную функцию
В силу известной теоремы Лебега (стр. 124), для того чтобы
некоторая функция у = Ф(х19 х2, ..., хт) входила в классификацию Бэра,
необходимо и достаточно, чтобы, какова бы ни была порция (а, Ь)
области с?у, множество точек М(xv х.2, ..., хт)> для которых мы имеем
неравенство a<Zy <С^, было измеримо В.
Применим этот критерий к неявной функции z/t. Пусть
У1 = еЛ*)> •••> yv=gP{t)
есть регулярное параметрическое изображение множества &; мы
предполагаем, что все функции /< и gt непрерывны и определены на
порции (0,1) области r7f.
Так как функция gi(t) непрерывна, множество значений, для
которых a<lgi{t)<Zb> измеримо В; обозначим это множество буквой е.
Если мы заставим t пробегать е, то множество соответствующих точек
М(х19 х±у ..., лгт) «з Е необходимо измеримо Ву так как двум
различным точкам е отвечают две различные точки Е (стр. 142). Но это
множество точек М есть как раз то, для которого мы имеем неравенства
в<ф<(*1» х2, ..., хт)<Ь.
Следовательно, неявная функция ^ = Ф^ входит в классификацию
Бэра (ч. т. д.).
Остается лишь сделать одно замечание, касающееся неявной
функции Ф{. В настоящий момент эта функция определена лишь на области
существования Е. Но мы можем закончить ее определение, полагая ее
равной любому постоянному С вне Е. Так как Е измеримо Ву то
функция Ф<, дополненная таким образом, заведомо входит в классификацию
Бэра. Следовательно, мы можем рассматривать неявную функцию г^ка*
часть явной функции классификации Бэра, всюду определенной, но
рассматриваемой только на множестве Е, измеримом В. Таким образом, мы
приходим ко второму закону (L2) Лебега:
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
197
Теорема II. Если система уравнений допускает единственное
решение для каждой точки области существования^ то это решение
состоит из функций yiy входящих в классификацию Бэра.
Случай I, когда одна из неявных функций однозначна1. В общем
случае система уравнений (I) не допускает единственного однозначного
решения, и, следовательно, существуют точки M(xlt xt9 ..., хт) из Еу
которым соответствует несколько систем значений у19 у.,, , ур. В этом
случае по крайней мере одна из неявных функций уи у2, ..., ур
многозначна.
Мы изучим тот интересный случай, когда одна из неявных функций,
например yiy остается однозначной.
Область существования. В противоположность тому, что мы нашли
в предыдущем случае, эта область может быть произвольным
аналитическим множеством, значит, неизмеримым В.
Чтобы убедиться в этом, возьмем в области <УХ произвольное
аналитическое множество Е. Пусть f(x) — произвольная функция
классификации Бэра. Возьмем в области <Эгху множество Н точек Р(х, г/), для
которых ордината у имеет значение, определенное уравнением #=/(*)>
а абсцисса пробегает данное аналитическое множество Е.
Легко видеть, что множество Н есть аналитическое. В самом деле,
если х= <р (t) есть непрерывное параметрическое изображение Еу то
уравнения
х = ?(*)> У =/[<?(*)}
дают параметрическое изображение Н при помощи функций
классификации Бэра. Следовательно (стр. 125), Н есть аналитическое
множество.
Установив это, возьмем в трехмерной области 3xyz множество <£,
измеримое Ву ортогональная проекция которого на плоскость XOY
совпадает с Н. Пусть F{x, z/, z) есть функция, равнгая 0 на & и 1 вне §.
Так как & измеримо 5, то функция F(x> у, г) входит в классификацию
Бэра. Но если мы рассмотрим уравнение
F(x, у, z) = 0,
то область существования неявных функций у и z, очевидно,
совпадает с Еу причем неявная функция у однозначна, так как она равна
f(x) на £ и не существует вне Е.
Таким образом, мы констатируем, что если одна из неявных
функций (но не все) однозначна^ то область существования может быть
неизмерима В.
Следовательно, закон (Lx) Лебега не сохраняется.
Природа однозначной неявной функции. Пусть
У=У*(Х1> *2> ••♦> Хт)
1 Это* случай бык релспмггрен в моей заметке „Sur W р**Ыёте des functions
implicites" (Comptes Rendus, 8 июля 1929 г.).
198
Н. Н. ЛУЗИН
есть неявная функция, однозначная всюду в области существования £.
Если мы геометрически изобразим эту функцию в т -*- 1-мерной
области <?х#в ...хпйо мы получим аналитическое множество (стр. 191)//,
ортогональная проекция которого на область о7хх...Хт совпадает с Е.
Так как неявная функция г/< однозначна, то каждая параллель Dm
к оси OYiy проведенная через точку М из Еу пересекает аналитическое
множество Н в одной и только одной точке. Отсюда следует, что две
различные точки Н имеют различные проекции. Из этого вытекает
(стр. 141), что аналитическое множество Н измеримо В в том и только
в том случае, когда область существования Е измерима Ву что является
частным случаем. Значит, вообще говоря, изображающее множество Н
неизмеримо В* Тем не менее мы констатируем тот неожиданный факт,
что в области о7хх...Хт можно провести однозначную поверхность Sy
измеримую Ву
(S): У*=/{хи х2, .. .9х w),
которая проходит через все точки //.
Другими словами, однозначная неявная функцияу определенная
на области существования Е, совпадает с некоторой функцией
классификации Бэрау определенной всюду на о7хх...Хт.
Мы видим, что это и есть второй закон (Z,2) Лебега.
Этот факт есть прямое следствие одного общего предложения из
геометрии.
Теорема. Если S есть аналитическое множествоу расположенное
в m-t- 1-мерной области g^*,...*^, такоеу что каждая параллель
к оси OY пересекает S не более чем* в одной точкеу то существует
функция у(х1У>х2У ..., хт)у входящая в классификацию Бэрау всюду
определенная и такаяу что множество S лежит на поверхности Sy
определенной уравнением y = <?(xv х2У ..., хт).
Чтобы доказать это, возьмем непрерывное параметрическое
изображение s
Xl = ?l(t)> *2=Ъ(*)> •••> **. = ?* (Of » = Ф(0-
Обозначим через Si множество точек области Q'х ...Xmyf
расположенных под S.. Ясно, что координаты всех точек S1 можно записать
в виде
*l = <Pl(')i *2 = ?*(')» •••> Xm = <?m{t), y = ty{t)+*y
где t — любое отрицательное число.
Аналогично, обозначим через S2 множество точек, лежащих над S;
все точки S2 можно получить, приняв в предыдущих формулах за *
любое положительное число.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
199
Очень легко доказать, что множества Sx и <§2— аналитические;
достаточно заполнить кривой Пеано t = g (и), -z = h (и) область (0 < t < 1,
—оо < х < 0). Уравнения
*1 = ?1 [g (««)], *2 = ?2 [^ («)], • • > ЛГт = ?т [# (**)],
очевидно, дают параметрическое изображение <§1в Точно так же
доказывается аналитичность множества £2.
Так как аналитические множества &-*-ё1 и £2 не имеют общей точки,
то они отделимы В. Пусть Н есть множество, измеримое Ву
содержащее S-*-&l и не имеющее общей точки с <£2. Точно так же пусть Н2—
множество, измеримое В9 содержащее &-*-&2 и не имеющее общей
точки с &!* Пусть Н—общая часть Нх и //2. Ясно, что Н есть
множество, измеримое Ву содержащее £ и такое, что всякая параллель
к оси О У, проведенная через точку £, пересекает Н в одной и только
одной точке.
Установив это, обозначим через Q множество точек области Jx .. .х у,
расположенных на всех параллелях к оси QYy каждая из которых
пересекает Н по крайней мере в двух различных точках. Так как
ортогональная проекция Q на область о/х .. ,в есть аналитическое
множество (стр. 143), то и самое Q есть аналитическое множество.
Отсюда следует, что общая часть V множеств Q и Н есть
аналитическое множество. Но мы заметили, что каждая прямая, параллельная
оси ОY и проведенная через точку из £, пересекает Н в одной
и только одной точке. Значит, аналитические множества V и & не имеют
ни одной общей точки. Отсюда следует, что существует множество
S, измеримое В, содержащее £ и не имеющее общей точки с V.
Обозначим через S общую часть S' и //. Так как множества S' и Н
измеримы В, то и S будет таковым.
Легко видеть, что не существует ни одной параллели к оси О У,
которая пересекает S в двух различных точках, В самом деле, если
прямая Z), параллельная оси О У, пересекает Sb двух различных точках,
то прямая D пересекает Н в двух различных точках, а значит, D
принадлежит к Q. Следовательно, все точки Ну расположенные на Dt
принадлежат к V, что невозможно, так как среди этих точек есть
точки S9 а множества S и V не имеют общей точки.
Отсюда следует, что множество S есть множество, измеримое Ву
содержащее & и такое, что каждая параллель к оси OY пересекает S
не более, чем в одной точке. Поэтому проекция S на о7х • • •* есть
множество, измеримое В; обозначим его через а.
Очевидно, что функция <р (xl9 x2,..., хт), равная любой постоянной
вне с и равная координатам у точек S на а, есть функция
классификации Бэра. С другой стороны, однозначная поверхность у = <р (х1У х2у..., хт)у
очевидно, проходит через все точки множества S (ч. т. д.).
200
Н. Н. ЛУЗИН
Природа множества точек, в которых неявная функция имеет
единственное значение. Рассмотрим какую-нибудь неявную функцию
j/i (х19 x2i ..., хт) и возьмем в области с?' х х.. ,х у представляющее
ее множество //<. Все значения, которые принимает у{ в какой-либо
точке М области существования Еу можно получить, пересекая
множество Н{ параллелью Dm к оси OYi9 проведенной через М.
Отсюда следует, что функция у{ имеет единственное значение
в точке Му когда прямая Dm пересекает Hi в одной и только одной
точке.
Так как множество //< есть проекция <§ на область ^v "*m* >
то Hi есть произвольное аналитическое множество.
Итак, все сводится к определению природы множества Е тех точек
области <?&•••»> в которых параллели к оси OY пересекают данное
аналитическое множество //, лежащее в о/х.. .х у, в одной и только
одной точке.
Мы докажем, что Е' есть разность двух аналитических множеств.
Чтобы убедиться в этом, обозначим через Е проекцию Н на область
о/х.. .х и через Е" — множество точек этой области, в которых
параллели к оси О Y пересекают множество Н не менее чем в двух
различных точках. Так как множество Н аналитическое, то и множества
Е и Е" будут аналитическими (стр. 143). Но рассматриваемое множество £'
есть, очевидно, разность Е — Е", что и доказывает наше предложение
(ч. т. д.).
С другой стороны, обратное предложение, очевидно, также
справедливо: каждое множество точек, являющееся разностью двух
аналитических, может быть рассматриваемо как множество точек, в которых
параллели к оси OY пересекают некоторое аналитическое множество
в одной и только одной точке.
В общем случае разность двух аналитических множеств не есть
ни аналитическое множество, ни аналитическое дополнение; это
множество новой природы.
Легко видеть, какова природа множества, представляющего
единственные значения неявной функции. Достаточно рассмотреть множество
тех точек //, проекции которых принадлежат к Е'. Так как множество Н
аналитическое, и так как множество точек //, проекции которых
принадлежат к Еиу тоже аналитическое, то рассматриваемое изображающее
множество есть разность двух аналитических множеств.
Таким образом, мы заключаем, что множество тбчек области
<3?v • *хтуу изображающих единственные значения неявной функции yi,
есть разность двух аналитических множеству равно как и
ортогональная проекция этого изображающего множества на qJх.. .х х.
1 Мы увидим в конце этой главы, что если изображающее множество Н для
неявной функции у измеримо В (а не произвольное аналитическое множество),
то множество» которое изображает единственные значения gt, а также и проекция
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
201
Теперь легко узнать природу множества, образованного из точек
области существования £, в которых уравнения (I) допускают
единственное решение. Это множество есть, очевидно, общая часть
множеств Е., /=1, 2,..., р, каждое из которых есть разность двух
аналитических: Е] = Е — Е"г Так как эту разность можно представить
в виде Е-СЕ", и так как общая часть конечного числа аналитических
дополнений есть опять аналитическое дополнение, мы заключаем, что
множество точек области существования Е} в которых уравнения
(/) допускают единственное решение, есть разность двух
аналитических множеств.
Изучение многозначных неявных функций со счетным
множеством значений
Случай П9 когда все неявные функции многозначны и имеют
не более счетного множества значений1. Этот случай аналогичен
случаю Лебега.
Область существования. Легко видеть, что эта область измерима
В и, следовательно, первый закон (L}) Лебега сохраняется. В самом
деле, множество £, измеримое В, имеет своей проекцией область
существования £", и притом каждая точка Е есть проекция не более
чем счетного множества точек &. Известно (стр. 150), что в этих
условиях множество Е измеримо В.
Природа неявных функций. Гораздо труднее установить природу
неявных функций. Д\я того чтобы ее изучить, мы вынуждены
рассмотреть структуру непрерывной гсолурегулярной функции.
Пусть y=zf(x) есть непрерывная и полурегулярная функция,
определенная на порции (0,1) области о7х; это значит, что, каково бы
ни было действительное число у0> уравнение Уо=/(х) имеет не более
счетного множества корней.
Итак, возьмем любое i/0 на оси OY. Пусть Fy есть множество
корней уравнения i/o =/(*)• Так как /(х) непрерывна и полурегулярна,
то множество Fp счетно (или конечно) и замкнуто в J %. Отсюда
следует, что если мы возьмем последовательные производные от этого
множества, мы придем к некоторому производному множеству, которое
будет пустым (лишенным точек). Пусть ау есть наименьшее трансфи-
ннтное число второго класса (или конечное), такое* что производное
множество от Fv порядка лр лишено точек. Это число аУо мы назовем
индексом остановки, соответствующим точке у0.
этого множес!ва ва <&х • •« оказываются оба аналитическими дополнениями.
Это очень важный факт, доказательство которого представляет значительные трудности.
1 См< П. С. Новиков. Sur les fonctions implicites mesurables В (Fund. Math.,
XVH, 1931).
202
Н. Н. ЛУЗИН
Установив это, мы докажем, что индексы остановки ограничены
для каждой непрерывной полу регулярной функции f (x). Это значит,
что существует трансфинитное число второго класса (или конечное) р,
которое превосходит всякий индекс остановки о.у, какова бы ни была
точка у0 на оси OY.
Допустим обратное; это значит, что каково бы ни было
трансфинитное число ^ второго класса, найдется точка г/, для которой ау^>7.
Я теперь утверждаю, что на о/х существует два интервала Бэра,
\ и 82, без общих точек и такие, что, как бы велико ни было т>
производное порядка f от F у эффективно содержит точки в \ и 82,
если только у выбрано надлежащим образом.
В самом деле, мы можем выбрать точку у так, чтобы производное
порядка т от Fу содержало не менее двух различных точек. Пусть \
и 82— Ава интервала Бэра без общих точек, причем каждый из них
эффективно содержит точки производного Fy. Так как существует
лишь счетное множество пар интервалов Бэра, тогда как
трансфинитных чисел if несчетное множество, то пара 8, и 82 с указанным
свойством должна существовать.
Установив это, допустим, что существует к интервалов Бэра 8lf
&2> •••»&* попарно без общих точек и таких, что, как бы велико
ни было ?, производное порядка -j от Fу эффективно содержит точки
в каждом из этих интервалов, если только у выбрано надлежащим
образом. Мы докажем, что в этих условиях существует в каждом Ь{
два интервала Бэра 8' и о" без общих точек и таких, что система из 2к
интервалов 8^, 8J, ..., Ъ', 8* обладает тем же свойством.
В самом деле, на основании свойства интервалов 8lf ..., 8*, как бы
велико ни было ?, можно найти точку у такую, что производное
множество порядка 7 от Fy содержит по крайней мере две различные
точки х( и л:? в каждом 8<# Заключим эти точки х'. и х': в два
интервала Бэра 8^. и 8J без общих точек и содержащихся в 8i# Так как
существует лишь счетное множество систем интервалов Ь'. и 8", / = 1,
2, ..., к> и так как трансфинитных чисел 7 несчетное множество,
мы заключаем, что существует система из 2к интервалов Бэра
8[, 8", . #., 8^, 8£, обладающая указанным свойством.
Из предшествующего мы заключаем, что на <7Х существует такое
совершенное множество Р, что, каково бы ни было л, совершенное
множество Р содержится в 2я интервалах Бэра попарно без общих
точек 8lf 82, ...,8^, таких, что каждый из этих интервалов эффективно
содержит точки замкнутого множества Fу при надлежаще выбранном у.
Кроме того, порядок интервалов Бэра 8lf 82, ..., 82л можно
предполагать как угодно высоким.
Так как f(x) непрерывна на o7xt отсюда следует, что /(х) постоянна
на Р. В самом деле, в противном случае мы имели бы две точки Р, хг
и х2, такие, что f{x-)^f{x^. Эти две точки заключены в двух
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
203
различных интервалах 5< и о, системы 8„ о2, ..., о2п. Так как длина
этих интервалов стремится к нулю, когда п неограниченно возрастает,
то отсюда следует, что множества значений f(x) на о, и Ьу не имеют
общей точки. Но это невозможно, так как множество F9 для
некоторого у имеет точки в о< и bj одновременно.
Таким образом, мы приходим к заключению: если индексы
остановки ау не ограничены, то существует точка у, для которой
множество Fу несчетно, а следовательно, функция /(х) не будет
полурегулярной. Итак, в рассматриваемом нами случае индексы остановки
ограничены (ч. т. д.).
Прежде чем приступить к изучению природы множества,
измеримого В, пересекаемого каждой параллелью к некоторому данному
направлению не более чем в счетном множестве точек, мы докажем
следующую лемму: если & есть множество, измеримое В, лежащее
& 3х х • • •* и такое* что всякая параллель к оси ОУлерепекает j§
не более чем в счетном множестве точек, то множество Е тех
точек области g?^. . .с , для которых параллели к оси OY
пересекают <§ в одной и только одной точке, измеримо В.
Чтобы доказать это, возьмем на оси OY все рациональные
точки г19 г2, ..., гп, ... Пусть &' и <§'' — части &, для которых
координата у соответственно меньше или больше г№. Эти множества
<£' и <§" измеримы В и таковы, что каждая параллель к оси OY
пересекает их не более счетного числа раз. В силу предшествующего
{стр. 150) проекции Е' и Е" множеств &' и &" на область <7Х х
измеримы В. Это же имеет место для общей части Е'пЕГп и для суммы S
всех этих общих частей, где п = 1, 2, 3,... Но множество S есть,
очевидно, множество всех точек области 3а х • • • % > Аля которых
параллель к оси OY пересекает S по крайней мере в двух точках.
С другой стороны, проекция Е множества S на с7**а.. .*w также
измерима В; поэтому то же справедливо и для разности Е — S.
Но эта разность, очевидно, совпадает с рассматриваемым множеством
Е (ч. т. д.).
Установив это предварительное предложение, возратимся к изучению
структуры непрерывной полурегулярной функции /С*). Мы хотим
доказать следующее предложение: если функция /(х) непрерывна
и полурегулярна, то кривую у=/(х) можно разложить на счетное
множество множеств, измеримых В и однозначных по отношению
к оси OY. Это значит, что всякая параллель к оси ОХ пересекает
каждое из этих множеств не более чем в одной точке.
Чтобы доказать это важное предложение, рассмотрим в области о/ху
все прямоугольники Бэра R19 R2> • • •> Rn> • • • Обозначим через Qn
множество точек кривой у =/(*)> лежащих в R». Рассмотрим
множество всех параллелей к оси ОХ, пересекающих Qn в одной и только
204
н. н. лузин
одной точке. Пусть /Л есть множество точек Qn, лежащих на этих
прямых. В силу предыдущих рассмотрений Z,(n0) есть множество,
измеримое В.
Удалив из кривой у =/(х) все точки, принадлежащие множествам/Я
мы получим в области Jху множество <?п, измеримое В; это множество
получается непосредственно, если провести все параллели к оси ОХ
и удалить из каждой из этих параллелей изолированные точки тех
линейных замкнутых множеств, по которым эта параллель пересекает
кривую.
Мы можем повторить эту операцию и удалить из <§0 все
изолированные точки, лежащие на параллелях к оси О Ху что дает нам счетное
множество новых множеств U\\ U\\ . . . L^\ ..., измеримых В
и однозначных по отношению к оси OY, Легко видеть, что эту
операцию можно повторять и что мы не встретимся ни с каким
препятствием до тех пор, пока все точки кривой у=/{х) не будут удалены.
Но это, несомненно, случится после счетного множества указанных
операций, так как индексы остановки а ограничены.
Итак, мы можем рассматривать кривую у=/{х) как соединение
счетного множества множеству измеримых В: Lv L2, ..., Lny ...,
однозначных по отношению к оси OY.
Этими рассуждениями наше предложение доказано, но мы хотим
еще уточнить выбор однозначных множеств Ln.
Прежде всего мы можем предполагать, что множества Ln попарно
без общих точек. Чтобы убедиться в этом, достаточно сохранить в Ln
точки, которые не принадлежат ни одному из предыдущих множеств L]9
Z,2, ..., Ln-т, что не уничтожает измеримости В множества сохраненных
точ^ек.
Установив это, преобразуем множества Ln следующим образом:
возьмем L: и прибавим к Lx все точки Ln> проекции которых на ось OY
не принадлежат ни к одной из проекций предшествующих множеств
Li, i<^n. Если мы произведем эту операцию дая каждого л, мы
получим множество, измеримое В, однозначное по отношению к оси OY,
проекция которого на OY совпадает с проекцией кривой z/=/(jc).
Обозначим это однозначное множество через Л,; ясно, что точки Aj
принадлежат к кривой у=/{х) и что Лх содержит L}.
Удалим из каждого из членов последовательности L]y L2, ..•
, Ln, ... все точки, принадлежащие к Aj; первый член будет полностью
удален. Но с остающимися частями множеств Lm n > 1 мы можем
повторить ту же операцию, и таким образом мы получим множество Л^,
однозначное и измеримое В, без общей точки с LT. Ясно, что сумма
AjH-Ag содержит Ll-¥-L2 и что проекция А2 на QY в точности
совпадает с множеством тех точек Е> в которых параллели к оси ОХ
пересекают кривую у=/(х) по крайней мере в двух точках1.
Напомним, что Е есть проекция кривой y='f(x) на оеь ОК.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
205
Ясно, что если мы возобновим эту операцию и будем ее повторять
неограниченно, мы получим конечную или бесконечную
последовательность множеств, измеримых 5,
^)у ^2> • • •> ^я> • • •
попарно без общих точек, однозначных по отношению к оси OY,
причем их соединение совпадает в точности с самой кривой у =/(х).
Важно заметить, что проекция Л,^ на О У содержится в проекции Аи.
Но разность этих двух проекций есть множество тех точек оси OY,
в которых параллели к оси ОХ пересекают кривую у=/(х) равно
в п точках. Значит, это множество также измеримо 5.
Произведем другое преобразование множеств L]f Z^, ..., Lny •..
Прежде всего прибавим к Ьл точки всех тех Lny n >1, проекции
которых на О К не принадлежат ни к одной из проекций
предшествующих множеств ЬЛУ L2, •. •> Ln^y. Этим способом мы получим множество,
измеримое 5, однозначное и проекция которого на О К совпадает с Е;
пусть \ — это множество. На плоскости XOY мы можем провести
однозначную кривую &л% которая содержит множество \ и задана
уравнением х = ф, (у), где &} есть однозначная функция классификации
Бэра, всюду определенная на области е7у.
Установив это, обозначим через L и V части множества L„,
расположенные соответственно ниже и выше однозначной и всюду
определенной кривой J2V Очевидно, мы можем возобновить указанную
операцию над последовательностями однозначных множеств L\y L'v ...
и L2> L'v ..., что дает нам две новые кривые, однозначные и
определенные всюду на О К, пусть &г и ^з» из которых первая целиком лежит
ниже .2?!, а вторая целиком выше 2?х. Важно заметить, что соединение
кривых J2?j, &г и &z содержит L} и L2. Построенные кривые &2 и &%
задаются уравнениями x = ty2(y) и x = tyz(y)y где <j>2 и Фз СУТЬ одно-
значные функции классификации Бэра, определенные всюду на OY.
Три построенные таким образом кривые «S?j, &2 и &ъ Аелят плоскость
XOY на четыре части, и мы можем возобновить указанную операцию
над частями множеств L3, Liy ..., содержащимися в этих частях
плоскости; таким образом, мы получим четыре новые кривые &i9 «^s»
-2?в, ^7, однозначных и всюду определенных на О У.
Важно заметить, что соединение предыдущих кривых и этих кривых
содержит кривые Lly L%, Lj.
Продолжая таким же образом, мы получим неограниченную (или
конечную) последовательность кривых «2^, ^2,..., &пу •..,
однозначных относительно оси OY и всюду определенных, соединение
которых непременно содержит все точки рассматриваемой кривой
у=/(х); каковы бы ни были две кривые ^ и &j из этой
последовательности, одна из них расположена ниже другой. Кроме того, всякая
кривда &п задается уравнением x = tyn(y)y где <Ь„ есть однозначная
функция классификации Бэра, определенная всюду на ОУ.
206
Н. Н. ЛУЗИН
В итоге точки кривой у=/(х), где f есть непрерывная и полу*
регулярная функцияу распределяются на не более чем счетном
множестве однозначных относительно OY кривых; каждая из этих
кривых задается уравнением х = ф (у), где ф есть однозначная
функция классификации Бэрау всюду определенная на OY; наконец,
каждая из этих кривых лежит либо нижеу либо выше другой.
После того как этот важный частный случай изучен подробно»,
мы рассмотрим несколько более общий случай. Требуется доказать,
что всякое множество &, измеримое Ву расположенное в плоской
области о/ ху и такое у что каждая параллель к оси OY пересекает
<§ не более чем в счетном множестве точек, есть соединение-
счетного множества множеству измеримых В и однозначных
относительно оси ОХ.
Чтобы убедиться в этом, достаточно взять непрерывное регулярное
изображение множества S:
x = g{t), y = h(t),
где, если это нужно, мы пренебрегаем счетным множеством точек &*
Так как всякая прямая х = const пересекает & не более чем в
счетном множестве точек, то функция g(t) полурегулярна. Следовательно*
уравнение x = g(t) определяет t как обратную функцию аргумента ху
и легко видеть в силу полученного результата, что эта обратная
функция есть соединение счетного множества явных однозначных функций
t = ul(x), * = ш2(х),..., / = шя(х)...,
входящих в классификацию Бэра; кроме того, каждая из этих функций шл
рассматривается лишь на некотором множестве еп> измеримом Ву
расположенном на <7W.
Подставляя t в уравнение
U = h(t),
мы получаем счетное множество явных однозначных функций
У = h К ML У = Л К МЬ • • •> У = h К МЬ • • -э
входящих в классификацию Бэра. Заставляя хв уравнении */ = Ма)п(*)]
пробегать множество епу мы получим в плоскости XOY множество Lni
однозначное относительно оси ОХ и измеримое В* Ясно, что данное
множество & есть соединение этих множеств Ьп(ч. т. д.).
Перейдем теперь к общему случаю. Мы докажем следующую общую
теорему1:
Теорема. Если & есть множество точеку лежащих в т-+~1-мер~
ной области о/\... хту> измеримое В и такоеу что каждая параллель
1 См. мою заметку „Sur la representation parametrique semiregulfire des ensemb*
lesa (Comptes Rendus, 29 июля 1929 г.).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
207
к оси OY пересекает § не более чем в счетном множестве точек,
то точки & распределяются на счетном множестве однозначных
поверхностей Sn> измеримых 5, определенных уравнениями
y=fn(xi, х2У.. ., хп)у где каждая /я есть однозначная функция
классификации Бэрау определенная всюду в области с7*,*,...*т; кроме того,
про любые две поверхности S< и Sj можно утверждать, что одна из
них лежит под другой.
Чтобы доказать это, преобразуем m-мерную область с7*,... хщ в
линейную область qJх при помощи взаимно однозначного и взаимно
непрерывного преобразования (стр. 144).
Пусть
*i=*iM> х2 = g2(x)y..., xm = gm(x)t
x = G(xly хъ ..., хт) |
— уравнения, определяющие это преобразование; функции gt и G
непрерывны.
Если мы прибавим к этим уравнениям тождество
У = У>
то получим взаимно однозначное и взаимно непрерывное
преобразование /л-н 1-мерной области с/*,*,... %^ в плоскую область о7жу. Известно
(стр. 144), что множество, получаемое при таком преобразовании из
множества, измеримого В, само измеримо В и того же класса и подкласса;
кроме того, ясно, что множество, однозначное по отношению к оси ОХ
в области о/хуу преобразуется во множество, также однозначное
относительно области о/хх... лщ в о/*,... xmgy и обратно.
Установив это, обозначим через £' результат преобразования <£.
Очевидно, что £' есть плоское множество, измеримое Ву и что каждая
параллель к оси OY пересекает & не более чем в счетном множестве
точек. Следовательно, множество &' есть соединение счетного
множества множеств L\y L2>..., измеримых Ву однозначных относительно
оси ОХ. Следовательно, данное множество <£, будучи прообразом £\
есть соединение множеств Lly L2y...y Ln...; здесь мы через Ln
обозначаем прообраз Ln. Все эти множества однозначны относительно
области о/хх..,хт и измеримы В.
Если над полученными однозначными множествами Ll9 L2,... мы
будем оперировать так, как мы это делали раньше в случае
полурегулярной функции у=/(х)у мы придем к последовательности поверхностей
Sly S2y..., Sny..., содержащих точки данного множества § и
удовлетворяющих формулировке предложенной теоремы (ч. т. д.).
Установив это, вернемся к исследованию данной системы
уравнений (I):
Л \Хц х2у • • •> хм; Уху у29..., ур)=^0у
fq \Xi, x2>..., хш\ у^ У%> • • •> Ур)=z и. )
208
Н. Н. ЛУЗИН
Мы предполагаем, что каждой системе чисел х1У х2>..., хт
соответствует не более чем счетное множество систем чисел у1У У2У--.,ур9
удовлетворяющих этим уравнениям.
Возьмем две области о/хх...гт и о/у{...ур и преобразуем их
соответственно в две линейные области <Р'х и о/у при помощи двух взаимно
однозначных и взаимно непрерывных преобразований. Пусть
xi = gi{x), x2 = g2{x)y...y xm = gm(x)y
X = U \Х±У Х2У - • •> Х1П)
и
У\ = ^1 (у), у2 = h (у),..., ym = hm (у),
у = Н(у1У у2У..., ур)
— уравнения, устанавливающие эти два преобразования.
Легко видеть, что уравнения (1) и (2), взятые вместе, устанавливают
взаимно однозначное и взаимно непрерывное преобразование тон-/>-мер-
ной области о7х{...хтУк...ур в плоскую область Jzy. Отсюда следует, что
множество &\ являющееся результатом преобразования <?, есть
множество, измеримое Ву расположенное на плоскости XOY и такое, что
всякая параллель к оси OY пересекает <£' не более чем в счетном
множестве точек.
Пусть Lly L2,..., Liy... суть множества, измеримые В, однозначные
по отношению к оси ОХ и такие, что их соединение совпадает с <£'.
Мы предполагаем, что Lt-расположено на однозначной кривой у = й){(х),
где функция &i{x) всюду определена и входит в классификацию Бэра.
Если мы подставим найденное значение */ = ч(дс) в уравнения (2) и
затем возьмем значение х из уравнений (1), то мы придем к решению
предложенной системы (I), выраженному при помощи функций,
входящих в классификацию Бэра, от аргументов хх, дс2,..., хт:
yi = hi{"i\G{xl9 x2,..., хт)])у
yP = hp{ui[G(xly х2У..., хт)]}.
Ясно, что написанные здесь сложные функции входят в
классификацию Бэра и что полное решение предложенной системы (I) мы
получим, полагая i = 1, 2, 3,.. .
Итак, мы приходим к следующему заключению: полное решение
предложенной системы уравнений образовано из счетного множества
систем из р функций «р^, <?2'\..., <р^, входящих в классификацию
Бэра; каждая из этих систем удовлетворяет предложенным
уравнениям на некоторой части £* области существования Еу причем эта
часть измерима В.
Итак, закон (L2) Лебега в этом случае сохраняется.
Случай Ш, где одна из неявных функций многозначна и имеет
не более счетного множества значений. Этот случай аналогичен
случаю I, где одна из неявных функций однозначна.
(1)
(2)
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
209
Область существования. Эта область, вообще говоря, неизмерима В,
так как рассматриваемый случай содержит, как частный случай,
случай I, а в случае I область существования может быть неизмерима В.
Итак, первый закон (Lx) Лебега уже не применим здесь.
Природа рассматриваемой неявной функции. Напротив, второй
закон (L,) Лебега остается в силе. В самом деле, мы увидим, что
рассматриваемая неявная функция принимает значения со счетного
множества однозначных неявных функций, входящих в классификацию Бэра.
С этой целью мы докажем следующую теорему из геометрии:
Теорема. Если <S есть аналитическое множество, лежащее
в т -+- 1-мерном пространстве о7^ ... хщу и такое, что каждая
параллель к оси OY пересекает <$ не более чем в счетном множестве
точек или не пересекает его совсем, то множество £ можно
рассматривать как часть некоторого множества Н, измеримого В и
обладающего тем же свойством.
Прежде всего д\я упрощения доказательства этой теоремы мы
сведем общий случай m-ь 1-мерной области gZx,...*^ к случаю плоской
области о7х6.
С этой целью преобразуем /п-мерную область с7а,...7т в линейную
область q/w при помощи взаимно однозначного и взаимно непрерывного
преобразования. Пусть
*i = &(*)> х2 = g*{x),..., xm = gm{x),
x=G{xl9 х2,..., хт)
— уравнения, устанавливающие это преобразование; функции gt и G
непрерывны.
Если мы прибавим к этим уравнениям (1) тождество
У = У,
то мы получим взаимно однозначное и взаимно непрерывное
преобразование т -+- 1-мерноЙ области SfXx... х^ в плоскую область о/ху. Если &
есть аналитическое множество, расположенное в ^...х»* и такое, что
каждая параллель к оси OY пересекает § не более чем в счетном
множестве точек, то образ &' множества <§ есть аналитическое множество,
обладающее тем же свойством.
Допустим, что рассматриваемая теорема справедлива для плоской
области и, следовательно, существует плоское множество Н\
измеримое В, содержащее аналитическое множество &' и такое, что каждая
прямая, параллельная оси OY, пересекает Н не более чем в счетном
множестве точек. Ясно, что прообраз Н множества Н измерим В,
содержит & и обладает опять тем же свойством.
Итак, все сводится к доказательству теоремы д\я плоского
аналитического множества <£.
Мы начнем с того, что рассмотрим в трехмерной области <5fхуж
элементарное множество (стр. 121)> проекция которого на плоскость XOY
(1)
210
Н. Н. ЛУЗИН
совпадает с данным аналитическим множеством <§. Мы предполагаем
(стр. 161), что элементарное множество Q есть общая часть сумм
параллелепипедов рангов 1, 2, 3,..., таких, что каждый параллелепипед
ранга п содержит счетное множество параллелепипедов следующего
(л-1-1)-го ранга, причем их проекции на ось OZ образуют
возрастающую последовательность сегментов. Верхние грани этих
параллелепипедов образуют решето (стр. 162) С, называемое элементарным и
определяющее аналитическое множество &.
Пусть тс— один из этих параллелепипедов. Обозначим через Qz
часть Q, содержащуюся в тс, через С„ — часть С, содержащуюся в тс,
и через <£к — проекцию QK на плоскость XOY. Легко видеть, что Сп
есть решето, определяющее аналитическое множество &к.
Пусть х — любая точка линейной области о/Л и пусть Рх—
перпендикуляр из точки х к оси ОХ> лежащий в плоскости XOY. Так как
множество £ пересекается каждым Рх не более чем в счетном
множестве точек, то дополнение С<§п измеримо В на Рх.
Отсюда следует, что общая часть CSr и Рх содержится в счетном
множестве конституант, измеримых В> на которые разлагается
дополнение С&ъ* Отсюда мы заключаем, что для каждого Рх существует
конечное или трансфинитное число второго класса ссМ такое, что сумма
конституант с индексами, превосходящими или равными а^), содержит
лишь счетное множество точек на Рху причем это число а£) нельзя
уменьшить, не теряя этого свойства.
Если мы рассмотрим все решето С, а не его часть, лежащую в
некотором параллелепипеде тс, то мы обозначим просто через лх
трансфинитное число, которое мы только что определили.
Установив это, мы докажем, что числа <хх ограничены, т. е. что
существует трансфинитное число р второго класса, превосходящее
каждое ал, каково бы ни было х в области о/х*
С этой целью допустим обратное, т. е. что числа сих не ограничены.
В этих условиях мы рассматриваем систему из к параллелепипедов тсг,
~2> • • -» тс*> проекции которых на плоскость XOY не имеют попарно
общих точек, и которые обладают следующим свойством: каково бы
ни было трансфинитное число ?, существует точка х такая, что
у каждого множества C£r.i(f = 1, 2, ..., к) по крайней мере одна
конституанта с индексом, превосходящим 7> имеет несчетное множество
точек на Рх. Такие системы тсь тг2,..., ък существуют, так как вся
область ofхуя является такой системой (к = 1).
Мы докажем, что каждый параллелепипед ^(/ = 1, 2, ..., к) содержит
пару параллелепипедов тс/ и тс^' такую, что система из 2к
параллелепипедов тс/, тс/',..., тс'к, тс'^ обладает тем же свойством.
Чтобы доказать это, возьмем любое трансфинитное число if. Пусть т*
есть трансфинитное число, превосходящее произведение *у ' й)Ш» В силу
гипотезы о параллелепипедах тсх, тс2,..., щ существует точка х, обла-
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
211
дающая следующим свойством: каждое аналитическое дополнение
С£щ(1 = 1, 2, ..., к) имеет конституанту 0< индекса, превосходящего *('>
которая содержит несчетное множество точек на Рх. Так как общая
часть *% • Рх несчетна, то на Рх найдется такой сегмент А,, что часть Ь{ • РХ1
содержащаяся в Д<, несчетна, тогда как часть bi • Pzy лежащая вне А<,
счетна, причем А#. есть наименьший сегмент, обладающий атим свойством.
Установив это, возьмем целое положительное л, настолько большое,
чтобы все параллелепипеды ранга л, содержащиеся в параллелепипеде ъ1у
имели ребра меньше, чем -^ длины А^ каково бы ни было / = 1, 2, ..., к.
Разделим каждый сегмент At. на три равные части и удалим
центральную часть. Каждый из двух остающихся сегментов содержит несчетное
множество точек Ь{ • Рх. Выберем произвольно точку множества Ь4 • Рл
в каждом из этих сегментов; пусть М\ и М'1 — эти точки. Легко видеть,
что существует несчетное множество таких пар точек М\ и Л/,'.
Проведем через точки М{ и М'{ прямые, параллельные оси OZ; пусть Df
и D'l — эти параллели. Так как точки М\ и М'1 принадлежат к
конституанте &{> отсюда следует, что прямые D\ и D"{ пересекают решето Сч
по двум вполне упорядоченным множествам RM' и RM"y каждому из
которых соответствует трансфинитное число, превосходящее "['. Но
проекции параллелепипедов ранга л на ось OZ образуют вполне
упорядоченное множество сегментов, которому соответствует трансфинитное
число о)я. Отсюда следует, что существует по крайней мере два
параллелепипеда ранга п таких, что частям RM' и RM''> содержащимся
соответственно в этих параллелепипедах, соответствуют два трансфинитных
числа, превосходящих т» Очевидно, что проекции этих двух
параллелепипедов ранга л на плоскость XOY не имеют общей точки, так как
эти проекции содержат соответственно точки М\ и М[ и имеют стороны,
1 А
длины которых меньше, чем -^ длины &{.
Так как существует лишь счетное множество пар параллелепипедов
ранга л, и так как, с другой стороны, существует несчетное
множество пар точек М\ и Л/,", мы заключаем, что в каждом
параллелепипеде ^ существует два параллелепипеда тс'4 и ъ"{ ранга л такие, что
прямые D\ и ZX', проведенные через точки М\ и Л/", пересекают
решета С'п С'ъ по вполне упорядоченным множествам, которым
соответствуют трансфинитные числа, превосходящие 7, причем таких
точек М\ и М'! несчетное множество.
Другими словами, мы доказали, что, каково бы ни было
трансфинитное число 7> перпендикуляр Рх содержит несчетное множество точек
двух конституант с индексами, превосходящими ?> V и &п"9
аналитических дополнений С&%\ и CS^; здесь аналитические множества £%
212
Н. Н. ЛУЗИН
и £г" суть проекции элементарных множеств Q^ и QTC"> содержащихся
в параллелепипедах \ и тс7.
Из предшествующего следует, что система из 2к параллелепипедов
k'v rcj', ..., тг^, тг^ обладает тем же свойством, как и начальная система к
параллелепипедов [24].
Установив это, вернемся к доказательству формулированной теоремы.
Выше мы определили для каждого перпендикуляра Рх трансфинитное
число ах и предположили, что числа ах не ограничены, когда х
пробегает область <JX. При этой гипотезе мы доказали, что каждая система
из к параллелепипедов п1У тг2,..., ъку обладающая специальным свойством,
содержит систему из 2к параллелепипедов п'1У ^', ..., ~'къ"к, обладающую
тем же свойством. Так как проекции параллелепипедов т^, ~2, ..., ък на
плоскость XOY попарно не имеют общих точек и все имеют точки на
одной и той же параллели к оси OYy то, повторяя этот процесс
неограниченно, мы получим совершенное множество, содержащееся в
элементарном множестве Q, проекция которого на плоскость XOY есть
совершенное множество, лежащее на прямой, параллельной оси OY.
Но это невозможно, так как проекция Q на плоскость XOY есть
аналитическое множество £, а мы знаем, что каждая параллель к оси OY
пересекает & не более чем по счетному множеству точек.
Итак, трансфинитные числа ах ограничены.
Установив это, возьмем трансфинитное число Р второго класса,
превосходящее все а^. Рассмотрим все конституанты аналитического
дополнения CS, индексы которых меньше р. Пусть S есть соединение этих
конституант; множество S, очевидно, измеримо В. Обозначим через Н
дополнение ко множеству S; множество Н также измеримо В. Ясно,
что Н содержит данное аналитическое множество <§*
Я теперь утверждаю, что множество Н пересекается каждой
параллелью к оси О У не более чем в счетном множестве точек. В самом
деле, в противном случае мы бы имели перпендикуляр Рх, содержащий
несчетное множество точек из //. Эти точки образуют множество,
измеримое В. Значит, это множество содержится в счетном множестве
конституант С<§, причем эти конституанты имеют индексы,
превосходящие р. Отсюда следует, что существует конституанта индекса,
превосходящего Р, которая имеет несчетное множество точек на
перпендикуляре Pw. Но это невозможно, так как р превосходит ая.
Итак, мы определили множество //, измеримое В} содержащее
данное аналитическое множество & и такое, что каждая параллель к оси OY
пересекает Н не более чем в счетном множестве точек, а это и
доказывает высказанную теорему (ч, т. д.).
Из доказанной теоремы следует, что всякое аналитическое
множество St лежащее q т-*-1-мерной области Л,...*,^ и такое, что
каждая параллель к оси OY пересекает & не, более чем в счетном
множестве точек, есть соединение счетного множества аналитиче-
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
213
ских множеств &1У 62> —, &и> —> расположенных соответственно
на однозначных поверхностях у = ъ(х1У х.1У..., хк)у где ?* суть явные
функции классификации Бэра, определенные всюду на 7жг...хт.
Чтобы применить этот результат к изучению неявных многозначных
функций с не более чем счетным множеством значений, достаточно
заметить, что многозначная неявная функция у4 имеет в качестве
геометрического образа аналитическое множество S{t\ лежащее в
области o7Zx...zmui и получаемое проектированием множества £ на эту
область. Если мы предположим, что неявная функция у{ имеет не более
счетного множества значений, то аналитическое множество $%*
удовлетворяет условиям предыдущего результата.
Итак, счетнозначная неявная функция у{ разлагается на счетное
множество однозначных функцийу входящих в классификацию Бэра>
а это показывает, что второй закон (L2) Лебега частично сохраняет
силу.
Изучение общего случая в проблеме неявных функций
Общие замечания. После того как были изучены естественно
представлявшиеся частные случаи, мы переходим к общему случаю.
Изучение этих частных случаев показало нам, что область
существования неявных функций бывает в зависимости от того или иного
случая измерима или неизмерима В. Итак, первый закон Лебега иногда
сохраняется, а иногда не сохраняется в этих частных случаях.
Напротив, второй закон (Z,2) Лебега в этих частных случаях всегда
сохраняется хотя бы частично. Точнее говоря, предполагая одну из
неявных функций, например yiy имеющей не более счетного множества
значений, мы видели, что можно каждой точке М(х1У xv ..., хт)
области существования Е привести в соответствие единственное число ср,
выбранное среди значений этой неявной функции гд- в точке М так,
что определенная этим способом однозначная функция ср (х19 х2У ..., хт)
совпадает с некоторой функцией классификации Бэра.
Но мы увидим, что в общем случае, где относительно неявных
функций ничего не предполагается, определение такой однозначной
функции ф (х1У х2У ..., л:т) становится невозможным. Это значит, что
хотя мы всегда можем образовать однозначную функцию у(х1У хъ ...
..., л:т), выбирая соответствующим образом ее значения среди
значений рассматриваемой неявной функции (стр. 192), но эта функция f
не совпадает на области существования Е ни с какой функцией
классификации Бэра.
Эта невозможность становится почти банальной, если область
существования Е неизмерима В. Чтобы убедиться в этом, возьмем уравнение
F(x, y) = 0
такое, что область Е существования неявной функции у неизмерима 5*
Так как F входит в классификацию Бэра, то множество & точек
214
Н. Н. ЛУЗИН
плоскости XOY, в которых F обращается в нуль, измеримо В. Область
существования Е есть ортогональная проекция £ на ось ОХ. Если
существует однозначная функция <р (л:), определенная на Ef
удовлетворяющая уравнению F=0 и совпадающая на Е с функцией, входящей
в классификацию Бэра, то общая часть Н множества £ и кривой
У = <?(х) есть однозначное множество, измеримое В. Следовательно,
проекция Н на ось ОХ должна быть измерима В9 что невозможно, так
как эта проекция совпадает с областью Е (ч. т. д.).
Итак, изучение случая, когда область существования неизмерима В9
не представляет никаких затруднений. Но не так обстоит дело, когда
область существования измерима В. Однако мы увидим, что есть
случаи, когда область существования измерима В (и даже совпадает
с основной областью о/х^..*^) и где тем не менее невозможно
определить однозначную функцию <р (х19 лг2, ..., л:т), входящую в
классификацию Бэра, значения которой выбираются из значений
многозначной неявной функции.
Эти случаи очень важны, но, чтобы доказать, что такие случаи
эффективно существуют, мы нуждаемся в некоторых предварительных
рассмотрениях.
Прежде чем перейти к доказательству, мы заметим, что речь идет
о решении следующей проблемы из геометрии:
Найти множество £9 измеримое В, расположенное в т -ь
1-мерной области с7«1ж,...хту, проекция которого на 3*,...%» совпадает со всей
этой областью и которое обладает следующим свойством: не
существует никакой поверхности S, определенной уравнением
где <р входит в классификацию Бэра, и такой, что каждая точка S
принадлежит к £.
В «самом деле, пусть F(xl9 х2, .., хту у) есть характеристическая
функция для множества £. Так как £ измеримо В, то F входит в
классификацию Бэра. Так как каждая точка М{х19 х19 ..., хт) области о/x^..zm
есть проекция точек £> то уравнение F(xl9 ..., хт9 у) = 0 допускает по
крайней мере одно решение у для каждой системы чисел х19 ..., хт.
Но в силу предполагаемого свойства множества £ ясно, что не
существует никакого однозначного решения у = <?(х19 х2, ..., хт), где <р
входит в классификацию Бэра (ч. т. д.).
Итак, все сводится к решению только что поставленной
геометрической проблемы.
Точки единственности1* Для решения предложенной проблемы из
геометрии нам понадобится одно важное понятие, а именно понятие
о точках единственности.
1 В качестве метода для анализирования общего случая неявных функций я взял
изучение точек единственности; см. мою заметку в Comptes Rendus Acad. Sci.»'
26 сентября 1929 г. „Sur les points d'unicite d'on ensemble mesurable Bu.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
215
Пусть ё— любое множество точек, расположенное в области г7хх...х^.
Мы скажем, что точка N(xly ..., хту у) из £ есть точка единственности
относительно оси OY, если параллель к этой оси, проведенная через N,
не пересекает 5 ни в какой точке, отличной от N. Множество всех
точек единственности называется множеством единственности для ё и
будет обозначаться через §1Л
Пусть Е — проекция ё на область о7хх...хт. Пусть
есть однозначная функция, определенная на Еу и *S— поверхность,
определенная уравнением у = у(х1У ..., хт).
Ясно, что если каждая точка из S принадлежит к <£, то эта
поверхность непременно должна пройти через всякую точку единственности
для S; это значит, что множество ё\ должно принадлежать к
поверхности S.
Метод дая разрешения поставленной проблемы из геометрии состоит
в том, чтобы построить множество ё, измеримое Ву у которого
множество единственности ёх таково, что a priori невозможно провести
через ё\ однозначную поверхность S, определяемую при помощи
функции классификации Бэра.
Заметим, что легко установить природу множества
единственности ёх для множества ё, измеримого В: это — аналитическое
дополнение,
В самом деле, мы видели (стр. 143), что точки М(х1... хт)
области 0/хх%,.хту
в которых параллель к оси OY пересекает ё по крайней
мере в двух точках, образуют аналитическое множество. Пусть Е2 —
это множество. Так как ё измеримо Ву то все точки ё, проекции
которых принадлежат к Е1У образуют множество <§2, которое должно быть
аналитическим. Следовательно, точки ё, не принадлежащие к ё2,
образуют аналитическое дополнение. Но ясно, что это множество
совпадает с ёг (ч. т. д.).
Проекция множества единственности. Проблема о природе этой
проекции и ее редукция. Мы видели, что очень легко установить
природу самого множества единственности ё^ Напротив, очень трудно
узнать природу проекции Ех множества единственности ёг. Следующие
страницы имеют целью констатировать тот замечательный факт, что
множество Ех есть также аналитическое дополнение.
Чтобы избежать второстепенных осложнений в наших рассуждениях,
мы начнем с редукции проблемы, упрощая природу множества £а.
Пусть ё — множество, измеримое Ву расположенное в ш+ 1-мерной
области g^...*„#, и <§\ — множество единственности для ё. Пусть Е
и Е1 — соответственно проекции ё и ё± на область о/^...^.
Мы уже видели, что можно установить взаимно однозначное и
взаимно непрерывное соответствие между точками области о/хл.^жт и точ-
216
Н. Н. ЛУЗИН
ками новой линейной области <Э'х> причем это соответствие
устанавливается формулами
*1=Л(*)> *2 = Л(*)> •••> *m = /m(*)>
X Г \Х^у Х2, . . •, Хт)у
где все функции /, и F непрерывны.
Мы видели, что в этом соответствии двух областей с7Х) ,%тт и <3 х
каждому множеству, измеримому В, соответствует множество,
измеримое В того же класса, и что каждое аналитическое множество
преобразуется в аналитическое.
Прибавляя к предыдущим уравнениям (1) тождество
У = У>
мы получаем преобразование т -+■ 1-мерной области oJXx%_Jmll в плоскую
область Jxy. Пусть £, е1э е и ех — образы множеств <£, 6\, £ и Ех.
Ясно, что £ измеримо В, ^ — множество единственности для е, е
и ех — проекции е и ^ на ОХ. Для того чтобы Ег было аналитическим
дополнением, необходимо и достаточно, чтобы ех было аналитическим
дополнением.
Итак, все дело сводится к плоской проблеме. Но мы увидим, что
возможно ее еще упростить.
С этой целью рассмотрим регулярное и непрерывное
параметрическое изображение множества е (пренебрегая, быть может, счетным
числом его точек). Пусть
это изображение; функции <р и & непрерывны на .7*.
Рассмотрим на плоскости ХО Т кривую jt = cp(f). Множество
значений <р (t)f очевидно, совпадает с еу тогда как ех есть множество всех
тех точек х, в которых прямая, параллельная оси О Т, пересекает
кривую один и только один раз.
Итак, все сводится к выяснению природы множества ег тех точек х>
в которых параллель к оси ОТ пересекает кривую х = <? (t) один и
только один раз, причем функция <р непрерывна на <Р\. Это и есть
редукция проблемы.
Природа проекции множества единственности» Итак, надо
изучить природу множества Е тех точек у> для которых
уравнение y = f(x) имеет единственный корень, причем f{x) непрерывна на о/х>
Пусть о19 о2, ..., Ьп9 ... — все интервалы Бэра порядка 1 в интервале
(0<х<С1). Пусть еп — множествво значений /(х) на Ьп и пусть Д„ —
наименьший сегмент, содержащий еп; Дя расположен на оси OY. Так
как множества еп аналитические, то к любым двум из них, например
к е4 и ej, можно применить второй принцип. Обозначим через е^ общую
часть е4 и в/, через Rj и Rj4 разности е4 — e4j и ej — в^. В силу вто^-
а)
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
217
рого принципа можно найти два аналитических дополнения H{j и HJ{
без общих точек, содержащие соответственно R{J и RJim Очевидно,
можно предположить, что Нц содержится в Д,, a Hj4 в Ду.
Установив это, фиксируем индекс / и заставим j пробегать все
целые положительные числа, исключая /. Пусть //, — общая часть всех
ЭТИХ Hijl
Hi = Hn ' Ия • • • Hit,_! • Н. .+1...
Ясно, что Hi есть аналитическое дополнение, содержащееся в *\. Легко
видеть, что все эти //Д/=1, 2, 3,...) не имеют попарно общих
точек.
Главное свойство //< состоит в том, что это множество заведомо
содержит все те точки у, для которых уравнение y=/(jt) имеет один
и только один корень, причем этот корень лежит в Ь{.
В самом деле, каждая точка у, удовлетворяющая этому условию,
принадлежит всем RiJy значит, всем Нц- и, следовательно,
множеству Н{.
Кроме того, для всякого у> принадлежащего к Hif все корни
уравнения у=/(х) принадлежат к 8i#
Таким образом, мы получили счетную последовательность Ни Н>,...
. .., Нп... аналитических дополнений попарно без общих точек; их
соединение содержит множество Ег. Мы назовем эти множества Нп
аналитическими дополнениями порядка 1.
Чтобы определить аналитические дополнения порядка 2> мы берем
любое множество Hi и соответствующий интервал Бэра 8^. Мы делим о, на
все интервалы Бэра порядка 2; пусть 8^, 8^, ..., 8^,. .. — эти интервалы.
Обозначим через ек множество значений /(х) на 8^ и через
А^—наименьший сегмент оси О У, содержащий ек.
Мы можем оперировать с множествами ек таким же образом, как
с ранее определенными множествами е4 и мы таким образом получим
счетную последовательность аналитических дополнений Нк попарно без
общих точек, содержащихся в соответствующих &к и в Hiu
Важно заметить, что Нк содержит все точки у, для которых
уравнение у=/(х) имеет один и только один корень, причем этот корень
принадлежит к Ъ'к.
Кроме того, для каждого у, принадлежащего к Н[, все корни
уравнения у=/(х) принадлежат к 8^.
Все так определенные для каждого Hi множества Нк мы назовем
аналитическими дополнениями порядка 2.
Описанный нами процесс неограниченно продолжается и дает нам
аналитические дополнения всех порядков»
Обозначим через Sn сумму всех аналитических дополлений порядка п;
множество Sn есть аналитическое дополнение. Пусть, наконец, Н есть
общая часть всех *£»; множество Н есть, очевидно, аналитическое
дополнение.
218
Н. Н. ЛУЗИН
Я теперь утверждаю, что Не точности совпадает с множеством Ех,
природу которого мы хотим определить.
Прежде всего Н содержит Еи так как каждое Sny очевидно,
содержит Ег.
С другой стороны, пусть у0 есть точка //; так как Sn есть сумма
аналитических дополнений попарно без общих точек, то у0 принадлежит
одному и только одному из них. Пусть hn — это аналитическое
дополнение, оп — наименьший сегмент, содержащий Л*, и йя — интервал Бэра
порядка п, соответствующий h^ В силу свойства аналитических
дополнений порядка п все корни уравнения Уо=/(х) содержатся в &„.
Заставляя изменяться л, мы получаем неограниченную
последовательность интервалов Бэра $lf fr2, ...,$„,... порядков соответственно
1, 2, 3,..., содержащихся друг в друге. Следовательно, существует
иррациональная точка л:0, принадлежащая всем &„.
Я теперь утверждаю, что #о=/(«*<>)• В самом деле, обе точки уь и
/(jc0) принадлежат к &„, каково бы ни было я, а так как длина Ьп
стремится к нулю, когда п неограниченно возрастает, то постоянные
точки у0 и /(х0) должны совпасть.
С другой стороны, х0 есть единственный корень уравнения
^/0=/(х0). В самом деле, все корни этого уравнения содержатся в &я,
каково бы ни было л, а длина &п стремится к нулю.
Значит, множества Н и Ех тождественны и, следовательно, Ег есть
аналитическое дополнение (ч. т. д.)*
Таким образом, мы приходим к следующему результату:
Теорема. Каково бы ни было множество &, измеримое В>
множество &х его точек единственности и проекция Е1 этого множества
единственности являются оба аналитическими дополнениями.
Важно заметить, что проекция Е множества точек единственности £г
есть произвольное аналитическое дополнение.
Чтобы убедиться в этом, ограничимся случаем множества &,
измеримого В и лежащего на плоскости.
Пусть Ех — совершенно произвольное линейное аналитическое
дополнение, лежащее на оси ОХ. Множество СЕг есть аналитическое
множество. Значит, существует плоское множество //, измеримое Ву проекция
которого на ось ОХ совпадает с СЕг. Обозначим через S соединение Н
и параллели к оси ОХу не пересекающей //. Такие параллели всегда
существуют, так как мы можем предположить, что множество Н лежит
между прямыми г/ = 0 и у=1* Легко видеть, что & измеримо В и
имеет Ег проекцией своего множества единственности.
Однако нельзя утверждать, что всякое плоское аналитическое
дополнение 0, пересекаемое не более чем в одной точке каждой
параллелью к оси OY% служит множеством единственности дая некоторого
плоского множества &, измеримого В.
В самом деле, если бы это было так, то проекция 8 на ось ОХ
<)ыла бы непременно аналитическим дополнением. Но в силу нсследо-
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
219
ваний Мазуркевича, которое мы изложим в главе V, проекция
однозначного аналитического дополнения может в некоторых случаях быть
произвольным аналитическим множеством.
Второе доказательство существования двух аналитических
дополнений, неотделимых В. Доказательство предыдущей теоремы
о природе проекции множества единственности и пример, который мы
только что привели, дают нам вполне ясное указание на существование
таких аналитических дополнений.^
В самом деле, допустим противное, т. е. что всякие два аналити-
тических дополнения Н и Н" без; общих точек отделимы В. В этих
условиях любые два множества, взаимно отделимые при помощи
аналитических дополнений, просто отделимы В. Отсюда следует, что в
предыдущем доказательстве мы можем предполагать все отделяющие
множества Hij просто измеримыми В. Из этого вытекает, что множества //,.
всех порядков, а следовательно, и суммы Slf S2, ..., S^ ... также
измеримы В, Но множество Н есть общая часть всех Sn (п = 1, 2, 3, .. .)•
Поэтому Н измеримо В, и мы отсюда заключаем, что проекция
множества единственности всегда измерима £.
Но это невозможно, так как мы показали, что проекция множества
единственности может быть произвольным аналитическим дополнением,
а следовательно, неизмеримым В (ч. т. д.).
Общий случай неявных функций* Отступление в сторону проекций
множеств единственности было сделано с целью разрешения ранее
поставленной проблемы из геометрии: найти в пространстве OXYZ
множество &, измеримое Ву проекция которого на плоскость XOY
совпадает с этой плоскостью и которое обладает следующим свойством:
не существует никакой поверхности Sy определенной уравнением
z =F(xy у), где F входит в классификацию Бэра, причем каждая точка S
принадлежит к ё.
Мы теперь дадим решение этой проблемы.
С этой целью возьмем функцию с? (л*, *), которую мы определили
выше (стр. 126). Эта функция обладает следующими свойствами: 1° она
определена для всех х и t> принадлежащих интервалу (0,1), и входит
в класс 2 классификации Бэра; 2° какова бы ни была функция /(*),
определенная на (0 < х < 1) и непрерывная для всякого
иррационального х, существует такое иррациональное t0, что мы тождественно
имеем
Установив это, возьмем в пространстве OXYZ множество точек
М(х> у, z), координаты которых удовлетворяют уравнению
x = ?(z9 у).
Это множество, очевидно, измеримо В; мы его обозначим через //.
Легло видеть, что Н расположено ниже плоскости z = l. Важно
220
Н. Н. ЛУЗИН
заметить, что множество Н пересекается плоскостью у = Уъ по любой
кривой, непрерывной для каждой иррациональной точки z.
Возьмем теперь на оси ОХ произвольное множество е, измеримое В.
Мы можем определить функцию /(z), непрерывную для всякого
иррационального z и такую, что уравнение х =/(z) дает регулярное
параметрическое изображение множества е (с точностью до счетного
множества точек е)у когда z пробегает иррациональные точки от 0 до -г ,
и дает в то же время регулярное параметрическое изображение (с
точностью до счетного множества точек) дополнения Се> когда z пробегает
иррациональные точки от у до 1. Но так как существует всегда
число у0 такое, что мы тождественно имеем
f (z, y<>)=f{z),
то мы отсюда заключаем, что плоскость у = у0 пересекает множество Н
по однозначной кривой
z = g(x),
где g есть функция, обратная для f(z). Следовательно, эта функция g(x)
входит в классификацию Бэра.
Я теперь утверждаю, что эта функция g(x) может быть как
угодно высокого класса.
В самом деле, рассмотрим множество тех ху для которых мы имеем
неравенство
0<g(x)<j.
Очевидно, что это множество в точности совпадает с множеством е
А так как множество е может быть выбрано из любого класса
классификации Бэра, то мы заключаем1, что класс функции g(x) может
быть предположен как угодно высоким, если только е выбрано
надлежащим образом.
Следовательно, множество Н пересекается некоторыми плоскостями
у = Уо по однозначным кривым, входящим в классификацию Бэра и как
угодно высоких классов.
Отсюда немедленно вытекает, что невозможно провести через точки
единственности множества Н однозначную поверхность z = F(x, y)r
где F входит в классификацию Бэра, так как, если бы это было
возможно, то класс этой поверхности был бы вполне определенным чис-
1 Речь идет о следующим предложении Лебега: для того чтобы всюду
определенная функция f была класса а, необходимо и достаточно, чтобы, каковы бы ни
были а и Ь, множество точек, где мы имеем а < / < Ь, было класса < а и чтобы
оно было эффективно класса о. для некоторых значений а и Ь („Sur les fonctions
representables analytiquement", стр. 167, теорема IV).
Это предложение докадывается трансфияатной индукцией (см. также-стр. 124
настоящего тока. — Ред.).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
221
лом а, и все плоскости у = const пересекали бы эту поверхность по
кривым классов, не превосходящих а. Но мы видели, что классы этих
кривых могут быть как угодно высоки.
Нам остается дополнить множество //, прибавляя к нему новое
множество ff> измеримое В, так чтобы сумма Н-*-Н имела те же точки
единственности, как и //, и чтобы в то же время проекция Н на XOY
совпадала со всей этой плоскостью.
Но это возможно в силу теоремы о природе проекции множества
единственности. В самом деле, обозначим через £х множество точек
единственности для Н и через Ех — его проекцию на плоскость XOY.
Мы знаем, что Ех есть аналитическое дополнение. Значит, его
дополнение СЕ^ есть аналитическое множество. Поэтому существует
множество 0а> измеримое 5, лежащее под плоскостью z = l, проекция
которого на XOY совпадает с СЕ. Обозначим через 0.2 множество,
симметричное с 0L по отношению к плоскости z = l.
Установив это, обозначим через Н сумму 0t -+- 02. Множество
(§ = И ч-//7, очевидно, измеримо В и имеет своей проекцией на XOY
всю эту плоскость. А так как множество единственности для &>
очевидно, совпадает с множеством единственности для //, то мы получили
решение поставленной проблемы (ч. т. д).
Третье доказательство существования двух аналитических
дополнений, неотделимых В. Мы теперь непосредственно укажем два
аналитических дополнения без общих точек, неотделимые 5.
Возьмем снова функцию
у = <?{х, t),
указанную выше. Свойства этой функции, которые нам будут нужны,
таковы: 1° функция <?(дг, /) входит в классификацию Бэра; 2° какова бы
ни была функция /(*), непрерывная в каждой иррациональной точке,
существует такое число £0, что мы имеем тождество
?(*, h)=f{x).
Эта функция z/ = 'f (л:, /) геометрически изображается в виде
однозначной поверхности, расположенной в пространстве OXTY; мы
обозначим эту поверхность через S.
Установив это, проведем плоскость дг = у. Эта плоскость делит
нашу поверхность на две части, Sx и S%.
Обозначим через £ множество всех точек поверхности S, в которых
прямая, параллельная оси ОХ> пересекает S в одной и только одной
точке. Легко видеть, что множество & есть множество единственности
для поверхности S по .отношению к оси ОХ.
Пусть ё' и §" — аналогичные множества единственности
соответственно,для. поверхностей St и *%. Обозначим через £, Е' и Е"
соответственно проекции &, S' и £" на плоскость TOY. В силу тборекш
222
Н. Н. ЛУЗИН
о природе проекции множества единственности множества Е, Е* и Еп
суть аналитические дополнения.
Пусть Нх есть общая часть Е к Е', а Н2— общая часть Е и £":
гл i = Е * Е , //2 ^ Е ' Е .
Эти множества //а и Н2 являются также аналитическими
дополнениями. Легко видеть, что Нх и Н2 не имеют общей точки. В самом
деле, если бы М принадлежало к Н± и Нъ то параллель к оси ОХу
проходящая через М, пересекала бы 5 в одной единственной точке,
что невозможно, так как она должна пересекать и Sx и S2.
Се
/i
Рис. 8.
Мы докажем, что Нх и Н> неотделимы В.
С этой целью возьмем любое линейное множество е, измеримое В;
пусть Се — его дополнение. Существует такое число tQ, что
функция <р (х, t0) разнозначна на порции (0, 1) области <5f z и что ее значения
образуют на порции (О, у) множество е, а на порции (у, 1)
множество Се.
Если мы проведем плоскость t = t0, мы увидим, что она пересекает
множество Hj no e и множество Н2 по Се.
Если бы Нх и Н2 были отделимы В, то существовало бы два
множества Ьх и 02, измеримые В, без общих точек и содержащие
соответственно Нх и Н2. В этих условиях плоскость t = t0 пересекала бы
множества бг и 62 по Двум множествам, которые, очевидно, совпали бы
сей Се. Но это как раз невозможно, так как плоское множество bi
есть множество вполне определенного класса а. Следовательно,
пересекая 0! плоскостями t = const, мы получим линейные множества
классов, не превосходящих а. Но множество е выбрано произвольно, значит,
можно предполагать, что его класс выше а (ч. т. д.).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
223
Метод П. С. Новикова. Выше мы доказали (стр. 213 и 219), что
в общем случае неявных функций второй закон (L2) Лебега больше не
применим. Это значит, что не существует никакой явной однозначной
функции, входящей в классификацию Бэра и принимающей значения
среди значений рассматриваемой многозначной неявной функции. Мы
знаем (стр. 214), что этот вопрос сводится к построению множества £,
измеримого By лежащего в пространстве OXYZy проекция которого на
плоскость XOY совпадает со всей этой плоскостью, и такого, что не
существует ни одной однозначной поверхности S, входящей в
классификацию Бэра, каждая точка которой принадлежит к <?. Мы построили
такое множество, пользуясь свойствами множества единственности и
его проекции.
П. С Новиков решил эту проблему, опираясь на существование
двух аналитических дополнений, неотделимых В1.
Вот метод П. С. Новикова:
Рассмотрим в плоскости XOY два аналитических дополнения Ех и £.,
без общих точек и неотделимые В.
Возьмем в пространстве OXYZ два множества, измеримых Ву пусть
Н1 и H^y из которых первое лежит ниже плоскости z = 0 и имеет
проекцией дополнение СЕХ к множеству Elf а второе лежит выше
плоскости 2 = 0 и имеет проекцией дополнение СЕ2 к множеству £2.
Соединение Н=^Н1-^-Н2 есть множествОу измеримое Ву которое
дает решение поставленной проблемы.
Вот доказательство П. С. Новикова:
Допустим, что существует однозначная поверхность S> заданная
уравнением z~F{xy y)y где F входит в классификацию Бэра, причем
каждая точка S принадлежит к Н. Части Sy расположенные
соответственно ниже и выше плоскости z = 0, обозначаются через Sx и *£>.
Множества Sx и S2, очевидно, однозначны и измеримы В.
Отсюда следует, что проекция а1 множества Sx на плоскость XOY
измерима В, так же как и аналогичная проекция о2 д\я S±. Пусть о —
общая часть о1 и о2, а-^а^- а2; множество а, очевидно, измеримо В.
Пусть 6Х есть разность ох — а и соответственно в2 — разность з2— а.
Ясно, что 0Х и 02 измеримы В и не имеют общих точек.
Мы докажем, следуя методу П. С. Новикова, что \ и 02 отделяют
множества Ех и Е2»
В самом деле, пусть М есть точка Ег. Параллель к оси OZ,
проведенная через My не пересекает поверхность Sl9 но пересекает
поверхность S2; следовательно, М принадлежит к о2. А так как М не
принадлежит к olf то она принадлежит к 62.
Итак, множество Ех содержится в б2# Так же доказывается, что £.>
принадлежит к 61# Следовательно, множества Ьх и 02 измеримы В и
1 Построение которых было дано им самим; см. его исследования о неявных
функциях „Sur les fonctions implicites mesurables Bu (Fund. Math., XVII, 1931).
224
Н. Н. ЛУЗИН
отделяют множества Е2 и Е1У что противоречит сделанной гипотезе
<ч. т. д.).
Замечание
В качестве работы, касающейся вопросов, связанных с вопросами,
изученными в настоящей главе, отметим: F. Vasilesco. Essai sur les
fonctions multiformes de variables reelles (Диссертация, защищенная
в мае 1925 г. в Париже).
Точка зрения, принятая автором в его изящной диссертации,
существенно отличается от нашей. Ф. Василеско рассматривает
многозначные функции как неразложимые организмы и старается изучить их и
классифицировать, в то время как мы рассматриваем многозначную
функцию как очень сложный объект, составленный из однозначных
функций, быть может, идеальных (в смысле Адамара), и которых, вообще
говоря, несчетное множество.
ГЛАВА V
ПРОЕКТИВНЫЕ МНОЖЕСТВА
Определение проективного множества, его преобразование
Введение. В этой главе мы рассмотрим новое семейство точечных
множеств, называемых проективными; их геометрическое
происхождение очень ясно. Это важное семейство множеств содержит как частный
случай все аналитические множества и их дополнения.
В математической литературе можно найти лишь очень немногие
сведения о проективных множествах. Тем не менее те минимальные
результаты, которые мы имеем, показывают, что мы имеем дело
с чрезвычайно важным семейством множеств, имеющих почти
парадоксальные свойства.
Операция проектирования является одной из наиболее простых и в то же
время наиболее важных операций в геометрии; эта операция позволяет
образовывать новые множества, которые можно получить, отправляясь
от уже известных множеств.
Рассматривая проектирование (Р) как операцию и комбинируя ее
с операцией (С), позволяющей переходить от множества к его
дополнению, мы получаем, отправляясь от множеств, измеримых В, сначала
все аналитические множества £, потом, отправляясь от их дополнений
Се, новый класс множеств РСЕ совершенно не известной природы;
потом, отправляясь от их дополнений СРСЕ, новые множества РСРСЕ,
и так далее. Это и будут проективные множества.
Это общее определение проективного множества я дал в своих
первых заметках по проективным множествам1. В этих заметках я стал
на философскую точку зрения и указал те принципиальные трудности,
которые вызываются теорией этих множеств, а также сомнения, касаю-
1 „Sur les ensembles projectifs. . ." (Comptes Rendus Acad. Sci.» 25 мая 1925 г.J.
См. также мои заметки в Comptes Rendos „Sur un ргоЫеше de M. Emile Borel et
les ensembles projectifs.. .* (4 мая 1925 г.); „Les proprietes des ensembles projectifs44
(15 июня 1925 г.); „Sur les ensembles non-mesurables В et Temploi de la diagonale. . ."
(20 июля 1925 г.); „Sur nn probleme de M. Borel ©t la methode des resolvantes"
(17 августа 1925 г.), „Remarques snr les ensembles projectifs4* (24 октября 1927 г.).
226
н. н. лузин
щиеся законности их определения, если стать на точку зрения
Бореля \
Я опустил в этих заметках и в своем мемуаре „Sur les ensembles
analytiques" 2 формулировки и доказательства положительных
результатов об этих множествах, так как изложение их, казалось, должно было
быть длинным и представлять лишь копию теории аналитических
множеств 3.
С другой стороны, Серпинский опубликовал в Fund Math.4 статью
„Sur une classe cTensembles", где он очень ясно указал на трудности,
возникающие при изучении даже весьма простых точечных множеств:
не известно ничего ни об измеримости в смысле Лебега, ни о
категории проекций плоских аналитических дополнений. Позднее Серпинский
в заметке „Sur quelques proprietes des ensembles projectifs" 5
формулировал первые теоремы из этой теории и дал их доказательства в ряде
статей, появившихся в Fund. Math.6
В этой главе я изложу некоторые положительные результаты из
теории проективных множеств. При этом в формулировках и
доказательствах я буду выдерживать возможно более полную аналогию
с теорией аналитических множеств. Метод, которому я буду следовать,
геометрический; именно этим методом я несколько лет тому назад дал
техническое изложение теории проективных множеств7.
Определение проективных множеств* Мы называем проективным
всякое множество точек, которое можно получить, отправляясь от
множества, измеримого Ву при помощи двух основных геометрических
операций, повторенных конечное число раз:
1°. Взятие ортогональной проекции уже определенного множества Е
на область меньшего числа измерений
РЕ. (Р)
1 Е. В or el. Sur les definitions analiti^ueb et sur Tillusion du transfini (Bull, de la Soc.
Math, de France, 47» 42, 1919); его же „Sur Integration des fonctions non bornees et
sur les definitions constructives" (Ann. de l'Ecole Norm. Super., 1920); его же. nLe
calcul des integrates definies" (Journ. de Math., 1912).
2 Fund. Math., X, 1926.
3 Теория проективных множеств была предметом моих лекций, прочитанных
в 1924—1925 гг. в Московском университете. Я сохранил в своих заметках и своем
мемуаре лишь следы предложений, которые, однако, предполагают теорию
проективных множеств достаточно разработанной. Таковы предложения о существовании,
а также о сумме и о произведении проективных множеств.
^ Том 7, 1925, стр. 237—243.
•r> Comptes Rendus, 24 октября 1927.
6 Том XIII, стр. 228 „Sur les families inductives et projectives d'ensembles"; см.
также т. XI, стр 117 „Sur les projections des ensembles complementaires aux
ensembles (A)u и т. XI, стр. 123 „Sur les produits des images continues des ensembles (CA)a.
7 Я намеревался дать полное изложение лекций о проективных множествах,
прочитанных мною в 1924—1925 гг. в Московском университете, в работе „Memoire sur
les ensembles analytiques et projectifs", первая часть которого появилась в Матем.
Сборнике, 33, 327, 1926 (стр. 317 настоящего тома. — Ред.).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ 227
2°. Взятие дополнения уже определенного множества Е
СЕ. (С)
Это определение проективного множества, естественно, приводит
к определению класса проективного множества.
Мы скажем, что некоторое множество точек есть проективное
множество класса п, если его можно представить в виде
РСР ...РЕ
ИЛИ
СРС ...РЕ,
где Е есть множество, измеримое В, лежащее в области любого
числа измерений, и где буква Р, чередуясь с буквой С, написана
ровно п раз, причем такое изображение уже невозможно, если число
п заменить меньшим числом.
Чтобы иметь возможно более полную аналогию с теорией
аналитических множеств, их дополнений и множеств, измеримых В, мы будем
различать в каждом классе прооктивных множеств три различных
рода множеств:
I. Проективное множество <$ класса п мы назовем множеством первого
рода, если его можно представить в виде
РСР ...РЕ
и если его невозможно представить в виде СРС ... РЕ, где буква Р
в обоих случаях написана ровно п раз. Для сокращения мы будем
говорить в этом случае, что проективное множество & есть
аналитическое множество порядка л, и примем для него обозначение (Л*).
Эти множества во всех отношениях аналогичны обыкновенным
аналитическим множествам, неизмеримым В.
II. Проективное множество S класса л мы назовем множеством
второго рода, если его можно представить в виде
СРС ...РЕ
и если его нельзя представить в виде РСР ... РЕ, где буква Р
в обоих случаях написана ровно п раз. Для сокращения мы скажем
в этом случае, что проективное множество £ есть аналитическое
дополнение порядка л, и примем для него обозначение (СЛП)(25].
Эти множества во всех отношениях аналогичны обыкновенным
аналитическим дополнениям, неизмеримым В.
III. Проективное множество & класса п называется множеством
третьего рода, если его возможно представить одновременно в обоих
видах
РСР ... РЕ и СРС ... РЕ',
228
Н. Н. ЛУЗИН
где буЛва Р в обоих случаях написана ровно л раз, а множества Е и
Е" измеримы В. Для сокращения мы будем говорить в этом случае
что проективное множество S есть двустороннее порядка п или
измеримое В порядка п; мы будем его обозначать через (Вп).
Эти множества аналогичны множествам, измеримым В в обычном
смысле.
После того как эти определения установлены, легко видеть, что
всякое аналитическое множество, неизмеримое В, есть множество (Лх),
что его дополнение есть (СА^)> а каждое множество, измеримое В, есть
(/?х), и обратно. Итак, теория аналитических множеств содержится
в теории проективных множеств. Это замечание показывает, что
понятие проективного множества является совершенно естественным.
Преобразование определения проективного множества. Прежде
чем перейти к доказательству эффективного существования проективных
множеств каждого класса и, в частности, множеств (Aft), (САП) и (Вп)
в отдельности, мы преобразуем предложенное определение проективных
множеств.
Вот каково это преобразование. Мы ввели операцию (Р), которая
состоит в том, чтобы брать ортогональную проекцию множества точек,
лежащего в /я-мерной области, на область меньшего числа, например т\
измерений. Это число т не обязательно равно т—1.
Тем не менее, мы покажем, что, не уменьшая общности определения
проективного множества класса л, можно предполагать, что каждая
операция (Р)9 фигурирующая в этом определенищ уменьшает число
измерений в точности на одну единицу, в результате чего, если §
есть проективное множество класса л, лежащее в m-мерной основной
области, то множество & можно рассматривать как получившееся из
множества Е, измеримого В и лежащего в области т-*-п измерений.
Мы начнем со следующего замечания: если MQ(x\, х\> ..,, х°) есть
точка рь-мерной области <7Х х , то ее проекция ^Vq(*J, *!!, • • •> *?) на
v-мерную область Л,*,,.. ^, где v <^ р, получается сохранением v первых
координат точки М и отбрасыванием всех остальных.
Установив это, возьмем проективное множество <§ класса л,
расположенное в лг-мерной области <?*&...хт» Мы предполагаем, что & по*
лучается из некоторого множества £, измеримого В, лежащего в р-мер-
ной области ©^...«р. Пусть М(х19х2У -.., хр) есть переменная точка,
пробегающая область Л,*,...^.
Так как каждая операция Р уменьшает число координат на несколько
единиц, то координаты точки М мы можем разделить на несколько групп:
{ххх2 ... хт) (*т+1 ... *V|) (*vl+i • • • xhJ • • • (-^vi^+i • • • xp)>
где число групп равно л-t-l.
Рассмотрим любую из этих групп, следующую за первой; пусть это
будет группа xv +1 ... xv . Мы можем установить взаимно
однозначное и взаимно непрерывное преобразование области о?*, -ы...*. на об-
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
229
ласть о7Ук. Мы, таким образом, получаем взаимно однозначное и взаимно
непрерывное соответствие между областью о7х1хг...хр и некоторой новой
областью g7Xix, ... zmjji • • • »п- Это преобразование областей ставит в
соответствие множеству Е, измеримому В и лежащему в области с/»,...*^...^,
множество Е'у также измеримое В и лежащее в области (7*,... Mmgi... *,.
Если мы будем применять поочередно к множеству Е> измеримому В,
операции (Р) и (С), для того чтобы в конце концов получить из него
данное проективное множество £, то мы последовательно уничтожим
все скобки, начиная с последней, и мы придем к первой скобке (хх... хт),
содержащей координаты точек множества £.
Так как каждой из исчезнувших скобок соответствует одно и только
одно число у, то ясно, что, применяя к множеству Е', измеримому В,
те же операции (Р) и (С), мы в итоге придем к тому же
проективному множеству S.
Итак, мы приходим к следующему результату: можно предполагать,
что в определении проективного множества класса п каждая
операция (Р) уменьшает число измерений только на одну единицу.
В частности, каждое линейное проективное множество класса п
получается из п -+- 1-мерного множества £, измеримого В.
Мы дополним этот результат следующим замечанием: изучение
проективных множеств, лежащих в многомерной области, сводится к
изучению линейных проективных множеств.
В самом деле, пусть & есть проективное множество, лежащее в
области g7*t ... xm» Соответствие
Xi = giti)> x2 = g2{y)y ,.., xm = g»(y);
y = G{xlf x2, ..., xm),
где gt и G непрерывны, установленное между точками рассматриваемой
области <?мг...хт и новой линейной области <7Я, преобразует данное
проективное множество S в линейное множество £'. В силу предше-
ствующего очевидно, что преобразованное множество &' есть
проективное множество того же класса и того же рода, как и &.
Простейшие свойства проективных множеств
Проекции. Из результатов предыдущего параграфа следует, что
проекция множества (Ая) есть либо проективное множество класса
ниже л, либо множество (£*), либо множество (An). Точно так же
проекция множества (Вп) либо класса ниже л, либо (Вя), либо (Лй).
Только проекции Множеств {СAn) могут дать проективные множества
высшего* класса именно: (А,-ц) или (Дн-i).
В самом деле, если § есть (Ап) или (Вя), то его можно представить
в виде
РСР ...РЕ,
(1)
230 н. н. лузин
где буква Р фигурирует п раз. Если мы проектируем <£, то получаем
множество вида
РРСР ... РЕ.
Но двойная операция (РР), очевидно, тождественна с простой
операцией (P)t уменьшающей число измерений по крайней мере на две
единицы. Следовательно, результирующее множество можно записать,
повторяя букву Р не более чем п раз (предыдущий параграф); значит,
это множество либо класса < я, либо (Bn)t либо {Ап) (ч. т. д.).
Легко видеть, что установленное предложение аналогично теореме
из теории аналитических множеств: проекция аналитического множества
или множества, измеримого 5, есть множество либо аналитическое,
либо измеримое В; каждое аналитическое множество есть проекция
множества, измеримого В.
В силу полной аналогии между множествами (Ап), (САп)у (Вя)9 с
одной стороны, и множествами аналитическими, их дополнениями и
множествами, измеримыми By с другой стороны, естественно возникает
большое число важных проблем.
Чтобы поставить некоторые из этих проблем, удобно предварительно
ввести следующую терминологию: мы скажем, что множество L,
лежащее в плоской области о/хуу есть однозначная кривая, если каждая
параллель к оси О Y пересекает L в одной и только одной точке. Точно
так же мы скажем, что & есть однозначное множество относительно
оси ОХу если всякая параллель к оси OY пересекает & не более чем
в одной точке.
Установив эти определения, мы немедленно встречаемся со
следующими вопросами:
Если <§ есть плоское множество (Вп)> однозначное относительно оси
ОХу должна ли проекция Е множества <S на эту ось быть непременно
множеством (Вп) или класса < п?
Имеет ли однозначное плоское множество класса п—1 своей
проекцией множество (Вп) или класса <С.п? [26].
Можно идти дальше. Мы видели, что каждое однозначное
аналитическое множество содержится в однозначной кривой, измеримой В
(стр. 198) и что каждое множество Еу измеримое Ву пересекаемое
всякой параллелью к оси О К не более чем в счетном множестве точек,
составлено из счетного множества однозначных множеств, измеримых
В (стр. 212).
Вполне естественно поставить аналогичные вопросы относительно
проективных множеств (А„) и {Вп).
Точно так же вполне естественно спросить себя, будет ли всякое
плоское множество (А,), пересекаемое каждой параллелью к оси OY не
более чем по счетному множеству, содержаться во множестве (Вп),
обладающем тем же свойством.
И, аналогично, было бы чрезвычайно интересно доказать, что всякое
плоское множество (САп)у пересекаемое каждой пераллелью к оси OY
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
231
не более чем по счетному множеству, является соединением счетного
множества однозначных {САп) [27].
Проективное множество как множество значений некоторой
функции. Мы видели, что всякое линейное аналитическое множество
можно рассматривать как множество значений, принимаемых на У*
некоторой непрерывной на ,71 функцией /(/).
Аналогично, мы докажем, что всякое линейное множество (Ан) или
(Ви) можно рассматривать как множество значений, принимаемых на
некотором проективном множестве Н низшего класса функцией
f(t)y непрерывной на <7/.
В самом деле, линейное множество Е вида (Ап) или (Вл) можно
рассматривать как проекцию плоского множества S вида (CAn-J. Мы
предполагаем, что <§ расположено в области Jzy и что Е есть проекция
& на ось ОХ.
Преобразуем Q\y в новую линейную область Ыt при помощи взаимно
однозначного и взаимно непрерывного преобразования:
* = <?№, y = 1t(t), I
t = F(x,y)y J
где <р, ф и F непрерывны.
Известно, что в этом преобразовании каждому проективному
множеству соответствует проективное множество того же класса и того же
рода. В частности, множество <S преобразуется в линейное множество И
вида (САп~х), лежащее в области Jt.
Легко видеть, что непрерывная функция х = <р(/) пробегает данное
проективное множество Еу когда t пробегает проективное множество Н
(ч. т. д.).
Если Е есть проективное множество (Ая), лежащее в m-мерной
области с7^г,...хт, то мы преобразуем эту область в линейную область о7х
при помощи формул
*l = gl(x)> *2 = &(■*)> •••> *m = gtn(x); \ ц)
X = G(X19 Xoy . .., *m)> I
где gi и G непрерывны.
Образ £' множества Е есть линейное множество (Ап). Следовательно,
Е' есть множество значений, принимаемых непрерывной функцией
х = <р (t) на некотором множестве Н вида {САп-^). Если мы в функции gi (х)
вместо х подставим <p(f), то мы придем к следующему результату:
Всякое проективное множество (Ап) или (Вп), лежащее в т-мерной
области о/^*..^ можно рассматривать как геометрическое место
последовательных положений подвижной точки М(хх, х^, *.., **»),
координаты которой являются функциями переменного параметра t>
непрерывными на g7*:
232
Н. Н. ЛУЗИН
причем t пробегает проективное множество (САп-г).
Таким образом, мы получили параметрическое изображение
множеств (Ап) и (Вп); легко видеть, что оно аналогично параметрическому
изображению аналитических множеств.
Но как только эта аналогия констатирована, естественно поставить
следующие вопросы: можно ли для каждого множества Вп найти
регулярное параметрическое изображение?
С другой стороны, если S есть множество (Лп), допускающее
регулярное или полурегулярное параметрическое изображение, должно ли оно
непременно быть множеством (2?я)?[28].
Множества параллелей* Лая дальнейшего нам понадобится узнать
природу множеств, образованных из точек, лежащих на прямых,
перпендикулярных некоторой области и проходящих через точки некоторого
проективного множества, лежащего в этой области.
Пусть Е есть проективное множество класса л, лежащее в области
Л,*,... «т- Будем рассматривать эту область как часть области е7в|ва... Г|пГ
и проведем через каждую точку Е прямую, параллельную оси ОУ\
Пусть & есть множество точек, лежащих на всех этих прямых. Надо
узнать природу &.
Так как множество Е есть проективное множество, то мы можем
его получить, отправляясь от множества 6, измеримого В, и лежащего
в области efzfr... <Lp p измерений:
Е= ... РСРЬ.
Мы можем предполагать, что здесь каждая операция (Р) уменьшает
число измерений на одну единицу.
Пусть М(х19 х2, ..., хт) есть любая точка области е?^*,... *т. Точки Nr
лежащие на прямой, проходящей через М и параллельной оси О Y, имеют
координаты уу х1у х29 ..., хту где у есть любое число.
Если точка ЛТ (х19 ..., хт, ..., хр) пробегает множество 6,
измеримое В9 то множество точек N' (у9 х1У ..., хр), где число у произвольно^
пробегает множество 6', также измеримое В. Если мы применим ко
множеству 6 последовательные операции (Р) и (С), то мы в конце концов
придем к данному проективному множеству Е. Те же операции,
примененные ко множеству 6', дают нам, очевидно, множество <£, природу
которого мы стремились узнать.
Итак, множество <§, образованное из точеку лежащих на
параллелях, есть проективное множество того же класса и того же рода*
как Е.
Сумма и произведение проективных множеств* Мы внаем, что
сумма счетного множества аналитических множеств и общая часть
счетного множества аналитических множеств суть опять аналитические
множества. Аналогичный результат имеет место и для аналитических
дополнений.
Мы имеем в виду доказать следующую теорему:
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
233
Сумма и произведение конечного или счетного числа множеств (Ап),
или (Вя) или класса <л есть (Ая) или (5П), или класса <С л*
Аналогичный результат имеет место для (СAn) и (Вя).
Мы начнем с доказательства этой теоремы для суммы.
Пусть S=E1-+-E2-t- ... -ь£*-ь ... есть сумма счетного
множества множеств (Ап) или (Вя). Мы предполагаем, что Et есть линейное
множество и является проекцией плоского проективного множества St
класса <л. Пусть £ есть сумма множеств St»
Предложенная теорема верна для л = 1. Допустим, что она верна
д\я всех классов <^п, и докажем, что она тогда верна и для п.
В силу сделанной гипотезы множество Е есть проективное множества
класса ниже п.
С другой стороны, множество *S, очевидно, есть проекция £.
Следовательно, S есть либо (Ап), либо (£„), либо класса <л (ч. т. д.).
Рассмотрим теперь общую часть
Р = Ег- Е2 ... Ек ...
счетного числа множеств (Ап) или (Вя).
Прежде всего мы можем предположить, что множества Et линейные,,
так как мы видели, что каждое проективное множество можно
преобразовать в линейное проективное множество того же класса и рода при
помощи преобразования многомерной области в линейную, причем это»
преобразование областей не зависит от операций, при номощи которых
получены проективные множества. Итак, предположим, что все Et
лежат в линейной, области о7в.
В силу предшествующего мы можем рассматривать Et как
множество значений функции fk (xk), где fk непрерывна на о/% , а переменная
точка xt пробегает проективное множество Ht вида (CA*—^.
Установив это, возьмем неограниченную последовательность
непрерывных на <2ft функций
*i = ?i(')i *2=?Л*)> ••> ** = ?*(')• •••
таких, что, какова бы ни была последовательность чисел jcJ, jtjj, .. #
.. ^ х\у ... в о/я, существует иррациональное *0, заключенное между О
и 1, для которого мы имеем
**(<•)=••*» №=1.2,3, ...)•
Сложные функции /*[?*(')] непрерывны на (0, 1) области g7/.
Следовательно, множество точек t, для которых удовлетворяются
одновременно равенства
Л[?1(0]=ЛЫ')]= ... =ЛЫ')]= •••>
есть замкнутое на g7* множество. Обозначим его через Г.
Обозначим через % множество всех точек t, для которых <р* (t)
принадлежит к Ht. Установим природу 6к.
234
Н. Н. ЛУЗИН
С этой целью рассмотрим кривую хк = <?к (t) в области <з7^*.
Линейное множество Нк расположено на оси ОХк. На основании
предыдущего параграфа множество точек, лежащих на всех прямых,
параллельных оси ОТ и проведенных через точки Нк, есть плоское множество
{CAn-i). Обозначим это множество через Qk. Рассмотрим дополнение CQk
к множеству Qk; это множество (Д,^).
Мы предполагаем, что теорема верна для всех классов ниже п.
Отсюда следует, что общая часть CQk и кривой ** = ?(£) есть
множество (An-i) или (бя-х), или класса ниже <С п. Значит, проекция этого
множества на ось ОТ есть (Ап-^ или (Bw_1), или класса <Сп— 1. Но
множество Ьк есть, очевидно, дополнение к этой проекции. Значит,
% есть (САп-г) или (Д,^), или класса <С п—1.
Установив это, вернемся к доказательству предложенной теоремы.
Так как мы предположили теорему верной а^я всех классов, ниже я,
то общая часть
0=ГЛЛ ... 6* ...
есть (САп-^ или CBw_i), или класса < п — 1.
Если точка t пробегает 6*, то <р* (0 принадлежит к //*, значит, Д [срд. (£)]
принадлежит к £*. И так как * принадлежит к Г, то все значения
/*[?fc(0] равны между собой. Значит, любая из этих функций /*!?*(£)],
например первая, /i[<Pi(*)L принимает на 0 значения, принадлежащие Р.
С другой стороны, множество Р содержится во множестве
значений /i[<Pi(01 на &• В самом деле, пусть М0 — некоторая точка из Р.
Так как М0 принадлежит к £*, то существует число х\, принадлежащее
к Нк и такое, что точка fk(x°k) совпадает с Ми#
Но в силу свойства функций <p*(tf) существует иррациональное /0
такое, что <рл(?0) = х:£ для всякого к. Эта точка /0 непременно
принадлежит к Ту так как все значения fk [<p* (/0)] равны между собой. Кроме
того, /0 принадлежит каждому из 6Ь так как <р*(0 принадлежит к Нь
Отсюда следует, что tQ принадлежит к 6, значит, множество Р
тождественно со множеством значений fl [cpx {t)\ на 6. Так как 9 есть
проективное множество (САп-.г) или (Вп^), или класса < п — 1, то это же
•справедливо для множества точек, расположенных на параллелях к оси ОХ
и проведенных через точки Ь. Отсюда следует, что тЬчки кривой
* = /i[<Pi(0L расположенные на этих параллелях, образуют плоское
множество Л вида (CAn-J или (5Я_1), или класса <^п—1. А так как
рассматриваемое множество Р есть, очевидно, проекция Л на ось ОХ,
то мы видим, что Р есть (Ап) или (Вп), или класса <л—1.
Итак, мы установили ту часть формулированной теоремы, которая
касается множеств (Ап).
Так как каждое (САп) есть дополнение к некоторому (Ап)9 и так
-как мы имеем очевидные формулы:
С(Егч-Е2ч- ...) = СЕгСЕ2 ..., С(Е1-Е2 . ..) = СЕг-*-СЕ2-+- ...,
ЛЕКиИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
235
-го мы видим, что и часть теоремы, относящаяся ко множествам (САЯ)Г
доказана.
Остается рассмотреть лишь множества (В„). Но по самому
определению каждое множество (Вп) может быть представлено одновременно
в двух видах:
PC ... CPE и СР ... СРЕ.
Из предыдущих рассуждений следует, что сумма и общая часть
счетного множества множеств (Вп) может быть представлена в этих
двух формах, а потому она либо (Вл), либо класса </г (ч. т. д.).
Мы дополним этот результат следующим замечанием: мы доказали,
что сумма и общая часть множеств (Вп) (или класса <С л) есть также (Вя)
(или класса <С п). Но легко видеть, что лаже сумма двух множеств
класса п — 1 может быть эффективно множеством (Вп).
Чтобы убедиться в этом, возьмем множество (Л„_1), лежащее на (0, -у)
в области g7V, пусть Ег — это множество. Пусть £2 — множество (СЛ*-^),
лежащее на (л-,1 в 7 х. Обозначим через Е ьуищ Ег-+-Е2.
Я теперь утверждаю, что Е есть эффективно множество {Вм), но не
класса ниже п. В самом деле, если £ класса <Ся, то Е есть либо (Д|_х),
либо (CAn—i). Пусть, например, Е есть (Ап—Х). Но часть Е, лежащая
на порции ("2~>1)> есть (СД,^), что противоречит условию. Значит, £ —
в точности проективное множество класса п [291. Значит, Е — в
точности (В„) (ч. т. д.).
Итак, существуют эффективно множества (Д,), которые можно
получить при помощи операций суммирования и взятия общей части,
отправляясь от проективных множеств класса ниже п.
Возникает теперь вопрос, можно ли получить всякое (Вп),
отправляясь от проективных множеств классов ниже л, при помощи операций
•суммы и общей части, повторенных счетное множество раз? [30].
Теорема С. Мазуркевича. Обобщение В* Серпииского
Исследования С. Мазуркевича* Мы обязаны С. Мазуркевичу
результатом чрезвычайной важности1, непосредственно связанным с
предыдущими рассмотрениями и касающимся теории аналитических
множеств и их дополнений.
Для определенности мы, излагая результат Мазуркевича, ограничимся
рассмотрением плоской области о/%у.
Пусть Н есть множество, измеримое В, лежащее в <7ху. Мы скажем,
что точка М0 (jc0, y0) есть нижняя точка множества Ну если М0
принадлежит к Н и если не существует никакой точки М(лг0> у) из Н
с ординатой у> меньшей чем у yQ.
1 См. Mazurkiewiez. Sur une propritte des ensembles С A (Fund. Math., X,
172—174).
236
Н. Н. Л У 3 И Н
Установив это определение, легко узнать, какова природа
множества всех нижних точек некоторого множества Н, измеримого В.
Обозначим через //*** множество всех нижних точек множества Н-
Очевидно, это множество H{i) можно получить следующим образом.
Возьмем прямую у = р, где р—рациональное число. Обозначим через//
множество всех точек Н, лежащих ниже этой прямой. Пусть Лр есть
множество параллелей к оси OY, проходящих через все точки Н?.
Множество всех точек о/ху, принадлежащих к Лр, есть, очевидно,
аналитическое множество. Следовательно, то же имеет место и для
множества 0( всех точек Н, лежащих выше прямой у = ? и принадлежащих
к Лр.
Установив это, заставим р пробегать все рациональные числа; сумма Ь
всех множеств 6р есть, очевидно, аналитическое множество,
принадлежащее к Н. Отсюда следует, что разность Н — 6 есть аналитическое
дополнение, которое в частных случаях может оказаться измеримым В.
Но это множество, очевидно, совпадает с рассматриваемым
множеством Н^\ А так как всякая параллель к оси OY пересекает H{i) не
более чем в одной точке, то мы приходим к следующему результату
Маэуркевича:
Множество Н^ всех нижних точек множества Н, измеримого Вг
есть аналитическое дополнение, однозначное относительно оси ОХ.
Прежде чем идти дальше, полезно доказать следующие две леммы,
принадлежащие Серпинскому:
Лемма 1. Сумма Ех-ь-Ег-¥- ... -+-£„-+- ... счетного множества
линейных множеств попарно без общих точек, каждое из которых
есть проекция однозначного аналитического дополнения, обладает
тем же самым свойством.
В самом деле, если Еп есть проекция однозначного аналитического
дополнения Ля> то сумма Л1-*-Л2-ь ... -ьДя+ ... есть, очевидно,
однозначное аналитическое дополнение, имеющее проекцией заданное
множество-сумму Е1-+-Е2-*- ... -+-ЕП-*- ... (ч. т. д.).
Лемма 2. Общая часть Ех- Е2 ... Еп ... счетного множества
линейных множеств, каждое из которых есть проекция однозначного
аналитического дополнения, также обладает этим свойством.
Пусть Ля есть аналитическое дополнение, однозначное относительно
оси ОХ, проекция которого на эту ось есть Еп.
Если мы преобразуем область о/ху в порцию (0, 1) линейной области с7*
при помощи взаимно однозначного и взаимно непрерывного соответствия:
у=<И0, О)
t = F(x,y),
то образ Хп множества Ля есть аналитическое дополнение. Легко видеть,
что функция <р(£) разнозначна на \ и что Еп есть множество ее
значений на Х„.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
237
Установив это, рассмотрим бесконечную последовательность
непрерывных на о7т функций
'i=/iW, '«=/iW, •-., *.=/„(-), ••-,
обладающих следующим свойством: какова бы ни была
последовательность иррациональных чисел f°v /°, ..., ?п)..., заключенных между 0 и lf
существует одно и только одно иррациональное число Xq, заключенное
между 0 и 1, для которого /м (х0) = £ (л = 1, 2, 3, ...).
Так как функции /я непрерывны на с7т, множество &„ точек х, для
которых /п(х) принадлежит к Хя, есть аналитическое дополнение. Отсюда
следует, что общая часть 0 всех Ьп есть также аналитическое
дополнение.
Рассмотрим теперь множество Т точек х, для которых
удовлетворены равенства
Так как функции <р[/я(х)] непрерывны на п7т> то легко видеть, что 7
замкнуто на с7т.
Множество Т • & есть, следовательно, аналитическое дополнение.
Повторяя рассуждение (стр. 234), мы видим, что Е есть множество
значений <р L/lf (/)] на Ь • Т.
С другой стороны, очевидно, что функция <р[/*(х)] разнозначна
на Т • Ъ.
Обозначим через Л множество точек области с/^, принадлежащих
кривой * = <Р [Л (х)]> причем х принадлежит к Т • Ъ. Это множество есть,
очевидно, плоское аналитическое дополнение. Но функция <р [fx (х)]
разнозначна на Т • $. Следовательно, множество Л однозначно относительно
оси ОХ, что и доказывает лемму (ч. т. д.).
Перейдем теперь к доказательству основного результата Мазурке-
зича.
Теорема (Мазуркевич). Всякое аналитическое множество есть
проекция однозначного аналитического дополнения.
Так как область о?^...*** может быть преобразована в плоскую
область о/цуу мы ограничимся рассмотрением линейных аналитических
множеств.
Пусть Е — линейное аналитическое множество, лежащее в области о7*.
-Мы можем рассматривать Е как проекцию элементарного множества <?,
построенного следующим образом (стр. 161): & есть общая часть
S^- S2 •.. Sn ..., где Sn есть сумма прямоугольников Бэра ранга л,
попарно без общих точек; проекции прямоугольников Бэра ранга п на
ось OY попарно не имеют общих точек и образуют на этой оси вполне
упорядоченное множество интервалов, причем порядок соответствует
положительному направлению оси OY. Кроме того, каждый
прямоугольник ранга п содержится в одном и только одном прямоугольнике ранга
л — 1 и содержит счетное множество прямоугольников ранга п -+- 1.
238
Н. Н. ЛУЗИН
Так определенное элементарное множество <$ есть множество,
измеримое Bf и легко видеть, что Е есть проекция его нижних точек, что
и доказывает теорему Мазуркевича (ч. т. д.).
Сам Мазуркевич ограничился тем, что вывел из своей теоремы лишь
следующий результат: всякое множество Е> являющееся разностью
двух аналитических множеству есть проекция однозначного
аналитического дополнения.
Серпинский указал1, что применение двух предыдущих лемм
позволяет получить следующий более общий результат:
Всякое множествОу которое можно получить, отправляясь от
аналитических множеств и их дополнений и повторяя счетное
Множество раз операцию взятия суммы или общей частиу есть
проекция однозначного аналитического дополнения.
Так как каждое линейное аналитическое дополнение можно
рассматривать как проекцию тождественного с ним множества, то можно было бы
думать, что рассматриваемое предложение уже доказано. Но следует
принять во внимание, что здесь идет речь о сумме в широком смысле,,
следовательно, ее члены могут иметь попарно общие точки. Между
тем, лемма 1 Серпинского доказана лишь для суммы в узком смысле*
Чтобы устранить эту трудность, немедленно доказывают, что можно
получить те же самые множества, если взять за две основные
операции суммирование в узком смысле и взятие общей части. Это
замечание заканчивает доказательство теоремы (ч. т. д.).
Сделаем еще следующее замечание: каждое множество Еу которое
можно получить таким способом, отправляясь от аналитических множеств
и их дополнений, есть, очевидно, множество (В2). Возникает вопрос,
будет ли всякое множество (В2) проекцией однозначного аналитического
дополнения и можно ли распространить теорему Мазуркевича на
проективные множества высших классов? [31].
Обобщение теоремы о параметрическом изображении
проективных множеств* Мы видели, что всякое проективное множество (Ап)
можно рассматривать как геометрическое место последовательных
положений подвижной точки М(х1У jc2, , хт)у координаты которой являются
функциями переменного параметра t:
*1 =/l (')> *2 = Л (')> . . •> Xm=fm {*)>
непрерывными на области <Р\у причем t пробегает проективное
множество (CAn—i).
Мы докажем, что семейство множеств (Ап) не расширится, если
за функции fi принять произвольные функции классификации Бэра
и если заставить t пробегать любое проективное множество класса <Сл,
лежащее в g7/.
1 См. W. Sierpinski. Sur les images continues et biunivoques des compieraeatai-
res analytiques (Fund. Math., ХП, 211—213).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ 239
В самом деле, пусть /<(i = l, 2, ..., т) — любые функции
классификации Бэра, определенные на с7*, и Н—любое проективное
множество класса <[ л, лежащее в о/(.
Рассмотрим в m-t-1-мерной области Jx,...*mt множество £ точек
N(xly 232, хт> t)y удовлетворяющих уравнениям
*l=/l(0, *2 = Л(0, ...,XM = fm(t).
Это множество <S необходимо измеримо В.
Установив это, отметим на оси ОТ данное множество И и
рассмотрим в области <7х,... xmt множество всех тех точек, для которых
координата t принадлежит к //. Пусть V— это множество. Выше мы доказали
(стр. 232), что V есть проективное множество того же класса и того же
рода, как Н*
Следовательно, общая часть множеств V и <£ есть проективное
множество класса <Сл, и, следовательно, его проекция в область o/^...хщ
есть проективное множество (Ап) или (Вп), или класса <л (ч. т. д.).
Заметим, что мы придем к тому же результату, если множество Н
есть (Ап) или (£я).
Вспомнив аналогию между множествами (Вп) и множествами,
измеримыми В9 естественно поставить вопрос:
Если дано параметрическое изображение
*i = /i(0. *2=Л(0> ♦.., xm = fm(t)
из функций классификации Бэра, причем оно регулярно или полурегулярно
на Н, где И есть (5Я), будет ли множество, допускающее это
параметрическое изображение, непременно (Вп) или класса <^п? (см. [28]).
Проективные функции. Д\я определенности мы ограничимся
рассмотрением функций одного независимого переменного.
Введем следующее определение:
Мы скажем, что однозначная, всюду определенная функция / (х)
есть проективная функция, если множество точек области <Эxv> лежа-
щих на изображающей кривой у=/ (х)у есть проективное множество.
Проективные функции / (х) можно классифицировать по классам и
родам проективных множеств.
Как только понятие проективной функции введено, возникают
важные вопросы относительно параметрического изображения множеств
при помощи проективных функций.
Среди этих многочисленных проблем мы ограничимся указанием
некоторых: если дана проективная функция / (х), являющаяся плоским
аналитическим дополнением, каково множество ее значений на с?*?
Известно, что это множество есть (Л2) или {В2)9 или проективное
множество класса 1, но мы не знаем, можно ли всякое (А2) представить
таким образом.
Больше того, мы не знаем, можно ли всякое аналитическое
дополнение, неизмеримое Ву представить в этой форме.
240
Н. Н. Л У 3 И Н
Ответ положителен и до некоторой степени банален, если это
аналитическое дополнение содержит совершенное множество: этот
результат можно получить, отправляясь от предыдущей теоремы
Мазуркевича. Но если не делать никакой гипотезы, то ничего не
известно.
В заключение мы хотим привлечь внимание математиков к одной
проблеме первостепенной важности.
Дана проективная функция f (x) однозначная, всюду
определенная и такая, что изображающая ее кривая L есть аналитическое
дополнение; узнать, содержит ли непременно L совершенное
множество? [22].
Чрезвычайная важность этой проблемы вызвана тем, что если ее
решение отрицательно, то знаменитая проблема континуума решается
положительно.
В самом деле, множество L есть сумма несчетного множества
конституант, измеримых В и перенумерованных при помощи конечных и
трансфинитных чисел второго класса по Кантору
L = £0 -+- Sx -+- £2 -*-...-*- £ш ч-... -ь £в -ь... | Q.
Так как L не содержит никакого совершенного множества,, то каждая
его конституанта Е есть счетное множество, и такова же будет ее
проекция Еа на ось ОХ. Но проекция кривой L на ось ОХ в точности
совпадает с этой осью. Следовательно, мы имеем
(—со, 4-co) = EQ-+-El-*-...+Ei3y-*-...-i-Ea4-...\Q,
что и доказывает, что мощность континуума есть К1#
Проективные решета. Мы теперь обобщим результаты, относящиеся
к аналитическим решетам (стр. 151).
Легко показать, что мы не выходим за пределы проективных
множеств, производя операцию, которая состоит в том, чтобы брать
множество, просеянное при помощи проективного решета.
Теорема. Всякое множество, просеянное при помощи
проективного решета класса п, есть проективное множество (^n+i) или
класса ^ п.
Чтобы убедиться в этом, достаточно следовать доказательству,
относящемуся к аналитическим решетам (стр. 151). В самом деле, если
дано проективное решето С класса п, то множество Е, просеянное при
помощи С, есть множество значений непрерывной функции <pl/i(t)j
на 6 • Н. Но множество 6 измеримо В. С другой стороны, мы имеем
Н= Hi • Н2... //**..
Так как Нъ есть результат непрерывного преобразования С, то Ни
есть проективное множество класса ^л, каково бы ни было к.
Следовательно, 6 • Н есть также проективное множество класса ^ к, и,
следовательно, Е есть С4*-ц) или проективное множество класса ^л
(ч. т. д.).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
241
Обратно, всякое множество (4п+1) можно рассматривать как
просеянное при помощи решета (САп). Это замечание весьма банально,
так как каждое множество Е вида (4я+1) есть проекция множества Н
вида {САп). Если мы обозначим через Нк множество {САп), лежащее
между прямыми у= к_^^ и i/ = ~, проекция которого на ось ОХ
совпадает с £, то ясно, что Е просеяно при помощи суммы //j -ь Н2 -+-
-+- ... ч-Нк-*-..., а эта сумма есть множество (САп) (ч. т. д.).
Среди проективных решет наиболее интересны счетные: это такие
проективные решета С, что каждая прямая, параллельная вертикальной
оси, пересекает С не более чем по счетному множеству точек. К
сожалению, по этому вопросу известно очень мало.
Известно, что каждое аналитическое множество можно
рассматривать как просеянное при помощи счетного решета, измеримого В.
Но не известно, можно ли каждое множество {А2) рассматривать как
просеянное при помощи счетного решета (Я2). Не известно даже,
можно ли каждое счетное решето (В.,) разложить на счетное множество
однозначных множеств (52).
С этими рассмотрениями можно связать понятие прямолинейного
решета. Счетное решето С называется прямолинейным, если оно
составлено из счетного множества множеств, лежащих на параллелях
к оси ОХ. Было бы чрезвычайно интересно узнать, каковы линейные
множества (А2), которые могут быть получены при помощи
прямолинейных решет (В.2).
Я должен отметить одну работу Е. А. Селивановского, относящуюся
к этому вопросу. Этот молодой автор рассматривал семейство множеств,
которые можно получить, отправляясь от множеств, измеримых В, при
помощи двух операций: прямолинейного решета и взятия дополнения
повторенных неограниченно. Эти множества носят название множеств (С)
и разбиваются на бесконечное множество классов, перенумерованных
при помощи всех конечных чисел и всех трансфинитных чисел второго
класса по Кантору [33].
Селивановский доказал, что все эти множества измеримы и имеют
определенную категорию, но связь этого семейства множеств с
семейством проективных множеств остается неизвестной1.
1 См. заметку Е. А. Селивановского „Sur une classe d'ensembles definis
par une infinite denombrabie de conditions" (Comptes Rendus 30 мая 1927 г.).
Исправляя корректуры, я добавлю, что исследования, относящиеся к этой
проблеме, были предприняты недавно двумя учениками Г. М. Фихтенголъца Канторовичем
и Ливенсоном; они показали, что множества (С) суть проективные множества в то*
рого класса; см. их заметки в Comptes Rendus. Канторович и Ливенсон.
Sur les ensembles projectifs de deuxieme classe 30 декабря 1929 г.; Sur les o>fonctions
de M. Hausdorff (10 февраля 1930 г.); Sur les ensembles projectifs de M. Lusin
(12 мая 1930 г.) [34].
242
н. н. лузин
Отделимость. Одна из наиболее важных проблем теории
проективных множеств, ожидающая еще своего решения, есть проблема их
отделимости.
Известно, что любые два аналитических множества без общих точек
всегда отделимы В. Было бы очень важно доказать, что любые два
множества (А,) без общей точки всегда отделимы {Вп).
Точно так же мы знаем, что если удалить их общую часть из двух
аналитических множеств, то оставшиеся части отделимы при помощи
двух аналитических дополнений. Естественно, возникает вопрос,
сохранится ли этот принцип, если заменить аналитические множества
через (Ап)у а их дополнения через (САп)> Эта проблема, несмотря на
свою трудность, заслуживает того, чтобы привлечь внимание
математиков.
Кроме того, важно было бы узнать, существуют ли два
множества (СА„), которые неотделимы (Д,) [35].
Существование проективных множеств всякого класса
и всякого рода. Универсальные множества
Теперь пора восполнить пробел, доказав существование проективных
множеств всякого класса и рода. Мы отложили это доказательства
к концу теории проективных множеств для того, чтобы некоторые
предварительные очень полезные предложения были уже доказаны1.
Сделаем сначала одно очень простое замечание: чтобы доказать
существование множеств (5П), достаточно доказать существование
множеств (Ля_1) и (CAn-J. В самом деле, мы видели (стр. 235), что сумма
двух множеств, из которых одно (Ап-г)9 а другое (САп^)9
расположенных в двух неперекрывающихся порциях области п7х, необходимо имеет
вид (Вн). С другой стороны, если Е есть (Ап), то его дополнение СЕ
есть (САп). Итак, все сводится к доказательству существования
проективных множеств (Ап).
Метод, позволяющий нам доказать это существование, опирается на
построение универсальных плоских множеств различных типов.
Мы называем универсальным множеством типа (Ап) всякое плоское
проективное множество U вида (Av) или (5Я), или класса <С л,
обладающее следующим свойством: всякое линейное множество (Ап) или {Вп)у
или класса <л можно получить, пересекая U подходяще выбранной
параллелью к оси OY.
Легко видеть, что каждое универсальное множество U типа (Ап)
само является эффективным примером множества (<4П). В самом деле*
пересечем U диагональю у = х. Пусть е есть множество точек U>
лежащих на этой диагонали, и пусть е есть проекция е на ось OY.
1 См. также мою заметку „Les proprietes des ensembles projectifs" (Comptes
Rendus 15 июня 1925 г.) (стр. 307 настоящего тома.—Ред.).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
243
Прежде всего дополнение Се заведомо не может быть получено,
если пересекать U параллелями к оси OY. Этот важный факт мы уже
видели на стр. 111.
Отсюда следует, что линейное множество е есть эффективно
множество (Ап). В самом деле, в противном случае это множество есть
либо (Вп)у либо класса <С л. Следовательно, линейные множества е и Се
одной и той же природы, что невозможно, так как в этом случае Се'
можно было бы получить, пересекая U параллелью к оси OY.
Итак, мы уже имеем пример линейного множества (Ап): это
множество е. Но можно утверждать нечто большее: самое множество U
есть множество (Ап). В самом деле, если бы U было {Вл) или класса < л,
то его часть в, лежащая на диагонали */ = х, была бы той же природы.
Итак, все сводится к построению универсальных множеств типа (Ам)>
каково бы ни было целое положительное л.
Прежде всего на стр. 125 мы построили универсальное
аналитическое множество U. Его дополнение CU есть, очевидно,
универсальное аналитическое дополнение, так как каждое линейное аналитическое
дополнение (и, в частности, каждое множество, измеримое В) можно
получить, пересекая CU параллелью к оси ОК.
Установив это, применим метод простой индукции.- Итак, допустим,
что мы построили множество £/„-i> лежащее в плоскости ХОТ ъ
являющееся универсальным множеством типа (Лп_х). Его дополнение CUn^x
есть, очевидно, универсальное множество типа (САП~-).
Возьмем функцию
класса 2 по классификации Бэра, определенную всюду над с/*- и такую,
что всевозможные функции /(х) класса 1 классификации Бэра можно
получить, выбирая подходящим образом значение т0 параметра т:
/(х) = <р(х, т0).
Такие функции <р мы строили на стр. 126.
Установив это, преобразуем множество Un-X и функцию <р во
множество !/„_} и функцию ф таким образом, чтобы получить новую пару
(!/„_,, ф), в некотором роде дважды универсальную.
С этой целью возьмем две функции:
t = g(y) и х = А(у),
непрерывные на с7„ и обладающие следующим свойством: каковы бы
ни были два иррациональных числа t0 и т0э найдется такое
иррациональное уп, что t0 = g(y()) и т0 = Л(уп).
Чтобы получить множество Vn-ly возьмем преобразование области o/tx
в новую область о/уху данное формулами
х = х, t = g(y).
Множество Vj,_j есть, по определению, образ множества £/*_-!• Ясно,
что Vj,-! есть плоское проективное (An-i)*
244
Н. Н. ЛУЗИН
С другой стороны, преобразуем функцию ср (jc, т) в новую
функцию ф (дг, у) при помощи подстановки ~ = h(y):
■Нх, y) = iU, Л (у)].
Множество 14-1 и функция ф образуют дважды универсальную пару,
так как, выбирая подходящим образом число г/0, мы получаем
одновременно произвольное линейное множество {Ап-Х) или (5Я_Х), или класса
<^л—1, как результат пересечения Уп-г прямой у=у0> и любую
функцию /(х) класса 1 при помощи равенства f(x) = 6 (ху y0).
Установив это, рассмотрим трехмерную область о7хуг. Пусть S есть
поверхность, определенная уравнением
* = Ф(*> У)-
Возьмем на горизонтальной плоскости XOY множество CVn—x и
обозначим через S множество тех точек S, проекции которых на
плоскость XOY принадлежат к CVn—l. Ясно, что & есть (САп—^) или (5п_г),
или класса <^п — 1. Следовательно, проекция & на плоскость ZOY
есть проективное множество (Ап), или (5Я), или касса <С л.
Я теперь утверждаю, что так определенное множество Е есть
универсальное множество типа (Ап).
В самом деле, мы знаем, что всякое линейное множество е вида (Ап)
или {Вп)у или класса <С.п можно рассматривать как множество значений
некоторой функции f(x)y непрерывной на о/х> когда х пробегает
линейное множество Н вида (Ci4„_1) или (Вп—\)> или класса <^п — 1.
Но, выбирая соответствующим образом у0, мы получим множество Ну
пересекая С]/п-.г прямой у = Уо, и функцию /(*), подставляя г/ = i/0
« ф<х, у)*
Отсюда можно заключить, что наперед заданное множество е рода
(Ан) или (Вп) или класса <л можно получить, пересекая Е
прямой у = у$, а это и доказывает, что Е есть универсальное множество
типа (Ап) (ч. т. д.).
Резольвенты
Резольвенты. Мы скажем, что некоторая проблема Р теории
функций поставлена в резольвенту если мы можем назвать множество
точек Е такое, что проблема Р решается положительно, каждый раз
как можно назвать точку из Еу и решается отрицательно, если можно
доказать, что Е пусто *. Самое множество точек Еу от которого зависит
окончательное решение предложенной проблемы Р, называется
резольвентой проблемы Р.
1 О методе резольвент см. мою заметку wSur le probleme de M. Emile Borel et
la methode des re'solvantes" (Comptes Rendus Acad. Sci., 17 августа 192S г#» стр. 312
настоящего тома. —Ред.) и цитированный мемуар „Sur les ensembles analytiques** (Fund.
Math., X, 91).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
245
Среди проблем теории функций, решение которых, по-видимому,
представляет трансцендентные трудности, большинство может быть
поставлено в резольвенту, причем важно заметить, что все эти
резольвенты оказываются проективными множествами. Среди этих проблем
наиболее интересны следующие: эффективное вполне упорядочивание
континуума и отыскание аналитического обозначения, лишенного
двусмысленности, для всех трансфинитных чисел второго класса по
Кантору. Этой последней проблемой мы обязаны Борелю; мы сейчас
объясним, в чем ее смысл.
Известно, что среди трансфинитных чисел второго класса по Кантору
„маленькие" трансфинитные числа могут быть написаны при помощи
буквы ш. Это значит, что существует много трансфинитных чисел,
в некотором смысле близких к о>, которые могут быть написаны в виде
многочленов или показательных функций от ш. Все эти трансфинитные
числа вполне определены. Но таким способом нельзя определить все
трансфинитные числа второго класса. В самом деле, какие бы
определения мы ни дали (определения, содержащие конечное число символов),
найдутся трансфинитные числа, которые не подпадут под эти
определения, но могут быть определены другими символами в конечном числе
и так до бесконечности1.
Итак, в настоящем состоянии науки мы не имеем никакого алгорифма»
позволяющего написать все трансфинитные числа второго класса. Тем
не менее, существует алгорифм, позволяющий написать все
действительные числа: достаточно напомнить разложение в бесконечную
десятичную дробь.
Вышеуказанная проблема Бореля состоит именно в том, чтобы найти
алгорифм, составленный из счетного множества символов и
позволяющий написать все трансфинитные числа второго класса.
Проблема Э. Бореля была бы решена, если бы мы умели
перенумеровать все действительные числа при помощи совокупности
трансфинитных чисел второго класса или, по крайней мере, назвать часть
континуума, перенумерованную этим способом. Но в первом случае самая
проблема континуума была бы полностью решена, а во втором случае
мы имели бы решение проблемы о сравнении двух мощностей:
мощности континуума и мощности Кх2.
Вернемся теперь к резольвентам. Самое введение понятия
резольвенты тесно связано с идеями Э. Бореля. В своем сообщении IV
Математическому конгрессу (Рим, апрель 1908 г.) Борель говорит: „Чтобы
дать понять мою точку зрения, я укажу проблему, кажущуюся мне
одной из наиболее важных в арифметической теории континуума:
можно ли определить множество Е такое, что нельзя назвать ни одного
1 См. Е. В о г с 1. La philosophie mathematique et Tinfini (Revue du Mois, август
1912 г.).
1 См. письмо Лебега: „Cinq lettres sur la theorie des ensembles4* (Bull, de la
Soc. Math, de France, декабрь» 1904 г.).
246
Н.Н. ЛУЗИН
индивидуального элемента этого множества Е, т. е. без
двусмысленности отличить его от всех остальных элементов Е" *.
Цель дальнейших рассмотрений состоит в том, чтобы указать
проективные множества, образованные из точек сегмента (0, 1) и которые
я рассматриваю как решение только что цитированной проблемы Бореля.
Эти проективные множества являются резольвентами некоторых
проблем, решение которых в абсолютном смысле, по моему мнению,
выходит за пределы классической теории множеств.
Среди многочисленных проблем теории функций я ограничусь
рассмотрением только двух и построю резольвенты этих проблем.
Проблема I. Узнать, не будут ли все аналитические
дополнения либо счетнЫу либо иметь мощность континуума.
Интерес этой проблемы вызывается тем, что если допускать
существование всех трансфинитных чисел второго класса, то можно
безукоризненно доказать, что всякое несчетное аналитическое дополнение,
не содержащее совершенного множества, необходимо является
соединением несчетного множества счетных множеств попарно без общих
точек, перенумерованных вполне точно при помощи всех трансфинитных
чисел второго класса. Следовательно, если этот логически возможный
случай практически реален, то можно будет утверждать, что
существование всех трансфинитных чисел второго класса есть факт как бы
экспериментального характера.
Резольвента Е этой проблемы есть проективное множество
класса не выше 3. Если можно назвать точку из £, то такое
необыкновенное аналитическое дополнение существует, и обратно.
Перейдем теперь к построению этой резольвенты.
Возьмем трехмерную область о/хуя и рассмотрим в плоскости XOZ
универсальное аналитическое множество U> т. е. такое, что
всевозможные линейные аналитические множества можно получить, пересекая U
параллелями к оси OZ.
С другой стороны, возьмем в плоскости YOZ множество U' такое,
что всевозможные линейные совершенные множества и только их можно
получить, пересекая U' параллелями к оси OZ. Такое множество И
построить очень легко [46].
Обозначим через ё множество точек области q/xvz> проекции
которых на плоскость XOZ принадлежат к U. Аналогично, пусть &' есть
множество точек <9fхуеу проекции которых на плоскость YOZ
принадлежат LT,
Ясно, что ё есть аналитическое множество и что &' есть либо (А2),
либо {В2)9 либо класса 1. Значит, общая часть & • ё' есть либо
множество (А2)9 либо (B2)t либо класса 1.
Произведем над ё • ё' операции, указанные в следующей формуле:
Е1 = РСР(ёё,)У
1 См Е. В о г е 1. Lemons sur la theorie des fonctions, 3e6d. 1928, стр. 162.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
247
где мы проектируем £ • £' на XOY, затем берем дополнение к этой
проекции и, наконец, проектируем это дополнение на ОХ.
Ясно, что так полученное проективное множество Е} есть либо (Л3),
либо (Bz), либо класса <^2.
Установив это, возьмем в плоскости YOZ множество £/", измеримое
В, такое, что всевозможные счетные линейные множества можно
получить, пересекая U" параллелями к оси OZ. Чтобы получить такое
LF'y достаточно взять бесконечную последовательность непрерывных
«функций /г(у)9 /2(у), .. ♦, fn(y)> ••• таких, что, какова бы ни была
система иррационных чисел z\, z% ..., z°, . .., существует число у^
для которого при всяком п имеем z*=fn(yQ). Если мы проведем в
плоскости YOZ все эти кривые z=fn{y), я = 1,2,3, . . ., то их
соединение и есть, очевидно, искомое множество [/'.
Заметив это, обозначим через §" множество точек ■?гхуя> проекции
которых на плоскость YOZ принадлежат к U'. Ясно, что 6" измеримо
В и что сумма £н-£" есть аналитическое множество.
Произведем над S-*-£" операции, указанные формулой
E2 = PCPC(S + S"),
где дополнение берется в области о?хуж; затем мы проектируем на XOYy
затем берем дополнение и, наконец, проектируем на ОХ.
Легко видеть, что так полученное проективное множество Е2
есть либо (Л3),; либо (В3)> либо класса ^2.
Отсюда следует, что множество-сумма Ех -+- Е2 есть проективное
множество класса <^3. Значит, если мы обозначим через Е
дополнение к этой сумме, то множество Е есть также проективное и
класса ^3.
Я теперь утверждаю, что множество Е есть резольвента
поставленной проблемы. Это значит, что если бы мы умели указать точку
во множестве Е, то мы бы получили несчетное аналитическое
дополнение без совершенной части; а если бы удалось доказать, что Е
пусто, то было бы доказано, что таких аналитических дополнений
не существует.
В самом деле, если мы расшифруем смысл несколько сложных
построений двух линейных проективных множеств Ех и Ег, то мы
найдем, что £г есть множество тех точек jc, в которых параллели
к оси OZ пересекают универсальное аналитическое множество U по
обыкновенным аналитическим множествам, дополнения к которым
содержат каждое по совершенному множеству; точно так же Е2 есть
множество тех точек х, для которых соответствующие аналитические
множества имеют счетные (или конечные) дополнения: это также
обыкновенные дополнения.
Если мы удалим из оси ОХ все точки множеств Ег и £2, мы,
разумеется, получим точки х, которые соответствуют необыкновенным
аналитическим дополнениям.
248
Н. Н. ЛУЗИН
Итак, в конечном итоге мы здесь имеем лишь чисто логическую
трудность, хорошо запрятанную под квазигеометрической внешностью.
Проблема II. Узнать, существует ли функция f(x), всюду
определенная и такая, что изображающая ее кривая г/=/(х) есть
аналитическое дополнение без совершенной части.
Важность этой проблемы объясняется тем, что в случае положительного
ответа мощность континуума окажется равной #х (стр. 240).
Кроме того, эта кривая y = f{x) не может быть измерима
в смысле Лебега. В самом деле, если бы эта кривая была измерима
в смысле Лебега, то на оси ОХ существовало бы совершенное
множество Р, на котором f(x) была бы непрерывна. Это значит, что рас*
сматриваемая кривая у=/(х) содержит совершенное множество, что
противоречит сделанной гипотезе.
Чтобы не утомлять читателя, повторяя одни и те же операции, мы
просто укажем путь построения резольвенты предложенной проблемы.
Прежде всего мы возьмем в области Sfлуг аналитическое
универсальное множество U трех измерений, такое, что всевозможные плоские
аналитические множества получаются при пересечении U плоскостями,,
параллельными XOY.
Обозначим через Нх множество точек прямых, параллельных оси
OY и не пересекающих дополнение CU к U. Точно так же пусть Н2
есть множество точек прямых, параллельных оси OY, каждая из кото-
рых пересекает CU не менее двух раз. Пусть Ех и Е2 соответственно
проекции Нх и Н2 на ось OZ. Так как Н1 есть либо {СА2), либо {В2)>
либо класса <2, а Я2 либо (А2), либо (В2), либо класса < 2, то Е
есть проективное множество класса ^3, Е2 — проективное множество
класса <12.
Обозначим через Еь множество таких точек С оси OZ, что каждая
плоскость z = C пересекает U по аналитическому множеству,
дополнение к которому либо счетно (или конечно), либо имеет мощность
континуума. Чтобы получить множество Ez, достаточно преобразовать
взаимно однозначно и взаимно непрерывно область о/ху в область с7л
при помощи уравнений
t = F(x, у)Л
z = z. )
Образ U множества U при этом преобразовании есть плоское
аналитическое множество и плоскости, параллельные XOY, преобразуются
в прямые, параллельные оси ОТ.
Отсюда следует, что дополнение к множеству Ег тождественно
с резольвентой предшествующей проблемы. Значит, Еь есть
проективное множество класса ^3.
Если удалить из оси OZ множества Е19 Е2 и Ez, то множество Е
оставшихся точек есть, очевидно, проективное множество класса ^3.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
249
Это проективное множество Е и есть резольвента поставленной
проблемы.
Мы видим, что лицо, которое сумело бы назвать точку во
множестве Еу сумело бы перенумеровать все точки оси ОХ при помощи
всех трансфинитных чисел второго класса.
Анализ мемуара Лебега „Sur les fonctions representables
analytiquement"
Этот мемуар Лебега, появившийся в 1905 г.1, крайне богатый
идеями, методами и общими результатами, еще далеко не изучен. В частности,
вся теория аналитических множеств имеет своим началом этот мемуар.
На следующих страницах мы укажем некоторые пункты этого
мемуара, тесно связанные с предметом наших рассмотрений. В то же
время мы хотели бы привлечь внимание аналистов к одному методу
употребленному Лебегом для построения точечных множеств.
Природа этого метода очень сложна и несколько загадочна. С одной
стороны, он совершенно избегает рассуждения Цермело. С другой
стороны, базируется на совокупности всех трансфинитных чисел второго
класса. Важно заметить, что самый способ пользования этой
совокупностью крайне замечателен и существенно отличается от способов,
употребляемых во всех известных рассуждениях.
В самом деле, есть много точечных множеств, которые могут быть
определены при помощи совокупности трансфинитных чисел второго
класса: таков, например, случай аналитических дополнений (стр. 163),
а также проективных множеств. Но мы видели, что каждый раз, как
эта совокупность появляется, ее можно исключить при помощи
отрицательных определений. Например, любое решето С определяет
аналитическое дополнение положительным образом: это множество точек,
где перпендикуляры пересекают решето С по вполне упорядоченным
множествам, которым, вообще говоря, соответствуют все более и более
высокие трансфинитные числа. Итак, все трансфинитные числа второго
класса эффективно вошли в это определение. Тем не менее, если мы
хотим избежать понятия трансфинитного, достаточно определить
аналитическое дополнение как множество почек, которые не принадлежат
данному аналитическому множеству. Ясно, что здесь совокупность
трансфинитных чисел заменена отрицательной операцией: взятием
дополнения к уже определенному множеству.
Но употребление совокупности трансфинитных чисел в методе Лебега
совершенно другое и весьма замечательное. Лебег пользуется
трансфинитной последовательностью действительных чисел, определенных
не одновременно, а после до вате льноу таким образом, что
определение каждого из этих чисел существенно зависит от предыдущих
численных определений.
1 Journ. de Math., стр. 139—216, 1905.
250
Н. Н. ЛУЗИН
Этот замечательный способ пользоваться совокупностью
трансфинитных чисел делает чрезвычайно затруднительным исключение этой
совокупности при помощи отрицательных определений. Может случиться,
что такое исключение является даже абсолютно невозможным.
Если это так, то метод Лебега, безусловно, явится началом ряда
работ, посвященных изучению смысла этого метода, так как множества,
определенные этим методом, совершенно новой природы и тем не менее
„эффективны", так как рассуждение Цермело избегнуто (см.[21]).
Понятие достижимых множеств и их роль в образовании
множеств у Лебега. Мы начнем с выявления тех пунктов мемуара
Лебега, которые тесно связаны с главой II. В этой главе понятие
элемента класса а играло существенную роль. Напомним сначала, что
мы назвали достижимым сверху всякое множество Е класса а,
являющееся общей частью счетного числа множеств класса ниже а. Мы
назвали элементом класса а множество £, достижимое сверху,
дополнение которого СЕ недостижимо сверху.
Мы знаем, что элементы класса а играют существенную роль в
теориях главы И. И, в частности, теорема об отделимости любых
элементов класса а при помощи множеств класса ниже а выявляет очень
важное свойство элементов класса а, во всех отношениях аналогичное
отделимости В дая аналитических множеств1.
Если мы внимательно проанализируем мемуар Лебега, мы там уже
найдем идею множества достижимого сверху, а также и немедленные
приложения этого понятия.
Прежде всего процитируем одно место в этом мемуаре (стр. 161,
строка 8):
„Я назову множеством ранга ос всякое множество, которое можно
рассматривать как общую часть конечного или счетного числа
множеств F класса ниже а, причем это невозможно, если заменить <х
меньшим символом. Если а первого рода, то множества ранга а заключены
среди множеств класса а—1".
„Если а второго рода, то множества ранга а суть одновременно
F и О класса а; это верно при всяком а".
Мы видим, что в этих строках идея множества, достижимого сверху,
ярко выявлена. Классификация множеств, данная Лебегом, и та,
которой мы руководились в этой книге, различны: в классификации Лебега
множество F класса а есть множество E[f{x)^ а] — значений
переменного ху для которых функция f(x) класса а не меньше некоторого
числа а. Легко показать по индукции, что множество F класса а
в классификации Лебега есть множество класса ан-1, достижимое
сверху, в классификации, принятой в этой книге. Множество же ранга
а есть достижимое сверху множество класса <х.
1 См. мою статью „Analogies entre les ensembles mesurables В et les ensembles
analyti4uesa (Fund. Matn., XVI, 1930) (стр. 470 настоящего тома. —Ред.).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
251
Идея множества, достижимого сверху, дана Лебегом, и он извлек
из нее следствия, которые почти совпадают с некоторыми из
результатов главы II.
Среди этих следствий мы цитируем главное, которое можно найти
на стр. 173, строка 4:
„X. Для того чтобы функция f была класса а^>0, необходимо
и достаточно, чтобы, каково бы ни было е, область, где f
определена, могла быть рассматриваема как сумма счетного множества
множеств ранга не выше а, на каждом из которых / с точностью
до е класса ниже а, или же на каждом из которых колебание /
не больше е".
Легко видеть, что, несмотря на большое различие двух
классификаций, эта теорема Лебега почти тождественна с теоремой главы II:
Всякое множество точек класса Ка есть сумма счетного множества
элементов класса ^а попарно без общих частей, дополненной
предложением (стр. 68) этой книги.
Необходимое и достаточное условие для того, чтобы сумма
счетного множества элементов класса ^ <х без общих частей была класса
^а, состоит в том, чтобы она была частью некоторого полного
разбиения всей области о/ на счетное множество элементов
класса ^ а без общих частей.
В самом деле, преобразуем формулировку Лебега, относящуюся
к функциям, в формулировку, относящуюся к множествам. С этой
целью допустим, что / есть характеристическая функция некоторого
множества Е класса а. В силу цитированной теоремы Лебега область,
где / определена, можно рассматривать как сумму счетного множества
множеств ранга не выше а, на каждом из которых колебание /
не больше е.
Но так как / принимает лишь значения 0 и 1, то эта функция
постоянна на каждом из этих множеств ранга а. Следовательно, вся
область, гда / определена, разлагается на множества ранга ^ а,
принадлежащие либо к Е, либо к СЕ.
Другими словами, рассматриваемое множество Е есть часть полного
разбиения всей области на счетное множество множеств ранга ^а.
Но в этой форме формулировка Лебега совпадает с нашей
формулировкой, так как множество ранга а в смысле Лебега есть множество,
достижимое сверху.
Непрерывность (а) у Лебега. Кульминационный пункт теории
Лебега есть понятие непрерывности (а) и теорема о функциях класса а,
формулировка которой совпадает с теоремой Бэра о функциях класса 1.
Лебег определил непрерывность (а) следующим образом (стр. 191,
строка 3):
„Функция называется непрерывной (а) на совершенном
множестве Е в точке Р из Е, если каждому положительному
числу е можно привести в соответствие интервал, содержащий
252
Н. Н. ЛУЗИН
внутри точку Р, где Е можно рассматривать как сумму счетного
множества множеств ранга не выше а, на каждом из которых f
постоянна с точностью до s, причем все эти множества, кроме
одного у содержащего Р, нигде не плотны на Е".
С этим определением Лебег смог доказать следующее предложение
(стр. 191, строка 21):
„XVII. Для того чтобы функция f была класса не выше а,
необходимо и достаточно, чтобы она была точечно разрывна (а) на
всяком совершенном множестве".
Было бы интересно отыскать идею непрерывности (а) и теорему
Лебега в понятиях главы II.
Дескриптивный метод Лебега для определения множеств
конечных классов. Важным пунктом мемуара Лебега, который надо
очень внимательно изучить, является способ эффективно получить все
функции конечных классов классификации Бэра при помощи функций
многих переменных непрерывных по каждому из них.
Лебег доказывает следующую теорему, касающуюся этих функций
(стр. 201, строка 10):
„XX. Функция от п переменных, непрерывная по каждому из
них, будет класса не выше п — 1".
Из этой теоремы следует, что если /(хг, х2, ..., хп) есть такая
функция, то функция f(x, х, ..., х), которую мы получим, полагая
х\ == х2 == • • • z= Xn =z ху
есть функция класса не выше п — 1.
Установив это, цитируем один отрывок из Лебега (стр. 202,
строка 1):
„Правда, можно спросить себя, возможно ли, чтобы найденный для
класса верхний предел был фактически достигнут. Ответ
положителен; в самом деле, мы докажем, что. . .
„XXI. Если f(t) есть функция класса п, то существует функция
y(xi> х2у • • •> xn+i)> непрерывная по каждому из своих лн-1
переменных и такая, что f(t) тождественна с y(t, t, ..., /)".
Рассмотрения Лебега относятся к функциям. Если мы применим их
ко множествам, то вот что мы получим:
Если <§ есть множество точек, лежащее в п -+- 1-мерной области
о?** * * и такое, что, какова бы ни была точка М этой области,
существует фигура, составленная из лн-1 прямолинейных интервалов,
параллельных осям ОХх, ОХ2, ..., ОХп+х и проходящих через точку
М1, причем эта фигура либо целиком принадлежит к &, либо не имеет
с S ни одной общей точки, — тогда линейное множество Е, которое
получается при разрезании S прямой хх = х2 =• •. = хп, есть мно-
Точка М есть внутренняя в узком смысле для каждого из этих интервалов.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
253
жество класса не выше п> и каждое множество конечного класса п
может быть получено этим способом.
Итак, метод Лебега позволяет получить все множества конечных
классов дескриптивным путем, не употребляя никакого оперативного
процесса.
Было бы желательно распространить метод Лебега на множества
трансфинитных классов. Но следует заметить, что невозможно
непосредственно обобщить метод Лебега. В самом деле, д\я этого пришлось
бы рассматривать функции счетного множества переменных хх> х2> .. .,
хиу .. ., непрерывных по каждому из них. Но если определять функцию
j{xu х2> ..., хп, —,) от счетного множества переменных как
соответствие между числом у и бесконечной последовательностью х19 х2> .. .,
х,п ..., то можно тотчас же придти к следующему отрицательному
результату: можно определить функцию f{xv х2, ..., хП1 ...),
непрерывную по каждому из переменных и такуюу чтоу полагая х = хг =
= х± = ... = хп = .. ., мы получим совершенно произвольную функцию
/(х) переменного х.
Этот факт показывает нам, что для обобщения результата Лебега
надо идти другим путем.
Метод Лебега для доказательства существования функций всех
классов* Перейдем теперь к той части мемуара Лебега, где он
доказывает существование функций всех классов и функции, которая не
допускает никакого аналитического изображения.
Вот метод Лебега.
Пусть а — любое число, конечное или трансфинитное второго класса.
Требуется определить функцию /й (t, x) двух действительных
переменных /их, входящую в классификацию Бэра и такую, что каждую
заранее данную функцию F(x) класса а можно заведомо получить,
выбрав подходящим образом значение £0 параметра t:
fa(tu,x)=F(x).
Чтобы получить такую функцию /e (t> x)> делаются следующие
рассмотрения1:
Каждая функция /(х) класса ^1 классификации Бэра есть предел
последовательности полиномов
f(x) = \\mPn(x\
где можно предполагать, что полином Рп(х) имеет степень <^л.
Обозначим через a(fcw) коэффициенты полинома Рь (х),
* = 0, 1, 2, ..., л.
С другой стороны, рассмотрим счетное множество функций <p$.M)(f)»
определенных на порции (0,1) области Qfh непрерывных в каждой точке
1 Я позволяю себе слегка изменить метод Лебега в его технической части, чтобы
<осветить основные принципы.
254
Н. Н. ЛУЗИН
этой порции и обладающих следующим свойством: какова бы ни была
система чисел а(£\ найдется такое иррациональное /0 между 0 и 1, что
^^W^^» каковы бы ни были пик.
Эти функции f^]{t) определяют то, что Лебег называет „кривой,
заполняющей целую область в пространстве счетного числа измерений"
(стр. 211, примечание).
Если мы в полиномах Рп (х) заменим коэффициенты а^
соответствующими функциями <p(kW)W> мы получим функцию фн(*, л:) двух переменных
t и х, непрерывную по совокупности этих переменных и совпадающую,
очевидно, с заранее заданным полиномом относительно х степени л,
когда значение £0 параметра t выбрано надлежащим образом.
Установив это, вернемся к данному трансфинитному числу а.
Чрезвычайно важно заметить, что Лебег предполагает это число а не только
названным, но данным в некотором смысле эффективно, именно так,
чтобы вместе с ним задан был пересчет ах, а2, ... всех трансфинитных
чисел, которые предшествуют а. Известно, что в теории трансфинитных
чисел смысл символа
где аир два трансфинитных числа, определяется по индукции, Лебег
выводит из простой бесконечной последовательности alt a2...,
образованной из всех трансфинитных чисел, предшествующих а, новую
вполне определенную последовательность, также простую бесконеч-
ную> Pi> (32, ..., составленную из всех трансфинитных чисел,
предшествующих о)"1.
В этом заключается основной пункт, так как этот факт позволяет
построить множество точек F, линейное, замкнутое и вполне
упорядоченное в положительном направлении прямой, содержащей F, причем
ему соответствует трансфинитное число wa.
Главное свойство числа u)a заключается в том, что если мы
рассмотрим последовательность производных множеств для F:
F, F, F", ..., Я"\ ..., Ят), ..., | Я«>,
то производное множество F{a) состоит из одной и только одной
точки х, следовательно, дальнейшие производные будут пусты.
Заметив это, установим взаимно однозначное соответствие между
изолированными точками F и всеми непрерывными функциями tyn(t, x)+
Так как мы умеем перенумеровать все точки F при помощи целых
чисел, то мы можем эффективно получить это соответствие.
Установив это, будем действовать следующим образом: прежде всего
каждой изолированной точке с первого производного множества F' мы
приведем в соответствие вполне определенную функцию переменных t
1 Знаменитый автор производит эту нумерацию при помощи очень важного
нового метода, плодотворность которого наиболее ярко проявилась в первых же
исследованиях по теория аналитических множеств: это метод „кортежей индексов" („Sur
les fonctions representables analitiquement", стр. 209).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
255
и х класса ^ 1, получаемую, если взять предел последовательности
функций ^я(/, х)у соответствующих изолированным точкам ;х, ;2, ..., ;v
из Fy стремящимся к рассматриваемой точке ; из F.
Допустим, что каждой изолированной точке каждого из производных
множеств F^\ предшествующих множеству F^\ приведена в
соответствие вполне определенная функция переменных tux класса ^^, и
установим аналогичное соответствие для изолированных точек самого
множества F^K
Следует различать два случая.
В первом случае число 7 первого рода 7 = 7*н~1- В этом случае
мы приводим в соответствие каждой изолированной точке ; из F^
?
т • • • •—•—•—i Mi«« |
Рис. 9.
вполне определенную функцию переменных t и х класса ^7>
получаемую, если взять предел последовательности функций,
соответствующих изолированным точкам 11У с2, .. #> £v, .. ., из F^*\ стремящихся
к рассматриваемой точке I из F^\
Во втором случае число 7 второго рода. В этом случае мы начнем
с того, что заключим все изолированные точки ; из F1 в
последовательность интервалов о, неперекрывающихся и таких, что каждый
интервал & содержит одну и только одну изолированную точку Е из ,РТ •
Так как мы имеем вполне определенную нумерацию дая точек
множества F при помощи целых чисел, то мы можем определить дая
каждой изолированной точки £ из F последовательность точек Е1Э ;2» —»
£v, ..., лежащих в соответствующем интервале о, и таких, что точка ;м
есть изолированная точка производного множества F($n)y где
последовательность Pi "СРг^ • • • ^Ря'С-• • стремится к 7» Точке £ мы
приведем в соответствие вполне определенную функцию переменных /их,
являющуюся пределом функций, соответствующих точкам Ъх, £2> • • •» ^п> • • *
Очевидно, что, действуя дальше таким же образом, мы в конце
концов придем к единственной точке из F и мы приведем ей в
соответствие вполне определенную функцию класса ^ а; это и будет
искомая функция /а (/, х).
Чтобы увидеть это, достаточно доказать, что, выбирая надлежащим
образом значеняе t0 параметра ty мы получим для изолированных точек
производного множества F^ произвольно данные функции класса ^ 7
переменного ху каково бы ни было ч-
С этой целью заметим, что это верно дая 7= 1> так как функции
ф„(/, х) представляют собой произвольные полиномы относительно х
степени пу если только удачно выбрать параметр t.
256
Н. Н. ЛУЗИН
Случай, когда 7 первого рода, 7 = 7*-*-1 не представляет никаких
трудностей. В самом деле, по гипотезе можно выбрать параметр t так,
чтобы функции, соответствующие изолированным точкам производного
F^\ обратились в произвольные функции переменного х класса <^7*«
В этих условиях рассматриваемый случай тождественен со случаем
т = 1.
Случай, когда 7 второго рода, несколько более сложен. Чтобы
устранить трудности, мы определим в каждом интервале о, содержащем
изолированную точку I из F т, последовательность интервалов 8', 8", .. #>
Ь[п\ ... попарно без общих точек и содержащих соответственно внутри
(в узком смысле) точки $1Э с2, . . ., ;я, . . . В этих условиях мы, очевидно.
«/
8"
h
Г"
iT4
Т4
~>^-^
ч, «
Рис. 10.
можем выбрать значение t так, чтобы точкам ^, Е2, ..., £„.. . отвечали
заранее данные функции класса соответственно ф19 |32, • • •> К> • • •> и так для
всех изолированных точек S из Fт. Из этого немедленно следует, что
изолированным точкам ; из F1 соответствуют заранее данные функции
класса ^7-
Итак, процесс Лебега приводит нас к единственной функции,
которую мы обозначим через /а (t> х) и которая отвечает
единственной точке производного множества Р*. Предыдущее рассуждение
показывает, что, выбирая надлежащим образом значение параметра t>
мы получаем произвольно данную функцию класса <1а.
Представляется еще одна трудность, которую важно устранить.
Функция /а(/, х) не всюду определена, ибо для некоторых значений t
пределы, которыми мы пользовались, могут не существовать. Чтобы
преодолеть эту трудность, мы просто заменим операцию lim (переход
к пределу) через операцию lim (верхний предел). Так как операция
lim есть частный случай операции lim, мы заключаем, что ни один из
случаев перехода к пределу (когда он возможен) не будет потерян.
Но в случае, когда переход к пределу невозможен по причине
наличия расходящихся последовательностей функций, операция lim,
заключающаяся во взятии верхнего предела, дает нам всегда вполне
определенный результат. Мы видим, что таким образом мы приходим к
функции fa(t, х), всюду определенной на (—оо <х < -+■ °°, 0<*<С1)-
Покажем, что функция /e (t, x) входит в классификацию Бэра.
Это очевидно дая функций tyn(t, x), так как они непрерывны по
совокупности переменных. А так как операция lim, произведенная над
функциями классификации Бэра, всегда приводит к функциям этой класси-
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
257
фикации, то мы заключаем, что функции, соответствующие
изолированным точкам производных множеств 7^т, все принадлежат классификации
Бэра. В частности, и fa(t, x) входит в эту классификацию.
Отсюда мы заключаем, что функция переменного х
/«(*> х)
входит в классификацию Бэра и ее класс меньше или равен классу
Л С х)1.
Мы докажем, что класс функции /в (х, х) не может быть меньше а.
В самом деле, допустим, что класс /в(лг, л:) будет <Са; пусть р —
этот класс. Функция <р„(*)> определенная равенством
будет класса меньшего или равного $2. Следовательно, предельная
функция
<р (х) = lim <?я (х)
будет класса не выше а, так как р-+-1^а. Но это невозможно, так
как, если класс <р (х) не превосходит а, мы можем выбрать значение
/0 для t так, чтобы fa(t0> x) = y(x) при всяком х. Полагая в этом
тождестве х = t0, мы приходим к невозможному равенству /в (t0> /0) =
= ср (/0), так как каждый раз, как/а(/0, /0) отлично от нуля, мы имеем
<р (/0) = 0, и обратно.
Итак, нам удалось назвать функцию, класс которой заведомо
не ниже а; это функция fa(xy x).
Отсюда следует, что существуют функции класса, в точности
равного а, так как, если бы таких функций не было, функция /в (х, х)
не могла бы существовать3.
Прежде чем идти дальше, сделаем следующее важное замечание:
функция /в(х, х) построена при помощи счетного множества переходов
к пределу. Эти переходы расположены во вполне упорядоченную
последовательность, которой соответствует данное трансфинитное число а,
и они налагаются друг на друга, т. е. они проделаны последовательно
один за другим, но так, что знание численного результата одного
1 В самом деле, не представляет никаких затруднений доказать при помощи
трансфинитной индукции, что если Ф (аг, у) есть функция класса < а, то это же имеет
место аля Ф (х, х).
2 Речь идет о теореме Лебега: если функция ? (*l» t^. . ., tp) будет класса О,
а функции Д, /2, . . .Jp^ класса не выше а, то Ф=<р(/Ъ /2, . . м fp) будет класса
не выше п („Sur les fonctions representables analytiquement44, стр. 153, строка 17).
Доказательство такое же: методом трансфинитной индукции.
3 См. также заметки в Comptes Rendus от 13 ноября 1922 г. и от 22 января
1923 г. Серпинского и Куратовского: „Sur I'existence de toutes classes d'ensembles
mesurables Bu et „§ur I'existence effective des fonctions representables. analitiquejnent
de toute classe de Baire".
258
Н. Н. ЛУЗИН
из переходов к пределу существенно предполагает знание численных
результатов всех предшествующих переходов к пределу.
А так как трансфинитное число а может быть как угодно большим,
то очень вероятно, что нельзя назвать функцию /e (х> x) без того,
чтобы знать все численные результаты предшествующих переходов
к пределу, т. е. без того, чтобы построить самое это трансфинитное
число а.
Метод Лебега для построения функции, не допускающей
никакого аналитического изображения* Перейдем теперь к последнему
пункту мемуара Лебега, а именно к тому, где он указывает функцию-
индивидуум, неизобразимую аналитически.
Прежде всего цитируем текстуально несколько отрывков из Лебега
(стр. 213, строка 25):
„Я предполагаю, что рациональные числа, заключенные между 0 и 1,
расположены в некотором порядке, который я не уточняю, но
предполагаю вполне определенным; пусть zl9 z2> ... — рассматриваемая
последовательность, Я беру некоторое значение /, заключенное между
О и 1, и записываю его по двоичной системе счисления, употребляя,
если это возможно, цифру 1 только конечное число раз; выражение
для г вполне определено, как только t известно,
°1 62
г— 2 -+-22 н-...
„Вычеркнем из последовательности zly z2, ... все те zt, которые
соответствуют индексам i цифр 6^, равных нулю; пусть zv zv ... —
оставшиеся z. Возможно, и так всегда будет, если чисел z лишь
конечное число, что можно найти символ класса а, обладающий
следующим свойством: можно установить соответствие между числами z и
всеми символами [3, меньшими а, так, чтобы одному z отвечало только
одно (3, и обратно и чтобы, если числам р и 3' отвечают z ($) и z((3'),
то z ((3) < z фг) всякий раз, как (3 меньше (31# Тогда мы назовем а
символом, соответствующим t. Кроме того, каждому символу |3([3<а)
соответствует вполне определенное целое число i — индекс
соответствующего z; следовательно, если расположить р в порядке, давая им
в качестве номеров эти целые г, мы получим последовательность ар
<х2, .. и> образованную из символов, меньших а. Следовательно,
рассматриваемому значению t мы можем привести в соответствие функцию
<рв (х) класса а; дая этого достаточно применить вышеуказанный
процесс; эту функцию <ра(г), которая еще не определена, когда дано а,
но становится определенной, когда задано /, если этому /
соответствует символ а, мы назовем <р (/, х). Если числу I не соответствует
никакой символ а, я положу <р(£, дс) = 0.
„Я утверждаю, что функция ср(£, л:) не допускает никакого
аналитического изображения...".
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
259
Если построение Лебега мы переведем на геометрический язык, то
получим следующее: в пространстве трех измерений берется система
прямоугольных осей координат ОХТУу и рассматривается на плоскости
OTY прямолинейное решето Г. Прямые, на которых лежат отрезки
решета, перенумерованы.
Далее рассматриваются на оси ОТ те точки t, в которых прямая,
параллельная оси OY, пересекает решето Г по вполне упорядоченному
множеству. Пусть & — это множество и Е — его дополнение.
Рис. 11.
Установив это, заставляем t пробегать ось ОТ. Если точка /0
принадлежит множеству Е9 то полагаем
Т(*0,*) = 0.
Если tl принадлежит к <§у то прямая t = tl пересекает решето Г по
вполне упорядоченному множеству, и таким образом ему соответствует
трансфинитное число а.
Важно заметить, что во втором случае знание /х влечет за собой
знание последовательности схх> а2,..., образованной из трансфинитных
чисел, предшествующих а. В самом деле, решето Г образовано из
счетного множества прямолинейных отрезков, параллельных оси ОТ и
расположенных в простую бесконечную последовательность. А так как
каждому трансфинитному числу, меньшему а, отвечает один и только
один составляющий отрезок решета Г и, следовательно, одно целое
число, то эти трансфинитные числа уже перенумерованы. Но это нам
позволяет применить построение Лебега аая функции /а (ху х) и
положить
9 (*i> х) =/• (*> *)•
260
Н. Н. ЛУЗИН
Таким образом, получается поверхность
y=<?(t,X),
всюду определенная и дающая пример функции, аналитически неизо-
бразимой.
В самом деле, пересекая эту поверхность плоскостями t = const,
мы получаем кривые, измеримые В, как угодно высоких классов, что
было бы невозможно, если бы ср (t, x) была функцией классификации
Бэра и, следовательно, входила в некоторый вполне определенный
класс этой классификации.
Анализ функции, построенной Лебегом. Если мы будем пытаться
анализировать процесс, при помощи которого Лебег построил свою
функцию <р (t> x), не допускающую никакого аналитического
изображения, то вот что мы найдем: построение этой функции разбито на две
части, а именно: 1° определение <р(£, х) для точек /0; 2° определение
<р (/, л:) дая точек tx.
В первом случае Лебег полагает y{t0, jc)=0. Но точки t0
образуют линейное множество Е> лежащее на оси ОТ и. определенное при
помощи решета Г. Следовательно, это множество Е, которое, кстати,
во всем построении Лебега играет вспомогательную роль, являясь
лишь промежуточным инструментом при поисках функции ср (ty x), есть
аналитическое множество, неизмеримое В.
Это первый пример аналитического множества, неизмеримого В,
который встречается в математической литературе и в определении
которого посредством бинарного решета Г содержится, как в
зародыше, вся теория аналитических множеств (стр. 165—178).
Отсюда мы заключаем, что теоретически одного этого множества Е
было бы достаточно знаменитому автору дая достижения конечной
цели: назвать функцию, не входящую в классификацию Бэра (см. [20]).
Во втором случае Лебег полагает^ (^, х)=/а(х, х). Так как точки tx
образуют дополнение к Е, то построение функции ср (£, х) полностью
закончено. Поверхность у = ср (tf х) таким образом определена при
помощи совокупности трансфинитных чисел второго класса по Кантору.
Но употребление совокупности трансфинитных чисел здесь крайне
замечательно и совершенно отлично от того, которое имеет место
в теории аналитических и проективных множеств. В самом деле, мы
видели, что в области проективных множеств трансфинитное всегда
может быть исключено и заменено эквивалентным отрицательным
определением. Здесь же не видно, как можно было бы исключить
трансфинитное из определения Лебега дая функции ср (t, x). Трудность
состоит именно в том, что численные значения /в (х, х) получаются
в результате бесконечного множества переходов к дределу,
наложенных друг на друга и расположенных в трансфинитную
последовательность; не известно, как можно было бы получить численные значения
fa(x, x) непосредственноt не переходя через эти предварительные
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
261
переходы к пределу. Этим важным замечанием мы обязаны Борелю *.
Итак, метод Лебега основан на употреблении трансфинитных
последовательностей действительных чисел, каждое из которых имеет
численное определение, существенно зависящее от численных определений
предыдущих членов.
По этой же причине чрезвычайно вероятно, что поверхность
9 (t, х) Лебега не может быть определена без привлечения
трансфинитного. Если это так, то природа этой поверхности совершенно новая,
более интересная, чем у проективных множеств, и, без сомнения, она
скоро привлечет внимание математиков. Изучение точечных множеств,
которые можно назвать без рассуждения Цермело, но при помощи
бесконечного множества последовательных численных определений,
зависящих друг от друга, может нас привести к совершенно
неожиданным результатам [21].
И тем не менее, загадочная вещь, хотя кривую <р (t, х) нельзя
задать непосредственно, не пользуясь предварительными переходами
к пределу, но совокупность этих кривых может быть представлена сразу
и без привлечения трансфинитного.
Точнее говоря, хотя координаты у поверхности Лебега
У' = <? (*> *)
не могут быть численно определены без того, чтобы осуществить все
переходы к пределу, приводящие к численному значению <р (/, х)у так как
этих переходов к пределу трансфинитное число, зависящее от t и от
ху тем не менее можно сразу без малейших затруднений и без
привлечения трансфинитов назвать проективную поверхность
которая пересекается плоскостями t = const по всем возможным
кривым y=f(x)> измеримым В> и, в частности, по всем кривым г/=/а(л:, х)
Лебега.
Чтобы получить эту проективную поверхность, мы отправляемся от
универсального аналитического множества Е, лежащего в трехмерном
пространстве OXTY и пересекаемого плоскостями /^ const по всем
возможным плоским аналитическим множествам.
Пусть РЕ есть проекция множества Е на плоскость ХОТ;
рассмотрим дополнение СРЕ этой проекции и спроектируем его на ось ОТ*
Множество 60
% = РСРЕ,
полученное таким образом, есть линейное проективное множество класса
не выше 2. Если tQ есть точка оси ОТ> принадлежащая %, то ясно, что
плоскость t=t0 заведомо содержит прямую, параллельную оси OY и
не пересекающую универсальное множество Е.
1 Е. В о г е 1. Sur las definitions analitiqaes et sur i'illusion du transfini (Bull,
de la Soc. Math, de France, 47, стр. 42, 1919).
262
Н. Н. ЛУЗИН
С другой стороны, обозначим через Н множество точек M(t, x)
плоскости ХОТ таких, что параллель к оси О К, проведенная через М,
пересекает универсальное множество Е по крайней мере в двух
различных точках. Известно (стр. 143), что Н есть аналитическое
множество. Значит, проекция 82 множества Н на ось ОТ
Ь2 = РН
есть линейное аналитическое множество. Если t2 есть точка оси ОТ,
принадлежащая 62, то ясно, что плоскость t = t2 заведомо содержит
прямую, параллельную оси OY и пересекающую универсальное
множество Е по крайней мере в двух различных точках.
Рис. 12.
Отсюда следует, что множество 6L тех точек, которые мы получим,
удаляя из оси ОТ точки множеств 60 и 02, есть проективное
множество класса 2. Если tx есть точка из Ь19 то ясно, что плоскость t = tb
пересекает универсальное множество Е по однозначной кривой #=/(.*:)>
«определенной для каждого значения х. Так как точки этой однозначной
кривой образуют аналитическое множество, то это множество по
«еобходимости измеримо В9 и, следовательно, функция у—/(х) входит
в классификацию Бэра (см. стр. 537. — Ред.),
С другой стороны, так как аналитическое множество Е универсально,
то мы, очевидно, можем получить всякую кривую #=/(x)> измеримую В,
выбирая подходящим образом точку ty множества 8г и пересекая Е
плоскостью t = tx.
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
263
Установив это, мы возвратимся к предыдущему методу Лебега
{стр. 260). Мы определим однозначную поверхность
y = <f{t9x)
следующим образом:
1° Если точка ? принадлежит множеству-сумме ^0 н- 02, мы просто
лоложим
W,x) = Q.
2° Если точка t" принадлежит множеству 0г, мы полагаем
где однозначная функция/(л:) определяется однозначной кривойy=f(x),
измеримой By которую мы получим, пересекая множество Е
плоскостью t = t".
Ясно, что так построенная однозначная поверхность у = 6 (t, x)
всюду определена. Я теперь утверждаю, что эта поверхность проек-
тивна. Это значит, что множество точек трехмерного пространства
OXTY, принадлежащих этой поверхности, есть проективное множество.
Чтобы убедиться в этом, заметим прежде всего, что рассматриваемая
поверхность y = ty(t9 х) составлена из следующих двух частей: 1°
первую часть мы получим, если возьмем общую часть плоскости ХОТ и
множества плоскостей, параллельных плоскости XOY и проведенных
через точки множества 60 -+- 02, так как множество 60 -+- 62 проективное
класса ^2, то такой же будет и рассматриваемая часть поверхности
y = ty(t,x); 2° вторую часть мы получим, если возьмем общую часть
аналитического множества Е и множества плоскостей, параллельных
плоскости XOYy проведенных через точки множества 61# Так как это
последнее множество проективное класса ^ 2, то такой же будет и
рассматриваемая часть поверхности y = ty(t9 х).
Таким образом, мы приходим к следующему заключению:
однозначная поверхность y = ty(ty x)y построенная таким способому есть
проективное множество класса <^ 2. Пересекая эту поверхность
плоскостями t = const, мы получим только одозначные кривые
y=f(x), измеримые В, и каждая однозначная кривая, измеримая Ву
может быть получена таким образом.
Наличие парадокса не подлежит сомнению. И объяснение его
не легкое, оно, по-видимому, глубоко скрыто. Вот что я могу
придумать. Кривые у =/в (х, х)9 определенные Лебегом и получаемые при
пересечении поверхности Лебега i/ = cp(£, л:) плоскостями / = const,
разумеется, находятся среди разрезов проективной поверхности у = ф (t, x)
плоскостями £ = const. Но они там сдвинуты в направлении,
параллельном оси ОТ так, что разрез . поверхности y = <?(tt x) Лебега
плоскостью £ = /' становится разрезом проективной поверхности
у = ф (t9 х) при помощи плоскости t = f", где t" =^= *'.
264
Н. Н. ЛУЗИН
Но в этих условиях трудность получить кривую #=/e(x, x)y
соответствующую данному транс финитному числу а, сколь угодно
большому, преобразуется в трудность получить точку t". Чем
больше нам нужно совершить предварительных переходов к пределу,
чтобы определить функцию о (t'y *)=/а (л:, л:), тем труднеее нам будет
вычислить численное значение соответствующего t"> так как функция
•Ь (t, х) относительно проста. Мы возвращаемся, таким образом, к идеям
Бореля.
Понятие континуума приобретено геометрической интуицией \ При
изучении континуума не встречается никаких трудностей до тех пор,,
пока мы стоим на чисто геометрической точке зрения; все точки
прямой тождественны, так как они все имеют одни и те же свойства;
трудности появляются лишь с арифметическими определениями, так как
узнавание этих общих свойств становится менее легким2. Полное
арифметическое понятие континуума требует того, чтобы
геометрический континуум рассматривался как множество точек и, следовательно,,
арифметический континуум как множество чисел, причем каждой точке
континуума соответствует некоторое действительное число. Но
геометрический континуум существенно однороден, тогда как
арифметический континуум не имеет никакой однородности. Правда, каждое
действительное число, заключенное между 0 и 1, может быть
представлено в виде бесконечной десятичной дроби
О, ага2... ап...,
но было бы иллюзорно думать, что эта дробь есть определение
действительного числа. Действительные числа, которые могут быть
определены таким способом, очень немногочисленны. Всех их таким
способом получить нельзя. Мы убедились в том, что истинное
определение числа t" требует трансфинитного числа предварительных
переходов к пределу, и, следовательно, эффективное определение
каждого десятичного знака числа t" не может быть достигнуто прежде,,
чем будет проделано трансфинитное число предварительных операций*
Мы видим, что в этих условиях десятичное разложение ни на что
не годно.
Но как только мы констатировали, что арифметический континуум,
совершенно разнороден и что существуют действительные числа t"y
определение которых требует трансфинитной бесконечности
предварительных операций, соответствующих как угодно большому
трансфинитному числу, становится вероятным, что в геометрическом
континууме имеются точки, которые не допускают никакого
арифметического или аналитического изображения.
1 Е. В^о г е 1. Sur les principes de la theorie des ensembles.
Доклад, сделанный на IV Международном математическом конгрессе (Рим*
апрель, 1908 г.).
2 Е. В or el. L'antinomie du transfini (fteVue philosophique, .1900).
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
265
Из таких точек можно образовать множество. Но нельзя назвать
ни одной индивидуальной точки в таком множестве. Мы даже не будем
знать, „существуют" ли точки в таком множестве. Таков случай
множеств-резольвент (стр. 244), и таков, на мой взгляд, случай
большинства проективных множеств. Определение этих множеств, хотя
оно и конечно, зависит от отрицательных операций и строго
эквивалентно трансфинитному.
Аналитическое выражение. Являются ли функции классификации
Бэра единственными, которые допускают аналитическое изображение?
Этот вопрос, на мой взгляд, не имеет никакого абсолютного смысла,
так как, очевидно, надо уточнить, какие операции мы допускаем.
Чтобы убедиться в этом, мы докажем, что если допустить в
качестве аналитического выражения классическую операцию,
состоящую во взятии верхнего предела некоторой функции Urn Ф, то можно
изобразить аналитически^ отправляясь от полиномов9 однозначную
функцию f{x), не входящую в классификацию Бэра.
С этой целью возьмем плоскость XOY и рассмотрим на оси ОХ
линейное аналитическое множество Еу неизмеримое В.
Характеристическая функция f(x) множества £, равная 1 на Е и 0 вне Е> очевидно,
не входит в классификацию Бэра.
Установив это, обозначим через &п элементарное множество, лежащее
в плоскости XOY между прямыми у = п и 1/ = л-ь1 и такое, что его
ортогональная проекция на ось ОХ совпадает с данным аналитическим
множеством Е. Известно (стр. 122), что &п измеримо В и класса ^2.
Значит, сумма Н= Si ■+- &2 "+-••• "|"<?пн~* • • тоже измерима В и класса
^2. Отсюда следует, что характеристическая функция Ф(х, у)
множества Н есть функция класса ^2 классификации Бэра. Значит, мы
можем изобразить функцию Ф (дг, у) в виде двойного предела полинома
от х и у:
Ф(х, y) = \im \1тРт„(х, у).
С другой стороны, возьмем любую точку х0 оси ОХ. Следует
различать два случая:
Первый случай. Точка х0 не принадлежит к Е. В этом случае
прямая, параллельная оси OY и проведенная через лг0, не встречает
множества Н. Значит, функция Ф (х0, у) переменного у тождественно
равна нулю, Ф(х0, */) = 0.
Второй случай. Точка х0 принадлежит к Е. В этом случае прямая
jc = jc0 пересекает множество Н в бесконечном множестве точек,
ординаты которых неограниченно возрастают. Следовательно, верхний
предел функции Ф(х0, #) переменного у заведомо равен 1, когда у
стремится К +00.
Итак, мы можем написать
/(х)=йюФ(*о>у)
266
Н. Н. ЛУЗИН
и, следовательно, окончательно
f(x) = lim lim lim Рт,п(х, у)>
у->+со и-*+со w->+oo
где буква Р обозначает полином относительно х и у и где f(x)
не входит в классификацию Бэра.
Следовательно, при помощи классических операций lim и lim,
употребленных конечное число раз, можно записать функцию, не
входящую в классификацию Бэра.
Кроме того, можно доказать, что этим способом можно записать
все проективные функции и только проективные функции. Но если
повторить эти две операции счетное множество раз, то мы заведомо
выйдем из семейства проективных функций. Но мы не будем
останавливаться на этом пункте, так как, согласно замечанию Бореля, в
данном случае тот факт, что функция допускает аналитическое
изображение, есть в некотором роде побочное обстоятельство, не
прибавляющее ничего к ее первоначальному логическому определению *.
Замечание
Некоторые интересные исследования, касающиеся проективных
множеств, были предприняты недавно Канторовичем и Ливенсоном.
Полученные результаты формулированы в Comptes Rendus 30 декабря
1929 г., 10 февраля, 12 мая и 2 июня 1930 г. Подробный мемуар
опубликован в Fund. Math., XVIII и XX.
1 Ё. Borel. Le calcul des integrates dlfiaies (Jonrn. de Math., 1912).
ЗАКЛЮЧЕНИЕ
Чтобы не покидать области математики, я избегал глубоко входить
в те философские дискуссии, которые могли быть вызваны многими
из встреченных вопросов; да будет мне позволено в этом кратком
резюме сказать все же настолько ясно, насколько я смогу это сделать,
каковы, на мой взгляд, наиболее важные проблемы, которые сейчас
можно поставить более четко, чем несколько лет тому назад.
На предыдущих страницах были изложены многие теории,
касавшиеся различных семейств точечных множеств. В двух первых главах
я старался продолжить и распространить работы Бэра, остановленные
на изучении множеств класса 3. Была дана общая теория множеств,
измеримых jB; она привела к арифметическому результату о
множествах класса 4, вполне аналогичному результату Бэра. В других
главах целью являлось изучение семейств точечных множеств,
выходящих из классификации Бэра.
Интерес исследований такого рода заключается главным образом
в том, что с точки зрения принципов математического анализа можно
сравнивать роль множеств, измеримых Ву с ролью рациональных
чисел, уподобляя множества, неизмеримые В, числам иррациональным.
Хотя идея наиболее общего иррационального числа содержит в
зародыше наиболее сложные аналитические трудности (Борель), однако
неоспоримо, что существуют иррациональные числа, представляющиеся
естественно. Непосредственным примером такого числа служит
диагональ квадрата со стороной 1: это случай иррационального числа,
тесно связанного со свойствами нашего организма (концепция
конгруэнтности, различение направления).
Мы изучали открытие Лебега, который назвал множество,
неизмеримое В. Чтобы найти множество точек вне классификации Бэра и
представляющееся так же естественно, как квадратичное
иррациональное число, мы образовали довольно многочисленные примеры мно-
.жеств вне классификации Бэра, названных при помощи простых
логических законов, где трансфинитное явным образом не входит. Тем
не менее, автор вовсе не считает, что он приблизился к решению этой
важной проблемы. Различные средства, которые он мог придумать,
чтобы определить такое множество, все сводятся к тому, чтобы
предполагать данной совокупность иррациональных чисел (актуальная
бесконечность, имеющая мощность континуума) или употреблять
268
Н. Н. ЛУЗИН
отрицательные определения, аналогичные понятию точки сгущения,,
принадлежащему Линделефу.
Но если мы будем стремиться изгнать эти отрицательные
определения, мы неизбежно наткнемся на совокупность всех чисел второго класса
по Кантору (трансфинитное). Таким образом, отрицательное понятие
может стать эквивалентным трансфинитному.
Дебаты по поводу реальности актуальной бесконечности не новы.
Самая идея актуальной бесконечности была хорошо известна в средние
века (infinitum in facto esso) и всегда вызывала живые возражения
формального или метафизического характера. Математики эпохи
Возрождения, по-видимому, забыли эту идею. Лишь во второй половине
XIX в. эта идея воскресла и была введена в область математики
главным образом благодаря усилиям Г. Кантора. Среди математиков
XIX в., восставших против этой идеи, следует назвать Пуанкаре и
Бореля.
Борель не ограничился опровержением этой идеи, он попытался
уточнить ее истинное значение.
Для него актуальная бесконечность есть просто несовершенная
математическая модель, предназначенная д\я изображения колоссально
большого целого числа, конечного „в себе" и не допускающего в
действительных условиях никакого конечного изображения. Конечное
число может ускользать от всякого вида конечного изображения, и
в то же время еще большее число может быть изображено конечным
образом. Кажется, этим важным замечанием мы обязаны Архимеду
(Аренарий). То, что мы называем актуальной бесконечностью, есть
не что иное, как конечное, но фиксированное и очень большое.
Автор этой книги становится на эмпирическую точку зрения и
склонен рассматривать построенные им примеры как словесные
образования, определяющие не действительно законченные объекты, а лишь
виртуальности. В частности, он рассматривает проективные множества
как объекты, определение которых не может быть вполне закончено:
это чисто отрицательные понятия, которые ускользают от всякого
вида положительного определения. И много шансов за то, что эти
понятия попарно неприводимы. Например, автор рассматривает как
неразрешимый вопрос о том, все ли проективные множества измеримы
или нет, так как, на его взгляд, самые процессы определения
проективных множеств и меры в смысле Лебега являются несравнимыми
понятиями, и, следовательно, они лишены логических
взаимоотношений [35]. Короче говоря, область проективных множеств есть область,
где принцип исключенного третьего уже неприменим, хотя всякое
проективное множество формально определимо при помощи счетного
множества условий.
Но если допускать все множества, измеримые В, то необходимо
допустить проективные множества, как справедливо заметил Лебег.
Следовательно, если желать ограничивать математический анализ лишь
ЛЕКЦИИ ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ, ЗАКЛЮЧЕНИЕ 269
изучением вполне законченных объектов и вполне определенных
взаимоотношений, то нужно, с точки зрения эмпиристов, пожертвовать
некоторыми множествами, измеримыми В, и даже некоторыми
иррациональными числами. В конечном итоге, и вопреки возражениям, вполне
определимых иррациональных чисел имеется лишь счетное множество, хотя
их перенумерование и не может быть осуществлено при помощи
математического закона. Таким образом, арифметический континуум
заведомо содержит неопределимые точки. Эти точки, каждая из которых
имеет бесконечное определение, являются паразитическими во всяком
рассуждении, которое можно сделать эффективно, и таком, что оно
устанавливает вполне определенную связь между уже определенными
объектами. Можно было бы отметить, что в истории математической
науки введение идеальных элементов оказало важные услуги, чего
никто не станет отрицать. Но на это легко возразить, что истинно
полезные идеальные элементы индивидуально различимы, чего нет
в данном случае. Исключение этих точек создало бы большое
упрощение в методах математического анализа (Борель). Однако в данный
момент из таких неопределимых точек можно образовать множества,
которые можно назвать, но нельзя ни назвать индивидуальную точку
такого -множества, ни узнать, „существуют" ли точки в таком
множестве, ни узнать его свойства. По мнению автора, таков случай
большинства проективных множеств. В самом деле, по-видимому, в этом
и заключается единственное естественное объяснение трудностей
теории проективных множеств.
В конечном счете вопрос будет разрешен определенно лишь
усилиями научной мысли, т. е. наблюдением математических фактов.
Философские рассмотрения всегда неопределенны и служат лишь л^я
того, чтобы отличить истинно плодотворное направление от
бесконечного множества других. Только два случая возможны:
Или дальнейшие исследования приведут когда-нибудь к точным
соотношениям между проективными множествами, а также к полному
решению вопросов относительно меры, категории и мощности этих
множеств. С этого момента проективные множества приобретут в
математике право гражданства наравне с наиболее классическими из
множеств, измеримых В.
Или указанные проблемы из теории проективных множеств
останутся навсегда нерешенными, и к ним добавится множество новых
проблем, столь же естественных и столь же недоступных. В этом
случае ясно, что пришло время произвести реформу в наших идеях
об арифметическом континууме.
О КЛАССИФИКАЦИИ БЭРА*
В настоящей статье я намерен указать некоторые следствия из
результатов Суслина.
1. Функциональные приложения. Заметим, прежде всего
что каждая определяющая система (Л-система. — Ред.) может быть
заменена определяющей системой o:=:{SW|¥..,^ }, обладающей следующими
свойствами:
1°. Концы отрезков &*,...«* лежат в рациональных точках.
2°. Отрезок &!*,...wfct*ifc+l содержится в отрезке 8M|...njk.
3°. Длина отрезка ^...п* ранга к меньше, чем -г. Мы называем
регулярной системой всякую определяющую систему, обладающую
указанными свойствами.
Установив это, рассмотрим произвольное Л-множество, лежащее
на оси у.
Обозначим это множество через Е. Пусть 5= {§n,...Hfc} —
регулярная определяющая система для множества Е.
Возьмем на оси х отрезок (0^лг^1). Обозначим через о/
множество иррациональных точек отрезка (O^x^Tl). Пусть £— точка
из о7, изображенная непрерывной дробью (04, а2>. .. аку...), где целые
числа ах, а2>. .. являются неполными частными. Рассмотрим отрезки
8в|, 8в1в„ ..., 8ftl...afc,...; так как эти отрезки замкнуты и их
бесконечное множество, то в силу свойств 2° и 3° существует одна и только
одна точка у\, общая им всем. В силу определения Л-множества эта
точка принадлежит Е. Итак, каждой точке ; из g7 соответствует одна
и только одна точка у\ из Е. Обратно, каждой точке у\ из Е
соответствует по крайней мере одна точка $ из о7.
Рассмотрим ординату г\ как функцию абсциссы $: т] =/($). Если
множество Е даноу то функция f{x) определена без аксиомы Цермело
во всех точках о7.
В силу свойства 3° функция f(x) непрерывна в каждой точке </
относительно g7; множество значений f(x) на о/ есть данное
множество Е. Определим значение функции f(x) для рационального х как
максимум функции f{x) в х относительно <?7. После этого функция
f(x) определена без аксиомы Цермело во всякой точке отрезка
• „Sur la classification de M. Baire". Comptes Rendus, Paris, 91—94, 1917.
О КЛАССИФИКАЦИИ БЭРА
271
(O^x^l). Легко видеть, что /(х) непрерывна (в обычном смысле)
в каждой иррациональной точке отрезка (0^л:^1); значит, /(л:) —
функция, измеримая В и первого класса классификации Бэра.
Значения f{x) во всех рациональных точках образуют, очевидно, счетное
множество. Отсюда:
Теорема I. Всякое А-множество с точностью до счетного
множества есть множество значений некоторой функции f(x)
первого класса, определенной на (0^.х^\) и разрывы которой лежат
лишь в рациональных точках.
В силу теоремы I предшествующей статьи1 имеем:
Теорема Г. Всякое множество, измеримое В, с точностью до
счетного множества, есть множество значений функции /(х)
первого класса, разрывы которой лежат лишь в рациональных точках.
В силу теоремы II предшествующей статьи имеем:
Теорема II. Существует (без употребления аксиомы Цермело и
трансфинитных чисел) вполне определенная функция (в логическом и
точном смысле слова определенная) класса 1, непрерывная в каждой
точке х отрезка (О,1), кроме рациональных точек, такая, что
множество ее значений на (О,1) есть множество, измеримое В.
00
Следствие. Существует ряд полиномов 2 Л»(*)> сходящийся
всюду на (О,1) такой, что множество значений его суммы есть
множество, неизмеримое В.
Если ввести трансфинитные числа в счетном числе, то можно
исключить2 из формулировки теоремы I (и Г) слова с точностью до
счетного множества. Следствие доказывается без употребления аксиомы
Цермело; чтобы эффективно построить ряд полиномов из следствия,
нужно употребить трансфинитные числа в счетном числе (т. е. те,
которые меньше некоторого из них).
Для теоремы 1 имеется обратное утверждение:
Теорема III. Множество значений всякой функции f{x),
входящей в классификацию Бэра, есть А-множество.
2. Неявные функции. Установим следующее определение: мы
говорим, что определяющая система {&*,...„*} для множества Е есть
однозначная система, если для каждой точки х из Е существует одна
и только одна последовательность целых положительных чисел
ai> а2> • • •> afc> • • • такая, что точка х содержится во всех отрезках
Зв1, 8в|(Ч, ..., 8в1...в;ь ... Установив это определение, мы можем,
употребив метод Суслина, доказать следующее утверждение,
характеризующее множества, измеримые В.
1 Имеется в виду теорема о том, что всякое множество, измеримое £, есть
-4-множество (ссылка сделана на статью Суслина, Comptes Rendus, 88, 1917. — Ред.}
(см. 114|).
2 Это замечание принадлежит Суслияу.
272
Н. Н. ЛУЗИН
Теорема IV. Для того чтобы А-множество было измеримо В,
необходимо и достаточно, чтобы оно обладало однозначной
системой.
Это утверждение позволяет доказать, что все результаты Лебега
относительно аналитической изобразимости неявных функций
сохраняются1; но доказательства сложны и используют совокупность всех
трансфинитных чисел второго класса,
3. Л-множества. Можно доказать следующие теоремы об Л-мно-
жествах:
Теорема V. Всякое А-множество измеримо L.
Теорема VI. Если множество Е, которое есть А-множество,
образованное из точек совершенного множества Р, есть множество
второй категории на Р, то существует интервал, содержащий
точки Р, в котором дополнение к Е относительно Р есть первой
категории (на Р. — Ред.),
В силу этих теорем Л-множества могут быть использованы в теории
функций (например, в теории интегрирования).
Наконец, Суслин показал, что всякое А-множество либо счетно,
либо содержит совершенное множество. Мощность множеств,
дополнительных к Л-множествам, не известна; эти множества не являются
обязательно Л-множествами.
1 В доказательствах Лебега („Sur les fonctions representables analytiquement"
Journ de Math, pures, appl., 1905) содержится ошибка. — Ред.
О НЕКОТОРЫХ СВОЙСТВАХ А-МНОЖЕСТВ *
В заметке „Об определении множеств, измеримых В, без помощи
трансфинитных чисел" (Comptes Rendus, 8 января 1917 г.) Суслин ввел
важный класс множеств, названных им ^-множествами. Эти множества
определяются счетным множеством условий и являются более общими,
чем В-множества. Многие свойства Л-множеств были изучены Суслиным
в указанной заметке1, некоторые другие были отмечены Лузиным в
заметке, напечатанной в том же самом выпуске Comptes Rendus.
Дальнейшие исследования Суслина и Лузина, касающиеся Л-множеств, пока
не опубликованы.
В настоящей работе мы дадим упрощенное доказательство
основной теоремы Суслина об Л-множествах2, основанное на разложении
множества, дополнительного к Л-множеству, на сумму fr^ множеств,
измеримых В. При помощи этого разложения мы построим несчетное
множество, которое преобразуется в множество меры нуль при всяком
взаимно однозначном и непрерывном преобразовании содержащего его
интервала (и, следовательно, не содержит никакого совершенного
подмножества).
Наконец, мы дадим доказательство следующей теоремы: всякое
Л-множество измеримо в смысле Лебега, и укажем одно обобщение
этой теоремы.
Этот мемуар написан так, чтобы его могли понять и лица, не
знакомые с работами Суслина и Лузина об Л-множествах.
* Sur quelques proprietes des ensembles (Л): Bull. int. Acad. Sci., Cracovie,
серия A» № 4-5a, 35—48, 1918 (Совместно с В. Серпинским. Представлено В. Сер-
пинским на заседании 8 апреля 1918 г.).
1 Наиболее важные свойства Л-множеств, найденные Суслиным, таковы: всякое
линейное Л-множество есть ортогональная проекция на ось абсцисс некоторого
плоского множества, измеримого В% и обратно. Всякое множество, измеримое В, является
Л-множеством, иг не наоборот. Чтобы Л-множество было измеримо В, необходимо и
достаточно, чтобы его дополнение было Л-множеством. Всякое несчетное
Л-множество содержит совершенное подмножество.
2 Доказательство Суслина (основанное на геометрических рассмотрениях) не было
опубликовано; его основная теорема сформулирована в указанной заметке (Comptes
Rendus, 8 января 1917 г.).
274
Н. Н. ЛУЗИН
1. Допустим, что каждой конечной системе натуральных чисел
л,, я?, . .., Пк поставлен в соответствие интервал ^»]1>,...пк; мы будем
говорить тогда, что задана определяющая система
Рассмотрим множество Е для всех точек х> для каждой из которых
существует по крайней мере одна бесконечная последовательность
индексов л,, л2, лп, ... такая, что точка х принадлежит всем интервалам
Мы скажем, что множество Е определено системой S.
Суслин называет А-множеством всякое множество, допускающее по
крайней мере одну определяющую систему.
Определяющая система называется регулярной, если каждый
интервал V«*...»'fc«jt+i содержится в интервале otv,t...MJtJ. Можно было бы
доказать без труда, что всякое Л-множество допускает по крайней мере
одну регулярную определяющую систему. (Если бы мы допускали
интервалы, сводящиеся к одной точке, и пустые интервалы, и если бы
мы считали, что пустой интервал содержится в любом интервале, то
для получения регулярной определяющей системы было бы достаточно
заменить каждый интервал Кхщ...ык системы S пересечением всех
интервалов 8Wl, 8WiMl, ..., 8M|Wt...,IJfe.)
2. Пусть Е — данное Л-множество, и пусть 6*= {ищи,...»**} — его Р^
гулярная определяющая система. Рассмотрим точку х, не
принадлежащую к Е. Мы скажем, что интервал й,^,,...*^ системы S имеет индекс О
относительно точки х> если х не принадлежит этому интервалу. Если х
принадлежит интервалу %ущ...пк> то мы назовем индексом интервала
%,*,... *fc по отношению к точке л: и обозначим через Ind^o,*,,,,...^
наименьшее число (натуральное или трансфинитное), превосходящее все числа
lndxKxv^..vku (л=1, 2, 3, ...)J.
Легко видеть, что если х — точка, не принадлежащая
множеству Еу то всякий интервал 8Mi„t#..nfc из системы *S,
определяющей £, имеет в точке х определенный индекс,
являющийся либо натуральным числом, либо
трансфинитным числом второго класса.
Действительно, допустим, что интервал оР[Рг,^Рт не имеет
определенного индекса в точке х или что этот индекс не является ни целым ко-
1 Всегда можно было бы предполагать, что длины интервалов &-го ранга,
Ьнн ###п., стремятся к 0 при k—> со\ однако в наших рассуждениях вто ограничение
не является необходимым»
2 Понятие индекса было введено Сусляным (в геометрической форме) и затем
упрощено Лузиным. Многие свойства индексов были изучены Сусляным и Лузиным»
О НЕКОТОРЫХ СВОЙСТВАХ ^-МНОЖЕСТВ
275
нечным числом (^0), ни трансфинитным числом второго класса.
Очевидно, что в этом случае по крайней мере один из интервалов
°PiPu..Pmn (Л=1, 2, 3, ...)
обладает тем же свойством1. Повторяя это рассуждение, мы пришли бы
к бесконечной последовательности интервалов из системы S:
°J>iPi. -./',„> °Р>Р-:...ртРт+1> °/'»^--ЯтЯт-иЯя+»> • • •> (1)
в которой ни один интервал не имеет определенного индекса в точке х
или имеет индекс, не являющийся ни конечным числом (^0), ни
трансфинитным числом второго класса. Ясно далее, что в этом случае каждый
из интервалов (1) должен содержать точку jc; но так как система S
регулярна, то х принадлежит и каждому из интервалов (которые
содержат интервал ъР]...рт)
и, следовательно, х принадлежит всем интервалам регулярной
последовательности интервалов из S:
S ^ «Ч N
°Р\> °PiPi> • • •> °РЛ.-Л»» °р1Рг-"Р»гРрг+>> • • •>
следовательно, является точкой множества Я, что противоречит нашему
предположению.
3. Назовем индексом системы S относительно точки х (не
принадлежащей Е) и обозначим через Ind^ наименьшее натуральное или
трансфинитное число, превосходящее все индексы интервалов SHiN2>_WJk
из S (относительно точки х). Легко видеть, что Indz*S является
наименьшим числом, превосходящим все индексы Indzon (л = 1, 2, 3, ...);
следовательно, Indx S является (для каждой точки х9 не принадлежащей Е)
натуральным числом или трансфинитным числом второго класса.
Для каждого данного числа а, натурального или трансфинитного
второго класса, обозначим через Р<*> совокупность всех тех точек х
(не принадлежащих Е), для которых
Ind^AS^a;
мы покажем, что все множества /*в) измеримы В.
Это утверждение верно для а = 1, ибо Р**1 является множеством
точек дг, не принадлежащих ни одному из интервалов 8^ &2> &3, — ,
Пусть теперь Р — число натуральное или трансфинитное второго
класса ^> 1; предположим, что наше утверждейие справедливо, каковы бы
ни были число а<СР и определяющая система S.
1 Чтобы убедиться в этом, достаточно сослаться на теорему, согласно которой
лля всякой бесконечной (счетной) последовательности чисел первого или второго
класса существует число второго класса, превышающее- все члены данной последо-*
вательности.
276
Н. Н. ЛУЗИН
Дкя всякого данного натурального р обозначим через S^ систему
•^H^L.nb О)
где
*$,...**= *!»«"■•••"*» для ni» л1э..., nfr = l, 2, 3,..,
Пусть £(Р) — множество, имеющее S^P) своей определяющей системой;
через Р*а) обозначим множество всех точек дс, не принадлежащих Е&\
для которых
lndT#p> = a.
В силу предположения все множества Р£в)(а<С?; Р —1> 2» 3, ...)
измеримы 5.
Легко проверяется следующая формула:
P(W:
(Здесь ^ обозначает суммирование, распространенное на все натураль-
ные и трансфинитные числа, меньшие ^.)
В силу принятого предположения множества Р^] и PW (<*<СР)
измеримы В; так как сумма и пересечение счетного числа множеств,
измеримых Ву и разность двух множеств, измеримых Ву измеримы Ву то из
•формулы (4) следует, что множество РФ) измеримо В. Итак, формула (4)
позволяет доказать методом трансфинитной индукции, что все
множества Р(в) измеримы В, что и требовалось доказать.
Обозначая теперь через СЕ дополнение к множеству £, очевидно,
лолучим формулу
С£ = Р(1)-*-Р(2)ч-.. ,+ ^ + ^-h... -*-Р(в)н-... (а<2) (5)
(неравенство а <^ 2 обозначает, что суммирование распространено на
все натуральные числа и трансфинитные числа второго класса).
Формула (5) показывает, что дополнение к Л-множеству
всегда является суммой Sx множеств, измеримых В (или
пустых), и, следовательно, что всякое Л-множество есть
пересечение ^ множеств, измеримых В (на основании
формулы Е-
ЦСР*А.
Мы покажем теперь, что а ля того, чтобы Л-множество Е
было измеримо В, необходимо и достаточно, чтобы,
начиная с некоторого, все члены ряда (5) были пусты (т. е.
чтобы последовательность (5) содержала лишь конечное или счетное
число непустых множеств). Очевидно, что высказанное условие
достаточна (так как в этом случае СЕ является суммой конечного иди
счетного числа множеств, измеримых В, и потому само измеримо В, а зна-
О НЕКОТОРЫХ СВОЙСТВАХ А.МНОЖЕСТВ
277
чит, таково же и Е); поэтому достаточно доказать, что это условие
необходимо. Но предварительно мы докажем одну общую лемму.
4. Пусть М—некоторое подмножество данного множества СЕ. Назовем
индексом системы S (соответственно интервала 8И1м,...и4) относительно
множества М и обозначим Ind VS (соответственно Ind v о т ) наименьшее
целое число (конечное или трансфинитное), превосходящее индексы Indx»S
(соответственно Ind* оП),,2 .WJt) для всех точек х из множества М. Так как
индексы Inda S суть числа первого или второго классов, то очевидно,
что для всякого подмножества М из СЕ индекс Indj, S всегда является
конечным или трансфинитным числом ^2, где 2 обозначает наименьшее
число третьего класса. Мы докажем следующую лемму:
Лемма. Если S—регулярная система, определяющая
множество Е, М — подмножество множества СЕ, и если М есть А-мно-
жествоу то мы имеем
Ind„S<<2.
Доказательство. Пусть S' = (Ъчь.-./'к)—регулярная система,
определяющая множество М. Обозначим вообще через M(nv л2, . .., nq)
подмножество М, определяемое системой
S' = (n1,ni,...,ng)={^--^},
где
tev.p?)= ци,..,уЛ...Рк (*ля Pv Р2--> Р* = 1> 2, 3, ...).
Очевидно, будем иметь
М = М(\) + М(2) + М(Ъ)+... (6)
и
M(nlf /i2, ...tnq) = M(nl9 л.>, .. ., ngi 1)ч-М(п1У п,у .. ., nqy 2) -ь.. . (7)
Допустим, что
lndMS=U. (8)
В силу (8) и из определения символа Ind^^S легко обнаружить, что
существует по крайней мере одно натуральное число n'v для которого
ШЯЪЯ.=Я. (9)
Но из (9) и (6) следует также, что существует по крайней мере
одно число р[9 для которого
Из (10) мы заключаем, что существует натуральное число л'2, для
которого
278 н. н. лузин
и, наконец, в силу (7) существует р2, для которого
Вообще мы получим таким образом две бесконечные
последовательности натуральных чисел
и
Pv Рг> Pv • • •>
такие, что
Indjr(F;.p;.....г1,)%;.... »*=2, для s=1, 2> 3> ••• ^
Между тем, множество М{р\, />!„ ...,р^) (имеющее своей
определяющей системой
содержится, очевидно, в интервале ^ >> > (ибо вследствие регулярности
системы S* все интервалы
/*•••'•=■,.. .
содержатся в интервале TpV .у); таким образом, формула (11)
показывает, что интервалы 7ру...р' и V?/...t/ имеют общие точки.
Мы приходим таким образом к двум бесконечным
последовательностям интервалов:
о * Ь *', Ь ' > >
V я!«° "iW • • •
и
таким, что каждый интервал содержит все последующие и пересекается
с интервалом того же ранга в другой последовательности. Легко видеть,
что в этом случае найдется по крайней мере одна точка д:0,
принадлежащая всем интервалам обеих последовательностей.
Но тогда точка х0 принадлежала бы множествам Е и Л/,
определенным соответственно системами S и *У, что невозможно, ибо М
содержится в СЕ> Значит, равенство (8) влечет за собой противоречие; этим
лемма доказана.
5. Допустим теперь, что множествр СЕ является Д-множеством.
Тогда из леммы п. 4 следует, что
значит, для каждого х из СЕ
\ndxS<*{),
О НЕКОТОРЫХ СВОЙСТВАХ Л-МНОЖЕСТВ
2?9
а потому (в силу определения множеств Р^>) все множества /*"> пусты
при а^а0> откуда следует, что ряд (5) содержит лишь конечное или
счетное множество непустых слагаемых. Так как члены ряда (5) измеримы JB,
то мы заключаем отсюда, что СЕ (которое есть сумма счетного числа
множеств, измеримых В) также измеримо В. Таким образом, мы
доказали, что если СЕ является ^-множеством, то оно измеримо В. Но тогда,
очевидно, Е тоже измеримо В. Итак, если СЕ есть Л-множество, то Е
измеримо В. Так как обратное тоже справедливо (ибо, как доказал
в указанной заметке Суслин, всякое множество, измеримое В, является
Л-множеством1), то мы получаем теорему:
Теорема Суслин а. Для того чтобы А-множество было
измеримо Ву необходимо и достаточно^ чтобы его дополнение СЕ было
также А-множеством.
6. Суслин построил Л-множество £, дополнение к которому СЕ
{относительно интервала (0, 1)] не есть Л-множество2; соответствующий
ряд (5) содержит в этом случае несчетное множество (мощности Кх)
членов P(0t), которые являются непустыми множествами. В каждом из
этих множеств выберем по точке; мы получим таким образом
несчетное множество точек Q (мощности Кх), лежащее на интервале (0, 1).
Мы утверждаем, что множество Q имеет меру нуль (по Лебегу).
Всякое А-множество измеримо в смысле Лебега; подробное
доказательство этого мы дадим в п. 7. Отсюда следует, что всякое
дополнение к Л-множеству также измеримо L. В то же время известно, что
всякое множество, измеримое Z,, является суммой множества меры нуль
■и счетной совокупности замкнутых или пустых множеств (следовательно,
измеримых В). Можно, следовательно, положить
CE = N +-M, * Мо + Л/з-ь..., (12)
где т (N) = 0 [m(N) обозначает лебеговскую меру множества N] и где
Ml9 M2, M3i ... множества, измеримые В, значит, тем более Л-мно-
жества.
В силу леммы п. 4, л\я всякого натурального п имеем:
1пс1^5=аи<о.
1 Это следует немедленно из следующих трех свойств Л-множеств: 1° всякий
интервал есть Л-множество; 2° сумма счетного числа Л-множеств есть Л-множество;
3° пересечение счетного числа Л-множеств есть Л-множество. Ср. заметку В. Сер-
пннского „Об аксиоматических определениях множеств, измеримых В", напечатанную
,в предыдущем номере Comptes Rendus.
2 Класс всех Л-множеств имеет, очевидно, мощность континуума; поэтому при
помощи хорошо известного процесса Кантора (при помощи которого доказывают, что
множество всех точечных множеств на интервале имеет мощность, большую мощности
континуума) можно построить такое множество £q, которое не является Л-множеством.
Но, как доказал Суслин, дополнение к втому множеству СЕ§=Е\ есть Л-множество.
Доказательство Суслина, упрощенное Лузиным, будет опубликовано в другом ме-
.муаре*
280
Н. Н. ЛУЗИН
Это значит, что для о.^ап множества Р(а) не пересекается с Мп*
Формула (5) дает тогда (так как Мп — подмножество СЕ)
мп= 2 mj*>
и, следовательно,
MnQ= £ MJX'>Q. (13)
Но из определения множества Q следует, что каждое из
множеств P^Q содержит не более одной точки; следовательно, сумма (13)
содержит не более счетного множества точек, а, значит, множество MnQ
имеет меру нуль. Мы приходим, таким образом, к выводу:
m(MnQ) = 0 для /г=1, 2, 3, .. . (14)
С другой стороны, формула (12) дает (в силу того, что Q —
подмножество СЕ)
откуда, вследствие (14) и того, что т (N) = 0,
m(Q) = 0,
что и требовалось доказать.
Пусть теперь <р — взаимно однозначное и непрерывное отображение
интервала (0, 1). Будем обозначать через <р (х) точку, в которую
переходит точка х при отображении <р, а через <р(М)— то множество,
в которое отображается множество М. Пусть далее *S= {^и*...^}—
определяющая система множества Е; каждый интервал ^п,...^ этой
системы преобразуется в интервал <р (^м»...**), а система *S—в
систему <p(*S). Легко видеть, что <?(S) будет определяющей системой для
множества <р (Е) и что <р (Р^) есть множество всех тех точек х из
<р {СЕ) = С<? (£), а^я которых
мы получим таким образом формулу
cpfCE^^P^-bcp^ (<*<*■*),
которая нам позволит [доказать точно так же, как это было доказано
для Q, исходя из (5), что у (Q) имеет меру нуль.
Мы доказали тем самым, что существует несчетное множество*
которое переходит в множество меры нуль при любом взаимно
однозначном и непрерывном отображении интервала1. Таким образом, это
свойство ни в коей мере не является характеристическим лая счетных
множеств.
1 Наше доказательство, очевидно, использует принцип произвольного выбора»
О НЕКОТОРЫХ СВОЙСТВАХ А -МНОЖЕСТВ
281
Основываясь на доказанном свойстве множества Q> легко
обнаружить, что Q не содержит никакого совершенного подмножества (ибо
всякое совершенное множество может быть отображено на множество-
положительной меры при помощи подходящего взаимно однозначного и
непрерывного преобразования всего интервала, содержащего данное
множество*).
Итак, мы имеем пример несчетного множества, не содержащего
никакого совершенного подмножества*.
7. Теперь мы докажем следующую теорему:
Те орема3. Всякое А-множество измеримо L.
Доказательство. Пусть Е — данное Л-множество и пусть S =
= {?>"i*>--wj} — его регулярная определяющая система. Мы будем
обозначать через £Plf>2'"p8 множество, определенное системой
oiPiPt-.-Pe) f*iP\P:---P*)\
где
Qnlfh!/.nk =:°piPi...jwi"i...w* Для ninn •••» ")[-1) 2, 3, ...
Множество Е р7" лежит, очевидно, в интервале ^р,л...я,. Легко-
видеть также, что мы имеем
Е = £<*> -ь Е& -+- £<*> -н ... {15}
и
niPxPt. ♦. Р$) pifxPi ---Ps1) . r(PiP*-••?$*) , H6V
Из теории меры Лебега известно, что для всякого множества Е
существует содержащее его множество Му измеримое L, такое, что его
мера равна внешней мере множества Е, т. е.
т(М) = тё(Е). (17)-
Будем обозначать через №***--**' множество, измеримое L, лежащее
в интервале oPlP2...p8y содержащее множество Е ***"*' и такое, что
m(M(rj"-Pt))=m.(E<fJ"-l")). (18)-
Положим
Г = Л^1)-1-М^-|-М<3>н-... (19>
и
1 Ср. ааметку В. Серпинского („Об одном общем свойстве точечных множеств"),
напечатанную в Comptes Rendus, 162 (8 мая 1916 г.).
2 Проблема существования таких множеств была поставлена Л. Шеффером и
решена (при помощи аксиомы Цермело) Ф. Бернштейном. Ср. A. Schoenfliess.
Entw. der Mengelehre и т. д., I половина (1913)» стр. 361.
* Эта теорема уже была анонсирована Н. Лузиным в указанной заметке.
1H2
Н. Н. ЛУЗИН
Эти множества являются измеримыми множествами как суммы
счетного числа измеримых множеств. Положим еще
R = M—T, (21)
piPtPt • • • Ps) _ ДЛУМ • • • Л) j<P\Pt --Ps) iiyy\
M
N=R + 2iR{p*' "'Ps\ (23)
где суммирование V производится по всем конечным системам нату
ральных чисел р19 р2, • • • , /V
Заметим прежде всего, что при любом натуральном значении п
множество Л/(,,) содержит множество EW; отсюда мы заключаем, в силу (15)
и (19), что множество Т содержит множество Е. Следовательно,
множество
Q = M — R (24)
также содержит Е [так как, в силу] (21) и (24), имеем Q=MT, где
множества МиГ содержат Е]. В то же время, в силу (21) и (24),
•Q измеримо; отсюда, на основании (24) (Q содержит Е), имеем
m.(£)<m(Q)<m(M),
а потому, в силу (17),
m(Q) = m(M). (25)
Но в силу (21), R содержится в М; поэтому формулы (24) и (25)
дают нам
m(R) = 0.
Аналогично, исходя из формул (16), (18), (20) и (22) [вместо (15),
417), (19) и (21)], получим
А\я любой конечной системы натуральных чисел р19 р2, .. ., р9.
Таким образом, в силу (23), множество N есть сумма счетного числа
множеств меры нуль; следовательно, имеем
т(ЛО = 0. (26)
Положим теперь
P = M — N; (27)
* силу (26), будем иметь m(P) = m(M); значит, на основании (17)
m(P) = m$(E). (28)
Теперь мы покажем, что множество Р содержится в Е.
Действительно, пусть х — точка множества Р. Так как Р содержится в мно-
О НЕКОТОРЫХ СВОЙСТВАХ /1-МНОЖЕСТВ
283
:жестве М, на основании (27), то х есть точка множества М. С другой
стороны, из (27) и (23) заключаем, что х не принадлежит множеству /?,
т. е., в силу (21), множеству М— 7\ Таким образом, х принадлежит М
и не принадлежит М— Т; следовательно, х принадлежит множеству 7,
-т. е., в силу (19), по крайней мере одному из множеств М*> (л =
= 1, 2, 3, —). Пусть дг — наименьшее из натуральных чисел такое,
что х принадлежит множеству Лг7 •
Из (27) и (23) следует, что точка х не принадлежит множеству /?lVl\
-т. е., в силу (22),—множеству М{Ях)—Т*Ях); поэтому х принадлежит Ля '*
и не принадлежит ЖЯх — ТЯх; отсюда следует, что х принадлежит
множеству j1\ т. е«, на основании (20), множеству
7Ч»,)=М(„1)н_Л^./,2)_ьМ(„3,+ _.
следовательно, х принадлежит по меньшей мере одному из множеств
№ (л=1, 2, 3, )♦ Через q2 обозначим наименьшее натуральное
число такое, что х принадлежит множеству АГЫг*
Вообще предположим, что мы уже определили индексы д19 q2y ..., 9*
•и что точка х принадлежит множеству Af<™'-4 Вследствие (27) и (23),
х не принадлежит множеству J?™**"9* f т# е., вследствие (22),
множеству М™*""4**—yw*...?*). как и раньше? мы заключаем отсюда, что х
принадлежит множеству р*1**""** и потому, в силу (20), по крайней
мере одному из множеств Л/^1*2" *у*'° (л=1, 2, 3, ...). Через qk+x мы
обозначим наименьшее натуральное число такое, что х принадлежит
ъсножеству A^**u7fc+l).
Таким образом, мы определим последовательность qx, q2i <7з> • • •>
причем при любом натуральном к точка х принадлежит множеству
а, следовательно, и интервалу °^5...^« Значит, х принадле-
.жит каждому из интервалов бесконечной последовательности
поэтому х является точкой ядра Е определяющей системы
Мы доказали, что каждая точка множества Р принадлежит £,
вследствие чего
m(P)^mi(E) (29)
{здесь 1щ(Е) обозначает внутреннюю меру множества Е\.
Из формул (28) и (29) следует, что
/*.(£)<*!,(£),
284
Н. Н. ЛУЗИН
откуда следует измеримость L множества Е.
Таким образом, наша теорема доказана1.
8. Мы подошли к обобщению только что доказанной теоремы.
Пусть каждой конечной системе натуральных чисел пи л2, . . ., %
соответствует линейное множество iiinlYit... Hfc»
Обозначим через Е множество всех таких точек х, для каждой из
которых найдется по крайней мере одна последовательность индексов.
л1э /г2, л3, ..., такая, что х принадлежит каждому из множеств
Мы будем говорить, что Е есть результат Л-операции, примененной
к системе множеств
(Всякое Л-множество может быть, таким образом, рассмотрено как
результат Л-операции, примененной к системе интервалов £= {&1у*...«к},
и наоборот, Л-операция, примененная к системе интервалов, всегда
приводит к Л-множеству2.)
Можно было бы без труда показать, что Л-операция содержит как
частные случаи сумму и пересечение счетной совокупности множеств,,
так же как верхний и нижний пределы последовательности множеств.
Предположим теперь, что множества ЕЩпг...пк системы ^={ЕП1пг...пк}
все измеримы L. Д\я такой системы можно дословно повторить все
доказательство п. 7, заменяя лишь интервалы o„|t4#>.njk множествами
Еп^...П1г Таким образом, получим теорему:
Теорема. А-операция> примененная к системе множеств, изме~
римых L> всегда приводит к множеству, измеримому L.
1 Из доказанной теоремы легко следует, что Л-множества н их дополнения
переводятся всяким взаимно однозначным 'и непрерывным преобразованием содержащего
их интервала в множества, измеримые L.
2 Н. Лузин доказал, что Л-операция, произведенная над системой Л-множеств,
всегда приводит к Л-множествам.
ОБ ОДНОМ МНОЖЕСТВЕ, НЕИЗМЕРИМОМ Б*
По известной теореме Бэра1 каждая функция, представимая
аналитически, точечно разрывна на каждом совершенном множестве, если
пренебречь множеством первой категории относительно этого множества.
„Возникает очень важный вопрос, — пишет А. Лебег в своем мемуаре
^,Sur les fonctions representables analytiquement",— является ли
необходимое условие, данное теоремой XVI, достаточным? И, если это не так,
существуют ли функции, которые ему не удовлетворяют? Я не пытался
ответить на эти трудные вопросы".
В 1914 г. Лузин показал, что свойство Бэра не является
достаточным, если мощность континуума есть алеф-один2. Он доказал тот же
•факт в 1917 г. при помощи аксиомы выбора без применения гипотезы
•континуума3. Целью настоящего мемуара является эффективное
определение функции, не представимой аналитически, но обладающей
свойством Бэра.
Мы докажем, что такой функцией является характеристическая
«функция множества Е, определенного следующим образом:
Пусть
г, г2, г3,. .. (Г)
— бесконечная последовательность, состоящая из всех рациональных
чисел, содержащихся в интервале (0,1).
Пусть х — действительное число интервала (0,1);
х = (со> с\у с2> сз • • • /21= со ~*~ ~2 ~+~ 22~*~ 23 ~*~ • • ' Q'
— его конечное или бесконечное двоичное разложение. Обозначим
через Е (х) множество, образованное из всех тех чисел гп
последовательности (Г), для которых в разложении (2') (или, по крайней мере,
в одном из двух двоичных разложений числа х, если их два) с„ = 1.
* „Sur un ensemble non-mesurable B, Journ. Matb. pures, appl." серия 9, 2,
53—72, 1923. (Совместно с В. Серпинским)
1 Н. Lebesgue. Journ. de Math., серия 6, I, 138, 1905 (теорема XVI).
3 Comptes Rendus» 158, 1259 (заметка от 4 мая 1914 г.).
з Fund. Math., II, 157, 1921.
286
Н. Н. ЛУЗИН
Пусть Е будет множество всех чисел х интервала (0,1), дкл которых
множество Е(х) не вполне упорядочено (если его упорядочивают по-
возрастающей величине рациональных чисел, которые оно содержит)..
Следует заметить, что множество Е (относительно которого мы
докажем, что оно неизмеримо В) определено без использования
операций сложения и умножения, исходя из несчетного множества множеств,
что существенно отличает наш пример от примера функции, не пред-
ставимой аналитически, найденного Лебегом (loc. cit.)1.
Можно также доказать (чего мы не делаем в этом мемуаре), что
множество Е есть ортогональная проекция плоского множества,
измеримого В {F класса 1), которое можно определить эффективно.
Существование множеств, измеримых В, проекции которых неизмеримы Ву.
было доказано Суслиным2.
Только глубокий анализ теории Л-множеств, созданной Суслиным,.
позволил нам получить результаты, изложенные в этом мемуаре.
1. Обозначим через R множество всех рациональных чисел г,
удовлетворяющих неравенству 0<V<[1. Если каждому числу г множества R
поставлено в соответствие замкнутое (или пустое) множество F2 m-мер-
ного пространства, то мы скажем, что нам задана определяющая
система £= (/%■}• Мы назовем ядром системы S множество всех точек р
рассматриваемого пространства, для которых существует по крайней
мере одна бесконечная убывающая последовательность чисел
множества R:
гг > г2 > гз> • • •
таких, что р принадлежит каждому из множеств
Гтху Гг3, Гги . . .
Мы назовем Л-множеством всякое множество, которое является
ядром определяющей системы3.
Пусть Е—ядро определяющей системы £={/%.}. Положим (для
каждого г из R)
F°r = F;> ft)
Гг = РГх*Ъ1Т\ (2>
если а — трансфинитное число первого рода; сумма 2 распространяется
на все числа р множества R, которые <^г и
лв=пле, о)
1 Ср. A. Lebesgue. Notice sur les travaux scientifiques. Toulouse, 1922, стр. 61»
2 Comptes Rendus, 8 января 1917 г.
3 Это определение Л-множества не совпадает с классическим определением (см.
С у ел и н. Comptps Rendus, 8 января 1917 г.), во можно доказать, что оно ему
эквивалентно; впрочем, это не будет необходимо для нашей цели.
ОБ ОДНОМ МНОЖЕСТВЕ, НЕИЗМЕРИМОМ В
287
если а есть трансфинитное число второго рода; произведение Ц рас-
иространяется на все трансфинитные числа ?<<*.
Множества F", определенные таким образом при помощи
трансфинитной индукции, очевидно, измеримы В для каждого числа г из R и
каждого трансфинитного числа а<2 (2 обозначает наименьшее
трансфинитное число третьего класса).
Согласно (2) и (3), находим:
F^F* при а О. (4).
Положим
г
суммирование 2j распространяется на все числа г множества R. Все
г
множества S* измеримы В для д <С -. Согласно (4) имеет место
S'DS' для а О. (6>
2. Мы покажем, что
£=П^. (?)
Пусть /? — точка множества Е. Так как Е есть ядро системы {/vj,
то существует бесконечная убывающая последовательность чисел
множества R:
Гг>г2>г3>... (8)
такая, что
р 6 Л* для /7 = 1, 2, 3,-,.1 ДО-
Согласно (1), мы имеем
р 6 /^ Для л = 1, 2, 3,... (Ю>
Предположим, что имеет место
p£Fr\ (/2 = 1,2,3,...) (11>
для всех трансфинитных чисел ЕО, где а —данное трансфинитное
число > 1.
Пусть /г — данный индекс. Если а — число первого рода, то имеем,
согласно (2),
f^CSC1- (12>
Согласна предположению, (11) верно для £ = а— 1, следовательно^
p6/va"L и pff^1. Но, согласно (8), имеем гя+1<гя, и, следовательно^
1 х£Х обозначает, что х есть элемент множества X.
288
Н. Н. ЛУЗИН
FrtH.l является членом суммы ^ F* , которая содержит, таким обра-
9<гп
зом, точку р. Следовательно, р есть точка множества (12).
Если а есть число второго рода, мы имеем, согласно (3),
К= П Fb
следовательно, согласно (11),
Таким образом, при помощи трансфинитной индукции формула (И)
установлена для всех £<2. Из этого, согласно (5), следует:
p£S* ДАЯ а<2;
следовательно, р£Р, где
p = ILs*. аз)
Пусть теперь р — точка множества (13). Мы имеем тогда
p£S* для а < 2;
тогда, согласно (5),
р€ШК лая a<Q.
г
Из того, что сумма 2 содержит счетное множество членов F*y мы
г
заключаем, что существует по крайней мере одно число гх множества R
такое, что формула
реп:
справедлива для несчетного множества трансфинитных чисел a <C 2,
следовательно, согласно (4), для всех а<2.
Следовательно, мы имеем для каждого a < 2
pGF?1;
следовательно, согласно (2),
Р £ 2 F? Аля a < 2.
Из того, что сумма 2 содержит счетное множество членов
Fa(p<rj), заключаем, как и выше, что существует число г2<^г1 из R
такое, что
р*П
ОБ ОДНОМ МНОЖЕСТВЕ. НЕИЗМЕРИМОМ В
289
для несчетного множества чисел <х<С^> следовательно, для всех а<2.
Продолжая рассуждать таким образом, мы получим бесконечную
убывающую последовательность чисел множества R> гг ^>г2> г3^> ...
таких, что
p£F;n для а<2; Л = 1, 2,3...
В частности, для a = О, находим, согласно (1),
P$Frn (« = 1, 2, 3,...),
откуда следует, что р есть точка множества Е.
Мы доказали таким образом, что Е=Р, и формула (7) установлена.
* (* 1
3. Пусть теперь j£ и Е—ядра соответственно систем {Fr) и {/V/, и
предположим, что имеет место
S*-E=£0 для а<2. (14)
Мы покажем, что из этого следует, что
Из (14) и из формулы
аналогичной формуле (7), следует, что
S*-S*=£0 дкя а<2; р<2. (15)
Пусть Р — трансфинитное число <2. Согласно (5), формула (15)
дает
2f;-£V0 для а<2.
г
Из того, что сумма 2 содержит счетное множество членов, заключаем,
г
что существует число г((3) множества /? такое, что неравенство
Fr\ -JSVO (16)
г(3)
имеет место для несчетного множества трансфинитных чисел а,
следовательно, согласно (4), для всех a < 2.
Так как /? счетно, то множество всех чисел г(Р), соответствующих
трансфинитным числам Р <С 2, не более чем счетно. Итак, из того, что
формула (16) справедлива для всех a < 2 и всех [J < 2, следует, что
существует число ra множества Я, не зависящее от (3 такое, что
FP"-$V0 Для a<2, р<2. (17)
290
Н. Н. ЛУЗИН
Пользуясь формулой для S^y аналогичной формуле (5), и рассуждая
так же, как и выше, из (17) делаем вывод, что существует число г\
множества R такое, что
F'-F^O для а<2, р<2. (18)
i
Согласно (18), мы имеем в таком случае
F"+1-K^Q для *<U, ?<";
следовательно, согласно (12),
Из того, что 2j содержит счетное множество членов, заключаем, как
и выше, что существует число г2^гг из R такое, что
^•^■^Одля а<2, ?<2.
Заменяя в этой формуле fi на Р -+-1 и рассуждая, как и выше,
доказываем существование числа r^ <C ^i из R такого, что
F*-FT]-Fl--H^0 Для *<Q> $<£•
Продолжая рассуждать таким образом, мы получим две
последовательности чисел множества R г1 > г2 > г:{ > .. . и ^ ^> ^ ^> Гз > ...
таких, что
К-К----- Кп ■ К ■ К ■ • • • ■ Н-¥= 0 для а < й, р < 2, „ = 1, 2, 3,...;
следовательно, в частности, д\я а = р = 0, согласно (1),
Fr,Fr,---- Frn ■ Kh- ■ ■ • • Кп¥-0 для п = 1, 2, 3,... (19)
*
Так как множества Fr и Т7^ замкнуты, то из формулы (19) (по
известной теореме Кантора) следует существование общей точки р у всех
*
множеств F' и F/ (п = 1, 2, 3...), следовательно, у множеств Е и Е
п п
(ч. т. д.).
Мы доказали таким образом, что если Е • Я = 0, то формула (14)
имеет место не для всех а < 2. Следовательно, тогда существует индекс
*<2 такой, что 5е £=0, т. е. EczCS*.
ОБ ОДНОМ МНОЖЕСТВЕ. НЕИЗМЕРИМОМ В
291
В частности, если дополнение к Еу СЕ, есть Л-множество, мы м#-
*
жем положить Е = СЕ> и тогда для некоторого а<2 СЕ С CS\
следовательно, ZTZ)*S\ а тогда, согласно (7), E = S*. Следовательно:
Если Е и СЕ суть Л-множества, то Е измеримо В1.
4. Пусть Е — ядро системы {Fr} и р — некоторая точка
(принадлежащая или не принадлежащая множеству Е). Обозначим (для а < 2) череа
R* (р) множество всех чисел г из R таких, что
Согласно (14), мы имеем, очевидно,
Я» =>#(/>) Аля а<В. (20)
Но множества R* {р) не более, чем счетны (как подмножества /?)
следовательно, из (20) вытекает существование (для каждой данной
точки р) наименьшего индекса р. = р.(/?)< 2 такого, что
Л^О^Я^О»). (21)
Пусть г — число из Т?*"*"1^), тогда p£F$+\ и, согласно (2) (для
a = |iH-l), существует число гх<Сг из R такое, что p£F*;
следовательно, согласно (21), pQF^+19 откуда, согласно (2) (для а = р,н-2)т
p£Ff+2. Следовательно, г принадлежит /J*1"1"2 (/?). Таким образом, имеем
R^l(p)(ZRXJh2(p); следовательно, согласно (20), Яч'1(р) = 1?+*(р).
Из (3) и (20) при помощи трансфинитной индукции без труда
находим, что
R* (р) = R» (р) для а > (х = а (р). (22)
Положим для а<£2
r=2(F;-F;+1). (23)
Это, очевидно, множества, измеримые В. Если р £ 7**, то для
некоторого числа г из R имеемр £ /\£ и P~£F?+l'> следовательно, #* (/?) ^= Z?*4"1 (р),
откуда, согласно (22), <*<!*(/?)•
Пусть тепер /? — такая точка, что Н-(/>)><*; в таком случае, согласно
определению индекса н-(р), /?а (/>) =^= Я*"1"1 (/>) и, согласно (20),
существует число г из R такое, что p£F? и p£F? ; следовательно,
согласно (23), />6 Т\
Мы доказали, что
Г = £И/>)>*| для всех а<2. (24)
v
1 Суслин. Loc. cit.; N. Lusin et W. Sierpinski. Sur queues proprie-
tes des ensembles (A) (Bull, de TAcademie de Sciences de Cracovie, 1918), стр. 4'2'f
теорема Суслина.
292
Н. Н. ЛУЗИН
(E[W(p)\ обозначает множество всех точек р рассматриваемого про-
\р
странства, удовлетворяющих условию W(p).\
Пусть р — точка Е такая, что р(р)^ь. Согласно (7), мы имеем
Е С S*f следовательно, р 6 »$*; но, согласно (24), р £ Т*> следовательно,
рЫ—Г. _
Наоборот, пусть p£Sa— Га; мы имеем, следовательно, р £ 7**; тогда,
согласно (24), pip)^.* и, согласно (22),
ff(p) = R*(p) для р>а. (25)
Так как р £ Sa, то существует, согласно (5), число г множества R
такое, что р £ F?; следовательно, согласно (25), мы имеем р £ F& для
р^а; следовательно, согласно (6), дая всякого (3<С&; отсюда,
согласно (7), р£Е. Мы имеем таким образом
^_Г = £-£[иЫ<а] (для а<2). (26)
р
Так как дая всякой точки р имеет место р(р)<С&> то из (26)
немедленно выводим формулу
Е= 2 (5е—Г*). (27)
Формулы (7) и (27) доказывают, что всякое Л-множество есть
произведение, а также сумма ^ множеств, измеримых В.
5. Из определения ядра Е системы {Fr} непосредственно вытекает,
что дая того, чтобы точка р принадлежала Е> необходимо и достаточно,
чтобы множество R°(p) не было вполне упорядочено по возрастающей
величине рациональных чисел, которые в него входят.
Пусть р — точка СЕ. Множество R0 (р) тогда либо вполне
упорядочено, либо пусто; пусть a — его порядковый тип. (Мы рассматриваем
пустое множество как вполне упорядоченное множество типа 0.) Если
R (р) пусто, мы имеем, очевидно, р (р) = 0. Но предположим, что a > 0,
и пусть
ro<rl<r2<...<rz<...(l<a) (28)
— числа множества /?, входящие в R° (p) и расположенные в порядке
возрастания. Пусть X — некоторое трансфинитное число; мы покажем,
что множество R (р) совпадает с множеством И всех чисел
г^ где X<S<a.
Равенство
R\p) = Hx (29)
*ерно аая Х = 0; предположим, что оно верно дая всех трансфинитных
чисел Х<(5.
ОБ ОДНОМ МНОЖЕСТВЕ. НЕИЗМЕРИМОМ В
293
Пусть Р —число первого рода, г —число из множества R?(p).
Согласно (20), г содержится в множестве R°(p), следовательно, г — член
последовательности (28); пусть г = гь где 0^Е<а. Мы имеем тогда
P^F- и» согласно (2), рб 2 F"1; следовательно, в R существует
число р<гЕ такое, что p^F^~l9 следовательно, р£/??-1(р); отсюда
следует, что /-£ не есть первый элемент множества R?~l (p), которым
является, по предположению,/-^ [так как (29) верно для Х = Р— 1]. Но,
согласно (20), гг есть число из /?3-1 (р); мы имеем, следовательно,
£ ^> Р — 1> т. е. £ ^ Р. Следовательно,
R4p)(ZtP. (30)
Пусть, наоборот, г*— число из Нл\ мы имеем тогда r->r;*_i. Из
предположения, что (29) верно для Х = р— 1, следует, что г^г и г^г^
принадлежат R?~l(p); следовательно, pG-F/"1 и p£F?~l, что Дает*
согласно (2), p£F?, т. е. r^^R^ip). Тогда Н* CR;i{p); следовательно,
согласно (30), R:'(p) = HK
Пусть теперь р — число второго рода, г — число из R? (/>). Как и
выше, мы находим г = п, где 0^£<а. Если £<СР> то (так как р
второго рода) ; н-1 < р. Так как формула (29), по предположению, верна
для ^<СР> следовательно, для Х = £-ь1, То можно заключить, что г- не
принадлежит //5"1"1 = R*+1 (p); следовательно, согласно (20), тем более
не принадлежит R^(p), что противоречит предположению. Мы имеем,,
следовательно, 5 ^ Р, следовательно (так как £ < а), г* принадлежит /^.
Следовательно, имеет место включение (30).
Пусть, наоборот, г^ — число из Н\ тогда имеет место р ^ £ <Z а, и,
так как формула (29), по предположению, верна для ^ <С Р> то г\
принадлежит всем множествам R (р) при ^<СР; следовательно, p£F, при
Х<Р, что дает, согласно (3), p£Fl> следовательно, г56/??(р). Имеем,
следовательно, H^(ZR3{p) и, согласно (31), R*(p) = H?.
Равенство (29) таким образом доказано при помощи трансфинитной
индукции для всех чисел К Из этого следует, что множества к(р)
(О^Х^а) различны (образуют убывающую последовательность
множеств) и что множества R {р) пусты при Х^а. Следовательно, имеем
|*(/>) = <х.
Мы доказали таким образом, что если р £ СЕ, то R° (p) есть вполне
упорядоченное множество типа |а (р).
Пусть теперь Е есть Л-множество, дополнение к которому СЕ —
также Л-множество. Мы показали выше, что в этом случае существует
трансфинитное число а<2 такое, что E = Sa. Пусть р — точка СЕ.
Если р (р) > а, то, согласно (24), р £ Т%, следовательно, тем более р G $а
(потому что, согласно (23) и (5), Т* С Sa). Однако это невозможно,
потому что Sa = E и р — точка СЕ.
294
Н. Н. ЛУЗИН
Мы доказали, следовательно, что если Е и СЕ суть Л-множества,
то существует трансфинитное число а <^ S такое, что имеет место
1х(р)^а Для всех точек СЕ.
Этот результат позволит нам построить Л-множество, дополнение
к которому не является Л-множеством.
6. Пусть
*Ч, r2> rz>... (31)
— бесконечная последовательность всех чисел множества /?. Пусть х —
действительное число интервала (0, 1) и
х = (с0, сХ9 с2, с3...) (32)
— его конечное или бесконечное двоичное разложение.
Пусть г — некоторое число из множества R; оно является,
следовательно, числом из последовательности (31) и мы имеем г = гпУ где
п — некоторое натуральное число. Обозначим через Fr множество всех
действительных чисел х интервала (0, 1), которые имеют в
разложении (32) (или по крайней мере в одном из двух двоичных разложений
числа х, если они существуют) ся=1. Множества Fr таким образом
определены для всех чисел г, принадлежащих /?, и легко видеть, что
они замкнуты (так как Fr есть сумма 2"-1 замкнутых интервалов).
Пусть Е — ядро системы {Fr}l.
Пусть а — трансфинитное число <С^. Так как всевозможные
подмножества /?, упорядоченные по возрастающей величине содержащихся
в них чисел, представляют все счетные порядковые типы, то
существует подмножество множества R — тип а, пусть это будет
rtV Гтг Гта> • • • (33)
Положим
1 11.
Х = 1 1 Ь ....
oW*j 0"Ц *)т3
Легко видеть, что х — число интервала (0, 1), имеющее единственное
двоичное разложение [так как множество (33) упорядочено по
величине чисел, которые его образуют, и вполне упорядочено по типу
а^о)]. Из определения множеств Fr следует, что x(r/v для всех чисел г
последовательности (33) и только для них. Следовательно, множества (33)
совпадает с множеством R°(x)> и
Р (*) = «•
Так как а может быть любым трансфинитным числом <С 2* то мы
заключаем, что не существует никакого трансфинитного числа а<^2
такого, что \ъ (х) ^ а для каждой точки х множества СЕ. Отсюда
следует, как мы показали выше, что СЕ не является Л-множеством.
1 Легко видеть, что Е—то самое множество, которое было определено во вво-»
деыин.
ОБ ОДНОМ МНОЖЕСТВЕ, НЕИЗМЕРИМОМ В
295
Мы имеем таким образом эффективный пример Л-множества,
дополнение к которому не является Л-множеством.
7. Мы докажем, что всякое Л-множество Суслина является Л-мно-
жеством в нашем смысле.
Пусть Е0 есть Л-множество Суслина; £0 есть ядро определяющей
системы
S= \°*v*h >*}>
где Kvn7 vie суть замкнутые множества (соответствующие конечным
системам натуральных чисел п19 л2, •.., л*) и где всегда
3|«|, М3, ... 9 ttfc, Hjc+i С °Wp II., ...,«*• (34)
Следовательно, р есть точки множества Е0 в том и только том
случае, когда существует бесконечная последовательность натуральных
чисел
п\> п2> Л3 » • • • (35)
«таких, что
/> б8*!."» ....** А** £ = 1,2,3,... (36)
Пусть N—множество всех конечных систем натуральных чисел
(п\> п2> • • •> пк)у упорядоченных таким образом, что
(п19 л2, ..., л*, л*+1) "^ (лх, л2, ..., лк) -<С
"^(ЛЦ Л2, . . ., Пъ-х, Л* -♦- 1, Л*+1, . . ., #1*-н) (37)
(для всех натуральных чисел ку I и л1э л2, . .., л*+<).
Легко видеть, что порядковый тип множества N — тот же, что и
множества R (упорядоченного по возрастающей величине чисел г);
следовательно, существует отображение множеотва N на /?, которое
сохраняет относительный порядок соответствующих элементов Ч
Пусть Ри,,*,, ...,«* — число из множества R, которое соответствует
при этом отображении системе
(nlf л2, ..., л-f).
Мы определяем теперь систему {Fr} следующим образом.
Пусть г — данное число из множества R. Число г определяет систему
(nv л2, ..., л*) из множества N такую, что г = pW|fHat ...,**• Мы положим
Ft = F?Hv Пг> .... wfc = &"i, м, i,t. (38)
Пусть Е — ядро системы {Fr}; мы докажем, что £ = £0.
Пусть р — точка Е0 и (35) — бесконечная последовательность
натуральных чисел, аля которых P6^»i. ...»п*. Согласно (37), мы имеем
(п19 л2> .. ♦, л*+1) -< (лх, л2, ..., л*) Аля к = 1, 2, 3, ...;
1 Такое соответствие легко может быть определено эффективно.
296
Н. Н. ЛУЗИН
следовательно,
P»V»'a, .... «*+, \ P»'i, и» «fcl^— 1> 2, 3, . . .).
/
Согласно (36) и (38), заключаем, что
r* = P«„»i, >* (&=1> 2, 3,...)
есть бесконечная убывающая последовательность чисел из R таких, что
Р6Л, (* = 1, 2, 3, ...)•
Это значит, что р есть точка ядра Е системы {Fr}. Следовательно,
доказано, что Е0 d E.
Пусть, наоборот, р — точка Е и
ri>r2>rs>... (39)
—бесконечная убывающая последовательность чисел из R таких, что
p£Fr, (/ = 1,2,3,...)- (40)
Согласно (37), имеем
(1)-< (2)-<(3)-<...;
следовательно,
Pi < р2 < Рз < • • •;
но если (nl9 /z2, ..., щ) — некоторая данная система из множества N>
то имеет место
(п19 п2У ..., пк) -«< (пг ■+-1),
следовательно,
Рир м2, ...,vjc \ Pxt+i;
существуют, следовательно, индексы m такие, что рт }> г1#
Пусть /лх— наименьший индекс, такой, что pWt превосходит
некоторый член последовательности (39); легко видеть, что для некоторого
индекса ^ имеет место
Pm,-1 < Г/< рт, МЯ У>Н-! (41)
(pmi_i должно быть заменено нулем, если /п1 = 1).
Согласно (37) мы имеем
(ш1-1)-<К, 1)-<К, 2)-<...-<(/п1);
следовательно,
Р*п,-1 < рж„ 1 <С Pm1§ 2 <С • • • < Рт,-
Из (37) легко вытекает, что аля всех чисел г = ри„ w„ ...,и*
множества /?, лежащих между pm,—i и pWj, имеет место лх = т19 следовательно,
Г <С P^h, n^-l.
ОБ ОДНОМ МНОЖЕСТВЕ. НЕИЗМЕРИМОМ В
297
Следовательно, существует наименьший индекс т2 такой, что pw„ m.
превосходит некоторый член последовательности (39). Мы имеем тогда
для некоторого индекса |а2
?mlt m7-\ < Tj < pw„ пц ДЛЯ j ^ (12.
Рассматривая последовательность
rmlt т<х—1
получаем таким же образом индексы тг и [х3 такие, что
ртр ж„ тз-1 <С /у <С Р»Ч, т,, т3 ДЛЯ у ^ ^3>
и так далее. Таким образом, можно получить бесконечную
последовательность натуральных чисел т19 т2, /п3, ... таких, что
ДАЯ j > JJ.k,
и, в частности,
^mp ..., mfc-.,, mfr-1 ^ r^fc ^ Pm1% ..., mfc» V*^>
г^ как число из множества R может быть записано в форме
ГИ&=Р к к к у
и, согласно (42) и (37), мы находим:
п\ = т1; пк2 = т2; .. .; пкк = тк;
согласно (40), (38) и (34), находим
Р£р9щ,т, «t=8«u«i "к (* = 1» 2, 3, ...)•
Отсюда следует, что р принадлежит множеству Е0. Мы имеем таким
образом Е С Е0. Отношения E0dE и Е С Е0 дают нам Е0 = £ (ч. т. д.).
Каждое множество, измеримое В, есть Л-множество Суслина;
следовательно, каждое множество, измеримое В, есть Л-множество в
нашем смысле.
Отсюда следует, что если Е измеримо В, то Е и С£ суть Л-мно-
жества. Это утверждение, обратное теореме, которую мы доказали
выше.
Следовательно, множество Еу которое мы построили выше и
дополнение к которому не есть -Д-множество, неизмеримо В. Таким
образом, построен эффективный пример множества, неизмеримого В.
8. Мы намереваемся теперь доказать, что всякое /4-множество
обладает свойством Бэра.
298
Н. Н. ЛУЗИН
Пусть Р — данное совершенное множество. Мы скажем, что
множество М—первой категории на Р в точке р (принадлежащей или не
принадлежащей множеству Р), если существует сфера S, окружающая р
и такая, что множество Р • М • S первой категории на Р; если не
существует такой сферы, мы скажем, что М—второй категории на Р
в точке р.
Пусть Мц = М± -+- М2 ■+- Mz -+-... — сумма счетного числа множеств Мъ;
обозначим через Nk (k = 0, 1, 2, ...) множество всех точек р
множества Р, в которых Mjc — первой категории на Р. Легко доказать,
что множество
K=(P-Na)-Nl-N2-N,...
нигде не плотно на Р.
Пусть теперь Е — данное Л-множество, которое является ядром
системы *S= {Fr}> P — данное совершенное множество такое, что Е—
второй категории на Р в каждой точке множества Р.
Если р — число из Р, то обозначим через S? систему, которая
получается из S заменой каждого множества Fr9 где г ^ р, пустым
множеством. Обозначим через Е? ядро системы *Sp; легко проверить
формулу
E = 2Fr-E„ (43)
г
так же как формулу
£r=2/v£P (*ля rW (44)
Пусть г1э г2, ...,/-*— некоторая конечная убывающая
последовательность чисел R; обозначим через 7Vri, r„ ...,rfc множество всех точек Р,
в которых множество Fri • Frt • • Fn • Erjc — первой категории на Р,
то положим
Н= Пл^г -ь t \(Р - Nri. г, к) ■ П Nri, Г1 „ Р], (45)
где произведение IX распространяется на все числа г из множества Р,
г
*
произведение XI —на все числа р<Сг* из Р, суммирование 2и— на все
конечные убывающие последовательности rlf r2, . .., rfc чисел из Р.
Так как множество Е, по предположению, — второй категории на Р
в каждой точке множества Р, то множество TV точек Р, в которых
Е — первой категории на Р, пусто, следовательно, Р — N=P. Из (43)
и из определения множества Nr следует, как мы знаем, что множество
Xl7Vr нигде не плотно на Р.
г
Пусть rJf г2, ♦.., гк — данная конечная убывающая
последовательность чисел из Р. Согласно (44), мы имеем
Егк= 2 F9E9;
ОБ ОДНОМ МНОЖЕСТВЕ. НЕИЗМЕРИМОМ В
299
следовательно,
Frr Frr - • • • Frk • Erk=Z> Fr{ • Ft,- ... • FTk - F,t • E ,
откуда, как мы знаем, следует (по определению M.„rs гк. Р), что
множество
{P-Nr„r, г*)П^г,.г... .г».р
Р T|f
*
нигде не плотно на Р. Так как сумма 2 содержит счетное множество
членов, то из (45) следует, что множество Н — первой категории на Р.
Мы докажем, что
P-H<ZE. (46)
Пусть р — точка Р — //. Тогда
/>€"#. (47)
Следовательно, согласно (45), рТПМ-; тогда существует числом
г
из множества R такое, что
P*Nri. (48)
»
Но из (47) и (45) следует, согласно определению суммы 2., что
pT(P-Nr)J{Nru9,
рО|
откуда, согласно (48),
РТ. ПЖи
p<ri
Существует, следовательно, число г2<^г{ из множества R такое, что
Точно так же из (47) и (45) следует, что
PtiP-N^rdTlNrvr*,.
Отсюда заключаем, согласно (49), что существует число г3<г2 из R
такое, что р~£ Nrit rt, r3.
Рассуждая таким1 же образом, получаем бесконечную убывающую
последовательность чисел гх > г2 > г3> ... таких, что
р*Я„гь...,гк для * = 1, 2, 3,... (50)
Из определения множества 'Nrvrt п и (50) следует, что множество
FriFr3...FrkErk — He первой категории на Р в точке р. Отсюда
следует, что р есть точка накопления множества FriFrt - - - FrkErk,
следовательно, тем более множества Fr^; так как последнее замкнуто, то
300
Н. Н. ЛУЗИН
отсюда вытекает, что р £ Fr(c. Мы доказали, следовательно, существо-
вание бесконечной убывающей последовательности гг ]> г2 > ... чисел
из R таких, что
p£Fn (* = 1, 2, 3, ...).
Отсюда следует, что р принадлежит ядру Е системы {Fr}.
Таким образом, формула (46) доказана. Отсюда следует, что
Р — Ed Ну и так как Н—первой категории на Р, то Р — Е — первой
категории на Р.
Следовательно, мы доказали, что если Е есть Л-множество и
Р—совершеннее множество, в каждой точке которого Е — второй
категории на Р, то Р — Е — первой категории на Р. Отсюда следует,
что каждое Л-множество обладает свойством Бэра. Следовательно,
характеристическая функция Л-множества непрерывна на каждом
совершенном множестве, если пренебречь множествами первой категории
относительного этого совершенного множества, значит, обладает
свойством Бэра, сформулированным в теореме XVI мемуара Лебега „Sur
les fonctions representable analytiquement". Характеристическая функция
Д-множества, неизмеримого В, определенного выше, представляет собой,
следовательно, эффективный пример функции, не представимой
аналитически и в то же время обладающей свойством Бэра.
ПРОЕКТИВНЫЕ МНОЖЕСТВА И МЕТОД РЕЗОЛЬВЕНТ*
(Об одной проблеме Бореля, проективных множествах
Лебега и аналитических множествах)
В сообщении, сделанном на IV Международном математическом
конгрессе (Рим, апрель 1908 г.), Э. Борель сказал: „Чтобы дать
представление о моей точке зрения, вот проблема, которая мне кажется
наиболее важной в арифметической теории континуума: можно ли
определить множество Е такое, что нельзя назвать никакой
индивидуальный элемент этого множества £, т. е. отличить его без
двусмысленности от всех других элементов Е". Известно, что множество
абсолютно нормальных чисел не является, вероятно, совсем адекватным
этой проблеме, как, впрочем, и все множества метрического характера.
Цель последующих рассмотрений — указать множество Е
дескриптивного характера, образованное из точек сегмента [0, 1), которое точно
решает проблему Э. Бореля.
1. Аналитические множества. Теория аналитических множеств
возникла из мемуара Лебега „Sur les fonctions representables analyti-
quement", появившегося в „Journal de Jordan", 6 серия, 1, стр. 139.
Знаменитая функция, не определяемая аналитически, названа автором
без использования аксиомы выбора, однако при помощи аксиомы
разбиения1, и явилась истинным началом серии исследований, которые
связаны с понятием аналитического множества.
В 1916 г. Суслин и я, стремясь осуществить программу Лебега
изучения наиболее общих функций, которые могут быть названы
(loc. cit., стр. 215), ограничиваясь новым классом множеств,
выводящим нас за пределы класса 5-множеств, тесно связанных, однако,
с рядами полиномов, мы приняли терминологию, уже употребленную
самим Лебегом2. В пределах ограниченных размеров наших заметок
* „Sur un probleme de M. Emile Borel et les ensembles projectifs de M. Henri
Lebesgne; les ensembles analytiques*4. Comptes Rendus, 180, 1318—1320, 192S.
1 Аксвома разбиения—см. мою статью „Об аналитических множествах", гл. Ill,
п. XIV, 65 стр. (стр. 447 настоящего тома.—Ред.)
2 Цитируем текстуально это место Лебега (loc. cit.» стр. 165): „Из того, что
будет доказано в последующем, следует, что множества, измеримые В* суть те.
302
Н. Н. ЛУЗИН
в Comptes Rendus1, где имеются все принципиальные результаты об
аналитических множествах, сформулированные без доказательств, мы
назвали аналитические множества более кратко: А-множествами.
Суслин пользовался методом индексов, который восходит к Лебегу
(loc. cit., стр. 209), а я употреблял только чисто геометрические
рассмотрения. Но важно заметить, что первый пример аналитического
множества, неизмеримого В> встречающийся в математической
литературе, — это пример, который Лебег сам построил и использовал как
промежуточный инструмент на пути построения индивидуальной
функции, не допускающей никакого аналитического представления (loc, cit.,
стр. 213—214). Ввиду вспомогательной роли, которую играло там это
множество, знаменитый автор опустил углубленное изучение этого
множества при построении функции, не определимой аналитически,
поскольку этот анализ казался излишним для конечной цели
(см. [20]).
Скоропостижная смерть Суслина и трудности международных связей
помешали публикации подробного изложения теории аналитических
множеств. Серпинский независимо нашел доказательства многих
предложений этой теории и опубликовал их в серии работ, появившихся в
журнале Fundamenta Mathematicae. Метод, которому следовал Серпинский, —
тоже метод индексов [36].
Одной из фундаментальных идей, которой мы обязаны Борелю,
является понятие функции, определенной при помощи счетного числа
элементов („Lecons sur la theorie des fonctions", l"e ed., 1898;
добавление I, стр. 109 и добавление III, стр. 126). Таковы непрерывные
функции, а также функции, разрывные только при счетном числе значений
переменной (счетно-разрывные функции). Это идея, которая играет
весьма существенную роль в геометрической теории аналитических
множеств 2.
которые могут быть определены при помощи аналитических равенств или
неравенств; поэтому их следует назвать аналитическими множествами".
Обратное предложение (т. е. что всякое множество, определяемое при помощи
аналитических равенств или неравенств, есть множество, измеримое В) не было
никогда сформулировано им: Лебег не написал ни единой фразы, ни простого намека
о возможности этой инверсии (см. [3]).
1 S о u s 1 i n. Sur une definition des ensembles mesurables В sans nombres trans-
finis; моя заметка „Sur la classification de M. Baire". Comptes Rendus, 164, 88 и
91, 1917.
2 Я не знаю, является ли концепция функции^ определенной счетным числом
условий, адекватной концепции функции^ которую можно назвать в смысле Лебега,
б настоящее время не известно никакой называемой функции, которая не была бы
определяемой счетным числом условий. Практически всякий раз, когда математики
констатируют существование индивидуальной функции, они умеют определить ее при
помощи счетного числа условий. Это важный факт, ибо мы увидим, что даже
функция, не определимая аналитически, которая была названа Лебегом посредством
трансфинитного процесса, является функцией, определимой счетным числом условий
таким же образом, как всякая непрерывная функция.
ПРОЕКТИВНЫЕ МНОЖЕСТВА И МЕТОД РЕЗОЛЬВЕНТ 303
Пусть & — евклидово пространство т измерений. Мы назовем
аналитическим множеством в пространстве S геометрическое место
последовательных положений подвижной точки M(xv х2, . .., хт),
координаты которой являются счетно-разрывными функциями
переменного параметра t, определенными в области D~■ (0<С/<С 1):
xl=/i{t)9 x2=f2(t)y ..., xm = fm(t). При этом мы не расширим данного
определения аналитического множества, беря в качестве f{ (t)
произвольные функции классификации Бэра: легко доказать, что все такие
множества — аналитические в указанном смысле. Из самого определения
аналитического множества следует, что всякое аналитическое множество
точек пространства т измерений определимо посредством т простых ]
рядов полиномов, которые абсолютно сходятся к /,(/) при всяком
значении t из D. Отсюда название — аналитическое множество. Если
функции fi(t) таковы, что двум различным значениям t соответствуют
две различные точки в пространстве £, то аналитическое множество Е
обязательно является 5-множеством, и обратно, всякое несчетное 5-мно-
жество пространства § может быть получено таким образом. Отсюда
следует, что аналитическое множество в пространстве m-t-1
измерений, определенное равенствами: x1=fl(t), х2 = f2(t), ..., xm=fm(t)y.
xm+i= t> является всегда 5-множеством, следовательно:
Всякое аналитическое множество в пространстве т измерений
есть ортогональная проекция некоторого В-множества9
расположенного в пространстве т ■+- / измерений.
Обратное предположение также верно:
Ортогональная проекция В-множествау расположенного в
пространстве т измерений^ на пространство т измерений (т < т)
является аналитическим множеством.
1 Т. е. не трансфинятных. — Pej.
О ПРОЕКТИВНЫХ МНОЖЕСТВАХ ЛЕБЕГА*
1. Теория аналитических множеств представляет совершенную
гармонию 1: всякое аналитическое множество либо является учетным, либо
имеет мощность континуума; всякое аналитическое множество никогда
не является множеством третьей категории (мы так называем
множества, которые не являются множествами типа Z по Лебегу или
неисчерпаемыми множествами по Данжуа); наконец, всякое
аналитическое множество измеримо.
Имеется только один важный пробел: не известно, имеет ли
несчетное аналитическое дополнение (т. е. дополнение к
аналитическому множеству) мощность континуума.
Усилия, которые я прилагал д\я решения этого вопроса, привели
меня к такому неожиданному результату: существует семейство,
допускающее отображение на континуум [37| эффективных
множеств таких, что не известно и никогда не будет известно, имеет ли
произвольнбе несчетное множество данного семейства мощность
континуума, является оно или нет множеством третьей
категории; измеримо ли оно. К тому же указанное семейство содержит
семейство аналитических множеств, очень естественным обобщением
которого оно является, — это семейство проективных множеств Лебега.
Остается только выяснить природу этого нового факта.
Пусть в евклидовом пространстве & т измерений дана какая-нибудь
система прямоугольных осей
О \Xi, Х^у . • ., Хт),
которую мы будем считать неподвижной.
По определению, множество Е точек пространства & называется
аналитическим, если оно является геометрическим местом
последовательных положений подвижной точки
М(хи х2, ..., хт),
координаты которой являются счетно-разрывными функциями
переменного параметра /, определенными в области D = (О <С t <C 1):
* „Sur les ensembles prejectifs de M. Henri Lebesgue". Comptes Rendus, 180,
1572, 192S.
i Cm. Comptes Rendus, 180, 1318, 1925.
О ПРОЕКТИВНЫХ МНОЖЕСТВАХ ЛЕБЕГА
305
Так как всякая счетно-разрывная функция (т. е. разрывная только
в счетном числе значений переменной) определяется счетным числом
элементов1, ясно, что семейство F всех аналитических множеств
пространства S (принимая в расчет повторения) допускает эффективное
отображение на континуум. К тому же из теории аналитических
множеств известно, что это семейство F содержит все Б-множества,
расположенные в пространстве £, и бесконечное число других множеств,
которые не являются ^-множествами.
Наиболее замечательной теоремой, которая представляет собой одно
из важнейших предложений геометрической теории множеств, является
следующая: всякое аналитическое множество евклидова пространства
S т измерений является ортогональной проекцией В-множества,
расположенного в эвклидовом пространстве £'т-+-1 измерений,
содержащем пространство <§, и обратно: проекция В-множества всегда
является аналитическим множеством. Это теорема, которая может
служить определением аналитического множества.
2. Известно, что свойства аналитических множеств привлекли
внимание Лебега, который дал замечательное расширение теории
аналитических множеств, в высшей степени естественное.
В эпоху, когда символическая теория аналитических множеств была
формально завершена, т. е. в 1916—1917 гг., предложение: всякое
аналитическое множество есть проекция В-множества было доказано,
но в действительности это предложение никогда не играло
существенной роли в этой теории. Суслин и я не придавали никакой особой
важности этому предложению, рассматривая его скорее как
любопытное, чем полезное, и если оно было явно сформулировано2, то, как
легко видеть, это было сделано а^я того, чтобы рассеять некоторое
недоверие в существовании множества, неизмеримого В: если допустить
существование ZJ-множеств, то признание существования множеств,
неизмеримых В, становится неизбежным. Но самая идея рассматривать
проекцию как операцию была чужда нам. Именно Лебег подчеркнул
большой теоретический интерес изучения проекции как одной из
наиболее простых и в то же время наиболее важных операций
геометрии— операции, позволяющей строить новые множества, которые
можно назвать, отправляясь от уже известных эффективных
множеств 3.
Следуя именно этой идее Лебега, получают сначала из В-множеств
все аналитические множества Е; затем из их дополнений СЕ — новый
класс множеств РСЕ совсем не известной природы, но таких, которые
можно назвать; отправляясь от дополнений последних СРСЕ> jioxy-
чают новые множества РСРСЕ, которые еще можно назвать, и т. д.
Это проективные множества Лебега [38].
1 См. Е. Borel. Lecons sur la theori© des fonctions. Iе ed.t Not© III, стр. 125.
2 Суслин. Comptes Rendus, 164, 88, 1917.
3 Ann. de l'Ecole Norm. Super., серия 3, 35, 242, 1918.
306
Н. Н. ЛУЗИН
Таким образом, мы приходим к новому понятию: классам
проективных множеств. Для определенности мы ограничимся линейными
множествами.
Пусть Е — какое-нибудь множество точек евклидова пространства £ т
измерений, т^>1. В последующем мы будем обозначать через СЕ
дополнение к множеству Е относительно £ и через РЕ ортогональную
проекцию Е на евклидовское пространство £' т — 1 измерений,
расположенных в пространстве £.
Установив это, примем следующее определение:
Будем говорить у что линейное множество является проективным
множеством Лебега класса л, если оно может быть представлено
в форме
PC... РЕ или СРС...РЕ,
где Е есть В-множествоу расположенное в евклидовом пространстве
п-+-1 измерений, и буква Р, чередующаяся с буквой С, написана
в точности п раз, и если такое представление невозможно при
замене п меньшим целым положительным числом.
Приняв это определение, мы немедленно обнаруживаем, что всякое
аналитическое множество или его дополнение есть проективное
множество первого класса, и наоборот. Следовательно, теория аналитических
множеств содержится в теории проективных множеств Лебега. Это
замечание позволяет оценить важность понятия проективного множества.
СВОЙСТВА ПРОЕКТИВНЫХ МНОЖЕСТВ*
Сначала мы, применяя диагональ Кантора, без труда доказываем,
что существуют проективные множество всех классов. Но более
замечательным и одним из наиболее важных является следующее
свойство: все множества, неизмеримые В> которые известны до сих пор,
как те, которые задавались „естественно", так и те, которые были
названы без употребления рассуждения Цермело (аксиомы выбора) при
построении примеров всех родов, суть проективные множества. Этот
результат, не удивительный на первый взгляд, становится более
удивительным, если вспомнить, что среди множеств, неизмеримых 5,
которые можно назвать, имеются такие множества, в определение каждого
из которых должны эффективно войти все транс финитные числа
второго класса, а не только те, которые меньше некоторого
фиксированного трансфинита (аксиома разбиения).
Знаменитая функция Лебега <р (/, х), не допускающая никакого
аналитического представления, может служить поразительным примером
такого рода. Способ, при помощи которого известный автор назвал эту
функцию у (/, х)> состоит в следующем: сначала сегмент (0, 1]
разлагается в трансфинитную совокупность множеств ЕаУ имеющих каждое
мощность континуума и занумерованных трансфинитными числами второго
класса; затем осуществляются одновременные отображения семейств Fa
функций f(x) класса а на соответствующие множества £а; все это
делается без применения аксиомы выбора. Именно этим методом Лебег
получил функцию <? (tj х).
Известно, что Борель, следуя своей идее иллюзии трансфинитного,
счел | необходимым критиковать эту функцию <?(t, x) за использование
незаконной совокупности всех трансфинитных чисел. Однако из теории
проективных множеств следует, что множество, образованное из точек
поверхности z = <?(t, x)y является проективным множеством
(конечного класса) в пространстве трех измерений. Таким образом видно,
что существует проективная функция ф(/, х), численно равная
функции <р(/, х) ^Лебега при всех значениях /их. Следовательно,
трансфинитное опять исключено.
Трудности теории проективных множеств. Я давно указывал1,
* „Les proprietes des ensembles projectifs". Comptes Rendu*, 180, 1817, 1925.
1 См. мою заметку „Sur la classification de Baire" (Comptes Rendus, 164, 91, 1917).
308
RH. ЛУЗИН
что вопрос: имеет ли несчетное аналитическое дополнение (проективное
множество первого класса) обязательно мощность континуума,
представляет большие трудности. Но эти трудности бесконечно возрастают, когда
речь идет о проективных множествах второго класса. Не известно и
никогда не будет известно, имеет ли несчетная проекция двумерного
аналитического дополнения мощность континуума или она не является
множеством, „которое не есть множество типа Z", ни даже
измерима ли она1. Эти трудности и самая легкость, с которой
обнаруживается исключение трансфинитного, заставляют нас исследовать более
внимательно законность этих множеств, равно как и существование
множеств, неизмеримых В [39].
Ср. замечание о статье Серпинского в моей предыдущей заметке.
О МНОЖЕСТВАХ, НЕИЗМЕРИМЫХ £, И ОБ
УПОТРЕБЛЕНИИ ДИАГОНАЛИ КАНТОРА*
Диагональ Кантора. Прежде чем начать изучение вопроса
о существовании множеств, неизмеримых В, следует привести
некоторые определения и предложения, которые мы используем в дальнейшем.
Множество Е называется аналитическим, если оно является
геометрическим местом положений подвижной точки, координаты которой
являются счетно-разрывными функциями некоторого параметра.
Семейство F аналитических множеств пространства & т измерений
содержит все 5-множества, лежащие в пространстве <?.
Легко доказать, что ортогональная проекция аналитического
множества \Е в евклидово пространство &' т измерений, содержащееся
в S, т<^ту является аналитическим множеством в &'.
Наконец, вот еще важное свойство, принадлежащее Лебегу: если
функция /(*!, лг2, ..., ATm-x) представима аналитически, то множество,
образованное из точек поверхности xm=f(xv x>, —, хт—г),
расположенной в £, является В-множеством.
Установив это, возьмем плоскость XOY [и дадим следующее
определение: аналитическое множество U точек плоскости XOY называется
универсальным, если можно получить все линейные аналитические
множества, пересекая U прямыми, параллельными оси ОУ\
Дополнение CU ко всякому универсальному множеству V не может
быть аналитическим множеством. Действительно, если
CU—аналитическое множество, то его часть, расположенная на диагонали Д, у = х>
есть также аналитическое множество, равно как и ее проекция Р на
ось OY. Так как множество U универсальное, то существует
параллель оси OY, х = х0, такая, что часть U, расположенная на этой
параллели, имеет проекцией на ось OY множество Р. Кроме того, точка
М (jc0, л:0) диагонали Д не может принадлежать к множеству U, потому
что в этом случае проекция точки М на ось OY должна содержаться
в Р, что противоречиво. Точка М не может также принадлежать к
множеству CU, потому что в этом случае проекция точки М на ось OY
не должна принадлежать Р, что также противоречиво.
* Sor les ensembles non-mesu rabies B et Temploi de la diagonale de Cantor.
Comptes Rendus, 181, 95—96, 1925.
310
Н. Н. ЛУЗИН
Все сводится к доказательству действительного существования
универсального аналитического множества С/. Всякое линейное
аналитическое множество Е есть множество значений, которое принимает в
области £) = (0<О<С1) функция f(t)y счетно-разрывная в этой области.
Такая функция /(/) является функцией первого класса классификации
Бэра. Все сводится, следовательно, к определению функции з (t, х) от
двух переменных (t и х) такой, что из нее можно получить все
функции переменного t первого класса, давая х частные значения х0.
Всякая функция /(f) первого класса может быть представлена в виде
ряда полиномов с рациональными коэффициентами. Достаточно взять
ряд, общий член которого есть непрерывная функция переменных t и х:
Ъ (х) Р, (t) . ?4 (х) Р, (0 +-. .. .- ?„ (х) Р„ (t) • I- .. .,1
где Ри /\> . . . есть совокупность всех полиномов от i с рациональными
коэффициентами, a <?i(x)y <р2М> ••• — кривая Пеано, заполняющая при
O^jc^I фундаментальный куб со стороной, равной единице, в
пространстве счетного числа измерений. Обозначим через SH(t, x) сумму л
первых членов этого ряда. Функция <р (/, jc), определенная равенством
v (t> x)= lim 5Я (/, *), обладает желаемыми свойствами и является функ-
П->00
цией не более чем второго класса классификации Бэра. Следовательно,
поверхность (S), y = ?(t> х) представима аналитически. Множество
точек, которые принадлежат этой поверхности (5), измеримо В (Лебег).
Проекция U поверхности (S) на плоскость XOY есть аналитическое
множество, которое, очевидно, универсально (ч. т. д.).
В предыдущих рассуждениях имеется лишь один уязвимый пункт:
употребление дополнения С(/.
Задано ли на самом деле это дополнение? Аналитическое выражение
lim Sn (ty x) „дано" уже тем, что оно написано. -А поскольку поверх-
ность (5) дана, естественно рассматривать как заданную ее проекцию U
на плоскость XOY\ К тому же мы имеем чисто аналитическое
представление множества U: оно является геометрическим местом точек
М(х, у), где x=fl(t), y=f2(t) и /{9 /2 являются счетно-разрывными
функциями переменного t. Таким образом, мы имеем положительное
определение множества U. Но мы не можем сделать ничего подобного
для дополнения CU; это множество, не поддающееся положительному
определению, названо посредством чисто отрицательного свойства:
это совокупность точек, которые не... . Множество CU бесконечно,
но нам не дан закон этой бесконечности. По моему мнению, нельзя
назвать закон, позволяющий на каждой из параллелей оси OY выбрать
одну и только одну точку (если она существует) множества СИ (лебе-
говский выбор) [40].
Верно, ни один математик, которому приходится строить множество
точек Е, не задается вопросом: будет ли при этом иметь положительное
О МНОЖЕСТВАХ. НЕИЗМЕРИМЫХ В. И ОБ УПОТРЕБЛЕНИИ ДИАГОНАЛИ КАНТОРА 311
определение дополнение СЕ множества Е\ он изучает свойства
множества СЕ, не беспокоясь об этом вопросе. Однако надо соблюдать
осторожность, если только речь не идет, как обычно в классических
разделах математики, о множествах, измеримых В. Ибо, если Е
измеримо Ву то его дополнение СЕ также измеримо В. Следовательно,
если даже множество СЕ определено отрицательным образом, мы имеем
для СЕ и положительное определение: х =/г {t), #=/2(^)1 потому что СЕ
является в этом случае аналитическим множеством. Но когда речь идет
о множестве, неизмеримом В, мы находимся в необычном положении.
Не известно, существует ли множество Еу неизмеримое В, с
положительным и конечным определением такое, что его дополнение СЕ имеет
также положительное и конечное определение. Смысл такой теоремы
Суслина: Если множество Е и его дополнение СЕ являются оба
аналитическими множествами, то они измеримы В, становится
поэтому особенно ясным.
Эти трудности бесконечно возрастают, когда мы проектируем
СЕ и берем дополнение этой проекции, чтобы ее проектировать
в свою очередь, и т. д.
О ПРОБЛЕМЕ БОРЕЛЯ И МЕТОДЕ РЕЗОЛЬВЕНТ*
Настоящая заметка имеет связь с заметками, которые я
представил на рассмотрение Академии 4 мая, 25 мая, 15 июня и 13 июля;
логически она следует за третьей заметкой.
В настоящем сообщении я продолжаю заниматься решением
проблемы Бореля1, формулировка которой была приведена в первой из этих
заметок.
1. Резольвенты. Будем говорить, что некоторая проблема Р
теории функций поставлена в резольвенту, если мы можем назвать,
в смысле Лебега, множество точек Е такое, что мы умеем
утвердительно решить проблему Р всякий раз, когда можем назвать точку
множества Еу и умеем решить ее отрицательно всякий раз, когда можем
доказать, что множество Е пусто. Самое множество точек Е, от
которого зависит окончательное решение рассматриваемой проблемы Ру
будет называться резольвентой проблемы Р.
Среди проблем теории функций, решение которых, по-видимому,
представляет трудности трансцендентного порядка, если можно так
выразиться, в большинстве случаев может быть поставлено к резольвенту,
и, важно заметить, что все эти резольвенты суть проективные
множества. Среди этих проблем наиболее интересны те, которые
исследуют эффективным образом вполне упорядоченный континуум или
аналитическое определение для всех трансфинитных чисел второго класса
способом, лишенным двусмысленности (Борель).
Именно проективные резольвенты этих проблем я считаю
убедительными решениями вышеуказанной проблемы Бореля.
2. В ограниченных рамках настоящего сообщения мы упомянем
только об одной проблеме немного искусственного характера, важность
которой проявляется в том, что речь идет, согласно определению
аналитических множеств, только о рядах полиномов с целыми
коэффициентами, которые сходятся абсолютно при всех значениях jc, 0<Цх<^Ъ
Выяснить, не имеют ли все дополнения к аналитическим
множествам или счетную мощность, или мощность континуума.
* „Sur le probleme de M. Emile Borel et la methode des resolvantes". Comptes
Rendus, 181, 279—281, 1925.
1 См. сообщение Бореля на IV Международном конгрессе математиков
(Рим, апрель 1908 г.).
О ПРОБЛЕМЕ БОРЕЛЯ И МЕТОДЕ РЕЗОЛЬВЕНТ
313
Интерес проблемы состоит в том, что если встать на точку зрения
идеалистов, т. е. принять существование всех трансфинитных чисел
второго класса, то можно безукоризненно доказать, что всякое несчетное
аналитическое дополнение, которое не содержит никакого совершенного
множества, является точным объединением несчетного множества счетных
множеств, не имеющих попарно общих точек и занумерованных вполне
определенным образом, без возможной двусмысленности, посредством
всех трансфинитных чисел второго класса. Следовательно, если этот
логически возможный случай осуществляется практически1, то можно
утверждать, что существование всех трансфинитных чисел второго
класса есть факт как бы экспериментального порядка. Это
единственная точка зрения, которая мне представляется заслуживающей
наименования реализма.
Резольвентой Е этой проблемы является проективное множество
не более чем третьего класса; если мы умеем назвать точку
множества Е> то мы имеем такое необыкновенное аналитическое дополнение,
и наоборот. Частью (опять проективной) множества Е является
множество Е1У являющееся резольвентой другой проблемы, которая,
по-видимому, представляет большой интерес: если только мы умеем назвать
точку множества Ev то мы получаем несчетное множество точек,
выбранных индивидуально каждая из континуума и занумерованных без
двусмысленности посредством всех трансфинитных чисел второго класса
(Лебег).
3. Этот метод является общим. Многие проблемы могут быть
поставлены в резольвенту. Таковы, например, проблемы меры и категории
проективных множеств второго класса, такова даже проблема вполне
упорядоченности континуума. Резольвенты всех этих проблем суть
проективные множества. Тот, кто назвал бы точку резольвенты Е
последней проблемы, занумеровал бы без двусмысленности все точки
сегмента [0, 1] посредством всех трансфинитных чисел второго класса.
Это одно из решений проблемы континуума2.
4. Вопрос теперь состоит в том, чтобы знать, должны ли мы
рассматривать эти проективные множества как данные (вполне
определенные). Мы этого не думаем. „Эффективность" проективных множеств,
несмотря на то, что они названы, только кажущаяся, потому что
операция, состоящая во взятии дополнения к множеству, является чисто
отрицательной.
1 Исходя из делимости целых положительных чисел, можно получить
арифметический пример аналитического множества, неизмеримого В (см. стр. 315
настоящего тома.—Ред.).
2 Мы будем иметь другое решение, если встанем на точку зрения
непротиворечивости (Гильберт). Было бы очень интересно знать, является ли предложение:
„мощность континуума есть алеф-два" непротиворечивым, так же как предложение:
„мощность континуума есть алеф-один".
.314
Н. Н. ЛУЗИН
В письме к Адамару, двадцать лет тому назад, Бэр писал: „...то, что
множество дано, для меня не значит, что нужно рассматривать
как данные у части этого множества". Нам кажется, что это
утверждение должно быть распространено следующим образом: если
множество дано, то ошибочно рассматривать как данное его
дополнение.
В настоящем состоянии науки В-множества являются единственными
множествами, которые конструируются при помощи положительных
операций, так же как и их дополнения1.
1 Напомним, что всякое множество точек, в определении которого фактически
-употребляются все трансфинитные числа второго класса, является проективным
множеством. Трансфинитное определение, положительное по внешнему виду,
преобразуется, следовательно, если придерживаться конечных определений, в чисто
отрицательное определение.
АРИФМЕТИЧЕСКИЙ ПРИМЕР ФУНКЦИИ,
НЕ ВХОДЯЩЕЙ В КЛАССИФИКАЦИЮ БЭРА*
1. Известно, что Бэр дал чисто арифметический пример функции
третьего класса его классификации.
Вот этот пример.
Рассмотрим основной интервал (0, 1) и в нем какое-нибудь
иррациональное число ху изображенное в виде непрерывной дроби
1
х= 1
'l + aTT- =(«„ *>, ..., *„, ...),
1
где а19 а2, а3, .. ., ая, ...—натуральные числа. Каждому
иррациональному числу х однозначно соответствует определенная
последовательность натуральных чисел ар а,, ..., <хя, .. ., и обратно, каждая такая
последовательность определяет единственное иррациональное дс.
Достаточно положить теперь, согласно Бэру, /(jt) = l, если эта
последовательность натуральных а19 а,, . .., а„, стремится к
бесконечности, и положить f(x) = 0 в противном случае.
Так определенная функция /(*), согласно исследованиям Бэра
'(см. Acta Math., 30), является функцией в точности третьего класса.
2. Для построения арифметическим путем аналогичной функции/(jc),
не содержащейся в классах Бэра, введем следующее определение:
Будем говорить, что последовательность натуральных чисел
аи а2> • • •> ая> • • • является с ос тавной9 если среди ее членов имеется
бесконечное множество чисел а, делящихся одно на другое: .. ,ап^: ая^: ая;
в противном случае скажем, что данная последовательность л}> о^,. ..
-.., ая, ... является пр ос той»
Определяемая таким образом функция f{x) не входит в
классификацию Бэра [41].
3. Переходя к доказательству этого, назовем решетом всякую
счетную совокупность С замкнутых отрезков а, параллельных оси
* Sur un examples arithmetique <Tune fonction n© faisant pas partie de la
classification de M. Rene Baire. Comptes Rendus, 182 (1926), 1521—1522.
316
Н. Н. ЛУЗИН
ОХ, расположенных внутри основного квадрата К, уравнения сторон
которого суть
х = 0, х = 1, у=0, у = 1.
Обозначим через & совокупность всех точек х интервала (0 < х < 1)
таких, что перпендикуляр Рх, восставленный к оси ОХ из точки х,
пересекает решето С по вполне упорядоченному множеству Rx, если
считать, что Rx упорядочено в положительном направлении оси OY.
Множество точек интервала (0<С*<С1)> не принадлежащих
совокупности &, обозначим через Е. Именно это множество Е (а не &) мы
будем называть множеством, определяемым решетом С.
Введем важное понятие, позволяющее различать решета:
Говорят, что С есть ограниченное решето, если
существует счетное вполне упорядоченное множество W, порядковый
тип которого больше порядкового типа множества Rz при любом х,
не принадлежащем к определяемому решетом С множеству Е.
Будем говорить, что решето С имеет ле бего в с кий тип,
еслщ каково бы ни было подмножество Yl счетного множества Y,
составленного из ординат сегментов о решета С, найдется точках,
для которой множество Rw совпадает с Уг.
Для того чтобы решето С было ограничено, необходимо и
достаточно, чтобы множество Е было измеримо В. Никакое множество,
определенное при помощи решета лебеговского типа, не может быть
измеримым В-множеством.
4. Множество Е точек, для которых f(x) = l, является
множеством, определенным при помощи решета лебеговского типа. Чтобы
убедиться в этом, достаточно поставить в соответствие каждому
интервалу Бэра о7(а1, а2, ..., ая) сегмент 3(04» а2> • • •> а«)> следующим
образом определенный:
1°. Проекция о на ось ОХ совпадает с с/.
2°. Ордината отрезка з(<х1У ..., я„) есть рациональное число вида
!± + h+ .4 °*-i , е*
2 22 2Я~1 2" '
где 0Я=1, а для i<^n имеем ^ = 0, если а{ есть делитель дя, и 0^ = 1
в противном случае.
Совокупность всех таких сегментов о составляет решето С
лебеговского типа, определяющее множество [/(*) = 1].
Таким образом, среди законов арифметики можно найти такие,
которые приводят к множествам, неизмеримым В.
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ
МНОЖЕСТВАХ*
Введение
I
Современное состояние математического анализа убедительно
показывает, до какой степени желательно установить точное разграничение
между математическими объектами, рассматриваемыми как
„существующие", и теми, реальность которых только видимая.
С одной стороны, логические построения в современной теории
множеств являются источником неисчислимого множества
математических объектов, существование которых на самом деле только
словесное.
С другой стороны, в последние годы стараются, становясь на почву
непротиворечивости в стиле Гильберта, узаконить эти объекты путем
отождествления того, что непротиворечиво в себе, с тем, что имеет
несомненную реальность.
Именно это разграничение является темой известных „Cinq lettres
sur la theorie des ensembles" Адамара, Бэра, Лебега и Бореля, и
именно на его необходимости очень настаивал Борель в своих
последующих сочинениях.
Это разграничение между математическими объектами, действительно
существующими, и теми, которые кажутся реально существующими, но
в действительности не имеют никакого substractum, и которым не
соответствует никакой интуитивный образ, в настоящее время очень
необходимо, но его близкая реализация при современном состоянии науки
представляется мало вероятной.
Тем не менее, исходя из необходимости сохранить классические
части математики, можно наметить в общих чертах естественный очерк
одной из таких реализаций.
С одной стороны, при современном состоянии науки кажется
затруднительным отрицать право рассматривать сегмент [0, 1] как законное
множество точек.
* „M6moire sur les ensembles analytiques et projectifs". Матем. сборник, 33, 3f
237—290, 1926.
318
Н. Н. ЛУЗИН
С другой стороны, допустив его законность, необходимо
рассматривать как законные и все множества, которые получают из сегментов
при помощи неограниченного повторения следующих двух позитивных,
операций:
1°. Образовать сумму счетного числа множеств, определенных
ранее:
£, f E2 ч ... -+-£„-+- ...
2°. Взять общую часть счетного числа данных множеств:
а.| • /So • ... е,п ' ...
Отрицание законности множеств, которые получаются при помощи
этих элементарных и позитивных операций, полностью упраздняет самый
математический анализ.
Таким образом, кажется неоспоримым, что нет смысла сомневаться
в реальности множеств, измеримых В, по крайней мере тех из них,,
которые получают, делая первые шаги в применении указанных
операций. Постоянными объектами математического анализа как раз и
являются множества (и функции), измеримые В, по крайней мере те из
множеств, измеримых В> которые получают из сегментов при помощи
относительно небольшого числа указанных операций.
II
Можно ли расширить область математического анализа за пределы
поля множеств, измеримых В, с такой же степенью безопасности и без
привлечения каких бы то ни было сомнительных элементов?
Известно, что именно этот вопрос являлся темой великолепного-
мемуара Анри Лебега1, вышедшего двадцать лет тому назад,
добившегося утвердительного решения его при помощи одного нового
понятия, которое он ввел, понятия, которое кажется логически
неопределимым, но которое выражают только словом назвать.
Мы не будем стараться дать определение слову назвать (nommer)r
нам кажется, что это достаточно примитивное понятие ji,\n того, чтобы
его определение было по меньшей мере бесполезно; можно только
постараться объяснить при помощи примеров смысл этого слова.
Назвать функцию, множество это значит однозначно указать эту
функцию индивидуальным образом без каких бы то ни было возможных
двусмысленностей.
Одна из основных идей, которой ^мы обязаны Лебегу, — это точное
различение двух понятий: называемое и неназываемое множество.
Мы уже знаем, что следует понимать, по Лебегу, под названным
множеством: это множество точек, [которое можно назвать, т. е. можно-
1 Н. Lebesgue. Sur les fonctions representables analytiquement. Journ. de
Math, pures» appl., 1905.
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ИЮЕКТИВНЫХ МНОЖЕСТВАХ
319
охарактеризовать без возможных неясностей при помощи надлежащего
определения. Называемые множества это как раз те, которые
представляют собой, по Лебегу, необходимые объекты математического
анализа. Что касается до слов неназываемые множества, то они
обозначают в своем наиболее общем смысле все множества, которые не
могут быть названы. К тому же известно, что при современном
состоянии науки неназываемыми множествами являются те множества, которые
получают при помощи аксиомы Цермело или применением аналогичного
рассуждения.
Именно эти неназываемые множества Лебег рассматривал как
сомнительные: они могут быть введены в науку только при том обязательном
условии, что они окажутся интересными, применимыми, полезными и
эффективными при решении какой-нибудь классической проблемы. Но
в общем содержанием математического анализа является по
преимуществу область определяемых объектов. Такова концепция
математического анализа, предложенная Лебегом.
В частности, в цитированном мемуаре Лебегом были даны примеры
называемых объектов, неизмеримых В. Но все они были названы
автором посредством совокупности всех трансфинитных чисел второго класса.
Лебег заканчивает свой мемуар призывом изучать общие свойства,
принадлежащие всем математическим объектам, которые можно назвать.
Этот призыв автора является столь же необходимым с точки зрения
его концепции математического анализа, как и естественным, так как,
изучая множества, измеримые В> настолько полно, как это было
возможно в ту эпоху, Лебег практически пришел к постановке проблемы
об изучении объектов, которые можно назвать по крайней мере
„непосредственно "следующих за объектами, измеримыми В, как,
например, тех, которые называют, используя совокупность всех
трансфинитных чисел второго класса, считая эту совокупность уже названной.
III
Известно, что Борель в силу своего убеждения в иллюзорности
трансфинитного вынужден был направить упреки на примеры
называемых объектов, неизмеримых В> данных Лебегом. Здесь неуместно
вдаваться в обсуждение высказанных аргументов. Мы ограничимся
дословным цитированием одного отрывка из Бореля: „Я оставлю в
стороне возражения, которые можно сделать по поводу существования
функции, „называемой" Лебегом, который, впрочем, сам настаивал на
различении понятий назвать и определить функцию; я охотно буду
более категоричным, чем он: повсюду, куда бы ни должны были эффективно
входить все трансфинитные числа второго класса (а не только те,
которые меньше одного из них, фиксированного заранее), мне
представляется выход из области математики" 1.
1 Е. Во г el. Le calcul des integ/ales definies. Journ. de Math., 208, 1912.
320
ri. H. ЛУЗИН
Так как многие превосходные умы не считают совокупность всех
трансфинитных чисел второго класса законным математическим
объектом, потому что невозможно полностью описать этот объект, примеры
Лебега еще далеки от того, чтобы всеми математиками единодушно
быть принятыми. Основной вопрос: можно ли расширить область
математического анализа за пределы множеств, измеримых В,— оставался
нетронутым.
В 1916—1918 гг. Суслин, Серпинский и я, стремясь выполнить
цитированную программу Лебега: изучить наиболее общие множества
которые можно назвать, — пришли к изучению нового класса множеств,
наверняка выходящего за пределы класса множеств, измеримых В, и
тем не менее образованного из множеств, определимых без
применения какого бы то ни было трансфинитного числа. Ввиду тесной связи
между множествами и рядами полиномов, эти множества (по
предложению Лебега) получили название аналитических множеств 1.
Первые изложения теории аналитических множеств были совершенно
символическими и довольно сложными. Я теперь отказываюсь от
символических рассуждений и перехожу к геометрическим рассуждениям.
Геометрический путь мне кажется более поучительным.
I. Множества, измеримые В
Генетическое определение. Обычно различают две основные
категории математических определений, смотря по тому, является ли
существенный момент определения конструктивным или логическим:
первая категория представляет собой то, что называют генетическими
определениями, между тем как вторая категория содержит
аксиоматические определения. Для множеств, измеримых Ву существуют
определения как одной, так и другой категории.
Обычно множеством, измеримым Ву называют каждое множество
точек, которое может быть получено, исходя из интервалов,
повторным применением двух основных операций (сложения счетного
числа множеств и взятия общей части счетного числа множеств).
Легко видеть, что это определение генетическое.
Сформулированное определение, несомненно, кажется особенно ясным,
когда речь идет о множествах, уже реализованных; но это
определение не имеет еще достаточной четкости, чтобы фигурировать в
математическом доказательстве, в котором делаются заключения о
множестве, измеримом В7 реализация которого возможна. Если намереваются
изучать общие свойства множеств, измеримых В> то немедленно
возникает необходимость производить такие рассуждения, и тогда стараются
уточнить это определение при помощи дополнительных фраз.
С этой целью, сформулировав рассмотренное определение, обычно
сообщают, что две основные операции, при помощи которых из интер-
г См. 114] и 131.
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ 321
валов строят множества, измеримые В, можно комбинировать весьма
сложным образом, так как, чтобы получить желаемое множество Е,
измеримое В, очень часто нужно сначала подготовить бесконечное
множество других предварительных множеств, также измеримых В,
композиция которых посредством основных операций приводит нас
в конечном счете к результирующему множеству Е.
Эти объяснения необходимы, если намереваются изучать множества,
измеримые В, в их общности; они к тому же ясно обнаруживают всю
сложность общего понятия множества, измеримого В. Но самые эти
объяснения позволяют понять, что предыдущее определение, взятое само
по себе, не имеет никакого ощутимого смысла: действительно, что без
дополнительных объяснений выражают слова: повторное применение
основных операций? Таким образом, эти объяснения неотделимы от
предыдущего определения, скорее, именно эти объяснения и являются
самим определением множества, измеримого В.
Если мы попытаемся проанализировать эти объяснения, то придем
к следующему заключению: мы исходим из интервалов, которые нами
рассматриваются как данные; затем нам нужно было бы заготовить
бесконечное число промежуточных множеств, которые наверняка
зависят друг от друга.
В каком порядке нужно их брать, чтобы быть уверенным, что можно
получить их все, не заблудившись в неисчислимом множестве
их и не впадая в порочный круг?
С этим вопросом впервые встречаются, когда приступают к
изучению функций и принимают следующее определение: функция /(х)
называется элементарной, если она может быть получена, исходя из
действительного переменного и констант, повторным применением
основных операций (сложения, вычитания, умножения, деления, ^
log, sin и т. д.). Невозможно не поражаться аналогией между этим
определением и предыдущим определением множества, измеримого В.
Но это только чисто формальная аналогия.
В случае понятия элементарной функции каждая из основных
операций применяется не более чем к двум функциям, ранее
определенным; множество промежуточных функций тоже очевидно конечно. Именно
на этом основании эти функции можно разместить в некотором
порядке таким образом, что можно определить при помощи основных
операций последовательно все промежуточные функции, не исключая
ни одной из них и не повторяя ни одной из них несколько раз, чтобы
придти в конце концов к желаемой функции. Именно в силу этой
упорядоченности невозможно впасть в порочный круг, и, следовательно,
данное определение элементарной функции является настоящим
определением.
Совсем другая картина в случае понятия множества, измеримого В.
В этом случае число предварительных множеств бесконечно, и порядок,
в котором эти множества располагаются, значительно более важен,
322
Н. Н. ЛУЗИН
чем самое определение множества, измеримого В. Без знания этого
порядка мы будем обычно находиться в положении математика, который
хочет иметь в своем распоряжении всевозможные целые
положительные числа, не зная, однако, принципа полной индукции. Именно этот
порядок промежуточных множеств является истинным нервом всех
генетических определений множества, измеримого В. Теоретическая
необходимость генетических определений множества, измеримого В, на почве
общих рассуждений перерастает, следовательно, в математическую
необходимость точного определения порядка промежуточных
множеств.
Известно, что все процессы, эффективно устанавливающие этот
порядок, поддаются общему исследованию, которое впервые было
проделано Кантором в связи с последовательными производными данного
множества и которое ведет к понятию трансфинитных чисел второго
класса. Самое трансфинитное число есть не что иное, как сокращенное
обозначение д\я того, чтобы указать порядок, в котором должно
производиться счетное множество операций, допуская счетное число
последовательных и суперпозированных переходов к пределу1. Если не
ограничивать поле математики изучением определенной категории
множеств, измеримых Ву происходящих, например, из функций конечного
класса Бэра, то в определение должны быть введены сколь угодно
большие трансфинитные числа. В этом смысле совокупность всех
множеств, измеримых Ву есть нечто, совершенно адекватное совокупности
всех трансфинитных чисел второго класса.
Борель подверг глубокой критике этот вопрос. Эта критика стала
слишком классической д\я того, чтобы была необходимость подробно
излагать ее доводы; мы ограничимся беглым напоминанием
существенных пунктов, на которых она основана.
Имеется много исходных законов совокупностей. Например, можно
рассуждать о всех точках, содержащихся внутри данного интервала,
или о всех непрерывных функциях, так как эта возможность
узаконена вполне конечным определением действительной точки или
непрерывности функции, введенным Коши. Таким образом, получаются
общие свойства совокупности; но в действительности никогда не
рассуждают об определенном индивидууме этой совокупности, если только
дело не идет об очень частном индивидууме, который можно отличить
от всех других при помощи конечного определения2. К тому же, если
каким-нибудь законом задают индивидуум совокупности, то мы можем
post factum определить его регулярным приемом, используя, например,
1 Это определение принадлежит Борелю (см. „Le calcul des integrates definies".
Journ. de Math., 177, 1912). Имеется несколько теорий трансфинитных чисел:
теория Кантора „порождения типов", номиналистические теории Бэра и Лебега,
формальная теория Расселя—Серпинского.
2 См. E.^Borel. La philosophie mathematique et Tinfini (Revue du Mois, август
1912 г.).
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ 323
подходящим образом выбранные десятичные разложения или
полиномиальные аппроксимации.
Наоборот, множество всех точечных множеств является незаконной
совокупностью. Когда говорят об этой совокупности, не указывают
ни закона, ее задающего, ни способа назвать ее. Если некоторым
способом задан индивидуум этой совокупности, то не существует никакого
регулярного метода для того, чтобы получить его post factum, даже
если слово трансфинитное при помощи смелого обобщения
приобретает столь же ясный и столь же универсальный, лишенный
двусмысленности смысл, как принятый в настоящее время смысл слова
безгранично. В настоящее время мы не знаем никакого способа определения
совокупности всех точечных множеств; когда мы говорим о ней, мы
фактически представляем себе только различные приемы, которые можно
придумать для определения очень сложных множеств, за неимением
конечного определения, которое позволило бы охватить их одним
взглядом. Но с момента, когда дело касается человеческой возможности
создавать приемы определения и системы соглашений, уравнивание ее
в правах, сознательное или несознательное, с совокупностью с
конечным определением должно совершенно исчезнуть, и мы находимся
в области субъективного. Следовательно, совокупность всех точечных
множеств, представляемая по-своему каждым математиком, не имеет
в объективной науке, каковой являются классические части математики,
другого существования, как чисто словесное; следовательно, невозможно
ее рассматривать как истинный математический объект, который может
быть включен в рассуждения. Именно в силу этой невозможности
область математики ограничивают изучением классов точечных множеств
с конечными определениями: только эти классы можно рассматривать
как предмет исследования.
Так же как за совокупностью всех точечных множеств необходимо
признать только словесное существование, нужно включить в область
незаконного самую совокупность действительных чисел. Так как
каждое действительное число должно иметь конечный закон, необходимый
Л\я его определения, исходя из единицы \ то ясно, что в обоих
случаях мы останавливаемся перед одной и той же трудностью: нельзя
охватить одним взглядом математические объекты, определенные, исходя
из неизменных условий, при помощи самых различных конечных
законов, не зная закона задания этих законов. Теперь необходимо сказать
несколько слов о понятии континуума. Может показаться
парадоксальным отделение совокупности точек от совокупности чисел путем
признания первой и отрицания второй; однако это очень естественный
круг идей. Понятие континуума приобретено при помощи геометрической
1 Мы напомним здесь важное понятие высоты данного действительного числа,
введенное Э. Борелем (см. „Le calcul des integrales definles*4. Journ. Math., 163,
1912). Будет очень интересно сравнить с этими взглядами Бореля новые взгляды
Д. Гильберта (см. „Logische Grundlagen der Mathematik." Math. Ann., S3).
324
Н. Н. ЛУЗИН
интуиции !; знание единицы длины ни в коей мере не необходимо для
фиксации на прямой одной вполне определенной точки; неподвижная
точка вполне определена на прямой уже тем, что она находится на
прямой там, где она есть. При изучении континуума нет никаких
трудностей, если оставаться на чисто геометрической точке зрения;
все точки прямой совершенно идентичны, так как они обладают одними
и теми же общими свойствами; трудности представляются только
в связи с арифметическими определениями, так как познание этих общих
свойств является более трудным2. К тому же известно, что полное
арифметическое определение континуума требует признания законности
счетного числа последовательных и произвольных выборов, в то время
как эта законность сомнительна. Следовательно, континуум никогда не
появляется как данный в своей арифметической полноте3. Одна из
наиболее важных проблем теории функций действительного
переменного состоит теперь в преобразовании совокупности чисел в
законную совокупность (с конечным определением) или в том, чтобы
назвать при помощи конечного определения класс чисел, инвариантных
относительно всех преобразований классического анализа и алгебры:
именно этот класс чисел будет представлять собой практический
континуум, который используют математики4.
Возвращаясь к совокупности всех трансфинитных чисел и всех
множеств, измеримых Ву мы мало что можем добавить: обе совокупности^
конечнОу незаконны. Трудность, которая имеется при возникновении
концепции этих совокупностей, связана с тем, что можно
сформулировать эффективно только конечное число условий, и что как бы далеко
эти условия не позволяли идти, объекты (множества, измеримые В,
трансфинитные числа), которые они позволяют эффективно получить,
ничем не отличаются от тех, которые получаются из них, но которые
могут быть определены конечным числом других условий; причем этот
процесс никогда не заканчивается5. Концепция конструктивной
совокупности множеств, измеримых Ву хотя и непротиворечива в себе, но
не является действительной математической концепцией, так как при
помощи конечного числа соглашений невозможно точно описать
конструкцию такой совокупности: чтобы установить это понятие способом,
лишенным двусмысленности, потребуется бесконечное число абсолютно
независимых друг от друга условий.
1 См. Е. В orel. Sur les principes de la theorie des ensembles (IVе Congres
international des mathematiciens, Rome, 1908).
2 Cm. E. В ore I. L'antinomie du transfini (Revue philosophique, 1900).
s Cm. E. В orel. Sur les principes de la theorie des ensembles (IVе Congres
international des mathematiciens, Rome, 1908).
4 См. Е. В or el. Les „Paradoxes" de la theorie des ensembles (Ann. de PEcole
Norm. Sup&r., октябрь 1908 г.).
5 См. Е. В orel. L'infini mathematique et la realite (Revue du Mois, 10 июля
1914 г.).
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ 325
Но тогда немедленно возникает математическая необходимость
овладеть главными свойствами, общими всем множествам, измеримым 5.
Если при помощи конечного определения дана совокупность некоторых
объектов, то свойства, общие всем этим объектам, получают
непосредственным анализом самого определения (предполагаемого конечным)
предложенной совокупности. Безукоризненный пример такого способа
действия представляет собой случай функций первого класса Бэра.
Но как нужно действовать в случае совокупности, лишенной
конечного определения? И прежде всего каким образом возможны- такие
свойства?
Пытаясь рассуждать о несовершенной совокупности, лишенной
конечного определения, как о совокупности с конечным определением,
можно проводить только общие или символические рассуждения, в
которых рассматриваемая совокупность представлена одним только
символом. В таких рассуждениях, как рассуждения общего характера,
допустимы моменты, которые свободны от противоречий, но в то же время
лишены всякого точного содержания1. Чтобы иметь возможность дать
им содержание, нужно точно установить неизменное обозначение а^я
элементов совокупности, а именно это невозможно. Теория совокупностей,
лишенных конечного определения, неизбежно ограничивается чем-то
вроде логической алгебры, символы которой не скрывают никакого
доступного реального факта. Различные математики не могут быть
уверены в том, что они находятся в согласии относительно этого
реального факта, так как они не имеют общего представления о нем2.
Такой способ действия, очевидно, приемлем в том смысле, что мы
всегда имеем право создать словарь и при помощи этого словаря
построить логическое здание; но такой способ действия бесплоден с точки
зрения открытия новых фактов, которые одни только и двигают
вперед нашу науку. Следовательно, мы не имеем права создать себе
иллюзию относительно реального значения таких общих рассуждений:
отсутствие логического противоречия недостаточно, чтобы
охарактеризовать конструкцию как научную3.
Именно в силу этого предпочитают с неоспоримым успехом
следовать другим путем. Если математику не ограничивают изучением
специального класса множеств, порожденных функциями конечного
класса Бэра (чего для большей части приложений достаточно), то
метод остается тем же и всегда состоит в получении новых
множеств из множеств, уже определенных; только, вместо того чтобы
исходить из интервалов и продолжать конструкцию постепенно, пред-
1 См. Е. В or el. La philosophie mathematique et Tinfini (Revue du Mois>
август 1912 г.).
2 См. Е. В or el. Sur les principes de la theorie des ensembles (IVе Сongres
international des mathematiciens, Rome, 1908).
3 Cm. E. В or el. L'infini mathematique et la realite (Revue du Mois, 10 июля
1914 г.).
326
Н Н ЛУЗИН
полагают, что конструкция проведена до некоторого места и обладает
некоторыми свойствами, и доказывают, что эти свойства
сохраняются при продвижении на новый шаг. Такой способ действия
непреложен с логической точки зрения, и, что еще более важно, он
безупречен по отношению к математической реальности. К тому же он
плодотворен: большая часть ценных свойств (мера, категория), общих
всем множествам, измеримым В, получается этим методом. Установка
этого метода, следовательно, теоретически очень сильна 1.
Практически же она значительно слабее. Достаточно указать, что
такой способ действия ведет в то же время к потере такого свойства,
общего всем несчетным множествам, измеримым В, каким является
свойство иметь мощность континуума. Так как это обстоятельство,
быть может, не очень тривиально, нам кажется, что интересно
остановиться на этом пункте.
В работе Лебега („Sur les fonction representables analitiquement")2
указано много основных свойств, общих всем несчетным множествам,
измеримым В. Автор получил все эти свойства однообразным
применением предыдущего метода: они проверяются для интервалов, и
доказывается, что эти свойства инвариантны относительно основных
операций (сложения, общей части). Но среди этих свойств не
встречается важное свойство, которое устанавливает существование
совершенного множества в каждом несчетном множестве, измеримом В. Это
свойство было впервые открыто Александровым и Хаусдорфом через
десять лет после появления мемуара Лебега.
Суть дела в следующем. Все свойства, выведенные Лебегом,
индуктивны, а свойство, найденное Александровым и Хаусдорфом, не
является таковым; мы увидим в этой работе, что это свойство вовсе
не инвариантно относительно второй основной операции (общей части)
счетного числа множеств и, следовательно, не может быть получено
предыдущим методом. Отсутствие этого свойства в мемуаре Лебега
не представляет, следовательно, никакой случайности.
Итак, имеет место очень важный факт: существуют неиндуктивные
свойства, общие всем множествам, измеримым В. Но как, однако, могут
существовать такие свойства?
Мне кажется, что ответ напрашивается сам собой. Существует
конечное определение совокупности множеств, измеримых В, в силу
которого эта совокупность становится законной совокупностью (с
конечным определением). Именно в силу этого конечного определения должны
существовать неиндуктивные свойства множеств, измеримых 5. Знание
этого определения достаточно, чтобы иметь все свойства, индуктивные
и неиндуктивные, множеств, измеримых В.
1 См. Е. В or el. Le calcul des integrales definies (Journ. de Jordan, 183f
1912).
2 Journ. de Math., 1905.
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ 327
Чтобы узаконить это утверждение, нам достаточно эффективно
преобразовать конструктивную совокупность множеств, измеримых В,
в совокупность с конечным определением. К сожалению, мы должны
будем войти для этого в область аксиоматики. Но не следует
удивляться [этому: невозможно полностью преобразовать ложное понятие
в истинное при помощи способа, безупречного с точки зрения
математической реальности.
II. Принцип минимума
Аксиоматическое определение. В качестве путеводителя,
который нам позволит по аналогии найти аксиоматическое
определение совокупности множеств, измеримых Ву мы возьмем арифметику.
Известно, что одной из наиболее прекрасных концепций
арифметики является понятие тела чисел> восходящее в Галуа. Телом чисел
называется произвольная система чисел, такая, что, произведя над
несколькими числами системы четыре основные операции: сложение,
вычитание, умножение, деление (исключая деление на нуль), мы
получим в результате этих операций числа, также принадлежащие этой
системе. Числовое тело задано, если множество его элементов есть
множество с конечным определением; такое тело называется
эффективным телом.
Первым примером эффективного тела является множество всех
рациональных чисел; его называют областью рациональности. Второй
лример эффективного тела, заслуживающий значительно большего
интереса, есть тело, полученное из области рациональности
присоединением данного несоизмеримого числа. Вот что под этим надо
понимать.
Пусть R — область рациональности; прибавим к ней вполне
определенное несоизмеримое число а (например число е); мы имеем тогда
новую систему чисел:
■которая не образует тела; тело получим только, если к ней присоединим
также числа, которые возникают, когда а соединяется с элементами R
при помощи основных операций. Таким образом, мы получаем более
•обширное тело, содержащее R и а и вполне определенное посредством R
и а; мы назовем его телом R (а) и будем говорить, что R (а) получается
яз R присоединением а.
В этих разъяснениях сразу узнаем генетическое (конструктивное)
определение. Как в аналогичном случае совокупности всех множеств,
измеримых В9 это определение, строго говоря, незаконно. Но вот
корректное определение: тело R(a) есть множество всех
рациональных функций от ос с целыми коэффициентами.
Именно благодаря этому вполне конечному определению тело R (а)
вполне эффективно.
328
Н Н ЛУЗИН
Что именно во втором определении делает нашу концепцию тела R (а)
законной? Не изучая глубоко этот затруднительный вопрос, мы хотим
отметить, что это в конечном счете факт обладания совершенно ясным
представлением о натуральной последовательности целых чисел1.
1, 2, 3, 4, ...
Если, наоборот, мы не обладаем четким и ясным представлением
о неограниченной последовательности целых чисел (что является только
чистым предположением, так как если бы не было вполне ясного
понятия о неограниченности9 то не существовало бы математики), остается
только сформулировать третье, вполне аксиоматическое определение
тела /?(а):
Это тело есть наименьшее из телу содержащих данное число а.
Закончив эти предварительные рассмотрения, мы можем теперь
сформулировать a prioril следующие определения:
Мы будем называть телом множеств такую систему линейных
точечных множеств, что две основные операции (образование суммы
счетного числа множеств, взятие общей части счетного числа
множеств), произведенные над некоторыми множествами системы, всегда
приводят к множеству, принадлежащему той же системе.
Аксиоматическое определение. Мы назовем В-телом
наименьшее тело множеств, содержащее все открытые интервалы с
рациональными концами. Линейное множество называется измеримым В>
если оно принадлежит телу В.
Это определение, к которому нас естественным образом привела
аналогия с предыдущим, покажется, без сомнения, ясным читателю,
слишком привыкшему к идее актуальной бесконечности; но одна из
идей, на которых мы хотим основать наш мемуар, состоит в том, что
во всех вопросах, куда входит „актуальная бесконечность", нужно
крайне недоверчиво относиться к мнимой ясности: нет ничего более
опасного, чем позволить себе довольствоваться пустыми словами
в подобных случаях. Мы должны отметить это, используя указанное
определение.
Мы не можем не поражаться наличием существенных различий
между гэтим определением и тем, которое мы установили в случае
арифметического тела. Следует подчеркнуть только одно из этих
отличий: наименьшее из арифметических тел, содержащих а, существует,
очевидно, потому, что существует множество рациональных функций
от а с целыми коэффициентами; следовательно, третье (аксиоматическое)
определение тела R{o) можно узаконить, опираясь на законность
второго (конечного) определения этого тела. В случае тела множеств это
1 См. Е. В or el. L'infini mathematique et la rSalite (Revn-e du Mois» 10 июля
1912 г.).
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ
329
отнюдь не так: мы не имеем для 5-тела конечного определения,
аналогичного второму определению тела /?(<*)•
Мы подошли, таким образом, к постановке следующего вопроса:
Какими средствами можно узаконить аксиоматическое определение,
предложенное для В-тела? И, прежде всего, как можно доказать
существование этого тела? Неуместно дискутировать истинность этого
определения как определения; нельзя сказать: оно истинно только
потому, что оно написано; нужно отыскать реально существующий объект
который описывается этим определением.
Попытка такого рода, которая кажется наиболее естественной и
имеет то преимущество, что она крайне проста и элементарна,
осуществляется следующим рассуждением:
„Ясно, что имеются тела множеств, содержащие все интервалы
с рациональными концами, так как множество всех точечных
множеств представляет собой одно из них; очевидно, что если
рассматривать множество F всех тел, содержащих рациональные интервалы, то
множество-делитель F (делитель конечного или бесконечного числа
множеств Е есть множество элементов, общих для всех Е) есть тело
той же природы; это наименьшее тело. Таким образом,
существование Б-тела — установлено".
Эти доводы не новы; их можно прочитать с незначительными
изменениями в первых строках известного рассуждения Цермело,
относящегося к вполне упорядоченным множествам1. Я применял уже однажды
этот прием рассуждения2, приступая к теории аналитических множеств;
в то время я сильно колебался между точкой зрения Адамара и
точкой зрения Бореля и Лебега. Теперь я склоняюсь ко второй и не
рассматриваю больше это рассуждение как убедительное.
Чтобы подтвердить правильность предыдущего рассуждения,
необходимо прежде всего строго доказать существование тел множеств,
содержащих рациональные интервалы. А ведь приведенный выше
пример множества всех точечных множеств поистине выбран плохо: не
существует никакого реального объекта, который соответствовал бы
этому понятию. Это понятие, изменяясь от математика к математику,
каждый раз имеет только чисто субъективный субстрактум; оно,
следовательно, по выражению Бореля, — „вне математики". Существование
тел множеств будет косвенно следовать из теории аналитических
множеств: мы увидим, что семейство аналитических множеств есть
эффективное тело. Другим пунктом этого рассуждения, легко подвергаемым
1 См. хорошо известную статью Бореля nLe continu bien ordonne d'apres
M. Zermelo" („Lecons sur la theorie des functions". 2e ed., стр. 148).
2 Именно этот способ рассуждения я использовал в доказательстве теоремы:
каждое множество^ измеримое В, есть аналитическое множество; см., например,
статью Суслина „Sur une definition des ensembles mesurables В sans nombres
transfinis" (Comptes Rendus, 8 января 1917 г.)-
330
н. н. лузин
критике, является использование совокупности всех тел множеств: эта
совокупность также незаконна.
Все, чего можно ожидать от этого рассуждения, — это
единственность 5-тела; так как общая часть двух каких-нибудь тел есть также
тело, то 5-тело, если оно существует, есть тело, определенное
однозначно без возможной двусмысленности.
Не имея возможности в настоящее время доказать существование
5-тела, мы это примем временно как своего рода постулат и назовем
его принципом минимума.
Правда, с этим принципом связаны особые трудности, первая из
которых следующая: право образовывать множество только из ранее
построенных объектов. Легко видеть, что определение 5-тела
предполагает обратное; это определение располагает, следовательно, вещи
в порядке, совсем обратном тому, в котором они должны были бы
следовать: здесь не только не образуется совокупность при помощи
элементов, но именно элементы определяются при помощи совокупности,
которую предполагают уже определенной. Тем не менее, удобно
временно принять этот принцип как промежуточный инструмент,
актуальной пользой которого не следует пренебрегать, но который следует
рассматривать только как средство преобразования ложных
совокупностей в совокупности с конечным определением, составляющие
единственную реальность, которую мы можем познать. Важно то, что
рассмотрение этого принципа никогда не может привести к неточным
представлениям, парадоксам или противоречиям; здесь не встречается
трудностей вариационного исчисления. К тому же пробел
незамедлительно будет заполнен: существование В-тела будет доказано при
последующем развитии теории аналитических множеств.
Следствия из принципа минимума. Определение В-тела
влечет за собой совершенно непосредственное следствие:
Сумма счетного числа множеств, измеримых В, есть множество,
измеримое В. Общая часть счетного числа множеств, измеримых В,
есть также множество, измеримое В.
Мы теперь естественным образом подошли к поискам других
операций над множествами, которые сохраняют измеримость В.
Прежде всего необходимо исследовать с этой точки зрения две
борелевские операции предельного перехода и в особенности тонкую
операцию вычитания.
Верхним пределом множеств Ev Е2,.. .называется, согласно Борелю,
множество, образованное из точек, которые принадлежат бесконечному
числу из них. Нижним пределом множеств Ех, Е2, ... называется
множество, образованное из точек, которые принадлежат всем этим
множествам, кроме, быть может, конечного числа из них.
Если дана последовательность множеств Е19 Ег, ..., то оба
предельных множества вполне определены и не зависят от порядка ее чле-
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ 331
нов; мы обозначим, согласно обыкновению, через lim Еп верхний предел,
«=00
а через Нт Еп нижний предел. Очевидно, что нижний предел содержится
t/=oo
в верхнем пределе, но обычно не совпадает с ним; если они
совпадают, то последовательность Еи £2, ..., называется сходящейся,
я этот общий предел обозначается через lim £„.
w=co
Д\я обоих пределов имеем следующую символическую запись:
lim Еи = (Ег -+- £2 ч- £3-+-...)(£>"»" £з-+■ • • •) (£з ■+" • • •) • • •;
»/=ОЭ
lim Еи = (£х• £2 • £3 -.. Q ч- (£2 • £а -...)-«- (£3 -...) -ь ...,
»/=J0
где через £г-1-£2-н... обозначают сумму множеств £lf £2, ..., а через
£2 • £2 • .. . — их общую часть.
Из этого непосредственно заключаем, что верхний и нижний пределы
счетного числа множеств, измеримых В, суть множества,
измеримые В. Предел счетного числа множеств, измеримых В, если он
существует, также измерим В.
Остается исследовать только одну операцию. Разностью двух
множеств Е и S называется множество, образованное из тех точек £,
которые не принадлежат S; впрочем, это определение ни в коей мере
не предполагает, что множество £ содержит <§. Это множество-разность
обычно обозначают через £ — 8.
Если через Сё обозначить дополнение к §, то имеем
£ — £ = £. CS;
следовательно, операция вычитания может быть заменена второй
основной операцией (операцией общей части) и новой операцией,
позволяющей переходить от множества к его дополнению. Это замечание будет
немедленно использовано.
Теорема. Дополнение к множеству, измеримому В, есть также
множество, измеримое В.
Для доказательства1 назовем регулярным множеством каждое
множество, измеримое В, дополнение к которому измеримо 5. Очевидно,
что каждый интервал, имеющий рациональные концы, есть регулярное
множество. Я утверждаю теперь, что если множества Е19 £2, ...
регулярны, то то же самое имеет место и д\я их суммы и общей части.
Действительно, если положить S= Ег -и £2 -+■. • • и Р = Ег • £2 • ...,
то, очевидно, будем иметь:
CS=CEX • С£2 •..., СР = СЕХ-+-СЕ2+...
1 Это доказательство принадлежит В. Серпинскому; см. статью В. Серпинского
„Sur les definitions axiomatiques des ensembles mesurables Bu (Bull, de Г Acad, des
Sci. Cracovie, январь—март 1918 г.).
332
Н. Н. ЛУЗИН
Следовательно, S и Р регулярны. Но тогда семейство регулярных
множеств будет телом множеству содержащим все интервалы с
рациональными концами. Согласно принципу минимума fi-тело содержится
в этом теле. Следовательно, все множества, измеримые В> регулярны,.
и т. д.
Из этой теоремы следует, что множество-разность двух множеству
измеримых By измеримо В.
Необходимо сказать несколько слов об этом следствии; имеется
существенное отличие между этим следствием и тем заключением,
которое мы должны были сделать в случае борелевских операций
предельного перехода. Множества-пределы также принадлежат всем телам
множеств, так как операции предельного перехода сводятся к основным
операциям (суммы, общей части), но ничего подобного нет для
вычитания: дополнение к множеству, являющемуся элементом тела, вообще
говоря, не принадлежит этому телу. Мы увидим эффективные примеры
такого рода. Даже несколько удивительно, что дополнение всегда
принадлежит Л-телу; рассматриваемое свойство не индуктивно. Мы
приходим к следующему заключению:
Если дополнение к множеству точек не принадлежит телу
множеству содержащему все интервалы с рациональными концамиу то
это множество наверняка неизмеримо В.
Как мы увидим, это имеет место в случае тела аналитических
множеств.
III. Определение аналитического множества. Л-тело
В своих работах по интегрированию Лебег пришел к идее деления
интервала изменения функции и рассмотрения множества ее значений. Именно
на этой идее основана большая часть последующих рассмотрений.
Сначала мы ограничимся случаем однозначной функции одного
действительного переменного /(х)9 определенной в открытом интервале,
за который мы можем взять интервал (0,1). Мы будем называть этот
открытый интервал (0,1) областью и будем обозначать его знаком D
или DXy если необходимо будет явным образом отметить независимое
переменное.
Если функция f(x) непрерывна в каждой точке областиу то
множество ее значений совсем просто; непосредственно видно, что
возможны только четыре случая: 1° множество значений функции есть
открытый интервал; 2° полусегмент (т. е. сегмент, закрытый только
с одного из своих концов); 3° замкнутый сегмент; 4° одна точка.
Если функция /(х) имеет в области D только конечное число
точек разрыва, то множество ее значений также очень просто: это,
очевидно, соединение четырех предыдущих элементарных видов
множеств, взятых в конечном числе.
Теперь естественно исследовать с этой точки зрения функции / (х),
разрывные только на счетном множестве значений переменного.
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ 333
Борель уже давно привлек внимание к этим функциям, класс которых
следовало бы изучать непосредственно после класса непрерывных
функций1; я их назову д\я краткости счетно-разрывными функциями.
Совокупность этих функций, как и совокупность непрерывных функций, явно
законна, так как обе они имеют конечное определение.
Основным понятием, из которого вытекают все рассмотрения,
развитые в этом мемуаре, является понятие аналитического множества.
Аналитическим множеством называют множество значений счетно-
разрывной функции; совокупность всех аналитических множеству
включая в нее пустое множество^ называется аналитическим телом.
1 Цитируем дословно несколько отрывков из Бореля („Lecons sur la theorie des
fonctions'% Iе ed., 1898, Note I, стр. 109; Note III, стр. 126):
„ . . . в этом исчислении можно пользоваться функцией только в том случае,
когда она определена при помощи счетного числа элементов. Токов случай
непрерывных функций, а также функций, разрывных только на счетном множестве
значений переменного. Такие функции действительно могут быть определены при
помощи счетного множества условий. . .
„ . . . если они различны, то мы можем быть уверены в том, что это всегда
заметим. Ничего подобного нет лая разрывных функций (здесь рассматриваются
наиболее общие разрывные функции): такая функция определена несчетным
множеством условий; практически это значит, что ее невозможно определить. Среди
наиболее общих разрывных функций, которые представляется целесообразным
исключить, по крайней мере в настоящий момент, из математических рассмотрений,
следовало бы различать функции, разрывность которых подчиняется ограничениям.
Эти ограничения должны быть такого рода, чтобы функция могла быть
полностью определена счетным множеством условий. Множество функций,
удовлетворяющих этим ограничительным условиям, имеет такую же мощность, как и
континуум. Среди функций, удовлетворяющих ограничительным условиям такого
рода, я приведу функции, разрывные только на счетном множестве точек, которые
с пользой рассматриваются некоторыми математиками".
Было бы очень интересно узнать, адекватна ли борелевская концепция функции,
определенной счетным числом условий, лебеговской концепции функции, которую
можно назвать („Sur les fonctions representables analitiquement", стр. 215).
По-видимому, невозможно найти называемую функцию (т. е. функцию-индивидуум),
которая не была бы определима счетным множеством условий; практически всякий
раз, когда математики констатировали существование функции-индивидуума, они
умели определить ее счетным числом условий. Это важный факт: мы увидим, что
функция, не определимая аналитически, которая была названа Лебегом, есть функция,
определенная счетным числом условий таким же образом, как каждая непрерывная
функция. Но нам кажется небесполезным еще раз подчеркнуть трудность, состоящую
в пересчете условий в общем случае, как только дана индивидуальная функция,
заданная точным законом, даже если каждое условие переводится на факт задания
целого числа. Перед этой же трудностью мы останавливаемся, когда хотим
установить конечное число операций, необходимых для определения исходя, из единицы,
данного действительного числа (например тс). На этих соображений Борель ввел
важное понятие высоты числа (см. его „Lecons sur la theorie de la croissance" и
его „Sur le calcul des integrates definies", Journ. de Jordan, 1914). Можно
сопоставить с этим понятием понятие „функционального ранга", недавно введенное П. Бер-
найсом.
Но и там мы сталкиваемся с трудностями, которые далеки от того, чтобы быть
разрешенными.
334
Н. Н. ЛУЗИН
Название: аналитические множества дано этим множествам согласно
предложению Лебега называть аналитическими множествами все
множества, которые могут быть определены аналитическими равенствами
или неравенствами1. Легко убедиться в том, что все множества, кото*
рые мы только что определили, допускают хорошее аналитическое
представление.
Действительно, каждая счетно-разрывная на области D функция f{x)>
очевидно, точечно разрывна на каждом совершенном множестве.
Следовательно, по известной теореме Бэра, можно эффективно построить
ряд полиномов:
Р1(х) + Р2{х)+...ч-Ря{х)ч-...,
1 Цитируем дословно этот отрывок иэ Лебега („Sur les fonctions representables
analytiquement", стр. 165):
„Из того, что будет доказано впоследствии, следует, что множества, измеримые В,
это те, которые могут быть определены при помощи аналитических равенств или
неравенств; из этих соображений они заслуживают быть названными аналитическими
множествами".
Обратное утверждение (т. е. что каждое множество, определенное аналитическим
равенством или неравенством, есть множество, измеримое В) никогда не
высказывалось им: Лебег не написал ни одной фразы, ни простого намека на возможность
такого обращения. Именно поэтому Суслин и я, придавая большое значение
выполнению программы Лебега: изучить наиболее общие функции, которые можно назвать*
как только мы познакомились с новым классом множеств, тесно связанных с рядами
полиномов, — приняли терминологию, уже установленную самим Лебегом. Но в то
же время мы воздержались от того, чтобы дать такое же наименование
аналитических множеств дополнительным множествам: эти последние, будучи
определенными чисто отрицательным образом как совокупности точек, которые не . . .,
нуждались в специальной проверке их аналитичности в смысле Лебега. А ведь частный
пример дополнительного множества, полученный попутно самим Лебегом, ясно
обнаружил невозможность существования положительного и конечного определения
дополнительных множеств, что в дальнейшем было подтверждено теорией: во всяком
положительном определении дополнительного множества неминуемо должны принять,
участие все трансфинитньте числа второго класса (а не только те, которые меньше
одного из них, фиксированного заранее) или нечто, полностью адекватное этой
незаконной совокупности. Значение этого факта станет особенно ясным, когда мы
вплотную подойдем к изучению множеств, которые я называю проективными и*
первая идея о которых принадлежит Лебегу (см. пять моих заметок в Comptes
Rendus, относящихся к аналитическим и проективным множествам: от 4 мая, 25 мая,
15 июня, 13 июля и 25 августа 1925 г.) (см. стр. 301 настоящего тома.—Ред.).
В ограниченных рамках наших заметок в Comptes Rendus de l'Academie des.
Sciences (Souslin. Sur une definition des ensembles mesurables В sans nombres-
transfinis N. Lusin. Sur la classification de M. Baire, 164, 88 и 91, заседанне-
8 января 1917 г.), где имеются все принципиальные результаты об аналитических,
множествах, сформулированные, впрочем, без доказательства, мы называли
аналитические множества кратким названием yl-множества. В силу существования
аналогичных наименований в самых разнообразных случаях (так, Борель использовал то же-
наименование А множеств для вполне определенных множеств, которые все
измеримы В; см. „Le calcul des integrales definies", стр. 184; см. также Л-множества.
Валле-Пуссена: „Integrates de Lebesgue fonctions d'ensembles, classes de Bairea,
стр. 135) я хотел бы дать сокращенному названию Л-множества его первоначальный;
смысл: аналитическое множество (см. (3]).
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ 335
сходящийся при каждом значении х из области D, сумма которого
есть f(x). Мы видим таким образом, что каждое линейное
аналитическое множество есть множество значений, которые принимает
в области D сумма сходящегося ряда полиномов.
К тому же обратное утверждение также безусловно верно:
действительно, мы увидим, что определение аналитического множества нисколько
не расширится, если рассматривать таким же образом множество
значений, которые принимает произвольная функция классификации
Бэра на произвольном множестве, измеримом В (и даже на
произвольном аналитическом множестве); такое множество также будет
аналитическим. Это утверждение показывает важность аналитических
множеств и заставляет нас ожидать, что они имеют большое
число интересных аналитических свойств; мы отметим некоторые
из них.
Первый пример аналитического множества, неизмеримого Ву
который упоминается в математической библиографии, это множество,
построенное Лебегом1 и использованное им как промежуточный инструмент
при конструировании индивидуальной функции, никаким способом не
поддающейся аналитическому представлению („Sur les fonctions represen-
tables analytiquement", стр. 213—214).
Ввиду вспомогательной роли, которую это множество там играет,
знаменитый автор, занятый быстрейшим завершением конструкции
функции, не определимой аналитически, охотно согласился опустить
глубокий анализ этого множества, так как казалось, что он должен быть
длинным и утомительным для читателя и в то же время излишним д\я
достижения конечной цели2. Тем не менее это множество представляет
большой интерес3, так как, полностью решая проблему Лебега о
конструкции индивидуальной функции, не представимой аналитически, оно
дает в то же время полное решение другой проблемы, также
принадлежащей Лебегу („Sur les fonctions representables analytiquement",
стр. 188), формулировка которой следующая: найти индивидуальную
функцию, которая не принадлежит классификации Бэра, но которая
обладает в то же время необходимым свойством Бэра — быть точечно-
разрывной на каждом совершенном множестве, если пренебречь
множеством первой категории на этом совершенном множестве.
Действительно, мы увидим, что для получения такой функции достаточно
рассмотреть характеристическую функцию аналитического множества,
неизмеримого В, ранее указанного Лебегом [функция f(x) называется
характеристической дая данного множества Е, если f(x) равна 1 для
точек множества Е и равна 0 вне Е].
1 См. [14] и [201.
* Там же.
s Глубокий анализ этого примера Лебега дан в моей работе „Sur le ensembles
analytiques" (Fund. Math., X) (см. стр. 380 настоящего тома.—Ред.).
336
н. н. лузин
Возвратимся к представлению аналитического множества рядом
полиномов. Может показаться, что ряд полиномов
/W = P1(x) + P.2w + ... + ^w + ...,
для которого множество значений его суммы f(x) неизмеримо В, должен
представлять крайнюю экстравагантность с точки зрения его
сходимости. Никоим образом. Мы увидим, что, не меняя данного
аналитического множества, можно всегда предположить, что этот ряд сходится
абсолютно при всех значениях х. Но, вообще говоря, этот ряд ни
на каком интервале не сходится равномерно.
Тело аналитических множеству будучи совокупностью с конечным
определением, является законной совокупностью.
Простейшие свойства аналитических множеств. Мы
отметим сначала наиболее простые свойства аналитических множеств.
Все эти свойства индуктивны, т. е. сохраняются при применении
основных операций (суммы, общей части); мы покажем в дальнейшем (в п. IV),
что имеются свойства, которые не индуктивны, т. е. не инвариантны
относительно основных операций.
Каждый открытый интервал (а, Ь) с различными рациональными
концами есть аналитическое множество; в этом мы немедленно
убеждаемся, беря в качестве счетно-разрывной функции f{x) линейную
функцию а -+- {Ь — а) х.
Множество, состоящее из единственной точки, — аналитическое
множество; достаточно взять функцию f(x), равную ординате *этой
точки на всей области D.
Каждое счетное множество точек — аналитическое множество.
Если у 1У у2У ..., упу - • • — ординаты этих точек, то достаточно построить
функцию f(x), равную числу*>уп, для точек полусегмента (——Г^-^^^Ь
функция /(х), определенная таким образом на области D, очевидно,
счетно-разрывна на D.
Для дальнейшего нам потребуется ввести новое понятие, относя1
щееся к способу представления аналитического [множества различными
счетно-разрывными функциями.
Пусть Е — аналитическое множество, рассматриваемое как множество
значений счетно-разрывной функции f(x), определенной на области D.
Чтобы точка г/0, расположенная на оси ординат, содержалась в Е,
необходимо и достаточно, чтобы уравнение f(x) — у0 = 0 имело корень
в области D.
В общем случае это уравнение имеет несколько корней; это сложный
случай. Следовательно, естественно начать изучение аналитических
множеств с внимательного исследования наиболее простого случая, когда
уравнение f(x) —1/0 = 0 имеет один и только один корень в области D.
В этом случае данной точке у0 аналитического множества Е
соответствует единственная точка х области D; назовем эту точку у0 точкой
единственности аналитического множества Е.
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ 337
Таким образом, мы пришли к формулировке следующего
определения:
Будем говорить у что функция действительного переменного f(x)y
определенная на области Z), является разнозначной функцией, если
она не принимает одного и того же значения для двух различных
значений х и х\ x'=£x"y независимого переменного х.
Мы назовем однозначным аналитическим множеством множество
значений счетно-разрывной разнозначной функции.
Это определение, к которому мы подошли естественным образом,
несомненно, покажется читателю, еще не освоившемуся с теорией
аналитических множеств, бесполезно усложненным по сравнению с данным
ранее простым определением аналитического множества. Тем не менее,
оно принципиально важно для последующего развития теории множеств,
измеримых В: мы увидим, что каждое однозначное аналитическое
множество обязательно измеримо В. К тому же обратное утверждение
также безусловно верно: мы докажем, что каждое несчетное множество,
измеримое В, является однозначным аналитическим множеством. Из
множеств, измеримых By только счетные (или конечные) множества не
являются однозначными множествами.
Закончив эти предварительные рассмотрения, отметим сначала
совершенно элементарные свойства однозначных аналитических множеств.
Каждое однозначное аналитическое множество имеет мощность
континуума. Очевидно, что если Е есть множество значений
разнозначной на области D функции /(х), то уравнение у=/(х) должно
устанавливать взаимнооднозначное соответствие между Е и D.
Более важно следующее предложение:
Множество Е'> получающееся из однозначного аналитического
множества Е путем удаления точек счетного множества А, также
является однозначным аналитическим множеством. Действительно,
пусть /(х) — разнозначная счетно-разрывная на области Dt функция,
множество значений которой есть Е. Уравнение
9=/(t)
ставит в соответствие каждой точке / области Dt точку у множества Е,
и наоборот. Это соответствие должно преобразовать счетное множество А
во вполне определенное множество &, содержащееся в области D% и также
счетное. Пусть К—счетное множество точек, всюду плотное на Dt
и не содержащее ни одной точки Ь; выбор множества К безразличен,
лишь бы только он был сделан вполне определенным образом, что в
рассматриваемом случае всегда возможно.
Установив это, возьмем новую область Dx независимого
переменного х, Dx = (О <С х <С 1)» и обозначим через R множество рациональных
точек этой области. Так как счетные множества АГ-+-& и R подобны,
то существует преобразование / = ф(х) замкнутого сегмента [0^/^1]
в замкнутый сегмент [O^x^l], которое устанавливает подобие между
338
Н. Н. ЛУЗИН
двумя счетными множествами АТ-+-& и R; функция ф (х) непрерывна на
замкнутом сегменте [0 ^ х ^ 1] и является возрастающей в узком смысле;
имеет место ф (0) = 0 и ф (1) = 1.
Исходя из этого, установим взаимно однозначное соответствие между
всеми точками t{ множества К:
*\У *2> *3> • • •> *П9 • • • \К)
и всеми рациональными числами ру области Dx:
Pi, Р2э Рз> • • •> ?пу • . . (R)
таким образом, чтобы два соответствующих элемента tt и pj были сколь
угодно близки к паре точек, соответствующих им в преобразовании / = ф(дг),
когда индексы i и j неограниченно возрастают. Но необходимо принять
меры предосторожности, чтобы наверняка исчерпать все точки К и все
рациональные числа множества R. Д\я этого будем действовать методом
чередования. Возьмем точку tx множества К и найдем в бесконечной
последовательности (R) первый элемент ря1, отличающийся от х, ^ = ф(х),
на величину, меньшую чему; затем, вычеркнув в последовательностях (К)
и (R) полученную пару (tly рЯ1), возьмем число р1 в R и найдем в
бесконечной последовательности (К) первый элемент tn , который отличается
1 2
от ty £ = ф(р1), на величину, меньшую чем-т-. Продолжим неограниченно
вычеркивать в последовательностях (К) и (R) полученные пары (tly ря ),
(Pi> ^«о)> (*2> Рп3)>... и брать поочередно в одной из последовательностей (К)
и (R) первый из оставшихся элементов и ставить ему в соответствие
в другой последовательности первый элемент, который отличается от
соответствующего числа пары (/, х), £ = ф(дг), на величину, меньшую
1
чем 2т-и 1 гДе т — число пар, уже построенных ранее; мы исчерпаем
все точки К и все числа R. Легко видеть, что соответствие,
установленное между элементами К и R, есть взаимно однозначное
соответствие, обладающее указанным свойством.
Установив это, рассмотрим множество всех пар (/, х), связанных
преобразованием t = ty(x), когда значение х иррационально, и
соответствие, установленное между К и /?, когда х принадлежит R. Ясно, что
это множество определяет функцию действительного переменного х:
определенную в области Dz, счетно-разрывную и разнозначную на этой
области, множество значений которой есть дополнение к S. Но тогда
сложная функция
будет также счетно-разрывной, разнозначной на области D^ функцией,
множество значений которой есть множество-разность Е — Д. Следова-
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ 39
тельно, это множество есть однозначное аналитическое множество
(ч. т. д.).
Также очевидно, что:
Множество точек Е\ которое получается присоединением к
однозначному аналитическому множеству Е точек счетного множества А,
есть также однозначное аналитическое множество. Действительно,
пусть f{x) — счетно-разрывная разнозначная на области D функция,
множество значений которой есть Е. Заметим, что мы можем
предположить, что счетное множество А не имеет ни одной общей точки с
множеством Е.
Пусть
У11 У2у • • •> Ум • • •
— последовательность, образованная из всех различных точек
множества А; имеет место утфую когда т^п. Отметим теперь в области D
все точки вида
_ J_
где т — целые положительные числа, и определим в этой области новую
функцию fi(x) при помощи следующих условий: /х(х) совпадает с f(x)
ДЛЯ каЖДОЙ НеОТМечеННОЙ ТОЧКИ Jt, fx (*2m-l) =/(*m) и /(х2т) = Ут-
Очевидно, что таким образом определенная функция есть счетно-разрыв-
ная и разнозначная на области D функция, множество значений которой
есть множество-сумма £-+-Д. Следовательно, это множество является
однозначным аналитическим множеством (ч. т. д.).
Эти две теоремы очень важны, так как мы показали, что при
изучении однозначных аналитических множеств можно беспрепятственно
пренебрегать счетным множеством точек. Счетные множества точек
играют таким образом по отношению к однозначным множествам ту же
роль, что и бесконечно малые по отношению к конечным величинам.
Одно из наиболее полезных приложений предыдущих рассмотрений
относится к совершенным множествам. В элементарной теории доказано,
что если из любого совершенного множества Р удалить все правые
концы смежных к нему интервалов, то получим множество, подобное
сегменту [0,1]. Это соответствие между точками множества Р и всеми
точками х сегмента [0,1] определяет на этом сегменте счетно-разрывную
и возрастающую в узком смысле функцию у=/(х). Следовательно, по
предыдущей теореме само совершенное множество Р есть однозначное
аналитическое множество. Из этого немедленно заключаем, что всякое
точечное множество, полученное из совершенного множества
добавлением к нему произвольного счетного множества точек и
одновременным вычеркиванием произвольной счетной части его элементов, есть
однозначное аналитическое множество.
340
Н. Н. ЛУЗИН
Закончив эти предварительные рассмотрения, мы направим наше
внимание на наиболее общие аналитические множества; мы докажем для
этого две фундаментальные леммы.
Лемма I. Сумма счетного числа аналитических множеств есть
аналитическое множество. Более того, если эти множества являются
однозначными аналитическими множествами или счетными
множествами и не имеют попарно общих точек> то их сумма есть также
однозначное аналитическое или счетное множество.
Пусть Ех, Е2, ... — аналитические множества, расположенные на
оси у; пусть Еп есть множество значений счетно-разрывной функции
i/ = /n(jc„), определенной на области Dn независимого переменного хп,
D„ = (0 <С *п < 1)« Вычеркиваем из области Dn ее середину у.я, ^я = -^- •
остаются два открытых интервала, левый из которых мы обозначим
через gn, а правый — через dn. Возьмем теперь новую область D
независимого переменного jc, D = (0 <С х <С 1) и рассмотрим в этой области
все открытые интервалы im вида
1т~ \m-4-l <*-< т)>
где т — целое положительное число. Если мы поставим в соответствие
каждому открытому интервалу gn открытый интервал /2п_1 и каждому
открытому интервалу dn открытый интервал i2ny и если мы осуществим
линейное преобразование интервалов gn и dn в соответствующие
интервалы z, мы получим однозначную функцию у=/(х) действительного
переменного х, определенную всюду на Dy кроме точек вида х = =- >
и построенную из кусков функций /я с линейно преобразованными
аргументами; мы завершим определение полученной функции /(х), полагая
/(—^Гт)=/»("2~) для каждого значения л.
Ясно, что таким образом определенная функция f(x) счетно-разрывна
на области D и что множество ее значений совпадает с множеством-
суммой Ех -t- Е2 ■+-... . К тому же, если множества Е19 Е2, ... не имеют
общих точек, и если все функции ДС^), Ata)» ••• разнозначны, то
то же самое имеет место и аая /(х).
Очевидно, что доказательство совершенно не изменится, если вместо
бесконечной последовательности множеств Е19 Е2, ... имеется некоторое
конечное число их; чтобы убедиться в этом, достаточно разбить первую
область Dx на бесконечное число открытых интервалов S при помощи
произвольной последовательности убывающих положительных чисел \,
стремящихся к нулю, и затем оперировать интервалами & и точками X*
тем же способом, как мы оперировали перед этим интервалами g и d
и серединами iv
Это замечание завершает доказательство (ч. т. д.).
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ 341
Чтобы продолжить изучение второй основной операции — общей
части, нам понадобится одно предварительное замечание.
Первая трудность, которая представляется в элементах
математического анализа, следующая: если функция действительного переменного
определена как соответствие между числом у и числом х> to когда
можно рассматривать ее как данную? Действительно, совершенно ясно,
что если рассматривают только конечное число значений аргумента х,
то задать функцию — это значит задать все значения у, не исключая
ни одного. Можно ли принять такое определение, когда значение jc
может быть каким угодно: должно ли выражение: задать функцию
для всех значений действительного переменного рассматриваться как
имеющее смысл?
Известно, что задать однозначную функцию действительного
переменного /(х) это значит при современном состоянии науки назвать ее;
этим хотят сказать, что должен быть дан вполне конечный закон L,
согласно которому дая всякого числа х число f(x) получается путем
непосредственного вычисления или применения закона исключенного
третьего. Наиболее классической функцией, значение которой дая каждого
значения переменной не может быть получено при современном
состоянии анализа непосредственным вычислением, является часто
рассматриваемая функция х(х)у которая равна 0 или 1, смотря по тому, является ли
переменное х рациональным или иррациональным числом; мы в
настоящее время не знаем никакого способа определить значение х(х) Для ^»
^ = 2,71... и тс = 3,14... Именно благодаря знанию закона L слова:
функция действительного переменного f(x) задана приобретают дая
нас вполне точный смысл.
Итак, знать функцию действительного переменного это значит знать
ее значения в ранее указанном смысле. Но тогда, если уже
сформулировано, по Коши, определение функции, непрерывной в точке,
множество S точек разрыва данной функции f(x) должно быть
рассматриваемо как определенное точным, не допускающим двусмысленностей
способом уже самим знанием значений /(*).
Но теперь какой смысл имеет постоянно употребляемое выражение:
счетно-разрывна? Имеется колоссальное разнообразие законов L, при
помощи которых называют функции действительного переменного,
и будет слишком преждевременным пытаться их классифицировать.
Исходным пунктом дая рассуждений при современном состоянии науки
может служить только лишь утверждение о знании значений функции
без проникновения в природу закона L для нее. Но тогда множество Е
ее точек разрыва необходимо представляется в стационарной и аморфной
форме. Откуда же следует возможность расположить элементы
множества S в последовательность Ъ19 £.,, ..., £я, —? Является ли эта
последовательность произвольной или она извлекается из самого знания
значений рассматриваемой функции, каков бы ни был закон L,
определяющий ее?
342
Н. Н. ЛУЗИН
Пусть f(x) — заданная функция действительного переменного,
определенная на области D. Возьмем положительное число £ и обозначим
через Зс множество точек, в которых колебание f(x) больше или равно г
Это множество есть часть Е, и, кроме того, как известно, оно замкнуто
на области ZX
Рассмотрим теперь открытые интервалы с рациональными концами,
которые принадлежат области D; мы предположим, что эти интервалы
расположены в некотором порядке, который мы не уточняем, но
который предполагается вполне определенным; пусть
Pi, Р2> Рз> • • •> Ря> • • • (S)
— рассматриваемая последовательность.
Установив это, поступим следующим образом: вычеркнем сначала из
последовательности S все открытые интервалы, каждый из которых
не содержит двух каких-нибудь различных точек, принадлежащих
множеству Et, заботясь в то же время о том, чтобы удалить из Ее точки,
содержащиеся в вычеркнутых р; затем вычеркнем из
последовательности (S) все оставшиеся интервалы р, каждый из которых не содержит
двух каких-нибудь точек, сохранившихся в Зе, удаляя в то же время
из Ее точки, содержащиеся в этих новых вычеркнутых р1э и т. д.
Бесполезно утомлять читателя, постоянно повторяя одни и те же
слова. Если под этим „и т. д." разуметь, что одна и та же операция
{вычеркивание из (S) всех тех из оставшихся р, которые не содержат
никакой пары точек, сохранившихся в Ег> и удаление из Е£ точек,
содержащихся в этих вычеркнутых р] повторяется столь далеко, сколько
это возможно, то получим точки Ее> расположенные в простую
бесконечную последовательность Е^, Е(2°, ..., определенную точным, не
допускающим двусмысленностей способом при помощи самой
последовательности (S); для этого достаточно поставить в соответствие каждой
точке $(&J множества Зе индекс того интервала р из (S), вычеркивание
которого из последовательности (S) влечет удаление этой точки № из
множества Ее; или, если среди интервалов последовательности (S) имеются
невычеркиваемые интервалы р, то точки, не удаленные из Ев, очевидно,
образуют совершенное множество, в этом случае множество Ее имеет
мощность континуума.
Нам скажут: вы описали лишь только начало метода, но вы не
описали его целиком, а чтобы это сделать, необходимо употребить
трансфинитные числа; и так как процесс может продолжаться как угодно
далеко, то здесь предположено предварительное существование
совокупности всех трансфинитных чисел второго класса.
Никоим образом! Прежде всего здесь не рассматривается трансфи-
нитность, а рассматривается неограниченность; действительно, наш
метод на каждой ступени регулируется самой последовательностью (5),
и каждый действительно новый шаг этого метода состоит в точности
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ 343
в том, что эффективно вычеркивают из последовательности (S) вполне
определенные интервалы р; следовательно, на каждом шагу мы
обнаруживаем, что множество оставшихся \> наверняка уменьшилось. А ведь
таких истинных уменьшений может быть только столько, сколько имеется
целых положительных чисел, следовательно, этот процесс действительно
продолжается неограниченно.
К тому же предварительное существование трансфинитных чисел
отнюдь не постулируется нами даже неявным образом. Здесь нет транс-
финитных чисел. Идеалисты пренебрегали этим и столкнулись с
неразрешимыми проблемами, список которых, и в настоящее время очень
внушительный, в будущем грозит бесконечно удлиниться.
Трансфинитные „числа" не являются настоящими числами. Они не существуют
сами по себе. То, что при современном состоянии науки мы называем
трансфинитным числом, является только меткой для того, чтобы
узнавать и отличать промежуточный шаг неограниченного регулярного
процесса, употребляемого д,\я получения решения предложенной
математической проблемы. В каждом действительно научном исследовании
трансфинитные „числа" всегда вводятся только таким способом, т. е.
в счетном числе, и, кроме того, порождаются каждый раз тем самым
регулярным процессом, который является инструментом исследования;
они служат, следовательно, метками промежуточных шагов регулярного
процесса, который наверняка не ограничен. Везде, куда бы ни входили
счетные вполне упорядоченные множества (которые являются
сегментами одного из них, фиксированного заранее), мне кажется, должны
применяться трансфинитные „числа". Существование вполне
упорядоченных счетных множеств отнюдь не базируется на постулате
существования трансфинитных „чисел": это математический факт,
который не базируется ни на каких априорных рассмотрениях. И именно
потому, что существуют вполне упорядоченные счетные множества,
существуют и трансфинитные „числа". Чтобы пойти дальше, нужно дать
словам экстраординарный, расширенный и, добавлю, обманчивый
смысл.
Чтобы лучше оттенить те разногласия в оценке, которые я вижу,
я напомню предложение, приведенное в начале этих общих рассуждений:
всякое замкнутое множество, не содержащее совершенного
множества, есть счетное множество. Я лучше показал бы разногласия
в оценках, сказав, что я не понимаю того, что хотят сказать, когда
говорят о положительном доказательстве этого утверждения,
проведенном без помощи аксиомы Цермело и без помощи трансфинитных
чисел. Предыдущие рассмотрения не приводят ни к чему, как только
к отрицанию существования такого доказательства.
Существует только одно единственное доказательство этого
предложения, которое совершенно не использует трансфинитных чисел. Это
хорошо известное важное доказательство принадлежит Линделефу.
Но хотя- оно не использует ни трансфинитных чисел, ни произвольного
344
Н. Н. ЛУЗИН
выбора1, оно носит совершенно отрицательный характер, так как
опирается на бесспорно отрицательное понятие точки конденсации. Все
другие математические работы, в которых имеются счетные вполне
упорядоченные множества, более протяженные, чем последовательность
положительных целых чисел 1,2,3,4,5,6,..., решительно должны
быть рассматриваемы как реализованные при помощи трансфинитных
„чисел", даже если такие слова, как трансфинитное числоу
трансфинитно, не написаны там авторами явным образом. Когда мне говорят
об эффективном исследовании без помощи иррациональных чисел, и когда
я усматриваю в нем диагональ квадрата со стороной 1, я становлюсь
очень недоверчивым, так как не вижу здесь заметного прогресса.
Мы уже говорили, что эти „числа" всегда порождаются тем самым
регулярным и неограниченным процессом, который должен входить
в исследование, что при этом не предполагают не только существования
их совокупности, но ничего не предполагают об их существовании: их
строят самим процессом.
Если теперь хотят избавить данный метод от взглядов лица,
осуществившего его (правда, это некоторым образом зависит от этого лица),
достаточно снова повторить слово в слово первое рассуждение Цермело,
относящееся к возможности вполне упорядочить каждое множество; это
рассуждение представляется здесь законным, так как основной метод
безграничен и регулярен. Но это модифицированное доказательство
является только усложнением предшествующего, столь наглядного
доказательства усложнением, скрытым под логическим аппаратом. Здесь мы
не говорим явным образом „трансфинитные числа", но читатель не
будет введен в заблуждение: они неявно проникают в доказательство-
вместе с вполне упорядоченными множествами, но всегда в счетном
числе.
Итак, возьмем снова замкнутое множество 2t и простую
бесконечную последовательность (S)
Pi» ?2> РЗ» • • •» Рп, . . м (Ф
образованную из всех открытых интервалов с рациональными концами,,
принадлежащих области D.
Мы скажем, что вполне упорядоченное множество Е, образованное из
различных интервалов р последовательности (S), представляет собой
цепь, если, каков бы ни был сегмент о' вполне упорядоченного
множества Е, элемент р' множества Е, который определяет о7, совпадает с
первым интервалом р^ последовательности (S), который не содержит
никаких двух точек, принадлежащих St, но не принадлежащих никакому
интервалу р сегмента <*'. Ясно, что цепи существуют, так как одну из них
составляет первый интервал последовательности (S), который не
содержит двух точек замкнутого, нигде не плотного множества 2в; очевидно,.
1 Мы отвергаем то, что называют счетной формой аксиомы Цермело.
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ
34S
что если рассматривать две цепи Е и Е\ то они либо совпадают друг
с другом, либо одна из них составляет отрезок другой. Отсюда
следует, что каждой цепи £, не являющейся наибольшей цепью, можно
поставить в соответствие положительное целое число / таким образом,
что двум различным цепям соответствуют наверняка различные числа;
достаточно для этого рассматривать данную цепь Е как сегмент о'
цепи £, более обширной, чем £', и поставить в соответствие Е' индекс /,
который присвоен в последовательности (S) элементу р' цепи Е,
определяющему сегмент о'. Мы можем, следовательно, нумеровать все эти
цепи Е' при помощи положительных целых чисел; очевидно, что
совокупность этих цепей Е' счетна; следовательно, она существует.
Образуем объединение всех этих цепей Е'\ пусть <§ — таким образом
составленное множество. Ясно, что это множество <§ вполне упорядоченно
и что каждая из цепей Е' есть отрезок &; следовательно, это
множество является цепью. Это наибольшая цепь; к тому же может
существовать лишь одна и только одна цепь такого рода. Если множество
элементов S совпадет с множеством элементов последовательности (S),
то все точки замкнутого множества Et перенумерованы при помощи
положительных целых чисел самой нумерацией элементов цепи <$, так
как каждый элемент р' цепи <§ содержит не более одной точки
множества Зе, которая не принадлежит никакому из интервалов р сегмента з',
определенного посредством р', и каждая точка St может быть получена
таким образом. Если <§ — собственная часть последовательности (S), то
точки Et, которые не принадлежат никакому из интервалов р множества £9
образуют, очевидно, совершенное множество (ч. т. д.).
Таким образом, очевидно, что если мы имеем однозначную функцию
действительного переменного /(jc), значения которой даны для всех
действительных значений переменного, то можно указать регулярный
прием, который позволит либо расположить точки, где колебание f(x)
больше или равно е, в простую бесконечную последовательность, либо
при помощи конечного или эффективно перечислимого числа операций
убедиться в том, что их множество Eg содержит совершенное
множество.
Установив это, дадим е значения —, где п — целое число, и
рассмотрим последовательность множеств
S 31 Е1 Si
2 3 а
ясно, что множество, образованное посредством объединения этих
множеств, совпадает с множеством Е точек разрыва функции/(х). Для того
чтобы функция f(x) была счетно-разрывной, необходимо и достаточно,
чтобы никакое Ех не содержало совершенного множества, и так как
п
в этом случае мы умеем расположить точки каждого множества Е^_
346
Н. Н. ЛУЗИН
в простую бесконечную точным образом определенную последователь.
(Г) II)
ность £}я', Ч > > то нумерация самого множества л не
представляет никаких затруднений.
Отсюда следует, что знание значений функции действительного
переменного f(x) либо влечет за собой вполне определенную
нумерацию (при помощи целых положительных чисел) ее точек разрыва,
либо мы сумеем определить совершенное множество, составленное
из точек разрыва.
Укажем приложение предыдущих рассуждений.
Пусть Е — аналитическое множество, расположенное на оси у и
рассматриваемое как множество значений счетно-разрывной функции y = F(t)t
определенной на области Df Расположим при помощи предыдущего
приема точки разрыва функции F{t) в простую бесконечную
последовательность; пусть
Х1> Т2> Т3> • • •> Тп> • • • \Г)
— эта последовательность точек разрыва. Предположим, что
рациональные точки, содержащиеся в области Д, расположены в порядке,
который мы не уточняем, но который предполагаем вполне определенным;
пусть
Pl> Р2> Рз> • • •» Рп> • • • (Р)
— рассматриваемая последовательность. Возьмем теперь объединение
двух последовательностей (Т) и (р); это всюду плотное на области Dt
множество точек, нумерация которого при помощи целых
положительных чисел вполне определенна; обозначим это множество через К.
С другой стороны, возьмем новую область Dx независимого
переменного ху Dx = (0<Cx <C 1)> и обозначим через R множество
рациональных точек г этой области; мы можем расположить точки г множества R
в простую бесконечную последовательность
г1> г2> г3> • • •» гя> • • •» (К)
определенную точным образом. Множество R всюду плотно на Dx.
При этих условиях множества К и R подобны, так как их подобие
определено без каких бы то ни было возможных двусмысленностей
самой нумерацией К и R. Это подобие определяет отображение / = <р (jc)
замкнутого сегмента [0^ ^^ 1| на замкнутый сегмент [0 ^дс ^1].
Функция <р (х) непрерывна на замкнутом сегменте [O^x^l] и возрастает
в узком смысле; если х принадлежит /?, то точка t = <p (х)
принадлежит АГ, и наоборот; кроме того, имеем ср(0) = 0 и <р(1) = 1#
Исходя из этого, рассмотрим сложную функцию # =/(*),
определенную равенством f(x) = F(<? (x)). Ясно, что множество значений f(x) есть
данное аналитическое множество Е и что /(х) непрерывна во всех
иррациональных точках х области Dx.
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ
347
Таким образом, каждое линейное аналитическое множество есть
множество значений функции, все точки разрыва которой
рациональны.
Мы можем теперь приступить к доказательству второй основной
леммы.
Лемма II. Общая часть счетного числа аналитических множеств
-есть аналитическое множество. Кроме того, если множества являются
однозначными аналитическими множествами или счетными
(конечными) множествами, то их общая часть является также
однозначным аналитическим множеством или счетным (конечным)
множеством.
Пусть Еи Е2> ... — аналитические множества, расположенные на оси у,
где Еп — множество значений функции y = fn(xn)> определенной на
области Dn независимого переменного хп, D„ = (О <С х < 1), и
непрерывной в каждой иррациональной точке этой области. Чтобы точка z/°,
расположенная на оси у, была общей для всех аналитических множеств Е1У
Е2,..., необходимо и достаточно, чтобы все счетное число уравнений
у°=Л <*i)=/. (*«) = ..-=/. (*„) = ■ • •
удовлетворялось частными значениями переменных х19 х2> ..., хп> .. .,
где хп принадлежит области Dn. Очевидно, что точки у°9 для которых
одно из предыдущих уравнений имеет рациональный корень, образуют
счетное множество. Опустим эти точки и постараемся удовлетворить
предыдущим уравнениям при помощи иррациональных значений
переменных х1У х2> ..., хпу ...
Иррациональное число хп области Dn представимо вполне
определенным образом бесконечной непрерывной дробью
где каждое число a„v есть неполное частное, следовательно,
положительное целое число.
Мы можем бесконечным числом способов расположить члены
таблицы с двойным входом:
a21tt22a23 * * ' a2v • • #
ая1ая2а«3* ' ,anv« • •
в простую последовательность рх, р2> • ••, Ря> ••• Выберем определенный
метод (впрочем, все равно какой) такого преобразования; положим
* = (Pi, Р2,-.мР*---)
и поставим в соответствие иррациональную точку /, расположенную
в новой области Du А = (0<<<1), бесконечной последовательности
348
Н. Н. ЛУЗИН
иррациональных точек хи х2, -. ., расположенных соответственно в
областях Д, D>, ....
Ясно, что знание этой последовательности xv x2, ... определяет /
единственным образом, и, обратно, знание t однозначным образом
определяет последовательность х19 х2, Мы можем, следовательно,
написать
*i = cPi(0; ^2 = ^2^); •••; -*» = <?••(*)>•••
где, каково бы ни было положительное целое число л, функция cpe(f)
определена л^я. каждого иррационального числа t области Д; д\я
рациональных t функция <ря(0 не имеет никакого смысла; к тому же
множество значений <рм(0 совпадает с множеством иррациональных чисел
области Dn. Если мы обозначим через J множество иррациональных чисел
области Д, то заметим, что функция yn(t) непрерывна в каждой точке /о
множества о/ относительно множества d/. Отсюда следует, что
сложная функция
•МО = /„(?.«))
также непрерывна в каждой точке t0 множества о/ относительно мно-
ства g7.
Установив это, рассмотрим неограниченную последовательность
совместных равенств
<М*)='М')='1»»(0=... = Ф. (')=•••
и обозначим через & множество значений £, которые удовлетворяют
всем этим равенствам.
В силу относительной непрерывности функции фя очевидно, что это
множество & замкнуто относительно множества о/; к тому же
множество <§ содержится в о/. Отсюда непосредственно следует, что из
предельных точек & только рациональные предельные точки не
принадлежат множеству &. Следовательно, множество &-*-&', замкнутое
в абсолютном смысле на сегменте [O^tf^l], отличается от <§ только-
не более чем счетным множеством точек; здесь £' обозначает
производное множество множества &.
Если это множество & счетно и конечно, то общая часть всех
данных аналитических множеств Е19 Еъ — наверняка счетна или конечна;
следовательно, в этом случае лемма доказана.
Если множество & несчетно, то оно отличается от совершенного
множества не более чем счетным множеством точек, следовательно,
согласно ранее доказанному предложению S есть однозначное
аналитическое множество. Отсюда следует, что существует счетно-разрывная
разнозначная функция £ = а)(х), определенная в новой области Д
D=(0<x<l), такая, что множество ее значений совпадает с
множеством &.
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ
349
Исходя из этого, рассмотрим сложную функцию у=/(л:),
определенную равенством
/(*)=<WH*)).
Очевидно, что f(x) непрерывна в классическом смысле во всех
точках непрерывности функции и(х); к тому же, если все данные функции
Л (х\)> Л (хг)> • • • разнозначны, то и функция f(x) такова же. Так как
множество значений у функции f(x) совпадает, очевидно, с общей частью
всех данных аналитических множеств Е1У Е2У ..., если пренебречь
счетным или конечным множеством, то сформулированная лемма доказана
(ч. т. д.).
Следствия из основных лемм. Как непосредственное
следствие имеем предложение:
Аналитическое тело инвариантно относительно двух основных
операций (образования суммы счетного числа множеств и взятия
общей части счетного числа множеств).
К тому же аналитическое тело содержит все интервалы с
рациональными концами. Возвращаясь к определению В-тела, мы заключаем
отсюда, что аналитическое тело содержит В-тело, или, что сводится
к тому же:
Каждое множествОу измеримое В, является аналитическим
множеством.
Чтобы истолковать результаты, относящиеся к однозначным
аналитическим множествам, нам понадобятся новые определения.
Выше мы ввели, вместе с Лебегом, две основные операции:
сложение (образование суммы счетного числа множеств) и общую часть
(взятие общей части счетного числа множеств). Мы хотим теперь
ограничить, следуя идее Бореля, первую операцию применением к множествам,
попарно не имеющим общих точек. Дкя этого мы сформулируем
следующее определение:
Мы назовем сложением в узком смысле операцию, которая состоит
в образование суммы счетного числа множеству попарно не имеющих
общих точек.
Вторую операцию: взятие общей части, мы сохраним неизменной.
Из рцределения таким образом измененной первой операции
непосредственно вытекает, что аналитическое тело и В-тело, тем более
инвариантны относительно сложения в узком смысле. В таком случае
возникает вопрос, состоящий в том, чтобы узнать, будет ли В-тело по
определению наименьшее относительно прежних операций: сложения
в широком смысле и взятия общей части, наименьшим также и
относительно операции сложения в узком смысле и взятия общей части.
Ответ получается немедленно и является утвердительным.
Теорема. В-тело есть наименьшее тело множеств, содержащее
все открытые интервалы с рациональными концами и инвариантное
350
Н. Н. ЛУЗИН
относительно двух операций: сложения в узком смысле и взятия
общей части.
Для доказательства применим принцип минимума, называя ZJ'-телом
наименьшую из совокупностей множеств, содержащую все открытые
интервалы с рациональными концами и инвариантную относительно
сложения в узком смысле и взятия общей части. Это iJ'-тело можно
назвать В-телом в узком смысле.
Легко видеть, что согласно самому определению В'-тело содержится
в В-теле.
Впрочем, верно и обратное: 5-тело содержится в #-теле. Чтобы
в этом убедиться, назовем регулярным множеством каждое множество Е
5-тела, которое принадлежит, так же как и его дополнение С£, /?'-телу.
Очевидно, что каждый открытый интервал является регулярным
множеством.
Общая часть счетного числа регулярных множеств есть
регулярное множество. Действительно, пусть Е19 Е2> ——счетное число
регулярных множеств. Очевидно, что их общая часть Е1 • Е2 •...
принадлежит iJ'-телу, так как ZJ'-тело инвариантно относительно этой операции»
С другой стороны, имеем
С(ЕХ • Ег • £3 • • • •) = СЕ1ч- СЕгч-СЕъ-+~... =
v_/Zli ~т~ а-гл * \*ri-dо ■" 1 * ^2 * ^^3 • • • ■ Hi^ ' IL2 * • • • ' *-*п—l * ^^п ~~• • • •
Так как все члены этой суммы принадлежат В'-телу и попарно не
имеют ни одной общей точки, то множество С (Е1 • Е.г • Ez • ...)
принадлежит #'-телу. Следовательно, множество Е1 • Е2 •... регулярно.
Сумма в широком смысле счетного числа регулярных множеств
есть регулярное множество. Действительно, из тождеств
Е^ -+- Е2 -+- £3 -I-... = Ег ■+■ СЕХ • Е2 -+- СЕХ • СЕ2 • Ez -+-...
.. .-I- С£а • С£2 • • • • • СЕп^1 •Еп-¥- —
и
С^-ьЕ,-*-^-1-- • -) = СЕг • С£2 • СЕг •...
мы заключаем, что сумма в широком смысле El-*-E.1-t~... регулярных
множеств £L, ZT2, ... (которые, вообще говоря, имеют общие точки)
является также регулярным множеством.
Следовательно, совокупность регулярных множеств образует
совокупность, содержащую все открытые интервалы и инвариантную
относительно основных операций: сложения в широком смысле и взятия
общей части. Отсюда заключаем, что эта совокупность содержит 5-тело
(я. т. д.).
Установив это, сформулируем основное определение, имеющее
принципиальную важность для всего последующего*
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ 351
Назовем аналитическим телом в узком смысле совокупность
однозначных аналитических множеству включая в нее все счетные1
множества, все конечные множества и пустое множество.
Легко видеть, что это определение конструктивно (а не является
аксиоматическим определением). Из доказанных выше основных лемм
выводим, что аналитическое тело в узком смысле содержит все
открытые интервалы и в то же время инвариантно относительно двух
операций: сложения в узком смысле и общей части. Следовательно,
аналитическое тело в узком смысле содержит В-тело, или, что сводится
к тому же:
Каждое несчетное множество, измеримое В, является
однозначным аналитическим множеством.
Имеет место и обратное утверждение; мы увидим, что каждое
однозначное аналитическое множество необходимо измеримо В. Имеется,
следовательно, абсолютная идентичность между конструктивным
определением (аналитическое тело в узком смысле) и аксиоматическим
определением (5-тела). Эта идентичность придает законность аксиоматическому
определению и в то же время самому принципу минимума в некотором
частном случае. Но доказательства требуют нового определения и
представляют некоторые трудности.
Мощность множества, измеримого В. Пусть Е —
однозначное аналитическое множество, расположенное на оси у. Пусть y = f(x) —
счетно-разрывная, разнозначная на области D функция, множество
значений которой совпадает с Е. Обозначим через 3 множество точек
разрыва функции f{x); множество 2 счетно. Исходя из этого, возьмем
какое-нибудь совершенное множество Р, принадлежащее области D и
не имеющее ни одной общей точки с множеством 3; обозначим через Q
множество значений, которые принимает функция f(x) на совершенном
множестве Р. Так как f(x) разнозначна и в классическом смысле
в каждой точке совершенного множества Р, то очевидно, что
множество Q также совершенно. Отсюда заключаем, что:
Каждое однозначное аналитическое множество содержит
совершенное множество, следовательно, имеет мощность континуума.
Так как В-тело содержится в аналитическом теле, в узком смысле,,
отсюда выводим, что:
Каждое множество, измеримое В, есть либо счетное {конечное)
множество, либо содержит совершенное множество.
1 Мы учитываем повторения счетных множеств. Существование множества всех
счетных множеств, взятого без повторений, мне кажется очень сомнительным. Это
существование вытекает из приложения аксиомы разбиения, представляющее здесь,
по моему мнению, огромные трудности. Но множество счетных множеств, включающее
повторения, наверняка существует; каждая пеановская кривая ?i (x), ?2(•*)«•••»
заполняющая для 0 < х < 1 основной куб со стороной 1 в пространстве счетного
числа намерений, представляет особенно ясное доказательство такого рода
существования.
352
Н. Н. ЛУЗИН
Это теорема Александрова—Хаусдорфа.
Отсюда следует, что никакое множество Е> измеримое В, не может
обладать на совершенном Множестве Р несчетным множеством
точек, не имея на этом совершенном множестве Р совершенного
подмножества Рх. Действительно, общая часть Е и Р, будучи
измеримой В и несчетной, необходимо содержит совершенное множество Pv
Мы назовем это свойство множества точек свойством Александрова—
Хаусдорфа. Является ли это свойство общим свойством множества
точек? Я не буду пытаться ответить на этот трудный вопрос, потому что
я не знаю, можно ли назвать индивидуальное множество, которое не
обладает этим свойством; мы увидим, что всякое аналитическое
множество, даже неизмеримое В, наверняка обладает этим свойством. Правда,
при помощи идеалистических рассуждений можно „доказать14
существование множества точек, не обладающего этим свойством; но применять
свободный выбор, это значит, по моему мнению, жонглировать
соединениями пустых слов, смыслу которых не соответствует никакой
интуитивно доступный факт.
Свойство Александрова—Хаусдорфа не является индуктивным
-свойством. Здесь не может возникнуть противоречия с предыдущим:
свойство аналитичности, значительно более частное, чем свойство
Александрова—Хаусдорфа, наверняка является индуктивным.
Действительно, мы увидим, что вторая основная операция (взятие
-общей части) не сохраняет этого свойства.
Абсолютная сходимость рядов полиномов. Мы уже
имели случай отметить, что каждая счетно-разрывная функция х =/(/),
определяющая аналитическое множество Е, может быть представлена
рядом полиномов
f(t) = Px{t)-*rPt® + ...-+-P.{t) + ...,
сходящимся в каждой точке области Dt = (Q<C.t <^ 1). Но нельзя
утверждать, что каждая счетно-разрывная функция может быть представлена
абсолютно сходящимся рядом полиномов 1. Тогда возникает вопрос: узнать,
можно ли рассматривать каждое аналитическое множество как
множество значений сумм абсолютно сходящегося ряда полиномов?
Мы увидим, что эта проблема решается положительно. С этой целью
мы преобразуем счетно-разрывную функцию х =/(/), которая
определяет аналитическое множество Е, в другую счетно-разрывную функцию
х = g(t), определяющую то же аналитическое множество, но предста-
вимую абсолютно сходящимся рядом полиномов.
Если данное аналитическое множество Е конечно или счетно, оно
наверняка является множеством значений суммы абсолютно
сходящегося ряда полиномов. Действительно, если а9 #!, д2> • • •> яя, ... — точки
1 См. W. Sierpinski. Sur les fonctlons developpables en series absolument
convergentes de fonctlons continues (Fund. Math., II, 19).
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ
3S3
множества £, положим /\^^—^ = ая и f(t) = a в других точках /. Так
как все точки разрыва функции, определенной таким образом,
изолированы, то /(/) наверняка разложима в абсолютно сходящийся ряд
полиномов.
Итак, предположим, что данное аналитическое множество Е
несчетно, и пусть а — такая точка £, что как часть множества £,
расположенная выше а, так и та часть, которая расположена ниже а,
несчетны. Так как обе части, очевидно, являются аналитическими
множествами, то отсюда заключаем, что множество Е может быть определено
счетно-разрывной функцией /(£), равной а при t = -~ и определяющей
верхнюю часть Е при /<^у и нижнюю часть при t^> ~о • Очевидно, что
если Е есть однозначное аналитическое множество, то можно
предполагать, что функция /(/)> определенная таким образом, разнозначна, так
как каждая из рассматриваемых частей есть однозначное множество.
Исходя из этого, определим три функции Л(0> Л(0> Л (О ПРИ по~
мощи условий: /х (t)=f(t) при *<Ст и Равна нулю в других точках;
«М~2~)~а и/2(0 = 0 в других точках; наконец, У3(0=/(0 Для *>~2
и равна нулю в других точках. Очевидно, что три функции,
определенные таким образом, счетно-разрывны и что имеет место равенство
Так как функция /2(0 наверняка представима абсолютно сходящимся
рядом полиномов, то достаточно изучить возможность аналогичного
представления а^я первой функции fl(t). Мы можем предположить, что
она непрерывна в каждой иррациональной точке /, так как в топологии
существует преобразование, которое преобразует сегмент [0, 1]в самого
себя таким образом, что все точки разрыва функции f(t) становятся
рациональными.
Исходя из этого, возьмем в интервале (О, -^\ два счетных всюду
плотных множества А0 и \ без общих точек, содержащих только
иррациональные точки. Пусть # = {piP2> ..., Р»}—множество всех
рациональных точек интервала (О, у] и J — множество его иррациональных
точек.
Отметим на интервале (О, -Л точки ■§" * Т ' # ' м л"' •••и определим
в области (0, 1) функцию Ф(*) условиями: Ф (^"^J^/i (р*)> л = 1,2,3,...
и *(*)=/!(*) вне R-+-\-*-\. Чтобы определить функцию Ф(*) в
других точках, рассмотрим сначала рациональные точки р интервала (0, у К
в которых функция Ф(0 еще не определена; пусть р*, р*, .. ., р*, .. . —
354
Н. Н. ЛУЗИН
множество этих точек. Обозначим через ц* минимум функции /(f)
в точке р*, предполагая, что переменная t принадлежит с7. Так как мно-
жество Д0 всюду плотно на ((}> у Ь то каково бы ни было целое
положительное число /2, в множестве Д0 существует точка хя такая, что
значение /^J отличается от ц* не более чем на еп1 где ем — сколь
угодно малое положительное число. Всегда можно предположить, что
00
ряд 2 Еп сходится и что точки in различны дая двух различных значе-
ний целого числа л. Положим в таком случае Ф(р*) = /1(ти).
Остается только определить функцию Ф(£) на множестве А0-нЛ1к
Дая этой цели обозначим через Д' множество точек множества Д0 (если
они существуют), которые не принадлежат последовательности t19 x2, .. „
. .., тя, ... Так как множество &х счетно и всюду плотно на (0, -у), то
оба множества Д0-1-Д1 и Д|)-4-Д1— подобны. Преобразование множества
Д|)-+-Д1 на множество Д0-+-Дд может быть определено таким образом,
что разности значений fx (t) в каждой паре (t, t') соответствующих точек
образуют абсолютно сходящийся ряд. Выбрав это наложение, мы дадим
функции Ф(/) в точке t суммы Д0-1-Д1 значение, равное значению /x(f)
в точке ( множества Д^-ьД^ которая соответствует /.
Очевидно, что таким образом определенная функция Ф (t) есть не
что иное, как преобразование функции fx (t), которая сохраняет все
значения /г(0 [принимает каждое из них точно один раз, если функция fx(t)
разнозначна на (О, -у 1] и не вводит к тому же никаких новых значений.
Функция Ф(0> очевидно, счетно-разрывна. Мы увидим, что Ф(г*) пред-
ставима абсолютно сходящимся рядом полиномов.
В самом деле, пусть m{f) — минимум функции Ф(£) в точке t
области (О, 1). Очевидно, что m(t) полунепрерывна снизу на (О, 1) и
ограничена снизу. Отсюда следует, что m(t) представима абсолютно
сходящимся рядом полиномов1. Рассмотрим разность Ф(£) — m{t). Она,
очевидно, равна нулю в каждой точке ty которая не принадлежит
счетному множеству /?-ь,До~»- \\ к тому же абсолютные значения этой
разности в точках этого множества, не принадлежащих последовательности
~о~* т, • • •, — 1 • • •> образуют абсолютно сходящийся ряд.
Установив это, обозначим через d± (t) функцию, равную Ф(£)— m(t)
1 1 1
в точках -j > • • •, "4" , • • м ~ > • • • и равную нулю в других точках, и
через d2(t) функцию, равную нулю в точках -г- > — . . ., —, ... и
1 См. W. Sierpinski. Sur les fonctions developpables en series absolument
convergentes de fonctions continues (Fund. Math., II, 15).
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ 355
равную Ф(/) — m(t) в других местах. Очевидно, что функция d1 (t) пред-
ставима абсолютно сходящимся рядом полиномов, так как каждая точка
разрыва dl (t) есть изолированная точка; dt (t) также разложима в
абсолютно сходящийся ряд полиномов, так как это счетно-разрывная
функция, колебания которой в точках разрыва образуют абсолютно
сходящийся ряд.
Отсюда заключаем, что функция Ф(/) может быть представлена
абсолютно сходящимся рядом полиномов. Преобразовывая таким же
образом функцию /з(0> получим таким образом следующее утверждение:
Каждое аналитическое множество есть множество значений суммы
абсолютно сходящегося ряда полиномов; к тому же, если данное
множество есть однозначное множество, то можно предполагать, что
сумма этого ряда полиномов есть разнозначная функция.
Заметим наконец, что согласно общей теоремы И. Хлодовского1
можно всегда предполагать, что коэффициенты этого ряда суть целые
числа.
IV. Множества точек в /я-мерном пространстве
Предыдущие исследования линейных точечных множеств нам были
необходимы, чтобы ясно осветить роль счетно-разрывных функций в
определении множеств, измеримых Ву и аналитических множеств. Настало
время ввести новые понятия, относящиеся к множествам точек
пространства нескольких измерений, понятия, которые, как мы увидим,
позволят нам установить общие свойства аналитических множеств и
очень облегчат изучение смежных вопросов.
Мы вернемся, следовательно, с совершенно общей точки зрения
к вопросам, изученным в предыдущих параграфах, рассматривая случай
/п-мерного пространства. Имея в виду приложения к классическому
анализу, мы рассмотрим пространство евклидовой геометрии.
Множества, измеримые В. Пусть S(x1x2y ..., хт) — какая-
нибудь система прямоугольных координат в m-мерном пространстве,
которую мы будем считать неподвижной. Система S позволит нам
определить точечные множества, измеримые В> и аналитические множества.
Назовем открытым т-мерным параллелепипедом множество точек
М(х19 х2, ..., хт), удовлетворяющих условиям
ai<*i<6i> а2<^х2<^Ь2У ..., ат<хт<Ьт,
где число Xi обяз ательно заключено между неравными числами а< и biy
не совпадая ни с одним из них2.
1 Каждая функция первого класса Бэра, определенная на (0<* < 1), исключая
концы, разложима в ряд полиномов с целыми коэффициентами. Это предложение
И. Хлодовского (1. Chlodovski. Une remarque sur la representation des fonctions
continues par des polynomes a coefficients entiers. Матем. сборник, XXXII, 3, 1925).
2 Следовательно, мы никогда не рассматриваем вырожденных интервалов, для
которых ai равно Ь{.
356
Н. Н. ЛУЗИН
Открытый /п-мерный параллелепипед называется рациональным^ если
все числа aiy Ь{ рациональны. Из этого определения заключаем, что
в одномерном пространстве понятие открытого рационального
параллелепипеда совпадает с понятием открытого интервала (а, Ь) с
рациональными концами. Сформулировав это определение, перейдем теперь к
понятию множества, измеримого Ву в m-мерном пространстве; чтобы
определить его, мы используем принцип минимума.
Аксиоматическое определение. Назовем т-мерным В-те-
лом наименьшую совокупность точечных множеств т-мерного
пространства у содержащую все т-мерные открытые рациональные
параллелепипеды и инвариантную относительно двух основных
операций: сложения в широком смысле и взятия общей части. Множество
точек т-мерного пространства называется измеримым Ву если оно
принадлежит В-телу.
Две основные операции, при помощи которых определяют понятие
тела, измеримого Ву состоят в образовании суммы счетного числа
множеств, которые, вообще говоря, имеют общие точки (сложение в
широком смысле)у и во взятии общей части счетного числа множеств (взятие
общей части).
Сформулированное определение множества, измеримого Ву требует
от нас оправдания этого понятия путем доказательства независимости
его от выбранной системы координат S(xly х.>, ..., х1П). Чтобы доказать
это, сделаем совершенно очевидное предварительное замечание: если
дано конечное или счетное число множеств, Е1У Е1У .. ., принадлежащих
Л-телу, то наименьшая совокупность точечных множеств, содержащая эти
данные множества и инвариантная относительно двух основных
операций, наверняка содержится в В-теле.
Заметив это, изменим систему координат, беря вторую систему
координат S(xu х2^ ..., х'т). Назовем В'-телом совокупность точечных
множеств в системе Sy совершенно аналогичную той, которую мы
определили для первой системы S и которую мы назвали В-телом. Так как
каждый открытый параллелепипед с ребрами, параллельными осям
координат системы Sy будучи суммой рациональных открытых
параллелепипедов, ориентированных по осям Sy является, очевидно, множеством,
измеримым В относительно первой системы Sy то легко видеть, согласно
предыдущему замечанию, что В'-тело содержится в 5-теле. В силу
симметрии обратное также имеет место. Следовательно, факт измеримости В
точечного множества не зависит от выбора прямоугольной системы
координат (ч. т. д.).
Перейдем теперь к важному вопросу взаимного соотношения
измеримости В относительно пространств различного числа измерений.
Пусть . ё — то-мерное евклидово пространство, 1 < то, и пусть &' —
то'-мерное, 1 ^ т < то, евклидово пространство, содержащееся в
пространстве §j Всякое ли множество Еу содержащееся в £' и
измеримое В относительно £', измеримо В и относительно пространства S?
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МН02КЕСТВАХ 357
Легко видеть согласно предыдущему замечанию, что ответ будет
утвердительным. Действительно, очевидно, что каждый яг'-мерный
рациональный открытый параллелепипед, содержащийся в пространстве S' и
рассматриваемый как часть пространства S, является множеством,
измеримым В относительно этого пространства, так как он является, очевидно,
общей частью счетного числа параллелепипедов т измерений,
содержащихся в &. Следовательно, согласно предыдущему замечанию В-тело
множеств, образованное для пространства £', необходимо составляет
часть более широкого В-тела, образованного д\я пространства & (ч. т. д.).
Другой вопрос, значительно более важный, чем предыдущий, состоит
в следующем: всякое ли множество Е, содержащееся в пространстве S'
и измеримое В относительно &у является также измеримым В
относительно пространства £'? Ответ также утвердительный. Чтобы
доказать это, нам достаточно рассмотреть совокупность /Г,
образованную из всех множеств Е вида
Е = еч-е\
где е — множество точек, измеримое В относительно пространства £ и
не имеющее общих точек с пространством <£', а е—множество точек,
содержащееся в пространстве §' и измеримое В относительно этого
пространства; в частности, множества е и е' могут быть пусты.
Согласно предыдущему множество е необходимо измеримо В
относительно пространства £. Следовательно, совокупность К содержится
в 5-теле относительно этого пространства £. С другой стороны,
пространство <£', рассматриваемое как множество точек пространства §>
очевидно, измеримо В относительно S; следовательно, каков бы ни был
открытый m-мерный параллелепипед, содержащийся в &, множество
точек этого параллелепипеда, не входящих в пространство <§', является
множеством, измеримым В относительно пространства <S. Отсюда
следует, что совокупность К содержит все открытые m-мерные
параллелепипеды, принадлежащие пространству &. К тому же легко видеть,
что совокупность К инвариантна относительно двух основных операций:
сложения в широком смысле и взятия общей части. Отсюда
непосредственно заключаем, что совокупность К совпадает с 5-телом
относительно пространства £. Следовательно, каждое множество точек £,
содержащееся в £' и измеримое В относительно <£, наверняка должно
быть измеримо В относительно £' (ч. т. д.).
Одно из важнейших приложений предыдущих рассмотрений
относится к плоским множествам; если Е — плоское множество точек> из-
меримое Ву и если мы проведем в плоскости Е прямую /,
пересекающую множество £, то общие точки Е и I образуют линейное
множество, измеримое В*
Это предложение будет очень полезно в последующем.
Сделаем последнее замечание; обращаясь к п. П, читатель увидит,
что все рассуждения этого параграфа без всяких изменений применимы
358
Н. Н. ЛУЗИН
также в случае евклидова пространства любого конечного числа
измерений.
Отсюда непосредственно заключаем, что:
Нижний предел, верхний предел и предел {если он существует)
счетного числа измеримых В множеств т-мерного пространства
также измеримы В.
Дополнение к множеству, измеримому В, и разность двух
множеств, измеримых В, также измеримы В.
Аналитические множества. Мы теперь совершенно
естественным образом обобщим понятие линейного аналитического множества,
рассмотренное в предыдущем параграфе, стараясь его распространить
на случай m-мерного евклидова пространства.
Для этого мы сформулируем следующее определение:
Назовем аналитическим множеством в т-мерном пространстве
геометрическое место последовательных положений движущейся точки
М(хг,х2, ..., Хт), координаты которой являются счетно-разрывными
функциями переменного параметра t, определенными в области D =
= (0<*<1): Xi=A(t), x2=/2{t), ..., xm=fm(t). Совокупность
аналитических множеств, включая в нее пустое множество, называется
аналитическим телом относительно т-мерного пространства.
Легко видеть, что сформулированное определение совершенно
конструктивно, следовательно, законно.
Нам остается только оправдать данное понятие аналитического
множества в /п-мерном пространстве, доказав, что оно не зависит от
выбранной системы координат S(xu x2, ..., хт). Чтобы доказать это,
изменим систему координат, беря вторую систему координат *S'(*^ х2^ ,..
. . м х'т). Формулы преобразования координат суть хорошо известные
соотношения, выражающие новые переменные х'1щ) х'2, . . ., х'т как
функции прежних координат х19 л:2, ..., хт (и обратно); так как эти
соотношения линейны относительно х1У х2, ..., хт и имеют постоянные
коэффициенты, то новые координаты х'и х2%1 ..., хт суть
счетно-разрывные функции параметра t. Следовательно, факт аналитичности
точечного множества не зависит от выбора системы прямоугольных
координат (ч. т. д.).
Отсюда следует, что аналитичность точечного множества, будучи
независимой от выбора системы координат, является свойством этого
множества относительно самого пространства. В таком случае возникает
вопрос, является ли множество точек Е\ содержащееся в т'-мерном
евклидовом пространстве &' и аналитическое относительно этого
пространства, аналитическим также и относительно более обширного
т-мерного, т' < т, пространства 8, содержащего <§'. И наоборот, является ли
множество точек Е, содержащееся в &' и аналитическое относительно
данного пространства <§, аналитическим также и относительно <£'. Ответ,
и при том утвердительный, получаем непосредственно.
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ 359
Чтобы убедиться в этом, выберем в пространстве ё систему
координат S(x19x2, ..., хт) такую, что д\я всех точек пространства §'
имеют место равенства
Хтп'н-1=0, *тЧ-2 = 0, . . ., Jtm = 0.
Легко видеть, что в этой системе координат условия, при которых
множество точек, содержащееся в пространстве £', будет аналитическим
относительно §' или относительно &, являются всегда одинаковыми:
это равенства
/--.и (0 = о, Л,+1 W=о, ..., /м (о=о,
которые должны выполняться для всех значений / области £>*(ч. т. д.)
Важным приложением этого предложения является следующее: Если
Е — плоское аналитическое множество и если мы проведем в
плоскости прямую I, пересекающую множество Е, то точки, общие Е
и I, необходимо образуют линейное аналитическое множество.
Именно это следствие предыдущих предложений даст нам
возможность совершенно строго установить существование аналитического
множества, неизмеримого В.
Так как каждая счетно-разрывная функция представима рядом поли
номов с рациональными коэффициентами, сходящимися в каждой точке,
то легко видеть, что все точечные множества, которые мы хотим
определить, допускают четкое аналитическое представление:
*i = 2 К (0, *2 = 2 г? О» • • •> *» = £ Ф О-
п=1 п=1 и=1
К тому же, обращаясь к концу предыдущего параграфа, читатель
легко докажет, что, не изменяя данного множества точек, можно
предположить, что эти т рядов сходятся абсолютно для каждого значения t
яз области D. В связи именно с этим представлением мы и назвали
эти точечные множества аналитическими согласно предложению
Лебега 1.
Из сформулированного определения непосредственно заключаем, что:
Каждое конечное или счетное точечное множество т-мерного
пространства является аналитическим множеством.
Чтобы убедиться в этом, достаточно разбить область Z) = (О <С *<С 1)
на счетное или конечное число открытых интервалов и полусегментов2,
попарно не имеющих общих точек, и взять функции /х (t) /2(0> • • •> /т (*)>
равные на этих частях надлежащим образом выбранным константам.
1 См. начало п. III (см. [3|).
2 Полусегментом называют каждый замкнутый сегмент, лишенный одного из
своих концов.
360
Н. Н. ЛУЗИН
Понятие однозначного аналитического множества обобщается очень
естественным образом; достаточно сформулировать следующее
определение:
Если счетно-разрывные функции x1=fl(t), x2 = f2(t), ..., хт =
~fm (0» которые определяют аналитическое множество точек Е
т-мерного пространства, таковы, что двум различным значениям
переменного параметра t соответствуют две различные точки
пространства, то множество Е называется однозначным
аналитическим множеством.
В силу этого определения ясно, что:
Каждое однозначное аналитическое множество содержит
совершенное множество, следовательно, имеет мощность континуума.
Чтобы усмотреть это, достаточно образовать совершенное
множество Р, расположенное в области D = (0 <С *<С 1) и не содержащее точек
разрыва функций /*(£) (что наверняка возможно, так как мы можем
перенумеровать при помощи целых положительных чисел соединение
множеств точек разрыва этих функций), и заставить t пробегать
множество Р. Множество Q соответствующих точек m-мерного
пространства будет, очевидно, совершенным множеством (ч. т. д.).
Д\я однозначных аналитических множеств пространства т
измерений имеет место предложение, совершенно аналогичное тому, которое
мы доказали раньше д\я линейных множеств.
Каждое точечное множество т-мерного пространства, полученное
из однозначного аналитического множества прибавлением к нему
произвольного счетного (или конечного) множества точек и
одновременным удалением произвольной счетной (или конечной) части его
элементов, является однозначным аналитическим множеством.
Чтобы установить это, достаточно подвергнуть область D = (0<^
<С^<С1) переменного параметра t тому же преобразованию, которое
было осуществлено для пространства Dt и D в случае линейных
множеств (см. п. III) (ч. т. д.).
Так как счетные (или конечные) множества являются наиболее
простыми из аналитических множеств и так как среди несчетных аналитических
множеств однозначные аналитические множества также являются
наиболее простыми, то довольно естественно охватить их, объединяя их
в одно семейство. Таким образом, мы пришли к введению следующего-
определения:
Назовем аналитическим телом в узком смысле совокупность
однозначных аналитических множеств, включая в нее все счетные
множества1, все конечные множества и пустое множество.
Это определение, к которому мы подошли естественным образом,,
очевидно, конструктивно (а не является аксиоматическим определением);
оно играет очень существенную роль во всем последующем.
1 Предполагаем, кроме того, что учитываются повторения счетных множеств.
Относительно аксиомы разбиения см. аналогичное примечание к п. III.
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ 361
Мы увидим, что в /п-мерном пространстве аналитическое тело в узком
смысле также совпадает с 5-телом, определение которого является
совершенно аксиоматическим. Именно совпадение этих двух понятий и
дает законную силу частному случаю самого принципа минимума.
По самому определению:
Аналитическое тело содержит аналитическое тело в узком смысле.
К тому же, обращаясь к п. III, читатель непосредственно увидит,
что все рассуждения, при помощи которых мы доказали две основные
леммы этого параграфа (лемму I и лемму II), без серьезных изменений
применимы также и в случае евклидова пространства любого конечного
числа измерений. Таким образом, мы имеем два важных предложения:
Лемма I. Сумма счетного числа аналитических множеств т~мер-
ного пространства является также аналитическим множеством.
Более того, если множества являются однозначными аналитическими
множествами или счетными (конечными) множествами, попарно не
имеющими общих точек, то их сумма также является однозначным
аналитическим или счетным (конечным) множеством.
Лемма II. Общая часть счетного числа аналитических множеств
т-мерного пространства является аналитическим множеством.
Более того, если множества являются однозначными аналитическими
множествами или счетными (конечными) множествами, то их общая
часть также является однозначным аналитическим множеством
или счетным (конечным) множеством.
Впрочем, если мы не хотим делать никаких, даже малейших
изменений в вышеприведенных доказательствах этих лемм, то для того,
чтобы их распространить на случай m-мерного пространства, достаточно
ввести комплексные числа с т мнимыми единицами ily i2l ..., zw:
a\h ■+■ a±h -*--..-+- amim.
Условившись писать
если имеют место равенства аг = Ь19 а2=62> • • •> ат = Ьт; таким
образом, уравнения между комплексными величинами сводятся к т
уравнениям между действительными величинами. При этих условиях каждое
аналитическое множество Е представимо одной мнимой функцией f(t):
f W =Л (*) h -*- ft W h -+-.../.(<) im
действительного параметра t, счетно-разрывной на области D = (<C0<^
<£<1), и предыдущие доказательства двух основных лемм остаются
неизменными (ч. т. д.).
Отсюда непосредственно заключаем, что:
Аналитическое тело инвариантно относительно двух операций:
сложения в широком смысле и взятия обшей части. Аналитическое
362
Н. Н. ЛУЗИН
тело в узком смысле инвариантно относительно двух операций:
сложения в узком смысле и взятия общей части.
Операция сложения в узком смысле состоит в образовании суммы
счетного числа множеств, попарно не имеющих общих точек.
Чтобы сравнить В-тело с аналитическим телом и с аналитическим
телом в узком смысле, остается только доказать, что каждый
открытый т-мерный параллелепипед принадлежит аналитическому телу
и аналитическому телу в узком смысле.
Что касается аналитического тела, то это замечание крайне банально,
так как пеановская кривая х1 =/г (0> *2 =Л(0» • • •» xm=fm(/),
заполняющая открытый /п-мерный параллелепипед, непосредственно доказывает
сформулированное замечание. Но для аналитического тела в узком
смысле такой способ действия совершенно не приемлем, так как
согласно работе Лебега1 каждая пеановская кривая, заполняющая
открытый /n-мерный параллелепипед, необходимо имеет в этом
параллелепипеде кратные точки. Следовательно, естественно искать другое
доказательство этого основного предложения.
Лемма III. Каждый открытый т-мерный параллелепипед является
однозначным аналитическим множеством.
Так как для каждой пары открытых m-мерных параллелепипедов тс
и тс' существует преобразование Т:
Х1 = Ш1 (*1, **, • • V* J, • • ч *т = "т (*1, *2, • • -, Хт\
линейное относительно переменных х19 х2, ..., xmf преобразующее
параллелепипед тс в параллелепипед тс', то легко видеть, что достаточно
доказать сформулированную лемму для случая основного открытого
параллелепипеда тс:
я = (0<*1<1, 0О8<1, .... 0<*W<1).
Исходя из этого, зафиксируем некоторые из переменных хи х2, ...
..., хт, беря их равными фиксированным рациональным числам,
произвольно [выбранным между 0 и 1, и будем варьировать другие
переменные, давая им соответственно все иррациональные значения,
содержащиеся между 0 и 1; мы получим таким образом множество точек,
которое составляет вполне определенную часть параллелепипеда тс;
обозначим ее через Е'. Мы можем теперь утверждать, что Е есть
однозначное аналитическое множество.
Действительно, предположим]для определенности, что буквы xv x2, . ♦.
..., Хт' — переменные, а остальные — фиксированные; пусть
х = о' х = eft*—™')
1 ,rSur les correspondences entre les points de deux espacesa (Fund. Math.» П).
См. также „Le theoreme de Schoenflies" (там же, VI» 96, 1924).
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ
363
Иррациональное число д^ представимо вполне определенным образом
бесконечной непрерывной дробью
*« = (ал, в«, ..-, а*о •••),
где каждое число &in — неполное частное, следовательно, целое
положительное число.
Рассмотрим теперь таблицу из т бесконечных строк:
&n, a12, an, .. ., аЬ/, .. .
<*2i, а22, а2з, ..., а2м, . . .
т'1-> т'Ъ т'З") • • •> m'ni * * *
и расположим члены этой таблицы в простую бесконечную
последовательность рх, (32, ..., (Зь ...
Непрерывная дробь
* = (Pi,P2> •--, Р* •••)
дает нам вполне определенную иррациональную точку х, расположенную
в новой области Z)T = (0<Cx <С1)- Обозначим через <э7 множество
иррациональных точек этой области.
Ясно, что знание х1У хъ ..., хт* определяет х однозначным образом,
и, наоборот, знание т однозначным образом определяет л^, -х^, ..., xw'.
Мы имеем, следовательно,
где каждая функция <р*(х) определена для всех точек с7; к тому же
легко видеть, что <рДх) непрерывна в каждой точке х множества з7
относительно этого множества.
Так как линейное множество о7 есть однозначное аналитическое
множество (см. п. III), то существует счетно-разрывная разнозначная
функция х = и>(£), определенная в новой области Dy Z) = (0<C*<C 1)>
множество значений которой совпадает с о7. Отсюда немедленно заключаем,
что сложная функция /,(*) = <?<(">(*)) определена всюду в области D;
более того, она счетно-разрывна в этой области.
Отсюда следует, что множество точек га-мерного пространства,
определенное уравнениями
*i=/iW, *2=Л(')> • ••> x«=f«(t), хт,+г=9', ...,хт=Р<—г
является однозначным аналитическим множеством. Так как оно,
очевидно, совпадает с ранее определенным множеством £', то наше
утверждение доказано.
364
Н. Н. ЛУЗИН
Установив это, вернемся к параллелепипеду тт. Мы уже видели, что
рассматриваемое множество Е' составляет часть параллелепипеда тс и
что оно полностью определено выбором (из букв х:, x2> ..., хт)
фиксированных букв и выбором их рациональных значений. Так как
существует счетное число таких выборов и так как различным выборам
соответствуют множества, попарно не имеющее общих точек, мы можем
написать
где D — множество точек ~, у которых все координаты рациональны.
Следовательно, D счетно.
По лемме I отсюда заключаем, что параллелепипед тс является
однозначным аналитическим множеством (ч. т. д.).
По-видимому, эти рассмотрения могут представлять некоторый
интерес, так как они показывают нам, что если отказаться от
непрерывности соответствия между двумя множествами, даже в счетном числе
точек, то нет существенной разницы между множествами,
содержащимися в одномерном пространстве, и множествами, содержащимися
в пространстве двух (или трех...) измерений.
Чтобы сравнить теперь 5-тело с аналитическим телом в узком смысле,
осталось только сделать такое замечание:
В-тело есть наименьшая из совокупностей точечных множеств
т-мерного пространства, содержащих все т-мерные открытые
рациональные параллелепипеды и инвариантных относительно двух
операций: сложения в узком смысле и взятия общей части.
Доказательство этого предложения остается тем же самым (см. п. III).
Отсюда непосредственно заключаем, что:
В-тело образует часть аналитического тела в узком смысле и
тем более часть аналитического тела.
Отсюда следует, что каждое несчетное множество, измеримое В>
является однозначным аналитическим множеством. Следовательно,
Каждое несчетное множество, измеримое В, содержит
совершенное множество, следовательно, имеет мощность континуума.
Как видно, это и есть предложение Александрова—Хаусдорфа.
Неиндуктивное свойство. Мы назвали в п. I свойством Александрова-
Хаусдорфа свойство точечного множества Е% формулировка которого следующая:
каково бы ни было совершенное множество тс, если множество Е обладает на я
несчетным множеством точек, то оно обладает на тс совершенным множеством Е\.
Обозначим это свойство через Р$.
Легко видеть, что каждое аналитическое множество Е наверняка обладает этим
свойством Р^у так как общая часть множеств Е и я, будучи аналитическим
множеством и в то же время по предположению несчетным, должна обязательно содержать
совершенное множество Е\ (п. IV).
Между тем, воспроизводя рассуждения идеалистов, основанные на континуум*
гипотезе (т. е. на нумерации всех точек континуума при помощи трансфинитных чиоел
второго класса)» без всякого труда можно образовать последовательность мяо-
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ
36S
жеств Ely Е<1Л. . .,обладающих свойством Р0, общая часть которых не обладает этим
свойством, хотя и является несчетной.
Чтобы доказать это, запишем все точки ,и евклидова пространства & в виде
вполне упорядоченного множества
н< н< н »*., fv- •. IQ. 0)
где а есть трансфинитное число второго класса. Рассмотрим, с другой стороны,
множество всех совершенных множеств к% расположенных в S и неплотных на этом
пространстве:
Пусть {а0 — первый элемент последовательности (I), принадлежащий ^. Если
точки {Jfl, i^i, [i^,. . •»Н-а«- • • I Э <С а I определены, мы обозначим через jj.a первый
элемент последовательности (I) (если он существует), принадлежащий множеству т:а и
яе принадлежащий никакому предыдущему совершенному множеству гсд, ji < a . . .
Последовательность
Hfb f*i. 1*2 Лл !*«.• • -lQ- (HI)
наверняка содержит несчетное множество точек. Пусть Н — это множество.
Из самого определения множества Н следует, что это множество несчетно и
содержит не более чем счетное число точек в каждом совершенном неплотном
множестве 71, расположенном в пространстве £. К тому же непосредственно убеждаемся
в том, что Н не обладает свойством Р^.
Установив это, возьмем в этом пространстве <£ счетную последовательность
совершенных неплотных множеств
Пь По, П3 П*
попарно не имеющих общих точек и таких, что сумма их всюду плотна на
пространстве S. Обозначим через Е^ бесконечное объединение:
Я -+- Пк -ь П^ -+- Пл+2 -*-
Очевидно, что каждое Ek наверняка обладает свойством Р$ и что общая часть
определенных таким образом множеств
Е\ч Eoi» • • Eic%» • •
не обладает свойством Pq, так как их общая часть совпадает с множеством И.
V. Проекции и их приложения к изучению
аналитических множеств.
Детально разъяснив определения множеств, измеримых 5, и
аналитических множеств, последующее изложение мы можем сделать более
кратким.
Проекции. Возьмем в /и-мерном евклидовом пространстве &
точку М и /и'-мерное евклидово пространство ё\ где 1^т <т.
Опустим из точки М перпендикуляр на пространство £'; основание
опущенного перпендикуляра называется проекцией точки М на
пространство <§'.
Пусть Е — некоторое множество точек в m-мерном пространстве;
множество проекций всех точек Е на пространство &' называется
проекцией данного множества Е на пространство £'.
366
Н. Н. ЛУЗИН
Проектировать множество Е на пространство £', это значит взять
его проекцию на &''. Это одна из наиболее простых и в тоже время
наиболее важных геометрических операций, и было бы очень
желательно, чтобы исследования, относящиеся к этой основной операции
были обширными и постоянно продолжалисьг.
Первый из вопросов, касающихся проекций, это вопрос о природе
этих множеств. Если данное множество Е является аналитическим
множеством, какова будет его проекция? Будет ли эта проекция также
аналитическим множеством? Ответ, и при этом положительный, следует
непосредственно.
Чтобы установить это, выберем в пространстве & прямоугольную
систему осей координат S(xl9 лг2,. • •, хт) такую, что оси хг, jc2,. .., хт'
принадлежат пространству <£'; эти оси образуют систему координат дая
пространства <§'; обозначим ее через S' (xv лг2,..., хт'). При этих
условиях проекция |а0 точки М°(х^ *!},..., *°), взятой произвольно в
пространстве <§, на пространство &' имеет в качестве координат
относительно системы S' соответственно числа х\, х\,.... х**т,. Отсюда следуем
что, каково бы ни было аналитическое множество Е>
*l=/l(*)> X2=f2(t)y . ..,*m'=/m'(0> ...,*т=/т(0,
расположенное в пространстве &> проекция Е на пространство S есть
множество точек пространства <£', координаты которых имеют вид:
*1 = Л (')> *2 =f* (0> • • •> *m' =/„.' (*)•
Очевидно, что это аналитическое множество. Таким образом:
Ортогональная проекция аналитического множества точек т-мер-
ного евклидова пространства на т-мерное евклидово пространство*
т <^т, является аналитическим множеством.
Мы можем сказать, в частности, что:
Проекция множества, измеримого Ву является аналитическим,
множеством.
Как мы увидим, в этой формулировке слово аналитическое не может
быть заменено словами измеримо В.
Другой вопрос, значительно более сложный, чем предыдущий, однако
более достойный внимания, состоит в следующем: не будет ли
аналитическое множество проекцией множества особенно простой природы?
Мы ответим положительно на этот вопрос, доказав мало вероятное,
на первый взгляд, предложение: каждое аналитическое множество
является ортогональной проекцией множествау измеримого Ву и даже
не слишком сложного множества^ измеримого В. Чтобы оценить простоту
этого множества, нам потребуется новое определение.
1 Ср. Н. Lebesgue. Remarques sur les theories de la mesure et de Tintegrale»
(Ann. sdentifiques de l'Ecble Norm. Super, 242 1918); см. Comptes Rendus, 25 мая
192S г.
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ 367
С этой целью возьмем яг-мерное евклидово пространство S. Пусть
в этом пространстве имеется некоторая прямоугольная система осей
координат, которую мы предполагаем неизменной и выбранной раз
навсегда и которую мы обозначим через S(xlt x>, ..., лгт).
Установив это, представим себе в этом пространстве S вполне
определенную счетную или конечную последовательность m-мерных
замкнутых рациональных параллелепипедов \ ориентированных по осям
системы S и попарно не имеющих общих точек; эти замкнутые
параллелепипеды будем называть параллелепипедами ранга 1. Представим себе
в каждом из этих параллелепипедов ранга 1 вполне определенную
счетную или конечную последовательность m-мерных замкнутых
рациональных параллелепипедов, ориентированных по осям системы S и попарно
не имеющих общих точек; эти замкнутые параллелепипеды будем
называть параллелепипедами ранга 2. Очевидно, что множество,
образованное из всех параллелепипедов ранга 2, счетно. Вообще, каково бы
ни было положительное целое число я, я>1, будем мыслить в каждом
параллелепипеде ранга п — 1 вполне определенную счетную или
конечную последовательность замкнутых параллелепипедов, также попарно
не имеющих ни одной общей точки, и будем называть их для
сокращения параллелепипедами ранга п> и т. п.
Так как имеется счетное (или конечное) число параллелепипедов
ранга п и они попарно не имеют общих точек, то их множество-сумма
необходимо измерима В; обозначим ее через Sn. Отсюда
непосредственно следует, что общая часть всех множеств-сумм Sv S2>*. ;Sn>...
неизбежно является множеством, измеримым В; обозначим его через Е
и сформулируем следующее определение:
Определение. Построенное таким образом множество Е мы
будем называть элементарным множеством, измеримым В,
Мы видим, что каждое элементарное множество, измеримое В, есть
множество не слишком сложной природы, но это, строго говоря, только
очень относительно2.
1 т-мерным замкнутым параллелепипедом называют множество точек М (Jtlt
ДГ2, ...» Хт) пространства <£, удовлетворяющих условиям а\ < хх < &i» a% < х% < &2, . . .,
От < Хт < km, где каждое число xi содержится между существенно неравными
числами а% и &»*, {а%<? Ы) или совпадает с одним из них.
т мерный замкнутый параллелепипед называется рациональным, если все числа
a», hi рациональны.
Каждый замкнутый m-мерный параллелепипед, очевидно, измерим Вл так как
он является общей частью счетного числа m-мерных открытых рациональных
параллелепипедов.
Я никогда не буду рассматривать вырожденные образования, такие, что для
некоторого значения /, а% равно Ъ%.
2 „Простота" элементарного множества, измеримого £ч кажется нам очень
иллюзорной. Перевод определения элементарного множества, измеримого В, на
язык арифметики сталкивает нас со всеми противоречиями, относящимися к теории
роста. Правдоподобно, что все трудности теории проективных множеств содержатся,
как в зародыше, в элементарных множествах, измеримых В.
368
Н. Н. ЛУЗИН
Множество, образованное одной единственной точкой, является,
очевидно, элементарным множеством, измеримым В.
Изолированным множеством называют каждое множество точек
m-мерного пространства, каждый элемент которого является
изолированной точкой. Из этого определения следует, что изолированное
множество является элементарным множеством, измеримым В.
Именно в силу тесной связи между наиболее общими аналитическими
множествами и элементарными множествами, измеримыми 5, мы ввели
эти последние.
Теорема. Каждое аналитическое точечное множество т-мерного
евклидова пространства & можно рассматривать как ортогональную
проекцию элементарного множества, измеримого В, расположенного
в (т н- \)-мерном евклидовом пространстве, содержащем &.
Чтобы доказать это важное утверждение, следует сначала сделать
предварительное замечание.
Пусть /х (t), /2 (/), ..., /w (t) — некоторые однозначные функции
действительного переменного ty определенные в открытом интервале В.
Я утверждаю теперь, что если колебание каждой из этих функций
в любой точке интервала Ь меньше положительного числа с, то мы
можем удалить из открытого интервала Ь счетное число точек, не
имеющих предельной точки, внутренней в узком смысле а^я9 Ь таких,
что в каждом из оставшихся открытых интервалов общее колебание
каждой функции /<(~) также меньше г. Действительно, разобьем сначала
интервал 8 его серединой ц0 на два равных интервала; затем разобьем
правый и левый из этих интервалов соответственно при помощи их
середин |а—1 и j^; затем мы также разобьем самый левый и самый правый
из полученных интервалов при помощи их середин |*_2 и р2
соответственно, и так безгранично. Очевидно, что переменные точки {*_„ и \in
стремятся соответственно к правому и левому концам интервала о,
когда п неограниченно возрастает; открытый интервал о, следовательно,
полностью разбит на счетное число полусегментов [^^t<С^»"+■ lb
попарно не имеющих общих точек, где индекс / возрастает от —схэ
до -1-00, пробегая целые значения1.
Рассмотрим теперь замкнутый сегмент [^ ^ t ^ Уч+1], гДе z —
некоторое целое число. Так как колебание каждой из функций f\{t\
/2(0» •••>/!» (О наверняка меньше s во всякой точке замкнутого сегмента
[\Lt ^ t ^ Рчч-iL то этот сегмент можно разбить на конечное число рядом
лежащих интервалов, таких что максимальное полное колебание
функций AWjAW» •••>/»» (t) в каждом из них строго меньше з. Отсюда
непосредственно заключаем, что соединение точек (* и точек, которые
служат точками деления замкнутых сегментов [Нч^*^1Ч-нЬ составляет
1 Ниже мы всегда будем обозначать через [а, в] сегмент (замкнуты^), через
(а, в) — интервал (открытый,) через [а, в] — сегмент, открытый со стороны в
{полусегмент) и через (а, в] — интервал, замкнутый со стороны а (полуинтервал).
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ 369
счетное множество точек, обладающих ранее сформулированным
свойством (ч. т. д.).
Установив это, возьмем теперь произвольные счетно-разрывные
фу нкции /х (t), f2(t),..„ fm(t), определенные на области £>=(0</<1).
Я утверждаю, что если е — заранее данное сколь угодно малое
положительное число, то мы можем определить в D приводимое
(следовательно, счетное) множество Нг, такое, что в каждом из интервалов,
смежных к Н%, полное колебание каждой функции /< будет меньше £.
Действительно, обозначим через 2е множество точек области D, в
которых колебание по крайней мере одной из функций fx, /„ ...,/„, больше
или равно s; это множество счетно, и известно, кроме того, что оно
замкнуто на области D. Пусть и1У и2, ..., ик, ...— последовательность
интервалов, смежных к множеству Нь. Так как колебание каждой из
функций /х, /о, ...,//л во всякой точке интервала ик меньше г, то мы
можем удалить из щ счетное множество точек Qk, не имеющее ни одной
предельной точки внутри (в узком смысле) щ и такое, что
максимальное полное колебание функций }х, /,, ..., /м в оставшихся открытых
интервалах меньше г. Очевидно, что соединение Ht множеств 2. и
Q\y Qz> • • •> Qky • • • составляет приводимое множество, удовлетворяющее
предыдущему условию (ч. т. д.).
В результате мы подошли к следующему предложению, цоторое
является следствием всего предыдущего:
Если даны т счетно-разрывных функций fx (t), fi(t), • ••>/♦*(*)»
определенных в области D, и некоторый открытый интервал о,
принадлежащий области D, то можно определить в о приводимое
множество Н значений t, стремящихся соответственно к двум
концам интервала о и такое, что в каждом интервале, смежном к И
и расположенном на Ьу полное колебание каждой функции j{ будет
меньше е, где е — произвольное сколь угодно малое положительное число.
Чтобы доказать это, достаточно обозначить через Н множество,
образованное путем соединения ранее определенных точек ая, и точек Нг,
принадлежащих 8.
Определение. Будем говорить, что открытый интервал о
разделен регулярным образом на множество частичных открытых
интервалов, если из о удалено приводимое множество, предельными
точками которого являются только концы интерзала о.
Приняв это определение, мы можем следующим образом
сформулировать следствие, к которому мы пришли перед этим: каково бы ни было
положительное число £, всякий открытый интервал, принадлежащий
области D, можно регулярным образом разбить на множество
частичных открытых интервалов таким образом, что на каждом
из них максимальные полные колебания данных счетно-разрывных
функций fly /2> .. ., /т будут меньше г.
Установив это, вернемся к сформулированной теореме. Чтобы
доказать ее, возьмем какое-нибудь аналитическое множество Е, располо-
370
Н. Н. ЛУЗИН
женное в m-мерном евклидовом пространстве & и определенное
уравнениями
Х1 = Л (')> *2 = к (0» • • •> *т =fm (Of
гАе Л> Л» •••» /т — функции, счетно-разрывные на области Z> = (0<С^ <С 1).
Зададим убывающую последовательность положительных чисел еа>
£>, . •., еп >• • •» стремящихся к нулю.
Сначала область D разобьем регулярным образом на множество
открытых интервалов, таким образом, чтобы полные колебания
функций /{ на каждом из них были меньше ех; эти открытые интервалы
будем называть интервалами ранга 1. Затем разобьем регулярным
образом каждый из этих интервалов ранга 1 на множество открытых
интервалов таких, чтобы полные колебания функций fi на каждом из
этих последних интервалов были меньше £2> эти открытые интервалы
будем называть интервалами ранга 2. Вообще, если определены
все (открытые) интервалы ранга п — 1, мы разобьем регулярным
образом каждый из них на множество открытых интервалов таких, чтобы
полные колебания функций ft на каждом из этих последних были
меньше вя; эти открытые интервалы будем называть интервалами
юанга пу и т. д.
Исходя из этого, возьмем (т -н 1)-мерное евклидово пространство $у
содержащее пространство <§. Пусть S' (хх, х2>,.., хту хт+1) —
прямоугольная система координат пространства <§", включающая систему
координат S(xly х2> , хт)> взятую в пространстве &; ось хт+г,
следовательно, есть прямая, проведенная через начало О системы S и
перпендикулярная пространству £. На этой оси мы возьмем закрытый
сегмент [0 ^jcw+1 ^ 1], определенный координатами своих концов дстЧ.1=0
и хт+1 = 1.
Возьмем теперь на этом сегменте [0 ^ xm+i ^ 1] вполне
определенную бесконечную последовательность замкнутых сегментов, попарно
не имеющих ни одной общей точки и стремящихся к верхнему концу
*m+i — 1 этого сегмента; эти замкнутые сегменты будем называть
сегментами первого ранга 1. В каждом из этих сегментов первого
ранга мы поместим вполне определенную бесконечную
последовательность замкнутых сегментов, попарно не имеющих общих точек,
которые расположены по отношению к этому замкнутому сегменту так же,
как множество сегментов первого ранга по отношению к сегменту
[0^дгт+1 ^1|; эти замкнутые сегменты будем называть сегментами
второго ранга. Вообще, если определены сегменты ранга п — 1, поместим
в каждом из них вполне определенную бесконечную последовательность
замкнутых сегментов, не имеющих попарно общих точек и стремящихся
к верхнему концу этого сегмента; эти замкнутые сегменты будем
называть сегментами ранга л, и т. д. Очевидно, мы можем предположить,
что все эти замкнутые сегменты имеют рациональные концы и что
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ
371
максимальная длина сегментов ранга п стремится к нулю, когда я
неограниченно возрастает.
Установим для каждого значения п взаимно однозначное
соответствие между ранее определенными открытыми интервалами ранга п
области £> = (0<С*<1) и замкнутыми сегментами ранга л,
расположенными на оси хт+11 таким образом, чтобы каждому открытому
интервалу о ранга л, содержащемуся в открытом интервале 8' ранга п — 1,
соответствовал замкнутый сегмент з ранга л, содержащийся в сегменте о\
соответствующем 8'.
Для этого установим взаимно однозначное соответствие между
открытыми интервалами первого ранга области D и замкнутыми
сегментами первого ранга, расположенными на оси лгтч.х, затем между
открытыми интервалами второго ранга и замкнутыми сегментами второго
ранга, содержащимися соответственно в соответствующих друг другу
открытых интервалах и замкнутых сегментах. Таким же образом
продолжаем неограниченно брать в каждой паре о', а\ образованной из
открытого интервала 8' ранга л— 1 на области D и соответствующего
замкнутого сегмента <з' ранга п — 1 на оси хт+г, все открытые интервалы В
ранга п и все замкнутые сегменты о ранга л, содержащиеся
соответственно в 8' и о', и определенным образом ставить в соответствие
каждому о сегмент <з, и обратно. Ясно, что, продолжая таким образом,
мы установим искомое взаимно однозначное соответствие между
открытыми интервалами области D и замкнутыми сегментами оси хт+х ранга
12 3
Установив это, возьмем в области Z) = (0<C*<C1) какой-нибудь
открытый интервал 8 ранга л. Так как полное колебание функций
*l=/l(')> *2=Л(')> •••> Xm=fm(t)
в открытых интервалах 8 меньше ея, то мы можем определить т
замкнутых сегментов о1э о2> ..., ow> расположенных соответственно на осях xlf
jc2, ..., хт, меньших е„ и непустых, таких что множество значений,
которые функция *<=/*(/) принимает на интервале 8, будет
содержаться в о*. Следовательно, рассматривая открытые интервалы ранга
1, 2, 3, ..., содержащиеся в области D = (О <С t <C 1), мы можем
поставить в соответствие каждому из них вполне определенную систему т
сегментов, расположенных соответственно на осях х1У х2,..., хт.
К тому же, как легко видеть, мы можем предполагать, что эти сегменты
рациональны и что если 8' — открытый интервал ранга лч-1,
содержащийся в открытом интервале 8 ранга л, то т замкнутых сегментов а[ >
02, ..., а которые соответствуют о', содержатся соответственно в
замкнутых сегментах о1У <?2, ..., <*т, соответствующих 8.
Предыдущие рассмотрения, касающиеся замкнутых интервалов,
расположенных на оси хт+1 и на осях х1У х2, ..., хт, были необходимы
нам, чтобы приступить к конструкции элементарного множества, изме?
римого В, в т-н1-мерном евклидовом пространстве &\ ортогональная
372
Н. Н. ЛУЗИН
проекция которого на пространство S совпадает с данным
аналитическим множеством. Настало время осуществить эту конструкцию.
Возьмем в области £) = (0<С^<С1) произвольный открытый
интервал 8 ранга л, где положительное целое число п произвольно. Пусть
^i» а2> • • •» °т — система т замкнутых сегментов, расположенных
соответственно на осях jCj, лг2, .. ., хту соответствующая Ъ; и пусть о —
замкнутый сегмент ранга л, расположенный на оси хт+х и соответствующий
интервалу &; все эти (т ■+-1) замкнутых сегментов определены
единственным образом, если только известен интервал о. Так как точки
M(xv x2f . •., хт, jcm+1) пространства £', координаты которых хи х2, ...,
хт, хт+1 принадлежат соответственно замкнутым сегментам оХ9 о2, . ..,ow,
<Wi> образуют (га-+-1)-мерный замкнутый рациональный параллелепипед,
то с каждым открытым интервалом о ранга л области /) = (0<О<1)
связан вполне определенный замкнутый параллелепипед пространства <§'♦
назовем его для сокращения замкнутым параллелепипедом ранга л.
Очевидно, что имеется счетное число замкнутых параллелепипедов ранга
п и что они попарно не имеют общих точек; каждый из замкнутых
параллелепипедов ранга п содержит бесконечное число замкнутых
параллелепипедов ранга /2-bl, и каждый замкнутый параллелепипед ранга п
содержится в одном и только одном параллелепипеде ранга п—1, если
.целое положительное число п больше 1.
Установив это, обозначим через Sn множество-сумму всех замкнутых
параллелепипедов ранга п пространства &' и через Q — общую часть
всех множеств-сумм Slf S2> ...,5Я, ... . Очевидно, что множество Q
является элементарным множеством, измеримым В.
Непосредственно из самой конструкции множества Q выводим его
основное свойство: ортогональная проекция множества Q на
пространство & является частью данного аналитического множества Е>
и обратно: каждая точка множества Е является проекцией точки
множества Q, кроме> возможно, точек *i=./i(~)> -*2=/2(x)> • • •>
jc,n=/m(t) множества Е, соответствующих числам т, каждое из
которых принадлежит только конечному числу интервалов & ранга
1, 2, 3, ... области Z? = (0<г*< 1).
Все сводится к тому, чтобы добавить к элементарному множеству Q,
измеримому В, соответствующим образом выбранные точки. Так как
при каждом значении п точки / области Dt не принадлежащие никакому
открытому интервалу S ранга л, образуют приводимое множество,
то ясно, цто имеется только счетное число чисел т, таких что точка
■*,г=Л(х)> •*2=/2-(t)> ••■•> Xm=fm{z) множества Е не принадлежит
проекции множества О. Расположим эти числа в простую бесконечную
последовательность *v т2, ..., хп> .. „ и рассмотрим в пространстве <§' счетное
множество точек Л/1; М^ . .., Мп> ..., координаты которых определяются
следующими равенствами:
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ
373
Очевидно, это счетное множество точек является изолированным
множеством; следовательно, соединение этого множества и множества Q
также является элементарным множеством, измеримым В.
Ясно, что ортогональная проекция этого соединения на
пространство ё совпадает с данным аналитическим множеством Е (ч. т. д.).
Лебеговский выбор. Пусть М— множество, составленное из
непустых множеств М\ попарно не имеющих общих элементов, и
определенное точным образом при помощи вполне конечного закона А.
Первая из наиболее важных при современном состоянии науки проблем,
которая возникает в связи с множествами М\ следующая:
Узнать, существует ли множество, образованное из элементов
множеств М' и содержащее в каждом множестве М' по одному и
только одному элементу т.
Хорошо известно, что категорическое утверждение действительного
существования во всех случаях такого множества является сущностью
знаменитого принципа произвольного выбора, часто называемого
аксиомой Цермело. Именно Цермело принадлежит слава явно
сформулировать и попытаться узаконить в области бесконечных множеств способ
рассуждения, который многие математики с непреложным успехом
применяли к конечным множествам задолго до него. Этот способ
рассуждения состоит в следующем: в каждом множестве М можно ad
libitum выбрать отдельный элемент т, и так как выбор, проведенный
в каждом из множеств М, может быть проведен для множества М этих
множеств, то и получается множество Z, имеющее в каждом
множестве М один и только один элемент т.
Такой образ действия вполне законен, когда речь идет о конечном
числе множеств AT; но, как известно, он очень подвергается критике,
так только речь заходит о бесконечной совокупности множеств М\
Я не буду больше останавливаться на этом, так как после появления
знаменитых Пяти писем1 мне не кажется, чтобы при современном
состоянии науки к ним можно было добавить что-нибудь новое; я только
хочу разъяснить положения, извлеченные из этого мемуара.
Прежде всего, если дан конечный закон Л, определяющий
множество М множеств М, то в большинстве классических случаев мы можем
вывести из А новый вполне конечный закон \ который позволит
точным образом и без возможных двусмысленностей определить множет
ство Z, содержащее по одной и только одной точке в каждом из
множеств М. Если эта возможность вывода такого закона X действительно
имеет место, мы скажем, что мы имеем случай лебеговскою выбора.
Лебеговский выбор не является ни новой аксиомой, ни новым
соглашением: это просто факт математического анализа, законность которого
каждый раз вне сомнения.
1 См. „Cinq lettres sur la theorie des ensembles". E. В or el. Lemons sur la theorie
dbs fonctions, 2e ed., Note IV, стр. ISO.
374
Н. Н. ЛУЗИН
Если такой возможности не существует, мы скажем, что мы имеем
случай цермелистского выбора. Чтобы в этом случае говорить о
„действительном существовании** множества Z, имеющего по одной и только
одной точке в каждом множестве Му нужно дать словам
экстраординарное и, добавлю, слишком мало кронекеровское, для того чтобы
приписать им смысл, толкование.
Но здесь следует выделить важный частный случай, когда
множество М счетно. Именно в этом случае обязательным является
лебегов с к и й выбор, так как a priori невозможно получить самые
множества М, перенумерованные при помощи целых положительных чисел,
не имея предварительно закона \ который определяет выбранные
элементы — по одному в каждом множестве М — и нумерует их
аналогичным образом. Когда речь идет о „счетной форме" аксиомы Цермело,
допускают, сознательно или несознательно, отождествление с
последовательностью замкнутых поверхностей (каждая из которых содержит
элементы), перенумерованных при помощи номеров 1, 2, 3,..., которые
приклеены по одному на эти поверхности без пропусков и без
повторения какого-нибудь из них несколько раз. Но это отождествление,
на мой взгляд, совершенно незаконно: множеству не соответствует
никакая поверхность, и номер, который ему предназначается, не
может быть приклеен на несуществующую поверхность, а должен
быть приклеен к отдельному элементу, выбранному в этом
множестве. Фраза: „Вот счетная последовательность множеств"
неизбежно предполагает предварительное существование конечного закона
X, осуществляющего выбор отдельного элемента в каждом из этих
множеств.
Этому случаю можно противопоставить другой важный случай, когда
множество М эффективно имеет мощность континуума. Дальше я
укажу очень простой пример такого рода, где мы не имеем, с моей
точки зрения, лебеговского выбора. Мы не будем больше
распространяться о происхождении и природе этого факта; мы ограничимся
кратким замечанием, что возможность существования множеств М',
перенумерованных при помощи действительных чисел, без существования
лебеговского выбора связана, на мой взгляд, с тем, что
понятие действительного числа является вторичным понятием по
отношению к понятию целого числа и что континуум не может быть
представлен во вполне упорядоченной форме в кронекеровском
смысле.
Закончив эти общие рассуждения, обратим наше внимание на
элементарное множество, измеримое В, ортогональная проекция которого
«а пространство S есть данное аналитическое множество Е. Пусть Ег —
элементарное множество, измеримое 5, расположенное в (т -+- 1)-мерном
пространстве <£'. Пусть М — некоторая точка пространства & и Рм —
перпендикуляр из точки М к пространству &. Так как Е —
ортогональная проекция множества Е19 то, следовательно, общая часть перпен-
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ
37S
дикуляра Рм и множества Е1 содержит точки в том и только том
случае, когда точка М принадлежит множеству Е. Обозначим через ем эту
общую часть. Так как множества eMJ очевидно, попарно не имеют
общих точек, то возникает вопрос, существует ли лебеговский выбор
одной и только одной точки в каждом из этих множеств еу?
Мы хотим дать положительный ответ на этот вопрос, показав, что
можно указать закон, который позволит назвать одну и только одну
точку N в каждом ем.
Так как множество ем необходимо содержит точки, то среди
параллелепипедов первого ранга, определяющих элементарное множество Ev
существует параллелепипед с наименьшим индексом, содержащий
точки ем. Пусть тсх — этот параллелепипед. Среди параллелепипедов
второго ранга, содержащихся в гс1э обязательно имеются
параллелепипеды, содержащие точки множества ем. Пусть ^2 — тот из этих
параллелепипедов, индекс которого наименьший, и т. д. Продолжая
безгранично этот процесс, мы образуем последовательность параллелепипедов,
имеющих соответственно ранги 1, 2, 3,. •.:
^1» ^2» ^3» • * * 9 ^т • • • >
каждый из которых содержится в предыдущем, и которые наверняка
содержат точки на перпендикуляре Рм. Следовательно, точки
перпендикуляра Рм, принадлежащие их общей части, образуют замкнутый
сегмент (с различными или одинаковыми концами), расположенный на Рм.
Центр этого сегмента является, очевидно, точкой множества ею
которая таким образом названа.
Итак, лебеговский выбор в этом случае осуществлен, и,
следовательно, мы имеем названную поверхность (S), которая пересекается
с каждой прямой, параллельной оси дст+1, в одной или большем числе
точек и ортогональная проекция которой совпадает с данным
множеством Е.
Не останавливаясь пока что на изучении природы этой поверхности
(*У), рассматриваемой как множество точек в (т -+- 1)-мерном
пространстве <§', мы хотим сделать только одно замечание: a priori видно, что
эта поверхность (S) не является однозначным множеством, если данное
аналитическое множество Е не является однозначным множеством.
Действительно, если бы (S) было однозначным множеством, то первые т
уравнений его параметрического представления
Х1 = gl (0> Х2 = 22 (')> • • •» Xm = gm (0> *п»-Н = fti+i (')»
давая параметрическое представление самого множества £, определяли бы
его как однозначное множество.
Принимая во внимание идентичность совокупности всех однозначных
множеств с совокупностью множеств, измеримых В (идентичность будет
376
Н. Н. ЛУЗИН
доказана впоследствии), мы видим, что невозможно a priori реализовать
лебеговский выбор при помощи функции переменных х19 х2У...}хту
входящей в классификацию Бэра, если данное аналитическое
множество Е неизмеримо В.
Свойства аналитических множеств.
Если дано какое-нибудь множество точек, то немедленно возникают
три основных вопроса: Будет ли это множество счетным или оно
имеет мощность континуума? Измеримо ли это множество? Какова
его категория? Мы хотим теперь исследовать свойства аналитических
множеств по отношению к этим вопросам.
Мощность.
Пусть Е — некоторое аналитическое множество, относительно
которого известно только, что оно несчетно. Пусть е — элементарное
множество, проекция которого совпадает с множеством Е.
Так как диаметры параллелепипедов ранга п стремятся к нулю,
когда п неограниченно возрастает, и так как Е несчетно, то существует
настолько большое целое положительное число л, что среди
параллелепипедов ранга п имеются два параллелепипеда к и к', обладающие
следующими свойствами:
1°. Проекции к и к' не имеют общих точек.
2°. Проекции частей е, заключенных в гс и в тс', также несчетны.
Следовательно, мы находимся в тех же условиях, что и раньше,
и мы можем определить в каждом из двух параллелепипедов тс и тс' два
новых параллелепипеда, обладающих теми же свойствами; мы получим
таким образом четыре определенных параллелепипеда. Повторим такие же
операции в каждом из них и получим восемь определенных
параллелепипедов, обладающих теми же свойствами; будем продолжать этот
процесс неограниченно.
Ясно, что множество точек, принадлежащих каждая бесконечному
числу параллелепипедов, определенных таким образом, является
совершенным множеством и содержится в элементарном множестве е.
К тому же проекции двух различных точек этого множества всегда
различны.
Отсюда следует, что проекция этого совершенного множества также
является совершенным множеством. И так как это последнее
содержится, очевидно, в данном аналитическом множестве Е, то мы получаем
следующее предложение:
Каждое несчетное аналитическое множество необходимо содержит
совершенное множество^ следовательно, имеет мощность
континуума 1.
1 Это результат Суслина. См. мою звметку „Sur la classification de M. Baire".
Comptes Rendus, 8 января 1917 г. (стр. 270«настоящего тома. — Ред.)
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ 377
Измеримость.
Пусть Е — любое аналитическое множество, относительно которого
известно только, что его внешняя мера не равна нулю, теЕ^>0.
Прежде всего мы сделаем совершенно тривиальное замечание: дая
доказательства измеримости любого множества точек £, внешняя мера
которого не равна нулю, нужно установить, что оно содержит
замкнутое множество F> мера которого больше, чем твЕ—е, где г — сколь
угодно малое положительное число; и этого достаточно.
Действительно, с одной стороны, можно покрыть точки множества Е
рядом параллелепипедов (интервалов, прямоугольников), общая
протяженность (длина, площадь, объем) которых меньше, чем т,£н-£.
С другой стороны, все точки, не принадлежащие множеству Е>
очевидно, входят в ряд параллелепипедов, внешних относительно
замкнутого множества F, полная протяженность которых меньше, чем 1 —mF-+-e.
Следовательно, полная протяженность обоих этих рядов
параллелепипедов меньше, чем теЕ -+- е ч- 1 — mF-+- £ <С 1 -+- 3s. Следовательно, Е
измеримо. Несмотря на свою крайнюю банальность, это замечание
будет нам очень полезно.
Еще одно замечание. Если мы имеем последовательность Еи Е.2,...
каких-нибудь множеств, не подчиняющихся никаким ограничениям, то
верхняя мера множества-суммы первых п членов последовательности
стремится к верхней мере соединения всех членов последовательности,
когда п неограниченно возрастает.
Отсюда следует, что можно взять настолько большое число лх
параллелепипедов первого ранга, что часть элементарного множества е,
содержащаяся в этих параллелепипедах, имеет проекцию, внешняя мера
которой больше, чем т^Е— ^
Будем поступать таким же образом с параллелепипедами второго
ранга, содержащимися в выбранных параллелепипедах первого ранга;
мы можем взять настолько большое число п2 параллелепипедов второго
ранга, чтобы часть еу содержащаяся в них, имела проекцию, внешняя
мера которой больше, чем теЕ — ех — е2, и т. д.
Таким образом, составляем совокупность К1У
л»» ^з> * * •
параллелепипедов соответственно рангов 1, 2, 3,..., каждая из
которых состоит из конечного числа параллелепипедов и лежит внутри
предыдущей, таких, что проекция части элементарного множества е,
содержащаяся в параллелепипедах совокупности Кп> имеет внешнюю
меру большую, чем тД — \ — е2 — • • • — еп1 здесь ряд положительных
чисел еа ч- е2 ч-.. . сходится и имеет сумму е, где е сколь угодно
мало.
Отсюда следует, что проекция точек совокупности Кп является
совершенным множеством, мера которого больше, чем mji — е:
обозначим его через F.
С другой стороны, общая часть совокупностей Кг> Къ... является,
очевидно, замкнутым множеством точек, и ясно, что множество F
378
Н. Н. ЛУЗИН
является проекцией последнего. Следовательно, множество F
содержится в данном аналитическом множестве Е.
Мы пришли таким образом к следующему предложению:
Каждое аналитическое множество измеримо1.
Категория.
Речь идет о том, чтобы доказать, что никакое аналитическое
множество никогда не является тем, что А. Лебег иногда называл
множествами, которые не суть Z, или, если воспользоваться снова
терминологией А. Данжуа, что аналитическое множество никогда не исчер-
паемо без остатка.
Другими словами, нужно показать, что, каково бы ни было
совершенное множество Р, существует порция те множества Р такая, что
либо данное аналитическое множество Я, либо его дополнение СЕ
является множеством первой категории на те.
Очевидно, достаточно установить, что если данное аналитическое
множество Е не является множеством первой категории ни на какой
порции множества Р, то дополнительное множество СЕ является
множеством первой категории на Р.
Прежде всего в (т н- 1)-мерном пространстве, где расположено
элементарное множество е> мы будем рассматривать основной куб как
единственный параллелепипед нулевого ранга.
Начнем с вычеркивания всех параллелепипедов, каков бы ни был
их ранг, таких, что принадлежащие им части е имеют проекции,
являющиеся множествами первой категории на Р; ясно, что останутся
параллелепипеды всех рангов.
Установив это, с каждым из оставшихся параллелепипедов, каков бы
ни был его ранг, будем поступать следующим образом: пусть А— этот
параллелепипед; рассмотрим часть элементарного множества е, которая
принадлежит А. Так как А — один из сохранившихся параллелепипедов,
то проекция этой части е не является множеством первой категории
на Р. Следовательно, в Р существует вполне определенное замкнутое
множество F такое, что эта проекция никогда не является множеством
первой категории ни на какой порции те множества Р, не содержащей
точек F; и это не имеет места, если порция те содержится в Р.
Установив этот первый пункт, определим для каждого
сохранившегося параллелепипеда Д\ содержащегося в А и имеющего
непосредственно следующий ранг, соответствующее замкнутое множество F.
Ясно, что общая часть всех этих замкнутых множеств F не плотна
на каждой порции те множества Р, не содержащей точек множества Р.
Следовательно, множество точек, общих всем множествам Г и не
принадлежащих Р, является множеством, не плотным на Р; обозначим его
через //(А).
1 Теорема V моей заметки (1917): „Каждое Л-множество измеримо L"; см. также
N. Lusin etW. Sierpinski. „Sur quelques proprietes des ensembles (A)a. Bull, de
l'Acad. des Sci., Cracovie, серия A, № 4—5A, 44, 1918.
МЕМУАР ОБ АНАЛИТИЧЕСКИХ И ПРОЕКТИВНЫХ МНОЖЕСТВАХ
379
Таким образом, каждому параллелепипеду А, каков бы ни был его
ранг, соответствует вполне определенное множество, //(А), не плотное
-на Р. Отсюда следует, что соединение всех таких множеств //(А)
является множеством первой категории на Р. Обозначим его
через Н.
Мы докажем сейчас, что каждая точка q множества Р, не
принадлежащая Ну является точкой данного аналитического множества Е.
Действительно, так как q не принадлежит f/(An), где А0 есть
основной куб, то в А0 существует параллелепипед At ранга 1 такой, что
точка q будет внешней для замкнутого множества Fx,
соответствующего Aj; так как q не принадлежит //(AL), то в \ существует
параллелепипед А2 ранга 2 такой, что q будет внешней относительно
замкнутого множества F2> соответствующего А^, и т. д.
Таким образом, выбираем параллелепипеды Д0, Др А,,,..., ранги
которых соответственно равны 0, 1, 2,..., каждый из которых ^.ежят
внутри предыдущего, и таких, что точка q не принадлежит никакому
из замкнутых множеств Fn.
Следовательно, точка q обязательно принадлежит проекции каждого
из параллелепипедов А0> Ди Д2).. .. Отсюда заключаем, что точка q
есть проекция точки элементарного множества е, следовательно,
принадлежит Е1 (ч. т. д.).
Аналитическая форма, которую можно придать этому предложению,
быть может, сделает его более ясным; рассмотрим в /n-мерном
евклидовом пространстве произвольное аналитическое множество Е. Пусть
j—функция, равная 1 для точек множества Е и равная 0 вне Е.
Если Р — какое-нибудь совершенное множество, расположенное
в рассматриваемом пространстве, то имеются порции множества Р,
на которых либо Е, либо его дополнение СЕ является множеством
первой категории. Следовательно, таким образом определенная
функция / обладает необходимым свойством Р. Бэра, принадлежащим всем
функциям его классификации, т. е. / точечно-разрывна на каждом
совершенном множестве, если пренебрегать множествами первой
категории относительно этого совершенного множества Р.
Примечание. Мы дополним эти результаты следующим
замечанием. Если некоторое множество измеримо, то его
дополнение также измеримо, и мы имеем то же заключение д\я свойств
быть множеством типа Z. Следовательно,
Дополнение к аналитическому множеству измеримо и является
множеством типа Z (не исчерпаемо без остатка).
1 Теорема VI моей заметки (1917): „Если множество Еу которое является
множеством (А)% образованным при помощи точек совершенного множества Я,
является множеством второй категории на Р, то существует интервал^
содержащий точки Р% в котором дополнение множеству является множеством
первой категории Р". См. также N. Lusin etW. Sierpinski. Sur un ensemble non
mesurable B. Journ. 4e Math., П, 68, 1923; 0. Nikodym. Fund. Math., VII, 1S3.
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ*
Введение
В 1905 г. Лебег в своем мемуаре „Об аналитически представимых
функциях" дал убедительное построение некоторого точечного
множества, которое употреблялось им как переходный инструмент при
отыскании индивидуальной функции, ускользающей от какого бы то ни было
аналитического представления. По причине вспомогательной роли,
которую играет это множество Е9 знаменитый автор, желая поскорее
закончить определение функции, не определимой аналитически, опустил
углубленный анализ этого предварительного множества Еу так как он
казался длинным и утомительным для читателя и в то же время
совершенно излишним а^я конечной цели (см. [20]).
Именно эта не определимая аналитически функция, названная
автором без применения Аксиомы выбора, и стала истинным источником
ряда изысканий, из которых все яснее и яснее выявлялось понятие
аналитического множества.
В настоящее время, когда теория аналитических множеств формально
закончена, важно признать, применяя обычные рассуждения теории
функций, что именно это вспомогательное множество Е Лебега и
является само аналитическим множеством, не входящим в семейство
множеств, измеримых 5, и что в его построении содержится, как
в зародыше, вся теория аналитических множеств.
Глава первая
ПОСТРОЕНИЕ ЛЕБЕГА И ЕГО ОБОБЩЕНИЯ
I. Построение Лебега
1. Вот построение вспомогательного множества Е. Мы
воспроизводим здесь почти текстуально этот отрывок из статьи Лебега1:
„Мы предполагаем, что все рациональные числа, заключённые
между 0 и 1, расположены в некотором порядке, которого мы точно
* „Sur les ensembles analytique". Fund. Math.» X, 1— 95, 1927.
1 „Sur les fonctions representables analytiquement" (Journ. de Jordon, 1905,
стр. 213, строки 25—32, и стр. 214, строки 1—17). Для наибольшего упрощен**
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА I
381
не указываем, но считаем его определенным; пусть г,, г _>,...—
рассматриваемая последовательность. Возьмем некоторую величину х,
заключенную между 0 и 1, и запишем ее в двоичной системе счисления,
употребляя бесконечное множество раз цифру 1; разложение х вполне
определено, как только дано л::
* = ■£-«-?-*-••••
Вычеркнем из последовательности г{> г2,... все г„
соответствующие индексам / тех цифр 0., которые равны нулю; пусть r'v г'„...—
оставшиеся г. Отметим на интервале (0, 1) все точки, имеющие эти
r'v rv... в качестве абсцисс.
Возможны только два случая:
Первый случай: Отмеченные точки образуют на (0, 1) вполне
упорядоченное множество, согласно условию, что ранг этих точек
соответствует порядку, в котором мы их встречаем, пробегая слева
направо интервал (0, 1).
Второй случай: Отмеченные точки не образуют такого
множества на (0, 1).
Обозначим через § совокупность точек интервала (О <С х <С 1), Аля
которых выполняется первый случай, и через Е множество точек х>
для которых имеет место второй случай".
Множество Е является дополнительным для совокупности £, и легко
видеть, что совокупность S определена Лебегом положительным
образом, а определение множества Е только отрицательно.
Но в дальнейшем мы увидим, что имеет место как раз обратное:
мы покажем, что множество Е Лебега является аналитическим
множеством и, следовательно, есть множество положительного и конечного
определения. Что же касается совокупности £ Лебега, то мы не имеем
никакого другого положительного определения этой совокупности,
кроме определения Лебега.
П. Каноническое решето Лебега
2. Геометрическая форма, которую можно дать этому построению
Лебега, может быть сделает его более ясным. Рассмотрим две взаимно-
перпендикулярные оси и квадрат, стороны которого заданы
уравнениями
х = 0, х = 1у у = 0, у = \.
рассуждений мы позволяем себе сделать только незначительное изменение в
построении Лебега, относя дееся к применению во всех случаях разложений с бесконечным
Множеством цифр 1, благодаря чему ко множеству Е Лебега могут добавиться
только рациональные точки.
382
Н. Н. ЛУЗИН
Отметим на левой вертикальной стороне л: = 0 квадрата все
рациональные точки Гр г2,.. .; их множество R всюду плотно на этой
стороне.
Проведем внутри квадрата через точку гп параллель оси х и,
разделив ее на 2П равных интервалов, перенумеруем их при помощи целых
чисел 1, 2, 3,..., 2П слева направо. Если мы вычеркнем из этой
параллели все интервалы, имеющие нечетные номера, то множество
оставшихся точек будет образовано всеми точками замкнутых
равноотстоящих отрезков числом 2П~1, общая длина которых равна 1:2.
Таким образом, мы видим, что на каждой из параллелей у = г1У
у = г2,..., у = г„,... помещены, в конечном числе, замкнутые отрезки,,
не имеющие общих точек.
Соединение всех этих отрезков мы назовем каноническим
решетом Лебега и обозначим его через С.
3. По самому определению каноническое решето С есть счетное
множество определенных замкнутых отрезков, параллельных оси ху
распределенное специальным образом внутри квадрата; к тому же
ясно, что это множество всюду плотно на этом квадрате.
Название решета легко оправдать. В самом деле, пусть х — про*
извольная точка, принадлежащая полусегменту1 О <С х ^ 1 оси OXt
следовательно, точка х расположена на нижней стороне квадрата.
Обозначим через Рх перпендикуляр, восставленный в этой точке х
к оси ОХ. Ясно, что этот перпендикуляр пересекает решето С самое
большее в счетном множестве точек; обозначим его через Rz. Так как
все ординаты точек множества Rx являются рациональными числами,,
то ортогональная проекция множества Rx на ось ОY содержится
во множестве R рациональных точек, которые принадлежат стороне
х = 0 квадрата.
Но гораздо более важное замечание, относящееся к одному из самых
прекрасных свойств канонического решета С Лебега, есть следующее:,
точка гп стороны х = 0 квадрата принадлежит проекции множества Rx
на ось OYj если 9Л=1, и только в этом случае.
Отсюда следует, что счетное множество Rx образует на
перпендикуляре Рх вполне упорядоченное множество для всех точек х
совокупности <?, причем ранг точек множества Rx соответствует
порядку, в котором они встречаются на перпендикуляре Рх,
пробегаемом снизу вверх, и Rx не является вполне упорядоченным
множеством при принятом условии о ранге ни для какой точки х
множества Е.
Отсюда мы немедленно заключаем, что для каждой точки х
множества Е Rx содержит часть, не имеющую начального элемента;
следовательно, в этом случае возможно будет определить убывающую
1 Полусегментом называется всякий замкнутый отрезок, из которого выброшен*
одна и только один из его концов.
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА 1
383
последовательность а1У а2,..., образованную элементами множества
Rx, так что каждый последующий лежит ниже предыдущего, и
которые, очевидно, стремятся к некоторой точке р., расположенной на
перпендикуляре Pz. Таким образом, в этом случае точки множества Rz
допускают обратное движение, и ясно, что среди предельных точек
множества Rx> в каждой из которых Rx имеет обратное движение, мы
имеем самую низкую точку; обозначим через ^ (лс) ординату этой точки.
Резюмируем: самая совокупность замкнутых отрезков С
просеивает автоматически точки основного интервала О <С л: <Г 1> пропуская
точки совокупности £; остаются одни только точки множества Е. Отсюда
название решета.
Мы назовем множеством, просеянным посредством решета С, или
просто просеянным множеством, это множество Е (а не
совокупность &).
Заметим, наконец, что отныне множество Е представляется
определенным положительным образом, так как свойство множества Rx иметь
обратную предельную точку \*-(х) есть чисто положительное свойство.
III. Аналитичность множества Е Лебега
4. Мы называем аналитическим множеством всякое линейное
множество точек, которое является множеством значений некоторой
функции, разрывной только для счетного множества значений
переменного г.
1 См. мою заметку в Comptes Rend us, 1917 г. Борель уже давно привлек
внимание к этим функциям, класс которых заслуживает быть изучаемым немедленно
после класса непрерывных функций. Процитируем текстуально некоторые отрывки
из книги Бореля („Lecons sur la theorie des fonctions". Iе ed., 1898; Note I, стр. 109
н Note III, стр. 126): n . . . в исчислении можно пользоваться функцией только если
она определена при помощи счетного множества элементов. Таков случай
непрерывных функций, а также функций разрывных, но разрывных только для счетного
множества значений переменного. В самом деле, такие функции могут быть определены
посредством счетного числа условий. . .
„ . . . Если они различаются, то при достаточной настойчивости мы обязательно
это заметим. Ничего подобного нет для разрывных функций (здесь речь идет
о самых общих разрывных функциях): такая функция определена несчетным
множеством условий; практически это сводится к тому, что ее невозможно
определить. Среди самых общих разрывных функций, которые кажутся, по крайней
мере на момент, подлежащими исключению из математических рассмотрений, следовало
бы различать функции, разрывность которых подчинена ограничениям. Эти
ограничения должны быть такого рода, чтобы функция могла быть всецело
определена счетным множеством условий. Тогда множество функций, удовлетворяющих
этим ограничительным условиям, имеет мощность континуума. Среди функций,
удовлетворяющих ограничительным условиям такого рода, я процитирую функции,
разрывные только в счетном множестве точек, которые были с пользой рассмотрены
несколькими математиками".
Было бы очень интересно знать, соответствует ли принадлежащее Борелю
понятие функции, определенной счетным множеством условий, понятию функции,
которую можно назвать, принадлежащему Лебегу. Вряд ли возможно найти инди-
384
Н. Н. ЛУЗИН
Основание для этого названия очень ясно: так как каждая функция
x=f(t),
разрывная только в счетном множестве точек основного интервала
(0<C,t <С1)у является функцией первого класса по классификации Бэра,
то существует ряд многочленов от / с целыми коэффициентами1
Px(t) + P2(t) + ... + P„(t)4-... у
сходящийся для каждого значения / интервала (О <С ^ <С 1)> сумма
которого равна f(t). Итак, каждое линейное аналитическое множество есть
множество значений, которые принимает на некотором интервале сумма
сходящегося ряда многочленов с целыми коэффициентами, и,
следовательно, оно определено при помощи аналитического равенства2.
Установив это определение, мы обратим свое внимание на
множество Е Лебега, определенное при помощи канонического решета С.
Очень легко доказать, что это множество является аналитическим
множеством.
5. Для доказательства этого предложения рассмотрим в
плоскости XOY каноническое решето С Пусть о — произвольный отрезок,
принадлежащий С; в силу предыдущего з есть замкнутый отрезок,
параллельный оси ОХ.
Опустим из обоих концов отрезка о перпендикуляры на ось ОХ;
мы получим таким образом прямоугольник Q, основание которого
находится на оси ОХ. Так как отрезков з решета С — счетное множество,
видуально называемую функцию (fonction nommable), которая не была бы
определима счетным множеством условий.
В „Lecons sur les fonctions de variables reelles" (1905) Бореля мы находим
первые исследования о функциях, разрывных только в счетном множестве точек
(стр. 94—98).
1 Всякая функция первою класса по Бэру, определенная на (0<^х <^\),
исключая концы* разложима в ряд многочленов с целыми коэффициентами. Это —
предложение И. Н. Хлодовского.
2 Название аналитического множества дано, следуя предложению Лебега:
называть аналитическими множествами все множества, которые могут быть
определены аналитическими равенствами, или неравенствами.
„Из того, что будет доказано далее, следует, что множества, измеримые В,
это те, которые могут быть определены аналитическими равенствами, или
неравенствами; в силу втого они заслуживают быть названными аналитическими
множествами" („Sur les fonctions representables analytiquement", стр. 16S).
Обратное предложение (т. е. что всякое множество, определенное аналитическими
равенствами или неравенствами, есть множество, измеримое В) неверно.
В ограниченных рамках наших заметок в Comptes Rendus (S о u s 1 i n. Sur une
definition des ensembles mesurables В sans nombres transfinis; N. Lusin. Sur la
classification de M. Rene Baire. Comptes Rendus, 164, 88 и 91, 1917 г.), где можно
найти все основные результаты об аналитических множествах, сформулированные,
впрочем, без доказательств, мы называли аналитические множества кратким
названием: (ЛЬмложсства (см. [З]).
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА I
385
мы можем перенумеровать все построенные прямоугольники при помощи
целых положительных чисел:
Qi> Q„ ..., Q*, ... (l)
Обозначим через хк абсциссу правого конца основания
прямоугольника Qfc.
Установив это, займемся построением функции f{t)y разрывной только
в счетном множестве точек интервала (0<*<1), множество значений
которой совпадает с лебеговским множеством Е.
Пусть t — произвольное иррациональное число, заключенное между О
и 1 и определенное разложением вида
t =
а2
где аг, а2, а3, ... — определенные целые положительные числа.
Поставим в соответствие t вполне определенную
последовательность
*3„ л:р2, ..., л:эп, ..., (2)
образованную правыми концами оснований некоторых прямоугольников Q,
определенную следующим рекуррентным соотношением:
1° р1 = а1; следовательно, мы имеем х?1 = х*1;
2° если число xf, определено, рассмотрим все прямоугольники Q,
1 т—1
которые являются внутренними по отношению к прямоугольнику Qp ;
их множество образует часть последовательности (1); следовательно,
оно тоже является последовательностью. Число х0 будет определено
как равное члену ранга ат этой последовательности (т. е. лгр есть
абсцисса правого конца проекций соответствующего прямоугольника. —
Ред.).
Ясно, что последовательность (2), образованная положительными
числами, убывает; следовательно, она имеет предел. Так как этот
предел определен единственным образом заданием t, то мы обозначим его
через f(t).
6. Легко доказать, что построенная таким образом функция f(t)
непрерывна в каждой иррациональной точке £0 относительно
множества всех иррациональных точек.
В самом деле, обозначим через </ множество всех иррациональных
чисел интервала (0<*<1). Функция f(t) определена всюду на о7;
пусть t0 — произвольная точка множества 7, которую мы будем
предполагать фиксированной.
386
ri. H. ЛУЗИН
Заставим подвижную точку t множества ^7 стремиться к *0; число TV
первых неполных частных разложения t в непрерывную дробь, которые
совпадают с соответствующими неполными частными разложения t{)>
безгранично растет. Следовательно, последовательность (2) для точки t
и последовательность (2) для точки t0 обе имеют сколь угодно большое
число соответственно равных первых членов. Значит, члены
последовательности (2), которые следуют за произвольным членом х* , все
являются точками, принадлежащими основанию прямоугольника Q^ . Так
как длина основания прямоугольника Qjt стремится к нулю, когда к
неограниченно растет, то число /(/) стремится к /(/0)> когда точка /
стремится к /0, оставаясь все время на с7, что и доказывает
относительную непрерывность функции f(t).
7. Установив это, мы хотим изучить множество значений функции /.
Рассмотрим прямоугольники, соответствующие членам
последовательности
QPl. Q;v •■•• <&.• ••• (3)
Так как каждый прямоугольник Q,3W содержит последующий, то это
последовательность прямоугольников, вложенных друг в друга и
основания которых, расположенные на оси ОХ, стремятся к нулю. Высоты
этих прямоугольников очевидно убывают. И так как точка x=f(t)>
являясь пределом последовательности (2), принадлежит всем основаниям
прямоугольников (3), то ясно, что решето С определяет на
перпендикуляре Рх нисходящую последовательность точек множества Rx>
Следовательно, каждое значение f(t) функции / является элементом лебе-
говского множества Е.
Очевидно, что обратное тоже имеет место: каждая точка лебегов-
ского множества Е может быть получена таким образом.
Итак, множество значений, которые принимает функция f(t) для
иррациональных значений переменного t, совпадает с лебеговским
множеством Е.
$. Нам остается только закончить определение функции / во всех
рациональных точках интервала (О <С ^ <Г 1), не нарушая ни множества £
ее значений, ни ее непрерывности в иррациональных точках [42].
Чтобы удовлетворить этому требованию предположим, что все
рациональные точки интервала (0<*<[1) расположены в определенном
порядке; пусть tlf t2y ... — рассматриваемая последовательность.
Обозначим через Мп максимум функции / в точке tn относительно
множества <Э'.
Так как функция / ограничена на g7, мы легко замечаем, что все
числа М19 М2, ... конечны; мы представим их точками интервала
(0<х<О), на котором расположено лебеговское множество Е.
Теперь достаточно взять для каждой точки Мп точку Мп> которая
принадлежит множеству Е и сколь угодно близка к Мпу когда п неог-
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА I
387
раниченно растет; функция /(f), подчиненная условию, что в точках
tl9 tv ... она соответственно равна абсциссам соответствующих точек
MJ, M'v ..., очевидно удовлетворяет всем желаемым условиям (ч. т. д.).
9. Итак мы пришли к следующему предложению:
Лебеговское множество точек Е есть аналитическое множество.
Так как определение математического объекта при помощи всюду
сходящегося ряда многочленов с целыми коэффициентами является
положительным и конечным определением, то мы можем сказать, что
лебеговское множество Е может быть рассматриваемо как
определенное положительным и конечным образом.
IV. Решето общего вида.
10. Здесь возникает очень важный вопрос. Мы только что убедились,
что лебеговское множество Е есть аналитическое множество.
Измеримо оно В или нет? И если оно неизмеримо В, то каким
механизмом рассуждения мы можем открыть его неизмеримость В?
Но прежде чем приступать к этим трудным вопросам, полезно
несколько обобщить понятие канонического решета С Лебега.
Возьмем, как мы делали раньше, две взаимно-перпендикулярные
оси XOY и квадрат Ку стороны которого заданы уравнениями
х = 0, х = 1; у = 0> у = 1.
Мы назовем решетом всякое счетное соединение С замкнутых
отрезков о, параллельных оси ОХ и расположенных внутри
квадрата К.
По аналогии с предыдущим мы обозначим через & совокупность
точек х интервала (0<C.t<^l), Аля которых перпендикуляр Рху
восставленный в л: к оси ОХ> пересекает решето С по множеству точек,
вполне упорядоченному при условии, что ранг точек будет
соответствовать положительному направлению оси OY.
Множество точек интервала (0< х < 1), которые не принадлежат
совокупности £, мы обозначим через Е.
По определению множества £, перпендикуляр Рх в каждой точке х
множества Е пересекает решето С в счетном множестве Rxt которое
не вполне упорядочено, при том же условии для ранга. Следовательно,
в этом случае можно определить убывающую последовательность а19
а2, ..., образованную точками множества Rx, так что каждая
последующая ниже предыдущей, и которые стремятся к некоторой точке р.,
расположенной на перпендикуляре Рх. Итак, в этом случае множество Rx
находится в обратном движении, и ясно, что среди предельных точек р.
перпендикуляра Pxt в каждой из которых множество Rx имеет обратное
движение, имеется самая низкая точка; мы обозначим ее ординату
через н- (х).
Именно это множество Е (а не совокупность S) мы назовем
множеством, просеянным посредством решета С.
388
Н. Н. Л У 3 И Н
Решето С Лебега, которое мы рассмотрели прежде, мы назовем
каноническим решетом.
11. Прямая теорема. Мы обобщим теорему об аналитичности лебе-
говского множества Е.
Теорема (прямая). Каждое множество точеку просеянное
посредством решета общего вида> есть аналитическое множество.
Чтобы доказать это, мы опять применим тот же метод рассуждения.
Но необходимо принять некоторую предосторожность, чтобы быть
уверенным, что все рассуждения в этом доказательстве, данном для случая
канонического решета, еще приложимы к случаю общего решета.
Следующие свойства канонического решета сделали действительным
предшествующее рассуждение:
1°. Длина основания прямоугольника Qn стремится к нулю, когда п
бесконечно возрастает.
2°. Каково бы ни было число л, в прямоугольнике Qn существует
прямоугольник Qm, высота которого строго меньше высоты
прямоугольника Q„.
Итак, все сводится к доказательству того, что можно преобразовать
данное общее решето С в другое, обладающее двумя вышеуказанными
свойствами канонического решета, не нарушая при этом множества Ef
просеянного посредством решета С.
Перенумеруем замкнутые отрезки данного решета С при помощи
целых положительных чисел; пусть
— эта последовательность. Начнем с целого положительного числа л.
Мы разделим основной интервал (О <С х <С 1) на 2м равных частей и
спроектируем 2л концоь первых п отрезков последовательности (о')
на ось ОХ.
Если мы отметим на интервале (О <С х < 1) точки деления и эти
проекции, мы получим конечное соединение точек; обозначим его через Zn.
Разделим, наконец, замкнутый отрезок а'п на конечное число маленьких
замкнутых отрезков о" точками, абсциссы которых принадлежат Zn.
Установив это, заставим л изменяться. Множество всех этих
полученных таким образом маленьких замкнутых отрезков о" образуют,
очевидно, новое общее решето С", которое обладает теперь первым свойством
(1°) канонического решета, и очевидно, что просеянное множество Е
остается нетронутым.
12. Итак, все сводится к удовлетворению второго свойства (2°)
канонического решета. Напомним, что каждой точке х просеянного
множества Е соответствует относительно решета С" вполне определенное число,
зависящее от этой точки и которое мы обозначили через и. (х).
Следовательно, мы имеем вполне определенную кривую
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА I
389
определенную на просеянном множестве Е.
Установив это, удалим из решета С все его замкнутые отрезки з",
все точки которых имеют ординаты, меньшие или равные ординатам
точек кривой i/ = |x(x), обладающих теми же абсциссами. Так как
просеянное множество Е предполагается не пустым, то существуют
неудаленные отрезки а'', и даже в счетном числе. Их множество образует
новое решето, которое мы обозначим через С".
Вполне очевидно, что решето С" обладает свойствами 1° и 2°
канонического решета, и что просеянное множество Е опять остается
нетронутым.
С этого момента все рассуждения предыдущего доказательства
аналитичности множества, просеянного посредством канонического решета
Лебега, примененные к решету С", становятся строгими (ч. т. д.).
Резюмируем: если Е просеяно посредством решета общего вида,
то множество Е является аналитическим множеством.
13. Преобразование точек разрыва. Мы должны спросить себя,
является ли найденное условие того, чтобы множество было просеяно
посредством некоторого решета, достаточным. Мы покажем, что
необходимое условие быть аналитическим множеством является в то же
время достаточным.
Для доказательства следует сделать сначала несколько
предварительных замечаний.
Пусть Е — аналитическое множество, расположенное на интервале
(0<ix <Cl). По самому определению существует такая функция
x=f(t), определенная на интервале (0<С'<С1) и разрывная только
в счетном множестве точек, что Е есть множество всех ее значений.
Я теперь утверждаю, что всегда можно предполагать функцию /(f)
разрывной только в рациональных точках интервала (О <С * <С 1)»
В самом деле, пусть D — множество точек разрыва функции /;
D счетно. Известно, что среди преобразований Analysis Situs
замкнутого отрезка [0^*^1| в самого себя существуют такие, которые
преобразуют данное произвольное счетное множество в часть множества
рациональных точек. Если д\я множества D мы выполним такое
преобразование, мы, очевидно, получим функцию от t, обладающую
указанным свойством.
Чтобы избежать трудностей второстепенного порядка, мы отныне
будем предполагать функцию f{t) разрывной только в рациональных
точках.
14. Регулярные разбиения* Мы покажем, что если не принимать
во внимание счетного множества точек множества Е, то можно
предполагать функцию f(t) непрерывной справа на (0<^<С1) в каждой
точке t% без всякого исключения, даже в рациональных точках и
в начале координат О.
Для доказательства достаточно подвергнуть функцию f(t)
специальному преобразованию. Прежде всего введем полезное определение:
390
Н. Н. ЛУЗИН
мы скажем, что открытый интервал & разбит регулярным образом
на бесконечное множество открытых частных интервалов^ если
из Ь удалено приводимое множество, имеющее предельными точками
только концы интервала Ъ.
Установив это определение, мы покажем, что каждый открытый
интервал Ь может быть разбит регулярным образом на бесконечное
множество таких частных интервалов, что на каждом из них
колебание (полное) функции / меньше е, где е — сколь угодно малое
положительное число,
В самом деле, так как / разрывна только в рациональных точках,
то множество точек интервала о, где мера разрывности функции /
не меньше е, есть замкнутое приводимое множество; обозначим его
через Ft. Из определения множества Ft следует, что колебание функции
/ в каждой точке интервала 5, не принадлежащей Ft> строго меньше е.
Отсюда мы заключаем, что каждый из открытых частных интервалов
можно разбить регулярным и вполне определенным образом так, чтобы
колебание (полное) функции / ца каждом из них было меньше е.
Очевидно, что соединение всех частных интервалов, определенных на
каждом из смежных интервалов множества F*> образует искомое
регулярное разбиение интервала 5 (ч. т. д.).
Установив это, зададимся последовательностью положительных
чисел еа, е2, ..., стремящихся к нулю. Начнем с основного интервала
(0<С<С1)- Согласно предыдущему мы можем разбить (0<С*<1)
регулярным образом на бесконечное множество таких частных интервалов,
что на каждом из них колебание (полное) функции / меньше е1#
Обозначим через /?е, приводимое множество, для которого все эти частные
интервалы являются смежными. Заметим, что мы можем предполагать
длину каждого из этих смежных интервалов меньшей е1#
Разобьем каждый из смежных интервалов множества Rtl регулярным
образом на бесконечное множество таких частных интервалов, что на
каждом из них колебание (полное) функции / меньше s2. Обозначим
через /?е, приводимое множество, д\я которого все эти частные
интервалы являются смежными. Мы можем предполагать длину каждого
из этих смежных интервалов меньшей е2.
Вообще, если приводимое множество Rz определено на (0 <С t <C 1)>
разобьем каждый из смежных интервалов множества Rt регулярным
образом на бесконечное множество таких частных интервалов, что на
каждом из них колебание (полное) функции / меньше ея. Обозначим
через Rlfl приводимое множество, дая которого все эти частные
интервалы являются смежными; мы можем предполагать их длины
меньшими е,«
Таким образом, мы образуем неограниченную последовательность
/\t, > /Vgj > • • •» *Wn> * * •
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА I
391
приводимых множеств, расположенных на (0<*<1), каждое из
которых содержит предшествующие.
15. Преобразование функции f(t). Возьмем полусегмент
0<т<1
и разобьем его точками Ми М2, ..., Мк> ..., стремящимися к 1, на
бесконечное множество частных полусегментов, каждый из которых замкнут
слева и открыт справа. Эти полусегменты будут называться
полусегментами ранга 1. Точно так же разобьем каждый из полусегментов
ранга 1 точками, стремящимися к его правой границе, на бесконечное
множество частных полусегментов, каждый из которых замкнут слева
и открыт справа; эти полусегменты будут называться полусегментами
ранга 2. Вообще, определив все полусегменты ранга п — 1, мы разобьем
подобным образом каждый из них на бесконечное множество частных
полусегментов, замкнутых слева и открытых справа; эти частные
полусегменты будут называться полусегментами ранга п. И т. д.
Заметим, что длину каждого из полусегментов ранга п можно предполагать
меньшей 1 : п.
Установив это, для каждого значения п установим взаимно
однозначное соответствие между смежными интервалами ко множеству R€ft
и полусегментами ранга п так, чтобы каждому интервалу о, смежному
ко множеству R^ и содержащемуся в некотором интервале о', смежном
ко множеству Rtn,iy соответствовал полусегмент d ранга л, также
содержащийся в полусегменте а" ранга п — 1, который соответствует
интервалу &'.
Для этого установим взаимно однозначное соответствие между
смежными интервалами ко множеству Rh и полусегментами ранга 1; потом
между смежными интервалами ко множеству Rh и полусегментами
ранга 2, содержащимися соответственно в парах о, d интервалов,
смежных ко множеству /?,,, и соответствующих полусегментов ранга 1.
Продолжаем таким образом неограниченно: в каждой паре S', d\
образованной некоторым интервалом &', смежным ко множеству Лп_„ и
соответствующим полусегментом d' ранга п — 1, возьмем все интервалы,
смежные ко множеству Rifl1 и все полусегменты ранга я, содержащиеся
соответственно в о' и d\ и заставим соответствовать определенным
образом каждому о некоторое d> и обратно. Ясно, что, продолжая
таким образом, мы установим искомое взаимно однозначное
соответствие между смежными интервалами ко множествам RhJ Rti, /?«„ ... и
полусегментами ранга 1, 2, 3, ....
Установив это, возьмем на полусегменте
0<^<1
произвольную точку х. Так как точка х принадлежит некоторому
определенному полусегменту dx ранга 1, некоторому определенному
392
Н. Н. ЛУЗИН
полусегменту d2 ранга 2 и так далее, то мы имеем вполне определенную
бесконечную последовательность
d\, d>, d:i, ...
полусегментов соответственно рангов 1, 2, 3, .. ♦, каждый из которых
вложен в предшествующий, и стягивающихся, очевидно, к точке х,
расположенной внутри них или в их левом конце.
Этой последовательности соответствует, очевидно, бесконечная
последовательность
Oj, О.,, 03, ...
интервалов, смежных соответственно ко множествам Rtx> Rtzy Rhy ...,
каждый из которых вложен (в узком смысле) в предшествующий и
которые, очевидно, стремятся к некоторой точке t, расположенной
внутри них (в узком смысле).
Следовательно, мы имеем
Ясно, что определенная таким образом функция ср (х) есть функция,
определенная в каждой точке х полусегмента (0^х<^1). Так как
точка / не принадлежит ни одному из приводимых множеств /?€|, /?е.,
/?£j, ..., и так как каждая точка t основного интервала (О <Сх <С 1)> не
принадлежащая ни одному из этих приводимых множеств, может быть
получена таким образом, то очевидно, что соотношение
устанавливает взаимно однозначное соответствие между точками
полусегмента (0^х<^1) и точками интервала (О <С*<С 1)> которые не
принадлежат счетному множеству D> образованному соединением множеств
Л„ Rt2> • • •
Установив это, рассмотрим сложную функцию ^(х), определенную
на полусегменте (О =С х <^ 1) равенством
Так как каждой точке х, принадлежащей определенному
полусегменту d ранга л, соответствует некоторая точка t интервала 8,
смежного ко множеству Ren и соответствующего полусегменту с/, то легко
видеть, что колебание (полное) функции F(*) на d меньше ея.
Следовательно, функция F(t) непрерывна справа в каждой точке х
полусегмента (0^х<1) (ч. т. д.).
16# Обратная теорема. Рассмотрим множество Е' значений сложной
функции
* = F{r),
которые она принимает на полусегменте (0<^х<1). Мы сейчас пока-
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА I
393
жем, что Е' есть множество^ просеянное посредством решета общего
вида.
Для построения возьмем произвольный полусегмент d ранга л.
Пусть Н и А — соответственно максимум и минимум функции F{") на а1.
Восставим в правом конце полусегмента d перпендикуляр к оси т
и отметим на этом перпендикуляре две точки, ординаты которых равны
Н и Л. Таким образом, мы получим вполне определенный замкнутый
отрезок а, расположенный на этом перпендикуляре и имеющий своими
концами отмеченные точки; этот отрезок з вертикален, следовательно,
параллелен оси лг-ов.
Если мы выполним это построение для каждого полусегмента d
ранга п и будем изменять целое положительное число л, мы получим
счетное множество замкнутых отрезков а, параллельных оси лг-ов.
Следовательно, мы имегм некоторое решето общего вида С.
Рассмотрим множество точек оси лг-ов, просеянное посредством этого
решета С". Мы обозначим это множество через Е'\ Для того чтобы
какая-нибудь точка лг оси ОХ принадлежала множеству Е", необходимо
и достаточно, чтобы она содержалась в проекциях на эту ось
бесконечного множества замкнутых отрезков о решета С", абсциссы которых
образуют убывающую последовательность. И так как сложная функция
F(t) непрерывна справа в каждой точке t полусегмента (0^~<С1),
мы отсюда заключаем, что множество Е" совпадает с множеством Е'
значений функции F (~).
Нам остается лишь сравнить данное аналитическое множество Е
с множеством Е'.
Из самого вида функции F(t)
следует, что Е' является частью множества Е. И так как функция
*=?(т)
принимает каждое значение ty принадлежащее интервалу (0<О<С1)>
кроме элементов приводимых множеств /?.,, /?ч, ..., мы легко
констатируем, что множество Е отличается от множества Е\ быть может,
только счетным множеством точек х19 лг2,
Теперь их легко прибавить ко множеству Е, произведя небольшое
изменение решета С В самом деле, отметим на интервале (1<СТ<С2)
счетное множество точек тх, х2, т3, ... стремящихся к 2. Если для
каждого целого положительного числа т мы построим решето Ст>
имеющее единственную просеянную точку лгт и такое, что все абсциссы т
замкнутых отрезков, составляющих Сж, принадлежат интервалу (^, ^,-ы),
то легко видеть, что соединение решета С и всех решет Ст есть
некоторое решето общего видау для которого просеянное множество
в точности совпадает с данным аналитическим множеством Е.
394
Н. Н. Л У 3 И H
Итак, мы доказали важное предложение:
Теорема (обратная). Каждое линейное аналитическое множество
есть множество, просеянное посредством некоторого решета общего
вида.
Соединяя это предложение с прямой теоремой, мы приходим к еле*
дующему предложению:
Семейство всех линейных просеянных множеств тождественно
с семейством всех линейных аналитических множеств.
V. Проекции.
VI. По самому определению аналитическим будет каждое линейное
множество точек Е, которое дано нам как множество значений
некоторой функции f{t)y разрывной только для счетного множества значений t.
Геометрическая форма, которую можно придать этой формулировке,
сделает ее, быть может, более ясной. Рассмотрим две прямоугольные
оси и кривую, уравнение которой
Очевидно, функция / точечно разрывна относительно любого
совершенного множества, значит, является функцией первого класса по Бэру.
Следовательно, разность
x-f(t)
является функцией двух переменных /их, представимой аналитически.
При этих условиях из одной теоремы Лебега вытекает, что множество
точек плоскости ТОХ, в которых эта разность равна нулю, есть
наверняка плоское множество, измеримое В.
Роль, которую играет это плоское множество, становится ясной,
если мы заметим, что данное линейное аналитическое множество Е
является ортогональной проекцией этого плоского множества на ось ОХ.
Чтобы оценить простоту этого плоского множества, удобно установить
следующее общее определение*
18. Возьмем эвклидово пространство <§ т измерений. Пусть в этом
пространстве дана какая-нибудь система прямоугольных осей координат,
которую мы обозначим через S (х1У х,у ..., хт). Вообразим в этом
пространстве <§ вполне определенную счетную или конечную
последовательность замкнутых параллелепипедов т измерений, ориентированных по
осям системы S и попарно без общих точек: эти параллелепипеды
будем называть параллелепипедами ранга 1.
Вообразим в каждом из этих параллелепипедов ранга 1 вполне
определенную счетную или конечную последовательность замкнутых
параллелепипедов, ориентированных по осям системы S и попарно без
общих точек; эти замкнутые параллелепипеды будем называть
параллелепипедами ранга 2; легко видеть, что множество, образованное из
всех параллелепипедов ранга 2, является счетным.
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА I
395
Вообще, каково бы ни было целое положительное число л, л>1,
возьмем в каждом из параллелепипедов ранга п — 1 вполне определенную
счетную или конечную последовательность аналогичных замкнутых
параллелепипедов попарно без общих точек и назовем их для сокращения
параллелепипедами ранга п. И т. д.
Так как множество всех параллелепипедов ранга п счетно (или
конечно), их множество-сумма необходимо измеримо В; обозначим его
через Sn. Отсюда немедленно следует, что общая часть всех множеств-
сумм Sly S2, S3, .. . обязательно есть множество, измеримое В;
обозначим его через е и установим следующее определение:
Определение. Мы назовем элементарным множеством
построенное таким образом множество е.
Мы видим, что каждое элементарное множество является множеством,
не слишком сложным по существу, но, строго говоря, это только
весьма относительно1.
Заметим, что множество, образованное из единственной точки, является,
очевидно, элементарным; точно так же каждое изолированное
множество (т. е. такое, что каждая его точка является изолированной точкой)
также элементарно.
19. Установив это определение, мы докажем следующее предложение:
Каждое линейное аналитическое множество является
ортогональной проекцией некоторого плоского элементарного множества»
Для того чтобы доказать это, достаточно рассмотреть функцию
F(t), непрерывную справа в каждой точке, которую мы определили
прежде (п. 15).
В самом деле, возьмем произвольный полусегмент d ранга п. Пусть
И и h—соответственно максимум и минимум функции F(^) на d. Точки
плоскости, абсциссы которых принадлежат замкнутому отрезку d
(включая правый конец), а ординаты заключены в отрезке (А ^ х ^ Н),
образуют замкнутый прямоугольник, ориентированный по осям т и х; мы
назовем его прямоугольником ранга п.
Итак, каждому полусегменту d ранга л, расположенному на (0 ^ ~ <С 1),
соответствует в плоскости прямоугольник ранга л, и, очевидно, что
два из этих прямоугольников никогда не пересекаются друг с другом; но
они могут иметь общую границу. Так как каждый полусегмент d ранга п
содержит счетное множество полусегментов а1' ранга л-*-1, которые не
имеют попарно ни одной общей точки, то каждый прямоугольник ранга л
содержит счетное множество прямоугольников ранга л-ь1, которые
никогда не пересекаются друг с другом, но могут иметь общую границу,
и т. д. Если это последнее обстоятельство имеет место, мы можем,
1 „Простота" элементарных множеств нам кажется весьма обманчивой. Перевод-
определения элементарного множества на язык арифметики наталкивается на
всевозможные противоречия, относящиеся к теории роста. Правдоподобно, что все
трудности теории проективных множеств содержатся в элементарных множествах,
как в зародыше.
396
Н. Н. ЛУЗИН
очевидно, предположить, что эти прямоугольники немного сжаты в
направлении оси т без изменения их проекций на ось л:, так чтобы все
прямоугольники одного ранга не имели ни одной общей точки.
В этих условиях мы получим плоское элементарное множество еу
и очевидно, что его ортогональная проекция на ось лг-ов совпадает
с множеством значений функции F(t); значит, данное аналитическое
множество Е отличается от этого последнего множества только
счетным (или конечным) числом дополнительных точек, которые мы можем
рассматривать как проекции изолированных точек плоскости. Это
замечание заканчивает доказательство предложенной теоремы (ч. т. д.).
VI. Решета нескольких измерений.
20. Лая определенности ограничимся случаем решета в пространстве
трех измерений.
Возьмем евклидовское пространство трех измерений и рассмотрим
три прямоугольных оси OXYZ и фундаментальный куб К со стороной 1>
точки которого М (л:, у, z) удовлетворяют неравенствам
0<х<1, 0<у<1, 0<z<l.
Определение. Мы назовем решетом в пространстве
трех измерений всякое счетное соединение С замкнутых
прямоугольников, параллельных плоскости XOY, ориентированных по
осям ОХ и OY и расположенных внутри куба К.
По аналогии с предыдущим мы обозначим через <§ совокупность
таких точек М(х, у) нижней грани куба ЛГ, что перпендикуляр Рм>
восстановленный в М к плоскости XOY, пересекает решето С во
множестве точек, которое вполне упорядочено относительно
положительного направления оси OZ.
Множество точек, которые не принадлежат совокупности S, мы
обозначим через Е.
По определению множества Е перпендикуляр Ру в каждой его точке
пересекает решето С в счетном множестве Rm> которое не вполне
упорядочено, принимая тот же способ упорядочивания. Следовательно,
в этом случае возможно определить нисходящую последовательность
ат, а2,..., образованную точками множества Rm, каждая из которых
ниже предшествующей и которые стремятся к некоторой точке и,
расположенной на перпендикуляре Рх. Таким образом, в этом случае
множество Rm обладает обратным движением, и ясно, что среди
предельных точек [х множества Rm, в каждой из которых множество Rm
обладает обратным движением, найдется самая низкая точка; мы обозначим
через \ъ (х, у) ее координату z.
Именно это множество Е (а не совокупность £) мы назовем
множеством, просеянным посредством решета С, расположенного в
пространстве трех измерений, или, проще, просеянным множеством.
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА I
397
21. Просеянные множества нескольких измерений тесно связаны
с аналитическими множествами в пространстве нескольких
измерений. Но необходимо сначала определить эти последние.
Определение. Мы называем аналитическим множеством в
пространстве т измерений геометрическое место последовательных
положений подвижной точки М(х1У х2,..., хт)> координаты которой
являются функциями переменного параметра t> определенными на
интервале (О <С t <С 1) " разрывными только для счетного множества
значений t:
*i=/i(')> х4=/2(*),... xn=fm(t).
Легко видеть, что это определение является вполне естественным
обобщением понятия линейного аналитического множества. Следующее
предложение оправдывает введение этого обобщения:
Для того чтобы множество точек в евклидовском пространстве
т измерений было просеянным, необходимо и достаточно, чтобы
оно было аналитическим в этом пространстве.
22. Условие необходимо. Для определенности ограничимся случаем
плоского просеянного множества Е(т = 2).
Пусть С — решето в пространстве трех измерений, определяющее
множество Е. Мы будем рассматривать каждый из замкнутых прямо"
угольников Sn решета С как верхнюю грань некоторого
параллелепипеда Р,п ориентированного по осям OXYZ и имеющего основание в
плоскости z — 0.
Установив это, мы начнем с преобразования данного решета С
в некоторое другое решето С", которое обладает двумя свойствами
канонического решета Лебега.
1°. Диаметр основания параллелепипеда Рп стремится к нулю,
когда п неограниченно возрастает.
2°. Каково бы ни было число п, в параллелепипеде Рп существует
некоторый параллелепипед Рт, высота которого строго меньше
высоты параллелепипеда Pw.
Метод осуществления этого преобразования остается тот же, который
был использован в случае линейного множества Е: достаточно заменить
слова „отрезок" и „прямоугольник" соответственно словами
„прямоугольник" и „параллелепипед".
Все рассуждения доказательства аналитичности лебеговского
множества Е становятся приложимыми к преобразованному решету С" (ч. т. д.).
23. Условие достаточно. Пусть Е — плоское аналитическое
множество, содержащееся в квадрате, стороны которого заданы
уравнениями
х = 0, х = 1, z/ = 0, z/=l.
По определению Е есть геометрическое место последовательных
положений подвижной точки М (jc, у), координаты которой являются
398
Н. Н. ЛУЗИН
функциями переменного параметра t> определенными на интервале
(О <С t <С 1) и разрывными только а^я счетного множества значений /:
*=/('), y = g(t)-
Кроме того, как мы сказали (п13), всегда можно предполагать
функции / и g разрывными только в рациональных точках интервала
(0</<1).
Отсюда следует, что каждую иррациональную точку t интервала
(О, 1) можно заключить в такой открытый интервал 2, что колебания
(полные) обеих функций / и g на о будут меньше е, где е положительно
и сколь угодно мало. Отсюда мы заключаем, что, каков бы ни был
открытый интервал о, можно определить на о такое приводимое
множество #е, что колебания (полные) обеих функций / и g на каждом
из интервалов, смежных к /?а, будут меньше £, где е сколь угодно
мало (п. 14).
В этих условиях все рассуждения, проделанные в случае одной
функции /, становятся приложимыми к случаю двух функций fug.
Бесполезно утомлять читателя, повторяя все время одни и те же
слова: приложение предыдущих методов (п. 15) оправдано.
Таким образом, мы придем к сложным функциям
* = F(t)=/ [<р (т)] и y = G(T) = *t<p(T)],
определенным на полусегменте
0<~<1
и непрерывным справа в каждой точке т этого полусегмента, без
всякого исключения, даже в рациональных точках и в начале координат О.
Эти функции F и G таковы, что их колебания (полные) на каждом из
полусегментов d ранга п будут в точности меньше ея- \J2.
Кроме того, если изменять т на полусегменте 0^т<1, все
множество Е' точек М(ху у) будет содержаться в данном аналитическом
множестве Е и будет отличаться от Е быть может только счетным (или
конечным) числом дополнительных точек.
Мы немедленно докажем, что это плоское множество Е' просеяно
посредством некоторого решета С, расположенного в пространстве
трех измерений.
Лая его построения рассмотрим три прямоугольные оси OX, OY и
О" и возьмем какой-нибудь полусегмент d ранга п. Так как полные
колебания обеих функций F(x) и G(^) на d меньше еи, то в плоскости
XOY можно определить такой малый квадрат q со стороной длины £,„
что подвижная точка М(х, у) остается в q, когда параметр ~
изменяется на d. Если мы будем рассматривать теперь квадрат q как
ортогональную проекцию на плоскость XOY квадрата Q, параллельного
этой плоскости и находящегося на расстоянии, равном координате '
правого конца полусегмента dy мы поставим в соответствие каждому из
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА 1
399
полусегментов d ранга п вполне определенный квадрат Q,
параллельный плоскости XOY и расположенный в фундаментальном кубе
0<х<1, 0<у<1, 0<х<1.
Если мы выполним это построение квадрата Q для каждого
полусегмента d ранга п и будем менять л, мы получим в этом кубе счетное
множество замкнутых квадратов Q, параллельных плоскости XOY и
ориентированных по осям ОХ и OY. Следовательно, мы имеем
решето С в пространстве трех измерений.
В силу непрерывности справа функций F и G в каждой точке
множество^ просеянное посредством этого решета С", в точности
совпадает со множеством Е'. И так как данное аналитическое множество Е
отличается от Е не больше чем на счетное множество
дополнительных точек, мы немедленно заключаем (п. 16), что аналитическое
множество Е само является просеянным множеством (ч. т. д.).
Таким образом, мы пришли к следующему предложению:
Семейство всех точечных множеств в пространстве т измерений^
просеянных посредством решета в пространстве т -+-1 измерения^
тождественно с семейством всех аналитических множеств в
пространстве т измерений.
24. Проекции. Вернемся к элементарным множествам в
пространстве нескольких измерений (п. 18). Мы можем извлечь из предыдущего
доказательства крайне важное следствие.
Мы видели, что каждому полусегменту d ранга л, расположенному
на оси 0^, соответствует вполне определенный малый квадрат q,
расположенный в плоскости XOY (п. 23). Итак, рассмотрим множество
точек в пространстве трех измерений, проекции которых на плоскость
XOY и на ось Ос принадлежат соответственно квадрату q и
полусегменту d, который предполагается замкнутым (следовательно,
отрезку d). Очевидно, что это множество образует замкнутый
параллелепипед, ориентированный по осям триедра OXYt; мы назовем его
параллелепипедом ранга п.
Всех параллелепипедов ранга п счетное множество, и они никогда
не налегают друг на друга; но они могут иметь общую грань. Если
имеет место это последнее обстоятельство, мы можем, очевидно, сжать
их в направлений оси Ch, не изменяя их проекций на плоскость XOY,
так чтобы они не имели попарно ни одной общей точки.
Так как каждый параллелепипед ранга п содержит, очевидно,
счетное множество параллелепипедов ранга л-«-1, мы можем посредством
параллелепипедов рангов 1, 2, 3,... образовать элементарное
множество €у и очевидно, что плоское множество Е' является ортогональной
проекцией множества е на плоскость XOY. А так как данное
аналитическое множество Е отличается от Е' только счетным множеством
дополнительных точек, мы можем прибавить к е счетное множество точек
400
Н. Н. ЛУЗИН
таким образом, чтобы Е стало ортогональной проекцией некоторого
элементарного множества.
Мы пришли таким образом к важному предложению:
Каждое аналитическое множество точек в евклидовом
пространстве <S m измерений может быть рассматриваемо как ортогональная
проекция некоторого элементарного множества, расположенного в
евклидовом пространстве шн-1 измерений, содержащем &1.
Это предложение чрезвычайной важности в теории аналитических
множеств, так как именно отсюда следуют основные свойства
аналитических множеств: мощность, мера, категория.
25. Мощность. Пусть Е — произвольное аналитическое множество,
о котором известно только, что оно несчетно. Пусть е — элементарное
множество, проекция которого совпадает с Е. Так как диаметр
параллелепипеда ранга п стремится к нулю, когда п неограниченно
возрастает, и так как Е несчетно, то существует такое достаточно большое
целое положительное число п, что среди параллелепипедов ранга п
существуют два параллелепипеда к и тс', обладающие следующими двумя
свойствами:
1° проекции параллелепипедов тс и тс' не имеют общих точек;
2° проекции частей множества е, заключенных в тс и тс', обе также
несчетны.
Итак, мы находимся в тех же условиях, что и раньше, и в каждом
из двух параллелепипедов тс и тс' мы можем определить два новых
параллелепипеда, обладающие теми же свойствами; мы получим таким
образом четыре определенных параллелепипеда. Мы продолжаем
оперировать подобным же образом в каждом из них, и мы получим восемь
определенных параллелепипедов, обладающих теми же свойствами, и
так до бесконечности.
Ясно, что множество точек, принадлежащих каждая бесконечному
множеству определенных таким образом параллелепипедов, является
совершенным множеством, содержащимся в элементарном множестве е.
Кроме того, проекции двух его точек, предполагающихся различными,
также всегда различны.
Отсюда следует, что проекция этого совершенного множества есть
также совершенное множество. А так как это последнее, очевидно,
содержится в данном аналитическом множестве Е, мы получаем
следующее предложение:
Каждое несчетное аналитическое множество необходимо
содержит некоторое совершенное множество, следовательно, имеет
мощность континуума 2.
1 Теорема Суслина: „Каждое А-мнэжество есть ортогональная проекция
некоторого В множества класса Iй; см также W. Sierpinski. Les projections des
ensembles mesurables (B) et les ensembles (A). Fund. Math., V, 159.
2 Это результат Су едина; см. мою заметку „Sur la classification de M. Baire".
•Comptes Rendus, 164 (1917).
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ, ГЛАВА I
401
26. Мера. Пусть Е — произвольное аналитическое множество, о
котором известно только, что оно имеет положительную верхнюю меру
теЕ>0.
Сначала сделаем следующее довольно тривиальное замечание: для
того чтобы доказать, что произвольное множество точек Е с
положительной внешней мерой измеримо, надо установить, что оно
содержит некоторое замкнутое множество F, мера которого больше
тёЕ — г, где е — сколь угодно малое положительное число; и этого
достаточно.
В самом деле, с одной стороны, точки множества Е можно
заключить в последовательность параллелепипедов (интервалов,
прямоугольников), полная протяженность (длина, площадь, объем) которых меньше
С другой стороны, все точки, не принадлежащие множеству £,
очевидно содержатся в последовательности параллелепипедов, внешних
к замкнутому множеству Fy полная протяженность которых меньше
1 — mF-i- е. Следовательно, полная протяженность обеих
последовательностей параллелепипедов меньше m,£-+-e-+-l— mF-\- e<C 1 н-Зе;
следовательно, Е измеримо. Несмотря на свою чрезвычайную
банальность, это замечание нам будет весьма полезно.
Еще одно замечание: если мы имеем последовательность EXi E2i...
произвольных множеств, не подчиненных никакому ограничению,
внешняя мера множества-суммы п первых членов последовательности
стремится к внешней мере совокупности всех членов последовательности,
когда п безгранично возрастает.
Отсюда следует, что можно взять число пг параллелепипедов ранга 1
достаточно большим для того, чтобы часть элементарного множества е,
содержащаяся в этих параллелепипедах, имела проекцию, внешняя мера
которой больше теЕ — ех.
Оперируем подобным же образом с параллелепипедами ранга 2,
содержащимися в выбранных параллелепипедах ранга 1; мы можем взять
число п2 достаточно большим для того, чтобы часть множества ef
содержащаяся в них, имела проекцию, внешняя мера которой больше т^Е —
— £i — V> и т- А-
Мы образуем таким образом такие соединения К19 Къ Kz,...
параллелепипедов соответственно рангов 1, 2, 3,..., каждое из которых
составлено из конечного числа параллелепипедов и лежит внутри
предшествующего, что проекция части множества е, содержащейся в
параллелепипедах совокупности Кпу имеет внешнюю меру, большую чем
тД — ех — е2 — . ..-f- ея.
Здесь ряд с положительными членами ег -+- е2 -+- s3 -н... сходится и имеет
сумму е, где е сколь угодно мало.
Отсюда следует, что проекция точек совокупности Кп есть
совершенное множество меры, большей чем mji — е; мы обозначим его
через F.
402
Н. Н. ЛУЗИН
С другой стороны, общая часть совокупностей К1У К2,... есть,
очевидно, замкнутое множество точек, и ясно, что множество F
является проекцией этого последнего. Следовательно, множество
Fсодержится в данном аналитическом множестве Е.
Мы пришли таким образом к следующему предложению:
Каждое аналитическое множество измеримо1.
11. Категория* Речь идет о том, чтобы доказать, что никакое
аналитическое множество никогда не принадлежит к тем, которые Лебег
называл множествами, не являющимися множествами типа Z, или, если
принять терминологию А. Данжуа, что аналитическое множество
никогда не будет неисчерпаемым.
Другими словами, следует показать, что, каково бы ни было
совершенное множество Ру существует такая часть тс множества Р, что
первой категории на тс будет: или данное аналитическое множество Е, или
его дополнение СЕ.
Очевидно, достаточно констатировать, что если данное
аналитическое множество Е не будет первой категории ни на какой части
множества Ру то дополнительное множество СЕ будет первой категории на Р.
Рассмотрим сначала в пространстве т-н1 измерений, где
расположено элементарное множество в, фундаментальный куб как
единственный параллелепипед ранга 0.
Мы начнем с того, что исключим все такие параллелепипеды, каков
бы ни был их ранг, что принадлежащие им части множества е имеют
проекции первой категории на Р; ясно, что сохранятся параллелепипеды
всех рангов.
Установив это, оперируем с каждым оставшимся параллелепипедом,
каков бы ни был его ранг, следующим образом: пусть А— этот
параллелепипед; мы рассмотрим часть элементарного множества в, которая
принадлежит А. Так как А — один из сохранившихся параллелепипедов,
то проекция этой части множества е не будет первой категории на Р.
Следовательно, на Р существует такое вполне определенное замкнутое
множество F, что эта проекция никогда не будет первой категории ни
на какой порции тс множества Р, которая не содержит точек
множества F, и это не имеет места, если порция тс содержится в F.
Установив этот первый пункт, определим дая каждого
сохранившегося параллелепипеда А', содержащегося в А и непосредственно
следующего ранга, соответствующее замкнутое множество /^.
Ясно, что общая часть всех этих замкнутых множеств F' есть
множество, нигде не плотное на каждой порции тс множества Р, которая
не содержит точек множества F. Следовательно, множество точек,
общих всем множествам F и не принадлежащих множеству F, есть
множество, нигде не плотное на Р; мы обозначим его через //(А).
1 Теорема V моей заметки (1917): „Каждое А-множество измеримо (L)u\ см.
также N. Lusin et W. Sierpinski. Sur quelques proprietes des ensembles (A).
Bull, de TAcademie des Sciences, Gracovie, 44, 1918.
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА I
403
Итак, каждому параллелепипеду А, каков бы ни был его ранг,
соответствует вполне определенное множество Н(±), нигде не плотное на Р.
Отсюда следует, что совокупность всех этих множеств //(А) является
множеством первой категории на Р. Обозначим его через //.
Мы сейчас докажем, что каждая точка т множества Р, не
принадлежащая множеству //, является точкой данного аналитического
множества Е.
В самом деле, так как т не принадлежит множеству Н(\)> где
Л0—фундаментальный куб, то в Д0 существует такой параллелепипед \
ранга 1, что точка т будет внешней относительно замкнутого
множества Fly соответствующего параллелепипеду Дх; так как т не
принадлежит множеству Н(\), то в А1 существует такой параллелепипед Аг
ранга 2, что точка т будет внешней относительно замкнутого множества
р2, соответствующего параллелепипеду А2) и т. д.
Мы образуем таким образом такие параллелепипеды А0, Д1э А2>
рангов, соответственно равных 0, 1, 2,..., каждый внутренний к
предшествующему, что точка т никогда не принадлежит никакому из
замкнутых множеств Fn. Следовательно, точка т необходимо принадлежит
проекции каждого из параллелепипедов А0> Д1э А2,.... Мы заключаем
отсюда, что точка т является проекцией некоторой точки
элементарного множества в, следовательно, принадлежит множеству Е1.
28. Аналитическая форма, которую можно дать этому предложению,,
сделает его, быть может, более ясным: рассмотрим в евклидовом
пространстве т измерений произвольное аналитическое множество £. Пусть
/—функция, равная 1 в точках множества Е и равная 0 вне Е.
Если Р — какое-нибудь совершенное множество, расположенное в
рассматриваемом пространстве, то существуют порции множества Р, на
которых или самое Е> или его дополнение СЕ будут первой
категории. Следовательно, определенная таким образом функция / обладает
необходимым свойством Р. Бэра, которое принадлежит всем функциям
его классификации, а именно:
/ точечно разрывна на каждом совершенном множестве Р, если
не принимать во внимание множеств первой категории относительно
этого совершенного множества Р.
29» Замечание. Мы дополним эти результаты следующим
замечанием. Если некоторое множество измеримо, его дополнение также
измеримо, и мы можем сделать то же самое заключение для свойства
быть множеством типа Z. Следовательно,
Дополнение к аналитическому множеству измеримо и является
множеством типа Z (не является неисчерпаемым множеством)*
1 Теорема VI моей заметки (1917): „Если множество Ел которое является А-
множеством, образованным при помощи точек совершенного множества Р, второй
категории на Р% то существует интервал, содержащий точки множества Р> на
котором дополнение к Е относительно Р будет второй категории"; см. также
N. Lusin et W. Sierpinski. Sur un ensemble non mesurable (B). Journ. de Math.
П, 68, 1923; O. N i с о d у m. Fund. Math. VII, 1S3.
404
Н. Н. ЛУЗИН
Г л а в а вторая
ИЗМЕРИМОСТЬ В
VII. Идеи Бореля
30. Понятие множества, измеримого В. Настало время
рассмотреть соотношения между просеянными (аналитическими) множествами и
множествами, которые называются измеримыми В.
Мы не будем стараться дать общее определение понятия
„измеримое В": нам кажется, что здесь возникает достаточная опасность того,
что общее определение будет применяться без крайней
предосторожности.
Обычно называют множеством, измеримым В, каждое множество
точек, которое может быть получено повторяющимся применением
двух основных операций (сложение счетной совокупности множеств,
общая часть счетной совокупности множеств), отправляясь от
интервалов.
Это определение, несомненно, кажется особенно ясным, когда дело
идет об уже реализованных множествах; но оно еще не имеет
достаточной ясности, чтобы фигурировать в математическом доказательстве,
в котором рассуждают о множестве, измеримом В, реализация которого
еще только возможна. Необходимость в таких рассуждениях
немедленно возникает, если мы намереваемся изучать общие свойства
множеств, измеримых В. И тогда мы стараемся уточнить это определение
посредством дополнительных фраз.
Дая этой цели, сформулировав рассматриваемое определение, обычно
показывают, что две основные операции, посредством которых при
помощи интервалов строятся множества, измеримые В, могут взаимно
комбинироваться чрезвычайно сложным образом, потому что, чтобы
получить требуемое множество F, измеримое В, очень часто нужно сначала
подготовить бесконечное множество других предварительных множеств,
также измеримых В, построение которых посредством основных
операций приводит нас, в конце концов, гк результирующему множеству Е.
Эти пояснения, впрочем, необходимые, если мы намереваемся
изучать множества, измеримые В, в их общности ясно показывают всю
сложность общего понятия множества, измеримого В. Но сами эти
пояснения заставляют понять, что предыдущее определение множества,
измеримого В, взятое само по себе, не имело никакого ясного смысла:
что в самом деле без них обозначают эти слова: повторяющееся
применение двух основных операций? Таким образом, эти пояснения
неотделимы от предыдущего определения; или, скорее, именно эти
пояснения и являются самым определением множества, измеримого В.
Если мы постараемся проанализировать эти объяснения, то мы
констатируем следующее: мы отправлялись от интервалов, которые
рассматривали как данные; потом нам надо было подготовить бесконечное
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА II
405
множество промежуточных множеств, которые, несомненно, зависят
друг от друга. В каком порядке следует их брать, чтобы быть
уверенным в том, что мы получим их все, не запутавшись в их
безграничном многообразии и не совершив порочного круга?
В первый раз мы встречаемся с этим вопросом в элементах, когда
приступаем к изучению функций и обычно принимаем следующее
определение: функция f(x) называется элементарной, если ее можно
получить повторяющимся применением основных операций (сложе-
т
ние, вычитание, умножение, деление, у, log, sin и т. д.), отправляясь
от действительного переменного х и констант. Нельзя не
поразиться аналогией между этим определением и предшествующим
определением множества, измеримого В. Но эта аналогия чисто формальная.
В случае понятия элементарной функции каждая из основных
операций применяется не более чем к двум предварительно определенным
функциям; следовательно, множество промежуточных функций,
очевидно, конечно. Именно по этой причине можно расставить эти
функции в некотором определенном порядке таким образом, чтобы
при помощи основных операций можно было определить все
промежуточные функции одна за другой, не исключая ни одной и не повторяя
ни одну из них несколько раз, чтобы, в конце концов, придти
окончательно к искомой функции. Именно по причине этого порядка
невозможно впасть в порочный круг, и, следовательно, данное определение
элементарной функции является настоящим определением. Совершенно
иначе обстоит дело для случая понятия множества, измеримого В.
В этом случае совокупность предварительных множеств бесконечна
и порядок, в котором расставлены эти множества, гораздо более важен,
чем самое это определение множества, измеримого В. Не зная этого
порядка, мы вечно будем находиться в положении математика,
считающего, что он обладает всевозможными целыми положительными числами,
не зная, однако, принципа полной индукции. Именно этот порядок
промежуточных множеств и является истинным нервом всех
конструктивных определений множества, измеримого В. Следовательно,
теоретическая необходимость конструктивных определений множества,
измеримого В, превращается на почве общих рассуждений в
математическую необходимость строгого определения порядка промежуточных
множеств.
Известно, что все процессы дая эффективного установления этогсх
порядка поддаются общему изучению, которое было проделано впервые-
Кантором в связи с последовательными производными данного
множества и которое привело к понятию трансфинитных чисел второго
класса.
Самое трансфинитное число есть не что иное, как сокращенное
обозначение для указания порядка, в котором должно быть выполнено
счетное множество операций, допускающих счетное множество после-
406
Н. Н. ЛУЗИН
довательных или суперпозированных переходов * к пределу. Если не
ограничивать области математики изучением определенной категории
множеств, измеримых Ву происходящих, например, от функций
конечного класса классификации Бэра, можно ввести в определение
множества, измеримого Ву сколь угодно большие трансфинитные числа.
Это и есть причина, по которой совокупность множеству измеримых В,
есть нечтОу несомненно адекватное совокупности трансфинитных
чисел второго класса.
3L Критические замечания Бореля. Борелю принадлежит
глубокая критика этого предмета. Эта критика стала слишком классической,
чтобы была необходимость излагать в деталях ее доводы; мы
ограничимся тем, что кратко напомним основные пункты, на которых она
основана.
Во-первых, существует много объектов, которые кажутся при
современном состоянии науки законными совокупностями (т. е. истинными
множествами). Например, представляется затруднительным отрицать
возможность при работе в области теории функций рассуждать о всех
точках у заключенных в данном интервале, или о всех непрерывных
функциях; эта возможность кажется узаконенной известным полностью
конечным определением действительной точки или непрерывности
функции, принадлежащим Коши. Мы получаем таким образом общие
свойства совокупностиу но в действительности никогда не рассуждаем
об определенном индивидууме этой совокупности, если только дело
не идет об очень частном индивидууме, который может быть отличим
от всех других посредством конечного определения2. К тому же, если
посредством какого-нибудь закона задается индивидуум совокупности,
то мы можем определить его post factum при помощи регулярного
процесса, например применяя подходящие десятичные разложения или
приближения многочленами.
Напротив, множество всех точечных множеств является
незаконной совокупностью. Когда мы говорим об этой совокупности, мы
не указываем ни закона этой бесконечности, ни способа ее назвать.
Если мы зададим каким-нибудь образом индивидуум этой совокупности,
то не существует никакого регулярного процесса, чтобы получить его
post factum, даже если бы слово трансфинитное путем смелого
синтеза приобрело такой же ясный и так же универсально лишенный
двойственности смысл, как и принятый теперь смысл слова
бесконечное. Мы не знаем в настоящее время никакого способа для
определения совокупности всех точечных множеств; когда мы говорим о ней,
мы фактически представляем различные приемы, которые можно изо-
1 Этим определением мы обязаны Э. Борелю („Le calcul des integrales definies".
Journ. de Math., 177, 1912). Существует несколько теорий трансфинитных чисел:
теория Кантора эманации типов, номиналистские теории Бэра и Лебега;
формальная теория Рёсселя—Серпинского.
2 Е. В orel. La philosopbie mathematique et l'infini (Rev. du Mois, авг. 1912),
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА 11
407
•брести для определения очень сложных множеств, за неимением
конечного определения, которое позволило бы охватить их единым взглядом.
Но как только дело идет о человеческой возможности создавать
процессы определения и системы условий, ассимиляция, сознательная
или бессознательная, с совокупностью, данной конечным
определением, должна полностью исчезнуть, и мы находимся в области
субъективного. Таким образом, совокупность всех точечных множеств,
меняясь от математика к математику > не имеет в области
объективной науки, как, например, классические разделы математики,
другого существования, кроме чисто словесного) следовательно, невозможно
рассматривать ее как настоящий математический объект, который можно
вводить в рассуждения.
Точно так же, как необходимо приписать совокупности всех
точечных множеств чисто словесное существование, нужно отнести к области
незаконного и самую совокупность действительных чисел. Так как
каждое действительное число должно подчиняться некоторому конечному
закону, необходимому для его определения, начиная с единицы1, то
ясно, что в обоих случаях нас останавливает одно и то же
затруднение: нельзя объять единым взглядом математические объекты,
определенные при помощи фиксированных условий посредством самых
разнообразных конечных законов, не зная закона определения этих
законов. Однако необходимо сказать несколько слов о понятии
континуума. Может показаться парадоксальным отделение совокупности
точек от совокупности чисел путем узаконивания первой и отрицания
второй; однако этот образ мыслей чрезвычайно естественен. Понятие
континуума приобретено посредством геометрической интуиции2, знание
единицы длины вовсе не необходимо для того, чтобы фиксировать на
прямой единственную вполне определенную точку: неподвижная точка
вполне определена на прямой уже тем, что она есть на прямой таму
где она есть. При изучении континуума не возникает никакого
затруднения, пока мы остаемся на чисто геометрической точке зрения; все
точки прямой тождественны, потому что все они обладают одними и
теми же общими свойствами; затруднения возникают лишь при
арифметических определениях, так как познание этих единых общих свойств
•становится тогда менее легким. Кроме того, известно, что полное
•арифметическое понятие континуума требует, чтобы мы
допустили законность счетного множества произвольных
последовательных выборов, а эта законность весьма сомнительна. Таким образом,
континуум никогда не появляется как заданный во всей своей арифме-
1 Мы наломинаем здесь важное понятие высоты данного действительного числа
принадлежащее Борелю („Le calcul des integrates definies". Journ. de Math., 163,
1912). Было бы очень интересно приблизить к этим идеям Бореля новые идеи
Гильберта („Logische Grundlagen der Mathematik". Math. Ann., 88).
•2 Cm. E. BoreL Sur les principes de la theorie des ensembles (IV* Congres
international des matheraaticiens, Rome» 1908).
408
Н. Н. ЛУЗИН
тической общности 1. Одна из наиболее важных проблем теории
функций действительного переменного состоит теперь в том, чтобы
преобразовать совокупность чисел в некоторую законную совокупность
(с конечным определением) или указать некоторый класс чисел
с конечным определением, инвариантный относительно всех
преобразований классического анализа и алгебры: именно этот класс
чисел и составит практический континуум, которым пользуются
математики 2.
Возвращаясь к совокупностям трансфинитных чисел и тех множеств,
измеримых В} которые были определены выше, нам остается сказать
очень немного: обе совокупности, несомненно, незаконны.
Затруднение в приобретении концепции этих совокупностей состоит в том, что
эффективно можно сформулировать лишь конечное число условий, и
что, как бы далеко ни позволили идти эти условия, объекты
(трансфинитные числа, множества, измеримые В), которых они позволяют
эффективно достичь, являются ничем по отношению к тем, которые от
них ускользают, но смогут быть определены посредством других
условий в конечном числе, никогда не доходя до конца3. Концепция
конструктивной совокупности множеств, измеримых В, хотя и не
является внутренне противоречивой, не является настоящей
математической концепцией, потому что невозможно точно описать построение
такой совокупности при помощи конечного числа условий:
потребовалось бы бесконечное множество условий, абсолютно не зависящих
друг от друга, чтобы зафиксировать ими обозначение лишенным
двусмысленности образом4.
Именно по этим причинам Борель предложил при изучении множеств,
измеримых В, всегда ограничиваться рассмотрением открытого тела
множеств, измеримых В; знаменитый автор дал это название
совокупности множеств, измеримых В, которые соответствуют трансфинитным
числам, меньшим некоторого заранее фиксированного трансфинитного
числа, следовательно такой, что она, несомненно, может быть
расширена повторением основных операций. Этой концепции Борель
противопоставляет концепцию замкнутого тела, т. е. совокупности, которая
не может быть расширена повторением тех же операций, рассматривая
последнюю как неясную и незаконную5.
Именно эта форма парадокса трансфинитного и заставила нас
избегать столь деликатного понятия, как трансфинитное число.
1 См. Е. Во г el. L'antinomie du transfini (Revue philosophlque, 1900).
2 Cm. E. Borel. Les „Paradoxes" de la theorie des ensembles (Ann. de i'Ecole
Norm. Super., 1903).
3 Cm. E. Borel. L'infini mathematique et la realite (Revue de Mois, 10 июля
1914 г.).
4 См. Е. Borel. La philosophie mathematique et Tinfini (Revue de Mois»
август 1912 г.).
5 См. E. Borel. Lecons sur la tbeorie des fonctions. 2e ed., Note VI,
235-236.
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА II
409'
Правда, выше мы были вынуждены прибегнуть к вполне упорядочен-
ным множествам (всегда образованным рациональными точками, ранг
которых соответствует положительному направлению прямой), но
существование таких частных множеств нам кажется несомненным, будучи
просто достаточно примитивным математическим фактом, для того
чтобы его объяснение было по меньшей мере бесполезным. В случае
понятия трансфинитного числа дело обстоит совершенно иначе: это
понятие кажется нам совершенно второстепенным, будучи произведено
(может быть, трудно определимым путем) от такого совершенно ясного
образа, каким мы себе представляем (или думаем, что представляем)
вполне упорядоченное множество рациональных точек. Но тогда, само
собой разумеется, нужно разъяснить понятие трансфинитного.
32. Тем не менее немедленно возникает математическая
необходимость иметь общие свойства, присущие всем множествам, измеримым В.
Если дана совокупность конечного определения каких-либо объектов,
можно получить свойства, общие всем этим объектам, при помощи
непосредственного анализа самого определения (предполагаемого
конечным) предложенной совокупности. Прекрасным примером этого
образа действий является случай совокупности функций первого класса
классификации Бэра. Но как надо поступать в случае совокупности,,
лишенной конечного определения? И прежде всего как возможны
такие свойства?
Когда мы пытаемся рассуждать о несовершенной совокупности,
лишенной конечного определения, так же как о совокупности конечного
определения, мы можем проделывать лишь общие, или символические,,
рассуждения, в которых рассматриваемая совокупность представляется
единственным символом. Такие рассуждения в качестве общих
рассуждений допустимы с того момента, как они свободны от противоречия^,
но в то же время они лишены какого-либо точного содержания 1. Д\я
того чтобы дать им содержательный смысл, нужно было бы уточнить
единообразное обозначение элементов совокупности, а именно это и
невозможно. Теория совокупностей, лишенных конечного определения,
поневоле приводится к некоторого рода логической алгебре, символы
которой не отражают никакой достижимой реальности, и различные
математики не могут быть уверены, что они одинаково понимают эту
реальность, потому что они не имеют о ней общего представления.
Этот образ действия, очевидно, допустим в том смысле, что мы всегда
имеем право создать некоторый словарь и при помощи этого словаря
построить логическое здание; но этот образ действия бесплоден
с точки зрения открытия новых фактов, которые одни только двигают
нашу науку. Следовательно, не надо создавать себе иллюзий по поводу
истинной ценности этих символических рассуждений2.
1 См. Е. В о г е 1. Sur les principes fie la theorie dts ensembles (IVе Congrsv
international des mathematicians. Rome, 1908).
2 Там же.
410
Н. Н. ЛУЗИН
Именно в силу этих причин было предпочтено с неоспоримым
успехом следовать по другому пути. Если не ограничивать
математиков изучением специального класса множеств, измеримых В>
происходящих от функций конечного класса классификации Бэра (чего
достаточно для большинства приложений), то метод остается тем же самым
и состоит в том, чтобы получать новые множества из уже
определенных множеств; только вместо того, чтобы отправляться от интервалов
и следовать построению шаг за шагом, мы предполагаем, что
построение сделано до некоторого пункта и обладает какими-то определенными
свойствами, и мы доказываем, что эти свойства продолжают
существовать, когда мы продвигаемся еще на один шаг. Этот образ действия
непогрешим с логической точки зрения и, что еще важнее, безупречен
по отношению к математической действительности. Кроме того, он
плодотворен: большая часть прекрасных свойств (мера, категория),
общих всем множествам, измеримым В, обязана этому методу.
Следовательно, позиция этого метода теоретически очень сильна1.
Практически она значительно слабее. Достаточно указать, что этот
•образ действия привел однажды даже к потере одного такого свойства,
•общего всем несчетным множествам, измеримым В: свойства иметь
мощность континуума. Так как это обстоятельство, возможно, мало
известно, нам кажется, что будет интересно остановиться на этом
«опросе.
В известной работе Лебега („Sur les fonctions representables analy-
tiquement") мы находим много основных свойств, общих всем
несчетным множествам, измеримым В. Все эти свойства знаменитый автор
получил единообразным применением предшествующего метода:
проверял, их для интервалов и показывал, что они инвариантны по
отношению к двум основным операциям (сложение, общая часть.) Но среди
этих свойств мы не встречаем важного свойства, которое
устанавливает существование некоторого совершенного множества точек в каждом
несчетном множестве, измеримом В. Это свойство было открыто
впервые Александровым и Хаусдорфом через десять лет после
появления мемуара Лебега. Основное обстоятельство состоит в следующем:
все свойства, полученные Лебегом, индуктивны, а свойство найденное
Александровым и Хаусдорфом, не такой природы; это свойство не
инвариантно относительно второй основной операции (взятие части,
общей счетной совокупности множеств) и, следовательно, не может
•быть получено этим методом2. Таким образом, отсутствие этого
-свойства в мемуаре Лебега объясняется совершенно естественно, ибо
это было неизбежным.
1 См. Е. В or el. Le calcul des integrales definies (Journ. de Jordan, 183,
1912).
2 Однако существует индуктивное свойство (инвариантное относительно двух
основных операций), которое влечет за собой свойство Александрова и Хаусдорфа:
хм. W. Sierpinski. Fund. Math., V, 166—171, 1924.
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ, ГЛАВА II
411
Этот факт чрезвычайно важен: существуют не индуктивные
свойства, общие всем множествам, измеримым В. Но как могут
существовать такие свойства?
33. Ответ, нам кажется, напрашивается сам собой: существует
вполне конечное определение совокупности множеств, измеримых 5,
в силу которого эта совокупность становится законной (с конечным
определением). Этому конечному определению мы и обязаны
существованием неиндуктивных свойств множеств, измеримых В. Знание этого
определения достаточно для получения всех свойств, индуктивных и
неиндуктивных, множеств, измеримых В.
Чтобы узаконить это утверждение, нам достаточно будет
эффективно преобразовать конструктивную совокупность множеств,
измеримых Ву в совокупность конечного определения. И во избежание какого-
либо порочного круга мы последуем вот какому методу изложения:
мы не будем пытаться постигнуть сущность наиболее общего
множества, измеримого В, ни даже определить соответствующее понятие.
Наоборот, мы начнем с того, что не будем отделять общего понятия
множества, измеримого В, от более конкретного понятия индуктивного
свойства, и мы, в конце концов, придем к такому частному
индуктивному свойству, что каждое им обладающее множество точек может
быть получено из интервалов посредством бесконечно повторенных
основных операций (сложение, общая часть).
Все это будет выполнено без использования понятия трасфинитного
числа; по самому определению, каждое множество точек, обладающее
этим частным свойством, будет измеримо 5.
Именно это свойство узаконивает совокупность множеств,
измеримых В, так плохо постижимую с чисто конструктивной точки зрения.
VIII. Первое индуктивное свойство: аналитичность
34» Мы назовем индуктивным всякое свойство Р, которое
принадлежит всем параллелепипедам (прямоугольникам, интервалам) и
инвариантно относительно двух основных операций: взятия суммы счетной
совокупности множеств и взятия общей части счетной совокупности
множеств.
По определению прилагательного „измеримое В" каждое индуктивное
свойство необходимо принадлежит всем множествам, „измеримым В",
но оно может принадлежать и многим „другим" множествам.
Установив эти определения, нам важно рассмотреть свойство
точечных множеств, которое состоит в следующем: такое-то множество
имеет решето.
Мы сейчас докажем чрезвычайно важное предложение, относящееся
к этому свойству.
Теорема. Свойство иметь решето есть индуктивное свойство.
Д\я облегчения рассуждений мы считаем семейство просеянных
множеств тождественным с семейством аналитических множеств.
412
Н. Н. ЛУЗИН
Во-первых, каждый замкнутый параллелепипед А, расположенный
в пространстве т измерений, является аналитическим множеством1;
достаточно взять пеановскую кривую xl=fl (t), x2=f2(t)9..., xm=fm(t)r
заполняющую А, где функции f4 непрерывны на интервале (0<£<1)г
Установив это, рассмотрим первую операцию — сумму.
Пусть Е19 Е2,... — аналитические множества в пространстве т
измерений. По самому определению аналитического множества, Е„
является геометрическим местом последовательных положений
подвижной точки М(хх, х2, ..., лгт), координаты которой имеют вид
*i =Л'° (О. **=Л"> (О. •••.*. =ЛИ) (О.
где функции /М непрерывны на интервале (0<С£Я<С1)> кроме точек
некоторого счетного множества.
Возьмем новый параметр т и разделим интервал его изменения
О <^" <С 1 на счетное множество интервалов точками у, -«-, .... Если
мы преобразуем линейно интервал (0<С£ц<С1) в интервал f « <СХ<С~-)г
мы получим систему т новых функций параметра т:
*l=/l(T)> *2=Л(Х)> •• > ^m=/m("c),
определенных на интервале (0<СХ<С1)> кроме точек т > Т ' ' * * и Раз~
рывных только в счетном множестве точек.
Для того чтобы получить функции /, определенные всюду на
интервале (0<СХ<С1)> достаточно, очевидно, установить взаимно-однозначное
/ 1 1\
соответствие между серединами интервалов I—г, — J и соединением:
этих середин и точек у, -^, ... ; приписывая функциям /» в каждой'
точке этого соединения значения, соответственно равные их значениям
в соответствующей середине, мы, очевидно, получим функции /<, опре~
деленные всюду на интервале (О <Сх <С 1)- Так как эти функции fi раз-
рывны только в счетном множестве точек, то геометрическое место
подвижной точки М(х1У х27 ..., хт)у координаты которой
*1=Л(Х)| *2=Л(Х)» •••» *т=/т("0,
является аналитическим множеством2. Кроме того, ясно, что оно
совпадает с совокупностью данных аналитических множеств Е19 Е2,. —
Остается лишь рассмотреть вторую из основных операций: общую
часть.
Как мы указали выше (пп. 13 и 23), мы можем предполагать
функции
*i =ЛИ) (О. х* = Лв) (О. •.., х. =/£) (О,
1 Лемма 1 Суслина: „Каждый интервал (а, в) есть А~множестзои''.
1 Лгюса 2 Суслина: „Пусть £lt E2i . . . — счетная совокупность А-множеств;
их множество-сумма Е = Е\-+-Е2-*~ ...— также А-множество.
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА II
413
которые служат дая определения аналитического множества £я,
разрывными только в рациональных точках интервала (О <Z tn <С 1).
Установив это, возьмем какую-нибудь иррациональную точку tn
интервала (0<Оя<1); пусть
— ее разложение в непрерывную дробь, где a„,v— целые
положительные числа. Мы умеем бесчисленным множеством способов расположить
члены таблицы с двойным входом
*1,1 <*г, 2 . . .
*2.i а2,2 ...
в простую последовательность р1э |32, ..., рь ... Выберем определенный
метод (впрочем, произвольный) дая выполнения этого преобразования;
мы положим
' = (Pl, h, ..м fc, .-.)
и поставим иррациональную точку /, расположенную в новой области
(0<С*<С1)> в соответствие бесконечной последовательности
иррациональных точек tlt t.„ ..., расположенных соответственно в интервалах
(0<^<1), (0</2<1),....
Ясно, что значение этой последовательности tly tly ... определяет t
единственным образом, и, обратно, значение t определяет единственным
образом последовательность tly t2, ....
Следовательно, мы можем записать
'l = ?l(')> ^2 = ?2(0> •••, 'п = ?«(')> ...,
где, каково бы ни было целое положительное число л, функция <ря(0
определена для каждого иррационального числа области (0<О<О);
для рационального t <р„ не имеет никакого смысла. Если мы обозначим
через о/ множество иррациональных точек области (0 <^ t <C 1), мы
можем заметить, что функция <?„{t) непрерывна в каждой точке t0
множества о/ относительно этого множества. Отсюда следует, что
сложная функция
ф(«> (0 =/« [?„(/)]
также непрерывна в каждой точке t0 множества о/ относительно ./.
Установив это, рассмотрим т бесконечных последовательностей
совместных равенств:
<ЙЦ (')=♦? '(0=^(0= ••• =^(0= ....
и обозначим через Н совокупность точек t множества с7, которые
удовлетворяют всем этим равенствам.
414
Н. Н. ЛУЗИН
В силу относительной непрерывности функций ^w) легко видеть,
что это множество Н замкнуто относительно ^7; кроме того, Н
содержится в о)'.
Из этого мы немедленно заключаем, что среди предельных точек
множества Н одни только рациональные предельные точки не
принадлежат Н. Следовательно, множество Н отличается от замкнутого
в обычном (абсолютном) смысле на отрезке (0^/^1) множества
не более, чем счетным множеством дополнительных точек. Наконец,,
так как общая часть множеств Е19 Е2, • .. несчетна, то и множество И
также несчетно. В этих условиях множество //, очевидно, допускает
эффективное отображение на континуум (О <С^ <^1) посредством функции
t = *>(*),
определенной на интервале (О <С ~ <С 1) и разрывной только в
рациональных точках этого интервала1.
Установив это, рассмотрим систему т сложных функций /г,/29. • .,/т
параметра т, определенных равенствами
/1(х) = фа)[«,(х)], /,(x) = f[<o(T)l, .../m(t) = fm)hW].
Из непрерывности функций ф и со в каждой иррациональной точке
следует, что функции / разрывны только в рациональных точках.
Следовательно, геометрическое место подвижной точки М(х19 лг2, ..., хт)
с координатами
*1 = Л (Т)> *1 =Л (*), ...Хт =/т (х)
является аналитическим множеством; обозначим его через Е.
Процесс, который мы только что применили д\я определения
множества Е, указывает нам, что Е образовано точками, которые
принадлежат всем данным аналитическим множествам Ех> Е2, ... и
соответствуют иррациональным значениям всех представляющих параметров
^i> *2> • • •> 'п> • • • • Следовательно, множество Е отличается от общей
части всех множеств Е19 Еъ ... только дополнительными точками,
которые соответствуют рациональным значениям параметров t19 f2> •••> **> •••*
но тогда эти точки образуют не более, чем счетную совокупность.
Следовательно, рассматриваемая общая часть, будучи соединением
аналитического, значит, просеянного множества и счетного множества
точек, сама является просеянным, следовательно, аналитическим
множеством2 (ч. т. д.).
Приложения.
35. Приложение к мощности множества, измеримого В. Одно
из важных следствий предыдущего предложения состоит в том, что;
1 Для того чтобы выполнить это отображение, достаточно сделать
незначительное изменение в доказательстве известной теоремы: Всякое совершенное линейное
множество имеет мощность континуума, данной Борелем; см. его „Lecons sur
les fonctions de variables reelles", стр. 14—16.
2 Лемма 3 Суслина: „Пусть Е±л Е^ ... — счетная последовательность А-мно'
жесте; их общая часть Е=Е\Еъ% . . . также является А-множествомл'.
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА II
41S
Каждое множество, измеримое В, является просеянным,
следовательно, аналитическим множеством 1.
Но мы видели выше (п. 25), что каждое аналитическое множество
или конечно, или счетно, или содержит совершенное множество^
Отсюда следует, что:
Каждое несчетное множество, измеримое В, содержит
совершенное множество, следовательно, имеет мощность континуума.
Таким образом, мы получаем предложение Александрова—Хаус-
дорфа.
Легко видеть, что свойство точечных множеств, о котором идет
речь, в этом предложении не является индуктивным свойством.
В самом деле, обозначим вообще через Р0 следующее свойство
точечных множеств: каково бы ни было совершенное множество ~,
если множество Е несчетно на тс, то оно содержит совершенное
множество Ех, принадлежащее к.
Каждое аналитическое множество Е, несомненно, обладает этим
свойством Р0, так как общая часть множеств Е и тс, будучи
аналитическим множеством (п. 34) и по предположению несчетным, необходимо
должна содержать совершенное множество Ег.
Следовательно, повторяя рассуждения идеалистов, основанные на
гипотезе континуума (т. е. нумерации точек континуума посредством
трансфинитных чисел второго класса), мы без всякого затруднения
образуем последовательность множеств Ег, Ег, ..., которые все
обладают свойством Р0, но их общая часть им не обладает, хотя она и
несчетна2.
36. Приложение к проекциям множеств. Мы определим
аналитическое множество как геометрическое место подвижной точки М(хх>
х2,..., хт), координаты которой удовлетворяют равенствам
*l=M*)f *«=/«(*)>•••» Xm=fm(t),
где функции / разрывны лишь в счетном множестве точек.
1 Теорема I Суслина: „Каждое множество, измеримое Вч является А-мно-
жеством" (см. [14]).
2 В силу одного замечания Серпинского а\я нашей цели достаточно взять
вместо свойства Pq свойство Pi точечных множеств, определенное следующим
образом: множество Е обладает свойством Р^ если оно счетно, или содержит
некоторое совершенное подмножество.
Опираясь на аксиому Цермело (без допущения гипотезы континуума), можно
без труда показать, что общая часть двух множеств, обладающих свойством Plt
не обладает необходимо этим свойством. В самом деле, из аксиомы Цермело
вытекает существование на интервале (0, 1) некоторого множества Е% несчетного и не
содержащего никакого совершенного подмножества. Далее, обозначим через М
множество всех действительных чисел > 1, а через N—множество всех
действительных чисел <0 и положим Ei = E-*-M, E2 = E-*-N. Мы видим без труда, чт*
множества Е± и Е<ь обладают свойством Pi, но их общая часть (которая, очевидно,
есть множество Е) этим свойством не обладает. Следовательно, свойство Рх не
является индуктивным.
416
Н. Н. ЛУЗИН
Предложенное определение аналитического множества обязывает нас
оправдать это наименование, доказав, что оно не зависит от
выбранной системы координат S(xly х2У.. ., хт).
Для доказательства изменим систему координат, взяв вторую систему
координат S'(x[y х'2> • • •> х'т). Формулы преобразования координат
являются хорошо известными соотношениями, которые выражают новые
координаты xv х2У..., х'т в функции старых координат х1У х2У..., хт
{и обратно); так как эти соотношения линейны относительно х1У х2У..., хт
и имеют постоянные коэффициенты, то новые координаты х[, х2У.. ,ух'т
являются функциями, разрывными лишь в счетном множестве точек
интервала (О <С ^ <Г 1); следовательно, факт аналитичности точечного
множества не зависит от выбранной декартовой системы координат.
Установив это, возьмем в евклидовом пространстве & т измерений
аналитическое множество Е и спроектируем его ортогонально на
некоторое евклидово пространство §' тп измерений, 1 ^ rn <^ /л, произвольно
взятое в данном пространстве &. Так как аналитичность множества Е
не зависит от выбранной системы координат S(xly лг2, —, хт)у мы можем*
взять в пространстве £ такую систему прямоугольных осей S(xiy х2У..., хт)у
что оси х1У х2У..., хт принадлежат пространству §'\ эти оси образуют
в пространстве <§' систему координат; обозначим ее через S'(х19 лг2,..., х'т).
В этих условиях ортогональная проекция р° точки P°(xJ, х\у..., х°т)у
произвольно взятой в &у на пространство <§' имеет координатами
относительно S' соответственно числа х[у х\у..., х*т,. Отсюда следует, что,
каково бы ни было аналитическое множество Е:
*i=/i(*)t x2=/2{t)y...y xm>=fm>(t)y xm=fm(t),
расположенное в пространстве &у ортогональная проекция Е на
пространство &' есть некоторое множество точек пространства <£',
координаты которого имеют вид
*l=/l(0f *2 =/2 (')»•••» Xm'=fm'(t).
Легко видеть, что это — аналитическое множество.
Итак:
Ортогональная проекция аналитического множества точек в
евклидовом пространстве т измерений на евклидово пространство т из*
меренийу т <^т, является аналитическим множеством1.
Так как все множества, измеримые Ву являются аналитическими
множествами, мы можем, в частности, сказать, что:
Ортогональная проекция множествау измеримого Ву является
всегда аналитическим множеством.
Эта теорема чрезвычайно важна, потому что она показывает нам,
что, проектируя элементарные множества, которые все измеримы В
>(п. 18), мы получаем только аналитические множества. И так как,
1 Теорема Суслина: „Если S есть А-множестао% то его проекция — также
А-множес тво и.
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ, ГЛАВА II 417
с другой стороны, каждое аналитическое множество может быть
получено проектированием надлежащим образом определенного элементарного
множества (п. 24), мы имеем таким образом три совершенно
эквивалентных метода для определения аналитических множеств:
1° просеивать посредством общего решета;
2° писать параметрические уравнения л\-=/,(£);
3° проектировать элементарные множества (см. [18]).
37. Приложения к функциям. Мы определили аналитическое
множество посредством параметрических уравнений
где fi разрывны лишь в счетном множестве точек области (О <С t <C 1)«
В этих условиях функции fi являются функциями первого класса
классификации Бэра.
Естественно постараться теперь распространить только что данное
определение на высшие классы Бэра1.
Рассмотрим систему т произвольных функций классификации Бэра:
/i(0> fi (')»•••» /m(0» определенных на интервале (0<*<С1)» и
обозначим через Е геометрическое место последовательных положений
подвижной точки М(хи х2,..., хт), координаты которой удовлетворяют
уравнениям
*l=/l(0i X2=f2(t),..., XM=fM(t).
Требуется выяснить природу множества Е.
Для этой цели возьмем евклидово пространство <£' т -+-1 измерений,
содержащее пространство S т измерений. Пусть &(х1У х2,..., xmyt) —
система прямоугольных осей координат в пространстве £', содержащая
систему координат S(xu х.2,..., хт)у взятую в пространстве S;
следовательно, осью t будет прямая, проведенная через начало О системы S
перпендикулярно пространству £.
Установив это, рассмотрим функцию F(x1,x2, ..., xm,/) т-+-1
переменного, определенную равенством
F= к -Л С)]2 ч- [-, -Л WI*+...[*•-/. (012.
Так как функции /1Э /2, ..., /т принадлежат к классификации Бэра,
функция /* также ей принадлежит. Следовательно, функция F
аналитически представима. Между тем, хорошо известная теорема Лебега
утверждает, что множество точек пространства, в которых
аналитически представимая функция равна нулю, необходимо является
множеством, измеримым В2. Следовательно, множество точек N(xl9 лг2, ..., хт, t)
в пространстве & тч-1 измерения, координаты которых х19 х2, ...
. •., х„, г удовлетворяют уравнениям
1 См. Е. В о г е 1. Lecons sur les fonctions de variables reelles, стр. 100.
2 См. H. Lesbegue. Sur les fonctions representables analytiquement,
стр. 1S6.
418
Н. Н. ЛУЗИН
*i=/i(')» x2=f2(f), . .., xm=fm(t),
является множеством, измеримым В.
Отсюда следует, что ортогональная проекция этого множества на
евклидовом пространстве & т измерений является аналитическим
множеством. Но эта проекция есть не что иное, как геометрическое место
подвижной точки М{хи х2, ..., хт) пространства &, координаты
которой могут быть представлены в параметрической форме
*i=/iW» x2=f2(t), ..., xm=/m(t).
Мы приходим таким образом к следующему предложению:
Мы нисколько не расширяем определения аналитических множеству,
рассматривая геометрическое место положений, последовательно
принимаемых подвижной точкой, координаты которой являются
произвольными функциями параметра, принадлежащими классификации
Бэра \
IX. Второе индуктивное свойство: однозначность.
38. Однозначные множества. Итак, вернемся к данному
первоначально определению аналитических множеств. Пусть Е — аналитическое
множество в пространстве § т измерений, заданное параметрическими
уравнениями
Xi=fi(t), x2=f2(t), ..., xm = fw{t)9
где функции / разрывны лишь на счетном множестве точек.
Из самого определения следует, что необходимое и достаточное
условие для того, чтобы произвольная точка М° (лг°, х\, ...а:^), взятая в
пространстве §, принадлежала аналитическому множеству Е, состоит в том,
чтобы существовал хотя бы один общий корень t° уравнений
*!=/,(<). А=Ш> ■••><=/„(*).
Но в общем случае эти уравнения допускают несколько общих
корней; это сложный случай.
По этой причине естественно подвергнуть внимательному анализу
сначала самый простой случай, когда предыдущие уравнения имеют
один и только один общий корень, какова бы ни была точка
№(х\, \х\, ..., л:^), принадлежащая аналитическому множеству Е.
В этом случае каждой точке М° множества Е соответствует единствен-
ное значение *° на интервале (0 < t <C 1).
Таким образом, мы приходим к следующему определению:
Если функции xl=f1(t), x2=f2(t)9 ..., xm=fm(t), разрывные лишь
в счетном множестве точек интервала (0<О<О)> определяющие
аналитическое множество Е, таковы, что двум разным значениям
1 Теорема III моей заметки (1917 г.): „Множество значений каждой функции
f(x), которая входит в классификацию Бэра, есть А-множество"*.
'ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА II 419
переменного параметра t соответствуют две различные точки
множества Еу это множество называется однозначным множеством.
Из этого определения легко видеть, что каждое однозначное
множество является аналитическим множеством, быть может, очень
своеобразного вида.
Чтобы уточнить своеобразие однозначных множеств, заметим сперва,
что никакое конечное или счетное множество не может быть
однозначным множеством. В самом деле, параметрические уравнения jc1=/1(tf),
jt2 = /2(0> • • •> •*m=/m(0> которые служат для определения понятия
однозначного множества Е> осуществляют, очевидно, взаимно
однозначное соответствие между точками множества Е и точками интервала
(CKCf^l) таким образом, что каждому числу t интервала (0<С?<С1)
соответствует одна и только одна точка М множества Е и, обратно,
каждой точке М множества Е соответствует единственное число t этого
интервала. Таким образом, мы имеем отображение множества Е на
континууму осуществленное посредством системы т функций,
разрывных лишь в счетном множестве точек.
Следовательно:
Каждое однозначное множество имеет эффективно мощность
континуума.
Чтобы исследовать природу однозначных множеств, докажем
следующее важное предложение:
Теорема. Свойство точечных множеств — быть конечным мне-
жествому или счетныму или же однозначным множеством — есть
индуктивное свойство.
Во-первых, сумма счетной совокупности однозначных множеству
не имеющих попарно общих точеку есть однозначное множество.
Чтобы это увидеть, достаточно заметить, что доказательство,
данное выше (п. 34) для случая аналитических множеств, прилагается без
всякого изменения и к случаю однозначных множеств, так как, если
система т параметрических уравнений
допускает один и только один общий корень /°, то, каково бы ни было
целое положительное число л, полученная система
также допускает один и только один общий корень х0#
Далее, общая часть счетной совокупности однозначных множеству
если она не является ни конечным, ни счетным множествому есть
также однозначное множество.
Чтобы это увидеть, достаточно сделать аналогичное замечание
(см. п. 34).
Следовательно, остается только доказать, что каждый замкнутый
параллелепипед Р т измерений является однозначным множеством.
420
Н. Н. ЛУЗИН
Чтобы это доказать, необходимо принять некоторую
предосторожность, потому что предыдущее рассуждение (п. 34) больше не
применимо: каждая пеановская кривая, заполняющая Р, несомненно допускает
кратные точки.
Итак, возьмем параллелепипед Р. Так как для каждой пары
параллелепипедов т измерений Р и Р' существует преобразование Т
линейное относительно переменных х1У х2, ..., хту которое
преобразует Р в Р', легко видеть, что достаточно доказать сформулированное
предложение а^я фундаментального куба К:
(0<дг1<1, 0<х2<1, ..., 0<хш<1).
Установив это, фиксируем некоторые из букв xiy x2i . .., х„> взяв
их равными также фиксированным рациональным числам, произвольно
выбранным между 0 и 1, и будем изменять остальные буквы, давая им
соответственно все иррациональные значения, заключающиеся между О
и 1; мы получим таким образом множество точек, которое составляет
вполне определенную часть куба ЛГ; обозначим его через /Г.
Мы можем теперь утверждать, что К' является однозначным
множеством.
В самом деле, повторяя рассуждение, данное выше (п. 34) для
случая „пространства с бесконечным множеством измерений" (здесь речь
идет о бесконечном множестве параметров tv t2, ..., tn> • • •> которые
изменяются независимо друг от друга во множестве иррациональных
чисел g7, и об их представлении последовательностью функций одного
переменного t:
мы констатируем, что К' есть множество, гомеоморфное множеству 3
иррациональных точек интервала (0<*<С1)» следовательно, К есть
однозначное множество.
Установив это, вернемся к фундаментальному кубу К. Мы уже
видели, что рассматриваемое множество 1С является частью куба Ку и что
оно совершенно определено выбором фиксированных букв из букв xlt
*2* • • •» хп и выбором их рациональных значений.
Так как этих выборов счетное множество и разным выборам
соответствуют множества К' попарно без общих точек, мы можем написать
где D — множество точек куба К со всеми рациональными
координатами. Следовательно, D счетно.
Число фиксированных букв может быть равно нулю.
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ, ГЛАВА II
421
В силу теоремы п. 34 мы заключаем отсюда, что фундаментальный
куб есть однозначное множество (ч. т. д.).
39. Из этой теоремы следует, что:
Каждое множество, измеримое В, является или конечным множе-
ствоМу или счетным, или же однозначным множеством*.
Но гораздо более замечательна следующая теорема, относящаяся
к самой природе множеств, измеримых В:
Если дана система т параметрических уравнений с
единственным общим корнем, мы можем получить однозначное множество Е,
определенное этой системой уравнений, отправляясь от
параллелепипедов, посредством ряда основных операций: сумма, общая часть,
занумерованных посредством целых положительных чисел, нумерация
которых извлекается из данной системы параметрических уравнений.
Чтобы доказать эту важную теорему, следует сначала изучить
некоторые предварительные вопросы.
X. Отделимость В.
40. Вполне полуупорядоченные вшожестаа. Во-первых, мы введем
некоторые понятия, которые нам будут весьма полезны в дальнейшем.
Определение. Натуральный ряд Е целых чисел 1, 2,3,
...называется полуупорядоченным, если согласно какому-то закону каждому
элементу (п) последовательности Е соответствует ее конечная, или
бесконечная (или пустая) часть Еп, составленная из элементов,
называемых „предшествующими** (п), причем принято условие, чтобы
соотношения: (Ь) „предшествует** (с) и (а) „предшествует*4 (Ь),
влекли за собой: (а) „предшествует" (с)2.
Определение. Натуральный ряд Е целых чисел 1,2,3, ...,
предполагаемый полу упорядоченным, называется вполне
полуупорядоченным, если не существует никакой бесконечной
последовательности аи а2, а3, .. .элементов ряда Е, такой что, каково бы ни было
целое положительное число n, aw+1 „предшествует" ап.
Установив эти определения, мы докажем следующее предложение:
Теорема. Каждую вполне полуупорядоченную натуральную
последовательность Е можно представить во вполне упорядоченной
форме Е таким образом, что если в последовательности Е (а)
„предшествует" (Ь) согласно принятому закону^ то во вполне
упорядоченном множестве Е' ранг (а) меньше ранга (Ь).
Лая доказательства этого предложения достаточно будет обратиться
ко второму рассуждению Цермело, относящемуся к возможности
представить каждое множество во вполне упорядоченном виде; это рассу-
1 Теорема IV моей заметки (1917 г.): пДля того чтсбы А-мнсжество было
измеримым В, необходимо и дсстстсчнс, чтсбы сно было однозначным
множеством11.
2 Можно сопоставить это понятие с понятием частично упорядоченных множеств
Ф. Хвусдорфа: см. „Theorie den Mengenlebre", 1914, стр. 139.
422
Н. Н. ЛУЗИН
ждение здесь совершенно законно, потому что в рассматриваемом
случае речь идет совсем не об аксиоме выбора, а о фактически
реализуемых выборах.
В самом деле, пусть Ег есть произвольная часть натуральной
последовательности Е. Так как эта последняя вполне полуупорядочена,
то существуют такие элементы Elf „предшествующие" которым (если
они существуют) не принадлежат Elf и среди этих элементов мы
найдем первый; пусть ег — этот элемент Ev При помощи этого метода мы
получим во всевозможных частях Ех последовательности Е вполне
определенные различные элементы ег из Е±. Следовательно, правило выбора дано.
Из самого метода определения реализации этого выбора следует, что,
какова бы ни была часть Ег натурального ряда Е, ни один элемент Ех
не будет „предшествующим" соответствующему ему элементу ех
совокупности Ег. Вообще, упорядочение некоторого множества М путем
выбора в его подмножествах Мх различных элементов т1У в каждом по
одному, таково, что каждый элемент т множества М является
отличным от других элементов в подмножестве, образованном элементами
множества М, ранг которых больше или равен рангу га1. Отсюда
следует, что упорядочение множества Е путем указанного правила выбора
удовлетворяет формулировке предложенной теоремы (ч. т. д.).
41. В этом рассуждении имеется серьезный изъян: а именно,
необходимость рассматривать произвольную часть Ех натурального ряда £.
Тогда предпочтительнее первое рассуждение Цермело, потому что речь
идет только о частях ряда Еу перечисленных при помощи целых
положительных чисел.
Итак, назовем цепью каждое вполне упорядоченное множество С,
образованное из элементов натурального ряда Е и обладающее
следующим свойством: каков бы ни был элемент е цепи С, если удалить из Е
все элементы цепи С, ранг которых в С меньше ранга е, то первый
из остающихся элементов последовательности Е, для которого все
„предшествующие" (если они существуют) не будут остающимися элементами,
совпадает с е.
Ясно, что цепи существуют, так как первый элемент
последовательности Еу не имеющий никаких „предшествующих", уже составляет цепь.
Очевидно, что если даны две разные цепи, одна является точным
отрезком другой. Отсюда следует, что если С0 — цепь, но не самая большая,
ей соответствует некоторое вполне определенное целое положительное
число л0, которое является элементом некоторой большей цепи Ci9
непосредственно превосходящим все элементы цепи С0. Кроме того,
обратное также имеет место: каждому элементу последовательности Е
соответствует одна и только одна цепь, которая не является наибольшей.
Отсюда мы немедленно заключаем, что совокупность цепей, каждая из
1 См. Е. В orel. Lemons sur la theorie des fonctions. 2e ed., IV, n° III. — Le
continubien ordonne d'apres M. Zermelo, стр. 148—149.
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА II
423
•которых не является наибольшей, эффективно существует, так как это
есть множество, занумерованное посредством целых положительных
чисел. Следовательно, существует совокупность всех этих цепей. Но эта
•совокупность, увеличенная, если нужно, одним последним остающимся
элементом последовательности Е, является, очевидно, наибольшей целью.
Очевидно, что эта наибольшая цепь удовлетворяет формулировке
предложенной теоремы (ч. т. д.).
42. Множества, отделимые В. Из доказанной теоремы мы получим
важные следствия. Дая этого следует сперва ввести одно чрезвычайно
лолезное понятие.
Определение. Мы скажем, что два точечных множества Е и Е',
не имеющие общих элементов, отделимы В, если из определений
множеств Е и Е' мы умеем получить два ряда основных операций:
яумма, общая часть, занумерованных посредством целых
положительных чисел, которые позволяют построить, отправляясь от
параллелепипедов, два множества Н и Н, не имеющие ни одной общей
точки и заключающие соответственно множества Е и Е'.
Введя это понятие, мы можем доказать следующую теорему:
Теорема. Два аналитических множества, не имеющие ни одной
общей точки, всегда отделимы В.
Рассмотрим два произвольных аналитических множества Е и Е', для
определенности линейные.
Пусть С и С — два решета, расположенные в фундаментальном
квадрате, стороны которого имеют уравнения
х = 0, х = 1, у = 0, у = 1,
посредством которых заданы Е и Е'.
Оба решета С и С образованы соответственно счетным множеством
замкнутых отрезков av a2, а3, ... и a'v o'v а^, ###, параллельных гори'
зонтальной оси ОХ.
Я утверждаю теперь, что всегда можно предполагать эти отрезки
такими, что проекции двух произвольных отрезков на ось ОХ или вло-
.жены одна в другую, или не имеют общей внутренней точки. В самом
деле, если дано целое положительное число п, достаточно разбить
отрезки ап и о'п на конечное число замкнутых отрезков посредством точек,
абсциссы которых совпадают с концами проекций In отрезков olf a2, ...
„.., ап и о\у о\, ..., а^; два новых решета, образованные соответственцо
этими частями отрезков оп и о'пУ когда мы изменяем п, удовлетворяют,
очевидно, .высказанному условию1.
1 Кроме того, мы можем предполагать, что длины отрезков о„ и оя стремятся
к нулю, когда п неограниченно растет. В самом деле, достаточно перед только что
описанным разбиением отрезков оп и оя разделить их на л равных частей и,
изменяя л, перенумеровать полученные таким образом замкнутые отрезки посредством
целых положительных чисел. Важно отметить, что все эти преобразования нисколько не
изменяют jp.eineT С я С с геометрической точки зрения.
424
Н. Н. ЛУЗИН
43. Установив это, рассмотрим все пары [а, а'] замкнутых отрезков:
а и а', взятых соответственно в решетах С и С, проекции которых на
ось ОХ вложены одна в другую. Ясно, что этих пар счетное
множество; следовательно, мы можем их перенумеровать посредством целых
положительных чисел. Пусть
[11, И, ..., [п], ...
— их последовательность, где символ [л] обозначает пару [о, а']; мы
прибавим сюда пару [0], образованную дважды повторенной стороной у = 1
фундаментального квадрата.
Установив это, условимся в следующем: мы будем говорить, что
пара 1пх] = [ах, а^] „предшествует" паре [л2] = [з2, а2], если проекция
отрезка ох содержится в проекции отрезка а2, а ордината ах меньше
ординаты а2, и если мы имеем аналогичные соотношения между о\ и o't.
После того как введено это определение, ясно, что условия: [6]
„предшествует" [с\ и [а] „предшествует" [Ь] влекут: [а] „предшествует" [с]-
Мы заключаем отсюда, что последовательность
[01, [11, 12], ..., In], ... (1>
полу упорядочена. Кроме того, эта последовательность вполне
полуупорядочена, так как иначе мы имели бы такую бесконечную
последовательность [ах], [а2], ..., что [ая+1) „предшествует" [ая], каково бы ни было
целое число л, что как раз невозможно, так как множества Е и Е' не
имеют ни одной общей точки.
В силу предыдущей теоремы (п. 40) последовательность (I) может
быть эффективно представлена во вполне упорядоченной форме таким
образом, что если [а] „предшествует" [6], то ранг [а] в этой вполне
упорядоченной форме будет меньше ранга [Ь\. Кроме того, так как
каждая пара [л], л<1 „предшествует" паре [0], то ранг пары [0] в этой
вполне упорядоченной форме больше всех других рангов.
Установив это, возьмем функцию ц(лг), определенную ранее (пп. 3,.
10 и 20) на множестве Е посредством решета С; пусть |i' (х) —
аналогичная функция, определенная на £' посредством решета С Наконец,,
если дана пара [а, а'), [обозначим через [е, е\ соответствующую пару,.
образованную двумя точечными множествами и определенную
следующим образом: е есть множество тех точек Е> которые принадлежат*
проекции отрезка о на ось ОХ и для которых р(х) меньше ординаты
отрезка а; е определено аналогичным образом посредством Е' и а'.
В этих условиях каждому элементу [п] рассмотренного выше вполне
упорядоченного множества соответствует пара множеств; следовательно,,
мы имеем вполне упорядоченное множество (П) соответствующих пар
множеств. Кроме того, среди этих пар множеств имеется одна пара,,
обладающая самым высоким рангом: это, очевидно, пара [£, Е%
соответствующая [0].
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА II
42S
44. Я утверждаю теперь, что каждая пара множеств [е, е]
отделима В.
Это справедливо для первой пары [е, е'] вполне упорядоченного
множества (И)#
В самом деле, пусть [a, d\ — соответствующая пара отрезков. Так
как эта пара является первой во вполне упорядоченном множестве пар
отрезков, то не существует никакой другой пары отрезков, которая ей
„предшествует". Установив это, рассмотрим множество таких отрезков х
решета С, что их проекции содержатся в проекции отрезка а, а их
ординалы меньше ординаты а. Пусть Н—сумма проекций этих отрез-
ков х# Мы обозначим через Н аналогичную сумму, относящуюся к
решету С и отрезку о'. Так как у пары [а, а'] нет никакой
„предшествующей" пары, множества Н и Н не имеют ни одной общей точки, кроме,
можеа быть, концов проекций, которых счетное множество. А так как
множества е и е\ очевидно, содержатся соответственно во множествах
Н и Н (кроме, может быть, четырех концов проекций отрезков а и а'),
то легко видеть , что е и е отделимы В.
Предположим утверждение верным для всех пар множеств, ранг
которых меньше ранга пары [е, е]у и распространим его на [е, е']. Пусть
[а, с']—соответствующая пара отрезков.
Обозначим через х отрезок решета С, проекция которого содержится
в проекции отрезка а, а£ордината меньше ординаты а; точно так же
обозначим через х' отрезок решета С, обладающий аналогичными
свойствами относительно а'. Пусть т\—совокупность точек множества ЕТ
принадлежащих проекции отрезка х, в которых [х (х) меньше ординаты х;
пусть г( — совокупность точек множества £', обладающих аналогичными
свойствами относительно проекции отрезка ц' и функции ji/ (х).
Я утверждаю, что т\ и т\ отделимы Ву и что нами получены
множества Н и Н', которые осуществляют это отделение.
В самом деле, если проекции отрезков х и х' вложены одна в
другую, пара отрезков [х, х'], несомненно, „предшествует" паре [а, о'];
следовательно, в этом случае множества г\ и ч\ отделимы по
предположению. Если же, наоборот, проекции отрезков х и х' не имеют ни одной
общей точки (кроме, может быть, одного конца), отделение т] и ч)'
производится посредством самих проекций отрезков х и х'#
Я утверждаю теперь, что множества i] п е отделимы В, и что мы
знаем отделяющие множества.
В самом деле, зафиксировав отрезок х, будем изменять отрезок х'
всеми возможными способами и возьмем общую часть всех множеств Нг
соответствующих различным отрезкам х\ Пусть h — эта общая часть.
Ясно, что множество h не содержит ни одной точки множества е\ так
как каждая точка множества в'(кроме, может быть, обоих концов проекции
отрезка а*) принадлежит, очевидно, хоть одному из множеств rf.
Я утверждаю наконец, что е и е отделимы В* В самом деле, чтобы
осуществить это отделение, достаточно образовать сумму S множеств hr
426
Н. Н. ЛУЗИН
соответствующих различным отрезкам ~, и прибавить, если это нужно,
оба конца проекции отрезка о; так как каждая точка множества е или
является концом проекции отрезка а, или принадлежит одному из
множеств Т|, то легко видеть, что множество-сумма S' содержит множество е
и не содержит ни одной точки множества е. С другой стороны, если
отрезок х фиксирован и мы составим сумму S' множеств //',
соответствующих различным отрезкам V, и возьмем общую часть Р сумм S',
соответствующих всевозможным отрезкам t', мы получим, очевидно,
множество, не имеющее ни одной общей точки с S и содержащее
множество е (кроме, может быть, концов проекции отрезка т').
Следовательно, искомое отделение осуществлено (ч. т. д.).
Следствие. Если два аналитических множества Е и Е' взаимно
дополните льны у то из определения Е и Е' мы умеем осуществить
их построениеf отправляясь от параллелепипедов, посредством
операций: сумма, общая часть1.
XI. Эффективное построение, отправляясь от
параллелепипедов, каждого однозначного множества.
45. Мы можем приступить теперь к изучению однозначных множеств.
Теорема: Каково бы ни было однозначное множество Е, мы
можем извлечь из определения Еу отправляясь от параллелепипедов,
его построение посредством операций: сумма, общая часть2.
В самом деле, пусть Е — однозначное множество, расположенное
в евклидовом пространстве т измерений и заданное параметрическими
уравнениями
где функции /4 разрывны каждая лишь в счетном множестве точек
области (0<С*<С1)» Кроме того, как мы видели (пп. 13 и 23), всегда
можно предполагать, не уменьшая общности однозначных множеств,
функции fi разрывными только в рациональных точках области
(0<*<1).
Возьмем положительное число г. Так как функции /^ непрерывны
в каждой иррациональной точке ty то в области (0<^t<Cl) можно
определить такое замкнутое приводимое множество рв рациональных
точек, чтобы колебания (полные) всех функций /,- на каждом из
смежных интервалов к ре были меньше е (п. 14).
Дадим е последовательность убывающих значений г1? г2,.. #, гя,. #.,
стремящихся к нулю. Мы получим последовательность соответствующих
замкнутых приводимых множеств р6, р.,..., Ре,««- Установив это, мы
возьмем последовательность новых приводимых множеств /?г> /?2>-«»> Яя>...,
1 Теорема III Суслина: „Если множество Е и его дополнение СЕ являются оба
А-множествами<, они измеримы В",
2 Теорема IV моей заметки (1917): „Для того чтобы А-множестзо было
измеримо В% необходимо и достаточно, чтобы оно допускало систему единственности".
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА II
определенных следующим рекуррентным соотношением: первое
множество /?! совпадает с приводимым множеством ре; если множество Rn_x
определено, мы образуем множество Rn, прибавляя к /?„_! множество piw
и разбивая каждый смежный интервал этой совокупности правильным
образом (п. 14).
Мы образуем таким образом бесконечную последовательность
множеств
приводимых на (О <С t <Z 1), содержащихся каждое в последующих и
таких, что колебания (полные) функций /< на каждом смежном к Rn
интервале будут меньше £я. Важно отметить, что каждый из смежных
к /?я+1 интервалов является внутренним в узком смысле к некоторому
интервалу, смежному к Rnf таким образом, что они не имеют общих
границ. Отсюда мы немедленно заключаем, что, несомненно, существуют
точки интервала (О <С £ <С 1)> общие всем открытым интервалам
смежным соответственно множествам /?lf R.l9..., /?„,... и каждый
внутренний к предшествующему.
Закончив эти предварительные рассуждения, вернемся к данному
однозначному множеству Е. Пусть п — данное целое положительное
число. Возьмем приводимое множество /?я, и пусть о и о' — два разных
произвольных смежных к Rn интервала. Если мы будем изменять
параметр t сначала на о, а потом на 8', система параметрических уравнений
*1=Л(*)» *2=Л(*)»--м Xm=fm(t)
дает нам два аналитических множества е и е у не имеющие ни одной
общей точки. Следовательно, мы можем извлечь отсюда два
множества Н и //, отделяющие соответственно е и е. Если мы
зафиксируем смежный интервал 8 и будем изменять смежный интервал о',
по-прежнему отличный от 8, мы получим счетную совокупность
множеств //, содержащих е. Следовательно, общая часть всех этих
множеств Ну несомненно, содержит множество е; мы обозначим ее через Л.
Из этих рассуждений очевидно следует, что каждому интервалу 8,
смежному к Rn> соответствуют некоторое очень малое аналитическое
множество е и некоторое множество А, содержащее е. Так как
множества А, соответствующие различным 8, не имеют, очевидно, попарно
ни одной точки, мы имеем одновременное отделение всех е посредством
множеств А. Кроме того, мы можем предполагать множества А также
очень малымщ так как в силу того, что колебания (полные) функций /,-
на 8 меньше вя, соответствующее множество е имеет очень малый диаметр.
Установив это, обозначим через Sn сумму всех этих множеств А,
прибавив к ней счетную совокупность точек множества £,
соответствующих точкам приводимого множества Rn.
Ясно, что данное однозначное множество Е содержится в Snf
каково бы ни было целое положительное число л. Следовательно,
428
Н. Н. ЛУЗИН
общая часть всех множеств Sx, S2y..., несомненно, содержит Е;
обозначим эту общую часть через Р.
Я утверждаю теперь, что Р совпадает с Е. В самом деле, пусть
М—некоторая точка множества Р. Нужно доказать, что М
принадлежит множеству Е.
Это очевидно, если М принадлежит одному из дополнительных
счетных множеств, которые мы прибавляем к суммам множеств Л:,
в этом случае М является некоторой точкой множества £, которую»
мы получаем, давая t значение, принадлежащее некоторому
приводимому множеству Rn.
Итак, предположим, что М не принадлежит ни одному из этих
дополнительных множеств. В этом случае М принадлежит одному к
только одному из множеств А, каково бы ни было целое положительное
число п; пусть Ьп — соответствующий смежный к Rn интервал.
Мы приходим таким образом к бесконечной последовательности
открытых интервалов ~ * *
смежных соответственно множествам /?х, /?2,... и таких, что если мы
будем изменять параметр t на оя, точка М, несомненно, будет
принадлежать множеству Ля, содержащему малое аналитическое множество ея,
которое соответствует интервалу оя.
Пусть t0— точка, общая всем \, 82>. #., &„,... Так как функции/^
непрерывны в /0 и диаметр множества hn стремится к нулю, когда п
неограниченно растет, очевидно, что мы получим точку М, давая t
значение t0; следовательно, М принадлежит множеству Е.
46. Понятие множества, измеримого В. Предыдущие рассуждения
чрезвычайно важны, потому что они нам показывают, что если
пренебречь конечными и счетными множествами, то нет существенной
разницы между однозначными множествами и множествами, называемыми:
измеримыми В. В дальнейшем мы подробнее остановимся на
возможности постичь „другие" множества; в этой главе нашей единственной
целью было: несколько уточнить понятие множества, измеримого В~
Таким образом, мы приходим к следующему заключению: мы начали
с чисто конструктивного определения множества, измеримого В, к
констатировали, что понятие, которое возникает из этого определения,,
еще не обладает достаточной ясностью, чтобы фигурировать в
математическом рассуждении, так как самая совокупность определенных таким
образом множеств является лишь одной из форм парадокса
трансфинитного. Тогда мы пошли следующим путем: мы доказали, что свойство
точечных множеств — быть однозначными множествами, или счетнымиу
или же конечными, есть индуктивное свойство, следовательно, такое»
что в каждом частном построении, выполненном посредством двух,
основных операций, если следовать этому построению шаг за шагом,
каждое промежуточное множество обладает этим свойством, так же как
и финальное множество. На этом основании довольно естественно
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА II
429
считать это свойство, как, впрочем, и каждое индуктивное свойство,
принадлежащим всем множествам, измеримым В, хотя у нас и нет
определения этих множеств. С другой стороны, мы доказали, что
каждое однозначное множество может быть построено, отправляясь от
параллелепипедов, посредством двух основных операций, повторенных
счетное множество раз, причем последовательность этих операций и их
порядок вытекают из параметрических уравнений предложенного
однозначного множества.
Таким образом, мы пришли к следующему заключению:
Каждое множество, измеримое В, является или конечным
множеством, или счетным, или же однозначным множеством.
Нам кажется, что введенное понятие обладает большим
преимуществом— быть менее метафизическим, так как, поскольку трудно
отрицать существование совокупностей всех точек интервала (0, 1), всех
непрерывных функций, всех функций, разрывных только в
рациональных точках, постольку представляется трудным отрицать и
совокупность всех аналитических множеств; следовательно, если мы добавим
дополнительное условие: чтобы разным значениям t соответствовали,
несомненно, разные точки, законность соответствующей совокупности
не может быть уменьшена.
Заметим наконец, что введенное понятие облегчает наше представ-
ление о наиболее обм,ем множестве, измеримом В.
В самом деле, среди множеств, имеющих бесконечную мощность,
самыми простыми и естественными являются множества^ элементы
которых могут быть перенумерованы посредством целых
положительных чисел.
Это счетные множества.
Также среди несчетных множеств самыми простыми и
естественными являются множества, элементы которых могут быть
перенумерованы посредством действительных чисел, при условии, что всегда
употребляются соответствия, разрывные не более чем в счетном
множестве точек.
Это множества, измеримые В.
Приложения.
47. Приложения к проекциям множеств. Мы имеем приложение
предыдущей теоремы к проекциям множеств, вполне аналогичное
приложению п. 37.
Теорема. Ортогональная проекция множества, измеримого В,
в евклидово пространство т измерений, т! <С т, является
множеством, измеримым В, если проекции двух разных точек
множества различны.
Чтобы убедиться в этом, возьмем доказательство соответствующей
теоремы п. 36. Так как в данном случае две точки проекции
*i=/i(')>*a=/i(')>..•> xM>=fm.{t)
430
Н. Н. ЛУЗИН
рассматриваемого множества, измеримого В, соответствующие двум
разным значениям переменного параметра t, различны, предложенная
теорема доказана (ч. т. д.).
48. Приложения к функциям. Это приложение тоже аналогично
приложению п. 37.
Теорема: Если система т произвольных функций
классификации Бэра xl=/l{t)y x>=f2(t),..., xm=fm(t) такова, что двум разным
значениям переменного параметра t соответствуют две различные
точки пространства т измерений, то множество Е, определенное
посредством этих параметрических уравнений, наверняка
измеримо В.
В самом деле, рассмотрим в пространстве ё' /ин-1 измерений
систему S(x!, лг2,..., хт, t) прямоугольных осей координат. В силу
цитированной теоремы Лебега (п. 37) множество Е' точек
пространства <£', которые обращают в нуль аналитически представимую
функцию /п-4-1 действительных переменных х1У х2,. •., хт, i
[*i-/iWP-+-[**-/»W]8-b...-b[*«-/«WP,
есть множество, измеримое В. Из свойства системы функций /+ следует,
что каждый перпендикуляр к пространству & т измерений,
определенному осями х19 х2,. •., хт, пересекает множество Е' не более чем
в одной точке. Следовательно, в силу предыдущей теоремы
ортогональная проекция множества Е' на евклидово пространство £ является
множеством, измеримым В. Значит, это последнее, очевидно, совпадает
с предложенным множеством Е (ч. т. д.).
49. Замечание. Очень легко дать предыдущей теореме полезное
расширение, распространяя ее на случай, когда за область
определения функций fi вместо фундаментального интервала (0<C^<O)t
берется произвольное множество, измеримое В.
В самом деле, пусть Н, расположенное на интервале (0<С*<С1)> —
множество, измеримое В, на котором определена система т
произвольных функций
*i=/i(0> x2=f2{t),...9 xm=fm(t)
классификации Бэра.
Предположим, что двум разным значениям переменного параметра ty
взятым на множестве Н, соответствуют две различные точки
пространства S т измерений, и что мы ничего не знаем, если берем
значения t, не принадлежащие множеству //. Нужно доказать, что
множество Е точек пространства S, которые соответствуют всем
значениям t, взятым на Н и только на Н, есть множество, также
измеримое В.
Это тривиально, если Н—конечное или счетное множество. Итак,,
предположим, что Н несчетно.
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ ГЛАВЛ И
431
Так как Н предполагается измеримым В, то существует
параметрическое представление
*=ср(т)
множества //, устанавливающее взаимно однозначное соответствие
между точками множества Н и точками интервала (О <Сх <Г 1)? где
функция ср (т) разрывна лишь в счетном множестве точек.
Установив это, рассмотрим сложные функции
хх =Л [? W1 *2 =Л [? WL. •., *. =/. [? W].
Ясно, что функции определены на всем интервале (0<~<1) и
принадлежат классификации Бэра. Так как двум разным значениям х
соответствуют две различные точки пространства &, то очевидно, что
множество Е измеримо В.
XII. Неявные функции
50. Проблема Лебега. Пусть & — евклидово пространство т-*-р
измерений, отнесенное к системе
о(хх> лг2,..., хту Уи г/2>* • •> Ур)
прямоугольных осей координат.
Обозначим через &х и §у два евклидова пространства
соответственно т и р измерений, которые содержат, одно — систему
S(xly х2,...> хт), а другое — систему S(yly y2,..., ур) прямоугольных,
осей координат.
Установив это, рассмотрим аналитические соотношения
Fl(xly лг2,..., хт, у1У у29..., Ур) = 09
F2(x]y х2У..., хт, у1У г/.2,..м Ур) = 0,
FQ(xly х2У..., хту у19 у2,..., уР) = 0,
где функции F являются функциями классификации Бэра,
определенными во всем пространстве £.
Тогда вопрос ставится так: узнать, разрешимы ли эти
соотношения относительно у-ов, и если разрешимы, то какова природа
неявных функций у, им удовлетворяющих?1.
51. Область существования неявных функций. Прежде всего
функция т-\-р действительных переменных
очевидно, входит в классификацию Бэра. Следовательно, множество
1 См. Lebesgue. Sur les functions representables analytiquement, стр. 192.
432
Н. Н. ЛУЗИН
точек Е всего пространства &, которые обращают эту функцию
в нуль, есть множество, измеримое В1.
Отсюда следует, что ортогональная проекция Ех множества Е
в евклидово пространство &х является аналитическим множеством.
Кроме того, так как множество Е может быть произвольно взятым
в пространстве S множеством, измеримым В, его ортогональная
проекция Ех является самым общим аналитическим множеством.
Итак:
Область существования неявных функций является самым
произвольным аналитическим множеством.
52* Однозначные неявные функции. Теорема Лебега. Установив
это, рассмотрим классический случай Лебега, когда ни одна из неявных
функций у не является многозначной функцией.
В этом случае ортогональные проекции двух разных точек
множества Е на частное евклидово пространство &х будут наверняка
различны. Отсюда немедленно следует (п. 47), что ортогональная
лроекция Ех множества Е на частное пространство &х является
множеством, измеримым В.
Следовательно:
Область существования однозначных неявных функций есть
множество, измеримое В.
53. Установив это, рассмотрим природу этих неявных функций.
Чтобы устранить тривиальный случай, когда Е конечно или счетно,
«мы предположим множество Е несчетным.
В этом последнем случае, так.как Е измеримо 5, мы можем записать
•его в параметрическом виде
*i=/i(f)» **=/>(')»•--i xm=fm(t), yi=gl(t)y y2 = g2(t),..., Ур = 8р%
где функции / и g разрывны лишь в счетном множестве точек
интервала (0</<1).
Рассмотрим какую-нибудь неявную функцию уь. В силу известной
теоремы Лебега, для того чтобы произвольная функция у(хх, х7,.. .,хт)
входила в классификацию Бэра, необходимо и достаточно, чтобы,
каковы бы ни были а и Ь, множество
£(<z<y<6)
было измеримо В2.
Применим этот критерий к случаю неявно? функции.
Так как функция gv(0 разрывна лишь в счетном множестве точек
интервала (0 <С t < 1), она входит в классификацию Бэра. Следовательно,
множество точек t интервала (О <С t <C 1), для которых мы имеем
a<gk(t)<b
*есть множество, измеримое В; обозначим его через е.
1 См. Н. Lebesgue. Sur les fonstions representables analytiqueraent, стр. 157.
2 См. там же, стр. 167.
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА II
433
Из замечания п. 49 следует, что если мы будем изменять t на
множестве е, множество точек
*i =Л (0. х* =Л (0..• •> *.. =/« С)
необходимо будет множеством, измеримым В.
Но очевидно, что это множество совпадает с множеством
Следовательно, неявная функция у^ входит в классификацию
Бэра.
Мы пришли таким образом к теореме Лебега относительно
однозначных неявных функций *.
Теорема (Лебег). Однозначная функция, неявно определенная
при помощи аналитического выражения, может быть выражена
аналитически явным образом2.
54. Многозначные неявные функции. Изыскания П. С. Новикова
(см. [23]). В случае многозначных неявных функций дело обстоит
сложнее. Теорема Лебега относительно однозначных неявных функций
позволит нам по аналогии приступить к изучению многозначных
неявных функций3.
Прежде всего здесь следует отметить один важный частный случай,
который HMfeT много сходного с классическим случаем Лебега
однозначных неявных функций, а именно случай, когда множество значений,
которые может принимать каждая из многозначных неявных функций
в точке (х[у х2, ..., хи), не более, чем счетно.
Вот результаты исследований П. С. Новикова, относящиеся
к этому важному случаю:
I. Область Ех существования неявных функций у^ также является
множеством, измеримым В.
П. Существует, по крайней мере, одна система р однозначных
функций y°v у\,.. ♦, */°, определенных в области Ех и входящих
в классификацию Бэра, которые удовлетворяют заданным аналитическим
соотношениям
^i = 0, F2 = 0,..., Fg = 0.
1 Н. Lebesgue. Loc. cit., стр. 192.
2 Чтобы уточнить пределы применимости рассуждения, нам достаточно было
сделать изменение в формулировке Лебега, относящееся к добавлению слова
„однозначная". Впрочем, сам Лебег всегда рассматривал только однозначные неявные
функции.
3 Лебегу принадлежит набросок программы изучения многозначных неявных
функций.
„С атой теоремой (речь идет о теореме относительно однозначных функций)
можно связать и другие теоремы о многозначных функциях. Я указываю лишь,
природу этих предложений" (loc. cit., стр. 192—193).
434
Н. Н. ЛУЗИН
III. Полная система у1У у,у.. ., ур многозначных неявных функций,
которые удовлетворяют заданным уравнениям 7^ = 0, /^ = 0,
Fq = 0, может быть рассматриваема как совокупность счетного
множества систем р однозначных функций классификации Бэрау
удовлетворяющих каждая заданным уравнениям.
Лая сокращения изложения мы ограничимся только формулировками
этих интересных результатов.
Резюмируем: если ограничиться рассмотрением многозначных
неявных функций со счетным множеством значений, то по-прежнему
имеет место теорема Лебега.
55. Общий случай. В общем случае многозначных неявных функций
с несчетным множеством значений результат совершенно иной.
Прежде всего область Ех существования неявных функций
является в этом случае самым общим аналитическим множеством
(п. 50).
Остановимся несколько на этом факте. Пусть М(х1У лг2,..., хт) —
произвольная точка области существования Ех. Так как предложенные
уравнения
РЛХ1> «*2> ' • •! *m, ffl, 1/21 • • •> yp) = Qf
Г2\х\* Х2> " • •» Хт> У\> 1/2» • • м Ур) '==m Vy
*q\xli Х2У • • •» Xmi У\* 1/2' • • •» Ур) "
по предположению разрешимы относительно уг> у2, ..., ур в каждой
точке М(х^ х2, ..., хт)у принадлежащей Ех> то существуют системы
чисел у19 у2 ,. .., уР, удовлетворяющие одновременно этим уравнениям.
Так как каждая система чисел уи у2, ..., уР является точкой в евкли-
довском пространстве <§у, очевидно, что множество всех точек
М{у\, у2> • • •> Ур) пространства £у, которые удовлетворяют
предложенным уравнениям, есть множество, измеримое В: достаточно рассмотреть
Множество точек 7V, которые обращают в нуль функцию
/Г2_4_ F2-i hf2
где числа х1У х2У ..., хп фиксированы. Мы обозначим множество этих
точек N через Ем.
В общем случае множество Ем несчетно, следовательно, оно имеет
мощность континуума; и среди точек М множества Ех эффективно
имеются такие, что JZM не будет счетным или конечным.
После этих геометрических соображений ясно, что пытаться
удовлетворить предложенным уравнениям посредством однозначных
функцийу значит пытаться выбрать в каждом из множеств Ем одну
и только одну точку N.
Теперь возникает интересный вопрос:
Возможна ли эффективная реализация этого выбора?
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА III
435
И если она возможна, существуют ли однозначные функции
классификации Бэра, которые реализуют этот выбор?
Вот результаты П. С. Новикова по этому поводу:
I. Всегда можно назвать, в смысле Лебега, систему р
однозначных функций уи у2, .. ., ур, которые удовлетворяют предложенным
уравнениям.
II. Можно эффективно определить такую систему аналитических
уравнений FY = О, F, = 0, ..., Fq = О, что не существует никакой
системы однозначных функций, входящих в классификацию Бэра,
которые удовлетворяют этим уравнениям1.
56. Системы со счетным множеством уравнений. Могут ли быть
эти рассуждения распространены на случай счетного множества
уравнений Г{ = 0, содержащих счетное множество л>ов и у-ов? Само собой
разумеется, это зависит от определения функции счетного множества
переменных и от понятия „классификации Бэра" в этом случае.
Необходимо принять следующую предосторожность: функция f(xx,
х2,.. •> хп,.. .) счетного множества переменных х{, непрерывная
относительно каждого из этих переменных, может стать абсолютно
произвольной функцией ср(лг) действительного переменного х, если положить
х =: х\ == х2 :== XZ=Z' * *:= хп =' ' '
Но вот определение функции счетного множества переменных:
f(xlf х2, ..., хп, ...) = limfn(xl9 x.>, ..., хп).
п -> со
Если принять это определение, основная теорема Лебега,
относящаяся к однозначным неявным функциям, снова имеет место.
Г л а в а третья
НАИБОЛЕЕ ОБЩИЕ АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
XIII. Критерий измеримости В
57. Углубленное изучение лебеговского множества Е. Вернемся
к главной цели настоящего исследования: к изучению аналитического
множества Е, определенного Лебегом (см. [20]). Прежде всего мы
получим важные следствия из доказательства теоремы п. 42, относящейся
1 Существование такой системы уравнений получено П. С. Новиковым из
существования двух множеств Е\ и Е^ дополнительных соответственно к двум
аналитическим множествам, которые неотделимы Ву хотя они и не имеют общих
точек. П. С. Новиков нашел пример такой функции F (лг, у) второго класса, что
существует однозначная функция <р (дг), удовлетворяющая для каждого
действительного х уравнению F [дг, т,(дг)]=0, но не существует никакой однозначной функции
<р(дг>, входящей в классификацию Бэраг которая удовлетворяла бы (а^я каждого
действительного х) этому уравнению. •
436
Н. М. ЛУЗИН
к отделимости В двух аналитических множеств Е и £', не имеющих
общих точек.
Пусть С и С — два решета, посредством которых соответственно
определены аналитические множества Е и Е'. Пусть х и х—две
произвольные точки, принадлежащие соответственно множествам Е и Е'.
Обозначим через Rj и Rx> два счетных множества, в которых
перпендикуляры Рх и Р£; восставленные соответственно в точках х и х
к оси ОХ, пересекают решета С и С. В силу п. 10 множества R^
и RX' вполне упорядочены в положительном направлении оси OY.
Установив это, мы имеем следующее предложение:
Теорема. Если даны решета С и С", то можно назвать вполне
упорядоченное множество W, образованное целыми положительными
числами и более протяженное, чем вполне упорядоченные
множества Rx и /?,', каковы бы ни были точки х и х\ принадлежащие
соответственно множествам Е и Е\
Чтобы доказать это, достаточно обратиться к доказательству
теоремы п. 42. В самом деле, обозначим через W вполне
упорядоченную форму, к которой приведена последовательность (I) п. 43, таким
образом, что если [а] „предшествует" [6], следуя закону, принятому
б (I), ранг [а] в W меньше ранга [Ь] (см. п. 43). Пусть х — точка
Множества Е, которая не является концом проекции на ось ОХ
Ни одного из замкнутых отрезков, составляющих решета С и С".
Отсюда следует, что перпендикуляр Рл, восставленный в л: к оси ОХ>
пересекает отрезки решет С и С только во внутренних точках.
Следовательно, если а и с'— два каких-нибудь отрезка, которые
принадлежат соответственно решетам С и С и пересекают перпендикуляр Ра,
их проекции на ось ОХ вложены одна в другую (п. 42); это
показывает, что пара [з, о'] является элементом W.
Установив это, возьмем такую последовательность ои а2, а3, .,., ап9 . ..
отрезков решета С, которая пересекает перпендикуляр Рх в нисходя
щей последовательности соответствующих точек av а2, а^, ..., ап> ...
(п. 10); кроме того, мы можем предполагать, что проекция отрезка ап+\
содержится в проекции ая, каково бы ни было целое положительное
число п. Так как точка х принадлежит Еу ясно, что такие
последовательности <*!, о2, ... существуют.
Заметив это, рассмотрим все пары вида
где п — целое положительное число, а а'— отрезок решета С,
пересекающий перпендикуляр Рх; пусть Wx — их множество. Ясно, что
Wi — вполне упорядоченное множество, так как оно является частью
вполне упорядоченного множества W. Мы будем сравнивать вполне
упорядоченные множества Rz и Wx. Заметим, что каждому элементу
[а«* а] множества Wx соответствует одна и только одна точка
множества Rx: это точка перпендикуляра Рху которая принадлежит о'.
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА III
437
Чтобы осуществить это сравнение, начнем с начального элемента
[°м0> ао] множества 4^1 • Я утверждаю, что соответствующая точка
множества Rx имеет конечный ранг. В самом деле, в противном случае
мы могли бы определить точку перпендикуляра Рх конечного ранга,
достаточно большого для того, чтобы проекция соответствующего
отрезка а' содержалась в проекции отрезка а^1; следовательно, в этом
случае пара [\+г9 °'] „предшествовала быа паре [а о^], что как раз
и невозможно.
Вообще, какова бы ни была точка р множества Rxy среди тех
элементов-пар вполне упорядоченного множества Wly дкя которых
соответствующие точки вполне упорядоченного множества Rx имеют в Rx
ранги, большие или равные рангу р> первый, в Wly соответствует
точке р1 множества Rxy ранг которой превосходит ранг р на конечное
число единиц.
Мы немедленно заключаем отсюда, что если р — такой элемент
множества Rxy что существует бесчисленное множество элементов Rxy
ранги которых больше ранга р, отрезок множества Rxy определенный
элементом ру подобен некоторой части множества Wy следовательно,
подобен некоторому отрезку W.
Отсюда следует, что, если прибавить ко вполне упорядоченному
множеству W вполне упорядоченное множество, подобное натуральному
ряду целых положительных чисел, мы получим вполне упорядоченное
множество, более протяженное, чем каждое вполне упорядоченное
множество Rx и, в силу симметрии, RXy каковы бы ни были точки х и х'9
которые принадлежат соответственно Е и Е' и не совпадают ни с одной
проекцией концов отрезков а и а', составляющих данные решета С и С.
Но этих последних счетное множество, так же как и отрезков решет С
и С.
Следовательно, если мы прибавим ко вполне упорядоченному
множеству W одно за другим вполне упорядоченные множества Rx и Rx>t
определенные для проекций х и х этих концов, перенумерованных
посредством целых положительных чисел, мы получим фиксированное
вполне упорядоченное множество, более протяженное, чем вполне
упорядоченные множества Rx и Rjy каковы бы ни были точки х и У,
принадлежащие соответственно Е и Е (ч. т. д.).
58. Установив это, вернемся к лебеговскому множеству точек Е
(п. 1), определенному посредством канонического решета Лебега (п. 2).
Мы уже выяснили, что Е — аналитическое множество (III, пп. 5—8),
Напомним, что совокупность2 точек х интервала (О <С х < 1), которые
не принадлежат Еу была названа лебеговской совокупностью и £ыла
обозначена через & (п. 1).
1 Мы предполагаем, что как бы мало ни было £, решета С и С содержат лишь
конечное число замкнутых отрезков, длины которых превосходят е; см. сноску п. 42.
2 Это слово совокупность должно быть вз-ято в возможно более широком смысле.
438
Н. Н. ЛУЗИН
Главным результатом настоящего мемуара является следующий:
Основная теорема. Допуская возможность назвать решето
для лебеговской совокупности &у мы придем к противоречию.
В самом деле, пусть названо решето С", указанное для лебеговской
совокупности <§. Так как лебеговское множество Е и лебеговская
совокупность S не имеют общих точек, легко видеть, что в силу
предыдущей теоремы мы можем назвать счетное вполне упорядоченное
множество Wy более протяженное, чем всякое вполне упорядоченное
множество точек Rxy какова бы ни была точка х, принадлежащая
лебеговской совокупности £.
С другой стороны, выражение х вполне определено, как только
дано
• Gi h (J3 ()n
x— 2 -^-2i 2 ' ' ' 2" "•
По определению (п. 1) множество Rx образовано рациональными
числами, записанными в виде последовательности
ri* ri* ^з> * • •> ^я» • * *
и обладающими тем свойством, что их индексы равны индексам тех
цифр 0^, которые равны 1.
Так как последовательность ги г2, ... содержит все рациональные
числа, заключенные между 0 и 1, ясно, что Rx является самым общим
множеством, образованным рациональными числами на (0, 1).
А так как среди наиболее общих множеств, образованных
рациональными точками, содержатся, в частности, вполне упорядоченные
множества, протяженные как угодно, желаемое противоречие получено.
Чрезвычайно важно отметить, что в конце концов, вопреки
правдоподобию, принципом этого доказательства является как раз
свободная человеческая возможность мыслить счетные
вполне упорядоченные множества, протяженные как
угодно (ч. т. д.).
Следствие. В предположении, что лебеговское множество Е
входит в семейство множеств, измеримых В, заключается
противоречие.
В самом деле, утверждать, что множество Е измеримо В, значит
утверждать, что мы умеем назвать1 построение Е, отправляясь
от интервалов, посредством операций: сумма, общая часть. Как только
мы умеем назвать это построение множества Е, мы умеем назвать
аналогичное построение лебеговской совокупности- <§, так как эта
последняя является дополнением к Е. Как только мы умеем
реализовать это построение £, мы умеем назвать параметрическое
представление x=/(t) совокупности <£, где / разрывна лишь в счетном
множестве точек (п. 34), следовательно, мы умеем назвать решето для &г
1 Мы не бу,дем пытаться постичь понятие множества, измеримою В, иезавит
само от ращей возмржности назвать такое построение.
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ, ГЛАВА III
439
что как раз и невозможно в силу предшествующей основной теоремы
(ч. т. д.).
Таким образом, мы пришли к следующей формулировке:
Понятие произвольного аналитического множества не совпадает
с понятием произвольного множества, измеримого В.
59. Ограниченные и неограниченные решета. Мы дадим
некоторое расширение результатов, которые составляют предмет двух
предшествующих пунктов, распространяя рассуждение, проделанное дая
случая лебеговского множества Е.
Прежде всего мы установим существенное различие между разными
решетами.
Определение I. Будем говорить, что С является
ограниченным решетом, если мы умеем назвать счетное вполне
упорядоченное множество W, более протяженное, чем множество Rx, каково бы
ни было х, не принадлежащее множеству Е, просеянному
посредством С.
Определение II. Решето С называется неограниченным, если
не существует счетного вполне упорядоченного множества, которое
было бы более протяженным, чем множество Rx, каково бы ни было х,
не принадлежащее множеству Е, просеянному посредством С.
Определение I, очевидно, законно, потому что возможность назвать
не доказывается, а констатируется; мы ее можем наблюдать или не
наблюдать1. Что же касается определения II, мы не будем пытаться узнать,
ни является ли оно абсолютно обратным определению I, ни является ли
оно достаточно кронекеровским, чтобы приписать ему некоторый смысл.
Вот предложение, относящееся к определению I:
Теорема. Для того чтобы решето С было ограниченным,
необходимо и достаточно, чтобы мы умели назвать построение
просеянного множества Е, отправляясь от интервалов, посредством
операций: сумма, общая часть (т. е. чтобы Е было множеством,
эффективно измеримым В).
Условие необходимо. В самом деле, пусть W—счетное
вполне упорядоченное множество, более протяженное, чем каждое
вполне упорядоченное множество Rx, какова бы ни была точка х,
не принадлежащая множеству Е, просеянному посредством С. Мы
предположим, что это решето помещено внутри фундаментального
квадрата К, стороны которого имеют уравнения
jt = 0, x=l; у = 0, у = 1.
Пусть olf а2, ..., аи, ... — отрезки, составляющие решето С; это
замкнутые отрезки, параллельные оси ОХ и расположенные внутри
квадрата К.
1 См. J. Had a mar d. Lettre a M. Emile Borel (Bull, de la Soc. Mat. de
France, 1904).
440
Н. Н. ЛУЗИН
Обозначим элементы вполне упорядоченного множества W через е-
пусть ех — начальный элемент множества W.
Установив это, введем счетную совокупность точечных множеств
расположенных внутри К, которые мы обозначим через \еу ая] и
которые определены следующим рекуррентным законом:
1°. По определению [е1У о,] совпадает с замкнутым отрезком ая.
2°. Если элемент е множества W первого рода [е, о„] является
суммой ортогональных проекций на а„ множеств (У, а,], где а. — отрезок
решета С, ордината которого строго меньше ординаты о1П а
е—элемент W, непосредственно предшествующий е.
3°. Если элемент е множества W второго рода [е, о,] является
общей частью всех множеств [е\ ая], где е — элемент множества Wy
предшествующий е.
Так как вполне упорядоченное множество W предполагается пере*
нумерованным посредством целых положительных чисел, легко видеть,
что множеств [е> <*п] — счетное множество, и все они эффективно
измеримы Ву так как мы назвали построение каждого из них,
отправляясь от отрезков, посредством операций: сумма, общая
часть.
Обозначим через [е] сумму ортогональных проекций на ось ОХ
множеств [е, ая], где е фиксировано, а п =1, 2, 3, .... Обозначим,,
наконец, через Е общую часть всех [е]. Легко видеть, что Е
эффективно измеримо В.
Я утверждаю теперь, что Е совпадает с Е.
В самом деле, если точка х принадлежит Е, она, очевидно,
принадлежит проекции на ось ОХ каждого множества [е, ow], где ордината а„
больше |i (х) (см. п. 10). Следовательно, х принадлежит Е.
Наоборот, если х не принадлежит Е> множество Rx вполне
упорядочено. И так как Rx менее протяженно, чем Wy существует такой
элемент е множества W, что х не принадлежит ни одной проекции,
на ось ОХ множеств [е, ая], каково бы ни было я. Следовательно, х
не принадлежит Е.
Таким образом, множества Е и Е тождественны* Мы заключаем
отсюда, что Е эффективно измеримо В.
Условие достаточно. В самом деле, если Е является
множеством, эффективно измеримым Ву мы умеем назвать решето С для
множества, дополнительного к Е (п. 58, следствие). Но тогда в силу
теоремы п° 57 мы умеем назвать множество W, образованное целыми
положительными числами и более протяженное, чем Rxy где
х—произвольная точка дополнения к Е.
Следовательно, данное решето С ограничено.
Можно без всякого затруднения распространить все эти
предложения на случай решет нескольких измерений (п. 10).
6в. Вот заключение, к которому мы приходим: мы теперь знаем
критерий для того, чтобы какое-нибудь решето С было ограничено*
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА III
441
Но для определения II предшествующего пункта нет ничего подобного.
Мы не знаем даже, имеет ли оно смысл.
Правда, это определение сформулировано в таких терминах, как
„не существует... вполне упорядоченного множества, более
протяженного, чем... которые, несомненно, покажутся все объективными,
но возникает вопрос, не является ли эта объективность скорее
кажущейся, чем действительной.
В этой формулировке глагол „существовать" употреблен в
абсолютном смысле; но нам кажется, что наука по самому своему
характеру может употреблять это слово только в относительном смысле,
заранее указывая каждый раз поле законов, по отношению к которому
констатируются „существования" и „несуществования" математических
объектов, точно так же как нельзя говорить о неприводимости или
приводимости алгебраического уравнения в абсолютном смысле, не
указывая заранее числового тела, относительно которого констатируют
неприводимость (или обратное) этого уравнения. Кронекер прибавил даже
требование конечного регулярного процесса для выполнения приводимости.
Если мы не всегда находим, когда говорят о существовании, явные
сведения, приносящиеся к полю законов, по отношению к которому
рассматривается существование или несуществование, то это по
причине крайней ясности самой единственности такого поля: таков,
например, случай существования интеграла дифференциального уравнения.
Но в общем случае сведения о поле законов необходимы, так же как
и кронекеровская регулярность, в этом поле процессов, которые можно
предполагать конечными или бесконечными; но в последнем случае эти
процессы должны быть необходимо счетными, потому что, когда речь
идет о бесконечности, только натуральный ряд целых положительных
чисел
X у £у О, ", • • •
дает совершенно ясное и положительное1 изображение. Понятие
несчетной бесконечности является чисто отрицательным понятием2,
не имеющим никакой объективной реальности; это понятие, вызванное
лишь человеческой способностью создавать доказательства „от
противного", не соответствует никакой достижимой реальности и меняется
от поля к полю.
Если мы будем изменять поле законов, „существования" и
„несуществования" математического объекта полностью меняют смысл и
могут даже быть переставлены, так же как кронекеровская
регулярность в некотором поле.
Теперь, когда мы детально исследуем определение, мы находим его
недостаточно кронекеровским, чтобы приписать ему смысл.
1 См. Е. В о г е 1. L'infini mathematique et la realite" (Revue du Mois, 10 июня
1914).
2 Cm. E. В о r e 1. Les „Paradoxes" de la theorie des ensembles (Ann. de I'Ecole
Norm. Super., 1908).
442
Н. Н. ЛУЗИН
Правда, при современном состоянии науки нельзя полностью
избежать применения некронекеровских понятий, но важно отметить, что
существуют „более" и „менее" кронекеровские понятия, и важно
различать разные степени интенсивности этого качества.
Например, понятие расходящегося ряда (с положительными членами)
или понятие иррационального числа являются, несомненно, некронеке-
ровскими понятиями. Но если ряд с положительными членами или
действительное число даны, можно узнать при помощи счетного числа
операций, является ли ряд сходящимся или число рациональным.
Следовательно, степень указанного качества счетна.
Для понятия „неограниченного" решета нет ничего подобного:
невозможно фиксировать такой метод, что если данное решето С не
ограничено, мы в этом наверное убедимся в результате счетного
множества операций; это происходит оттого, что дополнение & к множеству Е
не является ни счетным, ни даже измеримым В; следовательно,
необходимо взять все вполне упорядоченные множества Rx, где х —
произвольная точка S, и их сравнить; практически это все равно, что
сказать, что невозможно определить понятие неограниченного решета:
Вот чисто объективное затруднение: если дано произвольное
решето С, то невозможно указать метод, который позволил бы
назвать точку в дополнении & к Е (см. [43]).
В случае аналитического множества дело обстоит совсем иначе
•(п. 11), и если решето С дано, мы умеем эффективно построить
параметрическое представление *=/(/) множества Е; тогда, полагая t = -^y
мы получим единственную и вполне определенную точку просеянного
множества Е. Но назвать точку дополнения & невозможно, даже если
мы убедились каким-нибудь гипотетическим методом, что решето С
не ограничено и, следовательно, что существуют точки
совокупности §. Именно по причине этой невозможности невозможно ни найти
совершенное множество, содержащееся в 6\ ни даже определить его
мощность без всякой двусмысленности.
Этого затруднения не существует, если данное решето С является
решетом единственноети, т. е. таким решетом, что, какова бы
ни была точка х множества Е, множество Rx имеет одну и только
одну предельную точку, к которой Rx имеет обратное движение (п. 10);
в силу теорем пп. 38 и 45 каждое множество Е, эффективно
измеримое Ву допускает решето единственности, и это единственные
множества, которые обладают этим свойством. Следовательно, если
множество Е просеяно посредством решета единственности, мы умеем назвать
решето дая его дополнения S и, следовательно, осуществить
параметрическое представление x=/(t). Тогда, полагая £ = ,у> мы получим
точку x0=^g\-^\t наверное принадлежащую &.
Но в общем случае, когда С не является решетом единственности,
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ, ГЛАВА III
443
этот способ рассуждения становится совершенно непригодным, и
назвать точку совокупности S невозможно.
Среди самых общих „неограниченных" решет, которые, по-видимому,
должны быть исключены из математических рассмотрений, по крайней
мерз в настоящее время, следовало бы различать „неограниченные"
решета, для которых соответствующие вполне упорядоченные
множества Rx подчинены некоторым ограничениям. Эти ограничения должны
быть такого рода, чтобы утверждение несуществования „границы"
множеств Rx могло быть получено из столь неопределенной концепции
самого общего множества, образованного рациональными точками.
Мы называем плотным в себе всякое счетное линейное множество,
ни одна из точек которого не имеет последующей точки. Известно, что
каждое счетное линейное множество, плотное в себе, подобно
множеству рациональных точек интервала (0, 1), включая концы или исключая.
Установив это, рассмотрим какое-нибудь решето С. Пусть 3f —
множество ординат всех отрезков а, составляющих решето С.
Рассмотрение канонического решета Лебега (пп. 2 и 58) приводит нас
к тому, чтобы предложить следующее определение:
Мы скажем, что решето С—лебеговского типа, если мы умеем
мазватъ часть о/1 множества g7, образованную соединением множества Z),
плотного в себе, и фиксированного вполне упорядоченного множества И
(принимая обычное условие порядка), таким образом, что какова бы
ни была часть Di множества Z), на (О <С х <С 1) существует такая
точка ху что соответствующее множество Rx содержит Пг и будет
содержаться в o/v
Не настаивая на общности этого определения, мы заметим, что
доказательство теоремы п. 58, относящееся к тому, что каноническое
решето Лебега не может быть ограничено, распространяется без
всякого изменения на решето лебеговского типа. Таким образом,
ни одно из множеств, определенных посредством решета лебеговского
типа, не входит в семейство множеств, измеримых В.
Мы немедленно применим это замечание.
61. Модификация примера Лебега1. Известно, что Бэр дал чисто
арифметический пример функции третьего класса его классификации.
Вот этот пример.
Возьмем основной интервал (0, 1) и рассмотрим произвольное
иррациональное число Ху представленное непрерывной дробью:
х = —j = (<*!, а2,..., ая>.. .),
1
^
апч- .
1 См. мою заметку в Comptes Rendus, 182, 1521 (заседание от 21 иювя-
1926 г.).
444
Н. Н. Лузин
где а1? о^, Од, ...—целые положительные числа. Каждому
иррациональному числу х соответствует вполне определенная последовательность-
целых положительных чисел
а1> а2> • • •» ал> • • *>
и обратно, такая последовательность определяет единственным,
образом число х.
После того как это установлено, нам будет достаточно* следуя-
Бэру, положить
/(*) = !,
если целые положительные числа а1э а2, ..., ая, ... стремятся к беског
нечности, и положить
/(*) = 0
в противном случае.
Как показал Бэр1, функция f(x), определенная таким образом,
является в точности функцией третьего класса.
62. Чтобы назвать чисто арифметическим образом аналогичную
функцию f(x), не входящую в классификацию Бэра, установим
следующее определение:
Мы скажем, что последовательность ах, а2, а3, ..., ая, ..., целых
положительных чисел является сложной, если среди ее членов имеется
бесчисленное множество чисел а, делящихся друг на друга
оц^-.а^: а„3: ... ; в противном случае мы скажем, что данная
последовательность о^, а2, аа, .. ., ая, ... проста.
Установив это определение, мы определим функцию f(x)
равенствами
/(*) = !,
если последовательность о^, а2, а3, ..., ап, ... сложная, и мы положим
}(х) = 0,
если последовательность av а2, а3, .. ., ал, ... проста.
Чтобы доказать, что определенная таким образом функция /(х)
не входит в классификацию Бэра, достаточно отметить, что множество
точек х = (ь1, а2, а3, ..., ая, ...), которые соответствуют сложным
последовательностям, есть множество, просеянное посредством
решета С лебеговского типа.
Чтобы построить это решето, напомним некоторые обозначения
Бэра (loc. cit.). Символ с7 (чх, а2, ..., ая) обозначает так называемый
интервал ранга п, концы которого рациональные и даны двумя
конечными непрерывными дробями:
1 Acta Math., 30. Важно отметить, что Бэр всегда воздерживается от применения-
метода диагонали Кантора (т. е. от отображения на континуум), посредством
которого Лебегу удалось указать примеры функций всех классов („Sur les fonctions rep-
resentables analytiquement", стр. 212).
Лебег любезно указал мне, что, если отвергнуть этот метод, проблема
существования функции класса 4, несмотря на свою трудность, заслуживает того, чтобы
привлечь внимание математиков.
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА III
445
1 Г
а2-н .
1 1
ая ап -*- 1 *
Известно, что все интервалы 07 ранга п не имеют попарно общих
точек и целиком покрывают интервал (0<х<1). Кроме того, каждый
интервал ранга я, g?^, a2, ..., ап), разбит на бесчисленное множество
янтервалоя ранга /г-н1:
c7(ai> a2> • • -f an, 1), o7{dly a2, ..., a„, 2), ...
Наконец, каждая последовательность njly >72, .. ., 7Я,... интервалов
соответственно рангов 1, 2, 3, .. ., каждый внутренний к
предшествующему, будет необходимо вида <7 (лг)9 c7(alf a,), g7 (alf a2, gl,), ...;
иррациональная точка (alf a2, a3, ...) будет единственной точкой, которая
лрингдлежит всем этим интервалам.
Напомнив это, рассмотрим произвольный интервал о7(^, а.„ ..., а„)
ранга л. Мы поставим в соответствие этому интервалу замкнутый
-отрезок, расположенный внутри фундаментального квадрата и
параллельный оси ОХ9 который мы обозначим через a{&i, a.>, • • •> ам) и
определим следующим образом:
1° Проекция отрезка a(alf a2, ..., ая) на ось ОХ совпадает с
интервалом о7'(лх, а,, „. ., ая), исключая концы;
2° Ординаты отрезка a(ai, a2, ..., <*«) есть рациональные числа
вида
ui
-^
2 2Z 2я-1 2**
-определенные тем условием, что 0Я = 1, а лая i<^n мы имеем 8< = 0Э
•если at. является делителем an, и 0^ = 1 в противном случае.
Так как «интервалов J(Oj, a2, ..., aB) счетное множество, множество
отрезков с образует решето С, которое определяет некоторое
просеянное множество £.
В силу построения решета С легко видеть, что это решето — лебе-
ловского типа, и что множество Е, просеянное посредством С,
совпадает с множеством точек, в которых /(дс) = 1, кроме, быть может,
грациональных точек (я. т. д.).
Итак, среди законов арифметики существуют такие, которые
приводят нас к множествам, не входящим в семейство множеств, измери-
'МЫХ В1.
1 Вот почему было бы чрезвычайно интересно поставить проблему чистой ариф-
•метики, разрешение которой существенным образом зависит от некоторого множества,
«неизмеримого В.- По видимому, разрешение такой проблемы, если такие существуют,
.должно представлять чрезвычайные трудности.
Это имеет отношение к следующему вопросу: узнать, в какой мере уже
известные проблемы арифметики связаны с множествами, не измеримыми В.
446 Н. Н. ЛУЗИН
63. Диагональ Кантора. Мы получим аналитические множества,
неизмеримые By исходя из идей совершенно другого порядка.
Известно, что, какова бы ни была счетная последовательность
и1У и1У..., игп ... действительных чисел, Кантор указал такое
действительное число и, которое не входит в эту последовательность. Метод,
который он применил, является методом диагонали.
Известно, что этот диагональный метод Кантора был применен
Борелем для случая семейств, отобразимых на континуум ] [37], и что
он позволил сделать выводы: Борелю — о существовании функций,
которые ни класса а, ни меньшего класса2, а Лебегу — о существовании
функций любого класса классификации Бэра3.
Именно этот метод позволит нам сейчас сделать вывод о
существовании аналитического множества, неизмеримого В.
Но необходимо принять вот какую предосторожность: если мы будем
исходить из одного из отображений семейства всех аналитических
множеств на континуум, мы только можем оттуда получить
неаналитическое и, следовательно, неизмеримое В множество; но отсюда мы не
можем еще сделать вывода о существовании аналитических множеств,
неизмеримых В.
Чтобы избежать этого затруднения, мы введем следующее понятием
Аналитическое множество U точек плоскости XOY называется
универсальным, если, пересекая его прямыми, параллельными оси OYr
мы получаем все линейные аналитические множества, которые
только возможны.
Дополнение CU каждого универсального множества U не может
быть аналитическим.
В самом деле, если CU— аналитическое множество, то его часть,
расположенная на диагонали А, х = уу тоже будет аналитическим
множеством (п. 34), так же, как и проекция Р этой части на ось OY. Так
как множество Uуниверсально, то существует такая параллель оси OY
x = xQ> что часть U, расположенная на этой параллели, имеет своей:
проекцией на ось OY множество Р.
Значит, точка М (х0У х0) диагонали Д не может принадлежать
множеству U, так как в этом случае проекция точки М на ось OY должна
содержаться в Р, что противоречиво; точка М не может принадлежать
и CU, так как в этом случае проекция М на ось OY должна
принадлежать к СРУ что также противоречиво.
Все сводится к доказательству реального существования
универсального аналитического множества £/.
Каждое линейное аналитическое множество Е является множеством
значений, которые принимает на интервале (0<О<С1) функция /(()>
1 См. Е. Borel. Lemons sur la theorie des fonctions, Iе ed., 1893, Note II*
стр. 107.
2 См. Е. Borel. Lecons sur les fonctions de variables reelles, 1905, Note III.
3 См. Н. Lebesgue. Sur les fonctions representables analytiquement, стр. 212.
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА III
447
разрывная лишь в счетном множестве точек. Такая функция f{t)
является функцией класса 1 классификации Бэра.
Следовательно, все сводится к определению такой функции <?(tyx)9
чтобы, приписывая х частные значения х°, мы получили из нее все
функции переменного t класса 1, какие только возможны.
Любая функция f{t) класса 1 может быть представлена рядом
многочленов с рациональными коэффициентами; достаточно взять ряд, общий
член которого является непрерывной функцией tux:
?iW-Pi(') + ?!W-aW + - + ?.W-P»(') + ..-
где последовательность Р1У Р2,... есть множество всех многочленов
от t с рациональными коэффициентами, а <р2 (л:), <р2 (дг),... — пеановская
кривая, заполняющая для 0 ^ х ^ 1 фундаментальный куб с ребром 1
в пространстве счетного множества измерений.
Обозначим через Sn (t, x) сумму п первых членов этого ряда: это
непрерывная функция tux. Функция ср (t, x), определенная равенством
<Р (/, х) = lim Sn (t, x)y
п= х>
обладает, очевидно, требуемым свойством и является функцией класса
не выше 2 классификации Бэра. Следовательно, поверхность
аналитически представима; множество точек в пространстве трех
измерений, которые принадлежат этой поверхности (S)> измеримо В
(Лебег), проекция U поверхности (S) на плоскость XOY является
аналитическим множеством, которое, очевидно, универсально (ч. т. д.).
Замечание I. Таким же образом можно доказать, что и в евкли-
довском пространстве трех измерений OXYZ существует
универсальное аналитическое множество U: это такое аналитическое множество,
что, пересекая его плоскостями, параллельными плоскости XOY, мы
получаем все плоские аналитические множества, какие только возможны.
Замечание II. В силу соображений, изложенных нами в другом
месте (Comptes Rendus, 181, 95, 1925), и к которым мы не возвращаемся,
метод диагонали Кантора, хотя и не трансфинитный на первый взгляд,
представляется нам на самом деле адекватным употреблению трансфи-
нитов, так как каждое аналитическое множество, неизмеримое В> тесно
связано с совокупностью всех вполне упорядоченных счетных
множеств (п. 59). Кроме того, трудности, связанные с этим методом,
безгранично возрастают, когда дело идет о множествах, называемых
проективными.
XIV. Трансфинитное
64. Аксиома выбора. Чтобы уточнить понятие трасфинита, следует
сначала рассмотреть аксиому выбора.
448
Н. Н. ЛУЗИН
Пусть М—множество, образованное непустыми точечными
множествами М попарно без общих точек и точно определенное посредством
вполне конечного закона Л.
Мы скажем, что мы находимся в условиях лебеговского выбора, если
из Л мы можем получить новый вполне конечный закон ^, который
позволяет точно и без всякой двусмысленности определить множество
точек L, содержащее одну и только одну точку в каждом из множеств М'.
Если такой возможности не существует, мы скажем, что мы
находимся в условиях цермглистского выбора. Знаменитый принцип
произвольного выбора, часто называемый аксиомой Цермело, категорически
утверждает во всех случаях реальное существование некоторого
множества Z, имеющего одну и только одну точку в каждом М, давая
,словам чрезвычайное и расширенное значение, недостаточно кронеке-
ровское, для того чтобы ему можно было, по моему мнению, приписать
некоторый смысл.
Но здесь следует отличать один важный частный случай, случай,
когда множество М счетно. В этом случае имеет место лебеговский
выбор, так как, по нашему мнению, a priori невозможно получить
самые множества М', перенумерованные посредством целых
положительных чисел, не имея предварительного закона, который определяет
выбранные точки, по одной в каждом из множеств М, и перенумерованные
аналогичным образом.
Теперь возникает чрезвычайно важный вопрос: имеет ли место
необходимо лебеговский выбор также и в случае, когда множество М
эффективно имеет 1 мощность континуума?
Другими словами, если допустить, что мы не можем констатировать
перенумерование множеств М' посредством целых положительных
чисел, не реализовав предварительно определенного выбора одной и только
одной точки в каждом М' одновременно с аналогичным
перенумерованием выбранных элементов, — в какой мере перенумерование
множеств М' посредством действительных чисел предполагает
выполненным аналогичное перенумерование выбранных элементов по одному,
и только по одному в каждом М'?
Этот вопрос, к которому мы естественно пришли, несомненно
покажется очень легким, если не иметь в виду, что мы должны быть
уверены в том, что мы имеем эффективное отображение множества М
на континуум.
В самом деле, возьмем за множества М' такие множества точек
некоторой прямой D, чтобы расстояние между двумя произвольными
точками множества М' было рационально, а расстояние между двумя
точками, из которых одна принадлежит М', а другая — вне М', было
иррационально. Легко видеть, что если даны два множества М, то они
или тождественны или не имеют общих точек.
1 Это означает, что мы умеем назвать некоторое отображение множества 3/на
континуум.
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА III
449
Пусть М—множество всех этих различных множеств М'.
Каждое множество М, очевидно, счетно, будучи множеством точек
вида л:=ь — , где х — точка ЛГ.
С другой стороны, прямая D полностью разложена на множества Л/'.
Кажется довольно естественным заключить отсюда, Зто множество М
имеет мощность континуума. Однако выбор некоторой точки в каждом ЛГ
представляет чрезмерные трудности.
В действительности мощность множества М (если законно о ней
говорить) совершенно не известна: мы не умеем назвать
отображение М на континуум. Сверх того, Серпинский доказал, что если бы
мы умели назвать простое упорядочение множества М, какова бы ни
была мощность М, то мы умели бы назвать неизмеримое в смысле
Лебега множество точек1.
Но можно указать другой такой пример множества М, эффективно
имеющего мощность континуума, что лебеговский выбор во множествах М'
представляет непреодолимые трудности..
В самом деле, возьмем универсальное аналитическое множество U,
которое мы построили в п. 63. Пусть Е — множество таких точек х
оси ОХ, что перпендикуляр Рх, восставленный в л: к оси ОХ>
пересекает дополнение CU множества U в непустом множестве точек.
Очень легко видеть, что Е содержит некоторое совершенное
множество; следовательно, Е эффективно имеет мощность континуума*.
Однако лебеговский выбор дая каждой точки х множества Е, одной и
только одной точки из множества CU, имеющей х абсциссой, очевидно
адекватен выбору одной точки в дополнении к каждому линейному
аналитическому множеству (п. 60).
Таким образом, имеется существенная разница между случаем,
когда М перенумеровано посредством целых положительных чисел9 и
случаем, когда М перенумеровано посредством действительных чисел.
Возможность получить множества М\ перенумерованные посредством
действительных чисел, не имея лебеговского выбора, зависит, по нашему
мнению, от того, что континуум не может быть эффективно вполне
упорядочен.
65. Аксиома разбиения. Мы указали выше (п. 30, сноска), что
существует несколько теорий трансфинитных чисел. Чтобы увидеть
логическое происхождение трансфинитного, примем точку зрения
формальной теории Рёсселя—Серпинского, которая представляется наиболее
законченной.
Пусть R — бинарное (с двумя членами) симметричное (т. е. если xRy
верно, yRx также верно) и транзитивное (т. е. если xRy и yRz
1 Bull. Acad. Sci., Cracovie, 147,1918.
2 Это — следствие известной теоремы Кантора—Бернштейна; См. Е. В о г е 1.
Lecons sur la throrie de fonctions. Note I, стр. 106.
450
Н. Н. ЛУЗИН
верны, xRz также верно) соотношение, представляющее вполне
определенный смысл для всех точек х и */, взятых в континууме1.
Назовем полной системой относительно R всякое множество точек &у
такое что соотношение xRy верно, каковы бы ни были точки х и у,
взятые в £, и неверно всякий раз, когда одна из этих двух точек,.
х и у у принадлежит £, а другая — его дополнению С<§.
Ясно, что если даны две полные системы, S и ё1У то они ила
тождественны или не имеют общих точек.
Аксиома разбиения2 утверждает реальное существование сово~
купности Т различных полных систем, которая полностью
исчерпывает континуум.
Все доводы, которые могут быть приведены в пользу этой аксиомы,,
имеют психологический характер, как и в случае аксиомы выбора, и
имеют не большую ценность3; конечное соединение фраз, которое
составляет соотношение /?, давая нам возможность ^определять
частные полные системы, само очень далеко от того, чтобы дать нам
полное разложение континуума.
Все обстоит совершенно иначе в особом случае, когда мы можем*
получить из R конечный закон А, который определяет множество точек L>
обладающее двумя следующими свойствами:
1° xRx неверно, если точки х и х (х=^=х) принадлежат L;
2° какова бы ни была точка у, взятая в континууме, существует
такая точка х множества L, что xRy верно.
Мы назовем лебеговским разбиением всякое разбиение, которое
обладает этими двумя свойствами.
Только в этом случае совокупность Т реально существует, будучи
завершенной; следовательно, она законна.
Но в общем случае, когда мы имеем дело с не лебеговским
разбиением, совокупность Т является, по нашему мнению, совершенно
незаконной: она является лишь виртуальностью.
Именно эта аксиома при изменении соотношения R порождает
бесчисленное множество квазиэффективных потенциальных возможностей,
и имеется много шансов за то, что большей частью они попарно не-
приводимы *.
66. Трансфинитное. Согласно формальной теории трансфинитных
чисел мы называем трансфинитным числом второго класса всякое
множество &> составленное из всех попарно подобных вполне упоря-
1 Можно было бы, например, взять за R фразу: „Чтобы расстояние |*—у\ был*
соизмеримым".
2 В логике этот метод доказательства существования называется принципом
абстракции.
3 Я должен указать на интересные беседы по атому поводу с А. Н.
Колмогоровым и П. С. Новиковым.
* Напомним, что мы сказали в п. 64 о мощности виртуальности Л/, происходящей
от соотношения „чтобы расстояние \х—у\ было рационально".
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА III
4S1
доченных множеств, образованных рациональными точками интервала
(CKC^/^l)» причем ранг точек соответствует положительному
направлению оси OY.
Отправляясь именно от этого определения, мы строим прекрасную
теорию трансфинитных чисел второго класса.
В силу предшествующего ясно, что „трансфинитное число** этой
теории является не чем иным, как полной системой относительно
симметрического и транзитивного соотношения „быть подобным".
Следовательно, совокупность трансфинитных чисел второго класса
происходит от применения аксиомы разбиения, что, по нашему мнению,
представляет огромные трудности1.
67* Геометрическая форма, которую можно дать этой формулировке,
сделает ее, быть может, более ясной.
Рассмотрим в плоскости XOY фундаментальный квадрат К со
стороной 1. Пусть С—каноническое решето Лебега (п. 2), расположенное
в К. Возьмем лебеговское множество Е и лебеговскую совокупность <S;
известно, что Е просеяно посредством С, а £ является дополнением к £.
Если переменная точка х пробегает совокупность £, мы получим
всевозможные вполне упорядоченные множества Rz (образованные
рациональными точками и упорядоченные в положительном направлении
оси ОУ). После этого немедленно применяется понятие трансфинитного
числа формальной теории, и оно может быть интерпретировано чисто
геометрическим образом.
Д\я этого достаточно объединить в одну систему все точки х
оси ОХ, для которых соответствующие множества Rx попарно подобны.
Мы получим таким образом вполне определенное множество е, и оно
уже полностью определено, если мы знаем только одну его точку х.
Легко видеть, что эти множества-соединения е все попарно без
общих точек, и что лебеговская совокупность <§ является суммой всех
этих множеств-соединений е.
Согласно формальной теории легко видеть, что это множество-
соединение е и есть по определению трансфинитное число, точно
так же как действительное число является по определению множеством
рациональных точек, удовлетворяющих хорошо известным условиям
теории Дедекинда. Совокупность трансфинитных чисел является
совокупностью этих множеств-соединений е, и важно отметить, что
существование этой совокупности целиком обусловливается аксиомой
разбиения, так как именно это разбиение лебеговской совокупности &
1 Я не знаю, существует ли корректный пример несчетного вполне
упорядоченного множества, образованного произвольными элементами. Существование таких
множеств мне представляется весьма спорным. Напротив, теорема: Каждое
вполне упорядоченное множество необходимо является счетным мне кажется
весьма правдоподобной. Но доказательство этого предложения представляет,
по-видимому, при современном состояния науки большие трудности, так как мы еще
не классифицировали всех методов упорядочения множеств.
452
Н. Н. ЛУЗИН
на множества-соединения е и создает эту совокупность трансфинитных
чисел.
Эти множества-соединения е могут быть расположены вполне
упорядоченным образом: достаточно сказать, что одно из них, е9 предшествуете',
если вполне упорядоченное множество RX9 соответствующее некоторой
точке л: множества е> менее протяженно, чем множество RX't
соответствующее некоторой точке х множества е. При этом условии
совокупность множеств е представима во вполне упорядоченной форме (й?):
е0У е19е29...,еш,...,еа9... {W)
Заметим, наконец, что какова бы ни была точка множества еХ9 вполне
упорядоченное множество Rx подобно отрезку совокупности (*У)У
определенному посредством ех.
68. После того как это установлено, возникает чрезвычайно
важный вопрос: какова природа этих множеств-соединений е?
В наших доказательствах мы применим следующую лемму:
Лемма I. Если мы умеем назвать точку множества еаУ то
мы умеем назвать различные точки во всех множествах е . которые
предшествуют еа.
В самом деле, пусть х — названная точка множества еа. Вполне
упорядоченное множество Rx также названо. Пусть е& — элемент
совокупности W9 предшествующий еа. Так как каждое вполне
упорядоченное множество RX9 где х—точка множества е~у подобно одному и
тому же вполне определенному отрезку множества Rxy и так как этот
отрезок является, очевидно, некоторым /?т, легко видеть, что
названная точка £ принадлежит е . Таким образом, мы имеем различные точки
во всех множествах е (ч. т. д.).
Установив эту лемму, докажем следующую теорему, относящуюся
к поставленному вопросу:
Теорема. Для того чтобы можно было назвать построение
множества ел9 отправляясь от интервалов, посредством операций-
сумма, общая часть, необходимо и достаточно, чтобы мы могли
назвать некоторую точку множества еЛ.
Условие необходимо. Действительно, если мы умеем назвать
такую конструкцию для еа9 то мы умеем назвать параметрическое
представление x=/(t) множества еа. Тогда, положив /=-^-, мы
получим называемую точку в еа.
Условие достаточно. В силу предшествующей леммы, если
мы умеем назвать некоторую точку в еа9 например х09 мы умеем
назвать определенную точку х' в каждом е9 предшествующем еЛ.
С другой стороны, мы видели (см. теорему п. 59), что если дано
счетное вполне упорядоченное множество Wl9 то множество точек х
дополнения к £, л\я которых соответствующие Rc де превосходят Wv
является множеством, эффективно измеримым В (т. е. мы умеем
указать построение этого множества) 144]. Взяв за W± вполне упорядочен:
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА III
453
ное множество RzQy мы получаем как следствие, что сумма всех е\
которые предшествуют ев+1, является множеством, эффективно
измеримым В,
Это рассуждение применимо также и к каждому множеству е\
предшествующему еа, так как мы умеем назвать некоторую точку х!
множества е'.
Отсюда следует, что сумма множеств е\ предшествующих еа, также
эффективно измерима В. Следовательно, еа эффективно измеримо В.
Если некоторое множество еа не содержит ни одной точки,
которую можно назвать, то еа является множеством, измеримым 5, не
заданным конструкцией, так как мы никогда не сумеем назвать
построение еа.
69. Парадокс трансфинитного. Этот парадокс состоит в том, что
мы не можем определить все трансфинитные числа посредством
обозначений последовательных или суперпозированных переходов к пределу,
так как невозможно установить единообразное обозначение всех
трансфинитных чисел1.
Уточним несколько этот парадокс.
Лемма II. Для того чтобы можно было назвать некоторую
точку множества еа, необходимо и достаточно, чтобы мы умели
получить одну и только одну фундаментальную последовательность
для каждого из предельных элементов совокупности W, не превоо
ходящих еа.
Условие необходимо. В самом деле, если х — названная точка
множества еху Rx является указанным вполне упорядоченным множеством.
Кроме того, мы умеем назвать перенумерование множества Rx
посредством целых положительных чисел, так как Rx образовано
рациональными точками. Так как отрезок совокупности W> определенный
посредством еаУ подобен Rx, мы умеем перенумеровать элементы е* этого
отрезка посредством целых положительных чисел:
/ / / г
е1> £%у ^3> • * "» еп ' " '
Пусть е—предельный элемент совокупности W, не превосходящий еа.
Возьмем в предыдущей последовательности первый элемент, меньший е\
пусть это будет е[у \^\. Возьмем, далее, в ^первый элемент,
больший е[ и меньший е; пусть это будет е^> \^>\. Можно продолжать
применение метода до бесконечности. Мы образуем таким образом
последовательность
которая, очевидно, является фундаментальной для е\
Условие достаточно. Чтобы получить названную точку мно-*
жества еаУ достаточно уметь назвать перенумерование отрезка со*
вокупности W> определенного при помощи еа, посредством целых
1 См. Е. В or el. La philosophic mathematique et l'infini (Revue du Mois, 1912),
454
Н. Н. ЛУЗИН
положительных чисел. В самом деле, при этих условиях мы можем
определить вполне упорядоченное множество р, образованное
рациональными точками (причем ранг соответствует положительному направлению),
которое подобно этому отрезку. Так как это множество является
некоторым Ri9 мы имеем точку £, названную в еа.
Следовательно, все сводится к тому, чтобы назвать
перенумерование этого отрезка.
Я утверждаю, что известно определенное перенумерование отрезка,
определенного посредством ер, если известно одно и только одно
перенумерование отрезка, определенного каждым из элементов е',
предшествующих ер.
В самом деле, если ер — первого рода, мы получаем перенумерование
отрезка, определенного посредством ер, из перенумерования отрезка,
определенного посредством ер_i:
/ / / /
^1> ^2> ^8* * * *> ^и> * • •>
прибавляя к этой последовательности единственный элемент ep_i:
/ / / /
е$—1> е\> еч> eV • • *> е*> ' • #
Если ер — второго родау мы имеем для него, по предположению,
единственную фундаментальную последовательность
ex,, ex,,..., ex*,...
Осуществим определенное и единственное перенумерование отрезка,
определенного каждым ел* (что, по предположению, возможно), и
рассмотрим полученную таким образом таблицу с двойным входом*
Если мы расположим элементы этой таблицы в простую
последовательность и вычеркнем повторяющиеся элементы, мы получим, очевидно,
определенное перенумерование отрезка, определенного посредством ер.
Мы заключаем отсюда, что известно определенное перенумерование
отрезка совокупности Wy определенного посредством ев (ч. т. д).
Установив это, вернемся к парадоксу трансфинитного.
Обозначение непредельных трансфинитных чисел, имеющее вид
а-н/2, очевидно, единственно. Предельные числа представляют трудности
для обозначения.
Так как каждая фундаментальная последовательность является не
чем иным, как переходом к пределу, легко видеть, что мы имеем
единственное обозначение всех трансфинитных чисел, меньших некоторого е^
в котором мы можем назвать некоторую точку.
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА III
455
Следовательно, парадокс трансфинитного сводится к тому, чтобы
назвать одну и только одну точку в каждом из элементов еа
совокупности W, следовательно, к реализации лебеговского выбора (п. 64)
so всех еа.
70. Можно без всякого затруднения распространить предыдущие
рассуждения на случай произвольного решета (не канонического).
Пусть С — произвольное решето, Е— множество точек, просеянное
посредством С, и & — дополнение к Е.
В силу рассуждений п. 67 мы можем написать
£ = е()ч-е1+ ...-н^-ь . . н-ев-н ...,
где все Rx подобны, когда х остается в еа, и не подобны, когда х
выходит из еа.
Все заключения остаются такими же; если мы можем назвать
некоторую точку множества еа, то мы умеем его построить,
отправляясь от интервалов (параллелепипедов). Единственное различие между
общим случаем и предшествующим состоит в том, что некоторые из
множеств-соединений еа могут быть пустыми.
Если данное множество Е измеримо В, все члены трансфинитной
последовательности
начиная с некоторого, пусты* Если данное множество Е неизмеримо В,
рассматриваемая последовательность существенно трансфинитна.
Так как совокупность § является суммой всех еа, мы легко
замечаем, что если хоть один из членов трансфинитной
последовательности является несчетным множеством, то существует
совершенное множество, содержащееся в этом члене и, следовательно,
содержащееся в <§.
Итак, в этом случае дополнение к Е имеет мощность континуума.
Существует только один особый случай, когда каждое множество еа
счетно или состоит из единственной точки.
Тогда проблема ставится так: узнать, является ли этот особый
случай реально возможным? Это „проблема" о мощности множеств,
дополнительных к аналитическим множествам.
В силу соображений предыдущего пункта легко видеть, что эта
„проблема" является лишь одной из форм парадокса
трансфинитного [45].
Эти соображения тесно связаны с методом диагонали Кантора.
XV. Проективные множества1
71. Лебег первый указал на большой теоретический интерес,
который представляет изучение проекции как одной из простейших
1 Я ограничиваюсь кратким изложением свойств проективных множеств. См. мои
заметки в Comptes Rendus от 4 мая, 25 мая, 15 июня, 13 июля и 17 августа 1955 г.
(см. стр . 304, 307, 312 настоящего тома. — Ред.).
456
Н. Н. ЛУЗИН
и в то же время важнейших операций геометрии, операции,
позволяющей образовывать новые множества, которые можно назвать*
отправляясь от эффективных уже известных множеств1. Следуя этой
идее Лебега, мы получаем сначала, отправляясь от множеств,
измеримых В, все аналитические множества Е; затем, отправляясь от их
дополнений СЕ, новый класс множеств РСЕ совершенно неизвестной
природы, но которые можно назвать; затем, отправляясь от их
дополнений СРСЕ, новые множества РСРСЕ, которые опять можно
назвать, это проективные множества [38].
Установим определение класса проективных множеств. Для
определенности мы ограничимся случаем линейных множеств.
Пусть Е — произвольное множество точек в евклидовом
пространстве S т измерений, т^>1. Мы обозначим через РЕ ортогональную
проекцию множества Е на евклидово пространство &' т — 1 измерений,
расположенное в пространстве S, и через СЕ — дополнение к Е
относительно <§.
Установив это, сформулируем следующее определение:
Будем говорить, что линейное множество является проективным
множеством класса п, если его можно представить в виде
PC ...РЕ или СРС ...РЕ,
где Е — некоторое множество, измеримое В, расположенное в
евклидовом пространстве лн-1 измерений, а буква Р, чередующаяся
с буквой С, написана в точности п раз, и если это невозможно*
когда мы заменяем целое положительное число л меньшим числом.
Установив это определение, мы немедленно усматриваем, что каждое
аналитическое множество или его дополнение является проективным
множеством класса 1, и vice versa; следовательно, теория
аналитических множеств совпадает с теорией проективных множеств класса 1.
Это замечание позволяет понять интерес, который представляет понятие
проективного множества.
72. Прежде всего, применяя диагональ Кантора, нетрудно доказать,
что существуют проективные множества любого класса. Кроме того,
сумма конечного числа проективных множеств и общая часть конечного1
числа проективных множеств также являются проективными множествами.
Но гораздо более замечательное свойство, и одно из важнейших, еле-*
дующее: все построенные до сих пор для всякого рода примеров
множества, неизмеримые В, представлялись ли они „естественно** или были
названы без применения рассуждения Цермело (аксиома выбора),
являются проективными. Этот результат, не изумляющий с первого
взгляда, удивит больше, если вспомнить, что среди множеств,
неизмеримых В, которые можно назвать, существуют такие множества, что
в определении каждого из них должны были бы эффективно применяться
1 Ann. de le'Ecole Norm, super., 242, 1918.
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ГЛАВА III
457
все трансфинитные числа (аксиома разбиения), а не только те, которые
меньше одного из них, фиксированного заранее.
Теория проективных множеств представляет большие трудности.
Правда, и теория множеств, дополнительных к аналитическим
множествам, представляет существенное затруднение, относящееся к мощности
такого множества; но трудности безгранично возрастают, когда дело
идет о проективных множествах: не известно, например, имеет ли
проективное множество класса 2 мощность континуума, имеет ли оно
определенную категорию (т. е. является ли оно Z-множеством), кни даже
измеримо ли оно в смысле Лебега (см. [39]).
Эти трудности и самая легкость, с которой мы исключаем трансфи-
ниты, заставляют нас более внимательно изучить вопрос о законности
этих множеств.. Трудности теории проективных множеств происходят
оттого, что операция: „взять дополнение" является чисто
отрицательной операцией.
73. Мы укажем некоторые любопытные примеры проективных
множеств.
Первый пример. Возьмем евклидовское пространство OXYZ
и в плоскости XOZ универсальное аналитическое множество U (п. 63).
Пусть U' — такое расположенное в плоскости YOZ множество,
измеримое В9 что, пересекая его прямыми, параллельными оси OZ, мы
получаем все линейные совершенные неплотные множества, какие только
возможны. Можно без всякого затруднения определить такое
множество U' (см. [46]).
Установив это, обозначим через Е множество таких точек в
пространстве трех измерений, что их ортогональные проекции на плоскость
XOZпринадлежат С/. Пусть Е—аналогичное множество, относящееся kU'.
Легко видеть, что Е является аналитическим множеством и что Е
ивмеримо By следовательно, аналитично. Мы заключаем отсюда, что
общая часть множеств Е и Е является аналитическим множеством;
обозначим его через Е • Е\
Спроектируем Е - Е на плоскость XOY: мы получим плоское
аналитическое множествоР(Е- Е). Возьмем дополнение к этому множеству и
спроектируем его на ось ОХ: мы получим линейное проективное множество
* = РСР(ЕЕ).
Установив это, рассмотрим такое множество (f\ измеримое В
и расположенное в плоскости YOZ, что, пересекая его прямыми,
параллельными оси OZy мы получаем все счетные множества, какие только
возможны. Пусть Е' — множество точек в пространстве трех
измерений, проекции которых на плоскость YOZ принадлежат U"; это
множество, измеримое В. Мы заключаем отсюда, что сумма Е-+-Е'
является аналитическим множеством.
Воаьмем додолаение к множеству Е-+-Е* и спроектируем его на
йлооюоть XOY- мы получим проективное множество PC (£-*-£").
458
Н. Н. ЛУЗИН
Возьмем его дополнение и спроектируем его на ось ОХ: мы получим
линейное проективное множество
Ъ = РСРС(Е + Е").
Установив это, возьмем на оси ОХ сумму
и обозначим через е дополнение к w-t-8; это, очевидно, проективное
множество.
Это проективное множество е обладает следующим интересным
свойством:
Если бы мы умели назвать точку множества еу мы имели бы
линейное аналитическое множество, дополнение которого несчетно
и в то же время не содержит никакого совершенного множества.
В самом деле, если мы расшифруем смысл очень сложных
построений двух линейных проективных множеств гс и Ъ, вот что мы найдем:
л является совокупностью точек х, в которых параллели оси OZ
пересекают универсальное множество U в тривиальных аналитических
множествах, дополнение к которым содержит совершенное множество,
а ^ является совокупностью точек ху для которых соответствующие
линейные аналитические множества имеют дополнениями не более чем
счетные, т. е. опять тривиальные множества. Если мы удалим из
оси ОХ все точки множеств ^ и 8, мы получим, само собой разумеется,
точки х, которые соответствуют экстраординарным аналитическим
множествам.
Второй пример. Возьмем в пространстве OXYZ такое
аналитическое множество U> что, пересекая его плоскостями, параллельными
плоскости XOYy мы получим все плоские аналитические множества,
какие только возможны (п. 63, замечание 1).
Пусть Е — совокупность таких точек оси OZ, что плоскости,
параллельные плоскости XOY и проведенные через эти точки, пересекают U
по плоским аналитическим множествам, дополнения к которым несчетны
и не содержат никакого совершенного множества.
С другой стороны, пусть Е— совокупность таких точек оси 0Z,
что плоскости, параллельные плоскости XOY и проведенные через эти
точки, пересекают U по плоским аналитическим множествам,
дополнения к которым пересекают каждую прямую, параллельную оси ОY,
в одной и только одной точке.
Соображения, аналогичные предшествующим, показывают нам, что Е
и Е являются линейными проективными множествами. Следовательно,
общая часть е множеств Е и Е также является проективный
множеством.
Легко видеть, что человеку который сумеет назвать точку линейг
ного проективного множества е, будет иметь все точки некоторой
ОБ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ. ДОБАВЛЕНИЕ
4S9
лрямой, параллельной оси ОХ, перенумерованными без
двусмысленности посредством всех трансфинитных чисел второго класса1.
Достаточно будет немного терпения, чтобы описать построение,
дающее самые экстравагантные множества, но это „построение" будет
содержать несколько суперпозированных операций С (взять дополнение)
и ни к чему не приведет. Можно убедиться, что эта операция С, будучи
чисто отрицательной, вводит множества, не определенные реально2.
Добавление
Два основных результата об аналитических множествах,
сформулированных без доказательства, можно найти в двух заметках в Comptes
Rendus de ГAcademie des Scinces de Paris: M. S о u s 1 i n. Sur une
definition des ensembles mesurables В sans nombres transfinis; N. L u s i n.
Sur la classification de M. Baire (заседание от 8 января 1917 г J,
Преждевременная смерть Суслина и трудности международных
сношений помешали опубликованию подробного изложения теории
аналитических множеств.
Серпинский независимо нашел доказательства многих предложений
этой теории и опубликовал их в ряде работ, появившихся в журнале
Fundamenta Mathematicae.
Теория проективных множеств была предметом лекций, которые я
читал в 1924—1925 гг. в Московском Университете; часть результатов,
относящихся к проективным множествам, была опубликована мной в пяти
заметках в Comptes Rendus (4 мая, 25 мая, 15 июня, 13 июля
я 17 августа 1925 г.). Но Серпинский указал несколько ранее, в статье
в Fundamenta Mathematicae, 1925, трудности, которые вызывают
проективные множества класса 2.
1 Нельзя сказать ни что е пусто, ни что е непусто, так как это зависит от поля
законов*
2 См. мою заметку в Comptes Rendus: „О проблеме Э. Бореля н методе резольвент*
*т 17 августа 1925 г. (см. стр. 312 настоящего тома. — Ред).
ЗАМЕЧАНИЯ
О ПРОЕКТИВНЫХ МНОЖЕСТВАХ*
1. В 1898 г. Борель писал в своих первых „Lemons sur la theorie
des fonctions": „...если рассматривать какое-либо множество как
данное, то можно рассматривать как „данные" все множества той же-
мощности". Именно этот принцип позволяет нам рассматривать как-
данное множество Е значений, которые принимает „данная" функция f(x)r
если мы рассматриваем как данное множество (—оо, -ноо),
образованное из всех действительных чисел. Смысл этого принципа совершенно
ясен: мы получаем произвольный элемент множества Еу совершая
операцию f(x) над произвольным элементом х множества (—оо, н-оо)^
которое рассматривается как данное. Но ничто не оправдывает
распространение этого принципа на множества „дополнительные" к множествам
„данным", если мы не можем преобразовать отрицательное
определение такого множества в определение положительное. Тогда как глы
получаем все элементы Е> совершая операцию /над всеми
действительными числами, мы не обладаем никаким регулярным процессом, чтобы
узнать, принадлежит ли данное действительное число у0 дополнению
к Е или нет; и можно сильно сомневаться в том, что можно дать общее
решение этой проблемы. Таков в точности случай проективных множеств.
2. Трудности возникли уже в случае аналитических множеств.
Известно, что всякое линейное аналитическое множество Е может быть
определено как множество значений, которые принимает функция f(x)r
непрерывная справа в каждой точке х. Кроме того, каждая из этих
функций f{x) разрывна только для счетного множества значений х
и, очевидно, полностью определена, если известны ее значения только-
в рациональных точках. Таким образом, функция / и множество Е с его»
дополнением СЕ—все определены при помощи эффективно
перечисленного множества условий. Но решение проблемы: узнать, принадлежит
ли данное действительное число у0 к СЕ или нет, требует счетного
множества операций, расположенных во вполне упорядоченную
последовательность, дая которой верхняя грань не известна заранее. Эта
грань существует наверняка, если множество Е измеримо В> и ве
существует в противном случае, так что полное познание множества СЕ
* „Remarques sur les ensembles projectifs" Comptes Readus* 835—SS^ 192X-
ЗАМЕЧАНИЯ О ПРОЕКТИВНЫХ МНОЖЕСТВАХ
461
в этом случае строго эквивалентно познанию совокупности всех транс-
финитных чисел второго класса.
3. Но более того: всюду, где математическая проблема представлена в
конечной форме, т. е. объекты этой проблемы определены каждый при
помощи конечного числа условий и даны в конечном числе, можно
яадеяться получить конечное решение этой проблемы.
Таков, например, случай проблемы: узнать, совместна или нет
данная система из т линейных уравнений с п неизвестными.
Бесконечное множество испытаний, имеющее мощность континуума, не
предоставляется истинным решением проблемы. Мы имеем аналогичный
случай и А^я проблемы: узнать, сходится ли данный ряд с
положительными членами или нет. Эта проблема имеет счетный характер, и было бы
неправильно рассматривать как решение бесчисленное множество
испытаний, имеющее мощность континуума.
Так как всякое аналитическое множество определяется при помощи
эффективно перечислимого множества условий, то естественно искать
решение, имеющее счетный характер д\я каждой из трех следующих
лроблем:
I. Если f(x) дана, узнать, является ли дополнительное множество СЕ
пустым или нет.
II. Если возможно СЕ непусто, узнать, счетно оно или нет.
III. Если множество СЕ несчетно, узнать, содержит ли оно
совершенное множество.
В действительности не существует никакого регулярного алгоритма,
использующего только значения / в рациональных точках, который
дает решение одной из этих трех проблем.
4. Предмет становится значительно более сложным, когда дело
-касается проективных множеств и функций.
Если кривая У=/{х) есть плоское проективное множество, то
невозможно узнать при помощи счетного множества операций, имеет ли
уравнение Уо=/С*) корень или нет: необходимо осуществить множество
операций, мощность которого континуум, и много шансов за то, что
эти испытания независимы одни от других, хотя / определима при
помощи счетного множества условий.
Неприменимость классических способов рассуждения к решению
указанных проблем происходит, по моему мнению, от того, что
проективные множества используют одну отрицательную операцию: взятие
дополнения, и не являются истинными множествами, несмотря на их
счетный характер.
5. В довершение я должен указать, что я обязан Лебегу первой
идеей проективного множества. Но первые публикации по этому
предмету принадлежат Серпинскому, который отметил ранее меня очень
ясно в своей статье в Fund. Math., VII („Sur une classe des ensembles'*)
трудности, к которым Приводят простейшие проективные множества [38].
О ДОСТИЖИМОСТИ ТОЧЕК*
„Что касается вопроса о природе множества достижимых точек1,,
то вот рассуждение, на мой взгляд довольно простое [47].
Пусть F—замкнутое точечное множество, расположенное внутри
квадрата XOY. Возьмем евклидово пространство четырех измерении
XlYlX2Y2 и пеановскую кривую, заполняющую основной куб, ребра
которого лежат на осях координат и равны 1:
*i = <Pi (0; #i = фх С); *2 = ?2 (0; ah = Ф2 (')■
где <р и ф непрерывны в [0 ^ t ^ 1]. Формулы
5 = ?l(*)4-tf[?,W-?i(f)]; Ч = Фх С)-*-^/[Ф, С)-+!<<)].
где O^f/^1, представляют I и у\ как непрерывные функции от t и [/:
& = Ф(*,*/); 4 = V('.^.
Пусть /—множество всех точек M{t9 U) таких, что
соответствующие точки р(Е, ?]) плоскости ЛГОУ принадлежат /Г. Очевидно, что
множество / замкнуто. Ясно, что часть этого множества лежит заведомо
на прямой U=l, т. е. на верхней стороне квадрата плоскости TOU> —
а именно, точки (t> 1) такие, что кривая
* = ?»('), у = М*)
определяет точки из множества F на плоскости ХОY. Очевидно, что
эти точки (tt 1) образуют линейное замкнутое множество, например /2,
лежащее на прямой U= 1.
Ясно, что мы получим все линейно достижимые точки множества
F и только такие точки, если будем проводить внутри квадрата TOU
прямые, параллельные оси OU, упирающиеся верхними концами в
множество /2 и, кроме того, не пересекающиеся с множеством /. Очевидно,
что множество таких t имеет тип G8. Заставляя t пробегать это С8, при
помощи кривой
• „Sur l'accessibilite des points". Fund. Math., XII» 158—159, 1928.
i Ср. О. Nikodym. Fund. Math., VII, 250.
О ДОСТИЖИМОСТИ ТОЧЕК
463
мы, очевидно, получаем аналитическое множество, образованное всеми
достижимыми точками множества F плоскости XOY (ч. т. д.).
Очевидно, что этот метод остается применимым, если F—проективное
множество и речь идет о достижимости посредством алгебраических
путей или спрямляемых жордановых путей. При этом следует
пользоваться „универсальными множествами1* (т. е. наложением на
континуум). Но это совсем просто. Кроме того, наши рассуждения не
выводят за пределы семейства проективных множеств".
Николай Лузин
Париж, 19 ноября 1925.
О ПУТЯХ РАЗВИТИЯ ТЕОРИИ МНОЖЕСТВ*
За последние годы эти пути немало обсуждались благодаря
большому спору, возникшему между идеалистами и реалистами, о принципе
исключенного третьего и благодаря появлению теории Д. Гильберта,
названной знаменитым автором „теорией математических доказательств".
Ввиду крайне неполных сведений, относящихся к этой теории, я
ограничусь кратким указанием личных заключений, к которым я пришел по
этому поводу, не входя в обсуждение всех высказанных
доводов.
Чтобы не запутаться в метафизических дискуссиях о смысле слова
„бесконечный", я удовольствуюсь обсуждением частного вопроса,
который, без сомнения, привлекает внимание всех математиков: это попытка
разрешить удовлетворительным образом то, что называют проблемой
континуума, поставленной уже лет шестьдесят тому назад Георгом
Кантором.
В теории функций имеется много эффективных соответствий между
очень различными множествами. Например, если мы рассмотрим
предложение: множество всех непрерывных функций f{x) имеет мощность
континуума, то каждый человек, обладающий математической культурой,
понимает, что речь идет о взаимно однозначном соответствии между
множеством всех непрерывных функций / (х) и множеством всех
действительных чисел [0^£^1], так что каждому действительному
числу t соответствует непрерывная функция /(*), и обратно, причем
это соответствие установлено для всех действительных чисел t
независимо от того, можно или нет рассматривать отдельное
действительное число £0.
Вопрос состоит в том, чтобы узнать, существует ли, или, можно ли
указать, аналогичное соответствие между множеством действительных
чисел [0 ^ t ^ 1] и совокупностью всех трансфинитных чисел второго
класса 0, 1, 2,..., ш,..., а,... |Q, предполагая эту последнюю
совокупность законной.
Вот краткое изложение идей Д. Гильберта.
• „Sur les voles de la th^orie des ensembles". Atti del Congresso Internationale
•del matematici, 3—10 septembre. Bologna, Zanichelli, 1, 295—299, 1929.
О ПУТЯХ РАЗВИТИЯ ТЕОРИИ МНОЖЕСТВ
465
Каждый шаг человеческой деятельности в математическом анализе
может быть формализован, т. е. представлен соединением простых
символов в конечном числе. Среди них находятся символы логики-
&, V, -*, -, (х), (£,),
и, или, следует, нет, каково бы ни было, существует;
<§(А), Z{a) N(a)
произвольный вы- „а— целое поло- „а— число вто-
бор в логике; жительное число" рого класса";
и математические символы:
= > а
равно, следующее число.
Следовательно, существует основная область D9 на которую
проектируются наши математические мысли, и проекция в D доказательства
некоторой теоремы Т математического анализа есть „фигура",
образованная простыми символами, повторяемыми таким образом, что каждому
шагу рассуждения соответствует часть этой фигуры, образованная
согласно определенным правилам, установленным для простых символов.
После этих общих рассуждений переходим к проблеме континуума.
Итак, речь идет о нумерации иррациональных чисел отрезка [0, 1] при
помощи трансфинитных чисел второго класса, или, что то же самое,
об аналогичной нумерации целочисленных функций /(п) целого
положительного аргумента с целыми положительными значениями, так как, если
х—иррациональное число, мы имеем
1
х= 1
/(D-7(2^—
Вот что делает знаменитый автор, если я правильно понял его
мысль. Он исследует способ образования каждой отдельной
целочисленной функции /(л) и ставит в соответствие функции / ее определение
в области D. Если рассматриваемая целочисленная функция /(я) задана
индуктивно, т. е. отправляясь от п определима посредством
алгебраических подстановок и совместных последовательных рекурсий, то ее
определение в области D можно преобразовать таким образом, чтобы
оно содержало только конечное число последовательных рекурсий.
Следовательно, если мы формально заменим в этом определении знак Z'
на N, определение функции / становится определением некоторого
определенного трансфинитного числа второго класса. Опуская
технические трудности, мы приходим таким образом к взаимно однозначному
соответствию в области D между определениями индуктивных
целочисленных функций и определениями трансфинитных чисел второго класса.
466
Н. Н. ЛУЗИН
Мы поступаем подобным же образом, опять-таки если я правильно
понял, и в случае неиндуктивной целочисленной функции /(л), т. е.
такой, что ее определение в области D содержит один или несколько
раз знак <§ произвольного выбора в логике. Гильберт даже записывает
полученное таким образом соответствие между определениями в виде
функции
С (а, л),
так что мы получаем все целочисленные функции /(я), заставляя букву а
пробегать все трансфинитные числа второго класса.
Будет ли принято это решение единодушно всеми математиками, как
идеалистами, так и реалистами? Хотя я и очень далек от идеализма
в смысле Цермело, я в это не верю: идеалисты найдут это решение,
право, „слишком психологическим".
Ж. Адамару принадлежат следующие слова, написанные уже двадцать
три года тому назад в известных „Пяти письмах по теории множеств44:
„Я бы не очень хотел ставить вопрос, подобно Гильберту, на почву
непротиворечивости, что мне представляется обращением к психологии
и введением в рассмотрение свойств нашего мозга".
Смысл этих слов становится теперь совершенно ясным: основная
область Гильберта есть не что иное, как живой математический мозг,
но, право, слишком идеализированный. Настоящий мозг с конечным
числом клеток является полем физических и химических процессов
всегда в конечном числе, даже если бы он бесконечно обновлялся:
с этой точки зрения математики индивидуально всегда будут
рассматривать лишь ограниченное число элементов некоторой природы.
Но основная область Гильберта имеет несколько отличные и в общем
почти парадоксальные свойства: с одной стороны, она может содержать
произвольный член последовательности
О, О', О", О'",...,О"'"',...
которая есть не что иное, как последовательность целых
положительных чисел) и в то же время она является полем интуитивного
индуктивного процесса; с другой стороны, в этой области D никак нельзя
применять методы обыкновенной математической рекурсии.
Наиболее тонким пунктом всей этой теории является существенная
разница между интуитивной индукцией и математической индукцией,
и в этом пункте я охотнее всего согласился бы с Вейлем, так как
многие математики, включая Анри Пуанкаре, не делают никакой
разницы между этими двумя видами индукции. Кажется неоспоримым, что
математики нашей эпохи близки к тому, чтобы потерять чувство
глубокой разницы между тем, что интуитивно очевидно, и тем, что
становится очевидным после простого рассуждения.
Но если не делать этого различия, то мы немедленно приходим
к нумерации в области D всех определений как действительных чисел,
О ПУТЯХ РАЗВИТИЯ ТЕОРИИ МНОЖЕСТВ 467
так и трансфинитных, при помощи целых положительных чисел и,
следовательно, попадаем таким образом в затруднения типа рассуждения Ришара.
Каждая фигура в области D> которая служит дая определения
действительного числа, может быть описана посредством фраз на некотором
определенном языке. Следовательно, если мы будем рассматривать
буквы этого языка как цифры некоторой системы счисления, то каждое
определение станет просто целым положительным числом,
написанным в этой системе счисления.
Мне кажется таким образом, что идеалисты найдут несколько опасной
эту близость рассуждения Ришара и метода Д. Гильберта — всегда
восходить к основным определениям. Впрочем, каждое трансфинитное число
второго класса имеет несчетное множество математических определений:
это происходит оттого, что каждое предельное число второго класса
может быть представлено многими способами как предел восходящей
последовательности:
а\ < До < аз < • • •
трансфинитных чисел. По-видимому, метод Гильберта опирается на
возможность указать одну последовательность этого вида, и именно
этот факт трудно принять как идеалистам, так и реалистам. Борелю
принадлежит указание, что парадокс трансфинитного именно и состоит
в невозможности выбора такой единственной последовательности.
Природа метода Гильберта существенно отличается от природы
классических методов теории функций, которые устанавливают наиболее
полезные соответствия (как, например, цитированное выше соответствие
между действительными числами и непрерывными функциями). Таким
образом, возникает необходимость различать среди проблем теории
функций те, в которых можно избежать метода восхождения к основным
определениям. Например, Серпинский и я доказали, что континуум
[O^x^l] может быть разложен многими способами на бесконечное
число множеств, измеримых Ву перенумерованных при помощи
трансфинитных чисел второго класса. Но в большинстве случаев мы
констатировали, что классы этих множеств, измеримых 5, не ограничены, т. е.
стремятся к 2. Является ли метод основных определений необходимым
дая того, чтобы установить существование случая, когда классы
ограничены? Это, очевидно, ослабленная проблема континуума, так как мы
находим полное разрешение проблемы континуума Кантора, если каждое
5-множество в указанном разложении континуума приводится к одной
точке.
В системе Гильберта формальное противоречие, т. е. коллизия слов,
исключено; мы никогда не встретим фразы: единица не равна единице
(1 =^= 1). Но вопрос состоит в том, чтобы узнать, какая реальность
скрывается за этими словами.
Однако теория Гильберта является величайшим событием в
математике: у нас есть способ анализировать математические доказательства.
468
Н. Н. ЛУЗИН
Например, если я правильно понял, хотя аксиома Цермело и не
противоречива, как показал Гильберт [48], но без нее можно обойтись в
каждом рассуждении, относящемся к конечным вещам, так же как в алгебре,
можно исключить букву, которая нам мешает.
Точка зрения, противоположная идеализму, это точка зрения реализма.
Мне кажется, что мы приходим к этому роду идей скорее из-за
нагромождения неразрешимых проблем, чем из-за парадоксов теории
множеств.
Впрочем, именно усталость от „канторовского рая" сыграла известную
роль: огромное количество новых понятий без приложений и всегда
без связи с другими ветвями классической математики, многочисленные
работы на явно искусственные темы и по крайней мере не соразмерные
с их полезностью — все это требовало крайней осторожности.
Точка зрения реализма выявилась в полном свете в споре об аксиоме
Цермело, появившейся в известных „Пяти письмах по теории множеств".
Дальнейшее развитие этой точки зрения хорошо известно: именно
сомнения В. Брауэра относительно закона исключенного третьего наиболее
ясно выражают эту точку зрения. Впрочем, все в этих же „Пяти
письмах" уже имеются строки, которые нужно рассматривать как начало
атаки на принцип исключенного третьего: это слова Лебега, которые
долгое время оставались несколько загадочными: „хотя я сильно
сомневаюсь, чтобы когда-либо было названо множество, которое не было бы
ни конечным, ни бесконечным, невозможность существования такого
множества мне не кажется доказанной". Но именно Брауэру мы обязаны
научной критикой этого принципа.
Успех теории В. Брауэра имеет своей истинной причиной не смелость
(хотя в этих вещах надо быть бесконечно смелым), но уже указанную
искусственность рассуждений, основанных на понятии актуальной
бесконечности.
Я не рассматриваю теорию В. Брауэра ни как некоторый запрет, ни
как попытку создания новой логики: даже а^я нас, математиков,
привычных к существованию многих геометрий, существование многих
логик было бы, право, очень печальной роскошью. Мне кажется, что
построение новой логики в настоящее время крайне преждевременно.
Мне кажется, что идеи В. Брауэра будут иметь следствием более
осторожное применение принципа математической индукции.
Неиндуктивная теория целых положительных чисел еще не построена,
и в этом направлении мы имеем лишь крайне разрозненные результаты.
Здесь нужно проделать большую работу, подобно той, которую
проделал Серпинский в области теории множеств, классифицируя
предложения, которые можно доказать без аксиомы Цермело, и те, которые мы
не умеем доказать таким образом.
Загадочное сопротивление, которое испытывают ученые, пытающиеся
установить связь между числовыми константами, например между я и
&t трудности теории проективных множеств — все это приводит нас
О ПУТЯХ РАЗВИТИЯ ТЕОРИИ МНОЖЕСТВ 469
к мысли, что в классической математике, возможно, имеется больше
постулатов, чем это обычно думают.
Великий спор, возникший между Деламбером и Эйлером о понятии
произвольной функции, становится спустя века спором о произвольном
действительном числе и даже о произвольном целом положительном
числе.
АНАЛОГИИ МЕЖДУ МНОЖЕСТВАМИ, ИЗМЕРИМЫМИ Я,
И АНАЛИТИЧЕСКИМИ МНОЖЕСТВАМИ*
Существует реальная аналогия между множествами, измеримыми 5,
и более общими аналитическими множествами. Сущность этой аналогии
состоит в том, что можно рассматривать каждое аналитическое
неизмеримое В множество как множество, измеримое В> класса а, где буква а
обозначает неопределенное трансфинитное число второго класса
„чрезвычайно большое", так что невозможно никакое его конечное
представление1.
Эта формулировка, к которой естественно приходят, следуя идеям
Бореля, кажется, без сомнения, неясной и даже лишенной смысла
читателю, слишком привыкшему к рассуждениям идеалистов: но одна из
идей, которую мы предложим тем, кто интересуется современной теорией
функций, состоит в том, что во всех вопросах, где входят
трансфинитное или отрицательные определения, не следует бояться рассуждений,
кажущихся „сомнительными" с точки зрения абстрактной логики: это
не более, чем, следуя голосу абстрактной логики, поплатиться за это
бесплодностью и утратить плодотворные предложения, необходимые для
всех, включая идеалистов. Мы можем это констатировать, обозревая
факты.
Вот эти факты: в теории множеств, измеримых В, и аналитических
множеств имеется род двойственности, которая некоторым образом
аналогична двойственности, которую мы находим в проективной геометрии.
Чтобы уточнить эту двойственность, удобно ввести следующее
определение: мы скажем, что точечное множество Е какого-либо класса
классификации Бэра—Валле-Пуссена является элементом класса а, если
Е есть общая часть счетного числа множеств Е1У Е2У ..., Enf ... классов,
низших, чем а, и если такое представление невозможно для его
дополнения СЕ. Можно обнаружить без труда, что элементы эффективно
существуют в каждом классе классификации Бэра—Валле-Пуссена.
* „Analogies entre les ensembles mesurables В et les ensembles analytiques".
Fund. Math., XVI, 48—76, 1930.
1 Вместо буквы а можно писать букву Q, которой идеалисты обычно обозначают
то, что называется наименьшим числом третьего класса. На самом деле
единственная роль, которую в действительности играет это понятие, состоит в том, что она
служит для выражения идеи, которая в классическом анализе называется всегда
„бесконечностью".
АНАЛОГИИ МЕЖДУ МНОЖЕСТВАМИ. ИЗМЕРИМЫМИ В. И АНАЛИТ МНОЖЕСТВАМИ 471
Установив это определение, вот как можно сформулировать
указанную двойственность.
Из каждого предложения, относящегося к элементам класса а, где
а — произвольное число второго класса Г. Кантора, получается
предложение а^я аналитических множеств путем замены всех выражений:
„элемент класса а" выражениями: „аналитическое множество" и выражений:
„множество класса, низшего, чем а" выражениями: „измеримое 5-множе-
ство". Обратно, из каждого предложения для аналитических множеств
получается предложение, относящееся к элементам класса а, где а —
произвольное число второго класса Г. Кантора, путем осуществления
всюду в формулировке и в доказательстве обратной замены указанных
выражений.
Предложения, которые получают таким образом \ будут называться
двойственными или соответствующими в двойственности.
Вопрос состоит в том, чтобы узнать, каковы конечные основания
этой двойственности. Не собираясь решать поставленную проблему
относительно этой двойственности, мы ограничимся следующими
замечаниями.
Единственное логическое определение, которое мы имеем для
„наименьшего числа третьего класса" 2, это чисто отрицательное свойство:
невозможность пересчета трансфинитных чисел, предшествующих 2, при
помощи натуральных чисел. А ведь эта невозможность в
действительности имеет место для некоторых чисел второго класса Г. Кантора,
потому что иметь пересчет чисел, низших чем а, это значит иметь
конечное представление числа а. Между тем, числа а, которые могут
быть записаны таким образом, образуют счетное множество, что не
имеет места по отношению к тем числам, которые не поддаются такому
представлению: имеется несчетное множество чисел второго класса
Г. Кантора, постижимых а^я идеалистов, для которых мы не имеем и
не будем иметь никакого конечного представления и, следовательно,
никакого пересчета. Идеалисты рассматривают этот пересчет как
существующий „в себе", который мы никогда не сможем осуществить. Это
во всяком случае одна из форм парадокса бесконечности, на котором
♦столько раз настаивал Борель. Ясно, что элементы Е такого класса а,
будучи измеримыми В для идеалистов, обладают в действительности
-свойствами более общих аналитических множеств.
1 Необходимо заметить, что нужно принять меры предосторожности, чтобы
•быть, уверенным в правильном применении двойственности: надлежит, чтобы
рассматриваема предлоигние не содержало множеств классов, высших чем а; точно
так же слово „существование" требует большого внимания, потому что его смысл
(даже конструктивный) часто неопределенен. К тому же предосторожность
необходима, чтобы с уверенностью устанавливать использование аксиомы Цермело
в предложениях теории множеств, как это было отмечено с полным основанием
В. Серпинским.
472
Н. Н. ЛУЗИН
Эта возможность мыслить трансфинитные числа, которые являются
числами второго класса Г. Кантора и которые в действительности
обладают третьей мощностью, по моему мнению, является доказательством того,
что мы не имеем достаточно ясной концепции актуальной бесконечности,
хотя это понятие может быть определено в терминах абстрактной логики.
„Нет актуальной бесконечности44 (Анри Пуанкаре1), и то, что мы
называем в наших рассуждениях актуальной бесконечностью, есть не
что иное, как „конечное, очень большое" (Борель). Мы обязаны Борелю
этой важнейшей идеей2. Борель сам дал процесс построения некоторого
натурального числа, совершенно аналогичный трансфинитному процессу
Г. Кантора3.
В действительности каждое фиксированное количество, каждая
постоянная величина, каждое определенное число необходимо конечны.
Мы не владеем идеей бесконечного иначе, как беря конечное и
заставляя его расти. Всегда, следовательно, имеется неопределенность,
которая является истинной идеей бесконечности. Таким образом, мы
возвращаемся к языку классического математического анализа, который
употреблялся до трудов Г. Кантора.
Но надлежит очень хорошо понимать истинный смысл понятия
актуальной бесконечности. Вот идеи Бореля в этом отношении4.
1 Henri P о in care. Les derniers efforts des logisticiens (Science et Methode*
212, 1912).
2 Emile В о r e 1. La philosophic mathematique et l'infini (Revue du MoisT август
1912 г.).
3 Процитируем текстуально это важное высказывание Бореля („L'infini
mathematique et la realite". Revue du Mois, 10 июля 1914 г.):
„Если ввести подходящие символы, станет возможно аффективно записать
очень простым способым некоторые числа, которые в десятичной системе не могут быть
записаны человеком. Если мы обозначим, например, через (л) число из п. цифр, то ((п))
будет числом, у которого число цифр само является числом, имеющим л цифр, так что
((10j) означает число с 10 миллиардами цифр. Записывая скобки далее, обозначим
через (((10))) число, у которого число цифр само имеет 10 миллиардов цифр. Можно
продолжать так дальше и представить себе, что записаны тысячи скобок, нала*
гающиеся таким образом; после того как имеет место эффективная запись этих
скобок, обозначим через \п\ число (( . . . ((10)) . . . )) в случае, когда имеется rt
скобок; налагая квадратные скобки, будем иметь обозначение, еще более сжатое,
и т. д. Нельзя не поражаться аналогии между определением этих арифметических
символов и последовательным процессом Георга Кантора дая конструирования
трансфинитных чисел. В обоих случаях мы сталкиваемся с теми же трудностями;
нельзя сформулировать эффективно ничего, кроме конечного числа условий, и как.
бы далеко эти условия ни позволяли заходить, числа, которые они позволяют
достигать, практически ничтожны по отношению к тем, которые от них ускользают.
В случае, когда будет достигнуто установление таких условий, что можно будет
записать на нескольких страницах колоссально большое число, будут существовать
еще большие числа, которые при тех же условиях не смогут быть определены.
иначе, как записью, требующей миллиарды тонн бумаги".
* Эмиль Борель изложил эти идеи в своих (глубоких) лекциях по теории
вероятностей, прочитанных им в течение первого семестра 1929/30 уч. года на
факультете наук (la Faculte des Sciences) Парижского университета.
АНАЛОГИИ МЕЖДУ МНОЖЕСТВАМИ. ИЗМЕРИМЫМИ В. И АНАЛИТ. МНОЖЕСТВАМИ 473
Человеческая возможность фактически определять числа, вопреки
видимости, очень ограничена, даже если допустить безграничную
продолжительность человеческого рода. Согласно исчислениям А. С. Зддинг-
тона, наибольшее из всех небесных тел не может никогда превзойти
некоторый конечный предел, потому что в противном случае давление
излучения превысило бы ньютоновское притяжение. Таким образом, мы
не имели бы никогда, каковы бы ни были физические условия
существования, достаточного количества „миллиардов тонн бумаги", для
того чтобы записать числа, достаточно большие и тем не менее
конечные. Обычно возражают, что нет никакой необходимости эффективно
записывать числа, для того чтобы они были определены; достаточно
мыслить их. Но между тем следует отметить, что очень трудно
пренебрегать устройством наших мозгов, подчиняющихся всегда конечным
физическим процессам и законам прерывистости частей. В этих
условиях, если мы захотим исключить соображения, слишком фантастические,
и сохранить в науке ее главную цель: рассматривать доступные
наблюдению явления при помощи доступных наблюдению объектов, несомненно*
что идея актуальной бесконечности является просто математической
моделью, назначение которой — представить колоссально большое число,
„конечное в себе", которое не поддается никакому конечному
представлению1.
Мы вернемся теперь к указанной аналогии между множествами,
измеримыми В, и аналитическими множествами и дадим примеры пар
двойственных предложений. Но прежде чем сформулировать явно
соответственные предложения, я хотел бы сначала изложить некоторые пункты
теории множеств, измеримых Ву принципы которой я давно указал2.
1 Конечное число может ускользнуть of всех способов конечных представлений*,
и в то же время большее число может быть представимо конечным путем.
До-видимому, мы обязаны этим важным замечанием Архимеду; см. его „Arenaire".
2 См. заметку Лаврентьева, „Sur les sous-classes de la classification de
M. Rene Baire" (Comptes Rendus, 12 января 192S г.).
Я предпринял построение этой теории, имея целью решение проблемы
определения мощностей аналитических дополнений: я не распознал в то время истинного
характера этой проблемы, невозможности рассматривать ее как подлинную проблему на*
уки. Так как каждое аналитическое дополнение £, определенное решетом С, разлагается
на трансфинитное число множеств, измеримых В% Е = Е$ -+- Ei -+- Е^ -+-... -+- Е{0 -+•
■+-. . . -ь Ea-h- . . . |Q, был поставлен вопрос: узнать, каковы классы конституант Еа.
Именно для определения классов Еа я ввел понятие элемента класса и рассматривал
роль элементов класса а в образовании других множеств класса а. Поскольку
каждое множество Е класса а может рассматриваться как рассеянное множество
элементов класса а, я пришел к определению подклассов классификации Бэра—
Валле-Пуссена.
Очень важный вклад, который внес в эту теорию Лаврентьев,—строгое
доказательство того, что эта подклассификация не является чисто абстрактной, т. е.,
что эффективно существуют множества каждого класса а и каждого подкласса Р,
каково бы ни было трансфинитное число второго класса $.
474
Н. Н. ЛУЗИН
Теория множеств, измеримых В, базируется на следующих
соображениях *.
Фундаментальное пространство. Прежде всего, для того
чтобы логические законы были сформулированы в наиболее простой
«форме, мы исключим из рассмотрения все рациональные точки. Мы
предполагаем таким образом, что все линейные точечные множества, которые
мы рассматриваем, образованы иррациональными точками. Множество
всех иррациональных точек мы будем называть фундаментальным
пространством и обозначать через <7.
Порции. Мы будем называть порцией фундаментального
пространства (7 множество иррациональных точек, содержащихся между двумя
данными рациональными точками а и Ьу и будем обозначать ее через
(а, Ь). Фундаментальное пространство о/ будет рассматриваться как
порция и будет обозначаться в этом случае через (—оо, -ч-оо). Если
с — рациональное число, то (—со, с) и (с, -ьоо) также являются порциями.
Начальный класс. По определению множество начального класса
или класса К0 — это каждое точечное множество Еу которое является
суммой конечного или бесконечного числа порций, так же как и его
дополнение СЕ.
Фундаментальная операция. Фундаментальная операция,
которая используется в этой теории и которую мы введем сообразно
идеям Валле-Пуссена2, — это переход к пределу. Назовем сходящейся
последовательностью каждую безграничную последовательность
точечных множеств
■^1» ^2> • • •> *^пу • • • (1)
какую, что каждая точка х пространства о7 либо принадлежит, либо не
принадлежит всем Еп, исключая ограниченное число их, зависящее от
х. Множество Е называется пределом сходящейся последовательности
множеств, если Е есть множество всех тех точек jc пространства <з7,
каждая из которых принадлежит всем Ет начиная с некоторого места,
зависящего от х. Мы говорим в этом случае, что Е определяется
сходящейся последовательностью (1) при помощи операции предельного
перехода, и мы обозначаем его через lim En.
« = 00
Алгебраические обозначения3. Мы применим по отношению
к множествам иррациональных точек классические соглашения
относительно алгебраических обозначений: сумма Ех -+- Е2> общая часть Ех - £2»
разность Е2 — Еи равенство и включение ЕХ = Е2> ElCZF2, E = 0 и
дополнение СЕ. Таким образом, мы будем иметь Е2 — Е1 = Е2- CEV
1 Полное изложение этой теории было дано в моей книге „Лекции об
аналитических множествах" (см. стр. 9 настоящего тома.—Ред.).
2 Ch. de la Vallee-Poussin. Sur l'integrale de Lebesgue (transactions of
the American Mathematical Society, 1915); Ch. de la Vallee-Poussin. Integrates
-de Lebesque, fonctions d'ensembles, classes de Baire, 1916, стр. 8.
a Cm. Ch. dela Vallee-Poussin. Loc. cit.
АНАЛОГИИ МЕЖДУ МНОЖЕСТВАМИ, ИЗМЕРИМЫМИ В, И АНАЛИТ. МНОЖЕСТВАМИ 475
Пусть Р(х1У х2 ..., хп)— полином относительно х1у х2у ..., хпу имеет
коэффициенты, равные 1. Если мы подставим вместо переменных х1У х2У ...
♦ . ., хп соответственно какие-либо точечные множества Е1У Е2. ..., Еп
и если мы будем рассматривать знаки операций -+- и • как сумму и
общую часть этих множеств, то полином будет вполне определенным
-точечным множеством, которое мы обозначим снова через Р{Е1У Е2У ...
..., £я). В этом случае значение Р(Е19Е2У ..., Еп) нисколько не зависит
от порядка членов Р.
Если полином Р{х1У х.1У ..., хп) имеет коэффициенты -н 1 и —1
и если первый член Р положителен, мы можем получить снова
интерпретацию Р {Е1У Е2у •. ., Еп) в области множеств, если положим
U— V— W= {U— V) — Wy
где Uу V и W — какие-либо точечные множества. В этом случае
значение выражения Р(Е1У Е29 ..., Еп), естественно, зависит от порядка
•членов полинома Р(х1У х2у ..., хп).
Ряды множеств. Назовем рядом множеств бесконечный символ
^-|-^2-ь...-ь£/я-ь..., (2)
тде буква Un означает точечное множество со знаком н- или —
впереди.
Точечное множество, которое получается отбрасыванием знака члена
Uny будем называть абсолютной величиной U„; мы обозначим это
множество через \Un\.
Мы скажем, что ряд множеств (2) сходится, если последовательность
Sly S2y ..., Snf ..., где Sn — сумма первых п членов этого ряда,
сходится. В этом случае предельное множество S этой последовательности
«будет называться суммой ряда (2), и мы будем записывать равенство
S= иг-*- £/2н- ... -I- Un-+-...
Мы будем рассматривать только сходящиеся ряды; эти ряды имеют
лоложительный первый член, потому что в противном случае сумма
Sn первых п членов не имела бы никакого смысла.
Мы займемся знакопеременными убывающими рядами: эти ряды
ямеют вид
Ег - Е2 -н Ег - £4 -+- ...-Н- D"+1 •£»-+-•• -,
где точечные множества Е1У Е2У ... образуют убывающую
последовательность £jD E2Z) ... Z) EnZD ... .
Для того чтобы знакопеременный убывающий ряд множеств Е1 —
— Et-+-Ez—... был сходящимся, необходимо и достаточно, чтобы его
общий член стремился к нулю:
lim£e = 0.
476
Н. Н. ЛУЗИН
Классификация множеств. Начиная с начального класса К0>
мы будем определять при помощи фундаментальной операции lim
последовательные классы Бэра—Валле-Пуссена формально шаг за шагом:
Ко> ^l» K2f ..., К^, ..., Ktl, ..., Ка, ... |2.
Класс Ка определен здесь логически (формально) как множество
всех таких точечных множеств Е, не входящих ни в один
предшествующий класс, которые являются пределами, Е = \\тЕ„, множеств Еп пред-
»/=-СО
шествующих классов.
Классы классификации Бэра—Валле-Пуссена не имеют попарно
общих элементов.
Совокупность множеств, принадлежащих классам этой
классификации, совпадает с совокупностью множеств, измеримых В.
Если какое-либо множество Е принадлежит классу К*, мы будем!
записывать равенство
cl£ = a,
и мы скажем, что Е есть множество класса а.
Если точечное множество Е класса *, тр его дополнение СЕ также
класса а.
Сумма Ег -+- Е2 -+- ... -+- Еп и произведение Ех • Е2- ... - Еп конечного
числа множеств являются множеством класса самое большее равного
наибольшему из классов, составляющих множеств Е{.
Достижимость. Мы скажем, что множество Е, принадлежащее
классу Ка, достижимо сверху, если Е является общей частью
счетного числа множеств классов, низших чем а. Точно так же мы скажем,,
что множество Е класса а достижимо снизу, если Е есть сумма
счетного числа множеств классов, низших чем а.
Если множество Е класса а достижимо сверху, то его дополнение
СЕ достижимо снизу, и наоборот.
Множество Е класса а называется двусторонним, если оно
достижимо сверху и в то же время достижимо снизу; множество класса а
называется односторонним, если оно достижимо сверху или достижима
снизу и не является двусторонним.
Наконец, скажем, что множество Е класса а недостижимо с обеих:
сторон, если оно недостижимо ни снизу, ни сверху.
Каждый класс Ка+г первого рода образован множествами
односторонними и множествами, недостижимыми с обеих сторон. Каждый класс
Ка второго рода образован множествами двусторонними,
односторонними и недостижимыми с обеих сторон.
Классы первого рода Ка+1 не могут содержать двусторонних
множеств. Каждый класс второго рода эффективно содержит
двусторонние множества.
Множество всех двусторонних множеств класса Ка второго рода
называется базой класса ЛГа; база класса К% будет обозначаться
через Ва.
АНАЛОГИИ МЕЖДУ МНОЖЕСТВАМИ. ИЗМЕРИМЫМИ В. И АНАЛИТ. МНОЖЕСТВАМИ 477
Предел множеств базы Ва никогда не может принадлежать классу
Если точечное множество Е является суммой знакопеременного
ряда множеств классов <а, то £ либо класса <[ а, либо принадлежит
базе Ва.
Элементы. Чтобы проанализировать структуру более общих
множеств класса а, мы возьмем в качестве инструмента односторонние
достижимые сверху множества Ка. Эти множества будут называться
элементами класса а.
Имеется реальная аналогия, с одной стороны, между обычными
точками и элементами класса а и, с другой стороны, между порциями
фундаментального пространства 3 и множествами базы Ва.
Элементы класса а играют очень существенную роль в образовании
множеств класса а:
Необходимое и достаточное условие для того, чтобы точечное
множество Е было класса <^<*, состоит в том, чтобы Е, так же
как его дополнение СЕ> было суммой счетного числа попарно не
пересекающихся элементов классов ^а:
Е = е1 н- е2 ■+" • • • ~,-£п -*-..., СЕ = \ ■+- т]2 н- ... -ь гы ...,
где £»• и \ — элементы классов ^а, попарно не пересекающиеся.
Отделимость (а). Два произвольных точечных множества Ех и
Ео называются отделимыми относительно класса КЛ или просто
отделимыми (а), если существуют два множества Нх и Н2 классов <Za
или базы ВаУ не пересекающиеся и содержащие соответственно
множества Е1 и Е2: Ех С Н1У Е2 С Н2. Эти множества Нх и Н2
называются отделителями1.
Первый малый принцип. Точка, взятая в отдельности,
является, очевидно, элементом класса 1. Две различные точки хг и х2,
разумеется, отделимы при помощи двух порций фундаментального
пространства \ и 82э попарно не пересекающихся. То же предложение
имеет место для элементов класса ЛГа; мы назовем это важное
предложение первым малым принципом. Вот его формулировка.
Первый малый принцип: Два непересекающихся элемент а
класса а всегда отделимы (а).
Роль, которую играет этот принцип, очень важна. Вот
доказательство этого принципа.
Пусть Е и § — два элемента класса а без общих точек. По самому
определению Е и 8 являются соответственно пределами двух
убывающих последовательностей:
и
Sx D £2 D ... D ёп Э - • •
множеств классов <Са: Е = \\тЕпу ё = \\т§п.
1 Я заимствовал эту терминологию у Лебега.
478
Н. Н. ЛУЗИН
J J
г ^ «
Е; — %,
S
i^:
J J
r \
Е,— S,
\
b^h
Запишем теперь две вертикальные схемы и возьмем все
произведения двух букв, расположенных на одной и той же наклонной прямой
со знаком -+- и произведения двух букв, расположенных на одной и
той же горизонтальной прямой, со знаком —. Мы получим таким
образом два знакопеременных убывающих ряда множеств классов <^*:
г>7 ' Е\ — Ei&i ~*~ &\Е2 — Е2&2 ~*~ • • •
и
o7<?i — £\Е\ ~*~ Е \<S 2 — (§2^2 -*-...
Эти два ряда множеств, очевидно, сходящиеся, потому что Е и <Г
не имеют общих точек и, следовательно, общий член в обоих рядах
имеет пределом нуль.
Пусть Н1 — сумма первого ряда и Н2 — сумма второго. Согласно
предшествующей теореме о знакопеременных рядах множеств классов
<Са оба множества Нг и Н2 являются
множествами либо класса <Са, либо базы Ва.
Установив это, возьмем произвольную
точку х пространства с7. Предположим, что
х принадлежит к членам левого столбца и
/ членам правого столбца предыдущей
вертикальной схемы. Очевидно, что ^1 и
1^1. Если к = 1> точка х не принадлежит
ни Н19 ни Н2; она принадлежит Нг или Н2
в зависимости от того, имеем ли мы к^>1
или к <С /• Таким образом, множества Нх и Н± не имеют общих точек и
содержат соответственно Е и <£, что и доказывает первый малый
принцип.
Изолированные множества элементов. Очевидно, что
различные точки х1У х2, . • •> хп в конечном числе одновременно отделимы
при помощи соответствующих попарно не пересекающихся порций olf
\у . • •> К* Точно так же попарно не пересекающиеся элементы ех>
е2У ..., еп класса а всегда одновременно отделимы при помощи
множеств-отделителей Аг, А2, ..., hn класса <^а или базы Ва.
Но счетное число точек х1У х2, ..., хп, ... допускает такое
одновременное (равномерное) отделение только в том случае, если их
множество Е является изолированным множеством: это означает, что
каждая точка х множества Е изолированна в £, т. е. может быть
заключена в порцию о, которая не содержит никакой другой точки £•
Аналогичным образом будем рассматривать счетное множество Е
элементов е19 е21 ..., еп, ... класса а. Элемент е из Е называется
изолированным в Е, если существует множество-отделитель Н класса
<^а или базы Ва, содержащее элемент е, которое не содержит точек
других элементов из Е> кроме е. Самое множество Е называется
изолированным, если каждый из его элементов изолирован в Е,
АНАЛОГИИ МЕЖДУ МНОЖЕСТВАМИ. ИЗМЕРИМЫМИ В. И АНАЛИТ. МНОЖЕСТВАМИ 479
Для того чтобы счетное число элементов класса а
еа &<>> • • •> епч • • •
попарно без общих точек допускало равномерное отделение,
необходимо и достаточно, чтобы множество Е было изолированным
множеством.
Рассеянные множества элементов. Одно из важных
понятий, которым мы обязаны Данжуа, — это определение рассеянного
множества. Мы уже знаем, что следует понимать, согласно Данжуа,
под рассеянным множеством точек: это счетное точечное множество £,
каждая часть которого Ех содержит точку, изолированную в Ех.
Известно, что каждое рассеянное точечное множество Е может быть
преобразовано во вполне упорядоченное
-*0> х19 х>у • • •» Хкму . . ., ATv, . . ., f)y {l)^
соответствующее трансфинитному числу 0 второго класса Кантора
таким образом, что член Ху является изолированной точкой в той
части множества Еу которая получается выбрасыванием из Е всех
точек Ху'у которые предшествуют хт, т'<Ст; здесь число т —
произвольное число, предшествующее б. Другими словами, вполне упорядоченной
последовательности точек (1) мы можем поставить в соответствие вполне
упорядоченную последовательность
%> 81, К • . •» К • • •> °7> • • •» 1°> @)'
образованную порциями пространства cJ и такую, что, каково бы
ни было число т, предшествующее б, порция от содержит
предшествующую точку Ху и не содержит никакой последующей точки jct", *f"^>7-
Известно, что понятие рассеянного множества является очень
полезным инструментом при изучении счетных множеств *.
Точно так же мы назовем рассеянным множеством элементов
класса а всякое счетное множество Е элементов класса а попарно без
общих точек, каждая часть Ех которого содержит элемент,
изолированный в Е}. Каждое рассеянное множество Е элементов класса а
может быть преобразовано во вполне упорядоченное множество
е0> ^1» *2> •••> е"» •••> ет> • • •> 1^ (I)
соответственно трансфинитному числу 0 второго класса Кантора таким
образом, что существует вполне упорядоченная последовательность
множеств-отделителей класса <^а или базы Ва
А0, hly А,, ..., Ло>, ..., Лт, ..., |0. (II)
1 Г. М. Фреше перенес понятие рассеянного множества в топологические
пространства; см. „Les espaces abstraits", 1928, стр. 174 и его труды в Fund. Math.v
1927—1929.
480
Н. Н. ЛУЗИН
такая, что, каково бы ни было число 7, предшествующее 0, множество-
отделитель Лт содержит соответствующий элемент ет и не содержит
никакого последующего элемента ет", 7"^>7*
Понятие рассеянного множества элементов играет весьма
существенную роль в изучении более общих множеств класса а. Вот каковы
основания для этого.
Точка пространства 7f взятая отдельно, является, очевидно,
элементом класса 1. В общем случае счетное множество Е является
множеством класса 2 (достижимым снизу). Для того чтобы счетное
точечное множество Е было класса 1, необходимо и достаточно, чтобы
множество Е было рассеянным в смысле Данжуа.
Точно так же в общем случае счетное множество Е элементов
класса ^<% попарно без общих точек является множеством класса а-ь-1
(достижимым снизу). Для того чтобы множество Еу измеримое Ву
было класса ^а, необходимо и достаточно, чтобы множество Е
можно было рассматривать как сумму счетного числа элементов
класса ^а попарно без общмх точек, множество которых является
рассеянным множеством в ранее данном смысле1:
£ = ^ + ^ + «2+...+^+...+^+... |О, (III)
Подклассы- Итак, множество Е> измеримое В, класса а всегда
можно представить в виде рассеянного ряда элементов классов ^а,
взятых в счетном числе:
Е = е0 -+- ех -+- е2 ч- ... ■+- е» -н ... -+- ет -+- ... |0, (Ш)
1 Мы определили ранее рассеянные множества, образованные элементами точно
класса а (а не классов < а). Если ограничиться этим определением, теорема в тексте
может быть сформулирована следующим образом:
Каждое множество Е класса < а. является суммой двух множеств Е\ и Е%>
из которых первое достижимое снизу класса а, а второе образовано счетным
числом элементов точно класса а попарно без общих точеку множество которых
является рассеянным множеством в ранее определенном смысле. Обратно% сумма
двух множеств указанной формы является множеством класса < а.
Но кажется предпочтительным немного расширить данное определение, введя
понятие множества, рассеянного относительно класса а: это будет в том случае,
когда все множества-отделители Лу являются множествами класса < а или базы Ва1
каковы бы ни были соответствующие элементы еу классов < а.
Очевидно, что, применяя это определение, мы сможем упразднить множество Е\ч
потому что каждое множество е из Е\ класса, низшего чем а, и мы сможем
предположить, что оно совпадает с соответствующим множеством-отделителем А. В
результате, если мы будем нумеровать элементы Е\ при помощи чисел, оставляя
трансфинитные индексы аля элементов Е2% мы получим рассеянное разложение (III) текста.
Множествам, рассеянным относительно класса а, можно противопоставить
множества, рассеянные в абсолютном смысле: это те множества, которые мы получим
в том случае, когда каждое множество-отделитель Лт является множеством либо
класса, точно предшествующего классу соответствующего^ элемента еу, либо того же
класса, что и этот элемент.
Понятие множества, рассеянного в абсолютном смысле, очень важно, потому что
оно позволяет нам изучать аналогичным образом структуру двусторонних множеств
каждого класса а второго рода.
АНАЛОГИИ МЕЖДУ МНОЖЕСТВАМИ, ИЗМЕРИМЫМИ В. И АНАЛИТ. МНОЖЕСТВАМИ 481
который соответствует трансфинитному числу 6 второго класса
Кантора. Так как каждое множество Е класса а допускает бесконечное
число различных разложений (III), множеству Е соответствует
бесконечное число различных чисел 0. Среди этих чисел 6 имеется одно
наименьшее; мы обозначим его через (3. Таким образом, каждому
множеству Е класса а соответствует вполне определенное трансфинитное
число р.
Мы условимся говорить, что множества Е класса а, которые
соответствуют одному и тому же транофинитному числу (3, образуют
подкласс Р. Мы можем произвести теперь теоретическое распределение
множеств класса а классификации Бэра—Валле-Пуссена на
трансфинитное множество подклассов, перенумерованных трансфинитными числами
второго класса Кантора.
Легко видеть, что определенные таким образом подклассы не имеют
попарно общих элементов и что каждое множество Е, измеримое В,
принадлежит одному определенному классу а и одному определенному
подклассу р.
Было бы очень желательно, чтобы имелись какие-либо общие результаты
для таким образом определенной подклассификации измеримых В множеств.
Подклассификация и теорема Бэра. Бэру принадлежит
важнейший результат, который дает нам необходимое и достаточное
условие для того, чтобы можно было рассматривать функцию /(л:),
определенную для числовых значений сегмента (0 ^ л: ^ 1) как предел
непрерывных функций, т. е. как функцию первого класса его
классификации. Известно, что главная часть доказательства самого Бэра состоит
в построении регулярного оперативного процесса, позволяющего при
помощи счетного числа операций по отношению к числовым значениям
/(х) узнать, принадлежит ли f(x) первому классу или нет, и в первом
случае эффективно найти последовательность непрерывных функций
Л(*)> Л(*)> •••> стремящуюся к f(x).
Тем не менее оперативный процесс Бэра, хотя и счетный, является
существенно трансфинитным, потому что последовательные шаги этого
процесса нумеруются при помощи трансфинитных чисел Кантора в
счетном числе. Вот почему Лебег и Валле-Пуссен дали другие
доказательства теоремы Бэра без введения трансфинитных чисел1. Известно, что
1 См. статью Лебега в Bull, de la Societe math, de France, 1904; см. также
заметку Лебега „Demonstration d*un theoreme de M. Baire" в „Lecon sur les
fonctions de variables reeles", 1905 г. Бореля* и мемуар Лебега „Sur les fonctions
representables analytiquement" (Journ. de Math., 183, 1905); Валле-Пуссен „Integrates
de Lebesgue, fonstions d'ensembles, classes de Baire", 1916, стр. 125; ср. К. Кура-
товский, Fund. Math., Ill, 104.
Я указывал, что в 1903 г. Борель в заметке „Sur la representation effective
de certaines fonctions descontinues, comme limites de fonctions continue "(Comptes
Rendus, 137, 903, 1903) настаивал, что получение доказательства теоремы Бэра
без введения трансфинитных чисел имело бы интерес, и указывал, что имеются
прецеденты в случае* теоремы, называемой теоремой Кантора—Бендиксона.
482
Н. Н. ЛУЗИН
трудности доказательства этой теоремы были преодолены ценой потери
регулярного оперативного процесса: т. е. было получено только
существование последовательности непрерывных функций fl{x)y /2(jc), ...
стремящихся к f(x), но не было эффективного построения каждой из
функций /й (х), /2(х), .. Л
Если мы вернемся теперь к оперативному процессу Бэра, мы
немедленно заметим, что продолжительность процесса Бэра различна для
разных функций: эта продолжительность целиком зависит от
рассматриваемой функции /(х). И так как продолжительность процесса Бэра
измеряется определенным трансфинитным числом второго класса Кантора,
то естественно классифицировать функции /(х) класса 1 соответственно
продолжительности оперативного процесса Бэра. Мы подошли таким
образом к распределению функций класса 1 на подклассы,
перенумерованные при помощи трансфинитных чисел Кантора 2.
Если мы применим теперь оперативный процесс Бэра к функциям
f{x) класса 1, не принимающим других значений, кроме 0 и 1, мы
сможем констатировать следующее: такая функция f{x) определяет
множество Е точек, для которых функция имеет значение 1; это множество Е
класса 1 (или 0) в классификации множеств Бэра—Валле-Пуссена. Но
главное состоит как раз в том, что оперативный процесс Бэра,
примененный к такой функции f{x), идентичен с разложением множества Е
в рассеянный ряд (III), образованный элементами класса 1, т. е.
составленный из точек и совершенных множеств в счетном числе. Это то
разложение множества класса 1 в рассеянный ряд замкнутых множеств,
которое составляет подлинную сущность принадлежащего Бэру
доказательства его теоремы. К тому же подклассы, произведенные процессом
Бэра, совпадают с подклассами, определенными при помощи рассеянного
1 В своем мемуаре „Sur les fonctions representables analatiquement" (Joura. de
Math., 183, 1905) Лебег сделал интересное замечание, поставив вопрос на почву
реализма; „Всякий оперативный процесс, относящийся к наиболее общим функциям,
предполагает, что эффективно известны некоторые операции, относящиеся к этим
функциям. Нет никакого вопроса, как бы он ни был прост, который можно было
бы решить а^я наиболее общей функции, заданной произвольным образом; каждый
операторный процесс иллюзорен, когда его пытаются применять в общем случае.
Процесс Бэра не избегает этой критики, ибо он предполагает, что известно, как
найти точки разрыва функции на совершенном множестве, в то время как не известно,
как это. сделать в общем случае. Но так как чаще всего это можно эффективво
сделать, то процесс Бэра практически полезен во всех случаях, когда требует лишь
конечного числа операций. Когда он требует бесконечного числа операций, он может
все еще быть полезным, уже, собственно говоря, не как оперативный процесс,
а как цутеводцтель доказательства".
2 Данжуа отметил интерес, который представляет, распределение тотализуевсых
функций на классы соответственно длине тотализации. Распределение, данное
Данжуа в 1916 г. в его „Memoir* sur la totalisations des nombres derives
non-somB}able& (A»iu de l'Ecote Norm. Super., .S3), очень походит на указанное
распределение фушедвй первого класса согласно длавье оперативного процесса
Бора.
АНАЛОГИИ МЕЖДУ МНОЖЕСТВАМИ; ИЗМЕРИМЫМИ В. И АНАЛИТ. МНОЖЕСТВАМИ 483
разложения, и, следовательно, процесс Бэра образует рассеянные ряды
наименьшей длины.
Так .как каждое множество класса а, каково бы ни было ос, конечное
или трансфинитное второго класса Кантора разложимо в рассеянный
ряд элементов, мы заключаем, что оперативный процесс Бэра
сохраняется для высших классов.
Метод арифметических определений Бэра. Известно, что
сам Бэр никогда не использовал метод отображения на континуум [37]
для доказательства существования функций всех классов. Эта
предосторожность вполне естественна с точки зрения строгого реализма,
потому что рассматривать как данную функцию f(x) класса а,
полученную отображением на континуум семейства F, образованного всеми
функциями классов, низших чем а, это значит считать известной каждую
функцию, входящую в семейство Fy чего нельзя принимать всерьез,
если мощность семейства F несчетна1.
По этой причине сам Бэр предпочитал построить фактически
определенную функцию рассматриваемого класса, дав ей арифметическое
определение. Именно этим методом Бэр конструктивно доказал суще-'
ствование функций класса 3. Вот функция Бэра:
если разложить в непрерывную дробь иррациональное число ху за*
ключенное между 0 и 1:
1
х = ~
1
Н
ап+ #
то функция /(х)у равная 1, если негголные частные ах> а2, ..., аиу ...
стремятся к бесконечности, и равная 0 в противном случае, является
точно функцией класса 3.
Известно, что исследования Бэра2 ограничились изучением функций
класса 3. Но идеи, на которых базируется рассматриваемая теория В
1 Метод наложения на непрерывное был применен: Эмилем Борелем в Note III
его „Lemons sur les f о notions de variables reeles", 1905 г. для установления
существования функций каждого конечного класса; Анри Лебегом аля установления
существования функций каждого класса (Jour*, de Math., 1905); Ш. де ла Валле-
Пуссеном („Integrales, fonctions, classes de Baire, стр. 145); см. также заметку
В.Серпинского: „Sur l'existence de toutes les classes d'ensembles mesurables Bu (Comptes
Rendus, ноябрь 1922 г.) и заметку К. Куратовского: „Sur l'existence effective des
fonctions representables analytiquement de toute classe de Baire" (Comptes Rendus»
январь 1923 г.).
Другой метод, ари-роду которого, пожалуй, трудно уточнить, дан В. Серцин-
схям и автором; см. нашу заметку „Sur les classes des constituantes d'un comple*
mentaire aaalytique" (Comptes Readus, 12 ноября 1929 г.).
2 См. era глубсмвй м ем yap .„Sur la representation des fonctions discontinues",
вторая часть (Acta Math., 32, 1909).
484
Н. Н. ЛУЗИН
множеств и часть которых заимствована Лебегом1 и самим Бэром
позволяют очень естественно продолжить исследования Бэра дальше
класса 3 и проникнуть в структуру множеств высших классов.. В
частности, имеется возможность дать арифметическое определение функций
высших классов. Вот очень интересный результат исследований Л.
Келдыш в этом направлении:
если разложить в непрерывную дробь иррациональное число х
заключенное между 0 и 1:
1
х= Г"
«1-*-
1
Н
то функция f(x)y равная 1, если среди неполных частных alf a2,
,.., art, ... имеется бесконечное число различных неполных частных, каждое
из которых повторяется бесконечное число раз, и равная 0 в
противном случае, является функцией точно класса 4.
Было бы очень интересно дать арифметический пример функции
произвольного конечного класса Бэра и, в частности, класса 5 [49].
Исследования М. Лаврентьева. Вернемся теперь к подклас-
сификации множеств класса а. Можно задаться вопросом, не является
ли эта подклассификация чисто идеальной, т. е. существуют ли
эффективно множества в различных ранее определенных подклассах. М.
Лаврентьев дал предшествующей теории фундаментальный результат, без
которого излагаемая теория была бы чисто формальной: эффективна
существуют множества класса а всех подклассов2.
Кроме того, он доказал, что подклассы остаются инвариантными
при всех гомеоморфных преобразованиях.
Отделимость (Са). Мы ввели ранее понятие отделимости (а).
Затем мы доказали одно фундаментальное предложение, которое мы
назвали первым малым принципом и которое состоит в том, что два
произвольные элемента класса а без общей части всегда отделимы (а).
Естественно искать обобщения этого важного факта и
распространить теорию отделимости на другие множества класса а. Естественно
начинать построение этой теории с изучения отделимости при помощи
дополнений к элементам класса а, т. е. при помощи множеств,
достижимых снизу, класса а.
Сформулируем следующее определение.
1 Важное понятие элемента класса а дано Анри Лебегом; знаменитый автор
называл множеством ранга а, то, что мы называем теперь элементом класса а; и указал
очень четко важную роль этих множеств в теоремах X и XVII его фундаментального
мемуара »Sur les fonctions representables analytiquement" (Journ. de Math., стр; 173и 191).
zCm. заметку Лаврентьева: „Sur les sous-classes de la classification de M. Rtne
Baire" (Comptes Rendus, 12 января 1925 г.).
АНАЛОГИИ МЕЖДУ МНОЖЕСТВАМИ. ИЗМЕРИМЫМИ В. И АНАЛИТ. МНОЖЕСТВАМИ 485
Мы скажем, что два точечных множества £х и Е2 одновременно
отделимы (Са), если существуют два множества Нх и Н2 класса а,
достижимые снизу, не имеющие общих точек и содержащие
соответственно Ег и Е2.
Прежде чем указать принципы этой теории, следует сделать
следующее замечание1. Было бы бесполезно вводить понятие
одновременной отделимости при помощи двух элементов Нх и Н2 класса а, потому
что в этом случае рассматриваемые множества Ех и Е> были бы просто
отделимы (а). Наоборот, важно ввести отделимость (Са), потому что,
как мы увидим, существуют два множества Нх и Н2 класса а,
достижимые снизу, не имеющие общих точек, которые не являются
отделимыми (а).
Второй малый принцип. Теория отделимости (Са) базируется
на следующем фундаментальном предложении, которое мы называем
вторым малым принципом.
Второй малый принцип. Если Ех и Е2 — два элемента
класса а, то множества /?х и /?.>, которые получают удалением из
Ех и Е2 их общей части у являются всегда одновременно
отделимыми (Са).
Для доказательства возьмем две предыдущие вертикальные схемы,
где больше не будем предполагать, что данные элементы Е и & класса а
не имеют общих точек.
Положим
H^iJ.E^E,- S,) н- (Sx -Et-€t.El + ...
H2 = (<y-gl — Sx-El)-*-(El-e2 — gfEJ+...
Очевидно, что Нх и Н2У определенные таким образом, являются:
либо множествами классов <С&, либо множествами базы Вв, либо
односторонними множествами, достижимыми снизу. И так как Н1 и Н> не
имеют общих точек и содержат соответственно множества Rx и R2,
которые получаются удалением из Е и & их общей части, то
сформулированный принцип доказан.
Множества многих измерений. Для определенности мы
ограничимся множествами в пространстве двух измерений.
Возьмем евклидово пространство £ двух измерений. Пусть в этом
пространстве дана какая-либо система взаимно перпендикулярных осей,
которую мы обозначим через XOY.
Назовем фундаментальным пространством двух измерений множество
всех точек М(х> у) плоскости XOY> у которых обе координаты х и у
иррациональны. Фундаментальное пространство двух измерений будет
обозначаться через g7*, у.
Все плоские множества, которые мы будем рассматривать,
образованы точками фундаментального пространства о7*,#.
1 Ср. с моей заметкой: „Sur un principe general de la theorie des ensembles
analytiques" (Comptes Rendus, 2 сентября 1929 г.).
486
Н. Н. ЛУЗИН
Назовем порцией пространства 7х,# множество точек М(ху у) этого
пространства, координаты которых х и у принадлежат каждая
соответственно порциям (а, Ь) и (с, d)y расположенным соответственно
в линейных фундаментальных пространствах о7'х и Уу.
Говорят, что точечное множество Е пространства ?7х,у является
множеством начального класса К0 или класса 0, если множество Е и
его дополнение СЕ (относительно о7х,р) являются каждое суммой
конечного или бесконечного числа порций фундаментального пространства с7*,у.
Если мы постараемся проанализировать все определения и
рассмотрения, которые мы ранее делали относительно линейных множеств, мы
констатируем, что они все применимы без всяких изменений к
пространствам многих измерений.
В частности, мы будем иметь классы Бэра—Валле-Пуссена
^о» л^ лГ2, ..., К(оУ ..., Ка, .., |2,
и в каждом классе Ка мы будем иметь элементы, односторонние
достижимые снизу множества и множества, недостижимые с обеих сторон;
если класс Ка второго рода (т. е. предельный класс), мы будем иметь
в этом классе двусторонние множества, множество которых называется
базой Ва класса а.
Определение подклассов и их свойства остаются такими же в
пространстве многих измерений.
К тому же фундаментальное пространство двух измерений о/х,у и
линейное фундаментальное пространство c7ty очевидно, гомеоморфны,
и вследствие этого мы имеем одновременные равенства, определяющие
этот гомеоморфизм:
* = ?('). У = ♦('),
t = F(x, у),
где функции <р и ф непрерывны на о7/ и функция F(xy у) непрерывна
на о/Ту у»
Преобразование (Т) ставит в соответствие каждому точечному
множеству Е в о/х,у линейное множество е в о/и и наоборот. Ясно, что
это преобразование (Т) сохраняет класс и подкласс, если множество
Е или е измеримо В.
Множества универсальные и дважды
универсальные. Пусть Е — какое-либо точечное множество, расположенное в
пространстве двух измерений о7^у. Возьмем произвольную точку х0 в <9гх
и проведем прямую х = х0, параллельную оси OY. Прямая х = х0
пересекает множество Е по некоторому линейному множеству, которое мы
обозначим через е.
Очевидно, что если Е — множество класса а, то множество е,
рассматриваемое как линейное множество, является множеством класса
^а. Если Е — элемент класса а, то линейное множество е является
либо множеством класса <Са, либо множеством класса а, достижимым
сверху; если Е — множество-дополнение к элементу класса а, то линей-
(Т)
АНАЛОГИИ МЕЖДУ МНОЖЕСТВАМИ. ИЗМЕРИМЫМИ В. И АНАЛИТ. МНОЖЕСТВАМИ 437
ное множество е либо класса <а, либо класса а, достижимое снизу;
если Е — множество базы 5а, то линейное множество е либо класса
<а, либо базы Ва.
Сформулируем следующее определение.
Определение. Элемент Е класса ^расположенный в 7*%lh
называется универсальным, если в пересечении его с параллелями оси
0Y можно получить все линейные множества класса <[ а и все
множества, достижимые сверху, класса а.
Существуют универсальные элементы каждого класса; таково
важное предложение Лаврентьева, которое он получил в ходе своих
исследований относительно эффективного существования множеств всех
подклассов1. Точно так же существуют универсальные дополнения
к элементам каждого класса: достаточно взять дополнение к
рассматриваемому универсальному элементу класса а.
В противоположность этому, невозможно получить универсальное
множество класса а, каково бы ни было а. Точно так же невозможно
получить универсальное двустороннее множество Е класса а, каково бы
ни было а второго рода.
Действительно, предположим, что Е — универсальное множество
класса а. Это значит, что все линейные множества е класса ^а
получают пересечением Е с параллелями оси OY. Проведем диагональ
х = у и обозначим через в множество тех точек этой диагонали,
которые не принадлежат Е; пусть ц— проекция 9 на ось OY. Очевидно,
что i\> рассматриваемое как множество точек пространства о7у, является
множеством класса ^а. Таким образом, существует параллель оси
О К, х = х0, которая пересекает множество Е точно по т], что
невозможно (рассуждения методом канторовской диагонали).
Точно такими же рассуждениями доказывают невозможность
существования двустороннего универсального множества предельного
класса а.
Сформулируем одно очень полезное определение. Пара (Е1У Е>)
элементов класса а, расположенных в пространстве 7*,#, называется
дважды универсальной у если, каковы бы ни были линейные множества
е1 и ег класса <^а или класса а, достижимые сверху, существует
прямая лг = лг0, параллельная оси OY> которая пересекает Ег и £2
соответственно по ех и е22.
Имеются дважды универсальные пары. Дая доказательства
рассмотрим в пространстве двух измерений q7x,v универсальный элемент
Е. Это значит, что все линейные множества класса <Са или класса а,
достижимые сверху, получают в пересечении Е с параллелями t = t0
оси OY. Установив это, возьмем новое фундаментальное пространство
1 Comptes Rendus, 12 января 1925 г.
2 Ср. с моей заметкой: „Sur un principe general de la theorie des ensembles
analytiques" (Comptes Rendus, 2 сентября 1929 г.).
488
Н. Н. ЛУЗИН
двух измерений oftvtt и рассмотрим его гомеоморфное преобразование
в линейное пространство с/х. Пусть
x = F(tlyt2)
— это преобразование; здесь функции <р и ф непрерывны на <УХ и
функция F непрерывна на o7t},i2.
Рассмотрим теперь преобразование пространства с7/, у в с7х,у,
определенное равенством / = <р(лг), у = у.
Пусть Ех — образ Е. Аналогичным образом, установив
' = <И*)э У = У>
мы преобразуем пространство oft,у в о/х,ь\ пусть Е2— образ Е.
Очевидно, что Ех и Е2 — элементы класса а. Легко видеть, что пара (El9 Е.,)
дважды универсальна. Действительно, всегда существует jc0 такое, что
прямая х = х0 пересекает Е1 и Е2 по двум наперед заданным линейным
множествам ех и е2 класса <^а или достижимым сверху класса а.
Существование двух дополнений к элементам класса а,
неотделимых (а). Мы сможем теперь приступить к доказательству этого
существования. Возьмем в пространстве g7*, у дважды универсальную
пару (Е19 Е>) элементов класса а и применим второй малый принцип
к элементам Ех и Е2. Пусть Rx и R2— множества, которые получаются
удалением из Ех и Е2 их общей части. Согласно принципу, существуют
два достижимых снизу множества класса а Нх и //2, не имеющих
общих точек и содержащих соответственно Rx и R2.
Я утверждаю теперь, что множества Нх и Н2 неотделимы (а).
Действительно, если бы существовали два множества 9t и 92 класса
<а или базы Ва без общих точек, содержащих соответственно Нх и
Н21 каждая параллель оси OY пересекала бы Qx и в2 по двум
линейным множествам класса <С<* или базы Ва. Но пара (Ei9 E2) дважды
универсальна. Это значит, что, каково бы ни было линейное множество
е класса <Са или базы Ва> существует прямая х = х0> которая
пересекает Ег и Е2 соответственно по е и Се. Таким образом, множество
Ех является множеством базы Ва и универсально, а это противоречит
условию1 (ч. т. д.).
Общие свойства множеств, измеримых В. Изучение
множеств, измеримых Ву с точки зрения отделимости2 вызвано
настоятельной необходимостью. Здесь мы будем иметь бесчисленное множества
очень интересных проблем, и среди этих проблем мы найдем проблемы
большой важности.
1 Это доказательство идентично доказательству существования двух
аналитических дополнений, неотделимых В; см. мою заметку: wSur un principe general de
la theorie des ensembles analytiques" (Compter Rendus, 2 сентября 1929 г.).
2 Мы обязаны Хаусдорфу введением общей идеи отделимости, такой
плодотворной в топологии и в теории множеств.
(Т)
АНАЛОГИИ МЕЖДУ МНОЖЕСТВАМИ. ИЗМЕРИМЫМИ В. И АНАЛИТ. МНОЖЕСТВАМИ 489
Идея, которая мной руководила, — это польза, казавшаяся мне
очевидной, различать среди множеств, какие из них являются очень
отдаленными друг от друга и какие являются очень близкими друг другу.
Мера отдаленности может быть дескриптивной, т. е. выраженной при
помощи некоторого трансфинитного числа.
Рассмотрим два какие-либо точечные множества Е и £ без общих
точек и отделимые В, Пусть Н—измеримое В множество, которое
содержит множество Е и не содержит ни одной точки множества £;
мы назовем множеством-отделителем это множество Н. Среди
множеств-отделителей Н имеются такие, класс которых наименьший. Пусть
а — этот класс.
Мы рассматриваем данные множества Е и £ как более близкие
друг к другу, если это число а велико1.
Предположим, что множества Е и £ измеримы В; пусть f — класс
Е и S — класс £. Мы скажем, что Е и £ удалены одно от другого,
если номер ос, таким образом определенный, строго меньше f и &.
В противоположность этому, если мы имеем a=-f или a = 8, множества
Е и £ будут называться асимптотическими по отношению друг к другу.
Множества Е и £ должны рассматриваться как наиболее удаленные
одно от другого в случае, когда а = 0. Таков, например, случай, когда
множества Е и £ просто расположены в различных порциях (а, Ь) и
(с, d) фундаментального пространства с7, не имеющих общих точек.
Закончив эти предварительные замечания, перенесем наше
внимание на элементы класса а. Мы знаем, что любые два элемента Е и £
класса а всегда ^отделимы (а). Это значит, что существует множество-
отделитель И либо класса <а, либо базы ВаУ которое содержит
элемент Е и которое не содержит ни одной точки элемента £. Это
приводит нас к введению следующего определения.
Мы скажем, что два произвольных элемента Е и £ класса а, не
имеющие общих точек, являются смежными по отношению друг к другу,
если, в случае когда а первого рода, a = a*-bl, не существует
множества-отделителя класса <Са*> а в случае когда а второго рода, не
существует множества-отделителя класса <Са-
Оказывается, что каков бы ни был элемент Е класса а, где а
произвольно, существует элемент £ класса а, не имеющий общих точек
с Е и смежный с £. Исключением является случай, когда дополнение
СЕ к элементу Е счетно.
Это предположение кажется, без сомнения, очень банальным, так
как можно рассуждать следующим образом: мы возьмем в порции (1, 2)
два абсолютно произвольных элемента Е' и £' класса а, не имеющих
общих точек. С другой стороны, разобьем порцию (0, 1) на два
дополнительные по отношению друг к другу множества е и у\ класса а*,
1 Можно также измерять „расстояние* между двумя произвольными множествами,,
рассматривая подкласс множества-отделителя //.
490
Н. Н. ЛУЗИН
если а = а*н-1, или базы Ва, если а второго рода. Суммы е + £' и
г\ -+- &' являются, очевидно, элементами класса а, смежными по
отношению .друг к другу.
Но элемент е-*-Е' класса а, таким образом определенный, не
является абсолютно произвольным элементом класса а, потому что он
содержит лишнюю часть е в порции (0, 1), имеющую класс, низший
чем а.
Предложение становится очень трудным в случае, когда
рассматривают элементы, называемые каноническими класса а, которые не имеют
ни одной лишней части1. Такие канонические элементы, не гомеоморф-
ные один другому, имеются в числе двух в классе 1, в числе двух
в классе 2. Не известно их число в классе 3. Проблема определения
числа канонических элементов, попарно не гомеоморфных, в каждом
классе Ка классификация Бэра—Валле-Пуссена является очень
значительной проблемой в современной теории функций2.
Другая проблема состоит в следующем: существует или нет
дополнение <£-элемента класса а, смежное к наперед заданному дополнению Е
элемента класса а. Мы доказали прежде, что в каждом классе Ка
имеется- пара (Е, £) дополнений элементов класса а, смежных по
отношению-друг к другую т. е. не имеющих общих точек и не отделимых (а).
Ставится вонрос, аоеможно ли брать произвольно дополнение Е.
После того как изложены принципы указанной теории измеримых В
множеств, мы вернемся к аналвгии между множествами, измеримыми В,
и аналитическими множествами, неизмеримыми В. Вот некоторые пары
двойственных предложений.
Существует плоский универ- Существует плоское
универсальный элемент класса а. сальное аналитическое множество.
Первый малый принцип. Первый принцип. Два ана-
Два элемента класса а, не имею- литические множества, не
имеющие общих точек, всегда отде- щие общих точек, всегда
отделимы (а). лимы В.
ъ Мы говорим, что элемент Е класса а имеет лишнюю часть, если существует
множество 6 класса (J, нязпъего чем а, такое, что общая часть в • Е была бы класса
7, промежуточного между а и {J, Э <Г "У <С а- По поводу этого определения я указывал
мою беседу с Б. Кнастером.
2 Л. Келдыш, которая рассматривала трудности этой важной проблемы,
сообщила мне, что, по ее мнению, в каждом классе Ка существует конечное число (и при
.©том ограниченное) канонических элементов, попарно не гомеоморфных, таких, что
каждое измеримое В множество класса а является суммой счетного числа
канонических элементов классов < а.
Эта идея выбора в каждом классе Кл конечного числа канонических элементов,
различных типов в смысле гомеоморфии, и представления каждого измеримого В
.множества асак-счетаой суммы, -элементов, выбранных типов представляет живой инте-
рее [50].
АНАЛОГИИ МЕЖДУ МНОЖЕСТВАМИ. ИЗМЕРИМЫМИ В. И АНАЛИТ. МНОЖЕСТВАМИ 491
Второй малый принцип.
Если Ех и Е2— два элемента
класса а, то множества Rx и /?2,
которые получаются удалением
из Ех и Е2 их общей части, всегда
«одновременно отделимы (Са).
Существует пара (£,, Е2)
дополнений к элементам класса а, не
имеющих общих точек и не
отделимых (а).
Второй принцип. Если Ех
и Е2— два аналитических
множества, то множества RY и R2,
которые получаются удалением
из Е} и Е2 их общей части, всегда
отделимы С А.
Существует пара (Е19 Е.2)
аналитических дополнений, не
имеющих общих точек и не
отделимых В.
Невозможно не удивляться аналогии, которую представляют
элементы класса а и аналитические множества, неизмеримые В, В обоих
.случаях мы имеем те же самые предложения. Мы приходим теперь
-естественно к рассмотрению аналитических множеств, неизмеримых В,
как элементов класса а, колоссально большого, так что нет никакой
«человеческой возможности ни записать это число а, ни определить его
лри помощи конечной системы обозначений или условий. Не забудем,
что символ 2, который имеют обыкновение писать идеалисты, в
действительности есть не что иное, как обозначение невозможности
перенумеровать при помощи натуральных чисел все трансфинитные числа,
предшествующие 2. А эта невозможность может быть либо
объективной, либо субъективной. Однако, каков бы ни был метафизический
интерес к проведению этого различия, практически это одно и то же,
потому чтЪ в обоих случаях получаются одни и те же цепи дедукций.
Так мы объясняем указанную аналогию.
Но имеется большее: в обоих случаях мы имеем не только
одинаковые формулировки, но и одинаковые доказательства. Это главный
пункт, практически очень важный, так как, для того чтобы расширить
наше знание об аналитических множествах, неизмеримых В, нам
достаточно углубить наши знания о множествах, измеримых В, и затем
преобразовать, следуя правилам двойственности, результаты, полученные
лая множеств, измеримых В, в предложения относительно более общих
аналитических множеств. С этой точки зрения каждому шагу в
изучении измеримых В множеств соответствует прогресс в наших знаниях
об аналитических множествах.
Дая примера мы рассмотрим первый и второй принцип теории
аналитических множеств, а чтобы выделить идеи, ограничимся
рассмотрением линейных аналитических множеств.
Прежде всего следует представить данное аналитическое
множество Е в форме элемента класса 2; мы будем предполагать, что Е рас-
лоложено на оси ОХ.
Дая этого достаточно взять в плоскости XOY решето С,
образованное счетным числом прямолинейных интервалов, параллельных оси ОХ.
492
Н. Н. ЛУЗИН
Известно1, что прямая х=х0, параллельная оси OY и проходящая
через точку х0 множества Е> пересекает решето С по счетному
множеству е , которое не является вполне упорядоченным, если мы
условимся, что порядок точек ех соответствует положительному
направлению оси OY. В противоположность этому, если х0 не принадлежит Ег
множество ех вполне упорядочено при тех же условиях и
соответствует вполне определенному конечному числу или трансфинитному
числу второго класса Кантора (^.
Обозначим теперь через Еа множество всех точек х0 оси ОХ, д\я
которых множество ех либо не является вполне упорядоченным
соответственно положительному направлению оси О Y, либо вполне упоря-
доченно и Рж ^а, Известно, что ЕаУ таким образом определенное,
измеримо В и что, если Е не измеримо В, то убывающая последовав
тельность
(/ = £0=)£1Z)£2Z)...D£(O=)...D£eZ)...^
существенно трансфинитна (несчетна). Это значит, что эта
последовательность продолжается трансфинитно без появления, начиная с
некоторого ранга 7» равенства Е^ = £т-ц = Ех+2 = ...
Известно, что данное аналитическое множество Е является общей
частью всех членов Еа рассматриваемой трансфинитной
последовательности.
Раз это так, то для получения первого принципа теории
аналитических множеств нам достаточно взять две предыдущие вертикальные
схемы, продолженные трансфинитно:
• \ :
Рис. 14.
н образовать два „знакопеременных" транс финитных ряда:
g . El-El. ^н-Sx. Ег-Ег. £2-ь. ..
и
<з7 • S\ — &t* Е1ч~Е1 • St — Ег • £2 -+-... .
1 Читатели, желающие больших технических сведений, могут обратиться к моему
мемуару „Об аналитических множествах* (см. стр. 380 настоящего тома.—Рел-) илл
к моим „Лекциям об аналитических множествах* (см. стр. 9 настоящего тома. —
Р*Д.).
АНАЛОГИИ МЕЖДУ МНОЖЕСТВАМИ. ИЗМЕРИМЫМИ В. И АНАЛИТ. МНОЖЕСТВАМИ 493
Доказано, что суммы Нх и Н2 этих двух рядов являются
множествами, измеримыми В.
Чтобы иметь второй принцип, нам достаточно образовать, как в
случае соответствующего малого принципа, два трансфинитных ряда с
„положительными" членами:
{<У'Е1 — Е1- Ях)-+-(«! • Е2 — Е, • £2) н- ...
я
{3 - Sl — <Sl - Ег) -+- (Ех • £2 — £2 • £2) н-... .
Доказано, что суммы Н{ и Н2 этих двух рядов являются
аналитическими дополнениями. Это завершает доказательство обоих принципов.
Получив эти трансфинитные доказательства, легко на следующем
этапе работы ликвидировать все следы трансфинитного и,
следовательно, дать строгое доказательство второго принципа, где трансфи-
яитное явно не вводится. Это доказательство будет опубликовано
в другой статье этого журнала1.
Мы дополним эти соображения следующим замечанием. Мы говорим,
что дая каждого наперед заданного элемента Е класса а существует
элемент <£ класса а, смежный с Е, за исключением случая, когда СЕ
счетно. Двойственное предложение является невозможным
предложением, потому что оно предполагает, что мы можем указать точку,
яе принадлежащую данному аналитическому множеству.
Но было бы очень интересно исследовать природу проблемы,
двойственной ранее поставленной проблеме относительно дополнений
элементов класса а.
Эта двойственная проблема:
если дано аналитическое дополнение Е, найти другое
аналитическое дополнение &у не имеющее общих точек с Е и не отделимое В
от Еу может иметь в области абстрактной логики вполне определенное
решение, потому что мы имеем здесь две отрицательные сущности Е и £>
отношения которых могут быть вполне определены в области
абстрактной логики.
1 См. „Лекции об аналитических множествах11 (стр. 9 настоящего тома. —
Ред.).
СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ
ФУНКЦИЙ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО*
Начиная с середины прошлого века, заботы математиков
направились к достижению абсолютной строгости в их работах. Эта тенденция
привела к ряду изысканий, объединяемых одним общим именем „теория
функций действительного переменного". Несмотря на то, что
образующие ее исследования крайне многочисленны и имеют в настоящее
время даже свой собственный орган, они группируются около
сравнительно небольшого числа идей. И сообразно этому теория функций
действительного переменного может быть разделена на три области:
метрическую, дескриптивную и топологическую. Ввиду того что
топология послужит предметом специальной статьи, мы коснемся в
настоящем обзоре лишь достижений, сделанных в последнее время первыми
двумя областями.
I
Успех интеграла Лебега (Н. Lebesgue), ставшего классическим
инструментом анализа, и все возрастающее число его применений
в самых разнообразных ветвях математики, естественно, вызвали
появление ряда работ, имеющих своею целью дальнейшие обобщения
понятия интеграла. Среди этих попыток выйти за границы
интегрирования в смысле Лебега наблюдается большое разнообразие в отношении
идей, так как самые различные свойства интеграла Лебега брались
как точки отправления путей обобщения. И следует заметить, что
многие из этих путей, не примыкая ни к какой общей и четко поставленной
проблеме, выдвинутой какой-либо теорией, отличной от теорий
интегрирования, являются, следуя выражению Лебега, не чем иным, как
„пустым удовольствием обобщать ради обобщения". Поэтому
естественно проследить вкратце ход идей, приведших в свое время к
открытию Лебега2, дабы, идя дальше по этому пути, встретить проблемы,
* Доклад, сделанный на I Всероссийском съезде математиков в Москве-
29 апреля 1927 г., дополненный автором для настоящего издания. Впервые
напечатано в Москве в 1933 г.
1 Для составления этой речи мы воспользовались содержанием курса Лебега»
читанного им в College de France в 1925/26 уч. году, о теориях интегрирования,,
та» же как его сообщением^ сделанным К^пенгагенекому математическому обществу:
„Sur le developpement de la notion dlntegrale" (Mathematisk Tidsskrift, 1926).
СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ ФУНКЦИЙ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО 495
Требующие уже не искусственных дальнейших расширений * понятия
интеграла.
Идеи К о ш и (Cauchy). До Коши не имелось никакого „определения"
в современном смысле понятия интеграла: делались лишь простые
указания на то, что необходимо складывать или вычитать площади, дабы
получить интеграл
\f(x)dx.
II
Следовательно, в этом круге идей отправлялись от концепции площади
как интуитивно непосредственной и самоценной.
Коши первый вышел из этого круга идей: он первый заявил о
необходимости определения интеграла, отправляясь прямо от понятия
величины и числа и не прибегая к геометрическим интуитивным данностям.
Это же самое он требовал и от других понятий, усвоенных математикой,
начиная с эпохи Возрождения. В сущности, с Коши начинаются заботы
о строгости, столь характерные для современной науки. Шаг,
сделанный Коши, имеет такую философскую важность, что не будет
излишним здесь несколько задержаться.
Часто заявляется, что Декарт свел геометрию на алгебру; но это,
собственно, несколько неточно. То, что осуществил Декарт, — это
сведение при помощи метода координат всякой геометрии к геометрии
прямой линии, каковая, употребляя понятие непрерывности и
иррационального числа, дозволила алгебре достигнуть широкого ее
применения. Но чтобы эта редукция всяких геометрий к прямой была
окончена, необходимо было исключить известное число самых основных
для геометрии величин, среди которых важнейшими являлись длина
кривой, площадь, объем. Это, собственно, и было сделано Коши. После
Коши было достаточно лишь построить линейный континуум при помощи
целого числа, чтобы арифметизация науки была закончена.
Эта арифметизация математики, на которой так настаивает
современная наука, является научным течением неоспоримой ценности,
связанным с глубочайшим философским вопросом: может ли быть
сведенным всякое математическое познание к целому числу? Не пытаясь
в данный момент вынести определенный и решающий приговор по этому
делу ни путем утверждения, что всякий математический факт есть
просто' отображение соответствующего свойства целых чисел и может
быть выраженным исключительно в терминах арифметики, ни путем
указания на наличие не сводимых на арифметику математических
фактов, о котором говорит нарождающееся в последнее время течение
„деарифметизации анализа", мы удовольствуемся лишь указанием на
то, что концепция интуитивного или экспериментального характера
обычно всегда имеет действительный интерес, даже в том случае,,
если она не очень хорошо поддается логическому определению, и что-
496
Н. Н. ЛУЗИН
обычно имеет большую важность ее всестороннее изучение, и что,
напротив, огромное большинство чисто логических сущностей и понятий,
встреченных на путях логического порядка, обычно бесплодны и не
могут оказать никакого влияния на прогресс науки. Именно в полной
мере является справедливым то давно уже сделанное замечание, что
на логических путях исследования как раз не встречают тех понятий,
которые наиболее ценны, и если бы мы ограничились лишь
исследованиями строго логического характера, мы никогда бы их не имели.
Возвращаясь к определению интеграла, данному Коши, следует
заметить, что оно имелось в виду его автором лишь д\я непрерывных
функций: после определения непрерывной функции, сделанного Коши
так, как сейчас это делает современный анализ, интеграл
L
\f{x)dx
а
от непрерывной функции f(x) определяется как предел сумм S:
s=2/ex*«-i-*«).
Суммы этого рода давно до Коши употреблялись землемерами и
математиками для оценки (приближенной) площадей. Новое, что сделал
Коши, это было доказательство существования предела сумм S и
вытекшая отсюда возможность логического определения интуитивного
понятия площади.
Уточнения Римана и Дарбу. Определение Коши оказалось
приложимым к некоторым разрывным функциям. Отсюда естественно
родилась мысль Римана об отыскании полной границы приложимости
определения Коши.
Обозначим через /» и /< верхнюю и нижнюю границы функции f(x)
на интервале (xi9 x»+l). Тогда сумма Коши S заключена между
s= 2/, fo+1—х{) и s= 2л (*<+i—х{).
Риман показал, что достаточно, чтобы разность *S—S стремилась
к нулю для одного частного способа деления интервала (а, Ь) на все
•более и более мелкие интервалы (xiy xi+l), чтобы определение Коши
оказалось приложимым. Дарбу доказал, что суммы S и S при всякой
функции f(x) стремятся к определенным пределам, совпадающим, когда
интеграл Коши—Римана существует.
Критика определения Коши. Каким бы логически
безупречным ни было определение интеграла Коши—Римана, можно с
уверенностью сказать, что для разрывных функций оно фактически не
служит ни к чему. Действительно, лая интегрируемости f(x) нужно
установить стремление разности
3-5=2(7«-/«) (*«.,-*«)
СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО 497
к нулю. Это стремление разности S—S к нулю теоретически еще
ясно для непрерывной функции /(л:), потому что достаточно разбить
(ау Ь) на столь малые интервалы (xiy xi+l)y дабы все разности /,.— fi
оказались малыми, как вся разность *S—S сама в свою очередь станет
малой. Но для случая разрывной f{x) мелкость разбиения (а, Ь) уже
не служит ни к чему, потому что в этом случае разности fi —fi вообще
весьма велики и не стремятся к нулю с уменьшением (xiy *Vh). Для
разрывной функции f(x) соседство лг> и jci+l еще не означает
близости f(Xi) и /(л^и). Напротив, соседними /(*») и f(xj) могут
оказаться величины функции /(х) для весьма удаленных друг от друга
х{ и Xj. В соответствии с этим в сумме Коши
близкими друг к другу по величине оказываются вовсе не те
слагаемые, которые имеют соседние нумера, а те, которые имеют близкие
друг к другу множители /(;,) и /(;}), т. е. величины функции f(x)
в точках, выбранных в далеких вообще друг от друга делениях (xiy дгт)
И (Xjf *;+,).
Это обстоятельство навело Лебега на мысль о перегруппировке
слагаемых в сумме Коши S для наиболее компактной оценки ее
величины, подобхЮ тому как, прежде чем оперировать с каким-нибудь
многочленом, имеющим очень большое число членов, является
целесообразным сначала выполнить приведение подобных членов. Сумма Коши 5
для разрывной функции f(x) похожа на многочлен с беспорядочно или
случайно выписанными членами, где соседство членов в строчке никак
не связано с соседством их степени.
Идеи Лебега. Дабы проследить генезис идей Лебега,
рассмотрим эффект перегруппировки членов в сумме Коши дая непрерывной
функции; более того, рассмотрим сперва самый простой из всех
случай— тот, когда f(x) непрерывна и имеет только конечное число maxima
и minima. Имея в виду соседство величин членов суммы S, т. е.
близость значений функции /(*), мы разбиваем интервал на оси Y>
содержащий все значения функции f{x), принимаемые ею на (а, Ь), на малые
части (yiy yi+x)- Всякому такому малому интервалу (yiy yi+i) отвечает
на оси X определенное множество точек Е{— тех, в которых значения
функции / попадают в (yiy yi+l). В силу того, что maxima и minima
функции f(x) имеются лишь в конечном числе, множество Е{ есть
конечное число интервалов (на чертеже — четыре). Если мы теперь
сгруппируем вместе все те члены суммы Коши Sy интервалы которых
образуют множество Eiy то их общая сумма ничтожно мало отличается
от величины т\%- X длина Eiy где т\{ есть какая-либо величина, взятая
в интервале (yiy yi+A)y а длина Е{ есть сумма длин всех интервалов,
498
Н. Н. ЛУЗИН
образующих множество £,; мы, следовательно, уже просуммировали
указанную группу членов суммы Коши S.
После этих замечаний ясно, что сумма Коши S после
перегруппировок и суммирований каждой группы напишется в виде
S' = 2 Ъ > длина Е{.
Эта сумма носит имя суммы Лебега. Ясно, что предел суммы S'
Лебега есть тот же самый, что и предел суммы Коши, т. е. это есть
интеграл
\f(x)dx.
Рис. IS.
Это обстоятельство, т. е. совпадение предела суммы S' с пределом
суммы Коши 5, кажется сначала обескураживающим, так как,
естественно, спрашивают себя, зачем
производить перегруппировку членов в
сумме Коши S с тем только, чтобы
придти снова к тому же самому
результату? На самом деле это не так:
сумма Лебега S' обладает столь
большой гибкостью по отношению даже
к разрывным функциям, какую нельзя
было и представить дая сумм Коши.
Это делается понятным, если
заметить, что сумма Лебега »У совпадает с суммой Коши S лишь
для таких непрерывных функций /(дг), у которых* имеется только
конечное число maxima и minima. Д\я общего же случая непрерывной
функции f(x) не только нет такого совпадения, но даже самое понятие
суммы Лебега S' становится на первых порах не имеющим никакого
математического смысла, так как ведь не известно тогда, что
понимать под „длиной Et*\ особенно когда Е( есть очень сложное
множество. И то обстоятельство, что для того, чтобы интегрировать методом
Лебега произвольную непрерывную функцию, сначала пришлось
преодолеть эту трудность, т. е. научиться отыскивать „длину" сложных
множеств,—это обстоятельство оказалось целиком в пользу нового
метода, потому что по приобретении умения отыскивать „длины"
множеств стали тем же самым приемом Лебега (т. е. переходом к пределу
суммой S') доступными для интегрирования не только непрерывные
функции, но и такие разрывные, о способности которых подвергнуться
„интегрированию" невозможно было раньше и думать.
Известно, как это произошло исторически, Сначала Э. Борель
указал, исходя из геометрических соображений, на „естественность"
приписывания некоторой положительной „протяженности" или „меры" даже
таким множествам, которые не содержат никаких отрезков, и указал
СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО 499
процесс получения этой „Протяженности" множества, исходя из той
манеры, которой нам дано это множество. Впоследствии эти множества
точек, для которых приложим процесс Э. Бореля, получили название
„множеств, измеримых В". А затем сам Лебег дал новое определение
„меры" множества, столь логически совершенное и тонкое, что, несмотря
на все усилия, мы до сих пор еще не имеем неизмеримых в смысле
Лебега множеств. В соответствии с этим всякая ограниченная
функция f(x) фактически оказывается интегрируемой в смысле Лебега.
Таким образом, окончательно интеграл Лебега явился определенным
как предел суммы Лебега S':
S = 2d гч * mes En
где mes E{ обозначает меру множества Ev
Неделимые. Геометры XVII в. рассматривали интеграл не как
предел суммы, а как самое сумму „элементов" площади, за которые
принимали просто ординаты кривой. Короче, говоря языком Кавельери,
интеграл для них был просто суммой неделимых.
Мы видим, что эти неделимые подсчитываются в сумме Коши S
в том порядке, который обусловливается их следованием по оси X в
вовсе независимо от их природы и величины. В методе же Лебега
подсчет неделимых совершается по группам, соединяя в одну группу те
неделимые, величина которых одна и та же. В методе Коши, говорит
Лебег, „...оперируют так, как это делает коммерсант сильно
неопытный, который подсчитывает монеты и кредитные билеты,
предоставляя все случаю, т. е. сообразно тому, как они попадают под руку;
тогда как мы оперируем, как уже опытный и методический коммерсант,
говорящий:
у меня mes£l монет по 1 франку, стоящих 1 Xmes^;
у меня mes Е2 монет по 2 франка, стоящих 2 X mes E2;
у меня mes2T3 билетов по 5 франков, стоящих 5 X mesi^
итого: у меня 1 Xmes£1 + 2Xmes£2-b5 X mes^-h... франков.
Конечно, тот и другой коммерсант придут к одному и тому же
результату, как бы велико ни было состояние, которое они подсчитывают,
ибо число франков конечно. Но в случае суммк неделимых, число
которых бесконечно, разница двух манер подсчитывать капитальна".
Первые расширения интеграла Лебега. Эти
расширения относятся прежде всего к возможности определить кратный
интеграл Лебега. Формула остается та же самая:
[("/(*•> y)dxdy = lim^f)i • mesEt,
х, у^ z) dx dy dz = lim 2 Ъ " mes E*
и т. д., только тгод mes£< надо понимать уже меру плоского или
трехмерного множества.
/<
500 и. н. лу зин
Затем дальнейшим расширением явилась возможность
интегрировать функцию не по отрезку, а по множеству, т. е. иметь
\f(x)dx.
Формула, определяющая этот символ, остается еще та же самая, только
здесь Е{ есть всегда часть множества Еу по которому интегрируют.
С другой стороны, определение Лебегом „меры44 плоского множества
позволило возвратиться к концепции интеграла эпохи до Коши, но уже
пользуясь точными определениями в современном смысле. Именно,
обладая функцией у = /С*)» мы можем определить интеграл
h
\f{x)dx
а
по формуле
ь
I f(x) dx = mes Ep — mes ЕП9
а
где Ер есть совокупность точек плоскости, образованная
положительными ординатами у, а Еп — отрицательными.
Это определение интеграла, каким бы наивным оно ни казалось,
влечет новое важное расширение интеграла, именно интегрирование
неограниченных функций /(л:).
Действительно, наличие определенной конечной „меры" у плоского
множества Е вовсе не требует непременной его ограниченности.
Отсюда, считая Ер и Еи неограниченными множествами, но
имеющими конечную плоскую меру, мы умеем интегрировать некоторый класс
неограниченных функций /(х). Лебег назвал их суммируемыми
функциями.
Впрочем, интеграл от суммируемой функции f(x) может быть
определен опять по формуле Лебега как предел сумм Лебега S':
•У = 2 Ъ • mes Ei9
в которой только знак суммы Е надо понимать в смысле абсолютно
сходящегося ряда, происходящего от разбиения всей оси Y на малые
интервалы (у,-, у,-н)« Отсюда получаются аналитические необходимые и
достаточные условия дая суммируемости функций /(*).
Дальнейшее расширение интеграла Лебега было предпринято
молодым французским ученым, убитым на войне, Гато (R. Gateaux)1, впер-
1 R. Gateaux. Bull, de la Societe Math, de France, 1919; P. Levy. Lemons
d'analyse fonctioneile, 1922; N. Wiener. Proc. of the London Math. Soc, 1922;
M. Frccbet. Bull, de la Societe Math, de France, 1915; T. Daniell. Ann. of
Math., 1918, 1919.
СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО $01
вые определившим интеграл функции бесконечного числа переменных.
Эти изыскания, продолженные П. Леви (Levy) и Норбером Винером
(Norbert Wiener), стоят в связи с аксиоматическими попытками Фреше
(Frechet) и Даниэля (Daniell), расширяющими на абстрактные множества
указанные выше определения.
Но, чтобы указать самое ценное и самое естественное направление
работ по теории интегрирования после Лебега, нам необходимы
рассмотрения иного уже рода.
Неопределенный интеграл Лебега как функция
области. Обычно называют неопределенными интегралами функции ^(л*),
F(x, y)y ..., даваемые формулами:
X
F(x) = C + \f{x)dx;
а
* У
Fix, y) = Cl(x) + C2(y) + \\f(x, y)dxdy...
ар
Нужно, однако, отметить, что это наименование создалось лишь на
почве неправильного употребления речи. Притом первоначальный смысл
термина „неопределенный интеграл" был совсем иной и к тому же
совершенно естественный. Первоначально называли „определенным
интегралом" и „неопределенным интегралом" одно и то же самое
выражение
ь
\/(x)dx,
а
смотря по тому, очень ли было важным считать интервал (а, Ь)
фиксированным или он должен быть, напротив, произвольным.
Мы хотим возвратиться к этому первоначальному смыслу слов.
Д\я этого, отметив, что между понятиями „неопределенного интеграла"
и „определенного интеграла" такое же взаимоотношение, как между
функцией и ее частным значением аля фиксированного значения
аргумента, мы назовем неопределенным интегралом от /(х) выражение
jf(x)dx,
где Е есть некоторое множество, измеримое1 и притом произвольное,
на которое распространен интеграл Лебега. Следовательно,
„неопределенный интеграл" есть просто функция области ф(£), которая
заставляет отвечать всякому множеству Е число ф(Я).
1 Мы повторяем, что до сих пор не известно хотя бы одно неизмеримое
жество; не известно, следовательно, имеются ли такие множества.
502 н. н. лузин
Сказанное немедленно расширяется на понятие кратного
неопределенного интеграла: это есть опять просто функция ty(E) области Е, по
которой интегрируют в пространстве двух, трех, ... измерений:
<!»(£) = J [/(*, y)dxdy,
b(E) = \\\f(x,y,z)dxdydz, ...
Чтобы иметь единообразный язык и единообразие обозначения, не
связанного с числом измерений, мы вместо многих предыдущих формул
пишем общую формулу
*(£) = ]/(P)rfmes(*)f
употребив символ /(Р) для понятия функции точки.
Данное определение отнюдь не является только вопросом слов,
потому что здесь пред нами уже новая концепция: движимые ею, мы,
естественно, спрашиваем себя, всякая ли функция области есть
неопределенный интеграл и какова связь ф с /?
Ответом на первый вопрос служат два необходимых и достаточных
свойства функции ty(E): полная аддитивность и абсолютная
непрерывность *.
Ответом же на второй вопрос является формула
нш Щ =/(Р),
А-^0 mes A
где А есть, в зависимости от кратности интеграла, определяющего ^ (Д),
или отрезок, или круг, или сфера, имеющие своим центром точку Р.
Это равенство имеет силу почти всюду, т. е. всюду, кроме
исключительного множества точек Р меры нуль.
Это равенство обобщает ту классическую теорему, в силу которой
неопределенный интеграл от непрерывной функции есть ее примитивная.
Функция области и реальность. Новая концепция функции
области, восходящая, правда, еще к Коши, имеет основное значение
дая натурфилософии. В частности, Коши был хорошо известен только
что описанный способ дифференцирования функции области.
1 Термины Ш. де ла Валле-Пуссена (СЬ. ds la Vallee-Pou>sin) и Д». Витали
(G. Vitali): функция области ^ (Е) есть вполне аддитивная, если любое разбиение
области Е на конечное или счетное число неперекрываю дихся областей Е\% Е%% . . •
дает место равенству
Ф 15) = Ф (*i) ■+-♦ №2) ■+-+ (^ -н . . . ;
функция области ty(E) есть абсолютно непрерывная, если lim ^ \Е) = 0 всякий раз,
как lim mes E = 0.
СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО 503
Коши назвал „сосуществующими" величины, определенные в одно и
то же самое время, т. е. в равных условиях. Если, например, мы имеем
какую-нибудь неоднородную материальную среду и обозначим через D
<ее часть, то: объем V(D) этой части материи, ее масса М(D) и
количество тепла Q(D), необходимое аая поднятия температуры части D
на 1°, предполагая ее изолированной, суть функции области.
Отнюдь не случайно выдвинулась в последнее время в науке
концепция функции области. Например, нужно удивляться, что она заставила
себя так долго ждать. Следует, в самом деле, заметить, что всякая
физическая величина всегда дается непосредственным образом как
функция области и оттого не как функция точки. И притом, это полностью
относится не только к телам, доступным нашим органам чувств, но и
к телам чисто математической концепции, когда в рассматриваемую
величину привходят непг ,редственные данные (каковы: время,
температура etc.)*
Что же касается <рУнкЦи^ точки, то введение их в рассмотрение
всегда происходит отнюдь не непосредственным образом, а путем
предельного процесса: эти функции суть или производные, или, более
обще, пределы отношения двух сосуществующих величин. Так, например,
1. масса |. кол. теплоты
плотность = lim — ; удельная теплота = lim .
объем - J масса
Таковы же суть функции точки: скорость, давление и т. д.
Итак, геометрия и физика заинтересованы в самостоятельном
развитии теории функций областей таким же точно образом, как анализ
заинтересован теорией функций действительного переменного; причем
в физике функции области даются первоначально и лишь идеальным
предельным процессом вводятся функции точки. Казалось бы поэтому,
-что теория функций области должна иметь в геометрии, механике и
физике преобладающую роль. На самом же деле не только нет, но,
напротив, даже там, где введение в рассмотрение функции области
фактически почти уже осуществилось,— там всегда замечается
сильнейшая тенденция к исключению этой концепции и к замене ее
обыкновенным понятием функции точки, что достигается тем, что берут области
частичного вида—параллелепипеды, ориентированные по осям,— и этим
самым ограничиваются рассмотрением функций от параметров, хотя эта
замена не всегда удовлетворительна для простоты дела.
Причина этому лежит, без сомнения, в совершенной неизученности
математиками функций области и в полном отсутствии самых основных
обозначений д\я них и, следовательно, необходимой алгебры. Дая того
чтобы оценить важность этого замечания Лебега, достаточно указать на
то обстоятельство, что хотя формула
<b(£) = j/(P)c/mes(e)
Е
504 и н. лузин
и дает алгебраическое обозначение для функции области •) (£), однако эта
функция области, будучи неопределенным интегралом, должна обладать
специальными свойствами. Большинство же функций области,
рассматриваемых физикой, не обладают этими специальными свойствами и,
значит, не будучи неопределенными интегралами Лебега, не подпадают
уже под указанное алгебраическое обозначение.
Интеграл Радона (Radon). Предшествующие рассмотрения,
естественно, привели нас к новой, чрезвычайно широкой и важной
концепции интеграла, полностью развитой Радоном в 1913 г. Правда,
эта концепция была известна уже в 1894 г. Стильтьесу (Stiltjes),
употребившему ее в его исследованиях по анализу и арифметике; хотя,
таким образом, Стильтьес может быть рассматриваем как первый
изобретатель этого расширения интеграла, однако арифметическая форма
его изложения замаскировала его физическое значение и, следовательно>
его естественный генезис. Много поэтому было употреблено усилий
различными авторами для того, чтобы понять то, что теперь столь
очевидно.
История этих усилий связана с именами Риса (F. Riesz), Лебега,
Юнга (W. Н. Joung), Фреше, Валле-Пуссена (Ch. de la Vallee-Poussin)L
и обнаруживает соперничество в остроумии, проницательности и также
то, что в конце концов движение идей происходило вслепую.
В указанном ходе идей интеграл Радона появляется одновременно
со следующими вопросами, к которым мы теперь пришли.
Если дифференцирование такое, какое мы выше описали, возможно
относительно меры области, то нет ли более широкой идеи
дифференцирования по отношению ко всякой другой сосуществующей функции
области? Какой алгорифм явится обратным к этому релятивному
дифференцированию? Нет ли возможности заменить функцию области mes (е)
в определении интеграла Лебега какой-либо другой функцией области
и, следовательно, говорить уже об интеграле, дающемся символом
\f(P)d<?(e).
Е
Утвердительный ответ на первый вопрос непосредственно ясен. Что же
касается третьего вопроса, то а^я ответа на него приходится ввести
новую идею — измеримости множества Е по отношению к данной
функции области ф (е), затем потребовать измеримости предложенной к
интегрированию функции f(P) относительно функции области <р (е) и, наконец,
сходимости ряда S' = 2 Нч? (£»)• В этом случае, когда все это выполнено
1 J. R a d о п. Sitz. d. Kais. Ak. d. Wiss. in Wien, 122, 1913; T. J.: S t i 11 j e s. Ann. de
la Faculte de Sci. de Toulouse, 1894; F. Riesz. Comptes Rendus, 1909; H. Lebesgue.
Idem., 1910; W. H. Joung. Proc. of the L. M. S., 1913; M. Frechet. Nouv. Ann.
des Math., 1909; Qhr de la Vallee-Poussin. Integrate, fonctions, classes de
Baire.
СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО $05
и когда на функцию области 'f (е) наложено условие быть с
ограниченным изменением 1, определение релятивного интеграла Радона от
функции точки f(P) относительно функции области з (е) делается в точности
так же, как и определение интеграла Лебега: это есть по-прежнему
предел суммы S. Таким образом, определяется интеграл Радона
\f(P)dr(e).
К
Введение интеграла Радона естественно потому, что физики никогда,
в сущности, и не рассматривали иного интегрирования, кроме
интегрирования относительно функций области.
Например, если хотят вычислить количество теплоты ср (D),
необходимой для поднятия на 1° температуры тела Z), надо разделить D на
малые тела Dlf D2> ..., имеющие массами М(Д), М(Д>), ..., взять
в каждом из них по точке Р1У Р2, ... и написать приближенную сумму
f(P1)M{Dl)^/(P,)M(D2)-t-...,
где /(Р) есть удельная /теплота материи в точке Р. Значит, имеем
вычислить интеграл Радона
<?(D) = \f(P)dM(e).
2)
Сами математики, в сущности, никогда не переставали
рассматривать интегралы Радона: криволинейный интеграл \f(xfy)dx есть инте-
с
грал Радона относительно функции 9 (*)> определенной как длина
проекции на ось ОХ дуги кривой С. То же самое следует сказать об
интегралах поверхности. То обстоятельство, что имеют чаще всего дело
не с одиночным интегралом, а с суммой вида
J/(x, y)dx-+-g{x, y)dyy
о
только показывает, что имеют дело с еще более общей концепцией:
интегрированием относительно нескольких функций областей. Несмотря
на частные результаты Геллингера (Hellinger) и Теплица (Toeplitz)2,
общее изучение еще не начато.
1 Функция области <? (е) есть функция с ограниченным изменением, если при
любом способе разбиения Е на счетное множество неперекрывающихся частей £lt
Еъ . . . ряд ^ | <р (Ei) I сходится.
Заметим, что в силу данного выше определения всякая вполне аддитивная
функция есть тем самым функция с ограниченным изменением. Систематических
попыток освободиться в интеграле Радона от ограниченности изменения функции
области ^> (е) до сих пор не производилось.
* Journ. de Crelle, 144.
S06
Н. Н. ЛУЗИН
Нерешенные проблемы. Изучение интеграла Радона не только
еще не выполнено, но здесь не разрешены и даже не поставлены самые
основные задачи. Первая среди них — та, которая спрашивает, каким
образом по данной функции точки /(Р), являющейся производной
относительно известной функции области ср(е) от некоторой примитивной
функции области Ь(Е)У отыскать эту примитивную?
Не известно, каким образом решается это проблема» По-видимому,
интеграл Стильтьеса совершенно недостаточен. В самом деле, идеи
Стильтьеса относятся лишь к функциям с ограниченным изменением,
а определение релятивной производной вовсе не предполагает такого
ограничения.
Не известен также произвол в определении примитивной; не известно,
каким образом должна быть поставлена общая задача о разыскании
примитивной, дабы быть вполне определенной.
Идеи Данжуа (A. Denjoy). Возвратимся от этих общих
рассмотрений к обращению задачи дифференцирования: зная, что /(х) есть
точная производная, найти ее примитивную F(x).
Если данная производная f(x) конечна в каждой точке, произвол
примитивных F(x) не очень велик: все они отличаются друг от друга
на некоторую постоянную величину. Таким образом, требование, чтобы
кривая у=/{х) прошла через начало координат, т. е. чтобы имели
0=/г(0), вполне определяет примитивную F(x). Отсюда совершенно
уместен вопрос, каким образом получить эту единственную примитивную
прямо через величины функции /(л:), т. е. через ординаты кривой
Известно, что А. Данжуа указал некоторый правильный процесс
для этой цели, манипулируя которым, приходят через счетное число
шагов к знанию примитивной у=/(х); процесс этот назван им тота-
лизацией» Тотализация есть предельный процесс, в состав которого
входят интегрирования в смысле Лебега, располагаемые уже в
трансфинитном порядке. Процессу тотализации подпадает всякая точная
производная /(х), конечная для всякого х. Но имеется бесчисленное
множество функций, совершенно не тотализируемых. Интересно отметить,
как это выяснено недавними работами в Москве, среди нетотализи-
руемых функций имеются и точные производные, бесконечные в
некоторых точках (множество которых имеет всегда меру нуль). Если
заметить,, что интеграл Лебега дает всегда примитивную, когда данная
точная производная /(х) везде конечна и интегрируема в смысле Лебега,
процесс тотализации А. Данжуа является подлинным расширением
интегрирования Лебега.
Успех полного решения обращения задачи дифференцирования
внушил А. Данжуа рассмотреть еще другую задачу: определить
коэффициенты тригонометрического ряда по его сумме.
Известно, в самом деле, что два тригонометрических ряда, имеющих
для всякого х одну и ту же самую конечную сумму, являются тожде-
СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ ФУНКЦИЙ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО $07
ственными (Кантор). Отсюда знание суммы тригонометрического ряда
должно каким-то образом определять его коэффициенты. Данжуа
поставил себе задачей открытие процесса, определяющего коэффициенты
через сумму. Так как сумма S(x) тригонометрического ряда
00
S(x) = -£• '*' ^. ап cos пх ч- Ьп sin пх>
сходящегося везде к конечному числу S(x)f есть вообще нетотализи-
руемая функция, то ясно, что процесс, определяющий коэффициенты
[и, прибавим, совпадающий с тотализацией, когда S(x) тотализируема],
должен быть рассматриваемым как еще более общий, чем тотализация
А. Данжуа. Этот процесс, открытый А. Данжуа в 1921 г.1, назван
автором тотализацией с двумя индексами, потому что он позволяет
непосредственно переходить от данной суммы S(x) сходящегося всюду
тригонометрического ряда
CD
S(x) = -у- -+- ^ ап cos пх -+- Ьп sin пх (I)
t«=i
к сумме S.>(x) такого тригонометрического ряда, который получают,
интегрируя формальным образом почленно дважды тригонометрический
ряд (I):
^^x)=^^c1x^c0-f;fl"co,iMr^ri,i"> (id
в котором есть две произвольные постоянные и в котором
тригонометрический ряд есть заведомо абсолютно сходящийся, так как ап и Ьп
стремятся к нулю в силу того условия, что S(x) есть сумма
сходящегося всюду тригонометрического ряда (Кантор—Лебег).
Прогресс, внесенный Данжуа, состоит в том, что им указан
процесс, позволяющий непосредственно подняться от S(x) к функции iS2(x),
минуя всякие тригонометрические ряды. И так как S2(x) есть функция
с ограниченным изменением (a variation Ьогпёе), то разложение ее в ряд
формы (И) хорошо известно, так что коэффициенты —§• и -^f-
определены, а значит, определены и самые коэффициенты ап и Ьп.
Благодаря личной любезности А. Данжуа я имею возможность
сообщить, что в самое недавнее время им найден процесс, позволяющий
непосредственно переходить от данной функции S{x)y являющейся суммой
сходящегося всюду тригонометрического ряда, к функции ^(л:),
долженствующей быть суммой того тригонометрического ряда
О / \ П . °0Х __._ V1 An SJTl ПХ — Ьп COS ПХ /тттч
У Comptes Rendus, 172, 1921,
508
Н Н. ЛУЗИН
который получается формальным интегрированием почленно
тригонометрического ряда (I). В силу того что lim an = lim bn = 0y когда п
стремится к бесконечности, ряд (III) сходится почти всюду [Фату (Fatou)]
и определяет функцию Sx (x) с интегрируемым квадратом. Разложение
найденной функции St (х) в ряд (III) хорошо известно, раз S1 (x) имеет
интегрируемый квадрат. Отсюда прежняя возможность иметь
коэффициенты аи и Ь„.
Этот процесс перехода от S(x) к Sx (x) назван А. Данжуа тотали-
зацией с одним индексом. Тот факт, что функция Sx (x), получаемая
процессом тотализации с одним индексом, есть вообще функция
разрывная от ху этот важный факт, по словам автора, как будто бы
указывает на то неожиданное обстоятельство, что „всякая общая теория
интегрирования, преследующая не кажущуюся гладкость и
подражательное сходство с прежним, но имеющая в виду истинный прогресс в решении
очень точно поставленных и естественным образом выдвинутых проблем,,
необходимо должна нас приучать к мысли, что неопределенный интеграл
есть вообще всюду разрывная функция своего верхнего
предела".
К этим идеям А. Данжуа, естественно, присоединяются работы
польских и наших московских математиков о единственности
изображения функций тригонометрическими рядами.
Исходная точка идей А. Данжуа — это полная определимость
коэффициентов тригонометрического ряда через его сумму. Но для этого
приходится отправляться от тригонометрических рядов, сходящихся
всюду, и, значит, от функций S(x), служащих суммой
тригонометрического ряда в каждой точке х, так как в основе всего лежит та теорема
Кантора, что нет двух различных тригонометрических рядов,, сходящихся
в каждой точке к одной и той же самой функции S(x). Но это
требование представляет значительные неудобства, так как в теории
интегрирования Лебега, например, всегда пренебрегают множествами меры
нуль, что значительно развязывает руки при исследовании многих
частных вопросов. Однако дальнейшие исследования обнаружили, что лежащая
в основе теорема Кантора лишь с чрезвычайным трудом поддается:
расширению и притом неполному.
Если, с одной стороны, работы Юнга и Валле-Пуссена показали,
что всегда можно пренебрегать множеством точек х счетной мощности,
то работа Д. Е. Меньшова, наоборот, обнаружила, что имеется
тригонометрический ряд, сходящийся к нулю вне некоторого определенного
совершенного множества Р меры нуль и имеющий коэффициенты не^
все нули. Этот удивительный результат Д. Е. Меньшова приобретает
тем большую остроту, что множество точек, где тригонометрический
ряд, рассматриваемый произвольно, не сходится к нулю, есть непременно?
множество, измеримое 5, и как таковое, в силу теоремы Александрова—
Хаусдорфа, есть либо счетное множество, либо содержит совершенна
множество меры нуль.
СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ ФУНКЦИЙ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО 509
Вместе с тем в последнее время обнаружен и диаметрально
противоположный факт, неожиданным образом разрушающий гармонию в наших
представлениях о серьезности явлений в тригонометрических рядах:
одновременные и независимо проведенные в Варшаве и в Москве работы
доказали, что некоторыми совершенными множествами меры нуль
невозможно пренебрегать таким же точно образом, как в теории Лебега
пренебрегают всяким множеством меры нуль.
Отсюда, естественно, возникает проблема о точном распознании тех
-множеств, которыми еще возможно пренебрегать.
Эта теория представляет еще до сих пор чрезвычайные трудности
лаже в отношении качественном: мне лично думается, что при
определении необходимых и достаточных признаков множеств, которыми можно
лренебрегать, доминирующую роль играют диофантовы законы [51].
Но Райхман недавно сообщил мне, что его предчувствия иные и что,
ло его мнению, все дело решится не диофантовым анализом, а в
обычных теоретико-функциональных понятиях и терминах.
Как бы то ни было, процессы тотализации Данжуа со временем должны
будут учесть возможность пренебрежения некоторыми множествами
мощности континуума.
II
Квазианалитические и почти периодические функции.
Недостаток места не позволяет мне коснуться другого важного процесса
метрической теории функций действительного переменного — открытия
■и изучения двух больших и чрезвычайно важных классов функций:
квазианалитических и почти периодических, так тесно связанных с
именами их первых авторов и исследователей — Сергея Натановича Берн-
штейна и Бора.
Следует, впрочем, сказать, что эти функции, открывая
неограниченную перспективу самых разнообразных приложений основной важности
к различным ветвям естествознания, лежат, в сущности, на границе
уже самого классического анализа, так как изучение их выполняется
теми самыми тотальными приемами, которые так характерны лая
классического анализа и которые отличаются от тех по преимуществу
микроскопических методов, которые употребляет теория функций
действительного переменного.
III
Дескриптивная теория функций. Нам осталось рассмотреть
наиболее деликатный пункт теории функций действительного
переменного — успехи ее дескриптивной части. Уже с первых же шагов мы
должны оговориться: слово „успех" имело очень ясный смысл по
отношению к метрической ветви теории функций, обозначая в ней, как,
впрочем, и во всякой другой ветви математики, установление новых
фактов и таких сближений и аналогий, которые не сразу бросаются
510
Я. й. лузйН
в глаза, но которые обнаруживаются пытливой мыслью за сменой
явлений и течением вещей. В этом отношении слово „успех" для
дескриптивной ветви теории функций имеет совсем особый смысл, так как
трудно, на самом деле, дать имя успеха такой деятельности, которая
сводится к разрушению установленных ранее фактов, путем ли
заявления об ошибочности их или путем до такой степени последовательного
отрицания какого-либо смысла за ними, что необходимо встает вбпроб
о ненужности целой хорошо развитой ветви науки и о тщетности более
чем полувековых усилий многочисленной плеяды ученых, работавших
в ней. Вопрос стоит в настоящее время до такой степени остро, что
не нашлось протестующих голосов против произнесенных уже слоа
„кризис теории функций".
Недоумения и недоразумения начались уже давно, еще со времени:
знаменитого спора относительно так называемой „Аксиомы Цермело"
(принцип произвольного выбора). В 1904 г. Цермело „доказал"* что»
всякое множество, в частности и континуум, „может быть сделано"'
вполне упорядоченным. Это рассуждение Цермело немедленно было
опротестовано частью ученых, причем математики с изумлением конста^
тировали радикальное отсутствие единомыслия в своей среде: все
в математике до сих пор заставляло думать, что всякое наличие
разногласия обусловлено либо недостаточностью сведений, либо плохой
постановкой вопросов. Здесь же оказалось непримиримое различие взглядов,
при полной внутренней очевидности дела. Эта разница взглядов получила
наиболее точное и наиболее яркое выражение в тех знаменитых „Cinq
lettres sur la theorie des ensembles" l, которыми обменялись по поводу
рассуждения Цермело между собой Адамар, Борель, Бэр и Лебег
в следующем 1905 году.
Какими бы ни были личные симпатии того или иного автора этих-.
„Cinq lettres" и его философские вкусы, каждому из них непререкаемо^
ясно было одно: рассуждение Цермело отнюдь не устанавливает мощности:
континуума; если ввериться рассуждению Цермело, мощность конти^
нуума есть, в самом деле, алеф; но найти ее местоположение на шкале
алефов не только не допускалось рассуждением Цермело, но, напротив
того, это представлялось абсолютно безнадежным делом, и не вследствие
сложности обстановки, а напротив, благодаря ее простоте. Не следует
упускать из вида, что рассуждение Цермело много бы потеряло в своей
сомнительности и остроте, если бы из него вытекли новые математические
факты, устанавливающие новые соотношения между давно известными
вещами или, по крайней мере, новые привлекательные богатые соотно-
шениями перспективы. Но этого не было: просто утверждалось, что
мощность континуума находится на алефической шкале, без того чтобы
знать точно, в каком именно ее месте. И так как вся обстановка ука-
1 См., например, Е. В о г е 1. Lemons sur la theorie des fonctions, 2e ed., Note IV,.
стр. ISO.
СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО 511
зывала на то, что никакое указание не может быть достигнуто
конечным путем, то впервые в математике встал вопрос во всей его остроте
о существенной необходимости делать различие между „тем, что есть
на самом деле" (= реальность) и „тем, что может быть доказуемо для
человеческого интеллекта" (= познание) — вопрос, мало новый для
философии, прибавим. Едва только появился на горизонте этот вопрос, как
не стало обычного единомыслия математиков, тотчас же разбившихся
на толки. Для одних, получивших название „идеалистов", все это
слишком антропоморфично: надо ни на минуту не забывать о самом предмете
и поменьше говорить о человеческой возможности его охватить, —
говорит же нам палеонтология о фауне третичной эпохи или астрофизика —
о строении всей поверхности луны, хотя в первом случае тогда не было
человека, и во втором случае имеется невидимая половина у нашего
спутника. Это мнимое злоупотребление категориями времени и
пространства не мешает быть упомянутым дисциплинам истинными науками.
„Мало ли вещей на свете, о которых мы не знаем и о которых мы
никогда не узнаем. Вот, например, капля воды. Число молекул конечно,
но какое оно? Я не знаю и никогда не узнаю, — и это еще не резон
уничтожать кинетическую теорию материи. Все это слишком
антропоморфично" (А дам ар).
Для других, по иронии судьбы получивших прозвище реалистов,.
необходимо избегать жонглирования с символами, которые не
соответствуют ничему. Истинная наука никогда не будет сборищем пустых
слов и чисто логических понятий без концепции. Наука не есть лого-
махия. За словами всегда должна скрываться сама реальность.
Рассуждение Цермело— только греза, так как каждый из идеалистов,,
говоря о выборах, выбирает и грезит по-своему, и нет не только
возможности сообщить своему собеседнику о проделанных в бесконечном,
количестве выборах, но и быть согласным даже с самим собой.
Построение, которое нельзя описать, рассуждение, не могущее быть
выполненным во всех его шагах до конца, — все это находится вне науки-
Победы и горести в мире призраков не окажут никогда никакого эффекта—
ни задерживающего, ни ускоряющего — на ход науки, занятой открытием*
конечных соотношений между вещами мира чувств или мира концепций
(Б о р е л ь).
Эта к изумлению самих математиков обнажившаяся разница взглядов,
с течением времени не смягчилась, но была просто отмечена и
констатирована. По молчаливому соглашению решено было не настаивать,
на ней и не углублять ее, но подождать новых фактов.
Так прошло около двух десятков лет. За это время произошло*
следующее: не только не выяснилась математическая природа рассуждения
Цермело, но, напротив того, к проблеме установления места континуума
на алефической шкале были прибавлены еще и другие проблемы, частью
связанные с трансфинитными числами, частью свободные от них, —
проблемы, вся обстановка которых представляет ту же самую степень-
512
i-L H. ЛУЗИН
безнадежности в смысле разрешения конечным рассуждением, каковая
имеется в вышеуказанной проблеме об алефе континуума. При этом
нисколько не смягчившемся положении дела вполне следовало ожидать
возобновления спора. Не нужно думать, что здесь доминирующую роль
играет психологический момент, связанный с не удавшимися попытками
разрешения и с немногими имеющимися в науке прецедентами
„доказательств невозможности". Всякая наука имеет свои собственные временно
недоступные проблемы, решения которых приходится иногда ждать
веками, — теория чисел, например. Но обстановка таких проблем всегда
в высшей степени сложная, и внимательный глаз, исследующий ее,
вскоре подмечает многочисленные нити, тянущиеся от исследуемой
проблемы к многим вопросам и проблемам — решенным или нет — самых
разнообразных математических областей, на первый взгляд совершенно
чуждых области рассматриваемой проблемы. Ничего похожего нет
в обсуждаемой обстановке: рассматриваемые проблемы теории функций
характеризуются крайней простотой и полной изолированностью
обстановки. Нет никаких нитей, связывающих их с проблемами вне теории
функций: каждая из этих проблем формулирована в терминах теории
функций и должна решиться в этих же терминах и методами и
рассуждениями только теории функций. Решение должно произойти внутри
области почти простыми средствами элементарной логики, причем число
испытуемых комбинаций обычно весьма ограничено. И если такого
решения уже вскоре же не находится, то в этом и повод к тревоге
за прочность основ области.
Возобновление спора произошло в два-три последние года, и это
произошло в столь подчеркнутой и ни перед чем не останавливающейся
форме, что дало повод Адамару говорить о подлинном „землетрясении
в математике". И при том это потрясение отнюдь не ограничивается
„окраинными владениями математического царства", что было бы простой
болезнью роста науки, связанной с неладами и неустройствами [при
недавней ассимиляции какого-нибудь нового понятия, но идет в самую
глубь его, опрокидывая и разрушая все, что считалось прочным со
времени Ренессанса.
Атака повелась „реалистами" на этот раз на принцип исключенного
третьего, и авторами ее явились Брауэр (Brouwer) и Вейль (Weyl).
Этот принцип поставлен ими под категорическое сомнение. Так как он
все-тжи действенен для текущей жизни, то Брауэр считал его
законным лишь для конечных множеств, отрицая его применимость к каким
бы то ни было бесконечным множествам, включая сюда и натуральный
ряд. И дабы объяснить его действенность в области обыкновенной
логики, Брауэр изменяет порядок вещей, объявляя логику лишь частью
теории конечных множеств.
Дабы дать некоторое представление об аргументации этих
„неокартезианцев", как -характеризует это течение Адамар, рассмотрим один
пример Вейдя.
СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ ФУНКЦИЙ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО 513
Речь идет о целых и положительных числах вида
2м+ \, где п = 1, 2, 3,...
„Мнение, будто либо все эти числа суть простые, либо среди них
должно иметься составное число, основывается вот на чем: станем
исследовать одно за другим эти числа; если встретимся с составным,
вопрос уже решен; если же мы не встретим такого числа, в чем мы
будем уверены лишь тогда, когда переберем одно за другим все числа,
вопрос тоже решен. Но неразумно думать, что мы можем исчерпать
бесконечность числа" (В е й л ь).
С точки зрения последователей этого учения, получившего
название интуиционизма, принцип исключенного третьего неприменим ни
к какому бесконечному множеству: следует признать заблуждением
всякое математическое предложение, в доказательстве которого имеется
фраза: „так как случай, когда все элементы е множества Е имеют
свойство Р, уже приводит нас к истинности доказываемого
предложения, то нам остается рассмотреть случай, когда это не так. Пусть же
е есть элемент Е, не обладающий свойством Р; в этом случае.. .и
я т. д.
Ясно, что с запрещением пользоваться такого рода доказательствами
разрушительный вихрь проносится нами над большинством классических
рассуждений, не говоря уже о теории функций, от развалин которой
остается столь мало, что возникает вопрос: „стоит ли восстанавливать
то, что осталось после этого землетрясения, тем более что почва
продолжает еще колебаться" (А д а м а р).
В частности, геометрическая точка на прямой есть не что иное, как
•бесконечная последовательность стягивающихся интервалов. Отсюда ясно,
•с какой осторожностью приходится оперировать с точками, дабы не
попасть в положение, в котором мы будем вынуждены применить принцип
'исключенного третьего к бесконечной последовательности. Но такое
незаконное применение необходимо будет иметь место, если мы будем
настаивать на концепции континуума как множества точек. Следовательно,
необходимо отказаться от этой концепции.
Континуум не есть множество точек: это есть чистая протяженность,
в которую мы можем помещать точки, стягивая интервалы, но которая
не состоит из точек. „Континуум — это есть среда свободного
становления" (В е й л ь).
Общего обмена мнений по поводу выступлений Брауэра и Вейля
•еще не произошло. В печати высказался лишь один Адамар в тонкой
пессимистически написанной статье1. В ней он, констатируя
возвращение математики к матафизике средних веков и появление среди нас
элеатов и Пиррона, еще раз настаивает на полном прекращении каких-
1 Статья является предисловием к книге: G о n s e t h. Les fonde meats des mathema-
*iques, Paris, 1926.
514
Н. Н. ЛУЗИН
либо споров, которые здесь, по его мнению, совершенно бесполезны.
Принцип исключенного третьего для него столь же ясен, как и принцип
тождества, и столь же ясно, что никто никогда не может обходиться
без них, даже когда называют себя интуиционистами. Ввиду
совершенной ясности и непреложности для него логики Port г^оуаГя, различие
мнений должно обусловливаться, по словам Адамара, не заблуждением,
а тем обстоятельством, что в соприкосновение вошли по-иному
устроенные умы. Наше воспитание сообщает известное однообразие нашему
мозговому устройству, открывая вследствие достигнутой этим ценной
однородности нашим мозгам возможность общения между собой. Наше
воспитание и образование — это не что иное, как феномен
приспособления, и никогда не следует забывать о его регулирующей силе. Но,
несмотря на значение воспитания, достигающаяся им однородность
мозгов не носит абсолютного характера, и там, куда регулирующие
силы еще не успели внести однородность, там сказывается природная
естественная неоднородность. „Кто знает, мое различие мнений с Лебегом
об идеализме и реализме — не обусловливается ли оно некоторой
разностью осмотического давления ph в той или иной категории клеток
моего мозга и мозга Лебега? „После беглых указаний на то, что манера
обходиться без тех или иных принципов пришла из геометрии, где
имеет смысл при доказательствах первоначальных предложений („все
прямые углы равныа и т. д.) забывать об имеющихся соотношениях
и понятиях", Адамар говорит, что подобное „забвение" никогда не может
быть исключением в столь больших вещах, какоиы принцип тождеств
и принцип исключенного третьего, и что petitio principii здесь неизбежно.
Не с критикой Брауэра и Вейля, но с направленной против их учений
большой теорией выступил Д. Гильберт (D. Hilbert). Целью его усилий,
по его собственным словам, были сохранение всего того „цветущего
прекрасного математического рая, который был открыт и предоставлен
для нас нашими предшественниками". Согласно теории Гильберта,
следует признать существующим все то, что непротиворечиво. И в
соответствии с этим главные усилия автора направлены на выработку метода
доказывать непротиворечивость той или иной системы основоположений.
Теория автора им полностью еще не изложена, но по предварительным
очеркам дело представляется в следующем виде: всякий акт
математической мысли может быть формализован, т. е. записан в виде символов.
Самые нормы мышления, т. е. „аксиомы" логики, также могут быть
выписаны в виде формул, аксиомы арифметики — также.
Всякое математическое доказательство есть просто конечная система
или цепь формул, выводимых в момент его создания согласно нормам
мышления, т. е. согласно выписанной системе аксиом логики и другим
принятым аксиомам предметного (не формального) характера. Если
система аксиом противоречива, то должно иметься доказательство
с противоречивым выводом, за который всегда можно принять 1=0.
И автор сообщает, что начертание и свойства формальных символов
СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ ФУНКЦИЙ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО $15
логики и арифметики таковы, что не может осуществиться никогда
такое конечное сцепление символов логики и арифметики, которое было
бы развито согласно выписанным аксиомам логики и'арифметики и
которое привело бы к выводу 1=0.
Это обстоятельство доказывает, по мнению Гильберта,
непротиворечивость аксиом не только арифметики, но и самой логики, притом
без какого-либо petitio principii.
В частности, имея в виду нужды теории функций, автор набрасывает
эскиз доказательства непротиворечивости аксиомы Цермело аксиомам
логики и арифметики, удостоверяя этим право пользоваться ею в анализе
невозбранно, не опасаясь могущего последовать какого-нибудь
противоречия. Наконец, в своем последнем мемуаре „L'infini" (Acta Mathematica,
48), следуя своей обычной манере искать доказательства
непротиворечивости, Гильберт сообщает, что ему удалось найти доказательство
непротиворечивости того, что мощность континуума есть алеф, следующий
за счетным (алеф-один) (см. [48]).
Сейчас является еще преждевременным, до полного изложения теории
Гильберта, высказываться о ее действенности. Сделаем только несколько
замечаний общего характера относительно теории Гильберта, поскольку
это дозволяют определившиеся ее контуры.
Прежде всего привлекательным в этой теория является ее творческий
характер, хотя несколько и своеобразный: в то время, когда теории
Брауэра и Вейля имеют, собственно, только разрушительный характер
и, не созидая новых соотношений и новых предложений, воздвигают
всюду бесчисленные баррикады в виде непрерывной цепи запрещений, —
в это самое время теория Гильберта несет в себе интересные творческие
возможности. Одну из них автор указывает как уже реализованную:
это установление места мощности континуума на алефической шкале.
С другой стороны, именно как раз своеобразие творческих
возможностей теории Гильберта и заставляет быть очень осторожным в ее
оценке; в частности, для мощности континуума автором сделано не
совсем то, что нужно для теории функций.
Для теории функций мало знать, что совпадение мощности континуума
с первым за счетным алефом непротиворечиво: для теории функций
необходимо фактическое знание индивидуального перечисления точек
трансфинитными числами второго класса Кантора. А этого как раз нет
в теории Гильберта. Совпадение мощности континуума с алеф-один
непротиворечиво; но исключается ли этим возможность того, что
совпадение мощности континуума с алеф-два также непротиворечиво?
И что произойдет, если будет доказана в самом деле и эта последняя
непротиворечивость? Первое, что приходит на ум, это то, что
установление мощности континуума есть дело свободной аксиомы, вроде аксиомы
о параллелях для геометрии. Но в то время как при инвариантности
всех прочих аксиом геометрии Евклида и при вариировании аксиомы
о параллелях меняется самый смысл произнесенных или написанных
516
Н. Н. ЛУЗИН
слов: точка, прямая etc., смысл каких слов меняется, если мы делаем
мощность континуума подвижной на алефической шкале, все время
доказывая непротиворечивость этого движения? Мощность континуума,
если только мыслить его как множество точек, есть единая некая
реальность, и она должна находиться на алефической шкале там, где она на
ней есть; нужды нет, если определение этого места затруднительно
или, прибавил бы Адамар, „даже невозможно для нас, людей41.
Аналогичная трудность проистекла бы для анализа, если была бы доказана
непротиворечивость того, что эйлерова постоянная С есть рациональное
число, без того чтобы указать, каково оно, или, еще хуже, если
одновременно с этим доказать непротиворечивость и того, что С есть ква-
дратическая иррациональность.
Таким образом, для творческих возможностей теории Гильберта,
по-видимому, серьезно встает вопрос о том, что именно достигают
в отношении реальности, устанавливая непротиворечивость того или
другого и ограничиваясь только этим?
Относительно же самого существа теории Гильберта какие-либо
суждения еще затруднительны ввиду отсутствия полных о ней сведений.
Наиболее деликатным моментом является, без сомнения, вопрос о peti-
tio principii: избегнуто ли это? Без сомнения, некоторые движения
нашей мысли могут быть „формализированы", т. е. отмечены символами.
Гильберт говорит о превращении в символы всякой математической
мысли. Без сомнения, мы имеем возможность оперировать живой мыслью,
непосредственным (несимволизированным) рассуждением над этими
символами, как бы над некоторыми окаменелыми остатками некогда также
живой мысли. Нет сомнения, далее, что мы, как это делается в теории
инвариантов, можем приходить, принимая во внимание форму и вид этих
символов, к определенным заключениям о возможности или невозможности
иметь „правильное" сочетание этих символов, оканчивающееся фигурой
1=0. Нет сомнения, что все это можно проделать без petitio principii.
Но когда мы хотим вывести отсюда определенные заключения об
отсутствии противоречия в живой мысли внутри ее самой, мы должны
оживить эти окаменелости, превратив их в процессы живой мысли. Имеется ли
гарантия, что на некотором месте ожившего узора мы не встретим
конфликта живой мысли с самой собой? [52].
На затруднении иметь аксиоматику целых чисел без petitio principii
весьма настаивал в свое время А. Пуанкаре, который выражал сомнения
относительно возможности без petitio principii определить число 2,
когда число аксиом арифметики заведомо более двух. По этому поводу
памятен вопрос А. Пуанкаре, обращенный к математику, пытавшемуся
символически обосновать ему арифметику: „Как я могу сомневаться
в существовании числа, раз вы мне тут написали &?"
Следует еще обратить большое внимание на основное положение теории
Д. Гильберта, связанное у него с моментом символизирования до конца
всякого математического рассуждения: наша мысль конечна. Обычно
СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО 517
философы как будто протестуют против такого рода заявлений, утверждая,
что они лишены какого-либо содержания и смысла. Различие категорий-»
конечного и неконечного осуществления тогда, когда мысль направлена
на внешний мир или мир концепций, но когда мысль направлена на
самое себя, эти категории утрачивают всякий смысл. Формация концепций
есть иррациональный акт; хотеть, чтобы он был „конечным", — это
значит желать, чтобы он перестал быть самим собой.
С другой стороны, присоединиться к точке зрения Брауэра и Вейля
также представляется затруднительным. Интуиционизм в тех его формах,
которые он принял у последователей Брауэра и Вейля и в которых,
прибавим, неповинны его инициаторы, представляет собой, скорее, игру
ума, чем науку. Он есть, в сущности, смесь обостренной критики
и догматизма теологического характера. Он возводит конечное в догму;
но та „революция", которую он обещал внести в математику, является
не освобождением мысли, но загромождением путей исследования, т. е.,
в сущности, одним из реакционных запретов мысли. Притом в самое
последнее время получены оттиски имеющего появиться в Bulletin de
TAcademie de Bruxelles небольшого мемуара двух бельгийских
математиков— Bap39Ha(Barzin)n3ppepa(Errera). В этой работе авторы выводят,
отправляясь от принципов теории Брауэра, выраженных ими
символически, формальное противоречие логике Аристотеля: терциональное
состояние р' какого-либо предложения р влечет его ложность ~ />. Так как
терциональное состояние при известных условиях все-таки, как будто, имеет место
(мы уже указывали на случай предложения о существовании
параллельной прямой при сохранении остальных аксиом геометрии Евклида), хотя
оно и должно сопровождаться, в случае замены терционального состояния
положительным или отрицательным предложением, изменением смысла
всех терминов, необходимо подождать дальнейшего выяснения значения
результатов Барзэна и Зррера [53].
Лично мне кажется, что мнение Адамара о необходимости
прекращения бесполезных и не могущих ничего выяснить споров вполне справедливо.
Необходимо, в самом деле, подождать новых фактов, касающихся
возможности полной арифметизации континуума. Из всех тезисов Брауэра
и Вейля самым интересным является утверждение, что континуум не
есть множество точек. Эта идея в истории мысли не представляет первой
новизны: она восходит еще к Аквинату, дабы не цитировать древних.
Притом до появления работы Кантора, с которого начинается перевод
всех основных понятий математики на язык множеств, большинство
математиков, чтобы не сказать все, именно и мыслили континуум как
чистую бесточечную протяженность. И еще после Кантора А. Пуанкаре,
обсуждая смысл теоремы Кантора о том, что континуум имеет мощность,
высшую счетной, усумнился в том, имеет ли он вообще какую-либо
мощность.
Недостаток места не позволяет мне изложить более подробно
результаты ведущихся в настоящее время в Москве исследований по арифмети-
S18
Н. Н. ЛУЗИН
зации континуума1. По-видимому, если только здесь нами не сделано
каких-либо упущений, установленное нами существование индивидуально
определенных проективных множеств, пустота или непустота которых
оказывается зависящей от специальной аксиомы, явится, если
только мы не ошибаемся, experimentum crucis в пользу упомянутого
тезиса Брауэра.
Обычно длящаяся деятельность вулкана не препятствует, все-таки,
окрестному населению заниматься текущими делами. Так же точно
текущая работа дескриптивной теории функций продолжается, несмотря
на колебание ее основ. Из главного мы остановимся на немногом.
Здесь прежде всего следует весьма отметить систематическую
деятельность сильной и прекрасно организованной польской школы, поставившей
себе задачей установление новых фактов из теории алефов и континуума
без ограничения себя определенным кругом методов. Этим в самом
деле полнее всего может быть характеризована математическая природа
таких рассуждений, каково рассуждение Цермело.
Из результатов этого рода упомянем прежде всего работу Банаха
(Banach) и Тарского (Tarski) о разбиении сферы. Оказывается, можно
разбить сферу радиуса R на конечное число таких неперекрывающихся
частей, перемещая которые, как твердые тела, и прикладывая их друг
к другу надлежащим образом, можно получить новую сферу вдвое
большего радиуса (= 2/?), причем мы не теряем ни одной точки
прежней сферы и не вводим новой. Конечно, эти части суть неизмеримые
множества (в смысле Лебега) и, следовательно, пока получаемые при
помощи аксиомы Цермело. Этот факт, которым, без сомнения,
воспользовался бы Зенон, если бы он ему был известен, имеет большую важность:
если бы мы могли без аксиомы Цермело указать или определить (nom-
mer) эти множества, это послужило бы поводом дая избежания парадоксов
ввести какую-то атомистическую структуру для пространства.
Далее проф. В. Серпинский (W. Sierpinski) доказал, что множество
значений, каждое из которых непрерывная везде функция / (х) принимает
несчетное число раз, может быть произвольным аналитическим
множеством и, в частности, любым множеством, измеримым В; и так как эти
последние образуют классы Бэра (Baire), то явилась возможность
расклассифицировать по классам Бэра и непрерывные функции, что было
до сих пор осуществлено лишь для разрывных функций.
Эти результаты стоят в близкой связи с вопросами о возможности
получать непрерывные функции путем итерации или суперпозиций
функций, течение которых и свойства хорошо известны, например функций
с ограниченным изменением. На этом пути Г. М. Фихтенгольцем получены
ценные результаты о суперпозиции двух абсолютно непрерывных функ-
1 См. мои предварительные заметки о проективных множествах от 4 мая,
25 мая, IS июня, 20 июля и 17 августа (Comptes Rendus), а также мемуар „Sur les
ensembles analytiques* (Fund. Math., X, 1927) („Об аналитических множествах",
см. стр. 380 настоящего тома.—Ред.).
СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ ФУНКЦИЙ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО $19
ций, положенные им в основу теории замены переменных в интеграле
Лебега. Эти рассмотрения были продолжены учеником Г. М. Фихтен-
гольца, Зарецким, поставившим вопрос о характеристических свойствах
таких суперпозиций; частично эти последние рассмотрения совпали
с результатами польских и московских математиков.
ДОПОЛНЕНИЕ
Предыдущая статья, дающая обзор состояния теории функций
действительного переменного, написана в 1927 г. В настоящее время мне
остается указать вкратце лишь самое направление работ по ней за истекшие
лять лет, насколько это позволяет столь незначительный срок1.
I
Как я уже указал в предыдущей статье, значительное число идей
в теории функций действительного переменного было сосредоточено
около понятия интеграла в направлении его расширения наиболее „есте-
•ственным" путем за пределы интеграла Лебега.
За истекшие пять лет попытки в этом направлении продолжались.
Здесь мы имеем прежде всего продолжающееся изучение той группы
определений интеграла („определения Д й и С*, следуя терминологии
Данжуа), которые были предложены еще в 1919 г. А. Данжуа2, и
попытка систематического изучения которых была потом предпринята
Боксом (Т. J. Boks)3. Все эти определения имеют в виду получение
интеграла Лебега и его расширений „чисто римановским путем", т. е.
дроблением на уменьшающиеся до нуля части не оси OY зависимого
леременного, а оси ОХ аргумента.
Так как вопрос относительно первого определения интеграла
(„определение Аи) выяснился лишь в самое последнее время после ряда
предшествовавших сообщений Кемписти4 (Kempisty) в результате совсем
недавней работы А. Данжуа5, то для характеристики указанного
направления следует остановиться на этой последней.
ь
Интеграл Коши. Известно, что интегралом Коши J f(x)dx от функ-
а
цяк f(x), непрерывной в каждой точке отрезка [а^дс^б], называется
лредел суммы
•?=2/в) '(*<+!-*<). (1)
1 Полного нового „обзора" состояния теории дать, конечно, невозможно, так
лак для этого необходимо иметь некоторое историческое расстояние. В этом
отношении вполне целесообразна практика математических международных
конгрессов, хотя и собирающихся через каждые четыре года, но не ставящих обзорные
.доклады подряд, каждый раз по одной и той же самой ветви математики.
2 Comptes Rendus, 169, 219—22 J, 1919.
3 Rendiconti del Circolo matematico di Palermo, 1—54, 1921.
4 Comptes Rendus, 180, 812—815, 1011—1014, 1925 и 185, 749—751, 1927.
5 Comptes Rendus, заседание 19 октября 1931 г.
520
Н. Н. ЛУЗИН
когда наибольший из отрезков [а, д:^, [л^, лг2], ..., \х{, xt+1], ..., [хп_1э Ь]
стремится к нулю, здесь ^ обозначает любую точку отрезка [х{, х,'+\].
Если /(л:) есть какая-нибудь функция, определенная на отрезке
[а^дг^б] и конечная в каждой его точке, то сумма S хотя и имеет
конечную величину, однако, вообще говоря, не стремится ни к какому
конечному пределу, когда наибольшее из делений [л:,-, xi+l] стремится
к нулю. Открытие Коши, исторически вполне подготовленное, и состояло-
в установлении того первостепенной важности факта, что сумма *S в
указанных условиях всегда имеет предел, когда функция f(x) есть не
какая-нибудь, а непрерывная в каждой точке отрезка [а, Ь\ включая его
концы. В этом случае сумма S имеет единственный вполне
определенный предел, совершенно не зависящий ни от употребляемого способа
разделения отрезка [а, Ь] на части [а, дсх], [х19 х2], ..., [xn—lf b\ ни от
выбора точки 1; на делении [л:,, xi+l\; влияние этих произвольных
элементов на сумму S ощутительно, но исчезает в пределе, так что он
уже перестает зависеть от этих употребительных элементов.
Из самого определения интеграла Коши следует, что процесс его*
вычисления есть счетный. Этим мы хотим сказать, что, зная величину
функции /(х) в каком-нибудь счетном, всюду плотном множестве точек Ег
мы узнаем величину интеграла Коши
ь
\f(x)dx
а
посредством простого однократного перехода к пределу. Например, взяв
за Е множество всех точек, происходящих от разделения
рассматриваемого отрезка [а> Ь] на равные части, мы можем определить величину
интеграла Коши как предел среднего арифметического:
Г/<«) +/(« - ^)-- • • -/ (« -- ^ ') -• • .-/(в ч- *=«„)1
когда целое положительное п безгранично возрастает.
Условия Римана. Заслуга Римана заключается в том, что он
точным образом определил условия применимости процесса
интегрирования Коши к произвольной функции /(л:), а не только к непрерывной.
На современном языке теории множеств условия эти выражаются
следующим образом:
1°. Функция f(x) должна быть ограниченной.
2°. Множество разрывов функции f(x) должно иметь меру нуль.
Совокупность обоих этих условий является необходимой и
достаточной для применимости к рассматриваемой функции f(x) процесса Коши
в этих и только в этих условиях предел суммы
■S=2/e>-(*m-*<)
(1)
СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ ФУНКЦИЙ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО $21
не зависит от употребленных точек деления х{ и от выбора на делениях
[xh Хм\ точек Е...
Указанные условия иногда чрезвычайно удобны лая приложений, так
как дают немедленный ответ на вопрос: интегрируема ли
рассматриваемая функция f(x) процессом Коши. Так, например, сразу ясно, что
всякая функция f(x) со счетным лишь множеством Е точек разрыва есть
интегрируемая процессом Коши.
В частности, следовательно, интегрируемой процессом Коши
окажется всякая монотонная (т. е. возрастающая или убывающая) функция.
Но в общем случае, когда рассматриваемая функция f(x) имеет
несчетное множество Е точек разрыва, вопрос об интегрируемости в смысле
Коши функции f(x) сводится к вопросу о мере множества Е. Лая
определения же этой меры у нас не имеется никакого счетного процесса,
и следовательно, констатирование равенства нулю или отличия от нуля
меры множества Е должно как-то следовать из самого задания
функции /(*), минуя счетные процессы.
Тем не менее, если мы уже знаем, что рассматриваемая функция /(*),
непрерывная или разрывная, интегрируема процессом Коши, то самое
ь
вычисление интеграла \/(x)dx требует лишь счетного процесса: дая
а
этого достаточно просто хотя бы взять предел предыдущего среднего
арифметического (2).
Метод Дарбу. Известно, наконец, что интеграл Коши—Римана
подвергся пересмотру геометром Дарбу, который дал ему новое
освещение. Пусть/(х) — какая-нибудь ограниченная функция, определенная
на отрезке [а^лг^б]. Обозначим через Mi и /я,- соответственно
верхнюю и нижнюю границы рассматриваемой функции f(x) на отрезке
[х<, xi+l] и составим две суммы Дарбу:
S=2Mt(xt+l-xd (3')
и
*=2 т* (xi+i—*<)• <3">
Дарбу доказал, что когда наибольший из отрезков [xiy х<+г]
стремится к нулю, то обе указанные суммы S и s стремятся к вполне
определенным пределам, зависящим только от самой функции f(x) и от
отрезка (а, Ь) и совершенно независящим от употребляемого способа
разделения отрезка [а, Ь] на части [а, х{\, [х1У х2]9 ..., [хп-19 Ь].
Пределы эти получили названия верхнего и нижнего интегралов Дарбу и
ь ь
обозначаются через \/(x)dx и I f(x)dx, причем мы имеем очевидное
а «
неравенство:
6 Ь
522
Н. Н. ЛУЗИН
В случае, когда оба эти предела равны друг другу
/, ь
\f(x)dZ=\f(x)dx,
а а
тогда функция /(х) интегрируема в смысле Коши—Римана, и мы имеем
общую величину обоих этих пределов просто равной интегралу Коши.
Если же эти пределы отличны друг от друга, то функция f(x) не
интегрируема процессом Коши. Это обстоятельство преобретает совершенно
ясный смысл, если мы заметим, что при надлежащем выборе точки it
на отрезке [х», xi+l] сумма Коши (1) может быть сколь угодно
приближена, смотря по желанию, либо к первой сумме S, либо ко второй
сумме s Дарбу.
Следует отметить то обстоятельство, что обе суммы Дарбу 5и s
содержат меньше произвольных элементов, чем сумма Коши (1), так как
в них уже не встречается произвольно избираемая на делении [xiy х^г]
точка £t: она заменена у Дарбу числом М,- в сумме S и числом т%
в сумме s, определяемыми единственно через отрезок [xiy х»-^].
Интеграл А. Напомнив это, перейдем к рассмотрению последней
работы Данжуа. Пусть f(x) есть какая-нибудь измеримая функция,
определенная на отрезке [а, Ь] и конечная почти всюду на нем. Пусть [с, d\
есть какой-нибудь отрезок, лежащий на [а, Ь].
Назовем максимумом до & функции /(х) на отрезке |с, d\ вполне
определенное действительное число, обозначаемое через М(/у с, dy S) и
получаемое в силу следующего определения:
1°. Имея на отрезке [с, d\ фиксированное множество точек Е меры,
£
меньшей d_c > мы ищем верхнюю границу функции f(x) на
дополнительном до отрезка [с, d] множестве СЕ; обозначим через М(/, с, dy Ey S)
эту верхнюю грань.
2°. Заставляя всяческим образом изменяться указанное множество £,
мы ищем нижнюю грань чисел М(/, с, с/, £, &) и обозначаем ее через
М(/у су dy £). Эта нижняя грань Л/(/, с, d9 <§) и есть максимум до S
функции /(х) на отрезке [с, d].
Аналогично минимумом до <§ функции f(x) на отрезке [с, d]
называется число т (/, с, dy <§)y получаемое следующим образом:
1°. Имея на [с, d\ фиксированное множество Е меры, меньшей -г^,
ищем нижнюю грань функции /(х) на дополнении СЕ; обозначаем через
ш(/, с, dy Ey &) эту нижнюю грань.
2°. Заставляя всячески изменяться множество Е на [с, d]y ищем
верхнюю грань чисел т (/, с, dy Ey £)у которую и обозначаем через
т (/, с, dy <£). Это и есть минимум до &.
Установив эти определения, разделим данный отрезок [а, Ь]
произвольным образом на части [а, хг]у [х1У х.г]у ..., [*,, xi+1], ..., [xn-v b)
СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ ФУНКЦИЙ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО $23
и, обозначив через Mi($) и тДа) соответственно максимум до р и
минимум до а функции f(x) на отрезке [х{, xi+l\; составим две суммы Дарбу-
Данжуа:
S$) = ZMi(?)-(xi+l-xi) (4')
s(a) = Vm,(a).(xm-X;), (4")
где числа а и Р есть два какие-нибудь положительные числа, столь
малые, чтобы их сумма ан-р была меньше единицы, ач-Р<1.
Вот теперь основное определение Данжуа:
Функция f{x) называется интегрируемой А на [а> Ь]9 если обе
суммы S($) и s(a) при каком-нибудь выборе чисел а и Р стремятся
к одному и тому же пределу, когда наибольший из отрезков [л\, лг1Ч_,]
стремится к нулю.
В этом случае этот общий предел сумм S($) и s(a) называется
интегралом А от функции f(x) на отрезке [а, Ь] и обозначается через
ь
\/(x)dx.
-a
На первый взгляд может показаться, что предел сумм *S(p) и s(a),
предполагая, что он существует, должен зависеть от чисел а и ?.
В действительности никакой зависимости этого предела от чисел аир
нет, и если интегрируемость А наступает хотя при одной паре чисел a
и Р, то она имеет силу и для всех пар аир. Основным результатом
работы Данжуа является следующий.
Для того чтобы какая-нибудь функция f(x) была интегрируема А
на отрезке [а, Ь], необходимо и достаточно, чтобы f(x) была сумми-
//
руемой в смысле Лебега; в этом случае интеграл A j f(x) dx численно
а
Ь
равен интегралу Лебега (L) \f(x)dx.
а
Анализ интеграла А. Я не вступаю на почву фактического
доказательства только что приведенной теоремы Данжуа, для которого
отсылаю читателя к последнему сообщению Данжуа Академии наук2,
и перехожу теперь к рассмотрению самой цели, которая преследуется
„интегралом А".
Уже самое название указанного сообщения Данжуа (о римановском
определении интеграла Лебега) показывает, что имелось в виду
получение интеграла Лебега „чисто римановским" путем, т. е. как простого
предела суммы S Коши:
при надлежащем выборе точки Е, на отрезке [xiy дг<+1].
1 A. Den joy. Sur 1а definition riemannienne de l'integrale de Lebesgue. Comptes
Rendus, 19 октября 1931 г.
S24
Н. Н. ЛУЗИН
Для достижения этой цели автор отправляется от представления
римановского интеграла, данного Дарбу, как общего предела сумм
s=2AM*«-i —*<) (зг>
*=2>< (*<-и — *<). (3">
где Mi и rrii обозначают соответственно верхнюю и нижнюю границы
функции f(x) на сегменте [xiy xi+l]. Беря в качестве модели или образца
указанное представление Дарбу, автор вводит вместо чисел М< и т<
числа М»-ф) и шДа), названные им соответственно «максимумом до (3» и
«минимумом до а» функции / {х) на сегменте [xiy х{+л\, и, построив две
суммы
s(a) = 2m#(a).(jcm-jc<), (4»>
аналогичные суммам Дарбу, определяет интеграл Лебега как общий
предел этих сумм. Числа аир предполагаются положительными к
такими, что <хн-(3<С1.
Нельзя не видеть, что аналогия с представлением римановского
интеграла Дарбу получилась в самом деле полная.
Действительно, если мы положим а = р —0 и не позволим себе при
определении «максимума до (3» и «минимума до а» функции f(x)
пренебрегать никаким множеством точек (не только меры нуль, но даже
содержащими хотя бы одну только точку), то тогда М,(р) становится
просто Mi и тДа) делается равным т^ В этом случае суммы Данжуа
переходят в суммы Дарбу, являющиеся таким образом их естественным
частным случаем, и в результате достигают получения интеграла Лебега
методом, скопированным с метода Дарбу.
При анализе этого интересного результата следует вспомнить о тех
причинах, которые послужили поводом для возникновения этой попытки
и других менее удачных попыток, сделанных раньше в этом
направлении 1.
Общей причиной их является некоторое неудовлетворение,
сознательное или бессознательное, процессом Лебега.
1 Огромная заслуга Данжуа состоит в том, что числа Mi (p) и mi (а) определены
им эффективно, т* е. единственным образом при задании отрезков [*», Jft+i] и
функции f (х) без употребления аксиомы Цермело. Попытки определить интеграл Лебега
суммами, аналогичными суммам Дарбу, делались весьма рано и восходят еще к
работам Риса (1910 г.). Но во всех таких попытках неизменно употреблялась аксиома
Цермело, которая, помимо вносимого ею ничем не ограниченного и не направляемого
никаким правилом произвола, была должна по самой своей природе ставить дело так,
что для того, ичтобы. получить интеграл Лебега способом Дарбу, т. е. как предел
суммы типа 2^(-**-И. — •*•)» надо было знать числа р.», а для знания этих чисел ja*
нужно было предварительно знать величину интеграла Лебега и других
сопутствующих ему чисел той же самой природы.
•СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО 525
Д\я того чтобы видеть, какой оно природы, предположим
функцию/(х) ограниченной на отрезке 1а<лг<6], и пусть мы имеем
Л</(х)<В
для всякой точки х отрезка [а, Ь]. Процесс самого Лебега состоит
в следующем: отрезок [Л, В\> помещаемый на ось OY зависимого
переменного Г, Y=f(x)y делится на части [A, YJ, [Yl9 К2], .. ., [Yiy У,+1|, ...
..., 1Уя-+-1> В\* и множество точек х, удовлетворяющих неравенству
У<<Ях)<У»л,
обозначается через Я<. Обозначим через и-,- меру множества Et:
H.< = mes£,, / = 0, 1, 2, 3, . .., (л — 1).
Лебег определяет свой интеграл просто как предел суммы
когда наибольший из отрезков [А> Yx], [Yu Y2\> ..., [Yly Yi+l]> ...
.. .y[Yn-ly В] стремится к нулю.
В случае если данная функция f(x) есть неограниченная на отрезке
(а, Ь]у то в формуле (5) конечная сумма 2 должна быть заменена
бесконечным рядом и деления [Yiy К»-+1], (—оо</<-*-со) всей оси OY
должны равномерно стремиться к нулю.
В смысле формальной простоты определение Лебега не оставляет
желать ничего большего. И в самом деле, вначале было непривычным
лишь деление на части оси зависимого переменного OY9 а не оси
аргумента ОХу как это делается в методе Коши—Римана.
Следовательно, вначале были затруднения лишь психологического
порядка1. Но потом стали выступать на передний план соображения
принципиального характера. И поиски римановского изображения
интеграла Лебега обусловлены не одним лишь стремлением возвратиться
к привычному приему деления на части оси аргумента ОХ.
Чтобы понять сущность дела, нужно обратить внимание на то, что
самый процесс вычисления интеграла Лебега вовсе не заключается
1 Интересно отметить, что деление оси зависимого переменного OY было
впервые сделано для интегрирования непрерывных функций („слишком волнистых,
чтобы применение обычного- метода Коши было практичным") инженерами еще до
появления работ Лебега. На этом основании в литературе проскользнули было
признаки попыток отнести к ним приоритет открытия интеграла Лебега. Но эти
аопытки не удержались ввиду того, что хотя процесс Лебега и был отчетливо
употреблен инженерами, однако ими ничего не было сделано в смысле возведения
их приема в принцип, таким образом, этот прием получил у них характер частного,
как бы случайно проделанного процесса, каких появляется очень много*
Ни естественность деления оси зависимого переменного OY в свете неделимых
Кавальеры обратил внимание сам Лебег.
526
Н. Н. ЛУЗИН
в одном лишь действии перехода к пределу. Это действие составляет
лишь финальную часть интегрирования по Лебегу, главная же часть
процесса Лебега состоит в вычислении коэффициента |\ в сумме с
Лебега (5), т. е. в определении мер множеств Et.
Определение меры mes E какого-нибудь множества точек Е> лежащего
на отрезке [а, А], состоит из двух действий: 1° определения верхней меры
mes Е множества Е; 2° определения верхней меры mes СЕ множества СЕ,
дополнительного к £ до отрезка [а, Ь\.
Если окажется, что mesf-i-mes CE = b — а, то множество Е
измеримо по Лебегу, и в этом случае его мера mesE полагается равной
верхней мере mes E рассматриваемого множества £".
Если же оказалось бы, что mes E -+- mes СЕ ^> Ь — а, то такое
множество Е неизмеримо по Лебегу и такое множество [и порождающая
его функция f(x)\ не может служить ни к чему1.
Таким образом, определить число ц,- в сумме Лебега (5) — это
означает: найти верхнюю меру множества Et. Но определение верхней меры
какого-нибудь несчетного множества Е является операцией существенно
трансцендентной, для которой мы не имеем никакого счетного процесса2.
Отсюда следует, что главное затруднение при доведении до конца про-
1 До сих пор не известно ни одного множества, не измеримого по Лебегу.
Самое существование таких множеств не признается бесспорно установленным»
2 Чтобы учесть трудность этой операции, достаточно сделать следующие
наблюдения. Назовем покрышкой данного линейного множества точек Е систему Е
неперекрывающихся попарно интервалов 5» = (а», о4) с рациональными концами,
содержащую целиком в себе множество Е.
Обозначим через и длину покрышки £, т. е. сумму длин всех входящих в нее
интервалов Ьц ясно, что число и зависит от покрышки £ и изменяется, вообще
говоря, с изменением этой покрышки. Если мы станем теперь всячески изменять
покрышку £ данного множества £, то нижняя граница полученного множества и
чисел и называется верхней мерой множества.
Легко сообразить, что все сводится к определению нижней границы некоторой
положительной функции /(/). Действительно, системы £, составленные из не
перекрывающихся попарно интервалов с рациональными концами, образуют
множество, имеющее мощность континуума, и можно фактически привести их во взаимно-
однозначное соответствие с точками отрезка [0 < f < 1|; пусть £/ будет системой,,
соответствующей действительному числу t.
Определим теперь функцию <f (t) следующими двумя условиями:
1°. <р {t) = Ь—а, если система £/ не содержит множества £.
2°. <р (t) равно длине системы £/, если £/ содержит Е.
Ясно, что функция <f>(£), определенная на отрезке [0 < t < 1|, есть
положительная ограниченная. Ясно, наконец, что нижняя граница функции <р (t) есть в точно*
сти верхняя мера mes E множества Е.
Определение нижней границы заданной функции <р (/) не есть счетная операция,,
хотя она и разбивается на счетное число следующих шагов: имея рациональное
число г, узнать, справедливо ли для всех точек х отрезка [а> Ь\ неравенство
/(*)>г; однако невозможно каким-либо счетным процессом констатировать л^л
разрывной функции f{t) соблюдение неравенства /(.*)> г вр всех точках отрезка
СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО 527
цесса вычисления интеграла Лебега состоит вовсе не в переходе к
пределу суммы Лебега о, а в вычислении ее коэффициентов р4 еще до
перехода к пределу.
Именно это наличие столь тягостной трансцендентной операции
заставляло и теперь еще заставляет исследователей искать иных
определений интеграла Лебега и прежде всего влечет их на покинутый путь
Коши—Римана. Здесь же заметим, что мы пока еще не имеем
определения интеграла Лебега строго римановским путем: то, что сделано
в рассматриваемой работе Данжуа, есть, собственно, путь Дарбу, а не
Римана.
Строго римановским путем было бы определение интеграла Лебега
как простого (не общего) предела суммы S Коши
при надлежащем выборе точки ;< на отрезке [xiy Arm]. Этот путь был
еще недавно испробован Рисом, но эффективного определения точек ?#
тогда не удалось сделать, не употребляя аксиомы Цермело и не зная
заранее численной величины интеграла Лебега.
Не имеем мы указанного выбора точек ^ и в рассматриваемой работе
Данжуа; следовательно, в ней, собственно, нет римановского пути
в точном смысле этого слова. Но путь Дарбу проведен с большим
искусством и силой.
Если мы теперь проанализируем коэффициенты М,(Р) и шДа), то
тотчас же заметим, что хотя определение их и эффективное, но оно
требует д^я своего выполнения процесса/ еще более тягостного, чем
отыскание меры Лебега: здесь мы имеем и определение верхней границы
функции на фиксированном множестве, и затем отыскание нижней
границы получающихся^ таким образом величин при изменяющемся
множестве. Короче говоря, определение чисел Данжуа Л/ДР) и mt(ot)
требует операции гораздо более сложной, чем у Лебега.
Отметим здесь же, что лишь у Коши и у Римана мы имЪем одну
лишь операцию простого перехода к пределу.
Но даже у самого Дарбу определение его чисел Mt и т<
представляет огромную трудность и не может быть выполнено никакой счетной
операцией, так как вычисление коэффициентов Дарбу М{ и т{ является
отысканием верхней и нижней границ разрывной, вообще говоря, функ-
ции /(л:), т. е. распадается на континуум элементарных процессов.
Здесь уместно ввести следующие обозначения: обозначим через о (Е\
операцию отыскания верхней грани счетного точечного множества Е и
через 0(E) операцию отыскания верхней грани несчетного множества £.
С этим обозначением, учтя все то, что было нами изложено выше, мы
теперь можем сказать:
Интеграл Коши—Римана требует лишь одной операции о; интеграл
Дарбу —одной операции О и одной операции о; интеграл Лебега —
одной операции О, осложненной отысканием покрышек для множеств,.
528 н. а лузин
и двух операций о; интеграл А — двух осложненных операций О и
одной операции о.
Сказанное, конечно, не мешает признать по справедливости работу
Данжуа чрезвычайно интересной и имеющей значение для дальнейших
попыток: если бы удалось определить числа, аналогичные числам
Дарбу Mi и rrii другим образом, пусть сколь угодно сложным, лишь бы
эффективным, и если новое определение дало бы существенное
расширение интеграла Лебега, например с охватом метода тотализации, тогда
это было бы значительным успехом, оправдывающим все усилия,
затраченные на преодоление сложности *.
Взаимоотношение мер Бореля и Лебега. В этом же
круге идей стоит еще не разрешенный вопрос о взаимоотношении мер
Бореля и Лебега. Что вопрос о мере множеств стал в центре внимания,
в этом нет удивительного, так как вычисление интеграла Лебега,
охватывающего большинство случаев, нужных математическому анализу,
сводится просто к вычислению меры множеств, как мы это видим из
формулы (5). Коснемся прежде всего некоторых общих соображений.
То, что называется в настоящее время теорией функций
действительного переменного, есть совокупность предложений, тесно
соединенных между собой связями следующего характера.
Предложение Р* говорит о том, что некоторая проблема А будет
разрешена до конца, если будут разрешены проблемы Ву В'у В'\ В'"у ...,
из которых основной (и чаще всего единственной, стоящей в центре
внимания) считается проблема В,
Предложение Р*-х говорит о том, что проблема В доводится
решением до конца, если будут разрешены проблемы С, Оу С'у С", ..., из
которых основной признается проблема С, а об остальных либо
забывают, либо умалчивают, считая их решения индивидуальными в
различных частных случаях.
Предложение Р*_2 говорит о том, что проблема С решится
немедленно, .если будут решены проблемы Dy D'y D'y D'"> ..., из которых
центральная есть Z), и т. д.
Это можно иллюстрировать на любой частной теории, входящей
в состав теории функций действительного переменного. Например,
а
в теории, интегрирования по Лебегу интеграл Лебега I f(x)dx будет
ъ
найден, если мы умеем определять меру множеств и выполнить
операцию о; мера множества найдется, если мы умеем находить верхнюю меру
множеств; верхняя мера множеств найдется, если мы умеем найти нижнюю
границу множества (операция О) и находить покрышки для множества.
1 В этом смысле очень интересны определения В и С, дающие несомненное
. расширение интеграла Лебега; см. указанное сообщение Данжуа (Comptes Rendas,
1919) и цитированный мемуар Бокса.
СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО 529
Набранная жирным курсивом проблема обычно не ставится, потому что
признается, что в различных частных случаях мы сумеем довести дело
до конца, смотря по создающейся обстановке, поступая в каждом
случае по-разному.
Короче говоря, в теории функций действительного переменного
необъятно многие проблемы рассматриваются как слишком элементарные,
и о них либо совсем умалчивают, либо считают как-то разрешаемыми.
Если приглядеться к делу, то идеалом считается тот случай, когда
удается отбросить все на проблемы арифметики, т. е. на натуральный
ряд чисел. Так, например, проблема о том, имеется ли рациональная
точка, принадлежащая всем отрезкам 81э о2, . .., оя, ..., охватывающим
эйлерову постоянную С и стремящимся по длине к нулю,—эта
проблема уже выходит из области теории функций.
Таким образом, в теории функций действительного переменного
молчаливо стараются фактически использовать закон исключенного
третьего там, где он скрывается в форме: проблема А разрешена, потому
что решение проблемы В должно иметь единственный ответ.
В этом отношении теория функций действительного переменного
имеет много общего с общей теорией функционалов: так, например,
верхняя мера mes Е множества Е есть просто функционал от переменного
множества Е. Такая точка зрения, безраздельно опирающаяся на
принцип исключенного третьего, вполне законна. Но здесь возникают
трудности вот какого порядка: пока функционал привлекается к
разрешению фактической (это слово употреблено в том смысле, в каком
английские математики, работающие в теории функций, употребляют слово
„материальный") проблемы теории функций, и пока он фигурирует
в единственном числе, все идет хорошо. Но когда проблема начинает
ставиться о взаимоотношении двух функционалов, тут чаще всего
встречаются непреодолимые трудности, проистекающие, на мой личный взгляд,
из необходимости отхода от формального принятия функционала и из
необходимости по удалении формального покрова функционала войти
глубоко в сущность тех операций и возможностей, которые он
молчаливо предполагает. Такова, например, проблема о существовании
неизмеримых множеств по Лебегу.
Ввиду сказанного в теории функций стараются всегда избавиться от
операций несчетного характера и сводить все дело к употреблению
операции о, взятой в конечном или счетном числе. И здесь прежде всего
сталкиваются с проблемой взаимоотношения меры Бореля и меры
Лебега.
Определение меры Лебега есть несчетная операция.
Мы видели, что она сводится к операции О, примененной к
специальной функции или множеству. Стремление удержать удаляющуюся
от математического анализа теорию функций в его пределах заставило
Бореля до начала работ Лебега предложить иную концепцию меры
множеств.
S30
Н. Н. ЛУЗИН
Борель отказывается с самого начала от концепции произвольного
точечного множества как такой, которая лежит „вне математики".
Согласно его взглядам, ввиду абсолютно различных в качественном смысле
способов определять множества, ввиду невозможности иметь
однородную рамку для удержания в ней всех качественно разнородных
определений различных индивидуальных множеств, необходимо сосредоточить
свое внимание лишь на определенных классах множеств, существенных
дая развития математического анализа.
Ясно, что этот прием есть истинно научный, тот, который приводил
математический анализ к его лучшим открытиям.
Достаточно вспомнить хотя бы эллиптические функции. Согласно
Борелю, стремление создать общую теорию точечных множеств вполне
беспредметно, не менее чем попытка создать общую теорию всех
приемов мышления.
Семейство множеств, выделенное Борелем, оказалось необычайно
плодотворным и творческим. Это так называемые множества,
измеримые В.
Не касаясь сейчас несравнимой ни с чем роли, которую играют эти
множества в математическом анализе, ни их классификации, я
ограничусь лишь необходимым дая указания проблемы меры.
Множество точек £, лежащих на отрезке [O^at^I], называется
измеримым Ву если оно определимо, отправляясь от отрезков, при
помощи следующих двух операций, повторенных конечное или счетное
число раз:
1°. Образовать разность двух множеств Ех и Е29 ранее уже
определенных и таких, что Е1 содержится в £.,:
tin) E*\'
2°. Образовать сумму счетного числа множеств Е1У £2, . . ., Еп, ... >
ранее уже определенных и не имеющих попарно общей точки:
Е^ -+- £2 н- ... -+- Еп н- ... .
Указанные две элементарные операции могут комбинироваться между
собой как угодно сложно, лишь бы не была допущена никакая новая
третья операция. Всякий раз, как мы получим два или счетное число
множеств Е1У Е29 > ЕпУ ..., измеримых Ву составляя разность Е2 — Ех
или сумму EY -+- Е2 -+- "+- Еп -+-..., мы выводим новые множества,
измеримые By и т. д.
Данное определение, обязанное самому Борелю, имеет несколько
расплывчатый характер, потому что не делает ясным ни переплетение
указанных операций, которые надо повторно проделывать, чтобы получить
искомое множество £, измеримое Ву ни говорит о том, какие по пути
промежуточные множества, также измеримые Ву придется образовать
дая получения в окончательном итоге искомого множества.
СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО $31
Более точно определение ставится так:
Множество Е называется измеримым В, если оно является
последним членом счетной вполне упорядоченной последовательности (цепочки)
множеств:
Е0> Elf Е2>..., £(|),..., £а,..., £, (6)
всякий член которой, не являющийся отрезком, выводится: либо из двух
предыдущих применением операции разности (1°), либо из счетного числа
предыдущих применением операции суммы (2°).
Данное определение ясно указывает, что множество Е> измеримое
Ву получается счетным числом условий, т. е. счетной операцией.
Естественно думать, что и мера множества Е определима счетным
процессом.
Борель ответил на этот вопрос утвердительным образом. Вот его
мероопределение:
I. Всякому отрезку [а, Ь\ лежащему на [0, 1], приписывается мера,
равная его длине Ь — а.
И. Если мы уже определили меры тЕг и тЕ2 множества Е1 и Е2Т
и если Ех содержится в £2, то т (Е2— Е1) = тЕ2— тЕ1У т. е. мера
разности равна разности мер.
III. Если мы уже определили меры тЕ1У тЕ2> ..., тЕп... множеств
Elf Е.1у ..., ЕПУ и если эти множества не имеют попарно общей точки, та
m (EY -+- Е2 ■+ ... -ь Еп -»-...) = mEl -§- тпЕ2 н- ... -+- гпЕп-+-...,
т. е. мера суммы равна сумме мер.
Ясно, что, идя по последовательности (6), мы таким образом шаг
за шагом будем находить в силу мероопределения Бореля меры ее
членов, пока наконец, придя к последнему ее члену 2Г, мы не получим
его меры тЕ.
Мы видим, что процесс получения меры Бореля есть счетный. Но
здесь может встретиться три и только три возражения:
1° применение операции разности мер II пгЕ2—тЕх может дать
отрицательный результат;
2° применение операции суммы мер III mEl-*-mE2-+-...-*-тпЕп
может дать расходящийся ряд;
3° ни откуда не следует, что мероопределение Бореля даст для
множества Е, измеримого Ву единственный результат: a priori возможно,
что, определяя одно и то же самое множество Еу измеримое В, двумя
различными цепочками (6), мы придем к численно разным мерам Бореля.
Впрочем, более подробный анализ показывает, что преодоление этих
трех затруднений сводится лишь к одному: невозможности получения
отрицательной меры для какого-нибудь члена цепочки (6). Однако до
сих пор эта невозможность, оставаясь при употреблении лишь счетных
процессов, еще не обнаружена. Это и есть знаменитая проблема меры
Бореля.
S32
Н. Н. ЛУЗИН
Однако, если мы допустим употребление несчетных процессов
в частности, мероопределения Лебега, все три указанные затруднения
устраняются мгновенно. Чтобы в этом убедиться, достаточно просто
констатировать, что мера Лебега mes Е есть по самому своему
определению единственное для данного множества Е неотрицательное число.
Далее, уже не в силу соглашения, а в силу теорем, вытекающих
немедленно из определения меры Лебега:
1° мера Лебега отрезка [а, Ь] равна его длине Ь — a, mes [а, 6] =
= Ь-а;
2° мера Лебега разности mes (Е2 — £\) равна разности мер Лебега,
mes (Е, — £\) = mes Е> — mes Ex 1;
3° мера Лебега суммы mes (2^ н-£.>"*"•• -~*-Ен-*- ...) равна сумме
мер Лебега, mes (EY -+~ Е, -+-...) = mes Е{ -+- mes Ег -+-...2
Таким образом, для меры Лебега мы имеем и неотрицательность, и
8аведомую сходимость ряда mes Ех -+- mes £>-*-..., и, наконец, по
самой природе его определения единственность.
Отсюда следует, что, применяя к цепочке (6) мероопределение
Лебега, мы будем двигаться по ней, все время получая численно те же
самые меры Лебега ее членов mes ЕаУ которые давал и метод Бореля,
тЕа. Следовательно, имеем mes E= тЕ, и таким образом доказывается,
что счетный процесс мероопределения Бореля не может встретить
никаких указанных выше затруднений и даст в результате то же самое
число /п£, которое дает и метод Лебега mesE:
тЕ = mes E.
Эта необходимость обращения к несчетному процессу Лебега, для
того чтобы оправдать счетный по своей природе процесс Бореля,
представляется загадочной. Имеем ли мы здесь лишь трудности технического
лорядка, или же здесь дело глубже и касается принципов? Ответ, без
сомнения, будет дан дальнейшими изысканиями.
'Другие изыскания по метрической теории функций.
Мы сосредоточили свое внимание на так называемых „теориях
интегрирования*4. Эти теории до сих пор являются одним из центральных
нервов метрической теории функций: проблемы, разрешаемые в этом
направлении, и вопросы, ставящиеся здесь, ясно говорят, что речь идет
вовсе не об „интегрировании" все более и более широких классов
функций, а об открытии нового предельного процесса, не опирающегося на
понятие трансцендентного числа и столь могущественного, что один он
был бы достаточен д\я разрешения столь разнородных задач, каковы
отыскание примитивных, определение коэффициентов тригонометрических
рядов. Еще Данжуа заметил, что работа в метрической теории функций
1 Предполагаются, разумеется, те же самые условия, что и у Бореля, т. е.
ято £| содержится в Е<ь*
2 Ет не имеет общей точки с Еп при т Ф п.
СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ ФУНКЦИЙ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО 533
сильно напоминает изучение микроструктур. При изучении работ по
теориям интегрирования и близким к ним областям открывается трудно
поддающееся описанию богатство взаимоотношений математических
микроструктур; эти взаимоотношения математических микроструктур
в последнее время начинают все чаще и чаще служить моделями уже
для взаимоотношений в математическом мире конечного.
Однако за истекшие пять лет не было недостатка в работах и в
других направлениях метрической теории функций.
Здесь прежде всего упомянем о работах по дробному числу
измерений и по расширению понятия линейной меры плоских множеств (Бе-
зикович, Цермело); метрическому строению плоских множеств [Булиган
(Bouligand), Келлог (Kellog), Василеско (Vasilesco)]; асимптотическому
изучению точечных множеств [Леви (P. Levy)); теории интегрирования
и меры множеств [Руссель (Roussel), Риддер (Ridder), Юнг (L. С. Joung)];
непрерывным преобразованиям с ограниченным изменением [Стоилов
(Stoilow)]; функциям a jcart fini [Брай (Bray)]; по тригонометрическим
рядам [Гилл (Hille) и Тамаркин, Szasz, Вольф (Wolf), Гарди (Hardy),
Литтльвуд (Littlewood), Алекситс (Alexits), Коплэнд (Copeland), Гагаев].
Мы оставляем в стороне работы по почти периодическим и
квазианалитическим функциям как более близкие к классическому анализу.
II
Нам осталось рассмотреть те направления, по которым двигалась
в течение последних пяти лет дескриптивная теория функций.
Здесь мы имеем работы, гораздо более многочисленные и более
принципиального значения, чем в метрической теории функций, где
технический момент играет все же заметную роль.
Большая часть работ по дескриптивной теории функций отведена
вопросам обоснования аналида, обоснования теории множеств [Стьюди
(Е. Study), Френкель (A. Fraenkel), Ласло (Laszlo), Кальмар (Kalmar),
Сцего (Szego), Баэр (Ваег), Гейтинг (Heyting), Нейман (v. Neumann)»
Брауэр (L. E. J. Brouwer), Горак (Horak), Ло (Leau), Кассина (Cassina)*
Лагаж (Lagage), Аккерман (Ackermann), Бернайс (Bernays), Шенфинкель
(Schonfinkel), Менгер (Menger), Гербранд (Herbrand), Жегалкин]. Затем:
следуют работы по вполне упорядоченным множествам [Журдэн (Jour-
dain), Френкель, Патаи (Patai)]; по общим свойствам функций
действительного переменного [Вереис (Vereis), Бэр (Baire), Ло, Фрода (Froda),
Скоцга (Scozza), Серпинский (Sierpinski)]; по теории эффективных
точечных множеств [Блю (Blue), Хаусдорф, Гуревич (Hurewiez), Куратовский
(Kuratowski), Серпинский и работы польской школы; в СССР: Лузин»
Колмогоров, Канторович, Ливенсон, Новиков, Келдыш, Селивановский].
Не претендуя на полноту списка, мы опускаем все работы по
топологической теории множеств ввиду естественности отнесения их к
топологии как ее приложений.
534
Н. Н. ЛУЗИН
Мы ограничимся здесь тем, что коснемся лишь работ по
обоснованию анализа. Центральное место в этих работах занимают по
объективной важности и по уделяемому всеми вниманию теория Д. Гильберта
и критика его взглядов и диаметрально противоположных взглядов
Л. Брауэра.
Трудно найти достаточно сильные слова, которые охарактеризовали
бы всю существенную важность этого направления. Важность и ценность
самой теории Гильберта и поднявшейся сейчас полемики вокруг его
взглядов и взглядов Брауэра могут быть сравнены с важностью того
момента (1904 г.), когда Цермело дал свою знаменитую „теорему" о том,
что всякое множество может быть „сделано" вполне упорядоченным,
и важностью тотчас же поднявшейся полемики (1905—1914 гг.). В обоих
этих моментах имеется много общего, не говоря уже о том, что самые
истоки теорий и споров — одни и те же.
Я уже достаточно полно высказался по поводу взглядов Гильберта
и Брауэра в моей предыдущей статье1, к которой и отсылаю читателя
за подробностями: новейшие работы не только не пролили света на
чрезвычайно глубокие и еще совсем темные пункты теории Гильберта,
но, напротив, запутали дело, потому что там, где была кажущаяся
ясность, в настоящее время оказывается либо проблема, либо дефект.
Здесь мы укажем лишь один пункт, стоящий в тесной связи с
генезисом идей Гильберта и Брауэра.
Известно, что Максвелл в целях наиболее яркой интерпретации своих
взглядов прибег к помощи некоторого воображаемого существа,
получившего у физиков имя Bai|xtov Максвелла: это воображаемое существо,
находясь у форточки, проделанной в перегородке, разделяющей сосуд
с газом, пропускает в одну сторону перегородки лишь молекулы с
большой скоростью и в другую сторону — молекулы, имеющие малую
скорость; в результате в сосуде без затраты работы одна половина будет
горячей, другая — холодной.
Это воображаемое существо было привлечено для наглядного
изображения его идей.
Аналогично, если анализировать взгляды творцов современной теории
функций, легко подметить, что каждый из них в процессе своей работы
исходит из определенной концепции возможного и допустимого, за
пределами которого кончается область математики и начинается область,
лежащая, по выражению Бореля, „вне математики" („en dehors des
1 Однако, по-видимому, моя личная точка арения представляется не совсем ясной.
По поводу этого я должен сказать, что я не рассматриваю ни теории Гильберта, ни
взглядов Брауэра достигшими той степени зрелости, начиная с которой можно
уверенно говорить о математической теории как осуществившейся. Всякая
осуществившаяся теория характеризуется творчеством новых теорем, открытием новых фактов,
которые одни только и могут служить к ее признанию. Теория, не дающая новых
фактов, ни к чему не может служить и в дальнейшем осуждена на забвение [54].
СОВРЕМЕННОЕ СОСТОЯНИЕ ТЕОРИИ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО 535
mathematiques"). Если, следуя примеру Максвелла, приписать область
возможного и исполнимого того или иного автора соответствующему
воображаемому существу, то получится следующая схема:
1. oatpav Б pay эра. Его область есть область целого конечного и
притом ограниченного путем указания верхнего конечного предела. За
этой областью все лежит „вне математики".
2. oat^iajv Бэра. Его область есть просто область целого конечного
без указания верхней конечной границы. Бесконечное —это лишь fa$on
de parler и находится „вне математики".
3. oai|xu)v Бореля. Его область есть область счетной бесконечности.
Всякое несчетное множество—„вне математики".
4. oat[xu)v Лебега. Его область есть область мощности континуума.
Всякая операция, требующая континуум простых шагов, доступна этому
oatpcDv'y; поэтому определение верхней меры еще лежит в области
математики, но мощность 2**1 — мощность совокупности всех функций — уже
отрицается Лебегом и не по силам его oatjxitfv'y.
5. Batjxujv Ц е р м е л о. Его поле операций — всякие мощности; в
частности, всякое множество oatjiujv Цермело может „сделать" вполне
упорядоченным.
Мы видим, что по мере увеличения нумера этого воображаемого
существа все увеличивается его „сила". И однако при всей логической
стройности точки зрения Цермело наличие „ Н^-парадокса" и других
служит непреодолимым препятствием дая принятия всерьез этой точки
зрения. Но, отступая с этой позиции на более „умеренную", трудно
вследствие отсутствия принципиальных соображений где-либо
остановиться посередине, и вот таким образом здесь, вероятно, кроется
причина, по которой часть математиков оказывается вместе с Брауэром:
в указанной классификации нет места соображениям умеренности и
интересны лишь ее фланги.
Соображения этого порядка и привлекли внимание Гильберта.
Гениальный мыслитель задумал спасти все положительное, что
сделано было в анализе и теории функций, путем создания глубокой
логической теории, стремящейся оправдать все то, что непротиворечиво, и
с ним все положительное анализа и теории функций.
В настоящее время трудно судить об истинности взглядов Гильберта
и ценности его теории.
Сведения, поступающие из литературы, весьма неполны, отрывочны
и туманны; сведения, идущие с мест, противоречивы. Без личного
контакта с деятелями в теории Гильберта нет возможности составить себе
правильное представление о сущности этой теории. Поэтому будет
правильным подождать дальнейших, уже по существу, сведений.
В этом же самом направлении протекают в настоящее время работы
у нас, в СССР, И. И. Жегалкина, с тем лишь различием, что, исходя,
как и Гильберт, из системы Ресселя (Russel), И. И. Жегалкин ищет
исключить из нее произвол и случайность и внести в нее алгорифм,
536
Н. Н. ЛУЗИН
который позволил бы в некотором роде алгебраически разрешать
Entscheidungsproblem Гильберта.
На этом пути автором получены чрезвычайно интересные и ценные
результаты. Объем и глубина их могут быть оценены лишь по
установлении точных взаимоотношений теорий Гильберта и И. И. Жегал-
кина [55].
С другой точки зрения, к исследованию объема математического
анализа подходит то направление дескриптивной теории функций,
которое ищет расширения пределов „эффективизма" множеств.
Сюда относятся и наши работы. Течение это ищет осуществить более
медленным путем нахождения фактов то, к чему стремятся теории,
исходящие из априорных соображений.
НЕКОТОРЫЕ ЗАМЕЧАНИЯ О КРИВЫХ, ЯВЛЯЮЩИХСЯ
АНАЛИТИЧЕСКИМИ ДОПОЛНЕНИЯМИ*
1. Назовем униформной кривой в плоскости XOY всякое точечное
множество С, которое пересекается каждой прямой, параллельной оси
OY в одной и только одной точке. Если N1 — какая-либо точка
множества С, определенная координатами х и z/, то ордината у является,
очевидно, величиной, зависящей от х, и является, таким образом,
однозначной функцией действительного переменного /(*), определенной для
всех значений х бесконечного интервала (—со < х <С~*- °°). В этом
случае равенство
У=/(х)
называется уравнением кривой С.
Обозначим через / и S два множества точек плоскости XOY,
определенные кривой С и расположенные соответственно ниже и выше этой
кривой. По точному определению / есть множество точек М(х> у)
плоскости, координаты которых удовлетворяют неравенству у<^/(х). Точно
так же S есть множество точек М(х> у), для которых у^>/{х). В
результате плоскость XOY разбита на три множества /, С и 5, не
имеющие попарно общих точек. Совершенно очевидно, что среди трех
множеств У, С и S одно вполне определяет два других.
2. Установив это, приведем теперь основные факты, которые
следуют из работ Бэра, Бореля, Лебега и Валле-Пуссена:
I. Если функция f(x) входит в классификацию Бэрау то три
множества /, С и S измеримы В.
II. Если одно из Двух множеств J и S измеримо 5, то функция
f(x) входит в классификацию Бэра.
Мы дополним эти основные результаты следующим свойством:
III. Если множество С аналитическое, в частности измеримое В,
то функция f(x) обязательно входит в классификацию Бэра1.
Доказательство получается немедленно, если применить теорию
аналитических множеств. В самом деле, известно, что необходимое и
достаточное условие а^я того, чтобы функция действительного пере-
* „Quelques remarques sur les courbes qui sont des complementaires analytiques".
Mathematica, Cluj, 10, 70—80, 1934.
1 W. S i e r p i n s k i. Fund. Math., II, 78 и 79, 1921.
538
Н. Н. ЛУЗИН
менного f(x) входила в классификацию Бэра, состоит в том, что одно
из четырех множеств
£(/>Д), Е(/<А), Е(/>А), £(/<Л)
было измеримо В> каково бы ни было А1.
Проведем в плоскости XOY прямую у = Ау параллельную оси ОХу
и обозначим через С часть данной кривой С, которая расположена
ниже этой параллели; пусть С" — множество остальных точек С. Так
как множество С по предположению аналитическое, то множество
С тоже аналитическое, потому что общая часть двух аналитических
множеств (С и открытой полуплоскости, определенной параллелью
у = А) является также аналитическим множеством2. Точно так же
множество С" аналитическое, будучи общей частью множества С и
замкнутой полуплоскости, определенной прямой у = А.
Установив это, спроектируем два множества С и С" на ось ОХ и
обозначим через е и е" соответствующие проекции множеств С и С". Так
как кривая С униформна, множества е и е" не имеют общих точек и
их сумма е-+-е" совпадает с осью ОХ. Но множества С и С"
аналитические; из этого следует, что их проекции е' и е" на ось ОХ являются
аналитическими множествами3.
С другой стороны, множества е и еиу будучи аналитическими и не
имея общих точек, отделимы В*. Это означает, что существуют два
множества Н и Н"у измеримые Ву не имеющие общих точек и такие,
что Н содержит е и соответственно Н" содержит е". Так как
множества е и е" являются взаимными дополнениями, они необходимо
совпадают с соответствующими отделяющими множествами Н и Н". Мы
заключаем отсюда, что два рассматриваемых множества е и е"
измеримы В.
Но из самого определения множества е мы имеем тождество
е' = Е(/<А),
и так как е измеримо Ву мы заключаем, что рассматриваемая функция
/(х) входит в классификацию Бэра (ч. т. д.).
Важно заметить, что если и ввести ограничительное предположение
относительно измеримости В рассматриваемой кривой С, все же нет
другого доказательства, не привлекающего теорию аналитических
множеств. Было бы очень интересно суметь дать другое доказательство,
1 См. Ch. de la Vallee-Poussin. Integrales, fonctions, classes de Baire,
стр. 32.
2 См. мои „Лекции об аналитических множествах" (в настоящем издании стр. 119—
Ред.).
3 Там же (в настоящем издании стр. 123—Ред.),
4 Там же (в настоящем издании стр. 133— -Ред.).
НЕКОТОРЫЕ ЗАМЕЧАНИЯ О КРИВЫХ, ЯВЛЯЮЩИХСЯ АНАЛИТ. ДОПОЛНЕНИЯМИ 539
позволяющее вывести без помощи теории аналитических множеств,
непосредственно из измеримости В кривой С, тот важный факт, что
«соответствующая функция /(х) входит в классификацию Бэра1.
Предположения I, II и III можно рассматривать как положительные
предложения, т. е. такие, которые дают положительный ответ на
поставленный вопрос, и было бы очень желательно, чтобы последующие
исследования всегда продолжались и распространялись в таком же
направлении. Но на этом пути мы сталкиваемся с определенно
отрицательными результатами.
Прежде всего мы видели, что из аналитичности множества С
следует, что функция f(x) входит в классификацию Бэра. Но мы не
можем получить аналогичного результата из предположения
аналитичности множества J или S:
Аналитичность одного из двух множеств J или S не влечет за
собой измеримость В кривой С, и функция f(x) может не быть
функцией классификации Бэра.
Чтобы это увидеть, достаточно рассмотреть следующий пример.
Пусть Е— какое-либо аналитическое множество, неизмеримое В,
расположенное на оси ОХ. Пусть f(x) — характеристическая функция
множества Е% т. е. равная 1 в точках множества Е и равная 0 в
остальных точках. Обозначим через С кривую, определенную уравнением
г/=/(лг). Я утверждаю теперь, что плоское множество J является
множеством аналитическим. Действительно, множество / является,
очевидно, объединением двух частей Jx и /2, имеющих общие точки:
первая часть Jx представляет собой множество точек М(х, у) плоскости,
у которых отрицательна ордината, следовательно, множество /г есть
открытая полуплоскость, а значит, измеримо В и таким образом есть
аналитическое множество. Вторая часть /2 является множеством
точек М(х> у) плоскости, абсцисса которых входит в данное
аналитическое множество Еу а ордината у меньше 1, у<^1. Легко доказать, что
множество /2 аналитическое.
Чтобы увидеть это, возьмем параметрическое представление
x = ?(t) (1)
данного аналитического множества Е; здесь ? (t) — функция,
определенная для всех иррациональных значений t интервала (0<О<1) и
непрерывная в каждой точке2. Если мы напишем одновременно два
уравнения:
1 По мнению Серпинского, эта проблема трудна, даже если предположить, что
С является множеством типа G$.
2 См. мои „Лекции об аналитических множествах" (в настоящем издании стр. 116—
Ред.).
540
Н. Н. ЛУЗИН
мы получим, очевидно, параметрическое представление множества J2r
осуществленное при помощи двух функций ф(/) и 1 — и1 двух
действительных переменных / и ц, которые явно входят в классификацию Бэра.
Мы заключаем отсюдах, что рассматриваемое множество У2 является
аналитическим множеством.
Отсюда следует, что самое множество J—множество
аналитическое, так как мы имеем J-=Jx-\-J^1,
С другой стороны, так как данное аналитическое множество Е
неизмеримо Ву характеристическая функция /(х) множества Е не может
входить в классификацию Бэра (ч. т. д.).
3. Итак, множество У, определенное какой-либо кривой С, может
быть аналитическим без того, чтобы соответствующая функция /(х)
входила в классификацию Бэра. Точно так же аналитичность множества
S не влечет за собой измеримость В соответствующей кривой С, так
как множество У, определенное для кривой
у =/{*).
является, очевидно, множеством S для кривой
У = -/(х).
Но важно заметить, что одновременная аналитичность множеств J и
S влечет положительное утверждение, которое гласит:
IV. Если оба множества J и S аналитические, то функция f{x)
входит обязательно в классификацию Вэра.
Чтобы показать это, предположим сначала, что только множество J
аналитическое, и рассмотрим новую кривую, которую мы обозначим
через Ое), определенную уравнением
У =/(*)+-£>
где функция /(х) соответствует данной кривой С, а е — произвольное
положительное число. Пусть У(в) и S^— множества, определенные кривой С
и расположенные соответственно ниже и выше этой кривой. Ясно, что
множество У(с)—не что иное, как множество У, перемещенное в
положительном направлении оси OY на положительную величину. Отсюда
следует, что оба множества J и /{t) одной природы. Так как множество J
по предположению аналитическое, то множество У(е) также
аналитическое.
Будем теперь придавать £ бесконечную убывающую
последовательность значений elf е2, ..., ея ..., стремящуюся к нулю. Так как
множество У£> аналитическое, каково бы ни было натуральное число л,
1 См. мои „Лекции об аналитических множествах" (в настоящем издания
стр. 116 — Ред.).
2 Там же (в настоящем издании стр. 119 —Ред.).
НЕКОТОРЫЕ ЗАМЕЧАНИЯ О КРИВЫХ, ЯВЛЯЮЩИХСЯ АНАЛИТ. ДОПОЛНЕНИЯМИ $41
пересечение аналитических множеств /<■»>, /(6i),..., J^\ ... является снова
множеством аналитическим1. Но это пересечение, очевидно, есть не
что иное, как сумма двух множеств / и С. Таким образом, если мы
предполагаем множество / аналитическим, то сумма /-«-С является
обязательно аналитическим множеством и, следовательно, множество S
является аналитическим дополнением.
До сих пор мы делали единственное допущение, что множество /
аналитическое. Мы вывели из этого, что множество S является
аналитическим дополнением. Из этого следует, что если мы сделаем второе
допущение и предположим множество S аналитическим, мы придем
к выводу, что множество S заведено измеримо В и, следовательно,
функция f{x) входит в классификацию Бэра (ч. т. д.).
Из самого доказательства предыдущей теоремы мы видели, что
аналитичность множества J влечет за собой аналитичность суммы ]-\-С.
Но и обратное предложение опять-таки имеет место:
Аналитичность суммы J-*-C влечет за собой обязательно
аналитичность множества J.
Чтобы убедиться в этом, достаточно рассмотреть кривую Св,
определенную при помощи
где £ — произвольное положительное число и функция f(x)
соответствует данной кривой С. Обозначим через /t и S% два множества,
расположенные соответственно ниже и выше кривой Се. Ясно, что
множество ]г и кривая Сг являются не чем иным, как множеством / и
данной кривой С, перемещенными в отрицательном направлении оси OY
на положительную величину е. Отсюда следует, что оба множества-
суммы Jz-*-Ct и /+С являются множествами одной природы, и
следовательно, если множество /-*-С аналитическое, то и множество /tH-Ct
также аналитическое.
Будем придавать теперь £ бесконечную убывающую
последовательность значений ер г2,..., ея,..., стремящуюся к нулю. Так как
множество Jtn-*-Ctn аналитическое, каково бы ни было натуральное число л,
сумма множеств /ем -§- С*п (л = 1, 2, 3 ...) является также
аналитическим множеством1. Но это множество-сумма совпадает, очевидно, с
исследуемым множеством /, что и доказывает аналитичность / (ч. т. д.).
Точно так же аналитичность С н- S влечет аналитичность S.
4. Желая изучать различные кривые С с точки зрения чисто
геометрической, следует начать с различения наиболее простых кривых.
Очевидно, что среди кривых С наиболее простыми являются кривые,
измеримые Ву и что тем более простой является кривая С, чем меньше
класс множества С.
1 См. мои „Лекции об аналитических множествах" (в настоящем издании стр. 119—
Ред.).
2 Там же (в настоящем издании стр. 119 — Ред.).
542 н. н. лузин
Казалось бы, что наиболее простыми кривыми С, идущими вслед
за кривыми, измеримыми В, являются аналитические кривые,
неизмеримые В. Но изучение таких кривых было бы ложным шагом, потому что,
как мы видели, не существует таких кривых: каждая
аналитическая кривая обязательно измерима В.
Следовательно, здесь имеется нечто вроде разрыва, скачка, и
наиболее простыми кривыми, идущими за кривыми, измеримыми В,
по-видимому, являются аналитические дополнения.
Следует заметить, что точка зрения чисто геометрическая очень-
заметно отличается от точки зрения аналитической. С точки зрения
анализа характеристическая функция /(х) аналитического множества Еу
неизмеримого В, является функцией довольно простой и может
рассматриваться как немедленно следующая за функциями классификации
Бэра. В противоположность этому, геометрия рассматривает кривую С,
соответствующую функции
у =/(*),
как кривую очень сложную, потому что ее геометрическая природа
представляет собой объединение, части которого имеют между собой
отношения сложные и трудно уловимые: действительно, эта кривая С
не является ни аналитическим множеством, ни аналитическим
дополнением, будучи суммой двух множеств, одно из которых аналитическоег
а другое аналитическое дополнение.
Исходя из этого, ставится вопрос, узнать, существуют ли в
действительности кривые С, которые являются аналитическими
дополнениями, неизмеримыми В. Этот вопрос является тем более
естественным, что не имеется аналитических кривых, неизмеримых В.
И очень важная теорема Мазуркевича1 дает нам ответ определенно
положительный. Вот формулировка этой теоремы: каково бы ни было
аналитическое множество Е, расположенное на оси ОХ, существует
униформное аналитическое дополнение Н, расположенное в плоскости
XOY, ортогональная проекция которого на ось ОХ совпадает с Е.
Чтобы хорошо понять смысл этой теоремы, следует отметить, что
униформным называют всякое множество точек плоскости XOY,
которое пересекается каждой прямой параллельно оси OY не более чем
в одной точке. В первую минуту этот важный результат С. Мазуркевича
кажется весьма парадоксальным, потому что всякое аналитическое
дополнение, расположенное на измеримой В кривой С, имеет проекцией
аналитическое дополнение, и потому что имеется очень обширное семейство
униформных аналитических дополнений, которые не могут быть
помещены на измеримой В кривой С и тем не менее имеют в качестве
1 См. S. Mazurkiewicz. Sur une propriete des ensembles С (A). Fund. Math.r
X, 172—174. „Лекция об аналитических множествах" (в настоящем издании стр. 235—
Ред.).
НЕКОТОРЫЕ ЗАМЕЧАНИЯ О КРИВЫХ, ЯВЛЯЮЩИХСЯ АНАЛИТ. ДОПОЛНЕНИЯМИ 543
проекций на ось ОХ аналитические дополнения: а именно, таким является
множество точек единственности плоского измеримого В множества б\
т. е. множество точек £, лежащих на параллелях оси О К, пересекающих 6
в одной и только одной точке1.
Теорема Мазуркевича доставляет нам средство аля отыскания
униформной кривой Су являющейся аналитическим дополнением,
неизмеримым В. В самом деле, возьмем на оси ОХ какое-нибудь аналитическое
множество, неизмеримое В. Пусть Н—униформное аналитическое
дополнение, расположенное над осью UX, проекция которого на эту ось
совпадает с данным аналитическим множеством £.
Возьмем в качестве униформной кривой С множество, состоящее из
точек Н и из точек оси иХ, которые не входят в £. Ясно, что С
является суммой двух аналитических дополнений: И и СЕ. Таким
образом, С является аналитическим дополнением. С другой стороны,
очевидно, что С неизмеримо В, потому что часть Н кривой С,
расположенная над осью иХу была бы в противном случае множеством,
измеримым Ву что невозможно, ибо проекция Е множества И—заведомо
неизмеримое В множество2.
Итак, существуют неизмеримые В кривые С, которые являются
тем не менее аналитическими дополнениями.
Из этого предложения следует, что аналитичность суммы J+-S
не влечет за собой измеримости В кривой С, и функция /(х) может
не быть функцией классификации Бэра.
5. Так как можно рассматривать кривые С, являющиеся
аналитическими дополнениями, как наиболее простые вслед за измеримыми В
кривыми, было бы очень желательно, чтобы имелись какие-либо общие
результаты относительно соответствующих функций /(л:). Первая из
проблем, которые ставятся в связи с функциями /(х), — проблема о
природе множеств J и S. Являются ли эти множества всегда проективными
множествами? Положительный ответ нетруден и почти очевиден. Но
строгие исследования относительно точной природы множеств / и S
кажутся представляющими большие трудности.
Пусть С—кривая, являющаяся аналитическим дополнением, и /(х) —
соответствующая функция. Возьмем последовательность rlf r2, .. ♦ > г„, ...
всех рациональных чисел и проведем в плоскости XOY прямую у = гп>.
параллельную оси ОХ. Пусть Сп — часть С, расположенная над этой
параллелью; ясно, что Сп — аналитическое дополнение, измеримое В или
неизмеримое В. Обозначим через еп проекцию С„ на ось ОХ; ясно, что
еп — проективное множество, которое может быть представлено в форме
РСРЕу где Е — измеримое В множество, так как множество Сл, являю-
1 См. мои „Лекции об аналитических множествах" (в настоящем издании стр. 235—
Ред.),
2 Проекция униформного измеримого В множества всегда измерима В; см. мои»
„Лекции об аналитических множествах" (в настоящем издании стр. 203— Ред.).
Н. Н. ЛУЗИН
щееся аналитическим дополнением, может быть записано как СРЕ1.
Таким образом, множество еп является множеством (А2). Отсюда следует,
что линейное дополнение множества еП9 которое мы обозначим через
т1я, является проективным множеством (СЛ2). Согласно теореме о
множествах параллелей2 мы заключаем, что множество Нп точек М (х, у)
плоскости, абциссы которых х принадлежат t]n и ординаты у < гя, является
плоским проективным множеством (СЛ2). Теперь, если мы будем изменять
00
натуральное число п, л=1, 2, 3, ... и возьмем сумму V //„, мы будем
иметь плоское проективное множество, которое снова является
множеством (СЛ2), так как сумма счетного числа множеств (САп) является
проективным множеством и самое большее (САп)3. Но, очевидно, что
сю
множество-сумма ^] Нп совпадает с множеством /, определенным для
данной кривой С. Таким образом, множество / проективно и самое
большее (СА.г).
Так как множество S, определенное дая кривой г/=/(лг), является
множеством / дая кривой у = —/(•*)> мы заключаем, что множество S
также проективно и самое большее (СА2)- Так как данная кривая С
является аналитическим дополнением, а значит (САХ)> то отсюда следует,
что множество-сумма С -+- S является самое большее (СА2), и значит,
дополнительное множество J не более, чем (А2). Так как множество /
является одновременно {СА.г) и (Л2), мы заключаем, что множество J
не более, чем (52). То же заключение имеет место и дая множества S.
Итак: если кривая С является аналитическим дополнением, то
два соответствующих множества J и S являются проективными
множествами не более, чем (В2).
Между тем вероятно, что это — грубое определение природы / и S
и что дальнейшие исследования будут проведены со всей точностью.
В случае кривой Мазуркевича природа множеств J и S может быть
уточнена. В самом деле, если дано какое-либо аналитическое множество Е
«а оси ОХу Мазуркевич строит в плоскости КОY множество &,
измеримое В, проекцией которого на ось ОХ является данное аналитическое
множество Е, Следует отметить, что каждая прямая, параллельная
оси О К, проведенная через какую-либо точку х множества Е, пересекает
множество & по множеству &х точек, нижняя ?рань которого [* является
обязательно точкой множества <§х. Мазуркевич доказал, что
множество Н точек [i-y, соответствующих точкам множества /Г, является
аналитическим дополнением, которое, очевидно, униформно. И легко
доказать, что множество 0 точек М (дс, у) плоскости, расположенных
над точками \*<Ху является множеством аналитическим.
1 См. мои „Лекции об аналитических множествах" (в настоящем издании стр. 225—
.Ред.).
2 Там же (в настоящем издании стр. 232—Ред.).
3 Там же (в настоящем издании стр. 233—Ред.).
НЕКОТОРЫЕ ЗАМЕЧАНИЯ О КРИВЫХ, ЯВЛЯЮЩИХСЯ АНАЛИТ. ДОПОЛНЕНИЯМИ 545
Действительно, множество 0 обладает параметрическим
представлением с двумя переменными:
* = ?('). y = v(t)+u\ (3)
где уравнения * = cp(f), i/ = со (f) дают параметрическое представление
плоского измеримого В множества <?, а и — произвольный параметр.
С другой стороны, ясно, что множество всех точек М (х, у)
плоскости XOY> абсциссы которых х принадлежат £, является плоским
аналитическим множеством; пусть D — это множество. Наконец, обозначим
через G множество точек М (л:, у) плоскости, абсциссы которых х не
принадлежат Е и ординаты у отрицательны. Ясно, что G является
плоским аналитическим дополнением. Далее очевидно, что исследуемое
множество / представляется следующей формулой:
/=G-+-(£> —0) = G-+-£>C6.
Из этого следует, что / есть сумма аналитического дополнения и общей
части аналитического множества и аналитического дополнения. Таким
образом, множество / является множеством (52) очень частного вида,
будучи составлено из аналитических множеств и их дополнений при
помощи двух операций: суммы и пересечения,, повторенных конечное
число раз1.
6. Теперь ставится интересный вопрос: обязательно ли отделимы В
две кривые, являющиеся аналитическими дополнениями, одна из которых
находится под другой? Ответ, очевидно, зависит от самого определения
отделимости В-кривых* Здесь можно дать следующие три определения
отделимости В-кривых.
Первое определение. Две произвольные кривые С\ и С2, одна
из которых расположена над другой, называются отделимыми В при
помощи кривой, если можно провести в плоскости промежуточную
кривую С2, измеримую Ву которая расположена под одной и над другой
из данных двух кривых Сх и С2.
Это определение не может представлять, очевидно, никакого интереса,
потому что, какова бы ни была кривая y:=zf(x)y проведенная в
плоскости XOY и неизмеримая Ву можно указать такую положительную
величину е, чтобы две кривые у =/(х) и у=/(х)ч-г были неотделимы В
в смысле первого определения. Действительно, в противном случае легко
видеть, что если придавать э убывающую последовательность
значений elf е2, ..., ея, ..., стремящуюся к нулю, то функция /(х) является
пределом последовательности промежуточных функций /г (х), /2 (х), ...,
/п(х)} ..., входящих в классификацию Бэра, равномерно сходящейся к/(х).
Таким образом, функция/(х) и сама входит в классификацию Бэра.
Второе определение. Две произвольные кривые Сх и С2
называются отделимыми В при помощи двух множеству если можно
1 Там же (в настоящем издания стр. 233 — Ред.).
2 Ср. Ch. de la Vallee-Poussin. IntSgrales, Fonctions, Classes de Baire,
стр. 128.
546
Н. Н. ЛУЗИН
найти два множества Нг и //>, измеримые Ву не имеющие общих точек
и такие, что Сх содержится в Нх и соответственно С2 содержится в //2.
В связи с этим определением можно указать без труда, что существуют
две кривые Сх и С2, являющиеся аналитическими дополнениями и
неотделимые В в смысле второго определения.
Чтобы убедиться в этом, возьмем в интервале (О <С х < 1) оси ОХ
два аналитических дополнения <§\ и £2, которые неотделимы В с точки
зрения отделимости В точечных множеств. Известно, что такие
аналитические дополнения существуют г.
Пусть Нх — униформное аналитическое дополнение, расположенное
под осью ОХ, проекция которого на эту ось совпадает с линейным
аналитическим множеством С£х. Точно так же, пусть Н2 — униформное
аналитическое дополнение, расположенное над осью ОХ, проекция
которого на ось ОХ совпадает с линейным аналитическим множеством С§^
Исходя из этого, мы определим две функции действительного
переменного fi(x) и />(х) следующим образом: /х(х) равна нулю на &х и
ординатам точек униформного множества Нх вне &г; /2{х) равна нулю на
<§2 и ординатам точек униформного множества Н2 вне £2.
Совершенно очевидно, что Л (*) <СЛ («*)> каково бы ни было х; что
кривые Сг и С2, определенные соответственно уравнениями у =/2 (*)
и у =/2 (х), являются аналитическими дополнениями и что Сх и С2
неотделимы В в смысле второго определения.
Третье определение. Две произвольные кривые С\ и С2, одна
из которых расположена под другой, называются отделимыми В при
помощи множества, если существует в плоскости XOY измеримое В
множество Е, расположенное между двумя данными кривыми Сх и С2>
которое пересекается обязательно каждой прямой, параллельной оси 0Yf
по крайней мере в одной точке.
С точки зрения этого определения ничего не известно об
отделимости кривых, которые являются аналитическими дополнениями. Можно
только заметить, что каждое плоское измеримое В множество содержит
униформизирующее множество Н, которое является аналитическим
дополнением2 и что униформизирующая кривая С множества Е должна быть
расположена между двумя данными кривыми Сх и С2, равно как и
отделяющее множество Е.
Замечу, что вопросы, очень близкие к тем, которые рассматривались
в настоящей статье, излагаются в работе: W. Sierpinski. Sur certains
ensembles plans (Mathematica, IV, 178, Cluj, 1931).
1 См. мои „Лекции об аналитических множествах" (в настоящем издании стр. 221—
Ред.); см. также П. С. Новиков. Sur les fonctlons implicites mesurables В (Fund*
Math., XVII, стр. 8).
2 См. работы по униформизации множеств W. Sierpinski. Sur certains
ensembles plans, и N. Lusin. Sur le probleme de M. Jacques Hadamard d'uniformisation
des ensembles (Mathematica, IV, 62 и 178, Cluj, 1930).
НЕСКОЛЬКО ЗАМЕЧАНИЙ О КРАТНОЙ ОТДЕЛИМОСТИ*
1. О сообщении П. С. Новикова. В предыдущем сообщении,
озаглавленном „Об одном свойстве аналитических множеств",
П.С.Новиков вводит весьма интересное и обещающее быть ценным новое
понятие, которое естественно назвать кратной отделимостью.
Как известно х9 два какие-либо множества точек Ех и Е2У не имеющие
общей части, называются отделимыми Ву если можно найти такие два
множества точек Нх и Н2у измеримые В, которые также не имеют
общей точки и которые соответственно содержат данные множества Е1
и Е2У. т- е-
Ех С Нх и Е2 С#2.
Этот случай отделимости двух множеств П. С. Новиков
рассматривает лишь как самый простой, вводя вслед за ним более общее понятие
кратной отделимости трех, четырех и большего числа множеств.
Случай трех множеств формулируется так:
три какие-нибудь множества точек Ех, Е2 и £3, не имеющие части,
общей им всем, называются отделимыми В9 если можно найти такие
три множества точек НХУ Н2 и //3, измеримые В, которые также не
имеют общей им всем части и которые соответственно содержат данные
множества Е19 Е2 и ЕЗУ т. е.
Ех СНХУ Е2СН2 и £3 С//3.
Это определение было П. С. Новиковым распространено на любое
конечное число множеств Е1У Е2У ..., Ет; А. А. Ляпунов расширил
его на случай счетного числа множеств.
2. Это определение оказалось не только точно копирующим по своей
внешней форме обыкновенную (т. е. а^я двух множеств) отделимость Ву
но и другие далеко идущие результаты обнаруживают, что в этом
определении мы имеем дело с полной и глубокой аналогией отделимости
двух множеств.
Так, совершенным аналогом теоремы, названной нами „первым
принципом" :
два аналитические множества Ег и Е2У не имеющие обшей точки,
всегда отделимы Ву является предложение П. С. Новикова:
• ДАН СССР, 2, № S, 280—284, 1934.
1 См. стр. 132 настоящего тома.—Ред.
548
Н. Н, ЛУЗИН
три аналитические множества E]f Е2 и £3, не имеющие общей
им всем точки, всегда отделимы В, расширенное им на любое
конечное число аналитических множеств. Это предложение было распространено
А. А. Ляпуновым на счетное число множеств.
Ввиду этой аналогии естественно желать исследовать, сохраняется
ли она в столь же совершенном виде и при других свойствах множеств
при формулировке которых фигурирует обычная отделимость двух
множеств. Целью настоящего сообщения является указание на
некоторые относящиеся сюда предложения, от которых следует ожидать такой
аналогии.
3. ЬЦ этом пути мы прежде всего встречаемся с вопросом о
переносе понятия кратной отделимости на о тделимость посредством
аналитических дополнений.
Известно1, что наряду с отделимостью В имеется также отделимость
посредством аналитических дополнений („отделимость СА"), причем эта
отделимость имеет отнюдь не формальное значение, так как
действительно существуют непересекающиеся аналитические дополнения Ех и
Е2, которые уже неотделимы В. Напротив, отделимость посредством
аналитических множеств не имеет никакого реального значения, так как
всякие два непересекающиеся аналитические множества Ех и Е2 всегда
отделимы В- Известно2, наконец, что отделимость посредством
аналитических дополнений имеет не только существование в действительности,
но приобретает уже чисто математическое значение благодаря
приложениям к теории неявных функций, основывающимся на теореме,
названной нами „вторым принципом"3:
если уничтожить из двух аналитических множеств Ех и Е2 их
общую часть Ех • Е2У оставшиеся их части отделимы посредством
двух непересекающихся соответственных аналитических дополнений
СНЛ и СН2У т. е.
Егсснг и Е2асн2.
Легко видеть, что эта теорема получает немедленное расширение
на случай трех аналитических множеств следующим образом:
если уничтожить из трех аналитических множеств Elf Е2 и Еь
их общую часть Ех- Е2- Еъ, оставшиеся их части отделимы
посредством трех соответствующих аналитических дополнений СН19 СН2
и СНЗУ не имеющих точкиу общей им всем> т. е.
Е2 С СНи Е2 С СН2 и £3 С С#3.
Доказательство. Пусть Е19 Е2 и Ez — какие-нибудь три
аналитические множества. Пусть Е есть их общая часть, E = Ej • E2EV
1 См. стр. 174 настоящего тома.—Ред.
2 См. стр. 225 настоящего тома.—Ред.
8 См. стр. 175 настоящего тома. —Ред.
НЕСКОЛЬКО ЗАМЕЧАНИИ О КРАТНОЙ ОТДЕЛИМОСТИ
54£
Удаляя ее из каждого аналитического множества £, (i = l, 2, 3), мы
получаем остаточные множества Ri9 /?. = £<— Е. Предложение, которое
мы имеем в виду, таково: существует три такие аналитические
дополнения СНХ, СН2 и С7/3, которые не имеют общей им всем точки и для
которых Rx С СН1У R2 С С#2, #3 С СН3.
Чтобы убедиться в этом, рассмотрим сначала два аналитических
множества Ех и £2-ь£3. Общая их часть Ег- (E2-+-Ez) есть опять
аналитическое множество. В силу второго принципа множества-остатки
Ег • СЕ2 . CEZ и (£2-ь£3) ■ СЕХ
отделимы посредством двух непересекающихся аналитических
дополнений СКХ и СК2, т. е.
E1CE2^CEzdCKl и (£2-k£3)-C£iCCA:2,
где Кх и К2 суть некоторые аналитические множества и где СКг X
хсл:2=о.
Аналогично имеем:
Et-CE1-CE^c:CLl и {El4-Ez)CE2(zCL,
и
Еь • СЕг • С£2 с СМХ и (^н-f.,) • С£3 с СМ2>
где Llf L2, М± и М2 суть аналитические множества и где CLX- CL2 = 0
и СМ1-СМ2 = 0.
Мы имеем таким образом три аналитических дополнения:
СКХ • CL2 • СМ2, CLX • СК2 • СМ2 и СМг • (Ж2 • CL2,
соответственно содержащих множества-остатки
EY • СЕ2 • С£3, £2" С-^1" С£3, £з * С£х • С£2
и попарно не пересекающихся.
Таким же точно образом рассмотрим два аналитических множества £t
и £2-£3. Общая их часть £, £ = £1-£2-£3 есть опять аналитическое
множество. В силу второго принципа множества-остатки
R1 = El — E и £2-£3 —£
отделимы посредством двух непересекающихся аналитических
дополнений CUX и CU2y т. е.
Rl = E1 — EczCU1 и £2£3 —£cCf/2,
где £/х и £/2 суть некоторые аналитические множества и где С11л X
ХС£/2 = 0.
sso
н. н. лузин
Аналогично имеем:
R2 = E2 — E<zCVl и Ех-Е2 — E(zCV2
Rz = Ez — E(zCW1 и Ex-E2 — E(zCW2y
где Vx% V2, Wx% W2 суть аналитические множества и где
CV^CV2 = 0 и CWx-CW2 = 0.
Мы получаем таким образом три новых аналитических дополнения:
си2 • cvx • cw» cv2 • си, • cwx и cw2. сих • ci/lt
очевидно» соответственно содержащих множества-остатки
Е2 • Е% — Еу Е, • £3 — ^ и ^i' Е*2 — Е
и попарно не пересекающихся.
В этих условиях очевидно, что три аналитические дополнения СН19
СНг и С//3, определенные равенствами:
снх=скх • ol2 . см2-^ст/2 • стл • cwl4-cw2. сгл • ci/lf
CHt=CLx • c/:2 • см2+си2 • сц • cif, h-cip; . С£л. ci/lf
CH, = CML • CAT2 • CL2 + CU2 • CVX • СИ^Ч- Cl/2 • CUX • dTlf
не имеют общей им всем точки и содержат соответственно множества-
остатки R{, /?2 и /?3, т. е.
Rx С С//1Э /?•> С СН2 и /?3 С СЯ3
(ч. т. д.).
Таким образом, расширение второго принципа на случай трех
аналитических множеств Ev E2 и Ez, у которых удалена общая им всем
часть Ех- Е2- EZf действительно имеет место. Употребленный дая этого
случая элементарный прием, вероятно, распространяется и на случай
любого конечного числа аналитических множеств, у которых удалена
общая им всем часть, так как, по-видимому, доказательство этой теоремы
не требует введения каких-либо новых рассмотрений, но лишь просто
комбинаторного искусства и удачных обозначений.
Например, расширение теоремы, о которой идет речь, на случай
счетного числа аналитических множеств Еи Е2> ..., £я, ..., у которых
удалена общая им всем часть, по-видимому, требует рассмотрений
принципиально иной природы, вероятно, связанных с конституантами
аналитических дополнений.
4. В связи с этим стоит вопрос о реальности кратного отделения
яосредством аналитических дополнений. Дая установления того важного
факта, что кратная отделимость посредством аналитических дополнений
имеет не только формальное, но и действительное значение, необходимо
НЕСКОЛЬКО ЗАМЕЧАНИЙ О КРАТНОЙ ОТДЕЛИМОСТИ
S51
доказать существование ! трех таких аналитических множеств, которые
по удалении общей им всем части, дали бы остатки, неотделимые В.
Сюда же относится вопрос об „односторонней отделимости44.
Известно2, что если имеем два множества ёх и £2 таких, что gx
отделимо от ё2 ПРИ помощи некоторого аналитического множества Ег, т. е.
^с^и S2(ZCEU
и одновременно с этим &2 отделимо от ёх также при помощи
некоторого аналитического множества £2, т. е. &2 С Е2 и ёг С СЕ2, то тогда
Si и ё2 одновременно отделимы друг от друга при помощи двух взаимно
яе пересекающихся аналитических дополнений СНХ и СН2> т. е. <§г С СНХ
и ёх С С#2, где СНХ • СЯ2 = 0.
Спрашивается, в какой форме должна выражаться односторонняя
кратная отделимость?
Далее, сюда же относится вопрос о втором принципе не для самих
аналитических множеств, а для их дополнений. Известно3, что если
СЕ1 и СЕ2 суть некоторые два аналитических дополнения, то,
удаляя из них общую им часть СЕХ • СЕ2> мы получаем множества-
остатки, отделимые при помощи аналитических дополнений.
Спрашивается, имеется ли аналогичное предложение при кратной
отделимости?
Наконец, укажем мимоходом, что первый и второй принципы для
аналитических множеств допускают приложение к множествам,
измеримым Ву и что тогда они называются5" „малыми принципами"4.
Спрашивается, имеется ли среди множеств, измеримых В, также и кратная
отделимость?
5. О сообщении А. А. Ляпунова. Мы уже указывали, что
в своем предыдущем сообщении, озаглавленном „Об отделимости
аналитических множеств", А. А. Ляпунов полностью разрешил проблему об
отделимости В счетного числа аналитических множеств, не имеющих
общей всем им точки. Этого прекрасного результата ему удалось
достигнуть благодаря следующей замечательной лемме:
если находящиеся в счетном числе в евклидовом пространстве
аналитические множества Elt Е2, ..., Еп, ... не имеют общей им
всем точки, и если дополнение к каждому из них разбито на
конституанты, тогда минимальный номер конституанты во всякой
точке пространства остается меньше некоторого фиксированного
трансфинитного числа второго класса.
Лемма эта глубока и, по-видимому, имеет применимость, далеко
выходящую за пределы того огромного приложения, которое ей дал
автор.
1 См. етр. 221 настоящего тома.—Ред.
2 См. стр. 174 настоящего тома. — Ред.
3 См. стр^ 175 настоящего тома. —Ред.
* См- стр. 477 настоящего тома. — Ред.
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ
ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИИ*
Целью настоящего доклада является наложение результатов новых
изысканий в области дескриптивной теории функций. Результаты эти
составляют содержание работ, выполненных в течение 1934/35 акад.
года в отделе теории функций действительного переменного
Математического института им. В. А. Стеклова при Академии наук СССР.
Работы эти были выполнены частью мною лично, частью же ученым
специалистом названного института доктором Петром Сергеевичем
Новиковым. Результаты, полученные им, столь глубоки и сильны, что,
собственно говоря, должны были бы составить содержание двух
отдельных докладов сессии.
Тесное расположение конституант
1. Происхождение проблемы. Конституанты аналитических
дополнений изучались внимательно в течение ряда лет. Работами как
математиков СССР, так и Польши были обнаружены чрезвычайные тонкость
и сложность их строения, влекущие большое богатство свойств,
касающихся их самих и их расположения. Из этих свойств в первую очередь
упомянем о следующем.
Пусть <§ есть аналитическое дополнение, лежащее на оси ОХ, Мы
предполагаем соответствующее ему аналитическое множество Е
заданным посредством решета С, лежащего на плоскости XOY и состоящего
из счетного числа прямолинейных интервалов, параллельных оси ОХ.
Пусть х есть какая-нибудь точка оси ОХ, Рх— перпендикуляр
в точке х к оси ОХ и Rx— пересечение решета С с
перпендикуляром Рх.
В этих условиях, если х принадлежит к Еу множество Rx не есть
вполне упорядоченное по отношению к положительному направлению
оси OY; если же х входит в <£, множество Rx есть вполне
упорядоченное и имеет вполне определенный тип ^х.
Если мы через &а обозначим множество тех точек ху где fs = a> то
&а и есть „<х-ая конституанта" аналитического дополнения <£.
Конституанты эти дают место равенству
£ = £0-+-£i4-£2h-. ..-ь^ч-...^-t- |2, (1)
1 Впервые напечатано в 1935 г., Москва.
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИИ 553
называемому „разложением аналитического дополнения & по
конституантам".
Известно, что конституанта <§а всегда измерима В. Известно также
следующее важное свойство конституант <§а.
Каково бы ни было аналитическое, в частности измеримое Ву
множество точек Н, лежащее на оси ОХ и содержащееся в S, оно
содержится целиком в сумме заведомо счетного числа
конституант £а.
Из этого предложения сразу же следует, что необходимым и
достаточным условием для того, чтобы аналитическое дополнение & было
неизмеримо В, является существенная трансфинитность
разложения (1), т. е. чтобы имелось несчетное число непустых конституант Sa
(иначе говоря, действительно содержащих точки). Таким образом, для
того чтобы S было измеримым В, необходимо и достаточно, чтобы все
конституанты &а были пустые, начиная с некоторого индекса р.
Большое математическое и философское значение имеет вопрос, ко-
торый мы формулируем как „первую проблему".
Проблема I. Узнать, существует или нет решето С такоег
что всякая конституанта &0 состоит из одной и только одной
точки?
Философское значение этой проблемы состоит в том, что
утвердительное решение ее ответило бы на важный вопрос о сравнимости
мощности континуума с и мощности алеф-один (tfi). До сих пор не только
этот вопрос не разрешен, но еще не известно, в каком направлении
вероятнее всего ожидать решения: с одной стороны, метод рассуждения
математиков-идеалистов, состоящий в ничем не ограниченной свободе
применения аксиомы Цермело дает множества точек мощности Si и>-
значит, утверждает сравнимость с и ^ в смысле
c>Sx.
С другой же стороны, наблюдение математиков-реалистов говорит
о том, что до сих пор ни одному математику еще не удалось открыть
индивидуального множества точек, имеющего мощность tfi> что до сих
пор все математические процессы, приводящие к индивидуальным
множествам точек, давали лишь несчетные множества, имеющие
совершенные части, и что еще ни один раз не удалось образовать множества-
индивида точек, имеющего мощность ^, Исходя из этого, они
выражают свое мнение, что не только „до сих пор", но и „всегда" так
будет и что, следовательно, не существует множеств-индивидов точек
мощности Ki* И так как неравенство с ^ Si <>ни понимают лишь в смысле
наличия в континууме части-индивида мощности Ni> TO отсюда они и:
выводят свой тезис о несравнимости c»(t
Математическое значение этой проблемы состоит в том, что
обладание множеством-индивидом точек мощности Si доставило бы возмож-
'554
Н. Н. ЛУЗИН
ность построения других множеств и функций с самыми разнообразными
свойствами, до сих пор еще не установленными ни для одной функции-
индивида или множества-индивида точек.
Ввиду сказанного было бы чрезвычайно важным утвердительное
решение проблемы I. Но и отрицательное решение ее было бы также
весьма важным, потому что это значило бы, что всякое несчетное
аналитическое дополнение & всегда имеет конституанту &а по крайней
мере с двумя точками. И в таком случае самый механизм
доказательства этого предложения о наличии &а по крайней мере с двумя
точками позволил бы вывести нечто большее: наличие конституанты <£в
с несчетным числом точек, т. е. с совершенным ядром.
О значении же этого мы скажем при рассмотрении следующих проблем.
К сожалению, проблема I не поддается при настоящем состоянии
науки никаким усилиям, и это по причинам, которые трудно понять.
При таком положении вещей, естественно, искать ослабить проблему I,
-заменив ее такой, более слабой:
Проблема II. Узнать, существует или нет решето С такое,
что всякая конституанта <§а есть, самое большое, счетная?
Философское значение этой проблемы состоит в том, что всякое
до сих пор построенное множество-индивид точек есть: или конечное,
мли счетное, или содержащее совершенное ядро. И так как в силу
теоремы Кантора—Бернштейна всякое множество точек, содержащее
совершенное ядро, приводится эффективным образом во взаимно
однозначное соответствие со всеми точками оси ОХ, то отсюда следует,
что до сих пор мы из несчетных множеств точек знаем лишь
множества, имеющие эффективную мощность континуума. Математики-реалисты
утверждают, что и всегда так будет, т. е. что среди множеств-индивидов
точек нет несчетного множества без совершенного ядра, и что,
следовательно, самый акт установления несчетности, по существу, есть
тот же самый, которым устанавливается несчетность точек отрезка,
потому что совершенное множество подобно отрезку (с утратой, самое
^большое, счетного числа точек). Если бы это оказалось действительно
так, это было бы своеобразным решением знаменитой проблемы
континуума, потому что показывало бы, что мощность континуума есть
непосредственно ббльшая счетной, потому что множества
промежуточного, т. е. неконечного, несчетного и без совершенного ядра иметь
(индивидуальным образом) невозможно.
Математическое значение этой проблемы состоит в том, что
наличие аналитического дополнения § несчетного и без совершенного
ядра позволило бы построить индивидуальным образом бесчисленные
случаи функций и множеств-индивидов с самыми парадоксальными
свойствами, которых сейчас нет ни у одного множества, и функции
индивида. Но еще важнее — это то, что при утвердительном ответе
(„такое решето есть") на проблему II было бы построено множество-
индивид, относительно которого можно было бы,- употребив аксиому
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИЙ
Цермело, доказать, что оно мощности «i; употребление аксиомы Цермело
здесь было бы своеобразным, так как оно потребовалось бы не для
построения множества (потому что оно было бы индивидуально
определено решетом С), а лишь для обнаружения некоторого его свойства.
И столь важным был бы отрицательный ответ („такого решета нет") на
проблему И, потому что это значило бы, что всякое несчетное
аналитическое дополнение § обладает несчетной конституантой ga и, значит,
содержащей совершенное ядро, так как вообще всякое несчетное
множество, измеримое В, содержит совершенное ядро. Поэтому тогда
аналитические дополнения имели бы такое же точно свойство, как
и множества, измеримые В, или аналитические множества: быть или,
самое большое, счетным, или обладать совершенным ядром.
К сожалению, мы столь же далеки от какого бы то ни было
решения проблемы II, как и проблемы I. При настоящем состоянии науки
мы не имеем ни малейших указаний на вероятность решения проблемы
II в том или другом направлении [56].
Это дает мысль заменить проблему II еще более слабой проблемой:
Проблема III. Узнать, существует или нет решето С такое,
что всякая конституанта ёа есть множество, измеримое В, класса
не выше, чем некоторое фиксированное число К?
Смысл этой проблемы следующий: множества, измеримые В, делятся
на классы: класс О, класс 1,..., класс ш,.т. , класса а,.#. 2.
Счетные множества суть множества, измеримые В, классов <^2.
И если имеется такая трудность, превосходящая наши силы, для того
чтобы получить решето С, дающее счетные конституанты, то,
спрашивается, будет ли трудность столь же значительной для получения
решета С, дающего хотя бы и несчетные конституанты &а, но зато
ограниченных классов, например не превышающих данного числа К?
И если бы такое решето удалось найти, спрашивается, не удалось
ли бы, видоизменив его, получить решето С, решающее утвердительно
проблему II или даже проблему I?
Таким образом, интерес проблемы III есть интерес механизма
утвердительного ее решения. Но и само по себе положительное
решение ее имеет чрезвычайный научный и философский интерес, так как
никому еще не удалось до сих пор найти не только Xi точек, но и Si
множеств ограниченных классов, т. е. меньших некоторого числа К.
Отрицательное решение проблемы III означало бы, что классы
конституант <§а при всяком решете не ограничены, и, значит, заведомо имеется
конституанта класса ^3. Но всякое множество, измеримое В, класса ^3
содержит совершенное ядро. Это показывает, что отрицательное
решение проблемы III влечет за собой решение проблем II и I.
К сожалению, проблема III Представляет те же самые трудности,
как и проблемы II и I. Но здесь выступает на сцену новый момент,
которого не было в проблемах I и И: д\я тех было сразу ясным, что
все решета, которые изучены до сих пор, оказываются имеющими
556
Н. Н. ЛУЗИН
несчетные конституанты &а> раз аналитическое дополнение & несчетно.
Этого обстоятельства вначале не было для проблемы III, так как
долгое время о поведении конституант ёа совсем ничего не было известно
даже для самых простых решет С: зная что для них имеются
несчетные конституанты &а, долгое время ничего не было известно о
поведении их классов, т. е. о том, ограничены ли их классы или не
ограничены.
Этот дополнительный вопрос к проблеме III был недавно решен
проф. Серпинским и мной. Мы подвергли детальному обследованию один
весьма важный класс решет (получающийся из пространственных
универсальных решет при свертывании трехмерного пространства oxy'z в
плоскость xoz преобразованием Пеано: х' = <р (х), у =ф (х)> z' = (z) и смогли
установить, что классы конституант <§а в этом случае монотонно возрастают
до 2, когда индекс а стремится к 2.
Но при этом мы не могли обнаружить случаев решет С, когда
классы конституант &а> будучи не только не ограниченными, но
и стремящимися к 2 как к пределу, были бы хотя бы немонотонно
приближающимися к 2. Тривиальный случай пустоты несчетного числа
конституант &а нами, понятно, отбрасывался.
Такое положение вещей, естественно, заставляет отступить еще
болое назад и искать проблем еще более слабых, чем проблема III,
в надежде встретиться не только со случаями решет, не обладающих
свойством, требуемым проблемой, но и с решетом, уже имеющим это
свойство.
Этот метод постепенного ослабления жесткости свойства, налагаемого
на решето С, представляется целесообразным, так как в тот самый
момент, когда указанное свойство будет уже настолько ослабленным,
что допустит положительное решение, в этот самый момент можно
будет понять характер трудности предыдущих проблем.
Одной из таких постепенно ослабляемых форм проблемы I является:
Проблема IV. Узнатьу существует или нет решето С такоеу
что все его конституанты &а могут быть соответственно заключены
в не перекрывающиеся попарно множества На ограниченных классов?
В этой проблеме не требуется нисколько ограниченность классов
самих конституант: класс конституанты £а может вместе с индексом а
возрастать до 2; здесь требуется лишь ограниченность классов мяо-
жеств-покрышек НаУ отделяющих конституанты &а одну от другой.
Конституанты решета С, не допускающие наличия таких покрышек,
следует рассматривать как представляющие чрезвычайно тесное рас-
положение^
К сожалению, проблема IV, видимо, еще недостаточно ослаблена*
чтобы стало возможным ее положительное решениеу пользуясь
известными сейчас методами* Напротив, исследование важнейшего класса
решет обнаруживает, что их конституанты как раз и представляют
указанное тесное расположение.
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИИ 557
Но, а^я того чтобы иметь этот результат, необходимо более
детальное изучение конституант вообще и, в частности, изучение особого
класса решет, дающих „пустые'* аналитические множества.
2. Определения. Множество называется пустым, когда оно не
содержит ни одного элемента. Пустое аналитическое множество измеримо В.
Поэтому решето С, определяющее пустое аналитическое множество,
дает место разложению
(_оо1+оо) = (?0-Ь(?1-Ь(52-ь...-»-(5О)-ь...-н5а-н...|^ (2)
состоящему из счетного числа конституант.
Число Р такое, что оно есть наименьшее из чисел р', для которых
конституанты £р, £g+1 12 суть пустые, называется степенью
решета С. Если степень Р решета С есть число первого рода, т. е.
если p = p*-t-l, тогда конституанта £\ является последней непустой
конституантой; в том случае она называется высшей конституантой.
Решето С, составленное из прямолинейных интервалов, параллельных
оси ОХ и находящихся в счетном (или конечном) числе, называется
вполне упорядоченным, если его проекция на ось OY есть вполне
упорядоченное множество.
Тип 7 проекции вполне упорядоченного решета С на ось OY
называется типом решета С. Ясно, что имеем
Р<Т-ь1-
Таким образом, для случая вполне упорядоченного решета типа т
нумер р* высшей конституанты не может превысить т.
Первой и важнейшей задачей является определение природы
конституанты <§г в случае вполне упорядоченного решета типа т.
3. Обозначения трансфинитных чисел* Известно, что если аир
суть какие-нибудь трансфинитные числа такие, что р^ а, то существует
одно и только одно трансфинитное число т (или конечное), которое
удовлетворяет равенству а = р-ьт. В этом случае мы условливаемся
писать
Это обозначение удобно и естественно. Мы должны предупредить, что
оно расходится с обычной манерой писать д\я трансфинитного числа а
первого рода его непосредственно предшествующее число в виде а — 1.
Эту последнюю привычку мы считаем за психологический недосмотр.
С вводимым нами обозначением мы всегда имеем равенство а — 1=а
для всякого трансфинитного числа а. Известно далее, что всякое
трансфинитное число а может быть написано в виде
а = о)а -+- v,
где v есть конечное число. Условимся писать
- а
а = — .
О)
SS8
Н. Н. ЛУЗИН
Этот символ имеет смысл в том и только том случае, когда а^ш.
Известно, наконец, что всякое трансфинитное число а может быть
изображено в виде
a = wi-i-ii)i4-(i)1'+1,,-+- со**,
где а ^ ах ^ а2... ^ а*, и где целое к — положительное (конечное) число.
Условимся писать
a = log,, a
или просто
a = log a.
Это обозначение оправдывается очевидным равенством
log (a&) = log a н- log (3
и еще тем, что
lim(£ — log a) = 2,
когда a возрастает трансфинитно, т. е. когда lima = Q.
4* Оценка высшей конституанты* Для того чтобы выполнить-
оценку этой конституанты, необходимо напомнить классификацию
множеств, измеримых 5, сделанную Валле-Пуссеном.
Классификация эта такова:
АГ0> Л], АГ2, ..., л(!, ..., Ка> | 2,
где за основной класс принимается семейство множеств, каждое из
которых состоит из сумм порций иррациональных чисел, как и
дополнительное к нему множество (рациональные точки предполагаются
удаленными). За производящую операцию принимается переход к пределу: lim.
Доказывается, что ни один из классов не есть пустой. Полезно
ввести следующее определение и обозначение: множество Е класса К9
называется достижимым сверху, если оно есть общая часть множеств
Е19 Е2, ..., Еп... классов К*>, предшествующих классу Ка, т. е. если
а <[ а. Для множества Еу которое есть или класса <^ а или
достижимое сверху класса а, будем писать знак равенства-неравенства:
£<^supa.
Вот теперь предложение, выполняющее оценку высшей
конституанты £у для вполне упорядоченного решета С типа 7:
Теорема. Всякое вполне упорядоченное решето С типа 7 имеет
конституанту £у удовлетворяющей условию
£T<sup[(21ogT-+-l) — 1].
И обратное также верно: всякое множество Sv произвольно
заданное и удовлетворяющее этому равенству-неравенству, есть высшая
конституанта вполне упорядоченного решета типа 7> надлежаще
подобранного.
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИЙ 55£*
5. Тесное расположение конституант* Рассмотрим универсальное
решето U, находящееся в трехмерном пространстве OXYZ. Мы
предполагаем, что U составлено из счетного числа плоских множеств
класса 0, лежащих на плоскостях, параллельных горизонтальной
плоскости XOY. 1 акое решето пересекается всякой плоскостью у = у0 по
плоскому решету [/Уо, составленному из линейных множеств класса 0^
параллельных оси ОА9 и важно заметить, что всякое плоское решето,
состоящее из линейных множеств класса 0 в счетном числе,
параллельных оси ОХ, может быть получено таким образом. Заметим, что мы,,
понятно, предполагаем элементы всех решет лежащими на прямых или
на плоскостях, пересекающих вертикальную ось в рациональных точках.
Пусть Е есть аналитическое множество, определенное решетом £/,.
и 5—у его дополнение. Мы имеем разложение
S = £<) ■+- ё\ ■+■ 6*2 ■+■ • • • И" £,, "+■ ..."+- ёа "+- | 2 (3)'
по конституантам.
Мы теперь утверждаем, что разложение (3) как раз и дает тесное
расположение конституант. Действительно, если бы имелась
трансфинитная последовательность плоских множеств классов <^р
//0, Нг, Нг>..., Нш, ..., На |2,
не имеющих попарно общих точек и таких, что На содержит
конституанту Saf то плоскость у = у0 разрезала бы множества На по линейным
множествам (На)Уо классов <р, отделяющих друг от друга линейные
конституанты:
определяемые решетом Uyo.
Но среди решет £/Уо имеются всевозможные вполне упорядоченные
решета. И, в частности, среди таковых имеются решета типа т с
высшей конституантой (£т)*0 класса, в точности равного
(21ogT-+-l)-l.
Эта высшая конституанта, являясь последней, должна совпадать с
покрывающим ее множеством (На)Уа1 что невозможно, так как выражение
(21ogY-bl) — 1 превысит число fi при достаточно великом ?.
Таким образом, разложение (3) есть разложение с тесными
конституантами.
Чтобы иметь плоское С, определяющее разложение с тесными
конституантами, достаточно свернуть пространство OXYZ в плоскость XOZ^
преобразованием Пеано
л: = <р(*'), y = ty(x')y z = z.
Тогда пространственное универсальное решето U будет свернуто*
в плоское решето С, дающее тесно расположенные конституанты.
'560
Н. Н. ЛУЗИН
Постановка проблем
6. Идеи Ж, Драша. Невозможно при настоящем состоянии науки
понять истинную причину трудности поставленных проблем. Вероятнее
всего, эту трудность следует отнести за счет какой-то неопределенности
понятия, выражаемого символом 2, и одновременно за счет аналогичной
неопределенности понятия „все точки континуума". Но полное
разъяснение сущности этой неопределенности еще не по силам современной
науке.
Возьмем в качестве образца проблему II о существовании или
несуществовании решета С, определяющего аналитическое
дополнение, измеримое 5, с одними только счетными конституантами.
Наша точка зрения состоит в том, что проблемы такого рода
заставляют отказываться от традиционного взгляда на смысл слов: „р е-
шение проблемы".
Обычно под словами: „решить проблему" имеют в виду составление
такой счастливой комбинации формальных алгебраических приемов и
средств абстрактной логики, которая позволила бы или сказать „в о т
нужное решето", или вывести из наличия такого решета
словесное противоречие. Но известно, что, несмотря на все усилия,
никто не смог до сих пор ни получить нужное решето, ни придти к
формальному противоречию.
В настоящий момент я рассматриваю как невозможное удержание за
словами: „решение проблемы" их обычного традиционного смысла.
Указанная неопределенность понятий „2" и „континуум" делают, по
нашему мнению, то, что мы оказываемся в категорической
необходимости дать этим словам другой смысл, не становясь, впрочем, на почву
-идей Гильберта о непротиворечивом", которая мне кажется мало
счастливой.
В качестве исходной точки зрения я беру идеи Ж. Драша об
алгебраических числах. Известно, что под алгебраическим числом
разумеется корень неприводимого алгебраического уравнения с целыми
коэффициентами
а0хп -ь аххп-1 -+- а2хп~2 -*-... -+- ап^хх -+- ан = 0. (А)
Ж. Драш рассматривает алгебраическое число как „идеальное число"
и вводит дая обозначения этих идеальных чисел символ
(а0, а19 а2, ..., ая).
Самое важное в идеях Ж. Драша есть то, что идеальные числа нам
никогда не даны прямо; мы не можем их фактически достигнуть
„коснуться их" в действительности (следуя удачному выражению Е. Бореля).
Они нам даны лишь посредством уравнения (А) и, значит,
посредством символа Ж- Драша. И если мы можем еще говорить о „сумме",
^разности", „произведении" и „частном" идеальных чисел, то никто не*
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИИ
должен обманываться на этот счет: производя над идеальными числами
указанные арифметические операции, в действительности оперируют
исключительно лишь с целыми числами, выводя из нескольких символов
Ж. Драша (а£, а(, а\... а£) единый окончательный символ (а0, а1У ..., ап).
И точно так же, как позволено Ж. Драшу говорить об идеальных
числах, писать их в виде совершенно определенных конечных символов
и рассуждать над ними, точно так же мы считаем себя в праве
говорить об идеальных аналитических дополнениях1, неизмеримых В и
со счетными конституантами, и рассуждать над ними, не боясь никакого
формального противоречия, не могущего придти в силу указанной
неопределенности понятий „2" и „континуум".
Вопрос на этом пути сводится лишь к выбору символа, который
мог бы описать так же хорошо какую-нибудь совокупность „идеальных
аналитических дополнений", как символ Ж. Драша (а0, а19 а2, ..., ап)
описывает совокупность „идеальных чисел", определенных
алгебраическим уравнением (Л).
7. Универсальные и полууниверсальные плоские аналитические
дополнения. Как инструмент дая создания такого символа может
служить плоское универсальное аналитическое дополнение //.
Назовем идеальным линейное аналитическое дополнение,
неизмеримое В и со счетными (или конечными) конституантами. В
противоположность этому, все остальные линейные аналитические дополнения
будут называться реальными; среди реальных аналитических
дополнений мы различаем: (а), содержащие совершенное множество, и (Ь)
счетные или конечные.
Обозначим через Нр совокупность всех точек х оси ОХ таких, что
прямая х = х0 пересекает плоское универсальное аналитическое
дополнение Н по линейным аналитическим дополнениям с совершенною частью.
Точно так же обозначим через Нл совокупность точек х0, дая которых
прямая х = х0 пересекает множество Н в счетных или конечных
линейных множествах. Легко видеть, что оба множества Нр и Hd
определены очень простой геометрической конструкцией.
Чтобы убедиться в этом, возьмем в пространстве трех измерений
координатный триэдр OXTY и поместим в плоскости XOY
универсальное аналитическое дополнение Н. Поместим в плоскости TOY
универсальное множество Р дая всех линейных совершенных множеств;
известно, что Р может быть выбрано измеримым В. Сделав это,
обозначим через СН плоское аналитическое множество, дополнительное к //,
и через СН совокупность точек, лежащих на прямых, проведенных
1 Прилагательное „идеальный" не нмеет ничего общего ни с какой философской
системой. В равной мере „идеальными" могут быть названы фильтрующиеся вирусы
или бактериофаги, потому что они невидимы, но подчинены тем же самым опера-
цияму как и обыкновенные видимые микробы. Идеальные числа Ж. Драша или
идеальные числа Куммера в этом отношении подобны ультрамикробам.
562
Н. Н. ЛУЗИН
через точки множества СН параллельно оси ОТ. Точно так же
обозначим через Р множество точек, лежащих на прямых, проведенных
через точки множества Р параллельно оси ОХ. Пусть СН X Р есть
общая часть множества СН и Р. Ясно, что это есть пространственное
аналитическое множество. Пусть т. есть проекция его на плоскость ХОТ
и Ск — плоское дополнение множества гс. Ясно, что Ск есть
аналитическое дополнение, которого проекция на ось ОХ и есть наше
множество Нр. Таким образом, Нр дается геометрической конструкцией и
есть проективное множество типа А2 (т. е. типа РСРЕ> где Е
измеримо В).
С другой стороны, поместим на плоскость XOY опять
универсальное аналитическое дополнение //, а на плоскость TOY множество Q,
измеримое Ву дающее при пересечении его прямыми, параллельными
оси О У, только счетные (или конечные) множества и притом все такие
множества; таким образом, множество Q есть универсальное по
отношению к конечным и счетным множествам. Пусть СН есть множество
точек, лежащих на прямых параллельных оси ОТ и проведенных через
точки множества СН; аналогично Q есть множество точек, лежащих
на прямых, параллельных оси ОХ и проведенных через точки
множества Q. Ясно, что сумма СН-*- Q есть пространственное аналитическое
множество. Поэтому формула РСРС(СН-+- Q), где первая буква Р
означает проекцию на ось ОХ и вторая — на плоскость ХО Т> дает
проективное множество типа Az. Но очевидно, что это множество и есть Н^
Таким образом, Hd дается геометрической конструкцией и есть
проективное множество типа Az.
Установив это, обозначим символом (Нр> Hd) совокупность точек
оси ОХ, не принадлежащих ни к Нру ни к Не- Это суть идеальные
точки прямой ОХ и получают все идеальные линейные аналитические
дополнения, рассекая множество Н прямыми, параллельными оси ОК и
проведенными через точки множества {Нр> Hd).
Здесь мы должны считаться с возражением. Нам могут сказать:
„Вы уничтожили на оси ОХ сначала все точки множества Нр и затем
все точки множества Hd- Но если Н& есть дополнение к Нру то вот на
оси ОХ этим самым будут уничтожены все возможные точки, и,
следовательно, совсем не останется никаких идеальных точек и вместе с ними
идеальных аналитических дополнений".
Этот аргумент, по видимости сильный, в действительности не может
служить препятствием. В самом деле, если серьезным образом
рассматривают Hd как дополнение к Нр> то нельзя забывать о том, что тип
множества Нр есть А2> и, значит, тип его дополнения должен быть СА2;
тип же множества Hd есть не СА2У но Л3, и притом никакие попытки
понизить его до типа СА2 путем формальных преобразований самого
определения множества Hd не увенчались успехом и, по-видимому, не
могут никогда быть успешными вследствие грубости и бедности фор-
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИИ 563
мальных средств. Если же опасаться неформальных преобразований
определения множества Hd> то тогда необходимо должны будут,
выполняя такие преобразования, употребить, действительно, все точки
прямой ОХ и среди них также и идеальные точки. Следовательно, circulus
vitiosus в этом случае налицо. Я считаю, что не приходится бояться
того, что кто-нибудь впоследствии придет к формальному противоре-
чиЮу допустив, что Нр и Hd не суть взаимно дополнительные
множества, так же точно так не приходится бояться того, что кто-нибудь
впоследствии в один прекрасный день откроет, что математика
противоречива.
Возвращаясь к существу дела, мы отмечаем, что точно так же, как
в случае „идеальных чисел" Ж. Драша, мы можем рассматривать
„идеальные" аналитические дополнения как определенные формально и
описанные символом
(Нр> Hd)
таким образом, что всякая операция над идеальными аналитическими
дополнениями есть в действительности не что иное, как просто
операция над двумя совершенно реальными и вполне ясными геометрическими
конструкциями, определяющими множества Нр и Hd. Напомним, что
конструкции эти совершенно прозрачны, так как речь идет лишь о
таких простых действиях, как составление суммы двух множеств, их
пересечения, проектирование и взятие дополнения.
Такая точка зрения не представляется бесплодной, так как на этом
пути встречаем такие вопросы, которые нельзя встретить при другом
ходе рассмотрений.
В качестве простейшей иллюстрации возьмем понятие
полууниверсального аналитического дополнения: таким именем мы называем такое
плоское аналитическое дополнение ff, которое всякой прямой х = х0
пересекается по линейному аналитическому дополнению, заведомо либо
счетному (конечному), либо содержащему совершенное множество,
причем всякое заранее данное такое линейное аналитическое дополнение
может быть получено рассечением Н надлежаще подобранной
прямой х = х0.
Д\я того чтобы иметь полууниверсальное аналитическое
дополнение //, достаточно взять триэдр OXTY, построить на плоскости XOY
универсальное аналитическое дополнение //, построить на плоскости TOY
множество Р, измеримое В и универсальное по отношению всех
линейных совершенных множеств. Пусть Й есть совокупность точек,
лежащих на прямых, проведенных через точки множества Н параллельно
оси О Г, и пусть Р есть совокупность точек, лежащих на прямых,
проведенных через точки множества Р параллельно оси ОХ. Множество-
сумма Й-+-Р есть, очевидно, пространственное аналитическое
дополнение. Свертывая трехмерное пространство OXYT в плоскость XOY/
564
Н. Н. ЛУЗИН
посредством преобразования Пеано: x = f(x), t = b(x), у = у\ мы
получаем в полосе (0<С* '<1> —°° <*/'<-*- °°) плоскости ЛГОУ'плоское
аналитическое дополнение, пересекаемое прямыми х = х0' для О <С х0' <С 1
по линейным аналитическим дополнениям с совершенным ядром и только
по таковым. Если мы теперь к полученному таким образом плоскому
аналитическому дополнению прибавим в полосе (—1 <С * <С 0, —со <^ у <^
<^-+-оо) множество, измеримое В, универсальное по отношению ко всем
счетным (и конечным) линейным множествам, то этим самым и
заканчивается построение полууниверсального аналитического дополнения.
8* Новые проблемы. Идя по указанному пути, мы встречаемся не
только с новыми проблемами, но и с новыми принципами, которые
могут показаться совсем невероятными при другом ходе идей.
Прежде всего, вводя идеальные аналитические дополнения,
естественно рассмотреть то, что можно назвать непрерывностью высшего
рода прямой линии, представляющей явную аналогию с обычной
непрерывностью Коши—Дедекинда. Но эта непрерывность приводит нас к двум
следующим предложениям, которых истинность мне кажется вне сомнений:
Предложение I. Всякое множество точек мощности **х есть
аналитическое дополнение.
Предложение II. Всякое множество точеку получаемое
суммированием конституант в трансфинитном числе аналитического
дополнения, есть опять аналитическое дополнение.
К этим двум предложениям, кажущимся мне несомненными, я
присоединил бы еще одно предложение, истинность которого кажется мне
правдоподобной:
Предложение III. Сумма трансфинитного числа множеств,
измеримых В и занумерованных трансфинитными числами второго
класса, есть проективное множество типа Аг. Если же указанное
перенумерование есть эффективное, тогда эта сумма есть
проективное множество типа В2.
Я прибавлю, что известно, что всякое множество типа А2 разложимо
в Ях не перекрывающихся множеств, измеримых В, но разложение это
не есть эффективное, и что до сих пор не открыто множеств,
разложимых на *5lf множеств, измеримых В, которые не оказались бы
типа А2 [57].
9. Две гипотезы континуума. Остается сказать лишь несколько
слов о так называемой „гипотезе континуума*'. Под таковой
чаще всего понимают гипотетическое равенство Г. Кантора
Мы будем его называть „гипотезой Кантора" или, лучше, „первой
гипотезой континуума*4.
Известно, что Д. Гильберт, оставаясь целиком на излюбленной им
Яочбе „непротиворечивого", дал обещание представить формальное
^доказательство непротиворечивости гипотезы Кантора (см. [48]).
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИИ S6S
Между тем, гипотеза Кантора вовсе не есть единственная гипотеза*
и это даже тогда, когда ограничиваются писанием алефов. Единствен-*
ное средство установить истинность гипотезы Кантора — *то дать
взаимно однозначное и эффективное (т. е. описанное совершенно
точным образом, без какой-либо неопределенности или двусмысленности)
соответствие Z между точками прямой линии, с одной стороны, и
трансфинитными числами второго класса, с другой стороны. Эта
эффективность имела бы огромное значение, интерес и важность, потому что
в этом случае эффективность соответствия Z была бы первопричиной
и источником многочисленнейших и важнейших-арифметических,
алгебраических, геометрических и аналитических соотношений. Но известно, что
не только мы не можем ожидать, что будущий прогресс науки нас
приведет к такому эффективному соответствию Z, но что, наоборот,
становится все очевиднее и очевиднее, что, на самом деле, будет иметь
место как-раз обратный факт: может быть, в один прекрасный день
ресурсы теории Гильберта настолько будут подвинутыми вперед, что
можно будет с успехом атаковать доказательство несуществования такого
соответствия Z, хотя существование неэффективного соответствия Z
и непротиворечиво.
Но гипотеза Кантора без эффективности соответствия Z
утрачивает почти всякую важность. Одно лишь преодоление трудности
при доказательстве непротиворечивости гипотезы Кантора может
представлять привлекательность для аналистов. Вне же этого соблазна
разрешение гипотезы Кантора (причем мы все время имеем в виду, говоря
это, лишь неэффективное Z) не даст науке почти ничего, так как все
разрешится в необозримое количество самых парадоксальных и патало-
гических примеров функций и множеств, не имеющих индивидуального
существования, но имеющих квази-существование лишь в смысле аксиомы
Цермело.
В математической литературе не раз проскальзывали намеки на то,
что возможны и другие гипотезы континуума. Среди них наиболее
интересной мне представляется та, которая выражается алефическим
равенством
Мы не станем доискиваться, с каким именем связано самое первое
начертание этого равенства автором, который, действительно, серьезно
мыслил его возможность. Мы назовем его пока „второй гипотезой
континуума".
Эта гипотеза континуума вполне согласуется с выставленными нами
в п. 8 гипотетическими предложениями I, II и III.
Вторая гипотеза континуума мне представляется в той же самой
степени изъятой от противоречий, как это имеет место и дая первой
гипотезы континуума. Мне думается, что со временем прогресс теории
Гильберта будет настолько значительным, что позволит с успехом ата-
566
Н. Н. ЛУЗИН
ковать доказательство непротиворечивости и этой второй гипотезы
континуума.
А тогда пред нами предстанет необходимость выбирать между
различными гипотезами континуума, в равной мере изъятыми от
противоречия. И этот выбор, вне всякого сомнения, будет продиктован одним
только наблюдением фактов.
Мы видим, насколько были проницательны слова Э. Бореля, писавшего:
„Следует различать подлинную математику от чисто словесных
логических спекуляций, в которых озабочены лишь одним совершенно
отрицательным качеством: свободой от словесного противоречия*4 („Теория
меры и теория интегрирования", § 3, 1914).
Исключение трансфинитного
10. Проблема исключения трансфинитного* Проблема эта возникла
впервые под влиянием критики Э. Бореля всех тех математических
рассуждений, в которых вводятся, действительно, все трансфинитные числа
второго класса (и не только те, которые меньше некоторого
определенного трансфинита, наперед заданного): Э. Борель рассматривает
совокупность всех трансфинитных чисел второго класса как совокупность
незаконную, так как она не может мыслиться как завершенная, в
отличие от натурального ряда, где дан закон его образования. Поэтому
Э. Борель опротестовывает все трансфинитные числа второго класса и
рассматривает как недоказанные все следствия, вытекающие из
подобных рассуждений.
Первая серьезная попытка систематического исключения
трансфинитных чисел из математических рассуждений была сделана польским
математиком Куратовским в статье: „Une methode d'elimination des nombres
transfinis des raisonnements mathematiques" (Fund. Math., Ш, 1—33,1921)1.
Но, насколько можно понять, автор заменяет рассмотрение
трансфинитных чисел введением вполне упорядоченных множеств. И так как их
типы в каком-нибудь математическом рассуждении могут быть сколь
угодно великими, то все возражения против этого рассуждения
остаются в силе и после работы Куратовского.
Другая попытка исключения трансфинитного была сделана лично
мной, но не для всяких вообще математических рассуждений, а лишь
для некоторой группы их, именно для тех, на которых была основана
теория аналитических множеств. После возражений Э. Бореля было
естественно желать освободить от подозрительных рассуждений эту
теорию.
1 Следует, однако, отметить еще две попытки, правда, удавшиеся, но совершенно
частного характера исключения трансфинитного. Одна из них принадлежит Линделефу,
исключившему трансфинитное нз теоремы Кантора—Бендиксона, другая принадлежит
Лебегу,- исключившему трансфинитное из теоремы Бэра.
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИИ 567
Это освобождение протекло очень легко и было сделано немедленно.
Но лишь один пункт, именно теорема Суслина:
„Два аналитических множества, взаимно дополнительные одно
к другому, измеримы В", продолжал держаться упорно и доставил
много забот.
Это важное предложение было доказано Суслиным помощью очень
сложной конструкции, в которой трансфинитная индукция играла
исключительно важную роль и была совершенно неизбежна в этом
рассуждении. Употребление существенно трансфинитной индукции, которую
нельзя свести к „полной индукции" обыкновенной арифметики, просле-
дующей лишь по всем натуральным числам, весьма характерно для
рассуждения Суслина, которое без этого употребления не могло состояться.
Таким образом, предстояло передоказать теорему Суслина, исходя
из совершенно иных начал и не употребляя трансфинитных чисел ни
явно, ни неявно в замаскированном состоянии (в виде вполне
упорядоченных множеств). Для этой цели я обратился к идее отделимости
множества, восходящей еще к Хаусдорфу, который первый дал понятие
отделимости множеств одного семейства посредством множеств другого
семейства [58].
Для целей освобождения теории аналитических множеств от
трансфинитного в теореме Суслина я ввел понятие множеств, отделимых В.
Это новое понятие позволило весьма скоро совершенно прямым путем,
без какого-нибудь употребления ни трансфинитных чисел, ни вполне
упорядоченных множеств и без использования теоремы Суслина,
доказать теорему:
„Всякие два аналитические множества, не имеющие общей точки,
отделимы В", из которой предложение Суслина вытекало сразу же
как простое следствие. Таким образом, здесь трансфинитное было
радикально исключено введением понятия „отделимости В".
Сделанный новый шаг в теории аналитических множеств показался
мне настолько существенным, что я искал охарактеризовать его тем
или иным выразительным именем: поэтому я назвал доказанную теорему
об отделимости В аналитических множеств первым принципом
отделимости.
Идеи Э. Бореля относительно абсолютной неопределенности
понятия „Qu и незаконности его введения в математику, а также еще и та
его замечательная идея, что 2 есть не что иное, как просто
трансфинитное число Р второго класса, только „невыразимо большое", „очень
большое" („tres grand et echappant a nos notations et a notre
imagination"), естественно вызывали желание провести аналогию1 между
аналитическими множествами, неизмеримыми Ву и множествами, измери-
1 гСм. мою работу „Analogies entre les ensembles mesurables В et les ensembles
analytiques" (Fund. Math. XVI, 48, 1930) (стр.470 настоящего тома.—Ред.).
568
Н. Н. ЛУЗИН
мыми By „очень большого" класса (3. И так как аналитическое
дополнение £9 неизмеримое В, дает место разложению
с? = б'о-+-<?i-»-(?2 ■+-• • •-*-£<о~|-" •-•-£,-+-. *-12
по конституантам, измеримым 5, классы cl£a которых необходимо
удовлетворяют неравенству 1
с16,<2^--н1
и, значит, могут лишь постепенно возрастать до 2, то естественно
было рассматривать аналитическое дополнение £ как аналог множеству,
измеримому Ву достижимому снизу (т. [е. разлагающемуся на сумму
множеств, измеримых В низших классов, меньших „весьма большого"
класса р). Следовательно, самое аналитическое множество £,
неизмеримое В, дополнительное к £, следовало рассматривать как sup В,
точнее как „элемент" класса (3 (т. е. как множество класса (3,
достижимое сверху и недостижимое снизу).
Указанная аналогия аналитических множеств и множеств,
измеримых By заставила искать принципов отделимости уже среди множеств,
измеримых В, Естественно было их называть в этом случае „малыми
принципами", сохраняя название „больших принципов" для теории
аналитических и проективных множеств.
Аналог первому большому принципу был немедленно найден в виде
следующего предложения, которое мы назвали „первым малым
принципом^:
„Два элемента класса Р, не имеющие общей точки, всегда
отделимы ф)а.
Здесь под отделимостью (Р) имеется в виду понятие, аналогичное
отделимости В: два какие-нибудь множества Ех и Е2 называются
отделимыми (J3), когда имеются два множества Нг и //2, не имеющие
общей точки и содержащие соответственно Ех и Е2у причем HY и Н,
суть либо множества класса <С Р, либо двусторонние множества класса (3.
Самое доказательство первого малого принципа есть немедленное:
пусть Е' и Е" — два элемента класса Р, не имеющие общей точки. По
самому определению элемента класса (3, существуют две
последовательности монотонно убывающие множеств классов <^ (3
/=>£;=>£;=>...d£;,d... (4>
/d£;'d£;'d...d£;'d..., (5>
1 Я должен отметить, что сотрудница Математического института им. В. А. Стек-
лова АН СССР Л. В. Келдыш недавно указала точный верхний предел &\я класса
конституанты <£а, уже достигаемый при векоторых решетах и, значит, не могущий
быть далее пониженным.
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИИ
имеющие данные элементы Е и Е" соответственно своим пределам.
В этих условиях строят два альтернативных убывающих ряда множеств.
//=/• £;-£;<£;'-+- е^е\—е% >е2 + ... ч-
+К-е^-е^-е;-*-... (6)
и
Н'=1-е';-е,;-е'1+е'1-е';-е';-е'2-1-...ч-
ч-к-е^-е:+1-е:+1+.... (?)
Эти альтернативные ряды сходятся, потому что элементы Е и Е" не
имеют общей точки и, значит, общие члены этих рядов имеют
пределом нуль (т. е. пустое множество).
Очевидно, что множества Н и Н" соответственно содержат
множества Е и Е" и не имеют общей точки. И так как они могут быть
написанными каждое одновременно в двух видах:
н'=(1-е[-е[. £;')-*-(£;' •£;-£; •£;')+... (8)
Ff = I.E'-[(E[-E';-E';.E't)4-(E'i-F;-EZ-E,J+...l (9)
то Н есть или множество класса < р, или двустороннее множество
класса р. То же самое следует сказать и о Н\ что и доказывает
первый малый принцип.
Сделанное рассуждение важно вот в каком отношении: оперируя
над множествами, измеримыми В, гораздо легче придти к
определенным математическим заключениям, чем при рассмотрении аналитических
и проективных множеств. И когда теоремы фактически уже получены
для множеств класса Р, то формально, делая замену числа р символом 2,
мы в результате этого своеобразного „перехода к пределу" получаем
теоремы для самих аналитических или проективных множеств, уже
неизмеримых В. Понятно, что, д\я того чтобы полученные теоремы имели
ценность в теории аналитических и проективных множеств, нужно, чтобы
их формулировки перестали содержать трансфинитное, т. е. чтобы
теоремы эти были выражены на конечном языке аналитических и
проективных множеств. Это достигается процессом исключения
трансфинитного.
Рассмотрим в качестве примера второй малый принцип. Он имеет
силу для множеств, измеримых В класса р, и формулируется так:
„Удаляя у Двух пересекающихся элементов класса р их общую
часть у мы получаем два множества, отделимые (Ср)".
При этом два каких-нибудь множества Е1 и Е2 называются
отделимыми (СХ когда имеются два множества Нг и Н2У не имеющие общей
towh и содержащие соответственно Ег и Е2> причем Ht и Н2 суть»
множества класса Р, достижимые снизу.
570
Н. Н. ЛУЗИН
Для доказательства второго малого принципа достаточно обратиться
к первому малому принципу и к его доказательству.
В самом деле, пусть Е и Е"— два каких-нибудь элемента класса р,
вообще уже имеющие общие точки. Пусть эти элементы Е и Е"
определены как пределы монотонно убывающих последовательностей
IZ)E[Z)E2Z>...Z)E'uZD... (4)
И
/DEi'DEjD.-.H-f;;!).... (5)
Мы теперь определяем два множества Н и Н" разложениями:
#={(/• е[-е[-е';)ч-(е;. e\-e\-ed -*-... +
#"={(/• £';-£;' • £;)-ь(£; • £;'-£; • £;)-♦-...-♦-
4-(^-^+i-^i-^i) + ---}- (9')
Для того чтобы второй малый принцип стал уже доказанным,
достаточно просто "Заметить, что множества Н и Н\ определенные
формулами (8') и (9'), суть или' множества класса <С Р» или множество
класса р, достижимое снизу. И так как ясно, что множества Н'-
и Н"> определенные формулами (8') и (9'), не имеют общей точки и
содержат в себе соответственно множества-разности Е' — Е'Е" и Е" — Е'Е\
то этим второй малый принцип является уже вполне доказанным.
Теперь, если желают переделать второй малый принцип во второй
большой принцип, дая этого прежде всего необходимо представить
данные аналитические множества Е и Е" как трансфинитные пределы
соответственно двух монотонно убывающих последовательностей (4*)
в (5*)
/D£;z>£;=)...=>£:=)...3£.D \Q (4*)
/d£;'d£;'d...3£:z»...d£;'d \Q (5*)
множеств, измеримых В.
Сделать это очень легко, раз аналитические дополнения €' и £"
данных множеств Е' и Е" разложены в трансфинитные ряды по их
конституантам:
£'=#;-+- §;+^;+...+^'-i-...+5;+ \q (io)
€"=-ё;.+ £';-^;-*т.„+&^+...+€';-+- \q. (и)
При этом *мы предполагаем, ,что аналитические множества Е и Е"
заданы соответственно решетами Г' и Г", составленными из счетного
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИИ 571
числа интервалов, параллельных оси ОХ; поэтому все конституанты
разложений (10) и (11) измеримы В.
Для того чтобы иметь монотонные трансфинитные
последовательности (4*) и (5*), достаточно положить
^. = /-(^"Ь«;+...-1-<Гш + ...-|-г;н-..-.|а) (12)
и
^ = /-(^о-ь^>.-.-нС-+-...-+-67-н...|«). (13)
Формулы (12) и (13), очевидно, можно написать в виде
£;=£'-+- (<§: -н<§:+1-ь \Q) (12-)
£:=г+(с+с+ I2). (1зо
В этих условиях множества-разности Е'—Е'Е" и Е" — Е'Е"
отделимы, очевидно, двумя множествами Н и Н", не имеющими общей
точки и определяемыми двумя трансфинитными разложениями:
// = (/• Е\ — Е\-Е'[) -ь...-ь
и
н"=(1-е-;—E';-E[)4-... ■+■
-b(£;-£;'+1-£:+1-£;+1)+ \q. р*)
Для того чтобы второй большой принцип был доказан, нужно,
чтобы было установлено, что Н и Н" суть не что иное, как
аналитические дополнения.
Следовательно, имея заданными разложения (8*) и (9*), т. е.
написанными при помощи совокупности всех трансфинитных чисел второго
класса, нужно исключить из них трансфинитное.
Таким образом, проблема исключения трансфинитного приобретает
уже не только теоретический, но и совершенно конкретный смысл, так
как, если мы умеем исключить трансфинитное из трансфинитных рядов,
то этим самым мы имеем возможность получать новые теоремы в теории
аналитических и проективных множеств, выраженные в „конечном"
виде.
Таким образом, проблему исключения трансфинитного вполне законно
сравнить с классической проблемой математического анализа
суммирования в конечном виде бесконечных рядов, бесконечных произведений
или вычисления в конечном виде определенных интегралов: и в этих
классических проблемах происходит также, ведь, исключение, но уже
не трансфинитного, а инфинитного (т. е. просто бесконечного).
572
Н. Н. ЛУЗИН
В частности, исключение трансфинитного из рядов (8*) и (9*)
делается следующим образом: сначала пишут общий член ряда (8*) в виде
что после формул (12') и (13') дает
[E'-(S'a+l-i-S:+^...\Q)]-S:;
следовательно, трансфинитный ряд (8*) можно написать так:
/f=2 [£'-(С+1+ ... 1^]-С- (14)
Теперь, чтобы „просуммировать" трансфинитный ряд (14), обозначим через
х какую-нибудь точку оси ОХ, через Рх — перпендикуляр в точке х
к оси ОХ и через Rx и R'^— соответственно пересечения решет Г'и Г"
перпендикуляром Рх. Следовательно, R'x и R^ суть счетные (или
конечные) множества.
Так как в точке х множества Е' множество R'x не есть вполне
упорядоченное, а в точке х конституанты §' оно будет вполне
упорядоченным и типа 7? то отсюда множество Н получает очень простой
геометрический смысл: это есть совокупность всех точек дг,
принадлежащих к <§" таких, что R'x не подобно части (в широком смысле)
множества R"x. А относительно этого множества доказывается, что оно
есть аналитическое дополнение (см. мою книгу: „Лекции об
аналитических множествах") (стр. 181. настоящего тома. — Ред.). Следовательно^
Н и аналогично Н1 суть аналитические дополнения. Этим второй
большой принцип является вполне доказанным.
Мы видим таким образом, что проблема исключения трансфинитного,
подобная классической проблеме суммирования рядов, представляет
существенный интерес даже в том частном виде, который мы ей здесь
придали: суммирования трансфинитных рядов, написанных как
комбинации множеств, снабженных индексами.
Но еще больший интерес являет проблема исключения
трансфинитного, когда она ставится в более общей форме. Эта же последняя
такова:
Имея заданным множество точек Е, определенное при помощи
совокупности всех трансфинитных чисел второго класса, узнатьг
возможно или нет преобразовать первоначальное определение
множества в другое, не содержащее никаких следов (ни явных, ни
неявных) трансфинитного?
И. Два семейства множеств. Среди множеств точек Е,
определяемых при помощи совокупности всех трансфинитных чисел второго
класса, следует различать два семейства множеств, природа которых
совершенно различна*
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИЙ 573
Первое семейство состоит из множеств Е, определяемых
трансфинитным числом операций, абсолютно не зависимых одна от
другой. Самые операции, определяющие множество Е, занумерованы
трансфинитными числами второго класса, но абсолютно не зависят одна
от другой.
Множества этого семейства мы будем называть множествами
первого рола, или множествами со свободными операциями.
Простейшим примером множества со свободными операциями является,
например, множество Е, определенное формулой
£=<?;+<?;' -i-w -н...<?ж-ь... <§'& |2,
где 8'а и 8'^ суть конституанты двух произвольно заданных решетами Г'
и Г" аналитических дополнений 8' и 8". A priori неясно, какой природы
множество Е и может ли здесь трансфинитное быть исключено. Мы
в следующем параграфе увидим, что оно есть проективное множество
и типа не сложнее А? (т. е. разности двух аналитических множеств).
Второе семейство состоит из множеств Е, определяемых
трансфинитным числом операций, существенно зависящих одна от
другой. Самые операции, определяющие множество Е, и в этом
случае занумерованы трансфинитными числами второго класса, но на этот
раз уже существенно зависят одна от другой. Множества этого
семейства мы будем называть множествами второго рода, или множествами
со связанными операциями.
Множества второго рода, вероятно, совсем не допускают
исключения трансфинитного, в противоположность множествам первого рода.
Они, по-видимому, не могут быть ни проективными, ни просто
выразимыми без помощи совокупности всех трансфинитных чисел второго
класса. Короче говоря, множества второго рода определяются
существеннейшим образом трансфинитной индукцией, проследующей по всем
трансфинитным числам второго класса и, вероятно, не могущей быть
сведенной ни на обычную арифметическую индукцию, идущую только
по натуральным числам, ни на усеченную трансфинитную индукцию,
т. е. идущую хотя и по трансфинитам, но лишь только до некоторого
трансфинитного числа, известного нам или не известного.
Первый пример множества, которое, по-видимому, есть истинное
множество второго рода, не допускающее исключение трансфинитного,
дан А. Лебегом (в его знаменитом мемуаре „Sur les fonctions repre-
sentables fcnalytiquement (Journ. de Math., 1905). Там знаменитый автор,
задавшись целью дать эффективный пример функции, не входящей
в классы Бэра, строит сначала как вспомагательный инструмент решето,
определяющее ему аналитическое множество, неизмеримое В, и затем
определяет путем существенно трансфинитной индукции, по-видимому,
совершенно не допускающей исключения трансфинитного, некоторую
поверхность y = <?{t, x), рассекаемую плоскостями t = t0 по кривым,
S74
Н. Н. ЛУЗИН
измеримым В, и по всем таким кривым. Эта вот поверхность и была
определена А. Лебегом при помощи существенно зависимых друг от друга
операций, составляющих предмет трансфинитной индукции. Есть много
данных думать, что поверхность y = y(t, х) Лебега и есть истинное
множество второго рода, т. е. не только имеющее его внешнюю форму,
но и не сводимое к множествам первого рода[59].
12* Множества первого рода. Мы уже указали в предыдущем
пункте, что множествами первого рода являются прежде всего те,
которые изобразимы как суммы трансфинитных рядов, члены которых
суть полиномы от аргументов, снабженных трансфинитными индексами;
эти же аргументы суть конституанты наперед заданных аналитических
дополнений.
Как мы сказали, простейшим случаем таких трансфинитных рядов
является, например, ряд
£=ед+<?><?;'-н...сс+..--ьСС+ lfi. as)
где ё'а и &'^ суть конституанты двух аналитических дополнений &' и §"у
определенных решетами Г' и Г".
Легко доказать, что множество первого рода Е> определенное
формулой (15), есть проективное множество типа не сложнее А? (т. е.
разности двух аналитических множеств).
Чтобы видеть это (и тем самым показать на конкретном примере
процесс исключения трансфинитного), напишем разложения
аналитических дополнений §' и <?" в ряд по их конституантам:
£' = <?; ч-£;-ь£;-н...-+- £'» + ... -*-£>- \Q
g» = gl + g'> -4-£;'ч-... + &1 н-...-ь^н- |2.
Обозначим через Н множество точек л: аналитического дополнения
&' • §" таких, что R'x не подобно части множества Rx ; аналогично
пусть Н" есть множество точек х множества <§' • &" таких, что R'^ не
подобно части множества R'x. Мы уже указали, что оба эти множества
Н и Н" суть аналитические дополнения.
Но по определению &'а есть множество точек х> где R'z есть вполне
упорядоченное и имеет а своим типом; то же самое имеет место и для Е"^ по
отношению к R'^%
Отсюда следует, что множество Н изобразимо двойной
трансфинитной суммой
н=ъ $:■£■;. (16)
Точно так же для Н' мы имеем
*<3 р
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИЙ 57S
Отсюда ясно, что данное множество £, изображенное трансфинитной
суммой (15), допускает еще и другое изображение, на этот раз уже
не трансфинитное, но конечное в виде формулы
Е = #.ё" — {Н'-*-Н"). (18)
И так как &', &'', FT и Н" суть аналитические дополнения, то
множество Е есть не сложнее типа А?. Таким образом, из
первоначального определения множества Е трансфинитное является
исключенным совершенно.
13. Естественно после этого желать исключить трансфинитное из
рядов типа
Е = S'0 - <££(0) н- ё'г • ££(1) -+- ... £'ш • ££(со) н-
+...«:•«;.,+ i2> с»)
где £', ё" суть конституанты двух наперед заданных аналитических
дополнений £' и S" и где ср (а) есть любая наперед заданная
возрастающая функция трансфинитного аргумента.
Здесь при решении вопроса о том, возможно или нет определить
в конечном виде множество £, заданное трансфинитной формулой (19),.
т. е. исключить из его первоначального определения трансфинитное,,
мы наталкиваемся на характерную трудность, заключающуюся в том,
что сначала нужно выяснить, что значит выражение: „задать
возрастающую функцию <р (а) трансфинитного аргумента а"?
Заметим, что относительно самих конституант £' и £'' вопроса
этого совсем не возникает, потому что они появляются вполне
определенными, раз заданы решета Г' и Г"; таким образом, вопрос о задании
всех конституант £' и <§'' сводится к заданию решет Г' и Г". И так
как решета эти состоят из счетного числа интервалов, параллельных
оси ОХ и имеющих своими концами точки с рациональными
координатами, то так далеко заходить, чтобы поднимать вопрос о задании
решет, мы не будем.
Совсем иное дело — вопрос о задании трансфинитной возрастающей
функции ср (а). Таковая, понятно, задана, если задано множество ее
значений. Значит, все дело сводится к заданию, т. е. умению задавать
различные части совокупности всех трансфинитных чисел
О, 1, 2, ...ш, ...а |2.
Важно при этом отметить, что это умение задать часть чисел
второго класса должно исходить из предположения, что это задание
направляется лишь счетным числом условий. Действительно, если
условий, каждое из которых фиксируется „произвольно", будет несчетное
число, то тогда вообще слово „задание" утрачивает смысл, потому чта
А^я задания части трансфинитных чисел второго класса было бы
достаточным задать в отдельности всякое ее число. Итак, задание транс-
576
Н. Н. ЛУЗИН
•финитной функции ср (а) должно быть сделано лишь счетным числом
условий.
Не следует при этом бояться утраты какой-нибудь части чисел
второго класса, не поддающейся заданию путем выбора, т. е. фиксации
счетного числа условий, так как ничто не доказывает, как было уже
указано, неверности второй гипотезы континуума;
я значит, выбирая трансфинитные функции <р (а) счетным числом
условий, мы можем даже с точки зрения математика-идеалиста (каковы,
например, Ж. Адамар, Ф. Хаусдорф, Цермело) получать их все.
При этом надо еще учесть и то обстоятельство, что задание
функции <р (а) одними лишь арифметическими операциями, проделываемыми
над трансфинитными числами и комбинированными между собой,
является в высшей степени бедным. По верному замечанию П. С.
Новикова, всякий арифметический закон, составленный д\я трансфинитов
второго класса, автоматически и без малейшего изменения переносится
на трансфинитные числа третьего, четвертого и вообще любого класса.
Таким образом, задание функции ср(а) одними лишь арифметическими
законами является нецелесообразным.
14. Ввиду сказанного мы предприняли такой путь задания
трансфинитной функции <р (а) счетным числом условий.
Возьмем на плоскости XOY универсальное плоское аналитическое
дополнение U и еще какое-нибудь индивидуальное плоское множество //,
названное нами каким-нибудь законом, лишь бы этот закон не содержал
в себе трансфинитного (ни явно, ни неявно).
Пусть х есть какая-нибудь точка оси ОХ) далее пусть Рх. есть
перпендикуляр в точке х к оси ОХ; пусть, наконец, Ux и Нх будут
линейными множествами, получающимися пересечением плоских множеств U и
Н перпендикуляром Рх.
Множество U предполагаем заданным вполне определенным
пространственным решетом Г, состоящим из плоских прямоугольников,
параллельных плоскости XOY, ориентированных по осям ОХ и ОУ,
находящихся в счетном числе. Пусть Тх есть пересечение решета Г плоскостью,
проведенной через точку х оси ОХ перпендикулярно к этой оси.
Пусть
U=Ub + Ui + ... + Un + ... + Ub + |2 (20)
есть разложение универсального аналитического дополнения по
конституантам: всякое Ua есть плоское множество, измеримое В.
В этих условиях ясно, что
£/* = (£/«)*-»-(£Л)* -*-... + №.+ ...+ (U.). -+■ \Q (21)
есть разложение по конституантам линейного аналитического дополне"
ния Ux\ здесь (Ua)x обозначает линейное множество, образующееся
пересечением плоского множества Ua перпендикуляром Рх.
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИИ 577
Возьмем теперь линейное множество Ня. Оно, вообще говоря,
содержит в себе целиком (т. е, без раздробления) трансфинитное, число
конституант {Ua)x; другие же конституанты (Ua)x являются: или
раздробленными, т. е. частью входящими в Нх и в то же самое время
частью выходящими из него, или не имеющими с Нх общей точки.
Сосредоточим свое внимание на конституантах (Ua)x, целиком без
раздробления содержащихся в Нх. Пусть их нумера отмечены среди
множества всех конечных и трансфинитных чисел второго класса; в
таком случае они составят часть совокупности трансфинитов второго
класса (присоединяя к ним и конечные числа) и, значит, определят
собой некоторую возрастающую трансфинитную функцию, которую мы
обозначим теперь через <р(л:, а).
Эту самую функцию <р(л:, а) мы и будем рассматривать как
заданную нам через задание действительного числа х и>
следовательно, как определенную счетным числом условий.
Ясно, что при заданном плоском множестве Н семейство
трансфинитных функций <р(лг, а) вполне определено. Чем „больше" плоское
множество Н содержит в себе линейных множеств Нх (т. е. чем
обильнее множество Н линейными множествами Нх\ надо иметь в виду, что
за Н можно взять, например, какое-нибудь плоское множество,
измеримое Ву но можно взять и универсальное аналитическое множество,
и т. д.), тем большее разнообразие мы имеем трансфинитных функций
?(•*» <*)• Притом плоские множества U и Н всегда можно взять за
дважды универсальную систему (см. мои „Лекции об аналитических
множествах")1. Трансфинитную функцию <р(дс, а) назовем проективной,
если исходное плоское множество Н было проективным.
15. Естественно, после того как мы определили, какие
трансфинитные функции <р (а) мы рассматриваем как заданные, написать ряд (19)
в виде
Ex = Sq • £f0R,o)-,-£i • ^,1) + " ••-+-£«• ££(*.«,)-*- • • • ■+-
-ь*:-^.)-*- i2 (w*>
и спросить, возможно или нет исключить из этой формулы транс-
финитное, дав множеству Ех конечное определение, т. е. свободное
от следов трансфинитного?
Ответ получается вполне определенный и утвердительный: такое
исключение возможно. Это делается на основе следующих предложений,
которые мы укажем, не приводя их доказательства.
Прежде всего будем рассматривать как „решето* всякое вообще
плоское множество К, определенное без помощи трансфинитного.
Обозначим через L совокупность всех точек л: таких, что Рх пересекает
плоское множество К по линейному множеству Кх, не вполне
упорядоченному в положительном направлении оси OY; обозначим через Л
1 См. стр. 187 настоящего тома.—Ред.
578
Н. Н. ЛУЗИН
совокупность всех точек х таких, что Кх есть вполне упорядоченное
в указанном направлении. Если мы обозначим через Аа множество
точек х, где Кх есть вполне упорядоченное и имеет своим типом число а,
то ясно, что имеем, вообще говоря, трансфинитное разложение
А = А0+А1 + ,„ + Ал+,.1 + Ав + | 2. (22)
Мы его будем называть разложением, соответствующим плоскому
решету К, по конституантам Лв.
Ясно, что множества L и Л взаимно дополнительные.
Введя эту терминологию, мы имеем предложения:
2 Q
Теорема I. Если разложения 2^ и 2 -^1 определены реше-
а—О а=0
^
тами К* и К", тогда разложение 2 ^1^4' происходит от решёта Ку
а=0
определенного проективным образом, отправляясь от данных решет
К' и К", причем Ла = -Л/-Л^'.
я
Теорема И. Если разложение 2 Лв происходит от решета Ку
а=0
и если непустые конституанты Л^ образуют последовательность
Л?(а)> гДе <Р (°0 есть трансфинитная возрастающая функция, тогда
разложение 2 ^<р(«) происходит от решета К', определяемого проек-
а=0
тивным образом, отправляясь от решета К, причем Л^ = А,
Эта последняя теорема имеет еще ту важность, что из
трансфинитной возрастающей функции р = ср (а) дает возможность получить
обратную функцию а = ф ((3) проективным путем.
Комбинированное применение указанных общих теорем к частному
случаю разложения (19*) приводит к предложению:
разложение, определяемое трансфинитным рядом
£,=«i'«;,M+^r^.i+-+^,^,)+ i2 (w*>
допускает исключение трансфинитного, причем сумма Ех этого ряда
есть сечение перпендикуляром Рх некоторого плоского множества Еу
определяемого проективно, отправляясь от заданного множества Н~
Как следствия этого предложения мы имеем:
Следствие I. Если трансфинитный ряд
« = ^ + ^ + 1, + ,,, + ^ + ... + ^+ |2
есть разложение аналитического дополнения по конституантам*
происходящее от обыкновенного решета С, составленного из
интервалов, тогда множество
ёх-н&о -+- <£to* -+-...-+- <§а><и ч- ... -+- <£шо -ь | 2
есть проективное.
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИИ $79
Следствие II. При тех же самых условиях множество
•О ei *? Hi> ta i
есть опять проективное множество; здесь индексы е0, е1э ... еа, ...
суть так называемые „числа 8", удовлетворяющие равенству юе = £,
расположенные в возрастающем порядке; начальное число 80 есть
предел последовательности со, юш, wwtl\ .. .
Самый вывод этого следствия очень прост: положим в равенстве (19*)
конституанты £7 и <§7 тождественными между собой. Тогда указанное
равенство напишется в виде
E, = S0-S9ix>0)^S1-S,(x>l)4-...4-Sa-Sf{Zia)4- |2 (19**)
где<£^ = (£^ = <? есть конституанта некоторого аналитического
дополнения <§> заданного обыкновенным решетом С.
Так как все конституанты аналитического дополнения € попарно не
имеют общей точки, то лишь только те члены траясфинитного ряда (19**)
не будут пустыми, где мы имеем удовлетворенным равенство
a=cp(jc, a). (23)
Следовательно, трансфинитный ряд (19**) есть разложение
множества Ех по конституантам аналитического дополнения £ с индек-
солш, являющимися корнями уравнения a = <p(jc, a).
Наконец, полагая по определению
ср(дг, a)=u>a,
мы имеем плоское множество Н проективным и состоящим «з
тождественных сечений. Следовательно, транофинитдаый ряд
£г+ё^ёч+...-*-ё^+... + ё^ |Q
имеет своей суммой проективное множество.
Было бы весьма интересно иметь пример множества Е первого рода
(т. е. со свободными операциями), которое не допускало бы исключения
трансфинитного.
J6. Множества второго рода* До сих пор мы имеем только один
дример множества второго рода, описанный А. Лебегом в его знамени-?
том мемуаре „Sur les fonctions representables analytiquement" (Journ.
de Math., 1905, стр. 214, строка 2 сверху). Самый трансфинитный
процесс со связанными операциями, который дает А. Лебег при описании
своего множества второго рода, очень сложен и настолько темен, что
в течение более тридцати лет математики не решались анализировать
этот процесс, вероятно считая, что расшифровка процесса слишком
трудна и не стоит затраченного времени, так как дело может кодчиться
580
Н. Н. ЛУЗИН
пустяками. А между тем, подобно тому как вспомогательное множество,
употребленное А. Лебегом как временный инструмент при построении
его универсальной поверхности у = ?(^, x) дая всех кривых,
измеримых В, и определенное им при помощи бинарного решета Г, впервые
описанного им же, оказалось аналитическим множеством,
неизмеримым В, подобно этому и трансфинитный процесс со связанными
операциями, открытый А. Лебегом, представляет выдающееся явление. Есть
много данных полагать что процесс этот, являющийся не чем иным,
как трансфинитной лндукцией в ее полном объеме, в которой всякий
следующий шаг обусловлен всеми без исключения предыдущими шагами,
дает эффективные множества существенно новой природы, совершенно
отличные от проективных множеств и их деривативов.
Желая насколько возможно более приблизиться к пониманию самой
сущности процесса А» Лебега, мы подвергнем его расщеплению,
отколов от него детали проективного характера, не представляющие
большого интереса.
17э Мы вместе с А. Лебегом отправимся от бинарного решета Г.
Под таковым понимается множество отрезков, параллельных оси ОХ
и определенных следующим образом: отмечают на интервале 0<^у<^1
оси OY все рациональные точки, которые затем выписывают в виде
бесконечной последовательности рл, р2, ..., р„, .... Потом берут
прямую у=^рп и делят ту ее часть, которая содержится в основном
квадрате ((X-K^l» 0<Cy<C^) плоскости XOY на 2л равных отрезка,
сохраняя из них лишь те, которые имеют четные нумера при последовательной
нумерации их слева направо. Наконец, заставляя число пробегать все
целые и положительные числа 1, 2, 3, ... и отмечая в основном
квадрате все сохраненные отрезки, в результате получают то, что
называется бинарным решетом Г.
Вот основное свойство бинарного решета: какова бы ни была
подпоследовательность рп, р , ... рациональных чисел, всегда имеется такая
точка х0 на отрезке [O^x^l] оси ОХу что перпендикуляр РХо
пересечет бинарное решето Г по линейному множеству точек, ординаты
которых образуют множество, тождественное с заданной
подпоследовательностью р^, рщХ ...
Пусть Е есть аналитическое множество, определенное бинарным
решетом Vf и 8 — его дополнение. Так как из рациональных точек можно
составить вполне упорядоченное множество любого наперед заданного
типа, то отсюда заключаем, что аналитическое дополнение разлагается
п ряд своих конституант
^^-н^-н^-н...-*-^-,-.. .ч-£вч- 2,
на которых ни одна не есть пустая.
Для дальнейшего нам необходимо следующее определение:
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИЙ $81
Мы называем частной производной Му по оси OY данного плоского
множества М совокупность всех предельных точек множества Му
берущихся лишь вдоль прямых, параллельных оси OY.
На основании теоремы о точках единственности множества,
измеримого В (см. мои „Лекции об аналитических множествах") (стр. 218
настоящего тома.—Ред.) имеем следующее предложение:
Теорема. Частная производная плоского множества,
измеримого Ву есть аналитическое множество.
Чтобы идти дальше, введем определение: мы называем какое-нибудь
плоское множество М множеством со счетными сечениями^ если
всякая прямая, параллельная оси О У, пересекает множество М, самое
большее, в счетном числе точек.
С этим определением мы имеем предложение:
Теорема. Частная производная плоского множества,
измеримого Ву со счетными сечениями есть множествоу измеримое 5.
Приложим эту теорему к бинарному решету Г, мы заключаем, что
частная производная Г'у есть множество, измеримое В.
Обозначим через D множество точек частной производной Vyy
лежащей на прямых у = риу где л = 1, 2, 3, ... . Ясно, что D есть
измеримое В9 и что его проекция d на ось OY также измерима В. Отсюда
следует, что множество-разность
S-d
есть аналитическое дополнение. Геометрический смысл этого множества
очень прост.
§ — d есть совокупность точек интервала (О < х <С 1) оси ОХ,
для которых линейное множество Rx есть вполне упорядоченное и для
которых производное множество Rx не содержит точки с
рациональной абсциссой.
Заметим, что для ху принадлежащего к множеству-разности Е — dy
линейное множество Rx состоит из одних лишь изолированных точек,
потому что Rx состоит из точек с рациональной ординатой, a Rs не
содержит точки с рациональной ординатой.
Обратимся теперь к множеству-сумме S трансфинитного ряда
S=E(o+Ea>t+.. .н-£шЦ>-н.. .-ь£шан- |2
Мы уже сказали, что S есть проективное множество (см. п. 15).
Поэтому множество
K=S-(E-d)
есть также проективное. Проективным же будет множество К у
составленное из точек прямых, параллельных оси OY и проведенных через
точки линейного мнржества К. И так как множество Г-нГ# есть изме-
582
Н. Н. ЛУЗИН
римое ZJ, то, наконец, проективным будет плоское множество //,
определенное формулой
#=£-(г-нг;).
Геометрическое свойство точек множества Н есть следующее:
прямая линия дс = х0, пересекающая множество Н, пересекает его по
замкнутому вполне упорядоченному множеству Нх типа а>вн-1;
изолированные точки линейного множества Нх имеют рациональную
ординату; предельные точки множества Н^ имеют все
иррациональную ординату; заставляя точку х0 пробегать все точки множества К,
мы получаем всевозможные замкнутые вполне упорядоченные
множества типа o>a-hl(a = l, 2, | Щ с описанными свойствами
изолированных и предельных точек.
18. Идея процесса Лебега. Рассмотрим трехмерное пространство
и в нем координатный триэдр OXYZ. Поместим на горизонтальную
плоскость ХОТ только что построенное проективное множество Н.
Теперь процесс Лебега есть следующий:
1. Рациональным точкам р1э р2, *.. р„, ... интервала (О <^у <С 1) оси 0Y
заставляем соответствовать некоторые заданные заранее действительные
числа />!, р2, .. .ря> • • •> благодаря этому всякой изолированной точке М
сечения Нх множества Н прямой х = х0 будет отвечать определенное
действительное число pif которое мы изобразим в виде апликаты точки /V,
проектирующейся в М. Таким образом, всякой изолированной точке М
линейного множества Нх отвечает определенная пространственная точка TV,
имеющая точку М своей проекцией.
2. Допустим процесс Лебега продвинутым так, что изолированные
точки М производных множеств N{£ получают соответствующие им
пространственные точки /V, имеющие отвечающие им точки М своими
проекциями, и допустим, что сказанное имеет силу уже аля всех производных
множеств Н£\ порядок т которых меньше числа а. Покажем, что
указанный процесс захватит изолированные точки и производного
множества №*\
3. Если число а есть первого рода, т. е. если
а=а*н-1,
то всякую изолированную точку М производного множества Иха) можно
окружить столь малым интервалом 8, в котором будут находиться лишь
изолированные точки М* производной Н^*\ для которых уже имеются
отвечающие им пространственные точки TV,-, имеющие Л/< своими
проекциями. Пусть zt есть апликата точки Л^. Тогда мы заставляем отвечать
точке Му являющейся пределом точек Miy наибольший из пределов z
чисел zi9 Полученное число мы рассматриваем как апликату точки 7V,
соответствующей точке М и имеющей М своей проекцией.
4. Если число а есть второго рода, тогда имеется возможность ука»*
вать фактически одну (и тольтео одну) простую (инфиннтгную) воара-
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИИ 583
стающую последовательность чисел at < a2 <[... < а< <..., имеющую
число а своим пределом. Действительно, пусть М есть изолированная
точка производного множества Н[*\ Точка М, очевидно, не принадлежит
вдолне упорядоченному множеству Rx и, будучи предельной его точкой,
отсекает некоторый сегмент о множества R . Но этот сегмент о состоит
из одних только рациональных точек pt; поэтому элементы сегмента a
занумерованы целыми положительными числами совершенно
определенным образом. С другой стороны, сегмент а подобен сегменту ог вполне
упорядоченного множества Rx-+-R'x, отсекаемому точкой М; поэтому
элементы сегмента а1 также занумерованы целыми положительными
числами. Но этот сегмент ох заведомо содержит точки всех производных
множеств Н[£ для т <^ а. Беря первую точку в каждом производном
множестве Н^ для 7 <С а> мь* имеем, очевидно, занумерованными целыми
положительными числами все числа f меньшие числа а. И так как а есть
число 2-го рода, то такое занумерование немедленно влечет определение
лростой возрастающей цепочки ^ <^а2<^... <^at <С .. •» имеющей число а
своим пределом. Окружая точку М последовательностью вложенных
друг в друга интервалов Ь19 Ь2У ..., &<..., длина которых стремится
к нулю, и выбирая в 8t. первую точку ЛГ< производного множества ff?*\
мы имеем последовательность точек Mi9 стремящуюся к точке М как
лределу. Так как a;<^a, точка Mi имеет отвечающую ей
пространственную точку Ni с апликатой z,-. Обозначая через z наибольший из
пределов чисел zi(i=lf 2, 3, ...), мы заставляем отвечать точке Мчисло z,
которое мы рассматриваем как апликату точки TV, соответствующей
точке М и имеющей М своей проекцией.
19. Определенный таким образбм трансфинитный процесс может
продолжаться вплоть до 2, и он действительно продолжается до 2, потому
что имеются точки л:0 на множестве AT, для которых тип вполне
упорядоченного множества Нхестъ ч>а-*--1, где а есть любое число второго
класса.
Но дая каждого отдельного числа х0 указанный процесс непременно
заканчивается на определенном трансфините, потому что раз тип вполне
упорядоченного множества Нх есть ша-н1, то это значит, что
производная Н^] состоит из одной только точки, которую мы обозначим
через Мж. Ясно, что на ней процесс Лебега и будет закончен, поставив
•ей в соответствие пространственную точку N с апликатой z(x0) и
имеющую Мх своей проекцией.
Таким образом, на всякой прямой л: = х0, пересекающей
проективное множество //, имеется самая верхняя точка Мх> совокупность
которых образует, очевидно, проективное униформное плоское множество,
которое мы обозначим через Ш-
Каждой точке М проективного множества ЭД отвечает определенная
пространственная точка Nx с апликатрй z(xq). Обозначим совокупность
■определенных таким образом точек NXa через 91.
584
Н. Н. ЛУЗИН
Это самое [пространственное множество 91 и есть определенное
трансфинитным процессом Лебега, со связанными операциями, и ничто
не заставляет думать, что 91 есть проективное множество, и что
множество 91 можно определить еще каким-нибудь другим путем>
при котором трансфинитное окажется совершенно исключенным.
Обозначим через 21 проекцию пространственного множества 91 на
плоскость XOZ. Ясно, что 21 есть униформное множество, лежащее
на плоскости XOZ и имеющее проективное множество 2Ti своей
проекцией на ось ОХ. Всякая точка т этого плоского множества 21 имеет х^
своей абсциссой и z(xQ) своей ординатой.
Ничто a priori не доказывает, что 21 есть проективное
множество.
20. Окончательная форма процесса Лебега* Тем не менее иногда
определенное выше множество 21 может оказаться проективным. Чтобы понять
причины этого, достаточно заметить, что множество 21 зависит от
взятых в начале процесса действительных чисел ри р2, ..., рп> • • •> которые
мы сделали отвечающими рациональным точкам р1э р2, ..., рп,... интервала
(0<Су<С1) оси OY. Например, если действительные числа рп взяты
все равными между собой: p=Pi = P2 = ••• =Рп — ••• = 1» то ясно, что
множество 21 будет конгруэнтно множеству К и, следовательно, само
будет проективным.
Чтобы избежать этого, Лебег делает следующее: множество
рациональных точек рр р2, ..., ря, ... интервала (0<Су<С1) он разбивает на
счетное число всюду плотных на интервале (0 <*/<!) множеств Dly
D<l, ..., U^j ...:
А = <р.и» p.* -.•>■„. •••}■
D2 = Ks?nn>--- ?«„> —К
и затем, расположив заранее все многочлены с рациональными
коэффициентами от действительного аргумента t в простую бесконечную
последовательность
МО. МО. .--МО. •••.
Лебег заставляет отвечать [каждой рациональной точке Ря<(*=1>
2, 3, ...) множества Д,, один и тот же самый многочлен МО*
Так как совокупность чисел п^ совпадает с натуральным рядом 1,
2, 3, ..., то всякая рациональная точка р* интервала (0<С*/<С1) имеет
отвечающее ей действительное число /?„(0, зависящее от аргумента t.
Вследствие этого само плоское униформное множество 21 теперь
оказывается уже зависящим от аргумента t, равно как и функция z(x0),
определенная на проективном множестве К в итоге всего тртнсфинит-
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИЙ $8S
ного процесса. Поэтому становится целесообразным написать
полученную функцию в виде
X = Ф (t, *),
где х есть точка множества К.
Из самого определения функции Лебега <р(/, х) ясно, что для всякого-
фиксированного дг0, принадлежащего к проективному множеству К,
функция <?{t, x0) аргумента t входит в классификацию Бэра, и что каждая
заранее заданная функция f(t) аргумента t> входящая в классификацию
Бэра, может быть получена из функции Лебега, при надлежащем выборе
точки х0, т. е. так, чтобы имелось тождество
f(t) = ?(ttx0)
дая всякой величины аргумента t.
Поэтому, если функцию Лебега z = <? (ty x) изобразим а виде
униформной поверхности в трехмерном пространстве OXTZ> то эта
поверхность разрезается плоскостями х = х01 где л:0 принадлежит к
проективному множеству К по всем возможным униформным кривым,
измеримым fi, и только по кривым, измеримым В. Следовательно, поверхность-
z = y(t> x) есть универсальная по отношению ко всем кривым,
измеримым В.
Но поверхность эта определена существенно с трансфинитной
последовательностью операций, из которых каждая зависит от всех
предыдущих, и ничто не доказывает, что трансфинитное может быть исключено.
Если невозможность исключения трансфинитного здесь будет строга
установлена, среди семейства множеств этого рода можно ожидать
встретить множества с удивительными свойствами.
21* Примечания. К сказанному полезно прибавить следующее:
задача построения эффективной поверхности, универсальной по отношению
ко всем кривым, измеримым Ву представляет неоспоримый, интерес».
когда хотят, чтобы эта поверхность была наипростейшего типа.
В моих „Лекциях об аналитических множествах" (см. стр* 263
настоящего тома. — Ред.) я доказал, что такой поверхностью служит
некоторая специально построенная проективная поверхность класса не выше 2-
Проф. В. Серпинский недавно пошел много дальше, показав, что
такую поверхность можно построить соединением двух униформных и
не перекрывающихся множеств, одно из которых есть типа А?> а
другое — аналитическое дополнение.
Была бы интересно иметь искомую универсальную поверхность-
одноро лишь типа А,, или еще интереснее было бы иметь ее одним
лишь аналитическим дополнением.
Второе замечание относится к конституантам. Мы всюду в
предыдущем говорили лишь о конституантах &а аналитического дополнения <§f
т. е, о так называемых внешних конституантах. Но само аналити—
586
Н. Н. ЛУЗИН
ческое множестве Е также разбиваете* на свои собственные
конституанты ЕаУ* называемые внутренними конституантами. Сотрудник
Математического института им. В. А. Стеклова АН СССР А. А.
Ляпунов недавно привлек мое внимание на то, что результаты теории
исключения трансфинитного сохраняют свою силу и для внутренних конституант
Так, например, можно сразу же утверждать, что ряды
Ех -+- Е(-> н- Ею* -+-...-+- Еюш -+-... ■+- Еша -+- I 2,
л другие суть проективные множества. Для этой цели А. А. Ляпунов
устанавливает, что если мы применим теорему С. Мазуркевича и
изобразим данное линейное аналитическое множество Е как проекцию
униформного аналитического дополнения //, то всякая конституанта На
аналитического дополнения Н проектируется во внутреннюю
конституанту Еа аналитического множества Е. Это замечание позволяет без
новых рассуждений перенести результаты теории исключения на
внутренние конституанты.
Изыскания П. С. Новикова
22. Характер исследований. Изыскания эти посвящены главным
образом переносу принципов отделимости теории аналитических
множеств на множества других семейств.
В этом отношении нашим автором были подвергнуты исследованию
три семейства множеств:
(а).— С-мноместза;
(Р)— проективные множества класса 2;
(7) — множества, являющиеся проекциями униформных аналити"
ческих дополнений.
Известно, что принципы отделимости аналитических множеств
формулируются так:
Принцип I. Всякие два аналитических множества отделимы (В).
Принцип II. Удаляя общую часть двух пересекающихся
аналитических множеству мы имеем оставшиеся от них части
отделимыми друг от друга аналитическими дополнениями.
Известно далее, что всякое аналитическое множество есть проекция
множества, измеримого В, что аналитические дополнения совпадают
с аналитическими множествами лишь в случае измеримости В, и что
проективные множества класса п разделяются на 3 семейства:
1°. Семейство РСРС.. .РЕ9 где Е измеримо В> и где буква Р,
обозначающая операцию проектирования и чередующаяся с буквой С,
обозначающей операцию взятия дополнения, написана в точности п раз;
это семейетво обозначается символом Ап, и множества^ образующие
его, называются аналитическими множествами класса п.
2°. Семейство СРСРС... РЕ, где буква Р написана п раз,
обозначается символом САп; множества, образующие его, называются
аналитическими дополнениями класса п.
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИИ $87
3°. Семейство множеств, которые суть одновременно и Ап и САт
обозначаются символом Вп; множества, образующие его, называются
измеримыми В класса п.
Ясно, что, делая л=1, мы получаем обычные аналитические
множества, аналитические дополнения и множества, измеримые В.
Известно наконец, что эта классификация есть не только
формальная, так как, каково бы ни было число л, фактически существуют
множества, входящие в отдельности в любое из множеств: Ап, СЛ*, Впу
я которое не принадлежит ни к одному из предыдущих классов.
Целесообразным является введение еще особых символов для
обозначения проекций униформных множеств САп-х: семейство таких
множеств обозначаем через А'пл Семейство дополнительных к ним
множеств обозначаем через СА'п. И, наконец, семейство множеств,
которые суть одновременно и А'п и СА'п> будет обозначаться через В'и.
Наконец, семейство „С-множеств", введенное преждевременно
скончавшимся геометром Евгением Августовичем Селивановским, определяется
следующим образом.
Прежде всего вводится „операция решета": она состоит.ja том, что
на прямых, параллельных оси ОХ и взятых в счетном числе, помещаются
некоторые заранее данные множества точек; затем полученное плоское
множество со счетными сечениями рассматривается как решето Cf
определяющее линейное множество £, образованное теми точками х
оси ОХ, где перпендикуляр Рх встречает решето С в множестве точек
R99 которое не есть вполне упорядоченное по отношению к
положительному направлению оси OY. Полученное множество Е и называется
множеством, определенным операцией решета, проделанной над
заданными множествами, помещенными на указанных прямых, параллельных
оси ОХ.
Семейство „С-множеств" определяется теперь так: это есть
наименьшее из семейств, содержащих интервалы, и инвариантное по
отношению к двум операциям: операции решета и операции взятия
дополнения.
Семейство всех С-множеств допускает точную классификацию того
же самого трансфинитного характера, как и классификация Бэра.
Именно, все семейство С-множеств разбивается на классы
^0> ^1» ^2> • • • > ^ш> * * * » ^а> I >
тде начальный* класс С$ обозначает совокупность всех аналитических
множеств и где каждый класс Св обозначает совокупность всех
множеству не входящих в предыдущие классы и получаемых
операцией решета, проделанной над множествами предыдущих классов
и их дополнениями'.
Такая класснфакан^я была предложена Е. А. Селивановским, 4ока"
завшим непусаготу каждого класса», измеримость Лебега и свойство
Бара всякого С-множества (см. [3Q])u
588
Н. Н. ЛУЗИН
Нам нужно еще одно определение: пусть S есть некоторое семейство
множеств, инвариантное по отношению к операциям счетной суммы и
счетного произведения; пусть В9 есть совокупность всех множеств,
входящих в Sy так же как и их дополнения.
Условимся, согласно П. С. Новикову, назвать В» максимальным
телом В в семействе S. Ясно, что в семействе всех аналитических
множеств максимальным телом В будет совокупность всех множеств,
измеримых 5.
В качестве приложения этого понятия обозначим через Sa
совокупность всех С-множеств, содержащихся в классе Са и во всех
предшествующих классах; легко видеть, что Sa есть семейство множеств,
инвариантное по отношению к операциям счетной суммы и счетного-
произведения. Обозначим В9л максимальное тело В в семействе Sa.
Очевидно, нужно ждать, что свойства этого максимального тела В8а имеют
много общего со свойствами совокупности всех множеств, измеримых В>
по отношению к семейству всех аналитических множеств. Исследования
нашего автора вполне оправдывают это ожидание.
23. После введения этих понятий, определений и обозначений
возвратимся к изысканиям П. С. Новикова.
Как уже было указано, они относятся в первую очередь к переносу
принципов отделимости теории аналитических множеств на множества
трех семейств: 1° С-множества, 2° множества А2 и СА2 и 3° множества
А2 и СА'Г
В этом отношении автором получены результаты исключительного
значения, так как проблема отделимости проективных множеств
при современном состоянии науки казалась совершенно безнадежной»
Проблема эта более 10 лет ждала своего решения и только в работах
П. С. Новикова получила точное и совершенно неожиданное решение.
Забегая вперед, мы теперь же отмечаем глубину изысканий нашего
автора и большую силу его результатов. Это можно усмотреть хотя
бы из того факта, что если проблема отделимости С-множеств решена
автором в направлении, которого все ожидали и которое можно было
предвидеть («всякие два множества Св, не имеющие общей точки,
отделимы посредством множеств 5*ва, „всякие два перекрывающиеся
множества Св по удалении общей части отделимы двумя дополнениями
к множествам Саи)> так что здесь были нужны лишь настойчивость и
терпение, то, наоборот, проблема отделимости проективных множеств
второго класса решена автором в том направлении, которого никто
не ожидал и которое для всех явилось удивительным: совершенно
естественно было ждать отделимости В2 для двух Аъ не имеющих
общей точки. И, однако, это как-раз и оказалось неверным, так как
отделимы (В^ не два не перекрывающихся Л2, а два не перекрывающихся.
СА2* Оказывается, что все законы отделимости, имеющие силу в теории
аналитических множеств, продолжают быть действительными и для
проективных множеств второго класса, но только, в обратном смысле»
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИИ 589
«говоря образно: „навыворот"; роль аналитических множеств играет
не А2> а САъ роль аналитических дополнений играет не СА2, а самое
А2; и лишь роль В2 аналогична, до известной степени впрочем, роли
множеств, измеримых В.
Подобная инверсия законов отделимости во втором классе
проективных множеств является сюрпризом; такой отделимости никто не
ожидал, и после этих результатов автора делается понятной безуспешность
всех делавшихся попыток открыть отделимость в теории проективных
множеств второго класса: попытки эти, оказывается, делались в том
направлении, где успех был невозможным, так как отделимость лежала
в диаметрально противоположном направлении. Чтобы сделать эти
открытия, нужны были исключительные проницательность и глубина.
Достаточно указать, что даже такие острые исследователи проективных
-множеств, каковы ленинградские талантливые молодые математики:
Канторович и Ливенсон, выработавшие особые тонкие приемы
исследования проективных множеств второго класса и внесшие важную долю
в прогресс их теории („всякое С-множество есть проективное
множество второго класса"), даже и они были вынуждены отступить
перед трудностями теории отделимости в проективных множествах второго
тсласса. Эта отделимость лежала так глубоко, что для ее открытия
необходимы были математические инструменты - очень большой силы,
которых не было в руках других исследователей: д\я более слабых
средств теория эта недоступна. Одним из таких сильных инструментов
является, например, понятие минимального индекса пространственного
решета относительно прямощ введенное нашим автором.
Не следует притом упускать из вида особого свойства той области,
тде протекали эти изыскания, которое делало их действительно
трудовыми: в этой области обычно уже самая постановка проблемы делает
сразу же ясным путь к ее решению; но если в самой постановке
проблемы не содержится указаний на такой путь, проблема выглядит
безнадежной и может десятки лет ждать своего решения. В этом
отношении эта область исследований имеет много общего с исследованиями
но труднейшим проблемам Теории чисел.
Характер исследований П. С. Новикова другой, чем характер
исследований, изложенных нами ранее: эти последние имеют целью лишь
наметить новые пути изысканий и поэтому не имеют характера
законченности. Тогда как результаты П. С. Новикова по своей законченности
приближаются к классическим.
В дальнейшем мы лишь вкратце изложим результаты П. С. Новикова,
так как дело говорит само за себя и не нуждается в комментариях.
24# Пошггие правильного решета. Это понятие является первым
Ленным инструментом, выработанным автором для проведения его
изысканий.
Решето называется правильным, если всякая прямая, параллельная
вертикальной оси, встречает решето: либо во вполне упорядоченном
590
Н. Н. ЛУЗИН
множестве по отношению к положительному направлению этой оси,
либо во множестве точек, которое не есть „clairseme" (в смысле А. Дан-
жуа).
Теорема. Всякое аналитическое множество определимо
правильным решетом, составленным из счетного числа интервалов,
параллельных оси ОХ.
Предложение это весьма важное и лежит в основе всех дальнейших
рассуждений автора.
25. Максимальное тело. Другим ценным вспомогательным
инструментом исследователя является понятие максимального тела В,
содержащегося в данном семействе S множеств.
Максимальное тело В в данном семействе S обозначается
символом Вв.
По самому определению, максимальным телом В в данной системе
S множеств называется совокупность множеств системы S,
инвариантная по отношению к операциям: сумма, разность и
произведение, и такая, которая не может быть пополненной ни одним
множеством из системы S, без того чтобы не утратить указанную
инвариантность.
Когда само данное семейство S инвариантно по отношению к
операциям: счетная сумма и счетное произведение, тогда
существование и единственность максимального тела В$ доказывается немедленно:
тело В* получается, беря в семействе все такие и только такие
множества Е, дополнения которых СЕ также входят в семейство S.
В семействе S всех аналитических множеств максимальное тело Bs есть
совокупность всех множеств, измеримых В.
Определение других максимальных тел в данной системе множеств S
(например, максимального аналитического тела и т. д.) не требуется
в работе П. С. Новикова.
26. Теория отделимости в семействе С-множеств [60]. Мы уже
указали, что работами Канторовича и Ливенсона установлена
принадлежность всех С-множеств к семейству проективных множеств
второго класса.
Поэтому изучение С-множеств является как бы вступлением в теорию
проективных множеств второго класса и вследствие этого представляет
существенный интерес. Несмотря на то, что классификация С-множеств
аналогична классификации множеств, измеримых В, оставалось до сих
пор не известным, имеют ли силу для С-множеств теоремы отделимости.
В мемуаре Канторовича и Ливенсона на это не содержится ни
малейших указаний. Для П. С. Новикова область С-множеств является
как бы пробой его сил. Пользуясь исключительно элементарными
геометрическими образами, П. С. Новиков с большой глубиной
исследует их свойства; как результат его анализа вытекает то ваастое
следствие, что в теории С-множеств имеют место те же -самые теоремы
отделимости,' как и для аналитических множеств и stx доиголяевей. Ваокйо
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИЙ S91
заметить, что отделимость С-множеств и аналитических множеств
происходит в том же самом смысле (а не в обратном).
Ключом в теории отделимости С-множеств является следующее'
важное предложение:
Лемма. Пусть даны два решета С" и С", составленные из
С-множеств или класса <<*, или класса а и принадлежащих к
максимальному телу этого класса, причем множества эти расположены
на прямых, параллельных оси ОХ; тогда множества тех точек х,
где R'% подобно части R"x, есть С-множество класса а.
Раз эта основная лемма доказана, из нее тотчас же вытекают
следующие два принципа отделимости Сгмножеств:
Принцип I. Каждые два С-множества класса а без общей точки
отделимы двумя С-множествами максимального тела класса а.
Принцип II. Если у двух пересекающихся С-множеств класса а
удалить их общую часть, тогда оставшиеся части отделимы
множествами, дополнительными к С-множествам класса а.
Так же точно остается в силе кратная отделимость, как показывают
теоремы:
Теорема. Пусть Ех Е2, .. ♦ есть счетная последовательность-
С-множеств класса а, для которой Ех- Е2- = 0; тогда имеется
счетная последовательность С-множеств максимального тела
класса а, Нх, Н2, ... такая, что £< С //< и Н1Н2... = 0.
Теорема. Если у С-множеств Е1У Е2, ... класса а удалить юб-
щую всем им часть, то оставшиеся части кратно отделимы
множествами, дополнительными к С-множествам класса а, т. е. имеются
множества Ну, Н2, ..., дополнительные к С-множествам класса а,
такие, что Е+ С //» и Ну • Н2 * ... = 0.
Мы напоминаем, что максимальным телом класса а называется
максимальное тело В»л семейства aS^, составленного из С-множеств
классов <а из самого Са.
27. Теория отделимости в семействе проективных множеств
второго класса [35]. Мы уже указали, что результаты этой работы
П. С. Новикова, трактующей законы отделимости всех вообще
проективных множеств класса 2, представляют исключительную ценность для.
современного состояния науки. Автор устанавливает в этой работе
законы отделимости для проективных множеств второго класса, причем
совершенно неожиданным является тот его результат, что отделимость,
эта совершается в обратном смысле, чем д\я аналитических множеств
и их дополнений. Именно, множества А2 оказываются аналогичны не
самим аналитическим множествам, а их дополнениям; множества же СА2
оказываются аналогичными самим аналитическим множествам, что же
касается до множеств В2, то они аналогичны множествам, измеримым В*
Результат этот, совершенно экстраординарный, должен сделать,
понятной неудачу тех многочисленных попыток, которые делались.
для проективных множеств второго класса, где искали установлениж
'592
Н. И- ЛУЗИН
законов отделимости в том же самом смысле, как и для аналитических
множеств и их дополнений, а не в обратном.
Здесь рассмотрения автора являются еще более глубокими и
сильными, чем в предыдущей работе.
Основным инструментом, который открывает дорогу дая дедукций
автора, является сильное и прекрасное понятие индекса
пространственного решета относительно данной плоскости.
Пусть в пространстве OXYZ имеется какое-нибудь множество
точек С, которое мы рассматриваем как пространственное решето, т. е.
как просеивающий аппарат для точек М плоскости XOY, для
которых R м есть вполне упорядоченное множество по отношению к
положительному направлению оси OZ. Обозначим через П^ плоскость,
проведенную через точку л: оси ОХ перпендикулярно к этой оси. Эта
плоскость Пд. пересечет пространственное решето С по плоскому
решету, которое естественно обозначить через Сх> Это плоское решето
определяет линейное аналитическое дополнение §х, являющееся
разрезом плоского аналитического дополнения &, определенного
пространственным решетом С, перпендикуляром Рх, лежащим в плоскости XOY
и восстановленным в точке х оси ОХ к этой оси. Обозначим через лх
индекс наименьшей к онституанты, фактическиимеющей
точки на перпендикуляре Рх. Если таких точек совсем
нет, т. е. если Рх не пересекает плоское аналитическое
дополнение &, тогда мы полагаем по определению а* = 2.
Это число &х и называется индексом пространственного
решета С относительно плоскости Пл.
Ключом в теории отделимости проективных множеств второго класса
служит следующее важное предложение:
Лемма. Пусть даны два пространственных решета О и С",
составленные из счетного числа прямоугольников, параллельных
плоскости XOY и ориентированных по этим осям; предполагается,
что решета эти правильные и такие, что нет точки х0, для
которой а^ = а^<^2. В этих условиях совокупность точек х, для
которых a'9<Za^y есть множество типа Л2.
Раз эта основная лемма доказана, из нее тотчас же вытекают
следующие два принципа отделимости проективных множеств второго
класса:
Принцип I. Всякие два множества СА2 без общей точки
отделимы (В2).
Принцип И. Если у двух пересекающихся множеств СЛ2
удалить их общую часть, тогда оставшиеся части отделимы (А2);
если у двух пересекающихся множеств Аг удалить их общую часть,
тогда оставшиеся части отделимы (А2).
Кратная отделимость, введенная впервые П. С. Новиковым, также
протекает в обратном смысле, чем в теории аналитических множеств.
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИИ 593
Теорема. Пусть Е19 Е2, есть счетная последовательность
множеств С А,, для которой Ех • Е2 • .. .=0; тогда имеется счетная
последовательность множеств В» Н1У Н>, ..., такая, что Е{ С Н{
и НГНг...=0.
Теорема. Если удалить общую часть счетной
последовательности множеств СА2, Е1У Е2>..., оставшиеся части кратно
отделимы множествами (А,).
28. Теория отделимости в семействе проекций униформных
аналитических дополнений. Свойства этих проекций [61]. Эти
изыскания П. С. Новикова являются, собственно, центром всей его работы
по теории отделимости. Здесь автор, ободренный удачей предыдущих
исследований, приступает и доводит до конца изыскания, которые при
современном состоянии науки можно было считать безнадежными.
Давно уже было известно после исследований С. Мазуркевича и
В. Серпинского, что всякое аналитическое множество есть А'2 (т. е.
проекция униформного аналитического дополнения. Мы напомним
обозначения п. 22: А'2 есть семейство всех проекций униформных
аналитических дополнений; СА2 есть семейство дополнений к множествам,
образующим семейство А2; и В'2 есть семейство всех множеств, входящих
одновременно в^ив СА'2. Это составляет основной результат С.
Мазуркевича. Серпинский распространил его на все те множества,
которые получаются из аналитических множеств и их дополнений путем
двух операций:
1° сумма счетного (конечного) числа неперекрывающихся множеств
(т. е. сумма в узком смысле);
2° произведение счетного (конечного) числа множеств.
Из этих исследований С. Мазуркевича и В. Серпинского вытекает,
что все множества минимального тела, содержащего аналитические
множества и их дополнения [иначе говоря, минимальной системы множеств,
содержащей все аналитические множества и их дополнения и
инвариантной по отношению к операциям суммы (в широком смысле) и
произведению счетного числа множеств; по отношению же к операции
разности двух множеств эта минимальная система будет автоматически
инвариантна, т. е. без каких-либо добавочных условий], суть опять А2,
Эти результаты В. Серпинского были обязаны двум следующим леммам,
им доказанным:
Лемма I. Если Е}, Е1У ... суть множества А'2 и если они попарно
не перекрываются, то сумма их Ех -+- Е2-+-... есть также А'г
Лемма II. Если Ех, Е>9 ... суть множества A'v то произведение
их Ег • Е2 •... есть также А'г
В этом виде теория проекций униформных аналитических
дополнений долгое время оставалась без изменения. Атаки, которые велись на
лемму I В. Серпинского, с тем чтобы уничтожить в ней слова: „если
594 н. н. л у з и н
они попарно не перекрываются%\ до сих пор оставались
безуспешными.
Чтобы пробить брешь в этом труднейшем вопросе, П. С. Новиков
ввел новое, очень простое и глубокое понятие точки трансфинитной
единственности.
Содержание его следующее: пусть в пространстве п измерений
ОХх Х.г. .. Хп находится аналитическое дополнение о, определенное
решетом С, находящимся в пространстве ОХ1 Х2. .. Xn Y, число
измерений которого есть /2 —•— 1. Мы предполагаем решето С состоящим из
прямоугольных частей л измерений, ориентированных по осям ОХи
ОХ2,..., ОХп и находящихся в счетном числе. Если М (х1У х.1У ..., хп)
есть точка пространства ОХх Х2... Хн и Рм — прямая параллельная
оси OY и проходящая через точку М, то через Rm мы обозначим
линейное счетное множество, являющееся пересечением решета С
прямой Рм- Аналитическое дополнение $ есть совокупность всех точек Му
таких, что Rm есть вполне упорядоченное множество в положительном
направлении оси ОК.
Пусть S = So-i-<§1-i-S2+ ... -+-£,„-*- ... -+-£«-§- |й (24)
есть разложение аналитического дополнения <§ по его конституантам;
здесь £а есть совокупность точек М таких, что тип вполне
упорядоченного множества Rm в точности равен а.
Введя эти обозначения и данные, обозначим через Н 0 0 0 часть
пространства п измерений ОХгХ2 ... Хиу получающуюся, фиксируя
первые т координат подвижной точки М(хг, х2, ..., хтУ хт+1, ... хп)>
полагая jt1=jt°, x2 = xl, ..., xm=-xQm и заставляя оставшиеся
переменные хт+1, — х„ изменяться независимо друг от друга от —со до -i-co;
движущаяся точка М опишет в этом случае рассматриваемое
многообразие Я0о о у число измерений которого, очевидно, равно разности
п—т. Здесь мы предполагаем, что l^m^n — 1.
Многообразие И 0 о о содержит в себе точки данного аналитиче-
х\х2 ' ' • хт
ского дополнения £; мы обозначаем через £ 0 о о часть множества £,
и г\* ЛА*§ "• • • А2») часть кон-
принадлежащую к И 0 о о. Обозначая через ev x l mJ
Х1Х2 * • ' Хт а
ституанты £., находящуюся в многообразии Н 0 о 0 > мы> очевидно,
Л\Х2 " ' хт
имеем разложение
+ Г2 WV ... |Q. (25)
Многообразие // 0 о л называется критическим,
*1*2 ' ' ' Тт
/,00 0\
если первая непустая конституанта S разложе-
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИИ 595
ния (25) состоит из одной только точки, которую
обозначим через Mq и которую будем называть точкой
трансфинитной единственности аналитического дополнения <£.
Ясно, что точка Л/0 имеет своими первыми т координатами числа
jcj, х2У .. ., х^, определяющие рассматриваемое критическое
многообразие Н о о л>; ясно далее, что остальные п—т координат х , ...х
%\*Ъ ' ' tn m+l w
точки М0 определены единственным образом знанием первых т
координат х°, х!?, • • • > х°т. Поэтому, если все координаты точки М0
обозначим через xj, x!j, ..., хЦ, то имеем
Ясно, наконец, что функции эти ср1э ср2, . . ., <p„_w определены вообще
не для всякой системы т действительных чисел хг, х2, . .., хту потому
что не всякое многообразие Нх& ... хт есть критическое.
Совокупность всех точек М0 трансфинитной
единственности в пространстве ОХгХ2 ... Хпу получаемая
допустимым изменением координат х\у х°, ..., хЦ,,
называется множеством трансфинитной единственности
аналитического дополнения &. Мы его обозначим через 2^1 0
значки 1, 2, ..., т должны напоминать о том, что рассматриваются
критические многообразия п—т измерений, получаемые
фиксированием т первых координат; подобным же образом символом $ftk k k
обозначают множество трансфинитной единственности, получаемое
отбором точек трансфинитной единственности в критических
многообразиях Н о о о .
Понятие точки трансфинитной единственности оказывается весьма
острым инструментом, приводимым в действие следующим важным
предложением:
Лемма. Множество точек трансфинитной единственности
аналитического дополнения есть опять аналитическое дополнение.
Раз эта основная лемма доказана, из нее тотчас же вытекает давнр
ожидаемое расширение леммы I В. Серпинского в виде предложения
первостепенной важности:
Теорема. Сумма конечного или счетного числа множеств А>
есть опять множество А2.
Но центральным и совершенно парадоксальным результатом П. С.
Новикова является тот, который дается предложением:
Теорема. Существует униформная поверхность^ которая есть
аналитическое дополнение и которая есть универсальная по
отношению ко всем плоским униформным аналитическим дополнениям.
Из этой блестящей теоремы сразу же следует, что существует
такое плоское множество точек А2> которое является
596
Н. Н. ЛУЗИН
универсальным по отношению ко всем линейным
множествам точек Аг
Отсюда следует, что пересечение прямой х = у этого
плоского универсального А'2 дает такое линейное А2
дополнение которого уже не есть А'2. Следовательно,
существуют А'2У которые не суть В'2.
Но, с другой стороны, дополнение к множеству В> есть опять
множество В2. Поэтому: семейство А2 не тождественно с семейством В2л
Но каково в действительности взаимоотношение А'2 и В2У
содержится ли какое-нибудь из них в другом или же они только
перекрываются, — это не известно. Вопрос этот исключительной трудности.
29. Ключом в теории отделимости множеств A'v СА'2 и В'2 является
следующее важное предложение об униформизации плоских
аналитических дополнений с конечными сечениями.
Лемма. Всякое плоское аналитическое дополнение с конечными
сечениями может быть униформизировано аналитическим
дополнением.
Это предложение означает, что если & есть плоское аналитическое
дополнение, пересекающееся всякой прямой, параллельной оси ОУу
не более чем в конечном числе точек, тогда всегда можно отыскать
такое униформное аналитическое дополнение £, содержащееся в <£,
которое имеет ту же самую проекцию на ось ОХу как и все данное
множество <§.
Доказывается эта лемма на основании предыдущей леммы
относительно множеств трансфинитной единственности.
Раз эта основная лемма доказана, из нее тотчас же вытекают
следующие два принципа отделимости множеств А2, СА'2 и В2:
Принцип I. Каждые два множества СА'2 без общей точки
отделимы (В2).
Принцип И. Если у двух пересекающихся СА2 удалить их
общую часть, оставшиеся части отделимы (А2); если у двух
пересекающихся А2 удалить их общую частьу тогда оставшиеся части
отделимы {А^.
Кратная отделимость выражается предложениями:
Теорема. Всякая счетная последовательность множеств CAi,
для которой EY • £2 • .. . = 0, допускает кратную отделимость
множествами В'г
Теорема. Если удалить общую часть счетной
последовательности Е1У Е2У ... множеств СА'2У оставшиеся части кратно
отделимы множествами А2.
Из этих теорем мы видим, что законы отделимости для множеств
А2У СА2 и В2 абсолютно тождественны с законами отделимости для
множеств А2У САг и В,у т. е. также протекают в обратном смысле,
чем в теорий аналитических множеств.
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИИ $97
Это обстоятельство заставляет весьма серьезно поставить вопрос:
не существует ли в действительности тождества семейств
А2 и А2?
Проблема о тождестве или различии А2 и А2 представляет
исключительные трудности [62].
3i). Частная попытка приблизиться к разрешению этого вопроса
сделана П. С. Новиковым, поставившим вопрос о
взаимоотношении семейства Аг и с еме йст в а С-м нож е ств.
Этот вопрос им разрешен до конца. Предложение, служащее
ключом к этой проблеме, есть, в сущности, не что иное, как уточненная
лемма II. В. Серпинского. Это уточнение дается П. С. Новиковым
в следующем виде:
Лемма. Если Е1У £2, ... суть проекции плоских униформных
аналитических дополнений £1У &2У ..., определенных решетами
С1У Со ..., тогда произведение Е1Ег- ... есть проекция плоского
униформного аналитического дополнения &> определенного таким
решетом С, что в каждой точке М, принадлежащей к £, тип RM
в точности равен сумме типов RM, R^, ..., соответствующих
решетам С, С", — в точках Мг> М2, ... множеств <§\, £2> .. •>
лежащих на прямой L, проходящей через М и параллельной оси OY*
Доказательство этой леммы получается непосредственно из
рассмотрения рассуждений В. Серпинского о том, что проекция счетного
произведения А2 есть множество А'г То решето, которое там получается а^я S9
в этом рассуждении как раз удовлетворяет условиям леммы П. С. Новикова.
Из этой леммы П. С. Новикова после длинных и технически
сложных рассуждений следует предложение, представляющее
самостоятельный интерес:
Теорема. Всякое С-множество есть AY
Это предложение есть большое заострение предложения, впервые
установленного Канторовичем и Ливенсоном о том, что „всякое С-
множество есть проективное множество второго класса".
И вместе с тем делается еще более ясной необходимость или
отыскать такое А2> которое не есть Av или установить тождество
семейств А2 и Аг
31. Общая униформизация плоского аналитического дополнения.
Мы видели (см. п. 29), что плоское аналитическое
дополнение & с конечными сечениями униформируется опять
аналитическим дополнением.
Естественно поставить вопрос, нельзя ли униформизировать вообще
всякое плоское аналитическое дополнение <§, не делая никаких
частных предположений относительно его сечений прямЬши, параллельными
оси OY/
П. С. Новиков ответил утвердительно на этот вопрос, доказав
следующее важное предложение:
598
Н. Н. ЛУЗИН
Теорема. Всякое плоское аналитическое дополнение мотет быть
униформировано множеством А*-
Процесс, который дает П. С. Новиков, существенно трансфинитен
и позволяет во всяком непустом аналитическом дополнении указать
индивидуальную точку. Но, как показывает самый финальный результат,
трансфинитное, в конце концов, исключимо, и в итоге мы имеем
проективное множество и даже А.>.
Отмечу, что проблема об указании индивидуальной точки в непустом
аналитическом дополнении мной была поставлена около двадцати лет
тому назад, причем я неоднократно настаивал explicite в печати на ее
значении как математическом, так и философском.
Совершенно очевидно, что здесь представляется самая настоятельная
необходимость сделать дальнейшие изыскания о природе этого процесса,
указывающего индивидуальную точку в непустом аналитическом
дополнении, и должны быть выведены отсюда по возможности все следствия.
Сейчас пока преждевременно делать какие-нибудь выводы и
заключения.
32. Попытка классификации эффективного. Изложенные
результаты П. С. Новикова составляют содержание трех первых глав его
диссертации, представленной в рукописи Академии наук СССР на
соискание звания доктора чистой математики. Насколько материал этих глав
работы П. С. Новикова является законченным, давая совершенно ясную
и точную картину исследуемых явлений и свойств, настолько последняя,
четвертая глава работы представляется сырой и незаконченной даже
в самом своем замысле. Впрочем, глава эта, трактующая о
множествах эффективных, в смысле А. Лебега лишь весьма косвенно связана
с проективными множествами вообще.
Основная идея этой главы состоит в разыскании такой
классификации множеств, которая охватила бы не только проективные, но и
вообще все множества, которые можно индивидуально определить1.
В этой главе автор приступает к исследованию сюжета, который
современная наука считала преждевременным даже формулировать и
ставить в проблему.
Вкратце содержание этой главы следующее: автор строит весьма
естественным образом такую классификацию множеств, за пределы
которой мы не умеем выйти, употребив даже столь могущественный прием,
каким является применение диагонали. Классификация эта идет по
трансфинитам третьего класса, и остается неизвестным,
распространяется ли она действительно на все трансфинитные числа
третьего класса или же только на их сегмент.
1 Лебег в своем знаменитом мемуаре „Sur les fonctions representables analytique-
ment" (стр. 21S) пишет: „Игак, можно назвать (nommer) функцию» непредставимую
аналитически, и то исследование, которое мы только что предприняли, не следует
смешивать с изучением функции, кэтэрыг мужнЬ назявзть (fDnctions qu'on peut
nommer), т. е. с исследованием, к которому было бы интересно приступить".
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИИ 599
При настоящем состоянии науки и имея в руках лишь указанный
сырой материал, является преждевременным какое-нибудь умозаключение
об удаче этой смелой попытки П. С. Новикова. Но самое построение,
даваемое им, и проблемы, с ним связанные, столь интересны, что весь
замысел этой четвертой главы следует, безусловно, рассматривать как
начало большой и очень важной работы. Здесь интересно отметить, что
решение вопроса о том, доходит ли его классификация до первого
трансфинита четвертого класса или кончается раньше, является
чрезвычайно интересным, так как и в том и в другом случае получили бы
также решения проблемы, которые нам сейчас кажутся безнадежными.
33. Ввиду значительного интереса этой попытки П. С. Новикова мы
приводим ее здесь целиком, отбросив, впрочем, некоторые детали, которые
нам кажутся лежащими в стороне от главной идеи. Сам автор посвятил этому
предмету всего лишь три страницы, дав на протяжении их только контур
своего замысла. Так как восстанавливать всю конструкцию приходится
лишь по ее скелету, то само собой разумеется, что лично на меня
должна падать ответственность за возможное непонимание или
искажение смысла.
/. Вполне упорядоченная система униформных множеств.
Возьмем плоскость XOY и на ней систему S={E) униформных множеств Е.
Мы предполагаем:
1° что никакие два множества Е' и Е" системы S не имеют
общей точки;
2° что проекции П' м П" двух любых множеств Е и Е" системы S
содержатся одна в другой;
3° что если обозначим через Е совокупность всех точек XOY
плоскости, лежащих соответственно строго ниже точек множества
Е', то, если множество Е" содержит хотя бы одну точку
множества Е, тогда оно должно содержать точку множества Е на
каждой прямой Рх, проходящей через точку х произведения ГГ • II".
К пояснению описанных свойств системы униформных множеств S
следует добавить, что сказанное в пунктах 1°, 2° и 3° выражает лишь
то обстоятельство, что из двух любых множеств Е' и Е" системы S
одно непременно лежит ниже другого, и что если Е лежит ниже Е" и
Е" расположено ниже £"', то Е' находится ниже Е"'~
Таким образом, система S={E} униформных множеств Е,
обладающая свойствами 1°, 1° и 3°, есть система упорядоченная.
Система *У= {£} униформных множеств называется вполне
упорядоченной, если всякая ее часть имеет первый элемент, т. е. если всякая
часть SY системы S имеет самое нижнее в ней униформное множество Ех.
В дальнейшем мы будем рассматривать исключительно одни лишь
вполне упорядоченные системы S={E) униформных множеств Е. Мы
особенно настаиваем на том, что факт полной упорядоченности
системы S в силу свойств 1°, 2° и 3° есть чисто геометрический факт
и что поэтому одна и та же самая система -5* униформных множеств не
600
Н. Н. ЛУЗИН
может оказаться и вполне упорядоченной, и не вполне упорядоченной:
здесь должно иметься что-либо только одно (ср., например, множество
всех рациональные точек, которое можно рассматривать: и как не вполне
упорядоченное, и как вполне упорядоченное, в зависимости от
предварительного определения порядка следования элементов множества один
за другим; в системе *S этой неопределенности быть не может, потому
что этот порядок следования определяется свойствами 1°, 2° и 3°,
следовательно, чисто геометрически, и раз система S геометрически дана
своими отдельными множествами-элементами Е, то этим самым уже
установлен порядок следования один за другим ее элементов, и, значит,
факт полной упорядоченности системы S есть чисто геометрический
факт, не зависящий ни от каких других дополнительных условий).
II. Мощность вполне упорядоченной системы S. Первый вопрос,
подлежащий выяснению, это вопрос о том, какую мощность может
иметь вполне упорядоченная система S униформных множеств Е?
Легко видеть, что ее мощность не может превосходить X].
Для того чтобы видеть это, обозначим через Н совокупность точек,
принадлежащих множествам системы S. Следовательно, Н есть
соединение всех множеств Е системы S. В силу того, что система S есть
вполне упорядоченная, плоское множество точек Н есть множество
с вполне упорядоченными сечениями, которые поэтому должны быть
счетными.
Обозначим через А проекцию плоского множества Н на ось ОХ.
Если х принадлежит к Л, перпендикуляр Рх встретит плоское
множество Н во вполне упорядоченном множестве Rx типа -\х. Обозначим
через ha совокупность точек х множества А, для которых *[х = а-
Ясно, _что в силу этих обозначений мы имеем трансфинитное
разложение
Л = Л1н-Л2-1- ... + А,0-н ... + Аа-+- \Q. (26)
Обозначим через На совокупность точек множества Ну имеющих
свои проекции принадлежащими к множеству Аа. Ясно, что имеем
разложение
Н = Н1 + Н2+ ... +ЯШ+ ... +Я.+ \Q. (27>
Так как перпендикуляр Рх, когда х пробегает множество Аа,
встречает множество Иа по вполне упорядоченному множеству Rx типа,
в точности равного а, то это множество На можно представить как
соединение счетного числа униформных множеств е, На={е)> каждое
из которых имеет проекцию на ось ОХ тождественной множеству Ав,
идущих вверх вполне упорядоченным множеством типа, в точности
равного а.
Мы теперь утверждаем, что множества Еу составляющие систему S
и имеющие точки на множестве еу образуют счетное множество»
Действительно, если бы дело было иначе, тогда среди множеств е
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИИ
имеется самое нижнее, пусть е^, содержащее точки несчетного числа
множеств Е; пусть этими множествами Е будут
Ех, £?1, ... Ек, ... Е?а, \Q,
где
Po<Pi ••• <L< ^;
мы при этом вовсе не предполагаем, что (30, ра, ... суть
трансфинитные числа второго класса: это может оказаться фактически неверным.
То, что мы вправе предположить, это именно то, что ни одно из
множеств Е^ не имеет точек ниже множества еа ; действительно,
множества Е^ имеющие точки ниже множества е , могут иметься лишь
в счетном числе, потому что иначе е^ не было бы самым нижним
множеством соединения На, содержащим точки несчетно многих
множеств Е; но раз так, то мы можем из последовательности Е?(, ЕРуУ .. .
..., EpUi, ... £ра, |2 просто вычеркнуть все те множества,
которые имеют точки ниже множества еа, и перенумеровать заново
остальные индексами |30, ^, (32 ..., рш, ... рв, | 2.
И так у ни одно из множеств Е$а не имеет точек ниже множества еч.
Пусть М0 есть точка множества Е^, лежащая на е^; мы обозначим
через т0 проекцию точки М0 на ось ОХ. Пусть Мх есть точка
множества Eq9 принадлежащая к множеству е • пусть тх есть ее
проекция на ось ОХ. Мы утверждаем, что перпендикуляр Рт„ не встречает
множества Е%. Действительно, эта встреча невозможна, очевидно,
ни ниже точки М1У ни выше ее, ни в самой Мх. Отсюда следует, что
тг не принадлежит к проекции множества Е*. Но проекция
множества Ер0 в таком случае должна содержаться в проекции множества Е$г
Это значит, что точка т0 принадлежит к проекции множества Е^ и,
значит, перпендикуляр Рто встречает наверное множество Е^. Ясно,
что встреча эта должна быть выше точки М0, т. е. должна произойти
в некоторой точке Nu лежащей на кривой е^ где ^^>а0. Пусть
теперь М2 есть точка множества £pj, принадлежащая множеству е^
пусть т2 есть ее проекция на ось ОХ. По-прежнему точка т2 не может
принадлежать проекции множества Е&. Значит, точка т0 заведомо
принадлежит к проекции множества £&, и поэтому перпендикуляр Рт,
наверное пересечет множество £&. Ясно, что эта точка пересечения,
пусть N2, должна быть выше точки Nv т. е. должна находиться на
кривой е«„ о^^^^а^ И так далее.
Вообще точка М{ множества £, принадлежащая множеству е^, не
имеет своей проекции ту на ось ОХ> входящей в проекцию
множества £р0. Поэтому точка гщ заведомо принадлежит к проекции
множества Efy и, значит, перпендикуляр Рт0 наверное пересечет
множество Efy обозначим эту точку пересечения Рт0 с Е^ через 7V7; ясно,,
что она должна быть выше построенных ранее точек Af0 = 7V0, Nlr
Nfr ... I т, т. е. должна находиться на множестве e*v где а0 < ах <^
$02
Н. Н. ЛУЗИН
<С ао <С ♦ •• <Саг Таким образом, мы приходим к тому, что
перпендикуляр Рт пересекает несчетно много множеств еа , е^ , ... е , | Q
что невозможно, так как точки пересечения 7V0, Nly N2> ..., 7VY, | Q
образуют вполне упорядоченное множество.
Вернемся к первоначальному положению вопроса. Мы установили
что точки множества Иа могут принадлежать лишь счетному
(конечному) числу множеств Е системы S. И так как число а обязательно
есть либо конечное число, либо трансфинитное число второго класса
то множества £, имеющие свои точки на Ну находятся, самое большее,
в мощности ^х. А так как, действительно, всякое множество £,
входящее в состав системы Sy фактически имеет все свои точки на
множестве Ну то отсюда следует, что мощность системы *S не
превышает Si (ч. т. д.).
Как следствие мы получаем:
Тип вполне упорядоченной системы S униформных множеств Е
есть транс финитное число третьего класса, или ниже.
Отметим при этом, что самое доказательство этого предложения дает
больше, чем содержится в его формулировке, именно: вполне
упорядоченная система S униформных множеств Е всегда может быть
эффективно перенумерована числами конечными и трансфинитами второго
класса.
В дальнейшем мы будем обозначать этот тип через символ ^в.
Итак, мы имеем строгое неравенство
где Й* обозначает первый трансфинит четвертого класса (по обычной
символике: 2 = 2Х и 2* = 22; мы не пользуемся ею, так как самое
существование трансфинита четвертого класса 22 нам представляется
еще более условным, чем существование самого 2).
III. Обратная проблема о типе вполне упорядоченной системы 5.
Здесь следовало бы поставить обратную проблему: дано
произвольное т р а н с ф и ни тно е число третьего класса и; узнать,
существует ли такая вполне упорядоченная система S>
составленная из униформных множеств £, S={E}9 тип
которой в точности равен 1*, ^« = 1*?
Здесь тонкость обратной проблемы состоит в определении самого
•смысла слов: „дано трансфинитное число третьего класса". Мы это
понимаем так: сегмент порядковых чисел, отсекаемый „данным"
трансфинитным числом [х третьего класса, перенумерован
трансфинитными числами второго класса, И самое „задание" трансфинита
третьего класса ^ есть не что иное, как задание определенной
нумерации сегмента порядковых чисел,
предшествующих числу ^ при помощи трансфинитов второго класса.
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИИ
Мы видим, что тонкость обратной проблемы сводится на еще
большую тонкость, состоящую в определении тех средств, при помощи
которых мы можем иметь фактически такие перенумерования.
Инструмент в виде вполне упорядоченной системы S униформных
множеств Е> введенный П. С. Новиковым и описанный в начале п. 33,
понятно, является весьма важным инструментом, но не следует
переоценивать его силу. В самом деле, если вполне упорядоченная система
*£={£} нам дана чисто геометрически, т. е. только как множество всех
точек плоскости, ей принадлежащих, и, следовательно, еще в
расщепленном виде на униформные множества Е, то ничто нам не позволяет
выполнить такое расщепление из одних только геометрических
соображений, и, следовательно, мы в этом случае совсем не имеем никакого
трансфинита иж. Для того чтобы трансфинит третьего класса р.,
появился, система S должна быть нам заранее заданной в расщепленном
виде на униформные множества Е. Только тогда мы можем
констатировать, есть или нет рассматриваемая система S вполне упорядоченная,
и в этом последнем случае, как показывает II п. 33 (см. стр. 600),
произвести фактическое перенумерование трансфинитами второго класса
сегмента чисел, отсекаемого типом |хв.
Таким образом, процесс перенумерования сегмента, отсекаемого
типом |xs, трансфинитами второго класса производится лишь после того,
как будет произведено расщепление системы на униформные множества
Е, т. е. перенумерование сводится к расщеплению.
Весьма вероятно (мы думаем, что дело здесь совсем элементарно, и
-что остановка лишь за техникой нужного построения), что верно и
обратное, т. е. что любое заранее „фиксированное" перенумерование
сегмента, отсекаемого трансфинитом ^ третьего класса, помощью транс-
•финитов второго класса, влечет совершенно определенное построение
вполне упорядоченной системы *S, уже расщепленной на униформные
множества Е, S={E) такой, что y.f = ^.
Если это правильно (а это кажется верным, если судить по
аналогии с существованием вполне упорядоченных систем S> тип которых |х,
•есть наперед „заданный" трансфинит второго класса ^ = а), то тогда
вопрос о задании трансфинита |х третьего класса есть лишь вопрос
о построении вполне упорядоченной системы S и о расщеплении ее на
униформные множества Еу S={E).
IV. Задание систем S униформных множеству перенумерованных
трансфинитами второго класса. За математический аппарат, задающий
такие системы Sy П. С. Новиков берет пространственные решета.
Пусть в трехмерном пространстве OXYZ имеется некоторое
пространственное множество С, которое рассматривается как решето. Пересекая
его всевозможными вертикальными прямыми (т. е. прямыми,
параллельными оси OZ)> мы отбираем все те и только те прямые, которые
пересекают решето С во вполне упорядоченном множестве точек относительно
положительного направления оси OZ. Обозначим через S пересечение
604
Н. Н. ЛУЗИН
всех этих прямых с горизонтальной плоскостью XOY. Ясно, что имеем
трансфинитное разложение на конституанты плоского множества точек S:
S=S0 + Sl-*-S2+...4-Sll> + ...-+-Sa + |Q, (28)
где *Уй обозначает совокупность точек М плоскости XOY таких, что
перпендикуляр Рм пересекает решето С во вполне упорядоченном
множестве типа, в точности равного ос.
Если всякая непустая конституанта Sa есть униформное множество,
мы тогда вправе рассматривать множество S как систему, составленную
из униформных множеств Еу т. е. как S={E}y и соответственно писать
5=£0н-£1ч-£2н-...-ь£шн-...-1-£а-ь \Q9 (29)
где мы полагаем Ea = Sa.
Важно отметить, что система S={E) униформных множеств Е
является в разложении (29) сразу данной нам в виде, уже
перенумерованном трансфинитами второго класса.
Если эта система S униформных множеств есть вполне
упорядоченная (в смысле I, п. 33; см. стр. 599), тогда трансфинит \ь8 третьего
класса является нам заданным, потому что осуществлено не только
расщепление системы S на униформные множества, но даже
перенумерование этих множеств трансфинитами второго класса. Отметим при
этом, что это перенумерование, даваемое нам решетом С, может совсем
не совпадать с тем перенумерованием вполне упорядоченных систем S
униформных множеств, которое мы нашли в II п. 33 (см. стр. 600). Но
это несовпадение не представляет ни малейшего неудобства, потому что*
самой важной для нас вещью является тип у-« вполне упорядоченной системы
S униформных элементов, который, понятно, совершенно не зависит от
манеры перенумеровывать сегмент чисел, отсекаемый типом i*«.
В дальнейшем мы будем предполагать решето С всегда выбираемым
так, чтобы система S была составлена из униформных конституант Е
и чтобы она была вполне упорядоченной в смысле определения, данного
в I п. 33; перенумерование же униформных множеств Е мы берем то
самое, которое дается решетом С, т. е. разложением (29).
В этом случае тип ц, системы S можно считать „заданным", потому
что перенумерован сегмент, отсекаемый (х* помощью трансфинитов
второго класса.
Таким образом, „задание" трансфинитов третьего класса сводится
к заданию трехмерных решет С.
V. Выбор основных операций. Начиная с этого момента, изложение
нашего автора, до сих пор бывшее конспективным, становится неясным
и нерешительным. После того как был выбран инструмент, вводящий
непосредственным образом в математические конструкции трансфиниты
третьего класса, наступает время строить классификацию множеству
идущую по этим трансфинитам. Но для такой классификации необходимы.
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИЯ
605
производящие операции и, значит, необходим выбор основных,
независимых производящих операций.
Автор в этом пункте как раз и обнаруживает колебания: отправляясь
от одного списка операций, рассматриваемых им как основные, автор
в течение своего изложения изменяет этот список, выбрасывая
некоторые операции и вводя другие. Поэтому изложение автора в этом
чрезвычайно важном и ответственном пункте становится смутным и
нерешительным.
Операции, упоминаемые автором на протяжении всей работы в
различных ее местах, суть следующие:
Счетное суммирование, разность, гомеоморфные
преобразования, проектирование на пространство низшего
числа измерений, 5-преобразование, дополнение,
диагональ, решето, свертывание пространства в плоскость
и обратное развертывание плоскости в пространство,
соответствие Кантора—Бернштейна и, наконец, особая операция,
вводимая автором, трансфинитного характера, утилизирующая
совокупность всех чисел второго класса (и только одни эти числа) и
позволяющая относить лебегову бинарному решету Г определенное
пространственное множество; для краткости мы в дальнейшем будем называть эту
операцию „2-отн есением".
Относительно фундаментальной операции „счетное
произведение" автор не упоминает совершенно.
Если мы пробежим этот список операций, кстати сказать, не
выбираемый автором в этом его виде за основной, то мы немедленно
замечаем, что многие операции разложимы на более простые, фигурирующие
в этом списке. Так, например, разность сводится к
произведению и дополнению по формуле
Гомеоморфные преобразования суть частный случай 5-преобразова-
ний. Проектирование на пространство низшего числа
измерений есть опять частный случай В~преобразования. Но
и самое £-преобразов ание разложимо на последовательные ступени,
каждая из которых есть проектирование плоского множества
на прямую линию, т. е. совсем элементарная форма
проектирования. Диагональ разлагается на произведение, дополнение
и проектирование плоского множества на прямую.
Решето разлагается на произведение и5-преобразования.
Свертывание пространства в плоскость и обратное
развертывание плоскости в пространство происходят при помощи одних
лишь B-np eобразований. Соответствие Кантора—Бернштейна
разложимо на суммирование, разность и В-преобразования;
кроме того, оно и не нужно, так как может быть заменено операцией
606
Н. Н. ЛУЗИН
свертывания пространства в плоскость, как это будет нами
сделано. Остается лишь одна операция П. С. Новикова: „^-отнесение".
Таким образом, в качестве действительно основных операций следует,.
по нашему мнению, оставить на первых порах лишь следующие:
1° счетное суммирование;
2° счетное произведение;
3° проектирование плоского множества на прямую;
4° дополнение и
5° ^.-отнесение.
Мы помещаем на предпоследнем месте операцию: дополнение^
так как она совершенно особенного характера, будучи абсолютно
отрицательной.
К сказанному мы прибавим следующее примечание: операции 1°, 2\
3°, 4° и 5° предполагают, что интересуются лишь линейными и
плоскими множествами. Если интересуются как финальным
результатом одними лишь линейными или плоскими множествами, тогда нет
надобности выходить и во время промежуточных построений за пределы
операций 1°, 2°, 3°, 4° и 5°. Если же желают принимать во внимание и
множества, расположенные в пространствах конечного или счетного1
числа измерений, или если имеют некоторые опасения, что операция 3°
недостаточна, тогда следует заменить операцию 3° операцией 3*
следующего вида:
3*. Проектирование в пространствах конечного или счетного числа
измерений; или
3**. В-преобразования с конечным или со счетным числом
переменных.
VI. Общий вид классификации эффективного (Classification de
Teffectif). Общий вид этой классификации, задуманной П. С.
Новиковым, таков:
К0, Кл, /С2,... КЦ1 , /С, ... Ка |u*r (30>
где остается до сих пор еще не известным, имеем ли мы неравенство
|х* < 2* или же равенство ц* = 2*; здесь 2* есть „первый трансфинит
четвертого класса". В этой классификации общий член написан в виде
КаУ где а есть: или конечное число, или любой трансфинит второго
класса, или трансфинитное число третьего класса, любое при рь* = 2 и
меньшее числа (а*, если и* есть трансфинит третьего класса.
1 Мы не рассматриваем „пространств с числом измерений выше счетного", так
как считаем, что привлечение таковых имеет всегда лишь чисто вербальный интерес
(если в финальном результате нет терминов этих пространств). В особенности же
в Дескриптивной теории функций это представило бы крупную методологическую
ошибку и явный circulus vitiosus, так как вся цель Дескриптивной теории функций
как раз и состоит в исследовании кардинальной проблемы: что такое несчетные
множества и как они возможны?
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИИ (,Q7
Важнее всего заметить, что каждый класс Ка составлен из линейных
множеств, представляющих собой всевозможные разрезы некоторого
совершенно определенного плоского множества £,, прямыми,
параллельными оси OY. Таким образом, всякий класс Ка состоит из
эффективного континуума (с повторениями) линейных множеств.
Итак, классификации (30) эффективных множеств („ensembles qu'on
peut nommer"), следуя выражению Лебега, имеют параллельную ей
трансфинитную последовательность индивидуальных плоских множеств
£0, £17 £2, ..., £,, ,£.,,.. .,£., !<х*, (31)
и задача сводится теперь к фактическому построению плоских множеств
трансфинитной последовательности (31) помощью тех или других
производящих операций, отправляясь от начального множества Е{).
VII. Выбор начального множества. За начальное множество Еи мы
берем плоское множество, универсальное по отношению ко всем
линейным проективным множествам и всем остальным, которые получаются
из них помощью операций 1°, 2° и 3°, повторенным конечное или
счетное число раз. Такое плоское множество Е0 определить индивидуально
не представит ни малейшего затруднения, и мы больше к этому вопросу
не станем возвращаться.
VIII. Случай первый. Число а есть первого рода: а = а* -н 1. Мы
предполагаем классификацию (30) продвинутой вплоть до класса АГД*,
который уже фактически имеем. Задача сводится к определению
следующего класса K**+i. Итак, мы предполагаем, что имеем плоское
определенное множество £а*. Мы одновременно с плоским множеством Е**,
которым мы уже обладаем, рассматриваем дополнительное плоское
множество СЕа* и образуем всевозможные линейные множества,
получаемые из линейных вертикальных множеств, входящих в состав Еа* и СЕа*>
помощью операций 1°, 2° и 3°, повторенных конечное или счетное число
раз. Легко теперь построить определенное плоское множество £/,
универсальное по отношению к образованным линейным множествам.
Мы не станем останавливаться на фактическом построении
множества U; это построение не представляет труда. Полагая
Еа*Ч-1 = Uу
мы имеем классификацию (30) получившей новый класс КаУ а = а*-н1.
IX. Случай второй. Числа о есть второго рода. Случай этой есть
самый интересный. Д\я того чтобы овладеть трудностями, с ним
связанными, мы одновременно с трансфинитной последовательностью (31)
плоских множеств рассматриваем так же точно последовательность
я» w» я?» .... К, , и^..... w« 1«Л (32)
составленную из четырехмерных индивидуальных множеств, лежащих
в пространстве O'XY'Z'T и так, что пересечение четырехмерного мно-
608
Н. Н. ЛУЗИН
жества Wa трехмерными многообразиями t' = t'0 дает всегда трехмерное
множество (Wa)t' , получающееся из сечения плоского множества Е
некоторой прямой х = х0 помощью ^-преобразования, и обратно, всякое
5-преобразование вертикального разреза плоского множества в
трехмерное получается, пересекая четырехмерное множество Wa надлежаще
подобранным трехмерным многообразием t' = t'0.
Иначе говоря, Wa есть универсальное четырехмерное множество для
всех В-преобразований линейных вертикальных сечений плоского
множества Ев в трехмерные множества.
Введя трансфинитную последовательность (32) четырехмерных
универсальных множеств Way мы возвращаемся к случаю предельного
числа а.
Мы предположили, что наша классификация (30) доведена до
предельного класса КаУ причем самый этот класс еще не определен.
Следовательно, мы уже имеем определенными плоские множества
£о> ^i> £*> • • •> £«» > ^2> • • •» Е$у 1а
и четырехмерные множества
W0, W„ IV2, .... 1Г„, , Ws, .... Wp I a.
Число a есть предельное, и здесь возможны два случая:
Случай 1. Нет такого трехмерного множества (й^),', Р<Са,
которое, будучи решетом в трехмерном пространстве OX'YZ'y дало бы на
плоскости XOY' вполне упорядоченную систему S униформных
множеств типа (ху, в точности равного а, т. е.
Если этот случай имеет место, то мы просто останавливаем наше
построение и, полагая
считаем классификацию законченной на этом предельном трансфините.
С л у ч а й 2. Имеется такое W§, Р < а и такое действительное число t'^
что трехмерное множество (й?р) f, рассматриваемое как решето в про-
о
странстве OX'Y'Z'y дает на плоскости XOY' вполне упорядоченную
систему S униформных множеств, тип которой в точности равен а, т. е.
Если этот случай представляется нам, мы начинаем с того, что среди
индексов р с таким свойством мы берем наименьший; пусть он. равен р.
Делаем дальше построение чисел £ таких, что решето (У^1 дает
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИЙ 609
вполне упорядоченную систему S униформных множеств типа, в
точности равного а; их, вообще говоря, имеется бесчисленное множество.
Пусть t'0 есть одно из них В этом случае мы применим к лебегову
бинарному решету Г, лежащему в вертикальной плоскости UOV триэдра
OUVW, операцию „^-отнесения", введенную П. С. Новиковым.
Вот эта операция. Бинарное решето Г Лебега, лежащее в
плоскости (/01/, определяет в интервале (0 < и < 1), находящемся на оси OU>
аналитическое дополнение <£, разлагающееся на ^ конституант
§ = S0 ■+- 6\ -ь £2 -*-... -+- Si0 -+■... -+- £у н- | ^\
причем ни одна из этих конституант не есть пустая.
С другой стороны, пространственное решето {*Vt)t Д*ет нам вполне
1о
определенное перенумерование всех трансфинитов (3, предшествующих
рассматриваемому трансфиниту а
О, 1, 2, ..., а), , Q, ...3, (а,
помощью одних только трансфинитов второго класса
О, 1, 2, ..., о), |2,
потому что решето (!^)/ дает вполне определенную систему б1
униформных множеств, занумерованных трансфинитами второго класса, причем
система S есть вполне упорядоченная и имеет а своим типом.
Но, раз сегмент чисел
о, 1, 2, .... о), , а, ..., Р, к
отсекаемый числом а, перенумерован трансфинитами второго класса, то
точно так же перенумерована подобная ей последовательность плоских
множеств
•^о> ^\у ^2> • • •> ^о>» > ^у> • • •» ^3> I а>
нами уже определенных.
Пусть
Р = ?<7)
есть рассматриваемое перенумерование; здесь г есть любое из чисел
конечных и трансфинитов второго класса:
О, 1,2, ...о), , |И, т<2
и ,3 есть соответствующее число сегмента чисел:
О, 1, 2, ..., о>, , 2, ..., р, , |а,
усеченного числом а. Каждому числу г < 2 отвечает определенное
число Р<Са> и обратно, каждому такому числу [3 отвечает одно и только
одно число 7> Т^^-
610
Н. Н. ЛУЗИН
Это дает нам возможность выполнить операцию „^-отнесения".
Для этого поступим так: через всякую точку щ конституанты £..
проведем плоскость, перпендикулярную к оси OU, и поместим на этой
плоскости плоское множество £?(т)-
Если мы это проделаем дая каждой конституанты Sv мы будем
иметь в пространстве OUVW пространственное множество, которое мы
обозначим через Н?\ индекс t'0 указывает на то, что не нужно забы-
о
вать о том, что все построение проделано помощью решета (И^з)л опре-
о
деленного, в свою очередь, единственно знанием действительного
числа t'0.
Полученное трехмерное множество Н( обладает тем замечательным
свойством, что:
a) не пересекается плоскостью и = щ> если щ не принадлежит к
аналитическому дополнению £;
b) если точка и0 принадлежит к аналитическому дополнению &>
плоскость ц = ц0 наверное пересекает пространственное множество Ht*
в точности по одному из плоских множеств
£0, Е]у £.,, ..., £и), , Ец> ..., £з> 1а;
с) каждое из этих плоских множеств -Е$ может быть получено как
пересечение множества Ht* плоскостью и = и0 при надлежащем подборе
о
действительного числа щ.
Установив это, свернем трехмерное пространство OUVW в
плоскость UOW при помощи преобразования Пеано
w=f(u'), v = g(u')y w = wf.
Ясно, что пространственное множество Ht* свернется в плоское мно-
0
жество Htf, обладающее тем замечательным свойством, что
о
a) или оно совсем не пересекается вертикальной прямой и=и0;
b) или оно пересечется прямой и=и'0 по одному из вертикальных
сечений некоторого плоского множества £р ({3 <^ а);
c) всякое прямолинейное вертикальное сечение любого из плоских
множеств £р (Р <Са) может быть получено пересечением плоского
множества Hj вертикальной прямой.
о
Короче говоря, плоское множество Н > есть универсальное по отно-
шению ко всем вертикальным сечениям всех плоских множеств
Е0У Ех, £2, ..., £^, Eq, ..., Е$> |а.
Теперь нам осталось лишь освободиться от числа t'Q, что достигается
следующим образом: рассмотрим пространство OU'V'T трех измерений
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИЙ 511
и проведем через точку t'0, взятую на оси ОТ плоскость,
перпендикулярную к этой оси. Если точка /о такова, что трехмерное решето (W$)t'f
которое было нами определено выше, или не дает вполне
упорядоченной системы S униформных множеств, или хотя и дает такую систему Sy
но £ не имеет своим типом числа а, тогда на этой плоскости £ = *оп
проведенной в пространстве OU'VT\ мы не помещаем ничего. Если же
точка t'Q такова, что трехмерное решето (И^р)/ даст вполне упорядо-
о
ченную систему S униформных множеств, имеющую своим типом транс-
финит а, мы поместим в этом случае на плоскости t' = £q построенное
нами выше плоское множество Hf.
о
Ясно, что этот процесс даст в трехмерном пространстве OU'VT
уже единственное и совершенно определенное, не зависящее ни от ка~
ких параметров, пространственное множество, которое мы обозначим,
через <Щ.
Очевидно, что Ш есть универсальное по отношению ко всем
вертикальным сечениям всех плоских множеств
^-Of ^\у **•>» • • •> ^и > > ^Qy • • ♦> ^h I a*
Но множество ЭД есть пространственное; оно покоится в
пространстве OU'VT. Свернем это трехмерное пространство в плоскость XOY
преобразованием Пеано
н"=/М, i/' = g(x), t' = y.
Ясно, что после такого свертывания трехмерного пространства OU'VT
в плоскость XOY пространственное множество ЭД свернется в плоское
множество Sft, универсальное по отношению ко всем вертикальным сече-
ниям всех плоских множеств
£0, Е19 Е2У .. ., Е(,, , Еяу . .., £р, (а.
Вот это-то плоское множество vJt мы и обозначим через Еа и скажем,-
что оно получено операцией „2-отнесения" их всех предыдущих
множеств Е$> где р <С а-
Таким образом, трансфинитная последовательность (31)
индивидуальных плоских множеств
Е0, Ev Е,, ..., £,„, , Ев, .... Е„ Ь* (31)
получает вполне определенное плоское множество ЕаУ где а —
предельное число, и, следовательно, беспрепятственно определяется член за
членом дальше вплоть до предельного трансфинита [**, которого
перешагнуть уже невозможно.
И вместе с трансфинитной последовательностью (31) является
определенной и вся „классификация эффективного"
К0, Ки К» ..., Кю, Кя, ..., К, Ift*. (30)
612
Н. Н. ЛУЗИН
К сожалению, без углубленного анализа остается неизвестным, равно ли
число [а* „первому трансфиниту четвертого класса" 2* или \х* меньше
его.
X. Точка зрения 77. С. Новикова. Для того чтобы точнее изложить
взгляд автора на значение классификации эффективного, лучше всего
представить ему самому слово.
Мы цитируем дословно окончание его диссертации:
„Итак, мы построили классы множества Ка; каждый класс содержит
континуум множеств, и трансфинитные числа принадлежат 1-му, 2-му и
3-му классу. Является вопрос, представляет ли совокупность трансфи-
нитов а множество всех чисел 1-го, 2-го и 3-го класса или же
составляет часть его? Иначе говоря, будет ли наименьший трансфинит,
превышающий все а, который мы назовем ц*, меньше 22 или равен ему?
Вопрос этот очень труден. Мы не имеем эффективного соответствия,
хотя бы такого, в котором разным точкам континуума отвечают не
обязательно различные множества. Поэтому выход из системы
построенных множеств затрудняется тем, что в этих условиях не удается
приложить диагональ Кантора. С помощью аксиомы Цермело можно
показать, что построенные множества не исчерпывают всех точечных
множеств.
Доказательство того же положения без аксиомы Цермело провести
не удается, и поэтому относительно построенной совокупности множеств
законна гипотеза о том, что эта совокупность множеств содержит все
вообще множества, которые можно построить эффективно в смысле
Лебега.
Заметим, что разрешение вопроса о соотношении трансфинитов ц*
и 22 приведет к важным результатам. Если будет доказано, что рь* < 22,
тем самым решен один из вопросов, на которые указал Н. Н. Лузин:
существует ли хоть одно из множеств мощности &$i> не являющееся
в то же время аналитическим дополнением?
Из допущения [а* < 22 вытекает, что действительно существует такое
множества из Si точек, которое не является аналитическим
дополнением и даже больше; тогда можно утверждать, что найдется множество
точек мощности Хи не проективное вообще".
XI. Критические замечания к „классификации эффективного44,
предложенной /7. С. Новиковым. Откладывая углубленный и
детальный анализ интересной попытки П. С. Новикова „классифицировать
эффективное" до появления более осязательного материала, мы в
настоящее время ограничимся лишь краткими замечаниями по поводу
данного автором первого наброска этой классификации.
Этот набросок очень неполон и являет собой лишь скелет
классификации эффективного или точнее: программу работы в этом направлении.
Автор в своем устремлении остается верен идее Лебега о ценности
предпринять изучение множеств „qu'on peut nommer". В этом
заключается неоспоримая и очень большая заслуга автора.
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИЯ 613
О самом же существе этой попытки судить сейчас невозможно:
материал очень недостаточен; по имеющемуся скелету сказать можно лишь
очень немного, да и то лишь с известной степенью вероятности.
Существенным нам представляется следующее.
В математической литературе не раз проскальзывала мысль о
составлении такого списка операций, чтобы минимальная система множеств,
содержащая отрезки и инвариантная относительно операций этого списка,
оказалась неспособной к дальнейшему расширению диагональю Кантора.
Я уже указал выше (см. V, п. 33. Выбор основных операций), что
самая диагональ Кантора разлагается на следующие операции:
произведение, дополнение и проектирование на прямую так, что здесь особенно
трудного момента нет никакого. Но диагональ Кантора предполагает
наличие эффективно названного плоского множества, т. е. наличие
выполненного „application sur le continu" Лебега. И весь центр тяжести
проблемы именно в этом application sur le continu. Несомненно, что это
есть какая-то операция, которую мы иногда умеем проделать; иногда
этого умения у нас нет. Вообще говоря, этот пункт наиболее
загадочный во всей Дескриптивной теории функций; напомним, что сам Лебег
оказался в силах построить эффективно функцию, не входящую в
классификацию Бэра, лишь тогда, когда ему удалось осуществить
application sur le continu семейства всех функций классификации Бэра. До
Лебега у нас не было такого умения. Если какое-нибудь семейство S
множеств допускает application sur le continu, пусть даже с
повторениями, т. е. с наличием тождественных экземпляров, тогда мы. говорим,
что семейство S имеет эффективную мощность континуума (кратную,
если учитывать повторения). Если доказано, что семейство S допускает
вообще application sur le continu, но назвать его не умеем, тогда мы
говорим, что S имеет неэффективную мощность континуума.
Но если установлено, что семейство S совсем не допускает
никакого application sur le continu, тогда мы уже говорим, что семейство S
имеет мощность выше континуума.
Таким образом, искать такого списка операций, чтобы минимальная
система, содержащая отрезки и инвариантная по отношению ко всем
операциям этого списка, оказалась не способной к расширению общей
(т. е. всякой) диагональю Кантора, — это значит требовать, чтобы в этом
списке фигурировало в самом общем виде application sur le continu как
операция. Так обычно это всегда и делалось implicite explicite. И так
как свойства этой операции загадочны, то вполне естественно, что дело
с этими рассмотрениями не подвигалось.
Теперь в списке П. С. Новикова диагональ Кантора входит
полностью, хотя и в раздробленном состоянии: я уже указал выше (V,
п. 33), что диагональ Кантора составляется у автора из операций 1°,
2°, 3° и 4°. Но гораздо важнее отметить, что implicite предполагается
осуществленным application sur le continu, выполненный Л-преобразо-
ваниями. Понятно поэтому, что минимальное семейство (Е) автора, содер-
614
Н. Н. ЛУЗИН
жащее все отрезки и инвариантное по отношению к операциям 1°, 2°, 3°
(или 3*, или 3**) и 4° автора, оказывается не способным к расширению
диагональю Кантора предшествуемой application sur le continu, сделанным
/^-преобразованиями. Таким образом, семейство (£) П. С. Новикова все в
целом не допускает application sur le continu, сделанного ^-преобразованием,
и потому такая (частная) диагональ Кантора, в самом деле, не даст
никакого расширения. Но отсюда еще очень далек вывод, что всякое
application sur le continu должно осуществляться лишь ^-преобразованиями:
минимальное семейство (£) автора прекрасно может оказаться
допускающим другое application sur le continu, которое уже не осуществляется
/^-преобразованиями, но каким-нибудь иным способом. Ведь, было время,
когда (стадия до Лебега) думали, что одни лишь множества,
измеримые Ву и имеют индивидуальное существование, или что (стадия до
Эрмита) всякое иррациональное число есть непременно алгебраическое.
При этом мы оставляем в стороне операцию 5° „2-отнесение",
введенную автором: к ее природе мы еще возвратимся.
Пока же нас интересует следующий пункт: мы видели (IX, п. 33),
что для трансфинитной последовательности (31) плоских множеств
£0, Е1У Е2, ..., Ew, , Eg, ..., £e, 1р.* (31)
имеется коррелятивная к ней трансфинитная последовательность (32)
четырехмерных множеств
W» W„ \УЪ ..., !Уа, №, ... W„ W*, (32)
причем всякое четырехмерное Wa получается из соответствующего
плоского Еа некоторым преобразованием, как и обратно: из Wa
получается Еа обратным преобразованием.
Мы видели, что если а есть число предельное, то плоское
множество Еа получается применением операции „2-отнесения" из некоторого
предыдущего четырехмерного множества W§ (J3 <^ а) следующим образом:
пересекая W-^ трехмерным многообразием ^ = t'oy где t'0 надлежаще
подобрано (предполагая, что оно имеется), получают трехмерное решето
{Н^)/, дающее нужную нам вполне упорядоченную систему S
униформных множеств типа цл, в точности равного а, ^ = а.
Эта система S нам нужна не сама по себе, а только тем, что дает
ценного для дальнейшего перенумерования трансфинитных чисел,
предшествующих числу а, помощью трансфинитных чисел второго класса.
Пользуясь же этим перенумерованием, мы строим плоское
множество ЕаУ где а есть предельное.
Резюмируя сказанное, мы видим, что построение плоского
множества Еа удается благодаря тому, что в четырехмерном множестве W^
существует такой разрез трехмерным многообразием г' = ^, который
лает решето типа а.
О НЕКОТОРЫХ НОВЫХ РЕЗУЛЬТАТАХ ДЕСКРИПТИВНОЙ ТЕОРИИ ФУНКЦИИ 615
Введем теперь определение: мы скажем, что четырехмерное
множество \У$ есть множество с ограниченными типами, если всякий его
разрез (Wb)? или не дает никакого типа, или дает тип не выше некоторого
фиксированного трансфинита третьего класса ft(i><;<22). В противном
•случае множество Wp есть множество с неограниченными типами.
Мы теперь утверждаем, что необходимым условием дкя того, чтобы
а* = 22, является существование четырехмерного множества IV^ с
неограниченными типами.
Действительно, пусть каждое \У$ есть множество с ограниченными
типами; более точно, пусть типы разрезов множества W$ не
превосходят числа третьего класса ftp. Обозначим через 0;, наименьшее из чисел,
превосходящих все числа
К К К •••> «и. Ч -.-IP.
Ясно, что % есть трансфинит третьего класса или ниже, и что 0^ не
убывает с возрастанием индекса (3. Имеются две возможности.
Если 6р не возрастает до 2.,, тогда Ьр <С &, где 0 есть фиксированный
трансфинит третьего класса. Ясно, что тогда множество Е$ уже нельзя
определить, и р.* < 0, т. е. |** <[ 22.
Если % возрастает с р до 22, то мы полагаем
&(» = ?№).
В этом случае, положив
Р, = «р(Р), P* = ?(Pi), k=?(W. ••., iWi = ?(&,), •••>
5(ы имеем
— возрастающую цепочку типа и> чисел третьего класса, предел
которой т, lim ря ^= 7 есть трансфинитное число третьего класса.
Ясно, что типы разрезов множеств
W0, Wv VPlt .... Wa, , Wu, ...It
меньше 7, т. е. процесс П. С. Новикова должен остановиться, и мы
имеем р.* < т <С ^2-
Итак, необходимым условием л^я того, чтобы р.* = 22 является
существование множества й?р с неограниченными типами.
Это условие является и достаточным, если слегка видоизменить
построение „классификации эффективного" П. С. Новикова.
Заметим, что пока еще не известно, ограничено или нет даже
четырехмерное множество W> универсальное по отношению к всевозможным
трехмерным решетам, определяющим плоские аналитические множества.
Если бы такие неограниченные множества W нашлись, они, вероятно,
:могли бы сыграть ту же самую роль, какую играет плоское решето,
определяющее аналитическое множество, неизмеримое В.
616
Н. Н. ЛУЗИН
Сделаем последнее замечание: если а есть число 1-го рода а = а*ч ]
тогда плоское множество Еа*+\ определяется через предыдущее плоское
множество Еа* помощью суммирования, произведения и В-преобразова-
ний, все это в счетном числе. Следовательно, переход от Еа+ к £а*-ы
осуществляется непосредственно, т. е. без всяких трансфинитных чисел.
Рассмотрим теперь операцию „2-отнесения". Она выполняет переход
от множества Еа к Еа, где а есть предельное число, и где
четырехмерное множество lV7j допускает трехмерный разрез (>^)/'» дающий систему
униформных множеств, вполне упорядоченную и типа, в точности
равного а.
Эта операция по внешнему виду представляется существенно
трансфинитной. Но ничто не доказывает, что она, в самом деле, такова и что
трансфинитное здесь не может быть исключено хотя бы одним из тех
методов, которые мы указали в начале нашего доклада. Если это
исключение, в самом деле, можно сделать, переход от Ер к Еа будет так же
нетрансфинитен, как переход от Еа* к Еа*+ь В этом случае вся
классификация эффективного П. С. Новикова будет состоять из множеств,
образуемых каждое в отдельности нетрансфинитным процессом. Если
прибавить сюда, что вероятен тот факт, что уже первое четырехмерное
множество \У0 есть множество неограниченное и, значит, всегда Р = 0,
то вся классификация П. С. Новикова будет развертываться лишь из
начального члена £0.
В этом случае ц* = 22 и вся классификация эффективного, вероятно,
допустит application sur le continu и, значит, не включит в себя всего
эффективного. Если же исключение трансфинитного невозможно, то вся
классификация представит пример (второй после Лебега) трансфинитного
процесса со связанными операциями, о которых мы говорили раньше.
Таким образом, случай ц* <С ^2 представляется мало вероятным.
Напротив, имеется большая вероятность наличия application sur le
continu всех множеств, входящих в „классификацию эффективного".
ЭФФЕКТИВНЫЙ ВЫБОР ТОЧКИ В ПРОИЗВОЛЬНОМ
АНАЛИТИЧЕСКОМ ДОПОЛНЕНИИ, ЗАДАННОМ ПОСРЕДСТВОМ
РЕШЕТА*
Метод этого построения предложен П. Новиковым; мы излагаем
здесь упрощенную редакцию Н. Лузина.
1. Пусть Е— непустое аналитическое дополнение, расположенное
в интервале (0<С*<С1)- Предположим, что Е определено посредством
решета С, образованного бесконечным множеством интервалов
К Ь>> 83> • • •> Ьп> • . м (1)
параллельных оси ОХу проекции которых, пр. о„, на эту ось являются
интервалами Бэра. Обозначим через Сп часть С, расположенную строга
ниже Ьп.
Пусть
Е = Е0 -+- £2 -ь Е., -+■... -#- Ем -+-... -+- Еа -+- ... | 2
— разложение Е в трансфинитную последовательность конституант
определенное решетом С. Пусть Еу — первая непустая конституанта,
0^т<[2; обозначим ее через Е \ Е7 = Е{)-
2. Вот искомый процесс.
Первый шаг. Пусть 8W| — первый интервал в
последовательности (1) такой, что множество-пересечение Нх = пр. оМ| • Е[ =^=0.
Если х — точка из И1У то перпендикуляр Рх в точке х к оси ОХ
пересекает решето С«, по вполне упорядоченному множеству; пусть 7i —
минимальный тип этого множества, когда х пробегает Нх. Обозначим
через Е множество точек из Н1У соответствующих fi-
Второй шаг. Пусть 8И„ п.2^>пи первый интервал в
последовательности (1) такой, что множество-пересечение //2 = пр. о„2 • £ Ф 0.
Если х принадлежит Н2У то Рх пересекает решето Си, по вполне
упорядоченному множеству; пусть ?2 — минимальный порядковый тип этого
множества, когда х пробегает //2- Обозначим через Е( } множества
точек из //2, соответствующих т2.
* „Choix effectif d'un point dans un complementaire analytique abritraire, donne
par un crible". Fund. Math., 25, 109—131, (1935). Совместно с П. С. Новиковым.
Сообщение, сделанное Н. Н. Лузиным в Академии наук СССР 8 сентября 1935 г.
€18
Н. Н. ЛУЗИН
£-й шаг. Пусть о„к9 пк^>пк-{у первый интервал в
последовательности (1) такой, что множество-пересечение//л=: пр. o,/Jt • £^-1) =т^0. Если
х принадлежит //*, то Рл пересекает решето CUfc по вполне
упорядоченному множеству; пусть 7fc— минимальный порядковый тип этого
множества, когда х пробегает Нк . Обозначим через Е множество точек
из Hicy соответствующих 7*--
Интервалы пр. о;/1, пр. oMj, ..., пр. <Ц, ... обязательно содержат
некоторую точку ;. Именно эта точка ; принадлежит первой непустой
конституанте £г
3. Чтобы убедиться в этом, покажем сперва, что Р^ не пересекает
никакого интервала от, отличного от %к. Действительно, если щ^ <^
<С т<Спку то np.ow наверняка содержит точки из Е . Кроме того,
*%к есть первый интервал в (1), который следует за Кк_} и проекция
которого, пр. Кку содержит точки из Е . Следовательно, т = пъ.
Добавим, что Р* пересекает в действительности все интервалы Ъ„к.
4. Остается лишь установить, что относительный порядок ординат
интервалов 8„ совпадает с порядком следования трансфинитных (или
конечных) чисел 7л-
Чтобы убедиться в этом, возьмем два любых интервала о,;/ и S^.;
предположим, что Ъщ расположен ниже, чем bnj..
Пусть к — любое целое положительное число такое, что £>/ и
k^>j. Если х — точка из Е , Р, пересекает решета С^ и Cuj по двум
множествам, вполне упорядоченным по типам 7* и 7у соответственно.
И так как решето C„t является частью решета CWy, то очевидно, что
7*<Ст.;> поскольку равенство между этими числами невозможно.
С другой стороны, очевидно, что все числа 7я меньше, чем 7> потому
что Е является частью £г Отсюда вытекает, что Р. пересекает
данное решето С по вполне упорядоченному множеству типа ^7- Так
как Еу — первая непустая конституанта, мы заключаем, что тип этого
вполне упорядоченного множества в точности равен 7> что и
требовалось доказать.
Вскоре появятся другие применения описанного выше процесса.
II цикл
ОБ ОДНОМ РАЗЛОЖЕНИИ КОНТИНУУМА*
Цель этой заметки — дать эффективный пример разложения
интервала на алеф-один непустых множеств, измеримых В и попарно без
общих точек.
Пусть X—множество всех действительных чисел х>
удовлетворяющих неравенству 0<!л:^1, a R— множество всех рациональных чисел
интервала (0, 1). Расположим числа, принадлежащие R, в бесконечную
последовательность
г1э г2, га, . . . . (1)
Пусть х — число, входящее в множество X; как известно,
существует единственное разложение числа х вида
x = ± + JL+^ + •••> (2)
г\Ш\ л1»; O^.t
где /я* (Аг~1, 2, 3, .. .) — бесконечная возрастающая
последовательность натуральных чисел.
Итак, каждое число х множества X определяет, следовательно,
соответствующую последовательность т1У т2У т.л> ..., следовательно,
и последовательность рациональных чисел
извлеченную из последовательности (1). Обозначим через R0(x)
(линейное) множество рациональных чисел (3), соответствующее таким образом
числу х множества X1.
Пусть задано порядковое число а первого или второго класса,
и предположим, что мы уже определили множества Rc(x) для 0^£<Са.
Если а — число первого рода, обозначим через Ra(x) множество,
которое мы получаем из Ra^l(x)} выбрасывая из этого множества его
нижнюю границу [если она ему принадлежит; если нет, #a(x) = /?a_1(x)l.
Если а — второго рода, положим
* „Sur une decomposition du continu". Comptes Rendus, 175, 357—359, 1922.
Совместно с В. Серпинским.-
1 Н. Lebesgue. Journ. de Math, серия 6, I, 213, 1905.
^622
Н. Н. ЛУЗИН
Таким образом, множества Ra(x) определены посредством
трансфинитной индукции дая каждого порядкового числа а<^2 (где 2
обозначает наименьшее трансфинитное число третьего класса), и очевидно мы
имеем
/?„(*)=>£,(*) для а<р.
Так как множества Ra(x) не более чем счетны (как состоящие из
рациональных чисел), то отсюда следует существование (для каждого
числа х множества X) такого наименьшего порядкового числа а —
= у.(х)<С^, что
#ii М = #,ги С*) [следовательно, R: (х) =£ R^x (x) для ;<>|.
Впрочем, множество R^(x) может быть пустым.
Пусть а — данное порядковое число <С^; обозначим через Е% мно~
жество всех таких чисел х множества X, что р* (х) = а. Очевидно, мы
будем иметь
ЕаЕ^ = 0 для а=^В
и
Х=Е9ч-Е1 + Ег + ... + Еа + Е№+1ч-...Е.ч-... (а<У). (4)
Обозначим (дая каждого данного числа г из множества R) через
Qa{r) множество всех чисел х множества Х> дая которых множество
Ra (x) содержит число г, и обозначим через Sa (r) множество-сумму всех
множеств Qa(p), где суммирование распространяется на все числа p<V
множества R.
Для каждого числа г множества R нетрудно проверить формулу
Q.(r)=Q^(.r)-s.-Ar), (5)
если a — число первого рода, и формулу
<2.0-) = П^(г)> (б)
где ol—число второго рода.
Тогда положим
Ти=-2[0Лг*)-0.ъЫ; (7>
к=1
нетрудно убедиться, что Та есть множество всех чисел х множества Хт
дая которых /?a(x)=7^=/?a+1(jc), и мы находим формулу
Е. = Т1Т1-Т. №
для каждого порядкового числа a<^Q.
Qo(r*) есть множество всех чисел х множества Ху для которых
разложение (2) содержит член ^f; следовательно, это сумма l~x интер-
ОБ ОДНОМ РАЗЛОЖЕНИИ КОНТИНУУМА 623
валов (без левых концов). Значит, все множества Q^(r) измеримы В»
Формулы (5) и (6) позволяют без труда доказать посредством
трансфинитной индукции, что множества Qa(r) измеримы В (для каждого
числа г множества R и каждого порядкового д <[ £2). Отсюда следует
в силу формул (7) и (8), что множества Еа все измеримы В для а <^ 2.
Так как последовательность (3) представляет некоторое
подмножество множества /?, пусть это будет £/, а число х определено
формулой (2), мы, очевидно, будем иметь R0(x) = U. Тогда всевозможные
подмножества множества R, упорядоченные по величине чисел, которые
они содержат, могут представить все четные порядковые типы.
Следовательно, для каждого данного порядкового числа а<<2 существует
такое число х множества Ху что R0(x) будет вполне упорядоченное
множество типа а. Нетрудно убедиться, что для такого х мы имеем
а(;с) = а, следовательно, Еа=£0. Следовательно, все множества Еа
непусты дкя а<^2.
Итак, формула (4) представляет желаемое разложение.
ОБ ОДНОМ СЕМЕЙСТВЕ АНАЛИТИЧЕСКИХ ДОПОЛНЕНИЙ*
Это семейство состоит из аналитических дополнений <St конституанты
которых &а принадлежат классам, „стремящимся" к -2 вместе с а.
1. Чтобы лучше объяснить, в чем состоит интерес рассмотрения этих
множеств, мы рассмотрим сначала плоскость ХОУ и на ней
прямолинейное решето Г, состоящее из счетного множества отрезков а,
параллельных оси ОХ. Пусть Е — линейное аналитическое множество, просеянное
решетом Г, а & — его дополнение. Без ограничения общности
последующих рассмотрений можно предположить, что отрезки о решета Г
имеют концы с рациональными координатами.
В этих предположениях рассмотрим разложение дополнения & в ряд
из конституант
Из числа этих конституант мы исключим те, которые пусты, т. е.
не содержат точек. Если классы оставшихся конституант не стремятся
к 12, то существует трансфинитное число р такое, что имеется несчетно
много непустых конституант <§аУ классы которых меньше, чем р. В этом
случае мы получим совокупность множеств, измеримых В,
занумерованных всеми трансфинитными числами второго класса, классы которых
ограничены. Из этого следовало бы, что ограниченная проблема Лебега
имеет положительное решение1.
2. К сожалению, мы не можем указать таких случаев. Наоборот, мы
можем констатировать существование таких аналитических дополнений &у
у которых не пустые конституанты имеют классы стремящиеся к 2 при
трансфинитном возрастании а2. Мы их назовем обыкновенными
дополнениями. Целью настоящей заметки является доказательство
существования таких дополнений.
* „Sur une famille de complementaires analytiques". Fund. Math., XVII,
4-7, 1931.
1 Эта проблема состоит в выяснении того, можно ли указать трансфинитную
(до Р.) последовательность множеств $а% непустых измеримых В, ограниченных
классов.
2 Мы будем говорить, что трансфинитная функция f(a) стремится к Q вместе
с а, если имеет место /(а)>Р» каково бы ни было число (J второго класса, когда а
достаточно велико.
ОБ ОДНОМ СЕМЕЙСТВЕ АНАЛИТИЧЕСКИХ ДОПОЛНЕНИЙ 625
3. Мы будем отправляться от заметки Серпинского, который
предложил весьма полезную конструкцию универсального решета U.
Это универсальное решето Серпинского U расположено в
пространстве трех измерений XYZ и образовано счетным множеством
прямоугольников, параллельных плоскости ХОУ и имеющих вершины в точках
с рациональными координатами. Каждая плоскость у= const пересекает
решето U по прямолинейному плоскому решету, состоящему из
отрезков, параллельных оси ОХ, концы которых имеют рациональные
координаты. Но что гораздо более замечательно, так это следующий
действительно важный факт: каждое прямолинейное плоское решето,
образованное отрезками, параллельными ОХ с рациональными концами,
может быть получено таким способом, при подходящем выборе плоскости
у = const. Благодаря этому решето U и названо Серпинским
универсальным.
Обозначим через Е аналитическое множество, расположенное в
плоскости ХОУ и просеянное универсальным решетом U. Пусть S —
дополнение к Е. Обозначим через
<$ = <$о ■+■ Si-*- • - • -«- Slo -+ ... -+ £в -ь ... | 2
разложение дополнения S в ряд из конституант, определенных решетом U.
Мы покажем, что классы этих конституант стремятся к & вместе с а.
4. Чтобы доказать это, возьмем на оси ОХ произвольное линейное
множество е, измеримое В. Его линейное дополнение Се также
измеримо В. Обозначим через Г прямолинейное решето с вышеуказанным
свойством, определяющее Се (как множество, задаваемое решетом Г.)
Мы можем считать, что решето Г находится под осью ОХ. Так как
дополнение к е измеримо В, то решето Г есть ограниченное решето.
Это значит, что существует трансфинитное число второго класса 3
такое, что каждая прямая L, параллельная оси OZ и проходящая через
точку из е, пересекает решето Г по вполне упорядоченному множеству,
трансфинитный тип которого а/, меньше f), v.l<^$.
Установив это, присоединим к решету Г счетное множество D
прямых, параллельных оси ОХ, расположенных выше этой оси и
образующих множество, вполне упорядоченное в положительном направлении
оси OZ, Пусть т — трансфинитное число, соответствующее D. Мы
всегда можем считать, что 7 — произвольное трансфинитное число,
превосходящее ри).
Объединение Г и D, очевидно, представляет собой новое решето,
посредством которого просеяно рассмотренное множество Се; обозначим
это решето через Г1# Легко видеть, что всякая прямая L, параллельная
оси OZ и проходящая через какую-либо точку множества е> пересекает
решето 1\ по вполне упорядоченному множеству, трансфинитный тип
которого строго равен ?.
Так как решето U универсально, то существует постоянная с такая,
что плоскость у=с пересекает U точно по Г1#
626
Н. Н ЛУЗИН
Проведем в плоскости ХОУ прямую у = с. В силу предыдущего легко
видеть, что все точки множества S, лежащие на этой прямой,
принадлежат конституанте <£ . Следовательно, конституанта S1 пересекается
прямой у = с точно по е. Таким образом, всякая конституанта £т
пересекается прямой, параллельной оси ОХу выбранной подходящим образом,
в точности по наперед заданному множеству еу измеримому В, если
только 7 достаточно велико.
Но если некоторая конституанта £г пересекается с прямой по
множеству е> то класс этой конституанты не меньше, чем класс е. А так
как множество е — произвольное множество, измеримое Ву то мы
заключаем отсюда, что классы конституант £т стремятся к 2 вместе с *;'
(ч. т. д.).
5. Мы дополним этот результат следующим замечанием. Каждое
аналитическое дополнение & может быть разложено в последовательность
конституант
S = £0 -+- £т -+- ... н- £ш -+-...-+- <Sa -*- ... | Q,
среди которых несчетное множество пустых. Чтобы убедиться в этом,
достаточно взять решето Г, расположенное ниже оси ОХ, и
присоединить к нему простую возрастающую последовательность прямых,
параллельных оси ОХ и расположенных выше этой оси. Легко видеть, что
решето 1\, определенное таким образом, дает нам разложение <£, в
котором все конституанты, отвечающие трансфинитным числам первого
рода, пусты.
Добавлю, что метод, использованный в этой заметке, принадлежит
В. Серпинскому (см. мою заметку „Sur les classes des constituantes
d'un complementaire analytique". Comptes Rendus, 12 ноября 1929 г.)
О КЛАССАХ КОНСТИТУАНТ АНАЛИТИЧЕСКИХ
ДОПОЛНЕНИЙ *
Общие замечания о проблеме континуума. Известно, что
знаменитая проблема континуума состоит в определении ранга
мощности континуума в цепочке алефов в предположении, что эта последняя
определена.
Известно также, что все усилия решить эту проблему, оставаясь
на почве идей Кантора и аналистов, таких как Жак Адамар и Феликс
Хаусдорф, были тщетны, если не считать одного весьма скромного
отрицательного результата: мощность континуума не есть ни а„, ни
какой-либо другой алеф, „конфинальный" <d (И. Кениг).
Последние работы Давида Гильберта, преследующие ту же цель,
выходят уже за пределы этого круга идей. Его метод не может быть
проанализирован на нескольких строках; мы ограничимся здесь указанием
наиболее существенных его моментов.
Чтсбы показать, что утверждение: „мощность континуума есть >^
непротиворечиво в области математического анализа, Давид Гильберт
устанавливает взаимно однозначное соответствие между самыми
определениями иррациональных чисел, с одной стороны, и трансфинитными
числами второго класса, — с другой. Таким образом, его метод
существенно отличается от ранее указанного круга идей, где пытались
доказать наличие (или отсутствие) соответствия между самими
иррациональными и трансфинитными числами, не вникая в способ нашего
восприятия иррациональных и трансфинитных чисел. Короче, в круге идей
Кантора и аналистов, которые были согласны с ними, совершенно
не касались математических рассмотрений.
В ожидании новых публикаций на пути, открытом идеями Д.
Гильберта, мы сделаем здесь два замечания.
Прежде всего, анализируя самые способы определения различных
иррациональных чисел, метод Д. Гильберта использует математические
выражения, именуемые функционалами: иррациональное число
определяется при помощи функционала, и метод Д. Гильберта производит
классификацию этих функционалов. Однако, прежде чем перейти к точ-
% „Sur les classes des constituantes des complementaires analytiques". Ann. Scix
norm, snper., Pisa, серия 2, 2, вып. 3, 269—282, 1933. (IX Международный конгресс
математиков, Цюрих, 1932).
628
Н. Н. ЛУЗИН
<ным объяснениям, остается выяснить, почему мы можем быть уверены
* том, что действительно исчерпаны все возможные виды функционалов,
и почему не может случиться, что иррациональное число, определение
которого не познано в настоящее время, ускользнет в наших
последующих рассуждениях.
Далее, некоторые опасения может внушить известная близость метода
Д. Гильберта и способа рассуждений И. Ришара. Несомненно, такое
рассуждение: „Возьмем все математические определения иррациональных
чисел и занумеруем их при помощи целых положительных чисел, затем
сделаем то же с определениями трансфинитных чисел, и т. д." было бы
чересчур упрощенным, ибо самая эта нумерация не относится, вероятно,
к области математики. Однако рассуждения И. Ришара являются
доказательством для тех, кто хочет проникнуть в тайны бесконечного, как
справедливо отмечает Э. Борель.
Оставляя теперь область попыток, пока что больше философских,
чем математических, я хочу отметить, что в математическом анализе
употребляются многочисленные соответствия между элементами
множеств без анализа их определений. Так, в вариационном исчислении мы
разыскиваем непрерывную функцию двух независимых переменных
9 (х, /), которая при произвольном изменении параметра / давала бы
всевозможные функции с ограниченной вариацией ср (л:), полная
вариация которых не превосходит некоторого положительного числа А.
С этой точки зрения, даже если бы проблема континуума была
полностью решена в смысле непротиворечивоети, по-прежнему остался бы
открытым чисто математический вопрос:
установить, можно ли построить эффективное взаимно
однозначное соответствие между иррациональными числами и трансфи-
иитными числами второго класса, не привлекая определений этих
чисел?
С этой точки зрения легко видеть, что мы не только не знаем
такого соответствия, но даже не можем назвать tfi точек континуума.
Проблема разыскания эффективного множества из >$i точек является в
настоящее время ослабленной формой проблемы континуума, и она тоже
далека от своего решения. На этом пути встречается несколько других
проблем, являющихся все более и более ослабленными формами
проблемы континуума.
В 1905 г. Лебег дал весьма замечательный способ эффективно
строить Xi попарно не пересекающихся точечных множеств. Сила этого метода
исключительна, и природа его загадочна. Сам автор писал:,. Я доказал
существование (в некронехеровском смысле, с трудом поддающимся
уточнению) измеримых множеств, неизмеримых В". Еще до сих пор мы
не поняли полностью природы этого метода. Я напомню, что
последующее изучение этого метода привело к открытию аналитических и
проективных множеств; природа и свойства этих последних загадочны еще
и теперь.
О КЛАССАХ КОНСТИТУАНТ АНАЛИТИЧЕСКИХ ДОПОЛНЕНИЙ
629
Именно этим путем Лебега Серпинский и я (в 1922 г.) разложили
континуум на KL непустых множеств, измеримых В. Если бы каждое
из этих множеств содержало по одной точке или, во всяком случае, не
более чем счетное множество точек, то проблема континуума была бы
решена.
В силу этого было бы интересно изучить природу и классы этих
конституант. Кстати, всякое дополнение к аналитическому множеству.,
неизмеримому 5, разлагается на сумму ^ попарно не пересекающихся,
измеримых В непустых конституант, и отыскание аналитического
дополнения, все конституанты которого счетны, также было бы решением
ослабленной проблемы континуума.
Еш,е более слабой формой проблемы континуума является задача,
отыскать Xj измеримых В множеству классы которых ограничены
в совокупности.
Мы полагаем, что исследования на этом пути представляют живой
интерес, так как здесь мы встречаемся с сущностью загадок и
трудностей самой проблемы континуума.
В этой статье я собираюсь рассмотреть один случай, когда классы
конституант монотонно возрастают до 2. Это нам дает новое
доказательство существования множеств, измеримых В всех классов, без
использования рассуждений, проводимых от одного класса к другому.
Перейдем теперь к детальному изложению.
1. Прямоугольное решето. Возьмем евклидово пространство двух
измерений. Пусть в этом пространстве введена -прямоугольная система
осей, которую мы обозначим XOZ.
Назовем фундаментальным квадратом множество всех точек
М{х> z) плоскости XOZ с обеими иррациональными координатами х
и z, удовлетворяющими неравенствам
0<*<1, 0<*<1.
Этот фундаментальный квадрат будем обозначать через Q.
Назовем прямоугольником Бэра порядка к в фундаментальном
квадрате Q множество точек из Q, координаты х и z которых принадлежат-
каким-нибудь двум интервалам Бэра* порядка к, лежащим соответственно
в интервалах 0<д:<1 и 0<z<l. Из свойств интервалов Бэра
следует, что фундаментальный квадрат Q разделен на прямоугольник»
Бэра порядка 1 и что каждый прямоугольник Бэра порядка к разделе»
на прямоугольники Бэра порядка А-ь1; если два прямоугольника Бэра,
R в R*> разных порядков имеют общую точку, то одни вэ них
содержит другой, если же^и^ имеют один и тот же порядок, то он»
1 Вообще, если дана система целых положительных натуральных чисел,
расположенных в определенном порядке: а1% а2, . . ., ль то интервалом Бэра (а\% аъ . . .» я*)
называют множество иррациональных точек, представление* которых при помощи^
непрерывных дробей начинается с (aj, a%% . . ., а*). Этот интервал называется
интервалом „порядка к".
630
Н. Н. ЛУЗИН
Совпадают; каждая неограниченная последовательность прямоугольников
Бэра различных порядков
*м> *vj> • • •> Кт, .. .,
содержащихся каждый в предыдущем, сходится к некоторой точке из Q,
принадлежащей всем этим прямоугольникам.
Назовем прямоугольным решетом конечную или счетную
совокупность прямоугольников Бэра; прямоугольное решето будем обозначать
через Г.
Если дано прямоугольное решето Г, то мы будем различать в Г
прямоугольники рангов 1, 2, 3, ... . По самому определению, ранг 1
имеет всякий прямоугольник /?, не содержащийся ни в каком другом
прямоугольнике этого решета; прямоугольник R решета Г называется
прямоугольником ранга т, если он содержится в прямоугольнике /?
ранга т — 1 и если он не содержится ни в каком другом прямоуголь-
«нике этого решета, содержащемся в /?'. Из этого определения следует,
что каждый прямоугольник решета Г имеет вполне определенный
конечный ранг; прямоугольники одного ранга не имеют попарно общих точек.
Обозначим через Sm объединение всех прямоугольников ранга т
решета Г, рассматриваемое как точечное подмножество квадрата Q,
и через 9—общую часть всех Smi
ту = Sj • о2 • *>з * ... • Sт • ... .
Таким образом, определенное множество 9 называется элементарным
множеством точек фундаментального квадрата Q. Ортогональную
проекцию 9 на ось ОХ обозначим через Е; это — множество иррациональных
точек интервала
(0<*<1).
Известно, что Е — аналитическое множество и что всякое
аналитическое множество, расположенное в интервале (0<С*<С1)> —
измеримое В или нет, — может быть получено таким способом. Обозначим
через £ дополнение к Еу т. е. множество тех иррациональных точек
интервала (0, 1), которые не принадлежат Е:
ё = СЕ.
2» Явный индекс и минимальное решето. Пусть х0 —
иррациональная точка интервала (0, 1) оси ОХ, аР^ — прямая х = х0, параллельная
оси OZ, проведенная через х0.
Будем говорить, что прямоугольник R решета Г имеет явный индекс
в точке х09 равный нулю, если РХ(> не пересекает прямоугольника R.
Будем говорить, что прямоугольник R решета Г имеет в точке х0
явный индекс, равный л, а > 0, если Р*0 пересекает прямоугольник R
и если а — наименьшее из чисел, конечных или трансфинитных второго
О КЛАССАХ КОНСТИТУАНТ АНАЛИТИЧЕСКИХ ДОПОЛНЕНИЙ 631
класса, превосходящих явные индексы в точке х0 всех
прямоугольников R! решета Г, содержащихся в R. В этом случае мы будем писать
Indapp vR = a.
Прежде чем идти дальше, напомним одно определение из области
трансфинитных чисел. Если дано множество //, состоящее из конечных
или трансфинитных чисел второго класса в конечном или счетном числе,
то верхней гранью множества Н называется наибольшее из чисел Н,
если такое существует, или, если оно не существует, то наименьшее
из чисел, превосходящих все числа из И.
Назовем, в соответствии с этим определением, явным индексом
решета Г в точке х0 верхнюю грань множества, образованного явными
индексами в точке х0 всех прямоугольников R решета Г; этот индекс
обозначим
Indapp ^Г.
Из этого определения следует, что Ind app; Г не может существовать
нигде, кроме точек х0 аналитического дополнения £, и в каждой из
таких точек является вполне определенным числом — конечным или
трансфинитным второго класса.
Как следствие имеем разложение аналитического дополнения S
в сумму составляющих множеств &а:
S = S0^S14-S24-...^(S^4-...-HSa^...\i^ (1)
где <$а обозначает множество тех точек х0 из 6\ для которых имеем
Indapp. Г = а; эти множества Sa будем называть явными
конституантами аналитического дополнения &.
Явные конституанты &а разложения обладают теми же свойствами,
что и действительные конституанты 1 аналитического дополнения &.
Мы ограничимся здесь указанием двух следующих свойств:
1° явные конституанты измеримы В;
2° каково бы ни было аналитическое множество Elt содержащееся
в &> оно принадлежит лишь счетному числу явных конституант £а.
1 Выражения явный индекс и явная конституанта употребляются для
противопоставления действительному индексу и действительной конституанте,
которые • определяются следующим образом.
Прямолинейным решетом Г на плоскости XOZ называют счетную совокупность
интервалов, параллельных оси ОХ,
Пусть Тх — множество точек, которые получают, пересекая Г прямой x = xq.
Если Тх вполне упорядочено в положительном направлении оси OZ, то
соответствующее число, конечное нли трансфинитное, называют действительным индексом
решета Г в точке х0, Ind reels Г. Действительной конституантой £л называют
множество точек х , л^я которых мы имеем Ind reel* Г = а,
О "
Так как вычисление действительных индексов кажется нам сложным и трудным»
мы предпочитаем здесь употребление явных индексов.
632
Н. Н. ЛУЗИН
Отсюда следует, что необходимым и достаточным условием того
чтобы аналитическое множество Е было измеримо Z?, является условие
чтобы все явные конституанты &а разложения (1°), начиная с
некоторой <£*0, были пусты.
Этот результат весьма просто приводит к углубленному изучению
явных конституант.
Возьмем произвольное множество Еу измеримое Ву определенное
некоторым прямоугольным решетом Г, и дадим следующие определения.
Назовем явным индексом прямоугольного решета Г верхнюю грань
чисел Ind арр^Г, когда переменная точка х0 пробегает аналитическое
дополнение <§; этот индекс будем обозначать через Ind арр Г.
Назовем явным индексом множества Ef измеримого В>
Ind арр Е
наименьшее из чисел Ind арр Г, когда буква Г пробегает множество
всех прямоугольных решет> определяющих рассматриваемое
множество Е,
Легко видеть, что явный индекс множества £, Ind арр £, есть вполне
определенное число и зависит лишь от самой природы данного
множества Еу измеримого В. В последующем мы найдем связь между
природой множества Е и Ind арр £.
Прямоугольное решето Г, определяющее множество Еу
измеримое В, для которого Ind арр Г совпадает с Ind арр Е, называется
минимальным решетом.
3. Неравенства Серпинского. В одном из своих писем 1917 г. об
аналитических множествах В. Серпинский указал важные соотношения
в форме неравенств между явными индексами множеств Е1У Е2, ..., Еи> ...,
их- суммы и общей части, с одной стороны, и между числом а и
классом суммы &0 ч- £1 н- ... -н £р •+- ... | а, — с другой стороны. Этот
параграф посвящен изложению самих результатов Серпинского1;
последующие же — рассмотрениям, которые связаны с этими неравенствами и
которые мы привлечем для точного определения классов конституант £в
в одном особенно интересном случае.
Заметим прежде всего, что явный индекс множества £, измеримого В7
Ind арр Е9 авляется предельным трансфинитным числом или равен нулю.
Действительно, допустим, что Ind арр£ = а-+- 1, и возьмем минимальное
прямоугольное решето Г, определяющее данное множество Е.
Удалим из Г все его прямоугольники ранга 1; мы получим новое
прямоугольное решето 1\, определяющее, очевидно, то же множество Е.
И так как теперь мы имеем Ind арр 1\ ^ а, то мы пришли к
противоречию. Итак, всегда имеем
Ind арр Е = wot,
1 Эти результаты никогда не публиковались, так как для них не было видно
непосредственных приложений. Одно из них мы дадим в нижеследующем.
О КЛАССАХ КОНСТИТУАНТ АНАЛИТИЧЕСКИХ ДОПОЛНЕНИИ 633
где а — трансфинитное число второго класса или конечное число, а^О.
Установив это, перейдем к неравенствам Серпинского.
Пусть
£], Ь.2У £3 • • •> Еп, ...
— неограниченная последовательность каких-то множеств, измеримых В;
мы обозначим через ая явный индекс множества £„, Ind app Еп = ая. Вот
первые три неравенства Серпинского:
Ind app (El -+- Е2 -+-... ч- Е„ н- ...) ^ верхи, грани чисел а„; (I)
Ind app (£т Е.> • ... • Еп • ...) ^ верхи, грани чисел ап, (II)
если среди чисел а1э а2, ..., ая, ... нет наибольшего или если такое
число входит в эту последовательность не более чем конечное число
раз;
Ind app (Ex • Е2 • . .. • Еп • . ..) ^ (верхн. грани чисел <хп) -+- ш, (III)
если среди чисел а1У <х2, ..., ая, ... есть наибольшее и если оно
встречается в этой последовательности бесконечное число раз.
Первое неравенство. Доказательство этого неравенства весьма
просто: достаточно разделить фундаментальный квадрат на бесконечное
множество полос, параллельных оси ОХ> и внутри этих полос
поместить соответственно минимальные решета Гя, л = 1, 2, 3, ... . Тогда,
очевидно, объединение решет 1\, Г2, ..., Гя... образует прямоугольное
решето Г, определяющее множество-сумму EY -ь Е2 -+- Е2 -+-.. ,-ь Еп -+-... .
Первое неравенство (I) следует тогда немедленно из определения
построенного таким образом решета Г.
Второе и третье неравенства. Трудность доказательства
состоит здесь в эффективном построении прямоугольного решета Г,
определяющего пересечение Е1 • Е2 •...£„•... . Вот его конструкция.
В качестве прямоугольников ранга 1 искомого решета Г берем
прямоугольники ранга 1 минимального решета 1\. Пусть Rx — один такой
прямоугольник. В качестве прямоугольников ранга 2 решета Г,
содержащихся в Rly возьмем прямоугольники Бэра, у которых каждая сторона
есть пересечение двух сторон, из которых одна принадлежит какому-
нибудь прямоугольнику ранга 2 решета 1\, входящему в Rly другая —
какому-нибудь прямоугольнику ранга 2 решета Г2. Вообще, если с
помощью прямоугольников Ry R'y ..., R{n) рангов л, принадлежащих
соответственно решетам 1\, Г2, ... Гп, построен прямоугольник ранга п,
Rn решета Г,4 то в качестве прямоугольников ранга п -*-1 решета Г,
содержащихся в Rny возьмем все такие прямоугольники Бэра, у которых
стороны суть пересечения п -+-1 сторон каждая, из которых первые п
суть соответственно стороны п прямоугольников ранга л-*-1 решет Т1Г
1\> ..., Гя, содержащихся соответственно в прямоугольниках /?', R\ |...
..., R{n\ а последняя есть сторона какого-нибудь прямоугольника ранга
л-ь-1 решета IV*., „
634
Н. Н. ЛУЗИН
Очевидно, имеем Ind appz /?м = О в том и только в том случае, когда
Ind appA R{%) = 0. Следовательно, трансфинитная индукция дает нам не-
равенство
Ind арр^Ли < Ind app^'),
каково бы ни было / = 1, 2, . . ., л. Отсюда следует, что если л:0—
точка дополнения к общей части Ех • Е., • Е$; • . ♦. • Еп • ... и если х() не
принадлежит определенному сомножителю £ff, то будем иметь
Ind app #n <! Ind app • Ек -+- (А: — 1).
Поскольку А: — конечное число, то мы закончили доказательство второго
и третьего неравенств Серпинского (ч. т. д.).
Четвертое неравенство. Прежде чем формулировать это
неравенство Серпинского, мы должны напомнить следующие определения1,
Рассмотрим классы Бэра—Валле-Пуссена:
АГ0, Кх. ЛГ2, ..., АГШ, ..., Ка, ... | 2.
Начальный класс К0 этой классификации состоит из множеств Е,
являющихся, так же как- их дополнения СЕ, суммами интервалов
Бэра. Основной операцией, которая служит для определения
последовательных классов этой классификации, является операция lim перехода
к пределу. Каждый класс Ка этой классификации содержит множества
трех родов. Прежде всего множества, именуемые достижимыми снизу
множествами класса а. Это множества, которые являются суммами
счетного числа множеств классов, предшествующих а; обозначим их
через Infa% Затем множества, называемые элементами класса а; это
множества, недостижимые снизу и в то же время являющиеся
пересечениями счетного числа множеств предыдущих классов; мы их
обозначаем через ela. Наконец, прочие множества класса а, именуемые
недостижимыми с обеих сторон множествами класса а; мы их
обозначаем Inac а.
Главную роль в классификации Бэра—Валле-Пуссена играют
элементы: каждое множество Infa есть сумма счетного числа элементов
классов <Са> и каждое множество Inac a есть сумма счетного числа
элементов классов ^ а, причем элементы обоих сумм не имеют попарно
общих точек.
Условимся теперь в следующем. Если некоторое множество Е
неизвестной природы, но мы знаем, что Е либо принадлежит классу <Са»
либо есть Inf а, то будем писать Е ^ Inf a. Точно так же, если Е
принадлежит классу <а, или есть Infa, или, наконец, является ela, будем
писать £^ela. Наконец, если просто известно, что Е имеет классе а,
то будем писать £^ Inac a.
См. мои „Лекции по аналитическим множествам", вторая глава.
О КЛАССАХ КОНСТИТУАНТ АНАЛИТИЧЕСКИХ ДОПОЛНЕНИЙ
63S
Напомнив это, перейдем теперь к четвертому неравенству Серпин-
ского. Пусть Е — произвольное аналитическое множество и § — его
дополнение; пусть
S = S0 + gl -ь£2-1- ... -*-£«-+-... | Q
— разложение множества £, осуществленное при помощи некоторого
прямоугольного решета Г. Мы обозначаем через за сумму конституант,
номера которых меньше а:
°а = £0 ■+■ 6\ -н ё2 -+- . .. ■+■ £р -+- ... | а.
Очевидно, al = g0} a з0 есть пустое множество.
Четвертое неравенство имеет следующий вид:
а ьа < Inf 2а, а^п < 61 (2а Н- 1), (IV)
где п — целое положительное (конечное) число, л^1.
Доказательство четвертого неравенства просто. Прежде всего
множество Oj, очевидно, либо имеет класс 0, либо есть 611. Так как
неравенство <J(oa^Inf2a следует из неравенства аш?ч^ ^ el (2р-+-1) в
предположении, что это последнее выполняется, когда Р <С а, и так как случай
<Wf-w при л }> 1 немедленно сводится к случаю 0<и«+м—ь если заменить
решето Г другим решетом 1\, которое получается из Г удалением
всех его прямоугольников ранга 1, то ясно, что все сводится к случаю
аша+ь Случай же o^^i получается следующим образом: если Rlt R2» .. •
..., Rn> ... — прямоугольники ранга 1 решета Г, то через Нп обозначаем
множество всех тех точек ху для которых Ind арр R < <*>а. В силу
предположения, //Я<Г Inf 2a. И так как, очевидно, имеем
то окончательно получаем cwn ^ el (2a -ь 1) (ч. т. д.).
4. Вычисление явных индексов множеств, измеримых В.
Неравенства Серпинского позволяют полностью определить явные индексы
всех множеств, измеримых 5.
Пусть a — конечное число или трансфинитное второго класса, и пусть
л' — наибольшее предельное число, не превосходящее а. Тогда имеем
где л— конечное целое число, л^О. Если a — конечное число,
полагаем а' = 0.
Вот формулы, определяющие явные индексы множеств, измеримых В:
ЛТа, {Ind арр = d>a, |
Ки,+ъ (Ind арр = a) (а' н- л),
Inf Ind арр = а) (а'и-л), { (2)
*ач-2п-ы] ё1 lnd aPP = 4' + " + 1)»
Inac Ind арр = ш (а' н- л -н 1).
636
Н. Н. ЛУЗИН
Чтобы доказать эти формулы, заметим сначала, что множества
класса 0 и Infl имеют явный индекс, равный нулю, и обратно: если
Ind арр £ = О, то множество Е имеет класс 0 или есть Infl.
Первые три неравенства Серпинского показывают лишь, что явные
индексы множеств, измеримых Ву никогда не могут превзойти величин,
написанных в правых частях формул (2). Дая полного же вычисления
нам нужно воспользоваться четвертым неравенством.
Пусть Е— множество, измеримое fi, явный индекс которого равен юа:
Inf app E = сна. (3)
В силу самого определения явного индекса существует минимальное
прямоугольное решето Г, определяющее множество Еу явный индекс
которого равен соа, Inf app Г = а>а« Следовательно, разложение
дополнения S к множеству Е может быть написано в форме
ё = ё0-*-€г-+-£ъч-... -•-£&-«-...-н£и)в, (4)
ибо все следующие конституанты пусты. Отсюда следует, что
дополнение & есть а(1а-ц, и на основании четвертого неравенства Серпинского
имеем £<^ё1 (2а-ь 1). Как следствие1, получаем
£<Inf(2a+l). (5)
Установив это, рассмотрим случай, когда a — предельное число,
a = a'. В этом случае Е ^ Inf (a' -+-1), ибо мы имеем, очевидно, 2а' = а'.
Я утверждаю теперь, что мы имеем либос1/Г = а', либо Е = Inf (a' -+-1),
Действительно, если бы выполнялось неравенство с\Е <^а\ мы можем
написать cl£ = (3'-i- m> где $' — предельное число (или нуль) такое, что
р' <С а', и т — конечное целое число, т ^ 0. Из неравенств (2) следует, что
Ind арр Е ^ о) ф' -к |х),
где и — вполне определенное конечное число. А так как Р' < а\ то мы
выводим отсюда $' ч-\ь<^а' и, следовательно,
Ind арр Е <С <°а' = а>а,
что противоречит (3).
Таким образом, формула (2), относящаяся к Ка*у доказана. Чтобы
доказать прочие формулы (2), достаточно воспользоваться методом
полной индукции по целым числам. Если формула (2) доказана для
a^a'^-p, где ja — конечное целое, р^О, то нам нужно рассмотреть
два случая.
Предположим сперва, что ^ — четное число, |х = 2/п, и что
Ind арр Е = a) (af -i- m).
1 Это следует из того факта, что S есть пересечение множеств ^ Inf 2а, £ ^
r=U (^ Inf2a) и, следовательно, Е = CS = 2 ( < •! 2а) ^ (Inf2a -+-1).
О КЛАССАХ КОНСТИТУАНТ АНАЛИТИЧЕСКИХ ДОПОЛНЕНИИ 637
Формула (5) дает нам Е <Ы (а' -н 2т -+- 1). Таким образом, если класс
множества Е превосходит а = а'-ь2т, то Е может быть лишь Ы(а'-н
н-2т-н1). Если Ind app E = ш (а' -ь /п -ь 1), то формула (5) дает нам
Е ^ Inf (а' -ь 2т -+- 2). Поэтому, если не имеет место равенство cl£ =
= а' -+- 2^ -+- 2, то необходимо имеем cl Е = а' -ь 2т +-1, что и
доказывает ЧаСТЬ формулы (2), ОТНОСЯЩУЮСЯ К ЛГа'+2т-«-1.
То же рассуждение служит нам для доказательства части формулы (2),
относящейся к АГа'+2т. Допустим, что |х нечетное, |i = 2m— 1, и что
Indapp £ = ш(а' ч-т). Формула (5) дает нам £<[ Inf (a' -+- 2т -+- 1).
Поэтому, если не имеют места равенства ни Е = Inf (а'-н 2т-*- 1), ни £ =
= el(a'-i-2m—1), ни Е = 1пас (а' ч-2т—1), то необходимо имеем
с1£ = а'-к2т, что доказывает часть формулы (2), относящуюся
К АГа' + 2т (ч. Т. Д.).
5* Максимальное решето* Решето Г, определяющее аналитическое
множество Еу называется максимальным, если все конституанты
S0, £„..., £.,... | а
дополнения £ к множеству Е имеют наивысшие возможные классы.
Таким образом, если Г* — произвольное решето, определяющее
некоторое аналитическое множество £*, и если конституанты дополнения <£*
к множеству £* суть
vo /** v* с* | о
то кмеем неравенства
с1<£<с1£„
каково бы ни было число а — конечное или трансфинитное второго
класса.
Отсюда следует, что если Г и Г' суть какие-то два максимальные
решета, то необходимо
где Sa и &а, — конституанты номера а, определенные решетами Г и Г".
Очевидно, что аналитическое множество Е, определенное
максимальным решетом Г, не может быть измеримым 5.
Нашей целью теперь является полное вычисление классов
конституант £а максимальных решет и доказательство того, что эти классы
монотонно стремятся к 2 вместе с а.
Но предварительно нужно заполнить один пробел в наших
рассуждениях: самое существование максимальных решет еще не доказано.
Дкя доказательства их существования рассмотрим трехмерное
евклидово пространство и в нем — прямоугольную систему координат OXYZ.
Так как прямоугольники Бэра всех возможных рангов в
фундаментальном квадрате Q плоскости XOZ образуют счетное множество, мы
можем их занумеровать натуральными числами:
R\i #2> ^3> • • •> Яг» (6)
638
Н. Н. ЛУЗИН
Рассмотрим теперь фундаментальный куб К
(0<х<1, 0<у<1, 0<г<1).
в пространстве OXYZ1 и поставим в соответствие каждому интервалу
Бэра (п19 л2,..., л*), расположенному в интервале (О <С */ <С 1) на оси OYr
прямоугольники Бэра /?Я|, #«,,..., Rnk. Пусть к19 ^2»'-м т"к —
параллелепипеды, содержащиеся в фундаментальном кубе AT, ортогональные
проекции которых на ось OY и на плоскость XOZ суть соответственно
интервал Бэра (п1э я2,. .., л*) и прямоугольники Бэра /?„,, /?„,,..., /?я
Если мы сделаем это построение для всех интервалов Бэра, лежащих
в (0<С*/<С 1)> то мы получим счетную совокупность параллелепипедов::,
множество которых образует в трехмерном пространстве решето из
параллелепипедов Г.
Легко видеть, что, пересекая так построенное из параллелепипед
доврешето^ плоскостями у = const, параллельными плоскости XOZr
можно получить всевозможные прямоугольные решета ГМ.
Обозначим через Е плоское аналитическое множество, определенное
решетом Г, и через & его плоское дополнение относительно квадрата
(0О<1, 0<z/<l). Пусть
S = S04-gl-*-gi+ ... ч-£а-н ...\Ц (7)
— разложение & на бесконечную совокупность явных конституант §аГ
каждая из которых представляет собой плоское точечное множество.
Очевидно, что можно получить все конституанты
$>*>, <^>--- ^.-••lQ
— дополнения Sw) к линейному аналитическому множеству £(у>,
определенному прямоугольным решетом Г^
£(*) = £Мн-£(/')н- ... -н£Ы-*- ...\Q,
попросту пересекая прямыми у = const все конституанты <Sa разложения (7)
дополнения £.
Это доказывает, что плоская конституанта £а есть множество,
измеримое 5, класс которого не ниже, чем класс линейной конституанты S%\
получаемой при помощи прямоугольного решета Г^, каково бы ни было
иррациональное число у из интервала (0 <^у <С 1)-
Итак, Г есть максимальное решето2.
1 Координаты х% у и z всегда иррациональны.
2 Правда, конституанты §а плоские. Но устанавливая взаимно однозначное и
взаимно непрерывное соответствие между точками основного квадрата (0<jr<lr
О <Су <С 1) и иррациональными точками нового интервала (0 </<!)» ыы получаем,
очевидно, линейное максимальное разложение.
О КЛАССАХ КОНСТИТУАНТ АНАЛИТИЧЕСКИХ ДОПОЛНЕНИИ 639*
6. Исследование классов конституант максимальных
разложений* Рассмотрим сначала конституанту £„ номер $ которой есть
предельное число:
(3 = ша, а = а' н-л;
Здесь а' — предельное число, an — конечное целое, л ^ 0. Если о.л есть
сумма конституант £т разложения (7) с номерами 7» меньшими чем 'р9.
то четвертое неравенство Серпинского дает нам
а^<Ы2а, аш,+т<ё1(2а-ь1)э
где т — целое конечное число, т^1.
Так как а = а'-нл, мы имеем
°„.<Ы(а'н-2л) и сфа+1^е\(а,-^2пч-\)
и, следовательно,
^.<ё1(а'-ь2л-1-1).
Отсюда следует, что все сечения <£М плоского множества ё^ пря-*
мыми у = const, параллельными оси ОХ и лежащими в плоскости ХОУу.
суть множества ^ ё1(а' -ь2л-1- 1):
5«Й<ё1(а' + 2п + 1).
С другой стороны, в силу формулы (2) всякое множество
Inf (а'-+-2л-+-1) имеет в качестве явного индекса ш(а'н- л). Следовательно,,
если мы возьмем такую плоскость у = const, что Eil/) = Inf (a' -+- 2л н- 1),.
то получим
el (а' ч- 2п -ь 1) = £« ■+- 5?" -+■... -ь #&„..)•
И так как ^^^ ^ Inf (a' -+- 2л), то получаем
^U., = «l(«'-b2n-Hl).
Итак, окончательно имеем
5ш(ач-п) = el (a' -+- 2л -+-1),
что можно записать в окончательном виде
£и.а = ё1(2а-ь-1). (8)'
Теперь остается только исследовать природу конституант Swa+mi где
т — конечное целое положительное число. К сожалению, исследование
природы множества ёшл+т представляет, по-видимому, трудности; мы
ограничимся здесь лишь тем, что выясним класс конституанты 8иЛ+т.-
Прежде всего, так как мы имеем
°ша-ь»+1<4(2«-«-1) и ошв+и<ё1(2а-ь1),
640
Н. Н. ЛУЗИН
то множество-разность <*„.,+,„+1 — ашв+т есть множество класса не выше
2ач-1. Значит,
с1£.оа-и»<2а-ь1. (9)
Возьмем, с другой стороны, плоскость */ = const такую, что
£(^=Ы(2а+ 1).
В силу формулы (2) имеем
Indapp£0/) =ma.
Кроме того, очевидно, всегда можно считать множество £М
расположенным в интервале Бэра порядка m-hl, так чтобы соответствующее
минимальное решето Г(^ содержалось в прямоугольнике Бэра порядка
/п-к1, лежащем в фундаментальном крадрате плоскости z/ = const.
Установив это, присоединим к решету Г(^ те т прямоугольников
Бэра порядков 1, 2,..., т, которые содержат решето ГМ. Таким
способом мы получим новое решето Г,, определяющее множество £<*) —
= Inf(2a-i-l) и такое, что
Ind арр \\ = wa -+- т.
Следовательно, существует другая плоскость у = const,
пересекающая плоское множество &им+т точно по множеству £(L(X, т. е.
следовательно, в силу (8), по множеству el (2a +-1). Отсюда следует, что
с1£ша+,„>2а-|-1. (Ю)
Сравнение неравенств (9) и (10) дает нам желаемое равенство
cl £„.+„, = 2а ч-1. (И)
Объединение формул (8) и (11)
где т — конечное, т ^> 0, определяет классы всех конституант <Sa
максимального разложения (7) (ч. т. д.).
Предыдущие рассмотрения показывают нам, что если речь идет
о существовании В-множеств различных классов, то нет
необходимости применять „рассуждение шаг за шагом", ибо каждое
максимальное разложение дает нам измеримые В конституанты сразу всех
возможных нечетных классов, конечных и трансфинитных, по одной
д\я каждого класса, и так, что они охватываются единым взглядом,
>сразу, без того чтобы продвигаться шаг за шагом.
О КЛАССАХ КОНСТИТУАНТ АНАЛИТИЧЕСКИХ ДОПОЛНЕНИИ 641
Мы приходим к следующему выводу: мы можем определять
максимальные решета, производя весьма простое геометрическое построение;
конституанты соответствующих максимальных разложений суть
множества, измеримые В, классы которых монотонно возрастают до -.
Кроме того, мы можем быть уверены, что таким способом получаются
все нечетные классы, конечные и трансфинитные. Остается выяснить,
существует ли разложение, которое не является максимальным
разложением и конституанты которого принадлежат классам, немонотонно
стремящимся к 2, каков бы ни был номер, с которого рассматриваются
конституанты: эта проблема представляет, по-видимому, большие
трудности.
И, наконец, значительные трудности при современном состоянии
науки представляет задача — выяснить, существует ли разложение,
конституанты которого непусты и принадлежат классам, не
стремящимся к Й. Весьма вероятно, что порядок трудностей этой последней
проблемы таков же, как и в проблеме континуума.
О СТАЦИОНАРНЫХ ПОСЛЕДОВАТЕЛЬНОСТЯХ*
1. Определения* Последовательности, о которых будет речь, имеют
своими членами различные совокупности точек и перенумерованы
натуральными числами, а также трансфинитными числами второго класса.
Поэтому они будут иметь вид
^о> ^i> £>> • • •> £,i»• • •» £<»» М- (1)
Всякая такая последовательность называется возрастающей, если
каждый ее член содержится в любом следующем члене:
E0<zE1C...cEaC...\Q;
последовательность называется убывающей, если каждый ее член
содержит любой следующий член:
£0э£,з ...d£,d ...|2.
Возрастающие и убывающие последовательности объединяются в одном
имени монотонных последовательностей.
Монотонная последовательность называется предельной, если
каждый ее член Еа, имеющий своим индексом а число второго рода,
есть предел предшествующих членов 2Tr, j3 <Cа- Из этого определения
следует, что если последовательность (1) есть предельная и
возрастающая и если а есть число второго рода, член Еа есть соединение всех
предшествующих членов £3, p <С&; напротив, член Еа есть общая часть
всех предшествующих членов £?, когда последовательность (1) есть
предельная и убывающая.
Классическим примером предельной убывающей последовательности
является последовательность всех производных совокупностей F{a\
образованных одна за другой, исходя от заданной замкнутой
совокупности F-
F, F, F',..., ЯЧ..., Я«>, |2. (2)
Для дальнейшего мы нуждаемся в следующем основном определении:
Последовательность
^0» ^1» ^2> • • '> ^и.» ' * •> ^а> I
* Труды физ-мат. ин-та, отд. мат., 5, 125—147, 1934.
О СТАЦИОНАРНЫХ ПОСЛЕДОВАТЕЛЬНОСТЯХ 643
называется стационарной, если существует такое число 7»
начиная с которого, все члены последовательности являются
тождественными, т. е. когда имеем
£т = £7+i = £т+2 = | &.
2. Основная проблема. Только что данное основное определениег
без сомнения, покажется слишком простым тому, кто не знаком с
трудностями теории совокупностей.
Чтобы рассеять это впечатление кажущейся простоты, достаточно
заметить, что математический анализ в каждом индивидуальном
теоретическом вопросе всегда имеет дело с совокупностями, измеримыми В
и притом всегда ограниченных классов. Но, несмотря на значительные
усилия, продолжающиеся более тридцати лет, еще никому не удалось
найти последовательности, образованной из совокупностей ограничен-»
ных классов, которая не была бы стационарной: как основной факт,
природа которого остается непонятной, является то, что всякая такая*
последовательность на деле всегда оказывается стационарной.
Например, последовательность (2) производных совокупностей стационарна»
в силу известной теоремы Кантора — Бендиксона. До сих пор никто еще-
не видел последовательности, образованной из совокупностей
ограниченных классов, которая была бы нестационарнойх.
Бесполезно при настоящем состоянии науки пытаться разгадывать*
что именно лежит в основе этого замечательного, но непонятного факта:
есть ли это просто эффект рутины и недостаточное богатство
воображения, бессильного пока указать правило составления такой
последовательности, или же здесь скрывается чрезвычайно глубокая причина,
связанная с нашим непониманием самой сущности трансфинитного числа,
выяснение которой повлечет изменение наших взглядов на самые
основные понятия математического анализа. Здесь мы удовольствуемся
указанием на чрезвычайный интерес разрешения вопроса в ту или
другую сторону.
Действительно, если нестационарных последовательностей из совот
купностей ограниченных классов нет, то уже это одно влечет
необыкновенные следствия. Например, отсюда вытекает, что мощность
континуума и мощность совокупности трансфинитных чисел второго класса
суть несравнимые между собой мощности, в противность тому, что
1 Положение вещей радикально изменяется, когда дело идет о последовательности,
образованной из совокупностей, хотя и измеримых Z?, но неограниченных
классов: здесь оказываются осуществимыми и нестационарные
последовательности. В сообщении, сделанном на IX Международном математическом конгрессе
в Цюрихе (1932 г., сентябрь), я дал правило строить нестационарные последователь^
ности, в которых класс совокупности Еа возрастает и стремится к & вместе с
индексом а; см.: N. L u s i n. Sur les classes des constituantes des complementaires analy-
tiques. Annali della R. Scuola Normale Superiore di Pisa, серия II, П, 1933 (стр. 624
настоящего тома.—Ред.).
644
Н. Н. ЛУЗИН
утверждали Кантор и его последователи Цермело и Хаусдорф. В самом
деле, в этих условиях не может иметься в континууме ни одной части
мощности алеф-один.
И в то же самое время наличие нестационарных последовательностей
из совокупностей ограниченных классов представляется совсем
невероятным, потому что среди самых могущественных средств современной
науки нет ни одного, которое можно было бы рассматривать хоть
сколько-нибудь приближающимся к построению такой
последовательности: все известные до сих пор приемы кажутся качественно
неадекватными этому построению.
Мы не имеем в виду заниматься здесь разрешением этих трудных
вопросов. Ограничимся лишь указанием на то, что современная наука
обладает многими ресурсами строить последовательности совокупностей,
измеримых В; например, как мы увидим далее, теория аналитических
совокупностей приводит к весьма простым таким последовательностям,
которые притом являются монотонными и предельными. Поэтому
естественно желать изучить a priori такие последовательности, с тем
чтобы определить природу тех совокупностей Еа> измеримых 5,
которые могли бы сделать нестационарной рассматриваемую
последовательность.1
3. Изыскание Бэра. Первым, кто стал на эту дорогу, был Рене
Бэр. Ему принадлежит замечательная теорема, позволяющая
констатировать стационарность всякой убывающей последовательности,
образованной из замкнутых совокупностей. Этот замечательный результат
является глубоким расширением указанной теоремы Кантора — Бендиксона
и будит многочисленные отзвуки как в математическом анализе, так и
в теории функций.
Сам Рене Бэр дважды доказал эту теорему: один раз для обычных
евклидовых пространств, другой раз для того отвлеченного
пространства, которое он называл „пространством измерения нуль". С
геометрической точки зрения это последнее является просто обычной
прямой, из которой удалены все рациональные точки. Это пространство
представляет существенную разницу с обычным евклидовым: общая
часть бесконечности замкнутых совокупностей может оказаться пустой.
Ввиду исключительной важности теоремы Бэра мы восстанавливаем
ее доказательство, пригодное сразу д\я обоих указанных случаев.
1 Указания на то, что то же самое происходит со всякой еще не разрешенной
проблемой теории чисел, например со знаменитой теоремой Ферма, мне не кажутся
особенно убедительными: теорема Ферма проста лишь своей формулировкой, на дележе
является в высшей степени богатой по содержанию. Указанная же проблема
нестационарной последовательности проста по форме и, в сущности, крайне бедна по
содержанию, так как здесь отсутствует вся полнота богатства и сложности свойств
натуральных чисел, а фигурирует лишь соотношение немногих и совершенно общих
понятий.
О СТАЦИОНАРНЫХ ПОСЛЕДОВАТЕЛЬНОСТЯХ
645
Теорема Бэра. Всякая убывающая последовательность
замкнутых совокупностей необходимо стационарна.
Пусть
£0^£i3£p...D£wD...D£lD \& (3)
— последовательность, составленная из замкнутых совокупностей.
Назовем порцией совокупность точек, заключенных между двумя
какими-нибудь рациональными точками. Из этого определения следует,
что совокупность всех порций есть исчислимая. Обозначим через
К 8*...Л>... (4)
все те порции, каждая из которых содержит точки самое большое
исчислимой совокупности членов Еа последовательности (3). Отсюда
следует, что для всякого натурального числа п имеется такое
трансфинитное (или конечное) число ая, что порция 8„ уже не содержит никакой
точки члена Ей . Обозначим через [3 трансфинитное (или конечное) числоу
которое непосредственно превосходит все числа alt <х2, а3,..., ая,...
Положив это, уничтожим в рассматриваемом пространстве все
порции (4) и обозначим через Е совокупность оставшихся точек. Яснр,,
что Е есть замкнутая совокупность (или пустая). Мы теперь
утверждаем, что, начиная с индекса 8, все члены последовательности (3)
тождественны замкнутой совокупности Е> т. е. что имеем
Е = Е$ = /?р-ц = £р+2 = |2.
Действительно, прежде всего порции (4) не содержат никакой точки
членов Е$у £р-и, Е$+2, |2; поэтому замкнутая совокупность Е
необходимо содержит каждый из этих членов. С другой стороны, если
индекс 7 превосходит все числа а1У о^,..., ая,..., совокупности Е
содержится в члене Ег Чтобы видеть это, обозначим через х какую-
нибудь точку совокупности Еу не принадлежащую к£т; так как £7 есть
замкнутая совокупность, существует порция 8, содержащая точку х и не
содержащая никакой точки совокупности Ev Значит, порция 5 есть
одна из порций (4), что, очевидно, невозможно.
Мы заключаем из этого, что имеем ЕГ = Е, каков бы ни был
индекс 7> больший или равный числу (3. Этим теорема Бэра доказана (ч. т.,д.).
К этой теореме Бэра мы присоединим следующее коррелятивное
предложение, являющееся почти очевидным:
Теорема. Всякая возрастающая последовательность замкну
тых совокупностей необходимо стационарна.
Пусть
Е9сЕЛсЕас...сЕЛс..сЕЛс: \Q (5)
— последовательность, составленная из замкнутых совокупностей.
Возьмем все порции о, которые не содержат ни одной точки
членов Еа последовательности (5); пусть
8', 8", 8"',...,&<">,... (6)
646
Н. Н. ЛУЗИН
будут эти порции. Если мы уничтожим в рассматриваемом пространстве
все порции (6), мы получим некоторую замкнутую совокупность,
составленную из оставшихся точек; пусть будет Е эта совокупность. Из
самого определения совокупности Е следует, что каждый член Еа
последовательности (5) содержится в Е, каков бы ни был индекс а.
Мы утверждаем теперь, что всякая точка х совокупности Е
принадлежит всем членам Ел последовательности (5), начиная с известного
индекса (3. Действительно, если бы это не было верно, то, приняв во
внимание, что члены Еа суть замкнутые совокупности и идут в
последовательности (5), возрастая, мы заключили бы, что наверное имеется
порция Ьу содержащая точку хине содержащая никакой точки членов Еа
последовательности (5); но это последнее обстоятельство является
невозможным, так как такая порция Ь была бы одной из порций (6).
Установив это, возьмем какую-нибудь исчислимую совокупность D
точек, всюду плотную на совокупности Е; пусть
Xj, Х-2» ATj, . . ., Xni . . . y/J
будут точки совокупности Z), взятые все. Обозначим через ая
наименьший из индексов таких, что точка хп принадлежит члену Еа . Пусть ^
будет число, непосредственно превосходящее числа аи <х2, *3,.. .,ая,....
Ясно, что совокупность D образует часть члена Ev Но обе
совокупности Е и Еу суть замкнутые, и совокупность Z), содержащаяся в Ev
является всюду плотной на Е. Отсюда следует, что совокупность Е
сама, в свою очередь, является частью совокупности Ег и,
следовательно, всех членов Еа последовательности (5), каков бы ни был
индекс а, превосходящий число 7-
Мы заключаем окончательно, что имеем
Е = Еу = Еу+х = Еу+2 = 12.
Этим теорема установлена (ч. т. д.).
Прежде чем идти дальше, является полезным соединить обе эти
теоремы в одну, ограничившись рассмотрением одних лишь убывающих
последовательностей.
С этой целью заметим сначала, что если последовательность каких-
нибудь совокупностей
Zs0, Ь1У h2,. . ., £ш,..., ЬаУ |и
есть возрастающая, соответствующая ей последовательность
дополнительных совокупностей
есть убывающая, как и обратно; здесь £а есть дополнение
совокупности Еа9 т. е. &а = СЕй. С другой стороны, известно, что дополнение
замкнутой совокупности есть открытая совокупность; обратное
также имеет силу.
О СТАЦИОНАРНЫХ ПОСЛЕДОВАТЕЛЬНОСТЯХ 647
Вследствие только что сказанного теорема Бэра и коррелятивное
ей предложение могут быть объединены следующим образом:
Всякая убывающая последовательность замкнутых или
открытых совокупностей необходимо стационарна.
Здесь уместно будет вспомнить о символах Хаусдорфа,
представляющих некоторые удобства, когда дело идет о совокупностях, измеримых В,
малой сложности. Согласно предложению Хаусдорфа обозначают
замкнутые совокупности буквой F, а их дополнения (т. е. открытые
совокупности) буквой G. Далее, обозначают символом F9 совокупности,
являющиеся соединением исчислимой бесконечности совокупностей F,
и соответственно через Ge обозначают совокупности, которые суть
общая часть исчислимой бесконечности совокупностей G.
При таком обозначении теорема Бэра и ее коррелятив выражаются
весьма сжато:
Убывающая последовательность совокупностей F или G
стационарна.
4. Расширение результатов Бэра. Естественно спросить, можно ли
продолжить изыскания Бэра и расширить его результаты за замкнутые
и открытые совокупности? Мы имеем в виду ответить здесь
утвердительным образом, показав, что теорема Бэра о стационарности
продолжает сохранять силу для всех без исключения совокупностей
класса 1 классификации Валле-Пуссена и для некоторых совокупностей
класса 2 той же самой классификации.
К этому мы прибавим следующее: если теорема Бэра о
стационарности будет иметь силу для всех совокупностей класса 2, то это
повлечет, как было сказано, столь удивительные заключения, какова,
например, несравнимость мощностей континуума и алеф-один. Если же
теорема Бэра о стационарности окажется заведомо ложной хотя бы д\я
некоторых совокупностей класса 2, то это будет значить, что мы
в состоянии строить нестационарные последовательности весьма простых
совокупностей. В настоящем же состоянии науки это кажется весьма
парадоксальным, потому что невозможно вообразить, какими
средствами будет осуществлено построение столь необыкновенной
последовательности.
Расширение теоремы Бэра, которое мы имеем в виду, выражается
предложением:
Теорема. Всякая предельная убывающая последовательность
совокупностей F9 необходимо стационарна.
Пусть
£0э£1э£2=)...э£а)з...:э£аэ |2 (I)
будет данной предельной убывающей последовательностью
совокупностей Еа9 всякая из которых есть соединение исчислимой бесконечности
замкнутых совокупностей.
648
Н. Н. ЛУЗИН
Доказывая от противного, предположим последовательность (I)
нестационарной.
Покажем прежде всего, что мы имеем право предположить каждую
из совокупностей-разностей Еа—£а-ц непустой, т. е. действительно
содержащей точки, каков бы ни был индекс а. В самом деле, если бы
последовательность (I) имела отрезки £3 — £|Э-и = • •.> состоящие из
равных членов, мы просто могли бы взять лишь одни только первые
члены этих отрезков, не заботясь об остальных. Отобранные первые
члены при условии сохранения среди них прежнего порядка составят,
очевидно, предельную убывающую последовательность, которая не
будет иметь двух равных членов и поэтому также не может быть
стационарной. Таким образом, рассмотрение данной последовательности (])
заменено рассмотрением другой последовательности той же самой
природы, но еще лишенной равных членов.
Установив это, обозначим через ;а какую-нибудь точку разности
Если мы заставим индекс а пробежать все конечные числа и
трансфинитные числа второго класса, мы получим трансфинитную
последовательность
У у к У 'г \Г\
^о> ^i» ?2> . . ., so,, . . ., <;а, | *
попарно различных точек. Обозначим через 3 совокупность всех точек
этой последовательности.
Мы утверждаем теперь, что совокупность 3 есть первой категории
на всякой совершенной совокупности. В самом деле, предположим,
что 3 не есть первой категории на некоторой совершенной
совокупности Н. Мы можем предположить, что 3 всюду плотная на Н. Возьмем
исчислимую часть совокупности 3, также всюду плотную на //; пусть D
есть эта часть. Так как совокупность D есть исчислимая, имеется такое
число f> чт0 член £у не содержит никакой точки совокупности Z).
С другой стороны, всякий член Еа последовательности (1) есть
соединение исчислимой бесконечности замкнутых совокупностей;
следовательно, мы можем писать
£а — я^-btfp-i- ... -ь />)-ь ...,
где всякий F£] есть замкнутая совокупность. Если а^у, член Еа не
содержит никакой точки совокупности D. Так как D есть всюду
плотная на совершенной совокупности Н и так как F^ не содержит никакой
точки совокупности Dy каковы бы ни были числа п и а, а^*[> то
отсюда мы заключаем, что всякая замкнутая совокупность F^ есть
нигде не плотная на //. Значит, Ей есть первой категории на //;
a fortiori будет первой категории на//рассматриваемая совокупность 3,
потому что она составляет часть совокупности £а, за исключением
может быть, исчислимой бесконечности ее точек (ч. т. д.).
О СТАЦИОНАРНЫХ ПОСЛЕДОВАТЕЛЬНОСТЯХ
649
В приведенном рассуждении полезно отметить один пункт: если
совокупность л есть всюду плотная на какой-нибудь совершенной
совокупности Я, всякая совокупность Еа есть первой категории
на Ну когда индекс а будет превосходить некоторое определенное
число 7»
Установив это, возвратимся к доказательству предложенной теоремы.
Пусть Р есть совокупность всех точек уплотнения (в смысле Линде-
лофа) совокупности 2. Известно, что Р есть совершенная совокупность,
что 3 есть всюду плотная и всюду неисчислимая на Р и что точки
совокупности Е, не принадлежащие к Р, имеются, самое большее,
в исчислимой бесконечности. Мы должны теперь изучить распределение
точек совокупностей Еа на этой совершенной совокупности Р.
Прежде всего, раз совокупность S есть всюду плотная на Р,
существует такое число 7i> чт° совокупность Еь есть первой категории
на Р. Значит, мы можем писать,
Р • Еь = Pi, а -к Plt 2 -+-... -+ Р,,„ -н ..., (8>
где всякое слагаемое Р\гП есть замкнутая совокупность, содержащаяся
в Р. Мы утверждаем теперь, что имеем право предполагать:
1° что замкнутые совокупности Pi,w суть совершенные;
2° что совокупности Pi,w попарно не имеют общей точки;
3° что совокупность S есть всюду плотная и всюду неисчислимая
на всякой совокупности Pi,*, каково бы ни было натуральное число л.
Чтобы удостоверить это, укажем сначала на то, что всякая
замкнутая совокупность Pi,w заведомо есть нигде не плотная в абсолютном
смысле, потому что она есть нигде не плотная на Р. Отсюда следует,
что совокупность-сумма
Р\Л -Ь Pi, 2 -Ь . ..Н- Pi, n-\
есть нигде не плотная в абсолютном смысле. Но известно, что
совокупность-разность двух замкнутых нигде не плотных совокупностей
есть сумма исчислимой бесконечности замкнутых совокупностей, не-
имеющих попарно общих точек. И так как мы, очевидно, имеем право
написать
P-Eb = %[Pl,H— Pl,n(Pl,l-bPl,2-H...-*-Pl,n-l)l,
tt=l
то отсюда мы заключаем, что Р • Еь есть сумма (и не только
соединение) исчислимой бесконечности замкнутых совокупностей, не имеющих
попарно общих точек. С другой стороны, всякая замкнутая
совокупность есть либо исчислимая (конечная), либо разбивается на
[совершенную совокупность и на исчислимую совокупность точек. Отсюда мы
окончательнозаключаем, что все совокупности Pi,n могут быть
предположены либо совершенными, либо состоящими из единственной.
.650
Н. Н. ЛУЗИН
точки и притом все Pi,„ попарно не имеют обиден точки. К тому же,
раа. совокупность 3 есть неисчислимая и всюду плотная на Р,
совокупность Р • Еь имеет эти же самые свойства. Следовательно, среди
совокупностей Pi,w заведомо имеется исчислимая бесконечность
совершенных совокупностей.^ сумма которых есть всюду плотная на
рассматриваемой совершенной совокупности Р,
Установив это, возьмем какую-нибудь совершенную совокупность P]>w
и рассмотрим точки совокупности Е, принадлежащие к Pi,w. Эти точки,
очевидно, составляют общую часть E-Plf„; предположим ее
неисчислимой. В этом случае совокупность всех точек уплотнения (в смысле
Линделофа) совокупности 2 • Р1>п есть совершенная совокупность,
которую мы обозначим чрез ^i,„. Совокупность тч,« составляет
часть совокупности Pi,»<, и ясно, что Е есть всюду плотная
и всюду неисчислимая на k1iU> и что точки совокупности S,
содержащиеся в Pi,M и не принадлежащие к tt1i70 имеются, самое большее,
в исчислимой бесконечности. Отсюда следует, что совокупность-раз-
нсгсть Pi,w — щ,п есть сумма исчислимой бесконечности совершенных
совокупностей, из которых каждая содержит точки совокупности Е,
самое большее, в исчислимой бесконечности.
Если поступают указанным образом со всеми совершенными
совокупностями Pi,n, каждая из которых содержит точки совокупности S
в неисчислимой бесконечности, тогда получат следующее разбиение
рассматриваемой- совокупности Р • Еь:
Р • Еъ = icx -I- ъ2 -ь к3 -н... -н ъп -н .. .
... -*- Pi -+- ?2 ■+■ Рз -*- •••-»- Р» ■+---• > (9)
где каждая ~„ есть совершенная совокупность, на которой Е есть
всюду плотная и всюду неисчислимая, и где каждое слагаемое ря
есть либо отдельная точка, либо есть совершенная совокупность,
содержащая точки совокупности Е, самое большее, в исчислимой
бесконечности.
Из самого построения совокупностей ^ и ру явствует, что все они
не имеют попарно общей точки между собой и друг с другом, каковы бы
ни были / и у. Так как Е есть всюду неисчислимая на Р, первая сумма
формулы (9) есть всюду плотная на совершенной совокупности Р#
Ясна, что мы можем предположить диаметры обеих совокупностей ^„
1
и р* меньшими, *ем —, потому что в противном случае мы можем всегда
разделить всякую данную совершенную совокупность на конечное число
совершенных совокупностей, из которых каждая содержится в
интервале длины, меньшей, чем е; г— здесь положительное число, малое как
угодно.
О СТАЦИОНАРНЫХ ПОСЛЕДОВАТЕЛЬНОСТЯХ
651
Мы можем теперь окончить построение разложения (8) совокупности
Р - Еь таким образом, чтобы совершенные совокупности Pi,„ (п = 1, 2,3,...)
обладали всеми тремя указанными свойствами (1°, 2° и 3°).
Для этого присоединим сначала к совокупности р< бесконечность
совокупностей ^ так, чтобы полученная таким образом сумма
-оказалась совершенной совокупностью, на которой pj есть нигде не
плотная, и значит, чтобы эту сумму можно было обозначить буквой Pi, i.
Чтобы иметь эту совокупность Pi, i, достаточно построить в каждой
порции ок совокупности Р, смежной к рр исчислимую бесконечность
лорций
а' а" п(т)
3Jb °к у ' • •» а* » ' • •
совокупности Р, стремящуюся к концам порции оку и взять в каждой
из этих порций о^) совокупность тс>, в ней целиком содержащуюся:
сумма, составленная из рх и из всех выбранных таким образом ~у, будет,
очевидно, желаемой совокупностью Pi,l
Раз совокупность Pi.i составлена, мы зачеркиваем в формуле (9)
совокупность рх и все те тс>, которые пошли на образование
совокупности Pi,i> и поступаем таким же точно образом с р2: мы присоединяем
к р2 известные совокупности itv, чтобы составить нужную нам
совершенную совокупность Pi, 2, и так далее. Поступая все время таким же
точно образом, мы получим совокупности Pi, 1, -Pi, 2, Pi,n,.. .,Pi,n,....
Если, по завершении процесса, у нас останутся некоторые
совокупности ?гт, которые не послужили нам для образования совокупностей
Pi, 1, Pjf>,...» мы пишем такие кт еще как Pi,fc, совершая новую
нумерацию. Эта метода дает нам, очевидно, желаемые разложения (8), где
все совокупности Pi,n удовлетворяют поставленным выше
требованиям 1°, 2° и 3° (ч. т. д.).
Установив это, мы можем теперь перейти к окончанию доказательства
предложенной теоремы.
Прежде всего вот заключение, к которому мы пришли: Р есть
совершенная совокупность, на которой совокупность 2 есть всюду
плотная и всюду неисчислимая. Из одного этого факта мы вывели,
что всякий член Еъ данной последовательности (1) может быть написан
да Р в виде
Р • £Tl =Pi.i-b Р\л+ ... -bPi.n-н ...,
где Р],и суть совершенные совокупности, не имеющие попарно общих
точек и такие, что совокупность Е есть всюду плотная и всюду
неисчислимая на каждой из этих PilW, когда индекс тх достаточно велик.
Как только мы это установили, мы оказываемся опять в прежних
условиях, и значит, мы можем снова начать предшествующие
рассуждения. Отсюда следует, что если индекс ^2 достаточно велик, 72^>7]> мы
можем писать
Р-£Ti=P2,l-»-P2, 2 "*-...-+-Р2.П-Н...,
652
Н. Н. ЛУЗИН
где Рг, п суть совершенные совокупности, не имеющие попарно общей
точки и такие, что совокупность £ есть всюду плотная и всюду
неисчислимая на всякой из этих Pi,„. И так далее.
Окончательно, если мы поступаем указанным образом, мы получим
исчислимую бесконечность следующих разложений:
P-£Tl=PlfH-P1,,-b...-4-Pi,H-b... j
Р . £7,= P2,i н-Р,,, ~+- . . . -+- Р2,„ -ь .. .
• Р • Еь= Рз, 1 Н- Р:». 2 Н- • • • Н- Рз. „ И- . . . I (JJV
у)
в которой совершенные совокупности PitJ образуют таблицу с двойным
входом. Совершенные совокупности Р<, i, Pi, о,.. ., Pi, >lf..., написанные
в одной и той же горизонтальной линии, попарно не имеют общих
точек, и всякая совокупность Рт,и, /п^>1, наверное, содержится
целиком в одной и только в одной совокупности Pm—hs предыдущей
горизонтальной линии. Важно заметить, что на всякой из совокупностей Рт>п
совокупности Ряи-1,к следующей горизонтальной линии образуют
совокупность всюду плотную и первой категории. Что же касается до-
индексов 7i> 72» • • •> Тп> • • •> они образуют, очевидно, возрастающую
бесконечную последовательность
Т1<Т2<Тз<---<7п<....
Отсюда следует, что число, непосредственно большее всех чисел ^ПТ
является пределом их, т. е. числом второго рода; обозначим его через рг
P = lim7*.
П-+СО
Так как данная последовательность (1) есть предельная и
убывающая, член Ер есть общая часть совокупностей £Tl, Еь,.. ♦, £Tw,... *
Значит, имеем
Р.£3 = Р.£Т1.Р.£Т,....Р.£Ь.....
Мы теперь переходим к наиболее важному пункту рассуждения. Так
как Яр есть сумма исчислимой бесконечности замкнутых
совокупностей, общая часть произведений Р • Еы является совокупностью
той же самой природы. Но всякая совокупность, являющаяся суммой
исчислимой бесконечности замкнутых совокупностей, есть, самое боль*
щее, класса 2 классификация Валле*Пуссена. Отсюда следует, что
общая часть Р • Еь • Р • Еь • ... есть, самое большее, класса 2 в этой
классификации.
С другой же стороны, отнесясь к работам Бэра и, в частности,
к его примеру функции класса 3 (см. его мемуар „Sur la representation
des fonction discontinues'4, Acta Math., 30, 44), немедленно усматриваем*
О СТАЦИОНАРНЫХ ПОСЛЕДОВАТЕЛЬНОСТЯХ
653
что общая часть Р • ЕЬР -Еь- .. . есть в точности совокупность
класса 3 классификации Валле-Пуссена, потому что ее
характеристическая функция/(л:), равная 1 на Р • Еъ • Р • Еь • ... и 0 вне, есть
заведомо функция класса 3 классификации Бэра.
Таким образом, мы пришли к противоречию, предположив данную
последовательность (1) нестационарной, что и доказывает предложенную
теорему (ч. т. д.).
Доказанная теорема содержит в своей формулировке символ Хаус-
дорфа Fa. Легко видеть, каким образом изменится эта формулировка
при переходе к обычной классификации совокупностей (Валле-Пуссена).
С этой целью сделаем сначала следующее замечание: всякая
совокупность точек, которая является пределом замкнутых совокупно-
стейу есть сумма исчислимой бесконечности замкнутых
совокупностей. Обратное утверждение верно и очевидно.
Действительно, пусть совокупность точек Е есть предел замкнутых
совокупностей
так что имеем
Е = \\тЕп
при /2, безгранично возрастающем. Так как предел lim Еп, исчислимой
простой последовательности совокупностей Еп(п = 1, 2, 3, ...) по самому
своему определению совпадает с предельной совокупностью в узком
смысле^ \\тЕП9 то мы имеем право написать
E = \imEu = (Ex-E2-Ez...)-*-(E2-Ez .. .)-*-(Ez.. .)-н ... . (10)
Но совокупности Еп суть замкнутые, и общая часть исчислимой
бесконечности замкнутых совокупностей есть опять замкнутая совокупность
(или пустая для случая пространства Бэра). Поэтому из формулы (10)
следует, что совокупность Е есть сумма исчислимой бесконечности
замкнутых совокупностей, т. е. Fa, что и требовалось установить
(ч. т. д.).
Коррелятивным предложением является: всякая совокупность точек,
которая является пределом открытых совокупностей, есть общая
часть исчислимой бесконечности открытых совокупностей.
Обратное утверждение верно и очевидно.
Действительно, если Е = YimEn> имеем очевидно Е = lim£n, т. е.
£ = 11^£я = (£1-н£2-н£3-н ...)*(Е2 + Е3+ ...)(Ей + •••)••• • (П)
Предположим, что совокупности Еп все открытые. Так как
соединение исчислимой бесконечности открытых совокупностей есть также
открытая совокупность, формула (11) говорит, что Е есть общая часть
исчислимой бесконечности открытых совокупностей, т. е. G$, что и нужно было
установить (ч. т. д.).
654
Н. Н. ЛУЗИН
Напомним, наконец, следующую важную теорему Валле-Пуссена:
всякая совокупность класса 1 есть одновременно предел и замкну-
тых и открытых совокупностей. Обратное является также верным.
Иначе говоря, для того чтобы совокупность Е была класса 1,
необходимо и достаточно, чтобы она была одновременно и F,h G$.
Так как теорема о стационарности имеет силу для всех F3, то как
частный случай она сохраняет свою справедливость и для таких G3r
которые являются одновременно и Fr Таким образом, мы заключаем:
Всякая предельная убывающая последовательность совокупностей
класса 1 необходимо стационарна.
Так как совокупности вида F и G являются, в свою очередь, лишь
весьма частными случаями совокупностей класса 1, то отсюда видно,,
что указанное предложение представляет естественное расширение
теоремы Бэра.
Ближайшим вопросом, естественно становящимся на очередь, был бы
коррелятивный вопрос о стационарности возрастающих
последовательностей совокупностей Fa или, что все то же самое, убывающих
последовательностей совокупностей Gs. К сожалению, при настоящем
состоянии науки мы ничего не можем сказать о таких последовательностях;
мы не знаем даже, разрешима ли вообще эта проблема, так как,
возможно, что самая ее формулировка является неполной. К тому же,
может быть, здесь нам понадобятся дальнейшие ограничения,
наложенные на самую последовательность. Одним из таковых могло бы быть
требование, чтобы совокупность-разность Е3 — ЕЛ ПРИ ?^>а никогда не
была совокупностью F,9 если данная последовательность Е{), F{1 ...,
Et,, ..., ЕаУ ...2 совокупностей Fy есть возрастающая[63\.
Другая проблема, уже совершенно выводящая нас из области
математики в область чистой логики, состоит в требовании разбить
отрезок 10, 1] на алеф-один непустых совокупностей В ограниченных
классов; при этом относительно мощности континуума не предполагается
ничего, кроме того, что это есть мощность вполне упорядоченной
совокупности. Мы ограничиваемся здесь лишь формулировкой этой
проблемы [64].
5* Приложение к теории решет. Рассмотрим на плоскости
прямоугольную декартову систему координат XOY. Термином „решето" мы
обозначаем всякую исчислимую бесконечность отрезков Дя, лежащих
на этой плоскости и параллельных оси ОХ. Решето мы будем
обозначать буквой С, а составляющие его отрезки Ам А3> • • •> ^п> ••• будем
называть элементами рассматриваемого решета С. Для большей
определительности мы будем предполагать расстояние рп отрезка Дп до оси ОХ
ноложительным и рациональным, а самые концы отрезка Ая — имеющими
рациональные координаты. Кроме того, для той же самой цели наибольшей
определительности мы будем предполагать, что два различных отрезка Ат
и Ал> т=^=пу расположены на разных расстояниях от оси ОХ, так что
Рт^Ря, если тфп.
О СТАЦИОНАРНЫХ ПОСЛЕДОВАТЕЛЬНОСТЯХ
655
Из данного решета С, которое мы будем называть начальным (или
производящим) решетом и которое будем обозначать буквой С0, мы
выведем трансфинитную последовательность решет
С=С0, С„ С,,..., С„,..., С, |9. (III).
Решета эти мы будем называть производными решетами от данного
решета С и будем образовывать их по следующему правилу:
1°. Элементы каждого из этих решет суть некоторые совокупности
точек, лежащие на прямых y = pJlf где я = 1, 2, 3, ...
2°. Если число а есть первого рода, так что а = а*-н1, то элемент
решета Са, лежащий на прямой z/ = pw, получается следующим образом:
на элемент решета Са«, лежащий" на прямой # = pw, проектируем точки
элементов этого решета, лежащих ниже прямой i/ = pm, и удерживаем
на рассматриваемом элементе лишь точки этих проекций, выбрасывая
все другие его точки; совокупность удержанных точек рассматриваемого
элемента решета Са* есть по определению элемент решета Са.
3°. Если а есть второго рода, то получают элемент решета СаГ
лежащий на прямой у = рту беря общую часть всех элементов
предыдущих решет CV, p <C a> лежащих на этой прямой.
Данное правило является, очевидно, достаточным, для того чтобы
формально определить всю последовательность (III) производных решет.
Так как при определении элементов производных решет, мы не
встречаем никаких других операций, кроме проектирования совокупностей,
лежащих на прямых, на прямые, параллельные им, соединения
совокупностей и взятия общей части совокупностей, фигурирующих всегда лишь
в исчислимой бесконечности, — мы заключаем отсюда, что все элементы
производных решет суть всегда совокупности, измеримые В, и что
последовательность элементов производных решет, лежащих на одной и той же
прямой у = рт,
е(гп) з е[щ з ei«) з ... 3 е^ Z) .. . 3 <m) D | (Л (IV>
есть предельная убывающая последовательность совокупностей,
измеримых 5.
Заставляя т пробежать весь натуральный ряд чисел, т = 1, 2, 3, ...,
мы, очевидно, получим исчислимую бесконечность предельных
убывающих последовательностей совокупностей, измеримых В. Заметим,
что указанная метода есть наипростейшая получать такие
последовательности совокупностей.
Легко видеть, какой геометрический смысл имеет указанное правило
образования производных решет. Для этого возьмем какую-нибудь
точку х на оси ОХ и проведем через нее параллель оси OY; обозначим
через Рх полученную прямую, перпендикулярную к оси ОХ Далее
обозначим через Н{£ совокупность точек, образующуюся при
пересечении решета Са перпендикуляром Ра. Так как все элементы производных.
456
Н. Н. ЛУЗИН
решет лежат на прямых z/ = pw, то отсюда следует, что совокупность Н[*>
есть исчислимая. В зависимости от частного положения точки х на
оси О К совокупность Н^] может оказаться конечной или даже пустой.
Последнее будут обозначать, что перпендикуляр Рх не пересекает
решета Са.
Так как элементы (IV) производных решет образуют убывающую
последовательность, то отсюда следует, что Н{£] СН(*\ если а<^|3.
Следовательно, на всяком перпендикуляре Р(а] к оси ОХ мы также
сбудем иметь убывающую последовательность
щ* D^D^D...DWHD...D^D I Q. (у)
Вследствие того что последовательность (IV) есть предельная,
предельной, очевидно, будет и рассматриваемая последовательность (V).
Так как ее члены суть исчислимые совокупности (или конечные),
последовательность (V) необходимо стационарная.
Легко видеть, что последовательность (V) образуется по следующему
правилу: всякие два соседних члена, Н^и Н£~*~1\ могут отличаться не
•более чем на одну только точку, а именно если в совокупности H**]
имеется самая нижняя точка, то такая точка уже не фигурирует в
совокупности 1~Р*+1\ удерживающей в себе все другие точки совокупности Н^^]
•если же совокупность Н^ не имеет самой нижней точки, то тогда
совокупность /^аЧ_1) тождественна с совокупностью Н£\
В справедливости этого правила мы удостоверяемся немедленно,
когда относимся к данному выше правилу образования производных
решет: при применении этого правила из элементов решета Са
удаляются все те и только те точки, которые не имеют лежащей под ними
•точки решета Св.
Из найденного правила составления последовательности (V) легко
усмотреть тот момент, начиная с которого эта последовательность
становится стационарной: стационарность наступает в тот самый момент,
когда совокупность Н^ или лишается вообще всех своих точек,
становясь пустой, или когда она лишается самой нижней точки; в этом
последнем случае совокупность Н^ бесконечна, но самая нижняя предельная
к ней точка уже более не входит в нее.
Легко теперь определить, зная один лишь начальный член /^0)
последовательности (V), момент наступления стационарности. Здесь возможны
•только два случая.
1°. Совокупность Н^] есть вполне упорядоченная в направлении
•снизу вверх. Пусть (3 есть то порядковое (конечное или трансфинитное)
число, которое соответствует этой вполне упорядоченной совокупности.
Ясно, что стационарность наступает в точности с индекса (В, так что
имеем
0 = Н® = Щ+1> = \Q9
О СТАЦИОНАРНЫХ ПОСЛЕДОВАТЕЛЬНОСТЯХ
657
и что предыдущие члены //*', а<з, не являются пустыми, фактически
содержа точки.
2°. Совокупность Н^] не есть вполне упорядоченная по
направлению снизу вверх. В этом случае совокупность Н£] заведомо допускает
предельные точки, являющиеся пределами для простых бесконечных
последовательностей точек совокупности /^х0), идущих сверху вниз, т. е.
для „падающих" простых последовательностей точек совокупности Н^\
Ясно, что среди таких предельных точек для совокупности Н^ имеется
самая нижняя; обозначим ее через jv И ясно, что точки совокупности И^\
лежащие на замкнутом отрезке [л:, \ьТ] перпендикуляра Рх, образуют
вполне упорядоченную совокупность и что самая точка \ьх есть предел
простой падающей последовательности точек совокупности Н^ (т. е.
имеющей убывающие ординаты). Обозначим через 3 то порядковое число
(конечное или трансфинитное), которое соответствует вполне
упорядоченной части совокупности Н^\ находящейся на замкнутом отрезке [л:, \ьх].
Ясно, что именно с этого индекса (3 и начинается стационарность
последовательности (V), т. е. что имеем
H® = Hf™ = |2,
тогда как для чисел а <^ 8 мы не имеем еще стационарности, потому что
замкнутый отрезок [ху p-J еще продолжает содержать точки члена Н^\
когда а<|3.
Из общей теории аналитических совокупностей известно, что точки jc,
для которых совокупность Н[^ не есть вполне упорядоченная по
направлению снизу вверх (для которых, следовательно, точка \i£
фактически существует), образуют аналитическую совокупность; обозначим
ее через Е. Напротив, точки ху для которых совокупность Н1^ есть
вполне упорядоченная в указанном направлении, образуют дополнение
к аналитической совокупности, обозначаемое обычно буквой <§; <§=СЕ.
Аналитическая совокупность Е и ее дополнение & разбиваются на
попарно не прекрывающиеся совокупности, измеримые Ву находящиеся
в количестве, самое большее, алеф-один и называемые
конституантами В:
Е = Е0-*-Ех-*-Е2ч- ... -*-£„-!- ... -ь£.-+-
и
g = g04-£1 + St-*- ... -ь£шн- ... -+■£.-+-
причем совокупности Еа называются внутренними конституантами
аналитической совокупности Еу тогда как совокупности <Sa называются
ее внешними конституантами. Правило, определяющее все эти
конституанты, состоит в следующем: в конституанту Еа входят все точки
и только такие точки ху для которых вполне упорядоченная часть
совокупности Н^\ принадлежащая к замкнутому отрезку [х, pj, соответ-
\Q
6S8
Н. Н. ЛУЗИН
ствует порядковому числу а. Аналогично конституанта &а составлена
из всех точек и только таких точек х, для которых вполне
упорядоченная совокупность Н^] соответствует порядковому числу а.
Внешние конституанты &а довольно хорошо изучены и обладают
несколькими замечательными свойствами. Среди этих последних важно
то свойство, в силу которого всякая аналитическая совокупность Ау
содержащаяся в дополнении &, всегда целиком содержится в сумме,
самое большее, исчислимой бесконечности внешних конституант £а.
Отсюда следует, что необходимым и достаточным условием дкя того,
чтобы дополнение £ (и, значит, самая аналитическая совокупность Е)
было измеримым Ву является требование, чтобы все внешние
конституанты &а, начиная с достаточно большого индекса а, были пустыми%
т. е. не содержащими точек.
Что же касается до внутренних конституант £а, то они далеко не
так изучены, как внешние. Известно только, что измеримость В
аналитической совокупности Е отнюдь не требует, чтобы внутренние
компоненты Еа были все пустыми для достаточно большого индекса а. Но
если указанное имеет место, тогда совокупность Е необходимо
измерима Ву и значит, тогда и внешние конституанты £а становятся
необходимо пустыми, начиная с достаточно большого индекса а.
Основной и еще не разрешенной проблемой теории аналитических
совокупностей, по-видимому представляющей огромные трудности, является
вопрос: могут ли все конституанты, внутренние и внешние, быть
ограниченных классов?
Легко связать этот вопрос с вопросом о классе элементов
производных решет Са.
Чтобы видеть это, укажем прежде всего соотношения между
конституантами (внешними и внутренними), с одной стороны, и элементами
производных решет, — с другой стороны.
Пусть Са есть производное решето. Мы уже знаем, что переход
от какого-нибудь производного решета Су к следующему С^+{ состоит
в уничтожении самой нижней точки всякой совокупности НХЛ\ по
которой решето Сг пересекается перпендикуляром Рх, какова бы ни была
точка х оси ОХу если только такая нижняя точка имеется у
совокупности //£>; в противном случае мы имеем тождество Н£) = Н£+1К Отсюда
следует, что точки л:, в которых Рх не пересекает решета Са, являются
такими, для которых совокупность Н%\ по которой Рх пересекает
начальное решето С0 (= С), есть вполне упорядоченная и соответствует
порядковому числу, не большему числа а; обратно, перпендикуляр Рх,
восставленный в таких точках jc, не пересечет решета Са.
Заметив это, обозначим элемент решета Св, лежащий на прямой у = ?ту
через е^; не произойдет никакого ущерба, если мы той же буквой е^п)
обозначим и ортогональную проекцию элемента е^ решета Са на ось ОХу
потому что вследствие параллельности прямой у = рт оси ОХ элемент е^
О СТАЦИОНАРНЫХ ПОСЛЕДОВАТЕЛЬНОСТЯХ
659
имеет проекцию, ему конгруэнтную. Приняв это обозначение и учтя
предыдущее замечание, мы можем написать очевидное равенство
*.+.=с 2«& -с 2*0, (13)
2«,=с 2<"'Ь (12)
4=0 \ж=1 /
где буквой С мы обозначаем взятие дополнительной совокупности.
Из равенства (12) следует равенство
\т=\
определяющее внешнюю конституанту &a+Y через элементы
производных решет Са и Са+Х.
Чтобы найти выражение внутренней конституанты Еа через элементы
производных решет, рассмотрим решето Са и его элементы
р(1) е(2) Лт)
помещенные соответственно на прямых
*/ = Pi> */ = Р2> • • •> */ = Р*и ...
Возьмем натуральное число т и рассмотрим выражение
01я"=с-1' • П Се*] ■ 2 е« \ <14)
где произведение JJ распространено на такие числа р среди чисел 1,
р
2, 3, ..., /и, для которых рр^рщ, и где сумма 2 распространена на
такие числа </ среди чисел 1, 2, 3, ..., т, д\я которых p^^>pm+i; здесь
в формуле (14) е^ обозначает, разумеется, проекцию элемента е^ на
ось ОХ.
Геометрический смысл формулы (14) ясен: Q*em) обозначает
совокупность таких точек х, в которых перпендикуляр Р*, при пересечении
с элементами е^\ е^\ ..., е^\ e^w+1) имеет самой нижней точкой этого
пересечения точку, лежащую на элементе е(ат_и), заведомо при этом
пересекая элементы е?\ е[?\ ..., е[т\
Заметив это, рассмотрим предельную совокупность в широком смысле,
lim Q^m), последовательности
($\ <зг» Qim), •••
Обозначим эту предельную совокупность через Qa; Мы можем писать
<?.=lto QL-^дач- 0»ч- <£> +...) • (Qm-ь Q<»>-i- ...)• (Ql3) -ь •••)•• •
m-*oo
Из самого определения совокупности Qa следует, что Qe есть
660
Н. Н. ЛУЗИН
совокупность всех таких точек х> в которых перпендикуляр Рх, пересекая
решето Сл, не имеет в этом пересечении самой нижней точки. Отсюда
ясно, что
2£T = Q„ (15)
7=0
й значит, мы имеем равенство
£e+1 = Q1+l-Q„ (16)
определяющее внутренюю конституанту Еа+Х через элементы
производных решет Са и Са+Х.
Из формул (13), (14) и (16) вытекает такое важное заключение:
Если элементы производных решет имеют классы ограниченными,
тогда все конституанты первого рода, внутренние и внешние,
Еа+Х и £а+х, также имеют классы ограниченными.
Легко видеть, что то же самое заключение имеет силу и дая
конституант &а и ЕЛ с индексом а второго рода (т. е. с предельным
индексом).
Действительно, если а есть число второго рода, а есть предел
возрастающей последовательности
а1<Л2< •-• <av< —
В этих условиях из формулы (12) следует, очевидно, равенство
^а оо ^а /00 \ 00 / оо \
*.= 2*т-2 2Ч=с 2<4m) -2c 24? • 07)
7=# ' *=1 т=0 ' \ет=1 ] v=l \m=l /
Аналогично формула (15) дает
^а Ш ^av оо
^=2£т-2 2£t=Q.-2Qs- (18>
7=0 v=l т=0 v=l
Формулы (17) и (18), соединенные с формулами (13), (14) и (16),
показывают, что все конституанты, внутренние и внешние, Еа и £в,
при всех индексах а, предельных или нет, имеют классы ограничен-
ными, когда элементы производных решет имеют классы
ограниченными.
Введем, наконец, последние определения: последовательность
производных решет
С9, CL, Cj, ..., Сш, ..., Са, [ 2 (III)
называется стационарной, если существует такое число ?, начиная
с которого все решета последовательности (III) являются
тождественными, т» е. когда имеем
О СТАЦИОНАРНЫХ ПОСЛЕДОВАТЕЛЬНОСТЯХ
661
Так как тождество двух решет выражается тождеством всех их
элементов, то отсюда следует, что дая стационарности последовательности
решет (III) необходима и достаточна стационарность всех
последовательностей (IV).
еЬп) Am) р{т) р(т) (щ) Ю Ал/\
(т = 1, 2, 3, ...) их элементов.
Назовем, далее, начальное (производящее) решето С(=С0)
стационарным, если определяемая им последовательность производных решет
есть стационарная.
Легко видеть, что всякое стационарное решето С определяет
аналитическую совокупность Е, измеримую В.
Действительно, если данное решето С есть стационарное и если
Су = Стч-1> то, очевидно, всякий перпендикуляр Рху пересекающий
решето Сг, имеет совокупность Н^ лишенной самой нижней точки.
Отсюда следует, что
т. е. Е есть совокупность, измеримая В. Обратное, очевидно, не верно:
нестационарное решето С может определить аналитическую
совокупность Еу измеримую В.
Назовем, наконец, начальное решето С особым, если оно
нестационарно и если все элементы производных от него решет Са имеют
классы ограниченными.
Основная проблема теории решет состоит в установлении
существования или несуществования особых решет С Так как последовательности
элементов производных решет суть предельные и убывающие, то отсюда
следует, что все элементы производных решет особого решета не
могут быть ни совокупностями F> ни G и ни FQ.
Этот скудный отрицательный результат показывает, что все
внимание должно быть сконцентрировано на той гипотезе, что элементы
производных решет суть совокупности G5. Соответствующий этому случаю
анализ представляет большую тонкость.
О ПУСТЫХ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ*
1* Пустые аналитические множества* Множество называется пустым,
если оно не содержит элементов. Пустые аналитические множества
задаются с помощью прямолинейных решет С, которые с каждой
прямой, параллельной оси OY, пересекаются по множеству, вполне
упорядоченному в положительном направлении оси OY.
Так как пустое аналитическое множество измеримо В, то его
дополнение (—оо, -i-со) разлагается на сумму счетного (или конечного) числа
измеримых В конституант:
(—оо, -+. оо) = ^0-н6\н- ... -ь£а-ь ... /3. (1)
Наименьший из индексов р таких, что все конституанты &^ <$;иЛ, ... /2
пусты, называется порядком решета С, определяющего пустое
аналитическое множество. Если порядок р рассматриваемого решета С
первого рода, (3 = р*-н1, то конституанта &у* непуста, ёр^О; она
называется верхней конституантой. Если же порядок (3 — число второго
рода, то никакой верхней конституанты в разложении (1) нет.
2. Вполне упорядоченные решета* Наиболее простыми среди решет,
определяющих пустые аналитические множества, являются так
называемые вполне упорядоченные решета Г.
По самому определению вполне упорядоченным называется решето Г,
ортогональная проекция которого на оси 0Y вполне упорядочена. Мы
ограничимся здесь рассмотрением таких прямолинейных решет, элементы
которых суть множества класса 0 или, попросту, суть порциих, взятые
в счетном (или конечном) числе и расположенные на прямых,
параллельных оси ОХ
Обозначим через G ортогональную проекцию решета Г на ось 0Yy
через ? — трансфинитное (или конечное) число, соответствующее вполне
упорядоченному множеству G. Мы будем говорить, что f есть тип
вполне упорядоченного решета Г.
Ясно, что
Р<Т-ь1. (2)
* „Sur les ensembles analytiques nuls". Fund. Math., XXV% 109—131, 1935.
1 Порция—интервал с рациональными концами. — Ред.
О ПУСТЫХ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
663
и что среди вполне упорядоченных решет Г типа 7, действительно,
существуют такие, для которых порядок 3 в точности равен 7-ь1.
Чтобы убедиться в этом, достаточно взять решето Г типа f> состоящее
из элементов, тождественных между собой, за исключением их
расстояния до оси ОХ.
Рассмотрим теперь такие вполне упорядоченные решета Г данного
типа Т> порядок которых 3, действительно, достигает своего
максимума ^ = -[-ь1. В этом случае наивысшая конституанта реально
существует и совпадает с <SV £т=^0.
Это множество £у зависит, несомненно, от решета Г и, безусловно,
измеримо В. Теперь важно точно определить возможную природу этого
множества.
8« Производные решета. Мы начинаем прежде всего с
рассмотрения общего случая.. Возьмем произвольное прямолинейное решето С,
определяющее некоторое — измеримое В или нет — аналитическое
множество Е. Дополнение £ к аналитическому множеству Е полностью
распадается на свои конституанты, все — измеримые В:
£ = S0-h6V*-£2h- ... -*-£.+- .../9. (3)
Чтобы исследовать природу конституанты <£а, мы ^образуем
последовательность производных решет, происходящих из данного решета С:
C = -CiV\ С(-\ .... С1", .../а- (4)
Напомним, что если а первого рода, а = а*н-1, то производное
решето С получается из уже построенного решета (у , исключением
из каждого элемента решета (уа} тех точек, абсциссы которых не
принадлежат ни одной из проекций на ось ОХ элементов С* , лежащих
ниже рассматриваемого элемента. Если же а второго рода, то решето (у
составляют из элементов пересечения соответствующих элементов ранее
определенных решет Су , а' < а.
Возьмем теперь произвольную иррациональную точку на оси ОХ
и обозначим через Рх проведенную через х прямую, параллельную
оси О У. По самому определению производного решета ясно, что
прямая не пересекает решета Cw в том и только в том случае, когда х
принадлежит сумме
5о + 6\ + ^+ -•- -+-6V-+- ••• К (5)
где а — произвольное трансфинитное число, а а'<^а.
Таким образом, множество-сумма £0 ■+- S1 ■+- . ♦ • -*-€л.-+- • • • /а
совпадает с дополнением к проекции на ось ОХ решета С •
4. Четвертое неравенство Серпинского. Интересующая нас
проблема состоит в выяснении природы конституанты £а. Но из предыдущего
664
Н. Н. ЛУЗИН
ясно, что исследовать природу &аУ значит оценить природу суммы
£о ч~ <§\"+" • • • / а и, в конечном счете, определить природу элементов про-
изводного решета С •
Проблема, которую мы себе ставим, получила уже давно почти
полное решение в работах Серпинского1: таков именно смысл его важных
четырех неравенств. Необходимо, однако, обратить внимание на то,
что эти неравенства применимы лишь к случаю явных конституант;
в случае же действительных конституант ничего не известно.
Совокупность первых трех неравенств Серпинского дает нам основу
для отыскания нижней грани возможных классов явной конституанты <$аг
в то время как четвертое неравенство Серпинского дает — и притом уже
непосредственно — верхнюю грань этих классов.
Пока что мы удовлетворимся распространением четвертого
неравенства Серпинского на действительные конституанты.
Предварительно, однако, необходимо сделать несколько замечаний,
чтобы разъяснить символическую форму, которую мы избрали для этого
неравенства.
В качестве базы наших рассмотрений мы возьмем совокупность
иррациональных точек, удалив с оси ОХ рациональные точки. Это
фундаментальная область. Множество иррациональных точек, содержащихся
в некотором интервале (а, Ь) с рациональными концами, называется
порцией фундаментальной области.
Мы рассмотрим классы Валле-Пуссена
Кй, К„ ...,*„,..., К., ... /2. (6)
Начальный класс ЛГ0 этой классификации состоит из множеств,
которые, так же как и их дополнения, являются суммами порций.
Основной операцией, при помощи которой определяются последовательные
классы этой классификации, является операция перехода к пределу,
обозначаемая lim. Каждый из классов этой классификации содержит
множества трех родов. Во-первых, множества, называемые
достижимыми снизу множествами класса а: это суммы счетного числа
множеств предыдущих классов; мы их будем обозначать через Infa. Далее
множества, называемые элементами класса а; это множества, не
достижимые снизу, которые являются в то же время пересечениями
в счетном числе множеств предшествующих классов; будем обозначать
их через el ос. Наконец, остальные множества, называемые
недостижимыми с двух сторон множествами класса а- мы их будем обозначать
через Inaca.
Множества, играющие основную роль в классификации Валле-
Пуссена, — это элементы: каждое множество Infa является суммой
1 См. мое Сообщение, сделанное на IX Международном конгрессе математиков
(Цюрих, 1932), „О классах конституант аналитических дополнений", вышедшее в Ап-
nalidellaR. Scuola Norm. Super, di Pisa, серия II, II, стр. 276, 1933 (стр. 625
настоящего тома. — Ред.).
О ПУСТЫХ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
66S
счетного числа элементов классов <а, и всякое множество Inaca есть*
сумма счетного числа элементов классов <^а, причем в обеих суммах
элементы попарно не пересекаются.
Условимся теперь в следующем. Если множество Е — не известной
нам природы, но мы знаем, что Е — либо класса <<х, либо является
Inf a, мы будем писать
£<Infa.
Аналогично, если Е принадлежит классу <а, или является двусто'
ронним1 в классе а, или есть ё1а, то пишем
£<ё1а.
Наконец, если известно просто, что Е — множество класса ^ а, то
пишем
cl£<a.
Напомнив это, перейдем к четвертому неравенству Серпинского,
которое мы можем написать в символической форме:
^У I Каждый элемент решета С ^ 61 (2а).
I Каждый элемент решета С^"1"*0 ^Inf(2ач- 1), п^\
(п — конечное).
Доказательство. Заметим прежде всего, что в соответствии
с предположением элементы исходного решета С(1) суть множества
класса 0. Отсюда следует, что элементами производных решет С***
(при целом положительном и конечном л) являются либо множества
класса 0, либо достижимые снизу множества класса 1, что мы
записываем в форме символического неравенства ^Inf 1. Это показывает,
что четвертое неравенство Серпинского удовлетворяется при ос = 0.
Предположим, что неравенство (IV) верно дая всех чисел а',
меньших а; покажем, что тогда оно будет выполняться и для числа а.
Следует различать два случая.
Первый случай: число a — второго рода. В этом случае мы
имеем a = lima*, где a1<^a2</-«<[aJt<^---. Так как мы предположили
неравенство (IV) справедливым дая решета С *к, то, записывая fy
в форме cljc = toa* н- ^, где vt — конечное число, получим:
элементы решета С{*к) < 61 (2afc), если vJfc = 0;
элементы решета C(a/f)<Inf (2а*н-1), если vfc>0.
С другой стороны, последовательность аи а2, ..., аку ... —
возрастающая. Отсюда следует, что числа л19 а2, ..., afc, ... сами образуют
1 Множество класса а называется двусторонним, если оно есть одновременно
и Inf а и пересечение счетного числа множеств классов <С *. Двусторонние
множества существуют лишь в классах Ка, где a — второго рода.
666
Н. Н. ЛУЗИН
возрастающую или стационарную последовательность. Откуда
заключаем, что число а, которое является пределом последовательности
а2, а.,, .. ., аь ..., удовлетворяет равенству
а = ша. (7)
Но элементы решета С являются, очевидно, общими частями
элементов предшествующих решет С *к. Это приводит нас к искомому
символическому неравенству
элементы решета С * ^ 61 (2а),
где а удовлетворяет равенству (7).
Второй случай: число а — первого рода. В этом случае мы имеем
а = ша ч- л,
где л — целое положительное. Поскольку ша<^а, то на основании
неравенства (IV) мы имеем символическое неравенство
элементы решета С <^ё1(2а).
В силу самого определения решета С * дая случая а первого
рада мы заключаем немедленно, что выполнены следующие
символические неравенства:
элементы решета Qiiua+1) ^ Inf (2a -+- 1)
элементы решета С J ^ lnf (2a -+- 1)
элементы решета С(цД+)^Inf (2a-+-1)
Окончательно мы получим
элементы решета С ^ Inf (2a -+- 1),
где а = ша + л, л ^ 1 (конечное) (ч. т. д.).
5. Первая оценка верхней конституанты* Четвертое неравенство
Серпинского позволяет нам сделать первую оценку верхней
конституанты.
Действительно, в силу неравенства (IV) мы приходим к заключению,
что для проекции решета Сша+", v ^ 0 (v — конечное) имеем единое
леравенство
проекция С*"**0 на OX <Inf (25-Ы), (8)
каковы бы ни были а, конечное или трансфинитное, и целое
положительное конечное v^ 0.
О ПУСТЫХ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
667
Но мы видели, что сумма £0 -+- б\ -+-.. ./а совпадает с дополнением
к ортогональной проекции решета С(а) на ось ОХ. Отсюда немедленно
выводим, что имеют место два совместные неравенства
^o-|-^i-+-^./a<el(2a-bl)
и
£ н-£вн-£«+1-§-...^<hf (25 н-1).
Таким образом, мы получаем окончательно
£о-*-6\+ .../а<ё1(2ач- 1),
cl£.<2a-Hl,
где a = coa -+- v, v ^ 0 (v — конечное).
В частности, если ^=u>y-f-v, v^O (v — конечное), получаем
с1£т<27-»-1. (Ю)
Это и есть искомая оценка.
6. Обозначения трансфинитных чисел. Известно, что если аир
суть произвольные трансфинитные числа, подчиненные единственному
условию {3<Са> то существует трансфинитное (или конечное) число т
такое, что
а=рч-Т.
Мы можем условиться записывать это равенство
7 = «-Р. (И)
Это есть просто удобное обозначение.
Необходимо, однако, предупредить читателя, что принятая нами
теперь форма записи не совпадает с классической, согласно которой
число, непосредственно предшествущее трансфинитному числу а первого
рода, обозначается
а-1,
в то время как в принятой нами форме записи имеем равенство
a = a — 1,
каково бы ни было трансфинитное число а. Нам кажется
неоспоримым, что классическое обозначение a — 1, непосредственно
предшествующего числу а первого рода, обязано скорее психологической
иллюзии, чем теоретическим соображениям.
Перейдем теперь к другим обозначениям трансфинитных чисел.
Известно, чтд каждое трансфинитное число <х может быть записано
в форме
а= а>а-+- v,
(9)
668
Н. Н. ЛУЗИН
где v — целое положительное (конечное), v ^ 0.
Мы условимся писать
а = —>
(12>
употребляя эту форму записи лишь в случае а ^ а>.
Кроме того известно, что всякое трансфинитное число может быть*
записано в форме
где а^ 04 ^ а2 ^ ... ^ аь к — целое положительное число (конечное),.
Мы можем условиться писать
5 = bg^ а,
или просто
а = log а. (13)
Легко видеть, что в этих обозначениях
log (ар) = log а -ь log p
и что
1ш1(т — 1о£а)=2>
когда а возрастает трансфинитноу т. е. если lima = 2.
Условившись в этом, вернемся к оценке (10) для верхней
конституанты Sy. В соответствии с принятыми обозначениями мы можем
записать окончательное неравенство (10) предыдущего пункта в следующей
форме:
с1£т<2^-н-1. (14)
Однако мы увидим, что эта оценка является еще весьма грубой,.
и что вполне достаточно логарифмического члена log?- Нельзя не
обратить внимания на следующий факт: мы еще не ввели в рассмотрение
предположения полной упорядоченности рассматриваемого решета С.
7. Вторая оценка верхней конституанты. Рассмотрим
произвольное вполне упорядоченное решето Г, элементы которого суть множества
класса 0. Пусть ? — тип решета Г и £г — верхняя конституанта, <§т=^=0.
Оценка класса конституанты £т основана на нижеследующих
рассмотрениях.
Лемма I. Если т=<*>\ то £т <^ £1 {[2 (log т)— 1]н-1}.
Доказательство. Наиболее естественно здесь доказательство
по индукции.
Утверждение справедливо а^я 7 = 1. Действительно, в этом случае
решето Г имеет тип "> и состоит из элементов еп класса 0. Очевидна,
О ПУСТЫХ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
669
что верхняя конституанта £ш рассматриваемого решета Г является
верхним пределом последовательности множеств е1У е2, ..., ет, ...,
следовательно, является множеством ё1(2). Имеем таким образом
неравенство £<0 <J! el (2).
Допустим, что наше утверждение справедливо дая всех f, 7'<Т»
и докажем его справедливость д\я самого 7*
Будем различать два случая.
Первый случай. 7 — число первого рода; 7 = 7* "^l- В атом
случае вполне упорядоченное решето Г как имеющее тип го** • го может
быть разложено в сумму частичных вполне упорядоченных решет
*\> Г-2> ..., Гт, ..., имеющих каждое тип го7 , так что каждое
следующее решето, Гт+1, лежит выше предыдущего Гт.
Проделав это, обозначим через ё(т) верхнюю конституанту
частичного решета Гт. В силу предположения имеем
£<"■>< ё1 [(2т*-1)-*-1]. (15)
Обозначим через Н верхний предел множеств £(1), £(2), ..., £(т), ....
Если х есть точка из //, то х принадлежит бесконечному числу
множеств &т\ Следовательно, перпендикуляр Рх пересекает бесконечное
множество решет Гт по вполне упорядоченному множеству типа шт .
Значит, Рх пересекает решето Г по вполне упорядоченному множеству
типа го7 • го = гот. Мы заключаем отсюда, что х принадлежит верхней
^конституанте £т решета Г.
Если х не принадлежит //, то перпендикуляр Рх пересекает не более
чем конечное число частичных решет Гт по множествам типа гот .
Следовательно, Рх пересекает данное решето Г по множеству типа,
заведомо меньшего 7> гДе Т = соТ '®* Поэтому точка х не принадлежит
верхней конституанте <£т решета Г.
Отсюда следует, что множество Н совпадает с £т,
Но множество Н является верхним пределом множеств &{1\ £(2),
, glm\ ... , из которых каждое удовлетворяет неравенству (15),
Из этого следует, что верхний предел множеств £(т) должен быть
записан в форме <^ё1[(2т*— 1)~*~3].
Из этого мы можем заключить, что множество Н может быть
записано в форме
Я<«1{[2(1о8П)-1К1}.
it окончательно имеем
«7<«l{[2aojTT)-lRl>- <16>
Второй случай. 7 — второго рода: 7 = Hni7m> гДе Т1<Л2<Лз<
<С.. .<7т<**- • В этом случае наше вполне упорядоченное решето Г
как решето, имеющее тип ? = <от = lim «>Tm, может быть разбито на
счетное множество вполне упорядоченных решет 1\, Г2, ..., Гт, ...,
$70
Н. Н. ЛУЗИН
имеющих тип соответственно f i = ^\ 7-> = 0) » • • •> 7 т = ш ,. • •; это можно
сделать так, чтобы каждое следующее решето Гт+1 лежало выше
предыдущего, Гт.
Установив это, обозначим через &W верхнюю конституанту решета Г^.
В соответствии со сделанным предположением имеем
^w)<el[(2Tm-l)-f-lJ. (17)
Здесь т = 1, 2, 3, ...
Через Н обозначим верхний предел множеств &V\ Si2\ ..., S^'\ ...
Те же рассмотрения, что и в предыдущем случае, показывают, что
верхняя конституанта данного решета Г есть верхний предел Н
множеств &т)(т = 1, 2, 3, ...), т. е.
£т = #.
Но верхний предел множеств <§(1), <§(2\ .. ., <£(т), ... ,
удовлетворяющих неравенству (17), необходимо должен быть
ё1[(2т-1)-1].
Отсюда следует, что
£T<el{[2(logT)-lRl} (18)
(ч. т. д.).
Лемма П. Каково бы ни было трансфинитное число *[> имеем
£т<ё1{[2(1о<гТ)-1]ч-1}.
Доказательство. Известно, что всякое трансфинитное число f
тяожет быть записано в форме
где 7 S^ 7i ^ 7i> ^ • • • ^ Tfc>* ^ — целое положительное (конечное).
Разобьем теперь рассматриваемое вполне упорядоченное решето Г
на кч-1 частных решет Г0, \\у ..., Тку типы которых соответственно
<°\ о)71, ..., со1*, и обозначим их верхние конституанты соответственно
через £<°\ £<1>, ..., &*>.
Ясно, что верхняя конституанта £т данного решета Г представляет
собой пересечение множеств S{0\ <§(1), ..., &^> т. е.
Поскольку
<§<'><ё1[(2,т<-1)-«-1] (i = 0, 1, 2, .... к),
то, очевидно,
^<6l{l2(logT)-l]-*-l} (19)
(ч. т, д.)
О ПУСТЫХ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
671
Лемма III. Всякое множество S, измеримое В9 такое что
£<ёИ(2т-1) + 1],
может служить верхней конституантой £wT некоторого вполне
упорядоченного решета Г, тип которого равен ш7.
Доказательство. Утверждение верно для *у = 1. Действительно,
очевидно, что каково бы ни было данное множество 6\ g ^61 (2), £
может быть рассмотрено как верхняя конституанта подходящим образом
выбранного вполне упорядоченного решета Г типа о>, элементы которого
суть множества класса 0.
Предположим теперь, что утверждение справедливо дая всех
номеров Y> предшествующих данному числу т, и докажем его дая самого f.
Нам предстоит рассмотреть два возможных случая.
Первый случай. f—первого рода: f = 7*"•" 1- В этом случае
данное множество & есть верхний предел бесконечной
последовательности элементов
Sa\ £(*\ ..., £<w>, ...
классов строго ниже, чем (2^ — 1)*. Здесь мы имеем
2т —1 = (2т*-*-2) —1.
Согласно принятому предположению каждое из этих множеств £(т)
является верхней конституантой некоторого вполне упорядоченного
решета Гт типа <^о>7 . Мы можем считать эти решета Гш
расположенными так, что решето Гт+1 находится выше предшествующего решета Гш
при любом целом положительном т.
Обозначим через Г объединение решет Гш, /л = 1, 2, 3, ... • Ясно,
что Г — вполне упорядоченное решето типа о>7, и что верхней
конституантой Г является данное множество &.
Второй случай: т — второго рода. 'Тогда данное множество &
является верхним пределом последовательности элементов
ё*\ £(2), ..., £(w), ...
классов строго ниже ?. Пусть классы этих элементов суть
соответственно ти ?2> ..., Тж, ...; мы можем считать, что Тх<Т2<Тз<
Обозначим теперь через Гт вполне упорядоченное решето типа ш т,
дая которого множество ё(т) является верхней конституантой. Будем
считать эти решета Гш выбранными указанным выше способом:
решето Гт+1 расположено выше решета Гт.
1 См. мои „Лекции об аналитических множествах" (стр. 58 настоящего тома.—
Ред.).
672
Н. Н. ЛУЗИН
Объединение Г решет Гт представляет собой вполне упорядоченное
решето Г типа шт, и легко видеть, что данное множество <§ является
верхней конституантой Г (ч. т. д.).
Мы можем объединить теперь все три доказанные леммы следующим
образом:
Теорема. Всякое вполне упорядоченное решето Г типа 7
обладает верхней конституантой <?т, для которой
6\<ё1{[2(1о8Т)-1К1};
обратно, всякое множество £у измеримое В и удовлетворяющее
неравенству & ^ el {[2(log f) — 1] —•— 1}, является верхней
конституантой некоторого вполне упорядоченного решета Г типа f«
8* Применение к изучению конституант аналитических
множеств, неизмеримых В. Результаты, полученные в предыдущем пункте
относительно пустых аналитических множеств, дают нам средство
глубже проникнуть в природу следования конституант в случае
аналитических множеств, неизмеримых В.
Пусть С—прямолинейное решето, определяющее аналитическое
множество £, неизмеримое В. Дополнение к Е обозначим через £>
и пусть
£ = £0ч-£1н-...н-£ич-... + £.-ь...^ (А)
.— разложение множества & на конституанты.
Так как £ неизмеримо В, то среди конституант £а разложения (А)
имеется несчетное множество непустых конституант.
В связи с разложением (А) может быть поставлена следующая
проблема большой важности:
Проблема I. Выяснить, можно ли построить такое
прямолинейное решето С, для которого каждая конституанта в
разложении (А) состояла бы ровно из одной точки?
Известно, что среди проблем теории аналитических множеств эта
задача рассматривалась как наиболее трудная.
Чаще упоминается в качестве достойной внимания и в то же время
яе менее трудной, чем предыдущая, следующая задача:
Проблема II. Выяснитъу можно ли построить прямолинейное
решето С, для которого каждая конституанта £а в разложении (А)
была бы счетной (или конечной)?
Эту проблему можно рассматривать как ослабленную форму
проблемы I, утверждение которой более ограничительно.
Дальнейшее ослабление задачи приводит к следующей проблеме III:
Проблема III. Выяснить^ возможно ли построить
прямолинейное решето С, для которого классы всех конституант в
разложении (А) ограничены в совокупности?[56].
Трудности, связанные с решением этой проблемы, по-видимому,
ртоль же значительны, как и в случае проблем I и II; известно, что
О ПУСТЫХ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
673
до сих пор не удалось открыть ни возможного закона образования
таких решет, ни доказательства невозможности такого закона; в то же
время нам известны законы построения таких решет, для которых
классы конституанты &а не ограничены. Совместно с Серпинским
мы исследовали классы конституант в некоторых наиболее классических
случаях и констатировали:
1° что классы конституант &а не ограничены;
2° что классы конституант £а стремятся к 2 равномерно, за
исключением тех случаев, когда имеется несчетно много пустых конституант;
3° что классы конституант §а стремятся к 2, возрастая.
Кроме того, в случае явных конституант удается иногда
непосредственно определить их классы: они даются следующей формулой:
Можно далее еще больше ослабить формулировку проблемы III,
предлагая проблему IV:
Проблема IV: Выяснить, возможно ли построить
прямолинейное решето С, для которого все конституанты &а можно было бы
соответственно заключить в попарно не пересекающиеся
множества На, классы которых ограничены в совокупности?
Следует заметить, что существование множеств-отделителей И0
ограниченных классов никоим образом не предполагает ограниченности
классов самих конституант &а: классы последних могут при этом
стремиться к 2.
Возможно, что эта проблема более доступна, ибо мы вовсе не
настаиваем на эффективном построении множеств-отделителей На: мы
спрашиваем лишь об их существовании. Тем не менее, пока что видимые
трудности этой проблемы те же, что и в трех предыдущих проблемах.
Мы ограничимся здесь доказательством следующего утверждения,
ясно показывающего, как тесно могут быть расположены
конституанты &а в некоторых случаях:
Теорема: Существуют прямолинейные решета С такие, что
соответствующие конституанты &а не могут быть заключены
в множества-отделители ограниченных классов.
Доказательство. Мы начнем с рассмотрения решета С,
называемого универсальным, которое расположено в трехмерном
пространстве OXYZ и имеет своими элементами двумерные множества класса 0.
Такое решето С пересекается с произвольной плоскостью у = у0 по
прямолинейному решету С9о> элементами которого являются линейные
множества класса 0; важно отметить, что таким способом может быть
получено произвольное линейное решето С, элементы которого имеют
класс 0.
Пусть Е — аналитическое множество, определяемое универсальным
решетом С, и & — его дополнение; S — двумерное точечное множество,
лежащее в плоскости XOY.
674
Н. Н. ЛУЗИН
Пусть
S = SQ + el + et + ...-*-£„+...+ €a + ...\Q (А')
— разложение дополнения S на последовательность конституант; все
конституанты &а измеримы и двумерны.
Я утверждаю теперь, что эти плоские конституанты Sa не могут
быть заключены одновременно в не пересекающиеся множества //в,
классы которых были бы ограничены сверху числом (3, где Р — наперед
заданное фиксированное число, конечное или трансфинитное (второго
класса).
Действительно, возьмем произвольное линейное множество L,
измеримое В9 класс которого X превышает р:
с11 = Х, Х>р.
В силу теоремы пункта 7, каково бы ни было т, удовлетворяющее
неравенству
b<[2(logT)-lRl, (20)
найдется такое вполне упорядоченное линейное решето Г типа f> верхняя
конституанта которого <?т совпадает с множеством L:
©7 = -Ь»
Но неравенство (20) во всяком случае будет удовлетворено, если
положить
Т>^- (21)
Таким образом, каково бы ни было трансфинитное число 7i>
превосходящее и> , существует прямолинейное вполне упорядоченное решето Г
типа 7> верхняя конституанта которого £7 совпадает с L.
Установив это, возьмем теперь такое у0, что соответствующее
решето Ср0 совпадает с выбранным вполне упорядоченным решетом Г.
Ясно, что пересечение конституанты <£7 в разложении (А') с прямой
У = Уъ, х = 0 совпадает с верхней конституантой вполне упорядоченного
решета СУо, СУо=Т, а значит, совпадает с множеством L.
Если теперь через &%о) обозначить пересечение конституанты <Sa
в разложении (А') с прямой у = у09 z = 0, то имеем равенство
(—оо, ч-со) = £<*о) -+- <§Ш -|- ... ч- £<W;
при этом все &%°\ у которых а>7, пусты.
В силу этого равенства ясно, что множество-отделитель Hv
содержащее конституанту <£7 разложения (А'), должно содержать также и
пересечение ё^\ Поэтому Н^ должно содержать точки некоторых из
предыдущих множеств g§*\ S{?°\ £^tt)v..|T> ибо класс отделителя Нл
не превышает (3, в то время как класс множества S^°\ &&<>) = L равен'Х,
где X превышает р.
О ПУСТЫХ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ 675
Мы пришли таким образом к противоречию, что и доказывает, что
плоские конституанты &а в разложении (А') не могут быть заключены
соответственно в множества-отделители На ограниченных классов.
Теперь остается только получить разложение (А) на линейные
конституанты &а9 которые нельзя погрузить в множества-отделители На
ограниченных классов. Но лая этого достаточно преобразовать
множество двух измерений <9г*,* в линейное множество q/i при помощи
взаимно однозначного и непрерывного в обе стороны преобразования1
* = ?(*), у = И*),\
i = F(x, у). I
Ясно, что если к этим уравнениям добавить тождество
z-=z,
то мы получим преобразование трехмерной области о/хуУ,г в плоскую
область g7/, »♦ Очевидно, что образ универсального решета С представляет
собой прямолинейное решето С, лежащее в плоскости TOZ, с элементами
класса 0, так что конституанты решета С суть преобразованные
конституанты разложения (А'). Поскольку преобразование области <з7*, у
в с7* взаимно однозначно и непрерывно в обе стороны, то ясно, что
образ разложения (А') есть разложение (А) на линейные конституанты,
обладающее требующим свойством (ч. т. д.).
Мы дополним этот результат следующим определением: конституанту &а
разложения (А) будем называть изолированной, если существует
множество Нш класса меньше а, целиком содержащее &а и не содержащее
ни одной точки конституанты <£«', отличной от &а, а=£й'.
Вот, наконец, последняя проблема:
Проблема V. Выяснить, можно ли построить прямолинейное
решето С, конституанты которого £а были бы изолированы, начиная
с некоторого номера?
Во всех проблемах речь идет, понятно, лишь о таких решетах С,
которые определяют аналитические множества, неизмеримые В.
9. Проблемы и общие замечания* Теперь мы вновь обратимся
к задачам, поставленным в предыдущем разделе, притом с весьма общей
точки зрения, и в особенности к проблеме II.
Мы видели, что эта проблема состоит в том, чтобы выяснить,
можно ли построить прямолинейное решето С, -все конституанты
которого &а в разложении
ё = £0-*-&1 + ёъ+...+ £«+...+ &9-*-...\& (А)
были бы не более чем счетны?
1 Плоское множество с7*, у—Это Плоскость XOY за вычетом тех точек, у которых
хотя бы *>дна яюордаиата* раДОЖ&льна; аявейвое множество 671 — это множество ирра-
цио вальв ых точек оси ОТ,
(22)
676
HL H. ЛУЗИН
Эта проблема имеет, большой теоретический интерес в связи с тем,
что всякое совершенное множество Р, содержащееся в &, полностью
покрыто счетной (а не трансфинитной) совокупностью конституант <§а
из разложения (А), в силу чего по крайней мере одна иа этих
конституант несчетна и, значит, сама содержит совершенное множество Р1э
РХ^Р. Отсюда следует, что необходимым и достаточным условием
того, чтобы в дополнении <§ к аналитическому множеству Е не
содержалось никакое совершенное множество, является условие, чтобы все
конституанты £й были не более чем счетны.
Как известно, эта проблема еще не получила своего решения.
Слово „решение*4 я употребляю здесь в обычном смысле, т. е.
в смысле удачной комбинации алгебраических (формальных)
операций и средств абстрактной логики, позволяющей либо получить
нужное формальное противоречие, либо построить это необыкновенное
решето С. Так вот известно, что, несмотря на многолетние усилия,
не получено ни формального противоречия, ни способа построения
искомого решета.
В течение ряда лет я не видел иного смысла слова „решение",
кроме обычного, указанного выше; в этот период я колебался между
положительным и отрицательным ответом на этот вопрос. Теперь же
я понял, что невозможно ограничиваться этим смыслом слова „решение"
и категорически необходимо дать другой смысл этому слову, если не
находиться на почве некоторого заведомо непротиворечивого
фундамента в духе Гильберта. Я не буду приводить здесь полного
обоснования этого, так как подробнее его изложение может оказаться весьма
длинным; я хотел бы лишь кратко наметить мои личные заключения
об этом предмете, не входя в обсуждение всех возможных аргументов.
Тем не менее, я безусловно сохраняю за собой полную ответственность
за все, что может вызвать критику в рассмотрениях, которым посвящены
эти строки.
Мы будем исходить из идей Ж. Драша, относящихся к
алгебраическим числам. Алгебраическим числом называется всякий корень
алгебраического уравнения с целыми коэффициентами:
а0хп -ь а^*1 -+-... ч- ап-^х ч- ап = О (В)
Ж. Драш рассматривает алгебраические числа как идеальные числа
и вводит д\я обозначения совокупности идеальных чисел, определяемых
уравнением (В), символ
(а0, аг,..., ап).
Таким способом каждое рациональное число записывается в виде
(яо> ai)> причем а0 и ах могут быть рассматриваемы здесь как
знаменатель и числитель этого рационального числа*
Однако особенно важным обстоятельством, вытекающим из идей
Ж. Драша, является соображение, что идеальные числа никогда
О ПУСТЫХ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
677
не бывают даны нам непосредственно; мы не можем получить их
эффективно, реально „коснуться" их: они даны лишь посредством
алгебраического уравнения (В), т. е. посредством символа Ж. Драша
{а0, ах,..., ап). Тем не менее, мы можем все же говорить — и вполне
законно — о сумме, разности, произведении и частном идеальных
чисел: никто из читателей не ошибется, ибо очевидно, что, осуществляя
над идеальными числами основные операции: Сложение и умножение,
мы имеем дело по существу лишь с целыми числами, выводя из
нескольких символов (а^}, a(*j,..., а[*}) Ж. Драша один окончательный"
символ (А0У А19 А>,..., Ап)у.
Точно так же мы будем называть идеальным аналитическим
дополнением всякое неизмеримое В аналитическое дополнение, не
содержащее совершенного подмножества. Прочие аналитические дополнения
назовем реальными.
В полном соответствии с тем, как идеальные числа Ж. Драша
формально определяются алгебраическим уравнением (В) и записываются
символами Ж. Драша, идеальные аналитические дополнения могут быть
формально определены посредством двумерного универсального
аналитического дополнения &. Известно, что такое дополнение & может
быть получено непосредственно при помощи прямой и весьма простой
геометрической конструкции.
Роль этого универсального дополнения <£ вполне сравнима с ролью
алгебраического уравнения (В). Действительно, если ё лежит в
плоскости XOY, обозначим через Нр совокупность таких абсцисс х0, что
соответствующие прямые х = х0 пересекают <§ по реальным
аналитическим дополнениям, содержащим совершенные подмножества. Далее
через Hd обозначим множество тех -абсцисс лс0, для которых
пересечение & с прямой х = х0 не более чем счетно. Известно, что множество
Нр есть проективное множество типа А2(=РСРЕ) и что Hd — тоже
проективное множество типа А$(=РСРСРЕ). Важно заметить, что
множества Нр и Hd вполне определены двумя весьма несложными
геометрическими конструкциями.
Обозначим теперь через (Нр, Hd) множество точек оси ОХу не
принадлежащих ни Нру ни Hd. Это идеальные точки оси ОХу и всякое
линейное идеальное аналитическое дополнение может быть получено как
пересечение универсального дополнения & с прямыми, параллельными
оси О Y и проходящими через точки множества (Hp,Hd).
Здесь небесполезно подчеркнуть одно обстоятельство. Могут
сказать: „Вы удалили с оси ОХ точки множества Нр и Hd- Но если Нd
является дополнением к множеству Нру то с оси ОХ удалены все точки,
поэтому идеальных точек нет, а следовательно, нет и идеальных
дополнений". Однако, как ни убедительно это рассуждение с первого взгляда,
оно не является по существу серьезным возражением. Действительно,
если допустить, что Hd есть дополнение к множеству Нру то тип Нн
должен быть СА2( = СРСРЕ)У а не А^( = РСРСРЕ). Но нет никаких
678
н. н. луэин
формальных преобразований самого определения (конструкции)
множества Hd> которые бы позволяли снизить полученную иным способом
оценку класса Hdy именно Az, до класса СА2. Опасаясь неформальных
преобразований определения Hd, мы употребляем необходимо
всевозможные точки оси ОХу и между ними идеальные точки; следовательно,
мы обретаем верный circulus vitiosus.
Со своей стороны я полагаю, что, принимая, что Н<л не является
дополнением к Нр, мы должны опасаться противоречия не больше, чем
математики, занимающиеся продвижением математического анализа,
опасаются угроз теории Гильберта, которая, может быть, установит когда-
нибудь противоречивость всего математического анализа!
Вернемся теперь к идеальным аналитическим дополнениям. Как и в
случае идеальных чисел Ж. Драша, можно считать, что идеальные
дополнения формально определены и описаны символом
(Ир> Д*),
так что всякое действие с идеальными* дополнениями есть лишь
действие с множествами Нр и Н^ вполне реальными и определенными при
помощи весьма прозрачной геометрической конструкции, использующей
такие лишь элементарные понятия, как: универсальное множество,
сумма, пересечение, проектирование и операция перехода к
дополнению.
Можно думать, что этот путь не является бесплодным, ибо здесь
возникают проблемы, которые не встречаются при исследованиях в
других направлениях.
Среди таких проблем находится проблема полууниверсального
множества. Полууниверсальным будем называть плоское множество &,
составленное из всех реальных линейных аналитических дополнений,
лежащих на прямых х=с, и не содержащее вовсе идеальных дополнений.
Можно доказать, что S является все еще плоским аналитическим
дополнением, к тому же полностью реальным; с другой стороны, такое
полууниверсальное & должно существенно отличаться от универсального
аналитического дополнения, которое содержит идеальные дополнения.
Но более того: на этом пути встречаются проблемы и принципы,
которые могли бы показаться совершенно неправдоподобными на* всяком
другом пути.
Прежде всего, вводя в рассмотрение идеальные дополнения,
естественно рассматривать то, что можно назвать высшей непрерывностью
числовой прямой и что представляет собой некоторую аналогию
обычной непрерывности Коши — Дедекинда. Именно этот род непрерывности
приводит нас к двум следующим предложениям, справедливость
которых представляется мне несомненной:
Предложение L Всякое множество точек, мощность которого
равна алеф-одину является аналитическим дополнением.
О ПУСТЫХ АНАЛИТИЧЕСКИХ МНОЖЕСТВАХ
679
Предложение II. Всякое множество точек, выбранных случайно
из конституант §а разложения (А) в трансфинитном числе, все
еще является аналитическим дополнением.
Но вот предложение, которое кажется мне в данный момент лишь
вероятным:
Сумма трансфинитного числа множеств, измеримых В,
занумерованных транс финитными числами второго класса, есть
проективное множество класса ^2. Кроме того, если эта нумерация
эффективна, сумма является проективным множеством класса В2.
Добавлю, что известно, что каждое проективное множество типа А2
является суммой трансфинитной совокупности множеств, измеримых В,
занумерованных трансфинитными числами второго класса; однако эта
нумерация не является эффективной. Кроме того, не известно ни одно
проективное множество класса ^3, представляемое в виде суммы алеф-
одного множества, измеримого В, и ни одно непроективное множество,
обладающее этим свойством.
Теперь остается лишь сказать несколько слов по поводу континуум-
гипотезы. Как кажется, обсуждение континуум-гипотезы представляет
значительные трудности, и все-таки говорить о континуум-гипотезах
вынуждает математическая необходимость. Первой среди возможных
континуум-гипотез и наиболее элементарной из них является гипотеза Кантора
2*> = *.
Будем называть ее гипотезой Кантора или первой
континуум-гипотезой.
Известно, что Гильберт обещал дать формальное доказательство
отсутствия противоречия в гипотезе Кантора, оставаясь на
непротиворечивом основании, и что Серпинский подверг тщательному
исследованию всевозможные следствия этой гипотезы в своей важной работе
„Континуум-гипотеза". Эта книга, столь богатая следствиями из гипотезы
Кантора, из которых многие принадлежат Серпинскому и его школе, не
может быть проанализирована на нескольких страницах; все те, кто
интересуются философией континуума, не преминут прочесть и обдумать
«е. Между тем именно вследствие важности работы Серпинского мне
кажется необходимым отметить то, что мне представляется
недоразумением: гипотеза Кантора не является единственной континуум-гипотезой
{что, впрочем, явно указывает и Серпинский), даже если условиться огра^.
ничиваться алефами. Единственное доказательство справедливости
гипотезы Кантора могло бы состоять в нахождении взаимно однозначного
соответствия Z и притом эффективного, т. е. описанного вполне
определенно и без возможности двусмысленного понимания, между
точками прямой линии и трансфинитными числами второго класса.
Эта эффективность представляла бы значительный интерес и
большое значение, ибо в таком случае она явилась бы источником боль-
680
Н. Н. ЛУЗИН
шого числа арифметических, алгебраических, геометрических и
аналитических соотношений. Однако, как известно, не только нельзя ожидать,,
что прогресс науки приведет нас к такому эффективному соответствию
Z, но, наоборот, представляется гораздо более вероятным обратное:
что когда-нубудь средства теории Гильберта, может быть, будут
развиты настолько, что можно будет с успехом пытаться доказать
отсутствие всякого эффективного соответствия Z, хотя бы существование
неэффективного соответствия Z и не было противоречиво.
Но без эффективности соответствия Z ценность гипотезы Кантора
значительно снижается: только трудности, связанные с доказательством
непротиворечивости, привлекают аналистов; вне этих трудностей
решение гипотезы Кантора (в положительном смысле и по-прежнему без
эффективности Z) не дает ничего, исключая, понятно, массу весьма
парадоксальных примеров. Именно в этом смысле часто говорят о
действительной важности других математических проблем.
Однако в математической литературе имеются указания и на
возможность других гипотез континуума; среди них наиболее интересной
является гипотеза, которая может быть записана в следующей формег
Мы не будем пытаться найти имя автора, первым принявшего
серьезную возможность такой гипотезы; здесь мы будем ее называть
простое/порой континуум-гипотезой.
Вторая континуум-гипотеза, родственная проблемам и предложениям
этого раздела, кажется мне лишенной противоречия в той же мере, что-
и первая континуум-гипотеза, и можно надеяться, что успехи теории
Гильберта позволят когда-нибудь доказать непротиворечивость второй
гипотезы континуума.
В этом случае дая нас возникнет необходимость делать выбор
среди различных континуум-гипотез, в равной мере непротиворечивыхг
и выбор этот будет продиктован лишь наблюдением фактов.
Хорошо видно, сколь глубоки слова Эмиля Бореля, говорившего,,
что следует „отличать реальную математику от чисто словесных
логических спекуляций, в которых речь идет лишь об отрицательном
качестве: об отсутствии противоречийи 1.
1 Е. В о г е 1. La theorie de la mesure et la theorie de Integration, Introduction, II„
ctp. 222.
Ill цикл
ОБ ОДНОЙ ПРОБЛЕМЕ БЭРА*
1. 'Известно, что Бэр дал общее свойство функций, входящих в его
■классификацию. Всякая функция определенного класса является точечно
разрывной на всяком совершенном множестве, если пренебречь
множествами первой категории относительно этого совершенного множества.
Ъ этой связи возникает вопрос — является ли это условие, необходимое
для того, чтобы функция входила в классификацию Бэра, также
достаточным. Этот вопрос был поставлен самим Бэром. Цель настоящей
заметки — показать, что если мощность континуума есть алеф-один, то
существуют функции, обладающие этим необходимым свойством Бэра
•и не входящие в его классификацию.
2. Теорема 1. Если мощность континуума есть алеф-один,
то существует в интервале (О, 1) множество Е мощности
континуум такое, что всякое совершенное множество, нигде не плотное
£ (0, 1), содержит не более чем счетное множество точек Е.
Допустим, что мощность континуума есть алеф-один. [Мы можем
-тогда выписать все точки х из интервала (0 ^ х ^ 1) в виде вполне
упорядоченного множества
Xq, JCj, Х2,. . ., Хп, . • ., Хи у . . ., ДСа,. . . | Ьб, \1)
тде а — числр второго класса. Рассмотрим, с другой стороны,
множество всех совершенных множеств тс, нигде не плотных в (0 ^ х ^. 1).
Известно, что это множество имеет мощность континуума.
Следовательно, можно выписать все эти совершенные множества тс в виде
зполне упорядоченного, множества
тс0, *!, *2> ...,*», .. ., *«„, . . ., ire; . . . | Q. (2)
Возьмем первое совершенное множество тс. Точки тс0 образуют в
множестве (1) вполне упорядоченное множество. Обозначим через Е0
первый элемент этого множества и удалим из (1) все точки тс0. Среди
множеств тс из (2) существует в (2) первое (пусть тсв1, ах>0),
содержащее не удаленные точки из (1). Точки из тсар не удаленные из (1),
юбразуют в (1) вполне упорядоченное множество. Обозначим через £х
первый элемент этого множества и удалим из (1) все точки тса1.
* „Sur un probleme de M. Baire". Comptes Rendus, 15S, 1258—1261, 1914.
684
Н. Н. ЛУЗИН
Среди множеств к из (2), существует первое (пусть тса2, °-2^>o-i)w
содержащее не удаленные точки из (1). Не удаленные из (1) точки ^
образуют в (1) вполне упорядоченное множество. Обозначим через $,
первый элемент этого множества и удалим из (1) все точки к^.
Применение этого метода можно продолжать неограниченно. Таким образом,,
образуется счетное множество точек !|0, Е1Э £2, ..., £я, ...,
соответствующее счетному множеству совершенных множеств ^0, я1э ^2» • • •> г»>
(О <С а1э <С а2- • • < ап <С • • •)• Объединение совершенных, нигде не
плотных множеств тс0, тга1, тсЛг> ..., tz0Lhj ... является множеством первой
категории в (0 ^ х ^ 1). Следовательно, если удалить из (1) точки
множеств ~0, яв1, ^а,, ..., ^аи, ..., то в (1) останется еще несчетное
множество точек. Поэтому среди множеств ъ из (2) существует первое
(пусть тгац)> аш }> aw), содержащее не удаленные точки из (1).
Эти точки из ~яш образуют в (1) вполне упорядоченное множество.
Обозначим через Ьш первый элемент этого множества и удалим из
(1) все точки тсва). Так как объединение множеств тс0, тса1> тс^, .. ., тг^, . т шу>
..., гсва) является множеством первой категории в (O^x^l), то
существует среди множеств к из (2) первое (пусть *аш+1, a(0+i>O»
содержащее не удаленные точки из (1).
Приходим таким образом к определению Ьш+19 и т. д. Продолжая
таким же образом, мы в результате определим некоторое множество Е
точек из (0<1л:^1).
имеющее мощность континуума. Очевидно, что каждое совершенное,
нигде не плотное множество в (0^дс<^1) (например ъа) содержит не
более чем счетное множество точек из Е (что и требовалось доказать).
Всегда можно предположить, что множество Е содержит только*
иррациональные точки; в противном случае удалим из Е все
рациональные точки, что не изменит ни интересующих нас свойств £, ни его
мощности.
Теорема II. Если мощность континуума есть алеф-один, то
в интервале (О, 1) существует множество G мощности континуума,
являющееся множеством первой категории на всяком совершенном
(плотном или нет) множестве, расположенном в (О, 1).
Возьмем в интервале (0^лг<^1) множество К всех точек, предста-
вимых неограниченными непрерывными дробями, в которых неполное
частное ранга п неограниченно возрастает вместе с л. Бэр установил
взаимно однозначное соответствие между множеством S всех
последовательностей положительных целых чисел (i\, /2, /3> • • •> 4> • • •) и
множеством К, обладающее особыми свойствами (Acta mathematical
XXX, 42). Рассмотрим, с одной стороны, множество всех
иррациональных точек области (0^г/^1). Любая иррациональная точка этой
области (0<^г/<^1) представима вполне определенным образом неограни-
ОБ ОДНОЙ ПРОБЛЕМЕ БЭРА
685
ценной непрерывной дробью (/\, /2, /3» • • •> '» • • •)> и обратно, таким
юбразом, что имеется взаимно однозначное соответствие между
множеством иррациональных чисел области (0 ^ у ^ 1) и множеством S
•бесконечных последовательностей целых положительных чисел (/,, /.,,
4> • • м 4> • • •)• Мы установили таким образом некоторое вполне
определенное взаимно однозначное соответствие между множеством всех
иррациональных точек области (0^г/^1) и множеством К,
обладающее особыми свойствами. Обозначим это соответствие через Z.
Установив это, возьмем в области (0^1/^1) множество Е> не содержащее
рациональных точек и обладающее свйствами, указанными в теореме I.
Соответствие Z отображает множество Е области (0^г/^1) на вполне
определенное множество G, содержащееся в множестве К и имеющее
мощность континуума.
Это множество G и является множеством первой категории на
всяком совершенном (плотном или нет) множестве, расположенном в
интерзале (0 ^ х <^ 1). Мы опускаем доказательство этого факта, потому что
-оно довольно длинно. Заметим только, что можно всегда предположить
множество G неизмеримым В. Действительно, множество всех множеств
измеримых В, имеет мощность континуума. С другой стороны, так как
<G имеет мощность континуума, то множество всех подмножеств G
мощности континуума имеет мощность, превышающую континуум.
Следовательно, существует подмножество Н множества G неизмеримое В
я имеющее мощность континуума. Это множество //, очевидно,
удовлетворяет утверждению рассматриваемой теоремы.
Теорема III. Если мощность континуума есть алеа>один, то
.существует функция, обладающая необходимым свойством Бэра и
не представимая аналитически.
Возьмем, в самом деле, в (0 ^ х ^ 1) множество G по теореме II.
Функция /(jc), равная 1 на G и равная нулю вне G, аналитически не
представима, потому что множество G неизмеримо В. С другой стороны,
каково бы ни было (плотное или нет) совершенное множество Р
-в (0<^х<^1), функция/(х) равна 0 повсюду в Р, кроме множества
первой категории в Р. Следовательно, f(x) точечно разрывна (и даже
равномерно непрерывна) на всяком совершенном множестве, если
пренебречь множествами первой категории относительно этого
совершенного множества (ч. т. д.) [65].
О РАЗБИЕНИИ ИНТЕРВАЛА НА НЕСЧЕТНОЕ МНОЖЕСТВО
НЕИЗМЕРИМЫХ МНОЖЕСТВ*
Целью этой заметки является доказательство существования
разбиения интервала (0, 1) на множество мощности континуума попарно не
пересекающихся множеств таких, что внешняя мера каждого из этих
множеств равна 1. Доказательство использует теорему Цермело,
согласно которой существует вполне упорядоченное множество
мощности континуума.
Пусть 2 — наименьшее трансфинитное число такое, что множество
всех трансфинитных чисел а<2 имеет мощность континуума. Тогда
существует вполне упорядоченное множество типа 2.
хХУ *о, х3, ..., *,.» ..., х3, . .. (а < Q), (iy
содержащее один и только один раз каждую точку интервала (0, 1).
Но так как множество всех совершенных множеств, содержащихся
в (0, 1), имеет мощность континуума, то существует вполне
упорядоченное множество типа 2 совершенных множеств
Л, Р„ Р3,..., Р^, .., Р., ... («< 2), (2>
содержащее каждое совершенное множество интервала (0, 1) континуум
раз.
Возьмем теперь первую точку рх последовательности (1),
содержащуюся в множестве Р19 затем первую точку р2 последовательности (1)г
содержащуюся в Р2 и отличную от р1; дальше первую точку pz из (1)г
содержащуюся в Р3 и отличную от рх и р.2, и так по трансфинитной'
последовательности. Вообще пусть а — данное конечное или бесконечное
порядковое число < 2; обозначим через ра первую точку
последовательности (1), содержащуюся в Ра и отличную от всех точек
Pi» Р2> • •> Ли» • • •> Pv • • • (&<<*)• (3)
[Легко видеть, что д\я всякого числа а <^ 2 такая точка ра существует
в Ра, так как совершенное множество Ра имеет мощность континуума,
* „Sur une decomposition d'un intervalle en une infinite non-denombrable d'ensembles
non-mesurables". Comptes Rendas, 165, 422—424, 1917. Совместно с В. Серпннским,
Представлено Адамаром.
О РАЗБ. ИНТЕРВАЛА НА НЕСЧЕТНОЕ МНОЖЕСТВО НЕИЗМЕРИМЫХ МНОЖЕСТВ 687
а (3) есть множество типа а <^ 2, следовательно, во определению числа
2, мощности ниже континуальной].
Мы определили, следовательно, вполне упорядоченное множество
различных точек интервала (0, 1)
Pi» Ргу Рз» • • •» Р<и, • • .» Ра* • • • (а < 2) (4)
типа 2.
Пусть теперь Р—совершенное множество, расположенное в
интервале (0, 1). Последовательность (2) содержит Р континуум раз.
Множество последовательных индексов а, удовлетворяющих условию
Ра = Р, будет, очевидно, типа 2.
Пусть alf a2, a3, ..., аш% ... a$t .. . ф <; 2)— эти индексы, и
положим
p*.f = q9(P) (для p<Q).
Каждому совершенному множеству интервала (0, 1) соответствует,»
следовательно, вполне упорядоченное множество различных точек
яЛР), яЛР),.... яЛР)>..... ч,(Р), ••• (Р<2) (5)
типа 2; множество (5) будет, очевидно, подмножеством Р, и разным
множествам Р будут всегда соответствовать непересекающиеся мно~
жества (5).
Положим теперь для каждого данного числа Р<]2
Р
суммирование распространяется на все совершенные множества
интервала (0, 1). Легко видеть, что множества Q? и Q$> не пересекутся при
Р =т^ Р' и что каждое множество Qp будет содержать по крайней мере
одну точку из каждого совершенного множества интервала (0, 1).
Но без труда можно доказать, что каждое множество, лежащее
на интервале (0, 1) и содержащее по крайней мере одну точку из каждого
совершенного на (0, 1) множества, имеет верхнюю (лебегову) меру,
равную единице. Действительно, пусть Е — такое множество; если
верхняя мера Е меньше 1, Е можно будет заключить (в узком смысле^
в счетное множество интервалов, сумма длин которых меньше 1; точки
интервала (0, 1), не внутренние ни д\я какого из этих интервалов,
образуют, следовательно, замкнутое множество положительной меры,
следовательно, содержащее совершенное множество. Существует, следо-
вательно, в (0, 1) совершенное множество, не пересекающееся с Е
вопреки свойству множества Е.
Обозначим через Q0 множество всех точек интервала (0, 1) (если
они существуют), не вошедших ни в одно из множеств Qp(P<C^
688
Н. Н. ЛУЗИН
{можно было бы, впрочем, без труда доказать, что множество Q0 пусто);
множества
Qo+Qx, Q» Q3. .... <2Ш..... &> ••• Ф<2)
дадут, следовательно, искомое разбиение интервала (0,1) на континуум
попарно не пересекающихся множеств, каждое из которых имеет
внешнюю меру, равную 1. Легко видеть также, что внутренняя мера каждого
из этих множеств равна нулю.
Мы укажем в нескольких словах отличный от предыдущего способ
разбиения интервала. Пусть, как и выше, 2 — наименьшее
трансфинитное число, соответствующее мощности континуума, и
Slt St, St,..., £_, .... Sa, ... (a<2)
— трансфинитная последовательность типа £, образованная из всех
совершенных множеств, содержащихся в (0, 1).
Возьмем точку s'x в Sv две новые точки S^ и S^ в S2, три новые
точки s"9. s£ и s£ в *^з> и так по трансфинитной последовательности
-(вообще возьмем в Sa точки Sj(a), s!f\ ..., s£°). Д\я каждого данного
порядкового числа a < Q точки
eM, stM-D, ***■*>, ..., ,<**•>, ..., sJh-П, .... (Р<2)
образуют, как легко видеть, множество Еа} обладающее общими
точками с каждым совершенным множеством, лежащим на интервале (0, 1)
(так как каждое совершенное множество содержит континуум
совершенных подмножеств).
Множества Еа(&<С&) имеют внешнюю меру, равную 1, и попарно
яе пересекаются.
ОБ ОДНОМ СВОЙСТВЕ КОНТИНУУМА*
1. Теорема. Если континуум разбит на сумму двух множеств,
то по крайней мере одно из этих множеств имеет мощность
континуума.
Доказательство. Пусть Мх и М.> — два множества, сумма
которых М есть множество, имеющее мощность континуума. Множество
М может быть приведено во взаимно однозначное соответствие с
множеством Р всех точек квадрата К; пусть Рх и Р2— подмножества Р,
которые соответствуют Мх и М2. Разобьем квадрат К на континуум
параллельных сегментов. Если среди этих сегментов имеются такие,
все точки которых принадлежат множеству Pv то последнее, очевидно,
содержит подмножество мощности континуума. Если таких сегментов
не существует, то это означает, что каждый из наших сегментов
(множество которых имеет мощность континуума) содержит по крайней
мере одну точку множества Р2; выбирая на каждом из наших сегментов
точку множества Р2, мы получим множество мощности континуума,
которое будет подмножеством множества Р2. Следовательно, по крайней
мере одно из множеств Рг и Р2 содержит подмножество мощности
континуума, откуда без труда вытекает наша теорема.
2. Слегка изменяя предыдущее рассуждение, получаем
доказательство замечательной теоремы Кёнига:
Мощность континуума не есть яш; ясно также, что это будет
также доказательством классической теоремы Кантора:
Мощность континуума не есть So-
Достаточно, очевидно, доказать, что сегмент (0, 1) не является
суммой Е1 -+- Е2 -+-... -+- Еп -+-... счетного числа множеств, мощности
которых ниже мощности континуума.
Произведем разбиение сегмента (0, 1) на семейство F мощности
континуума совершенных попарно не пересекающихся множествх. Пусть
мощность Ех ниже мощности континуума, тогда существует в семействе
F совершенное множество Рх, не содержащее Никакой точки Ех.
Такое же разбиение совершенного множества Рг на семейство Fly
* „Sur une propriety du contlnu". Comptes Rendus, 165, 498—500 (1917). Совместно
с В. Серпинским. Представлено Адамаром. Ср. заметку В. Серпинского в Comptes
Rendus Soc. Sci., Varsovie, 4, 55, 1911.
1 Для ©того достаточно применить кривую Пеано.
690
Н. Н. ЛУЗИН
имеющее мощность континуума, совершенных попарно не
пересекающихся множеств приводит к совершенному множеству Р2,
содержащемуся в Ра, которое не содержит никакой точки £2. Продолжая этот
процесс, получаем последовательность
(О, 1) 3 Рх 3 Р2 3 Р3 3 ... 3 Рп 3 ...,
где Р{ суть совершенные множества; множество Рп не содержит
никакой точки множеств Еи Е.1У £3> ..., Еп.
Из сказанного заключаем, что существуют точки, которые входят
в Р„, каково бы ни было п; это точки сегмента (0, 1), которые не
входят ни в какое из множеств Еп каково бы ни было л, что
противоречит тому факту, что сегмент (0,1) есть сумма Е1 н- Е2 -+■ Е3 -+-...
Итак, гипотеза: с = Ки) приводит к противоречию.
Заметим, что теорема Кёнига может быть доказана без аксиомы
выбора, так как предположение, что она ложна (т. е. предположение,
что с = Nu) оправдывает все выборы, которые производились в нашем
доказательстве (как выборы из вполне упорядоченного множества).
Мы дадим еще другое доказательство теорем пунктов 1 и 2.
Пусть Мх и М> — два множества, сумма которых М есть множество
мощности континуума. По известной теореме Кантора (которая
доказывается без аксиомы выбора) множество М можно привести во взаимно
однозначное соответствие с множеством Р всех точек квадрата К; пусть
Рх и Р2 — подмножества множества Р, которые соответствуют
соответственно подмножествам Мх и М2 множества М. Предположим, что
мощности обоих множеств М1 и М2 ниже мощности континуума; тогда
мощности множеств Р1 и Р2 будут также меньше континуума.
Обозначим через Хг множество абсцисс всех точек Р1 (оси координат
пусть будут параллельны сторонам квадрата К) и через У2 множество
ординат всех точек Р2. Множества Х1 и У2 как проекции соответственно
множеств Рх и Р2 имеют мощности соответственно не выше мощностей
этих множеств, следовательно, ниже мощности континуума.
Множество X абсцисс всех точек множества Р (как множество
абсцисс всех точек квадрата) имеет, очевидно, мощность континуума,
следовательно, так как множество Хх имеет мощность ниже мощности
континуума, мы заключаем, что существует абсцисса х0,
принадлежащая X, но не принадлежащая множеству Хг. Таким же образом мы
заключаем, что существует во множестве У ординат всех точек Р
ордината у0, которая не принадлежит У2. Точка (дс0, у0) принадлежит,
очевидно, множеству Р, но она не может принадлежать ни Pl9 mi P2, потому что
она отличается от каждой точки множества Рг своей абсциссой, а от
каждой точки множества Р2 своей ординатой. Следовательно, мы
получили противоречие, потому что Р = Р1-+-Р2. Следовательно, множества
М1 и М2 не могут оба иметь мощность ниже мощности континуума.
Но множества Мг и М2 как подмножества М имеют мощность не выше
мощности континуума. Из этого следует по теореме Кантора—Берн-
ОБ ОДНОМ СВОЙСТВЕ КОНТИНУУМА
691
штейна (которая доказывается без аксиомы выбора), что по крайней
мере одно из множеств Мг и М2 имеет мощность континуума, что и
доказывает теорему пункта 1.
Заметим, что это доказательство применимо также к разбиению
континуума на счетное число множеств, потому что счетно-мерное пространство
можно поставить во взаимно однозначное соответствие с одномерным
пространством.
Из этого следует новое доказательство теоремы Кёнига.
Заметим, что наше доказательство опирается на аксиому выбора.
В самом деле, мы использовали в нашем доказательстве утверждение,
что проекция множества точек имеет всегда мощность, не
превосходящую мощности множества, которое проектируют, — утверждение,
которое не умеют доказать иначе, как выбирая дая каждой точки проекции
точку проектируемого множества.
Обратим внимание на то, что теорема пункта 1 эквивалентна
следующему: Если множество М мощности континуума расположено
в интервале d и если d разбит на два интервала dx и d2, то по
крайней мере один из них содержит подмножество множества М
мощности континуума.
О СУЩЕСТВОВАНИИ НЕСЧЕТНОГО МНОЖЕСТВА ПЕРВОЙ
КАТЕГОРИИ НА ВСЯКОМ СОВЕРШЕННОМ МНОЖЕСТВЕ*
В 1914 г. я показал, что если мощность континуума есть алеф-один,
то на интервале (0, 1) существует несчетное множество G первой
категории на любом совершенном множестве, лежащем в интервале (0, 1) *.
Целью этой заметки является доказательство того же утверждения без
предположения, что
2*° = *,
Из аксиомы произвольного выбора следует, как известно,
существование вполне упорядоченного множества G типа 2 (£ обозначает
наименьшее число третьего класса)
*i> x2f х3, ... хш, х^-н, .. ., ха, .. . (а < 2) (1)
непрерывных дробей
1 I 1 I И
такого, что дая любой системы из двух порядковых чисел <(2, а и
(3>а, существует номер р=/>(а, р) такой, что
4*)>а<в*> для *>р2.
Мы покажем, что множество G—первой категории на всяком
совершенном множестве.
Пусть Р — данное совершенное множество (линейное). Если
множество G не является нигде неплотным на Р, то Р является суммой
конечного или счетного числа порций, в которых G плотно, и множества
R такого, что GR нигде не плотно на Р. Пусть Q — одна из этих пор-
* „Sur Texistence d'un ensemble non-denombrable qui est de premiere categorie
dans tout ensemble parfait". Fund. Math., II, 155—157, 1921. Эта заметка,
содержащая результаты, полученные Лузиным в 1917 г., публикуется под ответствениостью
Серпинского.
1 N. Lusin. Sur un probleme de M. Baire, Comptes Rendus, 158, стр. 1259
(Note du 4 mai 1914), (стр. 683 настоящего тома.—Ред.).
2 См. A. Schoenflies. Entwickeiun£ den Mengenlehre. Erste Hafte. Leipzig,
1913, стр. 221.
О СУЩЕСТВОВАНИИ НЕСЧЕТНОГО МНОЖЕСТВА 1 КАТЕГОРИИ
693
Вий. Чтобы доказать наше утверждение, очевидно, достаточно будет
доказать, что множество G— первой категории на Q.
Так как G плотно на Q, то существует счетное подмножество G,
плотное на Q, скажем
(2)
Так как индексы аи а2, а3, ... образуют счетную последовательность
порядковых чисел первого или второго класса, то существует, как
известно, трансфинитное число ц<^2, превосходящее каждое из чисел
«II а2> а3- • • •
Так как множество всех ха1 где а^р», не более чем счетно, то
достаточно показать в дальнейшем, что множество G^ всех тех хв, для
которых а]>р, первой категории на Q.
Множество Сц, очевидно, является частью множества
где Еп обозначает множество всех тех дробей
x=\v^\vH^U'--' <3>
для которых
д(*)>в») при *>л. (4)
Достаточно, очевидно, показать, что множество Еп нигде не плотно
на Q. Лая этого, как легко видеть, достаточно доказать, что каждая
точка последовательности (2) находится на положительном расстоянии
от множества 2v
Итак, пусть т — заданное натуральное число. В силу определения
числа ^ и последовательности (1) существует такое натуральное число
Рт, ЧТО
аЫ>аЫдля Гс^рт. (5)
Пусть q = max (л, рт); в силу (4) и (5) для каждого х из Еп1
представленного разложением (3), мы будем иметь
Таким образом, разложения чисел х и хЛт в непрерывные дроби
различаются в q-м знаменателе. Отсюда сразу следует, что дг«ад не может
быть предельной точкой множества Ея. Но так как множество (2) плотно
в Q, то отсюда следует, что Еп нигде не плотно в Q (ч. т. д.).
Мы показали таким образом, что несчетное множество G есть
множество первой категории на каждом совершенном множестве.
Положим теперь f(x) = 1 д\я точек х из G и /t*) = 0 для всех
остальных действительных х. Множество всех чисел х, для которых
694
Н. Н. ЛУЗИН
/(.*)> О совпадает, очевидно, с множеством G; это множество, таким
образом, несчетно и первой категории на каждом совершенном
множестве. Но такое множество неизмеримо /?, так как в силу одной
теоремы Александрова—Хаусдорфа всякое несчетное множество,
измеримое Ву содержит совершенное подмножество, на котором оно,
очевидно, не может быть первой категории. Следовательно, функция f(x)
не может быть аналитически изобразимой. С другой стороны, /(х)
очевидно, является непрерывной функцией ( = 0) на всяком
совершенном множестве, если пренебречь множеством G, которое является
множеством первой категории на этом совершенном множестве. Итак,
условие Бэра, необходимое дая того, чтобы функция могла быть
аналитически изобразимой1, не является достаточным.
1 V. Н. Lebesque. Sur les foncttons represantables analitiquement. burn, de
M*th., XVI, 188, 1905.
ОБ ОДНОМ ВОПРОСЕ, КАСАЮЩЕМСЯ СВОЙСТВА БЭРА*
Вы спрашиваете мое мнение по следующему вопросу:
Всякое ли множество, обладающее свойством Р. Бэра1, является
обязательно измеримым?
Вот оно.
Да, ибо я вовсе не верю в существование неизмеримых множеств.
Когда я слышу разговор о законе, определяющем одно множество, „не
обладающее свойством Бэра" или „неизмеримое" и т. д., я бываю весьма
недоверчив, ибо мне не известны такие законы. Но это лишь дело
рутины. После некоторого размышления я уже вижу трудности, столь же
значительные, на мой взгляд, в рассуждениях, касающихся множеств,
неизмеримых В; не известно, возможно ли назвать множество,
неизмеримое 5, определенное положительным образом2, так, чтобы в этом
определении не участвовало явно или неявно понятие трансфинитного
числа. Таким образом, я полагаю, что всякое действительно
определенное точечное множество обязательно измеримо и, может быть, даже
измеримо В.
Нет, если мы покидаем почву математической реальности в пользу
почвы чисто словесных логических дедукций. Допустим же на одно
мгновение, что когда мы произносим слово „трансфинитный", то, кроме
звуковой волны, в нем содержится некоторая ощутимая реальность, и
примем „гипотезу континуума", т. е. предположим, что все точки
сегмента [0, 1] занумерованы трансфинитными числами второго класса:
х0, х1У х2, ..., х^, ха, ... | 2. (1)
Так как семейство всех совершенных множеств, лежащих на отрезке
[О, 1], имеет мощность континуума, то мы можем считать их тоже
занумерованными тем же способом:
*0> «1» • • •> *»» • • -f ТС«> • • • I 2, (2)
где тс0 обозначает весь сегмент [0, 1].
Каждому совершенному множеству тиа поставим в соответствие вполне
определенную сумму оа счетного числа совершенных множеств я,
* „Sur une question concernant la propriete de M- Baire". Fund. Math., IX,
116—118, 1927. (Выдержка из письма В. Серпинскому).
1 Речь идет о следующем свойстве множеств Е: каково бы ни было совершенное
множество тс, найдется такая его порция 7сх, что 'либо Е% либо его дополнение СЕ
имеет первую категорию на тсх. В силу теоремы Рене Бэра и Анри Лебега всякое
множество, измеримое В% обладает свойством Бэра.
2 Трансфинитное иногда бывает глубоко спрятано в определениях, имеющих
конечную, но отрицательную форму: таков, например, случай проективных множеств.
696
Н. Н. ЛУЗИН
содержащихся в тса и не плотных на этом множестве тсв так, чтобы
мера суммы оа была равна мере множества тса. Легко видеть, чта
множество оа имеет первую категорию относительно тсв; следовательно,
дополнение к ов, т. е. множество точек из тса> не входящих в ааУ
является остаточным множеством (Арно Данжуа) меры нуль; обозначим
его через Еа.
Установив это, укажем следующий закон построения:
1°. В трансфинитной последовательности (1) берем первую точку ^
принадлежащую множеству <*0.
2°. Если точки $0, ?!, ..., ?з> • • • определены для всякого р,
предшествующего числу а, мы обозначим через 5а первую точку (если она
существует) в последовательности (1), принадлежащую ов, но не
принадлежащую ни одному из остаточных множеств Е$, Р<Са и отличную
от уже определенных точек ?р.
Ясно, что если множество тса имеет ненулевую меру, то наверняка
имеется точка £а, ибо в этом случае множество тса имеет положительную
меру, а сумма всех остаточных множеств £р, Р<Са> каждое из которых
имеет меру нуль, также есть множество меры нуль.
Отсюда мы заключаем, что множество всех таким образом
определенных точек f;
«о» *i, *»,.... **,..., $.,... \Q (S)
имеет мощность континуума, ибо множество всех совершенных множеств
тсв ненулевой меры имеет, очевидно, мощность континуума. Множество
этих точек 5 мы обозначим через 2.
Я утверждаю, что множество S есть множество первой категории
на каждом совершенном множестве тс. Действительно, пусть тс—
произвольное совершенное множество, лежащее на отрезке [0, 1]. Ясно,
что это тс есть некоторое вполне определенное ^, где ? — конечное
или трансфинитное число. Из самого определения множества 2 следует,
что всякая точка £в, принадлежащая тс, каково бы ни было а,
превосходящее т, есть точка множества от. Таким образом, часть множества
2, содержащаяся в тс, состоит из части, входящей в ат, и, возможно*
из счетного множества точек £р, имеющих индексы (3, меньшие чем 7-
Следовательно, общая часть тс и 2 есть множество первой категории
на тс.
Я утверждаю теперь, что множество 2 неизмеримо. Действительно,,
множество 2 заведомо имеет точку в каждом совершенном множестве
тс ненулевой меры. Поэтому 2 не может иметь внешней меры, отличной
от 1. Но внутренняя мера 2 равна 0, ибо в противном случае 2
содержало бы совершенное множество, что невозможно, потому что 2 является
множеством первой категории на каждом совершенном множестве.
Таким образом, поскольку множество 2 имеет первую категорию на
каждом совершенном множестве, оно заведомо обладает свойством Бэра
и в то же время неизмеримо.
Москва, 18 июля 1926-
О НЕСЧЕТНОМ МНОЖЕСТВЕ, ЯВЛЯЮЩЕМСЯ МНОЖЕСТВОМ
ПЕРВОЙ КАТЕГОРИИ НА ВСЯКОМ СОВЕРШЕННОМ МНОЖЕСТВЕ*
Существование несчетного множества, являющегося множеством
первой категории на всяком совершенном множестве, было доказано
Н. Лузиным . Цель этой заметки — дать доказательство существования
такого множества, основанное на другой идее, именно на теории
аналитических множеств.
Пусть Е — аналитическое множество, неизмеримое В. Как известно,
имеет место формула
СЕ = %Еь (1)
где Ei (£ <С 2) суть множества, измеримые Ву Ei С Еп для % < т\ и где
разложение (1) обладает следующим свойством (Р).
Если Н есть множество, измеримое 5, и если H(ZCEf то
существует порядковое число а<^2 такое, что H(ZEa2.
Так как множество Е9 а следовательно, и множество СЕ
неизмеримы В9 то существует несчетное множество членов
последовательности (1), не содержащихся в сумме всех предшествующих членов.
В каждом из этих членов выберем точку, не принадлежащую никакому
из предшествующих членов: полученное таким образом множество N
будет, очевидно, несчетным (мощности ^i)> а множества N • Е$. будут
не более чем счетными для £<[2.
Мы докажем, что множество N—первой категории на всяком
совершенном множестве.
Действительно, пусть Р — совершенное множество, и допустим, что
множество N не есть множество первой категории на Р. Тогда, как
известно, существует порция Р0 множества Р такая, что N всюду
второй категории на Р0. Множество СЕ Z) N будет поэтому и подавно
* „Sur tin ensemble non-denombrable qui est de premiere categoric sur tout
ensemble parfait". Comptes Rendus Acad. Lincei, 7, серия 6а, 3, 214—215, 1928.
Совместно с В. Серпинским. Представлено корресп.Л.Тоннелли на заседании 5февраля1928г.
* Fund. Math., II, 155. 1921. В 1914 г. (Comptes Rendus, 158,1259) Н. Лузин
доказал то же самое, использовав континуум-гипотезу.
* N. Lusin et W. Sierpinski. Bull. Acad. Cracoyle, 39, 1918; см. также
Journ. de Math., II, 56-60, 1923.
698
Н. Н. ЛУЗИН
всюду второй категории на Р0. Так как множество СЕ9 будучи
дополнением к ^-множеству,, обладает свойством Бэра1, то множество Е —
первой категории на,Ро, и можно положить
P0£ = Q14-Q2H-Q3-b---. (2)
где Qn (л = 1, 2,3, ...) суть множества, не плотные на Р0,
Следовательно, замыкания Qn = Qn -+- Q'u множеств Qn также не плотны на Р0;
их сумма
будет поэтому множеством первой категории на Р0. Кроме того,
множество (3) есть, очевидно, типа Fay Р0 — S есть типа G$; из (2) и (3)
следует, что Р0Е С S, что дает Рп — S С СЕ. Поэтому, в силу свойства
(Р) существует индекс а < Q такой, что Р0 — S С Еа. Кроме того, как
нам известно, множество N-Ea не более чем счетно; следовательно,
множество N • (Р0 — S\, не . более чем счетно [N • (Р0 — S)(ZN • Еа].
Так как множество - N-PQ-S является [в силу свойства
множества (3)] множеством первой категории на Р0, отсюда следует, что
множество N • Р0 = TV * Р0 • 5-н 7V • (Р0 — *S) имеет первую категорию на
Ро^чем доказывается, чхо N,первой категории на Р0, вопреки допущению.
Итак, мы доказали, что множество N имеет первую категорию на
всяком совершенном множестве (ч. т* д.).
Риму февраль 1928.
1 Jounr. d* Ма%Ь., Hf 68, 192S; см также Fund. Math.» VH. 153 и Х, 26.
О МНОЖЕСТВАХ ВСЕГДА ПЕРВОЙ КАТЕГОРИИ*
Серпинский сообщил мне формулировку Вашей проблемы о
множествах всегда первой категории. Я прошу Вашего разрешения адресовать
Вам некоторые размышления, на которые она меня наводит.
Прежде всего вопрос о множествах всегда первой категории тесно
связан с вопросом Лебега. В своем знаменитом мемуаре „Sur les fonc-
tions representables analitiquement" *, приведя формулировку Бэра:
XVI. Всякая аналитически представимая функция точечно
разрывна на всяком совершенном множестве, если пренебрегать
множествами первой категории на этом совершенном множестве,
Лебег пишет:
„Теперь возникает очень интересный вопрос: является ли
необходимое условие, выраженное теоремой XVI, также достаточным? И если
:это не так, существуют ли функции, которые не удовлетворяют ему?
Я не буду пытаться ответить на эти трудные вопросы..." .
Важно заметить, что сам Лебег разделяет проблему на две части:
1° установить, неважно каким образом — может быть, даже применяя
рассуждение Цермело (AZ)> — недостаточность условия XVI; 2° назвать
функцию /(х), которая удовлетворяет этому условию и которая не
входит в классификацию Бэра.
Мы впервые встречаемся с вопросом о множествах всегда первой
категории2, когда рассматриваем первую часть проблемы Лебега и
допускаем существование множества точек Е> имеющего мощность
.континуума и всегда первой категории. Это значит, что, каково бы
ни было совершенное множество Р, совокупность точек множества Еу
принадлежащих Р, есть первой категории на Р. Действительно, если Е
^всегда первой категории, то таковой же будет и каждая часть Ех
множества £. Из этого следует, что характеристическая функция /х(х)
множества Е}9 равная 1 в точках множества Ех и 0 в точках, не
принадлежащих £г, наверняка удовлетворяет условию XVI. С другой
стороны, совокупность множеств Ev очевидно, бесконечна и мощность ее
* „Sur les ensembles toujours de premiere cat^gorie". Fund. Math., XXI, 114—126,
1933. (Из письма Куратовскому).
i Journ. de Math., 188, 1905.
2 Я употребляю здесь- Г ellipse temporelle, говоря „множество всегда первой
категории*, так же как говорят ellipse d'espace, говоря о множестве, нигде не плотном.
700
Н. Н. ЛУЗИН
выше мощности континуума. Между тем, множество всех функций,
входящих в классификацию Бэра, имеет мощность континуума. Таким об*
разом, мы должны заключить, что условие XVI является достаточным;
это значительно разъясняет первую часть проблемы Лебега*
Таков путь, посредством которого я давно1 пытался ответить на
первый вопрос Лебега, определяя множество Е всегда первой
категории посредством такой сильно ограничительной гипотезы: мощность
континуума есть алеф-один. С тех пор произошло многое. Сначала
появилась теорема2, которая гласит, что всякое несчетное измеримое В
множество Е необходимо содержит совершенное множество и, следовательно,,
не является одним из множеств всегда первой категории;
следовательно, совсем не необходимо иметь множество мощности континуума*
которое всегда первой категории, чтобы быть уверенным в
недостаточности условия XVI: всякое несчетное множество Е всегда первой
категории, какова бы ни была его мощность, конечно, имеет
характеристическую функцию /(дг), которая обладает свойством XVI, но не
входит в классификацию Бэра. Позже были эффективно определены3
примеры функций /(лг), удовлетворяющих условию XVI и не входящих
в классификацию Бэра: всякое аналитическое множество Е,
неизмеримое В, имеет характеристическую функцию/(х), удовлетворяющую
условию XVI и не входящую в классификацию Бэра. Таким образом,
второй вопрос Лебега нашел полное решение.
Все эти вещи хорошо известны, и если я позволяю себе
останавливаться на них, то только потому, что хочу подчеркнуть один особенно»
интересный факт: ничего не известно о существовании множеств всегда
первой категории, имеющих мощность континуума, если даже
употреблять произвольный выбор (AZ). Я прошу Вашего разрешения немного»
остановиться на этом пункте.
Когда применяют рассуждение Цермело, то, с точки зрения
реалистов, нет никакой разницы между различными формами выбора.
Напротив, с точки зрения чисто логической (идеалистов), надо делать
большое различие между случаем выбора различных элементов в множествах^
которые не имеют никаких попарно общих элементов, и случаем, когда
эти множества могут пересекаться друг с другом* потому что логисты,
склонны рассматривать рассуждение Цермело k$lk операцию. С этой,
точки зрения, в первом случае рассуждение Цермело является
ограниченной операцией (AZ)> которую можно обозначить через (AZ)'; во
втором случае не накладывают никаких ограничений на характер выбора;
это самая общая операция (AZ). Ясно, что в абстрактных пространствах
это различие становится иллюзорным; но в евклидовом пространстве-
1 См. мою заметку „О проблеме Бэра" (Comptes Rendus, 4 мая 1914 г.).
2 Эта теорема была доказана Александровым и Хаусдорфом в 1916 г.
3 См. Н. Лузин и В. Серпинский. Об одном множестве, неизмеримом К
(Journ. de Math., II, 68, 192$).
О МНОЖЕСТВАХ ВСЕГДА I КАТЕГОРИИ
701
это различие может проявляться очень заметно, и важно заметить, что
существование большей части „особых" множеств было установлено
применением именно ограниченной операции (AZ)'; таков, например,
случай существования неизмеримого множества Витали или Ван Флека.
Было бы интересным дать пример множества Е всегда первой
категории, имеющего мощность континуума, применяя только ограниченную
операцию (AZ)'.
Другая представляющая интерес проблема, значительно более про.
•стая, чем предыдущая, состоит в том, чтобы узнать, может ли быть
неизмеримым множество всегда первой категории. Я рассматривал этот
вопрос в Сообщении, сделанном на I Русском математическом конгрессе
(съезде математиков) (Москва, 27 апреля — 4 мая 1927 г., стр. 226) Ч
Я воспроизвожу здесь только один пункт этого Сообщения.
Предположим, что все точки сегмента [O^x^l] занумерованы
посредством конечных чисел и трансфинитных чисел второго класса
Кантора:
•*0> *^1> "*2> • • • » *^и)> * * * У Х&> л • • I » \-V
-и возьмем все совершенные множества Р, расположенные в [0 ^ х ^ 1]
я занумерованные таким же образом:
Р0, Ри Р.г, ..., Рш, ..., Р., ... | 2- (И)
Пусть
#0, Ни //„...,#„,,..., H.,...\Q (III)
-суть все множества типа G8, расположенные в [O^jc^I] и меры нуль.
Возьмем первое совершенное множество Р0. Если mesPo=0, мы
исключаем из (I) все точки множества Р0 и переходим к Рх. Если
tnesP0>0, мы берем в (I) две первые точки множества Р0, — мы их
обозначаем через £0 и т\0,— и исключаем из (I) все точки первого
множества //0 последовательности (III), которое всюду плотно на Р0, за
исключением точек пары (?0; у\0); затем переходим к множеству Рг
Продолжаем применение этого процесса трансфинитно. Рассмотрев
все множества Рт, Т <Са> мы переходим к множеству Ра. Если mesPa = 0,
-мы исключаем из (I) все точки множества Рв, за исключением
точек пар (£f; т|т), соответствующих множествам Р7, mesPr^>0. Если
mesPa>0, мы берем в (I) две первые точки множества Pa, отличные
ют точек уже определенных пар (Sr; т)т); мы их обозначаем через Sa и
т\а и исключаем из (I) все точки первого множества Дза
последовательности (III), всюду плотного на Ра, за исключением точек пар (^; ?)г) и
i$a'> ^a)» и переходим к множеству Ра + 1.
Вполне очевидно, что так определенные точки Е образуют несчетное
множество S и что 3 всегда первой категории. Однако, поскольку вся-
1 Ср. Fund. Math., IX, 117, 1927, и Saks. Fund. Math., XI, 277, 1928; см. также
.недавнюю заметку. Серцинского: „Sur un ensemble, lineaire non denombrable qui est
«de premiere categorie sur tout ensemble parfait". Comptes Rendus Soc. Sci., Varsovie,
Ю2—105, 1933.
702
Н. Н. ЛУЗИН
кое совершенное множество Р, имеющее положительную меру, необхо-
димо содержит одну точку множества 2 и одну точку, которая
наверняка не принадлежит множеству Е, то множество Е неизмеримо.
Если мы употребим простой язык и рассмотрим множества всегда
первой категории как крайне „тощие" (не в смысле точной
терминологии Данджуа, а в совсем общем смысле, т. е. как множества,
бесконечно бедные точками, очень слабые, мало заметные, очень
незначительные в смысле количества их точек), то мы тотчас же заметим, что
отсутствие меры у множества точек обусловлено исключительно
крайней неправильностью распределения его точек, потому что
существуют множества всегда первой категории, которые не
являются измеримыми множествами.
Таким образом, мы очень естественно приходим к рассмотрению
Вашей важной проблемы, которую можно сформулировать следующим
образом:
Можно ли различить среди несчетных множеств всегда первой
категории теу которые богаче или беднее точками, и найти
множества всегда первой категории, которые, с одной стороны,
наиболее массивны и, с другой стороны, наиболее разрежены.
Серпинский сообщил мне, что Вы взяли в качестве критерия
бедности точками следующее определение.
Опр ед еле ни е. Множество точек Е называется разреженным,
если всякая счетная часть D множества Е может быть заключена
в множество типа G8, не содержащее никаких других точек
множества Е.
Действительно, немедленно убеждаемся, что всякое разреженное
множество является множеством всегда первой категории. Чтобы убедиться
в этом, возьмем какое угодно совершенное множество Р. Если
рассматриваемое множество Е не первой категории на Р, то существует
порция Рх множества Р такая, что точки множества Е, принадлежащие Ри.
образуют множество, всюду плотное на Р19 не являющееся множеством
первой категории на Рх. Пусть D есть счетная часть множества Ег
всюду плотная на Р1# Поскольку Е есть разреженное множество,
существует множество Н типа G8, которое содержит D и не содержит
никаких других точек множества Е. Между тем, множество D всюду
плотно на Р19 и, следовательно, Н всюду плотно на Рх. Отсюда
следует, что точки множества Р19 не принадлежащие //, образуют
множество первой категории на Р1# Отсюда заключаем, что точки множества Е,
принадлежащие множеству Р19 образуют множество первой категории
на Р19 что противоречиво. Таким образом, мы убедились, что всякое-
разреженное множество является множеством всегда первой
категории.
С другой стороны* Вы отметили, что большая часть множеств всегда
первой категории, известных до настоящего времени, является именно
разреженными множествами, так что возникает вопрос: существуют ли
О МНОЖЕСТВАХ ВСЕГДА 1 КАТЕГОРИИ
703
множества Е всегда первой категории, которые не являются
разреженными множествами?
Это и есть Ваша проблема.
Определение. Множество Е называется массивным, если
всякая счетная часть его D, не являющаяся рассеянным
множеством, не может быть заключена в множество типа Gb, не
содержащее никаких других точек множества Е.
Я не знаю, существуют ли массивные множества всегда первой
категории. Поэтому в настоящее время я довольствуюсь констатацией
существования множеств всегда первой категории, не являющихся
разреженными. Множество всегда первой категории я определил в 1914 г.
в моей уже указанной заметке (loc. cit.). Поскольку в этой заметке
я опустил все доказательство, ибо детальное изложение мне казалось
слишком длинным, чтобы быть опубликованным в Comptes Rendus,
я прошу Вашего разрешения воспроизвести здесь все необходимые
рассуждения. Извините меня за подробность. Я буду точен.
Прежде всего главным средством доказательства там было одно
очень важное соответствие, определенное Бэром в его мемуаре „Sur la
represantation des fonctions discontinues" (Acta Math., 30, 42).
Рассмотрим вместе с Бэром множества, совершенные и нигде не
плотные на сегменте [O^x^l], обозначенные через РЯ1,я, nk, где к целых
чисел пх, л2, ..., П]с принимают все целые положительные значения.
Диаметр множеств РП1,щ,...,пк стремится к нулю, когда к неограниченно
растет.
Множество Рп„ла,...,пл,пк+х содержится в Рп,,*,.....** и нигде не плотно
на нем.
Множества Pnl,nt,...,nk при фиксированном к не имеют попарно общих
точек.
Объединение всех множеств Pnl,n2t...,nk,nk+lt где к, лх, л2,..., пк
фиксированы, образует множество Qn„n„...,nfc, всюду плотное на множестве
Объединение всех множеств Р^н,,...,^,»^, где к фиксировано,
образует множество Qfc. Общая часть всех Qk будет обозначена через К:
K=QX-Q%-...(&... .
Отметив это, рассмотрим в сегменте [0 ^ у ^ 1] иррациональную
точку у, абсцисса которой представляется бесконечной непрерывной
дробью
у = (пи л2, ..., пк, ...),
и возьмем общую часть соответствующих множеств
tlt> /ЯрИ* ...» 4П|,*2».-.»Як> • • • •
704
Н. Н. ЛУЗИН
Поскольку диаметр множеств Pnvn^...tnk стремится к нулю вместе с -г,
эта общая часть содержит только одну точку, которую мы обозначим
через xi
Таким образом, мы устанавливаем вполне определенное взаимно
однозначное соответствие между множеством S всех иррациональных точек у
сегмента [0^г/^1] и множеством К
x = Z(y),
непрерывное в каждой точке у множества S относительно S.
Установив это, возьмем на сегменте [0^г/^1] множество Е
иррациональных точек, всюду несчетное на этом сегменте и обладающее
таким замечательным свойством: множество Е не более чем счетно на
всяком нигде не плотном на отрезке [О^у^.1] множестве. Я
показал, как можно определить такое множество Еу исходя из определенной
нумерации всех точек сегмента [0 ^ у ^ 1] посредством всех конечных
чисел и трансфинитных чисел второго класса Кантора. Пусть G есть
множество значений, которые функция Z(y) принимает на множестве Е,
G = Z(E). Легко видеть, что G есть множество точек, расположенных
на сегменте [O^x^l]*
Я утверждаю теперь, что так определенное множество G есть
множество всегда первой категории.
В самом деле, пусть Р есть произвольное совершенное множество,
расположенное на отрезке [0^лг<^1]. Через Н обозначим множество
таких точек уу что значения х функции Z(y) принадлежат множеству Р:
H=[Z(y)(ZP\.
Легко видеть, что множество Н содержится в множестве S и
замкнуто относительно S. Общая часть Н • Е является, очевидно,
прообразом общей части множеств Р и G, Р • G.
Если множество Н-Е нигде не плотно на [0^г/^1], то оно не
более чем счетно, и, следовательно, таким же является множество Р • G.
Следовательно, в этом случае множество G первой категории на Р.
Если множество НЕ плотно на [0^1/^1], то множество
Неточностью до множества рациональных точек является суммой конечного
или счетного числа интервалов Бэра ix> i'2> ..., i'm, .. ♦, лишенных
рациональных точек, и нигде не плотного множества F
ff=(/;+r8+...+i;+...)+F.
Поскольку общая часть F • Е не более чем счетна, среди образов
Z(V^, Z(Q, .*., Z(/jJ, ••• существует наверняка такое множество, ко-
О МНОЖЕСТВАХ ВСЕГДА I КАТЕГОРИИ
70S
торое не первой категории на Р, потому что множество Р • G не первой
категории на Р. Пусть Z(i') — этот образ.
Если мы запишем интервал Бэра /' в форме
^ = (Л!, Л>, . . ., Пк)у
то мы легко заметим, что соответствующее ему совершенное
множество Рщщ пк не содержится в Р. В самом деле, когда точка у
пробегает часть множества S9 содержащуюся в интервале Бэра (л1э л2, • • •> пк)>
соответствующая точка xf x = Z(y), пробегает все точки совершенного
множества л п,я,...яи» Поскольку множество Е всюду плотно в интервале
О^л.,, ..., пк) и не содержит никакой рациональной точки, образ G • Рпхт...пк
множества i'p% E всюду плотен на Рпхпг...пк. Следовательно, совершенное
множество РП1пг...пк составляет часть совершенного множества Р.
С другой стороны^ множество G является частью множества К.
Между тем, множество К первой категории на всяком совершенном
множестве РЯ1п,...мк, потому что К содержится в Qninx...nk, а множество
V< Л,Я;.. . Яь первой категории на РП1п7...пк. Отсюда следует, что точки
множества G, принадлежащие РП1п7...пк, образуют множество первой
категории на
Рп\Уг... Яь
и тем более на Р, что противоречит предположению
о том, что образ множества i'n • Е не первой категории на Р.
Я утверждаю теперь, что множество G всегда первой категории не
является разреженным множеством.
Чтобы обнаружить это, возьмем какую-нибудь счетную часть А
множества Е> всюду плотную на [0<Cz/<^l].
Пусть D есть образ множества А. Все сводится к доказательству
того, что, каково бы ни было множество М типа Сг, расположенное на
[О ^ х ^ 1] и содержащее D, оно наверняка содержит точки множества Е,
не принадлежащие к D.
Обозначим через N прообраз множества М, M = Z(N). Ясно, что
это множество есть также множество типа G$, расположенное на
[0^1/^ 1]. Поскольку N содержит А, множество N плотно на отрезке
[O^y^l]. Следовательно, на [0^г/^1] существует сегмент а такой,
что N всюду плотно на о. Отсюда следует, что точки сегмента а, не
принадлежащие N9 образуют множество первой категории на а. Между
тем, всякое множество первой категории на [0^1/^1] содержит точки
множества Е не более чем в счетном числе. Так как множество Е
всюду несчетно на [0^1/^1], существует несчетная совокупность
точек множества Еу принадлежащих множеству N. Следовательно,
множество М необходимо содержит несчетную часть множества G и,
следовательно, точку, не принадлежащую Z), что и доказывает нам, что
рассматриваемое множество G не является разреженным множеством (ч. т. д.).
Я оставляю теперь массивные множества и перехожу к все более и
более разреженным множествам. Было бы очень интересно пройти по
лестнице множеств всегда первой категории и остановить внимание на
706
Н. Н. Л У 3 И Н
бесконечно разреженных множествах. Однако это понятие в настоящее
время кажется пустым, потому что, несмотря на то, что оно
соответствует совершенно ясному интуитивному представлению, в настоящее
время не представляется возможным представить его в форме точного
определения. И это интуитивное представление есть представление о
точечном множестве, которое невозможно отличить от счетного множества,
следовательно от множества, которое является „почти счетным". Поэтому
я ограничусь здесь следующим замечанием.
Рассматриваемый вопрос представляется мне тесно связанным с
убывающими трансфинитными последовательностями множеств типа FQ:
Е0 Z) Е, => Е2 D ... Z) Еа Z)... D Ea Z)... | 2, (1)
где каждый член Еа есть вполне определенное множество типа Fa.
Примем следующее общее определение:
трансфинитная последовательность каких-угодно множеств
£0> <§\, <§2> • • •> £i., ..., £а, ...|*
называется стационарной, если существует некоторое число *[,
начиная от которого все рассматриваемые множества тождественны,
т. е.
<5у = О т-м = . . . I *.
Первые результаты на этом пути принадлежат Бэру. Именно он
доказал весьма замечательную теорему, позволяющую констатировать, что
всякая убывающая последовательность замкнутых множеств необходимо
стационарна. Эта важная теорема является глубоким обобщением
известной теоремы Кантора—Бендиксона. Она имеет многочисленные
применения в математическом анализе и в теории функций.
Известно к тому же, что эта теорема Бэра допускает немедленно
следующее обобщение:
Всякая монотонная последовательность (убывающая или
возрастающая) замкнутых множеств стационарна.
Тогда возникает вопрос, существуют ли нестационарные убывающие
последовательности множеств типа F,1. Я рассмотрел этот вопрос
в статье „О стационарных последовательностях", которая появилась
в книге, изданной в память нашего умершего друга Гербрандта. Я
нашел там довольно общее условие для того, чтобы убывающая
последовательность множеств типа F, была стационарной, — условие, которое,
повидимому, должно быть очень полезным при изучении решет. В на^
стоящий момент я ограничусь следующими соображениями.
1 Существование таких последовательностей было отмечено Залвассером, Fund
Math.,Ш, 45, 1922; см. также Серпинский. ComptesRendus dela Soc. des Sci. et des
Lettres de Varsovie, XXV, 103, 1932, где имеется доказательство существования
возрастающей трансфинитной последовательности множеств типа G$.
О МНОЖЕСТВАХ ВСЕГДА 1 КАТЕГОРИИ
707
Пусть $а есть точка множества-разности Еа —Еа+1. Я утверждаю, что
множество Е точек £а, выбранных таким образом, является
множеством всегда первой категории.
Действительно, пусть D есть какое-нибудь заданное счетное
подмножество множества Е, D = (Ра„ Ра„ P«,.. .)• Существует порядковое
число р-<2, такое что и->^ для £=1, 2, ... (потому что а*<2 для
Л = 1, 2, ...). Из определения точек Ра сразу следует, что Рак ^Е^для
& = 1, 2, .... Следовательно, DcCE^. Между тем, из определения
точек Рак следует, что Ра£Е^ для а ^ р.. Отсюда следует (из
определения множества Е и из неравенства у < 2), что множество В • СЕ„ не
более чем счетно. Следовательно, всякое счетное подмножество D
множества Е содержится в множестве СЕ^ типа Gb, которое содержит не
более чем счетное множество Е • СЕ^ точек множества Е. По теореме
Серпинского1 множество Е является, следовательно, первой категории
на всяком совершенном множестве (ч. т. д.).
Теперь возникает вопрос большой важности:
существуют ли в действительности множества всегда первой
категории? Другими словами: можно ли назвать несчетное
множество всегда первой категории?
При настоящем состоянии науки я не вижу никакого способа
ответить утвердительно на этот жгучий вопрос, и поэтому я не считаю
установленным самое существование таких множеств при помощи
предыдущих рассуждений.
Я рассматриваю вопросы существования, как Вы хорошо знаете,
с точки зрения натуралистов, как это делает Борель — великий
натуралист нашего времени. С этой точки зрения нет никакой разницы между
применением рассуждения Цермело во всей его полноте и
употреблением так называемой „гипотезы континуума". Все эти вещи одинаково
нереальны.
Если я трачу время на рассмотрение этих вещей, то не потому, что
считаю их действительно серьезными, а потому, что через множества
чисто словесных „существований", слишком легких, чтобы принимать
их всерьез, я вижу слабый свет настоящей интуиции, могущей привести
нас к совершенно неожиданным фактам, которые мы не обнаружим,
если следовать другому пути.
Бэр имеет все основания говорить, что в конечном счете, несмотря
на видимость, все должно сводиться к конечному. Я только добавлю,
что я не знаю, обладает или нет конечностью хорошее определение.
По-видимому, надо принимать меры предосторожности относительно са.
мой полной индукции. Если не считать установленными предыдущие
существования, я вижу также очень значительные трудности в некотот
рых рассуждениях о целых положительных числах.
*• W. Sicrpinski. Loc. cit., стр. 104.
im
H. H. ЛУЗИН
Несмотря ни на что, я не могу рассматривать как данное множество
целых положительных чисел, потому что самая идея актуальной
бесконечности мне кажется мало естественной, чтобы рассматривать ее в себе.
Однако критика бесконечности ужасно трудна, и мы начинаем понимать,
какие трудности видел Борель, когда он писал:
„Кажется неоспоримым, что математики делают или думают, что
делают, из этой неограниченной последовательности
1, 2, 3, 4, 5, 6, ... (S)
совершенно ясную идею".
Слова „или думают, что делают" очень характерны для точки зрения
натуралиста.
Представляется трудным пройти мимо новых идей, к которым нас
приводят кванты и исследования Дэситтера и Лемэтра.
Фундаментальная проблема состоит в том, чтобы выяснить, является ли
последовательность целых положительных чисел вполне объективной? Кажется,
что она почти объективна, и что имеются следы несомненной
субъективности, такой, что нельзя говорить о последовательности целых
положительных чисел всегда, во всех случаях, в одном и том же смысле.
Однако в данный момент слишком преждевременно ставить жгучую
яроблему о единственности последовательности целых
положительных чисел и говорить о конечных недостижимых числах, отправляясь
от 1. Современная теория чисел весьма униформизирована методом
полной индукции. И тем не менее, наука о числах благополучно
существовала в XVII в. В то время существовали другие умственные привычки,
которые не дошли до нас.
С точки зрения натуралвета, трансфинитные числа являются только
очень большими конечными числами. Исследования о множествах —
классификация Бэра и другие — приобретают совершенно новый аспект.
Это исследования о конечных выборах, но надо принимать указанную
предосторожность относительно слова „конечное".
В теории аналитических и проективных множеств имеются странные
вещи. Ситуация очень напоминает нам вопрос о существовании
совершенного нечетного числа. Однако из теории проективных множеств
сразу видно, что имеются объекты, которые никогда никем не будут
реализованы. Такое ли положение сейчас в вопросе о целых
положительных числах?
Я не считаю бесполезными усилия в изучении классов Бэра,
аналитических и проективных множеств: они не являются в точности
объектами, имеющими самостоятельную ценность, но движениями мысли,
которые, будучи перенесенными в область целых положительных чисел,
позволят нам по аналогии открыть новые феномены, недостижимые
другими методами. Но я Вам уже писал об этих вещах.
Москва^ 14 мая 1933 г.
О ЧАСТЯХ НАТУРАЛЬНОГО РЯДА*
Известные работы Ренэ Бэра об изображении разрывных функций
в самой своей глубине являются исследованиями о безграничной
последовательности целых положительных чисел
1, 2,3, 4, 5, 6, ....
Эти работы, остановленные болезнью и преждевременной смертью
автора, по-видимому, дают возможность естественного их продолжения
как в дескриптивном отношении, так и в метрическом.
1. Первые определения. Когда пишут натуральный ряд чисел
12 3 4
его представляют себе как простую, не имеющую конца
последовательность. Мы будем его обозначать через R. Если ^ есть неотрицательное
целое число, мы можем обозначить через R множество чисел
И--н1, ^н-2, |А-ьЗ, ни-4, ...,
которое мы называем остатком натурального ряда R. Ясно, что R0 = /?.
Если М есть конечное множество целых положительных чисел
(не пустое или же лишенное элементов), мы пишем М=0. Если М не
пустое, мы будем обозначать через М наибольший из элементов,
принадлежащих к М. Если М лишено элементов, мы пишем М=0.
Установив эти обозначения, мы видим, что при М=|* остаток R^ не
содержит элементов, принадлежащих к М; значит, мы имеем равенство М= О
на остатке R^
По преимуществу мы рассматриваем бесконечные части Е
натурального ряда/?. Если£и£'— такие части, мы пишем Е'<^Е, когда
все элементы части Е\ за исключением конечного числа таковых
(каковое может быть и нулем), принадлежит к части Е. В этом случае мы
имеем Е' — £ = 0. Если Е' — Е = )ху мы имеем очевидное неравенство
Е <^Е на остатке /?к
Две бесконечные части Е и £ натурального ряда называются
ортогональными одна к другой, когда Е£ = 0; если Е£ = ц, части Е
и £ не имеют общих элементов на R^.
Два какие-нибудь множества 3)1= {Е} и 3t = {<£}, составленные из
бесконечных частей Е и £ натурального ряда, называются ортого-
♦ ДАН СССР, 40, No 5, 195—199. 1943.
710
Н. Н. ЛУЗИН
нальными одно к другому (вообще неравномерно), если все их
элементы Е и <§ взаимно ортогональны, Е& =^0; в этом случае мы пишем
2Ш = 0.
2. Отделимость. Пусть Зй = {Е} и 9^ = {&} — два каких-нибудь
множества, составленные из бесконечных частей Е и & натурального ряда.
Мы пишем 2)£<9£, когда отношение Е<^<§ удовлетворено для всех
соответственных элементов Е и & этих множеств. Если множество 91
будет состоять лишь из единственной бесконечной части Н натурального
ряда, тогда написать 4)1 <^Н, это означает написать отношение Е<^Н
для всех элементов Е данного множества 9№. В этом частном случае
бесконечная часть Н натурального ряда называется покрышкой
множества ЗЯ.
Два каких-нибудь множества Ш и 9i, составленные из бесконечных
частей натурального ряда, называются отделимыми, если среди всех
их соответственных покрышек Н к К, Ч)1<СН и У1<^К имеются
ортогональные покрышки: НК = 0. Такие ортогональные покрышки Н и К
для множества 2К и 9£ называются их отделителями.
При установленных определениях мы имеем вполне очевидное
предложение:
Условием, необходимым для того, чтобы два каких-нибудь
множества 9К и 9t были отделимы, является их ортогональность одного
к другому: 2)Ш = 0.
В частных случаях условие это оказывается и достаточным. В этом
мы удостоверяемся теоремой, начало которой восходит к известному
рассуждению Поля дю Буа-Реймонда:
Теорема (Поль дю Буа-Реймонд). Если два множества 3№ м Я,
составленные из бесконечных частей натурального ряда и
ортогональные одно к другому, суть счетные (или конечные), они наверное
отделимы.
Доказательство. Согласно предположению мы можем писать
3№ = {£1, Е2, ..., Ея, ...} и 9l = {Sl9 £2, ..., £п, ...}. Так как 2ft и #
ортогональны одно к другому, ЗКЗ^ = 0, мы имеем Ер&я = 0 для всех
р и q, какие только возможны.
Обозначим через /(л) наибольшие из 2я неотрицательных целых
чисел SyEn и Е^&п, где v не превосходит п (прием Поля дю
Буа-Реймонда), и определим две бесконечные части Н и К натурального ряда
следующим законом:
Н = ExRf(l) -+- E2Rm ч- ... -+- EnRm -н ...
и
К= £х/?/(1) -+- S2Rm -+- ... -+- <SnRm -+-
Прежде всего Еи<Н и §Л<^К, каково бы ни было целое
положительное п, и, значит, мы имеем удовлетворенными отношения 9Й<// и
91<СК. Следовательно, Н и К суть соответственные покрышки д\я
множеств SK и 9t.
О ЧАСТЯХ НАТУРАЛЬНОГО РЯДА
711
Но бесконечные части Н и АГ, определенные таким образом, не имеют
никакого общего элемента. В самом деле, если целое положительное е
принадлежит части Н и части К, оно необходимо принадлежит
некоторому члену EpRf(p) суммы Н и одновременно некоторому члену
<§gRf{q) суммы К. Следовательно, е принадлежит общей части Е & , и,
значит, если п есть наибольшее из двух чисел р и q9 то мы имеем
е^/(п)- С другой стороны, е принадлежит общей части R^Rf^ и,
в конце концов, остатку R^n) натурального ряда, что противоречит
предыдущему неравенству. Следовательно, мы имеем//ЛГ=Ои a fortiori
//АГ=0. Отсюда следует, что Н и К суть отделители и данных
множеств 5Й и 3? (ч. т. д.).
Возникающий теперь вопрос формулируется так:
В общем случае является ли взаимная
ортогональность 2Щ = 0 двух данных множеств 2R и Ш достаточным
условием дая отделимости 9)£ и 5ft?
Этот вопрос важно решить. Ибо если его разрешают в
положительном смысле, тогда можно утверждать, что, обладая двумя
заданными взаимно ортогональными множествами, всегда умеют эффективно
отыскать их отделители. Если же, наоборот, поставленный вопрос
разрешают в отрицательном смысле, тогда должны существовать два
несчетных множества, ортогональные одно к другому, которые уже
нельзя отделить.
Не приступая к рассмотрению глубины этого вопроса, который будет
разрешен лишь наблюдением фактов, я удовольствуюсь некоторыми
аусвалическими рассуждениями, т. е. основанными на аксиоме
произвольного выбора Цермело (Auswahlprinzip).
3* Продолжение ортогональных последовательностей. Среди
открытий, которыми мы обязаны Георгу Кантору, наиболее важным
является относящееся к мощности континуума: континуум не есть
счетное множество. Точная форма, которую можно дать этой
формулировке, сводится к возможности продолжить всякую
безграничную последовательность xL, x.,y ..., хя, ...
действительных чисел, определяя эффективно новое
действительное число х, заведомо не принадлежащее
этой последовательности.
Проследуем теперь аналогией и назовем ортогональным в себе
всякое множество, составленное из бесконечных частей натурального
ряда, все элементы которого ортогональны один к другому. Множество
Ш = {Е}9 ортогональное в себе, называется открытым, если к нему
можно присоединить новую бесконечную часть & натурального ряда
такую, которая ортогональна к каждому элементу Е множества Ф£,
ИЛЕ = 0. В противном случае множество 2К называется замкнутым,
т. е. не могущим быть расширенным путем присоединения к нему
какого-либо нового элемента под условием удержания его
ортогональности в себе.
712
Н. Н. ЛУЗИН
Конечное ортогональное в себе множество может оказаться
замкнутым; но если оно фактически счетно, оно никогда не может
быть таковым. Это вполне элементарное предложение, самая идея
которого восходит к основателю теории множеств:
Теорема (Георг Кантор). Всякая безграничная
последовательность попарно ортогональных элементов всегда может быть про-
должена.
Доказательство. Пусть Е19 Е2> ..., Еп, ...— безграничная
последовательность бесконечных частей натурального ряда,
ортогональных одна к другой ЕрЕя = 0, если p=£q. Обозначим через /(л)
наибольшее из -уп (п — 1) целых неотрицательных чисел ЕрЕя> где р и q
не превосходят п, p^q. Ясно, что на остатке /?/(Я) части Е1У Е2У ..., Еп
не имеют попарно общих элементов. Следовательно, мы можем
эффективно отыскать такой элемент еп последней части Еп, который имеет
сколь угодно большую величину и который заведомо не
принадлежит никакой из предыдущих п — 1 частей Е19 Е2> ..., Еп^^
Здесь легко узнают известный диагональный процесс
Георга Кантора.
В этих условиях определенные таким образом элементы
е1 < е2 < е3 < • • • < еп <
образуют эффективную бесконечную часть Е натурального ряда, такую
которая наверное ортогональна ко всем элементам Е19 Е2> ..., Епу ...
данной безграничной последовательности: ЕпЕ^0 при всяком п;
к тому же, разумеется, целые положительные Е„Е = еп попарно
различны (ч. т. д.).
4. Неотделимые ортогональные множества. Предыдущая теорема
заставляет соответствовать всякой безграничной последовательности
бесконечных попарно ортогональных частей Е1У Е2У ..., Еп, . ..,
эффективно перенумерованных натуральными числами 1, 2, 3, ..., одну и
только одну эффективную часть Е9 ортогональную ко всем этим частям,,
без единого исключения.
Трансфинитное повторение этой теоремы приводит к
несчетной вполне упорядоченной последовательности
^0> ^1) *^2> * • •» ^ш> • * •> ^а> • • •> ^
бесконечных частей натурального ряда, ортогональных одна к другой;
к тому же благодаря самому способу образования этой трансфинитной
последовательности, т. е. диагонали Кантора, целые положительные
ЕрЕ^ для всякого фиксированного а и переменного [3, меньшего чем
а> Р <С а> все различны.
Установив это, разобьем произвольным образом
рассматриваемую трансфинитную последовательность на две последовательности,,
обе несчетные и без общих элементов; мы обозначаем через 5JI и 91
О ЧАСТЯХ НАТУРАЛЬНОГО РЯДА
713
два несчетных множества, соответственно образуемые элементами этих
последовательностей:
Ш = {Е., Е., .... Е., ...,£<, ...|2}
*о h *<d тв
и
й = {£», Е.., ..., Е.; .... Е.., ...|2),
т0 'l Тш 7а
где значки Ya и Т« суть различные конечные и трансфинитные числа,,
расположенные в порядке возрастающей величины их.
Ясно, что эти множества 2R и 5ft ортогональны одно к другому:
2Ш = 0.
Мы утверждаем теперь, что ЭД£ и Я неотделимы. Проследуем
рассуждением от противного и предположим, что Н и К суть
отделители множеств 2R и Я. Тогда мы имеем: Е < <^НУ Е »<iK и НК=0*
A fortiori мы будем иметь £'АГ=0 и Е "// = 0, какого бы ни было а
•а Та
меньшее, чем 2, а<^2. Мы заключаем отсюда, что существует
счетная бесконечность индексов р таких, что имеем Е^К<^тпу
где m есть фиксированное целое положительное число; мы можем
предположить эти индексы р меньшими некоторого фиксированного-
трансфинитного числа р*, р* <^ 2. Отсюда ясно, что можно найти
фиксированное трансфинитное число X, Х<^2, такое, что имеем
Т^ <С т'х- На остатке /?да части £ ' и А^ не имеют общего элемента.
И так как мы имеем отношение Е»<^К> то должен существовать
такой остаток R^9 на котором мы имеем неравенство Е » <С.К. Пусть
теперь /п* будет наибольшим из двух чисел m и \ь; на остатке /?*»* нет
элементов, общих частям Е > и Е». С другой стороны, мы имеем
Тр <С Тх> и» как мы Уже сказали, такие индексы имеются заведомо
в бесконечном числе, что, очевидно, невозможно, будучи в
противоречии с диагональю Кантора.
Математикам, интересующимся преимущественно самой техникой
математических рассуждений и допускающим существование всех
трансфинитных чисел второго класса, рассмотрения, содержащиеся в тексте,
позволяют поставить большое число трудных вопросов, встречающихся:
на этом пути и которых нельзя на*йти на других дорогах: таковы,
например, вопросы, относящиеся к отделимости 5-множеств,
ортогональных в себе, среди которых заведомо имеются множества мощности
континуума и т. д.
Но работа, гораздо более трудная и которую предстоит еще
целиком сделать, состоит в постижении того действительного и точного
смысла, который скрывается за рассуждениями текста, основанными,
фактически лишь на чисто словесном столкновении терминов:
конечное и бесконечное.
О ЧАСТЯХ НАТУРАЛЬНОГО РЯДА
"В работе даются доказательства предложений, формулировки которых были
опубликованы в 1943 г. в Докладах Академии наук СССР*).
Обозначения* Натуральный ряд чисел 1, 2, 3, 4, . .. обозначаем
буквой /?. Остаток т-+-1, /л-+-2, тн-3, т-1-4, ... натурального
ряда, где т — целое неотрицательное число, обозначаем через Rm.
Рассматриваем различные части Е натурального ряда. Если Е — пустая
* часть, пишем обычное равенство £ = 0. Если Е — конечная часть,
пишем символическое равенство £ = 0, обозначая для непустой Е
через Е наибольший из ее элементов; для пустой Е мы полагаем Е = 0.
Ясно, что при Е = т мы имеем на остатке Rm равенство Е = 0.
Преимущественно здесь рассматриваются бесконечные части
натурального ряда. Если две части Е и & тождественны, пишем обычное
равенство- Е-= &. Если они отличаются одна от другой лишь конечным
числом элементов, пишем символическое равенство Е ~£. Если каждый
элемент части Е входит в- &> пишем обычное неравенство Е<^<§.
Если же всякий элемент части £, за возможным, но не обязательным,
исключением конечного числа их, входит в <£, пишем символическое
неравенство Е^£. Две части Е и & называются взаимно
ортогональными, когда для их произведения имеем Е£ = 0. Символическое
неравенство Е*$&9 очевидно, эквивалентно взаимной ортогональности Е и
.дополнения CS части <£, т. е. отношению Е • CS = 0. Ясно, что при
ЕС<§ = т имеем на остатке Rm обычное неравенство Е<^&, причем
такой остаток уже нельзя расширить путем уменьшения числа т.
Два каких-нибудь множества 2К = {£} и 9? = {£}, составленные из
частей Е и <§ натурального ряда, называются ортогональными одно
к другому (вообще: неравномерно), если все их элементы Е и &
взаимно ортогональны, т. е. если имеем всегда Е •£ = (). В этом
случае мы пишем 2R • У1 = 0.
Если для множеств ЯК = {£} и 31 = {£} имеем отношение Е^ё
между всякими двумя их элементами, мы пишем ЗИ << 31. Если У1 состоит
из единственной бесконечной части Н натурального ряда, тогда
соотношение Ш-<Н эквивалентно системе всех соотношений E^Hf где
Е пробегает все элементы множества 9Й. В этом случае Н называется
покрышкой множества ЗК.
* Иав. АН СССР, серия мат., И, № 5, 1947.
О ЧАСТЯХ НАТУРАЛЬНОГО РЯДА
71S
Два множества Ш {Е} и 5t {<§} называются отделимыми друг от
друга, если у них имеются покрышки без общего элемента, т. е. когда
имеем одновременно Ш^Н, У1^К и //-ЛГ=0.
Прямое предложение: если множества ЧЛ и ЬЛ отделимы друг
от друга, они ортогональны одно к другому, т. е. 2К-5К = 0 является
вполне тривиальным.
Обратный вопрос: всякие ли два взаимно ортогональные
множества Ш и %1, ЗЯ!К = 0 отделимы друг от друга? — требует
внимательного анализа.
Теорема П. дю Буа-Реймонда. Если оба взаимно
ортогональные множества 9И = {£} и У1 = {£} счетные, то они наверное
отделимы друг от друга.
Доказательство. Имеем Ш = {Е1У Е2, ...,Ер,...} иУ1={&1, <§2,...,
..., Sq} ...}, где всегда Ер £^=0. Обозначим через <р(/:) наибольшее
из к2 чисел Ер£я, где 1<^<^£ и 1<^^/:. Мы полагаем
Н= ExR9(i) -+- E2R9p) -+- ... ч- ЕьКф) -+-...,
Очевидно, что Ш*$Н и З^ЦАГ. Остается доказать, что Н-К = 0.
Общий элемент е покрышек Н и К должен войти в произведение
EpR9(py&qR<p(q). Обозначим через /: наибольшее из двух чисел р и q.
Ясно, что R<p(p)-R9(g) = R<?(k). С другой стороны, очевидно, что е<^ср(&)
и значит, е не может войти в R9{ky Полученное противоречие
доказывает равенство Н-К=0, т. е. отделимость 25! и Л (ч. т. д.).
Внутренне ортогональные множества. Это название мы
даем множеству У)1 = {Е), неважно какой мощности,
бесконечных частей Е натурального ряда, взаимно ортогональных между собой,
т. е. когда имеем Е' • Е" = 0 для любых двух различных элементов
Е и Е" множества Ш.
Такое 2R = {Е) называется полным, если не существует никакой
бесконечной части S натурального ряда, ортогональной ко всем
элементам Е множества 5К. Неполное ЭД£ всегда может быть пополнено
новым ортогональным элементом <§.
Конечное внутренне ортогональное множество 3W может оказаться
полным, например Ф£ = {£, СЕ). Но счетное внутренне ортогональное
множество 2К = {Е19 Е2, ..., Ек, •..} никогда не может быть полным.
Чтобы видеть это, введем важное определение:
Бесконечная часть & натурального ряда называется
соприкасающейся к последовательности Е19 Е2, ..., Ек, ... каких-нибудь
бесконечных частей натурального ряда, если, во-первых, она ортогональна
к каждой из них, т. е. £*£ = 0, и если, во-вторых, £*£->н-со при
возрастании к.
Теорема Кантора. Всякая последовательность Ev Е2,..., Еь, ...
попарно ортогональных бесконечных частей натурального ряда
716
Н. Н. ЛУЗИН
допускает соприкасающуюся к ней бесконечную часть <§
натурального ряда.
Доказательство. Обозначим через у (к) наибольшее из ^
чисел Ер9 Eqy где 1<^/> <?<[£. Ясно, что на остатке R^k) части
Е19 Е2у ..., Eic не имеют попарно общего элемента. Нужная нам часть
£={е19 е>, ..., ек, ...} строится так: ех есть первый элемент части
Е19 ек есть первый элемент части Ек, принадлежащий остатку R9(k) и
больший, чем ек—г.
Из этого построения части § следует, что д\я каждого
фиксированного к имеем Ек<§ = 0у Ек& = ек, и что поэтому Ekg^>-*-co, когда
к возрастает (ч. т. д.).
Трансфинитное повторное применение теоремы Кантора дает вполне
упорядоченную последовательность типа 2 попарно ортогональных
бесконечных частей натурального ряда
£„£, ... Еш ... Е? ... Еа \Q
и притом такую, что всякий ее член Ев есть бесконечная часть
натурального ряда, соприкасающаяся к сегменту этой последовательности
{2Гр}, |3<Са> отсекаемому членом £а. Иначе говоря, мы имеем Еа-Е$ = 0
при любых а ф (3 и Е$Еа -> -+- оо для всякого фиксированного а и при
переменном |3, (3 < а.
Два неотделимые взаимно ортогональные
множества, каждое мощности алеф-один. Чтобы иметь такие
множества 2К и 9£, возьмем две какие-нибудь последовательности типа й
возрастающих индексов:
Тп<Ь< ... <Т„>< ••• <7.< \&,
%<\< ... <К< ... <h< ^,
соблюдая лишь ту предосторожность, чтобы в них обеих не содержался
один и тот же индекс.
Мы полагаем 3)i = {Eu} и 9t={£3J. Ясно, что имеем взаимную
ортогональность 2R и 9J, 2Й • 91 = 0. Мы теперь утверждаем
неотделимость 2Jt и 9i друг от друга.
В самом деле, пусть Н есть какая-нибудь покрышка для Ш,ЧЛ < Н.
Имеем Eia < Н при всяком а, а<^й.
Значит, 2?у -С// = 0 и символ £Y * С//всегда есть число натуральное
(или нуль). Поэтому существует такой фиксированный трансфинитный
индекс X и такое фиксированное натуральное число ру что равенство
справедливо д\я бесконечно многих индексов а, меньших
чем X, а <^Х.
С другой стороны, является очевидным существование такого
фиксированного трансфинитного индекса ^, чтобы было удовлетворено
неравенство fx <С V Мы теперь утверждаем, что никакой элемент Ец множества
91 не может быть ортогональным к покрышке //, когда P>V-
О ЧАСТЯХ НАТУРАЛЬНОГО РЯДА 717
В самом деле, возьмем фиксированное р, р > ^ и предположим, что
JJ'EZq = 0. Тогда символ HEb^ = q есть число натуральное. Пусть
т — наибольшее из двух чисел р и д. Ясно, что на остатке Rm
натурального ряда мы имеем Еъ$ < СН и в то же самое время £Te</f для
бесконечно многих а, а<Х. Но, очевидно, имеем Ta<Tx<CS <V
Отсюда на фиксированном остатке Rm части Еу и £8о не имеют общего
Те °р "-*
элемента, и, значит, имеем £Та • Еь^ ^ т. Но это противоречит
требованию иметь Еи - Еь$ -> -+- оо при переменном а, ^а^С^.
Теперь, если бы Ш и 9i были отделимы друг от друга какими-нибудь
покрышками Ни К, ЧЯ<Н, У1<К, НК=0, то приняв во внимание,
что Ш = {Е1а) и Sft={£^}, мы должны были бы иметь ЕЬ^К и,
значит, Н • £ц = 0 7Г/>м всяком р, что, как мы видели, невозможно уже
при Р > р., где р. — фиксированное число (ч. т. д.).
Как резюме полученного мы имеем:
1. Всякие два счетные взаимно ортогональные множества 9К и
VI всегда отделимы.
2. Имеются пары взаимно ортогональных множеств 9R и 91,
каждое мощности алеа>один, которые наверное неотделимы друг
от друга.
Естественно возникает вопрос о важном смешанном случае:
Проблема I. Установить отделимость или найти примеры
неотделимости друг от друга двух взаимно ортогональных
множеств 4R и 91, одно из которых счетное, а другое — мощности
•алеф-один.
Монотонные трансфинитные последовательности.
Последовательность бесконечных частей натурального ряда
£в£, ...£„...£. \Я (1)
называется возрастающей, если имеем Еа -^ £з при а < 3. Она
называется существенно возрастающей, когда имеется фиксированная
грань \ Х<2, за которой нельзя встретить соотношения Ea = E{i дкя
Х<^а<^р. Аналогичные определения имеем для убывающих и
существенно убывающих последовательностей. Возрастающие и
убывающие последовательности носят объединяющее их название монотонных
последовательностей.
Последовательность называется стационарной, когда за
фиксированной гранью X всегда имеем соотношение Еа = Ер при X <^ а <^ р.
Всякая возрастающая нестационарная последовательность (1)
содержит в себе существенно возрастающую трансфинитную
последовательность.
Это замечание вполне тривиально, ибо достаточно удалить из
последовательности (1) все интервалы стационарности, внутри
зсаждого из которых имеем Еа = Е$9 оставив неудаленным один лишь
718
Н. Н. ЛУЗИН
левый конец каждого из них; оставшиеся члены образуют, очевидно,,
существенно возрастающую последовательность типа 2.
Имеются существенно возрастающие трансфинитные
последовательности,
В целях лишь ускорения изложения (и не в порядке метода) мы
прибегаем к геометрическим образам. Возьмем какую-нибудь
трансфинитную последовательность
/.(»)/l («) ••/» •-./.(«) I2
арифметических функций П. дю Буа-Реймонда натурального аргумента п>
т. е. такую, что /а(п) есть натуральное число при всяком а и
/р(л)—Л(л)->-+- оо, если а<£), когда п безгранично возрастает. На
плоскости XOY мы наносим кривую у=/а(х) и нумеруем
натуральными числами 1, 2, 3, 4, ... все точки М(х, у) плоскости XOY+
имеющие координаты х, у, равные натуральным числам. Наконец,,
обозначаем через Еа ту часть натурального ряда R, которая
соответствует точкам М{хуу)у лежащим ниже кривой у=/а(х)»
Ясно, что трансфинитная последовательность частей ряда
E9<Et4 ... <Е,0< ... *Е.< \Q (2>
есть существенно возрастающая^ что и требовалось доказать.
Отделимые встречные трансфинитные
последовательности. Если мы возьмем две какие-нибудь бесконечные части
//и fC натурального ряда, не имеющие общего элемента, Н'К = 0, и
установим взаимно однозначное соответствие сначала между
элементами натурального ряда А* и элементами части //, а потом между
элементами ряда R и части К, то в этом случае трансфинитная
последовательность (2) порождает сразу две встречные существенно
возрастающие последовательности типа 2
Eb<EY< ... <ЕШ< ... <Еа< ...|... ><§?> ...
... >SM> ... >SX>€0,
отделимые друг от друга покрышками Н и К, ибо их члены Ел и <§$_
удовлетворяют соотношениям
Еа<Я, S?<K, H-K=0.
Поэтому мы имеем £а-<§^ = 0, а<2 и Р<2 любые, и, следовательно,
наши встречные отделимые последовательности взаимно ортогональны.
Неотделимые встречные взаимно ортогональные
последовательности. Чтобы иметь их, достаточно предположить
что всякий член <$^ правой последовательности есть бесконечная часть
натурального ряда, соприкасающаяся к соответствующему сегменту
{Еа}, а<Р, левой. Мы утверждаем, что две такие встречные
возрастающие последовательности заведомо неотделимы одна от другой*
О ЧАСТЯХ НАТУРАЛЬНОГО РЯДА 719%
В самом деле, пусть Н—какая-нибудь покрышка для левой
последовательности, Еа^Н, a <Q —любое. Поэтому £а-С7/=0 и, значит,,
имеются фиксированные: трансфинитный индекс X и натуральное
число р такие, что уравнение ЕаСН=р удовлетворено дая
бесконечно многих а, а <[ X.
Значит, на остатке Rp имеем Ea<iH для всех таких а. С другой
стороны, соотношение £^Н= О невозможно для Р>Х. Действительно,
если бы оно осуществилось, мы бы имели g^H=q, где q—
натуральное. Значит, на остатке Rq имели бы <§^ < СУ/. Обозначая через т
наибольшее из двух чисел р и q9 на остатке Rm мы имели бы Еа§^ = 0,.
т. е. Еа§р^т для бесконечно многих а, меньших фиксированного
Р, ос <^р. А это невозможно, ибо свойство соприкосновения части &~
к сегменту {Еа}, а<СР> требует, чтобы £в£|Н-► н-со при переменном а.
Итак, покрышка Н дая левой последовательности и всякая часть
<§$> $^>\ правой имеют бесконечно много общих элементов, что
несовместимо с наличием отделяющей покрышки К для правой
последовательности (ч. т. д.).
Итак, все сводится к построению встречных трансфинитных
последовательностей со свойством соприкосновения каждой части £^ правой
к соответствующему сегменту {Еа}9 &<СР> левой.
Предположим, что мы получили два встречных взаимно
ортогональных вполне упорядоченных множества типа а:
Е0<Ег< ... <Е^< .. |а J... >ё,> ... >ёг>ё0, (3).
имеющие нужные свойства:
1° Е^ = 0 дая р<а и Т<а,
2° £г соприкасается к сегменту {Е^}, Р <С Т-
Докажем, что можно продолжить построение, определив члены Еа
и <§а с сохранением свойств 1° и 2°. Предстоит рассмотреть два
случая.
Число а непредельное: а = а*-ь1. Применение теоремы
П. дю Буа-Реймонда дает покрышки Н и К такие, что Е^^НУ.
<?у<$ЛТ, Н-К=0 при любых Р<Са и Т<Са- В этом случае мы просто
полагаем Еа = Н и Sa = K, ибо ясно, что К соприкасается ко всему
левому множеству (3).
Число а предельное: ^Ч^^^ ••• <Cav<C • • •> °Ч^а ПРИ
v -*н- со. Сохраняя те же покрышки П. дю Буа-Реймонда Н и AT,
обозначим через 5V совокупность индексов (3, для которых E$K=v,
где Р <Са» Если Д, при всяком натуральном v есть конечное
множество, К соприкасается ко всему левому множеству, и мы по-прежнему
полагаем Еа = Н и <§а = К. Если дая фиксированного v множество 5V
бесконечно, оно, очевидно, имеет тип w и конфинально числу а.
В этом случае, уничтожая в 5V индексы р, меньшие чем av, мы
обозначаем совокупность удержанных в В„ индексов р через 5* и.
ISO
H. Н. ЛУЗИН
составляем сумму В* = В\-*-В\-*- ... н- Z^-ь .... Ясно, что 5* имеет
тип и) и конфинально числу а. Следовательно, можно написать
£*={£*, р*, ..., pj, ...}, где все $*к расположены в возрастающем
порядке. Значит, имеем Еа*<Ел**$ ... <Е7*< ..., причем эту последо-
вательность всегда можно предполагать существенно возрастающей,
ибо таковым мы можем предполагать все левое множество (3). Это
означает, что в £г* входит бесконечно много элементов, не входящих
в предыдущую часть Е ♦ . Отсюда следует, что всегда можно определить
Pfc—1
такую бесконечную часть Е* натурального ряда £* = {в*, в*, ..., е£, ...},
элементы е£ которой расположены в возрастающем порядке, причем е\
входит в часть Е • и заведомо не входит ни в одну из предыдущих
частей Е *, £ •, ..., £ * . В этих условиях ясно, что имеем £^* •£* = е*
для всякого А:. Очевидно, что найденная бесконечная часть Е*
натурального ряда ортогональна ко всякому элементу £р, Р <С а> левого
множества (3). Поэтому, вынув из Н все элементы части £*, т. е.
составив разность Еа = Н— £*, мы убеждаемся в том, что £р ^ £e, Р <С а,
причем мы не можем иметь £р = £а. Ясно, далее, что, присоединив
к покрышке К все элементы части £*, т. е. составив сумму £а = АГ-*-£*,
мы имеем £а>*£7, 7 "С01» причем соотношение <£€ = £Y невозможно.
Затем мы имеем £а • <£а = 0, откуда Еа - <£т = 0, 7 <С а и £?<£а — 0>
р<*.
Наконец, неравенство Е$ • <§а^Е$ К показывает, что имеем
£р£а -^-ьоо при р переменном, но остающемся меньше некоторого
фиксированного Р0<Са. А неравенство £ *£а ^ £ *£* = е£, где e£-*-+-oot
когда £ безгранично возрастает, удостоверяет, что, приняв во
внимание самое определение части £*, имеем Е$&а -> -+- оо при всяком
возрастании переменного индекса р и стремлении его к пределу ос.
Отсюда мы заключаем, что &а соприкасается ко всему левому
множеству (3), и что поэтому построенные Еа и <§а пополняют наши
встречные вполне упорядоченные множества (3), продолжая их при
сохранении нужных нам свойств 1° и 2°, что и требовалось доказать.
Как резюме изложенного, мы имеем:
3. Всякие две встречные существенно возрастающие и взаимно
ортогональные последовательности прямого и обратного типов
и) и о>* всегда отделимы друг от друга.
4. Имеются пары встречных существенно возрастающих и
взаимно ортогональных последовательностей прямого и обратного
типов 2 и 2*, которые заведомо неотделимы друг от друга.
Таким образом, и здесь проявляется давно известный
математическому анализу феномен Пифагора, состоящий в невозможности
вставить между двумя идущими навстречу друг другу специально
подобранными последовательностями рациональных точек рациональную
О ЧАСТЯХ НАТУРАЛЬНОГО РЯДА
721
точку. Если мы будем называть реальной точкой все бесконечные
части Е\ £", ... натурального ряда, конгруэнтные друг другу, т. е.
Е~Е"^ . .., то на построенной таким образом трансфинитной
прямой (при отбрасывании реальных точек, не помещающихся на ней)
наблюдается тот же самый феномен Пифагора „трансфинитной
иррациональности".
Далее естественно возникают следующие важные проблемы.
Проблема II. Установить отделимость или найти примеры
неотделимости друг от друга двух встречных существенно
возрастающих и взаимно ортогональных последовательностей прямого
и обратного типов о) и 2* (или 2 и <*>*).
Проблема III. Установить (или опровергнуть) существование
двух встречных существенно возрастающих и взаимно
ортогональных последовательностей прямого и обратного типов 2 и 2* таких,
что между ними можно вставить лишь одну реальную точку.
Наконец, наиболее интересная из всех проблем:
Проблема IV. Установить (или опровергнуть) наличие такой
существенно убывающей последовательности бесконечных частей
натурального ряда
E0>EV>E2... >ЕЮ> ... >Еа> |2,
которая не допускает никакой бесконечной части Е натурального
рядау удовлетворяющей соотношению Еа^Е при всяком а, а<^2.
Все эти проблемы, представляющие собой дериваты
континуум-проблемы, по нашему убеждению, не могут иметь решения при
существующих взглядах на трансфинитное и натуральный ряд чисел.
Примечание. Изложенное выше не следует рассматривать как
желание приблизиться к конструктивному решению
континуум-проблемы. Многое в этом отношении можно было бы сказать, но здесь
мы ограничимся лишь несколькими тезисами. Континуум-проблема
утратила научное значение еще задолго до последних изысканий о
непротиворечивости континуум-гипотезы, стоящих, по справедливому
замечанию Адамара, более на почве физиологии мозга, чем на почве
математики. Континуум-проблема переросла в вопрос первой важности: как
возможен натуральный ряд чисел?
Автор держится русла идей Пуанкаре и Бореля, стремившихся
отрицать актуальную бесконечность во всех ее видах. К сожалению,
Пуанкаре под влиянием доктрины Канта о синтетических суждениях
a priori в арифметике, по-видимому, колебался совсем отказать
натуральному ряду в актуальной бесконечности, — то, от чего свободен
Борель, рассматривающий трансфинитное и все затруднения с ним как
дериват гипотезы актуальной бесконечности натурального ряда.
В этом русле идей для нас теперь безразлично употребление или
неупотребление аксиомы Цермело— различение, поведшееся от Лебега.
Близость в арифметике той реформы, которую выполнил Лобачевский
722
Н. Н. ЛУЗИН
в геометрии, зависит от проницательности мыслителей, становящихся на
этот путь, а также, по справедливому замечанию акад. И. П.
Павлова, от смелости их концепций.
Эти размышления — я не имею необходимости об этом говорить —
складывались у меня постепенно, и прямое действие на них имели
личные беседы с Вацлавом Константиновичем Серпинским и с проф.
Владимиром Семеновичем Федоровым.1
Поступило 2 VI. 7947
1 Я не должен пройти мимо переписки по некоторым затронутым здесь вопросам
с И. В. Поповым и указания на письма, присланные мне по поводу проблемы I
И. М- Максимовым.
Приложения
КОММЕНТАРИИ К РАБОТАМ Н. И. ЛУЗИНА
|1] Пространством Бэра R называется топологическое пространство, элементами
которого являются всевозможные последовательности целых положительных чисел
д = (ль /i2, . . . ль . . .)•
Окрестностью в R является множество тех точек /?, у которых первые k анаков
фиксированы. Это множество — обозначим его Ьп . . . Ьп —называется интервалом
Бэра порядка k. Пространство R взаимно однозначно и взаимно непрерывно
отображается на множество всех иррациональных точек, заключенных в отрезке
(О, 1|, а следовательно, и на множество <г?х всех иррациональных точек оси ОХ.
Для доказательства достаточно заметить» что каждое иррациональное число,
заключенное между 0 и 1, может быть представлено в виде непрерывной дроби.
1
х= Т
л1-*- 5~
л*-*-———
2 лз-*-
В пространстве Бара вводится расстояние- между двумя точками (х9 у)
следующим образом: если первые k знаков п^ п2, . . ., njc у элементов х и у одинаковы,
a (fe-t-l)-e знаки различны, то
1
Определенное таким образом пространство R является полным метрическим
пространством, в отличие от пространства иррациональных точек с евклидовым
расстоянием между двумя точками. Н. Н. Лузин рассматривает основную область о7*
как множество всех иррациональных точек оси ОХ, не касаясь ее топологическое
структуры. Однако он фактически неоднократно на нее опирается, используя
тот факт, что бесконечная убывающая последовательность интервалов Бэра всегда
содержит точку.
[2] Нельзя согласиться с утверждением автора о причине простоты изложения
дескриптивной теории множеств в пространстве <^х» Эта простота, связана не с тем
обстоятельством, что пространство & л более однородно, тогда как .классическая
числовая прямая содержит разнородные элементы, а с тем, что пространство е?т
нульмерно,(не содержит никакой связной части). Выбросив из оси ОХ
произвольное всюду плотное счетное множество Е, мы получим пространство R% на
котором построение дискриптивной теории множеств будет в точности таким же*
как в пространстве & %л независимо от арифметической структуры элементов
множества Е.
726
КОММЕНТАРИИ К РАБОТАМ Н. Н. ЛУЗИНА
(3] Лебег подразумевал под словами „аналитически иэобраэимые функции" функции
классификации Бэра, в силу того, что они получаются счетно-кратным
применением операции перехода к пределу, исходя от непрерывных функций.
Термин „аналитическое множество" встречается у Лебега в мемуаре „Sur les fonctions
representables analytiquement" (Journ. Math., 1905), на стр. 165, в сноске, где он
замечает, что множества, измеримые В, которые могут быть определены
аналитическими равенствами или неравенствами [Е (а </)♦ Е (а < /)], могут
заслуживать названия „аналитических множеств'. Однако в дальнейшем Лебег этим
термином не пользуется.
[4| Область <з7'ху является топологическим произведением с?х X & у областей <Р' х и <г^,
а порция области <^Ху ~~ топологическим произведением (а, Ъ) X (о» d) двух
порций соответственно областей <&х и <&у. Интервалом Бэра порядка Ди##'вЯ
области о/ху называется топологическое произведение двух интервалов Бара
порядка к областей <з7' х и о?у. Заметим, что все области & ху% &' ху» и т. д. гомео-
ыорфны области о/х. Для доказательства достаточно сначала установить взаимно
однозначное соответствие между интервалами Бэра порядка 1 области &я и
интервалами Бара порядка 1 области ^ху- После того как установлено
соответствие между интервалами порядка к— 1, установить взаимно однозначное
соответствие между всеми интервалами Бэра порядка к области <&х% содержащимися
в интервале о* н*—1«> и всвми\ интервалами Бэра порядка £ области <&ху%
содержащимися в интервале Бэра Д^5л, т*- « соответствующем Ь'х .
Важно заметить, что области <а7я, ^^у. . . ., <?х я имеют размерность 0. Как
мы уже указывали (см. [2]), этим и объясняется то обстоятельство, -что
дескриптивная теория множеств в этом пространстве становится особенно простой
■ стройной. Употребляемый Н. Н. Лузиным термин „область тп измерений4*
^«,«1 х относится только к расположению области <& х в евклидовом
пространстве, а не к размерности этой области. Следует отметить, что, используя
области of~%aaX % лежащие в евклидовых пространствах нескольких измерений,
Н. Н. Лузин достигает чрезвычайно большой геометрической ясности при
исследовании очень сложных вопросов теории множеств.
[5| Бар дал первоначально классификацию функций, определенных на евклидовой
прямой. Н. Н. Лузин рассматривает здесь функции, определенные на & х. Классы
Бэра для таких функций определяются следующим образом. Функции,
непрерывные на е?в> принадлежат к классу 0. Функция принадлежит к классу в, если она
не принадлежит ни к какому классу <*'<<*, и является пределом сходящейся на
<?х последовательности функций классов < а:
/W = lim/,W; el/,(*)<».
Изучая функции, определенные на области <&х% естественно потребовать, чтобы
эти функции принимали только иррациональные значения, т. е. рассматривать
отображения области о?х в область ofy. Тогда кривая, изображающая функцию
g=f(x)% содержится в области <з7«у. Лебеговскими множествами для функции f(x)
называются множества [/(*)> г] н [fix) <г] тех точек оси ОХ% где выполняются
неравенства соответственно /(лг)>г или f(x)<^r% причем г — рациональное
число.. Если функция f(x) принадлежит к классу а классификации Бэра, то
ее лебеговские множества являются измеримыми В множествами класса а,
и обратно (см. Ляпунов, /^-функции. Успехи матем. наук, V, вып. S (39), ПО
1950).
[б] Понятия математики в силу своей абстрактной природы, вообще говоря, являются
законными и осмысленными в определенном круге вопросов при соблюдении
КОММЕНТАРИИ К РАБОТАМ Н. Н. ЛУЗИНА
727
определенных предпосылок. Вне этих условий эти понятия могут становиться
фиктивными и терять смысл. Это относится, в частности, к понятию
существования математического объекта. Н. Н. Лузин относится критически к
утверждению существования тех объектов, которые порождаются принципом произвольного
выбора, и также к тем, в основе которых лежит утверждение о существовании
всех трансфинитных чисел второго и тем более высших классов.
По существу, мы здесь имеем дело с гносеологическими трудностями, которые
порождает идея актуальной бесконечности, выраженная в теоретико-множественной
форме. Трудности эти наиболее ярко выражаются в вопросах, связанных с
принципом выбора и совокупностью всех трансфинитных чисел хотя бы только второго
класса.
В своих трудах Н. Н. Лузин постоянно вскрывал и анализировал указанные
трудности. В этой книге он также неоднократно возвращается к этому анализу.
(7] Элементы класса 2 были изучены П. С. Урысоном и П. С. Александровым (Math.
Annalen. H. 1, 1927). Бэр указал конструкцию элемента класса 3 (Acta Math.,
30, 1950). Л. В. Келдыш показала, что элементы, построенные Бэром, являются
каноническими („О гомеоморфности канонических элементов третьего класса",
Мат. сборник, 41, 2, 1934). Канонические элементы класса Ка найдены Л. В.
Келдыш. Оказалось, что в каждом классе /Св, а > 2 есть один род канонических
элементов. Они между собой гомеоморфны, топологически инвариантны,
и каждый элемент класса Ка есть сумма одного канонического элемента класса Кл
и не более чем счетного множества элементов классов <^а (см. Л. В. Келдыш.
Структура В-множеств. Труды Мат. ин-та им. В. А. Стеклова АН СССР, XVII,
1944).
[8] Канонические элементы класса 2 рода 1° гомеоморфны каноническим элементам
рода 2°, как показали П. С. Александров и П. С. Урысон (Math. Annalen, H. 1,
1927). Поэтому топологически эти два рода эквивалентны. Заметим, что
канонические элементы класса 2 гомеоморфны области <з7 и, следовательно, гомеоморфны
некоторым множествам класса 0 и некоторым множествам класса 1. Это
происходит в силу того, что сама фундаментальная область <& есть абсолютное G$,
которое не есть Fg. Для а > 3 элементы класса Ка топологически инварианты,
как показал М. А. Лаврентьев (Fund. Math., VI, 1924).
Если объединить в один род канонические элементы рода 1° и рода 2° и назвать
каноническим элементом класса 2 элемент класса 2, который получается
выбрасыванием из совершенного множества Р всюду плотной на Р суммы счетного
множества нигде не плотных на Р замкнутых множеств, то имеет место
следующее: каждый элемент класса 2 является суммой! одного канонического
элемента класса 2 и одного множества класса о < 1.
Заметим, что для случая а > 2 в настоящее время доказано более слабое
утверждение. Именно: каждый элемент) класса а, а>2 является суммой одного
канонического элемента класса а и не более чем счетного множества множеств
классов <а (Л. В. Келдыш. Структура В-множеств. Труды Мат. ин-та
им. В. А. Стеклова АН СССР, XVII, 1944). Вопрос о возможности
представления произвольного элемента класса а в виде суммы одного канонического
элемента класса а и одного множества класса < а остается открытым до настоящего
времени.
[9] Для того чтобы существовала иррациональная точка £, общая всем тс»п, достаточно,
чтобы каждая порция 7tm была высечена из соответствующего определяющего
множества при помощи интервала Бэра, что, очевидно, всегда возможно.
[10] Доказательство достаточности можно провести значительно проще: часть Е%
принадлежащая произвольному совершенному множеству Р, содержит первый
элемент £ft. Пусть rcft — порция /\ отделяющая ^ от всех остальных точек
728
КОММЕНТАРИИ К РАБОТАМ Н. Н. ЛУЗИНА
множества Е • Р. В порции тг- найдется порция 1?д множества Р, не содержащая
точки ^ и, следовательно, целиком принадлежащая к СЕ, Следовательно, Е есть
множество класса < 1.
[11] Когда х пробегает интервал Бэра Д, то t пробегает часть 7\ заключенную
в соответствующем интервале Бэра о. Но эта часть Т получается выбрасыванием
из о счетного множества интервалов Бэра Ь'. Когда t пробегает о', то функция Fi (t)
пробегает часть Е% класса < а. Так как функция F% регулярна, то часть Ей
которую пробегает Fi (t)% когда t пробегает 7\ получается выбрасыванием из
части Е%% которую пробегает Fi(t)4 когда t пробегает все Ъ, всех частей Е%у
которые пробегает Fi(t)% когда t пробегает все о'. Отсюда следует, что когда
/ пробегает множество 7\ то каждое F%(t)% а значит и F(t)4 пробегает либо
множество класса <[<*, либо множество базы 2?а, либо элемент класса а.
[12] Речь идет о построении трансфинитной функции, которая каждому
трансфинитному числу а ставила бы в соответствие пересчет 1 всех трансфинитных
чисел, меньших а. Автор говорит о невозможности построения такой функции
без аксиомы Цермело. Термин „данное число аи употребляется автором в том
смысле, что число а задано каким-то законом, так что вместе с ним дан пересчет
всех чисел, меньших а.
[13] Заметим, что здесь доказано существование сколь угодно высоких подклассов*
но не доказано существование всех подклассов. На самом деле, не все подклассы
существуют. Легко видеть, что если трансфинитное число (3 имеет вид р' •+- пу
где п — конечное число, большее 1, п > 1, то подкласса Р не существует, так
как множество, которому при некотором разложении в рассеянную
последовательность элементов класса о соответствует число (3, можно представить в виде
рассеянной последовательности, которой соответствует число {З'-t-l. Для этого
достаточно объединить сумму элементов %'+1 "+" "Чрч-г "•" ••• ~*~ %'+и в °ДИН эле"
мент ф3'+ь
[14] Употребляемое автором название „аналитическое множество" не является
общеупотребительным. В литературе эти множества известны под названием
А-множеств или суслинских множеств, ^-множествами называются множества,
которые могут быть получены, исходя из интервалов при помощи некоторой
теоретико-множественной операции, носящей название Л-операции. Впоследствии было
выяснено, что Л-операция над интервалами пространства <з/х эквивалентна
операции непрерывного отображения пространства о?х- Л-операция была введена
П. С. Александровым (Comptes Rendus, 323t 1916). П. С. Александров показал,
что всякое ^-множество, лежащее в о?х* может быть получено при помощи
Л-операции над интервалами, и использовал это для доказательства теоремы
о мощности ^-множеств. Затем Н. Н. Лузиным был поставлен вопрос: можно ли
при помощи Л-операции над интервалами получить множества, которые не
являются .S-множествами? Суслин дал утвердительный ответ на этот вопрос,
показав, что существуют А-множества% которые не являются В-множествами*
[15] Легко заметить, что элементарное множество Е есть замкнутое множество
в пространстве <& хул так как каждая сумма Sn состоит на параллелепипедов Бэра
одного порядка, и, следовательно, дополнение к Sn есть сумма параллелепипедов.
Бэра того же порядка, т. е. Sn есть множество класса 0. Следовательно, Е есть,
самое большее, элемент класса 1 в пространстве <^ху% т. е. замкнутое в <&ху
множество.
(16] Это легко доказать по индукции. Если S — множество класса 0, то это
непосредственно следует из теоремы Лебега, Пусть теперь утверждение верно для
всех аг<<х и S—множество класса а. Тогда & = lim &п% причем £п—множества
КОММЕНТАРИИ К РАБОТАМ Н. Н. ЛУЗИНА
729
класса <<*. Тогда, по условию, прообраз множества €п • Q, где Q — множество
значений функции /, измерим В. Но прообраз множества & • Q есть предел
прообразов £я • Е:
/-1 (S ■ Q) =/-l [lim <?„ • Q] = lim f-\ (<£„ . Q).
и, следовательно, есть также множество, измеримое В.
[17] См. П. С. Новиков. Sur les fonctions implicites mesurables В. Fund. Math.,
XVII, 1931.
[18] Первоначально аналитические множества, или иначе Л-множества, были
определены при помощи введенной П. С. Александровым Л-операции над системой
множеств, когда эти множества являются порциями пространства <з?х я. #
Л-операция может быть произведена над счетной системой множеств
произвольной структуры и определяется следующим образом. Пусть дана счетная система
множеств, занумерованных при помощи конечных кортежей индексов
где &=1, 2, ... до бесконечности и для каждого k% л^ = 1, 2. . . до
бесконечности. Система (Еп „А называется А-системой.
Множества Еп с одним индексом называются элементами А-системы первого ранга,
и вообще множества Enn^ n с к индексами называются элементами ранга к.
Если кортеж множества En n n получается присоединением одного индекса
п]С+1 к кортежу множества Еп ...„.» то элемент Еп ^ пп называется
подчиненным элементу Еп п п . Последовательность элементов А системы
я,* щпг♦ »х»»ая^» * * * ^пхпг , . . п^% *^пхпг . . Я£Я^+1* • • •» ^А/
каждый последующий из которых подчинен предыдущему, называется цепью».
Множество называется результатом А-операции над системой {Еи ъ .. ,пи}>
если оно определяется равенством
где сумма ^\ берется по всем возможным цепям (1). Таких цепей, очевидно,
континуум. В том случае, когда все множества Еп „ я являются параллелепипедами
Бэра пространства о?'% v х , множество 2Г, которое является результатом
операции над системой (1), называется А-множеством, Покажем, что А-множества
тождественны с аналитическими множествами* Для этого мы покажем, что
Л-операция над системой параллелепипедов Бэра ^П1пг...пк в области ^*,г, ...*т
эквивалентна операции проектирования в область &%%%л% %% л лежащего в
пространстве области <^«-. ~ и элемента класса 2 классификации Бэра. Действи-
тельно, пусть дана система параллелепипедов Бэра области ^XiTt z
\\"i... »'fc/
н множество Е является результатом Л-операции над этой системой. Каждому
элементу первого ранга оя мы поставим в соответствие т -+- 1-мерный
параллелепипед 7iWi в области ^^...х^у так' чтобы проекции кщ в область <2?'ад Хт
совпадали с Ьп , а проекции параллелепипедов пп на ось OY были интервалами
Бэра области е?у и не пересекались между собой. Параллелепипеды те^
называются, параллелепипедами первого ранга» После того как построены m-н
1-мерные параллелепипеды Kfl n ран*а к, соответствующие параллелепипедам
730
КОММЕНТАРИИ К РАБОТАМ Н. Н. ЛУЗИНА
^п п. я ранга &, т -и 1-мерные параллелепипеды г.п ранга к •+• 1 строятся
следующим образом:
Iе все параллелепипеды ъп ^ я , соответствующие параллелепипедам о nfcn^ >
подчиненным Б„ , содержатся в параллелепипеде т: # ^ я , соответствующем
2° проекции на ось OY параллелепипедов
Кщ...пк\* */!,.. «fc2 *W| ..nj^fc+i' "••
являются интервалами Бэра в области <&у и попарно не пересекаются; лежащее
в области <^ХК х „ множество £, определенное равенством
*=П 2 *..л....к. <3>
является, очевидно, элементом класса 2 классификации Бэра.
Легко видеть, что проекция множества 6{ в области <?х.т х совпадает с
множеством Е, которое является результатом Л-операции над системой |ЬЯ \
Действительно, каждой цепи
м,' w,n2» * * *♦ ЩЩ • • • nk* м«я* • • • nknk+^' * * *
соответствует убывающая последовательность параллелепипедов
^л* —^ ^jfa* * * * ^"iM» • • • nfc* r"inJ • • • nfcnfc+l • • •»
и обратно, причем Ьп ^ п есть проекция в область &rXix7...xmy
параллелепипеда 7tn п . Следовательно, множество Е есть проекция множества £ и, значит,
результат Л-операции над системой (Ьп п ^ \ тождественен с результатом
проектирования множества, измеримого В% следовательно, Е—аналитическое
множество.
Обратно, если Е есть аналитическое множество, определенное как проекция
множества <£, заданного равенством (3), то мы немедленно построим Л-операцию,
определяющую Е, Для этого достаточно каждому параллелепипеду пп ^ ^ ^ в
области ^XZa...*my поставить в соответствие его проекцию &я ^ в область
^ад ..х,» и считать, что элемент \nt... пр^ подчинен *„,»,... nfc, если
4«i.. • Vk-и с°ДеРжится в *„,«,... v Очевидно, что Л-система (о^ # # ^}
определяет множество £, которое является проекцией S.
Геометрическая форма определения Л-множества, введенная Н. Н. Лузиным,
оказалась чрезвычайно плодотворной при изучении множеств, лежащих в евклидовом
пространстве, так как она позволяет пользоваться геометрическими образами.
Следует, однако, отметить, что первоначальная форма определения Л-множества
при помощи Л-операции, данная П. С. Александровым и определенная
формулой (2), дает возможность изучать не только множества, лежащие в
пространствах Евклида, но также и множества, лежащие в абстрактных пространствах.
[19] М. Я. Суслив аля определения Л-множества пользовался Л-операцней. Другие
способы задания Л-множества были найдены позже.
Суслин непосредственно доказал сформулированную теорему. Данное в тексте
доказательство принадлежит Н. Н. Лузину и дано значительно позже, когда им было
введено понятие об отделимости и доказан первый принцип отделимости В для
Л-множеств.
КОММЕНТАРИИ К РАБОТАМ Н. fi. ЛУЗИНА
731
120] Нельзя согласиться с Н. Н. Лузиным, приписывающим Лебегу открытие
Л-множеств.
-4-множества, которые Н. Н. Лузин называет аналитическими, Лебегу в то время не
были известны и были открыты Суслиным, исходя из Л-операции, построенной
П. С. Александровым (см. [14]). Позднее, когда Л-множества были уже известны,
анализируя построенный Лебегом (Journ de Math., 1905), пример множества,
неизмеримого В, которое отнюдь не является Л-множеством, Н. Н. Лузин показал,
что из этой конструкции можно извлечь решето и определенное им Л-множество.
Это решето Н. Н. Лузин и называет „бинарным решетом Лебега", а
определенное им Л-множество — первым примером ^-множества.
121] Природа поверхности Лебега была изучена Нейманом и Куратовским. Оказалось,
что эта поверхность представляет собой проективное множество второго класса,
точнее — пересечение Л-множества и дополнения к -4-множеству.
[22] Доказательство Н. Н. Лузина теоремы о сравнении решет, изложенное в
следующем параграфе оригинала книги, содержит неточность. В самом конце
доказательства автор, используя построенную им в предыдущем параграфе систему
кривых L%% приписывает ей более сильное, чем ей присуще, свойство
универсальности, которым она не обладает. С целью исправления этого доказательства мы
вводим в текст этот параграф, отмеченный звездочкой. Полностью сохраняя идею
автора, изложенную в предыдущем номере, н лишь вводя необходимые
технические усложнения, мы строим систему кривых £% ' " , удовлетворяющих
требуемому условию. После этого доказательство следующего параграфа сохраняется
почтя полностью. Небольшие изменения, введенные нами в тексте следующего
параграфа в связи с заменой кривых автора Ln на кривые LJ,1 * * * *&", отмечены
в тексте звездочками в начале и в конце. Весь остальной текст следующего
параграфа является точным переводом с оригинала книги.
123] См. П. С. Новиков. Sur les fonctions implicites mesurables В. Fund. Math.,
XVII, 1931.
(24] Здесь доказательство содержит небольшую неточность. Построенная система
параллелепипедов tcj, 7ilf . . ., тг^, ък еще не удовлетворяет требуемым свойствам.
Пока доказано только, что, каково бы ни было трансфинитное число 7» суще-
ствует такая точка х и такая система параллелепипедов nv к1% . . ., кк% rfc, что
прямая Рх содержит несчетное множество точек на каждой из конституант Ъ^
Ьг'\ 1 = 1, 2, . . ., &, причем индексы всех этих конституант превосходят Т.
' ' " ' " я
Точка х и система параллелепипедов ъ1% т^, . . ., пк, т.к зависят от числа *[. Для
того чтобы выбрать требуемую систему параллелепипедов, достаточно заметить,
■что различных чисел f — несчетное множество, тогда как различных систем
параллелепипедов k'v т^', . . ., **, Кц существует лишь счетное множество.
Поэтому среди этих систем параллелепипедов найдется такая, которая
соответствует несчетному множеству различных чисел 7- Эта система, очевидно, уже
обладает требуемым свойством.
125) Термины „аналитическое множество" порядка п и „аналитическое дополнение*
порядка п не привились. В литературе употребительны термины проективное
множество класса (Ап) и проективное множество класса (САП).
[26] Оба эти вопроса решены отрицательно для п = 2 в работе: К о n d о. L'unifor-
misation des complementaires analytiques, Proc. Imp. Acad. Tohoku, ХШ, 1937.
Кондо доказал следующую теорему: всякое проективное множество класса {А2)
или (В2) есть проекция однозначного аналитическою дополнения. Эта теорема
732
КОММЕНТАРИИ К РАБОТАМ Н. Н. ЛУЗИНА
получена как следствие следующей теоремы: Каково бы ни было плоское С А-
множество Е, в нем содержится такое однозначное СА-множество S
SdE,
что проекция S на ось ОХ совпадает с проекцией Е.
[27] Вопрос о покрытии однозначного плоского множества класса (А2) однозначным
плоским множеством класса (В2) решается отрицательно. Это непосредственно-
следует из теоремы П. С. Новикова о существовании двух непересекающихся
множеств класса А2 неотделимых посредством множеств класса В2. (П. С. Н о-
в и к о в. Sur la separabilite des ensembles projectifs de seconde classe. Fund. Math.,
XXV, 459—466, 1935). В самом деле, пусть Ег и Е2 — два непересекающихся
множества класса (А2), неотделимых посредством множества класса (В2). Пусть,
далее, 6 — плоское множество класса (А2)% лежащее в области <Рху и состоящее
из множества £1э положенного на прямой у = ^1% и множества Е2, положенного-
на прямой у = т}2» li <С ^2 и ll и Т\2 иррациональны. Очевидно, что S —
однозначное относительно оси ОХ плоское множество класса (А2). Покажем, что S нельзя
покрыть однозначным множеством класса (В2). Действительно, если бы это было
возможно, то существовало бы плоское множество Н класса (#2), однозначное
относительно оси ОХ и содержащее £. Пусть Н\ — пересечение Н с прямой.
у = т\1% а Н2 — пересечение Н с прямой у = т\2. Очевидно, что
^СЯ1И£2С И2
и оба множества Н^ и Н2 являются множествами класса (В2). А так как
множества Е и Е неотделимы посредством (BJ» то найдется прямая Р.. ,
параллельная оси OY, пересекающая как //1% так и Н2. Но //х и Н2 принадлежат к Н,
следовательно, прямая Рх пересекает Н в двух точках, и, значит, множество Н
не однозначно относительно оси ОХ, вопреки предположению. Итак, мы показали,
что существует однозначное плоское множество класса (А2), которое нельзя
покрыть однозначным плоским множеством класса {В2).
Совершенно так же можно показать, что существует плоское С А-множество,
однозначное относительно оси ОХ, которое нельзя покрыть множеством,
измеримым В, однозначным относительно оси ОХ.
Для п^>2 вопрос не решен в классическом смысле.
Исследование проективных множеств более высоких классов связано, как указывал.
Н. Н. Лузин (см. заключение) с трудностями, по-видимому, не преодолимыми
методами теории множеств. Большинство проблем здесь нельзя решить в
классическом смысле, т. е. дать положительный или отрицательный ответ на
поставленный вопрос. Но тогда можно ставить вопрос о непротиворечивости того или
иного утверждения теории множеств (см. предисловие). Такая задача может
решаться методами математической логики. П. С. Новиков показал, что
непротиворечиво предположение, что существует число Д/>2 такое, что для
всякого л > N существуют два множества класса (Ап)% неотделимые посредством
множеств класса (Вп). Отсюда, рассуждая так же, как для п = 2, заключаем,
что непротиворечиво предположение^ что для всякого п > N существует
однозначное плоское множество класса (Ап), которое нельзя покрыть однозначным:
плоским множеством класса {Вп).
Все остальные поставленные 'вопросы остаются открытыми даже для случая л = 2.
[28] Для п—2 отрицательный ответ на этот вопрос непосредственно следует из.
теоремы Кондо (см. примечание [26]). Именно: Каждое множество класса {А2)
допускает регулярное- параметрическое изображение. Действительно, пусть Е
есть линейное (А%\% лежащее в области в7ш,- В силу теоремы Кондо Е есть про-
КОММЕНТАРИИ К РАБОТАМ Н. Н. ЛУЗИНА
733
екция однозначного СЛ-множества <?, лежащего в области <&ху. Пусть теперь
функции
* = ?(*). # = <М>).
t = G(x, у)
осуществляют гомеоморфное отображение области о7Хч на область <з7/. Образ &'
множества S при этом отображении есть линейное СЛ-мн<>жество, лежащее в
области о/1. При этом в силу однозначности £ разным значениям t из множества S'
соответствуют разные значения д:, и х пробегает множество £, когда г пробегает
множество 6'. Следовательно, функция jr = <p(f) осуществляет регулярное
параметрическое изображение множества Е.
Для п > 2 вопрос остается открытым.
(29] Это рассуждение предполагает» что существуют множества (САп^ и (An—rf.
Доказательство этого факта изложено в одном из последующих параграфов
текста. Множества же (Вп) являются по определению одновременно РС.РЬ и
СР...Р0', где операция Р употреблена ровно п раз.
Чтобы показать, что Е есть (Вп), покажем, что оно есть одновременно проекция
(СЛ„__i) и дополнение к проекции (САп—{). Выберем в области <&%у проективное
множество 6' класса п — 2, проекция которого в оТ'х совпадает с Е\. Множество
S' -+- E<i есть, очевидно, плоское (CAn—i)% и проекция его в <Рх совпадает с Е.
Следовательно, Е есть проекция (С4„—{). Теперь покажем, что Е есть также
дополнение к проекции (€Ап—{). Для этого достаточно показать, что СЕ есть
проекция (СЛЯ_!). Выберем плоское проективное множество 8" класса п — 2,
проекция которого в о/% совпадает с разностью
и рассмотрим множество (0, -о") — Е\-+-S". Это, очевидно, плоское {САп—{).
Проекция его в &х% очевидно, совпадает с дополнением к Е относительно (0, 1).
Следовательно, Е есть дополнение к проекции (САп—\). Итак, Е есть
одновременно проекция (CAn—i) и дополнение к проекции (CAn—i)% следовательно,
Е есть (Вп).
[30] Этот вопрос решается отрицательно: в каждом классе п проективных множеств
существуют множества класса (#я), которые нельзя получить, исходя из множества
класса п — 1 счетно-кратным применением операций суммы и пересечения
(см. Л. В. Канторович и Е. М. Ливенсон. Memoir on the analytical
operations and projective sets. Fund. Math., XVIII, 1932 и XX, 1933). He только
применением операции пересечения и суммы, но и счетно-кратным применением
Л-операции и операции взятия дополнения, исходя из множеств класса п — 1
нельзя исчерпать всех множеств класса Вп. А. Н. Колмогоровым были
определены новые, более сложные операции над множествами: ^-операции, частным
случаем которых является Л-операцня. Эти операции изучены Ливенсоном и
Канторовичем в упомянутой статье и А. А. Ляпуновым в статье „^-множества"
(Труды Мат. ин-та им. В. А. Стеклова АН СССР, XL, 1953). Множества,
которые могут быть получены, исходя из множеств, измеримых В при помощи /?-опе-
рации, повторенной счетное множество раз, носят название ^-множеств. А. А.
Ляпунов показал, что ^-множества разбиваются на Hj классов. Все С-множества,
(получаемые яз множеств, измеримых В счетно-кратным применением Л-операции
и операции взятия дополнения) входят в первый класс /^-множеств. А. Н.
Колмогоров и А. А. Ляпунов показали, что все /^-множества измеримы и входят
734
КОММЕНТАРИИ К, РАБОТАМ Н. Н. ЛУЗИНА
в класс (В2). П. С. Новиков показал, что предположение о существовании-
в классе (В2) неизмеримого множества не может привести к противоречию („О
непротиворечивости некоторых положений дескриптивной теории множеств". Труды
Мат. ин-та им. В. А. Стеклова АН СССР, XXXVII, 31S, 1951, теорема 4). Отсюда
следует, что невозможно доказать, что R множества исчерпывают класс (В2).
Точнее: непротиворечиво предположение, что в классе (Во) содержится множество,
ие входящее в класс /^-множеств.
[31] Положительный ответ на первый из поставленных вопросов следует из теоремы
Кондо (см. [26]). Что же касается до распространения теоремы Мазуркевича на
проективные множества высших классов, то для случая п = 2, как уже указано, имеется'
более сильная теорема — теорема Кондо.! Для случая же п > 2 вопрос сводится
к проблеме о структуре однозначного множества, которое можно выделить из
плоского множества класса (САп—\) так, чтобы проекция его в о7х совпадала
с проекцией данного (САп—\)- Однако едва ли можно надеяться на решение этой
задачи в классическом смысле.
(32] В классическом смысле эта проблема не решена. Как указывает Н. Н. Лузин
(стр. 246), эта проблема, по-видимому, принадлежит к числу тех проблем,
решение которых в рамках теории множеств невозможно. Привлекая методы
математической логики, можно ставить вопрос о ее непротиворечивости. П. С. Новиков,
доказал непротиворечивость утверждения, что существует проективная
функция f(x) однозначная, всюду определенная и такая, что изображающая ее
кривая L есть СМ^множество, не содержащее совершенного множества (П. С.
Новиков. О непротиворечивости некоторых положений теории множеств. Труды
Мат. ин-та им. В. А. Стеклова АН СССР, XXXVIII., 1951, теорема 2). Заметим,,
что кривая t^=ri(y) П. С. Новикова есть проективная кривая класса (А2),
Однако из нее немедленно извлекается и СЛ-кривая L. Для этого достаточно
заметить, что кривая t = vi(y)4 лежащая .в плоскости e^ty* есть проекция
однозначного относительно <?ty Сл4-множества Z/, лежащего в пространстве <?tys-
Множество L представляет собой пространственную кривую, которая является
С/4-множеством и определена для всех значений у области <7у. Чтобы получить
плоскую кривую L% достаточно гомеоморфно отобразить пространство <&tyg на
пространство <&ty при помощи преобразования
у = д% t=G(t% z).
Кривая П. С. Новикова t=^ri(y) строится средствами классической теории
множеств. Но для доказательства непротиворечивости предположения, что эта кривая
не содержит совершенного множества, он опирается на результат Гёделя о
непротиворечивости континуум-гипотезы (см. Гедель. Совместимость аксиомы
выбора и обобщенной континуум-гипотезы с аксиомами теории множеств,
пер. В. А. Маркова. Успехи мат. наук, Ш, вып. 1 (23), 1948). Поэтому
дальнейшие заключения Н. Н. Лузина о выводимости континуум-гипотезы из
отрицательного решения указанной проблемы здесь теряют смысл.
[33] Из теоремы Кондо (см. примечание [26]) непосредственно следует, что каждое
множество £ класса (^2) можно рассматривать как просеянное при помощи
счетного решета (СА). Для этого достаточно в каждой полосе (—<^У <С __ 1 ]
области <з/Лу поместить однозначное СА множество Ещ проекция которого в
область o7<t совпадает с £. Множество S просеяно при помощи плоского решета (СА)
Е = Ei -+- Е2 •+• ... -н Еп ■+■ ... .
Что же касается до рассеивания при помощи прямолинейного решета С,
составленного из (В2) множеств, или, что то же, ^операции над. множествами класса (В2)%
КОММЕНТАРИИ К РАБОТАМ Н. Н. ЛУЗИНА
73S
то, как показали Канторович и Ливенсон, она всегда приводит к множествам
класса (£2) (см- Kantorovitch and L i v e n s о п. Fund. Math., XVTO и XX).
Множества, которые получаются из А- и С А- множеств при помощи
счетно-кратного применения Л-операции и операции взятия дополнения, носящие название
С-множеств, были введены А. Н. Колмогоровым. Им же независимо от £. А. Се*
ливановского были доказаны их измеримость и наличие свойства Бэра. Однако
работа А. Н. Колмогорова осталась неопубликованной. Она будет опубликована
в журнале „Успехи мат. наук".
[34] Результаты Конторовича и Ливенсона опубликованы в статье „Memoir on the
analytical operations and projective sets" (Fund. Math., XVIII, 1932 и XX, 1933).
[35] Проблема об отделимости проективных множеств второго класса была решена
П. С. Новиковым („Sur la separabilite des ensembles projectifs de seconde classe".
Fund. Math., XXV, 459—466, 1935). Законы отделимости здесь оказались обра*
щенными, т. е. они получаются из законов отделимости1 для Л-множеств, если
заменить ^-множества через С^-множества, а С А множества через Ау
множество. Основные принципы отделимости во втором классе проективных множеств
формулируются так:
Теорема I. Два множества класса (СА.}) без общих точек всегда отделимы при
помощи двух множеств класса (£2).
Теорема II. Если удалить из двух множеств (СА2) их общую часть, то
оставшиеся части отделимы при помощи А^множеств.
Теорема III. Если удалить из двух множеств (А?) их общую часть, то
оставшиеся множества отделимы при помощи множеств (Лг).
Теорема IV. Существуют два множества (А2) без общих точек, неотделимые
при помощи множеств (#2).
Для случая п > 2 в классическом смысле ничего не доказано. Однако П. С. Новиков
показал, что непротиворечиво предположение, что л^я всех л, больших
некоторого TV, в /z-м классе проективных множеств принципы отделимости такие же,
как и во втором классе (т. е. обращенные по отношению к классу Л-множеств}
(см. Новиков. О непротиворечивости некоторых положений дескриптивной
теории множеств. Труды Мат. ин-та им. В. А. Стеклова АН СССР, XXXVIII,
1951).
[36] Метод индексов, на который здесь ссылается автор, есть не что иное, как
первоначальный способ задания ^-множеств при помощи Л-операции (см. [18]).
[37] Термин „отображение на континуум" некоторого семейства множеств (или
функций) был введен Лебегом (Journ. de Math., 206—207, 1905). Семейство множеств,
допускающее отображение на континуум, есть, следуя Лебегу, семейство F
точечных множеств, для которого можно установить взаимно однозначное
соответствие между элементами семейства и точками отрезка [0, 1]. Для этих семейств
методом диагонали Кантора может быть доказано существование множества,
не принадлежащего к F»
[38] Нельзя согласиться с Н. Н. Лузиным, приписывающим Лебегу идею проектиг»
ного множества» Лебег, действительно, впервые употребил операцию
проектирования при изучении неявных функций, определенных при помощи функций
классификации Бэра в Journ. de Math., 1905. Здесь, на стр. 191, Лебег делает
неверное утверждение, что „проекция ^-множества есть /^-множество". Затем
Суслин показал (Comptes Rendus, 1917), что всякое А-множество есть
проекция некоторого В-множества, и что существуют А-множества,
неизмеримые В. После этого в статье в Ann. de Г Ecole Norm, super., 242, 1918, Лебег
указывает различные операции, при помощи которых можно, отправляясь от
множеств, измеримых В, назвать множество, неизмеримое В. В числе
736
КОММЕНТАРИИ К РАБОТАМ Н. Н. ЛУЗИНА
этих операций он указывает и операцию проектирования, опираясь на указанный
результат Суслина.
Характерно, что в числе операций, указанных Лебегом, нет операции
взятия дополнения к множеству. Между тем, в определении проективных множеств,
которое принадлежит Н. Н. Лузину, существенную роль играет именно
чередование операции проектирования с операцией взятия дополнения.
Открытие проективных множеств явилось результатом изысканий Н. Н.
Лузина, направленных на то, чтобы найги класс множеств, которые можно назвать
(в смысле Лебега), но для которых нельзя было бы средствами теории множеств
решить проблему их измеримости, категории и мощности. Операции взятия
дополнения Н. Н. Лузин придавал здесь большое значение как операции,
определенной чисто отрицательно (см. статью „О проблеме Бореля и методе
резольвент", стр. 312 этого тома). Независимо от Н. Н. Лузина и почти одновременно
к определению проективного множества в несколько иной форме пришел Сер-
пинский.
[39] Предположение Н. Н. Лузина о невозможности доказать измеримость
проективных множеств в настоящее время полностью оправдалось. Именно, П. С.
Новиков построил проективное множество класса (52), относительно которого
непротиворечиво утверждение, что оно неизмеримо (П. С. Новиков. О
непротиворечивости некоторых положений дескриптивной теории множеств. Труды Мат.
ии-та им. В. А. Стеклова АН СССР, XXXVIII, 315, 1951, теорема 4). Отсюда
следует, что невозможно доказать измеримость проективных множеств. Однако
вопрос о возможности доказательства методами теории множеств существования
неизмеримого проективного множества в настоящее время еще остается открытым,
так как пока не доказана непротиворечивость утверждения об измеримости
проективных множеств.
[40] В данном случае Н. Н. Лузин ошибся. Лебеговский выбор по одной точке
на каждой параллели оси OY из плоского СМ-множества осуществляется в силу
теоремы Кондо (см. [26]).
[41] Предполагается, что f (х) есть функция, характеристическая для множества всех
точек, которые изображаются непрерывными дробями, у которых совокупность
неполных частных <*i, a2% . . ., а„, ... образует составную последовательность
натуральных чисел.
[42] Трудности, связанные с определением функции / в рациональных точках, сильно
загромождают изложение в атом мемуаре. В „Лекциях об аналитических
множествах" Н. Н. Лузин освободился от этих трудностей, рассматривая множества,
лежащие на совокупности всех иррациональных точек прямой или точек п. мерного
пространства, все координаты которых иррациональны.
[43] Вопреки предположению Н. Н. Лузина о невозможности указания метода для
выбора точки в дополнении к Л-множеству, такой метод был впоследствии
указан П. С. Новиковым (см. статью Н. Лузина и П. Новикова „Эффективный
выбор точки из произвольного аналитического дополнения, заданного посредством
решета", стр. 617 настоящего тома).
[44] Легко заметить, что все множества [е] в п.59 являются проекциями частей
решета С, полученных в процессе последовательного отбрасывания нижних точек
у множеств /?<t» если такие точки есть. Поэтому дополнение к [е] и есть
множество тех точек, для которых соответствующие Rx не превосходят W^. Каждое
множество еа есть разность двух множеств [е] и [е'], где элемент е'
непосредственно следует за е. Следовательно, еа измеримо В.
[45] В классическом смысле эта проблема не решена. П. С. Новиков построил
множество-£, дополнительное к Л-множеству, для которого непротиворечиво пред-
КОММЕНТАРИИ К РАБОТАМ Н. Н. ЛУЗИНА
737
положение, что оно не содержит совершенного подмножества (см. П. С. Н о в и-
ков^О непротиворечивости: некоторых положений дескриптивной теории множеств.
Труды Мат. ия-та им. В. А. Стеклова АН СССР, ХХХУП, 1951).
(46] Для построения U' рассмотрим в плоскости YOZ построенный выше
универсальный, элемент Е класса 1, т. е. плоский элемент класса 1, который пересекается
с прямыми, параллельными оси OZ по всевозможным линейным замкнутым
множествам (см. стр. 109). Обозначим через Егхгг часть множества Е+ заключенную
в полосе (r!<z<r2), а через егхгг множество тех точек М области <з7у% для
которых прямая Р*и% проходящая через М параллельно оси OZ% пересекает Егг
не более чем в одной точке. Все множества еГГщ являются аналитическими
дополнениями (стр. 218). Рассмотрим множество.
H=CPE+J\err -PErr,
Легко видеть, что Н есть множество всех тех точек М области «з^у, в которых
прямая Р^ либо вовсе не пересекает множества Е, либо же пересекает его по
множеству, содержащему хотя бы одну изолированную точку, т. е. несовершенному.
Так как все множества РЕ„Г аналитические, а е_„ —аналитические дополнения,
то множество Н есть либо множество класса (A%\% либо (£2), либо проективного
класса 1. Пусть теперь Н — множество всех точек области &yj% проекция
которых в с?^ принадлежит к И, Очевидно, что И' есть либо (Ло), либо (В2), либо
проективного класса 1. Положим теперь
1Г = Е-+- #'.
Очевидно, что всякая прямая, параллельная оси OZ* пересекает U по
совершенному (в <а7ж) множеству, и что U универсально а^я всех линейных совершенных
множеств. Так как Е—элемент класса 1, а ЬГ—либо множество класса (Л2),либо (£2),
либо класса 1, то и U есть множество либо класса (Л2)» либо (52), либо класса 1.
|47] Н. Н. Лузин пользуется здесь следующим понятием достижимой точки:
точка р плоского множества F называется линейно достижимой, если
существует отрезок \pq], один конец которого есть р, а все остальные точки лежат
вне F.
(48] Гильберт заявил утверждение о непротиворечивости аксиомы Цермело и
континуум-гипотезы, ио доказательство им дано не было. Доказательство этих
утверждений принадлежит Гёделю (см. Гёдель. Совместимость аксиомы выбора
и обобщенной континуум-гипотезы с аксиомами теории множеств, пер. Маркова.
Успехи мат. наук, Ш, вып. 1 (23), 1948).
[49] Арифметические примеры множеств, измеримых В всех конечных классов и
класса се, были построены Л. В. Келдыш (Труды Мат. ин-та им. В. А. Стеклова
АН СССР, ХУП, 1944).
[SO] Л. В. Келдыш доказала существование канонических элементов класса а
(см. Л. В. Келдыш. Структура ^-множеств. Труды Мат. ин-та им. В. А.
Стеклова АН СССР, ХУП), пользуясь, однако, другим определением канонического
элемента класса а. Именно, — элемент Е класса а называется каноническим, если
любая его непустая часть, высеченная порцией, гомеоморфна Е.
Определение, данное Н. Н. Лузиными сноске на стр. 490, однако является
неудачным, так как не существует канонических элементов класса <2 в атом
смысле. Действительно, в силу известной теоремы Гуревича (Fund. Math., XVI)
для каждого СЛ-множества S не типа Gj, а следовательно, и для каждого эле-
738
КОММЕНТАРИИ К РАБОТАМ Н. Н/ ЛУЗИНА
мента класса о, а > 2, существует совершенное множество Я такое, что
пересечение Р • £ есть счетное плотное на себе множество, т. е. множество второго
класса. Такое счетное множество, очевидно, представляет собой „лишнюю часть"
в смысле определения в сноске на стр. 490. Л. В. Келдыш показала, что построен*
ные ею канонические элементы являются универсальными в следующем смысле:
если Е — канонический элемент класса a, a е—произвольное множество,
измеримое В класса <а или элемент класса а, то существует такое совершенное
множество Р, что пересечение Р • Е гомеоморфно е. Остается открытым вопрос:
не является ли универсальным каждый элемент класса а?
(51] Интересно отметить, что предвидения Н. Н. Лузина о роли единственности
разложения функций в тригонометрический ряд полностью оправдались; см. по атому-
поводу:
Н. К. Бари. Проблема единственности разложения функции в
тригонометрический ряд (Успехи мат. наук, IV, вып. 3, 38, 1949).
И. И. Пятецкий-Шапиро. Дополнение к работе „К проблеме
единственности разложения функции в тригонометрический ряд" (Ученые записки!
Моск. Университета, математика, VII, 88, 1954).
R. Salem et A. Zygmund. Sur une theoreme de Piatecki-Schapiro (Comp-
tes Rendus, 140, 2040-2042, 1955).
[52| Можно сказать в настоящее время, что дальнейшее развитие математической,
логики в какой-то мере подтверждает высказанные здесь мысли. Именно, Г еде ль.
показал, что в каждой формальной системе в смысле Гильберта, содержащей,
арифметику, возникают формальные высказывания, недоказуемые и
неопровержимые в этой системе. В частности, утверждение о непротиворечивости такой,
системы может быть записано на ее формальном языке, но не может быть
доказано ее средствами. Вместе с тем эти не разрешимые внутри формальной системы
формализованные утверждения и их отрицания не являются просто независимыми
аксиомами, подобно постулату о параллельных. Выбор между утверждением и его-
отрицанием осуществляется однозначно и доставляет новые арифметические
истины, лежащие вне рассматриваемой формальной системы. Отсюда мы можем
заключить, что арифметика во всей своей полноте не может быть формализована
в смысле Гильберта.
[53] Как выяснилось очень скоро, упомянутая работа Барзона и Эррера является
ошибочной. Дело в том, что в логике без закона исключенного третьего имеет
место теорема о невозможности терциального состояния. Вместе с тем из нее
не вытекает закон исключенного третьего.
[54] Последующее развитие вопросов основания математики показало, что и теория
Гильберта и теория Брауэра, обнаружившие весьма важные стороны в вопросах
основных взаимоотношений математики и логики конечного и бесконечного*
вместе с тем являются обе односторонними крайностями. Однако каждое из этих,
учений породило соответствующую систему взглядов и разногласия в этих двух,
направлениях не исчезли до настоящего времени.
[55] В настоящее время известно, что не существует алгоритма аля решения
известной в логике проблемы разрешимости, которую Н. Н. Лузин здесь называет
„Entscheidungsproblem Гильберта". Вместе с тем результаты, полученные в
направлении этой проблемы разными авторами, в том числе И* И. Жегалкиным*
действительно весьма важны и интересны.
J56] В классическом смысле ни одна из проблем I, II, III не имеет решения. В статье
„О взаимоотношении второго класса проективных множеств и проекций
униформных аналитических дополнений" (Изв. АН СССР, серия математ., № 2, 1937),
на стр. 241—242, П. С. Новиков доказал следующую редукцию: если существует
КОММЕНТАРИИ К РАБОТАМ Н. Н. ЛУЗИНА
739
несчетное С А-множество, не содержащее совершенною подмножества, то
существует несчетное СА-множество, все конституанты которого состоят
ле более чем из одной точки.
В статье „О непротиворечивости некоторых положений дескриптивной теории
множеств" (Труды Мат. ин-та им. В. А. Стек^ова АН СССР, XXXVIII, 1951)
П. С. Новиков доказал непротиворечивость утверждения, что существует
несчетное СА-множество, не содержащее совершенного подмножества. Отсюда,
в силу редукции, цитированной выше, следует, что непротиворечиво
предположение, что существует несчетное СА-множество, каждая конституанта
которого содержит не брлее одной точки.
157] В силу теоремы Кондо (см. [26]), разложение множества Е типа Ао на консти*
туанты эффективно, так как конституанты Е являются проекциями конституант
однозначного СЛ-множества, которое проектируется на Е.
{58] Хаусдорф рассматривал лишь отделимость замкнутых множеств или точек
посредством открытых множеств. Общее же понятие отделимости множеств введено
Н. Н. Лузиным.
(59] Исключение трансфинитного из определения поверхности Лебега было сделано
Куратовским, который показал, что поверхность Лебега есть проективное
множество (см. Comptes Rendus, 202, 1239, 1936).
{60] См. П. С. Новиков. Отделимость С-множеств (Изв. АН СССР, серия ма-
темат., № 2, 1937).
{•61] См. П. С. Новиков. О взаимоотношении второго класса проективных
множеств (Изв. АН СССР, серия математ., № 2, 1937).
{62] Этот вопрос впоследствии был решен утвердительно в работе Кондо (см. [26]
{63] При помощи аксиомы Цермело легко строится нестационарная возрастающая
последовательность счетных множеств типа F0. Так как, в силу теоремы Гёделя
(см. Гёдель. Совместимость аксиомы выбора и обобщенной
континуум-гипотезы с аксиомами теории множеств, пер. Маркова. Успехи мат. наук, Ш, вып. 1
(23), 1948), аксиома Цермело непротиворечива, то отсюда следует, что
невозможно доказать стационарность произвольной возрастающей последовательности
множеств типа F0.
{64] Хаусдорф доказал, с использованием аксиомы Цермело, что отрезок [0, 1] можно
представить в виде возрастающей последовательности *i множеств типа о§
(см. Fund. Math., XXVI, 241—255, 1938).
{65] Работа Н. Н. Лузина „Об одной проблеме Бэра" напечатана в 1914 г.,
т.* е. до открытия Суслиным Л-множеств. Характеристическая функция для
Л-множества обладает свойством Бэра и строится без аксиомы Цермело
(см. статью „Об одном множестве, неизмеримом Ви).
СПИСОК РАБОТ Н. Н. ЛУЗИНА В ОБЛАСТИ ДЕСКРИПТИВНОЙ
ТЕОРИИ МНОЖЕСТВ
Sur un probleme de M. Baire. Comptes Rendus Acad. Sci., Paris, 158, 1258—126U
1914.
Sur la classification de M. Baire. Comptes Rendus Acad. Sci., Paris, 164, 91—94,
1917.
Sur une decomposition d'un intervalle en une infinite non-denombrable d'ensemble
non-mesurables. Comptes Rendus -Acad. Sci., Paris, 165, 422—424, 1917
(совместно с В. Серпинским).
Sur une propriete du continu. Там же, стр» 498—500 (совместно с В. Серпинским)
Sur quelques proprietes des ensembles (A). Bull. Int. Acad. Sci., Cracovie, серия А
№■ 4—5'A, 35—48, 1918 (совместно с В. Серпинским).
Sur l'existense d'un ensemble non-denombrable qui est de premiere categorie dans tout
ensemble parfait. Fund. Math., П, 155—157, 1921.
Sur une decomposition du continu. Comptes Rendus Acad. Sci., Paris, 175, 357—
359, 1922 (совместно с В. Серпинским).
Sur en ensemble non-mesurable B. Iourn. de Math, pures, appl., серия 9, 2, 53—72,
1923 (совместно с В. Серпинским).
Sur un probleme de M. Emile Borel et Ies ensembles projectifs de M. Henri Lebesque;
les ensembles analytiques. Comptes Rendus Acad. Sci., Paris, ISO, 1318—1320,
1925.
Sur les ensembles projectifs de M. Henri Lebesque. Там же, стр. 1572—1574.
Les proprietes des ensembles projectifs. Там же, стр. 1817—1819.
Sur les ensembles non-mesurables В et l'emploi de la diagonale de Cantor. Comptes
Rendus Acad. Sci., Paris, 181, 95—96, 1925.
Sur le probleme de M. Emile Borel et la methode des resolvantes. Там же, стр. 279—
281.
Memoire sur les ensembles analitiques et projectifs. Матем; сборник, 33, 3, 237—290,
1926.
Sur un exemple arithmetique d'une fonction ne faisant pas partie de la classification
de M. Rene Baire. Comptes Rendus Acad. Sci., Paris, 182, 1521—1522,
1926.
Sur une question concernant la propriete de M. Baire. Fund. Math., IX, 116—118,
1927.
Sur les ensembles analitiques. Fund. Math., X, 1—95, 1927.
Remarques sur les ensembles projectifs. Comptes Rendus Acad. Sci., Paris, 185»
835—837, 1927.
Sur Taccessibilite des points. Fund. Math., XII, 158—159, 1928.
Sur un ensemble non-denombrable qui est, de premiere categorie sur tout ensemble
parfait. Comptes Rendus Acad. Lincei, 7, 3, 214—215, 1928 (совместно с В.
Серпинским).
Sur les voies de la theorie des ensembles. Atti del Congresso Internationale dei ma*
tematici, 3—10 settembre, Bologna, Zanichelli, 1, 295—299, 1929.
СПИСОК РАБОТ Н. Н. ЛУЗИНА
741
Sur le problem© des fonctions implicites. Comptes Rendus Acad. Sci., Paris, 189»
80—81, 1929.
Sur la representation parametrique semireguliere des ensembles. Там же, стр. 229—
231.
Sur les fonctions implicites a une infinite denombrable des valeurs. Там же, стр. 313—
316.
Sur nn priircipe general dans la theorie des ensembles analytiques. Там же, стр. 390—-
392.
Sur les points d'unicite d'un ensemble mesurable В. Там же, стр. 422—425.
Lecons sur les ensembles analytiques et leurs applications. Collection de monographies
sur la theorie des fonctions publiee sous la direction de M. Emile Borel. Paris»
Gauthiers-Villars, 193, 328.
Analogies entre les ensembles mesurables В et les ensembles analytiques. Fund.
Math., XVI, 48—76, 1930.
Sur le probleme de M. J. Hadamard d'uniformisation des ensembles. Comptes Rendus
Acad. Sci., Paris, 190, 349—351, 1930; то же, Mathematica, Cluj, 4, 54—66,
1930.
Sur une famille de complementaires analytiques. Fund. Math., XVII, 4—7, 1931.
Современное состояние теории функций действительного переменного. М.—Л*, ГТТИ»
1933, 58 стр.
Sur les classes des constituantes des complementaires analytiques. Ann. Sci., Norm.
Super., Pisa, серия 2, 2, вып. З, 269—282, 1933.
Sur les ensembles toujours de premiere categorie. Fund. Math., XXI, 114—126,
1933.
О стационарных последовательностях. Труды фиэ.-мат. ин-та, отд. матем., 5, 125—
147, 1934.
Несколько замечаний о кратной отделимости. ДАН СССР, 2, № 5, 280—284,
1934.
Sur les suites stationnaires. Paris, Hermann et Cie, 19, 1934 (Actualites scientifiques
et industrielles. 149. Exposes mathem. publies a la memoire de Jacques Her-
brand. V).
О построении множеств, неизмеримых В, В кн.: Лебег. Иьгсгрвроваяие и
отыскание примитивных функций. Ми—Л*т ГТТИ, 1934, стр. 310—321.
Sur une propriete nouvelle des ensembles mesurables B. Comptes Rendus Acad. Sci.,
Paris, 198, 1116—1118, 1934.
Sur quelques problemes difficiles de la theorie des fonctions. Там же, стр. 1296—•
1298.
Sur la decomposition des ensembles. Там же, стр. 1671—1674,
Quelques remarques sur les courbes qui sont des complementaires analytiques.
Mathematica, Cluj, 10, 70—80, 1934 (Bull. Soc. Sti., Cluj, 7, 599—609).
Современные проблемы теории функций действительного переменного (тезисы до*
клада). В кн.: „Бюллетень II Всесоюзного съезда математиков в Ленинграде
24—30 июня 1934 г.а Л., изд. АН СССР, 1934, стр. 8—10.
О некоторых новых результатах дескриптивной теории функций. М.—Л., изд.
АН СССР, 1935, 86 стр.
Sur les ensembles analytiques nuls. Fund. Math., XXV, 109—131, 1935.
Choix effectif d'un point dans un complementaire analytique arbitraire, dorme par un
crible. Там же, стр. 559—560 (совместно с П. С. Новиковым).
Sur un raisonnement nouveau dans la' theorie des fonctions descriptives. Comptes
Rendus Acad. Sci., Paris, 201, 638—640, 1935.
О частях натурального ряда. ДАН СССР, 40, № 5, 195—199, 1943.
О частях натурального ряда. Изв. АН СССР, 11, 403—410, 1947.
СОДЕРЖАНИЕ
Стр.
От редакторов тома 3
I цикл
Лекции об аналитических множествах и их приложениях 9
Глава I. Общие понятия о множествах, измеримых В 11
Область. Порции. Начальный класс 12
Операции над множествами 14
Алгебраическое обозначение 19
Понятие множества, измеримого В 23
Преобразования определения множества, измеримого В 42
Глава II. Исследования о структуре множеств, измеримых В 52
Классификации множеств, измеримых В 52
Достижимость 55
Структура классов 58
Отделимость 61
Первые сведения о структуре множества точек данного класса ... 68
Множества класса 0 и 1. Исследования Бара 74
Конструктивное существование множеств 1, 2, 3 и 4-го классов ... 80
Понятие рассеянного множества (по Данжуа) 92
Процесс Бэра в высших классах 98
Подклассы, их существование 107
Глава III. Аналитические множества 116
Определения и простейшие свойства 116
Проекции 121
Свойства аналитических множеств 128
Первый принцип аналитических множеств. Отделимость В 132
Изучение регулярных и полурегулярных изображений аналитических
множеств 138
Решета. Бинарное решето Лебега 150
Второй прицип аналитических множеств. Отделимость (СА) 174
Глава IV. Неявные функции 189
Общие замечания о неявных функциях 189
Изучение однозначных неявных функций. Исследования Лебега . . . 195
Изучение многозначных неявных функций со счетным множеством
значений 201
Изучение общего случая в проблеме неявных функций 213
Глава V. Проективные множества 225
Определение проективного множества. Его преобразование 225
СОДЕРЖАНИЕ 743
Простейшие свойства проективных множеств 229
Теорема С. Мазуркевича. Обобщение В. Серпинского 235
Существование проективных множеств всякого класса и всякого рода.
Универсальные множества 242
Резольвенты 244
Анализ мемуара Лебега „Sur les fonctions representables analitiquement" 249
Заключение 267
О классификации Бэра 270
О некоторых свойствах А-множеств 273
Об одном множестве, неизмеримом В 295
Проективные множества и метод резольвент 301
Об одной проблеме Бореля, проективных множествах Лебега и.
аналитических множествах 301
О проективных множествах Лебега 304
Свойства проективных множеств 307
О множествах, неизмеримых В, и об употреблении диагонали Кантора 309
О проблеме Бореля и методе резольвент 312
Арифметический пример функции, не входящей в классификацию Бэра 315
Мемуар об аналитических и проективных множествах 317
Об аналитических множествах 380
Глава первая. Построение Лебега и его обобщения 380
I. Построение Лебега 380
II. Каноническое решето Лебега 381
III. Аналитичность множества Е Лебега 383
IV. Решето общего вида 387
V. Проекции 394
VI. Решета нескольких измерений 396
Глава вторая. Измеримость^ 404
VII. Идеи Бореля 404
VIII. Первое индуктивное свойство: аналитичность 411
IX. Второе индуктивное свойство: однозначность 418
X. Отделимость В , 421
XI. Эффективное построение, отправляясь от параллелепипедов каждого
однозначного множества 426
XII. Неявные функции 431
Глава третья. Наиболее общие аналитические множества. . 435
XIII. Критерий измеримости В 435
XIV. Трансфинитное 447
XV. Проективные множества 455
Добавление 459
Замечания о проективных множествах 460
О достижимости точек 462
О путях развития теории множеств 464
Аналогии между множествами, измеримыми В, и аналитическими
множествами 470
Современное состояние теории функций действительного переменного . . . 494
Некоторые замечания о кривых, являющихся аналитическими
дополнениями ,.....,......, 537
Несколько замечаний о кратной отделимости ..»«.»••.- 547
О некоторых новых результатах дескриптивной теории функций 552
Эффективный выбор точки в произвольном аналитическом дополнении, за-
данном посредством решета » 617
W
СОДЕРЖАНИЕ
II ЦИКЛ
Об одном разложении континуума 621
Об одном семействе аналитических дополнений 624
О классах конституант аналитических дополнений 627
О стационарных последовательностях 642
О пустых аналитических множествах ♦ • ■ • 662
III цикл
06 одной проблеме Бэра 683
О разбиении интервала на несчетное множество неизмеримых множеств 686
Об одном свойстве континуума 689
О существовании несчетного множества первой категории на всяком
совершенном множестве 692
Об одном вопросе, касающемся свойства Бэра 695
О несчетном множестве, являющемся множеством первой категории на
всяком совершенном множестве 697
О множествах всегда первой категории 699
О частях нотурального ряда 709
О частях натуральною ряда 714
П ржложенкя
Комментарии ж работам И, //. Лузина 725
Список работ //. И, Лавина в области дескриптивной, теории множеств ♦ 740
Н. И. Лузин
Собрание сочинений. Том II
Печатается по постановлению
Редакционно-издателъскою совета
Академии Наук СССР
•
Редактор-шдахельстм В. Я. Арсенин. Технический редактор Г. И. Шевченко
РИСО АН СССР J* 8—5В. Сдано в'набор 8/» 1957 г. Иодпжс. it печати" 10/Ш 1958 г; Формат 70Xl08Vi».
46t5 new* A*—6V0 <У<"- ***• *• ЗД1 уч.-яад л. Тира* ЗООЭ »кж. Ивд. № 1745. Тип. аак. J* 382.
Цеха 38 рдб, 60 хрп.
Иэдатехьство Аж&дешш нвуж СССР, Москва* Б-64, Подсосенской пор., 21
1-»тше..я»д..АН СССР. Ленинград. В-34. 9 линия, д. 12..
Ис правления
Стр.
27
87
88
89
91
Строка
6 св.
9 св.
16 ся.
5 сн.
4 св.
8 сн.
(
1
1
Напечатано
всюду
выходят
плотный
Должно быть
всё
выходит
густой
Н Н Луаии, т. 2