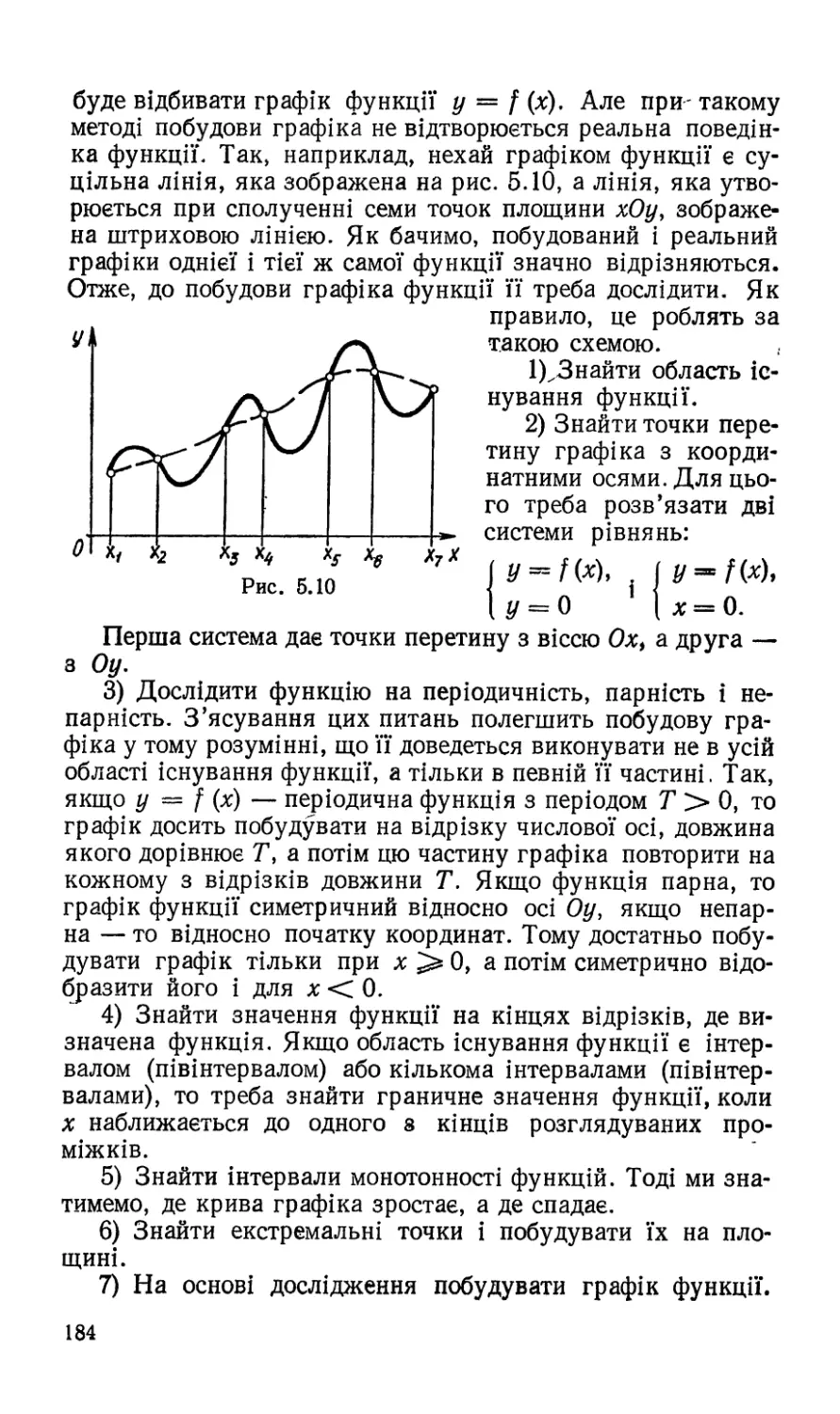
Автор: Шкіль М.І. Слєпкань З.І. Дубинчук О.С.
Теги: математика алгебра навчальний посібник видавництво вища школа початок аналізу
Год: 1992
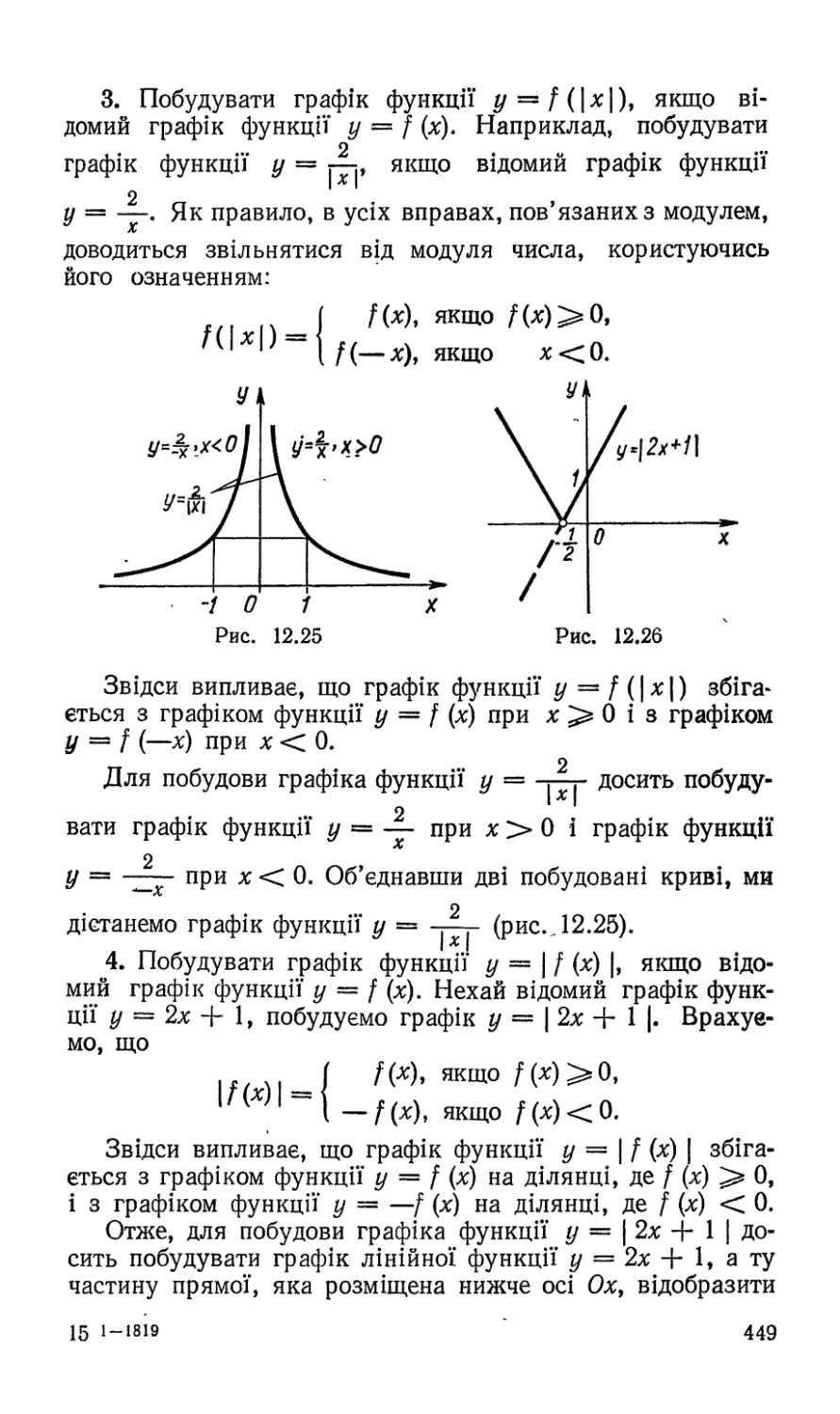
Текст
АЛГЕБРА
М. І ШКІЛЬ
З І. слєпкднь
О С ДУБІЛНЧУК
0 ПОЧЖЇЖИІ
М. І. ШКІЛЬ
3.1. СЛЄПКАНЬ
0. С. ДУБІ/1НЧУК.
ЯЕИ
П ГПОЧ1ЖТКМ]
КИЇВ
«ВИЩА ШКОЛА»
1992
ББК22.14я722
Ш 66
УДК 512(07)
Рекомендовано Міністерством
народної освіти України
як навчальний посібник
для учнів середніх
професійно-технічних училищ
Викладений матеріал відповідає діючій програмі з алгебри і
початків аналізу для середніх ПТУ. В основу покладено принцип
взаємозв’язку загальноосвітньої і професійно-технічної підготов-
ки майбутніх кваліфікованих робітників.
До кожного розділу подано запитання і завдання для само-
контролю та вправи для самостійного розв’язання, що дозволяє
використовувати посібник без спеціального збірника задач.
Для учнів середніх ПТУ.
Изложенннй матеріал соответствует действующей програм-
ме по алгебре и началам анализа для средних ПТУ. В основу по-
ложен принцип взаимосвязи общеобразовательной и професіо-
нально-технической подготовки будущих квалифицированньїх
рабочих.
К каждому разделу даньї вопросьі и задания для самоконт-
роля, а также упражнения для самостоятельного решепия, что
позволяет пользоваться пособием без специального сборника за-
дач.
Для учащихся средних ПТУ,
Рецензент и: канд. фіз.-мат. наук, доц. /. П. Ганжела,
канд. пед. наук, доц. Г. М. Ганжела (Кіровоградський держав-
ний педагогічний інститут), викладач математики середньої
школи № 223 м. Києва С, П, Кирик
Редакція літератури з математики і фізики
Редактор Г. Г, Рубан
1602040000—210
М2И(04)—92
73—91
І8ВМ 5-11-002589-4
© М. І. Шкіль, 3. 1. Слєпкань,
О. С. Дубинчук, 1992
ВІД АВТОРІВ
Вступаючи до професійно-технічного училища, дехто сподівається,
що йому не доведеться вивчати математику, інші навіть думають,що май-
бутньому робітникові вона взагалі не потрібна. Насправді це не так.
Вивчення математики сприяє формуванню певної системи знань, нави-
чок І умінь, які мають служити не лише основою для успішної праці в
конкретній галузі виробництва, а й забезпечити майбутньому робітни-
кові можливості для самостійного поглибленого вивчення теоретичних
питань, пов’язаних з освоєнням нової техніки і технології.
У практичній діяльності сучасного робітника все більшого значен-
ня набувають елементи розумової праці при одночасному підвищенні
вимог до швидкісних і точнісних характеристик діяльності. Вивчення
математики сприятиме формуванню в учнів цих здібностей.
Видатний російський учений М. В. Ломоносов вважав, що матема-
тику хоча б тому треба вивчати, що вона розум у порядок приводить,
Справді, доводячи теореми, розв’язуючи задачі, учні навчаються логіч-
но мислити, обгрунтовувати кожне своє твердження, не сприймати на
віру те, що на перший погляд є очевидним. А саме це і є ознаками розу-
мового' розвитку.
Математичні знання потрібні для засвоєння курсів фізики, хімії,
загальнотехнічних і спеціальних дисциплін. Математичні розрахунки
широко застосовують також під час виробничого навчання.
Серед майбутніх робітників є чимало юнаків і дівчат, які в школі
мало уваги приділяли вивченню математики, відчували труднощі в ово-
лодінні матеріалом і втратили віру в свої сили. Але ніколи не пізно сер-
йозно взятися за подолання прогалин у знаннях і налагодити «добрі від-
носини» з математикою.
Цей посібник допоможе вам повторити призабуте чи заново вивчити
окремі геми, які з певних причин не були засвоєні в основній школі. Усі
необхідні відомості можна знайти у розділі 12, де зосереджено матері-
ал для повторення. Треба лише порадитись з викладачем, як краще ор-
ганізувати роботу з цим матеріалом, на яку допомогу ви можете розра-
ховувати, на чому необхідно зосередити увагу.
Виклад нових тем у цьому посібнику відрізняється від звичного для
вас. Теоретичні відомості подано в системі, з необхідними обгрунтуван-
нями, до тексту внесено зразки розв’язання типових для кожної теми
вправ, Ці вправи необхідно докладно розібрати і записати в зошит,
З
Необхідно звернути увагу на те, як подані завдання для самостій-
ного розв’язання. За ступенем складності вони мають три рівня. Завдан-
ня, позначені буквою А, відповідають обов’язковим результатам нав-
чання, і їх виконання оцінюється балом «З». Відповідно завдання, поз-
начені буквами Б і В, відповідають оцінкам «4» і «5».
Хто відчуває, що засвоїв теоретичний матеріал теми і розібрався
у розв’язанні типових вправ, може лише переглянути завдання рівня А.,
усно «прикинути» іх розв’язання і безпосередньо перейти до завдань
рівня Б. Якщо хто вважає себе підготовленим до виконання завдань
рівня Б, він починає розв’язувати завдання рівня В. Якщо ж виявить-
ся, що новий матеріал ще не повністю засвоєний і необхідні додаткові
роз’яснення, треба звернутися за допомогою до викладача або товари-
шів, ще раз продумати все і приступити до виконання завдань рівня А.
Якщо цей етап пройдено успішно, то за порадою викладача можна до-
датково розглянути деякі завдання рівня Б або ж розв’язати ще кіль-
ка простіших завдань.
Кожен розділ посібника містить запитання і усні вправи для само-
перевірки. Після засвоєння матеріалу з певної теми треба звернутися до
відповідних запитань і обов’язково дати відповіді'на кожне з них. Після
опрацювання всього розділу ще раз треба перевірити себе, виконуючи
всі завдання.
У посібнику вміщено відомості про застосування певних матема-
тичних фактів і закономірностей у споріднених загальноосвітніх пред-
метах, а також у загальнотехнічних дисциплінах, які вивчають майбут.
ні робітники.
Автори сподіваються, що поза увагою учнів не залишаться вміщені
в книзі історичні довідки, а також відомості про вчених, які зробили ва-
гомий внесок у розвиток математики.
РОЗДІЛ 1
ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ
§ 1. Тригонометричні функції кута
У курсі геометрії 8 класу було введено означення три*
гонометричних функцій — синуса, косинуса і тангенса
гострого кута як відношення сторін у прямокутному три-
кутнику
Синусом гострог кута а прямокутного трикутника
(позначається зіп а) називається відношення протилеж-
ного катета а до гіпотенузи с (рис. 1.1)
а
зіп а = — .
с
Косинусом гострого кута а прямокутного трикутника
(позначається соз а) називається відношення прилеглого
катета Ь до гіпотенузи с
ь
соз а = — .
с
Тангенсом гострого кута а прямокутного трикутника
(позначається а) називається відношення протилежного
катета до прилеглого
і а
-у .
Було доведено, що синус і косинус гострого кута три-
кутника залежать лише від величини кута і не залежать від
довжини сторін трикутника, його розміщення, тобто синус,
косинус, а значить і тангенс є функціями кута. Пізніше
для кутів від 0е до 180° означення цих функцій було введе-
но за допомогою кола радіуса /? у системі координат (коор-
динатний спосіб означення).
Синусом кута а називається відношення ординати у
точки Ра (х; у) кола до його радіуса К (рис. 1.2)
у
зіп а =
Косинусом кута а називається відношення абсциси х
точки Р& (х; у) кола до його радіуса К
X
соз а = -5- .
5
Тангенсом кута а називається відношення ординати у
точки Ра (х; у) кола до абсциси х
І£сс = — .
& X
Для а кут а = 90° виключають, бо при а = 90° абс-
циса дорівнює 0, а ділити на 0 не можна.
При такому означенні соз 90° — 0, зіп 180° = 0,
соз 180° = —1, 180° = 0. Якщо взяти до уваги, що про-
мені, які збігаються, утворюють кут 0°, то зіп 0° = 0,
соз 0° = 1, 0° = 0.
Нагадаємо, що для будь-якого кута 0°<а<180’
зіп (180° — а) = зіп а, соз (180° — а) = —соз а. Для ку^
та а 90° (180° — а) = —а.
У курсі-алгебри 9 класу ці означення були поширені
на кути, числове значення градусної міри яких для синуса
і косинуса може бути довільним числом (як додатним, так
і від’ємним), а для тангенса — довільним числом, що не
дорівнює 90° + 180°п, де п £ 2. Було введено також озна-
чення котангенса.
Котангенсом кута а називається відношення абсциси
х точки Ра (х; у) кола до ординати у
сі§ а = — .
& у
Кути довільної величини описують стрілки годинника,
точки обертових частин механізмів тощо.
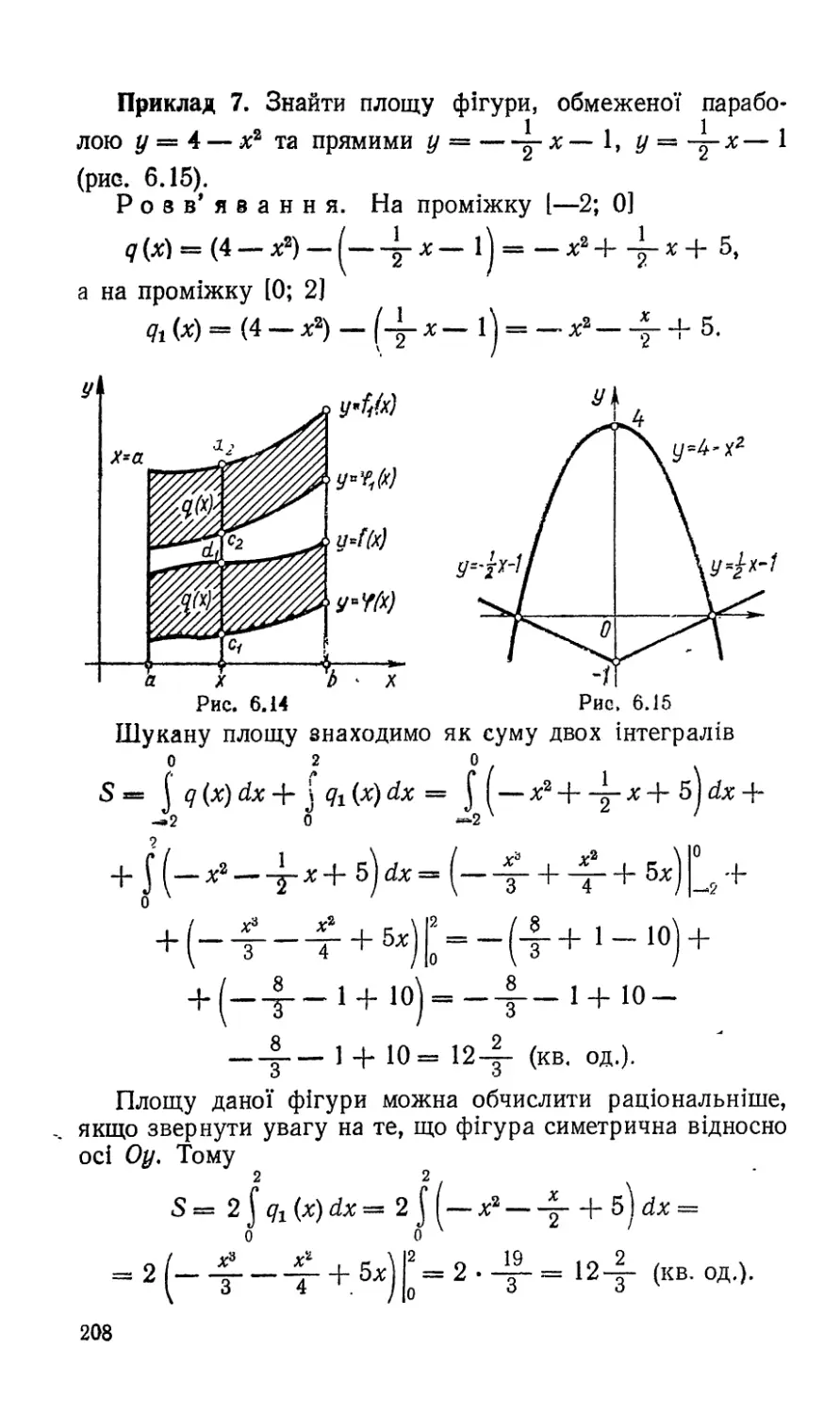
Приклад 1. Записати кут Р у вигляді Р = а + 360°п,
де п £ 2, а — додатний кут, менший від 360°, якщо: 1) Р =
2000°; 2) р = —490°.
Р о з в’ я з а н н я. 1) Поділимо 2000° на 360°. Отже, да-
ний кут складається з 5 повних обертів і ще 200°. Тому р ==
= 2000° = 200° + 360° -5, п = 5, а = 200°;
6
2) 3 рівності —490° — а + 360°и знайдемо умову,
яку має задовольняти п, щоб кут а був додатним. Розв’я-
жемо останнє рівняння відносно а : а = —490° — 360°п.
За умови а > 0 маємо —490° — 360°га > 0. Розв’яже-
490°
мо цю нерівність відносно п: 360°п < —490°; п <------360^'
або п < —1 -од-.
□О
Найближче ціле число п, яке задовольняє цю нерівність,
є п = —2. З рівності а = —490° — 360°« знайдемо а,
підставивши значення п. Маємо ч
а = —490° — 360° • (—2) = —490° + 720° == 230°;
— 490° = 360° • (—2) + 230°, п = — 2. а = 230°.
Приклад 2. Стрілки годинника показують рівно 12 год.
Через який найменший проміжок часу хвилинна стрілка
знову суміститься з годинниковою?
Розв’язання. Хвилинна стрілка робить повний
оберт, тобто повертається на кут в 360°, за 60 хв. Тому за
1 хв вона повертається на -^д- = 6 . Годинникова стрілка
робить повний оберт за 12 год, або за 720 хв. Отже, за 1 хв
360° п со ч
вона повертається на = 0,5 .
Коли годинник показує 12 год, то найменший відмін-
ний від нуля кут між годинниковою і хвилинною стрілка-
ми дорівнює 360°. Позначивши шуканий проміжок часу
у хвилинах через х, дістанемо рівняння 6х-^-х = 360°.
5 5
Звідси х = 65 (хв), або І год 5 -у хв.
Отже, хвилинна стрілка суміститься з годинниковою
5
щонайменше через 1 год 5-д-^хв.
У геометрії термін «кут» вживають для позначення двох
понять: 1) геометричної фігури, утвореної двома променя-
ми із спільним початком; 2) величини, що характеризує
міру відхилення одного променя від іншого (0° а
180°), або однієї прямої від іншої при їх перетині (0°
а 90°), або кута повороту (—оо < а < оо).
- Коли йдеться про аргумент тригонометричної функції,
то термін «кут» (синус кута, косинус кута) вживають у ро-
зумінні величини, а не фігури.
Відомо, що кожному центральному куту відповідає пев-
на дуга кола заданого радіуса. Якщо розгорнутий централь-
ний кут поділити на 180 рівних частин (величина кожної
7
Рис. 1.3
частини називається градусом), то і відповідна дуга (пів-
коло) теж ділиться на 180 рівних частин. Величину кожної
з дуг, на які розіб’ється півколо, теж називають градусом.
Інколи для кута вживають термін «кутовий градус», а для
дуги — «дуговий градус».
Існують різні системи вимірювання кутів і дуг. Крім
градуса, його частин (мінути, секунди) в геометрії за оди-
ницю вимірювання кутів використовують прямий кут.
Цю одиницю позначають буквою й. На-
приклад, величину кута а, що дорівнює
30°, в одиницях прямого кута познача-
1 ,
ють так: а = -%-а.
В астрономії за одиницю вимірюван-
ня кутів взято кутову годину. Це вели-
1
чина кута, який становить -у частину
прямого.
У техніці за одиницю вимірювання
кутів взято повний оберт. Мова йде про
число обертів вала, шківа, махового колеса тощо.
В артилерії кути вимірюють у так званих поділках ку-
томіра. Велика поділка кутоміра — це частина повного
оберту. Мала поділка кутоміра дорівнює частині вели-
кої поділки. Кут, виміряний у таких одиницях, записують
так: 28—32, що означає 28 великих і 32 малі поділки куто-
міра.
Моряки вимірюють кути в румбах. Ця одиниця дорів-
нює частині величини розгорнутого кута.
У картографії в деяких країнах за одиницю вимірюван-
ня кутів взято град. Град дорівнює частині величини
розгорнутого кута і позначають його знаком Наприклад,
АОВ = 5*.
§ 2. Радіанна система вимірювання кутів і дуг
У математиці, астрономії, фізиці, техніці використову-
ють радіанну систему вимірювання кутів і дуг, яка має
певні переваги перед іншими системами. До введення ра-
діанної системи привела така властивість дуг, що відпові-
дають кожному центральному куту: якщо розглянути два
концентричних кола радіусів і\ і г2 (рис. 1.3) і два різних
8
центральних кути / АОВ = а° і /_ВОС = £° з відпо-
відними дугами 4 і 12, 1\ і І2, то за відомою формулою довжи-
ни дуги маємо
1 ла°гх 1 __________ ла°г2 / ______ г____ л[Зог2
ч ~ 180° ’ ~ 180° ’ ~ 180° ’ /2 ~ 180° ’
Поділивши обидві частини кожної з цих чотирьох рів-
ностей на відповідний радіус, дістанемо
па? 12 __ па? . Ч _ лрс . ^2 __ зт(3°
77— “180^ ’ 77 — 180° ’ гх ~ 180° ’ 77 — Лвб3" ‘
Звідси — = — = т; — = — = п. Якщо а°> р°, то
Г1 Г2 Г1 Г2
т> іг. Отже, для даного центрального кута відношення
довжин дуг концентричних кіл до довжин відповідних ра-
діусів є величиною сталою. Це відношення залежить від
величини кута, тому може служити характеристикою вели-
чини центрального кута.
Отже, для довільного центрального кута = а. Число
а характеризує величину даного центрального кута. Якщо
І = г, то а = 1. Тому у радіанній системі за одиницю ви-
мірювання кутів і дуг взято величину центрального кута,
для якого довжина відповідної дуги дорівнює довжині
радіуса.
Оскільки довжина півкола радіуса г дорівнює ,яг, то ра-
ПГ
діанна міра розгорнутого кута дорівнює — = я радіанів*
Враховуючи, що градусна міра розгорнутого кута стано-
вить 180°, а його радіанна міра дорівнює я радіанів, то
1 рад = , а 1° = рад 0,01745 рад.
Нехай сс° — градусна міра деякого кута, а а — його
радіанна міра. Оскільки градусна міра кута, утвореного
при одному оберті точки Ро (1; 0), дорівнює 360°, а його ра-
о 360° 2л
діанна міра дорівнює 2я, то - .
о . ла° .о сг-1800 - . ,
Звідси а = і а = —----------------, тобто ми дістали фор-
мули переходу від градусної міри кута до радіанної і нав-
паки.
Використовуючи ці формули для обчислення радіан-
ної і градусної мір кута, слід враховувати правила набли-
жених обчислень. Навіть у тому разі, коли наперед задати
точне значення градусної чи радіанної міри кута (це мо-
же бути лише у теоретичних розрахунках), обчислені за фор-
9
мулами переходу значення будуть Наближеними з точністю,
яка залежить від вибору наближеного значення числа я.
Приклад 1. Визначити радіанну міру кута у 108°.
„ , ,, ла° я • 108°
Розв язання. Маємо а = тоКо, а = —гоЯо— =
1оО 1оО
= 4- л. При я « 3,14 а ^4- ’ 3,14 = °>6 • 3,14 =
5 г ’ 5 ’ ’ ’
= 1,884 « 1,88 рад, якщо вважати, що градусна міра
задана точним значенням.
Приклад 2. Визначити градусну міру кута, радіанна
міра якого наближено дорівнює 2,3 рад.
Г> ЛД О а • 180° о 2,3 • 180°
Розв язання. Маємо а = —-—, а л? -2—.
П О 1Л 2,3 • 180° , ЛЛО , ПЛО
При я « 3,14 а « 3 14— « 132 130 .
У радіанній системі не було введено позначення оди-
ниці вимірювання, тобто позначення радіана. Тому, коли
кут як аргумент тригонометричної функції виміряний у
радіанах, під знаком тригонометричної функції записують
тільки числове значення величини кута. Наприклад,
• Л «ГЕ
81П 2, СО8 .
Специфікою радіанної міри є і те, що її одиниця (один
радіан) міститься у розгорнутому куті не ціле число разів,
як наприклад 1°, а ірраціональне: я ж 3,14.
Перевага радіанної міри перед іншими полягає в тому,
що для малих кутів, виміряних у радіанах, виконуються
наближені рівності зіп а ж сс, а а.
Справді, нехай а = 3°. За таблицею переходу від градус-
ної міри до радіанної знаходимо, що 3° & 0,0524 рад. За таб-
лицями значень тригонометричних функцій для кутів, вимі-
ряних у градусній мірі, зіп 3°^ 0,0523. Якщо кут а виміря-
но у радіанній мірі, то зіп 0,0524 ж 0,0523, тобто зіп а « а.
У градусній мірі аналогічна наближена рівність зіп 3° ж
3 не має смислу. Вказана перевага радіанної міри зна-
ходить широке застосування у математичному аналізі
та інших науках.
Перевага радіанної міри полягає ще і в тому, що відома
з геометрії формула довжини дуги, виміряної у градусах,
/ = 1РП-О і формула площі сектора 5 = -а^— у радіанній
1оО оОМ
і о аг2
мірі спрощуються і мають вигляд І = га, 8 = , де
г — радіус кола, а — радіанна міра дуги.
Радіанна міра дає змогу ввести поняття тригонометрич-
ної функції довільного числового аргументу.
10
§ 3. Тригонометричні функції числового аргументу
Перш ніж вводити означення тригонометричних функ-
цій числового аргументу, згадаємо, що в курсі алгебри
9 класу зверталась увага учнів на незалежність значень
синуса, косинуса, тангенса і котангенса довільного кута
від радіуса 7? кола. Тому покладемо 7? = 1, а відповідне
коло назвемо одиничним (рис. 1.4).
Виконаємо таку вправу: побудувати на одиничному ко-
лі точки, на які відображується початкова точка Ро (1; 0)
при повороті навколо центра кола на кут а радіанів, якщо
а) а = 0; б) а = в) а=—г) а ='—1; д) а = 2.
Р о з в’ я з а н н я: а) числу 0 на одиничному колі
(рис. 1.5) відповідає точка Ро (1; 0) — початок відліку;
б) оскільки кут 90° дорівнює -у рад, то, поділивши на
З кут -у рад, будемо мати кут обертання -у рад, якому відпо-
відає на колі точка Р_л , що ділить дугу Р0Р на три рівні
6 2
частини;
в) відомо, що кути, градусна чи радіанна міра яких вира-
жається від’ємним числом, відкладають від радіуса ОР0
за годинниковою стрілкою; розділимо прямий кут, тобто
кут -у рад, навпіл і відкладемо кут — -у від радіуса ОР0
у IV чверті, дістанемо точку Р п;
~ Т
г) куту 1 рад відповідає дуга одиничного кола, довжина
‘ л 3 14
якої дорівнює радіусу Я = 1; оскільки -у- & « 0,78,
а -у- 1,57, то точка Рг лежить вище від точки
4!
П
Ря, точка Р^\ буде симетричною до. неї відносно осі Ох і
т
буде розміщена на одиничному колі у IV чверті;
д) щоб знайти на одиничному колі точку досить від*
класти від початкової точки у напряму, протилежному
ДО руху ГОДИННИКОВОЇ стрілки, ДВІ дуги РцР-і послідовно.
Розв’язуючи цю вправу, помічаємо, що кожному дійс-
ному числу а на одиничному колі відповідає точка Ра, по-
ложення якої залежить від числа а.
Кожній точці Ра на одиничному колі відповідають певна
абсциса і ордината, які також залежать від а.
Отже, маємо залежності між дійсним числом а і абсци-
сою та ординатою відповідної точки одиничного кола, в яку
відображується початкова точка Ро (1; 0) при повороті
навколо центра кола на кут а рад. ЦІ залежності дістали
назву тригонометричних функцій числа, або тригоно-
метричних функцій 'числового аргументу.
Оскільки Р = 1, то означення тригонометричних функ-
цій як відношення ординати і абсциси до радіуса, які були
введені дляч довільних кутів а і Р, спрощуються
Синусом числа а називається ордината точки Ра оди-
ничного кола, в яку переходить початкова точка Ро (1; 0)
при повороті навколо центра кола на кут а рад, і познача-
ється зіп а.
Косинусом числа а називається абсциса точки Р& оди-
ничного кола, в яку переходить початкова точка Ро (1; 0)
при повороті навколо центра кола на кут а рад, і позна-
чається соз а.
Тангенсом числа а називається відношення а
соз а
.соз а
котангенсом числа а— відношення ——, і позначаються
8іп а*
вони відповідно а і сІ£ а.
гх । зіп а . соз а
Отже, за означенням , сі£ а = .
’ & соз а ’ ° зіп а
Оскільки кожному дійсному числу х можна поставити у
відповідність дійсні числа зіп х і соз х, то вважатимемо,
що на множині Р задано функції у ~ зіп х і у — соз х.
Оскільки у = х = -5їп * визначений для всіх х, крім
тих, при яких соз х = 0, то кожному дійсному числу X,
крім х = у + лп, п 6 відповідає єдине число х (зна-
чення у залежить від х), тобто вважатимемо, що задана
функція у = X, де X #= -у + лп, п 6 2.
12
• Можна вважати, міркуючи аналогічно, що на множині
В, х шг, п £ надана функція у = сі§ х.
Для побудови^графіків функцій у = х і у = сі§ х та
розв’язання деяких інших задач доцільно ввести поняття
про лінії тангенсів і котангенсів
Проведемо дотичну і до одиничного кола у гочці (1;
0) (рис 1 6) Для довільного числа а, якщо пзз а =# 0, від-
повідна точка (соз а» зіп а) не лежить на осі Оу, а тому
промінь ОРа перетинає дотичну в деякій точи і Та з абсци-
сою, що дорівнює 1
Для знаходження ординати точки Та скористаємось рів-
нянням прямої, що проходить через початок координат,
оскільки пряма ОРа є такою прямою. Воно має вигляд
у = кх, де к — кутовий коефіцієнт прямої, який дорівнює
тангенсу кута нахилу прямої з додатним напрямом осі
Ох, тобто к = а. Оскільки абсциса точки Та дорівнює 1,
то, підставляючи значення х і к у рівняння прямої ОРа, ді-
станемо у = а
Таким чином, ордината точки перетину прямої ОРа з
прямою і дорівнює тангенсу кута а. Тому дотична / дістала
назву лінії тангенсів.
Щоб ввести поняття лінії котангенсів, проведемо дотич-
ну 9до одиничного кола у точці Р п (рис. 1.7). Для довіль-
Т
ного числа сс, якщо зіп а #= 0, відповідна точка (соз а;
зіп а) не лежить на осі Ох, а тому промінь ОРа перетинає
пряму 9 у деякій точці з ординатою, що дорівнює 1.
Знайдемо абсцису цієї гочки.
Скористаємося рівнянням прямої, що проходить через
початок координат. Воно має вигляд у = кх, де к = а
Оскільки ордината точки (?а дорівнює 1, то, підставляючи
значення к і у у рівняння у = кх, дістанемо рівність 1 =
= х сс. Звідси х = а.
13
Таким чином, абсциса точки перетину прямої ОРа з
прямою дорівнює котангенсу кута а. Тому дотична д
дістала назву лінії котангенсів.
- Оскільки кожному дійсному числу а на одиничному ко-
лі відповідає певна точка Ра, а цій точці відповідають певні
абсциса і ордината зіп а і соз а, то областю визначення
функцій у = зіп х і у = соз х є множина всіх дійсних чи-
сел Р. Оскільки абсциса і ордината точки Ра одиничного
кола змінюються від —1 до 1, то
областю значень цих функцій є
відрізок [—1; 1].
Областю визначення функції
у — х є множина всіх чисел,
для яких соз х =/= 0, тобто мно-
жина всіх дійсних чисел крім чи-
сел X = у + пп, де п — будь-яке
ціле число, тобто п € X.
Областю визначення функції
у = сі§ х є множина всіх дійсних
чисел, для яких зіп х Ф 0, тобто множина всіх дійсних
чисел, крім чисел X = пл, де п £ X.
Областю значень функцій у = х і у = сі§ х є множи-
на всіх дійсних чисел. Справді, якщо а — довільне дійсне
число, йому відповідає на лінії тангенсів (рис. 1.6) точка
Т (1; у0) така, що / ТОх = у0, а на лінії котангенсів — точ-
ка 0. (у»', 1) така, що сі§ / ООх = уй (рис. 1.7). Отже, функції
у = х і у = сі§ х набувають будь-яких дійсних значень у0.
Приклад 1. Знайти значення синуса, косинуса, тангенса
і котангенса числа
<5
Розв’язання. Числу у- на одиничному колі від-
повідає точка Рп (рис. 1.8). Щоб знайти зіп і соз до-
з 6
сить знайти ординату і абсцису точки Рп. У прямокутному
Т
трикутнику ОЛР_„ / 0Р_пА — -у рад, або / ОР пА =
зз з
= 30°. Оскільки у прямокутному трикутнику катет, що
лежить проти кута 30°, дорівнює половині гіпотенузи,
то О А = у. За теоремою Піфагора Р я А = 1/~ ОР^ — ОА2;
РпА = 1/" 1---у = 1/"1 — -у-. Отже, зіп у =
-д— Г г 'і <6 О
14
У З л 1 о , зіп а
— —соз -5- = П5-- За означенням іе а = --------------------, тому
2 3 2 _ ь соз а ’ ’
. 31 /З
81П —--
СОЗ о п
1 _ /з
~ Уз з
Таблиця 1,1
а 0 (0°) О / в £[<о О** Ю о со 3* о о в* о 00 Е Зл ~тр-(27°°/ о”4 о со со і
зіп а 0 1 2 Г~2 2 Гз 2 1 0 — 1 0
соз а 1 Гз 2 /2 2 1 2 0 — 1 0 1
0 /3 3 1 /3 Не існує 0 Не існує 0
сі§а Не існує У~з 1 /3 3 0 Не існує 0 Не існує
Аналогічно можна знайти значення тригонометричних
функцій чисел -у, що дорівнюють тригонометричним
функціям відповідних кутів у градусній і радіанній мірах.
Доцільно пам’ятати ці значення, як і значення функцій
для чисел (кутів) 0, я, 2л, оскільки їх часто вико-
ристовують при розв’язанні задач. Значення тригономет-
ричних функцій таких чисел (кутів) систематизовані у
табл. 1.1.
Зл
Приклад 2. Знайти зіпсс, соз а, сі§а, якщо а =
Розв’язання. Нехай точка Р.х здобута з точки
Ро(1; 0) при повороті на кут -4—(рис. 1.9), точок А і В—
проекції точки Ра на осі координат. У прямокутному
трикутнику РаА0 /_РаОА = ~, ТОМУ Д Ра.А0 рІВНОбеД-
15
рений/ Оскільки Д РаЛО = Д РпСО, то Р^А = РЯС =
т т
= 8Іп-~, АО = ОС = соз ~ . Відомо (див. табл. 1,1),
. я /^2 л 2 о
що зіп—г- = —і соз-т-= —х— . За означенням соза і
4 2 4 2
зіп а є відповідно абсцисою і ординатою гочки Р^. Тому
. Зл У'2 Зл |/ 2
зіп = —у- , соз -у- =----------- , оскільки ординати то-
чок II чверт додатні, а абсциси — від’ємні.
о зіп а
За означенням шсс =---------, тому
° соз а 7
Приклад 3. Дослідити зміну соз а при зростанні числа
а від 0 до 2л.
Розв’ язання, За означенням соз а є абсцисою
точки Ра одиничного кола, в яку переходить початкова
точка Ро (1; 0) при повороті навколо центра кола на кут
а рад.
Якщо а збільшується від 0 до л (І і II чверті), то абсци-
са зменшується від 1 до — 1. Отже, при зростанні аргументу
від 0 до л функція косинус спадає від 1 до —1,
Якщо а збільшується від л до 2л (III і IV чверті), абс-
циса збільшується від —1 до 1, тобто при зростанні аргу-
менту від л до 2л функція косинус зростає від —1 до 1.
Аналогічно досліджують зміну функції синус.
16
Характер зміни тангенса і котангенса легко дослідити,
користуючись лініями тангенса і котангенса.
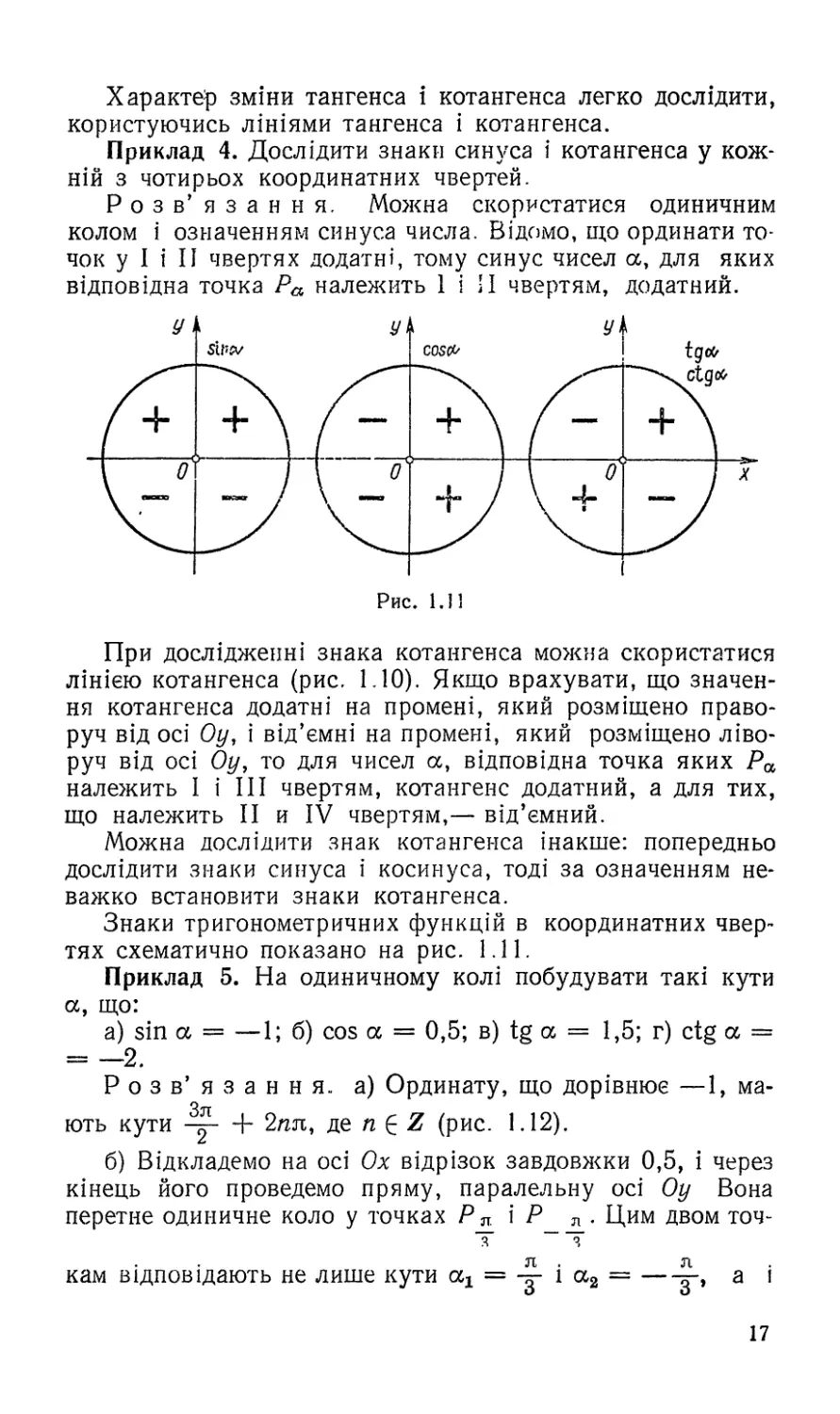
Приклад 4. Дослідити знаки синуса і котангенса у кож-
ній з чотирьох координатних чвертей.
Розв’ язання. Можна скористатися одиничним
колом і означенням синуса числа. Відомо, що ординати то-
чок у І і II чвертях додатні, тому синус чисел а, для яких
відповідна точка Ра належить 1 і II чвертям, додатний.
Рис. 1.11
При дослідженні знака котангенса можна скористатися
лінією котангенса (рис. 1.10). Якщо врахувати, що значен-
ня котангенса додатні на промені, який розміщено право-
руч від осі Оу, і від’ємні на промені, який розміщено ліво-
руч від осі Оу, то для чисел а, відповідна точка яких Ра
належить 1 і III чвертям, котангенс додатний, а для тих,
що належить II и IV чвертям,— від’ємний.
Можна дослідити знак котангенса інакше: попередньо
дослідити знаки синуса і косинуса, тоді за означенням не-
важко встановити знаки котангенса.
Знаки тригонометричних функцій в координатних чвер-
тях схематично показано на рис. 1.11.
Приклад 5. На одиничному колі побудувати такі кути
а, що:
а) зіп а = —1; б) соз а = 0,5; в) а = 1,5; г) сі§ а =
= —2.
Р о з в’ я з а н н я., а) Ординату, що дорівнює —1, ма-
Зл
ють кути + 2ші, де п £ X (рис. 1.12).
б) Відкладемо на осі Ох відрізок завдовжки 0,5, і через
кінець його проведемо пряму, паралельну осі Оу Вона
перетне одиничне коло у точках Р п і Р л . Цим двом точ-
т т
л . л
кам відповідають не лише кути = -х- і а2 = —х-, а і
о о
17
всі кути, радіанна міра яких дорівнює ±-у- + 2пл, п^Х9
в) На одиничному колі побудуємо лінію тангенсів і на
ній від точки Ро відкладемо відрізок Р0Т завдовжки 1,5
(рис. 1.13). Через кінець відрізка проведемо пряму Ті,5О,
яка перетне коло у двох точках Рг і Р2. Шуканими є кути
РцОРх = &х і РьОР2 = а2, а також всі кути ах + 2/гя і
а2 + 2пл, де п С X. Оскільки а2 = ах + я, то а2 + 2пя =»
Рис. 1.12 Рис. 1.13
= ах + я + 2пя = <хх + (2и + І) я. Дві формули ах + 2пя
і ах + (2/г + 1) я можна об’єднати в одну ах + де
к£Х.
Отже, шуканими є кути виду ах + кзі, де к £2.
г) На лінії котангенсів вліво від осі Оу відкладемо від-
різок РС завдовжки 2 Через кінець С проведемо пряму
2
СО, яка перетне коло у двох точках Рг і Р2. Шуканими є
кути РцОРі = ах і Р^ОР2 = а2, а також всі кути ах
+ кп, де к^Х.
§ 4. Періодичність тригонометричних функцій
До поняття періодичної функції приводять періодичні
процеси, у яких стан певних змінних повторюється. Прик-
ладами таких процесів є рух колінчастого вала і поршня
у двигунах внутрішнього згоряння, різні обертальні рухи
та ін
Нарис. 1.14 зображено простий пристрій, який перетво-
рює обертальний рух у прямолінійний. Колесо, яке оберта-
ється і насажене на вісь, з’єднане за допомогою «пальця»
Р з рамкою Р. При обертанні колеса «палець» Р здійснює
обертальний рух, захоплює за собою рамку /?, яка руха.
18
ється вздовж бічних напрямних станин і виконує прямолі-
нійний періодичний рух (якщо колесо обертається рівно-
мірно). Якщо позначити ОР = г, а точку дотику рамки до
станин через Р19 то шлях О^Рг кінця рамки змінювати-
меться залежно від зміни кута а, який утворює радіус
кола з горизонтальним діаметром Оскільки ОуРг = АР =
= г зіп а, то, позначивши ОГР^ через у, дістанемо у —
= т зіп а, тобто періодичну функцію. Через кожний оберт
Рис. 1.15
Рис. 1.14
колеса (через 2л) положення точки Р повторюється. Тому
найменший додатний період функції у = г зіп а дорів-
нює 2л.
Функція у = / (х) називається періодичною з періодом
Т =/= 0, якщо для будь-якого х з області визначення функ-
ції числа х 4- Т та х — Т також належать області визна-
чення і виконується умова
Неважко довести, що коли Т-період функції у = / (х)е
то всі числа виду пІ\ № п £ Я, п =/= 0, також є періодами
функції.
Справді, застосовуючи кілька разів означення періо-
дичної функції, дістанемо
/(х + ЗТ) = /((х + 2Т) + Т) = /(х + 27) =
= Н(х+Т) + Т) = Цх + Т) = Цх).
Використовуючи означення синуса, косинуса числового
аргументу та враховуючи їх геометричну інтерпретацію
на одиничному колі, маємо
зіп (х + 2л) = зіп х, соз (х + 2л) = соз х.
Будь-яке число виду 2пл, де п £ Я, п 0, є періодом
синуса і косинуса.
19
Використовуючи лінії тангенсів і котангенсів, неважко
зробити висновок, що (х + л) = х, сі§ (х + л) =
= х. Це ж саме можна довести, користуючись означен-
ням тангенса і формулами зведення
і§(х + п) = _5ІП = = І£Х.
ь ' соз (а -[ л) — соз х &
Будь-яке число виду /?л, де я 6 2, я =/= 0, є періодом
тангенса та котангенса
Доведемо, що найменшим додатним періодом синуса та
косинуса є число 2л, а тангенса — число л
Доведення виконаємо методом від супротивного.
1) Вище було показано, що число 2л є періодом синуса.
Припустимо, що існує додатне число І < 2л таке, що
зіп (х + І) = зіп х. Нехай х = тоді зіп =
= зіп -у- = 1. Але синус може дорівнювати 1 лише в точці
Рл_(рис. 1.15), яка відповідає на одиничному колі числам
2
+ 2пл, де п £ 2 Отже, + І = + 2пл, звідки
І — 2пл. Проте за припущенням 0 < І < 2л, тобто 0 <
< 2пл < 2л. Поділивши всі частини подвійної нерівності
на 2л, дістанемо 0 < п < 1, що суперечить умові, оскіль-
ки п С а між 0 і 1 немає жодного цілого числа.
Отже, припущення неправильне, 2л — найменший до-
датний період синуса.
2) Відомо, що число л є періодом тангенса. Припустимо,
що існує додатне число І < л і (х + /) = х Нехай
х = 0, тоді (0 + І) = 0 = 0. Але тангенс дорівнює
нулю лише у двох точках Ро і Рг одиничного кола, які від-
повідають числам виду пл, де п £ 2 Тому І = пп. За при-
пущенням 0 < І < л, тобто 0 < пл < л. Звідси 0 < п, < 1,
що суперечить умові.
Отже, припущення неправильне, л — найменший до-
датний період тангенса.
Самостійно доведіть, що найменшим додатним періодом
косинуса є 2л, а котангенса — число л.
20
Не слід думати, що періодичними є лише тригонометрич-
ні функції. Прикладом періодичної є функція у = {х} (у
дорівнює дробовій частині х) (рис. 1.16). Найменшим до-
датним періодом цієї функції є число 1.
Лінійна функція у = кх 4- Ь є періодичною при к = 0
Для неї періодом є будь-яке дійсне число Т =# 0, оскільки
/ (х 4- Т) = І (х) = Ь. Найменшого додатного періоду
ця функція не має.
За найменшим додатним періодом тригонометричних
функцій у = зіп х, у = соз х, у = х, у = сі§* х можна
знайти найменший додатний період складної тригономет-
ричної функції, проміжним аргументом якої є, зокрема,
лінійна функція.
Приклад 1. Знайти найменший додатний період функції
у = зіп (кх + Ь), де к, Ь — числа.
Р о з в’ я з а н н я. Нехай Т > 0 — шуканий період.
За означенням періодичної функції
зіп (к (х 4- Т) 4- Ь) = зіп (кх 4- /;),
або
зіп (кх 4- кТ + Ь) = зіп (кх 4- Ь).
Позначимо Хї = кх 4- Ь і підставимо значення хх замість
кх 4- Ь в останню рівність Дістанемо зіп (хх + кТ) =
= зіп хх.
Оскільки найменшим додатним періодом синуса є 2л,
то І к | • Т = 2л, звідки Т =
1 І
Користуючись здобутим результатом, можна стверджу-
вати, що найменшим додатним періодом функції у = зіп 2х
2л , .1 2л А
Є -у = л, функції у = зіп X — ЧИСЛО -у- = 4л,
т
, ... . , 2л
функції у = ЗІП кх — ЧИСЛО
Спираючись на властивість періодичності тригоно-
метричних функцій, можна знаходити значення функцій
будь-якого аргументу через значення функцій аргументу
0 < х < 2л для синуса і косинуса і 0 < х < л для танген-
са і котангенса.
Приклад 2. Звести до однойменних функцій гострого
кута:
1) соз 1827°; 2) і§978°; 3) Зіп (—800°); 4) сі§ 1305°;
г-. . 26л , 7л . ( 33л \
б) 8Ш— ; 6) ; 7) сЦ------д-) .
Розв’язання:
1) соз 1827° = соз (360е • 5 + 27°) = соз 27°;
21
2) 978° = (180° • 5 + 78°) = 78°;
3) зіп (— 800°) = зіп (360° • (— 2) — 80°) = зіп (— 80°);
4) 1305° = (180° • 7 + 45°) = сі§ 45° = 1; /-
• 26л . /г- .1 \ . ІА , / . 1 \\
5) 8Ш—=— = ЗІП 5л +-Г-Я =81П 4л + л я 11 =
О \ О/ у І О / /
. / І 1 \ .1
= ЗІП Я + -р- Л = — ЗІП я;
\ ^ / а
6) 4-=Н2п+-т)== у*
7) (я • (— 4) + -у я) = я.
Приклад 3. Обчислити значення тригонометричних
функцій:
1)созИ25°; 2) зіп(—315°); 3) -у-я);
л \ 13 л
4) соз—.
' 6
Розв’яза ння:
1) соз 1125°= соз (360° • З 4- 45°) = соз 45° = ;
2) зіп (— 315° + 360°) = зіп 45° = ;
3) -----у-я) = (-6) += =/3;
V О І \ о / о
л\ 13л /о І Л \ Л Кз
4) соз —= соз 2 л + -г- = соз = -V- .
7 6 \ 6 / 6 2
§ 5. Побудова графіків тригонометричних функцій
Графік кожної з тригонометричних функцій досить по-
будувати на проміжку, що дорівнює найменшому додат-
ному періоду, а потім його можна продовжити на всю
область визначення. При побудові графіків за точками ско-
ристаємось геометричним тлумаченням кожної з тригоно-
метричних функцій на одиничному колі.
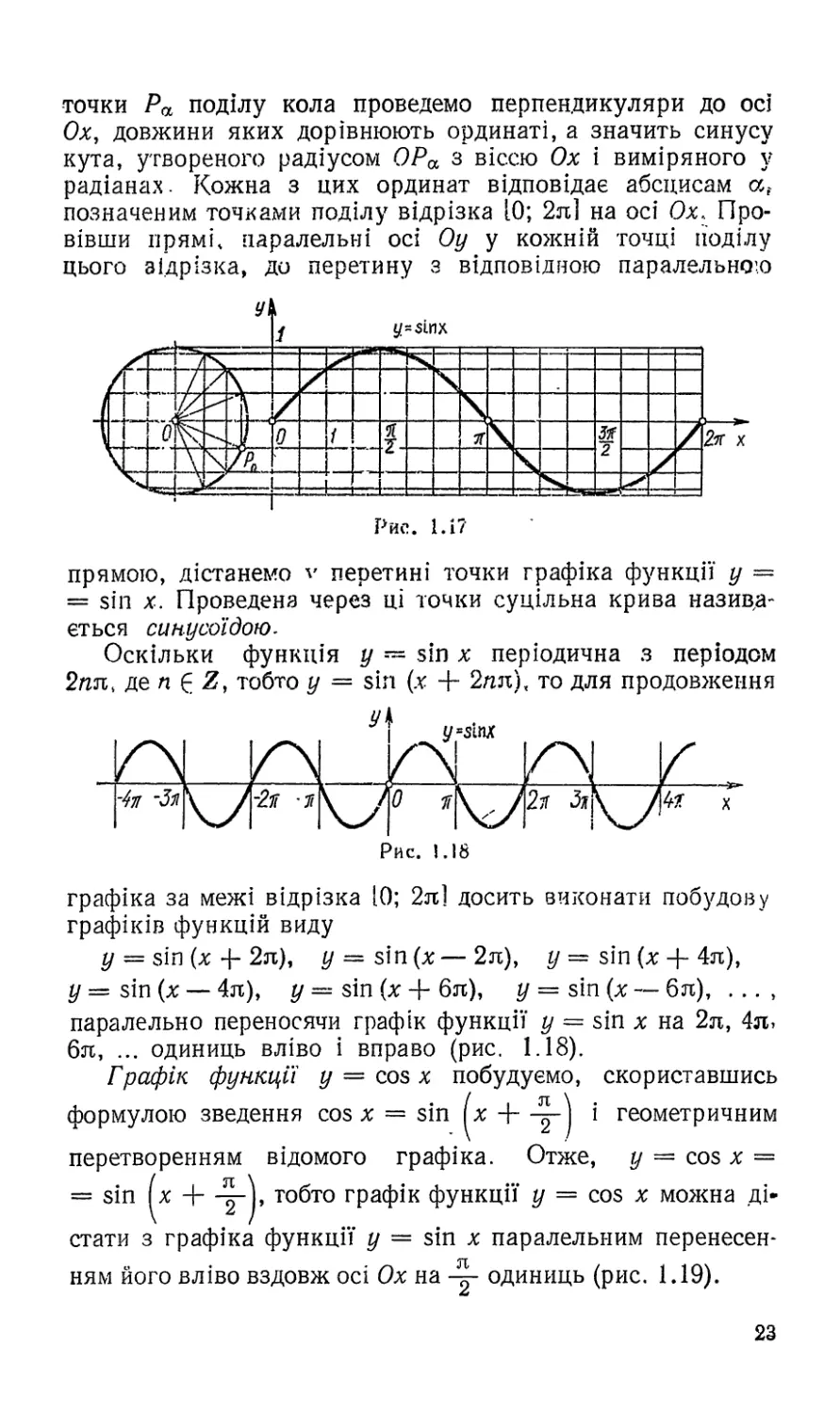
Графік функції у = зіп х побудуємо на відрізку [0; 2я].
Оскільки синус числа а — це ордината точки одиничного
кола, в яку переходить точка Ро (1; 0) при повороті навко-
ло центра на а рад, то побудуємо систему координат. По-
значимо на осі Ох відрізок [0; 2л], довжина якого наближено
дорівнює 2л 2 • 3,14 = 6,28 (рис. 1.17). Побудуємо
також поза цим відрізком коло з центром на осі Ох і радіу-
сом, що дорівнює 1. Довжина кола також наближено дорів-
нює 2л 6,28. Розіб’ємо відрізок [0; 2л] і коло, починаю-
чи від точки Ро, на 16 рівних частин. Через кожну точку
поділу кола проведемо прямі, паралельні осі Ох. З кожної
22
точки Ра поділу кола проведемо перпендикуляри до осі
Ох, довжини яких дорівнюють ординаті, а значить синусу
кута, утвореного радіусом ОРа з віссю Ох і виміряного у
радіанах. Кожна з цих ординат відповідає абсцисам а?
позначеним точками поділу відрізка 10; 2л] на осі Ох. Про-
вівши прямі, паралельні осі Оу у кожній точці поділу
цього відрізка, до перетину з відповідною паралельною
прямою, дістанемо V перетині точки графіка функції у =
= зіп х. Проведена через ці точки суцільна крива назива-
ється синусоїдою.
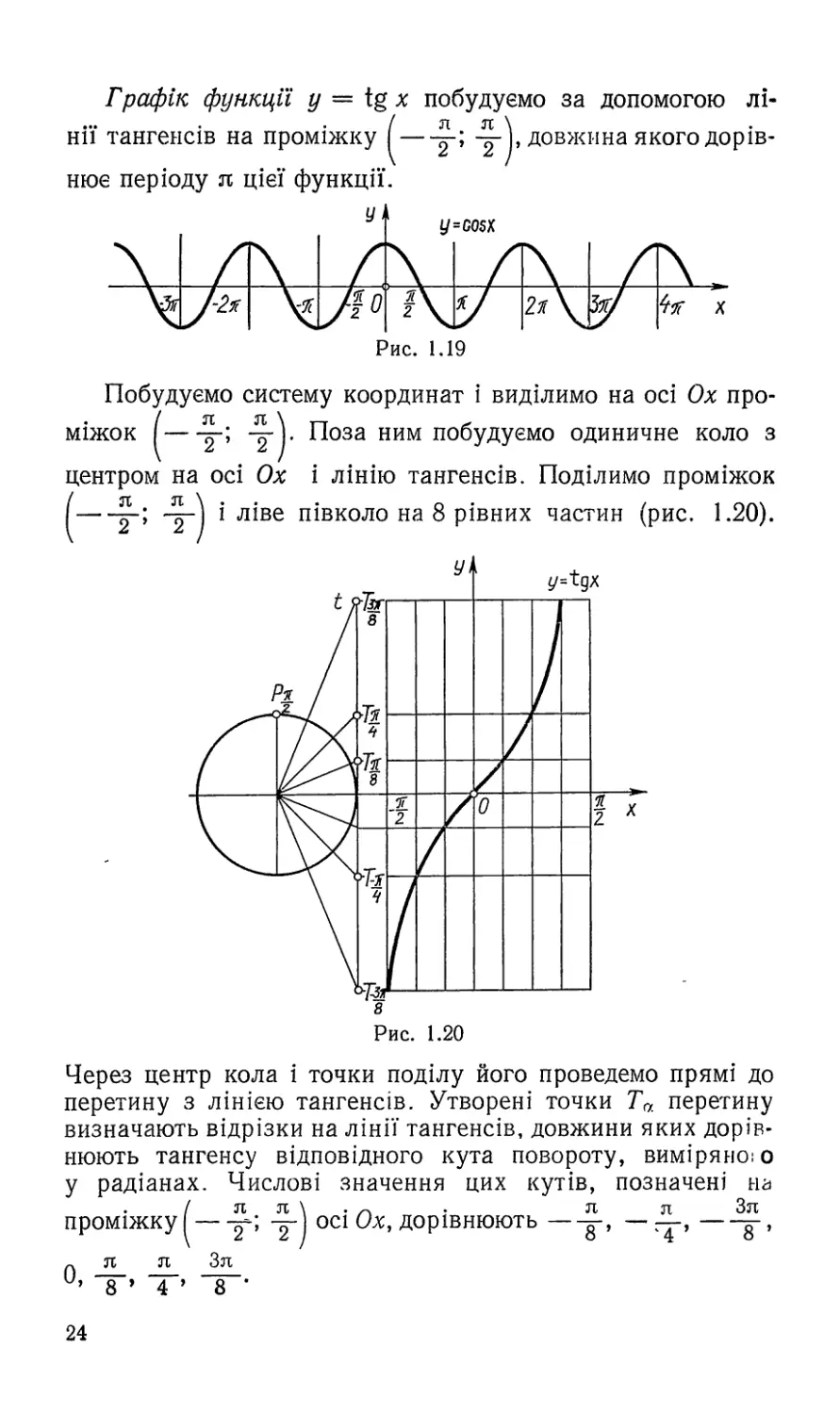
Оскільки функція у — зіп х періодична з періодом
2пл> де п £ 2, тобто у = зіп (х + 2пл), то для продовження
Рис. !.18
графіка за межі відрізка 10; 2л] досить виконати побудову
графіків функцій виду
у = 8ІП (х 4- 2л), у = зіп (х — 2л), у ~ зіп (х + 4л),
у = зіп (х — 4л), у = зіп (х + 6л), у = зіп (х — 6л), . .. ,
паралельно переносячи графік функції у = зіп х на 2л, 4л,
6л, ... одиниць вліво і вправо (рис. 1.18).
Графік функції у = соз х побудуємо, скориставшись
формулою зведення соз х = зіп (х + і геометричним
перетворенням відомого графіка. Отже, у = соз х =
= зіп (х + тобто графік функції у = соз х можна ді-
стати з графіка функції у = зіп х паралельним перенесен-
ням його вліво вздовж осі Ох на одиниць (рис. 1.19).
23
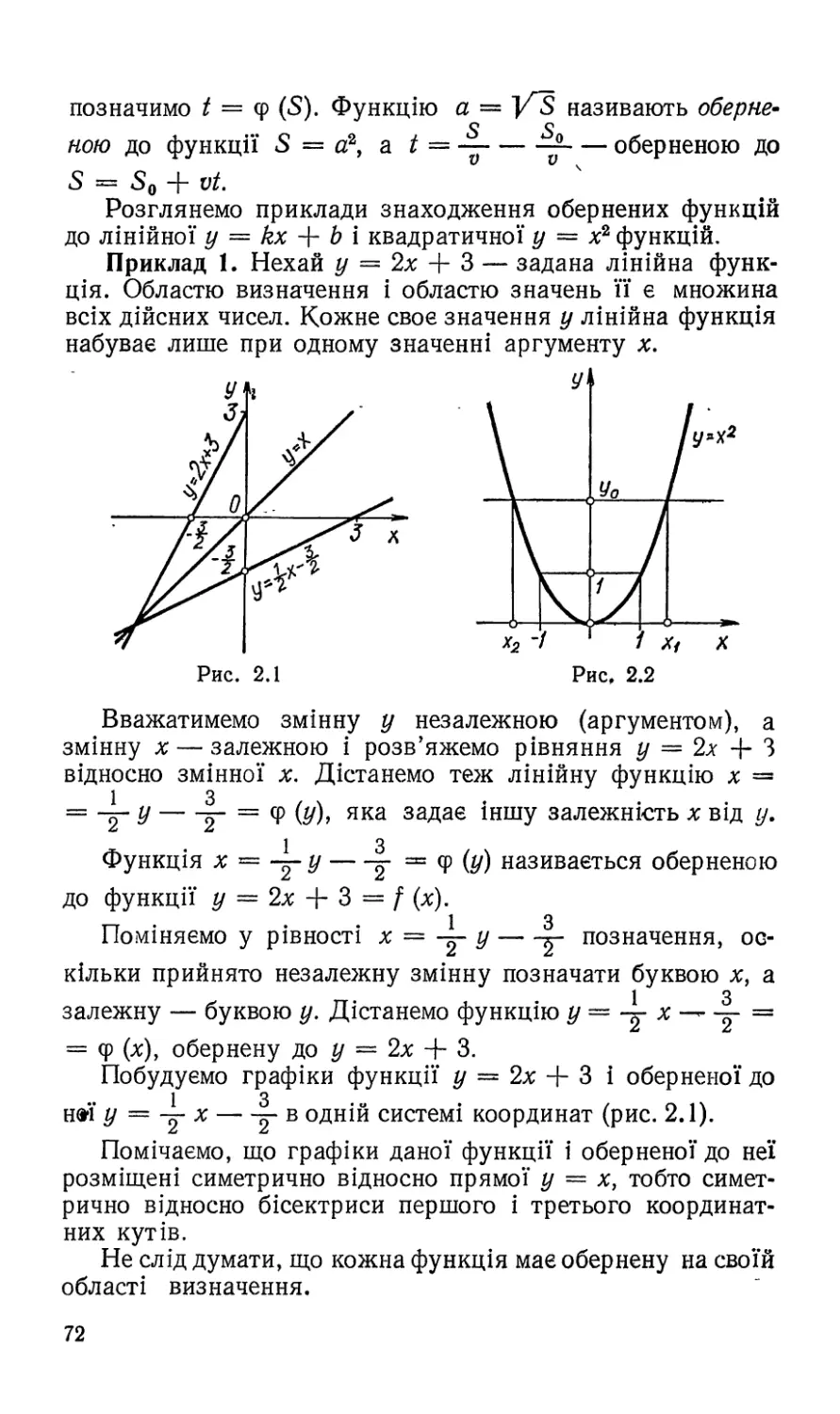
Графік функції у = х побудуємо за допомогою лі-
нії тангенсів на проміжку (—довжина якого дорів-
нює періоду л цієї функції.
Рис. 1.19
Побудуємо систему координат і виділимо на осі Ох про-
міжок —-2-; 4^. Поза ним побудуємо одиничне коло з
центром на осі Ох і лінію тангенсів. Поділимо проміжок
[----5-; -2-І і ліве півколо на 8 рівних частин (рис. 1.20).
Через центр кола і точки поділу його проведемо прямі до
перетину з лінією тангенсів. Утворені точки Та перетину
визначають відрізки на лінії тангенсів, довжини яких дорів-
нюють тангенсу відповідного кута повороту, виміряної о
у радіанах. Числові значення цих кутів, позначені на
. / Я Я \ . • я я Зя
проміжку —у І осі Ох, дорівнюють —— —,--------------------
.о. я я Зя
1Г’ Т’ "8"*
24
Через точки Та на /іінії тангенсів проведемо прямі, па-
ралельні осі Ох, а через точки поділу проміжка (—-у) —
паралельні осі Оу. Перетин цих паралельних прямих ви-
значають точки, що належать графіку функції у = х.
Провівши плавну криву через ці точки, дістанемо графік
функції у = х на проміжку І----Щоб побудувати
графік за його межами, досить скористатися періодичністю
функції тангенс, тобто тотожністю (х + ил) = х.
Отже, треба виконати побудову функцій виду у = (х + л),
У = — л), у = (х + 2л), у = (х — 2л), у = (х +
+ Зл), ... паралельним перенесенням графіка функції
у = х на я, 2л, Зл, .. одиниць вліво і вправо (рис. 1.21).
Графік функції у = х називають тангенсоїдою.
Графік функції у = сі§ х легко дістати, скориставшись
формулою зведення (х + = — сі§ х, сі§ х =
= — ^х + і двома геометричними перетворення-
ми — паралельним перенесенням тангенсоїди на -у одиниць
вліво і перетворенням симетрії утвореного графіка від-
носно осі Ох (рис. 1.22).
Приклад 1. Користуючись одиничним колом і графіком
функції у = зіп х, відповісти на такі запитання:
25
1) як змінюється значення функції у = зіп х при зміні
аргументу від 0 до 2л у кожній координатній чверті?
2) які знаки мають значення функції у — зіп х у кожній
чверті?
3) при яких значеннях аргументу функція дорівнює
нулю на проміжку [0; 2л]?
4) чому дорівнює у — зіп х при х, рівному —у, —-у-,
бзт
"Т’* '
5) назвати відповідні числа з проміжку [0; 2л], синус
1 1 А Кз /З , і Ґ2
яких дорівнює -у,-----у, 0, -у-,-----2~, 1, —1,
6) яких найбільших і найменших значень набуває функ-
ція у = зіп х на відрізку [0; 2л], при яких значеннях ар-
гументу вона набуває цих значень?
Р о з в’ я ? а н н я. 1) Оскільки синус числа а — це
ордината точки одиничного кола, то при збільшенні числа
а (а значить і кута повороту) від 0 до у (І чверть) ордина-
та (зіп а) збільшується від 0 до 1. При дальшому збільшенні
аргументу від л до у- (II чверть) синус продовжує змен-
шуватися від 1 до 0. При збільшенні аргументу від я до
-у (III чверть) синус продовжує зменшуватися від 0 до
Ззт
—1. При збільшенні аргументу від -у до 2л (IV чверть)
26
значення функції синуса збільшується від —1 до 0. Аналіз
графіка функції у = зіп х підтверджує такий характер змі-
ни значення цієї функції: у І чверті синусоїда піднімається
вгору, у II і III чвертях опускається вниз, у IV чверті —
знову піднімається вгору.
2) Знаки функції синуса в координатних чвертях ви-
значає знак ординати точок одиничного кола: у І і II чвертях
синус додатний, в НІ і IV — від’ємний.
3) Значення синуса дорівнює нулю при тих значеннях
аргументу, при яких ординати точок одиничного кола
дорівнюють нулю, тобто при х = 0, я, 2л.
4) Користуючись означенням синуса та одиничним ко-
лом або графіком функції у = зіп х, зробимо висновок, що
• 5л і і л । я । ।
зш = зіп 12л — І = 1.
тт я 11л а я 5я я Зя
5) Це числа — 0, л, —, —, .
6) Аналіз зміни значень функції у = зіп х на одиничному
колі і за графіком показує, що найбільшого значення 1
функція набуває при значенні аргументу, що дорівнює
а найменшого — 1 — при значенні аргументу, що до-
Зл
рівнює .
Приклад 2. Побудувати графіки функцій у = зіп 2х,
. 1
у = зш -у х.
Роз в’ язання. Використаємо геометричне пере-
творення відомого графіка функції у = зіп х. Якщо зіп х =
27
= / (х), то зіп 2х = / (кх). Відомо, що графік функції у = / (кх)
можна дістати з графіка функції у = [ (х), стискаючи його
до осі Оу при к > 1 і розтягуючи від осі Оу при 0 < к < 1.
Отже, графік функції у = зіп 2х можна дістати, сти-
скаючи у 2 рази (рис, 1.23, а), а графік у = зіп х — роз-
тягуючи у 2 рази відомий графік функції у = зіп х
ірис. 1.23, б).
Приклад 3. Побудувати графік функції у ~ 3 соз^2х —
л \
2/
Розв’ язання. Перетворимо вираз даної функції
так, щоб перед аргументом у дужках залишився коефіцієнт,
що дорівнює 1,, тобто подамо у вигляді у = 3 соз 2 [х-—
Це дасть змогу пізніше використати побудову графіка
функції у = І (х — а), де а > 0, паралельним перенесен-
ням у напрямі осі Ох вже відомого графіка функції.
Послідовність побудови шуканого графіка може бути
такою:
будуємо відомий графік функції у = соз х;
будуємо графік функції у = соз 2х, стискаючи графік
функції у = соз х у 2 рази до осі Оу ;
будуємо графік у = 3 соз 2х, розтягуючи у 3 рази від
осі Ох графік функції у — соз 2х;
будуємо шуканий графік у = 3 соз 2 (х----пара-
лельно. переносячи раніше побудований графік у =
== Зсоз2х вправо вздовж осі Ох на одиниць (рис. 1.24).
28
§ 6. Властивості тригонометричних функцій
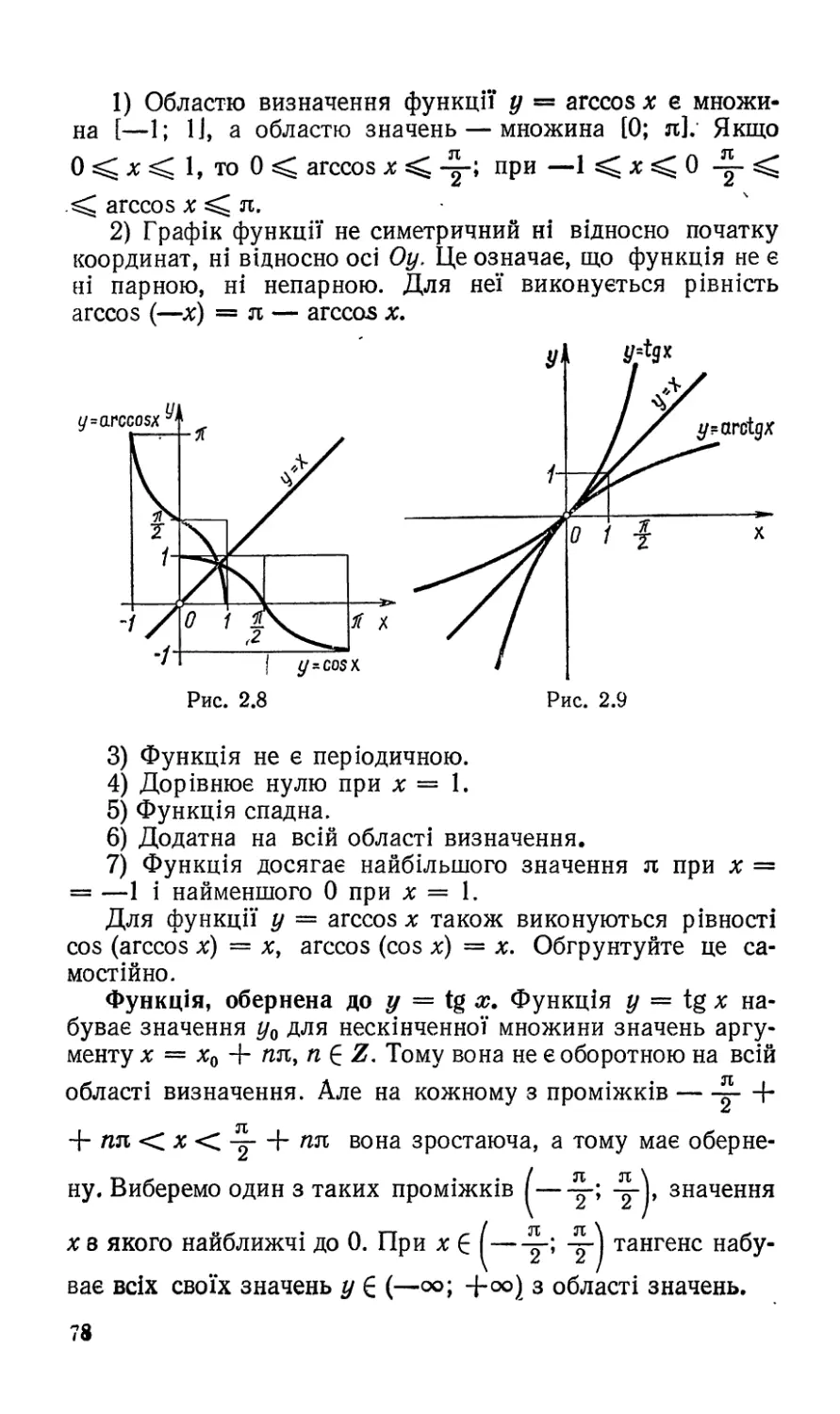
Функція у = ЗІП х. 1) Оскільки синус існує для будь-
якого дійсного числа і як ордината точки одиничного кола
(див. рис 1.2) змінюється на відрізку від —1 до 1, то об-
ластю визначення цієї функції є множина Р всіх дійсних
чисел, а областю значень — відрізок [—1; 1].
2) Графік функції симетричний відносно початку коор-
динат (див. рис. 1.18), тобто функція у = зіп % непарна.
РаА = Р-аА, а катет
Доведемо це для відрізка [0; 2л],
користуючись одиничним колом.
Оскільки областю визначен-
ня функції у = зіп х є множина
7?, яка симетрична відносно по-
чатку (нуля) відліку, го зали-
шається довести, що зіп (—а) =
= — зіп а
Позначимо на одиничному ко-
лі точки Ра і Р_а, які відповіда-
ють числам а і —а (рис. 1.25).
Оскільки прямокутний трикут-
ник Д РаОА = Д Л_а0Л, то катет
ОА — спільний Отже, абсциси точок Ра і Р_а рівні, а орди-
нати — протилежні числа. Тому зіп (—ос) = — зіп а.
3) Функція у = зіп х періодична з періодом 2/гл, де
2, п =А=0 Справді, означення синуса числа як ординати
точки одиничного кола і графік функції свідчать про те,
що кожне своє значення функція повторює через повний
оберт. Вище вже було доведено, що найменшим додатним
періодом цієї функції є число 2л.
4) Функція набуває значення, що дорівнює 0 (нуль
функції), при х = &л, де к £ 2, оскільки ординати точок
одиничного кола перетворюються в нуль на відрізку [0;
2л] у двох точках <хх = 0 і а2 = л, а функція періодична.
Числа 0 + 2/гл = л + 2/гл, ... утворюють множину
Ал, де к £ 2.
5) Проміжки зростання функції — відрізки —у +
+ 2/гл; + 2/гл , де п £ 2. Оскільки у = зіпх— функція
періодична, досить довести зростання на одному з вказа-
них відрізків, наприклад на у^ Скористаємось озна-
ченням зростаючої функції. Нехай хх 6-----к~; -тт І, *2 (і
І " І
29
€ ----тр -у- і Х2 > ХР Доведемо, що різниця [ (х2) — / (хх)
додатна. Справді, / (х2) — / (хх) = зіп хг — зіп хг =
= 2соз - Х1 зіп -2 ~ %1- > 0, оскільки за умовою х2 —
Я Я Я Хі 4-Х*
— Хх>0, —тому------------------------------2" < - "7 ’ <
Я л Хі — Хп Я Ха —І-” Х-і - л •
<. 0 < 2~ • < -д-, а значить соз —- 2 > 0 і
зіп -2 ~ Х1 > 0. Отже, зіп х2 > зіп хх.
Довести самостійно, що синус спадає на проміжках
|^-у + 2пл; 4* 2плф де п £ 2.
6) Проміжками, де синус додатний, є (2пл; л + 2пл),
оскільки на відрізку [0; 2л], довжина якого дорівнює най-
меншому додатному періоду 2л, функція додатна на про-
міжку (0; л). Синус від’ємний на проміжках (л -|- 2гал;
2л + 2/гл), оскільки на відрізку [0; 2л| він від’ємний на
проміжку (л; 2л). Враховуючи періодичність функції,
дістанемо всі можливі проміжки знакосталості.
7) Синус досягає максимумів, що дорівнюють 1, у точках
+ 2пл, де п £ 2, а мінімумів, що дорівнють —1, у точ-
ках + 2пл, де п £ 2, оскільки на відрізку І0; 2л] орди-
ната точки одиничного кола дорівнює 1 при а = -£- і —1
Зл
при а = —.
Функція у = соз ж. 1) Областю визначення функції є
множина всіх дійсних чисел /?, а областю значень — відрі-
зок [—1; 11, оскільки косинус існує для будь-якого дійсно-
го числа і як абсциса точки одиничного кола (див. рис. 1.4)
змінюється на відрізку [—1; 1].
2) Графік функції симетричний відносно осі Оу (див.
рис. 1.19), отже, функція парна. Доведемо це для відрізка
10; 2л], користуючись одиничним колом.
Оскільки областю визначення функції у = соз х є мно-
жина /?, симетрична відносно початку (нуля) відліку, то
залишається довести, що соз (—х) = соз х.
Позначимо на одиничному колі точки Ра і Р_а, які відпо-
відають числам а і —а (див рис. 1.25) Вище було показано,
що абсциси цих точок однакові, тому соз (—а) = соз а.
3) Функція у = соз х періодична з періодом 2пл, де
п £ 2, оскільки означення косинуса числа як абсциси точки
одиничного кола (див. рис. 1.5) і графік функції (див.
3.0
рис, 1.19) свідчать про те, що кожне своє значення функція
повторює через повний оберт. Раніше було доведено, що
найменшим додатним періодом функції є число 2я.
4) Функція набуває значень, що дорівнюють 0 (нулі
функції), при х = -у + йя, де к £ 2, оскільки абсциси то-
чок одиничного кола на відрізку 10; 2л] дорівнюють 0 у
двох точках = у і а2 = у. Додавши до цих чисел
період 2/гя, матимемо дві множини чисел, які разом дають
множину -у + кп.
5) Проміжки зростання функції — відрізки [—я +
+ 2/гя; 2/гя], де п С £ Оскільки функція у = соз х періо-
дична, то досить довести зростання на одному з вказаних
проміжків, наприклад на відрізку [я; 2я].
Нехай хг £ [я; 2я], х2 £ ія; 2я] і х2 > х1. Доведемо, що
різниця / (х2) — / (хх) додатна. Справді, / (х2) — { (хх) =
= соз х2 — соз хг = —2 зіп —- зіп > 0, оскіль-
ки за умовою я Хі < 2я, х2 — х±> 0. Тому я <
Х9 -4- X, о п Хо — Хг Я . Хі + Хо _
< -у—— < 2я, 0 < —- < -у, значить зш ---у 2- <
< 0, зіп *2 ~ Х1 > 0. Отже, соз х2 > соз хх.
Довести самостійно, що косинус спадає на відрізках
[2/гя; я + 2/гя], де п £ 2,
6) Проміжками, де косинус додатний, є (—у + 2/гя;
-у + 2/гя), а від’ємними є (у + 2/гя; у + 2/гя), де
п £ 2. Справді, у І і IV чвертях, тобто на проміжку —у;
-у , косинус набуває додатних значень, а у II і III, тобто
на проміжку (-у; -у), —- від’ємних. Враховуючи періодич-
ність функції, дістанемо всі можливі проміжки знакосталості.
7) Косинус досягає максимумів, що дорівнюють 1, у
точках х = 2/гя, де /г £ 2, а мінімумів, що дорівнюють —1,
у точках х = я + 2/гя, де /г Є 2,
Функція у = х. 1) Областю визначення функції є
множина всіх дійсних чисел, крім тих, косинус яких до-
рівнює 0, тобто чисел у + /гя, де /г £ 2', областю значень
є множина
Зі
2) Графік тангенса (див. рис. 1.21) симетричний віднос-
но початку координат, тобто функція непарна Довести це
твердження можна, користуючись непарністю синуса і
парністю косинуса Справді, область визначення танген-
са — множина, симетрична відносно нуля — початку від-
ліку, і
= 5ІП (~х) == = - 21ГД- _ _ іох
® ' СОЗ (— х) СОЗ X СОЗ X Ь
3) Функція у = х — періодична з періодом пп, де
п £ 2, оскільки кожне своє значення, як довжину відрізка
лінії тангенсів, вона повторює через половину оберту
(див. рис. 1.6). Вище було доведено, що найменшим додат-
ним періодом тангенса є число л.
4) Функція набуває значень, що дорівнюють 0 (нулі
функції), при х = пл, де п £ оскільки тангенс дорівнює
нулю у тих точках, де синус дорівнює нулю, а косинус не
дорівнює нулю. Про це свідчить інтерпретація .на одинич-
ному колі і графік функції.
5) Проміжки зростання функції + /гл; + ял),
де п £ 2.
Враховуючи періодичність функції, досить довести зро-
стання на одному з проміжків, наприклад на (—-2-).
Доведемо цю властивість.
Нехай хг^[------у ; х2є(— -у-; -у-) > хі>х1. До-
ведемо, що різниця / (х2) —/ (хх) додатна.
Справді,
ї М - / (хх) = х2 — %х = -----
1 4 і 17 Ь 2 Ь 1 СО8 Х2 СО8 X]
__ 8ІП Х2 СО8 Хх —СОЗ Х2 ЗІП Хх _ ЗІП (Л2 — Хх) д
СОЗ Х2 СОЗ х2 СОЗ X] соз х2 :
оскільки за умовою — у < < у , 0 < х2 — хх < л,
то СОЗ Х2 > 0, соз хх > 0, зіп (х2 — хх) > 0. Отже, х2 >
> ХХ.
Оскільки тангенс набуває додатних значень у І і III
чвертях, то (пл; + пл) і --------+ пл; пл^ є відповідно
проміжками, де тангенс додатний і від’ємний. Врахову-
ючи періодичність тангенса, дістанемо всі можливі проміж-
ки знакосталості.
32
6) Функція у — х не має екстремумів, бо на кожному
з проміжків, де вона визначена, тангенс зростає від —оо
до -|-оо.
Функція у = сі£ х. Обгрунтуйте самостійно всі власти-
вості функції котангенс.
1) Областю визначення є множина всіх дійсних чисел,
крім х = пл, де п £ 2.
2) Функція непарна.
3) Періодична з періодом пл, п£ 2; найменшим додат-
ним періодом е число л.
4) Функція набуває значень, що дорівнюють 0 (нулі
функції) при х = у 4 пл, де п £ 2.
5) Проміжками спадання є (пл; я 4- пл), де п Є 2.
6) Проміжками, де котангенс додатний, є ^пл; у 4-пл),
а від’ємний—(—— плі пл^ при п£2.
7) Функція не має екстремумів.
Приклад 1. Знайти область визначення функцій:
і) у = іїпх1-! і 2) у = І^соГх; з) у = ;
£>111 А» — X Л
4)У = І2(*—-г)>
Р о з в’ я з а н н я. 1) Дріб ( існує, якщо знамен-
ник зіп х — 1 5і 0. Звідси зіп х =/= 1. Користуючись гра-
фіком синусоїди, знаходимо точки, в яких зіп х = 1. Ви-
кидаючи їх, дістанемо х =£ — -у-; х #= у, х =И= -у-,... .
Записуючи всі ці числа у вигляді однієї формули, маємо
х ¥= (4А 4- 1) к € 2.
2) Вираз Ксоз х існує при соз х 0. Вище було доведе-
но, що соз х > 0 на інтервалах (-у 4- 2пл; у 4* 2пл^ і
соз х = 0 у точках х = -5- 4- пл, де п Є 2. Об’єднавши ці
А
множини чисел, маємо соз х 0 на відрізках [—у 4*
4- 2пл; у 4- 2пл^ Ці відрізки є областю визначення
функції у « И соз х.
3) Вираз -^у існує при всіх х, для яких існує сі§ х і
сі§ х #= 0. Котангенс існує при х ф кл, а не дорівнює нулю
2 1-1819 33
при всіх х =/= (2й + 1) -у-. Якщо записати першу множину
чисел кл у вигляді 2к • то можна об’єднати обидві мно-
жини, враховуючи, що всі парні (2/г) і непарні (2Л + 1)
числа утворюють множину цілих чисел. Отже, областю ви-
значення функції у = —— є множина всіх чисел х таких,
Сї§ X
ЩО X =£ п -у-, де п $ 2.
4) Вираз І х----5- ] існує, якщо х-^^(2п-{-1)-5-,
тобто х=£(2п + 1)4г + -7-• Звідси х#= 2п • -£- 4- 4- -2- ,
ТГ £ £ тг
Зл
або х —|- пзт, де п £ 2.
Приклад 2. Знайти область значень функції:
1)у=-^-созх; 2) у = зіпх 4- 1; 3)у = соз2х+1і
4) у — ~ ї§2х + 1; 5) у = зіп 2х.
Розв’язання. 1) Оскільки соз х змінюється від
—1 до 1, то областю зміни функції у = соз х є відрізок
Г____1_. _1_1 ч
[ 2 ’ 2 ]•
2) У виразі зіп х + 1 найменше значення першого додан-
ку —1, а найбільше 1. Тому найменшим значенням виразу
зіп х + 1 є число 0, а найбільшим — число 2. Отже, об-
ластю значень функції у — зіп х 4- 1 є відрізок (0; 2].
3) У виразі соз2 х 4* 1 перший доданок змінюється від
0 до 1, а весь вираз — від 1 до 2. Отже, областю значень
функції у — соз2 х + 1 є відрізок [1; 2].
4) Перший доданок виразу -^-1§2х4- 1 змінюється від
0 до +оо, оскільки і§х змінюється від —оо до 4-°°, а
і§2 х — число невід’ємне. Тому областю значень функції
у = і§2 х є множина [0; 4-°о).
5) При будь-яких дійсних значеннях х областю значень
функції у = зіп 2х є множина І—1; 1].
Приклад 3. Яке число більше:
1) зіп-у чи зіп-^- ; 3) чи ї£—;
2) соз -у чи соз -5- ; 4) сі§ ~ \ чи сі§ (— ?
34
Розв’язання. 1) Числам ах =і аа = -^- відпо-
відають точки одиничного кола Ра, і Раг, які належать
І чверті, де синус зростає. Оскільки ~ > -у-, то зіп >
п
>8Ш^.
її я
2) Косинус у І чверті спадає, тому соз < соз -д-.
3) Числу ах — відповідає точка Раі, яка належить
яг * ЗіС р,
І чверті, а числу а2 = -------точка Раг, яка належить
II чверті. Оскільки тангенс у І чверті додатний, а у
II — від’ємний, то -5- > .
4) Числам-----~ і-----відповідають точки Раі і Ра2,
які належать IV чверті, тобто проміжку -----у; 0^. Ос-
кільки котангенс — функція спадна на кожному з проміж-
• • я я
ків області визначення, а------х->------, то
о о
Приклад 4. У яких чвертях може закінчуватися кут
а, якщо:
1) | зіп (— а) | = — зіп а; 2) | соз а ( = — соз а;
3) І а | = а; 4) | сі§ (— а) | = — сі§ а?
Р о з в’ я з а н н я. 1) Оскільки синус — непарна
функція, то дану рівність можна записати у вигляді
| —зіп сс | = —зіп а. Модуль будь-якого числа — число
невід’ємне, тому невід’ємним має бути вираз —зіп а. Це
означає, що зіп а 0. Тому кут а може закінчуватися у
III або у IV чверті.
2) За означенням модуля числа модуль від’ємного числа
дорівнює протилежному числу. Тому соз а за умовою набу-
ває лише від’ємних значень. Це означає, що кут а може
закінчуватися у II або у III чверті.
, 3) За означенням модуля а — число невід’ємне. Тому
кут а може закінчуватися або у І, або у III чверті.
4) Оскільки сі§ (—а) = — сі§ а, то згідно з означен-
ням модуля —сі§ а має бути числом невід’ємним. Тому
кут а може закінчуватися у II або у IV чверті.
Приклад 5. Побудувати графіки функцій:
і) у = —
2*
35
2) 0 = 2003 -2-).
Розв’язання. 1) Графік даної функції побудуємо
за допомогою геометричних перетворень відомого графіка
функції у =* х.
Якщо X “ / (х), то — І£ (х + / (х + д), да
а ™ Застосуємо відомі алгоритми побудови графіків
перетворень: а) побудуємо
за допомогою геометричних
графік функції / (х) = х; б) побудуємо графік функції —
— / (х) = — х, відобразивши попередньо побудований
графік симетрично відносно осі Ох; в) побудуємо шуканий
графік, паралельно перенісши здобутий графік на -2- оди-
ниць вліво уздовж осі Ох (рис. 1.26).
2) Щоб побудувати графік функції у — 2соз (-у----у)
ва допомогою геометричних перетворень відомого графіка
функції у = соз х, треба перетворити формулу, що задає
функцію так, щоб перед аргументом х був коефіцієнт 1.
Це дасть змогу використати побудову графіка у = Ь[ (х —
— а), якщо відомий графік у = / (х). Отже, у = 2соз(-^-
---— 2соз^-^-^х-------Послідовність побудови така.
Будуємо графіки: а) у = соз х; б) у = соз -у х (розтяг
графіка у — соз х удвоє від осі Оу); в) у = 2 соз -у х (роз-
36
тяг графіка у = соз -у- х удвоє від осі Ох); г) у =-
» 2єоз (х-------(паралельне перенесення графіка
у -» соз -і- х уздовж осі Ох на відстань -у одиниць вправо)
Приклад 6. Знайти залежність між фазами <рг і <р8 для
миттєвих значень струмів, що проходять по двох паралель-
них вітках мережі, якщо іх = /тах зіп (гоі 4* <рх) і ї2 =
= /тах зіп (йу/ 4- <ра) за умови, що 4- і2 = ізаг; гзаР = 0.
Розв’язання. З умови випливає, що /тах X
X ЗІП (да/ + фх) 4- /тах 8ІП (МІ + ф2) = 0; ЗВІДСИ ЗІП (йУІ 4~
4- фі) 4- зіп (йу/ 4- ф2) = 0; зіп йу/ соз фх 4- соз йу/ зіп фх 4*
+ зіп а)і соз ф2 4- соз иіі зіп ф2 = 0; зіп да/ (соз фх 4- соз ф2) 4*
4- соз уві (зіп фх 4* зіп ф2) = 0; зіп хші • 2 соз Ф1 + Фа х
X соз —<Ра- 4- соз • 2 зіп соз <Ріі- = 0;
СОЗ <Р1~ 8ІП (йу/ 4- 2~"'2== 0-
Звідси соз ф1~ фг = 0; 4- лй, к £ 2',
Фі — Ф2 = я. 4- 2йл; фх — Ф2 = (2к 4- 1) я, к $ 2.
Отже, фази фх і ф2 відрізняються на (2й 4- 1) я.
з?
Приклад 7. За графіками синусоїдальних струмів
(рис. 1.28), що проходять в обмотках котушок трифазної
системи, визначити параметри, що їх характеризують.
Відповідь. В обмотках проходять синусоїдальні струми
з однаковими амплітудами і однаковою кутовою частотою
(о = 2л/), фази яких зміщено на періоду.
§ 7. Співвідношення
між тригонометричними функціями
одного й того самого аргументу
При вивченні тригонометричних функцій гострого кута у
8 класі за теоремою Піфагора було доведено основну триго-
нометричну тотожність
зіп2 а + соз2 а =1. (1)
Вона виконується для, тригонометричних функцій будь-
якого кута і тригонометричних функцій ДОВІЛЬНОГО число-
вого аргументу. Доведемо це. Якщо косинус числа а — це
абсциса точки Ра одиничного кола, а синус числа а — ор-
дината цієї точки, тобто х = соз а, у — зіп а, то точка
Ра (я; у) віддалена від центра кола на відстань, що дорів-
нює 1. Відомо, що відстань точки від початку координат
визначається за формулою х2 + у2, = г2 Оскільки г = 1,
то х2 + у2 = 1, тобто зіп2 а + соз2 а = 1.
Означивши тангенс і котангенс через синус і косинус,
ми ввели ще два незалежних співвідношення:
। зіп а . /оч
щ а =------; (2)
ь соз а 4 '
д. СОЗ 0& /О\
ь зіп а 4 '
З тотожностей (1) — (3) як наслідок випливають ще
кілька співвідношень, які часто використовують при об-
численні значення тригонометричних функцій через дане
значення однієї з них та в інших задачах.
Перемноживши почленно рівності (2) і (3), дістанемо
а • сі§ а = 1, звідки
сЇ£ а = ~г~— , І£ а = —г-ї— .
ь і&а & сі&а
Поділивши обидві частини рівності (1) на соз2 а, діста-
немо
зіп2а , соз2,а 1 . 2 1
—5— Ч-------=-------2— > або 1 + І£2 а = —»— •
соп2 а * соз2 а соз2 а ’ 1 ® соз2 а
38
Поділивши обидві частини рівності (1) на зіп2 а, діста-
немо
_8ІГ?О_ соз2 а = 1 б і . х 2 = 1
. зіп2 а ' зіп2 а зіп2 а ’ + б зіп2 а
Тотожність (1) виконується для будь-якого значення
аргументу, тотожності (2) і (3) — для всіх значень, крім
тих, для яких соз а #= 0 і зіп а 0.
Покажемо приклади застосування основних тригоно-
метричних тотожностей для обчислення значень тригоно-
метричних функцій за відомим значенцям однієї з. них
Вони ілюструють спрощення і обчислення тригонометрич-
них виразів і показують шляхи доведення інших тригоно-
метричних тотожностей.
Приклад 1. Знайти значення всіх тригонометричних
З Ззт
функцій аргументу а, якщо а = — і л < а <
Розв’язання. У III чверті, де на одиничному колі
розміщено точки, які відповідають числу а, тангенс і ко-
тангенс додатні, а синус і косинус від’ємні.
За тотожністю 1 + і§2а = —— знаходимо соз2а =
СОЗ ос
1 О 1 16 і/иГ
= Г+Ї^’ с°з а = ——9“ = 25 , а соза==— |/ =
+ 16
4
5 ‘
За тотожністю (1) маємо зіп2а=1— соз2а, зіп2а =
. 16 9 З о
= 1 “-2Г = -25- ’ 8Ша = - И -25~ = --Г- За Т0Т0Ж-
ністю (4) знаходимо сі§а = -|-.
У табл. 1.2 подано формули, які зв’язують тригономет-
ричні функції одного й того самого аргументу. У наведених
формулах перед знаком радикала треба взяти знак плюс
або мінус залежно від того, в якій чверті лежить кут а, а
саме так, щоб знак тригонометричної функції, який стоїть
у лівій частині, збігався із знаком величини, що стоїть у
правій частині рівності.
Приклад 2. Спростити вирази:
1) ? С°3 — 1 І 2) 1 + зіп2 а — соз2 а;
9 зіп а + соз а ' ‘
3) 1—зіп а сі§ а соз а; 4) (1 + соза)і§2а(1—соза);
зіп2 а — 1 зіп а 8Іп В і о . п <
5) -і---5— ; 6) -------сі£ 6 сЬ 2а + 1;
7 1 — соз2 а 1 соз а соз 0 ь г & *
г 7) зіп2 а — зіп2р — соз2р — соз2 а;
39
8) зіп4 а — соз* а 4- 2 соз2 а.
п , < ч 2 соз2 а — 1 2 соз2 а — зіп2а - соз2 а
Р О З В Я 3 а Н Н Я. 1) ----і----= -------:----:--------- =
7 8іп а + соз а зіпа + соз а
соз2 а — зіп2 а (соз а — зіп а) (соз а + зіп а) :
= ---------;----= к;-----------V--------—----- = соз ос — зіп сс;
зіп а + соз а зіп а 4- соз а
2) 1 + зіп2а— соз2а = (1 — соз2а) + зіп2 а = зіп2 а 4-
4- зіп2 а = 2 зіп2 а;
Таблиця 1.2
Функ- ції зіп а соз а а сі£а
зіпа ±К1 — соз2 а , .... .лгт—.—г=г- ± V 1 4- і§2 а ± V 1 4- сі§2 а г 1 сіда соза ± V 1 — зіп2а ~ —— ± V 1 4- і§2 а ± У 1 4- сі§2 а зіп а ± — соз2 а 1 1§а ±уі — зіп2а соза сі^а сі§а ± /1 — 5Іп2« соза 1 зіпа ±/1—соз2а *§а
3) 1 — зіп а сі§ а соз сс = 1 — зіп а С05 — соз сс =« 1 —
7 ° зіп а
— соз2 а = зіп2 а;
4) (1 4- соза)і§2а(1 —соза) = (1 — соз2а) і§2а
= зіп2аі§2а;
гх зіп2 а — 1 __ — (1 — зіп2а) _ соз2а __ 42.
7 1 — соз2 а ~~ 1 — соз2 а зіп2 а с § а»
6) созасТзВ' 1 = і§аі§Рсі§рі§а= 1§2а 4-
+1 = -V-;
1 соз2 а
7) зіп2 а — зіп2 р — соз2 р — соз2 а = зіп2 а — соз2 сс —
— (зіп2 Р 4- соз2 Р) = зіп2 а — соз2 а — 1 = — 2 соз2 а;
8) зіп4 а — соз4 а 4- 2 соз2 а = (зіп2 а 4- соз2 а) (зіп2 а —
— соз2 а) 4~ 2 соз2 а = 1 — соз2 сс — соз2 сс 4- 2 соз2 а = 1.
Приклад 3. Дано зіп а 4- соз а = т. Знайти зіп а соз ос.
Розв’язання. Піднесемо обидві частини даної
рівності до квадрата. Маємо
(зіп а 4- соз а)2 = т2,
або
зіп2 а 4- 2 зіп а соз сс 4- соз2 а = /тА
/?22 —- 1
Звідси 1 4- 2 зіп а соз а — т2, отже, зіп а соз а = —я—.
40
Приклад 4. Обчислити 5ЇП а С05 а— при
к зіп2 а — соз2 а г & 2
Розв’язання. Треба даний вираз спочатку впра-
вити через а, а потім обчислити його значення. Для цього
поділимо чисельник і знаменник даного дробу на соз2 а:
' зіп а сов а
зіп а соз а ______соз^а_______
зіп2 а — соз2 а зіп2 а соз2 а і£2 а — 1 *
соз2 а соз2 а
5
п . 5 і£а 2 10
При і§а— 2 1§2а_1 — 25 ~ 21 ’
4 —1
Приклад 5. Довести, що вираз 1 “2 а • 1
не залежить від а, тобто є величиною сталою.
п , і£а сЬ*2а—1 і£а *£2а
Розв язання.г=^-.4іі7Г-==т=^.—— =
і§а
. 1 —а _ , 1 — а _ .
1 — і§4 а ‘ 1 1 — і§2 а 12 а
Приклад 6. Довести тотожність
7 /~ 1 + соз а 1/1 — соз а о , Л _ л
І/ ---------І/ -ти------= 2сі§а при 0<а<-х-.
г 1 - соз а г 1 соз а ь г 2
Розв’язання. Доведення тригонометричних то-
тожностей можна виконувати різними способами:
1) за допомогою тотожних перетворень треба показати,
що одну частину рівності (ліву чи праву) можна подати у
вигляді другої;
2) кожну частину рівності звести до одного і того самого
виразу;
3) скласти різницю лівої і правої частин рівностей і за
допомогою тотожних перетворень показати, що ця різниця
дорівнює 0.
Дану тотожність доведемо, користуючись першим спо-
собом:
1/” 1 + С03 а 1 /" 1 — соз а л/" (14~ соз а)2 _
У 1—соз а У 1 4-соз а У (1—соз а) (1 4-соз а)
__і/ (1 — соз а)2 __ і / (1 4~ соз а)2 _
У (1—соз а) (1 + соз а) У 1 — соз2 а
41
_і Г (1 — соз а)2 __ і Г (1 + соз а)2 і / (1 — соз а)2
И 1—соз2 а V зіп2 а V зіп2 а
_ | 1 + соз а | 11 — соз а | і соз а 1 — соз а
| зіп а | | зіп а |_зіп а зіп а
= І+соза-1+соз» = 2 сій а
зіп а ь
Оскільки синус і косинус при 0 < а < -у додатні, 1 —
— соз а 0, тому | зіп а | == зіп а, | 1 + соз а | = 1 4-
4- соз а, | 1 — соз а | = 1 — соз а (косинус за модулем не
перевищує 1).
§ 8. Обчислення значень тригонометричних функцій
і тригонометричних виразів за допомогою
мікрокалькуляторів
1. Функції у = зіп х, у = соз х. у = і&х. Значення цих
функцій обчислюють за програмами:
х Р зіп; х
Р соз; х
ід
Р
При обчисленні значень функції у = сій х використо-
вують тотожність сі§ х = Тому програма обчислен-
ня має вигляд
х р ід Р 1/х
Мікрокалькулятор дає змогу обчислювати значення
тригонометричних функцій для значень аргументу як у
градусній, так і у радіанній мірах, причому перед обчислен-
ням перемикач «Г—Р», який розміщено на корпусі кальку-
лятора, треба встановити у відповідне положення.
Зазначимо, що при обчисленні значень тригонометрич-
них функцій або виразів з ними аргумент х використову-
ють у межах 0° х 90° (у градусній мірі), або 0 х
1,57 (у радіанній мірі); для тангенсів відповідно у ме-
жах 0° < х < 90°; 0 < х < 1,57.
Якщо аргумент х задано цілим числом градусів, то
спочатку це число вводять у регістр індикації (на екран),
а потім натискують послідовно клавіш і клавіш відповід-
ної тригонометричної функції.
Приклад 1. Знайти зіп. 75°.
Програма: 75 Р зіп.
Відповідь, зіп 75° « 0,9659.
2
Мікрокалькулятори типів «Злектроника МКШ-2», «Злек-
троника БЗ-32», «Злектроника БЗ-18» обчислюють значен-
ня тригонометричних функцій з точністю до чотирьох пра-
вильних десяткових знаків. У розглянутому прикладі вось-
мирозрядне число на індикаторі округлене до чотирьох
правильних десяткових знаків.
Якщо аргумент подано у градусах і мінутах, то міну-
ти попередньо перетворюють у частини градуса, а значення
аргументу записують десятковим дробом, що містить цілу
і дробову частини градусів. Наприклад, нехай х = 24° 12'.
12 12°
Оскільки 12' становлять -^у частин градуса, то х = 24 -уу.
12
Перетворення у десятковий дріб числа 24 уу виконують за
програмою
12[Т] 60 ГП 24 П
Відповідь, х — 24,2°.
Програма обчислення значення зіп 24° 12' має вигляд
12 [Т| 60 □ 24 □ СЕІ
Відповідь, зіп 24° 12' 0,4099.
7л
Приклад 2. Обчислити соз у-.
Встановлюємо перемикач на режим роботи у радіанній
мірі. Оскільки соз у- = соз у-, то програма має вигляд
Р тг +
З = І Р соз
! Відповідь, соз -х- = 0,5.
о
2л
Приклад 3. Обчислити соз
о
./ Зазначимо, що мікрокалькулятор обчислює лише мо-
дулі значень тригонометричних функцій. Тому знак мінус
треба набирати додатково, натискаючи клавіш /-у залежно
від координатної чверті для конкретного аргументу. Ос-
2л л
кільки соз -х- = — соз то можна скласти програму
О о
р 7Г -г 3 | = | Р СОЗ |*~*|
' Відповідь, соз -х- = —0,5.
* о
43
2. Обернені тригонометричні функції ЯГС8ІП X, агссоз X,
агсід х. Значення цих функцій обчислюють відповідно за
такими програмами:
X
Р зіп""1; х Р соз"1* х Р ід"1
Залежно від того, в якому вимірюванні (градусному чи ра-
діанному) ми будемо знаходити значення оберненої триго-
нометричної функції, встановлюється відповідне положен-
ня перемикача «Г—Р».
Аргумент х при цьому не може виходити за межі 0 х
1 для арксинуса і арккосинуса та 0 х 500 для
арктангенса.
Приклад 4. Обчислити агсзіп 0,75 з точністю до 10*"2
у градусній мірі.
Попередньо встановлюємо перемикач «Г—Р» на режим
роботи у градусній мірі і обчислюємо значення агсзіп 0,75.
Програма:
0,75 Р зіп"1
Відповідь, агсзіп 0,75 « 48,59°.
Приклад 5. Обчислити з точністю до 10*~3 агссоз 0,578 у
радіанній мірі.
Встановлюємо перемикач «Г—Р» на режим роботи у ра-
діанній мірі і обчислюємо шукане значення за програмою:
0,578 Р соз"1
Відповідь, агссоз 0,578 « 0,955.
3. Обчислення значень виразів, що містять тригоно-
метричні функції. Розглянемо два приклади.
Приклад 6. Обчислити зіп а, а і сі§ а, якщо соз а «
« 0,52 і 0 < а <
І спосіб. Можна скористатися основними тригономет-
ричними тотожностями і знайти наближені значення функ-
цій за формулами:
1) зіп а = К1 — соз2 а, зіпа^Кі— 0,582^0,85;
х зіп а . 0,85 « ~
3). с1§ а = 1^’ сіб а « « 0,61.
44
/ Усі три значення функцій можна знайти, користуючись
неперервною програмою
1Е0 0,52 0 х! 0,52 00 1/х
II спосіб. Можна використати суміщений клавіш соз-1 за
такою схемою:
а) за даним значенням косинуса знайти кут а, послідов-
но натискуючи клавіші Г і соз-1;
б) надіслати знайдене значення а у пам’ять і одночасно
обчислити за ним синус, послідовно натискуючи клавіші
і зіп;
в) викликати на екран з пам’яті значення а і обчислити
а, натискуючи клавіші Е і і§;
г) обчислити сі§ а за відомим тангенсом, послідовно на-
тискуючи клавіші Е і 1/х
Програма:
Р
Р
Р
0,52 Е
соз"1 П ГІЕ
зіп |ИП| Е їд Е 1/х
Шукані значення функцій записують з екрана після
натискання клавішів зіп, 1/х.
Відповідь, зіп а « 0,85; а яз 1,6; сі§ а « 0,61.
Приклад 7. Обчислити значення виразів: 1) зіп 25° +
+ соз 70°; 2) а = -ЦЦЛ при Ь ж 25, а « 28°, р « 65°.
1 ' ЗІП р г г
Програми:
1) 25] Е |зіп +| 70 1 Е |соз| —
2) 25 X 28 Е зіп т 65 Е зіп =
Відповідь. 1) 0,7646; 2) 12, 950039 « 13.
Якщо у цих двох прикладах аргумент тригонометричних
функцій був би виражений у градусах і мінутах, то дове-
лося б використовувати регістр пам’яті. Адже при обчис-
ленні значень кожної з тригонометричних функцій опера-
45
ційний регістр зайнятий, а його необхідно одночасно вико-
ристовувати і для виконання дій над тригонометричними
функціями (у даних прикладах додавання і ділення).
Приклад 8. Обчислити значення виразів:
1) зіп 25° 20' + соз 70° 12'; 2) а = 25,00 5КІ"2£154 •
7 1 ’ 7 81П 65 42'
Програми:
Відповідь. 1) 0,7666; 2) 12,983322 ж 12,98.
Обчислення двох останніх виразів можна виконувати
неперервним ланцюгом, не звертаючись до пам’яті, якщо
використати клавіші ( і ) . Відповідні програми мають
вигляд:
2О^6О025005Іп0|7]і206ОН7ОШ Р~ІСО£Г”І
250Ш1506О028Н [V] зіп .0 ОН600 65 □
Е зіп | в |
Перевірте відповіді, здобуті за цими програмами.
Розглянемо приклади обчислень більш складних ви-
разів.
Приклад 9. Знайти з точністю до 1 сторону в Д АВС,
у якого а « 36, с ж 52, / В ж 48°.
За теоремою косинусів
Ь = Ка2 + с2 — 2ас соз В,
Ь « V 362 + 522 — 2 • 36 • 52 соз 48°.
Здобутий вираз можна обчислити кількома способами.
Без використання регістра пам’яті послідовність обчис-
лень буде такою:
1) знайти добуток 2 • 36 • 52 соз 48° і змінити знак ре-
зультату за допомогою клавіша
46
2) додати до здобутого числа квадрати чисел 36 і 52 за
допомогою клавіша х2;
3) із здобутого результату добути квадратний корінь.
Програма:
20 36 5248 |~Е~]сб5 рП (77) Зб|~Р~| х2Я 52|~Е~] Xа
= Р
Відповідь. Ь « 38,662349 « 39.
Приклад 10. У Д АВС сторони Ь яз 28, с.« 39, /_ С «
яз 128°. Знайти з точністю до 1° кут В.
За теоремою синусів зіп В — &8Іп<? . Звідси
Д В = агсзіп
бзІпС
с
= агсзіп
28 зіп 52°
39
Програма:
28 X 52 Р зіп + 39
Р зіп-1
Відповідь. /_В яз 34°.
Приклад 11. Обчислити величину заряду д кульки, яка
має масу т = 2,0 г і обертається навколо нерухомого точ-
кового заряду на нитці довжиною/ = 1,2 м, якщо період
її обертання Т = 3,2 с, а кут відхилення від вертикалі
а = 25°.
Після розв’язання задачі дістанемо відповідь у вигляді
формули
д = І зіп а
4л2 , . .
----Ті- 1 8Ша),
де 80 = 1,000594, д = 9,8 м/с2.
Після підстановки числових значень треба обчислити
вираз
д— 1,2 зіп 25° х
X |/4л • 1,000594 • 2,0 (9,8 25° — • 1,2 зіп 25°) =
= 1,2 зіп 25° і / 8л • 1,000594 (9,8 і§25°— -1,2 зіп 25°).
47
Програма:
4 X
Р~|тг[~р]хйГ7]з<2[~Е~| х*[х] 1,2 [х] 25 [Т| 8іп
П 9,8 X
Е ід - ИП X 1,000594 X Е Я
ЯИуФП 1,2 |~Х] 2Б |~Р~| ііпрЯ
Відповідь. <7 «4,1 Кл.
§ 9. Основні тригонометричні формули
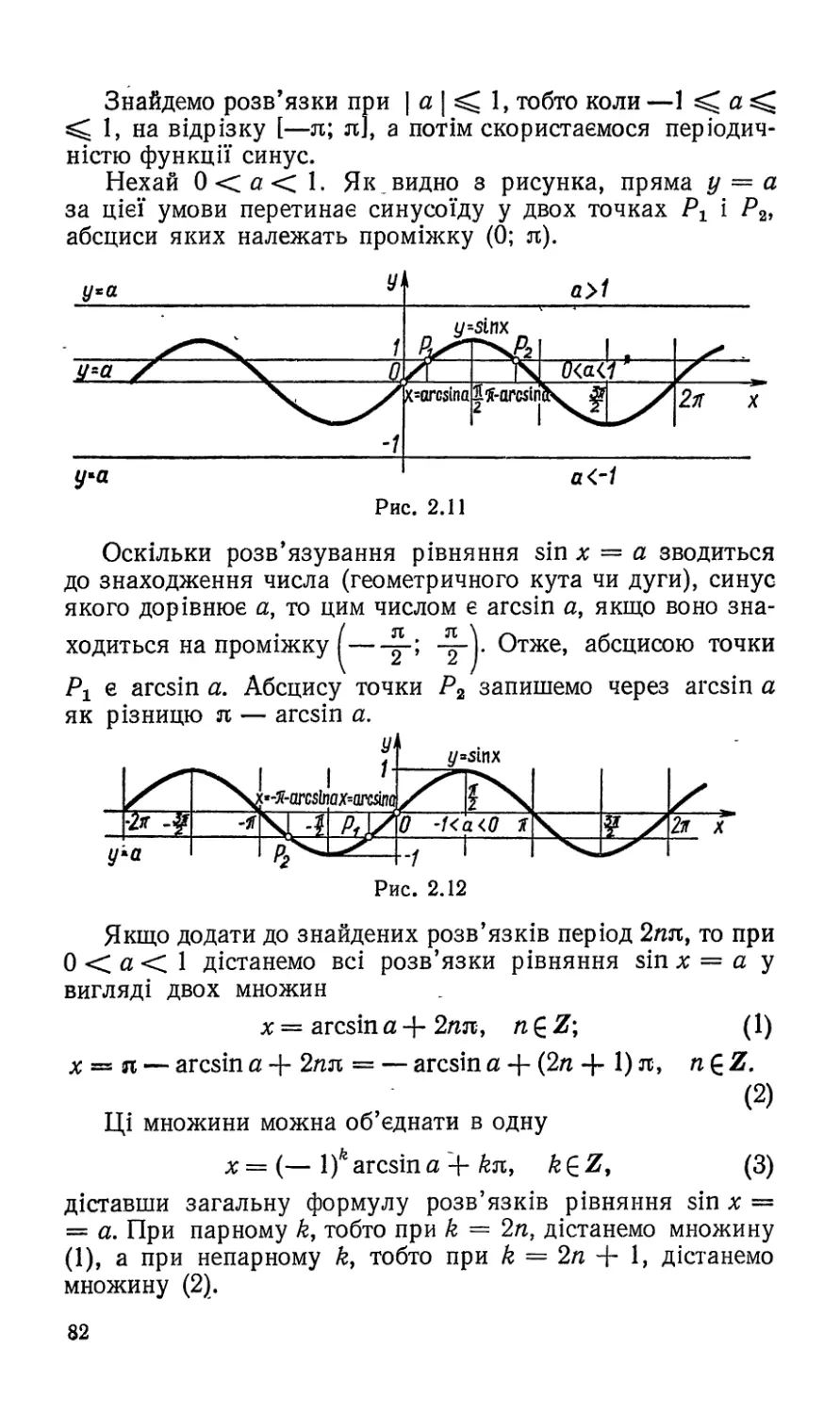
1. Формули додавання:
соз (а 4-Р) = соз а соз р— зіп а зіп Р; (1)
соз (а — Р) = соз а соз р + зіп а зіп Р; (2)
зіп (а + Р) = зіп а соз р + соз а зіп р; (3)
зіп (а — Р) = зіп а соз р — соз а зіп Р; (4)
+ ' <5>
Доведемо формулу (1), з якої
неважко дістати решту.
Нехай а і Р — будь-які числа.
Виберемо на одиничному колі точки
Ра, Р-р і Ра+р, які дістали з точки
Ро (1; 0), повернувши її відповідно
на кути а, —Р, а 4- Р (рис. 1.29).
Враховуючи означення синуса і ко-
синуса, можна записати коорди-
нати вибраних точок: Ра(соза;
Рис. 1.29 зіп а), Р_р (соз (—Р); зіп (—Р)),
Ра+р (соз (а 4- Р); зіп (а 4- Р)).
Хорди Р0Ра+р і Р-рРа рівні, ОСКІЛЬКИ рІВНІ ВІДПОВІД-
НІ їм дуги кола. Знайдемо довжини цих хорд за формулою
відстані між двома точками
Ро^а+Р = (1 — СОЗ (а 4- Р))2 4- (зіп (а 4- Р))2;
Р-рРа = (соз (— Р) — соз а)2 4- («іп (— Р) — зіп а)2.
Оскільки Р0Ра+р = Р-рРа, ТО Р0Ра+р = Р_рР£.
Тому
(1 — соз (а 4- Р))2 4- (зіп (а 4- Р))2 = (соз (— р) — соз а)2 4*
4- (зіп (— Р) — зіп а)2.
48
Скориставшись властивістю парності косинуса і непар-
ності синуса, формулою квадрата двочлена, дістанемо
1 4- 2 соз (а 4- 0) 4- соз2(а 4- Р) 4- зіп2 (а 4- р) =
= соз2 р — 2 соз а соз р 4- соз2 а 4- зіп2 Р 4-
4- 2 зіп а зіп р 4- зіп2 а.
Використовуючи основну тригонометричну тотожність,
маємо
2 — 2 соз (а 4* Р) — 2 — 2 соз а соз р 4- 2 зіп а зіп р.
Виразивши з останньої рівності соз (а 4- Р), дістанемо
формулу для косинуса суми двох аргументів
соз (а 4- Р) = соз а соз р — зіп а зіп р.
Формулу (2) можна дістати, замінивши у формулі (1) р
на —р і скориставшись парністю косинуса і непарністю
синуса,
соз (а 4- (— Р)) = соз а соз (— Р) — зіп а зіп (— Р),
соз (а — Р) = соз а соз р 4- зіп а зіп р.
Формулу додавання для синуса неважко дістати з фор-
мули (1) і формули зведення зіп х = соз (-2---
Вказану формулу зведення можна дістати і з форму-
ли (1), поклавши а = ~ . Справді, соз(-^-----------Р) =
= соз -у- СОЗ р 4- ЗІП -у- ЗІП Р = 0 ’ СОЗ р 4- 1 зіп Р = ЗІП Р
Отже,
СОЗ -----р) = ЗІП р. (6)
Замінивши у формулі (6) р на -----------а, дістанемо
(Л / Л \\ • [ Л \ у* • / Л \
-2--1"2—а 1= зіпі-^----а » або соз а = зіп І-----а .
Отже,
зіп І ---а = соз а.
Виразимо зіп (а + |3), скориставшись формулою (6) від
носно числа (а + 0) у зворотному порядку,
зіп (а 4- Р) = соз ----(а 4- Р)] = соз ----а] — р) =
49
= соз -----соз Р + зіп --------а) зіп Р =
= зіп а соз р + соз а зіп р.
Отже,
зіп (а + Р) = зіп а соз р + соз а зіп р.
Формулу (4) дістанемо, замінивши у формулі (3) Р
на —р і скориставшись парністю косинуса і непарністю
синуса,
зіп (а + (— Р)) = зіп а соз (— Р) + соз а зіп (— Р),
звідки
зіп (а — р) = зіп а соз р — соз а зіп р.
Формулу додавання для тангенса можна дістати за
означенням тангенса і формулами додавання для синуса
і косинуса:
+ / । гп 81П (а + Р) 5ІП а С05 Р + С05 а зіп р
8 \ "г Р/ соз (а + Р) соз а соз р — зіп а зіп р
Розділивши почленно чисельник і знаменник правої
частини на вираз соз а соз Р (поясніть, чому він не дорів-
нює 0), дістанемо
зіп а соз Р соз а зіп Р
соз а соз р + соз а соз р а + р
(а "Ь Р) соз а соз Р зіп а зіп Р 1 — а р
соз а соз р соз а соз Р
Отже,
І£(а + 6) = 18?_+ЧР.
Якщо замінити у формулі (5) р на —р і врахувати непар-
ність тангенса, то
-іб(а_0) = .
6 ' 1 + а р
Самостійно довести формули додавання для котангенса.
2. Формули зведення. Формули зведення для довільних
кутів вивчали у курсі алгебри 9 класу. Властивість періо-
дичності тригонометричних функцій будь-якого числового
аргументу дає змогу звести обчислення їх значень до об-
числення значень функції для аргументу від 0 до 2л (для
синуса і косинуса) і від 0 до л (для тангенса і котангенса)
за допомогою формул зведення.
50
/ Нехай, наприклад, треба обчислити соз 0, де я < 0 <
< Запишемо 0 у вигляді 0 = я + а, де 0 < а < -у.
За формулою (1) додавання для косинуса дістанемо
соз (я + а) = соз я соз а — зіп я зіп а = — соз а.
Формула соз (я + а) = —соз а виконується при будь-яко-
му а і називається формулою зведення.
Таблиця 1.3
Функ- ції 90° 4-а л . 180° 4- а п 4- а і 270° 4- а Зл , —+ <Х в 1 90° — а л 180° — а л — а 270° — а Зл — •— а 2
зіп и соз а — зіп а — соз а — зіп а созсх зіп а — соз а
соз и — зіп а — соз а зіп а соз а зіп а — соз а — зіп а
— сі§ а — сІ£ а — сі§ а — і§а сі§а
сі&и — — і§а — сі£а - -сі§а
Будь-яку з формул зведення, що наведено у табл. 1.3,
можна вивести за допомогою формул додавання.
Довести самостійно, що
зіп + а) = — соз а, + а) = — сі£а,
с!§ (я — а) = — сі§ а.
Щоб записати будь-яку формулу зведення, коли 0 <;
< а < у, зручно користуватися такими правилами:
1) якщо кут а добудовується відносно вертикального
діаметра (рис. 1.30) (це кути, що відповідають числам -у ±
Зл \ .. .
± а; -у ± а І, то назва даної функції змінюється на ко-
функцію (синус на косинус, тангенс на котангенс і нав-
паки); якщо кут а добудовується відносно горизонтального
діаметра (рис. 1.31) (це кути, що відповідають числам я ±
± а), то назва даної функції не змінюється;
2) перед утвореною функцією ставиться той знак, який
має функція, що перетворюється за формулою зведення.
3. Тригонометричні функції подвійного аргументу. Це
формули, які виражають функції 2а через функції аргумен-
ту а. їх можна здобути з формул додавання.
61
Поклавши р = а у формулі (3), дістанемо формулу си-
нуса подвійного аргументу
зіп 2а = 2 зіп а соз а. (7)
З формули (1) при р = а дістанемо формулу косинуса
подвійного аргументу
соз 2а = соз2 а — зіп2 а.
Рис. 1.30
Якщо замінити за допомогою основної тригонометричної
тотожності зіп2 а + соз2 а == 1 функцію соз а на зіп а або
зіп а на соз а, то матимемо ще дві формули для соз 2аі
соз 2а = 2 соз2 а — 1, соз 2а = 1 — 2 зіп2 а.
Формула (5) при р = а дає формулу тангенса подвій-
ного аргументу
(§2а = т2-^ (9)
Формули (7) і (8) виконуються для будь-яких значень
аргументу, а формула (9) — лише для тих, для яких існу-
ють 2а, а і 1 — і§2 а 0.
4. Тригонометричні функції половинного аргументу. За-
пишемо дві відомі формули
соз 2х = СОЗ2 X — ЗІП2 X, 1 = СОЗ2 X -|- зіп2 X.
При х = -у ці формули матимуть вигляд
п • а а « п ос . • 9 а
соза = соз2 ----81п 2 » * = соз2“2’ + 81п ~2~ ’
Додавши почленно ці дві рівності і віднявши від першої
рівності другу, дістанемо такі дві формули:
1 + соз а = 2 соз2 , 1 — соз а = 2 зіп2-^- .
52
Виразивши з них квадрати функцій, матимемо формули
половинного аргументу для квадратів синуса і косинуса
» а 1 4- соз а . » а 1 — соз а
С05 -Г = — 2------’ 81П V =--------2---
Звідси
а . 1 / 1 4- соз а . а , 1 / 1 — соз а
соз -у = ± |/ —2--------, зіп-у = ± у --------.
Ці формули дають змогу замінити квадрати тригономет-
ричних функцій на перші степені функцій. Тому їх нази-
вають також формулами пониження степеня.
Розділивши почленно дві останні рівності, дістанемо
формули для квадрата тангенса і котангенса половинного
аргументу
, 2 а 1 — соз а , 2 а 1 + соз а
® 2 1 -|- соз а ’ С° 2 1 — соз а
Звідси
. а , і/~ 1 — соз а . а , 1 /” 1 4- соз а
= ± И 14-соза ’ с1§"2- = ± V Т-соза' ’
5. Формули суми і різниці однойменних тригонометрич-
них функцій. Ці формули дають змогу виражати суму й різ-
ницю однойменних тригонометричних функцій через добу-
ток тригонометричних функцій і навпаки.
Щоб перетворити суму зіп а + зіп р у добуток, позначи-
мо а = х + у, р = х — у і використаємо формули додаван-
ня для синуса
зіпа+ ЗІП Р — зіп (X + у) 4- зіп (х — у) = 8ІПХСОЗЇ/ +
+ соз х зіп у + зіпхсоз//— соз х зіп у — 2зіпхсозг/.
Враховуючи введене позначення, розв’яжемо систему
І х + у = а,
|х —у = р
. . т-т. &+ Р а - Р
відносно х і у. Дістанемо х = —, у = —.
Отже,
зіп а + зіп Р = 2 зіп соз . (10)
Замінивши у формулі (10) р на —Р і врахувавши непарність
синуса, дістанемо
. о п . а - В а + р
зіп а — зіп р = 2 зіп —2^” С08 —•
53
Таким самим способом знаходимо
соз а + соз0 = соз (х-Ь у) + соз (я — у) —
= соз х соз у — ЗІП X ЗІП у + СОЗ X СОЗ у + зіп х зіп у ==
о о <%+ 6 а — 6
= 2 соз х соз у = 2 соз —соз —.
Отже,
> о п а 4- Р а— 6
соз а 4- соз р — 2 соз —соз —.
соз а — соз р = соз (х 4- у) — соз (х — у) =
= СОЗ X соз у — зіп X зіп у — СОЗ X соз у — зіп х зіп у =
= — 2зіпхзіпг/ = —2зіп зіп .
Таким чином,
соз а — соз р = — 2 зіп зіп •
Користуючись означенням цієї функції, знайдемо суму й
різницю тангенсів
*8« + і§Р =
зіп а , зіп р ______ зіп а соз р + соз а зіп Р _____
соз Р соз а соз Р
зіп (а + Р) .
соз а соз р *
зіп Р ___ зіп а соз р — соз а зіп Р ____
соз а соз Р соз а соз Р
__ зіп (а — р)
соз а соз Р
соз а
зіп а
— і§Р =
Отже,
і§а-Н§Р =
і§а — і§Р =
зіп (а Р)
соз а соз р *
зіп (а — Р)
соз а соз р
6. Формули перетворення добутку тригонометрич-
них функцій у суму. При розв’язанні деяких задач дово-
диться добуток двох тригонометричних функцій заміняти
сумою (чи різницею) функцій. Щоб вивести формулу пере-
творення добутку двох косинусів, почленно додамо рІВНОСг
ті
соз (а — Р) = соз а соз р + зіп а зіп Р;
соз (а 4- Р) = соз а соз р — зіп а зіп р.
54
Дістанемо
созасозр = соз(а-Р) + соз(а + Р) :. (1
Якщо відняти ці самі рівності, матимемо
. о соз (а — 6) — соз (а 4- 6)
зіп а зіп р =-----------і----1 .
Щоб дістати формулу добутку синуса на косинус, додамо по-
членно рівності
зіп (а + р) = зіп а соз Р + соз а зіп р,
зіп (а — Р) = зіп а соз Р — соз а зіп р.
Після додавання матимемо
о зіп (а 4- р) 4- зіп (а — р)
зіп а соз р =-----------* 2---1~ ’
7. Формули перетворення синуса і косинуса кута через
тангенс половини цього кута. Маємо
а а
2 зіп -у соз у
зіп а = 2 зіп соз .
2 2 а „а
зіп8 ~2~ + соз2
Поділимо чисельник і знаменник утвореного дробу на
соз2-5- за умови, що соз2-^-=#0. Звідси + кп,
де к £ X, і
а
2 2
зіп а =------------. (12)
Таким же способом виразимо соз а через
сс а а
соз2 -X- — зіп2 ~5" 1 — ід2 -5-
» а . » а * * 2
соз а == соз2 -а-зіп2—х- =------------------=------------.
2 2 . а . „ а „а
51П ~2~ + со8 ~2~ 1 + *§ “2~
Отже,
соза= -------------------------. (13)
і + і£2-у
55
Якщо поділити почленно рівності (12) і (13), то дістанемо
1§а =-------— •
1-^Т
Виведені формули широко використовують для спро-
щення виразів і обчислення їх значень, доведення тотож-
ностей, розв’язування тригонометричних рівнянь і нерів-
ностей та ін.
Приклад 1. Обчислити значення виразів, не застосовую-
чи таблиці тригонометричних функцій і мікрокалькулятори»
1) соз 75°; 2) зіп ; 3) ; 4) соз 210°;
5) зіп 75° 4-зіп 15°; 6) 8Іп22°30'’’
8) 9) зт-^-зш-^-; 10) соз—,
Н9 ; Зл
якщо соз а = і те < а < .
Р о з в’ я з а н н я. 1) Нехай 75° = 45° + 30°. Тоді
соз 75° = соз (45° 4- 30°) = соз 45° соз 30° — зіп 45° зіп 30° =
ҐЗ /2 1 _ /б — |/2
“2'2 2 ’ 2 ~ 4
л\ • 7 її , / її । її ) * її її
2) 8іп-іу= зіп 4--47 = зіп —соз -^-4-
. її , її /з /2 . 1 /2 /2 Л<Л . 1ч
+ соз X®іП'4~ = ~2--Х"+х' Л-=-1-<|ЛЗ+
Іе— +
. 1-І84-І24-
о
3)
1 . /З
_ 3 = 3 + /3 .
~ і Кз з—/з ’
з
4) соз 210° = соз (180° 4- 30°) = соз 180° соз 30° —
— зіп 180° зіп 30°= —
ех • -7ЕО , • 1ЕО О • 75° + 15° 75° —15°
5) зіп 75° + зіп 15 = 2 зіп-у----соз----------
= 2 зіп45°соз30° = ]/2 • ;
6) = 1§<13° + 47’>= 1£60°=
56
соз 45°
"2
2
і зт
1 — соз-----
4
1 + соз —
4
7) 8іп22° ЗО'
К2 —/2
= 2
(знак плюс перед коренем взято тому, що кут 22° ЗО' нале-
жить І чверті, а синус у І чверті додатний);
ЕЕ
(2 — /2)8 2 — К2 =
(24-/2) (2-/2) ~ /2
8) =
/2 • — /2
У2
5я • я 1 І
9) зіп—810-^- = ^-^
я \\ 11 Я .
-24-)) = -НСО5~ + сО8
я
24
5я
"24
10) СО8 ~ = —
119
169
З----
і/ 228 _____і/ 144 _ 12
V 169 • 2 ~ V 169 — 13 *
Приклад 2. Спростити виразні
соз а соз 0 — соз (а + 0) .
соз (а — 0) — зіп а зіп 0 ’
8іп^-2- + а) — соз (а — л) — 1§(а — а) 4- —а
і? 27° + 18 18° ,
І8 27° 18 18 - 1 ’
8)
4) соз4 а — 6 соз2 а зіп2 а зіп4 а;
б) 2 зіп2 -у- + соз а;
л\ £іп + зіп 9а + зіп Юа + зіп 11а + зіп 12а
' соз 8а + соз 9а + соз 10а + соз 11а + соз 12а *
Розв’язання.
й С05 06 соз 0 — соз (а + Р) __
' соз (а — 0) — зіп а зіп 0
__ соз а соз 0 — соз а соз 0 + зіп а зіп 0 зіп а зіп 0 , . «
соз а соз 0 + зіп а зіп 0 — зіп а зіп 0 соз а соз 0_® ® Р’
57
2) зіп^- + «у*— соз (а — я) —.і§(а — я) + ау ==
= соз а — соз (а — я) —і§ (а — я) + сі§ (-у-а) =
= соз а 4- соз а — і§ а + і§ а = 2 соз а;
о\ 27е-(-18е ____ 27е + 18е __ . /97° . іоо\_
27° І& 18° — 1 — 1-і£27°і£ 18° “ Т
= — і§45°= — 1;
4) соз4 а — 6 соз2 а зіп2 а + зіп4 а = (соз4 а —
— 2соз2азіп2а + зіп4 а) — 4 соз2азіп2а = (соз2а — зіп2а)2—
— (2 зіп а соз а)2 = соз2 2а — зіп2 2а = соз 4а;
5) 2зіп2-^- + соза = 1 — соза + соза = 1;
дч зіп 8а + зіп 9а + зіп 10а + зіп 11а + зіп 12а '
' соз 8а + соз 9а + соз 10а + соз На + соз 12а
__ (зіп 8а + зіп 12а) + (зіп 9а зіп 11а) + зіп 10а
(соз 8а + соз 12а) + (соз 9а + соз 12а) + соз 10а
__ 2 зіп 10а соз 2а + 2 зіп 10а соз а + зіп 10а
2 соз 10а соз 2а + 2 соз 10а соз а + соз 10а
__ зіп 10а (2 соз 2а + 2 соз а + 1) _± і л
соз 10а (2 соз 2а + 2 соз а + 1) а‘
Приклад 3. Подати вираз у вигляді добутку або дробуї
1)1 — соз -у а; 2) 1 + зіп За; 3) 1 — соз а + зіп а;
4) 1 + 1§а; 5) а зіп а + Ь соз а; 6) 3—і§2а.
Розв’язання.
1) 1 — соз -у- а = 2 зіп2 а;
2) 1 + зіп За = 1 + соз ---За) = 2 соз2 (-^--а) ;
3) 1 — соз а + зіп а = (1 — соз а) + зіп а = 2 зіп2 -у -Ь
. о . а а п . а / . а . а \
+ 2 ЗІП-х- СОЗ -х~ = 2зіП-^- 81П-К- + СОЗ -н- =
~ . а/, а , . І я а \\ п. а.,
= 2 ЗІП^ЗІП у + 31П^“2-----2"/) = 2зтт х
а л _____ а а ___ л . а
„ . ~2~'~ Т ~ 2 . . а
X 2 ЗІП------2------С08-------2------= 4 ЗІП -д- X
я /а я \ п і гк се (а я \
X зіпсоз ^-2-----Ї-) = 2и 2 зіп ~2~ соз 1^2-4-);
58
4) 1 + --------/-
соз -2- соз а
У2 соз а соз а
5) а зіп а + Ь соз а = а (зіп а + соз в
= а (зіп а + і§ ф соз а) = а (зіп а + соз а) =
______ зіп а соз <р + соз а зіп ф а зіп (а 4- ф)
соз ф соз ф ’
де ~ ф, оскільки будь-якому числу, в даному ви-
* л • •
падку —, при а=/=0 відповідає тангенс деякого кута ф.
Кут ф завжди можна обчислити за відомим значенням тан-
генса за допомогою таблиць чи мікрокалькулятора;
6) 3-і§2а = (ГЗ)2-і§2а=і§24-і§2а =
. ( я А
= (*ба- *б-т)(18а + ^-т) =------:-----я~ х
соз а соз -д-
а —
соз2 а
зіп І а + —)
X-----і-------
соз а соз —
З
Приклад 4. Довести тотожності:
1) зіп (а + Р) соз (а — Р) = зіп а соз а + зіп р соз Р;
2) і§аі§р + (і§а + і§Р) сі§(а + Р) = 1;
зіп 2а соз а ____, а *
' 1 + соз 2а ’ 1 + соз а 2 *
соз — — зіп —
2 2 1 .
4) ---------------------------а;
7 а .а соз а ь
созД-4-зіпД-
6) і§(45°4-а)= С05К + 2?п” -
' ь ' ' 7 соз а — зіп а 9
+-^-1 (і+5іп«)
= сі§а.
6)
соз а
59
Доведення. 1) Перетворимо ліву частину рівності
за формулою (11)
соз (а 4- Р) соз (а — £) =
_ зіп (а + Р + а — Р) + «іп (а + р — а + Р) зіп 2а 4- віл 2р
~ 2 2 —
2 зіп а соз а 4- 2зіп В соз В . , . о о
------------с = зіп а соз а 4- 8іп р соз р;
2) і§аі§Р + (^а+1:§Р)сі§(а + Р) =
-‘е “‘8 р + "Ітйтг =‘е “ р +
+ (‘8а + і8Д + ;Г‘8Р’ ° + 1 -«Є«>ЄР = 1;
зіп 2а соз а 2 зіп а соз а соз а
' 1 + соз 2а 1 + соз а 2 соз2 а * „ а я
2 соз2 -у
2 зіп соз -2-
2 2
О 2 06
2 соз2 -у
соз2 — — 2 зіп соз -2- + зіп2
2_________2 2 2
о а „а
соз2 — — зіп2 -у
1 — зіп а___ 1 ,
соз а соз а ® *
гч соз а + зіп а — зіп (90° — а) + зіп а
' соз а — зіп а зіп (90° — а) — зіп а
о сіп 90° —а + а 90° —а —а
2 зіп------------!--соз
2
зіп 45° соз (45® — а)
соз 45° зіп (45° — а)
---------------2----------------------=
90° — а + а 90° — а — а
2 соз----------2-----зіп-------§------
= 45° СІ§ (45° — а) = (90° — 45° + а) = 1§ (45° + а);
6)
зіп а
я
_ ^(1+соз(4--а
зіп а
60
зіп а
соз а
зіп а
сі§а.
Історична довідка
Термін «тригонометрія*, який походить від грецьких слів «три-
гон» — трикутник і «метрео» — вимірюю і означає у перекладі «вимі-
рювання трикутників», був запропонований у 1595 р. німецьким мате-
матиком В. Б. Пітіском (1561—1613).
Тригонометрія, як астрономія і географія, зародилася та розвивала-
ся у Вавілоні, Єгипті, Китаї, Індії та інших країнах. Значного розвитку
тригонометрія як частина астрономії набула у Стародавній Греції. Гре-
ки першими почали розв’язувати прямокутні трикутники, у зв’язку з
чим склали тригонометричні таблиці. У цих таблицях містилися дов-
жини хорд, що відповідали центральним кутам круга сталого радіуса.
Фактично це були таблиці синусів, оскільки лінія синусів дорівнює по-
ловині хорди.
Перші тригонометричні таблиці було складено давньогрецьким ас-
трономом-математиком Гіппархом (біля 150 р. до н. е.). Він ввів також
географічні координати — широту і довготу, визначив віддаль від Зем-
лі до Місяця.
Таблиці синусів складали також індійські астрономи, які розгля-
дали і лінію косинуса.
Тригонометричні таблиці високої точності було складено у XV ст.
середньоазіатським вченим ал-Каші (XIV—XV ст.) та німецьким аст-
рономом і математиком Регіомонтаном (1436—1476).
В Росії перші тригонометричні таблиці, в складанні яких брав
участь Л. Ф. Магницький (1669—1739), було видано у 1703 році.
Вчення про тригонометричні функції почало розвиватися ще у IV—
V ст. у працях індійських вчених. Термін «зішіз» хоч і було введено ла-
тинською мовою у XII ст., але переклали його з індійського «архаджи-
ве», що означає «половину хорди».
Термін «косинус» походить від скорочення двох слів «зіпиз сотріе-
шепіі» (синус доповнення зіп (90° — %)), які вживав Регіомонтан.
У IX—X ст. середньоазіатські вчені ввели поняття тангенса, котан-
генса, секанса (величини, оберненої до косинуса) і косеканса (величини,
оберненої до синуса). Термін «тангенс» було введено у 1583 р. німець-
ким математиком Т. Фінком (1561—1656). Латинське слово «іап^епз»
означає «той, що дотикається». Термін «котангенс» походить, як і коси-
нус, від словосполучення «іап^епз сошріешепіі».
Сучасного вигляду вчення про тригонометричні функції набуло
в працях Леонарда Ейлера (1707—1783) — математика, фізика і аст-
ронома, швейцарця за походженням, який довгий час працював у Петер-
бурзькій Академії наук. Л. Ейлер розглядав тригонометрію як науку
про тригонометричні функції. Ці функції він тлумачив як відношення
відповідних тригонометричних ліній до радіуса, що дало можливість
розглядати їх не лише як функції кутів і дуг, а й як функції дійсних чи-
сел. Л. Ейлер вперше доступно виклав відомості про знаки тригономет-
ричних функцій у кожному з квадрантів, дослідив їх області визначення,
61
ввів позначення функцій зіп х, соз х, іап& х, сої х, сторін а, Ь, с і про-
тилежних до них кутів А, В, С у трикутнику. Він — автор ряду триго-
нометричних формул.
Запитання і завдання для повторення
1. Сформулювати означення тригонометричних функцій гострого
кута у прямокутному трикутнику.
2. Сформулювати означення синуса і косинуса довільного кута*
3. Як означаються тангенс і котангенс кута?
4. Які існують системи вимірювання кутових величин?
5. Що покладено в основу введення радіанної системи вимірюван-
ня кутових величин?
6. Що таке радіан?
7. Які переваги і особливості радіанної системи вимірювання куто-
вих величин перед іншими системами?
8. Яка залежність між градусною і радіанною мірами кута?
9. Сформулювати означення синуса і косинуса довільного числа*
10. Як означаються тангенс і котангенс числового аргументу? Яка
геометрична інтерпретація їх на одиничному колі?
11. Назвати числові значення тригонометричних функцій чисел
я л я
ТР Т’
12. Дослідити зміну соз а при зростанні числа а від 0 до 2л.
13. Дослідити зміну зіп а при зростанні числа а від 0 до 2л.
14. Як змінюється а і сі£ а при зростанні числа а від 0 до 2л?
15. Назвати знаки тригонометричних функцій у кожній з коорди-
натних чвертей.
16. Яка функція називається періодичною? Навести приклади пе-
ріодичних функцій.
17. Довести, що найменшим додатним періодом синуса і косинуса
є число 2л.
18. Довести, що найменшим додатним періодом тангенса і котанген-
са е число л.
19. Як побудувати графіки тригонометричних функцій числа? По-
будувати графіки функцій у — зіп х і у = х.
20. Побудувати графіки функцій у = соз х і у = сі§ х.
21. Назвати властивості функції у = зіп х. Довести властивість
спадання на певних відрізках.
22. Назвати властивості функції у = соз х. Довести властивість
парності цієї функції.
23. Назвати властивості функції у = І£ х. Довести, що функція
непарна на проміжках області визначення.
24. Назвати властивості функції у = сі§ х. Довести, що вона спад-
на на всіх проміжках області визначення.
25. Довести основну тригонометричну тотожність зіп2 х +
+ СОЗ2 X = 1.
26. Які ще співвідношення між тригонометричними функціями од-
ного і того самого аргументу існують?
27. Довести, що 1 4~ х = —; 1 + сі£2 х = —Д— .
° СОЗ2 X ЗІП2 X
28. Як обчислюються значення тригонометричних функцій за до-
помогою мікрокалькулятора?
29. Скласти програми для обчислення значень всіх тригонометрич-
них функцій за відомим значенням однієї з них,
62
ЗО. Скласти програми для обчислення сторони трикутника за тео-
ремою синусів.
31. Скласти програму обчислення сторони трикутника за теоремою
косинусів.
32. Довести формулу додавання для косинуса.
33. Довести формулу додавання для синуса.
34. Довести формулу додавання для тангенса.
35. Сформулювати правило користування формулами зведення.
36. Довести формули тригонометричних функцій подвійного ар-
гументу.
37. Записати формули тригонометричних функцій половинного ар-
гументу.
38. Довести формули суми і різниці синусів.
39. Довести формули суми і різниці косинусів.
40. Довести формули суми і різниці тангенсів,
Вправи
1. Подати кут Р у вигляді Р = а + 360°п, де £, а а — додатний
кут, менший від 360°, якщо: а) Р = —180°; б) р = —780°; в) Р = 1580°;
г) Р = 7242°; д) Р = —1690°.
2. Зобразити на колі у системі координат кут Р = а+ 360°п при
таких значеннях п і а: а) п = 3, а = 40°; б) п = —2, а = 30°; в) п =
= 5, а = —25°; г) п = — 3, а = 48°.
3. Колесо машини за 2 с робить 6 обертів. Записати у градусах кут,
на який повернеться колесо за 1 с, 10 с.
4. Через скільки хвилин після того, як годинник покаже 3 год, хви-
линна стрілка наздожене годинникову?
5. Записати у радіанній мірі кути: 15°, 22® ЗО', 51*, 157® ЗО', 162а.
2л
6. Подати у градусній мірі кути, що виміряні у радіанах: •
~ ; 1,5; 2,50.
о о
7. Побудувати на одиничному колі точки Ра, на які відображується
початкова точка (1; 0) при повороті кола навколо центра на а рад,
. л л , 5л
якщо: а) а == — . б) а = 2,5; в) а = 2; г) а = —,
♦ о
О гт /лі Л Уз , Л Уз, , л
8. Показати, що зіп = у ; соз -у = -у = -у-» сі£ =
= /3.
9. Знайти зіп а, соз а, а, сі£ а, якщо а = —9
10. Обгрунтувати знаки синуса у кожній з чотирьох координатних
чвертей.
11. Дослідити характер зміни зіп а і а при зростанні числа а від
0 до 2л.
12. На одиничному колі побудувати кути а такі, що:
1/ з
а) зіп а = Д—— ;
2 г
в) соз а = — 0,5;
б) = — 2;
г) сі£ а = 1,5,
63
13. Визначити знаки зіп а, соз а, І£ а, і сІ£ а, якщо!
а) а = 0,3; б) а = я; в) а = 2; г) а = — 2^- .
7 о
14. Чи можлива рівність: _
а)зіпа = -1-; б)зіпх =— -^1— ї в)єозх«=1,2;
5 З
15. Що більше:
а) зіп 1 чи зіп 1,5; б) соз 2 чи соз 2,1;
В) І&-5- чи г> чй
6 4 3 3,2
16. Обчислити:
1) 3 соз л —-2-зіп;
2) 2 зіп 4-/2і§Л_+ 1 соз-ї-}
О 4 & 4
3) 2зіп4—соз
6 4 6
4) зіп-Ї- +соз "
о 4 о
17. Знайти найбільше і найменше значення виразів:
, 1) 2созх;
2) —5 зіп я;
4) 2зіпх— 3;
5) 5 соз і + 1;
7)
8)
З — соз2 х;
1
3) 3 + 2 зіп х;
18. За допомогою
а) зіп 29°;
2 + соз х
і
З — зіп х
калькулятора (або таблиць) знайти:
б) зіп 0,48; в) 1,5; г) — сі& 2,5;
6) 2 + Ззіп2х;
9)
д) е) зіп 48° 32'; є) —соз 0,7; ж) сі& 100° 42'.
19. Звести до однойменних функцій гострого кута:
1) зіп 425°; 2) і 3) соз(— 1750°); 4) сі§ ;
6 з
5) зіп-4-я; 6) соз (—1125°); 7) сі§ (—12,5л); 8) 600°.
20. Довести, що найменшим додатним періодом функції у =
2зт
= соз (кх + Ь) е число Т = у-т-г, а функції у = (кх + Ь) — число
1 **
РІ '
21. Які з даних функцій періодичні? Знайти для періодичних функ-
цій найменший додатний період: 1) Зх; 2) ^ == 5; 3) у ~ соз — І
4) £ = {Зх}; 5) у= [х].
іе(--у- л) + с°з(_!^-)
22. Обчислити: —-----------------------і л
26л
зіп ——
64
23. Спростити! '
1) _____________зіп2 (За + 6л)___________ л
і£2 (2л + За) + і£ (5л + За) сі£ (За + л)
2) зіп (а 6л) сі§ (5 л — а)
зіп (2л — а) сі£ (5л + а)
А
24, Користуючись одиничним колом і графіком функції у — соз х
на відрізку [0; 2л], відповісти на шість запитань, які наведені у при-
кладі щодо функції у — зіп х (с. 25—26),
25. Побудувати графіки функцій:
а) У = і£ (х — -2-] $ б) у»2созх;
\ о /
Б
26. Користуючись одиничним колом і графіком функції у = х,
дослідити знаки функції, характер зміни її значень та нулі на проміжку
(0; 2л).
27. Побудувати графіки функцій:
а) у = 8іп(-1-а: — Л-) } б) =
в) у = соз (-2-х — -2-) І Г)у==і81х|.
в
28. Знайти період функції у = зіп ^2х-і відповісти на питан-
ня, які пропонувались у прикладі щодо у = зіп х (с, 25—26),
29. Побудувати графіки функцій:
а) у =» — 2зіп (-2_ — Зх^ ; б) у » | соз | х ЦІ
зіпх
в) У = "Иіїх" ; г) 8ІП х ~ 005 х'
80. Знайти область визначення функцій:
1) У = -3— 5 2) у= ------!— ; 3) г/ = зіп-*_; 4) У = ~ .
ЗІП X зіп X — 1 X І£ X
31. Знайти область значень функцій:
1) У “ СОЗ 2х; 2) у = х + 1;
3) у = 2 сі£2 х + 3; 4) у = соз х + 1.
32. Яке з чисел більше:
1) соз-2— чи соз-2-; 2) зіп ( — -2-^ чи зіп(— —-Ь
5 4 \ 6 / \ 5 /
3) чи І 4) сі84- чи сі84-?
5 о 4 5
З 1-1819
65
33. У яких чвертях може закінчуватися кут а, якщо:
1) | соз (—а) | = — соз а; 2) | сі£ а | = сі§ а;
3) | зіп а | = — зіп а; 4) | (— а) | = — а?
34. Розставити у порядку зростання числа:
а) соз 15°; соз 70°; соз (—25°); соз 230°; соз (—130°);
б) соз 1,5; соз (—1,3); соз; соз (—2); соз ; соз 2;
2 о,
В) сі83; сі8(-120°); і82{ і8(-3); 120°,
35. Знайти проміжки знакосталості і нулі функцій:
1) у = зіп 2х; 2) у =• —Д— ; 3) у = соз -ДД ;
’ зіп х З
4) у = зіп2х; 5)^ = і8-І_; 6)^ = сі82х.
36. Побудувати графіки функцій:
А
1 ( тс \
1)0 = соз — х; 2) у — | созх |; 3) 0 = зіп Іл— —І ;
2 \ 4 ]
4) 0 = -іе(* + 4-)’
\ о / -
Б
4) у = -1-зіп 2х; 5) у ------Ц* + ;
6) у = 2 соз (х — А-) ; 4) у = | 2 зіп ;
В
7) 0 = 2зіп|х|; 8) у —-----1-соз ^2х —-2-р
9)0 = |І£Х|; 4) у = — зіп^Зх — Л-) ,
37. Спростити вирази:
А
1) 5 2) ;~5ЇП^.. + асі8а,
1 + а - 1 — соз2 а
3) соз а а + зіп а; 4) а- Р ;
сі£ а + сі£ 0
5) зіп2 а + соз2 а + сі§2 а; 6) 1 -Д- № сс — і&2 а (соз2 а—1).
Б
7) —1-— — і£2а(соз2а+1);
соз2 а
8) зіп4 а 4- зіп2 а соз2 а — зіп2 а + 1 ;•
66
9) зіп8 а Ю) ІЄ« . _
1 4- соз а зіп а
1П . 1 с1£2 а •
7 1 —1£2 а ' сі£ а
зіпа
сі£а
12) і£«4
соз а;
соз3 а — зіп3 а
(1 + зіп а соз а) соз а
В
13) 1 — 8Іп6 а + со$е а • 14) 5Іп а + *£ а . 1 — со$ а а.
7 1 — зіп4 а — соз4 а соз а + с!§ а 1 — зіп а
15) а - 5Іп2оі-^ .) соз2 а сі§2 а;
\ _________соз2 а /
“і Г______8___ । 8
У 1 + соз а 1 — соз а
38. Дано: а + сі§ а = /п. Знайти: 1) І£2 а + сі&2 а;- 2) і§3 а +
+ сЩ9 а.
39. Обчислити: а) зіп2 а — зіп а соз а, якщо сі§ а == ;
1 З
б) , якщо і£ а = —-,
зіп а соз а 4
40. Довести, що вираз ——1—----4- — не залежить
-1 + і£2 а 1 + сі£2 а
від а.
41. Обчислити значення решти тригонометричних функцій за даним
значенням однієї з них:
1) соз а ----< а < я; 2) х = 2; я < х < ;
3) СІ2 X = -1- , 180° < X < 270°;
4) зіпх------{1, -^<х<2л.
10 ~
42. Довести тотожності:
А
1) зіп4 а — соз4 а == зіп2 а — соз2 а;
2) (1-і§а)2 + (Ц-і§а)2----------*----?
соз2 а
3) (сі£2 а — соз2 а) і£2 а = соз2 а; 4) І£2 а — зіп2 а = зіп2 а і§2 а,
Б
ех сі£2 а 1 + і&2 а __ 1 + сі^4 а ч
1 + сіу2 а І£2 а І£2 а + сі£2 а ’
6) і/" 1 + С08 а _ 1 + €оз а .
У 1 — соз а | зіп а |
соз3 а — зіп3 а __
і) , «і •“ СО8 0& *““ ЗІП
1 + зіп а соз а
8) 2ій2а = 1-8і^а-соз«а ,
соз4 а
З*
67
в
10) зіп8 а (1 + а) + соз8 а (1 + а) = зіп а + соз а}
Ц) 1 । 5*п4 а + він2 а соз2 а . 1 .
соз2 а соз2 а
12) 1 — (зіп6 а + соз® а) «= 3 зіп2 а соз2 а;
13) со5а + с|§ « -|_і=2 він3 а +.2 со«2 а 4- зіп а,
сі§а
43. Обчислити зіп а, і£а, сі§ а, якщо соз а « 0,48 і 0 < а< *
44. Обчислити з точністю до 1(Г~3 значення виразів;
п 12,3 зіп 28°20' .
} зіп 49°40'
2) а = К35,22 + 47,б2 — 2.35,2.47,6 соз 25°50';
3) 95,2 зіп 43°40' .
' зіп62°30'
4) с = У 41,252 + 72,732 -2 - 41,25.72,73 соз 37°28'.
45. Знайти з точністю до 1° кут <р, якщо:
1) соз <р = соз а соз (3, де а = 28°, £ = 56®;
2) кут А в Л АВС, якщо а = 42, Ь = 65, с = 28;
3) кут ф, якщо зіп ф = зіп а зіп р, де а = 42®36', (3 = 65°12';
4) кут А в Л АВС, якщо с = 53,2, /С = 59°20', а — 32,7.
46. Знайти радіус кулі, вписаної у правильну трикутну піраміду,
за формулою
/ ’ ~ а~
а - / 1 2
г=-0-|/ ------— , якщо а = 28,6, а = 68°40,у,
Г 1 + ш—
47. Обчислити початкову швидкість руху електрона за формулою
V = 1/ —, де І = 25 см, е = 1,6 • 10“"9 Кл,
г тії зіп а
Зауваження. У запропонованих вправах значення ліній-
них елементів і кутів вважають наближеними, хоча і вжито знак точ-
ної рівності. Знак «=» можна вживати для наближених даних, коли всі
цифри правильні. Результат обчислення треба округляти за правилами
наближених обчислень.
48. Обчислити значення виразів, не застосовуючи тригонометрич-
ні таблиці і мікрокалькулятори:
1) соз 15°;
4 3 еГС
2) соз (а — Р), якщо зіпа = -—, созр = —, —— <а<я,
5 - 5 2
0<р<Л_;
ЇХ
68
ю а
4) 8ІП * соз* ід *
и £ £
ЯКЩО ВІДОМО, ЩО зіп х» 0,62,
<х< я;
5) зіп І а — -5-І, якщо зіпа «= — 0,8;
\ /
6) 1.+-^4 х£4Л° ; 7) соз2 22°30‘ — зіп» 22°30«;
49° — і£ 4°
8) “я—5 я; 9) зіп 16в зіп 34°; 10) зіп — соз .
12 12 4 12
49. Спростити вирази:
А
1) зіп а зіп (а + Р) + соз а зіп (а + 0);
2) соз (а + 0) + соз (а — 0) ,
соз (а — р) — соз (а + 0)
3) 8*п * 1° С05 *5° + соз 11° зіп 15° , Щ 7а — За
зіп 18° соз 12° + соз 18° зіп 12° ’ І# 7а . і£ За + 1
5) соз2 а — 4 зіп2 — соз2Л_; ,6) V 1 + соз 8а*
2 2
зіп а соз а оч • . • । о».
7) -------------— ; 8) зіп х + зіп 2х + зіп Зх,
1 — 2 зіп2 а
Б
дч (1—соз 2а) соз а . ^ч зіп (45° — а) зіп (45° + а) .
зіп а ’ соз (45е — а) соз (45° + а)
--------------- 12 (а+ А я) -сі2 («+ 4 "
П) У4—гсоз4а; 12) ~і—г\—і—їгі
Г 2 2 сіЦа+^Я) + Ца+-^
13) (І£ а + сі£ а) зіп 2а; 14) -і-— — а —• зіп2 а;
соз2 а
15) соз За + соз 4а + соз 5а . 1 — зіп 2а
зіп За + зіп 4а + зіп 5а 1 (зіп а — соз а)2
В
17)
18)
19)
20)
21)
1
— 8ІП 4- — Ззт І — СОЗ2 — + ЗІП2 -5_ ;
\ 2 І 4 4
1 + соз а + соз 2а + соз За .
соз а + 2 соз2 а — 1_________*
-‘8е 4") (сі§»-4-1)5
зіп 2а + соз 2а — соз 6а — зіп 6а ,
зіп 4а + 2 зіп2 2а — 1
]/~ 2 зіп 'якщо л< а <3 2л;
г 2 зіп а + 5Іп 2а
69
22) зіп8 (« + Р) + зіп2 (а — Р) д
2 соз2 а соз2 (З
50. Записати вирази у вигляді добутку або дробу:
А
о
1) зіп (а + р) + $іп (а — £); 2) 1—соз-—а; 3) 1 + зіп5а;
4) 1 — а; 5) 1 — зіп а — соз а; 6) а -|~ 2а —• І£ За.
Б
7) .* + С03 ; 8) зіп х + зіп 2х + зіп Зх + зіп 4х;
1 — соз (а — Р)
9) /3— 2 соз 20°; 10) 1/ 1 + -----,2 , . ;
г а + сі§ а
11) зіп2 (а + Р) — зіп2 а — зіп2 Р; 12) 1 — 3 і&2 а.
В
13) зіп2 2а—4 зіп2 а . 14) с4§2 2а — і^2 2а — 8 соз 4а сі§ 4а;
зіп2 2а + 4 зіп2 а — 4 •
15) 2__________зіп 8а_______ . 10) соз 2а —- зіп 4а — соз 6а
зіп4 2а — соз4 2а ’ соз 2а + зіп 4а — соз 6а
51. Довести тотожності:
А
соз а соз Р (і£ а + і£ Р) = зіп (а + р);
1)
2)
3)
4)
5)
6)
зіп (а + Р) —зіп (а—• Р) == _а.
соз (а + р) — соз (а — Р)
1 + 2 соз 2а + соз 4а = 4 соз2 а соз 2а;
2 зіп 2а зіп а + соз За = соз а;
1 + сІ& 2а
1 — сі£ 2а
2 зіп а — зіп 2а
2 зіп а + зіп 2а
= і§2-т
Б
7) ---------------------зіп 2а;
а а 4
—сі§ —
8) зіп За = 3 віп а — 4 зіп3 а; .
соз2 (а — Р) — зіп^(а — Р)_ = а р.,
4 соз2 а соз2 Р
10) соз4 а — зіп4 а = соз 2а;
11) * + соз а + соз 2а + соз За _= а.
зіп 2а + 2 зіп а соз 2а
12) р^І + зіп а — V1 — зіп а = 2 зіп ;
13) 4 зіп2 а — 3 = 4 зіп
1
70
і8 _2_
2 2
14) 4---------------------= а,
в
15) 1+8І9п2ст----і§(4-+аЬ
соз 2а \ 4 )
16) ЄО82 + 8іп2(4-+-тй — 4- =
\ 6 2 / \ 6 2 І 2
«= —28ІП-2-8Іп(-Ц- + 4") 5
2 V З 2 /
17) зіп 2а + зіп 4а — 2 зіп За соз За = 4 зіп а зіп 2а зіп За;
18) з*п а + 2 зіп За + зіп 5а^ в зіп За ,
' зіп За + 2 зіп 5а + зіп 7а зіп 5а
л лля / \ пі** / зіп За
19) 4 соз —- — а І зіп І —- — а І = —:-- ;
\ 6 / \ 3 / зіп а
20) зіп2 а + зіп2 |3 + 2 зіп а зіп (3 соз (а + (3) = зіп2 (а + 0);
22) с05 4а ~ 5*п
соз 4а сі£ 2а + зіп 4а
РОЗДІЛ 2
ТРИГОНОМЕТРИЧНІ РІВНЯННЯ
§ 1. Поняття про обернену функцію.
Обернені тригонометричні функції
При розв’язуванні різних задач часто доводиться об-
числювати значення функції за даним значенням аргу-
менту. Наприклад, обчислювати площу 5 квадрата за дов-
жиною його сторони за формулою 5 = а2, яка задає залеж-
ність (функцію) площі від довжини а сторони квадрата.
Проте часто доводиться розв’язувати обернену задачу!
якою має бути сторона квадрата а, щоб площа 5 мала напе-
ред задане значення а = К«5, або обчислити час /, який
витрачено тілом при рівномірному русі, якщо воно пройшло
шлях певної довжини. Якщо 5 = 50 Ч- V/ (де V — стала) —
формула шляху, яка задає лінійну функцію, то 5 =
= / (/) — функція аргументу /. Якщо визначити і з фор-
мули шляху, то дістанемо іншу функцію і = —-------
також лінійну але аргументу 5, яку в загальному вигляді
71
позначимо і = <р (5). Функцію а = ]Л$ називають оберне-
8 8
ною до функції 5 = а1 2, а і = —----------оберненою до
5 = 5в ~|- VI.
Розглянемо приклади знаходження обернених функцій
до лінійної у = кх + Ь і квадратичної у = хй функцій.
Приклад 1. Нехай у = 2х + 3 — задана лінійна функ-
ція. Областю визначення і областю значень її є множина
всіх дійсних чисел. Кожне своє значення у лінійна функція
набуває лише при одному значенні аргументу х.
Вважатимемо змінну у незалежною (аргументом), а
змінну х — залежною і розв’яжемо рівняння у = 2х +• З
відносно змінної х. Дістанемо теж лінійну функцію х =
13,, . . .
— — У------2~ ~ яка заДає іншу залежність х від у.
1 з
Функція х = -у у-----% = <р (у) називається оберненою
до функції у = 2х + 3 = / (х).
Поміняємо у рівності х = у у------1- позначення, ос-
кільки прийнято незалежну змінну позначати буквою х, а
1 з
залежну — буквою у. Дістанемо функцію у = -у х —- у =
= ф (х), обернену до у = 2х + 3.
Побудуємо графіки функції у — 2х + 3 і оберненої до
1 з
неї у = х------2“ в одній системі координат (рис. 2.1).
Помічаємо, що графіки даної функції і оберненої до неї
розміщені симетрично відносно прямої у = х, тобто симет-
рично відносно бісектриси першого і третього координат-
них кутів.
Не слід думати, що кожна функція має обернену на своїй
області визначення.
72
Приклад 2. Нехай задано функцію у = х2. Областю визна-
чення її є множина всіх дійсних чисел, тобто Я, а областю
аміни — множина невід’ємних чисел, тобто [0; +оо).
Графік функції (рис. 2.2) показує, що кожне своє зна-
чення у0 (крім у0 = 0) вона набуває при двох значеннях
аргументу хх і х2. Якщо розглянути залежність х від у,
то вона не буде функцією, оскільки одному значенню у0
відповідає два значення х. Це означає, що функція у = х2
на всій області визначення не має оберненої. Проте, якщо
розглянути підмножини області визначення, наприклад
(—со; 0] або [0; +оо), то на цих підмножинах функція
у = х2 кожне своє значення набуває лише при одному зна-
ченні аргументу. На першій з цих підмножин функція
спадає, а на другій — зростає. На кожній з них існує
функція, обернена до у = х2.
Знайдемо, наприклад, функцію, обернену до у = х2,
якщо х 6 (—00; 01, тобто х — недодатне. Тут областю ви-
значення є множина (-^оо; 0], а областю значень — множи-
на невід’ємних значень у, тобто у £ [0; +°°).
Будемо вважати тепер у незалежною змінною, ах — за-
лежною і розв’яжемо рівняння у = X2 відносно змінної
х. Це — квадратне рівняння. Воно має два корені х =
= ± У у. Але за умовою х — недодатне, тому х =
= — Уу = Ф (у).
Функція х = — У У = <Р ЇУ) є оберненою до функції
у = х2 за умови х < 0.
Поміняємо у рівності х =— Уу позначення незалежної
і залежної змінних. Дістанемо функцію у = — Ух = (р (х),
обернену до у = х2, х 0.
Областю визначення оберненої функції у = —Ух є
множина [0; +оо), бо х в арифметичному корені невід’ємне,
а областю зміни — множина (—оо; 0].
Помічаємо, що області визначення і зміни взаємно обер-
нених функцій помінялись множинами.
Побудуємо графіки функцій у = х2, х^0 і у = —Ух
в одній системі координат .(рис. 2.3). Побудовані графіки
теж симетричні відносно прямої у = х.
Функція /, яка має обернену, називається оборотною.
Необхідною і достатньою умовою існування оборотної
функції / є така: вона має набувати кожного свого значення
лише для одного значення аргументу.
Достатньою умовою існування оберненої функції для
даної функції є її монотонність, тобто зростання або спадан-
ня на всій області визначення.
73
Наприклад, будь-яка лінійна функція у = кх 4- Ь при
к Ф 0 є оборотною, тобто має обернену. Такою ж є функція
у = х3, бо вона зростаюча на всій області визначення.
Оберненою до даної оборотної функції у = / (х) назива-
ється така функція х = <р (у), що кожному у із множини
значень функції у = / (х) ставить у відповідність єдине чис-
ло х із її області визначення.
Рис. 2,4
Якщо поміняти позначення незалежної і валежної змін-
них, то обернену функцію до у = / (х) запишемо у вигляді
У = ф <х).
Розглянемо алгоритм знаходження формули функції,
оберненої до даної.
1) З’ясовуємо, чи є функція у = / (х) оборотною на всій
області визначення. Якщо ні, то виділяємо підмножину
області визначення; де існує обернена функція до у =
= / (х).
2) Розв’язуємо рівняння у = / (х) відносно змінної X,
тобто знаходимо функцію х = <р (у), яка є оберненою до
У = ї (х).
- 3) Міняємо позначення змінних: незалежну змінну по-
значаємо через х, а залежну — через у. Дістаємо функцію
у = ф (х), обернену до у = / (х) у прийнятих позначеннях
змінних.
Можна довести загальне твердження: графік функції ер,
оберненої до функції симетричний до графіка ї відносно
прямої у — х. >
Доведення. Якщо у = / (х) — дана оборотна функ-
ція, то х = ф (у) — обернена до неї. Це означає, що коли
точка М (х; у) належить графіку у = / (х), то точка
N (у\ х) належить графіку х = ф (у) (або у = ф (х)). Але
ці дві точки розміщені у системі координат симетрично
відносно прямої у = х (рис. 2.4).
74
Сформулюємо без доведення таку властивість оберненої
функції: якщо функція ? зростаюча (спадна) на проміжку
І, то вона оборотна. Обернена до / функція ф, визначена в
області значень /, також є зростаючою (спадною).
Функція, обернена до у = зіп х. Введемо обернену функ- -
цію, користуючись загальним алгоритмом знаходження
функції, оберненої до даної.
1) Із властивості періодичності і графіка функції у =
зіп х (рис. 2.5) випливає, що кожне своє значення у0 вона
набуває для нескінченної множини значень аргументу х =
= х0 + 2пл. Це означає, що функція не є оборотною на
всій області визначення. Разом з тим на всіх проміжках,
де вона зростає або спадає, до неї існує обернена. Виберемо
такий із проміжків монотонності, значення х у якому най-
ближчі до 0. Це проміжок
~ синус набуває всіх своїх зна-
чень у ([—1; 1] і зростає.
2) Вважатимемо у незалежною
змінною (аргументом), ах—за-
лежною і розв’яжемо рівняння
у = зіп х відносно х. Це означає,
що треба знайти таке число х (кут
або дугу), синус якого дорівнює
у. На обраному проміжку таке
число буде єдине. Для його позна-
т . Дійсно, при х Є — -п-;
І І
Рис. 2.6
чення використовують символ
х = агсзіп у = <р (у). Отже, під знаком агсзіп знаходиться
значення синуса, а х = агсзіп у — функція, обернена до
• ЇТ ЯТ ”]
у = 81П X При X 6-----2~; ~ •
3) Поміняємо позначення незалежної і залежної змін-
них. Дістанемо функцію у = агсзіп х — ф (х), обернену
до у — зіп х при х Е [--2-; записану у прийнятих по-
значеннях змінних.
76
у — ЗІП ХПрИХ £ -у-;
Помічаємо, що і для будь-яких взаємно обернених функ-
цій області визначення і значень цих функцій помінялись
множинами. Для у = агсзіп х х — значення синуса і х£
€ І—1; 1], а у — число (кут або дуга), синус якого дорів-
• /** Г "1
НЮЄ X, і -------г; Т •
Графік функції у — агсзіп х дістанемо з графіка функції
перетворенням симетрії віднос-
но прямої у = х (рис. 2.6).
Розглянемо властивості функції у = агсзіп х.
1) Областю визначення функції у = агсзіп х є множина
[—1; 1], областю значень — множина ----При цьо-
му, якщо 0 х1, то 0 агсзіп х а якщо — 1
х 0, то-------2~^ агсзіп х 0.
2) Графік функції симетричний відносно початку коор-
динат (функція непарна), тобто агсзіп (—х) — —агсзіп х.
Довести цю властивість можна так. Область визначення —
множина, симетрична відносно 0. Доведемо, що / (—х) =
— — / (х). Враховуючи область значення арксинуса, маємо
------агсзіп (—х) —, агсзіп х
Помножимо всі три частини останньої нерівності на —1,
матимемо — -у — агсзіп х -у. Запишемо синуси ви-
разів агсзіп (—х) і агсзіп х. Дістанемо зіп (агсзіп (—х)) —
= —х, зіп (— агсзіп х) = —зіп (агсзіп х) = —х. Але як-
що два числа належать одному і тому самому проміжку і
синуси їх рівні, то і числа рівні в силу монотонності синуса
на цьому проміжку. Отже, агсзіп (—х) — — агсзіп х.
3) Функція не є періодичною.
4) Дорівнює нулю при х = 0.
5) Зростаюча за теоремою про властивість оберненої
функції.
6) Додатна при х £ Ю; 11 і від’ємна при х Є [—1; 0].
7) Набуває найбільшого значення, рівного -у при х = 1
і найменшого —у при х — —1.
Якщо в рівності х = агсзіп у замінити у на зіп х, оскіль-
ки у = зіп х, то агсзіп (зіп х) = х,-у- х
Якщо від рівності у = агсзіп х перейдемо до оберненої
76
функції х = зіп у, а в останній рівності замінимо у на
агсзіп х, то дістанемо ще одну рівність зіп (агсзіп х) = х.
Рівності агсзіп (зіп х) — х і зіп (агсзіп х) — х' викори-
стовують у різних тригонометричних обчисленнях. Згідно
в цими рівностями зіп
1 • І /2\
-у, агсзіп І зіп І —
Ґ2
2 •
Функція, обернена до у = соз х. Із властивості періодич-
ності і графіка функції у = соз х (рис 2.7) випливає, що
кожне своє значення у0 функція набуває для нескінченної
множини значень аргументу х = х0 + 2«я. Це означає,
що функція не є оборотною на всій області визначення.
Разом з тим на всіх проміжках, де вона зростає або спадає,
вона має обернену функцію. Виберемо один з них, зокрема
проміжок [0; я]. При всіх х £ [0; я] косинус набуває всіх
своїх значень у 6 І—1; її з області значень.
Вважатимемо у незалежною змінною (аргументом), а
х — залежною і розв’яжемо рівняння у = соз х відносно
змінної х. Це означає, що треба знайти таке число х (кут
або дугу), косинус якого дорівнює у. На обраному проміж-
ку таке число єдине і позначається х = агссоз у. Очевидно,
що х = <р (у). Отже, під знаком агссоз знаходиться значен-
ня косинуса, а функція х — агссоз у обернена до у = соз х
при х Є [0; я].
Поміняємо позначення незалежної і залежної змінних.
Дістанемо функцію у = агссоз х = ф (х), обернену до у = созх
при х 6 10; я],-записану в прийнятих позначеннях змінних.
Областю визначення функції у = агссоз х є множина
[—1; 1], а областю значень — [0; я].
Графік функції у — агссоз х дістанемо з графіка у =
= соз х при х 6 [0; я] перетворенням симетрії відносно пря-
мої у = х (рис. 2.8).
Вкажемо властивості функції у = агссоз х, що випли-
вають з її графіка. їх можна обгрунтувати так само, як
і для функції у =•= агсзіп х.
77
1) Областю визначення функції у = агссоз х є множи-
на [—1; 1], а областю значень — множина [0; як Якщо
0 х «С 1, то 0 агссоз х при —1 х 0 -у
агссоз х л.
2) Графік функції не симетричний ні відносно початку
координат, ні відносно осі Оу. Це означає, що функція не є
ні парною, ні непарною. Для неї виконується рівність
агссоз (—х) = л — агссоз х.
3) Функція не є періодичною.
4) Дорівнює нулю при х = І.
5) Функція спадна.
6) Додатна на всій області визначення.
7) Функція досягає найбільшого значення я при х =
= —1 і найменшого 0 при х = 1.
Для функції у = агссоз х також виконуються рівності
соз (агссоз х) — х, агссоз (соз х) = х. Обгрунтуйте це са-
мостійно.
Функція, обернена до у = х. Функція у — х на-
буває значення у0 для нескінченної множини значень аргу-
менту х = х9 + гал, га 6 2. Тому вона не є оборотною на всій
області визначення. Але на кожному з проміжків----+
+ гал < х <. + гал вона зростаюча, а тому має оберне-
ну. Виберемо один з таких проміжків (— -у), значення
х в якого найближчі до 0. При х Є (—тангенс набу-
ває всіх своїх значень у £ (—оо; 4-оо) з області значень.
78
Вважатимемо у незалежною змінною (аргументом), а
х — залежною змінною і розв’яжемо рівняння у = х від-
носно х. Це означає, що треба знайти таке число (кут або
дугу), тангенс якого дорівнює у. На обраному проміжку
це число буде єдиним і позначається х — агсі§ у. Очевидно,
Що х = ф (у).
Отже, під знаком агсі§ знаходиться значення тангенса, а
функція х = агсі£ у обернена до у — х при х 6 (—-уУ
Поміняємо позначення
незалежної і залежної змін-
них. Дістанемо функцію
у = агсі§ х = ф (х), оберне-
ну до у — х при х б
(ЗТ зх \
-----2*‘> —1> записану в
прийнятих позначеннях
змінних.
Графік функції у =
= агсі§ х дістанемо з гра-
фіка у = х при х С
симетрії відносно прямої у = х (рис. 2.9).
Розглянемо властивості функції у = агсі§ х, що випли-
вають з її графіка.
' 1) Областю визначення функції у = агсі§ х є множина
(—оо; Ч-оо), а областю значень — множина (-------у).
Якщо 0 х < +°°, то 0 агсі§ х < а при —оо <;
< х 0--------у < агсі£ х 0.
2) Графік функції симетричний відносно початку коорди-
нат, це означає, що функція непарна, тобто агсі§ (—х) =
= — агсІ§ х.
3) Функція не є періодичною.
4) Дорівнює нулю при х —-д.
5) Функція зростаюча.
6) Додатна при 0 < х < +°° і від’ємна при —оо <
< х < 0.
7) Функція не досягає найбільшого і найменшого зна-
чень. Для функції у = агсі§ х також виконуються дві рів-
ності (агсі§ х) = х, агсТ§ (і§ х) = х. Обгрунтуйте це
самостійно.
79
Функція, обернена до у = сі£ х. Функція у = сі§ х не
є оборотною на області визначення, але має обернену на
проміжках спадання. Виберемо один з них, наприклад
(0; я). При х С (0; я) котангенс набуває всіх своїх значень
у Є (—°°; +«>).
Розв’яжемо рівняння у = сі§ х відносно змінної х. Ді-
станемо функцію х = агссі§ у — <р (у), а обернену до у =
— сі&х при х £ (0; я).
Поміняємо позначення змінних. Матимемо функцію
у = агссі§ х — <р (х), обернену до у = сі§ х при х 6 (0; я),
записану в прийнятих позначеннях.
Областю визначення функції у = агссі§ х є множина
(—оо; 4-со), областю значень — проміжок (0; я).
Графік функції на проміжку (0; я) дістанемо з графіка
у — х, симетрично відобразивши його відносно прямої
у = х (рис. 2.10).
Самостійно назвіть властивості функції у = агссі§ х за
її графіком.
Приклади. Обчислити!
1 / 1/^2 \ /—
1) агсзіп-у-; 2) агссоз І--у-1 | 3) агсі§(—у 3);
4) агссІ£І; 5) агсзіп 0,8192; 6) 2 агссоз (-;
7) агсі§ 0 + агсі:§ (-•; 8) агсзіп (зіп 'І;
9) соз (агссоз 1); 10) І£^агсі§^-’
Р, 1 \ • 1 «ТС • • «П> 1
озв язання. 1) агсзіп-й-=оскільки зіп-т-=;
7 2 6 6 2 ’
о. ( /2 \ /2 я Зл
2) агссоз І-у-І = я — агссоз = я-----------^- = -у ,
я /2 /2 я
оскільки соз -г- = ; агссоз -4— = -т- ;
4 2 ’ 2 4
3) агсі§(—КЗ) = —агсі§ ]/3 = — у, оскільки і§у=
= р^З, агсІ§ Кз = -Ц- ;
О
4) агсі§ 1 = -у, оскільки сі^-у = 1;
5) агсзіп 0,8192 « 0,9599, оскільки за таблицями зна-
чень тригонометричних функцій кутів, виражений у радіа-
нах або за мікрокалькулятором, синус числа 0,9599 дорів-
нює 0,8192;
6) 2 агссоз (--1-) — агссоз -4- = 2 [ я — агссоз Л-) —
80
1 О О 1 1
— агссоз — = 2л — 2 агссоз ----агссоз -у =
= 2л — 3 агссоз -у = 2л — 3 • -у- = л;
7) агсі§0 +агсІ§(—^) = О — асгі§(—^-) = — •£-,
. X Гз я
оскільки агсі£ Лт- = ;
О 0
8) агсзіп згідно з рівністю агсзіп (зіп х) = х;
9) соз (агссоз 1) = 1 згідно з рівністю соз (агссоз х) = х;
10) і§^агсі§(--£”)) =---1“ зг’дн0 3 рівністю
(агсі:§ х) = х.
§ 2. Розв'язування найпростіших
тригонометричних рівнянь
Тригонометричними рівняннями називаються рівняння,
у яких невідома (змінна) входить лише під знак тригоно-
метричної функції. Наприклад, зіп х — соз х = 0; 2 зіп х +
з
+ соз х = у зіп2 2х; соз 4х соз 2х =* соз 5х соз х; 5х +
4- Зх = 0.
Тригонометричні рівняння, у яких змінна входить ли-
ше-під знак тригонометричної функції, або зовсім не мають
розв’язків, або мають безліч їх внаслідок властивості періо-
дичності тригонометричних функцій.
Не існує загального способу розв’язування будь-якого
тригонометричного рівняння. Однак деякі способи розв’я-
зування окремих видів тригонометричних рівнянь можна
вказати. Як правило, розв’язування будь-якого тригоно-
метричного рівняння зводиться до розв’язування прості-
ших рівнянь зіп х = а, соз х = х = а. Рівняння
сі§х = а рівносильне рівнянню = тому немає
потреби розглядати його окремо.
Розглянемо розв’язування найпростіших тригонометрич-
них рівнянь.
Рівняння зіп х = а. Розв’яжемо це рівняння спочатку
графічно, побудувавши в одній системі координат графіки
функцій у = зіп х і у = а.
При | а\ > 1, тобто при а>\ і а <—1, пряма і
синусоїда не перетинаються. Тому рівняння зіп х = а не
має розв’язків (рис. 2.11).
81
Знайдемо розв’язки при | а [ 1, тобто коли —1 а
1, на відрізку [—я; я], а потім скористаємося періодич-
ністю функції синус.
Нехай 0 < а < 1. Як. видно з рисунка, пряма у = а
за цієї умови перетинає синусоїду у двох точках Рг і Р2,
абсциси яких належать проміжку (0; я).
Оскільки розв’язування рівняння зіп х = а зводиться
до знаходження числа (геометричного кута чи дуги), синус
якого дорівнює а, то цим числом є агсзіп а, якщо воно зна-
ходиться на проміжку (---Отже, абсцисою точки
є агсзіп а. Абсцису точки Р2 запишемо через агсзіп а
як різницю я — агсзіп а.
Рис. 2.12
Якщо додати до знайдених розв’язків період 2пя, то при
0 < а < 1 дістанемо всі розв’язки рівняння зіп х = а у
вигляді двох множин
х = агсзіп а + 2пя, п£2; (1)
х = я — агсзіп а + 2пя = — агсзіп а + (2п + 1) я, п £ 2.
(2)
Ці множини можна об єднати в одну
х=(—І)6 агсзіп а + кл, к£2, (3)
діставши загальну формулу розв’язків рівняння зіп х =
= а. При парному к, тобто при к — 2п, дістанемо множину
(1), а при непарному к, тобто при к — 2п + 1, дістанемо
множину (2).
82
Нехай —1 < а < 0. З рис. 2.12 видно, що за цієї умо-
ви пряма у — а перетинає синусоїду теж у двох точках
Р± і Р2, абсциси яких належать проміжку (—я; 0). Абсциса
першої точки належить проміжку (— тому є агсзіп а.
Абсцису другої Р2 можна записати через агсзіп а як різни-
цю —я — агсзіп а. Якщо до знайдених розв’язків додати
період функції синуса, то дістанемо всі розв’язки рівняння
зіп х = а при —1 < а < 0 у вигляді двох множин
х = агсзіп а + 2пл, п £ X,
х = — п — агсзіп а + 2пл = — агсзіп а + (2п — 1) я, п £ X.
Об’єднавши ці дві формули в одну, запишемо
х = (— 1)* агсзіп а + к£Х.
Отже, дістали ту саму загальну формулу розв’язків
рівняння.
Якщо а = 0, то пряма у = а перетинає синусоїду в точ-.
ках, абсциси яких дорівнюють пл. Отже, рівняння зіпх =
= 0 май множину розв’язків х — ил, де п £ X.
Якщо а — 1, то пряма дотикається до синусоїди у точ-
ках з абсцисами х = -у- + 2пл. Отже, рівняння зіп х = 1
має множину розв’язків х = -у + 2пл, п Є X.
При а = — 1 х ==------+ 2пл, п, £ X.
Неважко довести, що при а = 0, а = 1 і а = —1 ті ж
самі множини розв’язків можна знайти і за загальною фор-
мулою (3).
Загальну формулу розв’язків рівняння зіп х — а при
| а | 1 можна знайти і за допомогою одиничного кола.
Нехай 0 < а < 1. Оскільки а як значення синуса є ор-
динатою точки одиничного кола, то відкладемо на осі Оу
відрізок, що дорівнює а, і через кінець його А проведемо
пряму, паралельну осі Ох (рис. 2.13). Вона перетне коло
у двох точках РА і Р2. Оскільки треба знайти таке число
(кут або дугу), синус якого дорівнює а, то таких чисел,
яким відповідають точки Рг і Р2 одиничного кола, вияви-
лось два. Перше з них, яке знаходиться на проміжку (—
є агсзіп а, а друге дорівнює л — агсзіп а. Враховую-
чи періодичність функції синус, дістанемо дві множини
83
розв’язків рівняння зіп х = а при 0 < а < її
х = агсзіпа4- 2пл,
х = л — агсзіп а + 2пл = — агсзіп а + (2п + 1) л.
Після їх об’єднання дістанемо загальну формулу роз-
в’язків
Нехай —1 < а < 0. Відповідні точки Рг і Р2, що зо-
бражують числа на одиничному колі, належать нижньому
півколу (рис. 2.14). Точка Рг зображує число, яке нале-
жить проміжку (—-2-^, і є агсзіп а. Точка Ра зображує
число, яке дорівнює —я — агсзіп а.
Враховуючи періодичність синуса, дістанемо дві мно-
жини розв’язків рівняння зіп х = а при —1 < а < 0:
х = агсзіп а + 2пл,
х = — л — агсзіп а 4~ 2пл = — агсзіп а -|- (2п — 1) л.
' Об’єднуючи їх, дістанемо загальну формулу розв’язків
рівняння
х—(—І)6 агсзіп а + кя, к£%.
Рівняння соз х = а. Розв’язування його графічним спо-
собом показує (рис. 2.15), що при | а | >> 1 рівняння не
має розв’язків. Знайдемо розв’язки рівняння на проміжку
[—л; л], довжина якого дорівнює періоду 2л.
Нехай 0 < а < 1. Проведемо пряму х — а. Вона перет-
не графік функції у = соз х на відрізку [—л; л] у двох
точках Рг і Р2. Оскільки треба знайти таке число (кут або
дугу), косинус якого дорівнює а, то таких чисел, яким від-
повідають точки Рг і Р2) виявилось два. Перше з них нале-
жить проміжку (0; л) і є агссоз а, а друге — протилежне
84
йому і дорівнює — агссоз а в силу парності функції коси-
нус. Враховуючи періодичність функції косинус, дістанемо
дві множини розв’язків рівняння соз х = а при 0 < а < 1
х = ± агссоз а + 2/гя. (4)
Нехай —1 < а < 0. З рис. 2.16 видно, що пряма у = а
перетинає графік косинуса у двох точках Рг і Р2. Абсциса
точки належить проміжку (0; я) і тому дорівнює агссоз а,
абсциса другої точки Р2 дорівнює — агссоз а. Додавши
до знайдених розв’язків період 2/гя, дістанемо дві множини
розв’язків, які можна записати у вигляді однієї формули
х — ± агссоз а + 2/гя, п £ 2.
Отже, дістали ту саму загальну формулу (4) розв’язків
рівняння соз х = а при —1 < а < 0.
При а = 0 пряма у = а перетинає графік косийуса у точ-
ках з абсцисами 2/гя, 2. При а = 1 пряма дотикається
до графіка косинуса у точках з абсцисами 2/гя, п £ 2, при
а — — 1 дотикається у точках з абсцисами (2/г + 1) я, /г £
6 2.
Доцільно запам’ятати «особливу» форму запису розв’яз-
ків рівняння соз х — а для окремих випадків:
якщо соз х == 0, то х = -^- + /гя, п£2\
якщо соз х = 1, то х = 2/гя, п £ 2.
Неважко показати, що ці ж множини розв’язків для
окремих значень а можна дістати із загальної формули
85
розв’язків х = ± агссоз а + 2гал, Справді, при а = 0
агссоз а = , а х = ±-^- + 2пл = (4га ± 1) -у, га Є 7.
Проте вираз 4л ± 1 при п £ 7 дає множину всіх непар-
них чисел, як і вираз 2га 4- 1, що входить до формули
х=^-+пл = (2га+ 1)і.
Загальну формулу розв’язків рівняння соз х = а при
(а | 1 за допомогою одиничного' кола можна вивести так
само, як і для рівняння зіп х = а. ~ '
, Як видно з рис. 2.17, а, при 0 < а < 1 пряма, паралель-
на осі Оу і проведена у кінці А відрізка осі абсцис довжиною
а, перетинає коло у двох точках Рг і Р2. Точка відповідає
числу, що належить проміжку (0; я), тобто є агссоз а, дру-
га точка Р2 відповідає числу — агссоз а в силу парності
функції косинус. Додавши період до обох чисел, дістанемо
загальну формулу (4) розв’язків рівняння соз х = а при
0 < а < 1і
х = ± агссоз а + 2пя, п £
При —1<а<0 пряма, проведена у кінці відрізка
ОА паралельно осі Оу, теж перетинає коло у двох точках
Рх і Р2 (рис. 2.17, б). Точка Р± відповідає числу, що нале-
жить проміжку (0; я) і є агссоз а, а Р2 відповідає числу —
агссоз а. Додавши період до обох чисел, знов дістанемо ту
саму (Загальну формулу розв’язків рівняння созх = а.
Рівняння ж = а. Оскільки областю значень функції
у = х є множина всіх дійсних чисел, то знайдемо роз-
в’язки рівняння при будь-якому а на проміжку (—тН'т)»
довжина якого дорівнює періоду я, а потім скористаємося
періодичністю функції тангенса.
86
Графічний спосіб розв’язування рівняння і&х = а
(рис. 2.18) показує, що на інтервалі -у; пряма у — а
перетинає графік тангенса лише в одній точці, абсцисою
якої є агсі§ а. Враховуючи періодичність функції у =
= х, дістанемо загальну формулу розв’язків рівняння
х — а, тобто множину
х = агсі§а 4* ял, п£2.
(5)
Розв’язування рівняння х — а за допомогою одинич-
ного кола на проміжку (— -у; -у) приводить до тієї самої
множини. Оскільки а — це
ордината точки Та перетину
прямої ОРа з лінією тангенсів
(рис. 2.19), а пряма ОТа перетинає одиничне коло у двох точ-
ках Ра, і Раі, то в інтервал (—-у) потрапляє лише одна
в них Ра, яка відповідає числу агсі§ а. Всі інші розв’язки
дістанемо, додавши до цього числа період гал, га £ 2, тобто
х — агсі§ а + гал.
Отже, маємо загальні розв’язки трьох найпростіших
тригонометричних рівнянь:
зіпх = а, х=(—1)"агсзіпа4- пл, п£2,
созх = а, х— ±агссоза+ 2пл, п^2,
х = а, х = агсі§а 4- пл, п£2.
Покажемо застосування здобутих формул.
Приклад 1. Розв’язати рівняння зіп х = —.
Розв’язання. Оскільки значення синуса за умо-
. ( Кз\ л
вою від ємне, то агсзіп І-~~і вибираємо на проміжку
87
X
— ~2 "> о). Тому агсзіп (— Ху) = —у, а за формулою (3)
= (—1)*(—4)+*я = (—і)*+14+*я> к^г-
\ о / о
Приклад 2. Розв’язати рівняння зіп х — .
Розв’язання. Оскільки значення синуса за умо-
вою додатне, то значення агсзіп у вибираємо на проміжку
^0; у). Отже, агсзіп у = -у, тому за формулою (3) х —
= (— 1)*у+ кп, ке 2.
т/*2
Приклад 3. Розв язати рівняння созх “-у-.
Розв’язання. Оскільки значення косинуса за
/2 -
умовою додатне, то агссоз -^у- вибираємо з проміжку
(о; -у), тобто агссоз = -у. Отже, за формулою (4) х =
= Ч~ -у 2мп, п Є
Приклад 4. Розв’язати рівняння соз х = —у .
Розв’язання. Оскільки значення косинуса за
умовою від’ємне, то агссоз (—-у) вибираємо з проміжку
(-2-; я). Отже, за формулою (4) агссоз (— у^ = я —у =
= , тому х = ± ~ + 2пя, п Є
о <5
1/*3
Приклад 5. Розв’язати рівняння х = .
Розв’язання. Оскільки значення тангенса за
умовою додатне, то агсі§ вибираємо з проміжку ^0;
-уУ Отже, агсі§Д^- = -~, тому за формулою (5)х = -^- +
+ пл, п С 2.
Приклад 6. Розв’язати рівняння ї§х =— 1.
Розв’язання. Оскільки значення тангенса за
умовою від’ємне, то агсі§ (—1) вибираємо з проміжку
(—; 0^. Отже, агсі§ (—1) = —, тому за формулою (5)
х 2.
88
Приклад 7. Розв’язати рівняння соз х = —0,3257.
Розв’язання. Оскільки значення косинуса за
умовою від’ємне, то агссоз (—0,3257) вибираємо з проміж-
ку (-5-; я). За формулою (4), використовуючи таблиці або
мікрокалькулятор, маємо
х = ±1,9044 + 2пп, п£2.
1 До розв’язування найпростіших тригонометричних рів-
нянь безпосередньо зводять розв’язування тригонометрич-
них рівнянь виду зіп (кх 4- ф) — а, соз (кх 4- ф) = а,
(кх + <р) = а. Формули (3) — (5) застосовують для зна-
ходження виразу кх + ф, а після цього знаходять х із
здобутого рівняння.
Приклад 8. Розв’язати рівняння зіп 2х -----.
Р о з в’ я з а н н я. За формулою (3) 2х = (— 1)* (— 4*
4- кл,
2х= + х = к^г.
(2 л \ 1
---5“ -----о •
О О / £
Розв’язання. За формулою (4) х---------5- = ± 4*
О О о
4- 2пл;
-і-х — ±. 4- 4- 2пл; х = ± я 4- -т" 4- Зпя, п £ 2.
О О О тг
§ 3. Деякі способи
розв'язування тригонометричних рівнянь,
які відрізняються від простіших
Розглянемо окремо способи розв’язування деяких три-
гонометричних рівнянь на прикладі одного рівняння і
спробуємо обгрунтувати доцільність використання кож-
ного з них.
Розв’яжемо рівняння
8ІПХ — СОЗ X = 0. (1)
1. Спосіб зведення до однієї тригонометричної (функ-
ції (алгебраїчний спосіб). Цим способом розв’язують рів-
няння, до складу яких входять різні тригонометричні функ-
ції одного і того самого аргументу. Використовуючи основ-
89
ні тригонометричні тотожності, всі функції виражають
через одну функцію, а потім розв’язують алгебраїчне рів-
няння відносно цієї функції.
Отже, перенесемо соз х- у праву частину рівняння і
виразимо його через зіп х за формулою соз х =
= ± 'И1 — зіп2 х. Дістанемо рівняння
зіп X — ± V1 — зіп2 X.
(2)
Піднесемо обидві частини рівняння
(2) до квадрата. Дістанемо зіп2 х =
= 1 — зіп2 х, або 2 зіп2 х = 1, звід-
ки зіп2 х — у . Добудемо квадрат-
ний корінь з обох частин рівнян-
ня, використовуючи тотожність
= | а- |. Маємо | зіп х | — уД.
Звідси здобули два простіших три-
гонометричних рівняння;
к 1^2
х = (— 1) агсзіп -у—йл,
або х — (— 1/ у- -ф кл, к£2,
зіп х =-----, х = (— 1)* агсзіп (-------
або х = (— 1)*(— + = 1)*+1Д_ + )ь, к£2.
Оскільки ми виконували піднесення обох частин рів-
няння (2) до квадрата, то можливі порушення рівносиль-
ності, тобто рівняння зіп2 х = 1 —зіп2 х, а значить і
81П 2 X =, можуть мати сторонні розв язки.
Щоб відкинути сторонні розв’язки, зробимо перевірку
на відрізку довжиною 2л, зокрема на [0; 2л], враховуючи,
що найменшим додатним періодом синуса і косинуса є
число 2л. Для цього зручно використати одиничне коло.
Нанесемо на одиничне коло всі точки, які відповідають
числам, що містяться у знайдених серіях розв’язків
(рис. 2.20), у
X = (— 1/ -ї- + кл і х = (— 1)/і+І у- + кл, к£2.
90
Перша формула при к = 0, ±1, ±2 дає точки , Рзл •
Т 4
Друга формула при к = 0, ±1, ±2 дає точки
Р5л » ,
4
Підставимо кожне із здобутих чисел у дане рівняння»
я : я я |/2 И2лла
При X = — 8Ш —-----СОЗ— = ----------2~ = °; ° =
Зя - Зя Зя У~2 І У^Х -./75 , А
при х = — зіп------соз —=-^2-----у 2^*0;
я . І я \ І - я \ У~2
при X =-----— ЗІП------7- — СОЗ-----т- =---------
г 4 \ -4 / \ 4 / 2
---^- = -Г2#=0;
5я . 5я 5я У 2 І УИ \
при X = — зіп -------СОЗ — =----------------2~* / =
= 0; 0 = 0.
Отже, дане рівняння задовольняють лише розв’язки -
з двох множин:
х=-^-Н-2пл, і х =-^-+ 2/гя,
їх можна записати однією формулою, якщо перетворити
другу формулу так:
х = + 2/гя = ~ + я + 2/гя = -^- + (2п + 1) я.
У першій серії до -2- додають число 2/гя, а у другій —
(2п + 1) я. Парні і непарні числа утворюють множину ці-
лих чисел. Тому об’єднана формула розв’язків матиме
вигляд
х = + кл, к£ 2.
Способом зведення до однієї функції можна розв’язува-
ти, наприклад, такі рівняння: 6 соз2 х — 5 зіп х + 5 = 0,
х + 2 сі§ х = 3, соз2 х + 2 зіп2 х — соз х = 0 та ін.
2. Спосіб розкладання на множники. При розв’язуванні
тригонометричних рівнянь цим способом всі члени рівняння
переносять у ліву частину і подають утворений вираз у
вигляді добутку. Далі використовують необхідну і достат-
ню умови рівності нулю добутку тригонометричних вира-
зів: добуток двох або кількох співмножників дорівнює
нулю тоді і тільки тоді, коли принаймні один із співмножни-
ків дорівнює нулю, а інші при цьому не втрачають смислу.
91
У даному рівнянні всі члени знаходяться у лівій части-
ні. Запишемо соз х через зіп(-^- — х) і застосуємо формулу
різниці синусів
зіп х — зіп -------х) = 0;
х+"-х *-"+х
2 СОЗ-5--зіп--Я--- = 0.
Звідси 2 соз зіп (х---= 0 . Оскільки 2 соз-у- =
= 2 х -^-=#0, то зіп(х-------= 0. Отже, х—= кл,
а х = ~ + кл> к£2.
Дістали ту саму множину розв’язків, що й при розв’я-
зуванні першим способом, але коротшим шляхом. Крім
того, при розв’язуванні не було порушення рівносильності
рівнянь, тому в перевірці немає потреби.
3. Спосіб розв’язування однорідних рівнянь. Цей. спо-
сіб застосовують при розв’язуванні однорідних тригоно-
метричних рівнянь, тобто таких, у яких ліва частина є мно-
гочленом, у кожному члені якого сума показників степенів
синуса і косинуса одного і того самого аргументу однакова,
а права — нуль. В загальному випадку однорідне тригоно-
метричне рівняння можна записати так:
Я8ІПП X + &8ІПЛ~1 ХСО5Х-Н •••
• • • + т зіп х соз'1”’1 х + І созл х = 0.
Однорідне рівняння п-го степеня відносно синуса і ко-
синуса розв’язують діленням обох частин на созп х. Але
попередньо треба довести, що соз х =Н= 0. Використаємо для
цього метод доведення від супротивного. Припустимо, що
соз х = 0. Тоді, підставивши у дане рівняння замість соз х
число 0, дістанемо а зіпп х = 0, звідки зіп х = 0. Але це
суперечить властивостям синуса гкосинуса одного і того ж
самого аргументу, оскільки при соз х = 0 зіп х = 1. Поді-
ливши на соз71 х Ф 0 обидві частини однорідного рівняння*
дістанемо алгебраїчне відносно функції тангенса рівняння
а х + Ь х + ... + /п х + / = 0.
Дане рівняння зіп х — соз х = 0 однорідне. Доведемо,
що соз х #= 0. Це так, бо при соз х = 0 мала б виконува-
тись рівність зіп х = 0, а це неможливо для одного і того
самого аргументу.
Поділимо обидві частини рівняння на соз х =£ 0. Діста-
немо х — 1 =0, або х = 1, звідки х = агсі§ 1 + кл,
або х = -^ + кл, к£ 2.
92
Не слід думати, що при розв’язуванні однорідних рів-
нянь завжди можна ділити на соз" х. Наприклад, якщо у
рівнянні а соз2х 4- Ь зіп х соз х = 0 поділити обидві ча-
стини на соз2 х, то можна загубити серію розв’язків х =
= -^- + /гл. Причина полягає в тому, що в цьому рівнянні
соз х може дорівнювати нулю, тому його треба розв’язу-
вати способом розкладання на множники: соз2 х (а 4*
+ Ь х) = 0 і т. д.
4. Спосіб введення допоміжного аргументу. Запишемо
дане рівняння у вигляді зіп х — 1 • соз х — 0. Замінимо
1 через . Дістанемо зіп х — і§-^-соз х = 0, зіп х —
зіп -2-
------- соз х = 0. Помножимо обидві частини рівняння
соз 4-
на соз-^-#= 0. Дістанемо зіп х соз—зіп-^-соз х = 0,
або зіп ^х —= 0. Звідси х —^- = £л, х =
£ €
Спосіб введення допоміжного аргументу застосовують
при розв’язуванні лінійних тригонометричних рівнянь,
якими називаються рівняння виду а зіп х + Ь соз х = с.
Дане рівняння є окремим випадком лінійного.
Розглянемо у загальному випадку розв’язування лі-
нійного тригонометричного рівняння способом введення
допоміжного аргументу. Винесемо за дужки з лівої ча-
стини рівняння |/а2 + Ь2. Дістанемо
а . . Ь \
ЗШ X Н-7....СОЗ X = с.
. V а2 + &2 / а2 + б2 )
-=^=|<1 і І-^
/ а2 + *21 І / а2 -
/ Ь \2
\ V а2 + Ь2
Очевидно, ЩО
(—а —V 4
\ К а2 + б2 І
а
означає, що при
Ь
» = соз ф матимемо т/ 2 . ~ = 8Ш Ф-
а2 + Ь2 ж у а2 + Ь2
Підставимо у попереднє рівняння ці вирази. Дістанемо
У а2 Ь2 (соз <р зіп х зіп <р соз х) = с,
або У а2 4- Ь2 зіп (х 4- ф) = с,
За умов"' и°
або с2 а2 4- Ь2, останнє тригонометричне рівняння має
93
розв’язок х + <р — (— І)6 агсзіп у р
= (— 1)* агсзіп - с - — ф + Айв, де
V а2 + Ь2
зіп (р . Ь
ОСКІЛЬКИ -----— = І£ ф = -----.
соз ф ь а
Отже, перед розв’язуванням лінійного
Ь Ал, або х =
Ф = агєі§-£-,
тригонометрич-
ного рівняння треба перевірити, чи виконується умова
с2 а2 + Ь2. Зафіксуємо здобуту формулу при розв’язу-
ванні даного рівняння: а зіп х + Ь соз х = У а2 + Ь2 X
Хзіп(х + ф). Будемо нею користуватися при розв’язуванні
інших задач, пов’язаних з тригонометричними функціями.
Застосовуючи цей загальний спосіб розв’язування, зо-
крема здобуту формулу (3), до даного рівняння зіп я —
— соз х = 0, дістанемо V2 зіп (х = 0, бо агеі§ 1 =>
= -г-. Звідси зіп х------— = 0, х-------т- = пл, х = -з- 4-
4 \ 4 / ’ 4 ’ 4 1
-|- ПЛ, П £
Лінійне тригонометричне рівняння можна розв’язати
ще кількома способами. Зокрема, можна звести його до
! о X . 9 X
однорідного, ВВІВШИ заміну 1 =СОЗ^-2-----ЗІП2 — ЯК МНОЖ-
НИК с і замінивши зіпх та созх за формулами подвійно-
. о . х х 9 х
ГО аргументу; ЗІП X = 2 ЗІП “2” СОЗ , СОЗ X = соз2 -------
• 9 X
-51П2—.
Можна також замінити зіп х і соз х через тангенс поло-
винного кута за формулами
зіп X =------------, СОЗ X =-------------.
1 + 1 + 122"Т
5. Спосіб піднесення до квадрата. Рівняння (1) можна
розв’язати способом піднесення обох частин до квадрата.
Отже,
(зіп х — соз х)2 — 0, зіп2 х — 2 зіп х соз х + соз2 х = 0,
1 — зіп 2х — 0, зіп 2х =1, 2х = 4 + 2йл,
х — 4 +
94
У цьому разі піднесення до квадрата не спричиняє по-
яву сторонніх розв’язків.
6. Графічний спосіб. Запишемо дане рівняння у вигля-
ді зіп х = соз х і введемо функції у = зіп х та у = соз х.
Побудувавши в одній системі координат графіки цих функ-
цій, знайдемо розв’язки рівняння як абсциси точок пере-
тину графіків (рис. 2.21).
Порівнюючи розглянуті способи розв’язування рів-
няння зіп х — соз х = 0, неважко зробити висновок, що
найменш раціональним є перший (алгебраїчний) спосіб,
який привів до появи сторонніх розв’язків і потребує
перевірки.
§ 4. Приклади розв'язування деяких інших типів
тригонометричних рівнянь
Розглянемо приклад рівняння, розв’язання якого ви-
магає виключення сторонніх розв’язків.
Приклад 1. Розв’язати рівняння зіп 2х Зх сі§ (х —
— -у)=0.
Розв’язання. Дорівнявши до нуля кожен із спів-
множників, розв’яжемо здобуті рівняння, а із знайдених
розв’язків виключимо ті, при яких інші співмножники втра-
чають смисл:
зіп 2х = 0, 2х — кл, х = к-^г , к£ 2\
іе Зх = 0, Зх = пл, х = п -2- , п, С
О
(х—-у) = 0, і§(-=----х + -т)=°- 4-* +
і л । 5л 5л ।
Ь -у = тл, — х 4- -у = тл, х — -у 4- рл, р£ 2.
95
Оскільки синус існує для будь-яких аргументів^ то із
знайдених розв’язків треба виключити ті, при яких не
Існують Зх І СІ£ ^Х----у). Для цього розкладемо форму-
ли, за допомогою яких записано розв’язки кожного з трьох
мули розв’язків виду
рівнянь, на елементарні (елементарними називають фор-
х = а + 2ші, де 0 а 2л) і зо-
бразимо їх на одиничних колах
(рис. 2.22). Це можна зробити,
оскільки період 2л є спільним для
всіх трьох співмножників.
Перевірка показала, що із Ю
елементарних формул розв’язків,
* зображених на рисунках, шість ви-
явилися сторонніми для даного рів-
няння (вони перекреслені), оскіль-
ки для таких чисел тангенс і котан-
генс не існують.
Отже, розв’язки рівняння запи-
шемо у вигляді _.
Рм
Р&Г
У
р*
ря
Ріг
2
X
Р-2Я
Рл З
2
Рис, 2,22
Ро
РіІ7Г
т
х = тя, х = —з—тя, т£2.
О
Рівняння, що містять тригонометричні функції у зна-
меннику, як і дробові раціональні рівнянця, зводять до ви-
/ (х)
ду = 0. Далі використовують необхідну і достатню
Ф (X)
умову рівності дробу нулю, яку для тригонометричних вира-
зів формулюють так: дріб дорівнює нулю тоді і тільки тоді,
коли чисельник дорівнює нулю, а знаменник при значен-
нях змінних, які перетворюють у нуль чисельник, не дорів-
нює нулю і не втрачає смислу.
Наприклад, у рівнянні - = 0 чисельник дробу
1 І X
дорівнює нулю при х = -у + пл, п 6 2, але при цих зна-
ченнях втрачає смисл знаменник, бо х не існує.
Приклад 2. Розв язати рівняння । соз х- = 8Ш ,
Розв’язання.
ЗІП X — ЗІП (1 + соз х)
зіп х . х Л 2 п
1 + соз х 8 П 2 ’ 1 + соз х * *
ЗІП X — зіп-н- (1 + соз х) == 0,
£
96
зіп х + 2 соз2 -у зіп = 0,
зіп х — зіп х соз = 0, зіп х 1 — соз = 0,
1)зіпх=0, х—кл, к£2,
2) 1 —сову — 0, созу = 1, -у = 2пл, х = 4пл, п£2.
З множини розв’язків х = кл треба виключити ті, при
яких знаменник 1 + соз х перетворюється у нуль, тобто
при яких соз х перетворюється у —1. Відомо, що соз х до-
рівнює —1 при всіх непарних к. Отже, треба залишити
лише розв’язки х = 2пл.
Множину розв’язків х = 4пл включають до множини
х = 2пл. Отже, розв’язками даного рівняння є х = 2пл,
Рівняння, до складу яких входять добутки зіп а зіп Р,
соз а соз р, зіп а соз р, зручно розв’язувати за такими фор-
мулами:
зіп а зіп р = -у (соз (а — р) — соз (а + Р));
соз а соз р = -у (соз (а — Р) + соз (а + р));
зіп а соз Р = -у (зіп (а — Р) + зіп (а + Р)).
Приклад 3. Розв’язати рівняння зіп х зіп Зх + зіп 4х х
X зіп 8х = 0.
Ровв’явання.
-у (соз (х — Зх) — соз (х + Зх)) + -у (соз (4х — 8х) —
— соз (4х + 8х)) = 0, -у (соз 2х — соз 4х) -ф
+ -у (соз 4х — зіп 12х) — 0,
соз 2х — соз 4х + соз 4х — соз 12х = 0, соз 2х — соз 12х = 0,
/-ч ♦ 2х —І— 12х • 2х 12х л • п • г" г\
— 2 81П-------81П---2---= 81П ^Х • 8Ш = 0-
Звідси маємо два рівняння:
зіп7х = 0, 7х=кл, х = к-^~, к^2\
зіп 5х = 0, 5х = пл, х == л , п £ 2.
О
4 1-1819
97
Тригонометричні рівняння, до складу яких входять
алгебраїчні суми виду зіп х 4- зіп 2х + зіп Зх + ... 4*
+ зіп пх або соз х + соз 2х + соз Зх + ... + соз пх, і§х4-
4- + ... пх, або інші аналогічні комбінації аргу-
ментів, розв’язують, групуючи члени і застосовуючи фор-
мули додавання тригонометричних функцій. Але робити це
треба так, щоб після перетворення у добуток кожної пари
доданків з’являвся спільний множник. Далі рівняння роз-
в’язують, розкладаючи його на множники.
Приклад 4. Розв’язати рівняння зіп х — зіп 2х 4-
+ зіп 5х + зіп Зх = 0.
Розв’язання. Згрупуємо члени таким чиномі
(зіп х + зіп 5х) + (зіп 8х — зіп 2х) = 0. Застосуємо фор-
мули суми і різниці синусів і використаємо властивість
парності косинуса
2 зіп Зх соз 2х 4- 2 соз 5х зіп Зх — 0,
2 зіп Зх (соз 2х 4- соз 5х) = 0.
Ще раз перетворимо у добуток суму косинусів
7 З
2 зіп Зх 2 соз -у х соз -у х = 0.
Звідси дістанемо три рівняння:
зіпЗх=0, Зх = кл, х—к-%~, к^2‘,
О
7 А 7 л. .
СОЗ-уХ=0, -у X = -у + пл,
-у + 2п-^= (2л+1)-^-, п$2;
соз х = 0, у х = -у 4- піл,
^-4-2ту-==-у(2/п4-1), т$2.
Остання множина розв’язків входить до множини х =
ь
= -х-л. Отже, розв язками даного рівняння є числа х —
= £у, к Є 2, х = у (2п 4- 1), п € 2.
Тригонометричні рівняння, до складу яких входять пар-
ні степені функцій зіп х, соз х, доцільно розв’язувати, зни-
жуючи степінь функції за формулами зіп2 а ==------,
98
Приклад 5. Розв’язати рівняння 6 зіп2х + 2 зіп22х = 5.
Розв’язання Якщо зробити заміни зіп2 х =
=----2-----» 81П 2х == 1 — соз2 2х, то дістанемо рівняння
6 * 1 “~є°52^ 4-2(1 — соз2 2х) = 5, або 3 — 3 соз 2х + 2 —
— 2 соз2 2х— 5 = 0. Звідси 2 соз2 2х + 3 соз 2х = 0. Має-
мо квадратне рівняння відносно соз 2х. Розв’язуючи його
способом розкладання на множники, дістанемо соз 2х х
X (2 соз 2х + 3) = 0. Звідси соз 2х = 0, 2х = ~ + пл,
х ~ Т+ п Т =Т(2п + 1)1 гаЄИ; 2 008 2^ + 3 = 0,
2 соз 2х = —3, соз 2х = —у не має розв’язків, оскільки
| соз 2х | 1.
Отже, розв’язками даного рівняння є числа х =
= -у (2п + 1). Це рівняння можна було б розв’язати інак-
ше, замінивши зіп2 2х на 4 зіп2 х соз2 х, а соз2 х на 1 —
— зіп2х. Після цього дістанемо квадратне рівняння відносно
зіп х. Але цей спосіб більш громіздкий.
При розв’язуванні тригонометричних рівнянь слід па-
м’ятати про можливі випадки порушення рівносильності
рівняння, тобто про втрату і появу сторонніх розв’язків.
Зокрема, при піднесенні до квадрата обох частин рівняння
можуть з’явитися сторонні розв’язки. При розв’язуванні
однорідних рівнянь необгрунтоване ділення на созп х може
призвести до втрати розв’язків. Доводиться включати сто-
ронні розв’язки і при розв’язуванні рівнянь, що містять
добутки і дроби у лівій частині і нуль — у правій.
Наведемо ще два приклади втрати розв’язків.
Приклад 6. Розв’язати рівняння зіп х — соз х =
= /7.
Розв’язання Це лінійне рівняння. Використаємо
підстановки зіп х =------, созх =--------. Дістанемо
1 + ^2| 1+і§24
1 + ^4
-----X У7 Г = Оскільки 1 + І§2 у Ф
2Цу------------* + 1§2Т
=0= 0, то
24— уї (і - 4-)=К7 (і + 4-).
99
Звідси = V?, -у- = агсі§ 1^7 4- кл, х = 2 агсі§ Г7 4-
“Р 2йл, к £ %.
Неважко перевірити, що дане рівняння задовольняють
і числа х = (2п + 1) л. Втрата розв’язків сталася внаслі-
док застосування підстановки і переходу до алгебраїчного
рівняння відносно тангенса. Його не задовольняють числа,
при яких не існує, тобто числа = (2п + 1)-^ , або
х = (2п + 1) я. Але ці числа задовольняють дане рівняння.
Тому при використанні підстановки, яка виражає синус і
косинус через тангенс половинного кута, необхідно переві-
ряти числа х = (2/г + 1) я. Якщо вони задовольняють дане
рівняння, то їх слід приєднати до знайдених розв’язків.
Тому остаточно запишемо розв’язок у вигляді х =
= 2 агсі§ К? + 2йя, к б 2, х = (2п + 1) я, п £ 2.
Приклад 7. Розв’язати рівняння Н—£"") +
+ -т) = 2 *•
Розв’язання. Застосуємо формули
(а 4- В) = + їй (а — В) =
8 + Р) 1 — а р ’ 81 Р-* 1 — а 3 ’
, 1
Сій а = ---.
5
Дістанемо
<8* 4-1 і§х— 1 _ 2
1 —1 4-х і§х ’
і§х((і§х4- 1)24-(і§х— 1) (1 — 1§х)) —2(1 —і£ах)
(1 — і£2х)і£х
Після спрощення маємо
3 =0, Зі§2х—1=0, 1§2х = 4-,
(1—і£2х)і£х ь ’ & З
= х=±-^-4~пя, п£2.
При цих значеннях х не втрачає смислу і не перетворю-
ється у нуль знаменник дробу. Проте неважко перевірити,
що дане рівняння задовольняють також числа виду х =
= -у + пл, п С 2, Втрата цих розв’язків сталася внаслідок
застосування теореми додавання для функції тангенс. Фор-
мули тангенса суми і різниці двох чисел а і £ виконуються
іоа
лише за умови, що мають смисл вирази а, р і (а +
+ |3). Якщо х = -у + пл, то х не має смислу, тому ці
розв’язки було втрачено. Якщо дане рівняння розв’язати
за формулою суми тангенсів двох чисел, то вказані розв’яз-
ки не будуть втрачені.
В результаті розв’язування одного і того самого триго-
нометричного рівняння різними способами можна дістати
різні загальні формули розв’язків рівняння. їх еквівалент-
ність можна довести,‘перетворивши формули та об’єднав-
ши кілька формул в одну. Можна також довести рівність
знайдених множин розв’язків, записавши у розгорнутому
вигляді прогресії, п-м членом яких є формула розв’язку
тригонометричного рівняння. Проте обидва ці способи гро-
міздкі. Доцільно записати дане тригонометричне рівняння у
вигляді І (х) = 0, знайти найменший додатний період / функ-
ції у = / (х) і показати, що на проміжку [0; /] кожна з утво-
рених формул дає одну і ту саму множину розв’язків.
Зручним виявляється також геометричний спосіб доведення
рівності множин розв’язків за допомогою одиничного кола.
Якщо різні формули на одиничному колі дають однакові
множини точок, що зображують частинні розв’язки рів-
няння, то ці множини рівні. Проте така геометрична інтер-
претація можлива тільки тоді, коли періодом функції,
що входить до лівої частини рівняння / (х) = 0 (не обов’яз-
ково найменшим додатним), є число 2л.
§ 5. Розв'язування найпростіших
тригонометричних нерівностей
Розв’язування будь-яких тригонометричних нерівнос-
тей, як правило, вводиться до розв’язування найпрості-
ших нерівностей:
зіп х а або зіп х а\
соз х а або соз х а*
х а або х а\
сі§ х а або сі§ха.
Як і найпростіші тригонометричні рівняння, нерівності
природно розв’язувати графічно. Розглянемо приклади.
Приклад 1. Розв’язати нерівність зіп х ,
Розв’язання. Позначимо функції, які стоять у
лівій і правій частинах, через у = зіп х і у = і побуду-
101
ємо схематично їхні графіки (рис. 2.23). Розв’язками нерів-
ності будуть абсциси всіх точок графіка синусоїди, які
вище прямої Враховуючи періодичність функції
синус, досить знайти розв’язки на будь-якому відрізку об-
ласті визначення довжиною 2л і додати до знайдених чисел
період 2пл, п £ 2. Виберемо, наприклад, проміжок 10; 2л].
З рисунка випливає, що множиною значень х з відрізка
[0; 2л], для яких відповідні точки графіка синусоїди вище
точок прямої у = у, буде • Додавши до цих
чисел період 2пл, дістанемо множину всіх розв’язків даної
нерівності -у + 2пл < х < + 2пл,
Графічний спосіб є досить наочним, але незручність
полягає в тому, що кожного разу (хоч і схематично) треба
будувати графіки тригонометричних функцій.
Дещо зручнішим є спосіб розв’язування найпростіших
тригонометричних нерівностей за допомогою одиничного
кола. Для даної нерівності розв’язування цим способом
проводять аналогічно розв’язуванню простішого тригоно-
метричного рівняння.
Побудуємо одиничне коло (рис. 2.24). Відкладемо на осі
Оу ординату у і через кінець відрізка проведемо пряму,
паралельну осі Ох.
Розв’язання даної нерівності зводиться до знаходження
на одиничному колі всіх точок, у яких ординати більші
у. Ці точки відповідають шуканим числам а, що є розв’яз-
ками даної тригонометричної нерівності. З рисунка випли-
ває, що такими точками є точки дуги кола, які розміщено
над прямою у і відповідають числам множини )
на відрізку [—л; л], довжина якого дорівнює періоду 2л.
Додаючи до цих чисел період функції 2пл, дістанемо
1
множину ВСІХ розв ЯЗК1В нерівності 8ШХ>у.
102
Розглядаючи розв’язання нерівності виду зіп х > а
у загальному випадку, необхідно накласти обмеження на
число а. Якщо 1, то нерівність зіп х > а розв’язків
не має, бо при будь-якому х завжди | зіп х | 1. Якщо ж
а <—1, то нерівність зіп х > а виконується при будь-
якому х, тобто множиною розв’язків такої нерівності є мно-
жина /?.
У загальному випадку нерівність зіп х > а, де —1
розв’язують аналогічно (рис. 2.25). Точки
Лгсзіпа і Лі-агсзіпа зображують числа агсзіп а і я —
— агсзіп а. Розв’язками нерівності на відрізку [—я; я] є
множина (агсзіп а\ я — агсзіп а), а множиною всіх розв’яз-
ків будуть проміжки
агсзіп а + 2пл < х < я — агсзіп а + 2ля, п £ 2,
Аналогічно розв’язують нерівність зіп х < а. На
рис. 2.26 показано дугу, що відповідає розв’язкам цієї
нерівності.
Приклад 2. Розв’язати нерівність соз х ~ .
Розв’язання. Знайдемо спочатку розв’язки на
відрізку [—я; я]. Розв’язання даної нерівності зводиться
103
до знаходження на одиничному колі всіх точок Ра, що ма-
ють абсциси, які менші або дорівнюють—~ (рис. 2.27).
Всі ці точки відповідають на одиничному колі числам а,
які є розв’язками даної нерівності.
Відкладемо на осі Ох відрізок ОА, що відповідає абсци-
сі — і проведемо через його кінець А пряму, паралель-
ну осі Ог/.
Шукані точки одиничного кола
... .. 1
лежать лівіше від прямої х = —
або на самій прямій і належать ду-
зі Р 2л Р 4Л . Отже, МНОЖИНОЮ рОЗ-
“з~ ~
в’язків нерівності, що належить
відрізку І—л; лі, є — < х •
Додавши до цих чисел період ко-
синуса, дістанемо всі розв’язки не-
Рис. 2.28 рівності
^5—р 2пл х —х—Н 2пл, п б 2.
о о
Приклад 3. Розв’язати нерівність х < КЗ.
Розв’язання. Враховуючи періодичність танген-
са, знайдемо розв’язки даної нерівності спочатку на проміж-
ку —у» у'У Якщо а — розв’язок даної нерівності, то
ордината точки Та лінії тангенсів (рис. 2.28), що дорівнює
а, повинна бути менша КЗ. Всі такі точки лежать на
ДОТИЧНІЙ нижче ТОЧКИ 7\. Відповідні точки Ра одинично-
Т
го кола належать дузі, позначеній на рисунку. Ці точки
відповідають числам а, що належать проміжку----< а <
л
Додавши до знайдених чисел період тангенса, дістанемо
всі розв’язки даної нерівності
її । її . пр
----п- + /гл<х<-^-4- пл, п £ 2.
£ о
Більш складні тригонометричні нерівності розв’язують
способами, що аналогічні до способів розв’язання тригоно-
метричних рівнянь такого ж типу.
104
Запитання і завдання для повторення
1. Яка функція називається оборотною?
2. Сформулювати означення функції, оберненої до даної оборот-
ної функції.
3. Як розташовані графіки двох взаємно обернених функцій?
4. Сформулювати алгоритм знаходження формули функції, обер-
неної до даної. Знайти функцію, обернену функції: а) у — 2х— 1;
б) у = х1 2 при 0 < х < +°°; в) у = х\
5. Сформулювати теорему про властивість оберненої функції.
6. Ввести функцію, обернену до у = зіп х. Назвати її властивості.
7. Ввести функцію, обернену до у = соз х, і назвати її властивості.
8. Ввести функцію, обернену до у — х, і назвати її властивості.
9. Як побудувати графіки обернених тригонометричних функцій?
10. Довести, що функції у = агсзіп х і у = агсі& х непарні.
11. Як виразити агссоз (—х) через агссоз х?
12. Обчислити значення виразів:
1) агсзіп 1; 2) агссоз (—3) агсі£ ---------агсі§’/З:
5) агссоз 0,7986; 6) 2 агсзіп —=•— агсзіп 1;
У2
7) агссоз + агссоз ~ ; 8) агссоз ( соз ; 9) ( агсі§ ( — ))
І І 2 \\
10) СІ£ І агссІ£І — — II.
ІЗ. Яке рівняння називають тригонометричним?
14. Яка особливість розв’язків тригонометричних рівнянь?
15. Вивести формули розв’язків рівнянь зіп х = а, созх=а,
ї&х= а.
16. Назвати способи розв’язування окремих видів тригонометрич-
них рівнянь.
17. Які тригонометричні рівняння називають однорідними? Як ї>.
розв’язують?
18. Які тригонометричні рівняння називаються лінійними? Колі’
існують розв’язки таких рівнянь?
19. Як розв’язують лінійні тригонометричні рівняння?
20. Як розв’язують тригонометричні рівняння виду І (х) ф (х) ...
4>(х)=0 і -Ц^-= 0?
<р (х)
21. Коли при розв’язуванні тригонометричних рівнянь може пору-
шитись рівносильність?
22. Як розв’язати нерівності виду зіп х я, зіп х а?
23. Як розв’язати нерівності виду соз х а, соз х^ а за допомо-
гою одиничного кола?
24. Як розв’язати нерівності виду х > а, х а за допомо-
гою одиничного кола?
Вправи
1. Розв’язати рівняння:
1) зіпх = 0; 2) соз х = —0,4827; 3) і£х = 0;
4) х = — 0,5; 5) соз х = 0; 6) зіп 2х = ~ 1;
105
7) зіп х = - ; 8) зіп — 30°) + 1=0; 9) соз х = 1. ;
10) 2созЗх—1 =0, 11)1§х=ҐЗ; 12) 3 (х + 1) — КЗ = 0;
13) соз х = — -£2- ; 14) 2 зіп^-|- —х^—1 =0;
15) і§х = - У?- ; 16) 2 соз Зх + /З = 0;
17) і§х = —0,6009; 18) Зі§22х+1 =0; 19) зіп х = 0,2753;
20) 2 зіп2 Зх — 1 = 0.
2» Розв’язати рівняння:
А
1) соз х 4-зіп х = 0; 2) соз 2х соз х = зіп 2х зіп х;
3) зіп3 х + 2 зіп х — 3 = 0; 4) соз 2х = 2 зіп2 х;
5) зіп 2х = соз х соз 2х; 6) зіп х 4- зіп 2х + зіп Зх = 0;
7) 2 зіп2 х + 3 соз х = 0; 8) зіп х + 1^3 соз х == 1;
9) соз 2х = соз 6х; 10) 1 + С03 2х = 0;
соз X
11) зіп + соз х = 1; 12) 1 + зіп х зіп 2х = соз х соз 2х;
13) х + 5 сі§ х = 6; 14) . х = 1.
1-КЗійх
Б
15) 31§2х —-----1—= 1; 16) зіп4 х + зіп4/х + ~^~) = —;
соз2х \ 4/4
17) зіп4 х — соз4 х = зіп 2х; 18) ,..-8?п х-= зіп — ;
1 + соз х 2
19) 1 — соз (л - х) + зіп — = 0; 20) 3 зіп х — 3 соз х = 5;
21) 1 + зіп х + соз х 4- х = 0; 22) 4 зіп х + 5 соз х = 4;
23) -і8х = 1 + х;
24) 5 зіп2 х + зіп х соз х = 5 — 6 соз2 х;
25) 4 зіп4 х + зіп2 2х = 2; 26) (1 + соз х) = 0;
27) 1 — соз х = зіп х зіп ; 28) соз2 х — 3 зіп х соз х 4- 1 = 0;
29) 2 зіп -р зіп — х^ 4“ 8іп2 х = 0;
30) і£3 х — і&2 х 4- х = 1.
В
31) соз х 4- соз 2х 4- соз Зх 4- соз 4х 4~ соз 5х = 0;
32) (1 — х) (1 4- зіп 2х) = 1 4~ х;
33) 6 х 4- 5 сі£ Зх = 2х; 34) 1 4~ зіп3 х 4- соз3 х = зіп 2х;
106
35) 1 + соз ІОх соз 6х = 2 соз2 8х + зіп2 Зх;
36) зіп 2х — 3 соз 2х = 3;
37) зіп4 х + соз4 х — зіп х соз х = 0; 38) 5*п хл—!- = 1;
соз4 х
39) Кзіп2 х — 1 + V 1 — зіп2 х — зіп 2х;
40) ]Ґ2 — 3 соз 2х — Vзіп х;
41) С08. = 0; 42) зіп2 х + зіп2 2х = зіп2 Зх + зіп2 4х.
х
5ІПТ
3. Розв’язати нерівності:
1) зіпх < ; 2) І£х> — 1; 3) зіпх>2; 4) і§х^2;
1 Кз і
5) соз х < -у- ; 6) | зіп х | > 2 ; 7) со8х> у- ;
8) соз2 х < .
4
РОЗДІЛ З
ГРАНИЦЯ І НЕПЕРЕРВНІСТЬ ФУНКЦІЇ
§ 1. Границя числової послідовності
1. Поняття про границю числової послідовності. У кур-
сі «Алгебра і початий аналізу» вивчають досить важливі
властивості функцій, які не можна дослідити елементарни-
ми способами. В основі методів, за допомогою яких вда-
ється дослідити ці нові властивості, лежить поняття грани-
ці функції, одне із фундаментальних понять сучасної мате-
матики. Існує окрема дисципліна, яка називається «Мате-
матичний аналіз». В ній досить грунтовно вивчається тео-
рія границь. У цьому розділі ми розглянемо лише окремі
питання цієї теорії, які будуть необхідні нам у подальшому.
З’ясуємо поняття границі на простішому випадку функ-
ціональної залежності, коли областю визначення функції
у = / (х) є множина натурального ряду чисел N. Таку функ-
цію називають числовою послідовністю і позначають через
Уп = Нп). п=1, 2, ....
Числову послідовність ще записують у вигляді ряду
чисел
Уп , Уп, • • • ,
в якому у± називають першим членом послідовності, у2 —
другим і т. д., уп — п-м або загальним членом послідовно-
107
сті. Числову послідовність вважають заданою, якщо задано
її загальний член.
Для числових послідовностей застосовують ще і таке
позначення (уп) або (ап), де уПі ап — /г-ні члени послідов-
ностей.
Прикладами числових послідовностей є арифметична
і геометрична прогресії. Тут загальні члени задають та-
кими формулами:
Уп = Уі + <Цгі — 1), уп = УіЯп~\ п=1, 2,...,
де й — різниця арифметичної прогресії; д — знаменник
геометричної прогресії.
Ую У 5 У 4 Уз У 2 Уі
І-о------о—о------о-----о-----------------------о-**
п 1 1 1 1 1 / X
и 10 5 Ч 3 2 *
Рис. 3.1
Розглянемо ще приклади числових послідовностей.
Приклад 1. Нехай загальний член послідовності задано
формулою
1 1 П
Уп п » 1» 2, . . . .
Тоді, надаючи п значень і, 2, ..., дістанемо числову
послідовність
Помічаємо, що члени даної послідовності із збільшенням
числа п спадають: кожний наступний член менший за по-
передній, тобто для всіх п = 1, 2, ... виконується нерів-
ність Уп-\-\ < уп.
Із збільшенням числа п відповідні члени послідовності,
залишаючись додатними числами, стають ближчими до
числа нуль. Так, другий член послідовності (1) знаходить-
ся до нуля ближче, ніж перший член цієї ж послідовності,
третій член послідовності знаходиться до нуля ближче,
ніж другий, і т. д., п + 1-й член — ближче до нуля, ніж
п-й член (рис. 3.1).
Що означають слова: «члени послідовності із збільшен-
ням числа п стають все ближчими і ближчими до числа
нуль?» Це означає, що із збільшенням числа п відстань
між відповідними членами послідовності і числом нуль
стає все меншою і меншою. Оскільки відстань між двома
дійсними числами а і Ьу або, що те саме, між двома точками
138
а і Ь числової осі дорівнює додатному числу | а — Ь |, то
в даному разі модуль різниці
\Уп-0| = 4-
при зростанні п стає все меншим і меншим. Зокрема, цей
модуль може бути меншим, наприклад, за числа 0,1; 0,01;
0,001 і т. д. Для цього в послідовності (1) досить взяти від-
повідно члени з номерами, більшими за 10, 100, 1000 і т. д.
Таблиця 3.1
Є 0,1 0,01 0,001 0.0001 0,00001 0,000001
N 10 100 1000 10 000 100 000 1 000 000
А якщо взяти, наприклад, довільне, як завгодно мале до-
датне число 8 (грецька буква «епсілон»), то чи знайдеться
в послідовності (1) її член (його номер к) такий, щоб для
всіх наступних членів цієї послідовності виконувалася не-
рівність
Відповідь стверджувальна. Для цього досить брати чле-
ни послідовності упі у яких номер п задовольняє нерівність
Позначимо через уп такий член в послідовності (1), що
при виконується нерівність
\Уп — 0 І <8.
Зрозуміло, що для кожного окремого значення числа є
існує своє натуральне число N. У табл. 3.1 для різних
значень є наведено відповідні значення N.
Приклад 2. Розглянемо послідовність, загальний член
якої заданий формулою
Уп = "~^2~ » я = 1, 2, ,...
Дістанемо таку числову послідовність:
У послідовності (2) її члени із зростанням числа п спа-
дають і наближаються до числа нуль. І чим більше число
109
п, тим відповідний член послідовності знаходитиметься
ближче до нуля. Іншими словами, відстань | уп — 0 | при
зростанні п стає як завгодно малою, тобто у послідовності (2)
знайдеться її член уп, такий, що для всіх п> N буде
справджуватися нерівність
\уп - 0| <0, (3)
де є — довільне, як завгодно мале додатне число. Надаючи
є довільних додатних значень, кожний раз матимемо шу-
кане число N.
Таблиця 3.2
1 1 1 1 1 1_ 1
4 9 16 25 100 Ю0( 10 000
N 2 3 4 5
10
31 100
Щоб знайти N для будь-якого наперед заданого додат-
ного числа є, підставимо в нерівність (3) значення уп і
розв’яжемо здобуту нерівність відносно п. Дістанемо
(4)
о • 1
Звідси гг>—т=-.
у 8
Отже нерівність (3) буде справджува-
тися для всіх значень п, які задовольняють нерівність (4).
Тому за число N можна взяти число , якщо воно ціле,
V е
або найбільшу цілу частину цього числа, якщо це число
є дробовим. Проілюструємо сказане за допомогою табл. 3.2.
Приклад 3. Нехай у числовій послідовності загальний
член уп задається формулою
Уп = —ТТ’ я = 1, 2, ... . (5)
п +1 7
Тоді маємо числову послідовність
12 3 п.
2 9 3 9 4 9 ”* ’ п+ 1 ’ * ’ ’ ’
(6)
Помічаємо, що із зростанням числа п члени послідов-
ності (6) зростають і наближаються до числа 1, залишаю-
чись меншими 1. І чим більше число п, тим ближче відповід-
ний член послідовності (6) стоїть до 1.
Розглянемо задачу: чи існує таке натуральне число /V,
щоб при п> N члени послідовності (6) задовольняли не-
110
рівність
\Уп-і\<^ (7)
де є — будь-яке як завгодно мале додатне число? Щоб від-
повісти на це питання, треба розв’язати нерівність (7) від-
носно п Для цього у ліву частину цієї нерівності підста-
вимо значення уп із (5) і зробимо певні перетворення.
Маємо
І п і І І п — п — І — і \
----і~і--1 < в, --------г-: < 8, ----г-г- < 8,
| П + 1 І І П + 1 І | п + 1 І *
1
---і—Г
п+1
Звідси п > 1 •
Якщо 0 < 8 < 1, то N = 18 , коли число ці-
8 - 8
ле, і N дорівнює найбільшій цілій частині числа 8 ,
коли воно є дробове число. При 8^ 1 ціла частина чис-
ла 1 ~8 менша або дорівнює нулю. Тому за число N
можна взяти будь-яке натуральне число, зокрема числа
1, 2, ... .
Для позначення найбільшої цілої частини числа т вво-
дить спеціальний символ Е (т) (Е — перша буква від фран-
цузького слова епііег, що означає «цілий»).
Так, наприклад, Е (0) = 0, Е (1) = 1, Е (0, 5) = 0,
Е (3, 2) = З, Е (—1, 1) = —2, Е (1Ї000) = 31.
У цьому прикладі число N можна було знайти простіше,
використавши так званий прийом «підсилення нерівності».
Ідея полягає в тому, що коли 5 < 12, то й поготів 3 < 12.
Оскільки для всіх п = 1, 2, ...
і 1
«4-1 < п ’
то, розв’язавши нерівність — <8 .. 1 більша, ніж —гп-, дістанемо п п 4- 1 = ЕШ- Пр" — < е й поготів нерівність - , в якій ліва частина > — . Візьмемо АГ = є виконується нерівність 1 ——г- <8, а значить п -1- 1 ’
111
Тоді для числа N у першому і другому прикладах має-
мо такі формули*
І 8 ) І г«)
Дамо означення границі числової послідовності.
Число а називається границею послідовності уи у2,
у3, • ••, Ум •••> якщо для будь-якого як завгодно малого додат-
ного числа в існує таке натуральне число N = N (є), що
для всіх п> N виконується нерівність
\уп—а\<е. (8)
Символічно це записують так:
ііт уп = а, або уп -» а.
Ми будемо користуватися першим позначенням (Ііт —
від латинського слова «іігпез», що означає «границя»).
Отже, у розглянутих прикладах границі послідовностей
(1), (2), (6) відповідно дорівнюють 0; 0; 1.
Приклад 1. Показати, що границя функції уп = ,
, . .4 7 3п+1
або, що те саме, послідовності-р , у, ДОР1В'
Зп+ 1 З
2/7 — 1 “ 2 *
нює-І-, тобто Ііт
П-4-ОО
Ро з в’ я з а н н я. Згідно з означенням границі треба
показати, що для будь-якого числа в > 0 знайдеться таке
число N = N (є), що для всіх п> N виконується нерів-
ність
З
Уп 2
< 8.
Справді, підставивши у дану нерівність значення уПІ
дістанемо
І Зп +1 ЗІ, І 1 \
І 2н—1 2 |<8’ аб° |2(2п— 1)|<8‘
3вІДСИ 11(2^ <Є'
Розв’язавши здобуту нерівність відносно іг, знаходимо
1 + 2в
п >—т—.
4е
Отже, існує шукане число N = Е^1 ^2Є) Тому
Ит уп = .
112
Приклад 2. Показати, що Ііш_____2п2 + 3 = 2.
М->оо П* 1 2 + п — 1
Роз в’ яз а н н я. Справді, при п З
I п2 + п — 1 I п2 п — 1 п
Тому [ ---21 і поготів буде меншим за є,
якщо -|~ <8, або п>-|- . Отже, N = Е
Значення п 3 взято тому, що за цієї умови дріб
] набуває додатних значень. (На означення гра-
ниці це обмеження не впливає.)
Приклад 3. Показати, що границя сталої послідовності
уп — а, п = 1, 2, дорівнює числу а.
Розв’язання. Нехай маємо сталу послідовність
а, а, ..., а, ... . Тоді \уп — а | = 0, п = 1, 2, .... Отже,
яке б мале число 8 >> 0 ми не взяли, для всіх п = 1, 2, ...
виконується нерівність \ уп — а | = 0 < є.
У цьому разі за число N можна взяти будь-яке нату-
ральне число, наприклад, числа 1, 2 і т. д.
Якщо числова послідовність має границю, тобто для
будь-якого 8 > 0 можна вказати натуральне число М, то це
число не єдине. Будь-яке число, більше за N. теж підходить
Приклад 4. Показати, що послідовність із загальним
членом уп = (—1)п не має границі.
Р о з в’ я з а н н я. Покажемо це, користуючись мето-
дом доведення від супротивного. Нехай задана послідов-
ність має границю, яка дорівнює числу а. Отже, яке б ми
1
не задали додатне число е, наприклад число & = , існує
таке N. що при п > N виконується нерівність | уп — а | <
< 2 *
Оскільки уп при непарному п набуває значення —1, >
при парному п — значення І, то виконуються нерівносі1
Тоді
2 =|1 = !(«_(_ 1))+(1-й)|<
<|(-1)-аН |1 -а|<4- + ^= 1.
Отже, 2 < 1. Дістали протиріччя.
113
2. Нескінченно малі числові послідовності. Серед функ-
цій натурального аргументу особливе місце належить так
званим нескінченно малим послідовностям.
Послідовність уп = І іп\ п == 1, 2, ..., називається не-
скінченно малою, якщо Ііт уп — 0. Таку числову послі-
довність називають нескінченно малою числовою послідов-
ністю.
Наприклад, послідовності /-Ц, є нескінченно
малими.
Якщо у нерівності (8) покласти а = 0, то дістанемо
нерівність | уп | < в, п> N Тому нескінченно малу число-
ву послідовність можна означити ще й так.
Числова послідовність (уп) називається нескінченно ма-
ною, якщо для будь-якого як завгодно малого додатного чис-
ла 8х існує натуральне число N таке, що для всіх п> N ви-
конується нерівність | уп | < 8.
Отже, члени послідовності (//п), починаючи з певного
номера і для всіх наступних номерів, стають за модулем
як завгодно малими.
Не треба плутати нескінченно малу числову послідов-.
ність з досить малим числом. Окремі члени нескінченно ма-
лої числової послідовності можуть бути як завгодно вели-
кими. Так, наприклад^ послідовність ^2°^ є нескінченно
1101ип І
( < е при п, більшому, наприклад, від
10і0 д . 1')Ю 10і" • 2 102 • З
числа ----. Але окремі значення —у-, —=—, ——
є / □ ю
не є малими числами.
Нескінченно малі послідовності позначають через ап,
|3П, уп і т. д.
Наступні теореми встановлюють тісний зв’язок між
функцією уп, яка має границю, і нескінченно малою функ-
цією.
Теорема 1, Якщо Ііт уп = а, то послідовність ап =
И->оо
= уп — а є нескінченно малою.
Доведення. Яке б не було ЧИСЛО 8 > 0, знайдеться
таке /V, що для всіх п> N виконуватиметься нерівність
\Уп — а | < 8, або | ап | < є (п > У), тобто ап — нескін-
ченно мала функція.
Справедлива і обернена теорема.
Теорема 2. Якщо різниця між уп і числом а є нескінченно
малою послідовністю, то а є границею послідовності уп.
114
Доведення. Позначимо ап = уп — а. Тоді уп —
— а є нескінченно малою послідовністю. Отже, для будь-
якого числа 8 >> 0 знайдеться таке /V, що для всіх п> N
виконується нерівність | ап | < 8, або, що те саме, | уп —
— а | <С 8. Отже, згідно з означенням границі Ііт уп =
= а. Доведені теореми дають змогу навести ще й таке озна-
чення границі послідовності.
Число а називається границею числової послідовності
(уп), якщо різниця між уп і числом а є нескінченно малою
послідовністю, тобто уп — а = ап.
Нескінченно малі функції (послідовності) мають такі
властивості.
Властивість 1. Алгебраїчна сума скінченного числа не-
скінченно малих послідовностей є нескінченно малою послі-
довністю.
Заради простоти припустимо, що маємо дві нескінченно
малі послідовності ап і |3П. Треба показати, що послідов-
ність уп = ап + |3П є також нескінченно малою. Для цього
задамо довільне число е > 0. Оскільки ап є нескінченно ма-
лою послідовністю, то для числа існує таке число Л^,
що для всіх п> Л\ виконуватиметься нерівність | ап | <
. Існує також і число М2» Що для всіх п> N2 викону-
ватиметься нерівність І рл| Су . Візьмемо тепер число /V,
яке більше за числа Л\ і Л/2. Тоді для всіх п> N одночасно
виконуються обидві нерівності
І І е Ш 1^ 8
| ап І ~2~ > І Рп І \ ~2~ •
Використавши властивість модуля суми, дістанемо
Іїл| = |ал + Рп|< І«П 1 + ІРп|-
Згідно з попередніми нерівностями
І їп І < Є, (П> її).
Використавши метод математичної індукції, можна до-
вести справедливість цієї властивості і для будь-якого
(певного) числа нескінченно малих послідовностей.
Приклад. Довести, що послідовність із загальним
членом
Уп = -п-^— , П= 1, 2, ... (9)
е нескінченно малою.
115
Р о з в’ язання. У правій частині рівності (9) вико-
нуємо ділення. Маємо уп = — + • Кожний доданок
тут є нескінченно малою числовою послідовністю. Згідно
з властивістю 1 робимо висновок, що послідовність (9) є
нескінченно малою.
Перш ніж сформулювати наступну властивість, наведемо
таке означення.
Послідовність (уп) називається обмеженою, якщо існує
число М > 0 таке, що для всіх значень п = 1, 2, ... викону-
ється нерівність
\Уп\<М.
Наприклад, послідовність ((—1)п) є обмеженою. Тут
| (—1)п | = 1. Тому за число М можна взяти, наприклад,
число 2. Тоді для всіх п = 1,2,..., буде справджуватиметься
нерівність | (—1Г |.< 2.
Послідовність уп = созп , гг=1,2,..., єтакожобме-
женою. Тут| СО8П 1, и= 1, 2, ..., тоді як послідов-
ність уп = /г2, п= 1, 2, не є обмеженою. (Чому?)
Властивість 2. Добуток нескінченно малої числової послі-
довності на обмежену послідовність є нескінченно малою
числовою послідовністю.
Нехай (і/л) є обмеженою послідовністю, а ап — нескін-
ченно малою. Покажемо, що |3П = уп • ап є нескінченно
малою числовою послідовністю.
Оскільки (уп) є обмеженою послідовністю, то існує таке
число Л4, що для всіх п справджується нерівність | уп\ <
<М.
Оскільки ап є нескінченно малою послідовністю, то яке
б ми не взяли число, зокрема число , де є > 0, знайдеться
таке число /V, що для всіх п> N виконується нерівність
І І < М '
Тоді
|рп| = |^|.|ап|<Л4.^- = є> (/г > А/).
З нерівності | рп ї < е, (п > П), випливає справедли-
вість доводжуваного твердження.
3. Основні теореми про границі. Знаходження границі
числової послідовності на основі тільки означення границі
116
викликає часто певні труднощі, оскільки: треба наперед
знати «підозріле» на границю число; не кожного разу за
заданим е можна знайти N.
Тому на практиці для знаходження границі числових
послідовностей користуються такими теоремами.
Теорема 1. Нехай послідовності (хп) і (уп) мають відпо-
відно границі а і Ь. Тоді сума (хп + уп) має границю а + Ь.
Доведення. Якщо а і Ь є відповідно границі хп і
Уп, то хп = а + ап, уп = Ь + рп, де ап і рп — нескінчен-
но малі послідовності.
Додавши почленно ці рівності, дістанемо
Хп + Уп ~ а 4“ 4~ ап + Рп-
Отже, послідовність (хп + уп) подано у вигляді суми
сталого числа а + Ь і нескінченно малої послідовності
ап + Рп- Тому існує Ііт (хп + уп) і дорівнює а + &,
п->оо
тобто
Ііт (хп + уп) = Ііт хп + Ііт уп = а + Ь.
П-+ОО п-+<х> П-*оо
Теорема 2. Нехай послідовності хп і уп мають відповідно
границі а,Ь. Тоді їхній добуток має границю, яка дорівнює
а • Ь, тобто
Ііт (хп • уп) = Ііт хп Ііт уп-
П-*(Х) П-+ОО п->оо
Доведення. Послідовності Хп і Уп за умовою да-
ної теореми можна подати у вигляді хп = а + ап, уп —
= Ь + рп, де ап і Рп — нескінченно малі послідовності.
Тоді
хп • Уп = аЬ + арп + Ьап + апРп-
У даній рівності сума останніх трьох доданків є нескін-
ченно малою послідовністю. Тому
Ііш (хп • Уп) = аЬ.
П->оо
Теорему доведено.
Зазначимо, що теореми 1 і 2 справедливі й для більшо-
го числа доданків (співмножників). З теореми 2 випливають
наслідки.
Сталий множник можна виносити за знак границі. Справ-
ді, нехай хп = с, а уп має границю. Тоді
Ііт (хп • уп) = 1ітхп • Ііт уп = с!ітуп.
П-їОО п-*оо п-><х>
117
Якщо Ііт = а і к — натуральне число, то
П-4-ОО
Ііш (Хп) — (Ііт хп)* = а*.
П-*<х> П~юо
Теорема 3. Нехай послідовності (хп) і (уп) мають скін-
ченні границі, які відповідно дорівнюють Ііт хп = а,
П-+СО
Ііт уп = Ь, причому Ь =/=0. Тоді і їх відношення | —]
мав скінченну границю, яка дорівнює у .
Доведення. Оскільки Ііт уп =£ 0, то можна бу-
п->оо
ло б довести, що знайдеться таке /V; що при п> N викону-
ється нерівність | уп | > г > 0, де г — стале число.
Надалі обмежимося тими значеннями членів послідов-
ності уПі які наперед задовольняють нерівність. Тоді
_3>_____= а + к«_______- _1_ (ьа — ав А
Уп Ь ь + ?,п Ь - Ьуп (°ап а№'
де ап, рп — нескінченно малі послідовності.
Покажемо, що послідовність правої частини поперед-
ньої рівності є нескінченно малою. Справді,
і 1
ІЬупІ <
Отже, послідовність () є обмеженою. Послідовність
Ьап — а(5л є нескінченно малою.
Таким чином, послідовність уп = ~г-—(&ап— а$п) €
0Уп
нескінченно малою. Тому+ уп, Теорему дове-
Уп 0
дено.
Сформулюємо без доведення ще дві важливі теореми, які
стосуються існування границі числової послідовності.
Теорема 4(Вейєрштрасса). Зростаюча або спад-
на обмежена послідовність має границю.
Теорема 5. Якщо послідовність (хп) має границю а, то ця
границя єдина.
і
Приклад 1. Знайти Ііт Н—зіпп2 + ), а>ї.
п-юо \ П
(За означенням п\ = 1 • 2 • З...П.)
Р оз в’ язання. Використаємо теорему про грани-
цю суми. Для цього з’ясуємо, чи існують границі додан-
118
„..11
ків Послідовності —, е нескінченно малими, тобто
Ііт —==0 і Ііт Л = 0. Послідовність (зіп п1 2) є обме-
П-юо п п
женою: | зіп п2 | 1. Отже,
і
Ііт —у- зіпп2 = 0, Ііта'2 =1.
П-*оо п~*<х>
Границі доданків існують. Тому
і
Ііт (— Н—т- зіп п2 + а п) = Ііт — -ф
„-«А П ге1 ЛМ-00 п
1
+ Ііт -у-зіпп2 + Ііт а" = 1.
Н-*-0О Г2-4-ОО
Приклад 2. Знайти
Ііт
п-^оо
Розв’язання. Для знаходження цієї границі
використаємо теорему про границю частки. Для цього знай-
демо окремо границю чисельника і знаменника, викори-
стовуючи при цьому формулу суми п членів геометричної
прогресії:
Отже, границі послідовності у чисельнику і знаменнику
заданого дробу існують, причому границя знаменника не
дорівнює нулю. Тому
§ 2. Границя функції неперервного аргументу
1. Поняття про границю функції. У попередніх парагра
фах ми ознайомилися з поняттям про границю числової
послідовності, або з границею функції натурального аргу-
119
менту. У таких функціях аргумент змінюється розривно
(дискретно), набуваючи значень 1, 2, ..., п, ... .
Розглянемо функцію у = / (х), де аргумент змінюєть-
ся неперервно (пробігає всі точки певного проміжку
(а; Ь) крім, можливо, однієї внутрішньої точки даного
проміжку).
Наведемо два приклади.
Приклад 1. Простежимо, як поводить себе значення
функції / (х) = у х2 + 2,
коли значення аргументу х як
завгодно близько наближається
до числа 2. Символічно це позна-
чають так: х 2. З рис. 3.2 вип-
ливає, що ко'іи х —> 2 зліва або справа, то відповідні зна-
чення функції / (х) як завгодно близько наближаються до
числа 4, тобто ці значення будуть досить мало відрізнятися
від числа 4,
У такому разі кажуть, що функція /(х)=уХ1 2+2
має границею число 4, якщо х -> 2, або в точці х0 = 2.
Символічно це записують так: Ііт (-^-х2 + 2^ = 4.
х->2 \ 2 /
Приклад 2. Простежимо, як поводять себе значення
л-2 ____________ О
функції / (х) = х_~д-, коли х -> 3. На відміну від попе-
реднього прикладу у точці х0 = 3 функція не визначена.
Проте за графіком (рис. 3.3) неважко зробити висновок,
що коли х —> З, то відповідні значення функції наближа-
ються до числа 6. У такому разі також вважаємо, що число
х2 ______________________________9
6 є границею функції / (х) = , коли х ->3, або в
1 Тут і далі символом (а; Ь) будемо позначати будь-яку множину
чисел: інтервал (а; Ь), відрізок [а; д], множини [а; Ь) або (а; Ь\
120
точці х0 = 3, тобто
Ііт
г-+3
Xі — 9
х — 3
= 6.
Отже, коли число А є границею функції у = ? (х) при
х -> х0, то значення функції / (х) як завгодно близько на-
ближаються до числа Л, коли значення аргументу х як
завгодно близько наближаються до числа х0.
З’ясуємо, як математично записати сформульовану
властивість числа А. Повернемось до
Задамо наперед як завгодно мале
додатне число є і побудуємо на осі
Оу відрізок ММ завдовжки 2є, се-
рединою якого є точка 4. Цей відрі-
зок називають є-околом точки 4
(рис. 3.4).
Всі значення функції, які міс-
тяться в е-околі точки 4, тобто в
середині відрізка ММ, задовольня-
ють нерівність 4 — 8< / (х) < 4 +
+ 8, або — є < / (х) — 4 < е, або
першого прикладу,
У*
м
4*&
4
4-£-£-
/V
2
рівносильну нерівність
(1)
о
-ф^ЬР&О-
___£
’Т
Рис. 3.4
х
Проте поведінка функції зале-
жить від значень, яких набуває аргумент х. З’ясуємо гео-
метрично, для яких х виконується нерівність (1). Для цього
через точки М і N проведемо перпендикуляри до осі Оу і че-
рез точки С і О перетину цих перпендикулярів з графіком
функції проведемо перпендикуляри до осі Ох. Відрізок РС£
містить крім точки 2 всі значення аргументу х, відмінні від
х0 = 2, для яких виконується нерівність (1).
Очевидно, що РР > Рф. Довжину меншого відрізка /«’ф
позначимо через 6 і побудуємо б-окіл точки 2. Усі значення
аргументу х, які містяться у б-околі точки 2, задовольня-
ють нерівності 2 — б < х < 2 + б, або —б < х — 2 < б,
або рівносильну нерівність
|х-2|<б. (2)
Отже, для тих значень х, які задовольняють умову | х —
— 2 | < б, виконується нерівність | / (х) — 4 | < 8. Гео-
метрично це означає, що як тільки значення аргументу
х, яке прямує до числа 2, потрапляє у б-окіл точки 2, то від-
повідне значення функції /(х)=уХ2 + 2 потрапляє у
в-окіл точки 4.
121
' За б-окіл точки 2 взято довжину меншого відрізка Рф,
тому, що коли б за 6 взяти довжину більшого відрізка РР,
то в побудованому б-околі точки 2 знайшлись такі значення
х, для яких відповідні значення / (х) не потрапила б в е-окіл
точки 4.
Значення б > 0 для будь-якого наперед заданого е > 0
можна знайти і алгебраїчним способом, розв’язавши відпо-
відну нерівність | / (х) — А І < є відносно | х — х01.
Рис» 3,5 Рис. 3,6
Покажемо це для другого прикладу. Задамо наперед
є > 0 і поставимо на меті знайти відповідне б > 0, таке,
щоб для всіх х 3 і таких, що | х — 3 | < б, виконувала-
ся нерівність | / (х) — 6 | < е.
Підставимо в останню нерівність вираз, що задає функ-
цію. Матимемо
—9 с І _ /оч
т^т~6|<е- (3)
Розв’яжемо нерівність (3) відносно | х — 3 |. Врахо-
вуючи, що х =/= 3, а тому х — 3 0, і скоротивши дріб на
х — 3, дістанемо | х + 3 — 6 | < є, або | х — 3 | < є.
Отже, в даному прикладі за 6 можна взяти 6 = 8
(рис. 3.5).
Тепер сформулюємо означення границі функції у —
= / (х), визначеної на проміжку (а; Ь) при х ->х0 або,
що те ж саме, у точці х0.
Число А називається границею функції у = [(х) у точці
х0, якщо для будь-якого як завгодно малого числа в > 0
існує таке число 6 (є) > 0, що для всіх х Є (а-, Ь), х =£ х0
і таких, що | х — х01 < 6, виконується нерівність | / (х) —
— А | < 8.
Символічно це записують так:
Ііт / (х) = А, або /(х) А.
122
В означенні границі функції словосполучення «х =£х0
і таких, що | х — х0 | < 6» можна записати скорочено у
вигляді нерівності 0 <С | х — х0 | < 6.
Умову х х0 накладають для того, щоб підкреслити не-
залежність границі функції від точки х0 і охопити цим озна-
ченням випадки, коли в точці х0 функція не визначена, але
при х ->х0 мас границю число А.
На рис. 3.6 наведено геометричну інтерпретацію гра-
ниці функції у = / (х) у точці х0 в загальному випадку.
Наведемо приклади застосування означення границі
функції для доведення існування границь у певних точках.
Приклад 3. Довести, що Ііт (кх + Ь) = ка + Ь,
х-ьа
к =£ 0.
Щоб довести дану рівність, треба показати, що для будь-
якого (як завгодно малого) додатного числа є існує додатне
число 6, таке, що з нерівностей 0 < | х — а | < 6 випли-
ває нерівність
| (кх + Ь) —• (ка + Ь) | < є. (4)
Знайдемо число 6. Для цього в лівій частині нерівності
(4) виконаємо тотожні перетворення
|&х + Ь — ка —Ь | < є, | к(х — а) < 8, | к | • | х — а \ <8,
звідки
і 8
Іх — а І< Тм" •
8
Отже, якщо взяти 6 =
вольняють нерівності
то для всіх х, які задо-
О<ІХ — а|<6 = -7-7-7- ,
1 1 ЇМ
справджується нерівність (4).
Приклад 4. Довести, що Ііт (2х + 1) = 3.
Розв’ язання. Під знаком границі є лінійна
функція у = кх + Ь (к = 2, Ь = 1). З попереднього прикла-
ду випливає, що лінійна функція у = кх + Ь у будь-якій
точці х = а або, що те саме, при х а має границю А.
Границя дорівнює значенню цієї функції у точці х = а, тоб-
то А = ка + Ь. Отже, у даному прикладі А = 2 • 1 + 1 =
= 3. Задача розв’язана.
г / 1
Ііт у
Ро з в’ язання. Задамо додатне число є і знайдемо
число 6 > 0, таке, щоб для всіх х =^= 2 і таких, що | х —
х2 + 2 = 4,
Приклад 5. Довести, що
123
— 2 | < б, виконувалася нерівність
|(4-х2Н-2)-4|<е. (5)
Щоб знайти б, треба розв’язати останню нерівність від-
носно | х — 2 |. Проте за допомогою тотожних перетворень
це вдається зробити для лінійних функцій. У даному при-
кладі застосується прийом підсилення нерівності.
Виконаємо тотожні перетворення у лівій частині нерів-
ності (5). Дістанемо
їх2 — 4
І 2
Iх—2 І • І х + 2 І
< 8, або ------<8. (6)
Підсилимо нерівність (6), замінивши множник | х + 2 |
на число, якого він не перевищує. Для цього накладемо
на шукане б обмеження б 1. Це завжди можна зробити,
оскільки б залежить від 8, а число 8 можна задавати як зав-
годно малим. Але тоді | х — 2 | < 1 або —1 < х — 2 < 1.
Додавши до всіх трьох частин останньої нерівності число 4,
дістанемо 3 < х + 2 < 5, тому | х 4- 2 | < 5.
Замінивши в нерівності (6) множник | х + 2 | на число
5, вимагатимемо виконання нерівності
Якщо виконується нерівність (7), то й поготів викону-
ється нерівність (6) і рівносильна їй (5).
З нерівності (7) дістанемо
їх —2і<4-є-
1 1 5
і
2
Отже, за б можна взяти менше з двох чисел 1 і -=- 8.
□
Якщо х #=2 і | х — 2 | < б, то
х2 4- 2 — 4 І < є.
Приклад 6. Довести, що
Ііт х2 —2
хч-2 X2 + 1
З
5 •
Яким має бути б, щоб для значень х, які задовольняють
нерівність 0 < | х — 2 | < б, виконувалась нерівність
1 !_І <0 00Р
х24-1 5 І <-м’ииі-
Розв’язання. Задамо довільне число є > 0 і пока-
жемо, що існує таке число б, що з умови 0 < [ х — 2 [ •< б
124
випливає нерівність
І х2 — 1 ЗІ
І Xі + 1 5 І < є'
(8)
Виконуючи у лівій частині нерівності (8) тотожні пере-
творення, дістанемо рівносильну нерівність
2 | х — 2 | * |х + 2 |
5 (х2 + 1)
(9)
< 8.
Шукатимемо 6 таке, що 0< б ^.1. Оскільки має бути
\х — 2 | < б, то | х — 2 | < 1, звідси —1 < х — 2 < 1,
або 1 < х < 3. Отже, 3<х + 2< 5,
а 1 < х2 < 9, тому 2 < х2 + 1 < 10.
Якщо у лівій частині нерівності (9)
множник | х + 2 | замінити на заві- ґ
домо більше число 5, а вираз | х2 + 11 / / и
у знаменнику на напевно менше число 4-------5—
2, то дістанемо нерівність \ ° І
’-гтІ— <е. ПО)
у якої ліва частина більша, ніж у не- рис
рівності (9). З нерівності (9) дістане- ис’
МО І X — 2 | < 8.
Отже, за 8 можна взяти менше з двох чисел 1 і б = 8.
Поклавши 8 = 0,001, дістанемо б = 0,0001.
Розглянемо приклад, який широко застосовують
при знаходженні границь функцій.
Приклад 7. Довести, що
Ііт
8ІП X
X
(Н)
Нехай х > 0. Оскільки х розглядається у малому околі
нуля, то можна припустити, що 0<х<-^
Покажемо^ що для будь-якого як завгодно малого числа
8 > 0 існує таке число б > 0, що з нерівності | х | < б випли-
ває нерівність
І 8ІП X
І *
Доведемо спочатку допоміжну нерівність, а саме: пока-
жемо, що при 0 < х < -^-справджується нерівність
зіпхСх <
— 1 І < е.
125
Візьмемо коло з центром у довільній точці 0 з радіусом,
що дорівнює одиниці (рис. 3.7), а також гострий кут ЛОВ,
хорду АВ і дотичну АС до кола у точці Л. Тоді площа
Д ЛОВ < площі сектора ЛОВ < площі Д АОС,
Якщо х — радіанна міра / АОВ, то довжина дуги АВ
дорівнюватиме добутку радіуса на радіанну міру кута,
тобто дорівнюватиме х. Співвідношення між площами за-
пишемо у вигляді
• 1 • 1 • зіп х < • 1 • 1 • х < • 1 • 1 • х.
Після множення усіх трьох частин нерівності на 2, діста-
немо
зіп х < х < х.
Оскільки в цьому разі зіп х >0, то, поділивши всі члени
останньої нерівності на зіп х, дістанемо
1 _ X і а і зі п X
1 < —:-----<С-------- або 12> ---------> соз х.
81П X СОЗ X. X
Розглянемо рівність 1 = 1 = 1. Віднявши почленно від
цих рівностей попередні, маємо
п 1 ЗІП X _ ,
0 <С 1---------< 1 — соз х,
X
або
0 < 1---------< 2 зіп2 -тг- < 2 зіп -тг- < х.
х 2 2
Отже,
Оскільки х>0, то —х<1---------------
7 V
<х. Останні не-
рівності можна записати у вигляді
Отже,
якщо | х
Тому, ВЗЯВШИ 6=8, ЯКЩО 0<8<-^- (КОЛИ 8^-^-,
то можна взяти 6 = , помічаємо, що з нерівності |х| <
<6 випливає нерівність
ЗІП X
X
— 1 <8.
126
Задачу для х > 0 розв’язано.
Нехай тепер-----Введемо нову змінну х'>-0
за формулою х= —х'. Тоді
1іт-^± = цт = Ит = 1.
х->0 х х^О х х'-+0 х х'-*0 Х
Зазначимо, що при розв’язанні цієї задачі ми не роби-
ли жодного припущення про те, що х є строго аргументом.
Тому рівність (11) записують ще й так:
,. зіп а .
Ііт-----= 1,
а->0 а
де а може бути функцією від х.
Приклад 8. Знайти Ііт 8ІП .
х->0 х
Розв’ яз анн я. Позначимо а = Зх. Тоді при х ->0
і а —> 0. Якби у знаменнику було Зх, то границя поперед-
нього виразу дорівнювала б 1. Тому, домноживши чисель-
ник і знаменник на 3, дістанемо
Ит = Ііт 3 8ІП = 3 Ііт = 3.
х-+0 6 х-^0 (Зх) а-*-0 а
Сталий множник можна виносити за знак границі.
У попередніх прикладах розглянуто випадки, коли
функція у — ?(х) у точці х0 мала границю. Можна навести
приклади, коли у = / (х) у точці х0 границі не має. Для
цього розглянемо, наприклад, функцію Діріхле
( 1, якщо х — раціональне число,
О (х) = л
10, якщо х—ірраціональне число.
Припустимо, що О (х) у точці х0 має границю А, тобто
Ііт О (х) = А.
Тоді згідно з означенням границі для будь-якого числа
є > 0, зокрема для числа в = -±-, існує число б > 0 таке,
що для всіх х, які задовольняють нерівність | х — х0 | <
< б (х х0), виконується нерівність
|Р(х)-Л|< *
о
Нерівність | х — х0 | < 6 означає інтервал (х0 — 6;
х0 + 6), в якому містяться як раціональні, так і ірраціо-
нальні числа, що не дорівнюють х0. Нехай хх — раціональ-
127
не число (хг Ф х0), а х2 — ірраціональне число (х2 х0),
які належать зазначеному інтервалу. Тоді згідно з нерів-
ністю | / (х) — А | < є справджуються такі нерівності:
п-^<4, і/іі<4.
Отже, 1-|(1-4) + Л|<|1-Л|+МІ<4- + 4“
о О
= — , тобто 1 < -у .
Дістали протиріччя. Отже, у точці х0 функція £> (х) гра-
ниці не має.
Вище ми розглянули границю функції неперервного ар-
гументу, коли він наближається до фіксованої точки х0.
Припустимо, що функція у = / (х) визначена, напри-
клад, на множині всіх додатних чисел, і нехай х необмеже-
но зростає (позначається це так: х->+оо). Тоді може
трапитись, що значення функції наближаються як завгодно
близько до числа А. У цьому випадку число А називають
границею функції у = / (х) при х +оо і позначають
Ііт / (х) = Л.
Число А називається границею функції у = / (х) при
х -> + оо, якщо для будь-якого як завгодно малого додатного
числа 8 існує таке додатне число М, що з нерівності х> М
випливає нерівність | / (х) — А | < е.
Аналогічно означають границю функції при х —оо.
Число В називається границею функції у = } (х) при
х -> —оо, якщо для будь-якого як завгодно малого є > 0
існує таке від'ємне число N, що для всіх х < N виконується
нерівність
|/(х) —В|<е.
Наприклад, Ііт -^- = 0, Ііт (— хЗ^ = 3.
—оо х-*—оо \ X /
2. Нескінченно малі функції. Основні теореми про
границі. Нехай функція у = / (х) визначена на проміжку
(а\ Ь), крім, можливо, точки х0 Є Ь).
Функція у = / (х) називається нескінченно малою у точ-
ці х0, якщо існує границя функції у даній точці, і вона до-
рівнює нулю.
Нескінченно малу функцію в точці ще називають нескін-
ченно малою величиною.
Так, наприклад, нехай у = 1 — х. Тоді Ііт (1 — х) =
= 0. Отже, функція у = 1 — х в точці х — 1 е нескінчен-
но малою.
128
Зазначимо, що розглядувана функція у = / (х) може
бути нескінченно малою у даній точці і не бути такою в ін-
шій точці. Може трапитися, що функція е нескінченно
малою у кількох точках. Так, наприклад, функція у —
= х (х — 1) (х — 2) є нескінченно малою у точках 0; 1; 2.
Якщо х0 внутрішня точка проміжку (а; Ь), то, скори-
ставшись означенням границі функції в точці, нескінченно
малу функцію означимо так.
Функція у = ! (х) називається нескінченно малою у
точці х0, якщо для будь-якого числа г>0 існує число б >
> 0 таке, що для всіх х 6 (а; Ь}, (х =/= х0), які задовольняють
нерівність | х — х0 |< б, виконується нерівність | / (х) | < є.
Оскільки число є може бути як завгодно малим, то з по-
передньої нерівності випливає, що значення нескінченно
малої функції поблизу даної точки х0 є по модулю як зав-
годно малі. Але не слід плутати нескінченно малу функ-
цію в точці з досить малим числом. Значення нескінченно
малої функції можуть бути за певних значень як завгодно
великими числами. Наприклад, функція у — х2 в точці
х = 0 є нескінченно малою, але її значення при досить
великих по модулю значеннях х є теж як завгодно великі.
Нескінченно малі функції, аналогічно нескінченно ма-
лим числовим послідовностям, мають властивості, які ми
сформулюємо у вигляді теорем.
Теорема 1. Сума (різниця) двох нескінченно малих
функцій у даній точці є нескінченно малою функцією.
Цю теорему пропонуємо довести самостійно.
Функція у — ? (х) називається обмеженою на проміжку
(а; Ь}, якщо існує число М > 0 таке, що для всіх значень х
із цього проміжку виконується нерівність | / (х) | < М.
Так, наприклад, функція у — зіп х в інтервалі (—оо;
+ оо) є обмеженою (| зіп х | 1). Обмеженою на відріз-
ку [—1; 1] є також функція у = х2 (| х2 | 1). Однак
функція у = х2 в інтервалі (— оо; + оо) не є обмеженою.
Теорема 2. Добуток нескінченно малеч функції на обме-
жену функцію є функцією нескінченно малою у даній точці.
Доведення . Нехай а (х) у точці х0 є нескінченно
малою функцією, а / (х) — обмеженою. Тоді існує окіл
0 <. | х — х01 < бі точки х0 такий, що для всіх х із цього
околу справджується нерівність
|/(Х)І<М, (12)
де М > 0.
Візьмемо число 8] = , де є — довільне додатне чи-
сло. Тоді, оскільки а (х) є нескінченно малою в точці х0>
5 1-1819 129
для числа Єі існує таке число б2, що для всіх х х0, які
задовольняють нерівність І X — х01 < б2, виконується не-
рівність
|а(х)|<е1. (13)
Нехай 6 — число, менше за числа' б! і б2. Тоді для всіх
х =/= х0, які задовольняють нерівність | х — х0 | •< б, вико-
нуватимуться нерівності (12), (13). Отже, для всіх х =£= х0,
які задовольняють нерівність І X — х0 | < б, виконується
нерівність
| а (х) • / (х) | < Ме,х = в.
Ця нерівність і доводить теорему. Зазначимо, що тео-
рему 1 можна узагальнити і на більшу кількість доданків.
Теорема 3. Для того щоб функція у = / (х) у точці
х0 € (а; Ь) мала границею число А, необхідно і достатньо,
щоб різниця ї (х) — А була нескінченно малою функцією
у цій точці.
Доведення. Необхідність. Нехай ііт / (х) = А.
Х-*Х9
Тоді для будь-якого числа е > 0 існує таке число б >* 0,
що для всіх х Е (а; Ь} (х Ф х0), які задовольняють нерів-
ність |х— х01 < б, виконується нерівність |/(х) —
— А І < 8.
Позначивши а (х) = { (х) — А, дістанемо | а (х) | <7 8.
Достатність. Нехай а (х) = / (х) — А є нескінченно
малою у точці х0, тобто | а (х) | <2 е, або, що те саме,
| / (х) — А І < є.
Тоді А є границею /(х) у точці х0. Теорему доведено.
Виходячи з цієї теореми, можна дати таке означення
границі функції в точці.
Число А називається границею функції у = / (х) в точ-
Ці х0 Е (а; Ь), якщо різниця між цією функцією і числом
А є нескінченно малою функцією в цій точці.
Звідси випливає, що поблизу точки х0 справджується
рівність
/ (х) = А + а(х),
де А — границя функції / (х) в точці х0, а а (х) — нескін-
ченно мала функція в точці х0.
Користуючись цим означенням границі функції, а також
властивостями нескінченно малої функції, можна довести
основні теореми про границі.
Теорема 4. Якщо функції [ (х) і <р (х) в точці х0 мають
границі, то сума і добуток цих функцій також мають у
130
цій точці границю, причому
Ііт {[(х) + ф(х)) = 1іт/(х) 4- Ііт ф(х), (14)
Ііт (/ (х) • ф (х)) = Ііт / (х) • Ііт ф (х). (15)
X -*0 х*+х0 х^х0
Теорема 5. Якщо функції ї (х) і ф (х) в точці х0 мають
границі і Ііт ф (х) Ф 0, то й функція має в цій точ-
Х-+Х, Ф \х)
ці границю, яка дорівнює
Ііт / (х)
Ііт = 4^ , . . (16)
Х-»Х. 1іт<р(х)
Х-І-Хо
Доведемо, наприклад, рівність (15) (рівності (14), (16)
пропонуємо довести самостійно).
Нехай Ііт / (х) = А, Ііт ф (х) = В. Тоді справд-
х-*хв х-+х0
жуються рівності
/ (х) = А 4- а (х), ф (х) = В 4- Р (х), (17)
де а (х), р (х) — нескінченно малі функції в точці х0.
Перемножимо почленно рівності (17)
І (х) • ф (х) — АВ 4-Й • Р (х) 4- В • а (х) 4- а (х) • Р (х)). (18)
Покажемо, що сума останніх трьох доданків у рівності
(18) є нескінченно малою функцією у точці х0. Для цього
досить довести, що а (х) • р (х) є нескінченно малою функ-
цією у точці х0 (А • р (х), В • а (х) — нескінченно малі
функції згідно з теоремою 2).
Оскільки а (х) — нескінченно мала функція в точці
х0, то для будь-якого додатного числа, наприклад, числа
де 8 >• 0, існує число 6Х > 0 таке, що для всіх х0, які
задовольняють нерівність 0 < | х — х0 | < 6Х, справджу-
ється нерівність
|а(х)|<К'е. (19)
Існує також число 62 > 0 таке, що для всіх х, які за-
довольняють нерівність 0 < | х — х0 | < 62, справджу-
ється нерівність
ІР(Х)|<РТ. (20)
Візьмемо число 6 > 0 меншим за числа бх і 62. Тоді для
всіх х, які задовольняють нерівність 0 < | х — х0 | < 6,
будуть одночасно справджуватися нерівності (19), (20)
5*
131
і для цих значень х буде виконуватися нерівність
І а (х) • Р (х) І с И 8 • К 8 = 8.
Ця нерівність і доводить, що добуток а (х) • Р (х) е не-
скінченно малою функцією у точці х0.
Отже, згідно з рівністю (18) добуток функцій / (х) • ф (х)
зображено у вигляді суми числа А • В і нескінченно малої
функції. Тому число А • В є границею функції / (х) • ф (х)
в точці х0, тобто
Ііт (/ (х) • ф (х)) = Ііт / (х) • Ііт ф (х) = А • В.
Рівність (15) доведено.
Як і для числових послідовностей, для функцій можна
довести теорему:
Теорема 6. Якщо при х->х0 функція у = /(х) має
границю А, то ця границя єдина.
Приклад 9. Користуючись основними теоремами про
границі, знайти границі:
1) Ііт (2(х + 3)---Ц-'); 2) Ііт Зх» + 2х2-х .
х-*4 \ X — £ у_ 5х >
3) Ит ; 4) Ііт ^^ -2 ..
' х-5 * + 5 хч-1 /2-х- 1
Розв’язання. 1) Застосуємо теорему про границю
суми. Тоді Ііт (2 (х + 3)) =14, Ііт (—= 2.
х-*4 х—4 \ х 1 /
Отже,
Ііт (2(х + 3)--^М = Ііт 2(х 4-3) — Ііт —=
\ л £ і х-*4 х->4 х £
= 14 — 2= 12.
2) У цьому прикладі безпосередньо не можна викори-
стати теорему про границю частки, бо границя знаменника
дорівнює нулю. Оскільки в означенні границі сказано, що
при х —> х0 обов’язково вимагається, щоб х х0, то на
різницю х — х0 =/= 0 можна скорочувати чисельник і зна-
менник.
Тому
Ііт +Л'— -Пт
хм-0 &Х х-*0
Зх24-2х — 1 1
5 — 5 ’
3) У цьому прикладі приведемо скорочення дробу на
X — 5:
Ііт х* ~ >5.. = ііт .(-« — 5) (* + б), = ііт (х 4- 5) = 10.
х-*5 х—0 х-5 х — 5 Х-.5
132
4) Знищимо ірраціональність у чисельнику і знамен-
нику. Матимемо
Ііт /5^2 = ИтР_-Л_-.4Н^+1) =
х-и /2-х—1 х-*1 (2 — х — 1) (/5 — х2)
- Ііт (1-х)(/Г^+1) _ 2 _1_
х-1 (1 —х)(/5 —х + 2) 4 2
§ 3. Неперервність функції в точці
Неперервність функції в точці — одна в важливих вла-
стивостей, інтуітивне уявлення про яку ми вже дістали,
будуючи графіки різних
функцій, коли знаходили
кілька окремих точок
графіка і через них про-
водили суцільну лінію.
Виникає питання — чи
правомірною операцією
є проведення такої лінії
навіть тоді, коли функ-
ція визначена на всій
числовій прямій або в
усіх точках деякого про-
міжку (а; Ь)? Чи Існують функції, графіки яких не є суціль-
ними лініями на всій області визначення чи на деякому про»
міжку (а; Ь) і чи є такі реальні функції на практиці, в су-
міжних предметах? Відповідь на це питання позитивна.
Розглянемо приклад. Візьмемо кубик свинцю, який має
об’єм 1 дм3 при 0 °С і рівномірно нагріємо його. Дослід
показує, що зміна об’єму кубика відбувається так: при
нагріванні від 0° до 327° об’єм свинцю збільшується від
1000 см3 до 1030 см3 поступово, без стрибків, тобто об’єм
набуває при цьому проміжних значень. При і = 327° (точ-
ка плавлення свинцю) об’єм різко (стрибком) зростає до
1067 см3 і при подальшому нагріванні від 327° до 500° знов
поступово, без стрибків, зростає від 1067 см3 до 1088 см3,
знаходячись при цьому в рідинному стані. Графік зміни
об’єму свинцю залежно від температури подано на рис. 3.8,
звідки видно, що при 0° < і < 327° графік є неперервною,
суцільною кривою АВ, а при і = 327° відбувається стри-
бок від точки В (327; 1030) до точки С (327; 1067), причому
точка В належить графіку, а точка С йому не належить.
При 327° < і 500° графік знов є неперервною, суціль-
ною кривою СК.. Тут вісь АМ лежить вище осі абсцис
(Л (0; 1000) належить осі ординат, але не збігається з почат-
133
ком О). Тому відрізки ВС і ЛГМ не будуть ординатами то-
чок В і М.
Отже, графік залежності між температурою і об’ємом
свинцю є функцією V — Ці), яку задано на відрізку [0°,
500°], і є розривною в точці і — 327°, хоч і визначена в кож-
ній точці відрізка.
Спробуємо знайти границю функції в точці ій — 327°.
З рисунка видно, що при і > 327 і і -> 327 значення функ-
ції V як завгодно близько наближаються до числа 1030,
тобто V (327) = 1030 є границею функції. При і > 327
і і -> 327 значення V як завгодно близько наближають-
ся до числа 1067, тобто це число є теж границею функції.
Але якщо границя в точці існує, то вона має бути єдиною.
Отже, при і ->-327 функція V = Ці) не має границі.
Це і стало причиною існування розриву функції в точці-
і = 327, хоч в цій точці функція визначена.
Якщо розглянути ще кілька функцій, серед яких багато
відомих (рис. 3.9, а—г), то неважко з’ясувати причину
розриву їхніх графіків у певних точках. Справді, функ-
1 —— 1
Ції у = — і / (х) = х _ і (рис. 3.9, б, г) мають розриви від.
повідно в точках х0 = 0 і х0 = 1, бо в цих точках вони не
134
визначені. Функції / (х) = [хі і
_ 1, х<о
(рис. 3.9, в, д) розривні, відповідно перша при всіх цілих
значеннях х, а друга при х = 0, бо в цих точках вони не
мають границі. Функція
[ Xі 4-1, х=/= 0,
^(Х)==| 2,- х = 0
(рис. 3.9, е) визначена в точці х = 0, має границю А = 1
при х —0, але ця границя не дорівнює значенню функції
/ (0) = 2 в цій точці.
Лише функція / (х) = х2 неперервна в будь-якій точці
х0 області визначення, оскільки в кожній точці х0 існує
значення функції / (х0), існує границя функції в цій точці
і вона дорівнює / (х0).
Виконання цих трьох необхідних умов забезпечує до-
статню умову неперервності функції / (х) = X2 в точці х0.
Сформулюємо означення неперервної функції в точці.
Функція у = ї (х) називається неперервною в точці
х0 Є Ь), якщо існує границя функції в цій точці і вона
дорівнює значенню функції в точці х0.
Отже, функція у = / (х) в точці х0 буде неперервною то-
ді і тільки тоді, коли виконуються умови:
1) функція у = / (х) визначена в точці х0, тобто існує
число / (х0);
2) існує границя Ііш (х) функції в точці х0;
3) границя функції дорівнює значенню функції в цій
точці, тобто
(1)
Ііт /(х) = /=(х0).
Х-*Х0
Разом всі ці умови є необхідними і достатніми для того,
щоб функція у — [ (х) була неперервно в точці х0.
Приклад 1. Показати, що степенева функція у — х", де
п — ціле додатне число, є неперервною у будь-якій точці
числової осі.
Розв’язування. Степенева функція при цілому
додатному показнику визначена на всій числовій осі. Візь-
мемо довільну точку х0 Є (— оо; 4* °°)- Тоді / (х0) = Хо.
Знайдемо
Ііт х" = Ііт (х • х....х) = х?.
Х-*ХЛ х-*хл
135
Отже, Ііт 7 (х) = 7 (х9). Тому функція у = х" є не
Х-ЇХО
перервною у будь-якій точці х0 £ (—оо; 4-оо).
Приклад 2. Довести, що многочлен
У — ао + аіх + • ’ • + .
є неперервною функцією у будь-якій точці числової осі.
Розв’язання. Задана функція визначена в усіх
точках числової осі, тобто при х Є (— оо; + оо). Візьмемо
довільну точку х0 Є (— оо; + оо). Тоді
7 (*0) = ао + аіхо + • • • + «п4.
Використавши основні теореми про границі, матимемо
Ііт (а0 + аіх + • • • + ОпХп) = а0 + агх0 + • • • +апх%.
х-*х0
Отже,
Ііт 7(х) = 7(х0).
х-+х0
Приклад 3. Дослідити на неперервність функцію
7(х) =
1*1 , г\
, ЯКЩО Х5^о,
0, якщо х = 0,
в точці х = 0.
Розв’язання. Задана функція визначена в інтер-
валі (—оо; + оо), зокрема 7 (0) = 0. Проте в точці х = 0
ця функція не має границі. Справді, при х > 0
7(х)= = —= 1,
' ' ' X X ’
а при х < 0
7(х) = -Ш- = = — 1.
1 4 ' X X
Тут правостороння границя дорівнює 1, а лівосто-
роння —1. Отже, задана функція в точці х = 0 не є непе-
рервною.
Якщо функція у = / (х) неперервна в точці х0, то роль
границі функції в точці х0 відіграє число / (х0). Тому,
використавши означення границі функції в точці, можна
дати таке означення неперервності функції в точці.
Функція у = / (х) називається неперервною в точці х0,
якщо для будь-якого як завгодно малого числа є > 0 існує
таке число 6 > 0, що для всіх х б Ь)> які задовольняють
136
нерівність | х — х01 < б, виконується нерівність | / (х) —
— / (*о) | < є.
Зазначимо, що на відміну від означення границі тут
ми не ставимо умову | х — х01 > 0, бо в даному разі
х = Хд в точці Хд визначена, а нерівність | х — х01 < б при
х = Хд справджується.
Приклад 4. Користуючись наведеним означенням, пока-
зати, що функція у — зіп х неперервна в кожній точці
числової осі.
Розв’язання. Візьмемо довільну точку х06 (—
+оо). Тоді для будь-якого числа є > 0 повинно існувати
таке число б > 0, що нерівність
| ЗІП X — ЗІП Хд | < е
(2)
виконується для всіх х Є (—о°; + оо), які задовольняють
нерівність | X — Хд І < б.
Покажемо, що таке число б існує. Для цього ліву части-
ну нерівності (2) запишемо у вигляді
| зіп х — зіп Хд | — 21 соз *°
зіп - 2 х°
2 Зіп--у-2- ,
Іх + хв І
СОЗ--у-2- рС 1 •
Значення х розглядаються поблизу точки х0. Тому,
згідно з нерівністю зіп х < х < х (§ 2, п. 1, приклад 5),
І. X — Хп X — Хп
Отже,
І ЗІП X — Зіп хо К І X — Хд |.
Таким чином, для того щоб виконувалася нерівність (2),
достатньо, щоб | х — х01 < е. Поклавши б = є, переко-
нуємося в тому, що з нерівності | х — Хд | < б випливає
нерівність
|зіпх— 8ІПХ0|<8.
Це й доводить неперервність функції у = ЗІП X у довіль-
ній точці числової осі.
На практиці при дослідженні функцій на неперервність
часто користуються означенням неперервності функції,
яке базується на понятті приросту функції в точці.
Нехай функція у = / (х) визначена в усіх точках деяко-
го проміжку (а‘, Ь). Візьмемо дві довільні точки з цього
проміжку Хд І Хд 4- ДХ, ДЄ ДХ = X -- Хд.
137
Тоді число Дх називають приростом аргументу, а чис-
ло Дг/ = / (х0 + Дх) — / (х0) — приростом функції ї (х) в
точці х0.
Так, нехай в прикладі про плавлення свинцю надамо
аргументу і в точці і0 — 327° приросту Д/ > О.Тоді і зна-
чення функції набуде приросту До >0, = ЕІЇ, До =
— МР (див. рис. 3.8).
Якщо Д/ -> 0, то точка N прямуватиме до точки Е, точ-
ка М — до точки С, тому приріст До = МР буде прямува-
ти до границі, що дорівнює довжині відрізка ВС, і, отже,
відмінної від нуля. Символічно це запишемо так: Ііт До#= о-
ЛҐ-»
Якби Ііт До = 0, то точка С збігалась би з точкою
&і-*0
В і графік у точці і = 327 ° не мав би розриву.
Сформулюємо тепер таке означення неперервної в точці
х0 функції у = / (х).
Функція у — [ (х) називається неперервною в точці х0,
якщо
ііт Ді/ = 0. (3)
Дх-+0
Так, функція у = х2 неперервна в довільній точці, бо
Ііш Д(/ = Ііт (2х0Дх + Дха) = 0.
Вважатимемо, що коли функція у = / (х) неперервна
в кожній точці проміжка (а; 6), то вона називається непе-
рервною на цьому проміжку.
Наприклад, функція у = х2 неперервна на проміжку
2
(—оо; +оо), а функція у = — неперервна на кожному з
проміжків (—оо; 0) і (0; 4* оо), що утворюють область визна-
чення функції.
Сформулюємо без доведення теорему про арифметичні
операції над неперервними функціями.
Теорема. Якщо дві функції у = [ (х) і у — § (х) визна-
чено в одному і тому самому проміжку {а\ Ь) і обидві непе-
рервні в точці х0, то в ній будуть неперервні і функції ї (х) ±
± 8 (х), ї (х) • § (х), (остання за умови, илр § (х0) =/=
=#= 0).
Зазначимо, що поняттям неперервності функції в точці
часто користуються при знаходженні границі функції
в цій точці: якщо функція у = / (х) є неперервною у точці
х0, то, як це випливає з (1), для знаходження Ііт [ (х)
досить знайти / (х0).
138
Приклад. Користуючись співвідношенням Ііт / (х) =
= / (х0), знайти границі функцій:
1) 1іт(х2-|-х—2); 2) ііт 8Іпх.
х-*а я
х~¥ Т
' Р о з в’ я з а н н я. 1) Оскільки функція / (х) = ха +
4-х — 2 е неперервною у будь-якій ТОЧЦІ числової осі,
то вона є неперервною і в точці х = а. Тому
Ііт / (х) = / (а) = а2 4- а — 2.
х=а
2) Функція у = зіп х е неперервною у будь-якій ТОЧЦІ
числової осі. Тому
Ііт зіпх=== зіп-^-= 1.
Запитання і завдання для повторення
1. Що таке числова послідовність? Навести приклади.
2. Сформулювати означення границі числової послідовності.
3. Яка послідовність називається нескінченно малою? Навести
приклади.
4. Сформулювати теореми про властивість нескінченно малих по*
слідовностей.
5. Сформулювати основні теоремй про границі числових послідов-
ностей .
6. Сформулювати означення границі функції в точці. Навести прик-
лади границь, якщо в точці функція існує, якщо не існує.
7. Яка функція називається нескінченно малою функцією?
8. Сформулювати теореми про властивості нескінченно малих
функцій.
9. Сформулювати означення неперервної в точці функції, Навести
приклад неперервної і розривної в точці функції.
10. Яка функція називається неперервною на проміжку (а; Ь)?
Навести приклади.
Вправи
1. Довести рівності:
Ііт ?? * = -2- | починаючи з якого п9
П-юо 5п-Н 5 \
З І \
— _ не перевищує 0,0001?
1) Ііт _* = 0; 2)
п-*со оП
ІОЯ і
-=—гт-
5п + 1
3) Ііт (— 1)п -А_ = 0; 4) ііт = 1(а> 1).
П->оо П п-*со
5) Ііт -^- = 0; 6) Ііт (уТ+Т —К»)*=0.
139
2. Довести, що задані послідовності нескінченно малі:
Уп в ---П ’ 2) Уп
П X
2п ви2 4-1 11і + п2 — п
Користуючись основними теоремами про границі, знайти гра*
ниці послідовностей, у яких члени з номером п (п = 1, 2, ...). дорівню-
ють:
1)
1)
3)
5)
3.
п«4-2 ’’
1 зіп п2;
3)
4.
Уп= _1_ + 2" ; 2) уп= ’ созп3——31—;
2па Зп + 1 2п 6п + 1
о — 1)" 1 •’ 4) и — 1 4-О н-а2 + ••• +а"
Уп — \ Уп — -----і і----------------і *
Л „1.1 І
і + — + Іб-+ • • • +-^г
1) Довести, що Ііт (2х— 1) = 3. Яким повинно бути б, щоб з
х-*2
нерівності 0 < І х — 21 < б випливала нерівність | / (х) — 3 | < 0,01?
1 1
2) / (х) = —---- . Довести, що ііт / (х) =-Яким має бути
х2 + 2 х-+2 2
б > 0, щоб з нерівності 0 < | х — 2 | < б випливала нерівність
|/(х)--1- <0,001?
3) / (X) = Зх — 5. Довести, що Ііт / (х) = 4. Яким має бути б, щоб
з нерівності 0 < | х — 3|< б випливала нерівність | / (х) — 4 | <-
< 0,001?
4) Довести, що Ііт х3 = 1.
х-И
5. Знайти границі
1) Ііт 25ІП —; 2) Ііт .8ІП7П*..
Х->0 х х-*0 8ІП ПХ
6. Користуючись основними
ниці функцій:
1) ііт (х5 * — 5х + 2 +
х-і\ х /
3) Ііт 2^3--2х2 + х-о1_ ;
7 х_ь] х8 — х2 + Зх — З
5) Ііт К* + 1 — (* +,.1).;
+ 1 — 1
7. Користуючись означенням неперервності функції в точці, знай-
ти границі функцій:
теоремами про границі, знайти гра-
2) Ііт
Х-+2
4) Ііт-
х-*1
х2 5х 4~ 6
х2 — 12х + 20
X — К X .
У~Х — 1
6) Ііт
%->о х2
1) Ііт (х^-|-х4 + х3х2 4- 1); 2) Ііт зіп х.
х-И х->0
8. Користуючись означенням неперервності функції через приріст
функції, довести що:
140
1) функція у = | х | неперервна на всій числовій осі;
2) функція у = у є неперервною в кожній точці х 0;
3) функція у = Ух є неперервною в кожній точці 0;
4) функція у = соз х е неперервною на всій числовій осі;
5) дробово раціональна функція
у = ао 4~ аіх + * • * +
Ьо + М+ ••• +ЬтХт
є неперервною в усіх точках числової осі, крім тих точок, в яких зна-
менник дорівнює нулю;
6) функція у = х є неперервною в усіх точках числової осі, крім
тих точок, в яких СОЗ X == 0.
РОЗДІЛ 4
ПОХІДНА
§ 1. Задачі, які приводять до поняття похідної
1. Задача про миттєву швидкість. Розглянемо рівномір-
ний прямолінійний рух. Відомо, що закон (залежність дов-
жини шляху 5 від часу ї) рівномірного руху виражається
лінійною функцією
8=аі+Ь, (1)
де а і & — сталі числа.
Розглянемо два різні моменти часу: і і і + А/ (А£ > 0)
(приріст часу). Довжину шляху, який матеріальна точка про-
ходить за час А/, позначимо через Д5 (приріст довжини
шляху). Тоді згідно з рівністю (1)
А5 = а (і + А/) + Ь — (аі 4- &) = «А?.
Знайдемо відношення :
Д5 __ аАі __
~5Г ~ “дГ “ а'
Відомо, що —середня швидкість оо. Отже, для
рівномірного руху
и*=а (2)
є сталою і не залежить від часу АЛ Вона залишається тією
самою у будь-які моменти часу. Тому природно середню
швидкість для рівномірного руху вважати миттєвою швид-
141
кістю, або швидкістю у даний момент часу. Оскільки у
будь-які моменти часу миттєва швидкість однакова, то її
називають швидкістю рівномірного руху.
Розглянемо нерівномірний рух. Нехай, наприклад, мате-
ріальна точка М падає у середовищі без опору. Відрахову-
ватимемо час і від початку падіння. Тоді, як відомо, закон
09—-----
5
-------
45
Мр-------
Рис, 4.1
такого руху виражається формулою
5=-4", (3)
де § = 9,81 м/с — прискорення вільного па-
діння.
Поставимо задачу: обчислити швидкість
руху точки у момент часу /0 = 4 с, якщо точка
знаходиться у положенні М ( рис. 4.1).
Розв’яжемо цю задачу, користуючись по-
няттям середньої швидкості. Для цього вико-
наємо чотири кроки.
1) Надамо аргументу /0 приріст Д£, тобто крім моменту
часу /0 розглянемо момент часу /0 + Д/ (Д/>0). Нехай
у момент часу /0 + рухома точка знаходиться у положен-
ні Л4і.
2) За час Д/ точка пройде шлях, який позначатимемо
Д5 і називатимемо приростом шляху (на рис. 4.1 цей шлях
дорівнює довжині відрізка ММ-^, Спираючись на (3), об-
числимо приріст
д5= + _
= & (іА -+
44
3) Знайдемо середню швидкість
= = + <4>
Покладемо і0 = 4 с, а = 1; 0,1; 0,01; 0,001 с... Об-
числимо за формулою (4) відповідні значення ос, взявши
для спрощення обчислень § л; 10 м/с2. Здобуті значення за-
пишемо в табл. 4.1,
Отже, на відміну від рівномірного руху, середня швид-
кість у розглядуваному випадку вже не є сталою. Вона при
фіксованому моменті часу і0 залежить від приросту часу
Лі. При різних значеннях середня швидкість набуває
різних значень.
142
4) Нехай М ->0. Чим менший проміжок часу Д/ після
моменту часу і0, тим точніше середня швидкість буде ха-
рактеризувати швидкість точки у момент і0. З таблиці
випливає, що значення середньої швидкості прямують до
числа 40, якщо Дї -> 0. Тому природно за швидкість точки
у момент часу і0 = 4 с взяти границю ц, при Д/ ->0. Отже,
оо = ііт -^- = Ііт 4-
д*->о Д*->0 \ 2 /
Швидкістю точки у момент часу і називається границя
середньої швидкості за проміжок часу А/, коли &і пря-
мує до нуля.
Таблиця 4Л
•5 Л) А/ *о4-Д* 5 (і0 + ДО Д<$ (/0) Д5 ((,) с д;
80 1 5 125 25 45
80 0,1 4,1 84,05 4,05 40,5
80 0,01 4,01 80,4005 0,4005 40,05
80 0,001 4,001 80,040005 0,040005 40,005
80 0,0001 4,0001 80,00400005 0,00400005 40,0005
Перейшовши у формулі (4) до границі при А/ ->0, маємо
Ііт ц, - Ііт {£і0 +
д/->о дл+о \ г І
При і0 = 4 с, § ж 10 м/с2 маємо Ііт щ = 40 м/с;
д/-*о
при /0 = 5 с Ііт Vо = 50 м/с.
д/->о
Отже, швидкість точки, яка вільно падає, у момент
і0 дорівнює
У = §*0-
Зазначимо, що при фіксованому значенні /0 границею
середньої швидкості є число. Але для різних значень /0 ці
числа різні. Отже, оскільки кожному значенню /0 відпові-
дає єдина певна границя, то можна стверджувати, що гра-
ниця є функцією /, тобто
и{ = Ііт і)в = Ііт (еі 4-
Дістали відому формулу з курсу фізики.
Розглянемо загальний випадок. Нехай матеріальна
точка рухається прямолінійно, а закон руху її задано дея-
кою функцією
(6)
143
Поставимо задачу: знайти швидкість точки у момент
часу і. Використаємо наведене вище означення. Тоді швид-
кість V точки, яка рухається за законом (6), у момент часу
і визначається співвідношенням V = Ііт оо. Підстав-
А/->0
дз • <
ляючи значення ус = дістанемо формулу
х о=1іт-дГ. (7)
д/->о
Знайдемо приріст шляху Д5. Для цього часу і надамо
приросту Дї. Тоді із (6) дістанемо вираз для приросту
шляху
Д5 = Ці + Д0-/(/)• (8)
Підставивши у (7) значення Д5, остаточно матимемо та-
ку формулу:
р==Пт /(/+А/) ~/(/) .
дмо М ’
Приклад 1. Нехай точка рухається рівномірно приско-
рено з прискоренням а і початковою швидкістю а0. Знайти
її швидкість у момент часу і.
Розв’язання. Відомо, що залежність шляху
від часу при рівномірно прискореному русі виражається
формулою
5 = ц/+4-. (10)
1) Надамо і приріст ДЛ
2) Знайдемо приріст
до /4 । д। а (*+ # і \
Д5=о0(? + Д/)+ -*-Т.. /--.
Спростивши вираз у правій частині, дістанемо
Д5 = а0Д/ + аіМ + = Д^(о0 + аі + .
3)' Знайдемо середню швидкість як відношення приросту
функції 5 до приросту аргументу і'.
Д5 , , , аД<
аі ~1~ 2
4) Перейшовши в останній рівності до границі при Д/ ->
->0, знаходимо
и—а0 + аі, (11)
тобто дістаємо відому формулу з курсу фізики основної
школи.
144
Приклад 2. Нехай точка рухається так, що закон її
руху виражено формулою 8 = /® — 5/2 4- і 4- 2. Визначи-
ти: 1) середню швидкість точки на проміжку від 4 = 5 с до
4 = 10 с; 2) знайти швидкість точки на початку і в кінці
цього проміжку.
Розв’язання. Яків першому прикладі, надамо
аргументу і приросту А/ і знайдемо приріст шляху А8.
Для цього розглянемо два моменти часу і і і 4- А 4 Тоді
Д8 = (і + А/)3 — 5 (і 4- А/)2 + (і + М) +
_|_ 2 — (/3 — 5/2 + / 4-2),
або після спрощення
А8 = Зі (А/)2 4- 3/2А/ 4- (А*)3 — 10/А/ — 5 (А/)2 4- М.
Обчислимо середню швидкість на проміжку
уа = -^- = 3/А/4-3/24-А/2 —Ю/ —5Д/4-1. (12)
Підставивши сюди значення і = 4» А^ = 4 — 4> зна-
ходимо середню швидкість на проміжку від 4 = 5 с до
4 = 10 с: п0 = 101 м/с.
Знайдемо швидкість у будь-який момент часу і. Для цього
у рівності (12) перейдемо до границі при А/ ->0. Маємо
V = З/2 — 10/4- 1. (13)
Підставляючи у формулу (13) окремі значення і, кожно-
го разу діставатимемо відповідні значення швидкості. Зо-
крема, підставивши у (13) значення 4 = 5 с та 4 — Ю с,
знаходимо V — 266 м/с, V = 201 м/с.
2. Задача про величину змінного струму, який про-
ходить по провіднику. Нехай по провіднику за час / через
поперечний переріз проходить кількість електрики д,
яка з часом змінюється. Зміна задається відповідною
функцією
<7 = <7(0- (14)
Треба знайти величину сили струму, який проходить
через провідник у момент часу /.
Для розв’язання цієї задачі застосуємо той самий спо-
сіб, що й при розв’язуванні задачі 1.
1) Надамо / приріст А/ > 0;
2) Знайдемо приріст кількості електрики = д (і 4-
+ А/) - д (і}-,
3) Визначимо відношення приросту функції до приросту
аргументу:
_Дд_ _ <7(/4-а/)-9(0 ,. ~
д/ — д/ '1е>'
145
(це відношення називається середньою силою струму за
проміжок часу А/ і позначається /с);
4) Знайдемо границю середньої сили струму при А/ ->
->0:
Ііт /в = Ііт
ДЄ-.0 Д/-.0
Границя середньої величини сили струму за проміжок
часу Аї
Ііт 4 = Ііт 4г (16)
А/->0 &-+0
називається силою струму в даний момент часу.
Отже, якщо через / позначити величину сили струму в
момент часу /, то для її обчислення маємо таку формулу:
або
І = Ііт /в,
а^о
7= Ііт 41= Ііт +
Д/->0 д/-*п
(17)
Приклад 3. Нехай в момент часу і через поперечний пе-
реріз провідника проходить кількість електрики
9= ҐТТ7. (18)
Знайти силу струму у момент і = 2 с.
Р о з в’ я з а н н я. За формулою (15) знайдемо серед-
ню величину сили струму за проміжок часу Д#
ї /2 + * + А/ — /2 + / =_____________1_________
с А/ /2 4- / + А/ + УТ+~і
Перейшовши до границі при Д/ ->0, знаходимо величи-
ну сили струму у довільний момент часу і
І = Ііт Л---------==- = -----4= . (19)
д^О /2 + / + ДЇ + К2+/ 21/24-/ '
Підставивши у формулу (19) значення і = 2, дістанемо
/ і л
відповідь: І = А.
3. Задача про дотичну до кривої. З поняттям дотичної до
кривої у даній точці ми знайомилися в курсі геометрії при
вивченні кола. Було наведено означення дотичної до кола
як прямої, яка має з колом одну спільну точку. Але це
означення є окремим випадком. Його не можна поширити,
наприклад, на незамкнені криві. Справді розглянемо пара-
болу, рівняння якої у = хІ 2 (рис. 4.2). Вісь абсцис Ох і вісь
ординат Оу мають з кривою у точці О по одній спільній
146
точці. Отже, кожна з них згідно з означенням має бути
дотичною до кривої у точці О. Проте це не так.
Розглянемо ще один приклад. Нехай розглядувана кри-
ва є синусоїдою у = зіп х (рис. 4.3). Тоді пряма у = 1 має
з даною кривою безліч спільних точок (а не одну 1), І вона
є дотичною до даної кривої, наприклад, у точці М. Це ж
саме стосується і прямої у — —1, яка є дотичною до кривої,
наприклад, у точці ЛЦ і має безліч
спільних точок з кривою.
Тому, як випливає із наведених
прикладів, треба дати загальне оз-
начення дотичної, яке б охоплюва-
ло як замкнені, так і незамкнені
криві.
Отже, нехай маємо деяку довіль-
ну криву Ь (рис. 4.4). Візьмемо на
ній дві точки Л40 і і через них
проведемо пряму МйМх, яку назива-
тимемо січною. Якщо тепер точка
Мг рухатиметься уздовж кривої, то
січна МпМ1 повертатиметься навколо точки Л40. Нехай точ-
ка ЛЦ, рухаючись вздовж кривої, наближається до точки
Л40. Тоді довжина хорди Л40ЛЦ прямує до нуля. Якщо при
цьому й величина кута МгМйТ прямує до нуля, то пряма
М0Т називається граничним положенням січної МйМг.
Отже, маємо таке означення.
Дотичною до кривої Ь у точці Мо називається граничне
положення М0Т січної МоМі, якщо точка М1 прямує уз-
довж кривоі до злиття з точкою Мо.
Зазначимо, що з якого б боку точка Мг не наближалася
по кривій до точки Л40, січна Л40^і ПРИ цьому має наближа-
тися до того самого її граничного положення (до тієї самої
прямої). Тільки у цьому разі кажуть, що у точці Лїо крива
має дотичну. Не кожна крива у розглядуваній точці має
дотичну. Граничного положення січної може і не існувати.
Із рисунка видно, що з якого б боку точка по кривій
не рухалась би до точки Л40, січна М0Ми обертаючись
147
навколо точки Мо, при цьому наближається до тієї самої
прямої М0Т.
Якщо січна УИ0Мі наближається до різних прямих
(рис. 4.5) залежно від того, з якого боку Мг -* Мо, кажуть,
що в даній точці дотичної до кривої не існує. Так, дотичної
до кривої у точці Мо не існує, бо коли точка Мі -> Мо і
д знаходиться справа від Л40,
/ то січна М.гМй наближаєть-
ся до прямої М0Т±. А якщо
ЛІ!-»-Л40 і знаходиться злі-
/ \ ва, то січна Л^Мд наближа-
/ Vх .ється до прямої Л40Т2.
дг / /у Поставимо задачу: про-
/ вести дотичну до графіка
функції у — } (х) в точці
Мо (х0; у0).
рис> 4 4 Положення дотичної до
кривої у заданій точці ціл-
ком визначається кутом нахилу її з додатним напрямом осі
Ох. Отже, треба знайти цей кут.
Для цього виконаємо такі чотири кроки:
1) Надамо абсцисі х0 приросту Ах. Нове значення абс-
циси х0 + Ах визначає нове значення ординати у0 + Дї/.
Цим самим від точки Мо (х0; у0) перейдемо до точки Мг (х0+
+ Ах; у0 + А#) (риє. 4.6).
2) Визначимо приріст ординати, тобто приріст функції
&у. Для цього досить від нового значення функції / (х0 4*
-|- Ах) відняти попереднє значення / (х0):
А^ = /(х0 +Ах)—/(х0).
Геометрично Ау дорівнює довжині відрізка тобто
приросту ординати при переході від точки 2И0 до точки Мг.
148
3) Складемо відношення -^г — —£&).
З АЛ^АШі випливає, що це відношення дорівнює тангенсу
кута <р нахилу, утвореного січною Л4ОЛ4Х 3 додатним напря-
мом осі Ох, тобто
4) Нехай тепер Дх ->0, тоді і Ду ->0 (внаслідок непе-
рервності функції у = / (х)), а тому точка М1Г рухаючись
по кривій, буде прямувати до точки Л40, а січна М.0Мг пря-
муватиме до свого граничного положення, тобто до поло-
ження дотичної М0Т. Це означає, що кут ф нахилу січної
Л40Л41 буде прямувати до кута а нахилу дотичної М0Т, а
Ф а, якщо Дх 0.
Отже,
Ііт — Ііт ф = а = к,
Дх-М) Дх-*-0
де к — кутовий коефіцієнт дотичної Л40Т.
Знаючи а, можна знайти кут а і побудувати дотичну
до кривої у = І (х) у точці Мо (х0; у0).
Проаналізувавши розв’язання розглянутих трьох задач
(про миттєву швидкість, про величину сили змінного струму
у провіднику і задачу про проведення дотичної до кривої
у певній точці), приходимо до висновку, що всі вони розв’я-
зувались одним і тим самим способом, який складається з
чотирьох кроків:
1) незалежній змінній х надаємо приросту Дх;
2) знаходимо приріст залежної змінної Ду;
3) складаємо відношення ;
4) знаходимо Ііт .
Відношення при цьому виражає середню швидкість
зміни функції, а Ііт — швидкість зміни функції при
даному значенні аргументу х, або, ще те саме, у точці х.
Оскільки за допомогою Ііт розв’язують крім роз-
глянутих ще й багато інших важливих задач (наприклад,
про швидкість протікання хімічної реакції, знаходження
лінійної густини неоднорідного стержня, теплоємності ті-
ла при нагріванні, кутової швидкості тіла, що обертається
та ін.), то доцільно всебічно вивчити цю границю, зокрема,
149
вказати способи її обчислення. При цьому змінні х і у дово-
диться розглядати абстрактно, не вкладаючи в них конкрет-
ного смислу, тобто доводиться узагальнити спосіб розв’я-
зання розглянутого виду задач. Цю границю в математиці
називають похідною.
§ 2. Похідна. Механічний
та геометричний зміст похідної
1. Означення похідної. Правило знаходження похід-
ної. Нехай функція у = / (х) задана на деякому інтервалі
(а; Ь). Візьмемо довільну точку х0, що належить цьому ін-
тервалу. Виконаємо відомі чотири кроки:
1) надамо значення х0 довільного приросту Дх (число Дх
може бути як додатним, так і від’ємним), але такого, щоб
точка х0 + Дх належала інтервалу (а; &);
2) обчислимо в точці х0 приріст Ду = Д/ (х0) функції
Дг/ = Д/ (х0) = / (х0 + Дх) — / (х0);
3) складемо відношення ~;
4) знайдемо границю цього відношення при Дх -> 0;
тобто
Ііт = Ііт = Ііт ./^ + у-/(х) .
Дл~0 Дх Дх-0 Дх Дх—0 Д*
Якщо дана границя існує, то її називають похідною
функції у = / (х) в точці х0 і позначають /' (х0) або у*.
Похідною функції у = / (х) в точці х0 називається гра-
ниця відношення приросту Ау функції до приросту Ах ар-
гументу за умови, що приріст Ах аргументу прямує до ну-
ля, а границя існує, тобто
г (х0) = Ііт 4*- = Ііт +
°' Дх-»0 Д* Д^О
Кроки 1) — 4) фактично визначають правило знахо-
дження похідної.
Застосовуючи поняття похідної до розглянутих вище
трьох задач, які привели до поняття похідної, можемо
стверджувати, що миттєва швидкість нерівномірного руху
є похідною від шляху 5 = / (0. тобто о = 5' = /' (ї0)-
У цьому полягає механічний зміст похідної.
Задача про дотичну дає змогу з’ясувати геометричний
зміст похідної: похідна /' (х0) дорівнює кутовому коефіці-
єнту к = а дотичної до кривої, проведеної у точці
М0(х0; уа).
150
Зазначимо, що коли похідна знаходиться у певній точ-
ці х0, то вона як границя є певним числом /' (х0). Але для
різних значень х0 такі числа можуть бути різними і кожному
х0 відповідатиме своє число /' (х0). Зокрема в задачі про мит-
тєву швидкість при /0 = 4 с V = 40 м/с, а при /0 = 5 с V =
= 50 м/с.
Отже, похідна функції у = / (х), якщо вона існує в кож-
ній точці інтервалу (а\ Ь), є теж функцією аргументу х. То-
ді її позначають символом (х) і за означенням
Г(х) = Ит Ііт +
Якщо функцію задано формулою, наприклад, у = х2,
то похідну позначають також символом (х2)'.
Наведемо приклади застосування означення похідної
для знаходження похідних окремих функцій. Оскільки на
кроці 1) правила знаходження похідної ніяких обчислень
фактично не доводиться виконувати, то при знаходженні
похідних починають з кроку 2) Якщо похідну треба зна-
йти у будь-якій точці х з (а; Ь), то правило залишається тим
самим, тільки замість х0 ставимо х.
Приклад 1. Знайти похідну від функції у = х2 у точці
хв = 1.
Розв’язання. Користуємося наведеним правилом.
Знаходимо приріст Д.у функції у = х2 у точці х:
Дг/ = (х 4- Дх)2 — х2 = 2хДх 4- (Дх)2 = кх (2х 4- Дх).
। Складаємо відношення
Д^= Дх(2х4-Дх) =г2х+Дх
Дх Дх
і знаходимо границю
ііт 4^- = Ііт (2х + Дх) — 2х.
Дх-»0 Дх->0
Отже, похідна функції у = х2 у точці х існує і (х) =
<= 2х. При х = 1 (1) = 2.
Приклад 2. Знайти похідну функції у = х3 + х2 + 4х 4-
4- 1 у точці х0 = 0.
Розв’язання. Знаходимо приріст Ду у точці х0 = 0:
Ду = (Дх)3 4- (Дх)2 4- 4Дх = Дх ((Дх)2 4- Дх 4- 4).
Тоді
д^ ~ Дх,((Дх)2 4-^47.1)- = (Дх)2 4- Дх 4- 4.
Дх Дх » / • *
153
Обчислимо границю
Ііт 4т- = Нт ((Дх)2 + Дх + 4) = 4.
АХ-+0 Дх->0
Отже, похідна функції у = х8 + х2 4- 4х + 1 у точці
х0 = 0 існує і /' (0) — 4.
Приклад 3. Знайти похідну функції
У =
х2 зіп -і-, якщо х Ф 0,
0, якщо х = 0,
у ТОЧЦІ х0 = 0.
Розв’язав
= 0:
н я.
Знаходимо приріст Ді/у точці х0 =
Тоді
Дг/ = (Дх)2 зіп .
Ду
Дх
(Дх)2 зіп —1—
__________Дх
Дх
= Дхзіп-^— .
Дх
Обчислимо границю
Ііт -т^-= Ііт (Дхзіп-^—ї = 0.
Дх-0 Дх->0 ( Дх )
Отже, похідна заданої функції в точці х0 — 0 існує
Г (0) = 0.
Приклад 4. Довести, що функція у = | х | у точці х = 0
похідної не-має.
Розв’язання. Знаходимо приріст заданої функції
у точці х = 0. Маємо Дг/ = | Дх |.
Знайдемо відношення
Ду _ | Дх| _ [ І» якщо Дх> 0,
Дх — Дх ~ | —1, якщо Дх<0.
Звідси випливає, що відношення при Дх -> 0 границі
не має.
Зазначимо, що з графіка функції у = | х | (рис. 4.7) ви-
пливає, що в точці О (0;0) провести дотичну не можна, у цій
точці крива, яка є графіком даної функції, має злам.
Приклад 5. Враховуючи геометричний зміст похідної,
виведемо рівняння дотичної до графіка функції у = І (х)
в точці Мо (х0; у0).
152
вигляд
(1)
прохо-
У
0 х
Рис, 4.7
Рівняння прямої з кутовим коефіцієнтом к має
у = кх + Ь. Оскільки для дотичної к — ? (х0), то
У = ї'(х0)х + Ь.
Щоб знайти Ь, скористуємось тим, що дотична
дить через точку Мо (х0; у0). Це означає, що її координати
задовольняють рівняння дотичної, тобто / (х0) = (х0) х 4-
+ Ь, звідки Ь — ? (х0) — /' (х0) • х.
Підставимо значення Ь у рівнян-
ня (1). Дістанемо
у = Г (х0) х — Г (х0) х0 + / (х0)
або у = / (х0) + /' (х0) (х — х0). (2)
Отже, рівняння (2) є шукане рів-
няння дотичної.
Використовуючи рівняння до-
тичної і формулу (X2)' = 2х, доведемо, що дотичною до Па-
раболи у = х2 у точці Мо (0; 0) є вісь Ох.
Справді, оскільки ) (х0) = (х2)х„=о = 0, (х0) =
= (2х)х„=о — 0, то, підставляючи значення / (х0) і /' (х0)
у рівняння (2) дотичної, дістанемо у = 0 + 0 • (х — 0);
звідки у = 0, а це і є рівняння осі Ох.
Наведемо таке означення.
Функція у = / (х) в точці х0 називається диференційов-
ною, якщо в цій точці вона має похідну І' (х0).
Якщо функція у = / (х) є диференційовною в кожній
точці деякого інтервалу (а; &), то вона називається диферен-
ційовною на цьому інтервалі.
Природно поставити запитання: який існує зв’язок між
неперервністю функції в точці і диференційовністю її у цій
точці? Зокрема, якщо функція неперервна в точці, то чи
буде вона в цій точці диференційовною? Щоб дати відповідь
на ці запитання, розглянемо приклад.
Функція у = | х | в точці х = 0 є неперервною, бо
Ііт Ду = 1і т | Дх | = 0,
Дх->0 Дх-*0
але вона не є в точці х = 0 диференційовною. Отже, не будь-
яка неперервна функція в точці є в цій точці диференційовною.
Справедлива така теорема.
Теорема. Якщо функція у = / (х) в точці х0 є диферен-
ційовною, то вона в цій точці неперервна.
Доведення. Нехай у — І (х) в точці х0 має похідну
/' (х0), тобто
1Іт ^- = ^(хо)-
Дх-*0
153
Запишемо приріст функції ку в точці х0 у вигляді
Дг/ — • Дх.
Дх
Тоді
Ііт Дг/ = Ііт (-• Дх') =
Дх-»-0 Дх-»-0 \ А* ]
= Ііт • Ііт Ах = /' (х0) -0 = 0.
Дх->0 Дх-*0
Отже, границя приросту функції в точці х0 дорівнює
нулю. Тому функція у = / (х) в точці х0 є неперервною. Тео-
рему доведено.
З цієї теореми випливає, що неперервність функції в
точці є тільки необхідною умовою диференційовності функ-
ції в даній точці.
§ 3. Похідні елементарних функцій
Виведемо формули для похідних елементарних функцій,
причому на відміну від попередніх прикладів,' знаходити-
мемо похідну в довільній точці.
1. Похідна сталої функції у = с = соп$1:. Нехай на де-
якому проміжку (а\ Ь) задано сталу функцію у = с = сопзі.
Тоді її значення у точках х і х + Ах рівні між собою при
будь-якому х. Тому приріст Ау = 0, а отже, й = 0.
Перейшовши до границі в останній рівності при Ах ->0,
знаходимо
Ііт = Ііт 0 = 0.
Дх-*>0 &Х Дх-*0
Отже, границя відношення-^- при Дх->0 існує і до-
рівнює нулю. Тому існує і похідна цієї функції в довільній
точці х, яка теж дорівнює нулю, тобто якщо у = С = СОП5І,
то у' = 0, тобто с' = 0.
Похідна сталої функції дорівнює нулю. Наприклад,
якщо у = 2, то у' = 0.
2. Похідна степеневої функції з цілим показником. Роз-
глянемо спочатку окремі приклади.
Приклад 1. Знайдемо похідну функції у = х у довіль-
ній точці х.
Знайдемо приріст цієї функції Ау в точці х
Ду = х + Дх — х = Дх.
154
Тоді
Ду _ А* .
Дл: Дх
Знайдемо границю
Ііт = Ііт 1 = 1.
Дх->0 Дх->0
Отже, похідна у' функції у = х у будь-якій точці х існує
і дорівнює 1, тобто х' = 1.
' Вище доведено, що похідна функції у = X2 в точці х до-
рівнює 2х, тобто (х2)' = 2х.
Приклад 2. Знайдемо похідну функції у = х3 у довіль-
ній ТОЧЦІ X.
Знайдемо приріст функції
Ду = (х + Ах)3 — х3 = Зх2Дх + Зх (Ах)2 + (Дх)3.
Тоді '
= Зх2 + ЗхАх + (Дх)2.
Перейдемо у цій рівності до границі при Дх -> 0. Діста-
немо
Ііт -4^- = Ііт (Зх2 + ЗхДх 4- (Дх)2) = Зх2.
Отже, похідна у' функції у — х3 в точці х існує і дорів-
нює у' = Зх2, тобто (х3)' = Зх2.
У розглянутих прикладах помічаємо таку закономір-
ність: похідна степеневих функцій х, х2, х3 дорівнює показ-
нику степеня, помноженому на цю функцію в степені, на
одиницю меншому:
У = х, у' = 1 • х°,
У = х2, / = 2 • х,
у = х3, у' = 3 • х2.
Переконаємося, що дана закономірність є справедливою
для степеневої функції у = хп з будь-яким натуральним по-
казником:
у = хп, у' = п-хп~'. (1)
Формулу (1) виведемо у наступному параграфі.
Розглянемо ще приклади.
Приклад 3. Знайти похідну функції у = у будь-якій
точці х ф 0.
155
Надамо х довільного приросту Ах, але такого, щоб х 4-
+ Ах =/=0. Тоді і функція у дістане приросту
д ___ 1 __ 1 ___ — Дх
У х 4- Дх х х (х + Дх)
Знайдемо
Ду __________1
Дх х (х 4- Д*)
Перейдемо в цій рівності до границі при Ах -> 0. Ді-
станемо
Ііт 4^- = Ііт —г-дгт V' =-------1- = — х*2.
Дх-0 Дх Дх-0 * (* + Дх) х
Отже, похідна у' функції у = = х"1 існує і дорів-
нює у' = — х“2.
Приклад 4. Знайти похідну функції у = у будь-якій
точці х 0.
Надамо х такого приросту Ах, щоб х + Ах #=0. Тоді і
функція у дістане приросту
д________1_________1 ___ 2хДх 4- (Дх)2 _____Дх (2х + Дх)
У (х 4- Дх)2 х2 х2 (х 4- Дх)2 х2 (х 4- Дх)2 ’
Знайдемо
Ду ___ 2х 4~ Дх
Дх х2(х4-Дх)2 ’
Перейдемо у цій рівності до границі при Ах -> 0. Ді-
станемо
Ііт = Ііт(------------------------1- = — 2х*"3.
дх-о д* Дх-*о\ х2(х4-Дх)2/ % х3
Отже, похідна у' функції у = = х“*2 існує і дорів-
нює у' = — 2х~3.
Із прикладів 3, 4 можна зробити такий висновок: похід-
на у' функції у = х~к, де 6 > 0 — ціле число, існує у кож-
ній ТОЧЦІ X =/= 0 і дорівнює
у'^-кх^. (2)
Формулу (2) також виведемо у наступному параграфі.
Формули (1), (2) дають змогу сформулювати таке твер-
дження: похідна степеневої функції у = хт з цілим показ-
ником існує і дорівнює показнику степеня, помноженому
156
на цю функцію у степені, на одиницю меншому, тобто
у' = /пл/"-1 (3)
(при т < 0 х не може дорівнювати нулю).
Так, наприклад,
у = х10, у' = 10х9, у = х-6, у' = — 5х-6.
3. Похідні тригонометричних функцій. Похідна функ-
ції у — зіп х. Надамо х довільного приросту Дх =/= 0. Тоді
функція у дістане приросту
Дї/ — 8ІП (х 4* Дх) — зіп X = 2 зіп СОЗ (х + .
Знайдемо відношення
* І . X 3*Д£-
До / . Дх ) 2
ПГ- = соз х 4---я- ---------.
Ах \ 2 І ьх
2
Перейдемо у цій рівності до границі при Дх 0. Вна-
слідок неперервності функції соз х
Ііт соз (х 4- ДгД = соз ( Ііт і х 4- ДгД) = со3 *•
Дх-*0 \ 1 І \Дх-»0 \ 2 //
п • Ах
Для другого співмножника, позначивши —5- = а,
маємо
зіпДі- ,
Ііт -----1_ = Ип1^=і.
Дх^.0 Дх а-*о а
.2
Тому
/ 8ІП-^- \
Ііт Д^- = Ііт і соз (х 4- -Д—)------— І = соз х.
Дх-*о Ах Дж-*0 і ' ' &х І
Отже, похідна функції у = зіп х існує у довільній точці
х€ (—ооі 4-оо) і дорівнює соз х, тобто
(зіп х)' = соз х. (4)
Похідна функції у = соз х. Аналогічно доводиться, що
похідна функції у = соз х у довільній точці х 6 (—оо; 4*оо)
існує і дорівнює —зіп х, тобто
(соз х)'= — зіп х. (5)
167
Похідна у = х. Візьмемо довільну точку х Є (а; Ь),
де (а; Ь) — область визначення функції х. Знайдемо при-
ріст
д ____ ЗІП (X + Дх) зіп X __
СОЗ (X + Дх) СОЗ X
___ зіп (х + Дх) СОЗ X — зіп X СОЗ (х 4- Д*) зіп Дх__
СОЗ (х + А*) СОЗ X____________________________________СОЗ (X + Дх) СОЗ X
зіп Дх
І складемо відношення -4^- =-------.
* кх соз (х + Дх) соз х
Перейдемо до границі при Дх -> 0:
зіп Дх
Ііт = Ііт ---------. д .-------= —.
Дх-0 &Х 008 "І- Д*) с08 Х СОЗ2 Х
Отже, похідна функції у = х існує і дорівнює
(*£*)' • (6)
Похідна функції у = х. Аналогічно доведемо, що
похідна функції у = сі§ х існує у довільній точці х б (я; Ь),
де (а\ Ь) — область визначення сі§ х, і дорівнює
(сі§ х)' ----Д— .
Виконайте доведення самостійно.
(7)
§ 4. Теореми про похідні алгебраїчної суми,
добутку і частки функцій
Доведемо ряд теорем, які широко використовують для
знаходження похідних функцій.
Похідна суми. Теорема 1. Якщо функції (х) г /2 (х) в
точці х мають похідні, то функція у = (х) ± /2 (*) в Цій
точці також має похідну, яка дорівнює
у' = (71 (X) ± /з (х))' = /і (X) ± Л (х).
Доведення. Надамо х деякого приросту Дх. То-
ді функції (х) і /2 (х) матимуть прирости Д/х (х) і Д/2 їх),
а функція у матиме приріст
Аг/ = А/і (х) ± Д/з н).
Знайдемо відношення
А» = 4/1 (X) Д/г (х)
Дх Дх ”с Дх ’
158
Перейдемо у цій рівності до границі при Дх -> 0. Ос*
кільки А (х) і А (х) У точці х за умовою теореми мають по-
хідну, то
1іт-^- = Л(х), Ит-^£1 = А(х).
Дх->0 Дх->0
Тому
Ит-^= 1іт(-^-±-^_) =
Дх->о Дх->о \ Ах Ах )
= Ііт ± Ііт = А (х) ± А (х).
Дх->0 Дл->0
Отже, ЗГІДНО З означенням ПОХІДНОЇ у ТОЧЦІ X Існує ПО"
хідна функції у, яка дорівнює
У' = А(х)4-А(х). (1)
Теорему 1 можна узагальнити для будь-якої скінченної
суми функцій: похідна суми скінченного числа функцій до-
рівнює сумі похідних від цих функцій, якщо похідні даних
функцій існують, тобто
(А(х)4-А(х)4- ... 4-А(х))' =
= А (х) + А (х) + ••• + А (х). (2)^
Приклад 1. Знайти похідну функції у = зіп х + созх4~
+ х + 5.
Розв’язання. За формулою (2) маємо
у' = (зіп х + соз х -|- х + 5)' = (зіп х)' 4- (соз х)' 4*
+ (*§ х)' 4- (5)'.
Знаючи похідні кожної функції, дістанемо
у' = соз х — зіп х 4--5—.
а 1 СО82 X
Похідна добутку. Теорема 2. Якщо функції А(х) і А (х)
в точці х мають похідні, то в цій точці функція у = А (х) х
X 'А (х) також має похідну, яка дорівнює
У’ = /і (х) А (х) 4- А (х) А (х). (3)
Доведення. Надамо х деякого приросту Дх. Тоді
функції Д (х), А (х) матимуть приріст ДА (х), ДА (х), а функ-
ція у дістане приросту
&у = (А (х) 4- ДА (х)) (А (х) 4- ДА (х)) — А (х) А (х) =
= А (х) (х) 4- А (х) ДА (х) + ДА (х) ДА (х).
і 59
Знайдемо відношення
# = Ш • ^- + ГМ + -АІИ-. д/ї(х).
Перейдемо у цій рівності до границі при Дх ->0. За умо-
вою теореми
Ііт = А (х), Ііт = А (X),
Дх-.в Дх-0
а Ііт ДА (х) = 0, бо А (х) неперервна в точці х.
Дх->0
Отже,
Ііт = А (х) А (х) + А (х) А (х).
Дх-*0
Зазначимо, що коли один співмножник, наприклад
А (х) = с = сопзі, то А (х) = 0 і формула (3) набуває ви-
гляду у = с/г (х). Якщо в добутку один співмножник ста-
лий, то похідна від такого добутку дорівнює сталому спів-
множнику, помноженому на похідну змінного співмнож-
ника.
Дану теорему, можна узагальнити і на випадок п спів-
множників. Зокрема, для похідної від добутку трьох функ-
цій
(А (х) • А (х) . /з (х))' = (х). А (х) • А (х) +
+ А (х) • А (х) ’ А (х) + а (х) • А (х) • А (х).
Приклад 2. Знайти похідну функції у = х8 зіп х.
Р о з в’ я з а н н я. За формулою (3)
у' = х3 соз х 4- Зх2 зіп х.
Приклад 3. Знайти похідну функції у = 10 сі§ х 4-
+ 5 соз х + х® х.
Розв’язання.
у' = 10 (сі§ х)' 4- 5 (соз х)' 4- (х6 х)' = — —
— 5зіпх4- с0^ + бх6 і§х.
Приклад 4. Довести, що функція у = хп, де п — нату-
ральне число, має похідну
у’ = пх"”1. (5)
Розв’язання. Скористаємося методом математич-
ної індукції. Цей метод грунтується на такому прин-
160
ципі: якщо деяке твердження А (гі) відносно натураль-
ного числа п правильне для п = 1 і з припущення, що воно
правильне для п = А, випливає, що воно правильне для
наступного числа л=£+ 1, то це твердження правильне
для будь-якого натурального числа п.
Щоб довести твердження методом математичної індук-
ції, треба:
1) перевірити правильність твердження для п = 1;
2) припустити, що воно правильне для к, і на підставі
цього припущення і вже відомих тверджень довести, що
твердження правильне для іг = к + І;
3) зробити висновок, що згідно з принципом математич-
ної індукції доводжуване твердження правильне для будь-
якого натурального числа п.
Доводжувана формула у' = (хп)' = /їх”-1 є тверджен-
ням відносно натурального числа п. Виконаємо три кроки:
1) переконаємося, що формула правильна для п = 1.
У § 3 було доведено, що у' = (х)' = 1. Отже, (х1)' = 1 X
X х1-1 = х° = 1, тобто для п = 1 формула (5) правильна;
2) припустимо, що формула (5) правильна для п = к,
тобто правильна формула у' = (х*)' = кхк~їі і доведемо,
що формула (5) правильна для п = к + 1.
Справді, використовуючи теорему про похідну добутку
двох функцій і припущення, дістанемо
у' = (х*+1у = (х . X*)' = X . ЙХ**"' + / -
= &/ + / = (£+1)?.
3) згідно з принципом математичної індукції формула
у' = (%«)' = пхп~' виконується для будь-якого п.
Похідна частки. Теорема 3. Якщо функції (х) і Ь (х)
г (х)
в точці х мають похідні і (х) 0, то функція у =
також у точці х має похідну
, їа (х) і'і (х) — Її (х) (*) .д.
• =---------ЛЙР---------- • <6)
Доведення. Надамо х приросту Дх. Тоді функції
/і (х) і їа (*) матимуть відповідно прирости Д/х (х), Д/2 (х),
а функція у матиме приріст
_ /і(х)+А/і(х) _ Л(х) /2(х) -іїіху^іх)
У ~ Іа (X) + Д/а (х) /а (х) (/а (х) + Д/а (х)) /2 (х) •
6 1-1819 161
Знайдемо відношення
/2 (X) . --Л (х) . А7з(*).
Дг/____________Дх_____________Дх
Дх “ (А (X) + Д/2 (х))/8 (х)
За умовою даної теореми функції (х) і (х) в точці х
мають похідні, а це означає, що
Піп -А^-х)- = /і (х), Ііт = І2 (х).
Дх->-0 ах Дх->0 йх
Крім того, Ііт Д/2 (х) — 0, оскільки функція /2 (х) неперерв-
Дх->0
на. Тому
Дг/ _ /г (*) /і (*) — А. (*) /г М
д™ Дх ~ а2(х))«
З останньої рівності й випливає формула (6).
Приклад 5. Знайти похідну функції у = •
Р о з в’ я з а н н я. За формулою (6)
, _ (х* + 2) (ха + 1)' - (х2 + 1) (х4 + 2)' _
» ~ (х4 + 2)2 “
__2х (х4 + 2) — 4х3 (х2 -|- 1) 2х (2 — х4 — 2х)
~ (х4 + 2)2 (х4 + 2)2 -
Приклад 6. Користуючись формулою (6), знайти похід-
ну функції у = і:§ х, у — сі§ х.
Р о з в’ я з а н н я. Знайдемо похідну функції у = х
(для у = сі§ х похідну знаходять аналогічно). Подамо х
у вигляді у = Тоді згідно з формулою (6)
, _ СОЗ х (зіп х)' — зіп х (соз X)' _ СОЗ2 X -|- ЗІП2 X _ 1
У СО32Х СО32Х СО32Х ’
Приклад 7. Вивести формулу похідної функції у =»
= де с— соті, а /(х) і в точці х має похідну.
Розв’язання. Використаємо формулу (6), вважа-
ючи Д (х) = с, /2 (х) == / (х). Маємо
_ Цх) - є'—с Г (х)______с/' (х)
у (Ш)а (/(*))’ '
Це і є шукана формула.
Приклад 8. Знайти похідну функції у =
Р о з в’ я з а н н я. За формулою (7)
,____________ (соз х)' ____ зіп х __ х
V СОЗ2 X СОЗ2 X соз X '
(7)
162
,/ Аналогічно можна довести, що похідна функції у =
дорівнює
, СОЗ X СІЄ X
и =-------5— =--------—.
ЗІП2 X ЗІП X
Приклад 9. Знайти похідну функції у = х~к, де А — ці-
ле число.
Розв’язання. Запишемо дану функцію у вигляді
у = -у. Тоді згідно з формулою (7)
г (хкУ кхм
У х2к '
Після скорочення на хк~] дістанемо
иг - = — кх^
Це і є формула (3) § 3.
Похідна складної функції. Спочатку з’ясуємо, що таке
складна функція. З прикладами складної функції нам вже
доводилося зустрічатися при побудові графіків функцій
виду у = / (Ах), у = / (х ± а). Наприклад, функцію у =
і
= V"х — 5 = (х — 5)2 можна розглядати як степінь
лінійної функції и = х — 5 = Н (х). Щоб обчислити зна-
чення складної функції при певному значенні х, доведеть-
ся виконати дві операції:
1) обчислити значення різниці х — 5; 2) добути арифме-
тичний корінь із значення цієї різниці.
Перша операція кожному х ставить у відповідність пев-
не число. Отже, маємо одну функцію и = Н (х) = х — 5.
Друга операція знайденому числу ставить у відповідність
також певне число. Маємо другу функцію у = § (и) =
= Уи = V Н (х) = § (Нх) = / (х).
Функцію у = / (х) = § (Н (х)) називають складною функ-
цією аргументу х. Змінну и назвемо проміжною змінною.
Областю визначення функції и = И (х) = х — 5 є мно-
жина дійсних чисел /?, областю визначення функції, у =
= £ (м) = У и є множина невід’ємних значень и. Отже,
значення и мають задовольняти умову и 0 або х — 5
0. Звідси х > 5.
Отже, областю визначення складної функції у — { (х) =
= У5 —хе множина [5; Н-оо).
6* 163
Треба навчитися у складній функції визначати проміж-
ну змінну, яка є також функцією. Наприклад, для функції
/ л\
у — зіп 12х + ~4~І проміжною змінною и є лінійна функція
и — 2х + -£. Для функції у — ]/х2 — 5х + 6 проміжною
змінною є квадратична функція и — х2 — 5х + б, при цьо-
му задані функції можна записати у вигляді у — зіп и, у =
= Уи.
Строге доведення теореми про похідну складної функ-
ції міститься у курсі математичного аналізу. Ми наводимо
доведення з певними обмеженнями, які його спрощують.
Нехай функція и = к (х), де и — проміжне значення
для складної функції, має похідну у точці х0, а функція у =
= § (и) має похідну у точці и0 = к (х0). Це означає, що іс-
нують границі Ііт і Ііт
Надамо значенню х0 приросту Дх. Тоді змінна и набуде
.приросту Ди, який, в свою чергу, зумовить приріст Ду функ-
ції у = / (х) = § (и), де и = к (х).
Щоб знайти похідну у' = (х0), треба обчислити
Ііт 4^- Припустимо, що при досить малих Дх =^0 відпо-
Дх->0 Лх
відне Дп також не дорівнює нулю. Подамо відношення
у вигляді
ку ку ки
кх ки * Ах
За теоремою про границю добутку
Ііт4^ = Ііт 1іт4^-,
Дл-М) &х Д«->0 Дх->0 &х
оскільки Дц ->0 при Дх ->0. Справді, функція и = к (х)
диференційовна, а тому неперервна.
Оскільки обидві границі, що стоять в правій частині
рівності, за умовою існують, то існує і границя Ііт =
Дх-И) Лх
= ґ (*<>)• Отже> Л М = ОМ • Л' (х0).
Позначимо §' (и0) = у'и, щоб підкреслити, що похідну
функції § шукають по и, а /і' (х0) = их, бо похідну функції
к шукаємо по х. Тоді формулу похідної складної функції
У = / (х) запишемо скорочено у вигляді
У' == у'и- и'х,
164
тобто похідна складної функції дорівнює добутку похідної
цієї функції по проміжній змінній и на похідну проміжної
вмінної и по змінній х.
Проілюструємо застосування цієї теореми.
Приклад 10. Знайти похідні функцій:
1) У = Ух — 5;__2) у — (5х8 4- З)4; 3) у = зіп 2х;
4) у = х — У 1 — х8; 5) у = (х3 — 1) У 2 — х;
6) У-------7Х Є-
соз І Зх — “4/
Розв’язання. 1) Тут у =Уй, и — х— 5, тому
У = • (х — 5)' = '_ ;
* 2/и ' 2/х—5
2) позначимо и — 5х2 + 3, тоді у = и4. Тому у' =
«= 4г? (5х8 4- 3)' = 4 (5х8 4- З)3 • Юх = 40х (5х3 4- З)8;
3) покладемо и = 2х, тоді у = зіп и, отже, у' =
= сбз и • (2х)' = 2 соз 2х;
4) маємо різницю функцій, з яких друга складна, за те-
оремою про похідну різниці та формулою похідної склад-
ної функції, де и = 1 — х8, а у = х — У и, дістанемо у' —
к і _ 1 . (1 х3¥ = 1 4- 3x8
2 Ні - х3 ' + 2 У 1 —х3’
5) у другому співмножнику покладемо и = 2 — х, тоді
у = (х3 — 1) Уи, а у' = (х3 — 1)' Уи — (Уй)' • (х3
= Зх2 У~й--------(х3 — 1) = Зх2 У2=~х —
-77^7 “ ЗІ‘ +
= 6х3 (2 — х) 4- (х3 — 1) — 5х3 4- 12ха — 1
= 2/П^х 2/П^Т
(X3)' ЄО8 (зх-5-— (воз ^Зх — Xа
вО83(зх——
\ 4 /
6) у' =
165
Наведемо основні формули похідних:
(с)' = 0, с — стала;
(хУ = 1;
(хп)' = пх"-1, де п £ АГ;
= х>°;
(1^)'=-^-, х>0;
п V хп~1
І X V 1 , п
І — І ------5“ , х=^=0;
\ X / X2 ’ V- »
І С \ СЇ' (х)
І7со) = де с~стала;
(/ (х) ± (ф (х))' = /' (х) ± ф' (х);
(/ (х) ф (х))' = / (х) ф' (х) + ф (х) /' (х),’
(с/(х))'= с/'(х), де с — стала;
/ /(х) V /' (х) <р (х) — <р' (X) / (х)
\ ф (х) І (ф (х))2 ’
(зіп х)' = соз х;
(созх)' — —зіпх;
(і§ х)' = —І—;
К & ' СОЗ2 X
, х 1
СШХ =-----7-2- 5
4 ь ' 81П2 X
Ух^Уи* и'х, де у = и = Л(х), тобто у = /(й(х)).
Запитання і завдання для повторення
1. Що називається законом руху?
2. Що називається середньою швидкістю прямолінійного руху точ-
ки?
3. Чому дорівнює середня швидкість: а) прямолінійного рівномір-
ного руху; б) рівномірно прискореного руху 15 = І?
4. Що називається миттєвою швидкістю рухомої точки, закон руху
якої описується законом 5 — / (/)?
5. Чому дорівнює миттєва швидкість:
а) рівномірного руху;
б) рівномірно прискореного руху 15 = ;
166
в) рівномірно сповільненого руху
с) руху, закон якого описується формулою 5 = а/3 + ЬР + сі +
</?
6. Що називається силою струму? Чому сила струму дорівнює, як-
що кількість електрики, що проходить по провіднику, виражається фор-
мулою д = -ркг ?
7. Яка пряма називається січною до кривої?
8. Яка пряма називається граничним положенням січної?
9. Яка пряма називається дотичною до кривої?
10. Чому дорівнює кутовий коефіцієнт дотичної до кривої, заданої
рівнянням у = / (х), у точці Л40 (х0; £0)?
11. Написати рівняння дотичної до кривої у = / (х) у точці
Мо (*оі Уо)-
12. Що називається швидкістю зміни функції у = / (х) у точці х0?
13. Сформулювати означення похідної функції в точці.
14. Який механічний зміст похідної?
15. Який геометричний зміст похідної?
16. Сформулювати правило знаходження похідної функції.
17. Сформулювати означення диференційовної функції: а) в точці;
б) в інтервалі (а; Ь).
18. Чи буде: а) неперервна функція в точці диференційовною в цій
точці; б) диференційовна функція в точці неперервною в цій точці?
19. Чому дорівнює похідна сталої функції?
20. Чому дорівнює похідна степеня з натуральним показником?
21. Чому дорівнює похідна степеневої функції з цілим показником?
22. Чому дорівнює похідна тригонометричних функцій у = зіп х,
у = СОЗ X, у — X, у — СІ§ X.
23. Сформулювати теорему про похідну суми (різниці) двох функ-
цій.
24. Сформулювати теорему про похідну добутку двох (трьох) функ-
цій.
25. Чому дорівнює похідна добутку двох функцій, у якому один із
співмножників сталий?
26. Сформулювати теорему про похідну частки від ділення двох
функцій.
27. Чому дорівнює похідна дробу, у якого чисельник сталий?
28. Чому дорівнює похідна складної функції?
Вправи
1. Користуючись означенням похідної і правилом, що випливає з
нього, знайти похідну функцій:
А
1) у = Г (1); 2) у = 5х2 + 1, Г (3)5
3) у = С08Х, 4)у= ‘ , /'(2).
\ 4 / х8
2. Знайти миттєву швидкість рухомої точки в момент часу і = 1 с,
якщо закон руху задано формулою у = /8 — 2/2+ 2.
З, Написати рівняння дотичної до кривої у = х2 у точці Л40 (1; 1),
167
Б
4. Знайти похідні функцій у заданій точці
1) у = ах» + 1, ? (- 1); 2) у = /~х, ?' (3)}
3)у = х* + 3х+1, /'(1); 4) у = V х, Г (4).
5. Знайти рівняння дотичної до синусоїди у = зіп х в точці
Л4о(-£; 1).
6. Довести, що дотична до прямої у = кх + Ь у будь-якій точці
збігається з самою прямою,
В
7. Знайти похідні функцій
1) У=*Л /'(1); 2) у=х\х\, ?$)-,
3) у = 4) у = х.
8. Знайти рівняння дотичної до параболи у = 2 — — х! в точці
перетину з віссю ординат.
9. Відомо, що точка рухається за законом 5 = -т—1—— . Знайти
3/*Т8
миттєву швидкість руху точки в момент часу і = 2 с.
10. Знайти похідні функцій, використовуючи формули і теореми
про похідні:
А
4) у =» ; б) у = х2 зіп х; 6) у = (1 + зіп х)2}
7)у = /7 + /‘2; 8)ув^; 9)у=_£±’;
2а х— 1
10) у==р/Гсо8х; 11) у = (х — І)2 (х + 1); 12) — 2х$
13)^=7ГТГГ: 14)У = сі§3х;
15) у = (/7+ 1) (Зх2 — 5х + 1); 16) у =
Б
17) у = (х» + 1) (Зх - 2) (1 - х3); 18) у = 1
ат + от2
2х2 + х-Н 5
19) у = х2 _ х ; 20) у — у— ;
21) у = (а + &)/3 + (а + 6)3; 22) у = 5і§ Л- + Ш 21 ?
/ і і уЯ \8
23) у = ах3 + + ^іх У точці х == а; 24) у = —а ;
168
25) у = „ 1 . у точці х = — 1; 26) у = ?5ІГ|ІЖ-.}
х8 — 1 соз 2х
27) у = 2x1 ; 28) у = 2+ 8ІП 2х ;
’ - X8 + 1 1 - зіп 2х
29) у = хвіп — х2 созх; ЗО) у = (х2 + 1)п, де
31) у = Х8ІП* , ; 32) у = соз (Зх2 — 1) + зіп 4.
1 + і§х
В
з,— І 3/ /"ТХ
33) у ж=(1 + /1) ^1- уу + 3|/ — у
34) » = ( та + п У; 35) у = —--------- 3 *-;
\ р / (1 — х2) (1 — 2х8)
36) у = 1 ^у-} і _ у-* : 37> у = І -І- соз 4х 5 *
38) у = соз2 х8; 39) у = і§8 - + 3* ~ ;
5
40) у = (соз 2 ...* + *. — зіп 0,8х ,
11. Знайти кут, під яким синусоїда перетинає вісь Ох, проходячи
через початок координат.
12. Під яким кутом перетинаються криві, задані рівняннями у ==
» ж2 і у = ~ ? Враховувати, що під кутом перетину двох кривих розумі-
ють кут між дотичними, проведеними до кожної кривої в точці їх пере-
тину.
13. Із тотожності
1 + х + х2+ ... +хп = -£—— , х^Ь
знайти формулу для суми 1 + 2х + Зх2 + ,.. + лх”"*"1.
РОЗДІЛ 5
ЗАСТОСУВАННЯ ПОХІДНОЇ
§ 1. Зростання, спадання функції.
Екстремальні точки
1. Поняття зростаючої і спадної функції в точці. Мак-
симум і мінімум функції. Введемо ряд означень. Для цього
припустимо, що функція у = / (х) визначена на деякому
проміжку (а; Ь), а х0 є внутрішньою точкою цього проміжку.
Функція називається зростаючою в точці х^, як-
що існує інтервал (х0 — 6; х0 + 6), де 6 > 0, який знахо-
169
даться у проміжку {а\ Ь} і такий, що ї (х)< ї (х0) для всіх
х з інтервалу (х0 — 8; х0) і ї(х) >/(х0) для всіх х з інтер-
валу (х0; х0 + 8).
Приклад 1. Довести, що функція у = х3 є зростаючою у
точці х0 = 0.
Роз в’я з а н н я. Функція / (х) = х3 визначена на всій
числовій осі, тобто на інтервалі (—оо; + оо). Візьмемо де-
який інтервал, наприклад, (—1; 1), в якому знаходиться
точка х0 = 0. Тоді для кожного х з інтервалу (—1; 0) маємо
[ (х) <0, а для кожного х з інтервалу (0; 1) / (х) > 0.
Оскільки / (0) = 0, то задача розв’язана.
Приклад 2. Довести, що функція у = зіп х у точці х0 =
= 0 є зростаючою.
Розв’язання. Візьмемо інтервал
л л \ <*
---Г’Т’ ЯКИИ
містить точку х = 0. Тоді для кожного х з інтервалу --
0^ зіп х < 0, а для кожного х з інтервалу ^0; -у) зіп х > 0.
У точці х0 = 0 зіп х = 0.
Функція у = / (х) називається спадною у точці х0, як-
що існує інтервал (х0 — 6; х0 + 8), 6 > 0, який міститься
у проміжку (а\ Ь) і такий, що ї (х) > / (х0) для будь-якого
х з інтервалу (х0 — 6; х0) і ї (х) < [ (х0) для будь-якого х з
інтервалу (х0; х0 + 8).
Приклад 3. Довести, що функція у = зіп х у точці х =
= л є спадною.
Розв’язання. Візьмемо інтервал (0; 2л), який
містить точку я Тоді для всіх х з інтервалу (0; я) зіп х >
> 0, а для всіх х з інтервалу (я; 2я) зіп х < 0. У точці
х = я зіп х = 0.
Приклад 4. Довести, що функція у = -^-у точціх = 1 є
спадною.
Роз в’ язання. Візьмемо інтервал (0; 2). Тоді для
всіх х з інтервалу (0; 1) / (х) = -і-> 1 = / (1), а для всіх
х з інтервалу (1; 2) ?(х)< 1.
Якщо існує інтервал (х0 — 6; х0 + 8), де 8 > 0, який
міститься у проміжку (а\ Ь) і такий, що / (х) < / (х0) для
всіх х з інтервалу (х0 — 8; х0 + 8) (х хр), то точку х0 на-
зивають точкою максимуму функції у = / (х), а саме число
/ (хо) — максимумом функції у = / (х).
Приклад 5. Довести, що точка хо=О є точкою максиму-
му функції у = соз х.
170
Розв’язання. Візьмемо інтервал
я п \
2-і — .який
містить точку х=0. Оскільки /(х) = созх у точці х = 0
дорівнює одиниці, а для всіх х з інтервалу І------5-; -й-і
(х =# 0) соз х < 1, то х = 0 є точкою максимуму функції
у = соз х. Число 1 є максимумом функції у = соз х.
Приклад 6. Довести, що точка х = 0 є точкою максимуму
функції
/(*)= і+х»-
Роз в’ язання. Візьмемо інтервал (—1; 1), який
містить точку х = 0 (тут 6 = 1). Тоді / (0) = 1, а для всіх
х з інтервалу (—1; 1) (х =И= 0) / (х) < / (0). Отже, точка х =
= 0 є точкою максимуму функції у = а число 1 є
максимумом заданої функції.
Якщо існує інтервал (х0—6; х0 + 6), який міститься у
проміжку {а; Ь) і такий, що І (х) > { (х0) для всіх х з інтер-
валу (х0 — 6; х0 + 6) (х =#= х0), то точку х0 називають точ-
кою мінімуму функції у = І (х), а саме число [(х0) — мі-
німумом функції у = / (х).
Приклад 7. Нехай / (х) = х2. Довести, що точка х = 0
є точкою мінімуму даної функції.
Роз в’ язання. Візьмемо інтервал (—1; 1). Тоді
} (0) = 0, але для всіх х маємо х2 > 0. Тоді точка х = 0 є
точкою мінімуму функції у = х2, а число / (0) = 0 — мі-
німумом заданої функції.
Приклад 8. Довести, що точка х = 1 є точкою мінімуму
функції / (х) = | х — 1 |.
Роз в’ язання. Візьмемо інтервал (0; 2) (6 = 1).
У кожній точці цього інтервалу / (х) > 0, а в точці х = 1
І (X) = 0. ,
Отже, х = 1 є точкою мінімуму функції у = І х — 1 |,
а число 0 — мінімумом- заданої функції.
Зазначимо, * що точки максимуму і мінімуму функції
називають ще екстремальними точками, а
максимум і мінімум називають екстремумом функ-
ції (екстремум походить від латинського слова ехітетиш,
що означає «крайній»).
Графік точок зростання (спадання) та екстремальних то-
чок зображено на рис. 5.1.
Якщо функція є зростаючою (спадною) у кожній внутріш-
ній точці проміжку {а\ Ь), то вона називається зростаючою
(спадною) на цьому проміжку.
171
Наприклад, функція у = х8 є зростаючою в інтервалі
(—оо; 4-оо), а функція у == -і-----спадною у півінтерва-
лі (0; -Ьоо). Проте є функції, для яких у розглядувано-
му проміжку є як точки зростання, так і точки спадання,
а також екстремальні точки. Прикладом такої функції
ця функція зростає, а в інтервалі спадає. Точ-
ки -----у- є точками екстремуму (див. рис. 1.17)'.
Для функції, яка має похідну, існують прості достатні
ознаки зростання (спадання) її в точці.
Теорема 1. Якщо функція у = / (х) у внутрішній точці
х0 проміжку (а; Ь) має похідну Г (х0) і (х0) > 0 (/' (х0) <
< 0), то функція у = ( (х) в точці х0 зростає (спадає).
Доведення. Розглянемо випадок, коли /' (х0) >
> 0. Доведемо, що в такому разі функція у = / (х) в точці
х0 зростає. Скористаємось означенням похідної
/' (х0) = Ііт ./(^о + у-/(-»о). ,
Дх->0
де Дх = X — х0.
Тоді з попередньої рівності та умови теореми випливає
така нерівність:
Ііт /(*)-/(*») >0
Х-^Хц Х Х0
При цьому знайдеться інтервал (х0 — 6; х0 + 6), 6 > 0>
точки х0, такий, що для всіх х з цього інтервалу, крім,
можливо, точки х = х0, справджуватиметься нерівність
Нехай х0 — 6 < х < х0. Тоді з попередньої нерівності
випливає, що й / (х) > / (х0).
172
Нехай х0 < х < х0 + 6. Тоді з тієї самої нерівності ма-
ємо / (х) > / (х0).
Отже, існує інтервал (х0 — 6; х0 + б) такий, що для всіх
х з інтервалу (х0 — 6; х0) матимемо ї (х) < / (х0), а для всіх
х з інтервалу (х; х0 + б) матимемо / (х) > / (х0), а це й
означає, що в точці х0 функція є зростаючою. Теорему дове-
дено.
Аналогічно доводить-
ся теорема і для /' (х0) <
<0.
Приклад 9. Довести,
що функція у = агсі§ хє
зростаючою в інтервалі
(—°° і 4"°°).
Розв’ язання.
В курсі математичного
аналізу доведено, що
(Х) в 1 +хя •
У кожній точці інтервалу (—оо; Ч-оо) ? (х) > 0. От-
же, за попередньою теоремою функція у = агсІ§ х є зро-
стаючою у кожній точці даного інтервалу. Це видно з графі-
ка цієї функції (див. рис. 2.9).
Приклад 10. Знайти інтервали зростання і спадання
функції:
а) /(х) = х3 + 2х —5; б) /(х) = .
1 І Л
Р о з в’ я з а н н я. а) Знайдемо похідну /' (х) = Зха 4-
+ 2. Неважко помітити, що при будь-якому х з інтервалу
(—оо; +оо) /' (х) > 0. Отже, функція / (х) = х3 4- 2х — 5
на всій числовій осі є зростаючою.
б) Обчислимо похідну
Г (г\ — 9 (1 Ч- х2) — х . 2х _ р 1-х2
(1-|_Х2)2 — (14-хЯ)а •
Знайдемо точки, в яких (х) > 0. Це всі точки, в яких
1 —х2>0. Розв’яжемо нерівність х2< 1, |х|< 1, або
—1 <х< 1.
Отже, в інтервалі (—1; 1) функція зростає. Тоді в інтер-
валах (—оо; —1), (1; -|-оо) функція спадає. Звідси робимо
висновок, що точка х = —1 є точкою мійімуму, а точка х =
= 1 — точкою максимуму даної функції. Мінімум функції
дорівнює / (—1) = —1, а максимум / (1) = 1 (рис. 5.2).
173
§ 2. Локальний екстремум функції
У § 1 дано означення екстремальних точок і екстремуму
функції. Далі будуть доведені теореми, за допомогою яких
можна знаходити екстремальні точки, а отже, і екстремум
функції. Іншими словами, ці теореми дадуть змогу дослі-
джувати функції на екстремум.
Спочатку зазначимо, що екстремальні точки, як випливає
з означення, це такі точки, в яких функція набуває відпо-
відно найбільшого чи найменшого значень порівняно із
І значеннями функції, яких вона набу-
1 ває в точках, досить близьких до екст-
I У=*5 ремальної. Такий екстремум назива-
/ ють локальним екстремумом (слово
І «локальний» походить від латинського
/------у слова Іокаїіз, що означає «місцевий»).
У' Отже, не слід плутати локальний
/Ияї Т максимум (мінімум) з найбільшим (най-
< меншим) значенням функції, якого
/ вона набуває (досягає) на проміжку.
І Локальних максимумів і мінімумів
/ функція може мати кілька, а найбіль-
I ше значення (його ще називають абсо-
Рис. 5,3 лютним максимумом), якщо воно іс-
нує, єдине. Це саме стосується і най-
меншого значення (абсолютного мінімуму) функції. Окремий
локальний мінімум може бути більшим за окремий локаль-
ний максимум, як це показано, наприклад, на рис. 5.10.
Функція, графік якої тут зображено в точці х4, має мінімум,
більший за максимум, якого вона набуває в точці хг.
Розглянемо необхідні умови існування екстремуму
функції. Доведемо теорему.
Теорема 2. Якщо функція у = (х) у внутрішній точці
х0 проміжку (а\ Ь) має екстремум, то в цій точці похідна
Ґ (*о)> якщо вона існує, дорівнює нулю.
Доведення. Доведемо теорему методом від супро-
тивного. Нехай в точці х0 £ (а; Ь), яка є екстремальною для
у = / (х), існує похідна (х0) і (х0) 0. Припустимо, що
/' (х) > 0. Тоді за теоремою 1 у = / (х) в точці х0 зростає.
Отже, х0 не є екстремальною точкою. Якщо (х0) < 0, то
// == / (х) в точці х0 спадає. Дістали суперечність. Отже,
теорему доведено.
З цієї теореми випливає такий факт: коли в точці х0 іс-
нує похідна (х0) Ф 0, то у = { (х) в точці х0 екстремуму
мати не може.
174 ,
Звідси дістанемо таку необхідну умову існування екс-
тремуму: екстремум може існувати в таких точках, де похід-
на, якщо вона існує, дорівнює нулю.
Внутрішня точка х0 проміжку (а\ Ь} називається ста-
ціонарною точкою функції у = / (х), якщо в цій точці
/ (*о) = о*
Отже, згідно з попередніми міркуваннями функція мо-
же мати екстремум в стаціонарних точках. Проте не слід
вважати, що функція кожного разу в стаціонарній точці
має екстремум, оскільки в цій точці виконується тільки
необхідна умова існування екстремуму. Стаціонарні точки
можуть бути точками, в яких функція зростає або спадає.
Приклад 1. Нехай / (х) = х3. Тоді (х) = Зх2. В точці
х = 0 похідна (0) дорівнює нулю. Отже, необхідна умова
існування екстремуму виконується. Проте задана функція
в точці х = 0 екстремуму не має, вона в цій точці зростає
(рис. 5.3).
З наведеного прикладу випливає, що стаціонарні точки
функції не обов’язково є екстремальними. Вони є екстре-
мальними, якщо в цих точках виконуються достатні умови
існування екстремуму. Доведемо таку теорему.
Теорема 3. Нехай х0 —стаціонарна точка функції у =
= / (х), яка в цій точці є неперервною, і існує окіл точки
(х0 — б; х0 + б), в якому у = І (х) має похідну (х). Тоді:
1) якщо в інтервалі (х0 — б; х0) похідна (х) > 0, а в ін-
тервалі (х0; х0 + б) похідна (х) < 0, то х0 є точкою мак-
симуму функції у = І (х); 2) якщо в інтервалі (х0 — б; х0)
/' (х) < 0, а в інтервалі (х0; х0 + б) (х) > 0, то х0 є точ-
кою мінімуму функції; 3) якщо в обох інтервалах (х0 — б; х0)
і (^о» Хо + 8) похідна і' (х) має той самий знак (набуває тіль-
ки додатних, або тільки від'ємних значень), то х0 не є екс-
тремальною точкою функції у = / (х).
Доведення: 1) Нехай (х) > 0 в інтервалі (х0 —
— б; х0), а в інтервалі (х0; х0 + б) (х) < 0. Тоді для всіх
х Є (х0 — б; х0) функція у = { (х) зростає, а для всіх х £
€ (х0; х0 + б) у = / (х) спадає. При х0 — б < х < х0 справ-
джується нерівність / (х) < / (х0), а прих0 < х < х0 + б —
нерівність / (х) < / (х0).
Отже, існує окіл точки х0, а саме інтервал (х0 — б; х0 +
+ б) такий, що для всіх х £ (х0 — б; х0 + б), крім х = х0,
значення функції в х менші за значення функції в точці х0,
а це й означає, що х0 є точкою максимуму функції у = ? (х).
2) Нехай в інтервалі (х0 — б; х0) похідна /' (х) < 0, а в
інтервалі (х0; х0 + б) похідна (х) > 0 і для всіх х £ (х0 —
— б; х0) функція у = І (х) спадає, тобто / (х) > / (х0), для
175
всіх х € (х0; х0 + 6) функція у = [ (х) зростає, тобто / (х) >
> / (х0). Отже, інтервал (х0 — б; х0 + б) має'ту властивість,
що функція у = І (х) при х0 — б<х<х0Н~б набуває
значень, більших ніж / (х0), а це й означає, що х0 є точкою
мінімуму функції у = / (х).
3) Нехай, наприклад, в інтервалах (х0 — б; х0), (х0; х0 +
+ б) похідна /' (х) > 0. Тоді функція у = / (х) в цих ін-
тервалах зростає і при х0 — б < х < х0 справджується не-
рівність / (х) < / (х0), а при х0 < х < х0 + б — нерівність
/ (х) > /= (х0).
Отже, функція у = / (х) в точці х0 зростає, тобто х0 не є
екстремальною точкою.
Якщо /' (х) в обох інтервалах (х0 — 6; х0), (х0; х0 + 6)
набуває від’ємних значень, то, як і у попередньому випадку,
можна показати, що // = / (х) в точці х0 спадає. Теорему до-
ведено.
Із доведених теорем випливає така схема дослідження
функції на екстремум.
1) Необхідно знайти стаціонарні точки даної функції.
Для цього треба розв’язати рівняння /' (х) = 0, причому
з коренів даного рівняння вибрати тільки дійсні і ті, які є
внутрішніми точками області існування функції.
Стаціонарні точки і точки, в яких похідна першого по-
рядку не існує, називаються критичними. Якщо
критичних точок функція у = / (х) не має, то вона не має
і екстремальних точок. Така функція не має екстремуму.
Якщо критичні точки є, то їх треба досліджувати далі.
2) У кожній стаціонарній точці треба перевірити зміну
знака похідної. Якщо /' (х) при переході через стаціонарну
точку (зліва направо) змінює знак з «+» на «—», то ця точ-
ка є точкою максимуму. Якщо (х) змінює знак з «—» на
«+», то ця стаціонарна точка є точкою мінімуму. Якщо при
переході через стаціонарну точку знак похідної не зміню-
ється, то розглядувана точка не є екстремальною точкою да-
ної функції.
Приклад 2. Дослідити функцію / (х) = х8 на екстремум.
Розв’язання. Використаємо наведену схему.
Знайдемо похідну (х) = Зх2. Розв’яжемо рівняння (х)= 0,
Зх2 = 0, звідки дістанемо одну стаціонарну точку х = 0.
З’ясуємо, чи є зміна знака похідної. Оскільки Зх2> 0 для
всіх х =/= 0, то (х) не змінює знак при переході через точку
х = 0. Отже, х0 = 0 не є екстремальною точкою. Функція
у = х3 екстремуму не має.
Приклад 3. Дослідити функцію / (х) = х2 на екстремум.
Розв’язання. Знаходимо /' (х) = 2х і розв’язу-
176
ємо рівняння 2х = 0, звідки дістанемо одну стаціонарну
точку х = 0.
Перевіряємо достатні умови. Для цього візьмемо по-
близу точки х = 0 від’ємне значення х, наприклад х = —Н
(И > 0 — дійсне число) і обчислимо похідну /' (—И) = —2И.
Оскільки Н > 0, то —2Н < 0. Отже, зліва від точки х = 0
похідна /' (х) має від’ємний знак.
Обчислимо /' (х) в точці х = Н. Маємо (/і) = 2к > 0.
Отже, справа від точки х = 0 похідна /' (х) має додатний
знак.
Таким чином, похідна (х) при переході через точку
х = 0 змінює знак з «—» на «+». Звідси х = 0 є точкою мі-
німуму, а сама функція в точці х = 0 має мінімум. Щоб
знайти цей мінімум, треба знайти значення функції в цій
точці. Дістанемо / (0) = 0. Зазначимо, що перевірку до-
статніх умов у випадку, коли функція має скінченну множи-
ну стаціонарних точок, можна дещо спростити. Справді,
нехай, наприклад, хр х2, ..., хк — стаціонарні точки функ-
ції у = / (х), які занумеровано в порядку зростання, тобто
Хі < Х2 < ... < Х/г-1 < Хк.
Розглянемо інтервали
(а; хх), (хх; х2), ... , (х*_і; хЛ), (хЛ; &),
де числа а і Ь належать області визначення функції. Тоді в
кожному з інтервалів не має екстремальних точок. Отже, в
цих інтервалах похідна /' (х) має сталий знак. Тому, обчис-
ливши похідну у будь-якій точці інтервалу, можна зробити
висновок про знак похідної в усьому інтервалі.
Приклад ’ 4. Дослідити на екстремум функцію / (х) =
= (х + І)2 (х — 2)3.
Розв’язання. Знайдемо
/'(х) = 2(х+ 1)(х —2)3 + 3(х+ 1)2(х —2)2 =
= (х+ 1)(х-2)2(2х-4 + Зх+3) =
= (х+ 1)(х — 2)(5х— 1).
Розв’яжемо рівняння (х) = 0: (х + 1) (х — 2)2 (5х —
— 1) = 0. Звідси знаходимо стаціонарні точки хх = —1,
х2 = 4-, х3 = 2. Розглянемо інтервали
О
(_оо;_і), (4~; 2)> (2;+со).
Для визначення знака похідної обчислимо останню
в довільних точках, які належать даним інтервалам.
177
Візьмемо, наприклад, такі точки: —2; 0; 1; 3. Тоді
/'(—2) = — 42 (—11) > 0 (+);
Г (0) = —4<0 (-);
/'(1) = 8>0 (+);
(3) = 4 • 14>0 (+).
Отже, При переході через точку Хі = —1 похідна змі-
нює знак з «+» на «—». У цій точці функція має максимум,
який дорівнює / (—1) = —27.
При переході через точку х2 = -у- похідна змінює знак
з «—» на «+». У цій точці функція має мінімум =
324
~ 125 •
При переході через стаціонарну точку х3 = 2 похідна
знака не змінює. Точка х3 = 2 не є екстремальною для за-
даної функції.
§ 3. Знаходження найбільшого
і найменшого значень функції
Нехай на відрізку [а; &] задана неперервна функція у =
= / (х). Тоді, як доводиться в курсі математичного ана-
лізу, серед множини значень такої функції є найбільше і
найменше числа. Ці числа і називаються відповідно най-
більшим і найменшим значенням функції. Постає питання:
як знайти точки відрізка [а; Ь], в яких функція набуває
свого найбільшого і наймен-
шого значень?
0 о. С? Ь х
Зазначимо, що функція може набувати свого найбіль-
шого і найменшого значень як на кінцях відрізка, так і у
внутрішніх його точках.
Так, на рис. 5.5 зображено графік неперервноїфункції,
яка у внутрішній точці сг відрізка [а; Ь] набуває найбіль-
шого значення, а у внутрішній точці с2 — найменшого.
178
На рис. 5.4 зображено графік функції, яка на кінцях від-
різка набуває найменшого і найбільшого значень.
Може статися і так, що одного із значень функція набу-
ває всередині відрізка, а другого — на одному з кінців.
Так, на рис. 5.6 зображено графік неперервної функції, яка
в лівому кінці відрізка (точці а) набуває найменшого зна-
чення, а у внутрішній точці (точці с) — найбільшого.
Якщо функція набуває найбільшого (найменшого) зна-
чення всередині відрізка, то це найбільше (найменше) зна-
чення є одночасно і локальним
максимумом (мінімумом) за- /Т\
даної функції. Звідси випли- / \
ває спосіб знаходження точок, / \ /
в яких функція набуває най- /
більшого (найменшого) зна- ?
чення.
Щоб знайти найбільше
(найменше) значення неперерв- _______________________►
ної функції на відрізку [а\ Ьі, 0 ас 6 х
треба знайти всі локальні мак- Рис, 5.6
симуми (мінімуми) і порівняти
їх із значеннями функції, яких вона набуває на кінцях від-
різка. Найбільше (найменше) число серед утвореної множини
і буде найбільшим (найменшим) значенням функції, заданої
на відрізку [а; Ь].
Оскільки неперервна функція обов’язково набуває сво-
го найбільшого (найменшого) значення і воно може досяга-
тися тільки в стаціонарних точках і на кінцях відрізка, то
немає потреби перевіряти достатні умови існування екстре-
муму функції в стаціонарних точках. Досить обчислити
значення функції в цих точках і порівняти їх із значеннями
функції на кінцях відрізка, тобто з числами / (а) і / (Ь). Най-
більше і найменше з усіх чисел і будуть відповідно найбільшим
і найменшим значеннями функції у = }(х) на відрізку [а; Ь].
Якщо між точками (кінця відрізка) а і Ь знаходиться
тільки одна критична точка х0£(а; Ь) і в ній функція має мак-
симум (мінімум), то без порівняння з числами / (а) і / (&) мож-
на стверджувати, що цей максимум (мінімум) і є найбіль-
шим (найменшим) значенням функції на відрізку [а\ Ь].
У цьому разі не треба обчислювати значення функції на
кінцях відрізка, а дослідити відразу точку на екстремум.
Значення функції в цій точці й буде відповідно найбіль-
шим (найменшим) значенням функції.
Приклади. Знайти найбільше і найменше значення
функції: і
179
1) ї (х) = 2х8 — Зх2 — 12х — 1 на [— 2; -у]'.
2) / (х) = зіп2 х на [0; 2л].
Р о з в’ я з а н н я. 1) Знайдемо стаціонарні точки. Для
цього знайдемо похідну /' (х) = 6х2 — 6х — 12. Розв’язу-
ючи рівняння 6х2 — 6х — 12 — 0, дістанемо стаціонарні
точки х4 = —1, х2 = 2.
Обчислимо значення функції в точках хх, х2, а також на
5
кінцях відрізка, тобто в точках х3 = —2, х4 = -у. Маємо
Н- 1)=8.
/(2) =-19; /(-2)=-3; /(4) =
= -16-1-.
Отже, найбільше значення дорівнює / (—1) = 8, най-
менше — / (2) = —19.
2) Знайдемо стаціонарні точки з рівняння
(х) = 0, зіп 2х = 0.
Звідси х = -£ к, к — 0, ± 1, ± 2, ....
Ми повинні взяти точки, які б належали відрізку [0;
2л]. Такими точками є: хх = 0, х2 — -у, х3 = л, х4 =
х6 = 2л.
Отже, маємо три стаціонарні точки -у, л, 4. Точки0
і 2л збігаються з кінцями. Обчислюємо значення функції в
цих точках: І (0) = / (л) = / (2л) = 0; / (у-) = / (4) = Е
Найменше значення функції дорівнює нулю, найбільше —
одиниці.
Розглянемо кілька практичних задач, розв’язання яких
зводиться до знаходження найбільшого чи найменшого зна-
чення певної функції.
Задача 1. Нехай маємо квадратний лист заліза із сто-
роною а. Треба в кожному куту його відрізати такі квад-
рати, щоб після згинання країв можна було одержати ящик
найбільшої місткості.
Р о з в’ я з а н н я. Позначимо через х довжину сторони
того квадрата, який треба відрізати (рис. 5.7), а через V
об’єм ящика. Тоді V є функцією від х, яка виражається фор-
мулою
V (х) = (а — 2х)2 х, '
180
причому х змінюється на відрізку [О; -у1. Оскільки V(х)
є неперервною функцією на відрізку р; , то вона
набуває на ньому найбільшого значення. На кінцях від-
різка V (х) не може 'набувати найбільшого значення, бо в
цих точках V = 0. Отже, шукана точка знаходиться всереди-
ні відрізка. Знайдемо її. Для цього обчислимо спочатку
похідну
V' (х) = — 4 (а — 2х) х 4- (а — 2х)2 = (а — 2х) (а — 6х)
і розв’яжемо рівняння (а — 2х) х
X (а — 6х) = 0.
Звідси дістанемо корені хх = і х2 = . Точка Хі
не є стаціонарною, бо це кінець відрізка, на якому розгля-
дається функція V — V (х). Точка х2 знаходиться всереди-
ні даного відрізка. Отже, точка х2 = -|- є стаціонарною і
точкою максимуму. У ній функція V = V (х) набуває най-
більшого значення, яке дорівнює V а9.
Задача 2. Нехай електрична лампочка переміщається
(наприклад на блоці) уздовж вертикальної прямої ОВ
(рис. 5.8). На якій відстані від горизонтальної площини
треба її розмістити, щоб в точці А цієї площини освітленість
була найбільшою (ОА = а)?
Розв’язання. З курсу фізики відомо, що освітле-
ність прямо пропорційна зіп <р і обернено пропорційна квад-
рату відстані АВ = г, тобто Е = к де к — коефіці-
єнт пропорційності, який залежить від сили світла лампи.
За незалежну змінну візьмемо висоту х = ОВ. Тоді
8ІПф= -у-,
г =Ух2 + а2, ОсхСЧ-00-
181
Отже,
Е = к-------Х~Г
(Xі + а2)2
Знайдемо похідну від Е (х)
а2 — 2х2
Т
(х2 + а2) 2
Е’ (х) = к
і розв’яжемо рівняння
(л» + аг)2
• . а
звідси знаходимо стаціонарну точку х = -уу-.
Оскільки функція Е (х) має тільки одну стаціонарну
точку, а в умові задачі сказано, що існує положення лампоч-
ки, при якому освітлен-
ня в точці А найбільше,
то х є шуканою точкою.
Задача 3. Визначити
_розміри такого відкрито-
го басейну з квадратним
дном і об’ємом V = 32 м3,
щоб на облицьовування
його стін і дна було ви-
трачено найменшу кіль-
кість матеріалу.
Розв’язання.
Позначимо довжину сторони основи через х, а довжину висо-
ти через у. Тоді V (х; у) = х2у = 32.
Площа бічної поверхні басейну разом із площею дна до-
рівнює 5 = х2 + 4ху. Знайшовши з попередньої рівності
у і підставивши в останню рівність його значення, дістане-
мо таку функцію від х:
О / \ 2 І 128
5 (х) - х2 + -у- •
Знайдемо похідну цієї функції
128
X2
5' (х) = 2х
Розв’язуючи рівняння
2х 128
0,
X2
знаходимо стаціонарну точку х = 4.
182
Оскільки існує тільки одна стаціонарна точка, то вона
і буде точкою мінімуму. Отже, найменші розміри басейну за-
даного об’єму V = 32 м8 такі: х = 4 м; у = 2 м.
Задача 4. Посудина з вертикальною стінкою і висотою
И стоїть на горизонтальній площині (рис. 5.9). На якій гли-
бині треба розмістити отвір, щоб дальність вильоту води з
отвору була найбільшою (швидкість рідини, що витікає за
законом Торрічеллі, дорівнює У де х — глибина роз-
міщення отвору, § — прискорення вільного падіння)?
Роз в’ язання. Позначимо через Н відстань отво-
ру в посудині від горизонтальної площини, а через І — від-
стань точки А від стіни посудини. Тоді І = Уі, де і — чає
вильоту води з отвору на площину (у точку А).
З курсу фізики відомо, що
і= а6о
Тоді
/ (х) = КУ 2 ~ — 2 Ух(Н — х), 0<.х<_Іі.
Знайдемо похідну
Розв’язуючи рівняння
й — 2х ___0
х (й — х) ’
й
знаходимо стаціонарну точку х = — .
Оскільки це єдина стаціонарна точка, то вона і буде шу-
каною.
§ 4. Загальна схема дослідження функції
та побудова її графіка
Нехай на відрізку [а; Ь] задана неперервна функція у =
= / (х), графіком якої є деяка лінія. Виникає питання: як
побудувати цей графік? Один з методів побудови графіка
функції є побудова за точками. При такій побудові графіка
на площині будують кілька точок, координати яких задо-
вольняють рівняння у — ? (х), а потім ці точки сполучають
суцільною лінією. Зрозуміло, чим більше таких точок буде
нанесено на площину, тим точніше лінія, що їх сполучає,
183
буде відбивати графік функції у = / (х). Але при-такому
методі побудови графіка не відтворюється реальна поведін-
ка функції. Так, наприклад, нехай графіком функції є су-
цільна лінія, яка зображена на рис. 6.10, а лінія, яка утво-
рюється при сполученні семи точок площини хОу, зображе-
на штриховою лінією. Як бачимо, побудований і реальний
графіки однієї і тієї ж самої функції значно відрізняються.
Отже, до побудови графіка функції її треба дослідити. Як
правило, це роблять за
такою схемою.
1)„3найти область іс-
нування функції.
2) Знайти точки пере-
тину графіка з коорди-
натними осями. Для цьо-
го треба розв’язати дві
системи рівнянь:
( У=Ч(х), і У^Нх),
І у = 0 ( х = 0.
Перша система дає точки перетину з віссю Ох, а друга —
з Оу.
3) Дослідити функцію на періодичність, парність і не-
парність. З’ясування цих питань полегшить побудову гра-
фіка у тому розумінні, що її доведеться виконувати не в усій
області існування функції, а тільки в певній її частині. Так,
якщо у — { (х) — періодична функція з періодом Т > 0, то
графік досить побудувати на відрізку числової осі, довжина
якого дорівнює Т, а потім цю частину графіка повторити на
кожному з відрізків довжини Т. Якщо функція парна, то
графік функції симетричний відносно осі Оу, якщо непар-
на — то відносно початку координат. Тому достатньо побу-
дувати графік тільки при х 0, а потім симетрично відо-
бразити його і для х < 0.
4) Знайти значення функції на кінцях відрізків, де ви-
значена функція. Якщо область існування функції є інтер-
валом (півінтервалом) або кількома інтервалами (півінтер-
валами), то треба знайти граничне значення функції, коли
х наближається до одного з кінців розглядуваних про-
міжків.
5) Знайти інтервали монотонності функцій. Тоді ми зна-
тимемо, де крива графіка зростає, а де спадає.
6) Знайти екстремальні точки і побудувати їх на пло-
щині.
7) На основі дослідження побудувати графік функції.
184
Приклади. Дослідити функції та побудувати їхні гра-
фіки:
У3
а) у = 2х4 — Xа + 1; б) у =^~ГГ\-
Р о з в* я з а н н я. а) Дослідимо функцію у — 2х4 —
— Xа + 1 за наведеною схемою.
1) Вона є многочленом, областю існування якого є вся
множина дійсних чисел, тобто інтервал (—оо; +оо).
2) Знаходимо точки перетину графіка з координатними
осями. При перетині з віссю Ох (у = 0) маємо рівняння
2х4 — ха + 1 = 0. Це рівняння дійсних коренів не має,
тобто крива осі Ох не перетинає. Для знаходження точок
перетину графіка з віссю Оу покладемо х = 0. Маємо у =
= 1. Отаке, в точці (0; 1) графік функції перетинає
вісь Оу.
3) Функція неперіодична, але парна. У подальшому
будемо досліджувати задану функцію тільки при х 0.
4) Многочлен є функцією, неперервною на всій число-
вій осі.
5) Досліджуємо функцію на кінцях інтервалів. У точці
X = 0 маємо у = 1.
6) Для знаходження інтервалів монотонності треба роз-
в’язати нерівність у' > 0, у' < 0. У точках, де у' > 0,
функція зростає, а де у' < 0 — спадає.
Обчислимо
у' «вх8 — 2х = 2х(4ха — 1), х(4ха— 1)>0.
Оскільки х>0, то 4х®—1>0. Звідси ха>-т- або
4
1 ~ . І 1 . \ і
Отже, в інтервалі ; +°°) функція зростає,
тоді в інтервалі (О; вона спадає.
7) Досліджуємо функцію на екстремум. Для цього розв’я-
жемо рівняння х (4х2 — 1) = 0. Дістанемо такі стаціонарні
точки: хх = 0, х2 = (від’ємні значеннях не розглядаємо).
Неважко показати, що хх = 0 е точкою максимуму, а х2 =
1 . .
== -^-мінімуму, причому
{/так = / (0) ж 1,
(1 7 \
-у- ; -§-) — екстре-
мальні. Графік заданої функції зображено на рив. 5.11.
185
б) 1) Знаходимо область існування функції. Оскільки
задана функція дробово-раціональна, то вона не існує в тих
точках, де знаменник дорівнює нулю, тобто х2 — 1 = 0,
звідки х = ±1.
Отже, областю існування функції є об’єднання множин
(-оо; -1) 0 (-1; 1) и (-1; + оо).
2) Визначимо точки перетину графіка з осями коорди-
нат. Нехай: у = 0, тоді х — 0; х = 0, тоді у = 0. Отже,
графік перетинає координатні
осі в точці О (0; 0), тобто гра-
фік проходить через початок
координат.
3) Функція неперіодична.
Вона непарна, тому розгля-
датимемо тільки х > 0.
Рис. 5.12
Рис. 5.11
4) Чисельником і знаменником є многочлени, які непе-
рервні на всій числовій осі. Функція неперервна на всій
числовій осі крім точки х = 1.
5) Знаходимо похідну
/__ (х2 — 1) • Зх2 — х8 • 2х _ х2 (ха — 3)
У ~ (X2 — І)2 “ (X2 — І)8 ‘
х2 (х2_3)
Розв’яжемо нерівність у' > 0; ^2__ ^2 - > 0. Помно-
живши обидві частини нерівності на додатні множники
і (х2 — І)2, дістанемо ха — 3 > 0, звідки х > КЗ. Отже,
в інтервалі ("И3; +°°) функція зростає, а в інтервалах (0; 1),
(1; V3) — спадає.
6) Знайдемо екстремальні точки. Розв’яжемо рівняння
/ = 0:
х2(х2-3) п
(Xі— і)2 ’
звідки знайдемо стаціонарні точки Хі = 0, х2 = V3.
_При переході х через точку Хі похідна знака не змінює,
а при переході х через точку х2 похідна у' змінює знак з «—»
186
на «+». Тому Хі не є екстремальною точкою, а х3 е точкою
мінімуму і
Утіп = /(/3) = -ф- .
7) Графік даної функції зображено на рис. 5.12.
Запитання І завдання для повторення
1. Яка функція називається зростаючою (спадною) в точці?
2. Яка функція називається зростаючою (спадною) на інтервалі?
3. Сформулювати ознаку зростання (спадання) функції в точці,
4. Сформулювати ознаку зростання (спадання) функції на інтер-
валі.
5. Яка точка називається точкою максимуму (мінімуму) функції?
6. Що називається максимумом (мінімумом) функції?
7. Яка точка називається екстремальною для функції у = / (х)?
8. Яка точка називається стаціонарною для функції у = / (х)?
9. Чи буде стаціонарна точка екстремальною для функції у = / (х)?
Навести приклади.
10. Сформулювати необхідну умову існування екстремуму функ-
ції.
11. Сформулювати правило дослідження функції на екстремум.
12. Що називається найбільшим і найменшим значеннями непе-
рервної функції, заданої на замкнутому відрізку?
13. В яких точках відрізка неперервна функція може досягати сво-
го найбільшого і найменшого значень?
14. Сформулювати правило знаходження найбільшого і наймен-
шого значень функції.
Вправи
1. Знайти інтервали зростання і спадання функцій:
А
1) у = х4; 2) у = (х — 2)2; 3) у = 2 — х3;
4)г/=14-—; 5) у — ах2 + Ьх + с; 6) г/= 1<х?
З 1 1
7) У = х —2 ! 8) У = ~х8 +~2'х2 + х— 2!
Б
9) ((х) = (х-3) Ух; 10) Г (х) = -фр ; 11) /(х) = х-х»і
12) / (х) = Ух2 — 2х; 13) / (х) = х3 + Зх2 + х — 8;
14) § (х) = х4 — 4х + З,
В
х3
15) у = х4—2х2 —3; 16) і—х і 17) у =/х — 4х3;
18) у = І/'х3 — Зх; 19) у = зіп х — -1- х; 20) у = (х — І)3 (2х + З)2.
2. Знайти локальні екстремуми функцій:
187
А
1)і/ = 4х— х2; 2) # = 2х7 8 9 + 6х2—12х + 100; 3) у =-1_х>
х
4) у = 1ґх; 5) £/= зіп х; 6) у «= (а — х) (а — 2х),
Б
7) Цх) = 3х'-Ь*- 8) /(х)= * 4-Х;
4 х
9) / (х)-х8-2х + 2 10 } = _ 2)4}
X— 1
Н)/ (*) = зіп х + соз х; 12) / (х) = (х + 1) Кх,
В
13) у = * (х- 12)2; 14) у = -4=3 5
х2 — 4х
15)^=~2Т^"’
- 4
17) У = V з зіп X — соз х; 18) у = -у==-.
3. Знайти найбільше і найменше значення функцій:
1)
2)
3)
4)
б)
6)
А
у = -А- х2 — 2х2 + 3 на відрізку [— 1; 2];
у = х4 — 8х2 + 3 на відрізку — 2; 2];
у = -2- х — зіп х на відрізку 0; .
2
Б
гз
у = —. — 6х2 + 32х; на відрізку [0; 9)}
о
^ = х + К*ї на відрізку [1; 4];
У = „ 1 , на відрізку
Xі — 1
1 . 1
2 1 2
В
7) у =—х4 + 2х2 + 3 на відрізку [—0,5? 0,7);
2
8) у » х 3 (х — 2) на відрізку [— 8; — 1 ];
9) у = х + сі£ х на відрізку — -2-; 4г •
І 0 о і
4. Розв’язати задачі на знаходження найменшого та найбільшого
значень функцій:
А
1) Знайти число, яке, будучи додане до свого квадрату, має наймен-
шу суму.
2) Знайти найбільшу площу прямокутника, вписаного в круг раді-
уса г,
3) 3 квадратного листа жерсті зі стороною а треба виготовити бак
з квадратною стороною без кришки найбільшого об’єму,
188
Б
4) Є проволока довжиною а метрів. Треба огородити цією проволо-
кою прямокутну ділянку землі, одна сторона якої прилягає до будинку,
так, щоб площа огородженої ділянки була найбільпїою.
5) Із всіх кругових секторів, що мають даний периметр, знайти сек-
тор з найбільшою площею.
Вказівка: периметр сектора р = 2г + аг, де г — радіус сек-
тора і а — відповідний центральний кут.
В
6) Друкований текст (разом з проміжками між рядками) однієї сто-
рінки книги повинен займати 5 см2. Верхні і нижні поля сторінки по-
винні мати ширину а см, бічні — Ь см. Які найвигідніші розміри сто-
рінки, якщо враховувати лише економію паперу?
В
7) Із всіх прямокутників, що мають периметр 20 см, знайти той, у
якого діагональ найменша.
8) Міцність балки прямокутного перерізу пропорціональна її
ширині і квадрата її висоти, тобто р = кху2. Який периметр повинен ма-
ти брус, вирізаний з циліндричної колоди радіуса /?, щоб його міцність
була найбільшою?
9) Вартість (за годину) утримання баржі складається з двох ча-
стин: вартості палива, яка пропорційна до куба швидкості баржі, і вар-
тості амортизації баржі (заробітна плата команди, обладнання та ін.).
Загальна вартість утримання баржі за годину, таким чином, виразить-
ся формулою 5 = ау2 + Ь, де V — швидкість судна в км/год; а і Ь — ко-
ефіцієнти, задані для кожного судна.
Визначити, при якому V загальна сума утримання на 1 км шляху
буде найменшою, якщо а = 0,005, Ь = 40.
5. Дослідити функції і побудувати графіки:
А
1) ^ = Х2 —5x4-6} 2) у = 1 — 2х2 —
3) у = — х2 4- 5х — 4; 4) у = х4 — 2х2 — 3.
Б
5) ^ = -х4 + 2х2 + 3; '6) у = хЄІ-1;
7) у ~п~ ; 8) У = +
х (X і;
В
9) у == х4 — 10х2 4-9; 10) у = 2 | х | — х2;
П) у = зіп 2х 4- 2 зіп х; 12) у = .
х2— 1
РОЗДІЛ 6
ІНТЕГРАЛ І ЙОГО ЗАСТОСУВАННЯ
§ 1. Первісна. Таблиця первісних
Звернемо увагу на те, що кожна дія (операція), яку ви-
вчали у шкільному курсі, має обернену: додавання — відні-
мання; множення—ділення; піднесення до степеня —
189
добування кореня; множення одночлена на многочлен — роз-
кладання многочлена на множники способом винесення
спільного множника за дужки та ін. При цьому деякі з
обернених операцій виявилися неоднозначними. Наприк-
лад, дія добування квадратного кореня з додатного числа,
яка є оберненою до дії піднесення до квадрата, є двознач-
ною. Справді, існує два значення квадратного кореня з чис-
ла 25, а саме числа 5 і —5, бо 52 = 25 і (—5)2 = 25.
Основною операцією диференціального числення є зна-
ходження похідної у' = (х) даної функції у = і (х). Про-
те при розв’язуванні різних задач, зокрема фізичних і гео-
метричних, іноді треба виконати обернену задачу: за відо-
мою похідною у' = /'(*) деякої функції знайти (відновити)
саму функцію, яку називають первісною для відомої функ-
ції у = / (х).
Приклад 1. Нехай дано функцію / (х) — х2, яка є по-
хідною невідомої функції Р. Треба знайти функцію Р, тоб-
то знайти формулу, що задає цю функцію. Щоб це зробити,
спробуємо відповісти на питання: похідна якої функції до-
рівнює х2?
Неважко зробити висновок, що похідна функції Р (х) =
= -у дорівнює х2, тобто — = X2.
Первісною для даної функції у = / (х) на заданому про-
міжку Ь) називається така функція Р, похідна якої для
всіх х з цього проміжку дорівнює / (х), тобто Р' (х) = / (х)
для всіх х Є Ь).
Виникає ще одне запитання: чи існують інші функції,
похідні яких дорівнюють X2?
(^3 \
=х2, а і
о /
(4 + 5У= *2’ (4 - °’2)'= *2> (4 + Ух}' =*2.............
Отже, існує безліч функцій, похідні яких дорівнюють
х2. їх можна записати у вигляді однієї множини у + С, де
С — довільна стала (число). Якщо Р (х)—одна первісна,
то Р (х) + С — загальний вигляд первісної для функції
У = / (*)•
^8
Геометричне тлумачення первісної Р (х) = -у для даної
функції у = х2 зробити неважко — це кубічна парабола,
графік якої дістаємо з графіка функції у = х3, стискаючи
його у 3 рази до осі Ох. Загальним виглядом первісної для
функції у = х2 є множина парабол, які дістаємо з графіка
190
X8
у (х) = —, паралельно переносячи його вгору вздовж осі
Оу чи вниз на відстань С — залежно від знака С (рис. 6.1).
Отже, у загальному вигляді первісною для у = х2 є множи-
X8
на — + С кубічних парабол.
Операція знаходження первісної Р для даної функції
у = / (х) на певній множині (а; Ь) називається інтегру.
ванням. Вона є оберненою до
операції диференціювання.
Отже, операція інтегрування
є багатозначною.
Приклад 2. Для функції
/ (х) = на інтервалах (—оо;
0) і (0; +оо) первісною є функ-
ція Р (х) = — -р бо (—4-) =
= (—х-1)'------=
= х-2 = і.
X2
Приклад 3. Для функції
/ (х) = 4= на інтервалі (0;
У х
+°о) первісною є Р (х) =
= 2 Ух, бо (2 Ух)' = (2x2)
2 2*
Користуючись таблицею похідних, заповнимо таблицю
первісних для функцій, похідні яких відомі (табл. 6.1).
Таблиця 6.1
Функція у «В / (X) Загальний вигляд первісної Р (х) 4- С
к, де к— стала
кх-[-С
уЛ-Н
хп9 де п£ 2, п=/= — 1
ЗІП X
СОЗ X
1
СОЗ2 X
1
зіп2х
— соз х + С
зіп х + С
— сі&с + С
191
Розглянемо дві задачі фізичного і геометричного смислу,
які приводять до поняття первісної. Розв’язання цих за-
дач допоможе з’ясувати фізичний та геометричний смисл
довільної сталої С.
?Задача ((обернена до задачі, яка при-
вела до поняття похідної). Тіло рухається
прямолінійно із швидкістю V = £ м/с, де § « 10 м/с2. Тре-
ба знайти закон руху, якщо за перші 4 с тіло пройшло 80 м.
Розв’ язання. Шуканий закон руху є функцією
часу і. Позначимо її через 5 = 5 (/). Оскільки швидкість
прямолінійного нерівномірного руху є похідною функції
5 = 5 (і), то 5' (/) =
Отже, треба знайти функцію 5 = 5 (/), таку, що 5' (і) =
= £/, а 5 (4) = 80 (м).
Множина функцій, похідні яких дорівнюють має ви-
гляд 5 (і) = + С, де С — довільна стала (число). Коли
б в умові задачі не вказувалось, що за перші 4 с тіло про-
йшло 80 м, то стала С залишалась би невизначеною. Але за
вказаною додатковою умовою можна обчислити значення С
і тим самим з множини функцій 5 (і) = + С вибрати
ту, яка відповідає умові задачі.
За умовою при і = 4 5 (І) = 80. Підставляючи ці зна-
чення і і 5 (і) у попередню рівність, дістанемо 80 =
= —2— + С, звідки С = 0.
Підставляючи знайдене значення С у формулу загаль-
ного вигляду первісної, дістанемо 5 (/) = Це закон руху
вільно падаючого тіла.
Задача 2 (обернена до задачі про про-
ведення дотичної до кривої у певній
точці). Знайти рівняння кривої, що проходить через точ-
ку М (1; 2), якщо кутовий коефіцієнт проведеної до неї
дотичної дорівнює 4х3.
Розв’ язання. У цій задачі треба знайти формулу,
що задає функцію Р, похідною якої є функція / (х) = 4х3,
тобто треба знайти первісну функції у = 4х3. Крім того,
відомо, що графік шуканої функції проходить через зада-
ну точку М (1; 2).
Множина первісних функцій у = 4х3 має вигляд У7 (х) =
= х4 + С. Щоб виділити з цієї множини первісну, графік
якої проходить через точку Л4 (1; 2), врахуємо, що при х =
= 1 значення функції Р має дорівнювати 2. Підставляючи
у рівність Р (х) = х4 + С замість х число 1, а замість Р (х)
192
число 2, дістанемо 2 = 1 + С, звідки С = 1. Підставляючи
значення С в ту саму рівність, дістанемо Р (х) = Xі + 1 —
шукане рівняння кривої, яка проходить через точку М (1; 2).
У курсі математичного аналізу доведено таку теорему.
Сформулюємо її без доведення.
Теорема, Будь-яка неперервна на відрізку [а; 6] функція
у = / (х) має первісну функцію.
§ 2. Основна властивість первісної
Наведемо без доведення допоміжну лему, яку будемо ви-
користовувати при доведенні основної властивості первіс-
ної.
Лема. Якщо Р (х) = 0 на деякому проміжку (а; 6), то
Р (х) = С на цьому проміжку, де С — стала.
Геометричне тлумачення цієї леми випливає з геомет-
ричного змісту похідної. Оскільки Р' (х) = 0, то дотична
до графіка функції у = Р (х) у кожній точці паралельна осі
Ох. Тому її графік збігається з відрізком прямої, паралель-
ної осі Ох. Цю лему доведено в курсі математичного аналізу.
Основну властивість первісної сформулюємо і доведемо
у вигляді двох теорем.
Теорема 1. Якщо на проміжку (а\ Ь) функція Р (х) є пер-
вісною для ? (х), то на цьому проміжку первісною для ї (х)
буде також функція Р (х) + С, де С — довільна стала
(число).
Доведення. Нехай Р (х) — первісна для / (х).
Згідно з означенням первісної Р' (х) = / (х), але тоді і
(Р (х) + С)' = } (х). Теорему доведено.
Теорема 2. Будь-які дві первісні функції для однієї і тієї
самої функції відрізняються одна від одної на сталий дода-
нок.
Доведення. Нехай Р (х) і Ф (х) — дві первісні
для однієї і тієї самої функції / (х) на проміжку (а; Ь), тоб-
то за означенням Р’ (х) = / (х) і Ф' (х) = / (х).
Знайдемо похідну різниці даних функцій
(Ф (х) — Р (х))' = Ф' (х) — Р’ (х) = / (х) — І (х) = 0.
Згідно з лемою функції Ф (х) — Р (х) стала на проміж-
ку (а; Ь), тобто Ф (х) — Р (х) = С, де С — довільна стала.
З попередньої рівності випливає, що Ф (х) = Р (х) +
+ С.
Теорему доведено.
7 1-1819
193
§ 3. Правила знаходження первісних
Оскільки операція знаходження первісної (операція
інтегрування) є оберненою до операції знаходження похід-
ної (операція диференціювання), то правила знаходження
первісних випливають з відповідних правил знаходження
похідних. Розглянемо три таких правила.
1) Якщо Р (х) є первісною для / (х), а О — первісною
для § (х), то Р (х) + 6 (х) є первісною для / (х) + £ (х).
Справді, оскільки Р' (х) = / (х), а 6' (х) = § (х), то
(Р (х) + с (х))' = р' (х) + О' (х) = / (х) + § (%)•
2) Якщо Р (х) є первісною для [ (х), а к — стала, то
кР (х) є первісною для к[ (х).
Дійсно, оскільки сталий множник можна виносити за
знак похідної, то (кР (х))' = кР' (х) = Л/ (х).
Отже, сталий множник можна виносити за знак первіс-
ної.
3) Якщо Р (х) є первісною для / (х), а к і Ь — сталі (чис-
ла), причому к =/= 0, то ±-Р (кх + Ь) є первісною для [(кх +
+ й).
Справді, за правилами диференціювання
Р (кх + &)) = Р' (кх + Ь) • к = / (кх + Ь).
Ці правила використовують для знаходження первіс-
них.
Приклад 1. Знайти загальний вигляд первісної для
функцій:
1) х2 Н—V 5 2) х3 — зіп х; 3) —.
7 1 х2 ’ 7 ’ 7 СО82х
Розв’язання. 1) Оскільки однією з первісних для
функції Xі є — , а для функції -------функція-----— ,
то за першим правилом знаходження первісних функцій
одна з первісних для функцій х2 Н-----г дорівнює “5--
X <3
1 X3 1
------, а первісна має загальний вигляд --------р С.
X О X
X4
2) Одна з первісних для функції х3 дорівнює — ,
тоді за другим правилом знаходження первісних одна з пер-
2х4 х4
вісних функції 2х3 дорівнює = -у-, а одна з первіс-
194
них для функції зіп х дорівнює —соз х. За першим прави-
лом одна з первісних для функції 2х3 — зіп х дорівнює -
— ('— соз х) = — + соз х, а у загальному вигляді первіс-
на дорівнює -у- + созх+ С.
3) Одна з первісних для функції х дорівнює ї§х.
Для функції —і=- однією з первісних є 2 ]ґх. За третім пра-
у х
вилом знаходження первісних одна з первісних для функ-
ції у.? дорівнює V 7х + 2.
Отже, за першим правилом одна з первісних функції
75^7- + дорівнює х + И7х+2. Отже,
загальний вигляд первісної х + У7х + 2 + С.
Приклад 2. Швидкість руху точки задано рівнянням V =
= 7 зіп і. Знайти рівняння руху, якщо в момент часу і =
= 0 точка знаходиться на відстані 12 м від початкового по-
ложення.
Розв’язання. Закон руху 5 = 5 (і) точки зна-
ходимо, інтегруючи функцію, що виражає швидкість. Пер-
вісна для функції V = 7 зіп і дорівнює —7 соз і + С. От-
же, 5 (і) = —7 соз і + С, де С — довільна стала інтегру-
вання. Для обчислення С використаємо умову 5 (/) = 12
при і = 0. Підставимо ці значення і і 8 (/) у рівняння
8 (/) = —7 соз і + С, дістанемо 12 = —7 + С. Звідси С =
= 19.
Підставляючи значення С в те саме рівняння, дістанемо
шуканий закон руху 8 (і) = —7 соз і + 19.
Приклад 3. Точка рухається вздовж прямої із сталим
прискоренням а. Знайти рівняння руху 8 = 8 (/), якщо ві-
домо, що в момент часу і — 0 точка знаходилася на відста-
ні 80 від початкового положення і'мала початкову швид-
кість V =
Розв’язання. Оскільки прискорення а є похід-
ною від невідомого закону зміни швидкості V, то закон змі-
ни швидкості знаходимо, інтегруючи функцію прискорення,
тобто V = аі + Сх, де Сг — стала інтегрування.
Для обчислення Сх покладемо в останньому рівнянні
і = о і V = у0. Дістанемо и0 = а • 0 + Сг. Звідси Сх =
Підставивши значення Сх в рівняння V = аі + Сх, ді-
станемо закон зміни швидкості V = у0 + аі-
7*
195
Закон руху 5 = 5 (ї) знайдемо, визначивши первісну
функції V = у0 + аі. Вона дорівнює 5 (/) = + -у- +
+ С2. Підставивши в останнє рівняння замість і значення
і = 0, а замість 5 — значення 50, визначимо С2. Отже, 30 =
= V, • 0 + ^ + с2. Звідси Са = 50.
Підставивши значення С2 в загальний вигляд первісної,
дістанемо закон руху
5 (і) = 50 -|- ц0/ 4- .
Приклад 4. Матеріальна точка масою 3 кг рухається
вздовж осі Ох внаслідок дії сили Р. В момент часу і сила
Р (і) = 2і — 1. Знайти закон руху х = х (і), якщо відомо,
що при і = 1 с швидкість руху точки 5 м/с, а координата
х = 3, де Р — сила у ньютонах, і — час у секундах, х —
шлях у метрах.
Розв’язання. За другим законом Ньютона Р —
= та. Звідси
' Оскільки швидкість є первісною для прискорення руху
точки, то
/А 2 1 4 , & 1 , ,
3 ’ 2 з /+С1“ З з
Щоб знайти Сь врахуємо, що при і = 1 є швидкість дорів-
/2
нює 5 м/с. Підставивши ці значення у рівняння V(ї)= -
---і + Сх, дістанемо 5 = ^- + С1( звідки' С\ = 5.
Підставивши в те саме рівняння, знайдемо закон зміни
швидкості
/2- 1
Р+5-
Закон руху х = х (і) є первісною для швидкості. Тому
/З /2
= ------1-+ 5/+ С2.
За умовою при і — 1 с х = 3. Підставляючи ці зна-
чення в останнє рівняння, знаходимо 3 = -^-4- 5 4-
4* б?2. Звідси С2 =-.
196
Підставляючи Са в те саме рівняння, дістанемо закон
руху
г--г + «—ТГ’
§ 4. Інтеграл
1. Приклади задач, що приводять до поняття інтеграла.
До поняття інтеграла, як і багатьох інших математичних
понять, привели потреби розв’язання задач геометрії, фі-
зики та багатьох практичних задач. Розглянемо дві такі
задачі.
Задача 1 (п р о площу У | „ ___——
криволінійної тра-
п е ц і ї). У шкільному курсі л'хУ
геометрії розглядаються спо- /
соби обчислення площ невели- /
кої кількості фігур лише пев-
ного виду (многокутників,
круга та його частин). Вини- ——І—А—4-------—Ь-4—------
кає питання! як обчислити 0 а *' х2- х
площу плоскої фігури, обме- Рис. 6.2
женої будь-якою кривою? Ви-
являється, що розв’язання такої задачі існує за певних умов.
Розглянемо спочатку плоску фігуру, обмежену графіком
неперервної і невід’ємної на відрізку [а; Ь] функції у — } (х),
відрізком [а; &] і прямими х — а і х = Ь (рис. 6.2). Ця фі-
гура дістала назву криволінійної трапеції. Обчислимо її
площу. Для цього розіб’ємо відрізок Іа; Ь] на п рівних від-
різків точками
а = х0 < Хі < ха < • • • < хк-і <хк<
* * * Хп^ві Хц = Ь.
Довжини будь-якого з відрізків Іха-ь хЦ, на які роз-
бито відрізок [а; Ь], однакові і дорівнюють
Дх = Ь~а — хк — х^і, де к — 1, 2, ... , п — 1, п.
Побудуємо на кожному з відрізків [х*_і; хкІ як на ос-
нові прямокутники з висотою, що дорівнює значенню
/ (хй-і) функції у лівому (або правому) кінці відрізка.
Площа кожного такого прямокутника дорівнює
/(хА„і) • Дх = /(х/^і) • ,
197
а площа східчастого многокутника, утвореного всіма прямо-
кутниками, дорівнює сумі площ прямокутників
5п = /(х0).-^- + /(хх).-Ц^-+
•. • + = (/(%„) + /(Хх) + •..
... + /(%„_!)) • •
Якщо П->ОО, то Ах = ~ Д І оскільки функція
У = ї (х) неперервна, то східчаста фігура буде все менше від-
різнятися від криволінійної трапеції. А тому площа 5 кри-
волінійної трапеції буде все менше відрізнятися від 8п тоб-
то 8п яз 5. При досить великих п ця наближена рівність
виконується з будь-якою точністю. Тому природно за пло-
щу криволінійної трапеції за означенням взяти границю
площі східчастого многокутника за умови п -> оо, тобто
8 = Иш 8П.
П-+оа
У курсі математичного аналізу доведено, що для будь-
якої неперервної функції у = [ (х) (не обов’язково не-
від’ємної) така границя існує і дорівнює певному числу.
Введений метод обчислення площ плоских фігур можна
застосувати і для тих фігур, формули площ яких було вве-
дено у шкільному курсі геометрії (многокутники, круг і
його частини), але можливості нового розглядуваного мето-
ду значно ширші.
Наведемо приклади обчислення за цим методом площ
трикутника і фігури, обмеженої параболою.
Приклад 1. Обчислити площу трикутника, обмеженого
віссю Ох, прямими х = к і у = 2х (рис. 6.3).
198
Розв* язання. Тут криволінійна трапеція має ви-
гляд прямокутного трикутника, причому а = 0, Ь == к, а
функція у = 2х, графік якої обмежує трикутник, додатна
і неперервна на [0; &].
Розіб’ємо відрізок 10; к] на п рівних частин. Довжина
кожного з утворених при цьому відрізків дорівнює хк —
— х*_і = Дх = Абсцисами правих кінців кожного з
відрізків є:
хх = Дх; х2 = 2Дх; х3 = ЗДх, ... , хк =
= £Дх, ... , хл = пДх ,= к.
Утворимо добутки / (хЛ) Дх і знайдемо суму
5Л = ^(х1)Дх+/(ха)Дх+ ••• +/(хй)Дх,
8п = 2Дх • Дх + 2 < 2Дх • Дх + 2 • ЗДх • Дх + • • •
... 4- 2пДх • Дх= 2(Дх)8(1 + 2+3+ ... +и) = 2 • х
п (п + 1) _ , 2 . »+ 1
п п ’
враховуючи, що 1 + 2+ 3+ ••• + п = . (Ос-
танню формулу неважко довести методом математичної ін-
дукції.)
Звідси
5 = Ііт 8„ = к2 Ііт —— ? = к2 Ііт [14—і-] = к2 (кв. од.).
Обчисливши площу трикутника за відомою з геометрії
формулою (площа прямокутного трикутника дорівнює по-
ловині добутку його катетів), дістанемо той самий резуль-
тат.
Задача 2. Обчислити площу фігури, обмеженої парабо-
лою у — х2, віссю Ох і прямою х — к (рис. 6.4).
Розв’язання. Розіб’ємо відрізок [0; к] на п рів-
них частин і обчислимо суму
5П = (Дх)2 • Дх + (2Дх)а • Дх +
+ (ЗДх)2 • Дх + • • • + (пДх)а • Дх —
= (Дх)3 • (Iа + 22 + 32+ ••• + п2) => (Дх)8.1}6(2п+=
__ к? п (л + 1) (2п 1)
6 ’
199
враховуючи, що 1 + 22 + З2 + • • • + п2 = п •
(Доведіть останню формулу самостійно методом математич-
ної індукції.)
Отже,
5 = Ііт 8„ = X Ііт + =
* 6 па
П-+ОО П->0О
&8 14 /і » 1 \ /П І 1 \ Л’ о / \
= ~± 1 + ~ 2+” = — ,2шт <кв-од->-
П.—ЮО \ / \ /
2. Задача про масу неоднорідного стержня. Обчислимо
масу неоднорідного стержня, тобто такого, в якому густина
____________о_____о змінюється від точки до точки
0 М і х на ділянці [0; /] (рис. 6.5).
Рис. 6.5 Якщо позначити через х від-
стань точки М стержня від лі-
вого його кінця, то кожному значенню х відповідатиме пев-
не значення густини р. Отже, густина р е функцією від х,
яку позначимо р == р (х).
Щоб знайти масу стержня, розіб’ємо відрізок [0; І] на
п рівних частин точками
0 = Хо < < Х2 < • • • < Х*-і <Хк< • • • < Хп-1 <
«С хЛ == /.
Довжина кожного з утворених відрізків [хл>—і; х^і до-
рівнює хк — х*__і = Дх =
Якщо п -> оо, то Дх -> 0. На досить малій ділянці стер-
жня густину його можна вважати однаковою і такою, що
дорівнює, наприклад, значенню функції р = р (х) на ліво-
му чи правому кінці відрізка. Тоді маса кожного з відріз-
ків дорівнює р (%/г—і) Дх, а сума
тп = р (х0) Дх + р (хх) Дх 4- ♦ • • р (хЛ_і) Дх
дасть наближене значення маси т всього стержня [0; І].
Тому за означенням природно вважати, що маса т неодно-
рідного стержня дорівнює Ііт тп, тобто т = Ііт тп.
П-+еа П-+оо
2. Означення інтеграла. Обидві розглянуті задачі роз-
в’язували одним і тим самим методом, яким розв’язують
багато інших задач (обчислення роботи змінної сили, кіль-
кість електрики та ін.). Узагальнити його можна так.
Розглядають неперервну функцію у = / (х), невід’єм-
ну на відрізку [а\ Ь]. Відрізок [а; 6] розбивають на п рів-
них частин точками
а = х0 < хх < х2 < • • • < х^і <хк<С • • • < хп = Ь.
200
Довжина кожного з відрізків [х*_г, хк] дорівнює хк—
— Хк-і = Ь~а = Ах. Утворюють добутки /(х0) Дх,
[(х^&х, , ї(хп-\)Ьх і знаходять їх суму
5п = Г(х0)Ах + /(х1)Ах + /(х2)Ах+ ••• + / (хп-і) Ах.
Обчислюють Ііт 8п.
П-+ОО
За означенням цю границю називають інтегралом функ-
ь
ЦІЇ У = ї (х) від а до Ь і позначають / (х) сіх (читають так:
а
«інтеграл від а до & еф від ікс де ікс»).
Числа а і Ь називають межами інтегрування: а — ниж-
ньою межею, Ь — верхньою межею. Символ У називають
знаком інтеграла, функцію у = / (х) — підінтегральною
функцією, вираз / (х) йх — підінтегральним виразом, змін-
ну х — змінною інтегрування. Отже, за означенням
ь
Ііт 8п = С / (х) сіх.
Зазначимо, що відрізок [а; Ь] можна було б ділити на п
не обов’язково рівних частин. Але у цьому разі довжина
найбільшого з відрізків розбиття повинна прямувати до 0
при п -> оо.
Застосовуючи поняття інтеграла до двох розглянутих
ь
задач, можна стверджувати, що 5 = £ / (х) <іх — площа
а
І
криволінійної трапеції, а т =§ р (х) сіх — маса неоднорід-
ні
ного стержня.
3. Формула Ньютона — Лейбніца. Безпосередньо за
означенням інтеграли легко обчислювати лише для най-
простіших функцій, таких, як у = кх, у = х2 (див. дві по-
передні задачі про обчислення площ). Для інших функцій,
наприклад тригонометричних, обчислення границь сум ус-
кладнюється.
Виникає питання: чи не можна обчислювати інтеграли
іншим способом? Такий спосіб був знайдений ще у XVII ст.
англійським вченим Ньютоном і німецьким математиком
Лейбніцем. Строге доведення формули Ньютона — Лейбні-
ца дають в курсі математичного аналізу. Ми лише проілюст-
руємо справедливість формули геометричними міркування-
ми.
201
Нагадаємо задачу про площу криволінійної трапеції
ь
(рис. 6.6). Було встановлено, що 5 = £ / (х) б/х.
а
Виберемо довільну точку X є Іо; Ь] і проведемо через неї
перпендикуляр хК до осі Ох. Площа фігури аАКх зміню-
ється із змінною х, тобто є функцією від х. Позначимо цю
функцію через 5 (х) і покажемо, що існує її похідна, при-
чому 5' (х) == / (х), де у =
= / (х) — підінтегральна функ-
ція, графік якої обмежує кри-
волінійну трапецію. Іншими
словами, покажемо, що 5 (х)є
первісною для / (х).
Надамо змінній х приросту
Дх, вважаючи (для спрощення
міркувань), що Дл > 0. Тоді і
функція 5 (х) набуде приросту
Д5 (х). У курсі математичного
аналізу доводиться, що непе-
рервна на проміжку [а; &] функція у — [ (х) досягає на ньо-
му найбільшого і найменшого значень. Оскільки підінтег-
ральна функція у — { (х) неперервна на проміжку [х; х +
+ Дх], то вона досягає на цьому проміжку найменшого т
і найбільшого М значень. Отже,
/пДх < Д5 (х) < МДх.
Поділивши всі частини цієї нерівності на Дх > 0, діс-
танемо
' Д5 (х) ..
т <_ —т-і-і- <М.
Дх
За неперервністю функції у = / (х)
Ііт т = Ііт М = /(х).
Дх->0 Дх-*-0
Але тоді
Оскільки Ііт —т——= 5' (х), то 5' (х) = } (х), тобто
функція 5 (х) є однією з первісних функцій У = І (х).
Позначимо через Р (х) будь-яку первісну для функції
у — І (х). За основною властивістю первісної будь-які пер-
вісні однієї і тієї самої функції можуть відрізнятися лише
сталим доданком С. Тому
5(х) = Р(х) + С. (1)
202
При х = а криволінійна трапеція вироджується у від-
різок аА, тому 5 (х) = 0.
Підставивши у рівність (1) замість х число а, а замість
5 (х) число 0, дістанемо С = —Р (а).
Підставивши замість С у рівність (1) його значення, діс-
танемо
8(х) = Р(х) — Р(а). (2)
При х — Ь площа криволінійної трапеції дорівнює чис-
лу 8 = 8 ф). Крім того, при х = Ь із рівності (2) дістаємо
8ф) = Рф)-Р(а).
Раніше було встановлено, що площа 8 криволінійної
ь
трапеції дорівнює значенню / (х) сіх. Тому можна зробити
а
ВИСНОВОК, ЩО
Ь
І(х)сіх= Р ф) — Р (а),
а
Це і є формула Ньютона — Лейбніца, яка показує, що
значення інтеграла на відрізку [а; Ь] дорівнює різниці зна-
чень первісної підінтегральної функції при х = Ь і х = а.
Різницю Р (Ь) — Р (а) позначають Р (я) |д. Тому рів-
ність
ь
^(х)сіх = Рф) — Р(а)
а
можна записати так;
ь
У р (х) сіх — К(х)£.
а
Розв’язання розглянутих у попередньому параграфі
двох задач про площі трикутника і фігури, обмежені пара-
болою, значно спрощується, якщо використати формулу
Ньютона — Лейбніца. Справді,
к
8^оав = ] 2хсіх = х2 |о == к2 — 0 = А2 (кв. од.);
о
к
С їй ЬЗ ЬЗ
80вс — хЧх = — ---0 = —(кв. од.).
V о ю о о
о 1
Приклад 1. Обчислимо за формулою Ньютона — Лейбніца
площу фігури, обмеженої зверху синусоїдою у — зіп х,
203
знизу—віссю Ох, а з боків—прямими х = і х= -2-
(рис. 6.7).
Ров в’язання.
Я
2
5 = У зіп хіх =» — соз х
я
4
л
2
— соз
л
4
= —(0--------(кв- од-)’
Запишемо символічно основні властивості інтеграла, які
випливають із властивості первісної і формули Ньютона —
Лейбніца. їх неважко довести,
користуючись означенням інтег-
рала:
ь
а
Ь
ь
а
а
& ь
2) § к[ (х) (їх — к^ { (х) йх, де к £ Я.
а а
Ь а Ь
3) ] 7(х)(їх+ У }(х)(ІХ, тобто якщо відрізок
а а б
{а; &] розбито на два відрізки точкою с, то інтеграл на відріз-
ку [а; 6] дорівнює сумі інтегралів на відрізках [а; с] і [с; Ь];
Ь кЬ+р
4) ? (кх + р) (їх =§ І(і)(іі, де р$Я, к£ії.
а ка-}-р
Доведіть самостійно перші три властивості. Останню вла-
стивість доведено в курсі математичного аналізу.
я
4
Приклад 2. Обчислити £ (я8— созх)йх.
о
Розв* язання.
4
4 - 4
У (Я3 — СОЗ X) СІХ = У
0 о
— л4 . л л4 К2 л
— 5ШХ04 — “1024 81П-4 І024 2“ « — 0,698.
Л4
о
я4
»•
204
2
Приклад 3. Обчислити ]*(*+ 2)2сіх.
Розв’язання.
2 2 2
У (х + 2)2 д,х = § (х2 + 4х + 4) сіх = У х2сіх +
1 1 1
+ 4хйх + У 4(іх = -у- 1
(4-т)+2<4-‘)+
+ 4(2 - 1) = 4- +
+ 6+4=12І.
Я
2
Приклад 4. Обчислити £ зігпЗх-1 йх.
Я 7
4
Роз в" язання.
1 ( 5я я \
зДеоз-з----соз-у ==
« 0,235.
4. Застосування інтеграла. Обчислення площ плоских
фігур. Два приклади обчислення площ трикутника і пара-
болічного сегмента ми вже розглянули. Наведемо ще кіль-
ка прикладів.
205
Приклад 5. Обчислити площу фігури, обмеженої! 1) си-
нусоїдою у = зіп х і відрізком [0; я] осі Ох (рис. 6.8); 2) ку-
бічною параболою у — х?, віссю Ох та прямими х — 2 і х —
= 5 (рис. 6.9).
Розв’язання.
ЗІ
1) 5 = £ зіп хсіх — — СОЗ X |о = — (СОЗ я — соз 0) =
= — (— 1 — 0) = 2 (кв. од.).
5
2) 5 = У хМх = 415 = -і- (54 - 52) = (52 — 5) (52+ 5) =
2
Виникає питання, як обчислити площу фігури, обмеже-
ної графіками двох неперервних функцій у = / (х) і у =
— ср (х) (рис. 6.10).
ь ь
Неважко помітити, що «Я^двв, = 7(х) (іх — ' <р (х) Лх =
г? а
Ь
= У (/ (х) — ф (*)) йх за першою властивістю інтеграла.
а
Приклад 6. Обчислити площу фігури, обмеженої кривими
у = X2 і у = X3.
Розв’язання. Побудувавши ескізи графіків функ-
цій (рис. 6.11), з’ясуємо, площу якої фігури треба знайти
(цю фігуру виділено штриховкою), графіки яких функцій її
обмежують, і визначимо межі інтегрування. У даному ви-
падку / (х) — х2, ф (х) = х3, а = 0, Ь = 1.
5=
111, ч
= -3--^-=-^ (КВ. од.).
206
Виникає питання: чи можна застосувати формулу 5 =
ь •
= У (/ (*) — Ф (*)) якщо фігура, площу якої треба об-
числити, розташована частково чи повністю під віссю Ох
(рис. 6.12)? Виявляється, що можна. Щоб переконатися в
цьому, досить перенести дану фігуру паралельно вздовж
осі Оу на відстань т так, щоб вона розмістилася над віссю
Ох (рис. 6.13). Але таке перетворення означає, що дані функ-
ції У = / (х) і у = Ф (х) ми замінили новими функціями
Л (х) = / (х) + т і фі (х) = ф (х) + т. Площа фігури, об-
межена графіками цих функцій, дорівнює площі даної фі-
гури. Тому шукана площа
д ь
5 = і (/і (*) — Фі (*)) ( ((/ (/) + т) — (ер ус) + т)) (їх =
а а
Ь
= Ц (/(х) — <р(х)) (їх.
а
Ь
Якщо позначити / (х) — ф (х) — д (х), то £ д (х) йх. Це
означає, що для обчислення значення площі важливою є
не форма фігури, а довжина відрізка д (х) ординати, що до-
рівнює різниці ординат точок графіків відповідних функцій
у = / (х) І у = Ф (х). Отже, якщо взяти дві інші функції
У = /і (*) і У = Фі (х), які задовольняють умову (х) —
— Фі (х) = д (х) у будь-якій точці х £ [я; Ь], то площа фігу-
ри, обмеженої графіками цих функцій, буде дорівнювати
площі фігури, обмеженої графіками функцій у = $ (х) і у =
= ф (х) (рис. 6.14).
207
Приклад 7. Знайти площу фігури, обмеженої парабо-
лою у = 4 — х2 та прямими у =------і- х — 1, у = -^-х— 1
(рис. 6.15).
Р о з в’ я в а н н я. На проміжку [—2; 0]
д (х) = (4 — х2) — (-х — 1) — — х2 + -у- х + 5>
а на проміжку [0; 2]
Уі (х) = (4 — х2) — {Ц- х — = — х2-----у + 5.
Шукану площу знаходимо як суму двох інтегралів
0 2 0
5 = ( у (х) &х + і (х) <іх = ] І — х2 + -у х + 5] йх +
-»2 0 -2 ' '
+ ((-*’—г*+5)'ь=(~тг + т+5*)|1г +
°+(-4-4+5^^-(4+і-іо)+
+ (--г-1 + |о)--т-1 + 10-
---і- 1 + 10- 12-ї- (кв. од.).
О О
Площу даної фігури можна обчислити раціональніше,
якщо звернути увагу на те, що фігура симетрична відносно
осі Оу. Тому
2 2 '
5 = 2 У дг (х) сіх = 2 У (— х2-у + 51 йх —
о о ' 7
СІ X* Xі . с А І2 „ 19 10 2 . .
= 2 (- -з---г +.5х) |0 = 2 • — = 124Г (кв- од->-
208
Зазначимо, що коли криволінійна трапеція розміщена
ь
ПІД ВІССЮ Ох (рис. 6.16), ТО У / (х) (їх — від’ємний. Тоді
а
Ь
вважатимемо, що 5 = | і (х) сіх .
а
Обчислення об’ємів тіл. Задача про обчислення об’єму ті-
ла розв’язується аналогічно задачі про площу криволіній-
ної трапеції.
Нехай задане тіло Т і коор-
динатна пряма Ох у просторі
(рис. 6.17). Проведемо площи-
ни, перпендикулярні до пря-
мої Ох так, щоб вони перети-
нали тіло Т або дотикались до
нього. Дотичні площини, що
обмежують тіло, перетнуть
вісь Ох у точках а і &, а будь-яка площина між ними перетне
тіло в точці х. Позначимо площу перерізу тіла цією площи-
ною через 5. Кожному значенню х з відрізка \а\ Ь] відпові-
датиме певне значення площі перерізу 8 = 8 (х). Площина
перерізу буде відтинати тіло, об’єм якого є також функцією
х, тобто V — V (х). Тому можна стверджувати, що на відріз-
ку [а; Ь] визначена функція 5 (х). Якщо вона неперервна
на відрізку [а; &], то функція V (х) є первісною для функції
ь
8 (х) і виконується формула V ~ § 8 (х) сіх.
а
Строге доведення цієї формули дано у курсі математич-
ного аналізу. Наведемо лише геометричні міркування, які
приводять до вказаної формули.
Розіб’ємо відрізок [а; і] на п рівних частин точками
а = х0 < Хі < х2 < • • •
<С Х£—і хк • •
• • • < Хп—] < ХЛ = Ь.
Позначимо довжини кожного з відрізків розбиття через
= = хк — Хй-і, де 6= 1, 2, ... , п. Через кожну
точку розбиття проведемо площину, перпендикулярну до
осі Ох. Проведені площини розіб’ють тіло Т на шари Об’єм
шару, що знаходиться між площинами, які проходять че-
рез точки хк-\ і хк при досить малих Дх (тобто досить вели-
ких п), наближено дорівнює добутку площі 5 (Хп-і) на
209
Дх. Якщо утворити суму
V„= 8 (х0) Дх + 5 (хх) Дх + ••
•.. + 5 (х„_і) Дх = (5 (х0) + 5(хх) + • • • + 5(х„_0)
то Уп ж V. Ця наближена рівність виконується з будь-якою
точністю при досить великих п. Отже, цілком природно,
що
V = Ііт уп = Ит (5(х0) + 5 (хх) + • • • + 5(хп_,))-^ .
«-♦•ОО «-+ОО П
Рис. 6.17
Границю такої суми, як і в задачі про площу криволі-
нійної трапеції, називають інтегралом і позначають
ь ь
У 5 (х) йх. Тому V = У 5 (х) сіх.
а а
Наведемо приклади застосування формули для обчис-
лення об’ємів різних тіл.
Приклад 8. Знайти формулу об’єму кулі радіуса 7?.
Роз в’язання. Оскільки в перерізі кулі завжди
утворюється круг, то розмістимо її так, щоб точка О від-
ліку збігалася з проекцією центра Ох кулі (рис. 6.18) на
координатну пряму.
З Д ОгКР, де / ОіКР = 90°, за теоремою Піфагора
РР2 = ОХР2 — Ох№. Оскільки ОХР = Р, ОгК = х, КР =
— т — радіус круга, який утворюється в перерізі, то г2 =
= Р2 — х2, а 5 (х) = я (Р2 — х2). Отже,
я к
V — [ 5 (х) сіх = ї я (Р2 — х2) сіх —
-я -я
210
е ґ \ / „ Х3 \ |«
= Я І ] Я2(ІХ — і Х2(ІХ 1 — Я -
-"(«•-4+«--Я=тя«’’
Приклад 9. Знайти формулу об’єму кругового циліндра
з площею основи 5 і висотою Н.
• Розв’язання. У кругового циліндра (похилого
чи прямого) (рис. 6.19 а, б) будь-яка площа паралельних
перерізів стала і дорівнює 5. Тому координатну пряму Ох
проведемо перпендикулярно до площини основи, а точку
відліку виберемо в точці її перетину з площиною основи.
Вісь Ох перетне площину другої основи в точці —
висота циліндра. Тоді
н
Уу=\8<1х=8х\а=8Н.
0
Формула Уу = 8Н виявилась однаковою і для похилого,
і для прямого кругового циліндрів.
Приклад 10. Знайти формулу об’єму піраміди з площею
основи 5 і висотою Н.
Розв’язання. Нехай координатна пряма Ох про-
ходить через вершину піраміди перпендикулярно до пло-
щини її основи (рис. 6.20). Виберемо за точку відліку вер-
шину піраміди.
Перетнемо піраміду площиною, паралельною площині
основи на відстані х від вершини. Площа перерізу є функ-
211
цією відстані х. За відомою теоремою в геометрії про від-
ношення площ таких перерізів (вони є многокутниками,
подібними основі піраміди)
£ (х) _ І х С /у\ _____ „2
• 5 ~ я ; ’ и) — #2 * •
Тому
н н н
V = § 5 (х) йх = -Д- х2(іх = У хЧх =
0 0 0 -
_ $ х? н
~ Н2 ’ З
= Ц-5Я.
о 6
Отже, об’єм будь-якої піраміди дорівнює третині добутку
площі основи на висоту.
Приклад 11. Знайти формулу об’єму тіла обертання
(так само можна знайти формулу об’єму конуса).
Роз в’язання. Розглянемо криволінійну трапецію
аАВЬ, обмежену графіком не-
перервної функції у = / (х)
(рис. 6.21).
При обертанні трапеції навколо осі Ох утвориться тіло
обертання. Будь-яким перерізом тіла обертання є круг ра-
діуса г = / (х). Площа перерізу 5 (х) = № = я/2 (х),
тому об’єм тіла обертання знайдемо за формулою
ь ь
V = У я/2 (х) (їх = я р (х) (їх.
а а
За цією формулою обчислимо, наприклад, об’єм прямого
кругового конуса (рис. 6.22), радіус основи якого дорівнює
7?, а висота Н.
Для цього треба знайти спочатку рівняння прямої ОВ,
що проходить через точки О (0; 0) і В (В; /?). З курсу гео-
212
метрі! відомо, що рівняння прямої має вигляд ах 4- Ьу 4-
4~ с — 0.
Оскільки точки О і В належать цій прямій, то їхні ко-
ординати задовольняють рівняння прямої. Підставляючи
координати у рівняння, дістанемо дві рівності
Підставляючи с — 0 у другу рівність, дістанемо аН 4-
4- і>К — 0. Звідси а —---
гі
Підставимо значення а і с у рівняння прямої. Дістанемо
— х Ьу — 0.
Поділивши обидві частини цієї рівності на Ь, матиме-
о
мо----X + у 0. Звідси у =?= —&• х — рівняння прямої О В.
Отже, І (х) = х, а
н
17 „ С Я2 ** Н "Я2 Н* 1
Н2 х^х—^р“^ з о Н2 * 3 ~ "З
о
тобто об’єм конуса дорівнює одній третині добутку площі
основи л7?2 на висоту Н.
За допомогою формули об’єму тіла обертання можна об-
числити об’єм кулі і циліндра.
Приклад 12. Знайти об’єм тіла, утвореного обертанням
параболічного сегмента з висотою Н і основою 27? навколо
осі симетрії (рис. 6.23).
Ро з в ’я з а н н я. При такому виборі осей коорди-
нат рівняння параболи має вигляд у2 = кх. Щоб знайти к>
врахуємо, що точка А (Н; 7?) належить параболі, тому її
координати задовольняють-рівняння параболи. Підставля-
213
ючи у рівняння замість х число Н, а замість у число 7?, ді-
р2
станемо /?2 = кН. Звідси к = -тг-. Підставляючи значення
п
2 я*
х у рівняння параболи, матимемо у* = х.
Шуканий об’єм тіла знайдемо за формулою V =
н
= я У /2 (х) <іх, де г/ = ї (х):
о
н
т, С Я2 . я#2 X2 |Н я/?2 Н* я/?2//
= -----ГІо ----------Г'==~2—*
о
Застосування інтеграла у
фізиці. Обчислення шляху за
відомим законом зміни швид-
кості. Раніше було встановле-
но, що закон руху 5 = 8 (і)
є первісною для функції V =
= V (/), яка виражає закон
зміни швидкості. Оскільки
шлях, який пройде тіло за про-
міжок часу від /і до і2, є при-
ростом функції 8 — 8 (і) (при-
ріст первісної), який виражається через інтеграл за фор-
^2
мулою Ньютона — Лейбніца, то 5 = V (і) Лі за умови,
І
що функція V = у(і) неперервна.
Наведемо приклад застосування цієї формули.
Приклад 13. Тіло рухається прямолінійно із швидкіс-
тю, яка змінюється за законом V = 2і + 1 (м/с). Знайти
шлях, який пройшло тіло за проміжок часу від = 1 сдо
= 3 с.
Розв’язання.
с І & \ з
5 = ) (21+ 1)^=(2.-|-+ і = (9 + 3-(1+ 1)) =
= 10 (м).
Обчислення роботи змінної сили. Нехай тіло, що роз-
глядається як матеріальна точка, рухається під дією змін-
ної сили Р (х), направленої вздовж осі Ох. Знайдемо форму-
лу для обчислення роботи при переміщенні з точки х = а
у точку х — Ь.
214
Нехай А (х) — робота при переміщенні тіла з точки а
у точку х. Надамо х приросту Дх. Тоді А (х + Дх) —
— А (х) — робота, яка виконується силою Р (х) при пере-
міщенні тіла з точки х у точку х + Дх. При Дх -> 0 силу
Р (х) на відрізку [х; х + Дх] вважатимемо сталою, що до-
рівнює Р (х). Тому А (х + Дх) — А (х) а Р (х) • Дх, звід-
ки Л(х + М-4(х) р }
кх ' 7
Тоді
Ііт л<* +У-/.(*) = Л(х),
Дх-+0 &х
або за означенням похідної А' (х) =
= Г(х).
Остання рівність означає, що А (х) є
первісною для функції Р (х). Тоді за фор-
мулою Ньютона — Лейбніца
ь
а
Р (х) сіх — А(Ь) — А(а) = А(Ь) = А, Рис. 6.24
• оскільки А (а) — 0.
Отже, робота змінної сили Р (х) при переміщенні тіла
, ь
з точки а в точку Ь дорівнює А = Р (х) (їх.
а
Приклад 14. Обчислити роботу, яку треба виконати, щоб
викачати воду з ями глибиною 4 м, що має квадратний пере-
різ із стороною 2 м. Густина води р = 103 кг/м3.
Розв’язання. Спрямуємо вісь Ох вздовж діючої
сили (рис. 6.24). Значення сили Р (х), що діє на переріз
прямокутного паралелепіпеда площею 4 м2, визначають ва-
гою шару води, що знаходиться вище цього перерізу. От-
же, Р (х) = 4р£ (4 — х), де х е [0; 4], § ж 9,8 м/с2.
4 4
А = 4р£ (4 — х) д.х = 4р§^(4 — х) сіх = 4р§[іх — -у-
6 о >
== 4Р£(і6_8) = 32 • 103 • 9,8 = 313,6 • 103 (Дж) ж
а 3,1-Ю5 (Дж).
Обчислення маси неоднорідного стержня. За означен-
ням лінійна густина р неоднорідного стержня дорівнює по-
хідній функції т = т. (І), що виражає масу стержня як
функцію його довжини. Отже, р = т’ (І), тобто функція
т — пг (І) є первісною для р = р (/). Звідси випливає, що
215
масу стержня на відрізку [/г; /2] можна обчислити за форму-
ла
лою т = у р (І) йі.
її
Приклад 15. Знайти масу стержня довжиною 35 см, як-
що його лінійна густина змінюється за законом р (/) =(4/ +
+ 3) кг/м.
Розв’язання.
0,35
т = | (41 + 3) аі = (21і + 3/) |о’35 = 1,295 «1,3 (кг).
0
Обчислення кількості електрики. За означенням сила
струму є похідною від кількості електрики 0 = 0 (/), де
і — час, тобто ] (і) = 0' (/). Але тоді функція 0 = 0 (0
є первісною для функції (і), тому кількість електри-
ки, що проходить через поперечний переріз провідника за
І2
час від до і2, можна знайти за формулою ф = У (/) йі.
Приклад 16. Знайти кількість електрики, що проходить
через поперечний переріз провідника за 10 с, якщо сила
струму змінюється за законом / (і) = (4і + 1) (Л).
Розв'язання.
ю
в = [ (4і + 1) <Ц = (21і + і) |о° = 210 (Кл).
6’
Застосування інтеграла в економіці і техніці. Інтеграл
широко застосовують при розв’язанні фізико-технічних
задач різного характеру, а також задач економічного змі-
сту.
Приклад 17. Експериментально встановлено,-що про-
дуктивність праці робітника наближено виражається функ-
цією
/(/) = — 0,0033/* — 0,089/ + 20,96,
де / — робітничий час у годинах. Обчислити обсяг випуску
продукції за квартал, вважаючи робочий день восьмиго-
динним, а кількість робочих днів у кварталі 62.
Розв’язання. Обсяг випуску продукції протягом
зміни є первісною від функції, що виражає продуктивність
праці. Тому
8
о
216
Протягом кварталу обсяг випуску продукції становити-
ме
8 8
І/ = 62 С /(/) аі = 62 У (— 0,0033/2 __ 0,089/ + 20,96) Ш =
о о
= 62 (— 0,0033 . — 0,089 • + 20,96/) |® =
= 62 (- 0,001 • 512 — 2,848 + 167,68) = 62 - 164,27 «
яі 10 185 (од.).
Приклад 18. Завод випускав за рік 15 000 верстатів, а
потім збільшив їх випуск на 55 верстатів щорічно. Визна-
чити суму амортизаційних відрахувань за 10 років при нор-
мі амортизації 5 %, якщо вартість одного верстата стано-
вить 1745 крб.
Зауважимо, що випуск верстатів можна виразити фор-
мулою і/ = 15 000 4- 55/, де / — число років.
ю
Розв’язання. V — § (15 000 4- 55/) йі.
о
Приклад 19. Експериментально встановлено, що залеж-
ність витрати бензину автомобілем від швидкості на 100 км
шляху визначається формулою ф = 18 — 0,3ц 4- 0,003и*,
де 30 о ПО. Визначити середню витрату бензину при
швидкості руху 50—60 км/год.
Розв’язання. Середня витрата бензину становить
60
{ (18 — 0,Зо 4-0,0030а) йо
50
т 60 — 50
18а — 0,3 • ----0,003
10
60
50
= -^(18 - 60 — 0,3 • 1800 4-0,003-72 000 — 18-50 4-
4- 0,3 - 1250 — 0,003 - 41 667) = -^-(1080—540 4- 216 -
- 900 4-,375 — 125) = 10,6 (л).
Отже, автомобіль на 100 км шляху, рухаючись із швид-
кістю 50—60 км/год, витрачає в середньому 10,6 л бензину.
Історична довідка
Ключовими поняттями математичного аналізу, початки якого ви-
вчають в школі, € поняття функції, границі, похідної та інтеграла.
Термін «функція» вперше запропонував у 1692 р. видатний німець-
кий філософ і математик Готфрід Вільгельм Лейбніц (1646—1716) для
характеристики різних відрізків, що з’єднують точки деякої кривої.
Перше означення функції, яке вже не було пов’язане з геометричними
217
уявленнями, сформулював Йоган Бернуллі у 1718 р. Пізніше, у 1748 р.
дещо уточнене означення функції дав учень Й. Бернуллі Леонард Ейлер
(1707—1783). Ейлеру належить і символ функції / (х).
В означеннях Бернуллі і Ейлера функцію ототожнювали з аналі-
тичним виразом (формулою), яким вона задається. Ейлер вважав також
за можливе задавати одну і ту ж функцію на різних множинах різними
аналітичними виразами. Ці так звані «кусково задані функції» широко
застосовуються на практиці.
Вже в часи Ейлера стало зрозумілим, що ототожнення функції з
її аналітичним виразом звужує саме поняття функції, бо, по-перше, од-
ним і тим же виразом можна задати різні функції, по-друге, не завжди
функцію можна задати аналітично. Вже Ейлер припускав можливість
задання функції лише графіком.
Дальший розвиток математичного аналізу і практичних застосу-
вань математики привів до розширення поняття функції. У 1834 р. ви-
датний російський математик М. І. Лобачевський сформулював озна-
чення функції, в основу якого було покладено ідею відповідності: «За-
гальне поняття вимагає, щоб функцією від х називати число, яке даєть-
ся для кожного х і разом з х поступово змінюється. Значення функції
може бути задане або аналітичним виразом, або умовою, яка подає за-
сіб випробування всіх чисел і вибору одного з них; або, нарешті, залеж-
ність може існувати і залишатися невідомою».
Вже через три роки німецький математик Лежен Діріхле (1805—
1859) зробив таке узагальнення поняття функції: «у є функція змінної
х (на відрізку а х Ь), якщо кожному значенню х відповідає ціл-
ком певне значення у, причому не має значення, яким чином встановле-
на ця відповідність — аналітичною формулою, графіком, таблицею або
навіть просто словами».
У другій половині XIX ст. після відкриття теорії множин до озна-
чення функції крім ідеї відповідності було залучено ідею множини, а
тому сучасне означення функції формулюють гак: «Відповідність між
множинами X і У, при якій кожному елементу х множини X відповідає
певний елемент у множини У, називають функцією».
У XX ст. відбулось подальше розширення поняття функції, викли-
кане потребами фізики. У 1930 р. англійський фізик Поль Дірак (1902—
1984) ввів поняття так званої дельта-функції, а у 1936 р. радянський ма-
тематик і механік С. Л. Соболєв (1908—1990) ввів більш широке понят-
тя узагальненої функції, яке охоплює і дельта-функцію.
Отже, поняття функції продовжує розвиватись і розширюватись
відповідно до потреб розвитку математичної науки та її практичних за-
стосувань.
Походження поняття границі, на якому грунтується весь матема-
тичний аналіз і корені якого сягають глибокої давнини, пов’язане з об-
численням площ криволінійних фігур, об’ємів тіл, обмежених кривими
поверхнями. Ідею границі вперше було використано стародавнім грець-
ким математиком IV ст. до н. е. Евдоксом Кнідським. Метод Евдокса,
який був названий «методом вичерпування», використовували Евклід,
Архімед та інші вчені стародавнього світу.
Перше означення границі дав у середині XVII ст. англійський ма-
тематик Джон Валліс (1616—1703). Але тоді ще не було чіткого розу-
міння основних понять, пов’язаних з теорією границь. Зокрема, тер-
мін «нескінченно мала» розуміли як вказівку на розмір величини, а не
характер її зміни.
Термін «границя» і відповідний символ Ііт вперше було введе-
но англійським математиком і механіком Ісааком Ньютоном (1643—
1727).
218
Строге означення границі і неперервності функції сформулював у
1823 р. французький математик Огюстен Луї Коші (1789—1857). Озна-
чення неперервності функції ще раніше Коші сформулював чеський ма-
тематик Бернард Больцано (1781—1848). За цими означеннями на базі
теорії дійсних чисел було здійснено строге обгрунтування основних по-
ложень математичного аналізу.
Відкриттю похідної і основ диференціального числення передува-
ли роботи французького математика і юриста П’єра Ферма (1601—1665),
який у 1629 р. запропонував способи знаходження найбільших і най-
менших значень функцій, проведення дотичних до довільних кривих,
що фактично спиралися на _________к----------------- —-------------—
застосування похідних. Цьо- .... /X-----------.-у/к-------------—
му сприяли також роботи Ре- / Х^______________1_—V-----------------
не Декарта (1596—1650), 1 Х^.-------------1----X—--------------
який розробив метод коорди-ч /__________Х^----1-------Хч^-.--------
нат і основи аналітичної гео- ------------X, у.--------------------
метрі!’. Лише в 1666 р. Нью- І______________X X
тон і дещо пізніше Лейбніц ф1 Фг
незалежно один від одного
побудували теорію диферен- *
ціального числення. Ньютон
прийшов до поняття похідної, розв’язуючи задачу про миттєву швидкість,
а Лейбніц, — розглядаючи геометричну задачу про проведення дотичної
до кривої. Ньютон і Лейбніц досліджували проблему максимумів і міні-
мумів функцій. Зокрема, Лейбніц сформулював теорему про достатню
умову зростання і спадання функції на відрізку.
Ейлер в роботі «Диференціальне числення» (1755 р.) розрізняв ло-
кальний екстремум і найбільші та найменші значення, функції на пев-
ному відрізку. Він перший почав використовувати грецьку букву А для
позначення приросту аргументу Ах = х2 — хт і приросту функції Аг/ =
= у2 — Уі-
Позначення похідної у' і /' (х) ввів французький математик Жозеф
Луї Лагранж (1736—1813).
Інтегральне числення і саме поняття інтеграла виникли з потреб
обчислення площ плоских фігур і об’ємів довільних тіл. Ідеї інтеграль-
ного числення беруть свій початок у роботах стародавніх математиків.
Про це свідчить «метод вичерпування» Евдокса, який пізніше викори-
став Архімед у III ст. до н. е. Суть цього методу полягала в тому, що для
обчислення площі плоскої фігури (об’єму тіла) навколо них вписували
і описували ступінчасті фігури і, збільшуючи кількість сторін многокут-
ника (граней многогранника), знаходили границю, до якої прямували
площі (об’єми) ступінчастих фігур. Проте для кожної фігури обчислен-
ня границі залежало від вибору спеціального прийому. А проблема за-
гального методу обчислення площ і об’ємів фігур залишалась нерозв’яза-
ною. Архімед ще явно не застосовував загальне поняття границі і інте-
грала, хоча в неявному вигляді ці поняття використовувались.
У XVII ст. Йоганом Кеплером (1571—1630), який відкрив закони
руху планет, було успішно здійснено першу спробу розвинути ідеї Ар-
хімеда. Кеплер обчислював площі плоских фігур і об’єми тіл, спираю-
чись на ідею розкладання фігури і тіла на нескінченну кількість не-
скінченно малих частин. З цих частин в результаті додавання складалась
фігура, площа (об’єм) якої відома і яка дає змогу обчислити площу
(об’єм) шуканої. На відміну від Кеплера італійський математик Бонавен-
туро Кавальєрі (1598—1647), перетинаючи фігуру (тіло) паралельними
прямими (площинами), вважав їх позбавленими будь-якої товщини, але
додавав ці лінії. В історію матемаїики увійшов так званий «принцип
219
Кавальєрі», за допомогою якого обчислювали площі і об’єми. Цей прин-
цип дістав теоретичне обгрунтування пізніше за допомогою інтеграль-
ного числення. Для площ плоских фігур принцип Кавальєрі формулюва-
ли так: якщо прямі деякого пучка паралельних прямих перетинають фі-
гури Фг і Ф2 по відрізках однакової довжини, то площі фігур і Ф2 рів-
ні (рис. 6.25).
Ідеї Кеплера, Кавальєрі та інших вчених стали тим грунтом, на
якому Ньютон і Лейбніц відкрили інтегральне числення. Розвиток Ін-
тегрального числення продовжили Ейлер та великий російський мате-
матик П. Л. Чебишов (1821 — 1894), який розробив способи інтегрування
деяких класів ірраціональних функцій.
Сучасне означення інтеграла як границі інтегральних сум нале-
жить Коші. Символ / усіх було введено Лейбніцем. Знак / нагадує роз-
тягнуту букву 5 (першу букву латинського слова зшита — «сума»).
Термін «інтеграл» походить від латинського слова іпіе^ег — «цілий» і
був запропонований у 1690 р. Й. Бернуллі. /
Запитання і завдання для повторення
1. Сформулювати означення первісної для функції у = / (х) на
множині (а; Ь).
2. Який геометричний зміст загального вигляду первісної?
3. Які задачі фізичного змісту приводять до поняття первісної?
4. Яка задача геометричного змісту приводить до поняття первіс-
ної?
5. Сформулювати основну властивість первісної.
6. На яких твердженнях грунтується доведення основної власти-
вості первісної?
7. Довести основну властивість первісної.
8. Сформулювати правила знаходження первісних. Довести, що
первісною для функції // = / (кх + Ь) є — Р (кх + Ь),
к
9. Які задачі приводять до поняття інтеграла?
10. Сформулювати означення інтеграла.
11. Записати формулу Ньютона—Лейбніца і прокоментувати її.
12. Назвати властивості інтеграла.
13. Назвати відомі вам застосування інтеграла.
14. Як обчислити за допомогою інтеграла площу плоскої фігури,
обмеженої графіками двох функцій?
15. Як обчислити за допомогою інтеграла площу плоскої фігури,
якщо вона розміщена під віссю 0x7
16. Як обчислити за допомогою інтеграла об’єм тіла?
17. Записати формулу об’єму тіла обертання за допомогою інте-
грала.
Вправи
1. Довести, що функція Р є первісною для функції / на всій число-
вій прямій:
1) Р (х) = -1— Xі, /(*) = _!_№; 2) Р (х) = 2х + 5, / (х) = 2;
16 4
3) Р (х) = х2 3 4 — З, / (х) = 2х;
4) р (х) — 12 соз Зх + 1^2, / (х) = — 4 зіп Зх;
220
5) Р (х) = зіп -і- х — 3, ? (х) = -1- соз-і- х;
6) /(х) = --^ при хЄ(0; +оо)
5х2 5х3
2. Довести, що функція Р є первісною для функції / на вказаному
проміжку:
1)/?(х)=А, Г(х)=------£, хЄ(0;4-оо);
„ з<-
2) Р (х) = . — 1, / (х) = /х, хЄ (—оо; 4-оо);
4
3) Р(х) =7і§х— 1, Цх)=—7—_, ХЄЯ, х^Л-4-пл;
СОЗ2 X 2
4) /?(х) = --Л_, Цх) = Л_, х£(-оо; 0) І) (0; 4-оо),
3. Знайти загальний вигляд первісної для функції / на 7?:
1) / (х) = х; 2) / (х) = 2 соз х; 3) / (х) = _2- зіп х;
4)Ш = —^7’
5) [ (х) = — —1, х пл; 6) / (х) = соз 2х;
ЗІП2 X
7) Дх) = — зіп Зх; 8) / (х) = х4.
4. Знайти функцію /, якщо відомий загальний вигляд первісної
Р (х) + С:
1) Р(х) +С = 3х2 + С; 2) /7(х)+С = —і§х + С;
3) Р (х) + С = — 4 зіп х + С; 4) Р (х) + С = сі§ х + С.
5. Швидкість руху точки задається рівнянням V = 7х2 — 1 (м/с).
Знайти рівняння руху 5 = 5 (/), якщо 5 = 12 у момент часу і — 2с.
6. Швидкість руху точки задається рівнянням и = 3 соз і (м/с).
Знайти рівняння руху, якщо у початковий момент часу точка знаходи-
лась на відстані 2 м від початкового положення.
7. Точка рухається по прямій із сталим прискоренням 12 м/с. Знай-
ти швидкість руху точки, якщо у початковий момент швидкість ц, =
= 100 м/с.
8. Точка рухається по прямій із сталим прискоренням а = 8 м/с2.
Знайти рівняння руху 5=5 (/), якщо відомо, що в момент часу І — 0.
точка знаходилась на відстані 24 м від початкового положення і мала
початкову швидкість 5 м/с.
9. Точка масою т = 6 кг рухається по осі Ох під дією сили, спря-
мованої вздовж осі Ох. У момент часу і ця сила дорівнює Р (/) =2/ — 1.
Знайти закон руху х — х (/), якщо при і — 3 с швидкість V — 2 м/с, а
координата х = 12, де Р — сила у ньютонах, і — час в секундах, х —
шлях у метрах.
10. Обчислити інтеграли:
А
2 8 / з 2
1) у (Зх — 1) Ох; 2) $ \2х 4- -у=-1 Ох; 3) С (5х 4- 1)а ах;
=1 з ' х -і
221
я я
2 2 З
5 зіп хйх\ 5) § (х + 2)3 сіх; 6)
я о я
4 6
я
з з
\ (Xі —2 /х) ах-, 8) \ —5— ах;
Л Л соз2 х
і о
~^—0х-
8ІП2Х
Я
З
9) соз 2х<іх.
о
Ю)
х2
(ІХ;
И)
12)
4 /
я
б
§ (1+ соз
п
13)
б
V2х —~3с1х;
2
14)
о
<їх;-
16)
2іїх
зіп2
17)
19)
18)
^К(4 — Зх)3ах; 20)
0
із
Г (ІХ
1 о 4_____________
К (1 + 2х)2
Я
11. Обчислити площі плоских фігур, обмежених:
2
\ ЗІП
4
4
2
А
1) лініями, зображеними на рис, 6.26, а та рис. 6.26, б;
2) лініями у = х2, у = 4;
222
3) дугою косинусоїди у = 2 соз х на відрізку — -і ;
4) лінією у = х3, віссю Ох і прямою х = 2;
5) параболою у — 1 — х2 і віссю Ох;
6) параболою у = х3 і прямою у = х + 1,
Б
7) графіком функції у = —х2 + 4 і прямою х + у = 4;
8) графіками функції у = —х2 — 2х + 8, у = х? + 2х + 2;
9) параболою у == х2 + 1 та прямою 5х + Зу — 25 = 0;
10) лініями у = 0, у = —х2 + 3, х = 1, х = 1,5;
11) кривою у = х3 і прямими у — 1, х= —2;
12) прямою у = х і параболою у = 2 — х2;
В
13) лініями у = (х + І)2 і. у = 4 — х;
14) прямою у = 4, параболою у = Зх2 — Юх + 7 та дотичною до
цієї параболи, проведеною через точку з абсцисою х0 = 2;
15) параболою у = х2 + 2х — 8 і віссю Ох;
8
16) графіком функції у = —х3, у — -^-ух\у~3.
12. Знайти об’єм тіла, утвореного:
1) обертанням навколо осі Оу фігури, обмеженої прямими у = 2х,
х — 0, у = 5;
2) обертанням навколо осі Ох фігури, обмеженої синусоїдою і пря-
мими х = 0 і х = —;
2
3) обертанням навколо осі Ох фігури, обмеженої кривою у = х* і
прямими х — 1 і х = 2;
4) зрізаного конуса з радіусами основ і\ і г2 І висотою Я.
13. Тіло рухається прямолінійно із швидкістю V (і) (м/с). Обчис-
лити шлях, який пройшло тіло за проміжок часу від до /2, якшо:
1) V (0 = 5/ — З, /і = 0, /2 = 3;
2) V (0 = /2 — 5/, і± =1, і2 = 2;
3) V (0 = 1 — 3/, іі = 2, = 5;
4) V (0 = /2 __ 5/ + = 0, І2 = Е
14. Обчислити роботу, яку треба затратити, щоб викачати воду з
циліндричної цистерни, радіус якої дорівнює Я, а висота Н.
223
15. Обчислити роботу, яку треба затратити, щоб розтягнути пру-
жину на 0,06 м, якщо сила 12 Н розтягує її на 0,01 м.
Вказівка. За законом Гука сила Р пропорційна розтягу або
стиску пружини, тобто Р = кх, де х — величина розтягу або стиску.
З умови задачі можна знайти к. Оскільки при х = 0,01 м сила Р дорів-
нює 12 Н, то к = —; к = —— = 1200. Отже, Р = кх = 1200х.
к 0,01
16. Обчислити роботу, яку треба затратити для стиску пружини,
якщо сила в 4 Н стискає цю пружину на 2 см.
17. Знайти масу неоднорідного стержня довжиною 40 см, якщо його
лінійна густина змінюється за законом р (/) = 2і2 + 1 (кг/м).
18. Знайти кількість електрики, яка проходить через поперечний
цереріз провідника за 20 с, якщо сила струму змінюється за законом
/ (0=2/+ 1 (4).
19. Продуктивність праці бригади робітників протягом зміни на-
ближено визначається формулою / (/) = —2,53/2 + 24,75/+ 111,1, де
/ — робочий час у годинах. Визначити об’єм продукції, виготовленої
бригадою на п’яту робочу годину.
РОЗДІЛ 7
СТЕПІНЬ З РАЦІОНАЛЬНИМ ПОКАЗНИКОМ
§ 1. Корінь п-го степеня і його властивості
1. Поняття кореня л-го степеня. В курсі алгебри 8 кла-
су було введено поняття квадратного кореня: квадратним ко-
ренем з числа а називають число, квадрат якого дорівнює а.
Наприклад, числа 3 і —3 — квадратні корені з 9, бо
З2 = 9 і (—З)2 = 9; -|- і (—— квадратні корені з
. / 2 \2 4 / 2 \2 4
б° ( 5 ) 25 ( 5 ) , 25 ’
Квадратний корінь з 0 дорівнює 0, бо О2 = 0, корінь з
0 єдиний. Квадратний корінь з —25 не існує, бо немає та-
кого дійсного числа,квадрат якого дорівнював би —25.
Отже, існують два квадратні корені з додатного числа:
один додатний, а другий від'ємний. Додатний квадратний
корінь з додатного числа а називають арифметичним квад-
ратним коренем і позначають а. Знак називають зна-
ком арифметичного квадратного кореня; вираз, що стоїть
під знаком кореня,— підкореневим виразом.
Додатні числа разом з числом нуль називають невід'-
ємними числами. Надалі поняття арифметичного квадратно-
го кореня вживатимемо стосовно невід’ємних чисел.
Арифметичним квадратним коренем з невід'ємного чис-
ла а є невід'ємне число, квадрат якого дорівнює а.
224
З цього означення випливає, що при а < 0 вираз не
має смислу (наприклад, К—16, V—49, К—1,44).
Використовуючи введене позначення, запишемо корені
рівняння х2 = 81: хх = К81, х2 = —К81.
Якщо треба добути квадратний корінь з алгебраїчної
суми, то не можна добувати його з кожного доданка окремо.
Наприклад, 1^9 + 16 = ]/25 = 5, але ]/9 + К16 =
= 3 + 4 = 7.
Отже, дія добування кореня відносно додавання (і від-
німання) не має розподільної властивості. Те саме можна
сказати і про дію піднесення до степеня.
Ми нагадали найважливіші відомості про квадратний
корінь, або корінь другого степеня.
Розглянемо корінь будь-якого степеня. Рівність б3 =
= 125 можна прочитати так: число 5 є кубічним коренем
(коренем третього степеня) з 125.
Аналогічно з рівності (—4)3 = —64 випливає, що число
—4 є кубічним коренем з —64, а з рівності (—З)4 = 81 —
число —3 є коренем четвертого степеня 81.
Добування кореня — це операція, обернена до опера-
ції піднесення до степеня.
Коренем п-го степеня з числа а називається таке число,
п-й степінь якого дорівнює а (п — натуральне число).
Нехай п — непарне число. Корінь непарного степеня з
числа завжди існує і до того ж тільки один: при а > 0 цей
корінь додатне число, при а = 0 він дорівнює нулю, а при
а < 0 корінь — від’ємне число.
Для його позначення використовують знак а (читають
«корінь п-го степеня з а»). Число п називають показником
кореня, число а — підкореневим виразом.
Нехай п — парне число. Якщо а > 0, то існує два про-
тилежних числа, які є коренями п-го степеня з а.
Додатний корінь п-го степеня з а позначають у цьому
«/—
випадку знаком у а, тоді протилежне йому число дорівнює
п —
— Пг-
При а = 0 існує єдиний корінь п-го степеня з а; у 0 =
= 0, бо 0" = 0.
При а •< 0 корінь п-го степеня з а не існує. Інакше ка-
п >--------- .
жучи, вираз у а, де п — парне і а < 0, не має смислу.
Отже, якщо п непарне число, то вираз у^а має смисл при
будь-якому а; якщо а парне число, то вираз а має смисл
лише при а 0.
8 1-1819 225
Очевидно, при всіх значеннях а, при яких вираз у^а має
смисл, справджується рівність (уґ а)п = а.
Якщо а 0, вираз уЛа завжди (як при парному, так і
при непарному п)’ має смисл.
Арифметичним коренем /2-го степеня з невід’ємного чис-
ла а називається невід’ємне число, /2-й степінь якого дорів-
нює а.
Корінь непарного степеня з від’ємного числа можна ви-
разити через арифметичний корінь того самого степеня з
протилежного (додатного) числа. Наприклад, У—125 =
= —У Ї25.
Взагалі, якщо а < 0 і к — непарне число, то -]/~а =
26—1 у-
= — у — а.
Справді
—1 у—. 1 , —1 у---. 97? 1 . ч
( уау* = а\ (— у — = — (— а) = а.
Надалі користуватимемося арифметичними коренями.
Зазначимо, що за показник кореня можна взяти будь-яке
натуральне число. Проте показник кореня, що дорівнює
1 Л~-
одиниці, не розглядатимемо, бо за означенням кореня у а ~
— а.
Найменший з натуральних показників, які розглядають,
дорівнює 2, його не пишуть.
2. Властивості коренів. За означенням кореня /2-го сте-
пеня можна довести такі твердження:
1) Для будь-яких невід’ємних чисел а і Ь і будь-якого
натурального числа п виконується рівність
уГа • Ь = УаЬ.
(1)
Добуток коренів /2-ГО степеня з чисел а і Ь дорівнює ко-
реню /2-ГО степеня з їхнього‘добутку.
Це твердження можна узагальнити: для будь-яких на-
• п г~~
туральних чисел п і г і невід ємних чисел 62Х, ..., аг\ у а2 X
п г- П/— П у---------
X у а2 ... у аг == у Наприклад,
Уг . 1/8 = >/І6 = 2, бо 24 = 16;
>/27 • |/9 = >/243, бо З8 = 243;
У^8 • УІ25 = У- 1000 = — 10, бо (— 10)3 = - 1000;
У 2 • У 4 • у 16 = у 128 = 2, бо 2’ = 128.
226
2)' Для кожного невід’ємного числа а, кожного додат-
ного числа Ь і натурального числа п виконується рівність
Частка коренів п-го степеня з чисел а і Ь дорівнює ко-
реню /2-го степеня з їх частки. Наприклад;
3/3
27 = 3, бо 33,= 27;
“ 27 ‘
3) Для кожних цілого числа к, додатного числа а і нату-
рального числа п виконується рівність
^а)к = Уак. ’ (3)
Якщо к— натуральне число, то рівність виконується
і для а = 0, тобто для будь-якого невід’ємного числа а.
Якщо к = п, то (ЇЛ а)л = У сГ = а.
Приклади.
а) (Уз)4 = Уз4 = УП; б) (—Уїї)6 = — УїР = — 11;
в) (3УіГЗ)® = З6УНЗ)5 = З5 • (— 3) = — 3е = —729;
г) (_/7)3=-У75=-У343.
4) Для будь-яких натуральних чисел т і п, кожного не-
від’ємного числа а виконується рівність
}/У16= 2Уі6 = /16 = 2; У/1024 = 5'р/1024 =
= ’У ОТ = 2.
8*
227
5) Для будь-яких натуральних чисел т, п і р і кожного
невід’ємного числа а виконується рівність
Наприклад:
|/9« = /9 = 3; И25® = /(б5? = /б1"2 = б3 = 125
або |<256 = /(253)2 = /253 = V 25а - 25 = 125;
1/215 = 22 = 4;
уҐР6 = З3 = 27.
Доведемо для прикладу рівність (1). Позначимо у/~а і і/~Ь
відповідно через х і у. Очевидно, х > 0, у 0.
За означенням кореня п-го степеня а = хп, Ь = уп, звід-
ки
аЬ = хпуп = (ху)п.
Числа а, Ь невід’ємні. Отже, і аЬ невід’ємне число, а то-
му існує єдине невід’ємне число, яке є коренем п-го степе-
ня з аЬ.
Беручи до уваги, що ху 0, дістанемо аЬ = ху або
= /а • /&, що і треба було довести.
Пропонуємо самостійно довести цим самим способом
рівності (2) — (5).
Зазначимо, що для практики обчислень важливо вміти
читати деякі з наведених вище рівностей справа наліво.
Щоб добути корінь п-го степеня з добутку невід'ємних
чисел, треба добути корінь того самого степеня з кожного
множника і результати перемножити:
уґ аЬ = у4а • у/И. (1)
Наприклад:
|<343Т8 = ]/~343.1/8 = 7-2 = 14;
/їб~/8І = /іб • з/ЇЇТ = 2-3=6;
У32 • 243 = )Л32 • і<243 = 2-3 =6;
|/32 • 0,00001 = |/32 • V0,00001 = 2 - 0,1 = 0,2.
228
Щоб добути корінь п-го степеня з частки від ділення не-
від’ємного числа а на додатне число &, треба добути корінь
того самого степеня з діленого і дільника і перший резуль-
тат поділити на другий:
На окрему увагу заслуговує рівність (5), яка виражає
основну властивість арифметичного кореня: при діленні і
множенні показника кореня і показника степеня підкорене-
вого виразу на одне й те саме число значення кореня з невід'-
ємного числа не змінюється.
Доведемо це твердження. Нехай а 0, т, п, р — нату-
ральні числа. Треба довести, що у атр = у ат.
Позначимо атр = х (х 0), у^ ат = у (у 0). Тоді
за означенням кореня хпр = атр, уп = ят, значить, і упр =
= атр. Звідси хпр = упр. Оскільки х > 0, у > 0, те х = г/,
що і треба було довести.
При доведенні показник кореня і показник степеня під-
кореневого виразу ділимо на одне й те саме число. В тако-
му разі кажуть, що показники кореня і підкореневого ви-
разу скорочено на одне й те саме число.
З цього твердження дістанемо наслідок: щоб добути ко-
рінь із степеня, треба показник степеня підкореневого ви-
разу поділити на показник кореня, якщо можливе ділення
без остачі.
Справді, нехай а 0, т, п, р — натуральні числа і т =
= пр. Тоді за основною властивістю кореня маємо ат =
= апр = ар. Наприклад: у^363 = 6 363 = у^Зб;
і^253 = 4У^253 = /25;
229
^7Ї-2 = В^ = ^=^49;
V 16й .= /(2і)5 = /(2й)4 = /2й = /32.
Читаючи рівність ’/о™» = /ат справа наліво, тобто
п , — ир/ ---
}/ ат = / атр, дістанемо таке твердження: при множенні
показника кореня і показника степеня підкореневого вира-
зу на одне й те саме число значення кореня з невід’ємного
числа не змінюється.
За цим твердженням можна зводити радикали з різними
показниками до спільного показника. Наприклад:
/б"2 = 3-/52-2 = /5і; /2=2-/2і = 1/бТ
у— З у— 4 У—
Звести до спільного показника радикали: V 2, у 2 і у 2.
Найменше спільне кратне всіх показників радикалів 12.
Додаткові множники: для першого радикала 6, для другого
— 4 і для третього — 3. Отже,
/2 _'-^ = '^16;
/2 =
Перетворення радикалів доводиться виконувати над ви-
разами, які мають від’ємні числа. При цьому треба уважно
стежити за знаками.
Слід пам’ятати, що основна властивість арифметичного
кореня не завжди справджується. Наприклад: ]/—27 =
= —3; /Р=27р = °/ 729 = 3. Але —3 3, отже,
8/=27 /(—27)2.
3. Найпростіші перетворення радикалів. Винесення
множника за знак радикала. У випадках, коли підкореневий
вираз розкладається на множники так, що з одного або з
кількох з них можна добувати точний корінь, ці множники,
після добування з них кореня, можна записати перед зна-
ком кореня.
Наприклад: /75 = /25 • 3 = 5 /3;
/98а3Ь = /49 • 2 • а2 • аЬ = 1а /2а&;
/375х’у2 = /125 • Зх°ху2 = 5х2 /Зху2;
4 / 32а66 4 / 16 • 2а4а26 2а </-о~2Г
V ~мГ = V - м = лг
230
При винесенні буквених множників з-під знака радикала
під всіма буквами слід розуміти лише невід’ємні числа.
Зокрема, в розглянутих вище прикладах а 0, Ь 0, х
0, у 0, с 0, сі 0. Якщо а < 0 і Ь < 0, то вираз
]/ 98я36 має зміст, але не дорівнює 7а У2аЬ.
Щоб дізнатися, з яким показником степеня можна вине-
сти за знак кореня множник, а які множники і з якими по-
казниками степенів залишаться під коренем, досить по-
казник степеня множника, що стоїть під коренем, поділити
на показник степеня радикала:.частка покаже, в якому сте-
пені цей множник буде стояти перед коренем, а остача пока-
же, в якому степені цей множник залишиться під знаком
радикала.
За допомогою винесення множника з-під знака радика-
ла можна звести дробовий підкореневий вираз до цілого.
Для цього досить помножити чисельник і знаменник під-
кореневого виразу на один і той самий множник так, щоб
і /""Зх*
із знаменника добувався точний корінь. Наприклад: у — =
3 / За2х 3 Г За2х • 256 1 з /-
V ~ V 5^2 • 256 “ ~ЬЬ~ Ьх-
Введення додатних множників під знак радикала. Пе-
ретворення, обернене до виведення множників з-під знака
радикала, називається введенням множників під знак ра-
дикала.
Щоб ввести множник під знак радикала, треба піднести
його до степеня, показник якого дорівнює показнику коре-
ня, і записати результат під знаком кореня.
Так, запис а^Ь = апЬ можна розглядати як перетво-
рення, обернене до виведення множника за знак кореня.
Наприклад:
2]ЛЗ^ = У^^Зх = /І2х;
5а уг2х = (5а)3 • 2х = 125а3 • 2х = 250а3х;
За2 4 / 2&3 _ 4 / 81а8 2&3 _4,/ 18а6
Ь V 9а3 ~ V Ь* • 9а3 — V Ь •
2а^~х = У2паіпх.
Зазначимо, що введення множника під знак радикала
використовують при порівнянні виразів. Наприклад, що
231
більше: 2/5 чи 5/2? Ввівши множник під знак кореня,
дістанемо 2/5 = /22 • 5 = /20; 5 /2 = /5«Т2 = /50.
Отже, 5/2 >2/5.
Таке перетворення буває корисним при виконанні на-
ближених обчислень. Нехай треба обчислити 5 К2 з точні-
стю до 0,01. З таблиць знайдемо К2 « 1,41 (з точністю до
0,01). Наближене значення 5 ]Ґ2 = 5 • 1,41 = 7,05. Але
похибка знайденого добутку у п’ять разів більша за похиб-
ку наближеного значення К2. Щоб точніше обчислити ви-
раз 5 |/2, доцільно ввести множник 5 під знак кореня.
Дістанемо 5 ]Ґ2 = ]/50 ж 7,07. Отже, внаслідок вве-
дення множника 5 під знак кореня дістали точніше значен-
ня виразу 5 ]/2.
Під знак радикала можна вводити як числові, так і бук-
вені множники, тільки треба пам’ятати, що буквений множ-
ник не може бути від’ємним.
Зведення радикалів до найпростішого (нормального) ви-
гляду. Вважатимемо, що радикал зведений до найпрості-
шого вигляду, коли: підкореневий вираз не містить дробів;
раціональні множники винесені за знак радикала; показ-
ник кореня і показник степеня підкореневого виразу ско-
рочені на їхній найбільший спільний дільник. Якщо підко-
реневий вираз є добутком кількох множників, показники
яких мають спільний множник з показником кореня,то по-
казники кореня і співмножників поділені на цей множник.
Наведемо приклади зведення радикалів до найпрості-
шого вигляду:
Зх2г/ уГ-^- = У~'£у = У^У = 6х /Зху;
* **у * л у
о\/”3аг о3,/ За2 • 2 З/-—
2 ]/ — = 2 )/ -^^2- = /6а2;
”| Г а \ Ь ___ “і / а2 б2 __ 1 /~ (а2 + Ь2) аЬ _
V V аЬ “ V аЬТіїЬ
= -^-/а&(а24-Ь2). !
4. Подібні радикали. При спрощенні виразів, які мають
суму радикалів, користуються зведенням подібних радика-
лів. Воно аналогічне зведенню подібних членів. Проте оз-
начення подібних радикалів відрізняється від означення
подібних членів.
Радикали називають подібними, якщо після зведення їх
до найпростішого (нормального) вигляду вони мають рів-
232
ні підкореневі вирази і однакові показники. Наприклад,
подібними є радикали:
3/2, — 0,7/2, а&/2, (х— у)/2;
-і- у/~аЬ, — 3 уґаЬ, -х^~2 аЬ;
х^У Ух+ у, -±- ху /х +у-
Раціональний множник, що стоїть перед знаком радика-
ла, називають коефіцієнтом.
Якщо радикали не зведені до найпростішого вигляду, то
не можна нічого сказати про їхню подібність. Щоб це з’я-
сувати, треба їх спростити, тобто: звільнитись під радика-
лом від дробів; винести за знак радикала ті множники, з
яких добувається точний корінь; показник кореня і степе-
ня підкореневого виразу скоротити на найбільший спіль-
ний дільник.
' ч Розглянемо приклади на доведення подібності радикалів.
3)’//
Розв’ язання.
3) /4^
Отже, радикали подібні.
4) V; 5)4/а2—ь2.
Ро з в’ я з а»н н я.
4) 1/а+^ = 1/-^^=—* /Н^Я
' V а — Ь г (а — Ь)2 а — Ь г
Отже, радикали подібні.
6) і^Тб; 7) /4Я, 8))/б4--
Розв’язання. 6) /16 = 2^2;
7) /4ав = а /4 = а /2;
Отже, радикали подібні.
233
5. Дії над радикалами. Додавання і віднімання. Дода-
вання і віднімання радикалів виконують так само, як дода-
вання і віднімання раціональних одночленів: радикали спо-
лучають знаками «+» або «—» і зводять подібні члени, якщо
вони є.
У багатьох випадках при додаванні і відніманні радика-
лів доводиться спочатку виявляти подібні члени, а потім
їх зводити. Для виявлення подібних членів треба звести
радикали до найпростішого вигляду. Наприклад: 4 /б +
+ 7 /54 = 4 /б + 7]/ 9“Т~6 = 4/6 + 21 И 6 = 25/6;
+ ЗЬ ]/~= 2 у^аЬ + 3 у^аЬ = 5 /аЬ.
Множення і ділення радикалів. Щоб перемножити кіль-
ка радикалів з однаковими показниками, треба перемножи-
ти підкореневі вирази і написати добуток під знаком коре-
ня з тим самим показником. Наприклад. /7 • /5 • /2 =
= 1^76;
2 /Зах • / За = /9а2х = а /х.
Щоб поділити радикали з однаковими показниками, тре-
ба поділити їх підкореневі вирази і записати частку під зна-
ком кореня з тим самим показником. Якщо перед радикала-
ми є коефіцієнти, то їх треба поділити. Наприклад:
27 тЛЇІ5 : 9^5 = 3'/23;
-9а 1/ 1/^ =
г х Ь * 2ох2
= --^- =_3& = _
За г х (а — Ь)
Якщо треба помножити або поділити радикали з різни-
ми показниками, то їх спочатку зводять до одного показ-
ника. Наприклад:
/4а2: /2а = / 16а4: /8а3 = /2а;
а^2х • 4 /+ • ^7^ = а У~2^ • А УX
X Ь У&Ї? = й2 У -2°'4 х<іх-- = Ь2 У 1728х’.
234
Якщо треба помножити або поділити радикали на раці-
ональний вираз, то досить на нього помножити або
поділити коефіцієнт радикала. Наприклад:
5х Зах2 х
X (— 2,5а) = — 12,5ах )/"Зах2; 8а2Ь2 У'ху ' аЬ =
= -8 ху = 12а& Уху.
2аЬ г
Піднесення радикала до степеня. Піднесення радикала
до степеня і добування кореня з кореня ми вже розглядали
при вивченні властивостей коренів- Розглянемо ще деякі
приклади.
Щоб піднести радикал до степеня, треба піднести до цю
го степеня підкореневий вираз, залишивши той самий показ-
ник радикала. Наприклад:
(|/* Зх2у)2 = У (Зх2у)2 = у4 9х4//2; (у^ 2а3)п = 2па3п.
Добування кореня з радикалів. Щоб добути корінь з
кореня, досить з підкореневого числа добути корінь з по-
казником, що дорівнює добутку двох даних показників.
Наприклад;
]/"а4 == І/7" у4а14 =
А у-- і г----- 3 /—
у аи-у а1 ==ау а (перший спосіб);
(другий спосіб);
а4ІЛа2 = V(а2а)2 = а2}/а (третій спосіб);
Зазначимо, що множення і ділення сум, що містять ра-
дикали, виконують за звичайними правилами множення і
ділення многочленів. При цьому широко застосовують фор-
мули скороченого множення і ділення. Наприклад:
(/т - /ЛЛ) (К5Г+ПГ + КЛЛ) = (КГ+Л)2-
— (Ух—І)2 = х + 1—%Н-1=2 при х> 1;
(Д-|/За — 5-|-а — 5/0;б&+ 5Ь.
235
Розкладаючи на множники вирази, що містять радика-
ли, застосовують не тільки розклад на множники підкоре-
невих виразів, а й запис раціональних виразів у вигляді
добутку радикалів. Наприклад:
а + Vа = ]/га (У а + І),
тут а подаємо як У а • а;
а + У"аЬ У а (V а + К5) Ка і Г а
Ь + ^аЬ УЬ (Уа + /5) ““ У"Ь ~ ~ *
' Зведення до раціонального вигляду членів дробових ір-
раціональних виразів. При обчисленні дробових ірраціо-
нальних виразів у деяких випадках доцільно звільнитись
від ірраціональності (тобто від радикалів) у знаменнику або
чисельнику. Це перетворення грунтується на основній вла-
стивості дробу: величина дробу не змінюється від множен-
ня його чисельника і знаменника на одне й те саме число.
Наведемо приклади, коли знаменник — одночленний ір-
раціональний вираз:
6 = 6/3 = 6/3 = 2 рГд.
/З (/З)2 З у ’
5 = 5’|/3~3 = 55/3~2 = бУз2 = 5%/27
г^/з2 2^3». тЛз2 2^/з® 6 6
Якщо у знаменнику двочлен, то можна звільнитись від
ірраціональності у знаменнику, використовуючи тотожність
(х — у) (х 4- у) = х2 — у2. Наприклад:
5 5 (4 — /її) = 5(4 —/ТТ) _
4-Ь/ТГ (4 +/її) (4 —/її) 16—11
- 5(4—Кїї) д4_КІТ;
О
4 == _4(/б + /3) = 4 (/б + /3) =
/6— /3 (/6— /3) (/6 + /3) 6 — 3
_ 4(/б'4-/3) .
~ З
14 =________14(5 /2 — 2/7)_______=
5/2 4-2/7 (5/2-|-2/7) • (5/2—2/7) “
14(5/2—2/7) 14 (5/2 — 2 /7)
(5/2)2—(2/7)2 ~ 50 — 28 —
_ 14(5/2—2/7) _ 7(5/2—2/7)
~ 22 — 11
236
В окремих випадках виникає потреба звільнитись від
ірраціональності у чисельнику. Перетворення' виконують
аналогічно, тобто чисельник множать на такий вираз, щоб
добуток став раціональним виразом. Наприклад:
З/2 = З }г2 /2 = 6 .
5 “ 5 /2 ~ 5/2 ’
2 уГа3 2 У а3 • У а 2а
За За4/а За У а
5 + /3 = (5 + /3) (5 - /3) вв 5а—(/З)2 =
4 4(5_/з) 4 (5— /3)
_ 25 — 3________22 11
— 4(5—/з) ~ 4(5_/з) “ 2(5 —/3)
§ 2. Ірраціональні рівняння
Найпростіші ірраціональні рівняння. Рівняння, в яких
змінна міститься під знаком кореня, називають ірраціо-
нальними. Інакше кажучи, рівняння називають ірраціо-
нальним, якщо в ньому крім дій додавання, віднімання, мно-
ження, ділення, піднесення до степеня з натуральним по-
казником зустрічається також добування кореня з алгеб-
раїчних виразів, які містять невідоме. Наприклад:
Ух = 3; У 8 — х + х = 2; *У 2х + 7 = 3;
З — 5х + 1 = 1; ]/" х + Ух2 — 5 = 2 та ін.
Будь-яке ірраціональне рівняння можна перетворити в
ціле алгебраїчне рівняння, яке є наслідком вихідного.
Доведення цього твердження у загальному вигляді
складне, і ми розглянемо лише окремі випадки.
При розв’язанні ірраціональних рівнянь, які містять
вирази з невідомими під знаком квадратного кореня, нама-
гаються позбутися коренів, підносячи до квадрата обидві
частини рівняння.
Приклад. Розв’язати рівняння У 8 — х + х = 2.
Розв’язання. Відокремимо радикал (залишимо
його в лівій частині), а решту членів рівняння перенесемо
у праву частину
У 8-х =2 — х.
Піднесемо обидві частини рівняння до квадрата
(]/8 — х)2 = (2 — х)2, звідки 8 — х = 4 — 4х + х2.
237
Зведемо утворене рівняння до нормального вигляду і
розв'яжемо його: х2 — Зх — 4 = 0, х2 = —1, х2 = 4.
Перевірка. Хі = —1. У лівій частині маємо
]/г8 —(—1) + (—!) = /8— 1 = 1/9 — 1 = 2.
Права частина теж дорівнює 2.
Отже, х = —1 є коренем даного ірраціонального рів-
няння.
х2 = 4. У лівій частині маємо
/8^4 + 4 = /4 + 4 = 6.
Права частина дорівнює 2. 6 =^= 2.
Отже, корінь х = 4 є стороннім для даного ірраціо-
нального рівняння, ми його відкидаємо.
Як виник сторонній корінь? Щоб з’ясувати це, розгля-
немо питання у загальному вигляді.
Нехай дано рівняння А = В, де А і В — деякі вирази,
що містять невідоме. Після піднесення до квадрата обох
частин рівняння дістанемо: А2 = В2, або (А + В) (Л —
— В) = 0. Маємо два рівняння: А — В = 0, тобто А = В,
і А + В = 0, тобто А — —В.
Перше з цих рівнянь таке саме, як вихідне, а корені
другого (якщо вони існують) можуть відрізнятися від коре-
нів даного. Тоді вони сторонні по відношенню до рівняння
А = В.
Тому, якщо при розв’язанні рівняння обидві його час-
тини підносять до квадрата (чи іншого степеня), то після
розв’язання утвореного рівняння треба вибрати з його ко-
ренів лише ті, які задовольняють початкове рівняння. Реш-
та коренів буде сторонньою.
Повернемось до рівняння У8 — х + х = 2. Із прове-
деного дослідження випливає, що сторонній корінь х = 4
має задовольняти рівняння К8 — х = — (2 — х). Це справ-
ді так, бо К8 — 4 = — (2 — 4); 2 = 2.
При піднесенні до квадрата обох частин рівняння А =
= В сторонніх коренів не буде, якщо рівняння А = —В не
має коренів.
В окремих випадках, не розв’язуючи даного ірраціо-
нального рівняння, можна з’ясувати, що воно не має ко-
ренів. Наприклад: Ух— 5 = —2 — рівняння не має ко-
ренів, бо арифметичний корінь не може бути від’ємним;
2 — Ух + 10 = 6 — рівняння не має коренів, цей ви-
падок стає очевидним, якщо рівняння записати у вигляді
КГ+То = —4}
238
]/х + Ух + 2 = 0 — рівняння не має додатних ко-
ренів, бо сума додатних чисел не може дорівнювати нулю
(бути від’ємними або одночасно дорівнювати іїулю ці чис-
ла не можуть);
Ух + 2 — Ух — 2 = 0 — рівняння не має коренів, бо
Ух + 2 і Ух 2 не можуть бути рівними ні при яких зна-
ченнях х;
Ух — 5 — У4 — х = 3 — перший радикал має смисл
при х — 5^0, тобто при х > 5, а другий — при 4 — х
0, тобто при х 4.
Ці нерівності несумісні, отже, дане ірраціональне рів-
няння не має коренів.
Розглянемо ще кілька прикладів розв’язання ірраціо-
нальних рівнянь.
Приклад 1. У+ 8 + УЗх — 2 = 2.
Розв’ язання. Маємо два радикали, позбутися
яких одночасно піднесенням до квадрата неможливо.. Тому
відокремимо один з радикалів, а потім піднесемо обидві
частини рівняння до квадрата:
/4x^8= 2 —/Зх —2, (/4х + 8)’= (2 — /3/^2)2,
4х “|” 8=4 — 4 /Зх — 2 -}" Зх — 2,
4/Зх=^2 = —х —6,
(4 /Зх — 2)2 = (— (х + б))2, 16 (Зх — 2) = х2 + 12х + 36,
х2 —36х + 68 = 0,
звідки хх = 2, х2 = 34.
Обидва ці корені для даного ірраціонального рівняння
є сторонніми (перевірте це).
Чи можна було, не розв’язуючи даного ірраціонального
рівняння, з’ясувати, що воно не має коренів?
Зазначимо, що при розв’язанні прикладів немає потре-
би заздалегідь з’ясовувати, чи з’являться сторонні корені
при піднесенні до квадрата. Підносимо до степеня стільки
разів, скільки треба для знищення радикалів, і перевіря-
ємо, чи задовольняють корені утвореного рівняння почат-
кове. _____
Приклад 2. У2х + 15 — Ух — 1=3.
Розв’язання. рл2х+15 = 3 + '|/х — 1,
(У2х+ 15)2 = (3 + /Г^ї)2,
2х+ 15- 9+ б/х^1+ х—1,
х + 7 = 6У х — 1,
23?
(х+7)2 = (бКх — І)2,
х2 + 14x4- 49 = 36(х—1),
х2—22x4* 85= 0, хх = 5, х2 = 17.
Перевіримо, чи є числа 5 і 17 коренями вихідного рів-
няння:
хх = 5,.у лівій частині дістанемо К25 — ]/4 = 3. Пра-
ва частина дорівнює 3. З = 3.
х2 = 17, у лівій частині дістанемо 1^49 — К16 = З,
3 = 3.
Отже, дане ірраціональне рівняння має два корені:
хх = 5, х2 = 17.
Розглянемо приклад рівняння з трьома радикалами.
Приклад 3'. 2 'Кх — 1 — К* + 2 = ]/5х — 10.
Розв’язання. . Піднесемо обидві частини рівнян-
ня до квадрата:
(2 — КГ+"2)2 = (У5х — 10)2,
4(х — 1)_4 /(х — 1)(х4- 2) 4- х4* 2 = 5х— 10.
Відокремимо радикал і зведемо подібні члени:
4 К(х — 1)(х,4* 2) = 8, К(х — 1)(х4*2) = 2,
(К(х— 1)(х+ 2))2 = 22, (х — 1) (х 4* 2) = 4,
х2 4* х — 6=0, хх = — З, х2 = 2.
Перевіримо здобуті корені за вихідним рівнянням:
хх = —3, у лівій частині вираз 2 К—3 — 1 — К —3 + 2
не має смислу. Отже, х, — —3 — сторонній корінь;
х2 = 2, ліва частина 2 У 2 — 1 — рЛ2 + 2 = 0, права
частина Кб • 2 — 10 = К10 — 10 = 0.
Отже, х2 = 2 — корінь даного ірраціонального рів-
няння.
Розв’язування складніших ірраціональних рівнянь.
Приклад 1. 2 іК2х + х3 + 15 — х — х + 2.
Р о з в’ я з а н н я. Відокремимо радикал
2 |^2х + х8 + 15 = 2х + 2, р^2х + х3 + 15 = х + 1.
Звільнимося від радикала
(•^2х+х3 + 15)3 = (х + І)3, 2х +х3+15 = х® +Зх2 +
+ Зх + 1.
240
Зведемо рівняння до нормального вигляду
Зх2 + х — 14 = 0, хх = — 2 -і-, х2 = 2.
Перевірка. хх = — 2, ліва частина
2]/2-(-24)+(-2т)‘+15+24-=
- 2У-24т-+2т=2 +2т-
Права частина — 2+ 2 ---------,------|- = —
тобто х — — 2 -у- є коренем даного ірраціонального рівняння.
х2 = 2, ліва частина
2^4 + 8+ 15 —2=2^27 —2 = 2-3 —2 = 4.
Права частина 2 + 2 = 4, 4 = 4, тобто х2 = 2, теж за-
довольняє дане рівняння. Отже, хх = —2-І-, х2 = 2.
О
Приклад 2. у/'х2 — 4}/х + 3 = 0.
Розв’ язання. Перший спосіб. Подамо
рівняння у вигляді 4Ух — Ух2 = 3 і піднесемо обидві ча-
стини до куба. При цьому формулу- куба різниці візьмемо
в такому вигляді:
(а — Ь)3 = а3 — Ь3 — ЗаЬ (а ~ Ь).
Маємо 64х — х2 — 12 )/х • }/х2 (4 )/х — у^х2) = 27.
Врахуємо, що іЛх • Ух2 = = х і- 4 і/х — у^х2 = З
(це випливає з умови).
Отже, перетворене рівняння має вигляд
64х — х2 — 12х • 3 = 27, х2 — 28х + 27 = 0,
Хі = 1, х2 = 27 — корені цього рівняння.
Підставляючи у початкове рівняння його корені, пере-
конаємося, що обидва вони його задовольняють.
Як бачимо, розглянутий спосіб розв’язання дуже гро-
міздкий.
Другий спосіб. Беручи до уваги, що (Ух)2 =
3 /—з . з г-
= у х2, можна ввести нову змінну, поклавши у х = у. То-
241
ді Ух2 = у2 і відносно нової змінної рівняння перетворю-
ється на таке: у2 — 4у + 3 = 0. Звідси у± = 1, у2 = 3. Але
х = у3 Отже, = 1, х2 = 27.
Розглянемо ще кілька прикладів розв’язання ірраціо-
нальних рівнянь способом введення допоміжного невідо-
мого. _____
Приклад 3. х2 + Их2 — 9 = 21.
Розв’ язання. Віднімемо від обох частин рівнян-
ня по 9:
х2_9+у х2_ 9= 12.
* Введемо допоміжне невідоме у = Ух2 — 9. Маємо у2 +
+ у — 12 = 0, г/і = — 4, у2 = 3. Коріньу± = —4 відки-
даємо як сторонній.
Підставляючи друге значення у в рівність Ух2 — 9 =
= у, знайдемо V х2 — 9 = 3, х2 — 9 = 9, х = ±ЗУ24
Приклад 4. 2]Ух2 — Зх 4- 11 — Ух2 — Зх + 3 = 5.
Розв’язання. Введемо нове невідоме у =
= Ух2 —Зх + 11, тоді х2 — Зх + 11 = у2 і х2 — Зх + 3 =
= У2 - 8.
Таким чином, відносно нового невідомого дане, рівнян-
ня має вигляд 2у — ]/ у2 — 8 = 5. Звільнившись від радика-
ла, дістанемо Зу2 — 20у + 33 = 0, звідки уг = 3, у2 =
= . Обидва корені задовольняють рівняння (перевірте
це). Далі, беручи до уваги, що х2 — Зх + 11 = у2, діста-
немо два рівняння відносно х:
Xі — Зх+ 11 = (-У")2’ *2 —3х+11 = 32,
або після спрощення
х2 —Зх---у- = о, х2 —Зх + 2 = 0.
9 ± 13
Перше рівняння має корені хі,2 =-------------» а АРУге
х^ •—: 1, х2 = 2.
Усі чотири корені задовольняють дане рівняння, у цьо-
му можна переконатися, підставивши їхні значення. От-
9+13 і п
же, ХЦ2 == ----0----- , х3 = 1, х4 = 2.
242
Приклад 5. ]/” 1,5 — х 'Кх2 — 5,25 = 2.
Розв’ язання. Піднесемо обидві частини рівнян-
ня до квадрата і виконаємо перетворення:
1,5 —х К*25,25 = 4,
х Vх2 — 5,25 = — 2,5, х2 (х2 — 5,25) = 6,25,
х4 - 5,25х2 — 6,25 = 0.
Введемо позначення х2 = у. Маємо у2 — 5,25// — 6,25 =
= 0; //і = —1, у2 = 6,25. Але х2 0, тому у± = —1 від-
кидаємо. Залишається х2 = 6,25, звідки = —2,5, х2 =
= 2,5.
При х = —2,5
|/"1,5 —х/х2 —5,25 = ]/1,5 + 2,5 /6,25 — 5,25 =
= /4 = 2.
При х = 2,5
У 1,5 —х/х2 —5,25 = У 1,5 —2,5 /6,25 — 5,25 =
= /=т,
але такого числа серед дійсних чисел не існує. Отже, дане
ірраціональне рівняння має єдиний корінь х = —2,5.
Приклад 6. х2 — х — р х2 — х + 13 = 7.
Розв’ язання. Додавши до обох частин рівняння
по 13, маємо
(х2 — х + 13) — /х2-х + 13 = 20.
Введемо позначення /х2— х + 13 = у, дістанемо
квадратне рівняння відносно у у2 — у — 20 = 0, корені
якого у і = —4 і у« = 5.
Але /х2 — х т Ід 0. Отже, уг = —4 відкидаємо і
беремо /х2 — х + 13 = 5. Маємо х2 — х + 13 = 25, х2 —
•— х — 12 = 0, Хї = —3, х2 = 4.
При х = —3: 9 + 3 — /9 4 3 + 13 = 12 — 5 = 7.
При х = 4: 16 — 4 — 1-16 — 4 + 13 = 12 — 5 = 7.
Отже, дане рівняння має два корені: хг = —3 і х2 = 4.
Приклад 7. /х + 6 — /х — 7 = 5.
Розв’язання. Помножимо обидві частини рів-
няння на /х + 6 + Ух—7 Дістанемо
(/^+6 - /Г—7) (/Г+6 + /Г-7) =
243
==5Ух+6 + Гх-7),
х 4- 6 — х + 7 = 5 (УТ+6 + /х^7),
звідки іЛг + 6 + Ух — 7 — -у- . Додаючи почленно це рів-
няння до даного, дістанемо
2 Ух + 6 = . Звідси х — (— 6 = 8 .
о І о ] 4о
/ 19 \2 11
* Підставивши значення х = -=— — 6 = 8 у дане
\ и І 40
рівняння, переконаємося, що воно його не задовольняє (зро-
біть це самостійно). Отже, дане рівняння не має розв’язків.
Як бачимо, крім загальних підходів при розв’язанні ір-
раціональних рівнянь можна застосувати штучні прийоми.
Системи ірраціональних рівнянь. Якщо серед рівнянь
системи є ірраціональні, то для розв’язання її треба звіль-
нитися від ірраціональності. При цьому застосовують ме-
тоди, які використовували при розв’язанні ірраціональних
рівнянь. Наведемо приклади розв’язування систем ірраці-
ональних рівнянь.
п і х + у + У х-*уу = 20,
пр“«і-и+ї>-ізб. . ______
Розв’язання. Введемо нову змінну г = Ух 4- у.
Тоді х + у = г2 і перше рівняння системи матиме вигляд
г2 + г — 20 = 0, звідки гх = —5, г2 = 4.
Вираз Ух 4 у = —5 не має смислу. З рівності
Ух + у = 4 знаходимо х 4* у = 16.
Визначимо з цього рівняння х і підставимо його у друге
рівняння системи:
х=16-у, (16 — у)2 4-у2 = 136,
256 — 32г/ 4- г/2 4- г/2 = 136, 2г/2 — 32г/ 4- 120 = 0,
у2— 16г/4- 60 = 0.
Корені цього рівняння Уі = 6, у2 = 10. Визначимо х:
хх = 16 — г/х, хг = 10, х3 = 16 — у3, х3 = 6. Відповідь.
(10; 6), (6; 10).
Приклад 2.
ТхТІ4- = 5,
X 4- у = 37.
Розв’ язання. Введемо позначення Ух + 1 = р,
і/ у — 3 = у, тоді х 4- 1 — У, У —’ 3 — у. Додавши по-
244
членно ці рівняння, дістанемо х + у — 2 = р9 + д9, х +
+ У = Р3 + <73 + 2-
З другого рівняння системи маємо 37 = р9 + д9 4- 2,
або р3 + (р — 35.
Розглянемо тотожність (р + д)3 — У + (р + Зрд (р +
4- д) і підставимо замість р9 4* д3 і р 4- д їхні значення р8 4~
4* ср = 35, р 4- д = 5. Отже,
58 = 35 4- Зрд • 5, 15рд = 90, рд = 6.
Маємо систему рівнянь
(>+9=5,
І РЧ = 6,
звідки рг = 2, 9х = 3, ра = 3, р2 = 2.
Повернемось до невідомих х і у, дістанемо
у> 4- 1 = 2, х + 1 = 8;
{/у^З = 3, у — 3 = 27;
1/7+1 = 3, х+1 = 27;
У>^3 = 2, у-3 = 8.
Маємо дві системи рівнянь
х+ 1 = 8, (х+1 = 27,
у —3=27 1 | 9 — 3=8.
Розв’язками першої системи є х = 7, у = ЗО, а другої —
X = 26, у = 11. Відповідь. (7; ЗО), (26; 11).
Приклад 3.
' х + у = 13.
Розв’язання. Запишемо суму х + у у вигляді
х + у = (Кх + Уур — 2 Уху.
За першим і другим рівняннями системи маємо
13 = (4^ї~2^> 13 = -§-х9-2К^,
ху — 2 Уху —13=0.
ОО
Позначивши Уху = г, дістанемо
25г2 —72г—13-36 = 0,
245
36±/362 + 36 • 13 • 25
21(2 — 25 ’
36 ± 6 |<36 + 325 36 ± 6 • 19
2,12 — 25 — 25
36 —6-19 , . . 36Ч-6.19 36+ 114
-----25----(не існує), г2 = -^25----------= - -
Отже, У~ху = 6. Підставимо значення Уху у перше
рівняння системи. Маємо Ух-і-Уу = -~ -6, Ух + Уу =
= 5.
Розв’язавши систему рівнянь
Ух + У у = 5,
. Ух -Уу =6,
дістанемо Ух = 2, У у = 3, звідки хг — 4, уг — 9 і У~х —
= З, Уу = 2. Звідси х2 = 9, у2 = 4. Відповідь. (4; 9), (9; 4).
_ . У1 + 5х + У5 — у = З,
Приклад 4. ;
ох— //=11.
Розв’язання. Позначивши У1 + 5х = « і
Уб — у = V, дістанемо систему рівнянь
1 и + V = З,
| /? + Vі = 17,
розв’язками якої єи=1,о = 2іи = 2, V = І (знаходимо
методом спроб).
Повертаючись до початкових невідомих, матимемо
/1 + 5х= 1, 1 + 5х= 1,
]/ 5 — у = 2, 5 — у — 16.
Дістанемо дві системи лінійних рівнянь:
| 1 + 5х = 1, | 1 + 5х = 16,
( 5— у= 16 ’ ( 5 —у= 1.
Розв’язком першої системи є х — 0, у — —11, а другої —
х = 3, у = 4. Відповідь. (0; —11), (3; 4).
Ж
Приклад 5.
І (х у У~Х + у2) Ух Аг у2 = 65,
\ (х — уУ'х-^г у2) |/х2 + г/2 = 185.
Ро з в’ я з а н н я. Ліві частини рівнянь системи запи-
шемо у вигляді
(^- + х^ + 1)-^/ГТ72=65,
. (-^-^^ + 1)-У2/Г+^=185.
Поділимо почленно рівняння системи
(-V + + 1) ! (-V — + Й = 65:185.
\ у2 у2 І \ у2 у2 І
Спростивши цю рівність, дістанемо «
37(^ + -^ + 1) = 13(-?--іЛ + 1)’
звідки 24 + 50 + 24 = 0,
або
12^- + 25-?— + 12 = 0.
у2 у 1
Ввівши нове невідоме -?у- = г, дістанемо
12г2 + 25г+12= 0,
— 25 ± V625 - 4 12 • 12 _ — 25 ± ^49 — 25 ± 7
24 24
__£ г-_А
4 ’ 21~ 3 ’
21,2 =
— 32
21 — 24
24
4
З ’
Візьмемо
г - ~18 -
22 — 24 "
З
4 '
4 . х х 16
-т- 1 знайдемо -о-. Маємо —т- = -г- ,
з г у2 9 ’
=
9х х
-77- ♦ Підставимо значення —т-,
ш у*
звідки у2 =
у перше рівняння перетвореної системи
/Л________________і. + ік Л ]/х+
\ 9 3 Ч 16 Г 1(
= 65,
/ X 2 9
—, 1 У
у 9 *
247
-V- • “ЇГ І^ТГ = 65> звідки
-^-•4^=65» -^-^ = 65,
-^-•х=1, х3= 642, х3 = (48)2 = (42)3, х = 42, х = 16.
Знайдемо у. Маємо ^16 =------------—, звідки у — — 3.
У &
Аналогічно, підставляючи значення г2 = —, знаходимо
х = 9, у = —4. Відповідь. (16; —3), (9; —4).
§ 3. Узагальнення поняття степеня.
Степенева функція.
Степінь з натуральним і цілим показником. Для узагаль-
нення поняття степеня нагадаємо основні йоняття і формули:
ап = аа ... а, якщо п — натуральне число, «>1}
п разів
ап = а, якщо п = 1;
ап = 1, якщо п = 0, а=/= 0;
ап = Ай » якщо п — ціле число, п < 0, а Ф 0.
а п
Нагадаймо властивості степеня з цілим показником.
При множенні степенів з однаковою основою а (а #=0)
їхні показники додають
ат • ап = огп+л.
При діленні степенів з однаковою основою а (а =/= 0) від
показника діленого віднімають показник дільника
ат г ап = ат~п.
Щоб піднести до степеня добуток, досить до цього степе-
ня піднести кожний множник і результати перемножити
(аЬс)п = апЬпсп.
Інколи цю рівність необхідно прочитати справа наліво!
щоб помножити степені з однаковими показниками, досить
перемножити основи і результат піднести до степеня з тим
самим показником
апЬпсп = (аЬс)п.
248
Щоб піднести до степеня дріб, треба піднести до цього
степеня чисельник і знаменник і перший результат поділити
на другий
\ Ь ) ьп *
Щоб піднести до степеня степінь, треба показники степе-
нів перемножити, а основу степеня залишити без зміни
Зазначимо, що у формулюванні цих правил ніде не вка-
зувалося, яким має бути показник степеня — натуральним
числом чи цілим. Це тому, що множина цілих чисел включає
множину натуральних чисел як свою частину. Отже, наве-
дені правила стосуються степенів з натуральним, нульо-
вим і від’ємним показниками. Зрозуміло, що для випадку
степеня з нульовим і цілим показниками ставиться додат-
кова умова, щоб основа степеня не дорівнювала нулю.
Степінь з раціональним показником. Введення степеня з
нульовим і від’ємним показниками було першим розширен-
ням поняття про степінь. При цьому нові означення степе-
ня з нульовим і від’ємним показниками було введено так,
що властивості степеня з натуральним показником за-
лишалися правильними і для степенів в цілим показни-
ком.
Введемо поняття степеня, показником якого може бути
1 2
будь-яке дробове (раціональне) число. Наприклад, 2 2, З3 ,
т
б0’9, тобто а п , де а > 0, т— ціле, а п — натуральне число.
Введення степеня з дробовим показником е дальшим роз-
ширенням поняття про степінь. Означення степеня з дробо-
т
вим показником а п має бути таким, щоб властивості степеня
з натуральним показником залишалися справедливими і
для степенів з будь-яким дробовим показником.
Означення дробового показника виникло у зв’язку з ба-
жанням узагальнити правило добування кореня на випадок,
коли показник підкореневого числа не ділиться на показ-
ник кореня.
___ т
Правило — ап дістали за умови, що т і п — нату-
ральні числа і т ділиться на п.
Це правило будемо застосовувати і тоді, коли п — будь-
яке натуральне, а т — будь-яке ціле число.
249
Якщо а — додатне, п — натуральне і т — будь-яке
ціле число, то степінь числа а з дробовим показником є
радикалом Уат, тобто
Показником кореня є знаменник, а показником степеня
підкореневого числа — чисельник дробового показника.
т
Якщо а = 0, а —----дробове додатне число, то а п = 0.
Згідно з цими означеннями
2 5 _2_ —і ___
б3 = 0,36 = 3 4 = 3 4 = / З^;
17 ------.
І і V’7 І і \10 ’іп / / і \17 4-
Ш =Ш =|/ Ш 5 0 =»
2 З 1
Вирази 0 5, (— 4)8 , (— 8)3 не мають смислу.
Обмеження, що накладається на основу а (а > 0), не-
т
обхідне при означенні степеня а п . Справді, якщо а <0, то
т
при п парному і т непарному вираз а п не має смислу. На-
з _________________________ _________
приклад, (—5)2 = (—5)3 = К—125 не існує.
Отже, введення степеня з дробовим показником дає змо-
гу зберегти правило добування кореня з степеня у ат для
випадку, коли т не ділиться на п. Але можна дати означен-
ня степеня з дробовим показником, не користуючись понят-
тям кореня.
т
Степенем а п невід’ємного числа називають невід’ємне
число, п-й степінь якого дорівнює ат.
За означенням степеня з дробовим показником справед-
лива така тотожність:
т
(а~)п = а\
Це означення степеня з дробовим показником зручно
використовувати для доведення основних властивостей сте-
т
пенів виду а п .
250
Подаємо ці властивості без доведення. При будь-яких
додатному а і раціональних значеннях р і д
а^О1 = аР+р, (1)
ар . а = аР—ч, (2)
(а^ = арч. (3)
Крім того, при а > 0 і Ь > 0 і раціональному значенні
р справедливі тотожності
(аЬ)р = арЬр,
(4)
= _аР_
\ Ь / ьр ’
(5)
З властивості (1) випливає, що для будь-яких додатного
а і раціонального р
З властивості (3) випливає, що при будь-якому раціо-
нальному р
п/— Л-
у аР = а п
(а > 0, п — натуральне число, п Ф 1).
Приклад 1. Записати у вигляді степеня з раціональним
показником такі вирази:
а) = ао.зч-(—ін-2,7 = а2;
1 і І __ 5 1 __ 5 1 _ 1
б) (X2)4 =х8 ; в) Ь вЬ3=Ь 6 3 =6 2 і
_А_ 1 _А £
8 \°’4 „0,25 , 8Ч5 4 Л 8’5 4
г) \сс ) • а — \сс } * сс —— сс * сс *
__і_ і
= а 4 • а4 = а° = 1.
Приклад 2. Обчислити:
б) 43 • 22 = (22)3 • 22 = 26 > 2а = 28 = 256.
251
Приклад 3. Спростити:
6-0,5 ’
ь 2
5 _ 1 Б 6 ± / М
б) (а12)1'2^ 3 )-1'5 = а12'6 3 А 2) =
1 1
2 . 2 і.
= и »а = 1,
_ 3 2 9 6 2 1 Л. 2_
в) (с 7Г0Л)8-с7/'2 =с“7 у^с'у* =с~7 7 X
6 , 1
X у 6 5 = с~'у~\
Приклад 4. Знайти значення виразу:
а) (81 • 16)~Т = (З4 • 24)~Т = 34’(’Т) • 2*т) =
__ о-1 9—1 _ 1 1 — 1
“ 6 * — 3 ’ 2 ~ 6 ’
1 1 1
б) 1000000’2 • 0,001 3 = (108)6 • (10-3)3 = 10 .10-1 = 1-
Приклад 5. Записати вираз у вигляді квадрата
з
а) а30 = (а18)2; б)а3 = (а2)2;
в) а“’8 = (а-9)2; г) а"3 = (а“ Т)2.
Приклад 6. Записати вирази у вигляді степеня з дробо-
вим показником:
= / V3 =/‘3 21 ;
в) с? а = )/'уга* а. = ]ЛКа8 = = а6;
г) Xі х~3 = (х2)4 х~3 = )^}/х8 • х~3 =
= І^І^х8 = ^х8 = х20 = х0>2В.
252
Приклад 7. Виконати дії:
і і і
а) (1 + а2 )(1 — а2) = І2 — (а2 )2 = 1-а;
і ___і_ £ 2____і_ _2_
б) (Xі +у 2)2=(х2)2 + 2х2у 2 +(У 2)2 = х +
+ + у-';
£ 1 2. 1 1 £ 1 і
в) (а3 +63)(а3 — а3 Ь3 + Ь3) = (а3 )3 + (Ь3 )8 =
= а 4- Ь.
3. Поняття про степінь з ірраціональним показником.
Розглянемо степінь а“, де а — будь-яке додатне число, а=#
=/= 1, а а — будь-яке ірраціональне число. Розглянемо такі
три випадки.
а) а > 1 і а — додатне ірраціональне число, наприклад
5^.
Позначимо через а, будь-яке раціональне наближене зна-
чення а, взяте з недостачею, а через а2 — будь-яке набли-
жене раціональне значення числа а, взяте з надлишком.
Тоді степінь Позначає таке число, яке більше будь-якого
степеня ааі, але менше будь-якого степеня Наприклад,
Б^2" означає таке число, яке більше будь-якого з чисел ряду
£-1,4 ^1,41 ці,414 $1,4142
в якому показники — десяткові наближення К2, взяті з
недостачею, але менші будь-якого з чисел ряду
$1,5 $1,42 £1.415 £1.4143
в якому показники—десяткові наближення |/2, взяті з
надлишком.
б) а < 1 і а — додатне ірраціональне число, наприклад
0,5у5.
Тоді під степенем аа розумітимемо число, яке менше
будь-якого степеня але більше будь-якого степеня сР*.
Так, 0,5^2 є число, менше будь-якого з чисел ряду
0,5і’4, 0,5і’41, 0,5і’414, 0,5і’4142, ,
але більше будь-якого з чисел ряду
0,5і’5, 0,5і’42, 0,5і’415, 0,5і’4143, ....
Таким чином, якщо додатне ірраціональне число а зна-
ходиться між двома раціональними числами і а2, то сте-
253
пінь а“ знаходиться між степенями а“< і і при а > 1, і
при а < 1.
в) а % 1 і а — від’ємне раціональне число, наприклад
5-Л (4Г5
Тоді виразу 0а надають того самого змісту, який мають
степені з від’ємними раціональними показниками. Тал,
с-аГ?____!_ __ і
“ 5^ Ч 3 / ~
\ з /
Можна довести, що дії над степенями з ірраціональними
показниками виконуються за тими самими правилами, які
встановлено для степенів з раціональними показниками
а • а = а , -о- = а , що) = а о , (а ) = а ,
аР
де а, Ь — додатні, а, |3 — ірраціональні числа.
4. Степенева функція. Як ми вже переконалися, для
будь-якого дійсного числа р і додатного х визначено чис-
ло хр.
Якщо показник степеня р — стале число, а основа х —
змінна величина, то у = хр є функцією аргументу х, тобто
ї (х) = ХР.
Функцію / (х) = хр, де р — стале дійсне число, а х (ос-
нова) — змінна величина, називають степеневою.
Області визначення і зміни степеневої функції, а також
її властивості залежать від числа р.
1. Нехай р — натуральне число.
Функція визначена на всій числовій прямій;
при х = 0г/ = 0іх=1 при у = 1;
при непарному р для всіх значень х < 0 і х > 0 знак
функції збігається із знаком аргументу; функція непарна
і зростає на всій області визначення.
Графіком є пряма при р = 1 і криві при р = 3, 5, 7, ...,
симетричні відносно початку координат, розміщені у І і III
координатних чвертях (рис. 7.1).
При парному р у > 0 для всіх значень х < 0 і х > О,
функція парна. При х < 0 функція спадає, при х > 0 —
зростає. Графіки у = хр (р = 2, 4, 6, ...) — криві, симет-
ричні відносно осі у, розміщені у І і II чвертях (рис.- 7.2).
2. Нехай р — ціле від’ємне число.
Функція- визначена на всій числовій прямій, крім точки
х = 0 (немає числа, оберненого до нуля). Графік склада-
ється з двох віток.
254
При х = 1 у = 1.
При р непарному (—Г, —3, —5, ...) для всіх значень
х < 0 і х > 0 знак функції збігається із знаком аргументу.
Функція непарна, спадна на всій області визначення. Гра-
фіком є криві, симетричні
відносно початку координат,
розміщені у І і III чвертях
(рис. 7.3).
При р парному (—2, —4; —6, ...) значенням х < 0 і х >
> 0 відповідають значення у > 0. Функція парна. При х <
< 0 функція зростає, при х > 0 спадає. Графіком є криві,
симетричні відносно осі у, розміщені у І і II чвертях
(рис. 7.4).
3. Нехай р = у, де к = 2, 3, 4, ...
Функція визначена для всіх значень х 0, при цьому
У 0, у — 1 при х = 1.
Функція зростає на всій області визначення. Графіки
розміщені у II чверті (рис. 7.5).
Степенева функція у = хр при р > 0 визначена і при
х = 0, бо 0р = 0. Вираз 0° не має смислу.
При цілих р степенева функція визначена і для х < 0.
При парних р функція парна, а при непарних р — непарна.
При р = 0 зи означенням степеня з нульовим показни-
ком у = 1 при будь-якому х 0. Графіком такої функції
є пряма, паралельна осі х і віддалена від неї на відстань,
що дорівнюй 1. З цієї прямої треба виключити точку, яка
відповідає абсцисі, що дорівнює 0 (рис. 7.6).
Степенева функція у = СхР. На практиці часто дово-
диться розглядати функцію виду у = Схр, де С — стала.
Це функції у = кх, у = кх2, у = кх3.
255
Наприклад: функція 5 «4,9/2 при вільному падінні ви-
ражає залежність між пройденим шляхом 5 тіла і часом £
функція = л7?2 виражає залеж-
ність між площею круга К і його
радіусом г,
За формулою Рг == СрРо&г. виз-
начають зусилля різання Рг при об-
точуванні залежно від і і 5, при постійній швидкості різання
V, тому самому оброблюваному матеріалі і незмінному різ-
ці. Ср — коефіцієнт, Хр і Ур — показники степенів, сталі
в цій задачі.
Історична довідка
Поняття степеня виникло у зв’язку з обчисленням площі квадрата
і об’єму куба (звідси пішли назви «квадрат», «куб» для позначення дру-
гого і третього степенів). Збереглися таблиці квадратів і кубів, складені
за 1700 р. до н. е. у Вавілоні.
Для позначення вищих степенів пізніше вживали вирази «біквад-
рат» або «квадрато-квадрат» для четвертого степеня, «кубо-квадрат» для
п’ятого і т. д,
256
Сучасні назви для позначення степенів запропонував голландський
вчений Сімон Стевін (1548—1620), який позначав степені у вигляді чи-
сел, зображених у крузі. Він почав систематично використовувати дро-
бові показники степеня для позначення коренів. У наш час для добуван-
ня кореня вживають два позначення: знак радикала і дробові показни-
ки (позначення за допомогою радикалів є даниною традиції).
Наближене значення квадратних коренів з цілих чисел уміли добу-
вати ще у Стародавньому Вавілоні близько 4 тис. років тому’ Вавілон-
ські вчені користувалися для цього таким методом: число а подавали у
вигляді суми Ь2 + с, де с — мале порівняно з Ь2 число, і писали У^а =
= 6 + -£- Наприклад, /І800= /1600 + 200= /402+ 200= 40 +
+ І 1
2 . 40 2 ’
Такий спосіб наближеного добування квадратного кореня називають
вавілонським методом.
Іранський математик і астроном ал-Каші (помер близько 1430 р.),
який працював у Самарканді в обсерваторії відомого узбецького астро-
нома і математика Улугбека (1394—1449), сформулював такі правила:
с^1 • ап = агл+п і ат : ап = ат~^п. Ал-КашІ вмів зводити до спільного по-
казника добутки радикалів і словесно сформулював правила а • Гу/гЬ =
= у сР • у Ьп = у атЬп. Він також описав загальний спосіб добу-
вання коренів з цілих чисел.
Назва «радикал» походить від латинських слів гасііх — корінь та
гадісаііз — корінний.
Починаючи з XIII ст. європейські математики позначали корінь
цим словом або скорочено г. У 1525 р. у книзі чеського математика Хрис-
тофа Рудольфа (1500—1545) «Швидка і красива лічба за допомогою
вправних правил алгебри», з’явилося позначення V для знака квадрат-
ного кореня; кубічний корінь позначався там як V V у.
У 1626 р. голландський математик Альберт Жірар (1595—1633) за-
2 З
мість знака г ввів позначення V, V.... При цьому над підкореневим
виразом ставили горизонтальну риску. Замість сучасного радикала
УТ+ь тоді писали V# + Ь. Сучасне позначення кореня вперше з’яви-
лося в книзі французького філософа, математика і фізика Рене Декарта
(1596—1650) «Геометрія», виданій у 1637 р.
Степені з від’ємними показниками ввів шотландський математик
Уїльям Уолліес (1768—1843).
Дробові показники степеня і найпростіші правила дій над степеня-
ми з дробовими показниками були описані ще в XIV ст. в працях фран-
цузького математика Нікола Орема (1323—1382), який застосовував та-
кож ірраціональні показники степеня. У своїй практиці «Алгоритм про-
порцій» (рукопис XIV ст.) Орем ввів поряд з подвійним, потрійними та
п-кратними відношення чверте і, полуторні та інші дробово-раціональні
2_ і2_
відношення, які відповідають теперішнім а 2 , а 4 , а 2 . Виходячи,
наприклад, з того, що 8 = У"в4, 4 = 1^64, Орем зробив висновок, що 8
з
знаходиться у полуторному відношенні до 4, тобто 8 = 4 2 , що запису-
Р • 1
1 • 2
ється так:
(р — перша буква від слова ргорогііо),
9 1-1819
257
Дробові відношення Орем називав ірраціональними. Він словесно
сформулював правила операцій з дробовими відношеннями типу
т 1 1 1 1 1 1 —
ап = (ап)т ; ап . Ьп = (аЬ)п \ ап :Ьп =[~у і
1
1 1 1 1 / п \тп
ат • Ьп = (апЬт)тп ; і
А і (’)'(І)
(ат) « = (атр) « = а К п 7 .
Створення формального алгоритму дробових відношень, а по суті
узагальнення дії піднесення до степеня на додатні дробові показники,
було важливим досягненням середньовічної алгебри. Хоча згаданий твір
Орема було надруковано лише у XIX ст., він був поширеним і в серед-
ні віки.
Дальшу розробку алгоритму Орема здійснив французький матема-
тик Нікола Шюке (1445—1500). Його рукописна праця «Наука про чис-
ла у трьох частинах» містить правила обчислень з раціональними чис-
лами, ірраціональними коренями, а також вчення про рівняння.
Розглядаючи рівняння, Шюке виходив із загального випадку, зводя-
чи всі рівняння до чотирьох «канонів»:
ахт = 6хт+п; ах” + ^+п = схт+2п;
ах”1 = Ьхт+п + схт+2п; ахт + схт+2п = Ьхт+п.
Праця Шюке залишилася в рукопису і не набула поширення.
П’єр Ферма (1601—1665) в середині XVII ст. запропонував загаль-
ний метод розв’язання ірраціональних рівнянь, зводячи їх до системи
цілих алгебраїчних рівнянь.
Запитання і завдання для повторення
1. Як називається дія, за допомогою якої, знаючи показник степе-
ня і степінь, можна знайти основу степеня?
2. Для якої дії добування кореня є оберненою?
3. Що називається коренем п-го степеня з числа а?
4. Що називається коренем п’ятого степеня з числа а?
5. Який знак має корінь непарного степеня: з додатного числа, з
від’ємного числа?
6. Яким правилом треба скористатися при визначенні знака коре-
ня непарного степеня?
З « з - 4 у-___
7. Чи правильні рівності: у/64 = 4; у —125 = —5; у 81 = 3;-
/36 = 6; /25 = —5; 1^4 — 2/3 = 1 — /З?
8. Що називається арифметичним значенням кореня (або арифме-
тичним коренем)?
9. Чи можна стверджувати, що а— арифметичний корінь з а2?
10. Чи правильно, що кубічний корінь з 125 має два знаки?
11. Вказати, яке з двох означень арифметичного кореня правильне:
258
1) арифметичним коренем називають корінь з невід’ємного числа;
2) арифметичним коренем називають невід’ємне значення кореня з
невід’ємного числа.
12. Чому дорівнює 17)9?
13. Що більше: (у^бб)8 чи (у^85)9?
14. Що більше: чи у^П?
15. Що менше: у^б чи у/ 36?________
16. Спростити вираз Кя4 + 2а2Ьа + б4, використовуючи основи}
властивість кореня.
17. Як добути корінь: з добутку, з дробу?
18. Як перемножити корені одного й того самого степеня?
19. Записати правило множення коренів з однаковими показника-
ми аналітично (у вигляді формули).
20. Записати аналітично правило добування кореня з дробу.
21. Як виконати ділення коренів однакового степеня? Записати це
правило аналітично.
22. Як добути корінь із степеня? Записати це правило аналітично
і проілюструвати його прикладами.
23. Як добути корінь Із кореня? Записати це правило аналітично і
проілюструвати його прикладами.
24. Перелічити властивості коренів. Кожну з них записати аналі-
тично.
25. Як винести множник за знак радикала (кореня)?
26. З яким показником степеня можна винести за знак кореня множ-
ник?
27. Які вирази називаються ірраціональними відносно якої-небудь
букви?
28. Які властивості коренів використовують при винесенні множ-
ника за знак кореня, якщо підкореневий вираз дробовий?
29. Як називається перетворення, обернене до винесення множни-
ка за знак кореня?
ЗО. На якій властивості кореня грунтується перетворення, що при-
зводить до пониження степеня кореня?
31. Яке з двох тверджень правильне:
1) степінь будь-якого кореня може бути понижений;
2) степінь не будь-якого кореня може бути понижений?
32. На якій властивості коренів грунтується зведення їх до спіль-
ного показника?
33. Чи треба понижувати степені коренів (якщо це можливо) перед
зведенням їх до спільного показника?
34. Сформулювати правило зведення коренів до найменшого спіль-
ного показника.
35. Що означає звести радикал- до найпростішого вигляду?
36. Дано корені а10/?6, 1/"-і, 32п£. Які з них зведені до
найпростішого вигляду, а які ні?
37. Які радикали називаються подібними?
38. Як додати (відняти) радикали? Проілюструйте на прикладах.
39. Як перемножити кілька коренів з однаковими показниками?
Проілюструйте на прикладах.
40. Як поділити корені з однаковими показниками степенів? Про-
ілюструйте на прикладах.
41. Як перемножити (поділити) радикали з різними показниками?
9*
259
42. Яка різниця між ірраціональним виразом та ірраціональним
числом?
43. Як звільнити знаменник дробу від ірраціональності, якщо цей
знаменник одночлен?
44. Як звільнити знаменник дробу від ірраціональності, якщо цей
знаменник двочлен з квадратними коренями? З кубічними коренями?
45. Як звільнитися від ірраціональності у тричленному знаменнику
дробу?
46. Як звільнитися від ірраціональності у чисельнику дробу? По-
яснити на прикладі.
47. Порівняйте числа (не виконуючи наближених обчислень): ’Из і
|/’2; У2 і |<4; V2^2 і }/ /19.
48. При яких значеннях букв правильні такі рівності:
а) У~5а2 = д/5; б) /7х2 = —л/7;
в) V 2Ь2 — 246 4* 72 = (6 — 6) /2;
г) _ 1 _____________________!_____?
/262 —246 4-72 (6—6)/2
49. Яке рівняння називається ірраціональним? Навести приклади.
50. Який смисл мають корені, що входять у ірраціональне
рівняння? _____
51. Чому Ірраціональне рівняння Ух—3= —2 не має розв’яз-
ків?
52. Як ірраціональне рівняння замінити раціональним?
53. Які перетворення ірраціональних рівнянь можуть привести
до появи сторонніх коренів?
54. У чому полягає метод введення нової змінної при розв’язуван-
ні ірраціональних рівнянь?
55. Які нерівності називають ірраціональними?
56. Який смисл мають корені, що входять в ірраціональну нерів-
ність?
57. Чи завжди нерівність / (х) < (р (х) рівносильна нерівності
(Ш)"< (<Р (*))"?
58. Записати аналітично (у вигляді формули) означення степеня з
дробовим показником.*
59. Що більше: 3 2 чи 9 4 ?
60. Чи можна, виконуючи дії над степенями з дробовими показни-
ками, користуватися правилами дій над степенями з цілими показни-
ками?
т
61. Яке обмеження накладають на основу а у виразі а п , деп —
парне число, і чим зумовлене таке обмеження?
62. Сформулювати властивості степеня з дробовим показником.
63. Сформулювати означення степеня з від’ємним раціональним по-
казником і записати його аналітично.
64. Чи можна степінь з дробовим показником замінити радикалом?
65. Записати за допомогою степенів з дробовим показником і об-
числити за допомогою мікрокалькулятора (з трьома знаками після ко-
з,-----1 Т<Ї2 8
ми): 110; с_____, ; о___ ; §_____•
У 15 уб У120
66. Записати основні властивості степеня з раціональним показ-
ником (множення, ділення, піднесення до степеня і добування кореня),
260
67. Як означається степінь з ірраціональним показником?
68. Дати означення степеневої функції з натуральним показником.
69. Які обмеження накладають на аргумент х функції як-
що п^О?
70. Які види степеневої функції вам відомі? Записати їх аналі-
тично.
71. Пригадати, які функції називаються непарними, Побудувати
ескізи графіків кількох непарних степеневих функцій з натуральним
показником.
72. Як розміщено на координатній площині графік функції у = х72,
якщо: п, — непарне, п — парне?
73. Назвати загальні властивості степеневих функцій.
74. Які властивості має степенева функція у = х“!? Пояснити за
ескізом її графіка.
75. Назвати властивості степеневої функції у = х^“2 за ескізом її
графіка.
1 і
76. Накреслити ескізи графіків функцій у=х2 і г/ = х 3 . Кори-
стуючись графіками, сформулювати властивості цих функцій.
77. Систематизувати властивості степеневих функцій у = х" за по-
казником п: а) п — натуральне число (1, 2, 3, ...); б) п — ціле від’ємне
число (—1, —2, —3, ...); в) п = де к = 2, 3, 4, ... .
к
78. Чим відрізняються між собою графіки функцій у = х3 і у —
= Зх3?
79. Порівняйте властивості функцій: а) у = х3 і у = хб; б) у = х
і у = х6; в) у = х“2 і у = х—3.
80. Дано функції / (х) — хИ ф (х) = х?. Не виконуючи обчислень,
порівняти з нулем: а) [ (25) — / (10); б) / (—20) — / (—15); в) / (0) X
X / (50); г) ф (11) - ф (7); д) ф (-5) . ф (-9); е) ф (15) ♦ ф (0).
81. Чи знайдеться таке натуральне значення р, при якому графік
функції у = хр проходить через точку: а) А (1; 4); б) В (У~3; 81);
в) С (—5; 6,25); г) О (—7; 343).
т
82. При яких значеннях х існує функція у — хп , т і п — цілі
числа і п — парне число?
__ А
83. Побудувати графік функції у = х * 2 і описати її властивості.
84. Побудувати графік функції у = х 3 — 1.
85. Чи належить функція у = Ух3 до непарних? Обгрунтувати
відповідь.
Вправи
А
1. Довести, що: 1) число 10 є арифметичним квадратним коренем із
100; 2) число —2 не є арифметичним квадратним коренем з 4; 3) число
0,3 не є арифметичним квадратним коренем з 0,9; 4) правильна рівність
/2^9"= 1,7.
261
2. Знайти значення кореня: 1) |^16; 2) /0,16; 3) р^0,0016;
4) /0,000016; 5).]/-||_; 6)^2^; 7)]/1_9_;
8) 1/3 _А_ ; 9)/3^24; 10) У 0,0121; 11) /2^5; 12) /ЦЙ.
' ло
Б
3. Знайти значення виразу:
1) 0,2/Ї4? + 0,3/Ї69; 2) — 9 /6/І66Г+ — /900;
15
3)/36+]/^; 4)
4. Записати за допомогою знака У корені рівняння і обчислити їх
значення: 1) Xі = 0,25; 2) у2 = 2,25; 3) г2 = 0,49;
4) ха = 1
9
В
5. Чи має смисл вираз: 1) }/"Ї96; 2) У—196; 3) —КІ96;
4) У(—49) • (—4); 5) 49 • 4? __
6. При яких значеннях а і х мають смисл вирази: 1)Уа; 2)У—а;
3) /^; 4) /=Ж; б) /~5; 6) ]/'—>?
• 6Х —
А
7. Знайти значення кореня: 1) |/ 1000; 2) р^вї; 3) Уз5;
4) уЧ; 5) 7У^Т, 6) іґд; 7) у^ООГ; 8) У-зА.
г 8
8. Які з поданих нижче коренів можна назвати арифметичними:
1) |<2І6 = 6; 2) |<=64 = —4; 3) ^625 = 5;__
5) /І++ <9 У+- +
Б
9. Знайти значення виразів:
а) 7у<64; б) 0,2^32 + ><—0,008;
в) 17 — 5><0,000216; г)
10. Подати корінь непарного степеня з від’ємного числа через ариф-
метичний корінь; 1) У—7; 2) р/^8; 3) У—2а, де а > 0,
В
11. Пояснити рівності:
хї/’ЗБ І . жч 2Н-1/-------- 2/Н-1/-Г
а) у аг* = | а |; б) у — а = — /а. ________________________
12. Знайти арифметичне значення кореня Уал — 12а + 36.
13. Яких значень набуває вираз —— при: а > 0, а < 0?
262
А
14. Знайти значення виразів:
1) Ріб • 100; 2) р2 . ><§;
15. Обчислити:.
• і^х2;
1)^8-125; 2) тЛ3)тА—.1—; 4)г/"12:Х
г ’ V 1000 У 8 2 ' У 7ІГ
16. Перетворити вирази:
1) (^ґа?)3; 2) (’рб)1 2 3 4; 3) у4/!.
17. Спростити вирази (знизити степінь радикалів):
1) У?2; 2) 3) ‘рЗб2; 4) 4раів*2*с82,
18. Звести радикали до спільного показника:
1) УЗ, рЗ, рЗ; 2) ^4аї, /2а.
Б
19. Знайти значення виразів:
т/3
1) ^Н-6 . ^4 . ^ТО»;
3) У 52'4 ' 2' 242 : 4) (^4)>; 5)^7 + /^
г о 1 • оУ
20. Спростити вираз К а4 + 2а2Ь2 + Ь*.
21. Обчислити:
1) (5^40 — 10І<5) • 0,5 . ^25;
2) УЗ (/5 + /б) + V5 (УЗ + /б)-/б (/З + /5),
22. Розмістити у порядку зростання числа 1^2, у^З,
В
23. Спростити вирази:
1) т+уЛат2-г’2; 2) с^-^Ь+ь2.
3) а + 2Уау3^а— 4^а— 4/а2 — Зу'а» —
24. Виконати дії:
1) Уз • У± . р4; 2) ^1 + У2 . І/3-2Г2;
3) (Уа + Ь + Уа^б) • (У^+~Ь — Уа^Ь);
4) К(5 — л)а при а >5; 5) К1 — 2х-\-х2 при х » 4 і х = -1-.
263
25. Довести, що
-----_ (За — 3 при бг < 3;
2а—У (а—З)2 = і „ ’
+ 3 при а > З,
26. Визначити знак рівностей:
1) ^/3 —1/4; 2) |/5 —^6.
27. Спростити і обчислити результати до 0,001
А
Винести множник за знак радикалів:
28. 1) V», 2) і<їб^й; 3) у
В
29. 1) ^24(т2 —п2)2(т + п); 2) а2п+3;
3) с?п2,~^; 4) 7/ апх^"2^3/12і3.
В
ЗО. Перетворити вираз при х > 0 і с > 0
2х3 п4/ 0,25с9
с2 У 2х '
Який результат дістанемо при х < 0 і о < 0? Чи можуть х і с мати
різні знаки?
31. Спростити вираз 7/*о7**^71 — Л71"*’1.
32. При яких значеннях х справедлива тотожність
Т^х2 — х* = — х 7^ 1 — х2?
А
33. Внести множник під знак радикалів:
1) 2^/3; 2) З 3) 2 |Л|_;
4) а -^2, де а>0; 5) 6^5, де Ь > 0; 6) (а-\-Ь)Уа-\- Ь,
34. Спростити вирази:
1) У'аУа при а > 0; 2) У^У^,
45 /"471
3) у х-у х, де х > 0; 4) у ау а, де а > 0.
35. Позбутися дробу під коренем:
«2,7т^--
Б
36. Внести множник під знак радикалів:
1) 2^^256; 2) (а + &)
264
37. Спростити вирази:
З Г о —
1) у ЬуЬ, де &>0;
~-2? 6 , де а > 2.
а— 2
38. Порівняти числа:
1) і У2^3; 2) У і У3^2'
В
39. Внести множник під знак радикалів:
і) —!_
х—у
х2
а3 (х — у).
40. Знайти значення виразу
р/7 — 4 /3 • К2 + /3.
Довести, що при а > 0 правильні рівності:
лі V ло 2п+,2/ 3у-3 ‘
41. У а у а = у а, 42. У я3 у а3 =
а3,
43. Чи можна стверджувати, що
€ радикалами найпростішого вигляду?
44. Звести до найпростішого вигляду корені:
45. Спростити корені:
_____________________; 2)
а2 + _|_ 2аЬ
а
а— 2Ь
4а2Ь2 4а&8
аЬ
А
Б
В
46. Звести до найпростішого вигляду вирази:
1)
; 2) (/х+ /а)2 + (/^+ /а3)2 (а>0,х>0).
47. Спростити ——— 1/ АП—4- —1_ при х > 2. Переві-
2 — х т х3 х
рити, що при 0 < х < 2 даний вираз перетворюється в Ух, Довести,
що при х 0 і х = 2 він втрачає смисл,
265
А
48. Чи подібні радикали:
1) 5 |/4 і 0,7^4; 2) і /б;
3)'^7 і /Ї5; 4) їА-у і 1^72?
49. Довести подібність радикалів:
1) |<250 і ^4 000 000; 2) 2 і
Б,
50. Довести подібність радикалів
2 а+Ь і ^'а«4-аЬ.
51. Чи подібні радикали
ЗЬ У ±+Ь і б^а^+І?
В
52. Довести подібність радикалів:
1/” —- — п; і/* — ї К/п3 — т4п, де т> 0, п> 0,
г т ' тп2
тп<Л.
53. Чи подібні радикали:
1)^42п+1 ( 2) !^Г^З+п^З+п ; р/"
Виконати дії:
А
54. 1) Зу'га*- бу'ТОа • 7><24а;
2) 8 / 14а«&8 і 10 ^аГ8; 3) ,
Б
55. 1) 15І|/’о»':51|/аї'Н-121у<а8.0,251|га8;
2) УаЬ* • Уай : 3) <У~а _ у^)2.
В
56. 1) / а^2И.5/5^; 2) і/" іЕ0^01^. + ;
______ _______4 -уГт 8
3) Ка + /& • Vа — Уь- Уа^ — ь.
Звільнити від радикалів знаменники дробів:
266
А
57. 1) ; 2) —— ; 3) ; 4) ОТ^Д і
3/2 ьУа 2пут
9 2
5) — ; 6) —т=---т=г .
5— У7 /54-/3
Б
13 „ 5а
58. 1) ?=-т=- ; 2) —т=---т=- ;
2/5-/7 а/7 —2/я
1 7/а —2/5
3) т=-----т=- ; 4) —4=--;
(1+/2)+/5 7/а + 2/б
7 , ох а3 — Xі
5) )<2-1 ’ ’ У~а-Ух '
В
б9‘ !) /24-/З—/5 ’ 2) /х2 — а2 — /х24~а2 ’
60. Звільнити від радикалів чисельники дробів:
А
П . ох . ох 3^5-2
*' 2а2Ь ’ ’ 5 ’ 6) 3/54-2 '
Б
4) 3 /7 - 2 /2 . 5) /Г+7? /;
11 X
В
4/6 4-/3-6/2 . _ х + /^Т
З * х — у х2 — 1
Розв’язати рівняння:
А
61. 1) /1=2; 2) /Т^~3=5; 3) /х — 4=0;
4) / 2х — 7 = 5; 5) /2 — х = /3 — 2х; 6) /х - а = Ь.
62. 1) х 4- /х + 5 = 7; 2) 3/х 4- 2 = 2х — 5.
63. 1) /х — 7 4- /17 - х = 4; 2) /2х 4- 1 4- /4х 4- 3 = 1.
64.1 ) /8х —5-/2x4-3=/6x4- 1; 2) з/х2 — 4 4-1 =
= Зх 4- 7.
Б
65. /7+3 4- /х^2 = /бх— 11;’
_____________ \/"2_______і/^ і
66. 1) /2х 4-ї 4-/4х 4-3 = 1; 2) 2^- =
267
67. 1) ^8х + 4 - ^8х — 4 = 2; _____
2) /8*4-1 - /2х — 2 = /7x4- 4 — УЗх —5;
3) У а — х + У Ь х = Уа + Ь\
4) х2 — х +Ух2 — 2х + 6 =в х + 6.
В
68. і) УбГ^П — /8^2х = К^Т;
2) 1/ 5х+2 — 1/ 7х—2
V 2х-4 V Зх —8 *
69. 1) /8 —х + /5+х = )/’9 + 5х + /4 —5х;
2> + -П.
V а + х — У а — х
70. 1) /х 4- Кх 4- /9 4- 24х = /3;
2) ^=-+ ? 6 =^=-.
/Зх + 10 /(х + 2) (Зх +10) /х + 2
71. 1) х — К*3— 4х— 7 = 1; 2) К4 — х/х24-8=2— х;
3) х2 — 9х + 12 = 4 У^х2 — 9х + 9;
4) /5а4-х + /5а— х = —7===-
У 5а + х
Пояснити, чому дані ірраціональні рівняння не можуть мати дійс-
них коренів:
А
72. 1) /2х2—3x4-5 = —4; 2) /Г="з4- /Г/З4-1=0.
Б
73. 1) /х4-2 — /хТ5 = її 2) /х^5 -|- /2Г=Й = 2.
В
74. 1) /х—3 = /2х —З-}-1} 2) /Зх—7 —/15х —11 = 2.
75. Розв’язати рівняння:
1) 2х + 1 = 3 Ух; 2) 1 — Ух = 2 + х і побудувати для них графік
лівої і правої частин.
Розв’язати системи рівнянь;
А
(У х + у у = 5,
76. а) 1 _ У
\Уху^=5\
\У~х + У~у^з,
ху — 4;
/^ । /у _ 5
/у /ї 2 ’
,х 4- у = 25;
|/ х2 4- 6/ = 2 4- х,
}3х 4- 4у = 23.
268
В) + 12, Г) (Ух + ^& = 4,
\ху = 64; їх 4- у = 28.
78. а)
в)
г)
\х У = 10,
ФСх + Уу — 2,5
5/ха — Зу — 14-/х + 6//= 19,
/ж-Ь/у _ а
У~х-У~у ь
,ху = (а2 — д2)2;
ЗУх2 — Зу — 1 = 1 +2Ух + 6уі
Ух + у + Ух —у — 6,
У(х + У)3 (х — у)2 = 8 (х > у).
Виконати дії:
79.
80.
81.
1)
4)
1)
1)
а2а6а8; 2) Л;2Лх4л; 3) б13: б10;
с^п: ?л;
(2х3ї/2г)4;
(а4)2; 2)
5) а": а"-’2; 6) &п+І : У*-1,
2) (—За264с?)3; 3) (--1-їі 4) (-£-ї
(__4^ї; 3) (ап~1)4; «(-.іГ.
\ / \ о /
82. 1) (За364)»; 2) (-*} 2 ; 3) .2 ; 4) 2і»: 24,
' \ о ] 2~2х
83. 1) а~т:а°; 2) (10«)“3; 3) (2а2Ь~3У, 4) 2х^4:х”7,
А
Б
84. 1) (а12а3: а4а7)3; 2) (— ЗаЬ2<?)*-, 3) (у2"-1)"1;
4) 1 5) (49-32 + 0,723е)3; 6) За7а’5 + 2,51°а^7а3.
85. Спростити вирази:
1) Г2 (&3)-3У ; 2) Зх"-1 • 5х"+І;
3) : 4) (5а-1 + Ь-Ь . (5а*1 - Ь~\
4 Іа °Ь
86. Піднести до квадрата ^2а3х 4-
В
87. Виконати дії:
в ії- аЧ ї • ( ас4 "Й • (( аЧ* ї • '2 Гі і
’ ІД \ М3) /‘ІД ) к ЬЧ ) г
2) (" с + х \т . / с — х \т *
\с — х ] \ а + д / к а— Ь ]
269
88. Обчислити значення виразу 125х2 (у2 — г2), якщо х « 2,24;-
у « 27,3; г « 12,8, за допомогою мікрокалькулятора.
89. Записати дріб + а за допомогою степенів з від’ємними
а264
показниками.
А
90. Подати вираз у вигляді степеня з раціональним показником:
1 1 1 1 з
1) х3х°'2х0,8; 2) а2 а3 а4 ; 3) Ь2 : Ь4 ;
__2_ 5 1 і
4) (а 5 )М; 5) (с3 ) 5 ; 6)
91. Спростити вирази:
2-2- 5 ^2_ і і
1) (X 3 )°-5 • х” 5 ; 2) рвІ9 4 /Г 7 <714 ; 3) (Ь~6)" 8 ,
92. Обчислити:
з з ±
1) 3я • З^”3" • 3Т; 2) [ ^...Г •
' к 125е /
93. Виконати дії:
7 П —|-
і) а~ 15 :а20; 2) -22-------.
аі,256~Т
64 \3
125 ) *
Б
94. Спростити вирази:
2__2_ ___]___2_ 2____2
1) (а3 )“ 2 • (а 4 ) 3 ; 2) (а4 х 3) . а0-7 • х°>8-
95. Обчислити;
4 4 2 1 2
1) 9” 3 • 273 . З3 ; 2) 646 . 43
96. Подати у вигляді куба:
і
У°. У^33, У*> У, у2 , у^1>5.
97. Скоротити дроби:
• 23 ; 3) ( ‘ . 125-1
_ 1 5
у 4,у°’1, Г6.
270
98. Подати вирази у вигляді суми:
і і і і
1) а2х2 (а2 +х2); 2) (2-у1’5) (2 + у1-5).
99. Спростити вирази:
1 1 _1_2_
1) (&2 _с2 ). (64 +с4); 2) (а2 -Ь2 ) - (а + а2 Ь2 +Ь).
100. Користуючись тотожністю а2 — Ь2 = (а — Ь) (а Ь), роз-
класти на множники вирази:
2 1 1
1) а2 = 3; 2) Ь 3 — 26; 3) (хТ)« —4; 4) а— Ь2 , де а>0.
В
101. Спростити вирази:
2) (х4 +04) • (х4 -у*) • (х2 +у2).
102. Довести, що при будь-якому а > 0 правильна рівність
103. Подати у вигляді суми:
1 1 Г 1 1 і
1) ((X4 +//4)(Х4 ))2; 2) ((X 2 -у4)^ 2 +я4))2.
104. Розкласти на множники:
1 2 4
1) а+а2\ 2) 125 —6, де д>0; 3) 183 — б3;
4) (2а) 2 — (5а) 2 .
105. Знайти значення виразу:
а2 —9а 6
і) -і-----Г
а3 —За6
при а = 64;
2) -А-
У4 -2
-т-8у— при у = 25.
106. Обчислити
У2 —4
0,027 3
2
271
РОЗДІЛ 8
ПОКАЗНИКОВА ФУНКЦІЯ
§ 1. Поняття показникової функції
Означення і графік показникової функції. Відомо, що
при додатному а для будь-якого числа х степінь ах має ціл-
ком певне додатне значення. Тому ах е функцією змінної
х, яка визначена на всій числовій осі.
При а = 1 кожне значення 1* дорівнює 1, тобто функція
\х— стала функція. Цей випадок нічого нового не додає до
означення показникової функції, а тому його виключають.
Функція у — ах, де а > 0 і а =/= 1, називається показ-
никовою (з основою а).
Так, функції у == 3х, у = 0,72х, у = (“13-і — показни-
кові.
Складемо таблицю окремих значень аргументу і відпо-
відних значень функції (табл. 8.1).
Таблиця 8,1
х —4 ‘ —3 —2 —1 0 1 2 3 4
1111 л л
*/ = 2* 16 8 4 2 0 2 4 8 16
Побудуємо на координатній площині точки за коорди-
натами, взятими з цієї таблиці, і сполучимо ці точки плав-
ною лінією (рис. 8.1). Дістанемо графік функції у = 2х.
Розглянемо тепер функцію у = 3х. Складемо аналогіч-
ну таблицю (табл. 8.2).
Таблиця 8.2
X —3—2—1 0 12 3
у __ Зл 27 9 з 1 3 9 27
Побудуємо в тій самій системі координат точки за коор-
динатами, взятими з таблиці, і сполучимо їх плавною лінією
(рис. 8.2). З рисунка випливає, що обидві функції зроста-
ють, але функція у = 3х зростає швидше (її графік зростає
«крутіше»).
272
Розглянемо тепер функцію у = .складемо таблицю
(табл. 8.3) і побудуємо графік (рис. 8.3).
/ 1 \х
Що є спільного у графіків функцій у = 2х і у = І у І ?
1) Областю визначення обох функцій є множина дійс-
них чисел.
2) Обидві функції додатні при будь-якому значенні ар-
гументу (графіки розміщені у верхній півплощині).
3) При х = 0 обидві функції набувають значень, що до-
рівнюють 1.
Таблиця 8.3
х —4 -=.3 — 2 0 1 2 3 4
_ , л л 1111
8420248 16
16
Ці три властивості спільні для будь-яких показникових
функцій.
/IV
Побудуємо тепер графіки функцій у = 2х і у = І у І в
одній і тій самій системі координат (рис. 8.4) і порівняємо
їх властивості. З рисунка випливає, що ці графіки розмі-
щені симетрично відносно осі ординат. Функція у = 2х —
11 V
зростаюча, а функція У — [2 І — спадна.
273
Проведемо через точку перетину графіків у = 2 і у =
1 V
у І пряму, паралельну осі абсцис (рис. 8.5), і порів-
няємо частини кривих, що лежать під цією прямою і над
нею. Які частини кривих відповідають значенням функцій:
меншим 1, більшим 1? При х < 0 (ліва півплощина) функ-
ція у = 2х набуває значень, менших 1, а при х > 0
(права півплощина) — більших 1.
/1 \*
Функція у = І у І при х<0 набуває значень, більших
1, а при х > 0 — менших 1.
Для більшої наочності подамо властивості функції у ==
= ах при а > 1 і 0 < а < 1 у вигляді таблиці (табл. 8.4).
Другий варіант викладу властивостей показникової
функції.
Як видно з означення показникової функції, на основу
а накладено певні обмеження, а саме: а > 0 і а =£ 1. Друге
обмеження ми вже з’ясували. Розглянемо перше а > 0.
При а = 0 і х 0 вираз ах не має смислу. Наприклад,
____________і_
вирази О”1, 0 8, 0° позбавлені смислу.
Якщо 0 < а < 1 і х— нескоротний дріб, знаменник яко-
го парний, то вираз ах не має смислу. Наприклад, степінь
з
(—2) = у (—2)3 — у —8 не можна виразити дійсним чис-
лом.
Для подальшого вивчення показникової функції треба
знати такі її властивості, які ми подаємо без доведення:
а) при піднесенні неправильного дробу до степеня з до-
датним показником дістаємо результат, більший 1, а при
піднесенні неправильного дробу до степеня з від’ємним по-
274
казником — результат, менший 1, наприклад;
(4)і=-?-=4ТГ: (4)’ ^ГМяЛ.15;
Таблиця 8,4
Зростає
При х < 0
менших 1
При х > 0
більших 1
набуває значень,
набуває значень,
При х<0
ших 1
При х>0
ших 1
набуває значень, біль-
набуває значень, мен-
б) при піднесенні правильного дробу до степеня з до-
датним показником дістаємо результат, менший 1, а при під-
несенні правильного дробу до степеня з від’ємним показни-
ком— результат, більший 1, наприклад:
Ш'-ТЯН (тГ -Ий0~0,84;
275
Властивості функції у = ах при а > 1 і 0 < а < 1 сут-
тєво відрізняються. Тому спочатку розглянемо загальні
властивості показникової функції, а потім окремо її влас-
тивості при а > 1 і 0 < а < 1.
Загальні властивості показникової функції. Областю
визначення показникової функції у = ах є множина всіх
дійсних чисел. Справді» при а > 0, а 1 вираз ах визна-
чений для будь-якого х, —оо < х < оо.
Показникова функція у = ах додатна при будь-якому
значенні аргументу, тобто ах > 0. _
Неважко переконатися в тому, що показникова функція
не може ні дорівнювати нулю, ні бути від’ємною, тобто об-
ластю її значень є множина всіх додатних чисел (0 < у <
< оо). Справді, ах може дорівнювати нулю лише тоді, коли
а = 0. Але ми домовилися, що а =# 0. Функція ах може бу-
ти від’ємною лише при а < 0 (при всіх значеннях х). Ми
ж домовилися розглядати показникову функцію лише при
а > 0. А при піднесенні додатного числа а до степеня х з
будь-яким дійсним показником завжди матимемо додатне
число.
Щоб переконатися в цьому, розглянемо всі можливі ви-
падки.
а) Нехай х = п, де п — натуральне число. Тоді ах =
= ап = аа...а > 0 як добуток додатних чисел.
б) Якщо х — дробове додатне число, тобто х = де
пі
— — нескоротний дріб, то ах = ап = 7/0'". Але ат > 0
(умова існування кореня п-го степеня).
в) Нехай х — додатне ірраціональне число. Позначимо
через аг і а2 наближені раціональні (додатні) значення з не-
достачею і з надлишком. Тоді значення ах міститься між
двома додатними числами і а“» і є додатним числом.
г) Нарешті, якщо х — деяке від’ємне число, наприклад»
х — —р, то ах = а~р — Але раніше було показано, що
276
при будь-якому додатному р ар >> 0. Отже, і ~-р > 0. Звід-
си випливає, що сформульована властивість справедлива
для будь-якого х.
Отже, графік показникової функції завжди лежить над
віссю абсцис (ординати всіх точок графіка додатні) і не пе-
ретинає її (у =/= 0).
При х = 0 показникова функція ах = 1. Це випливає
з того, що будь-яке число, крім нуля, в нульовому степені
дорівнює одиниці. Ми ж домовилися розглядати показнико-
ву функцію при а 0. З цієї властивості робимо висновок,
що графік функції у = ах завжди проходить через точку з
координатами х = 0; у = 1, тобто перетинає вісь ординат
на відстані 1 від початку координат.
Розглянемо властивості показникової функції у = ах
при а > 1 і 0 < а < 1.
Нехай а > 1. При а > 1 функція ах при зростанні х мо-
нотонно вростає (самостійно доведіть, що при а > 1 для
будь-якого х2 > Хі виконується нерівність ах* > ахі, тоб-
то ах^-х* >0).
При а > 1 при необмеженому зростанні показника х
функція у = ах необмежено зростає, а при необмеженому
спаданні показника х функція набуває значень, як завгодно
близьких до нуля.
При а > 1 функція у = ах більша 1 для всіх додатних
значень х і менша 1 для всіх від’ємних значень х, тобто ах >
> 1 для х > 0 і ах < 1 для х < 0.
Розглянемо можливі випадки для значень х,
а) Нехай х = п — натуральне число. Тоді ап > 1, бо
добуток чисел, більших 1, теж число, більше 1.
б) Якщо х = ~, де т і п — взаємно прості натуральні
числа, то
бо корінь будь-якого степеня з числа, більшого від 1 (ат >
> 1), є також число, більше від 1.
в) Якщо х — додатне ірраціональне число і а3 — на-
ближене раціональне значення х з недостачею, то 0а* > 1,
тому і ах > 1.
г) Якщо х — будь-яке від’ємне число, наприклад, х =
= —р, то ах = сг~р = але аР > 1. Отже, < 1, тобто
ах < 1*
277
Таким чином, ми довели, що при а > 1 а* х < 1 при х <,
< 0 і ах > 1 при х > 0. Ця властивість дає змогу встанови-
ти, в яких частинах координатної площини буде розміщений
графік функції у = ах при а > 1 (на рис. 8.8 ці частини за-
штриховано).
Нехай 0 < а < 1. Тоді функція ах при зростанні х моно-
тонно спадає.
При 0 < а < 1 функція у = ах при необмеженому зро-
станні показника х набуває значень, як завгодно близьких
до нуля, а при необмеженому спа-
данні показника х функція необме-
жено зростає.
При 0 < а < 1 показникова
функція ах більша 1 для всіх від’єм-
них значень х і менша 1 для всіх
додатних значень х, тобто ах > 1 для
х х < 0 і ах < 1 для х > 0.
Рис. 8.8 Справедливість цих тверджень ви-
пливає з того, що значення показни-
кової функції з основою, меншою 1, обернені до відповідних
значень показникової функції з основою, більшою 1$
Якщо 0 < а < 1, то > 1.
Для практичних застосувань показникової функції
важливими є такі її властивості (подамо їх без дове-
дення).
Якщо а > 0, а 1 і ах' = ах^ то хх = х2, тобто якщо
степені однієї і тієї самої додатної, відмінної від одиниці ос-
нови рівні, то рівні й показники степенів.
Якщо а > 0 і а 1, то, яке б не було додатне число N
існує, і до того ж єдине, таке значення х, що ах = N.
Іншими словами, за цих умов має розв’язок, і до того
єдиний, рівняння ах = N.
Властивості графіка показникової функції. Графік по-
казникової функції називається експонентою.
Складемо таблицю значень показникової функції у =
= 2х деяких значень х (х = —4; —3; —2; —1; 0; 1; 2;
3; 4) і побудуємо відповідний графік (див. рис. 8.1). Цей
графік у = 2х має такі властивості.
1) Графік розміщений у верхній площині, тобто там, де
ординати додатні.
278
2) Будь-яка пряма, паралельна осі Оу, перетинає гра-
фік, причому лише в одній точці.
3) Крива проходить через точку (0; 1), тобто при х =
= 0 функція чисельно дорівнює 1.
4) 3 двох точок графіка вище розміщена та, яка лежить
правіше.
5) На графіку є точки, які лежать вище будь-якої пря-
мої, паралельної осі Ох. На графіку є точки, що лежать ниж-
че будь-якої прямої, проведеної у верхній півплощині па-
ралельно осі Ох.
Лівою своєю частиною графік, якщо рухатись за ним
справа наліво, все ближче підходить до осі Ох, але не до-
тикається до неї.
6) Будь-яка пряма, що паралельна осі Ох і лежить у
верхній півплощині, перетинає графік, і причому в одній
точці.
Ми розглянули властивості графіка показникової функ-
ції у = а.х при а > 1 на прикладі функції у = 2х.
Самостійно проведіть аналогічні міркування для функ-
/1
ці» у = І у І . Які з розглянутих вище властивостей функції
у = ах при а > 1 і при 0 < а < 1 можна проілюструвати
за допомогою цих графіків?
Приклади застосування властивостей показникової
функції.
Приклад 1. Що можна сказати про числа т і п, якщо
5т < 5"?
Міркуємо так: оскільки основа степеня більша 1, то по-
казникова функція у = 5* із зростанням аргументу зрос-
тає. Отже, дана нерівність можлива при т < п.
Приклад 2. Що можна сказати про числа р і д, якщо
(0,3)р < (0,3)*?
Тут основа степеня менша 1, а тому із зростанням аргу-
менту показникова функція 0,3х спадає. Нерівність (0,3)р <
< (0,3)" можлива при р> д.
Приклад 3. Що можна сказати про додатну основу а,
якщо а7 > а10?
З даної нерівності випливає, що значення степеневої
функції ах із зростанням аргументу спадають. Це можливо
при а <_ 1.
Приклад 4. Який висновок можна вробити відносно до-
датної основи а, якщо а-7 > й-3?
Тут функція у = ах із зростанням аргументу спадає.
Отже, а < 1.
279
Приклад 5. Який висновок можна зробити про додатну
основу а, якщо а—3 < а~1>5?
Оскільки із збільшенням показника степінь збільшу-
ється, то основа степеня а > 1.
Приклад 6. Що можна сказати про число т, якщо 5т <
<4?
Тут основа а > 1. Отже, функція у = 5х є монотонно
зростаючою, причому 5т < 4 < 5, т < 1.
Приклад 7. На основі властивостей показникової функ-
ції замінити знак V в кожному з наступних випадків зна-
ком 2>, < або =.
а) 2,17“0’857 у 1. функція у = 2,17=~0,857 при від’єм-
них значеннях аргументу (х = —0,857) набирає значень,
менших 1. Отже, 2,17”0,8б7< 1.
/ \0,123 / \0,123
б) V 1- Функція у — І -ї£- І зростає і при
х>0.
в) 0,017 0,23 V !• Функція у = 0,017х при х<0 набу-
ває значень, більших 1. Отже, 0,017~°’23 > 1.
г) О,91олз V 3,б5’34; 0,91°’43 < 1, а З,65>34 > 1, тому
0,910'43 < 3,б5’34.
Приклад 8. Вказати, які з показникових функцій
У = 3х, у = (|<10)х, у = (4)". У = (4)‘ ’ У = °’018*
зростають?
Тут треба взяти до уваги, що функція у = ах зростає
при а > 1.
Приклад 9. Які з функцій
у=(Гз)х, у •= (47. у=(47 *у=0,24Л -
спадають?
Беручи до уваги властивості функцій у = а* при а <
/ з \*
приходимо ДО висновку, ЩО це функції у = І'“19“ І і у = 0,24*.
Приклад 10. Дано кілька зростаючих функцій:
У — 2х, {/= 1,4х, у = 4,1х, у = ГХ , У~ 5х, у= 1,11х.
280
Записати їх у порядку зменшення швидкості зростання при
і
0. Маємо у = 5х, у = 4,Г, у = 7 2 ,у = 2х, у = 1,4*,
У = і,нх.
Використання показникової функції під час вивчення
явищ навколишнього середовища. Багато процесів в при-
роді і техніці математично виражаються за допомогою по-
казникової функції.
Задача (про радіоактивний розпад). Не-
хай Т — проміжок часу, протягом якого кількість даної
радіоактивної речовини зменшиться удвоє внаслідок роз-
паду. Т називається періодом піврозпаду речовини (для
різних речовин Т має різні значення). Наприклад, Т =
= 4,56 млрд років для урану-238; Т = 1590 років для ра-
дію-226; Т = 3,81 дні для радону-222.
Позначимо відношення будь-якого проміжку часу і до
періоду піврозпаду даної речовини через; х*> х = (і і Т
вимірюють в одних і тих самих одиницях). Тоді х є міра
часу, що пройшов, за умови, що за одиницю часу взято пе-
ріод піврозпаду Відношення маси ш даної речовини після
проходження цього часу до початкової маси М позначимо
пг
через у- у = —.
Можна стверджувати, що у є частина речовини, яка за-
лишається внаслідок розпаду після х періодів піврозпаду.
Встановлено, що у є показниковою функцією від х тако-
го ВИГЛЯДУ;
Коли в цій формулі х змінюється в арифметичній прогресії
(х = 2, 3, 4, 5, ...), то у зменшується в геометричній прог-
... / 1111 \
респ = 4 , 8 , 16 ', 32 , ...
Більш загальною формулою, яка характеризує радіоак-
тивний розпад, є ш = де т — маса речовини, яка
розпалася; /п0 — маса речовини в початковий момент;
і — час; а і к — деякі сталі.
Задача (про зміну атмосферного тиску).
Атмосферний тиск змінюється в залежності від висоти й над
рівнем моря за законом р = де р0 — атмосферний тиск
на рівні моря; а — деяка стала.
Задача (про розмноження бактерій). Роз-
множення бактерій у певному середовищі відбувається так,
що їх число N змінюється з часом за законом N = N^0®,
281
де Уо — початкове число бактерій при і = 0; а і к — деякі
сталі.
Задача (про вакуумування). При вакуумував
ні кінцевий тиск пов’язаний з початковим тиском співвід-
ношенням
пі
р2 = (~РТ0~) Р1’
де р2 — кінцевий тиск, мм рт. ст.; р± — початковий тиск,
мм рт. ст.; /? — об’єму що підлягає відкачуванню, см3; ф —
об’єм газу, що відкачується насосом за один оберт, см3; п —
число обертів насоса, об/хв; і — час вакуумування.
Задача (про приріст деревини). Дерево рос-
те так, що кількість деревини збільшується з часом за за-
коном М = Моакі, де М — кількість деревини у даний мо-
мент, м3; Мо — початкова кількість деревини; і — час (у
роках), який відраховують з моменту Л40; к — деяка стала.
За скільки років об’єм деревини збільшиться в а разів?
М
Розв’ язання. Якщо в даний момент часу і -т-г- = а,
/Ио
то» поділивши обидві частини рівняння М = Моак1 на Мо,
дістанемо = а**, тобто ак1 = а = а1. Тоді кі — 1 і і = 4-.
/иір /г
Отже, об’єм деревини збільшиться в а разів за у років.
У практичному застосуванні показникові функції зу-
стрічаються здебільшого у вигляді у = Сакх.
Покажемо, що функцію у — акх+ь можна перетворити
до вигляду у = Сакх.
Справді, акх+ь = а^а6. Позначивши сР — С, дістанемо
акхаь _ Сакх. Наприклад, функцію у — 35*+3 можна по-
дати у вигляді у = З5* • З3, або у = 27 «З5*; функцію у =
, , і і
Ьх+— іх
= 25 можна подати у вигляді 25 • 25 , або у = 5 X
X 254Л.
Розглянемо деякі вправи на використання функції у —
= Сакх.
1) В якій точці перетинає вісь ординат графік функції
у = Сакх7 Відповідь. (0; С).
2) Яке значення коефіцієнта С функції у = Са**( якщо
її графік перетинає вісь ординат у точці (0; —3). Відповідь.
С = —3.
3) Яких значень (від’ємних чи додатних) набувають
функції: а) у = —ба**; б) у = 0,7а**? Відповідь, а) Від’єм-
них. б) Додатних.
282
4) При якому значенні С графік функції у = Сакх роз-
міститься над віссю абсцис? Відповідь. При С > 0.
5) При якому значенні С графік функції у = Сакх роз-
міститься під віссю абсцис? Відповідь. При С < 0.
6) Чи пройдуть через одну точку графіки функцій: уг =
— Сак'х, уг = Сак‘х, у3 = Са^х? Відповідь. Так, всі вони
пройдуть через точку (0; С).
Розглянемо ще деякі властивості функції у = Сакх.
Нехай у — Сакх, де С > 0. Якщо ак > 1, то графік має
вигляд, зображений на рис. 8.9. Це можливо у двох випад-
ках: 1) а > 1, к > 0; 2) 0 •< а < 1, к <_ 0.
Розглянемо функцію у = Сакх (С > 0), графік якої зо-
бражено на рис. 8.10. Це можливо, коли ак < 1, тобто у
двох випадках: або 0 < а < 1, к > 0, або а> 1, к <. 0.
При С < 0, к > 0 графік функції у — Сакх має вигляд,
зображений на рис. 8.11.
Основні показникові тотожності. При будь-яких дійс-
них значеннях х і у справедливі рівності:
ахс? = ах+9;
ау
Іпк\Х пХкх. ( 11 \Х аХ •
(ао) —а Ь » ) —— і
(а*)» =
Ці формули називають основними властивостями степе-
нів. Вони означають, що для функції ах, яка визначена на
всій числовій прямій, залишаються правильними властивос-
ті функції ах, яка спочатку була визначена лише для раціо-
нальних х.
Нагадаємо, що раціональні числа разом з ірраціональ-
ними утворюють множину дійсних чисел (числову пряму).
283
§ 2. Розв'язування показникових рівнянь,
нерівностей і систем
Показникові рівняння. Показниковими називають рів-
няння, в яких невідоме входить лише до показників степе-
нів при сталих основах.
Найпростішим показниковим рівнянням є
ах = Ь, а> 0, &> 0, 1. (1)
Якщо замість х у показнику степеня стоїть деяка функ-
ція / (х), то
ам = Ь, а>0, 6>0, а=/=1. (2)
Загального методу розв’язування показникових рівнянь
немає. Можна виділити кілька типів показникових рівнянь
і навести схеми їх розв’язання.
Деякі показникові рівняння можна звести до вигляду
(1) або (2) з допомогою основних показникових тотожно-
стей.
Найпоширенішим є спосіб зведення обох частин показ-
никового рівняння до спільної основи. Розглянемо прикла-
ди розв’язання рівнянь.
Приклади. 1) 5* = 53. Тут х = 3, бо з рівності степенів
при рівних основах випливає рівність їхніх показників.
2) 4х = . Подамо праву частину рівняння як сте-
пінь 4’ 4х == 4“2. Звідси х =—2.
3) 17х = 1, 17х— 17°. Звідси х==0.
. _ 2. іЛ 2
4) 5х = 5 }/25; 5 • 5 3 ; 5х = 5 3 . Звідси х = І у.
5) зх = _9_ зх = _; зх = 93 і 3х = З 3;
4
Зх = 33 = х = 4--
6) (0,1)* = 1000; (“іу-)*= Ю3; (Ю'“1)х = 103; — х =
= 3; х = — 3.
Спосіб зведення до спільної основи застосовують і при
розв’язанні рівнянь виду а№ = Ь.
7) З*2-*-2 = 81. Подамо праву частину рівняння як
степінь 3: З*2-*-2 — З4. Порівняємо показники степе-
нів у лівій і правій частинах: х3 — х — 2 — 4, х3 — х —
—6 = 0. Звідси = —2, х2 = 3.
284
Перевірка. При Хх = —2: ліва частина
а права частина 81 = З4. При х = 3 маємо
Отже, хг = —2, х2 — 3.
8) зх’-5х+6 * == і.
3*’-бх+6=3о; %2 _ 5х 4- 6 = 0; хх = 2;
! \2х2+л-0,5 1
7") /Г’
1 \2хг+х—0,5
з4+2’2 :== з4,
39“3-2
х2 = 3.
। \2х*+^0,6
/ 1 \2 ,
. Звідси 2х24-х — 0,5 = ,
2х24-х— 1 = 0,
Х1,2 =
У14-8 _ -1±3 . „ _ , у _ 1
4 — 4 > Л1-----‘> х2~~2~-
Обидва значення х є коренями даного рівняння.
Для розв’язування окремих видів рівнянь застосовують
спеціальні способи. Таким є, наприклад, спосіб, який нази-
вають зведенням до спільного показника.
> \ 3 ) \ 8 ) 64 •
Зведемо добуток у лівій частині рівняння до спільного
(2 9 V 27 І З \х ( З \3
-X- • -=- = -гт- > ТП = т .
З 8 / 64 ’ \ 4 / \ 4 )
Звідси х — 3.
11) 62*+4 = З3* • 2*+8. Перепишемо це рівняння у ви-
гляді 32х+4 * • 22*+4 = З3* . 2ж+8;
22х~1~4 9
^2х-і-4^3х_ 2х+8"*2^"”4« З4"”*_ 24~х*
4 — х = 0; х = 4.
В окремих випадках дане показникове рівняння пере-
творюють відомими методами: методами заміни, зведення до
квадратного рівняння та ін., а потім вже використовують
певну схему.
Х-Н І Х~1
12) З*-4 "* 3 = 1.
*+ 1 х— 1 о _1___п
х — 1 + «4-1 3
285
Зробимо заміну г = У> тоді * ? = — • Маємо
х і х і у
У + ±-----у-=0; Зу2 + 3- 10г/ = 0; Зу2-Юу 4-3 = 0;
= -§-і Уг = 3; * + ] = —, х — — 2;
Т^Г-3; х = 2.
ІЗ) (/3 4- 2/2) 4-(]/"з — 2/2)* = 6. Маємо суму
двох показникових виразів. Знайдемо їх добуток. Маємо
(|Лз + 2/2)ж • (]/з—2/2)* = (КЗ2- (/8)2)Х = 1-
Зробимозаміну(]/"34-2/2)* = /. Тоді (]/"3—2/2)*=
= -у-. Маємо і 4- -у- — б, звідки /2 — 6/ 4- 1 = 0, І —
= 3±2/2. Отже, (Уз+2^2)х = 3 4-2/2, звідки
х =2; (]/з+2/2)л =3 — 2/2, звідки х = — 2.
Розв’язування нерівностей, які містять показникову
функцію. Найпростішими є показникові нерівності виду
а/<*> >. а<р(«). При їх розв’язуванні використовують влас-
тивість монотонності показникової функції.
Функція у = ах при а > 1 — зростає, а при 0 < а <
< 1 — спадає.
При а > 1 більшому значенню функції відповідає біль-
ший показник. Отже, при а > 1 розв’язання даної нерів-
ності зводиться до розв’язання нерівності / (х) >» <р (х).
При 0 < а < 1 показникова функція спадає, тобто
більшому значенню функції відповідає менший показник.
Тому при 0 < а < 1 розв’язання нерівності >. цчх*?
зводиться до розв’язання нерівності / (х) < <р (х).
Розглянемо приклади розв’язуванйя нерівностей.
Приклади. 1) З2-* >• 27. Перепишемо дану нерівність
у вигляді З2-* > З3. Оскільки а = 3 і 3 > 1,то2 — х>
> 3. Звідси —х > 1; х < —1.
2) О.б5-2* < 8. Беручи до уваги, що 8 = О.б-'3, пере-
пишемо дану нерівність у вигляді 0,б5“2х < О.б’’’3. По-
казникова функція спадає, бо 0,5 < 1. Тому дана нерів-
ність рівносильна такій: 5 — 2х > —3. Звідси х < 4.
3) 25х+6 > 2х’. Оскільки а = 2 (2 > 1), то 5х 4- 6 >
> х2. Тепер розв’яжемо квадратну нерівність х2 — 5х —
— 6 < 0. Маємо (х 4- 1) (х — 6) < 0. Звідси —І < х < 6.
286
4) < 20х • . Зведемо дану нерівність до
СПІЛЬНОЇ ОСНОВИ!
54* & . 4х 1 . 5х 5х.22х .
23х в §3х 0 ’ ’ 24(*—1) * 23х *
р_у*<р_ух_4
Оскільки а < 1 (-у < 1^, то Зх>2х— 4, х~>— 4.
5) 5*2+2* > 53, а > 1 (5 > 1), тому показникова функ-
ція зростає і дана нерівність рівносильна нерівності
х2 + 2х > 3, х2 4- 2х — 3 > 0.
Розв’язком цієї нерівності, а значить і початкової, є
об’єднання інтервалів (—оо; —3) і (1; оо).
6) ("І")*-+ 3 < 0. Введемо нову змінну у ==
/ і у / і у
= І -у І , ТОДІ І-у І = у2 і нерівність набере вигляду
, №-------^-ї/+3<0; Зу2 —28у+9<0.
Розв’язком цієї квадратної нерівності є інтервал ^у; 9^,
тобто -у < у < 9.
Повертаючись до початкової змінної х, маємо:
<9 -ксШ'сШ'2
з з / ’ з у з) уз/ •
Функція спаДае- Отже, розв’язком останньої нерів-
ності будуть числа, які задовольняють нерівність —2 <
< х < 1.
7) 5 • З3х‘ > 3 • 53х\ Поділимо почленно цю нерівність
на добуток 5 • 3. Дістанемо З3*2-1 > 53*2-1
дЗж»—1 53я‘—1 дЗх2-1 / 3 \з^—і / з \0
53л«-1 '> 5ЗХ*-1 ’ 53*»-1 > 1»
Основа -у < 1. Отже, дана функція спадає і Зх2 —
1^-А 2 1 . І і 1 . /З _ Уз
— 1 <0, х < 3 , |х| < , 3 <х< 3 .
287
8) 3 • 4* 4* 2 • 9* < 5 • 6х. Перетворимо нерівність до
вигляду 3 • 22* + 2 • З2* — 5 • 2* • 3* < 0. Поділимо обид-
ві частини останньої нерівності на З2* > 0. Дістанемо З X
х(4Г + 2-5(4)’<»-
( 2 V
Зробимо заміну -х- = у, тоді Зг/2 — 5у 4- 2 < 0;
\ О /
Зг/2 — 5г/4-2 = 0; г/1і2 = -Ц^-; Е 4<
2 / 9 V
<У<1; 4<Ш <1; °<Л:<1-
9) 5 • З2^1 — 9Х“015 < 9х + 4 • 32*“2. Зведемо цю нерів-
ність до вигляду 5 • З2*-"1 — З2*"1 < З2* 4- 4 • З2*-2. Вине-
семо спільні множники за дужки:
З2*-1 (5 _ 1) < з2^2 (9 4- 4),
4 - З2*-1 < 13 • З2*""2,
З2*-1 13 . о 13
д2х—2 4 » 4 •
Отже, розв’язком є вся числова вісь.
10) 2^*“* х. Візьмемо до уваги, що вираз 2^1~*
має смисл при х 1. Тоді 2^/Г1~"* > 2° = 1. Звідси можна
зробити висновок, що 2^Г1“* :> х, бо х 1.
Історична довідка
До початку XVII ст. в математиці уникали вживання дробових та
від’ємних показників степенів. Лише в кінці XVII ст. у зв’язку з усклад-
ненням математичних задач виникла необхідність поширити область оз-
начення показника степеня на всі дійсні числа. Узагальнення поняття
степеня де п — будь-яке дійсне число, дозволило розглядати показ-
никову функцію у = ах на множині дійсних чисел і степеневу функцію
у — на множині додатних чисел (при цілих п степенева функція визна-
чена і для х < 0).
Питання, пов’язане з показниковою функцією, розробляв Леонард
Ейлер. У двох розділах своєї праці «Вступ до аналізу» він описав «по-
казникові і логарифмічні кількості». В ній, зокрема, зазначено, що по-
казникові кількості можуть бути різноманітними залежно від того, «чи
буде змінною кількістю один лише показник, чи, крім того, ще і кіль-
кість, ЯКІ підносять до степеня». До перших віднесено а2, до других у2.
Навіть і сам показник може бути показниковою «кількістю», наприклад
у виразах а?2, ау2, і/*2, ху2. Ейлеру належить відкриття зв’язку між по-
288
казниковою і тригонометричною функціями. Він довів, що ех^^1 =
= СОЗ X + К—1 8ІП X, звідки при X “ я 1 = соз Я + V —1 зіп я
або = —1, а також співвідношення = 1.
Показникову функцію виду у = ех почали вивчати з 40-х років
XVII ст. Іранський математик ал-Караджі (помер у 1016 р.) почав си-
стематично розглядати тричленні рівняння, квадратні відносно деякого
степеня невідомого, а також рівняння, що зводяться до них діленням на
степінь невідомого, тобто рівняння вигляду
ах2п + Ьхп = с, ах2п + с = Ьх\ Ьхп + с = ах2пі
ах?п+т = Ьх*+т + сЛ
Запитання І завдання для повторення
1. Дайте означення показникової функції у = ах. Чому в її озна-
ченні сказано, що а > 0 і а Ф 1?
2. Назвати область означення показникової функції ах.
3. Які з функцій у = х1’3; у == 2,75х; у — у = 5^2х; у == я**3;
{ 3 V 0
= Є показниковими?
4. Які властивості має функція ах при а > 1? Для відповіді побу-
дувати ескіз графіка цієї функції.
5. Які властивості має функція у = ах при 0< а< 1?Пояснити,
користуючись ескізом відповідного графіка.
6. Яка особливість розміщення графіків функції у = 10х і у =
= 0,1х?
7. За яких умов 3Х1 > 3х* і 0,7Х1 > 0,7х*?
8. Відомо, що аа > сР. Що більше: а чи Р при 0 < а < 1?
9. Відомо, що аа < бА Що більше: а чи р при а > 1?
10. Чи правильною є нерівність аХ1 > аХі при х^ > х2?
11. Які з показникових функцій
(7 \Х / д \Х
, <7 = 3х, ^= 4- , = 0,027х
11 / \ о /
зростають?
4 \х
ТУ/
12. Які з функцій у = 0,26х, у = (/3)х, у = =
спад^оть?
13. Порівняти показники к і /п, якщо правильна нерівність:
\ о / \ О /
г) (Ут— 1)*< (/7— І)”1.
в) СҐЗ — /2)й > (/3 — У2)т;
14. Чи можна, знаючи графік функції у = ах, побудувати графік
І і V
функції у = І — І ? Як це зробити?
10 1-1819
289
15. Порівняти число а з одиницею в кожній з таких нерівностей
и
а) а1,27 > а0,419; б) а“°>83 > а°‘14; в) а°’173<Г 4 ;
5 2
г) а 13 >а7 ; д) а”’4'2 > аГ*2,5; е) а~3 < а”-3’01.
16. Що можна сказати про знак числа к, якщо: а) 5* = 10; б) 7к =
= 1,003; в) (0,3)* = 100; г) (0,4)* = 18?
17. Побудувати на одному рисунку графіки функцій у = 2х, у =
= 2х”1, у = 2Х+1. Чому графіки цих функцій не перетинаються? Які
вони мають спільні властивості?
18. Якщо графіки функцій у = ах і у = Ьх симетричні відносно осі
ординат, то яке співвідношення існує між а і Ь?
/ 5 \*
19. Чи мають спільну точку графіки функцій у = 2х і у = І ?
(1
— І (а > 0,
а 1) один відносно іншого?
21. В якій точці перетинається графік функції у — 7,3"“0,3х з віссю
ординат?
22. На прикладах у = х2 і г/ = 2х пояснити, чим відрізняється по-
казникова функція від степеневої?
23. Які процеси в галузі техніки та природознавства виражаються
за допомогою показникової функції?
24. Довести, що коли показникова функція у — ах така, що х змі-
нюється в арифметичній прогресії, то відповідні значення у утворюють
геометричну прогресію. Знайти її знаменник.
25. У якій точці перетинають графіки функцій: а) у = 12х;
/ 2 \*
б) у — 0,07х; в) у = вісь ординат?
\ О І
26. У якій точці графік функції у = 3 • 27х перетинається з віс-
сю абсцис?
27. Побудувати ескізи графіків функцій; а) у = —5 • 3~0,2х, якщо
0 < а < 1; б) у = —За4х, якщо а > 1.
28. Чи правильне твердження: «Якщо одне із значень функції у =
= Сакх додатне, то функція набуває лише додатних значень, а якщо
від’ємне,— то лише від’ємних»?
29. Яке рівняння називається показниковим? Навести приклади.
ЗО. Чи має розв’язок показникове рівняння ах = у при у < 0?
31. У чому полягає спосіб зведення до спільної основи розв’язу-
вання показникових рівнянь?
32. У чому полягає спосіб винесення за дужки розв’язування по-
казникових рівнянь?
33. Як розв’язують показникові рівняння виду
Аа2х + Вах + С = <ії
34. Як розв’язати графічно рівняння: 2х = х + 3; 2х = х2\ 2х =
290
35. Записати в аналітичній формі показникову нерівність най-
простішого виду.
36. Якою властивістю показникової функції у = ах користуються
при розв’язанні показникових нерівностей? Розглянути випадки а > 1
і 0 < а < 1.
Вправи
1. Розв’язати показникові рівняння:
А
Застосувати спосіб зведення до спільної основи:
1) 2х = 64; 2) 22х = 512; 3) 2~х = 16;
4) 2х+І = 32; 5) З2*-1 = 81; 6) /б* = |^25;
7) 32*“‘ = 1; 8) ах’~7х+12 = 1; 9) а^~^х+2' = 1.
Застосувати спосіб зведення до спільного показника:
27
64 '
Розв’язати способом винесення спільного множника за дужки:
12) 2Х+2 — 2х = 96; 13) 7х — 7Х~1 = 6; 14) Зх+2 + 3х-1 = 28.
Розв’язати рівняння, зводячи їх до вигляду с?х + ах = Ь:
15) 4х + 2х = 72; 16) 72х —6 • 7х 4-5 = 0,
Б
10) 2х . 5х = 0,01;
8
17) ах+1 = Уах~2; 18)
19) 4А|Гх+і = 64 • 2^*+і; 20) (0,25)2-х = ;
21) 2Х—1 4- 2х-2 4- 2Х~3 = 448;
22) 2х+1 4-3 • 2х-1 — 5.2х 4-6 = 0;
23) • (-у-ґ-1=-у-; 24) =36ї
26) 2х- 5х = 0,1 (10х-1)5;
27) 5 • 32х_| — 9х-0,5 = 9х + 4.32х-2;
28) 23х—3 — 5 4- 6.23—3х = 0.
В
29) З2*-1 • 53х+2 = А . 52х • 32х;
5
ЗО) 3 • 4х 4- А . 9Х+2 = 6 • 4х+1-к • 9х+1;
3 2
31) 23(х-1) — 128 • 23(2”х’ = 48; 32) 22х”3 — 3.2Х“2 4-1=0;
33) 6.4х—13.6*4-6.9Х = О1
10*
291
34) (4 + /15)* + (4 - /15)* = 62;
35) (/5 4-2 /б/ 4- (/ 5 — 2/6)* = 10,
О Иілоп ’ ГГ П Л-ПТІ ГГЛТГЛПТТТІТГ^г, < ГТЛГ> .
2. Розв’язати показникові нерівності:
1)2* >-!-; 2) ІО3**2 > 100; 3) (0,3)* > 0,09;
1 а / 1 \2х«иеЗ
7) ^Г<49; 8)2*’>^
9) (/3)*<’« 10> 14
9 \ 4
*+ю
11) 0,75-2* <0,49; 12) 16*_|<і <0,125;
13) 0,78“*2 > 0,72*; 14) 3 • 9*“2 > (_1_)3*-15
15)(4'Г>^; 16) (/із)х!_2>(/ї4)х2’2;
17) 2*г-6*-2>5 <16/2; 18) 22*”"3 — 3 • 2*-2 + 1 < 0,
В
19) 8 • 72*ї—* — 7 • 82*’“*> 0;
20) 2 • 84-5*<(_1—Ґ+2 ; 21) 12х • 11/*—11* • 12/*<0;
\ 16 /
22) (44) Х < (/5>х2+3,75; 23) 9* + 6* > 22*+‘;
26) — Ч2х-1 + 4" > 0; 27) 22*+6 + 2*+7 > 17.
РОЗДІЛ 9
ЛОГАРИФМІЧНА ФУНКЦІЯ
§ 1. Логарифми
Поняття логарифма. Розглянемо рівність 43 = 64. В ній
число 3 є показником степеня, до якого треба піднести число
4, щоб дістати 64. Аналогічно в рівності 5““2 = число —2
є показником степеня, до якого треба піднести число 5, щоб
292
дістати У загальному випадку в рівності ах = N число
х є показником степеня, до якого треба піднести основу а,
щоб дістати число ЛЛ
Розглянемо рівняння а* = М, де а і /У — деякі числа,
причому а > 0 і а у= 1. При N 0 це рівняння не має ко-
ренів, бо значення показникової функції у = ах додатні
при будь-якому х.
При N > 0 рівняння має корінь, ідо того єдиний. Справ-
ді, областю значень показникової функції у == ах при а =^=
Ф 1 є множина додатних чисел (отже, корінь рівняння іс-
нує). Крім того, кожне своє значення показникова функція
набуває лише при одному значенні аргументу (отже, цей
корінь єдиний).
Корінь рівняння ах = N. де а > 0, а =£ 1, називають
логарифмом числа М за основою а.
Логарифмом числа N за основою а (а> 0 і а =£ 1) нази-
вають показник степеня х, до якого треба піднести а, щоб
дістати число N.
Слово логарифм заміняють символом 1о§, праворуч від
якого (трохи нижче) записують те число, яке називають ос-
новою.
Так, замість того, щоб писати «логарифм числа 81 за ос-
новою 3», скорочено пишуть 1о§3 81. Те, що число х є лога-
рифмом числа М за основою а, записують так: 1о§а N = х.
Цю рівність читають так: логарифм числа /V за основою а
дорівнює х. Наприклад, з рівностей 53 = 125, 6~"2 =
7° = 1, І-£-) , = 64 випливає: 1о§5 125 = 3, 1о§6 = —2,
1о§7 1 = 0, 1о§2_ 64 = —6.
2
Зазначимо, що вирази 1о§4 (—64), 1о§3 0 не мають смис-
лу, бо рівняння 4х = —64, 3х = 0 не мають коренів.
Вираз 1о£а М, де а > 0 і а 1, має смисл лише при N >
>0.
Логарифмічна 1о£а У = Ь і показникова аь = N рівності
виражають одне і те саме співвідношення між числами а, Ь
і N. За цими рівностями можна знайти одне з трьох чисел,
що входять до них, якщо задано два інші. Відповідно до
цього можна розв’язати три задачі.
1) Знайти число N за даним його логарифмом Ь за ос-
новою а.
2) Знайти основу аза даним числом N і його логариф-
мом Ь.
293
3) Знайти логарифм Ь даного числа N за даною основою а.
Широко вживають так звані десяткові логарифми, тобто
логарифми за основою 10. Для них застосовують позначен-
ня (без запису основи), наприклад 10 = 1, 100 =«= 2,
1§ 1000 = 3, 1§ 0,1 - —1.
Приклади. 1) Записати у вигляді логарифмічних рів-
ностей: а) 2’ = 128; ) 5~я = в) 216~ = 6.
За означенням логарифма даного числа за даною осно-
вою маємо:
а) 1о§2128 = 7; б) 1о§8— 3; 1о§31в6=-Ь.
2) За означенням логарифма перевірити справедливість
таких рівностей: а) 1о§6 625 = 4; б) 1о§ і — 5.
2
(1 \б 1
= -др
3) За означенням логарифма визначити, яке число має
логарифм 3 за основою 7.
За умовою 1о§7 х = 3, звідки х = 73, х = 343.
4) За якою основою логарифм числа 10 000 дорівнює 4?
Маємо 1о§х 10 000 = 4, звідки х4 — 10 000, х —
= ><ЇЇП)бб, х = 10.
5) Знайти: а) логарифм числа -дід' за основою 7; б) ло-
, О 1
тарифи числа 8 за основою —.
Маємо: а) = х, 7* =• , 7х = 7-3, х= — 3;
ОтгО ОтгО
/ 1 \Х / 1 \х / 1 V /і \~3
б) І03±8:-х, (4) =8, (4) = 23, 4-І =(4) ,
X = — 3. 2
6) Знайти основу х, якщо 1о§ж = — 2.
Маємо х~2 = -1-, = -&•, х2 = 49, х = 7.
7) Знайти число х, якщо: а) 1о§у2 х = 4; б) 1о§0д х =
= —1.
Переходячи від логарифмічних рівностей до показнико-
Г- І І \“1
вих, маємо: а) х = (]/2)4 = 4; б) х = І -ууі = 10.
8) За якої основи: а) логарифм числа 3 дорівнює 3; б)
логарифм числа -х- дорівнює -у-?
о о
204
а) 1°&» 3 = 3, або х3 = З, звідки х = у^З;
і
б) = 4-. або х3 =4-. Піднісши обидві час-
О О о
-і- / і \з
ТИНИ ЦІЄЇ рівності ДО степеня 3, дістанемо (х3 )3= І-д-1 ,
ЗВІДКИ X = .
9) Обчислити вирази! а) 31о§216 4- 41о§3
б) 1о§31о§327.
а) 31о§216 + 4 1о§3 = 3 • 4 4- 4 . (- 3) = 0;
б) позначимо 1о§31о§3 27 = х.
За означенням логарифма 3х = 1о§3 27, або З* = З,
звідки х = 1.
Основна логарифмічна тотожність. Розглянемо показ-
никову рівність
а* == N. (1)
За означенням логарифма
х = 1о§а№ (2)
Замінюючи у рівності (1) х на його значення з рівності
(2), дістанемо
Рівність (3) називають основною логарифмічною тотож-
ністю. Вона є стислим записом означення логарифма:
1о§а N є показником степеня, до якого треба піднести осно-
ву степеня а, щоб дістати N. Наприклад: б108'125 =
= 125, 10ій 1000 = 1000, Т =9-
Приклади. 1) За допомогою основної логарифмічної то-
тожності перетворити рівність 25 = 32.
Маємо 2ІО8ї32 == 32.
2) Обчислити! а) 1,9ІОЙІ-98; б) а2ІО8аЛ/.
Маємо! а) 1,91081.98 = 8; б) а І08а " = (а1®8* ")2 = №.
3) Обчислити! а) 4-'°8‘20; б) 5ІО8‘ 9-1О8‘ І0; в) 49і08’8.
а) за означенням степеня з від’ємним показником
і
л~> 1о£< 20 _ 4 1О£< 20 _ 1 .
* ~ 20 ’
295
б) у показнику маємо віднімання, а показники степенів
віднімаються при діленні. Отже,
КІО8» 9—Іое» 10 _ 5ІОЙ6 9 _ 9 .
“ 5ІОЙ6 10 — 10 ’
в) беручи до уваги, що 49 = Т2, дістанемо 49і08’8 =
= (7108’8)2 = 82 = 64. Отже, 49108’8 = 64.
4) Обчислити: а) 1 + 51О8|І 8; б) 21+3108‘5;
З 1оЄ. N 2 108- N
д) 101®2; е) Ю2+'8в-05.
а) 1 + 5ІОЙ‘8= 14-8=9;
б) 21+31О8’5 = 2 • 231082 5 = 2 • (2’08‘5)3 = 2 • 53 = 250;
а31оеаЛ,|а21°еа7У (аІО8“")з + (а1о8а")а № +№
~ №
= #4-1;
г) 810,57 = (З0,61о£’7)4 == З21о§3 7 = (З10*8 7)2 = 72 = 49;
д) 10182 = 2;
в) 102+ 18 0.05 = 102 . 1о18 0.05 = Ю0 • 0,05 = 5.
Основні властивості логарифмів. Практичне застосу-
вання логарифмів грунтується на ряді теорем, що виража-
ють основні властивості логарифмів.
Теорема 1. Логарифм добутку двох додатних множни-
ків дорівнює сумі їхніх логарифмів, тобто
^а(.N1N!і) = ^о§аN1+^о§аN2, де ^>0, ЛЇ2>0.
Доведення. Позначимо 1о§а Л\ = хх і 1о§а М2 =
= х2. За означенням логарифма = аХі, М2 = ах*. Пе-
ремножаючи почленно ці рівності, дістанемо 1УгМ2 —
= ах'+х‘. Тут хг + х2 є показником степеня, до якого тре-
ба піднести основу а,-щоб дістати число, яке дорівнює
добутку. Отже, 1о& (N1N2) = хг + х2.
Замінюючи хг і х2 їхніми виразами через логарифми, ос-
таточно дістанемо
1о§а (УДг) = 1о§а Л\ + ]о&аИ2.
Теорему доведено для окремого випадку — для двох
множників. Але її можна поширити і на будь-яке скінчен-
не число множників, бо при знаходженні добутку скінченно-
го числа степенів однієї і тієї самої основи показники сте-
пенів додаються.
Отже, 1о§а (#і#2#8 ... іїп) = \0§а + 1о&, + ... +
+ 1о& іїп, де #х >0, ТУ2 > 0, ..., > 0. (Пропонує-
296
мо самостійно довести теорему для випадку трьох множни-
ків.)
Зазначимо, що для доведення цієї теореми можна було б
скористатися основною логарифмічною тотожністю. Нехай
Мі == ах^ М2 = 3а основною логарифмічною тотож-
ністю
^ = а108«Л'*.
Перемножаючи почленно ці рівності, дістанемо
ВД. = а'°г“ • а1о8° = а1ое° ",+ ІО8<>
За означенням логарифма
1о& (^а) = Іо&ЛГі + 1о§Л2.
Теорема 2. Логарифм частки двох додатних чисел (дро-
бу) дорівнює різниці логарифмів діленого і дільника (чисель-
ника і знаменника), тобто
1О8а-^- = 1°бо^і —І0§аЛГ2, де ^>0, ^2>0.
Доведення. Нехай 1о§а А/'1 = %і і 1о§а Л72 = х2. Тоді
= аХі, N2 = аХг.
Поділимо почленно першу рівність на другу:
^2
Тут хх — х2 є показником степеня, до якого треба під-
нести основу а, щоб дістати число, яке дорівнює частці
-ф-. Отже, 1о§а = хг — х2. Замінюючи хг і х2 їхніми
виразами через логарифми, остаточно дістанемо
1о§а = 1о& — 1о§а
Наслідок. Логарифм дробу, чисельник якого дорів-
нює одиниці, дорівнює логарифму знаменника, взятому
з протилежним знаком, (Обгрунтуйте це твердження само-
стійно.)
Можна також довести теорему 2, користуючись основ-
ною логарифмічною тотожністю.
Теорема 3, Логарифм степеня додатного числа дорівнює
показнику степеня, помноженому на логарифм основи цього
степеня, тобто
= т\о%аМ,
де т — будь-яке число, N > 0.
297
4 Доведення. Нехай 1о§я N = х, тоді N = ах. Під-
несемо обидві частини останньої рівності до степеня т:
маємо — атх. Тут тх є показником степеня, до якого
треба піднести основу а, щоб дістати число, яке дорівнює
Мт. Отже, переходячи до логарифмів, дістанемо
>о§а (АП = тх.
Замінивши х його виразом через логарифм, остаточно мати-
мемо
1о&(ЛГ) = /п!о§аЛЇ.
Теорема 4. Логарифм кореня з додатного числа дорівнює
логарифму підкореневого числа, поділеному на показник
кореня, тобто
Доведення. Нехай треба знайти 1о§с у N. Замі-
нюючи радикал степенем з дробовим показником і засто-
совуючи теорему 3, дістанемо
1О&^ = 1о§лт = 4 = •
До основних властивостей логарифмів належать ще такії
І) Логарифм одиниці дорівнює нулю. Це випливає з
означення степеня з нульовим показником. При а 0
а° = 1, але тоді 1о§а 1 = 0.
2) Логарифм основи дорівнює одиниці, тобто 1о§о а = 1.
Це випливає з того, що а1 = а.
Основні властивості логарифмів широко використовують
при перетворенні виразів, що містять логарифми. Окремим
видом таких перетворень є логарифмування виразів.
Прологарифмувати одночлен означає виразити його ло-
гарифм через логарифми додатних чисел (позначених циф-
рами і буквами), що входять до його складу.
Користуючись теоремами про логарифм добутку, част-
ки, степеня і кореня, можна прологарифмувати будь-який
одночленний вираз.
Домовимося при логарифмуванні не писати основи, бо
подані нижче рівності справедливі за будь-якою основою
а, що задовольняє умови а > 0, а Ф 1.
Приклади. Прологарифмувати вирази:
1) х = 5ас (а > 0, с > 0).
Даний вираз є добутком , а тому за теоремою 1
1о§х = 1о§ 5 + 1о§а + 1о§о.
298
2) х = (т > 0, п > 0).
За теоремою 2 Іо§ х = 1о§ т — 1о§ п.
3) х (а > 0, Ь > 0, с > 0).
Даний вираз є часткою, а тому за теоремою 2
Іо§ х = 1о§ (7аЬ) — Іо§ (9с).
Застосовуючи до зменшуваного і від’ємника теорему
1, дістанемо 1о§ х = 1о§ 7 + 1о§ а + 1о§ Ь — (1о§ 9 4-
+ 1о§ с) = 1о§ 7 + 1о§ а + 1о§ Ь — 1о§ 9 — 1о§ с.
4) х = 11а2Ь3 (а > 0, Ь > 0).
За теоремами 1 і 3 1о§ х = 1о§ 11 +21о§ а + 31о§ Ь.
5) х = (а>0, 6>0, с>0).
1о§ х — 1о§ (а46) — 1о§ (7с6) = 4Іо§ а + 1о§ Ь — 1о§ 7 — 51о§ V.
6) х = За3Ь (а > 0, Ь >• 0).
За теоремою 4
1о§х = 4-1°§(За3&) = -|-1о§3 +-|-1о§а4--^-1о§&.
7) х = + ... де а>0, Ь>0, с>0, й>0.
|/(а — Ь)2сі2
1о§х = 41о§(а + Ь) 4- 1о§с------(21о§ (а — Ь) 4- 21о§<І).
8) Знайти х, якщо 1о§7 х = 1о£7 12 — 1о§7 4.
1о§7 х = 1о§7 ; 1о§7 х = 1 о§7 3.
Якщо логарифми чисел х і 3 за однаковою основою 7
рівні, то і числа будуть рівні. Отже, х = 3.
9) Обчислити без обчислювальних засобів:
а) 1о§3 2 4- 1о§3 4,5.
1о§3 2 4- 1о§3 4,5 = 1о§з (2 • 4,5) = 1о§3 9=2.
б) 1о§27 —1о§2-^-.
1о&7 — = 1о§3 —у— = 1о§216 = 4.
Тб"
10) Нехай 1о£а Ь = 0,45; 1о§а с = 0,4;
1о§а (і = 0,85; 1о§а к = — 0,25.
299
Знайти 1о£а х, якщо х — -
!о& х = 21о§а Ь + -і- 1о§а с — 1о§а а — 31о§а к =
= 0,9 + 0,05 — 0,85 + 0,75 = 0,85.
Деякі важливі логарифмічні тотожності. Доведемо то-
тожність
1о& а = ' аб° І0§ь а *1о& ь = Е
Нехай 1о§(, а = х. Тоді за означенням логарифма Ьх =
— а. Логарифмуючи цю рівність за основою а, дістанемо
х1о§а&=1, звідки X = , тобто 1о& а = .
Доведемо тотожн ість
1о&Л=1о§аХ
що має такий зміст: якщо число, що стоїть під знаком лога-
рифма, і основу логарифма піднести до будь-якого степеня,
то величина логарифма не зміниться.
Нехай 1о£д А/' = х. Тоді ах = N і акх = А^, або (ак)х =
= А^5. Тут х є показником степеня, до якого треба піднести
вираз ак, щоб дістати А^. Отже, х = 1о£а* ЛЛ
Підставляючи замість х його значення, остаточно діста-
немо
Іо&Л = Іо^ЛГ*.
що й треба було довести.
За цією тотожністю маємо, наприклад:
1о§2 5 = 1о§2» 53 = 1о§8125; 1о§3<- х = 1о§а х® = 31о& х.
У <2
Доведемо тотожність
іо§а^=4і°§л-
Нехай 1о£аП N = х, тоді апх = N. Піднісши обидві час-
1
тини останньої рівності до степеня —, дістанемо ах = Мп .
Тепер прологарифмуємо останню рівність за основою а.
Маємо х = 1о§а N. тобто 1о£аЛ N = 1о§0 N. що й
треба було довести.
300
Приклади. 1) Що більше: 1о§4 3 чи 1о§1в 9?
Іо§43 = 1о§4г32, отже 1о§4 3 = Іо§1в 9. .
2) Обчислити 1о§уз 8, знаючи, що 1о§12 3 = а.
1о§уз 8 = 1о§3 64 = 1о§3 43 = 3 1о§3 4 = 31о§з —- =
= 3 (1о§3 12 —1о§3 3).
Використовуючи залежність 1о§й а = , дістаємо
1о^12=йЬ-
Отже, Іо^д 8 = 3 (1 о§312 — 1о§3 3) = 3 3-1) =
= з р. _ = .
\ а І а
Потенціювання. Перетворення, за допомогою якого за
даним логарифмом числа (виразу) визначають саме число
(вираз), називають потенціюванням. Це перетворення є
оберненим до логарифмування.
Застосовуючи теореми логарифмування, іноді можна
вирази, що містять логарифми чисел або виразів, перетво-
рити у логарифм одного числа або виразу.
Приклади. 1) Знайти х за даним його логарифмом
1о§ х = 5 1о§ а — 31о§ с.
За теоремою про логарифм степеня Іо§ х = 1о§ о5 —
1о§ (?, За теоремою про логарифм частки 1о§ х = 1о§
Якщо логарифми виразів х і і при одній і тій самій
основі рівні, то вирази будуть рівні. Остаточно х =
(Самостійно зробити перевірку логарифмуванням.)
2) 1о§ з = 1о§ а — 1о§ 7 — 1о§ Ь.
Маємо 1о§ г = 1о§ ; г = .
Тут потенціювання виконали без проміжних записів.
3) 1о§ В — 1о§ А = 1о§ т — 21о§ п.
л* і В , іАп6 В у' пР
Маємо 1о§^- = 1о§ .
ЗОЇ
4) Спростити вираз 1о§ _|_ 10£ тіа^_пі +
Маємо 1о§ (. — аЬ і.. ,т , А,') = і0£ (т _|_ л).
ь \ а т2 — п* Ь ) & \ • л
5) Спростити вираз
о
1о§# = -£-1о§а — 21о2& — 1о§с 4- 1о§(а 4- &).
Маємо 1о§ N = 1о§ ~ » звідки N = .
Перехід від однієї основи логарифмів до іншої. Часто
необхідно здійснити перехід від логарифма за однією ос-
новою до логарифма за іншою основою.
Нехай відомо 1о§а N і треба знайти 1о§6 N — х (х — не-
відоме число), де а > 0, а 1, Ь > 0, &=/= 1.
За означенням логарифма Ьх = N. Прологарифмуємо
останню рівність за основою а. Маємо х 1о§а Ь — 1о§о М,
звідки х = , тобто
<»
Таким чином, логарифм будь-якого додатного числа N
за основою Ь дорівнює логарифму того самого числа за осно-
вою а, поділеному на логарифм числа Ь за основою а. Цю
залежність застосовують у такому вигляді:
1о§а УУ = 1о&> N • ІО£О (2)
Ще раз підкреслимо, що формули (1) і (2) справедливі,
якщо обидві їхні частини мають смисл, тобто а > 0
і а #= 1, Ь > 0, Ь #= 1.
Отже, будь-який логарифм можна подати у вигляді
відношення двох логарифмів, узятих за однією і тією самою
основою. Наприклад, 1о§5 10 можна подати за основами 2;
3; а (а > 0, а 1) так: 1о§6 10 = 1о§5 10 =
1о§6 10 = '°-
66 1о§о5 •
Приклади. 1) 1о§27 Зх подати за основою 3.
Маємо 10§87Зх = ^^-= ь&3 + 1о&^д2+1о&* ,
2) Знаючи 1о§и 2-а, знайти 1о& 16.
302
Маємо 1о§в 16 = Ц0§іа *6- = —1о81.а2Д = -,-1°1§1а^- =
88 10812 6 , п / 12 \ 1 — 1о§і2 2
4а
1 — а '
3) Обчислити 1о§9 5 • 1о§25 27.
Скориставшись залежністю 1о§ь N = » зведемо
логарифми до основи 10:
1о~ 5 Іог 27- ^27 - 1§б 31^3 - 3
ю§25^/- 1§9 ^25 - 21^3 21^5 - 4 .
Зазначимо, що в розрахунках найчастіше використо-
вують логарифми з основою 10, тобто десяткові логарифми.
Натуральні логарифми. В математичних дослідженнях
використовують логарифми з основою, вираженою ірра-
ціональним числом, наближене значення якого дорівнює
2, 718281 ... або яз 2,718. Російський математик, механік
та фізик Леонард Ейлер (1707—1783) запропонував позна-
чати це число буквою е. Його називають неперовим числом
на честь шотландського математика Джона Непера (1550—
1617).
Логарифми з основою е називають натуральними або не-
перовими і позначають Іпх. Тут основу е не пишуть, а лише
мають на увазі. Від назви «логарифм» залишили лише одну
букву /. Друга буква п є початковою в слові натуральний
(латинське — паіигаїіз).
Отже,
ІП X = 1о§в X. (1)
Наприклад, 1п е = 1, 1п 1 = 0, 1п 2 = 0,693, їй 3 —
~ 1,098, 1п 10 = 2,303.
За основною логарифмічною тотожністю для будь-якого
додатного числа
е1п а = а. (2)
Якщо відомі десяткові логарифми чисел, то можна, ви-
користовуючи формулу (2), обчислити відповідні натураль-
ні логарифми.
Цією формулою можна користуватися і для відшукання
десяткових логарифмів за натуральними. Маємо 1о§е х =
— 1о§10 х • 1о§е 10, але 10 ж 2,303, тому 1п х =
= 2,303 1§ х. Ця формула дозволяє обчислити натуральні
логарифми, якщо відомі десяткові. Нею можна користу-
ватися також і для відшукання десяткових логарифмів за
відомими натуральними. Для цього зручно переписати її у
303
вигляді:
І£ х = о * 1п х = 0,4341п х.
ВІДПОВІДНО ІП X = '0 434 1§ X.
Число М = е а? 0,434 називають модулем переходу
від натуральних логарифмів до десяткових. Отже, 1§ х —
= М їй х, 1п х = . Наприклад, 1п 2 = 1§ 2 • а#
а* 0,3010 • ; 2718 « 0,3010 • 2,303 « 0,6932. Натураль-
ний логарифм приблизно у 2,3 рази більший за десят-
ковий логарифм того самого числа.
§ 2. Логарифмічна функція, її властивості
і графік
Поняття логарифмічної функції. Кожному додатному
числу х відповідає певне значення його логарифма: 1о§а х
(основу а розглядаємо як дане стале додатне число, що не
дорівнює 1). _
Інакше кажучи, 1о§о х при заданому а (а > 0, а 1) є
функцією від х, визначеною на множині всіх дійсних чи-
сел. Функцію 1о§а х називають логарифмічною функцією
з основою а > 0, а=£ 1. Оскільки рівності у= 1о£а х і
х = а? за означенням логарифма визначають один і той са-
мий зв’язок між змінними х і у, то показникова і логариф-
мічна функції є взаємно оберненими, тобто логарифмічна
функція є функцією, оберненою до показникової.
Показникова функція у = ах відображує зміну степеня
числа залежно від зміни показника степеня.
Логарифмічна функція у = 1о£а х відображує зміну
показника степеня залежно від зміни степеня числа а.
Встановлено зв’язок між графіками показникової і
логарифмічної функцій з однією і тією ж основою а.
Вище було показано, що графік функції <р, оберненої до
функції /, симетричний графіку / відносно прямої у = х. Ско-
ристаємося цим для побудови графіка функції у = 1о£а х.
Графік функції у — 1о§а х можна -дістати з графіка
функції у = ах, симетрично відобразивши останній віднос-
но прямої у = х. Для цього досить для кожної точки
М (с; сі) графіка у = ах (рис. 9.1) побудувати точку М.г (д;
с), симетричну їй відносно прямої у = X.
Якщо на аркуші паперу накреслити чорнилом графік
функції у = ах, а потім, не давши йому висохнути, швидко
304
зігнути аркуш уздовж бісектриси І і III координатних ку-
тів, то відбиток буде графіком логарифмічної функції у =
= 1о§в X.
Побудуємо, наприклад, графік функції у = 1о§2 х. Для
цього знайдемо кілька точок, симетричних точкам графіка
у = 2х відносної прямої у = х (рис. 9.2). Такий вигляд
матиме графік логарифмічної функції за будь-якої основи
а> 1. Причому крива тим щільніше прилягатиме до осі
х, чим більше а (рис. 9.3). Якщо основа 0 < а < 1, то гра-
фік матиме інший вигляд. На рис. 9.4 зображено графік
логарифмічної функції у = х. Таку загальну форму
матиме графік логарифмічної функції у = 1о§а х за будь-
якої основи а <_ 1, причому крива тим щільніше приляга-
тиме до осі х, чим менше а (рис. 9.5).
Властивості логарифмічної функції. Знаючи властивос-
ті взаємно обернених функцій, можна легко дістати власти-
вості логарифмічної функції з показникової. Характер гра-
фіка показникової функції з основою а залежить від того,
буде а > 1 чи 0 < а < 1. Тому і характер графіка лога-
рифмічної функції з основою а залежить від тих же умов
305
Отже, для функції у = Іо§я х треба розрізняти два випадки:
а > 1 і 0 < а < 1 (рис. 9.6). У кожному з них властивості
логарифмічної функції випливають з властивостей показ-
никової, якщо врахувати ще зв’язок між графіками показ-
никової й логарифмічної функцій. Отже, маємо такі власти-
вості логарифмічної функції:
область визначення логарифмічної функції — множина
всіх додатних чисел;
область значень логарифмічної функції — множина всіх
дійсних чисел;
логарифмічна функція на всій області визначення
зростає при а > 1 і спадає при 0 < а < 1;
при будь-якому а > 0 (а =# 1) виконуються рівності:
а) 1о§а 1=0; б) 1о& а = 1;
Таблиця 9,1
Властивість у = ах у = 1о& а*
Область визначення
Область значень
Монотонність
а > 1
0<а< 1
Я
(0; оо)
Зростає
Спадає
(0; оо)
П
Зростає
Спадає
в) 1о£я (ху) = 1о§а х + 1о§а у при х > 0, у > 0;
г) ІО£О -у = 1о§а х — 1о§а у при % > 0, у > 0;
д) для будь-яких X > 0 і р Е 7? 1о§а хр — р 1о§а х.
Для порівняння наведемо властивості показникової
і логарифмічної функцій у вигляді табл. 9.1.
Систематизуємо властивості логарифмів, які треба за-
пам’ятати, щоб впевнено використовувати їх при розв’язу-
ванні різних вправ і виконанні практичних розрахунків.
Спільні властивості для а> 1 і 0 < а < 1:
306
будь-яке додатне число має логарифм і до того тільки
один;
від’ємні числа і число 0 не мають логарифмів;
логарифм одиниці дорівнює нулю;
логарифм основи дорівнює одиниці.
Властивості логарифмів чисел за умови а > 1:
якщо Л/х > М2, то і 1о§а > 1о£а тобто більше
число має більший логарифм;
логарифми чисел, більших 1, додатні; логарифми чисел,
менших 1, від’ємні;
якщо число зростає необмежено, то і логарифм його
вростає необмежено;
якщо число, залишаючись додатним, прямує до нуля, то ло-
гарифм його стає від’ємним і як завгодно великим за модулем.
Властивості логарифмів чисел за основою 0 < а < 1:
якщо > М2, то 1о§а < 1о§а Л^2, тобто більше
число має менший логарифм;
логарифми чисел, більших 1, від’ємні; логарифми чисел,
менших 1, додатні;
якщо число зростає необмежено, то його логарифм спадає
необмежено (умовний запис: 1о§о оо = — оо,) якщо число,
залишаючись додатним, прямує до нуля, то логарифм його
необмежено зростає (умовний запис: 1о§с 0 = оо).
Приклад 1. Які значення аргументу х є допустимими для
функції у = І0£а (3 — х)?
Оскільки логарифмічна функція має дійсні значення
тільки при додатних значеннях аргументу, накладемо умо-
ву З — х > 0, звідки х < 3. Отже, допустимі значення ар-
гументу для даної функції визначаються нерівністю х < 3.
Розглядаючи наступні приклади, перевіряйте всі твер-
дження за графіками логарифмічних функцій.
Приклад 2. Який висновок можна зробити щодо додат-
них чисел т і л, якщо 1о§б т < 1о§5 л?
т < л, бо за основи, більшої 1 (а = 5), меншому ло-
гарифму відповідає менше число.
Приклад 3. Який висновок можна зробити щодо додат-
ного числа т, якщо 1о§4 т — —3,7.
т< 1, бо за основи, більшої 1 (а = 4), від’ємними е
логарифми чисел, менших 1.
Приклад 4. Який висновок можна зробити щодо додат-
них чисел т і л, якщо 1о§ 2 т > 1о§2 л?
5 б
(2 \
а = — І, меншому лога-
рифму відповідає більше число.
307
Приклад 5. Який висновок можна зробити щодо додат-
ного числа су якщо 1о§£ с = —2?
4
1, бо за основи, меншої 1 (а = логарифми чи-
сел, більших 1, від’ємні.
Приклад 6. Який висновок можна зробити щодо основи
логарифма а, якщо 1о£о 8 = 0,3.
Якщо число, більше 1, має додатний логарифм, то основа
логарифма більша 1. Отже, а> 1.
Приклад 7. Який висновок можна зробити щодо основи
логарифма а, якщо 1о£а 7 < 1о§а 6?
Якщо більшому числу відповідає менший логарифм, то
основа логарифма менша 1. Отже, а < 1.
Приклад 8. За властивостями логарифмічної функції
визначити, що більше:
а) 1о£23 чи 1о§2 5? б) 1о§ і 5 чи 1о§ і З?
в) 1о§58 чи 1о§68? г) 1о§_і_5 чи 1о£_і_ 5?
З 2
д) ІО£45 чи 1о§54? є) 1о§2 1 чи 1о§6 1? є) 1о§33 чи 1о§7 7?
Р о з в’ я з а н н я. а) 1о§25 > 1о§2 3, бо а > 1;
б) 1о§2_ 3 > 1о§ і 5, бо а < 1;
Т ~
в) 1о§6 8 < 1о§5 8, бо при х > 1 графік функції у —
= 1о§в х лежить нижче графіка функції у — 1о§Б 8;
г) 1о§_і_ 5 > 1о§ і 5, бо графік функції у = 1о£_і_ 5 менше
Т Т з
віддалений від осі х, ніж відповідний графік у = 1о§_і_ 5;
2
д) 1о§4 5 > 1о§6 4, бо при х > 1 всі точки графіка у —
= 1о§4 х віддалені від осі х більше, ніж точки графіка
у = 1о§а х\
е) 1о§2 1 = 1о§5 1 = 0, бо логарифм одиниці за будь-
якої основи дорівнює нулю;
є) 1о§3 3 = 1о§7 7 = 1, бо логарифм основи дорівнює 1.
Приклад 9. Знайти області визначення функцій:
а) у = 1о§2 (5 — х); б) у = 1о§8 (х2 + 1);
в) у = 1о§2_ (5х — х2 — 6); г) у = 1о§в .
2
Розв’язання. Оскільки вираз, що стоїть під зна-
ком логарифма, має бути додатним, то для становлення
областей визначення даних функцій досить знайти значення
х, при яких вирази, що стоять під знаком логарифма, додатні.
а) 5 — х > 0; х <_ 5, тобто областю визначення функції
у = 1о§2 (5 — х) є проміжок (—оо; 5).
308
б) х2 + 1 > 1. Нерівність справджується для будь-яких
дійсних значень х, тому областю визначення даної функції
є (—оо; оо).
в) 5х — х2 — 6 > 0, або (х — 2) (х — 3) < 0, звідки
2 < х < 3, тобто областю визначення є проміжок (2; 3).
-г) 3Д->0, або(3 + %)(% — 5)>0, звідки —оо<
<х < —3, 5 < х < оо. Отже, областю визначення даної
функції є проміжки (—оо; —3) і (5; оо).
§ 3. Розв'язування логарифмічних рівнянь
і нерівностей
Логарифмічні рівняння. Приклади розв'язування лога-
рифмічних рівнянь. Логарифмічними називають рівняння,
які містять змінну під знаком логарифма. Наприклад:
1о§5х = 2, 1§х4-1§5 = 2, 1§(3х2+7) —1§(3х —2)= 1.
Рівняння х + 1о§2 7 = V 1о§4 5 не є логарифмічним,
бо воно не містить невідомого під знаком логарифма. Най-
простіше логарифмічне рівняння має вигляд 1о§а х = Ь,
де я > 0 і а =/= 1, Ь — будь-яке число, додатне, від’ємне
або нуль. Воно має єдиний розв’язок х = аь, який можна
дістати за допомогою потенціювання.
Розглянемо логарифмічні рівняння виду
1о& / (X) = І0§а ф (X) (а > 0, а =£ 1). (1)
Розв’язування цих рівнянь грунтується на тому, що
рівняння 1о§а / (х) = 1о§0 ф (х) рівносильне системі
р(х)>0,
ф (х) > 0, (2)
1/(х) = ф(х).
Інакше кажучи, рівняння 1о§а / (х) = 1о§а ф (х) рів-
носильне кожній із змішаних систем:
|/(х) = ф(х), |/(х) = ф(х),
|/(х)> 0, |ф(х)>0.
Для розв’язання рівняння (1) досить розв’язати
няння
/(х) = ф(х)
і його розв’язки підставити у систему нерівностей
і/(х)>0,
ІФ (х) > 0,
яка задає область визначення рівняння.
рів-
(3)
(4)
309
Коренями рівняння (1) є ті розв’язки рівняння (3), які
задовольняють систему (4), тобто належать області визна-
чення рівняння, заданій формулою (1).
При розв’язуванні логарифмічних рівнянь може ста-
тися розширення області визначення (з’являться сторонні
корені) або її звуження (зникнуть корені). Тому треба обо-
в’язково підставити корені рівняння (3) у систему (4). На-
приклад, рівняння х2 = 2 має два корені, бо за означен-
ням логарифма х2 = 102, х2 = 100, звідки хх = 10, х2 =
= —10.
Якщо спочатку винести показник 2 за знак логарифма, то
21§х = 2, 1§х= 1, х= 10.
Втрата другого розв’язку х = —10 сталася внаслідок
звуження множини допустимих значень х після винесення
показника за знак логарифма. Справді, у рівнянні 1§ х2 =
= 2, корінь х може бути додатним і від’ємним числом, а
в рівнянні 21§ х = 2 — лише додатним.
Навпаки, якщо даним було б рівняння 21§ х = 2, а
від нього ми перейшли до рівняння 1§ х2 = 2, а потім до
рівняння х2 = 100, звідки хг = 10, х2 = —10, то дістали б
сторонній розв’язок (х2 = —10) для даного рівняння. Сто-
ронній розв’язок з’явився внаслідок розширення множини
допустимих значень змінної х, що сталося після внесення
множника 2 під знак логарифма.
Взагалі не існує якогось універсального способу розв’я-
зування логарифмічних рівнянь. Здебільшого воно зводить-
ся до розв’язання алгебраїчних рівнянь і найпростіших
логарифмічних рівнянь вигляду 1о£а х = Ь.
Приклади. Розв’язати рівняння:
1) 1о§і_ х = —3.
2
Р о з в’ я з а н н я. За означенням логарифма х =
= (4 Л * -8-
2) 51о§2 х — 31о§7 49 = 21о§2 х.
Розв’язання. б 1о§2 х — 21о§2 х = 3 • 2,31о§2 х =
= 6, 1о§2 х — 2, х = 4.
Перевірка. 5 1о§2 4 — 3 1о§7 49 = 10 — 6 =4,
21о§2 4 = 4. Отже, х = 4.
3) 1о§5 х + 1о§5 (х + 7) = 1о§5 2 + 2 1о§5 3.
Розв’язання. Пропотенціюємо обидві частини
рівняння х (х + 7) = 2 • З2. Звідси х2 + їх — 18 = 0,
Хї = —9, х2 = 2.
Перевірка. Підставимо у дане рівняння замість не-
відомого числа —9. У лівій частині дістанемо вирази
310
1о§5 (—9) і 1о§5 (—2), які не мають смислу (логарифми
від’ємних чисел не існують). Отже, значення х = —9 є
стороннім коренем.
Тепер перевіримо, чи є коренем даного рівняння число
2. Ліва частина рівняння має вигляд
1о§5 2 4- 1о§8 9 = 1о§6 2 4- 1о§8 3а = 1о§5 2 4-21о§5 3.
Ліва частина рівняння дорівнює правій. Отже, х = 2 —
корінь даного рівняння.
Зауважимо, що прийом потенціювання широко застосо-
вують при розв’язуванні логарифмічних рівнянь.
4) 1о§2 (х2 + 4х 4- 3) = 3.
Р о з в’ я з а н н я. х2 + 4х 4- 3 = 23, або х2 4* 4х —
— 5 = 0. Коренями цього рівняння є: хх = —5, х2 = 1.
Перевірка показує, що обидва розв’язки задовольняють да-
не рівняння. (Перевірку зробіть самостійно.)
.5) 1о§7 (х - 2) - 1о§7 (х 4- 2) - 1 4- 1о& (2х — 7) = 0.
Розв’язання. Перенесемо два останні доданки у
праву частину рівняння:
1о§7 (х — 2) — 1о§7 (х 4- 2) = 1 — 1о§7 (2х — 7).
Беручи до уваги, що 1 = 1о§7 7, маємо
1о§7 (х — 2) — 1о§7 (х 4- 2) = 1о§7 7 — 1о§7 (2х — 7).
Тепер пропотенціюємо обидві частини рівняння:
х — 2 _ 7
х 4- 2 2х — 7
Після перетворень дістанемо квадратне рівняння х2 —
— 9х = 0, яке має корені хг = 0, х2 = 9.
Перевірка, х = 0 — сторонній корінь, бо вираз
1о§7 (0 — 2) не має смислу.
Підставимо у рівняння значення х = 9. Ліва частина
має вигляд 1о§7 7 — 1о§7 11 — 14- 1о£? 11 = 1 — ІО& 11 —
- 1 4- 1о§7 11 =0.
Права частина дорівнює нулю. Отже, х = 9 — корінь
даного рівняння.
6) 1о& (х2 — 2х 4-2) = 1.
Р о з в’ я з а н н я. х2 — 2х 4- 2 = х, тобто Xа — 3x4-
4- 2 = 0; Хі = 1, х2 = 2. Перевірка показує, що х = 1 не
може бути коренем даного рівняння, а число 2 є його ко-
ренем.
7) 1о§і_2х (ха — Зх 4-5) = 2.
Розв’язання. За означенням логарифма діста-
немо квадратне рівняння (1 — 2х)а = Xа — Зх 4- 5. Його
і 4
корені хх = — 1, х2 = -у.
811
Дане рівняння задовольняє лише значення х = — 1
(перевірте це).
8) 1о§1 х — 1о§4 х — 2 = 0.
Розв’язання. Нехай 1о§4 х = у, тоді дістанемо
квадратне рівняння у2 — у — 2=0, корені якого уг = —1,
у2 — 2. Дістанемо два рівняння: 1о§4 х = —1, 1о§4 х = 2.
З першого рівняння за означенням логарифма знаходи-
мо х4 = 4~1, Хх = З другого рівняння маємо х2 = 4а,
х2 = 16.
За допомогою перевірки з’ясовуємо, що обидва знайдені
значення х є коренями даного рівняння. (Перевірку зробіть
самостійно.)
9) х = 2 - 5.
Розв’язання. Запишемо 2 через 1§ 100. Дістане-
мо х — 1§ 100 — 1§ 5 або 1§ х = 1§ 20, звідки х = 20.
Тут використано таку властивість логарифмів: якщо ло-
гарифми двох чисел за однією і тією самою основою рівні,
то й самі числа рівні. '
Перевірка. 2 — 1§ 5 = 1§ 100 — 1§ 5 = 1§ =
= 1§ 20; 1§ 20 = 12 20.
10) 12 х + 18 (х + 21) = 2.
Р о з в’ я з а н н я. 12 х + І2 (х + 21) = І2 100, х (х 4~
+ 21) = 100, х2 + 21х — 100 = 0, Хх = —25, х2 = 4.
Перевірка. При х = —25 у лівій частині даного
рівняння матимемо вирази І2 (—25) і І2 (—4), що не мають
смислу. Отже, Хх = —25 не є розв’язком даного рівняння.
При Хх = 4 маємо І2 4 4- 25 = І2 (4 • 25) = І2 100 = 2.
Отже, х = 4 є коренем даного рівняння.
11) 123 (х-+ 1) + 122 (х + 1) - 2 12 (х + 1) = 0.
Розв’язання. Нехай І2 (х 4- 1) = у, тоді у3 +
+ у2 — 2у — 0, або у (у2 + у — 2) = 0, звідки дістаємо
два рівняння: у = 0; у2 + у — 2 = 0.
Розв’язавши ці рівняння, знаходимо: уг — 0, у2 = 1,
Уз = —2. Тоді: 1) 12 (х + 1) = 0; 2) 1§ (х + 1) = 1;
3) І2 (х + 1) = —2 і відповідно: 1) х 4~ 1 = 1; 2) х + 1 =
= 10; 3) х 4- 1 = 0,01.
З рівнянь 1) — 3) легко знаходимо, що хх = 0, х2 = 9,
х3 = —0,99.
Перевірка показує, що всі три знайдені значення х є
коренями даного рівняння.
12) 12 (2х2 4- 21х 4- 9) — 12 (2х 4- 1) = 1.
Розв’язання. І2~2х = 18 Ю- 3 рівності
312
| 21х ! 9
логарифмів випливає рівність чисел ----— = Ю-
Звідси 2х2 + х — 1=0; хх = — 1, х2 = -|~.
Значення = —1 не задовольняє рівняння, бо під
знаком логарифма дістанемо від’ємне число.
13) Х1е *-1 = 100.
Р о з в’ я з а н н я. (І£ х — 1) І£ х = 2. Поклавши
1§ х = у, маємо у2 — у — 2 = 0. Звідси уг = —1; у2 = 2.
Тоді І£ хг = —1 і 1§ х2 = 2 і х2 = 100.
Обидва значення х задовольняють рівняння.
Ми розглянули лише кілька способів розв’язування ло-
гарифмічних рівнянь: використання означення логарифма,
зведення до квадратного рівняння, введення допоміжного
невідомого.
Проілюструємо ще застосування способу логарифмуван-
ня обох частин рівняння.
14) Хі-іех = 0,01.
Розв’язання. Прологарифмуємо обидві частини
рівняння:
(1 — 1§Х) 1§х = — 2.
Нехай х = у, тоді (1 — у) у = —2, або у2, — у —
— 2=0. Знайдемо корені цього рівняння: уг = —1, г/2 = 2.
Дістанемо два рівняння: 1§ х = —1, 1§х = 2. Остаточно
Хі = 0,1, х2 = 100. Обидва значення х є коренями даного
рівняння.
Зазначимо, що у прикладах-13, 14 невідоме входило до
показника степеня під знаком логарифма. Такі рівняння
іноді називають показниково-логарифмічними.
Найчастіше показниково-логарифмічні рівняння роз-
в’язують способом логарифмування обох частин рівняння.
До окремих видів рівнянь зручно застосувати спосіб
зведення до спільної основи.
Приклади. Розв’язати рівняння способом зведення до
спільної основи.
1) ХІ8Х = Ю.
Розв’ язання. Прологарифмуємо обидві частини
рівняння, дістанемо 1§ х х = 1§ 10, 1§2 х = 1, звідки
1§ Хі = 1, 1§ х2 = —1, або хх = 10, х2 = 0,1.
Перевірка. При хг = 10 маємо 10Іе 10 — 10, 10 =
= 10. При х2 = 0,1 маємо 0,1’є 0,1 = 0,1-і = 10. Отже,
10 = 10, Хі = 10, х2 = 0,1.
2) —-— = —
' 2і0®» х 64 ’
313
Розв’язання. Зведемо обидві частини рівняння
_________________________З
до спільної основи. Дістанемо 210®1* = 2“6.
Прирівнюючи показники степенів, маємо — — — 6,
або Іо§3 х -, звідки х — 3 2, х = , або х =
_ /з 3
“ 3 •
- 3 з
Перевірка. 2 = 2 -у = 2~6, 2-6 = 2“6.Отже,
кз
З •
2 !гх
3) х 2 = 100.
Розв’язання. Прологарифмувавши обидві части-
ни рівняння за основою 10, дістанемо
(2 - = 1§ 100,
або 1§2х— 41§ х + 4 — 0, (1§х— 2)2 = 0. Звідси 1§ х = 2,
х = 100.
X =
О 1е 100
Перевірка. 100 2 = 1002-1, 100= 100. Отже,
х = 100.
4) 0,41е**+1 = 6,252-1е*’.
Розв’язання. Зведемо обидві частини рівняння
до спільної основи Дістанемо
або /АГМ-+"-таі!-3,вя.
Прирівнюючи показники степенів, дістанемо
— (1§2х+ 1) = 2(2 — 31§х), або 1§2х— 61§х + 5 = 0.
Розв’яжемо квадратне рівняння відносно 1§ х. Маємо
1§ Хі = 1, або Хі — 10; х2 = 5, або х2 = 100 000.
Перевірка показує, що обидва значення х є коренями
даного рівняння.
5) 1о§21о§31о§4 х = 0.
Розв’язання. Запишемо дане рівняння у вигляді
1о& (1о§3 х) = 0.
314
Число, що стоїть у дужках, за означенням логарифма дорів-
нює 2°, тобто 1. Отже, 1о§3 1о§4 х = 1.
Це рівняння перепишемо так: 1о§3 (1о§4) = 1. Число,
що стоїть у дужках, за означенням логарифма дорівнює 3.
Тоді 1о§4 х — 3, звідки х = 43, або х = 64.
Перевірка. 1о§21о§31о§4 64 = 1о§21о§3 3 = 1о§21 =*-
= 0, 0 = 0.
6) ІО§1# х + 1о§4 X + 1о§2 х = 7.
Розв'язання. Скористаємося формулою 1о§вх =
= і перейдемо в усіх доданках до логарифма за
ОСНОВОЮ 2;
Початкове рівняння набуває вигляду
4- 1о§2 Х + 4" І0& Х + І0§2% = 7’
звідки 1о§2 х = 4. Остаточно маємо х = 16.
Деякі логарифмічні рівняння вдається розв’язувати ли-
ше наближено. Одним із способів наближеного знаходжен-
ня коренів є графічний.
На рис. 9.7, 9.8 подано графічне розв’язання відповідно
рівнянь
1§х—1о§2_х+ 1 = 0 і 1§(х + 1) —1о§2х = 0.
2
Розв’язування систем логарифмічних рівнянь. При роз-
в’язуванні систем логарифмічних рівнянь в основному вико-
ристовують ті самі способи, що й при розв’язанні алгебраїч-
них систем.
Приклади. Розв’язати системи рівнянь:
1)
= 5,
—1§г/ = 3.
315
Р о з в’ я з а н н я. 2 х = 8, їй х = 4, х = 10 000,
1§У = 1. У = Ю-
2) (Xі + у2) = 2,
(1о§2 X — 4 = 1о§2 З — 1о§2 у.
Розв’ язання. Перше рівняння системи рівно-
сильне рівнянню х2 + у2 = 100, а друге — рівнянню
х З
, причому х > 0 і у > 0. Маємо систему
х24-у2= 100,
ху — 48.
Розв’язавши її з урахуванням умови х > 0, у > 0,
дістанемо два розв’язки: х = 8, у — 6; х = 6, у = 8.
'1о8. ^±^2,
-|-1о8.х 108.(1 + і/)а = -^.
Розв’ язання. Використовуючи властивості ло-
гарифма, перетворимо рівняння системи:
21о§2 х + -у 1о§2 (*/ + 1) — 1 = 2»
і 1о§2 х • 21о§2 (у 4- 1) = -і-,
41о§2 х + 1о£2 (у + 1) = 6,
1о§2 х • 1о§2 (у + 1) = 2.
Зробивши заміну 1о§2 х = «, 1о§2 (у + 1) = а, дістане-
мо систему
г4и 4- V = 6,
звідки
1о§2х=1, 1о§2х = —,
(у + 1) = 2; 1о§2 (у + 1) = 4.
Отже, дістали два розв’язки: х = 2, у = З і х = 1^2,
У = 15.
Логарифмічні нерівності. При розв’язуванні логариф-
мічних нерівностей виду
ІО£Й/(Х) $ І0§а ф (X)
насамперед враховують, що областю визначення логариф-
мічної функції є множина додатних чисел, тобто вирази,
які стоять під знаком логарифма, вважаються додатними.
При а > 1 логарифмічна функція зростає, тому біль-
шому логарифму відповідає і більше значення виразу, що
стоїть під знаком логарифма.
При а < 1 більшому логарифму відповідає менше зна-
чення виразу, що стоїть, під знаком логарифма.
При а> 1 нерівність (1) рівносильна системі нерівнос-
тей
/(•*) ф(х),
[Ф (х) > 0,
а при 0 < а < 1 — відповідно системі нерівностей
;/(х) $ ф(х),
Ф (х) > 0.
Приклади. Розв’язати логарифмічні нерівності:
1) 1о§2 х < 3; Маємо 0 < х •< 23, 0 < х < 8.
2) 1о£3 х > 4. Маємо х > З4, х > 81.
3) 1о§ і х<3. Маємо х>(-|-] > х>~їв~-
4) 1о§о,2 х > 5, 0 < х < 0,2е, х < 0,00032.
5) 1о§о,5 (2х + 3) > 0. 0 < 2х + 3 < 1, звідки —1,5 <
< х < — 1.
6) 2 — 1о§2 (х2 + Зх) > 0. 1о§2 (х2 + Зх) <2, х2 4-
+ Зх < 4, звідки х2 + Зх > 0 і х2 4- Зх < 4. Отже,
—4 < х < —3; 0 < х < 1.
7) (2х2 + 4х - 5) < (4 + х).
Розв’язання. Враховуємо, що а = 10 > 1. Маємо
|2х2 + 4х — 5 < 4 4- х, (2х2 4- Зх — 9 < 0,
(4 4- х > 0, |х > — 4,
2х2 4- Зх — 9=0, Хл = — 3, х2 = 1,5.
Отже, —3 < х < 1,5.
8) 1о§5 х 4- 1о§5 (х 4- 1) < ’о§5 (2х 4- 6).
Розв’язання. Вирази, що стоять під знаком ло-
гарифма у даній нерівності мають бути додатними. Отже,
справджуються нерівності:
х > 0; х 4- 1 > 0; 2х 4~ 6 > 0.
Запишемо дану нерівність у вигляді
1о§6 X (х 4- 1) < 1о§5 (2х 4- 6).
317
Тут основа а = 5 > 1, тому х (х 4- 1) < 2х + 6. Розв’я-
зання даної нерівності зводиться до розв’язання системи
чотирьох нерівностей:
х + 1 > 0,
2х + 6 > 0,
або
х(х-Ь 1)<2х4- б,
х> 0,
х> — 1,
х > — З,
Xі ~ х — 6<0,
'х>0,
х>— 1,
х > — З,
— 2<х<3.
Знаходимо значення х, при яких справджуються ці нерів-
ності.
Відповідь. 0 < х < 3.
9) 1о§ і (х2 — 8х + 12) > — 1.
Вираз, що стоїть під знаком логарифма, має бути додатним.
Тому х2 — 8х 4- 12 > 0. Запишемо дану нерівність у ви-
гляді
1о§ і (х2 — 8х + 12) > 1о§_і_
12 12
12.
І
Оскільки а = < 1, то х2 — 8х + 12 < 12. Залиша-
ється розв’язати систему двох нерівностей:
'х2 — 8х+ 12> 0,
х2— 8x4- 12 < 12,
— оо<х<2, 6<х<оо,
0<х<8.
Отже, 0 < х < 2 і 6 < х < 8.
10) 1о§| х 4* 3 1о§3 х 4- 2 < 0.
Розв’язання. Областю допустимих значень змін-
ної є х > 0. Позначивши у = 1о§8 х, дістанемо у2 4- Зу 4*
4- 2 < 0. Звідси —2 < у < — 1, або —2 < 1о§3 х < —1.
Отже, < х <
Історична довідка
Винайдення логарифмів значною мірою прискорено потребами удо-
сконалення обчислень. Винайшли логарифми і майже одночасно поча-
ли їх застосовувати шотландський математик Джоь. Непер і швейцар-
ський математик, астроном і механік Йост Бюргі (1552—1632). Проте
перший крок до спрощення обчислень за допомогою логарифмів зробив
німецький математик Михаель Штіфель (1487—1567), у якого поняття
логарифма з’явилося в результаті зіставлення геометричної і арифме-
тичної прогресій. Ця ідея бере свій початок у працях Архімеда (бл. 287—
212 р. до н. е.).
Розглянемо цю ідею на такому прикладі. Складемо таблицю. У верх-
ньому рядку маємо арифметичну прогресію з різницею 1, а в нижньо-
му — геометричну прогресію із знаменником 2* Зіставивши числа у від-
318
повідних колонках, помічаємо, що в першому рядку ми маємо логариф-
ми чисел другого рядка за основою 2. Наприклад, 1о§2 512 = 9 (бо 29 =
= 512), 1о£2 8192 = 13 (бо 213 = 8192) і т. д.
Користуючись даними таблиці і теоремою про те, що логарифм до-
бутку дорівнює сумі логарифмів співмножників, можна значно спрос-
тити знаходження добутків чисел, записаних у нижньому рядку таб-
лиці.
Нехай треба помножити 64 на 512. Знайдемо логарифм цього до-
бутку за основою 2. Маємо 1о£2 (64 - 512) = 1о§2 64 + 1о§2 512. З табли-
ці знаходимо 1о§2 64 = 6, 1о§2 512 = 9. Отже, 1о£2 (64 • 512) = 6 +
+ 9 = 15. Але числу 15 з першого рядка відповідає число 32 768 з дру-
гого. Отже, 64 • 512 = 32 768.
За теоремою про логарифм частки (дробу) аналогічно можна ско-
ристатися табл. 9 при діленні чисел.
Таблиця 9,2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
2 4 8 16 32 64 128 256 512 1024 2048 4096 8192 16 384 32 768
Наприклад, треба поділити 8192 на 128. Знайдемо логарифм цієї
частки за основою 2. Маємо
8192
1о§2 |28 = 8192 — 1о& 128 = 13 7 = 6.
Але числу 6 з першого рядка у другому рядку відповідає число 64. От-
же, 8192 : 128 = 64.
Можна скористатися таблицею і для піднесення чисел до степеня.
Наприклад, обчислимо 4б. Маємо 1о§2 4б = 5 1о§2 4 — 5 • 2 = 10.
Числу 10 з першого рядка таблиці відповідає число 1024 другого рядка.
Отже, 4Ь = 1024.
Як бачимо, дії другого ступеня (множення, ділення) звелися до дій
першого ступеня (додавання, віднімання) над відповідними логариф-
мами. При цьому доводиться виконувати дії з числами, значно мен-
шими.
Для практичного здійснення ідеї Штіфеля треба було скласти ге-
ометричну прогресію, яка б зростала дуже повільно, бо лише при цьому
вона може охоплювати значну кількість чисел. Бюргі взяв за знаменник
прогресії число 1,0001 замість 2 (як було у Штіфеля).
Пізніше основою таблиць почали називати той член, якому в ариф-
метичній прогресії відповідає число 1. У Бюргі основою був 10001-й
член геометричної прогресії, тобто 1,000110000, або (1 + 10“4)104 «
« 2,71814593 (в арифметичній прогресії йому відповідало число
0,0001 • 104).
Бюргі прийшов до логарифмів раніше, ніж Непер, але опублікував
свої таблиці лише у 1620 р. Таким чином, першою в 1614 р. з’явилася
праця Непера «Описання дивовижної таблиці логарифмів». Основою
таблиці логарифмів Непера є ірраціональне число, до якого необме-
(1 \п
1 + — і при необмеженому зростан-
ні п, Це число називають неперовим числом і з часів Ейлера позна-
319
чають так:
/ 1 \п
е= Ііт 1+— .
П-*оо \ * /
Непер склав таблиці, взявши дуже зручне наближення числа е, а саме:
/ 1 \Ю’
І 1 Н—[о?” І • Неперу належить і сам термін «логарифм».
Таблиці Непера вдосконалив англійський математик Генрі Брігс
(1561—1630). За згодою із самим Непером він спростив його систему
логарифмів і склав у десятковій системі числення таблицю логариф-
мів усіх цілих чисел від 1 до 20 000 і від 90 000 до 100 000 з 14 десят-
ковими знаками. Таблиці Брігса, опубліковані в 1624 р. і доповнені
А. Влакком у 1628 р., пізніше називали таблицями звичайних лога-
рифмів.
В Росії перші таблиці логарифмів було видано в 1703 р. за участю
російського математика і педагога Л. П. Магницького (1669—1739) —
«Таблиці логарифмів, синусів, тангенсів і секансів».
У зв’язку з появою сучасних ЕОМ обчислення за допомогою ло-
гарифмів втратили своє колишнє значення.
Запитання і завдання для повторення
1. Що називається логарифмом числа за даною основою?
2. За означенням логарифма вказати, яке з трьох тверджень спра-
ведливе: 1) логарифм — степінь; 2) логарифм — показник степеня;
3) логарифм — основа степеня?
2
3. Дано рівність 273 = 9, Що тут є логарифмом, якого числа і за
якою основою?
4. Довести, що 1о£а а = 1.
5. Подати в показниковій формі логарифмічні рівності:
1) 1о§6 = -3; 2) 1оЄ± 81 = —4.
З
р
6. Знаючи 1о&а Р = р і 1о£а (2 = д, знайти 1о§а -ур
х
7. Знаючи 1о§д N = 11, знайти 1о£а (№).
і
8, Знайти 1о£а (М 4 ), якщо 1о£д N = 4,28.
9. Знаючи 1о§а С = с, знайти 1о&о С,
10. Чи правильно, що 1о§а = —1о£а &?
11. Довести, що 1о£а 2 + 1о&а 0,5 = 0.
12. Чи правильно, що \о&а аЬ = 1 + 1о&а Ьї
2
13. Яку дію треба виконати, щоб з рівності 1о£ х = -х- 1о§ а дістати
о
рівність х =
14. Назвати дію, обернену до потенціювання.
15. Як дістати функцію, обернену до даної?
16. Яке перетворення системи координат приводить до зміни осей?
17. Вказати особливості розміщення графіків двох взаємно обер-
нених функцій.
320
18. Якщо графіки двох функцій симетричні один до одного віднос-
но бісектриси 1 і III координатних кутів, то чи означає це, що функції
взаємно обернені?
19. Як називається функція, обернена до показникової?
20. Обернення якої показникової функції приводить до логариф-
мічної функції у = ІО£3 X?
21. Дано експоненту-графік показникової функції у — ах. Як побу-
дувати графік оберненої їй логарифмічної функції у = 1о£а х?
22. Чому функція у = 1о£а х (при а > 1) існує лише в області до-
датних чисел?
23. Чому дорівнює 1о&з (—27)?
24. Чи може логарифм додатного числа при основі а > 1 бути від’-
ємним?
25. Вказати будь-яке число, логарифм якого при основі а = 9 біль-
ше 1о&9 15.
26. Які рівняння називають логарифмічними?
27. Якщо внаслідок виконуваних перетворень рівняння множина
допустимих значень невідомого звузилася, то що сталося з коренями
рівняння?
28. Яка причина появи сторонніх коренів при розв’язуванні ло-
гарифмічних рівнянь?
29. Які способи розв’язування логарифмічних рівнянь вам відомі?
ЗО. У чому полягає прийом потенціювання при розв’язуванні ло-
гарифмічних рівнянь?
31. Які рівняння називають показниково-логарифмічними?
32. Які способи використовують при розв’язуванні систем логариф-
мічних рівнянь?
33. Які властивості логарифмічної функції використовують при
розв’язуванні логарифмічних нерівностей виду
1О£а ЇМ £ І0£а ф (X)?
34. Якій системі нерівностей рівносильна нерівністьЛо&а / (х)
1о£о ф (х) при: 1) а > 1, 2) 0 < а< 1?
Вправи
А
1. Перевірити правильність рівностей: 1) 1о&4 16 = 2; 2) 1о&5 125 =
= 3; 3)1о§42 = 4-; 4) 1о£2-^- = -6; 5) І£ 1 = 0; 6) 1^100 = 2.
2. Використовуючи знак логарифма, виразити показник степеня з
рівностей: 1) З4 = 81; 2) 4"-2 = Д-; 3) 8~ = 2; 4) 3/27 = 3.
16
3. 'Знайти логарифми чисел: 1) 8; 2) -у-; 3) Г, 4) 0,5; 5) 512;
6) ~[2з" 83 основою 2.
4. Знайти: 1) 1о§3; 2) 1о& 64; 3) 1о& ; 4) 1о§^--8.
5. Знайти число х, якщо: 1) 1о§5 % = 2; 2) 1о£бх = 3; 3) 1о§ 1 х =
*= — 1; 4) 1о£13 х = 0; 5) 1о&4 х = 1,5; 6) І£ х = — 3.
6. Чи мають смисл вирази: 1) Іо&4 (— 64); 2) 1о£в 0; 3) 1о§2 (—- 4)6 * 8.
11 1-1819 ' 321
Б
/ О \~2
7. Записати у логарифмічному вигляді рівності: 1) — І
\ о /
-- 1 з
= 2,25; 2) 0,12 = 0,01; 3) 8 3 =-3-; 4) у343 = 7.
6) 7)у=-; 8)
9. Знайти х,
/- з
3) 1о&]/8 = —;
8. Знайти логарифми чисел: 1) 3, 2) _2_, 3) 81, 4) 1, 5) —1—,
леї
за основою 3.
2 1
якщо: 1) 1о§з^--х = — —; 2) 10^-^- = 4;
4) І0§ ! х = — 1.
10. Чи мають смисл вирази: 1) 1о§6 (—б)2; 2) —1о&8 16?
11. Обчислити: 1) 5 1о£б 25 — 4 1о£4 16; 2) 1о§2 1о&2 16,
12. Знаючи, що а2 = знайти 1о£а Ь.
В
13. Знайти логарифми чисел>1) 1о£0>225; 2) 1о£б0,04: 3) 1о§24рл2;
4) ІО£215 0,16; 5) 1о§а а-, 6) 1о£а 1; 7) 1о£а/а; 8) Іо§ауга?.
14. Знайти основи логарифмів: 1) 1о£х 3 = 0,25; 2) 1о&х 125 =«
= 3) 108x0,64=------2; 4) 1о&К2= 1 ї 5) 1о& (а2 + 2а +
2 4
+ 1) = 2; 6) 1о& * --------
У о
15. Знайти х з рівностей: 1) 1о£3х = — 1; 2) 1о^4 х = 2,5»
3) 1о&бх = 0; 4) 1о&49х = — 1,5; 5) 1о& і х = 3; 6) 1о& і х = — З,
16. Обчислити: 1) 1о£2(зіп-2-| ; 2) ІдЩ-^З.
\ 6 / \ 4 /
17. Розв’язати рівняння: 1) 1о£2х = 3; 2) 1о£07х = — 1;
3) 1о84х = -±; 4) 1о&(3-х) = 0; 5) 1оЄо>4 (6 — 7х) = Ц
6) 1о§2_ (5х —7) = — 3.
2
Знайти значення виразів:
А
18. 1) 210*810; 2) 51ог®16 7; 3) 1,3і0*1’3* ; 4) 1 + 710*7 2; 5) 4*“ІО*<7»
6)431в8‘2.
Б
19. 1) 1,71огі-75; 2) Я1ОЄя7Л; 3) б108*10"1; 4) 23108*4;
5) 2,41о82,4і°+1; 6) ю“18 19 °’8,
322
в
20. 1) 10ій 0і3; 2) Ю21®3; 3) Ю18 3—18 2; 4) 81 °*8,°8»7,
21. Порівняти за величиною: 1) З1’8*4 і б1®8' 4; 2) 41®8’7 і 71®8’ *і
8) З108’6 і 5ІО8’3.
22. Обчислити: 1) 210®’ 5+І°й* 2) 4 • б1"*08»2Б.
23. Довести тотожність т т »п п ,
Прологарифмувати вирази:
А
24. 1)!/«=-^-; 2) з.= _^_53)^ааИн)л=^§
Б
— 4 — 3/“Т"9
25. 1) х = а2УЬс—, 2) 2 /о2 ; в) х = 1о§ 0,6і;
З у (а-|-б)» УЬ
4) г = . ^1?.
В
26. 1) х = За><а8(а + *)’ 2) х = |/”]/ А 5
, ( а10 \~°’2
3) х == (-/а5!»)2; 4) х = І бг- 1 ; 5) х — 1о§3 V 16§, 3;
----------------- \ У а* /
а\ґ ьУ а \П>
о) х =-----------__ — .
Ь У а У Ь Уа
Знайти значення виразів:
А
27. 1) 1о§і2 5 + 1о§12 4; 2) 1о§5 15 — 1о& 3.
Б
_ 1^64-1^4
1648-їй 12 9
В
16 8 4-ІР 18
29. 1) іойо.з 9 2 1обо,з Ю» 2 їй 2 І£ 3 •
ЗО. Що більше: 1ой0ї6 13 + 1ойор6 12 чи 1ой0<6 (1,3 + 1,2) ?
Пропотенціювати вирази:
А
31. 1) Іой х = Іой 7 + 3 іой а — іой 5; 2) іойз У = 1о£з 1,5 + 1о£з 8;
3) іой у = "2“ 1°§ (а + д) — 2 іой а — 3
и 4) іой г = іой 2 — іой 3 + іой (а + Ь) — іой а.
11*
323
Б
12 2
32. 1) 1о$х у10£ (а — Ь) — у І0£ (а + Ь) — у 1о§а;
2) 1о& у □= 1о§ 2 + іо£ а + 3 1о£ Ь — 1о$ 3 — у 1о£ (Ь — а).
В
33. 1) 1о§ х = у Іоб (а3 * * * * + &*) + -у 1о§ (а + Ь) — 1о§ (а — &);
1 1 / 2 2
2) 1о£х = — у І0£а + — ІІ0£д — уІ0£а + уІ0£(а — 6) —
— у1о£(а + &).
34. Знайти х, якщо: 1) 1о£0>3 х = 2 1о£0,3 6 — 2 1о£0>3 12;
2) 1о£л х = 3 1о§л 4 — 2 1о$я 6.
35. Обчислити, не користуючись допоміжними засобами:
58
1) 1о§у-- 2 + 1о£б 6,25; 2) 1о§у- 25 — 1о§8 7 у- .
36. Обчислити значення: 1) е2; 2) -1—; 3) Уе; 4) е8; 5) Іпе3;
е
6) 1п20; 7) ІпЗ; 8) 1п7,5; 9) 1п 1,21.
А
37. Який висновок можна зробити щодо додатних чисел іп і п,
якщо: 1) 1о£б/п < 1о£б п; 2) 1о& 1 т>1о§1 п;
3) ІО£011 т < 1о§01 п?
38. Який висновок можна зробити щодо числа т > 0, якщо:
5 2
1) 1о§2 /и = — 0,32; 2) 1о§ ! т = у; 3) 1о£ ! т =— 3-у?
39. Який висновок можна зробити щодо основи логарифма а, якщо.
1) 1о£а 7 = 0,4; 2) 1о§а5 = —3) 1о§о4< 1о§а2}
2 2
4) 1о§а —> І0&-3-?
Б
40. За властивостями логарифмічної функції визначити, що більше:
1) 1о&2 5 чи 1о&2 8; 2) 1о£ і 6 чи 1о& і 8;
3) 1о&7 8 чи 1о£5 8; 4) 1о§ ! 11 чи 1о& і 11?
~ V
41. При яких значеннях х справедливі такі рівності:
1) 1И(а:2 + 5х-14) = 1§(х+7) + 1§(х-2);
2) 1£ (х2 — Юх + 25) = 2і£ (5 — х)?
42. Визначити знак добутку 1о§3 0,97 • 1о£2 0,98 • 1о§2 6,99,
324
в
4
48. Довести, що 1о£3 0,71 • 1о£3 ур • 0,95 < 0.
44. Яким співвідношенням пов’язані числа М і IV, якщо відомо,
ЩОІ£ М « 1,4153, а 1р N = 3,4153?
Знайти області визначення функцій:
А
45. 1) у = 1о& (2 + х); 2) у = 1о£3 (3 + х2);
3) У = 1о£4 (х2 + 1); 4) у = 1о£2 —х --.
Б
46. 1) 1о£0>1 (х2 — 4); 2) І02у-(6+х — х2); 3) 1о§8-^ру-;
2 + Зх
4) 1о£о,9 = 5 —2х *
В
47. 1) у = 1о& (Зх2-їх- 40); 2) у = (х2 - 2х- 3);
3) У = 1о§, ; 4) у = І023і1 Ч— Зх" : 5) у = Іо§21х І;
6) У = 1о§0,5|х|.
48. Для функцій, розглядуваних у зазначених проміжках:
1) У = ІО£3 (х — 1) при -д- < х < 10;
2) у = 1о£05-(х + 1) при — 0,75 < х < 7;
3) у = 1о£4 (х — 2) при 0,25 х 64;
4) у == 3 — 1о£б х при 0 < х < 625 — дати відповідь на запитан-
ня: 1) при яких значеннях х у < 0, у = 0, у > 0? 2) від якого наймен-
шого (найбільшого) і до якого найбільшого (найменшого) значення змі-
нюється у?
Зобразити схематично графіки функцій:
А
49. 1) у = 1о£а х; 2) у = 1о£ ! х<
Б
50. 1) у = ІО£3 х; 2) у == 1о£^ х; 3) у = 1о£0>3 х; 4) у = 1о£^— х.
В
51. 1) г/= їй х; 2) г/= 1п-у—; 3) г/== 1п (— х); 4)# = 1п/х|.
Розв’язати рівняння:
А
52. 1) 1О£2 (5-х) = 0; 2) 1о£(5х-7) = -3;
2
8) 1о§0і3(5 + 2х) = 1; 4) (х-1) = І£ (5х - 3);
325
5) 1о& (ха - х + 1) = 0; 6) 1ое^.і (ха - 5х + 10) = 2}
7) І08а х = 1оев 3 + І0Єд 5; 8) Іо^ х — 3 1о§, х;
9) 1б2х —51йх+6 = 0; 10) 1о§| х — ІО&, х — 2 = 0;
ІЄх+7
11) х‘« Х= 10000; 12) х 4 =х101+І8х;
13) 1§ 1§ 12 х = 0; 14) х18 *+2 = 1000.’
Б
63. 1) ІО8 । (2х — 4) = — 2; 2) = 2;
Т
3) І08а (х 3) = 3 — х; 4) І08х 3 — ІО2х 2 = % і
5) І02а X = І0£а 12 — 2 І08а 2;
6) і£(х + 6)-4-1§(2*-3) = 2-1825і
7) 12* х — 1012а х + 9 = 0; 8) V х18^* = 10;
9) ІО2Я (х2 4- 2х + 3) = 1о8п 6;
10) 2 1о2в (2 + х) + І02в (9 — 6х + ха) = 2;
11) — 9) 4-18/2x^1 =2;
12) 1о§3 4 4- 1о8з х = 1о8з (х — 6) — ІО23 (3 — х);
13) х18 х~3 = 0,01; 14) З2-*08’ х = 81х;
іех+7
15) х 4 =ЮІЙ*+1; 16) 100і®<х+20) = ЮООО.
В
64. 1) 1о2з (ха —Зх —5) = 1о8з (7 — 2х);
2) 12 (х* + 75) = 2 4- 18 (х — 4);
3) 18х —6 + 18x4-2 1:
4) 1о8з (х 4-1) 4- 0,5 1о82 (ха - 18х 4-16) = 1 4- 1о82 3;
ага.+18/7^=ііе(2.+1)!
7) ІО8І х 4- 1о80_2 х = 2; 8) 1о^ х — 91о8в х = 4;
9) Іоба х 4- 1о§* 2 = 5; 10) 1о^ (х 4- 1) — 1о8_]_ (х 1) = 5;
11) 81 1°8 — 1 = 0; 12) 518 * — з’г = З18 *+‘ — 5*8 *_'1}
Івдя 2(18 X)’-1-18* г__
13) х^=аах(а>0, а=^=1); 14) х 2 =/10.
Розв’язати системи рівнянь:
326
55. а) { ’ ’ 6П
'ІІ8х+І00 = 3; ’ 110x4-100=1}
/3* 4- Зд = 12, . П°& 729 = х 4- у,
’ ІІО& 27 = х + у; } ІЗ*-»-1 = 1.
Б
,а \ /1б + У*> = 2’ м Р°8« * 4- 1084 0 = 1 4- 1084 9,
бо. а) < о) (
ІІОЄ48 х 4-10848 0=1; І* 4- У — 20 = 0;
1о8_і_ х 4- 1°8_і_ 0 = 2,
, з з
в) , . .
ІО8 ! х— 108 10=4.
Т Т
В
рО8( (х4-0) = 2,
57. а) | —
11°8» (* — 0)
(у — ІО83*= 1>
} їх» = Зіа;
. (Іо09х4-1о8х0 = 25,
Д) 1 0-7
[ху — 27;
11оЧ-18(*+0) = бо,
2; Ч18(* — 0) 4-І8(*4-0) =2 — 105;
'ІО8Р* 4-108*0 = 2,
х2 — у = 20;
і
е)
к- , —1_____2
180-1 + 180 4-1 “
X
Розв’язати нерівності:
18»у-2* = 5.
А
58. 1) 1о88 х < 4; 2) 1о08 х> 2; 3) Іое і * < 3; 4) 1о0оз х > 3;
Т
5) І0 х < 10 3; 6) І0 х > -у-; 7) 10 х > 10 5; 8) 10 х > — 3;
9) 100. (ха — х — 4) < 3; 10) 1о03 (12 — 2х — х2) > 2;
11) 10x4-18 (*-3) < 1; 12) 10 (2x4-3) <18 (х - 1),
Б
59. 1) 108* 0,2 > 1о0х 3; 2) 2 І0х>10 (4x4- 21);
3) 1002 82п—і > Зп 4- 6; 4) 108о 5 162я“3 > х — 24;
5) І08в (5х — 8) < І08, (2х 4- 7); ’ 6) 1о80,з (*2 4- 1) < 1о80,з 2*;
7) 1о8зх+2 * < 1 ? 8) 1°8х-.і (5х 4- 3) > 1; 9) ІО0І х — 1о02 х 6;
10) 10ах4-210х>3; 11) 2100а (*—1) —І08а (2х—4) > 1;
12) 1о84 1°8а ІО08 х < 0,5.
В
60. 1) ІО02 0,25*,“'3 >1 — х2; 2) 1о0з х < 3 — ІО08 (12 — х);
3) 1о0 ! х < 100 ! (4 — х) — 1; 4) 1о02 (х2 — 9х 4- 8) < 3;
5) 1002 х > 1о04 (х — 1); 6) 1о0х,+4 (2ха — 5) < 1;
327
7) 12 (х2 - х + 8) > 1; 8) 1о8я (X + 1) + 1о8я х < 1о8я 2}
9) 1о§о,5 ~ 1; 10) 102-’ 1оЧб 1о8_і_ х >
11) 1о& (х + 2) > 2; 12) 1о8ж+1 (х + 3) > 1.
РОЗДІЛ 10
ПОХІДНА І ПЕРВІСНА ПОКАЗНИКОВОЇ
ТА ЛОГАРИФМІЧНОЇ ФУНКЦІЙ
§ 1. Похідна показникової функції
Вивчаючи показникову функцію, ми переконалися в
тому, що графіки показникових функцій мають вигляд
гладких кривих (без зломів), до яких у кожній точці можна
провести дотичну. Відомо також, що існування дотичної
до графіка функції в точці рівносильне її диференційов-
ності у цій точці. У вищій математиці доведено, що по-
казникова функція диференційовна у кожній точці, і по-
хідну показникової функції за основою е обчислюють дуже
просто, а саме:
= (і)
Нагадаємо, що 1п — натуральний логарифм, який об-
числюють за формулою
1п х = 1о§е х. (2)
В силу основної логарифмічної тотожності для будь-якого
додатного числа а виконується рівність
а = еіпа. (3)
Тому будь-яку показникову функцію можна записати
у вигляді
ах = ехіпа. (4)
Для цього треба піднести до степеня х обидві частини рів-
ності (3).
За допомогою формули (4) і застосовуючи правило об-
числення похідної складеної функції, дістанемо формулу
для похідної будь-якої показникової функції для будь-яко-
го показника х.
(ах)' = (ех 1п а)' = еХІпа (х 1п аУ = ах 1п а.
Отже, (а*)' — ах 1п а.
328
Приклади. Знайти похідні функцій:
а) у = еіх, у' = (е5*)' = е5х (5х)' = 5е5х;
б) у = ех\ у' = (/’)' = ех* (х8)' = Зх2е*’;
в) у = ех'+\ у' = (ехЧгУ = ех'+1 (х2 + 1)' = 2хе*’+1;
г) у = Зх, / = (Зх)' = Зх1пЗ;
д) у = 58іп х, у' = (58,п х)' = 58іп х 1п 5 (зіп х)' = 58іп х х
X Іпбсозх;
е) у = 73х’+х+1, у' = (73х2+^+1)' = 7*’+*+1 іп 7 (ЗдЛ 4- х +
4- 1)' == 7х2+х+' 1п7 (6х+ 1).
§ 2. Похідна логарифмічної функції
Розглянемо функцію у = 1п х і знайдемо її похідну.
Доведемо, що при будь-якому х > 0 виконується рівність
1п'х = -|-- 0)
За основною логарифмічною тотожністю х = е1пх при
всіх додатних х у цій рівності зліва і справа стоїть одна і та
сама функція (визначена на множині 7?^). Тому похідні
х і 1п х рівні, тобто
х' = (е1пх)'- (2)
Для знаходження похідної правої частини рівності ско-
ристаємося правилом знаходження похідної складеної
функції і тим, що показникова функція ех диференційовна
у кожній точці і (ех)' = ех.
Переконаємося, що логарифмічна функція диференці-
йовна у кожній точці. Справді, графіки функцій у =
= 1о§а х і у = ах симетричні відносно прямої у = х.
Оскільки показникова функція диференційовна у будь-
якій точці, а її похідна не перетворюється в нуль, то гра-
фік показникової функції має негоризонтальну дотичну
в кожній точці. Тому і графік логарифмічної функції
має невертикальну дотичну у будь-якій точці. Але це рів-
носильно диференційовності логарифмічної функції на
області її визначення.
Отже,
(ЄІп7 = е1пЧп'х=х1п'х.
329
х Взявши до уваги, що х' — 1 і підставивши знайдений
результат у рівність (2), дістанемо 1 = х 1п' х, звідки
Іп' х = —.
х
Розглянемо функцію у = 1о§а х і доведемо, що у' =
= 1 . 1
1п а х *
Справді, оскільки 1о£а х = то
(1о& хУ = (Іп хУ = . 4.
Отже,
Приклади. Знайти похідні функцій:
а) У = 1п Зх, у' = (Іп Зх)' = (Зх)' = ~
б) у = Іп (Зх + 5), у' = (Іп (Зх 4- 5))' = зттру • 3 =
з
~ Зх + 5 ’
в) у = 1п (х2 4- Зх 4- 9), У* — (Іп (х* 4- Зх 4- 9))' =
_ (х2 + Зх 4-9)' _ 2х-|-З
X2 4- Зх 4- 9 — х2 4- Зх 4- 9 ’
г) у = (х2 4- 3) Іп (2х 4- 1), у' — {Xі 4- 3)' 1п (2х 4- 1) 4-
4- (х2 4- 3) (Іп (2х 4- 1))' = 2х Іп (2х 4-1)4- (х2 4- 3) • =
= 2х1п(2х + 1) 4- :
д) у = Іо&х’ у' = (1о&х? = ( -їїНг)'=ТІНГ;
е) У = (1о& 4х)'-, у' = (1о§8 4х)' = =
__ 1
х 1п З
Приклад. Знайти похідну функції у = Іп -у.
Розв’язання. Функція визначена при х, для
яких -у > 0, тобто при кп < < у 4- кл
2кл <іх< (2к 4-1) я. к = 0, ± 1, ±2.
330
Обчислимо похідну
У' М = —Т" (1® "тї “ —
18-р 2 - 4-і-
1__________1-^________1
, х 2 зіп х
§ 3. Первісна показникової
та логарифмічної функцій
Функція ея е первісною для функції ех на 7?. Функція
є первісною для функції ах на 7?. Справді, 1п а —
стала. Тому
= -Д- (ах)' = ^—с?\па = ах
\ Іпа / Іпа ' ' Іпа
При будь-якому X. Цим доведено, ЩО є первісною для
функції 0х на 7?.
З рівності (ех)' = ех для будь-якого х випливає, що
ех є первісною для функції ех на 7?.
Приклади. Знайти первісні для функцій: а) 3х; б) 5 X
X 2х; В) 2е3х + 7 • 0,2х.
Розв’язання. Застосовуючи подані вище залеж-
ності, дістанемо:
3х . 5*2* . 2 л3х ( 0»2х
а) -ІгГз- ’ б) 1п2 ’ В) З Є + 7 * 1п 0,2 •
Приклад. Знайти площу фігури, обмежену лініями у —
= 2х; у = 0; х = —1; х = 3.
Розв’язання. Розглядувана фігура є криволіній-
ною трапецією (рис. 10.1). Знаходимо її площу 5 за форму-
лою площі криволінійної трапеції:
_______________8 £1__8_________1_____15
° 1 1П2 1п2_1п2 1п 2 21п 2 — 21п2 ‘
«и-1 •—1
Раніше було розглянуто похідну функції / (х) = 1п X
при будь-якому х і встановлено, що 1п' (х) = -у. Остання
залежність показує, що для функції на проміжку (0;
оо) будь-яку первісну можна записати у вигляді 1п х + С
Функція має первісну 1п (—х) і на проміжку (—оо; 0).
331
Справді,
(іп(-х))'=^ь.(-і)=4.
Оскільки | х | = х при х > 0 і | х | = — х при х< 0, то на
будь-якому проміжку, який не містить точку 0, первісною
для функції є 1п І X |.
Приклади. Знайти первісні для функцій:
а) Ц*) = ТГГ •
Первісні для цієї функції дорівнюють ІП І X + 5 | +С
на будь-якому проміжку, який не містить точку (—5);
б) / (я) = 5 2.2* ' Маємо -3^2" 1п | 5 — 2х | + С на будь-
якому проміжку, який не містить точку— (точку, де
5 - 2х - 0).
Приклад. Обчислити площу фігу-
ри, обмеженої графіком функції у =
= 1п х, прямою X = 2 І ВІССЮ X.
Розв 1 язання. Функцією, оберненою до у = ІП X,
є х = £. З рис. 10.2 випливає, що площа заштрихованої
фігури 5Х дорівнює різниці площ5 (прямокутника із сторо-
нами 2 і 1п 2) і 52 (криволінійної трапеції ОЛВС). Отже,
1п2
$2= У е^ = /|;п2 = еІп2—е° = 2— 1; 5 = 21п2.
0
Шуканою є площа 8Х = 5 — 5а = 2 1п 2 — 1.
§ 4. Дослідження показникової
та логарифмічної функцій
Нагадаємо достатню умову монотонності функції. Не-
хай функція / (х) визначена і диференційовна на проміжку
(а; Ь). Для того щоб функція була зростаючою на проміжку
332
(а; Ь), достатньо, щоб виконувалась умова Г (х) > 0 при
будь-якому х, що належить проміжку, (а; (з).
Точки, які належать проміжку (а; Ь) і в яких похідна
дорівнює нулю або не існує, називають критичними точка-
ми функції у = / (х).
З означення критичної точки випливає, що функція
змінює знак лише при переході через критичну точку. Та-
ким чином, проміжки спадання, зростан-
ня (проміжки монотонності) функції / (х) У 1 /
обмежені критичними точками. Отже, /
щоб знайти проміжки монотонності функ- /
ції, необхідно: 1) знайти критичні точ- /
ки / (х); 2) визначити знак похідної /
(х) всередині проміжків, обмежених 1 /
критичними точками. И-’ / _
Приклад. Дослідити на зростання і х
спадання функцію / (х) = хе~3х.
Розв’язання. Знаходимо по- Рис-10-3
хідну
Г (х) = (хе~3х)' ~ е~3х - Зхе~3х = е~3х (1 - Зх);
Похідна (х) існує на всій числовій прямій і перетворю-
ється в нуль у точці х = Точках =•-§- ділить числову
пряму на два проміжки: —оо; -|-) і (-І-; оо). Оскільки функ-
ція е~3х завжди додатна, то знак похідної визначає другий
множник.
Отже, на проміжку —оо; -|-) /' (х) > 0 (/(х) зростає),
а на оо) /' (х) < 0 (/(х) спадає).
Приклад. Дослідити функцію у = х2 Іп х на зростання
(спадання) та екстремум і побудувати її графік.
Розв’язання. Функція визначена при х > 0;
у = 0 при х = 1. Знайдемо похідну
у' — 2х Іпх + х2 = 2х Іпх -|- х = 2хНпх + -у-).
Оскільки х > 0, знак у' збігається із знаком рп х +
Звідси випливає, що у' > 0 на проміжку
і тому
Г 1
на проміжку І-р=-
оо) функція зростає; на проміжку
333
похідна у' від’ємна, тому у спадає на проміжку
. і
. У точці похідна міняє знак з мінуса на плюс,
отже це точка мінімуму.
На рис. 10.3 зображено графік функції у = х2 1п х.
Приклад. Знайти найбільше значення функції
І (X) = 7 + 2х 1п 25 — 5Х~‘ — 52“\
Розв’язання. Дана функція, диференційовна у
кожній точці х£ Я. Знайдемо точки, в яких похідна цієї
функції дорівнює нулю:
І' (х) = 2 іп 25 — 5Х~‘ 1п 5 — 52~* Іп 5,
І' (х) = 0, (4 — 5х-' 4- 52-х) Іп 5 = 0,
4 — -^ + = 0. 52х— 20 • 5* — 125 = 0.
5’5*
Розв’язавши це квадратне рівняння відносно 5х, діста-
немо 5х = 25, або 5* = —5. Друге з цих рівнянь розв’язків
не має, а перше має єдиний розв’язок х = 2. Оскільки по-
хідна
Пх) = --^(5х + 5)(5х-25)
додатна при х < 2 і від’ємна при х > 2, то на проміжку
(—оо; 2) функція / (х) монотонно зростає, а на проміжку
(2; оо) — монотонно спадає. Отже, в точці х = 2 дана функ-
ція набуває найбільшого значення / (2) = 1 + 8 Іп 5.
§ 5. Похідна степеневої функції
Нехай у = Л де р — довільна стала. Відомо, що будь-
якому додатному х відповідає число лЛ Тим самим на про-
міжку (0; оо) при фіксованому р визначена функція /, зада-
на формулою / (х) = лЛ Вона називається степеневою (з
показником степеня р).
Якщо р > 0, то степенева функція визначена і при х =*
= 0, бо 0р = 0.
При цілих р степенева функція визначена і для х < 0.
При парних р це — парна функція, а при непарних р — не-
парна. Тому дослідження степеневої функції досить вико-
нати лише на проміжку (0; оо).
334
Раніше було виведено формули для похідної функції
7 (х) = х° при цілих показниках степеня і при р = -у.
Виведемо формулу' для похідної степеневої функції
при довільному дійсному показнику р.
Якщо подати х у вигляді х = е1п х, то
7(х) = хр=(е1пТ = вр1пл.
Знайдемо похідну здобутої складеної функції:
г(х) = (ер 1п*)' = ер 1п*(р 1пх)' = £ • р . -р =
Отже, (х")' = рхр”1.
При р<0 степенева функція спадає на (0; оо), бо її
похідна рхр_| < 0 на цьому проміжку (рис. 10.4).
Нагадаємо, що при х = 0 степенева функція дорівнює
0 і хр —* 0 при х 0 і х > 0. Тому точку 0 приєднують
до проміжку зростання, тобто при р > 0 степенева функція
зростає на [0; оо).
Графіки степеневих функцій зображено на рис. 10.5,
10.6.
Приклади. Знайти похідні степеневих функцій:
а) У — х, у' = х = 1 • х1-1 = 1;
б) у = х7, у' = (х7)' = 7х7-1 = 7х®;
і . і
в) у = /х, / = (Кх)' = (х2 )' == -у X 2 =
і -4__і_________
~ 2 Х ~ 2/х ’
335
г) у = х^, у' = (хУ®)' = /3 хУз
д) у = У&, у’ = (Ух*)' = (х~)' = -£- х~ “’ =
1 / 1 \ — —1 1 __—
= -г(—2 (х+1)' = —г(х+1) 2 х
, __з_
Х1 = _^_(х+1) 2.
З формули (х^)' = рх^ випливає, що первісною сте-
пеневої функції / (х) = х? є степенева функція /' (х) =
= рхр~х.
Треба також мати на увазі, що: при р =/= —1 первісна
степеневої функції /(%)=/’ має загальний вигляд Р (х) =
%р~Н
= р-ц7'і + С; при р = —1 первісною для функції / е
функція вигляду ІП | X | + С.
Розглянемо функцію / (х) = х“ і скористаємося форму-
лою
І(х) »/(х0) +Л(х0)Дх . (1)
при х0 = 1 і х = 1 4- Ах. Дістанемо І (х0)= / (1) = 1 і
/' (х) = аха~1, звідки /' (х0) = /' (1) — а • Iа-1 = а.
За формулою (1)
ї(х) = (1 + Ах)а « 1 + аДх. (2)
Наближення буде тим точніше, чим менше Дх. Формулу
(2) застосовують, зокрема, для обчислення коренів.
Т-Г 1
Поклавши а = —, знаходимо
>/ТТЛ^ = (1 +Ах)^«1 + -^. (3)
Приклади. Обчислити наближене значення:
а) "/ТОЗ . Маємо 5/Т03 = (1 + 0,03)“ = 1 + 2- х
X 0,03 = 1 4- 0,2 • 0,03 = 1 + 0,006 « 1,006.
336
б) 3/64,ОЗ=]/64(1+Ь^-) = 43-/
~4(1 + 2_. Л°з\
(продовжіть обчислення за допомогою калькулятора).
§ 6. Диференціальні рівняння
При розв’язуванні багатьох практичних задач дово-
диться знаходити невідому функцію з рівняння, яке міс-
тить крім невідомої функції її похідні.
Рівняння, яке містить невідому функцію та її похідні,
називають диференціальним.
Порядок найвищої похідної, яка входить до диференці-
ального рівняння, називають його порядком.
Наприклад, рівняння у" + 4г/ = 0 є диференціальним
рівнянням другого порядку.
Якщо до рівняння входить незалежна змінна, невідома
функція і її перша похідна, то це рівняння називають ди-
ференціальним рівнянням першого порядку. Якщо, крім
того, до рівняння входить похідна другого порядку від
шуканої функції, то рівняння називають диференціальним
рівнянням другого порядку і т. д.
Будь-яку функцію, що задовольняє диференціальне рів-
няння, називають розв'язком або інтегралом цього рівняння.
Наприклад, функція у = ех є розв’язком диференціаль-
ного, рівняння у — у' — 0$ бо (ехУ = ех.
Функція у = соз х є розв’язком диференціального рів-
няння у" + у = 0. Справді, для функції у = соз х маємо
у" = — соз х. Підставляючи значення у" у рівняння у" +
+ у = 0, дістанемо —соз х + соз х — 0.
Аналогічно можна переконатися, що функція у =
= А зіп х + В соз х, де А і В — довільні сталі, також є
розв’язком даного рівняння. (Самостійно виконайте .необ-
хідні перетворення.)
Загальним розв'язком даного диференціального рівняння
називають розв'язок (якщо він існує), у якого число довіль-
них сталих дорівнює порядкові рівняння.
Розв'язок диференціального рівняння при певних значен-
нях довільних сталих називають окремим розв'язком цього
диференціального рівняння.
Так, у розглянутому вище прикладі у" + у = 0 розв’я-
зок у = А зіп х + В соз х є загальним, а розв’язок у =
= соз х — окремим.
337
На практиці здебільшого окремий розв’язок конкрет-
ного диференціального рівняння знаходять із загального
розв’язку, виходячи з деяких умов, яким має задовольня-
ти шуканий окремий розв’язок.
Умови, яким мав задовольняти окремий розв'язок даного
диференціального рівняння, називають початковими умовами.
Задачу відшукання конкретного окремого розв’язку
даного диференціального рівняння за початковими даними
називають задачею Коші.
Приклад. Знайти окремий розв’язок диференціального
рівняння
уу' + 2% = 0, (1)
яке задовольняє початковим умовам: у = 4 при х = 3, якщо
загальний розв’язок даного рівняння задано у вигляді
х2 + у2 = а2. (2)
Розв’язання. Підставивши у загальний розв’я-
зок (2) початкові умови, дістанемо значення довільної
сталої З2 + 42 = а\ звідки а = ±5.
Отже, шуканий окремий розв’язок диференціального
рівняння (1) при заданих початкових умовах є функція у,
задана рівнянням х2 + у2 = 25.
Дамо геометричну інтерпретацію розв’язання рівняння
(1). Оскільки кожний окремий розв’язок даного рівняння
є деякою функцією однієї змінної, то у прямокутній системі
координат на площині йому відповідає деяка лінія. Її на-
зивають інтегральною кривою даного диференціального
рівняння. Загальному розв’язку диференціального рівнян-
ня відповідає множина всіх інтегральних кривих цього
рівняння, яку називають сім’єю інтегральних кривих ди-
ференціального рівняння.
Встановлено, що окремим розв’язком рівняння уу' +
+ 2л = 0 за початковими умовами х — 3 і у = 4 є функ-
ція х2 + у2 = 25, а загальним розв’язком х2 + у2 = а2.
У системі координат на площині загальний розв’язок за-
дає множину концентричних кіл з центром у початку коор-
динат. Початкові умови означають, що серед цієї множи-
ни кіл треба взяти те, яке проходить через точку з коорди-
натами х = 3, у = 4. Це коло радіуса 5, тобто х2 + у2 = 25.
Багато фізичних законів визначаються диференціаль-
ними рівняннями. Інтегрування цих рівнянь — складна
справ'а. Одні диференціальні рівняння вдається розв’язати у
явному вигляді, тобто записати шукану функцію у вигляді
формули. Для інших ще й досі не знайдено досить зручних
формул. У цих випадках знаходять наближені розв’язки
338 '
за допомогою ЕОМ. Диференціальні рівняння досить про-
сто і повно описують виробничі процеси. Тому важливо не
лише вміти розв’язувати диференціальні рівняння, а й
складати їх.
Розглянемо приклади.
Приклад (розмноження б а к т е р і й). На до-
слідах встановлено, що швидкість розмноження бактерій
пропорційна їх кількості (якщо для них вистачає їжі). Вва-
жають, що з часом маса бактерій змінюється неперервно
(бо самі бактерії дуже малі, а їх кількість велика).
Тоді швидкість приросту маси бактерій називають швид-
кістю розмноження. Нехай х (і) — маса всіх бактерій на
момент часу і, тоді х' (/) є швидкістю розмноження, яка
пропорційна кількості бактерій. Існує таке к, що
і х (0 = кх. (1)
За умовою х (/) і х’ (/) — невід’ємні. Розглянемо лише
випадок, коли к > 0, бо при к = 0 ніякого розмноження
не відбувається.
Неважко перевірити, що будь-яка функція
х = Се1*, (2)
де С — деяка стала, є розв’язком рівняння (1).
Функція х = Се® є загальним розв’язком рівняння (1).
Коефіцієнт к залежить від виду бактерій і зовнішніх умов
їх існування. Якщо відомими є значення коефіцієнта к і
маса бактерій у деякий момент часу то за формулою
(2) знайдемо масу бактерій у будь-який момент часу і.
Отже, х (/0) = /и0, тоді /и0 = Сек\ С =
х (і) = т^ек{і~ій\
Розв’язування багатьох задач у фізиці, техніці, біології,
суспільних науках зводиться до математичної задачі зна-
ходження функції /, яка задовольняє рівняння
Г (*) = к{ (х), (3)
де к — деяка константа.
За властивостями похідних показникових функцій зна-
ходимо, що розв’язком рівняння (1) є будь-яка функція виду
/(Х) = СЛ (4)
де С — стала. Оскільки С — довільне, то розв’язків ди-
ференціального рівняння (3) нескінченно багато. Доведено,
що інших розв’язків, крім функції виду (4), у рівняння (3)
немає.
Приклад (рівняння механічного руху).
Нехай матеріальна точка маси т рухається під дією сили
339
Р вздовж осі х. Позначимо через і час її руху, V — швид-
р
кість, а — прискорення. Другий закон Ньютона а = — на-
буде вигляду диференціального рівняння, якщо записати
прискорення а як другу похідну а = х" (/).
Рівняння тх" (/) = Р називають рівнянням механічно-
го руху, де х (і) — невідома функція, т і Р — відомі вели-
чини.
Залежно від умов задач диференціальні рівняння меха-
нічного руху записують по-різному. Наприклад:
а) сила Р — стала, тоді рівняння руху має вигляд
Р
х (/) = — = а, де а = сопзі;
б) сила періодично змінюється за часом, наприклад, за
законом Р = Ро зіп со/, тоді рівнянням руху є
х" (/) = зіп со/;
'7 т 9
в) сила пропорційна зміщенню (рух ідеально пружної
пружини) Р = — кх, к > 0 (знак мінус вказує на те, що
напрям сили протилежний напряму зміщення). Маємо таке
рівняння руху:
Х"(0=-
х т
г) сила, обернено пропорційна квадрату відстані (вільний
політ), тоді рівняння руху має вигляд
*"(0 =----
Приклад (рівняння радіоактивного
розпаду). Нехай у початковий момент часу маса радіо-
активної речовини дорівнює
ти (0) = т0. (5)
Відомо, що швидкість зменшення маси речовини т (/)
з часом пропорційна її кількості, тобто виконується рів-
няння
т' (/) ~ — кт (/), де к > 0. (6)
Скористаємося (без доведення) встановленою залеж-
ністю т (і) = Се~кі. Константу С знайдемо з умови (5).
Маємо т (0) = Се°, тобто С = т (0) = т0, звідки т (/) =
= іще~кі.
Нагадаємо, що проміжок часу Т, за який маса радіо-
активної речовини зменшується вдвічі, називають періо-
340
дом тгіврозпаду цієї речовини. Отже, к і Т зв’язані рівняй-
_______ЬТ 1
ням е = -у, 3 якого дістаємо
= 2, кТ = 1п 2, к = -!2Д.
Для радію Т « 1550 років, тому к = а; 0,000447.
Через мільйон років від початкової маси радію т0 зали-
шиться
т (10е) = т0е-447 « 0,6 • 1О-194то.
Приклад (рівняння гармонічних коли-
вань). Розглянемо рівняння
/' + (О2% = 0, (7)
де (о — деяке додатне число.
1 Безпосередньою підстановкою перевіряємо, що функція
х = А соз (со/ + а) (8)
для будь-яких сталих А і а є розв’язком рівняння (7). Мож-
на показати, що інших розв’язків рівняння (7) не має.
Таким чином, функція (8) задає загальний розв’язок рів-
няння (7).
Функція (8) при будь-яких заданих А, со і а описує
гармонічний коливальний процес. Число | А | називається
амплітудою, а число а — початковою фазою, або просто
фазою коливання (8). Рівняння (7) називають рівнянням
гармонічних коливань, а додатне число со — частотою ко-
ливання.
Число коливань V за одиницю часу визначають за форму-
лою V = Як бачимо, загальний розв’язок (8) рівняння
(7) містить дві довільні сталі: амплітуду А і початкову
фазу а. Для їх визначення треба задати дві умови, напри-
клад,
% (У = ^0» % (^о) = (9)
Тоді для визначення сталих А і а дістаємо таку систему рів-
нянь:
( А соз (<в/0 4- а) = х0, 1())
І— Лсо зіп (а»/0 + а) = а0,
ЗВІДКИ
А2 соз2 (со/о + а) + А2 зіп2 (со^о + а) = хо + ,
V2
=
341
Можна вважати, що А > 0, тоді А = у Хо + Знаю-
чи амплітуду А, з системи (10) за тригонометричними фор-
мулами визначають початкову фазу а. З формули (8) можна
дістати інший вигляд загального розв’язку рівняння (7).
Справді,
х = А (соз аі соз а — зіп аі зіп а) = А соз а соз аі —
— А зіп а зіп аі.
Поклавши Ст = А соз а, С2 = — А зіп а, дістанемо
х = Сх соз аі 4- С2 зіп аі.
До такого диференціального рівняння приводять, на-
приклад, дві різні, на перший погляд, задачі з фізики —
коливання пружної пружини і розряд конденсатора через
котушку.
Зазначимо, що рівняння гармонічних коливань розгля-
нуто нами за умов, які реально не виконуються. Так, при
описанні коливання пружини треба врахувати тертя, а при
описанні розряду конденсатора — внутрішній опір. Тоді
у рівнянні коливань з’являється доданок, що залежить
від першої похідної (швидкості).
Історична довідка
В кінці XVII — на початку XVIII ст. різноманітні практичні і на-
укові проблеми привели до появи диференціальних рівнянь. Насампе-
ред це були диференціальні рівняння першого порядку, інтегрування
яких намагалися здійснити за допомогою функцій, що виражають скін-
ченне число алгебраїчних дій або таких, що включають елементарні
трансцендентні дії.
Найпростіші диференціальні рівняння з’явилися вже в працях Іса-
ака Ньютона (1643—1727) і Готфріда Лейбніца (1646—1716). Саме Лей-
бніцу і належить термін «диференціальне рівняння». Диференціальні
рівняння мають велике прикладне значення, вони є ефективним зна-
ряддям дослідження багатьох задач природознавства і техніки. їх ши-
роко використовують в механіці, астрономії, фізиці, у багатьох задачах
хімії і біології. Це пояснюється тим, що досить часто об’єктивні закони
записують у формі диференціальних рівнянь, а самі ці рівняння є засо-
бом кількісного дослідження цих законів.
Наприклад, фізичні закони описують деякі співвідношення між
величинами, що характеризують певний процес, і швидкістю зміни цих
величин. Іншими словами, ці закони виражаються рівностями, в яких
є невідомі функції та їхні похідні.
У XVIII ст. теорія диференціальних рівнянь відокремилася з ма-
тематичного аналізу в самостійну математичну дисципліну. Її успіхи
по’вязані з іменами швейцарського вченого Іоганна Бернуллі (1667—
1748), французького математика Жозефа Лагранжа (1736—1813) і особ-
ливо Леонарда Ейлера.
342
Перший період розвитку диференціальних рівнянь був пов’язаний
з успішним розв’язанням деяких важливих прикладних задач, що при-
водять до диференціальних рівнянь, розробкою методів інтегруван-
ня різних типів диференціальних рівнянь І пошуком класів рівнянь,
розв’язки яких можна подати у вигляді елементарних функцій або їх
первісних. Проте дуже швидко виявилося, що Інтегрованих диференці-
альних рівнянь зовсім небагато. Це привело до розвитку власне теорії
диференціальних рівнянь, яка займається розробкою методів, що доз-
воляють за властивостями диференціального рівняння визначити вла-
стивості і характер його розв’язку.
У зв’язку з проблемами практики поступово розроблялися і спо-
соби наближеного інтегрування диференціальних рівнянь. Ці методи
дають зручні алгоритми для обчислень з ефективними оцінками точ-
ності, а сучасна обчислювальна техніка дає змогу швидко довести роз-
в’язання кожної такої задачі до числового результату.
Запитання і завдання для повторення
1. За якою формулою обчислюють похідну показникової функції
при основі е?
2. Пояснити зміст рівності ах = ех[па,
3. За якою формулою обчислюють похідну показникової функції
для будь-якого показника х?
4. За якою формулою обчислюють похідну логарифмічної функції?
гт - і , 1
Пояснити зміст рівності ІП X = —,
5. Яка функція є первісною для функції ех на /??
ах
6. Пояснити, чому функція є первісною для функції ах на /??
7. Який вигляд має первісна для функції на проміжку (0; оо)?
8. Як дослідити показникову функцію на зростання і спадання?
9. Навести схему дослідження логарифмічної функції за допомо-
гою похідної.
10. Прокоментувати рівності: а) х = еіп *, б) хр = є*2111*.
11. Чому кажуть, що при р > 0 степенева функція / (х) = хр зро-
стає на проміжку [0; оо), тобто точка 0 приєднується до проміжку зро-
стання?
12. Який вигляд має первісна для степеневої функції / (х) = Хр
при р Ф —1, при р = —1?
Вправи
1. Обчислити наближені значення виразів:
А
і
1) уТоГ ; 2) ^8^03 ; 3) 48 2 }
Б
' 4) ‘^1026; 5) /б25 • 3 ; 6) у^ЗО.
343
в
7) |<24б; 8) /9^2 ; 9) .
2. Знайти похідні функцій:
А
1) у = ех\ 2) у = е7х\ 3) у — е~х', 4) = 5) у = 6 х’—1;
6) у = е2“3х; 7) у = 5х; 8) у = 101-*; 9) у = 32х+1;
10) у = 3 . 7х; 11) у = 2,1ЗЧ-4л:; 12) у =
13) у = Іп 2х; 14) у = Іп (2х— 3); 15) # = х81пх;
16) у =1о£7 х; 17) у = 1о£б 7х; 18) у = 1о£0>3 х.
Б
19) у = е~2х\ 20) у = е3—7х; 21) у~е2 ; 22) £/= е3*2-4х~2$
23) у = Зе2х — ех\ 24) у = 1' ; 25) у = 53х;
26) у = 6 • 2х; 27) у = 71~х; 28) у = 125“7х;
29) у = 2,34+5х; ЗО) у = 2Х СО8 X.
31) у = Іп (1 -|- Зх); 32) у = х8 Іп х; 33) у = ;
34) у == 35) у = У х Іп х; 36) у = Іп х соз х;
37) у = 1е§2 7х; 38) у = 1о& (3 - 2х); 39) І£ (3 + 4х);
40) у = 1о£0>3 (7х + 2); 41) у = І£ 5х; 42) у = /х І£ х.
В
Ку і і
43) у = е2х + 4е 2 ; 44) у = (х + 1) ех; 45) у ==-------------;
е
46) у — е~х*\ 47) у = 5е7х — Зе3х; 48) у = е005 5х;
49) г/ = 23х+х2; 50) у = (Зх + 5х2 + х3) • 4х; 51) у = г„ ;
4 + о
52) у = х2 • 2—*; 53) у = З5* — 7 • 25~7х; 54) у = ;
Ух
Х^
55) у = Іп (х2 + Зх + 2); 56) у = ;
57) у == ех+‘ Іп (х + 5); 58) у = ах‘ Іп (х2 + 4х + 12);
59) у = Іое, (2 + Зх); 60) у = 1о§0>2 (7 + Зх);
61) у= (Зх + 4) • 1о§6 (х24-х+ 1);’
62) у = 1о§п (х3 + 4 Ух -4-5); 63) у = 1§ (зіп Зх + 2х);
64 у = 1о£ । (х2 — 4х + 6).
3. Знайти первісні для функцій:
344
А
1) є2*; 2) 4х; 3) 3 • 5х; 4) Зех — 6 0,3х; 5)
X -р о
6) 2х — 5 : 7) 3x4-1 •
Б
8) 7.3х; 9)5.?*; 10) 4е3х — 5 • 0,2х; 11) ^!_8 8
і з 2
і2)іт=г; 13)-г+т+Г’
в
14) е7х; 15) ех (х — 1); 16) (х — —2—І}
Іп а \ Іп а /
17) -^(х+1).
4. Обчислити площу фігури, обмеженої лініями:
А
1) у = 2х, х = 1, х = 3, у = 0;
2)^ = “р> х=1, х = 4, г/ = 0,
Б
3) У = , х = З, х = 6, у = 0;
4) у = 3х, х = — 2, х = 2, у = 0,
В
5) у = (-1-) , у — 0, х = — 3, х = 2;
2 5 6 7
6) у = — , у = 0, х = 5, х=1.
5. Обчислити інтеграли:
За 0
, ч г сіх с сіх с &
1) ) X ; 2) ) X 3) ] 0,5x4-З ’
1 і —4
6. Написати рівняння дотичної до ^графіка функції:
1) / (х) = 2 • 6х у точці з абсцисою х0 = 0.
2) / (х) = 3 • 2х у точці з абсцисою х0 = 1.
7. Знайти проміжки зростання і спадання та екстремум функції
А
1) / (х) == 2хе~х\ 2) / (х) = х2е~~х*9 3) / (х) = Іп х, х С
4) / (х) = х — іп х х С (“7“; е] .
345
5) ї (х) = —е; 6) { (х) = х2 • 2 х; 7) / (х) = х 1п х;
8)/(х) = ТГГ.
В
9) (х) == Зх + е*, х є (- і; 1); 10) / (х) = 5
Х2+ 1
11) / (х) = Зх — 'У ; 12) } (х) = 2х2 — 1п х х € ; 1
8. Знайти похідні степеневих функцій:
А
1)
5)
7)
Н)
у = х100; 2) у = ух; 3)у = х*
у — хя; 6) у — — х°,
Б
у = — х20; 8)у = '?<х?; 9) у = _12_; 10)у = 2х2/х;
X
2 х2 + 3л? + ^
"к: №,-~кгтг-
В
; 4) г/ = хОіІ;
З і/\4 г-
13) (у = —14) у = -Г±_; 15) у = /х (2х + 5);
/х8 2
1 3
16) у = (Зх3 + 8х2— 5)2; 17) у = -/===•- ; 18) у = 5х3 /х ?
5 V 1 їх
19) у = Ух + — у^х3 + 5; 20) у = Vх + /х ;
21) у = У (Зх2 + 5х3)4 ; 22) у = І х5 * * + ? 1 » 4 і/ х2;
23) у = (ах3 + Ьх)ь; 24) у = Пп /х + Xі + ,
9. Перевірити, чи є розв’язком даних диференціальних рівнянь
записані поряд з ними функції:
1) хуп + 2у' — = 0, ху = С±ех + С2е^;
2) / — 2/ + у = 0, у = х4.
10. Знайти окремі розв’язки рівнянь:
1) (1 + х2) уп — 2ху' = 0, якщо у (0) = 0, у^(0) = 3;
2) УУЯ + у2 = 1, якщо у (0) = 1, у' (0) = 1.
11. Відомо, що за 1 год маса бактерій подвоюється, а швидкість
розмноження прямо пропорційна наявній кількості бактерій. Скласти
диференціальне рівняння розмноження бактерій і знайти його загаль-
ний розв’язок,
346
12. Відомо, що за 1 год маса радіоактивної речовини зменшується
на 1 %. Скласти диференціальне рівняння піврозпаду і знайти його за-
гальний розв’язок.
13. Знайти період піврозпаду радіоактивної речовини за умовою
попередньої задачі,
РОЗДІЛ 11
КОМПЛЕКСНІ ЧИСЛА
§ 1. Розширення множини дійсних чисел.
Поняття про комплексне число
У багатьох розділах математики та її застосуваннях не-
можливо обмежитися розглядом лише дійсних чисел. Вже
досить давно при розв’язуванні різних задач виникла по-
треба добувати квадратний корінь з від’ємних чисел. Але
чисел, які при піднесенні до квадрата дають від’ємні числа,
тоді не знали і тому вважали, що квадратні корені з від’єм-
них чисел не існують, тобто задачі, які до них приводять,
не мають розв’язків. Зокрема, так було при розв’язуванні
квадратних рівнянь з від’ємним дискримінантом. Напри-
клад: х2 — 4х + 10 = 0, %і,2 = 2 ± —6. Тому природ-
но постало питання про розширення множини дійсних
чисел приєднанням до неї нових чисел так, щоб у розшире-
ній множині, крім чотирьох арифметичних дій —додаван-
ня, віднімання, множення і ділення (за винятком ділення
на нуль), можна було виконувати дію добування кореня.
Це питання було успішно розв’язане лише у XIX ст.
Відповідно до прийнятих в математиці принципів при
розширенні множини дійсних чисел мають задовольнятися
такі вимоги:
1) означення нових чисел має спиратися на поняття
дійсного числа, і нова множина чисел має містити всі дійсні
числа;
2) для нових чисел повинні виконуватися п’ять законів
прямих арифметичних дій (пригадайте ці закони);
3) у новій числовій множині мусить мати розв’язок рів-
няння х2 = —1, бо в цій множині має виконуватися дія,
обернена до піднесення до степеня.
Оскільки існує вимога, щоб у новій числовій множині
рівняння х2 = —1 мало розв’язок, необхідно ввести деяке
нове число, вважаючи його розв’язком цього рівняння.
Число, квадрат якого дорівнює —1, позначають буквою і
і називають уявною одиницею (і — перша буква латин-
347
ського слова іта§іпагіи8 — уявний). Підкреслимо, що рів-
ність /2 = —1 вводять за означенням і не доводять.
До нової множини мають^належати числа виду Ьі (добу-
ток дійсного числа на уявну одиницю) і числа видула + Ьі
(суми дійсного числа а і добутку дійсного числа Ь на уявну
одиницю).
Отже, нова множина чисел має містити всі числа виду
а + Ьі, де а і Ь — довільні дійсні числа, а і — уявна одини-
ця. Такі числа називають комплексними.
Слово «комплексний» означає складений. Число а нази-
вають дійсною частиною комплексного числа, а вираз Ьі —
уявною. Число Ь називають коефіцієнтом при уявній части-
ні. Наприклад, у числі 6 + 7і дійсна частина дорівнює 6,
уявна — 7і. Коефіцієнт пр'и уявній частині дорівнює 7.
Дійсною частиною числа 0 + Зі є число нуль, а уявною —
вираз Зі. Коефіцієнт при уявній частині дорівнює 3.
Числа виду а +.3і ототожнюють з дійсними числами, а
саме вважають, що а + Зі = а. Далі замість а + Зі писа-
тимемо просто а. Зокрема, 0 + Зі = 0. Таким чином, вико-
нується обов’язкова для будь-якого розширення поняття
числа вимога, щоб попередній числовий «запас» входив
до нової числової множини як її частина. Множина дійсних
чисел є частиною (підмножиною) множини комплексних
чисел. Відповідно до вимог, що висуваються при будь-яко-
му розширенні поняття числа, при побудові множини
комплексних чисел треба ввести за означення умову рів-
ності нових чисел і правила виконання прямих дій — до-
давання і множення.
Два комплексних числа а + Ьі і с + <іі рівні між собою
тоді і тільки тоді, коли а = с і Ь = сі, тобто коли рівні
їхні дійсні частини і коефіцієнти при уявних частинах.
Поняття «більше» і «менше» для комплексних чисел не
має смислу. Ці числа за величиною не порівнюють. Тому
не можна, наприклад, сказати, яке з двох чисел більше:
10/ чи Зі, 5 + 2/ чи 2 + Зі.
Важливим є поняття про спряжені комплексні числа.
Числа а + Ьі та а — Ьі, дійсні частини яких рівні, а
коефіцієнти при уявних частинах рівні за модулем, але
протилежні за знаком, називають спряженими.
Можна сказати простіше: числа а + Ьі і а — Ьі, які відріз-
няються лише знаком уявної частини, називають спряжени-
ми. Наприклад, спряженими є комплексні числа 4 + Зі та
4 — 3/; 2 + і та 2 — і; —8 +7і та —8 —7і; —5 — і та —5 +і.
Якщо дане число Зі, то спряженим до нього буде —Зі.
До числа 11 спряженим є 11, бо 11 + 0/ = 11 — Зі.
348
§ 2. Дії над комплексними числами
Додавання комплексних чисел. Сумою двох комплексних
чисел а 4- Ьі і с 4- Лі називають комплексне число (а 4~ с) 4-
4- (Ь 4- Л) і, дійсна частина якого і коефіцієнт при уявній
частині дорівнюють відповідно сумі дійсних частин і кое-
фіцієнтів при уявних частинах доданків, тобто
(а 4- ЬІ) 4- (с 4- Лі) = (а 4- с) 4- (Ь 4- а!) і.
Приклади. Виконати додавання комплексних чисел:
.. а) (3 4- 21) 4- (—1 — 5/) = (3 - 1) 4- (2 - 5) і =
= 2 — Зі;
б) (4 - 5ї) 4- (2 — 0 = (4 4- 2) 4- (—5 — 1) і = 6 —
— Зі;
в) (2 4- ЗО 4- (6 — ЗО = (2 4-6) 4- (3 — 3) і = 8;
г) (10 — ЗО 4- (—10 4- ЗО = (Ю — 10) 4- (—3 4-3) і =
= 0 4- 0ї = 0.
З наведених прикладів випливає, що додавання комп-
лексних чисел ми виконуємо за правилом додавання много-
членів. У множині дійсних чисел справедлива рівність
а 4- о = а. У множині комплексних чисел нулем є число
0 + 0і. Справді, яке б не було число а 4- Ьі, справедлива
рівність
(а 4- Ьі) 4- (0 4- 00 = (а 4- 0) 4- (Ь 4- 0) і = а 4- Ьі.
За аналогією з дійсними числами для комплексних чи-
сел вводять поняття про протилежні числа: два числа а 4-
4- Ьі та —а — Ьі, сума яких дорівнює нулю, називають про-
тилежними.
Для додавання комплексних чисел виконуються пере-
становний і сполучний закони. Доведемо, наприклад, спра-
ведливість переставного закону додавання комплексних
чисел. Нехай Зі = а 4- Ьі, г2 = с 4- Лі. Тоді
гі 4- г2 = (а 4- Ьі) 4- (с 4- ЛІ) = (а 4- с) 4- (р 4- Л) і,
г2 4- гг = (с 4- Лі) 4- (а 4- Ьі) = (с 4- а) + (Л + Ь) і.
Оскільки для додавання дійсних чисел справджується
перестановний закон, тобто а + с = с + а; Ь 4~ Л = Л 4*
4- Ь, то
Зі 4- г2 = г2 4- *і, що й треба було довести.
Означення суми комплексних чисел поширюється і на
випадок трьох і більше доданків.
Пропонуємо самостійно довести справедливість спо-
лучного закону додавання для трьох комплексних чисел:
21 = а 4* Ьі, г2 = с 4- Лі, г3 = е 4- /і.
349
Віднімання комплексних чисел. Віднімання комплекс-
них чисел означають як дію, обернену до дії додавання, ко-
ли за даною сумою й одним із доданків знаходять другий,
невідомий доданок. ,
Різницею двох комплексних чисел = а + Ьі і га = с 4-
+ сіі називають таке комплексне число г3 = х + уі, яке в су-
мі а га дає 2Х.
Отже, гг — г2 — г3, якщо г3 + г8 = г1#
Можливість дії віднімання комплексних чисел та її
однозначність потребує доведення.
Доведемо, ЩО ДЛЯ будь-яких комплексних чисел ?! =
= а + Ьі і г2 = с + сіі різниця 2г — га визначена, і до
того ж однозначно. Доведемо, що існує, і до того ж єдине,
комплексне число г3 = х + уі, яке в сумі з га дорівнює гх.
За означенням дії віднімання
(с + сІІ) + (х 4- уі) = а + ЬІ.
Виконавши додавання у лівій частині рівності, дістане-
мо
(с + х) + (сі + у) і = а 4- Ьі. (1)
За умови рівності двох комплексних чисел
Іс 4- х = а,
\й + у = Ь.
Ця система має розв’язок, і до того ж єдиний: х = а — с,
у — Ь — сі. Отже, існує, і до того ж єдина, пара дійсних
чисел (х; у), яка задовольняє рівняння (1), що й треба було
довести. З доведення випливає, що віднімання комплексних
чисел виконують за таким правилом:
(а 4- Ьі) — (с — сії) = (а — с) + (Ь — ії) і,
тобто дійсна частина різниці двох комплексних чисел до-
рівнює різниці дійсних частин зменшуваного і від’ємника,
а коефіцієнт при уявній частині — різниці коефіцієнтів
при уявних частинах даних чисел.
Приклади. Виконати віднімання комплексних чисел:
а) (3 4- 4г) — (1 4- 2г) = (3 — 1) 4- (4 — 2) і = 2 4- 2ї;
б) (—5 4- 2г) — (2 4- г) = (—5 — 2) 4- (2 — 1) і =
= -7 4- г;
в) (6 4- 7г) — (6 — 5г) = (6 — 6) 4- (7 4- 5) і = 12г;
г) (0,3 4- 2,5г) — (—0,75 4- 1,5г) = (0,3 4- 0,75) 4-
4- (2,5 4-_1,5) і = 1,05_4- г;
д) (/3 - 2г) - (У2 4- Зг) = (/2 - У 2) 4- (- 2 -
— 3) і; = — 5г;
350
+ “Н * = ТТ + 1 "й-1-
При розв’язуванні прикладів на сумісне додавання і
віднімання комплексних чисел можна користуватися пра-
вилами додавання і віднімання многочленів.
Приклади. Виконати дії:
а) (7 + Зі) + (-8 - 5і) - (4 - 9і) - (1+ і) = (7 -
— 8 — 4—1) + (3 — 5 + 9 — 1) і = —6 + 67;
б) (2,3 + 1,57) — (0,9 — 2,47) + (—5,8 + і) — (—7,8 —
- 3,4/) = (2,3 — 0,9 — 5,8 4- 7,8) + (1,5 + 2,4 + 1 + 3,4) і =
= 3,4 + 8,Зі.
Множення комплексних чисел. Добутком двох комплекс-
них чисел а + Ьі і с + йі називають комплексне число
(ас — Ьй) + (ай + Ьс) і.
Суть, і доцільність цього означення стануть зрозуміли-
ми, якщо взяти до уваги, що цей добуток утворений так,
як виконується множення двочленів з дійсними коефіцієн-
тами, а саме:
(а + Ьі) (с + йі) = ас + айі 4- Ьсі 4- Мі2 =
= ас + (ай 4- Ьс) і 4- ЬйР.
Замінюючи за означенням і2 на —1, дістанемо Мі2 =
= —Ьй.
Відокремивши дійсну частину від уявної, остаточно ді-
станемо
(а 4- Ьі) (с 4- йі) — (ас — Ьй) 4- (ай 4- Ьс) і. (2)
Формулу (2) не слід намагатися механічно запам’ятати.
При множенні комплексних чисел треба користуватися ві-
домим правилом множення двочленів а 4- Ьі і с 4- йі з на-
ступною заміною і2 на —1.
Приклади. Виконати множення комплексних чисел:
а) (4 — 5і) (3 4- 2і) = 12 4- 8і — 157 — 10і2 = 12 4-
4- 10 — 7і_= 22 — 71;
б) (V3 — і) • (/2 4- 5і)_= /б — У2і 4- 5/Зі — 5і2 =
= (/6 4- 5)- (5 /3 4- /2)і;
в) 8і • Зі • /3 = —24 /3;
г) (2 — і) • (—5) = —10 4- 5і;
д) (—4 — Зі) • (—6і) = —18 4- 24І.
Дія^. множення комплексних чисел підлягає основним
законам множення, встановленим для дійсних чисел:
351
переставному і сполучному. (Пропонуємо самостійно довести
ці закони.).
Знайдемо добуток двох спряжених комплексних чисел.
Маємо
(а + Ьі) • (а — Ьі) = а2 — (Ьі)2 = а2 — Ь2і2 = а2 + &2,
тобто (а + Ьі) • (а — Ьі) = а2 + Ь2 Отже, добуток двох
спряжених комплексних чисел є дійсним невід’ємним чис-
лом, яке дорівнює сумі квадратів дійсної частини якогось
з даних чисел та коефіцієнта при уявній одиниці. Тому
при множенні спряжених комплексних чисел одразу писа-
тимемо результат.
Приклади. Обчислити добутки:
а) (3 + 5г) • (3 — 5ї)_= З2 + 52 = 34;
б) (4 + /Зг) • (4 — /Зї) = 42 + (/З)2 = 16 + 3 = 19;
в) (2 + 0 • (2 — 0 = 22 + І2 = 5;
г) (/х + Ууі) - (Ух — Ууі) = (Ух)2 + (Уу)2 = х + у,
ч / 3 , 2 л / 3 2 / З Л , / 2 9 ,
д) ( 4 + 5 Д 4 5 / ~ ( 4 ) + ( 5 ) ~ 16 +
. 4 289
25 400 ’
Читаючи рівність (а + Ьі) • (а — Ьі) = а2 + Ь2 справа
наліво, робимо висновок, що суму квадратів будь-яких
двох дійсних чисел можна подати у вигляді добутку комп-
лексно-спряжених множників.
Приклади. Розкласти на множники двочлен:
а) а2 + 9 = (а + ЗО (а — ЗО;
б) 16т2 + 25п2 = (4т + Бпі) (4т — 5пі);
в) 49 + 36 = (7 + 6/) (7 —_60;
г) а + 16 = (Уа + 40 (Уа — 4і)\
д) Ь + 7 = (УЬ + /70 (Ь - /70-
Ділення комплексних чисел. Ділення комплексних чи-
сел означають як дію, обернену до дії множення, коли за
даним добутком і одним із множників знаходять другий не-
відомий множник. Причому у множині комплексних чисел
залишається вимога, щоб дільник не дорівнював нулеві.
Часткою комплексних чисел = а + Ьі та г2 = с +
називають таке комплексне число г3 = х + уі, яке при
множенні на г2 дорівнює г1е
Можливість дії ділення комплексних чисел та її означ-
ність потребує доведення.
Доведемо, що частка комплексних чисел гх = а + Ьі та
г2 = с + Лі визначена, і до того ж однозначно, якщо
с + сіі Ф 0 + 0ї. Отже, доведемо, що за умови с + йі ф
352
Ф 0 + Оі існує, і до того ж єдине, комплексне число г3 =
— х + уі, яке при множенні на 2а дорівнює гг. За означен-
ням дії ділення
(с -|- Лі) (х + уі) = а + Ьі.
Виконавши у лівій частині цієї рівності множення, ді-
станемо
(сх — <1у) 4- (су + <іх) і = а-і- Ьі.
За умови рівності двох комплексних чисел
ісх— сіу = а,
су = Ь.
Система має єдиний розв’язок:
____ас + Ь4 " Ьс — аЛ
х ~ с2 + аг ’ У ~ с2+са2 •
Із доведення випливає, що ділення комплексних чисел
виконують за таким правилом:
а + Ьі асЬй ї Ьс — ай
с + <іі ~ 6* +4і + сл +4і •
Цей результат можна дістати, помноживши ділене і
дільник на число, спряжене до дільника. Покажемо це:
а + Ьі _ (а + Ьі) (с — йі) __ (ас + Ьс£) + (Ьс — ай) і __
с + йі (с + йї) (с — йі) ~ с2 + й2 ~
__ ас -\~Ьй Ьс — ай .
с2 + й2 с2 + й2
Цим прийомом користуються при розв’язуванні вправ на
ділення комплексних чисел.
Приклади. Знайти частку комплексних чисел:
. 2 + 5/ _ (2 + 5/)(3 + 20 _ (6 — 10) + (4 + 15) / __
3 — 2/ “ (3—20 (3 + 20 9 + 4 —
_ — 4 + 19/ _ 4 19.,
13 — 13 + 13
б) -1±£ = = _ Зі — і2 = 1 -Зг;
, 5 _ 5(1 + 20 ' 5+ 10/ _ , , 9,.
1—2» ~ (1 - 20 (1 + 20 5 - 1 З-
, 4і _ 4і (3 + 20 _ — 8 + 12» _ 8 12.,
Г' 3 —2»~ (3- 20(3 + 20 9 + 4 ~ 13 + 13 1'
12 1-1819
353
, 1-і _ (1-ї) (1 — о _ 1—21+і2 _ 1— 21 — 1 _
Д' 14-і ~ (1+0 (1—0 2 ~ 2
= — і;
- 2 /3 4- і (—2/3 -Ь 0 (1 - 2-/31) _
' 1+2/Зі (1+2/Зі)(1 — 2/Зі)
— 2/3+12І+І + 2/3 13І _
“ 1+12 — 13
Піднесення комплексних чисел до степеня. За означен-
ням і1 = і, і2 =—1, Користуючись рівністю і2 ——1,
визначимо кілька послідовних степенів уявної одиниці:
І3 = і2 . І = — 1 . і = — /; Iі = І? . І = — іі = — Iі = 1;
І5 = Iі . і = і; і6 = І6 . і — — 1; І’ = і« . і = — г;
г8 = г’ .1 = 1.
Оскільки Iі = 1, то значення степенів і періодично пов-
торюються із збільшенням показника на 4. Так,
/2 = і6 — — 1; і3 = і’ = — і; Iі = і& = 1 І Т. Д.
Щоб піднести число і до степеня з натуральним показни-
ком п, треба показник степеня поділити на 4 і піднести до
степеня, показник якого дорівнює остачі від ділення. В за-
гальному вигляді це можна записати так:
= 1; і4т+і = і; і4т+2 = — 1; ііт+3 = і3 = — і.
Приклади. Піднесення до степеня:
а) і19 = і4 4+3 = і16+1 = !.(=/;
б) і2і = і4’8+2 = ї32+2 = і2 = — 1;
в) ї65 = ї52+3 = 1 • і3 = — і.
Правила піднесення до степеня уявної одиниці застосо-
вують при піднесенні до степеня комплексних чисел.
Приклади. Піднести до степеня двочлени:
а) (2 + 5г)2 = 4 + 20г + 25г2 = — 21 + 20г;
б) (3 + 2г)3 = 27 + 54г + 36г2 + 8ї3 = —9 + 46г;
в) (1 + г)2 = 1 + 2г + г2 = 1 + 2г — 1 = 2ї;
г) (1 — г)2 = 1 — 2г + /2 = 1 — 2г — 1 = —2г;
Д) (1 _ іу = ((і _ і)2)2 = (—2г)2 = 4г2 = — 4;
е) (1 + г)е = ((1 + г)2)3 = (2г)8 = 8г3 = — 8г;
є) (1 _ 4)ю = ((1 — г)2)5 = (—2г)5 = —32г5 = — 32г
(рівності (1 + г)2 = 2г, (1 — г)2 = —2г корисно запам’я-
тати, бо їх часто використовують).
354
Добування квадратного кореня з від’ємних чисел. Роз-
в’язування квадратних рівнянь з від’ємним дискримі-
нантом. При побудові множини комплексних чисел було
забезпечено виконувані сть дії добування квадратного ко-
реня з від’ємних чисел. Розглянемо цю дію. Спочатку під-
креслимо, що існують два і тільки два значення квадрат-
ного кореня з —1, а саме: і та —і, Умовно це записують
так: /—1 = Аналогічно існують два і тільки два зна-
чення квадратного кореня з числа —а, а саме: Vаі та
—V аі, де під Vа розуміють арифметичний корінь.
Умовно це записують так: /—а = ±\^аі. Наприклад,
/=64 = ± 8/; /—0,0144 = ±0,12Л
Розглянемо розв’язання квадратних рівнянь з від’єм-
ними дискримінантами. Нагадаємо, що до введення множи-
ни комплексних чисел вважалося, що такі рівняння не ма-
ють коренів.
Нехай дано рівняння х2 + 8х + 17 = 0. Маємо хі-2 =
= — 4 ± /16—17, або хі,2 = —4 ± /—1 Враховуючи
попереднє, це можна записати так: хі,2 = —4 ± і. Корені
хх = —4+ і та х2 = —4 — і є спряженими комплексними
числами. Взагалі, будь-яке квадратне рівняння з дійсними
коефіцієнтами і від’ємним дискримінантом має два комп-
лексних спряжених корені Можна довести, що й для таких
рівнянь справедлива теорема Вієта. Наприклад, для роз-
глянутого вище рівняння хх + х2 = (—4 + І) + (—4 —
_ і) = —8; ххх2 = (—4 + і) (—4 — 0 = 16+1 = 17,
тобто сума коренів дорівнює коефіцієнту при х з проти-
лежним знаком, а добуток — вільному члену.
Приклади. Розв’язати рівняння:
а) х2 — 4х + 5 = 0; хі,2 = 2 ± /4 — 5 = 2 ±
± /+ = 2 ± /;
б) г2+6г+ 13 = 0; гЬ2= — 3± / 9-13= — 3± 2ї;
в) 4х2 + Зх + 1 = 0;
- з ± - 3 ± /л _ 3 /7 .
Хц2 — 8 — 8 8 ± 8 і-
Розглянемо приклад на складання квадратного рівнян-
ня з дійсними коефіцієнтами за його коренями.
Приклад. Нехай хх = 3 —^-і\ х2 = 3 + і.
хх 4~ х2 = ---+ (3 + = 6,
*1Х2 = (з- 4-Ф (з + = 9-Д-і2 == 94-.
12*
355
Числа і х2 є коренями рівняння х2 — 6х +'9-~ = 0. От-
же, шуканим є рівняння 4х2 — 24% + 37 == 0.
§ 3. Геометрична інтерпретація комплексних чисел
При вивченні комплексних чисел можна використовува-
ти геометричні термінологію і міркування, якщо встанови-
ти взаємно однозначну відповідність між множинами комп-
лексних чисел і точок координатної площини. Ця відповід-
ність може бути такою: кожному комплексному числу а +
+ Ьі поставимо у відповідність точку
М Ь) координатної площини, тобто
точку, абсциса якої дорівнює дійсній
частині комплексного числа, а ордина-
та — коефіцієнту уявної частини. Кож-
ній точці М (а; Ь) координатної площи-
ни поставимо у відповідність комплексне
число а + Ьі (рис. 11.1). Очевидно, що
така відповідність є взаємно однозначною.
Вона дозволяє інтерпретувати комплексні
числа як точки деякої площини, на якій вибрано систему
координат. Координатну площину називають при цьому
комплексною, вісь абсцис — дійсною віссю, бо на ній роз-
міщені точки, що відповідають комплексним числам а + 0/,
тобто відповідають дійсним числам. Вісь ординат називають
уявною віссю — на ній лежать точки, які відповідають
уявним комплексним числам 0 + Ьі.
Зручною є також інтерпретація комплексного числа як
вектора ОМ (рис. 11.1). Поставимо у відповідність кожному
комплексному числу вектор з початком у точці 0 (0; 0) і
кінцем у точці М (а; Ь). Такий вектор називають радіусом-
вектором, а його проекції на осі координат є координатами
вектора. Отже, можна сказати, що геометричними зобра-
женнями комплексного числа г = а + Ьі є радіус-вектор з
координатами а і Ь. Відповідність між множиною комплекс-
них чисел, з одного боку, і множиною точок або векторів
площини, з другого — дозволяє комплексні числа назива-
ти точками або векторами і говорити, наприклад, про век-
тор а + Ьі або про точку а + Ьі.
На рис. 11.3 вектори ОЛ, ОВ, ОС, ОД є відповідно гео-
метричними зображеннями комплексних чисел: гг = 2 +
+ 2ї; г2 = —3 + 4г; г3 = —4 — Зг; = 4 — 2і.
Протилежним комплексним числам відповідають про-
тилежні вектори. На рис. 11.2 зображено дві пари проти-
356
лежних векторів ОА і ОС, ОВ і ОД, що відповідають парам
протилежних чисел 3 + 4/ та —3 — 4ї; —2 + Зі та 2 — Зі.
Обидва способи геометричного зображення комплексних
чисел рівносильні, бо будь-якій точці А координатної пло-
щини відповідає певний радіус-вектор ОА. Навпаки, кож-
ному радіус-вектору ОА відповідає певна точка — кінець
Геометричне зображення суми і різниці двох комп-
лексних чисел. З геометричної інтерпретації комплексних
чисел у вигляді векторів випливає можливість геометрич-
ного зображення додавання комплексних чисел. Воно зво-
диться до знаходження суми двох векторів за відомим
правилом паралелограма.
Нехай дано два комплексних числа гг = аг + Ьгі та
г2 = а2 4- Ь2і, яким відповідають радіуси-вектори ОАг
та 0Л2 (рис. 11.4). Побудуємо на цих векторах як на сто-
ронах паралелограм. Тоді зображенням суми комплексних
чисел гг і г2 буде вектор ОВ (діагональ паралелограма).
Справді, при додаванні векторів їх відповідні координати
357
додають. Тому вектор ОАг має координати (а^, Ьг), а вектор
ОАЯ — (а8; &а), їхня сума — вектор ОВ матиме координати
(ах + а2; Ьг + &»)• Вектор ОВ відповідає комплексному
числу (аі + а8) + (Ьх + і, яке е сумою чисел гг і г,.
Віднімання двох комплексних чисел геометрично озна-
чає віднімання відповідних радіусів-векторів. Віднімання
векторів, що мають спільний початок, полягає в додаванні
до вектора-зменшуваного вектора, протилежного від’єм-
нику.
Нехай, наприклад, треба знайти геометричне зображен-
ня різниці гг — г2 комплексних чисел гх = 2 + Зі та га =
= —3 + 2г'. Будуємо вектор
ОА, що є зображенням числа
гь і додаємо до нього век-
тор ОВі , який зображає число
22 == 3 — 2і, протилежне від’єм-
нику (рис. 11.5). Шукану різницю зображують вектором
ОС, що є сумою векторів ОА і ОВ^ Йому відповідає комп-
лексне число 5 + і.
Приклади. Подати геометричне зображення суми і
різниці двох комплексних чисел:
а) (2 + 4г) + (4 + 2г).
358
Розв’язання випливає з рис. 11.6. Доданкам відпові-
дають радіуси-вектори ОА і ОВ, а сумі — радіус-вектор ОС.
б) Зі + (—4 —Зі) (рис. 11.7);
Будуємо вектор ОС, що відповідає сумі двох перших
доданків, і додаємо до нього вектор ОО, що зображує тре-
тій доданок. Сумі даних комплексних чисел відповідає
вектор ОЕ (рис. 11.9).
д) (—2 + ЗО — (—5 + ЗО (рис. 11.10);
е) (4 + 30 —(—2 + 30 (рис. 11.11).
§ 4. Тригонометрична форма
запису комплексних чисел
Запис числа г у вигляді а + Ьі називають алгебраїчною
формою запису комплексного числа. Крім алгебраїчної фор-
ми використовують ще інші форми запису комплексних чи-
сел — тригонометричну і показнико-
ву. Розглянемо тригонометричну фор-
му запису, а для цього введемо понят-
тя про модуль і аргумент комплексно-
го числа.
Модуль комплексного числа. Побу-
дуємо радіус-вектор ОА, що є геомет-
ричним образом комплексного числа
2-а + Ьі (рис. 11.12). Модулем комплексного числа г =
= а + Ьі називають значення Ус? + Ь2.
Число г = У с? + Ь2 перетворюється в нуль тільки за
умов а = 0, Ь = 0. Модуль комплексного числа а + Ьі поз-
начають символом | а + Ьі |. Отже, | а + Ьі | = У а2 + Ь2.
359
Якщо комплексні числа мають один і той самий модуль,
то кінці векторів, які зображують ці числа, лежать на колі
з центром у початку координат і радіусом, що дорівнює
їхньому модулю.
Приклади. Знайти модулі даних комплексних чисел:
а) 15 + 71 | = V 25 + 49 = /74;
б) | - 2— 3/| = 1^4 + 9 = /ІЗ;
в) |8+ 0і| = / 82 + 0 = 8;
г) |5і| = |5|.
Аргумент комплексного числа. Нехай радіус-вектор
ОА зображує комплексне число 2 = а + Ьі (див. рис. 12.12).
Позначимо через а кут, який утворює вектор ОА з додат-
ним напрямом осі х. Числове значення кута а, виміряного
в радіанах, називають аргументом комплексного числа
а + Ьі. Якщо комплексне число дорівнює нулю, то вектор
ОА перетворюється в точку (нуль-вектор) і говорити про
його напрям немає смислу. Тому вважають, що число нуль
не має аргументу. Кожне відмінне від нуля комплексне
число має нескінченну множину значень аргументу, які
відрізняються одне від одного на ціле число повних обер-
тів, тобто на величину 2шг, де п — довільне ціле число.
Значення аргументу, взяте в межах першого кола, тобто
від 0 до 2л, називають головним. Головне значення аргу-
менту а комплексного числа х = а + Ьі можна визначити
з рівності а = —. Справді, за знаками а і Ь можна ви-
значити, в якій чверті знаходиться кут а, і за величиною
а, використовуючи таблиці, знайти величину кута а.
Приклади. Знайти головне значення аргументу а комп-
лексних чисел:
а) г = 1 + і.
Маємо а = 1. Оскільки а = 1 та Ь — 1, то радіус-
вектор, який відповідає даному комплексному числу, на-
лежить І чверті. Тому а — гострий кут. Отже, а =
б) з = —2+ 2/ЗЇ .
Маємо і § а — 2_^23 = — /3. Тут а = — 2, Ь = 2 /З,
тобто радіус вектор, який відповідає даному комплексно-
2
му числу, належить II чверті. Отже, а = -д-л;.
в) 2 = —1 — і.
360
Маємо а — 1. Радіус-вектор, що відповідає даному
5
комплексному числу, належить III чверті. Отже, а =-уЛ.
г) 2 = 1 — КЗІ.
Маємо і§ а = — /3. Тут а = 1, Ь = — /З, тобто
радіус-вектор, що відповідає даному комплексному числу,
належить IV чверті. Отже, ос = -у я.
Тригонометрична форма комплексного числа. Нехай
—
вектор ОА є геометричним зображенням комплексного чис-
ла х = а + Ьі (рис. 11.12), модуль якого дорівнює г, а
аргумент а.
У прямокутному трикутнику А ОС а = г соз а, Ь =
= г зіп ос. Підставляючи у запис комплексного числа за-
мість а і Ь їхні значення, виражені через модуль і аргумент,
дістанемо
2 — г соз ос + г зіп а і = г (соз а + і зіп а).
Вираз г (соз а + і зіп а) називають тригонометричною
формою комплексного числа.
Будь-яке комплексне число а + Ьі, подане в алгебраїч-
ній формі, можна записати у тригонометричній формі.
Модуль г знаходимо за формулою г — Ка2 + Ь2, а кут
. , ь ,
ос визначаємо із залежності ос = —, яка випливає з фор-
а . . Ь
мул соз ос = — і зш а = —.
Приклади. Записати комплексні числа у тригонометрич-
ній формі:
а) х == —2 + З/.
г = у(— 2)а н- 3а = /13 ,
а=агсі§(-----1-) ^а<0, &>0,
За таблицями або за допомогою калькулятора знаходи-
мо а «124°. Отже, г_= /13 (соз 124° + і зіп 124°).
X б) г = —1 — /Зі.
г = V(- 1)2 + (-/3)а = 2, а = /З,
а = агсі§ /З, а = -у- + ял (п £ 7).
Оскільки радіус-вектор, який зображує число х = —1 —
— УЗ/, розміщений у III квадранті комплексної площини,
361
то за аргумент беремо а = -у 4- я. Отже, —1 — 1/~3і =
л / 4л ... 4л \
«2 ( СОЗ -X-Н І 81П -з- .
\ о о /
в) г =* 3 — Зі.
г = /32Д-(—З)2 = /18 = 3 /2.
Знайдемо
а З 1 /5 , Ь =
соз а = — — —т=- = —та— = -V-, зіп а — —
г 3/2 /2 2 '
_ -3________/2
3/2 2 ’
соза>0, а зіпа<0. Тому кут а належить IV чвер-
ті, а= -у- . Отже, 3 — Зі — 3 /2(соз-у- 4- і зіп -у-).
г) г = — 2/3— 2і.
г = )/"(- 2 /З)2 4- 22 - /Ї2+1 = 4.
Знайдемо
— 2/3 /з . — 2 1
СО5а =--------------, 51па = .
соз а < 0, зіп а < 0. Тому кут а належить III чверті, а =
= . Отже, — 2 /5 — 2І = 4 /соз 4- і зіп -5-').
о І о о /
д) г = і.
Тут а = 0, Ь = 1. Отже, 1. Вектор, що зображує
число і, утворює з віссю абсцис кут у- (поясніть чому).
Отже, І = СОЗ -у 4* і 8ІП -у.
е) 2 = 3.
Тут а = 3, 6 = 0. Отже, г = г, 3 = 3 (соз 0 4-і зіп 0).
Розглянемо приклади переходу від тригонометричної
форми комплексного числа до алгебраїчної.
Приклади.
а) 2 (соз 4- і зіп -у) = 2 (-у 4- -^у- і) = 1 4- /З і;
. ( 2л ... 2л \ . ( 1 . /З Д о ,
б) 4 (^соз — 4-»Зіп -у-^ = 4 | — -у 4- -у- ^ = — 2 4-
4- 2 /3 і.
Множення і ділення комплексних чисел, записаних
у тригонометричній формі. Тригонометрична форма запису
362
комплексних чисел виявляється дуже зручною при мно-
женні і діленні чисел. Нехай = гх (соз ах + / зіп ах) і
г2 = г2 (соз а2 + і зіп а2) — два числа, що записані в
тригонометричній формі. Тоді
гхз2 = гіг2 (соз аі соз а2 — зіп ах зіп а2 +
+ і зіп ах соз а2 + і соз ах зіп а2),
або
гхг2 = гхг2 (соз (ах + а2) + і зіп (ах + а2)).
Отже, справедливим є таке твердження: при множенні
комплексних чисел в тригонометричній формі модулі їх
перемножають, а аргументи додають.
Для знаходження частки множимо чисельник і знамен-
ник на число, спряжене до знаменника:
гх __ гг (соз ах + * зіп ах) (соз сс2 — * зіп аг) _
г2 га (соз а2 + і зіп а2) (соз а2 — і зіп а2)
_ гх соз (ах — а2) + і зіп (ах — а2) __ гх ( ( ,
“ 7~ соз2 а2 + зіп2 а2 ~ г2 ^С08 +
+ І зіп (ах — а2)).
Отже, при діленні комплексних чисел їх модулі ділять,
а аргументи віднімають.
Приклади. Виконати множення і ділення комплексних
чисел, записаних у тригонометричній формі:
а) = 3 (соз 7° 4- і зіп 7°), г2 = 8 (соз 15° + і зіп 15°).
Знайдемо г = Зі • г2. Маємо | г | = 3 • 8 — 24; 7° +
+ 15° = 22°, тобто г = 24 (соз 22° + і зіп 22°).
б) гх = У~7 (соз 50° 4- і зіп 50°), г2 = З К14 (соз 28° 4-
4- і зіп 28°), г3 = (соз 92° 4- і зіп 92°).
.— ------
Знайдемо г = Маємо | г | = у 7 • 3 у 14 • -у— =
= 6; 50° 4- 28° 4- 92° = 170°, тобто г = 6 (соз 170° 4-
4- і зіп 170°).
/ я
І СОЗ — — і 81П
В)------------7-
я я '
СОЗ — + І ЗІП -0-
Зя Зя \
СОЗ —4— + І ЗІП —4— І
Змайдемо модуль шуканого числа 1 • 2: 1^2 = К2 і
я . я Зл ' 11
аргумент —г4- --------Г "“ТГ11'
Отже, г = И2 / соз (--Ц- я'і 4- і зіп (-.
363
Подамо без доведення правила піднесення до степеня
комплексного числа, записаного в тригонометричній фор-
мі, і добування з нього кореня ?
При будь-якому натуральному п
(соз а + і зіп а)п = соз па + і зіп па.
Це твердження називають формулою Муавра.
Корінь п-го степеня з числа 2 = г (соз а + і зіп а)
обчислюють за формулою
п г- І а + 2£л С . . а 4- 2/гл \
СО = х/7 соз ——------ + І ЗШ —-2----- ,
V 1 ’у П П ) *
де к — деяке ціле число.
Підставляючи замість к зна-
чення 0, 1, 2, п — 1, діста-
немо п різних значень кореня.
Так, при п = 2, к = 2 матимемо
. а 4- 4л . а .
зіп -у—= ЗШ у 1 Т. д.
Приклади. Виконати дії під-
несення до степеня і добування
кореня з даних комплексних чи-
сел:
а) 2 = КЗ — ї. Обчислити г9.
Модуль даного числа дорівнює ]/"(Кз)2 + І2 = 2, ар-
гумент а = —у Отже, модуль числа 29 дорівнює 29, а
з
аргумент 9а = —п. Отже,
(]/3 — і)9 = 29 (соз (-+ і зіп (------= 5121.
б) Знайти всі значення уТ.
Оскільки 1 = 1 (соз 0 4- і зіп 0), то
5/7-7--7ГІ—• •< і І 0 4-2&Л . . . 0 4-2£л \
V 1 (соз 0 + і зіп 0) = 1 соз —---Ь і зш —,
к = 5, 1, 2, 3, 4.
Надаючи к послідовно значень 0, 1, 2, 3, 4, відповідно
дістанемо:
= 1 при к — 0;
г2 = соз -у + і зш -у при к = 1;
364
‘ІЗ І . . • 1 п
г3 = соз —~—Ь і зіп —г- при к = 2;
о □
~ 6л ... 6л і. о
2а = соз -її- + ь зіп —д- при к = 3;
□ о
8л ... 8л < л
гб = соз—+ і зіп —=— при к = 4.
о □
5г-
Цікавим є такий факт. Модулі всіх цих значень у 1 до-
рівнюють І. Отже, точки гь г2, г8, г4, г5 лежать на колі радіуса
1 з центром у початку координат. Побудувавши аргументи
значень гь ..., г5, помічаємо, що точки, які зображують
числа Хі, г5, є вершинами правильного п’ятикутника
(рис. 11.13).
Взагалі, точки, які відповідають значенням кореня п-го
степеня з комплексного числа г = г (соз <р + і зіп <р), роз-
міщуються у вершинах правильного п-кутника з центром
у точці 0.
Історична довідка
Комплексні числа виникли із практики розв’язування алгебраїч-
них рівнянь. При розв’язуванні квадратного рівняння у випадку, коли
його дискримінант від’ємний, корені не можуть бути дійсними. Те саме
спостерігалося і при розв’язуванні рівнянь вище другого степеня, тому
постала необхідність у розширенні поняття числа.
З комплексними числами вперше зіткнулися індійські вчені, які
вже мали поняття про квадратний корінь і від’ємні числа. Але вони вва-
жали, що квадратні корені з від’ємних чисел не існують, атому квадрат-
ні рівняння з недійсними коренями не розглядали.
У XVI ст. італійські математики зробили значний внесок у розви-
ток алгебри, розв’язавши в радикалах рівняння третього і четвертого
степенів. Зокрема, в опублікованій у 1545 р. праці італійського матема-
тика Джироламо Кардано (1501—1576) «Велике мистецтво» наведено
формулу алгебраїчних розв’язків кубічного рівняння х3 + рх + д —
= 0. Цікавим є такий факт: за умови, що всі коефіцієнти такого рівнян-
ня дійсні, усі корені дійсні, проміжні обчислення приводять до уявних
чисел (їх називали «фальшивими», «неіснуючими»). Відповідний випа-
док розв’язування згаданого кубічного рівняння називали «незвідним».
У зв’язку із застосуванням формули Кардано з’явилися символи виду
а ± К—Ь (Ь > 0), яким спочатку не надали будь-якого смислу, але ни-
ми оперували у проміжних викладках, поширюючи на них правила дій
з дійсними числами.
Інший італійський математик Раффаеле Бомбеллі (1530—1572)
вперше виклав правила дій над комплексними числами майже у сучас-
ному вигляді. Рене Декарт, який ототожнював дійсні числа з відрізка-
ми координатної осі, вважав, що для комплексних чисел не може існу-
вати жодного реального тлумачення, а тому вони назавжди залишаються
уявлюваними. Такого погляду дотримувалися й інші математики того
часу, у тому числі Ісаак Ньютон (1643—1727) і німецький учений Гот-
фрід Вільгельм Лейбніц (1646—1716).
У XVII ст. англійський математик Джон Валліс (1616—1703) у
своїй праці «Алгебра, історичний і практичний трактат» (1685) вказав
365
на можливість геометричного тлумачення уявних чисел. Лише у
XVIII ст. для розв’язання численних задач математичного аналізу,
механіки і геометрії виникла потреба у геометричній інтерпретації ком-
плексних чисел.
Початок застосування комплексних чисел в диференціальному та
інтегральному численні поклали Лейбніц і швейцарський математик
Іоганн Бернуллі (1667 — 1748), які ше в 1702 р. чисто формально викорис-
товували логарифми уявних чисел для інтегрування дробів з уявними
знаменниками. В 1712 р. між Лейбніцем га І. Бернуллі виникла супе-
речка щодо природи логарифмів комплексних і від’ємних чисел. Лейб-
ніц стверджував, що логарифми від’ємних чисел уявні, а І. Бернуллі
вважав, що вони дійсні. Це питання розв’язав у 1749 р. Ейлер на ко-
ристь Лейбніца. Формула (соз ф ± і зіп ф)л = соз пф + і зіп пф була
здобута у першій чверті XVIII ст. англійським ученим Абрахамом де
Муавром (1667—1754). У сучасному вигляді цю формулу навів Ейлер
у «Вступі до аналізу», користуючись замість символа і загальновживаним
у ті часи символом У — 1.
Цікаво що Лейбніц, називаючи комплексні числа «притулком бо-
жественного духу», заповів викарбувати на своїй могильній плиті знак
У—1 як символ потойбічного світу.
Символ і було введено Ейлером у 1777 р. (опубліковано у 1794 р.).
Поняття «модуль» і «аргумент» комплексного числа ввів французь-
кий учений Жан Лерон Д’Аламбер (1717—1783). Самі ж ці терміни було
введено у XIX ст. швейцарським математиком Жаном Робертом Арга-
ном (1768—1822) і французьким математиком Огюстеном Луї Коші
(1789—1857).
Геометричне тлумачення комплексних чцсел і дій над ними остаточ-
но закріпилось у математиці лише після виходу*, у 1831 р. праці німець-
кого математика Карла Фрідріха Гаусса (1777—1855) «Теорія біквадрат-
них лишків». Гаусе замінив назву «уявні числа» на термін «комплексні
числа».
В 70-х роках XVIII ст. Ейлер і Лагранж застосували поняття ком-
плексної змінної до розв’язання багатьох задач, зокрема задачі побудо-
ви геометричних карт. Комплексні числа застосовували у своїх роботах
з гідродинаміки Д’Аламбер та Ейлер.
За допомогою теорії функцій комплексної змінної, яка розвинула-
ся на основі комплексних чисел, було розв’язано багато проблем аеро-
і гідродинаміки, теорії пружності, радіотехніки та ін.
У нашій країні ці питання досліджували М. Є. Жуковський (1847—
1921), М. В. Келдиш (1911—1978), М. О. Лаврентьєв (1900—1980) та
інші вчені.
Запитання і завдання для повторення
1. Чи завжди можна добути корінь у множині всіх раціональних
чисел? У множині всіх дійсних чисел?
2. Сформулювати вимоги, яких треба дотримуватися при розши-
ренні множини дійсних чисел.
3. Сформулювати закони додавання і множення чисел, дотриман-
ня яких є обов’язковим на всіх етапах розширення поняття числа.
4. Чим викликана потреба розширення множини дійсних чисел?
5. Дати означення комплексного числа. Показати, що множина
дійсних чисел є підмножиною множини комплексних чисел.
6. Сформулювати умову рівності двох комплексних чисел. Чи мож-
на довести цю умову?
366
7. Дати означення спряжених комплексних чисел і навести прикла-
ди таких чисел.
8. Подати у вигляді формул правила чотирьох арифметичних дій
для чисел а + Ьі та с + <&’•
9. Чи може сума, різниця, добуток і частка двох комплексних чисел
дорівнювати дійсному числу? Навести приклади.
10. Чому дорівнює сума і добуток двох спряжених комплексних
чисел?
11. Розкласти на комплексні множники вирази: т2 + п2; х + у\
с + 3.
12. Скільки різних степенів має уявна одиниця?
13. Обчислити степені: і17, і18, і19, /20.
дроби: Д-; -к; -к; _к?
І І2 І3 г
14. Чому дорівнюють
15. Чи треба доводити справедливість основних законів прямих
арифметичних дій для комплексних чисел?
16. Чи коректним буде таке завдання: порівняти за величиною па-
ри чисел 4/ та 7і, К—5 та К—Ю?
17. Довести, що квадрат комплексного числа а + Ьі є дійсним чис-
лом тоді і тільки годі, коли або а = 0 або Ь = 0.
18. Скільки існує значень кореня квадратного з —1? Обгрунтуй-
те свою відповідь.
19. Довести, що теорема Вієта правильна для будь-якого квадрат-
ного рівняння з дійсними коефіцієнтами.
20. Відомо, що квадратне рівняння з дійсними коефіцієнтами має
один комплексний корінь. Що можна сказати про другий його корінь?
21. Яка відповідність існує між комплексними числами і точками
площини?
22. Як геометрично'можна інтерпретувати комплексні числа?
23. В яких чвертях містяться точки, що зображують комплексні
числа: 4 — /; —3 + 4г, —5 — 4 і; 6 — 7 і?
24. Які числа відповідають точкам осі х, осі у?
25. Що можна сказати про взаємне положення точок, які зобра-
жують спряжені комплексні числа, протилежні комплексні числа?
26. Як можна геометрично інтерпретувати додавання і віднімання
двох комплексних чисел?
27. Дати означення модуля комплексного числа. Який його гео-
метричний зміст?
28. Комплексне число помножили на 2. Чи змінився модуль цього
числа?
29. Чому дорівнюють модулі чисел: і; —£; 1; —1; 0.
ЗО. Що таке аргумент комплексного числа?
31. Як визначити головне значення аргументу числа г — Ьі?
32. Чи можуть аргументом комплексного числа бути одночасно ку-
ти а і —а?
33. Знайти геометричне місце точок площини, які зображують ком-
плексні числа з однаковими модулями.
34. Чи може модуль комплексного числа дорівнювати У—2?
35. Як розміщуються на площині точки, що зображують комп-
лексні числа з однаковими аргументами?
36. Як подати комплексне число виду а + Ьі у тригонометричній
формі? Як знайти модуль і аргумент цього числа?
37. Як перейти від тригонометричної форми комплексного числа до
алгебраїчної?
367
38. Вивести правила множення і ділення комплексних чисел, запи-
саних у тригонометричній формі.
39. За яким правилом виконують дію піднесення до степеня ком-
плексних чисел, записаних у тригонометричній формі?
40. За якою формулою можна обчислити корінь п-го степеня з чис-
ла з = г (соз а + і зіп а)?
Вправи
1. Виконати додавання і віднімання комплексних чисел:
А
1) (2+ 0+(3+ 0+ (—4+50; 2) (5+ ЗО — (2+ 0;
3) (0,8 — 0,2/) + (0,1 — 1,3/) — (1,5+ 0,7/) — (2,3 — 0,6/);
Б
4) 8 + (2 — 9/) + 4/ + (—2 — 8/);
/2 1 \ / 1 1 \
5) (т~ 5 12 ~ 4 ф
6) (5х — Зуі) + (— 2х + Зуі) — (2х — уі) + (7х — 2уі);
В
7) (2а — ЗЬі) + (— а — Ьі) + (4а + 2Ьі) - (2а — 5Ьі);
8) (2с — 84і) — ((5с — 2<іі) + (с — гіг) — (— 4с + ЗЛІ));
„ / 1 1 \ ( 3 2 \ / 3 5 \
9) (Т“Т /5" + Т ‘)+( 4 “ 6
2. Виконати множення і ділення комплексних чисел:
А
1) (3 + 7і) (2 + 0; 2) (У~2 - і) (1 + 2і);
3) (3 4- 4і) : (5 — 2г); 4) 5 : (1 + 2г); 5) (2 + Зі) (2 — Зі);
Б
6) (/2-і)(/3 + /2 і); 7) (-т + +')(4—4"‘):
8) (1 - і) : (1 + і); 9) (5 - /2 і) : (5 + /2 і);
і 7 З \І 7 3 \
10Ц 8 + 4 1Д 8 — 4 :
В
11) (4 + / Зі) (2 /З — /Зі); 12) (а + ЗЬі) (2а — Ьі);
13) (1 + /Зі) : (1 - /Зі); 14) (5 - 7і): (/3 + і);
15) (Vт + /пі) : (/й - /лі).
3. Подати вирази у вигляді добутку двох спряжених комплексних
чисел:
А
1) а2 + 962; 2) 0,64 + 0,49 х2; 3) а + 25;
Б
16 1
4)62 + -25-; 5)3 + х; 6)7 + -д-;
368
в
7) х4 + 4; 8) х* + у\ 9) 17.
4. Спростити вирази:
А
1) З/3; 2) 2/?;
Б
3) 7І24; 4) 5/У4;
В
5) 10/111; 6) 15+ 9/2 — /2і.
5. Піднести до степеня:
А
1) (3 + 2»)2; 2) (1 + О4; 3) (1 + і)»;
Б
4) (2 + /зо2; 5) (1 + о8; 6) (2 + 503;
В
6. Розв’язати рівняння:
А
1) х2 — 12х + 45 = 0; 2) 2х2 — х + 3 = 0;
Б
3) х2 + 6х + 18 = 0; 4) Зх2 + 2х + 27 = 0;
В
5) Зх2 + 7х + 5 = 0; 6) з2 — 2/г —5=0.
7. Виконати додавання і віднімання комплексних чисел у геомет-
ричній формі:
А
1) (2+ 3/)+ (1+ 4/); 2) (4+50-(2-ЗО;
Б
3) (-4 + 20 + (4 - 20; 4) (-4 + 0 - (1 + 40;
В
5) (2 + 40 + (3 — 50 + (-1 + 60; 6) (—2 + ЗО - (—5 + ЗОн
8. Знайти модулі і головні аргументи комплексних чисел:
А
1)г=1+/30 2)г = —І4-/З1;
Б
3)г=24-2/30 4) г = ——-ЕА 0
369
в
5) г = —і\ 6) 2^ -|- ?2, де 2$ = 3 -|- 4/, г2 = — 3 + 2/.
9. Подати у тригонометричній формі числа:
А
1) 2 = - /2 + 2) 2 = 5г, 3) 2 = 2;
Б
4) 2 = /3 — 1\ 5) 2 = —2/; 6) 2 = —3;
В
„— 10л 10л
7) г = — 1 — 1^3 і; 8) 2 = і17; 9) г = 1 -|- соз д + *8іп —' •
10. Подати у алгебраїчній формі комплексні числа, записані у три-
гонометричній формі:
А
\ п і) І» \
соз -у 4- і зіп -у І; 2) 2 = У 2 І соз — + і зіп —1 ;
Б
2л 2л \
3) г = 40 У ЗІ соз —у + і зіп -у-1; 4) г = 2 (соз 0 + і зіп 0);
В
5) г = 5 У2 (соз 315° + і зіп 315°); 6) 2 = 7 (соз л + і зіп л).
11, Виконати множення і ділення комплексних чисел, записаних
у тригонометричній формі:
А
1) Зі = 0,5 (соз 75° +/зіп 75°), г2 = 6 (соз 35°+ і зіп 35°);
, /*х ( Н . Л \ /-•— (ті Л
2) гг = У 2 І соз -у- + і зіп -у-1, г2 = У ЗІ соз -у- + і зіп -у
Б
3) = 10 (соз 107° + і зіп 107°), г2 = 13 (соз 42° + і зіп 42°);
5л 5л 13л 13л
4) 2і = соз -уу + і зіп -уу- , г2 = соз —уу + і зіп -- ; 5 * * * * * *
В
5) г, = 3 /2 (соз 100° + і зіп 100°), га = -ІЛ.
(соз 5° + і зіп 5°);
6) *ї =
СОЗ -у- — І ЗІП -у-еКЗ + 0
1
12. Піднести комплексні числа до степеня, користуючись форму-
лою Муавра:
[ 6л І 6л \\б
1) (1 +012; 2) 2= ^зіп-у+Ц 1 + соз -у .
370
13. Знайти значення кореня з комплексних чисел:
1) у о, де (ь = 16 (соз я + і зіп я);
2) 3/2=2І; 3) У=4.
РОЗДІЛ 12
ПОВТОРЕННЯ КУРСУ АЛГЕБРИ ОСНОВНОЇ ШКОЛИ
§ 1. Дійсні числа і дії над ними
!• Натуральні числа. Поняття натурального числа ви-
никло з потреб лічби та вимірювання величин. Числа 1, 2,
З, які використовують при лічбі, дістали назву нату-
ральних. Такими числами позначають також наближений
результат вимірювання величин, коли одиниця вимірю-
вання вміщується у вимірюваній величині ціле число разів.
Наприклад, довжина кімнати 5 м. Наближене значення
довжини тут виражене натуральним числом 5.
Поняття натурального числа, як і поняття точки, пря-
мої і площини в геометрії, належить до основних понять,
які вводять без означення.
Натуральні числа записують за допомогою десяти цифр
(символів) 0, 1,2, 3, 4, 5, 6, 7, 8, 9. При цьому викорис-
товують спосіб запису, який дістав назву десяткової си-
стеми. В його основу покладено поняття розряду і основна
властивість десяткової системи Назви розрядів у порядку
зростання такі: розряд одиниць, десятків, сотень, тисяч
і т. д. Відповідні назви мають одиниці розрядів: 1 — оди-
ниця розряду одиниць, 10 — одиниця розряду десятків,
100 — одиниця розряду сотень і т. д.
Якщо у числі немає одиниць якого-небудь розряду, то
на місці такого розряду записують цифру 0. Наприклад,
у числі 302 125 одиниць 5, десятків 2, сотень 1, тисяч 2,
десятків тисяч 0, сотень тисяч 3.
Кожні десять одиниць будь-якого розряду утворюють
одну одиницю вищого розряду, що стоїть поруч з ним зліва.
Основна з властивостей десяткової системи запису нату-
ральних чисел полягає в тому, що кожна одиниця певного
розряду у 10 разів менша одиниці сусіднього вищого розря-
ду, що стоїть ліворуч, і у 10 разів більша одиниці сусідньо-
го розряду, що стоїть праворуч (крім розряду одиниць).
З цієї властивості випливає, що значення кожної цифри за-
лежить від місця (позиції), яке ця цифра займає у запису
371
числа. Наприклад, цифра 2 у числі 6 302 872, що стоїть
на першому місці, рахуючи справа наліво, показує кіль-
кість одиниць. Та ж цифра 2, що стоїть на четвертому місці,
показує кількість тисяч.
У десятковій системі запису чисел для читання нату-
ральних чисел число розбивають на класи справа наліво.
Клас — це група цифр по три цифри у кожній Назва кла-
су походить від назви останнього розряду, який в даному
класі стоїть праворуч. Зокрема, клас одиниць містить циф-
ри трьох перших розрядів (одиниць, десятків, сотень),
клас тисяч включає цифри наступних трьох розрядів (ти-
сяч, десятків тисяч, сотень тисяч), наступний — клас
мільйонів і т. д.
Клас від класу прийнято відокремлювати невеликою
відстанню. Найвищий клас може виявитись неповним,
тобто може містити дві або одну цифру. Наприклад, число
6 302 872 має три класи: одиниць, тисяч і мільйонів.
У класі мільйонів — лише одна цифра 6.
Щоб прочитати багатоцифрове число, треба:
1) розділити число на класи по три цифри в кожному
справа наліво;
2) якщо найвищий клас містить три цифри, то прочитати
зліва направо кожний клас як тризначне число і додати
назву класу, назва останнього класу (класу одиниць) не
додається;
3) якщо найвищий клас містить одну або дві цифри, то
прочитати його як однозначне або двозначне число і дода-
ти назву цього класу.
При порівнянні багатоцифрових натуральних чисел
керуються такими правилами:
з двох натуральних чисел із різною кількістю цифр біль-
шим є те, у якому більше одиниць найвищого розряду;
якщо цифри найвищого розряду одинакові, то порівнюють
розряди на одну ступінь нижче і т. д.;
результат порівняння двох різних чисел записують
у вигляді числової нерівності за допомогою знаків «<»
(менше) або «>» (більше), наприклад, 12 <21; 132 >
>98.
Додавання натуральних чисел, використовуючи нату-
ральний ряд чисел, можна тлумачити так: додати два на-
туральних числа т і п означає знайти в натуральному ряді
число р (р > т), що знаходиться на п-му місці від числа
т, якщо лічбу починати з т + 1. Це число р називають
сумою чисел т та п і позначають т + п. Числа т і п при
цьому називають доданками.
372
Помножити число т на число п (п 2) означає знайти
суму п однакових доданків, кожний з яких дорівнює /тг,
т • п = т + т + ••• + т.
п доданків
При п = 1 за означенням вважаємо, що добуток т X
X п дорівнює першому співмножнику т, тобто т • 1 =
= пі.
Дії віднімання і ділення можна тлумачити як дії, обер-
нені до додавання і множення, а саме:
1) відняти від числа т число п означає знайти таке
число х, що х + п = т\ число т називають зменшеним,
п — від’ємником, число х, а також вираз т — п назива-
ють різницею;
2) розділити число т на число п означає знайти таке
число х, що п • х = т\ число т при цьому називають
діленим, п — дільником, число х, а також вираз т : п
називають часткою.
Будь-яке натуральне число можна записати у вигляді
суми розрядних одиниць. Наприклад,
6 302 872 = 6 000 000 + 300 000 + 2000 + 800 + 70 + 2.
На цій властивості грунтується розрядне додавання,
віднімання, множення і стовпчик. Приклади. а) , 2587 б) 867 698 + 369 “ 93 568 45 774 130 3001 ділення натуральних чис в) 5348 г) 623 455 х 605 ~ 470 26 740 1534 32 088 ~ 1410 ел у 235 2653
У множині 3 235 540 натуральних чисел завжди 1245 1175 705 — 705 0 можна викону-
вати дії додавання і множення, в результаті яких теж ді-
станемо натуральне число. Для цих дій виконуються
переставний і сполучний закони, а також розподільний
закон множення відносно додавання і віднімання:
а + Ь = Ь а, а • Ь = Ь • а,
(а + Ь) + с = а + (Ь + с), (а • Ь) • с = а • (Ь • с),
(а + Ь) • с = а • с + Ь • с9 (а — Ь) • с = а • с — Ь • с.
373
Якщо до множини натуральних чисел приєднати нуль,
то дістанемо розширену множину натуральних чисел. За
означенням
0-]~п=п-{-0 = п, 0 • п = п • 0 = 0,
0 + 0 = 0, 0-0 = 0, 01 п = 0.
На нуль ділити не можна.
Добуток одинакових співмножників, кожний з яких
дорівнює а, називається степенем числа а з натуральним
показником п 1:
а • а • а....а = ап.
п. співмножників
/ Вираз ап називається степенем, число а — основою
степеня, число п — показником степеня. За означенням
а1 = а.
При виконанні обчислень зручно користуватися озна-
ками подільності.
Ознака подільності на 2: на 2 діляться ті і тільки ті
числа, остання цифра яких парна.
Ознака подільності на 3 (9): на 3 (9) діляться ті і тіль-
ки ті числа, сума цифр яких ділиться на 3 (9).
Ознака подільності на 5: на 5 діляться ті і тільки ті
числа, у яких остання цифра або 5, або 0.
Ознака подільності на 10: на 10 діляться ті і тільки ті
числа, у яких остання цифра 0.
Якщо натуральне число ділиться на 1 і саме на себе (має
лише два дільника), то воно називається простим; якщо
число має хоча б один дільник, відмінний від одиниці і
самого себе, то воно називається складеним.
Будь-яке складене натуральне число можна розкласти
на прості множники лише єдиним способом. Звичайно, при
такому розкладі чисел використовують запис у стовпчик,
спираючись при цьому на ознаки подільності. При запису
у стовпчик дільники записують праворуч від вертикальної
риски, а частки — під діленим ліворуч від риски.
Наприклад, розклад чисел 4725 і 7875 має такий вигляд:
4725 3 7875
1575 3 2625
525 3 875
175 5 175
35 5 35
7 7 7
1 1
З
З
5
5
5
7
374
На практиці доводиться користуватись поняттям «най-
більший спільний дільник» і «найменше спільне кратне».
Дільником числа а називається число, на яке а ділиться
без остачі.
Запишемо всі дільники чисел 48 і 36: ,
1, 2, 3, 4, 6, 8, 12, 16, 24, 48; 1, 2, 3, 4, 6, 9, 12, 18, 36.
Випишемо спільні дільники для чисел 48 і 36:
1, 2, 3, 4, 6, 12.
Всі ці числа називають спільними дільниками чисел
48 і 36, а найбільший з них (число 12) називають найбіль-
шим спільним дільником і позначають О (36; 48) = 12.
Отже, найбільше натуральне число, на яке ділиться
кожне з даних чисел, називають найбільшим спільним діль-
ником цих чисел.
Щоб знайти найбільший спільний дільник двох або кіль-
кох чисел, необхідно:
1) розкласти дані числа на прості множники;
2) скласти добуток степенів всіх спільних простих
множників з найменшим показником;
3) знайти значення складеного добутку.
Приклад. Знайти О (4725; 7875).
Використовуючи наведений вище розклад даних чисел
на прості множники дістаємо
0(4725; 7875) = З2 • 52 • 7 = 1575.
Число Ь, яке ділиться на число а, називають кратним
числу а.
Запишемо у порядку зростання всі числа, кратні числам
6 і 9:
б, 12, 18, 24, ЗО, 36, 42, 48, 54 ...;
9, 18, 27, 36, 45, 54, 63, 72, 81 ....
Спільними кратними чисел 6 і 9 будуть 18, 36, 54, ... .
Найменшим із спільних кратних є число 18, яке позначають
так: К (6; 9) = 18.
Отже, найменше натуральне число, яке ділиться на кож-
не з даних чисел, називається найменшим спільним крат-
ним цих чисел.
Щоб знайти найменше спільне кратне двох чисел, необ-
хідно:
1) розкласти дані числа на прості множники;
2) скласти добуток степенів усіх простих множників
з найбільшим показником;
3) обчислити складений добуток.
375
Приклад. Знайти К (4725; 7875).
Використовуючи розклад даних чисел на прості множ-
ники, дістанемо
/<(4725; 7875) = З3 • 58 • 7 = 23 625.
2. Звичайні дроби. Всі дійсні числа можна поділити на
два класи: цілі і дробові. Дробові числа виникають у
зв’язку з необхідністю виразити числом результат вимірю-
вання різних величин (довжин, площ, кутових величин,
часу та ін.). Часто також доводиться знаходити частину
чисел чи кілька рівних
+ * ? ^”7 частин предмета (яблука,
0 ' з відрізка, прямокутника
Рис. 12.1 тощо).
Числа, які познача-
ють частину цілого, або разом ціле і частину цілого, діста-
ли назву дробових чисел.
Дробове число записують за допомогою звичайного дро-
бу або цілого числа і звичайного дробу. Наприклад,
1 1
2 ’ 5’3*
У звичайному дробі знаменник (число під рискою) пока-
зує, на скільки рівних частин розділене ціле, а чисельник
(число над рискою) показує, скільки таких частин взято.
Якщо чисельник звичайного дробу менший від знамен-
ника, то дріб називається правильним, а якщо чисельник
дорівнює або більший від знаменника, то дріб називається
2 3 12
неправильним. Дріб -у---правильний; дроби у, ------не-
правильні.
12
Зобразимо неправильний дріб -у на числовому промені
(рис. 12.1). З рисунка видно, що цей дріб має дві цілі оди-
ниці і ще одиниці. Отже, дробове число -=-можна запи-
□ о
12 2 2
сати у вигляді суми -у = 2 + у, а суму 2 + -----у ско-
2 12 2
роченій формі 2у, тобто — = 2у
Щоб виділити з неправильного дробу у цілу частину,
треба:
1) розділити чисельник т на знаменник и;
2) якщо остача від ділення т на п дорівнює 0, то не-
правильний дріб у зображує ціле число р;
376
3) якщо остача від ділення т на п дорівнює 7, то треба
записати дріб — у вигляді суми р + скорочено
14
Приклад. Виділити цілу частину дробу
14
Розв’ язання. 14:5 = 2 (остача 4); = 2 +
Отже, другим джерелом одержання дробових чисел є
ділення двох натуральних чисел, яке не виконується без
остачі.
Інколи доводиться виконувати обернене перетворення —
записувати число, що містить цілу і дробову частину, у
вигляді неправильного дробу. Для цього необхідно:
1) помножити ціле число на знаменник дробу;
2) додати до добутку чисельник дробу;
3) здобуту суму записати у чисельнику, а знаменник
залишити той самий.
2
Приклад. Перетворити у неправильний дріб число 5-уі
- 2 5 • 3 + 2 17
б— -------з— = —•
При порівнянні звичайних дробів з однаковими знамен-
никами більшим вважаємо той, у якого чисельник більший,
і меншим — той, у якого чисельник менший, рівними, якщо
чисельники обох дробів рівні. Тобто -у > якщо а>
а с а с
> с\ -т- = якщо а = с; -г- < -т-, якщо а < с.
о о о о
Щоб додати дроби з однаковими знаменниками, треба
додати їхні чисельники і залишити той самий знаменник,
тобто
а । с а-\- с
Ь ‘
Щоб відняти дроби з однаковими знаменниками, треба
від чисельника зменшуваного відняти чисельник від’ємни-
ка і записати той самий знаменник:
сс с а ~ с / ч
-г---т- = —т.— (а > с або а = с).
Ь о о ' '
Порівнюючи дроби з різними знаменниками використо*
вують означення: два дроби -у і називаються рівними,
377
1 1 тт 2 . 16
якщо аа = ос. Наприклад, дроби і рівні, оскільки
2 • 40 = 5 • 16.
Дроби з різними знаменниками порівнюють, попередньо
зводячи їх до спільного знаменника, 3 означення рівних
дробів випливає основна властивість звичайних дробів:
якщо чисельник і знаменник дробу помножити або розді-
лити на одне й те саме натуральне число, то дістанемо дріб,
рівнин даному: = -уу. Справді, дроби -у і уу рівні,
оскільки а • Ьт = Ь • ат.
Основну властивість дробу часто використовують для
скорочення дробів. Наприклад, дріб можна скоротити,
тобто розділити на найменший спільний дільник чисельни-
ка і знаменника, якщо вони не є взаємно простими числами.
Оскільки Р (16; 40) = 8, то 44 = т = 4г-
4 1 ’ 40 5-8 5
Основну властивість дробу використовують також при
зведенні дробів до спільного знаменника. Зводити дроби
до спільного знаменника необхідно при порівнянні дробів
з різними знаменниками, при їх додаванні і відніманні.
Якщо знаменники даних дробів взаємно прості числа,
то за спільний знаменник беруть добуток їх знаменників.
Наприклад, нехай треба звести до спільного знаменника
4 5
дроби -у і -у. Спільним знаменником даних дробів буде
5 • 7 = 35. Для зведення цих дробів до спільного знамен-
ника, досить чисельник і знаменник першого дробу помно-
жити на 7, а другого — на 5:
4 4-7 _ 28 е 5 _ 5 • 5 _ 25
5 ~ 5 7 ~ 35 ’ 7 “ 7 • 5 ““ 35 *
Якщо у знаменнику дробів маємо складні числа, то зви-
чайно дроби зводять до найменшого спільного знаменника.
Він дорівнює найменшому спільному кратному знаменни-
ків даних дробів.
Приклад. Звести до найменшого спільного знаменника
дроби і Маємо К (15; 12) = 3 • 5 • 22 = 60. Щоб
знайти додаткові множники, на які треба помножити чи-
сельник і знаменник кожного дробу, досить розділити
спільний знаменник на знаменник кожного дробу. Отже,
60 : 15 = 4 — додатковий множник першого дробу; 60 : 12 =•
= 5 — додатковий множник другого дробу. Тому
8 __ 8-4 _ 32 . 11 11 . 5 = 55
15 ~ 15 • 4 “ 60 ’ 12 ~ 12 . 5 ““ 60 ’
378
На практиці зручно користуватися таким правилом зве-
дення дробів до спільного знаменника:
1) знайти добуток знаменників даних дробів — їх спіль-
ний знаменник;
2) знайти додаткові множники до кожного дробу як до-
бутки знаменників решти дробів крім того, для якого шу-
каємо додатковий множник;
3) помножити чисельник кожного з дробів на відповід-
ний додатковий множник і записати спільний знаменник.
Щоб додати (відняти) дроби з різними знаменниками,
необхідно:
1) ввести кожний дріб до найменшого спільного знамен-
ника;
2) додати (відняти) чисельники утворених дробів, зали-
шивши той самий спільний знаменник;
3) скоротити здобутий дріб і виділити з нього цілу час-
тину, якщо це потрібно.
Приклади. Обчислити: 1) 4
Роз в’ язання.
7 . 7—7.5 7*4
12 ‘ 15 12 . 5 15 • 4
— 63 — 21
60 20
7 . 2ч 7 З
15 ’ "І?
8 ’
1) к (12; 15) = 22 • З • 5 = 60;
7
= 35 і 28
— 60 + 60
= 1 ~2б~ •
2) Я(12; 8) = 2* 3 = 24;
_ 14 9 5
~ 24 24 24 ’
При додаванні звичайних дробів, як і натуральних чи-
сел, виконуються переставний та 'сполучний закони:
а . с с , а /а . с\. т а . [с , т\
Т + "Г = Т + Т; + + = ~ + + —р
Щоб додати числа, що мають цілу і дробову частини,
треба:
1) записати кожний доданок у вигляді цілої і дробової
частини, звести дроби до найменшого спільного знамен-
ника;
2) відкрити дужки і, користуючись переставним і спо-
лучним законами, додати окремо цілі числа і дроби;
3) знайти суму здобутих результатів.
Щоб відняти числа, що мають цілу і дробову частини,
треба:
1) звести дроби до найменшого спільного знаменника;
379
2) відняти окремо цілі числа і дроби, якщо дробова час-
тина зменшуваного менша від дробу від’ємника, попередньо
одну одиницю зменшуваного зобразити у вигляді дробу і
додати її до дробу зменшуваного;
3) знайти суму здобутих результатів.
Приклади. 1) 5-|- +1 "ТГ (* 3 * 5 * 7 * * + 4) + (* + ‘к) =
— (5 + 1)4- 4~ ^2"] “ 6 4- 4- ~з§-) — 6 4- ~з§
с 29
6 36 ’
о\ і к І І і а 27 і£ 11*5 і 27 «З і р» 55
2) 15^- - 10^- = 15 -2ГТ- 10 -40ТТ= 15-120-
1Л 81 1л 175 1П 81 /ІЛ іт ! / 175
10 120 14 120 1 0 120 — (14 10 * *)4д !20
120 / ^ 60 60 ’
Щоб перемножити звичайні дроби, треба;
1) перемножити окремо їх чисельники і знаменники,
перший добуток записати у чисельнику, а другий — у
знаменнику;
2) скоротити утворений дріб і виділити в ньому цілу
частину, якщо це можливо.
п їх 3 5 13 5
Приклади. 1) — .-г = —= —;
9Х 2 7 _ 14 7 _ , 1
3 ‘ 4 12 6 6 •
Множення на дріб застосовують при знаходженні дробу
(частини) від числа: щоб знайти частину (дріб) від числа,
треба число помножити на цей дріб. х
Приклад. Знайти від: а) 75; б)
□ і
п ч 2 75 2 75 -2
Розв язання. а) 75 • -=- = —• -=- = —і—=- =
7 5 1 5 1-5
= = ЗО;
.,4 2 _ 4 • 2 _ 8
7 ' 5 7 • 5 ~ 35 *
При множенні чисел, що містять цілу і дробову части-
ни, їх необхідно попередньо перетворити у неправильний
дріб і перемножити за правилом множення звичайних
дробів.
380
п о 1 о 2 10 32 10 • 32 2 • 32
Приклад. З3-215— 3 • 15 — 315 — 3 . з —
_ 64 _ 7 1
~ 9 ~ ' 9 ’
При множенні дробів, як і натуральних чисел, викону-
ються переставний, сполучний і розподільний закони:
а с ____ с а , Iа с \ т ____ а І _2_ т \.
Ь (1 (і Ь 9 І Ь і Г п Ь \ сі п ) ’
( а _ с \ т __ а т __ с т
& сі ) п Ь п сі п ‘
При діленні на дріб використовують поняття взаємно
обернених чисел: два числа називаються взаємно оберне-
ними, якщо їхній добуток дорівнює 1.
Приклади. 1) Числа 2 і взаємно обернені, оскільки
9 А = А 1 _ 2 • 1 — і
’ 2 1’2 1-2
3 5 3 5
2 ) Числа -=- і -д- взаємно обернені, оскільки -=- . -д- =
о о о о
З . 5 _ .
5 • 3 ~
( Щоб розділити одне число на друге, треба ділене помно-
жити на число, обернене до дільника.
п 18 8 18 25 18-25 9-5
Приклади. 1) ——= -г^-=_==
= ^=ц2_.
4 4 ’
о\ 3 . л _ 3 , 6 _ 3 1 _ 3' 1 _ 1 .
4 ’ ° 4’1 4 ’ 6 ~ 4-6 8 ’
з) 124=12.4=4-.4=44 = 18.
Ділення на дріб використовують при знаходженні числа
за значенням його дробу (частини). Щоб знайти число за
даним значенням його дробу, треба задане число розділити
на цей дріб.
з
Приклад. поля становить 27 га. Знайти площу всього
поля.
п о_ З о- 4 27 4
Розвязання. 27: = 27 • -о- = —г- • -т- =
4 3 13
27-4 ч
= -утз- = 36 (га).
381
3. Десяткові дроби І наближені обчислення. До поняття
десяткового дробу можна прийти, поширивши праворуч
від розряду одиниць основну властивість десяткової систе-
ми запису чисел: кожна одиниця певного розряду у 10 ра-
зів менша одиниці вищого розряду, що стоїть ліворуч і
у 10 разів більша одициці сусіднього розряду, що стоїть
праворуч.
Навіщо треба розглядати розряди в 10, 100, 1000 разів
менші 1? Звернемося до метричної системи мір. Припусти-
мо, що ширина класу (з точністю до 1 дм) дорівнює
б м 1 дм. Запишемо ширину класу у метрах. Дістанемо
6 м 1 дм = 6~- м. Якщо виконати вимірювання з точністю
до 1 см, то дістанемо 6 м 15 см. Запишемо результат вимірю-
вання у метрах: '
1 5
6м15см = 6м + 1 дм + 5 см = 6 м + -ц)-м + м =
„ . 10 .5 „15
6м ** 100 М 100 М 6 1ОО м-
1 15
Дробові числа 6-уо" м і 6 м запишемо без знаменника
у вигляді 6,1 м; 6,15 м. Неважко помітити, що після цілої
частини числа і коми на першому місці стоїть розряд, оди-
ниця якого у 10 разів менша одиниці попереднього розря-
ду — розряду одиниць. На другому місці після коми стоїть
розряд, одиниця якого у 100 разів менша останнього роз-
ряду цілої частини і у 10 разів менша першого розряду
дробової частини. Відповідні назви розрядів після коми —
розряд десятих, розряд сотих і т. д. Таку форму запису
чисел називають десятковим записом числа, а самі числа,
записані у такій формі, дістали назву «десяткові дроби».
Цифри, що позначають розряди після коми, називають
десятковими знаками,
У скінченні десяткові дроби можна перетворити такі
числа, у яких знаменник дробової частини є або може бути
зображений одиницею з одним або кількома нулями. Якщо
знаменник дробової частини не можна так подати, то дро-
бове число перетворюється у нескінченний десятковий пе-
ріодичний дріб.
Щоб перетворити дробове число у десятковий дріб,
треба записати цілу частину, відділивши її комою, і знайти
дробову частину, поділивши чисельник дробу на знаменник.
У випадку нескінченного періодичного дробу ділення ви-
конують до певного десяткового знаку із заокругленням
частки.
382
Порівнюють десяткові дроби за тими ж правилами, що
і натуральні числа. Для цього треба:
1) порівняти цілі частини;
2) якщо цілі частини однакові, то порівнюють кількість
десятих частин;
3) якщо кількість десятих частин однакова, то порів-
нюють кількість сотих частин і т. д. Наприклад, 43,263 >
> 43,252.
Додавання і віднімання десяткових дробів, як і нату-
ральних чисел, виконують порозрядно у стовпчик. При
цьому треба стежити, щоб кома була розміщена під комою,
а однойменні розряди як цілої, так і дробової частин були
записані один під одним.
Приклади.
а) , 43,826 б) 23,825 в) 195,700
+ 8,523 — 7,947 — 28,425
52,349 15,878 167,275
Щоб перемножити два десяткових дроби, треба:
1) не звертаючи уваги на кому, виконати множення на-
туральних чисел;
2) в добутку відокремити комою стільки десяткових
знаків, скільки їх е в обох множниках разом.
Приклади.
а) 42,13 б) 2,03 в) 0,097
х 0,2 х 0,025 х 65
8,426 ,1015 , 485
+ 406 +582
0,5075 6,305
При множенні двох десяткових дробів першим множни-
ком зручніше записувати той, у якого більше цифр, не
враховуючи нулі на початку числа.
Ділення десяткових дробів на натуральне число і на де-
сятковий дріб виконують аналогічно діленню натуральних
чисел. При діленні на натуральне число, після того як
ділення цілої частини закінчено, у частці після останньої
цифри ставлять кому. Остачу перетворюють у десяті части-
ни і до них додають (зносять) число десятих з діленого і
т. д.
Щоб розділити число на десятковий дріб, треба в діле-
ному і в дільнику перенести кому праворуч на стільки
цифр, скільки десяткових знаків у дільнику, а потім ви-
конати ділення на натуральне число.
383
Приклади.
а) 283,015 23 б) 0,4212 8 в) 46,98; 1,16
_23 12,35 40 0,05265 4698 116
53 21 ~464 4^5
“46 . ~16 580
70 52 ~580
“69 ~ 48 0
115 40
~ 115 — 41 3
0 0
Наближені обчислення. Наближені обчислення вико-
нують тоді, коли компонентами дій є наближені значення
величин чи чисел, які здобуті шляхом заокруглення резуль-
татів вимірювання геометричних, фізичних, хімічних та
інших величин, використання .табличних значень, резуль-
татів виконання ділення, добування кореня з чисел, зна-
ходження значень тригонометричних функцій, логарифмів
чисел тощо.
У наближених обчисленнях доводиться користуватися
правилами округлення натуральних чисел та десяткових
дробів.
Правило. Щоб округлити натуральне число до певного
розряду, треба:
1) замінити нулями всі числа, що стоять після цього
розряду;
2) якщо наступна за цим розрядом цифра була 5, 6,7,8
або 9, то цифру розряду, до якого виконується округлення,
збільшити на одиницю; якщо наступна за цим розрядом
цифра була 0, 1, 2, 3 або 4, то цифру розряду, до якого ви-
конується округлення, залишити без змін.
Приклади. Округлити числа 752 781; 26436; 939 855;
6597; 4302: а) до розряду десятків; б) до розряду тисяч.
Р о з в’ я з а н н я. а) 752 781 « 752 780; 939 855 «
» 939 860; 26436 « 26440; 6597 « 6600; 4302 « 4200;
б) 752 781 ^753 000; 26436^ 26000; 939 855^940 000;
6597 ж 7000; 4302 4000.
При округленні десяткових дробів доцільно користува-
тися одним з двох правил.
Правило 1. Щоб округлити десятковий дріб до певного
розряду дробової частини (до певного десяткового знаку),
треба:
1) відкинути всі десяткові знаки, які стоять після цього
розряду; ,
384
2) якщо перта з відкинутих цифр була 5, 6, 7, 8 або 9,
то останню залишену цифру збільшити на одиницю;
3) якщо перша з відкинутих цифр була 0, 1, 2, 3 або 4,
то останню залишену цифру записати без змін.
Правило' 2. Щоб округлити десятковий дріб до певного
розряду цілої частини, вищого розряду одиниць, треба:
1) відкинути всі цифри дробової частини (всі десяткові
знаки);
2) цілу частину округлити за правилами округлення
натуральних чисел.
При округленні десяткового дробу до розряду одиниць
цифра цього розряду залишається без зміни чи збільшу-
ється на одиницю залежно від того, яким був перший з
відкинутих десяткових знаків.
У наближених обчисленнях використовують поняття
«абсолютна похибка», «відносна похибка» наближеного зна-
чення.
Абсолютною похибкою наближеного значення назива-
ється модуль різниці точного і наближеного значень числа
чи величини.
Якщо абсолютна похибка наближеного значення не пе-
ревищує числа й, то це значення називають наближеним
значенням з точністю до й.
Якщо х — точне значення і а—наближене значення
числа або величини, й — точність наближення, то викорис-
товують такий запис: х = а ± й.
Відносною похибкою наближеного значення називається
відношення абсолютної похибки до модуля наближеного
значення.
На практиці часто використовують правила наближе-
них обчислень без строгого урахування похибок, або так
званий спосіб підрахунку правильних цифр.
Правильною цифрою наближеного значення називають
цифру будь-якого розряду, якщо абсолютна похибка не
перевищує одиниці цього розряду.
Наближені значення-записують так, щоб усі цифри запи-
су були правильними. Такий запис дає уявлення про точ-
ність наближення. У таблицях усі значення записують ли-
ше правильними цифрами.
При виконанні дій додавання і віднімання в результаті
враховують кількість правильних десяткових знаків да-
них чисел. При цьому вважають, що дані наближені зна-
чення записані лише правильними цифрами.
Правило. При додаванні і відніманні наближених зна-
чень у результаті залишають стільки десяткових знаків,
13 1 — 1319
385
скільки їх має дане число з найменшою кількістю десятко-
вих знаків.
При виконанні дій множення і ділення в результаті під-
раховують кількість значущих цифр. Значущими цифрами
наближення, записаного у вигляді десяткового дробу,
називаються всі його цифри, крім нулів на початку числа.
Наприклад, у наближених значеннях 2,25; 0,317; 9,03;
12,0 по три значущі цифри; у наближеннях 76,28; 20,40;
0,009862 — по чотири значущі цифри.
-а а
ч---1—і—ьо—і---1---1-1---1—оч—і—і--н-
-5 -4 -3-2,7-2 -1 0 1 2 2}3 4 5 х
Рис. 12.2
Якщо наближене значення записане за допомогою нату-
рального числа, то його записують у стандартному вигляді
а • 10", залишаючи у десятковому дробі а лише правильні
цифри. Тут 1 10.
Наприклад, якщо у наближеному значенні 95 200 пра-
вильними є лише перші чотири цифри, то в стандартному
вигляді це число записують так: 9,520 • 104.
Правило. При множенні і діленні наближених значень
у результаті залишають стільки значущих цифр, скільки
їх має наближене дане з найменшою кількістю значущих
цифр.
При виконанні проміжних дій інколи користуються
«правилом запасної цифри»: в результатах проміжних дій
залишають на одну (запасну) цифру більше. В остаточному
результаті запасна цифра відкидається за правилами ок-
руглення.
4. Додатні і від’ємні числа. Додатні і від’ємні числа
були введені в математику в зв’язку з потребами практи-
ки — виражати числом значення величин, які можуть
змінюватися у двох протилежних напрямах (зміна темпера-
тури, рівня води у річці відносно умовного нуля, прибуток
і борг і таке ін.). В алгебру додатні і від’ємні числа було
введено у зв’язку з потребою виражати числом корінь рів-
няння виду а + х = Ь у випадку, коли Ь < а.
На координатній прямій (рис. 12.2) додатні числа зобра-
жують праворуч від точки, що зображує число 0, а від’єм-
ні — ліворуч.
Два числа, які відрізняються одне від одного лише зна-
ком, називаються протилежними. Наприклад: 5 і —5;
2,7 і —2,7; в загальному випадку а і —а. Протилежні числа
зображують на координатній прямій точками, симетрични-'
386
ми відносно початку відліку. Число 0 протилежне самому
собі.
Натуральні числа, протилежні їм числа і число 0 нази-
ваються цілими числами. Множину натуральних чисел
позначають буквою М, а множину цілих чисел — бук-
вою 2.
Цілі і дробові числа, як додатні, так і від’ємні, утво-
рюють множину раціональних чисел, яку позначають бук-
вою £. Будь-яке раціональне число, як ціле, так і дробове,
можна подати у вигляді дробу — де п — число натуральне,
а т — ціле.
Модулем числа а називається відстань точки, що зоб-
ражує число а на координатній прямій, від початку відлі-
ку — точки 0. Модуль числа позначають символом | а [.
Наприклад, | 2 =2, | —2 | = 2, | —2,73 | = 2,73. Для
числа 0 маємо 0 | = 0, оскільки точка 0, що зображує
число 0, збігається з початком відліку.
Протилежні числа мають рівні модулі: | 3| = | —3| =
= 3. Модуль будь-якого числа не може бути від’ємним.
У загальному випадку
а, якщо а>0,
а, якщо а<0,
0, якщо а = 0,
„ , . ( а, якщо а 0,
або |а І = {
(— а, якщо а<04
\а І =
Порівнюючи раціональні числа, зручно користуватися
їхніми зображеннями на координатній прямій. З двох чи-
сел меншим вважають те, для якого точка, що його зобра-
жує, розміщена на координатній прямій лівіше.
З двох додатних чисел більшим є те, у якого більший
модуль; з двох від’ємних чисел більшим є те, у якого менший
модуль.
Наприклад, —5 > —8, оскільки | —5 | < | —8 | і
на координатній прямій точка, що зображує число —8,
стоїть лівіше.
Правила дій з невід’ємними цілими і дробовими числами
розглядали вище. Щоб додати два від’ємних числа, досить
додати їх модулі і поставити перед результатом знак «мінус».
Наприклад,
'(- 5) + (- 12) = - (5 + 12) = - 17;
(_ з,2) + (— 8,9) = — (3,2 + 8,9) = — 12,1.
Щоб додати два числа з різними знаками, треба від
більшого модуля даних чисел відняти менший і постави-
ти перед результатом знак числа з більшим модулем.
13*
387
Наприклад,
32,7 + (— 16,8) = + (32,7 — 16,8) = 15,9;
— 6,42 + 3,2 = — (6,42 — 3,2) = — 3,22.
Існування додатних і від’ємних чисел дає змогу заміни-
ти дію віднімання дією додавання з числом, протилежним
від’ємнику.
Наприклад,
— 42 —21 = —42 4-(—21) = —(42 4-21)= —63;
62,5 — (— 12,4) = 62,5 4- 12,4 = 74,9.
У зв’язку з цим будь-який вираз, що містить лише зна-
ки додавання і віднімання, можна розглядати як суму.
Наприклад, —12 4- 7 — 18 — 23 4- 16 = (—12) 4-
4- 7 4- (-18) 4- (-23) 4- 16.
При додаванні і відніманні додатних і від’ємних чисел
теж виконуються переставний і сполучний закони. Це доз-
воляє раціоналізувати обчислення. У попередньому при-
кладі при обчисленні суми зручно використовувати спочат-
ку переставний закон, знайти окремо суму всіх додатних
і всіх від’ємних чисел, а потім знайти суму двох чисел
з різними знаками. Наприклад,
(- 12) 4- 7 4- (- 18) 4- (-23) 4- 16 = ((- 12) 4- (- 18) 4-
4- (— 23)) 4- (7 4- 16) = (— 53) 4- 23 = — (53 — 23) = — ЗО.
При обчисленні числових виразів часто доводиться ко-
ристуватися правилами розкриття дужок:
1) щоб розкрити дужки, перед якими стоїть знак «4-»,
треба відкинути дужки та цей знак «4-» і записати кожний
доданок, що стоїть в дужках, з його знаком.
Приклади. 1) 4,23 4- (—2,45 4- 6,48 — 3,19) = 4,23 —
— 2,45 4- 6,48 — 3,19;
2) а 4- (Ь — с 4- к) = а 4- Ь — в 4- к,
щоб розкрити дужки, перед якими стоїть знак «—»,
треба відкинути дужки та цей знак «—» і записати кожний
доданок, що стоїть у дужках, з протилежним знаком.
Приклади. 1) —2,5 4- 8,3 — (—6,9 — 8 4- 12) = —2,5 4-
4- 8,3 4- 6,9 — 8 4- 12;
2) а — (Ь — с 4- к) = а — Ь 4- с — к.
Множення і ділення від’ємних чисел зводиться до відпо-
відних дій над їх модулями:
щоб перемножити два від’ємних числа, треба пере-
множити їх модулі і результати взяти із знаком плюс;
щоб розділити від’ємне число на від’ємне, треба роз-
ділити модуль діленого на модуль дільника і результат
взяти із знаком «4-»;
388
щоб перемножити два числа з різними знаками, треба
перемножити модулі цих чисел і результати взяти із зна-
ком «—»;
щоб розділити два числа з різними знаками, треба роз-
ділити модуль діленого на модуль дільника і взяти резуль-
тат із знаком «—». _
Приклади. 1) (—27) • (—0,3) = 81; 2) (—125) : (—2,5) =
50;
3) (6,54) • (—0,3) = —1,962; 4) (—5,25) : 1,5 = —3,5.
Для раціональних чисел, як і для натуральних, вико-
нуються переставний, сполучний і розподільний закони
множення відносно додавання: "
а * Ь — Ь • а; (аЬ) • с = а • (Ьс)\ (а + Ь) * с~ ас 4- Ьс.
Так само виконуються дії з 1 і 0:
а • 1 = 1 • а = а; а • 0 = 0 • а = 0; 0: а = 0
(на нуль ділити не можна!).
Для розв’язання рівнянь важливе значення має обер-
нене твердження, що випливає з рівності а • 0 = 0 • а =
= 0: добуток дорівнює нулю тоді і тільки тоді, коли хоча б
один із співмножників дорівнює нулю.
5. Дійсні числа. Поняття числа в історії розвитку мате-
матики поступово розвивалось і розширювалось. Спочатку
було введено натуральні числа і нуль для лічби, потім
дробові числа для вимірювання величин і ділення натураль-
них чисел. Пізніше у зв’язку з потребами практики і роз-
в’язування рівнянь було введено від’ємні числа (дробові і
цілі), які разом із цілими і дробовими додатними числами
і числом 0 утворили множину раціональних чисел <2.
У множині раціональних чисел виконуються всі чотири
арифметичні дії — додавання, віднімання, множення і ді-
лення, крім ділення на нуль.
Кожному раціональному числу а на координатній пря-
мій відповідає єдина точка А (а). При цьому число а нази-
вається координатою точки А на цій прямій.
Виникає питання: чи виконується обернене твердження:
чи кожній точці координатної прямої відповідає раціональ-
не число, що є координатою цієї точки?
Вимірювання довжин відрізків, графічний спосіб роз-
в’язування рівнянь виду х2 = 2 приводять до висновку,
що не кожній точці координатної прямої відповідає раціо-
нальне число, що є її координатою. Тому виникає потреба
зобразити числом координати і таких точок.
Справді, розв’яжемо графічним способом рівняння
х2 = 2 (рис. 12.3). З рисунка видно, що мають існувати
389
два корені цього рівняння — абсциси точок Мг і М2.
З цього рівняння випливає, що розв’язками його є числа,
квадрати яких дорівнюють 2. Згідно з означенням квадрат-
ного кореня такими числами є х± = У 2 і х2 = —У 2.
У курсі алгебри доведено, що не існує раціонального числа,
квадрат якого дорівнює 2. Це означає, що числа У"2 і
— У 2 не є раціональними.
До такого ж висновку приводять і геометричні мірку-
вання. Побудуємо квадрат ОАВЕ, сторони якого дорівню-
Рис. 12.3
ють одиничному відрізку ип
на координатній прямій
(рис. 12.4). Довжина діагоналі
Рис. 12.4
ОВ цього квадрата за теоремою Піфагора дорівнює ОВ =
"= VОЕ2 — ВЕ2 = + 1 = 2. Якщо відкласти відрізок
на координатній прямій, то точці К має відповідати число 2,
яке не є раціональним.
Можна довести, що не існує раціонального числа, квад-
рат якого дорівнює 3, 5, 6, 7....Іншими словами числа
р^З, ]Ґ5, 'Кб'1^7, ... та протилежні їм числа —)/"3, —р 5,
— /б,— VI,.. . теж не є числами раціональними. У множи-
ні раціональних чисел рівняння х2 — 5 теж не має коренів.
Наведені приклади свідчать про те, що виникла потре-
ба доповнити множину раціональних чисел числами нової
природи, які дістали назву ірраціональних.
Ірраціональні числа записують у формі нескінченно-
го десяткового неперіодичного дробу. Зокрема, V^ —
= 1,4142135623... .
Не слід думати, що ірраціональні числа можна дістати
лише при добуванні коренів з чисел, з яких вони не добу-
ваються як точні числа.
Ірраціональним числом також є відношення довжини
будь-якого кола до його діаметра. Його позначають через
я, і дорівнює це число 3,1415926... . Ірраціональними чис-
лами є значення тригонометричних функцій багатьох кутів
390
(наприклад, зіп 60° = 60° = Кз та ін.), резуль-
тати виконання багатьох інших математичних операцій.
Ірраціональні числа можна дістати, утворюючи будь-
які нескінченні неперіодичні десяткові дроби. Наприклад,
2,12345..., 0,513114111....
Об’єднання множин раціональних та ірраціональних
чисел утворює множину дійсних чисел, яку позначають бук-
вою 7?.
Ірраціональні числа, записані у вигляді десяткового
дробу, порівнюють за тими ж правилами, що і десяткові
дроби, якими записують раціональні числа.
Правила дій над дійсними числами а і 0 у випадку,
коли вони належать до раціональних чисел, відомі. Проте
якщо одне або обидва числа є ірраціональними, то виконан-
ня дій над ними, як правило, зводиться до виконання дій
над їх раціональними наближеннями.
Приклад. Знайти суму чисел а і 0, якщо а = 4 =
= 0,333... , .0 = /2 = 1,41421... .
Запишемо нерівності:
0,33 <4- <0,34, 1,41 </2 < 1,42
0,333 <4-<0,334, 1,414 </2 < 1,415
О
................
Для знаходження суми 4 + 1^2 почленно додають ліві
і праві частини записаних нерівностей:
!<4-+/2<3,
□
1,7 <4-+ 1^2 <1,9,
1,74 < 4- + /2 < 1,76,
1,747 <4-+/2 < 1,749,
О
391
Утворення таких нерівностей і додавання їх дозволяє
знайти суму чисел + ]/*2 з точністю до будь-якого десят-
кового знака. Остання із записаних вище нерівностей забезпе-
чує у наближенні суми два перші правильні десяткові знаки.
Аналогічно виконуються інші дії над ірраціональними
числами. Після введення ірраціональних чисел і побудови
множини дійсних чисел 7?, встановлюється взаємно одно-
значна відповідність між множиною дійсних чисел і мно-
жиною точок координатної прямої. Це означає, що кожно-
му дійсному числу відповідає точка на координатній пря-
мій, для якої це число є координатою, і навпаки, кожній
точці координатної прямої відповідає дійсне число — коор-
дината цієї точки.
Означенню степеня з натуральним показником і його
властивості залишаються справедливими і для будь-яких
дійсних чисел. Нехай а — будь-яке дійсне число, п —
натуральне число, відмінне від 1. За означенням
ап = а • а • а • ... • а; при п = 1 а1 = а.
п співмножників
Виконуються такі властивості для степенів:
ат • а1 = ат+п, (ат)п = сГп, (аЬ)п = ап . Ь\
де а і Ь — будь-які дійсні числа.
Відношення і пропорції. Частка від ділення двох дійс-
них чисел називається відношенням.
Відношення показує, у скільки разів одне число біль-
ше від другого або яку частину одне число становить від
другого. Відношення записують так: 8 : 13 або ;
2,7 : 3,5 або ; /3 : 2 або .
Рівність двох відношень називається пропорцією. За
допомогою букв пропорцію можна записати так:
а: Ь = с і <1, або .
о а
Числа а і сі називаються крайніми членами пропорції/
числа Ь і с — середніми.
У правильній пропорції добуток крайніх членів дорів-
нює добутку середніх. Навпаки, якщо в пропорції добуток
крайніх членів дорівнює добутку середніх, то пропорція
правильна.
У буквенному запису: якщо а : Ь = с : сі — правильна
пропорція, то асі = Ьс, навпаки, якщо в пропорції а : Ь =
= с : сі, ай = Ьс, то ця пропорція правильна.
392
Властивості пропорції часто використовують при роз-
в’язанні задач.
Задача. Об’єм моделі металевої деталі 48 см3, її маса
374 г. Яка маса оригінала деталі, якщо його об’єм 8160 см3.
Розв’язання. 48 см8 — 374 г, 48 __ 374 .
8160 см3 —хг, 8160 х ’
8160 • 374 сосо , .
х -----------= 6358 (г).
Проценти. У практичних обчисленнях деякі дроби ді-
стали спеціальну назву, зокрема, одну другу називають
половиною, одну четверту — чвертю. Спеціальну назву
дістала одна сота. Вона називається процентом. Процент
позначають за допомогою знака %.
1 2
За означенням 1 % = -удо- = 0,01. Звідси 2 % = =
= 0,02; 5 % = = 0,05; 27 % = —- = 0,27; 100 % =
-452-=!; 243 % = 2-^ = 2,43 і т. д.
Взагалі, будь-яке число, наприклад -у , можна записа-
ти як-^-, , 80 %. Отже, проценти — це одна з можли-
вих форм запису чисел.
Проценти широко застосовують у фінансових операціях
(прибутки з капіталу, сплата внесків, різні касові операції
та ін.), для характеристики виконання виробничих планів,
при визначенні зростання чи зниження продуктивності
, праці, режиму економії, собівартості і якості продукції,
у госпрозрахунках. У сільському господарстві проценти
застосовують при визначенні питомої ваги окремих куль-
тур у загальних планах сільськогосподарського виробни-
цтва, при визначенні вологості, схожості насіння і т. д.
Проценти широко використовують і у шкільних курсах,
зокрема у математиці і фізиці при обчисленні відносної
похибки вимірювань і наближених обчислень, у хімії при
обчисленні концентрації розчинів.
Для розв’язування задач на проценти треба вміти запи-
сувати будь-яке число у вигляді процентів і розв’язувати
обернену задачу — виражати відоме число процентів у
вигляді дробового чи цілого числа.
Правило 1. Для того щоб перетворити дане число у про-
центи, треба це число помножити на 100.
Приклади. 1) 0,245 = (0,245 • 100) % = 24,5 %;
2) 0,009 = (0,009 • 100) % = 0,9 %;
393
3) А = (_3_ . юо) % = % = 42-^- %;
4) і А = (і А. іоо'і % = (4- • іоо5) % = % =
'4^4 ] ^4 ) 4
= 175 %;
5) 3 = (3 • 100) % = 300 %.
Правило 2. Для того щоб перетворити дане число про-
центів у дріб чи ціле число, треба розділити дане число про-
центів на 100.
Приклади. 1) 52 % = ;
2
27-5-
2} 27 — % =____— = 83 і 100 = 83_= 83 *
£1 3 /0 100 З . Ш З • 100 300 ’
3) 250 % = = 2,5.
Існують три основні задачі на проценти: 1) знаходження
процентів від числа; 2) знаходження числа за відомими
його процентами; 3) знаходження процентного відношення
двох чисел.
Знаходження процентів від числа. Задача. Місячна
зарплата робітника становить 280 крб. Крім того, він одер-
жав премію, яка становить 24 % від місячної зарплати.
Скільки карбованців становить премія.
Розв’язання. Перший спосіб. Визначимо, скіль-
ки карбованців становить 1 %. Для цього розділимо
280 крб. на 100. Дістанемо 2,8 крб. Обчислимо, скільки
карбованців становлять 24 % від 280. Для цього 2,8 крб.
помножимо на 24. Дістанемо 2,8 крб. • 24 = 67,2 крб.
Відповідь. Премія становить 67,2 крб.
Узагальнюючи цю задачу, дістанемо таке правило: щоб
знайти число Ь, що становить р % від числа а, треба число
а поділити на 100 і помножити на число Ь, тобто Ь = X р.
Другий'спосіб. Користуючись означенням процента як
дробу вимогу до задачі можна сформулювати так: знайти
24
= 0,24 від числа 280. Отже, знаходження 24 % від
24
числа 280 є не що інше, як знаходження дробу =
== 0,24 від числа 280. Відомо, що для цього досить число
280 помножити на дріб 0,24. Отже, 280 • 0,24 = 67,2 (крб.).
Звідси дістаємо правило: щоб знайти проценти від числа,
треба ці проценти записати звичайним чи десятковим дро-
бом і дане число помножити на здобутий дріб.
394
Знаходження числа за відомими його процентами. Зада-
ча. При помолі пшениці вихід борошна становить 80 %. Скіль-
ки пшениці треба змолоти, щоб одержати 520 кг борошна?
Розв’язання. При розв’язанні цієї задачі треба
знайти таке число, 80 % якого дорівнюють 520.
Перший спосіб. Знайдемо число, яке дорівнює 1 %. Для
520 13
цього 520 треба розділити на 80. Дістанемо .
13
Знайдемо число, яке дорівнює 100 %. Для цього число
треба помножити на 100. Дістанемо-^- -100 = 13 2100 =
= 650. Відповідь. Треба змолоти 650 кг пшениці.
Другий спосіб. Запишемо проценти у вигляді звичайно-
го
го чи десяткового дробу: 80 % = = 0,8. Отже, треба
знайти число, 0,8 якого становить 520, тобто знайти число
за відомим його дробом, що знаходиться шляхом ділення
даного числа на дріб. Розділимо 520 на дріб 0,8. Дістанемо
520 5200
— = —=65° кг.
. Звідси дістаємо правило: щоб знайти число за його про-
центами, треба проценти записати у вигляді звичайного чи
десяткового дробу і розділити дане число на цей дріб.
Знаходження процентного відношення двох чисел. За-
дачі такого типу розв’язують, наприклад, при визначенні
процентів успішності, відвідування, жирності молока,
вологості, усушки. Тут відношення двох чисел показує, яку
частину становить перше число від другого. При цьому
"важливо правильно зорієнтуватися, яке з двох чисел треба
вважати першим, а яке другим, тобто основним (за основ-
не беруть те, з яким порівнюють число).
Задача. З чотирьох деталей, які було заплановано, токар
виточив три. На скільки процентів токар виконав завдання?
Р о з в’ я з а н н я. Визначимо, яку частину завдання
З З
виконав токар. Дістанемо 3:4=-^-. Перетворимо у
з
проценти, для цього помножимо у на 100. Дістанемо
4 = 0,75 = 75 %.
4
Звідси дістаємо правило: щоб визначити процентне від-
ношення двох чисел, треба знайти їх відношення і виразити
його в процентах, тобто помножити знайдене відношення
на 100 і поставити знак процента. Між процентами і від-
ношеннями існує така залежність: збільшити число на р
процентів — це означає збільшити його у р разів. Іншими
395
словами, збільшення числа на р процентів слід розуміти не
як збільшення даного числа на р, а як збільшення цього
числа у р разів.
Наприклад, збільшення числа на 50 % — це збільшен-
ня його у 1,5 рази, оскільки 150 % = 1,5.
У загальному випадку: якщо число а збільшилось, на-
приклад, на 30%, то воно становить а 4- 0,3а = 1,3а,
тобто збільшилось у 1,3 рази.
Крім того, якщо величина зменшилась, наприклад, у
1,2 рази, тобто у раза, то воно становить свого попе-
/ 1 6 гт
реднього значення І оскільки 1 : Навпаки, якщо
• ~ 5
після зменшення величина становить свого попереднього
6
значення, то вона зменшилась у у раза. 1
Вказаною залежністю між процентами і відношеннями
можна пояснити такі факти: при зниженні трудомісткості
праці на 33 у % продуктивність праці (обернена величина)
збільшується на 50 %; при зниженні цін на 20 % ку-
півельна спроможність населення збільшується на 25 %
і т. ін.
Задача 1. В результаті вдосконалення верстата швид-
кість різання збільшилась з 120 м/хв до 135 м/хв. На скіль-
ки процентів збільшилась продуктивність праці?
Розв’язання. Продуктивність праці збільшилась
135 1
у = * 'я Раза> або у 1,125 раза, тобто становила 112,5 %
свого попереднього значення. Відповідь. 12,5 %.
Задача 2. За нормою на виконання виробничого завдан-
ня робітник повинен був витратити 4 у год, а фактично
він витратив 3 год. На скільки'процентів він перевиконав
норму?
Розв’язання. Час виконання завдання становить
З 3 2 2
—і— запланованого, тобто -к- = 3 • тг = -п . Візьмемо
.1 у у о
4Т ~2
2
норму за 1. Норма виконання з перевищенням у 1 ; — =
З
= — = 1,5 раза, тобто вона виконана на 150 %, а, переви-
конана на 50 %. Відповідь. 50 %.
Задача 3. Обсяг робіт на будівництві збільшився на 40 %'.
396
Як треба змінити кількість робітників, якщо передбачено
збільшити продуктивність праці на 10 %?
Розв’язання. Обсяг робіт збільшився у 1,4 раза,
тому і кількість робітників треба збільшити у 1,4 раза.
Вона буде становити 1,4 від початкової кількості, яку візь-
мемо за 1. Оскільки продуктивність праці треба збільшити
у 1,1 раза (на 10 %), то для виконання запланованого обся-
гу робіт кількість робітників треба зменшити у 1,1 раза.
Отже, необхідна кількість робітників повинна станови-
ти 1,4 : 1,1 = 1,27 від початкової кількості. Це означає,
що їх кількість треба збільшити на 27 %. Відповідь, Кіль-
кість робітників треба збільшити на 27 %.
Задача 4. Обсяг продукції заводу зріс за перший рік на
20 %, за другий — на 25 %. На скільки процентів зріс
обсяг продукції за два роки?
Розв’ язання. Нехай початковий обсяг продукції
становив р одиниць. Наприкінці першого року продукція
заводу збільшилась на 20 %, тобто у 1,2 раза, і становила
1,2 р одиниць. На кінець другого року обсяг продукції
збільшився на 25 %, тобто у 1,25 раза порівняно з 1,2 р,
і становив 1,2р • 1,25 = 1,5р. Це означає, що за два роки
вона збільшилась у 1,5 раза порівняно з р, тобто на 50 %.
Відповідь. 50 %.
Контрольні запитання
1. Як виникли натуральні числа?
2. Чи означається натуральне число?
3. Що таке десяткова система запису натуральних чисел і яка її
основна властивість?
4. Як прочитати багатоцифрове число?
5. Сформулювати правило порівняння багатоцифрових натураль-
них чисел.
6. Як тлумачити додавання натуральних чисел?
7. Що означає помножити натуральне число т на натуральне чис-
ло л?
8. Як тлумачити віднімання і ділення натуральних чисел?
9. Які дії можна виконувати у множині натуральних чисел?
10. Як формулюються закони дій з натуральними числами?
11. Як формулюються ознаки подільності натуральних чисел на
2; 3; 9; 5 і на 10?
12. Яке натуральне число називається простим, складеним?
13. Як розкласти натуральне число на прості множники?
14. Що таке дільник числа а? Що таке найбільший спільний діль-
ник двох або кількох чисел?
15. Як знайти спільний дільник двох або кількох чисел?
16. Яке натуральне число називається кратним певному числу?
Що називається найменшим спільним кратним двох або кількох чисел?
17. Як знайти найменше спільне кратне двох або кількох нату-
ральних чисел?
397
18. Які числа називаються дробовими?
19. Що таке чисельник і знаменник звичайного дробу?
20. Який звичайний дріб називається правильним, а який непра-
вильним?
21. Як виділити з неправильного дробу цілу частину? Як перетво-
рити неправильний дріб у число, що містить цілу і дробову частини?
22. Як порівнюються звичайні дроби з однаковими знамен-
никами?
23. Як додати (відняти) два дроби з однаковими знаменниками?
24. Як формулюється основна властивість звичайних дробів?
25. Як звести звичайні дроби до найменшого спільного знамен-
ника? і
26. Як додати дроби з різними знаменниками?
27. Як додати числа, що містять цілу і дробову частини?
28. Як відняти числа, що мають цілу і дробову частини?
29. Як перемножити звичайні дроби?
ЗО. Як розділити число на дріб?
31. Як можна прийти до поняття десяткового дробу?
32. Як порівняти два десяткові дроби?
33. Як виконують додавання і віднімання десяткових дробів?
34. Як перемножити два десяткові дроби?
35. Як розділити число на десятковий дріб?
36. Як округлити натуральне число до певного розряду?
37. Як округлити десятковий дріб?
38. Що таке абсолютна похибка наближеного значення?
39. Що таке відносна похибка наближеного значення?
40. Як додають (віднімають) наближені значення?
41. Яка цифра наближеного значення називається правильною?
42. Які цифри наближеного значення називають значущими?
43. Як формулюється правило множення і ділення наближених
значень?
44. Чому були введені додатні і від’ємні числа?
45. Які числа називають цілими? Як позначають множину нату-
ральних і цілих чисел?
46. Які числа називають раціональними? Як позначають раціо-
нальні числа?
47. Що називається модулем числа а?
48. Як порівнюють раціональні числа?
49. Як додати два числа з однаковими знаками?
50. Як додати два числа з різними знаками?
51. Як формулюється правило розкриття дужок?
52. Як формулюються правила множення і ділення раціональних
чисел?
53. Що спричинило до введення ірраціональних чисел? Які джере-
ла їх утворення?
54. Як утворилася множина дійсних чисел? Як її позначають?
55. Як виконують дії над ірраціональними числами?
56. Яке співвідношення існує між множиною дійсних чисел і мно-
жиною точок координатної прямої?
57. ' Що називається відношенням чисел?
58. Що називається пропорцією?
59. Як формулюється властивість пропорції?
60. Що називається процентом?
61. Які три основні задачі на проценти вам відомі? Як вони розв’я-
зуються?
398
Вправи
1. Обчислити значення виразу:
/З 8 \ / 1 З
0^2-у+ 0,15— 1 ”25“] : ^2 2 —1 4 +0,04
7 5 1
2) 1,456 :+-уу : 0,125 + 4-у • 0,8;
-4"-2,7 • 2-у
3) т—2Тлг;
6,2 — 1 5 : 7
З ~ 6
2. Знайти числове значення виразів:
і'
х^ + ху + у^ прь;
а) х = — 3; у =— 2; б) х = —0,4; г/= 0,5;
2 З 1
в) х = -у ; у = — — ; г) х = — -у ; у = — 0,25.
2) а^^+ 2Ь^ пРи:
З
а) а = — 4; 6 = — 1; б) а = — ; Ь = — 0,3;
2 1
в) а = — ~у ; Ь = 0,5; г) а = 1 “у ; Ь = — 1,5е
3. Знайти площу трапеції, основи якої а 4,6 см, Ь « 3,28 см і
висота Н « 3,0 см.
и
4. Знайти опір за формулою /?заг = Н—у, де Яі « 5,15 Ом,
12,5В , <7 « 2,ІД.
5. Радгосп продав державі 836 т м’яса, що становить 80 % пла-
ну поставок м’яса. Який план поставок м’яса?
6. Корова в колгоспі дала за рік 5500 кг молока жирності 4 %.
Скільки кілограмів масла можна одержати при переробці цієї кількості
молока?
7. Сума сторін трикутника дорівнює 85 см, а довжина третьої сто-
рони становить 80 % цієї суми. Визначити периметр трикутника.
8. Одна сторона трикутника 12 см, а дві інші становлять ЗО % цієї
сторони. Обчислити периметр трикутника. 1
9. На заводі 40 % всіх верстатів перевели на підвищені швидкос-
ті, внаслідок чого продуктивність праці збільшилась на ЗО %. На
скільки процентів збільшилось виробництво продукції на заводі?
10. Продуктивність праці підвищилась на 14 %. На скільки про-
центів знизилась трудомісткість праці?
(Трудомісткістю продукції називається кількість робочого часу, що
витрачається на одиницю продукції,)
399
11. Визначити процент виконання норми виробітку, якщо на дану
операцію встановлена норма часу 10,5 хв, а робітник протягом 5 днів
виконав 256 таких операцій.
(Кількість продукції, що виробляється за одиницю часу, називається
виробітком.)
12. На скільки процентів зміниться ціна товару, якщо спочатку
підвищити її на 20 %, а потім знизити на 20 %?
13. На скільки процентів збільшиться продуктивність праці, якщо
час на виконання певної операції скоротити на 20 %?
14. На скільки процентів збільшиться реальна зарплата, якщо ці-
ни на всі продовольчі і промислові товари зменшити на 20 %?
15. Скільки води треба долити до 7,5 кг 12-процентного розчину,
щоб дістати 10-процентний розчин?
§ 2. Тотожні перетворення виразів
1. Основні поняття. Вирази, складені з чисел, знаків
дій і дужок, називаються числовими виразами. Наприклад,
5 + 3,7; 5 - 102 Ч- 3 - 103 — /2; (27 — 3,5) • 12 — 67;
4_____1_
9 27
Якщо у числовому виразі можна виконати всі вказані
в ньому дії, то здобуте в результаті число називають число-
вим значенням даного виразу.
Вирази, до складу яких входять не лише числа, а й змін-
ні, позначені буквами, знаки дій, функції і дужки, назива-
ються виразами із змінними. Наприклад,
і о 2л 4- Ь зіп А і о ,« л і.
х + 2у; „ ; —г—; у а2 — Ь2 — 2аЬ соз у.
У3(а-Ь) Ь ' г *
Математичні вирази, в яких над числами і буквами, що
входять до виразів, виконуються дії додавання, відніман-
ня, множення, ділення, піднесення до натурального степеня
і добування арифметичного кореня, називаються алгебраїч-
ними виразами. Наприклад, алгебраїчними є вирази:
х~Уі ~ь=Т’ 5 + —’ -------------------------тщ—
Алгебраїчний вираз називається раціональним, якщо
відносно змінних (букв), що до нього входять, викону-
ються лише дії додавання, віднімання, множення, ділення
і піднесення до натурального степеня. Наприклад, -^а ;
12 т — Ц2 • тп;
400
Алгебраїчний вираз називається ірраціональним, якщо
в ньому виконуються дії добування арифметичного кореня
з букв (змінних) або виразів, що містять букви (змінні).
Наприклад,
+ /3^5;
У а3 — І
Раціональний вираз називається цілим, якщо він не мі-
стить дії ділення на змінну (букву) або на вираз, що міс-
7
тить змінну. Наприклад, цілими є вирази 2-^-—3; а— Ь\
X У . . оо
7 ’ 5 ’
У курсі алгебри вивчали два види цілих раціональних
виразів — одночлени і многочлени. Вирази, що не містять
інших дій крім дії множення і піднесення до натурального
степеня, називають одночленами. Наприклад, одночленами
є вирази 5,3; 7/п; у а&2; -у-. Многочленом називають су-
му одночленів. Наприклад, многочленами є вирази а2 +
+ 2аЬ + Ь2, 5 + ху.
Раціональний вираз називають дробовим, якщо він
містить дію ділення на змінну або на вираз, що містить змін-
2а 5 Зх
ну. Наприклад, дробовими є вирази-у; — — 6х; 1 .
У зв’язку з розглядом дробових виразів не слід ототож-
нювати поняття алгебраїчного дробу і дробового виразу.
Дріб — це вираз виду р де а і Ь — числові вирази
або вирази із змінними. Наприклад, вирази у; -у-і-у—;
^2__
-----— є дробами, але лише два останніх з них — дробові
вирази.
Вирази 5 —-у, 2’ Іх~ у — 5х — дробові, але вони не є
дробами, хоча і можуть бути шляхом перетворення зведені
до дробів.
Дріб — форма запису числового виразу або виразу із
змінними. Звичайні дроби є окремим випадком поняття ал-
гебраїчного дробу і теж є формою запису числового виразу.
У формі звичайного дробу можна записати як ціле, так і
, гд 10 12 2 45
дробове число. Наприклад, , -у, у, — .
Вирази, що містять зіп а, соз а, а, сі§ а, називають
тр и тонометр ичними.
40)
Два вирази із змінними називаються тотожно-рівними
на множині, якщо їх відповідні значення збігаються при
всіх значеннях змінних, що належать цій множині. Під
відповідними розуміють значення, які дістають при під-
становці у вирази однакових значень змінних.
Приклад. Вирази 5 (х + 2) і 5х + 10 — тотожно-
4а2 . 2а
рівні на множині всіх чисел; вирази і --------тотожно-
рівні на множині всіх чисел, крім нуля. Вирази а2 — Ь2 і
(а — Ь) (а + Ь) — тотожно-рівні на множині всіх пар чи-
сел.
Таблиця 12,1
Функ- 1ція] Аргумент
6 1 в 4- в 1 Е я н- а В 1 КІс» ео| Зя , —+“ і к
зіп соз а соз а зіп а — зіп а — соз а — соз а — зіп а
соз зіп а — зіп а — соз а — соз а — зіп а зіп а соз а
сій а — сі£ а — і§а Ій а сі§а — сій« — і&а
і§а — і§а — сі£ а сій а і§а — ій« — сі§ а
Тотожним перетворенням виразу називається заміна
виразу тотожно-рівним йому.
Рівність, в якій права і ліва частини — тотожно-рівні
вирази на певній множині, називаються тотожністю на
цій множині. Основними алгебраїчними тотожностями є
такі:
а2 — Ь2 = (а — Ь) (а + Ь); (а ± Ь)2 = а2 ± 2аЬ + Ь2\
(а ± Ь)3 = а3 ± За2Ь + За&2 ± б2;
а3 ± Ь3 = (а ± &) (а2 аЬ + б2);
У а2 = 1 а |, (К а)2 = а.
Основними тригонометричними тотожностями є:
: 2 । 2 і 4.^ зіпа . соза
8ііг а + соз2 а = 1; а =----------; сщ а = —------;
’ ь соз а ь зіп а
а * сі§ а = 1; 1 + і§2 а = —— ї 1 + сі§2 а = —— ..
& ’ 1 Ь соз2 а ’ & зіп2 а
При виконанні тотожних перетворень, обчисленні зна-
чень тригонометричних виразів широко використовують
402
тотожності, що дістали назву формул зведення (табл. 12.1),
а також тбтожності.
зіп (а ± Р) = зіп а зіп р ± соз а зіп Р;
соз (а ± Р) — соз а соз р =? зіп а зіп Р;
зіп 2а = 2 зіп а соз а; соз 2а = соз2 а — зіп2 а.
2. Тотожні перетворення цілих виразів. Одночлени
і многочлени. Стандартним видом одночлена називається
такий, якщо многочлен можна зобразити у вигляді добутку
коефіцієнта (числового множника) і степенів різних змін-
них, які взяті співмножником лише один раз. Наприклад,
2а2&3; —6,5 хг/3г; пг3п2; —хуг.
Щоб звести одночлен до стандартного виду, треба:
1) перемножити числові множини і поставити здобуте
число на перше місце в добутку;
2) перемножити степені однакових змінних і записати їх
як співмножники.
Зведення одночлена до стандартного виду — тотожне
перетворення. Тотожним перетворенням одночленів є також
множення одночленів і обернене йому перетворення — зо-
браження одночлена у вигляді добутку двох або кількох
одночленів, піднесення одночленів до степеня з натураль-
ним показником, зображення одночлена у вигляді степеня.
Приклад 1. Звести вираз до стандартного виду одночлена:
а) — 2-у- /п2п • -у- тп\ б) — 6А/ • (— ЗсМ2);
в) (—Зх2у3)2.
Розв’язання.
а) — 2 т2п ---1---1- /п3п2 = — т3и2;
б) 6сМ • (— Зс2<і2) = — 18сМ3; в) (— Зх2у3)2 = 9х4у3.
Приклад 2. Подати одночлени у вигляді добутку двох
яких-небудь одночленів: а) —12Л/2; б) д-а4&6; в)—0,25 піп2.
Розв'язання:
а) — 12х3г/2 = (— 2ху) • (6 х2у)’,
б) -|-а4&6 = (2а262) • (-|-а2&4');
о І о 1
в) — 0,25/тш2 = (0,5п) • (— 0,5/пга).
Приклад. 3. Перетворити вирази в одночлени стандарт-
ного виду: а) (2а&3)4; б) (—0,Зх2у4)3; в) {-^-т2п\ .
403
Р о з в’ я з а н н я. а) (2аЬ3)4 = 32аіЬ12;
б) (— 0,Зх2г/4)3 = — 0,027хБг/12; в) = і т2"4-
Приклад 4. Зобразити одночлени у вигляді степеня:
а) 9а2Ьв; б) — 0,027л:вг/9; в) -^-т2п2.
Розв’язання. а) 9а2Ьв = (За&3)2;
б) — 0,027х6г/9 = — О,3х2г/3; в) ^2«2 = тп) •
Простішим перетворенням многочленів є зведення їх
подібних членів, тобто членів, які відрізняються лише кое-
фіцієнтами.
Щоб звести подібні члени многочлена, треба додати їх
коефіцієнти і приписати до утвореного числа як співмнож-
ники степені змінних.
Основним перетворенням многочлена є зведення його
до стандартного виду. Для цього треба:
1) всі члени многочлена звести до стандартного виду;
2) звести подібні члени многочлена.
Приклад. Звести до стандартного виду многочлен
а8 + 2аЬа + Ь2а — 2ЬЬ — 2Ь2Ь.
Розв’язання.
а8 + 2аЬа + Ь2а — 2ЬЬ — 2Ь2Ь = а8 4- 2а2Ь + аЬ2 —
— 2Ь2 — 2Ь8 = а8 + 2а2Ь + аЬ2 — 2Ь2 — 2Ь8.
Якщо многочлен після зведення його до стандартного
виду перетворюється в нуль, то його називають нульовим
многочленом. Наприклад, многочлени 2х — 2х = 0; 5т2п —
— 7т2п + 2т2п — 0.
Степінь ненульового многочлена це найбільший із сте-
пенів одночленів, що входять у многочлен після зведення
його до стандартного виду. При цьому степенем одночлена
називається сума показників степенів змінних. Наприклад,
одночлен 7т2п має третій степінь. Многочлен Зху2 — 2ху +
+ 7г/4 є многочленом четвертого степеня.
До тотожних перетворень виразів, що мають у складі
многочлени і одночлени, належать:
1) перетворення добутку (множення) одночлена на мно-
гочлен у многочлен стандар тного виду і обернене до нього
перетворення — розкладання многочлена на множники
способом винесення одночленного множника за дужки;
2) перетворення добутку (множення) двох многочленів
у многочлен стандартного виду і обернене перетворення —
розкладання многочлена на множники, кожний з яких є
многочленом.
404
, Щоб помножити одночлен на многочлен, треба помножи-
ти цей одночлен на кожний член многочлена і утворені
добутки додати.
Приклад. Перетворити вираз у многочлен:
— 0,2л3 • (2,3л2у — 0,9л + 3).
Розв’язання. — 0,2 ? (2,3 х*у — 0,9 х + 3) =
= —0,46 х2у + 0,18л4 — 0,6 л3.
Щоб розкласти многочлен на множники способом ви-
несення спільного множника за дужки, треба:
1) знайти спільний множник всіх одночленів многочлена;
2) подати кожний член многочлена у вигляді добутку
двох одночленів — з яких один множник спільний;
3) винести спільний множник за дужки, використовую-
чи розподільний закон множення.
Щоб знайти спільний множник, треба знайти найбіль-
ший за модулем спільний дільник всіх коефіцієнтів одно-
членів і помножити його на кожну змінну в степені з най-
меншим показником, який вона має в даному многочлені.
Приклади.
1) 12л4 — 8л3 + 2л2 = 2л2 • 6л2 — 2л2 • 4л + 2л2 • 1 =
= 2л2 (6л2 — 4л + 1);
2) —9л4у2 — 18л2// + 12л3//2 = —Зл2// • Зл2// + (—Зл2// х
X 6 — — (—Зл2//) • 4л// = —Зл2// (Зл2// + 6 —’4ху).
Щоб помножити многочлен на многочлен, треба кожний
член одного многочлена помножити на кожний член дру-
гого многочлена, утворені добутки додати і звести здобутий
многочлен до стандартного виду.
Приклад. (2 — 2л + л2) (л + 5) = 2л — 2л2 + л3 +
+ 10 — 10л + 5л2 = л3 + Зл2 — 8л + 10.
Перетворенням, оберненим до множення многочленів,
є розкладання многочлена на множники, кожний з яких є
многочленом. Виконують це перетворення способом групу-
вання. Для цього групують члени многочлена так, щоб до-
данки у кожній групі мали спільний множник, а після ви-
несення спільного множника в дужках кожної групи ви-
явились однакові многочлени. Потім однакові многочлени
знову виносять за дужки.
Приклад. Розкласти на множники многочлен ху +
+ 2у — 2л — 4.
Розв’язання, ху + 2у — 2х — 4 = (ху + 2у) +
+ (—2л — 4) = у (х + 2) — 2 (л + 2) = (л + 2) (л — 2).
В цьому разі групування можна виконати інакше: ху +
+ 2у — 2л + 4 = (ху — 2л) +(2// — 4)==л(// — 2)+2(// —
-2) = (//-2) (л + 2).
405
При виконанні тотожних перетворень многочленів інко-
ли зручно використати формули скороченого множення
(а — Ь)(а+Ь) = а2— Ь2. (1)
Добуток різниці двох виразів на їх суму дорівнює різни-
ці квадратів цих виразів. Якщо записати цю тотожність
справа наліво, то матимемо рівність
а2 — Ь2 = {а — Ь) {а + Ь). (2)
Різниця квадратів двох виразів дорівнює добутку різни-
ці цих виразів на їх суму.
Формулу (1) використовують для скороченого множен-
ня різниці двох виразів на їх суму.
Приклад. (9т2 — 5п) (—9т2 — 5п) = —(9т2 — 5п) X
X (9т2 + 5п) = —(81т4 — 25п2) = 25п2 — 81т4.
Формулу (2) використовують для розкладу на множни-
ки різниці квадратів будь-яких двох виразів.
Приклад. 81Л/4 — 16а2 = (9ху2)2 — (4а)2 = (9ху2 —
— 4а) І^ху2 + 4а).
При піднесенні до квадрата суми і різниці двох виразів
використовують такі тотожності:
(а 4- &)2 = а2 4- 2аЬ 4- Ь2\ (3)
(а — Ь)2 = а2 — 2аЬ 4- Ь2. (4)
Квадрат суми (різниці) двох виразів дорівнює квадрату
першого виразу плюс (мінус) подвоєний добуток першого
і другого виразів, плюс квадрат другого виразу. Тотожності
(3) і (4) називають відповідно формулою квадрата суми (різ-
ниці) двох виразів. їх використовують при перетворенні
трьохчленів виду а2 ± 2аЬ 4- Ь2 у квадрат двочлена або при
розкладанні його на множники.
Приклад. -±-х2 4- 4ху 4- 16у2 = ’ ~1~х * 4# +
(1 \2
При множенні двочлена на тричлен певного виду зручно
використовувати такі тотожності:
(а 4- Ь) (а2 — аЬ 4- Ь2) = а3 4- і>3, (5)
(а — Ь) (а2 4- аЬ 4- Ь2) = а3 — Ь3. (6)
Добуток суми (різниці) двох виразів на неповний квад-
рат їх різниці (суми) дорівнює сумі (різниці) кубів цих вира-
зів.
406
Приклади. 1) (2х 4- у) (4х2 — 2ху + у2) — 8х3 4- у3;
2) (0,3 — 2с) (0,09 + 0,6с + 4с2) = 0,027 — 8с3.
Якщо використовувати тотожності (5) і (6) у зворотному
порядку при розкладанні двочленів певного виду на множ-
ники, то дістанемо такі формули суми (різниці) кубів:
а3 4- &з = (а + &)(а2 —аЬ + &2), (7)
аз_ &з = (а —&)(а24-а&4-62).'
Сума (різниця) кубів двох виразів дорівнює добутку су-
ми (різниці) цих виразів на неповний квадрат їх різниці
(суми).
Приклади. 1) 27х3 + 8у3 = (Зх)3 + (2г/)3 = (Зх + 2у) X
X (9х2 — бхг/ 4- 4г/2);
2) 8 —^?-а3= 23—(4- <2?*= (2— 4 аі(4 4- -%-а + -^а2}.
3. Алгебраїчні дроби та дробові вирази. Основними ви-
дами тотожних перетворень алгебраїчних дробів є:
скорочення = де Ь=И=О;
заміна дробу тотожно-рівними виразами за формулами
а ______________ — а , а а
~ ь~'> ~ь =ї;
зведення їх до спільного знаменника;
перетворення суми і різниці, добутку, частки, степеня
дробів у дріб, у якого чисельник і знаменник — многочле-
ни стандартного виду.
Як правило, алгебраїчні дроби намагаються звести до
простішого спільного знаменника. Щоб знайти простіший
спільний" знаменник двох або кількох дробів треба:
І) скласти добуток найменшого спільного кратного
коефіцієнтів знаменників даних дробів і степенів кожної змін-
ної (букви) з найбільшим показником, який має змінна у
знаменниках даних дробів;
2) знайти додатковий множник кожного' з даних дробів;
для цього треба представити спільний знаменник у вигляді
добутку двох многочленів, з яких один — знаменник даного
дробу, тоді другий буде її додатковим множником;
3) знайти добуток чисельника кожного дробу на додатко-
вий множник і записати спільний знаменник.
Приклад. Звести дроби до прості-
шого спільного знаменника.
407
Розв’язання. 1) Простіший спільний знаменник
для даних дробів е одночлен 3.6 аЧії?.
2) Визначимо додаткові множники дробів:
Зба^с8 = 662с • 6а2са, 6а2с2 — для першого;
36а262с8 — 12ос8 • Зой2, Зоб2 —для другого;
36а262с3 = 18а26 • 26с3 — для третього.
3) 5а 5а • 6а2я2 30а3с2
662а 6&2а • 6а2с2 36а262е3 7Ь _ 7Ь - Заб2 __ 9 21а63
12ас3 12ас® ЗаЬа 11с _ 11с-26с8 Зба^с3 ’ 22Ьс4
18а2& 18а2д • 2Ьс3 36а3Ь3с3 •
Додавання і віднімання алгебраїчних дробів з однакови-
ми знаменниками виконують аналогічно виконанню цих дій
для звичайних дробів.
Щоб додати (відняти) алгебраїчні дроби з однаковими
знаменниками, треба записати у чисельнику суму (різни-
цю) їх чисельників, а знаменник залишити спільний. Якщо
можливо, то здобутий дріб треба скоротити.
Щоб додати (відняти) дроби з різними знаменниками,
треба:
а) звести дроби до простішого спільного знаменника;
б) додати (відняти) здобуті дроби за правилом додавання
(віднімання) дробів з однаковими знаменниками.
Приклади. 1) Додати дроби:
2) Відняти дроби: +-------
лу у л, лд
Розв’язання.
12 — а . 6 __ 22 —а і § _
6а — 36 + 6а — а2 6 (а — 6) + а (6 — а) “
_ 12 — а_______6 _ 12а — а2 — 36 __
6 (а — 6) а (а — 6) 6а (а — 6)
— (а2—12а+ 36) = _(д —б)2 == 6-а
6а (а — 6) 6а (а — 6) 6а
2) 1 1 - __1____________!___=
> ху—у3 хг — ху у(х — у) X (х — у)
_ Х—у _ 1
ху (х — у) ху •
До перетворення суми або різниці дробів зводиться пе-
ретворення дробових виразів, які є сумою або різницею
408
цілого виразу і дробу. Для цього досить записати цілий ви-
раз у вигляді дробу із знаменником 1.
п » а2 + Ь2 а-\-Ь а2 + Ь2
Приклад, а + Ь - = -X-----------=
— + 6) (а — Ь) — (а2 + Ь2) ' а2 — Ь2 — а2 — Ь2 _
а — Ь а — Ь
_ — 2Ь2 _ 2Ь2
а — Ь Ь — а
Множення і ділення алгебраїчних дробів теж викону-
ють за аналогією з множенням звичайних дробів.
Щоб помножити дріб на дріб, треба окремо перемножити
їх чисельники і знаменники і перший добуток записати як
чисельник, а другий — як знаменник. Після цього здобу-
тий дріб треба скоротити, якщо це можливо.
„ Зй2 6с2 М2 • бс2 ібгі
Приклад. 21с3 ’ 7й ~ 21с3 • 7й 49с •
Щоб піднести дріб до степеня з натуральним показником,
треба піднести до цього степеня окремо чисельник і знамен-
ник і перший результат записати як чисельник, а другий —
як знаменник.
п ! 2а*Ь \з (2а36)3 8а’&3
Приклад. Зтп9 — (3отп8)8 — 27/п3п9 ‘
Щоб розділити один алгебраїчний дріб на другий, треба
перший дріб помножити на дріб, обернений до другого:
а т с а сі ай
Ь * сі Ь ’ с Ьс *
Приклад.
= Зх2 — 12у
х3 — 2х2у '
х2 — 2ху ____х2 — 4у Зу
Зу ху 9 х2 — 2ху
Основна задача тотожних перетворень раціональних
виразів загального виду, що містять цілі і дробові вирази,
полягає в зведенні виразу до дробу, у якого чисельник і
знаменник — многочлени стандартного виду. При цьому
порядок виконання перетворень аналогічний порядку ви-
конання дій у числових виразах.
Приклад. Спростити вираз_х — а^_х :
РЛ Л , ах а 4- х . ах2
озв’язання. х—у—і—+ -?_= х —
____ах а . ах3 х__________________а2х . ах2 ______
а — х * а 4- х а2 — х2 ==—Г а2 — х2 ‘ а2 —х2
409
х (а2 — х2) — ах2 ах* _________ Д2* — х3 — а2х + ох2
а2 — х2 а2 — х2
_ *2 (а ~*) ____ х2
(а — х) (а + х) а + х '
4. Ірраціональні вирази. Квадратний корінь і його
властивості. Квадратним коренем з числа а називаються
числа/ квадрат яких дорівнюють а. Наприклад, числа 4 і
—4 — квадратні корені з числа 16, оскільки 42 = 16 і
(—4)2 = 16. Квадратний корінь з числа 0 дорівнює 0.
Корінь з числа 0 є єдиним, оскільки у множині дійсних
чисел тільки О2 = 0.
Квадратний корінь з від'ємного числа не існує, оскіль-
ки у множині дійсних чисел не існує числа, квадрат якого
дорівнював би від’ємному числу. Наприклад, не існує
квадратного кореня з числа —25, оскільки при множенні
дійсних чисел не існує числа, квадрат якого дорівнював
би —25.
Дію добування квадратного кореня з числа використо-
вують при розв’язанні квадратних рівнянь, зокрема рів-
няння х2 = 16. За означенням квадратного кореня рів-
няння х2 = 16 має два розв’язки (корені), які є квадратним
коренем з числа 16. Додатний корінь 4 цього рівняння на-
зивають арифметичним квадратним коренем з числа 16.
Число 0 — корінь рівняння х2 = 0. Його також нази-
вають арифметичним коренем з числа 0.
У загальному випадку: арифметичним квадратним коре-
нем з числа а називають невід’ємне число, квадрат якого
дорівнює а, і його позначають У а.
Оскільки квадрат будь-якого числа невід’ємне число,
то при а < 0 вираз У а у множині дійсних чисел не має
смислу. Наприклад, не мають смислу вирази ]/*—16
Арифметичний квадратний корінь має такі властивості:
1) якщо а 0 і Ь 0, то У~аЬ = Vа • ]^Ь, тобто ко-
рінь з добутку невід’ємних множників дорівнює добутку
коренів;
2) якщо а 0, Ь > 0, то Л. = -р=-,
тобто корінь з
дробу, чисельник якого невід’ємний, а знаменник додатний,
дорівнює кореню чисельника, поділеному на корінь зна-
менника;
3) при будь-якому значенні числа а маємо іЛг2 = |а|.
Останню тотожність використовують при виконанні
410
тотожних перетворень ірраціональних виразів, при розв’я-
занні квадратних рівнянь і нерівностей. Зокрема, щоб
розв’язати простіше квадратне рівняння х2 = 16, треба
добути арифметичний квадратний корінь з обох частин
рівняння. Отже, /х2 = 16; | х | = 4. Звідси хг = 4;
х3 = —4, або Хі,2 = ±4.
Основним тотожним перетворенням ірраціональних ви-
разів, що містять квадратні корені із змінних, є: '
1) винесення множника з-під знака кореня;
2) внесення множника під знак кореня;
3) звільнення від кореня у знаменнику або чисельнику
дробу.
Приклад 1. Винести множник з-під знака кореня:
а) Ух9; б) /а3Ь3; в) -У а2Ь12е3; г) У а^Ь^.
Загальний підхід до розв’язування цих вправ полягає
в тому, щоб попередньо подати підкореневий вираз у вигля-
ді добутку двох співмножників, з яких один є квадратом
одночлена, і скористатися тотожністю про добування коре-
ня з добутку і тотожністю У а2 = | а\.
Розв’язання, а) Ух3 = У(х4)2 • х — У(х4)2 • Ух —
= Xі Ух;___
б) Уа^3 = У(а^)2 • Ь = /(о4^ • У~Ь = а46 УТ>,
оскільки за означенням арифметичного кореня змінна Ь
має бути невід’ємною, тобто Ь 0;
в) УіїЇЇЧ* = К(а3&6с)2 • с = /(<Л°с)2 • Ке =
= \а3\ЬесУ~с.
За умовою існування арифметичного кореня с 0,
а змінні а і Ь можуть бути будь-якими;
г) У а3Ь2 = У (а2Ь)2 • Ь — У(а2Ь)2 • Уа = а21 Ь | У~а.
Приклад 2. Внести множник під знак кореня: а) 5 У 2 ;
б) — 3 У~а; в) а У З; г) х ------.
Розв’язання. а) 5 /2 = /б2 • /2 = У52 • 2 = /50;
б) від’ємний множник — 3 не можна внести під знак
кореня, оскільки його не можна подати у вигляді арифме-
тичного кореня. Але вираз — ЗУа можна перетворити так,
щоб внести під знак кореня додатний множник 3; — ЗУа —
= —1 • ЗУа = —УЗ2 • Уа — — /9а;
в) якщо а 0, то а УЗ = У а2 • У~3 — У За2; якщо а <
<0, то_а/3 = — (— а) /3 = — У(— а)2 • /3 =
= — УЗа2;
411
г) % А = _(_Х). у—|_ = _]Л(_Х)2 х
X У ^- = —]Л-^-•хі = — У — 2х, де х<0
за умовою.
Приклад 3. Спростити вирази: а) ]/"(2 — ]/^2)2 +
Розв’язання. а) ]/" (2— У 2)2 + (У2— 1)2 =
= | 2 — /2 | +|К2 — 1 | = 2-/2 + /2 — 1 = 1;
б)_У(УЗ - 5)2 + К(1 - КЗ)2 = |/3-5| + |1-
_ /3 | = 5 — /3 + /3 — 1 = 4.
Арифметичним коренем /г-го степеня - з невід’ємного
числа називають невід’ємне число, п-й степінь якого дорів-
нює а, і позначають його так: у а.
Арифметичний корінь п-го степеня з числа а має смисл
як при парному, так і при непарному показниках п. Корінь
непарного степеня з від’ємного числа можна записати через
арифметичний корінь того ж степеня. Наприклад,—27 =
= —-^27 = —3.
Взагалі, якщо п — непарне і а < 0, то у а — — у —а.
Знак кореня п-го степеня використовують для запису роз-
в’язків рівнянь виду хп = а.
Наприклад, рівняння х8 = —48 у множині дійсних чи-
сел має єдиний корінь х = У—48 = —У48.
Арифметичний корінь п-го степеня має ті самі власти-
вості, що і 'арифметичний квадратний корінь:
1)
2)
0, &>0;
П Г п' /
_/ а у а
* ~~1Гь
, якщо а
.т
якщо а 0, пік — натуральні числа;
, якщо п, к і т — натуральні числа.
Степінь з раціональним показником і його власти-
3)
4)
5.
вості.
Означення. Степенем числа а з натуральним показни-
ком п, більшим 1, називається добуток п співмножників,
кожний з яких дорівнює а. Степенем числа а з показником
1 називається саме число а, тобто
ап — а - а - а.......а\ а1 = а.
412
Будь-який степінь з натуральним показником додатно-
го числа — завжди число додатне, непарний степінь від’єм-
ного числа є число від’ємне. Справді, З4 = 3 • 3 • 3 • 3 =
= 81; (—2)4= (—2)-(—2)-(—2)-(—2) = 16; (—З)3 = (—3)Х
X (—3) • (—3) = —27.
Якщо а — 0, то ап = 0. Наприклад, О3 = 0 • 0 • 0 = 0.
Степінь з натуральним показником має такі властивості.
1) Для будь-якого а і довільних натуральних чисел т
і п маємо ат • а1 = ат+п, тобто при множенні степенів з
однаковими основами показники степенів додаються, а
основа залишається тією самою.
2) Для будь-якого а і довільних натуральних чисел т
і п таких, що т> п, маємо ат : ап = ат~п, тобто при
діленні степенів з однаковими основами, відмінними від
нуля, від .показника степеня діленого віднімається показ-
ник степеня дільника, а основа залишається тією самою.
Будь-яке число (що не дорівнює нулю) у нульовому сте-
пені дорівнює одиниці, тобто а° = 1, а 0.
Після введення означення степеня з нульовим показни-
ком можна застосувати формулу ат • ап = ат+п і у ви-
падку, коли т = 0, або п = 0, або т = 0 і п. = 0 (при а Ф
Ф 0), а формулу ат : ігп = ат~п при т 0 (а 0).
3) Для будь-яких а і Ь і довільного натурального числа п
І а \п__ ап
У*”’
тобто при піднесенні до степеня добутку підноситься до цьо-
го степеня кожний множник окремо і результати перемно-
жаються.
Ця властивість виконується і для степенів з нульовим
показником, якщо основи відмінні від нуля.
4) Для будь-яких а 0, Ь Ф 0 і довільного натураль-
ного п,
/ а \»__ а>г
\ Ь )
тобто при піднесенні до степеня дробу окремо підносимо
до цього степеня чисельник і знаменник і перший результат
ділимо на другий.
5) Для будь-якого числа а і довільних натуральних чи-
сел т і п
= атп,
тобто при піднесенні до степеня показники степенів
перемножають, а основу залишають ту саму.
413
Якщо а Ф 0 і п — ціле від’ємне число, то
Наприклад, 3 2 = ,
Всі властивості степенів з натуральним показником ви-
конуються і для степенів з цілим показником за умови, що
основа степеня не дорівнює нулю.
Якщо а — додатне число, а —------дробове число (т —
т
ціле, п — натуральне), то а п = У ат.
За означенням
Степінь, що дорівнює нулю, означається лише для додат-
ного дробового показника: якщо —-додатне дробове
т
число (т і п — натуральні числа), то 0 п = 0. _
Для степенів з раціональним, зокрема дробовим, пс>
казником виконуються всі властивості, що встановлені для
степенів з цілими показниками.
Тотожні перетворення виразів, що містять арифметич-
ні корені будь-якого степеня і степені з дробовим показни-
ком, виконують на основі властивостей арифметичних ко-
ренів і властивостей степенів.
Приклад 1. Спростити вирази:
а) (УТ2----|-К75 + • ГЗ = /І2ТЗ-
— 4-К75Тз + 4-]/’зТз = 'И36---1-К225 +4-^9 =
О о О о
= 6-34-1 = 4;
ч -2 /4+/ї) гя - 4 г» -
-2/4“6+/ 44=»,-26+1:
1 1 1 1 1
в) (1 +с2)2 — 2с2 = 1 +2с2 + (с2)2 — 2с2 = 1
414
1 1 І 1 1 1 1
г) (а3 4-Ь3)2 —(а3 — Ь3)2=((а3 +Ь3) + (а3 —
і і і ± і і і
- Ь3) • ((а3 + Ь 3) — (а3 — Ь 3)) = (а 3 + Ь 3 4- а3 —
і і і і і і і і
— &3) • (а3 4- Ь3 — а3 + Ь3) = 2а3 - 2-Ь3 =4(аЬ)3.
Приклад 2. Обчислити значення виразу
( Ь'+ : № - Л)-(- !)
при хх 15,2, у & 3,25,
Розв язання. ——-і(х2у — у3) • —Т ---------1 =
2 \ \ ^ху /
_ І 5х2(х + #) | У (х + у) (х — у) \ х2 + %ху + у2 — 4ху _
\ 2 ’ 1 у 4ху
== 5*2 (* + £) - 1 е (х — у)2 = 5х2 (* + у) (х — у)2 =
%У (* + У) (х — у) * Ьху %ху2(х-{-у) (х — у)
= 5х(х — г/) ~ 5- 15,2(15,2 —3,25) 5 • 15,2 • 12,0 ~ 1П о
8//2 8 • 3,252 8.3,252 1У,б‘
Контрольні запитання
1. Які вирази називаються числовими? Що таке числове значення
виразу?
2. Що таке вираз із змінними?
3. Які математичні вирази називаються алгебраїчними?
4. Які алгебраїчні вирази називаються раціональними?
5. Які раціональні вирази називаються цілими?
6. Що називається одночленом?
7. Що називається многочленом?
8. Які раціональні вирази називаються дробовими?
9. Що таке алгебраїчний дріб?
10. Які вирази називаються тригонометричними?
11. Які два вирази називаються тотожно-рівними?
12. Що називається тотожним перетворенням виразу?
13. Що називається тотожністю на множині?
14. Який вид одночлена називається стандартним? Як звести од-
ночлен до стандартного виду?
15. Які основні види тотожних перетворень одночленів ви знаєте?
16. Які члени многочлена називаються подібними? Як звести по-
дібні члени многочлена?
17. Який вид многочлена називають стандартним? Як звести много-
член до стандартного виду?
18. Що називається степенем ненульового многочлена?
19. Як помножити одночлен на многочлен? Яке перетворення є
оберненим до нього?
20. Як знайти спільний множник одночленів даного многочлена?
21. Як розкласти многочлен на множники способом винесення
спільного множника за дужки?
22. Як перемножити два многочлени? Яке перетворення є оберне-
ним до множення двох многочленів?
415
23. Як розкласти многочлен на множники способом групування?
‘24. Чому дорівнює добуток різниці двох виразів на їх суму?
25. Чому дорівнює різниця квадратів двох виразів?
26. Чому дорівнює квадрат суми (різниці) двох виразів?
27. Чому дорівнює добуток суми (різниці) двох виразів на непов-
ний квадрат їх різниці (суми)?
28. Чому дорівнює сума кубів двох виразів?
29. Чому дорівнює різниця кубів двох виразів?
ЗО. Назвати основні види тотожних перетворень алгебраїчних
дробів.
31. Як знайти простіший спільний знаменник двох або кількох
алгебраїчних дробів?.
32. Як додати (відняти) алгебраїчні дроби з однаковими знамен-
никами?
33. Як додати (відняти) алгебраїчні дроби з різними знаменника-
ми?
34. Як перемножити два алгебраїчні дроби?
35. Як розділити один алгебраїчний дріб на другий?
36. В чому полягає задача тотожних перетворень раціональних
виразів?
37. Що називається квадратним коренем з числа а?
38. Який квадратний корінь з числа а називається арифметичним?
39. Назвати властивості арифметичного квадратного кореня.
40. Назвати основні види тотожних перетворень ірраціональних
виразів.
41. Що називається арифметичним коренем п-го степеня з числа а?
42. Як записати корінь непарного степеня з від’ємного числа че-
рез арифметичний корінь того ж степеня?
43. Що називається степенем числа а з натуральним показником п?
44. Чому дорівнює будь-яке число, що не дорівнює нулю, у нульо-
вому степені?
45. Назвати властивості степеня з довільним натуральним показ-
ником.
46. Сформулювати означення степеня числа, відмінного від нуля,
з цілим від’ємним показником.
47. Сформулювати означення степеня додатного числа а з дробо-
т
вим показником —, де т — ціле, а п — натуральне число.
48. Які вирази називаються тригонометричними?
Вправи
1. Перетворити у многочлен стандартного виду:
1) (5Х2 __ ^ху + у*) (2х — у2);
2) (0,2г/ - х) (х + 0,2г/) + (х - Зу) (Зу + х)\
3) _ 7 (^ _ Зх); 4) (За — Ь) (а + ЗЬ) — (Ь + а) (а — £);
/2 \/ 1 \
5) —-упі; 6) (0,їх + у)2ї
[ \ З7 \ /1
7) 1-у а— ~у Ь1 (14а — д); 8) І -у а—2Ь1 ;
9) (0,02х — 2,7г/) (1,5^ — 0,2х); 10) ІбаЬ — (За + 2Ь)2;
11) (1 4"в + 2-дп*)(4“в~ 1Г*)} І2> (о +2)2 — (« — 2)а;
416
13) (2,5т-0,3л) (2,5т —2л); 14) (х + 1) (х2 — х + 1);
15) ^2-ух— //^1-|-//— х^ ; 16) (2а— Ь) (4а2-\-2аЬ-{-Ь2};
( 2 \ / 2 \
17) 11 — -у X 1 + -у X ; 18) (а — 36) (а2 + Заб + 962);
/5 \ / 5 \
19) (— “з” — а* 11 — а3 І; 20) (2х + у) (4х2 — 2ху 4- у2),
2. Розкласти многочлени на множники:
1) а3Ь2 — б4; 2) 27 + х3; 3) 12а? — 4а36; 4) 1 — 8а3;
5) а (х — У) Ь (х — у); 6) а3 + б9; 7) т (3 — л) — Зл (п — 3);
8) 8 — а363; 9) 2х (а — 6) — (Ь — а); 10) 125а3 — 2763;
11) а2 + аЬ — ас — Ьс\ 12) а6 + 1; 13) Зх +, З// — ах — ау\
14) 1,1а3 — 1,1 б3; 15) а2Ь — ас2 + аЬ2 — Ьс2\ 16) 27х3 — у3;
17) ІОлгл — 25тр — бдл + 15рд; 18) 9а3 — 9 б3; 19) 9х2 — 16;
20) 2т2 — 4т + 2; 21) а2 — 2а + 1; 22) х3 — х2у + х2 + ху;
1
23) 2-у — у\ 24) 0,09х6 — 0,09//2; 25) 4а2 + 4а + 1; 26) а^ + 1.
3. Знайти значення виразу:
1) 15,2 . 14,8; 2) 9,92; 3) 552 — 452;
/ 1 \2 / 1 \2
4) 4а2 +9 — 12а при а — 2,5; 5) 14 -у 1 — 11 -у І ;
6) 3 (т. — І)2 + (т + 2) (т2 — 2т + 4) — (т + І)3 при т = 1,1;
7) 0,8492 — 0,1512;
8) а3 — (а — 2) (а2 + 2а + 4) + 5а при а = 0,6;
9) (100 — І)2;
10) (х + 2)3 — х (Зх + І)2 + (2х + О (4х2 — 2х + 1) при х = 2,
4. Розв’язати рівняння:
1) (3// + 1) (4у - 5) - (Ьу - 11) (2у - 7) = 24;
2) х (х + 2) — (х + 3) (х — 3) = 13;
3) (х + 2) (х2 — 2х + 4) — х (х — 3) (х + 3) = 26;
4) (х — 7)2 + 3 = (х — 2) (х + 2);
5) 15 (х2 — 4) 4- 5х (х - З)2 - 5 (х - І)3 = 5.
5. Виконати дії:
/ а \ / За2 \
аЦа+1 і_а2 у?
Ь — с аЬ — Ь2 а2 — с2
а 4-6 а2 — ас * а2 — б2 ’
/ 2т 4- 1 2т — 1 \ 4т
в) ( 2т— 1 ~ 2т + 1 /: 10т+ 5 5
З Зх — Зу І 2х—-3у п о \
х + у 2х — Зу Д х2 — у2 х + *
6. Обчислити значення виразу, попередньо спростивши його:
4а2 4- 8а6 4- 462 7 і о_г
а) 2а2___262 ПРИ а = 6 40 ’ = 1,375;
б3 — 6
б) (1 -)-а&)2 — (а + &)2 при а = — 56, Ь = 125,
7. Довести тотожності:
14 1 — 1819
417
ь
І аЬ 4- б2 \ 5а у,
б) ( 5^-5аГ + а6 + 62)- Т+Т ~-^Ь=ЬаЬ'
\ У х ] \ у х / \ х / х~У
( Х + У ?.( 1 1 2 І 1 1 \\
ГЦ ху ) Ц х2 + у2 + х + у ’ \ х + у ]] ““ Е
8. Винести множник з-під знака кореня: а) /5х2 , де х > 0;
6) 'У54а2 , де а < 0; в) /75 б4 , де Ь > 0;
9. Чи правильна рівність а = У5а2 , якщо: а) а = 3;
б) а = — 5; в) а = 2; г) а = — 7?
10. Внести множник під знак кореня: а) х У? , де х 0;
б) х У1, де х < 0; в) а -А- ; г) а .
11. Обчислити значення виразів з точністю до 0,01:
а) /50 + 2 /72 + /8 ; б) (/§ - 2) (/5 + 2);
в) /80 + -І-/20 + 3 /45 — /25; г) (1 +/7) (/7—1);
д) (/20 - /3 + /б) • /5 ; є) (5 /3 + 6)2;
е) (4/3-2/6-1) • 2/3; ж) ~ ~Г '
12. Спростити вирази:
а) /(2 - /2)2 + /(/2-І)2; б) (1 - /х) (1 + /х + х);
в) /(/І5 — 2)2 —/(/Ї5 — З)2 ; г) (/д + 2) (д-2/Н+4),
13. Звільнитися від знака кореня у знаменнику дробу:
1 — /х 2/3 — 3 4
а) ---т=—; б) —-—т=— ; в) —т=-------т=- ;
/х 5/3 ’ /Н—/7
2 /7 — 3 /2
Г) 3 /7 — 2 /2 ’
14. Обчислити:
а) ((-г)°)-0,5 — 7>5 • 4~ ~ — (—2)—4 + 81 °’25;
б) 0,027~ Т — (— "і")-2 + 256°’76 — 3-1 + (5,5)°-
15. Записати у вигляді суми:
1 1 і 1
а) а2 • Ь2 (а2 +&2); б) (2 — х1’5) (2 + х1-5);
1 1 1 1 2 1 1 2
в) (х 2 — 2) (х 2 + 2); г) (а 3 — Ь 3) (а 3 + а 3 Ь 3 + Ь 3).
418
16. Спростити вирази:
а)
і і і
г 2 , „ 2 ґ 2
х ~г У_________х_____ | ___У .
1 1 1 ~ _£ 1 ’
X2 х2 — у 2 х+х2у2
а ' ( Ь а-\-Ь
“ + ±± ~ УаЬ ’
а 2 Ь 2 + Ь а2 Ь 2 — а
§ 3. Рівняння і нерівності
1. Числові рівності і нерівності. Властивості числових
рівностей і нерівностей мають певну аналогію, але і суттє-
ві' різницю (табл. 12.2).
Означення, властивості числових рівностей і нерівностей
використовують при доведенні тотожностей і нерівностей.
Нагадаємо три основних способи доведення тотожностей:
1) скласти різницю лівої і правої частин тотожності і
шляхом перетворення здобутого виразу показати, що вона
дорівнює 0;
2) шляхом тотожних перетворень лівої частини показа-
ти, що ліва частина тотожності дорівнює правій, або, нав-
паки, шляхом тотожних перетворень правої частини пока-
зати, що вона дорівнює лівій;
3) ліву і праву частини тотожності окремо перетворити
у той самий вираз.
Приклад 1. Довести тотожність —~2 =
__ Ь Ь2 — аЬ
а — Ь а2 — Ь2 '
л а + Ь а — Ь Ь .
Доведення. - о-;- —7Т----ТГ7 ----------г+
2 (а — Ь) 2 (а + Ь) а — Ь1
, б2 — аЬ _ (а + Ь)2 — (а — Ь)2 — 2Ь {а + Ь) + 2 (Ь2 — аЬ) __
а2_ Ь2 — 2 (а2 — Ь2) ~
__ а2 + 2аЬ + Ь2 — а2 + 2аЬ — Ь2 — 2аЬ — 2Ь2 + 2Ь2 — 2аЬ _
~ 2 (а2 — Ь2)———————— —
=_____2____= 0-
2 (а2 - &2) '
Приклад 2. Довести тотожність а4 + а2 + 1 = (а2 -|-
+ а + 1) (а2 - а + 1).
Доведення, (а2 + а + 1) (а2 — а + 1) — ((а2 +
+ 1) + а) ((а2 + 1) — а) = (а2 + і)2 — а2 = а* + 2а2 +
4- 1 — а2 = а4 + а2 4- 1.
І4*'
419
Таблиця 12.2
Числові рівності
Числові нерівності
1. Число а називається рівним
числу Ь, якщо різниця а — Ь
дорівнює 0. Позначення: а = Ь
1. Число а називається більшим
від числа Ь, якщо а — Ь додатна.
Позначення: а > Ь.
Число а називається меншим від
числа Ь, якщо різниця а — Ь від’єм-
на. Позначення а <. Ь
2. При будь-якому а співвідно-
шення а = а правильне
3. При будь-яких а і якщо
а = Ь, то Ь = а
4. При будь-яких а, Ь і с, якщо
а — Ь і Ь ~ с, то а = с (власти-
вість транзитивності рівності)
5. Якщо а = Ь і с — будь-яке
число, то а + с = Ь + с
2. При будь-якому а співвідношен-
ня а > а і а < а хибні
3. При будь-яких а і Ь, якщо а > Ь,
то Ь < а. Навпаки, якщо а < Ь,
то Ь > а
4. При будь-яких а, Ь і с, якщо а <
< Ь і Ь < с, то а < с\ якщо а > Ь
і Ь > с, то а > с (властивості тран-
зитивності нерівностей)
5. Якщо а < Ь і с — будь-яке чис-
ло, то а + с < Ь + с\ якщо а > Ь
і с — будь-яке число, то а + с >
>Ь + с
6. Якщо а = Ь і с — будь-яке
число, то ас = Ьс
6. Якщо а <
якщо а < Ь
якщо а > Ь
якщо а > Ь і
Ь і с > 0, то ас < Ьс\
і с < 0, то ас > Ьс\
і с > 0, то ас > Ьс\
с < 0, то ас < Ьс
7. Якщо а = Ь і с = с?, то
а -Ь с = Ь 4“ (і
8. Якщо а — Ь і с = то ас =
= М. Наслідок: якщо а= Ь, то
Ь2
7. Якщо а < Ь і с < д,, то
а + с < Ь + якщо а > Ь і
Ос?, то а + О Ь + с?
8. Якщо а < д, с < (1 і а, Ь, с, (і —
додатні числа, то ас < М; якщо
а > Ь, о (і \ а, Ь, с, (і — додатні
числа, то ас > Ьд,
Наслідок: якщо а < Ь і а, Ь — до-
датні числа, то а2 < Ь2; якщо а> Ь
і а, Ь — додатні числа, то а2 > Ь2
9. Якщо а — Ь і а ф 0, & #= 0,
9. Якщо числа а і Ь — одного знаку
• и 1.1
і а < Ь, то —>-г*, якщо числа
а Ь
а і Ь одного знаку і а > то — <•
2
< ь
420
Приклад 3. Довести тотожність (а— Т+'ь + ^! (а —
_м _ а____________ь
' а-}-Ь Ь — а '
Доведення, (а---------+ Ь\і{а — Ь) =
\ а ~Г & /
— д (д + 6) — + Ь (а-\- Ь) 1 __
а-\- Ь а — Ь
а* 2 аЬ — 4аЬ + + № _____ (Д — &)2 _ а — Ь
(а + 6) (а — Ь) (а-}-Ь) (а — Ь) а-\-Ь ’
а Ь 2аЬ _____ а , Ь __
а-]~Ь Ь — а а2 — Ь2 а + Ь ' а — Ь
2аЬ ___________________ а (а — Ь) + Ь (а + Ь) — 2аЬ
(а — Ь) (а + Ь) (а — Ь) (а + Ь)
а — аЬ — аЬ Ь2 — аЬ____________ (а — Ь)2 ____ аЬ
(а — Ь) (а -\-Ь) (а — Ь) (а Ь) а-\-Ь '
Нерівності, складені за допомогою знаків > або <,
називають строгими нерівностями, а складені за допомогою
знаків або називаються нестрогими нерівностями.
Один із способів доведення строгих і нестрогих нерівностей
є спосіб, що грунтується на означенні числових нерівностей.
с 1
Приклад 4. Довести нерівність у -у .
Доведення. Складемо різницю лівої і правої ча-
стин даної нерівності і перетворимо її:
1 1 _ 2с— с2—1 _— (с2 —2с+1) _ — (с—і)2
+ 1 ~Т 2(с2+ 1) 2 (с2 + 1) ““ 2 (с2 +“1)"
<0.
Знаменник дробу при будь-якому с додатний, а вираз
(с — І)2 невід’ємний. Тому чисельник дробу недодатний,
а отже, і дріб при будь-якому с недодатний. Оскільки дове-
дено, що різниця лівої і правої частин нерівності недодатна,
ТО нерівність ВИКОНУЄТЬСЯ ПРИ будь-якому с.
2. Рівняння. Нерівності із змінною. Рівняння і
системи рівнянь. Рівність із змінною, відносно якої треба
встановити, при яких її значеннях (можливо, таких зна-
чень і не існує) рівність перетворюється у правильну число-
ву, називається рівнянням.
Наприклад, 5х — х = 28; х2 — 4 = 0; 2 (х 4* 3) =
= 5х — 7.
Коренем (розв’язком) рівняння з однією змінною нази-
вається значення змінної, при якому рівняння перетворю-
421
ється у правильну числову рівність, або, іншими словами,
при якому змінна задовольняє рівняння.
Розв’язати рівняння — означає знайти всі його корені
(розв’язки) або довести, що рівняння коренів не має. Рів-
няння, в якому ліва і права частини є раціональними вира-
зами, називається раціональним. Наприклад, 5 (х — 1) =
- 2х + 3; —Ц- = —
1 ’ х —5 %4-5
Якщо ліва і права частини раціонального рівняння —
цілі вирази, то рівняння називається цілим. Раціональні
рівняння, в яких хоча б одна частина рівняння є дробовим
виразом, називають дробовим. Наприклад, перше з наве-
дених вище рівнянь — ціле, а друге — дробове.
Два рівняння з однією змінною називаються рівносиль-
ними, якщо корені першого рівняння є коренями другого і,
навпаки, корені другого рівняння є коренями першого.
Рівняння мають такі основні властивості:
1) якщо до обох частин рівняння додати одне й те саме
число чи вираз із змінною, що не втрачає смислу ні при
яких значеннях змінної, то дістанемо рівняння, рівносиль-
не даному;
2) якщо обидві частини рівняння помножити або розділи-
ти на одне й те саме число, що не дорівнює нулю, чи на
вираз із змінною, який не перетворюється в нуль ні при
яких значеннях змінної і не втрачає смислу на . множині
допустимих значень змінної для даного рівняння, то діста-
немо рівняння, рівносильне даному.
З першої властивості випливає, що можна переносити
будь-який член рівняння з однієї його частини в іншу, змі-
нюючи попередньо знак цього члена на протилежний.
Розв'язком рівняння з двома змінними називається пара
значень змінних, яка перетворює це рівняння у правильну
числову рівність. Наприклад, для рівняння х — у — 5
пара (6; 1) є розв’язком.
Якщо треба знайти спільні розв’язки двох рівнянь з
двома змінними, то кажуть, що треба розв’язати систему
двох рівнянь з двома змінними, наприклад,
( 2х — у = 24,
(я + Зу = 5.
Розв'язком системи рівнянь з двома змінними назива-
ється пара значень змінних, яка перетворює кожне рів-
няння системи у правильну числову рівність. Наприклад,
пара х = 11, у = —2, або (11; —2) є розв’язком поперед-
ньої системи.
422
Розв’язати систему рівнянь означає знайти всі її розв’яз-
ки або довести, що система розв’язків не має.
Дві системи рівнянь називаються рівносильними, якщо
розв’язки першої системи є розв’язками другої і, навпаки,
розв’язки другої системи є розв’язками першої.
При розв’язанні систем рівнянь з двома змінними вико-
ристовують спосіб підстановки, спосіб алгебраїчного дода-
вання і графічний спосіб.
Приклад 1. Розв’язати систему
(ху = — 6,
їх — // = 7.
Розв’язання. Визначимо х через у з другого рів-
няння і підставимо замість х його значення у перше:
X = 7 + у; (7 + у) у = —6; у2 + 1у + 6 = 0.
Дістали квадратне рівняння відносно змінної у. Запишемо
. , — 7 ± /49 — 24 — 7 ±5
його розв язки: уі,2 =------; ух =
= —6; у2 = —1.
Визначимо х, підставивши послідовно значення ух і
у2 у рівність х = 7 + у. Маємо хх = 1; х2 = 6. Відповідь.
(1; -6) і (6; -1).
Приклад 2. Розв’язати систему
і 40х + Зу = 10,
( 20х — 7у = 22.
Розв’язання. Помножимо 'обидві частини друго-
го рівняння на —2, а перше залишимо без зміни:
і 40х + Зу = 10,
{ — 40х + 14у == 144.
Додамо ліві і праві частини обох рівнянь. Дістанемо
рівняння 17у = —34, яким замінимо одне з рівнянь Даної
системи
( 17у = —34, і
(20х — 7у — 22.
З першого рівняння здобутої системи знаходимо у =
— —2. Підставивши знайдене значення у в друге рівняння,
2 / 2 \
знайдемо х = Відповідь. —2).
5 15/
Приклад 3. Розв’язати систему
( ху = —6,
І X "І” У — 1
графічним способом.
423
Розв’язання. Побудуємо в одній системі коорди-
нат графіки рівнянь ху = —6; х + у = 1. Для цього вира-
зимо у кожному рівнянні змінну у через х. Дістанемо у =
= —у = 1 —х, Побудуємо графіки функцій, що зада-
ють ці формули,— гіперболу і пряму (рис. 12.5). Коорди-
нати (—2; 3), (3; —2) точок А і В перетину графіків функ-
цій є розв’язками системи. Отже, система має два розв’яз-
ки. Відповідь, (—2; 3), (3; —2).
3. Розв’язування нерів-
ностей і систем нерівностей.
Розв’язком нерівності з од-
нією змінною називається зна-
чення змінної, яке перетворює
її у правильну числову нерів-
ність. Наприклад, число 10 є
розв’язком нерівності 2% > 5.
Розв’язати нерівність з од-
нією змінною —означає знай-
ти всі її розв’язки або довес-
ти, що нерівність розв’язків
не має.
ся рівносильними, якщо роз-
в’язки першої є розв’язками другої нерівності і, навпаки,
розв’язки другої нерівності є розв’язками першої.
Областю визначення нерівності з однією змінною нази-
вають множину значень змінної, при яких ліва і права ча-
стини нерівності не втрачають смислу.
Нерівності з однією змінною мають такі власти-
вості:
1) якщо до обох частин нерівності додати одне й те саме
число або вираз із змінною, що не втрачає смислу в області
визначення нерівності, то дістанемо нерівність, рівносиль-
ну даній;
2) якщо обидві частини нерівності помножити або поді-
лити на одне й те саме додатне число або вираз із змінною,
який набуває додатних значень при своїх значеннях змін-
ної з області визначення нерівності, то дістанемо нерів-
ність, рівносильну даній;
3) якщо обидві частини нерівності помножити або поді-
лити на одне й те саме від’ємне число або на вираз із змін-
ною, що набуває від’ємних значень при всіх значеннях
змінної з області визначення нерівності, і змінити при цьо-
му знак нерівності на протилежний, то дістанемо нерів-
ність, рівносильну даній.
424
Якщо треба знайти спільні розв’язки двох або кількох не-
рівностей, то це означає, що треба розв’язати систему нерів-
ностей.
Розв'язком системи нерівностей з однією змінною нази-
вається значення змінної, яке перетворює кожну нерів-
ність системи у правильну числову нерівність.
Розв'язати систему нерівностей — означає знайти всі
її розв’язки або довести, що система не має розв’язків.
Способи розв’язання основних видів рівнянь і нерів-
ностей мають певну аналогію (табл. 11.3).
2 1
Приклад 1. Розв язати рівняння —------т—г = - . +
. 2х — 1
+ х3 + 1 •
Розв’язання. Помножимо обидві частини рів-
няння на спільний знаменник х3 + 1 = (х 4- 1) (х2— х 4-
+ 1). Дістанемо 2 (х + 1) = х2 — х 4- 1 + 2х — 1. Звід-
2 о л І "У 1 “І- 8 1 . З
си х2 — х — 2 = 0; Х1,2 =-----у- = -у ± -у; хх =
= —1; х2 = 2.
Прих = —1 спільний знаменник дробів перетворюється в
нуль, тому цей корінь треба виключити. При х = 2 спіль-
ний знаменник дробів не перетворюється в 0. Тому х = 2
є коренем рівняння. Відповідь, х = 2.
-1 х 11 9
Приклад 2. Розв’язати нерівність —~* -—<1.
Розв’язання.
х2 + * + 9 1 <2 0 ~Ь * — 9 — х 0 %а — д
X * X ’ X
Звідси
ч (х2 — 9 > 0, [ х2 — 9 < 0,
а) < б) і
Ь<0, 2 Ь>0.
Розв’яжемо графічно нерівність х2 — 9 > 0. Побудує-
мо графік функції у = х2 — 9 (рис. 12.6), звідки видно,
що множиною розв’язків нерівності х2 — 9 > 0 є об’єд-
нання двох проміжків (—оо; —3) і (3; +оо). Множиною
розв’язків системи* а) є спільна частина множин розв’язків
першої і другої нерівностей, тобто проміжок (—оо; —3).
З того ж графіка випливає, що множиною розв’язків
нерівності х2 — 9 < 0 є проміжок (—3; 3), а множиною
розв’язків системи б) — спільна частина множин розв’язків
обох нерівностей, тобто проміжок (0; 3) (рис. 12.7).
Отже, множиною розв’язків даної нерівності є об’єднан-
ня множин розв’язків систем а) і б), тобто множина (—оо;
—3) або (0; 3). Відповідь, (—оо; —3) або (0; 3).
425
Таблиця 12.3
Рівняння з однією змінною
Нерівності з однією змінною
1. Лінійним рівнянням з однією
змінною називають рівняння ви-
ду ах = Ь, це х — змінна, а і
Ь — числа
Якщо а Ф 0, то х — рівнян-
ня має один корінь
Якщо а = 0 і Ь = 0, то множи-
ною коренів рівняння є множи-
на всіх чисел
Якщо а = 0 і Ь Ф 0, то рівнян-
ня не має коренів, тобто множи-
на коренів — порожня множина
2. Квадратним рівнянням нази-
вається рівняння виду ах2 +
+ Ьх + с, де х — змінна, а, Ь,
с — числа, причому а 0
3. Якщо у квадратному рівнян-
ні хоча б одне з чисел Ь чи с,
або Ь і с одночасно дорівнює ну-
лю, то таке рівняння називаєть-
ся неповним квадратним рівнян-
ням. При с = 0 дістанемо непов-
не квадратне рівняння ах2 +
+ Ьх — 0. Його розв’язують спо-
собом розкладання лівої частини
рівняння на множники: х (дх +
+ Ь) = 0. Звідси х = 0; ах +
+ Ь = 0, х =------. Рівняння
а
має два корені х = 0 і х = —
1. Лінійною нерівністю з однією
змінною називається нерівність ви-
ду ах < Ь або ах > Ь (відповідно
ах Ь або ах Ь), де х — змінна,
а і Ь — числа
Якщо а Ф 0, то множиною розв'яз-
ків нерівності ах < Ь є або множи-
/ Ь \ / Ь
на —оо; — , або множина — ;
\ а / \а
+оо^
Якщо а = 0, то множиною розв’яз-
ків нерівності ах < Ь є або множина
всіх чисел (при Ь > 0), або порож-
ня множина (при Ь < 0)
Якщо а =Д 0, то множиною розв’яз-
ків нерівності ах > Ь є або множи-
/ Ь , \ х /
на —; +оо|, або множина —оо;
І а І І
І)
Якщо а = 0, то множиною розв’яз-
ків є або порожня множина (при
Ь > 0), або множина всіх чисел
(при Ь 0)
2. Квадратною нерівністю з однією
змінною називається нерівність ви-
ду ах2 + Ьх — с < 0 або ах2 +
•+ Ьх + с > 0 (відповідно ах2 +
+ Ьх + с 0, або ах2 + Ьх + с >
> 0), де х — змінна, а, Ь, с — чис-
ла, причому а Ф 0
3. Якщо у квадратній нерівності
хоча б одне з чисел Ь чи с, або Ь і с
одночасно дорівнюють нулю, то ді-
станемо неповну квадратну нерів-
ність. При с = 0 ах2 + Ьх > 0 (або
ах2 + Ьх < 0). Його розв’язують
способом розкладання лівої части-
ни на множники: х (ах + Ь) > 0.
Далі використовують твердження:
добуток двох співмножників додат-
ний тоді і тільки тоді, коли обидва
співмножники мають однакові зна-
ки. Отже, можна скласти дві систе-
426
Продовження табл. 12,3
Рівняння З ОДНІЄЮ ЗМІННОЮ
Нерівності З ОДНІЄЮ змінною
При Ь = 0 дістанемо квад- ратне рівняння ах2 + с= 0, яке розв’язують так: ах2 = = —С, х2 = — £. Якщо — £ > ’ а а > 0, то добуваємо арифме- тичний квадратний корінь з обох частин рівняння: Ух2 = = звідси |х| = Отже, X = І — X = «= рС_£, звідси х= — і/*— ми нерівностей: а) (х > 0, або б) (х < 0, \ах + 6 > 0 \ах + Ь < 0, які розв’язують відомим способом. Аналогічно розв’язують нерівність ах2 + Ьх < 0. При Ь = 0 маємо нер івн ість ах2 + с > 0 (або ах2 + . + с < 0), яку можна розв’язати так: при а > 0 ах2 > —с, х2 > —£. а
Рівняння має два корені х^ = Якщо —£> 0, то Ух2 > 1/"— а V а | х І > і/"—£, звідси X > £
що — £ < 0, то х2 = — £ не має а а або — х > 1/ — £., звідси х < г а
розв’язків, а тому і рівняння < — Отже, множиною роз-
ах2 + с = 0 не має коренів в’язків нерівності ах2 —с>0 є два числових проміжки: —оо; “/-і) аб° (/-?= +о°)- Якщо — — < 0, то нерівність ах2 + + с > 0 не має розв’язків. При а < < 0 х2 < — £. Якщо ~ > 0, то а а І х|< £, звідки — |/"_£< < х < 1/ —-. Якщо — £ < 0, то г а а с нерівність х“ < —не має розв яз- ків, тому і дана нерівність ах2 + + с > 0 не має розв’язків
4. Вираз £) = Ь2 — 4ас назива- ється дискримінантом квадратно- 4. Щоб розв’язати квадратну не- рівність ах2 + дх 4- 0 (або
427
Продовження табл. 12.3
Рівняння З ОДНІЄЮ ЗМІННОЮ
Нерівності з однією змінною
г'о рівняння ах2 + Ьх + с = 0.
Якщо О > 0, то квадратне рів-
няння має два різних корені, які
знаходять за формулою =
—ь ±
= —~2а------* Якщо м = 0, то
квадратне рівняння має два рів-
них корені, тобто фактично один
розв’язок х = —2^" • Якщо Р <
< 0, то квадратне рівняння не
має дійсних коренів
Квадратне рівняння будь-якого
виду можна розв’язати графічно,
побудувавши графік квадратного
тричлена — параболу. При £> >
> 0 парабола перетне вісь Ох у
двох точках, абсциси яких і бу-
дуть коренями даного квадратно-
го рівняння. При О = 0 пара-
бола дотикається до осі Ох. Аб-
сциса точки дотику — корінь
квадратного рівняння
5. Щоб розв’язати дробово-раці-
ональне рівняння, треба: 1) пе-
ренести всі члени рівняння у лі-
ву частину, тобто подати рівнян-
ая2 + Ьх + с < 0), її подають у
Ь с
вигляді X2 + — х + — >0 при
а а
Ь с
а > 0, або х2 Ч---х Ч----<0 при
а а
а < 0. Знаходять корені відповід-
ного квадратного рівняння х2 4“
Ь с
Ч- ~Ч~ — = 0. Якщо тричлен має
два різних корені х± і х2, то за тео-
ремою Вієта розкладають тричлен
на множники, подаючи дану нерів-
ність у вигляді (х — хх) (х — х2) >
> 0 або (х — хТ) (х — х2) < 0, і
розв’язують її або складаючи дві
системи лінійних нерівностей
їх — Хі > 0, або (х — хі < 0,
[х — х2 > 0, (х — х2 < 0,
або методом інтервалів. Якщо квад-
ратний тричлен не має коренів, то,
виділяючи квадрат двочлена, по-
дають його у вигляді а (х — т)2 Ч"
4* п > 0, де т = —Д-, п ~
2а
Ь2 — 4ас .
= —. Залежно від знака а і
4а
п роблять висновок про множину
розв’язків нерівностей
Квадратну нерівність зручно роз-
в’язувати графічно, побудувавши
графік квадратного тричлена, тобто
графік функції у = ах2 Ч- Ьх Ч~ с.
За графіком встановлюють, при
яких х значення функції перетво-
рюються в 0, в яких проміжках во-
ни додатні, а в яких від’ємні. Ці
проміжки і будуть множинами роз-
в’язків відповідних нерівностей
ах2 4- Ьх Ч- с > 0, ах2 + Ьх с<
< 0
5. При розв’язанні дробових нерів-
ностей не можна у загальному ви-
падку заміняти його цілою нерів-
ністю шляхом множення обох час-
428
Продовження табл. 12.3
Рівняння з однією змінною
Нерівніть з однією змінною
/ (х)
ня у вигляді = 0;
Ф (х)
2) скористатися тим фактом, що
дріб дорівнює нулю тоді і тіль-
ки тоді, коли чисельник дорів-
нює нулю, а знаменник не до-
рівнює нулю, тобто прирівняти
до нуля чисельник, розв’язати
здобуте рівняння / (х) — 0. Із
знайдених розв’язків виключити
ті, що перетворюють у нуль зна-
менник
Можна також подати дробово-ра-
ціональне рівняння у вигляді
/ (х) <7 (х) .
—< і скористатися умо-
ф (х) ф (х)
вою рівності двох дробів з одна-
ковими знаменниками, тобто при-
рівняти чисельники і розв’язати
здобуте ціле раціональне рівнян-
ня / (х) = д (х). Із знайдених роз-
в’язків виключають ті, які пе-
ретворюють знаменник в нуль
Можна нарешті записати дробо-
. / (х)
ве рівняння у ВИГЛЯДІ Д =
<р (х)
<7 (*) .
= Ф(х) скоРиставшись власти“
вістю пропорції, скласти рівнян-
ня [ (х) • ф (х) = ф (х) д (х). Роз-
в’язавши це рівняння, треба ви-
ключити ті корені, які перетво-
рюють в нуль хоча б один із
знаменників ф (х) чи ф (х)
тин на спільний знаменник дробів,
що входять до нерівності. Справді,
спільний знаменник при певних зна-
ченнях змінної може набувати від’-
ємних значень, і тоді при множенні
знак нерівності треба змінювати на
протилежний. Тому можна викорис-
тати такий спосіб:
1) перенести всі члени нерівності
у ліву частину, тобто подати не-
рівність у вигляді - > 0 (або
Ш< 0);
<р(х)
2) скористатися твердженням —
дріб додатний тоді і тільки тоді, ко-
ли чисельник і знаменник мають од-
накові знаки:
І/ (*) > 0, або (х) < 0,
ІФ (х) >0 1ф (х) < 0;
3) розв’язати здобуті системи;
4) об’єднати їх розв’язки, що дасть
множину розв’язків даної нерівнос-
ті
Можна також після запису нерів-
£ (дЛ
ності у вигляді —, < > 0 помножи-
ф (X)
ти обидві її частини на ф2 (х) > 0,
замінивши цим самим дробову не-
рівність на рівносильну цілу / (х) X
X Ф (х) > 0
При розв’язанні нерівностей вид^
0 або / (х) • ф (х) % 0
можна скористатись також методом
інтервалів
Дві чи декілька нерівностей з однією змінною утворю-
ють систему, якщо поставити задачу знайти всі спільні
розв’язки даних нерівностей.
Кожне значення змінної, при якому кожна нерівність
системи перетворюється у правильну числову нерівність,
називається розв’язком системи нерівностей.
429
Дві чи кілька нерівностей з однією змінною утворюють
сукупність, якщо поставити задачу знайти всі такі значен-
ня змінної, кожна з яких є розв’язком хоча б однієї з даних
нерівностей. і
Кожне значення змінної, при якому хоча б одна з нерів-
ностей сукупності перетворюється у правильну числову не-
рівність, називається розв'язком сукупності нерівностей.
Систему двох нерівностей з однією змінною записують
з допомогою фігурної дужки. Наприклад,
(2х — 3>13,
12 — х < 6х — 8.
Для запису сукупності нерівностей вживають квадрат-
ні дужки. Наприклад,
Г Зх + 1 < х,
[ 2х 4- 3 < х + 2.
При розв’язанні систем і сукупностей нерівностей з
однією змінною зручно використовувати графічну ілюстра-
цію на координатній прямій
Приклад 1. Розв’язати систему нерівностей
І 2х 4- 3 < 12 4- 5х,
} 2 — х < 22 — 6х.
Розв’язання. Розв’яжемо обидві нерівності окремо.
З першої нерівності дістанемо рівносильну нерівність
Зх > —9, звідки х > —3. З другої нерівності має-
мо 5х < 20, звідки х < 4. Отже, дану систему замінимо
430
рівносильною
х> — З,
х< 2.
Зобразимо на координатній прямій множини розв’язків
кожної нерівності здобутої системи і позначимо їх штрихов-
кбю різного нахилу. Множина розв’язків утвориться в
результаті перетину штриховки різного нахилу (рис. 12.8).
Відповідь. (-—'3; 2).
Приклад 2. Розв’язати сукупність нерівностей
2х + 7 > 5х — 2,
5х — 2 < 20 — 6х.
Розв’язання. Розв’язавши кожну нерівність ок-
ремо відносно х, матимемо сукупність
або
[11х<22, [х<2.
Множиною розв’язків останньої, а отже і даної сукуп-
ності, є інтервал (—оо; 2) (рис. 12.9).
4. Метод інтервалів. Розглянемо метод інтервалів
за допомогою прикладу на розв’язування нерівності
0- Ліва частина нерівності — раціональ-
ний дріб, який задає функцію / (х) = --2^_л._6
Після розкладу чисельника і знаменника на множники
маємо / (х) = (х'^2) ’ Ця ФУнкція перетворюєть-
ся в нуль при х = —5, х = 4 і не визначена при х = —З,
х = 2. Розмістимо ці чотири числа на координатній прямій.
Вони розіб’ють її на п’ять інтервалів (звідси назва «метод
інтервалів»): (—оо; —5), (—5; —3), (—3; 2), (2; 4) і (4; Н-оо).
При х > 4, тобто на інтервалі (4; +оо), всі чотири множни-
ки чисельника і знаменника додатні, тому і функція / (х) =
(х + 5) (х — 4) п
= + з) (72) Д°Датна- Рухаючись вздовж координатної
прямої справа наліво, помічаємо (це легко перевірити,
обчисливши значення функції при довільному х з кожно-
431
го інтервалу), що в кожній з чотирьох точок змінює знак
лише один з чотирьох множників, тому змінює знак і зна-
чення функції, тобто ліва частина нерівності. На кожному
з чотирьох інтервалів функція зберігає знак, тобто є знако-
сталою.
Зміну знаків функції зручно проілюструвати з допомо-
гою хвилястої кривої (рис. 12.10), яку креслять справа на-
ліво, починаючи зверху від координатної прямої. На тих
Рис. 12.10
інтервалах, де крива розміщена над координатною прямою,
/ (х) > 0, а там, де під прямою, / (х) < 0. Побудовану
криву називають кривою знаків.
Отже, множиною розв’язків даної нерівності є об’єд-
нання двох множин [—5; 3) і (2; 4]. Оскільки дана нерів-
ність нестрога, то точки —5 і 4 (нулі функції) включаємо
до множини розв’язків. Відповідь. 1—5; 3) або (2; 4].
Метод інтервалів використовують і при розв’язанні рів-
нянь, які містять невідоме під знаком модуля.
-5 0 1 2/ З х
Рис. 12.11
Приклад. Розв’язати рівняння |5 — 2х | + | х + 3 | =
= 2 — Зх.
Розв’язання. Дане рівняння містить два вирази
з невідомим під знаком модуля. Ідея розв’язання рівнян-
ня з модулем, як і нерівностей з модулем, полягає в тому,
щоб звільнитися від них і перейти до рівняння, яке не
містить модуля і розв’язується вже відомим способом.
Вирази з модулями, які входять у дане рівняння, пе-
ретворюються в нуль відповідно при х = -|- і х = —3.
(5 \
-у) розбивають координатну пряму на
(5 \ / 5 \
—З’ Т * ПГ’ "І"00 (Рис* 12.11).
Перетворимо вирази з модулями на кожному з трьох інтер-
валів, починаючи з лівого (—оо; —3).
1) При х < —3 маємо | 5 — 2х ] = 5 — 2х; | х + 3 | =
432
= — х — з: Після підстановки в дане рівняння значення
модулів рівняння набере вигляду 5 — 2х — х — 3 = 2 —
— Зх, або 2 = 2. Це означає, що будь-яке значення х з про-
міжку (—оо; —3) є розв’язком даного рівняння.
2) При —З х -|- маємо | 5 — 2х | = 5 — 2х; | х +
+ 3 | = х + 3.
Рівняння набирає вигляду 5 — 2х + х + 3 = 2— Зх.
Звідси 6х = 4; х = -|-'
На цьому відрізку рівняння має єдиний корінь х — —3.
3) При х > -у | 5 — 2х | = —5 + 2х; | х + 3 | = х + 3.
' Рівняння набирає вигляду — 5 + 2х + х + 3 = 2 —
— Зх. Звідси 6х — 4; х = Але х = -у не належить роз-
глядуваному інтервалу. Це означає, що на інтервалі
+ оо^ рівняння не має коренів. Відповідь. Множиною розв’-
язків даного рівняння є множина (—оо; 3).
Контрольні запитання
1. Коли число а називається рівним числу Ь? Коли число а назива-
ється більшим (меншим) числа Ь?
2. Сформулювати властивості числових рівностей.
3. Сформулювати властивості числових нерівностей, аналогічні
відповідним властивостям числових рівностей. Довести одну з них.
4. Які властивості числових нерівностей відмінні від відповідних
властивостей числових нерівностей? Довести одну з них.
5. Назвати способи доведення тотожностей.
6. Яку рівність із змінною називають рівнянням?
7. Що означає розв’язати рівняння з однією змінною? Що назива-
ється коренем рівняння з однією змінною?
8. Які рівняння називають цілими, дробовими?
9. Сформулювати основні властивості рівнянь та наслідок з них.
10. Які два рівняння називаються рівносильними?
11. Що називається розв’язком рівняння з двома змінними?
12. Що таке система двох рівнянь з двома змінними?
13. Що називається розв’язком системи рівнянь з двома змінними?
. Що означає розв’язати систему двох рівнянь з двома змінними?
14. Які дві системи рівнянь називаються рівносильними?
15. Назвати основні способи розв’язування систем рівнянь з дво-
ма‘змінними. В чому полягає кожний із способів?
16. Що називається розв’язком нерівності з однією змінною? Що
означає розв’язати таку нерівність?
17. Які дві нерівності називаються рівносильними?
18. Що називається областю визначення нерівності з однією змін-
ною?
19. Назвати властивості нерівності з однією змінною.
20. Що означає вимога: розв’язати систему нерівностей?
433
21. Що називається розв’язком системи нерівностей з однією змін-
ною?
22. Назвати основні види нерівностей з однією змінною.
23. Яка нерівність з однією змінною називається лінійною? Як роз-
в’язується така нерівність?
24. Яке рівняння називається квадратним?
25. Яка нерівність з однією-змінною називається квадратною?
26. Як розв’язується рівняння виду ах2 + Ьх — 0 і нерівності ви-
ду ах2 + Ьх > 0 (ах2 + Ьх < 0), ах2 + 0?
27. Як розв’язуються рівняння виду ах2 + с = 0 і нерівності виду
ах2 + с = 0?
28. Як розв’язуються квадратні рівняння виду ах2+дх+с =
= 0, де Ь Ф 0, с #= 0.
29. Як розв’язуються нерівності виду ах2 + Ьх + с > 0 (ах2 +
4- Ьх + с <. 0), де Ь Ф 0, с =# 0?
ЗО. Як розв’язуються дробові рівняння?
31. Як розв’язуються дробові нерівності?
32. Коли дві або кілька рівнянь утворюють сукупність рівнянь?
Що називається розв’язком сукупності рівнянь?
33. В чому полягає метод інтервалів розв’язування нерівностей?
34. Як застосовується метод інтервалів при розв’язанні цілих не-
рівностей, які містять невідоме під знаком модуля? *
Вправи
1. Розв’язати рівняння:
А
1) А X = 3; 2) х2 + 3 = 0; 3) 5х + 4 = 0;
5
4) 2х2 -|- 5х — 3 = 0; 5) 9х — 2 (х — 3,5) — 2х — 1,5;
6) 4х2 — 4х + 1 = 0; 7) х~ 1 — А- = 4;
5 З
8) хч _ 7х = 6 — 2х; 9) 5х2 = 0; 10) Зх2 — 5х — 2 = 0;
11)х(3+х) = 0; 12) х2—Зх + 4 = 0; 13) (х + 2) (х — 5) = 0;
14) х* ~ А-- = 0; 15) 6х2 — Зх =0; 16) -А— = —;
’ х + 2 ' ’ г/+ 5 у+5
17) 2х = Зх2; 18) 2* - = А ; 19) — 2х2 + 8 = 0;
1-Х X
20) **—6—=---------5--; 21) Зх2 = 27; 22) А + . = 1;
х — 1 1 — х х х + 2
23) х2 — 5 = 0; 24) 2у + 3 = .У~А .
2// — 1 У + З
Б
25) кх~— — 3*'+ 2 = —; 26) 8х2 + 2ах — За2 = 0;
к — 1 к+1 к — 1
27) 3(г/+ 1) - А=Х = -А±А+ 12;
2 о
28)х2 + 5|х| + 6 = 0; 29) _ 2 =
ЗО) 1,3х — 2 — (3,3х + 5) = 2х +1;
434
Зх 1 1 . з?) % ”І- __Я •
Т ~ Т “ ~ ~ ’ ' х—3 х~+~3 “" ~ ’
31)
оо' 6x4-7 . 80 4~4х ЗО—2х .
63) —__ + л =--------- -------,
34) 1 + —Ц_-_6^ = _3 . 35) ах + 6 = 2а + З*;
X — 1 X2 — 1 X + 1
36) _-__=_____2 — __1____;
ха — 4 ха + 2х 2х — ха
37) (х—4)а • (ха —х + 2) —(х —5)а.(ха + х— 1) = 22;
х | 1 1 — х х2 - 1 *
39) (х — а)2 + (х— Ь)2 = а2 + б2;
40) х+ 2 | 8x2 + 3 = а:+ 0,5 . 41) ха_____х
7 Зх — 1 ' 1 — 9х2 9х + 3 ' а Ь
42) ЗО 13 _ 7 + 18у
- У2-1 у2 + у + і У2-і
2х . х— 1 __ 4
Зп п — 1 п2 —
(х _ 2)3 + (1 — X)3 = -
1 । 2 .
х—1 х — 2 х — З
43)
45)
47)
2. Розв’язати системи рівнянь:
А
В
_ ; 44) |у-6|-|у-1| = 3;
1; 46) |х|+|х-1| + |х-2| = х;
3 - —А-; 48) х2 = |5х —6|.
Х^- 6
х + У = 6,
Зх — Зу — 2;
х2 + у2 = 34,
х— у = 2;
х2 — у = 14,
Зх + у = 4;
ґ х2 — у=18;
2) { у
[ х -}-2у = 0;
5) ( х + у = 12,
( ху = 35;
[ х2 4- у2 = 41,
8) ’
( У — х = 1.
[ Зх + 2у = 34,5,
( 2х — у == 12,5;
х + у2= 16,
х + Зу = 10;
Б
5х + 9г/ __ 2х + Зу
3 2
х — Зу __ 2х — Зу .
2 З
Ю)
х — а __ Ь
у — а с
х — Ь _ а + Ь .
у — с а + с
ґ х + у =120,
| х2 + у2 = 10 400;
12)
Ч-+—=2-
х+у х—у
-4— + —— = 7;
х+у х—у
13)
А-_2_=11,
X у
А + А. = 17;
х У
ґ Зх- 4~ 2г/ + у — 43,
1 х2 4~ 2хг/ 4" Зг/2 = 33.
435
в
19)
20)
ху = 80,
х + у _ 3 .
х — у 2 ’
ґ ху + х-\-у= 11
( х2у -|- ху2 = ЗО;
ґ & -+{/* = 17 (х + у)а,
16) І ху = 2 (х + {/);!
18) [Х + » = 5>
’ 1 х3 + у2 = 35;
1 _і_ ' 2 _з
2х — Зу Зх — 2у 4
2х — Зу Зх — 2у
х+у х — у = 5 ,
х—у ху 2
х2 + у2 = 20.
3. Розв’язати нерівності:
А
1) 0,4х>2; 2) (х— 11) (х — 3) < 0; 3) 4х — 7 > 0;
4) Х2 _ 2х _ з > 0; 5) 3 — 2х < 12 — 5х; 6) 9ха — 25 > 0;
7) 2х — 3 < 7 (1 + х); 8) 2х2 — Зх — 2 > 0; 9) 5 — 4х < 0;
10) х(х — 1) (х — 3) <0; 11) Зх —~ 5 < 2 (1 — х);
12) х (х — 4) (х + 4) < 0; 13) х2 — 4 < 0; 14) х + 2 < 0;
х — 5
15) х (3 — х) > 0; 16) 2х~ І. > 0.
х + 2
Б
17) —-|-<4х—3; 18) (х—-|_у + 21 > 0;
19) (х—1)24-7>(х + 4)2; 20) 2^-—>-Зх у 10 ;
21) 2,5(2 —і/) — 1,5(г/-4)<3 — у,
22) -2 + х = х < — (4 — х)2;
23) 0,2х2 — 0,2(х— 6) (х + 6) > 3,6х; 24) х2+|х| —2>0;
25) — --Уо~^-3 —у> 2; 26) З.~х < — ;
2 8 у ' х—З З
27) х + 4 — — < ; 28) ~ ! + х~3 > 2;
3 3 ’ Зх+ І т х + 3
29) — 1 х2 + х+-1->0; ЗО) .... <~3--->2;
З г 3 х2 — 5х + 6
31) 0,1х2—1,1х+1>0; 32) 3х-4-.-х.+.1 <5.
436
в
33) | 2x4- 1 | + |3х + 2|< 11; 34) х2 4-31 х | + 6 < 0;
О
35) | 2~5х|4-|*4-1|>* + 3; 36) .*2~^ + 1 >0;
37) *2(2*~ 9) (*— 1)8<О; 38) І х + 2 >1;
(х + 4)6 (2х — 6)« | х2 — 1
39) (х — —) 4-4(х——^4-ЗсО;
\ х ! \ х /
40) |х2 —Зх-4-2|>х43
4. Розв’язати системи нерівностей:
А
ґ 2(3х— 1) <3(4x4- 1)4-16,
І 4 (2 4- х) < Зх 4- 8;
2х>3 — 13*~2 .
х । 2 ( >7\ Зх — 20 ,
_ + —(х-7)<------— ,
§ 4. Функції. Огляд властивостей
раніше вивчених функцій
1. Означення функції. Зростаючі, спадні, парні і
непарні функції. Матеріальна єдність світу виявляється
у взаємозв’язку і взаємообумовленості різних явищ і про-
цесів, що відбуваються в природі. При їх розгляді дово-
диться враховувати залежності одних величин від інших.
Наприклад, залежність шляху від часу, залежність кіль-
кості купленого товару на певну суму від ціни, залежність
437
між площею круга і його радіусом. Необхідність вивчення
на практиці залежностей між змінними різної природи при-
вела до поняття функції в математиці.
Залежність змінної у від змінної х називається функцією,
якщо кожному значенню х відповідає єдине значення у.
Функцію позначають або однією буквою латинського
алфавіту /, В, або з допомогою рівності у = / (х), яка сим-
волічно означає залежність між двома
змінними.
5 .X Змінну х називають незалежною,
або аргументом, а змінну у — залеж-
X ною.
/ Значенням функції називають зна-
/ чення залежної змінної у, яке вона на-
/[ 1 , буває при деякому певному значенні х.
0____________6 х Множина значень, яких набуває
Рис. 12.12 незалежна змінна х, називається об-
ластю визначення функції.
Множина відповідних значень залежної змінної у, яких
вона набуває при всіх значеннях х з області визначення
функції, називається областю значень, або областю зміни
функції.
Приклад 1. Залежність шляху 5 тіла, яке рухається
рівномірно, від часу і е функцією, що задається формулою
5 = 50 + Де *$о— шлях, який пройшло тіло, V — швид-
кість, яка є сталою при рівномірному русі.
Приклад 2. Якщо учні групи, яка складається з 25 осіб,
чергують протягом січня, крім тих днів, які припадають
на неділю, то кожному з днів січня відповідає певний чер-
говий. Незалежною змінною тут є дні січня, залежною —
черговий. Маємо функцію, областю визначення якої є
множина днів січня (без тих, які припадають на.неділю),
а областю зміни — множина учнів групи.
Приклад 3. Активна електрична енергія, яка витрача-
ється в ланцюгу змінного струму за час /, є функцією часу
і при сталій потужності Р виражається формулою =
= Рі-
Нагадаємо основні способи задання функції: 1) за допо-
могою формули (приклади 1 і 3); 2) за допомогою таблиці
(наприклад, таблиці квадратів чисел, значень тригономет-
ричних функцій та ін.); 3) за допомогою графіка (наприк-
лад, якщо фіксувати протягом кількох років висоту дерева,
яке росте, то, зобразивши по осі Ох вік дерева в роках,
а по осі Оу висоту в метрах, дістанемо графік функції
(рис. 12.12)).
438
Не завжди формула задає функцію. Наприклад, форму-
ла І — (закон Ома) задає пряму пропорційність (функ-
цію від V) при сталому опорі в ланцюгу і змінній напрузі
і задає обернену пропорційність (функцію від 7?) при сталій
напрузі і змінному опорі. Проте якщо з цієї формули вира-
зити К, то 7? = -у-. Остання формула не задає функцію.
Справді, 7? — величина стала для даного провідника і не
залежить ні від напруги, ні від сили струму; якщо напругу
збільшити, наприклад, у 2 рази, то в 2 рази збільшиться і
сила струму, а відношення напруги до сили струму не змі-
ниться . Опір 7? є функцією (прямою пропорційністю у =
— кх) довжини провідника при сталій площі поперечного
перерізу і є функцією площі поперечного перерізу (обер-
.„ . .„ . .
неною пропорційністю у = — 1 при сталій довжині провід-
ника
де р — питомий опір; І — довжина провідника; 5 — пло-
ща його поперечного перерізу.,
Інколи функцію задають різними формулами на різних
множинах значень аргумента (так звані кусково-задані функ-
ції). Наприклад, якщо турист знаходиться в дорозі 9 год і в
перші 5 год рухався зі швидкістю 4,5 км/год, потім відпо-
чивав 0,5 год, а решту часу йшов зі швидкістю 4 км/год,
то функцію шляху 5 залежно від часу і запишемо у вигляді
4,5/ при 0^/^5,
5 =
22,5
при 5^/^5,5,
22,5 -|- 4/ при 5,5 і 9.
Функція у — } (х) називається зростаючою, якщо біль-
шому значенню аргументу відповідає більше значення
функції, тобто ДЛЯ будь-яких ДВОХ значень Хх і х2 змінної
х, взятих з області визначення і таких, що х2 > хх, вико-
нується нерівність / (х2) > / (Хі).
Функція у = / (х) називається спадною, якщо більшо-
му значенню аргументу відповідає менше значення функції,
тобто для будь-яких двох значень хг і х2 змінної' х, взятих
з області визначення і таких, що х2 > хх, виконується
нерівність / (х2) < / (хх).
Для дослідження функцій на зростання і спадання,
виходячи з їх означень, треба:
439
1) вибрати будь-які два значення хг і х2 з області визна-
чення функції такі, що х2 >
2) скласти різницю / (х2) — / (*і) і з’ясувати (якщо це
можливо), чи буде вона додатною (від’ємною) і, користую-
чись означенням нерівності, переконатися, що / (х2) >
> ї (*1) (чи / (*г) < / (*і))> а звідси зробити висновок про
зростання (спадання) функції.
У зростаючої функції графік піднімається вгору, у спад-
ної — опускається вниз.
Функція // = /(%) називається парною, якщо для будь-
якого значення х з області визначення значення —х також
належить області визначення і виконується рівність
? (—х) = ї (х). Інакше кажучи, у парних функцій їх зна-
чення для протилежних значень аргументу рівні. Графік
парної функції симетричний відносно осі Оу.
Функція у = / (х) називається непарною, якщо для будь-
якого значенням з області визначення значення —х також
належить області визначення і виконується рівність
/ (-Х) = Ч (Д
Тобто у непарних функцій їх значення для протилежних
значень аргументу протилежні. Графік непарної функції
симетричний відносно початку координат.
Приклади. 1) Функція у = 2х зростаюча і непарна у
всій області визначення (рис. 12.13). Графік її симетричний
відносно початку координат.
2) Функція у = х2 зростаюча при х £ [0; 4~оо) і спадна
при (—оо; 0]- Вона парна, її графік симетричний від-
носно осі Оу (рис. 12.14).
Щоб дослідити функцію на парність чи непарність, тре-
ба:
1) перевірити виконання умови: для будь-якого х з об-
ласті визначення —х також належить області визначення,
440
тобто перевірити, чи буде область визначення даної функ-
ції множиною, симетричною відносно точки 0;
2) перевірити виконання умови: / (—х) = / (х) чи
ї (-*) = -/ (X).
Якщо не виконується перша умова, то не має рації
перевіряти другу,
2. Огляд властивостей основних видів функцій. Л і -
н і й н а функція. Лінійною називається функція,
яку можна подати у вигляді у = кх + Ь, де х — незалежна
змінна, к і Ь — числа.
При Ь = 0 формула лінійної функ-
ції набирає вигляду у = кх. Ця форму-
ла при к У=0 задає пряму пропорцій-
ність. Графіком лінійної функції є
пряма (рис. 12.15).
Лінійна функція виражає залеж-
ності між змінними різної природи.
Наприклад: а) залежність шляху 5,
який пройде тіло при рівномірному
русі, від часу і визначають за форму-
лою 5 = 50 + оі, де 50 — початко-
вий шлях, V — стала швидкість; б) за-
лежність довжини металевого стержня від температури і
при нагріванні задають формулою І = /0 + де /0— Дов-
жина стержня при і = 0, к — коефіцієнт лінійного розтя-
гу; в) вартість N телеграми обчислюється за формулою N =
= 5х + 20, де х —кількість слів, 5 коп.— вартість одного
слова, 20 коп.— попередня оплата; г) вартість проїзду в таксі
можна обчислити за формулою Р = 20п + 20, де п— кіль-
кість кілометрів (відстань), що проїхав пасажир, 20 коп.—
вартість проїзду одного кілометра, 20 коп.— сума, яка ав-
томатично фіксується на лічильнику, коли пасажир сідає в
таксі.
Нагадаємо властивості лінійної функції.
1) Областю визначення лінійної функції, якщо вона за-
дана формулою у = кх + Ь без вказівки на характер за-
лежності між змінними х і г/, є множина всіх дійсних чисел.
2) Зростання чи спадання функції залежить від знака
коефіцієнта к. При к > 0 функція зростає. Доведемо це,
користуючись означенням зростаючої функції. Справді,
нехай х2 > Де € К, х2 Е К- Тоді / (х2) — / (хх) =
= кх2 + Ь — кх± — Ь = к (х2 — %і) > 0, оскільки к > 0
і х2 — х1 > 0 за умовою вибору к, х2 і х±. Тому / (х2) >
>/(Х1).
Доведіть, що при к < 0 лінійна функція спадна.
441
3) При к Ф 0 і Ь =/= 0 лінійна функція не є ні парною,
ні непарною. Справді, хоча для будь-якого х £ 7? і —х £ Р
(область визначення є множиною, симетричною відносно
точки 0), все ж таки / (—х) = —кх + 6 (х) і / (—х) =
= —кх + Ь #= — / (х).
При к =И= 0 і Ь = 0 лінійна функція є непарною, бо
/ (—х) = —кх — —{ (х). Графіком її за цієї умови є пря-
ма, що проходить через початок координат. Вона симетрич-
Рис. 12.16
на відносно початку коорди-
нат.
При к — 0 і будь-якому Ь
лінійна функція парна, бо
/ (—х) = Ь = / (х). Графік її —
пряма, що паралельна осі Ох
(або збігається з нею) і тому
симетрична відносно осі Оу.
к
Функція У — —• Ця
функція виражає обернено про-
порційну залежність. 1 * з * * * * *
Обернено пропорційною на-
зивається функція, яку мож-
на задати формулою у = -у, де х — незалежна змінна і
й=Н=О.
Графіком функції у = -у є гіпербола, яка складається
з двох віток. Гіпербола розміщується в І і III чвертях при
к > 0 і в II та IV чвертях при к < 0 (рис. 12.16).
, ... к ...
Функції у = — виражають залежності між різними
змінними. Наприклад: а) залежність кількості купленого
товару на задану суму грошей від ціни товару; б) залеж-
ність сили струму від опору провідника при сталій напру-
зі / = -4- (закон Ома); в) залежність між тиском газу і
А
об’ємом, який він заповнює,/? = — (закон Бойля — Маріо-
та), де к — стала; г) залежність часу від швидкості руху
і = —, де 5 — шлях, та ш.
V 9 9
Нагадаємо властивості функції у = -р
1) Областю визначення і областю зміни функції є всі
дійсні числа, за виключенням нуля, бо х =/=0 і у=^=0.
2) При к > 0 функція у = р спадає на множинах
442
(—оо; 0) і (0; +оо). Доведемо, наприклад, що при й>0
і х £ (—оо; 0) функція спадає.
Дійсно, нехай х2> х19 де хг £ (—оо; 0) і х2 Є (—0):
х2 > хх. Тоді /(х2)-/(хх) = =
<0, бо хг • х2 > 0 як добуток двох від’ємних чисел;
к > 0, хх — х2 < 0 за умовою вибору к, х± і х2. Тому / (х2) <
< / (хх). Так само доводимо, що при к > 0 і х £ (0; +оо)
функція спадає, а при к < 0 — зростає при х £ (—оо; 0)
і х £ (0; +оо).
Доведіть самостійно, що у = при к <; 0 зростає при
х£ (—оо; 0) і х (0; +°°).
3) Функція у == непарна. Справді, областю визначен-
ня її є множина, симетрична відносно точки О і / (—х) =
= — = — — = / (х).
— X X ' 4 7
к
Графік функції у = — симетричний відносно початку
координат.
Функція у = х2. Властивості цієї функції випли-
вають із властивостей степеня з парним натуральним по-
казником.
1) Областю визначення функції є множина всіх дійсних
чисел, тобто х £ Областю її зміни є множина невід’ємних
чисел, тобто у Є [0; +оо).
2) На множині (—оо; 0] функція спадає, а на [0; +оо) —
зростає.
Доведемо, що при х£ (—00; 0] функція спадає. Нехай
х2> хх, де хх£(—оо; 0] і х2^(—оо; 0)- Тоді / (х2) —
— / (%1) = Х2 — Х1 = (*2 — Х1) (Х2 + *1) < 0, бо Х2 — Хд > 0
за умовою, х2 + хх < 0 як сума двох чисел, з яких одне
від’ємне, а друге може бути недодатним. Тому / (х2) <
< / (*і)-
Доведіть самостійно, що при х £ [0; +оо) функція
у = х2 зростає.
3) Функція парна, оскільки область її визначення —мно-
жина, симетрична відносно 0 і / (—х) = (—х)2 = х2 = / (х).
Графік функції — парабола, симетрична відносно осі
Оу (рис. 12.17).
4) Оскільки при х = 0 і у = 0, то графік проходить че-
рез початок координат.
За допомогою функції у = х2 виражають залежність
площі квадрата від довжини його сторін. На практиці у фізи-
ці, техніці частіше застосовують функцію у = ах2, де а —
443
число. За допомогою цієї функції виражають наприклад:
а) залежність площі круга від радіуса з = лг2; б) залежність
між кінетичною енергією тіла від його швидкості К =
= в) залежність шляху вільно падаючого тіла від
лу2
часу 5 = (якщо опором середовища нехтувати).
Графіком функції у == ах2 є також парабола, симетрична
відносно осі Оу. При а > 0 вітки параболи спрямовані
вгору, при а < 0 — вниз.
Форму параболи у = ах2 має: лан-
цюг, що відтримує висячий міст з
допомогою великої кількості стержнів
(якщо вагою ланцюга нехтувати); тра-
єкторія снаряду, що летить, осьовий
переріз автомобільної фари, осьовий
переріз вільної поверхні рідини при
обертанні посудини з рідиною навколо
його, осі симетрії.
Функція у = х3. Ця функція
виражає, наприклад, залежність об’є-
му куба від довжини його сторони.
Нагадаємо властивості цієї функції,
що випливають з властивостей степеня
з непарним натуральним показником.
1) Області визначення і зміни функції — множина всіх
дійсних чисел.
2) Функція, зростаюча на всій області визначення.
Справді, нехай х2 > х19 де хх Є Я і х2 £ У?. Тоді / (х2) —
/ (^1) = ^2 Х1 = (-^2 ^1) (х2 ЯХХ2 “1“ Хі) (х2
— хі)(х2 + -у- хі+ -|- х?) > 0, оскільки х2 — хх > 0 за
. • / . 1 \2 , 3 2 *
умовою вибору Х± 1 Х2, сума Х2 + Хх + ~Х* ПРИ будь-
яких Хх і х2. Тому / (х2) > / (хх), тобто функція у = X8
зростаюча.
3) Функція у = х3 непарна, оскільки область її- визна-
чення симетрична відносно точки О множина і / (—х) =
= (—х)3 = —х3 = —/ (х). Графіком цієї функції є ку-
бічна парабола, яка симетрична відносно початку коорди-
нат (рис. 12.18).
4) При х = 0 і у == 0, тобто графік проходить через
початок координат.
На практиці використовують також функцію у = ох3,
яка має ті ж самі властивості, хоча коефіцієнт а дещовпли-
444
ває на форму графіка (рис. 12.19). Графік у = ах3 викори-
стовують проектувальники залізниць та автомобільних
шляхів при здійсненні плавного переходу від прямоліній-
них до криволінійних ділянок шляху.
Функція у = Ух. За допомогою цієї функції ви-
ражається, наприклад, залежність сторони квадрата від
його площі 5.
Властивості функції у = Ух випливають із властиво-
стей арифметичного кореня.
1) Області визначення і зміни функції — множина не-
від’ємних чисел, тобто х Є [0; 4~оо) і # € [0; +оо).
2) Функція у = V х зростає на всій області визначен-
ня. Дійсно, при х2 > хх, де х± £ [0; + оо) і х2 £ [0; + °°),
І (х2) - / (Хі) = |/Т2 - = (Ж2-/^)(Ж2 + Г^) =
У х2 + У х1
= —> 0, оскільки х2—хх>0 за умовою вибо-
V х2+у _
РУ *х, х2 і У х2 + Ухг > 0 як сума додатного і невід’ємного
числа. Отже, / (х2) > / (хх), тобто функція у = Ух зро-
стаюча.
3) Функція у = Ух не належить ні до парних, ні до не-
парних функцій, оскільки її область визначення — множи-
на, не симетрична відносно початку координат.
4) При х = 0 і у = 0, тобто графік проходить через
початок координат, а оскільки х і у — невід’ємні, то він
розміщений у І чверті (рис. 12.20). Графіком є розміщена
у І чверті вітка параболи, симетрична вітці параболи у =
= X2, X 0, відносно прямої у = X.
445
На практиці використовують функцію у ~ а Ух. Зокре-
ма, за допомогою цієї функції виражають залежність пе-
ріоду Т малих коливань математичного маятника від його
довжини І: Т = 2л де § — прискорення сили тяжіння.
Квадратична функція. Квадратичною нази-
вається функція, яка задається формулою у = ах2 + Ьх +
+ с, де а, Ь, с — дійсні числа, причому а =/= 0.
За допомогою квадратичної функції виражають залеж-
ність положення тіЛа у будь-який момент часу при прямолі-
СІ і2
нійному рівноприскореному русі: X = Хо + УохІ Н—,
де х0 — початкова координата, Оох — проекція початко-
вої швидкості на вісь Ох, ах — проекція прискорення.
Графіком квадратичної функції є парабола, вершина
. лл ь
якої знаходиться у точці Мо з координатами х0 = —
_4 де
у0 = ——— , Це можна показати, якщо подати форму-
лу у = ах2 + Ьх + с так: у = ах2 + Ьх + с = а ^х2 + х +
. С \ /І 2 і п & І Ь2 \ Ь2 . С \ /7 і
□ = а х2+2«-х-хН— т-2" Н = а х +
• а ) \\ 2а ' 4а2 / 4а2 1 а ) \\
Ь \2 ь2 4дс \ ( Ь \2 Ь2 — 4ас
+ -о—-------Г-5-- Ь= а X + -ту—---------л--.
1 2а І 4а2 І \ 1 2а І 4а
Звідси випливає, що графік квадратичної функції у ==
= ах2 + Ьх + с можна дістати з графіка функції у =
= ах2 шляхом таких геометричних перетворень: послідов-
ного паралельного перенесення параболи у = ах2 на —
одиниць вліво чи вправо по осі Ох залежно від того, яким
буде знак числа — і паралельного перенесення здобу-
Ь2 _ 4ас
того графіка по осі Оу вгору або вниз на------— оди-
Ь2~~ 4ас
ниць залежно від того, яким буде знак числа---.
Функції у = [а?] і у = {а?}. Кожне дробове число
можна подати у вигляді суми двох доданків, один з яких
ціле число, а другий — невід’ємний правильний дріб.
Наприклад: 10,7 = 10 + 0,7; /2^1+ 0,41; 0,5 = 0 +
+ 0,5; —2,25 = —3 + 0,75. Отже, за цілу частину
числа х візьмемо найбільше ціле число, яке не перевищує
х. Цілу частину числа х позначають символом [х], де х =
= п + д, /г £ 7, а 0 д < 1. Очевидно, що [х] = п.
446
При будь-якому х виконується подвійна нерівність
[х]<[х] + 1.
Формула у = [х], де [х] — ціла частина х, задає функ-
цію, областю визначення якої є множина всіх дійсних
чисел.
Побудуємо графік функції у = [х] (див. рис. 10.20).
З формул х = л + д, 0^</<1і [х] — п випли-
ває, що коли 0 х < 1, то
у = 0; якщо 1 х < 2, то
у = 1; якщо 2 <2 х < 3, то
у = 2; якщо —1 х < 0, то
у = —1 т. д. Взагалі, якщо
Рис. 12.22
п х<п + 1, де га — ціле число, то у — п. Отже, на кож-
ному з проміжків [п; п. + 1) значення функції у дорівнює п
(рис. 12.21).
Графік, подібний до графіка функції у = [х], дістане-
мо, якщо зобразимо графічно залежність між вагою ванта-
жу і вартістю його перевезення, якщо відомо, що за пере-
везення першої повної чи неповної тонни вантажу треба
платити 20 крб., а за кожну наступну повну чи неповну
тонну — 10 крб.
Дробовою частиною числа х називається різниця між
цим числом і його цілою частиною.
Дробову частину числа х позначають [х]. З означення
випливає, що {х} = х — [х].
Наприклад, {9, 7} = 9,7 — [9,7] = 9,7 — 9 = 0,7;
{—2, 3}= —2,3 — [2,3]= —2,3 — (—3)= —2,3 + 3 = 0,7.
Формулою у = {х}, або у — х — [х] задається функція,
областю визначення якої є множина всіх дійсних чисел.
При побудові графіка у = {х} враховуємо, що коли 0
< х < 1, то [х] = 0 і формула у = х — [х] набуває вигля-
ду У — х, а графіком функції у = {х} є частина прямої
у = х. При х = 1, у = 1 — 1=0, тобто відповідна точка
графіка буде на осі Ох. Якщо 1 х < 2, то [х] = 1 і у =
= {х} = х — [х] = х — 1, тобто графіком функції на
цьому проміжку буде частина прямої у = х — 1.
447
Взагалі, якщо п^х<п+1, де п £ то [х] = п,
а у = {х} = х — п, тобто на кожному проміжку [п\ п +
+ 1] графіком функції у = {х} є частина прямої у =
= х — п (рис. 12.22).
3. Побудова графіків функцій за допомогою геомет-
ричних перетворень відомих графіків функцій. У багатьох
випадках графік певної функції можна побудувати за допо-
Рис.£12423
могою геометричних перетворень (па-
ралельний перенос, симетрія відносно
прямої, стискання до осі, розтягуван-
ня від осітаін.) графіка відомої функ-
ції, через яку виражається дана.
1. Нехай дано графік функції у =
= / (х). Треба побудувати графік функ-
ції у = — / (х). Наприклад, треба по-
Рис. 12.24
будувати графік функції у = —х\ якщо відомий графік у =
= х2. Тут у = / (х) = х2, а у = —І (х) = — х2. Області
визначення обох функцій збігаються, аргумент х — одна-
ковий, а значення функції у відрізняється лише знаком.
Це означає, що кожній точці Л40 (х0; г/0), що належить гра-
фіку у — ї (х), відповідає точка М (х0; — г/0) на графіку
функції у = —/ (х), тобто точки шуканого графіка симет-
ричні точкам графіка функції у = / (х) відносно осі Ох.
Отже графік функції у = —/ (х) можна дістати з графіка
відомої функції у = / (х) за допомогою відображення си-
метрії відносно осі Ох (рис. 12.23).
2. Нехай відомий графік функції у = / (х), а треба по-
будувати графік функції у = / (—х). Наприклад, відомий
• графік у = /х. Треба побудувати графік функції у =
= К—х (рис. 12.24). Аргументи функцій у = / (х) і
у = / (—х) відрізняються знаками. Нехай точка Л40 (х0;
£/о) Знайдемо координати відповідної точки М (х\ у) £
Є / (—*)* Введемо підстановку х0 = —х, звідси х = —х0, у =
= / (—*) = / (хо) = У о Отже, точка М має протилежну абсцису
і ту саму ординату, тобто М (—х0; г/0)- Це означає, що графік
функції у = / (—х) можна дістати з графіка функції у = ? (х)
за допомогою, відображення симетрії його відносно осі Оу.
448
3. Побудувати графік функції # = /(|х|), якщо ві-
домий графік функції у — [ (х). Наприклад, побудувати
графік функції у = і—=, якщо відомий графік функції
Іх І
2
у = —. Як правило, в усіх вправах, пов язанихз модулем,
доводиться звільнятися від модуля числа, користуючись
його означенням:
/(х), якщо
Н—х), якщо
Дх)>0,
х<0.
/(И) = {
Звідси випливає, що графік функції у — / (| х |) збіга-
ється з графіком функції у = / (х) при х 0 і з графіком
У = / (—х) при х < 0.
2
Для побудови графіка функції у = -ч—ґ досить побуду-
2 |Х|
вати графік функції у — — при х > 0 і графік функції
2
у — при х < 0. Об’єднавши дві побудовані криві, ми
2
дістанемо графік функції у = -щ- (рис., 12.25).
4. Побудувати графік функції у — | / (х) |, якщо відо-
мий графік функції у = / (х). Нехай відомий графік функ-
ції у = 2х + 1, побудуємо графік у = | 2х + 1 |. Врахує-
мо, що
.. / Кх\ якщо /(х)>0,
( —/(х), якщо /(х)<0.
Звідси випливає, що графік функції у — | / (х) | збіга-
ється з графіком функції у = / (х) на ділянці, де / (х) 0,
і з графіком функції у — —} (х) на ділянці, де / (х) < 0.
Отже, для побудови графіка функції у = | 2х + 1 | до-
сить побудувати графік лінійної функції у — 2х + 1, а ту
частину прямої, яка розміщена нижче осі Ох, відобразити
15 1-1819
449
симетрично відносно осі Ох. Ламана, яка лежить вище осі
Ох, включаючи точку на цій осі, буде графіком функції
у = | 2х + 1 | (рис. 12.26).
5. Побудувати графік функції у = / (х) і; Ь, де Ь > 0,
якщо відомий графік функції у = / (х). Області визначен-
ня обох функцій збігаються, аргументи їх однакові, а
значення функції відрізняються на Ь чи —Ь. Це означає,
що всі точки, наприклад, графіка у = / (х) + Ь мають ті
самі абсциси, що і відповідні точки графіка у = / (х), а
ординати збільшені на Ь. Тому шу-
каний графік легко дістати з графіка
функції у — І (х) за допомогою пара-
лельного перенесення його у напрям-
ку осі Оу на Ь одиниць вгору.
Рис. 12.27 Рис. 12.28
Наприклад, графік функції у = х2 ± 3 можна дістати
з графіка функції у = Xі за допомогою паралельного пере-
несення його на 3 одиниці вгору для у = х2, + 3 і на З
одиниці вниз для у = х2 — 3 (рис. 12.27).
6. Відомий графік функції у — ? (х). Треба побудувати
графік функції у = ї (х ± а), .де а> 0. Нехай відомий
графік функції у — х2, побудуємо графік функції у —
= (х ± 2)2.
Розглянемо випадок побудови графіка функції у =
= / (х — а). Нехай Мо (х0; у0) 6 / (х). Знайдемо відповідну
точку М (х; у) € / (х — а). Введемо підстановку: х0 = х —
— а, звідки х = х0 4- а, у = / (х — а) = / (х0) = у0. Отже,
абсциса точки М (х0 + а; у0) на а одиниць більша від
абсциси точки Мо (х0; ул), а ордината та сама. Це означає,
що будь-яка точка графіка функції у = / (х) переходить
у відповідну точку графіка функції у — І (х — а) за допо-
могою паралельного перенесення її вправо у напрямку
осі Ох.
Обгрунтуйте самостійно побудову графіка у = ? (х + а).
Таким чином, графік функції у = (х ± 2)2 можна дістати
450
в графіка функції у — х2 за -допомогою паралельного пере-
несення його на 2 одиниці вправо по осі Ох при у = (х — 2)г
і на 2 одиниці вліво при у = (х + 2)2 (рис. 12.28).
7. Побудувати графік функції у = а/ (х), де а > 0,
якщо відомий графік у = } (х).
Наприклад, побудуємо графік функції у = 2х3 і у —
= -у х3, якщо відомий графік функції у = х3.
Області визначення і аргументи обох функцій однакові.
Значення функції при будь-якому х для функції' у = а} (х)
в а разів змінюється порівнянно з функцією у = / (х). При
а > 1 ордината збільшується в а разів, при 0 < а < 1
вменшується. Тому графік функції у = а/ (х) можна діста-
ти з графіка функції у = / (х) за допомогою розтягу його в
а разів від осі Ох при а > 1 і за допомогою стискання в а
разів до осі Ох при 0 < а < 1.
Наприклад, графік функції у = 2х3 можна дістати з
графіка у = х3 за допомогою розтягування від осі Ох ор-
динат точок функції у = х3 у 2 рази, а графік функції у —
= -£- х3 — за допомогою стискання до осі Ох у 2 рази
(рис. 12.29).
8. Відомий графік функції у = / (х). Побудувати графік
функції у = / (ах), де а > 0.
Наприклад, за відомим графіком функції у = (х) по-
будуємо графіки функцій у = {2х} та у = х|.
Оскільки над змінною х у другій функції виконується
дія множення на число а, введемо підстановку і знайдемо
координати точки М (х; у) £ / (ах), в яку перейде точка
15*
451
Таблиця 12А
1) Дано графік у = [ (х). Побу- дувати графік у = —( (х) Приклад. Дано // == ха Побудувати у == —х3 Алгоритм 1. Побудувати графік функції У = / (х) 2. Побудувати графік, відобра- зити симетрично осі Ох Дістанемо графік у = —[ (х) (див. рис. 12.23) 2) Дано графік у = / (х). Побуду- вати графік у = / (—х) Приклад. Дано у= х Побудувати у = Алгоритм 1. Побудувати графік функції У = / (х) 2. Побудувати графік, відобразити симетрично осі Оу Дістанемо графік у = { (—х) (див. рис. 12.24)
3) Дано графік у = / (х) Побудувати графік у — / (| х |) 4) Дано графік у = / (х) Побудувати графік у = | / (х)[
Приклад. Дано у = Приклад. Дано у = 2х + 1
„ Л 2 Побудувати у = Побудувати у = | 2х + 1 |
Алгоритм 1. Побудувати графік функції у == } (х) для х > 0 2. Відобразити його симетрично осі Оу Об’єднання двох графіків дасть графік у = / ( | х | ) (див. рис. 12.25) Алгоритм 1. Побудувати графік функції У = / (*) 2. Частину його, що розташована нижче осі Ох, відобразити симет- рично осі Ох. Об’єднанням графі- ків, розміщених вище осі Ох, є гра- фік (див. рис. 12.26)
5) Дано графік у = / (х)
Побудувати у = / (х) ± 6, де Ь >
Приклад. Відомо у = х* 1 2 7
Побудувати у = х2 ± З
Алгоритм
1. Побудувати графік функції
у = {(*)
2. Виконати паралельне перене-
сення побудованого графіка у
напряму осі Оу на Ь одиниць
вгору при у = / (х) + Ь і на Ь
одиниць вниз при у = / (х) — Ь
(див, рис. 12.27)_____________
6) Дано графік функції у — / (х)
0 Побудувати у = / (х ± «), де а > 0
Приклад. Дано у = х2
Побудувати у = (х ± 2)2
Алгоритм
1. Побудувати графік у = / (х)
2. Виконати паралельне перене-
сення побудованого графіка в на-
пряму осі Ох вправо на а одиниць
для у — І (х — а) і вліво на а оди-
ниць для у = ( (х + а)
(див. рис. 12.28)
7) Дано графік функції у = / (х)
Побудувати графік у == а/ (х),
де а > 0
Приклад. Дано у — х8
Побудувати графіки у = 2Х3 і
1 л
Алгоритм
1. Побудувати графік у = [ (х)
2. Розтягнути його в а разів
від осі Ох при а > 1 і
стиснути до осі Ох в а разів
при 0 < а < 1 (див. рис, 12.29)
8) Дано графік функції у = / (х)
Побудувати у = / (ах),
де а > 0
Алгоритм
1. Побудувати графік у = / (х)
2. Стиснути побудований графік
до осі Оу в а разів при а > 1, роз-
тягнути до осі Оу в а разів при
0 < а < 1
(див. рис. 12.30)
452
Мц (х0; у0) С ї (Д Нехай х0 = ах, звідси х = у =
= / (ах) = / (х0) = Уо- Отже, М г/0^. Це означає, що
будь-яка точка графіка функції у = / (х) перейде у точку
графіка функції у = / (ах) з абсцисою — і тією самою ор-
динатою. Очевидно, при а> 1 абсциса точки М зменшу-
ється в а разів, а при 0 < а < 1 збільшується. Це озна-
чає, що графік функції у = / (ах) можна дістати з графіка
функції у = / (х) за допомогою розтягу його або стискання
до осі Оу.
Графік функцій у = {2х} та у = зображено на
рис. 12.30.
Зведені відомості про побудову графіків функцій за
допомогою геометричних перетворень подано в табл. 12.4..
Контрольні запитання
1. Що називається функцією? Як позначають функції? Навести
приклади функцій.
2. Що таке область визначення функції?
3. Що таке область значень або область зміни функції? Навести
приклади.
4. Назвати основні способи задання функцій.
5. Чи будь-яка формула задає фукцію?
6. Яка функція називається зростаючою? Навести приклади.
7. Яка функція називається спадною? Навести приклади.
8. Як дослідити функцію на зростання або спадання за допомогою
означення?
9. Яка функція називається парною? Навести приклади.
10. Яка функція називається непарною? Навести приклади.
11. Як дослідити функцію на парність чи непарність?
12. Яка властивість графіків парної і непарної функцій?
13. Яка функція називається лінійною? Що є графіком лінійної
функції?
14. Назвати властивості лінійної функції. Довести одну з них.
15. Навести приклади залежностей, які задаються за допомогою
лінійної функції.
16. Яка функція називається оберненою пропорційністю. Прямою
пропорційністю? Навести приклади залежностей, які задаються за до-
помогою цих функцій.
Д7. Назвати властивості функції у = —. Довести властивість не-
парності функції.
18. Що є графіком функції у = —?
19. Назвати властивості функції у = хК Довести властивість спа-
дання функції на множині (—оо; 0],
453
20. Назвати властивості функції у = х3 і довести властивість її
зростання. Що є графіком цієї функції?
21. Назвати властивості функції у х. Довести властивість
зростання цієї функції.
22. Яка функція називається квадратичною? Навести приклад за-
лежності, яка задається за допомогою квадратичної функції.
23. Що є графіком квадратичної функції?
24. Довести, що вершиною графіка квадратичної функції е точка
М (- ьі - 4Ч.
\ 4а )
25. Побудувати графік функції у = [х].
26. Побудувати графік функції у = {х}.
27. Назвати основні види перетворень при побудові графіків функ-
ції шляхом геометричних перетворень графіків відомих функцій.
28. Як побудувати графік функцій у =» —/ (х), у =» / (—х), якщо
дано графік функції у = / (х)?
29. Як побудувати графік функцій у = | / (х) | і у = / (| х |), якщо
дано графік функції у ~ ї (х)?
ЗО. Як побудувати графіки функцій у = / (х) і а, у = / (х ± а),
якщо дано графік функції у — } (х)?
31. Як побудувати графіки функцій у~ к/ (х), у = } (кх), якщо
дано графік у = / (х), к > 0?
Вправи
1. Знайти область визначення функцій:
А
1)У=_6 ; 2)у = /7^2; 3) у = 1/ ^=5 ;
х —______ г х + 2
4) у = ]/" 5 ; 5) у = 2х :
7 У V 2х + 3 ’ У х2-5х + 6 ’
6) у = /х2+л;-і2; 7) у = —; 8)^ = 2—-------
х2 — 1 х х — 5
Б
9) /3-х; 10)
11) і, = К16 — Xа; 12) =/4-|х|;
2 3 '4
13) У = Х_1 + х + з ' 14) У = /25-х* ’
В
17>У° 4-КР : 18)^ = ^4^+^="2+т4т5
19) У = /9_р-| + : 20) У = їх І - і + V 1
454
21) у = /х8-6х + У5х* + 2х>, 22) у = т/ |х~41-,
г х— о
2. Дослідити на парність і непарність функції:
А
1)^х + х3; 2)г/«х2-2; 3) у ;
х2 + 1
4)у-х+±; 5)у=/Г^?; 6) у = і/?8,
X
Б
7) у = Xі — 2ж8 + 3; 8) у = /7; 9) у = У х;
10) у = х8-5х+1; 11) у = х*~*. ; 12)У = х8—|х|.
В
4 ха 2х
13) у~|хв|; 14) у = ----; 15) у =-^3-8
16) у--^.2* р 17) у = 1/;
*2 + І * І + 1 г *
18) у = >/!’+ х + V 1- а:.
3. Побудувати графік функцій:
А
4)у = /х; 5) у-----Кх + 1; 6)у = -К*-11
7)у = |х|; 8)у = |х —3|; 9)у = |х + 3|;
Ю)у = х8; 11)у = |х8| + 4; 12) у = | х3 | + 4;
13) у » ха — 5х + 6; 14) у «= ха — 5 | х | + 6;
15) у == — (х3 — 5 | х | + 6);
Б
16) у - і 17)у-=/Т^; 18) у = (х + З)8 + 1}
19) у = | х* — 5х-|-6|; 20) у = 2 —К^х; 21) у = | 2х + 3|;
22) у = х| - -*-) +1) 23) у = (2х + І)8; 24) у = | х8 - 11 -т3;
В
28)ї_т1_+.3; 26)»-^-;
28) у = /2-х; 29) у-К2х-1 + 3; ЗО) у = 2/1 - Зх;
31)у-|2х-3|; 32) у~-(х-І)8; 33) у-2—К1-|х|;
34)у--І£Ь; 35) у-|х+1|-х;
36) у = Г (* + 2)2 + V (х-2)».
ДОВІДКОВИЙ МАТЕРІАЛ
Властивості степенів
ах • а» = ах+«- ах -.а? == ах^-, (ахУ> = а*»;
(аЬ)х == ахЬх-, = —; 0° = 1; 0-* = —5
\ Ь ) ьх 0х
Многочлени
а2 — Ь2 = (а — Ь) (а + Ь);
а3 — Ь3 = (а — Ь) (а2 + аЬ + Ь2);
а3 + Ь3 = (а 4- Ь) (а2 — аЬ б2);
(а + Ь)2 == а2 + 2аЬ 4- Ь2',
(а — Ь)2 = а2 — 2аЬ + Ь2\
(а + Ь)3 = а3 + За2/? 4" За/?2 + Ь3 = а3 Ь3 + За/? (а 4~ Ь)\
(а — Ь)3 — а3 — За2Ь + За/?2 — Ь3 = а3 — Ь3 — За/? (а — /?);
ах2 + Ьх + с — а (х — хх) (х — х2), де хх і х2 — корені рівняння
ах2 + Ьх + с = 0.
Властивості арифметичного кореня
'У Ь, якщо 0 а <Ь.
Тотожні перетворення тригонометричних
виразів
Співвідношення між тригонометричними функціями одного й того
ж аргументу
8ІП2 X 4“ СО52 X = 1;
х = 51ПХ X — + пл, п^2
соз х 2
СІ£ х = 005 х , X Ф ПП, п С
ЗІП X
X • X = 1, X У= , п Е 2і
456
1 + і&2 х = —~, х =# + ял, я С Я;
1 & соз2 х 2 ‘
1 4- СІЙ2 х =-!— , х =# ял, п Е %\
ЗІП2 X
Формули додавання
ЗІП (х + у) = зіп X • СОЗ у + СОЗ X • зіп у;
зіп (х — у) = зіп X • соз у — СОЗ X • зіп у;
СОЗ (X + у) = СОЗ X • соз у — зіп X • зіп у\
соз (х — //) = соз х • соз у + зіп х • зіп у;
*є(а: + у) = -?єх + 1§.^ ; X, у, х + + пє^;
1 —• їй X • І£ у 2
іе(х-у)=-ї-ГіГх1еіо; х’У’х-у^^г+^ ^г-
Формули подвійного аргументу
зіп 2х = 2 зіп х соз х;
соз 2х = соз2 х — зіп2 х = 2 соз2 х — 1 = 1 — 2 зіп2 х;
, ; х^^ + к^--, к£Я- хф ” +пл;п€2.
1 їй х 4 х £
Формули половинного аргументу
»"4=±/
> X , і/ 1 — СОЗ X
І8т = ± V -Т+'созх-
X , 1 Г 1 + СОЗ X .
соз — = ± І/ —-----------------:
2 Г 2
X _ ЗІП X __ 1 — соз X
2 1 + соз х зіп х
Формули перетворення суми і різниці тригонометричних функцій
зіп х + зіп у = 2 зіп -- • соз х ;
зіп х — зіп у = 2 соз • зіп .х~ У •
2 2
СОЗ X + соз у = 2 СОЗ • СОЗ Х~^ ;
СОЗ X — СОЗ X = — 2 ЗІП У- . зіп Л.~ У...
2 2
+ = -?іп<* + У) ; х,г/^4- + пя’
соз х • соз у ~ 2
І£Х- ^У = .8Іп(*-У) . Хг л +пп> пег.
соз х • соз у 2
Формули перетворення добутку в суму
зіп х . зіп у = -А_ (соз (х — у) — соз (х +#));
соз х • соз у = -і- (соз (х — у) + соз (х + ї/));
зіп X • соз у = (ЗІП (X — у) + 8ІП (X + £/));
457
Співвідношення між зіп X, СОЗ X І 'Іе1 зіп х ж» , х (2л + 1) я, л Е соз х = , х =# (2л + 1) л, л 0,2} Ц-і2а-у- Формули зведення
и л , л 4- а Зл Л- — 4-а — а л — — а 2 л — а Зл "2 “
зіп и соз а — зіп а — соз а — зіп а соз а зіп а — соз а соз и —* зіп а — соя а зіп а соз а зіп а —соз а —зіп а І£ и — сі§ а а — сіє а — і£ а сі§ а — І£ а сі§ а сій и — і§ а сі§ а — а — сій а а — сій ® а Основні властивості логарифмів к>йа 1 = 0; 1ойоа=1; 1о§а (ХУ) = 1о§а * + 1о& У при х > 0, у > 0; 1о8а V = І0§а х~ 1О§° У при х> °’ У > 0; 1о£а хр ~ р 1о£а х при х > 0, р Е К} Іо§аХ= 1о^а при х>0, Ь>0, Ь#=1;
ІО£ X л
а а — х при х > 0.
Формули диференціювання
с( = 0, (х') =’ 1, (ха)' « аха-іі1 при а 1;
(зіп х)' = соз х, (соз х)' =« — зіп х, (і§ х)' «= - -- ;
(сій *)'=--=
(ех)' = ех, (ах)' = а* Іп а, (1пх)' = — , (1о»а х)' = —Л—
л л ні їх
(Уху = 2^-. , (/і (X) ± (Х)У = їі (X) ± /2 (X);
458
01 (X) • Г» (х)У = (X) . /2 (X) + їі (х) - (х);
(с/ (х))' - сГ (х), (І (кх + Ь)У = кГ (кх4- Ь);
/ їг (х) V /і (х) (х) — Л (х) /д (х)
І № І “ її (*> ’
0 (и (х)))' = (и) • и' (х).
Первісні
/(X) Xа . а =# — 1 5ІПХ соз X 1 СОЗ1 2 X 1 ЗІП2Х
р (X) 4- С Ха+1 + с а+ — соз х + С зіп *+ С 1§х + С — сі§х+С
/(х) 1 X ех а* / (ах + Ь)
р (X) + с 1п 1ХІ + С є*+ С 4—+С Іпв — =? (ах + Ь) (а¥=0)
Прогресії
Арифметична прогресія
ап в а! + сі (п — 1), — перший член, сі — різниця, п — число
членів, ап — п-й член;
а-і сіп 2а, «4- сі (п —— 1)
8п =----§----* п в-----£---2-------Пі $п ~’ сума п пеРших
членів,
а/г—**- + **+ , * = 2,з..........п-и
&к + ат == ар + аЯі де к + т » р + д.
Геометрична прогресія
Ьп = дп-~х* — перший член, д— знаменник, (д^О); п —
число членів, Ьп — п-й член;
8„ «= Лі 0 Т , п 1, 5Л — сума п перших членів;
1 — 0
1*^+1» ^«2, 3, ..., п—1;
Ьк . Ьт « Ьр . Ья, де к + т^ р + д}
1— я
чної прогресії.
8 — сума незакінченної геометри-
ВІДПОВІДІ
До розділу 1
1. 1) р = 180° + 360° . (— 1); 2) р = 300° + 360° ♦ (— 3); 3) р =
14° + 360° . 4; 4) -Р = 42° + 360° - 20; 5) р = 110° + 360е . (— 5).
4
4. 16-д-хв, 5. 0,262; 0,393; 0,890; 0,0174; 2,75; 2,83. 6. 72°;
216°; 600°; 86°; 143°. 10. 1) — 3 4-; 2) /З" — « 0,671;
* 4
3) 1— + УП « 0,870; 4) ЛЕЇ- — . а 1,891.
2 3 2 2
17. 1) 2; —2; 2) 5; —5; 3) 5; 1; 4) —1; —5; 5) 6; —4; 6) 5;
111 „«
2; 7) 3; 2; 8) 1; —; 9) ; 19. 1) зіп 65°; 2) ;
3) соз 50°; 4) сі§ (— -д-^ ; 5) зіп -д-; 6) соз (— 45°);
І 3 \ 1
7) с^І~“Ї0~лТ $ *&60 « 23. 1) —зіп2 6а; 2) 1. ЗО. 1) х=И=пл;
п 62) х Ф -у- + 2пл, п Е 2; 3) х =Л 0; 4) х = пл, п 6^
31. 1) [—1; 1]; 2) (—оо; + оо); 3) [3; + оо); 4) [0; 2]. 33. 1) У II
або III чверті; 2) У III або IV чверті; 3) У І або ПІ чверті;
4) У II або IV чверті; 5) У II або IV чверті. 35. 1) у' > 0 при
л л
пл < х < ~2~ + пл; у < 0 при -у пл < х < л -|- пл; у = 0 при
л
х = п -у , п Е 2. 2) у > 0 при 2пл < х < л 4* 2пл; у < 0 при л +
Зл
+ 2пл < х < 2л+2пл; нулів немає; 3) 0 при — + бпл < х <3
Зл Зл 9л
< —у + бпл; у < 0 при ~2~ + бпл < х < + бпл; у = 0 при
Зл
х — -у- Зпл, п Е 9 4) у > 0 при х =^= пл, у = 0 при х == пл,
460
5) у > 0 при 2ля < х < я + 2ля; у < 0 при я + 2ля < х <
_. ля я ля
2я + 2ля; у = 0 при х — 2ля; 6) у > 0 при — < х < + -Ї£~ ;
я ' ля я я я ля
У < о при — 4- ~2~ < * < — + л —; у = 0 при х = — +~2~ >
п^2. 37. 1) сі§а; 2) /-А ; 3) 2зіп а; 4) а 0; 5) -А
ОЦІ кЛ 0X11 Ц*
6) 1+зіп2а; 7) соз2 а; 8) -1; 9) 1— соз а; 10) 0; 11) 1; 12) 1;
4
13) 1; 14) 0; 15) 1; 16) . 38. 1) лг2 —2; 2) лі(лг2 —3).
11 24 З
39. а) —; б) 2 . 41. 1) зіп а = а = — 3 — , сі& а =
7 пх . 2
-----24 ; 2) 81П* — — уу >
1
СОЗ X =
~~уТ' с^х= 4-;
3) зіп х = — 2^, соз х ==— х = 4) соз х = — Дд- х =
= — 2 — , сі&х е — • 43. зіп а «0,88. а « 1,83, сі§а «
« 0,55. 44. 1) 7,658; 2) 22,105; 3) 74,100; 4) 47,210. 45. 1) 60°;
2)29°; 3)38°; 4) ЗГбО7. 46. 2,70. 47. V «2,5-Ю7 м/с.
48. 1) ; 2) — 3)2 — /3; 4)0,2/27;
4 25
0,1/22; 2; 5) — 0,4 — 0,3 /3 або —0,4+ 0,3/7; 6)1;
7) 8) 4+2/3"; 9) 1; 10) + .1.-, 49. 1)зіп(2а + Р);
2) сі§ а сі§ 0; 3) 2 зіп 26°; 4) їй 4а; 5) соз 2а; 6) | соз 4а | /2 ;
1 Зх х
7) "2“ 2а; 8) 4 соз х зіп -у- соз -тр ; 9) зіп 2а; 10) 1; 11) | соз 2а |;
12) соз 2а; 13) 2; 14) соз2 а; 15) сі&4а; 16) 1; 17) 4 зіпзіп +
+ соз ; 18) 2 соз а; 19) 2 |сі£а|; 20) 2 зіп 2а;
а За
21) — і£“; 22) і&а. 50. 1) 2 зіп а соз (3; 2) 2 зіп2—4— ;
/л 5а \ /7 зіп(-5- —а) __
3) 2 зіп21 -у + ~п~ ; 4)----------ї---------!— ; 5) 2 /7 зіп -5- х
\ 1 соз а
461
X ЗІП (у — у) ; — а 2а За; 7) сі&2 — у£- ; 8) 4 соз 0,5хХ
г— ( я \ І
X соз х соз 2,5х; 9) —4 зіп 25° зіп 10°; 10) у 2 соз І а—у ;
/я \ / я \
4 зіп [ — — а | зіп у + а
11) 2 соз (а + Р) зіп а зіп [3; 12) ---------------:-------2. ;
соз2 а
! я \ /я \
4 соз 4 а зіп -т- — 4а зіп у + 4а
ІЗ) 14), --------------ї-----—2--------1-------2-І
зіп2 4а
Ся а \ / я \
~4~ + ~2~/ 5 16) 1§2 (а — ~) ’
До розділу 2
1. 1) х = ля, п Е 2) ± (я — агс соз 0,4827) + 2ля, п Е 3) х =
я
= ля, п Е 4) х = — агс 0,5 4- ля, л Е Я; 5) х = 4~ пя,
пЕ^; 6)х = —у + лу, пЕ2; 7) х= (—І)п+1 у + ля,
2я я
п Е Я; 8) х = — —д— + 4ля, л Е 9) х = ± -у + 2ля, п Е
я 2 я
Ю) х = ± —+ уля, лЕ#; І1)х==— + ля, лЕ^; 12) х =
«=-у—1 + ля, пЕ^; 13) х = ± -у + 2ля, лЕ#; 14) х =
= (— І)”-*-1 + 4г* ЛЛ> Л Є 15) х = — “4“+ пя, п Е^; 16) х ==
= ±-у§- + —пя, п Е 17) х=: — агс0,609 + пя, пЕ^І
18) розв’язків немає; 19) х = (— 1)п агс зіп 0,2753 + ля, л Е Я; 20)
я ля я я
= -|2~ + —0— , лЕ^* 2. 1) x^ — — 4-ля, 2) х — -^- +
итс л л
+—3~, пЕИ; 3) х « -у- + 2ля, л Е 4) х = ± — + ля, п Е
я __і
5) Хі = “п- + ля, х2 = (— 1)* агс зіп -І— ------+ &я, л, £ Е 2;
2
ля 2я * 2я
6) X] = -у ; х2 = ± "у + 2&я, л, к Е 2\ 7) х = ± -у + 2ля,
462
м я я пл
п 6 7; 8) х = (— 1 )л — —- — + пя; 9) х = —— , п Е 10) роз-
а, зт
в’язків немає; 11)хх = 2пя; х2 = (—1) у + &л, п, к Е 12) х —
2 я
= у пя, пЕЯ; 13)хх=у 4-пя; х2 = агсі& 5 4-/гя, п, к, £2;
14) х а= — -у 4-пл, п Е 15) х = ± у 4-пл, пЕ2; 16) х =
.чЬ-ьі я , кл < „ я пя
= у + (— 1Г+1 у + у“ » 17)х = у4-— , пЕЯ;
4я
18) х = пл, пЕ2Г; 19) х1=я-}-2пя; х2 = ± -у 4- 46я, п, к£2;
я
20) розв’язків немає; 21) хх = л4-2пя, х2 = — у + Ц п, к£2;
я 1
22) хх = -у + 2пя; х2 = — 2 агсі&у + 2/гя, п, к£2; 23) х =
= — у- 4- пя, п Е 2; 24) х1 = -у 4- пл; х2 = — у- 4- кл, п, к£2,
і я____і/чТ
25) х = ± — агссоз---------------4~ пл, п£ 2; 26) х = 2пя, п Е 2;
2 ' 4
я
27) х = 2пя, п Е 2; 28) хг = у 4~ пл, х2 == агсі& 2 4- кл, п, к Е 2;
29) х = -^--і~пл, п^2; ЗО) х = — 4- пл, п£2; 31) хг = у 4-
пя я
4--у ; х2 = я 4~ 2яя, х3 = ± у 4- 2/пя, п, к, т£2; 32) Хі =
я 1 1
= — — 4- пл, х2 « кл, п, к Е 2; 33) хг = ± у агссоз у 4- пл;
х2 = ± у — агссоз у4- ^л, п, к Е 2; 34) Хі = — у + 2пл;
х2 = я 4- 2/?л, п, к Е 2; 35) х = у 4- "у , п Е 2; 36) хх = у 4-
1 2
4- пл, х2 = агсі£ 3 4- &л, п, к Е 2; 37) х = -у (— 1)* агсзіп у- 4~
пл я
4-у» п^2; 38) розв’язків немає; 39) у 4~ пл, п£2; 40) х—
я пл кл
== (— /гя, к^2;41) розв’язків немає; 42) хх = х2 == у:
463
л
х3 = -у тп, п, к, т£ 2, 3. 1)
4л
т
л
4 2/гл < х < -у 4- 26л,
л л
к С 2; 2) — — + ~ + ил, п
Є 2',
3) розв’язків немає?
л
4> -Т
л
л л 7л
5) — + 2/гл < х < -у 4-
л 2л 2л
4- 2пл, п € 2\ 6) — 4- 2/гл < х < —у 4- 2/гл, — -у + 2&л < х <
< — -у 4- 2&л, п, к С 2\ 7) — -у 4- 2/гл < х < у 4- 2/гл, /г 6 И;
л 2л
8) -у 4- ял < х < —у 4" ял, я Є И,
До розділу З
. 2 1
3. 1) д ; 2) — 2 5
3) 2 \
4 (1 — а)
при | а | < 1; не
має границі при |а|>1,
4.
О
6 == 0,005;
3) 6 = 4 • 10“3,
5.
4; • 6‘ 0 ~ Ь 2>
1
8 ;
3)
4“; 4) і;
5) - 1; 6) -у.
7.
1) 5; 2) 0.
До
1) 3;
розділу 4
ЗО; 3) - ; 4)
2)
— — , 2. — 1.
16
4. 1) За?
2)
1
2/З ’
3)
5; 4) - "Ь—; .
З ТХ16
4)
3)
__ 1
ЗІП2 X
1
4x4- — ; 4)
7. 1) -3; 2) 0; 3) 4*" ?
з
х8— -у х2 зіп 2х
10. 1) 10х94-5х44-1; 2)____________________5
X9 СОЗ2 X
5
Х=-; 5) 2х зіп х 4- Xі соз х; 6) 2 соз х +
1
З
8) -у С08 Зх; 9)
2
(х- І)2
+ зіп 2х; 7) ;
зіп х л 2
Ю) - ~ ~ --- ; 11) х2 4- 2х — 3; 12) —-тг- . —37===
2>СО8Х з ]У(5—2х)2
X3 СОЗ X — СОЗ X — Зх2 ЗІП X
1
(Xі- 1)а
1/П -з С08~х
ЗІП4 X
13)
464
2 — п
15) 15x2 ~ 15х + 12х /х — Юх + 1 . іб) _?_х п І7)_21хв+
2 Кх п
+ ,2х5 + 3= 18> (аЗ'2^ 5 19) -3*а + 2х + 2;
20) -~4= ; 21) (а + Ь) V; 22)-----Ц— ;
2хУ* 2со8“-£-
— Xе + 2х5 — Xі + 4х3 +
23) Зах2 4-За3х2 4-а3; 4а3 + За3; 24)
+ Xі + 2х + 1
(1-х)4
З
25) - —; 26)
4 соз 2х
28) (1 — 8ІП 2х)2
X (X2 + І)"-1;
зіп 4х 4 зіп 2х зіп2 х 4х — 2х4
соз2 2х ’ 27) (х3 + І)2 ;
29) (14- х2) зіп х — х соз х; ЗО) 2пх X
, . , . , зіп2х хзіпх
х (соз х 4- зіп х) 4~ зіп х 4~ '
' 1 ' 1 1 СОЗ X СОЗ^ X
(1 +І6Х)2
1 12 3
32) — 6х зіп (Зх2 — 1); 33) п лз/^ — —й-— ——-------7= — 3;
* ' Зу;2 2і^Г 2/Т^/ 2/рТ
л о ( ти 4- п \2 т _ — ЗОх4 4- 18х2 4- 6х 1
34) 3( р ) • р ; 35) ((1 - X2) (1 - 2х8))2 : 36)-^7г><
/1 І \ 4 зіп 4х
* ( (1 -|_ ут)2 “І* (1 _ |/Г)2 ) ’ '7) (1 + соз 4х)2 ’ 8) — Зх X
х2 + Зх — 1
6х + 9 5,п 5 / „ X +1
X зіп 2Х3; 39)--е-• ,------5——----------,-; 40) — соз2 —
0 х2 4- Зх — 1 \ х
соз'-1----Е-----
— зіп 0,8х). 11. 45°. 12. агсіеЗ. 13.
пх"+' — пхп — хп + 1
До розділу 5
1. 1) (—со; 0)— спадає, (0; 4-со)— зростає; 2) спадає на
(—оо; 2); зростає на (2; 4-оо); 3) спадає на (—со; 4-со); 4) спа-
ь
дає на (—оо; 0) II (0; 4~°°)і 5) зростає при х> — “2а~ , спадає
Ь
при х < — "2^“; 6) зростає на (0; 4~°°)і 7) спадає на (— оо; 2) (]
и (2; Н~оо); 8) зростає на (—оо; 4"°°)ї зростає на (1; .4-°°);
спадам на (—оо; 1); 10) спадає на (—оо; — 1) II (— 1; оо); її) зро-
стає на (— — 3 ; . 3 \ , спадає на [—оо; —. І у І-К? ;
\ 3 3/ \ 3 / \ З
465
+©ор 12) зростає на (1; +©о), спадає на (— оо; 1); 14) зростає на
(1; +°°)> спадає на (—оо; 1); 15) зростає на (—- 1; 0) (1; 4-00),
(З
1; у
/3 \ / 1 \
спадає на І “§“5 +°°Н 1?) зростає на (— оо; “2”), спадає на
+°°)» 18) зростає на (—оо; —1) 0 (1; +оо), спадає на
(—1; 1); 19) зростає на (—-у2ші; -у 4- 2пл^ , /г£2, спадає
на (-у- + 2пл; + 2пл) , л Є 2. 2. 1) г/тах = / (2) = 4; 3) «/тах «
== / (— 2) = — 4; #тіп == / (2) = 4; 4) не має локальних екстремумів;
я Зл
5) максимум в точках х = -у + 2пл; мінімум в точках х = -у- 4*
/ 3 \ а2
+ 2пл, г/тіп = -1; «€2,//тах=1; 6) {/тіп = /
7) 0ШІП = /(1) = -1; 8) »тах =/(-4)=-2; ї/тіп = /(4)=2;
5
9) ^=/^=-2; 0тіп = /(3) = —; 10) 0тіг, =/(0) = 0;
И) »тах = в точках X = + 2пл, </гпіп = —/7 в точках
х = ^-+2пп; 13) ут, = І (0) = 0; г/тах = / (8) = 65536; </т(|І =
= /(12)=0; 14) утІ11=/(-Г2) = --|- Ґ2; »тах = ? (/2) =»
З 1^2*
= — ; 15) функція не має екстремумів; 16) */тіп = / (3) = 3;
17) х = -у + 2&П, — точки тах; х = -у- + 2кл — точки тіп;
УтаХ~1’ 18> Утах =/(0) = »/2. 3. 1) найбільше
7
значення / (0) = 3, найменше значення / (2) = — — ; . 2) найбільше
значення І (0) = 3, найменше значення / (— 2) = / (2) = 3; 3) най-
більше значення / (0) = 0, найменше значення / ;
\ 3 / 6
4) найбільше значення / (9) = 25, найменше значення / (0) = 0;
5) найбільше значення / (4) = 3, найменше значення / (1) = 2; 6) най-
більше значення / (0) = — 1, найменше значення / ^~2“^ = — 4”)
4
= — -у; 7) найбільше значення / (0,7) — 3,9399; найменше значен-
ня / (0) = 3; 8) найбільше значення / (— і) = — 3, найменше значен-
466
ня Ц—8) = — 40; 9) найбільше значення /^-^-^ = 2, йайменше зна-
/ \ 1 Ср
3”--
4) — ; — ; 5) а == 2 рад., т = — ; 6) ширина сторінки Т/ +
4-2 4 V а
+ 26 довжина сторінки
+ 2а; 7) квадрат із стороною 5 см;
8) р =-47? К2 ; 9) V = 16 км/год.
До розділу 6
3. 1) 2) 2зіпх + С; 3) — Л-созх+С; 4) —Зі§х+С;
1 1 уб
5) сі£* + С; 6) -А-зіп2х + С; 7) — — созЗх + С; 8) -±- + С.
£, О О
4. 1) 6х; 2)—-----!—; 3) — 4созх; 4)——!------5. з(0 =
СОЗ2 X ЗІП2 X
= З*- — х — 4 — . 6. з (і) = З зіп і + 2. 7. V (і) = 12/ + 100.
З з
8. з (і) = 4/2 + 5і + 24. 10. 1) _2_ ; 2)55+12/2 — 6/3;
3) 74-2-; 4) 5 НУ 5) 60; 6) -4^3 ; 7) 10 —4/3; 8) 5/3;
9) У3.; 10)7,5; 11) У2.; 12) 21 + ^3 .; 13) -22- ;
4 2 3 4 3
14) _22_; 15) 8 (/3—1); 16) .3~^3 ; 17) 4л; —8 —/з .
6 3 64
18) 8 /3; 19) -22. ; 20) 3; 21) 1 + 21; 22) — ...К3 .
15 2 4
9 і
11. 2) Ю— (кв. од); 3) 4 (кв. од.); 4) 4 (кв. од), 5) 1--- (кв. од.);
О О
6) -5 (КВ, од.); 7) -2_ (кв. од.); 8) 21 _2_ (кв. од.);
0 0 о
9) 30 (кв. од.); 10) (кв. од.); 11) 6 3 (кв. од.);
162 24 4
12) 4,5 (кв. од.); 13) 3,5/21 (кв. од.); 14) (кв. од.);
108
15) 36 (кв. од.); 16) 36 (кв. од.). 12. 1) . З*»2** я. (куб. од.);
О
2) (куб. од.); 3) п (куб. од.); 4) -2_ пЯ (^ + гггг + г|).
13. 1) 13,5 (м); 2) -3!- (м;) 3) 28,5 (м); 4) — (м).
6 6
14. Д= (дж) 15. Д = 2,16 (Дж). 16. А = 100/2 (Дж),
де І — довжина пружини. 17. гп ж 0,44 (кг), 18. 420 (Кл), 19. « 171 од.
467
До розділу 7
2. 1) 4; 2) 0,4; 3) 0,04; 4) 0,004; 5) А ; 6) А ;
7) 1 — ; 8) 0,36; 9) 1,8; 10) 0,11; 11) 1,5; 12) 1,4. 3. 1) 6,3:
4
2) 1,91; 3) бА; 4) А. 4. 1) ±0,5; 2) ± 1,5; 3) ±0,7;
5 5
4) ± 1 -і- . 5. 1) так; 2) ні; 3) так; 4) так; 5) ні. 6. 1) а > 0;
2) а<0; 3) будь-які дійсні числа; 4) х^О; 5) х > 5; 6) х>4.
7. 1) 10; 2) 3; 3) 2; 4) 1; 5) — 1; 6) 0; 7) 0,1; 8) —1,5.
9. 1) 28; 2) 0*2; 3) 16,7; 4) —20. 10. 1) —1<7; 2) — у^;
3) — у^а, 12. | а — 6 |. 13. 1 при а > 0; — 1 при а <. 0 і п пар-
ному; 1 при а<0 і п непарному, 14. 1) 10; 2) 2; 3) х3; 4) 3;
5) -А; 6) 1,5. 15. 1) 10; 2) 0,3; 3) 1,5; 4) 3. 16. 1) ‘^а5;
2) ‘т<25; 3) |<2. 17. 1) /7; 2) ^25; 3) ,/36; 4) V
18. 1) у'Т6; у'З*; ‘^З3; 2) уПба*; т^8а3. 19. 1) 14; 2) А-;
3)2; 4)2; 5)3. 20. а2 + 21.1)0; 2) 2/Ї5. 22^6-, Г/8;
у^9. 23. 1) ат~п-, 2) са~ь; 2) а — 4^а. 24. 1) рЛА; 2) І;
3) 26 при а^Ь; 2а при а <6; 4) | 5 — а|; 5) 1—х при * = _!_;
х — 1 при х = 4. 26. 1), 2) Плюс. 27. 2 -|- /3.
28. 1) т2Ут^; 2) 262^аФ; 3) 1/ ;
29. 1) 2 (т + п) У З (т — п)2; 2) а2/а3; 3) а2(га 4) ахЬ3 Уа2г3.
4 г________
ЗО. х2 у 2сх8; якщо х < 0 і с < 0, то х3 < 0 і х2 > 0; тоді під-
кореневий вираз залишається додатним, але весь вираз — від’єм-
ний — х2-/"2сх3. Різні знаки х і с не можуть мати, бо в цьому випад-
ку під коренем четвертого степеня було б від’ємне число. 31. аЬ х
32. х < 0. 33. 1) |/24; 2) ^9; 3) |<4; 4) ^/Іа3;
5) ^бб1; 6) У(а + б)3. 34. 1) Уа3; 2) ^20; 3) 'Ух*; 4) У~аІ
35. 1) А_ 2) —А-----^т(а2+ б2)2. 36. 1) ^4?^;
с2 а2 + Ь2
2) т/ За2 (а-А.У .. 37. 1) 2) — /2а (а —2). 38. 1) |<5>
г СС и
2) 3/7 < У3^2. 39. 1) - |ЛА<у+**),;
2) у" 4а3 (х — у)4. 40. 1. 44. 1) — Уху; 2) 3) А- X
У Ьс
468
69?
І . , »?8® , . &Х , . , . 98<?8®І8 ,
+ ^9»? 98 гр —' /5І & ’ 9і ’88
г77
' Т+>8 (9 :§ (3 <8 :ет3в?»»5г9 (З ;гт® (І 48
/ І {і (І і (л£ , . * г9£ /
8 5 (|г ‘^Г (е -зі-01 (г :««-0 (1 88 ~Г (* (Є
, з® , . , і—«г8 , , , , вг93І ,
:^(2 :і (1 'г8 7^Г~ ь (8 :*л^~ (г
і8® (І 48 (? * і’^~~ & :9т®ет9»®ДЗ — (З !»М?і*9І (і ’08
+ (9 !г» (9 -и3 (? !8<? (8 ‘и2х (З "ат® (І ‘6Д ’(08 — ;?Є)
‘(? ІЗі) (а !г(9 —®) =р ‘г(<?+®) + (9 ‘8Д ‘(і -Я) '(її, 4) (л
!(і 49) ‘(?9 4) (я і(9 -03) ‘(03 :9) (9 і(і -б) ‘(б і і) (в ‘ДД
‘(8 ІЗ) ‘(З І8) (я !(І ‘4) ‘(? *•!) (9 !(б і?) *(? І6) (в ‘9Д
•звиан аінзбоя (г Ц і -у- (і -д£ і 4 !б ‘8 ‘і ‘0 (8 4 ! 0 (З
р £ 9
!8 І —— (І ‘ІД ‘39 (з ‘-0 (І ’ОД • ІГдог" (г :-Г— ! 1 — (і ’69
'9 (з ІЗ (І ’89 •£ ! І — (?•<? —І о (8 і-у- І -у“— (і 49 ’0
:9‘0 —(і ‘99 ‘9 ‘99 ‘З— (3 :звиан агаєв.вєосі (і -^9 ’д'О —
І8 ! 91 (і ‘89 ‘І (3 і? (І ‘39 ’г? + ® (9 4 (9 І9І (? І9І (Є І83
|(г.и • г(і ~ гуЛ ~ х) , , 96 + Зуі ?9 ~ 9уі 83 ~ 8/ 99
І Д?
, ХА + *х+хЛ . , (3/ 3 +Д/ 8) II , , г(3 + 9/8)
х ’ 99 І?
. 1-9/ . . , . з®
І (г 8 (1 09 ^о — ^Л + гх
(б
(З
(З
(9
(8
(З
‘ 08/+^+21^ (І .-69 •(£/+»/) +гп) (9 !(І + г/е +
+ М)2(3 ! г(9/5^//Д) (* :(0І/—9/—г/г+Є)/- (8
(®/З Ч-2/і ®) ®9 ’4/”І*9/3 (і 89 Є/ 9/ (9
і(Д/+9)^- (9 і-^Г(? із£4®8 (8 і^/у (З
О
І3/у(і ‘Д9 -9—3® (8 (з ігг®09І (і ‘99 ‘г£/6+ 3 — » (8
:г9із®/<. (З !в»у* 9 (І ‘99 ‘9®ЗЛ <?» (8 :з99®?1 Л 8‘0 (б
І^/ІОІЗ (і 49 ‘яві (г ‘.яві (і -£й -ін ‘19 ’!н (? ;!н (8
іін (г ‘-яві (і •§? •?/- ‘Д? •(з(® + ^®/ — х) + І)в(«/ + ^/) (З
О + V
‘АХ Д^ (І ‘9? ‘О (з !(9 +®) ®/|--------1— (І ‘9? ~Вг9®9 /| X
+ а*+І*+ 16Д_і> • 87. 1) с3; 2) 89. 2а~2&-2 +
13
+ а“1&-4. 90. 1) Xі; 2) а 12 ; 3) Ь 4 ; 4) а-4; 5) с2; 6) -її,
___________1 ___9_ 37 27
91. 1) х 15 ; 2) р 1 9 28 ; ' 3) б2. 92. 1) 3 8 ; 2) 27 125~2.
_61 2 19 2
93. 1) а 60; 2) 2а 863 . 94. 1) 1; 2) а 20 х 15 , 95. 1) 9; 2) 32;
1 ~
3) 15. 97. 1) (2 2 — 1)/5; 2) —2----; 3) —£-----.
х2 + 3 а2 — 1
і і і і з з
98. 1)ах2+а2х\ 2)4 —г/8. 99. І)/?4— с4 ; 2) а2—б2,
1 1 1 1 і
100. 1) (а — 3 2 ) (а + 3 2 ); 2) (Ь 3 — 5) (Ь 3 + 5); 3) (а3 — 2) х
і і і 1 і
Х(х3+2); 4) (а2 — Ь4 ) (а 2 + Ь4 ). 101.1)1; 2) х — у.
1 1 і 1 1
103. 1) х — 2х 2 у2 + у\ 2) х~2 — 2х^у 2 + у; 104. 1) а2 (а2 4-
1 і 2 і 2 і 2
+ 1); 2) (5 — Ь3 ) (25 + 563 4-Р ); 3) (183 — 63 )(183 +63 )?
1 1 1
4) а2 (22 — 52 ). 105. 1) 5; 2) 41. 106. 32.
До розділу 8
1. 1) 6; 2) 4,5; 3) —4; 4) 4; 5) 2,5; 6) -І-; 7) 2;
8) 3 і 4; 9) —2 і 1; 10) —2; 11) 3; 12) 5; 13) 1; 14) 1;
15) 3; 16) 0; 1о§, 5; 17) 11; 18) —4;, 19) 35; 20) 3; 21) 9;
22) 2; 23) 2; 24) 4; 25) 1о£я 2; 26) ; 27) розв’язків
немає; 28)| ; 29) —3; ЗО) — _1_; 31) 3; 32) 1
12; 33) — 1 і 1; 34) — 2 і 2; 35) — 2 і 2.
2. 1) х>— 1; 2) х>0; 3) х < 2; 4)х< —2; ж>3;
9
5) х>0; 6) х>3; 7) х > — ; 8) х < — 3; х > 1; 9) х < — 4|
10) розв’язків немає; 11) х<1,5; 12) 0 < х < 20; 13) — 4;
х>2; 14) х>-1_; 15) х> — 0,25; 16) —/Г<х</2; 17)- 1<
<х<7; 18) 1<х<2; 19) (—0,5; 1); 20) х>^--, 21) (0; 1);
22) (—оо; —7,5) і (—0,5; оо); 23) 0; 24) (—оо; 6); 25) (1,6; оо);
26) (1; оо); 27) (—3; оо).
470
До розділу 9
2. 1)4=1о§381; 2) — 2 = 1о§4-2_ ; 3) -2_ = ІО& 2; 4) -2-=
=1о§273. 3.1)3; 2)-1; 3)0; 4)—1; 5)9; 6)—7.
4. 1). — 2; 2) 3; 3) - 4; 4) 6. 5. 1) 25; 2) 216; 3) 2; 4) 1; 5) 8;
6) 0,001. 7. 1) 1о§ 2 2,25 = —2; 2) 1о§01 0,01 = 2; 3) 1о§3 — =
Т ’ 2
-----1_;--------------4) 1О83437 ---* 8. 1) 1; 2) -3; 3)4; 4)0;
О О
5) -5; 6) -2-; 7) --2_; 8) -2-І-. 9. 1) ; 2) ; 3)4;
4) 2. 10. 1) так; 2) так. 11. 1) 2; 2) 2. 12. 2. 13. 1) —2;
2) -2; 3) 2-2-1 4) — 2; 5)1; 6)0; 7) А; 8)
2 2 О
14. 1) 81; 2) -А-! 3) 1,25; 4) 4; 5) а+ 1; 6) 729. 15. 1) -2_;
З
2)32; 3)1; 4) _2_; 5) ’ ; 6)8. 16. 1) -1; 2)0.
343 216
17.1)8; 2)1-2-; 3)_2_; 4) 2; 5)0,8; 6)3. 18.1)10; 2)7;
3) 5; 4) 3; 5) -2-; 6) 8. 19. 1) 5; 2) 7,4; 3) 2; 4) 64; 5) 24;
6) 1,25. 20. 1) 0,3; 2) 9; 3) 1,5; 4) 7. 22. 1) 20; 2) —.
5
24. 1) 1о§ а + 3 1о£ Ь — 2 1о£ с\ 2) А- 1о& а — 1о£ Ь — 2 1о£ с\
5
3) 2 1о& а + А- 1о£ Ь\ 4) 3 1о£ а + -А. 1о& Ь + -А- 1о£ с — 2 1о§ (а + Ь).
О І
25. 1) 2 1о§а+4-І°й *+4-*°8с — 1°§8 —4-1°§ <а + ^); 2) 1°82-|-
2 2 о
-І-Аіоеа — _2_ІО8£; 3) 1о§0,6, 26. 1) 1о§3 + 1 -2- 1о§Д-Ь
4 £ о
+ -2-1о§(а + 6); 2) _2_(1°8а —1°8*); 3) -2- 1о§ а + -2_1о2 Ь\
о о- 2 2
4)-1-2_1о§а; 5)0; 6) (1о£Ь — 1о§а). 27. 1) 1о§12 20; 2)1.
6 8
28. -1і22- . 29. 1) 2; 2) 1$ 12. 31. 1) 2^- ; 2) 12; 3) + & ;
4 ________ 5 ' а2/?3
4) 2 (д + 6) _ 32 () Уа — Ь . 2) 2д63 .
За ^(а + б)2 • ^а2 ’ 3 {'Ь^а
33. 1) ; 2) 4 /_.6(д-6)2 2 . 34. 1) ±;
а~Ь V 3/72-/7(7=6) 4
2) 1 -2- • 85- 1) 2; 2) 4. 41. 1) —х>2; 2) х<5. 42. Додатний.
471
44. Число N у 100 разів більше, ніж число М. 45. 1) (— 2; оо);
2) (—оо; оо); 3) (—оо; оо); 4) (А ; 3) . 46. 1) (—2; 2);.
2) (-2; 3); 3) (-1; 2); 4) ; _|А 47. 1) (- оо;
— 2 А) ; (5; оо); 2) (—оо; —1);
4) — оо; ; (3,5; оо); 5) і
52. 1) 4; 2) 3; 3) — 2,35;' 4)
7) 15; 8) 1 і 125; 9) 100 і 1000;
(3; оо); 3) (—оо; —2,5); (1; оо);
6) х > 0 і х < 0, — оо < г/ < оо,
розв’язків немає; 5) 0; 1; 6) 3$
10) 9 і 11) 100 і 0,01; 12) 10;
13) 1010; 14) 10 і 0,001. 53. 1) 6,5; 2) 4,5; 3) 1;
6) 14 і 6; 7) 10; 0,1; 1000; 0,001; 8) 100 і 0,01;
4) 4- ’ 5) 3-'
4
9) 1; 10) 4;
11) 13; 12) коренів немає; 13) 10; 100; 14) А; 15) 0,0001 і 10;
16) 80. 54. 1) —3; 2) 95 і 5; 3) 100 і 108; 4) 1; 2; 5; 5) 3,5;
6) 4; 7) 25 і 0,2; 8) -1- і 16; 9) 2; 10) 3; 11) А * 9; 12) 100;
2 о
13) а-1 і а2; 14) 10 і А-. 55. а) (100; 10); б) (2; 5); в) (1; 2);
г) (2; 1). 56. а) (6; 8); (8; 6); б) (2; 18); (18; 2); в) (_1_ ; з).
57. а) ; — 12 А); б) (4,5; 0,5); в) (27; 4); (А_ ; — з);
г) (5; 5); д) (3; 9); (9; 3). 58. 1) 0<х<8; 2) х>25;
3) х>4~; 4) 0<х<0,027; 10) (— 3; 1); 11) 3<х<5;-
З / 1 \
12) розв’язків немає. 59. 1) (0; 1); 2) 15— ; — ЗІ; (7; оо);
3) п > 3; 4) х < 4; 5) 1,6 < х < 5; 6) х > 0, крім х = 1; 7) х > 0,
8) х>2; 9) (0; 0,001); (10; оо); 11) 2<х<3,3; х > 3; 12) 3<х<
<81. 60. 1) — Кб<х</5; 2) (— оо£_3); (9; 12); 3) х > 3;
4) 0<х<9; 6) — 3< х < — /2Д>; /2,5<х<3; 8) (0; 1);
9) 2<х<2,75; 10) 1/А<х<1; 11) (0; 1), (1; 2), (2, оо);
12) коренів немає.
До розділу 10
2. 1) а*; 2) 7ех; 4) 4x36*’; 5) Зх2е**-1; 6) — За2-3*; 7) 5Л1п5;
8) —101-х Іп 10; 9) 2 • 32л:+1 Іп 3; 10) 3 . 7х Іп 7;
11) 4 • 2,13+4* Іп 2,1; 12) 25х2+Л"1 Іп 2 (Юх + 1); 13) А;
X
14)—?—; 15) х2 (3 Іп х + 1); 16) А—; 17) —!—; 18)______!__;
2х—3 х1п7 х1п5 хіпО.З
19) — 2е~2х; 20) — 7є3’7л; 21)АєТ; 22) (6х — 4) є3лг2~4х~2;
472
23) 6е2*-<+ 24) - ; 25) 3-53*1п5; 26) 6-2Л їй 2;
27) — 71"* Іп 7; 28) - 7 • ІЗ5”7* Іп 12; 29) 5 • 2,34+5* Іп 2,3;
ЗО) 2х (Іп 2 соз х — зіп х); 31) _Л_ ; 32) х2 (3 Іп х + 1); 33) ІЗГ1”*;
1 + Зх ха
о., 2(х2+1)—(3+2х) Іп (3 + 2х) 2х . Кх І Іп х . .\ , □«, соз х
’ (3 + 2х) (х2+І)2 ’ '”П 2 /’ ’ х
— Іпхзіпх; 37) —1— ; 38) ----2—— ; 39) ;
х Іп 2 (3 — 2х) Іп 9 (3 + 4х) Іп 10
40) 7________• 4|) 1 42) У* 1 У
(7х+2)1п0,3 ’ хІпЮ х \ 2 х Іп 10 /
— л Цу
43) 2е2* + 2г2 ; 44) (х4~2) ех; 45) —— ; 46) — 2хе“х’;
е
47) 35е7* —9в3*; 48) — 5 зіп 5хеСО5 бх; 49) (2х + 3) • Іп 2;
50) 4х (3 + Юх + Зх2) + (Зх + 5х2 + х3) 4х Іп 4);
51)
Зх2 (4х + 5) — х3 • 4х Іп 4
(4х + 5)2
X З5* Іп 3 +49 • 25“2х . Іп 2; 54)
52) х • 2—' (2 — х Іп 2); 53) 5 X
— 0,3“* х Іп 0,3 /х — 0,3-х • —77=
2у х.
----------------------------------*9
X
55) ____х + 3___; 56) *(2 1п*~ 0 ; 57) е*+і
х2 + Зх + 2 3 Іп2 х
58) а? І2х Іп а Іп (х2 + 4х + 12) Н-----„ 2* + 4
\ х2 + 4х 4
= -------------; 60) --------!-------; 61) 3 1о& (X + 1+ х2) +
(2 + Зх) іп 7 (7 + Зх) Іп 0,2 ’ і т т / т
59) у'
+ - (Зх + 4) (2х+ 1) . 62) 2 Зх + Ух
(х2 4- * 4~ 1) 5 ’ (х3 4- 4 Ух + 5) Іп 11
63) е (3 СО5 Зх 4~ Іп 2) . 64) г. 3. 1) ‘
зіп Зх + 2х (х2 — 4х 4~ 6) ~4~
2) 4х , 3) 3 • 5х . Іп 4 Іп 5 ’ 4) зг-6- 5) Іп (х + 3); ІП 0,о
6) _1_1п(2х —5); 7) Іп (Зд: + 1); 8) ; 9) е4*;
£ о ІП о 4
10) -4-еЗЛ--і’л’Г ; “) 4- 1п(5х-8); 12) * 1п(4х-1)}
З ІП 0,2 5 4
13) 3 Іп х + 2 Іп (х+ 1); 14) 4-е7л:; 15) ех(х—2); 16) ;
• Іп2 а Іп3 а
17) е-х(х+2); 4. 1)-Д- ; 2) 1о& 4; 3) 1о& 6 - 1о& 3; 4) - ^° „ . ?
Іп 2 У Іп З
473
5)
7 Л
4
Іп —
6) 21п5; 5. 1) ІпЗ; 2)1пй(а>1);
3) 2 Іп 3 = Іп 9;
7. 11) спадає на
на (-1- ; сю | .
\ 9 )
4) 0, їх-°-9; 5)
9) — 10х~2;
6. 1) {/ = 2x4-2; 2) {/ = 6(1 4-1п2(х—1)).
(о; Л^,4.Л^ = ЛЛ 1п9 « 1,066, зростає
\ 9 / \ 9 / З З
2
8. 1) 100х"; 2) Лх" 3 ; 3) /Зх^-’і
О
___3_
ш/і-і. 6) _5х4. 7) _20х19; 8) Л_х 10 |
З з
10) 5х 2 ; 11) — ЛЛ 2 1
(2х 4- з 4- 7хв) Кх2 4-1 - (X24- Зх4-х’) 1ЛЛ_^- _±
12) ----------------—------------ЕЛ+1; 13) -х 3 ,
X2 + 1
І 1 1
14) Лх3 ; 15) Зх2 4- 2,5х~ 2 ; 16) 2 (—ЗхЧ-8х2 — 5) (9х2 4-16х)}
З
17) -‘ х~ 2 ; 18) Л_х2 3 ; 19) —*
5]/П 3 2}Гх
З__ 4
3-рЛх 4 /х
4
20) Л (х 4- 414- —V) 5 21) -12 (2Х + 5-)— !
5 \ 2 /х / 7 / (Зх2 4.5хз)з
4-Лх 5 * — 2х~3 1, 10. 1) у = х*4-3х; 2) у = х4-1. 11. х* =х1п2;
5 /
х =С . 2'. 12. х' = х Іп 0,99; х = С . 0,99', 13. Т = — ,1п-2- - ,
1п 0,99
До розділу 11
7
1. 1) 1 + 7/; 2) 3 + 2/; 3) —2,9 —1,6/; 4) 8—13/; 5) ~ —
— Л_і; 6) 8х-|-4{/г; 7) За + ЗЬі-, 8)—8с —2й(; 9)Л.-1А(;
2. 1) — 1 4-17(; 2)(/2 4-2)4-(2]/2-1)(; 3) Л 4- Л і-, 4) 1-21»
лУ 2<У
5) 13; 6) (Кб4-К2) + (2-КЗ)(; 7) Л-- * (; 8) -і?
1^6 1^
474
9) 10) А; 11) (8/З + 3) + (6 - 4 /3) І-,
27 27 64
12) (2а2 + 3&2) + 5аЬі; 13) — -А- + 7; 14) 5^3~7 _ 5+7 /3 ,
2 2 4 4
3. 1) (а + ЗЬі) (а — ЗЬі); 2) (0,8 + 0,7x7) (0,8 — 0,7аУ);
3) (/а + 57) (/а- 57); 4) (* + 4 іїї* - 4- '15 5) (/3 + /х 7) X
X (/?- /х 7); 6) (/7 + _1_ і) (/7 - /) ; 7) (х2 +27) (х2 - 27);
8) (х2 + г/2г) (х2 — 9) (4 + 7) (4 — г). 4, 1) — Зг; 2)—2/;
3)7; 4) —5; 5) — Юі; 6) 3-і. 5. 1) 5 +127; 2) —4;
3) — 2 + 2і 4)1+4/37; 5)16; 6) — 142 — 657; 7) — к + і-,
8) —64; 9) 1. 6. 1) 6±37; 2) А±_!_23_7; 3) — 3 ± 37;
4 4
4) — 5) —-2-± X11. 7; 6) 2 +і, —2 +і.
' З 3 6 6
8. 1) 2; 4-; 2) 2; 2 я; 3) 4; 4-; 4) 1; 5) 1; 1л;
О о О О О
6;
6)
соз 4- і зіп ; 2) 5 (со8-ї-+ і ;
3) 2 (соз 0 + ІзіпО); 4) 2 (соз 2А + 7зіп—; 5) 2 (соз — +
\ 6 6 І \ 2
4-/ зіп; 6) 3 (соз я 4~^ зіп я); 7) 2 [ соз —4- * зіп ;
2 ] \ З 3 / —
8) зіп 4- + 1С08 — ; 9) — 2соз — (соз+ (8Іп.
2 2 9 \ 9 - 9 /
10. 1) 2 /3 + 27; 2) 1 + 7; 3) — 20 /З + 607; 4) 2; 5) 5 — 57;
6) —7. 11. 1) 3 (соз 110° + 7 зіп 110°); -і" С08 40° + 18ІП 40°>ї
2) Кб(соз4- + '8Іп4Ь КА(соз4-+І8Іп4
\ 2 2/ 3 \ 6 6,
3)130 (соз 149° +
+ 7зіп149°); -А (соз 65° + 7 зіп 65°); 4) соз А- + і«іп — ;
1 О І!
йк А — і Зіп 4- ; 5) З (соз 105" + і зіп 105°); 6 (соз 95° + і зіп 95°);
О о
6) Уг(соз (- -А-)—18ІП (— ,2-!) — 64; 2) “32 СО86-^- х
X ^08-2-+'Зіп 4") • 13- 1) 2 (соз я + 2А;я + і ЗІП —+„2АП .) }
( 4~+2^я +2^я \
2) /8 І соз---£-------— і 8іп------£----1;
4/-_ ( я 4- 2&я я 4- 2&я \
3) /4 [соз--------------- 4-/зіп-------------р
475
До розділу 12
§ 1.1. 1) 2; 2)11,3; 3) — 2 ; 4) -14,75. 2. а) ® }
оо 19
б)-----— ; в)-----— ; г) ; д) — А ; е) 6 — ; є) — 3;
’ 21 73 ’ 37 ’ & 3 '
Я
ж) — -А-. 3. «12 см3. 4. «11,10м. 5. 760 т. 6. 220 кг.
о
7. «153 см. 8. 27 см. 9. 12 %. 10. 12,3%. 11. 112%.
12. Зменшиться на 4 %. 13. Зросте на 25 %. 14. Збільшиться
на 25 %. 15. 1,5 кг.
§2.1. 1) 10х3 — 6х2г/ + 2хї/2 — 5х2(/2 + Зхі/3 — 2) — 8,96г/2;
3) 21х2 + 182x0 — 6302; 4) 8а2; 5) 4т2 + 17 А пт — А л2;
9 2
6) 0,01х2 + 0,2x0 + 02; 7) 2Аа2 —6Аа* +А*2; 8)Аа2 —
— 2а* + 4*2; 9) 0,57x0 —0,004х2 —4,0502; 10) 4а* —9а2 —4*2;
11) а2 -|—А- аЬ — 1 А. б2; 12) 8а; 13) 6,25т2 — 5,75тл + 0,6л2;
14) х3 + 1; 15) ЗА-Х0-1 А02-_^_х2; 16) 8а3-*3}
17)1—Ах2; 18) а3 —27*3; 19) а6 — А. ; 20) 8х3 + 03.
2. 1) *2(а3 —б2); 2) (3 + х) (9 — Зх + х2); 3) 4а3(3а4-*);-
4) (1—2а) (1+2а 4-4а2); 5) (а+*) (х - 0); 6) (а + Ь3) (а2 - а*3 +
+ *6); 7) (3 — л) (т + За); 8) (2 — а*) (4 + 2а* + а2*2); 9) (а —
— *)(2х+1); 10) (5а —36) (25а2 + 15а*+ 9*2); 11) (а — с) (а+*)}
12) (а2+1) (а4—а2+1); 13) (3 — а) (х + у)-, 14) 1,1 (а - 6) (а2 +
+ а* + *2); 15) (а + 6) (а* — с2); 16) (Зх - у) (9х2 + 3x0 + 02);
17) (5т —3?) (2л —5р); 18) 9 (а — *) (а2 + аЬ + *2); 19)(Зх + 4)Х
X (Зх — 4); 20) 2 (т — І)2; 21) (1 + 02) (1 - 02) ;
22) х (х + 1) (х + 0); 23) (а-1)2; 24) 0,09 (х3 - у) (х3 + у);
25) (2а + І)2; 26) (а4 + 1) (а8 — а4 + 1). 3. 1) 224,96; 2) 98,01;
3) 1000; 4) 4; 5) 16; 6) 0,1; 8) 11; 9) 9801; 10) 31.
4. 1) 2; 2) 2; 3) 2; 4) 4; 5) 2. 5. а) -А~д ; б) — А ?
1 — 2а а
•> -Аг- ' г> 3<’~й- ’• а>1А б> < » >
б) |а[/б; в) 562 /3; г) 31 с3 | /3. 10. а) /7х2; б) —/7х2;
в) /5а; г) —/—5а. 11. а) « 25,45; 6)1; в) «31,22; г) 6;
д) 7,36; е) 214,20; є) 3,58; ж) 0,28. 12. а) 1; б) 1— х/х;
в) 1; г) а/5+ 8. 13. а) -У. х~-±. ; б) ААА ; в) /ТТ + /7;
X 6
Г) — К.1.4 , 14. а) 3; б) 32;. 15. а) а/* + */а; б) 4-х3}
в) х —4; г) а — *. 16. а) ——АЕІ------------; б) .
х (х — у) Ь — а
476
§ 3.1. 1) 15; 2) коренів немає; 3) —-А-; 4) —3; 1/2;
5
5) —1,7; 6) А; 7) — 9; 8)—1,6; 9)0; 10)—А; 2;
2 о
11) 0; —3; 12) коренів немає; 13) —2; 5; 14) —4; 4; 15) 0; А ;
16) 0; 1; 17) 0; А; 18) -1; А; 19) —2; 2; 20) 5; 21) —3; 3;
О 2
22) —1; 2; 23) — /5; /б; ' 24) — А і 25) при ^#=А
5 4
3-й
4й — З
О
при & =— розв’язків немає; при к = ± 1 рівняння
4
не має смислу;
З 1
26) при а > 0 х = — — а; при а < 0 х = а;
при а = 0 х = 0; 27) 6; 28) розв’язків немає; 29) ; 30) — 2;
125
31) 5; 32) ±6; 33) 0; 34) 2; 35) при а=#3 х = 2; при а = 3
х — будь-яке число; при а ^0, &#=0 х = ; 36) —1; 10;
о
37) А; 5; 38) 2; 39) 0; а + 6; 40) 1; -А ; 41) 0; А при
а==&==0 рівняння не має смислу; 42) —4; 9; 43) при п=Н=
_ Зп+ 12 .
Х 5п — 2
2
При п= -
5
рівняння розв’язків не має; при п = 0,
п — 1 не має смислу; 44) 1,2; 2,4; 45) розв’язків немає; 46) 1; 2;
47) 2; 48) —6; 1; 2; 3. 2. 1) (4; 2); 2) (4; 2);
(—4,5; 2,25); 3) (8,5; 4,5); 4) (—3; —5), (5, 3); 5) (5; 7), (7; 5);
6) (15; -1), (—20; 6); 7) (—6; 22); 8) (—5; —4); (4; 5)|
9) (0; 0); 11) (20; 100); (100; 20); 12) (1; 0); 13) ; А) }
14) (3; 2), (—3; —2); 15) (20; 4), (—20; —4); 17) (2; 3), (3,2);
(1; 5), (5; 1); 18) (2; 3), (3; 2); 19) (4; 2); 20) (—3/2; /2);
(З /2; —/2); (—3 /2; — /2), (3/2; /2).
ЗМІСТ
Від авторів ................... .............................. З
Розділ 1. Тригонометричні функції . « ........................ 5
§ 1. Тригонометричні функції кута............................ 5
§ 2. Радіанна система вимірювання кутів і дуг................ 8
§ 3. Тригонометричні функції числового аргументу............ 11
§ 4. Періодичність тригонометричних функцій..........., . . 18
§ 5. Побудова графіків тригонометричних функцій ...... 22
§ 6. Властивості тригонометричних функцій .................. 29
§ 7. Співвідношення між тригонометричними функціями одного
й того самого аргументу ...................................... 38
§ 8. Обчислення значень тригонометричних функцій і тригоно-
метричних виразів за допомогою мікрокалькуляторів , . . 42
§ 9. Основні тригонометричні формули ..............., . . . , 48
Запитання і завдання для повторення 62
Розділ 2. Тригонометричні рівняння .......................... 71
§ 1. Поняття про обернену функцію. Обернені тригонометричні
функції ................................................... 71
§ 2. Розв’язування найпростіших тригонометричних рівнянь . . 81
§ 3. Деякі способи розв’язування тригонометричних рівнянь,
які відрізняються від простіших ............................. 89
§ 4. Приклади розв’язування деяких інших типів тригономет-
ричних рівнянь .......................................... . 95
§ 5. Розв’язування найпростіших тригонометричних нерівностей 101
Запитання і завдання для повторення................ , , , . 105
Розділ 3. Границя і неперервність функції ................. 107
§ 1. Границі числової послідовності ...................... 107
§ 2. Границя функції неперервного аргументу .................119
§ 3. Неперервність функції в точці .........................133
Запитання і завдання для повторення , ................., . ♦ 139
Розділ 4. Похідна.......................................... 141
§ 1. Задачі, які приводять до поняття похідної............ 141
§ 2. Похідна. Механічний та геометричний зміст похідної . . . 150
§ 3. Похідні елементарних функцій ..........................154
§ 4. Теореми про похідні алгебраїчної суми, добутку і частки
функцій .................................................... 158
Запитання і завдання для повторення 166
Розділ 5. Застосування похідної ...................... . . . 169'
§ 1. Зростання, спадання функції. Екстремальні точки .... 169
§ 2. Локальний екстремум функції ......................... 174
478
§ 3. Знаходження найбільшого і найменшого значень функції . 178
§ 4. Загальна схема дослідження функції та побудова її графіка 183
Запитання і завдання для повторення ........................187
Розділ 6. Інтеграл і його застосування............, . . . , 189
§ 1. Первісна. Таблиця первісних ............................ 189
§ 2. Основна властивість первісної ..............е . . . , . 193
§ 3. Правила знаходження первісних .........................194
§ 4. Інтеграл ......................................... е 197
Запитання і завдання для повторення ........................220
Розділ 7. Степінь з раціональним показником.................224
§ 1. Корінь п-го степеня і його властивості ................. 224
§ 2. Ірраціональні рівняння ................................237
§ 3. Узагальнення поняття степеня. Степенева функція .... 248
Запитання і завдання для повторення ........................258
Розділ 8. Показникова функція .......................... 272
§ 1. Поняття показникової функції .........................272
§ 2. Розв’язування показникових рівнянь, нерівностей і систем 284
Запитання і завдання для повторення ........................289
Розділ 9. Логарифмічна функція . , » . .....................292
§ 1. Логарифми ............................................292
§ 2. Логарифмічна функція, її властивості і графік............ 304
§ 3. Розв’язування логарифмічних рівнянь і нерівностей , . * 309
Запитання і завдання для повторення .......................... 320
Розділ 10. Похідна і первісна показникової та логарифміч- , , .
ної функцій ....................................... 328
§ 1. Похідна показникової функції .........................328
§ 2. Похідна логарифмічної функції .........................329
§ 3. Первісна показникової та логарифмічної функцій ..... 331
§ 4. Дослідження показникової та логарифмічної функцій . , . 332
§ 5. Похідна степеневої функції.............................334
§ 6. Диференціальні рівняння ........................... 337
Запитання і завдання для повторення ........................343
Розділ 11. Комплексні числа................................... 347
§ 1. Розширення множини дійсних чисел. Поняття про комплек- .
сне число ............................................. 347
§ 2. Дії над комплексними числами ...................... . » . 349
§ 3. Геометрична інтерпретація комплексних чисел ...........356
§ 4. Тригонометрична форма запису комплексних чисел . . , 359
Запитання і завдання для повторення .......................» 366
Розділ 12. Повторення курсу алгебри основної школи . . . * . 371
§ 1. Дійсні числа і дії над ними . . . , ,............... • 371
§ 2. Тотожні перетворення виразів .......................... 400
§ 3. Рівняння і нерівності ................................... 419
§ 4. Функції. Огляд властивостей раніше вивчених функцій . , 437
Відповіді ............................................... • . 460
Шкіль М. І. та ін.
Ш66 Алгебра і початки аналізу; Навч. посібник / М. І.
Шкіль, 3. І. Слєпкань, О. С. Дубинчук. —К-1 Вища
шк., 1992. 479 с. і іл.
I8ВN 5-11-002589-4
1602040000—210
Ш М211 (04)—92 73““91
ББК 22.14я722
У че бное издание
Шкиль Николай Иванович
Слєпкань Зинаида Ивановна
Дубинчук Елена Степановна
АЛГЕБРА И НАЧАЛА АНАЛИЗА
Рекомендовано Миниспгерством
народного образования Украиньї
в качестве учебного пособия
для учащихся средних
профессионально-технических- училищ
Киев, «Вища школа»
На украинском язьіке
Оправа художника Є. Г. Рубльова
Художній редактор С. В, Аннвнков
Технічний редактор Л. Ф. Волкова
Коректор Л. Г. Любимова
ИБ № 14508
Здано до набору 29.03.91. Підписано до друку 18.12.91. Фопмат 84хЮ81/»2. Папір"
друк. № 2. Гарнітура літературна. Високий друк. Умов.-друк, арк 25,2 Умов,
фарбовідб. 25,46. Обл.-вид арк. 27,94, Тираж 15 000 пр Вид № 9336 Замовлення
№ 1—1819. Ціна 2 крб. 70 к.
Видавництво «Вища школа», 252054, Київ-54, вул. Гоголівська, 7.
Головне підприємство республіканського виробничого об’єднання «Поліграфкнига»
252057, Київ, вул. Довженка, 3.