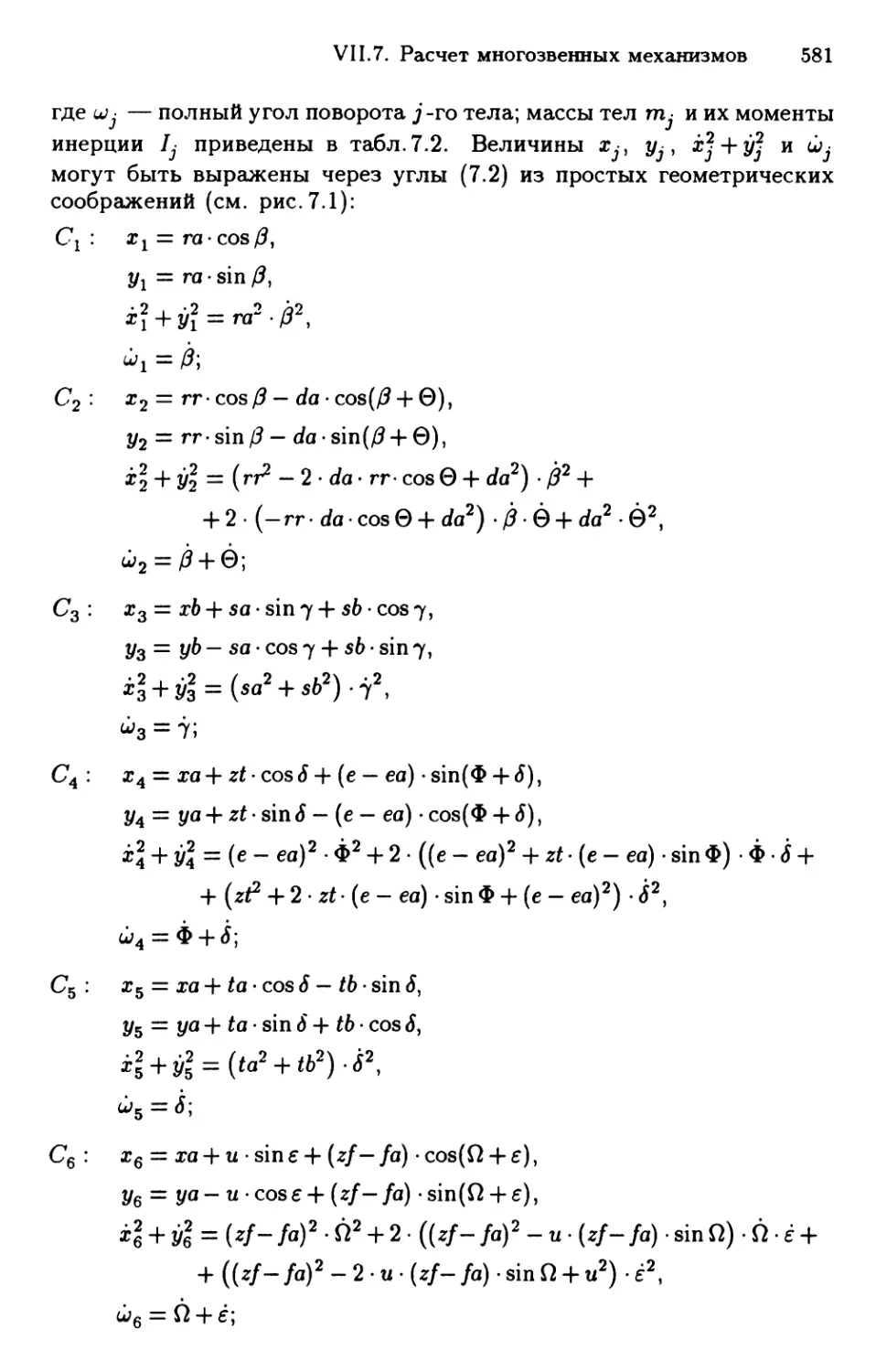Теги: дифференциальные, интегральные и другие функциональные уравнения конечные разности вариационное исчисление функциональный анализ математика дифференциальные уравнения
ISBN: 5-03-003117-0
Год: 1999
Текст
Э. Хайрер
Г. Ваннер
Решение
обыкновенных
дифференциальных
уравнений
Жесткие
и дифференциально-
алгебраические задачи
Перевод со второго английского издания
Е. Л. Старостина, И. А. Кульчицкой,
А. В. Тыглияна и С. С. Филиппова
под редакцией С. С. Филиппова
Москва «Мир» 1999
УДК 517.91
ББК 22.193 + 22.161.6
Х15
Хайрер Э., Ваннер Г.
X15 Решение обыкновенных дифференциальных уравнений.
Жесткие и дифференциально-алгебраические задачи. Пер. с
англ. — М.: Мир, 1999. — 685 с, ил.
ISBN 5-03-003117-0
Книга известных швейцарских специалистов по численному
анализу представляет собой продолжение для случая жестких задач
вышедшей ранее книги тех же авторов (в соавторстве с С.П. Нёрсеттом)
для случая нежестких задач (М.: Мир, 1990). Книгу отличают
методические достоинства: вначале приводятся примеры расчетов
прикладных задач из физики, химии и др. и обсуждаются возникающие
проблемы, а затем рассматриваются методы интегрирования,
излагаются теоретические результаты с доказательствами; приводятся
многочисленные литературные ссылки; каждый раздел сопровождается
задачами. Приложение содержит описание программ на Фортране.
Для всех, кто в своей работе встречается с решением
дифференциальных уравнений — для математиков-вычислителей, инженеров,
аспирантов и студентов.
ББК 22.193 + 22.161.6
Русский перевод книги выпущен в свет
издательством «Мир» совместно с ООО «Медицинские системы»
Редакция литературы по математическим наукам
ISBN 5-03-003117-0 (русск.) Originally published in English under
ISBN 3-540-60452-9 (англ.) the title: "Solving Ordinary Differential
Equations II" by E. Hairer and G. Wanner
Copyright © Springer-Verlag 1991, 1996
All Rights Reserved
© перевод на русский язык, «Мир», 1999
От редактора перевода
Предлагаемая Вашему вниманию книга представляет собой
перевод второго тома двухтомной монографии, посвященной
современным численным методам решения обыкновенных дифференциальных
уравнений, в развитие и исследование которых авторы — известные
специалисты по численному анализу и блестящие педагоги,
профессора Женевского университета Эрнст Хайрер и Герхард Ваннер внесли
большой вклад.
Первый том — «Нежесткие задачи» — содержит три главы:
одну, посвященную классической математической теории
обыкновенных дифференциальных уравнений, вторую — одношаговым методам
(Рунге—Кутты и экстраполяционным), третью — многошаговым
методам, а также приложение с текстами программ на фортране.
Перевод первого тома был выпущен издательством «Мир» в 1990 г. и
разошелся за один месяц, несмотря на значительный тираж A4 000
экземпляров). Когда в 1991 г. появился второй том, мы сразу же
приступили к его переводу в надежде, что ожидаемая читателями
книга сможет выйти в кратчайший срок. Но ... прошли долгие годы,
прежде чем наши усилия привели к цели. За эти годы издательство
«Шпрингер» выпустило второе издание сначала первого (в 1993 г.), а
затем и второго (в 1996 г.) тома, существенно переработанное
авторами и дополненное новыми результатами. Книга, которую Вы держите
в руках — перевод со второго английского издания. Поэтому номера
разделов, формул, теорем и т.п. из первого тома, ссылки на которые
имеются в книге, не всегда совпадают с соответствующими номерами
в русском издании 1990 г. (см. Дополнение в конце книги).
Я выражаю искреннюю признательность всем лицам и
организациям, содействовавшим появлению этой книги: авторам Г. Ваннеру и
Э. Хайреру за неоценимую помощь в преодолении трудностей,
возникавших при подготовке этого издания; руководству ООО
«Медицинские системы», финансировавшему издание; переводчикам —
сотрудникам Института прикладной математики им. М.В. Келдыша РАН,
которые, вопреки всему, не потеряли веры в то, что их труд будет
востребован; сотрудникам издательства «Мир» за ценные советы по
подготовке издания и оформлению книги; издательству «Шпрингер»,
неоднократно продлявшему срок действия лицензии на право
издания русского перевода. Хотелось бы поблагодарить также многих
будущих читателей, которые живо интересовались судьбой перевода
и этим даже в самые тяжелые времена поддерживали в нас
уверенность, что наш труд не напрасен. Замечания и предложения можно
направлять по электронной почте: filippov@spp.keldysh.ru
Июль 1999 г.
С.С. Филиппов
Посвящается Эфи и Мириам
Из предисловия к первому изданию
«Можно о чем-то сожалеть, но мы сделали все,
что могли.»
(Сэр Эрнст Шеклтон, на обратном
пути 9 января 1909 года, 88° 23' южной широты)
Брамс трудился 20 лет над своей первой симфонией. По
сравнению с этим те 10 лет, в течение которых мы работали над этими
двумя томами, могут показаться даже небольшим сроком.
В этом, втором томе рассматриваются жесткие
дифференциальные уравнения и дифференциально-алгебраические уравнения. Он
содержит три главы. Глава IV посвящена одношаговым методам
(Рунге—Кутты) для жестких задач, глава V — многошаговым
методам для жестких задач, а глава VI — сингулярно возмущенным и
дифференциально-алгебраическим уравнениям.
Каждая глава разбита на разделы. Обычно первые разделы
главы имеют вводный характер, в них объясняются явления,
наблюдаемые при выполнении расчетов, и приводятся численные результаты.
В дальнейших разделах каждой главы представлены исследования
более теоретического характера.
Как и в первом томе, здесь принята последовательная
нумерация формул, теорем, таблиц и рисунков в каждом разделе, причем
указывается и номер раздела. При ссылках на другие главы перед
номером раздела указывается еще номер главы (римскими цифрами).
Библиографические ссылки указывают «автора» и «год» в скобках.
Библиография и здесь содержит лишь работы, обсуждаемые в тексте,
и ни в коей мере не претендует на полноту.
Нам приятно поблагодарить Дж. Бутчера, Г. Далквиста, а также
С.П. Нёрсетта (соавтора тома I) за их интерес к предмету и за
многочисленные дискуссии с ними, весьма вдохновлявшие нас в нашей
работе. Мы чрезвычайно благодарны участникам нашего семинара в
Женеве (особенно К. Любиху, А. Остерману и М. Рошу), на котором в
течение многих лет докладывались и обсуждались все темы этой
книги. При подготовке рукописи большую помощь оказали Й. Штайниг,
К. Любих и А. Остерман, читавшие и перечитывавшие весь текст и
внесшие бессчетное количество поправок и предложений по его
улучшению. Мы выражаем им свою искреннюю благодарность.
Отдельные разделы смотрели и высказали неоценимые предложения и заме-
Предисловие 7
чания М. Крузе, П. Дойфлхард, К. Густафссон, Дж. Холл, В. Хундс-
дорфер, Л. Жэ, Р. Йелч, Й.-П. Каутен, X. Крайевангер, Р. Мерц и
О. Неванлинна. ... Несколько рисунков сделали наши дети Клаудиа
Ваннер и Мартин Хайрер, соревнуясь друг с другом в хэкерстве.
Восхитительная, совершенная и безотказная программа ТEХ
Д. Кнута позволила нам предоставить издательству «Шпрингер»
оригинал-макет книги, так что она могла быть издана быстро и по
разумной цене. Нам приятно выразить свою признательность группе
планирования и производства издательства «Шпрингер» за
множество советов по выбору шрифтов, стиля и по другим вопросам
изящного оформления книги.
Март 1991 г. Авторы
Предисловие ко второму изданию
Подготовка второго издания позволила нам улучшить книгу по
сравнению с первым изданием: переписать заново многие разделы,
устранить замеченные ошибки и опечатки. В частности, мы включили
новый материал по следующим вопросам:
- методы с расширенной областью устойчивости (чебышевские
методы) (разд. IV.2);
- новые компьютерные программы и новые численные тесты для
одно- и многошаговых методов (разделы IV. 10 и V.5);
- новые результаты о свойствах функций роста погрешностей
(разделы IV.11 и IV.12);
- квазилинейные дифференциальные уравнения с матрицей масс,
зависящей от состояния (разд. VI.6).
Мы полностью перестроили главу о
дифференциально-алгебраических уравнениях, разбив ее на две и включив три новых раздела,
посвященных
- методам понижения индекса (разд. VII.2);
- полуявным методам для систем индекса 2 (разд. VII.6);
- симплектическим методам для гамильтоновых систем со связями
и обратному анализу погрешностей на многобразиях (разд. VII.8).
Наши искренние благодарности адресованы многим лицам, помогшим
нам в нашей работе:
- всем читателям, любезно обратившим наше внимание на ряд
ошибок и опечаток в первом издании. Особого упоминания
заслуживают К. Бендтсен, Р. Чан, П. Шартье, Т. Эйрола, Л. Жэ, П. Капс,
Й.-П. Каутен, П. Леоне, С. Масет, Б. Оврен и Л.Ф. Шампайн;
8 Предисловие
- всем, кто читал черновые варианты новых материалов для
этого издания, за их бесценные советы. Это М. Арнольд, Дж. Каш,
Д.Дж. Хайам, П. Кункель, Кр. Любих, А. Медовиков, А. Муруа,
А. Остерман и Я. Фервер;
- сотрудникам женевского вычислительного центра и
математической библиотеки за их постоянную помощь;
- группе планирования и производства издательства «Шпрингер» за
множество советов по оформлению и стилю.
Все рисунки были получены на компьютере заново и отпечатаны
вместе с текстом на Postscript'е. Все расчеты, а также обработка текста
выполнены на рабочей станции SUN отделения математики
женевского университета.
Апрель 1996 г. Авторы
Предисловие к русскому изданию
Мы рады, что книга все-таки выходит, наконец, и на русском
языке. Мы отлично сознаем трудности, возникшие при подготовке
русского издания нашей книги в эти трудные для России годы. Мы хотим
сказать «Огромное спасибо!» всем, кто способствовал этому, и,
прежде всего, С.С. Филиппову — за все те усилия, которые он в течение
многих трудных лет предпринимал, чтобы подготовить и сделать
возможной публикацию этого перевода.
Май 1999 г.
Авторы
Глава IV
Жесткие задачи
— одношаговые методы
Настоящая глава знакомит с жесткими дифференциальными
уравнениями. Слово «жесткий» есть во всех языках: styv (в шведском
— в первую очередь!), steif (в немецком), stif (в исландском), stijf (в
голландском), raide (во французском), rigido (в испанском и
португальском), stiff (в английском и итальянском), капкеа (в финском),
SvaKafiTTTo (в греческом), merev (в венгерском), rigid (в румынском),
tog (в словенском), cvrst (в сербо-хорватском), tuhy (в чешском и
словацком), sztywny (в польском), jaik (в эстонском), stiegrs (в
латышском), standus (в литовском), stign (в бретонском), zurrun (в языке
басков), sert (в турецком), твърд (в болгарском), П^*й?р (в еврейском),
(в арабском), ^—г ^; (на урду), С^^^ч^^о (в персидском),
(на санскрите), ОпЗУ (на хинди), ng*|i (в китайском), fl^^^ (в
японском), с^^'^^ (во вьетнамском), ngumu — на суахили — В то время
как всем специалистам значение термина «жесткий» интуитивно
ясно, его корректное математическое определение продолжает вызывать
многочисленные дискуссии (см., например, Эйкен 1985, pp. 360-363).
Наиболее прагматическая точка зрения вместе с тем была и
исторически наиболее ранней (Кертисс и Хиршфельдер 1952): жесткие
уравнения — это уравнения, для которых определенные неявные
методы, в частности ФДН, дают лучший результат, обычно
несравненно более хороший, чем явные методы. При этом определенную
роль играют собственные значения матрицы Якоби df/dy, но важны
и такие параметры, как размерность системы, гладкость решения или
интервал интегрирования (разделы IV. 1 и IV.2).
Жесткие уравнения требуют введения новых понятий
устойчивости (А-устойчивость, разд.IV.3) и новых математических теорий
об ограничениях на порядок метода (порядковые звезды, разд. IV.4).
Жесткие уравнения требуют неявных методов. Поэтому в разделах
IV.5 и IV.6 мы сосредоточим внимание на неявных методах Рунге—
Кутты, в разд.IV.7 — на методах Розенброка (полуявных), а
полуявные экстраполяционные методы рассмотрим в разд. IV.9. Для
действительно эффективной реализации неявных методов Рунге—Кутты
надо решить ряд проблем, которые обсуждаются в разд. IV.8. После
этого в разд. IV. 10 сообщается о некоторых численных экспериментах
со всеми этими методами.
В разделах IV.11, IV. 12 и IV. 13 мы начинаем обсуждение
контрактивности (В-устойчивости) для линейных и нелинейных
дифференциальных уравнений. Глава завершается рассмотрением вопросов
существования и численной устойчивости решений для неявных методов
Рунге—Кутты (разд. IV.14) и теории сходимости, которая не зависит
от жесткости (В-сходимость, разд.IV.15).
IV. 1. Примеры жестких уравнений
«... Около 1960 года положение полностью
изменилось, и все осознали, что мир полон жестких задач».
(Г. Далквист в Эйкен 1985)
Жесткие уравнения — это задачи^), для которых явные
методы не работают. Кертисс и Хиршфельдер A952) объясняют свойство
жесткости на одномерных примерах, таких, как уравнение
у' = -50(у —cosx). A.1)
Л =1.974/50
/1=1.875/50
неявный Эйлер, /^ = 0.5 |
О 1
Рис. 1.1. Кривые решений A.1)
и решение неявным методом
Эйлера при t/@) = О.
О 1
Рис. 1.2. Решения явным методом
Эйлера при у@) = О, Л = 1.974/50
и 1.875/50.
Кривые решений уравнения A.1) показаны на рис. 1.1. Видно, что
вблизи г/« cos X имеется медленно изменяющееся решение, а все
другие решения подходят к нему после быстрой «переходной фазы».
Такие быстрые переходы типичны для жестких уравнений, но не
являются ни достаточным, ни необходимым их признаком. Например, у
решения с начальным значением 2/@) = 1 (точнее, 2500/2501) нет
переходной фазы. На рис. 1.2 показаны ломаные Эйлера для начального
значения у@) = О и длин шагов Л = 1.974/50 C8 шагов) и /i = 1.875/50
D0 шагов). Как только длина шага становится немного больше
критической величины (в данном случае больше 2/50), численное
решение уходит слишком далеко за равновесное, и возникают все более
сильные колебания.
В поисках лучших методов для таких дифференциальных
уравнений, как A.1), Кертисс и Хиршфельдер открыли метод ФДН (см.
разд.111.1): ведь аппроксимация t/«cosx (т.е., /(х,у) = 0)—это лишь
грубое приближение к медленно меняющемуся решению, так как про-
^' См. цитату на стр. 17. — Прим. ред.
IV. 1. Примеры жестких уравнений 11
изводная cos х не равна нулю; для данного значения решения у„
гораздо лучше поискать такую точку y^^i, где наклон векторного поля
направлен к у^ , т.е.
^^^^^y^ = /(^n+i.J/„+i)- A-2)
Это — неявный метод Эйлера. Пунктирная линия на рис. 1.1 состоит
из трех шагов неявного метода Эйлера и впечатляюще демонстрирует
хорошую устойчивость этого метода. Таким образом, уравнение A.1),
очевидно, является «жестким» в смысле Кертисса и Хиршфельдера.
Развитие только что изложенной идеи «с применением полиномов
более высокого порядка, использующих значения у в большем числе
точек», привело к ФДН-методам.
Системы, описывающие химические реакции
«Когда уравнения представляют поведение системы,
содержащей ряд быстрых и медленных регосций,
прямое интегрировгшие этих уравнений становится
затруднительным». (Робертсон 1966)
Следующий пример Робертсона A966) стал очень популярным в
исследованиях по численным методам (Уиллоуби 1974):
А > В (медленно),
В + В >^ С + В (очень быстро), A.3)
В + С -^ А + С (быстро),
что приводит к уравнениям
А: yi = - 0.04у1 + ЮЧузУз . I/i @) = 1,
В: j/2= 0.04j/i - 10%2J/3 -3107у2, У2{0) = 0, A.4)
С: Уз= 3 107у2, Уз(О) = 0.
После неудачного опыта с явным методом Эйлера в предыдущем
подразделе давайте попытаемся применить для этого примера
метод более высокого порядка и более усовершенствованную
программу D0PRI5 (см. том 1), Численные решения для i/j) полученные
с Rtol = Ю'^ B09 шагов), а также с Rtol = 10~^ B05 шагов) и
Atol = 10"^ • Rtol показаны на рис. 1.3. На рис. 1.4 представлены
длины шагов, использованные программой, а также оценки локальной
погрешности; все отброшенные шаги отмечены крестиками.
Мы видим, что решение Уз быстро достигает квазистационарного
положения в окрестности У2 = 0, которое вначале (при у^ = 1, t/g = 0)
находится около 0.04 « 3 • lO^j/j > следовательно, t/j ^ 3.65 • 10"^, и
затем очень медленно убывает опять до нуля. Однако численный метод
делает тысячи представляющихся ненужными шагов, интегрируя это
12 Гл. IV. Жесткие задачи — одношаговые методы
.000037
2/2
решение RADAU5: 13 шагов, То/ =: 10
— 1П"-2
решение D0PRI5: Rtol = 10"^, Rtol = 10"^
-переходная фаза
•«^^2.0 .1 .2 .3
Рис.1.3. Численное решение задачи A.4): программы D0PRI5 и RADAU5.
.002 F
Рис. 1.4. Длины шагов и локальные погрешности (DOPRI5, То1
гладкое решение. Более того, выбираемые длины шагов более или
менее независимы от выбранной погрешности. Следовательно, этот
выбор, по-видимому, делается исходя из требований скорее
устойчивости, нежели точности. Кроме того, здесь видно, что программа,
основанная на неявном методе Рунге—Кутты (такая, как RADAU5,
описанная в разд. IV.5 и IV.8), интегрирует это уравнение без всяких
затруднений.
Электрические схемы
«Такое поведение известно, по крг1йней мере отчасти,
любому опытному специалисту в данной области».
(Дж. Холл 1985)
Одно из простейших нелинейных уравнений, описывающих
электрическую схему, — это уравнение Ван-дер-Поля (см. разд. 1.16):
У1=У2 yi@) = 2
Уг = /^A-У1 )У2 - Vi УгСО) = О-
IV. 1. Примеры жестких уравнений 13
-.7
2/2
начальное значение
решение DEABM, 450 шагов
переходная фаза
решение RADAU5, 11 шагов
2/1
1.9994
1.9996
1.9998
2.0000
Рис. 1.5. Решение задачи A.5'): программа DEABM,
ЯЫ=10", ЛЫ = 10-^.
.000006
.000004 h
.000002 Й
^
т
1 . 1
длина шага
щ
1
1
\ порядок 1
У
К Rtol
1
= 10-2
1,1.
.0000
.0002
.0004
.0006
.0008
.0000 .0002
.0004
.0006
.0008
Рис. 1.6. Изменения длргаы шага и порядка метода для DEABM
f — in-2
(ЛЫ=10"^ и 10"^, ЛЫ = 5.10"^).
Мы видели в главе II, что это уравнение легко интегрируется для
умеренных значений fi. Но сейчас мы выберем // = 500, и есть подозрение,
что задача может стать трудной. Оказывается, период решения возра-
14 Гл. IV. Жесткие задачи — одношаговые методы
стает с ростом /i. Поэтому масштабируем решения, положив t = x/fi,
z^{t) = 2/i(x), Z2(t) =/^У2(^)- В полученном уравнении вторая
компонента правой части / пропорциональна /i^. Снова заменяя z иа. у, t
на а: и полагая ^^ = 1/6, получим
2/2 = /^^ (A - 2/1 )У2 - 2/i) ' ^2/2 = A - 2^1 J/2 - 2/1.
Стационарное приближение (см. том I, формула A.16.5)) становится
тогда независимым от fi.
Почему бы на этот раз не попробовать многошаговую процедуру?
Например, программу Шампайна и Уоттса DEABM, основанную на
методе предиктора—корректора Адамса. На рис. 1.5 и 1.6 показаны
вычисленное решение, длины шагов и порядки для первых 450 шагов.
В конце концов программа останавливается с сообщением /rftrf=: —4
(«задача оказалась жесткой»). Программа RADAU5, использующая
неявный метод Рунге—Кутты, интегрирует это уравнение на том же
самом отрезке за 11 шагов.
Диффузия
¦Застревающие численные процессы должны быть
неверны». (¦Золотое правило» Эйчи Брандта)
Другой источник жесткости доставляет превращение уравнений
диффузии в большую систему ОДУ путем аппроксимации
диффузионных членов разделенными разностями (метод прямых, см. разд. 1.1).
В качестве примера выберем брюсселятор (см. A6.12) из разд. 1.16) с
одной пространственной переменной х:
— = Л + Л-(В + 1)и + а;^^,
at ох^ /1 f*\
- = Bu-uv + a—,
С 0<х<1,Л=1,5 = 3, а= 1/50 и условиями на границах
ti@,0 = w(l,0 = 1, ^0,0 = v{\,t) = 3,
и{х, 0) = 1 -Н sinB7ra:), v(x, 0) = 3.
Заменив вторые пространственные производные конечными
разностями на сетке из Л^ точек х,= г'/(ЛГ-|-1) A<г<ЛГ), Дх = 1/(ЛГ-|-1),
IV. 1. Примеры жестких уравнений 15
Рис. 1.7. Решение и(х, t) системы A.6') с N=40 (программа ODEX).
Л2[
.09 [
.06 [
.03
0
8
6
4
2
порядок
"I 1 1
Ш1 11111В111111|111ШЛ1
ПИЯ 1 /||1И1 IIIIHMllillllll
То/= 10-2
" —' ^ . - ^- 1 - ^ ^ - 1
10 о
М!
i
длина шага
10
порядок
10 О
Рис. 1.8. Изменения длины шага и порядка метода
при интегрировании программой ODEX системы A.6*) с N=40,
16 Гл. IV. Жесткие задачи — одношаговые методы
мы получим из A.6)
"о@ = W;v+l@ = 1» ^o(<) = ^N+i@ = 3,
ti.@) = l-hsinB7rx,.), v,@)=:3, i = l,...,7V.
Таблица 1.1. Результаты счета A.6'); программа ODEX, О < ^
A.6'
<^< 10
Л^
10
20
30
40
40
То1
10-^
10-^
10-^
10-^
10~2
принято
шагов
21
81
167
275
266
отброшено
шагов
3
25
45
62
59
вызовов правых
частей
365
1138 ,
2459
4316
3810
На этот раз мы попробуем применить программу ODEX,
основанную на экстраполяционном методе (см. том I) и проинтегрировать на
отрезке О < ^ < 10 при Atol = Rtol = Tol. Количество необходимых
шагов возрастает любопытным образом вместе с ростом А^, как это
видно из табл. 1.1. Снова для большого N время вычисления почти
не зависит от допустимой погрешности, вычисляемые решения, тем не
менее, значительно различаются (см. рис. 1.7). Даже гладкое Ю"""*-
решение демонстрирует странные полосы, которые очевидным
образом не связаны с поведением решения. На рис. 1.8 показаны крайне
неровные изменения длины шага и порядка, которые имеют место в
этом примере.
Мы снова видим все признаки «жесткой» задачи, и
использование неявного метода обещает лучшие результаты. Однако, применяя
такой метод, необходимо возможно полнее использовать
преимущества ленточной или разреженной структуры матрицы Якоби. Иначе
объем вычислительной работы, связанной с линейной алгеброй, будет
возрастать как N^, т.е. точно так же, как и объем работы для явного
метода [N'^ для числа шагов и N для работы на шаге).
IV. 1. Примеры жестких уравнений 17
«Жесткий» стерлсень
«Хотя общепринято говорить о "жестких дифферешщальных
ургшнениях'', какое-либо уравнение само по себе не
является жестким, жесткой может быть конкретная задача Коши для
этого уравнения, причем в определенных областях, размеры
которых зависят от начальных значений и допустимой
погрешности». (Ч. Гир 1982)
Завершим наш ряд примеров
задачей из механики о движении
упругого стержня. Предположим,
что стержень тонкий,
нерастяжимый и имеет длину 1, т.е. мы
пренебрегаем сдвигающими
силами и инерцией вращения. Далее,
мы хотим позволить стержню
совершать произвольно большие
перемещения. В таком случае
наиболее естественной координатой для
наших целей будет угол в как
функция длины дуги S и времени
t. Пусть стержень закреплен при
5=0, а на его свободный конец
5=1 действует сила F = (F^, Fy).
Тогда движение стержня
описывается уравнениями
(Рисунок К. Ваннер)
x(s,i)= I cos^(G,<)dG, 2/E,^)= / sme(<T^i)dcT. A.7)
Уо Jo
Чтобы получить уравнения движения для этой задачи, применим
теорию Лагранжа A788). Она требует составления выражения L=T—U,
где Т — кинетическая и U — потенциальная энергия. Первая из них
равна просто
T=\l^{{x{s,t)f + {y{s,t)f)ds. A.8)
Потенциальная энергия складывается из энергии изгиба (зависящей
от кривизны) и из работы внешних сил следующим образом:
^"Uo i^'i''*))^'^'-^^tMht)-F^{t)y{l,t). A.9)
Здесь точки и штрихи обозначают производные по ^ и по 5
соответственно. Уравнения движения теперь получаются путем
«тривиальных» выкладок (мы благодарны нашему коллеге Ж. Деклу за то, что
18 Гл. IV. Жесткие задачи — одношаговые методы
он показаип нам, как это следует делать!) с применением принципа
Гамильтона (см. упр. 2), что приводит к следующей краевой задаче:
/ GE, сг) cos {e{s, t) - в{(т, t))в((т, t)da =
Jo
= e"(sj) -^cose{s,t)Fy{t) -sme(s,t)F^(t)- A.10)
-/ G(s,<T)sm{e(s,t)-e(a,t))(e((T,t)fd<T, 0<5<1,
Jo
(9@,0 = 0, l9'(l,<) = 0, A.11)
где
G(s, <t) = 1- max(s, a) A.12)
есть функция Грина для задачи —w"(s)=g(s), и;'@) = w;(l) =0. Если
мы заменим интегралы конечными суммами с помощью правила
средней точки
f^m<T,t))da=^j^f{e,), e,=e({k-\)^,t), k = h...,n,
A.13)
ТО уравнения A.10) - A.11) примут вид
п
E«//c^^=^'(^/-i-2^/+^/+i)+^'(cos^/F^-sin^^F,)-
к=1
Oo=-0l> ^n+l=^n. A.11')
где
(^ik=9ik^os(ei-e^), gif^=:n-\-^-m^x(l,k). A.14)
«Интеграция без подготовки приводит к крушению
надежд». (Преподобный Леон Салливгш)
Численное интегрирование A.10') представляется весьма
утомительным, так как уравнение не разрешено относительно компонент
ускорения в. Вычисление Of^ требует решения линейной системы
Ав=у. Благодаря специальной структуре Л, это может быть
проделано эффективно, поскольку, введя B={bif^)y Ьц^=^д1^ sin(^^—^^i^), имеем
A^iB= Alщ[e'^\...,e'^-^Gd\^g{e-'^\,,.,e-'^-^. A.15)
G-i =
IV. 1. Примеры жестких ургшнений 19
Матрица G={gii^) обладает замечательной обратной матрицей, трех-
диагональной и положительно определенной:
/1-1 \
-12-1
-1 •• A.16)
2-1
\ -13/
(естественное соответствие: G"^ представляет конечномерный
разностный оператор второго порядка, а G получается из функции
Грина задачи интегрирования уравнения второго порядка). Далее,
{A-^iB)'^=C + iD= diag(e*^S...,e*^'^)G-^diag(e-'^S...,€^'^'^),
а из равейств
AC-BD=zI^ AD-\-BC = 0 A.17)
следует, что Л"^ = С-\- DC~^D. Можно еще упростить член —^Idik'
sin(ei—ef^)el, в векторной записи имеющий вид —Вв^ , с помощью
соотношения A-'^B=—DC~^, которое вытекает из A.17). Ускорения $1^
теперь получаются из A.10') следующим образом.
a) Полагаем V/=n'*(^^_i—2^/4-^/^1 L-п2(costf^Fy—sin^fF^.).
b) Вычисляем w=Dv-\-e^ (D —двухдиагональная).
c) Решаем трехдиагональную систему Cu=w.
d) Вычисляем e=Cv-\-Du.
Таким образом, вычисление A.10') сводится к 0(п) операций (вместо
0{п^)), Мы выберем начальные условия
^(s, 0) = 0, ^(s, 0) = 0 A.18)
и приложим внешние силы
F, = -'p(t), F^ = <p{t), ^(<) = {j-5-^>"'^
0<t<ir
1T<t
A.19)
Полученная в результате система ОДУ была проинтегрирована для
0<t <5 программой DOP853 из т. I, хотя, строго говоря, метод имеет
излишне высокий порядок для такой задачи. Результаты
суммированы в табл. 1.2.
Мы наблюдаем то же самое явление, что и прежде: количество
необходимых шагов возрастает как 0(п2) (вычислительная работа
— как 0{п^)) и более или менее не зависит от выбранной
погрешности. Численное решение для п=40 показано на рис. 1.9.
Изображен только каждый 20-й из почти 9000 шагов (иначе рисунок был бы
совершенно черным). Вычисленное решение выглядит практически
гладким, и нет видимой причины для необходимости такого
большого количества шагов. Фактически, из-за недостаточной устойчивости
Рис. 1.9. Колебания стержня,
программа DOP853
при Tol = 10, п = 40,
показан каждый 20-й шаг.
Рис. 1.10. Колебания стержня,
программа DOP853
при Tol = 0.0075, п = 20,
показан каждый 5-й шаг.
Рис. 1.11. Высокочастотные
колебания стержня, DOP853
при Tol- КГ6, п= 10,
показан каждый 4-й шаг.
IV. 1. Примеры жестких уравнений
21
Таблица 1.2.
п
5
10
20
40
20
20
20
ТЫ
10-7
10-7
10-7
10-7
10-^
10-^
10-7
Результаты счета A.10')
принято
шагов
142
383
1397
6913
1486
1967
1397
отброшено
шагов
35
26
273
1347
450
266
273
; программа DOP853
вызовов правых
чахгтей
2091
4884
19769
97775
22784
26532
19769
численный метод дает маленькие колебания, которые невидимы при
Го/= 10" 7 и которые заставляют программу интегрирования
уменьшать размер шагов до такой степени. Если мы ослабим требование
высокой точности, эти осцилляции станут видимыми (рис. 1.10).
Высокочастотные колебания
Выберем теперь слегка возмущенные начальные значения для
уравнения колебаний стержня A.10'). Вместо A.18) положим
в, = ... = в„_, = о,в, = ол, в,^... = в„ = о.
A.18')
На этот раз корректное решение A.10') для п = 10, вычисленное с
точностью Го/=10"^ за более чем 2000 шагов, показано на рис. 1.11.
Решение колеблется с высокой частотой; поскольку система
консервативна, отсутствует демпфирование быстрых вибраций.
Следовательно, неявный метод, если требуется отследить все эти колебания,
должен сделать то же самое число шагов и нет, конечно, никаких
преимуществ в его применении. Таким образом, мы видим, что ответ на
вопрос, следует ли рассматривать задачу как жесткую или
нежесткую («... вот в чем вопрос!»), может зависеть также от выбранных
начальных условий. С другой стороны, мы увидим в разд. IV.2, что в
случае, если эти высокочастотные колебания нежелательны, неявные
методы представляют собой великолепный инструмент для их
подавления.
Упралснения
1. (Кертисс и Хиршфельдер A952): «Интересно отметить, что этот
метод интегрирования (неявный метод Эйлера) может
применяться в любом направлении».) Проинтегрируйте уравнение A.1)
назад с длиной шага —0.5 и начальным значением уA.5) = О на три
шага. Убедитесь, что численное решение остается устойчивым и
ложится на гладкое решение.
22 Гл. IV. Жесткие задачи — одношаговые методы
2. Выведите уравнения движения упругого стержня A.10) из A.8) и
A.9).
Указание. Если вы хотите избежать дифференцирования в
функциональных пространствах, то перейдите к конечным суммам,
скажем, таким образом:
} 3 л
Xj = As ^ cos ^,5, j/j = As ^ sin ^,t' i=l.-••."> As=-,
fc=i fc=i "
A.20)
j = l j = l /c = l
J = l fc = l fczrl
составьте функцию Лагранжа L=T—U и примените теорию Ла-
гранжа для п измерений [Лагранж A788), т. II, разд. VII и VIII];
очень наглядный вывод можно найти у Зоммерфельда A942), т. I,
§36:
d гдЬ\ дЬ _
dt\dej дв^ ^
или
Z-/ ^heA - ^Bk - ^Ht " Z-/ ^Bnefii • A-21)
/=i /=i
3. Примените программу, основанную на явном методе, к «Орегона-
тору» (гл. I, уравнение A6.15))
у; =77.27 (г/2+ 2/1 A-8.375x10-^1-Уз)).
2/2=77^(Уз-A + 2/1Ы. (^•^^^
у^ = 0.161(у1-уз)
и исследуйте ее работу.
4. а) Выведите уравнения движения висящей веревки длины 1,
используя результаты упр. 2. Потенциальная энергия должна быть
заменена на
и
= — / x{s, t)ds
Jo
IV. 1. Примеры жестких уравнений 23
Ответ.
1 G(s, а) cos{e(s, t)-e(<T, г))в(<т, i)dc = A.23)
Jo
= - I G(s, (T)sin{e(s, t)^e(a, t)) {в{а, i)L<T-- (l^s)sine(s, t)
Jo
для 0 < 5 < 1, ИЛИ после дискретизации
п П -
к=1
^=1
г^ДГ
Рис. 1.12. Движение висящей веревки, изображен каждый шаг.
Ь) Проведите численное интегрирование с помощью D0PRI5 или
DOP853. Выберите в качестве начального положение равновесия
подвешенной за оба конца веревки; в начальный момент
отпускается один ее конец.
Указание. Положение равновесия (в обычных координатах)
подвешенной в двух точках веревки удовлетворяет вариационной
задаче
/ ' y\/lTWVdx = min при / ' y/lT(y^dx = 1,
Jxq Jxq
которая после введения множителя Лагранжа переходит в
rXi
I \y-X)\/TT(y^dx= Stat.
Jxn
24 Гл. IV. Жесткие задачи — одношаговые методы
Применение формулы A.2.6) из разд. 1.2 приводит к уравнению
у — А = КуУ1-\-{]/У, решением которого является функция
У = Х + КсЬ{^).
Подходящий выбор параметров и замена координат (А'=1/2, Л =
= —/l'ch(a/A'), X —> у, у -> —х) приводит к начальному условию
вида
e(s, 0) = 7г/2- arctg(shBa) -25). A.24)
Ответ. DOP853 вычисляет решение за 203 шага для 0<t<b, п=60
и То/=10""^, а=0.6 (рис. 1.12). Количество шагов возрастает здесь
как 0(п), так что веревка, очевидно, менее жесткий объект, чем
стержень!
IV.2. Анализ устойчивости
для явных методов Рунге—Кутты
«... werden wir bei dem Anfangswertproblem hyperboli-
scher Gleichungen erkennen, dass die Konvergenz allgemein
nur dann vorhanden ist, wenn die Verhaltnisse der Gitter-
maschen in verschiedenen Richtimgen gewissen Ungleichun-
gen genugen».
«... в случае задачи Коши для гиперболических
уравнений мы увидим, что сходимость вообще имеется лишь
тогда, когда отношения размеров ячеек сетки по
разным направлениям удовлетворяют определенным
неравенствам». (Курант, Фридрихе, Леви 1928)
В известной работе Куранта, Фридрихса и Леви A928) впервые
был выполнен анализ явлений неустойчивости и получены
ограничения на длину шага для гиперболических уравнений. Позднее анализ
устойчивости проводился многими авторами, очень часто независимо
друг от друга, чтобы объяснить явления, которые нам встретятся в
настоящем разделе. Ранняя и прекрасная работа по этому вопросу —
Гийу и Лаго A961).
Анализ устойчивости для метода Эйлера
Пусть (р{х) — гладкое решение уравнения y' = f(x, у).
Линеаризуем / в его окрестности следующим образом:
у'(х) = fix, ф)) + |^(х, ф)){у(х) - ф)) + ... B.1)
И введем обозначение у{х)—(р{х)=у(х), тогда получим
Vix) = ^{х, ф)) -Vlx) + ... = J{x)y{x) + ... . B.2)
В качестве первого приближения положим матрицу Якоби J{x)
постоянной и пренебрежем остаточными членами. Опуская черточки,
придем к уравнению
у' = Jy . B.2')
Если теперь мы применим к B.2'), например, метод Эйлера, то
получим
2/^4-1= Л(Л^J/т. B.3)
где
R(z)=l-^z . B.4)
Поведение B.3) изучается с помощью приведения J к жордановой
канонической форме (см. разд. 1.12). Предположим, что J
может быть приведена к диагональному виду с собственными векторами
26 Гл. IV. Жесткие задачи — одношаговые методы
^1,..., г;„, и запишем Уо ^ этом базисе в виде
п
Подставив это в B.3), получим
у„ = Х:(Д(ЛА,)Га,..,, B.6)
1=1
где Л, — соответствующие собственные значения (см. также упр. 1
и 2). Ясно, что у^ остается ограниченным при m -> оо, если для всех
собственных значений комплексные числа z = h\ лежат в области
5 = {г G С; \R[z)\ < l} = |г G С; |г - (-1)| < l},
которая представляет собой круг радиуса 1 с центром — 1. Это
объясняет результаты, с которыми мы столкнулись в примере A.1). Там
мы имели Л = —50, и /lA G 5 означает, что О < /i < 2/50, в отличном
соответствии с численными наблюдениями.
Явные методы Рунге—Кутты
Явный метод Рунге—Кутты (П.2.3), примененный к B.2'), дает
t-i
Последовательно подставляя д, из первой строки во вторую, мы
получим
Ут+1 =R[hJ)ym.
где R[z) — многочлен степени < s\
Я(г) = 1 + г^6^. + г2^6^.а^., + .з^6^.а^.,а,^ + ... B.8)
J j.k j,k,l
Определение 2.1. Функция R(z) называется функцией
устойчивости данного метода. Она может быть интерпретирована как
численное решение после одного шага для задачи
y' = At/, уо=:1, z = /iA, B.9)
известной как тестовое уравнение Далквиста. Множество
5=:|zGC;|i?B)|<l} B.10)
называется областью устойчивости данного метода.
IV.2. Анализ устойчивости для явных методов Рунге—Кутты 27
Теорема 2.2. Если метод Рунге—Кутты имеет порядок р, то
Д(^) = 1 + г+| + ...+ ^ + 0(г''+1).
Доказательство. Точное решение B.9) есть е^ и, следовательно,
численное решение y^=R(z) должно удовлетворять условию
е' - R{z) = 0(ЛР+^) = Oiz^-^^) . B.11)
Другой довод состоит в том, что входящие в формулу B.8) суммы
появляются и в условиях порядка для «высоких» деревьев г, /ji) ^32'
^44' ^59' • • • (^^- табл. 2.2 в разд. II.2). Поэтому в B.8) коэффициенты
при гя равны l/q\ для всех q <р. П
Как следствие, все явные методы РК с p=s обладают функцией
устойчивости
Д(г)=:Ц-г + ... + ^ , B.12)
Соответствующие области устойчивости представлены на рис. 2.1.
Метод Дорманда и Принса DOPRI5 (разд. П.5, табл. 5.2) имеет
порядок 5 с 5=6 G-я стадия служит только для оценки погрешности).
Прямым вычислением получается следующий результат:
^2 гЗ г^ z^ z^
Я(г) = 1 + г + - + - + - + —+ —. B.13)
Для DOP853 (разд.11.5, рис. 5.3) R(z) будет
8 J
R{z) = 53 ^j- + 2.6916922001691 • 10" V + 2.3413451082098 • lO-'^z^°+
j=o •'•
+ 1.4947364854592 • 10"*z" +3.6133245781282 • 10-^°г^2 .
B.14)
Области устойчивости для этих двух методов показаны на рис. 2.2.
Экстраполяционные методы
Алгоритм ГБШ (см.разд. П.9, формулы (9.10), (9.13)),
примененный к 2/'=:A.v, у@) = 1, приводит, если положить z=HX, к
1/0 = 1, У1 = 1 + —,
У.+1 =У,_1+2 — у,-, г = 1,2,...,п^..
^i
B.15)
28 Гл. IV. Жесткие задачи — одношаговые методы
Рис. 2.1. Области устойчивости
явных методов Рунге—Кутты
порядка р^ S.
Рис. 2.2. Области устойчивости
для методов
Дорманда—Принса.
Области устойчивости для диагональных членов Т22, ^зз' ^44 ^ ^55
в случае гармонической последовательности
{п^} = {2,4,6,8,10,...}
(которая используется в ODEX) показаны на рис. 2.3. Нами
добавлены еще области устойчивости для методов без сглаживающего шага
A1.9.13с), при этом видно некоторое различие для отрицательных
вещественных собственных значений.
Анализ примеров из IV, 1
Матрица Якоби для реакции Робертсона A.3) имеет вид
(
-0.04 10%з Ю^Уз '
0.04 -104уз - б • 107J/2 -Ю^уз
О бЮ^уз О ,
IV.2. Анализ устойчивости для явных методов Рунге—Кутты 29
со сглаживающим шагом без сглаживающего шага
Рис. 2.3. Области устойчивости для экстраполяционных методов ГБШ.
В окрестности равновесия У1 = 1, У2 =0.0000365, у^=0 она равна
/-0.04 О 0.365 \
0.04 -2190 -0.365 ,
V О 2190 О J
а ее собственные значения суть
Ai =0, А2 = -0.405, A3 = -2189.6.
Третье из них и есть причина жесткости. Для устойчивости требуется
выполнение неравенства -2190/i > -3.3 (см. область устойчивости
D0PRI5 на рис. 2.2), следовательно, Л не должно превосходить 0.0015.
Это снова подтверждает численные наблюдения.
Матрица Якоби в примере A.6') (брюсселятор с диффузией)
представляет собой большую 2N x2N матрицу. Она состоит из членов,
отвечающих за реакцию, и диффузионных членов:
_ / diagB«..t;, -4) diag(«?) \ _о_ (К О \
•^ " V diagC - 2«..г;,) diag(-«?) J ^ {Ах^ \0 kJ' ^ ' ''>
30 Гл. IV. Жесткие задачи — одношаговые методы
где
(-1 1
1-2 1
А' =
1
\
B.17)
Собственные значения К известны
Mfc = -4(si
-2 ^ /
1 -2/
я-ik
sin
W
+ 2/
B.18)
(см. разд. 1.6, формула F.7Ь)). Следовательно, двукратные
собственные значения второй матрицы в правой части B.16) равны
причем они находятся между —4а(АГ-|-1J и нулем. Поскольку эта
матрица симметричная, ее собственные значения хорошо обусловлены, и
первая матрица в правой части B.16) с много меньшими
коэффициентами может рассматриваться как малое возмущение. Следовательно,
собственные значения J в B.16) будут оставаться вблизи собственных
значений невозмущенной матрицы и находиться в полосе,
прилегающей к отрезку [—4а(АГн-1J, 0]. Вычисления для 7^=40 показывают,
например, что наибольшее отрицательное собственное значение J
меняется между —133.3 и —134.9, в то время как невозмущенное
значение равно -4-412 .sin^D07r/82)/50 = —134.28. Так как большая часть
областей устойчивости для ODEX оканчивается вблизи —5.5 на
вещественной оси (рис. 2.3), это приводит к тому, что для iV=40 Л < 0.04
и число шагов должно быть > 250 (ср. с табл. 1.1).
Чтобы объяснить поведение уравнения колебаний стержня,
линеаризуем его в окрестности решения ^^=^^^=0, F^^-F^^^, Тогда A10')
примет вид
/-3 1
1 -2
GO = п"
1
1
\
-2
1
1
-1/
B.20)
так как при ^=0 имеем A=G и В=0. Подставляя теперь G~^ из
A.16), заметим, что элементы рассматриваемых матриц (за
исключением двух) совпадают с элементами ±К из B.17). Поэтому мы
аппроксимируем B.20) уравнением
в = -п*К'^0
B.21)
IV.2. Анализ устойчивости для явных методов Рунге—Кутты 31
Это уравнение второго порядка было проинтегрирювано в разд. IV. 1
как система уравнений первого порядка
Разрешив систему
(-„V 0@=40 ¦ <"^'
мы найдем, что А будет собственным значением Е тогда и только
тогда, когда А2 — собственное значение —п^К^. Таким образом,
формула B.18) показывает, что собственные значения Е лежат на мнимой
оси между —An^i и -{-An^i. Из рис. 2.2 видно, что область
устойчивости DOP853 захватывает мнимую ось между приблизительно —6г и
-Нбг. Следовательно, для устойчивости требуется Л<1.5/п2, и число
шагов на отрезке 0<<<5 должно быть больше, чем ^ Юп^/З. Это,
опять же, наблюдалось при численном интегрировании (табл. 1.2).
Автоматическое обнарулсение лсесткости
¦Абсолютно безупречного не бывает, но даже
несовершенный тест может оказаться весьма полезным, как это
можно показать на опыте ...» (Шампайн 1977)
Как видно, программы, основанные на явных методах, не
слишком эффективны в применении к жестким задачам, и оставшаяся
часть книги будет посвящена конструированию более устойчивых
алгоритмов. Чтобы избежать слишком больших напрасных затрат при
встрече «явной» программы с жесткостью (и дать возможность
переключаться на более подходящий метод), важно оснастить программу
дешевыми средствами обнаружения жесткости. Анализ, проведенный
в предыдущих подразделах, показывает, что, всякий раз, когда
нежесткая программа встречается с жесткостью, произведение длины
шага и доминирующего собственного значения матрицы Якоби
находится около границы области устойчивости. Мы укажем два способа
использования этого наблюдения для обнаружения жесткости.
Во-первых, мы приспособим идеи, которые высказали Шампайн и
Хиберт A977), к методу Дорманда и Принса порядка 5D),
приведенному в табл. П.5.2. У метода имеется оценка погрешности егг^^у^—^i,
которая в нежесткой ситуации имеет порядок O(h^). Однако в
жестком случае, когда метод работает около границы области
устойчивости 5, расстояние cfi=r/i—y(xQ Н-Л) до гладкого решения
равно приблизительно di^R(hJ)dQ, где J обозначает матрицу Якоби
для системы, R{z) — функцию устойчивости метода, а do=2/o"~2/(^o)-
Здесь мы пренебр)егли локальной погр)ешностью для начального
значения на гладком решении у(х). Подобная формула с заменой R на
32 Гл. IV. Жесткие задачи — одношаговые методы
R справедлива для вложенного метода. Оценка погрешности
удовлетворяет €rr^^E(hJ)dQ с E(z) = R(z)—R(z). Теперь основная идея
состоит в нахождении второй оценки погрешности efr^ (с €fr^^E(hJ)dQ)
такой, что
i) \ЁШ <^\E{z)\ на 95ПС" с небольшим в<1;
ii) err^=0(h^) при Л^О. _
Из условия (i) следует, что ||errj| <||errj|, когда ЛА оказывается
вблизи dS (задача, возможно, жесткая), а условие (ii) приводит к
ll^^ill^lk'^^ill ПР** длине шага, определяемой исходя лишь из
требований точности (когда задача нежесткая). Если ||^rj|<ЦеггЛ имеет
место последовательно несколько раз (скажем, 15 раз), то «жесткая»
программа могла бы оказаться более эффективной.
Для конструирования efr^ положим efr^ = /i(diA:i -h ^2*2 + • • • +
(f,/?^), где k^:=f{xQ-\'Cihygi) —значения функции, которые
вычисляются в данном методе. Коэффициенты cf,- определяются таким образом,
чтобш
5 5
53^< = 0, j;d,.c, = 0.02 B.24)
t = l
1 = 1
(так, чтобы выполнялось условие (ii) и в ъ (\) было минимально).
Численный поиск дал значения, которые были округлены до
B.25)
(fi = -0.08536, dj = 0.088, ^3 = -0.0096,
^4 = 0.0052, ^5 = 0.00576, d^ = -0.004 .
Значение 0.02 в B.24) выбрано так, что в в (i) получилось близким к
0.3 на больших кусках границы 5, но \E(z)/E{z)\ быстро становится
больше единицы, когда z приближается к началу координат.
Рис. 2.4. Линии уровня для E{z)/E{z).
IV.2. Анализ устойчивости для явных методов Рунге—Кутты 33
2/1
Уравнение Ван-дер-Поля A.5'),
€ = 0.003
2.0
Рис. 2.5. Обнаружение жесткости с помощью D0PRI5.
10-2 h
Рис. 2.6. Оценка постоянной Липшица с помощью D0PRI5.
На рис.2.4 показаны линии уровня \E(z)/E{z)\=:Const {Const=
4,2,1,0.5,0.3,0.2,0.14,0.1) вместе с областью устойчивости метода.
Численный эксперимент иллюстрируется на рис. 2.5. Мы применяли
программу D0PRI5 (см. приложение к т. I) к уравнению Ван-дер-
Поля A.5') с ?=0.003. Верхний график показывает первую компонен-
34 Гл. IV. Жесткие задачи — одношаговые методы
ту решения, на втором графике представлено частное Н^г^Ц/ЦеггЛ
для трех допустимых погрешностей То/=10~з, Ю"^, 10""^. На
последнем рисунке изображен график /i|A|/3.3, где h — текущая длина
шага, А — доминирующее собственное значение матрицы Якоби и 3.3 —
приближенное расстояние от dS до начала координат.
Вторая возможность для обнаружения жесткости заключается в
непосредственной оценке доминирующего собственного значения
матрицы Якоби данной задачи. Если через г; обозначить вектор,
приближенно равный соответствующему собственному вектору с
достаточно малой ||v||, то по теореме о среднем значении
'" м
будет хорошей аппроксимацией ведущего собственного значения. Для
метода Дорманда и Принса (табл. II.5.2) имеем Cq=^Cj=1 . Поэтому для
оценки |А| (т.е. постоянной Липшица) естественно выбрать величину
где Аг,=:/(хо+c,/i,5',) — значения функции на текущем шаге. Оба
значения, gj = yi и д^, аппроксимируют точное решение y{xQ-\-h), и
можно показать, разлагая в ряд Тейлора, что д^-'д^ = 0(Н^). Таким
образом, в общем случае эта разность достаточно мала. То же самое
рассуждение также показывает, что д^—д^=Е[кЗ)в,^, где J —
матрица Якоби линеаризованного дифференциального уравнения и E[z) —
многочлен, содержащий члены не ниже четвертой степени.
Следовательно, g-j—g^ — это, по существу, вектор, полученный за 4 итерации
степенного метода, примененного к матрице hj, Он будет хорошим
приближением к собственному вектору, соответствующему ведущему
собственному значению. Как и в описанном выше численном
эксперименте, мы применили программу D0PRI5 к уравнению Ван-дер-Поля
A.5') с е=0.003. На рис. 2.6 представлен график Лр/З.З, где h —
текущая длина шага и /> — оценка B.26). Имеется полное согласие с
точными значениями /i|A|/3.3 (см. третий график на рис.2.5).
Дальнейшие численные примеры показывают, что оценка B.26)
дает удовлетворительные приближения для |А| и тогда, когда
доминирующее собственное значение А комплексное. Однако если
требуется найти также и аргумент А, то можно расширить степенной метод,
как предложил Уилкинсон A965, р. 579). Этот алгоритм детально
разработали Соттас A984) и Робертсон A987).
Два описанных выше подхода позволяют обнаруживать области,
где устойчивость ограничивает длину шага. Чтобы решить, будет
ли жесткий метод интегрирования более эффективным, необходимо
сравнить затраты обоих методов. Изучение этого вопроса
предприняли Петзолд A983), Соттас A984) и Бутчер A990).
IV.2. Анализ устойчивости для явных методов Рунге—Кутты 35
Устойчивость управления длиной шага
Теперь перейдем к разъяснению еще одного явления,
встречавшегося нам в разд. IV. 1, а именно, разрывного поведения длины шага
(см., например, рис. 1.4 или 1.8); его исследование начал Дж. Холл
A985/86) и продолжили Дж. Холл и Хайам A988). Существуют ли
методы или жесткие уравнения, для которых длина шага Л^
изменяется плавно и не происходят частые отказы от шага?
Проведем численное исследование на примере задачи
у;=-2000( cosxyi-hsinxyjH-l)» yi@) = l,
У2 = -2000 (- sin X . T/i -hcosx . У2 + 1). УгСО) = О
B.27)
для о < X < 1.57, в которой собственные значения медленно
перемещаются по большой окружности от —2000 до ±2000г. Применив метод
Фельберга RKF5D) (табл. П.5.1) в режиме локальной экстраполяции
(т.е. продолжая интегрирование, мы используем решение,
доставляемое методом старшего порядка), а также программу D0PRI5 к этому
уравнению (с евклидовой нормой погрешности без нормирования),
получим поведение длины шага, представленное на рис. 2.7. Все
отброшенные шаги на рисунке отмечены крестиками C отброшенных шага
для RKF5D) и 104 — для DOPRI5).
.0020
.0015
0020
0015
.5
h
<
1
D0PRI5
1.С
)
1
1.5
>у л:
.5 1.0 1.5
Рис. 2.7. Длины шагов, выбираемые RKF5D) и D0PRI5 для B.27).
Чтобы объяснить такое поведение, рассмотрим (ну конечно же!)
для уравнения у'=\у численный процесс
36 Гл. IV. Жесткие задачи — одношаговые методы
у„+1 = Я(/»„А)у„,
err„ = ?'(h„A)y„, ^2.28)
(где егг^ —оценка погрешности, E(z) = R(z) - R{z), а = 1/(р+1) и
р — порядок R) как динамическую систему, неподвижные точки и
устойчивость которой надо изучить. Гарантийный фактор C^fac'' из
формулы (II.4.13)) легко может быть учтен в То/, и он не повлияет
на теорию. Анализ упростится, если ввести логарифмы:
r)„ = \og\yJ, x„ = bg/i„, B.29)
так что B.28) примет вид
»j„+i=log|^(e>'-A)H-r,„,
/ \ B.30)
где 7 — постоянная. Теперь это — отображение М^ -^ М^. Его
неподвижная точка (?;, х) удовлетворяет условию
|Я(е''А)| = 1, B.31)
которое определяет длину шага е^ таким образом, чтобы точка г =
= е^А лежала на границе области устойчивости. Далее,
T; = 7-log|?;(r)|
определяет rj. Матрицей Якоби отображения B.30) в этой
неподвижной точке будет
« = Re (—^ • г),
Прс^цдожение 2.3. Механизм управления длиной шага устойчив в
точке h\=iz, лежащей на границе области устойчивости у если и только
если спектральный радиус матрицы С B.32) удовлетворяет условию
р{С) < 1.
В этом случае метод назовем SC-устойчивым (Step-Control stable) в
точке Z. П
Матрица С не зависит от конкретного дифференциального
уравнения и от заданной допустимой погрешности. Поэтому она является
характеристикой численного метода и границы его области
устойчивости. Рассмотрим некоторые методы из разд. П.5.
IV.2. Анализ устойчивости для явных методов Рунге—Кутты 37
DOP853
I I I I I I 11 I М I I I
Рис. 2.8. Области устойчивого управления длиной шага.
a) RKF4E) (табл.5.1), а= 1/5:
о/ ч , •г^ -г^ 2^ 25 ^, , z5 гб
ДН = 1 + 2+у + у + 24+104' ^(^^=780-2080
b) DOPRIS (табл. 5.2), а= 1/5:
R{z) = see B.13), Е{г) =
97
13
¦z' +
1
B.33)
120000 40000' ¦ 24000"
c) RKF5D) (табл.5.1, с локальной экстраполяцией), а = 1/5:
Z Z 2^ Z^ Z^
Я(.) = 1 + 2+- + -+- + - + — ,
E{z) такое же, как и в B.33).
d) HIHA5 (метод Хайама и Холла, см. табл. 2.1 ниже), а = 1/5:
B.34)
г2 гЗ
ДB) = 1 + 2+у + -
''' 24 ¦*" 120 "^ 1440 '
E(z) = -
1
1200
z' +
1
2400
z' +
1
14400
B.35)
B.36)
Соответствующие области устойчивости показаны на рис. 2.8. Те
куски границы, для которых удовлетворяется неравенство р{С)<1,
изображены на рисунке жирными линиями. Можно видеть, что
эффекты, имевшие место на рис. 2.7, так же, как и описанные в
разд. IV. 1, подтверждаются в точности.
DOP853. Управление длиной шага в программе DOP853 (см.т.!)
чуть сложнее. Оно основывается на «растянутой» оценке погрешно-
38 Гл. IV. Жесткие задачи — одношаговые методы
сти (см. разд. 11.10), и для тестового уравнения у' = Ху это
эквивалентно замене \E(z)\ в формуле B.30) на
\E(z)\ =
^Щ^+олЩёШ^
B.37)
где Es(z)==R3(z)-R(z),E^(z) = R^{z)-R(z) и Яз(г),Д5(~') - Функ-
ции устойчивости вложенных методов третьего и пятого порядков
соответственно. Вышеизложенный анализ остается справедливым, если
выражение для v в B.32) заменить производной log |?'(е>^'^)| по \,
которая равна
v,\E,{z)\^ + Omv,\E,{zW B.38)
2^5 -
\E,(zW + O.Ol\E^(zW
где v^ = Re{zE^^(z)/E^(z)) и v^ = Re(zE'^(z)/E^{z)). При этом
поскольку при \z\ -^0 имеем \E(z)\ = 0(\z\^), в B.32) нужно взять
значение а = 1/8. Область 5С-устойчивости для DOP853 также показана
на рис. 2.8.
Табл. 2.1. Метод HIHA5 Хайама и Холла
0
2
9
1
3
1
2
3
5
1
1
У1
У1
2
9
1
12
1
8
91
500
11
20
1
12
1
12
2
15
1
4
0
27
100
27
20
0
0
0
3
8
78
125
12
5
27
32
27
32
27
80
8
125
36
5
4
3
4
3
2
15
5
125
96
125
96
25
48
5
48
5
48
1
24
0
1
10
SC-устойчивые пары Дорманда и Принса 5-го порядда. Из рис. 2.8
видно, что метод D0PRI5 не является 5С-устойчивым на
пересечении вещественной оси с границей области устойчивости. Поэтому
интересно найти пары явных методов Рунге—Кутты 5D)-го
порядка из семейства Дорманда и Принса A980) с большими областями
SC -устойчивости.
IV.2. Анализ устойчргоости для явных методов Рунге—Кутты 39
При выполнении упрощающего предположения (II.5.15) алгоритм
5.2 из разд. П.5 дает класс методов Рунге—Кутты с с^,с^,с^ в качестве
свободных параметров. Хайам и Холл A990) провели обширный
численный поиск хороших наборов этих параметров, чтобы иметь
разумный размер области устойчивости, большие куски 5С-устойчивости
и малую константу погрешности 6-го порядка. Оказалось, что чем
больше желаемая область 5С-устойчивости, тем больше
становится константа погрешности. Компромиссный выбор между Сциллой и
Харибдой, который вдобавок дает приятные рациональные
коэффициенты, получается при Сз = 1/3, с^ = 1/2 и с^ = 3/5. Это приводит к
методу, представленному в табл. 2.1 и имеющему удовлетворительные
свойства устойчивости, как можно видеть на рис. 2.8.
ПИ-управление длиной шага
«Мы увидели, что это было И-управление ..., а
любой специалист по теории автоматического управления
знает, что ПИ всегда лучше, чем И ...»
(К. Густафссон, июнь 1990)
В 1986/87 годах два студента, специализировавшихся по теории
управления, посещали курс численного анализа в университете Лунд.
В результате у них появилась идея преодолеть описанный выше
феномен неустойчивости в жестких вычислениях, используя понятие
«ПИД-управления» (Густафссон, Лунд и Сёдерлинд 1988).
Классический метод в теории автоматического управления — «ПИД-управле-
ние» (Каллендер, Хартри и Портер 1936) — мотивируется следующим
образом.
Пусть имеется задача непрерывного по времени управления, и вA)
— отклонение некоторой величины в момент времени t от ее
нормального значения. Этой величиной требуется управлять. Тогда можно
положить
e{t) = C(t)-'me{t), B.39)
где C(t) обозначает действие управления, а член —m9{t)
представляет эффект саморегулирования — такой, как у «сосуда на водяной
бане постоянной температуры». Проще всего было бы выбрать для
управления уравнение
--C(t) = n^e{t), B.40)
представляющее, скажем, клапан, открываемый или закрываемый в
зависимости от в. Уравнения B.39) и B.40) совместно приводят к
ё-f m^-f «1^ = 0, B.41)
всегда устойчивому при п^>0, т>0. Однако, если предположить, что
у нашей системы имеется некоторое запаздывание по времени (что
более реалистично), то тогда нужно заменить B.40) на
-С@ = П1^(<-Т), B.40')
40 Гл. IV. Жесткие задачи — одношаговые методы
и устойчивость процесса может быть нарушена. Это в точности тот же
эффект, что и неустойчивость уравнения A7.6) из разд. 11.17,
посвященного дифференциальным уравнениям с запаздывающим
аргументом, и рассматривается он подобным же образом. Чтобы сохранить
устойчивость, можно было бы заменить B.40') на
^C{t) = n^e(t-T) + п^в{^-Т) B.40")
или даже на
-C[t) = п^в{г-Т) 4- П2^(<-Т) + nJ(t^T) . B.40'")
Здесь первый член в правой части представляет собой
«интегральную обратную связь» (И), второй член — «пропорциональную
обратную связь» (П) и последний член есть «дифференциальная обратная
связь» (Д). П-член специально увеличивает константу m в B.41),
тем самым добавляя дополнительное трение в уравнение. Поэтому
естественно ожидать, что система становится более устойчивой.
Однако точная настройка параметров п^, rij, Пд — это долгая задача,
требующая много времени для аналитического исследования и
приобретения практического опыта.
Чтобы адаптировать модель непрерывного времени B.40") к нашей
ситуации, сделаем замены
C{t) i—У log Л„ ( «управляющая переменная»)
e{t) i—У log \err^ I — log Tol ( «отклонение»)
и заменим производные по t конечными разностями. Тогда формула
П1
Лп+1 = Лп
\\errjj
(см. B.28)), которую перепишем в виде
-(•ogЛ„+1 -log Л„) = г»!(log |егг„ l-log Tol) ,
соответствует B.40'). ПИ-управление B.40") перейдет в
-Oogft„+i-logA„) = f»! (log |сгг„l-log Го/)+
+ П2((log |етт„l-log Tol) - (log |егт„_1 l-log Tol)) ,
или, если разрешить относительно Л„^1,
'--"¦(^)"'(fef')"" '-'
Чтобы провести теоретический анализ этого нового алгоритма,
опять возьмем задачу у'=Ху и аналогично B.28) будем иметь:
г/п+1 = Л(Л„А)у„ , B.43а)
егг„ = ?;(Л„А)у„, B.43Ь)
IV.2. Анализ устойчивости для явных методов Рунге—Кутты 41
где a^nj-hrij, /?=П2. В обозначениях B.29) этот процесс запишется
как
'/„+i=bg|fl(e>'»A)| + »?„,
Xn+l=X„-c\og\E{e^•'X)\-aт,„+0\og\E(e>'•'-^\)\ + |Зт,„_^ + J
B.44)
С некоторой константой 7- Это можно рассматривать как
отображение {fln^Xn^Vn^vXn-i) -^{'Пп+i^Xn^v^n^Xn)' в неподвижной точке
(г)уХ)у которая снова удовлетворяет условию B.31), матрица Якоби
дается выражением
A и О О \
-а 1-QV 13 0V \ .^ ...
; ? S S
о 1 0 0/
с и и V такими же, как и в B.32). При а=1/р (где р — показатель
степени Л в главном члене выражения для оценки погрешности) и
/?=0.08 численное исследование спектрального радиуса р(С) вдоль
границ областей устойчивости для рассмотренных выше РК-методов
выявляет впечатляющее улучшение (см. рис. 2.9) по сравнению со
стандартным алгоритмом (рис. 2.8). Единственное исключение
составляет метод DOP853, который становится неустойчивым вблизи
вещественной оси, тогда как он был 5С-устойчивым при /3=0. Значение
/3=0.04 лучше подходит для этого метода.
На рис. 2.10 на примере задачи A.6') сравнивается поведение
длины шага у D0PRI5 при новой стратегии {/3=0.13) и при управлении
длиной шага без демпфирования (/3=0). Улучшение не нуждается в
комментариях. Чтобы сделать различие ясно видимым, мы
выбрали сверхбольшую допустимую погрешность Atol=Rtol=8 • 10"^. При
/?=0.13 численное решение становится гладким во временном
направлении. Зигзагообрг13ная погрешность в х-направлении
представляет собственный вектор, соответствующий наибольшему собственному
значению матрицы Якоби, и ее величина меньше Atol.
Man sieht dciss selbst der frommste Mann
nicht alien Leu ten gefcdlen kann.
(W. Busch, Kritik des Herzens 1874)
«Видать, и самый кроткий тоже
Всем сразу нравиться не может».
(В. Буш, Критика сердца^ 1874)
42 Гл. IV. Жесткие задачи — одношаговые методы
DOP853
Рис. 2.9. Области устойчивости управления длиной шага
с множителем стабилизации /3 = 0.08 .
без стабилизации (/3 = 0): со стабилизацией (/3 = 0.13):
294 шага, 212 принято, 82 отброшено 162 шага, 162 принято, О отброшено
Рис.2.10. Численное решение A.6') с Го/=8 10"'^.
IV.2. Анализ устойчивости для явных методов Рунге—Кутты 43
Исследование для малого h. В нежестком случае новая стратегия
выбора шага может оказаться несколько менее эффективной. Чтобы
понять это, предположим, что \егг^\ ^ Ch^, так что B.43с) переходит
или после логарифмирования
bg/in-Hi + (P<^-l)logA„ -p/?log/i„_i = (a-/?)log(-^) .
Этому линейному уравнению в конечных разностях соответствует
характеристическое уравнение
А2 + (ра-1)А-р/? = 0 , B.47)
корни которого определяют отклик системы на изменение С,
Очевидно, выбор а=1/р и /3=0 должен быть наиболее удачным, так как
при этом обнуляются оба корня, но это как раз и есть классическое
управление длиной шага. Поэтому приходится пойти на компромисс,
выбирая а и /? такими, чтобы матрица B.45) оставалась устойчивой
для больших кусков границы устойчивости, и в то же время
сохраняя корни B.47) значительно меньшими единицы. После некоторых
вычислений Густафссон A991) нашел достаточно хороший выбор:
а«0.7/р, /?«0.4/р. B.48)
Стабилизированные явные методы Рунге—Кутты
Явные методы с большими областями устойчивости могут быть
очень эффективны во многих задачах большой размерности, обычно
не очень жестких, и с собственными значениями, про которые
известно, что они лежат в определенной области. Мы рассмотрим здесь
методы с областями устойчивости, расширенными вдоль отрицательной
вещественной оси, которые поэтому особенно подходят для
интегрирования по времени систем параболических ДУЧП. По этому вопросу
имеется превосходная обзорная статья с дополнителными
подробностями и ссылками (Фервер 1996).
Наша первая задача заключается в нахождении для данного s
многочлена вида R(z) = 1-f г -h a2Z^ 4-... 4- а,2:* такого, чтобы
соответствующая область устойчивости в направлении отрицательной
вещественной оси была как можно большей. Главная составляющая
этих методов — многочлены Чебышева (Чебышев 1854)
Т, (х) = cos(s arccos х) B.49)
или
Т,{х) = 2хТ,_,(х)-Т,_,(х), То(х) = 1, Т,{х) = х. B.49')
44 Гл. IV. Жесткие задачи — одношаговые методы
cui 2™* 3'** 4*** П* 4*** 3"* 2™* 5*^
Рис. 2.11. Смещенный многочлен Чебышева Т9A -{- z/8l) и его нули.
Рис. 2.12. Области устойчивости для смещенных многочленов Чебышева при
5 = 2,3,4, 5 (пунктиром показан предельный случай 5 -^ оо, см. упр. 8 ниже).
Рис. 2.13. Области устойчивости для демпфированных
функций устойчивости Чебышева, е = 0.05.
При — 1 < Ж < 1 их значения заключены между —1 и -f 1, и среди таких
многочленов они имеют максимально возможное значение
производной Т,'A)=«2 (А.А. Марков 1890). Поэтому надо положить
R,{z) = T,(l + z/s') B.50)
(Саульев A960), аспирант Саульева Юань Чжао-дин A958),
Франклин A959), Гийу и Лаго A961)), и тогда Я,@) = 1, Щ@) = 1, причем
l-^iC-^^)! ^ 1 лля -2^2 < ^ < О (см.рис.2.11). В частности, имеем
R^(z
R^{z
R,(z
= 1 + г,
= 1 + ^+1^2,
"^"^'^'''32^ "^128^ "'"8192^
= 14-24- -^22 4- -^23 4- ^^ -^ 4-
— l-rzT 2Ъ^ -Г 3125'^ ^78125^ ^
B.50')
16
9765625* •
Соответствующие области устойчивости представлены на рис. 2.12.
IV.2. Анализ устойчивости для явных методов Рунге—Кутты 45
Демпфирование. В точках, где Г,A-f-j/s^) = ±1, полностью
отсутствует подавление высших частот, и область устойчивости имеет
нулевую ширину. Поэтому выберем малое е > О, скажем, е = 0.05 и
положим (как было предложено Гийу и Лаго A961))
Эти многочлены колеблются между примерно 1 —5и—Ц-еи опять
же удовлетворяют условию К^(г) = l-hZ'\-0(z^). Области
устойчивости становятся чуть короче (на величину De/i)s^), но их
граница располагается на безопасном расстоянии от вещественной оси (см.
рис.2.13).
Реализащ1Я Лебедева. Следующая наша задача — найти такие
методы Рунге—Кутты, в которых реализуются эти многочлены
устойчивости. Первая идея, упомянутая Саульевым A960), а также Гийу
и Лаго A961), состояла в том, чтобы записать
* 1
RAz) = Y[{l+Siz), где Si = , г,. — корни Я(г) B.52)
.=1 ^«
и представить метод РК как композицию явных эйлеровых шагов:
9о'=Уо1 9х ''=9i^i^hSJ{9i-i). (г = 1,2,..., s), 2/1 •=9s'
B.53)
Недостаток такой реализации состоит в том, что для первого из этих
корней, который по абсолютной величине много меньше, чем другие,
мы будем иметь очень большой эйлеров шаг, что определенно
нехорошо. Поэтому Лебедев A989, 1994) предложил сгруппировать корни
симметрично по два и представить соответствующий квадратичный
множитель
(Ц-(У,.г)A+($;г) = A + 2а,.г4-/?,г2) B.54)
в форме двухстадийной схемы
i7,: = i7,_i + K/(i/.-i)»
9Ui''^9i^haJ{g,)^ B.55)
9i+i • = 9U1 - ^"^Пх ifi9i) - fi9i-i)) =
= 9Ui^^iii9Ui -9i) - {9i-9i^i)).
которую дает B.54), если положить /3- = q?A — 7t)- Это уменьшает
почти вдвое длину самого большого эйлерова шага, а также
допускает комплексно-сопряженные пары корней. Для оценки погрешности и
выбора длины шага может быть использовано выражение (g^^i — 9i)~
"[9% -9i^i) ^ h^ot'iy" > При нечетном s остается один непарный
корень, который порождает эйлеров шаг B.53).
46 Гл. IV. Жесткие задачи — одношаговые методы
Наилучшее упорядочение. Теперь необходимо уделить некоторое
внимание решению вопроса, в каком порядке корни будут
использоваться (Лебедев и Финогенов 1976). Это делается посредством двух
требований: во-первых, выражающие устойчивость внутренних
стадий величины
3
Sj = maxjl -f (^1^1 Л |1 4-2а,г-[-/?,.г2|
t=i
должны быть < 1 (здесь max берется по вещественным z на отрезке
устойчивости метода). Во-вторых, величины
S
Q^. =тах Д |l-h2a.z-f/?.z2|,
которые описывают распространение ошибок округления, должны
быть как можно меньше. Полученное численным путем упорядочение
для случая 5 = 9 указано на рис. 2.11.
Методы второго порядка. Если многочлен устойчивости
аппроксимирует е^ с точностью до второго порядка, т. е. если
Я,(г) = 1 + гЧ-у + аз2:3-Ь...-Ьа,г% B.56)
то из B.8) можно видеть, что любая соответствующая схема Рунге—
Кутты также имеет второй порядок на нелинейных задачах. Лебедев
и Медовиков A994) получили аналитические выражения для таких
оптимальных многочленов в терминах некоторого эллиптического
интеграла. Их область устойчивости достигает —0.821842 • s^ при 5^1.
На практике они обычно определяются численным путем (Ремез 1957;
Лебедев 1995). Например, в случае s = 9 и для демпфирующего
множителя ?: = 0.015 получаем корни
^9 =-64.64238389, Zg =-60.67479347, Z7 =-53.21695488,
ге =-43.16527010, Zg =-31.72471699, ^4 =-20.25474163, B.57)
гз = -10.05545938, ^зд = -1.30596166 ±М.34047517.
Соответствующий многочлен устойчивости (он устойчив на отрезке
—65.15 < Z <0), область его устойчивости и наилучшее упорядочение
корней показаны на рис. 2.14. Видно, что теперь имеется пара
комплексных корней.
Лебедевская компьютерная программа DUMKA включает в себя
формулы рассмотренного выше типа с автоматическим выбором h и
S в широком диапазоне.
Численный пример. В качестве иллюстрации метод,
соответствующий B.55) и B.57), был применен к задаче A.6'). Теория
предсказывает устойчивость примерно для h < 65.15/135= 0.4826. Крайняя левая
картинка на рис. 2.15 вычислена при значении Л = 0.48865, которое
IV.2. Анализ устойчивости для явных методов Рунге—Кутты 47
р.985
Рис. 2.14. Аппроксимация Золотарева 2-го порядка и область устойчивости.
Рис. 2.15. Задача A.6'): Lebedev9, h=0.48865 (слева), DUMKA (в середине),
RKC (справа); показаны все внутренние стадии.
чуть великовато, что приводит к неустойчивости. Средняя картинка
получена программой DUMKA при То/ = 3 • 10"^.
Подход ван дер Хаувена и Соммейера. Ван дер Хаувен и Сом-
мейер A980) нашли элегантную идею другой реализации: применить
нормированные и смещенные многочлены Чебышева и использовать
формулу трехчленной рекурсии B.49') для задания внутренних
стадий. Поэтому, следуя Баккеру A973), положим
ЛЛ^) = а, + ^^,К + ^1^)> w^ = \-^els\ ?«0.15. B.58)
Условия второго порядка
Д,@) = 1, Д'Л0) = 1, д';(о) = 1
приводят к
B.59)
48 Гл. IV. Жесткие задачи — одношаговые методы
с демпфированием а^ -1- 6, « 1 — е/3 (см. упр. 9). Положим теперь для
внутренних стадий
Rjiz) = aj-\-bjTj{wQ-\-w^2), ;= 0,1,..., 5-1. B.60)
Соммейер (см. Соммейер и Фервер 1980) обнаружил, что эти Rj(z)
могут при J > 2 служить приближениями второго порядка в
определенных точках XQ-\-Cjhj если
Л,@) = 1, R'ji0) = cj, Лу@) = с?, B.61)
ЧТО дает
Rj(z)-l = bjiTjiwo + w,z)-Tj(w,)), 6. = ^Щ^. B.62)
Далее, трехчленное рекуррентное соотношение B.49') приводит к
где
/i, = T^-^, ^i = r^, ^• = -гГ-^' i = 2,3,...,5. B.63)
^ bj_i ^ bj_^ ^ bj^^
в случае системы нелинейных дифференциальных уравнений эта
формула позволяет определить схему
5^0 - 2/0 = 0)
</i-2/o = «i^/(^o)> B-64)
9j - 2/0 = /^i(^i-i - Уо) + ^j(9j-2 - Уо) + *^jf^f{9j^i) - (^j-if^jhf(9o).
которая, будучи второго порядка для j/ = Ау, имеет второй порядок
и для нелинейных уравнений (опять-таки вследствие B.8)). Для j = l
возможен только первый порядок, и выбор к^ произволен. Соммейер
и Фервер A980) предложили взять
^0 = ^2. ^=^2» что дает к^ = с^ = j;j^f^^.
Функции Rg{z) и /Zj(z), j = 2,..., 5— 1 вместе с областью устойчивости
Rg(z) показаны (как и выше, для 5 = 9) на рис. 2.16 («Венера Виллен-
дорфская») в том же самом масштабе, что и лебедевский многочлен
Золотарева на рис. 2.14. Видно, что область устойчивости
становится немного короче, но теперь у нас есть аналитические выражения в
замкнутой форме и более гладкое поведение коэффициентов с, (см.
правую картинку на рис. 2.15). Все внутренние стадии отвечают
условию |flj('2:)| < 1, и можно видеть, что метод обладает
удовлетворительной численной устойчивостью (см. Фервер, Хундсдорфер и Соммейер
A990)). Вышеприведенные формулы были использованы в
экспериментальной программе RKC («Рунге—Кутта—Чебышев»), которую
написал Соммейер A991). Как можно видеть из рис. 2.15, она хорошо
справляется с уравнением A.6'). В разд. IV. 10 будут представлены и
другие численные результаты.
IV.2. Ангшиз устойчивости для явных методов Рунге—Кутты 49
».95
Рис. 2.16. Функция и область устойчивости для метода RKC, 5 = 9, е = 0.15 ,
Упралснения
1. Докажите, что методы Рунге—Кутты инвариантны относительно
линейных преобразований y = Tz (т.е., если применить метод к
у'=/(х, у) и к г'=Т^^/(х, Tz) с начальными значениями,
удовлетворяющими yQ=TzQ , то получим yy=Tzi).
2. Рассмотрим дифференциальное уравнение у'^Ау и его численное
решение вида y^j^^=R{hA)y^. Пусть R{z) — Л-устойчивая
функция, т.е. удовлетворяет условию
|Я(г)|<1 при Rez<0.
Покажите, преобразовав А к канонической форме Жордана, что
a) если у^=Ау устойчиво, то множество {у„} ограничено;
b) у^—^0 при п -> ОС, если у*=Ау асимптотически устойчиво.
3. (Оптимальная устойчивость для гиперболических задач, ван дер
Хаувен A968); A977), р.99.) Дано т, найти многочлен Л^(-г) =
= 1 -I- г -f... степени m-fl такой, что |Я(гу)| < 1 при —/? <у<0 с
возможно большим /?.
Ответ. Решение (Зоннефельд и ван Лер 1985) имеет вид:
fim(^) = ^v;.-i@ + Kn(C) + ^v„+i(C), С=^, B.65)
где Kn(C)=^"*^m(C/0 —многочлены Чебышева с положительными
коэффициентами. R^[iy) устойчивы при —т<у<т. Первые Я^
таковы:
m
Я1(г) = 1+С + С',
Л2B) = l+2C^-2cЧ2c^
Лз(г) = l + ЗC + 5CЧ4CЧ4C^
^4B) = 1 + 4С + 8СЧ 12С^ + ее" + 8C^
Л5(г) = 1 + 5С + 13С^ + 20С^ + гее" + 16С^ + 16С^ .
B.66)
50 Гл. IV. Жесткие задачи — одношаговые методы
(см. Абрамовиц и Стиган, с.600). Как и многочлены Чебыше-
ва, они удовлетворяют рекуррентному соотношению R^^^=2(^Rj^-\-
-|-fl^_iG7i>2). Области их устойчивости показаны на рис. 2.17.
Рис. 2.17. Области устойчивости для гиперболических приближений.
4. Линеаризуйте уравнение колебаний веревки A.24) в окрестности
^=^=0 и проведите анализ устойчивости. Выведите заново
уравнение Лагранжа A.6.2) из линеаризованного уравнения, применив
преобразование координат
У =
1
V:
\
7
/ 1
-1
\
1
-1 1
\
7
у-
5. На рис. 2.18 показаны численные результаты классического
метода Рунге—Кутты 4-го порядка с постоянным шагом на отрезке
О < < < 5 в задаче о колебаниях стержня A.7)-A.20) при гг=:8.
Объясните результат с помощью рис. 2.1.
6. В примере упр. 5 явный метод Эйлера, хотя и сходящийся при
/г —> О, никогда не будет устойчивым (см. рис.2.19). Почему?
7. Пусть Л — собственное значение левого верхнего блока матрицы
С B.45), имеющего размерность 2x2 (т.е. матрицы С B.32)).
Обозначим его ансшитическое продолжение как собственного значения
С через Х{Р). Докажите, что
а) Если Re Л 7^ О, то для некоторого у ЕШ
A(/?)=A.(l-^(l-ReA) + 27?2/-fO(^2)) .
Отсюда видно, что |Л(/?)|<|Л| при малом /?>0, если КеЛ<1.
IV.2. Анализ устойчивости для явных методов Рунге—Кутты 51
425 шагов
430 шагов
421 шаг
Рис. 2.18. Классический метод Рунге—Кутты с постоянным шагом,
задача о колебаниях стержня.
h = 5/20000 h = 5/28000 h = 5/36000
Рис. 2.19. Явный метод Эйлера, задача о колебаниях стержня
(изображен каждый 50-й шаг).
Ь) Если А и ^ — два различных вещественных собственных
значения вышеупомянутого блока, то
^'« = ^('-^('-х)'л^-''<'''>)-
Указание. Выпишите характеристический многочлен С в форме
det{XI-C)=:X{Xp(X) + ;3q(X)) ,
где p(A)=det(A/—С) — характеристический многочлен С, и
продифференцируйте его по /?.
52 Гл. IV. Жесткие задачи — одношаговые методы
8. Покажите, что для функций устойчивости Чебышева B.50)
справедливо предельное соотношение
lim RAz) =cos(\/-22:).
Указание. Подставьте з.тссо8A — х^/2) ^ х в B.49) и B.50).
Соответствующая область устойчивости обозначена пунктирными
линиями на последней картинке рис. 2.12.
9. Покажите (например, с помощью B.49')), что для многочленов
Чебышева
10.
t:(i) = s\ t;'(i) =
52(s2_l)
И получите аи:имптотические значения (при ? -> О) для ly^, 6,, а,,
демпфирующего множителя и интервала устойчивости
многочленов Баккера B.58).
(Крестообразные области устойчивости, идея
Лебедева A996).) Положим Z = —Ь± \/а[(р— 1) Н-б^,
так что когда у? пробегает отрезок — 1 < ^ < 1,
Z двигается по кресту —26 < г < О и г = —6±гг/.
Таким образом,
R^M)-^Uip{z))
— функция устойчивости для собственных
значений, лежащих на крестах (как, например, в задаче
PLATE). Определите а в зависимости от 6 из
условия Д'@) = 1 и найдите максимальное значение у.
Ответ. R^,(z) = Т,{1 +z/s^ + гУ{2Ьб^)); у^,^ = уДЬ^-Ь^.
IV.3. функция устойчивости
неявных методов Рунге—Кутты
«Мне не нравились все эти "сильный", "совершенный'',
"абсолютный" , "обобщенный", "супер", "гипер", "полный" и т. п. в
математических определениях; я хотел чего-нибудь
нейтрального и, будучи под впечатлением "свойства Л" Давида Янга,
выбрал термин "Л-устойчивый"». (Г. Далквист, в 1979 г.)
«Существуют, по крайней мере, два способа борьбы с
жесткостью. Один — это создание лучшего компьютера, другой —
это создание лучшего алгоритма».
(X. Ломаке в Эйкен 1985)
Методы называются Л-устойчивыми, если при их применении к
уравнению y' = At/ с ReA<0 и Л>0 отсутствуют связанные с
устойчивостью ограничения. Это понятие было введено Далквистом A963)
для линейных многошаговых методов, но оно применимо также и к
методам Рунге—Кутты. Ил A968) и независимо Аксельссон A969)
исследовали Л-устойчивость неявных методов Рунге—Кутты и
предложили новые классы Л-устойчивых методов. Коллокационные
методы были изучены в замечательной статье Райта A970).
Функция устойчивости
Мы начнем с неявного метода Эйлера yi=yQ-\-hf(x^, у^). Этот
метод, примененный к уравнению Далквиста у'=\у, дает yi=^yQ-\-hXy^,
или (после разрешения относительно у^)
У1 = Л(/1А)уо с R{z) = j^,
На этот раз область устойчивости — это внешность круга радиуса
1 с центром в -1-1. Таким образом, область устойчивости целиком
покрывает отрицательную полуплоскость, а также и большую часть
положительной полуплоскости. Неявный метод Эйлера очень
устойчивый.
Прс^цдожение 3.1. Неявный метод Рунге—Кутты с s стадиями
S
л = 2/0 + л ^ aijf(xQ -^Cjh.gj), г = 1,..., 5 , C.1а)
S
yi=yo + hY,bjf(xo+Cjh,gj) C.1b)
при применении его к уравнению у'=Ху дает j/j =Я(ЛА)уо, где
R{2) = l + zb'^{I-zA)-4 C.2)
54 Гл. IV. Жесткие задачи — одношаговые методы
b^ = (b„...,b,), A = {a,j)lj^„ 11 = A,...,!)^.
Замечание. Как и в определении 2.1, R(z) называется функцией
устойчивости метода C.1).
Доказательство. Уравнение C.1а) с f(x, у) = Лу, z = hX
превращается в линейную систему для вычисления д^,.. .^д^. Решив ее и
подставив решение в C.1Ь), придем к C.2). П
Таблица 3.1. Функции устойчивости неявных методов РК из разд. II.7
Метод
R{z)
а)
Ь)
с)
d)
е)
П
g)
h)
i)
J)
tf-метод (II.7.2)
неявный Эйлера (II.7.3)
неявное правило средней |
точки (II.7.4) >
правило трапеций (II.7.5) J
Хам мера—Холлингсуорта
(II.7.6) ;
SDIRK, р=3 (табл. II.7.2)
Хаммера—Холлингсуорта,
порядок 4 (табл. II.7.3)
Лобатто III А, порядок 4
(табл. II.7.7)
Кунцмана—Бутчера, 1
порядок б (табл. II.7.4) j
полученная Бутчером
формула Лобатто
порядка 4 (табл. II.7.6)
полученная Бутчером
формула Лобатто
порядка 6 (табл. II.7.6)
Радо ПА, р=5 (табл.11.7.7)
1 + :гA-^)
l-z9
1
1-2
1 + ^/2
l-z/2
1 + 4г/6 + г^/6
1-2/3
1 + 2A-27) + 2^A/2-27 + 7^)
A-7^)'
1 + 2/2 4-^^/12
1-2/2 + 2^12
1+2/2 + 2^/10 + 2^/120
1-2/2 + 2*^10-2^/120
1 + 32/4 + 2^/4 + 2^/24
1-2/4
1 + 22/3 + 2 Уб + 2^/30 + 2^/360
1-2/3 + 2^/30
1 + 22/5 + 2^/20
1-32/5 + 32^/20-2^/60
Другое полезное выражение для R{z) указали Штеттер A973) и
Шерер A979):
Прсдаюжение 3.2. Функцию устойчивости для метода C.1) можно
представить в виде
det (I-zA-^-zUT)
R(z) =
dot (/-г/1)
C.3)
IV.3. функция устойчивости неявных методов РК 55
км
//
Г
Radau5 ф^^
1 F * R-Vl«^
. 1 , .
5
. . 1 . 1
10 1
Рис. 3.1. Области устойчивости неявных методов РК.
Доказательство. Применив метод C.1) к задаче B.9), получим
линейную систему
По правилу Крамера (Крамер 1750) знаменателем функции R(z)
является det (I—zA), а ее числителем
D
Функции устойчивости для методов из разд. п.7 представлены в
табл. 3.1, а соответствующие области устойчивости — на рис. 3.1.
Итак, для неявных методов Щг) — рациональная функция с
числителем и знаменателем степени < s. Мы будем использовать запись
P(z)
R{z) =
degP=fc, degQ = i .
C.4)
Q(z) '
Если метод имеет порядок р, то
е' - R(z) = Cz^-^^ Ч- Oiz^-^^) при z ^ О C.5)
(см. теорему 2.2). Постоянная С обычно ^0; в противном случае
будем увеличивать р в C.5) до тех пор, пока С не станет отличной от
56 Гл. IV, Жесткие задачи — одношаговые методы
нуля. Тогда R(z) назовем рациональной аппроксимацией е^ порядка
р, а С — ее константой погрешности.
А -устойчивость
Мы видим, что некоторые методы устойчивы на всей левой
полуплоскости С~ . Это как раз то множество собственных значений,
где тонное решение задачи B.9) также устойчиво (разд. 1.13,
теорема 13.1). Одно из желательных свойств численного метода состоит в
том, чтобы он сохранял это свойство устойчивости.
Опр€Ц1.еление 3.3 (Далквист 1963). Метод, имеющий область
устойчивости
5DCr={z; Re2:<0},
называется А -устойчивым.
Метод Рунге—Кутты с функцией устойчивости C.4) Л-устойчив
тогда и только тогда, когда
|jR(ij/)| < 1 при любых вещественных у C.6)
и
R(z) — аналитическая функция при Rez <0. C.7)
Это следует из принципа максимума, примененного к С~ . Допуская
некоторую вольность языка, будем называть в этом случае и саму
функцию устойчивости R(z) Л-устойчивой (многие авторы
предпочитают называть ее «Л-допустимой» (Ил 1968)).
Условие C.6) само по себе означает устойчивость на мнимой оси
и может быть названо I -устойчивостью. Оно эквивалентно
требованию, чтобы многочлен
Е{у) = |д(»1/)Р - |Р(»у)|2 = Qiiy)Q(-iy) - P(iy)P(-iy) C.8)
удовлетворял условию
Е(у) > О для всех у G М. C.9)
Предложение 3.4. Определенный в C.8) многочлен Е(у) имеет
четную степень^ не превышающую 2 max(deg Р, deg Q). Если R{z)
является аппроксимацией е' порядка р, то
Е{у) = 0(уР'^^) при 2/->0.
Доказательство. Взяв абсолютные значения в C.5), получим
Положив z=iy и учитывая, что [e'S'lrrl, придем к
\Q{iy)\-\P{iy)\ = 0{f+').
Результат теперь следует из тождества
Е{у) = {\Qiiy)\ + \P(iy)\){\Q(iy)\ - \Р{гу)\). П
IV.3. функция устойчивости неявных методов РК 57
Примеры 3.5. Для неявного правила средней точки, правила
трапеций, методов Хаммера—Холлингсуорта, Кунцмана—Бутчера и Ло-
батто IIIA (с, f, g в табл.3.1) имеем Е{у)=0, так как Q{z)=:P(—z).
Это также следует из предложения 3.4, поскольку p=2j.
Непосредственное вычисление показывает, что условие C.7) удовлетворяется.
Следовательно, эти методы Л-устойчивы.
Для методов d, h, i из табл. 3.1 имеем deg P>degQ, так что
коэффициент в члене старшей степени ъ Е — отрицательный. Поэтому
условие C.9) не может быть верно при у —>• оо, и эти методы не
являются Л-устойчивыми.
Для метода Радо ПА пятого порядка (случай j) Е(у) = у^/3600 у и
рассмотрение нулей Q{z) показывает, что метод Л-устойчив.
Для двухстадийных ОДНРК-методов (SDIRK, случай е) Е(у)
имеет вид
E(y) = {f-\y{4j-l)y\ C.10)
откуда видно, что метод Л-устойчив при 7^4 ' '^•^* "Р^ 7=C+\/3)/6
получаем Л-устойчивый метод третьего порядка, но при 7=C—\/3)/6
метод не является Л-устойчивым (см. рис. 3.1).
Следующий общий результат объясняет свойства /-устойчивости
рассмотренных выше примеров.
Прецщожение 3.6. Рациональная функция C.4) порядка p>2j—2
I-устойчива^ если и только если |Д(оо)| < 1.
Доказательство. Из |Л(оо)| < 1 следует, что k<j. Согласно
предложению 3.4, Е(у) должен иметь вид К • y^J . Устремляя у —> оо
в C.6) и C.9), видим, что |Д(оо)| < 1 эквивалентно К>0. П
L-устойчивость и л (а)-устойчивость
«Показано, что правило трапеций для численного ин-
тегрировалия обыкновенных дифференциальных
уравнений первого порядка обладает нежелательным свойством
на определенного типа задачах». (Гурлей 1970)
¦ Л-устойчивость — это не полный ответ на проблему
жестких уравнений». (Александер 1977)
Как представляется, некоторые из рассмотренных выше методов
являются оптимальными в том смысле, что область устойчивости в
точности совпадает с отрицательной полуплоскостью. Это свойство
не настолько желательно, как может покгьзаться, потому что для
рациональной функции
lim R(z)- lim Д(г) = lim R(z).
Z-^ — 00 Z-^00 2=iy,y-?00
58
Гл. IV. Жесткие задачи — одношаговые методы
Последний предел должен тогда равняться 1 по модулю, так как
|Д(гу)|=1 для всех вещественных у. Это означает, что для г, близких
к вещественной оси и с очень большой отрицательной вещественной
частью, \R(z)\ , хотя и <1, но очень близко к единице. Как следствие,
жесткие компоненты в B.6) демпфируются, но очень медленно.
Покажем это на примере задачи
у' = -2000(у-cosх), у@) = 0, О < х < 1.5 C.11)
— такой же, что и A.1), но с большей жесткостью. На рис. 3.2
численные результаты для правила трапеций даны в сравнении с
результатами для неявного метода Эйлера. Неявный метод Эйлера демпфирует
переходную фазу много быстрее, чем правило трапеций. Таким
образом, представляется желательным свойство метода, состоящее в том,
чтобы |Л('г:)| была много меньше чем 1 при z —>• —ос.
неявное правило трапеций (h = 1.5/40)
неявное правило трапеций {h = 1.5/80)
— неявный м. Эйлера {h= 1.5/40)
Рис. 3.2. Правило трапеций в сравнении с неявным
методом Эйлера, решение задачи C.11).
Определение 3.7 (Ил 1969). Метод называется L-устойчивым,
если он Л-устойчивый и если вдобавок
lim R(z) = 0. C.12)
2-+со
Среди методов из табл. 3.1 L-устойчивыми являются неявный
метод Эйлера, ОДНРК-метод с 7=B±>/2)/2 и формула Радо ПА (j).
Прсддоженне 3.8. Если неявный метод Рунге—Кутты с
невырожденной матрицей А удовлетворяет одному из следующих условий:
a,j=bj, j = l,...,s, C.13)
an=bi, i=l,...,s, C.14)
то Л(оо)=0. Это делает А-устойчивые методы L-устойчивыми.
IV.3. Функщш устойчивости неявных методов РК 59
Доказательство. Из C.2) следует, что
Л(оо) = 1-6^Л-4, C.15)
а C.13) означает, что Л^е,=6, где е, = @,.. .,0,1)^. Поэтому Д(оо) =
=zl—eji =1 — 1 = 0. В случае C.14) воспользуемся тем, что Ае^ = Ш^,
П
Методы, удовлетворяющие условию C.13), называются эюестко-
тонными (Протеро и Робинсон 1974). Они важны для решения
сингулярно возмущенных задач и для дифференциально-алгебраических
уравнений (см. главы VI и VII).
Как мы только что видели, определение Л-устойчивости, с
одной стороны, слишком слабое, но, с другой стороны, оно слишком
сильное в том смысле, что многие не так tptc плохие методы вообще
не являются Л-устойчивыми. Следующее определение слегка слабее;
оно окажется особенно полезным в главе, посвященной многошаговым
методам.
Определение 3.9 (Видлунд 1967).
Говорят, что метод А(а)-устойнив^
если сектор
S, = {z; |arg(-z)|<a, гфО}
содержится в области устойчивости.
Например, аппроксимация Паде Rq^(z) =(l~^"i""^'"':Tfl i^^-
C.29) ниже) Л (а)-устойчива при а < 88.23<>.
Численные результаты
Чтобы продемонстрировать на жестких примерах из разд. IV. 1, как
проявляются хорошие свойства устойчивости, возьмем трехстадий-
ную формулу Радо ПА (табл. 5.6 из разд. IV.5), которая, как мы
видели, Л-устойчива, Z/-устойчива и имеет достаточно высокий порядок.
Этот метод реализован в программе RADAU5 (см. Приложение),
которую подробнее мы обсудим позже (разд. IV.8). Эта программа
интегрирует все примеры из разд. IV. 1 за несколько шагов, и на графиках
рисунков 1.3 и 1.5 отличие ясно видно.
Уравнение колебаний стержня A.10') при п = 40 и Rtol = Atol =
= 10""^ (абсолютная величина допустимой погрешности) для гладких
начальных значений интегрируется за 28 шагов (рис. 3.3).
Поскольку использованный в RADAU5 метод L-устойчив, область
устойчивости покрывает также мнимую ось и большие части
правой полуплоскости С+ . Это означает, что высокочастотные
колебания истинного решения могут демпфироваться численным методом.
60
Гл. IV. Жесткие задачи — одношаговые методы
Рис. 3.3. RADAU5, уравнение
колебаний стержня A.10*),
изображен каждый шаг.
Рис. 3.4. RADAU5, затухание
ВЧ-колебаний при большом То1
A07 шагов, все показаны).
Этот эффект, иногда рассматриваемый как нежелательный (Линд-
берг A974): «опасное свойство ...»), может оказаться и полезным
как средство для подавления колебаний, не представляющих
интереса. Это продемонстрировано применением RADAU5 с очень
большой допустимой погрешностью (Rtol=Atol=l) к уравнению
колебаний стержня A.10*) при п=10 и с возмущенным начальным
значением tf„@)=0.4. Здесь высокочастотные колебания вскоре исчезают, и
численное решение становится совершенно гладким (рис. 3.4). Если,
однако, требования к точности повысить, то программа вынуждена
отслеживать все эти колебания, и картина остается такой же, как и
на рис. 1.11.
Функции устойчивости порядка > з
Рассмотрим рациональные функции R(z)=P(z)/Q(z), где Q@) = 1
и оба многочлена P(z) и Q(z) имеют степень не выше s. Если R{z)
— аппроксимация е' порядка > s, то из C.5) следует, что
e^Q(z) = P(z)-hCiz'+4C2^'+4... .
C.16)
Следовательно, многочлен P{z), а также постоянные Cj, С2,...
однозначно определены в терминах коэффициентов Q(z). Для
Qi^) = 9о + ^1^ + Я2^^ -I-... + q^z', qo = l
C.17)
IV.3. функция устойчивости неявных методов РК 61
разложение e'Q(z) в ряд по степеням z дает
и для констант погрешностей
C.18)
^¦=AТ1)!*!т+--^^Г+!т' ("^>
Jo I ^1 I I я,-I q,
(s + 2)!"^(s + l)!'^"'^ 3! 2!'
<:^2=7Г^ + 77тЧтТ+--+^ + ^- C-20)
Многочлен М(х). Если использовать многочлен
A/(x) = 9.+g._i^ + g._2^ + ... + go5. C-21)
формулы для Q{z) и P{z) принимают более симметричный вид:
Q(z) = M(*)@)-fM(*-^)@)z-h... + M@)z', C.22)
P{z) = M^'\\)^M^'-^\\)z-V.. . + M(l)z^ C.23)
а постоянные погрешностей представляются в виде
Ci=: / M{x)dx, С^= f (l~x)M(x)dar.
Jo Jo
Для функции устойчивости коллокационных методов имеется
следующий интересный результат:
Теорема ЗЛО (К. Райт 1970; СП. Нёрсетт 1975). Функция
устойчивости коллокационного метода с узлами с^, Cj,..., с, задается вы-
ражением R(z) = P(z)/Q{z), где Q{z) и P(z) — многочлены C.22) и
C.23) соответственно^ а М{х) имеет вид
C.24)
М(х) = 1П(^;-с,).
C.25)
Доказательство (Нёрсетт и Ваннер 1979). Положим Xq=0, /i=l,
А=2г, yQ = ly и пусть и(х) — коллокационный многочлен. Поскольку
u^{x)—zu(x) — многочлен степени s, который обращается в нуль в
узлах коллокации, существуют постоянные Kq и К такие, что
u'{x)-'Zu{x) = KoM(x) или (^1-^^и(х) = КМ(х). C.26)
Здесь D обозначает оператор дифференцирования и М{х) —
многочлен C.25). Разложение A —D/z)~^ в геометрический ряд дает
u(x) = x(l + ^ + ^ + ...+ —)М(Х), C.27)
62 Гл. IV. Жесткие задачи — одношаговые методы
так как М^^Цх)=0 для j>s. Из u{l)^R(z)u@) следует соотношение
R{z)=u{l)/u@), которое приводит к C.22) и C.23). П
Аппроксимации Паде для показательной функции
«Comme cela est sou vent le cas en ce qui conceme les
decouvertes scientifiques, leur inventeur n'est p2is H. Pade».
(C. Brezinski 1984, (Euvres de H. Fade, p. 5)
«Как это нередко бывает, когда дело касается научных
открытий, их изобрел не А. Паде».
(К. Брезински 1984, Труди А. Паде, р. 5)
Аппроксимации Паде (Паде 1892) — это рациональные функции,
которые для данных степеней числителя и знаменателя имеют
наивысший порядок аппроксимации. Своим возникновением они обязаны
теории непрерывных дробей; они играли фундаментальную роль в
доказательстве Эрмита A873) трансцендентности числа е.
Эти оптимальные аппроксимации для показательной функции е^
можно получить из C.22) и C.23) с помощью следующей идеи (Паде
1899): надо выбрать М(х) так, чтобы в C.22) и C.23) обращалось в
нуль как можно больше членов со старшими степенями г, т.е. взять
тогда М(»)@)=0 для г=0,...,А:-1 и MWA)=0 для i=0,...,i-l.
Теорема 3.11. (fe, j)-аппроксимация Паде для е^ дается
выражением
где
Я,,(.) = ^. C.29)
^kAZ) ^-^J_^_,^z-^(^J_^,щJ^k_¦^^ 2Г--^и+к)...и+1) к\'
о (Л-л J ,1 J(i-i) ^^ ,( ,4i J(J-1)-1 zi _
4kj(z)-l ^^j^+(;t + i)(ifc + j-l)'2! •••+^ '^(ifc + i)...(fc + l)j!-
= Pjki-z),
с погрешностью
е- -«.,(,) = (-1Г(.^ц,^^^.),^""-Ю(^^'^'). C.301
Это единственная рациональная аппроксимация для е' порядка j-fAr
такая, что к и j — степени числителя и знаменателя соответственно.
Доказательство. Подстановка C.28) в C.22) и C.23) дает
формулы для Pkj(^)iQkj{^) и C.30). Единственность следует из того факта,
что многочлен М{х) C.21) степени j-\-k должен иметь нуль
кратности Аг в точке а*=0 и нуль кратности j в точке х=1. П
IV.3. функция устойчивости неявных методов РК
63
Таблица 3.2. Аппроксимации Паде для е^
1
1
1
1-2
1
1-г+|^
1
1 r-U^^ ^^
1 + г
1
1 + 3^
1 2^ , 1 ^3
1 + |г
1 3^ , 1 ^3 1 ^3
1 + г + ^
1
1 _L 2^ , 1 г^
1-^
1 , 1^ , 1 г^
1 + ^^ + ш1г
1 3^ , 3 2^ 1 гЗ
В табл. 3.2 приведено несколько первых аппроксимаций Паде для
е^ . Как видим, функции устойчивости для многих методов из табл. 3.1
суть аппроксимации Паде. Диагональные аппроксимации Паде — это
такие, у которых k=j.
Упралснения
1. Пусть R{z) — функция устойчивости метода C.1) и Я*(г) —
функция устойчивости соответствующего присоединенного метода
(см. разд. П.8). Докажите, что
R'{z) = (R(-z))-\
2. Рассмотрите неявный метод Рунге—Кутты порядка p>s с
невырожденной матрицей А, не совпадающими с, и ненулевыми 6,.
Покажите, что
a) если справедливо упрощающее предположение C{s) и c^ = l, то
выполняется условие C.13);
b) если справедливо упрощающее предположение D(s) и с^=0, то
выполняется условие C.14).
В обоих случаях Д(оо)=0.
(Определения C{s) и D{s) см. в разд. IV.5.)
3. Покажите, что коллокационные методы могут быть L-устойчивы-
ми, только если МA) = 0, т.е. если один из узлов с (обычно с^)
равен 1.
64 Гл. IV. Жесткие задачи — одношаговые методы
4. (Паде A899), см. также Лагранж A776).) Покажите, что
непрерывная дробь
е' = 1 + ^
1-^ +
JL?1
1 3 4
2 А.^
1 +
1 ;
79"
1 + ...
дает диагональные аппроксимации Паде для е^.
Указание, Вычислите несколько первых подходящих дробей. Если
вам не удастся найти общее доказательство, прочитайте разд. IV.5.
Правило трапеций
О О
1/2 1/2
1/2 1/2
хотя и удовлетворяет условиям а,, =6,, но не обладает свойством
Я(оо)=0. Почему это не противоречит предложению 3.8?
Покажите, что обе формулы:
У1 = 2/0 + Л/(уо + в{у^ - уо)) и
являются нелинейными расширениями ^-метода. Найдите другие.
Композиция одного шага ^-метода длины ah с последующим
шагом ^'-метода длины A —2а)Л и еще одним шагом ^-метода длины
ah приводит к
_ /1Ч-агA-^)ч2 /l-f(l-2a)z(l-g04
^^ ^~V \-aze ) \ 1-A-2аJ^' ) *
Покажите, что этот метод при в'^\ — в имеет порядок 2, если
а =1 — ^2/2, и что он сильно А-усшойнив (т.е. Л-устойчив и
|Д(оо)|<1) при в>\/2. Авторы Мюллер, Проль, Раннахер и Ту-
рек A994) называют этот метод «дробным й-методом» и успешно
его применяют при интегрировании уравнений Навье—Стокса для
несжимаемой жидкости.
IV.4. Порядковые звезды
«Mein hochgeehrter Lehrer, der vor wenigen Jjdiren verstor-
bene Geheime Hofrath Gauss в Gottingen, pflegte in ver-
traulichem Gesprache haufig zu aussem, die Mathematik sei
weit mehr eine Wissenschaft fur das Auge als eine fur das
Ohr. Was das Auge mit einem Blicke sogleich iibersieht...»
«Мой высокочтимый учитель, скончавшийся всего
несколько лет назад в Гёттингене тайный надворный
советник Гаусс, бывало, часто в доверительной беседе
высказывал мнение, что математика в гораздо большей
степени наука для глаза, чем для уха. То, что глаз сразу
охватывает взглядом...» (Й.Ф. Энке 1861,
опубл. в Собрании сочинений Кронекера, т. 5, р. 391)
Порядковые звезды (order stars^)), открытые в поисках лучшего
понимания свойств устойчивости аппроксимаций Паде для е^ (Ван-
нер, Хайрер и Нёрсетт 1978), дали красивый и неожиданный
подход ко многим другим результатам: «второму барьеру» Далквиста,
предположению Даниела—Мура, наивысшему возможному порядку
для аппроксимаций с вещественными полюсами, сравнению областей
устойчивости (Йелч и Неванлинна 1981, 1982), ограничениям
порядков для гиперболических или параболических разностных схем
(например, Изерлес и Странг A983), Изерлес и Уилльямсон A983), Йелч
A988)).
Введение
«Когда я писал свою книгу в 1971 г., я хотел начертить
"области относительной устойчивости", но из-под пера
плоттера выходили странные звезды. Я подумал, что в
программе ошибка, и выбросил их...»
(Ч. Гир, в ,1979)
На рис. 4.1 представлены области устойчивости для
аппроксимаций Паде Дзз' ^24» ^15» ^об ^^ теоремы 3.11; все они —
аппроксимации 6-го порядка для ехрB:). Из рисунка видно, что Ддз ^ ^24
обладают приятным свойством Л-устойчивости, но две другие
функции этим свойством не обладают: для R^^ нарушается условие C.6),
а для Rqq — C.7). После некоторых размышлений над этими и
подобными рисунками, в попытках лучше понять эти явления, в конце
концов, возникло следующее
Опред^еленне 4.1. Множество
Л = {г€С;|Д(г)|>|е^|} = {г€С;|ф)|>1}, D.1)
где q{z)=R{z)/e^ , называется порядковой звездой для R.
^ Означает также «звезды орденов» (игра слов). — Прим. ред.
66 Гл. IV. Жесткие задачи — одношаговые методы
0
1 .0 . 1
1
-6 ' -3 1
i
0 1
1 '
1 '1
Рис. 4.1. Области устойчивости для аппроксимаций Паде.
В случае порядковой звезды I^C-sr)! сравнивается не с 1, как в
случае области устойчивости, а с точным решением |е^|=:е^; есть
надежда, что это могло бы дать больше информации. Поскольку мы
всегда предполагаем, что коэффициенты R{z) вещественные,
порядковая звезда симметрична относительно вещественной оси. Далее,
так как |e*J'| = l, то на мнимой оси А — дополнительное множество к
области устойчивости 5. Поэтому из условий C.6) и C.7) вытекает
Лемма 4.2. R{z) I-устойчива, если и только если
(i) Л П Ж = 0.
Далее, А-устойчивость R(z) равносильна выполнению условий (i) и
(и) все полюсы R(z) (= полюсы q(z)) лежат в С+ . П
На рис. 4.2 показаны порядковые звезды для тех же функций Rf^j ,
что и на рис. 4.1. Эти порядковые звезды демонстрируют красивое ре-
IV.4. Порядковые звезды 67
г ГШВШ№и\ \ \ \
Ш^Щ^Щшщ 3
K^^n:\
ИжВДВЙ^К^^^^^Зь*'''*'^ >yV
l^^^^j^"'''^ y^j
^P^.U«y
^^^::Ш^'М^^/-3
l^^^l^it^y
Ш^^^^^-7
-f^^V'-y \ 1' ¦-''•.'ч'. '• '•
Ьу ^'^''"^'^'Wb'''''^'
^ ' м'''|''|'' f '
>^ч^-^т^г^^л^;! ¦ 6
?\^>С^-'(Ш:1''' \
Mhs. /Я;^''///'/'
к-%5;;"/\ ' ' 'i/// / /
\У^Ш;1
WiL-A
Рис. 4.2. Порядковые звезды для аппроксимадий Паде.
гулярное поведение: справа имеется j черных лучей-«пальцев»,
каждый из которых содержит полюс Rf^^, а слева — к белых «пальцев»,
каждый из которых содержит нуль. Ровно две граничные кривые А
стремятся к бесконечности вблизи мнимой оси. Эти свойства —
следствие трех следующих лемм.
Лемма 4.3. Пусть R[z) — аппроксимация для е^ порядка р:
е' ~ R(z) = CzP+^ + 0(z''-^^), D.2)
где СфО. Тогда А при г -> О имеет звездообразный вид с р-|-1 сектора-
ми равной ширины 7г/(р+ 1), разделенными р-\-1 аналогичными
«белыми» секторами дополнительного множества. Положительное
направление вещественной оси лежит внутри черного (белого) сектора,
если и только если С<0 (С>0).
68 Гл. IV. Жесткие задачи — одношаговые методы
Доказательство, Деление выражения для погрешности D.2) на
е^ дает
ffl = l-Cz^+4C?(z'^+2).
Поэтому комплексная величина R[z)/e^ при малых \z\ обходит точку
1 столько раз, сколько zP+^ обходит начало координат, т.е. р-\-\ раз.
Таким образом, значение функции R[z)/e^ попеременно p-f-1 раз
оказывается внутри или снаружи единичного круга. При этом для малых
положительных вещественных z оно лежит внутри, когда С>0. П
Лемма 4.4. Если z = re*^ и г—>оо, то z Е А при 7г/2<^<37г/2 я
Z ^А при — 7г/2<^<7г/2. Граница ЗА имеет только две уходящие в
бесконечность ветви. Если
^(z) = /Cz40(z^-^) при z->oo, D,3)
эти ветви асимптотически стремятся к
x = log|/i:|-h^log|y|. D.4)
Доказательство. Первое утверждение — это хорошо известный
факт, что показательная функция при Re г ->^ ±оо растет (убывает)
гораздо быстрее любого многочлена или рациональной функции.
Чтобы показать единственность границ, рассмотрим при г -> ос две
функции
^J^) = |e^|2 = e2^^^«^ и
^M = \R{z)\^^R[re'')R{re-'') .
Дифференцирование дает
^ = -2rsin., ^ = 2гае(ге-.^). D.5)
Так как \R'/R\ -^ О при г -> ос, то
d d
— log^i(^)<—logy?2W при 9е[е,7Г'-е].
Следовательно, на этом отрезке может существовать только одно
значение в у для которого ^i{e) = <P2{9)* Формула D.4) получается из
D.3), если учесть, что
|^C|(x2 + y2)</2«e^ iog\K\ + ^ log(x4y2)«a;
И если пренебречь х^, что оправдано, потому что ж/у —>О, когда х-Ьгу
стремится к бесконечности, оставаясь на границе А. D
IV.4. Порядковые звезды 69
Из принципа максимума ясно, что каждый ограниченный «палец»
А на рис. 4.2 должен содержать полюс q{z). Более строгий результат
следующий:
Лемма 4.5. Каждое ограниченное подмножество F С А с общей
границей dF С дА, в которое входит т секторов в начале коорди-
нат, должно содержать не менее т полюсов q{z) (каждый полюс
считается с учетом его кратности). Аналогично, каждое ограниченное
«белое» подмножество F С С\А с т секторами в начале координат
должно содержать по крайней мере т нулей q{z).
Доказательство, Предположим сначала, что dF представлено с
помощью параметризованной положительно ориентированной петли
^(Oj ^0 ^^ ^ ^1- Пусть a = [c\(t)yC2[i)) — касательный вектор и п =
= (^2(О) ""^i@) — вектор внешней нормали. Запишем
q[z) = Г(Х, у) ' е''^^*' У\ Z:=:X'\' iy,
так что logq(z)=^\ogr(Xy y)+i<p{xy у). Поскольку г(ж, у) возрастает
внутри F, имеем
^<0. D.6)
Дифференциальные уравнения Коши—Римана для log q имеют вид
djlogr) ^д(р g(logr)^ д(р
дх ду' ду дх^
так что из D.6) вытекает неравенство
%<0. ,4.8,
Это неравенство — строгое, за исключением конечного числа точек,
так как q*{c{t)) • &{t) = i • q{c{t)) • д(р/да и число нулей q'{z) конечно.
Таким образом, аргумент q убывает вдоль с. Если кривая
контура c[t) возвращается в начало координат, где аргумент кратен 27г,
m раз, то вектор q[z) должен совершить по крайней мере m полных
оборотов в отрицательном направлении (рис. 4.3). Тогда принцип
аргумента (с которым мы уже встречались в разд. 1.13, см. т. I, ее. 89
и 349) гарантирует наличие по крайней мере m полюсов внутри F
(нули отсутствуют, так как их нет ъ А).
Если граничная кривая представлена несколькими кривыми, то
все числа вращений складываются. Для «белых» подмножеств
доказательство аналогично, только 9(log г)/9п > О и аргумент вращается
в другую сторону. П
На рис. 4.3 в качестве иллюстрации показаны две порядковые
звезды для ОДНРК-методов порядка 3 (табл.3.1, случай е). Здесь q[z)
имеет двойной полюс в z=l/7. Однако F (ограниченная компонента
70 Гл. IV. Жесткие задачи — одношаговые методы
/7 = C-V3)/6 '
' / / / / ¦¦ /
йЩ
'•^-\=^
^r|iE
^'$Щ
'^гШ
<г~Т
¦*щ —
'•'г—^
^ш.
!лГ -
"^'"-¦-•^..,_ '^~"ч^
^^^^(ЛЛГ^у.
^^^->^:>4Й?&Ш^^^^Й2
^yfcg^; i^ ^Лии'?^^ '' пШПтштат
шЯ^ё^^ ' ^"'^-«¦кмВЙИпЯВЗВ
ss^^^^. ^--^ ^^щршшшш
^<^^^^,>0С4^Ш^^
-7 = C + \/3)/б ^,..--^,.
„.---"' /
\
^Ч \ '
втам '
^Av
Y / /
/' /
/ 1
Рис. 4.3. ОДНРК-методы, порядок 3; стрелками показано направление q{z).
Л) при 7=C—\/3)/6 содержит только один сектор в начале
координат. Поскольку вектор q{z) совершает два оборота, то кроме начала
координат имеется еще одна точка на 9F, в которой arg(9) = 0, т.е.
arg(flB:)) = arg(e^) и, так как |Д(г)| = |е^| на 9Л, оказывается, что
R{z) — e^, Такие точки называют точками подгонки к экспоненте.
Отсюда — другой вариант леммы 4.5:
Лемма 4.5' (Изерлес 1981). Каждое ограниченное подмножество
F С А с дР С дА содержит в точности столько же полюсов^ сколько
точек подгонки к экспоненте имеется на его границе. П
Порядок и устойчивость
для рациональных аппроксимаций
В дальнейшем будем предполагать, что R[z) — произвольная
рациональная аппроксимация порядка рек нулями и j полюсами.
Теорема 4.6. Если R{z) А-устойчива, то p<2fci-|-2, где к^ —
количество различных нулей R(z) в С" .
Доказательство. По крайней мере [(р-|-1)/2] секторов А
начинаются в С" (лемма 4.3). В силу Л-устойчивости они должны быть
бесконечными и охватывать не менее [(р-|-1)/2]—1 ограниченных
белых «пальцев», каждый из которых содержит хотя бы один нуль, что
следует из леммы 4.5. Следовательно, [(р+1)/2]-1 < Аг^. П
Теорема 4.7. Если R{z) I-устойчива, то р< 2j\ , где j\
полюсов R(z) в С^ .
число
IV.4. Порядковые звезды 71
Доказательство. Не менее [(p-fl)/2] секторов А начинаются в
С+ . Они не могут пересекать гЖ и поэтому должны быть
ограниченными (лемма 4.4). Снова по лемме 4.5 имеем [(р-}-1)/2] < jj. П
Теорема 4.8. Пусть р> 2j-l я |Л(ос)| < 1. Тогда R(z) Л-устой-
чива.
Доказательство. Согласно предложению 3.6, функция R(z) I-
устойчива. Применяя теорему 4.7, получаем jy > j, так что из I-
устойчивости следует Л-устойчивость. П
Теорема 4.9 (Крузе и Рюамп 1977). Пусть р > 2j-2, |Л(оо)| < 1, и
коэффициенты знаменателя Q{z) имеют чередующиеся знаки. Тогда
R(z) А-устойчива.
Доказательство. Аргументация, подобная использованной в
предыдущем доказательстве, позволяет заключить, что в С~ возможен
не более чем один полюс; он был бы вещественным, и тогда его
существование противоречило бы предположению о знаках Q(z). П
Теорема 4.10. Предположим^ 4Top>2j—3, R[z) I-устойчива^ и
коэффициенты Q{z) имеют чередующиеся знаки. Тогда R{z)
А-устойчива.
Доказательство. Для р > 2j—3 аргументация предыдущего
доказательства остается справедливой. Однако предложение 3.6 более не
применимо, и необходимо предположить /-устойчивость. П
Из рис. 4.2 видно, что все полюсы и все нули для аппроксимаций
Паде должны быть простыми. В том случае, когда два полюса
совпадают, соответствующие секторы порождают ограниченный белый
палец между ними с неизбежным добавочным нулем. Таким образом,
наличие кратных нулей или полюсов связано с понижением порядка.
Теорема 4.11. Пусть R{z) обладает к^ различными нулями и Jq
различными полюсами. Тогда р < k^-^j^ .
Рис. 4.4. Порядковая звезда на сфере Гаусса.
72 Гл. IV. Жесткие задачи — одношаговые методы
Доказательство. Отождествим комплексную плоскость со
сферой Гаусса и порядковую звезду с CW-комплексной декомпозицией
этой сферы (рис. 4.4). Пусть «2 — число 2-ячеек /,-, s^ — число
1-ячеек /,- (путей) и Sq — число вершин. Тогда из формулы
Эйлера для многогранников («Si enim numerus angulorum solidorum fuerit
= 5, numerus acierum =Л et numerus hedrarum =Я, semper habetur
S-j-H=A+2, hincque vel 5=Л-|-2-Я vel Я=Л-|-2-5 vel A=S-\-H-2,
quae relationis simplicitas ob demonstrationis difficultatem.. .»^), Эйлер
A752)) следует
«о-«1+^2 = 2- D•^)
Современные версии имеются в любой книге по алгебраической
топологии (см., например, Масси A980), р. 87, следствие 4.4). Формула
D.9) верна, только если все /,- гомеоморфны дискам. В противном
случае они должны быть разрезаны на диски с помощью
дополнительных путей (пунктир на рис. 4.4). Итак, в общем случае имеем
Поскольку в каждую вершину входит по крайней мере 2 пути, а в
начало координат, согласно предположению, 2р-|-2 путей, и так как у
каждого пути есть две крайние точки, имеем
5i-5o>p. D.10)
Согласно лемме 4.5 каждая 2-ячейка, за исключением двух (двух
«бесконечных»), должна содержать по крайней мере один полюс или
нуль, так что имеем
«2<*o+io + 2. D.11)
Эти три неравенства дают р < ^o+Jo • О
Устойчивость аппроксимаций Паде
«... есть основания предположить, что это
единственные L-допустимые аппроксимации Паде для
показательной функции». (Ил 1973)
Теорема 4.12. Аппроксимация Паде Rf^j C,29) А-устойчива^ если
и только если к <j < fc-|-2. Все нули и все полюсы ее простые.
Доказательство. «Если5>-часть — это следствие теоремы 4.9.
«Только если»-часть следует из теоремы 4.6, поскольку p=zk-^j. По
той же причине теорема 4.11 показывает, что все полюсы и нули
простые. П
^ «Ибо если число телесных углов =5, число ребер =Л и число граней
=Я, всегда имеем 5-|-Я=А-|-2, откуда также 5=АН-2—Я, или Я=Л-|-2—5,
или Л=5-1-Я—2, — простые соотношения с трудным доказательством...».
— Лат.
IV.4. Порядковые звезды 73
Сравнение областей устойчивости
Da ist der allerarmste Мгшп Один — бедняк из бедняков,
dem ander^ viel zu reich, Другой слишком богат,
das Schicksal setzt den Hobel an Судьбы рубанок ровняком
und hobelt beide gleich. Строгает всех подряд.
(F. Raimund, das Hobellied) (Ф. Раймунд, Песня рубанка)
Йелч и Неванлинна A978) доказали следующую «теорему о
диске»: Если S — область устойчивости s-стадийного явного РК-метода
и D — диск радиуса s с центром —s (т.е. область устойчивости s
шагов явного метода Эйлера с длиной шага h/s), то
S^D, D.12)
за исключением случая, когда S = D и рассматриваемый метод —
метод Эйлера. Этот любопытный результат выражает тот факт, что
метод Эйлера «наиболее устойчивый» среди всех методов, требующих
одинакового объема вычислительной работы. После открытия
порядковых звезд стало ясно, что этот результат гораздо более общий и что
любой метод обладает тем же самым свойством (Йелч и Неванлинна
1981). В главе V мы увидим, что этот результат обобщается также
на многие многошаговые методы. Главным инструментом излагаемой
теории будет
Определение 4.13. Пусть Ri(z) и Дз!^) — рациональные
аппроксимации для е^, тогда их относительная порядковая звезда
определяется как
Здесь функция устойчивости для метода 1 сравнивается с
функцией устойчивости для метода 2 вместо точного решения е^. Следующие
соотношения для порядков
e'-R,(z) = C,zP^'^' + ...
e^^R,(z)=C,zP^^'-^...
приводят после вычитания к
^ = l-CzP^^ + ..., D.14)
где p=min(pi, Рз) и
{Cj — С2, если Pj = Р2'
С^, если Pi <Р2) D-15)
—Сз, если р^ > Р2-
74 Гл. IV. Жесткие задачи — одношаговые методы
Замечание 4.14. Утверждение леммы 4.3 остается неизменным для
В, если только Сфй. Поскольку дробь R^(z)/R2(z) не имеет
существенной особенности на бесконечности, у леммы 4.4 нет аналога.
Далее, в леммах 4.5 и 4.5' может быть опущено требование
ограниченности F {если ОС —полюс Д^(г)/Я2(г), то его тоже следует учитывать).
С учетом соответствий, представленных в табл. 4.1, утверждения
теорем 4.6 и 4.7 остаются в силе и для В.
Таблица 4.1. Соответствия между А и В
„^^«г,^^«^« ..«^.^тто А {л л\ V V / относительная порядковая
порадковая звезда Л D.1) f^ | ^^^^^^ ^ ^^^3)
мнимая ось i—> dS2
С~ i—у внутренность 52
i—у внешность 52
метод А-устойчив i—> Si Э 52
р <—> min(pi,p2)
Теорема 4.15. Если Ri{z) и R2{z) — полиномиальные функции
устойчивости степени s и порядков > 1, то соответствующие области
устойчивости не покрывают полностью друг друга:
5i0 52 и S,<tS,. D.16)
Доказательство. Предположим, что S^ D S2 (т.е. предположим
«Л-устойчивость» — с учетом табл.4.1). Тогда аналог теоремы 4.7
требует, чтобы у R^{z)/R2(z) выл полюс вне 82- Так как Rx(z) и
ЛзС-) имеют одну и ту же степень, у R^(z)/R2(z) нет полюса на
бесконечности. Поэтому единственные полюсы R^(z)/R2{z) — это нули
Дз!^) 1 и они находятся внутри S2 . Налицо противоречие, что и
доказывает первую часть D.16). Вторая часть получается перестановкой
/?i(z) и R2(z). П
Чтобы сравнивать численные методы, требующие разных объемов
вычислительной работы, рассмотрим нормированные области
устойчивости.
Определение 4.16. Если R(z) — функция устойчивости степени s
явного метод Рунге—Кутты (обычно 5-стадийного), то
5'"' = {г; \R(sz)\ < 1} = {--; s • ; € 5} = ^5 D.17)
будем называть нормированной областью устойчивости метода.
IV.4. Порядковые звезды
75
Теорема 4.17 (Йелч и Неванлинна 1981). Если Ri{z) и R2(z) —
функции устойчивости степеней соответственно s^ и «j Д^У^ явных
методов Рунге—Кутты порядков > 1, то
5J"^'2i55'^' и 5J"^'(^5^"^', D.18)
т.е. одяа нормированная область устойчивости никогда не может
целиком содержать другую.
Интересная интерпретация этого результата: для любых двух
методов существует дифференциальное уравнение у' = Ау, при
применении к которому первый метод оказывается эффективнее второго.
Никакой «чудодейственный» метод невозможен.
Доказательство, Сравним «2 шагов длины /i/sj методом 1 с
Sj шагами длины h/s^ методом 2. Обе процедуры при этом
требуют сравнимых объемов вычислений для одинакового продвижения на
длину шага Л. При их применении к у'=\у надо сравнивать
многочлены
имеющие одну и ту же степень. Тогда теорема 4.15 дает
S2-517^51-52, или 5Г'г5 5Г'.
Рис. 4.5. Нормированные области устойчивости методов Тейлора B.12).
В качестве иллюстрации этой теоремы на рис. 4.5 представлены
нормированные области устойчивости для методов Тейлора порядков
1, 2, 3, 4 (сравните с рис. 2.1). Отчетливо видно, что ни одна из них
не содержит в себе другую.
76 Гл. IV. Жесткие задачи — одношаговые методы
Рациональные аппроксимации
с вещественными полюсами
«Удивительный результат: наибольший достижимый
порядок равен m-fl».
(Нёрсетт и Вольфбрандт 1977)
Функции устойчивости диагонально неявных методов Рунге—Кут-
ты (методов ДНРК), т.е. методов с a,j=0 при i<j, имеют вид
"|"=A-..,)A-?;).м1-.,,)' <^"'
где 7t =^й (г=1,... ,5) и degP < s. Это сразу следует из
формулы C.3) предложения 3.2, так как детерминант треугольной матрицы
равен произведению ее диагональных элементов. Поэтому R(z)
обладает вещественными полюсами 1/7ц V72' - - -> ^lls • Такие
аппроксимации е^ возникнут также в следующих разделах в качестве функций
устойчивости методов Розенброка и так называемых однократно
неявных методов Рунге—Кутты. Таким образом, они заслуживают
более подробного изучения. Исследование этих аппроксимаций с
вещественными полюсами было начато Нёрсеттом A974) и Вольфбрандтом
A977). Многие результаты собраны в их совместной статье (Нёрсетт
и Вольфбрандт 1977).
Если порядок метода не меньше s, то P{z) дается формулой C.18).
Здесь и в дальнейшем мы очень часто будем записывать формулы для
5=3 без постоянных напоминаний, насколько тривиально их
обобщение для произвольного 5. Следовательно, для «=3
ши- ^"^HTT-fM^ К^-Ц^Ш^' 1з! " 2!-^Т! ~ oFJ
D.20)
где
Оо = 1, -^i = 7i + 72 ¦*¦ 7з' '^2 —7i72+7i73 + 7273i •^з —7i7273-
Константа погрешности при p=s имеет вид
^-4! 3!^2! !!• ^^'^^^
Теорема 4.18. Пусть R{z) — аппроксимация е^ порядка р,
имеющая только вещественные полюсы^ и пусть к — степень ее числителя.
Тогда
p</:-fl.
Доказательство. Если сектор порядковой звезды А оканчивается
полюсом на вещественной оси, то в силу симметрии комплексно
сопряженный сектор должен с ним соединяться. Поэтому все белые
секторы, лежащие между этими двумя, должны быть конечными (рис. 4.6).
IV.4. Порядковые звезды
77
То же самое верно для секторов, примыкающих к бесконечной части
А. Таким образом, с каждой стороны вещественной оси существует не
более нем один белый сектор, могущий быть бесконечным. Тогда,
согласно лемме 4.5, остальные р—1 белых секторов все вместе требуют
не менее р—1 нулей, т.е. имеем р—1 <к. П
Рис. 4.6. А11проксимащ1я с вещественными полюсами, 3 нуля, порядок 4.
Замечание 4.19. Если p>fc, то по крайней
мере один белый сектор должен быть неограниченным.
Тогда это или первый сектор на положительной
вещественной оси, или, в силу симметрии,
существует пара таких секторов. Как следует из
доказательства теоремы 4.18, эта пара единственная; назовем ее
«пробором Кэри Гранта».
Замечание 4.20. Если p=/:-fl (оптимальный случай), то
существует к-\-2 белых секторов, из них два бесконечных. Поэтому каждый
из оставшихся к секторов должен содержать в точности один корень
P(z). Следовательно, С<0 тогда и только тогда, когда P(z) не
имеет положительных вещественных корней между началом координат и
первым полюсом.
«Сэндвич» с вещественными полюсами
Займемся теперь более детальным анализом аппроксимаций D.19)
порядка р>5 (Нёрсетт и Ваннер 1979). Нас будут интересовать два
множества:
Определение 4.21. Назовем L множество Gi»-j7*) такое, что в
D.20) degP(^)<s-l, т.е. Л (ос)=О, если 7,-^ О (i=l,...,s).
Определение 4.22. Обозначим Я множество Gi» • Л*) такое, что
константа погрешности D.21) равна нулю, т.е. аппроксимация имеет
наивысший возможный порядок р=54-1.
78 Гл. IV. Жесткие задачи — одношаговые методы
Из теоремы 4.18 следует, что
ЬПН = т, D.22)
С учетом D.20) и D.21) запишем множества L и Н для случая 5=3
(обобщения для произвольного s очевидны):
г-и ^\ ^ 71+72 + 73 , 7172 + 7173-1-7273 717273 _ п\
L=|G1,72,73);5j 2! "^ 1! Or=V'
rr^U ч 1 71+72 + 73 . 7172 + 7173 + 7273 717273 _ л\
Я = |Gь72,7з);^ 3! "^ 2! Т^=^\'
D.23)
Теорема 4.23 (Нёрсетт и Ваннер 1979). Каждая из поверхностей Н
и L состоит из S отдельных связных листов
L = L^UL^U...UL, , Н = Н^иН^и.,.иН,. D.24)
Если направление rf= (E^,...,($,) выбрано так, что все S^^O и если к
из них положительны, то луч
^ = {G1, •..,7,); 7.=Ч-, 0<<<оо} D.25)
пересекает листы Я^, Z/j, Я2, Lj,..., Я^^, Lf^ в таком порядке и
никаких других листов не пересекает.
Доказательство. После того, как rf,- выбраны, подстановка 7, =<<^,
в D.23) дает
1 /i+<^2+<^3 . ^2^1^2-^^1^3"^<^2^3 43<^1^2<^3 _n
3! ^ 2! ^^ 1! ^ 0! """' D 26)
1 .^i+S^+S^ , .2<^1<^2+<^1^3"^Уз ^3<^1^2^3_n
4! 3! 2! 1!
для L и я соответственно. Это многочлены третьей (в общем случае
s-й) степени, положительные корни которых требуется исследовать.
Будем варьировать S и, следовательно, луч X, взяв для начала все
компоненты S отрицательными. Тогда у многочленов D.26) все
коэффициенты положительные и, очевидно, нет положительных
вещественных корней. Если теперь одна дельта, скажем Jg, меняет знак,
то старшие коэффициенты в D.26) при этом обращаются в нули, и
один корень каждого уравнения уходит в бесконечность,
удовлетворяя асимптотически
ДЛЯ L и Н соответственно. Таким образом, Я опускается вниз, а L
поднимается вверх. Но так как ЬГ\Н = 9 (см. D.22)), эти два корня
никогда не смогут пересечься и поэтому должны оставаться в этой
конфигурации (см. рис.4.7).
IV.4. Порядковые звезды
79
все Si < О 5^ = 0 S^ = 0 S^=0 все S- > О
Рис. 4.7. Образование «сэндвича».
Рис. 4.8. «Сэндвич» для 5=3
и для 5=5.
Если теперь последовательно изменять знаки ^2 и E^, то та же
самая ситуация будет повторяться снова и снова, два листа Н и L
будут располагаться всегда одинаковым образом и лежать на нижних
листах подобно ломтикам хлеба и ветчины в огромном сэндвиче. Так
как ЬПН=9, эти листы никогда не смогут пересечься, т.е. два
корня для L или Н никогда не смогут слиться и стать комплексными.
J аким образом, все корни остаются вещественными. Теорема
доказана. Расположение этих поверхностей в трехмерном пространстве
представлено на рис.4.8. П
80 Гл. IV. Жесткие задачи — одношаговые методы
Следующая теорема описывает форму соответствующей
порядковой звезды на всех этих листах.
Теорема 4.24. Пусть G^,..., G, — открытые связные компоненты
множества М*\Я такие, что L, лежит в G^y и пусть Gq —
компонента, содержащая начало координат. Порядковая звезда функции R(z)
D.20) имеет ровно к ограниченных «пальцев» справа от «пробора
Кэри Гранта» в том и только в том случае, если
G1,...Л,)€С^иЯ^.
Доказательство. Для доказательства воспользуемся
соображениями непрерывности при перемещении точки Gi> • • • ?Те) сквозь
«сэндвич». Поскольку «пробор Кэри Гранта» всегда существует (см.
замечание 4.19), число ограниченных секторов может измениться только
там, где константа погрешности С D.21) меняет знак, т.е. на
поверхностях Н^у Яз,..., Я^. На рис.4.9 дано несколько моментальных
снимков этого перемещения для 5=3 и 71=72=7з=7- В этом случае
уравнения D.23) принимают вид
Их корни
1^37 37^^7!^.
3! 2! 1! О! '
1^37 37^_7l_.
4! 3! "^ 2! 1!
Ai = 0.158984, А2 = 0.435867, A3 = 2.40515,
Xi = 0.128886, Х2 = 0.302535, Хз = 1.06858
D.28)
D.29)
чередуются, как требуется по теореме 4.23. Утверждение теоремы
4.24 для 5=3 можно отчетливо наблюдать на рис. 4.9.
Для доказательства общего утверждения мы также положим 7i =
.. .=7, =7 и исследуем два крайних случая.
1. 7=0: здесь R{z) —тейлоровский многочлен 1-[-г+.. .-f-z^/s!, у
порядковой звезды которого вообще нет ограниченных секторов.
2. 7"^ ОС- числитель R{z) в D.20) при 5=3 имеет вид
D.30)
При 7 "> ос последнее выражение переходит в
1_^C + С7ф)+^2C + С7ф)-«,3A + 0A)),
где zy=w, и все корни гу,- -> 1, т.е. г,- -f I/7 (см. последнюю
картинку на рис. 4.9). Поэтому слева от «пробора Кэри Гранта» не может
остаться ни одного нуля R{z), и мы имеем s ограниченных «пальцев».
IV.4. Порядковые звезды 81
7=2.40515
Рис. 4.9. Порядковые звезды для 7» перемещающегося сквозь «сэндвич».
82 Гл. IV. Жесткие задачи — одношаговые методы
Заключение теоремы 4.24 теперь следует из того, что между
этими крайними случаями имеется не более чем s пересечений
поверхности Н. П
Теорема 4.25. Функция R(z) D.20) может быть I-устойчивой тогда
и только тогда, когда
G1,...Л,)€Я^иС^иЯ^^1, если s = 2q^\,
и
G1,...,%)еС^иЯ^^1иС^^1, если s = 2q.
Доказательство. Обоснование этого результата сходно с
обоснованием теоремы 4.12. Если имеет место /-устойчивость, то мнимая
ось не может иметь пересечений с порядковой звездой и должна
поэтому достигать начала координат, находясь в «проборе Кэри Гранта».
Таким образом, /-устойчивость (а следовательно, и Л-устойчивость)
возможна только где-то в середине «сэндвича». Поскольку не более
[{р-\-2)/2] и не менее [(р-|-1)/2] из p-hl секторов А начинаются в С+ ,
то число к ограниченных «пальцев» удовлетворяет неравенствам
<к.
2
По определению, p=s-hl на Я и p=s на G. Подставляя эти значения
в наши неравенства, получаем требуемый результат. П
Аппроксимации с кратным вещественным полюсом
«... следующий основной результат: С принимает нал-
меньшее значение, когда все нули знаменателя
совпадают». (Нёрсетт и Вольфбрандт 1977)
Аппроксимации, у которых все полюсы совпадают, т.е. у которых
7j =72 = - • —75—7i называются аппроксимациями с кратным
вещественным полюсом (Нёрсетт 1974). Мы и здесь будем рассматривать
только аппроксимации, порядок которых > s. Они имеют вид (для
5 = 3)
где P(z) задается D.30), а их константа погрешности
Аппроксимации с кратным полюсом имеют много вычислительных
преимуществ: у всех линейных систем, которые требуется решать в
методах Розенброка или ДНРК, одна и та же матрица (см. разделы
IV.4. Порядковые звезды 83
IV.6 и IV.7)). Кроме того, оказывается, что у них еще и наименьшие
константы погрешности (Нёрсетт и Вольфбрандт 1977).
Теорема 4.26. На каждой из поверхностей L- и Н- (z = l,...,s)
константа погрешности С аппрокси\{ации D.20) минимальна (по
абсолютной величине), когда 7^ =72==- -=75 •
Доказательство. В нашем доказательстве используются
относительные порядковые звезды (подобные D.13))
B={zeQ \q(z)\ > l}, q(z) = ^^, D.33)
где Roidi^) — аппроксимация с вещественными полюсами, имеющая
порядок р=5+1 и соответствующая 7i) • • ^7, ? ^ ^newi^) получена в
результате бесконечно малого изменения значений 7- Предположим,
что не все 7i равны между собой, и покажем, что тогда константа
погрешности может быть уменьшена. Надлежащей перестановкой
индексов всегда можно сделать 7i=maxG,), и пусть 75<7i • По теореме
4.23 7i>0, так что l/7i представляет ближайший к началу координат
полюс на положительной вещественной оси. Вместо произвольных
изменений 7 мь1 будем уменьшать 7i, зафиксировав 72> • • -y^s-i' ^
определим 75 из уравнения, определяющего Я (см. D.23)).
Например, для 5=3 имеем
1 71+72 . 7i72
? а^ 2L.. D.34)
^ 71+72 I 7i72 ^
3! 2! "^ 1!
Поскольку полюсы и нули Roidi^) непрерывно зависят от 7, > полюсы
и нули q{z) рождаются всегда парами (назовем их диполями). Из
принципа максимума или из замечания 4.14 следует, что каждая
граничная кривая В, исходящая из начгила координат, должна пройти
по крайней мере через один диполь, прежде чем снова прийти в
начало координат. Поскольку имеется s+2=p-\-l диполей q(z) (одни и
те же полюсы Roidi^) и Rnewi^) и^ порождают диполь q(z)) и р-\-1
пар граничных кривых 5, исходящих из начала координат
(замечание 4.14), каждая такая граничная кривая проходит ровно через один
диполь прежде, чем вернуться в начало координат. Как следствие,
никакая граничная кривая В не может пересечь вещественную ось
нигде, кроме как в диполях.
Если константа погрешности Roid(^) удовлетворяет С^/^<0, то из
замечания 4.20 следует, что у Roid(^) иет нуля между l/7i и началом
координат. Поэтому у q{z) тоже нет диполя в этой области. Так как
полюс Rncwi^) С'^егка больше, чем l/7i (а это полюс Roidi^))^
вещественная ось между l/7i и началом координат должна принадлежать
дополнению В. Тогда из D.14) и D.15) следует, что C^^^-C^i^ > 0.
84 Гл. IV. Жесткие задачи — одношаговые методы
^Ш
I-
^o/d
Hnew
рисунки слева: C^/^ < 0
71 = 1.2
72 = 1.1
73 = 0.9455446
71 = 1.17
72 = 1.1
73 = 0.9628661
рисунки справа: C^/^ > 0
71 = 0.35
72 = 0.33
73 = 0.2406340
71 = 0.345
72 = 0.33
73 = 0.2440772
Рис. 4.10. Сравнение порядковых звезд Л и В.
Если C^i^ > О, то существует один дополнительный диполь q{z)
между l/7i и началом координат (см. замечание 4.20). Рассуждая
так же, как и выше, на этот раз мы заключаем, что C^cw^^^oid < 0.
В обоих случаях |C'„gy^|<|C^/^|, так как по непрерывности С^^^
близко к C^i^ . Отсюда следует, что никакой вектор Gi > •. • > Те) ^ ^»
у которого значения хотя бы двух компонент 7, не совпадают, не
может минимизировать константу погрешности. В то же время, если
хотя бы одна из компонент 7, стремится к оо, константа погрешности
становится большой по модулю. Это следует из теоремы 4.18 и из
того факта, что в этом случае R(z) стремится к аппроксимации, в
IV.4. Порядковые звезды 85
которой S заменено на s—1. Следовательно, минимальная по модулю
величина С будет достигнута, когда все полюсы совпадут.
В случае поверхности L доказательство такое же, только тогда
R(z) имеет s—l нулей и порядок p=s. П
Рис. 4.10 иллюстрирует порядковые звезды В в сравнении с Л.
Еще одно преимущество аппроксимаций с кратным вещественным
полюсом выявляет следующая
Теорема 4.27 (Килинг 1989). Фор\{ула D.20) дает минимальное
значение | Я(оо) | на каждой поверхности Я, П {Gi,. • • ,75)/ 7j>0}
при 7i=72 = --=7, •
Доказательство. Начало доказательства такое же, как и для
теоремы 4.26. Кроме l/7i и I/7,, в лучшем случае существует еще
четное число диполей на положительной вещественной оси справа от
l/7i. Как и в предыдущем доказательстве, заключаем, что правая
окрестность l/7i принадлежит В, так что ос должна лежать в
дополнении к В (ср. рис.4.10). Отсюда следует, что
I RneJoo) |<| Д„,^@0) I .
Поэтому никакой элемент множества Я П {Gi,. •, 7j) 5 7, >0} с хотя
бы двумя различными jj не может минимизировать | Д(оо) |. Если
7i —> оо, то I Д(оо) I тоже возрастает. Если же хотя бы одна из 7?
стремится к нулю, то | Я(оо) | стремится к бесконечности. Теорема
доказана. П
Упражнения
1. (Ил 1968.) Вычислите многочлен Е(у) для третьей и четвертой
субдиагонали Паде Rk^k.^{^) и Rk^k-H^^) (который, согласно
предложению 3.4, состоит только из двух членов). Покажите, что эти
аппроксимации нарушают условие C.6) и поэтому не могут быть
Л-устойчивыми.
2. Докажите общую формулу для аппроксимаций Паде Rf^j (j>k):
^ ¦"¦ r=[i±§±2] ^ '¦ ^'=1 ^
3. (Для фанатов математический точности.) Выведите следующие
формулы для корней А, и Xi уравнений D.28):
11 137Г X , /г /^ + 2я-\
^' = 2 + 7з'°'18"' A, = 1 + n/2cos(^-J,
86 Гл. IV. Жесткие задачи — одношаговые методы
1 1 257Г , . /?: /^ + 47г\
X2=2 + ^cos—, A2 = l4-v/2cos(>^-j,
X3=2 + ;^cos-, A3 = l4-V^cos(-J,
где в= arctg(V2/4).
Указание. Воспользуйтесь формулой Кардано—Виета (см.,
например, Хайрер и Ваннер A995), р. 66).
4. Докажите, что все нули многочлена
ТГ ~-^i A3Т)Т + ^2 GГ2)! - • • • ± 5,
вещественны и различны, когда вещественны все нули многочлена
Q{z) = l-zS,+z''S^-...±z'S,, 3,фО.
Кроме того, оба многочлена имеют одно и то же число
положительных (и отрицательных) нулей (Нёрсетт и Ваннер 1979; Бейлс,
Каракашьян и Сербии 1988).
Указание. Примените теорему 4.23. Это доставляет
геометрическое доказательство классического результата (см., например,
Пойа и Сегё A925), т. II, ч. V, JV? 65) и позволяет интерпретировать
R{z) как функцию устойчивости (вещественного) коллокационно-
го метода.
5. Докажите, что G, • ., 7) ^ ^ (определение 4.21), если и только если
L,(l/7)=0, где L^{x) обозначает полином Лагерра степени s (см.
Абрамовиц и Стиган A964), 22.3.9, или формулу F.11) ниже).
IV.5. Конструирование неявных
методов Рунге—Кутты
«Хотя, наверное, на данный момент большинство этих
методов предстгшляют главным образом теоретический
интерес...» (Ил 1968)
В разд. II.7 были представлены первые неявные методы Рунге—
Кутты. Как мы видели в разд. IV.3, не все они подходят для решения
жестких дифференциальных уравнений. Настоящий раздел посвящен
подборке из нескольких классов полностью неявных методов Рунге—
Кутты, обладающих хорошими свойствами устойчивости.
Конструирование таких методов существенно опирается на
упрощающие предположения
В(Р): i2^'i'i~' = l 9=h.
.=1 ч
.р;
с?
dv): Е«.Л-"^ = -' i=l,...,s, <,= !,.
'
.»/;
ЩО- ^6,сГ'а,,. = ^{1-ф, j=l,...,5, .7=1,..,С.
1=1 ^
Условие В(р) просто означает, что квадратурная формула F,, с,)
имеет порядок р. Важность двух других условий видна из следующей
фундаментальной теоремы, которая была выведена в разд. П.7.
Теорема 5.1 (Бутчер 1964). Если коэффициенты 6,, с,, а, • метода
Рунге—Кутты удовлетворяют условиям В(р), С(г)), D(C) и при этом
Р ^ ^+С -\-1 и р< 2r;-h2, то метод имеет порядок р. П
Гауссовы методы
Эти процессы, названные в разд. II.7 «методами Кунцмана—Бут-
чера», представляют собой коллокационные методы, основанные на
квадратурных формулах Гаусса, т.е. с^,..., с, являются нулями
смещенного полинома Лежандра степени s
Ради полноты в таблицах 5.1 и 5.2 представлены первые из этих
методов.
88
Гл. IV. Жесткие задачи — одношаговые \»« годы
Таблица 5.1. Гауссовы методы порядков 2 и 4
1 v^
2 6
1 v^
2 + -^
1
4
1 уД
4 + -6Г
1
2
1 уД
4 6
1
4
1
2
Таблица 5.2. Гауссов метод порядка 6
1 у/те
2 10
1
2
1 \/Т5
2 10
5
36
5 уДЕ
36 24
5 уДЕ
36 30
5
18
2 уДЕ
9 15
2
9
2 \/15
9 15
4
9
5 >/Г5
36 30
5 уДЕ
36 24
5
36
5
18
Теорема 5.2 (Бутчер 1964, Ил 1968). S-стадийный гауссов
метод имеет порядок 2s. Его функция устойчивости является (s,s)-
аппроксимацией Паде, и метод Л -устойчив.
Доказательство. Утверждение относительно порядка уже
было доказано в разд. II.7. Поскольку степени числителя и
знаменателя не выше s для любого 5-стадийного метода Рунге—Кутты,
функция устойчивости этого метода порядка 25 должна быть (s,s)-
аппроксимацией Паде согласно теореме 3.11. Л-устойчивость тогда
следует из теоремы 4.12. П
Методы Радо IA и Радо ПА
Методы Рунге—Кутты, основанные на квадратурных формулах
Радо и Лобатто, были представлены Бутчером A964). Он назвал
их процессами типа I, II или III в соответствии с тем, являются ли
Cj,..., с, нулями полиномов
I: ^j^(x*(x-l)^-^), (Радо левый) E.1)
II: ^^(х*-^(х-1)^), (Радо правый) E.2)
III: ^^(^x'-^x-iy-^y (Лобатто) E.3)
IV.5. Конструирование неявных методов Рунге—Кутты
89
Веса 6^,..., 6, выбираются так, чтобы квадратурная формула
удовлетворяла B{s), что влечет B{2s-l) в случае Радой BBs-2) в случае
Лобатто (см. лемму 5.15 ниже). К сожалению, ни один из этих
методов Бутчера не оказался Л-устойчивым (см., например, табл.3.1).
Идеи Бутчера развил Ил A969), который сконструировал методы
типов I, II и HI с превосходными свойствами устойчивости. Независимо
Аксельссон A969) нашел методы Радо ПА вместе с элегантным
доказательством их Л-устойчивости.
5-стадийный метод Радо IA — это метод типа I, где
коэффициенты а, (г, j = l,.. .,5) определяются из условия D(s). Это можно
сделать единственным образом, так как с, различны и 6, ненулевые.
В таблицах 5.3 и 5.4 представлены первые из этих методов.
Таблица 5.9
0
1
1
. Методы Радо IA порядков 1 и 3
Таблица 5.4.
0
е-у/б
10
6-Ь\/б
10
1
9
1
9
1
9
1
9
0
2
3
1 1
4 ~4
1 5
4 12
1 3
4 4
Метод Радо IA порядка 5
-1-V6
18
88 -h 7л/б 1
360
88Н-43>/б
360
1б-Н\/б
36
-1Ч-\/б
18
58 - 43>/б
360
88-7л/б
360
16-л/б
36
Процессы Ила типа II получаются, если наложить условие C(s).
По теореме II.7.7 это приводит к коллокационным методам на основе
нулей многочлена E.2). Они называются методами Радо ПА.
Примеры даны в таблицах 5.5 и 5.6. При s= 1 мы получаем неявный метод
Эйлера.
Теорема 5.3. S-стадийный метод Радо IA и s-стадийный метод
Радо ПА имеют порядок 2s—I. Их функция устойчивости [s—\,s) есть
субдиагональная аппроксимация Паде. Оба метода Л-устойчивы.
Доказательство. Утверждение относительно порядков следует из
теоремы 5.1 и леммы 5.4 (см. ниже). Поскольку для метода Радо IA
90
Гл. IV. Жесткие задачи — одношаговые методы
Таблиид 5.5. Методы Радо НА порядков 1 и 3
1
3
1
5
12
3
—
4
3
4
1
12
1
—
4
1
4
Таблица 5.6. Метод Радо НА порядка 5
4-\/б
10
4 + ^6
10
1
88-7\/б
360
296 -Ь 169>/б
1800
16-V6
36
16-V6
36
296 - 169лЛ
1800
88-Ь7\/б
360
16-fv/6
36
16-fv/6
36
-2Ч-3\/б
225
-2-3v/6
225
1
9
1
9
Cj=0, из D{s) для j=l и 8B8—1) следует C.14). Аналогично, для
метода Радо ПА из с, = 1 и C(s) следует C.13). Поэтому в обоих
случаях числитель функции устойчивости имеет степень < s—l согласно
предложению 3.8. Утверждение теперь следует из теоремы 3.11 и
теоремы 4.12. П
Лемма 5.4. Пусть s-стадийный метод Рунге—Кутты имеет
различные с^,..., Сд и ненулевые веса 6^,..., 6,. Тогда
a) из C(s) и B{s-\-i/) следует D(i/);
b) из D(s) и B(s-\-i/) следует C(i/).
Доказательство. Положим
4''-EVr'a.-f(l-el).
1 = 1 ^
Из условий C(s) и B{s-{'i/) следует
E.4)
^dfc']-' = 0 для к=1,...,
9 = 1,
, 1^-
Таким образом, вектор (dj ,..., с^* ) должен быть нулевым, как
решение однородной линейной системы с невырожденной матрицей типа
IV.5. Конструирование неявных методов Рунге—Кутты 91
матрицы Вандермонда. Это доказывает справедливость
предположения D{iy).
Для части (Ь) надо положить
«.'"-Е <¦.,»?-'-f
j = l ^
И провести аналогичное рассуждение для
я
^6,с*-'е,<''=0, k = l,...,s, 9 = 1,...,t/. П
» = 1
Методы Лобатто IIIA, IIIB и IIIC
Для всех процессов типа III с,- — нули многочлена E.3), а веса 6,
таковы, что удовлетворяется предположение BBs—2).
В методах Лобатто IIIA коэффициенты а,^ определяются из
условия C{s). Поэтому они являются коллокационными методами.
Методы Лобатто IIIB получаются наложением условия D(s). Наконец,
чтобы получить методы Лобатто II 1С, надо положить
а-^=Ь^ для г=1,...,5, E.5)
Таблица 5.7. Методы Лобатто IIIА порядков
0
1
0
1
2
1
2
0
1
2
1
2
0
1
2
1
0
5
24
1
6
1
6
0
1
3
2
3
2
3
2и4
0
1
24
1
6
1
6
Таблица 5.8. Метод Лобатто IIIA порядка б
0
5-уД
10
5 + v^
10
1
0
11 + \/5
120
ll-v/5
120
1
12
1
12
0
25-ч/б
120
25+13ч/5
120
5
12
5
12
0
25-13\/5
120
25-f n/5
120
5
12
5
12
0
-1 + \/5
120
-1-^5
120
1
12
1
12
92
Гл. IV. Жесткие задачи — одношаговые методы
Таблица 5.9. Методы Лобатто IIIB порядков 2 и 4
0
1
1
2
1
2
1
2
0
0
1
2
0
1
2
1
1
6
1
6
1
6
1
6
1
6
1
3
5
6
2
3
0
0
0
1
6
Таблиид 5.10. Метод Лобатто IIIB порядка 6
0
5-л/5
10
5 + л/5
10
1
1
12
1
12
1
12
1
12
1
12
-1-у/Е
24
25 + >/5
120
25 4-13\/5
120
11-\/5
24
5
12
-1 + \/5
24
25 - 13\/5
120
25-л/5
120
11 + \/5
24
5
12
0
0
0
0
1
12
а остальные а- определить из условия C(s—1). Ил A969) открыл
первые два класса и представил методы IIIC для s<3. Общее
определение методов IIIC дано Чипманом A971); см. также Аксельссон
A972). Примеры приведены в таблицах 5.7-5.12.
Теорема 5.5. Методы Лобатто IIIA, IIIB и IIIC при s стадиях
имеют порядок 2s--2. Функция устойчивости для методов Лобатто
IIIА и IIIB является диагональной {s-l^ s-l) -аппроксимацией Паде.
Для метода Лобатто IIIC она является (s-2, s) -аппроксимацией Паде.
Все эти методы А-устойчивы.
Доказательство. Сначала докажем, что методы IIIC
удовлетворяют предположению D(s-l). Из условия E.5) следует, что ^^^^^=0
(qf=l,.. .,5-1) для , задаваемых E.4). Условия C(s—l) и jBB5—2)
затем дают
J2^i^^^j'^=^ ^^^ А=1,...,5-1 и д=1,...,5-1.
Справедливость предположения D(s—l) докг13ывается, как в
доказательстве леммы 5.4. Все утверждения относительно порядков теперь
следуют из леммы 5.4 и теоремы 5.1.
IV.5. Конструирование неявных методов Рунге—Кутты
93
Таблица 5.11. Методы Лобатто II 1С порядков 2 и 4
0
1
1
2
1
2
1
2
I
2
1
2
1
2
0
1
2
1
1
6
1
6
1
6
1
6
1
3
5
12
2
3
2
3
1
6
1
12
1
6
1
6
Таблицд 5.12. Метод Лобатто II 1С порядка б
0
5->/5
10
5 + \/5
10
1
1
12
1
12
1
12
1
12
1
12
12
1
4
10 + 7л/5
60
5
12
5
12
n/5
12
10-7л/5
60
1
4
5
12
5
12
-1
12
Уз
60
-ч/5
60
1
12
1
12
Таблица 5.13. Полностью неявные методы Рунге—Кутты
метод
Гаусса
Радо IA
Радо ПА
Лобатто IIIА
Лобатто IIIB
Лобатто II 1С
упрощающие
предположения
В{2з) С{з) D{s)
BBs^l) C{s-l) D(s)
В{2з-1) С{з) DC-l)
ВBз-2) С(з) DC-2)
В{2з-2) СE-2) 0(з)
ВB5-2) СE-1) D{3-1)
порядок
25
25-1
25-1
25-2
25-2
25-2
функция
устойчивости
E,5)-Паде
E—1,5)-Паде
E—1, 5)-Паде
E—1, 5—1)-Паде
E—1,5 —1)-Паде
E—2, 5)-Паде
По определению, для методов П1А первая строка матрицы Л
метода Рунге—Кутты, а для методов 1ПВ последний столбец А состоят
из нулей. Знаменатель функции устойчивости поэтому имеет
степень <s—l. Ангипогично, для методов П1А последняя строка
матрицы Л—116^ обращается в нулевую, а для методов П1В обнуляется ее
94
Гл. IV. Жесткие задачи — одношаговые методы
первый столбец. Поэтому числитель их функции устойчивости
также имеет степень < s—l согласно формуле C.3). Теперь из теоремы
3.12 следует, что оба метода имеют в качестве функции устойчивости
E—1,5—1)-аппроксимацию Паде.
Для процесса IIIC обнуляются первый столбец и последняя строка
матрицы Л—116^. Тогда по формуле C.3) степень числителя
функции устойчивости не превосходит 5—2. Доказываемое утверждение
следует снова из теоремы 3.11 и теоремы 4.12. D
В таблице 5.13 суммированы утверждения приведенных теорем.
VT-преобразование
Теперь мы вплотную займемся конструированием всех тех методов
Рунге—Кутты, для которых справедлива теореЫа 5.1. Чипман A971)
и Берридж A978) первые заметили, что упрощающее предположение
С(т]) может быть записано в виде
/1
11
Г
\cisi
аь
ass -
/1
\1
ci
Cs
я-1
\
л-1 /
Cs 1
С1
\1 с.
Л
Cs I
Следовательно, если V — матрица Вандермонда
\i с.
/0 0 .
[10.
0 ^ .
{о 0 .
.. 0\
.. 0 \
.. 0
E.6)
^1
то первые ;; (при г)<$—1 ) столбцов матрицы K~MV должны иметь
специальную структуру (с большим количеством нулей) самой правой
матрицы в E.6). Это « V-преобразование» уже значительно упрощает
исследование порядков и устойчивости методов, для которых
выполнено предположение С{т}) с г/, близким к s (Берридж 1978). Таким
образом, коллокационные методы (rj^s) характеризуются матрицей
-/»о/« \
-Pi/s
/О
1
i/-Mv =
О
1/2
О
\
О -p,-2h
l/(s-l) -p,.jsj
E.7)
где р — коэффициенты многочлена М[1) = \\\^^{1—с^), которые
появляются, когда с\ в E.6) заменяются низшими степенями.
Всякий раз, когда некоторые из столбцов К"Ml/ не такие, как в E.7),
IV.5. Конструирование неявных методов Рунге—Кутты
95
удачная идея Нёрсетта позволяет интерпретировать метод как
возмущенный коллокационный метод (подробности см. Нёрсетт и Ваннер
A981)).
Однако у К-преобразования есть некоторые недостатки: оно не
позволяет аналогично характеризовать D(Q, и рассмотрение Л- и
Б-устойчивости остается довольно сложным (см., например,
вышеупомянутые работы). Тогда было обнаружено (Хайрер и Ваннер
A981), A982)), что более приятные результаты получаются, если
матрицу Вандермонда V заменить матрицей W, элементы которой —
ортогональные многочлены, вычисленные в точках с,. Поэтому
будем использовать (нестандартное) обозначение
к
'-'("=^^ <'*<'-"*)=^в-"'" G) СТ)
ДЛЯ смещенных полиномов Лелсандра, нормированных так, что
E.8)
P^,{x)dx=\.
Эти многочлены удовлетворяют интегральным формулам
L
[
о ^
Pk{t)dt = ^k+iPk+i{^)-ikPk-i{x), к = 1,2,...,
где
2\/4к'^-1
E.9)
E.10)
E.11)
(см. упр. 1). Теперь вместо E.7) имеем следующий результат:
Теорема 5.6. Пусть матрица W определена как
«'.¦i = ^'i-i(c.), i=l,...,s, j=l,...,s E.12)
и пусть А — матрица коэффициентов метода Гаусса порядка 2s.
Тогда
/1/2 Нг \
\V-^AW= ^2 ~-^G- E13)
Доказательство. Сначала запишем С(т}) в форме
Д гСг
^%P(^j)= P{^)<i^^ если deg(p)<77-l.
E.14)
96 Гл. IV. Жесткие задачи — одношаговые методы
что, с учетом E.10), эквивалентно соотношениям
' 1
j=i
E.15)
J2%^kicj) = ^k+iPk^i{ci)-^kPk^i(Ci). /:=:1,...,77-1.
i=l
При T] = s после подстановки E.12) в матричных обозначениях они
принимают вид
/а
11
au\ /^п ¦¦¦ «хЛ
\«и ••• ««/ V
E.16)
"»!
to
J
/-П ••• -, РЛс,)\ /f -^^ _^^
\«;„ ... w„ Р,{с,)/
\
О Ч,_1
С-1 О
Поскольку для процессов Гаусса Р^ (cj) =... = Р, (с,) = О, последний
столбец первой и последняя строка второй матрицы в правой части
могут быть опущены, и мы получаем E.13). П
В дальнейшем мы изучим аналогичные результаты для других
неявных методов Рунге—Кутты. Но сначала сформулируем
следующую лемму, которая является непосредственным следствием E.15)
и E.16).
Лемма 5.7. Пусть А — матрица коэффициентов неявного метода
Рунге—Кутты и W — невырожденная матрица с
Wij = Pj_^(Ci) для г = 1,...,5, j = l,...,r7+l.
Тогда предположение СG]) (при i]<s—l) эквивалентно тому факту,
что первые г} столбцов матрицы W~^AW равны первым т] столбцам
матрицы Xq в E.13). П
Упрощающее предположение второго типа, D[Q, теперь
записывается в форме
Y1 ^iTP^^i)^ij = h / Р(^)^^' если deg(p) < С - 1. E.17)
t=i ^cj
IV.5. Конструирование неявных методов Рунге—Кутты
97
Интегральные формулы E.10) совместно с условиями
ортогональности
/ PQ{x)dx = l, 1 P^(x)dx= I PQ(x)Pf^(x)dx = 0 для к=\.2....
Jo Jo Jo
показывают, что D((^) (т.е. E.17)) эквивалентно соотношениям
E.18)
1 = 1
5
E^*(^.)^«u= (^fc^*-i(S)-Wi^fc+i('^j))*i' /:=!,...,C-1.
1 = 1
Это может быть сформулировано как
Лемма 5.8. Пусть, как и в предыдущей лемме, W —
невырожденная матрица с
Wij=^ Pj^^{Ci) для г=1,...,5, j = l,...,C+l
и B=diag{b^, • • 1 ^а) с Ь-фО. Тогда D(Q (при (^<s —I) эквивалентно
условию, что первые С строк матрицы {W^В)А(\У^В)~^ равны
первым С строкам матрицы Xq E.13). (Если матрица В —
вырожденная, нижеследующая формула E.19) все еще остается справедливой.)
Доказательство. Формулы E.18), записанные в матричной
форме, дают
/1/2 4i \
^1 О •.
W'^BA =
^С-1
О
-^с
\ *
*/
W'^B.
E.19)
Теперь возникает естественный и интересный вопрос, могут ли
быть сделаны равными матрицы обоих преобразованиий в
предыдущих леммах, т.е. справедливо ли равенство
W'^B = W-^ или W'^BW = I. E.20)
Первый результат таков:
Лемма 5.9. Для любой квадратурной формулы порядка > 25—1
матрица
удовлетворяет равенству E.20).
E.21)
Пп, О
98 Гл. IV. Жесткие задачи — одношаговые методы
Доказательство. Если квадратурная формула имеет достаточно
высокий порядок, многочлены Р;^(х)РДх) (к-\-1 <2s—2)
интегрируются точно, т.е.
^6,Р,(с,)РЛс,)= / P,(x)P^(x)dx = S,r. E.22)
это равенство, однако, и есть просто W^BW = I. П
К сожалению, условие E.20) слишком ограничительно для многих
методов. Поэтому ослабим наши требования следующим образом:
Определение 5.10. Пусть заданы два целых числа г) и (^ между О
и 5—1. Будем говорить, что s х «-матрица W удовлетворяет условию
T(tjX) Лля квадратурной формулы F,-,с,),?_^, если
a) W невырожденная,
b) Wij = Pj_^(Ci), г = 1,...,5, j= l,...,max(r/,CL-l,
c) W-BW=(^j^ «),
где / —единичная (С+1) х (С-Ы)-матрица, тогда как R
—произвольная (s-^C"!) X E—С"" 1)-матрица.
Основной результат формулируется в следующей теореме.
Вместе с теоремой 5.1 она очень полезна при конструировании методов
высокого порядка (см. примеры 5.16 и 5.24, а также теорему 13.15).
Теорема 5.11. Пусть матрица W удовлетворяет условию ТG], Q
для квадратурной формулы (fc,,c,)*_i. Тогда для метода Рунге—
Кутты, основанного на F,, с^), у матрицы X = W~^AW
a) первые rj столбцов такие же, как у Xq <=> С(т]),
b) первые С строк такие же, как у Xq <^=> D[Q .
Доказательство. Эквивалентность (а) и С[г)) следует из леммы
5.7. Для доказательства (Ь) умножим E.19) справа на И^ и получим
W^BW •Xz::X'W'^BW,
где X — большая матрица из E.19). По условию (с) для T(rjX)
первые С строк X и X должны быть одни и те же (запишем их как
блочные матрицы). Утверждение теперь следует из леммы 5.8. П
До сих пор мы оставляли открытым вопрос о существовании W,
удовлетворяющей ТG;, Q. Следующие две леммы и теорема 5.14
дают ответ:
Лемма 5.12. Если узлы с- квадратурной формулы различны, все
веса положительны F, > 0) и ее порядок равен р, причем р > 277+1 и
р > 2С+1, то матрица
W
= fe.i(^,)). . , E-23)
IV.5. Конструирование неявных методов Рунге—Кутты 99
обладает свойством Т(т], Q и удовлетворяет E.20). Здесь Pj(x) —
многочлен степени j, ортонормированный относительно скалярного
произведения
5
(р, г) = ^6.р(с,)г(с,). E.24)
1=1
Доказательство. Положительность коэффициентов b позволяет
рассматривать E.24) как скалярное произведение в пространстве
многочленов степени < s—l. Из-за свойства порядка (ср. с E.22)) орто-
нормированные Pj{x) должны совпадать для j < maxG;. С) с
полиномами Лежандра Pj(x). Ортонормированность относительно E.24)
означает, что W'^BW = I. П
Лемма 5.13. Если узлы с, квадратурной формулы различны и ее
порядок р> 5-fC, то Wy определенная в E.21), обладает свойством
Доказательство. Так как р> 5-1-С» то равенство E.22) справедливо
для fc=0,...,s—1 и /=0,...,С- Это гарантирует выполнение условия
(с) в определении 5.10. П
Теорема 5.14. Пусть квадратурная формула имеет порядок р.
Тогда преобразование, обладающее свойством T(tj, Q, существует, если
и только если
p>77-hC-M и р>2С+1 E.25)
и не менее чем тахG;, С)+1 чисел среди с^,..., с, различны.
Доказательство. Положим i/=max(r/,C) и для столбцов
преобразования W введем обозначения w^,.. .,ги^. Благодаря условию (Ь)
для Т(т),(^) имеем
i^j = (/'j-.i(ci),...,Pj_i(cj) для i=l,...,i/-hl.
Эти 1/-{-1 столбцов линейно независимы лишь при условии, что не
менее чем i/-\-l среди с^,...,с^ различны. Далее, условие (с) для
Т{т]Х) означает, что w^,.. .,w^^i ортонормальны к Wi,...,w^
относительно билинейной формы vTBv. В частности, ортонормальность
1/;^,..., ty^^i по отношению к w^,..., w^^^^ (ср. с E.22)) означает, что
квадратурная формула является точной для всех многочленов
степени i^+C- Поэтому р> г/-|-С-1 (что то же самое, что и E.25)) —
необходимое условие для выполнения Т[г), Q.
Чтобы показать его достаточность, мы дополним w-^,...,w^,^^ до
базиса в R*. Затем новые базисные векторы w^^^2^ • • i й^,
спроектируем на ортогональное дополнение span(u;j,..., w;^^i) относительно
vTBv посредством процесса ортогонализации типа Грама—Шмидта.
100 Гл. IV. Жесткие задачи — одношаговые методы
Это приводит к
Wj = Wj-'^{wlBwj)Wf^ для ;; = i/-f 2,.. .,s.
kzzl
Конструирование неявных методов Рунге—Кутты
Чтобы с помощью теоремы 5.11 конструировать неявные методы
Рунге—Кутты, удовлетворяющие В{р), С{т}) и D(C), нам надо
сначала выбрать квадратурную формулу порядка р. Основной результат
для интегрирования по Гауссу представляет следующая лемма:
Лемма 5.15. Пусть с^,..., с, — вещественные и различные и пусть
6^,..., 6д определяются условием B{s) (т.е. имеем
«интерполяционную» формулу). Тогда эта квадратурная формула имеет порядок
2s—к у если и только если многочлен M(x) = (x"-cJ(x—Cj)... (х—с,)
ортогонален всем многочленам степени < s—Аг—1, т.е. если и только
если
М{х) = с(РЛх) + а,Р,_,{х) + ...^а,Р,_,(х)). E.26)
Идея доказательства указана в упр. 2. П
Из E.26) видно, что все квадратурные формулы порядка 2s-k
могут быть классифицированы в терминах к параметров а^, aj,..., а;^.
Далее, если целые числа т; и С таковы, что выполняются
неравенства т/Ч-^-Ы < 25—Аг и 2СН-1 < 2s—к (ср. E.25)), то, воспользовавшись
теоремой 5.14 (или одной из лемм 5.12 или 5.13), можно вычислить
матрицу W, удовлетворяющую Т[г}, Q. Наконец, матрица X
выбирается так, чтобы удовлетворялись условия (а) и (Ь) теоремы 5.11. Тогда
по теореме 5.1 метод Рунге—Кутты с коэффициентами A = WXW-^
имеет порядок не ниже minG;4-C-bl, 27)-\-2).
Пример 5.16. Найдем все неявные методы Рунге—Кутты,
удовлетворяющие B[2s—2), C{s—\) и jDE—2), т.е. согласно теореме 5.1
методы порядка не ниже 2s-2. Как и в E.26), положим
Л/(х) = с(РЛх) + а,Р,_,(г) + а2Р,_2(х)). E.27)
Если а^ удовлетворяет
S - 1 y/2s -h 1
то корни М вещественны и различны (см. упр. 7). Матрица W,
задаваемая E.21), согласно лемме 5.13 обладает свойством T{s—\, 5-2).
IV.5. Конструрфовалие неявных методов Рунге—Кутты
101
Наконец, положим
Х=:
/1/2
' ^1
\
-е,
0
?,-2
4,-2
0
^.-1
0s-r
а.
E.28)
(см. теорему 5.11) и получим для A=WXW'^ семейство неявных
методов Рунге—Кутты порядка 2s—2 с четырьмя параметрами а^, aj,
Все методы в табл. 5.13 (кроме Лобатто IIIB) должны представлять
собой частные случаи. Соответствующие значения параметров
указаны в табл.5.14 (о том, как их вычислять, см. упр.З). Если положить
а 1=0 и a2=—y/2s -f l/y/2s — 3 (квадратура Лобатто), то получим двух-
параметрическое семейство (Чипман 1976).
Таблинд 5.14. Частные случаи метода E.27), E.28)
Метод
Гаусса
Радо IA
Радо ПА
Лобатто IIIА
Лобатто II 1С
«1
0
у/2зТ1/у/2з-1
-ч/27ТТ/\/27^
0
0
«2
0
0
0
-^/2sTl/^Дз^
0S
0
VD3-2)
1/D5-2)
0
1/B5-2)
/3,-1
-6-1
-6-1
-6-1
0
-6-iB^1)/(^l)
Функция устойчивости
Попробуем выразить функцию устойчивости неявного метода РК в
терминах преобразованной матрицы Рунге—Кутты X = W~^AW. Из
пунктов (Ь) и (с) свойства Т{г), Q следует, что
Н'е, = ]1, Ж^5]1 = е1, ei=(l,0,...,0)^. E.29)
Следовательно, формулы C.2) и C.3) переходят в
R(z) = l + ze'({I-zX)-^e^, E.30)
det(I - zX + ze^ej)
^^'^- det(I-zX) •
E.31)
Функция устойчивости зависит только от X и не зависит от лежащей
в основе квадратурной формулы. Как следствие, функция
устойчивости методов из примера 5.16 зависит только от /?, и Р^^-^. Формула
E.31) станет более симметричной (Хайрер и Тюрке 1984), если ввести
арифметическое среднее матриц X и X — e^ej и определить
1 т
Y = X-^€,€i\ E.32)
что есть просто матрица X , у которой из элемента A,1) вычтена 1/2.
102
Гл. IV. Жесткие задачи — одношаговые методы
Пp€tII/Ioжeниe 5.17. Пусть для метода Рунге—Кутты C.1) W
удовлетворяет Т[г], С) Д«^^ некоторых rj, (^>0 и пусть Y задается E.32),
где X = W~'^AW. Тогда функция устойчивости имеет вид
R(z) =
1 + Шг)
где
1-1ф(г)'
E.33)
E.34)
Доказательство. Применяя метод Рунге—Кутты к тестовому
уравнению B.9), получим
д = Ьо-^ zAg, 2/i = % + ^f>^9'
Если положить W~^g =^=(^^,... ,^,)^ , то эти уравнения можно
переписать в виде
z^
(I - zY)g = ei(yo + 2^1), Ух = Уо + ^9i >
E.35)
где использовано E.29). Вычислив д^ из первого уравнения E.35) и
подставив его во второе, придем к требуемому результату. П
Если для метода Рунге—Кутты при некотором целом v
удовлетворяются условия B{2u'\-\), С[и) и D(v), то У принимает вид
У =
/0
^1
V
-^1
0
-4
у.
\
E.36)
/
(см. теорему 5.11). В этом случае вычисление E.34) для матрицы
Y размерности {s,s) может быть следующим образом сведено к
вычислению той же функции для меньшей матрицы У^^ размерности
E—I/, 5—г/):
Теорема 5.18. Если У имеет вид E.36), то функция ФB:) E.34)
может быть представлена в виде непрерывной дроби
где
^f,{z) = zeJ{I-zY,)-'e,.
E.37)
Доказательство. Пусть через У (для О < j < i/-\-l) обозначены
главные миноры У размерности {s—j, s—j), где выброшены первые
IV.5. Конструирование неявных методов Рунге—Кутты 103
j строк и столбцов. Разложение детерминанта I—zY^^ по первой
строке (и затем по первому столбцу) дает для j = l,..., i/
det(/ - гУ^.. J = det(/ - zY^)^i^.z^ det(/ - zY^^^). E.38)
По правилу Крамера функции Ф^(г) можно записать также в виде
гг. , det(/~2ry..i)
Ф,(.) = .е[(/ - .У,)-е, = ^^^^f^. E.39)
Деление E.38) на det(/—гУ^) приводит к соотношению
Повторное применение E.40) дает E.37), так как ФB) = Фо(^)- ^
Таким образом, мы естественным путем подошли к разложениям
в виде непрерывных дробей — технике, которая исторически была
наиболее ранней: Биркхофф и Варга A965) применили ее в своем
доказательстве Л-устойчивости диагональных аппроксимаций Паде.
Позднее Ил A969, 1973) пытался обобщить «доказательство Варги»,
чтобы проверить Л-устойчивость первой и второй субдиагоналей
таблицы Паде. («Это не увенчалось успехом, так как получившиеся
разложения в виде непрерывных дробей было нелегко соотнести друг
с другом».) Поэтому Ил A973), а также Ил и Пайсел A975)
доказали Л-устойчивость для первой и второй субдиагонали и некоторые
обобщения с помощью совершенно другого метода. В последующих
исследованиях Л-устойчивости (см. Бутчер A977), Хайрер A982),
Хайрер и Тюрке A984)) рассмотренное выше разложение в виде
непрерывной дроби использовалось вместе со свойствами
положительных функций.
Пололсительные функции
«Многие условия устойчивости численных методов
могут быть выражены в форме требований
положительности некоторой ассоциированной функции».
(Г. Далквист 1978)
Л-устойчивость неявного метода РК определяется свойством
|Д(г)|<1 при Rez<0. E.41)
Поскольку преобразование (l-hC)/(l-C)» входящее в E.33),
отображает отрицательную полуплоскость на открытый единичный круг, E.41)
эквивалентно условию
ЕеФ(г)<0 при Кег<0. E.42)
104 Гл. IV. Жесткие задачи — одношаговые методы
Это условие означает, что —Ф(—г) — положительная функция; для
рациональных функций понятие положительности может быть
определено следующим образом:
Определение 5.19. Рациональная функция /(г) называется поло-
эюительной, если
Re/(г) >0 для Re2:>0.
Прекрасный обзор о применении положительных функций в
численном анализе дал Далквист A978). Следующие леммы суммируют
некоторые свойства положительных функций.
Лемма 5.20. Пусть f(z) и g(z) — положительные функции. Тогда
a) af(z)-\-/}g{z) положительная, если а> О и /? > 0;
b) l/f(z) положительная;
c) f{g{z)) положительная. П
Обратите внимание, что полюсы положительной функции не
могут лежать в положительной полуплоскости, но возможны полюсы на
мнимой оси; например, функция l/z положительная.
Лемма 5.21. Положим
f(z) = --\.g(z) С g{z) = 0(l) при z^O
и g{z) ^ 0. Тогда f(z) положительная, если и только если с > О и
g{z) положительная.
Доказательство. «Если»-часть следует из леммы 5.20.
Предположим теперь, что f(z) положительная. Постоянная с должна быть
неотрицательной, так как для малых положительных значений z
имеем Re/(г) > 0. На мнимой оси (кроме полюсов) Reg(iy)=:Re f(iy) > О
или, точнее,
liminf Re^(z)>0 для j/GM.
Тогда из принципа максимума для гармонических функций следует,
что либо g(z) = О, либо g{z) положительная. П
Следствие этой леммы — следующее характеристическое свойство
А -устойчивости.
Теорема 5.22. Рассмотрим метод Рунге—Кутты, функция
устойчивости которого задается формулой E.33) с матрицей У E.36). Такой
метод А-устойчив, если и только если
Re^^B:)<0 для Rez<0, E.43)
где ^^(z) = zej{l-zy^)-^e^, как и в E.37).
IV.5. Конструирование неявных методов Рунге—Кутты 105
Доказательство. Рассмотрим субматрицы У матрицы У и
функции ^j{2) из E.39). Поскольку предпочтительнее иметь дело с
положительными функциями, положим
Xj(z) = -'ij{-z) = zeJ{I + zY,)-^e,. E.44)
Согласно условию E.42) Л-устойчивость эквивалентна
положительности Хо(^) ^ 21 условие E.43) означает, что Xi/(^) — положительная
функция. Соотношение E.40) можно записать в виде
ixj.i(z)r' = l+^jxj{z)-
Поскольку все Xj(^) ограничены вблизи начала координат и не равны
тождественно нулю (см. E.44)), из леммы 5.21 следует, что Xj(^) —
положительная функция, если и только если Xj-ii^) положительная.
Это доказывает теорему. D
Пример 5.23. Для метода Рунге—Кутты из примера 5.16 с
матрицей X, задаваемой E.28),
,(.) = ^^^^1
1-0.^-^,-Л-1^'-
Поскольку
(*,-2W)" = ;-^->^'-r:fe'
из леммы 5.21 и теоремы 5.22 следует, что метод Л-устойчив, если и
только если
/?,_!= О или (/?,^1<0 и /?, >0). E.45)
Сравнение этого результата с таблицами 5.14 и 5.13 приводит ко
второму доказательству Л-устойчивости диагональной и двух первых
субдиагональных аппроксимаций Паде для е^ (см. теорему 4.12).
Пример 5.24 (конструирование всех Л-устойчивых методов
Рунге—Кутты, удовлетворяющих условиям BBs—4), C(s—2) и D(s—3)).
Возьмем квадратурную формулу порядка 2s—4 и построим согласно
теореме 5.14 матрицу W, удовлетворяющую свойству T(s—2, 5—3).
Тогда матрица Рунге—Кутты Л имеет форму
с У, задаваемой E.36), i/=s — 3 и
106 Гл. IV. Жесткие задачи — одношаговые методы
Для исследования на Л-устойчивость нужно вычислить ^g_^(z) из
E.39). Разлагая det(/ —гУ^_з) "^ ^^^ первому столбцу, получим
где
E.46)
По лемме 5.21 и теореме 5.22 имеем Л-устойчивость, если и только
если либо ^qCz^^ztO, либо
-'^^0+^'^) E.47)
является положительной функцией, что эквивалентно условиям
^7о>0. 91 >0. /2>0, 9ofi-9i>0 E.48)
(см. упр.4Ь). Аналогичное характеристическое свойство
Л-устойчивых методов РК порядка 25—4 получено в работе Ваннера A980).
Упражнения
1. Проверьте правильность формул интегрирования E.10) для
смещенных полиномов Лежандра.
Указание. По свойству ортогональности Jq Pf^[t)dt должен быть
линейной комбинацией только P^t+i ^к ^ ^к-\ • Коэффициент при
Pf^ нулевой из-за симметрии. Для остальных просто посмотрите
на коэффициенты при х^"^^ и х^~^.
2. Дайте доказательство леммы 5.15.
Указание (Якоби 1826). Если f[x) является многочленом степени
2s—А:—1, а г[х) — интерполяционный многочлен степени s—1, то
f[x) = q[x)M[x) -f r[x), где deg q{x) <s — k — \.
3. Пусть R{z) — функция устойчивости метода Рунге—Кутты из
примера 5.16. Докажите следующие предложения:
a) Степень ее знаменателя < s—1, если и только если
/?,=/3,_i^,_.2Bs-3).
Указание. Воспользуйтесь формулой E.31) и тем фактом, что
det{I—zXQ) — знаменатель диагональной аппроксимации Паде.
b) Степень числителя R[z) < s—1, если и только если
0, = -0,_,i,_,2{2s-Z). E.49)
IV.5. Конструирование неявных методов Рунге—Кутты 107
c) Степень числителя R(z) < s—2, если и только если вдобавок к
E.49) выполнено равенство
/?, = l/Bs-2).
d) Проверьте правильность выражений в табл. 5.14.
4. а) Функция
siz) = —
при 7 > о удовлетворяет Res(z) > О для Re2: > О, если и только
если а>0, /3>0 и S>0.
Ъ) С помощью тождества
l + /i^ + /2^' 1 ^(fi-9i/9o) + f2^
z{9o+9i^) ^9о 9o-^9\Z
(для gQ > 0) докажите следующее предложение: функция E.47)
положительна, если и только если выполнены неравенства E.48).
5. Предположим, что
f{z) =cz-]-g(z) с g{z)=0(l) при z—^ оо
и g{z) ^ 0. С помощью преобразования z -> l/z в лемме 5.21
покажите, что /(г) — положительная функция, если и только если
с > О и g(z) положительная.
6. Дайте альтернативное доказательство критерия Рауса (теорема
13.4 из главы I): Все нули вещественного многочлена
p(z) = ao;j"-faiz'*-4... + a^ {а^>0)
лежат в отрицательной полуплоскости Re z < О, если и только если
с,о > О для г = 0, 1,...,п.
Здесь c^j — коэффициенты многочленов
Ро(г) = ао2:"+а22:'*"^ + ..., т.е. % = а2^-,
Pi(z) = a^z''-^-{-a^z''''^-\-..., т.е. c^j = a^j^^
и
Pi+iH = CioP,-i(-) - с.-1,о2Р,(^)' г = 1,..., п - 1. E.50)
Указание. Согласно принципу максимума для гармонических
функций, условие «p(z) ф О при Rez > О» равносильно
где
P(z)
< 1 при Re 2: > о
108 Гл. IV. Жесткие задачи — одношаговые методы
при условии, что Pq(z) и Pi(z) неприводимы. С помощью
преобразования E.33) покажите, что это эквивалентно положительности
Po(z)/pi(z). Теперь разделите E.50) на c,_i дРД^) ^ примените
рекурсивно результат из упр. 5.
7. Покажите, что
— достаточное условие для того, чтобы М(х) = Р^(х)-\-а^Р^_-^(х)-\-
+ct2^s-'2i^) имел вещественные и попарно различные корни.
Указание (см. «лемму 18» в работе Нёрсетта и Ваннера A981)).
Рассмотрите множество D всех пар (а^, aj), для которых корни
с^ многочлена М(х) вещественны и различны и соответствующая
интерполяционная квадратурная формула имеет положительные
6,. Проверьте, что (О, 0) G i^, и покажите, что для (а^, Q2) G дП
либо одно 6, обращается в нуль, либо совпадают два с-, но порядок
квадратурной формулы остается 2s—2. Поэтому она должна быть
формулой Гаусса порядка 2s—2 с s—1 узлами, и мы должны иметь
Р,{х) + а,Р,_,(х) + а^Р,_^(х) = с(х-/3)Р,_,(х). E.52)
Теперь примените трехчленную рекурсивную формулу
s^,P,{x) = (х-^-)Р,_,{х) - {s-m,_,P,_,(x) E.53)
(см. Абрамовиц и Стиган A964), р. 782 [в русском переводе A979)
см. с. 588 (прим. ред.)]; формула модифицирована), чтобы
исключить хР^_1 в правой части E.52). Затем путем сравнения
коэффициентов при Р,, Pg_i и Р,_2 находятся значения
Если /? — один из корней P,_i, то E.52) имеет двойной корень и
оценка E.51) для aj оптимальна.
IV.6. Диагонально неявные методы
Рунге—Кутты
«... Они назвали свои методы "диагонгипьно неявными",
использовав термин, зарезервированный здесь для специального случая,
когда все диагональные элементы равны...» (Александер 1977)
Продолжим цитировать эту прекрасную работу: «.. .При
интегрировании системы п дифференциальных уравнений неявный метод с
полной матрицей sxs требует решения системы ns уравнений (в
общем случае нелинейных) на каждом шаге по времени. (...) Один
из способов обойти эту трудность состоит в использовании методов
с нижней треугольной матрицей (a,j), у которой а,-,—^ "Р^ ^<iM
тогда уравнения могут быть решены за s последовательных стадий,
причем на каждой стадии нужно решить только систему размерности
п.» В согласии со многими авторами и в несогласии с остальными
(см. выше), мы называем такой метод диагонально неявным методом
Рунге—Кутты (DIRK или ДНРК).
«При решении систем размерности п с помощью итераций
ньютоновского типа на каждой стадии решаются линейные системы с
матрицей коэффициентов вида I—ha--df/dy. Если все а,, равны,
то можно надеяться многократно использовать одну такую матрицу,
хранимую в виде LU-разложения.» Чтобы подчеркнуть это
дополнительное свойство, мы будем называть такой ДНРК-метод однократно
диагонально неявным методом РК (SDIRK или ОДНРК) методом.
Любопытное совпадение: в начале семидесятых по крайней мере
четыре диссертации в большой своей части были посвящены
исследованию методов ДНРК и ОДНРК, при этом очень часто имелась в
виду их полезность для работы с дифференциальными уравнениями
в частных производных (Альт 1971; Крузе 1975; Курди 1974; Нёрсетт
1974). Классическую статью на эту тему написал Александер A977).
Условия порядка
«Традиционная задача выбора коэффициентов заводит в
нелинейные алгебраические джунгли, цивилизация и порядок в которые
были принесены в пионерской работе Дж.К. Бутчера и далее усо-
вершенствовсшы в диссертации М. Крузе». (Александер 1977)
Мы хотим сделать «джунгли» еще чуть более цивилизованными.
Идея состоит в следующем. Рассмотрим 5-стадийную схему ОДНРК
Cl
С2
С,
7
021
а,1
*1
7
0,2
ь, .
¦¦ 7
•• ь.
110 Гл. IV. Жесткие задачи — одношаговые методы
Условия порядка (см. т. I, разд. II.2) содержат суммы, такие как
E^«i^/ = i F.1)
Поскольку теперь в матрице А больше ненулевых элементов, чем в
случае явных методов, эта сумма содержит гораздо больше членов,
чем раньше. Трюк заключается в том, чтобы перенести все
выражения, содержащие 7. в правую часть F.1). В оставшуюся сумму,
обозначим ее ^ , тогда войдут только элементы, расположенные
ниже главной диагонали, как и в случае явных методов Рунге—Кутты.
Правая часть будет (в этом примере)
S4«i^/ = Z1 ^iK-fc -7<^>/с)(«ы -7<^ыI F.1')
j,k,l j,k,l
где 5ji^ обозначает символ Кронекера. Выполнив умножения,
получим
j,k,l j,k,l 3,1 j,k j
>
/•
•J
Таблица 6.1. Условия порядка для методов ОДНРК
t
•>
* «
' Wm
у;
Р@
1
2
3
3
4
4
4
4
прежние условия
Ebi = i
Y^bjajkdki = ^
J2bjajkakiajm = 5
^bjajkakiakm= и
J2^j^jkOklQlm = ^
упрощенные условия
Ebi = i
E4«i*=5-7
^'bjajkakl = ^-7 + 7^
E4^J^«i/^jm = ?-7+§7^-7^
E4^i'f«fc/«im = g-|7+f7^-7^
^'bjajkakiakm = T^-h-^h^-y^
E4'«i/f«^/^/m = ^-57+§7^~7^
IV.6. Диагонально неявные методы РК 111
Все суммы справа выразим через условия порядка (см., например,
теорему 2.1 из разд. И.2) и получим
EVi^«/c/ = b7 + 7^ F.Г)
Общее правило состоит в том, что возникает многочлен
относительно 7 с переменными знаками коэффициентов, которые суть суммы
l/j(u), где l/j(u) определено в разд. П.2 (см. определение 2.10) и
и пробегает все деревья, получающиеся «отключением» одной, двух,
трех и т. д. вершин t (исключая корневую). Полученные таким
способом условия для 4-го порядка собраны в табл. 6.1. Для 5=2, р=:3
и 5=3, р=4 в эти упрощенные условия входит очень мало ненулевых
членов, и уравнения становятся особенно простыми для решения (см.
упр. 1).
Жестко точные методы ОДНРК
Здесь нас будут интересовать, главным образом, методы,
удовлетворяющие условию
a,j = bj для j = l,...,5, F.2)
т.е. методы, для которых окончательная формула численного
решения t/i тождественна последней внутренней стадии. Первое следствие
этого свойства — это то, что Д(оо)=0 (см. предложение 3.8). Условия
порядка для таких методов можно упростить еще больше, чем F.1").
Снова рассмотрим пример F.1), который теперь можно записать так:
j,k,i
На этот раз вместо F.V) имеем
j,k,l J,kJ
j,kj jM j,l k,l
J к I
Подставив известные условия порядка, получим теперь
j,k,l
Общее правило похоже на предыдущее; различие в том, что теперь
нужно «отключать» все вершины (в том числе и корневую). На
112 Гл. IV. Жесткие задачи — одношаговые методы
рис. 6.1 приведена схема «отключения» в другом примере — для
дерева <42' которая приводит к следующей правой части:
8-Пз + 3 + ^-2 + б)+^B + ^-^ + ^-^ + 2 + 2 + 2)-
-7'A + 1 + 1 + 1)+7'' = ^-^7 + 47'-47^ + 7'.
Полученные таким способом условия порядка выписаны в табл. 6.2
для всех деревьев порядка < 4. Выражения для Y1' записаны явно
для удовлетворяющего условию F.2) метода ОДНРК с s=5:
7
021
а31
041
6i
6l
7
«32
042
b2
62
7
^43
Ьз
Ьз
7
б4
Ьа
7
7
^21 '
С2 = 02
^3 ~ ^31 ^" ^32 '
^4 = ^41+^42+^43-
F.3)
Видно, что они стгипи очень похожи на формулы A.11) из разд. П.1.
Таблица 6.2. Условия порядка для метода F.3)
-;
\',.
>'
J J
У''..
J2'o>J = ''1 +Ь2 +Ьз +64 =Р1
л ^»j^jk = Ьгсг + 63С3 + 64С4 = Р2
1^ 'osjajkCji = b-ic'2 + бзсз^ + Ь^с'^ = рз
IZ OtjajifOki = Ьзазгс'г + 64D424 + 04363) = Р4
53''»i''i*''i'°i'" =Ь2С2 +63С3 +64С4 =Р5
Ц 03jDk0jiaim = 63^303262 + 6404@4262+04363) =Р6
Ц o»jOjfeOfe/afc„, = 6303262 +64@4262 +04363 )=Р7
13 OijOj-fcafc/Oim = 64О43О3262 = Р8
F.4;1)
F.4;2)
F.4;3)
F.4;4)
F.4;5)
F.4;6)
F.4;7)
F.4;8)
Pi = 1 - 7
1 „ 2
P4=^-f7 + 37^-7^
Р5 = --27 + -7^-47^ + 7''
Рб = g - 37 + 47^-47^+7''
P7=-^-f + :2''^-'^'t^ + y^
Р8= 2^-3 "У+ 37^-4747"
IV.6. Диагонально неявные методы РК
113
1 ^
V'
V v'^' • ^
' •„ • :/ V
• Ь >
>
Ф^
•
\
Рис. 6.1. ¦Отключение» вершин для дерева ^42
Решение уравнений F.4). Рациональным образом исключая члены
из уравнений F.4;4) и F.4;6), а также (б.4;4) и F.4;7), получим
630324@4 - 4) = С4Р4 - Рб'
^44^4зD " 4) = 4^4 - Р7'
Перемножение этих двух уравнений с учетом F.4;8) дает
Р8*зD - 4)D - 4L = D^4 -Рб)DР4 -р?)-
Вычислим теперь frj» ^З' ^^4 ^^ F.4;2), F.4;3), F.4;5). Получим
'^з = (-Р244+РзD + 4) -Р5)/DD - 4)D - 4))^
F.5)
F.6)
а 62 и 64 — циклической перестановкой. Сравнение последних двух
уравнений приводит к
Сл =
Р8Рз4 - PsPb - 4РбР4 -^ РеР7
Р8Р2^2 - РвРз " 4Р4Р4 + Р4Р7
F.7)
Выберем теперь 7^ 4 ^ 4 ^ качестве свободных параметров. Тогда
С4 находится из F.7); 62, 63^ ^^4 — ^^ F-6), Ь^ — из F.4;1), 032 и 043
— из F.5), 042 — ^^ (б.4;4), и, наконец, Oj^, 031» ^41 — ^^ F.3).
Вложенная формула 3-го порядка. Для того, чтобы управлять
длиной шага, мы можем, следуя предложению Каша A979), добавить
к вышеприведенной формуле выражение третьего порядка
4
1=1
(опуская, таким образом, 65—7)- Коэффициенты 6^,..., 64
получаются просто из решения первых четырех уравнений табл. 6.1 (линейная
система). Непрерывные вложенные формулы 3-го порядка можно по-
114 Гл. IV. Жесткие задачи — одношаговые методы
лучить этим же способом (см. теорему 6.1 из разд. II.б):
4
1=1
Коэффициенты Ь^(в),... ,Ь^{9) получаются разрешением первых
четырех (упрощенных) условий табл. 6.1 с правыми частями,
замененными на
о, j-ie, ^-7^2+74 j-ie' + l'e
соответственно. Непрерывное решение, полученное таким способом,
при ^=1 совпадет с у^, а не с решением 4-го порядка у^. Поэтому
глобс1льное непрерывное решение окажется разрывным. Чтобы
избежать этой разрывности, мы добавим 65(^) ^ включим пятое уравнение
из табл. 6.1, но с правой частью
Функция устойчивости
Согласно формуле C.3) функция устойчивости R(z) для метода
ДНРК принимает форму
P(z)
так как детерминант треугольной матрицы равен произведению ее
диагональных элементов. Числитель P(z) является многочленом
степени не выше s. Если метод имеет порядок р> s, то этот
многочлен однозначно определяется формулой C.18). Он просто
получается из первых членов степенного ряда для (l—a^^z)... A—a,,z) • е^.
Для методов ОДНРК с ал = .. .=а^,=7 получим
^(^) = 7Г^' ^(") = (-1)' Е ^i'"'^ & i^^y F.9)
(см. также формулу C.18) с я. = (—7)j(y)) с константой погрешности
^^SV,(^). F.10,
^^r(-i)^
где
j=o ^•'z •'•
— полином Лагерра степени 5, а Li \х) обозначает его к-ю
производную. Поскольку функция F.9) при 7 > О будет аналитической в
IV.6. Диагонально неявные методы РК
115
С" , Л-устойчивость эквивалентна условию
Б{у) = Q(iy)Q{-iy) - P{iy)P{-iy) > О для всех у F.12)
(см. C.8)). Это четный многочлен степени 2s (в общем случае) и с
младшим членом степени 2j, где j=[(p-\-2)/2] (см. предложение 3.4).
Поэтому определим многочлен F(x) как
F(y') = E(y)/y'^, j = [(p+2)/2]
И проверим условие F(x)>0 для х>0, используя последовательности
Штурма. Полученные результаты, аналогичные тем, что
опубликовал Берридж A978), представлены в табл.6.3.
Таблнид 6.3. Л-устойчивость функции F.9), порядок р> з
S
1
2
3
4
5
6
7
8
А -устойчивость
1/2<7<оо
1/4 < 7 < оо
1/3 < 7 < 1.06857902
0.39433757 < 7 < 1.28057976
Г 0.24650519 < 7 < 0.36180340
t 0.42078251 < 7 < 0.47326839
0.28406464 < 7 < 0.54090688
0.21704974 < 7 < 0.26471425
А -устойчивость
и р = s-hl
1/2
C-Кл/3)/6
1.06857902
—
0.47326839
—
—
Для полноты изложения приведем здесь следующие явные
формулы для Е(у):
5=1, р=1 :
^ = у2B7-1);
5=2, р=2:
E = y4(-|-f 27-572+47з)=ИB7-1JG-i);
5=3, р=3:
^ = y^(i^-7 + 372-273)+y^(-^ + i-^ + ^-127467^)
5=4, р=4 :
1 ф ill! _ 322i +17^4 _ 8^5 j +
^=у'(^-^ + ^-=^ +
+
y'i-m
^ 18 36
. + Ш!_1Ш1 + 1^_227б+87^).
116 Гл. IV, Жесткие задачи — одношаговые методы
Л-устойчивость здесь означает, что все коэффициенты должны быть
неотрицательными. В общем же случае справедлива следующая
Лемма 6.1. Е-многочлендля F.8) с а^^ = .. .=а,,=7 и p>s
определяется формулой
E(y) = (^l-L,(^y){',yf'-
>-i fih F.13)
i=[(p+2)/2l •'O
Доказательство. Подставим формулу F.9) в определение Е{у):
E{y) = {l + 'r^y^r-P{iy)P{-iy)
к I ^ '
Равенство
2rL,(^)Li"+'-'^\x)dx = (-iy Yl (-l)'il'-*'(x)L('-')(x)
•^0 k+l=2j
оверяется интегрированием по частям. Поскольку
Y (-iyLi'-''H0)Li'-'){0) = (-iy('\
kJfl=2j
МЫ получаем требуемый результат. П
Аппроксимации с кратным вещественным полюсом
и с Я(оо) = О
Для методов, удовлетворяющих условию F.2), имеем Л(оо) = 0.
Поэтому старший коэффициент P[z) в F.9) равен нулю. Если
известно, что порядок метода р > s — 1, то остальные коэффициенты
P[z) все еще однозначно определяются 7, и мы имеем
p{z) = {-iyY.L^r^^{\)bzy F.14)
i=o '
с константой погрешности
<^=(-1)'^.(;O'- F.15)
Первые многочлены Е{у) F.12) теперь будут:
5=2, р=1:
IV.6. Диагонально неявные методы РК 117
5=3, р=2:
^ = у" (- 5 + 37 - 1272 + 187^ - 67") + У«7';
5=4, р=3:
^ = г/" (т5 - 3^ + 67^ - 87З + 27")+
+ 2/'(-5^ + ? - 67^ + ^ - 527" + 487^ - 127^) + yV-
Диапазоны изменения 7 Для Л-устойчивости (а также,
следовательно, и для L-устойчивости) представлены в табл. 6.4.
Таблиид 6.4. L-устойчивость R(z) для Р из F.14), порядок р > 5 — 1
S
2
3
4
5
6
7
8
L -устойчивость
B - ч/2)/2 < 7 < B -Ь V^)/2
0.18042531 < 7 < 2.18560010
0.22364780 < 7 < 0.57281606
0.24799464 < 7 < 0.67604239
0.18391465 < 7 < 0.33414237
0.20408345 < 7 < 0.37886489
0.15665860 < 7 < 0.23437316
L-устойчивость и p=s
7 = B±х/2)/2
7 = 0.43586652
7 = 0.57281606
7 = 0.27805384
7 = 0.33414237
—
7 = 0.23437316
Рис. 6.2. Константа погрешности и область А-устойчивости
для 5=5, р=:4.
118 Гл. IV. Жесткие задачи — одношаговые методы
Таблица 6.5. L-устойчивый
1
4
3
4
11
20
1
2
1
У1 =
У1 =
err =
1
4
1
2
17
50
371
1360
25
24
25
24
59
48
3
16
1
4
1
25
137
2720
49
48
49
48
17
96
27
32
метод
1
4
15
544
125
16
125
16
225
32
25
32
ОДНРК порядка 4
1
4
85
12
85
12
85
12
0
1
4
4
0
1
4
F.16)
Выбор метода
Определим теперь свободные параметры метода F.3) порядка 4 с
5=5. Для удобства хорошего выбора j мы построили на рис. 6.2
график константы погрешности С (в логарифмическом масштабе) и
указали области А' и Л (О)-устойчивости. График подсказывает, что 7
между 0.25 и 0.29 — подходяш;ий выбор. Метод при этом L-устойчив и
константа погрешности мала. Для разных значений 7 в этом
диапазоне мы определили (с помощью программы, реализующей нелинейный
алгоритм Гаусса—Ньютона) Cj и Сд для того, чтобы минимизировать
члены погрешности пятого порядка. Оказалось, что
с'з = 0.5, Сз = 0.3
близки к оптимальным. Для них мы запрограммировали два
различных варианта для 7- 7=4/15 = 0.2666 ..., что согласно вычислениям
лучше всего, и 7 = 1/4, что дает, в соответствии с формулами F.4),
F.5), F.6) и F.7), особенно хорошие рациональные коэффициенты.
Последние представлены в табл. 6.5. Мы включили в этот метод
непрерывное решение
которое имеет третий порядок для 0<^<1 и улучшает yj до четвер-
IV.6. Диагонально неявные методы РК
\
того порядка аппроксимации при в=1. Здесь
119
Упргклснения
3 72 36 9 '
11, 385,2 661,3 ,„м
= Т'-Тб-'+^'-^«''
128, 20125,2
18 432
8875
216
F.17)
85
85.
= _ii,+ 557 359 80
19 108 54 27
1. (Крузе и Равьяр 1980.) Рассчитайте методы ОДНРК (табл. 6.1)
для s=3, р=4. Для 5=2,р=3 получите еще раз также метод из
табл. 7.2, разд. II.7.
Ответ. Последнее условие порядка в обоих случаях — это просто
многочлен относительно 7 • Среди различных решений следующее
представляет Л-устойчивую схему:
7
1
2
1-7
7
1
2-7
27
S
7
1-47
1-2J
7
S
= ^МГ8^^^-'
тг \ 1
i8/''^2'
S =
6B7-1)
-П2-
F.18)
2. Проверьте все детали таблиц 6.1 и 6.2.
3. Четыре случая Л-устойчивых методов ОДНРК порядка р=5+1,
приведенные в табл. 6.3 (справа) — единственные существующие.
Этот факт до сих пор строго не доказан, поскольку
«доказательство», которое предложили Ваннер, Хайрер и Нёрсетт A978),
использует асимптотическую формулу без оценки погрешности.
Попробуйте сделать лучше.
4. Купер и Сейфи A979) вывели много методов ДНРК (которые они
называют «полуявными») высокого порядка. Их главной целью
было минимизировать количество неявных стадий, а не
максимизировать устойчивость. Вот один из их методов:
120
Гл. IV. Жесткие задачи — одношаговые методы
35
1
-6
41^
888Ч-607л/б
58Sb
3153--3082У^
R55T3
-325834-14638>/?
7гт—
126-161V?
1425
32134-1148у/?
28500
-171994-364%/?
2l0 ^
142S00
-2674-88%/б
5 А О ^
1329-544N/?
2500
6-у/б
"ТТГ"
-964-131V?
—ш
^
1е-у/б
1^ О
Покажите, что он 5-го порядка и Л-устойчив, но не L-устойчив.
5. Из табл. 6.4 можно видеть, что для 5=2, 4, 6 и 8 точка L-устой-
чивой сверхсходимости совпадает с правым концом интервала А-
устойчивости. Объясните это с помощью теории порядковых звезд
(рис. 6.3а).
Дгипее, для 5 = 7 точка сверхсходимости соответствует значению
7=0.20406693, которое промахивается мимо указанного
интервала Л-устойчивости менее чем на 2-10~^. Будет ли здесь также
применим предыдущий аргумент, и не произошла ли где-то тут
вычислительная ошибка? Изучите соответствующую порядковую
звезду для того, чтобы показать, что это не так (рис.б.ЗЬ).
в. \\V4\4.\\
а: 5=8, 7=0.23437316 Ь: 5=7, 7=0.20406693
Рис. 6.3. Порядковые звезды с кратными полюсами.
IV.7. Методы типа Розенброка
«Когда функции (^ нелинейны, неявные ургшнения в
общем случае можно решить только с помощью
итераций. Это крупный недостаток, tclk как к проблеме
устойчивости добавляется проблема сходимости
итерационного процесса. Альтернатива, которая обходит эту
трудность,...» (Розенброк 1962/63)
... рассматривается в этом разделе. Среди методов, уже покгизав-
ших удовлетворительные результаты для жестких уравнений, методы
Розенброка программируются легче всех. В этом разделе мы опишем
их теорию, которая и приведет нас к нашей первой «жесткой»
программе. Методы Розенброка принадлежат к большому классу
методов, которые стараются избежать нелинейных систем и заменяют их
последовательностью линейных систем. Поэтому мы называем эти
методы линейно неявными методами Рунге—Кутты. В
литературе такие методы часто называются «полунеявными» (или там было
«полуявный»?), или «обобщенными» или «модифицированными» или
«адаптивными» или «аддитивными» методами Рунге—Кутты.
Вывод метода
Начнем, скажем, с диагонально неявного метода Рунге—Кутты
S
i=l,...,s,
G.1)
1 = 1
примененного к автономному дифференциальному уравнению
У' = т- G.2)
Главная идея заключается в том, чтобы линеаризовать формулу G.1).
В результате получаются соотношения
9i = yo + 2^%l^j^
3 = 1
такие же, как при применении одной ньютоновской итерации с начгипь-
ным значением к\ ^=0 на каждой стадии в G.1). Вместо продолжения
итераций до сходимости рассмотрим G.3) как новый класс методов и
исследуем заново его свойства порядка и устойчивости.
122 Гл. IV. Жесткие задачи — одношаговые методы
Существенный вычислительный выигрыш получается при замене
матриц Якоби f'(gi) на J=/'(i/q), так что метод требует ее
вычисления только один раз (Калахан 1968). Ван дер Хаувен A973), Каш
A976) и Нёрсетт A975) вывели много методов этого типа и провели с
ними множество численных экспериментов.
Мы получим больше свободы, введя добавочные линейные
комбинации членов Jkj в G.3) (Нёрсетт и Вольфбрандт A979); Капе и
Рентроп A979)). Это приводит к следующему классу методов:
Определение 7.1. 5-стадийный метод Розенброка задается
формулами
^, = Л/ f г/о + X] », j *j ) + Л J ^ 7о kj. г = 1,..., S,
G.4)
где Q,^, 7,j, fr,- — определяющие коэффициенты метода, и J=f*(yQ).
Каждая стадия этого метода состоит из системы линейных
уравнений с неизвестными /:, и с матрицей I—h^a J • Особый интерес
представляют методы, у которых 7ii = - • =755=7» так что требуется лишь
одно LU-разложение на шаге.
HeaernqnoMHue задачи. Уравнение
y' = f{x,y) G.2а)
может быть преобразовано в автономную форму добавлением х'=\.
Если метод G.4) применяется к расширенной системе, то компоненты,
соответствующие переменной х, можно вычислить явно, и мы
приходим к
t-~\ ^ ( Л/ *
к^ = Н!(^х^-^а^к,у^Л^^а^^к^^^^^к'^ — [х^,у^)^
j=i j=i
s
2/1 = 2/0 +XI ^^j' G.4a)
j=i
где добавочные коэффициенты даются выражениями
J-1 t
^i = !]%•' ^=Y.^j' G-5)
Неявные дифференциальные уравнения. Предположим, что задача
записана в форме
My' = f(x, у), G.2b)
где М — постоянная матрица (пусть пока невырожденная). Если
формально умножить G.2Ь) на М""^, применить метод G.4а) и затем
IV.7. Методы типа Розенброка 123
умножить результирующую формулу на М, то получим
t— 1 л/ г^ f *
Mfc,. =/1/(хо+а,Л, Уо+1] o,j*j)+7./i^^(aro. 2/о)+/«^(хо, j/o) XI'''«J^J'
5
i=i
Преимущество этой формы записи в том, что не нужно обращать М, а
также в том, что сохраняется возможная ленточная структура матриц
М и df/dy.
Условия порядка
Условия, налагаемые на свободные параметры и гарантирующие,
что метод имеет порядок р, т.е. что локальная погрешность
удовлетворяет требованию
г/(хо+/1)-У1=0(/1''+М-
МОЖНО получить либо непосредственным дифференцированием, либо
с помощью теоремы о 5-рядах (разд. 11.12). Мы следуем здесь
первому подходу, так как он требует только знания разд. II.2. Идея
реализации второй возможности кратко обрисована в указании к упр. 2.
Как и в разд. II.2, запишем систему G.2) в тензорных
обозначениях, и метод G.4) примет вид^
к к
3
G.4')
J
Снова воспользуемся правилом Лейбница (ср. (II.2.4))
к к
G.6)
В дальнейшем читатель обнаружит много символов к в рг1зличных
значениях: с одной стороны, «fc» в формуле G.1), впервые появившееся в
работах Рунге и Кутты; с другой стороны, «fc» в качестве индекса
суммирования, как это обычно принято в численном анализе. И хотя в некоторых
формулах это выглядит порой странно, мы предпочитаем сохранить
обозначения предыдущих разделов.
124 Гл. IV. Жесткие задачи — одношаговые методы
и с помощью цепного правила получим (ср. разд.II.2, B.6;1), B.6;2)):
К
if'iffj))" = Е ficiigj) ¦ (</f)' • {gfY+Е fKiaj) ¦ igf)"
K,L К
И Т. Д. Подставив это в G.6), получим после выполнения рекурсий:
(*/)^°1л=о = 0. G.7; 0)
(*/)^^^Lo = /-'. G-7; 1)
(*/P^Lo=2E/к/'^E"i*+^E/к/^Eъ* =
к к к к
= 2Е/к/''ЕК* + Ъ*)' G-7;2)
к к
(*/)^'' 1/.=о = 3 Е fKLf4' Е "i*"i'+ G-7; 3)
K,L k,l
K,L k,l
И Т. Д. Все элементарные дифференциалы вычисляются в j/q •
Сравнивая производные численного решения (^ > 1)
J
с производными истинного решения (формулы A1.2.7;1), A1.2.7;2),
A1.2.7;3)), приходим к следующим условиям для третьего порядка:
Единственное отличие от условий порядка для методов Рунге—Кутты
состоит в том, что у соответствующих деревьев для вершин с одной
ветвью aji^ заменяются на а^^^Ч-7;^ь • На пути к общему результату
полученные формулы подводят к следующему определению:
Определение 7.2. Пусть t — помеченное дерево порядка q с корнем
j; обозначим через
*.w=E^i.M...
IV.7. Методы типа Розенброка 125
сумму по остальным q—l индексам Л,/,... и т. д. Под знаком суммы
стоит (fj^k.i,.. — произведение q—l множителей, равных
^ki + 7/с/) если / — единственный «сын» к;
af^i, если / — «сын» fc и у fc не меньше двух «сыновей».
Воспользовавшись рекурсивным представлением деревьев
(определение П.2.12), будем иметь Ф^(г) = 1 для единственного дерева
порядка 1 и, так же, как и в (П.2.19),
{Y. '^Jki-'^jkm^kAh)-'^kJ^m)^ ecли< = [^l,...,^J,
ки Лт т>2,
Х.Кл + 7iJ*fc(<i), если t = [t^l
G.9)
Теорема 7.3. Производные kj^ задаваемые G.4^), удовлетворяют
равенству
(Ф^Х=о= Е ymj(t)F4t){yol G.7;9)
teLTg
и для численного решения справедлива формула
iyin=o= Е 'rit)^ЬJфJ{t)F'(i)(yo), G.10)
t€LTq j
где F'^(t) — элементарные дифференциалы (определение 11.2,3).
Доказательство. Поскольку имеет место G.8), нам надо доказать
только первую формулу. Доказательство основано на индукции по q
и в точности следует линии доказательства теоремы П.2.11.
Применим формулу G.6), заменим выражение /'^{дЛ^^^^^ по формуле Фаа
ди Бруно (лемма П.2.8), для производных gj воспользуемся
формулой
к
И подставим индукционную гипотезу G.7;J) для S<q — 1. Это дает
(*/)^'^L=o=9 Е Е ••• Е 7(ti)...7(<„,)x
>< E"j*i^*.('l) • • •E°i*„.**n.('m)x
ki km
X E fL..Kjyo)F''4h){yo)-F''-iU{yo)+
Л 1,...,Л Л»
+я E 7(<i)E^^(*i)E/^(%)^''(^i)(i'o)-
126 Гл. IV. Жесткие задачи — одношаговые методы
Требуемый результат теперь получается благодаря однозначному
соответствию между множеством {(и, t^,.. .,t^)\u? LS^, tj G LT^ } , no
которому производится суммирование, и LT^, а также с помощью
рекурсивных формул G.9), (II.2.17), (II.2.18). D
Сравнивая теоремы 7.3 и II.2.6, получим следующий результат:
Теорема 7.4. Метод Розенброка G.4) с J=f(yQ) имеет порядок р,
если и только если
i ^(') D
Выражения Ф^@ упрощаются, если ввести обозначение
/?у=%+7о- G.12)
Условия порядка G.11) для всех деревьев вплоть до пятого порядка
даны в табл. 7.1.
Дальнейшее упрощение условий порядка G.11) возможно, если
7,., =7 для всех г. G13)
(К сожалению, в современной литературе буква 7 используется для
обозначения как коэффициентов в G.4), так и величины 7@ ^ G11),
но мы надеемся, что это не вызовет недоразумений.) Так же, как и
для методов ДНРК, суммы в выражениях для Ф,@ в 5-м столбце
табл. 7.1 содержат больше членов, чем соответствующие выражения
для явных методов Рунге—Кутты, так как матрица 7,j (а поэтому
и /?,j ) содержит ненулевые элементы на диагонали. Различие же
состоит в том, что здесь эти диагональные 7 появляются только для
вершин с одной ветвью (см. определение 7.2). Поэтому процедура,
которая была разъяснена в разд. IV.6 (см. формулы F.Г) и F.Г')),
должна быть слегка модифицирована, и она приводит к условиям
порядка в форме
5^'6,.Ф,.(<) = рЛ7), G.11')
3
где многочлены p^7) перечислены в последнем столбце табл. 7.1.
Функция устойчивости
Если применить метод G.4) к тестовому уравнению 2/'=Ау и
положить J=/'(t/q)=A, то численное решение будет у^=Е[к\)у^ с
R(z) = 1 -h г6^(/ - гБ)-^ И, G.14)
где использованы обозначения 6^ = F^,..., 6^) и В = {/3- )J ^^.
Поскольку В — нижняя треугольная матрица, то функция
устойчивости G.14) совпадает с функцией устойчивости метода ДНРК с РК-
матрицей В. Свойства таких функций устойчивости уже были
исследованы в разд. IV.6.
IV.7. Методы типа Розенброка 127
Конструирование методов 4-го порядка
Чтобы сконструировать 4-стадийные методы Розенброка порядка
4, мы для удобства выпишем сначала все восемь условий порядка (ср.
табл. 7.1):
6,+62 + 63 + ^4 = 1.
/ б2/?2 + Мз + М^=о-'У = Р21Ы.
V
*2<^2 + *з"з + ^4'>'4 = Q'
У М32^2 + Ь,@,20'2 + /?43/?3) = ^ - 7 + 7^ = Р32G),
\К Ь,а1 + Ьзо1 + Ь^а1 = -,
G.15а)
G.15Ь)
G.15с)
G.15d)
G.15е)
1 7
•^ ^з2/^2 + *4К2/?2+<*4з/'з)= 3-3=^42G)- G.15f)
У М32 + *4(/?42«i + 0430:1) = То " Т = Р4зG),
S
12 3
ЬЛ303202 = ^,-l; + h'-f'= Р44G).
G.15g)
G.15h)
24 2 2
Здесь мы использовали сокращения
Для управления длиной шага поищем также вложенную формулу
5
в которой используются те же самые величины к,, что и в G.4), но с
другими весами (Вольфбрандт A977); Капе и Рентроп A979)). Этот
метод должен иметь порядок 3, т.е. четыре условия G.15a)-G.15d)
должны удовлетворяться также для 6,. Эти уравнения составляют
линейную систему:
I \ (Ь\ (
/1 1 1
'о /?^ ff^
о оЗ, а\
/?4
Ь.
\0 о 42/?2 J:'04J0j/ \bj
1
1/2-7
1/3
\1/6-7 + 72,
G.18)
Если матрица в G.18) невырожденная, то из единственности
решения линейной системы следует, что fc,=6, (j = l,...,4), и
аппроксимация У1 не может использоваться для управления длиной шага.
128 Гл. IV. Жесткие задачи — одношаговые методы
Табл. 7.1. Деревья и условия порядка вплоть до порядка 5
p{t)
1
2
3
4
5
Г*
г
*?1
t31
h2
t4l
t42
Us
*44
^51
t52
*53
^54
*55
*56
^57
*58
*59
граф
•;¦
/
V ,
>
'•ф-"
•^^
'yr
>
'N?*
po
1
2
3
6
4
8
12
24
5
10
15
30
20
20
40
60
120
^jit)
1
^H.fijk
Hkj^^jk^'jl
Ylk,l)^jkfikl
T,k,l,m^Jk^Jl^Jm
T,k^,m^jf^(^kl^jrn
J2k^,mf^Jk^klOikm
J2k,l,mf^jk0klf^lm
J2^jkOijlQjmO(jp
^O^jk/^klOijmOijp
Y^OijkaklOkmOijp
Yl^Jkl^kl0lmOijp
Yl^Jf^f^l^l^JmPmp
^fijkOiklOikmOikp
^PjkQklfil
Yjl^jkl^kioimaip
El^jkl3kl0lml3mp
Ptil)
1
1/2-7
1/3
1/6-7 + 7^
1/4
1/8-7/3
1/12-7/3
1/24-7/2 + 37^/2-7^
1/5
1/10-7/4
1/15
1/30-7/4 + 7^3
1/20 - 7/4 + 7^/3
1/20 - 7/4
1/40-57/24 + 7^/3
1/60-7/6 + 7^/3
1/120-7/6 + 7^-27^ + 7^
Поэтому мы должны потребовать, чтобы матрица системы G.18) была
вырожденной, т.е.
3
(«-/?;а2)/?з2/?^ = (^^а2~/?^а2)^/?,./^.. G.19)
J=2
Это требование гарантирует существование вложенного метода 3-го
порядка G,17), разумеется, только при условии, что система
уравнений G.15) имеет решение. Вычисление коэффициентов а,-, /?, , 7^ 6, ?
удовлетворяющих G.15), G.16) и G.19), теперь проводится по
следующему плану:
Шаг 1. Выберем 7>0 такое, чтобы функция устойчивости G.14)
имела желаемые свойства устойчивости (ср. табл. 6.3).
IV.7. Методы типа Розенброка
129
Шаг 2. Выберем аз, ot^, ot^ и 6^, b^, 63' ^^4 таким образом, чтобы
выполнялись три условия G.15а), G.15с) и G.15е). Очевидно, что
для этого имеется четыре степени свободы. Обратите внимание, что
F-, а,) не обязательно должны быть коэффициентами стандартной
квадратурной формулы, так как не требуется выполнения условия
Шаг 3. Возьмем /?4з в качестве свободного параметра и найдем
/?32/?2 ^"^ G.15h), затем (/^42/^2"^/^43/^3) ^"^ G.15d). Эти выражения,
подставленные в G.19), доставляют второе соотношение между /?2, /?3' /?4
(первое — это G.15Ь)). Исключение (^4/^42+^3/^32) **з G.15d) и G.15g)
дает
ЬЛМ<^1 - Рз^1) = /?2Р43G) - С^1Рз2Ь)
— третье линейное соотношение для /?2, 0';^, /?4 • Полученная
линейная система не вырождена, если и только если 64/^43^27B7 ~ 1)^0.
Шаг 4' Коль скоро /?,• известны, мы можем найти /?32 и /?42? зная
величины /?32^2' (/^42/^2+/^4з/^з)' полученные на шаге 3.
Шаг 5. Выберем аз2, 0^42^ о^43 '^^^^ чтобы удовлетворялось
уравнение G.15f). Для этого имеется две степени свободы. И наконец, зная
величины а,, /й,-, найдем a,i, /?,i из условий G.16).
Табл. 7.2 Методы Розенброка порядка 4
метод
GRK4A (Капе и
Рентроп 1979)
GRK4T (Капе и
Рентроп 1979)
Шампайн A982)
ван Фельдхёйзен
A984)
ван Фельдхёйзен
A984)
L-устойчивый
метод
7
0.395
0.231
0.5
0.225708
0.5
0.572816
значения параметров
Q2 = 0.438, аз = 0.87,
б4 = 0.25
а2 = 27, G.22), 6з = 0
«2 = 27, G.22), 6з = 0
а2 = 27, G.22), 6з = 0
«2 = 27, аз =0.5,
6з = 0
«2 = 27, G.22), 6з=0
А(а).
устойч.
7г/2
89.3^
7г/2
89.5^
7г/2
7г/2
|Я(оо)|
0.995
0.454
1/3
0.24
1/3
0
Большинство распространенных методов Розенброка — это
специальные случаи такого построения (см. табл. 7.2). Обычно оставшиеся
130 Гл. IV. Жесткие задачи — одношаговые методы
свободные параметры выбираются следующим образом: если мы
потребуем, чтобы
«43 = 0, «42 = ^32 и а41 = аз1, G.20)
то аргумент / в G.4) будет один и тот же для г = 3 и г = 4.
Следовательно, количество вычислений функции сокращается на одно.
Далее, свободные параметры можно определить так, чтобы
удовлетворить нескольким условиям порядка для порядка пять.
Умножение условия G.15g) на Ofj и вычитание его из условия порядка для
дерева t^^ дает
^4^43<^з(<^3 - «2) = Р5бG) - 0^2Р4зЬ)' G-21)
Отсюда определяется /З^^- Условие порядка для fgi можно также
легко выполнить на шаге 2. Если а^=а^ (см. G.20)), то это приводит
к ограничению
_1/5-а2/4
В табл. 7.2 собраны некоторые хорошо известные методы. Все они
удовлетворяют G.20) и G.21) (единственное исключение: второй
метод ван Фельдхёйзена при 7=0.5 имеет /?4з = О вместо G.21)). В двух
первых столбцах даны значения оставшихся свободных параметров.
В последних столбцах отмечены некоторые свойства функции
устойчивости.
Методы высших порядков
Как и для явных методов Рунге—Кутты, конструирование
методов высших порядков облегчается использованием упрощающих
предположений. Во-первых, условие
S
Y,bAj^bj(l-aj), j = l,...,s G.23)
играет роль, аналогичную роли (П. 1.12) для явных методов Рунге—
Кутты. Из него вытекает, что условие порядка для левого дерева на
рис. 7.1 есть следствие условий для двух деревьев справа. Отличие
от методов Рунге—Кутты в том, что здесь вершина, расположенная
непосредственно над корнем, должна иметь больше одной ветви.
Второй тип упрощающего предположения (с /?/c=X^/=i P^i) такой:
i2^Jkl3k = ^^ i = 2,...,5. G.24)
Его эффект аналогичен (II.5.7). Как следствие G.24), условия
порядка двух деревьев на рис. 7.2 эквивалентны. Здесь тоже вершина,
помеченная стрелкой, должна иметь больше одной ветви.
IV.7. Методы типа Розенброка 131
Вышеприведенными упрощающими предположениями воспользо-
вгипись Капе и Ваннер A981) при конструировании методов вплоть
до 6-го порядка. Методы еще более высокого порядка потребовали
бы обобщения рассмотренных выше упрощающих предположений (по
аналогии с C(tj) и D(C) из разд. П.7).
да ... -> rV
хУ' ^ НИ нн '-¦¦¦] ^ '¦¦¦¦¦
Рис. 7.1. Редукщад с G.23). Рис. 7.2. Редукщ1я с G.24).
Реализация методов типа Розенброка
Непосредственная реализация G.4) требует на каждой стадии
решения линейной системы с матрицей / —/i7„J, а также умножения
матрицы на вектор: J•Yl^^j^^j• Последнего можно избежать, если
ввести новые переменные
t
^« = Zl^o''i' г = 1,...,5.
i=i
Если 7,i ^ О для всех г, то матрица Г=G,^) обладает обратной и fc,
можно восстановить по и^:
1 '"^
'^s^—^.-E^O-^i' ^= diagGr/,...,7,V)-r-^
'«• i=i
Подстановка этой формулы в G.4) и деление на Л дает
1-1 f-i ^
(—/-j)u, = /(yo + j;^a,_,.«^.) + 2;(-^^., , = 1,...,5,
/=* '=' G.25)
J'i = yo + JZ"'j«j.
где
{a,j) = {aij)r-\ {т„...,т,) = {Ь„...,Ь,)Г-К
По сравнению с G.4) формулировка G.25) метода Розенброка
исключает не только вышеупомянутое умножение матрицы на вектор, но
также п2 умножений для GйЛ)«/. Впервые подобные преобразования
были предложены Вольфбрандтом A977), Капсом и Ваннером A981)
и Шампайном A982). Формулировку G.25) можно найти в работе
(Капе, Пун и Буй 1985).
G.26)
132 Гл. IV. Жесткие задачи — одношаговые методы
Для неавтономных задач это преобразование примет вид
^/- ^(^0-yo)j «.• =/К+ «(/«. Уо+ 11 «.j«j)+
С а,- и 7,) задаваемыми G.5).
Для неявных дифференциальных уравнений в форме G.2Ь)
преобразованный метод Розенброка принимает форму
/1 Я f \ i~\
,_1 '"' G-27)
Программирование. Методы Розенброка почти так же легко
реализовать, как и явные методы Рунге—Кутты. Единственное отличие
состоит в том, что на каждом шаге нужно вычислять матрицу Якоби
df/ду и решать s линейных систем. Таким образом, можно взять
программу для явного метода РК (скажем, D0PRI5), добавить
четыре строки, в которых вычисляется df/dy методом конечных
разностей (или вызвать подпрограмму JAC, которую должен написать
пользователь и где запрограммированы аналитические формулы для
вычисления производных); добавить еще вызов подпрограммы DEC,
выполняющей разложение Гаусса и добавить на каждой
вычислительной стадии вызов SOL — подпрограммы решения линейной системы.
Коль скоро рассматриваемый метод имеет порядок 4C), формула
minje., max@.2, 0.9 • (То//егг)^/^) } G.28)
представляется вполне подходящей для предсказания длины шага.
Однако мы хотим, чтобы программа работала экономно и в
случае неавтономных задач, равно как и для неявных уравнений.
Далее, если размерность системы велика, то в линейной алгебре очень
важно применять ленточную форму всегда, когда это возможно. Все
эти возможности (автономное уравнение или нет, неявное или явное,
имеет ли df/dy ленточную структуру или нет, имеет В ленточную
структуру или нет, задается df/dy аналитически или нет «...— вот
в чем вопрос!») выливаются в 2^ разных случаев, и для каждого из
них программа содержит специальные части, обеспечивающие
высокую эффективность. Нет нужды говорить, что она хорошо работает
на всех жестких задачах из разд. IV. 1. Ее тестирование и сравнение с
другими программами будет детально обсуждаться в разд. IV. 10.
Л„,... = h
IV.7. Методы типа Розенброка 133
«Горб»
На некоторых очень жестких уравнениях программа, однако,
демонстрирует удивительное поведение. Рассмотрим уравнение Ван-
дер-Поля в сингулярно возмущенной форме A.5') с
5 = 10-^ t/i@)=2, У2@) = -0.66. G.29)
Далее, выберем метод GRK4T (табл. 7.2; любой другой метод здесь
ведет себя так же) и То/ = 7 10"^. На рис.7.3 показаны численное
решение у^, а также длина шага, выбираемая программой. Все
отброшенные шаги помечены х .
первая
компонента решения
Рис. 7.3. Длина шага GRK4T для ургшнения A5').
f^ "" I I imili "'I I llllllll ¦ ¦ "iiiil I I tmiil t/|Hi
10-^ 10-^ 10-^
L-устойчивый метод А^^~^
точная локальная погрешность
эценка локально^ погрешности
Рис.7.4. Исследование локальной погрешности для A.5') при х = 0.55139.
Без какой-либо видимой внешней причины происходят
удивительные резкие уменьшения длины шага (примерно в 10~^ раз). Кроме
134 Гл. IV. Жесткие задачи — одношаговые методы
того, эти уменьшения сопровождаются очень большим количеством
отброшенных шагов (вплоть до 20). Чтобы понять это явление, мы
представили на рис. 7.4 (слева) как тонную локальную погрешность,
так и оценку локальной погрешности Цу^—yjl при х = 0.55139 как
функции длины шага h (оба графика в логарифмическом
масштабе). Текущая длина шага отмечена крупным кружком. Погрешность
ведет себя как С - h^ только при очень малых h (< 10"^=б). Между
h=lO~^ и реально использовавшейся длиной шага (« 10"^)
погрешность более или менее постоянная. Всякий раз, когда эта постоянная
больше, чем То1 (горизонтальная пунктирная линия), программа
вынуждена уменьшать длину шага, пока она не станет hi^e. В качестве
простейшего средства мы ускорили этот долгий процесс, как это
сделал Шампайн A982), путем более радикального уменьшения длины
шага [h^^^=h/\Q) после каждых двух подряд отброшенных шагов.
Оказывается, что этот эффект исчезает в окрестности действительно
выбранной длины шага у L-устойчивого метода, когда /?(оо)=0 (см.
правую часть рис. 7.4). Методы, для которых не только Я(оо)=0, но
и Я(оо)=0, построили Капе и Остерман A990).
Более полное понимание этих явлений становится возможным при
рассмотрении сингулярно возмущенных задач (глава VI).
Методы с неточной матрицей Якоби (W-методы)
«Теперь уместен вопрос: каков самый дешевый тип
неявности, которую мы вынуждены требовать?»
(Штайхауг и Вольфбрандт 1979)
Вся вышеизложенная теория построена на предположении, что J
— точная матрица Якоби df/dy. Из этого следует, что матрица
должна вычисляться на каждом шаге, что может сделать вычисления
дорогими. Штайхауг и Вольфбрандт A979) предприняли следующую
попытку найти условия порядка, которые бы обеспечивали
классический порядок для люб'ыд: аппроксимаций А матрицы df/dy.
Последняя тогда сохраняется на протяжении нескольких шагов и
используется просто для гарантии устойчивости. Условия порядка теперь
должны выводиться немного по-другому: если J заменить на
произвольную матрицу Л, то формула G.6) превратится в
iФ^'^Лн=o=^^if'(9i))^'^-'\=o + чY.^iY.Ъkik^)^'^~'\=o^ G-30)
К к
где A = {Aj^Yj
К'=1' ^ ^^ получим
к к к к
IV.7. Методы типа Розенброка 135
После подстановки в G.8) первый член должен равняться
производной точного решения, а второй быть нулевым. Аналогично, вместо
G.7;3) получим
(^/)^'' 1л=о = 3 Е fLf4' Е ".'^«i'+ G-31; 3)
K,L k,l
K,L k,l K,L k,l
K,L k,l K,L k,l
И условия порядка для 3-го порядка примут вид
E*i = i-
/ E^"ifc = l/2,
E^'*j*'**'=^/^'
E^"ifc'^fc' = '^'
E*Afc"fe' = 0.
E^¦ъ¦*')'*'=o.
it
G.32)
Для графического представления элементарных дифференциалов в
G.31;q) и условий порядка G.32) нам потребуются деревья с двумя
различными видами вершин (одного вида для представления / и
другого — для А). Как и в разд. 11.15, будем пользоваться «тонкими» и
«толстыми» вершинами (см. определения П. 15.1 - П. 15.4). Но
теперь должны рассматриваться не все деревья с «тонкими» и
«толстыми» вершинами (Р-деревья). Из предыдущего вывода видно, что
«толстые» вершины должны иметь только одну ветвь (производные
постоянной матрицы Л равны нулю) и они не могут быть на конце
ветви. Поэтому воспользуемся обозначением
TW = { Р-деревья | концевые вершины — «тонкие»;
«толстые» вершины имеют одну ветвь },
G.33)
и если вершины помечены монотонно, то будем писать LTW.
136 Гл. IV. Жесткие задачи — одношаговые методы
Определение 7,5. Элементарные дифференциалы для деревьев t Е
TW определяются рекурсивно соотношениями Г-^(т)(у) = f-^(у) и
pJu>^iy>^^] '' ' " если < = ^[<1,...,<^] («тонкий» корень);
У^Л]^ • F^(/JB/), есяи1 = ^[i^] («толстый» корень).
к
Определение 7.6. Для i ? TW положим ^j{t) = 1 и
{ Y1 '^3k^'"'^3km^kSh)-"^kJ^m)^ ecли^ = J<l,...,/J;
Ф,@=<
Y^ljk^kih)^ если<=Д<1].
Заметим, что Т (множество деревьев, рассматриваемых для
методов Рунге—Кутты) — это подмножество TW, и что введенные выше
определения совпадают с определениями П.2.3 и II.2.9 (ср. также
формулы (П.2.18) и (II.2.19)). Теперь общий результат формулируется
следующим образом:
Теорема 7.7. Чтобы И^-метод G.4) с У=Л, где А — произвольная
матрица, имел порядок р, необходимо и достаточно, чтобы
J2^j^A^) = ^ длягет cp(t)<p и
^bJФJ{t) = 0 длягет\?\т с p(t) <р.
Доказательство, по существу, то же самое, что и доказательства
теорем 7.3 и 7.4. П
Количество условий порядка для 1У-методов весьма велико (см.
табл. 7.3), так как каждое дерево из Т с к вершинами, имеющими по
одной ветви, порождает 2^^ условий порядка (в случае симметрии
некоторые из них могут совпадать). Поэтому 1У-методы высших
порядков лучше всего получать с помощью экстраполяции (см. разд. IV.9).
Табл. 7.3. Количество условий порядка для W-методов
порядок р
кол-во условий
8 21 58 166 498 1540
IV.7. Методы типа Розенброка 137
Исследование устойчивости линейно неявных методов с Аф^{уо)
очень сложно. Если линеаризовать дифференциальное уравнение
(как в начале разд. IV.2) и принять матрицу Якоби постоянной, то
придем к рекурсии вида
y,=R{hf'[y^),hA)y^,
Поскольку в общем случае матрицы /'{Уо) и Л не могут быть диагона-
лизированы одновременно, рассмотрение скалярных тестовых
уравнений неправомерно. Исследования устойчивости для случая, когда
величина ||/'(t/o)—Л|| мала, будут проведены в разд. IV.11.
Упралснения
1. (Капе 1977.) Не существует метода Розенброка G.4) с 5=4 и ^=5.
Докажите это.
2. (Нёрсетт и Вольфбрандт 1979.) Обобщите вывод условий порядка
для методов Рунге—Кутты с помощью В-рядов (разд. 11.11, с. 263)
на методы Розенброка.
Указание. Докажите, что для В-ряда jB(a, Уо) с а : Т —У К,
удовлетворяющим условию а@)=О,
/1/'(УоM(а,Уо) = ^(а,2/о)
является тоже В-рядом с коэффициентами
j(,)^|p(Oa(*i).
если^ = [^1], и
в противном случае.
3. Купер и Сейфи A983) рассмотрели аддитивные методы Рунге—
Кутты
1-1 t
5^, = Уо + '^ XI ^/(^0 + S'*» 9j) + Л J X %9j' г = 1,..., 5 + 1,
yi=9s+u G.34)
t-i t
для коэффициентов которых 2_] ^ij — ^i» /J ^17 — 0•
a) Докажите, что G.34) эквивалентно G.4), если а^^^ ¦=b- и
(v.i)K) = K)Gu)- G-35)
138 Гл. IV. Жесткие задачи — одношаговые методы
Здесь размерности всех матриц равны (s-\-l) х (s-fl). Последнюю
строку G,j) определять не требуется, так как последний столбец
(а- ) нулевой.
Ь) Если коэффициенты G.34) для всех г удовлетворяют
требованию а, j_j 7^ О, то всегда можно найти эквивалентный метод типа
G.4).
4. (Фервер 1980; Фервер и Шольц 1983.) Выведите условия порядка
для методов Розенброка с «запаздывающей матрицей Якоби», т.е.
для методов типа G.4), в которых J, по предположению, имеет вид
f^(y(xQ—Luh)). Если LJ — отношение шагов h^i^/h, то это позволяет
использовать матрицу Якоби с предыдущего шага еще раз.
5. (Капе и Остерман 1989.) Покажите, что некоторые условия
порядка G.32) могут быть смещены в сторону высших порядков, если
предположить, что
f'(yo)-J = 0(h).
Это делает условия упражнения 4 независимыми от и;.
Ответ. Число смещений порядка равно числу «толстых» вершин.
IV.8. Реализация неявных методов
Рунге—Кутты
«До настоящего времени они не получили сколько-нибудь
широкого распространения. ..» (СП. Нёрсетт 1976)
«Однако трудности реализации этих методов стали препятствием
для их повсеместного использования; ...» (Вара 1979)
«Хотя методы Рунге—Кутты предстгшляют притягательную
альтернативу, особенно для жестких задач, ... распространено
мнение, что они никогда не составят конкуренции многошаговым
методам». (Берридж, Бутчер и Чипман 1980)
«Что касается методов Рунге—Кутты для жестких задач, то мы
только приступаем к их исследованию...»
(Шампайн в Эйкен 1985)
Если размерность дифференциального уравнения y'=f{x,y)
равна п, то s-стадийный полностью неявный метод Рунге—Кутты C.1)
включает в себя нелинейную систему размерности п • s относительно
неизвестных gi^'-yg^- Эффективное решение этой системы — это
главная проблема при реализации неявного метода РК.
Среди методов, рассмотренных в разд. IV.5, особенно
перспективными представляются предложенные Илом процессы Радо ПА,
являющиеся L-устойчивыми и имеющие высокий порядок. Большинство
возникающих вопросов (критерии остановки для упрощенных
итераций Ньютона, эффективное решение линейных систем, начальные
значения для итераций и выбор длины шага) обсуждается здесь на
примере одного метода Ила С5 = 3ир=5. По существу, это
рассмотрение представляет собой описание программы RADAU5 из
приложения. Адаптация описанной здесь техники для других полностью
неявных методов РК более или менее очевидна, если матрица Рунге—
Кутты имеет хотя бы одно вещественное собственное значение. Мы
кратко опишем также нашу реализацию диагонально неявного метода
0ДНРК4 (формула F.16)).
Иная запись нелинейной системы
Для того чтобы уменьшить влияние ошибок округления,
предпочтительнее работать с меньшими величинами
^.•=Л-2/о- (8.1)
Тогда C.1а) переходит в
5
^1 = ^]С ^••/'(^о + ^3^^ Уо + ^j)' г = 1,..., S. (8.2а)
Когда решение г^,...,г^ системы (8.2а) известно, C.1Ь) дает явную
формулу для У1. Ее непосредственное применение требует s допол-
140 Гл. IV. Жесткие задачи — одношаговые методы
нительных вычислений функции. Их можно избежать, если матрица
A={a^j) коэффициентов Рунге—Кутты невырожденная. В самом
деле, (8.2а) можно записать как
Л/(хо-[-с,Л,Уо-1-^,)-
и тогда легко видеть, что C.1Ь) эквивалентно уравнению
5
У1=% + Е'^.-^.' (8-2^)
t=i
где
{d„...,d,) = (b„...X)A-' . (8.3)
Для трехстадийного метода Радо ПА (табл. 5.6) вектор d есть просто
@,0,1), так как 6,=а,,- для всех г.
Еще одно преимущество формулы (8.2Ь) состоит в следующем.
Величины ^1,..., Z, вычисляются методом итераций, и поэтому они
неточны. Вычисление /(xq+ с,Л,Уо-1-'2^|) ^ формуле C.1Ь) сильно
увеличивает эти погрешности по причине большой константы Липшица
для /, и они тогда «могут стать катастрофически велики для жесткой
задачи» (Шампайн 1980).
Упрощенные итерации Ньютона
В случае нелинейного дифференциального уравнения общего
вида систему (8.2а) приходится решать итерационным методом. В
«каменном веке» жестких вычислений (т.е. до 1967 года) на ум
обычно приходил метод простых последовательных приближений. Но это
превращает алгоритм в явный метод и разрушает хорошие свойства
устойчивости. В своей статье Линигер и Уиллоуби A970) тогда
показали преимущества использования для этой цели метода Ньютона.
Метод Ньютона, примененный к системе (8.2а), требует на каждой
итерации решения линейной системы с матрицей
'^~^aii|^(xo + Ci/i,yo + ^i) ... -Ла1,|^(хо + с,/1,Уо + ^,)
Существенное упрощение достигается заменой всех матриц Якоби
|^(хоЧ-с,.Л,Уо-|-г,) приближенной:
J 9ff ^
IV.8. Реализадия неявных методов РК 141
Тогда упрощенными итерациями Ньютона для (8.2а) будут
(/ - ЛЛ (8) J)AZ^ = -Z^ -h h[A 01)F{Z^),
Здесь Z'^ = (zf,.. .,zj)^ — fc-e приближение решения, AZ^ =
= (Azf,..., Az^)'^ — приращения и
F(Z'^) = (/(xo + Ci/i, 2/0 +^f),...,/(^0 + ^,^.2/0 +^?))^'
Каждая итерация требует s вычислений / и решения линейной
системы размерности ns. Матрица (/ — hA 0 J) одна и та же для всех
итераций. Ее LU-разложение производится только один раз, но (для
задач большой размерности) оно требует обычно очень много
вычислений.
Начальные значения ддя итеращ[М Ньютона. Так как точное
решение (8.2а) Zi = 0{h)y то естественным и простым выбором для
начальных значений итераций (8.4) (или эквивалентных им (8.13), см.
ниже) было бы
zf = 0, г=1,...,5. (8.5)
Однако в общем случае возможен и лучший выбор. Если неявный
метод Рунге—Кутты удовлетворяет условию С(т;) (см. разд. IV.5 или
П.7) для некоторого г; < 5, то
Zi^y{xo-bCih)-yo'^0{h^^'). (8.6)
Предположим теперь, что с,- ф О (г=1,...,«) и рассмотрим
интерполяционный многочлен степени 5, определяемый условиями
д@) = 0, <7(с,.) = г,., 2=1,..., 5.
Поскольку погрешность интерполяции имеет порядок C?(/i*+^), то с
учетом (8.6) получим
yiXo + th)-y,-q{t)=Oih^+')
(см. теорему 7.10 из главы П для коллокационных методов). Мы
используем значения q{t) также и вне отрезка [0,1] и возьмем
2:? = g(l-hu;c.)-hyo-2/p г=1,...,5, w = h^^^/h^i^ (8.5')
в качестве начальных значений для итераций Ньютона на следующем
шаге. Численные эксперименты с трехстадийным методом Радо ПА
показали, что (8.5') обычно приводит к более быстрой сходимости,
чем (8.5).
Критерий остановки. Этот вопрос тесно связан с оценкой
погрешности итераций. Поскольку сходимость линейная, имеем
IIAZ'^-^^II < eilAZ'^ll в надежде, что 0 < 1. (8.7)
Применение неравенства треугольника к
142 Гл. IV. Жесткие задачи — одношаговые методы
где Z* — точное решение (8.2а), дает оценку
ll^'+'-^1l<Y^I|AZ''ll- (8-8)
Скорость сходимости 0 можно оценить, вычисляя величины
0, = ||Д7*||/||Д^''-Ч|, к>\. (8.9)
Ясно, что погрешность итераций не должна быть больше чем
локальная погрешность дискретизации, которая обычно
поддерживается вблизи То1. Поэтому мы останавливаем итерации, когда
г,,||Дг*||<к.Го/ с '?*=1^. (810)
и принимаем Z^-^^ в качестве приближения к Z*. Эта стратегия
может быть применена только после не менее чем двух итераций. Для
того чтобы иметь возможность остановить вычисления уже после
первой итерации (что особенно выгодно для линейных систем), мы
возьмем для к=0 величину
г/о = (maxG;^f^, Uround)f'^ ,
где Tj^i^ — последнее rjf^ с предыдущего шага. Остается сделать
хороший выбор параметра к в (8.10). Для этого мы испытали
программу RADAU5 со многими разными значениями к между 10 и 10"""* и
с разными допустимыми погрешностями То1 на нескольких
дифференциальных уравнениях. Наиболее эффективная работа программы
наблюдалась для значений к вблизи 10"^ или 10"^.
Наш опыт говорит о том, что программа становится более
эффективной, когда мы допускаем относительно большое число итераций
(например, к^^^ = 7 или 10). Во время этих к^^^ итераций
вычисления прерываются и начинаются заново с меньшей длиной шага
(например, с h:=h/2) в любом из следующих двух случаев:
a) встречается к такое, что 0/f > 1 (итерации «расходятся»);
b) для некоторого к оказывается, что
-t---l\AZ'\\>K.Tol. (8.11)
Выражение в левой части (8.11) представляет собой грубую оценку
погрешности итераций, ожидаемой после к^^^. — 1 итерации. Норма,
используемая во всех этих формулах, должна быть той же самой, что
и применяемая для оценки локальной погрешности.
Если потребовгипась только одна ньютоновская итерация, чтобы
удовлетворить условию (8.10), или если последнее 0^^ было очень
малым (скажем, < 10""^), то мы не перевычисляем матрицу Якоби на
следующем шаге. Вследствие этого для линейных задач с
постоянными коэффициентами матрица Якоби вычисляется только один раз
(если нет отброшенных шагов).
IV.8. Реализация неявных методов РК 143
Линейная система
Существенный выигрыш в вычислительной работе при решении
линейной системы (8.4) дает следующий метод, предложенный
независимо Бутчером A976) и Биккартом A977). Этот метод с
большой выгодой использует специальную структуру матрицы I—hA<S)J
в (8.4).
Идея заключается в том, чтобы предварительно умножить (8.4)
на (ЛЛ)""^0/ (мы предполагаем здесь, что Л имеет обратную
матрицу) и привести Л~^ к простому виду (диагональному, блочно-
диагональному, треугольному или к канонической форме Жордана):
Т-^А'^Т = А . (8.12)
В преобразованных переменных W^ = {T-^ ® I)Z^ итерации (8.4)
будут эквивалентны следующим:
W^-^^ = W^-\'AW'' . (8.13)
Заменим также Z^ и AZ'^ на W^ и AW^ в формулах (8.7)-(8.11)
(и этим сэкономим еще сколько-то работы).
Для дальнейшего предположим, что матрица А~^ имеет одно
вещественное собственное значение 7 и одну пару
комплексно-сопряженных собственных значений а±.гР. Такая ситуация типична
для трехстадийных НРК-методов — таких, как метод Радо ПА. При
'y=h''^y^a=h-'^a,P=h~^/i матрица в (8.13) будет
/yl-J О О \
О а/-J -/?/ , (8.14)
\ О 01 al^jj
так что (8.13) расщепляется на две линейные системы размерности п
и 2п соответственно. Возможно несколько подходов к тому, как
извлечь пользу из специальной структуры субматрицы 2пх2п. Самым
легким и наиболее устойчивым с вычислительной точки зрения
оказался следующий путь: преобразуем вещественную подсистему
размерности 2п в п-мерную комплексную систему
({a-{-if3)I-J)(u-\-iv) = a-\'ib (8.14')
и применим простой метод исключения Гаусса. Для машин без
комплексной арифметики нужно просто модифицировать подпрограммы
линейной алгебры. Тогда комплексное умножение будет состоять
из 4-х вещественных умножений и количество работы для решения
(8.14') составит примерно 4п^/3 операций. Таким обрс130м, общая
работа для системы (8.14) составит около бп^/З операций. По
сравнению с (ЗпK/3, что равнялось бы числу операций, необходимых для
разложения непреобразованной матрицы I—hA^J в (8.4), мы
выигрываем примерно в 5 раз по числу арифметических операций. За-
144 Гл. IV. Жесткие задачи — одношаговые методы
метьте, что такие преобразования, как Z^ = (T(S>I)W^ , требуют
только 0{п) сложений и умножений. Для методов, имеющих более трех
стадий, выигрыш получается еще более значительным.
Приведение к форме Хессенберга. Для больших систем с полной
матрицей Якоби J дальнейший выигрыш возможен, если привести J
к форме Хессенберга:
/* ... * ¦'
S''JS = H =
(8.15)
\
Первоначально эту процедуру предложил для многошаговых
методов Энрайт A978). Вара A979) распространил ее на случай методов
Рунге—Кутты. Программа ELMHES, взятая из пакета LINPACK,
выполняет это преобразование за 2п^/3 операций. Поскольку
умножение матрицы S на вектор требует только п^/2 операций (заметьте,
что 5 — треугольная), то, если известна матрица Хессенберга Я,
решение (8.13) находится за 0(п^) операций. Это преобразование
особенно выгодно, когда матрица Якоби J не меняется на протяжении
нескольких шагов.
Выбор длины шага
Экстраполяция по Ричардсону — это лишь одна из возможностей
выбора длины шага (см. разд. П.4). Здесь мы опишем использование
вложенной пары методов. Этот вариант легче запрограммировать, и
он делает программу более гибкой. Последующие формулы выведены
для специального случая трехстадийных методов Радо ПА, но те же
идеи применимы ко всем неявным методам Рунге—Кутты, матрица
Рунге—Кутты которых имеет хотя бы одно вещественное собственное
значение.
Вложенная формула. Поскольку наш метод имеет оптимальный
порядок, его невозможно эффективно встроить в метод более
высокого порядка. Поэтому мы ищем метод более низкого порядка в форме
^ 3 ^
У1=Уо + л(бо/(хо,Уо) + 1]№о + с.Л,^,)), (8.16)
1=1
где 9x^9219з — значения, полученные из метода Радо ПА, и bQ^O.
(Выбор 60=70=7"^) где 7 — вещественное собственное значение
матрицы А"^, снова экономит несколько умножений.) Разность
3
У1-У1= 7оЛ/(а:о, Уо) +1^(^ - f>i)f^f(^o + с,Л,^,),
1=1
IV.8. Реализация неявных методов РК 145
которая может быть записана также в виде
^1 -Ух =7оЛ/(а:о,Уо) + ^1^1+«2^2 + бз'2^3' (8-17)
служит тогда для оценки погрешности. Для того чтобы у^ — y^=0(h^),
коэффициенты должны удовлетворять условию
(е1-е2.ез) = у(-13-7ч/б,-13 + 7л/5,-1). (8.18)
К сожалению, для уравнения у'=Ху при ЛА —> оо разность (8.17)
ведет себя как ^i-~2/i^7o'^'^2/o' '^•^- ^"^ ^^ ограничена, и поэтому (8.17)
непригодна как оценка для жестких уравнений. Вместо этого будем
использовать
егг=(/-Л7о^)-Ч^1-У1) (8.19)
(идея Шампайна). LU-разложение {(hyQ)~^I—J) так или иначе
доступно из предыдущих вычислений, так что вычисление (8.19)
обходится дешево. При Л —> О мы все еще имеем err=0{h^), а при ЛА —> ос
получаем err—>¦—1 (если у^=Ху и J=A).
Это поведение (при ЛА —)¦ со) уже много лучше, чем у (8.17), но все
же недостаточно хорошо для того, чтобы избежать эффекта «горба»,
описанного в разд. IV.7. На первом шаге и после каждого
отброшенного шага, для которого \\€гт\\ > 1, мы будем поэтому для предсказания
длины шага вместо (8.19) использовать выражение
егг={1- hy^jy^ GоЛ/(а?о' % + ^^^) -Ь ^1 ^1 + ^2^2 + ^з^з)• (8-20)
Это требует одного дополнительного вычисления функции, но зато
етт-^ О при ЛА -> оо, как это имеет место для погрешности численного
решения.
Стацпдртная прои,€;лура управления длиной шага. Поскольку
выражения (8.19) и (8.20) ведут себя как O(h^) при Л->^0, стандартный
способ предсказания длины шага приводит к формуле
hne^=fcc-hM\\erf\\-'f\ (8.21)
•new
где
||егН| =
N
-ti—У
п f-f V sci )
и взято 5с,- = Aiol^ -h max(|t/o,|, \уц\)' Rtol^, как и в формуле D.11) из
разд. П.4. Но здесь мы предлагаем еще, чтобы множитель
безопасности jac зависел как от Newt (числа ньютоновских итераций на
текущем шаге), так и от максимального числа ньютоновских итераций
*^тах > например, так: jac = 0.9 х BАг^^^ -h 1)/B/:^^^ + Newt).
Чтобы сэкономить LU-разложения матрицы (8.14), мы сделаем
также такое добавление: если матрица Якоби не вычислялась заново
146 Гл. IV. Жесткие задачи — одношаговые методы
и если размер шага /inew определенный согласно (8.21), не вышел из
интервала
Cl^olcl<^new<C2^old (8-22)
(где, к примеру, с^ = 1.0 и Cj = 1.2), то мы оставим значение к^\^ для
длины следующего шага.
Предсказываюшдя проце^цура управления. Предсказание размера
шага по формуле (8.21) имеет тот недостаток, что уменьшение
размера шага более чем в fac раз невозможно без отказа от шага
(заметим, что /i^ew </^C'^old влечет \\err\\ > 1). Однако для жестких
дифференциальных уравнений часто требуется быстрое уменьшение
размера шага (как, например, в ситуации, показанной на рис. 8.1, где
размер шага сокращается с 10"^ до 10~^ за очень короткий
интервал времени). Обозначим через егг^^^ значение погрешности,
вычисленное на тг-м шаге длины h^ согласно (8.19) (или (8.20)).
Предсказания длины шага обычно выводятся из асимптотической
формулы
\\егг„^1\\ = СЛ- (8.23)
Стратегия (8.21) основывается на дополнительном предположении
^п+1 ^ ^п' которое, как мы видели, не всегда оправдано.
Густафссон A994) предпринял детальное исследование стратегий
управления длиной шага с точки зрения теории управления. Он
пришел к заключению, что лучше всего предполагать logC„ линейной
функцией п. Это означает, что logC„^i — logC„ — константа, или,
что эквивалентно,
Cn+i/Cn«Q/Cn-i. (8.24)
Подстановка Q и Q_i из (8.23) и C„^i из l=Q+i/i^ew ^ (8.24)
дает
в нашей программе RADAU5 мы берем минимум из двух длин шага
(8.21) и (8.25). Эта новая стратегия в упомянутой выше задаче (см.
рис. 8.1) уменьшает число отброшенных шагов с 27 до 7.
Численное исследование механизма управления длиной шага. В
качестве показательного примера мы рассмотрим решение уравнения
Ван-дер)-Поля A.5') при ?=10"^ и с начальными значениями yi@)=2,
2/2@)=—0.6 на отрезке интегрирования О < х < 2. На рис. 8.1
представлены четыре графика. На первом из них показана первая
компонента решения t/i(x) со всеми принятыми шагами интегрирования при
Atol = Rtol = 10""*. На следующем графике изображена вычисленная
программой RADAU5 длина шага как функция х. Непрерывная
кривая соответствует принятым шагам. Отброшенные шаги отмечены
IV.8. Реализация неявных методов РК 147
О 50 100 150 200 250 шаги
Рис.8.1. Решение, длина шагай ньютоновские итерации (RADAU5).
значком X. Обратите внимание на очень малые длины шагов,
которые требуются на быстрых переходах между гладкими участками
решения. На двух нижних графиках дано число ньютоновских
итераций, необходимых для решения нелинейной системы (8.2а), которое
представлено и как функция х, и как функция номера шага. На
последнем графике, кроме того, отмечены шаги, на которых матрица
Якоби вычислялась заново.
Другой численный эксперимент (рис. 8.2) иллюстрирует качество
оценки погрешности. Применив RADAU5 с Atol = Rtol = 10"^ и
начальной длиной шага Л=10~^ к той же задаче, мы для ряда
выбранных точек численного решения построили графики зависимости от Л
следующих величин:
a) точной локальной погрешности (отмечена мелкими кружками),
b) оценок (8.19) и (8.20) (отмечены значками -^ и и соответственно).
Крупными значками отмечены положения реально использованной
длины шага; Newt — число требуемых итераций Ньютона.
Интересно, что локальная погрешность ведет себя как O(h^)
(прямая линия с наклоном 6) только при h<e и при больших Л. Между
этими областями локальная погрешность с уменьшением Л растет
148 Гл. IV. Жесткие задачи — одношаговые методы
h IQr*
h 10^^. . .107^ . . ,
1(И
Л 10-*
NEWT=1
zr=
h 10^
10-»
h 1(Г*
10-»
Л \Qr^ 10"»
NSTEP=13
x = 0.0000157
NEWT=1
h 10-* 10"»
NSTEP=15
;c = 0.0005719
NEWt=i
h 10-* 10"»
NSTEP = 17
0.0361697
Л 10-* 10-»
h 10-* 10"»
Л 10-*
10-»
h 10-* 10-»
NSTEP = 28
jc = 0.7532679
NEWT'= 6
10"*
h 10^ 10-»
NSTEP = 31
NEWT = 5 ^ *"^
io-«
h 10-* 10-»
NSTEP = 33
;c = 0.8005135 JL .r^
NEWT = 5 ^ ^"
io-«
10-»2
10-«2
h 10-* 10-»
NSTEP = 34
jc = 0.8026597 7 ,rt^|
NEWt' = 5 ¦*¦ *"¦ '
10-" H
h 10-* 10-»
NSTEP = 36
x = 0.8049533j ,«^l
NEWT = 5 ¦** *" '
h 10-*
Л 10-*
10^1
io-«
NSTEP = 43
x = 0.8067309
NEWT = 210-12
10-»
-10^ H
10^
10^
10-»
NSTEP = 54
jc = 0.8070058
NEWT = 2 10-12
NSTEP =120
jt = 0.8070881
NEWT = 2
NEWT = 2
h 10-* 10-»
¦4 4 « M »
h 10-* 10-»
h 10-* 10-»
NSTEP = 146
x = 0.8070918
NEWT = 2
NSTEP = 148
x = 0.8070925 ,. ,,
NEWT = 2 *"^
h 10-* 10-»
NSTEP =153
x = 0.8071150
NEWt =
Рис. 8.2. Точная локальная погрешность и оценки (8.19) и (8.20).
IV.8. Реализация неявных методов РК 149
как 0(h''^). Это единственная область, где оценка погрешности (8.20)
значительно лучше, чем (8.19). Поэтому мы пользуемся более
дорогим выражением (8.20) только на первом шаге и после каждого
отброшенного шага. В любом случае обе оценки погрешности всегда
завышают действительную локальную погрешность, так что программа
обычно дает очень точные результаты.
Неявные дифференциальные уравнения
Во многих приложениях (например, для параболических
дифференциальных уравнений, дискретизированных по пространственным
переменным) часто возникают системы вида
My'= fix,у), у(хо) = Уо (8.26)
с постоянной матрицей М. В таких задачах мы формально заменяем
все / на M'^f, а получающиеся уравнения метода затем умножаем
на М. Формулы (8.13) и (8.19) тогда должны быть заменены на
{h'^\®M-I^j)AW^ = -h^^{A(S>M)W''-\-{T'^^I)F{{T®I)W^),
(8.13а)
€гг= ((Л7о)""^М- J)"^ {/{хоуУо) + (Л7о)"^Л^(ci^i + 622:2 + 632:3)) .
(8.19а)
Здесь матрица J снова является некоторой аппроксимацией df/dy.
Эти формулы могут быть даже применены к некоторым задачам
(8.26) с сингулярной матрицей М (подробности в главах VI и VII).
Решение линейной системы (8.13а) производится путем
разложения матрицы
V О (a + i/?)M-jj (^^^)
(ср. (8.14), (8.14')). Если М и J — ленточные или разреженные, то
матрицы 'yM—J и [a-\-i0)M—J тоже остаются ленточными или
разреженными. Программа RADAU5 из приложения может обрабатывать
ленточные структуры.
Программа ОДНРК
Воспользовавшись многими идеями, изложенными выше, мы
запрограммировали также формулу ОДНРК F.16) вместе с формулами
«непрерывного решения» F.17). Для этого метода тоже было очень
важно заменить оценку погрешности Ух—Ух на (8.19).
Здесь, в отличие от полностью неявных методов Рунге—Кутты,
можно обрабатывать стадии одну за другой. Такое последовательное
вычисление обладает тем преимуществом, что информация об уже
посчитанных стадиях может быть использована для того, чтобы удачно
выбрать начальные значения для ньютоновских итераций на
последующих стадиях. Предположим, например, что
150 Гл. IV. Жесткие задачи — одношаговые методы
Zi =lfhf(xQ-\--fh,yQ-\-z^),
^2 = 7^/(^0 -f Cj/i, % + ^2) + «21 f^fi^o + 7Л, % + ^1)
уже доступны. Поскольку
Zi = c,hf(x„ уо) + (X; %«^,)Л'{/х + fyf)(Xo, Уо) + 0{h^)
j
для всех i, то, решив линейную систему алгебраических уравнений
/ с, С2
найдем а^,а2 такие, что
a^z^ -\-a2Z2 = 2:зЧ-С?(Л^).
Выражение 2:3 ^ot^z^ -\-a2Z2 тогда служит начальным значением при
вычислении z^. На последней стадии в качестве начального
приближения при итерациях Ньютона для д^ = у^ можно взять уже
посчитанное к этому моменту у^. Вычисление z^yZ^^y^, осуществляемое
таким способом, не требует много ньютоновских итераций, а их
расходимость обычно обнаруживается уже на первой стадии.
Однако для вычислений на параллельных процессорах
использование треугольной структуры матрицы Рунге—Кутты может быть
менее желательным. В то время как при итерациях (8.13) все s
вычислений функции и большая часть линейной алгебры могут делаться
параллельно, это не проходит для методов ДНРК, в которых при
вычислении Zf^^^ используются ^1, . . . , Zij .
Методы ОНРК
4сТот факт, что у однократно неявных методов матрица
коэффициентов имеет одно собственное значение, является
ключевым для уменьшения количества операций в этих
методах до уровня, характерного для линейных
многошаговых методов». (Берридж, Бутчер и Чипман 1980)
Для того чтобы при написании программы обойти трудности,
вызываемые комплексными собственными значениями матрицы Рунге—
Кутты А, можно поискать методы с вещественными собственными
значениями, особенно с одним 5-кратным вещественным собственным
значением. Такие методы предложил Нёрсетт A976). Берридж A978)
снабдил их формулами для оценки погрешности; программы на
Алголе и Фортране приведены в статье (Берридж, Бутчер и Чипман 1980).
Методы, положенные в основу программы STRIDE этих авторов,
характеризует следующая лемма.
IV.8. Реализация неявных методов РК 151
Лемма 8.1. Для коллокационных методов (методов Рунге—Кутты,
удовлетворяющих условию C{s) из разд. IV.5) равенство
det(I'-zA) = {l-jzy (8.28)
имеет место тогда и только тогда, когда
Ci = yx., г = 1,...,5, (8.29)
где Xj,...,X, — нули полинома Лагерра Ь^{х) (см. формулу F.11)).
Доказательство. Многочлен d€t{I—zA) является знаменателем
функции устойчивости (формула C.3)), так что по теореме 3.10
М^'\0) -h M^"^^0)z + ...-f M{0)z' = A - yzY (8.30)
с многочленом М{х), задаваемым формулой C.25). Вычислив
значения МО)@) из (8.30), получим
1П(х^с,0 = М(х) = ^С)(-7Г^7^
^' ,=1 j=o ^^ ^' ^
что и приводит к (8.29). П
Функция устойчивости метода, о котором идет речь в лемме 8.1,
изучалась в разделах IV.4 (аппроксимации с кратным вещественным
полюсом) и IV.6. Кроме того, мы видели, что Д(оо)=0, когда х^-\-к
— точка коллокации (предложение 3.8). Это последнее означает, что
Сд = 1 или 7=l/iPg для ^G {1,.. .,s}, где О < х^ < ... < х, — нули
полинома L^{x). Но если мы заинтересованы в Л-устойчивых методах,
то теорема 4.25 налагает ограничение на положение этой точки: она
должна быть в середине (точнее: q^s/2 или s/2-l-l для 5 четного,
^ = E-|-1)/2 для S нечетного). Следствием этого (очевидно,
нежелательным) является то, что многие точки коллокации оказываются вне
отрезка интегрирования (например, для 5=5 и ^=3 имеем с^^О.ОТЗ,
С2=0.393, Сз = 1, С4 = 1.970, С5=3.515).
Поскольку эти методы с ')=\/х имеют всего лишь порядок p=s,
их легко встроить в метод более высокого порядка. Берридж A978)
добавил еще одну стадию
i=i
где c^^j и a^^i^^j —произвольные, а остальные a,^.ij определяются
так, чтобы E-1-1)-стадийный метод тоже удовлетворял условию C[s).
152 Гл. IV. Жесткие задачи — одношаговые методы
Чтобы избежать еще одного LU-разложения, выберем cis-^i,s-\-i—y-
Зафиксируем произвольный коэффициент с^^^, положив c,_j_^=:0. В
результате мы однозначно определим метод
5 + 1^
У1 = Уо + Л Y^^jf(xo -h cjh, gj)
i=i
порядка s-fl, вычислив коэффициенты интерполяционной
квадратурной формулы. Явная формула для матрицы Т, которая приводит
матрицу Рунге—Кутты А к канонической форме Жордана и Л"^ к
очень простой нижней треугольной матрице Л, приведена в упр. 1.
Она может быть использована для экономного решения линейной
системы (8.13).
Упралснения
1. (Бутчер 1979.) Докажите, что для коллокационного метода с
узлами с^,.. .yCg (8.29) при 5=4, например, справедливы формулы
1
1A1
1 1 1
Mill.
где преобразование Т имеет вид
а Lj_i(x) — полиномы Лагерра.
Указание. Воспользуйтесь тождествами
Ь;(х) = L'„_,ix) - L„_,ix), L„(x) = i„_i(x) + ^L'Jx)
и формулой Кристоффеля—Дарбу
которая в пределе у -> х переходит в
f;(L,.(x)J = („ + l)(L„^i(x)L;(x)-L;+,(x)L„(x)).
IV.9. Экстраполяционные методы
«Предстгшляется, что подходящий вариант НЭМ
(неявного экстраполяционного метода), который справится с
этими трудностями, может стать очень сильным
конкурентом любому общему методу дискретизации для
жестких систем из числа известных в настоящее время».
(Самое последнее предложение в книге Штеттера 1973)
Экстраполяция явных методов — это интересный подход к
решению нежестких дифференциальных уравнений (см. разд. П.9). Здесь
мы покажем, в какой мере идею экстраполяции можно применить
также и для жестких задач. Мы воспользуемся результатами разд. II.8
о существовании асимптотических разложений и применим их к
изучению таких неявных и линейно неявных методов, которые
представляются наиболее подходящими для вычисления решений жестких
дифференциальных уравнений. В этом разделе наш теоретический
анализ ограничивается понятием классического порядка при Л -> О,
изучением областей устойчивости и Л-устойчивости.
Большое затруднение, однако, создает тот факт, что
коэффициенты и остаточные члены асимптотических разложений могут
буквально «взрываться» при возрастании жесткости, а интервал тех
значений /i, для которых разложение имеет смысл, может стремиться к
нулю. Равномерно справедливые для класса произвольно жестких
задач оценки, ограничивающие сверху остаточный член, будут
рассмотрены позже в разд. VI.5.
Экстраполяция симметричных методов
Наиболее естественно начать с поиска симметричных одношаговых
методов как базовой схемы интегрирования. Обещающими
кандидатами выглядят правило трапеций
yi-^i = yi-^^{f(^i^yi) + f^vyi^i)) (9-1)
и неявное правило средней точки
J/.+1 = У< + hf(xi + -, - (у,+1 + 2/,.)). (9.2)
Возьмем некоторую последовательность чисел шагов п^ < П2 < Пз <
..., положим hj=H/nj и определим
Tji = y,,(xo + H) (9.3)
как численное решение, получаемое после выполнения п • шагов
длины hj . Затем экстраполируем эти значения согласно формуле
154 Гл. IV. Жесткие задачи — одношаговые методы
как это описано в разд. П.9. В результате получим экстраполяцион-
ную таблицу
Тп
ГТ1 пр /т-1 \\j .о f
^31 ^32 ^33
все элементы которой представляют собой диагонально неявные
методы РК (см. упр. 1). Благодаря симметрии базовых схем (9.1) и (9.2)
7^;^ есть метод ДНРК порядка 2к. Чтобы изучить свойства
устойчивости этих методов, применим их к тестовому уравнению у'=Ху. Для
обоих методов (9.1) и (9.2) получим
^ 2
так что функция устойчивости Rj^i^) метода Tjj^ рекурсивно
выражается следующим образом (z^HX):
/l-f-^X"*'
•j.
(9.6b)
2n
Уже Далквист A963) заметил, что для п^ = 1 и П2=2
5
> 1 при z^oo (9.7)
''''^'^-imr-m))
3
— нежелательное свойство при решении жестких задач. Штеттер
A973) предложил брать только четные или только нечетные числа
в последовательности чисел шагов {rij} . Тогда все функции
устойчивости экстраполяционной таблицы стремятся при 2 -> ос к 1 или — 1
соответственно. Но даже в этой ситуации экстраполяция
немедленно разрушает Л-устойчивость схемы, лежащей в основе (упр. 2). На
рис. 9.1 показаны области устойчивости {г; |Я;^|^(с)| < 1} для
последовательности {1,3,5,7,9,...}.
Сглалсивание
«Некоторые численные примеры обнаруживают силу
сглаживгшия в сочетании с экстраполяцией».
(Б. Линдберг 1971)
Другой возможностью преодолеть затруднение, встретившееся в
(9.7), является сглаживание (Линдберг 1971). Идея заключается в
IV.9. Экстраполяционные методы
155
.
'J>s^r>^^Sfci^^pM
-100
^.,..--^^^;;;;^^^^Ш
х<л^^Ш^^ШШШ|
^ВШ11
т
i
P2
Ш
-100
-
Рис. 9.1. Области устойчивости для экстраполированного правила трапеций.
том, чтобы заменить определение (9.3) на сглаживающий шаг Грэгга
^Л = 5л,К + Я), (9.8)
5/,(x) = i(%(r-A) + 2y,(x) + yJa: + /,)). (9.9)
Как и Уд(х), 5д(х) тоже обладает асимптотическим разложением по
четным степеням Л. Поэтому оправдана экстраполяция в
соответствии с (9.4). Функция устойчивости для Tji теперь имеет вид:
v...i|(S|)--..(;;S)-4J^)-)-
что является L-устойчивой аппрюксимацией показательной функции.
Все функции устойчивости Rjk{z), получаемые из (9.6b), обладают
свойством Rjf^{z)^0(z'''^) при z-voo. Для последовательности чисел
шагов
{п^} = {1,2,3,4,5,6,7,...}
области устойчивости для Rkki^) изображены на рис. 9.2.
(9.11)
156 Гл. IV. Жесткие задачи — одношаговые методы
Рис.9.2. Области устойчивости Rkk{z).
Линейно неявное правило средней точки
Экстраполяционные программы, основанные на полностью
неявных методах, трудно реализовать эффективно. После большого числа
вычислительных экспериментов Бадер и Дойфлхард A983) нашли,
что линейно неявное (типа Розенброка) расширение метода ГБШ из
разд. П.9 дает обещающие результаты для жестких уравнений. Этот
метод основан на двухшаговом алгоритме, так как одношаговые
методы Розенброка G.4) не могут быть симметричными для нелинейных
дифференциальных уравнений.
Мотивировка метода Бадера и Дойфлхарда базируется на
преобразовании Лосона A967)
у{х) = е-".с{х), (9.12)
где матрица J^f'[y), как можно надеяться, нейтрализует жесткость.
Дифференцирование дает
с' = е-^"". G(х,е-^^с), где д[х,у) = /(х,у) - Jt/. (9.13)
Решив теперь (9.13) с помощью алгоритма Грэгга (II.9.13b):
c,+i=c,_i+2/ie-^^«.(/(x,,e-^'«c,)
и выполнив обратную к (9.12) подстановку, получим
e-'-'y.+i =е"у.-1 +2Л<?(х,-у^). (9.14)
Далее, по очевидным соображениям вычислительной простоты,
заменим е^'*-^ приближениями I±hJ и, добавив соответствующий
начальный и конечный сглалсивающий шаги, получим
(/ - hJ)y^ = Уо + hg(xQ,yQ), (9.15а)
(/-./iJ)t/,^i = (/-fU)y,_,-f-2M^,,y,), (9.15b)
Sh{^)= oB/2m-i+2/2m+i)' где X = Xq-f 2m/i. (9.15c)
IV.9. Экстраполяционные методы 157
Подставив, наконец, д из (9.13) при x = Xo+2m/i, x, = Xo + 27i), мы
придем к формулам
(/- hJ){y^ - уо) = hf[x^,y^), (9.1ба)
[I - hJ){y,^, - у,) = -(/-f /iJ)(y, - у,_,) + 2/i/(x,, у,), (9.1бЬ)
5'л(^)= 2(^2^-1 "^^2m + l)» (^•16c)
где J — некоторое приближение матрицы Якоби |^(з?о,Уо)- Если
положить 7=0, то (9.16а) и (9.16Ь) становятся эквивалентными
соответствующим формулам метода ГБШ. Схема (9.16Ь) — это линейно
неявное (или полунеявное) правило средней точки, формула (9.16а)
— линейно неявный метод Эйлера.
Теорема 9.1 (Бадер и Дойфлхард 1983). Пусть /(х,у)
дифференцируема достаточное число раз, и пусть J — произвольная матрица;
тогда численное решение, определяемое формулами (9.16а,Ь,с),
обладает асимптотическим разложением вида
у{х) - S,(х) = J2 'J(^)'^"' + h^'^'C(x, h), (9.17)
где C{x, h) ограничена при Xq<x <x и 0<h<hQ. При J фО в общем
случае е^(х^) ф 0.
Доказательство. Как в доказательстве Штеттера для алгоритма
ГБШ, введем переменные
h*=2h, х^ = Хо + /:Л*, ио = ^о = Уо> Ч = У2к^
v^ = {I- hJ)y^^^^ -h hJy^,^ - hf(x^^, У2^ = (9.18)
= (/ -f Л7)У2Л-1 - hJy^,^ -h Л/(х2/,, У2^.
Метод (9.16a,b) можно тогда переписать в виде
где для У2к+1 ^^ получаем из (9.18) симметричное представление
Симметрия (9.19) иллюстрируется на рис. 9.3, и ее можно
проверить аналитически, сделав перестановки У'к+х ^ ^^к^ ^ife+i ^ ^/с >
158 Гл. IV. Жесткие задачи — одношаговые методы
2/2/е-|-2, = 3 + 1
\9{^2к^У2к)\
Р
У2к^1
'У2к\=^к
2/2;c+d
5'(^2fc + l'2/2yk-fl)
^(^2/с+2'2/2^ + 2)
У2к-\-3
)(/-л^)*
)(/-f/lJ)*
^2/с-1
^2к
''2/С + 1
^^2/с+2
^'2Jfe+3
Рис. 9.3. Симметрия метода (9.19) (см. (9.16Ь)).
Л* ^ —Л* и xj f^ xJJ Н-Л* . Метод (9.19) согласован с
дифференциальным уравнением
и' = /(аг, v) - y(t; - ii), u(xq) = уд,
v' = /(x, ti) -f J(t; - ti), t;(a:o) = Уо.
точным решением которого является u{x) = v{x)=y{x), где у(х) —
решение исходного уравнения 2/=/(ж,у). Применив теорему II.8.10,
получим
у(х) - ti,. (х) = Y1 ^(^)Л^'' + Л^'-^^Л(х, Л),
(9.20)
у(х) -1;,. (х) = Y^ bj{x)h'^ + Л^'+2В(х, А),
где а^(хо)=6^.(хо)=0. С помощью формул (9.18) можно выразить
численное решение (9.1бс) через и^ и v^ следующим образом:
^(^2^+1 + У2т-г) = (/ - Л^2)-» (v^ + h'J{f{x,^, и J - Juj),
и мы получаем
у{х) - S,(х) = (/ - Л^')-» (у(х) - «д. {х)-
- AV (/(X,«,. (х)) + J{y{x) - и,, (X)))) .
для x=XQ + 2mh. Подставляя разложения (9.20), находим (9.17). П
В качестве приложения этой теоремы мы получаем интересный
теоретический результат о существовании 1У-методов (методов G.4) с
неточной матрицей Якоби). Мы видели в томе I (упр. 1 из разд.11.9
IV.9. Экстралол$щионные методы 159
И теорема II.9.4), что все Tj f^ экстраполяционного метода ГБШ
представляют собой явные методы Рунге—Кутты. По аналогии
нетрудно догадаться, что Tj f^ для рассмотренного выше линейно неявного
правила средней точки представляют собой W-методы (подробнее см.
упр. 3) и справедливо следующее предложение о существовании таких
методов.
Теорема 9.2. Для четного р существует РУ-метод G.4) порядка р,
имеющий s=p(p-\-2)/4 стадий.
Доказательство. Из (9.20) следует, что для x=XQ-\-2mh численное
решение У^{^)=У2т обладает Л^-разложением вида (9.17) с е^(жо)=0.
Поэтому экстраполяция дает Ж-методы порядка 2к (в к-м столбце).
Взяв {п^} = {2,4,б,8,10,12,...} и сосчитав число необходимых
вычислений функции, приходим к утверждению теоремы. П
Для анализа устойчивости метода (9.16) надо применить его при
J=X к тестовому уравнению у' = \у. В этом случае формула (9.16Ь)
сводится к
_ \ + h\
^»+1"ТЛА^'-^'
и численный результат дается выражением
5.(хо + 2пгЛ) = ^^A±^)"'-',„, (9.21)
В точности таким же, как и полученное из правила трапеций со
сглаживанием (см. формулу (9.10)). Далее, надо выбрать
последовательность чисел шагов {rij). Ясно, что они должны быть четными:
п. =:2т . Бадер и Дойфлхард A983) предложили брать только
нечетные числа m , так как тогда S^(xQ-|-2m./i) в (9.21) имеет тот же
знак, что и точное решение е^'^^^^у^ , для всех вещественных ЛА < 0.
В результате они пришли к последовательности
{п-] = {2, б, 10,14,22,34,50,...}. (9.22)
Положив Tjl=Sf^ (xq-\-H) с hj=H/nj и определив Tjf^ согласно (9.4),
получим таблицу И^-методов G.4) (упр. 3). По теореме 9.1 Аг-й
столбец этой таблицы представляет собой методы порядка 2Аг — 1
независимо от выбора J (методы не имеют порядок 2Аг, потому что в (9.17)
еДдгд) фО). Функция устойчивости для Т,^ имеет вид
а функции устойчивости для 7'-;^ можно вычислить с помощью
рекурсии (9.6b). Исследование ?"-многочленов C.8) для этих рациональных
160
Гл. IV. Жесткие задачи — одношаговые методы
Таблищ 9.1.
90»
90» 90О
90» 90»
90» 89.34»
90» 88.80»
90» 88.49»
90» 88.43»
Л(о)-устойчивость экстраполированного
линейно неявного правила средней точки
90»
87.55»
86.87»
87.30»
87.42»
87.34»
86.10» 86.02»
86.61» 86.36» 86.33»
87.00» 86.78» 86.70» 86.69»
функций показывает, что Л-устойчивы не только Т^-^, но также Т22,
Тз2 и Тзз (Хайрер, Бадер и Любих 1982). Для некоторых дальнейших
элементов экстраполяционной таблицы (9.5) углы Л (а)-устойчивости
приведены в табл. 9.1. Области устойчивости Tf^j^ для А: = 2,3,4,5,б
изображены на рис. 9.4.
Рис. 9.4. Области устойчивости экстраполированного
линейно неявного правила средней точки.
Неявный и линейно неявный метод Эйлера
Почему бы не рассмотреть в качестве базовых схем
интегрирования также и несимметричные методы? Дойфлхард A985) сообщил об
экспериментах с экстраполяцией неявного метода Эйлера
2/.>1=У.+Л/(х,-^1,у,^1) (9.24)
и линейно неявного метода Эйлера
(/-Л7)(у,^.1-у,) = Л/(;с,,у,), (9.25)
где J — опять некоторая аппроксимация |^(^Со'2/о)- ^^и методы
несимметричны и обладают только Л-разложением своей глобальной
IV.9. Экстраполяционные методы 161
Рис. 9.5. Области устойчивости экстраполированного метода Эйлера.
погрешности. Поэтому мы вынуждены экстраполировать численные
решения в точке Xq-\-H по формуле
^i,fc+i ""^i.^"^
^i./c ""^j-i./g
(9.26)
(п^/п^_/с)-1'
так что Tji^ представляет собой метод порядка к.
У обоих базовых методов (9.24) и (9.25) функция устойчивости для
Tjf^ одна и та же и определяется рекуррентным образом:
R
:л(^)=A-^)"".
Rik+ii^) = Л,к(г + -^тЧ—\ 1 •
(9.27а)
(9.27b)
Взяв последовательность чисел шагов
{п^.} = {1,2,3,4,5,6,7,...}, (9.28)
мы изобразили на рис.9.5 области устойчивости Rk^i^) (левый
график) и Ri^ k-i(^) (правый график). Видно, что все эти методы
являются Л (а)-устойчивыми с а, близким к 90^. В табл. 9.2 даны
значения а (полученные численно) для Rj^i^) с j < 8.
В главе о дифференциально-алгебраических системах мы увидим,
что лучше использовать первую субдиагональ экстраполяционной
таблицы, вычисленной для последовательности (9.28). Это равносильно
использованию последовательности числа шагов {п,} = {2,3,4,5,...}.
Эффективное конструирование плотной выдачи лучше всего
можно мотивировать тоже при рассмотрении систем дифференциально-
алгебраических уравнений (разд. VI.5).
162 Гл. IV. Жесткие задачи — одношаговые методы
Таблищк 9.2.
~90^
90»
90»
90»
90»
90»
90»
90»
90»
90»
90»
90»
90»
90»
90»
Л{а)-устойчивость экстраполировалного метода Эйле
89.85»
89.90» 89.77»
89.93» 89.84» 89.77»
89.95» 89.88» 89.82» 89.78»
89.96» 89.91» 89.86» 89.82» 89.80»
89.97» 89.93» 89.89» 89.85» 89.83» 89.81»
Реализация
Экстраполяционные методы, основанные на неявной
дискретизации, вообще говоря, менее эффективны, чем основанные на линейно
неявной дискретизации. Причина этого в том, что решения
возникающих нелинейных систем необходимо вычислять с очень высокой
точностью, чтобы не разрушилось асимптотическое разложение
погрешности. Первой успешной экстраполяционной программой для
жестких диффе{9!енциальных уравнений стала программа METAN1 Бадера
и Дойфлхарда A983), основанная на линейно неявном правиле
средней точки (9.16). Формула (9.166) в ней на самом деле заменена на
равносильную формулу
Ду, = Ду,_,+2A-hjy' (hfixi, у,) - Ду,_,), Ду, = у,+1 -J/,, (9.29)
которая позволяет избежать одного умножения матрицы на вектор.
Выбор длины шага и порядка в этой программе описан в работе
Дойфлхарда A983); Шампайн A987) предложил модификации
управления длиной шага и порядком. Нами написаны следующие две
экстраполяционные программы (см. приложение).
Программа SODEX основана на линейно неявном правиле средней
точки (9.16), использует последовательность чисел шагов (9.22) и
математически эквивалентна METAN1. Выбор длины шага и порядка
в SODEX почти такой же (за исключением незначительных
изменений), что и в нежесткой программе ODEX из разд. II.9. Мы упомянем
лишь, что в формуле для вычислительной работы на единичном шаге
(II.9.26) число А^^ увеличивается на величину размерности дифферен-
цигипьного уравнения, чтобы учесть затраты на вычисление матрицы
Якоби.
Программа SEULEX реализует линейно неявный метод Эйлера
(9.25), используя последовательность чисел шагов {2,3,4,5,6,7,...}
(в программе можно выбрать и другие последовательности). Выбор
длины шага и порядка такой же, как и в SODEX. Программа-прототип
IV.9. Экстралоляционные методы 163
EULSIM, которую впервые обсуждал Дойфлхард A985), использует
тот же самый численный метод, но реализована иначе.
«Никакая программа не может решить задачу для
уравнения Ван-дер-Поля в лоб из-за переполнения...»
(Шампайн 1987)
Серьезную трудность при реализации экстраполяционных
методов представляет использование шагов «большой» длины. Во время
вычисления 7^^ можно легко попасть в беду из-за
экспоненциального переполнения при вычислении правой части дифференциального
уравнения. В качестве средства против этого мы предлагаем
следующие стратегии.
a) При формировании экстраполяционной таблицы мы сравниваем
оценку погрешности err =||7l-_i ^-^jll ^ предыдущей оценкой и
заново пересчитываем данный шаг с меньшим значением Я,
например, с Я=0.5 • Я, если erVj > errj^^ для некоторого j > 3.
b) Чтобы иметь возможность прервать процесс уже после первых
вычислений /, мы требуем, чтобы длины шагов /1 = Я/п, при 1 = 1
и г = 2 были достаточно малыми — такими, чтобы сошлись
упрощенные ньютоновские итерации, примененные к неявному методу
Эйлера y=^yo-{-hf(x^y), ж=ХоН-Л (идея Дойфлхарда «проверки на
устойчивость»). Первые две итерации будут
(/-Л7)До = Л/(хо.Уо). г/<'^ = Уо + До,
(/-Л7)Д,=/1/(хо + Л,у<»))-До.
Если ||Ai|| > ||Aq|| (расходимость итераций), то производится
пересчет шага заново с меньшим Я. Заметим, что для обоих методов
(9.16) и (9.25) не требуется никаких дополнительных вычислений
функции. Для линейно неявного правила средней точки мы имеем
простые соотношения До=Ауо» Ai = ^(At/i — Дуд) (см. формулу
(9.29)).
Неавтономные д||фференщ1альные уравнения. Имеется
несколько возможностей применить рассмотренные экстраполяционные аидго-
ритмы к неавтономному дифференциальному уравнению у' = /(х, у).
i) Можно непосредственно применить формулу (9.16) И1и (9.25) (это
оправдано, так как для неавтономных задач общего вида
справедливы все асимптотические рг13Ложения).
ii) Можно преобразовать дифференциальное уравнение в автономную
систему, добавив уравнение а:' = 1, и затем применить алгоритм.
164 Гл. IV. Жесткие задачи — одношаговые методы
Для линейно неявного метода Эйлера это дает
(/-Л^)(У,+1-г/.) = Л/(х,,у,) + Л2|^(хо,Уо) (9.31)
(производную ^(л^О'%) также можно заменить некоторым
приближением). Для линейно неявного правила средней точки
формулу (9.16а) надо заменить на (9.31) с г=0, формулы же (9.16Ь) и
(9.16с) не изменяются.
iii) Можно применить одну упрощенную итерацию Ньютона к неявной
дискретизации Эйлера (9.24). Это дает
(/-Л7)(у,+1 -у,) = Л/(х,+1,у,.). (9.32)
Использование этой формулы позволяет избежать вычисления
производной df /дх, но требует одного дополнительного
вычисления функции для каждого Т^^. В случае линейно неявного
правила средней точки замена (9.16а) на (9.32) разрушила бы симметрию
и разложения по степеням Л^.
Теоретическое изучение трех различных подходов для линейно
неявного метода Эйлера, примененного к уравнению Протеро—Робинсона
(см. упр. 4) показывает, что третий подход предпочтительнее.
Более глубокое теоретическое понимание этого вопроса достигается при
изучении сингулярно возмущенных задач (глава VI).
Неявные дщфферен1Ц1альные уравнения. Наши программы из
приложения написаны для задач вида
My'=fix,у), (9.33)
где М — постоянная квадратная матрица. Необходимые
модификации базовых формул получаются, как обычно, заменой всех / и J на
M'~^f и M~^J и умножением слева на М. Линейно неявный метод
Эйлера тогда имеет вид
(М - ЛУ)(у,+, - у,.) = ft/(x,, у,.), (9.34)
а линейно неявное правило средней точки переходит в
Ду, = Ду,,1 + 2(М - hjy' [hf[x,,y,) - MAy,_i), (9.35)
где Ду,=у,.^1-у,..
Упражнения
1. Рассмотрим неявное правило средней точки (9.2) в качестве
базовой схемы интегрирования и определим Tj/^ согласно (9.3) и (9.4).
a) Докажите, что Tjf^ представляет собой метод ДНРК порядка
p=2fc, имеющий 5=П1-|-П2Н-.. .-fn^ стадий.
b) Tjf^, определяемое формулами (9.8) и (9.4), эквивалентно
методу ДНРК порядка р=2к—1.
IV.9. Экстраполяционные методы
165
2. Пусть Rjk(z) задается формулой (9.6). Предположим, что
последовательность чисел шагов состоит только из четных чисел.
Докажите, что Rj2{z) не может быть Л-устойчивой. Точнее, покажите,
что не более чем конечное число точек мнимой оси может лежать
в области устойчивости Rj2(z) (объясните рис. 9.6).
Рис. 9.6. Как экстралоляция разрушает Л-устойчивость.
3. Докажите, что 5^(х), определяемое формулой (9.16), есть
численный результат 1У-метода G.4), имеющего Bп-|-1) стадий и
следующие коэффициенты {п=2т):
если j = 1 и i четное,
если 1 < j < г и г — j нечетное,
иначе;
"о = i 2/п,
U
_Г(-1).->/„,
если j = 1 или j = i,
если 1 < J < t;
^ = "n+i,.- + 7„+i,,- для всех i.
4. Примените три различные версии линейно неявного метода Эйлера
(9.25), (9.31) и (9.32) к задаче у'=\{у-<р(х))+<р'(х). Докажите, что
погрешности е,=1/,—у'(з;,) имеют вид e,-^j = A — ЛА)~'е,-|-<5д(х,),
где при h—?0 и ЛА-400
S,(x) = -hip'{x) + 0{h^) + 0{\-'),
S,ix) = -у^"(х) + {l-hX)-'h'X{^'{x)-<p'(xo)) +0{h^) +0(hX-'),
6,{x) = (l-h\)-' (^j<p"ix) + 0(h')^
соответственно.
IV. 10. Численные эксперименты
¦Теория не может выжить без практики, и смерть ее
наступает столь же скоро, сколь быстротечна ее жизнь».
(Леонардо да Винчи 1452-1519,
цит. по М. Kline, Mathematical Thought... 1972, p. 224)
«Sine experientia nihil sufficienter scrire potest». («Ничто
нельзя познать в должной мере без опыта».)
(Надпись над входом в оксфордский Ботанический
сад, цит. по The Latin Citation Calendar^ Oxford 1996)
После знакомства с множеством различных методов и идей
возникает правомерный вопрос: как все их теоретические свойства, что
рассмотрены в предыдущих разделах, влияют на эффективность
практических вычислений.
Использованные программы
Мы сравнивали перечисленные ниже программы, из которых
некоторые описаны в приложении.
RADAU5 и SDIRK4 — программы, реализующие неявные методы
Рунге—Кутты. Первая из них основана на методе Радо ПА
пятого порядка с 5 = 3 (табл. 5.6), вторая же использует метод ОДНРК
(SDIRK) четвертого порядка F.16). Оба метода L-устойчивы.
Детали их реализации описаны в разд. IV.8.
ROD AS и R0S4 — программы, реализующие методы Розенброка
четвертого порядка. Для оценки погрешности в них
используются вложенные методы третьего порядка. ROS4 реализует
методы из табл. 7.2; имеется ключ, позволяющий выбирать
различные наборы коэффициентов. В основу RODAS положен
метод, удовлетворяющий дополнительным условиям порядка для
дифференциально-алгебраических уравнений (см. разд. VI.4), но
вычислительные затраты на каждом шаге несколько больше.
R0DAS5 — это расширение RODAS на метод пятого порядка,
коэффициенты которого построила Ди Марцо A992).
SEULEX и SODEX — программы, использующие экстраполяцион-
ные методы. В первой реализован линейно неявный метод Эйлера
(Stiff EULer Extrapolation) (9.32), а во второй — экстраполяцион-
ный алгоритм, основанный на линейно неявном правиле средней
точки (9.16) (Бадер и Дойфлхард 1983). Оба метода обсуждались
в разд. IV.9.
В этом разделе приводятся также результаты численных
экспериментов с программой LSODE (Хайндмарш 1980), основанной на
методах ФДН (BDF). Эти методы относятся к классу многошаговых
методов, которым посвящена глава V.
Многие из решавшихся здесь задач очень жесткие, и явным
методам потребовались бы часы, чтобы вычислить решение. На некоторых
IV. 10. Численные эксперименты 167
примерах, однако, было все же интересно посмотреть и поведение
явных методов, особенно методов с расширенной областью
устойчивости (например, программа RKC Соммейера A991) реализует метод
Рунге—Кутты—Чебышева, рассмотренный в разд.IV.2), а также и
обычных методов Рунге—Кутты типа реализованного в программе
D0PRI5, которая была описана в томе I.
Двенадцать задач-тестов
«Man hiite sich, auf Grund einzelner Beispiele allgemeine
Schliisse iiber den Wert oder Unwert einer методе zu
Ziehen. Dazu gehort sehr viel Erfcihrung».
«He следует спешить с общими выводами о
достоинствах или недостатках некоторого метода на основании
отдельных примеров. Для этого требуется очень
большой опыт». (Л. Коллатц 1950)
Обширные численные эксперименты с жесткими задачами впервые
провели Энрайт, Халл и Линдберг A975). Их набор задач STIFF-
DETEST стал настоящим «должно» для поколений программистов
(см. также критические замечания Шампайна A981)). Энрайт и Халл
A976) предложили еще несколько пробных задач, в основном из
химической кинетики. Берн и Хайндмарш A987) написали интересную
обзорную статью, содержащую также задачи большой размерности.
Для наших тестов мы выбрали описанные ниже пробные задачи.
VDPOL — осциллятор Ван-дер-Поля (см. A5') и рис. 8.1):
y'l =2/2'
2/2=((l-2/?J/2-2/i)A. e = 10-^ A0.1)
2/1 @) = 2, У2@) = 0; arout = 1,2,3,4,..., 11.
ROBER — реакция Робертсона A966) (см. A.3) и A.4)):
у; = -0.042/1 + 10^1/22/3' yi@) = l,
2/2 = 0.04у1 - 104у22/з' - 3 . Wyl У2@) = О, A0.2)
2/з= 3.107у2, 2/з@) = 0,
один из наиболее известных примеров в «жесткой» литературе.
Обычно его рассматривали на отрезке О < х < 40, пока Хайндмарш не
обнаружил, что многие программы терпят неудачу, если х становится
очень большим (например, 10^^). Причина заключается в том, что
как только компонента численного решения г/2 случайно становится
отрицательной, она стремится к —ос, и выполнение программы
прекращается из-за переполнения. Поэтому мы выбрали
xout = l,lo,lo^lo^...,lo^^.
168 Гл. IV. Жесткие залами — одношаговые методы
OREGO — орегонатор, знаменитая модель с периодическим
решением, описывающая реакцию Белоусова—Жаботинского:
у'1=77.27(у2 + у,A-8.37510-«У1-2/2)).
у^ = 0.1б1(у1-2/з),
yi@) = l, У2@) = 2, Уз@) = 3, xout = 30,60,90,...,360
(Филд и Нойес A974); см. также Энрайт и Халл A976); рисунки см.
T.I, с. 124).
HIRES — эта химическая реакция с участием восьми реагентов
была предложена Шефером A975) для объяснения «роста и
дифференциации растительной ткани независимо от фотосинтеза при высоких
уровнях светового облучения». Готтвальд A977) предложил
использовать ее в качестве тестового примера. Соответствующие уравнения
имеют вид:
у[ = -1.71 • У1 + 0.43 • Уз + 8.32 • у^ + 0.0007,
Уз = 1-71 у,-8.75 Уз,
у^ =-10.03 • Уз-Ю.43 • У4 + 0.035 • У5,
у; = 8.32у2-Ц.71уз-1.12у4, A0.4)
у^ =-1.745 • У5-Ю.43 • Уб + 0.43 • У7,
у'е = -280 • УбУв + 0.69 • У4 -I-1.71 • У5 - 0.43 • Уе -I- 0.69 • у^,
г/7 = 280 УбУв-1.81 •У7,
г/8 = -г/?;
yi@) = l, уз@) = Уз@) = ... = У7@) = 0, У8@) = 0.0057,
и для выдачи были выбраны значения Xq^^ = 321.8122 и 421.8122 .
Е5 — еще одна задача о химической реакции, получившая имя "Е5"
в коллекции задач Энрайта, Халла и Линдберга A975). Она
определяется следующими уравнениями:
yi= ^Ау,-Ву,у^, yi@) = 1.76-10-3,
2/2= Лу^ -МСу^Уз, У2@) = 0> A0.5)
2/3 = Ау^ - Бу^уз - ^Су^у^ + Су4, Уз@) = О,
у'а= Ву^Уз -С'У4, У4@) = 0,
где Л = 7.89 10-10, В = 1.Ы07, С=1.13 103 и М = 10б. Как
видно из рис. 10.1, масштабы переменных имеют очень большой разброс
(У1 ^ 10-3 вначале, а значения остальных компонент не
превышают 1.46 • 10-1°), и «.. .задание скалярной абсолютной величины
допустимой погрешности здесь совершенно не годится» (Шампайн 1981).
IV. 10. Численные эксперименты 169
- 1 1
1 1 1 1 1
1 1 1 к 1 III 11
10-^
10-10
10-20
10-^ т^^ 10° ш^ 10^ ш^ 10» 10^0 10^
Рис. 10.1. Решение системы A0.5); обе шкалы логарифмические.
Дифференциальное уравнение имеет инвариант Уг ~ % ~ 2/4 — ^' ^ ^
подпрограмме вычисления функции рекомендуется использовать
соотношение Уз = У2 ~ У4 ' чтобы избежать возможной потери значащих
цифр.
Первоначально задача ставилась для интервала О < ж < 1000, но
Александер A997) обнаружил, что решение обладает интересными
свойствами на много большем интервале. Следуя этому указанию,
мы предусмотрели выдачу значений решения при
^out=lo,lo^lo^lo^...,lo^^.
PLATE — это линейный и неавтономный пример средней жесткости
и средней размерности. Он описывает движение прямоугольной
пластины под тяжестью проезжающего через нее автомобиля:
^+а;|^4-(тДДг/=:/(х,у,0. (Ю.б)
Пластина fi={(x,y) ; 0<х<2, 0<у<4/3} дискретизируется на сетке из
8x5 внутренних точек [х^—гк, yj=jh, Л=2/9), граничные и начальные
условия имеют вид:
ди
и\^^ = 0, Аи\^^ = 0, г/(х,у,0) = 0, ¦^(х,у,0) = О . A0.7)
Интервал интегрирования взят 0<<<7. Нагрузка f(x,y,t)
идеализированно представляется в виде суммы двух гауссовских кривых,
движущихся в X-направлении и соответствующих «колесам»:
/ 200(е-5(^-^-2)^ 4- e-5(^-^-5)^), если у=У2 или у^,
для иных значений у.
Оператор пластины ДД дискретизируется с помощью стандартной
«вычислительной молекулы»:
1
2-8 2
1 -8 20 -8 1
2-8 2
1
/(х,у,0 = | ^ Q
170 Гл. IV. Жесткие задачи — одношаговые методы
В качестве значений параметров трения и жесткости выбраны
величины а;=:1000 и G=100. В результате получается система, состоящая
из 80 дифференциальных уравнений и имеющая отрицательные
вещественные, а также комплексные собственные значения в диапазоне
-500 < КеЛ < О с максимальным углом а?^71® (см. определение 3.9).
BEAM — уравнение движения упругого стержня A.10) из разд. IV.1.
В уравнении A.10') мы положили п=40, так что получилась
дифференциальная система размерности 80. Интервал интегрирования
выбран О < / < 5. Собственные значения матрицы Якоби чисто мнимые
и заключены между —6400г и Н-6400г (см. уравнение B.23)).
Начальные условия A.18) и внешние силы A.19) выбраны так, что решение
выглядит гладким. Однако детальное численное исследование
показывает, что в точном решении присутствуют высокочастотные
колебания с периодом « 27г/б400 и амплитудой « 10~^ (см. рис. 10.2).
Рис. 10.2. Третьи конечные разности Д t/go/A^ решения
уравнения A.10') при п=40, О < х < 0.07 .
Рис. 10.3. «Катастрофа сборки», N = 32.
IV. 10. Численные эксперименты 171
CUSP — это комбинация из модели механизма прохождения
нервного импульса, включающей «катастрофу сборки» (—еу = у^-\-ау-]-Ь),
которую предложил Зиман A972), и осциллятора Ван-дер-Пол я (см.
рис. 10.3):
^ = 6 + 0.07г + ,т|^, A0.8)
at дх^
1^ = A - а2N - а - 0.42/ +0.0351; + <г|^,
где
"=^:Т0Л' « = B/-0-7)(У-1-3)-
Мы положили <т= 1/144 и сделали задачу жесткой, выбрав е=10~''.
Диффузионные члены мы дискретизировали с помощью метода
прямых:
щ = -iClyf + a,.j/,. + 6,) + D(y,._i -2у,. + j/<+i),
d, = 6,+0.07i;,-t-D(a,._i-2a,. + a,4.i), г=1,...,ЛГ, A0.8')
6i = A - a?N,- - a,- - 0.4y.. + 0.035t;, + ?)F,._i - 26,- + 6,.+i),
где
^ = ^^' "'^^I^fol' «.• = (y<-0-7)(%-1.3), Р = <тЛГ2 = ^,
И поставили периодические граничные условия:
2/0 •= Vn ' ^0 •= ^N ' ^0 •= ^лг 1
2/7V+1 -=2/1 ' «N+1 •=«! , 6jv^i :=6i .
Получилась система размерности ЗАГ=96. Мы взяли следующие
начальные условия:
у,@) = 0, a,@) = -2cos(^), M0) = 2sin(^), i = l,...,N
И назначили Xq^^^ = 1.1.
BRUSS — это уравнение A.6') с а = 1/50, с такими же начальными
условиями, как в разд. IV. 1, и интервалом интегрирования О < / < 10.
Но теперь положим А^=500, так что A.6') превратится в систему 1000
дифференциальных уравнений с максимгипьным (по абсолютной
величине) собственным значением, близким к —20000. Поэтому
уравнения становятся существенно жесткими. Матрица Якоби этой системы
имеет ленточную структуру с шириной верхней и нижней полосы,
равной 2 (если компоненты решения упорядочены так: т/^, v^, «з-^2, Wg,^з
и т.д.).
172 Гл. IV. Жесткие задачи — одношаговые методы
Рис. 10.4. Решение уравнения Курамото—Сивашинского.
A0.9)
KS — одномерное уравнение Курамото—Сивашинского
ди _ дЮ дЮ 1 ди^
dt ~~ дх^ дх^ 2 дх
с периодическими граничными условиями и{х -f i, <) == "(^» О > взятое
из работы (Коллет, Экман, Эпштайн и Штуббе 1983). Мы выбрали
L = 27г/д, q = 0.025, а в качестве начальных условий взяли
7/j = min(x/L, 0.1 — x/L),
U(x,0) = 16 • max@,ЩуГ)^, rj^, щ),
772 = 20(x/L-0.2)@.3-x/L),
7/3 = m\n(x/L -r 0.6,0.7 - x/L),
774 = min(x/L - 0.9,1 - x/L).
Член —д^и/дх^, соответствующий «обратному» уравнению
теплопроводности, порождает неустойчивость, но для колебаний высокой
частоты она стабилизируется таким же, как в уравнении колебаний
стержня, членом —d^U/dx^. Нелинейный член переноса dU^/dx
связывает различные моды колебаний и обеспечивает ограниченность
решения. Все это порождает удивительный хаос (см. рис. 10.4).
Уравнение A0.9) мы решаем с помощью псевдоспектрального
метода. Это означает переход к коэффициентам Фурье
Uj{t) = jf U(x,t)e-">^'dx, U(x,t) = TUj(t}e">^', A0.10)
так что уравнение A0.9) принимает вид бесконечномерной системы
обыкновенных дифференциальных уравнений
i9J,
^ = {{4i?-(qjY)U^-''f[U^U)^.
IV. 10. Численные эксперименты
173
10-
10-
10-
10-
\и,\
t = 0
\uji
I III I I HI III I ^"^^
lu,J
80
Рис. 10.5. Моды Фурье для уравнения Курамото—Сивашинского.
Мы обрываем эту систему следующим образом. При фиксированном
N, например, при N = 1024, рассматривается периодическая
последовательность u(t) = {uj(t)} с периодом N, которая получается при
решении обыкновенного дифференциального уравнения
u' = (d2-d>-|^-^vW«-:F-i«),
A0.11)
где d обозначает периодическую последовательность с периодом Л^,
которая определена так: dj = qj при \j\ < N/2 и d^^^/j = 0;
произведение последовательностей в A0.11) понимается как покомпонентное.
Дискретное преобразование Фурье Tj^ может быть вычислено с
помощью быстрого преобразования Фурье (FFT). Из того, что С/(х, t) —
вещественная функция, следует эрмитовость последовательности и,
т.е. u__j = Uj . Поэтому программа REALFT, описанная в книге (Пресс,
Фланнери, Теукольски и Веттерлинг 1986,1989), глава 12, наилучшим
образом подходит для вычисления правой части уравнения A0.11).
Поскольку do = d7V/2 = О, компоненты UQ{t) и г/^^/гСО являются
константами и их интегрировать не надо. Таким образом, на самом деле
наше обыкновенное дифференциальное уравнение оказывается
размерности N — 2= 1022. В качестве начальных значений мы берем
дискретные преобразования Фурье функций {U{jL/N,0)} , причем
{N/2)-я компонента полагается равной нулю. В наших испытаниях
мы решали дифференциальное уравнение A0.11) на отрезке 0<<< 100
(см. рис. 10.4).
Рисунок 10.5 показывает, что Фурье-моды стремятся к нулю при
i -> ОС, их поведение хаотично, а при вычислении их средних
значений за длинный промежуток времени доминирующими оказываются
моды, для которых qj w >/2/2.
BECK DO — это модель Беккера—Дёринга, описывающая систему из
большого числа одинаковых частиц, которые могут коагулировать,
образуя кластеры. Пусть у^ обозначает ожидаемое число кластеров
из к частиц в единице объема. Предполагая, что кластеры могут
терять или присоединять только по одной частице, мы получим еле-
174
Гл. IV. Жесткие задачи — одношаговые методы
дующую систему уравнений:
N-1
kzzl
Vk^Jk^i-Jk^ /: = 2,3,...,АГ-1,
A0.12)
где Ji^ zny^y^- 6;5^.i2/;j+i И б^^^^ = ехр(Аг2/з - (Л - 1J/3) Более
подробное описание этой системы дано в статье Карра, Дункана и Уолшо
A995). Это уравнение особенно интересно благодаря своей метаста-
бильностпи^ т.е. очень медленному изменению решения на очень
больших временных интервалах (см. рис. 10.6).
]|[50(Юу5ооо
Рис. 10.6. Решения уравнения Беккера—Дёринга A0.12).
В качестве начального условия мы взяли
yi@) = P, yjt@) = 0, для fc = 2,...,iV
A0.13)
(вначале кластеры отсутствуют). Посредством дифференцирования
можно убедиться, что плотность (полное число частиц в единичном
объеме)
N
E*2/it (=Р) A0.14)
к=\
является инвариантом системы A0.12). Большинство численных
методов интегрирования (в частности, методы Рунге—Кутты и
многошаговые методы) сохраняют такие линейные инварианты, если
отсутствуют погрешности округления. Если соотношение A0.14)
сохраняется неудовлетворительно, то существует возможность
восстанавливать его с помощью проекций (см. подраздел «Дифференциальные
IV. 10. Численные эксперименты 175
уравнения с инвариантами» в разд. VII.2). В описываемых здесь
численных экспериментах эта предохранительная мера не применялась.
Чтобы иметь возможность наблюдать метастабильные
состояния системы, ее размерность N должна быть достаточно большой.
Следуя экспериментам Карра, Дункана и Уолшо A995), мы взяли
N — 5000, р = 7.Ь и рассматривали решение на временном интервале
0<t < 10^^, сравнивая погрешности при х^у^^ = 1,10,10^, 10^,..., 10^^.
Матрица Якоби этой системы трехдиагональная с
дополнительными ненулевыми первой строкой и первым столбцом. Критерий Герш-
горина показывает, что ее собственные значения не могут быть
меньше — 10 (за исключением начальной фазы). Таким образом, в этом
примере жесткость обусловлена не большими собственными
значениями J, а крайне длинным интервалом интегрирования.
BRUSS-2D — двумерный брюсселятор, задача с реакциями и
диффузией из разд. 11.10:
A0.15)
в ее дискретизированной форме A1.10.14). Однако на этот раз мы
сделали задачу жесткой, увеличив коэффициент а (который был
0.002) до а = 0.1, а также увеличив число точек сетки до N = 128.
Это дает обыкновенное дифференциальное уравнение размерности
2N^ = 32768. Мы взяли начгильные условия
ii(x, у, 0) = 22 . уA - уK/2, v(x, у, 0) = 27. хA - xf^\ A0.16)
но система быстро забывает их из-за сильной диффузии (см. рис. 10.7
для < = 1). Поэтому мы полагаем, что неоднородность f(x, у, t),
определяемая формулой
f(xvt) = l^ при (х - 0.3J4-(у-0.6J < 0.12 и <>1.1,
Jy^y^j I Q g остальных случаях
моделирует добавление вещества и в малом круге. Для
выполнения линейно-алгебраических вычислений удобно использовать
подпрограмму двумерного быстрого преобразования Фурье. Чтобы
воспользоваться этой возможностью, мы заменили граничные условия
Неймана, которые были поставлены в разд. 11.10, периодическими
граничными условиями
u{x-\-l,y,t) = u(x,y,t), u{x,y'{'l,t) = u{x,y,i).
Для выдач мы выбрали точки ж^^^. = 1.5 и 11.5.
176 Гл. IV. Жесткие задачи — одношаговые методы
Рис. 10.7. Решение задачи «двумерный брюсселятор».
Обсулсдение результатов
Результаты работы рассмотренных выше программ для 12
примеров-тестов представлены на рисунках 10.8 и 10.9. Для каждого из
этих примеров мы очень аккуратно вычислили точное решение в
заданных точках вывода. Затем были применены рассмотренные выше
программы для множества различных значений допустимой
погрешности:
Tol = 10-^-'^/^ m = 0,1,2,..., 32.
Точнее, мы задали относительную допустимую погрешность Rtol =
= Tol и абсолютную допустимую погрешность Atol = 10~^ • Tol для
задач OREGO и ROBER, Atol = 10"^ • Tol для HIRES, Atol = Ю-з . Tol
для PLATE и BECKDO, Atol = 1.7 • lO'^^ для E5 и Atol = Tol для всех
IV. 10. Численные эксперименты 177
других задач. Несколько программ выдали численные результаты,
которые были значительно менее точными, чем требуемая точность,
в то время как другие методы оказались более надежными. Поэтому
в качестве разумного способа измерения эффективности мы выбрали
сопоставление двух характеристик. Регистрируются
- фактическая погрешность (норма, взятая по всем компонентам и
всем точкам вывода);
- время вычислений (на рабочей станции SUN Sparc 20) в секундах.
Полученные данные затем отображаются в виде ломаной линии на
диаграмме «точность — объем вычислений» с двумя
логарифмическими шкалами. Допустимые погрешности с целыми значениями
показателей 10~^, 10"^, 10~^,... отмечены увеличенными значками.
Значок для То1= 10""^ выделен особо: он темный. Чем правее
расположена такая линия, тем больше полученная точность; чем эта линия
находится выше, тем медленнее работала программа. «Наклон»
кривой выражает (эффективный) порядок формулы: методы более
низкого порядка дают более крутой подъем, чем методы более высокого
порядка. Рассмотрим теперь подробнее результаты, полученные для
каждой из 12 задач-тестов (рисунки 10.8 и 10.9).
VDPOL, ROBER, OREGO — очень жесткие задачи малой
размерности. Из рис. 10.8 видно, что программа RODAS, основанная на
методе Розенброка, — наилучшая при большой допустимой
погрешности (от 10~2 до 10"^), в то время как экстраполяционная программа
SEULEX превосходна при высокой требуемой точности. Из-за
дешевизны вычисления функций правой части многошаговая программа
LSODE требует, в общем, чуть больше вычислительного времени, чем
одношаговые программы. Отметим также, что для заданной
допустимой погрешности (например, для То1 = 10""^, что соответствует
серым значкам) программа RADAU5 дает самый точный результат, за
ней следуют RODAS, SEULEX и LSODE.
HIRES — эта задача менее жесткая, она может решаться и
явными методами. Время вычислений для «явной» программы D0PRI5
вначале совершенно не зависит от требуемой точности, кривая идет
горизонтально. Это, конечно, неудивительно, так как размер шага
ограничивается устойчивостью. Программа RKC, основанная на
методе Рунге—Кутты—Чебышева (явном, но стабилизированном),
демонстрирует значительное улучшение по сравнению с D0PRI5 для
больших допустимых погрешностей. «Жесткие» программы
остаются все же более эффективными.
Е5 — жесткая задача с плохими (очень сильно различающимися)
масштабами компонент решения, она интегрируется на очень
большом отрезке времени. Программы не могут правильно работать, если
абсолютная допустимая погрешность Atol слишком велика.
Наилучшие результаты дают программы RODAS (для низкой требуемой точ-
178 Гл. IV. Жесткие задачи — одношаговые методы
VDPOL
SEULEX
RADAU5
погрешность
faiiiii Liiiii кии biiiii biiiii liiii bun km
10°
10-'
— сек
г
iinCuu
ROBER /
RADAU5 ^
LSOQE y^i^/y^
ryi^y^^^ SEULEX
^^^^^^^^\^ RODAS
-O-""""^ погрешность
1 kuiiii Uiiii Liiii Liiii Liiii Liiii Liiii LI
10-3
10-*
10-^
10-
10-*
10-^
10°
10-'
сек
¦
V
II iuiM
biiii
OREGO / Й
RODAS 4 /
lsoqe/p Jy'
^j^t^ SEULEX
p^X^ RADAU5
P^ погрешность
nm kiuti kuiii luuiiiBiia.kiuii kiuj-biuii.kui У
10°
10-'
~'"
-
-
г
"
UUJ
сек
kui
HIRES / /
/ D0PRI5 у /^
RKC J iL^^T^
J^ „--V^^ SEULEX
ODE 4F^5^^\
Lf ^-je^^V; RADAU5
r^ X RODAS
_»i^* погрешность
1 LiiirCii.i Liiii Liiii Liiii Liiii Liiii Liiii Liiii I
10° 10-=
10-*
10° Ь
10-
h" E5 ^
и оьиьсл ¦¦ *^
" LSODE
L ^^^^'^^^^^ RADAU5
^—RODAS
(\J^ погрешность
uuLi Liiii Luii-kuui Lull Liii 1 km 11 kuui kiiiii kiim Liiii i
10-* 10
10^
10-* 10-* 10-'
10-3 10-* 10-^
Рис. 10.8. Диаграммы «объем вычислений — точность»
для задач с размерностью от 2 до 80.
IV. 10. Численные эксперименты 179
BEAM
SEULEX
RADAU5
(tuned)
\CP\r v^^ kf"^ погрешность
I |у||ип/м11111 I lumiM killH I luiimi hum i luii
10'
10°
-сек
' SEUI
lTL
CUSP у /
RKC у ^^.,^;//
.EX j^ Or^
Jw^l^p^ RADAU5
/>¦ LSODE
погрешность
11 Lull Liiii Lull Lull Lull Lull Lull Lmi
10-
10-^
10-^
io-«
10-9
BRUSS
RADAU5-
SEULEX
-RODAS
погрешность
mill Lull L Lull Lull Lull Lmi Liiii Liiii Lii
10-5
10^
10-^
KS
I SEULEX—^
X ^
L/ LSODE
-jLuiJLJ. llUlU 1 1 Juiu t t
1 iuiii
^ RADAU5
погрешность
.xj—limui.L...,kuiii J
10-^
10-^
lO^h
BECKDO
погрешность
Imiiiii Iujuj.i Lull Lull I Uiiii kiimi Imiiiii Uiiii
BRUSS-2D
10-3
10-^
10^
RADAU5
погрешность
Imiiiii I Luiiii I Lmi i Uiii i i Lm i i Lm i i Liiiii Imiii
10-3
10^
10-9
Рис. 10.9. Диаграммы «объем вычислений — точность»
для задач с размерностью от 80 до 32768.
180 Гл. IV. Жесткие задачи — одношаговые методы
ности) и RADAU5 (для То1 < 10""^). LSODE надежно работает только
при То1 < 10""^, тогда как у SEULEX возникают трудности с
погрешностями округления при высокой точности.
PLATE и BEAM — обе задачи типа у" = /(аг,г/,у'),
представленные как система уравнений первого порядка у' = v, v' ^ f{x, у, v).
Линейные системы, которые требуется решать в «жестких» программах,
имеют матрицы вида
A0.17)
(«' ^)
где / — единичная матрица. С помощью опции IW0RK(9)=N/2 (где
N — размерность системы уравнений первого порядка) наши
программы выполняют первые N/2 проходов для гауссовых исключений
аналитически, и размерность линейной системы уменьшается вдвое.
Без этой опции времена вычислений для программ RADAU5, RODAS и
SEULEX были бы больше примерно в 3.0, 1.7 и 2.6 раза
соответственно (числа указаны для задачи BEAM при То1 = 10~^). Здесь мы не
приводим результатов для LSODE, так как для нее мы не смогли
легко проделать такую редукцию. В задаче PLATE мы воспользовались
также ленточной структурой матриц df/dy и df/dv, задав MLJAC=16
и MUJAC=16.
«Явная» программа D0PRI5 тоже применима к обеим задачам. У
DOPRI5 на задаче PLATE возник любопытный феномен: как и
ожидалось, при низких требованиях к точности (То1 > 10"^) длина
шага, по-видимому, ограничивалась устойчивостью, программа показала
вычислительное время, не зависящее от То1, и выдала сообщение
«задача, по-видимому, жесткая». Но при более высоких требованиях к
допустимым погрешностям скорость работы программы
ограничивалась требуемой точностью, при этом неожиданно оказалось, что
время вычислений неожиданно намного превосходит время, требующееся
«неявной» программе RADAU5. Анализ задачи Протеро и Робинсона
A5.1) в разд. IV.15 дает объяснение этому факту. Мы увидим, что в
случае «явных» интеграторов жесткие задачи порождают не только
потерю устойчивости, но еще и потерю точности.
Эффективность программ может быть существенно повышена
путем настройки параметров^ особенно для задачи BEAM, требующей
«дорогой» линейной алгебры. Если для интегрирования с помощью
RADAU5 задать
W0RKC)=0.1 (не так часто пересчитывать матрицу Якоби),
W0RKD)=0.3 (раньше прекращать ньютоновские итерации),
W0RKE)=0.991 (не так часто изменять размер шага,
W0RKF)=2. J тем самым уменьшая число LU-разложений),
то время вычислений уменьшается в 2-5 раз. На рис. 10.9 видно
весьма существенное улучшение при счете с «настройкой».
IV. 10. Численные эксперименты 181
CUSP — матрица Якоби в этой задаче имеет вид
J =
Л2
Bn-
A0.18)
где A-, В-у С,, D, — матрицы 3 х 3, и эффективное решение линейной
системы требует особого подхода (см. упр. 1). Однако
рассмотренные методы, за исключением методов Розенброка, не требуют точной
матрицы Якоби. Поэтому простой способ значительного сокращения
вычислительного времени состоит в применении версий программ,
использующих ленточную структуру матриц, путем задания ML=MU=3.
При этом мы пренебрегаем D^ и D^ и получаем времена счета,
показанные на рис. 10.9. Если обращаться с матрицей Якоби как с полной
матрицей, то время счета для программ RADAU5, SEULEX и LSODE
возросло бы в 8.3, 6.6 и 4.8 раз соответственно (приведены числа для
То1 = 10"^). «Явная» программа RKC дает великолепные результаты
при низкой точности, в то время как результаты для D0PRI5 (более
чем 30 секунд) располагаются за пределами рисунка.
BRUSS — в этой задаче (реакция и одномерная диффузия)
использовалась «ленточная» версия линейной алгебры и
«аналитическая матрица Якоби». Задача очень жесткая (большая постоянная
диффузии и малая величина Да:), поэтому явный метод, такой, как в
D0PRI5, потребовал бы почти 60000 шагов интегрирования.
Программа RKC работает хорошо, хотя и менее эффективно, чем «жесткие»
интеграторы.
KS — решение этой задачи чувствительно к изменениям
начальных значений, — явление, уже встречавшееся в задаче LRNZ из
разд. П.10. Так же, как и там, точность возрастает только при То1
за определенным порогом. Матрица Якоби в этой задаче полная.
Численные эксперименты обнаружили, что программы работают
лучше всего, когда матрица Якоби заменена диагональной матрицей с
(qj)^ — (qjy на j-м месте. Методы Розенброка, которые требуют
точной матрицы Якоби, здесь неэффективны. «Явным» же программам
RKC и D0PRI5 нужно слишком много вычислительного времени.
BECK DO — в этой задаче «жесткие» программы (только они
справляются с ней) требуют решения линейных систем вида
где Vy W, Ь — (п — 1)-мерные векторы и Т — трехдиагональная
матрица. Поскольку подпрограммы линейной алгебры полностью
отделены от программ RADAU5, ROD AS и SEULEX, то они легко заменяют-
182
Гл. IV. Жесткие задачи — одношаговые методы
ся специальной подпрограммой, которая эффективно решает систему
A0.19) следующим образом:
, У^ ^ A0.20)
Сам «жесткий» интегратор изменять нет необходимости.
На рис. 10.9 видно, что RODAS, как обычно, лучше всех при
низкой точности, а RADAU5 предпочтительна при высокой. Необычно то,
что RODAS работает очень плохо при высоких требованиях к
точности. Мы объясняем это высокой чувствительностью линейной
системы A0.19) к погрешностям округления, или, как представил бы дело
Уилкинсон, она дает решение для неправильной матрицы Якоби. В
результате порядок метода Розенброка падает до 1.
Таблица 10.1. Число обращений к вычислению правой части
и время счета при То1 = 10~ для задачи BRUSS-2D
RADAU5
а = 10"^
а = 10-2
0 = 10""^
а=1
RKC
а = 10"-^
а =10-2
а = 10"^
а = 1
D0PRI5
а = 10-^
а =10-2
а=10-^
а=1
N = 16
3372/19.8
1286/7.7
1150/6.8
1195/7.8
N = 16
2367/4.7
1661/3.2
1899/3.6
4013/7.2
N = 16
976/2.0
784/1.6
4366/9.0
42832/90.6
ЛГ = 32
3233/84.9
1322/36.2
1131/30.9
1199/33.0
iV = 32
2277/18.6
1674/13.8
2823/22.5
7565/58.9
N = 32
1030/8.5
1894/15.4
17176/145.5
171010/1505.8
ЛГ = 64
3271/413.5
1295/167.4
1227/172.3
1247/177.3
N = 64
2249/76.3
2078/70.4
5047/176.8
14631/503.4
iV = 64
1408/48.5
6976/240.6
68446/2419.7
683836/24362.7
N=128
3290/2215.6
1381/868.8
1173/854.9
1242/945.9
Л^=128
2311/352.5
3379/511.5
9666/1446.2
29022/4328.8
N=128
3286/509.4
27478/4369.6
273568/43982.2
N = 256
3261/14902.1
1380/6459.3
1204/5664.9
1258/5961.2
N = 256
2911/1912.0
6259/4086.9
18911/12312.2
N = 256
11464/7704.2
BRUSS-2D — из-за большой размерности (п = 2 • 128^ = 32768) в
этой задаче не имеет смысла применять полную или даже
ленточную линейную алгебру. Поэтому мы решали линейные уравнения
(в программах с отделенной линейной алгеброй, см. соответствующее
замечание к задаче BECKDO) методами быстрого преобразования
Фурье, учитывая только диффузионные члены (жесткие) и пренебрегая
членами, описывающими реакцию (нежесткими в этой задаче). Мы
использовали программы быстрого преобразования Фурье, описанные
в книге (Пресс, Фланнери, Теукольски и Веттерлинг 1986, 1989) в
главе об уравнениях с частными производными. Здесь проявляется
IV. 10. Численные эксперименты 183
особое преимущество метода Радо, состоящее в том, что комплексная
алгебра, которая в любом случае используется в быстром
преобразовании Фурье, перемалывает комплексные собственные значения
матрицы Рунге—Кутты без дополнительных проблем.
Для этой задачи, которая является типичным параболическим
уравнением в частных производных с нежесткими нелинейностями,
мы выполнили детальное сравнение работы «неявной» программы
RADAU5, «стабилизированной явной» программы RKC и «явной»
программы DOPRI5 при различных значениях параметра дискретизации
Ах = Ду = 1/N и параметра диффузии а (см. уравнения A0.15) и
A1.10.14)). Результаты (число обращений к вычислению правой части
и время счета) представлены в табл. 10.1, где лучшие
характеристики выделены жирными цифрами. Можно видеть, как с
возрастанием жесткости «олимпийский огонь» передается от D0PRI5,
наилучшей при малой жесткости (aN^ ? 1)» сначала к RKC, а затем (при
aTV^ > 1000) к «неявной» программе RADAU5. Видно также, что
количество вычислений функции в правой части почти не зависит от
жесткости для RADAU5, ведет себя как Const у/а-N для RKC и как
Const. а. 7V2 для DOPRI5.
Сравнение программ сущего типа. Рисунки 10.8 и 10.9, своего
рода «уимблдонский финал», содержат только по одной программе для
каждого класса методов интегрирования (методы Радо, неявные
методы Рунге—Кутты, методы Розенброка и экстраполяционные методы).
Теперь мы приведем некоторые результаты сравнений внутри
каждого из этих классов.
Методы Радо. Для сравнения методов Радо различных порядков
мы написали программу RADAUP, которая позволяет устанавливать
программный флажок IW0RKA1)=3,5,7, чтобы выбирать s = 3, 5 или
7, т.е. порядок метода р = 5, 9 или 13. При 5 = 3 программа RADAUP
математически эквивалентна RADAU5, но чуть медленнее из-за
различий в реализациях. На рис. 10.10 можно видеть, как более высокий
порядок окупается при высокой точности, но при низкой точности
возникают проблемы из-за больших длин шагов и плохой
сходимости ньютоновских итераций. (См. также результаты Реймонда A989),
которые мы привели в первом издании.)
Неявные методы Рунге—Кутты. Долгое время считалось само
собой разумеющимся, что эффективно могут быть реализованы
только методы ДНРК и ОДНРК (DIRK и SDIRK). Наш опыт показал, что
диагонально неявный метод SDIRK4, построенный в разд. IV.6, дает
весьма ргьзочаровывающие результаты (см. рис. 10.11). Исключение
составляет задача BEAM с ее высокочастотно-колебательным
решением в микроскопическом масштабе. Так как у программы SDIRK4
нет опции для линейной алгебры «второго порядка», мы применили
184 Гл. IV. Жесткие задачи — одношаговые методы
сек VDPOL
-10"
RADAU5
10-3 10-6 10-9 10-3 10-6 10-5 10-* 10-9 10-»'
Рис. 10.10. Сравнение программ, реализующих методы Радо,
10-6 10-9 10-12 10-3 10-6 10-3 10-6 10-9
Рис. 10.11. Сравнение программ для неявных методов Рунге—Кутты.
гШГ
^10°
-
=-10-'
:
' tijA
ROBER^
RODAS—4>у^
j/y^KODkSS
^-R0S4.
^ бпогрешность
1 bun bill bun bun bun bun bull bllll
[ сек
Ио^
F
P
Uo'
Г\\Ы^
^T_ , ,Д - -, -П- ¦ ¦ -Д7
/^EAM y\
^y^'jJ^^RODASS
^-—RODAS погреши.
[^ BRuss уТ/
г """"^kiSy
L y^^RODAS5
1 RODAS ^^r
njfr^ погрешность
ia Ihiiii bull bun bun biiii biiii bun kai_bil
10-6 10-9 10-12 10-3 10-6 10-3 10-6 10-5
Рис. 10.12. Сравнение программ, реализующих методы Розенброка.
10-6 10-9 10-12 10-3 10-6 10-9 10-^ 10-* 10-9
Рис. 10.13. Сравнение программ, реализующих экстраполяционные методы.
IV.IO. Численные эксперименты 185
RADAU5 также без этой опции. Поэтому времена счета для RADAU5
отличаются от приведенных на рис. 10.9.
Методы Розенброка. Обычно нет большой разницы в
эффективности работы различных методов Розенброка (см. рис. 10.12). Среди
«классических» методов Розенброка 4-го порядка в целом самым
лучшим является второй метод из табл. 7.2 (отмечен индексом 2 на
рисунке), имеющий малую константу погрешности; он терпит, однако,
полную неудачу в задаче BEAM из-за отсутствия у него Л-устойчивости.
Шестой метод из табл. 7.2 отвечает набору коэффициентов, дающему
L-устойчивый метод. Однако программы RODAS5 E-й порядок) и
RODAS D-й порядок) часто дают наилучшие результаты, несмотря
на то, что реализованные в них методы имеют большее число стадий.
Экстраполяционные методы. Программа SODEX, основанная на
Л^-экстраполяции полуявного правила средней точки, заметно
превосходит SEULEX при низкой точности (см. рис. 10.13).
Противоположная ситуация возникает при более высоких требованиях к
точности; здесь мы наблюдаем явление понижения порядка, которое
объясняется ниже, в разд. VI.5. В эти испытания включена также
программа EULSIM Дойфлхарда, Новака и Пеле (poehle@sc.zib-berlin.de),
которая является другой реализацией экстраполированного
полуявного метода Эйлера с иной последовательностью длин шагов.
Чебышевские методы. На заключительной фазе этих
экспериментов мы получили программу DUMKA3 (написанную А. Медови-
ковым, nucrect@inm.ras.ru), в которой реализовано расширение до
третьего порядка оптимальных чебышевских методов Лебедева (см.
разд. IV.2). Эта программа находится еще на ранней
экспериментальной стадии, но уже дает очень обещающие результаты (см. рис. 10.14).
HIRES
10^ 10-' 10-'2 10-3 ,Q-« 10-9 10-3 10-6 1Q-9
Рис. 10.14. Сравнение программ для чебышевских методов и RADAU5.
186 Гл. IV. Жесткие задачи — одношаговые методы
Разделение и проекционные методы
«Большинство программ для решения жестких систем ...
тратят большую часть своего времени на решение систем
линейных уравнений...»
(Уоткинс и Хансон-Смит 1983)
Часто возможно еще более эффектное сокращение
вычислительной работы, относящейся к линейной алгебре. Одна из самых старых
идей заключается в разделении жесткой системы на (желательно)
небольшую жесткую систему и большую нежесткую часть:
Уа=/а{Уа^Уь) (жесткая),
Уь = МУа^Уь) (нежесткая),
чтобы к этим двум системам можно было применить два разных
метода: к первой — неявный, а ко второй — явный (см., например,
(Хофер 1976)). Как раз при исследовании свойств порядка таких
методов возникла теория Р-рядов (разд. 11.14). Трудность в этом
подходе, конечно, состоит в том, чтобы решить, какие уравнения следует
рассматривать как жесткие. Далее, жесткость может проявляться
в подпространствах, не параллельных координатным осям. Поэтому
мы сосредоточим внимание на процедурах, которые приспосабливают
к разделению уравнений не сами численные методы^ лежащие в их
основе, а только линейную алгебру. Превосходный обзор ранней
литературы по этим методам дал Сёдерлинд A981). Следующее
определение описывает особенно обещающий класс задач.
Определение 10.1 (Бьёрк 1983, 1984). Система 2/' = /(х,г/)
называется отделимо жесткой в точке х^,у^^ если матрица Якоби
J = |^(a:o,t/o) обладает к<п собственными значениями Ai,...,A^^
такими, что
min lA.I» max lAJ.
1<1<Дс' *' ^fe-fl<»<n *
Собственные значения А^,..., Aj^ называются оюесткими
собственными значениями^ а отношение
/i= min lAJ / max lA-l A0.22)
1<г</с' *' ' fc + l<t<n' *' ^
— относительным разделением. Пространство ?), натянутое на
жесткие собственные векторы, называется доминантным
инвариантным подпространством.
Например, задача Робертсона A0.2) имеет только одно жесткое
собственное значение (близкое к —2000), и поэтому она отделимо
жесткая с Аг=1. Задача CUSP A0.8') имеет размерность 96 и 32
больших собственных значения, лежащих в диапазоне между —20000 и
—60000 (за исключением переходных фаз). Все прочие собственные
IV. 10. Численные эксперименты 187
значения приближенно удовлетворяют неравенству |Л|<30.
Фактически это сингулярно возмущенная задача (см. разд. VI.1), а все
такие задачи отделимо жесткие. У других больших задач,
рассмотренных в этом разделе, собственные значения распределены
равномернее. А.Р. Кертис A983) отмечает, что на практике отделимо жесткие
задачи встречаются довольно редко.
Метод Гира—Сагщд. Неявные методы, такие как
(преобразованные) методы Рунге—Кутты или многошаговые формулы, требуют
решения линейной системы
Ах = Ь, где A=^I-J A0.23)
(как это принято в линейной алгебре, мы обозначили х неизвестный
вектор и г = Ь — Ах невязку). Выберем к линейно независимых
векторов ^1,..., ^/Р (обычно ортогональных) таким образом, чтобы их
линейная оболочка span {q^^..., g^}=D аппроксимировала доминантное
подпространство ?), и обозначим через Q матрицу fcxn,
сформированную из столбцов Qj:
Q = (gi,...,G,). A0.24)
Имеется несколько возможностей для замены решения х уравнения
A0.23) приближенным решением х Е D. Одна из наиболее
естественных — потребовать, чтобы невязка для х
г = Ь-Ах = А(х-'х), A0.25)
была ортогональна к ?), т.е. чтобы Q'^{b — Ax) = 0 (Саад 1981, Гир
и Саад 1983; фактически же — Галеркин 1915). Если записать х в
базисе A0.24) как х = Qy, то получим
Ну = О^Ь, A0.26)
где
H = Q^AQ, или QH = AQ. A0.27)
Это означает, что теперь надо решать линейную систему
размерности к с матрицей Н. Особенно хорюшим выбором для D является
подпространство Крылова, порождаемое произвольным вектором Гд:
D = span {го, Лго, А^г^,... А^'^г^} A0.28)
(обычно Tq — невязка хорошо выбранного начального приближения
Xq). Векторы A0.28) составляют последовательность, порождаемую
хорошо известным степенным методом. Поэтому в случае отделимо
жесткой системы, согласно анализу Хайама A989), пространство D
очень хорошо приближает пространство D, если его размерность
достаточно высока. В процессе Арнольди (Арнольди 1951) векторы в
188 Гл. IV. Жесткие задачи — одношаговые методы
A0.28) последовательно ортонормируются по Граму—Шмидту:
Я1 = Го/\\го\1
?2 = ^^1-^11^1, Ч2 = Ь1^21 с Л21 = 11^211
И Т. д., так что
Aq^ =/121^2+ '^ii9i)
М2 = ^32^3 + ^22^2 + ^12^1» A0.29)
и сравнение с A0.27) показывает, что Н имеет вид матрицы Хессен-
берга. При симметричной матрице А матрица Я тоже симметричная
и, следовательно, трехдиагональная; в этом случае метод
эквивалентен методу сопряженных градиентов.
Важны две особенности этого метода. Во-первых, не требуется ни
вычислять, ни хранить матрицу А. Все, что нужно — это матрично-
векторные произведения в A0.29), а они могут быть получены из
«производной по направлению»
Jv « [/(х, y-^Sv)^ fix, y)]/S, A0.30)
Поэтому некоторые называют такие методы «безматричными». Во-
вторых, не требуется знать размерность к: просто вычисляется один
столбец Я за другим и периодически оценивается невязка. Как
только эта оценка становится достаточно малой (или к слишком
большим), алгоритм прекращает свою работу. Упомянем еще два варианта
этого метода:
1. (Гир и Саад 1983, р. 595.) Перед началом вычисления
подпространства Крылова выполняется какая-нибудь начальная итерация
степенного метода для начального вектора Гд, при этом используется
или матрица А, или матрица J. Лопес и Триджианте A989)
сообщают о превосходных численных результатах этой процедуры.
2. Неполная ортогонализация (Саад 1982). Новый вектор Aqj ор-
тогонализуется только по отношению к предыдущим р векторам, где
р — некоторое небольшое целое число. Это превращает Я в
ленточную матрицу и экономит время вычислений и память. Для
симметричных матриц идеальный выбор, конечно, р=2, для матриц все
более и более несимметричных р обычно увеличивают до 10 или 15.
Метод ЭКБУХ (это не слишком благозвучное сокращение
образовано из первых букв фамилий Энрайт, Камел, Бьёрк, Уоткинс и
Хансон-Смит). В этом методе матрицы А и J ъ A0.23) заменяются
приближенными:
A=-^I-J, A0.31)
IV. 10. Численные эксперименты 189
причем нужно, чтобы J достаточно хорошо приближала J, и
чтобы было относительно легко вычислить обратную матрицу для А.
Матрица J определяется следующим образом. Представим себе
(теоретически), что векторы A0.24) дополнены до ортогонального базиса
(Q,Q) в М". В новом базисе J будет иметь вид
(^^)^(c?,Q) = (?;; ?-). A0.32)
при этом
Q'^JQ = T^^. A0.33)
Если spanQ=D приближает D, то Тц будет содержать жесткие
собственные значения, а Tji будет стремиться к нулю. Если D=D в
точности, то Т21=0 и A0.32) — блочное разложение Шура для J. Для
отделимо жестких систем ЦТззЦ будет малой по сравнению с (/17)"^ •
Поэтому определим J как
J = {Q,Q) (J^' ^^') (gr) =Q(TnQ^+^^) '' = '^ QQ'J-
Отсюда видно, что J — ортогональная проекция J ъ D. Обратная
матрица для А вычисляется как геометрическая прогрессия с
помощью разложения (/ — В)-^ = 1 + В + В^ + ...
А-^ = hf{l - hfQQ'^ J)~^ =
= hf{l + hiQQ^J + /iS^Q Q^JQ Q^J + ...) =
''" A0.34)
= h7(/+Q(^/-T'„)"'g^j),
ЧТО требует решения только «малой» системы с матрицей (I/h'y—T^^).
Последнее выражение называется формулой Шермана—Моррисона—
Вудбери.
Выбор Q:
— Бьёрк A983) вычисляет точный базис в D при помощи
преобразований Хаусхолдера с последующими блочными ^Я-итерациями.
Для отделимо жестких систем блок Tji сходится к нулю линейно с
коэффициентом fi"^, так что обычно достаточно двух или трех
итераций. Недостаток метода заключается в том, что оценка размерности
Аг подпространства D должна быть известна заранее.
— Энрайт и Камел A979) преобразуют J к форме Хессенберга и
прекращают преобразования, когда ||^2i II "^ 11^2211 становится
достаточно малой (отметим, что только последний столбец Tj^ отличен от
190 Гл. IV. Жесткие задачи — одношаговые методы
нулевого). Таким образом, размерность к может определяться
динамически. Энрайт и Камел комбинируют отражения Хаусхолдера со
стратегией выбора ведущего элемента и повторяющимися
перестановками строк и столбцов, чтобы сделать Т22 малой как можно быстрее.
Сначала было замечено при проведении расчетов (Карлссоном), а
затем показано теоретически (Сёдерлинд 1981), что эта стратегия
выбора ведущего элемента «нуждается в некоторых комментариях»: если
начать с A0.32), зная, что первые к столбцов матрицы
\^21 ^22/
имеют форму Хессенберга (с /iji ^^ О, /132 ^О,... ), и проанализировать
формулы A0.29) в обратном направлении, то видно, что пространство
D для метода Энрайта и Камела является подпространством
Крылова, порождаемым вектором q^ (Хайам 1989). Таким образом, только
первая перестановка влияет на результат.
— Уоткинс и Хансон-Смит A983) начинают с произвольного
набора взаимно ортогональных векторов Q(°) с последующим
выполнением нескольких шагов блочного степенного метода
JQ(») = Q(.>i)^(i+i)^ A0.35)
где Д(»+^) реортогонализует векторы произведения JQ(*). Большое
преимущество этой процедуры состоит в том, что не требуется ни
вычислять, ни хранить никаких больших матриц. Формулы A0.35), как
и A0.34), содержат только матрично-векторные произведения,
которые вычисляются с помощью A0.30). Недостатком же является то,
что должна быть известна размерность пространства.
Критерии остановки. Методы, описанные выше, нуждаются в
критерии того, насколько хороша аппроксимация J, чтобы решить,
достаточна ли размерность к. Предположим, что мы решаем
линейную систему A0.23) при помощи модифицированного ньютоновского
метода коррекции, который использует А в качестве «приближенной
матрицы Якоби»:
X = Xq-Ь А'^ {Ь-Axq).
Тогда сходимость этих итераций определяется условием
p{I'-A^'A)=p{A'^(A-A))=p(A-^{J^J))<l. A0.36)
Следовательно, разумным условием будет, чтобы спектральный
радиус р матрицы A'-^(J—J) был просто меньше единицы. Вычислим эту
величину для метода Бьёрка G*21=0). Поскольку собственные
значения любой матрицы С инвариантны относительно преобразования
IV. 10. Численные эксперименты 191
подобия Т^^СТ, имеем:
'<-'(-^))-((-^'-Ci''о'))"'A
^22
О
^22
На практике условие вида
11^7^2211 < 1,
A0.37)
где II • II — обычно норма Фробениуса yYlij ^Ij > гарантирует
разумную скорость сходимости. Для метода Энрайта—Камела аналогичное
условие рассматривается ниже, в упр. 3.
Упралснения
1. («Красно-черная редукция».) Матрица Якоби для модели
(периодической) катастрофы сборки A0.8') имеет вид
/ А, В,
В,
Ci \
\В
'2т-1
2т
^2т-1
^2т
Я
2т-1
^2т
A0.38)
где Д, Я,, С, — матрицы Cx3). Напишите программу,
которая решает линейные уравнения с матрицей A0.38) с
использованием «красно-черной редукции порядка». Это означает, что
Л^,Л3,^5,... используются как (матричные) ведущие элементы
для того, чтобы при помощи блочного метода исключения Гаусса
удалить С2,С^,...,В2,В^,...у расположенные выше и ниже.
Тогда результирующая система снова имеет такую же структуру, как
и A0.38), но с размерностью вдвое меньшей. Если размерность
исходной системы содержит 2* в качестве простого множителя, то
этот процесс может быть повторен к раз. Исследуйте на
модели A0.8*), как этот алгоритм позволяет повысить эффективность
работы программы RADAU5 и программы, реализующей метод Ро-
зенброка. Этот алгоритм допускает также высокую степень рас-
паргсллеливания.
Покажите при помощи численных экспериментов, что «кольцевой
нерв» A0.8') теряет свой предельный цикл, когда коэффициент
диффузии D становится или слишком малым (сигнал не проходит
через «водопад»), или слишком большим (тогда предельный цикл
сливается с началом координат).
192 Гл. IV. Жесткие задачи — одношаговые методы
3. (Критерий остановки для метода Энрайта и Камела (Хайам 1989).)
Предположим, что матрица J преобразована частично к форме
Хессенберга (см. A0.32)):
где Н — верхняя матрица Хессенберга и 6 — вектор-столбец.
Покажите, что критерий A0.36) тогда превращается в
p{hiB) < 1,
где
1 + п-к
С Н = {1 — hjH). Так как р(В) совпадает со спектральным
радиусом нижней главной подматрицы (l-hn-fc) х (Ц-п—Аг) матрицы В,
то достаточным условием сходимости будет
|Л7|у1Г
где у^ — Аг-я строка матрицы —Н'уН Ti2(b, ^22).
IV.ll. Контрактивность
для линеёных задач
чсТот, кто любит практику без теории, подобен моряку,
который садится на корабль без руля и компаса и
который никогда не знает, куда его может занести».
(Леонардо да Винчи 1452-1519,
Щ1Т. по М. Kline, Mathematical Thought.., 1972, p. 224)
Анализ устойчивости в предшествующих разделах был основан на
преобразовании матрицы Якоби J^df/dy к диагональной форме (см.
формулы B.5), B.6) из разд. IV.2). Однако матрица, реализующая это
преобразование, может быть плохо обусловленной (особенно в
многомерных задачах), что разрушает все полученные ранее прекрасные
оценки.
Пример 11.1. Дискретизация гиперболической задачи
ж=1 '¦¦"
с помощью метода прямых приводит к системе ОДУ
/-1 1 \
-1 ¦••
у' =Ау, Л = А
А = -^>0. A1.2)
Ах
1
V -1/
Все собственные значения матрицы А равны —Л, и развитый выше
анализ спектральной устойчивости показал бы быструю
асимптотическую сходимость к нулю. Однако ни решение уравнения A11),
которое представляет собой просто бегущую волну, ни решение системы
A1.2), когда ее размерность становится большой, не обладают этим
свойством. Таким образом, в настоящем разделе наш интерес состоит
в получении строгих оценок для численного решения
y„^,=R(hA)y„ A1.3)
(см. B.3)) в различных нормах в М'* или О*. Здесь R{z) обозначает
функцию устойчивости применяемого метода. Из A1.3) имеем
\\yrr.+i\\<mhA)\\-\\yJ\ A1.4)
(см. том I, разд. 1.9, формула (9.12)), и контрактивность^)
гарантирована, если
||Д(М)||<1.
^ Контрактивность означает невозрастание «расстояния» между
решениями. — Прим. ред.
194 Гл. IV. Жесткие задачи — одношаговые методы
Евклидовы нормы (теорема фон Неймана)
«Следует напомнить людям, занимающимся
математикой и [естественными] науками, что многое из
принимаемого сегодня как должное обязано своим происхождением
одному из самых выдающихся, наверно, людей
двадцатого столетия — Джону фон Нейману».
(Джон Импальяццо, цит. по SIAM News, сентябрь 1988)
Если рассматривать евклидову норму, соответствующую
скалярному произведению, которое будем обозначать (¦, •), то для решения
уравнения у^=Ау имеем
^||г/||' = -^{У, у) = 2Re {у, у') = 2Re (у, Ау). A1.5)
Следовательно, в этой норме решения затухают, если
Re{y,Ay)<0 для всех увС. A1.6)
Этот результат связан с теоремой 10.6 из разд. 1.10, так как
Ке<у,>1у><А*2(Л)|ЫР, A1.7)
где fJ'2{^) — логарифмическая норма матрицы А (см. формулу
A0.20) из разд. 1.10).
Теорема 11.2. Пусть рациональная функция R{z) ограничена при
Rez < О, я матрица А удовлетворяет условию A1.6). Тогда в
матричной норме, соответствующей скалярному произведению,
||Д(Л)||< sup \R{z)\. A1.8)
Re2<0
Замечание. Это конечномерный аналог результата, полученного
Дж. фон Нейманом A951). Краткое доказательство опубликовали
Хайрер, Бадер и Любих A982). Идея приведенного ниже
доказательства принадлежит М. Крузе (не опубликовано).
Доказательство, а) Нормальные матрицы могут быть приведены
к диагональному виду с помощью унитарной матрицы Q (см. упр. 3
из разд. 1.12). Следовательно, A = QDQ* ,тде D = diag{Ai,..., А^}. В
этом случае
\\R{A)\\ = \\QR{D)Q'\\ = \\R(D)\\ = . max |Д(А,)|,
И A1.8) следует из A1.6), потому что собственные значения А
удовлетворяют неравенству Re А, < О.
б) Для матрицы А общего вида рассмотрим матричную функцию
А{и;) = '^{А + А')+\{А-А').
IV. 11, Контрактивность для линейных задач 195
Из тождества
(v, A(u)v) = шКе (v, Av) + Ят (v, Av)
видим, что A{(jj) обладает свойством A1.6) при всех и с Recj > О,
так что собственные значения А{и;) также удовлетворяют
неравенству ReA(a;) < О при Rew > 0. Поэтому рациональная функция
(p{u;) = {u,R(A(u;))v)
[UyV фиксированы) не имеет полюсов в полуплоскости Reu; > 0.
Воспользовавшись тем, что АA)=Ау из принципа максимума получим:
(ti, R{A)v) = <p(l) < sup ip(iy) < sup ||fl(^Bj/))||||ti||||t;|| <
< sup |Я(.)|||г/||||г;||. ^ * ^
Rez<0
Последнее неравенство A19) следует из части (а) доказательства, так
как A(iy) — нормальная матрица (т.е. A{iy)A(iy)* =A(iy)*A(iy)).
Формула A1.8) теперь немедленно следует из A1.9) и из того факта,
что ||С|| = sup||„,|<ijl^ll<i{ti,Cv). П
Следствие 11.3. Если рациональная функция R(z) Л-устойчивая,
то численное решение y^^i=R{hA)y^ контрактивно в евклидовой
норме (т.е. ЦУп^хЦ < WVnlDf когда выполнено условие A1.6).
Доказательство. Л-устойчивость означает max |ДB:)| < 1. П
Rez<0
Слодствие 11.4. Если для матрицы А при любом v еС^
выполняется неравенство Re (t;, Av) < i^\\v\\^ , то
||Д(Л)||< sup \R(z)\. A1.10)
Rez<t/
Доказательство. Применим теорему 11.2 к функции Д(г)=Д(г-|-^')
и матрице A=^A—i/I. П
Функция роста погрешности для линейных задач
Руководствуясь полученной выше оценкой, определим функцию
^д(х):= sup |Д(г)|. A1.11)
Rez<x
Эта функция называется функцией роста погрешности {для
линейных задач). Она непрерывная и монотонно возрастающая. Если R{z)
аналитическая на полуплоскости Re г < х, то из принципа максимума
следует, что
(Pf^{x) = sup \R{x-\-iy)\.
196 Гл. IV. Жесткие задачи — одношаговые методы
Примеры.
1. Неявный метод Эйлера:
1 (RMi если -оо<х<1,
R{z) = -^, Ы^)= ,^ A112)
А — ^ к ОС, если 1 < а: .
2. Функция устойчивости ^-метода (или одностадийного метода Ро-
зенброка):
. /. _ оч Г |Л(ооI, если x<(q ,
^(^) = 1^вг ' ^^^""^ " 1 ^^''^' ^'''''' ^0 < ^ < 1/» ,
I со, если 1/^ < X ,
A1.13)
где ^о=A-2^)/B^A-^)) для О < ^ < 1 и ^о=-оо для 5 > 1.
3. @,2)-аппроксимация Паде:
^ Д(а;), если —оо < ж < О ,
_1
l-z + z^/2
Д(^)=1 .^.2/о- VhW=^
, если О < ж < 1 ,
I — X
оо, если 1 < X .
A1.14)
4. A,2)-аппроксимация Паде: ^(-2:) = :;—ТПГ^ГГТТ^ ^
1 — ZZ/O -г Z'^/0
||Д(х)|, если —оо < X < ^0 >
\/Зл/12х2-Ц2а:-Ь9+10а: + 7 ^ ^ ^_
2B^ГЙ ' ^^^^ ^0 < ^ < 2 .
оо, если 2 < X ,
A1.15)
где^о = -6-Зч/Г0.
. /^..ч т^ г,/ ч IH-2:724-^2/12
5. B,2)-аппроксимация Паде: ^(-2^) = - т^г;—ГГПТ'
1 — Z/Z -|- z^/lZ
1,
2х + л/9 -f 3x2
оо.
если —оо < X < 0 ,
если 0 < X < 3 ,
если 3 < X .
^д(^) = \ V , если О < X < 3 , A1.16)
Следующие две теоремы содержат некоторые общие результаты,
относящиеся к виду ^д(х).
IV. 11. Контрактивность для линейных задач 197
Теорема 11.5. Пусть R(z) — А-устойчивая аппроксимация е^,
имеющая точный порядок р, т.е. R{z)=e' —CzP-^^-^0(zP'^^) и СфО.
ПустЬу кроме того, |H(ij/)| < 1 при уфО и |Д(оо)| < 1. Тогда
a) если р нечетное^ то
^д(х)=е^Ч-0(х'^'^М при х^О; A1.17)
b) если р четное J то A1.17) имеет место только при {—1)р^^Сх > О, в
противном случае
(Рл{х) = е''-\-0{х'"^^) при х^О, A1.18)
где г — некоторое положительное рациональное числОу г < р/2.
Доказательство. Из условий теоремы следует, что при х -> О
максимум {|Л(х-|-гу)|;у G М} должен находиться около начала
координат. Далее, он должен лежать внутри порядковой звезды A={z G С;
\R{z)\ > |е^|}. Если р нечетное, порядковая звезда содержит р4-1
секторов вблизи начала координат (лемма 4.3) и, асимптотически при
Z —> со, все элементы А удовлетворяют неравенству |г|</)|х|, D<oo.
Поэтому
\R{z)\ = e^-\-0{\zf^^) = e'^0{x^-^^) при х-^ 0.
То же самое рассуждение справедливо и для четного р, когда
выполнено условие (—1)Р/2Сх > 0. В оставшемся случае (р четное и
[—1)р/^Сх < 0) максимум {|Д(хЧ-гу)|;2/ЕК} достигается вблизи
мнимой оси и необходим более детальный анализ (Хайрер, Бадер и Любих
1982). П
Теорема 11.6 (Хайрер и Дзеннаро 1996). Для А-устойчивой
аппроксимации е^ функция <Рл(х) сверхпоказательная, т.е. она
обладает свойствами ^д(О) = 1 и
У^я(^1) У^дС^г) < ^r(^i + ^2) A119)
для всех Xj и Xj, имеющих одинаковые знаки.
Доказательство. Так как Л-устойчивость равносильна условию
у?д@) = 1, то остается лишь удостовериться в справедливости
утверждения A1.19). Пусть Xi и Х2 фиксированы, оба > О (или оба < 0),
и предположим, что <Рл(х^ -f Xj) < ос. Идея состоит в рассмотрении
рациональной функции
S{z)=R(a-z)R{z),
где а Е С — параметр, удовлетворяющий неравенству Re а < х^ -h Xj.
Благодаря Л-устойчивости и условию (pjiix^ H-Xj) <оо, функция S{z)
аналитична в полосе О < Rez < х^ -j-Xj (или х^ -hXj < Rer < 0), и ее
модуль не превосходит ^r(xi-\-X2) на границе. Поэтому согласно
принципу максимума для всех z в рассматриваемой полосе имеем
\R{a-^z)R(z)\<<pj^{x,-\-X2).
198 Гл. IV. Жесткие задачи — одношаговые методы
Возьмем теперь на прямой Rez = X2 такое г, чтобы |ЯB:)| было
максимально; затем выберем на прямой Re а = х^ + Xj (т.е. Re(a — z) = x^)
такое а, что |Д(а —2:)| максимально (возможно, понадобится
предельный переход). Это и доказывает неравенство A1.19). П
Свойство A1.19) допускает интересную практическую
интерпретацию. Рассмотрим численное решение у^ , полученное с переменной
длиной шага. Повторное применение неравенства A1.4) и следствия
11.4 дает
m-l
к=0
если задача у' -=- Ау удовлетворяет условию A1.7) и ^ = А^2(^) • Д-^^
// < О и для А-устойчивого метода все сомножители (pjiihi^fi) меньше
единицы. Если вдобавок |Д(оо)| < 1, то эти сомножители близки к
единице только при /ij^ -> 0. Неравенство A1.19), записанное как
означает, что замена двух последовательных шагов одним большим
шагом размера hf^-^-hf^^^ приводит к увеличению верхней границы
A1.20). Поэтому, комбинируя (если необходимо) несколько
последовательных шагов, мы можем положить hf^>h>0 для всех к.
Отсюда следует, что \\у^\\ < р"*||Уо1| с р = (Рл{кр) < 1. Следовательно, для
любой сетки Хо,а?1,... с х^ —»• ос имеем асимптотическую
устойчивость, т.е. ||Уууг||->0 при т->оо. При дополнительных ограничениях
на длину шага могут быть получены более строгие оценки для \\у^\\
(упр.З).
Малые нелинейные возмущения
Приведенные выше оценки, справедливые только для линейных
автономных уравнений y'^Jy, могут быть распространены на задачи
с малыми нелинейными возмущениями, так называемые
полулинейные задачи
y' = Jy + G(^,y), A1.21)
где
(y,</y)</i||y||' и A1.22а)
\\9[x,y)-9[x,z)\\<L\\y^z\\ A1.22b)
с достаточно малым L.
При наличии нелинейностей свойства устойчивости выводятся
путем оценки расстояния между двумя соседними решениями у(х) и
у{х). Поэтому вместо A1.5) воспользуемся тождеством
IV. 11. Контрактивность для линейных задач 199
что дает, после подстановки A1.21) для t/ и у', с использованием
неравенства Коши—Шварца и оценок A1.22),
^\\y{x)-y(x)f<2{fi + L) \\y(x)-y{x)f. A1.23)
Таким образом, контрактивность имеет место, когда //-h L < 0.
Теперь мы хотим установить то же самое свойство для численных
решений. В принципе такие оценки могут быть выведены для всех
методов настоящей главы; однако здесь мы сосредоточимся на
методах Розенброка, поскольку множество замечательных свойств
неявных методов Рунге—Кутты будет рассмотрено в последующих
разделах.
Пример 11.7. Рассмотрим одностадийный метод Розенброка
2/1 = % + *^1
с 7 > О ь качестве свободного параметра. Его функция устойчивости
1 + A-7)^
1-fz '
И мы имеем Л-устойчивость при 7 > 1/2- Применение метода A1.24)
R(z) =
к уравнению A1.21) дает
y,=R{hJ)yo + (I-'rhJ)-'hg{xo,yo). A1.25)
По теореме фон Неймана \\{1— 'yhJ)~'^\\<{l'-yhfi)~'^ (следствие 11.4),
и ||/?(/iJ)|| < (Pfi(hfi) с (pf^^ определенной в A1.13). Если мы возьмем
второе численное решение у^, тоже определяемое формулой A1.25),
то разность между ним и у^ может быть оценена следующим образом:
llj/i-j/ill<(^(M + Y^)lli'o-%ll=(i + ^^r^)ll%-%ll
при ^Q< hfi<l/y, где ^0 определено в A1.13). Поэтому
контрактивность имеет место при //-ЬХ < О, что и было желательно.
Применяя общий метод Розенброка G.4) к задаче A1.21):
t
i=i
1-1 s
легко найти следующий аналог формулы вариации постоянных:
200 Гл. IV. Жесткие задачи — одношаговые методы
Теорема 11.8. Численное решение метода Розенброка,
примененного к уравнению A1.21)^ может быть записано в виде
S
2/1 = R(hJ)yo -f Л ^ bi{hJ)g(xo -h с.Л, t/,),
Til A1-26)
Ui = Ri{hJ)yQ + Л ^ aij{hJ)g{xQ -f Cjh, Uj), г = 1,..., s.
i=i
Здесь R{z) — функция устойчивости^ Ri(z) — так называемые
внутренние функции устойчивостиf а 6, (-г), а, • (z) — рациональные
функции ^ имеющие полюсы только в 1/j и удовлетворяющие условиям
6,.(оо)=0, а.^.(оо)=0. D
Замечание. Для многих классов линейно неявных методов
(например, для методов ван дер Хаувена A977), Фридли A978), Штремеля
и Вайнера A982) и др.) численное решение можно выразить в
форме A1.26) с некоторыми рациональными функциями. Таким образом,
последующий анализ может быть применен и к этим методам тоже.
Возьмем теперь второе численное решение Уо» 2,) у^ (тоже
определенное согласно A1.26)), возьмем разность j/i — Ух и применим
неравенство треугольника. Из предположений A1.22) с использованием
теоремы фон Неймана (следствие 11.4) выводятся следующие
неравенства:
S
\\У1 - yill < ^д(М1|Уо - Уо\\ + ЛХ,^(pf,.(hfi)\\ui - u,||,
A1.27)
11^.-^.11<^яЛМ11%-Уо11 + Л^1]^а.ЛМ1к2,—ti^ll.
i=i
Последовательная подстановка второго неравенства A1.27) в первое
приводит к следующей теореме.
Теорема 11.9. Если справедливы предположения A1.22), то
разность двух численных решений метода G.4) можно оценить
следующим образом:
\\У1-У1\\ < (?'д(М + сЛ1)||!/о -УоН. A1-28)
где (Рл(х) определяется формулой A1.11) (в которой R{z) — функция
устойчивости метода G.4)) и с — постоянная, гладко зависящая от
hL и hfi и не зависящая от \\J\\ (последняя представляет жесткость
задачи). П
Эта оценка означает, что при (рл[к^) -\- hL* < О имеет место
численная контрактивность. Теорема 11.5 показывает, что при выполнении
IV. 11. Контрактивность для линейных задач 201
определенных предположений (pj^(x)=l'\-x-\-o(x), так что
контрактивность имеет место, по существу, при fi-\'L* < 0. В любом случае из
Л-устойчивости при hfi < Const следует, что
11г/1-2/111<A+ЛС-)||уо-Уо11-
Здесь постоянная С* не зависит от жесткости уравнения A1.21).
Замечание. Поскольку рациональные функции 6, и а, в A1.26)
обращаются в нуль на бесконечности, то как (l—fhj)b^(hj), так и
(l—'yhJ)a^j{hJ) равномерно ограничены, если матрица J
удовлетворяет условию A1.22) и hfi<C<y~^ . Поэтому вместо второго условия
A1.22) можно потребовать, чтобы
\\{I-lhJ)-'h{g{x,y)-g(x,z))\\<e\\y-z\\, A1.29)
И утверждение теоремы 11.9 останется справедливым, если hL
заменить на ?. Видно, что предположение A1.22) влечет A1.29) с
?—hL/(l—^hfi). Однако в некоторых специальных ситуациях число
? может быть значительно меньше, чем hL. Соответствующую
технику использовали Хундсдорфер A985), а также Штремель и Вайнер
A987), чтобы доказать контрактивность и сходимость для линейно
неявных методов. Остерман A988) применил эти идеи к
нелинейным сингулярно возмущенным задачам, где hL=0{he~'^) с некоторым
очень малым е (e<^h), ио ? может быть ограничено независимо от
Контрактивность в нормах ||-||оо и ||-||i
Контрактивность в общих нормах исследовали, в основном, Спей-
кер A983, 1985) и его сотрудники. Сходную технику доказательств
развили также Болле и Крузе A978), изучая родственную проблему
(монотонность).
Следующая теорема дает условие, необходимое для
контрактивности именно специального уравнения A1.2) в норме || • ||оо или || • ||i.
Затем будет показано, что то же самое условие оказывается также и
достаточным для задач общего вида и для любых норм.
Теорема 11.10. Пусть А — п-мерная матрица A1.2) с
фиксированным А > 0. Чтобы для рациональной функции R(z) с /?@) = 1
выполнялось неравенство
\\R{hA)\\^ < 1 для всех размерностей п = 1,2,..., A1.30)
необходимо выполнение условия
К^^Цх)>0 для XG [-Л/1,0] я ; = 0,1,2,... A1.31)
(утверждение остается вернымj если в неравенстве A1.30) норму || • Цо^
заменить на \\ '\\i)>
202 Гл. IV. Жесткие задачи — одношаговые методы
Доказательство. Положим h=\ и запишем А в виде A=—\I-\-XN ,
где N — нильпотентная матрица. В подходящей норме ||Д^||
произвольно мала, и поэтому, воспользовавшись разложением Тейлора и
тем, что Л'"=0, имеем
ЩА) =
Это означает, что, например, при п=4 матрица R(A) имеет вид
/Д(-А) XR'{-X) ^R"(-X) ^R"'{-\)\
R(-X) АЯ'(-Л) |^Я"(-А)
R(-X) "аД'(-Л)
R(-X)J
Применение формулы A.9.1 Г) (или A.9.11")) показывает, что
неравенство ||Я(Л)||^ < 1 (или ||Я(Л)||1 < 1) эквивалентно условию
"-' XJ
A1.32)
V
ЕИП-А)|^<1.
j=o •^'
Если A1.32) справедливо для всех тг > 1, то ряд
Y^rU\_x)^ A1.33)
j>0 •'*
СХОДИТСЯ абсолютно, и поэтому
1 = Л@) = ^ Я(^)(-А)^ < J2 |Я<''(-А)|^ < 1,
j>0 •'* j>o •'¦
что влечет i?(-?)(—Л) > О для всех j >0. Поскольку разложение
Тейлора
(x-f A)^-J
k>j
{k-JV-
содержит при X > — X только неотрицательные члены, неравенство
A1.31) доказано. D
Следующая теорема показывает, что условие A1.31) достаточно
для контрактивности в произвольных нормах. Его легко можно
применить к системе A1.2), так как ее матрица удовлетворяет условию
\\А+Х1\\^=Х.
Теорема 11.11. Рассмотрим произвольную норму, и пусть матрица
Л такая, что для некоторого Л > О справедливо неравенство
\\Л-\-Х1\\<Х. A1.34)
IV. 11. Контрактивность для линейных задач 203
Если функция устойчивости метода удовлетворяет условию Я@) = 1
и
R^^\x)>0 для хе[-д^О] и ;=0,1,2,..., A1.35)
то при hX< д имеет место численная контрактивность: \\R(hA)\\ < 1.
Доказательство. Снова положим /i=l. Поскольку при О < Л < ^
имеем Я(-?)(—А) > О для всех j, функция
H(z) = ^flO)(-A)ii±^ A1.36)
удовлетворяет неравенству |Я(-г)| < Л(-А-}-г) для всех комплексных
Z в круге \z-^X\ < г. Из этого свойства и из A1.35) следует, что
никакие полюсы R(z) не могут лежать в круге |г-|-А| < А, так что радиус
сходимости ряда A1.36) строго больше, чем А. Поэтому из A1.34)
вытекает, что
Д(Л) = 5:Я<^)(-А)^^1±^. A1.37)
i>o •'•
Применение к A1.37) неравенства треугольника доказывает теорему.
П
Исследование порогового коэффициента
Определение 11.12. Наибольшее д, для которого справедливо
условие A1.35), называется пороговым коэффициентом R(z).
Пример 11.13. Неявный метод Эйлера, для которого
^'''^'^)=(l-x)i-H' •'¦ = 0'1'2'--
удовлетворяет A1.35) для всех ^ > 0. Он обладает пороговым
коэффициентом ^=оо.
Пример 11.14 (пороговый коэффициент для аппроксимаций Паде).
Производные многочленов
легко вычисляются; наиболее опасной из них является l-fz, поэтому
^=1 для всех к.
Аппроксимации Паде Rki(z) обладают только одним простым
полюсом, так что они могут быть записаны в виде выражения
а
Rf^i(z) — 7- -f многочлен относительно г,
204 Гл. IV. Жесткие задачи — одношаговые методы
имеющего только конечное число производных, которые могут менять
знак (см. пример 11.13). Полученные численные значения
представлены в табл. 11.1.
Функции Rk2{^) "^ имеют вещественных полюсов (см. разд. IV.4).
Однако свойство |Я(г)| < Щ—д-^г) для \z-\'g\ < г (см. доказательство
теоремы 11.11) означает, что максимум |Я(г)| в круге с центром —д
и радиусом г предполагается находящимся как раз на вещественной
оси. При возрастании г первый полюс, встречающийся с этим
кругом, должен быть поэтому вещественным и лежать справа от —^. В
данном случае это невозможно, и поэтому аппроксимации Rf^2i^) """
когда не удовлетворяют свойству A1.35). В табл. 11.1 это отмечено
звездочкой (*).
Все остальные значения в табл. 11.1, вычисленные с помощью
разложения R{z) на элементарные дроби, заимствованы из работ (Край-
евангер 1986) и (ван де Гринд и Крайевангер 1986).
Таблица 11.1. Пороговые коэффициенты аппроксимаций Паде
к
J
J
J
J
J
J
=0
=1
=2
=3
=4
=^
0
—
CO
*
0,584
*
0.353
1
1
2
¦
1.195
¦
0.770
2
1
2.196
*
1.703
*
1.081
3
1
2.350
¦
2.208
¦
1.424
4
1
2.477
*
2.710
*
1.794
5
1
2.586
*
3.212
¦
2.185
6
1
2.682
*
3.713
*
2.590
Любопытно отметить, что в этой таблице методы с наибольшими
пороговыми коэффициентами — как раз те, которые не являются А-
устойчивыми. Единственное исключение составляет неявный метод
Эйлера (А:=0, j = l), для которого ^=оо.
Абсолютно монотонные функции
«... on peut definir la fonction e^ comme la seule fonction
absolument monotone sur tout le demi-axe negatif qui prend
a Torigine, ainsi que sa derivee premiere [sic] la valeur un».
«... функцию e^ можно определить как единственную
абсолютно монотонную на всей отрицательной полуоси
функцию, которая принимает в нуле единичное значение
вместе со своей первой производной [^tc]».
(С. Бернштейн 1928)
Основательное изучение вещественных функций,
удовлетворяющих условию A1.35), было начато С. Бернштейном A914) и
продолжено Ф. Хаусдорфом A921). Такие функции называются абсолютно
IV.ll. Контрактивность для линейных задач 205
монотонными на [—^,0]. Позднее С. Бернштейн A928) дал
следующую характеристику функций, которые абсолютно монотонны на
(—00,0] (см. также Уиддер 1946).
Теорема 11.15 (Бернштейн 1928). Необходимым и достаточным
условием абсолютной монотонности функции Щх) на (—оо,0]
является представимость ее в виде
Щх)
/•ОО
= / e^4a{t), A1.38)
Jo
где a(t) — ограниченная и неубывающая функция, и интеграл
сходится при —ОО < X < О.
Это сильный результат, и это главный ключ для следующих двух
теорем. По-видимому, он не допускает элементарного и легкого
доказательства. Поэтому мы отсылаем читателя к оригинальной работе
С. Бернштейна A928). Более позднее изложение можно найти,
например в книге (Уиддер 1946, р. 160). Из этого результата мы немедленно
получаем «предельный случай Л -4 ос» теоремы 11.11, справедливый
тоже для произвольной нормы:
Теорема 11.16. Пусть R(x) абсолютно монотонна на (—оо,0],
Д@) = 1 и Л — матрица с неположительной логарифмической
нормой /i(^) < 0. Тогда
||Л(Л)||<1.
Доказательство. По теореме 1.10.6 для решения 2/(х)=е^^Уо
Уравнения у'=Ау справедливо неравенство ||2/(ж)|| < ЦуоН- Следовательно,
Це^^Ц < 1 при X > 0. Утверждение теоремы следует из того, что
/•ОО /«ОО лОО
||Л(Л)|| = ||/ e^Ua{t)\\< \\e^^\\da{i)< da{t)^R(Q) = h
Jo Jo Jo
поскольку a{t) — неубывающая функция. П
Следующий результат доказывает, что никакой метод Рунге—
Кутты порядка р>1 не может иметь функцию устойчивости,
абсолютно монотонную на (—оо,0].
Теорема 11.17. Если R(x) абсолютно монотонна на (-оо,0] и
R{x) = l + x-\-x^/2-^0(x^) при х->0,
то Я(х) = е^ .
Доказательство (Болле и Крузе 1978). Из A1.38) следует, что
/•ОО
R^^HO) = / t4a(t).
Jo
206 Гл. IV. Жесткие задачи — одношаговые методы
Так как R@) = R'{0) = R"@) = l, это дает
(l-tfdQ{t) = 0.
1
Jo
Следовательно, a{t) должна быть функцией Хевисайда {a{t)=0 для
^< 1 и Q{t) = l для t>l). Подстановка в A1.38) дает R(x)=e^. П
Упражнения
1. Докажите формулу A1.14). Для фиксированного х исследуйте
множество значений у, для которых |Д(х+гг/)| достигает своего
максимума.
2. Покажите, что функция роста погрешности A1.11) для
Л-устойчивой R(z) порядка р> 1 удовлетворяет условию
(Pfi(x) > е^ для всех х :^0.
Указание. Можно исследовать порядковую звезду на
параллельных линиях {x-f fi/,t/GM} (Хайрер, Бадер и Любих 1982) или
воспользоваться тем, что <Pfi(x) — сверхпоказательная функция.
3. (Хайрер и Дзеннаро 1996.) Пусть |Я(оо)| < 1. Рассмотрим сетку
Xq,Xi, ... с длинами шагов h,^ —^k-\-i '^ ^к ' причем Л^^^^ < chf^ (с>
1). Докажите, что существуют постоянные С> О и а > О такие,
что
1|Ут11<С(х^-^о)"''11г/о11 ДЛЯ т = 1,2
4. (Крайевангер 1986.) Пусть R(z) —многочлен степени $ такой, что
R{z)=€^-\-0(zP'^^). Тогда пороговый коэффициент д (определение
11.12) ограничен:
д< 5-p-f 1.
Указание. Докажите справедливость формулы
j=o ^
и выведите результат из равенств Л(р~^)@) = Д(р)@) = 1 .
5. Пусть р — пороговый коэффициент рациональной функции R{z).
Покажите, что ее область устойчивости содержит круг \z-\-p\<p.
IV.12. jB-устойчивость и контрактивность
«Затем мы нуждаемся в обобщении понятия
Л-устойчивости. Наиболее естественным обобщением было бы
рассмотреть случай, когда x{t) — равномерно
асимптотически устойчивое решение...в смысле теории
Ляпунова..., но этот случай, кажется, немного слишком
широк». (Г. Далквист 1963)
«Теоретический анализ применения численных
методов к жестким нелинейным задачам все еще далеко не
полон». (Г. Далквист 1975)
Здесь мы вступаем в новую эру — изучения устойчивости и
сходимости для общих нелинейных систем. Все «преступления» и разные
упущения, в которых мы были повинны в предыдущих разделах,
особенно в разд. IV.2, теперь будут исправлены.
В статье Дал к виста A963) видное место занимало обсуждение
возможности обобщения понятия Л-устойчивости на нелинейные задачи.
Его поиски достаточно общего класса нелинейных систем, в конце
концов, увенчались успехом 12 лет спустя. В своем докладе на
конференции в Данди в июле 1975 года он предложил рассмотреть
дифференциальные уравнения, удовлетворяющие одностороннему условию
Липшица, и представил некоторые первые результаты для многошаговых
методов. Затем Бутчер A975) распространил (во время обратного
полета с конференции) эти идеи на неявные методы Рунге—Кутты, и
родилось понятие Б-устойчивости.
Одностороннее условие Липшица
Рассмотрим нелинейное дифференциальное уравнение
у'= fix,у) A2.1)
такое, что для евклидовой нормы справедливо одностороннее условие
Литиица
{f(x,y)-f{x,z),y-z)<i^\\y-zf. A2.2)
Число и есть односторонняя константа Липшица для f. Это
определение оправдывает следующая
Лемма 12.1. Пусть f(x,y) — непрерывная функция,
удовлетворяющая условию A2.2). Тогда для любых двух решений у(х) и z(x)
уравнения A2.1) выполняется неравенство
11У(Х) - z(x)|| < \\y(x,) - z(xo)|| • е"''-^») при х>х,.
Доказательство. Дифференцирование т(х) = ||у(х)—г(х)|р дает
т'(х) = 2(/(х, y(x))-f(x, z(x)), y(x)--z(x)) < 2v m{x) .
Это дифференциальное неравенство можно решить и получить
т(х) <т(хо)е^''^^"''*^^ для х>х^
(см. теорему 1.10.3), что эквивалентно утверждению леммы. П
208 Гл. IV. Жесткие задачи — одношаговые методы
Замечания, а) На открытом выпуклом множестве условие A2.2)
эквивалентно /i(|^) < i^ (см. разд.1.10, упр. 6), если / непрерывно
дифференцируема. Лемма 12.1 тогда становится специальным
случаем теоремы L10.6.
Ь) Для комплекснозначных у и f условие A2.2) следует заменить
на
^e{f(x,y)-f(x,z),y-z)<u\\y-z\\\ y,zeC , A2.2')
и лемма 12.1 остается справедливой.
S-устойчивость и алгебраическая устойчивость
Если в A2.2) г/ < О, то расстояние между любыми двумя
решениями уравнения A2.1) — невозрастающая функция х. Желательно,
чтобы то же самое свойство было и у численного решения. Мы
рассмотрим здесь неявные методы Рунге—Кутты
2/1
= 2/о + Л^6,./(хо + с,/1,G,.) , A2.3а)
1=1
^=2/o + ^^a,.j/(xo-fc^./i,5'j) , г=1,...,5 . A2.3b)
Определение 12.2 (Бутчер 1975). Метод Рунге—Кутты называется
В 'устойчивым, если из условия контрактивности
(/(^,2/)-/(х,г),у-г><0 A2.2")
следует
\\У1-У1\\<\\Уо-%\\
при любых л > о. Здесь у^ и у^ — численные аппроксимации после
одного шага с начальными значениями t/g и щ соответственно.
Ясно, что Б-устойчивость влечет Л-устойчивость. Это видно,
если применить данное выше определение к уравнению у^ = Ху^ Л G С
или, точнее, к системе
(Й)=(?-/)(?)
Пример 12.3. Для коллокационных методов, основанных на
квадратуре Гаусса, возможно простое доказательство В-устойчивости
(Ваннер 1976). Обозначим через и{х) и й(х) коллокационные
многочлены (см. определение П.7.6, том I, с. 221) для начальных
значений у^ и yQ и продифференцируем функцию m(x) = ||w(a:)—w(x)||2. В
точках коллокации ^,=ХоЧ-с,Л тогда получим
IV. 12. В-устойчивость и контрактивность 209
Результат теперь следует из того факта, что квадратура Гаусса точно
интегрирует многочлен т'(х) (степени 25—1) и имеет положительные
веса 6,-:
11У1 - ^111^ = m(xo-l-/i) = m(xo) -h / m'(x) dx =
S
= т{х^) -h /i ^ 6,.m'(xo-f c,./i) < m(xo) = \\уо - Уо\\^ .
1=1
Алгебраический критерий 5-устойчивости нашли независимо Бер-
ридж и Бутчер A979) и Крузе A979):
Теорема 12.4. Метод Рунге—Кутты A2.3) является
В-устойчивым, если его коэффициенты удовлетворяют условиям
i) 6,. > О для г=1,..., 5 ;
И) матрица М=(т,^)=F,.а,-^-|-6^а^.,.-6,.6^),^^_1 неотрицательно
определенная.
Определение 12.5. Метод Рунге—Кутты, удовлетворяющий
условиям (i) и (ii) теоремы 12.4, называется алгебраически устойчивым.
Доказательство теоремы 12.4- Введем разности
^fi = h{f(xQ + Cih,gi)-f{xQ-^Cih,gi))
и вычтем друг из друга формулы Рунге—Кутты A2.3), записанные
для у и у:
S
А2/1=Ауо + Х)б.ДЛ, A2.5а)
«=1
S
Ag, = Ay,-b^a,jAf,. A2.5b)
Возведем теперь в квадрат формулу A2.5а):
||Дг/1||2 = ||Дуо||2 + 2^6,{Д/,,Дуо) + Х:^^6,6^.<Д/,,Д/,.) . A2.6)
1 = 1 1 = 1 j = l
Основная идея доказательства состоит в том, чтобы вычислить Ауд
из A2.5Ь) и результат подставить в A2.6). Это дает
\\Ay,f = \\Ayo\\' + 2J2bi{Af,,A9i)-i2i^m,j{Af„Afj) . A2.7)
» = 1 » = 1 J = l
Утверждение теоремы следует из того, что (Af-^Ag^) < О согласно
условию A2.2") и Ylij=i ^iji^fi^^fj) > О (см. упр. 2). П
210 Гл. IV. Жесткие задачи — одношаговые методы
Пример 12.6. Для метода ОДНРК из табл. 7.2 (глава II) веса 6,
положительны и матрица М имеет вид
М
-ьМ-\ -1)
При у >1/4^ эта матрица неотрицательно определенная, поэтому
метод Б-устойчивый. В точности это же самое условие было получено
при исследовании его Л-устойчивости (ср. C.10)).
Некоторые алгебраически устойчивые НРК методы
«La premiere de ces proprietes consiste en ce que tous
les Ak sont positifs».
«Первое из этих свойств состоит в том, что все Л/^
положительны». (Т.И. Стилтьес 1884)
Общее исследование гипгебраической устойчивости естественным
образом распадается на два шага: надо проверить положительность
весов квадратуры и удостовериться в неотрицательной
определенности матрицы М.
Теорема 12.7. Рассмотрим квадратурную формулу (с,,6,)*_i
порядка р.
a) Если р > 2s— 1, то 6,. > О для всех г.
b) Если с,- — нули многочлена E.3) (квадратура Лобатто), то 6, > О
для всех г.
Доказательство (Стилтьес 1884). Первое утверждение следует
из того, что при р> 25—1 многочлены степени 2s—2 интегрируются
точно, следовательно,
В случае квадратуры Лобатто (ci=0, с^=1 и p=2s—2) множители для
индексов j=l и j=s берутся без возведения в квадрат и применяется
то же самое рассуждение. П
Для проверки, выполнено ли условие (ii) теоремы 12.4, мы нашли
удобным воспользоваться 1У-преобразованием (см. разд. IV.5) и
рассматривать матрицу W^ MW вместо М. В векторных обозначениях
F=:Fi,.. .,bj^, J3=:diagFi,.. .,6,), A={a^j)) матрица М имеет вид
М = 5Л + Л^5-66^ . A2.9)
Если выбрать W согласно лемме 5.12, то W'^BW = I, а так как при
этом iy^6=:ei=(l, О,..., 0)^, то условие (ii) теоремы 12.4 равносильно
IV. 12. Б-устойчивость и контрактивность 211
утверждению, что матрица
W^MW = X -\- Х^ — е^е( неотрицательно определенная. A2.10)
Здесь X = W-'^AW=W'^BAW, как и в теореме 5.11.
Теорема 12.8. Предположим, что метод Рунге—Кутты, у
которого все с, различны и 6, положительны, удовлетворяет упрощающим
предположениям B{2s—2),C(s—l),D(s—l) (см. начало разд. IV.5).
Чтобы такой метод был алгебраически устойчив, необходимо и
достаточно, чтобы |Я(оо)| < 1, где R{z) — его функция устойчивости.
Доказательство. Поскольку порядок квадратурной формулы р >
> 25—2, матрица из W из леммы 5.12 имеет вид
W = WaD, ?> = diag(l,...,l,a-»),
A2.11)
где Wa = {Pj_,icMj^„ как в E.21), и a^ = ELl^>iPldci)фO. Вое-
пользуемся соотношением
X = W'^AW = D-^W^^AWaD = DWSbA(W^B)'-^D'\
которое выводится с учетом того, что W^BW = I. Применив лемму
5.7 с 7^=5—1 и лемму 5.8 с ^=5—1, получим
Х =
/1/2
^1
\
4i
0
^s-2 0
"^,-1
-<-1
/3
\
Если эту матрицу подставить в A2.10), то (о, чудесный сюрприз!) все
уничтожается за исключением /3. Поэтому условие (ii) теоремы 12.4
эквивалентно /? > О.
С помощью представления E.31) функции устойчивости получаем,
раскрывая определители,
|Я(оо)| =
det(X-eief)
detX
l3d,^i-c^4's-ids-2\
/3d,_i+«2^1^,-2 Г
A2.12)
где df^=k\/{2k)\ -детерминант матрицы Xq размерности к из E.13).
Поскольку Q^C]^ids-2 > О, выражение A2.12) не превышает единицы,
если и только если /? > 0. Это доказывает утверждение теоремы. П
Сопоставляя эти теоремы с таблицей 5.13, приходим к следующему
результату:
Теорема 12.9. Методы Гаусса, Радо IA, Радо ПА и Лобатто IIIC
алгебраически устойчивые, а поэтому также и В -устойчивые. П
212 Гл. IV. Жесткие задачи — одношаговые методы
AN -устойчивость
Теория Л-устойчивости основывается на автономном линейном
уравнении у* = \у, тогда как 5-устойчивость базируется на
нелинейных системах у^ =f{x, у) общего вида. Возникает вопрос, не
существует ли разумной теории устойчивости между этими двумя крайними
случаями. Естественным подходом было бы изучение скалярного
линейного неавтономного уравнения
t/' = A(x)y, ReA(a:)<0, A2.13)
где Х(х) — произвольно изменяющаяся комплекснозначная
функция (Берридж и Бутчер 1979; Шерер 1979). Несколько неожиданный
результат этого подраздела будет состоять в том, что устойчивость
на уравнении A2.13) для большинства методов РК эквивалентна В-
устойчивости.
Для задачи A2.13) метод Рунге—Кутты A2.3) будет (в векторных
обозначениях д =^{9ц -- -, д^)^ ^ Я = A,..., 1)^) иметь вид
д = ly^-^-AZg, Z = di^g{z^,,.,,zj, Zj = h\{xQ-\-Cjh). A2.14)
Выразив g из A2.14) и подставив в A2.3а), получим
у, = K{Z)yo, K{Z) = l-h6^Z(/-AZ)-^1 A2.15)
Определение 12.10. Метод Рунге—Кутты называется AN
-устойчивым ^ если
\KIZ)\ < 1 1^^^ ^^^^ ^ "^ diagB:i,,.., zJ с Re Zj < О
' ^ ^'- \и Zj=Zf^,KOrR8iCjZZC^ (j, Аг = 1, . . ., s).
Сравнивая A2.15) с C.2), находим, что
A'(diag(^,z,...,z)) = ^(z) A2.16)
— обычная функция устойчивости. Далее, рассуждая как для A2.4),
приходим к тому, что В-устойчивость влечет Л ЛГ-устойчивость.
Таким образом, получена следующая
Теорема 12.11. Для методов Рунге—Кутты имеем:
В-устойчивость ^ AN-устойчивость => А-устойчивость.
П
Для правила трапеций у^ = 2/о + |(/(^о>2/о)+ /(^i'2/i)) функция
K{Z) из A2.15) дается выражением
Положив, например, -^j = О и z^ -^ —ос, видим, что этот метод не
является ААГ-устойчивым. Имеется и более общий результат.
IV. 12. В-устойчивость и контрактивность 213
Теорема 12.12 (Шерер 1979). Методы Лобатто IIIA и Лобатто IIIB
не обладают AN -устойчивостью, следовательно, они не являются и
В -устойчивыми.
Доказательство. Как и в предложении 3.2, находим, что
По определению методов Лобатто IIIА, первая строка матрицы А и
последняя строка А — 116^ состоят из нулей (сравните также
доказательство теоремы 5.5). Поэтому знаменатель K(Z) не зависит от z^,
а числитель — от г,. Если положить, например, Zj = ... = г, = О,
то функция K{Z) неограниченна при 2:^ —> — ос. Это противоречит
AN -устойчивости.
Для методов Лобатто IIIB аналогичным образом используется
равенство нулю последнего столбца А и первого столбца А — 116^ . П
Следующий результат показывает, что, как уже упоминалось
выше, ЛЛГ-устойчивость оказывается гораздо ближе к В-устойчивости,
чем к Л-устойчивости.
Теорема 12.13 (Берридж и Бутчер 1979). Предположим, что
\KiZ)\<l (^•^«Bce^^ = diag(z„....zJcRez,<0
' ^ >" — [ ^ Kj I < ^ Д«^^ некоторого е> 0. ^ '
Тогда метод является алгебраически устойчивым (и, следовательно,
также и В-устойчивым).
Доказательство. При А/, := z^Ag^ и Дуо = 1 результатом
вычисления A2.5) будет Api = K{Z). Выкладки из доказательства
теоремы 12.4 (с учетом того, что z^ не обязательно действительные)
показывают, что
5 S
\K[Z)\^^\ = 2Y,biK^zM^- Е "^ij'idi'jdy A2.20)
»=1 tj=i
Здесь д '=^{9i^- • -^д»)^ — решение уравнения A2.14) с ур = 1 •
Чтобы доказать, что 6, > О, выберем z^=-—e<Q и z- = О при j / г.
Из предположения A2.19) и формулы A2.20) следует, что
-25b,|(/,|2-m,,e2|G,f <0. A2.21)
Если е достаточно мало, то д^ близко к единице, и тогда при 6,- ф О
второй член в A2.21) будет пренебрежимо мал. Следовательно, 6,
должно быть неотрицательным.
Чтобы удостовериться в справедливости второго условия
алгебраической устойчивости, возьмем чисто мнимые числа 2: = ге^ (^ G М).
Поскольку и здесь д^ = 1 Л'0{е) при е —> О, из A2.20) вытекает, что
214 Гл. IV. Жесткие задачи — одношаговые методы
Следовательно, матрица М = (т,^) должна быть неотрицательно
определенной. П
Комбинируя этот результат с теоремами 12.4 и 12.11, получим
Слоцствие 12.14. Для неконфлюентных методов Рунге—Кутты
(т.е. методов J у которых все Cj различны) понятия AN -устойчивости,
В-устойчивости и алгебраической устойчивости эквивалентны. П
Для конфлюентных методов РК эквивалентность 5-устойчивости
и алгебраической устойчивости доказать гораздо труднее (см.
теорему 12.18 ниже). Это и будет нашей следующей задачей, для
разрешения которой мы должны сначала обсудить приводимые методы.
Приводимые методы Рунге—Кутты
Для метода РК A2.3) может оказаться, что для всех
дифференциальных уравнений A2.1)
i) некоторые стадии не влияют на численное решение;
ii) несколько д^ совпадают между собой.
В обеих ситуациях метод Рунге—Кутты может быть упрощен до
«эквивалентного» метода с меньшим числом стадий.
Чтобы проиллюстрировать ситуацию (i), рассмотрим метод,
представленный в табл. 12.1. Его численное решение не зависит от ^2 ^
эквивалентно решению, получаемому неявным методом Эйлера. Для
метода из табл. 12.2 легко удостовериться, что д^ = ^2 всякий раз,
когда система A2.3b) обладает единственным решением. Таким
образом, метод эквивалентен неявному правилу средней точки.
Таблица 12.1. Таблица 12.2.
DJ-приводимый метод 5-приводимый метод
1
1/2
1
1/4
1
0
1/4
0
1/2
1/2
1/2 О
1/4 1/4
1/2 1/2
Ситуация (i) может быть формализована следующим образом:
Определение 12.15 (Далквист и Йелч 1979). Метод Рунге—Кутты
называется D J -приводимым, если для некоторого непустого
множества индексов Тс {1,...,«},
6^=0 для jeT и a,j = 0 для i^TJeT. A2.22)
В противном случае он называется D J -неприводимым.
Из условия A2.22) следует, что стадии j?Т не влияют на
численное решение. Это лучше всего видно, если переставить стадии так,
IV. 12. Б-устойчивость и контрактивность 215
чтобы элементы Т были последними (Купер 1985), как это сделано в
табл. 12.3.
Таблица 12.3. D J-приводимость
С1
С2
Ли
^21
^1
0
^22
0
С1
Ли
Далквист и Йелч A979) открыли интересное свойство ?)
J-неприводимых и алгебраически устойчивых методов Рунге—Кутты.
Теорема 12.16. D J -неприводимый алгебраически устойчивый
метод Рунге—Кутты обладает свойством
6,>0 для 1 = 1,..., 5.
Доказательство. Предположим, что bj=0 для некоторого
индекса j. Тогда rrijj = О по определению М. Поскольку М
неотрицательно определенная, все элементы в j-u столбце М должны обращаться
в нуль (упр. 11), так что 6,а,-^ = О для всех г. Отсюда следует A2.22)
для множества Т = {j\ bj = 0}, и мы получили противоречие с DJ-
неприводимостью. П
Алгебраический критерий для ситуации (ii) впервые (однако, не
полностью) дал Штеттер A973, р. 127 ^)) и окончательно
сформулировали Хундсдорфер и Спейкер A981). (См. также (Бутчер 1987, р. 319)
и (Деккер и Фервер 1984, р. 1082)).)
Определение 12.17. Метод Рунге—Кутты называется
S-приводимым, если для некоторого разбиения E^,..., 5^) (где г < s)
множества {1,..., s} справедливо равенство
keSm keSm
для всех / и т. В противном случае он называется S-неприводимым.
Методы, которые не являются ни D J-приводимыми, ни
5-приводимыми, называются неприводимыми.
Чтобы понять условие A2.23), предположим, что (быть может,
после некоторой перестановки стадий) / G 5/ для Z = 1,..., г. Рассмотрим
теперь г-стадийный метод с коэффициентами
k€Sj keSj
Применение ЭТОГО НОВОГО метода К уравнению A2.1) дает ^J, •. .,^J!,yJ,
и легко удостовериться, что д^ и у^, определенные равенствами
Л = Л* при ieSi, У1=у1,
^^ В русском издании см. с. 150 ид. — Прим. ред.
^ В русском издании см. с. 124 ид. — Прим. ред.
216 Гл. IV. Жесткие задачи — одношаговые методы
являются решением исходного метода A2.3). Для метода из табл. 12.2
имеем Si = {1,2}. Еще один пример 5-приводимого метода приведен
в табл. 12.4 в разд.П. 12 (S^ ={1,2,3} и 52 = {4}).
Теорема об эквивалентности
для 5-неприводимых методов
Теорема 12.18 (Хундсдорфер и Спейкер 1981). Для З-неприводи-
мых методов Рунге—^Кутты
В -устойчивость <=> алгебраическая устойчивость.
Доказательство, Так как следствие 12.14 охватывает почти все
имеющие практическое значение случаи и доказывается, к тому же,
намного проще, то эта теорема представляется малоинтересной с
практической точки зрения. Однако это интересный результат,
который угадывался многими исследователями на протяжении многих
лет, и поэток^у мы воспроизведем его доказательство, включающее
также три леммы 12.19-12.21. Контрпример из упр. 6 в конце
этого раздела показывает, что 5-неприводимость является необходимым
предположением.
Согласно теореме 12.4 достаточно доказать, что из
5-устойчивости и 5-неприводимости следует алгебраическая устойчивость. Для
этого возьмем s комплексных чисел z^,..., 2:, таких, что Re Zj < О
и 1-2:^1 < е для некоторого достаточно малого е > 0. Покажем, что
существует удовлетворяющая условию
Re{f{u) -/(v), u-v)<0 для всех u.vEC A2.25)
непрерывная функция f : С -? С такая, что для решений метода
Рунге—Кутты 2/1, д^ и у^, д^, соответствующих Уо = 0 и yQ = I при
Л = 1, выполняются соотношения
f{9i)-f{9i)=zM-9i). A2.26)
Это дает у^—у^ — ^(^)» где K{Z) определено формулой A2.15). В-
устойчивость тогда влечет |/^(-^)| < 1. По непрерывности K{Z)
вблизи начала координат тогда имеем |АГ(^)| < 1 для всех Zj, у которых
ReZj <0 и 1-2:^1 < е, так что из теоремы 12.13 следует доказываемое
утверждение.
Построение функции f. Обозначим через Д^,- решение системы
8
^gi^l + ^a^jZjAgj
i=i
(решение существует и единственно, если 1-2:^1 < е и е достаточно
мало). Положим
9^=4, /(,,) = .^, ^^^^^^
Qi = gi + Aflf,-, fidi) = f(gi) + г,-Дд,-,
IV. 12. В-устойчивость и контрактивность 217
где ^,77 — векторы из леммы 12.19 (см. ниже). Величины A2.27)
вполне определены для достаточно большого t (которое впоследствии
будет фиксированным), поскольку все т]^ различны. Ясно, что д^ и
д- представляют решение метода Рунге—Кутты для Уо = 0 и ^q = 1,
а соотношения A2.26) удовлетворяются по определению.
Теперь покажем, что неравенство
Re(/(«)-/(г) , w-!;)<0 при ифь A2.28)
выполняется для u^v Е D = {д^^... ^д^,д^,... ^д^}. Это следует из
построения ^, 7/, если г/, г; Е {5^1,..., 5^5} • Если и = д^ и v = д^, то это
следует из A2.26). В оставшемся случае u = g^,vED\ {^,,^,} имеем
{f(u)-f(v),u-v)=t\^i-^j)(n,-r,j) + 0{t) при <-^оо,
так что A2.28) удовлетворяется, если t достаточно большое.
Применяя лемму 12.20 (см. ниже), находим непрерывную функцию
/ : С -> С, которая обобщает A2.27) и удовлетворяет A2.25). П
Чтобы довести до конца изложенное выше доказательство, нам
нужны еще следующие три леммы.
Лемма 12.19. Пусть А — матрица коэффициентов
S-неприводимого метода Рунге—Кутты. Тогда существуют векторы ^ЕШ^ и 7] =
= А^ такие, что
{^i-^j){Vi-rij)<0 при i^j. A2.29)
Доказательство (Бутчер 1982). Предположим сначала, что
C=i-eAX где 11= A,1,..., 1)^,
и тогда
T)^A^ = Ai-eA^l,
Пусть с,- ^ Cj для всех г, j. Тогда ^,- — ^^- ^^^ О, и для достаточно малого
е мы будем иметь т;,- — rjj противоположного знака. Таким образом, в
этом случае неравенство A2.29) выполнено.
Чтобы провести доказательство во всех иных случаях, построим с
помощью рекурсии векторы Vq, ^i, ^2»• • • ** обозначим через Pf^
разбиение множества {1,..., s}, определяемое отношением эквивалентности
i^j <=» (t;,),-= (г;,),, для д = 0,1,...,Л. A2.30)
Для каждого разбиения Р множества {1,2, ...,5} введем
пространство
Х{Р) = {v е К'; (v),- = {v)j, если i ^ j относительно Р}.
Используя эти обозначения, можно утверждать, что метод 5-непри-
водим, если и только если
АХ{Р)(^Х{Р) A2.31)
для каждого разбиения, отличного от {{1}, {2},..., {s}}.
218 Гл. IV. Жесткие задачи — одношаговые методы
Построение начнем с Vq = 1 и Pq = {{\,.. .,s}} и определим
[и;, если Avf^ G Х(Р^) ,
где LJ — произвольный вектор из X(Pf^) такой, что Ли; ^ X(Pi^).
Такой выбор возможен в силу A2.31). После конечного числа (скажем,
т) шагов придем к Р^ = {{1}, {2},..., {s}} , так как число компонент
Pf^ увеличивается, причем строго увеличивается после каждого
второго шага. Следовательно, все элементы вектора
^ = VQ-ev,-^e^v^-...-\-(-erv^
различны (для достаточно малого 5 > 0) и неравенство A2.29)
удовлетворяется. П
Лемма 12.20 (Минти 1962). Пусть и^,.. ..Uf^ и f(u^),.. .,f{uf^)
принадлежат К", причем
Тогда существует непрерывное расширение / : М" -> М" такое, что
{/(и) — f(v)yU — v) <0 для всех w,i;GM".
Доказательство (Уоккер 1985). Определим
^ = ^^^ ГГ77—^—77—MI9 < О
и положим 9(и-) = 2'у f (и-)-и-, так что \\9(и^) - g(uj)\\ <\\и-- Uj\\.
Применение леммы 12.21 показывает, что существует непрерывное
расширение р : IR" —> М'* такое, что ||^(w) — ^(г)|| < ||w — г'|| (т.е.
отображение д — нерастягивающее). Тогда функция
f{u) = —(g{u)-{-u)
удовлетворяет требованиям леммы. П
Лемма 12.21 (Киршбраун 1934). Пусть и^,.. .,Uf^ и д{и^},.. .,g{ui^)
принадлежат Ш^, причем
\\9(Ui)'-g(uj)\\<\\Ui-Uj\\ для г, j = 1,..., А-. A2.32)
Тогда существует непрерывное расширение д : R" —> М" такое, что
\\g(u)'-'g(v)\\<\\u-v\\ для всех u,t'GlR". A2.33)
Доказательство. Некогда это был трудный результат в теории
множеств. Шёнберг A953) нашел особенно красивое доказательство,
«динамическую» версию которого мы здесь приведем.
а) Основная задача состоит в построении для одной заданной
точки р расширения д(р) такого, чтобы неравенство A2.33) оставалось
IV. 12. В-устойчивость и контрактивность 219
Y
">
/ \ ХХ ^ ^ ^^
V" \ у
Рис. 12.1. Построерше д{р).
справедливым. Будем перемещать точки и, в их образы д(и-) при
помощи аффинного отображения
г/.(Л) = г/. + Л(G(г/.)-и-), 0<А<1, г = 1,...,/:. A2.34)
Обозначим г, = ||w, -р\\ и для каждого А будем сжимать шары с
центрами u,(A) и радиусами r^fi до тех пор, пока их пересечение не будет
состоять только из одной точки
к
,i(A) := min{/i ; f|{u ; |К(А) - t/|| < r,/i} ^ 0}. A2.35)
t=i
Эта точка пересечения, обозначенная р(А) (см. рис. 12.1), зависит от
А непрерывным (за исключением возможного внезапного уменьшения
fiy если А = 0) и кусочно-дифференцируемым образом. Покажем, что
/х(А) не возрастает; это означает, что д{р) :=рA) — точка,
удовлетворяющая условию A2.33).
Рассмотрим векторы
Я,:=и,(А)-р(А). A2.36)
Согласно предположению A2.32) ||Я, - ^j||^ не возрастают,
следовательно, {R- - Rj, dR- - dRj) < О, или
{Ri,dRj)-^{Rj,dRi)>{Ri,dRi)-^{Rj,dRj). A2.37)
Как видно из рис. 12.1, не все точки w,(A) всегда «активны» в A2.35)
в том смысле, что р(\) лежит на границе сжатого шара с центром
в w,(A). В то время как для А = 0 (когда ||Я,|| = г,//) все четыре
точки активны, при А= 1/2 активными точками будут ^^(А), W2(A),
г(з(А) и, наконец, при А=: 1 активны только и^(\) и W2(A).
Предположим, что t/i(A),..., и^(Х) (т < к) — активны^ для данного А точки
220 Гл. IV. Жесткие задачи — одношаговые методы
(иногда может потребоваться надлежащее переупорядочение).
Ключевая идея Шёнберга основана на том факте, что р(Х) принадлежит
выпуклой оболочке гх^(Л),..., и^(Х), т.е. существуют положительные
величины Cj(А),..., с^(А) такие, что Yl^i ^%^х = ^ • ^'^^ означает, что
Теперь мы применим неравенство A2.37) к парам г, j и j, г, что дает
о = (Е,- с.Д,, Ei cj dR^) > Е.<Д.-, dR,){c, Е,- cj).
Поскольку по построению (см. A2.36)) все ||Д,.|| убывают или
возрастают одновременно с ^, а все с,- > О, мы видим, что d/i < О, т.е. /i не
возрастает.
Ь) Остальная часть стандартна (Киршбраун): выбираем счетную
плотную последовательность точек Р1,Р2'Рз> • • в М" и продолжаем
д непрерывно на эти точки, так что A2.33) всегда удовлетворяется.
Вследствие непрерывности (см. A2.33)) наша функция тогда
определена везде. Этим завершается доказательство леммы 12.21, а с нею и
доказательство теоремы 12.18. П
«Nous пе connaissons pas d'examples de methodes qui soient
J5-stables au sens de Butcher et qui ne soient pas Б-stables
suiv?uit notre definition».
«Мы не знаем примеров методов, которые в смысле Бут-
чера были бы Б-устойчивы и не были бы В-устойчивыми
согласно нашему определению». (М. Крузе 1979)
Замечание, Берридж и Бутчер A979) делают различие между
ВЛГ-устойчивостью (которая основана на неавтономных системах) и
S-устойчивостью (базирующейся на автономных системах).
Поскольку дифференциальное уравнение, построенное в вышеприведенном
доказательстве (см. A2.25)), автономное^ для неприводимых методов
оба понятия эквивалентны.
Функция роста погрешности
Во всей теории, которая излагалась до сих пор, контрактивность
рассматривалась только для случая нулевой односторонней
константы Липшица и в A2.2) (см. определение 12.2). Встает вопрос, можем
ли мы уточнить оценку, если известно, что i/ < О, и можем ли мы
получить оценки также и в случае, когда A2.2) справедливо только при
некотором I/ > О.
Определение 12.22 (Берридж и Бутчер 1979). Для заданного i/
положим х = hi/ (где Л — длина шага) и определим (рв(х) как
наименьшее число, для которого оценка
lll/i-J/ill<V'BWI|yo-yoll A2.38)
IV. 12. В-устойчивость и контрактивность 221
справедлива для всех задач, удовлетворяющих условию
Re(/(x,y)-/(x,z),y-z)<i/||y-z||2. A2.39)
Назовем (Ps{x) функцией роста погрешности датного метода.
Мы рассматриваем комплекснозначные функции f :RxC^ -^С^ .
Это не есть обобщение (любая такая система может быть записана в
вещественной форме, если отделить действительную и мнимую части,
см. уравнение A2.4)), но с задачами вида у* = Х{х)у и комплексно-
значной А(х) удобнее работать.
В случае линейной неавтономной задачи у* = А(х)у условие A2.39)
переходит в fi{A{x)) <и (где ^(•) обозначает логарифмическую норму,
см. разд. 1.10). Полагая Z,- := кА{х^ 4- с,Л), представим разность двух
численных решений в виде
2/1 - У1 = ^^'(^1» • • • > ^5)(% - %)>
где
A'(Zi,...,Zj = / + F^®/)Z(/®/-(A®/)Z)"^(n®/) A2.40)
и Z — блочно-диагональная матрица с Z^,..., Z, в качестве
диагональных блоков.
Теорема 12.23. Функция роста, погрешности неявного метода. Рун-
ге—Кутты удовлетворяет
Ы^)= s^P \\K{Z,,,,.,ZJ\\, A2.41)
/i(Zi)<r,...,/i(Z.)<2?
Доказательство. Оценка сверху. Разность Ду^ =у^—у^ двух
решений метода Рунге—Кутты удовлетворяет уравнению A2.5). Из
предположения A2.39) следует, что Re{Af-,Ag-)<x\\Ag-\\^.
Докажем, что существуют матрицы Z,- (г = 1,...,«) с /i(Z,) < х такие, что
Д/,. = Z^Ag^. Это влечет Ау^ = K[Z^,..., Z^)AyQ и, как следствие,
выражение в правой части A2.41) будет верхней гранью ^^{х).
Если Д^',- = О, то Д/,. = О, и мы можем взять произвольную
матрицу, удовлетворяющую условию /i(Z,) < х. Поэтому давайте
рассмотрим векторы /,д (причем ^ ^ 0) в С*, для которых Re (/,^) < xll^'IP.
Положим tij := ^/11^11 и дополним его до ортонормального базиса
г/^,..., ti„ в С*. Определим затем матрицу Z соотношениями
Zu^ '= f/Ml Zui := хщ - {UiJ)uJ\\g\l г = 2,..., п.
Тогда Zg = f и, как легко проверить, Re(Zv,v) < х|(г|р для всех
^ = ЕГ=1 ^i^i •
Оценка снизу. Рассмотрим сначала неконфлюентные методы
Рунге—Кутты. Для заданных Z^,...^Z^ с /i(^,) <х пусть А{х) —
непрерывная функция, удовлетворяющая условиям кА[х^-\-с^К) = Z,-, и
222 Гл. IV. Жесткие задачи — одношаговые методы
fi{A(x)) <х для всех х (А{х) может быть, например, получена
линейной интерполяцией). Тогда Ду^ = K[Z^,..., Z,)AyQ и, следовательно,
V?b(^)>II^'(^ii--->-2'J|| для всех Zi,...,Z, с //(Z,) <х.
Для конфлюентных методов доказательство сложнее. Без
ограничения общности можно предположить, что метод неприводимый,
так как ни величина ^^^(х), ни выражение в правой части
уравнения A2.41) не изменятся, если метод заменить на
эквивалентный. Теперь валено заметить, что леммы 12.20 и 12.21
справедливы для произвольней размерности. Рассмотрим матрицы Z^ ..., Z,
с А^(^,) < X такие, что линейная система Д^, = A2/o + Zlj=i ^ij^j^dj
имеет решение. Точно так же, как и при доказательстве теоремы
12.18, можно построить непрерывную функцию / : С" -> С" , которая
удовлетворяет условию A2.39) при и = х (положим Л=: 1), причем
f{9i) ~ f[9i) = ^%{9i -^9i)' Это завершает доказательство теоремы. П
Для одностадийных методов E=1) из теоремы фон Неймана
(следствие 11.4) вытекает, что в формуле A2.41) достаточно
рассмотреть скалярное комплекснозначное z^. Поскольку в этом случае
/\ (г) = R(z), имеем
(р^(х) = <Рл(х) для всех одностадийных методов. A2.42)
Можно ли при s>2 тоже ограничиться рассмотрением комплексно-
значных скаляров z, в формуле A2.41)? Для ответа на этот вопрос
надо обобщить теорему фон Неймана на функции более чем одной
переменной (Хайрер и Ваннер 1996). Мы вернемся к этому вопросу
несколько позже.
Теорема 12.24 (Хайрер и Дзеннаро 1996). Для В-устойчивых
методов Рунге—Кутты функция роста погрешности сверхпоказательная,
т.е. v?^@) = l и
*^b(^i) ^в{^2) ^ ^в(^1 + ^2) '^•^^ ^15 ^2 ^ одинаковыми знаками.
Доказательство. Свойство (^^(О) = 1 следует из определения 12.5.
Для доказательства неравенства рассмотрим рациональную функцию
S{z) = u'^K{Ai-zI,...,A,-zI)v^u-bK(B, + zI,...,B,+zI)vb,
где матрицы Aj, Bj — такие, что fi(Aj) < з^^ -l-Xj и fJL(Bj) < О, а w^,
г^д, и^у Vq — произвольные векторы в С" . С использованием
свойства А/(Л^-г/)=//(Л^.)-Ке2 итого, что ||С|| =sup||^ll^i U^U^i |и*Сг;|,
требуемое неравенство выводится точно так же, как в доказательстве
теоремы 11.6. П
Тот факт, что <Рв[^) — сверхпоказательная функция, вместе с
равенством <^^j(—ос) = |Л(оо)| (см. упр. 8) позволяет нам вывести те же
заключения об асимптотической устойчивости численных решений,
что и в разд. IV 11.
2 . , A2.43)
IV. 12. В-устойчивость и контрактивность 223
Вычисление ^в{х)
Идея состоит в поиске максимума ЦАуЛ с учетом ограничения
A2.39). Точнее, рассмотрим следующую задачу оптимизации с
ограничениями, заданными неравенствами:
||AyJ|2-^max,
Ке(Д/,,ДG.)<х||Д(/,||2, 1 = 1,..., 5.
Здесь Д/j,..., ДД трактуются как независимые переменные в С" ,
Ду^ и Ду, определяются из A2.5), а Дуд рассматривается как
параметр. Классический подход к решению задачи оптимизации A2.43)
заключается в том, что вводятся множители Лагранжа d^,...,dg и
рассматривается функция Лагранжа
?(Д/, D) = i||Aj/,||2 - J^ d,(Re<Д/,, Д</,> - х\\Ад,\\') =
где A/=(A/„...,A/J'',?> = diag(di,...,d,)H
a = -l-2iB''l>]!, A2.45а)
u = Di-b-2xA^DX A2.45b)
W = DA + A'^D-bb'^-2xA^DA. A2.45c)
Теорема 12.25 (Берридж и Бутчер 1980). Если при некоторых
значениях dj > О, ...,</,> О матрица
A2.44)
/ а + у?2 иТЛ
\ и W J
положительно полу определенная, A2.46)
то ||Aj/i|| < ^ЦДуоЦ для всех задач, удовлетворяющих условию A2.39)
при hv <х. Следовательно, <Рв{х) < у.
Доказательство. Вычитание ^2||Дуо|Р/2 из обеих частей
тождества A2.44) дает
1(||Дг/1||2-^2||Дуо1|2) -^^,(ае(дл,д<,,)-х||Д5,||^) <о.
1 = 1
Утверждение теоремы следует из cf, > О и Re(Д/,, Ду,) < х||Ду,|Р. П
С помощью этой теоремы Берридж и Бутчер A980) вычислили
оценки ^в{х) сверху для многих двухстадийных методов. Оказалось,
что для всех этих двухстадийных методов ^в[х) = ^к[х), где
<Рк(х)= sup \K<,z„...,z,)\. A2.47)
Re2i<r, ,Re2.<r
224 Гл. IV. Жесткие задачи — одношаговые методы
Возникает естественный вопрос: быть может, <Рв{^) = ^Рк(^) ^-^^
всех методов Рунге—Кутты? Если мы хотим удостовериться в
справедливости равенства <Рв{^)^^к{^) Д*^^ конкретного метода Рунге—
Кутты, надо найти неотрицательные множители Лагранжа d- такие,
чтобы условие A2.46) удовлетворялось. Для этой цели будут полезны
следующие леммы.
Обозначим через <2:i,...,2:J величины, для которых достигается
точная верхняя грань в уравнении A2.47). Согласно принципу
максимума z^ zzx-^iy^ (принимаем, что у^ = ос). Далее, обозначим z° =
= (zf,..., zj), и пусть djK(z^) — значение производной /i (-г^,..., 2г,)
по j'Uy аргументу в точке z^.
Лемма 12.26. Пусть х фиксировано и (pj^{x) < оо. Тогда
условие A2.46) с (р = <Рк(^) однозначно определяет множители Лагранжа
dj,..., d, (см. формулу A2.53)). Они вещественны и положительны.
Доказательство. Рассмотрим тождество A2.44) в частном случае,
когда Afj скаляр, Afj = ZjAgj и, следовательно, Ау^ = K{z^,..., г^).
Для Re Zj = X это тождество превращается в
№„...,гЛ^-^^ = -A,Дл(' "^)(д'/)- (^2.
48)
Подстановка (f := ^к(^) ^ -^j •= ^^ (^ конечном счете нужно
рассмотреть пределы) обращает в нуль выражение в левой части равенства
A2.48). Вместе с предположением A2.46) это влечет U'\-WAf = Q,
т.е.
DB ~ 6 - 2xA^Dl -h {DA -h A^D - 66^ - 2xA^DA) Д/ = 0.
После собирания подобных членов, с учетом равенств Д/ = Z^Ag и
Д^ = Л + AAf, где Zq = diag (-^J,..., zj), это соотношение принимает
вид
D Д(/ = (/ - A^Zl)-4. A:(zO). A2.49)
Покажем, что все компоненты Ад ¦= [I — AZ^)"^! отличны от
нуля, так что A2.49) однозначно определяет множители Лагранжа
di,...,(f,.
Разложив ЛГ(^1,..., Z,) в ряд Тейлора по z^ , получим
Л:(.?,...,2,.,...,г°) = /^(г°)A + ф,.-г9) + 0((г,.-г9J)),
где c = djK{z°)IK{z°). Так как \K{z4,. ..,Zj,.. .,zO,)\<\K(z°)\ при
Re Zj < Re z9, то с > 0 и, следовательно, также
д^K{z^)фQ, 0<djKiz°)/K(z°)<oo. A2.50)
Дифференцирование K{zi,...,z,)=:l + b'^Z(I — AZ)-^^i по Zj дает
djK(z°) = b'^{I-Z,A)-'ejeJ(I-AZ„)-'% A2.51)
IV. 12. Б-устойчивость и контргистивность 225
и из A2.50) получаем
b'^(I-Z,Ar'ej^O, Agj=eJ(I-AZo)-'l^O. A2.52)
так что rfj,..., с?^ однозначно определяются из A2.49). После деления
j-й компоненты A2.49) на Agj из A2.51) получаем
d, = |6^(/-Zo^)-ie,r^^^, A2.53)
И согласно A2.50) и A2.52) это есть строго положительное
вещественное число.
В этом доказательстве мы неявно предполагали, что все Zj
конечны. Если Zj = х-{- гоо для некоторого j, то нужно применить
стандартное преобразование Uj =x + l/{Zj — х), которое отображает
полуплоскость R^Zj < X на Rewj < х и ос в 0. П
Лемма 12.27. Если матрица W из уравнения A2.45с) с d^,..., d^,
определяемыми леммой 12.26, положительно полуопределенная, то
имеет место равенство (p^i^) = fxi^) •
Доказательство. Из
(см. A2.48)) и из того, что v'^Wv > О для всех v G М* следует, что
матрица в A2.54) положительно полу определенная. Утверждение
леммы тогда следует из теоремы 12.25. П
С помощью полученных выше результатов можно проверить,
удовлетворяется ли равенство ^в{^) — ^к{^) Д-^^ некоторого
конкретного метода Рунге—Кутты, пользуясь следующим алгоритмом:
• вычислить (p = (pj^(x) из уравнения A2.47) численно или с
помощью программы, выполняющей аналитические выкладки;
• вычислить множители Лагранжа d^,..., cf, из леммы 12.26;
• проверить, является ли матрица W из уравнения A2.45с)
положительно полу определенной. В этом случае согласно лемме 12.27
выполняется равенство <Рв{х) = (ff^(x).
Пример 12.28. Для двухстадийного метода Радо ПА (см. табл. 5.5)
функция K(z^,Z2) дается выражением
.0 .
226 Гл. IV. Жесткие задачи — одношаговые методы
Максимум 1^7-2:1,^2I на множестве Rez,- < х достигается при
хН-гоо для х<^,
. /45-42x4-8x2
"^^^V9+18x-8x2 Д^я^<х<3/2,
X для X < ^,
''^'— 8x2-6х-9 '- Для^<х<3/2.
И он выражается формулой
^, если х<^,
^^(^) = i 3 + 4х
' , если ^<х<3/2
V^C-2x)C-h4x-2x2) ^~ '
(^ = (9-3vT7)/8, это корень уравнения 9 + 18х-8х2 = 0). При х>3/2
функция /^(-2:1, z^ не ограничена на множестве Re г,- < х. Пользуясь
доказательством леммы 12.26, вычислим d^ и d^:
. _|C-х)E-2х) ^•™''^^^' .fsi ^"^"^^•
[4C + 4х-2х2) ^"^^^"' l4C + 4x-2x2) ^^«^^^-
Имея эти величины, можно непосредственно проверить, что матрица
W из уравнения A2.45с) положительно полуопределенная, так что
(р^{х) = ^/<'(х); см. также (Берридж и Бутчер 1980). На самом деле
матрица W невырожденная при х < ^, а при ^ < х < 3/2 ее ранг равен
единице.
Как показывает сравнение с формулой A1.15), при этом мы не
получим такую же оценку, как для линейных автономных задач.
Описанный выше алгоритм можно легко применить и к другим
двухстадийным методам. Например, для двухстадийного гауссова
метода получим
{1, если —оо < X < О,
2x + V9 + 3x2
, если и < X < 3,
3 —X ~*
а для двухстадийного метода Лобатто П1С
1
^в{^) = {
если —оо < X < О,
если О < X < 1 .
1 — х-|-х2'
1
I. 1-х'
Для методов с 5 > 2 явные формулы получить трудно; значения
zj^, при которых достигается точная верхняя грань в A2.47), находят
численными методами.
IV. 12. Б-устойчивость и контрг1Ктивность
227
Упралснения
1. Докажите непосредственно на основании определения 12.2, что
неявный метод Эйлера В-устойчивый.
2. Пусть М — симметричная матрица sx s и (•, •) — скалярное
произведение в М". Докажите, что М — неотрицательно
определенная матрица, если и только если
5 8
У^ У^ m^jiui, Uj) > О для всех и,- G К"*.
«=1 j=i
Указание. Воспользуйтесь представлением M = Q'^DQ, где D —
диагональная матрица.
3. Обобщая идеи примера 12.3, предложите простое доказательство
5-устойчивости методов Радо ПА.
Указание, Для квадратуры, основанной на нулях многочлена
E.2), имеем
'О .=1
где С<0 (см., например, (Абрамовиц и Стиган 1964), формула
25.4.31).
(Далквист и Йелч 1987.) Докажите, что метод I из табл. 12.4
является 5-приводимым относительно разбиения ({1},{2,3}).
Приведенный метод П сам D J-приводим и приводится к методу П1.
Для начальной задачи j/ = /(у), у@) = 1, где /(у) = у2 при у > О и
/(у) = О при у < О, и для Л = 2 методы I и П1 имеют единственные
решения, которые различны. Объясните это кажущееся
противоречие.
Таблица 12.4. Приводимость методов РК
0
1/2
1/2
0
0
0
1
0
1
1/2
6
0
-1/2
0
-ь
0
1/2
0
0
1
0
1/2
0
метод I
метод II
1
метод III
Дайте контрпример неприводимого ЛЛ/^-устойчивого метода,
который не является алгебраически устойчивым и, следовательно, не
будет и 5-устойчивым.
Указание. Начните с любого алгебраически устойчивого метода,
скажем, с двумя стадиями и модифицируйте его, как показано в
табл. 12.5. Найдите условия на свободные параметры d, е, а такие,
228 Гл. IV. Жесткие задачи — одношаговые методы
чтобы два метода были идентичны для уравнений г/ = Х(х)у. Это
гарантирует ATV-устойчивость второго метода. Затем поиграйте с
параметрами, чтобы разрушить алгебраическую устойчивость.
Таблнид 12.5. Построение ЛyV-устойчивого,
но не В-устойчивого метода
С1
^21 ^22 => <^2
^1 ^2
ап 012» ai2(l-a)
C2—d da d{l — a)
C2 — e eg e(l~a)
6i 62» 62A-a)
6. Покажите, что метод из табл. 12.1, будучи D J-приводимым, не
является 5-приводимым; покажите, что он алгебраически
устойчив вместе с приведенным методом.
Покажите, что метод из табл. 12.2, будучи 5-приводимым, не
является D J-приводимым; покажите, что он не является
алгебраически устойчивым, но приведенный метод алгебраически устойчив.
7. (Сандберг и Сичман 1968; Ванзелов 1979; Хундсдорфер 1985.)
Докажите, что методы Розенброка не являются В-устойчивыми в
смысле определения 11.2.
Указание. Примените метод к скалярной задаче y'=f{y)y Уо = ^у
где /(у) — невозрастающая функция, которая определяется
формулой (с малым е)
f( 1 = /"^' ^^^^ 1У-1|>2^'
^^^^ 1-1, если|у-1|<е.
8. (Хайрер и Дзеннаро 1996.) Для неприводимых алгебраически
устойчивых методов Рунге—Кутты функция роста погрешности
удовлетворяет неравенству
, , x/l-2x7A-р2)-2х7Р
где /?= |Д(оо)|. Здесь R{z) обозначает функцию устойчивости ме-
тода, 7=(E;=ifr7'^i)'' « (^i,...,t;,F = lim,^o6^H + ^/)-'.
Указание, Из A2.7) имеем ||AyilP < ||Ауо1Р + 2х^. 6.||Д(/.||2.
Далее вычислите Д/,- из A2.5Ь) (если матрица А обратима),
подставьте ее в A2.5а) и получите Ау^ = Д(оо)ДуоЧ-^^(Х],- f>i^ij)^9j >
где {(jJij) = Л. Неравенство Коши—Шварца дает J2i ^i\\^9i\\^ >
> 7(||Ayil| — р||АУо11) » ^то после подстановки в первую оценку
приводит к неравенству второй степени для Ду^.
IV. 12. В-устойчивость и контрактивность 229
9. Докажите, что для трехстадийного метода Гаусса при х > О
^bW>A + ^/2)/A-x/2).
Указание. С помощью формулы A2.18) вычислите значение K(Z)
при Zj —^ —ос, 22 = X, гд ^ —ос.
10. Если матрица W A2.45с) с 6fp...,d^, определяемыми леммой
12.26, невырождена, либо имеет ранг < 1, то <Рв(^) = ^Ki^"^) -
Указание. Воспользуйтесь тем, что выражение в формуле A2.48)
при (р = <Рк{х) неположительно для всех z, с Rez, <х.
П. Покажите, что для неотрицательно определенной симметричной
матрицы М =: (m^j) справедливо неравенство
IV. 13. Положительные квгцфатурные
формулы и 5-устойчивые методы
Рунге—Кутты
«Bien que le ргоЫёте (des quadratures) ciit une duree de deux cents
ans a peu pres, bien qu'il etciit Tobjet de nombreuses recherches
de plusieurs geometres: Newton, Cotes, Gauss, Jacobi, Hermite,
Tchebychef, Christoffel, Heine, Radeau [sic], A. Mcirkov, T. Stieltjes
[sic], C. Posse, С Andreev, N. Sonin et d'autres, il ne peut etre
considere, cependcint, comme sufRsamment epuise».
«Хотя проблеме (квадратуры) уже около двух веков, хотя она
была предметом многочисленных исследований многих геометров:
Ньютона, Котеса, Гаусса, Якоби, Эрмита, Чебышева, Кристоф-
феля, Гейне, Радо [sic], А. Маркова, Т. Стилтьеса [sic], К. Поссе,
К. Андреева, Н. Сонина и других, однако она не может
рассматриваться как достаточно исчерпанная». (В. Стек лов 1917)
Мы дадим конструктивную характеристику всех неприводимых
Б-устойчивых методов Рунге—Кутты (теорема 13.15). Теорема 12.16
показывает, что начать следует с изучения квадратурных формул с
положительными весами.
Квадратурные формулы и соответствующие
непрерывные дроби
Стеклов A916) доказал, что семейство интерполяционных
квадратурных формул сходится для всех функций, интегрируемых по
Риману, если все веса формул положительные («II faut remarquer
cependant que de tels theoremes generaux ne peuvent avoir aucune valeur
pratique...» — «Надо заметить, впрочем, что такие общие теоремы не
имеют никакой практической ценности...»). ТеоремаСтеклова,
которую Фейер открыл заново около 1922 г., положила нача^по обширным
поискам квадратурных формул с положительными весами. «Weiter
habe ich noch auf sehr kurzem Wege das folgende Resultat erhalten ...»
— «Далее я очень коротким путем получил еще следующий
результат» (Фейер 1933):
Если Pg(z) — полиномы Лежаядра, нормированные как в A3.4),
а Ср .. .,с, — нули многочлена M(z) = Р,(г) + ctiP,_i(z) -}-c^2^-2('2^)
с Qfj < О, то все веса Ь- положительны.
Теория В-устойчивых методов возродила интерес к
положительным квадратурным формулам, и Берридж A978) получил точную
границу
-^<4B.-Ш2!-3) ^''-'^
IV. 13. Положительные квадратурные формулы 231
для положительности 6,- в рассмотренном выше случае. Это то же
самое, что и условие E.51) при другой нормировке. Краткое
доказательство этого результата — «Лемма 18» в (Нёрсетт и Ваннер
1981) — привело в дальнейшем к полной характеризации
положительных квадратурных формул (Соттас и Ваннер 1982). Независимое
доказательство эквивалентного результата нашел также Пеерсторфер
A981). Ниже мы излагаем новый подходе использованием
непрерывных дробей.
Рассмотрим квадратурную формулу
i=i •'О
f{x)dx
с различными узлами с, и ненулевыми весами 6,. Основная идея
заключается в рассмотрении рациональной функции
j = l •'
где, как обычно, M(z) = (^ — с^) • • (z — с,). Сначала выразим порядок
квадратурной формулы в терминах функции Q{z).
Лемма 13.1. Квадратурная формула имеет порядок р, если и
только если функция Q{z), определенная формулой A3.2), удовлетворяет
условию
g(z) = -Iog(l-i)+o(^) при г-^оо. A3.3)
Доказательство. Подставив геометрический ряд для A — Cj/z)^^
в A3.2), получаем
fe>l\i=l /^
Q(z) =
к
Поэтому A3.3) эквивалентно
* 1
^б^с^-^^- для fc=l,...,p. П
i=i ^
Теперь изучим случай квадратурных формул Гаусса, где функция
A3.2) будет обозначаться Qf(z) = N^{z)/M^{z); здесь с,- — нули
сдвинутого полинома Лежандра степени s
нормированного так, что коэффициент при z' равен 1. Многочлены
A3.4) удовлетворяют рекуррентному соотношению
Р>^г(^)={^-\)Р,(^)-г,Р,-гИ, ^. = 5D^П) A3.5)
232 Гл. IV. Жесткие задачи — одношаговые методы
и Pq(z) = I, P^i(z) = О (см. E.53), или Абрамовиц и Стиган A979),
с. 588). Поскольку квадратурная формула Гаусса имеет оптимальный
порядок 25, из A3.3) следует, что
Aff(.) = -Mf(r)log(l-i)+o(^). A3.6)
Теперь подставим M^(z) = Pg{z) (см. A3.2)) в A3.5) и умножим на
log(l —1/z) (=0(l/z) при z-^oo). Сравнение с A3.6) показывает,
что многочлены N^iz) должны также удовлетворять рекуррентной
формуле A3.5) (с No(z) = О, N^(z) = 1). Поэтому из элементарных
свойств непрерывных дробей следует, что
(см. упр. 1 или Перрон A913), р. 4).
Для произвольной квадратурной формулы справедлива
Лемма 13.2. Необходимым и достаточным условием того, чтобы
неприводимая рациональная функция Q{z) = N(z)/M{z), у которой
deg М = S и deg N = 8—1, удовлетворяла соотношению A3.3) с р>
> 2E — Аг), является ее представимость в виде
ад=,-^-,-^'--,^-,^'. A3.7')
Z-
^-5 ¦¦¦ 1^-5 \т'
2 12 1*2
где deg f = к и degд <к — I.
Доказательство. Из леммы 13.1 мы знаем, что Q{z) = Qf{z)+
-fO(l/z2(*"'^)+i), т.е. первые 2{s — k) коэффициентов в разложениях
Q(z) и Qf(z) в непрерывные дроби должны совпадать. П
«Endlich sei noch die folgende Formel wegen ihrer haufigen
Anwendungen ausdrucklich hervorgehoben:»
«Наконец, специально отметим еще следующую формулу
по причине ее частого применения:»
(О. Перрон 1913, р. 5)
Лемма 13.3. Функции M(z) и N(z) из леммы 13.2 связаны с f(z)
и g(z) в формуле A3.7^) следующим образом:
Miz) = P,.,(z)f{z) - Л_,_,(г)^7(г),
N{z)=Nt,{z)f(z)-Nf_,_,{z)9{z).
Доказательство. Это следует из рекурсии A3.30) и упр. 1 ниже,
если положить там Ь^={), 6^ = ... = Ь^_^^ = г- 1/2, Ь^_^^^ = f{z) и
aj = 1, a^. = -r^._i(j = 2,...,5-Ar), а^^^^^ =-g(z). П
Решение линейной системы A3.8) относительно f(z) и g{z) с
использованием формулы из упр. 2 дает:
fiz) • Ti • •. r,_,_i = Niz)P,_,_,iz) - M(z)Nf_,_,(z),
9{z) ¦ T,. .¦T,_,_, = N(z)P,_,(z) - M{z)N^_,(z).
G . . A3.9)
IV. 13. Положительные квадратурные формулы 233
Число положительных весов
Для данной рациональной функции A3.2) веса определяются по
формуле
^'-Ш-у '"¦¦«'
Но мы хотим, чтобы наша теория работала также и для конфлюент-
ных узлов, для которых М'(с,)г=0. Поэтому предположим, что
Ci,...,Cy„ (m < s) — вещественные и различные нули M{z) крат-
ностей ^1,. •., /у71' ^ положим
'^ = Ш4~У '=Ь...,т. A3.10')
Для /,- = 1 это просто формула A3.10); в противном случае это веса
при наивысших производных в квадратурной формуле Эрмита (см.
упр.З).
Далее мы следуем работе (Соттас и Ваннер 1982), основная идея
которой состоит в рассмотрении контура, который описывает вектор
7(f) = (f(t),g{t)) на плоскости М^, где /ид — многочлены из
формулы A3.7'). При t —>• ±оо этот контур уходит на бесконечность с
горизонтальными предельными направлениями, так как степень / выше,
чем степень д. Уравнения A3.8) показывают, что для неприводимой
дроби Q(z) этот контур не проходит через начало координат.
Определение 13.4. Число вращений г для контура 7 есть целое
число такое, что гтг равно полному углу поворота вектора 7@ вокруг
начала координат, измеряемому в отрицательном направлении, т.е. по
часовой стрелке, когда t пробегает значения (—оо < < < со). Вращения
против часовой стрелки считаются отрицательными.
Можно дать и алгебраическое определение г:
i
где суммирование производится по всем вещественным нулям
нечетной кратности /, многочлена f{i).
Теорема 13.5 (Соттас и Ваннер 1982). Пусть Q{z) - N[z)/M[z)
— неприводимая рациональная функция как в лемме 13.2.
Предположим, что Ci,...,c^ — (различные) вещественные нули M(z)
нечетной кратности, и обозначим через п^ (соответственно п_ ) число
положительных (соответственно отрицательных) весов Ь-. Пусть,
далее, г — число вращений вектора 'у = [/,д) (определение 13.4). Тогда
п^ -п_ =s-k-\-r. A3.11)
234
Гл. IV. Жесткие задачи — одношаговые методы
Доказательство, Доказательство состоит в подсчете числа
пересечений векторов 7@ = (/(О ^^@) и /3@ = (Л-/с-1@)Л-;с@)
подобно пересечениям стрелок на швейцарских часах с кукушкой.
Из A3.9) мы видим, что когда t равняется нулю с, функции
Л/, эти два вектора параллельны {N(c-) > 0) или антипараллельны
GV(c,) <0). Из A3.8) видно, что M(t) — просто внешнее произведение
7@ X /^@ • С помощью элементарной геометрии и с учетом формулы
A3.10') получаем, что для каждого нуля с- нечетной кратности
i) 6, > О, если пересечение 7@ ^ /^@ происходит по часовой стрелке;
ii) 6, < О, если это пересечение происходит против часовой стрелки.
Нули М@ четной кратности не приводят к пересечениям.
Поскольку нули Pg^ff и Pg^if_i перемежаются (см., например,
теорему 3.3.2 в книге Сегё A939)), вектор /?@ поворачивается
(против часовой стрелки) на полный угол —{8 — к)тт (см. рис. 13.1).
Вектор 7@ поворачивается на полный угол гтг, измеряемый по часовой
стрелке (определение 13.4). Так как предельные направления 7@ ^
/9@ различны (горизонтальное для 7@ ^ вертикальное для P(t)),
то, когда t возрастает от —со до Ч-оо, вектор 7@ должен пересекать
вектор /9@ по часовой стрелке ровно на s-fc-hr раз больше, чем
против часовой стрелки. Это и дает формулу A3.11). П
Рис. 13.1. Путь вектора (P,_jfe_i(t), ^5-jfe@) Д-^^ 5 —А: = 7.
Следствие 13.6. В предположениях теоремы 13.5 все нули M{z)
будут вещественными и простыми, а 6, — положительными тогда и
только тогда, когда г = к.
Доказательство. Согласно A3.11) г = к означает, что n_^—n_=s.
Так как п_ > О и п^ < 5, то п_,_ = 5 и п_ = 0. П
Характеристика положительных
квадратурных формул
Следующая теорема дает конструктивную характеристику всех
квадратурных формул с положительными весами.
IV. 13. Положительные квадратурные формулы 235
Теорема 13.7. Пусть
(Ti<Pi<(T2<p2<"< Pk^l < <^к
— произвольные вещественные числа^ и С — положительная
постоянная. Тогда, положив
f(z) = {z-CT,)...(z-<r,), g(z) = C{z-p,)...{z-p,_,) A3.12)
Я вычислив M(z), N(z) из A3.8), получим все квадратурные
формулы с положительными весами порядка p>^{s — к) (а при C=T^_f^ —
порядка p>2(s — Ar)-flj, если в качестве узлов с^,..., с, взять нули
Л/(г), а веса 6, вычислить по формуле A3.10).
Доказательство. Функции f{z) и g{z) неприводимы, так что и
дробь N(z)/M(z) тоже неприводима согласно A3.9). Утверждение
теоремы вытекает из следствия 13.6, так как многочлены A3.12) —
это все возможные многочлены, для которых г = к. Утверждения
относительно свойств порядка следуют из леммы 13.2. П
Пример 13.8. Пусть с^,...,с, — нули многочлена
M{z) = P,(z) + a,P,_i(z) + a,P,_,(z). A3.13)
Чтобы исследовать, когда соответствующая квадратурная формула
имеет положительные веса, воспользуемся соотношением A3.5) и
запишем A3.13) в виде
M{z) = P,^,(z) (^ ~ i -f ai) - Р,_2(г)(г,_1 - аз).
Следовательно, /(г) = 2 — 1/2Н-а^, g(z) = r,_i — Ofj, и по теореме 13.7
заключаем, что нули M(z) вещественные и веса положительные в том
и только в том случае, если «2 "^ ^«-i • Таким образом, неравенство
A3.1) доказано.
При к>1 число вращений г вектора (/(<)>^@) может быть
вычислено с помощью алгоритма Штурма (лемма 13.3 из разд. 1.13).
Рассмотрим, например, многочлен
M{z) = P,iz) + aiP,_i(r) + 02Р,_2(г) + аз^',-з(г) =
= /',-2(^)[(^-5)(^-5 + "i) + «2-^,-i]-
-Ps-3i^)[r,-2i^-h+°'l)-°'3]-
Применение леммы 1.13.3 к /B:) = (г — |)B: — ^ Н-а^) Ч-о^з — т,.^ и
g(z) = т^_2{^ '~ 2"^^i)~^3 покг13ывает, что соответствующая
квадратурная формула имеет положительные веса тогда и только тогда,
когда
Т-,_2 ^ Г,_2/
Этот результат впервые получил Берридж A978).
236 Гл. IV. Жесткие задачи — одношаговые методы
Необходимые условия алгебраической
устойчивости
Обратимся теперь к алгебраической устойчивости. Здесь мы снова
воспользуемся обозначениями В(р), C(rj), D(^) из разд. IV.5.
Лемма 13.9 (Берридж 1982). Рассмотрим методы Рунге—Кутты,
которые удовлетворяют упрощающему предположению ВB) и
второму условию алгебраической устойчивости (т.е. матрица М
неотрицательно определена). Тогда
a) С(к) влечет ВBк-1);
b) D{k) влечет ВBк-1).
Доказательство. Вместо рассмотрения М будем работать с
преобразованной матрицей М = V^MV^ где V = (с^" )i 7=1 — матрица
Вандермонда. Элементы М определяются формулой
1=1 j=i j=i t=i 1=1 j=i
A3.15)
Далее, введем обозначение
так что В(и) эквивалентно условиям дг = 0 (г = 1,..., i/). Тогда С(к)
упрощает A3.15) до
Чг = ^ (^g+r + 1 - (i/g + Щдг + 1)), q<k,r<k.
Аналогично, D{k) влечет
1
т
= {9q+r-^dq'9r)^ Q<k, r<k.
Начнем теперь с предположения ВB), или В{21) для 1=1. Это
означает, что ^j = ... = ^2/ = О J так что в обоих случаях гпц = О. Но если
диагональный элемент неотрицательно определенной матрицы
нулевой, то соответствующий столбец должен быть тоже целиком нулевым
(см. упр. 11 из разд. IV. 12). Это приводит к равенству Qi^ = О при
q = 1,...,/:, означающему, что условие В{к -\-1) выполняется. Затем
мы повторяем рассуждение и по индукции приходим к В{2к — 1). П
Поскольку для 5-стадийных кол локационных методов B{s) и C{s)
выполнены (см. теорему 7.8 из главы П), то мы имеем
Следствие 13.10 (Берридж 1978). Всякий s-стадийный
алгебраически устойчивый коллокационный метод должен иметь порядок не
ниже^ чем 25 — 1. П
IV. 13. Положительные квадратурные формулы 237
Так как симметричные методы имеют четный порядок, то это дает
Следствие 13.11 (Ашер и Бадер 1986). Симметричная
алгебраически устойчивая коллокационная схема должна иметь гауссовы точки.
П
Следующий результат утверждает необходимость упрощающего
предположения С(к). Заметим, что согласно теореме 12.16 у DJ-ne-
приводимых алгебраически устойчивых методов веса 6, должны быть
положительными.
Лемма 13.12. Если метод Рунге—Кутты порядка р>2к-{-1 имеет
6,- > О для г = 1,..., 5, то условие С {к) выполнено.
Доказательство. Из условий порядка
t,j,m=l
(см. разд. П.2) следует, что
^ '* 2G+1'
1=1
* 1
.J^'^""^^'^ "Bg-fl)g'
ij = l
ri^'
для 2g + l <р. Поскольку все 6,- положительны, каждый член этой
суммы должен быть равен нулю, если q<k. (Далквист и Йелч A979)
приписывают идею доказательства Бутчеру.) П
Простое следствие этой леммы — существование следующих
порядковых барьеров для диагонально неявных методов — ДНРК (у
которых а• = О при i < j) и однократно диагонально неявных методов
— ОДНРК (с а-J = О при i < j и а,, = j для всех г).
Теорема 13.13 (Хайрер 1980).
a) Порядок метода ДНРК со всеми положительными 6, не выше 6.
b) Порядок метода ОДНРК со всеми положительными 6, не выше 4.
c) Порядок алгебраически устойчивого метода ДНРК не выше 4.
Доказательство, а) Предположим, что порядок выше, чем 6, и
пусть г — наименьший индекс такой, что с, /0. Тогда по лемме
13.12
W 2 ^г
ЧТО противоречит предположению с,^ О.
238 Гл. IV. Жесткие задачи — одношаговые методы
b) Аналогично, если порядок больше, чем 4, получим
с? с
«п^. = у или а,..= ^(^0).
Поскольку для методов ОДНРК имеем а,, = «ц , это приводит к с^ =
= Oil 7^ О, следовательно, г = 1. Но а^ = 0^/2 противоречит а^^ = с^.
c) Достаточно рассмотреть D J-неприводимые методы, так как
процесс приведения (см. табл. 12.3) оставляет класс методов ДНРК
инвариантным. По теореме 12.16 и лемме 13.12 получаем, что из
алгебраической устойчивости и из того, что порядок выше, чем 4, следует
«11 — ^1? «11^1 — у
и поэтому ajj =0. После подстановки в ш^^ это дает т^^ = — 6^ < О,
что противоречит неотрицательной определенности матрицы М. П
Для второго типа упрощающих предположений имеется
следующий результат, аналогичный лемме 13.12.
Лемма 13.14. Если метод Рунге—Кутты порядка р>2к+1
алгебраически устойчив и имеет Ь- > О для всех г, то условие D(k)
выполнено.
Доказательство основано на использовании 1У-преобразования
из разд. IV.5 и рассмотрении матрицы W^MW вместо М (см. также
доказательство теоремы 12.8). По теореме 5.14 существует
матрица 1У, удовлетворяющая условию Т(кук) (см. определение 5.10). С
помощью леммы 13.12 и теоремы 5.11а получаем, что первые к
диагональных элементов матрицы
W'^MW = (W'^BW)X 4- X'^iW'^BWf - e^ej A3.16)
нулевые. Поскольку М, а, значит, и W^MW — неотрицательно
определенная матрица, первые к столбцов и строк W^MW должны
состоять из нулей. Поэтому матрица (W^BW)X должна быть в этой
части кососимметричной (за исключением первого элемента).
Поскольку выполнено предположение С{к), первые к столбцов и строк
матриц (W^BW)X и X идентичны. Теперь результат следует из
теоремы 5.11. D
Характеристика алгебраически устойчивых методов
Из теоремы 12.16, леммы 13.12 и леммы 13.14 следует, что DJ-не-
приводимые и алгебраически устойчивые методы РК, порядок
которых р > 2Аг -f 1, имеют веса 6, > О для всех г, и для них выполнены
упрощающие предположения С{к) и D(k). Эти свойства позволяют
получить следующую конструктивную характеристику всех
неприводимых jB-устойчивых методов РК.
IV. 13. Положительные квадратурные формулы
239
Теорема 13.15 (Хайрер и Ваннер 1981). Рассмотрим квадратурную
формулу F,,с,)J
=1 порядка р с положительными весями, и пусть
матрица W при к = [{р— 1)/2] обладает свойством Т(к, к) из
определения 5.10. Тогда все алгебраически устойчивые методы Рунге—Кутты
р-го порядка, соответствующие этой квадратурной формуле,
задаются в виде
А = WXW-
A3.17)
где
/О 4i
^1 ¦••
(W^BW)X = -e,ej +
Q
A3.18)
/
И Q — произвольная матрица размерности s — fc, для которой Q -\- Q^
неотрицательно определенная. Для четного р необходимо
потребовать j чтобы gjj = 0.
Доказательство. Из алгебраической устойчивости и
положительности весов 6,- следуют С{к) и D(k) для fc = [(p—1)/2]. Матрица А
такого метода может быть записана в виде A3.17) с Х, задаваемой
согласно A3.18). Это следует из теоремы 5.11 и того факта, что
умножение на W'^BW не изменяет к первых столбцов и строк матрицы
X. Этот метод алгебраически устойчив, если и только если М {или
W^MW) — неотрицательно определенная матрица. В силу A3.16) и
матрица Q-\-Q'^ тоже неотрицательно определенная.
Обратно, любой метод Рунге—Кутты, заданный в виде A3.17),
A3.18) с неотрицательно определенной матрицей Q-\-Q^,
алгебраически устойчив и удовлетворяет С{к) и D{k). Поэтому из теоремы
5.1 в случае нечетного р=2к-\-1 следует, что метод Рунге—Кутты
имеет порядок р.
Если р четное, скажем, p = 2fc-|-2, то ситуация немного сложнее.
Так как
S
tj=l
то из SBAr-|-2), С(к), D{k) следует, что условие порядка A3.19) ниже
(при ^ = rj = к) эквивалентно q^^ = 0. Заявленный порядок р метода
РК теперь следует из леммы 13.16. П
В приведенном выше доказательстве мы воспользовались
следующей модификацией теоремы 5.1.
240 Гл. IV. Жесткие задачи — одношаговые методы
Лемма 13.16. Если коэффициенты 6,, c^,aiJ метода РК
удовлетворяют условию
И упрощающим предположениям В(р), C(ri), D(^) с р <т) + ^-{-2 и
р < 27/ + 2, то метод имеет порядок р.
Доказательство. Процесс редукции условий порядка с помощью
упрощающих предположений С(т]) и D(^), как описано в разд. П.7
(том I), приводит все деревья к «кустам», удовлетворяющим
упрощающему предположению В(р). Единственное исключение — дерево,
соответствующее условию порядка A3.19). П
Пример 13.17 (трехстадийные В-устойчивые методы ОНРК).
Выберем квадратурную формулу третьего порядка с положительными
весами, и пусть W удовлетворяет уравнению W^BW = /. Тогда
матрица A3.18) примет вид
Метод 5-устойчив, если матрица X'^-^-X — e^eJ неотрицательная,
т.е., если
а>0, rf>0, 4acf>(c + 6)^ A3.20)
Если мы хотим, чтобы этот метод был однократно неявным, то
характеристический многочлен матрицы А должен иметь вид
Это означает, что (см. A3.17))
- + a + rf=37,
aid , , « о
2 12 ^
Элементарные алгебраические выкладки показывают, что эти
уравнения можно решить, и неравенства A3.20) удовлетворяются, если
1/3 < 7 ^ 1.06857902, т.е. в точности если соответствующая
рациональная аппроксимация Л-устойчива (ср. табл.6.3; см. также (Хай-
рер и Ваннер 1981), где рассматривается аналогичный случай, но для
s = p=5).
IV. 13. Положительные квадратурные формулы 241
«Эквивалентность» Л- и J3-устойчивости
Многие Л-устойчивые методы РК не являются jB-устойчивыми
(например, правило трапеций, методы Лобатто IIIA и Лобатто IIIB;
см. теорему 12.12). С другой стороны, имеется знаменитый результат
Далквиста A978), говорящий, что каждый Л-устойчивый одноопор-
ный метод J9-ycтoйчив; это мы докажем в разд. V.6. Как мы только
что видели в примере 13.17, для определенного класса Л-устойчивых
методов всегда найдется 5-устойчивый метод с той же самой
функцией устойчивости. Универсальность этого результата прояснялась в
течение многих лет; суть его заключается в следующем.
Теорема 13.18 (Хайрер и Тюрке 1984; Хайрер 1986). Пусть R(z) =
= P[z)/Q[z) (где Р{0) = Q@) = I, degP < s, degQ = s) —
неприводимая А-устойчивая функция такая, что R{z) — е^= 0(zP-^^ ) для
некоторого р > 1. Тогда существует $-стадийный В-устойчивый метод
РК порядка р с R(z) в качестве функции устойчивости.
Доказательство. Поскольку R(z) — аппроксимация е^ порядка
р, она может быть записана в форме
ДЫ-1±1М фЫ-'U^'^''U +^*'-'''и^2гФ Ы
A3.21)
где к = [(р- 1)/2], ^? = 1/DDЯ- 1)) и ^,{г) = zg{z)lf{z), причем
^@) = /@) = 1, deg f <s-'k, degp < s — Ar — 1 (для четного p имеем еще
^'@) = /'@)). Для диагональной Паде-аппроксимации R^{z) порядка
2s это следует из теоремы 5.18cz/ = s—1 и ^^, = z:
Для произвольной R{z), удовлетворяющей предположениям теоремы,
A3.21) следует из того, что R[z) = R^{z)-\-0[zP-^^) или, что
эквивалентно, Ф(г) = Ф<^(гL-(!?B:Р+1).
Функция R[z) из A3.21) Л-устойчива в том и только в том случае,
если
Re^jt('2^)<0 для Кег<0
(теорема 5.22). Поэтому функция х(^) = ^'^k{~^h) положительная
(ср. определение 5.19), и по лемме 13.19 (см. ниже) существует
матрица Q размерности [s — k) такая, что
x{z) = e'-[[Q-\-zl)^^e^ и Q-\-Q^ неотрицательно определенная.
Зафиксируем теперь произвольную квадратурную формулу
порядка р с положительными весами Ь- и (для простоты)
различными узлами с,-. Пусть W — матрица, удовлетворяющая уравнению
W^BW^I и свойству Т{к,к) с Аг = [(р-1)/2] (ср. лемму 5.12);
определим коэффициенты Рунге—Кутты (а.) по формулам A3.17)
242 Гл. IV. Жесткие задачи — одношаговые методы
и A3.18). Построенный метод Рунге—Кутты алгебраически
устойчив (так как Q-?Q^ — неотрицательно определенная матрица), и он
имеет порядок р (заметьте, что из ^'@) = /'@) следует, что верхний
левый элемент Q равен нулю). Наконец, из теоремы 5.18 и равенства
\$^(^z) = —x{—l/z) = zej(l — zQ)''^ei следует, что функция
устойчивости этого метода есть R{z). П
Остается доказать следующую лемму.
Лемма 13.19. Пусть х(^) = ^(^)/Р(^) — неприводимая
рациональная функция с вещественными многочленами
a(z) = ^"-4aiz"-2-f..., /?(г)=г"-Ь^1^"-Ч.... A3.23)
Тогда необходимым и достаточным условием положительности
функции х{^) является существование п-мерной вещественной матрицы Q
такой, что
x(z) = e((Q 4- zl)~^e^ и Q-\- Q^ неотрицательно определенная.
A3.24)
Доказательство, а) Достаточность следует из того, что
Rex(z) = q(zy{I{^z.I+'^(Q + Q^)}q{z)
С q{z) = {Q-\- zl)'~^e^, так как Q-\-Q^ неотрицательно определенная.
Ь) Для доказательства необходимости (а это трудная часть)
воспользуемся леммой 6.8 из разд. V.6 (эта лемма — существенная
составляющая результата Далквиста об эквивалентности, и она будет
доказана в главе о многошаговых методах). Итак, лемма 6.8
утверждает, что положительность х{^) равносильна существованию
вещественных симметричных и неотрицательно определенных матриц А и
В таких, что для произвольных z^w ЕС имеет место равенство
a(zH{w) -ha{wH(z) = (г 4- w)z'^Aw -\- z'^Bw A3.25)
(здесь z= (-г:""^,..., -г, 1)^, u; = (u;""^,..., w;, 1)-^). Матрица A
положительно определенная, если a(z) и I3{z) взаимно простые.
Сравнив коэффициенты при w^ в A3.25), получим
a(z) = z'^Ae^. A3.26)
Заметим, что первый столбец А состоит из коэффициентов а(г). Для
верхней треугольной матрицы U в разложении Холецкого А = U^U
матрицы А мы, таким образом, имеем Ue^ = е^. Рассмотрим теперь
возможность вычисления матрицы Q из соотношения
(Q-fz/)[/?=/?(z).ei A3.27)
или равносильного ему
QUz = p[z)'e^-zUz. A3.28)
Правая часть A3.28) — известный многочлен степени п— 1, так как
[/е^ = е^. Поэтому сравнение коэффициентов в A3.28) дает матрицу
QC/, а следовательно, и Q. Остается доказать, что эта матрица Q
удовлетворяет требованиям A3.24).
IV. 13. Положительные квадратурные формулы 243
Воспользовавшись A3.26), тем, что Ле^ = U^Ue^ = f/^e^, и A3.27),
получим
ef (Q + zl)''e, .p{z) = e'{Uz = ejA^z = a{z), A3.29)
что доказывает первое условие A3.24). Далее, из A3.27) и a{z) = eJUz
получаем
z^U^iQ -f wI)Uw = a(z)/3{w).
Подстановка этой формулы и аналогичной ей (с переставленными
Z и w) в A3.25) дает О = ^"^(В-U'^{Q-\-Q'^)U)w и, следовательно,
В = U'^{Q-\-Q'^)U. Это доказывает второе условие A3.24), так как
матрица В симметричная и неотрицательно определенная. П
Упралснения
1. (Перрон A913) приписывает этот результат Валлису, Arithmetica
infinitorum A655) и Эйлеру A737).) Пусть последовательности
{Af^} 1л {Bf^} задаются соотношениями
Тогда
A3.30)
A3.31)
Указание, Пусть x = (xq,x^, ..., x^^^)'^ — решение линейной
системы Мх = (О,..., 0,1)^, где
/1 -fro -«1
1 -b^ -02
М =
Легко получить
\
1 -ь,
п-1
1
1 /
— = "о + i—-,—
= 6„ + ,-^ + ,
так что Xq/x^ равно правой части A3.31). Утверждение теперь
следует из того, что
{A_„Ao,...,AJM = {l,0,...,0),
E_i,5o,...,SJM = @,l,0 0),
а поэтому Xq = А„ и Xj = В„ .
244 Гл. IV. Жесткие задачи — одношаговые методы
2. Пусть Pg{z) — полином Лежандра A3.4) и N^{z) определяется
рекуррентным соотношением A3.5) с Nq(z) =0, N^{z) = 1.
Докажите, что
;vf_fc(.-)P,_,_i(z) - iVf_,_i(r)P,_,(z) = n • Г2 • • • r,_,_i.
Указание. Воспользуйтесь соотношением
t
i
f
Jo
3. Рассмотрите квадратурную формулу Эрмита
' f(r)dx = bJic,) + af(c,) + 0^ + 'r^^. A3.32)
Замените /'(cj) и /"(с^) на конечные разделенные разности,
основанные на f(c2-?), /(^2), 1(^2-\rs), чтобы получить
квадратурную формулу
f(x)dx = bj{c,) Ч- 62/(^2 - ^) + ^з/(^2) + ^4/(^2 + ^)' A3.33)
'о
a) Вычислите Q{z) для формулы A3.33) и, устремив е->0,
получите выражение, которое обобщает выражение A3.2) на
квадратурные формулы Эрмита.
b) Вычислите значения Ь^ и 63 Ci = 1)^2 — 3) в A3.10').
c) Покажите, что п^ — п_ (см. теорему 13.5) имеет одно и то же
значение для A3.32) и A3.33) при достаточно малом е.
Ответы.
Ь) 6^=6, (sic!), 62=7/3!.
4. Рациональная функция x{^) = 0[(^)/P{z) с a(z) = z-\-a^, /?(;:) = г--f-
-f/?j z-\- 02 положительна, если и только если выполнены условия
Qi > О, /?2 > О, /?1 - »! > О (сравните с E.48)).
a) Найдите вещественные симметричные и неотрицательно
определенные матрицы Л и В такие, чтобы выполнялось A3.25).
b) Покажите, что эти матрицы, в общем случае, не единственны.
c) Как в доказательстве леммы 13.19, вычислите матрицу Q такую,
чтобы выполнялось A3.24).
Указание. Начните с построения В, положив в A3.25) w^ —z.
IV. 14. Существование и ед[шственность
решений НРК
«Jusqu'a present, nous avons suppose que le schema admet-
tait une solution. Pour en demontrer I'existence. ..»
«До сих пор мы предполаггипи, что схема допускает
решение. Чтобы показать существование...»
(Крузе и Равьяр 1980)
«Поскольку контрг1Ктивность без осуществимости имеет
мало смысла...» (Спейкер 1985)
Поскольку все методы Рунге—Кутты, изученные в предыдущих
разделах, неявные, мы должны гарантировать, что численные
решения, для которых мы получили так много красивых результатов, еще
и реально существуют. Теория существования решений неявных
методов Рунге—Кутты, изложенная в томе I (теорема II.7.2), годится
только для нежесткого случая, когда hL мало (L — константа
Липшица). В жестком случае это предположение неприемлемо.
Здесь мы будем изучать существование решения уравнений метода
Рунге—Кутты, т.е. существование решения у системы
S
^,- = Уо + Л XI ^••''(^о + ^Л'^j)^ г = 1,..., 5, A4.1а)
5
2/i=% + ^Xb^./(xo+c^./i,G^) A4.1b)
для дифференциальных уравнений, удовлетворяющих
одностороннему условию Липшица
{f(x.y)-f{x.z),y^z)<u\\y-z\\\ A4.2)
Существование
Крузе и Равьяр A980) первые указали, что коэрцитивность^)
матрицы Рунге—Кутты А (или к ней обратной) играет важную роль в
доказательстве существования.
Определение 14.1. Пусть скалярное произведение определено так:
(tf, v)d = vTDv, где D = diag (d^,..., rf^) с d,- > 0. Будем обозначать
aj){A^^) наибольшее число a такое, что
{u,A''^u)p>a{u,u)jy для всех и G М*. A4.3)
Кроме того, введем в рассмотрение величину
ао(Л-^).= 8ира^,(Л-^). A4.4)
?>>0
' Определение 14.1 вводит а/)(Л~ ) и ао(Л~ ) — коэффициенты коэр-
цитиености матрицы Л^ . — Прим. ред.
246 Гл. IV. Жесткие задачи — одношаговые методы
Для сформулированной выше задачи первые результаты о
существовании решения получили Крузе и Равьяр A980), Деккер A982), а
также Крузе, Хундсдорфер и Спейкер A983). Их результаты можно
подытожить следующим образом.
Теорема 14.2. Пусть f — непрерывно дифференцируемая
функция, удовлетворяющая условию A4.2). Если матрица Рунге—Кутты
А обратима и
hu<aoiA-'), A4.5)
ТО у нелинейной системы A4.1а) существует решение (gi, - - ",9s) •
Доказательство. Оригинальные доказательства основаны на
«теореме о равномерной монотонности» или на подобных результатах.
Мы представим здесь более элементарную версию, которая, однако,
имеет недостаток, заключающийся в требовании дифференцируемо-
сти /. Идея состоит в том, чтобы рассмотреть гомотопию
S S
9i = yo-\'hY^aijf(xQ-\-Cjh,gj)-\-(T-l)hY^aijf{xQ-\-Cjh,yQ), A4.6)
i=i 3=1
которая построена таким образом, что при г = О система A4.6) имеет
решение д^ = j/q , а при г= 1 она эквивалентна A4.1а). Рассмотрим
д^ как функции т и продифференцируем A4.6) по этому параметру.
Этот дает
' 8f *
gi = h'^aij — {xQA-Cjh,gj)-gj-\-hY^aijf{xo'\-Cjh,yo)
или в векторной записи
(I-h(A®I){f^])g = h{A®I)fo, A4.7)
где использованы обозначения д = {дх^---^д,)^ (точнее, д должно
быть записано как (gj,..., fl'J')'^),
/о = (Л^о + с^Л, уо),..., Л^о + с^Л, уо)) ,
{4} = blockdiag(—(xo-hCi/i,yi),...,^(xo-fc,/i,yj).
Чтобы показать, что д можно выразить как д = G{g) с глобально
ограниченной G{g), возьмем некоторую D, удовлетворяющую
условию hi/< aj){A^^)y умножим A4.7) на g'^{DA^^ 0/) и получим
f{DA''^I)g-hg'^(D®I){fy}g = hf{D^I)fo. A4.8)
Оценим теперь отдельно три члена этого уравнения.
9^(DA-' ® 1)д > а^(А-') \\\д\\\1, A4.9)
где введено обозначение \\\д\\\}) =g'^{D® 1)д, совпадает с A4.3) в
случае скалярных дифференциальных уравнений (отсутствует «(g)/»).
{e^(x,z)u + o{e),eu)<ue'\\uf.
IV. 14. Существование и единственность решений НРК 247
В общем случае мы должны применить идеи упр. 1 из разд. IV.12
к матрице \{DA~^ -\-{DA''^)'^) — aj)[A~^)D, которая неотрицательно
определенная по определению 14.1. Из A4.2) при y = z + eu следует,
что
ду
Разделив на е'^ и перейдя к пределу е ->0, получим (w, ^(x,z)u) <
< i^\\u\\^ для всех {x,z) и всех и. Следовательно, мы имеем также
9'^(D^I){f^}g<u\\\g\\\l. A4.10)
Член в правой части A4.8) ограничен величиной ЛЩ^'ИЬ * 111/о11Ь ^^
гласно неравенству Коши—Шварца—Буняковского.
Подстановка этих трех оценок в A4.8) дает
{aj,(A-')-hu) М\1 <h\\m\D-\\\fo\\\D-
Это доказывает, что д может быть записана в виде д = G(g), причем
ftlll/olllp
ll|G(<7)llli,<
а?)(Л-^) -hi/'
Из теоремы 7.4 (разд. 1.7) следует, что это дифференциальное
уравнение с начальными значениями ^ДО)=Уо имеет решение при всех г, в
частности, также и при г = 1. Это доказывает существование решения
системы A4.1а). D
Замечание. Крайевангер и Шнайд A991, теорема 2.12) показали,
что условие A4.5) — «существенно оптимальное».
Контрпример
«После нашей дискуссии в тот понедельник (октябрь
1980 г.) во второй половине дня я пошел прогуляться,
и ко мне пришла идея контрпримера». (Спейкер)
Неравенство в A4.5) строгое, поэтому теорема 14.2 (даже с
учетом упр. 1, см. ниже) еще не отвечает на простой вопрос: всегда
ли будет S-устойчивый метод, примененный к контрактивной задаче
(т.е., когда i/ = 0), допускать решение? Первый контрпример к этому
утверждению привели Крузе, Хундсдорфер и Спейкер A983).
Простая идея построения другого контрпримера состоит в использовании
И^-преобразования (см. разделы IV.5 и IV. 13) следующим образом:
Положим S = 4 и возьмем квадратурную формулу с
положительными весами, скажем,
(с,) = @,1/3,2/3,1), F.) = а/8,3/8,3/8,1/8).
248
Гл. IV. Жесткие задачи — одношаговые методы
W.
-V3/3
V3
-1\
1
-1
1/
Затем сконструируем в соответствии с леммой 5.12 матрицу W,
удовлетворяющую свойству ТA,1). Для вышеуказанной квадратурной
формулы она будет иметь вид
/1 -л/3
1 -\/3/3
1 л/З/З
Vl v/3
Наконец, положим (взяв ^^ = 1/B\/3))
/1/2
Л = И^Х1У-' с Л'= Mj
\ О
При /?= 1/D^3) это дает точные рациональные коэффициенты для
матрицы Рунге—Кутты, а именно,
3 О
1
4i
О
О
О
о
о
о
о \
о
-/3
о /
^=48
y' = Jy + f{x) с J.
')•
6 9
5 18
12 15
Из теоремы 13.15 следует, что этот метод алгебраически устойчивый
и его порядок равен 4. Однако ±i/3 — это пара собственных значений
X и, следовательно, также и А.
Таким образом, мы выбираем дифференциальное уравнение
.^/0 -1/0'
VI//? о
которое удовлетворяет условию A4.2) с i/ = 0 независимо от выбора
/(х). Если мы применим вышеприведенный метод с Л = 1 к этой
задаче с начальными значениями Xq = О, t/q = @,0)^, то уравнение
A4.1а) станет эквивалентным линейной системе
(/-Л(8OM^ = (Л0/)/о,
где g = {9i,..^,94V и /о = (/(ci),...,/(С4))^. Матрица (/-Л0 7)
вырожденная, так как собственные значения / — Л 0 7 равны просто
1 ~ A/i, где X и /л — собственные значения матриц А и J
соответственно. Однако А — регулярная матрица, поэтому возможно
выбрать f(x) таким образом, чтобы у этой системы не было решений.
Влияние возмущений и единственность
Рассмотрим теперь, как возмущения в уравнениях метода Рунге—
Кутты влияют на численное решение. Начало исследованию этой
проблемы положили, независимо друг от друга. Франк, Шнайд и Ибер-
хубер (препринт 1981, публикация 1985) и Деккер A982),
IV. 14. Существование и единственность решений НРК 249
Как и выше, мы используем обозначения
\\\9\\\D = \ff\D®I)9, 5 6 Г"
И \\A\\q для соответствующей матричной нормы.
Теорема 14.3 (Деккер 1984). Пусть д^ и у^ —решения уравнений
A4.1), а возмущенные значения д^ и у^ удовлетворяют уравнениям
?, = Уо -+- л ^ a^jfixQ + Cjh,gj) + S^, A4.11a)
s
^1 = Уо + Л^6^./(хо-[-с^Л,?,.). A4.11b)
i=i
Предположим, что матрица Рунге—^Кутты А обратима, что
одностороннее условие Липшица A4.2) удовлетворяется и что hi/ < а?)(Л"^)
для некоторой положительной диагональной матрицы D. Тогда
справедливы следующие оценки:
1|У1 - 2/1II < \\Ь^А-'\\^ (l + ^^['^,'1}'^^^ IPIIb, A4.13)
где д:=[д^,,..,д^У, ?= (?i,.. .,?J^ я <J= (Jj,... ,<JJ^ .
Доказательство. Обозначив Д^ ^д — д и
А/= (/(a?o+^i^,?i)--/(a^o+Ci^,5'i),..-,/K+c,^,?J"-/(a:o-fc,/i,^Jj ,
разность A4.11а) и A4.1а) можно записать в виде
Д(; = Л(Л(8|/)Д/ + ^.
Как и в доказательстве теоремы 14.2, умножим это уравнение на
Д^^A)Л~^ ®/) и получим
Д(/^(ДЛ-^ ® 1)Ад - hAg'^iD 0 /)Д/ = Ag'^iDA'^ ® I)S. A4.14)
Это уравнение очень похоже на уравнение A4.8), и мы оценим его тем
же самым способом. Так как D — диагональная матрица с
положительными элементами, из A4.2) следует, что
A9'^(D®I)Af<^\\\Ag\\\l. A4.15)
Подставив A4.15) и A4.9) (где д заменим на Д^) в A4.14), получим
(а^,(Л-1)-М ЩД^ШЬ < \\\Ад\\\о lUA''® ЩЦ^,,
250 Гл. IV. Жесткие задачи — одношаговые методы
что влечет A4.12). Оценка A4.13) тогда немедленно следует из
y,-y,=h{b^^I)Af={b'^A-'(S>I){Ag-'S). П
Положив S = 0 ъ теореме 14.3, получаем следующий результат о
единственности:
Теорема 14.4. Если дифференциальное уравнение удовлетворяет
условию A4.2), а матрица Рунге—Кутты А обратима и к1/<а^{А~^),
то система A4.1а) имеет не более одного решения. П
Вычисление ао(А"
«.. .определение подходящей матрицы D ... На первый
взгляд эта задача не кажется легкой...»
(К. Деккер 1984)
В определении 14.1 ар{А-^) — наименьшее собственное значение
симметричной матрицы (^^/М-^Л-^/^ч-(Di/2^-iD-i/2)^)/2.
Вычислить ао(Л~^) труднее, так как в общем случае оптимгильная D не
известна.
Нетрудно указать верхнюю грань для ао(Л~^):
ao{A-')<,mm^w,i, A4.16)
где о;,-. — элементы А"^. Это следует из A4.3), если положить и = е,-
(е, — г-й единичный вектор).
Нижние грани для а^(А'''^) впервые нашли Франк, Шнайд и
Иберхубер в 1981 г. Ниже приводятся их точные значения (Деккер
1984; Деккер и Фервер 1984, с. 153-196; Деккер и Хайрер 1985; см.
также Лю и Крайевангер 1988; Крайевангер и Шнайд 1991).
Теорема 14.5. Для методов из разд. IV.5 имеем:
Гаусс a„(^->) = ^in^^-J_^.
{1, если 5=1,
;Т77^> если5>1,
2A-cj)
{1, если5 = 1,
^, если8>1,
Лобатто ШС ао(Л-М = 11' ^'''"'' * ^ о'
"^ ' I О, если S > 2.
Доказательство, а) Методы Гаусса. Записанная в
«симметричной форме» оценка A4.3) выглядит так:
i u'^iDA-^ + {DA-^f)u > au^Du.
IV. 14. Существование и единственность решений НРК 251
Очевидно, наиболее точные оценки получаются, когда D такая, что
матрица в левой части «настолько близка к диагональной, насколько
это возможно». Проделав большое количество численных расчетов,
Деккер получил приятный сюрприз: если взять D = 8@"^ — I), где
В = diagFi,.. .,6,) и С = diag(ci,.. .,с,), то матрица
DA-^ + [DA'^S^ = ВС^^ A4.17)
становится полностью диагональной. Тогда оптимальное значение а
получается просто испытанием единичных векторов и = 6^^ что дает
/ у* -1 \ -^ '^t 1
ап(Л ) = mm ^ ', = mm ^ ^, , ', -г = nim -—-: г-
» 2с?с/,- t 2с?6,.A/с,--1) t 2с,.A-с,)
Остается доказать равенство A4.17). Мы докажем эквивалентное
равенство
V^[A^D'\' DA - A^BC'-'^A)V = О, A4.18)
где V = {с{~ ) — матрица Вандермонда. У матрицы A4.18) элемент
(/,т) имеет вид
'•^ ' '•' ' A4.19)
С помощью упрощающих предположений C{s) и BBs) можно
показать, что выражение A4.19) равняется нулю.
b) Для методов Радо IA возьмем D = ВA — С) и покажем, что
DA-^ + (DA-^f = B + e^eJ. A4.20)
Формула для ao(i4""^) следует из О = с^ < Cj < ... < с, и неравенства
которое является простым следствием того, что Ь^ = l/s^ (см. (Абра-
мовиц и Стиган 1964), формула 25.4.31). Для проверки A4.20)
надо показать, что К^(?)Л~^ Н-A>Л"^)^ - S-e^ef)!^ = 0. При этом
используются следующие формулы: A'^Ve^ = Ь^^е^, V^e^ = е^ и
A-^Vej = {j-l)Vej^^ при>>2.
c) Аналогично, утверждение для методов Радо ПА следует при
D = ВС'^ из тождества
DA-^ 4- (DA-^f = BC^-^e^eJ.
d) Как и в части (Ь), для методов Лобатто ///С доказывается,
что
ВА'^ + {ВА'^)'^ = e.ej -f e,ej. A4.21)
Поскольку эта матрица диагональная, получаем ао(>1~^) = 1 при 5 = 2
и ао(Л-1) = 0 при 5>2. П
252 Гл. IV. Жесткие задачи — одношаговые методы
Для диагонально неявных методов Рунге—Кутты имеем
следующий результат:
Теорема 14.6 (Монтихано 1983). Для метода ДНРК с
положительными а,-,- имеем
ао(Л"-^)= min —. A4.22)
Доказательство. Выбрав D = diag A,5^, е"*,..., е^*"^), получаем
так что ао(Л"^) > min,- а,^^ -^О(е). Это неравенство при е ~> О вместе
с A4.16) доказывают утверждение теоремы. П
Методы с выролсденной матрицей А
В методах Лобатто IIIA первая стадия явная (первая строка А
состоит из нулей), а в методах Лобатто IIIB явной является последняя
стадия (последний столбец А состоит из нулей). Для этих методов
матрица Рунге—Кутты имеет вид
и мы имеем следующий вариант теоремы 14.2.
Теорема 14.7. Пусть f — непрерывно дифференцируемая
функция j удовлетворяющая условию A4.2). Если матрица Рунге—Кутты
имеет вид одной из матриц A4.23) с обратимой Л, то из
предположения ^
ки<ос^{А'^)
следует, что нелинейная система A4.1а) имеет решение.
Доказательство. Явная стадия не составляет проблемы для
существования решения. Чтобы получить результат, надо просто
повторить доказательство теоремы 14.2 для 5—1 неявных стадий (т.е. А
заменяется на А, и неоднородный член в A4.6) может быть иным). П
Явную формулу для а^{А^^) для методов Лобатто IIIB получили
Деккер и Фервер A984), а для методов Лобатто П1А — Лю, Деккер
и Спейкер A987). Результат таков:
Теорема 14.8. Для методов Лобатто IIIА и Лобатто IIIB имеем:
Лобатто ША: аоСЛ"') = {^i_i^_ 1Тл11>2,
Лобатто ШВ: aoM"^) = (?i \-i ^'^•^"« = 2'
"^ ' 1^A —с,) , если5>2.
IV. 14. Существование и единственность решений НРК 253
Доказательство. Для методов Лобатто IIIA положим D = BC^^ с
диагональными матрицами В = diag F3,..., 6,) и С = diag (cj,..., с,).
Тем же способом, что и в части (а) доказательства теоремы 14.5,
получаем
DA-' +{DA-'f = e,_,eJ_, + 2BC-\
откуда следует формула для Qo(A~^) , потому что 6, = {s(s — 1))"^ и
(l + 26J>6,/c,^i при 5>2.
Для методов Лобатто IIIB выбор D = В{1 — СУ (с матрицами В =
= diagFj,.. .,6,_i), C = diag(ci,.. .,c,_i)) приводит к равенству
DA-^ + {DA-^f = e^ef -f 25G - С).
Это доказывает второе утверждение. П
Методы с явными стадиями (такие, как Лобатто IIIA и IIIB) не
позволяют получить оценки численного решения при наличии
произвольных возмущений. Они обычно не являются ЛiV-устойчивыми,
и функция K{Z) у них не ограничена (см. теорему 12.12). Тем не
менее, имеется следующий результат о единственности.
Теорема 14.9. Рассмотрим дифференциальное уравнение^
удовлетворяющее условию A4.2). Если матрица Рунге—Кутты имеет вид
A4.23) с обратимой А и если hu < а^[А-^), то нелинейная система
A4.1а) имеет не более чем одно решение.
Доказательство. Предположим, что существует второе решение
Qi, удовлетворяющее уравнению A4.11а) при 6^=0.
a) Если первая стадия явная, то имеем д^ = д^. Разность двух
формул Рунге—Кутты тогда дает
Ag = h(A^I)Af
с ^g = (9i-9i)L2 и Д/ = (/(^о + С|'^'?|)-/(^о+С|'^'5',)),-=2- Повторяя
рассуждения из доказательства теоремы 14.3, мы тогда заключаем,
что Д^ = О.
b) Во втором случае мы можем применить теорему 14.3 к первым
S — 1 стадиям, что дает единственность ^i,. ., ^,_i. Ясно, что д^ тоже
единственное, так как последняя стадия явная. П
Методы Лобатто IIIC
Для методов Лобатто IIIC при s > 3 имеем а^(А^^) = О (см.
теорему 14.5). Поскольку эти методы алгебраически устойчивые,
естественно спросить, имеет ли нелинейная система A4.1а) также
решение для дифференциального уравнения, удовлетворяющего условию
A4.2) при I/ = 0. Положительный ответ на этот вопрос дали Хундс-
дорфер и Спейкер A987) для случая 5 = 3, а для общего случая 5 > 3
— Лю и Крайевангер A988) (см. упр. 6; см. также Крайевангер и
Шнайд A991)).
254 Гл. IV. Жесткие задачи — одношаговые методы
Упра^снения
1. Докажите, что для алгебраически устойчивых методов Рунге—
Кутты Qo(A) > О, а если матрица Л обратима, то и ао(Л""^) > 0.
2. Пусть А — вещественная матрица. Покажите, что о^{Л) < ReA,
где Л — собственное значение А.
3. (Хундсдорфер 1985; Купер 1986.) Докажите, что теорема 14.2
остается справедливой для вырожденной А, если hi/ < а и а
удовлетворяет условию
{u,Au)j)>a{Au,Au)j^ для всех wGM*.
Указание, Воспользуйтесь преобразованием g = i<S>yQ-\-(A<S> 1)к v
примените идеи доказательства теоремы 14.2 к гомотопии
S
^г = Л^о + с»^» % + Л XI ^0*^i) "^ (^ ~ ^)/(^о + с.Л, г/о)-
4. (Баркер, Берман и Племмонс 1978; Монтихано 1983.) Докажите,
что для любого двухстадийного метода условие
«и>0, ci22>0, det(>l)>0 A4.24)
эквивалентно условию ао(Л~^) > 0.
Замечание, Об обобщении этого результата на трехстадийные
методы см. (Крайевангер 1991).
5. Для двухстадийного метода Радо ПА имеем ао(Л"^) = 3/2.
Постройте дифференциальное уравнение у' = А(хJ/ с Re Х(х) = 3/2 -f в
{е > О произвольно малое) такое, что уравнения Рунге—Кутты
A4.1а) не допускают единственного решения при всех Л > 0.
6. Докажите, что для методов Лобатто IIIC (при s > 3) матрица
/-(Л0/O с J = blockdiagGp..., JJ
— невырожденная, если А*2(*^л) ^ О- Отсюда следует, что
уравнения Рунге—Кутты A4.1а) имеют единственное решение для всех
задач г/ = А{х)у-\- f(x) при H-2iM^))'?^-
Указание (Лю и Крайевангер 1988; Лю, Деккер и Спейкер 1987).
Пусть v = (v^,,. .,v^)'^ — решение уравнения (/ —(i4(S)/)J)t; =0. С
помощью равенства A4.21) сначала покажите, что v^ = v^=0.
Затем рассмотрите (s — 2)-мерную субматрицу А = (a,j)*ji2 ^
докажите, что Qq(A~^) > о, используя при этом диагональную матрицу
D = diagF,(cr'-in^.
IV. 14. Существование и единственность решений НРК 255
7. Рассмотрите алгебраически устойчивый метод Рунге—Кутты с
обратимой матрицей А и примените его к дифференциальному
уравнению у' = {J(x) -€l)y-f- f(x), где fi(J(x)) < О и е> 0.
Докажите, что численное решение yi(e) сходится к пределу при е-^0,
тогда как в сходимости внутренних стадий д^(е) надобности нет.
Указание. Разложите ^,E) вряд д^(е)=е''^д\''^^-^д^ ^+ед +•••
и докажите импликацию
g = [A<^I)Jg ==> F^0/)J(/ = O,
где 7 = blockdiag(J(xo-l-Ci/i),.. .,y(xo + c,/i)).
IVл5. В-сходимость
«При использовании Л-устойчивых одношаговых
методов для решения больших систем жестких нелинейных
дифференциальных уравнений мы обнаружили, что
— (а) некоторые Л-устойчивые методы дают сильно
неустойчивые решения, и
— (б) по-видимому, точность решений, полученных для
жестких уравнений, часто не связана с порядком
использованного метода.
Это заставило нас пересмотреть форму устойчивости,
требуемую при решении жестких систем уравнений, и
подвергнуть сомнению уместность понятия
(нежесткого) порядка точности для жестких задач».
(Протеро и Робинсон 1974)
Протеро и Робинсон A974) первые открыли явление снижения
порядка неявных методов Рунге—Кутты при применении их к жестким
дифференциальным уравнениям. Франк, Шнайд и Иберхубер A981)
ввели затем понятие В-сходимости^ которое доставляет оценки
глобальной погрешности, независимые от жесткости.
Феномен снилсения порядка
Для изучения точности методов Рунге—Кутты при применении
их к жестким дифференциальным уравнениям Протеро и Робинсон
A974) предложили рассмотреть задачу
у' = Х{у''ф))-\'<р'(х) , у(хо) = фо) . ReA<0. A5.1)
Она позволяет получить явные формулы для локальной и
глобальной погрешностей и открывает возможность нового, значительно
более глубокого понимания проблемы.
Применение метода Рунге—Кутты к уравнению A5.1) дает
S
9i = Уо + ^5^a,^AEfj- --v?K-fCjft)) 4-^'(^o+Cj.'i)|,
':' A5.2)
i=i
Если мы заменим здесь ^,',Уо и у^ на значения точного решения
^(хо+с,Л), у?(хо) и ^[х^-\-К) соответственно, то получим невлзкгу
(«дефект»), которая определяется уравнениями
IV. 15. Б-сходимость 257
Фо + с<Л) = <p{xq) + л 53 а^^^Чч + Cj/i) + A,-,ft (lo).
'-' A5.3)
4
V?(xo -f Л) = ^(xq) + лX)^jV^'K + S'M + Ао.лЮ •
i=i
Разложение функций в A5.3) в ряды Тейлора показывает, что
До.л(^о) = С?(Л''+^) , Д,,л(хо) = 0(Л'+^), A5.4)
где р — порядок квадратурной формулы F,-,^t)' ^ Ч — наибольшее
число, для которого выполнено условие C[q) (см. разд. IV.5), т.е.
^ с^
^а,.^.с^"^ = у для /:=:1,...,д и всех г. A5.5)
Меньшее из чисел ^ и р часто называют стадийным порядком метода
РК. Вычтя A5.3) из A5.2) и исключив внутренние стадии, получим
A5.6)
где использованы обозначения 2г=АЛ, iJ(z) = H-z6^(/ —2:Л)]1 (для
функции устойчивости) и Дд(х) = (Д1 ;j(a:),..., Д, д(х))^. Обозначим
J;j(x) локгальную погрешность^ которая получается из A5.6), если
положить j/o=^(^o)-
<5,(х) = -г6^(/-гЛ)-1Д,(х)-До,,(х) . A5.7)
Если мы повторим описанные выше выкладки для х^ вместо х^, то
получим рекуррентное соотношение
Уп^1-^[^п^1) = ^{^){Уп-Фп))^К{^п) , A5.8)
которое приводит к следующей формуле для глобальной
погрешности:
п
Уп+х-Фп^х) = Д(^)'^^Чуо-^Ю) +Е^(^Г"'^л(^,) . A5.9)
В классической (нежесткой) теории рассматривается случай, когда
z = 0(h); в этой ситуации глобальная погрешность ведет себя как
0{hP). При решении жестких дифференциальных уравнений
интерес представляют длины шага Л много большие, чем |А|""^. Поэтому
мы изучаем глобальную погрешность A5.9) в предположении, что
одновременно h—?0 и z = Xh—?оо. В табл. 15.1 собраны результаты
для методов Рунге—Кутты из разд.IV.5. В последнем столбце («Л
переменное») символы Лиг надо интерпретировать как max Л,- и
z=Amin/i,-. Заметим, что формулы A5.7) и A5.8) (но не A5.9))
остаются справедливыми для переменной Л, если z заменить на z^=h^X.
258 Гл. IV. Жесткие задачи — одношаговые методы
Таблица 15.1. Погрешности для ургшнения A5.1) при Л—>0 и z=hX-^oo
метод
Р ( S нечетное
^У^^ 15 четное
Радо IA
Радо ПА
Лобатто П1А { ' ZZIT
1S четное
Лобатто IIIB { ' Z^^^°^
15 четное
Лобатто П1С
локгшьная
погрешность
h'+i
h'
z-'h'+'
z-'h'+'
zh'-'
z-^h'
глобальная погрешность
h nocTostHHoe
\h'
h'
г-»Л'+1
Iz-'h'
\zh'-^
z-^h'
h переменное
h'
h'
z-'h'+^
z-^h'
zh'-^
z-'h'
Доказательство результатов, приведенных в таблице 15,1.
Методы Гаусса. Так как РК-матрица А обратима, —zb'^{I-zA)'-^ =
= b'^A'-^ -f (!?(z-^), и подстановка величин A5.4) в A5.7) дает Sf^{x) =
=(!?(Л*+^) (заметим, что q=s). Из A5.8) тогда следует (и для
постоянного, и для переменного Л), что глобальная погрешность ведет себя
как O(h^), потому что |ДB:)|< 1. Для нечетного s имеем Я(оо)=—1,
и оценка глобгильной погрешности может быть улучшена в случае
постоянной длины шага. Это следует из суммирования по частям
i=o ^ i=i
l-p
суммы в A5.9) и из того, что Sf^(xJ)Sf^{Xj_^)=0{hя+^).
Методцл Рдцо IA. Оценка локальной погрешности получается
таким же образом, как и для методов Гаусса. Так как R(z)=0{z~^),
то распространением погрешности в A5.8) можно пренебречь,
поэтому локальная и глобальная погрешности асимптотически ведут себя
одинаково.
Методы Рддо ПА и Лобатто ШС. У этих методов а,, =6, для всех
i. Поэтому последняя внутренняя стадия идентична численному
решению, и локальная погрешность может быть записана в виде
S,{x) = -eJ(I-zA)-'A,{x).
Так как матрица А обратима, то эта формула показывает наличие
г-^ в локальной погрешности. Здесь тоже Л(оо) = О, так что
глобальная погрешность, по существу, равна локальной.
Методы Лобатто IIIA. Первая стадия 5^1=2/0 — явная, она
выполняется без внесения погрешности. Поэтому А^ ^{х)=0 и (так как
IV. 15. В-сходимость 259
а^,=:6,) локальная погрешность имеет вид
S,(x) = -eJ_,(I-zA)-'A,(x),
где A = (aij)lj^2 ^ ^л=^(^2,Л'• • •'^«.л)'^- Результаты, приведенные в
табл. 15.1, теперь получаются так же, как и для методов Гаусса.
Методы Лобатто ШВ. Матрица А вырожденная (ее последний
столбец нулевой), поэтому два «г» в A5.7) не погашаются так просто
при г—^оо. Более детальный анализ (см. упр.5 ниже) показывает,
что локальная погрешность не ограничена, если z-^oo. Хотя они и
Л-устойчивы, эти методы не подходят для решения жестких задач.
D
Из табл. 15.1 видно, что порядок сходимости для задачи A5.1) с
большим А значительно меньше, чем классический порядок. Далее,
мы видим, что методы, удовлетворяющие условию а,,=6,- (Радо ПА,
Лобатто IIIA и Лобатто IIIC) дают асимптотически точный результат
при z—^oo. Протеро и Робинсон A974) называют такие методы оюест-
ко тонными. Важность этого условия проявится снова, когда мы
будем рассматривать сингулярно возмущенные и дифференциально-
алгебраические задачи (глава VI).
Локальная погрешность
«Das besondere Schmerzenskind sind die Fehler-
abschatzungen)^.
«Особенно болезненное дитя — это оценки
погрешности». (Л. Коллатц 1950)
Наша следующая цель — распространить изложенные выше
результаты на нелинейные дифференциальные уравнения общего вида
t/'=/(x, у), удовлетворяющие одностороннему условию Липшица
{f{x,y)-f{x,z),y-z)<u\\y-zf . A5.11)
Нижеследующий анализ, начатый Франком, Шнайдом и Иберхубером
A981), был детально разработан Франком, Шнайдом и Иберхубером
A985) и Деккером и Фервером A984). Локальную погрешность мы
опять обозначим
<5/»W = yi-y(^ + /i) ,
где у^ — численное решение с начальным значением у^^у[х) на
точном решении.
Преищожение 15.1. Рассмотрим дифференциальное уравнение,
которое удовлетворяет условию A5.11). Предположим, что РК-матрица
А обратима, а^(А^^) > О (см. определение 14.1) и что стадийный
порядок равен q .
260 Гл. IV. Жесткие задачи — одношаговые методы
a) Если ао(Л'"^) > О, то
ll<^^WII<Ch«+^ max ||у('+1)@|| для hu<a Ka^iA-') .
b) Если aj[y(A^^)=0 для некоторой положительной диагональной
матрицы D и и <0f то
1КМ11<ЙЛ' max ||у('+')@||.
В обоих случаях постоянная С зависит только от коэффициентов РК-
матрицы (и от а для случая (а)).
Замечания, а) Ключевой факт в этих оценках — это то, что правая
сторона зависит только от производных точного решения и не зависит
от жесткости задачи. Эти оценки полезны, когда надо
аппроксимировать «гладкое» решение жесткой задачи.
б) Предположение а?)(Л"'1)=0 (см. случай (Ь)) — более сильное,
чем ao(i4~^)=0 (см. упр. 4). Для методов Лобатто IIIC, для которых
ао(Л-1)=0 («>2), имеем а^^(Л-1)=0 при D=B (см. A4.21)). Для
жестко точных методов оценка для случая (Ь) может быть улучшена,
если вместо A4.13) использовать A4.12).
в) В оценках сформулированного выше предложения максимум
берется по ^ G [х, x+h]. В случае, когда неравенство 0<с,.<1 не
выполняется, этот отрезок, конечно, должен быть соответственно увеличен.
Доказательство. Положим У,=2/(хо+с,Л), так что соотношение
A4.11а) удовлетворяется с
5
Si=y(xo-\'Cih)-'y{xQ)'-hY^aijy'{xQ + Cjh) .
i=i
Разложение Тейлора показывает, что
11^,11 <С,Л'+1 max ||у('+»)(х)||,
где С,= (|с,.|9+1+(^4-1) ^*_^ |д.^.|. \cJ\я)/(q-\'l)\ — постоянная,
зависящая от метода. Аналогично, значение у^ в A4.lib) удовлетворяет
$
уК +/») - У1 = Фо + А) - у(хо) - л 5] bjV(xo + с^.Л) = 0(Л9+^) ,
A5.12)
так как у квадратурной формулы F,-,с,) порядок > д. Поскольку
PhW!l<llyi-yill + liyi-y(^o + A)||,
искомые оценки следуют из неравенства A4.13) теор)емы 14.3. П
IV. 15. В-сходимость 261
Распространение погрешности
В конце разд. IV. 12 мы вывели для отдельных методов РК точные
оценки вида
1|У1-г/111<^в(М1|Уо-%11- A5-13)
где Ух, t/i — численные решения, отвечающие Уо,2/о соответственно, и
где дифференциальное уравнение удовлетворяет условию A5.11). Мы
дадим здесь простое доказательство грубой оценки <pB{hi/), которой,
однако, будет достаточно, чтобы вывести интересные результаты о
сходимости.
Пре^пдожение 15.2 (Деккер и Фервер 1984). Предположим, что
дифференциальное уравнение удовлетворяет условию A5.11), и
применим алгебраически устойчивый метод РК с обратимой матрицей А
и ао(Л""^) >0. Тогда для любого а в интервале 0<а<ао(А"'^)
существует постоянная С > О такая, что
l|yi-yill<(l + C'/ii/)||j/o-2/oll Д^я 0</»/<а.
Доказательство. Из A2.7) имеем (используя обозначения
доказательства теоремы 12.4)
t = l »=:1 i = l
A5.14)
в силу алгебраической устойчивости последний член в A5.14)
неположительный, и им можно пренебречь. С помощью A5.11) и оценки
A4.12) с <^,=Уо"/о получаем
2Л J3 6,<Д/,, Д5,) < 2fti/J] 6, IIД<,,||2 <
1=1 1=1
< 2huC, \\\Ад\\\1 < ^^JJZ)lhu)^ \\^УоГ ¦
Подстановка этой оценки в A5.14) дает доказываемое неравенство:
ll^'""^('^»„(A-?-/,.)Oll^''°ll-
J3-СХОДИМОСТЬ при переменной длине шага
Теперь мы можем представить главный результат этого раздела.
Теорема 15.3. Рассмотрим алгебраически устойчивый метод Рун-
ге—Аутты с обратимой матрицей А и стадийным порядком q <р.
Предположим, что выполнено условие A5.11).
262 Гл. IV. Жесткие задачи — одношаговые методы
a) Если 0<a<Qo(^~^) и i/ > О, то для глобальной погрешности
справедлива оценка
11г/„-у(^„I1<Л'^^ rZ -^2 max ||у('+')(х)||
при hi/ <а .
b) Если ао(Л-^) >0 и 1/<0, то
1|2/п-2/(^пI1<Л^(^п-^о)С2 max ||у(^+1)(х)|| для всех Л > О .
хе[хо,хп]
c) Если aj){A~^) = 0 для некоторой положительной диагональной
матрицы D и 1/ <0у то
1|!/п-Ф„I1<Л'-^с(л+^1)(х„-Хо) max ||у"+^)(х)||.
\ \1/\/ Те[хо,Хп]
Константы С^, 6*2, С зависят только от коэффициентов матрицы Рун-
ге—Кутты. В случае переменной длины шага h должно
интерпретироваться как Л=max Л,.
Доказательство. Этот результат о сходимости получается в
точности тем же способом, что и для нежестких задач (теорема II.3.6).
Для перенесенных погрешностей Ej (см. рис. П.3.2) согласно
предложению 15.2 имеем оценку (при ^^ > 0)
||?;.||<еС.(х,-.,)||^^^__(^._Л|, .A5.15)
так как l-^-Chi/ < е^^^^. Теперь подставим в A5.15) оценку
локальной погрешности из предложения 15.1 и просуммируем перенесенные
погрешности Е,. Это дает желаемую оценку при i^ > О, так как
j = l •'^0
_ / (еС..(г,-«о) _ \I(Си) при I/ > О ,
х„ — Xq при 1/ = о .
={:
Если t/ < О, то имеем \\ЕА\ < \\Sf^ __^{xj_i)\\ в силу алгебраической
устойчивости, и применимы те же самые аргументы. П
Опираясь на этот результат, определим порядок Б-сходимости
следующим образом:
Определение 15.4 (Франк, Шнайд и Иберхубер 1981). Назовем
метод Рунге—Кутты В-сходящимся порядка г для задач j/ = f(x,y),
удовлетворяющих условию A5.11), если глобальная погрешность до-
IV. 15. В-сходимость 263
пускает оценку
1|Уп-2/(^пI1<^'*7К--^о.'^) max max Hy^-^'^lx)!!
j=i. ./ Хб[хо.Хп] A5.16)
при hi/ < а,
где Л = max Л,. Здесь 7 — функция, зависящая от метода, и а тоже
зависит только от коэффициентов метода.
Примером приложения доказанной выше теоремы служит
Теорема 15.5. Методы Гаусса и Радо ПА имеют В-сходимость
порядка S (число стадий). Методы Радо IA имеют В-сходимость
порядка 5—1. Двухстадийный метод Лобатто IIIC имеет В-сходимость
порядка 1. П
Для методов Лобатто IIIC с 5>3 стадиями (у которых ао(^"^)=0
и q = s—l) теорема 15.3 указывает на 5-сходимость порядка 5—2,
если 1/<0. Это не оптимальный результат. Спейкер A986)
доказал 5-сходимость порядка 5—3/2 для i/<0 при постоянной длине
шага. Шнайд A987) улучшил этот результат до 5 — 1. Позже Дек-
кер, Крайевангер и Шнайд A990) показали, что эти методы имеют
5-сходимость порядка 5—1 для произвольных последовательностей
длин шагов, если допустить, что функция 7 в определении 15.4
зависит также от отношения max Л, / min Л,-.
Методы Лобатто П1А и ПШ не могут быть ^-сходящимися, так
как они не являются алгебраически устойчивыми. Взаимосвязь этих
свойств будет предметом обсуждения в следующем подразделе.
jB-СХОДИМОСТЬ влечет алгебраическую устойчивость
Чтобы найти необходимые условия В-сходимости, рассмотрим
задачу
у' = Х(х)(у-ф))-\'^р'{х) , КеХ(х)<1/ A5.17)
с точным решением у(х)=<^(х)=х9+^ . Применим метод Рунге—Кутты
со стадийным порядком q и получим для глобальной погрешности
е^=у^ — ^{Xj^) простое рекуррентное соотношение
?„+1=А'B„)е„-Щ„)Л'+1 A5.18)
(ср. формулу A5.8) в начгипе этого раздела, где рассматривался
случай Л(х)=Л). Здесь Z^=diag(/iA(x„-hCi/i),.. .,/1Л(х„-|-с,Л)) и
K(Z) = l-\-b'^Z(I-AZ)'4, L(Z) = dQ-\-b'^Z(I^AZ)-4 . A5.19)
Функция K(Z) уже встречалась в определении 12.10, когда
рассматривалась ЛЛ^-устойчивость. В L(Z) скаляр d^ и вектор d =
264 Гл. IV. Жесткие задачи — одношаговые методы
=(^1,..., d,)^ характеризуют локальную погрешность и задаются
выражениями
do = 1 - (g-f 1) i2^^1 ' ^i = 'i^' - (9+1) E «O-^I • A5.20)
Заметим, что согласно определению стадийного порядка имеем либо
c/q ^ О, либо d^O (или и то, и другое). Теперь мы подготовлены к
доказательству следующей теоремы.
Теорема 15.6 (Деккер, Крайевангер и Шнайд 1990). Рассмотрим
DJ -неприводимый метод РК, у которого О < Cj < Cj < ... < с, < 1. Если
для некоторых г, / и 1/<0 глобальная погрешность удовлетворяет
оценке В-сходимости A5.16)^ то метод алгебраически устойчив.
Доказательство, Предположим, что метод не является
алгебраически устойчивым. Тогда по теореме 12.13 и лемме 15.17 (см. ниже)
существует матрица Z=diag {z^,., ,,z^) с Re г^ < О такая, что
\K(Z)\>1, L{Z)^0, A5.21)
и у матрицы (I—AZ) существует обратная. Рассмотрим отрезок
[О, A-|-^)/2] и последовательность длин шагов (h^)^~Q для четного
N, задаваемую формулами
h^ = 1/N {для четного п), Л^ = в/N (для нечетного п).
Если N достаточно большое, то можно определить такую функцию
А(х), у которой ReA(x) <i/ и
для четного п,
для нечетного п.
Соотношение A5.18) показывает, что глобальная погрешность г„ =
=у^—(р{х^) для задачи A5.17) удовлетворяет уравнениям
?„^1 = K{Z)en - h^'^^L{Z) для четного п,
e^^j =г K{Z)e^ — h^'^^L(Z) для нечетного п
(с h=l/N),гдe Z=diag{eZgy.. .^вг^). Следовательно,
е,^^, = I<(Z)K(Z)e,^ - Л9+1 (К{2)Ь{2) + в"^'L{Z)),
и погрешность в точке Х={\-?в)/2 выражается формулой
?jV =
1
ЛГ9+1 V V ; V ; v ;; K{Z)K{Z)-l ^
Если в достаточно мало, то K{Z) -^ 1 и L{Z) -f Jq, и в силу A5.21)
\K{Z)K[Z)\>\ и K(Z)L{Z)-{^в'i'^^L{Z)ф{) ,
Поэтому |б^| -^ со при N -?00 {N четное), что противоречит оценке
В-сходимости A5.16). П
IV. 15. В-сходимость 265
Для завершения данного выше доказательства приведем
следующею лемму:
Лемма 15.7 (Деккер, Крайевангер и Шнайд 1990). Рассмотрим
DJ -неприводимый метод РК и предположимj что
b^Z[I-AZy4 = Q A5.23)
для всех Z = diag (г^,..., г,) таких, что матрица I—AZ обратима.
Тогда d=0.
Доказательство. Определим множество
^ = (i I ^1«.1»2«Ыз • • •«»*-iu = О для всех к nil с i^=j} .
Положив fc = l, получим 6^=0 для j ЕТ. Далее, если i^T и j ^Т,
то существует набор индексов (г\,.. .,i^t) ^ ik^i такой, что
откуда следует, что a,j=0. Поэтому метод 1> J-приводим, если Тф^.
Таким образом, для докс1зательства утверждения достаточно
показать, что д,фй влечет Тф^.
После представления (I—AZ)"^ в виде геометрического ряда
предположение A5.23) становится эквивалентным следующему
предположению:
b^Z(AZf'^d = Q для всех к и Z = diag(zi,.. .,г,) . A5.24)
Сравнение коэффициентов при г,-^ • • г,-^ дает
E^.«.uV«i»-u»'^i»=0, A5.25)
где суммирование производится по всем перестановкам (jj,.. .,j/j) из
(г\,..., г'д^). Предположим теперь, что для некоторого индекса j
имеется c?j7^0, и докажем с помощью индукции по /:, что
^i^.i.'a ••^«ic-iu =0 длявсех 2^(^=1,...,*) с 2^=j, A5.26)
так что У G Т и, следовательно, Г^0.
Для к = \ это следует непосредственно из A5.25). Чтобы
доказать A5.26) для к-\-1 от противного, предположим, что существует
набор индексов (г^,..., i^^^J с г^^^=3 такой, что Ь-^а>^-^.. .а,^-^^^:^0.
Из соотношения A5.25) тогда следует существование перестановки
O'l' ••»^+i) из (г1,...,г;,+1) такой, что h-a
ilia • • • S**j*+i ^ ^ тоже.
Обозначим теперь через q наименьший индекс, для которого iqфЗq•
Тогда iq^Jr для некоторого г > д, и мы получаем
^,«..., • • •«.,-..,«jVi.+. • • «Ы.^. ^ о, A5.27)
ЧТО противоречит гипотезе индукции, так как выражение в A5.27)
содержит не более, чем к множителей. П
266 Гл. IV. Жесткие задачи — одношаговые методы
Правило трапеций
Правило трапеций
У^+1=2/^ + у[/К.2/^ + /К+пУ^+1)] A5.28)
не является алгебраически устойчивым. Поэтому (теорема 15.6) оно
не может быть 5-сходящимся в смысле определения 15.4. Тем не
менее, можно вывести оценки типа A5.16), если ограничиться
специальными последовательностями длин шагов (постоянными,
монотонными, ...). Впервые это доказал Штеттер (не опубликовано) и детально
исследовал Крайевангер A985).
Теорема 15.8 (Крайевангер 1985). Если дифференциальное
уравнение удовлетворяет условию A5.11), то глобальная погрешность
правила трапеций допускает при hji/<a<2 оценку
\\Уп-уМ\\<С max ||г/(з)(х)|| Х;{ П rnB.x{lhj/hj_Ahl .
Доказательство. Обозначим через у^, =:y(xi^) точное решение в
узловых точках. Из рг13ложения в ряд Тейлора тогда получим
yfc+i=J/* + Y(/(^fe.yfc) + /K+i.J/fc+i))+'Jfc . A5-29)
где
11«^Л<^Л^ max ||j/C)(x)|| . A5.30)
Основная идея доказательства состоит во введении промежуточных
значений
hf^ ,, , /li.
Ук+1/2 = Ук-^ у/К>Ул) = У/с+1 - y/(^fc+i'2/;c+i)
Переход У/е_1/2-^ У/с-|-1/2 » т.е
У/с + 1/2 = ^/с + у/(^/с ^Ук)-^^к = Ук + 1 - у/(-^^ + 1' ^/c + l)
A5.31)
Ук-\-1/2 = Ук-1/2 + 2 ('*^-1'^'^'^)'^(^'^' ^^)
можно тогда интерпретировать как один шаг ^-метода
С в =.h^^_^/[hf^_^-\'hj^) и длиной шага /i = (/i;j_j-f/i;j)/2. Аналогичное
вычисление показывает, что тот же самый ^-метод отображает yjt-i/2
в Ук+\/2-^к' Поэтому
\\Ук^\12 - Ук^1/2 -^к\\< У^в(М \\Ук^1/2 - Ук^1/2\\ '
IV. 15, В-сходимость 267
где функция роста погрешности <PB(hi/) выражается следующим
образом (см. формулы 12.42 и 11.13):
V?5(/ii/) = тах{A - в)/в, A -h A - 0)hu)/(l - Ohu)} =
1 1 A5.32)
= max{/i J/i;,_i, A -h ^h^u)/(l - -/i;,_it/)} =: (p,, •
Из неравенства треугольника получим также
1|У;с+1/2 - 2//C+1/2II < Гк\\Ук^1/2 - Ук-1/2\\ + 11*Л • A5.33)
Далее, из A5.31) при к=0 (учитывая, что Уо=Уо) следует, что
11У1/2-У1/211 = 11<^о11- A5.34)
Наконец, сделав последние шаги Уп^1/2 ~^ Уп ^ Уп-\/2 "^ Уп методом
Эйлера (см. A5.31)), получим
\\Уп-Уп\\< 7Г-Г1—ГТ 11^"-1/2-J'-i/2ll A^-35)
(снова используя формулу A1.13), на этот раз при ^=1). Комбинируя
A5.33), A5.34) и A5.35), придем к неравенству
\\Уп-Уп\\<., '^ . Е{ П ^ijll^^ll- A5.36)
Для i/ < О имеем (р/^ < тахA, /1;^/Л;р_ J, и утверждение теоремы
получается, если подставить A5.30) в A5.36). Для i/> О воспользуемся
оценкой (при hf^_^i/< 1)
1-^Л/с-1^ 1-^Л;,-1'^ l + i^^t-i'^
<e^"*-^'^.maxfl,—^) ,
откуда видно, что утверждение теоремы верно и С = е2*^(^«""^о)/12. П
Следствие 15.9. Если последовательность длин шагов (hi^)^^Q
постоянная или монотонная, то для Л = max Л,
\\Уп-У{'^п)\\<С max ||уC)(х)||-/,2. D
Хе[Хо,Хп]
Снижение порядка для методов Розенброка
Очевидно, что методы Розенброка (см. определение 7.1) не могут
быть S-сходящимися в смысле определения 15.4 (см. также упр. 8 из
разд. IV. 12). Тем не менее, интересно изучить их поведение на
жестких задачах, таких, как модель Протеро и Робинсона A5.1).
Поскольку это уравнение неавтономное, необходимо воспользоваться
формулировкой G.4'). Непосредственное вычисление показывает, что
глобальная погрешность е^=у^—(р{х^) удовлетворяет рекуррентному
соотношению
еп^1 = ЩФп+6,(х,)^ A5.37)
268 Гл. IV. Жесткие задачи — одношаговые методы
где R{z) — функция устойчивости G.14), а локальная погрешность
определяется выражением
<J^(x) = ^(x)-^(x-f/г) + 6^(/-г5)-^Д , A5.38)
где В = (а,^+7о), Ь = (^i, • • • ,*,Г, А = (Д„...,А,)^ и
Д. = z{(p{x) - (р(х-\-а^к) - 7,-V(^)) + V(^+ct,/i) -f 7,ЛV"(^) •
Разложение в ряд Тейлора дает следующий результат.
Лемма 15.10. Локальная погрешность S^i^) метода Розенброка,
примененного к уравнению A5.1), при /i->0 и z = A/i->oo имеет вид
S,{x) = E:6,a;.,.aj - l)^^"(r) + O(k') + o(^) ,
где Lj^j — элементы матрицы В^^. П
Замечания, а) Если метод Розенброка не удовлетворяет новому
условию порядка
S
Х;б.Ч,а?=1, A5.39)
то локальная и глобальная погрешности (при |Л(оо)|<1) имеют
порядок 0{h^). Поскольку ни один из классических методов Розенброка
из разд.IV.7 не удовлетворяет условию A5.39), то на задаче A5.1),
если Л очень велика, их порядок равен всего лишь 2.
b) Удобный способ удовлетворить условию A5.39) — потребовать,
чтобы
^M+7,i=b.- (*'=!> ••.^) и а,=:1 A5.40)
(это аналог условия а^, = 6^ для методов Рунге—Кутты), что влечет
не только A5.39), но даже
S,(x) = o{^),
так что такие методы дают асимптотически точные результаты при
г -> со.
c) Более глубокое понимание условия A5.39) станет возможным
при изучении погрешностей методов Розенброка для сингулярно
возмущенных и дифференциально-алгебраических задач (глава VI). Там
мы сконструируем методы, удовлетворяющие требованиям A5.40).
d) Шольц A989) записывает локальную погрешность Sf^(x) в виде
Ja(x) = J]C,.(z)/.V<^''(x) A5.41)
i>2
IV. 15. Б-сходимость 269
и исследует возможность иметь Су(г)=0 при i=2 (а также и при
j>2). Хундсдорфер A986) и Штремель и Вайнер A987)
распространили приведенный выше анализ на полулинейные задачи A1.21),
которые удовлетворяют условию A1.22). Изложение их результатов
довольно сильно осложнено специальной техникой и терминологией, но
эти результаты позволяют построить «Б-сходящиеся» методы
порядка р>1.
Упралснения
1. Докажите, что стадийный порядок метода ОДНРК не более
единицы, а метода ДНРК — не более двух.
2. Рассмотрите метод Рунге—Кутты cO<Ci<...<c, <1, имеющий
стадийный порядок q. Докажите, что такой метод не может быть
Б-сходящимся (для переменной длины шага) и иметь порядок,
равный ^+1.
Указание. Воспользуйтесь формулой A5.22) и докажите, что
отношение
K{Z)L{Z)-^e^^'L(Z)
K(Z)K(Z)-\
где
Z = diag(zi,...,zJ , Z = diag(?i,...,zJ
с Re г,. < О, Re ?, < О, не может быть равномерно ограничено (в
случае с^ = О и с, = 1 это надо доказывать с учетом
ограничений ?! = вг^, ?3 = ^^1). С этой целью рассмотрите значения z^-, z^ ,
близкие к началу координат.
3. (Берридж и Хундсдорфер 1987.) Предположим, что с^—с, не
является целым числом для всех 1 < г < j < 5 и что порядок
В-сходимости (при постоянной длине шага) метода РК равен ^-fl, где q
обозначает стадийный порядок. Тогда dg^^' ^ ^^^ компоненты
вектора d= (dj,.. .,rf,)^ одинаковы (определение d, дано в
формуле A5.20)).
Указание. Исследуйте функцию L(Z)/(K{Z) — 1) на предмет ее
равномерной ограниченности.
4. (Крайевангер.) Покажите, что для матрицы
/ О 1 0\
Л-^ = I -1 о 0 1 A5.43)
ао(Л''^) = 0, но не существует положительной диагональной
матрицы D такой, что а?)(Л~^) = 0. Для лучшего понимания см.
«следствие 2.15» в работе (Крайевангер и Шнайд 1991).
270 Гл. IV. Жесткие задачи — одношаговые методы
5. Докажите, что для методов Лобатто IIIB с матрицей Рунге-
Кутты
~W о)
доминирующим членом локальной погрешности A5.7) при Л-)-О и
z=hX—?oo будет
Здесь ^ = 5—2 — стадийный порядок метода и с= [с^,...,с^_^)'^.
Покажите, кроме того, что
а'^А-^с^ = 1 для Аг = 1,2,...^, A5.44)
а'^А-^с^ф! для k = q-\-l, A5.45)
Указание. Уравнение A5.44) вытекает из упрощающего
предположения C(q). Неравенство A5.45) можно доказать от противного,
предположив, что а'^А'^сЯ+^=1, откуда вместе с A5.44) будет
следовать, что для любого многочлена р(х) степени degp<gH-1=5—1,
удовлетворяющего условию р@)=0,
?<р{с.) = РA). где d'' = a''A-K
1 = 1
Многочлен
р{х) = (х-с^){х-с^)... (x-c,_i)
противоречит сделанному предположению.
Глава V
Многошаговые методы
для жестких з^цач
Многошаговые методы (ФДН) были первыми численными
методами, предложенными для жестких дифференциальных уравнений
(Кертисс и Хиршфельдер 1952). С появлением книги Гира A971)
основанные на этих методах программы приобрели наибольшую
известность и стали наиболее широко использоваться для всех жестких
расчетов.
В начале этой главы излагается линейная теория устойчивости
для многошаговых методов (разд. V.1), которая приводит к
знаменитой теореме Далквиста о том, что Л-устойчивые многошаговые
методы не могут иметь высокого порядка. Попытки преодолеть этот
барьер делаются, в основном, по двум направлениям: либо для этого
изучают методы с несколько ослабленными требованиями
устойчивости (разд. V.2), либо вводят новые классы методов (разд. V.3).
Теория порядковых звезд на римановых поверхностях (разд. V.4)
помогает распространить понятие барьера Далквиста на обобщенные методы
и объяснить различные свойства областей устойчивости. В разд. V.5
представлены численные эксперименты с несколькими программами,
реализующими рассмотренные методы.
Поскольку вся предшествующая теория устойчивости опирается
исключительно на линейные автономные задачи у^ = Ау, встает
вопрос о ее справедливости в общем случае нелинейных задач. Это
приводит к понятиям G-устойчивости для многошаговых методов
(разд. V.6) и алгебраической устойчивости для общих линейных
методов (разд. V.9).
Другой важный предмет исследования — оценки сходимости при
Л —> О, не зависящие от степени жесткости задачи (аналог
5-сходимости из разд.IV.15). Различные способы получения таких оценок мы
описываем в разд. V.7 (для линейных задач), а также в разделах V.6
и V.8 (для нелинейных задач). К их числу относятся:
использование G-устойчивости, матричная теорема Крайсса, метод множителей
и (последняя по порядку, но не по значению) дискретная формула
вариации постоянных.
V.l. Устойчивость
многошаговых методов
Общий fc-шаговый многошаговый метод имеет вид
Для него можно провести такой же анализ устойчивости, какой был
проведен в разд. IV.2 для метода Эйлера. Это означает, что мы
применяем метод A.1) к линеаризованной автономной системе
j/ = Jy A.2)
(см. (IV.2.2')), в результате чего получим формулу
Как и в разд. IV.2, для векторов у^,,., введем новый базис, состоящий
из собственных векторов матрицы J. Тогда в разложениях векторов
y^n^i мы получим для коэффициентов при каждом собственном
векторе V матрицы J точно такое же рекуррентное соотношение, как
A.3), но с заменой J на соответствующее собственное значение А.
Если обозначения у^^, сохранить и для этих коэффициентов, то мы
придем к формуле ^
К-/^/?^2/т+л+-- + К-Я/?оJ/т = 0, /i = hA, A.4)
которая совпадает с методом A.1), примененным к тестовому
уравнению Далквиста
у' = Ау. A.5)
Область устойчивости
Разностное уравнение A.4) можно решить методом Лагранжа (см.
том I, разд. III.3): подставив в A.4) у^ = С*' и разделив на С"^, мы
получим характеристическое уравнение
(afc-,i/?jC* + ... + (ao-/i/?o) = p(O-MC) = 0, A.6)
зависящее от комплексного параметра /i. Многочлены p{Q и a{Q —
это наши старые друзья из (III.2.4). Разностное уравнение A.4) имеет
устойчивые решения (при произвольных начальных значениях) тогда
и только тогда, когда все корни уравнения A.6) по модулю < 1. Кроме
того, кратные корни должны быть по модулю строго меньше единицы
(см. том I, разд. III.3, упр. 1).
^ В отличие от гл. IV, где произведение h\ всюду обозначгшось через z, в
этой главе мы будем писать /iА = /i, так как в теории многошаговых методов
(см. разд. II 1.3) Z обозначает преобразование Кэли для С-
V.l. Устойчивость многошаговых методов 273
Определение 1.1. Множество
5 =
^ 1С;(/^)| ^ I Д-^я всех корней C(fJ') уравнения A.6), 1
' 1С;(а^)| < 1 Д*^я кратных корней j
A.7)
называют областью устойчивости или областью абсолютной
устойчивости метода A.1). Если 5 D С~ , то говорят об А-устойчивости
метода.
Иногда желательно рассматривать 5jcaK подмножество
компактифицированной комплексной плоскости С. В этом случае при /i —> со
корни A.6) стремятся к корням уравнения G(C) = 0.
При fi = 0 уравнение A.6) переходит в p{Q =0. Таким образом,
обычная устойчивость (в смысле определения III.3.2) эквивалентна
требованию О G 5.
Теорема 1.2. Для линеаризованного уравнения A.2) с приводимой
к диагональному виду матрицей J все численные решения метода
A.1) ограничены тогда и только тогда, когда Л А G 5 для всех
собственных значений А матрицы J. D
Расчет области устойчивости мы поясним на частном примере
явного метода Адамса 4-го порядка (см. том I, разд. III. 1, формула
A.5')):
2/m+4 — 2/m+3 ¦^'*\^24*'^+3 24-'"^+2 "''24 "'¦^ 24 /
для которого уравнение A.6) примет вид
55 \,з 59 ,2 37 ^ 9
На рис. 1.1 показано сложное поведение корней этого уравнения.
Мы взяли значения /i, которые отмечены точками, окружающими
белую лошадь, и в С-плоскости нанесли соответствующие им значения
четырех корней С1»С2>Сз»С45 видно, что эти корни возникают из
корней 1,0,0,0 многочлена р.
Отображения, определяемые комплексными функциями,
являются конформными, т.е. сохраняющими углы и ориентацию. Угол
поворота и коэффициент растяжения такого отображения определяются
(локально) его производной. Дифференцируя A.8) по /i и полагая
затем /1 = 0 и С = 1 j получим
Л1)-с;(о)-стA)=о.
В силу условий согласованности метода //AO^0, сгA)=^'A) (см.
том I, уравнения (III.2.6)) отсюда следует, что Ci@) = 1- Этим
объясняется близость отображения /i»-^Ci к Ц-/х в окрестности точки
/i=:0, а также то, что Ci(A') сдвигается внутрь единичного круга,
когда pi сдвигается внутрь области С" .
<'-A+|.)с'+|к'-|к+|''=»- ('«I
274 Гл. V. Многошаговые методы для жестких задач
Кривая локуса корней. Ключевым для расчета 5 является то
обстоятельство, что вследствие линейности A.8) относительно /i
обратное отображение С^ И легко вычисляется и является однозначным:
^^^- ^ ^ A.9)
И =
^^' 24** 24 *> ^24^ 24
Внешность единичного круга в С-плоскости, будучи отображенной
по этой формуле обратно в /i-плоскость (серые лошади на рис. 1.1 —
наподобие фигур зодиака), дает запрещенные значения ^, для
которых хотя бы один из корней С,(/^) порождает неустойчивость. Образ
границы единичного круга С = е*^, О < ^ < 27г, называется кривой
локуса корней (геометрическое место граничных значений корней). Ее
следует рассматривать как ориентированную кривую, причем область
устойчивости — если она не пуста — должна лежать слева от нее.
плоскость
плоскость
Рис. 1.1. График функции устойчивости A.8) и кривая локуса корней.
Мы приходим к заключению, что область устойчивости явного
метода Адамса 4-го порядка — это маленькая область, заключенная
между началом координат и точкой ft = 2- 24/(-55 - 59 - 37 - 9) = -0.3
и своей формой напоминающая бриллиант, которую кривая локуса
корней обходит в положительном направлении.
V.l. Устойчивость многошаговых методов 275
Методы Адамса
Явные методы Адамса (III. 1.5) при применении их к уравнению
у' = Ху дают соотношения
^~1 15 3
или, после подстановки у^=(^^ и деления на С"»
C-l = .Go+7.(l-^)+7.(l-^ + ^)+...).
Следовательно, кривая локуса корней определяется формулой
С-1
^=^^
Ej:oSi(i-i/cy
С = е".
A.10')
При к = 1 мы получим метод Эйлера, т.е. кривая локуса корней — это
окружность с центром в — 1. Кривые локуса корней для t = 2,3,..., 6
изображены на рис. 1.2. Они показывают, что облахгти устойчивости
быстро уменьшаются в размере. Таким образом, эти методы заведомо
не подходят для жестких задач.
Рис. 1.2. Области устойчивости явных методов Адамса.
Рис. 1.3. Области устойчивости неявных методов Адамса и их сравнение
с областями устойчивости явных методов Адамса.
276 Гл. V. Многошаговые методы для жестких задач
Неявные методы Адамса (III. 1.8) приводят к соотношению
^ • 11
Подставив в него у^ =A^ и разделив на С^^^, получим:
fi=-T—^—^ , С = е'*. A.11')
При А: = 1 мы получаем неявное правило трапеций, которое является
Л-устойчивым методом. Однако при А = 2,3,..., 6 области
устойчивости хотя и намного больше, чем у явных методов, но они также не
покрывают С"* (см. рис. 1.3). Следовательно, эти методы не
являются Л-устойчивыми.
Схемы предиктор-корректор
«Неадекватность теории, учитывающей влияние
только уравнения корректора в методах
предиктор—корректор, была впервые обнаружена при
экспериментальных расчетах, которые проводились для модельного
линейного уравнения
У = /(^, у) = -ЮОу -f 100, у@) = 0.
(...) Получавшиеся при расчетах погрешности очень
слабо коррелировали с теми, которые ожидались,
исходя из свойств только уравнения корректора. Это и
побудило к развитию теории». (П.Э. Чейс 1962)
Как мы видели в разд. III. 1, классический способ вычисления у^^^
из неявных уравнений (III. 1.9') состоит в использовании t/*^i
(результата применения явного метода Адамса в качестве предиктора) в
члене /?it/(^n+i'2/n+i)- '^Р^ этом существенно ухудшаются свойства
устойчивости метода (Чейс 1962). Анализ устойчивости должен быть
изменен следующим образом. Формулу предиктора
надо подставить в формулу корректора
Уп+1=2/п+/^GоУп+1 +
+ 7Г(у;+1-Уп)+ ^^^^^
-Ь72B/п+1-22/п+Уп-1)+
+ 7з {Уп+1 - Ьп + 32/„-1 - 2/„-2) + •••)•
Поскольку /i входит и в A.12), и в A.13), на этот раз с помощью
подстановки у„ = С'* и деления на С^ мы получим квадратное уравнение
для /i:
Afi^-^Bfi'\'C = 0, A.14)
V.l. Устойчивость многошаговых методов
277
i=0 j=0
к
5=(i-c)E^;+cE^;(i-^)'.
}=0
3=0
С=1-С
При каждом значении С = ^'^ уравнение A.14) имеет два корня, что
порождает две кривые локуса корней, которые и определяют область
устойчивости. Эти кривые представлены на рис. 1.4 для схем РЕСЕ
(см. разделы III. 1, III.7 и III.8) в сравнении с кривыми исходных
неявных методов. Видно, что мы значительно теряем в устойчивости.
В частности, при Л = 1 правило трапеций переходит в явный метод
Рунге—Кутты второго порядка, и Л-устойчивость разрушается.
Чейс A962) исследовал только действительные собственные
значения; общий комплексный случай рассмотрели Крейн и Клопфен-
штайн A965), а также Крюх A966), представивший прекрасные
рисунки. Во всех трех статьях были предприняты также поиски процедур с
расширенными областями устойчивости. Эти исследования довел до
совершенства Штеттер A968).
Методы Нюстрёма
«Итак, мы видим, что с таким простым уравнением, как
у' = — у, у@) = 1, метод Милна не справится...»
(Р.В. Хамминг 1959)
«... Метод Милна имеет ряд достоинств,
отсутствующих у его основного соперника — метода Рунге—
Кутты. Они особенно важны в том случае, когда у
системы уравнений довольно высокий порядок {N от
10 до 30 или более)...» (Р.В. Хамминг 1959)
Рис. 1.4. Облги:ти устойчивости для схем предиктор-корректор (РЕСЕ)
и сравнение их с областями устойчивости исходных неявных методов.
278 Гл. V. Многошаговые методы для жестких задач
Явный метод Нюстрёма (III. 1.13) при к = I и 2 — это «явное
правило средней точки»
Уп+1 = Уп-1 + 2/1Д. A.15)
Ему соответствует кривая локуса корней, которая определяется
формулой
A.15')
/i= = isin(
Точки этой кривой лежат на мнимой оси между ±i, кривая
пробегает интервал (—t, -fг) вверх и вниз и оставляет в качестве области
устойчивости как раз этот интервал (см. рис. 1.5). Наличие любых
собственных значений внутри отрицательной полуплоскости
приводит к неустойчивости. Причина состоит в том, что второй корень
(— 1) многочлена р(С) выходит из единичного круга, если ^
сдвигается «на запад». Это примечательное явление, которое называют
«слабой неустойчивостью» правила средней точки, послужило отправной
точкой «карьеры» Далквиста в теории устойчивости (Далквист 1951).
Графики на рис. III.9.2 ярко демонстрируют (слабую) неустойчивость
численного решения.
Нюстрём, А: = 2 Нюстрём, А; = 4 Милн, /: = 3 Милн, /: = 6
..I.
Рис. 1.5. Кривые локуса корней для методов Нюстрёма и Милна.
Неявный метод Милна—Симпсона (III.1.15) при fc = 2 и 3 имеет
вид
2/„+1 = У„_1 + /^ (з-^п+1 + з-^п + 3-^n-i) •
Его кривая локуса корней
f" ie'O + l + ie-"
тт = 3»
cose + 2
A.16)
A.16')
V.l. Устойчивость многошаговых методов
279
пробегает вверх и вниз по мнимой оси интервал между ±iV3.
Следовательно, этот метод ведет себя подобно явному методу Нюстрёма,
только интервал устойчивости у него немного больше.
У методов Нюстрёма и Милна—Симпсона более высокого порядка
при обходе кривых локуса корней их ориентация оказывается
неправильной (см. рис. 1.5), так что их области устойчивости сокращаются
до наименьшего возможного (для устойчивых методов) множества,
состоящего только из начала координат.
Методы ФДН
Формулы дифференцирования назад ^j-i j^^Vn-^i = ^/n+i (^^•
том I, (III.1.22')) имеют кривые локуса корней, которые определяются
уравнением
= Е70-^-")'
A.17)
(см. рис. 1.6). При Аг = 1 мы имеем неявный метод Эйлера с областью
устойчивости S={fi\ Ia*—1|>1}. При к = 2 оказывается, что
величина Re(/i) = | —2cos^H- ^ cos 26 для кривой локуса корней
неотрицательна при любых значениях в. Следовательно, этот метод является
Л-устойчивым и имеет второй порядок. Однако, при fc = 3,4,5 и б
методы ФДН, как мы видим, все больше и больше теряют
устойчивость на части мнимой оси. При к>7 методы ФДН, как известно,
неустойчивы всюду, даже в начгипе координат.
__
si ^.,^^^
'¦ ¦^' '{^/Щш^
....1.1
Ш ^ J
l^^^ns
ЁгШщ
1 5
.... 1 .
5
Рис. 1.6. кривые локуса корней и области устойчивости методов ФДН.
280 Гл. V. Многошаговые методы для жестких задач
Второй барьер Далквиста
¦я долго вел поиски, пока, наконец, профессор Лаке
не показал мне теорему Рисса—Херглотца, и я понял,
что получил свою теорему». (Г. Далквист 1979)
Теорема 1.3. Если многошаговый метод A.1) А-устойчив, то
Re(^^)>0 при |С|>1. A.18)
Для неприводимых методов верно также и обратное: из A.18) следует
А -устойчивость.
Доказательство, Если метод А-устойчив, то все корни уравнения
A.6) должны удовлетворять неравенству |С| < 1 всякий раз, когда
Re /i < О. Логически эквивалентное утверждение (Re /i > О всякий раз,
когда ICI > 1) приводит к соотношению A.18), поскольку /i = /?(C)/<^(C)
в силу A.6).
Теперь предположим, что выполняется A.18) и метод является
неприводимым. Фиксируем fi = fiQ такое, что Re^o ^ О' ^ пусть Со
— корень уравнения A.6). Тогда сг{(^) ^ О (в противном случае
метод был бы приводимым). Итак, /Xq = р(Со)/^(Со) и из A.18) следует,
^то iCol ^ 1- Надо еще показать, что при |Со1 = 1 корень Со
является простым. Из A.18) по соображениям непрерывности следует, что
условия |Со1= 1 и Re/iQ <0 несовместимы. Поэтому остается
показать, что при RefiQ=:0 корень, удовлетворяющий условию |Со| = 1,
должен быть простым. В окрестности такого корня
а из A.18) следует, что С^фО. Однако такое возможно только в том
случае, если Со — простой корень уравнения A.6). П
Во всех предыдущих примерах мы не встретили ни одной
Л-устойчивой многошаговой формулы порядка р > 3. Объяснение этому
наблюдению дает следующая знаменитая
Теорема 1.4 (Далквист 1963). Любой А-устойчивый
многошаговый метод должен иметь порядок р < 2. Если порядок равен 2, то
константа погрешности удовлетворяет неравенству
Правило трапеций — это единственный А-устойчивый метод второго
порядка с константой погрешности С = —1/12,
Доказательство. Первое доказательство этой теоремы,
принадлежащее Далквисту, было сложным. Более простые варианты
появились в работе Видлунда A967), в записях лекций В. Линигера
(университет Нёшатель, 1971) и в книге (Григориефф 1977), vol.2, р.218.
V.l. Устойчивость многошаговых методов 281
Сначала напомним некоторые формулы из тома I. Формула (ii) в
теореме III.2.4 и формула (III.2.7) дают
p{e^)-h(T(e^)=:Cj,^^hP'^^-\-... при Л-^О. A.20)
Из условий согласованности (III.2.6) следует, что
;г,(е'*) = рA +/ц-...) = рA) 4-/(l)/i + ... = сгA)/1 + ....
Разделив A.20) на hp{e^), получим:
где С — константа погрешности (III.2.13). Если положить С = е'*,
это соотношение примет вид:
Возьмем в этой формуле р = 2. Если метод имеет более высокий
порядок, то С = 0. Для метода первого порядка доказывать нечего. Для
правила трапеций, у которого Ру(С) = С "" 1 > ^'^^(С) = |(С + 1) > та же
формула, полученная с помощью разложения в ряд (или с помощью
табл. III.2.1), принимает вид
А теперь вычтем из одной формулы другую и придем к равенству
Согласно A.18)
Re (-777 ) > О или, что равносильно. Re ( -777 ) > О при |С| > 1-
\G(С)/ ^P(Q^
A.25)
Решающим для нашего доказательства здесь является то
обстоятельство, что для правила трапеций эта величина Re(...) равна нулю
при ICI = 1, поскольку область устойчивости этого метода в точности
совпадает с С~ . Следовательно, из A.24) мы получим:
limRecf(C)>0 при |Со1 = 1. A26)
1С1>1
Полюса функции d(Q являются корнями p(Q, которые в силу
устойчивости не могут находиться вне единичного круга. Таким образом,
согласно принципу максимума соотношение A.26) остается
справедливым всюду вне единичного круга. Тогда, выбирая в A.24) С= 1+^,
где Re е > О и \е\ мал, мы видим, что либо —С — п -^ ^' «^^бо d(Q = О,
что и завершает доказательство. П
282 Гл. V. Многошаговые методы для жестких задач
Упралснения
1. При А = 4 и 5 методы Милна—Симпсона удовлетворяют
неравенству Re(p(C)/cr(C)) > О при 1^1 = 1. Поскольку их порядок выше
второго, это представляется противоречащим приведенному
доказательству теоремы 1.4. Дайте объяснение этому факту.
2. Ответьте на следующий вопрос: принадлежат ли множеству 5
конечные точки ±г области устойчивости для явного правила
средней точки A.15)? Исследуйте (возможную) устойчивость этого
метода при его применении с длиной шага Л = 1 к системе и' = v,
3. Для явных и неявных методов Адамса найдите наибольшее Ад G М
такое, что действительный отрезок [—Ао,0] принадлежит S.
Покажите, что для fc-шаговых явных методов Адамса Aq = 2/^;^,
где u^^Yl'jll'^hj (tii = l, ti2 = 2, ^3 = 11/3, «4 = 20/3, и^ =
= 551/45,...). С помощью производящих функций (см. разд. П1.1)
можно показать, что ряд
f„,,*=(_l + _l___l_)bg(l-20
имеет радиус сходимости 1/2. Это объясняет, почему области
сходимости уменьшаются так быстро.
Указание. Подставьте в = ж ъ формулу кривой локуса корней.
4. Докажите, что области устойчивости fc-шаговых неявных методов
Адамса имеют конечный размер при любом к>2.
Указание. Покажите, что (—1)'^(г(—1) <0 и, таким образом, а
имеет действительный отрицательный корень, меньший чем —1.
5. Покажите, что
a) все двухшаговые методы 2-го порядка задаются многочленами
Ж) = (С-1)К + 1-а),
'^(C) = (C-l)V + (C-l)a + (C + l)/2
(неприводимыми при а ^ 2/?);
b) такой метод устойчив в нуле, если и только если а > 1/2;
c) метод устойчив в ос тогда и только тогда, когда
а>1/2 и /?>а/2 A.27)
(примените критерий Шура—Кона из разд.П1.3, упр. 4);
d) метод Л-устойчив тогда и только тогда, когда выполнены
неравенства A.27).
Указание.
?@^1 i±l,tQ_^^ С-1
Ж) 2 С-1^ "i' аС+1-а'
V.2. «Почти» А-устойчивые
многошаговые методы
«Мы не пытаемся опровергнуть теоремы Далквиста, мы
стараемся обойти налагаемые ими условия...»
(Дж. Каш 1979)
Условие Далквиста р< 2, налагаемое на порядок Л-устойчивого
линейного многошагового метода, является серьезным ограничением
эффективных практических расчетов с высокой точностью.
Преодолеть этот барьер можно только двумя способами:
• либо ослабить условие,
• либо усилить метод.
На этих двух возможностях мы и сосредоточим наше внимание в этом
и следующем разделах.
Л(а)-устойчивость и лсесткая устойчивость
«Цель данной заметки — показать, что несколько иное
требование устойчивости допускает методы более
высокой точности». (О. Видлунд 1967)
«Угол а — это лишь один из ряда параметров,
предложенных для измерения протяженности области
устойчивости. Но он является, вероятно, наилучшей мерой...»
(Скил и Конг 1977)
Многие важные классы практических задач не требуют
устойчивости во всей левой полуплоскости С~ . Помимо этого, собственным
значениям на мнимой оси часто соответствуют сильно
осциллирующие решения, и тогда все равно приходится ограничивать длину шага
сообразно «с наивысшей из присутствующих частот, чтобы получить
правильное представление сигнала» (Гир 1971, р. 214).
Определение 2.1 (Видлунд 1967). Сходящийся линейный
многошаговый метод называют А{а) -устойчивым, О < а < 7г/2, если
5 D 5„ = {/i ; Iarg(-/i)| <а, fi^ 0). B.1)
Метод >1@)-устойчив, если он Л (а)-устойчив для некоторого
(достаточно малого) а > О.
Аналогично, Гир A971) в своем знаменитом определении
«жесткой устойчивости» потребовал, чтобы
SD{^i\ Re/i<-D} B.2)
при некотором D > О и чтобы метод был «точным» в прямоугольнике
— D<Re//<a, —в<\т^л<в при некотором а > О и в, близком к
7г/5. В данном определении многим не понравился неточный смысл
284 Гл. V. Многошаговые методы для жестких задач
слова «точный», и некоторые авторы впоследствии заменили его
другими требованиями. Например, Йелч A976) в дополнение к B.2) ввел
требование:
lCi(/i)l>ICHI, i = 2,...,/: при |Re/i|<a, |Im/i|<6, B.3)
где Ci(a*) — аналитическое продолжение главного корня ((^^@) = 1)
уравнения A.6). Кроме того, прямоугольник
|Im/i|<e, -DKRefiK-a
должен принадлежать 5.
Были предложены и другие идеи: метод Лд-устойчив, если
|СЛаг)|<1, г=1,...,Аг при -оо<х<0 B.4)
(Крайер 1973); метод Л-устойнив (шутка О.Неванлинны 1979), если
(~оо,0]с5. B.5)
Очевидно, что
Л@)-устойчивость => Лр-устойчивость => >{-устойчивость, B.6)
но ни одна импликация здесь не является обратимой (упр. 3; см.
также «Теорему 1» в работе Йелча 1976).
ФДН-методы (III.1.22*) удовлетворяют условию B.1) Л(а)-устой-
чивости и условию B.2) жесткой устойчивости при следующих
значениях параметров:
B.7)
Л(а)-устойчивые методы высоких порядков
«Дилл и Гир ..., а также Джейн и Сривастава ...
использовали компьютеры для построения жестко
устойчивых методов восьмого и одиннадцатого порядков
соответственно, но не сумели построить такие методы более
высоких порядков. Хотя мы и показали здесь, что
существуют Л о-устойчивые методы сколь угодно
высокого порядка, но есть подозрение, что не существует Л{0)-
устойчивых линейных многошаговых методов высших
порядков, скажем, больше двадцатого». (Крайер 1973)
Видлунд A967) показал, что для любого а < 7г/2, сколь угодно
близкого к 7г/2, существуют Л (а)-устойчивые многошаговые методы
порядка р=к при р = 3 и р=4. Возникает интересный вопрос:
существуют ли такие методы более высоких порядков? Ответ состоит
из новостей хороших и плохих.
к
а
D
1
90»
0
2
90»
0
3
86.03»
0.083
4
73.35»
0.667
5
51.84»
2.327
6
17.84»
6.075
V.2. «Почти» Л-устойчивые многошаговые методы 285
Начнем с хорошей новости. Предположение Крайера (см. цитату)
было вскоре опровергнуто с помощью комбинации Ло-устойчивых
методов Крайера с результатом Йелча A976), согласно которому
некоторые Л о-устойчивые методы являются также и Л (а)-устойчивыми.
Следующая теорема показывает, что можно даже выбрать а сколь
угодно близким к 7г/2.
Теорема 2.2 (Григориефф и Шролль 1978). Пусть задано а < 7г/2.
Тогда для любого к EN существует А(а)-устойчивый линейный
к-шаговый метод порядка р=: к.
Доказательство. Для р = к = 2 вопрос решает двухшаговый
метод ФДН, который является Л-устойчивым, а, следовательно, и
Л (аз)-устойчивым при любом aj < 7г/2. Для случая произвольного
к вставим к — 2 величины между а и 7г/2:
а < а;,_1 < а;,_2 < • • • < о^з < ^^2 < 2 (^'^^
и с помощью леммы 2.3 шаг за шагом расширим метод. П
Лемма 2.3. Пусть задан А(а)-устойчивый к-шаговый метод
порядка р, у которого
р(С)#0, если |С|=1, С 7^1, B.9а)
G@^^0, если |С|=1. B.9Ь)
Тогда для любого а < а существует А{а)-устойчивый
(АгН-1)-шаговый метод порядка р+ 1, который также удовлетворяет B.9).
Доказательство во многом повторяет ход рассуждений Йелча
и Неванлинны A982). Пусть p{Q и a{Q представляют заданный
А:-шаговый метод с условием порядка
^-«r(C) = Cp+i(C-l)'' + 0((C-ir'). B.10)
Умножив р и сг на (С - 1), мы формально увеличим порядок на
единицу и в то же время оставим кривую локуса корней без изменений.
Кажется, что этим все докг^зано. Однако новый р-многочлен будет
иметь двукратный корень при С = 1 и тем самым должен породить
неустойчивый метод. Поэтому выберем ? > О и умножим B.10) на
(С — l + e), при этом корень немного сдвинется внутрь единичного
круга. Тогда мы получим новый метод порядка p-f 1, если определим его
производящие многочлены следующим образом:
Ж) = Ж)(С-1+е),
5@ = <^(C)(C-H-e) + ?Cp^i(C-l)''. ^ ¦ '
Поскольку случай р = Аг-|-2 исключается (по теореме П1.3.9,
методы с р = /: -f 2 являются симметричными и нарушают предположение
286
Гл. V. Многошаговые методы для жестких задач
B.9а)), оба многочлена р и ? имеют степень, не превышающую к-\-1.
Далее, формула
Ж) Ж) Ж)(С-1+?)
B.12)
позволяет сравнить при малых е кривые локуса корней для этих двух
методов. Тот факт, что мы работаем с величиной G(е*^)/р(е*^) = l//i
вместо fi = р(е^^)/(т{е^^), не имеет значения, поскольку
преобразование /i •-> l//i отображает сектор из определения 2.1 на себя.
Согласно предположению B.9а) единица является единственным (простым)
корнем многочлена p(Q на единичной окружности, а поэтому
5(C) <т{0
т pio
< Се
|С-1|р-1
при С = ^
-je
B.13)
IC-i+f|
Лишь небольшое препятствие отделяет нас от «endless pleasure, endless
love, Semele enjoys above» ^), a именно, знаменатель |C — 1+6^1,
становящийся малым при 6—^0 и ^ —>^О. При р> 1 этот «малый» знаменатель
просто уравновешивается одним из множителей IC— 1| в числителе, и
мы получаем соотношение
то <г(С)|
т pio
< Се,
B.14)
которое означает равномерную поточечную сходимость ?(С)/р(С) к
<t(Q/p(Q при е-Ч'О. Поскольку величина a(Q/p{Q отделена от
начала координат в силу предположения B.9Ь), это также означает
равномерную сходимость углов.
Полученного результата уже достаточно для доказательства
теоремы 2.2, в которой всегда р > 2. Однако лемма 2.3 остается
справедливой и при р = 1. Критическая область имеется при ^ —> О, в этом
случае |^(е*^)/р(е»^)| и |?(е*^)/р(е»^)| стремятся к бесконечности как
Const/в. Вместо B.14) при р= 1 мы имеем
5(C) <т(С)
т />(с)
<
Се
1С-1+е|
= <)¦
Таким образом, угол между ?(С)/р(С) и (t(Q/p{Q (наблюдаемый из
начала координат) имеет порядок величины 0(e). П
Приблилсение методов низкого порядка
методами высокого порядка
Изложенное выше доказательство леммы 2.3 в действительности
показывает больше, чем ограниченность по углу кривой локуса кор-
' Желанной цели. — Прим. ред.
V.2. * Почти» Л-устойчивые многошаговые методы 287
ней, а именно, равномерную сходимость этой кривой для метода
высокого порядка к кривой метода более низкого порядка. Этот результат
приводит к следующей теореме Йелча и Неванлинны A982).
Теорема 2.4. Пусть имеется линейный устойчивый к-шаговый
метод порядка р с областью устойчивости S, удовлетворяющий
условию B.9а). Тогда для любого замкнутого множества П С Int 5 С С я
любого натурального К существует линейный (к -\- К)-шаговый
метод порядка р-\- К у область устойчивости S которого удовлетворяет
условию
Кроме того, если первый метод явный, то и метод более высокого
порядка тоже явный.
Доказательство похоже на доказательство леммы 2.3. Вместо
последовательности B.8) используется последовательность замкнутых
и открытых подмножеств, вложенных друг в друга между Q и S
(лемма Урысона). Предположение B.9Ь) исключается посредством
перехода к кoмJlaктифициpoвaннoй топологии замкнутой
комплексной плоскости С = Си{оо}. П
Замечание. Ни один имеющий практическую значимость метод с
непустым множеством Int5 не нарушает предположения B.9а). Тем
не менее, теорема 2.4 остается справедливой и без этого условия, но
тогда доказательство усложняется (см. Лемму 3.6 в работе Йелча и
Неванлинны A982)).
Теорема о диске
Другой способ ослабить требование Л-устойчивости состоит в том,
чтобы потребовать устойчивость в области
D, = {/i; |/i + r|<r}, B.15)
которая представляет собой круг («диск») радиуса г, лежащий в С"
и касающийся мнимой оси в начале координат. Для малых по модулю
собственных значений теоремы об устойчивости в D^ являются более
сильными, чем теоремы об Л (а)-устойчивости. Следующий результат
снова принадлежит Йелчу и Неванлинне A982).
Теорема 2.5. Пусть имеется линейный к-шаговый метод порядка
р с областью устойчивости S D D^ . Тогда для любого г<г и любого
К G N существует линейный (k-h К) -шаговый метод порядка р-\- К,
у которого область устойчивости S удовлетворяет условию S D D-^ .
Доказательство. Использованное в доказательстве леммы 2.3
отображение ^»-> l//i отображает внешность D^ на полуплоскость
{/i€C; Re/i>-^}. B.16)
288 Гл. V. Многошаговые методы для жестких задач
Поэтому равномерная сходимость, установленная в B.14),
распространяется также и на новую ситуацию, если р > 1. Однако случай
р= 1 требует более тщательного изучения, и здесь мы отошлем
читателя к оригинальной работе Йелча и Неванлинны A982, pp. 277-279).
а
Барьеры точности
для линейных многошаговых методов
Теперь перейдем к «плохим новостям»: >1(а)-устойчивые методы
высокого порядка при а, близких к 7г/2, не могут иметь
практического применения, или, иными словами, «нельзя разрушить второй
барьер Далквиста». Причина просто в том, что один лишь высокий
порядок не достаточен для высокой точности, поскольку тогда
методы имеют огромные константы погрешности. Йелч и Неванлинна
дают впечатляющее «стаккато» (от "теоремы 4.1" до "леммы 4.15" в
их работе) оценок снизу для констант погрешности и ядер Пеано
методов с большими областями устойчивости. Ядра Пеано — наиболее
серьезная мера погрешности — определяются формулами
/оо
Kg(-s)y^''+^\x + sh)ds= B.17)
¦ОО
к
=^T.{c^jy{^'^Jh)-hpjy'(x + jh)) B.18)
i=o
(см. том I, формулы (П1.2.15) и (П1.2.3)). Ядра K^(—s) = Kq{s) равны
нулю вне отрезка О < 5 < Аг и являются кусочно полиномиальными
функциями, заданными с помощью сложных формул (см. AП.2.16)),
которые выглядят не слишком привлекательно для работы с ними.
Однако формулы упрощаются, если использовать преобразование
Фурье J которое для функции f{x) определяется следующим образом:
т = /~ e-"^f(x)dx. B.19)
J — ОО
Чтобы получить преобразование Фурье L для B.17), надо подставить
определения, проинтегрировать по частям несколько раз и
преобразовать двойные интегралы. Тогда мы получим
1@ = Л'+'^,(ЛО • У^'ЧО = B.20)
=й^тт)''^'Ш), B.21)
а из B.18) получим
1@ = (р(е'''«) - iH<T{e">()) ¦ у{0- B.22)
Итак, B.20) и B.22) дают приятную формулу
^,(-0 = ^,@ = (Р(е'*) -«^ог(е'«))(гО-^'+^\ B.23)
V.2. 4сПочти» Л-устойчивые многошаговые методы 289
содержащую многочлены р и (Т, с которыми мы лучше знакомы.
Что же можно сказать о пользе К для оценок погрешности?
Равенство Парсеваля
11/1к^(-ос,оо) = ^ Шщ-с^.с) B-24)
(упр. 4) позволяет получить оценку погрешности в L^-норме
UWlh-oo.oo) < h"^'l|/^,IL- • У'^'Чь^ B.25)
как результат следующих преобразований:
2(-оо,оо) - 2^ ll^llL2(_oo,oo)
m\U-«.oo) = 7Г- l|i^lli.(-co,co) = (из B.24))
= -^7- / |Л',@| |У<'+'МО| «^^ < (из B.20))
1^,@1'- /~ \y^'40fd^= (оценка)
J -оо
Л2д+2
< —т— max
"¦ 27Г
/,2g+2 -^ -—.
= -2^ l|A',||i» • ||y('+i)|li, = (определения)
= h'^^'WK, Hi- • ||y('+^^||^. (из B.23), B.24))
Чтобы полученная оценка B.25) для L выражгипа фактическую
погрешность численного решения, примем в данном разделе
нормировку GA) = 1 (ср. с формулой (III.2.13)).
Приведем теперь теорему о том, что линейные многошаговые
методы порядка р > 2 с «большой» областью устойчивости не могут быть
точными.
Теорема 2.6 (Йелч и Неванлинна 1982). Рассмотрим к-шаговые
методы порядка р> 2 с нормировкой сгA) =. 1, для которых круг D^
B.15) принадлежит области устойчивости S. Тогда существует
постоянная С > О (зависящая от k^p.q, но не зависящая от г) такая^
что преобразование Фурье ядра Пеано К^ (д < р) удовлетворяет
неравенству
\\К\\оо>с{1У~'. B.26)
Доказательство Йелча и Неванлинны состоит из двух шагов,
а) Требование устойчивости вынуждает некоторые коэффициенты а^
многочлена R(z) быть большими (см. ниже лемму 2.7). Здесь, как
и в (III.3.17),
«w = (?)'K^) = Ev^ ("')
290 Гл. V. Многошаговые методы для жестких задач
к
^"> = (^) ЧЙ)=Е'.'^ («*)
Ь) ll-^'^^nlLoo ограничена снизу величиной max-а- (см. лемму 2.8).
Лемма 2.7. Если D^ С S и р>2, то
«fe-i>(9'''«*-i = @'''-2'-* для j = 2,...,p-l. B.29)
Доказательство. Устойчивость в D^, означает, что при fiE D^. все
корни уравнения р(С) - /^^(С) = О лежат в круге |С| < 1 •
Следовательно,
Ж)МС)^Я при |С|>1. B.30)
Применив «греко-латинское» преобразование (" = (г -f l)/(z - 1) и
учитывая B.16), мы увидим, что это означает следующее:
Re--^>-— при Re2:>0, B.31)
R(z) 2r
или
Ке^-Щ±^>0 при Re.>0. B.32)
Далее мы должны рассмотреть условия порядка (лемма HI.3.7 и
упр. 9 из разд. П1.3)
Эта формула показывает, что R{z) = 0(z^'^^), S(z) = 0{z^), ио 2S(z) —
—zR{z) = 0(z^^~^). Поэтому мы вычтем rz из неравенства B.32),
чтобы понизить степень числителя. Получаемая в результате функция
снова удовлетворяет соотношению
Re гB3(г)-.т)^Е(г) ^ ^ ,^, ^,^, B.34)
В силу равенства Re (rz) = О при z = iy и принципа максимума (это
похоже на рассуждение из леммы IV.5.21). Таким образом,
функция B.34) не может иметь нулей в С+ (поскольку согласно
разложению в ряд Тейлора все аргументы функции оказываются в
комплексной окрестности нуля). Поэтому числитель в B.34) должен иметь
неотрицательные коэффициенты (сравните с доказательством леммы
III.3.6). Перемножая B.33) и B.34), мы получим для коэффициента
при z^-J и <р— 1) следующее неравенство:
/1 4 \
О < r\^--ak_j^^ - — a,^^j^^ -...)-? af,^j,
V.2. «Почти» Л-устойчивые многошаговые методы
291
которое упрощается к виду
г
(ср. леммы III.3.8 и III.3.6). Используя равенства а,^_^ = 2^-^р^A) =
= 2^"^^ (см. лемму III.3.6), мы придем к утверждению B.29). П
Лемма 2.8. Существует постоянная С > О (зависящая от к,р и q,
где ^ = 0,1,..., рj такая, что если О G 5, то
U^IIloo > Cmaxaj.
B.35)
Доказательство. В формуле B.23) положим е*^ = С) ^ = —«bgC
с тем, чтобы максимум надо было брать по множеству |С| = 1 • Затем
сделаем преобразование ( = {z+ l)/{z — I) и возьмем максимум по
мнимой оси. С учетом B.27) и B.28) мы придем к формуле
\\К\\
gilL«>
: sup
t
R{
(i04iog
i-H)ll(a) ||'4i^)
-Я
Ф(<)
Ф@
B.36)
Теперь, подставив сюда при \t\ > 1 выражения (III.3.19), (III.3.21) и
(III.3.22), получим
где Pj^ — определяемый методом многочлен степени к и подстепени
р (см. лемму III.3.7). Поскольку мы хотим, чтобы наши оценки
были справедливы для всех методов, будем считать Pf^ произвольным
многочленом. Отделив действительную и мнимую части и подставив
1/< = S, получим
|Ф(<I' =\Qk-iis) + drs'-"' - ^3^*+' + - ... |Ч B.38)
+ \Qk{s) + d^s'^' - d.s'^' + - ... 1^ = \ФМ' + \bit)\\
где Qf^_i(s) и Qk(s) — произвольные (четные или нечетные)
многочлены степеней к—1 и к соответственно и подстепени р. Оба члена
оцениваются снизу по отдельности. Например, для первого из них
запишем неравенство
l^i(OI > IQfc-i(s) + d^+'l- Id^s'^^ -d5S*+5 + - ... |. B.39)
Поскольку /ij < ^3 < /ig < ... < 0 (cm. ниже упр. 6) и a,- > О, из (III.3.22)
получим
di<d^<d^<...<0 и ^2 < с?4 < ^б < • • • < 0. B.40)
292 Гл. V. Многошаговые методы для жестких задач
Поэтому второй член в B.39) оценивается сверху аргументом
знакопеременного ряда при О < 5 < 1:
Поскольку Q;j__i(s) — произвольный многочлен, его можно заменить
на \di\Qf^_i(s), так что величина |c/J станет общим множителем всего
выражения:
|*iW|>Kl(|Qfc-iW + *''+'|-«*"'')- B-41)
Это наводит на мысль определить константы
B.42)
где inf взят по всем многочленам Qfe~i(^) — ^/c-i^'^"^ "^^А:-з^'^"'^+
+^Л-5^'^"^ + - • • ^ Qki^)^^k^^ '^^к-2^^'~^'^^к-4^^~^'^ - ' ' СООТВеТСТВСН-
но, младшие члены которых имеют степень р. Два последних
множителя представляют Ф(^) из B.36). Поскольку при малых s величина
5*+^ превосходит 5^^+^, Dj и D2 являются положительными
константами (см. упр. 8). Тогда из B.38) и B.36) получим оценку
llA'JLoo > ^Jd\D\ + dlDl B.43)
Так как обе величины d^ и dj являются суммами а • с
отрицательными коэффициентами (см. (III.3.22) и лемму III.3.8), то ЦА^дЦ^^о должна
быть большой, если велик один из коэффициентов а-. П
Этим завершается доказательство теоремы 2.6, которое, кстати,
еще раз доказывает и теорему 1.4. П
Упражнения
1. Покажите, что не существует Л@)-устойчивых явных методов.
2. Покажите, что условие Р^/ос^^ > О является необходимым для
Л (а)-устойчивости линейного fc-шагового метода.
3. а) Покажите, что метод
2/п+2 "~2/п + 1 ~ ^v/n+2 "^/n+l +/n)
имеет область устойчивости, ограниченную параболой. Поэтому
он Ло-устойчив, но не является Л@)-устойчивым (Крайер 1973).
V.2. «Почти» Л-устойчивые многошаговые методы 293
Ь) Найдите «деформированную» схему ФДН 5-го порядка
5 J
с коэффициентом /?;^0.232 ..., которая будет Л-устойчивой, но не
будет Лд-устойчивой.
с) Найдите метод, который Лд-устойчив, но не устойчив на
бесконечности.
Указание к (с). «Lift up your heads, о ye gates.. .»^) Если вы
поднимете глаза (не к небесам, а всего на несколько строк выше), то
легко найдете ответ.
4. (Парсеваль 1799.) Докажите тождество B.24).
Указание. Подставьте определения в интеграл
/оо
•со
чтобы получить тройной интеграл. Два интеграла исчезнут при
использовании формулы обратного преобразования Фурье.
Замечание. Вас может удивить, что тождество Парсеваля старше,
чем ряды Фурье и преобразование Фурье. Дело в том, что
первоначально это тождество связывало бесконечную сумму и интеграл, а
позднее ему дали новую интерпретацию и обобщили, в результате
чего оно приняло современный вид.
5. Подставьте ^ = тг в формулу B.23), и вы легко получите оценку
снизу для ЦА' Ц^оо . Затем для методов, определенных в
доказательстве леммы 2.3 (с нормировкой <7A) = 1), вычислите значение
сг(—1) при малых е. Этим будет показано, что К становится
очень большим.
6. Используйте формулу
(см. доказательство леммы П1.3.8), чтобы показать, что /ii > /^з >
>/i5>...>0. ^
7. Покажите, что уравнение B.23) примет вид А'р(О) = C^^^i, если в
нем положить q = р, подставить i^ = h и использовать формулу
A.20) при h—yO. Здесь C^i является константой погрешности
(при<тA) = 1).
' «Поднимите ваши головы: о, врата...» — Англ.
294
Гл. V. Многошаговые методы для жестких задач
Тогда формула B.36) при р= к и < -> со дает оценку снизу для
константы погрешности (см. теорему 4.5 в работе Йелча и Неван-
линны A982)).
При р= k-^-l многочлены Qf^^i и Qf^ из B.42) тождественно
равны нулю, поскольку подстепень должна быть равна р. Вычислите
константы D^ и ?>2 для этого случая. Их легко вычислить также
и при р = А: — 1. В общем случае оптимальное решение
удовлетворяет условию типа «чебышевской альтернативы».
Ответы.
Случай р = к+1 (C = 0):
Di
g = 0
9=1
9 = 2
9 = 3
9 = 4
9 = 5
9 = 6
р = 3 р = 4 р = 5 р = 6
к = 2 к = 3 к = 4 к=:5
0.4742 0.5695 0.7020 0.8813
0.3876 0.4435 0.5298 0.6505
0.3524 0.3659 0.4152 0.4933
0.5000 0.3381 0.3459 0.3891
0.5000 0.3251 0.3275
0.5000 0.3131
0.5000
D2
q = 0
q=l
q = 2
q = 3
q = 4
q = b
q = 6
p = 3 p = 4 p=:5 p = 6
fc = 2 k = 3 k = 4 k = 5
0.3607 0.4501 0.5706 0.7319
0.2754 0.3347 0.4163 0.5263
0.2205 0.2570 0.3108 0.3852
0.1935 0.2075 0.2400 0.2888
0.1849 0.1956 0.2244
0.1770 0.1845
0.1698
Случай p = fc — 1 (в Q имеется одна свободная константа):
Di
q = 0
q = l
q = 2
q = 3
q = 4
q = 5
q = 6
p=:3 p = 4 p = 5 p = 6
k = 4 k = 5 k = e k = 7
0.0511 0.0362 0.0262 0.0193
0.0727 0.0499 0.0353 0.0256
0.1100 0.0709 0.0486 0.0344
0.2031 0.1070 0.0691 0.0474
0.1962 0.1041 0.0673
0.1894 0.1012
0.1828
D2
q = 0
q=l
q=2
q = 3
q = 4
(/ = 5
q = e
p = 3 p = 4 p = 5 p = 6
k=:4 k = 5 k = 6 k = 7
0.0195 0.0142 0.0104 0.0077
0.0269 0.0191 0.0138 0.0101
0.0384 0.0263 0.0186 0.0135
0.0583 0.0374 0.0256 0.0181
0.0567 0.0365 0.0250
0.0552 0.0356
0.0537
Случай p = A: — 3 (в Q имеются две свободные константы):
Di
q = 0
q=l
q = 2
q = 3
q = 4
q = 5
q = e
p = 3 p = 4 p = 5 p=:6
k = e k = 7 k = S k = 9
0.0030 0.0014 0.0007 0.0003
0.0066 0.0029 0.0014 0.0007
0.0160 0.0066 0.0029 0.0014
0.0457 0.0158 0.0065 0.0029
0.0448 0.0156 0.0064
0.0439 0.0154
0.0431
?»2
9 = 0
9=1
9 = 2
9 = 3
9 = 4
9 = 5
9 = 6
p=z3 p = 4 p = 5 p = 6
k = e k = 7 k = S k = 9
0.0007 0,0004 0.0002 0.0001
0.0015 0.0007 0.0003 0.0002
0.0034 0.0015 0.0007 0.0003
0.0082 0.0034 0.0015 0.0007
0.0081 0.0033 0.0015
0.0080 0.0033
0.0079
V.3. Обобщенные многошаговые методы
« Ограничение Дгшквиста на порядок Л-устойчивых
многошаговых методов, который не может быть выше
второго, стало императивом к выдвижению ... более слабых
свойств устойшсвости. ... Альтернативный способ
обойти ограничение Далквиста состоит в том, чтобы изменить
не свойство, а класс методов».
(Т.А. Биккарт и У.Б. Рубин 1974)
Поиск Л-устойчивых многошаговых методов более высокого
порядка ведется по двум основным направлениям:
¦ использование высших производных от решений;
• включение дополнительных этапов, промежуточных и
опережающих точек и другие подобные изменения, ведущие в широкую
область общих линейных методов.
Многошаговые методы Энрайта
со второй производной
«Формулы Эрмита заново открываются и публикуются
каждые четыре года». (П.Дж. Дейвис 1963)
Дифференцирование по х дифференциального уравнения
у' = /(х,у) C.1)
дает вторую производную решения
y" = h+fyf=-9(x,y), C.2)
которую мы обозначим через д. Теперь прямое обобщение как
многошаговых формул A.1), так и, например, метода рядов Тейлора (см.
A.8.13))
Уп+1=Уп + ^/п+2^9п
можно записать в виде
к к к
1 = 0 1=0 1=0
где Q,, /?,, 7f — параметры, которые должны быть выбраны
подходящим образом. Большая часть теории линейных многошаговых
методов (разд. III.2) может быть обобщена на этот случай без затруд-
296 Гл. V. Многошаговые методы для жестких задач
нений. Разложение в ряд Тейлора, подобное (III.2.5), показывает, что
метод C.3) имеет порядок р тогда и только тогда, когда
к к к
^a,t^=<,^^,,'-49(?-l)X^7,i'-^ C.4)
t=0 i=0 t=0
при о < g < p. Первые две из этих формул совпадают с (III.2.6), т.е.
они дают
рA) = 0, р'{1) = <гA). C.5)
Формула для константы погрешности имеет вид
к к к
(cm. формулу (III.2.13) и упр. 2 в разд.III.4). При поиске хорошего
набора свободных параметров а,-, /?,, 7i Энрайт A974) исходил из
следующих соображений:
(i) положим а^^ = 1, а^^_1 = -~1, а^^_2 = ... = ао = 0, чтобы обеспечить
приемлемую устойчивость в окрестности начала координат, как в
стандартных формулах Адамса;
(ii) положим 7л ?^ О J 7;^-1 = • • = 7о ^ О, чтобы обеспечить устойчивость
на бесконечности, как в формулах ФДН;
(iii) определим оставшиеся к-\-2 коэффициента 7/?, 0^, /?fc-i, • •, /?о из
уравнений C.4) при ^ = 1,2, ...,fc-f2 (при д = 0 C.4) выполняется в
силу условия (i)), чтобы обеспечить достаточно высокий порядок.
В результате был получен класс fc-шаговых формул порядка fc + 2
следующего вида:
к
1=0
Приведем первые несколько методов этого класса:
/307 19 1 '^ f \
^ - 3 : 2/n+i - Уп + Л[^fn+i + 40^- " 20-^^-1 ^ 1080^"-V ""
19 .2
80^"+^'
/3133 47 41 1
л - 4 : у„+1 - у^ "^'^15760^"+^ "^ 90-^" "" 480^""^ "^ АЬ^^-"""
17 , \ ?.2
"760-^"-^/ 32^"+^'
Общее выражение для этих методов дано ниже (см. формулу C.12) и
упр.1).
V.3. Обобщенные многошаговые методы
297
Анализ устойчивости методов со второй производной тоже
выполняется с помощью линеаризации, т.е. основан на использовании
уравнения
у' = Ау, для которого у" = Х^у. C.8)
Подстановка этих соотношений в C.3) дает вместо A.6)
характеристическое уравнение
к
^(а, - М- - /^S. )С =0, /i = /lA. C.9)
1=0
Это квадратное уравнение, если в нем положить С = ^'^, порождает
две кривые локуса корней, которые вместе описывают область
устойчивости. Методы Энрайта C.7) оказываются Л-устойчивыми при
А: = 1 и 2 (следовательно, при р = 3 и 4) и жестко устойчивыми при
Л = 3, 4, 5, 6 и 7. Соответствующие значения а (из определения А(а)-
устойчивости), D и константы погрешности С приведены в табл. 3.1.
Графики показаны на рис. 3.1.
Таблица 3.1. Характеристики устойчивости и константы погрешности
для методов Энрайта
к
р
а
D
С
1
3
90^
0.
0.01389
2
4
90^
0.
0.00486
3
5
87.88^
0.103
0.00236
4
6
82.03^
0.526
0.00136
5
7
73.10*
1.339
0.00086
6
8
59.95*
2.728
0.00059
7
9
37.61*
5.182
0.00042
X 10
. 5. . . .
-5
.^--^
-^sT^
1 1
5 1
\р = 9
1 - ' ' - ' 1
1 Р^ 1 1 1 1
Рис. 3.1. Области устойчивости методов Энрайта.
298 Гл. V. Многошаговые методы для жестких задач
Плотная выдача для методов ЭнраМта. В разд. П1.1 было
показано, что интерполяционная формула Ньютона с узлами в точках
^n+i'^n---^n-A:+i порождает
• неявные методы Адамса при интегрировании от х„ до х^^^,
• методы ФДН при дифференцировании в точке х^_^^.
Естественно применить ту же идею и к интерполяционной формуле
Эрмита (Аддисон 1979). Исходя из приобретенного опыта (см. выше),
выберем опорные точки следующим образом:
^п+1 (двукратный узел), х„, х„_р .. .,аг„_^^^^ (простые узлы).
C.10)
Это дает нам следующую схему разделенных разностей:
« = 1 /i
где x = x„ + sh. Для такого «вырожденного» (т.е. с кратными
точками) набора данных интерполяционная формула Ньютона принимает
вид
/(х„ + sh) = /,+(«- l)hf[ + E - l)\hf[ - V/i) +
Будем теперь интерпретировать / как производную /(Хуу(х))
решения, так что /' станет его второй производной. Проинтегрировав
C.11) от х„ до х„^1, получим
/с т-7, г / 'с \ /к
где
Wi = Уп + Л/п+, - л Е Щ^ (Е ''.) + f^"^n^^ ¦ (Е ".) • C.12)
-^=Г"""'"'^'?'"^''"^'''"'-"'Г"-"('т>'-
C13)
Таблнид 3.2. Коэффициенты методов Энрайта
t
щ
0
1
2
1
1
3
2
1
24
3
7
360
4
17
1440
5
41
5040
6
731
120960
7
8563
1814400
где
V.3. Обобщенные многошаговые методы 299
Первые несколько значений i/^ даны в табл. 3.2. Легко убедиться,
что коэффициенты в формуле C.12) совпадают с коэффициентами в
C.7). «Плотная выдача», конечно, получается при интегрировании
C.11) от х^ до x^ + eh:
Методы ФДН со второй производной
Если нас интересуют методы со второй производной,
аналогичные ФДН, надо заменить в C.11) все / на t/ и дважды
продифференцировать полученное выражение в точке х^^^. Тогда, положив
2/"(^n+i) =^п+1' получим методы
^1 = 1 ^ j = l i=j
которые мы назовем «ФДН-метподами со второй производной»,
сокращенно — ФДНВП (или SDBDF — Second Derivative BDF methods;
во избежание недоразумения предупреждаем читателей: Каш A981)
использует то же обозначение для класса «методов Энрайта»). При
анализе их устойчивости получены значения параметров,
приведенные в табл. 3.3. Кривые локуса корней показаны на рис. 3.2.
В полной аналогии с поведением неявных методов Адамса в
сравнении с методами ФДН, у методов ФДНВП константы погрешностей
больше, чем у методов Энрайта, но зато возможны жестко устойчивые
методы более высоких порядков.
Таблиид 3.3. Характеристики устойчивости и консталты погрешности
для методов ФДНВП
к
р
а
D
С
1
2
90^
0.
.1667
2
3
90^
0.
.0556
3
4
90^
0.
.0273
4
5
89.36'^
0.015
.0160
5
6
86.35^
0.128
.0104
6
7
80.82^
0.401
.0073
7
8
72.53^
0.886
.0054
8
9
60.71^
1.646
.0041
9
10
43.39^
2.770
.0032
10
11
12.34^
4.373
.0026
300
Гл. V. Многошаговые методы для жестких задач
Рис. 3.2. Кривые локуса корней для методов ФДНВП.
Смешанные многошаговые методы
Первоначальная мотивировка введения «смешанных методов:^
состояла в следующем (Скил и Конг 1977). Мы знаем, что для
нежестких задач очень хорошо выбирать методы Адамса
а для жестких задач — методы ФДН
- КУп+1 + "*-1Уп + • ¦ • + ЧУп-k+i) + Л/„+1 = 0. (B?)F(*))
Нежесткие задачи характеризуются тем, что в них величина —hdf/dy
мала, а жесткие — тем, что она велика (изначально это имеет смысл
только для скалярных уравнений, но применимо также и к
системам уравнений, если перейти к собственным подпространствам
матрицы Якоби df/ду = J). Идея состоит в том, чтобы использовать
взвешенное среднее двух методов — «смесь» (этот термин предложил
Ч.У. Гир) типа
{AMF^'"^^^] - y^''^hJ{BDF^''^} = О,
C.15)
где 7^*^^ — свободный параметр. Именно множитель -ЛУ, большой
или малый, определяет нужный вес, как того требует приведенная
выше мотивировка. Как показывает разложение в ряд Тейлора, при
любых значениях 7^*^ методы C.15) имеют порядок р = fc-h 1
(множитель h во втором члене увеличивает его порядок на единицу), даже
если J отличается от dj/ду. Таким обраизом, этот метод является
многошаговым аналогом 1У-методов, обсуждавшихся в разд. IV.7.
V.3. Обобщенные многошаговые методы
301
Пример. Возьмем в C.15) fc = 2 и подставим нужные величины из
формул (III. 1.8") и (III. 1.22"):
/5 _8^ ^ f \
/3 1 \ ^ ^ ^
Если теперь предположить, что наше дифференциальное уравнение
является линейным и автономным, т.е. у* = Jy, то Jy^^i = /n+t и
уравнение C.16) упрощается. Тогда особый интерес представляют
два конкретных выбора значения 7^^^ •
a) 7^^^ = 1/6; в этом случае f^^i и Jy^^i взаимно уничтожаются и
формула C.16) превращается ъ [к— 1)-шаговую формулу Энрайта
порядка А: + 1;
b) 7^^^ = 1/8; это «точка сверхсходимости» для линейных уравнений,
и мы получим Аг-шаговую формулу Энрайта порядка Аг + 2.
Оба свойства обобщаются на произвольное к; в первом случае надо
положить 7^^^^ = ""^7jt' ^Д^ 1к — величины из табл. III.1.2, а во втором
случае надо использовать 7^^^^ = ~ Х^»=о ^t» ^^^ ^ C.12).
Следовательно, смешанные методы обладают теми же превосходными свойствами
устойчивости, что и методы Энрайта, и в то же время, очевидно,
проще реализуются. Третья возможность — это выбрать 7^^^^ так, чтобы
сделать как можно больше угол а в определении А(а)-устойчивости.
Уравнение для кривой локуса корней в случае произвольного 7^^^^
принимает вид:
Таблица 3.4. Значения 7 и соответствующие углы а
для смешанных методов
к
1
2
3
4
5
6
7
8
9
10
11
Р
2
3
4
5
6
7
8
9
10
11
12
^ку1
.5
.1666667
.125
.1055556
.09375
.08561508
.07957176
.07485229
.07103299
.06785850
.06516462
а для
7('^) = -к,1
90^
90^
90^
87.88^
82.03^
73.10^
59.95^
37.61^
—
—
—
'^opt
[0,-hoo)
[.125,-boo)
[.12189, .68379]
.1284997
.1087264
.0962596
.08754864
.08105624
.07599875
.07192937
.06857226
а для
Лк) _ Лк)
1 'opt
90^
90^
90^
89.42^
86.97^
82.94^
77.43*
70.22''
60.68*
47.63*
28.68*
302 Гл. V. Многошаговые методы для жестких задач
j=0 i = i •'
Скил и Конг A977) тщательно вычислили оптимальные значения 7^^^^
(см. табл. 3.4; неточные значения в «столбце Энрайта» были
исправлены) и получили, таким образом, жестко устойчивые методы до
12-го порядка включительно.
Расширенные многошаговые методы Каша
Другая возможность обойти барьер Далквиста состоит в том,
чтобы вместо добавления высших производных добавлять дальнейшие
стадии, дополнительные узлы или промежуточные точки. Это ведет
нас в «гигантскую пустыню» (это — «басня К. Барриджа») общих
линейных методов, обсуждавшихся в разд. III.8. Новаторскими
результатами для жестких дифференциальных уравнений стали
«композитные многошаговые методы» Слоата и Биккарта A973), Биккарта и
Рубина A974), «гибридные» методы Ингланда A982) и
«расширенные» ФДН-методы Каша A980), сокращенно — РФДН (или EBDF —
Extended BDF methods). Рассмотрим более подробно основные идеи
последних. С целью повышения устойчивости ФДН-методов набор
их узлов расширяется путем добавления «забегающей вперед» точки
к
i=o
Коэффициенты здесь получаются из уравнений J2j ^jj^ — Я Y2j l^ji^~^
при g = 0, l,...,fc-l-l с условием нормировки а^^ = 1. Формула C.17)
используется следующим образом (см. рис. 3.3).
(i) Предположим, что значения решения Уп'2/n+i' • '^/n+fc-i
известны. Вычислим Vn^f^ как решение обычной ФДН-формулы
к
5]а^.т/„^^. = лД,Д^„ 3, = 1. C.17i)
j=o
(ii) Найдем y^+ife+i ^^^ решение той же ФДН-формулы, сдвинутой на
один шаг вперед (взяв у^^к ^ качестве у^^кУ-
к
Y^ Sj Уп+j+i = ЛД, /n+fc+1 {Уп+к •= Уп^к)^ C.17ii)
i=o
и положим 7n+fe + l =/(^n+)fe + pJ/n+/c-Hl)-
V.3. Обобщенные многошаговые методы 303
(iii) Отбросим Уп^к' подставим /„^;^+1 ^ уравнение C.17) и, решив его,
найдем новое значение Уп^^» которое и служит окончательным
численным решением метода.
Таким образом, продвижение численного интегрирования на один шаг
требует решения трех нелинейных систем размерности п. Для
стадии (i) и для стадии (iii) мы имеем отличные начальные приближения
— опережающую («забегающую вперед») точку предыдущего шага и
значение y^^k соответственно.
Лемма 3.1 (Каш 1980). Если формула C.17) имеет порядок /:-f 1,
а в C.17i) и C.17и) используется ФДН-метод порядка к, то в целом
алгоритм предиктор-корректор (i)-(m) имеет порядок fc -h 1.
Доказательство. Предположим, что значения 2/„, • • •, Уп+л-1 •^^"
жат на точном решении (рис. 3.3). Тогда простые выкладки (как в
доказательстве леммы III.2.2, см. также формулу (III.2.7))
показывают, что
уК+*)-|/п+* = С1Л*^^^*+^)(х„+,) + 0(Л''+2), C.18)
где Ci зависит от применяемого ФДН-метода. Теперь, если
невязка уравнения C.17) (при подстановке в него точного решения) равна
C2h^'^'^y^*^'^'^Wjу замена Л/(х^^^^^^, j/(x^^^^^i )) на hf(x
добавляет к ней выражение C.19), и мы получим:
+ 0(Л'^+3). C.20)
Таким образом, метод имеет порядок fc-|-l. В отличие от
линейных многошаговых методов, главный член погрешности состоит из
нескольких «элементарных дифференциалов», как в методах Рунге—
Кутты. П
Уп^к
J/n+fc + 1
Рис. 3.3. Погрешности алгоритма Каша.
304
Гл. V. Многошаговые методы для жестких задач
Модифицрфованные РФДН-мет(щы (МРФДН, или MEBDF). В
описанном алгоритме на стадиях (i) и (ii) нелинейные системы имеют
одну и ту же матрицу Якоби / — ЛД^ J, но для стадии (iii) матрица Якоби
иная: I — hPf^J. Это является недостатком алгоритма, так как
требует лишнего LU-разложения. Каш A983) предложил видоизменить
уравнение C.17) для стадии (iii) следующим образом:
к
Е^J2^n+i = Wn^k + КРк - РкIп^к -+¦ hp^^Jn^k^v C.17.mod)
J=0
При этом в приведенном доказательстве леммы добавляется еще один
член, пропорциональный ^^^+2, что не меняет порядка метода. Такая
модификация позволяет использовать в итерациях метода Ньютона
одну и ту же матрицу Якоби для всех трех стадий и, возможно,
сохранять ее также на прот51жении нескольких шагов.
Рис. 3.4. Области устойчивости МРФДН-методов Каша.
Таблица 3.5. Характеристики устойчивости МРФДН-методов Каша
к
р
а
D
1
2
90^
0.
2
3
90^
0.
3
4
90^
0.
4
5
88.36^
0.040
5
6
83.07*
0.246
6
7
74.48*
0.684
7
8
61.98*
1.402
8
9
42.87*
2.432
V.3. Обобщенные многошаговые методы 305
Анализ устойчивости. Подставим hfj=fiyj в C.17mod), C.17i)
и C.17ii), положим у„ = 1, y„+i = С» • •, Уп-^k-i = С""^ и, следуя
алгоритму (i), (ii), (iii), вычислим решение J/n+^—'C^- ^ результате
получим характеристическое уравнение
Л/х^ -h ^А^^ + C/i -h D = О, C.21)
где
?> = -Г,
я=Ё«/'' 5=Ё°/''"''- ^=Е'^/'-
J=0 j=0 7=0
При подстановке С = б*^ уравнение C.21) дает нам три корня /i,(^),
г = 1,2,3, которые описывают область устойчивости. На рис. 3.4
показаны эти кривые, вычисленные с помощью формулы Кардано.
Соответствующие характеристики устойчивости даны в табл. 3.5. Методы
являются Л-устойчивыми при р<4 и жестко устойчивыми до 9-го
порядка включительно.
Многошаговые коллокационные методы
«... теорема из глубокой древности ..., простая теорема
об интерпол5щии многочленами, на которую во многом
опирается практический численный анализ...»
(П.Дж. Дейвис, 1963, гл.II)
Существуют две основные возможности перенесения идеи колло-
кации, столь удачной в случае методов Рукге—Кутты (см. разд. П.7,
формулы (II.7.15)), на область многошаговых методов.
a) Как в подходе Нордсика, по заданным t/„,Лу^», /i^yJjV^, • • •
вычисляются y^^i, Лу^1ц.1, A2y^'^i/2,... В результате получается сплайн-
функция, глобально аппроксимирующая решение. К этому типу
относятся обобщенные однократно неявные методы Бутчера (Бутчер
1981). Обширное исследование таких методов провел Мюльтай A982).
b) Как в многошаговом подходе, по заданным у^ , t/„_i,.. •, y^Jk-^i
вычисляется y„^i, затем, как обычно, последняя точка y^^j^^i
отбрасывается и вычисления продолжаются. Этот вариант впервые
предложили и проанализировали Гийу и Суле A969). Ему посвящена
также статья Ли и Нёрсетта A989). Здесь мы уделим этому
подходу больше внимания. Являясь очевидным обобщением определения
II.7.б, метод задается следующим образом.
306 Гл. V. Многошаговые методы для жестких задач
Определение 3.2. Пусть заданы s действительных чисел Cj,..., с,
(обычно между О и 1) и Аг значений решения Уп'2/n-i' • •' 2/n-^c+i •
Определим соответствующий коллокационный многоилен и(х)
степени s-{- к — I формулами
u(xj) = yj, ; = п - * -h 1,..., n, C.23а)
u'(x„ + c,./i) = f(x^ -h c,./i, u(x^ + c./i)), г = 1,..., 5 C.23b)
(cm. рис. 3.5). Тогда численным решением является
Уп+1 :=t/(x,^i). C.23с)
Рис. 3.5. Коллокационный многочлен.
Если предположить, что производные г/'(х„Ч-с,Л) известны, то
уравнения C.23а) и C.23Ь) составляют интерполяционную задачу Эр-
мита с неполными данными: недостает значений функции в точках
x^-^c-h. Поэтому мы не имеем хороших формул. Сведем задачу к
системе линейных алгебраических уравнений. Введем безразмерную
координату t = (x — x^)/h, x = x^-\-th, узлы /^ = -/:-h 1,. • .,<)fe«i = -1,
/^^ = О и определим многочлены (p^(t) (г = 1,..., Аг) степени s-j-k — I
соотношениями
и многочлены V,@ (i = 1,. • ,s) соотношениями
если i ^ j,
если г = j,
j=l,...,s
j=l,...k,
C.24)
^.'(c,)={J;
j = h...,k,
если t = j,
если i ^ j,
i = l s-
C.25)
V.3. Обобщенные многошаговые методы 307
Заданные таким образом многочлены образуют (обобщенный) базис
Лагранжа, и многочлен и(х) легко записывается в виде
к S
u(x,-f</i)=:^V^^@2/„,,^,-f/i^^,@ti'K + ^/)- C.26)
в упр. 5 указан удобный способ вычисления многочленов <^,@ и V^,@
(заметим, что системы C.24) и C.25) не всегда имеют решения, см.
упр. 4). Положив t = c-, обозначив и{х^ + c-h) = v- и используя условие
коллокации C.23Ь), мы получим из C.26)
к 5
^- = T.^M)yn-k^j'^hJ2^M)fi^n-^Cjh.Vj). C.27а)
i=i j=i
к S
^п+1-Е^.A)^п-/с+,+лЕ^Л1)/(^п+с.Л,г;^.), C.27Ь)
т.е., в соответствии с формулами (П1.8.7), некоторый общий линейный
метод.
Теорема 3.3. Коллокационный метод C.23) эквивалентен общему
линейному методу
к S
^i = Yl^iJУn-kH'^^12^^ijf(^n'^Cjh.V^), г = 1,...,5,
-' - , C.28)
Уп+1 = 1^%+i,j Уп-k+j + /»S^*+i.j -^(^n ¦•¦ S''' ''i)'
где
^ij = Vj{Ci), biJ = фJ(c,), a,^,j = <pj(l), b,^,J = фJ{l), C.29)
a (fj {t), фJ (t) — многочлены J определенные в C.24) и C.25). Формула
C.26) дает в качестве результата «непрерывную выдачу». П
Прямое распространение доказательства теоремы П.7.9, опять-
таки с использованием формулы Грёбнера и Алексеева A.14.18),
приводит к следующей теореме.
Теорема 3.4 (Гийу и Суле 1969). Если квадратурная формула
C.27Ь) является точной для многочленов g(t) степени < 5 + fc -h г, т.е.
к
TO многошаговый коллокационный метод C.28) тоже имеет порядок
5-hAr-fr. D
308 Гл. V. Многошаговые методы для жестких задач
Методы «типа Радо»
¦Теперь мы будем изучать класс формул, обобщающий
обычные формулы Гаусса, Радо и Лобатто».
(Гийу и Суле 1969)
Возникает интересный вопрос: как выбрать узлы с,, чтобы
получить наибольший возможный порядок? Используя изящную идею
Крылова A959) (см. последнюю главу его книги об интегрировании),
Гийу и Суле A969), а также Ли и Нёрсетт A989) построили такие
методы с максимальным порядком p = 2s-\-k—l. К сожалению, эти
методы не являются жестко устойчивыми, и поэтому для жестких
задач они бесполезны. Чтобы обеспечить устойчивость на
бесконечности, зафиксируем с, = 1 и попытаемся определить с^,..., с^_^ так,
чтобы порядок был равным p=2s + k — 2. В силу теоремы 3.4
достаточно рассмотреть квадратурные задачи.
Теперь перейдем к идее Крылова для интегралов применительно
к нашей ситуации. Восполним пробел в данных для интерполяции
Эрмита, т.е. предположим, что значения функции v, =ti(x„ -hc,/i) (где
i=l,...,5—1) известны, и дополним соответствующим образом базис
Лагранжа. Сначала добавим многочлены Xi(Oj • iX^-ilO степени
2s -f fc — 2, которые должны удовлетворять следующим условиям:
Xi{tj) = 0,
X'i(cj)=0,
x.(c,) = {J;
i = i,.-
i = i,..
.,k,
.,s ,
C.30a)
C.30b)
i = l,...,s-l C.30c)
(обратите внимание, что последнее условие не налагается при j = s,
так как с, не является свободным узлом). Затем многочлены v?,@ ^
Фi{t) заменяются многочленами ^,(<)j V^t@ степени 25-1-А —2,
которые в дополнение к C.24) и C.25) должны удовлетворять равенствам
^,(cj) = 0 и ФiicJ) = 0, j = l,...,s-l. C.31)
Тогда формула C.26) заменяется на следующую:
к S"! 3
5(x,-h</i) = X^^,@y„-*+i+I]Xi@t^i+A^V^^.@ti>,+c.^
C.32)
V.3. Обобщенные многошаговые методы 309
и C.27Ь) превращается в формулу интегрирования вида
к «-1 S
yn-fi = E^.(^J/n-/c+i+E^i(i)^i+^E^i(i)^'(^n+s^). C.33)
порядок которой равен 25 4- Ar — 2. Если бы теперь все коэффициенты
)С A) чудесным образом обратились в нуль:
Х,A) = 0 0'=1,...,5-1), C.34)
то квадратурная формула C.27Ь) совпала бы с C.33), поскольку
оставшиеся коэффициенты <?,(!) и ^-A) вследствие их
единственности должны также равняться ^j(l) и Фj{l)'
Теорема 3.5. Если точки коллокации с^,...,с,_^ (при 0^ = 1)
выбраны так, чтобы многочлены <Pi{i),Фi{t) из C.24), C.25)
существовали и были единственными и чтобы выполнялось условие C.34), то
коллокационный метод C.28) имеет наибольший возможный порядок
28 +к-2. П
Вычисление узлов. Уравнения C.34) вместе с условиями C.30)
позволяют нам записать многочлены х,@ ^ простой форме
к 8
Xi(t)=Cl[(t-^tj)l[{t-Cj)\ C.35)
где С определяется равенством х,(с,) = 1. Это выражение
удовлетворяет требованиям (З.ЗОЬ) к производной во всех точках, кроме с,.
Однако Xi(c,) легко вычисляется из C.35), если перейти к
логарифмам, и условия Xii^i) ^ О приводят к следующим соотношениям:
^7377 + 13^ = ^'
j=i *^« Ъ j=i '^* '^3
1=1,...,5-1. C.36)
Пример. При S = 3 уравнения C.36) принимают вид
к
2 2^1
= —T + z] —Г
2 2 Л 1
-1 -Сз «2 - 1 ^._j С2 -tj
C.37)
(сз = 1). Эти два уравнения легко решаются относительно Cj и Cj,
и мы получаем кривые, показанные на рис.3.6 для k = Z и Л = 4.
310 Гл. V. Многошаговые методы для жестких задач
Мы видим, что возможно огромное число решений (точнее, ('^^7^)»
чтобы доказать их существование, Крылов воспользовался образом
заряженных электрических частиц в равновесии), но большинство из
них приводит к совершенно неустойчивым и поэтому бесполезным (в
смысле разд. III.3) методам. Итак, мы оставим только самые правые
на рис. 3.6 решения с,, для которых О < с^, Cj < 1; они представлены
в табл.3.6 (см. ниже). Кроме того, как показал Крылов (см.
книгу Крылова A959)), такой выбор приводит к наименьшей константе
погрешности (на этот раз устойчивость и малая погрешность не
противоречат друг другу!).
¦ г
-1 А^ ljxi.
¦ Н i ^
^3
--2
1
^^j-Nk-----<7
Lt<-rTTT. i....
/ ^
Рис. 3.6. Решения системы C.37): х — неустойчивые, а — устойчивые.
Рис. 3.7. Кривые локуса корней для многошаговых методов Радо E = 3).
V.3. Обобщенные многошаговые методы
311
Таблица 3.6. Коэффициенты и характеристики устойчивости
для многошаговых методов Радо {s = 3)
к
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Р
|1"
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
С1
0.155051025721682
0.177891722985607
0.192169638937766
0.202814874040288
0.211395456069620
0.218626151232186
0.224897548200883
0.230448266933707
0.235435607740434
0.239969169367303
0.244128606044551
0.247973766491964
0.251550844436705
0.254896295040291
0.258039429919700
0.261004194709515
С2
0.644948974278318
0.673235257220651
0.689317969824851
0.700407719104611
0.708798418188500
0.715507419158199
0.721072684914921
0.725812172023161
0.729928926504599
0.733560240031675
0.736803122952198
0.739728565298052
0.742390019356757
0.744828697795402
0.747077018862741
0.749160923778290
сз
1.
1.
1.
1.
1.
1.
1.
1.
1.
1.
1.
1.
1.
1.
1.
1.
а
90^
90*^
89.73^
89.13^
88.61^
88.14^
87.70'*
87.28^
86.89^
86.51^
86.14^
85.79^
85.44^
85.07^
84.68^
84.23**
D
0.000
0.000
0.016
0.084
0.178
0.278
0.376
0.467
0.555
0.649
0.763
0.917
1.135
1.462
1.995
3.037
Устойчивость методов типа Рцдо. Анализ устойчивости методов
Радо проводится с помощью подстановки t/' = Лу в C.28). Поскольку
с, = 1, мы имеем у^^^ = г^, и поэтому получаем (при s = 3) следующее
характеристическое уравнение:
1 - //622
*12
^22
^32
или
С" = @,0,1)
-A^6i2
1 - /1622
-/^'>32
П2
'22
^32
которое после умножения на det(/ —/х5) превращается в уравнение
третьей степени относительно fx. Для многошагового коллокационно-
го метода общего вида C.28) мы получим таким способом уравнение
9^^ЫС^ + 9;^-1(Ж*''+ •.. + 9оЫ = О,
где q^{fi) = det{I — fiB) и все g,(/i) — многочлены, степень которых
не превышает s.
Кривые локуса корней на рис. 3.7 вычислены с помощью
формулы Кардано. Коэффициенты и характеристики устойчивости приве-
312 Гл. V. Многошаговые методы для жестких задач
дены в табл. 3.6. Эти методы при fc = 1,2 (порядков 5 и 6)
являются Л-устойчивыми. Дальнейшие методы имеют удивительно большие
значения а при очень высоких порядках (примерно до 20-го), что
делает данный класс методов весьма перспективным.
Упралснения
1. Покажите, что коэффициенты i/ в C.13) для методов Энрайта
можно вычислять по рекуррентной формуле
1 ^'^ ' 1
'^• = >1)(;>2)-^5/^^^^-^' ^^^ ^'=gfc(/-fl-fc)'
Указание. См. доказательство формулы AП.1.7). Производящая
функция G(t)=Y^^Qi/jP здесь примет вид /^ (s—1)A-<)^~*с?5.
2. Формулы Энрайта жестко устойчивы при к <7 и не являются
таковыми при А = 8, fc = 9,... и т.д., что можно легко проверить,
например, с помощью графика, выполненного на компьютере.
Поэтому считают, что эти методы не являются жестко устойчивыми
при любых к>7. Однако строгого доказательства этого факта
(например, в духе доказательства теоремы III.3.4) найдено не было.
Почему бы Вам не попытаться найти его?
3. Докажите, что ФДН-методы со второй производной C.14)
неустойчивы (в смысле разд. III.3) при fc > 11.
4. а) Покажите, что при /: = 2, <^ = —1, t^ = 0^ s=l, с^ = —1/2 обе
системы C.24) и C.25) не имеют решений.
Ь) Покажите, что C.24) и C.25) всегда допускают единственное
решение, если все с,- различны и удовлетворяют условию с, > О.
Указание для (Ь). Если записать (р- (или гр-) в виде Yll=i ^/^'~^)
то C.24) и C.25) превращаются в линейные системы с одной и той
же матрицей и разными правыми частями. У соответствующей
однородной системы есть ненулевое решение тогда и только тогда,
когда интерполяционная задача
'<'>' = »¦ ' = ' *¦ C^39)
Р(^)=0' j=l,...,5
имеет ненулевое решение. Поскольку многочлен р'(<) имеет не
более fc Ч- 5 — 2 действительных нулей и (по теореме Ролля) каждый
интервал (^/,</^i) должен содержать по крайней мере один из них,
за точкой <fc = О не может быть более 5—1 нуля.
V.3. Обобщенные многошаговые методы 313
5. Удобный способ вычисления многочленов C.24), C.25) (описанный
здесь для случая s = 3) состоит в использовании следующего
представления многочлена <Pi{t):
к
<Pi{t) = (a,^a^i-^a^t''^a^t^) Ц (<-<^). C.40)
Покажите, что уравнения C.24) (при i = j) тогда превращаются в
следующую линейную систему:
«1 -f ^as + tfag + ^fa^ = l/r-, C.41)
sja, + {sjcj -f 1H2 + E^.c) -f 2с^.)аз + E^.cf+ 3c?)a4 = 0, j= 1,2,3,
к к .
где г. = J][ (<,• -^/), Sj = ^ ——. Кроме того, для
многочлена 'ф^{1) вида
ф^ (t) = {а, + a^t + a^V") \[[1 -1^) C.42)
;=i
уравнения C.25) принимают вид
о ч Г О, если j ф г,
*.«i + («^ + l)«2 + (*,c| + 2c>3 = (i/,._ ^^^Д. i = 1,2,3,
к к .
где г. = П(с..-<^), 5^.=^——.
/=1 /=1 S- W
б. Обобщите доказательство и заключение теоремы IV.3.10 на
многошаговые кол локационные методы.
Указание. Вместо КМ{х) в (IV.3.26) надо подставить
линейную комбинацию Ylizzi^t^ti^) ^ произвольными
коэффициентами ai,...,a;,, где М^(х) = М(х) ar^-i и М(ж) = ^П.*=1(^ ""^t)-
Тогда вместо (IV.3.27) мы получим выражение
Подстановка х = ^^,<2> • • • >^л» "^ife+i ^ ^(^) = Ух Д^^т
переопределенную систему для а^,..., а^^, которая имеет решение, только если
314 Гл. V. Многошаговые методы для жестких задач
определитель расширенной матрицы равен нулю. Если положить
в этом определителе Ух = 1, Уг = С) Уз = С^) • •) получится
характеристическое уравнение
det
которое является обобщением для (IV.3.22,23). Утомительное
разложение этого определителя по степеням С и /х (где многие
коэффициенты равны нулю) приводит к явному выражению (см.
теорему 7 в работе Ли A990)).
7. Докажите, что двухшаговый двухэтапный коллокационный метод
с С2 = 1 Л-устойчив тогда и только тогда, когда
С1>(л/17-1)/8.
Указание, а) Покажите, что характеристическое уравнение имеет
вид д2(Ж^ + 91(/^)С-1-^о(/^) = 0,где
(/2(/i) = -(9ci -h 5) -h fiCcl + 7ci + 2) - |i22ci(c, -h 1),
Gi(/i) = 12q+4-/i4(c2-l), C.44)
9o(/^) = -3ci-f l-f//ci(ci-l).
b) Примените критерий Шура A918) к характеристическому
многочлену, положив fi = it, < G М.
Критерий Шура. Пусть a(C) = a^tC''H-afc-iC''""^+ • - + «0 (чФ^) ~
многочлен с комплексными коэффициентами; рассмотрим также
многочлен
a'(C)=5oC*+5iC*... + a;t-
Все нули многочлена a(Q лежат внутри единичного круга тогда и
только тогда, когда
i) |aol<Kh
ii) все нули многочлена С"Ч^*@)^(С) —^@)а*(С)) степени k — l
лежат внутри единичного круга.
8. Докажите, что Ci = (\/T7—1)/8 является точкой сверхсходимости
для двухшаговых двухстадийных коллокационных методов с С2 = 1.
V.4. Пордцковые звезды
на поверхностях Римана
«Риман — человек блестящей интуиции. Своей всеобъемлющей
гениальностью он превосходит всех своих современников ... При
своих первых робких, неумелых выступлениях юный доцент, на
которого мы, пришедшие к жизни в науке после него, взираем kslk
на святого, был вынужден терпеть различные уколы и
ироническое отношение своих коллег».
(Ф. Клейн, Лекции о развитии математики в
XIX столетии. — М.—Л.: ОНТИ НКТП СССР, 1937, с. 288, 290)
В предыдущих разделах мы видели, что максимально возможный
порядок Л-устойчивых линейных многошаговых методов равен двум;
кроме того, было показано, что методы Энрайта со второй
производной, как и ФДНВП-методы, Л-устойчивы при р< 4; трехстадийные
многошаговые методы Радо Л-устойчивы при р< 6. В этом разделе
мы увидим, что эти наблюдения представляют частные случаи
общего принципа, так называемой «гипотезы Даниела—Мура» о том, что
порядок Л-устойчивого многошагового метода, содержащего либо s
производных, либо S неявных стадий, удовлетворяет соотношению
p<2s. Прежде чем приступить к доказательству этого
предположения, нам следует познакомиться с поверхностями Римана.
Поверхности Римана
«Во многих исследованиях, в частности, в исследованиях по
алгебраическим и абелевым функциям, удобно следуюхцим образом
представлять себе геометрически ветвление функции.
Представим себе, что по плоскости {х,у) разостлана некоторая другая,
совпадающая с нею поверхность (или же на плоскости уложено
некоторое бесконечно тонкое тело), однако, лишь там и только
там, где задана функция. При продолжении функции поверхность
будет также расстилаться дальше. В тех частях плоскости, в
которых имеются два или большее число продолжений, поверхность
ляжет два или большее число раз; она будет состоять из двух или
большего числа листов, из которых каждый будет изображать
некоторую ветвь функции. Около какой-нибудь точки ветвления
функции один лист поверхности, будучи продолжаем, переходит
в другой, так что в окрестности такой точки поверхность
представляет собой нечто вроде винтовой поверхности с осью, стоящей в
этой точке перпендикулярно к плоскости (х, у) и с бесконечно
малым шагом. Если функция после нескольких обходов переменной
Z вокруг точки ветвления возвращается к своему прежнему
значению (как, например, (г — а)"^'" , где т,п — взаимно простые
числа, после п обходов z вокруг а), то тогда, конечно, нужно себе
представить, что самый верхний лист поверхности продолжается
сквозь все остальные в самый нижний.
Многозначная функция имеет во всякой точке такой поверхности,
изображающей ее ветвление, только одно определенное значение
и поэтому может быть рассматриваема как вполне определенная
функция точки на этой поверхности».
(Б. Риман 1857; цит. по русск. изд. 1948, с. 88-90)
316 Гл. V. Многошаговые методы для жестких зацач
Рассмотрим в качестве примера ФДН-метод (III. 1.22") при к = 2 с
характеристическим уравнением
(|-.У-2С-Ь^ = 0. D.1)
Это квадратное уравнение выражает С как функцию /i (С и /х —
комплексные переменные). Из него сразу находим значения
2±^ЛT^ , .
^1-2- З-2/i • ^^¦'^>
которые определяют двузначную функцию^ т.е. при каждом fi?C мы
имеем два решения С- Они представлены на рис.4.1 линиями уровня
функций |Ci,2(A^)h в светлой области |Ci(a«)| > 1-
^^ , 2+унЗа
— з-л/ГТ^
3-2а* ^2 — З-2/i
Рис. 4.1. Два решения характеристического уравнения для метода ФДН2.
Рис. 4.2. Трехмерное изображение отображения D.4).
V.4. Порядковые звезды на поверхностях Римана 317
Отметим два существенных обстоятельства. Во-первых, Ci имеет
полюс в точке /i = 3/2 (а Сз не имеет). Это связано с присутствием
в D.1) множителя C/2 —/i), который представляет неявную стадию
метода. Во-вторых, на отрицательной части действительной оси
слева от точки —1/2 можно заметить странное нарушение
непрерывности. Это явление впервые было отмечено в знаменитой статье Пюизё
A850): «...а encore cet inconvenient, que и devient alors une fonction
discontinue...»^ Его причина заключается в поведении
комплексного квадратного корня -/1 -f 2/i: когда 1-|-2/х совершает один полный
оборот вокруг начала координат, комплексный квадратный корень
у/1 Ч-2/i делает только половину оборота и обменивает местами оба
наших корня. Поэтому мы не можем говорить в обычном смысле о двух
комплексных функциях Ci(a*) и СгСА*)- ^ здесь появляется великая
идея Римана A857): вместо изменения /i на комплексной плоскости
С представим изменение /i на двойном листе комплексных
плоскостей Си С (словами Римана: «бесконечно близких»). Значения /i на
верхнем листе отображаются в Ci > а значения /i на нижнем — в Сз •
При этом двузначная функция становится однозначной. На
«разрезе» слева от точки —1/2 два корня Ci и Сг переходят один в другой,
и мы должны представить себе, что верхний лист для Ci непрерывно
переходит в нижний лист для ^2 (оттененный на рис. 4.1) и наоборот.
Если мы обозначим полученное таким способом многообразие через
М, то отображение
становится всюду непрерывным и голоморфным (за исключением
полюса). Многообразие М называется римановой поверхностью
алгебраической функции /i »-> (^ .
Трехмерное изображение для отображения
представлено на рис. 4.2.
Более обище мето1Ц|1. Большинство методов, рассматривавшихся
в разд. V.3, являются так называемыми многошаговыми методами
Рунге—Кутты^ которые определяются формулами
2/п+. = Е^2/п+;-1 + ЛЕ^/К+с.Л,.^), D.5а)
к 5
^1'^ = Е^О- 2/n+i-i +ЛЕЬо- /(х„ +с,/1,г;5'^)). D.5Ь)
«... имеет еще такое неудобство: и становится тогда разрывной
функцией. ..» — Франц..
318 Гл. V. Многошаговые методы для жестких задач
Это именно тот подкласс общих линейных методов (см. пример
II 1.8.5), в котором внешние стадии представляют решение у{х) на
равномерной сетке. При использовании таких методов основную часть
вычислительной работы составляют неявные стадии D.5Ь).
Для анализа устойчивости мы, как обычно, положим /(х, t/) = Ау,
/iA=// и (у^,2/„^1,...,у„^;^) = A,С, ...,С''). Тогда уравнение D.5Ь) в
векторных обозначениях примет вид
гГ=(/-^В)-Чс, D.6)
где С = A, С) • • > С^""^)^ • Справа стоит рациональное по /i выражение
со знаменателем det(/ —//5). Подставляя это выражение в D.5а) и
умножая результат на этот знаменатель, мы получим
характеристическое уравнение вида
Q(/i,0 = д.Ш'+Як-гМС'-' + . • . + 9оЫ = о, D.7)
где q^ifi) = det{I — fiB) и все qj(fi) являются многочленами по /i
степени не выше s.
Другой класс методов — многошаговые методы со старшими про-
изводными — можно записать в виде
E'''E%-^J'n+. = 0 D-8)
j=o »=о
(М. Раймер 1967; Р. Йелч 1976), где вычисление старших
производных DJy производится по формуле (II.13.3). Для уравнения у' = \у
мы имеем D^y^XJy. Подставляя это выражение в D.8) вместе с
(Уп' Уп+1' • • •' Уп+к) = A,С,...,С"), мы сразу получим
характеристическое уравнение вида D.7). Здесь степень $ многочленов 9j(a*) равна
порядку самой старшей из присутствующих производных. Основная
часть вычислительной работы при расчете по формуле D.8)
состоит в определении y^^k ^^ неявного уравнения, содержащего y^^f^,
^Уп-\-к) • • •' ^^Уп-\-к • Если последняя из этих производных
присутствует (т.е. если а^^, ^ 0), то степень g^^(/i) в D.7) будет равна $,
Риманова поверхность М функции D.7) состоит из к листов, по
одному на каждый из к корней С, • Точками ветвления будут те
значения /i, при которых два или несколько корней уравнения D.7)
сливаются в m-кратный корень. Они являются корнями так называемого
дискриминанта (см. любой классический учебник по высшей алгебре,
например, знаменитый "Weber", Vol.1, §50)^; следовательно, для
неприводимого многочлена Q(/i,C) существует только конечное число
таких точек. Пюизё тщательно изучил, как движутся сливающиеся
корни С; у когда fi совершает оборот вокруг такой точки ветвления:
^ Или А.Г. Курош, Курс высшей алгебры (изд. 3-е) — М.: ГИТТЛ, 1953,
с. 236. — Прим. ред.
V.4. Порядковые звезды на поверхностях Римана 319
обычно они образуют то, что Пюизё назвал "systeme circulaire"
(круговой системой), т.е. при каждом обороте они совершают циклическую
перестановку, подобно значениям комплексной функции *>/?
вблизи начала координат. Риманова поверхность должна следовать этим
"монодромиям": листы ее должны быть разрезаны вдоль некоторых
линий и затем соединены соответствующим образом. Расположение
этих разрезов не определено однозначным образом.
Рис. 4.3. Различные разрезы для функции D.9) (Гурвиц и Курант 1925).
Например, для функции, которая определяется уравнением
e-il-fi^) = 0 D.9)
и имеет точки ветвления ±1 и ±i, две разных возможности выбора
разрезов показаны на классическом рисунке (рис. 4.3),
воспроизведенном из книги Гурвица и Куранта A925, р. 360).
Полюсы характеризуют вычислительные затраты
«Всего 85 (геогр.) миль до полюса, но, кажется,
предстоит жесткий переход в обе стороны; и все же мы еще
продвигаемся, а это уже кое-что».
(Р.Ф. Скотт, 10 января 1912 г.; первое упоминание в
литературе о взаимосвязи между полюсами и жесткостью.)
Мы только что видели, что степень s многочлена q/^ifi) в D.7)
отражает объем вычислительной работы (это либо число неявных
стадий, либо число производных в уравнении для нахождения
численного решения). Многочлен д^М будет иметь s нулей A^i, /i2) • • •»А** • Что
произойдет, если /i приблизится к одному из этих нулей? Уравнение
D.7) степени к (с к корнями Ci(/^)» • • мСл!/^)) внезапно превратится
в уравнение степени fc — 1, у которого только к — 1 корень. А куда
девается последний корень? Согласно теореме Виета он должен уйти
на бесконечность. Для определения его асимптотического поведения
предположим, что ^^(/^о) = О, 9^(а*о) т^ О' Як-Л^^о)^^ и что С велико.
320
Гл. V. Многошаговые методы для жестких задач
Тогда ^/j_i(/i)C*"^ доминирует над всеми членами g/f«2(A')C'^"'^> • •»
^oC/i), которыми теперь можно пренебречь. В результате получим,
что
С--
Як(^^о) /^-/^0
при
А^о.
D.10)
и, следовательно, алгебраическая функция C(fi) имеет полюс на
одном из своих листов. Если же qkif^o) =0 — кратный нуль функции
Яkip^)i то и соответствующий полюс функции C(fi) тоже будет
кратным.
Существует еще возможность, что рассматриваемый полюс
совпадает с одной из точек ветвления. Это происходит в том случае, когда,
кроме g^fe(/io) =0) ^Щв и Як-iif^o)^^' Тогда два корня Cj(fi)
стремятся к бесконечности, но более медленно^ как ±C(/i —/io)"^/^ (упр. 1).
Поэтому будем опять считать за один полюс оба «полуполюса»
вместе. Пусть с — некоторая кривая, служащая границей окрестности V
точки ^0 • Так как /ig — точка ветвления, кривая с окружает ее
дважды, прежде чем замкнуться. На этом пути аргумент функции С(^)
делает ровно один оборот по чгюовой стрелке. Рис. 4.4 иллюстрирует
этот факт примером.
Рис. 4.4. Поведение корней уравнения /if^ -Ь 2/iC + 2 ~ д« = О
вблизи точки |i = 0.
Вышеизложенному подводит итог следующая
Лемма 4.1. Римянова поверхность для характеристического
уравнения многошагового метода Рунге—Кутты с s неявными стадиями
на шаге (или неявного многошагового метода с s старшими
производными) содержит не более чем s полюсов алгебраической функции
V.4. Порядковые звезды на поверхностях Римана 321
Далее мы увидим, что лемма 4.1 остается справедливой для всего
класса общих линейных методов, но в данный момент мы «impatient
et joyeux d'aller au combat»^) (Asterix Legionnaire, pp. 29-30). Принцип
аргумента сохраняется и на римановых поверхностях; мы
сформулируем его следующим образом.
«On the left, isn't it ?» — «Right.»
«On the right ?» — «Left, leeeft!»
«Слева, не так ли?» — «Вы правы.»
«Справа?» — «Слева, сле-е-ева!»
(Джон Клиз, «По часовой стрелке»)
Лемма 4.2. Предположим, что область F С М не содержит нулей
функции Cif^)) ^^^ граница состоит из замкнутых контуров 7i,. •., 7^ •
Тогда число полюсов функции С(/^) > содержащихся в F, равно
общему числу оборотов по часовой стрелке, которые aTg(((fi)) совершает
при обходе контуров 7i»• • > 7г ^ таком направлении, что каждый раз
F остается слева от 7, •
Доказательство проводится с помощью разрезания F на
множество частей, каждая из которых гомеоморфна кругу в С, и суммиро-
вания числа всех оборотов, которые вдоль разрезов взаимно
сокращаются, поскольку смежные края обходятся в противоположных
направлениях. П
Порядок и порядковые звезды
«.. .denn das Klare imd leicht Fafiliche zieht ims an, das Verwickelte
schreckt uns ab».
«.. .ибо ясное и легко воспринимаемое привлекает нас, а
сложное — отпугивает». (Д. Гильберт, Париж, 1900 г.)
Руководствуясь идеями разд. IV.4, сравним теперь абсолютные
значения характеристических корней |Cil и IC2I для ФДН2-схемы D.2)
с показательной функцией le'^l = e^e/i ц определим множества
Л,. = {/х€С; |С^Ы1>|е''|}. i=1.2 D.11)
(Ваннер, Хайрер и Нёрсетт 1978). Они представлены на рис. 4.5,
масштаб которого точно такой же, что и у рис. 4.1.
Множества А^ непрерывно продолжаются при переходе через
разрезы таким же образом, как и корни, и поэтому естественно поместить
их на риманову поверхность М и определить множество
^ = {,ieM; |СЫ|>И'')|}, D.12)
где 7г: М —)• С — естественная проекция.
На рис. 4.5 для Ci(a^) ясно видна порядковая звезда с тремя
секторами, но для СгС/^) звезды нет, и можно предположить, что это
' «С нетерпением и радостью готовы идти в бой». — Франц.
322
Гл. V. Многошаговые методы для жестких задач
1 I
1 "^
: '
: ^-5
Рис. 4.5. Порядковая звезда D.14) для ФДН-метода второго порядка.
должно быть связано с порядком метода, который равен двум. Далее
будет приведена лемма 4.3, которая распространяет лемму IV.4.3 на
многошаговые методы.
Подставляя в D.5) А = 0 (и, следовательно, /i = 0 в D.7)) и полагая
(Уш Уп+1»• • м Уп+л-i) = A» li • •) 1)
(тогда в D.7) С = 1)) в силу согласованности метода мы должны
получить, что Vn^ff = 1 тоже, т.е. что Q@,1) = 0. Это соответствует
формуле рA) = 0 в многошаговом случае (см. (П1.2.6)). Но при Л = 0
разностное уравнение D.5а) устойчиво только в том случае, когда С = 1
является простим корнем полиномиального уравнения Q{OX) = 0-
Следовательно, должны выполняться соотношения
Q(o,i) = o, ^(о,1)#о.
D.13)
Аналитическое продолжение Ci (/^) этого корня в окр)естности начала
координат (если не встретится затруднений с точками ветвления)
назовем главным корнем^ а соответствующую поверхность — главным
листом М.
Лемма 4.3. Для устойчивых многошаговых методов Рунге—Кутты
(или методов со старшими производными) порядка р множество А
содержит звезду яз р -h 1 секторов на главном листе в окрестности
начала координат.
Доказательство, Фиксируем А G С, положим j/ = Ау и для Уо» • •
•iVk^i возьмем точные начальные значения 1,е'',.. .,6^^"^)^. Если
порядок метода равен р, это означает, что локальная погрешность
(см. рис.П1.2.1), т.е. разность между е^** и численным решением
У/^, найденным из D.5а), должна иметь вид С hP'^^ при Л —> О и,
следовательно, CA~''~^/iP+^ при |i->0. Таким образом, при замене
всех yj на е^> в формуле D.5) мы придем к выражению
Q(/i, е'^) = С^'"^' -f Oifi^-^^). D.14)
V.4. Порядковые звезды на поверхностях Римана 323
Вычтем D.14) из D.7), выберем в качестве C(/i) главный корень Ci(/^)
(для которого величина e^^ — Ci (//) мала при малых |/i|) и линеаризуем
результат. В итоге получим формулу
^@,1) к-С1Ы) = С/.''+Ч...,
разделив которую на ненулевую константу D.13), придем к
соотношению
e^-Ci(/i)=C'./i'^+40(/i''+2) при fi^O. D.15)
Оставшаяся часть доказательства проводится в полной аналогии
с доказательством леммы IV.4.3. В случае методов со старшими
производными разница также невелика. П
Постоянная С в D.15) называется константой погрешности
метода. Это согласуется с формулами (П1.2.6) и (П1.2.13) для
многошаговых методов и с (IV.3.5) для методов Рунге—Кутты.
Область устойчивости многошаговых методов Рунге—Кутты, а
также их Л-устойчивость определяется тем же способом, что и для
многошаговых методов (см. определение 1.1). Надо только под
Ci(a^)) ' • -Xki/^) понимать корни D.7).
«Догадка Даниела—Мура»
«Здесь предполагается, что ни один Л-устойчивый метод вида,
представленного уравнением 5-6, не может иметь порядок выше
чем 27-f 2 и что среди этих Л-устойчивых методов порядка 27 + 2
наименьшую константу погрешности дает метод Эрмита. ..»
(Даниел и Мур 1970, р. 80)
В то время, когда не было известно ни одного простого
доказательства Д41Я второго барьера Далквиста, найти его для обобщения
— предположения Даниела—Мура — казалось совершенно
безнадежным делом. И. Женен A974) построил Л-устойчивые многошаговые
методы со старшими производными, которые имели удивительно
высокий «порядок», противоречащий данному предположению. Позднее
Р. Йелч A976) прояснил эту загадку, показав, что в методах
Женена единица является кратным корнем многочлена р(С), и,
следовательно, «эффективный» порядок методов был более низким. В конце
концов, правильность гипотезы была доказана в 1978 г. с помощью
порядковых звезд.
Теорема 4.4. Наивысший порядок А-устойчивого многошагового
S-стадийного метода Рунге—Кутты (или метода с s производными)
равен 2s. Для А-устойчивых методов порядка 2s константа
погрешности удовлетворяет соотношению
324 Гл. V. Многошаговые методы для жестких задач
Доказательство. В силу А-устойчивости для всех корней на
мнимой оси выполняется неравенство |С;(*у)| ^ 1- Следовательно,
порядковая звезда А не может где-либо пересекать мнимую ось.
Рассмотрим Л"^ = ЛП7Г'"^(С"*') — часть порядковой звезды, лежащую над
С+ . Как и в лемме IV.4.4, множество Л+ должно быть конечным
на всех листах М. Граница Л+ может состоять из нескольких
замкнутых кривых. Как в лемме IV.4.5, аргумент функции (^(fi)/e^
монотонно растет при обходе 5Л"*". Поскольку в начале координат мы
имеем звезду с р-|-1 секторами (лемма 4.3) и среди них по крайней
мере [^7^] секторов лежат в С+ , то ограничивающие множество Л+
кривые должны пройти через начало координат не менее [^^] раз.
Следовательно, общее число оборотов не меньше чем [^у^], и из лемм
4.1 и 4.2 мы делаем вывод, что
Отсюда следует, что р < 25, и первое утверждение доказано.
Теперь нам нужна новая идея, чтобы доказать
ту часть теоремы, в которой речь идет о
константе погрешности. Здесь может быть полезным
следующее соображение: звезда А отражает тот факт,
что при обходе вокруг начала координат поверхность
|C(/i)/e^| поднимается и опускается, подобно
кружевным брыжам у Монтеня. Видимо, константа
погрешности должна быть связана с высотой этих волн.
Таким образом, если мы хотим сравнить константы
погрешности разных методов, надо сравнивать \(^{fi)/e^\ с |fl(/i)/e^|, где
R{fi) — характеристическая функция второго метода. При делении
одного выражения на другое е'^ сократится, и мы определим
множество
Ч'
в = ыем; ' ^(^^
1Я(тЫ)
> 1 }, D.18)
которое назовем относительной порядковой звездой. Для R{z)
выберем диагона^тхьную аппроксимацию Паде R^si^) с s нулями и s
полюсами (см. (IV.3.29)). Вычитая из формулы D.15) (в которой теперь
возьмем p = 2s) формулу (IV.3.30) (положив в ней j = fc = s), получим:
^^ V '
С
Известно, что |Л,,(гу)| = 1 при любом у GiR и все нули Д,,B) лежат в
С~ (теорема IV.4.12). Поэтому множество В D.18) не может
пересекать мнимую ось (как прежде), и отношение |С(^)/ЯGг(/х))| не имеет
других полюсов над С+, кроме полюсов С(а^)> число которых, как
V.4. Порядковые звезды на поверхностях Римана 325
мы знаем, не превосходит s. Следовательно, секторы относительной
порядковой звезды В должны иметь такие же цвета, что и секторы
классической порядковой звезды Л для диагональной аппроксимации
Паде (см. рис. IV.4.2). В противном случае был бы нужен лишний
полюс. Мы приходим к выводу, что константы погрешности должны
иметь одинаковые знаки (см. лемму IV.4.3), и поэтому выполняется
соотношение (-1)*С > О (см. IV.3.30), откуда и следует D.16).
Равенство С = О породило бы порядковую звезду В даже более
высокого порядка, что невозможно при s полюсах, если только оба
метода не совпадают. D
Замечания, а) Первая часть доказательства является, на самом
деле, излишней, поскольку из неравенства D.16) следует, что при
порядке 2s константа погрешности С ^^ О, а поэтому обязательно
выполняется соотношение p<2s. Мы оставили эту часть из-за ее красоты
и простоты, а также для читателей, не желающих разбирать вторую
половину доказательства.
Ь) В доказательстве нигде не используется целиком
предположение об Л-устойчивости; единственное нужное свойство — это
устойчивость на мнимой оси (/-устойчивость, см. (IV.3.6)). Таким образом,
теорема 4.4 допускает следующее усиление, в результате которого
теорема IV.4.7 распространяется и на многошаговые методы.
Теорема 4.5. Пусть I-устойчивый многошаговый s-стадийный
метод Рунге—Кутты (или метод с s производными) имеет
характеристическую функцию С (а*) с «1 полюсами в С+ . Тогда
p<25i, D.20)
а константа погрешности для всех таких I-устойчивых методов
порядка p=2s^ удовлетворяет неравенству
Другая интерпретация этой теоремы дает следующее утверждение
(ср. с теоремой IV.4.8), которое для случая 5=1 доказал Р. Йелч
A978):
Теорема 4.6. Пусть I-устойчивый методе s полюсами
удовлетворяет неравенству p>2s—l. Тогда он А -устойчив.
Доказательство. Если бы в С+ располагались только s — 1
полюсов, то мы пришли бы к противоречию: p<2s — 2. Следовательно,
все полюса функции С {/л) лежат в С"^ , и Л-устойчивость вытекает из
принципа максимума. П
Методы со «Свойством С»
Нельзя ли распространить доказательство теоремы 4.4 на любой
метод (отличный от диагонального метода Паде)? Главная трудность
326 Гл. V. Многошаговые методы для жестких задач
здесь встречается при задании множества В, поскольку определение
D.18) не имеет смысла, если R(fi) — многошаговый метод,
определенный на другой римановой поверхности. Идею преодоления этой
трудности подсказывает следующее наблюдение: во второй части до-
кг1зательства теоремы 4.4 мы имели дело только с С"*" — областью
неустойчивости метода, с которым проводилось сравнение.
Определение 4.7 (Йелч и Неванлинна 1982). Пусть задан метод с
характеристическим многочленом D.7), удовлетворяющим условиям
D.13). Обозначим область его устойчивости через 5^. Будем
говорить, что данный метод обладает Свойством С, если главный лист не
содержит точек ветвления вне 7Г''^Eд) (включая ос, если 5д
ограничена), а неустойчивость метода полностью определяется главным
корнем Ri (/i), т.е.
Дд :=55д = {^€С; |fii(/x)| = l}. D.22)
Примеры^ Все одношаговые методы, конечно, обладают Свойством
С Линейные многошаговые методы, у которых кривая локуса
корней просто замкнута, тоже имеют Свойство С. В этом случае все
корни, за исключением /ii(/i), по модулю меньше единицы при всех
// ^ 7г~^Eд). Таким образом, в этой области главный лист не может
иметь точек ветвления. Явный метод Адамса 4-го порядка не
обладает Свойством С (см. рис. 1.1). Неявные методы Адамса (см. рис. 1.3)
имеют Свойство С при fc < 5. Неявный метод Милна—Симпсона
A.16) 4-го порядка также обладает Свойством С,
Определение 4.7 позволяет заменить в доказательстве теоремы 4.4
Rggifi) на R^ (/i), С^" — на дополнение к 5д, мнимую ось — на Дд, в
результате чего получается следующая теорема (Йелч и Неванлинна,
5 апреля 1979 г., 5 часов утра, в Шампени; Ваннер, 5 апреля 1979 г.,
4.30 утра, в Урбане. Как стало возможным такое совпадение? В то
время e-mail (электронная почта) еще не вошла во всеобщее
употребление. Может быть, это была Ф-mail?).
Теорема 4.8. Пусть метод с характеристической функцией R(fi),
областью устойчивости 5д и порядком pj^ обладает Свойством С.
Если другой метод с характеристической функцией С(а') у областью
устойчивости S^ и порядком рл более устойчив, чем метод R, т.е.
если
S( D 5д, D.23)
ТО выполняется неравенство
p<2s, D.24)
где
р = тш(рд,р^) D.25)
из — число тех полюсов функции С(а^) (с учетом их кратности),
которые не являются полюсами главного корня Ri(fi) метода R(fi).
и
V.4. Порядковые звезды на поверхностях Римана 327
«... и попытались оптимизировать границу устойчивости. Однако
несмотря на все усилия мы не смогли превзойти л/З — границу
устойчивости метода Милна—Симпсона...» (К. Деккер 1981)
В качестве иллюстрации применения теоремы 4.8 найдем
наибольший отрезок устойчивости на мнимой оси /^ = [—гг, ir] С С для
многошагового метода 3-го порядка (ориентированного на решение
гиперболических уравнений). Поскольку в случае линейных многошаговых
методов 5 = 1, равенство р = 3 противоречит условию D.24).
Используя в качестве Д(/х) характеристическую функцию метода Милна—
Симпсона A.16), мы получим из теоремы 4.8 следующее утверждение:
Теорема 4.9 (Деккер 1981; Йелч и Неванлинна 1982). Если
линейный многошаговый метод порядка р>3 устойчив на 1^, то г < у/Ъ.
и
Вторая часть теоремы 4.4 также допускает расширение; напомним,
что существенным моментом в ее доказательстве был вопрос о знаке
константы погрешности для диагональной аппроксимации Паде.
Теорема 4.10. Рассмотрим метод с характеристическим
уравнением D.7), удовлетворяющим условиям D.13). Пусть р — его порядок
и С — константа погрешности. Предположим, что
a) метод обладает Свойством С,
b) главный корень R^ (/i) имеет s полюсов,
c) sign(C) = (-l)%
d) p>2s-l.
Тогда данный метод является «оптимальным» в том смысле, что
любой другой метод с s полюсами, устойчивый на Aj^ из D.22), либо
имеет более низкий порядок, либо при том же порядке имеет большую
(по абсолютной величине) константу погрешности. П
Примеры. Указанным условиям удовлетворяют аппроксимации
Паде — диагональные и из первой поддиагонали (см. формулу
(IV.3.30)). Можно применять также /-устойчивые линейные
многошаговые методы со Свойством С.
Замечание 4.11. Свойство С позволяет распространить теорему
IV.4.17 Йелча и Неванлинны на явные многошаговые методы. Таким
образом, у явных методов со сравнимыми вычислительными
затратами области устойчивости не могут содержаться одна в другой. Как
видно из упр. 4 (см. ниже). Свойство С является необходимым
условием. Напомним, что у всех явных методов их полюса находятся на
бесконечности.
328 Гл. V. Многошаговые методы для жестких задач
Общие линейные методы
В примере III.8.5 был введен весьма широкий класс общих
линейных методов. В очевидных матричных обозначениях эти методы
описываются уравнениями
1.„ = Л«„ + ЛВ/Ю. D.26а)
^„+i = Au„ + hBf(v„) D.2бЬ)
И, позволяя намного большую свободу, быть может, снимают
ограничение, которое Даниел и Мур сформулировали как предположение.
Далее, однако, мы убедимся, что это не так.
Основная часть вычислительной работы при решении D.26)
уходит на неявные стадии D.26а), и, следовательно, ее объем зависит от
структуры матрицы В. Подставляя у' = \у^ мы придем к уравнению
t/,^,=5(/i)ii„, D.27)
где
S{ti) = Л + ^хВ[1 - ^В)-^А. D.28)
Таким образом, устойчивость численного метода D.27)
определяется собственными значениями матрицы 5(//). Видно, что элементами
этой матрицы являются рациональные функции от /i.
Лемма 4.12. Если умножить характеристический многочлен
матрицы 3(/л) на det(/ — fiB), то он станет многочленом по степеням
det(C/-5(/i)).det(/-/i5) = (/,(;i)C4^,.i(/i)C'-4... + GoM = '-
= : Q(/i,C), D.29)
где ^0» • ¦»9jk — многочлены степени < s, причем q^if^) = det(/ — fiB).
Доказательство. Сначала предположим, что В приводится к
диагональному виду:
r-i5T = d;ag(/?i,...,/?,). D.30)
Тогда D.28) примет вид
S
S{^^)=A + BTdiлg{w^,...,w,)T-^A = A + ^WidicT, D.31)
1=1
где
1 = 1,...,5 D.32)
d, = i-й столбец матрицы ВТ,
с7 = г-я строка матрицы Т"М.
Запишем матрицу QI — S(^) через ее векторы-столбцы:
V.4. Порядковые звезды на поверхностях Римана 329
Ее определитель, характеристический многочлен для S{fi),
вычисляется с использованием пол и линейности определителя, причем С, w^
и с, рассматриваются как скалярные величины. Все члены,
содержащие одну из величин Wj в любой степени выше первой, взаимно
уничтожаются, поскольку соответствующий сомножитель является
определителем с двумя или более одинаковыми столбцами. Таким
образом, если умножить det(С/ —5(/i)) на YVi^i(^~'f^l^i) = ^^4^~f^^)^
мы получим многочлен вида D.29).
Матрица В, не приводимая к диагональному виду,
рассматривается как предел матриц, приводимых к диагональному виду.
Коэффициенты многочлена Q(/i,C) непрерывно зависят от В. D
Мы приходим к выводу, что лемма 4.1 остается справедливой и для
общих линейных методов. На римановой поверхности для
алгебраической функции, определяемой уравнением Q(/i,C) = 0) ^ полюсов
располагаются в точках // = l//?i,..., /i = 1//?,, где /З- — собственные
значения матрицы В,
Далее мы должны изучить условия порядка, т.е. аналог леммы
4.3. Напомним, что общие линейные методы должны быть
снабжены стартовой процедурой (см. (П1.8.4а)), которая в случае
дифференциального уравнения у' = \у будет иметь вид Uq = ф{(л) • у^, где
ф{0) ф 0. Здесь /i = ЛА, а V^(//) — это /:-мерный вектор многочленов
или рациональных функций от /i. В этом случгье схема, показанная
на рис. П1.8.1, превращается в схему, изображенную на рис. 4.6.
Ш)'е^
1 точное решение е^
Рис. 4.6. Применение общего линейного метода к уравнению у' = Лу.
Поэтому условие порядка (см. формулу AП.8.16) в лемме П1.8.11)
дает следующий результат:
Лемма 4.13. Если общий линейный метод D.26) имеет порядок р,
то выполняются следующие соотношения:
{е^ 1-3{и))ФМ=0{^м'') яря /Z -> О, D.33а)
Е{еЧ- S{fi)) ф{^х) = 0(ix^-^^) при ft-^ О, D.33b)
где Е определено в (IIL8.12), а S{fi) — в D.28). П
330 Гл. V. Многошаговые методы для жестких задач
Смысл формулы D.33) состоит, грубо говоря, в том, что ф(^г)
является приближенным собственным вектором матрицы S{fi), который
соответствовал бы собственному значению е^. Посмотрим теперь,
как можно использовать эту информацию, чтобы получить условия
порядка для истинных собственных значений S(fi).
Определение 4.14. Определим ? как число главных листов рима-
нова многообразия алгебраической функции, соответствующей D.29).
Иными словами, i является кратностью единицы как собственного
значения матрицы 5@) (при этом единица должна быть простым
корнем минимального многочлена в силу устойчивости метода). Число
? является также размерностью единичной матрицы / в формулах
(III.8.12) и рангом матрицы Е.
Теорема 4.15. Предположим, что существует вектор \l){^) (причем
ф{0) фО) такойf что общий линейный метод удовлетворяет условиям
D.33) при р> 1. Тогда ?-кратное собственное значение 1 матрицы
5@) непрерывно продолжаемо в ? собственных значений Cj(fi)
матрицы 5(/i), удовлетворяющих условиям
е^ - Cj{^) = 0(/хР>+^) при /i -^ О, D.34)
где
t
Примеры, а) Для матрицы
? = 2, а поэтому в D.33b) Е= I. Существует вектор ^(//) (отличный
от нуля при /i = 0) такой, что
(e'^/-5(/i))V(/i)=0{//«),
Т.е. р= 5. Для собственных значений
:.»=(>-?-T)*?V^
2 80
имеют место оценки ef* ~Ci(a^) = 0{^^), е^ — С2(/^) = ^(м) » т.е.
выполняются условия D.34) с Pi = 5 и Р2 = 0.
Ъ) Матрица
,.3
удовлетворяет условиям D.33), причем ^ = 2, р = 4. Ее собственные
значения Сх.гС/^) = 1+А*-/^^/2 удовлетворяют условиям D.34), где
Pi = Р2 = 2 •
V.4. Порядковые звезды на поверхностях Римана 331
с) Для
?=2 и р= 1 ъ D.33). Собственные значения (^ 2^ = l-f-/ii y/J^
удовлетворяют соотношениям D.34) с р^=р2 = 1/2. Этот пример
показывает, что Pj в D.34) необязательно должны быть целыми.
Доказательство теоремы 4.15. Введем матрицу
S(^^)=eЧ-S{^^), D.39)
которая имеет те же собственные векторы, что и S{^), а
соответствующие собственные значения равны
С^Ы = е''-С^Ы). D.40)
Теперь формулы D.34) и D.35) говорят просто о том, что
1
ПС,Ы = 0(//^^') при/i-^O. D.41)
Поскольку произведение собственных значений, как мы знаем, равно
определителю матрицы, будем искать информацию о det S{y).
Будем считать, что (после соответствующей замены координат с
помощью матрицы преобразования Т из (П1.8.12)) матрица 5 = 5@)
имеет жорданову каноническую форму. Выделим теперь блоки
размерностей i и к — l^ ъ результате чего получим
^-(,0 о)' ^('^)-i ад ОН))' ^^^^-изЫ;'^'''^
^'^-[sM SMj-yoM ОН))- ^'-''^
Важно отметить, что здесь 522@) —обратимая матрица, поскольку Е
собирает все равные единице собственные значения, и, таким образом,
522@) их не имеет, а 522@) не имеет нулевых собственных значений.
Теперь условия D.33) принимают следующий вид:
(Snit^) 5,Щ(ФМ\^@{и''^^)\
U2i(m) S,,(^^))UMJ V о(цр) )¦ ^ • ^
Положив В D.44) ^х = О, мы найдем, что V^2@) = 0- Таким образом, из
предположения ^'(О) ^0 вытекает, что по крайней мере одна
компонента вектора V'i(O) не обращается в нуль, например, j-я компонента
V^ij(O). Тогда по правилу Крамера
det5(/i)Vij(/i) = cletr(/i), D.45)
где T{pl) получается из матрицы S{yL) в результате замены ее j-ro
столбца на правую часть уравнения D.44). Легко убедиться, что
332 Гл. V. Многошаговые методы для жестких задач
deiT(fi) = 0{fiP'^^) (надо вынести множитель // из первых ? строк
и множитель /iP из j-ro столбца). Поскольку ^ij(O) ф О, это
означает, что det 5(/i) = 0{ii^'^^). Таким образом, мы доказали оценку D.41)
(а следовательно, и D.34), D.35)), поскольку Ci^i^ - • -Хк "^ сходятся
к нулю при /i -ч О. П
Следующая лемма исключает дробные порядки для
Л-устойчивых методов.
Лемма 4.16. Для I-устойчивых общих линейных методов порядки
Pj в D,34) должны быть целыми.
Доказательство. Разделим D.34) на е'^ и положим р^. -h 1 = т/г,
что дает
^ = l-C/i"'/^ + ....
_ .C/i"'/'- + .... D.46)
Предположим, что г > 1 и т, г — взаимно простые. Поскольку
величины e^—Cjif^) являются собственными значениями матрицы D.39)
и поэтому корнями некоторого аналитического уравнения,
присутствие корня ^"^/^ приводит к появлению всех ветвей fx^^^ • e'^^^Jf^
(j = 0,1,.. .,г—1). Следовательно, подставляя в D.46) значения
/i = ±iy = e^^^l'^y (с малыми у G К), мы получим 2г различных
значений
1 ^ Cy'^lr^±im^l2r ^2ii^j/r ^ ^ j = О, 1, . . ., Г - 1,
которые образуют правильную «звезду Мерседес», но с 2г
лучами. Тогда, каким бы ни был аргумент С, существует значение
C{±iy)^f^ c^^^^l^ (при некотором j, 0<j<r-l)c отрицательной
действительной частью. Поэтому из D,46) следует, что |Cj(±2l/)| > 1. Но
это противоречит предположению об /-устойчивости. П
А теперь сформулируем и докажем «гипотезу Даниела—Мура»
для общих линейных методов.
Теорема 4.17. Пусть характеристическая функция Q{fjX)
некоторого I -устойчивого общего линейного метода имеет s полюсов в С+ .
Тогда
р<Ъ. D.47)
Доказательство. Как и прежде, обозначим Л+= ЛП7г~^(С+)
часть порядковой звезды, лежащую над С+ . В силу
/-устойчивости Л+ не пересекает мнимую ось ^'""^(Ж) ни на одном листе.
Согласно теореме 4.15 кривые 7т > ограничивающие Л+ , попадают
в начало координат на различных главных листах не менее чем [^-^^]
раз (jf = l,...,^) (см. D.17)), где р^- —целые числа в силу леммы 4.16.
V.4. Порядковые звезды на поверхностях Римана 333
Таким образом, согласно лемме 4.2 выполняется неравенство
D.48)
Умножая его на 2, учитывая, что Pj < 2[^^^], и используя
неравенства D.35), мы получим утверждение теоремы: p<2s. П
Двойственные порядковые звезды
«А почему бы не поменять ролями эти две переменные, С и
/i...?» (Дж. Бутчер,
27 июня 1989 г., Вест Парк Холл, Данди, в летнюю полночь)
Рис. 4.7. Двойственные порядковые звезды D.53) для методов ФДН
(внизу - увеличенные фрагменты).
334 Гл. V. Многошаговые методы для жестких задач
Л-устойчивость означает, что для всех решений Cif^) уравнения
Q(fiX) = О мы имеем
Re//<0 => 1С>Ы1<1- D.49)
Логически это эквивалентно утверждению: для всех решений //,(С)
уравнения Q(/i,C) = 0 ^'^ имеем
|С|>1 => Re/i^.(C)>0 D.50)
(на самом деле, чистая логика дает знак ">" с обеих сторон, а знак
">" следует тогда из непрерывности). Далее, при переходе к
обратным функциям для главного корня условие порядка D.15)
переходит в
logC-/ii(C) = -C(C-l)''+4.... D.51)
Таким образом, теорию порядковых звезд можно во многом сделать
двойственной с помощью следующих замен:
с,
1,
единичная окружность , , ^^ч
м, ^'-''^
Arg ,
log .
Аналогом определенной в D.12) звезды становится множество
Л = {С; Re/i(C)<Re(logO} = {Ci R^MC)<bg|Cl}, D.53)
а аналогом относительной порядковой звезды D.18) — множество
В = {С; Re/i(C)<Re/i«(C)}. D.54)
В частном случае — для правила трапеций — последнее множество
имеет вид
в = {с ; R«//(C) < Re B^)} • D.55)
Множество А для методов ФДН2 и ФДНЗ изображено на рис. 4.7.
Этот рисунок еще раз объясняет, почему невозможно существование
Л-устойчивых методов порядка > 2s (см. упр. 5).
Еще одна возможность состоит в замене D.50) условием
|С|>1 => Re^>0, D.56)
которое, очевидно, является эквивалентным. В этом случае условие
порядка D.51) принимает вид
а)
Ь)
с)
d)
е)
f)
/*
0
мнимая ось
Re
Im
exp
V.4. Порядковые звезды на поверхностях Римана 335
поскольку как для log С, так и для /ii(C) имеет место разложение
(С — 1) + 0({С — 1)^). Порядковые звезды превращаются теперь,
соответственно, в множества
, = {С; Rejii>R.ji} D.58)
и
В={С; Re^> R.^--L}. ,4.5.)
Особое преимущество этих последних определений проявляется для
линейных многошаговых методов, у которых l//i = ^(С)/р(С) и
поэтому полюса рассматриваемых функций являются нулями р(С),
участвующими в определении обычной устойчивости (нуль-устойчивости,
см. разд. III.3). Это обстоятельство можно использовать для
получения геометрического доказательства теоремы III.3.5 (первого барьера
Далквиста), идея которого подсказана статьей Изерлеса и Нёрсетта
A984) (см. упр. 6).
Можно также заметить, что доказательство теоремы 1.4 [второго
барьера Далквиста) в разд. V.1 есть не что иное, как исследование
множества В из D.59), где //д(С) представляет правило трапеций.
Упралснения
1. Проанализируйте поведение характеристических корней
уравнения D.7) в окрестности полюса, совпадающего с точкой
ветвления, т.е. найдите асимптотическое решение D.7) для больших С в
случае, когда
Покажите, что эти корни ведут себя как ±C{fi'- ^Iq)"^^^ .
2. Для матриц 5(/i), заданных в D.36), D.37) и D.38), вычислите
приближенные собственные векторы ф{(л) такие, что
{e^'I-S(,л))ф(fл) = 0(^iP+').
Покажите, что указанные в тексте значения порядка являются
оптимальными.
3. Объясните с помощью порядковых звезд, почему двухшаговый
двухстадийный кол локационный метод с параметром Cj = 1 (см.
упр. 7 из разд. V.3) теряет Л-устойчивость как раз в тот момент,
когда значение с^ проходит через точку сверхсходимости (упр. 8
из разд. V.3).
4. В методе
336 Гл. V. Многошаговые методы для жестких задач
который при /? = 3/8 является методом Адамса 4-го порядка,
измените коэффициент /? таким образом, чтобы область устойчивости
стала строго больше. Этот пример показывает, что многошаговый
вариант теоремы IV.4.17 Йелча и Неванлинны требует
предположения о наличии «Свойства С».
5. Докажите гипотезу Даниела—Мура с помощью порядковой звезды
Л из D.53).
Указание. Множество А не может пересекаться с единичной
окружностью, а вдоль ограничивающих А кривых мнимая часть
bgC —А'(С) должна монотонно убывать (обратитесь к D.52) и к
доказательству леммы IV.4.5). Следовательно, граничная линия с
начгипом и концом в начале координат должна либо проходить
через полюс (который расположен внутри или на единичной
окружности), либо пересекать снизу вверх отрицательную часть
действительной оси (где Im(logC) увеличивается на 27г). Поскольку при
этом множество А должно находиться слева, такое возможно лишь
по одному разу на каждом листе.
6. Докажите теорему о первом барьере Далквиста с помощью
порядковых звезд, т.е. докажите, что устойчивые линейные
многошаговые методы удовлетворяют неравенствам р<к + 2 (при четных к)
и р< fc-f 1 (при нечетных к). Докажите также, что среди
методов оптимального порядка константа погрешности принимает
наименьшее значение для метода, у которого
Pnic) = i<-mc+i)'-\ D.60)
где к=: к (если к четное) и к = к—1 (если к нечетное).
Указание, Исследуйте порядковые звезды D.58) (при fi = ^f^) и
D.59), где fiji = <Тл1рл и рд задано формулой D.60) (для случая
fc = 6, р = 8, /?(С)=С^ —1 см. рис. 4.8). Вы должны показать, что в
окрестности точки С = 1 обе порядковые звезды имеют одинаковые
цвета. Вам помогут следующие наблюдения:
i) вблизи точки С = -1 (порожденной полюсом 1/(СЧ-1)'^""^) звезды
имеют противоположные цвета;
ii) из требования устойчивости следует, что все полюса функций
лежат на единичной окружности или внутри нее;
iii) граничные кривые множеств А и В пе могут пересекать
единичную окружность сколь угодно большое число раз, так как
^л(^^^) ^ ^в(^'^) являются тригонометрическими многочленами;
iv) исследуйте поведение А и В па, бесконечности.
V.4. Порядковые звезды на поверхностях Римана 337
Рис. 4.8. Двойственные звезды D.58) и D.59) для метода
pя(c)=(c-l)(c+l)^ Р(с)=г-1,
<тл (С) = B51С^ +273бС^ + 6957С^ + 10352С^ +6957С^ + 2736С + 251)/945
<т{С) = D1С^ + 216С^ + 27С^ 4- 272С^ + 27С^ + 216С + 41)/140 .
7. Докажите теорему о втором барьере Далквиста для линейных
многошаговых методов с помощью порядковой звезды D.55).
8. Для неявного многошагового метода третьего порядка постройте с
помощью компьютера порядковую звезду В, определяемую
формулой D.18), где R{fi) — максимальный корень метода Милна—
Симпсона A.17). Это даст вам возможность сразу понять, почему
справедлива теорема 4.9.
V.5. Эксперименты
с многошаговыми программами
«.. .мы знаем, что теория неспособна предсказать многое из
того, что происходит на пргистике в настоящее время, и
разработчикам программного обеспечения приходится искать
дорогу с помощью вычислительного эксперимента...»
(Дж.Р. Каш (см. Эйкен 1985))
¦Сравнение различных программ — это пользующаяся
дурной славой, трудная и неточная область..., однако есть
некоторые недвусмысленные результаты, которые могут...»
(Дж.Р. Каш 1983)
В данном разделе представлены численные результаты,
полученные при применении многошаговых программ к тем же самым
задачам, что и в разд. IV.10. Это, в порядке увеличения размерности,
задачи: VDPOL (уравнение Ван-дер-Пол я (IV. 10.1)), ROBER
(знаменитая задача Робертсона (IV.10.2)), OREGO (орегонатор (IV.10.3)),
HIRES (задача из физиологии (IV. 10.4)), Е5 (химическая реакция
(IV. 10.5) с переменными, отличающимися на много порядков), PLATE
(автомобиль проезжает по пластине, — единственная линейная и
неавтономная задача (IV.10.6)), BEAM (нелинейное уравнение
колебаний упругого стержня (IV.1.10') с п = 40), CUSP (катастрофа типа
сборки (IV.10.8)), BRUSS (брюсселятор (IV.1.6') с одномерной
диффузией, а = 1/50 и п = 500) и KS (одномерное уравнение Курамото-
Сивашинского (IV. 10.И) с п = 1022). Мы не включили сюда задачи
BECKDO и BRUSS-2D, поскольку они требуют особого обращения с
линейно-алгебраическими подпрограммами.
Как и в разд. IV. 10, для всех программ задавалась требуемая
точность
ДЫ = 10-^/^ т = 0,1,2,...
и Atol = Rtol (за исключением Atol = 10"^ • Rtol для задач OREGO и
ROBER, Atol = 10-4 • Rtol для HIRES, Atol = Ю'З . Rtol для PLATE, и
Atol = 1.7 • 10-^"* для Е5). Все программы компилировались с
одинаковыми опциями оптимизации. Результаты численных экспериментов
представлены на рисунках 5.1 и 5.2, где по осям отложены
полученные погрешности численных решений и процессорное время; как и
ранее, темными значками выделены точки, соответствующие
требуемой точности Rtol = 10"^.
Использованные программы
LSODE (Livermore Solver for Ordinary Differential Equations) —
«ливерморский решатель ОДУ»; эту программу разработал Хайнд-
марш A980, 1983). Поскольку мы имеем дело с жесткими
уравнениями, используются указатели «жестких» методов MF= 21,22,24 или
25, которым соответствуют методы ФДН с фиксированным шагом в
V.5. Эксперименты с многошаговыми программами 339
представлении Нордсика (см. разделы III.6 и III.7). Эта программа
возникла в результате длительной работы, начавшейся с
программы DIFSUB, которую создал Гир в 1971 г. Образцовый
пользовательский интерфейс и простота применения LSODE послужили примером
для многих последующих программ для ОДУ (включая наши).
Большинство задач решалось с аналитически заданной матрицей Якоби
и линейной гиягеброй для полных матриц (MF= 21); исключение
составили задачи BRUSS и KS (аналитическая ленточная матрица
Якоби, MF=24), BEAM (полная матрица Якоби, получаемая численно,
MF=22) и CUSP (ленточная матрица Якоби, получаемая численно,
MF=25).
С задачей Е5 программа работала правильно только при То1 <
< 10~^, для PLATE требовалась То1 < 10"*^. Для задачи BEAM,
имеющей собственные значения на мнимой оси, пришлось ограничить
максимальный порядок значением 2 из-за отсутствия Л-устойчивости у
методов ФДН более высоких порядков. На рис. 5.3 видно, сколь
катастрофичны последствия, если разрешить методы выше второго
порядка.
DEBDF — это драйвер (управляющая программа) Шампайна и
Уоттса для модифицированного варианта LSODE. Она включена в
семейство «DEPAC» (Шампайн и Уотте 1979). Как и следовало
ожидать, эта программа ведет себя почти так же, как LSODE (см. рис. 5.1
и 5.2). Она тоже требует ограничения порядка для задачи BEAM (см.
рис. 5.3).
VODE (Variable-coeffficient Ordinary Differential Equation solver) —
«решатель ОДУ с переменными коэффициентами»; программу
разработали Браун, Берн и Хайндмарш A989). Она основана на пакетах
EPISODE и EPISODEB (см. разд. III.7), использующих ФДН-методы
на неравномерной сетке (Берн и Хайндмарш 1975). Пользовательский
интерфейс VODE очень похож на LSODE; эта программа тоже
допускает выбор между полной и ленточной линейной алгеброй, между
аналитическим и численным определением матрицы Якоби. Результаты
численных расчетов по программе VODE для больших задач очень
близки к соответствующим результатам LSODE и DEBDF, однако на
задачах малой размерности она работает значительно медленнее (см.
рис. 5.1 и 5.2). Для задачи Е5 пришлось наложить ограничение на
требуемую точность {Rtol < 10"^). На задаче PLATE результаты
оказались намного лучше, чем у всех остальных программ. Для задачи
BEAM необходимо ограничение максимального порядка значением 2
(рис. 5.3).
SPRINT (Берзинс и Ферзеланд 1985). Этот пакет написал М. Берь
зинс; он включен в библиотеку NAG (раздел «subchapter D02N»).
Пакет содержит несколько модулей для процедуры пошагового интегри-
340 Гл. V. Многошаговые методы для жестких задач
\QP\-
VDPOL
VODE-
SPRINT
погрешность
lO bin JMini Ьщн biim Imiiii bim \mim knii Liiii iaiiii
LSODE
10-3
10-*
10-»
DEBDF
погрешность
II Уин Liiii Ум I hum 1ш»и Wiiui куим bum Liiii bill
10-3
10-6
10-*
10°
OREGO
io-«h
VODE
погрешность j L/'^"^ погрешность
шит Imiii biiii bun kuiii biiii kuw Jmiii kiiii biiii biiM.biml цп bim kiiii biiii bun biiii b»ii bmi bmi biiii bin
IQO 10-3 10^ 10-» 10-3 jo^ 10-» 10-^2
HIRES
SPRINT
10-» h
L сек
^¦
E5
VOQE
" spRI^n^.->^
HULLL-iuuE'j
Lull 11 krni
—DEBDF
-LSODE
погрешность
1 Uiiii Lull Lull Will Lull
10'
IQP
10-'
r
-
сек
•-a—-&
PLATE .^_^„j-i-^
SPRINT -==3?*-'"^
LADAMS \ LSODE
111 blULl
kZ^bbde ^J V
^"""^^ VODE
погрешность
biiiii kmii.kaLi-kuii-kmi kuiu Ltiti kul
10"
10-3
lO-*
10-^ 10-»
Рис. 5.1. Диаграммы побьем вычислений — точность»
для задач с размерностью от 2 до 80.
I0-»
V.5. Эксперименты с многошаговыми программами 341
BEAM ^^^^;
LSODE, and DEBDR
погрешность
mini t I Ь"|" ' ' liiiiii I t liimi I I liiim I I ..Imm i
K^"" CUSP
г SPRINT
г VODE цг-^^""^^
^^C;;^^!::^ DEBDF
11 Litii Uiiii Luiii Uuiii Liiii Uin
LSODE
погрешность
1 kuiii haiii.kui.i..iuuuJ
BRUSS
погрешность
b«uii km I Lull Lnii Imiiii Imiiii Utii iiiiiii JMiiiikiiiLi
10-
10-^
10-9
погрешность
Lllllini bum 1 1 luUU I i Imm I I liiiiti I I Imm i i Inn
IQO
10-5
Рис. 5.2. Диаграммы «объем вычислений — точность»
для задач с размерностью от 80 до 1022.
рования, в частности, модуль SBLEND. Это позволило нам
исследовать, как работают смешанные многошаговые методы C.15) Скила и
Конга A977). Как видно из табл. 3.4, эти методы Л-устойчивы до 4-го
порядка включительно. Поэтому мы ожидали, что они окажутся на-
хмного лучше остальных для колебательной задачи BEAM. На рис. 5.2
видно, что эта программа действительно дает отличные результаты
для данной задачи (ср. рис.IV.10.9). Положение серых значков
(соответствующих То1 = 10~5) на рисунках 5.1 и 5.2 показывает, что эта
программа при той же заданной точности дает лучшие результаты,
чем все остальные многошаговые программы. Однако порой она
работает довольно медленно (например, в задачах PLATE и KS).
342 Гл. V. Многошаговые методы для жестких задач
1 ^ LSODE
L ordJy \^а4 fjL ^
Г XLiJy^
: ml i~0Td2
Г10° ^^
1 погрешность
1 кип bill bill bill bill bill bill biiii ¦
1 V DEBDF^ ordS
г \ \^^^Jf J^S>T<i\ f
г V\ [f /
ИО' owi3>\Jr jC—ox^l
1-10° c#^
\_ погрешность
Г. L....L...Li...L...L....U..U..L..,d
реек yQpg
И(Я\ ^nN f J
P^'ordrvVv 1/ iT
P ^^ j(—01x12
Uo" Ap^
F dL/ погрешность
U.biii_bin Ьигаши bill buLimu bin У
IQO 10-' 10^ 10° 10-' 10^ 10° 10-'
Рис. 5.3. Работа программ LSODE, DEBDF и VODE
при ограничениях максимального порядка на задаче BEAM.
10^
F'^^'^ OREGO ^ д.
Г VODE—*^ ^CSECDER
п9С! y^Ki^^^
U \ ^^TLSbDE
. \v: g^ погрешность
¦111 ЮГкш bii bn bii bii bii bii bii bil
t ^^"^ HIRES
1 SECI^R
1 ^^R? Af^
HO-' 'C^^^Ji
\Jr^ «C—LSODE
y^ погрешность
hAiii bill bui bill Wii bui bill bill biiil
Реек
L-io'
Uo»
L r^
Xi bu bi
PLATE p,^^^,/"^^^^
-jj^^SE^DER
i-O LSODE
vbDE
погрешность
Liii Liii Ldi Lii Liii Liii Lii Lml
10° 10-' 10-* 10-» 10^ I0-» 10-12 10-' 10-* 10-»
Рис, 5.4. Сравнение программ SECDER, LSODE и VODE.
10-»^
¦LSODE погрешность
kUlLU liiiiiii 1 Uiiiii I luiiiil I lnilll.l.l—iui
10° 10-' 1(H 10-' 10^ 10-' 10-*
Рис. 5.5. Сравнение программ MEBDF, LSODE и VODE
(для задачи BEAM — при ограниченном максимальном порядке).
SECDER — эту программу написал в 1979 г. Ч.А. Аддисон (см.
Аддисон 1979); она реализует многошаговые методы со второй
производной (SECond DERivative) C.7) Энрайта. Высокий порядок методов
в сочетании с хорошей устойчивостью позволяют ожидать хорошей
работь^ при высокой заданной точности. Это было подтверждено на
задачах OREGO, HIRES и PLATE (см. рис. 5.4), однако последняя из
V.5. Эксперименты с многошаговыми программами 343
НИХ решалась очень медленно. Для больших задач мы эту программу
не использовали, поскольку в нее не включена ленточная алгебра и
требуется аналитическое задание матрицы Якоби.
MEBDF — эта программа (Каш и Консидайн 1992) реализует
МРФДН-методы (см. уравнение C.17mod) и табл. 3.5). Ее хорошая
работа продемонстрирована на рис. 5.5 на избранных примерах. На
задаче BEAM программа работает хорошо, если максимальный
порядок ограничен значением 4.
LADAMS — «Livermore Adams», т.е. LSODE с указателем метода
MF= 10. Этот вариант LSODE включен, чтобы показать, как
работает явный многошаговый метод на больших и (или) умеренно
жестких задачах. Он оказался конкурентоспособным при решении
некоторых больших задач (PLATE, BEAM). По сравнению с D0PRI5 (см.
рис. IV. 10.8) эта программа работает заметно медленнее, когда
вычисления / дешевы (CUSP), однако это не относится к задаче BEAM.
Программы LSODE, DEBDF, VODE и MEBDF доступны по
электронной почте: можно, например, по адресу «netlib@research.att.com»
послать текст «send Isode.f from odepack».
Упралснения
1. Поэкспериментируйте сами с перечисленными выше задачами и
сформулируйте свои выводы. Авторы будут рады предоставить
вам драйверы задач и подпрограммы вычисления функций.
V.6. Одноопорные методы
и G-устойчивость
«.. .формулировка анализа погрешностей для одноопор-
ных методов проще, чем для линейных мно1Х)шаговых».
(Г. Далквист 1975)
Первые результаты по устойчивости для нелинейных
дифференциальных уравнений и многошаговых методов были получены довольно
давно (Линигер 1956; Далквист 1963), — раньше, чем подобные
исследования были проведены для методов Рунге—Кутты. Большой
прорыв был совершен в 1975 г. (на конференции в Данди), когда
Далквист предложил рассматривать нелинейные задачи
у'= fix,у), F.1)
удовлетворяющие одностороннему условию Липшица
{fix,y)-f(x,z),y-z)<u\\y-zf F.2)
или, в случае комплекснозначных функций,
Re{f(x,y)- f(x,z), у- Z) <ф- zf F.2')
(см. разд. IV. 12). Далквист также обнаружил, что изучение
нелинейной устойчивости для общих многошаговых методов упрощается,
если рассматривать связанный с ними класс методов — так
называемые одноопорные (многошаговые) методы.
Одноопорные (многошаговые) методы
«... несколько ненормальное название
одноопорные методы...»
(Г. Далквист 1983)
«Je пе suis absolument pas capable de tra-
duire "one-leg'' en frcmgciis...imi-jambiste?»
«Я совершенно неспособен перевести на
французский язык "one-leg"...
одноногий?» (М. Крузе в 1987 г.)
«Signor mio, le gni поп hanno se non una
coscia ed una gamba...»
«Синьор мой, журавли ведь опираются
на одну ногу...» (Боккаччо, Декаме-
рон^ 1353; цитату предложил М. Крузе)
Предположим, что задан линейный fc-шаговый метод
к к
Е^.-2/т+.- =ЛХ;/?,/(х^^,,г/^^,), F.3)
1=0 1=0
производящие многочлены которого
к к
р(с)=Е«.с', ^(с)=Е'^.<'' F-4)
t=0 t=0
V.6. Одноопорные методы и G-устойчивость 345
имеют действительные коэффициенты, и у них нет общего лелителя
(см. разд. III.2). Мы будем также всегда предполагать нормировку
GA) = 1. F.5)
Тогда соответствующий одноопорный метод определяется формулой
к у к к ^
1=0 ^1=0 »=0 ^
в этом новом методе производная / вычисляется только в одной
точке, что делает его более простым для анализа.
Конечно, было бы интересно знать, как решения одноопорного
метода F.6) связаны с решениями его «многошагового двойника» F.3).
Если дифференциальное уравнение является линейным и
автономным, у' — Ау, то обе формулы — F.3) и F.6) — совпадают. Для схем
ФДН A.18) в многошаговом варианте всегда присутствует только
одно значение /, и, следовательно, уравнения F.3) и F.6) одинаковы.
Однако для общих методов и общих нелинейных уравнений эти
формулы не совпадают, хотя их решения связаны определенными
преобразованиями (см. упр. 3). Рассмотрим в качестве примера правило
трапеций, которое является двухопорным методом:
2/m + l " 2/m = 2 {jk^m ^ Ут) + /(^m+l' 2/m-f l)) • F7)
Соответствующий ему одноопорный метод — это неявное правило
средней точки
2/m+l - 2/m = ^f[ 2 ' 2 ) ' ^ ^^
Если {y^} — решение одноопорной формулы F.8), то пара значений
^ _ 1. ч - _ ^Г ^
Ут — 2 wm + 2/m+l J' ^m — 2 ^^'^ "^'^m+lj
удовлетворяет уравнению F.7). С другой стороны, если {y^,J^}
удовлетворяют F.7), то пара
Ут " Ут 2^^^^^^^^^ "^т ~" •^ш 2
является решением F.8). Эта связь уже использовалась при
доказательстве теоремы IV. 15.8.
Существование и единственность
Будем предполагать, что а^^ ^ О (как всегда) и что /?/с ^ О (иначе
метод будет явным). Многошаговые методы F.3) запишем теперь в
виде
у-г;-Л^/(х,у) = 0, F.9)
^к
где X задано, rj — вектор, составленный из известных величин, а
у = у^^1^ — неизвестный вектор. Одноопорную формулу F.6) с помо-
346 Гл. V. Многошаговые методы для жестких задач
щью преобразования у = 0кУт+к + • • + РоУт тоже можно привести к
виду F.9), так что все последующие результаты о существовании и
единственности решений будут справедливы как: для многошаговых,
так и для одноопорных методов. Для доказательства существования
решения уравнения F.9) заменим hPf^/a^^ на новую «длину шага» Л;
при этом получится не что иное, как неявный метод Эйлера. К нему
сразу можно применить все теоремы для неявных методов Рунге—
Кутты (теоремы 14.2, 14.3 и 14.4 из разд.IV.14), и мы придем к
следующим утверждениям.
Теорема 6.1 (Далквист 1975). Пусть f —непрерывно
дифференцируемая функция, удовлетворяющая условию F.2). Если
Л^<§^, F.10)
Ук
то нелинейное уравнение F.9) имеет единственное решение у. П
Теорема 6.2. Пусть у — решение уравнения F.9). Рассмотрим
возмущенное значение у, удовлетворяющее уравнению
g^rf^h^f(x,y)=S. F.11)
^к
Тогда при предположении F.10) выполняется соотношение
"^-""^i-wk»-"^"- '"^'
П
Замечание. Теоремы IV. 14.2, IV. 14.3 и IV. 14.4 верны для намного
более общего класса методов, чем просто неявный метод Эйлера,
который нам здесь понадобился. Читатели, которых не интересует более
общий случай, могут почти слово в слово переписать доказательства
из разд. IV. 14. Поскольку теперь имеется лишь одна неявная стадия,
все тензорные произведения исчезают, и формулы (но не идеи
доказательства) значительно упрощаются.
G-устойчивость
Если дифференциальное уравнение удовлетворяет
одностороннему условию Липшица F.2) (или F.2')) с константой i/ = О, то точные
решения являются контрактивными (лемма IV. 12.1). Теперь мы
исследуем, какие одноопорные (многошаговые) методы при этом тоже
имеют контрактивные решения. Поскольку численное значение у^^^
зависит от всех величин t/^^^^-i > •->Ут> ^^ имеет смысла требовать
выполнения неравенства \\Ут^к "Ут-\-к\\ < ЦУш+л-! - J/m+fc-ilb как в
одношаговом случае (определение IV. 12.2). Мы должны
рассматривать метод как отображение R^'^ -> Е" '^. Для этого введем
обозначение
>'m = (ym+fc-l.--.ymf F-13)
V.6. Одноопорные методы и G-устойчивость 347
и зададим в М*^ '^ нормы, порожденные скалярным произведением:
к к
\Ы\1 =^Yl9ij {ym-^i-.l.ym+j-l)^ F.14)
1 = 1 j = l
где (•,) — то же самое скалярное произведение в К'*, которое
использовано в F.2), а матрица
G={9ij)i,j=i,..,k
размерности к предполагается действительной, симметричной и
положительно определенной.
Определение 6.3 (Далквист 1975). Одноопорный метод F.6)
называется G-устойчивым^ если существует действительная
симметричная положительно определенная матрица G такая, что для двух
численных решений {Ут} и {у^} соотношение
\\Ут+1-Угг,+г\\с<\\Ут-УЛа F.15)
выполняется при любой длине шага Л > О и для всех
дифференциальных уравнений, удовлетворяющих условию F.2) или F.2') с
константой I/ = О.
Поскольку уравнение j/ = Ау при Re А < О удовлетворяет условию
F.2') с I/ = О, сразу получается
Теорема 6.4. Из G-устойчивости следует А-устойчивость. П
Пример 6.5. Рассмотрим двухшаговый ФДН-метод
3 1
22/т+2 - 2Ут+1 + 2^т = Л/(х^+2> Ут+г)- F16)
Возьмем второе численное решение {у^} и обозначим разность,
которую оно образует с {у^}, через Ау^ ^Ут^Ут- Применяя наше
предположение F.2') к F.16):
Re(/( ) - f{Xm+2 . Ут+а). Ут+2 ' Уш+з) < 0.
МЫ получим соотношение
?; = Re (|дг/„+2 - 2Ду„.+1 + ^ДУт . ДУт+г) < 0. F.17)
Идея состоит в том, чтобы привести это неравенство к требуемой в
F.15) форме, вычитая из него правильно подобранный
квадратичный член \\а2Ау^^2 +^i^2/m+i '+"^o^2/mlP- Если ввести обозначение
ДУ^ = (ДУт+1) ДУт)^ 1 ТО ЭТО означаст, что
Е = ||АУ^+111^ - \\AYJ\l + ||а2Ду^+2 + а,Ау^^, + а,Ау^\\\ F.18)
где G — положительно определенная матрица:
'^(922 92l\
\921 9п)'
348 Гл. V. Многошаговые методы для жестких задач
Произведи! умножение и сравнив коэффициенты при Ке(Ду,, Ду^) в
F.17) и F.18), мы получим шесть соотношений
3
2=^22 + «2' 0 = ^11-</22 + «1' 0 =-5^11+^0' F.19а)
-2 = 2(^21 + 20201, - = 20200, о = -2д^^ + 2oiOo. FЛ9Ь)
Сложение всех шести уравнений дает О = (oq -h о^ 4- aj)^, так что Gq^
-hOj +02 = 0. Из последнего соотношения вместе с F.19Ь)
определяются значения о,-: Oq = ±1/2, о^ = =р1» ^2 — ±1/2. Подставив их в
F.19), получим положительно определенную матрицу
4D 1)
F.20)
Так как согласно F.17) ?" < О, то из F.18) следует, что двухшаговый
ФДН-метод является G-устойчивым.
Алгебраический критерий
Алгебраические структуры предшествующих построений станут
намного яснее, если во всех членах в F.17) и F.18) сделать
формальную замену
И учесть, что
2Re (Ду^+,., ^Ут+j) = <ДУт+,-» ^Ут+j) + {^Ут+j . ^Ут-^г)'
В результате мы получим
Е = ^(р@<т{и>)+р{и,)<т{<:)), F.17')
к к к
Е = {Си>-1) Х: ^iC-V-4(X:a.C)(i;ay). F.18')
ij=l 1=0 j=0
Теперь можно сформулировать алгебраический критерий, который (в
других обозначениях) был дан уже в работе Далквиста A975).
Теорема 6.6 (Байокки и Крузе 1989). Рах:смотрим метод {р,сг).
Соответствующий одяоопорный метод является С-устойчивым, если
существуют действительная симметричная положительно
определенная матрица G и действительные числа Oq ,..., о^^ такие, что
\{р((:)<т{и)+р(и>)а{0) =
к к к {G)
= (Со; -1) х; 9ijC-'^'-'+(Е «.<•) (Е «i'^0 •
«,i=i i=0 j=0
Замечание. Множитель 1/2 в левой части соотношения (G) не
имеет существенного значения, и его можно заменить на любую другую
V.6. Одноопорные методы и G-устойчивость 349
положительную константу, что приведет лишь к иному
масштабированию коэффициентов g^j и а,.
Доказательство. Просто заменив в уравнении (G) С*ы-^
скалярным произведением {Ау^^^, Ay^_^j), получим
к к
Ке(^а,Ду^^,,^/?^-Ау^^^.) =
F.21)
= IIA^^n+l IIg - \\^Ут\\с + II Е ^г^УтН^'
1=0
Подставив затем сюда F.6) и использовав F.2') с константой «/ = 0,
придем к требуемой оценке ЦАУ^^Л^^ < ЦАУ^Ц^. П
Интересно выяснить, для каких методов (р, <т) выполняется
условие F.21). Согласно теореме 6.4 F.21) является необходимым
условием Л-устойчивости метода. Будет ли оно также и достаточным?
Эквивалентность Л-устойчивости и G-устойчивости
Далквист три года бился над этим вопросом. Ответ оказался
таким:
Теорема 6.7 (Далквист 1978). Если р и а не имеют общих
делителей^ то метод (р, а) А-устойчив тогда, и только тогда., когда
соответствующий одноопорный метод G-устойчив.
Доказательство. Здесь мы будем следовать изложению Байокки
и Крузе A989). Напомним сначала, что Л-устойчивость метода (/?, о")
означает, что
КеЖИС)>0 при|С|>1 (А)
(см. разд.УЛ). В силу теорем 6.4 и 6.6 достаточно доказать, что
из условия (А) следует существование действительной
симметричной положительно определенной матрицы G и действительных
чисел Oq, ..,, а;^ таких, что выполняется свойство (G). Доказательство
проводится в три этапа: а) вычисление Oq, .. .,а;^; Ь) вычисление G;
с) доказательство положительной определенности G.
а) Содержащий коэффициенты g^j член в (G) обратится в нуль,
если положить lj = l/Q. Поэтому рассмотрим функцию
Е{С) = ^(Ж)<^A/С) + РA/0<^(С)), F.22)
350 Гл. V. Многошаговые методы для жестких задач
которая имеет вид
F.23)
с некоторым г < к. Поскольку E(Q = ?"A/0, для каждого корня
(j многочлена С^Е{С) обратная ему величина 1/Cj также является
корнем той же кратности. Поэтому внутри единичной окружности
находится столько же корней, сколько и вне ее. Что касается корней
на единичной окружности, то для них согласно условию (А)
выполняется соотношение Е{С) = Кер(С)(т{С) > 0. Следовательно, все корни
на единичной окружности должны иметь четную кратность;
половину из них мы объявим расположенными «внутри» и половину —
«вне» окружности. Разумно собрать теперь все корни,
расположенные «вне» единичной окружности, в одно произведение. В результате
получим:
^@ = ^ П(с-д) П (с-с,) =
^ Cj вне С> внутри
= р П(с-с,) П(с-7:)= F.24)
=^<П(с-дП(^-с.).
Cj вне Cj вне
где К — некоторая константа. Но она должна быть
неотрицательной, что можно увидеть из следующих рассуждений: в силу условия
(А) E{Q неотрицательна на единичной окружности. Это же верно и
для функции, деленной на К^ так как каждому множителю (е*^ ""С/)
из первого произведения соответствует комплексно сопряженный ему
{е~^^ —Cj) из второго. Поэтому Е{С) в F.24) можно представить в
виде двух сомножителей:
J5(C) = a(C) 0A/0, F-25)
где
a{0 = VK П (С-С,) = :Х;а,С, F.26)
Cj вне 1=0
что и завершает этап (а) доказательства.
Ь) Из F.22) и F.25) следует, что многочлен
^'(С, w) = I {р{0<т{ш) + Р(ш)<г{0) - а(С)а(а>) F.27)
V.6. Одноопорные методы и G-устойчивость 351
обращается в нуль при Ct*' — 1 = О. Поэтому его можно записать в виде
к
Р(С,а;) = (Сы - 1) ^ 9ijC-'Lj^-'. F.28)
Коэффициенты g^j здесь являются действительными и
удовлетворяют условию g^j = gj^, поскольку P(C,t^) = Р((^, С) •
с) При рассмотрении F.28) на первый взгляд кажется сложным
доказать положительную определенность введенной там матрицы G =
= {g-j). Основная идея доказательства состоит в следующем: выберем
к комплексных чисел Ci > • • > Cjk (сначала произвольных) и произведем
в F.28) замену С *->^ Сд» ^ "^ С > ^то с учетом F.27) приведет к формуле
к
»"'*=1 F.29)
Здесь б^у. — элементы матрицы
B = V*GV,
где V = (Cj"^) — матрица Вандермонда. Таким образом, теперь нам
надо доказать положительную определенность В, что представляется
намного более простой задачей. Сначала разложим в ряд первый
множитель:
^^ = 1+С,С+С^Сг+С^Сг+--- F30а)
1-С,С
Ряд сходится, если
|С,|<1, 9 = 1,2,...,*. (б.ЗОЬ)
Затем потребуем, чтобы для всех q выполнялось равенство
p[Cq) + А(т(С^) = о при некотором А > 0. F.31)
За исключением конечного числа значений А, все к корней
уравнения F.31) различны. Из Л-устойчивости (предположение (А))
следует (б.ЗОЬ), потому что —А лежит внутри области устойчивости. Из
формулы F.29), подставляя в нее F.30а) и используя F.31), мы
получим для произвольного ненулевого вектора v = (г^,..., Vf^) следующее
выражение:
к оо к к
g,r=l fn=0 qf=:l g=l
которое выглядит вполне положительным. Оно не может равняться
нулю при гТ^ О, так как из F.31) следует, что <т(С^) ф О для всех q
(иначе р и <т имели бы общий множитель). Таким образом, tJ*5?>0,
352 Гл. V. Многошаговые методы для жестких задач
т.е. матрица В, а следовательно и матрица G положительно
определена. П
Стоит отметить, что приведенное доказательство дает
конструктивные формулы для матрицы G. В качестве иллюстрации снова
рассмотрим двухшаговый ФДН-метод F.16) с производящими
многочленами
функция E{Q (формула F.22)) принимает вид
и поэтому а(С) = ^{С— 1)^ • Подставляя это выражение в F.27),
получим
так что ^22 = ^/^^ 9x2 ^921 — "/2? 5^11 = 1/4. Полученные значения
совпадают с F.20).
Критерий для пололсительных функций
Докажем теперь критерий для положительных функций, которым
мы воспользовались при доказательстве леммы IV. 13.19 и который
является прямым следствием доказанной выше теоремы Далквиста
об эквивалентности.
Лемма 6.8. Пусть x[z) ^ a{z)/P[z) —неприводимая рациональная
функция с вещественными многочленами a(z) степени Kk — l и /3{z)
степени к. При этих условиях функция х(^) положительна, т.е.
Re x(z) > О при Rez> О, F.32)
тогда и только тогда, когда существуют действительная
симметричная положительно определенная матрица А и действительная
симметричная неотрицательно определенная матрица В такие, что
к к
a{z)l3(w)^a{w)l3(z) = (z-hw) ^ а.-^г'-^-Ч Y, К^^''^иР-\
t,i=i t,j=i
F.33)
Доказательство. Достаточность условия леммы станет сразу Ъче-
видной, если в F.33) положить w = z. Для доказательства
необходимости этого условия рассмотрим преобразования
2—1 С-1 W—1 и—1
И введем многочлены
V.6. Одноопорные методы и G-устойчивость 353
Поскольку преобразование F.34) отображает внешность единичного
круга Id > 1 на полуплоскость Rez > О, условие F.32) эквивалентно
предположению (А). Поэтому из теоремы 6.7 следует существование
действительной симметричной положительно определенной матрицы
G и действительных чисел Oq, ..., а^^ таких, что
к к к
\{р{0<т{ш)+р{ш)<т{0) = (Сы-1) f29ijC-''^'-' + (E«.<'')(S"i'^0•
«j=i «=o i=o
Возвращаясь к старым переменным, получим
^{a{z)p{w)-^a(w)f3(z))=: F.35)
к
к к
1=0 i=o
Перегруппировка членов по степеням z и w приводит к равенству
F.33). Получающаяся при этом матрица А положительно
определена, поскольку многочлены (г-М)»""^(г — l)'^"* при i= 1,..., Л линейно
независимы. Коэффициент при z^w^ во втором члене правой части
формулы F.35) должен быть равен нулю, так как степень a{z) не
превышает Л — 1. Заметим, что при таком построении ранг матрицы
В равен всего лишь единице. D
Оценки погрешности одноопорных методов
Применим полученные в этом разделе результаты об
устойчивости для получения оценок глобальной погрешности одноопорных
методов. Для дифференциального уравнения F.1) с точным решением
у{х) (гладким) естественно определить погрешность дискретизации
метода F.6) равенством
к к
SoLi^) = J2cciy{x^ih)-hf[x + 0h,'?fi,y{^ + if^)). F.36)
«=0 1=0
где /? = (т'A) = Е Щ • Для ФДН-методов Е,- Ау(^ + «*Л) = у(х -h/?Л),
поэтому F.36) равно
к
1=0
— погрешности аппроксимации производной в методе, так называемой
погрешности дифференцирования. Для методов, не удовлетворяющих
условию Et 1^{У(^ + *'*) = vix + Ph), правая часть формулы F.36) для
жестких задач может принимать очень большие значения, даже если
354 Гл. V. Многошаговые методы для жестких задач
производные решения ограничены константой умеренной величины.
В этом случае F.36) — неподходящая величина для оценки
погрешности. Далквист A983) предложил рассматривать наряду с Sp{x) еще
погрешность интерполяции
к
В нежестких задачах (с ограниченными производными функции /)
эти два выражения для погрешности связаны с Sqi^(x) следующим
соотношением:
Soii^) = SdH - ^^Щj (^. У(^))«5/(^) + 0{h\\Si{x)f).
Разложение функций F.37) и F.38) в ряд Тейлора показывает, что
Sj,(x) = 0(Л''°+1), Sj{x) = 0(Л'"+»), F.39)
где оптимальные порядки pj) и pj определяются некоторыми
алгебраическими условиями (см. упр. 1а). Из равенства /3 = о-'A) мы
всегда имеем pj > 1, а из условия согласованности следует, что Р?) > 1 •
Однако порядки pj) и pj могут быть значительно ниже, чем
порядок соответствующего многошагового метода (упр. 1). Константы в
членах 0{...) в F.39) зависят только от величин, ограничивающих
некоторую производную решения, но не от жесткости задачи.
Используя Sjy (х) и Sj{x), можно интерпретировать точное решение
задачи F.1) как решение возмущенной одноопорной формулы
к к
Y^ а, j/(x -Ь гЛ) - Sj, (х) = hf(x^-ph,Y, Ы^ + ih) - Sj (х)). F.40)
»=0 1=0
в следующей лемме, обобщающей результаты Далквиста A975) и
Неванлинны A976), исследуется влияние возмущений решения одно-
опорного метода.
Лемма 6.9. В дополнение к одноопорному методу F.6) рассмотрим
возмущенную формулу
к / '' \
^a,y^^,~J^=A/fx^-h/?/i,X^/?,y^+,~?^j. F.41)
t=0 ^ t=0 ^
Предположим, что для дифференциального уравнения F.1)
выполняется условие F.2')J а метод является G -устойчивым. Тогда разности
т
Ау, = у,- - у,, ДУ„ = {Ау^+к-1. • • •. ДУт)
в норме F.14) удовлетворяют следующему соотношению:
W^Y^+iWa < A + chu)\\AYJ\a + C{\\SJ\ + ||е„||) при О < /»/ < Const.
Постоянные с, С и Const зависят только от метода и не зависят от
дифференциального уравнения. Если i^ < О, то
IIAK^+iIIg < W^YJla + C{\\SJ\ + \\ej\) при любом Л > О.
V.6. Одноопорные методы и G-устойчивость 355
Доказательство. Сделаем дополнительное предположение о
непрерывной дифференцируемости функции /. Прямое доказательство
возможно и без него, но приводит к квадратичному неравенству для
IIAVm+lilG-
Идея доказательтва такова: вычтем F.6) из F.41) и воспользуемся
равенством
где
*''""/ 1^ ('''" "^ ^''' ' ^ ^••^'"+'' + (^ - ') Е ^<^"'+' - ^т)) Л.
В результате получим:
к к
«=0 t=0
Найдем из этого соотношения Ау^^/^:
^Ут+к = ^^т^к + {<^к - PkhJmY^Sm " hJ^^m)^ F-42)
где Дг^^^ определяется из уравнения
к к
1=0 1=0
а для J < m Н- А: по определению Azj = Ду^-. В силу нашего
предположения F.2') матрица J^ удовлетворяет одностороннему условию
Липшица Re(JyyjU,Ti) <i/||u|P (см. упр. 6 из разд. 1.10). Умножив ска-
лярно F.43) на Yl/^i^^m-^i ^ воспользовавшись формулой F.21), мы
получим в обозначениях F.13) следующее соотношение:
l|A^m+lllG - IIA^mllG < ^oHI Е A'^^m+Jl' <
(второе неравенство справедливо только при и>0; при
отрицательных значениях i/ заменим в F.2*) i/ на 0). Разделив последнее
соотношение на ЦД^уу^^Л^ + ЦД^^Ц^-, придем к оценке
\\^Z^+i\\G<{i + chu)\\AZj\a. F.44)
С помощью теоремы фон Неймана (разд. IV. 11) можно показать, что
второй член в F.42) ограничен величиной Con5^(||Jyy,||-|-||е^||).
Подставив ее и F.44) в F.42), мы получим требуемую оценку. П
356 Гл. V. Многошаговые методы для жестких задач
Доказанная лемма позволяет вывести утверждение о сходимости
одноопорных методов, аналогичное теореме о 5-сходимости для
методов Рунге—Кутты.
Теорема 6.10. Рассмотрим G-устойчивый одноопорный метод с
порядком дифференцирования Ро>р и порядком интерполяции pj >
>р—1. Предположим^ что дифференциальное уравнение
удовлетворяет одностороннему условию Липшица F.2^). Тогда существует
постоянная Cq>0 такая, что при hi/ < Cq выполняется неравенство
\\Ут - У(^тI1 < С max Ц - у{х^)\\ + Mh". F.45)
Константа С зависит от метода и (при i/>Q) от длины х^ — Xq
интервала интегрирования; константа М зависит, кроме того, от величин,
ограничивающих р-ю и (p-h 1)-ю производные точного решения.
Доказательство. Прямое применение леммы 6.9 к формуле F.40)
дает требуемую оценку погрешности только при Pi > р^ Поэтому,
следуя работе Хундсдорфера и Штайнингера A991), введем величину
у(х) = у{х) ~ Sf{x), и тогда F.40) примет вид
к к
^ а,.у(х -h ih) ~ S{x) = hf{x + Ph, Y, PiVi^ + ^h) - ?(^)). F-46)
1=0 i=0
где
к к
S[x)^S^{x)^Y.'^,Sj{x^ih), ?(х) = (^Их)-Х^/?Л(^ + ^*Л). F.47)
•=0 1=0
с учетом равенств р[1) = О и GA) = 1 формула Тейлора для этих
функций дает
rx-^-kh
Щх)\\ + т^)\\<с,н'> j^ IIj/C+^'COIK-
Таким образом, мы можем применить к F.46) лемму 6.9, в результате
чего получим
где At/j. = у[х^) — yj . Воспользовавшись неравенством A -f chuy <
< exp(ci/(xj — Xq)) , мы по индукции придем к соотношению
\\^Y^+i\\G<C\\AY,\\a + MhP.
Теперь утверждение теоремы следует из эквивалентности норм:
^oI|A>^oIIg < ,max^ W^Vjll < d,\\AY,\\a,
из оценки \\Ут-'У{^т)\\ < 1|Ут ~ 2/(^тI1 + ll^/B^m)ll " ИЗ ТОГО обстОЯ-
тельства, что ||<^/(Ху„)|| = O(h^). П
V.6. Одноопорные методы и G-устойчивость 357
Сходимость л-устойчивых многошаговых методов
В работе Далквиста A975) получено интересное отношение
эквивалентности между одноопорными и многошаговыми методами (см.
упр. 3). Оно позволяет вывести из полученного выше результата о
сходимости одноопорных методов соответствующее утверждение для
многошаговых методов (Хундсдорфер и Штайнингер 1991). Другой,
более прямой подход будет представлен в разд. V.8 (теорема 8.2).
Рассмотрим линейный многошаговый метод
к к
E^.-^m+i =ftE^./(^m+i,ym+i). F-48)
1=0 i=0
Пусть ж^ = х^ - /?Л. Тогда ^f^g /?,аг^^,. = х^, и с учетом формулы
F.54) мы определим {уо» У] i • • > Уг/с-х} ^^^ решение линейной системы
к к
J2^iyj+i = yj^ Y^^iyj+i = f^fi^j^yj)> i = 0,...,*r-l. F.49)
»=0 t=0
Эта система имеет единственное решение, поскольку многочлены p(Q
и сг((^) — взаимно простые. С полученными стартовыми значениями
определим теперь {у^п) (при т>к) как решение одноопорной
формулы
к к к
E^»2/m+i = Л/(Х)А^т+оЕ'^«2^т+.). F-50)
1=0 1=0 1=0
в силу второго соотношения в F.49) формула F.50) справедлива при
всех т>0. Следовательно (упр.За), выражение Х],=оАУт+«
является решением многошаговой формулы F.48). С учетом F.49) и
единственности численного решения мы получим, что
к
^Р{Ут^г = Ут "рИ ВСеХ Ш > 0. F.51)
1=0
Это соотношение позволяет доказать следующее утверждение.
Теорема 6.11. Рассмотрим А-устойчивый линейный многошаговый
метод порядка р. Предположим у что дифференциальное уравнение
удовлетворяет условию F.2'). Тогда существует постоянная Cq> О
такая J что при hi/ <Cq
\\Уп.-У{^Л\<СЫъ.х\\щ-у{х^)\\ + Нтг.хтх^,щ)-у'{^
Здесь константы С и М те же, что в теореме 6.10.
Доказательство. По теореме 6.7 из Л-устойчивости следует G-
устойчивость соответствующего одноопорного метода. Далее,
разложения Тейлора функций F.37) и F.38) показывают, что pj) > min(p, 2)
358 Гл. V. Многошаговые методы для жестких задач
и р/ > 1. Поскольку в силу второго барьера Далквиста р < 2, все
условия теоремы 6.10 выполнены. Таким образом, одноопорное решение
{Ут) удовлетворяет оценке F.45). Чтобы оценить Цуу — 2/(л:^)|| при
j < к, вычтем из F.48) выражения, определяющие Sd{x) и J/(x), и в
результате получим
к
t=0
к
1=0
Разрешая эти уравнения относительно j/, — у(аг^), придем к оценке
ma^xJ|j/,.-y(x,.)||<
< Со( тад \\yj-y{xj)\\ + Л тад \\f{xj,yj)-i/{xj)\\) + M^hP.
Она и доказывает утверждение теоремы, поскольку в силу F.51)
\\yn.-yi^rn)\\<i2^mym+i-yi^m+i)\\ + ?A^n,)\\- П
1=0
Упралснения
1. а) Докажите, что одноопорный метод F.6) удовлетворяет
условиям F.39) в том и только в том случае, если
к
^а^{^ = др^-' при 9 = 0,1,...,р^ , F.52)
1=0
к
Y,Pii'=^ при д = 0,...,р^. F.53)
1=0
Сравните это утверждение с теоремой III.2.4.
Ь) Вычислите порядки pj^ и pj для методов Адамса.
2. а) Покажите, что одноопорный метод F.6) можно записать в форме
общего линейного метода (разд. III.8).
b) Докажите, что порядок сходимости р этого метода вычисляется
по формуле
p = min(p^,p^-f 1),
где величины p^.Pj определены в F.39).
c) Порядок одноопорного метода никогда не превосходит порядка
соответствующего многошагового метода.
V.6. Одноопорные методы и G-устойчивость 359
3. (Далквист 1975.)
a) Пусть {Ут) и {х^ = XQ'\-mh} удовлетворяют (одноопорному)
разностному уравнению F.6); тогда значения
к к
Ут = ^2 ^зУт^З' ^m = Y. ^i^m+; F54)
i=o i=o
удовлетворяют (линейному многошаговому) разностному
соотношению F.3).
b) Обратное утверждение. Пусть многочлены
j=0 j=0
таковы, что при некотором целом / (О < / < fc) имеет место
равенство Р(С)^(С) — Я[Ор[0 = С • Тогда величины
/c-l k-l
j=0 j=0
k-l k-l
i=o i=o
удовлетворяют соотношению F.6), если {у^} и {х^} являются
решением F.3).
Указание для (а). Умножьте F.6) на /?^, замените m на m-hj,
просуммируйте от j = О до j = fe и поменяйте порядок
суммирования.
4. Одноопорные коллокационные методы (Далквист 1983).
a) Для заданного /3 существует единственный fc-шаговый одно-
опорный метод с Piy = к и pj = к.
b) Этот одноопорный метод имеет порядок р = fc -f 1 тогда и только
тогда, когда
c) Исследуйте численно нуль-устойчивость таких методов.
5. (Предложено М. Крузе.) а) Пусть R{z) = P[z)/Q(z) —
неприводимая рациональная функция, у которой degР<к^ degQ<k.
Покажите, что R{z) Л-устойчива тогда и только тогда, когда существу-
360 Гл. V. Многошаговые методы для жестких задач
ют многочлены а,(г), /3{z) с действительными коэффициентами
и степенями dega, < А - 1, deg/? < к такие, что
к
Q(z)Q{w) - P(z)P{w) = -(г-f ti;) ^а,(г)а,И + /?(г)^И. F.55)
t=i
b) Дайте новое доказательство теоремы фон Неймана (следствия
IV. 11.3), используя эту характеристику.
Указание. Доказательство части (а) можно провести по той же
схеме, что и для теоремы 6.7 и леммы 6.8. Заметим, что F.55)
сводится к многочлену Е (IV.3.8), если положить z = iy и w=—iy.
Для доказательства части (Ь) выведите из F.55) тождество
\\Q{A)uf - mA)nf = - ^ Re<а,(Л)«, Аа,{А)и) + ЩАМ'.
1 = 1
V.7. Сходимость для линейных згдач
Теоремы 6.10 и 6.11 дают удовлетворительные результаты для
сходимости G-устойчивых одноопорных методов и Л-устойчивых
многошаговых методов. Но таких методов немного, и их наивысший
порядок равен 2 (теорема 1.4). Поэтому желательно ослабить требование
Л-устойчивости и исследовать многошаговые и одноопорные методы
более высокого порядка. Данный раздел посвящен линейным
жестким задачам, а нелинейные задачи будут рассмотрены в разд. V.8.
Мы опишем здесь два различных подхода к исследованию
сходимости. Один из них опирается на дискретную формулу вариации
постоянных и будет изложен в конце этого раздела (см. далее лемму 7.9
и теорему 7.10). Другой подход основан на формулировке
исследуемых методов как одношаговых и использовании матричной теоремы
Крайсса.
Разностные уравнения для глобальной погрешности
Большую часть трудностей можно увидеть уже при изучении
одномерной задачи Протеро—Робинсона
2/' = Ay + 5f(x), у{хо) = Уо' G.1)
Предположим, что ReA < О, а решение у{х) является гладким в том
смысле, что достаточное число его производных ограничено
величинами, не зависящими от параметра жесткости А.
Применяя линейный многошаговый метод к задаче G.1), получим
формулу
к к к
Е^.-2/пг+.=ЛА5;/?,у^^,-ЬЛХ]/?,G(х^+,). G.2)
1=0 trrO 1=0
Легко видеть, что глобальная погрешность
^т=Ут-У{^т) G3)
удовлетворяет разностному соотношению
к
Y,{Oi - ЛА/?,)е„+, = -Si^m(^J, G.4)
1=0
362 Гл. V. Многошаговые методы для жестких задач
где
к к
<^ьм(^) = Е^«2/(х + гЛ)-Л;^^,2/'(х + гЛ) G.5)
«=о »=о
(сравните с формулой III.2.3). Отметим, что правая часть в G.4) не
зависит от жесткости (т.е. от А). Кроме того, если классический
порядок метода равен р, то Siji^(x) = 0{h^'^^).
Если мы применим метод в его одиоопорном варианте, го получим
формулу
к к
Е ^»2/т+.- = hXj2 PiVm^i + Ы^т + Р^), G.6)
1=0 1=0
где Х^/?, = 1 и ]^/3,г =/?. В этом случае глобальная погрешность
е^ = у^ — у[х^) удовлетворяет соотношению
к
Y,{C4 - ЛА/?,)е„+.- = hXSj{xJ - S^^x^), G.7)
1=0
где Sq(x) и Sj(x) определены в F.37) и F.38) соответственно. Если
условие 8j{x) = О (справедливое для ФДН-методов) не выполняется,
то уравнение G.7) не оправдывает ожиданий, поскольку его правая
часть становится большой в жестком случае (ЛА -ч ос).
Чтобы преодолеть эту трудность, Далквист A983) предложил
вместо е^ = Уу^ — у{х^) рассматривать величины
к
C^E'^.'^/n.+.-^m+W G.8)
1=0
(«...более адекватная мера глобгильной погрешности, чем обычная...»,
Далквист 1983). Замена в G.6) m на m-j-j, умножение на /3j и
суммирование дают формулу для погрешности
к
J2(a,-hX0,)e'^^, = -St^j^{x^ + lih), G.9)
1=0
где Sii^(x) определена в G.5). Теперь это разностное соотношение
имеет ту же силу, что и G.4).
В работе Хундсдорфера и Штайнингера A991) отмечено, что в
случае одноопорных методов обычно получаются лучшие оценки
погрешности, если рассматривать е^ = е^ -\-Sj(x^). В этом случае мы имеем
формулу
к
Y^{a, - ЛА/?,)с„+, = h\e(xj - S(xJ, G.10)
1=0
где е{х) и S(x) определены в F.47). Отметим, что е{х) = C)(/i^^'^^) и
?(ж) = 0(Л'"»"(Р^ + 1'Р/+2)^
V.7. Сходимость для линейных задач 363
Пр€и1.ставление в внд,е од^ошагового метода. Все соотношения для
погрешности G.4), G.7), G.9) и G.10) имеют вид
к
5](а..-ЛА/?,)е„+,=*л(х^). G.11)
1=0
Для оценки с„ удобно ввести, как в разд. III.4, вектор
^m = (em+fc-i.---.em+i.emf. G-12)
сопутствующую матрицу
/Cfe_i(/*) ••• Ci(/i) Со(ц)\
1
и вектор
о /
• '^""=-^ <'"'
Д™ = Л('».)/('>»-/'4).0 of. i, = h\. G.14)
Тогда формула G.11) примет вид
E^^,=C{hX)E„ + A„, G.15)
откуда получим:
т
E^^,=C(h\r^'E,-^^C{h\r-^Aj, G.16)
3=0
Для получения оценки Е^^^ надо, чтобы степени С(ЛА) были
равномерно ограничены по ЛА. Это и будет предметом рассмотрения в
следующем подразделе.
Матричная теорема Крайсса
4cAls Fakultatsopponent fur meine Stockholmer Dissertation
brachte Dr. G. D€dilqiiist die Frage der Stabilitatsdefinition
zur Sprache».
«B качестве фгисультетского оппонента моей
стокгольмской диссертадии д-р Г. Далквист поставил вопрос об
определениях устойчивости». (Х.-О. Крайсс 1962)
Следующая теорема Крайсса A962) служит мощным средством
для докг1зательства равномерной ограниченности степеней матриц
произвольного семейства.
Теорема 7.1 (Крайсс 1962). Пусть Т является семейством к х к-
матриц А. Тогда «степенное условие»
||Л'*||<М при п = 0,1,2,... я AeJ" (Р)
эквивалентно «резольвентному условию»
\\(A-zI)-'\\<j^ при И>1 я AeJ'. (R)
364 Гл. V. Многошаговые методы для жестких задач
Замечание. Доказать, что из (Д) следует {Р) — сложная задача.
В ее решение внес вклад ряд математиков (Рихтмайер и Мортон 1967;
Тадмор 1981). Левек и Трефетен A984) дали замечательный вариант
доказательства; лучшее, что мы можем сделать — это повторить его
почти буквально.
Доказательство. Необходимость. Если выполняется (Р), то
собственные значения матрицы Л лежат внутри замкнутого единичного
круга, и поэтому (А — zl)-^ существует при 1^1 > 1. Кроме того,
оо ^^ A/f
\\{Л ^ ./)-^|| = II Е A^z-^-'W <mY, W-' = т?гТ^ G-17)
п=0 п=0 1^' ^
И, следовательно, выполняется условие (Л), в котором С = М.
Достаточность. Предположим, что выполняется условие (Я),
так что все собственные значения А лежат внутри замкнутого
единичного круга. Матрицу А^ можно выразить через резольвенту с
помощью интеграла Коши (см. упр. 1):
где контуром интегрирования является, например, окружность
радиуса р>1 с центром в начале координат. Пусть и и v — произвольные
единичные векторы, т.е. ||и|| = ||г;|| = 1. Тогда
vM^ti=-^ f z''q(z)dz, где q{z) = v*(zl ^ А^^и.
27гг Ур
Интегрируя по частям, получим:
Теперь в качестве контура интегрирования фиксируем окружность
радиуса р = 1 -|- 1/(п-f 1). На ней |г"+^| < е, и поэтому будет
выполнено неравенство
Согласно правилу Крамера q(z) является рациональной функцией
степени к. Применяя лемму 7.2 (см. ниже), найдем, что интеграла
в G.19) ограничен сверху произведением Атгк на точную верхнюю
грань \q{z)\ на контуре Г, которая в силу условия {R) не превосходит
(п -Ь 1)С. Следовательно,
|vM"ti| < 2eJta
Поскольку ||Л"|| является точной верхней гранью для |v*>l*^it| повеем
единичным векторам w и v, оценка (Р) доказана, причем М = 2екС.
Q
V.7. Сходимость для линейных задач 365
В доказательстве использована следующая лемма, связывающая
длину дуги рациональной функции на окружности с ее максимальным
значением. В случае многочлена степени к этот результат является
следствием неравенства Бернштейна supi^. j \я'(^)\ ^ ^^^supi^.i \q(z)\
(см., например, книгу Мардена 1966).
Лемма 7.2. Пусть q(z) = p{z)/r(z) — рациональная функция, у
которой deg p<kj deg r<k, и предположим, что она не имеет полюсов
на окружности Г : |г| = />. Тогда
f W{z)\\dz\ < 47rfcsup|^)|. G.20)
Jr \г\=р
Доказательство. Заменив q{z) на q(pz), мы можем без
ограничения общности предположить, что /? = 1. Выполнив параметризацию
е*^ контура Г, введем
7@='/(е")- f'{t) = ie''q'ie'*).
Тогда
у it) = к'(е'')| • е'"'*), где g{t) = argG'(<))-
Интегрируя по частям, получим:
f\q'{z)\\dz\= r\q'{e'^)\dt= Г j'(t)e-'^(^)dt =
Jr Jo Jo
р2тс /.27Г
= i 'f{t)g'{t)e-'^^'Ut < supb{t)\. \g'{t)\dt.
Jo Jo
Остается доказать, что полная вариация д^ т.е. TV[^] = Jq^ \g^{t)\dt^
ограничена величиной Атгк. Для этого заметим, что zq^{z) —
рациональная функция степени BАг,2Аг), и ее можно записать в виде
произведения
3L aiZ-\'b-
Отсюда следует, что при z = е»*
(,(<) = arg(tV(z)) = ^ + ^arg(^^^^).
jzzl J 3
Поскольку преобразование Мёбиуса (аг-f 6)/(сг 4-с/) отображает
единичную окружность в некоторую другую окружность, полная
вариация aTg[{az-\-b)/{cz-\'d)) не превосходит 27г. Следовательно,
<4л-Аг.
TVM<i:Tv„g(^)
J=l »- J J
366 Гл. V. Многошаговые методы для жестких задач
Замечание. Левек и Трефетен A984) высказали предположение,
что оценка G.20) останется справедливой и в том случае, если
множитель An заменить на 27г. Спейкер A991) доказал, что их догадка
была правильной.
Некоторые применения матричной теоремы Крайсса
Теперь, следуя работе Далквиста, Миндью и Левека A981), мы
получим с помощью матричной теоремы Крайсса ряд утверждений о
равномерной ограниченности степеней матрицы C{fi), определенной
в G.13). Сходные результаты были независимо получены в работах
Крузе и Равьяра A980), а также Гекелера A979, 1984).
Лемма 7.3. Пусть 5 С С — область устойчивости метода (р, а).
Если область S замкнута в Су то существует константа М такая,
что
||C(/i)"||<M при ^eS и п = 0,1,2,....
Доказательство. В силу теоремы 7.1 достаточно доказать, что
\\{C{fi)-zir'\\< j?-^ при ties и и>1.
Для этого воспользуемся неравенством (Като A960), см. упр. 2)
Так как ||С(//)|| равномерно ограничена при ^ G 5, то достаточно
показать, что величина
|det(C(/z)-zJ)|
не может быть сколь угодно близка к нулю ни при каких значениях
fi ? S. При |2:|-^оо величина G.21) стремится к единице, поэтому
здесь трудностей не возникает. Заметим далее, что
к
|det(C(/i)-z/)| = |n(^-C,(/i))|, G.22)
i=i
где CjM — собственные значения матрицы C(fi), т.е. корни
уравнения
к
^(а,-М)С'' = 0. G.23)
1=0
По определению области устойчивости S при fi ? S значения С;(м)
принадлежат замкнутому единичному кругу, причем те из них,
которые лежат на единичной окружности, отделены друг от друга. Таким
образом, при фиксированном fiQ ? S только одно из значений Cj(f^o)
V.7. Сходимость для линейных задач 367
может быть близко к z, если |z| > 1. Соответствующий множитель в
G.22) ограничен снизу величиной |г| — 1, а остальные множители
отделены от нуля. В силу непрерывности Cj (/^) это имеет место для всех
//Е5 из достаточно малой окрестности V(|io) точки fiQ.
Следовательно, (p(fi) > а > О при fjL G V(/Lio) П5. Поскольку 5 является замкнутым
(компактным в С) множеством, его можно покрыть конечным числом
открытых множеств V(^q) . Поэтому (p(fi) > а > О для всех /i € 5, что
и завершает доказательство теоремы. П
Замечание. Предположение о том, что S замкнута в С, обычно
выполняется. Для методов, не удовлетворяющих этому
предположению (см., например, упр. 2 из разд. V.1 или работу Далквиста, Мин-
дью и Левека A981)), лемма остается справедливой на замкнутых
подмножествах D С S СС.
Оценку, даваемую предыдущей леммой, можно улучшить, если
рассматривать замкнутые множества D, лежащие внутри S.
Лемма 7.4. Пусть S — область устойчивости метода (/9, а). Если
множество D ClntS замкнуто в Су то существуют постоянные М и
к (О < /с < 1) такие, что
||C(/i)"||<M/c'^ при fieD и п = 0,1,2,....
Доказательство, Если fi лежит внутри S, то все корни уравнения
G.23) удовлетворяют неравенству |С;(/^)| < 1 (принцип максимума).
Поскольку множество D замкнутое, отсюда следует существование
е>0 такого, что
Dc5, = {/i€C; |C,(/i)|<l-2e, j = l,...,k}.
Рассмотрим теперь величину R{fi) = /c"^C(/i), где /с = 1 — е.
Воспользуемся тем, что собственные значения R(fi) удовлетворяют условию
\k-'^(j{/i)\ < A —2е)/A —?:) <!—€ при fiESg. Как и в доказательстве
леммы 7.3 (даже намного проще, поскольку R(^) не имеет
собственных значений, равных единице по модулю), мы делаем вывод о
равномерной ограниченности степеней матрицы R{fi) при /лЕ S^. Отсюда
следует утверждение леммы. П
Поскольку начало координат никогда не попадает внутрь 5,
добавим еще следующую оценку:
Лемма 7.5. Пусть метод (р, а) согласован и сильно устойчив (см.
разд. П1.9, предположение А1). Тогда существуют окрестность V
нуля и постоянные М и а такие, что
||C(/i)^||<Me^(^^^+^l'''') при ^ieV и п = 0,1,2,....
Доказательство. Поскольку метод является сильно устойчивым,
существует некоторая компактная окрестность V точки О, в
которой |Cy(/i)| < |Ci(/i)| при ; =2,...,fc (Cj(/i) — это корни уравнения
368
Гл. V. Многошаговые методы для жестких задач
G.23)). Тогда матрица R{fi) = Ci(^)^^C{n) имеет простое
собственное значение 1, а все остальные собственные значения строго меньше
единицы. Как в доказательстве леммы 7.3, мы получим неравенство
||fl(/i)'^|| < М и, следовательно, ||C(/i)^|| < M|Ci(/i)h при fxeV.
Теперь требуемая оценка вытекает из соотношения CiCa*) = ^^ "Ь^(А'^)-
П
Глобальная погрешность для задачи
Протеро—Робинсона
Доказанные выше леммы позволяют продолжить анализ формулы
G.16). Если рассматриваются такие значения Л и Л, что их
произведение АЛ остается в пределах замкнутого подмножества области 5,
то справедлива оценка
ll^m+ill<A^(ll^olKEllMi)
G.24)
j=0
(лемма 7.3). Если же ЛЛ остается в пределах замкнутого
подмножества, целиком расположенного внутри 5, то оценка улучшается:
m
ll^m+ill <m[k'"+'\\Eo\\ + J2'''"''W^jW) "Ри некотором к
<1
i=o
G.25)
(лемма 7.4). Получаемые в результате асимптотические оценки
глобальной погрешности е^^^^у^ — у(х^) при mh < Const представлены
в таблице 7.1 (р обозначает классический порядок, pj^ — порядок
дифференцирования, а р/ — порядок интерполяции, см. разд. V.6).
Таблица 7.1. Погрешность для задачи G.1) при hX-? оо и /» -> О
Метод
многошаговый
одно-
опорный
погрешность
Cm
(А)
(В)
Предполагается, что начальные значения заданы точно и что
одновременно ЛА —> ос и Л -> 0. Это наиболее интересная ситуация,
поскольку любой разумный метод для жестких задач должен интегрировать
уравнение с такой длиной шага Л, при которой ЛА велико. Будем
различать два случая:
(А) полубесконечный луч {ЛА ; Л>0, |ЛА|>с}и{оо} лежит в S
(можно применить лемму 7.3, т.е. формулу G.24));
V.7. Сходимость для линейных задач 369
(В) оо является внутренней точкой области S (можно применить
формулу G.25); глобальная погрешность ||^^||, по существу, равна
последнему члену суммы в G.25)).
Заметим, что глобаипьная погрешность многошагового метода
содержит множитель |А|~^, и поэтому погрешность убывает с ростом
|Л| («чем жестче, тем лучше»). Для одноопорных методов оценка в
случае (А) получена с использованием рекурсии G.10).
Сходимость для линейных систем с постоянными
коэффициентами
Полученные результаты легко распространяются на линейные
системы
у' = Ау-^д{х), у{хо) = Уо. G.26)
если предположить, что матрицу А можно привести к
диагональному виду. Приведенные ниже результаты получены в работе Крузе и
Равьяра A980).
Теорема 7.6. Предположим, что многошаговый метод (р, а) имеет
порядок Ру А(а)-устойчив и устойчив на бесконечности. Если
матрица А в G.26) может быть приведена к диагональному виду (т.е.
Т" ^ AT = diag (А^,..., А^^) j, а ее собственные значения отвечают
условию
|arg(-A,)|<a при г=1,...,п,
то существует постоянная М (зависящая только от метода) такая,
что при любом Л > О глобальная погрешность удовлетворяет оценке
M^J-yJ\<M\\T\\.\\T-^m^xJ\y(xj)-y^\\ + hp?"\^^^^^^
Доказательство. Преобразование у = Tz расщепляет систему
G.26) на п скалярных уравнений
z', = \z, + (T-'9Ux). G.27)
Поскольку это преобразование оставляет инвариантным численное
решение, достаточно рассмотреть уравнение G.27). Лемма 7.3 дает
ограниченность степеней:
1|С(ЛА,.)"*|| < Мо при Л>0, i = l,...,n и m > 0. G.28)
Погрешность дискретизации S]^j^(x) G.5) можно записать в виде
гк :^
SLMH = hP^4 K^{s)zl'^'\x-^sh)ds, G.29)
Jo
где Kp{s) — ядро Пеано многошагового метода (см. теорему П1.2.8).
В силу А(а)-устойчивости Qf^ уЗ^^ > О, так что \а^^ — ЛА,./?лр| < [а^^!"^ •
Отсюда с учетом G.29) следует соотношение
1|А^11<СЛ''Г'''|г.И')@Н^, G.30)
370 Гл. V. Многошаговые методы для жестких задач
в котором С зависит только от метода. Подставив оценки G.28) и
G.30) в G.16), мы придем к оценке глобальной погрешности в задаче
G.27) и, вернувшись к исходным переменным, завершим
доказательство. П
Благодаря присутствию экспоненциально затухающего члена
следующая оценка особенно полезна в случае, когда рассматриваются
длительные временные интервалы (или когда стартовые значения не
лежат на кривой точного решения).
Теорема 7.7. Пусть многошаговый метод {р, а) имеет порядок
р>1, A{q)-устойчив и сильно устойчив в нуле и на бесконечности
(т.е. из равенства G(C) = О следует, что |С| < l). Если матрица А в
задаче G.26) приводима к диагональному виду Т^ ^ AT = diag (А^,..., А„)
и ее собственные значения А,- удовлетворяют условию
I arg(~A,.)| < 7 < «, Re А, < -А < О,
то для заданного /iq > О существуют постоянные М и и > О такие,
что при О < Л < /iq справедлива оценка
M^J-yJ\<M-\\T\\-\\T-'\\-{e-'^^''''-''>).me.x^\\y{x^)-y^\\ +
Л" Г"'е-''('"-«)||г/(''+1)@1Н^).
fXo
Замечание. Постоянные Миг/ могут зависеть от j, А, h^ и от
метода, но они не зависят от собственных значений А, и длины х^ — Xq
интервала интегрирования.
Доказательство. Согласно лемме 7.5 существует такое г> О, что
||С(ЛА..)^|| < Мое~^'*^/2 при |ЛА,.| < г G.31)
(заметим, что |^|< Соп5^-|Ке/х|, если |arg(—/i)|<7<7r/2). Поскольку
множество
D={fi; |arg(-/i)|<7, |/i|>r}U{oo}
лежит внутри области устойчивости 5, из леммы 7.4 следует, что
\\C(hXir\\<M^p'^ при \h\-\>r G.32)
и некотором значении р<1. Объединив оценки G.31) и G.32), мы
получим:
||С(ЛА,.)^|| < Ме-"^^^ при О < Л < /iq, G.33)
где М = max(Mo,Mi) и i/= min(A/2, — Inp/Ag). Используя оценку
G.33) вместо G.28) и учитывая, что mh = x^ — Xq, мы тем же
способом, что и в доказательстве теоремы 7.6, получим доказываемое
неравенство. П
V.7. Сходимость для линейных задач 371
Матричный вариант теоремы фон Неймана
Интересный результат, относящийся к контрактивности,
получается с помощью следующего матричного варианта теоремы фон
Неймана (теорема IV. 11.2).
Рассмотрим евклидово скалярное произведение (•, •) в М'*, норму
К • 11^ в Ш^, задаваемую симметричной положительно определенной
матрицей G, и норму
и п =
i
к
J^diM^^'j) Д^я i/ = (tii,...,tiJ^GM^^ G.34)
I »j=i
Соответствующие операторные нормы будем обозначать теми же
символами.
Теорема 7.8 (О. Неванлинна 1985). Предположим, что элементы
матрицы C{fi) = (с, {fi))ij-i являются рациональными функциями от
/i. Если
I|C(/x)||g<1 пР^ Re/i<0, G.35)
то
II|CM)IIIg<i G.36)
для всех матриц А, отвечающих условию
Re{y,Ay)<0 при уеС, G.37)
Замечание. Если C(/i) — сопутствующая матрица G-устойчивого
метода (р, <т), утверждение следует из теоремы 6.7 и упр. 3 в конце
этого раздела («Было бы интересно иметь доказательство этого факта,
в большей степени опирающееся на теорию операторов.» — Далквист
и Сёдерлинд 1982).
Доказательство представляет собой прямое обобщение
доказательства теоремы IV.11.2, предложенного Крузе. Сначала
предположим, что матрица А — нормальная и, следовательно, может быть
представлена в виде А = QDQ*, где матрица Q — унитарная, а D —
диагональная: D = diag (А^,..., Л„). В этом случае мы имеем
соотношение
11|СИ)|||с= \\\{I®Q)C(D)iI®Q'ma=\\\C(D)\\\a. G.38)
С помощью матрицы перестановок Р = (/^е^,.. .,7® е„) (где / —
единичная матрица размерности Аг, а е^ — j-й единичный вектор
размерности п) матрица C{D) преобразуется к блочно-диагональному
виду:
P*C(D)P = blockdiag (C(Ai),..., C{XJ).
Так как Р* (G 0 /)i' = / ® G, то отсюда следует формула
P*C(D)*(G0/)C(D)P = blockdiag (C(Ai)*GC(Ai),...),
372 Гл. V. Многошаговые методы для жестких задач
а следовательно, и соотношение
irP)lllG=.maxJ|C(A,)||G. G.39)
Утверждение теоремы вытекает теперь из G.38) и G.39), так как
Re А,- < О соглг1сно условию G.37).
Для матриц А общего вида возьмем А{и) — ^{А + А*)-{• ^{А — А*)
и определим рациональную функцию
ip(Lj) = {щС{А(и))у)а = u*{G®I)C(A{lj))v.
Тогда утверждение теоремы можно вывести точно так же, как в
доказательстве теоремы IV. 11.2. П
Эту теорему можно использовать для вывода утверждения о
сходимости в случае дифференциальных уравнений G.26) с матрицей А,
отвечающей условию G.37). Действительно, если метод (р, (т) Л-ус-
тойчив, то сопутствующая матрица G.13) при Re^ < О удовлетворяет
условию ||C(/i)||E < 1 в некоторой подходящей норме (см. упр. 3).
Поэтому из теор)емы 7.8 следует, что |||С(ЛА)|||^< 1, и тогда формула
G.16) при замене А на А дает оценку
m
lll^m-MlllG<lll^olllG + Elll^llb- G.40)
Это соотношение доказывает сходимость, поскольку величины Д^
могут быть оценены, как в G.30).
Дискретная формула вариации постоянных
Другой подход к доказательству предложений о сходимости
линейных многошаговых методов состоит в использовании дискретной
формулы вариации постоянных. Этот подход является обобщением
классических доказательств для нежестких задач (Далквист 1956;
Хенричи 1962) на случай fi^O- Он был развит в работах Крузе и
Равьяра A976); позже этот подход исследовал Любих A988, 1990).
Рассмотрим уравнение для погрешности (ср. G.13))
к
?(о^,- - f^0i)^m+i = dm^k при m > о G.41)
i=0
И распространим его на отрицательные значения m, положив е^ = О
(при j <0) и определив rfo,..., d^^-i в соответствии с G.41). Основная
идея данного подхода состоит в том, чтобы ввести в рассмотрение
производящие степенные ряды
V.7. Сходимость для линейных задач 373
Тогда G.41) будет представлять т-е коэффициенты в тождестве
(Ж"М-МГ'))е(С)=Г*^{С). G.42)
Отсюда получим соотношение
е(С) = (Ж-М-МС-^))"^ГМС) = г(С,/^Ж), G.43)
позволяющее легко выразить е^ через dj :
т
3=0
Здесь г(^) —коэффициенты дискретной резольвенты
riC,и) = m-^^У'¦^)=J2ni^^)'^'' G.44)
з>о
где
'^(^)-?(?=^-^оС^ + ...+^,_,С+4- ^'-''^
Поскольку (p(C"'^)--/i^(C~M)^(C»A')=C"''^) коэффициенты г^(^)
можно интерпретировать как численное решение у- многошагового
метода, примененного к однородному уравнению у =^ fiy с длиной шага
Л=1 и стартовыми значениями j/_;j^i = .. . = у_1=0, 2/о = (<^л"~А'/?л)"^ •
Формулу G.43') можно использовать для оценки е^ , если
известны соответствующие оценки для коэффициентов rj{fi) дискретной
резольвенты. Эти оценки дает следующая лемма.
Лемма 7.9. Пусть 5 С С — область устойчивости многошагового
метода.
a) Если S замкнута в d то
М
kjMI< ^,^11 ^Р^ f^^S и ; = 0,1,2,...
b) Если область D ClntS замкнута в С, то существует постоянная
к (О < АС < 1) такая J что
h(A^)l< Y:j7ri "Р^ ^^^ » J = 0,1,2,...
c) Если метод сильно устойчив, то существует такая окрестность V
точки О, что
|r^.(/i)|<Me^*(^^''+^'^l') при fxeV и j = 0,l,2,...
Константы М, к и а не зависят от j и fi.
Доказательство. Оценки для |г^(/|)| в (а), (Ь) и (с) легко
выводятся из лемм 7.3, 7.4 и 7.5, поскольку г(^) является численным
374 Гл. V. Многошаговые методы для жестких задач
решением задачи у' = //у с длиной шага Л = 1 и стартовыми
значениями y_.k+i=" = y^i =0» Уо = К-/^/?^"^-
Как показано в работах Крузе и Равьяра A976), а также Любиха
A988), оценки леммы 7.9 можно доказать непосредственно, совсем
не обращаясь к матричной теореме Крайсса. Проиллюстрируем эту
идею доказательством утверждения (Ь) (доказательство утверждения
(а) см. в упр. 4).
Функция С'^(р(С~М ~ f^^iC~^)) в соответствии с определением
области устойчивости отлична от нуля при ICI < 1, если fiElntS.
Поэтому существует постоянная /с@</с<1) такая, что С^(р{С~^) —
—/i(T(C""^)) не имеет нулей в круге |С| < 1/«. Следовательно, при fi?D
выполняется соотношение
sup |(p(C-M-MrM)"V|<7^,
|С|<1/л 1 + 1/^1
и интегральная формула Коши
'M^hl (Ж-^)-МС-М)^Ч-Ч-^'-^^С G.46)
27гг У|с|=1/к
дает требуемую оценку. D
Использование дискретной резольвенты позволяет изящно
доказывать сходимость линейных многошаговых методов. Покажем это
для линейной задачи G.26), в которой матрица А отвечает условию
М
\\[sI-A)-'\\<-— при |argE-c)|<7r-a' G.47)
с некоторым с G М. (Это обычное предположение в теории
голоморфных полугрупп для параболических задач, см., например, работы Ка-
то A966) или Пейзи A983).) Если все собственные значения А,-
матрицы А удовлетворяют соотношению |arg(A, — с) — 7г| < а', то
выполняется условие G.47) с постоянной Л/, зависящей от матрицы А
(упр. 2). Следующая теорема, о которой нам сообщил Любих,
улучшает результаты Крузе и Равьяра A976).
Теорема 7.10. Пусть многошаговый метод имеет порядок р > 1,
является А(а)-устойчивым и сильно устойчивым в нуле и на
бесконечности. Если матрица А в уравнении G.26) отвечает условию
G.47), в котором а^ < а, то существуют постоянные С, Лд и 7
(причем 7 имеет тот же знак, что и с в G.47)), зависящие только от
М, с, а' и от метода, такие, что при Л < /iq глобальная погрешность
удовлетворяет оценке
11Фт)-Ут11<
0<j<fc ¦' J 7x0
Кроме того, если с < О, то Лд может быть выбрано произвольно.
V.7. Сходимость для линейных задач 375
Доказательство, Глобальная погрешность е^ = 2/(^т) "Ут УД^
влетворяет уравнению
к
]^(a.-/iA/?.)e^^. =d^+^,
1=0
где
?m^k\\ < Ch^ Г^' y'^'HmdC m > о, G.48)
a с?о> -'^iie-i являются линейными комбинациями векторов е и
ЛЛе с j < к; представим их в виде сумм
d^=:d[-{- hAd'l при i<k
таким образом, чтобы dj и d'l были линейными комбинациями
только векторов е (j < к). Кроме того, положим d'^ = d^ и d'^ = О при
?>к. Тогда анализ, проведенный в начале данного подраздела (см.
уравнение G.43)), показывает, что
е(С) = г(С, hA)d'{0 + г(С, hA)hAd"{C), G.49)
где, как и в скалярном случае,
г{С hA) = (S(C)I - hA)-'^^ = Yl 0(Л^К''' G.50)
Теперь применим лемму 7.11 (см. ниже), положив Ф{8) = {si — А)^^.
Согласно условию теоремы оценка G.57) выполняется при /? = 1, а
поэтому
||г^.(М)||<Се^^*. G.51)
Второй член в G.49) можно записать в виде
г(С, hA)hAiS@)-'6@^@ = г'(С, hA)d@, G.52)
где
r'iC,hA) = i6{QI-hAr'hA(S{C))-'-^^ = '?r'jihAK^,
^^ ^ '^-' G.53)
d(C)=<J(C)d"@ = E^/'-
Снова применим лемму 7.11, на этот рг13 положив
Ф(8) = (s/ - AY^As-'^ = {si - A)-'^ - $-4.
Условие G.57) выполняется при /? = 1, откуда следует, что
\\r'j{hA)\\ < CVJ*. G.54)
Коэффициенты <5, функции S{Q экспоненциально затухают,
поскольку все нули a(Q лежат в круге |С| < 1 • Следовательно,
||5,.||<к^Стах||е,|| G.55)
376 Гл. V. Многошаговые методы для жестких задач
с некоторым /с < 1. Коэффициент при С^ в G.49) дает формулу
m m
i=o i=o
Подставив в нее оценки G.48), G.51), G.54) и G.55), мы придем к
утверждению теоремы. П
Мы должны еще доказать оценки для rj(hA) и rj(hA). Для этого
возьмем некоторую аналитическую функцию ФE) (скалярную,
векторную или матричную) и рассмотрим коэффициенты выражения
Ф^О/Л) • -^ = h^<pj(h)C^. G.56)
^^ ^ i>o
Справедливо следующее предложение:
Лемма 7.11 (Любих 1991). Предположим^ что многошаговый метод
А{а)-устойчив и сильно устойчив в нуле и на бесконечности.
Предположим далее у что функция ФE) является аналитической в секторе
I argE — с) I < л- — а' (где а'<а, сЕШ) и удовлетворяет в нем условию
\\Ф(8)\\ < М' Isl'^ при некотором /? > 0. G.57)
Тогда коэффициенты <Pj{h) в G.56) могут быть оценены при h < h^
(где /iq достаточно мало) следующим образом:
\\'Pjm<C-(jhf-'e-^^'> при j>l, G.58)
а при j = 0 справедлива та же оценка^ что и при j = 1. Постоянные
С, 7 ^ Л о зависят только от а', с, М, /? и от самого многошагового
метода. Кроме того, если с<0, то и 7<0» ^ тогда оценка G.58)
справедлива при произвольном Hq .
Доказательство. В силу Л (а)-устойчивости имеем Р^/^к > О, а
поэтому значение 5{0)/h лежит в области аналитичности функции Ф
при Л < Ло. Интегральная формула Коши дает
4S{0/h) = ^ l^iSiO/h - А)-»Ф(А)^А, G.59)
где Г — подходящий контур, который проходит от «со • е"»(^-^')» до
«со • е'('^"'^')» внутри сектора аналитичности Ф, не проходя через
начало координат (см. рис. 7.1; отметим, что на бесконечности ФE)
затухает достаточно быстро). Умножив G.59) на С~*/<^(С~^) и сравнив
коэффициенты при равных степенях С > мы придем к представлению
<Pj (Л) = 2b X ""^ ('»А)Ф(А)с/А, i > О, G.60)
которое является дискретным аналогом формулы обращения
Лапласа. Положим теперь и; = jhX (при j = 0 положим о; = ЛА), так что Г
V.7. Сходимость для линейных задач 377
перейдет в Г = jhT и формула G.60) примет вид:
Используя теперь условие G.57), мы получим оценку
Wh)\\<^Uhf-'l^ |гД^)|.|и,|-^.|с/а;|. G.62)
Рис. 7.1. Контур Г в формуле G.59).
Нам еще надо показать, что интеграл в G.62) ограничен величиной
С' е^-?'*. Для этого разобьем его на две части. Первая часть
соответствует тем значениям и;, для которых uj/j лежит в замкнутом
подмножестве внутри области устойчивости метода. В этом случае
можно применить лемму 7.9Ь, согласно которой соответствующая часть
интеграла в G.62) ограничена величиной
j'K^ f\u;\'^-^\du\<Ce''^^
при
Л</1о.
У оставшейся части аргумент u/j = ЛА функции г^ в G.62) при
достаточно малом /iq лежит в окрестности V начала координат, где
справедлива оценка, даваемая леммой 7.9с. Таким образом, при jh > 1
мы получаем оценку
^Reu;+a№/j|^|-^|rf^| < Ce7iA
поскольку Reu; = j/iRe А, \(jj\^/j < jh • Const и |a;| > |A| отделена от
нуля. При малых jh контур Г^ становится сколь угодно близким к
началу координат, и тогда требуется более тонкая оценка. Ее идея
состоит в том, чтобы заменить в G.61) (а следовательно, также и в
G.62)) соответствующую часть Г^ эквивалентным контуром, который
не зависит от jh Е [Л, 1], находится на положительном расстоянии от
начала координат и остается в окрестности V. Тогда
соответствующий интеграл будет ограничен некоторой константой. П
378 Гл. V. Многошаговые методы для жестких задач
Замечание 7.12. В лемме 7.11 достаточно потребовать
аналитичности Ф(8) и выполнения оценки G.57) в секторе | arg(s — с)| < тг — а',
из которого удалена некоторая компактная окрестность начала
координат. Для этого надо взять в G.59) такой контур Г, который лежал
бы вне этой компактной окрестности нуля. В этом случае константа
7 может быть положительной также и при с < О.
Упралснения
1. Докажите интегральную формулу Коши G.18) в случае, когда все
собственные значения А матрицы А принадлежат замкнутому
единичному кругу, а контуром интегрирования является окружность
\z\ = p, где /?> 1.
Указание. Проинтегрируйте тождество
оо
j=0
2. (Като 1960.) Покажите, что для невырожденной к х Аг-матрицы В
в евклидовой норме выполняется неравенство
-i../IW"^
\в-
IdetSI
Указание. Используйте сингулярное разложение матрицы В,
т.е. B = [/^AV, где U и V — ортогональные матрицы, а Л =
= diag ((Tj,..., (Tf^), причем (т^ > (Tj > ... > сг^^ > О.
3. Метод (р, <т) называется А-контпрактивным в норме || • \\q^ если
\\СШ\о<^ при Re/i<0,
где C{fi) —сопутствующая матрица G.13) (Неванлинна и Линигер
1978-79; Далквист и Сёдерлинд 1982).
a) Докажите, что метод (р, а) Л-контрактивен при некоторой
положительно олределенной матрице G в том и только в том случае,
если он Л-устойчив.
b) Определите область контрактивности
{/ieC; ||С(я)||с<1}
для двухшагового ФДН-метода при заданной в F.20) матрице G.
Заметьте, что она строго меньше, чем область устойчивости.
Ответ, Областью контрактивности является {/i G С ; Re^ < 0}.
4. Дайте прямое доказательство леммы 7.9а.
V.7. Сходимость для линейных задач 379
Указание. Заметьте, что
где Ci(а*), . • •, СкМ — ^'^^ ^ нулей многочлена p{Q - /icr(C). Если
/ig G Int5, то существует окрестность U точки /ig такая, что
1С,(а*I ^ ^ < 1 лля всех i и fji EU. Следовательно, коэффициенты
rj{fi) ограничены. При ^д ?dS мы имеем равенство iCiCA'g)! = 1,
скажем, при г = !,...,?, где 1 < ^ < fc. Эти i нулей являются
простыми при всех /i из достаточно малой окрестности U точки
/ig, а остальные нули удовлетворяют условию \С{{и-)\ < а < 1 при
fiEU nS. Разложение на элементарные дроби
^(c.-.)=;:^(|:irf^-(c..))
показывает, что
ф) = ^^-^ ф<^М(СМУ + «,Ы), G.64)
где Sj(/i) —коэффициенту»! функции 5(С>А*)- Поскольку функция
5(С, /i) равномерно ограничена при |С| < 1 и /i G W П 5, из
интегральной формулы Коши с контуром интегрирования |С| = 1 следует
ограниченность 5 (/х). Таким образом, утверждение вытекает из
G.64) и того факта, что конечное множество окрестностей из
семейства {W}^^g5 покрывает S (лемма Гейне—Бореля).
V.8. Сходимость для нелинейных задач
в разд. V.6 была доказана сходимость одноопорных методов при
решении нелинейных задач, удовлетворяющих одностороннему
условию Липшица (теорема 6.10). В теореме 6.11 этот результат был
перенесен на линейные многошаговые методы. Другое (прямое)
доказательство этого результата будет первой нашей целью в настоящем
разделе. Однако этот результат справедлив, к сожалению, только для
Л-устойчивых методов (порядок которых не может превышать 2).
Поэтому последующие части этого раздела посвящены сходимости для
нелинейных задач при ослаблении условий, накладываемых на метод
(например, А(а)-устойчивость), но при этом класс рассматриваемых
задач сужается. Мы изложим здесь две разные теории: метод
множителей (Неванлинна и Одех 1981) и подход Любиха, основанный на
анализе возмущений с помощью дискретной формулы вариации
постоянных (Любих 1991).
Задачи, удовлетворяющие одностороннему условию
Липшица
Предположим, что дифференциальное уравнение у' = f{x^ у)
удовлетворяет условию
Ке(/(х,2/)-/(х,г), y-z)<u\\y-z\\\ (8.1)
записанному для некоторого скалярного произведения. Рассмотрим
линейный многошаговый метод
к к
Y1 ^i Ут+i = Л ]^ ^.. /(Х^+,, y^^i) (8.2)
t=0 1=0
вместе с его возмущенной формулой
к к
t=0 t=0
Возмущения d^^f^ можно интерпретировать как влияние округления,
как погрешность, возникающую при итерационном решении
нелинейного уравнения, или как локальную погрешность дискретизации (ср.
с формулой G.5)). Взяв разность между (8.3) и (8.2), мы получим
(при m > 0) следующую формулу:
к к
^а, Ду^^, = h^l3, Д/^^, -hd^^„ (8.4)
t=0 t=0
где мы ввели обозначения
Ayj=yj^yj, ^fj = fi^j^yj)-f{^j.yj)' (8.5)
V.8. Сходимость для нелинейных задач 381
Здесь нельзя прямо использовать одностороннее условие Липшица,
так как в (8.4) появляется несколько А/ (в отличие от одноопорных
методов). Чтобы выразить одно Af^ только через Ау , мы введем
формальные степенные ряды
Ау(С) = Х^Ау,.СЛ А/(С) = ^А/,.С^ d{C) = J2^J<''
j>o j>o j>o
Удобно предположить, что Ау^ = О, Afj = О, ^^ = О при отрицательных
значениях индексов, а dgj • • •»^л-i определяются по формуле (8.4) при
mG{—Аг,...,—1}. Тогда уравнение (8.4) просто связывает
коэффициенты при С"^ в членах тождества
р{С') Ду@ = hair') AfiO + C'diC). (8.4')
Разделив (8.4') на о'(С""^) и приравняв коэффициенты при С^, мы
получим формулу
'?S^_jAyj = hAf^ + d^, (8.6)
где, как и в G.45),
j=o
ПТ = '^@ = Е<^/' (8-7)
'^«-') ,>о
^d(C) = d(C)=l]rf/^ (8.8)
-(<") i>o
Теперь А/^ в (8.6) изолировано, что и требуется для того, чтобы
можно было скалярно умножить (8.6) на Ау^. Воспользовавшись
затем предположением (8.1), мы получим неравенство
m
Y^ S^^jRe {Ayj .AyJ< hu\\AyJ\' -f Re {d^ , Ay^). (8.9)
i=o
Oho позволяет доказать следующую оценку:
Лемма 8.1. Пусть {Ау^} я {Afj} удовлетворяют (8.6) при Sj,
заданных в (8.7). Если
R«(A/^, ДyJ<И|Дy^||^ m>0
И метод А -устойчив, то существуют такие постоянные С и Cq > О,
что при mh < Xgn^j — Xq и hi/ <Cq справедлива оценка
т
\\^yJ\<CY\\dj\l
Доказательство. Сначала преобразуем левую часть неравенства
(8.9). Для этого введем {АгЛ с помощью следующего соотношения:
к
Х^/?,Аг^^,=Ау^, т>0 (8.10)
»=о
382 Гл. V. Многошаговые методы для жестких задач
и предположим, что Azj = О при j < к. С учетом формулы Az(C) =
= YljAzjC^ это означает, что G(С""^)Дг(С) = Ду(С)- Следовательно,
мы также имеем соотношение
которое эквивалентно равенству
m к
'?^6^_jAyj = J2<^,Az„^,. (8.11)
j=0 «=0
Подставив (8.11) и (8.10) в (8.9), мы придем к неравенству
к к
1=0 1=0
II '^ 2 '^
<hi.\\j2Pi^^m^i\\ +Re(d^,E/?.^W.)-
1=0 t=0
По теореме 6.7 метод (р, а) является также G- устойчивым, и поэтому
можно применить формулу F.21). Как и в доказательстве леммы 6.9,
для AZ^ = (Дг^^^_1,..., Az^)'^ при 1/>0 мы получим неравенство
\\^Z^+i\\G<{^ + C,hu)\\AZJ\a + C,\\dJl
(если I/ < О, то заменим его на i/ = 0). Из него следует, что
m
1|А^.п+11Ь<Сз(||А^о11а + Е1К1|)-
i=o
По определению Дг мы имеем AZq = О. Теперь утверждение леммы
вытекает из того факта, что ||Ду^|| < С^ (УД^^+Л^ + ||Д^т11а) • О
Опираясь на эту лемму, можно дать прямое доказательство
сходимости Л-устойчивых многошаговых методов, сильно устойчивых на
бесконечности (ср. с теоремой 6.11).
Теорема 8.2. Рассмотрим А-устойчивый многошаговый метод
порядка р, сильно устойчивый на бесконечности. Предположим, что
дифференциальное уравнение отвечает условию (8.1). Тогда
существует такое Со > О, что при hi/ < Cq имеет место оценка
\\y^-y{^J\\ < С( max^l|yi-yK)ll + h m^xj\f{xj,yj)-j/(xj)\\) + МИГ
Постоянная С зависит от метода, а при i/ > О и от длины х^ — Xq
отрезка интегрирования; постоянная М зависит, кроме того, от
величин, ограничивающих (p-f 1)-ю производную точного решения.
Доказательство. Положим в (8.3) у^ = у(х^). Тогда возмущения
d^^^ становятся локальными погрешностями обрывания ряда:
к к
t=0 t=0
V.8. Сходимость для нелинейных задач 383
Если все нули многочлена a(Q лежат внутри единичной
окружности, то ряд из коэффициентов степенного разложения функции
С~^/^(С~^) является абсолютно суммируемым, и в силу соотношения
(8.8) мы имеем оценку
m т
E\\^j\\<c,J2\\dj\i
i=0 j=0
Теперь утверждение теоремы следует из леммы 8.1, неравенства
II^lm(^)II ^ Л/Л^"*"^ и того обстоятельства, что ^О' • • •»^k-i являются
линейными комбинациями векторов у^-'у(х^) и h{f(xj,yj)— i/(Xj))
при j <к. П
Метод мнолсителей
«...наилучшим из всех множителей был бы {1,—гу} с
очень малым г; > 0; ...» (Неванлинна и Одех 1981)
Приведенное выше доказательство сходимости основано на
формуле (8.6) и Л-устойчивости многошагового метода. Как можно
видоизменить это доказательство, чтобы получить результаты
относительно сходимости также и для тех методов, которые не являются
Л-устойчивыми? Это можно сделать с помощью так называемого
«метода множителей» (Неванлинна и Одех 1981), основу которого
составили идеи более ранних работ (Неванлинна 1977; Одех и Линигер
1977).
Основная идея состоит в следующем: вместо скалярного
умножения тождества (8.6) на Ау^ умножим его на сумму
m
Y^fim^jAyj ,
i=o
где {/i } — коэффициенты разложения «множителя» — некоторой
рациональной функции
где Г) и т — многочлены. В результате получим:
mm т
i=o i=o j=o
m
+ {4>Е^т-^Ду,)- (814)
384 Гл. V. Многошаговые методы для жестких задач
Теперь надо ввести новые переменные Дг с тем, чтобы левая
часть (8.14) приняла вид
mm Li
(E-^-i^^i' E^m-,Ay,) = (E«A^m+.- ЕДД^т+.>- (8-15)
j=0 j=0 1=0 1=0
Введем обозначения
t t
ж)=Е^.<''' ?(c)=E'^.<'- (s-i^)
1=0 1=0
Тождество (8.15) безусловно выполняется, если
Ж-^) Ay@ = <т(C-^) Ж-М Az(C), ^
77(Г^)Ау(С) = г(С-'M(С-МАг(С).
Деление одного соотношения на другое служит мотивировкой
следующего определения новых производящих многочленов:
Ж) = р{0ЛСIх{С,), Щ) = <г(С)Ж)/х(С). (8.18)
Здесь х(С) — наибольший общий делитель многочленов p{C)t{Q и
(T{Qr]{Q. Если положить по определению Az = О при j < О, а
остальные Az задать соотношением
X(Г^) Ay(C) = <т(С-1)г(С-1) Дг(С), (8.19)
ТО тождество (8.15) будет выполняться при всех т. Теперь
предположим, что многошаговый метод (Д, ?) Л-устойчив. Тогда левую часть
равенства (8.14) можно ограничить снизу значением из оценки F.21),
относящейся к G-устойчивости, и нам удастся получить результаты,
относящиеся к сходимости. Этим мотивируется следующее
Определение 8.3. Рациональная функция /i(C) в (8.13) называется
мноокителем для метода (р, ^), если //(С) ^^ р(С""М/сг(С~М и
определяемый формулами (8.18) метод (/?,?) является Л-устойчивым, т.е.
если
Продолжая начатый анализ, мы придем к следующему
утверждению о сходимости.
Лемма 8.4. Пусть {Ауу} и {А/^} удовлетворяют формуле (8.6) со
значениями Sj , определяемыми из (8.7). Если
N т
Y1 Y1 /^m-jRe (А/^ , Ау^.) < О для всех N > О
т=0 j=0
V.8. Сходимость для нелинейных задач 385
и если /i(C) является множителем для метода, то существует такая
постоянная С, что при mh < х^^^ — Xq
т
\\^Ут\\<С^,\Щ\.
i=0
Доказательство. Подставив (8.15) в (8.14) и воспользовавшись
оценкой F.21) для Л-устойчивого метода (р, ?), мы придем к
неравенству для AZ^ = i^z^^t^!»•••> ^^тУ '
т
7=0
, (8.21)
+ 1Ит1|-||ЕД-Д^.||-
1=0
Суммируя его от m = О до m = TV, получим соотношение
N
l|AZ^+ll|^ < С, Х; Ш\ ¦ (llA^m+lllo + IIA^mllG).
m=0
потому что AZq = о в силу (8.19). Отсюда, в свою очередь, следует,
что
м
max IIAZ^+ill^ < 2С, ^ Ц^^Ц • max IIAZ^^JI^.
ГЖМ ' ¦* т<.М
- т=0 ~
Деление на тахдг<д^ II^^tv+iIIg ^^^^ требуемую оценку, так как Ауд/
является линейно"Й комбинацией элементов AZj^^^. П
Теперь, применяя докгизательство теоремы 8.2 к Л-устойчивому
методу (р, ?), мы получим следующую теорему.
Теорема 8.5 (Неванлинна и Одех 1981). Рассмотрим линейный
многошаговый метод (8.2) порядка р, который сильно устойчив на
бесконечности и имеет множитель А'(С) • Предположим, что
дифференциальное уравнение удовлетворяет условию
N т
Е J2f'm^J^^{f{^m^^m)-f{^m^vJ,Uj-Vj)<0 (8.22)
m=0 j=0
при любых N >0 и любых последовательностях {uj} и {Vj}. Тогда
имеет место оценка
l|j/m-y(^m)ll < С( тад ||у,-у(х,.)|| + л max ||/(х_,., j/,.)-y'(x,)||) + Mh",
где постоянные С и М такие же, как в теореме 8.2. П
Re (П - i7e'04^) > О для всех t G ]
386 Гл. V. Многошаговые методы для жестких задач
Далее мы рассмотрим вопросы существования множителей и их
построения, а также попытаемся лучше понять условие (8.22).
Построение множителей. Очевидно, что /i(^) = 1 является
множителем тогда и только тогда, когда сам метод Л-устойчив. Кроме того,
переходя в (8.20) к пределу при |С| —)'Оо, мы видим, что ^@)
должно иметь такой же знак, как величина Qf^/ffj^ (которую мы всегда
считаем положительной). Поэтому простейший (и наиболее важный)
нетривиальный множитель имеет вид
Ж) = 1-'?С- (8.23)
Теперь предположим, что метод (р, (т) устойчив на бесконечности.
Тогда согласно принципу максимума для гармонических функций
(8.23) является множителем для метода (р,(т) тогда и только тогда,
когда l^yl < 1 и выполняется условие
V(e««)>
Это условие является поводом для изучения кривой
которую Неванлинна и Одех A981) назвали модифицированной
кривой локуса корней. В результате мы имеем следующий критерий.
Критерий 8.6. Рассмотрим устойчивый на бесконечности метод.
Функция (8.23) является множителем для (р, а) в том и только в том
случае, если |г;| < 1 и модифицированная кривая локуса корней лежит
справа от прямой, проходящей через начало координат и имеющей
наклон —l/rf.
На рис. 8.1 показаны модифицированные кривые локуса корней
для ФДН-методов при 2 < fc < 6. Оптимальные значения rj приведены
в табл. 8.1.
Предложение 8.7. Если fi(Q является множителем для метода
(/), а) и выполняется условие
|arg/i(C)l<|-a при |С|<1, (8.25)
то метод А(а)-устойчив.
Доказательство. Из условий (8.20) и (8.25) следует, что
|arg(^)-T|>a при |С|>1.
Но это условие и означает Л(а)-устойчивость. П
Простые выкладки показывают, что множитель (8.23)
удовлетворяет условию (8.25) с а = arccosr;. Для ФДН-схем мы включили эти
V.8. Сходимость для нелинейных задач
387
значения в таблицу 8.1 наряду со значениями а, характеризующими
линейную устойчивость.
Таблица 8.1. Множитель для схем ФДН
к Г] arccosr; Л (а)-устойчивость
2
3
4
5
б
0
0.0836
0.2878
0.8160
5.0130
¦nil
85.200
73.27»
35.32»
—
7г/2
86.03»
73.35»
51.84»
17.84»
it=6
-10 о 10 20 30 -10 1
Рис. 8.1. Модифицированные кривые локуса корней для схем ФДН.
Мнолсители и нелинейности
Нам предстоит еще выяснить, каким условиям должны
удовлетворять множитель /i(C) и функция /(х,у), чтобы неравенство (8.22)
выполнялось для любых последовательностей {и^} и {v^}. Чтобы
понять, что оно означает, рассмотрим сначала линейную задачу у' = Ау,
следуя работе (Неванлинна и Одех 1981).
Прецщожение 8.8. Если множитель /i(C) отвечает условию (8.25)^
а область значений матрицы А лежит в секторе \ arg(^t/, к) — 7г| < а
при всех и G С7*, то соотношение
N т
'?'?,i^_jRe{Au^,Uj)<0 (8.26)
m=0 j=0
выполняется для всех N >0 и любых последовательностей {uj}.
Доказательство. Непосредственное вычисление показывает, что
выражение в (8.26) равно
Re (^ ^" ^{e'^){Au^{t), uj,{t))dt^, (8.27)
388 Гл. V. Многошаговые методы для жестких задач
где
i=o
обозначает преобразование Фурье для (wq, Uj,..., и^). Из
предположений о /i(C) и А следует, что подинтегральное выражение в (8.27)
имеет неположительную действительную часть, что и доказывает
неравенство (8.26). D
Задачи, удовлетворяющие условию (8.22) с каким-либо
множителем /i(C), должны удовлетворять также одностороннему условию
Липшица (8.1) с i/ = 0 (это сразу видно, если в (8.22) положить N = 0).
Следующее предложение, в котором речь идет о задачах с
возмущениями, укг1зывает класс нелинейных задач, для которых выполняется
условие (8.22).
Предложение 8.9. Пусть /(х, у) = —Ау-\-Ад{х, у), где А —
симметричная и положительно полу определенная матрица. Предположим,
что в норме \\и\\^ =и^Аи выполняется неравенство
\\g{x,y)-g{x,z)\\^<L\\y-z\\^. (8.28)
Тогда условие (8.22) выполняется в том случае, если
L.maxHC)l<minReAi(C). (8.29)
Замечание, Для множителя (8.23) условие (8.29) эквивалентно
требованию Ь- (l-i-i]) <A — т)).
Доказательство. Для Wj = Uj — Vj тем же приемом, что и в
доказательстве предложения 8.8, получим соотношение
-Е Y.fm-j^^i^'^m.^j) = -Re :rz / ti(e'^){Aw^{t),w^{t))dt) <
m=Oj=0 ^^^JO ^
1 f^' ^
<-^oir {AWf,{t),Wf^(t))dt = -moY,{^^j'^j)' (8-30)
^^ •'0 i=o
где rriQ = minRefi{e^^). В то же время неравенство Коши—Шварца
дг1ет
N
J2 Re(A{g(x^,uJ,-gix^,vJ) , E^m-iK "«'j)) < (8-31)
m=0 j=0
^ N \^^^ / ^ II "^ ||2\ ^/^
^m=:0 ^ ^m=:0 j=0
V.8. Сходимость для нелинейных задач 389
Последний множитель в (8.31) можно оценить следующим образом
(положим здесь Wj = О при j > N):
^ ^, ^ ..9 1 гЗл-
m=o"j=0 "^ ^^ -^^ т>0 j=0
Г27Г „ ..9 ^
2
А
= ^ / "Ие-'')Г||Е^"''Ч|Г/'<Л/'Е1К11^ '
где М = max|/i(e"'**)|. Эти оценки вместе с (8.28) показывают, что
выражение в (8.22) можно ограничить сверху величиной
(L^M-^mo)f2\\uj-^Vj\\l
j=0
Если выполняется (8.29), то она неположительна. П
Дискретная вариация постоянных и возмущения
Теперь обратимся к основанному на анализе возмущений
подходу Любиха A991), который переносит идеи разд. V.7 (дискретная
вариация постоянных) на нелинейные задачи. Для этого рассмотрим
нелинейные дифференцигильные уравнения, записанные в форме
y' = Ay + g(t,y). (8.32)
Подставив это уравнение в формулы (8.2), (8.3) и (8.4), мы получим
к
J2(aJ - /iM)A2/m+.- = ЛД^„.+, +с/^+„ (8.33)
1=0
где
к
Д^т+fc = S ^« (^(^m+i' ^m+.) " </(^m+t > Ут+.)) (8-34)
1=0
при m>0. Положим теперь А|^^=:0 при j <к. Напомним, что dj (при
j > к) обычно представляют собой локальные погрешности
обрывания ряда, а rfg,. ., rf/c^i определяются из (8.33) при m G { —1,. •., —к}.
Тогда разности Ду являются глобальными погрешностями метода.
Если ввести формальные степенные ряды
j>0 j>0 j>0
то рекурсию (8.33) можно записать в следующем виде:
Ау@ = г(С, hA) {hAgiO + d{0). (8.35)
Резольвента г (С, ft Л) была введена в G.44) и G.50). Тогда
коэффициент при С" в (8.35) дает формулу
m m
Ay„ = ЛЕ'-—i(''^)^5i + E'-m-j(''M- (8-36)
390 Гл. V. Многошаговые методы для жестких задач
Вторую сумму в правой части (8.36) можно оценить так же, как в
разд. V.7. Чтобы оценить первую сумму, мы должны объединить
оценки для г (ЛЛ) с условием Липшица для д(х,у). Отсюда получим
неравенство типа неравенства Гронуолла, решение которого и дает
требуемые оценки для Ау^. Проиллюстрируем эту процедуру на
простой ситуации.
Теорема 8.10. Пусть многошаговый метод и матрица А отвечают
предположениям теоремы 7.10. Если нелинейность д(х, у)
удовлетворяет условию Липшица
\\gix,y)-g{x,z)\\<L\\y-z\\, (8.37)
ТО существуют постоянные С, /iq , 7 (^^^ ^ теореме 7.10) и А (причем
/iq и Л зависят от L) такие, что
Ы^т)-Ут\\<
- <Ce^^-(me.x\\y{xj)^yj\\-^hP Р e^(---^)||y('^-b^)@||d^).
\0<j<k Jxo ^
Доказательство. Из доказательства теоремы 7.10 и равенства
(8.36) следует, что
I т т
\\^yJ\ < hLC, Yiв^('"-^>||Д1/,|| + C,Yiе^С"--')^^., (8.38)
где (при О < к < 1)
ет = Со(«"* ^тах^\\Ayj\\ + Л" ^"^ ||y<''+')(OI|d^) •
Применяя к последовательности {е"'>"^'»||Ду^||} результат,
приведенный в упр. 1, мы придем к утверждению теоремы. П
Любих A991) показал, как можно улучшить приведенные
оценки, чтобы получить предложения о сходимости для сингулярно
возмущенных задач (см. разд. VI.2) и дискретизированных нелинейных
параболических уравнений. В следующем подразделе излагаются его
результаты для параболических задач.
Сходимость для нелинейных параболических задач
Мы будем рассматривать задачу Коши
уЧЛу = (/(<, 2/), у{0) = Уо. (8.39)
получаемую при дискретизации по пространственной переменной
дифференциального уравнения в частных производных параболического
типа. Предполагается, что матрица А удовлетворяет условию
\\{sI + A)-'\\ < -^ для |arg5| < 7г-а' (8.40)
V.8. Сходимость для нелинейных задач
391
при некотором а' G @,7г/2) (ср. G.47)). Чтобы мотивировать наши
предположения относительно g{t,y)i начнем с двух примеров.
Уравнение Бюргерса (Бюргере 1948). Для этой задачи
щ + ии^ = fiu^^ или "t + (у)^ = f^^xx^
мы рассмотрим дискретизацию
fi>0
4Дх
,•¦1 ^ Ц|>1-2ц,Ч-ц,-^1
(ДхJ
Она имеет вид уравнения (8.39), причем
А =
Да;2
/2-1
-1 2 -1
-1 2
V
-1
\
Vy
9(i^y)
1
4Дг
/ У2 - Уо
Уз-У?
\У^+1-Уп-
\
J
(8.41)
где /i > О — заданная константа, Ах = 1/(п -h 1) и (в случае
однородных краевых условий) t/g = у^^^ = О. Здесь удобно работать с
масштабированной нормой в R":
1Н1 = \/Д^ЕГ=1КР,
(8.42)
поскольку в пределе при п —^ ос она переходит в норму
пространства Z/^@,1). Так как собственные значения симметричной матрицы
А действительны и положительны, нетрудно проверить, что условие
(8.40) выполняется при любом а' > О равномерно относительно Дх.
Наличие знаменателя Дх у функции д{1уу) в (8.41) делает
невозможным выполнение условия Липшица (8.37) равномерно
относительно Дх > О (даже в окрестности точного решения). Однако
используя энергетическую норму ЦЛ^/^иЦ, которая уже содержит множитель
1/Дх, мы покажем, что
\\9{t, У) -9(t, z)\\ <и-'г- \\А''\у - z)\\ при WA'f'yW + \\A'/'z\\ < г.
(8.43)
Для доказательства этого неравенства рассмотрим билинейное
отображение 6 : К*^ X М'* —»^ К", г-я компонента которого определена как
bi(u,v) = DДх)-Н«,>1 -h«,_i)(v,+i -t;,.-.i)
(здесь мы тоже положили Uq = Vq = и^^^ = v^^j =0). Тогда
g{t. у) - g{t. z) = 6(у, у) - 6(z, z) = 6B/, у ~ z) -h 6(у - г, г), (8.44)
и нужно получить оценку для ||6(ri,i;)||. Используя неравенство
|(w,+i -htii-i)(t^,+i - v.-i)! < 2. |t;,.^.i -t;,._i| -maxj. \uj\
и оценки из упр. 3, мы получим, что
Щи, v)\\ < ||«|U • \\Dv\\ < /i-». \\A"\\\. \\A'/\\\, (8.45)
392
Гл. V. Многошаговые методы для жестких задач
где
D =
2Д1
/ О 1
-1 О 1
-1 О
\
(8.46)
-1 о/
представляет оператор первой центральной разности. Применение к
(8.44) оценки (8.45) доказывает неравенство (8.43).
Уравнения Навье—Стокса для несжимаемой эюидкости.
Движение вязкой несжимаемой жидкости в некоторой области ПсМ^
описывается уравнениями, которые сформулировали Навье A823) и Стоке
A845):
9и v-^ 9и ^
dt
divu = О,
(8.47)
t = l
где u = (wj,..., li^)^. Обозначим P оператор ортогонального
проектирования пространства ^^(fi)^ на X, где X — подпространство
функций, у которых divu = О (более точно: замыкание множества гладких
функций с равной нулю дивергенцией и содержащимся в П
носителем). Если применить оператор Р к уравнению (8.47), то gradp
пропадает, и мы получим
1=1 '
Эти уравнения имеют теперь точно такой же вид, как уравнение
(8.39), где А = —РА (или некоторая дискретизация этого оператора)
и 9(t,y) — правая часть (8.48). Условия Липшица для этого
нелинейного члена получили Соболевский A959), а также Фудзита и Като
A964). Они имеют вид
\\9{t,u)-g(t,v%_^<e(r)\\u-v\\^ при |Н|^ + |Н|^<г, (8.49)
где II • 11^ обозначает норму
||«||^ = |И^«||. (8.50)
В частности, ДЛЯ d=3 условие (8.49) выполняется при /3 = 1/2, 7>3/4
и при /? = 7 > 3/4 (Фудзита и Като 1964, pp. 272-273).
Основываясь на этих примерах, рассмотрим начальную задачу
(8.39) на М", предполагая, что А удовлетворяет условию (8.40) при
некотором а'Е@,7г/2), а нелинейный член g(t,y) удовлетворяет
условию Липшица (8.49).
Применяя к (8.39) линейный многошаговый метод, получим
к к к
Х1^«^т+.+Л^Х1^»^т+,=Л^/?,.(/(<^^.,у^^.). (8.51)
»=0
t=0
1=0
V.8. Сходимость для нелинейных задач 393
Вместо обычного сравнения численного решения {у^} с
аналитическим решением y(t) задачи (8.39), интересней сравнить численное
решение непосредственно с точным решением исходного уравнения в
частных производных. Для этого обозначим Tj{i) проекцию решения
уравнения в частных производных на рассматриваемое конечномер)-
ное пространство. В результате получим
где s(t) — погрешность дискретизации по пространственным
переменным.
Теорема 8.11 (Любих 1991). Рассмотрим задачу (8.39)^ где Л
^ 9{^^У) удовлетворяют соответственно условиям (8АО) и (8.49) с
7 < 1. Предположим J что многошаговый метод имеет порядок р,
A(q)-устойчив при некотором а > а' и сильно устойчив на
бесконечности. Тогда имеет место следующая оценка полной погрешности
дискретизации:
+ ||Л-»5@)||д + fj \\A-h4t)% dt^. (8.52)
Эта оценка справедлива для t^ = mh < Т при условии, что h <к^
и выражение, заключенное в скобки в правой части неравенства, не
превосходит е, где h^ и е достаточно малы. Постоянные С, h^ и е
зависят от niaxQ<^<j. ||77(/)||^ и от величины М из формулы (8.40), но
в остальном не зависят от А и от размерности системы; не зависят
они также от т и h.
Доказательство, а) При подстановке в (8.51) проекции ri[t)
решения уравнения в частных производных мы получаем
к к
«=0 »=0
где
Wdm^kh < ^oh' r^" h^'^-'Hrnp dt. m > 0. (8.53)
Повторение ра<:суждений, которые привели к формуле (8.36), теперь
даст соотношение для погрешности Ау^ = v(^rn) " Ут '
т т т
j=0 j=0 j=0
(8.54)
394 Гл. V. Многошаговые методы для жестких задач
Как и в (8.34), величины Д^^ и Asj определяются из формул
к
^^m+/c = l]/?,(^(Wi'^(W.))-^(Wi'2/m+.)).
»=0
к
1=0
при m > о, но Agj = О, Asj = О при j <к. Значения d^,.. .,d^_<^
определяются как обычно (см. их определение перед формулой (8.4')).
Три члена из правой части формулы (8.54) рассматриваются по
отдельности в следующих трех частях докгизательства.
Ь) Условие Липшица (8.49) может быть записано в виде
|И-^ E(<, у) - 9(t, Z)) 11^ < ^(г). Ну - z\\^ при ||j,||^ + ||z||^ < г.
Положим р = шаХо<^<7'11^@11/? и допустим, что при hm<T численное
решение у^ существует и ограничено: \\у^\\ < /?-Ы (это допущение
будет обосновано с помощью рекурсии в части (f) доказательства).
Тогда
к
1И-"Д5„,+Лд < ^B/»+ 1) • Е 1^.1 • W^Vm+ih- (8-55)
t=0
Следовательно, нам надо найти оценку для ||Гуу^_^.(—ЛЛ)Л'>||^ (для
матричной нормы, подчиненной векторной норме || • ||^, — см. разд. 1.9).
Отметим, что ||Гу^_^.(—ЛЛ)Л'^||^ = ||Л'^Гуу^_^.(—ЛЛ)||, и напомним, что
A'^r^[—hA) является коэффициентом при ^^ в ряде для
Л^г(С, -hA) = Л^ {S(C)I + ЛЛ)""^
Чтобы применить лемму 7.11, нужно оценить Ф{8) = A'^{sl-{-А)^^.
Если матрицу А можно привести к диагональному виду с помощью
ортогонального преобразования (как, например, матрицу (8.41)), то
при I arg s| < 7г — а' (О < а' < а) мы имеем
ЦА-^(si+ АГ'\\< sup ^<М,^\зГ-\
а>о \s-\-a\
По поводу общего случая мы отошлем читателя к работе (Хенри 1981,
pp. 26-28). Применение леммы 7.11 (см. также замечание 7.12) дает
||г^(-ЛЛМ^||^ < C,((i + 1)/.)-^ при j > 0.
Это неравенство вместе с условием Липшица (8.55) с L^C^- ^Bр+ 1)
дает оценку
m m
H|E''m-i(-/'^)A5i|| </»'-^iD"'--'' + l)"'II^J'jllr (8.56)
J=:0 ^ i=0
V.8. Сходимость для нелинейных задач 395
с) Второй член в (8.54) является коэффициентом при С"* в
выражении __
hr(C,-M)As(C) = r(C)As(C),
где мы ввели обозначения
^^ ' j>o
AsiO = 6@ Л'' As{0 = J2 ^^j c^-
Для оценки \\rj\\p (матричной нормы) заметим, что Цг^Ц^ = Цг^-Ц.
Чтобы применить лемму 7.11, мы должны рассмотреть матрицу Ф{$) =
= E/-|-Л)~М5~^ =s~^I-(sl + А)-^, норма которой в силу (8.40)
мажорируется величиной (M-h l)/|s|. Поэтому лемма 7.11 дает оценку
\\^j\\C ^ ^2- Далее, мы имеем формулу
As(Q = ^\A''As,C'-^ Е A-\Asj-Asj_,)C^),
причем ряд из коэффициентов функции J(C)/A—С) абсолютно
суммируем, поскольку все нули a(Q лежат внутри круга |С| < 1.
Объединив все эти оценки, мы получим
т т
HI Е'•-i (-''^) ^«i IL=IIЕ ^-i ^«i II <
<Сз(||Л-^Д.,||^+ J2 \\A-'(Asj-Asj_,)\\^)<
<c,{\\A-'sm\^+1^" \\A-' s'm^dt)
(8.57)
d) Последний член в (8.54) можно оценить тем же способом, что и
соответствующий член в доказательстве теоремы 7.10. Надо только
взять норму (8.50), и мы получим оценку
^ / Mm \
HI Л'т-А-'^ЩЦ < <^5(,тах \\yj-fi(tj)\\p + Л"! y^^'Hrn^dtj.
(8.58)
e) Подставив (8.56), (8.57) и (8.58) в (8.54), мы придем к оценке
m
IIA2/mlU < '^'¦' ^ Е(^ - > -^ 1)""' \\ЧЬ + ^б^т> (8.59)
i=o
где Cq = max(C4, Q) ^ ^т обозначает заключенное в скобки
выражение в правой части неравенства (8.52). Это неравенство типа Грон-
уолла при h < Hq и h\'^'^L < 1 может быть решено (см. упр. 2), в
результате чего мы придем к желаемому результату: ЦАу^пН ^ ^7^т •
396 Гл. V. Многошаговые методы для жестких задач
f) Докажем, наконец, с помощью рекурсии использованное в
пункте (Ь) предположение: ||у^||^ < /^+ 1 • Пусть неравенство \\yj\\p <p-f 1
выполнено при j = 0,l,...,m—1. Тогда по теореме о сжимающих
отображениях из h}"'^L < 1 следует, что решение у^ уравнения (8.54)
существует и единственно. Это решение удовлетворяет неравенству
\\Ут\\р < \Ы^т)\\р-^\\^Ут\\р<Р-^^^ ^^^^ значение е достаточно мало,
точнее, если С'^е < 1. П
Замечание. Леру A980) предложил другой подход к исследованию
сходимости многошаговых методов для нелинейных параболических
уравнений. Соответствующую теорему для методов Рунге—Кутты
доказали Любих и Остерман A993).
Упралснения
1. Пусть L>0. Рассмотрим две последовательности {uj} и {Sj}
неотрицательных чисел, отвечающих условию
m т
^m<^I'lZ^j+X^^i при т>0.
i=o j=0
Докажите, что при AL < 1 — С~^ выполняется соотношение
m
i=o
Указание. Покажите с помощью индукции, что из неравенства
^т ^ '^Л YlT=o ^i + ^ следует, что v^ < МA -|- ЛЛ)*^ < Ме^^^ .
2. Рассмотрите неравенство (8.59) при 7<1> L>0, €„1^^ ^ Л>0.
Докажите, что если Л < Лд и Hq^^L < 1, то существует постоянная
С такая, что ЦДу^Ц^ < Се^ для mh < Т.
Указание. Перенесите член h^"'^L\\Ay^\\ij в левую часть и
разделите неравенство на A - /i^^^L). Это дает:
\\^ym\\0<h''^Lj2irn-J)-^\\Ay^\\p+i при т>0.
i=o
Покажите, что HAy^yjIJ^ < eu{mh), где и(х) — решение
интегрального уравнения Вольтерры
и{х) = 1 -Ь L / (х - t)"^u{t) dt. (8.60)
Jo
Оцените решение этого уравнения (Хенри 1981, pp. 188-190).
V.8. Сходимость для нелине№ых задач 397
3. Пусть А и D — матрицы, определенные формулами (8.41) (при
// = 1) и (8.46). Докажите, что для любого к G IR" справедливы
неравенства
а) 1Н1оо<1И^^'«11- Ь) \\Du\\<\\A'f'ul
где ||и||^ = max,- |u,| и || • || — норма (8.42).
Указание, а) Положив Uq = О, примените неравенство Коши—
Буняковского—Шварца к щ = J2'j=i("j ~ "j-i) • Это даст
b) Неравенство и^Аи > ||?)it||2 является следствием
алгебраического тождества (при Uq = u^^i = 0)
1=1
n
= E(«.>i - 2^.- + ^«-i)" + 2"? + 2^n-
t=i 1=1
«=i
V.9. Алгебраическая устойчивость
обищх линейных методов
«Общие линейные методы первоначально были введены как
средство объединения и обобщения существовавших для
традиционных методов теорий». (Дж.Ч. Бутчер 1987)
В разделах IV. 12 и V.6 мы познакомились с теориями
нелинейной устойчивости методов Рунге—Кутты (S-устойчивость) и одно-
опорных методов (G-устойчивость). Естественно поставить вопрос:
нельзя ли эти теории объединить в рамках класса общих линейных
методов? Начало этой работе положили Берридж и Бутчер A980).
Рассмотрим дифференциальное уравнение у' = f{x,y), где у и f
— комплекснозначные векторы, и предположим, что выполняется
одностороннее условие Липшица
Re{f{x,y)-f{x,z), y-z)<^-zf. (9.1)
Общие линейные методы определяются следующими формулами (см.
пример 8.5 из разд. III.8):
u^^'^ = f2^ij''f-^f'ilf>ijf^^^ г-1,...,^, (9.2а)
^^''^=i2^iA^^-^^i2^^^^^^^ г = 1,...,5. (9.2b)
i=i i=i
Здесь u„ = {u^^,..., Uj^^)'^ содержит необходимую информацию с
предыдущего шага. Внутренние стадии (v^ % .. .,t;, '), определяемые
уравнениями (9.2Ь), служат для вычисления и^_^^ в (9.2а).
G-устойчивость
Как и в разд. V.6, мы будем рассматривать нормы, порожденные
скалярным произведением:
где G = [g^j) — действительная симметричная положительно
определенная матрица.
Определение 9.1. Общий линейный метод (9.2) называют
G-устойчивым^ если существует такая действительная симметричная
положительно определенная матрица G, что для двух численных решений
{и^} и {и^} соотношение
ll"n+l-Sn+lllG < \Wn-K\\G (9-4)
выполняется при любой длине шага Л > О и для всех
дифференциальных уравнений, отвечающих условию (9.1) с постоянной z/ = 0.
V.9. Алгебраическая устойчивость общих линейных методов 399
Для методов Рунге—Кутты, для которых fc=l и G = {!) (с
точностью до масштабирующего множителя), это определение сводится
к 5-устойчивости в смысле определения IV. 12.2. Для одноопорных
методов, у которых 5=1 и и^ = (l/n+jt-i' • ) VnV ) оно эквивалентно
определению 6.3.
Многие методы можно записать в виде общих линейных методов
рг1зными способами, и данное выше определение G-устойчивости
может зависеть от конкретной формулировки. Например, правило
трапеций
можно рассматривать как метод Рунге—Кутты (с и^= у^). В этом
случае оно не будет G-устойчивым (так как оно не является
j5-устойчивым, см. теорему IV.12.12). Но если положить и^ = {y^.hy^^), где
2/^ = /(Xyj, 2/„), то правило трапеций будет удовлетворять неравенству
(9.4) с матрицей
Действительно, если {у^} — решение, полученное с помощью
правила трапеций, то -гг^ = 2/п + 12/п будет решением, которое дает неявное
правило средней точки, а оно, как известно, обладает
5-устойчивостью (см. пример IV. 12.3 или теорему IV. 12.9). Поэтому справедливо
неравенство
которое и доказывает наше утверждение. Матрица G в (9.5)
вырождена и поэтому не является строго положительно определенной.
Однако Берридж и Бутчер A980) допускают в своем определении
G-устойчивости (которую они называют монотонностью) ненулевые
неотрицательно определенные матрицы G. Поэтому согласно их
определению правило трапеций G-устойчиво.
Алгебраическая устойчивость
Наряду с (9.2) рассмотрим другое численное решение, полученное
тем же методом, но с другими стартовыми условиями. Введем
следующие обозначения для разностей:
В следующей лемме доказывается тождество, которое будет играть
существенную роль при изучении G-устойчивости.
Лемма 9.2 (Берридж и Бутчер 1980). Пусть G является
действительной симметричной матрицей^ а D = diag (dj,..., d,) —
действительной диагональной. Тогда разность двух решений метода (9.2)
400 Гл. V. Многошаговые методы для жестких задач
удовлетворяет соотношению
l|A«„+i||^-||A«„||^ = 2X;d.Re(A//"),At;(">>- ^ m,j{w„Wj),
t = l t,j = l
где (ti;i,...,u;,^;t) = (Aw["\...,a4"\ A/{'*\ ..., Д/i"^), a матрица
M = (m^j) имеет вид
^^fG-ATGA ATD-ATGB \
Kda-btqa db + btd-btgb)
Доказательство. Рассмотрим тождество
» = 1
- x: d, (д//"\ дг^!" V i:'^. Ы"\ д/<")>
t=i t=i
и подставим в него формулы (9.2). В результате получим
f,j=i г=1 г=1 г=1 г=1
i,i=i »=1 ^=1 /=1
- Е'^.•(Ег«А«^"^+лЕ^vA/l"\ A/i")).
Выполнив умножения и приведение подобных членов, мы придем к
утверждению леммы. П
Опр€и1.еление 9.3. Общий линейный метод (9.2) называется
алгебраически устойчивым^ если существуют действительная симметричная
положительно определенная матрица G и действительная
неотрицательно определенная диагональная матрица D такие, что матрица М
в (9.6) будет неотрицательно определена.
Из леммы 9.2 и предположения (9.1) с константой ^^ = О
непосредственно вытекает следующая
Теорема 9.4. Из алгебраической устойчивости следует
G-устойчивость. П
Для конкретного метода может оказаться нелегко найти матрицы
D и G такие, чтобы матрица М из (9.6) была неотрицательно
определенной. Следующая лемма дает некоторые полезные соотношения.
V.9. Алгебраическая устойчивость общих линейных методов 401
которые справедливы, если метод предсогласоваи, т.е. если
существует такой вектор ^q 6 М'^ , что
^1^0 = Со- Мо = '^ (^•7)
(см. формулу (8.25) из разд.III.8).
Лемма 9.5. Если общий линейный метод предсогласован и
алгебраически устойчив^ то матрицы D и G удовлетворяют следующим
условиям:
i) {d„...,dy = Di = BTG^o,
и) [I — A'^)G^Q = 0, т.е. G^o является левым собственным вектором
матрицы А у соответствующим собственному значению 1.
Доказательство, х) Пусть г;бК* и е?Ж могут принимать
произвольные значения. Из неотрицательности матрицы М (9.6) следует,
что
а отсюда вытекает неравенство
il{G--A^GA)i^^-2er)^{DA-B^GA)i^^e'^ri^[DB-\-B^D-B^GB)^ > 0.
Поскольку не зависящий от е член обращается в нуль (потому что
Л^д =^о)' коэффициент при е должен равняться нулю, причем это
выполняется при любом т;, откуда и следует первое утверждение.
ii) Аналогичные рассуждения для неравенства
{iQ'^^iif[G-A^GA)[iQ'?ei{)>Q с произвольными ^iGM'', eGM
приводят ко второму утверждению леммы. D
AiV-устойчивость и эквивалентность
различных определений устойчивости
В каких ситуациях гипгебраическая устойчивость является также
необходимым условием G-устойчивости? Чтобы исследовать этот
вопрос, рассмотрим дифференциальное уравнение
у'= \{х)у, где ReA(ar)<0.
Если к этой задаче применить общий линейный метод (9.2), то
получится формула
«„+i = 5(Z)u„, (9.8)
где Z = diag{z^,...,z,), Zj = h\{x„ + Cjh) и
S{Z)=A + BZ{I-BZ)-^A. (9.9)
Далее мы будем предполагать, что абсциссы Cj связаны с другими
коэффициентами метода следующим соотношением:
(ci,...,c,f = c = A^i + Bi (9.10)
402 Гл. V. Многошаговые методы для жестких задач
(см. также замечание III.8.17). Здесь ^^ G М'^ — второй вектор
коэффициентов в функции точных значений
z{x,h) = y(x)^0 + hl/(xKi+O(h').
Это означает, что внутренние стадии приближают точное решение
векторами Vj^ = у(х^ 4- Cjh) -f- O(h^).
Определение 9.6. Общий линейный метод нг1зывается AN
-устойчивым, если существует такая действительная симметричная и
положительно определенная матрица G, что
\\S{Z)u\\^ < Ma f^^ ^^^^ ^ г "^'^^('i-"^^s)cRez,<0
"^-" "^ (J = 1,...,S) и Zj=Zk при Cj = Cf^.
Другие возможные определения ЛЛ^-устойчивости даны в работе
Бутчера A987). Например, если условие ||5(Z)w||(j < \\u\\q заменяется
условием ограниченности степеней матрицы S(Z), то метод
называется слабо AN -устойчивым. Однако это определение не допускает
изменения значений Zj = hX{x^ "+"^j^) "^ каждом шаге. В другой
модификации определения ЛЛ^-устойчивости рассматриваются
произвольные нормы (а не только порожденные скалярным
произведением). Бутчер A987) покгизал, что это определение не расширяет класс
ЛА^-устойчивых методов, но намного усложняет анализ.
Каковы же взаимосвязи между различными определениями
устойчивости? Следующие импликации:
алгебраическая устойчивость =^ G-устойчивость =>
=> ЛЛ/^-устойчивость ==> Л-устойчивость
являются либо тривиальными, либо следуют из теоремы 9.4. Мы
знаем также, что из Л-устойчивости метода, вообще говоря, не следует
его ЛЛ/^-устойчивость (см., например, теорему IV.12.12). Следующая
теорема показывает, что две другие импликации обратимы (почти
всегда).
Теорема 9.7 (Бутчер 1987). Для предсогласованных и не конфлю-
энтных (т.е. без кратных узлов, с отличными друг от друга
значениями Cj ) общих линейных методов имеет место следующая
эквивалентность определений устойчивости:
алгебраическая устойчивость ^==> G-устойчивость <=>
^=> AN-устойчивость .
Доказательство. Достаточно доказать, что из ЛЛ/^-устойчивости
следует алгебраическая устойчивость. Для этого возьмем матрицу G,
существование которой оговорено в определении ЛЛ/^-устойчивости, и
покажем, что матрицы D (из леммы 9.5i) и М (из формулы (9.6))
являются неотрицательно определенными.
Чтобы доказать, что dj>0, положим Zj =—е (^ > 0) и 2;^ = О при
кф j. Далее, положим Ati„ = ^q (это — вектор предсогласованности
V.9. Алгебраическая устойчивость общих линейных методов 403
из (9.7)) и Д//"^ = z^i^v^P^. Тогда Ati^^, = 5G)^0 и Дг;^^ = 1 + 0{е).
С учетом равенства
Со)-.
M|^-j=0, (9.11)
которое является следствием леммы 9.5, тождество из леммы 9.2
приводит к формуле
\\S{Z)io\?G-\\io\\b = -'i^d^ + 0(e').
Поскольку левая часть этого уравнения неположительна в силу AN ~
устойчивости, мы получим, что dj > 0.
Положим теперь z^ = ierji, где V = ('/i»• • •»'Z,)^ ^ К* —
произвольный вектор, а ? — малый действительный параметр. Кроме того,
положим Au^^^Q-^isfi, где fiER'^, а также Afi^=z^Avy^K
Отсюда, в свою очередь, следует, что Д^^"^ = 1-^0(е). Тождество из
леммы 9.2 с учетом равенства (9.11) дает формулу
\\SiZ)^o\\G - II^oIIg = -(^0 - «>/'. i^r, + 0{е'))М D+^(j'(^2)) =
Поскольку это соотношение выполняется при любых ^ и г;, матрица
М должна быть неотрицательно определенной. П
Пример 9.8. Исследуем на G-устойчивость многошаговые колло-
кациоиные методЫуЪведепиыевразд.У.З, Рассмотрим случай fc = 2 и
5 = 2 и зафиксируем одну точку коллокации при Cj = 1. Тогда метод
задается формулами
л
(.«).(.-.(!. W.,)(^._)
В
(vA_(l-<fi{c,) ^(Ci)W Уп \
(9.12)
А
+ h
VVi(l) ^2A) A fi^n + h,v:,) )'
404 Гл. V. Многошаговые методы для жестких задач
где
Из упр. V.3.7 нам известно, что этот метод Л-устойчив тогда и только
тогда, когда с^ >(\/l7—1)/8. Чтобы исследовать его на G-устойчи-
вость, предположим, что д^^ = 1 после соответствующего
масштабирования матрицы G. Тогда согласно лемме 9.5ii матрица G должна
иметь вид
(напомним, что ^q = A,1)^). Необходимым условием положительной
определенности G является неравенство det G > О. При с^ > О это
эквивалентно соотношению
Теперь воспользуемся леммой 9.5i, из которой следует, что
di=7V'i(l), ^2 = 7^'2A)- (9.15)
Подставив (9.13) и (9.15) в матрицу М (9.6), мы получим для ее
нижнего правого блока
(ф,{1) о \( 27Х,-1 (X2 + lO-lW^i(l) О \
V О V'2A)A(>:2 + 1O-1 27-1 Д О М^))'
(9.16)
где
^» - ф,{1) - 4'^^'' + ^^^^ ^''>' ^2 - ^2A) ~ 2Cс? - 1) •
Прямой подсчет (см. упр. 2) показывает, что эта 2х2-матрица не
может быть неотрицательно определенной при с^ > (y/Tf — 1)/8 и 7 >
отвечающем условию (9.14). Следовательно, рассматриваемые методы
никогда не являются G-устойчивыми.
В следующих подразделах мы покажем, как можно построить
алгебраически устойчивые общие линейные методы высокого порядка.
Многошаговые методы Рунге—Кутты
Интересное обобщение многошаговых коллокационных методов
представляют собой так нг1зываемые многошаговые методы Рунге—
V.9. Алгебраическая устойчивость обхцих линейных методов
405
(9.17)
Кутты. Они определяются следующими формулами:
к 8
и образуют подкласс общих линейных методов (9.2). Это становится
очевидным, если положить и^ = (у^, 2/„_i,. •., Уп-^k^iV • Тогда
функция точных значений равна
г(х, Л) = {у{х),у{х -h),...,y{x-{k- l)h)f.
Матрицы А к В для этих методов имеют специальный вид:
/ "fc\ /^ ••• *Л
1 О
А =
\
В =
О
\0
о
о/
(9.18)
1 О/
Условия порядка для таких методов получены в теореме III.8.14. Из
нее следует, что метод (9.17) имеет порядок р в том и только в том
случае, если
к S
l = '?aj{l^jr^'^^'^bjy'j(t) при <€Т, p{t)<p, (9.19)
Значения vj(/) заданы рекурсивно:
v,@ = Е%A ~Я^^^^ + E^i^i@- (9.20)
i=i i=i
Напомним, что согласно следствию II. 12.7
v;.{0) = o, v^(r) = i,
y'jit) = pit)yjit,)-...yj{tj, если < = [<„...,<J.
Условия порядка (9,19) образуют систему нелинейных уравнений
относительно коэффициентов метода. Ее решение без всяких
приготовлений может оказаться затруднительным. Поэтому введем
дополнительные предположения, упрощающие построение многошаговых
методов Рунге—Кутты.
Упрощающие предпололсения
Условия В{р), С{т]) и D(^) из разд. IV.5 оказались полезными
при построении неявных методов Рунге—Кутты высокого порядка.
Берридж A988) показал, как эти упрощающие предположения можно
распространить на общие линейные методы. Далее мы ограничимся
изложением его подхода для многошаговых методов Рунге—Кутты.
(9.21)
406 Гл. V. Многошаговые методы для жестких задач
Рассмотрим следующие упрощающие предположения:
S к
В{р): G^6^-cf4X;a^(l-jr = l, 9=1,...,р;
3 к
s
Da{0- яJ2b,cr% = aJil-(l-j)'^), </= 1,.. .,^ Vj ;
1 = 1
5
Ob@: ?^6,cr%=6j(l-cj), ?=l,...,e,Vj.
1 = 1
Условие B(p) эквивалентно условиям порядка (9.19) для деревьев-
«кустов». Условие С(г]) означает, что для v.(<), определяемых
уравнениями (9.20), справедливы равенства
yj{t) = cf^ при p{t)<r], (9.22)
Отметим, что условие предсогласованности (9.7) с вектором ^q =
= A,..., 1)^, а именно,
к к
^а^=1, X]3,j = l при г = 1,...,5 (9.23)
3=1 j=i
получается, если в В{р) и С{т}) положить ^ = 0. Условие D{^) для
методов Рунге—Кутты распадается на -0^@ и Dq((). Однако при
некоторых предположениях одно из этих условий выполняется
автоматически.
Лемма 9.9. Предположим^ что коэффициенты с^,..., с,
многошагового метода Рунге—Кутты все различны^ а 6,^ О. Тогда
i) Bi^k-l), С{к - 1), DsiO => D^iO,
И) Bi^ + s),C(s), D^iO ^Db@.
in) B{r, + s), D^(s), Db(s) => C{ri).
Доказательство. Первые две импликации являются следствием
тождества
i=i 1=1
j=i »=i
которое справедливо, если выполнены условия С(?) и B{q + ?).
Последнюю импликацию можно доказать аналогично. П
Следующая фундаментальная теорема обобщает теорему IV.5.1.
V.9. Алгебраическая устойчивость общих линейных методов
407
Теорема 9.10 (Берридж 1988). Если коэффициенты многошагового
метода Рунге—Кутты (9.17) удовлетворяют упрощающим
предположениям В(р), С{г)), Dj^(^), Db{^) при p<r) + ^-j-l я р< 277 + 2, то
метод имеет порядок р.
Доказательство. Условия СG7) и ?^^@» ^siO позволяют
производить редукцию условий порядка для определенных деревьев, как
это показано схематически на рис. 7.1 и рис. 7.2 из разд. II.7. При
ограничениях р<77 + ^ + 1 и р< 277 + 2 все условия порядка сводятся к
условиям порядка для деревьев-«кустов», а последние
удовлетворяют условию В{р). П
Напомним, что нас интересуют алгебраически устойчивые методы
высокого порядка. Согласно гипотезе Даниела—Мура (теорема V.4.4)
порядок ограничен значением p<2s. Поэтому естественно искать
методы, отвечающие условиям B{2s), C(s) и Dj^(s), Dq(s). Согласно
теореме 9.10 они будут иметь порядок 25, являясь обобщением
методов Рунге—Кутты, основанных на квадратурах Гаусса. Начнем с
анализа условия B{2s).
Квадратурные формулы
В силу равенств (9.23) условие В(р) из предыдущего подраздела
эквивалентно следующему:
E''i-'"(S) = E"i/ /(^М^- deg/<p-l, (9.24)
где / — многочлен степени не выше р — 1. Для построения таких
квадратурных формул полезно рассмотреть билинейную форму
ai?> = E^i/ fM9{x)dx=f u;(x)f{x)g(x)dx, (9.25)
^ Ji-j Ji-k
где u)(x) — ступенчатая функция, изображенная на рис. 9.1. При
предположениях
а^>0, с^;с + »;с-1>0'-> a;fe + ... + a2>0, a;, + ... + ai = l (9.26)
1-а,
1
аь
^/с+^/с.
¦jT
1-к 1-Jk+l l-k + 2 ... -1 О
Рис. 9.1. Весовая функция скалярного произведения (9.25).
408 Гл. V. Многошаговые методы для жестких задач
(jj{x) является неотрицательной, и (9.25) можно рассматривать как
некоторое скгилярное произведение, определенное в пространстве
действительных многочленов. Будем называть квадратурную
формулу (9.24) интерполяционной, если выполняется предположение B(s).
Отсюда следует, что
6,= /' ^{x)e,{x)dx, e,{x)=f[ ip^. (9.27)
Приведенные ниже результаты, относящиеся к квадратурам Гаусса и
ортогональным многочленам, являются классическими.
Лемма 9.11. Пусть М(х) = {х — с^) •... • {х — с^).
Интерполяционная квадратурная формула удовлетворяет условию ВE + т) в том я
только в том случае, если
к ^1
M{x)x^~^dx = 0 при g=l,...,m. П
к ^1
Пусть Pg{x) — многочлен степени 5, ортогональный ко всем
многочленам степени 5—1 в смысле (9.25). Тогда лемма 9.11
устанавливает, что квадратурная формула (9.24) имеет порядок 2s тогда
и только тогда, когда многочлен М{х) равен р^(х) с точностью до
числового множителя. Многочлены р,(^г), которые через
билинейную форму (9.25) зависят от а^,...,а^^, можно вычислить с помощью
стандартной трехчленной рекуррентной формулы:
Ро(^) = 1» p^{x) = x-0Q,
Ps+ii^) = i^ - /^в)РзИ -ЪРз-гИ^
где
{Ps^Ps) {Ps-^uPs-l)
Разумеется, это возможно только в том случае, если (Pj.Pj) Ф О при
j = 1,..., 5. При предположениях (9.26) данное условие, конечно,
выполняется.
Лемма 9.12. Если ol^,...,ol^ отвечают требованию (9.26), то все
нули многочлена р^(х) являются действительными, простыми и
лежат в открытом интервале A — fc, 1). П
При построении алгебраически устойчивых методов особый
интерес представляют квадратурные формулы с положительными весами.
Следующая теорема дает достаточные условия для этого свойства.
Теорема 9.13. Если квадратурная формула (9.24) имеет порядок
р > 2s — 1, а »!,..., а^^ отвечают условиям (9.26), то
6, > О при i=l,...,s. П
V.9. Алгебраическая устойчивость общих линейных методов 409
Алгебраически устойчивые методы порядка 2s
«... анализ свойств алгебраической устойчивости
многозначных методов ... не столь сложен, как это обычно
представляли...» (Берридж 1987)
Обратимся к статье Берриджа A987) и рассмотрим следующий
класс многошаговых методов Рунге—Кутты:
Определение 9.14. Пусть заданы ai,...,a^^ такие, что X]^j ~ ^'
ajij ^ О, а нули с^,..., с, многочлена р, (х) (формула (9.28)) —
действительные и простые. Будем обозначать jE^a^,.. .,а;^) многошаговый
метод Рунге—Кутты (9.17), коэффициенты которого вычисляются из
формул
2=1,...,S,
i= 1,...,5; j=l,...fc,
bij = f- ei{x)dx, i=l,...,5; j=l,...5,
где ^,(x) — функция из (9.27).
В силу леммы 9.11 из определений с,- и 6, следует, что
выполняется условие B[2s). Формулы для 5,-^ и 6,-^ эквивалентны
условиям Dj^[s) и Dq{s) соответственно. Поэтому из леммы 9.9iii следует
выполнение условия C[s)^ и теорема 9.10 завершает доказательство
того, что рассматриваемые методы имеют порядок 2s. Следующая
теорема дает достаточные условия алгебраической устойчивости этих
методов.
Теорема 9.15 (Берридж 1987). Если л^ > О при j=l,...,fc, то
метод Е{а^,...,а^^) G-устойчив с матрицей
G = diag A, Qj -f ... -f a^j,..., a^^_i -f a^^, a^^). (9.30)
Доказательство. Для многошаговых методов Рунге—Кутты
вектор предсогласованности равен ^q = AД > • • > 1)"'^ • Поэтому из леммы
9.5 с матрицей G (9.30) следует, что
d,= 6,. при f=l,...,s. (9.31)
Согласно теореме 9.13 отсюда следует, что d,- > О и, таким образом,
выполняется первое условие алгебраической устойчивости. Чтобы
убедиться в неотрицательной определенности матрицы М (9.6),
преобразуем ее с помощью подходящим образом подобранной матрицы.
Возьмем
V=U-').. , и a = (a„...,a,f. (9.32)
Прямые вычисления с использованием упрощающих предположений
410 Гл. V. Многошаговые методы для жестких задач
Dy^{s), D^{$) и 5B5) показывают, что
где
а v'r)«{i t)-{'o ;0"(о w)' ("')
IV=G0-г) .=..../>
и BArx 2/:)-матрица М имеет вид
^={z z)' ^ = cliag(ai,...,a,)-aa^. (9.34)
Поскольку а > о и ^ а = 1, из неравенства Коши—Шварца следует,
что
Поэтому матрица Z, а следовательно, и матрица М являются
неотрицательно определенными. Этим завершается доказательство
теоремы. П
Может возникнуть вопрос: какие преимущества имеют методы
E{ai,..., a^^) с к> 1 перед 5-стадийными гауссовыми методами Рун-
ге—Кутты порядка 25. Все эти методы имеют один и тот же порядок
и алгебраически устойчивы при otj>0.
• У гауссовых методов функция устойчивости на бесконечности
удовлетворяет условию |Д(оо)| = 1. В отличие от них, новые
методы допускают спектральный радиус /7E(оо)), меньший единицы,
что улучшает устойчивость на бесконечности. Численные
исследования показывают, например, что в случае 5 = 2, к = 2 спектральный
радиус p{S(oo)) имеет наименьшее значение у/2 — 1 ?^ 0.41421, когда
Qj = 12\/2 — 16 и а2 = 1 — а^ (см. упр. 7). Ряд фактов указывает на то,
что L-устойчивых методов не существует: если бы мы могли найти
метод, у которого какая-либо внутренняя стадия, скажем, v, ^
была бы равна 2/„^1, то он был бы L-устойчивым. К несчастью, это
означгило бы, что с, = 1, а это противоречит лемме 9.12 и условию
• У гауссовых методов собственные значения матрицы Рунге—
Кутты являются комплексными (за исключением одного
действительного собственного значения, когда s нечетно). Можно ли
надеяться, что при подходящем выборе Qj > О все собственные значения
В станут действительными? Расчеты, проведенные для случая 5 = 2
и Аг = 2, показывают, что это невозможно.
V.9. Алгебраическая устойчивость общих линейных методов 411
В -сходимость
Многие результаты из разделов IV. 14 и IV. 15 непосредственно рас-
пространимы на общие линейные методы. Теорема 9.16 соответствует
теоремам IV. 14.2, IV. 14.3 и IV. 14.4 и доказывается тем же способом.
Теорема 9.16. Пусть функция f непрерывно дифференцируема и
удовлетворяет условию (9.1). Если матрица В метода (9.2)
обратима и выполняется неравенство hi/ < аоE~^), то нелинейная система
(9.2Ь) имеет единственное решение. П
Следующие теоремы дают оценки локальной и глобальной
погрешностей. Мы сформулируем их только для многошаговых методов
Рунге—Кутты, поскольку в этом случае мы уже имеем определения
упрощающих условий С(т]) и В{р). По аналогии с методами Рунге—
Кутты будем говорить, что метод (9.17) имеет стадийный порядок д,
если выполняются предположения C{q) и B(q). Напомним, что в
определении локальной погрешности <J/|(x) = j/i—t/(x+/i)
предполагается, что значения yi = y{x-\-ih) при г = 1—Л,...,0 лежат на точном
решении.
Теорема 9.17. Пусть дифференциальное уравнение удовлетворяет
условию (9.1). Если матрица В обратима^ а^{В~^) > О и стадийный
порядок равен q, то локальная погрешность метода (9.17) имеет
оценку
\M^)\\<Ch^^\^, max ^^1|у(^+^)@11 при hu <а <а,{В-'),
где с зависит только от коэффициентов метода и от а. D
Этот результат, соответствующий предложению IV. 15.1,
представляет особый интерес для многошаговых коллокационных методов, у
которых стадийный порядок 7 = S-I-Л — 1 максимален. Глобальная
погрешность допускает следующую оценку, которая служит обобщением
теоремы IV. 15.3.
Теорема 9.18. В дополнение к условиям теоремы 9.17 предполо-
жиМу что метод (9.17) алгебраически устойчив.
a) Если 1/>0у то при hu<a< а^{В-'^) глобальная погрешность
удовлетворяет оценке
1|У„-У(^„I1<Л' р^- с, max ||y('+i>(x)||.
bit/ х€[*о,Гп]
b) Если 1/ <0t то
\\Уп - уМ\\ < Л'К - хо) с, max ||y('+i)(x)||
x?lxo,Xn]
при любом Л > О. Постоянные С^ я Сз зависят только от
коэффициентов метода и (в случае а) от а. П
В отличие от результатов, полученных в разд. IV. 15, данная
теорема справедлива только для реализаций с постоянной длиной шага.
412 Гл. V. Многошаговые методы для жестких задач
Упражнения
1. Покажите, что для методов Рунге—Кутты, для которых Л = A)
и Л = В, два определения алгебраической устойчивости (IV. 12.5 и
V.9.3) совпадают.
2. Дайте подробное доказательство утверждения из примера 9.8 о
том, что двухшаговые двухстадийные кол локационные методы с
коэффициентом Cj = 1 (и с^ ^ 1) не являются G-устойчивыми.
Указание. Из неотрицательности матрицы (9.16) следует 7 > 1/2,
а рассматривая ее определитель, мы получаем неравенство
7DX1-(l + X2)')>2(Xi-X2).
которое противоречит (9.14).
3. Если многошаговый метод Рунге—Кутты с отличными друг от
друга с,- и с,. > О отвечает условиям 5(s-fAr+^) и C(s-\-k-l)y
то он удовлетворяет также и условию D^ (^).
Указание. Покажите, что для всех многочленов г(х) степени
< 5 + Аг — 1, удовлетворяющих условию r(ci) = ...=: г(с^) = 0,
выполняется соотношение
E(9E^^r4i-«i(i-(i-j)'))('-(i)-'-(i-j))=o.
При заданном j постройте такой многочлен, который
удовлетворяет также условиям
r(l-j) = l, гA-г) = 0 при 1=1,..., Л и i^j.
4. Опровергните предположение Берриджа A988) о том, что для
любых к и S существуют нуль-устойчивые многошаговые методы
Рунге—Кутты порядка 25 Ч- Л ~ 1.
Указание. Рассмотрите случай 5 = 1, когда эти методы
эквивалентны одноопорным методам, и воспользуйтесь результатом Дал-
квиста A983).
5. (Берридж 1988.) Покажите, что существует нуль-устойчивый
многошаговый метод Рунге—Кутты с 5 = 2 и Л = 2, порядок которого
равен 5.
Ответ: с^^ = {у/7±у/2)/5 .
6. (Устойчивость на бесконечности.) Если многошаговый метод
Рунге—Кутты удовлетворяет условиям Dj^(s) и Dq{s), то, например,
при 5 = 2 и к = 2
Сформулируйте аналогичный результат для произвольных s и к.
7. Проверьте, что для метода Е(а^,а2) с 0<ai<l и а2=1 —а^
спектральный радиус p{S{oo)) минимален при а^ = 12\/2-- 16.
Глава VI
Сингулярно возмущенные задачи
и задачи индекса 1
(Рисунок Дж. Ди Марцо)
Сингулярно возмущенные задачи (СВЗ) образуют особый класс
задач, содержащих параметр е. Когда этот параметр мал,
соответствующее дифференциальное уравнение является жестким;
когда е стремится к нулю, дифференциальное уравнение переходит в
дифференциально-алгебраическое. В этой главе исследуются
способы численного решения таких сингулярно возмущенных задач. Это
позволит понять многие явления, наблюдаемые для очень жестких
задач. Многое разъясняет изучение предельного случая 6 = 0
(«приведенная система», или «задача индекса 1»), который обычно легче
исследовать.
Мы начнем с рассмотрения предельного случая е = О. В разд. VI. 1
исследуются два численных подхода — метод ?-вложения и метод
пространства состояний. Затем мы проанализируем в разд. VI.2
многошаговые методы, в разд. VI.3 — методы Рунге—Кутты, в разд. VI.4
— методы Розенброка и в разд. VI.5 — экстраполяционные методы.
Будет исследована сходимость этих методов для сингулярно
возмущенных задач и для полуявных дифференциально-алгебраических
систем «индекса 1».
VI. 1. Решение згдач индекса 1
Сингулярно возмущенные задачи (СВЗ) имеют несколько
источников в прикладной математике. Один из них связан с
гидродинамикой, где возникают линейные краевые задачи, содержащие малый
параметр е (коэффициент вязкости) таким образом, что при е —^ О
дифференциальное уравнение теряет высшую производную (см.
ниже упр. 1). Другие обязаны своим происхождением исследованиям
нелинейных колебаний с большими параметрами (Ван-дер-Поль 1926;
Дородницын 1947) и химической кинетики с медленными и быстрыми
реакциями (см. пример (IV. 1.4)).
Асимптотическое решение уравнения Ван-дер-Поля
В классической работе Дородницына A947) исследовано
уравнение Ван-дер-Поля (IV.1.5') при больших значениях //, т.е. малых е.
Анализ несколько облегчается, если воспользоваться координатами
Льенара (см. упр. 1.16.8). Перепишем уравнение (IV.1.5') в таком
виде:
ez"-f (г2-1)гЧг = 0 A.1)
и подставим в него тождество
rf / , .z^
""-^'-'-"''=s.("'+'y-'))^
Тогда A.1) примет вид
/.3 X A.2)
На рис. 1.1 показаны в плоскости {y,z) решения уравнения A.2) при
е = 0.03. Видны быстрые движения, направленные к определяемому
уравнением y=z^/3-'Z многообразию М, вблизи которого решение
становится плавным. Чтобы аппроксимировать решение при очень
малых г, положим в A.2) е = 0 и получим при этом так называемую
приведенную систему:
y' = -z =f{y.z),
0 = У- (^y-^j =9(y.z).
VI. 1. Решение задач индекса 1 415
. 1 . . .
1 "^
2
Ч, 1.
f г
-1
f(f^[\ I
^ "'Z
\z
-
,,.,л
1 1
Рис. 1.1. Решения СВЗ A.2).
Рис. 1.2. Приведенная задача A.2').
Уравнение A.2) не имеет аналитического решения, тогда как A2')
легко решается:
y' = -. = (z2-l)z',
ИЛИ
ln\z\-j = x + C.
A.3)
Систему A.2') называют дифференциально-алгебраическим
уравнением (ДАУ), так как она представляет собой комбинацию из
дифференциального уравнения (первая строка) и алгебраического
уравнения (вторая строка). Такая задача имеет смысл лишь в том
случае, если начальные значения согласованы^ т.е. лежат на
многообразии М. Принадлежащие М точки с координатами у = ±2/3, г = ^1
(рис. 1.2) представляют особый интерес: в этих точках частная
производная д^ = dg/dz обращается в нуль, и определяющее многообрг13ие
не «трансверсально» к направлению быстрого движения. Решений
задачи A.2') здесь уже не существует, а решения полной задачи A.2)
416 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
при е -> О с «бесконечной» скоростью перескакивают на
противоположную часть многообразия. При —l<z<l многообразие М
является неустойчивым для решений A.2) (здесь ^^ > 0), а в остальной
своей части М устойчиво [д^ < 0).
Мы продемонстрируем мощь приведенного уравнения, получив
ответ на вопрос: чему равен период Т решения уравнения Ван-дер-
Поля, соответствующего предельному циклу, при f ~> О ? Из рис. 1.2
видно, что асимптотическое значение Т равно удвоенному времени,
за которое z(x) в A.3) изменяется от г = —2 до 2: = — 1, т.е.
Т = 3-21п2. A.4)
Это первый член асимптотической формулы Дородницына. Мы
видим также, что z{x) достигает своих крайних значений (т.е.
пересекает сечение Пуанкаре г' = О, см. рис. 1.16.2) при z = ±2. Таким
образом, получается любопытный результат: предельный цикл уравнения
Ван-дер-Поля A.1) имеет при е —> О те же самые асимптотические
начальные значения г = 2 и г' = О, что и при ? -ч оо (см. уравнение
A.16.10)).
Метод в-влолсения для задач индекса 1
Исследуем теперь поведение численного решения при б -> О. Это
даст нам представление о многих явлениях, встречающихся у очень
жестких уравнений, и поможет понять, какие численные процедуры
полезны для жестких и дифференциально-алгебраических уравнений.
Пусть имеется произвольная сингулярно возмущенная задача:
l/ = f{y,z), A.5а)
?z'=g(y,z), A.5b)
где у и Z — векторы, и пусть f и д — достаточное число раз
дифференцируемые векторные функции той же размерности, что у и z
соответственно. Соответствующим приведенным уравнением будет ДАУ
У' = /(У,^), A.6а)
0 = 9(y,z), A.6b)
ДЛЯ которого начальные значения согласованы^ если 0 = giyQ^Zo). На
протяжении всей настоящей главы будем предполагать, что матрица
Якоби
dziy^^) обратима A.7)
в окрестности решения A.6). Тогда уравнение A.6b) имеет локально
единственное решение z = G(y) («теорема о неявной функции»),
которое, если его подставить в A.6а), дает так называемое «уравнение
в пространстве состояний»
y' = f{y,G{y)), A.8)
VI. 1. Решение задач индекса 1 417
являющееся обыкновенным дифференциальным уравнением. Если
выполнено условие A.7), то говорят, что уравнение A.6) —
дифференциально-алгебраическое уравнение индекса 1.
Интересный подход к решению A.6) состоит в том, чтобы
применить какой-либо численный метод к СВЗ A.5) и в получившихся
формулах положить 6 = 0. Проиллюстрируем этот подход на
примере методов Рунге—Кутты. Применяя такой метод к системе A.5),
получим
5
>;.=Уп-ЬЛ5];а,,./(>;,,^„,), A.9а)
S
eZ,, = ег, -f ft ^ а,,- д (У,,-, Z„,.), A.9b)
8
Уп+1 =yn + h^bj (У„.., Z„,), A.9с)
t = l
S
"n+i =ez„ + hY,bi9{Y„„Z„,). (IM)
1 = 1
Предположим теперь, что матрица РК-метода (а.) обратима. Тогда
из A.9Ь) следует, что
8
ftG(y„,,Z,,)=?5]u;,^.(Z„,.-zJ, A.10)
где о;,- — элементы матрицы, обратной к (a,j). После подстановки
этого выражения в A.9d) оказывается, что определение z^^^ не
зависит от е. Поэтому без'дальнейших затруднений можно положить
? = О и получить
8
Ущ = yn + hYl «О- / (ynpZ„j), A.11а)
0 = «,(y„..,Z„,), A.11b)
yn+i=yn + hi2^if(ynoZ„,), A.11c)
t = l
Здесь
8
1-5^6,а;,,. = Д(оо), (l.Ue)
где R(z) — функция устойчивости метода (см. формулу (IV.3.15)).
418 Гл. VI. Сингул5фно возмущенные задачи и задачи индекса 1
Метод пространства состояний
При предыдущем подходе численное решение [Vn^i i ^n-^i) обычно
не лежит на многообразии д{у, z) =0. Это, однако, легко поправить,
заменив A.1 Id) условием
0 = </(j/„+i,^„+i). A.12)
Тогда мы будем иметь не только Z^j = G(Y^j) (см.A.1 lb)), но и
Zn^i=G{yn^i). Вэтом случае метод A.11 а-с), A.12) идентичен
решению уравнения в пространстве состояний A.8) тем же самым методом
Рунге—Кутты. Этот прием называют методом пространства
состояний. Всю ситуацию подытоживает следующая диаграмма:
СВЗA.5) ^-^^ ДАУA.6) ^^^ ОДУ A.8)
РК
РК
f-чО
реш. A.9) >^ метод е-вложения
метод пространства состояний < реш. A12)
Здесь особенно важны оюестко точные методы, т.е. методы,
удовлетворяющие условиям
«51 =^- при i = l,...,s. A.13)
Это означает, что у^^^ = ^п*» ^n+i — ^п$ ^ A12) удовлетворяется
во всяком случае. Следовательно, для жестко точных методов метод
е-вложения идентичен методу пространства состояний. По этой
причине Грипентрог и Мерц A986) для таких методов ввели обозначение
IRK(DAE), или НРК(ДАУ).
Оба подхода имеют свои достоинства. Теоретические результаты,
полученные для метода ?-вложения, позволяют понять, как работает
метод в применении к сингулярно возмущенным задачам. Более
того, этот подход легко распространить на более общие ситуации, когда
алгебраическое соотношение не отделено явно от дифференциального
уравнения (см. ниже). С другой стороны, метод пространства
состояний имеет то преимущество, что он не ограничен выбором неявных
методов. В случае полуявных уравнений индекса 1 нет препятствий
для применения явного метода Рунге—Кутты или многошагового
метода к уравнению A.8). В этом случае нет надобности и в новой
теории.
VI. 1. Решение задач индекса 1 419
Рис. 1.3. Транзисторный усилитель. —
Транзисторный усилитель
«...обратить внимание на то удивительное
обстоятельство, что из Кенигсберга вышло исключительно большое
число знаменитых математиков...: Кант A724), Ришело
A808), Гессе A811), Кирхгоф A824), Карл Нейман A832),
Клебш A833), Гильберт A862)».
(Ф. Клейн, Лекции о развитии математики в XIX
столетии. — М.—Л.: ОНТИ НКТП СССР, 1937, с. 197)
Дифференциально-алгебраические задачи, возникающие на
практике, очень часто формулируются не сразу в полуявной форме A.6),
а имеют вид Ми' = y?(ti), где М — постоянная сингулярная матрица.
В качестве примера проведем расчет усилителя, покгизанного на
рис. 1.3, где и^{1) — напряжение на входе, Uf, = 6 — рабочее
напряжение, [/,(<) (г = 1,2,3,4,5)—потенциалы в узлах 1,2,3,4,5, причем
U^{t) — напряжение на выходе. Токи через сопротивления
удовлетворяют закону / = U/R (Ом 1827), а через емкости — I = С • dU/dt;
здесь R и С — постоянные и U — напряжение. Действие
транзистора как усилителя состоит в том, что ток между узлами 4 и 3 в 99
раз больше, чем ток между узлами 2 и 3, причем он зависит от
разности потенциалов U^ — U2 нелинейным образом. Закон Кирхгоффа
(открытый в Кенигсберге) гласит: сумма всех токов, приходящих в
некоторый узел, равна нулю. Применение этого закона к пяти узлам
на рис. 1.3 приводит к следующим уравнениям:
узел1: М1_Ь. + сЛЩ.и[) = 0,
Ял
Rn
узел 2: ^-uJ^ + ^)+C,iU[-U;,)-Omf(U^-U^) = 0,
420 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
узелЗ: ПЩ-Щ)-^-С^^Щ^О, A.14)
узел 4: -^ - -^ + С^ - f/^) - ОМПЩ - U^) = О,
/С^ -«14
узел 5: ~-^ + Сз(У^ ~ С/^) = 0.
Для констант мы возьмем значения, приведенные в работе (Рентроп,
Рош и Штайнебах 1989) для аналогичной задачи:
/(C/) = 10-(exp(-|-)-l),
^0.026
До = 1000, ^1 = ... = ^5 = 9000,
Cfc = ib•10-^ Jfe = 1,2,3.
Входной сигнал зададим в виде
t/J0 = 0.4sinB00:rt).
Уравнения A.14) имеют вид Ми' — tf>(u), где
Сг -С,
М=\ -Сг
-С.
\
3 ^3
^3 ~^з/
A.15)
очевидно, является особенной матрицей ранга 3. Суммы первых двух
и последних двух уравнений непосредственно дают два
алгебраических уравнения. Если ввести, например, обозначения
то уравнения A.14) преобразуются к виду A.6). Таким образом,
согласованные начальные значения должны удовлетворять уравнениям
(Pi{u)-\-(p2{u)=0 и <Р4{и)'\-<р^(У') = 0. Положив {/2@) = ?/з@), мы
получим /A/2@) — С/з@)) = 0. Поскольку и^{0) = О, согласованные
начальные условия легко находятся, например, в виде
t/i@) = 0, С/2@) = С^з@) = -^^. иМ = и„ и,{0) = 0.{1.Щ
Задачи вида Ми^ = (р{и)
Численные методы для задач вида
Ми' = (р{и) A.17)
с постоянной матрицей М можно вывести следующим образом.
Предположим, что М — регулярная матрица, применим численный метод
VI. 1. Решение задач индекса 1 421
к обыкновенному дифференциальному уравнению и' = М*" ^(u) и
полученные формулы умножим на М. Действуя таким образом, для
методов Рунге—Кутты мы получим
5
M{Uni-^n) = hJ2%<P{Unjl A.18а)
3 = 1
^n^i = (l- Е f^i^ij)^n^ i; b,u;,jU,j. A.18b)
где [u^j) опять обозначает матрицу, обратную к (a,j). Вторая
формула получена из
5
1=1
в точности тем же способом, что и выше (см. A.10)).
Оказывается, что формулы A.18) формально имеют смысл и в
том случае, если М — сингулярная матрица. В этом случае задача
A.17) математически эквивалентна полуявной системе A.6), и метод
A.18) соответствует методу A.11). Чтобы убедиться в этом,
разложим матрицу М (например, с помощью гауссова метода исключения
с выбором главного элемента), представив ее в виде
=<i 2)-.
W = S(^; 5jr, A.19)
где S и Т — обратимые матрицы, а размерность / равна рангу М.
Подставим это разложение в A.17), умножим на 5"^ и перейдем к
новым переменным:
Tu=(j^y A.20)
ЧТО дает
(^)=5-..(г-.0)) = :(/(-)), (>.:,
т.е. задачу типа A.6). Начальное значение Uq будет согласованным,
если (p{uq) принадлежит образу линейного оператора,
представленного матрицей М.
Аналогично, если подставить A.19) в A.18) и ввести переменные
уравнения A.18Ь) (для Z^^^) и A.18с) (для V^+i) приводят в
точности к уравнениям A.11). Это означает перестановочность, изобра-
422 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
женную на следующей диаграмме:
преобр. A.20)
задача A.17) > задача A.6)
метод
A.18)
метод
A.11)
A.23)
{«п)
преобр. A.22)
>
{Уп}^ {^п)
Из этой коммутативности вытекает важное следствие: все
результаты, справедливые для полуявных систем A.6) и метода е-вложения
A.11) (существование численного решения, сходимость,
асимптотические разложения, ...), применимы также к неявным задачам A.17) с
сингулярной матрицей М и к методу A.18).
Следовательно, все программы, имеющие опцию для неявных
дифференциальных уравнений типа A.17) (такие, как RADAU5) можно
применять непосредственно. Это мы и сделали для задачи A.14) с
начальными значениями A.16), интервалом интегрирования О < х < 0.2
и значением То1 = 10~^. Программа вычислила показанное на рис. 1.4
решение U^{t) за 556 (принятых) шагов. Сравнение с напряжением
на входе U^{t) показывает, что наш усилитель работает. Более
тщательно разработанный пример можно найти в работе (Хайрер, Любих
и Рош 1989, pp. 108-111).
Рис. 1.4. Численное решение задачи об усилителе A.14).
Сходимость методов Рунге—Кутты
Если метод является жестко точным, то численные решения A.11)
эквивалентны численным решениям обыкновенного
дифференциального у \>ъ,ъпеп1ля A.8). Поэтому сходимость решений описывается
теоремами II.3.4 и II.3.6 как
2,„-у(х„) = О{Л0. z„-z{x„) = Om^ A-24)
VI. 1. Решение задач индекса 1 423
где р — классический порядок метода (вторая формула следует из
условия Липшица для G). В случае методов общего типа оценка
A.24) остается справедливой для !/„, потому что A.11а,Ь,с) не
зависят от z^ и не меняются, если A.1 Id) заменить на A.12). Таким
образом, нам надо только доказать сходимость г„. Следующая теорема
существенно опирается на понятие стадийного порядка q метода, т.е.
на условие C[q) из разд. П.7 или IV.5.
Теорема 1.1. Пусть система, A.6) удовлетворяет условию A,7) в
окрестности точного решения (t/(x),z(x)), я начальные значения
согласованы. Рассмотрим метод Рунге—Кутты, имеющий порядок р,
стадийный порядок q и обратимую матрицу А. Тогда глобальная
погрешность численного решения (l.lla-d) имеет оценку
z^- z(x^) = 0(h^) при х^ —XQ=inh < Const, A-25)
причем
a) г = р, если метод жестко точный;
b) г = min(p, g + 1), если функция устойчивости удовлетворяет
условию — 1 < Л(оо) < 1 ;
c) г = min(p— 1,^), если Л(оо) = -f-1;
d) если |Я(оо)| > 1, то численное решение расходится.
Доказательство. Случай (а) уже был обсужден выше. Переходя к
рассмотрению остальных случаев, заметим прежде всего, что из того,
что выполнено условие C(q) и метод имеет порядок р, следует
5
^(х,Ч-е,Л) = г(х„) + /1^а,-^.г'(х„-Ьс^Л) + 0(Л^+М, A.26а)
8
zix,^,) = z(x„) + h'?b,z'{x„+c,h) + 0(hP^') . A.26b)
t = l
Поскольку матрица А обратима, из A.26а) можно вычислить
величину z^{x^ +^j'^) и подставить в A.26Ь), что дает
z(x^^,)=pz{xJ-^b^A-'Z^-^0{hP^')-^0(h<^^'), A.27)
гдер=1-6^Л-111=Я(оо) и Z„ = (z(x„-fci/i),...,z(x„-hc,/i))^.
Обозначим глобальную погрешность Az^ = ^п "" ^(^п) ^ ^^п ^ ^п'^^п-
Вычитая A.27) из A.1 Id), получим
Дг„^1=/>Аг„+6^Л-^Д^^-Ь0(ЛР+1)-|.0(Л^+М. A.28)
Обратимся теперь к оценке AZ„ . Для этого необходимо рассмотреть
2/-компоненту системы. Согласно A.11а-с) величины Уn^Уni — ^'^^
те значения, которые дает метод Рунге—Кутты, будучи применен
к уравнению A.8). Таким образом, как следует из теоремы П.8.1,
2/„ — y(x^) = е (х^)Лр-НС?(Л''+^). Заметим, что уравнение A.26а) оста-
424 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
ется справедливым, если в нем заменить z(x) на у(х), Вычитая
полученную формулу из A.11а), мы получим
откуда следует, что
>;.-2/К+с,Л) = С?(Л^') с i/ = min(p,(/-hl).
С учетом A.11b) получаем:
Zni - z(x„ + с,Л) = G{YJ - С{у{х„ + с,Л)) = О^,
так что уравнение A.28) примет вид
Az„+,=:pAz„+S„^„ где 6„^, = ОЮ. A-29)
Повторное применение этой формулы с учетом того, что Azq = О, дает:
А^п = Е^""Ч- A-30)
1 = 1
Таким образом, утверждение теоремы доказано при рф—1. В случае,
когда /?= —1, погрешность Az^ равна сумме разностей Sj^^ —Sj . Но
так как S^j^^ в действительности имеет вид S^^i = d(x^)h*^ + 0{h'^'^^) у
мы получаем, что Sj^^ —Sj = С?(Л'^+1), и утверждение теоремы
доказано и для этой ситуации. П
Снижение порядка для z-компоненты (для методов, не
являющихся жестко точными) впервые исследовала Петзолд A986) в более
общем контексте.
Упражнения
1. Вычислите решения граничных задач
ey'4y4j/=l и 5у"-уЧу = 1 A.31)
при у@) = уA) = 0 для е>0.
Заметьте, что при е -?0 решения имеют «пограничный слой» на
одном из концов отрезка [0,1] и что предельные решения при е = 0
удовлетворяют уравнениям
у'-|-у = 1 и -у'-|-у = 1
соответственно, так что одно из граничных условий теряется.
VI.2. Многошаговые методы
Цель этого раздела — изучить сходимость многошаговых
методов при применении их к сингулярно возмущенным задачам (методы
Рунге—Кутты будут рассмотрены в разд. VI.3). Мы будем
интересоваться равномерными оценками при е-^0. Результаты,
полученные в предыдущих главах, здесь не применимы. Поскольку
постоянная Липшица сингулярно возмущенной задачи A.5) порядка 0F"^),
оценки из разд. III.4 оказываются бесполезными. Односторонняя
постоянная Липшица в общем случае тоже имеет порядок 0(е^^),
поэтому результаты, полученные для сходимости в разд. V.8, тоже
нельзя применить. Начнем с рассмотрения приведенной задачи.
Методы для задач индекса 1
При применении к системе г/ = /(у, z), ez* = д{у, z) многошагового
метода мы получим уравнения
к к
YL'^iyn^i=hY,Pif{yn^i.z^^,). B.1а)
1=0 t=0
к к
»=0 t=0
Если положить 6" = о, они примут вид
к к
Е ^» 2/п+.- = л 5;^, nVn^i.z^^i). B.2а)
»=0 1=0
к
0 = E^.^B/n+i>^n+.) B.2b)
•=о
[метод е-влооюения)^ что позволяет нам применить многошаговый
метод к дифференциально-алгебраической системе A.6). Этот
подход впервые предложил Гир A971) для методов ФДН.
Теорема 2,1. Пусть система A.6) удовлетворяет условию A.7).
Рассмотрим многошаговый метод порядка р, устойчивый в начале
координат и на бесконечности (т.е. О и ос лежат в области
устойчивости) и предположим^ что погрешность стартовых значений у^, z^
(j = 0у.. .^к — 1) порядка O(h^). Тогда глобальная погрешность
метода B.2) удовлетворяет соотношениям
У„-у(х„) = 0{НП, z„-z{xJ = 0{hP)
при Xj^ — XQ = nh< Const.
426 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
Доказательство. Формула B.2Ь) является устойчивой рекурсией
для 5^ =д[у^^ z^), потому что ОС лежит в области устойчивости
метода. Из этого вместе с предположением о стартовых значениях
следует, что S^ = O(h^) при любых п > 0. По теореме о неявной функции
уравнение g{y^,z^) = S^ можно разрешить относительно г„ , что дает
z„ = G(y„) + Oih'>) B.3)
С той же функцией G(y), что и в A.8). Подстановка B.3) в B.2а) дает
многошаговую формулу для дифференциального уравнения A.8) с
0{h^'^^) в качестве возмущения. Тогда утверждение теоремы следует
из доказательства сходимости, приведенного в разд. П1.4. П
Для неявной задачи A.17) индекса 1 многошаговый метод
принимает вид
к к
Л^Е".«"+.=''ЕА-^К+.)' B.4)
t=0 »=0
и для методов, удовлетворяющих условиям теоремы 2.1, сходимость
без всякого понижения порядка вытекает из преобразования A.20) и
диаграммы A.23).
Для многошаговых методов также возможен подход, основанный
на методе пространства состояний. Надо только заменить B.2Ь) на
уравнение
9iy„+k^z„^k) = 0. B.2с)
Метод B.2а,с) эквивалентен решению уравнения A.8)
использованным выше многошаговым методом. Следовательно, его сходимость
такая же, как для нежестких обыкновенных дифференциальных
уравнений. Предположение со G 5 больше не требуется, и могут
применяться даже явные методы.
Сходимость для сингулярно возмущенных задач
Распространение погрешности исследовали Сёдерлинд и Далквист
A981), используя оценки G-устойчивости. Первые результаты по
сходимости получил Лётстедт A985) для методов ФДН. Любих A991)
получил приведенный ниже результат, основанный на гладкости
точного решения и поэтому равномерный по е, коль скоро мы остаемся за
пределами переходных фаз. Этот результат дает оптимальные оценки
погрешности для произвольных многошаговых методов.
Матрица Якоби системы A.5) имеет вид
{е\ e-^'gj
Как видно, ее доминирующие собственные значения близки к ?~^А,
где Л представляет собственные значения д^. По соображениям
устойчивости мы будем считать на протяжении этого подраздела, что
собственные значения д^ имеют отрицательную вещественную часть.
VI.2. Многошаговые методы 427
Точнее, мы предположим, что
собственные значения А матрицы g^iv, z) /л г\
лежат в области | arg А — 7г| < а \ - )
для (у, г), лежащих в окрестности рассматриваемого решения. При
этих условиях для метода B.1а,Ь) получен следующий результат:
Теорема 2.2 (Любих 1991). Пусть многошаговый метод порядка р
А{а)-устойчив и строго устойчив на бесконечности. Если задача A.5)
удовлетворяет условию B.5), то при h>e и nh<x — XQ имеет место
следующая оценка погрешности:
1|у„-у(^„I1 + 1к-Ф„I1<
< С( max \\yj - y{xj)\\ + Л" Г Wi'^'Hr)]] dx +
+ (h + p")mг^x\\zJ-z{xJ)\\+eh'> max \\z^'^'H^)\\),
0<j<k •' -' XQ<x<Xn /
где 0 < p < 1. Эта оценка справедлива при h < Hq (h^ достаточно
мало, но не зависит от е) и при условии, что стартовые значения
лежат в достаточно малой, не зависящей от h и е окрестности точного
решения. Постоянные С и р не зависят от е и h.
Доказательство. Доказательство разбито на несколько частей: в
части (а) мы выведем рекурсивные оценки для глобальной
погрешности, в части (Ь) мы решим полученные неравенства, а в части (с)
докажем одно неравенство, которое используется в части (а).
а) Прежде всего, подставим точное решение системы A.5) в
формулы метода B.1), что дает
к к
5^а,ф,^,) = hY,Pi /{у{^п^г).Фп+г))-^<-,к^ B.6а)
1=0 »=0
к , к
Е ^» ^(^n+t) = 7 Е^» 9{yi^n^i)^ ^(^п+.)) + ^n+fc, B.6b)
t=0 1=0
причем для возмущений d^^f^, е^^^^ можно получить (при п > 0)
следующие оценки:
1И„+Л < С^Л" Г^" UP^^\x)\\dx, B.7а)
l|e„+*ll<C2ft''+i max \\z(^^'\x)\\. B.7b)
Обозначим теперь глобальные погрешности Ду„ = Уп *"У{^п)^ ^^п —
= г„ ~ z{x^) и введем разности
к
i=0
428 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
Afj = О при j < к. Вычитая B.6а) из B.1а), получим для п > О
к
Используя уже имеющийся опыт (см. (V.7.41)), определим величины
doi" -i^k-i '^^К) чтобы B.8) выполнялось и при отрицательных п.
Разрешив это равенство относительно Ду„, получим
ДУп = л Е '•n-i(o) Д/, - Е г„_^@) dj,
jzzO j=0
где г^@) определены в (V.7.44). Эти числа являются
коэффициентами разложения в ряд функции г(С, 0) =С~'^/р(С~^) • Вследствие нуль-
устойчивости метода последовательность {rj{0)} ограничена.
Поэтому из условия Липшица для /(у, z) вытекает оценка
ПАУпИ < л J2(^\\4\\ + ^ll^^ili) + ^3 Е \№ B•^)
Для г-компоненты нужна более точная оценка. Возьмем разность
B.lb) и B.6b) и из обеих частей полученного равенства вычтем
величину
Л ^
j^p.JAz^^,, где J = 9Ayo^z,). B.10)
Это дает
где
'Г=о
* Л ,ч . Л
ЕК/ - /3< - ./) Д^„+.- = - Д5„+* - e„+fc , B.11)
1=0
к
Д^п+л = Е^.(^(^п+.>^п+Л~^/(уК+.),Фп+Л)-^А^п+^^^ B.12)
1=0
и Agj = О при j <к. Опять определим Cq, .. .,^^-1 так, чтобы B.11)
выполнялось и при отрицательных п. Разрешив B.11) относительно
Дг„, получим
Д^n=JE'•n-,G./)Дi/,-E'•n-i(^)ei. B13)
j=o i=o
где матрицы rjijJ) определены равенством
(см. формулу (V.7.50)), а S{Q —формулой (V.7.45). Воспользуемся
теперь неравенством, доказанным ниже, в части (с):
~||гД-j)||<Ck'^' при 0<«<1. B.15)
VI.2. Многошаговые методы 429
Подставив его в B.13), получим
l|A^nll<E«"'^W|Ayill + ^l|A^ill)+QjE B-16)
j=o j=0
Важно отметить, что постоянная Липшица ? может быть сделана
сколь угодно малой посредством сокращения рассматриваемого
интервала.
Ь) Чтобы разрешить неравенства B.9) и B.16), определим
последовательности {и^} и {г;^}:
u„ = hJ2{Muj + Nvj) + C^Y^\\dj\\,
B-17)
i=o j=o
По индукции доказывается, что при ?<1 и Л < Ло
\\AyJ<u„, ||Д^„||<.;„.
Перепишем теперь B.17) в виде
«п=«„-1 + ЛЛ/«„ + Л^г'„+Сз1К||, «_1=0,
«п = ««п-1 + ^«п +^v„ +С74 ре„||, v_i = 0.
Разрешив эту систему относительно «„, v„ , получим
(::)-«(:::;Lf:)' ^'*'=('оаГ .?%)•
B.18)
где р=к/{1-?)) и
К1<^AК11 + Фп11). l?„l<Q(|MJ| + |||e„||). B.19)
Итерируя B.18), придем к равенству
Если ? достаточно мала, так что р = к/A— ^)<1,и если Л < /iq , то
собственные значения A{h) различны, и A(h) может быть приведена
к диагональному виду:
.W=r-.«('-W ,,?„„)г,м, г,ч = (^,\, ад).
С учетом этого равенства из B.20) получаем:
п п
Утверждение теоремы теперь следует из B.19) и B.7), поскольку
^0'--»^л-1 являются линейными комбинациями Дуо, • •, Ду/с-!' ^
430 Гл. VI. Сингул$фно возмущенные задачи и задачи индекса 1
^O'-'^/c-i — линейные комбинации Azj и j^Zj. Вследствие
нашего предположения относительно i (а именно, что р = к/{\ — f)<\)
мы доказали теорему лля достаточно малых (но не зависящих от е)
интервалов. Компактные интервалы [хо,х] могут быть покрыты
посредством повторного применения полученных выше оценок.
с) Остается доказать неравенство B.15). Более общо, мы покажем,
что
1 II "^^ (? ^'^^' ^0 II - ^"^ "Р"" О < к < 1 B.21)
равномерно в некоторой компактной окрестности решения. Это
нужно, если полученные выше оценки применяются к нескольким подин-
тервалам. Чтобы доказать B.21), вспомним, что r^(jj) определяется
формулой B.14). Если мы сможем показать, что
-1 r-fc
\(Ls[QI-g^[y^z)y -|1^||<С при |С|<1//с, B.22)
то оценка B.21) немедленно следует из интегральной формулы Коши
е ^\е J 27Г|У,^,^1/^\Л ) G(С-^)
По определению области устойчивости S многошагового метода
значение J(C) лежит вне 5, если |С| < 1. Напомним, что метод
предполагается Л (а)-устойчивым и строго устойчивым на бесконечности, а
дифференциальное уравнение удовлетворяет условию B.5).
Поэтому, если (у, z) варьируют в некоторой компактной окрестности
решения, множество собственных значений g^iv^ z) отделено от множества
{l^[Q \ 7^1) 1С| ^ 1} • Более того, оно отделено даже от множества
{l^{0 \ 7 ? 1-) ICI ^ l/'^} при некотором /с < 1. Это и доказывает
неравенство B.22), если воспользоваться неравенством из упр. 2 разд. V.7.
D
Упралснения
1. (Любих 1991.) Докажите, что в случае схем ФДН оценка из
теоремы 2.2 (для п>к) остается справедливой, если в множителе
при 2-компоненте погрешностей в стартовых значениях заменить
(Л-!-/?") на ?(Ц-р^/Л).
Указание. Докажите это непосредственно для пб{^,...,2Л—1},
а затем примените теорему 2.2 к сдвинутым стартовым значениям
VI. 3. Эпсилон-разложения
для точных решений и для РК-решений
в предыдущем разделе мы доказали сходимость многошаговых
методов для сингулярно возмущенных задач. Но этот способ не дает
оптимальных оценок в случае методов Рунге—Кутты. Поэтому
исследуем более детально структуру решений сингулярно возмущенных
задач. Первое систематическое исследование качественных аспектов
таких задач дал Тихонов A952). Асимптотические разложения
исследовала затем Васильева A963). Классические книги на эту тему
написали Вазов A965), О'Малли A974) и Тихонов, Васильева и
Свешников A985).
Разлолсение гладкого решения
¦Теорема Тихонова — это только первый шаг...
Настоящее приближенное решение таких задач в виде ряда
остается трудной проблемой. Эта проблема анализировалась
в ряде статей Васильевой.. .¦ (В. Вазов 1965)
Будем рассматривать сингулярно возмущенную задачу
ez' = g{y,z), 0<6<1,
где /ид дифференцируемы достаточное число раз. Функции /,^ и
начальные значения у@), г@) могут иметь гладкую зависимость от
е. Мы не будем ее указывать, чтобы не усложнять обозначения. При
е = 0 соответствующая система
описывает приведенную задачу. Чтобы гарантировать разрешимость
C.2), будем предполагать, что матрица ^^(у, z) обратима (в некоторой
окрестности решения системы C.2)).
Нас интересуют, главным образом, гладкие решения C.1),
имеющие вид
У(х) = Уо(х)-\-€у^(х)'^€^У2(х) -I- . . . ,
Z(x) = Zq(x)'\-€Z^{x)-\-€^Z2(x) -f . . . .
2 , . . C-3)
Подставляя C.3) в C.1) и собирая члены с одинаковыми степенями
?, получим
1 y'l = /у(Уо.Ч)У1 + /ЛУо.'o)h \ ,„ ...
е : , . . , ч /. (бЛЬ)
г'о=9у(Уо>^о)У1+9г(Уо''о)^ j
432 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
^и. 2/i' = /yB/o''^oJ/i. + AB/o)^o)^t. + V?»/(yo.'2^o.--2/i.-i»^i.-i)l .^
<-1=^у(Уо>'г:о)У*.+5'гB/о.'2:о)г^+^^(Уо,'2:о,...,2/^_1,г^_1) J '
Как и следовало ожидать, из C.4а) видно, что у^{х), Zq{x)
является решением приведенной системы. Поскольку д^ обратима, второе
уравнение в C.4Ь) можно разрешить относительно z^. Подставляя
Zj в первое соотношение C.4Ь), получим линейное
дифференциальное уравнение для yi(x). Таким образом, yi{x) и z^{x) определены.
Аналогично получаем t/2(^)» -2:2C?) из C.4с) и т.д.
Это построение коэффициентов в C.3) показывает, что мы можем
выбирать произвольные начальные значения 2л@), но в выборе '2:@)
уже нет свободы. Следовательно, не каждое решение C.1) можно
записать в виде C.3).
Разлолсения, включающие члены пограничного слоя
«Чтобы построить равномерное асимптотическое
разложение, надо взять комбинацию из разложения Макло-
рена и другого разложения особого вида. Члены этого
разложения — показательные функции, имеющие
значительную величину внутри пограничного слоя, но
пренебрежимо малые вне его». (А.Б. Васильева 1963)
Пример 3.1. Рассмотрим задачу IV. 1.1, которую запишем в виде
ez' = -z-fcosx. C.5)
Ее аналитическое решение
2(ar) = (l-fe2)"^(cosa:-|-esinx)-fCe-'^/^ =
= cos ж 4- ^ sin ж — е^ cos ж — е^ sin х -f ... + Се"^^^
представляет собой суперпозицию гладкого решения вида C.3) и
быстро убывающей функции. Этот добавочный член (переходная фаза,
пограничный слой) компенсирует недостающую свободу выбора
начальных значений Zj @).
Этот пример является побудительным мотивом к поиску решений
общей задачи C.1), имеющих вид
^ J}' C.6)
j>0 j>0
где 2/;(х), Zj(x) определяются по формулам C.4), а относительно не
зависящих от е функций rjj, Cj мы предположим, что они
удовлетворяют условиям
Ihi^ll <«-"«, ||Cj(OII<e-''« C.7)
С некоторым /с > 0. Подставив C.6) в C.1) и воспользовавшись C.4),
VI.3. Эпсилон-разложения для точных и РК-решений 433
мы получим формально
j>0 V>o j>0 j>0 j>0 ^
S>o j>o '
j>0 S>o j>0 j>0 j>0 ^
-5(E^'j'iW-E^4w)- C.8b)
j>0 j>0 ^
Введем теперь вместо x «растянутую» переменную
i = xlt C.9)
и соберем члены с одинаковыми степенями е в C.8). Для е° это дает
Ш) = /(j/o@), ^о(О) + Со@) - /(j/o@), ^0@)), C.10а)
Со@=5(Уо@),го@)+Со@) --7(%@),^o@)). C.10b)
Здесь надо ввести некоторое предположение об устойчивости для
C.1), чтобы удовлетворить условиям C.7). Мы потребуем, чтобы
логарифмическая норма д^ удовлетворяла неравенству
А'EЛу.^))<-1 C11)
в некоторой не зависящей от е окрестности решения C.2) (любую
отрицательную границу можно привести к — 1, перемасштабировав
е\ Согласно теореме A.10.6) из уравнений (З.ЮЬ) и C.11) следует,
что
1Ко@11<11Со@)||е-«.
Поскольку /(у, z) удовлетворяет локальному условию Липшица,
правая часть C.10а), которую мы обозначим <^@) ограничена: ||^@11 ^
< L||Co@)||e~^ . Следовательно, есть только одно решение C.10а),
удовлетворяющее C.7) , а именно,
^@= / 4>{s)ds- / ^{s)ds. C.12)
Собирая в C.8) члены с е^, получим
'7'1@ = /у(г/о@),го@) + Со@)(У1@) + Ы@) + '?о(^)) +
+ /.(j/o@),2o@) + Co@)(^,@)+^4@) + Ci@)-
-/у(Уо@),го@))(у,@) + Ы@))-
-/z(j/o@),^o@))(^,@)+^za0)), C.13а)
C(@=5y(j/o@).^o@)+Co@)(j/i@)+^@) + '?o@) +
434 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
+ <?.(yo@),^o@) + Co@)Bi@)+^4{0) + Ci{0)-
-</Л^'о@)-^о@))(г/,@)+Ы@))-
-<7.(yo@),^o@))(^i@)+^zi@)). C.13b)
Уравнение C.13b) является линейным дифференциальным
уравнением для Ci (О • Если в нем заменить Ci на О, то невязка этого уравнения
ограничена величиной Се~^. Поэтому, применяя теорему 1.10.6,
получим
IICi(OII<e-4llCi@)li + CO,
откуда следует C.7) при любом /с < 1. Тогда правая часть C.13а)
ограничена величиной С^е"'^^ . Как и в C.12), мы получим
единственное решение уравнения C.13а), удовлетворяющее условию C.7). Эту
процедуру можно продолжить для получения всех дальнейших t)j(^) ,
С (О- На каждом шаге значение к в C.7) может уменьшаться, но
это не представляет серьезную трудность, потому что нас интересует
только конечная часть ряда C.6).
Подчеркнем, что при построении t)j(^)^ С (О ^^i можем выбирать
Cj@) произвольно, но не свободны в выборе rjj@).
В результате при произвольном начальном значении для C.1),
имеющем разложение
z{0) = z° + ez°+e'z° + ..., ^ ' ^
коэффициенты ряда C.6) можно построить следующим образом.
Положив в C.6) X = О, получим нужные соотношения:
Уо@) = Уо°- l/j@) + '?,_i@) = y°, z^.@)+<,.@) = z°. C.15)
Задав начальное значение у^{й) = Уо » найдем Zq{0) с помощью C.4а),
затем найдем Со@) из C.15), г]^{0) из C.12), у^@) из C.15), zjO) из
C.4Ь), Ci@) из C.15), 7/i@) из C.13а) и C.7), у^@) из C.15) и т.д.
Оценка остаточного члена
Приведенный ниже результат дает строгую оценку остаточного
члена в C.6) при обрывании ряда.
Теорема 3.2. Рассмотрим начальную задачу C.1), C.14) и
предположим, что условие C.11) выполнено в некоторой не зависящей от
е окрестности решения у^[х)^ ^q{^) (О < лг < х) приведенной задачи
(уд@) = Уо) • ^с-^и значения (t/o» -^^о) -^^^'^т в этой окрестности, то при
достаточно малых е задача C.1), C.14) имеет единственное решение
VI.3. Эпсилон-разложения для точных и РК-решений 435
при О <х <х, которое имеет вид
N N-1
y(x) = ^e^yj(x)-^e^e^rjj{x/e)-^0(e''^'),
7=0 7=0
ф) = ;^е^г.(х) + ^е%(хА) + 0(е^+М.
j = 0 j=:0
Коэффициенты yj(x), Zj{x), rjj(^), Cj@ определяются формулами
C.4), C.10), C.13) и удовлетворяют условиям C.7).
Доказательство. Обозначим оборванные ряды
Л^ N
j=o j=o
В соответствии с нашим построением функций у,(х), Zj(x), т),{^),
С (О "^ь! имеем:
y'(x) = f{y{x),z(x))+0(e''^'),
ez'(x) = g{y{x),z{x))+0(e''+').
Вычитая C.1) из C.18) и используя условия Липшица для /ид,
получим
D^.||j/(a:)-y(x)||<LJ|y(x)-y(x)|| + L2ll?(x)-z(x)|| + C,e^+i
eD^\\z(x)-z{x)\\<L:,mx)-y{x)\\-\\z(x)-z(x)\\ + C,e
Здесь D^ означает производную Дини, введенную в разд. 1.10. Мы
использовали неравенство D^||ti;(x)|| < ||w;'(x)|| (см. A.10.4)), а для
второго неравенстве C.19) — формулы A.10.17) и C.11).
Чтобы решить неравенства C.19), заменим < на = и при этом
получим
u' = L,u + L,v + C,e''+\ «о = ||у@)-у@)|| = 0E^+М- ,320)
ev' = L,u-v + C,e''^\ t;o =f ||?@)-г@)|| = 0(e^+^).
Эта система является квазимонотонкой. Следовательно (см. упр. 7 в
разд. 1.10),
\\у{х) - у(х)\\ < ti(x), 11%) - z(x)\\ < v(x). C.21)
Преобразовав C.20) к диагональному виду, легко найти
аналитические решения и убедиться, что на компактных интервалах
справедливы оценки и{х) = 0{е^'^^), v{x) = Oie^"^^). Подстановкой этого
результата в C.21) заканчивается доказательство теоремы. П
N+. C19)
где
и внутренние стадии задаются уравнениями
436 Гл.. VI. Сингулярно возмущенные задачи и задачи индекса 1
Разложение решения метода Рунге—Кутты
Теперь, разобравшись в структуре аналитического решения C.1),
обратимся к соответствующему ему численному решению.
Рассмотрим метод Рунге—Кутты
(t;)=(s)-'i:'.(l";)' <"^'
('c)=(ift::l::)) '^^"
сдаются уравнениями
(а)=E)-'|:->(':;)- "->
Если начальные условия произвольны, решение имеет переходную
фазу (описываемую теоремой 3.2), и численный метод в любом
случае должен использовать шаги малой длины 0(e). Поэтому
сосредоточим наше внимание на ситуации, когда переходная фаза пройдена
и метод вышел на гладкое решение с предписанной точностью. Тем
самым мы предполагаем, что начальные значения лежат на гладком
решении (т.е. справедливо разложение C.3)) и что длина шага h
велика по сравнению с е. Нашей ближайшей целью будет получение
?-разложения численного решения. Для этого мы запишем
формальное разложение всех входящих сюда величин в ряд по степеням е с
коэффициентами, не зависящими от е (см. Хайрер, Любих и Рош
1988):
Уп = Уп+^2/^+^'2/п+-> C.25а)
Ущ^Упг-^^Упг^^'Уы-^'-^ C.25Ь)
*n. = *n,+^^ii4-?2/:^, + ... C.25с)
и аналогично для z^ , Z„,-, ?„,•. Ввиду линейности соотношений C.22)
и C.24) мы получим
(l)=(i)-t""(S)
Подставив C.25Ь,с) в C.23) и собрав члены с одинаковыми степенями
е, мы получим:
VI.3. Эпсилон-разложения для точных и РК-решений 437
C.28с)
Поскольку C.23) имеет такой же вид, как и дифференциальное
уравнение C.1), очевидно, что формулы C.28) точно такие же, как и C.4).
Этот факт допускает следующую интересную интерпретацию:
коэффициенты г/2 , 2^ , у\, z\,,., представляют численное решение,
получаемое при применении метода Рунге—Кутты к дифференциально-
алгебраической системе C.4) (метод ^-вложения из ргизд. VI.1). Это
выражается в коммутативности следующей диаграммы:
C.3)
Задача C.1) > ДАУ C.4)
Р/\-
метод РК-
метод
C.29)
C.25)
Вычитая C.25а) из C.3), мы формально получаем
Уп-У{^п) = ^^''{Уп-Уи{^п))^
1/>0
1/>0
Чтобы исследовать эту погрешность, мы рассмотрим в следующем
подразделе сначала разности 2/}( — 2/^(л:„), z^ — z^^{x^). Затем будет
дана строгая оценка остаточного члена в C.29). Изложение следует
работе Хайрера, Любиха и Роша A988).
Сходимость РК-методов
для дифференциально-алгебраических систем
Первые разности г/^—г/о(^п)' ^n^^oi^n) ^ разложениях C.29)
представляют как раз глобальные погрешности метода Рунге-Кутты,
примененного к приведенной системе C.4а). В силу предположения
C.11) она является системой индекса 1. Поэтому нижеследующий
результат непосредственно вытекает из теоремы 1.1.
Теорема 3.3. Рассмотрим метод Рунге—Аутты порядка р
(классического) с обратимой матрицей коэффициентов {a^j), Пусть задача
C.4а) удовлетворяет условию C.11) и начальные значения
согласованы. Тогда
а) если метод является жестко точным (т.е. а^,- = 6, для / = 1,..., 5 j,
то для глобальной погрешности справедливы соотношения
Уп - УоМ = 0{hn, z° - Zo(xJ = Oih"); C.30)
438 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
Ь) если функция устойчивости удовлетворяет условию |Я(оо)| < 1 и
стадийный порядок равен q (q <р), то
Уп-Уо(^п) = ??(/."), r°-Zo(^„) = 0(ft«+M- C.31)
в обоих случаях оценки равномерны при nh< Const. П
Получить оценки вторых разностей t/^ - у^ (х„), z\ — z^ (х„) уже не
так просто, потому что увеличившаяся система C.4а,Ь) с
дифференциальными переменными y^.z^.y^ и алгебраической переменной z^
больше не является системой индекса 1. Как будет ясно из
дальнейшего (см. разд. VII. 1, упр. 5), в действительности это система индекса
2. В принципе, можно воспользоваться результатами, полученными в
разд. VII.4 (теоремы VII.4.5 и VII.4.6). Однако для конкретной
системы C.4а,Ь) возможно более простое доказательство. Его также легче
обобщить на задачи высших индексов C.4а-с).
Теорема 3.4 (Хайрер, Любих и Рош 1988). Рассмотрим метод
Рунге—Кутты порядка р, стадийного порядка q (q < р), с
обратимой матрицей (а, ) и функцией устойчивости, удовлетворяющей
условию |Я(оо)| < 1. Если выполнено условие C.11) и начальные
значения дифференциально-алгебраической системы C.4а-с) согласованы,
то для глобальной погрешности метода C.26)-C.29) при 1< и <q-\-l
справедливы оценки
у"п - у.(^„) = О!/»'-^'-"), < - z,K) = о(Л'+^-'').
Доказательство. Обозначим ргьзности между значениями
численного и точного решения
^Уп = Уп-Уи{^п)' Д< = <-2(,(а;„),
AC = >;Vy.U„+c,/i), AZ;;, = Z^-z,(x„ + c,A). C.32)
A^n,- = Ki - y>n + Cih), Дг-, = ^, - zl(x„ + с,Л).
Поскольку квадратурная формула с узлами с, и весами 6, имеет
порядок р, из C.26) мы получаем
Аналогично, из определения стадийного порядка следует, что
Из теоремы 3.3 вытекает (см. также доказательство теоремы 1.1), что
Ду°=0(ЛР), ДУ„'', = С7(Л'+1), Д*°, = С7(Л'+М,
Az°=0(h''+'), AZ°i = 0{h'>+'), AC = 0(h'').
а) Рассмотрим сначала случай и = I. Заменив в C.28Ь) У„^,, Z°,
на Уо(^п + ^«^) + ^^ni ^ ^oi^n + ^»^) + Д^т и вычтя уравнение C.4Ь),
VI.3. Эпсилон-разложения для точных и РК-решений 439
взятое при X =: х^-\- c^h, с помощью C.35) получим:
А*ы = fy (^п + с^к)^уУ + Л (х„ + с,Л) Д7', +
+ O(h0^' + Л'+Ч|ДУ„\.|| + Л«+1 WAZlW),
АС-= 5у (^п + с,Л)АУ„\ + <;.K +'^.•Л)Д^^.-+
+ 0(Л'+1 + Л'+Ч|ДУ„1,|| + Л'+Ч|Д2Г^,||).
Здесь введены сокращенные обозначения fy(x)=^fy(yQ(x), Zq{x)) и т. п.
Вычислив AZ^^ из второго соотношения C.36) и подставив его в
первое, найдем, что
А*Л.-(Л</;М(х„+с,л)дС =
Используя C.34), мы можем исключить АУ„\' и с помощью C.35)
получить
A/:i.- - (Л<7Г')(^„ + с.Л)Д4 = 0(\\Ay'J) + 0(h''+'). C.37)
Поскольку порядок величины А?^- есть О(Л^), мы имеем лишь
ДАг^^. = 0(||Ду1 II) -|-С?(Л''), и прямая оценка Дг/^ в C.33) привела бы
к соотношению Ду^ = 0(Л^), которое не является оптимальной
оценкой. Поэтому введем новую переменную
Aul, = Ayl,-(f,g:'){x„)Az°. C.38)
Из C.33) получаем
Д«^+1 = Au\ + hJ2bi(Afci, - (f,g:')(xJAO - C.39)
J = l
-((Лi/Г^Ж + Л)-(Л</Г^Ж))Дг°+^+C'(Л''+^).
Оценки C.35), C.37) и тот факт, что Дг/^ = Дг/^ -h С7(Л^"''^), приводят
к неравенству
1|А«и111<A + ^Л)||Д<|| + С?(Л9+2). C.40)
Применяя стандартные приемы, теперь легко показать, что Аи\ =
= 0(h^'^^) при nh < Const (заметьте, что начальные значения
предполагались согласованными, т.е. Auq = 0). Тогда из C.38) и C.35)
вытекает, что и Ду^ = 0(h^'^^), откуда следует ДЛ^, = O(h^) в силу
C,37) и ДУ„\ = 0(Л^+^) в силу C.34). Далее, второе равенство C.36)
показывает, что AZ^^ == O(h^). Чтобы оценить Az^, вычислим Д^^,
из C.34) и результат подставим в C.33). С учетом AZ^^ =:0(h^) это
дает
Дг>+, = A - 6^Л-111)Д4 +0(Л'), C.41)
и ИЗ ТОГО, ЧТО |1— 6^Л"^11| = |Д(оо)| < 1, следует Дг^ =0(Л^). Итак,
для случая 1/=1 теорема доказана.
Ь) Доказательство для общего i/ проводится по индукции. Мы
покажем, что соотношения
440 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
Дг;; = (!?(/1^+^-^), AZ^ = 0(/i^-^^-'^) *
справедливы при i/ = l,...,^-!-!. Основное отличие от случая и =: I
состоит в появлении добавочных неоднородностей v^^^ и ^^ в C.4с).
Используя их Липшиц-непрерывность, получаем в (З.Зб)
дополнительный член порядка (9(/i^"^^~^). В остальном доказательство точно
такое же, как и при и =1, D
Теперь мы обратимся к исследованию вопросов существования и
локальной единственности решения C.22)-C.24), получаемого
методом Рунге—Кутты. Затем мы рассмотрим влияние возмущений
численного решения в C.24). Это окажется важным для оценки
остаточного члена в разложении C.29).
Существование и единственность решения
метода Рунге—Кутты
Когда Л мало по сравнению с е, существование единственного
численного решения, т.е. решения уравнений C.23), C.24),
доказывается стандартным методом последовательных приближений, которые
сходятся к неподвижной точке (см., например, теорему II.7.2). Более
интересен случай, когда длина шага h велика по сравнению с е. В
приводимом ниже доказательстве существования (t/^^j, z^^^) мы
ввели обозначение (ту, Q для (у„, z„), которые предполагаются
известными.
Теорема 3.5 (Хайрер, Любих и Рош 1988). Пусть д{т]Х) = 0{h),
/i(^^ (г;, С)) < — 1 и собственные значения матрицы (а, ) метода Рунге—
Цутты имеют положительную вещественную часть. Тогда
нелинейная система
(Д-4))-|:"'Д^(^::|)) <^")
имеет локально единственное решение при Л < /iq ; ГДе Ло достаточно
мало, но не зависит от €. Для этого решения справедливы оценки
Yi-T, = 0{h), Z,-(: = 0(h). C.44)
Доказательство. Разделим второе уравнение нелинейной системы
C.43) на Л и применим к ней метод Ньютона. Тогда существование и
единственность решения могут быть выведены из теоремы Ньютона—
Канторовича (Канторович и Акилов 1959; Ортега и Рейнболдт 1970)
следующим образом. Для стартовых значений У^- = ^, Z^ =С
матрица Якоби системы имеет вид
(l + 0{h) 0(h) \
\ 0A) (e/h)I-A®9Av,0)- ^^¦^^>
VI.3. Эпсилон-разложения для точных и РК-рсшсний 441
Так как f^ig^dX)) < —1, то из теоремы фон Неймана для матрично-
значных функций (теорема V.7.8) следует, что
||(«/-Л®<?Л'7.С))"'||< max ||(/c/-/i^)-4|. C.46)
Re/i<--l
Правая часть неравенства C.46) ограничена постоянной, которая не
зависит от « > О, потому что мы предположили, что собственные
значения Л имеют положительные вещественные части. Следовательно,
обратная к C.45) матрица тоже равномерно ограничена при € > О и
h<hQ. Вместе с условием д{г]Х) — ^W это означает, что первое
приращение в методе Ньютона имеет порядок величины 0(h).
Следовательно, при достаточно малых Л условия теоремы Ньютона—
Канторовича выполнены. П
Влияние возмущений
Для случая, когда в методе Рунге—Кутты появляются
возмущения
мы имеем следующий результат.
Теорема 3.6 (Хайрер, Любих и Рош 1988). Пусть Yi,Zf
удовлетворяют уравнению C.43), а возмущенные значения У|-, Z, —
уравнению C.47). Пусть выполнены условия теоремы 3.5 и, кроме того,
fj-r] = 0{h), С - С = 0{h), Si = 0A) и $i = 0{h). Тогда при hKh^
m-Y,\\<ci\\fi-r,\\-i.e\\c-<:\\)+hcm\+m\h
\\Zi - Z,\\ < С{\Щ- vll + f НС - Cll) + С(Л||^|| + ii^ii), ^^'"^^
где8={5„...,&,)Т нв=(в„...,в,)Г.
Доказательство. В основу доказательства положена идея
рассмотреть гомотопию
(/i--b)-\|:4^S;tO-(i--<a,)' -'
связывающую систему C.43) при г = 0 с возмущенной системой C.47)
при г=1. Решение У,- и Z, системы C.49) является функцией т.
Если продифференцировать C.49) и разделить ее вторую строку на
h, мы получим дифференциальное уравнение
1, 0{\) M{e/h,Y,Z))\z)-\{elh)l-{^-0 + 6)' ^^•^"'
где ]1=A \)Т ,Y ^{Y„...,Y;iT ^ Z:=(Z„...,Z,)'r и
M{k,Y,Z)-kI-A®I\ . C.51)
442 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
Если ||У^- — rjWKd и ||Z,- — СИ ^ ^ для всех г, то
M{K,Y,Z) = Kl^A^g,(riX)-\-0(d), C.52)
и из C.46) следует, что при достаточно малых d M'^(k,Y,Z)
равномерно ограничена, когда /с > 0. Следовательно, матрица в C.50)
имеет обратную, для которой справедливо равенство
fl-\-0{h) 0[h) y'^(l^O[h) 0{h)\
\ 0(\) M{6/h,Y,Z)J -[ 0A) Oil))'
Тогда оценки C.48) вытекают из того факта, что
9-У= f Y{T)dT, Z-Z= f Z(T)dT. П
Jo Jo
Замечание 3.7. Если предположить только обратимость матрицы
А метода Рунге—Кутты, то результаты теорем 3.5 и 3.6 останутся в
силе при е < Kh^ где К — любая постоянная, меньшая чем
абсолютная величина наименьшего собственного значения А (т.е. Л" < |Aj^jj^|).
При этом правая часть C.48) тоже оказывается ограниченной, и
справедливо то же самое заключение.
Оценка остаточного члена в численном решении
Теперь мы имеем все необходимое для оценки остаточного члена
в C.29). Здесь получен следующий результат.
Теорема 3.8 (Хайрер, Любих и Рош 1988). Рассмотрим жесткую
задачу C.1)J C.11) с начальными значениями у@), г@), допускающими
гладкое решение. Применим к ней метод Рунге—Кутты C.22)-C.24),
имеющий классический порядок р и стадийный порядок q {l<q<p) •
Предположим^ что метод А -устойчив, его функция устойчивости
удовлетворяет условию |Л(оо)| < 1 я что собственные значения матрицы
коэффициентов А имеют положительную вещественную часть. Тогда
при i^<q-\-\ и е <ch, где с > О — любая фиксированная постоянная,
глобальная погрешность удовлетворяет оценкам
z„ - z(x„) = Дг°+eAzi + .. . + е''Дг;:+ 0(е''+7Л).
Здесь Ау°„ = уО- Уо(х„), Az° = zO- Zo(x„), ... (см. формулу C.32))
представляют глобальные погрешности метода при применении его к
системе C.4). Оценки C.53) равномерны при Л < Л^ и nh< Const.
Доказательство. В силу теоремы 3.4 достаточно доказать
результат для J/ = 9 + 1. Введем следующие обозначения для отрезков
рядов C.25):
Уп=Уп+еУ^+ ••• + ?" Уп-
У„, = F„° +еУУ +.. . + е''У„';., C.54)
VI.3. Эпсилон-разложения для точных и РК-решений 443
и аналогично ?„ , Z„,-, ^„,. Далее, обозначим
Aj/n = Уп-Уп' ^Ущ = Ущ - Ущ. А^п,- = ^п. - '^п.. • • C-55)
И используем C.3). Тогда, опираясь на теорему 3.4, легко показать,
что оценки C.53) эквивалентны следующим:
Ду„ = 0(е''+М, Az„ = 0{6^'+'/h). C.56)
a) Оценим сначала разности АУ„,, Д^„, внутренних стадий. Для
этого исследуем невязку, получающуюся при подстановке C.54) в
C.23). С помощью нашей конструкции C.28), учитывая C.42) при
i/ = 7 -h 1, получаем
^ ^ ^ (о.ОП
Из C.42) и C.27) мы знаем, что ^j;, = 0(/i-i). Тогда из C.27) следует
равенство
имеющее такой же вид, как C.47), и применение к нему теоремы 3.6
дает
1|АП.,|| < С(||Ду„|| +е||Д2„||) + 0(e^'+'),
\\AZJ[ < C(\\AyJ + ^||Дг„||) + 0(е''+7Л) ^^'^^^
при условии, что Ду„ и Az^ имеют порядок величины 0{h). Мы
дадим обоснование этого в части (с) доказательства.
b) Наша следующая цель — доказать рекурсию
(W^Vn+iW) ^(l + 0(h) 0(е) \(\\Ау„\\\ ( OCe^+i) ^
C.60)
где мы опять предполагаем, что Ду„ и Дг„ имеют величину 0{h).
Значение а < 1 будет определено ниже, в формуле C.63). Верхнее
соотношение C.60) получается из
Ду„^1 =Ду„ + Л^6,(/(У„,,7„,)-/(У„,,7„,)) +0(he^^+')
f = l
С использованием C.59) и условия Липшица для /.
Для того, чтобы доказать второе соотношение в C.60), вычтем
C.57) из C.23) и используем C.59) и C.42). Мы получим
?Д?„, = д,(XJAZ,, 4- 0(||АУ.,|| + Л||А^,,||) + 0{e^^'/h). C.61)
Здесь мы обозначили ^^(х) =5'г(%(^)'^о(^))* Подставляя в это
соотношение AZ„,. = Аг„ -^-h^a^jAl^j и используя снова C.59), получим
eAe„,-hJ2%9A'=.W.j = 9AxJAz,+0{\\AyJ+e\\AzJ)+0{e''+'/h).
444 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
Разрешив это уравнение относительно ЛА^„,, подставим результат в
Аг„^1 = Аг„4-/lE^-^^nz- (В силу C.46) матрица {s/h)I - A^g^(xJ
имеет ограниченную обратную.) Это дает
Az„^, = R{^эAxJ)Az, + 0{\\AyJ + e\\Az„\\) + 0{e^'+'/h), C.62)
где R(fi) — функция устойчивости метода. Благодаря условию C.11)
можно применить теорему фон Неймана (следствие IV. 11.4), что дает
оценку
||л( J дЛ^п)) II < s^p {|fi(/i)| ; Re/i < ^h/e} < a < 1. C.63)
Значение a строго меньше единицы, потому что |Я(оо)| < 1 и -h/e <
< —1/с < 0. Доказательство формулы C.60) заканчивается
применением неравенства треугольника к C.62).
c) Применение доказанной ниже леммы 3.9 к разностному
неравенству C.60) дает
Ду„ = 0(е''+7й)- Дг„ = Ole-'+Vft) C.64)
при nh < Const. Мы теперь можем обосновать сделанное в начале
доказательства предположение о том, что Дг/„ = 0(h) и Az^ = 0{/i),
воспользовавшись индукцией по п (AyQ = 0(e'^'^^), AzQ = 0{e'^'^^)) и
оценками C.64), потому что г/ = g-Н 1 > 2.
d) Формула C.64) доказывает желаемый результат C.56) для z-
компоненты. Однако оценка C.64) еще не оптимальна для ^/-компо-
ненты. Доказательство для корректной оценки аналогично
доказательству теоремы 3.4. Надо только более аккуратно работать с
выражением, которое порождает член 0(€^'^^/h) в C.61). С
использованием C.59) и C.64) такие же вычисления, что привели к C.61), теперь
дают
Afc„, = /, (xj ДУ„, + Л (rj Д^„, + 0(e^'¦''), C.65а)
eAe„,=g^ix„)AY„,-^-g,(x„)AZ„,+e^'+'er + 0{e^'+'). {3.65b)
Вычислим AZ^i из C.65а) и подставим в C.65Ь). Это даст
А<:„,-(Л5;^Ж)(еДг„,-?''+'С) =
= (/„-Л^/Г'5„Ж)АУ„. + С7(?''+М-
Руководствуясь этой формулой, положим
Д«„ = Ду„ - (Л5;МЮ(еДг„ -?"+><). C.67)
Поскольку
А«п+, = А«„ + ЛЕб,(Д^„.-(Л<7Г')(а:„)(?Д^„,-е''+'С))-
1=1
-((Л5;М(х„ + Л)-(Л5Г^Ж))Мг„+,-?''^^<+1)-
то из C.66), C.64) и C.42) следует, что
\\Au,^,\\<{l+ch)\\AuJ + 0(he''^'). C.68)
C.66)
VI.3. Эпсилон-разложения для точных и РК-решений 445
Отсюда, как и в доказательстве теоремы 3.4, мы выводим оценки
Дг/^ = С7(?^+1) и А2/„ = 0E*^+1). D
В приведенном выше доказательстве использована следующая
Лемма 3.9. Пусть {и^} , {v^} —две последовательности
неотрицательных чисел, покомпонентно удовлетворяющие неравенству
(:::;)^('^.й" „.%)(::)-"(?). <->
где 0<а<1 и М >0. Тогда при е <ch, h < h^ и nh < Const
справедливы следующие оценки:
Доказательство. Приведем матрицу в C.69) к диагональному
виду. Тогда получим
;")^-'(^" д)К;")-'|:-'(Т л^Ж?)'
где Ai=:H-0(/i), \2 = oi-]-0(e) — ее собственные значения, а матрица
преобразования Т, составленная из собственных векторов, имеет вид
._/ 1 0{е)\
~\0{1) 1 )¦
Теперь справедливость утверждения леммы при е <ch и nh < Const
следует из того, что (а + 0(е))^ = С?(а") + 0(e). П
Комбинируя теоремы 3.3, 3.4 и 3.8, мы получим такой результат:
Следствие 3.10 (Хайpep, Любих и Рош 1988). В предположениях
теоремы 3.8 для глобальной погрешности метода Рунге—Кутты
справедливы следующие оценки:
у„-у(а;„) = 0(Л'-) + (?(еЛ«+М, z„ - г{х„) = 0(Л'+1)- C.71)
Если, кроме того, а,,- = 6^ для всех г, то
z^-z{x„) = 0{h'>) + Oieh''). C.72)
Замечания, а) Если предполагать только обратимость матрицы
коэффициентов Л, отказавшись от требования Л-устойчивости, то
оценки из следствия 4.10 остаются в силе при в < Kh^ где /\ —
постоянная, зависящая от метода (см. замечание 3.7).
b) Если предполагается Л-устойчивость метода и обратимость
матрицы А, то отсюда следует, вообще говоря, положительность
вещественных частей собственных значений А. Иначе функция
устойчивости оказалась бы приводимой.
c) Для некоторых методов Рунге—Кутты, удовлетворяющих
условию а„. = 6,, оценка C.71) для у-компоненты может быть улучшена.
Например, для методов Радо ПА и Лобатто IIIC имеем у^ — у(х„) =
= O(h^) -f- C?(?^/i^). Это следует из табл. VII.4.1 (см. ниже).
d) Нипп и Штоффер A995) дали совершенно иное доказательство
оценок C.71). Они показали, что метод Рунге—Кутты, рассматрива-
446 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
емый как дискретная динамическая система, допускает
притягивающее инвариантное многообразие Мд ^, которое близко к
инвариантному многообразию М^ задачи C.1). Исследуя близость этих двух
многообразий, они получили оценки погрешностей C.71), не
рассматривая ?-разложения.
e) Для методов Розенброка аналоги теоремы 3.8 и следствия 3.10
можно найти в работе (Хайрер, Любих и Рош 1989).
f) Оценки для случая p = q даны ниже, в упражнении 3.
Численное подтверлсдение
Оценки из следствия 3.10 можно наблюдать в численных расчетах.
В качестве примера задачи C.1) возьмем уравнение Ван-дер-Пол я
y' = z,
ez' = {l-y^)z-y
при 6 = 10"^ и с начальными значениями
t/@) = 2, z{Q) = -0.6666654321121172 , C.74)
лежащими на гладком решении (см. упр. 2).
В табл. 3.1 приведены использованные в нашем численном
эксперименте методы вместе с теоретическими оценками их
погрешностей. На рис. 3.1 показаны относительные глобальные погрешности
при х^^^= 0.5 как функции длины шага Л, которая бралась
постоянной на всем интервале интегрирования. Благодаря использованию
логарифмических шкал по обеим осям кривые представляются в виде
прямых линий с наклоном г, когда поведение главного члена
глобальной погрешности подобно Const • Л**. Графики находятся в полном
согласии с нашими теоретическими результатами.
C.73)
Таблицд 3.1. Глобальные погрешности согласно следствию 3.10
Метод
Радо IA
Радо И А
Лобатто II 1С
ОДНРК (IV.6.16)
ОДНРК (IV.6.18)
Osi = bi
нет
да
да
да
нет
у-компонента
h^'-^-^-eh'
/,25-1 ^^2;,5
^2s-2^^2^s^l
hUeh"
h^-^eh^
г-компонента
h'
h^'-^+eh'
h^'-^+eh'-^
h'^ + eh
/.2
Возмущение начальных значений
При интегрировании сингулярно возмущенной задачи численное
решение аппроксимирует гладкое решение лишь с точностью до
заданной величины Tol. Поэтому представляет интерес исследовать
VI.3. Эпсилон-разложения для точных и РК-решений 447
h '"" 'О
Лобатто IIIC
10-2 10-
Л5
10-»2
грешность
h '"^ ">"'
^л^"*^
'Л^
1 . .....п1 . . ....
10-2 10-1
>/^10-5
vcr^ V%io-^
//^^jf 10-'
х/еЛ^
^ 10-12
погрешность
-
-
-
~
' I ¦ ii'iil . I 1 iiiitl i I I mill t I I mill I I I III
О метод (IV.6.18)
^ метод (IV.6.16)
io-'2
погрешность
1 1 1 1
h
a
.....1 . .
10-»
^
10-' 10-2 [0-1
^.O^^ 10-'
3^^ у
,--<S-<-^ '""^
^'^'^^eh^ 10^
io-»2
погрешность
-
-
_
у-компонента 2-компонента
Рис. 3.1. Глобальная погрешность как функция длины шага.
448 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
влияние возмущений в начальных значениях на глобальную и
локальную погрешности метода. Начнем с численного эксперимента.
Применим методы Радо ПА к задаче C.73), внеся в начальное
значение C.74) для z@) возмущение величиной в 10"^. Для глобальной
погрешности при з:^„^ = 0.5 получаются в точности те же
результаты, что и на рис. 3.1. Это показывает, что возмущение полностью
затухает на отрезке интегрирования. Но локальная погрешность
ведет себя иначе. Результаты расчетов представлены на рис. 3.2. Мы
видим здесь присутствие «горба», как на рисунках IV.7.4 и IV.8.2.
1 /j 10^ 10-5
Радо ПА
О «^=1
\^ ^ = 2
П ^ = 3
10^
.....J .
10-3
......1 J ...... 1
10-2 10-1 |_
r^fl"^ ^^и
у р
j/ /°"Т
-погпюшность и
1 /j 10-* 10-5
10^ 10-3 10-2 I0-»
г/^ 1^'^
^*^^??^*^^9Ц|^^
10-'2
погрешность
-
_'
-
:
Рис. 3.2. Локальная погрешность методов Радо ПА
(начальное значение возмущено).
Выясним причину этого явления. Обозначим (Уо?^о)
рассматриваемые начальные значения и (Ух^г^) численное решение после одного
шага длины Л. Точное решение у(х), z(x), проходящее через {у^, Zq) ,
будет иметь пограничный слой и (при соответствующих
предположениях, см. теорему 3.2) может быть записано в виде
^ у{х) = у(х)-^0(ее-'^'), г(х) = г(х)+ 0(е~^/^). C.75)
Здесь у{х), z{x) представляют гладкое решение задачи C.1).
Обозначим Уо = У@) J ^0 = ^(О) начальные значения, лежащие на этом
гладком решении, и (Ух^г^) численное решение, полученное тем же
методом с длиной шага h и начальными значениями (Уо'^о)- Тогда
локальную погрешность можно записать в виде
Z, - z{h) = (z,-z,) + (zi - z{h)) + (?(Л) - 2(Л)) C.76)
И аналогично для у-компоненты. Последним членом в C.76),
имеющим порядок величины 0(То/ •е~'*/^), можно пренебречь, если длина
шага Л значительно больше, чем е. Член z^ —z{h) представляет
локальную погрешность в «гладкой» ситуации и ограничен, по меньшей
мере, величиной порядка 0(Л^"^^) (можно применить следствие 3.10
с п = 1). Этот член проявляется на рис. 3.2 всякий раз, когда
величина Л или погрешность велики. Разность z^—z^ — это тот член,
который отвечает за нерегулярности на рис. 3.2. Используя теорему
3.6 (положив при этом E = 0, ^ = 0, fj-rj = 0(e' Tol), Q-(i = 0(Tol)) и
VI.3. Эпсилон-разложения для точных и РК-решений 449
идеи доказательства теоремы 3.8 (в частности, уравнение C.62)), мы
получим
z,-z, = R[f^9,@)){z,-z,) + O{e-Tol), ^^^^^
у,-у, = 0{еТо1).
При е < Л можно написать разложение
R{f^gA0))=R{oo) + C^9;'@) + o{{ff). C.78)
Следовательно, если Я(оо) ^^ О, то в локальной погрешности
должно проявиться не зависящее от h выражение Я(оо)B:о — ?о) = 0{То1).
Для методов с Я(оо) = О (таких, как Радо ПА) в члене z^ — z^
доминирующей частью будет C(€/h)gT^{0){zQ — Zq) = 0( Tol • e/h). Этот
член проявляется на рис. 3.2 как прямая линия с наклоном —1.
Таким образом, при уменьшении h в этом диапазоне локальная
погрешность растет как Л"^. Аналогичное возмущение, но умноженное на
6, наблюдается и для у-компоненты.
Однако описанное явление не следует считать серьезным
недостатком метода: оно сказывается лишь при тех длинах шага, когда
локальная погрешность меньше заданной допустимой погрешности Tol.
Упралснения
1. Докажите, что утверждение теоремы 3.2 останется справедливым,
если предположение C.11) заменить на следующее:
собственные значения А матрицы д^ (t/, z)
удовлетворяют условию Re Л < -1
для всех у, z в некоторой окрестности решения Уо{х)у Zq(x)
приведенной системы.
Указание. Разбейте их^тервал на конечное число малых
интервалов и для каждого из них постройте скалярное произведение и
соответствующую норму так, чтобы после перенормировки е
выполнялось неравенство C.11) (см. Неванлинна 1976).
2. Для уравнения Ван-дер-Поля C.73) при у@) = 2 найдите
соответствующее значение z{0) такое, чтобы решение было гладким.
Ответ,
2 10 292 2 1814 3 ^, 4ч
z@) = h —е е^ e^-^-Oie^).
^ ^ 3 81 2187 19683 ^ ^
3. Если в следствии 3.10 отказаться от предположения q < р (где р
— классический порядок, q — стадийный порядок), оценки
Уп-УМ = 0{кП, z,-z(x„) = 0(hn
останутся справедливыми. Докажите это утверждение.
Типичными примерами являются неявный метод Эйлера и ОНРК-метод из
леммы IV.8.1, для которых р= д.
Указание. Примените следствие 3.10 с q, уменьшенным на 1.
VI.4. Методы Розенброка
Этот раздел посвящен распространению методов Розенброка (см,
разд. IV.7) на дифференциально-алгебраические уравнения в
полуявной форме
2/' = /(у,^), 2/Ю = %' D.1а)
0 = 9(y^z), z(x^) = z^. D.1b)
Мы будем предполагать, что матрица д^ обратима (см. A7)), так
что задача имеет индекс 1. Для численного решения таких задач мы
получим новые методы и в то же время лучше разберемся в поведении
методов Розенброка для жестких дифференциальных уравнений. В
частности, получит объяснение явление, показанное на рис. IV.7.4.
Определение метода
Главное преимущество методов Розенброка перед неявными
методами Рунге—Кутты состоит в том, что нелинейные системы здесь не
возникают. Это преимущество утрачивается при использовании
метода пространства состояний, в котором D.1) преобразуется к виду
у' = /(у, G{y)). Это еще один аргумент в пользу рассмотрения метода
е-вложения. Для задачи A.5) метод Розенброка принимает вид
(?;)=КДГ^))^КЛ Л>'ф'0:)'
(:0=(^:)#^(';)' (^;)=(^:)ф(^)- '"^'
Если умножить вторую строку в D.2) на е и затем положить ? = О,
мы получим
(«0=К.'Й:;'0-К»: ;;)«»..ф,(';)- («ь.
Формулы D.3а) и D.3b) вместе и составляют распространение метода
Розенброка на задачу D.1). Впервые метод этого типа рассмотрел
Микельсен A976), работу которого цитируют Фенг, Холланд и Галлун
A984). Дальнейшие исследования проводил Рош A988). Заметим,
что вычисление (^,,^,) из D.3b) требует решения линейной системы
с матрицей
Л-74 -7Л/Л ,4 4)
где все производные вычисляются при (Уо^-^^о)- Если д^ неособенная
матрица, 7 отлично от нуля и Л > О достаточно мало, то матрица D.4)
обратима, в чем легко убедиться, разделив ее нижние блоки на 7^ и
положив затем /i = О.
VI.4. Методы Розенброка 451
Неавтономные уравнения. Если функции / и д в D.1) зависят
также от х, мы заменим D.3b) на
D.5)
(сравните с (IV.7.4а) и вспомните определение а,- и 7,- в (IV.7.5)). Все
производные вычисляются при начальных значениях (лтд, Уо»-^^о)-
Задачи вида Ми' = (р{и). Для случая регулярной М формулы
Розенброка для таких задач были получены в разд. IV.7 (формула
(IV.7.4b)). Эта формула применима также и для сингулярных М, что
можно объяснить следующим образом. Теоретически возможно
применить преобразование A.20), так что М станет блочно-диагональной
матрицей с блоками / и 0. Тогда метод (IV.7.4b) идентичен методу
D.3). Поэтому теория, которая будет развита в этом разделе, будет
верна и для метода Розенброка (IV.7.4b) при применении его к
задачам индекса 1, имеющим вид Ми' = (р{и).
Введя новый класс методов, мы должны изучить их условия
порядка. Как обычно, это делается с помощью разложений Тейлора
точного и численного решений (как в разд. П.2). При этом
получается хорошее соответствие между условиями порядка и определенными
корневыми деревьями с вершинами двух сортов (Рош 1988).
Производные точного решения
В отличие от разд. П.2, где мы использовали целые «орды
индексов» (см. предисловие Дьедонне к его «Основам современного
анализа»), чтобы указать путь через «woud met bomen»^ (выражение
Хундсдорфера), здесь мы будем записывать производные высших
порядков как полилинейные отображения. Например, выражение
2_] ^—-^— UjVf^ будет записываться как ^y^(w, v).
Это упростит последующие формулы.
Продифференцируем D.lb), что дает О = Qy у* -{-д^ • z', или, что
эквивалентно,
^' = i-9:')9yf. D.6)
Теперь будем последовательно дифференцировать D.1а) и D.6) по х,
используя при этом формулу
которая вытекает из равенства {А~^(х)У = —А~'^(х)А'{х)А^^{х) и
цепного правила. Это дает
у" = 4 • 2/' + л • г' = /,/ + л (-97 ^ )9yf, D.8)
«лес с деревьями». — Голл.
452 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
+{-97'){9yy{f,f)+9yAf,i-97')9yf) + D.9)
+{-97')9y{fyf + fA-97%f)-
Ясно, что такого рода выражения быстро становятся очень сложными,
так что желательно графическое представление членов в D.8) и D.9).
Деревья и элементарные дифференциалы
Мы будем отождествлять каждое вхождение / с «тонкой»
вершиной (точкой) и каждое дифференцирование / с выходящим из этой
вершины вверх ребром. Выражение {—д7^)д будет
отождествляться с «толстой» вершиной (кружком). Производные д в таком
выражении тоже будут указываться выходящими вверх ребрами.
Например, второй член в D.8) и первый член в D.9) соответствуют
деревьям, показанным на рис. 4.1. Тогда приведенные выше формулы для
у', -г:', у", 2:" примут вид:
Первый и четвертый члены в D.9) тождественны, потому что
dzyi^i'^) ^ 9уг{^^^)- ^'^^ хорошо согласуется с тем фактом, что
соответствующие деревья топологически эквивалентны. Самая нижняя
вершина дерева называется его корнем.
Мы видим, что производные у характеризуются деревьями с
корнем-точкой. Эти деревья будут обозначаться t или t^. Дерево,
состоящее только из корня (для у'), обозначим т^. Производные z имеют
деревья с корнем-круэюком. Они будут обозначаться и или w,, а
дерево для г' обозначим т^.
[-97^)9у {-97^)ду(/ Pf
{-9г^)9гу
Рис. 4.1. Представление элементарных дифферешщалов графами.
Определение 4.1. Будем обозначать DAT = DATyUDAT^
множество (дифференциально-алгебраических корневых) деревьев, которые
определим рекурсивно:
VI.4. Методы Розенброка 453
a) T^eDAT^, T^eDAT,]
b) [<i,...,<^,t/,,...uJj,G^r ,
если t^,...,t^eDATy и u^,.. ,u^e DAT,]
c) [<,,...,<^,ti„...,t/J,G^T,,
если<1,...,<^еШГ^,, u^,...,u^?DAT, и (m,n) ^«^ @,1).
Здесь [<i,...,<^,t/i,...,ujj^ и [<i,...,<^,Wi,...,wJ^ обозначают
неупорядоченные наборы из (т-\-п) деревьев.
Графическое представление этих деревьев таково: если мы
соединим m-hп ребрами корни деревьев ^^,...,<^, и^^.. ,,и^ с новой верь
шиной (новым корнем), мы получим дерево [<i, •. •,<,7i, ^i? • •»^Jy'
если новая вершина — точка, и дерево [<i, •. •, <у„ , t/j^,..., w„]^, если
новая вершина — кружок. Например, запись двух деревьев,
изображенных на рис. 4.1, выглядит так: [т,]^ и [т*^, t-J^ .
Опрс^деленне 4.2. Порядком дерева t G DAT у или и G DAT^,
(который будем обозначать p[t) или р[и) соответственно) будем называть
число его вершин-точек.
На примере D.10) видно, что это определение порядка совпадает с
порядком производных 2/(») и г(*) (по крайней мере, для производных,
представленных в D.10)).
Теперь дадим рекурсивное определение взаимно однозначного
соответствия между деревьями в D.10) и членами выражений D.8)
и D.9).
Определение 4.3. Элементарные дифференциалы F[i) (или F(u)),
соответствующие деревьям из DAT, определяются следующим
образом:
а) F{ry) = f, F{T,)^{^97')9yf.
^^ ^W = ^^ И^1)--"^(^-)' F(tx,),...,F(uj),
если < = [ti,...,<^, u^,...,u^]yeDATy,
с) F[u) = (-^J-i ^^ (f(<,), ..., F(tJ, F(tx J,..., F{uj) ,
если u=[t^,...,t^, «1>-)^п]г eDAT,.
Вследствие симметрии частных производных на это определение
не влияют перестановки ^^,..., <^ , w^,..., г/„, поэтому функции F{t)
и F{u) полностью определены.
Разлолсение Тейлора для точного решения
Чтобы глубже разобраться в процессе, началом которого являются
формулы D.8) и D.9), рассмотрим дифференцирование
элементарного дифференциала по х. В соответствии с правилом Лейбница
дифференцирование F{t) (или F{u)) дает сумму новых элементарных
454 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
дифференциалов, которая получается согласно следующим четырем
правилам:
i) к каждой вершине присоединяем ребро с Ту на конце
(дифференцирование / или ^ по у и добавление множителя у' = f)\
ii) к каждой вершине присоединяем ребро с т^ на конце
(дифференцирование / или д по Z vi. добавление множителя г'= [-'g7^)9yf)\
iii) каждую вершину-кружок расщепляем на две вершины-кружка
(соединенные новым ребром) и к нижней из них присоединяем ребро
с Ту на конце;
iv) как и в предыдущем правиле, каждую вершину-кружок
расщепляем на две вершины-кружка, но на этот раз к нижней из них
присоединяем ребро с т^ на конце.
Правила C) и D) соответствуют дифференцированию {—дТ^) и
получаются непосредственно из D.7). Мы видим, что
дифференцирование дерева порядка q (точнее, соответствующего ему элементарного
дифференциала) порождает деревья порядка q-\-\.
Как и в разд. II.3, некоторые из этих деревьев появляются в
производной несколько раз (например, первое и четвертое дерево для z"
в D.10)). Чтобы различать эти деревья, мы будем указывать
порядок генерации вершин-точек метками, как показано на рис. 4.2 для
первых трех производных у. Поскольку в описанном выше процессе
дифференцирования новая вершина-точка всегда является конечной
вершиной дерева, возникающие таким образом метки обязательно
возрастают от корня вверх вдоль каждого ребра.
3 .3
Рис. 4.2. Монотонно помеченные деревья (LDATy ).
Определение 4.4. Любое дерево t G DAT у (или и G DAT^), у
которого все вершины-точки имеют монотонно возрастающие снизу вверх
метки, называется монотонно помеченным деревом. Множества всех
таких монотонно помеченных деревьев обозначаются LDAT , LDAT^
и LDAT.
На монотонно помеченные деревья естественным образом
распространяются определения 4.2 (порядка дерева) и 4.3 (элементарного
дифференциала). Поэтому производные точного решения можно
записать следующим образом:
VI.4. Методы Розенброка 455
Теорема 4.5 (Рош 1988). Для производных точного решения DJ)
справедливы формулы:
У^'^Ю= Е F(<)(yo.Zo)= Y1 o{t)Fit)(yo,Zo),
t^LDATy,p{t)=zq teDATy,p{t)=q
^"Н^о)= E F(u)(y„z,)= E o{u)F{u)iyo,Zo),
ueLDAT^,p{u)=q и?ПАТг,р{и)=д
где целые коэффициенты a{t) и а [и) указывают число различных
возможных монотонных разметок данного дерева.
Доказательство. При д= 1 и q = 2 это как раз формулы D.1а),
D.6), D.8) и D.9). При произвольном q описанный выше процесс
дифференцирования деревьев порождает все элементы LDAT, каждый
элемент один и только один раз. Если берется сумма по DAT и
DAT2, надо добавить множители a[i) и а(и). П
Разлолсение Тейлора для численного решения
Нашей следующей целью будет доказательство аналога теоремы
4.5 для численного решения, даваемого методом Розенброка. Будем
рассматривать у^, г^ как функции длины шага к и вычислим их
производные. Из D.3а) следует, что
г/1''@) = Y.^ikf\% 4"@) = ЕМ1'^@)- D11)
Теперь надо вычислить производные к^ и i^. Это делается так же,
как для методов Рунге—Кутты (разд. II.2) или для методов
Розенброка в применении к обыкновенным дифференциальным уравнениям
(разд.1У.7).
Продифференцируем первую строку D.3b) по Л. С
использованием правила Лейбница (П.2.4) при Л = О это дает
^l'^=-/(/K--,))"-^>+(/,)o9E7o-*r^4(/jo</E7.i^i'"'^-
D.12)
Индекс О в (/у)о и (Д)о указывает, что производные вычисляются
при (Уо'^о)- Вторую строку D.3b) перед дифференцированием
разделим на Л. В результате получим (опять при Л = 0)
Производные f ^л д можно вычислить по формуле Фаа ди Бруно (лем-
456 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
ма II.2.8). Это дает
(Ль.t^.))'-"^=Е''"У;Г^ (-!"'¦ -^'"'''^'''¦¦¦'-1"') •
D.14)
где сумма взята по всем «специальным» деревьям LDATy порядка q.
Это монотонно помеченные деревья [<^,...,<^, и^,..., и^ , не
имеющие разветвлений, причем все их вершины — «тонкие» (т.е. вершины-
точки), за исключением корневых вершин у w^,..., w„. Целые числа
//^ и и2 — это порядки / и Wj соответственно. Они удовлетворяют
равенству ^^-\-,. ,-\-^^-^-i/^-^-.. .-\-i/^^q — \. Аналогично применяется
формула Фаа ди Бруно и к ^, что дает
(»(«..».))'"=Е '"У;;;""' с."" "-'. «-1-' «-l-')+
+S,(>'|."¦,)'»!'', (-lis)
где сумма взята по всем «специальным» деревьям LDAT^ порядка q.
Эти деревья определяются как и выше, но теперь все их вершины —
«толстые» (т.е. вершины-кружки). Целые числа//^, г/^
удовлетворяют равенству /ij -h • • • -f //^ -f i^i 4-... Ч- ^'^ = д'. Член с д^ выписан
отдельно, потому что [wj^ не является допустимым деревом (согласно
определению LDAT^).
Теперь мы можем вычислить производные к^ и ^,. Для этого
удобно ввести обозначения
/?0=%+^.i D.16)
(полагая а,-,- = 0), как в (IV.7.12). Нам понадобится также матрица,
обратная к (/?,^.), элементы которой мы обозначим и^^:
Di) = (Ai)-'- D.17)
Теорема 4.6. Производные Аг, я ^, даются формулами
t?LDATy,p{t)=q
, V - D.1о)
А^'^@)= Е 7(«)*,(«)F(«)(j/o,Zo),
u6L?)i4T,,p(ti)=g
где коэффициенты Ф,@ и Ф,(г/) имеют следующий вид: ^{(Ту) = 1,
VI.4. Методы Розенброка 457
Ф,(г,) = 1 и
для < = [<J ,...,<„, Up ..., «„)j, и m + п > 2
^%Ф,.(<1) для < = [<,]„,
Zl%*^j("i) Дляt = [u^]y,
. J
Ф.(<)=<
J,A»b ^/im.i^l,. ,i^n
для« = [tl,...,^^,Ul,...,wJ^ ит + п>2 ,
l^.(<i) для w = [<i], ,
a целые коэффициенты j^t) и 7(u) определены следующим образом;
7(т-у)=1. 7G-z) = l и
7(<) = p@7(<i) • • -litmhi^i) ¦ ¦ -ТЮ Д-^я < = [<1, ...,<„,«!,..., w„]j^,
7(u) = 7(<i) • • llitm) 7(«i) • • • 7Ю для « = [<i,...,<^, «1,..., uj,.
Доказательство. Из D.3a) имеем
Подставим D.19) в D.14), a затем получившуюся для (/(^,-,гу,.))(9~0
формулу — в D.12). Это дает
m+n>2 ^^ ''^ Ъ=1 i=l ^
D.20)
(все выражения должны вычисляться при Л = 0). Такие же выкладки
для второй компоненты D.3b) приводят к уравнению
0^ у- ^'"•^"р(Уо.го) '•"'
m+n>2
dy'^dz''
(Ёv^^•••.Ёv^^•••) +
D.21)
458 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
Суммы в D.20) и D.21) взяты по элементам LDAT точно так же, как
в D.14) и D.15). Из уравнения D.21) можно извлечь ij^\ используя
матрицу, обратную к (/?, ). Это дает
j = l т-\-п>2 ^ ^к = 1 к = 1 ^
+ ((-5Г^Mу)о*.-"- D-22)
Теперь формулы D.18) доказываются с помощью индукции по q. При
^ = 1 они следуют непосредственно из D.12) и D.13). Для
произвольного q мы подставляем индуктивное предположение в D.20) и D.22),
используем полилинейность производных и изменяем порядок
суммирования, как в доказательстве теоремы П.2Л1. П
Теперь производные численного решения окончательно
определены формулами D.11):
Теорема 4.7 (Рош 1988). Д,ля производных численного решения
D.3) справедливы формулы
teLDATy,p{t)=q « = 1
ueLDAT,,p{u)=q t = l
где коэффициенты 7 и Ф, определяются теоремой 4.6. П
Условия порядка
Сопоставляя теоремы 4.5 и 4.7, получаем:
Теорема 4.8. Для метода Розенброка D.3) имеем:
y(xQ -\- h) — у^= 0(/i^"'"^) тогда и только тогда, когда
Y1 ^•^«(^) = "т лля te DAT у при р[г) < р;
1=1
7(<)
z(xq-\- h) — z^ = 0(h^'^^) тогда и только тогда, когда
' 1
У^б^ФДц) = -г— ДЛЯ ueDAT^ при p(u)<q.
» = 1 Д /
Здесь коэффициенты Ф, и 7 определяются теоремой 4.6. П
Повторное применение индуктивного определения Ф, из теоремы
4.6 приводит к следующему алгоритму.
VI.4. Методы Розенброка 459
Составление условия порядка для заданного дерева: приписываем
каждой вершине-точке один индекс суммирования и каждой вершине-
кружку два индекса (один над другим). Тогда левая часть условия
порядка будет суммой по всем индексам, составленной из
произведений следующих множителей:
6,, если г — индекс корня (нижний индекс,
если корень — кружок);
а, , если j расположен непосредственно над г,
причем из i выходит более одного ребра;
/?• , если j расположен непосредственно над i
и из i выходит только одно ребро;
о;, , если i,j — два индекса вершины-кружка (г под j).
Рис. 4.3. Деревья с помеченными вершршами.
В качестве примера приведем условия порядка для первых двух
деревьев на рис. 4.3:
Е ^>i^ij'^ik^^lcAm = l, D.23)
J2 ^i'^ij^jk°'jt'^tm<^mn<^mp=^- D-24)
Условие D.23) можно еще упростить, воспользовавшись тем, что (^ij)
является матрицей, обратной к (/?,j). Действительно, D.23)
эквивалентно уравнению
которое является условием порядка для третьего дерева на рис. 4.3.
Используя такое упрощение систематически, мы придем к
следующему результату:
Лемма 4.9. Для метода Розенброка D.3) излишними являются
условия порядка^ соответствующие одной из следующих ситуаций:
a) из вершины-кружка исходит одно ребро,
b) из вершины исходит одно ребро, соединяющее ее с вершиной-
кружком. П
460
Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
Подмножество DAT , которое состоит из деревьев, имеющих
только вершины-точки, представляет собой просто Т — множество
деревьев из разд. П.2. Соответствующие условия порядка приведены в
разд. IV.7. Следовательно, метод Розенброка порядка р должен
удовлетворять всем «классическим» условиям порядка и, кроме того,
некоторому числу «алгебраических» условий. Первые из этих
новых условий порядка приведены в таблице 4.1. В последнем столбце
приведены многочлены рДт)? представляющие правые части условий
порядка при записи их в виде (IV.T.ir).
Таблица 4.1. Деревья и элементарные дифференциалы
Pit)
4
2
3
3
3
t
*45
ti21
1
ti32
3
граф
</
V
¦у
7@
4
1
1
2
1
фJ{t)
Y2 OijkOijt^emOimnOcmp
J^f^jkOikiOikm
Y^UfjkQklO^kmOikn
Yl f^jkOiktOlkm^mnCXnpOinq
ptb)
1/4
1
1
1/2-7
1
Сходимость
Прежде чем перейти к собственно построению нового метода
Розенброка, надо исследовать еще его свойства сходимости. Мы
воспользуемся при этом равенством
Л(оо) = 1 -6^5-^1= 1 -^6,0;,.^., D.25)
«J
где R{z) —функция устойчивости (IV.7.14).
Для локальной погрешности метода Розенброка D.3) введем
обозначения
^УыИ = У1 - У{^ + Л), Szf^ix) = zi - z(x Н- Л). D.26)
Здесь 2/1,^1 — численное решение, полученное с точными начальными
значениями t/q = У(^) > ^о = ^{^) •
Теорема 4.10. Пусть матрица д^ регулярна в некоторой
окрестности решения {у{х), г{х)) задачи D.1) и начальные значения (t/Q, z^)
согласованы. Если функция устойчивости такова, что |Л(оо)| < 1, я
локальная погрешность удовлетворяет условиям
Sy,{x) = 0{h''-''), 6г,(х)=.ОЮ,
D.27)
VI.4. Методы Розенброка 461
ТО метод Розенброка D.3) сходится с порядком р, т.е.
Уп - У{^п) = 0(hP), z^ - z{x^) = 0[h^) для x„ - xo = n/i < Const
Доказательство, Поскольку g^ регулярна, мы имеем
\\97\y,^)9{y,z)\\<S D.28)
ДЛЯ (у, z) в некоторой компактной окрестности U решения. Не
зависящее от h значение S может быть сделано сколь угодно малым
посредством стягивания U, Кроме того, предположим пока, что
численное решение и все его внутренние стадии остаются в этой
окрестности. Распространение локальных погрешностей будет исследовано
в части (а), а их накопление на всем интервале интегрирования — в
части (Ь) доказательства.
а) Рассмотрим две пары начальных значений (Уо» -^^о) ^ (Уо» ^о) (^'^^
значения могут быть несогласованными, но предполагаются
лежащими в W). Применив в каждом случае наш метод, покажем, что
\\y,-M<i^ + hL)\\y,-y,\\ + hM\\z^-z^\\,
lh-?ill<^lk-yoll + «lk-?ol!.
где /С < 1. Для ЭТОГО зафиксируем некоторую (достаточно малую)
величину шага h и рассмотрим yij-^^, /:,-,?,• как функции {Vq^Zq). Если
мы покажем, что
оУо "Ч
D.30)
ТО D.29) будет следовать из теоремы о среднем значении.
Оценим сначала к- и ?,•. Используя D.28), вычислим 1^ из второго
уравнения D.3b) и результат подставим в первое. Это дает к^=-0{К)
и ii^O[h-\-S) последовательно для всех внутренних стадий. Проводя
аналогичные выкладки с уравнениями D.3b),
продифференцированными по Уд либо по Zq , мы получим
^ = 0D, 11 = 0D,
Теперь оценки D.30) следуют из D.3а) и D.25).
Ь) Из леммы 4.9 следует (см. упр. 8), что распространение
локальных погрешностей rfy^(Xj_i), &Zf^(xj__'^) к решению в точке х^
ограничено величиной
С{\\6ун{х^_,)\\ + {^ + кГ-^)\\5г,{х^_,)\\). D.32)
462 Гл. VI. Сингул5фно возмущенные задачи и задачи индекса 1
Суммирование этих членов от j = l до j = n с использованием D.27) и
приводит к содержащимся в утверждении теоремы оценкам
глобальной погрешности, потому что Yll=i(^'^^^'''^) ^ Const.
Наше предположение о том, что численное решение и его
внутренние стадии лежат в U, теперь легко обосновать индукцией по
числу шагов. Численное решение остается С?(Л^)-близким к точному
и, следовательно, остается в И при достаточно малом /i. А тогда
giVj^Zj) = O(h^) при всех j, и поэтому ?¦ = 0{h) тоже. Таким
образом, (г;,-, w^) сколь угодно близки к точному решению. П
Жестко точные методы Розенброка
Мы имели уже несколько случаев убедиться в очень полезных
качествах жестко точных методов Рунге—Кутты (методов, у которых
а^- = Ь- для всех г, см. теорему 1.1 и следствие 3.10). Каково же
соответствующее условие для методов Розенброка?
Опр€;11,еление 4.11. Метод Розенброка называется эюестко тонным,
если
^M+7,,=fr,- (г=1,...,5) и а, = 1. D.33)
Напомним, что а^ = ^ а,^ . В конце разд. IV. 15 уже упоминалось,
что методы, удовлетворяющие условию D.33), дают асиптотически
точные результаты для задачи у' = \[у — <^(х)) 4- ^'[х). Еще одну
интересную интерпретацию этих условий дал Шнайдер A991). Он
рассуждал так: поскольку ДАУ сочетают в одной системе
дифференциальные и алгебраические уравнения, то численные методы для них
должны работать одинаково хорошо в обоих крайних случаях: как
для чисто дифференциального уравнения, так и для алгебраического
уравнения
х' = 1, ^ = 9[x,z), ^2 обратима. D34)
Преищожение 4.12. Жестко точный метод Розенброка^
примененный к D.34), дает
^1 = ^s-974^0^ ^о)'9(^0-\-h,w^).
Таким образом, численное решение z^ — это результат одной
упрощенной итерации по Ньютону для уравнения 0 = gix^-^-h,z) со
стартовым значением w^.
Доказательство. Из условия D.33) и J2i^^i = ^ следует, что 7, =
— Ylj 7jj = 0. Поэтому вторая строка D.5) дает
i
о = ^(хо + Л, w,)+g^(xo,Zo) ^7<j^j
VI.4. Методы Розенброка 463
(заметьте, что для задачи D.34) Аг, = Л). Подстановка получаемого
отсюда выражения для ^ • 7,j^j в равенство
S 8
доказывает предложение. П
Величины (г;,,It;,), полученные на последней стадии, часто
используют как вложенное решение для управления длиной шага. В
случае жестко точных методов это приводит к тому, что многие
алгебраические условия порядка выполняются автоматически. Это
вытекает из следующего результата.
Прсищоженне 4.13. Рассмотрим жестко точный метод Розенброка.
Для достаточно регулярных задач D.1) равенство
г1-г(хо + Л) = 0(Л^+М D.35)
справедливо тогда и только тогда, когда
v,-y{xo + h) = 0(h<') и w,-z{xo + h) = Om. D.36)
Доказательство. Воспользуемся теоремой 4.8 и тем, что
^^ * *J Ю иначе ^ ^
t
(uj^j определена в D.17)). Пусть равенство D.35) выполняется.
Согласно определению Фj{u) и 'У(и) для дерева « = [Гу,<2]2 с
произвольным <2 ^ ^^^у мь1 имеем
Е^*<(") = Е *.'^0"i"i***(<2) = T.<^.k^k{t2) D.38)
t ij,k к
И ^(и) = 7(^2) • Следовательно, условие порядка выполняется для и
в том и только в том случае, если оно выполняется для <2 • Так как
р(^2) = p(w) - 1, мы видим, что из D.35) следует v^ — 2/(а:о Н-Л) = 0{кя).
Рассмотрев и = [г , ti J^ с u^E DAT^ , мы выведем второе соотношение
D.36). Достаточность доказывается аналогичным образом. П
Заметим, наконец, что из D.25) и D.37) видно, что функция
устойчивости всякого жестко точного метода Розенброка удовлетворяет
равенству Л(оо) = О. При решении жестких и дифференциально-
алгебраических уравнений это свойство является весьма
желательным.
Построение RODAS —
лсестко точного влолсенного метода
Мы хотим построить вложенный метод Розенброка (у которого
у^ = Vgy z^ =w^) так, чтобы и основной, и вложенный методы были
464 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
жестко точными. Для этого требуется выполнение следующих
условий:
^ = ^5.=/^5-i,i (г=1,...,5-1), »,-1 = 1,
где, как обычно, /?,^ =a,^-|-7,j. Из предложения 4.12 следует, что
последние две стадии представляют упрощенные итерации по методу
Ньютона. Далее, оба метода должны иметь функцию устойчивости,
обращающуюся в нуль на бесконечности. Построить такой метод
порядка 4C) при 5 = 5, по-видимому, невозможно. Поэтому мы возьмем
5 = 6.
Ниже приводится список условий порядка, которые требуется
решить. Мы используем здесь сокращенные обозначения а,, /?,•, которые
определены в (IV.7.16), и коэффициенты а;., из D.17). Потребуем,
чтобы
y^-y{xo + h) = 0{h% ^-yixo + h) = 0{h% D.40)
Поскольку параметров имеется достаточно много, потребуем еще,
чтобы
v,_^-y{xo + h) = 0(h% w,_^-zixo + h)=0{h% D.41)
Тогда в силу предложения 4.13
z,-z{xo + h) = 0{h*), z^-z{xo + h) = Oih^). D.42)
Этого более чем достаточно, чтобы гарантировать сходимость с
порядком 4 (см. теорему 4.10). Итак, условия, обеспечивающие выполнение
D.40) и D.41), таковы (см. табл. IV.7.1 и табл. 4.1):
bi + ^2 + *з + ^4 + (*5 + *б) = 1. D-43а)
Ь2/?2 + ^3/^3 + ЬЛ + (*5 + *б)A - 7) = I - 7, D.43Ь)
b^al + b^al + 64QI + F5 + ^б) = i- D-43с)
6з-^32/?2 + ^4Е'/?4,/?; + (*5 + Ьб)(Ь27 + 72) = Ь7 + 72, D.43d)
b^al + b^al + 64»^ + (*5 + *б) = i. D-43е)
6з"з"з2/^2 + ^4«4ЕЧ/3; + (б5 + *б)E-7) = bi. D-43f)
^з/?32 + ^4 Е '/?4^"? + ibs + be){h-l) = h-}' D-43g)
M43^32/?i + {^5 + ^6)(Ы7 + 372-73) = ^-Hi72-7^ D.43h)
*30'322 + ^4 E,,j a4,'^.j"j + (^5 + ^б) = ?- D-43i)
2/^2 + "бз/?з + "б4/?4 = ^ - 27 + 7^, D.43J)
аб2 + "бз"з + "б4 = 3 ~ 7. D.43к)
Cs3032l3'2 + «64 Е ^4.-^1 = i - §7 + 37^ - 7^ D.431)
«52/32 + а53^з + 4)^4 = 5-7. D.43т)
VI.4. Методы Розенброка 465
ELi«5.E;=i'^<W=1- D.43n)
Чтобы решить систему уравнений D.39), D.43а-п), в качестве
свободных параметров можно взять 7» <^2' ^з > ^4' /^2 — /^21 > /^з ' /^4 • Тогда
остальные коэффициенты вычисляются следующим образом.
Шаг 1. Из D.39) следует, что 6g = 7- Остальные 6,- можно выбрать
так, чтобы удовлетворялись уравнения D.43а,Ь,с,е). При этом мы
имеем одну степень свободы, и ее можно использовать для того, чтобы
удовлетворить добавочному условию порядка ^, b^af = 1/5. Этот шаг
дает также /?g,. = b- для г = 1,..., 6.
Шаг 2. Из D.43cl,g) вычислим два выражения 63/^32"'" ^^4/^42 ^ ^4/^43 >
а затем вычислим /?32 из D.43h). Поскольку /?,• = Х1}=1 j3,j , это
определит все /3ij с г < 4. Напомним, что /?„• = 7 Д-^я всех г.
Шаг 3. Решим линейную систему уравнений D.43j,k,l)
относительно ag2, о^бЗ' ^64- И^ D.39) следует, что a^g = 7K, а^^ мы найдем из
условия ag = ^,- ag, = 1. Согласно D.39) мы при этом получим также
Р^. = ag,. Следовательно, на этой стадии будут определены все /?,-^- и
u)i^ , а также 6,- = /?5,- (г = 1,..., 5).
Шаг ^. Условия D.43m,n) вместе с ag = 1 образуют систему из
трех линейных уравнений с четырьмя неизвестными параметрами
^51' ^52 > ^53» ^54- И^ этом шаге мы имеем одну степень свободы.
Шаг 5. Оставшиеся два условия D.43f,i) образуют линейную
систему относительно трех неизвестных «32, <^42 > ^43 • ^^ имеем еще одну
степень свободы, которую можно использовать, чтобы удовлетворить
условию порядка для дерева [Ту, т^, [г^у]у. Тогда значения сс-^
определяются из уравнений а,- = Y^j^i ct^j , а значения 7tj из соотношений
Коэффициенты для программы ROD AS (см. Приложение) были
рассчитаны с помощью описанной выше процедуры. На шаге 4 мы
добавили условие
Yia,,u;,j = l, D.44)
которое будет разъяснено ниже, в упр. 3. Свободные параметры были
выбраны так, чтобы получить Л-устойчивый метод с малыми
константами погрешностей. При этом мы получили следующие значения:
7 =0.25;
а2 = 0.386, аз = 0-21» а4 = 0.63; D.45)
/?^ = 0.0317 , /3^ = 0.0635 , /?; = 0.3438 .
Мы не утверждаем, что эти значения оптимальные. Однако
приведенные в разд. IV.10 результаты численных расчетов (рисунки IV.10.8,
IV.10.9 и IV.10.12) являются обнадеживающими. Хотя новый метод
466 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
требует шести вычислений функций на шаг, он, вообще говоря,
превосходит классические методы из табл. IV.7.2, которые требуют только
трех вычислений на шаг.
Другой набор коэффициентов, основанный на той же процедуре
их построения, предложил Штайнебах A995). Свободные
параметры были им выбраны так, чтобы удовлетворялись условия Шольца
C2(z) =0 и Сз(г) = О (см. уравнение A5.41) в разд.IV.15).
Плотная выдача. Непрерывное численное решение для y(xQ -h Oh),
z(xq -h Oh) естественно определить следующим образом:
s s
У1(^)=% + Е^^*.' ^iW = ^o + X^6,m, D.46)
1=1 t=l
где Ь^(в) —многочлены, удовлетворяющие условиям 6,@) = О, 6,A) =
= 6,. Совершенно так же, как в теореме 4.8, мы будем иметь:
у{х^-\-вк) — ViiO) = 0(/i^"'"^), если и только если
^2Ь^(е)Ф,{1) = — для teDAT^, p{t)<p,
*"^ ^1 D.47)
z{xq -\-0h) — Zi{e) = C?(/i^"^ ), если и только если
^2Ь^{в)Ф-{и) = -— для ueDAT^, p{u)<q.
В нашем случае E = 6) легко удовлетворить этим условиям при р = 3
и g = 2. Дополнительное условие 6^ (в) = ')в делает решение
единственным.
Методы порядка 5. Шнайдер A991b) первый построил жестко
точные методы Розенброка порядка 5 с восемью стадиями (s = 8).
Затем Ди Марцо A992) аккуратно определила свободные параметры,
чтобы получить Л-устойчивость и малые константы погрешностей.
Получившийся метод воплощен в программе R0DAS5. Он дает
отличные результаты (см. разд.IV.10).
Несогласованные начальные значения
Даваемое методом Розенброка численное решение (?/„, 2„), вообще
говоря, не удовлетворяет уравнению д{у^, z„) = О, даже если
вычисления начаты с согласованных начальных значений. В этой связи
представляет интерес исследовать локальную погрешность также для
несогласованных начальных значений (у^, Zq) . Но что такое локальная
погрешность? С каким решением системы D.1) следует сравнивать
вычисленные значения? Если
\\i9:'9)(yo^z^)\\<8 D.48)
С достаточно малым S, то можно найти локально единственное
(благодаря условию A.7)) значение Zq, которое удовлетворяет уравнению
VI.4. Методы Розенброка 467
5(Уо'^о) = 0. Естественно сравнивать численное решение (j/i.Zj) с тем
решением D.1), которое проходит через (Уо>?о)-
Прежде всего, запишем это решение через элементарные
дифференциалы, вычисленные при (j/qi^o)- Используя равенство
^0 - -^0 = (-<?г"'д)(Уо. ¦^о) + 0{6^),
которое вытекает из О = 5B/0,^0)+5»(Уо>^о)(^о - ^о) +•• •> получаем:
у(хо + Л) = 2/0 + Л/(«/о, ?о) + O(h^) = D.49)
= Уо + Л/(Уо.^о) + Hh(-97')9)(yo.^o)+0{h^ + hS^),
г(го + /1) = го-|-Л(-5Г^уЛ(Уо.2'о) + С?(Л^) = D-50)
= ^0 + (-97^9){Уо^^о) + Н-97^9у/)(Уо'^о) +
+ Н-97^9гг (-97^9, -97^9yf))(yo'^o) +
+ Н-97^9уг (/. -97^9)){Уо, го) +
+ л(-<7;'«?„Л(-^г')»)(%.го)+с(лЧ*2).
Полученные выражения удобно интерпретировать с помощью
деревьев. Надо только добавить в индуктивном определении 4.1
дерево порядка О, которое состоит из единственной «толстой» вершины
(вершины-кружка). Обозначим это дерево 0^ и расширим
определение 4.3, положив ^'@г)(у,-г) = (—97^9)(Уу2). Тогда выражения,
входящие в D.49) и D.50), будут соответствовать деревьям рис. 4.4.
/ . /
\^ V )
Рис. 4.4. Деревья, которые надлежит рассматривать
в случае несогласованных начальных значений.
Численное решение тоже обладает разложением вида D.49), D.50)
с дополнительными коэффициентами, зависящими от метода. Его
первые несколько членов таковы:
«J
Чтобы понять вид этих новых коэффициентов, надо расширить
доказательство теоремы 4.6. 0кг1зывается, что элементарные
дифференциалы умножаются на 7@Z^t^»^t@ ^^^ "^ 7(") Z^t'^«^Д^)) где 7 и
Ф, определяются условиями 7@г) = Ь ^Л^г) — ^j^ij ^
рекурсиями теоремы 4.6. Приравнивая коэффициенты в точном и в численном
468 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
решениях, мы получим новые условия порядка для случая
несогласованных начальных значений. Из них несколько первых (а именно, те,
которые надо добавить к включенным в таблицы IV.7.1 и 4.1)
представлены в табл. 4.2.
Таблицд 4.2. Условия порядка для несогласованных
начальных значений
дерево
V
0
V
условие порядка
52fe,a,Q,ju;jfc = 1/2
^6,ы,-^ = 1
^biLOijajajkUJki = l
величина члена
погрешности
0{h^S)
0{S)
0{hS)
Замечанхля. а) Первое условие в табл. 4.2 в точности совпадает с
тем, которое нашел ван Фельдхёйзен A984) в ином контексте. Из
этого условия следует, что локальная погрешность у-компоненты имеет
порядок величины 0{h^'^^ -h h^S -f М^).
b) Условие Yli j K^ij = 1 означает, что функция устойчивости
удовлетворяет равенству Д(оо) = О. Если это условие не выполнено,
локальная погрешность z-компоненты содержит не зависящий от Л
член порядка величины S (которая обычно близка к значению То1).
Это проявляется в представленных на рис. IV.7.4 результатах
численных расчетов и объясняет феномен рис. IV.7.3.
c) Для методов Розенброка, удовлетворяющих условиям D.39),
второе и третье условия из табл. 4.2 выполняются автоматически.
Для таких методов локальная погрешность г-компоненты имеет
порядок величины 0(/i^'^^ -h h^S + S^).
Упралснения
1. (Рош 1989.) Рассмотрите применение неявного метода Рунге—
Кутты A.11) к системе A.6).
а) Докажите, что z^ — 2:(xo-f Л) = 0{h^'^^) тогда и только тогда,
когда
1
5]б,Ф,(и) =
1=1
7(г/)
для и G DAT2, р{и) < q,
где '){и) и ФДгл) определены как в теореме 4.6, но все
коэффициенты а,^. и /?,-^ заменены коэффициентами метода Рунге—Кутты а,..
Ь) Покажите, что все те деревья из множества DAT^, которые
имеют более одной вершины-кружка, являются излишними.
/'
Jo
VI.4. Методы Розенброка 469
2. Следствием упрощающих предположений D.39) является то, что
многие из (алгебраических) условий порядка удовлетворяются
автоматически. Охарактеризуйте соответствующие деревья.
3. Сформулируйте условие порядка для дерева [г , [7"у,02]г]г •
Покажите, что
a) соответствующий член погрешности имеет порядок величины
O(h^S), где S определено в D.48);
b) для методов, удовлетворяющих D.39), это условие
эквивалентно условию D.44).
4. (Остерман 1990.) Предположим, что метод Розенброка D.3)
удовлетворяет условиям D.37). Определите многочлены Ь^(в) степени
q = [{p+ 1)/2] из условий 6,@) =0, 6,A) = 6,- и
lEi'^oj "я при г=2,...,,-1.
Докажите, что погрешность формул плотной выдачи D.46) будет
порядка 0{кя+^),
Указание, Примените идеи упр. П. 17.5 к методам Розенброка.
5. Пусть некоторый метод Розенброка реализован в форме (IV.7.25).
Если он удовлетворяет D.39), то две последние его стадии
допускают очень простую реализацию.
Указание. Докажите, что
^_Г«5. при г=1,...,5-1, ^ --/^*-1,» "Р" г=1,...,5-2,
* \ 1 при г = 5 , ** \ 1 при г = 5 — 1 .
6. Разделяющиеся методы Розенброка (Рентроп, Рош и Штайнебах
1989). Рассмотрите метод D.3), в котором fy и Д заменены
нулями. Выведите необходимые и достаточные условия, при которых
такой метод будет иметь порядок р.
Замечание. В этой новой ситуации случай (а) леммы 4.9 остается
в силе. Однако деревья, соответствующие случаю (Ь), порождают
новые условия.
7. Чему равен «алгебраический порядок» рассмотренных в разд. IV.7
классических методов Розенброка 4-го порядка?
8. Пусть {и^} и {v^} — две последовательности неотрицательных
чисел, удовлетворяющие (покомпонентно) неравенству
где 0<«<1 и L,M,N — положительные постоянные. Докажите,
что при h<hQ и nh< Const справедливы следующие неравенства:
^п < С{и^ + К). ^п < ^(^0 + (Л + «")^о)-
Указание. Примените лемму 3,9, положив е = h и М = 0.
VI.5. Экстраполядионные методы
Приведенные в разд. IV. 10 результаты численных экспериментов
показали, что программа SEULEX является одним из лучших кодов
при очень высоких требованиях к точности. Целью настоящего
раздела является теоретическое обоснование положенного в основу этой
программы численного метода (экстраполированного линейно
неявного метода Эйлера) для сингулярно возмущенных задач как
представителей жестких уравнений.
Дискретизация с помощью
линейно неявного метода Эйлера
Линейно неявный метод Эйлера (IV.9.25), будучи применен к
сингулярно возмущенной задаче A.5), принимает вид
Здесь мы использовали для частных производных сокращенные
обозначения типа /у@) = /у(Уо)^о)- Напомним, что численные
приближения при Xq-\- Н (Я = nh) экстраполируются по формуле (IV.9.26).
В случае дифференциально-алгебраической задачи A.6) в
формуле E.1) надо просто положить ? = О, что дает
У -4@) -^^9гiO))Wl-ZiJ-''\9{Уi,Zi))¦ ^^'^
Возможности распространения метода на неавтономные задачи
обсуждались в разд. IV.9. Для задач вида Ми^ = (р{и) мы используем
формулировку (IV.9.34) и при сингулярной матрице М. Благодаря
инвариантности метода по отношению к преобразованию A.23) все
результаты этого раздела будут справедливы и для задач Ми' = (р(и)
индекса 1.
Поведение экстраполяционных методов тесно связано с
существованием асимптотического разложения глобальной погрешности.
Такие разложения хорошо изучены для нежестких дифференциальных
уравнений (см. ргьзделы П.8 и IV.9). А что будет в том случае, если
задача жесткая или дифференциально-алгебраическая?
«Как путь к более глубокому пониманию можно, как и
прежде, рекомендовать: продолжайте изучать
конкретные задачи...» (Э. Хопф 1950)
VI.5. Экстраполяционные методы 471
Пример 5.1. Рассмотрим тестовую задачу
2/' = 1, ez' = -z-\-g{y). E.3)
Метод E.1) дает точный результат у,- =х,- = Хо -1-гЛ для у-компоненты
и рекурсию
(е + Л)г,^.1 = ег, + Л(,(х,.) + ftV(xo) E.4)
ДЛЯ 2:-компоненты. Чтобы вычислить коэффициенты
асимптотического разложения (теорема II.8.1), подставим
Z, = z{x,) + hb,{х,) -h hH^ix,) + Л'бз(^,) + • • • E.5)
в E.4), разложим в ряд Тейлора и приравняем коэффициенты при
Ы . Эта процедура дает дифференциальное уравнение для Ь^{х):
eb[{x) + b,{x) = -'-z"{x)-z'{x)+g'{xo)
И аналогичные уравнения для 62B?), Ь^{х) и т.д. Полагая в E.5) г=0,
получим начальные значения 6,(хо) = О (для всех г). В общем
случае вычисление функций ^^(х), бгС^)» • • • довольно утомительно.
Поэтому дальнейшее рассмотрение нашего примера мы продолжим для
конкретного случая Xq = О, ^(х) = х^ + 2ех и Zg = О, когда точным
решением задачи E.3) будет г(х) = х^. Для этого случая мы получим
6j(x) = -3ee-^/-3?-2x,
E.6)
и т.д. Заметим, что при е -> О функция 62(^) становится разрывной
при X = О, а Ь^(х) не будет даже равномерно ограниченной.
Следовательно, разложение E.5) бесполезно для исследования
экстраполяции, если е мало по сравнению с длиной шага Я.
Идея устранения этой трудности состоит в том, чтобы отбросить в
E.6) члены, содержащие множитель е"^/^, потребовав, чтобы
функции 6,(х) были равномерно гладкими по ?, а вместо этого добавить
в E.5) дискретное возмущение /3^. Тогда для нашего примера мы
получим
z. = xf + ftC?-2x,.)-hft2-f/?i. E.7а)
Подстановка E.7а) в E.4) дает соотношение (s-\'h)l3^^^ = е/?,.
Значение /?о получается из E.7а) при f = 0. Таким образом, мы получаем
/?, = -(l + -)"'C?ft + ft2). E.7b)
При экстраполяции численного решения гладкие члены в E.7)
исключаются один за другим. Остается исследовать влияние экстраполяции
на возмущающие члены /?,. Если дифференциальное уравнение очень
жесткое (е <^ ft), то эти члены очень малы, и ими можно пренебречь
в широком диапазоне значений ft (заметьте, что г > п^).
472 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
Пример 5.2. Для дифференциально-алгебраической задачи
y' = h ^ = -z^9{y) E.8)
с начгипьными значениями у^ = х^, г^= di^o) численное решение,
даваемое формулами E.2), имеет вид
__ ( 9{xq) приг = 0,
* "" I 9(^i-.i) + ^^'(^о) при г > 1 .
Разложение второй строки (для г>1) дает
Z, = 9(х,) + ЛE'(хо) - </'(х,)) + у«;"{а^,) - у5"'(^.) + 0{h').
Если добавить возмущение
(i.^hl3l-\-h^(if-^h^pf-\-,., E.9)
(отличное от нуля только при г = О), то мы получим для всех i
3
Zi-9{Xi)=J2h4bM)+l3i) + 0{h'^), E.10)
где
b,(x) = g'{xo)-g'{x), Ь,{х) = У"(х), b^(x) =-^-д'" (х)
— гладкие функции, а возмущения имеют вид
Если добавить к E.8) еще одно алгебраическое уравнение,
например, 0 = и — k{z) и снова применить метод E.2), мы получим три
разных формулы для U,: одну для г = О, другую для г = 1 и еще одну
при г > 2. В разложении типа E.10) для и^ — к{д(х^)) возмущающие
члены будут присутствовать при г = О и г = 1.
Возмущенное асимптотическое разлолсение
В общем случае для дифференциально-алгебраических задач
имеется следующий результат:
Теорема 5.3 (Дойфлхард, Хайрер и Цугк 1987). Рассмотрим
задачу A.6) с согласованными начальными условиями (Vq^Zq), и пусть
выполнено условие A.7). Тогда глобальная погрешность линейно
неявного метода Эйлера E.2) имеет асимптотическое h-разложение
вида
м
yi-y{xi) = ^^{aj(x,)+ai)+0(h'^^'),
VI.5. Экстраполяционные методы 473
где aj{x), bj{x) — гладкие функции, а возл/у1ден11я удовлетворяют
равенствам
qI=Q^ af = 0, Qf = 0, /??=0 при г>0, E.12а)
/?f=:0 при г>1, E.12Ь)
Q'-=0 при i>j — 4 и i>4, E.12с)
/?/=0 при i>j-2 и ;>3 E.12d)
(см. таблицы 5.1 и 5.2). Члены погрешности в E.11) равномерно
ограничены при х, = ih < Н, если Н достаточно мало.
Таблица 5.1. Ненулевые а .
Таблиид 5.2. Ненулевые /3
УО
У\
У2
УЗ
У4
УЪ
h
0
0
0
0
0
0
J^
0
0
0
0
0
0
h^
0
0
0
0
0
0
h^
0
0
0
0
0
0
h^
¦
0
0
0
0
0
h^
¦
*
0
0
0
0
J^
¦
*
*
0
0
0
20
21
Z2
Z3
24
25
h
0
0
0
0
0
0
h^
*
0
0
0
0
0
h^
*
0
0
0
0
0
h^
*
*
0
0
0
0
J}L
*
*
*
0
0
0
JL
*
*
¦
¦
0
0
_h[
*
¦
*
*
*
0
Доказательство. В части (a) доказательства мы построим с
помощью рекурсии усеченные разложения
м
yi = y{x,) + '?h^aj(x,) + c4)+h'^^'af'+\
'м E.13)
i=i
так, чтобы невязка при подстановке у,, z^ в уравнения метода была
мала. Точнее, мы потребуем, чтобы
[ -4@) -л</Л0)А?.>1-?^-Ч5(у..?.)У ^
Для начальных значений мы потребуем, чтобы Уо = Уо» -о — -^о ^»^"'
что равносильно,
а^.@)Ч-а^о = 0, 6.@) 4-/?^ = 0. E.15)
Кроме того, предполагается, что возмущающие члены удовлетворяют
условиям
af->0, ^/->0 при г->оо E.16)
(в противном случае их предельные значения можно было бы
добавить к гладким частям). Тогда утверждение теоремы будет следовать
,М+2ч
474 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
из оценки устойчивости, которая выводится в части (Ь)
доказательства.
а) Для построения а,(х), bj{x), а^-, fij подставим E.13) в E.14) и
воспользуемся разложениями
Лу.-.?.) = /(уК). ^К)) +/s,K)(/»ai(^.) + hcl + ...) +
+ Л(х,Ж(^.) + л/?/ + ...) +
Vi+i - Vi = y(^i+i) - y(^i) + ^(aiK+i) - ai(Xi) + q?+i - q?) + ... =
= VW+у j/"(x,) + ... + /iVi(x,) + M«.>i-«<) + •••-
где fy{x) = fy[y[x), z{x)) и т.д., a также аналогичными разложениями
для g{yi,Zi) и z^^i — ?,, после чего соберем коэффициенты при Л^+i
(для j = О,..., М). Для каждой степени Л мы получим два равенства:
одно будет содержать гладкие функции, а другое — возмущающие
члены.
Первый шаг. Приравнивая коэффициенты при h^, получим
уравнения A.6) для гладкой части (вследствие согласованности метода) и
а\^^ — а| = О при г > О. Благодаря предположению E.16) мы получим
а] = О для всех i > О (ср. E.12а)).
Второй шаг. Коэффициенты при Л^ дают
a'Ax)+\^'{x)-f^{Qy(x)-fM^'{x) = 4(x)ai(x)+/,(xNi(x), E.17а)
-9уШ(х)-дМ^'{=^)-^9у{х)а,{х)+д,(х)Ь,{х), E.17Ь)
<1-«?-/Л0)(/?/+1-/?/) = Л@)/?/, E.17с)
-9.Ш0их-1^1)=9гт]- E.17d)
Заметим, что коэффициенты а\, /?/ должны быть не зависящими от
Л, так что в правых частях E.17c,d) Д@), Qzi^) нельзя заменить на
Л (^»)) 9z (^i) • Систему E.17) можно решить следующим образом.
Выразим Ь^{х) из E.17Ь) и подставим в E.17а). Это дает линейное
дифференциальное уравнение для а<^{х). Из E.15) и aj = О следует, что
начальное значение равно 0^@) = 0. Поэтому а^[х) и Ь^[х)
однозначно определяются уравнениями E.17а,Ь). Дифференцируя уравнение
g[y{x),z[x))^Q и полагая х = О, мы найдем, что при х = 0 левая часть
уравнения E.17Ь) обращается в нуль. Следовательно, мы получаем
6j@) = 0, а с учетом E.15) —также /?о =0. Далее, из E.17d) следует,
что /?/ = О (для всех г), а E.17с) и E.16) дают а^ = О (для всех г).
Третий шаг. По ангипогии со вторым шагом получим
a;.(x) = 4(z)a^.(x) + /,(xN,.(x) + r(x), E.18а)
а = 9у(х)а^{х)^9,(х)Ь^{х)Л-8{х) E.18Ь)
VI.5. Экстргшоляционные методы 475
(с J = 2), где г(х), s(x) — известные функции, зависящие от
производных у{х), z(x) и от а^(а:), Ь^(х) с ^< j —1. Далее, получим
«f+i-'^f = /.@)/?iVi. E18с)
0 = 9гт^1- E.18d)
Вычислим 02(г), Ь2{х) как во втором шаге. Однако в общем случае
6^@) :^ О, и здесь мы впервые вынуждены ввести возмущающий член
у^о ^ О. Тогда из E.18c,d) мы получим /if = О (при г > 1) и af = О (для
всех г).
Четвертый шаг. Сравнивая коэффициенты при h^, мы получим
E.18а,Ь) с j = 3 и E.18c,d) с верхними индексами, увеличенными на 1.
Как и выше, заключаем, что /}f = О (при г > 1) и af = О (для всех г).
Общий шаг. Условия для гладких функций по-прежнему имеют
вид E.18а,Ь). Для возмущающих членов мы получим
c4tl-'4^'=fziO)l3Ui+pi> E19с)
0 = </Л0)/^+1+<^', E.19d)
где Pi , сг- — линейные комбинации выражений, которые содержат
в качестве множителей otj^i, о^^'^, /?,^~^ с ?<j. Например, pf =
= fzzWiPfy и ^f — dzzWil^fy' Теперь E.12) доказывается
индукцией по j. Согласно индуктивному предположению при г > j — 3 мы
имеем /7- =0, aj =0. Следовательно, из E.19d) вытекает, что Pj_^^ =0
(при г > j —3), а из E.19с) и E.16) aj'^^ = О (при г > j —3), что,
собственно, и утверждается в E.12c,d).
b) Нам надо еще оценить остаточный член, т.е. разности Ау, =
= У{ — Ух у ^^i = ^i — ^i • Вычитание E.14) из E.2) и исключение Ду,^.!,
Дг,.^1 дает
// + 0(Л) 0{h) \(h{f(y„z,)-m,z,))\ @(h»+^)\
+ [ 0A) -<7ГЧ0)Д i7(y,,z,)-<;(y,,z,) ) + \0(h'^^^))-
Далее, применение условия Липшица для /(у, z) и д(у, г) дает
Л|ДУ.+111\<Л + 0(Л) Oih)\ (\\Ау,\\\ @{кМ+^)\ .5 20)
(,||Дг,^Л;^1, 0A) р ) [\\Az,\\) + [Oih^f^^)) ^ (^-20)
где |/?| < 1, если Н достаточно мало. Применяя лемму 3.9, мы
выводим отсюда, что ||Ау,|| + ||А2:,.|| = C?(/i^+^). П
Таблица порядков
Будем рассматривать E.2) как опорный метод для экстраполяции,
т.е. возьмем некоторую последовательность числа шагов п^ < Hj < ...,
476 Гл. VI. Сингул5фно возмущенные задачи и задачи индекса 1
положим Л = ^/^j и определим
Уп = УнМо + ^)^ Zji = z,^(xo + H) E.21)
— численное решение задачи A.6), полученное после п шагов длины
hj . Затем экстраполируем эти значения согласно (IV.9.26) и получим
Yjf^, Zji^. Каков будет порядок получаемых при этом приближений?
Теорема 5.4 (Дойфлхард, Хайрер и Цугк 1987). Для
гармонической последовательности {1,2,3,4,...} экстраполированные значения
Yjf^, Zjf^ удовлетворяют равенствам
Yj,-y{xo + h) = 0{H^'^-''), Zj,-z(xa + H) = 0(H'>^), E.22)
где Vji^, Sjf^ — дифференциально-алгебраические порядки,
приведенные в таблицах 5.3 и 5.4.
Таблица 5.3. Порядки rjk. Таблица 5.4. Порядки Sjk -
1 2
12 2 2
12 3 2 2 3
12 3 4 2 2 3 4
12344 22344
123445 223454
1234455 2234554
12344565 22345654
123445665 223456654
1234456765 22345 6i 7654
Доказательство. Воспользуемся разложением E.11). Из того, что
а] =/31=0 (для всех г >0) и E.15) следует, что aj(xQ) = 6i(xQ)=:0.
Поскольку aj{x) и bj(x) —гладкие функции, мы получаем a^lxQ-hН) =
= 0{H)i 6j(xQ-f Я) = (!?(Я); видно, что погрешности У^^, Zj^
имеют порядок величины О(Н^). Это доказывает правильность
первых столбцов в таблицах 5.3 и 5.4. Тем же способом выводится, что
a2(xQ + Н) = 0(Н). Однако, поскольку в общем случае /3q^0, из
E.15) следует, что 62(^0) т'^ О и член 62(^0 + ^) ^^его лишь порядка
0{1). Одна экстраполяция численного решения исключает из E.11)
члены с j = 1. Таким образом, погрешность имеет порядок величины
О(Н^) для Yj2, но лишь 0{Н^) для Z^2' Этим доказана
правильность вторых столбцов в таблицах 5.3 и 5.4. При продолжении
процесса экстраполяции гладкие части разложения погрешности E.11)
исключаются одна за другой. Однако возмущающие члены не
исключаются.
Для 2/-компоненты первым неисчезающим возмущением, когда
г > п^ = 1, будет а\. Поэтому диагональные элементы экстраполяци-
онной таблицы для у-компоненты (табл. 5.3) содержат член
погрешности порядка 0[Н^) (обратите внимание, что ос\ в E.11)
умножается на Л^). Элементы V^j_i первой поддиагонали зависят только от
УII = у„^ при t>2. Так как П2 > 2, то могут влиять лишь возмущения
VI.5. Экстраполяционные методы 477
aj с П2 > 2. Из E.12) видно, что первым неисчезающим возмущением
при 2 > 2 будет al- Это объясняет член погрешности 0[Н'^) в первой
поддиагонали табл. 5.3.
Для г-компоненты первым возмущающим членом при i > 1 будет
Pf. Поэтому диагональные элементы экстраполяционной таблицы
для Z-компоненты содержат погрешность 0(Н'^). Все остальные
элементы таблиц 5.3 и 5.4 проверяются аналогичным образом. П
Если мы рассмотрим последовательность числа шагов {п^},
отличную от гармонической последовательности, соответствующие
таблицы порядков будут выглядеть так: j-e диагонали новых таблиц —
это nj-e диагонали таблиц 5.3 и 5.4 соответственно. Тогда теорема 5.4
останется справедливой, но со значениями г ^^, s^^ , даваемыми этими
новыми таблицами. Это означает, что большее значение п^, скажем,
п^ = 2 повышает порядок экстраполированных величин. Численные
эксперименты показали, что последовательность
{2,3,4,5,6,...} E.23)
дает лучшие результаты, чем гармоническая последовтельность, и
поэтому она была рекомендована для программы SEULEX.
Представляет интерес исследовать влияние возмущающих
членов на экстраполированные величины. Предположим, что агц (или
/?ni) — ведущий возмущающий член в У^^ (или Z^^). При
рекурсии (IV.9.26) все Y^i^ будут содержать тогда член погрешности вида
Cf^H^aii^, тогда как Yjf^ (при j > к) не зависят от ani • Константы
погрешностей Cf^ определяются рекуррентными формулами
и с ростом Аг экспоненцис1льно стремятся к нулю.
Разложение погрешности
для сингулярно возмущенных задач
Нашей целью является распространение анализа примера 5.1 на
сингулярно возмущенные задачи общего вида:
.' = /(y.z). У@)=Уо-
ez' = g[y,z), ^@) = го, 0<е<1,
где решение у[х), z[x) предполагается достаточно гладким (т.е. его
производные до определенного порядка ограничены независимо от е).
Важным наблюдением, сделанным в примере 5,1, было
существование гладких решений (линейных) дифференциальных уравнений для
коэффициентов Ь^{х). В общем случае мы будем иметь дело с урав-
478 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
нениями вида
а' = /..Bг)а4-Л(хN + с(х,е),
E.26)
а' = 4(а:)аЧ-/Л^N + с(х,е),
еЬ' = gy(x)a-\-g^(x)b + d{x,€)
(коэффициенты fy{x) = fy{y(^)iz{^)) и т.п. гладко зависят от е,
потому что решение E.25) само зависит от е, даже если f и д не зависят
от е явно).
Лемма 5.5. Предположим^ что логарифмическая норма д^{х)
удовлетворяет условию
/^(^'гС^)) <-1 ПР^ 0<х<х, E.27)
При заданной величине
а@) = ag + eaj -h ... -f e^a^ -f 0(e^-^')
существует единственное (с точностью до членов 0{е^'^^))
представление
6@) = 6g + ?6J + ... + 5^6^ -f 0F^-^')
такое, что решения а(х), Ь{х) уравнений E.26) и их первые N
производных ограничены величинами^ не зависящими от е.
Доказательство. Подставим конечные разложения
N N
a{x) = ^e^a,(x), Ь(х) = ^,е%{х)
t=0 1=0
с не зависящими от е коэффициентами а,-(ж), Ь-(х) в E.26) и соберем
члены с одинаковыми степенями е (см. разд. VI.3). Это приводит к
дифференциально-алгебраической системе вида C.4).
Следовательно, Oq определяет 6q, они вместе с aj определяют 6q и т.д. Тогда
остаточные члены а(х) — а{х), Ь(х) — Ь{х) оцениваются, как в
доказательстве теоремы 3.2. П
Доминирующие возмущающие члены в асимптотическом
разложении погрешности линейно неявного метода Эйлера при применении
его к сингулярно возмущенной задаче выявляет следующая
Теорема 5.6 (Хайрер и Любих 1988). Предположим, что решение
задачи E.25) гладкое. При условии, что
||(/-7</Л0))-Ч|<т^ прилюбых 7>1 E.28)
(которое следует из E.27) и теоремы IV. 11.2), для численного решения
системы E.1) при е < h имеет место возмущенное асимптотическое
разложение вида
J/.. = y(Xi) + ha,{Xi) + h\^{xi) + 0{h^) - E.29)
- ef, @)9:'@) {l-j9.@))" {hb,@) + h4,@)) ,
VI.5. Экстраполяционные методы 479
Zi = г(х,.) + hby(Xi) + h4^[xi) + 0(h^) - E.30)
где X, = ih < Н и Н достаточно мало (но не зависит от е). Гладкие
функции а Ах), bj(x) удовлетворяют равенствам
а,{0) = О(?^), а,@) = О(е), Ь,@) = О{е), Ь^{0) = О{1).
Доказательство. Это доказательство построено по образцу
теоремы 5.3. В части (а) доказательства мы построим с помощью рекурсии
усеченные разложения (для М < 2)
м
У,=2/К) + 1]Л'КК)-+-ог^'),
так, чтобы
[ ^hg^iO) eI-hgMj[^i^i-^i)^ \9(Уо^г))^^^ ^'
E.32)
Ясно, что гладкие функции а^(х), bj{x) зависят от е, но они не
зависят от Л. Однако возмущающие члены а^, /3j (при i > 1) будут
гладким образом зависеть от е и от e/h. Как и в случае с е = О, мы
потребуем, чтобы выполнялись условия E.15) и E.16). Затем в части
(Ь) доказательства будут оценены разности у,. — у,, и z, — ?,.
а) Случай М = 0 очевиден. Действительно, величины у, =у(х,),
г, = z{x^) удовлетворяют E.32) с М = 0. Построение коэффициентов
в E.31) мы проведем в два шага.
Первый шаг {М = 1). Подставим E.31) в E.32) и приравняем
гладкие коэффициенты при h^. Это даст
а\{х)+^-у''{х)-/^{0)у'{х)-Г,(ОУ(х) = Цх)а,(х)+/Ах)Ь,(х)АЬ.ггг^)
?b\(x)+^-z"{x)-g^{0)y'{x)-gM^'M=9yi^iix)+9z{^iH-E-^^
Согласно лемме 5.5 начальное значение Ь^{0) однозначно
определяется значением а^{0). Дифференцирование уравнения sz' — g{y,z)
по X дает ez"[x) = ду(х)г/{х) + g2(x)z'(x), что, будучи подставлено в
E.33b), приводит к соотношению
9у{0)а,@)+9МЬЛ0) = О{е) E.34)
С известной правой частью.
480 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
Займемся теперь возмущающими членами. Собрав их (до членов
порядка 0(/i2)), получим
oUi-<^l-hfymal^-C'l}-hfAO)WUi-0l) =
E.35)
= hf^(x,)al-^hfAx,Hl
e(Phi -l3l)-h9ymal,-a})-h9,mi3Ui -^D =
Попытаемся определить, какие части здесь наиболее важны. Сначала
заменим hf {х^)а\ на hfy{{))a] и аналогично в трех других членах.
Это мотивируется тем, что мы ищем экспоненциально затухающие а-.
Поэтому при X, = ih
DК)-/у@))а/=О(Л).
Тогда в E.35) сократятся многие члены. Далее, заметим, что на е
умножается (i}^^ — /?/ , но не а]^^ — aj. Это говорит о том, что 01^^ на
порядок величины больше, чем а}^^. Поэтому пренебрежем а]^^ там,
где оно конкурирует с /?/^i, и таким образом придем к определению
<1-«.-= ft/. @)^+1 . E.33с)
ei0hi-l3l) = hgM0hi- E.33d)
Остается проверить апостериори, что действительно существуют
решения E.33a,b,c,d), которые дают член погрешности 0{h^) в E.32).
Из E.33d) получаем
^/ = (/-75Л0))~V^ E.36а)
Так как мы потребовали, чтобы а] —> О при г—»^оо, решение E.33с)
имеет вид
«•=^Л@)</;Ч0)(/-7</Л0))'Ч' E.3бЬ)
При г = О отсюда следует соотношение
al = efAO)974OHl E.37)
Предположение E.15) вместе с E.34) и E.37) однозначно определяет
коэффициенты а^@), ^^(О), aj, /?^. Заметим, что Ь^@) = 0(е) и
0^@) = 0(е^), Используя тот факт, что а] = 0(€^) и е < Л, легко
убедиться, что величины E.31) с М = 1 удовлетворяют E.32).
Второй шаг [М =2). Собирая в E.32) гладкие коэффициенты
при Л^, получим два дифференциальных уравнения для а2(х), Ь2{х)
вида E.26). Из леммы 5.5 следует, что начальные значения должны
удовлетворять соотношению
</„@)а2@) +5Л0)б2@) = 0[1), E.38)
VI.5. Экстралоляционные методы 481
в котором правая часть известна. Как и на первом шаге, потребуем,
чтобы для возмущений выполнялись соотношения
откуда получаются формулы вида E.36) и E.37), в которых вместо
а}, Р- стоят af, /3f. Значения а2{0), b^iO), а^, /?о здесь тоже
определяются однозначно из E.15), E.38) и E.37). Так как в правой
части E.38) стоит величина 0A), мы найдем лишь, что 62@) = 0A) и
а,{0) = О{е).
Нужно еще проверить, что E.32) выполняется при М = 2. В левой
части мы пренебрегли членами вида hf {0)(haj Ч-Л^а?). Это законно,
потому что а] = О(е^), а? = 0{е) и е < h. Наиболее опасен член,
которым мы пренебрегли в правой части E.32):
h{fAxi)-fAO))ih0} + h'l3f). E.40)
Однако fz(^i) ""Л@) = 0(гЛ), а из E.28) и е <h следует, что /3} =
= 0(e2~^)^ /?,• = (9B"»). Это показывает, что член E.40) тоже имеет
порядок величины 0{h^). Таким образом, E.32) выполняется и при
М = 2.
Ь) Чтобы оценить остаточный член, т.е. разности At/, = г/,- — у,-,
Дг,- = z^ — ?,, вычтем E.32) из E.1) и исключим Ду,-^! ^ ^^i+i • При
этом мы получим
+ [ 0(l) ij,I-g^@))-')[ 9{y„z,)-g(y„z,) ) + [0(h^^^^))-
Используя условие E.28) и учитывая, что е <h, получаем
неравенство
/+ {^1-9Л0)У\м\\ = ||(^- 7^^Л0))"|| < ^ < i. E.41)
Поэтому мы приходим снова к оценке E.20) с некоторым \р\ < 1 при
условии, что Я достаточно мало. Окончательный результат
выводится отсюда, как в доказательстве теоремы 5.3. П
В приведенном выше доказательстве можно, конечно, добавить и
третий шаг. Однако рекуррентные соотношения для af, Pf уже не
столь просты, как E.33) или E.39). Кроме того, возмущения в
формулах E.29) и* E.30) уже очень хорошо описывают встречающиеся на
практике ситуации. Мы проиллюстрируем это следующим
численным примером (см. также Хайрер и Любих 1988).
Рассмотрим уравнение Ван-дер-Поля B.73) с е = Ю"^ и
начальными значениями B.74), лежащими на гладком решении. Возьмем
последовательность чисел шагов E.23) и применим метод E.1) п
482 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
1 ^
10-5
\ 2C..fJ/\l
, ,,...,1 .
10-^
>%1
1 .
10-5
7=^2
j^
,..пм1
10-2
7 = 5
1
10-' я L
>й/Ж-з
//I *^
и 10-'
\ 10-'2
7=6
10-»5
-
-
io-»V
Рис. 5.1. Погрешность как функщ1я Н. Рис. 5.2. Зависимость Tjj от Н/е
раз с длиной шага Л = Я/п^ . Численный результат У^-^, Zj'^ при
этом экстраполируется по формуле (IV.9.26). На рис. 5.1 в
двойном логарифмическом масштабе показаны величины погрешностей
\Zjj — z[H)\ при j = 1,2,..., 6 как функции Я. Видно, что когда
погрешность становится больше чем е'^ = 10"^°, кривые переходят в
прямые с наклонами 2,2,3,4,5 и б соответственно. Если наклон прямой
равен ^, то log(error) « g log Я-|-Соп5^, или error^CH^, Получен-
ныо значения (за исключением последнего) соответствуют порядкам,
пр<»дсказываемым поддиагональю таблицы 5.4 для случая е = 0.
Чтобы понять причину нерегулярного поведения кривых, когда
погрешность становится меньше е^ = 10~^°, проанализируем влияние
экстраполяции на возмущающие члены в E.30). Поскольку 6^@)
содержит множитель 6, доминирующей частью возмущения в Z^^
будет (/ —(Л/?)^^@))"*^>/1^б2@), где 62@) — некоторая постоянная и
Л = Н/п-. Предположим, что матрица 5^2@) приведена к
диагональному виду, и положим ^^@) = — 1. Поэтому доминантное возмущение
в Zji будет e^Tj 162@), где
/Я\2/^ Н \-^i
E.42)
Вследствие линейности экстраполяции доминантное возмущение в
Z^j будет e^^Tjjb^iO), где Tjj получается из E.42) и (IV.9.26). Для
последовательности чисел шагов E.23) величины Tjj как функции
Н/е представлены графиками на рис. 5.2. При больших значениях
Н/е кривые переходят в горизонтальные линии. Это является след-
VI.5. Экстраполяционные методы 483
ствием нашего выбора п^ = 2 и того факта, что
-. = c,(f)-.((f))'
при >• ОС,
где Cj = 1, а остальные С^ получаются по рекуррентной формуле
E.24).
Теперь понятно, что погрешности, показанные на рис. 5.1,
получаются в результате наложения погрешностей, предсказываемых для
случая е = О (теорема 5.4) и показанных на рис. 5.2 возмущений,
масштабированных множителем 0[е'^).
Замечание. Как уже упоминалось в разд. VI. 1, дискретизация
неявным методом Эйлера обладает классическим асимптотическим
разложением для дифференциально-алгебраических задач A.6)
индекса 1 (случай ? = 0). Однако для сингулярно возмущенных задач
присутствуют возмущения такого же типа, как в E.29) и E.30).
Единственное отличие состоит в том, что в случае неявного метода Эйлера
все 6,@) содержат множитель е. Интересующихся подробностями и
численными экспериментами мы отошлем к работе Хайрера и Любиха
A988). Аналогичный анализ для несколько иного класса сингулярно
возмущенных задач провели Ауцингер, Франк и Мачек A990).
Плотная выдача
При интегрировании экстраполяционными методами, как
правило, выбирается очень большая длина базового шага. Поэтому важно,
чтобы метод обладал непрерывным численным решением. Первую
попытку получить плотную выдачу для экстраполяционных методов
сделал Линдберг A972). Однако его подход накладывает очень
сильные ограничения на выбор последовательности чисел шагов. Мы
опишем здесь плотную выдачу, которую предложили Хайрер и Остерман
A990) и которая существует для любой последовательности числа
шагов.
Основная идея (принадлежащая К. Любиху) состоит в
следующем. Вычисляя j-ю позицию в экстраполяционной таблице, будем
рассматривать не только У^^ = у^^ , но еще и разность (у„. — у^ _i)/ftj .
Поскольку эти выражения обладают Л-разложениями, их
экстраполяция дг1ет точное приближение к у'{х^-\-Н), Рассматривая
разности более высокого порядка, мы получим также приближения для
старших производных от у[х) в точке Xq-\- Н. Затем эти
приближения используются для эрмитовской интерполяции. Причиной,
почему следует вычислять производные только на правом конце базового
интервала, является присутствие возмущающих членов, описанных в
теоремах 5.3 и 5.6. Эти возмущения вначале велики (вблизи
начального значения), но с ростом i убывают экспоненциально. По этой
же причине нельзя использовать разности слишком высокого
порядка. На практике мы выбираем целое число А (обычно О или 1) и не
484 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
используем значения Ус • '2/ni+A~2 ^Р^ вычислении конечных
разностей. Заметим, что аналогичную идею использовали Дойфлхард и
Новак A987) при построении согласованных начальных значений для
дифференциально-алгебраических задач.
Приведем описание алгоритма плотной выдачи для линейно
неявного метода Эйлера (предполагается, что значение У^^ в качестве
численного приближения к у(хо + Я) было принято).
Шаг 1. Для каждого j G {1,..., к} вычисляем
^W^V^ при fc = l,...,j-A. E.43)
Здесь xif' — аппроксимация 2/(х,), полученная при вычислении У^^,
а Vy, = у, — у,_1 — оператор разности назад.
Шаг 2. Величину rj ' экстраполируем [к — к — Х) раз. Это даст
улучшенное приближение rW для у^^){х^-\-Н).
Шаг 3. Определим многочлен Р[в) степени к следующими
условиями:
Р@) = уо, PW = y..^
E.44)
P^^\l)^H^r^^^ при ik=l,...,/c-l.
Следующая теорема показывает, с каким порядком точности эти
многочлены аппроксимируют точное решение.
Теорема 5.7 (Хайрер и Остерман 1990). Пусть Л G {0,1}. Тогда в
случае нежесткого дифференциального уравнения для погрешности
интерполяционного многочлена Р{в) имеет место оценка
Р{в) - y{xQ -h вН) = 0(Я'^+^-^) при Я -> 0.
Доказательство. Так как Р{в) является многочленом степени /с,
погрешность, связанная с интерполяцией, имеет величину 0(Я'^+^).
Мы знаем, что У^^ — у(х^ -h Я) = 0(Я'^+^). Поэтому достаточно
показать, что
r^^^ = y^''\xQ-\-H) + 0{H''-''-'^-^^) при Л—1,...,/с-1. E.45)
Благодаря наличию асимптотического разложения у глобальной
погрешности у,- — у(х,), приближения rj тоже имеют разложения вида
rf) = yW(x, -^H)-h hja['^ + /i?4'^ + .... E.46)
Поэтому справедливость E.45) следует из того, что каждая
экстраполяция исключает одну степень h в E.46). П
Теперь исследуем погрешность плотной выдачи Р(9) для случая
жестких дифференциальных уравнений, как, например, в
сингулярно возмущенных задачах. Мы рассмотрим здесь предельный случай
VI.5. Экстраполяционные методы 485
6 = 0, который легче поддается анализу, но, тем не менее, много дает
для понимания структуры погрешности в очень жестких задачах.
Для дифференциально-гипгебраической системы A.6) плотная
выдача определяется точно так же, как и для обыкновенных
дифференциальных уравнений. Поскольку система A.6) разделена на у-
и Z-компоненты, удобно обозначить интерполяционные многочлены
для них Р{в) и Q{e) соответственно.
Теорема 5.8 (Хайрер и Остерман 1990). Пусть у{х), z(x)
—решение системы A.6). Предположим, что последовательность числа
шагов удовлетворяет условию п^ 4- А > 2, где А G {0,1} . Тогда имеют
место оценки
Р[в) - у(хо -f вН) = 0{Н^^'-') + 0[Н^^'),
где г и S — числа, стоящие в позициях (/с -f п^ -h А — 2, к) таблиц 5.3
и 5.4 соответственно.
Доказательство. Воспользуемся возмущенными
асимптотическими разложениями погрешности из теоремы 5.3. Для их гладких
членов полностью применимы рассуждения, приведенные в
доказательстве теоремы 5.7. Это дает члены погрешностей 0{Н'^^^~^) в E.47).
Вторые члены погрешностей в E.47) обязаны своим происхождением
возмущениям в E.11). Заметим, что при вычислении rj ^
используются только те значения г/, (или г,), у которых г > п — j -f А. Так как
Tij —j>n^ — l, то величины Ус • • •' ^п1+л-2 "^ войдут в формулы для
rj. \ а поэтому основное возмущение вносит y^^^x^i {или г^^^д^.^).
П
Р1нтересно, что при А = 1 второй член погрешностей в E.47)
имеет тот же порядок величины, что и погрешности численного решения
^кк' ^кк (^^- теорему 5.4). Однако в первом члене E.47) одна
степень Н теряется. С другой стороны, при А = 0 одна степень Н может
быть потеряна во втором члене погрешности. Оба выбора приводят к
дешевой (не требующей дополнительных вычислений функций /ид)
и точной плотной выдаче. Ее порядок точности при ^ G @,1)
уменьшается не более чем на единицу по сравнению с порядком точности,
получаемым при 6=1.
Упралснения
1. Линейно неявное правило средней точки, примененное к
дифференциально-алгебраической системе, выглядит так:
(i-hf,{0) -hfAO)\(y,^,-yA_
[ -4@) -f^9z@) J \ г.+i -zj - ^^¦^^>
486 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
Если вычислять Vi^z^ из E.2) и определить численное решение
при Xq-\- Н (Н = 2mh) посредством
Ул(^0 + Я) = ^B/2m-f 1 + 2/2m-l). ^л(^0 + Я) = ^{z^rn-^^ + 2:2^^1),
ТО этот алгоритм будет расширением (IV.9.16) на
дифференциально-алгебраические задачи.
a) Покажите, что этот метод интегрирует задачу E.8) точно.
b) Примените алгоритм к задаче
2/' = !, Q = u — y^, 0 = v — yu, 0 = w — yv, 0 = z — yw
с нулевыми начальными значениями и проверьте формулу
Замечание. Таким образом, погрешность z-компоненты содержит
не зависящий от h член порядка величины 0(Н^)^ на который
экстраполяция не влияет.
2. Рассмотрите метод из упр. 1 как опорный для некоторого Л^-
экстраполяционного метода. Докажите, что для
последовательности чисел шагов (IV.9.22) экстраполированные значения
удовлетворяют равенствам
С г ;j, Sjf^, приведенными в таблицах 5.5 и 5.6.
Указание. Интерпретируйте V^j, Zj^ как численное решение
методом Розенброка (упр. 3 из разд. IV.9) и проверьте выполнение
условий порядка, выведенных в разд. VI.4 (см. также Хайрер и
Любих 1988b; Шнайдер 1993).
Таблица 5.5. Порядки Vj^ . Таблица 5.6. Порядки Sjk -
1
1
1
1
1
1
1
3
3
3
3
3
3
5
5
5
5
5
7
7
7
7
7
7
7
7
7
7
2
2
2
2
2
2
2
4
4
4
4
4
4
5
5
5
5
5
5
5
5
5
5
5 5
5 5
VI.6. Квазилинейные задачи
Под квазилинейными дифференциальными уравнениями обычно
понимают уравнения, линейные относительно старшей производной.
В случае систем СДУ первого порядка они имеют вид
с{у)у'=т, F.1)
где С{у) — матрица пхп, В областях, где С{у) обратима, уравнение
F.1) может быть приведено к виду
y' = C{y)-'f(y), (б.Г)
И тогда к нему может быть применена любая программа,
интегрирующая ОДУ; надо лишь при каждом вызове функций решать
линейную систему. Однако это приведет к разрушению, например,
ленточной структуры матрицы Якоби, поэтому часто предпочтительнее
работать прямо с уравнением F.1). Если матрица С всюду
имеет ранг т [т<п)^ то уравнение F.1) представляет квазилинейную
дифференциально-алгебраическую систему.
Пример: двилсущиеся
конечные элементы
В качестве примера мы приведем
классическую идею «движущихся конечных
элементов», которую описали в своей работе
К. Миллер и Р.Н. Миллер A981).
Решение w(x,<) нелинейного уравнения в
частных производных
^ = L(t/(x,0), ii@,0 = гхA,0 = О, F.2)
где L(u) — неограниченный нелинейный
дифференциальный оператор,
аппроксимируется многоугольниками конечных
элементов t;(x,aj,5i,.. .,а„,5^), которые
удовлетворяют условиям v(sj,...) = а (рис. 6.1).
Эти многоугольники образуют 2n-мерное
многообразие в гильбертовом пространстве
L^@,1), которое параметризовано
величинами а^, Sj,..., a^j, Syj. Идея состоит в том,
чтобы двигать одновременно a{t) и s(t),
чтобы в любой момент решение в
конечных элементах как можно лучше
адаптировалось к уравнению F.2). Таким обргизом,
мы потребуем, чтобы невязка v — L(v) оста-
Рис. 6.1. Движущиеся
конечные элементы.
у.'
%¦¦
^2J,
/2i
[v-!(.))¦
-i,2fc — Jo :
— fl ^v
2k - Jo dsj
= !oL{v)'
ds,
dv .
daj
di
' ds
dv
dx = 0
dsk '
-dx,
к
dx.
488 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
валась всегда ортогональной к касательному пространству. Условия
l\v-L{v))--l^dx = 0, l\v-Liv))-^dx = 0 F.3)
приводят к системе типа F.1) с
%-1,2Л-1- Jo daj да^ "^'
^2j,2k-l = /о дТ^'д^^^^ ^2j,2k = /о дГ/ЪТ;^^' (^•'^)
/2i-l = /o^^0-^^^,
Для частных производных г», схематически показанных на рис. 6.1, те
из этих скалярных произведений, которые отличны от нуля, примут
вид
(б.5а)
%-l,2j-fl = % + l,2j-l=6^i + l' ^2i-l,2j42 = %>2,2j~l = "^j + l^j + l'
\ A 12л 2
%-,2j + l-%>l,2i —~6^j + l^j + l' %',2j42-%4-2,2j-6"^J-}-l^j + l~^ '
F.5b)
где
^3 == ^j "" ^i-i' ^j "= K- ~ ^j-i)/^j' j = 1,..., П -h 1.
Матрица С(у) — ленточная с шириной ленты 3 +1 + 3. Члены с е^
обязаны своим появлением штрафному члену «межузельной
вязкости» (объяснение см. Миллер и Миллер 1981), назначение которого
— регуляризировать относительное движение узлов, когда их
положение становится плохо обусловленным, что может происходить в
окрестности точек перегиба (см. рис. 6.2). При этом ожидается, что
узлы будут двигаться автоматически в критические области решений,
двигаться вместе с ударными волнами, которые могут возникнуть, и
что a(t) и s{t) станут гладкими функциями.
Приложение к уравнению Бюргеров. Это уравнение имеет вид
Щ = -ии^ + f^'^xx ИЛИ Щ = -(^^) +^^хг' F.6)
где /i = 1/Я, а R называют числом Рейнольдса. Это одно из
уравнений, которые первоначально построил Бюргере A948) как
«математическую модель, иллюстрирующую теорию турбулентности». Однако
вскоре Э. Хопф A950) предъявил аналитическое решение (см. ниже
упр. 1) и пришел к заключению, что «сомнительно, чтобы уравнение
Бюргерса полностью иллюстрировало статистику свободной
турбулентности. (...) Уравнение A) — слишком простая модель, чтобы
воспроизводить случайные флуктуации...». Но и в настоящее время
интерес к этому уравнению сохранился как к нелинейному
уравнению, сходному с уравнениями Навье-Стокса в динамике жидкости.
VI.6. Квазилинейные задачи
489
обладающему при больших R ударными волнами, а при Л -^ оо —
разрывными решениями. Для этого случая интегралы в F.4) примут
вид
f2j^i = Aj+fiBj, f2j=Cj'\^fiDj, j=l,...,n, (б.5с)
где
Aj = (a,..i ~a^.)(ia^. + ^--i)+ (a,- - a^.+i)|a^. + ^a^.^J,
F.5d)
(в случае Dj возникает произведение E-функции Дирака на
разрывную функцию; эти функции надо должным образом «смягчить»).
Выберем в качестве начального условия функцию
ti(x,0) = (sinC7rx)J.(l-x)^/2, F.7)
положим /i = 0.0003, а в качестве начальных положений возьмем
Sj = J/{n 4-1), aj=u(sj,0), i = 1,..., n, n = 100 .
Ha рис. 6.2 показано решение этой задачи со сглаживающим
параметром е = 10-2 при О < < < 1.9. Возникают две ударные волны, которые
позже сливаются в одну.
Рис. 6.2. Решение уравнения Бюргерса
методом движущихся конечных элементов.
490 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
Задачи индекса один
Если матрица С (у) обратима, то уравнение F.1) является
обыкновенным дифференциальным уравнением, и к нему применима
стандартная теория существования и единственности решения. Если же
матрица плохо обусловлена или даже вырождена, новое
исследование необходимо. Чтобы исключить уравнения с особенностями вроде
ху^ = {q-^bx)y (см. разд. 1.5), мы будем предполагать, что
С{у) имеет постоянный ранг т (т <п) F.8)
в окрестности решения. Тогда столбцы С(у) определяют т-мерное
подпространство ХтС(у), которое движется вместе с у. Понятно, что
нужны согласованные начальные значения, чтобы задача F.1) имела
смысл. Иными словами, надо потребовать, чтобы
ПУо)е1тС(уо). F.9)
Теперь мы покажем, как (при определенных условиях) это требование
может быть выполнено для всех х, и что при его выполнении решение
определяется единственным образом. Выберем неособенную матрицу
Т(у) = (^;{^;| ) такую, что Т(у)С(у) = (^^^^^^ ) . F.10)
Это означает, что строки Т2{у) должны служить базисом (п — т)-
мерного ортогонального дополнения к ХтС(у). Умножив уравнение
F.1) на Т(у), получим
(В,(у)\^.^(ТЛу)Пу)\ F 11)
так что условие, соответствующее F.9), примет вид T2{y)f(y) = 0.
Дифференцируя его и подставляя производную во вторую строку
F.11), получим
( В,(у) \ ,_({TJ){y)\ . .
Это уравнение будет регулярным квазилинейным уравнением, если
матрица
( В,(у) \
обратима. F.13)
Лемма 6.1. Пусть матрица С{у) удовлетворяет условиям F.8) и
F.13) у а начальные значения — условию F.9). Тогда квазилинейная
задача С{у)у' = /(у), у{хо) = t/q ^Af^^^ локально единственное
решение.
Доказательство. Условие F.9) означает, что Т2(уо)/(Уо) — О' ^
правая часть F.12) гарантирует, что [Т2{у[х))f(у{х)))' =0. Поэтому
(Т2/)(у(х)) = О для всех х, а решение F.12) является также решением
F.11) и F.1). D
VI.6. Квазилинейные задачи 491
Приведем теперь результат, который является следствием условия
F.13) и в дальнейшем понадобится при обсуждении осуществимости
вычислительных процедур.
Лемма 6.2. Пусть С(у) удовлетворяет условиям F.8) и F.13).
Если /(уо) = ^B/0J/0 ' ^о матрица
С(у) + Х{Г{Уо)-Г{уо,у'о))
обратима при достаточно малых ХфО и у, достаточно близких к у^ .
Здесь
г(у,г/') = |^(сЫу')-
Доказательство. Из условия F.13) следует, что матрица
T(y)CB/L-A(T/)'(j/o) обратима F.14)
при малых Л :^ О и у, близких к t/o • с учетом равенства Т'С -\- ТС = В'
мы получим
(Т'ЖУо) = Г'(уо)С(уо)у; = -Т(уо)Г(Уо. У'о) + 5'(Уо)Уо- F-15)
Поскольку В'[у^)у'^ не дает вклада в нижний блок матрицы F.14), то
эта величина выпадает после подстановки (Т/)' =:Tf'-\-T'f и F.15)
в F.14). Отсюда следует, что матрица
Пу)С[у) + ХТ{уо){Г(уо) - Г(уо, Уо)) обратима.
Утверждение леммы вытекает отсюда по соображениям
непрерывности. П
Численное решение уравнения С{у)у' = f{y)
Как уже говорилось, в случае обратимой матрицы С{у) можно, в
конечном счете, применить какой-нибудь явный численный метод к
уравнению F.Г). Однако если уравнение F.Г) жесткое, надо
применять неявный метод. В этом случае могут быть предпочтительнее
методы, не требующие вычисления матрицы Якоби для C{y)~^f(y).
Преобразование к полуявноИ форме. В случае, если уравнение
F.Г) жесткое или если С{у) — сингулярная матрица,
удовлетворяющая условиям F.8) и F.13), введем новую переменную z = у', так
что система F.1) примет полуявный вид:
y' = z,
F.16)
0 = C(y)z^f{y). ^ ^
Теперь можно применять все методы предыдущих разделов (по
крайней мере, формально). Вопрос о сходимости, однако, требует
дальнейшего исследования; потому что условие A.7) здесь уже не
выполняется.
492 Гл. VL Сингулярно возмущенные задачи и задачи индекса 1
Неявные методы Рунге—Кутты и многошаговые методы. При
использовании метода ?-вложения (см. формулы A.11) для
методов Рунге—Кутты и B.2) для многошаговых методов) мы приходим
к нелинейному уравнению, решая которое итерациями по Ньютону,
придется решать линейные системы с матрицей вида
(г(уо.^оГ-/'(г/о) с-ы}- ^^-^^^
Здесь а = {jh)"^» а 7 — собственное значение матрицы метода
Рунге—Кутты. В силу леммы 6.2 эта матрица обратима при достаточно
малых значениях Л > О. Тогда сходимость будет вытекать из
результатов, полученных в разделах VII.3 и VII.4 (см. упр. 2).
Методы Розенброка. Метод D.3), будучи применен к системе
F.16), приводит к уравнениям
U)=fe)^|-a;)• (^|)=(^:L;)'
F.1^
F.18а)
F.18b)
И в этом случае нетрудно видеть, что F.18Ь) представляет собой
линейную систему, регулярность матрицы которой гарантируется
леммой 6.2. Однако, поскольку условие A.7) не выполняется, нужна
новая теория для условий порядка локальной погрешности, а также для
сходимости глобальной погрешности. Эта теория показывает,
например, что для коэффициентов метода нужны новые условия порядка, и
объясняет, почему, скажем, программа RODAS при непосредственном
ее применении к F.16) не дает точные результаты. Все
подробности читатель может найти в оригинальной публикации (Любих и Рош
1990).
Экстраполяционные методы
Прежде всего, надо найти для уравнения F.1) подходящие линейно
неявные дискретизации по методу Эйлера, которые могли бы служить
опорным методом для экстраполяционного алгоритма (см. разд. IV.9).
Метод Дойфлхарда и Новака. Применяя линейно неявный метод
Эйлера (IV.9.15) к дифференциальному уравнению F.Г), мы получим
(/-М)A,,^., -г/,) = лс(г/,)-7(у.), F.19)
где
А^(С-'/)'(уо) = С(уоГ'{Г(уо)-Т(уо,у'о))
И Г(у,у*) такое же, как в лемме 6.2. Умножение F.19) на C(i/,) дает
(С(у,) - ЛСA/,)С(%)-'J)(y,+i - у,) = Л/(у,),
VI.6. Квазилинейные задачи 493
где J = Пуо) — ГB/о> Уо) • Дойфлхард и Новак A987) предложили
заменить С(у,)С(уо)~^ единичной матрицей, что «может быть
интерпретировано просто как внесение погрешности аппроксимации в
матрицу Якоби». Это приводит к дискретизации
(С{у,) - /iJ)(j/,+i - у,) = Л/(у,), F.20)
представляющей базовый шаг в программе LIMEX, которую описали в
своей работе Дойфлхард и Новак A987). Регулярность матрицы этой
линейной системы гарантируется тоже леммой 6.2.
Вычисление J требует некоторой аппроксимации для Zq = Уо • Т^"
кие согласованные начальные значения должны быть вычислены явно
для первых базовых шагов, а для последующих шагов они
получаются с помощью экстраполяции величины
^n = iyn-yn-i)/h. F.21)
Линейно неявный метод Эйлера для полуявной модели. Другая
возможность состоит в применении линейно неявного метода Эйлера
E.2) к дифференциально-алгебраической системе F.16). Это дает
[-hJ hC{yo)) V^ItI-^ij/B/i)~b(yJzJ' (^22)
где ^0 = 2/^= 2/(^о) • Первая строка дает z^^^ = {у^_^^ ~ y,)//i, а вторая
принимает вид
{С{Уо) - hJ){y,^, - у,) = Л/(у,) - (С(у,) - С(уо))(у^ - y._i). F.23)
Самый последний член обращается в нуль при 1 = 0, так что алгоритм
не использует значение у_ ^.
Асимптотические разложения. Для того, чтобы обосновать
теоретически использование F.20) или F.23) в качестве базового шага
в каком-либо экстраполяционном процессе, требуется исследование
асимптотического разложения соответствующих глобальных
погрешностей.
В ситуации, когда С{у) обратима, дискретизация F.20)
является непротиворечивой одношаговой дискретизацией уравнения F. Г) и
поэтому, в соответствии со стандартной теорией (теорема II.8.1),
обладает асимптотическим разложением, члены которого, однако, зависят
от жесткости. Для второй дискретизации F.23) из теоремы 5.3
выводится существование возмущенного асимптотического разложения,
поскольку система F.16) имеет вид A.6) и условие A.7) выполнено.
В ситуации, когда С{у) сингулярна, Любих A989) обнаружил
существование возмущенных асимптотических разложений для обеих
дискретизаций F.20) и F.23). За дальнейшими подробностями мы
отсылаем читателя к его оригинальной работе, содержащей, в
частности, исследование влияния этих возмущений на экстраполированное
численное приближение.
494 Гл. VI. Сингулярно возмущенные задачи и задачи индекса 1
Упралснения
1. Восстановите аналитическое решение, которое нашел Э. Хопф для
уравнения Бюргерса F.6).
Указание. Введите новую зависимую переменную
^(x,0=exp{-i-^ u{i,i)di- j^ с{т)Aт].
Покажите, что при подходящем выборе c{t) функция <^(х,<)
удовлетворяет одномерному уравнению теплопроводности. Тогда
решение u{x,t) уравнения F.6) получается из (p[x,t):
и = -2/i(logy?)^ = -2/i(^^/v?) .
2. Пусть выполнены условия F.8) и F.13). Исключая из уравнения
О = C{y)z — f(y) наибольшее возможное число компонент z,
преобразуйте систему F.16) в эквивалентную ей систему вида
2/' = F(t/,u), 0 = G(y),
где и обозначает остальные компоненты z.
a) Докажите, что методы Рунге—Кутты и многошаговые методы
инвариантны относительно этого преобразования.
b) Покажите, что матрица Gy{y)F^{yyU) обратима, так что
применимы результаты, полученные для сходимости в разделах УП.З
и VII.4.
3. (Квазилинейные задачи с массовой матрицей градиентного типа,
см. Хайрер, Любих и Рош 1989, р. 111.) Рассмотрите
электрическую цепь A.14), но пусть теперь емкости зависят от напряжений,
например, так:
C, = C,o/il-(U,-Uj)/U,)''',
так что выражения C/^{U- —Uj) в A.14) надо заменить
выражениями {Cff(Ui — Uj)y. Покажите, что соответствующие уравнения
имеют вид F.1) с
С(у) = Aq'iy),
где Л — постоянная матрица, а q{y) — известная функция у.
Покажите, что такие задачи можно эффективно решать, вводя в
качестве новой переменной q(y) = z, так что задача принимает
полуявный вид:
Az' = f{y), 0 = z-q(y).
Глава VII
Дифференциально-алгебраические
уравнения высших индексов
( (Рисунок к. Вгшнер)
В предыдущей главе мы рассматривали простейший частный
случай дифференциально-алгебраических уравнений — так называемые
задачи индекса 1. Однако многие задачи, представляющие
практический интерес, имеют более высокие индексы, и это делает их всё
более трудными для решения численными методами.
Мы начнем с классификации дифференциально-алгебраических
уравнений по индексам (индекс нильпотентности для линейных задач
с постоянными коэффициентами, индекс дифференцирования и
индекс возмущения для нелинейных задач общего вида); будут
представлены некоторые примеры, возникающие в приложениях (разд. VII. 1).
В разд. VII.2 обсуждаются несколько различных подходов к
численному решению задач с высшими индексами: понижение индекса
посредством дифференцирования в сочетании с подходящими
проекциями; методы, основанные на представлении в пространстве состояний;
рассмотрение систем как переопределенных или бесструктурных. В
разделах VII.3 и VII.4 изучаются свойства сходимости многошаговых
методов и методов Рунге—Кутты при непосредственном применении
их к системам индекса 2. Может случиться, что порядок сходимости
окажется меньше, чем для обыкновенных дифференциальных
уравнений (явление «снижения порядка»). Изучение условий,
гарантирующих определенный порядок сходимости — предмет рассмотрения в
разд. VII.5. Полуявные методы для задач индекса 2 особенно
подходят для механических систем со связями (разд. VII.6). В разд. VII.7
подробно рассматривается многозвенный механизм и его расчет
численным методом. Наконец, в разд. VII.8 мы обсуждаем симплекти-
ческие методы для гамильтоновых систем со связями и объясняем их
поведение на длительных временных интервалах с помощью
обратного анализа погрешностей для дифференциальных уравнений на
многообразиях.
VII. 1. Понятие индекса
и различные примеры
Наиболее общая форма дифференциально-алгебраической
системы — это неявное дифференциальное уравнение вида
F(t/',t/) = 0, A.1)
где F и и имеют одинаковую размерность. Мы всегда будем
предполагать, что F дифференцируема достаточное число раз.
Неавтономная система приводится к виду A.1) посредством добавления х к
вектору и и включения в систему уравнения х' = 1.
Если матрица дР/ди' обратима, то формально можно разрешить
уравнение A.1) относительно и' и получить обыкновенное
дифференциальное уравнение. В этой главе нас будут интересовать такие
задачи A.1), в которых матрица дР/ди' сингулярная.
Линейные уравнения
с постоянными коэффициентами
«Uebrigens капп ich die Meinung des Hm. Jordan nicht
theilen, dass es ziemlich schwer sei, der Weterstrass-schen
Analyse zu folgen; sie scheint mir im Gegentheil vollkommen
durchsichtig zu sein, ...»
«Впрочем, я не могу разделить мнение г-на Жордана^
будто следовать гшализу Вейерштрасса довольно трудно;
напротив, он кажется мне совершенно прозрачным,...»
(Л. Кронекер 1874)
Самыми простыми и лучше всего понятыми задачами вида A.1)
являются линейные дифференциальные уравнения с постоянными ко-
эффи циентам и
Bu'-^Au = d{x), A.2)
Разыскивая решения вида c^^Uq (когда d{x) = 0), мы приходим к
рассмотрению «пучка матриц» А Ч- ХВ. Если матрица А -\- ХВ особенная
при всех значениях А, то уравнение A.2) при заданных начальных
условиях либо не имеет решения, либо имеет бесконечно много
решений (упр. 1). Поэтому мы будем иметь лело только с регулярными
пучками матриц, т.е. с задачами, для которых многочлен det(^4-AJ5)
не обращается тождественно в нуль. Ключом к решению уравнения
A.2) является следующее одновременное преобразование матриц А и
В к каноническому виду.
VII. 1. Понятие индекса и различные примеры 497
Теорема 1.1 (Вейерштрасс 1868, Кронекер 1890). Пусть Л-\-ХВ —
регулярный пучок матриц. Тогда существуют неособенные матрицы
Р и Q такие, что
p^Q=(?;), pBQ=(^i oj, A.3)
где N = blockdiag (N^,.. .yNj^) и каждый блок N^ размерности m,
имеет вид
/о 1 0\
N.= • ; I. A.4)
\о о/
а матрицу С можно считать имеющей каноническую форму Жордана.
Доказательство (Гантмахер 1954 (гл. XII), см.также упражнения
2 и 3). Зафиксируем некоторое число с, при котором матрица А-\-сВ
обратима. Умножив матрицу
Л + Л5 = Л + с5 -f (Л ~ с) j3
на матрицу, обратную к ЛЧ-с5, и затем преобразовав [А-\-сВ)''^В
к жордановой канонической форме (теорема 1.12.2), мы получим
матрицу
в которой J^ содержит жордановы блоки с ненулевыми
собственными значениями, а Jj — ^ нулевыми (рс13мерность Jj равна как
раз степени многочлена dei{AЛ-\В)). Следовательно, матрицы J^
и I — CJ2 обратимы. Умножение матрицы A.5) слева на матрицу
blockdiag (Jf^(/-cJ2)-M
дает
Затем матрицы J^^[I — cJ^) и (I — cJ2)~^J2 можно привести к
канонической форме Жордана. Поскольку у матрицы (/ —cJ2)~^«/2 ^^^
собственные значения равны нулю, мы получим желаемое
разложение A.3). D
Теорема 1.1 позволяет получить решение уравнения A.2)
следующим образом. Умножим систему A.2) слева на Р и используем
преобразования
«=«(?)¦ ^ад=(*))-
При этом дифференциально-алгебраическая система A.2) распадется
на две:
у'-\-Су = ф), 7Vz4 Z = S(x). A.6)
498 Гл. VII. Дифференциально-алгебраические задачи высших индексов
Теперь для у мы получили просто обыкновенное дифференциальное
уравнение, а система для г, в свою очередь, распадается на к
подсистем, каждая из которых имеет вид
4 + ^1 =*iW'
• A.7)
где т = т^ из A.4). Здесь последнее уравнение определяет г^, а
остальные компоненты вычисляются рекурсивно повторным
дифференцированием. Таким образом, z^ зависит от (т—1)-й
производной S^ (х). Так как численное дифференцирование является
неустойчивой процедурой, наибольшее значение т,, встречающееся в A.4),
представляет меру трудности численного решения задачи A.2). Это
целое число (maxm,) называют индексом нильпотентности пучка
матриц А + ХВ. Он не зависит от конкретных преобразований,
используемых для приведения матриц к виду A.3) (см. упр.4).
Линейные уравнения с переменными жоэффшщентами. В случае,
когда матрицы А и В в A.2) зависят от х, исследовать решения
гораздо сложнее. Умножение уравнения A.2) на Р(х) и подстановка
и = Q{x)v приводят к системе
PBQv' -f {FAQ Н- PBQ')v = О, A.8)
откуда видно, что преобразование A.3) здесь уже не достигает
цели. Используя преобразования вида A.8), Кункель и Мерман A995)
вывели каноническую форму для линейных систем с переменными
коэффициентами.
Индекс дифференцирования
«Многие автомобили в Англии имеют рулевое колесо».
(Faulty Towers, Cleese and Booth 1979)
Начнем со следующего примера:
t/2 = 1.4.2/i+cosB.5.z) = /2(j/,z), ^^'^^f
0 = 2/? + У2^-1=^(у)- (l-9b)
«Переменную управления» z в A.9a) можно интерпретировать как
положение «рулевого колеса», сохраняющее направление векторного
поля [pi, У2) касательным к окружности у? + 2/2 = 1 > так что условие
A.9Ь) остается все время выполненным (см. рис. 1.1а).
Дифференцируя A.9Ь) и подставляя A.9а), мы должны поэтому получить
5уЫ/(у,г)=0. A.9с)
Это уравнение определяет «скрытое» подмногообразие цилиндра, на
котором должны лежать все решения системы A.9а,Ь) (см. рис. 1.1b).
VI1.1. Понятие индекса и различные примеры
499
Рис. 1.1а. Векторное поле A.9a,d). Рис. 1.1Ъ. Скрытое подмногообразие.
Мы пока еще не знаем, как с ростом х изменяется переменная г. С
этой целью можно продифференцировать A.9с) по х и из полученного
соотношения 9yy{fJ)-^Syfyf-\-9yfz^' = 0 извлечь
^' = "{ду/гГ' {gyyif. f)+9yfyf) (i.9d)
при условии, что матрица
9y{y)fz(y^^) обратима. A.10)
Мы смогли преобразовать дифференциально-алгебраическую
систему A.9а,Ь) в систему обыкновенных дифференциальных уравнений
A.9a,d) посредством двух аналитических дифференцирований
уравнения связи A.9Ь). На этом обстоятельстве основано следующее
определение, выкристаллизовавшееся в нескольких работах (Гир и Петзолд
1983, 1984; Гир, Гупта и Леймкулер 1985; Гир 1990; Кампбелл и Гир
1995).
Определение 1.2. Уравнение A.1) имеет индекс дифференцирования
d%=m^ если m — наименьшее число аналитических
дифференцирований
/г(^» = 0, —L^ = 0, ...,—^1^ = 0, A.11)
требующихся для того, чтобы из уравнений A.11) посредством
алгебраических преобразований можно было бы получить систему
обыкновенных дифференциальных уравнений явного вида и* = (р(и),
носящую название <аскрытое1^, или лежащее в основе ОДУ.
500 Гл. VII. Дифференциально-алгебраические задачи высших индексов
Примеры. Линейные уравнения с постоянными коэффициентами.
Легко видеть, что следующая задача:
4 + ^1 = ^1 4' + ^1 = ^1
4 + ^2=(J2 => 4" + 4' = *2 => 4=*'1-<^2+<5з" A12)
^3 — ^3 "~
имеет индекс дифференцирования, равный трем. Таким образом, для
линейных уравнений с постоянными коэффициентами индекс
дифференцирования совпадает с индексом нильпотентности.
Системы индекса 1. Дифференциально-алгебраические системы
y' = f{y.z), A.13а)
0 = (/(у,г), A.13Ь)
которые мы уже встречали в главе VI, не содержат z'.
Продифференцировав A.13Ь), можно получить уравнение
z'^-9:4y,2)g^{y,z)f{y,z) A.13с)
при условии, что матрица д^ обратима в окрестности решения.
Следовательно, задача A.13а,Ь) с обратимой матрицей д^ имеет индекс
дифференцирования, равный единице.
Системы индекса 2. Для системы
y' = f{y,z), A.14а)
0 = </(у), A14Ь)
В которой переменная z отсутствует в алгебраическом уравнении
связи (пример — система A.9)), путем дифференцирования уравнения
A.14Ь) мы получаем уравнение «скрытой связи»
Q = 9y{y)f(.y,z). A.14с)
Если условие A.10) выполняется в окрестности решения, то
уравнения A.14а) и A.14с) представляют собой задачу индекса 1.
Дифференцирование A.14с) дает недостающее дифференциальное
уравнение для Z, так что задача A.14а,Ь) имеет индекс
дифференцирования 2. Если начальные значения удовлетворяют уравнениям О = ^(уо)
и О = </у(Уо)/(%)'2^о)) и^ называют согласованными. В этом и только
в этом случае система A.14а,Ь) имеет (локально) единственное
решение.
Система A.14а,Ь) является представителем более широкого класса
задач типа A.13а,Ь) с сингулярное матрицей д^. Если допустить, что
д^ имеет постоянный ранг в окрестности решения, то можно
исключить некоторые алгебраические переменные из уравнения О = д{у, z),
пока система не примет вид A.14). Это можно осуществить
следующим образом. Из предположения о постоянстве ранга следует, что
либо существует компонента д^ для которой локально dgjdzi /О,
либо dg/dz^ обращается в нуль тождественно, так что д больше не
VI1.1. Понятие индекса и различные примеры 501
зависит от z^. В первом случае можно выразить z^ как функцию у и
затем исключить z^ из системы; повторяя эту процедуру для Zj, 23 и
т.д., мы придем к системе вида A.14). Это преобразование не изменяет
индекса. Более того, большинство численных методов инвариантны
относительно этого преобразования. Поэтому теоретическая работа,
проделанная для системы вида A.14), будет иметь силу и для более
общих задач.
Системы индекса 3. Задачи вида
г/' = /(у,г), A.15а)
г' = /:(г/,г.«), A.15Ь)
0=5(y) A.15с)
имеют индекс дифференцирования 3, если матрица
9yfz^xi обратима A16)
в окрестности решения. Дифференцируя A.15с) дважды, получим
0 = //,/, A.15d)
0 = 9yy{fJ)'^9yfyf + 9yfzk^ A.15е)
Уравнения A.15а,Ь), A.15е) вместе с условием A.16) имеют вид
задачи A.13а,Ь) индекса 1. Согласованные начальные значения должны
удовлетворять трем условиям A.15c,d,e).
Глубокое исследование пространства решений для,
дифференциально-алгебраических систем общего вида было проведено в работах
(Грипентрог и Мерц 1986; Мерц 1989, 1990). Эти авторы попытались
избежать предположений относительно гладкости задачи, насколько
это возможно, и заменить рассмотренные выше дифференцирования
тщательным исследованием подходящих проецирований, зависящих
только от первых производных F.
Дифференциальные уравнения на многообразиях
На языке дифференцируемых многообразий, необходимость
использования которого в теории ДАУ показал Рейнболдт A984),
уравнение связи (как, например, д(у) =0) представляет многообразие,
которое мы будем обозначать
A^ = {y€lR''|<7(y)=0}. A.17)
Будем предполагать, что ^ : R" —>• Ш^ (где т<п) является функцией,
дифференцируемой достаточное число раз, и что ее матрица Якоби
ду{у) имеет полный ранг при у?М. Для фиксированного у ЕМ
обозначим
T^M = {v€R''\g^{y)v = 0} A.18)
пространство, касательное к М ъ точке у. Это линейное
пространство, имеюшее ту же размерность п — т, что и многообразие М.
502 Гл. VII. Дифференциально-гшгебргшческие задачи высших индексов
Е
Рис. 1.2. Многообразие с полем касательных векторов,
карта и кривая решения.
Векторным полем на М называется отображение v\M-^W^, для
которого v[y) G ТуМ при всех у 6 Af. Для такого векторного поля
будем называть
j/' = t;(y), уем A.19)
дифференциальным уравнением на многообразии М.
Дифференцирование на (n—m)-мерном многообразии описывается с помощью так
называемых карт (р-: [/,• -> ?",, где области С/,, покрывают
многообразие Л<, а ?*,- — открытые подмножества в М'*"'" (см. рис. 1.2, а также
Ланг A962), гл.II и Абрагам, Марсден, Ратью A983), гл.III)i).
Локальную теорию обыкновенных дифференциальных уравнений можно
непосредственно распространить на векторные поля на
многообразиях (см. рис. 1.2):
проецируем векторы v{y) на Е^ с помощью карты ^,-,
умножая v{y) на матрицу Якоби отображения у?, в
точке у; затем применяем результаты стандартной теории к
проецированному векторному полю в R^~^ и
отображаем решение обратно в М.
Таким путем можно доказать (локально) существование решений у
уравнения A.19). Полученное решение не зависит от выбора карты.
Там, где решение покидает область карты, интегрирование следует
продолжить с помощью другой карты.
Заддчи шщекса 2. Рассмотрим систему A.14а,Ь) и предположим,
что условие A.10) выполнено. Это условие означает, что матрица
ду(у) имеет полный ранг, так что A.17) является гладким многообра-
^ Или В.И. Арнольд, Обыкновенные дифференциальные уравнения —
М.: «Наука», 1971, гл.5. — Прим, ред.
VIIл. Понятие индекса и различные примеры 503
зием. Кроме того, из теоремы о неявной функции следует, что
продифференцированное уравнение связи A.14с) можно разрешить
относительно Z (в окрестности решения), т.е. существует гладкая
функция ЛB/) такая, что
i/y(y)/(y,^)=0 ^^ ^ = Л(У). A.20)
Подставляя это соотношение в A.14а), получим
У' = /(У,ЛЫ). У€Л<, A.21)
ЧТО является дифференциальным уравнением на многообразии вида
A.17), потому что в силу A.20) /(у, Л(у)) G Т^уМ. Дифференциальное
уравнение A.21) эквивалентно системе A.14а,Ь).
Пример, Многообразие М для задачи A.9)
— одномерное (окружность). В точках, где у^ ф^
±1, можно получить локальное решение
уравнения A.9Ь) У2 = ±\/1 —j/i. Карту (р
составляет отображение (у^, У2) »-> Ух, которое является
биективным в окрестности рассматриваемой
точки. Подставляя в A.9а) z из решения уравнения
A.9с) и приведенное выше Уз, получим
уравнение вида yj = G(yi), которое и представляет
векторное поле, спроецированное в М^.
Заддчи ицдежса 3. Для системы A.15а,Ь,с) решения лежат на
многообразии
М = {{у, z) I д(у) = О, 9y{y)f{y, z) = 0}. A.22)
Из предположения A.16) следует, что матрицы ду{у) и 9y(y)fz(yiZ)
имеют полный ранг, так что М действительно является
многообразием. Касательное к нему в точке (у, z) прххтранство есть
^(у..)^ = {("'«') I Ф>=^^ 9yy{y){ny,z),v) +
+ Уу(у)(/,(У,г)« + Л(У.^Н=0}.
Решая уравнение A.15е) относительно и и подставляя результат в
A.15Ь), получим дифференциальное уравнение на многообразии М.
Уравнения A.15d,e) гарантируют, что полученное векторное поле
лежит в ках:ательном пространстве Т,у.^хМ при любых (у, z) G Л<.
Индекс возмущений
«Now fills thy sleep with pertm-bations». — «... сон твой
возмущает». {Дух Анны, — Шекспир, Ричард Шу акт V, сц. III)
Другая концепция индекса, выдвинутая в работе ХЛР89^,
интерпретирует индекс как меру чувствительности решений задачи к
возмущениям.
^ Работа (Хайрер, Любих и Рош 1989), напечатанная в «Lecture Notes»,
часто цитируется в дальнейшем, и ссылки на нее будут даваться в
сокращенном виде: ХЛР89.
504 Гл. VII. Дифференциально-алгебраические задачи высших индексов
Определение 1.3. Уравнение A.1) имеет индекс возмущений рг = т
вдоль решения и{х) на отрезке [0,х], если m — наименьшее целое
число такое, что для всех функций и(х), дающих невязку
F(u',u) = S(x), A.24)
на [0,х] существует оценка
||«(х)-«(хI|<с(||«@)-«@)||+ max 11^@11 + ...+ т^^^^
A.25)
при условии, что выражение в правой части достаточно мало.
Замечание. Мы намеренно не пишем в этом определении «Пусть
и(х) — решение уравнения F(u\ и) = S(x) ...», потому что
существование решения и(х) при произвольно заданном S(x) не
гарантировано. Мы отправляемся от й и вычисляем S как невязку уравнения
A.1).
Системы шщекса 1. Для вычисления индекса возмущений задачи
A.13а,Ь) рассмотрим возмущенную систему
y' = mz) + S^{x), A.2ба)
0 = 9iy,z) + S2(x). A.26b)
Здесь существенно, что разность z — z можно оценить с помощью
теоремы о неявной функции, не прибегая к дифференцированию
уравнения. Так как матрица д^ обратима по предположению, эта теорема
позволяет получить из сопоставления A.2бЬ) и A.13Ь) оценку
\\z(x) - z(x)\\ < с,(Шх) - у{х)\\ + \\S,{x)\\) A.27)
при условии, что правая часть A.27) достаточно мала. Вычтем теперь
A.26а) из A.13а), проинтегрируем от О до х, воспользуемся условием
Липшица для / и вышеприведенной оценкой для ?(x) — z{x). Это
дает следующую оценку для е(х) = \\у(х) — у(х)\\:
е(х)<е@)Ч-С2 / e{t)di + C^ f ||*2(<I|Л + 11 / S^(t)dt\
Jo Jo ¦' Jo '
в этой оценке для Jj берется интеграл от нормы, а для S^ — норма
интеграла. Причина заключается в том, что возмущения
алгебраического уравнения A.13Ь) более серьезны, чем возмущения
дифференциального уравнения A.13а). Наконец, применив лемму Гронуолла
(см. упр. 1.10.2), получим на замкнутом отрезке [0,х] оценку
тх)-у{х)\\ < С^ (||j/@)-j/@)|| +? \\S,{t)\\dt + max^ || j^ S,(f)л||) <
<(:^5(lly@)-y@)||+ max ||<52@||+ max ||<Jj@||).
Это неравенство вместе с неравенством A.27) показывает, что индекс
возмущений задачи равен единице.
VIM. Понятие индекса и различные примеры
505
Системы ицдекса 2. Для системы A.14а,Ь) рассмотрим такое
возмущение:
y^ = f{y.z)+S(x), A.28а)
0 = (/(у) + ^(х). A.28Ь)
Дифференцирование A.28Ь) дает
0 = 9уШ{У,^)+ду{т':) + 0'{х). A.29)
Если выполнено предположение A.10), можно использовать
оценки, полученные для случая задачи индекса 1, заменив S^ix) на
д^^{у(х))б{х) + $'(х), что дает
iiy(x) - у{х)\\ < с{\\т - ym\-^j\\m)\\+wmm).
\\Цх) - г[х)\\ < С(||у@) - у@)|| + max \Ш)\\ + тах^ ||^'@||) •
A.30)
Так как эти оценки зависят от первой производной в, индекс
возмущения этой задачи равен двум. Более строгая оценка для у-компоненты
дана в упр. 6.
Пример. Рис. 1.3 является иллюстрацией к задаче A.9а,Ь) индекса
2. Малые возмущения д{у), в одном случае вносимые разрывностью
первой производной (на рисунке слева), в другом —
колебательного типа (справа), приводят соответственно к разрывам или сильным
осцилляциям Z,
^У1 уу,
Рис. 1.3. Возмущения задачи индекса 2.
506 Гл. VII. Дифференциально-гилгебраические задачи высших индексов
Приведенные выше примеры могут создать впечатление, что
индексы дифференцирования и возмущений всегда равны. Следующие
контрпримеры показывают, что это не так.
Контрпримеры. Первый контрпример — задачу типа М[у)у' =
= f(y) — привел Любих A989):
у/ - УзУ2 + 2/22/3 = 0) Уг - У3У2 + У2У3 = О,
2/2 = 0, У2 = ез\пи;х, A31)
2/з = 0, у^ = ecosujx
с у.[0)=0 (г = 1,2,3). Подстановка У2 = esinux и y^rz еcosljx в
первое уравнение дает у/ = е^и, что делает при фиксированном е и
а; —>^ ОС оценку A.25) с т= 1 невозможной. Однако ясно, что при
m = 2 оценка A.25) применима. Таким образом, эта задача с
индексом дифференцирования, равным, очевидно, единице, имеет индекс
возмущений, равный двум.
Некоторое время считалось, что индексы дифференцирования и
возмущений могут отличаться не более чем на единицу (см. 1-е
издание, р. 479). Поэтому следующий пример, который привели Кампбелл
и Гир A995), оказался большой неожиданностью:
2/т^У' + У = 0. A.32)
Здесь N — нильпотентный жорданов блок размерности тхт
(верхняя треугольная матрица). Так как последняя строка N — нулевая,
то г/уу1 = О и, следовательно, индекс дифференцирования равен
единице. С другой стороны, добавление возмущения делает у^ отличным
от нуля. По этой причине индекс возмущения задачи A.32) равен т.
Задачи теории управления
Многие задачи теории управления приводят к обыкновенным
дифференциальным уравнениям вида t/ = /(у, и), где и представляет
множество управляющих параметров (функцию управления). Надо
выбрать управление таким образом, чтобы, как и в примере A.9),
решение удовлетворяло некоторому уравнению связи О = д{у, и). За
примерами численного решения таких задач управления мы отошлем
читателя к работам (Бренан 1983) (моделирование космического
челнока) и (Бренан, Кампбелл и Петзолд 1989).
Згщэчи оптимального управления формулируются так: в
дифференциальных уравнениях у' = /(у, и) надо выбрать управление и{х)
так, чтобы минимизировать некоторый функционал цены. При этом
уравнение Эйлера—Лагранжа часто становится дифференциально-
алгебраической системой (Понтрягин, Болтянский, Гамкрелидзе и
Мищенко 1961; Атанс и Фалб 1966; Кампбелл 1982). Мы
продемонстрируем это на задаче
У' = /(У,«), У@)=уо A.33а)
/¦
Jo
VI1.1. Понятие индекса и ргизличные примеры 507
с функционалом цены
J{u)= f ip{y(x),u{x))dx. (L33b)
При заданной функции и(х) решение у(х) определяется из A.33а).
Чтобы найти условия, которым должно удовлетворять управление
и{х), минимизирующее функционал J(u) в A.33b), рассмотрим
возмущенное управление и{х) -^ е5и(х), где Su(x) — произвольная
функция, а ? — малое число. Этому управлению соответствует другое
решение задачи A.33а): у{х) -^ eSy(x) -h 0{б^). Собирая члены с
одинаковыми степенями е, получим
Sy'ix) = fy[xNy[x) -h f^[xNu[x), 8y{Q) = 0, A.34)
где, как обычно, использованы обозначения /у{х) =^ fy{y{x),u(x)) и
т.п. Из A.33b), используя линеаризацию, получаем:
J(u -heSu) - J{u) = s {<Py{x)Sy{x) -f v?u{x)Su(x)^dx -f 0{e^),
Отсюда вытекает необходимое условие
U^ {х)8у[х) -h ^Лx)(Jii(x)) dx = О A.35)
того, чтобы и[х) было оптимальным решением нашей задачи. Чтобы
в A.35) выразить 8у через rfti, мы введем присоединенное
дифференциальное уравнение
v' = -fy{x)''v-<p^{xf, t;(l)=0 A.36)
С неоднородным членом (ру{х)'^. Тогда мы получим (см. упр. 7):
I <p^{x)Sy{x)dx = l v'^{x)f^(x)Su{x)dx. A.37)
Подстановка этого выражения в A.35) дает нужное нам условие:
I {v'^ix)f,{x) + <p,{x))Su{x)dx = 0. A.38)
Так как это соотношение должно выполняться при любых Su, мы
выводим отсюда требующееся нам соотношение v'^(x)f^(x) + <^u(^) = О,
опираясь на так называемую «фундаментальную лемму
вариационного исчисления».
Подведем итог. Мы доказали, что решение сформулированной
выше задачи оптимального управления должно удовлетворять системе
У' = /(У,«), 2/@) =Уо1
v' = -fy{y. ufv - ^^{у, uf, v[\) = О, A.39)
0 = ^^/и(У'^)+^и(У'«)-
508 Гл. VII. Дифференциально-алгебраические задачи высших индексов
Это дифференциально-алгебраическая задача с граничными
условиями. Ее можно также получить непосредственно из принципа
минимума Понтрягина, см. (Понтрягин и др. 1961; Атанс и Фалб 1966).
Дифференцирование алгебраического соотношения в A.39)
показывает, что если матрица
Ъ^Ш(У'-) + ^(У'-) A-40)
1=1
обратима на решении, то система A.39) имеет индекс 1. В упр. 8
представлена ситуация, когда система A.39) имеет индекс 3. Задача
индекса 5 этого же типа приведена в «примере 3.1» в статье Кларка
A988). Другие задачи теории управления с высокими индексами
обсуждаются в работе Кампбелла A995).
Механические системы
¦... berechnen wir T^VyL. Mehr brauchen wir von der
Geometrie und Mechauiik iinseres Systems nicht zu wissen.
Alias (ibrige besorgt ohne imser Zutun der Formadismus von
LAGRANGE».
¦... рассчитаем T^V^ L. Больше нам ничего не надо знать
о геометрии и механике нашей системы. Все остальное
обеспечит без налхего участия формализм ЛАГРАНЖА».
(Зоммерфельд 1942, §35)
Интересный класс дифференциально-алгебраических систем
возникает при механическом моделировании систем со связями. Лучший
метод для вывода уравнений движения механических систем — это
принцип Лагранжа—Гамильтона. Его долгая история восходит к
просто теологическим идеям Лейбница и Мопертюи. Пусть gi,..., ^„ —
координаты, описывающие положение системы, и w, = g, — скорости.
Предположим, что задана некоторая функция L{q,q). Тогда
уравнения Эйлера вариационной задачи
L{q,q)dt = т\п\ A.41)
имеют вид
или
/
n n
г=1 t=l
Великое открытие Лагранжа A788) состоит в том, что для
функции L = T—Uу где Г — кинетическая энергия и U —
потенциальная энергия, дифференциальные уравнения A.43) описывают
движение соответствующей «консервативной системы». Доказательство и
VII. 1. Понятие индекса и различные примеры 509
различные обобщения можно найти в любой книге по механике (см.,
например, Зоммерфельд A942), том I, §§ 33-37 или Арнольд A979),
часть II).
Пример 1. Для математического маятника длины ? мы выберем в
качестве координаты, описывающей его положение, угол б = д^, так
что Т = т?^в^/2 и [/ = —?тд cos Р. Тогда уравнение A.43) примет вид
хорошо известного уравнения маятника: ?в = —д sin в.
Движение^ ограниченное связями. Предположим теперь, что
имеются некоторые связи, которые ограничивают движение и задаются
уравнениями 5^1 (9) = О» • )9т{я) = О• Еще одна великая идея Лагран-
жа состоит в том, чтобы в этом случае изменить «функцию Лагран-
жа» следующим образом:
1 = Т-и-ХМч)---К9Лч). A.44)
Здесь к координатам добавлены «множители Лагранжа» А,;
важно, что ввиду независимости L от А, уравнения A.43) для
производных по А;^ превращаются просто в наши дополнительные условия
Пример 2. Опишем теперь маятник в декартовых координатах а:, у
с уравнением связи х^ -h2/^ — ^^ = 0. Это дает для A.44) выражение
L=y(i2-|-y2)-m</y-A(x2-h 2/2-^2),
и уравнения A.43) примут вид
т'х = —2жА,
ту = -тд - 2j/A, A-45)
0 = хЧу2-г'.
В этом примере физический смысл А — напряжение в стержне,
удерживающем материальную точку на требуемой орбите.
Общий вид механической системы A.43) со связями в векторных
обозначениях (и с заменой точек штрихами) таков:
q' = щ A.46а)
M{q)u' = f{q,u)-G'^[q)K A.46b)
О = (/(9), A.46с)
где M[q) = Tg^ = Т^^ — положительно определенная матрица, G{q) =
= dg/dq и g = (9i,...,gn)^, ti = (^i,.. .,g„)^, A = (A^,..., A^)^. Для
такой задачи возможны разные формулировки, и каждая из них
требует своего вычислительного подхода.
Формулировка в внде задэчи иццекса 3 (на уровне координат,
наглядная форма). Если формально умножить уравнение A.46Ь) на
510 Гл. VII. Дифференциально-алгебраические задачи высших индексов
М"^, то система A.46) примет вид A.15) с (g,w,A) в роли (у, г, к).
Условие A.16), записанное для системы A.46), будет таким:
GM-^G^ обратима. A.47)
Оно выполняется, если уравнения связи A.4бс) независимы, т.е. если
строки матрицы G линейно независимы. При этом предположении
система A.46а,Ь,с) оказывается задачей индекса 3.
Формулировка в виде згщдчи шщекса 2 (на уровне скоростей).
Дифференцирование уравнения A.46с) дает
Q^G[q)u. A.46d)
Если заменить уравнение A.46с) на A.46d), мы получим систему вида
A.14а,Ь) с [q^u) в роли у и А в роли z. Можно проверить, что
условие A.10) эквивалентно условию A.47), так что система A.46a,b,d)
представляет задачу индекса 2.
Формулировка в В1ще зги1.ачи шщекса 1 (на уровне ускорений).
Если дважды продифференцировать уравнение связи A.46с), то
полученное уравнение вместе с A.46Ь) дает
[G{q) О )[\)-[-q,,(q)(u,u))- (^^И
Это позволяет выразить и' и А как функции g,ti при условии, что
матрица в A.46е) обратима. Следовательно, уравнения A.46а,е)
составляют задачу индекса 1. Условие, накладываемое на матрицу в
уравнении A.46е), слабее условия A.47), потому что в этом случае
матрица M{q) не обязана быть регулярной.
Все эти формулировки математически эквивалентны, если
начальные значения согласованы, т.е. удовлетворяют уравнениям A.46c,d,e).
Однако если, например, система A.46a,b,d) индекса 2 интегрируется
численно, то уравнения связи первоначальной задачи уже не будут
выполняться точно. По этой причине Гир, Гупта и Леймкулер A985)
предложили другую формулировку для задач индекса 2 («...
интересный способ сведения задачи к индексу два и добавления
переменных, так что уравнения связи продолжают выполняться»).
Формулировка ГГЛ. Идея состоит в добавлении уравнения связи
A.46d) к первоначальной системе и введении дополнительного
множителя Лагранжа fi в уравнение A.46а). Для симметрии мы умножим
еще уравнение A.46а) на M(q)j так что вся система примет вид
M(q)q' = M{q)u-G''(q)fi,
M(q)u' = f{q,u)-G^{q)X,
0 = 9{q),
0 = G(q)u.
VII.l. Понятие индекса и различные примеры 511
Здесь дифференциальными переменными являются (д, и), а
алгебраическими (^, А). Система A.48) имеет вид A.14а,Ь), и предположение
об индексе 2 будет верным, если выполнено условие A.47).
Конкретная механическая система описана подробно вместе с
численными результатами для всех приведенных выше формулировок в
разд.УП.7.
Упранснения
1. Докажите, что начальная задача
5г/ЧЛи = 0, w@) = wo A.49)
имеет единственное решение тогда и только тогда, когда пучок
матриц А-\-ХВ регулярный.
Указание к части «только тогда». Если и имеет размерность п,
выберите произвольно п -h 1 различных чисел А,- и векторов v^ ^ О,
удовлетворяющих требованию (A-\'\B)v^ =0. Затем возьмите их
линейную комбинацию такую, что ]^a,t;,. = О, но ^a^e-^'^t;,- ^ 0.
2. (Стьюарт 1972.) Пусть А-\-\В — регулярный пучок матриц.
Покажите, что существуют унитарные матрицы Q и Z такие, что обе
матрицы
треугольные. Кроме того, все диагональные элементы у А22 и В^^
— единицы, а у В22 — нули.
Указание (сравните с разложением Шура в теореме 1.12.1). Пусть
Aj является нулем det(i4-hA5), а вектор ь^фО такой, что (А4-
-hAj5)i'i = 0. Проверьте, что Bv^ 9^ О и что
где Qi^Z^ — унитарные матрицы, у которых первые столбцы
соответственно Bv^ и v^. Пучок матриц А-\-ХВ тоже регулярный,
и эту процедуру можно продолжать до тех пор, пока не получится
det{A -f ХВ) = Const, из чего следует, что det В = 0. Тогда возьмем
вектор t;2 7^ О такой, что Bv2 = О, и преобразуем А + ХВ с
помощью унитарных матриц р2'^2' У которых первые столбцы
соответственно Av2 и ^2. О практическом вычислении декомпозиции
A.50) см. Голуб и Ван Лоун A989), разд. 7.7.
3. В предположениях упражнения 2 покажите, что существуют
матрицы S и Т такие, что
О /Д О A^J{0 l)-\ О A,J'
512 Гл. VII. Дифференциально-алгебра11ческие задачи высших индексов
\0 /До ВггДо Ч~\^ B,J-
Указание. Эти матрицы должны удовлетворять уравнениям
^11^4-^12 +5^22= О, A.51а)
^11^+^12 + SB^2 = О' A.51Ь)
и их можно вычислить так: первый столбец Т получается из
A.5lb), так как В^ обратима, а первый столбец 5^22 —
нулевой; затем первый столбец S определяется из A.51а), поскольку
Л22 обратима; тогда второй столбец 5J522 известен, и мы можем
вычислить второй столбец Т из A.5lb) и т.д.
4. Докажите, что индекс нильпотентности регулярного матричного
пучка А-\- \В не зависит от выбора матриц Р и Q в A.3).
Указание. Рассмотрите два разных разложения вида A.3) и
обозначьте возникающие в них матрицы Ci.Ni и С2, А^2- Покажите,
что существует регулярная матрица Т такая, что ^^2 = Т^^Л^^Т.
5. Докажите, что система (VI.3.4a,b) имеет индекс 2 (она имеет вид
A.14а,Ь) и удовлетворяет условию A.10)). Полная система (VI.3.4)
имеет индекс возмущения к.
6. (Арнольд 1993.) Рассмотрите задачу индекса 2 A.14) и ее
возмущенный вариант A.28). Докажите, что разность Ау{х) = у{х) —
—у(х) удовлетворяет неравенству
||Ду(х)|| < с(||Ду@)|| + max^d ? P(t)S{t) dt\\ +
+ 11^@11+ (ll<J(OII +Г Wll)'))
(где P{t) = /~ {fz{9yfz)^'^9y){y(t)^4t)) — оператор
проецирования) при условии, что величина, стоящая в правой части,
достаточно мала.
Указание. Линеаризуйте уравнение A.29) в окрестности (у,г),
выразите из него ? — z и найденную разность подставьте в
уравнение, которое получается в результате вычитания A.14а) из A.28а).
Член (/г (Яу/г)'^) B/(^)) z{x))e'(x) можно до интегрирования
заменить выражением ?{/Л9у/г)'Чу{^)^ФЫ^)) ^^Отх)]]).
7. Для линейной начальной задачи
у' = Л(х)у + /(х), у@) = 0
рассмотрите присоединенную задачу
v'=::-A(xfv-g{x), t;(l) = 0.
VII.l. Понятие индекса и различные примеры 513
Докажите, что / g(x)^y(x)dx = 1 v(x)^f(x)dx.
Jo Jo
8. Рассмотрите линейную задачу оптимального управления с
квадратичным функционалом цены:
y'=Ay-\-Bu^f(x), у{0) = Уо^
J [и) = ^[ (y{xfCy{x) -f и(х^Пи(х)) dx,
где матрицы С и D предполагаются положительно
полуопределенными.
a) Докажите, что J(u) минимален тогда и только тогда, когда
y' = Ay + Bu-^f{x), у{0)=Уо.
v' :=z-A^v-'Cy, v(l) = 0, A.52)
Q-B^v-^Du.
b) Если матрица D положительно определенная, то задача A.52)
имеет индекс 1.
c) Если Z) = О и матрица В'^СВ положительно определенная, то
задача A.52) имеет индекс 3.
VII.2. Методы понижения индекса
в разд. VI. 1 мы видели, что численное решение задач индекса 1,
сформулированных в полуявной форме A.13) или в форме уравнения
вида Ми' = (р(и), не намного труднее, чем решение обыкновенных
дифференциальных уравнений. Для задач высших индексов
ситуация совсем иная. Этот раздел посвящен исследованию нескольких
подходов, основанных на идее модифицировать задачу таким образом,
чтобы ее индекс понизился.
Понижение индекса дифференцированием
Наиболее очевидный способ понижения индекса — повторное
дифференцирование алгебраических уравнений связей (см. определение
1.2). В общем случае рекомендуется дифференцировать до тех пор,
пока не получится задача индекса 1. Например, задача индекса 2
A.14а,Ь) была заменена задачей A.14а,с); механическая система со
связями A.46а,Ь,с) — системой A.46а,Ь,е). Тогда получившаяся
задача решается методами гл. VI.
Мы проиллюстрируем этот подход на стандартном примере
маятника:
х' = и, ii'=-xA, B.1а)
у' = г;, г;' = -1-уА, B.1Ь)
0 = x2-f j/^-1. B.1с)
В такой форме задача имеет индекс 3. Дифференцирование
алгебраической связи два раза дает
0 = xu-hyv, B.2)
0 = -A(x2-hy2)-y4-u4i;2. B.3)
Уравнения B.1а,Ь) и B.3) представляют задачу индекса 1. Из
уравнения B.3) можно выразить А и подставить в уравнения B.1а,Ь). При
этом получится дифференциальное уравнение для х,у, i/,v, которое
можно решить стандартными методами.
.0002 г
.0001F- / x^u^+y^v^
25 50 75 100
Рис. 2.1. Погрешности в уравнениях связи
(программа D0PRI5, Atol = Rtol = 10"^ ).
VI 1.2. Методы понижения индекса 515
Явление сноса. Для примера мы решили с помощью программы
DOPRI5 задачу B.1а,Ь), B.3) индекса 1 с начальными значениями
oTq = 1, yQ = 0, Wq — О' i^Q =: О. Интересно было посмотреть, насколько
хорошо сохраняются связи B.1с) и B.2) в процессе численного
решения. Представленный на рис. 2.1 результат показывает, что
погрешность для связи B.2) растет лишь линейно, тогда как для связи B.1с)
она растет квадратично. Это явление можно объяснить следующим
образом.
Рассмотрим механическую систему со связями (см. A.46)):
q' = W, B.4а)
M{qW = f(q,u)^G'^{q)X, B.4b)
0 = 9{q). B.4с)
Дифференцируя уравнение B.4с) два раза, получим
(М{д) СГ{д)\(и'\_[ f{q,u) \
Это уравнение вместе с B.4а) представляет соответствующую задачу
индекса 1. Здесь важно отметить следующее обстоятельство:
задача индекса 1 имеет решение при любых начальных значениях ^q "
Uq. Как видно из второй строки в B.5), вторая производная g(q{t))
обращается в нуль, и вследствие этого решение задачи индекса 1
удовлетворяет соотношениям
9{Q{t)) = ^7(^о) + (< - <о)С(^о)"о' B-6а)
G{q(t))u{t) = G(qo)uo. B.6b)
Теорема 2.1. Если применить численный метод, имеющий
порядок р, к задаче индекса 1 B.4а), B.5) с согласованными начальными
значениями при tQ = 0, то численное решение (9„, ti„) для момента t^
(при t^—tQ< Const) удовлетворяет неравенствам
ЫЯп)\\ < h''{At„+Btl), \\G{q„)uJ < hPCt„ ,
где h представляет наибольшую из использованных длин шага.
Доказательство. Обозначим ^(<,<0'9о'^о) решение задачи
индекса 1 с начальными значениями (^О'^о) "Р^ < = <о- Поскольку
локальная погрешность q^^-^ ~"^(^j+i'^j'^j'^j) имеет величину порядка
0[Щ^ ) (и аналогично для w-компоненты), из B.6а) следует, что
lk(9('„-<i+i.9i+i."i+i))-5(9(<„.'i.9j-«i))ll<''r4^ + 2S(<„-<j+,)).
Суммируя эти неравенства от j = О до j = п - 1, мы получим
желаемую оценку для р(9„), потому что начальные значения согласованы:
^(д(<^, <Q, ^0) ^о)) ~0- Вторая оценка доказывается таким же способом.
П
Стабилиза1щя по Баумгарте. Исторически первым был способ
борьбы с явлением сноса, который предложил Баумгарте A972). Вме-
516 Гл. VII. Дифференциально-алгебраические задачи высших индексов
сто того, чтобы заменять уравнение связи B.4с) его второй
производной по времени, он предложил заменить B.4с) линейной комбинацией
0='д + 2ад + /3^д, B.7)
где у, у — производные по времени от B.4с), т.е.
д = g{q)^ д = G(g)ti, д = 9,,{q)(u, и) -f G{q) (/((/, и) - G^((/)A) .
Уравнение B.7) вместе с B.4Ь) определяет и' и А как функции от
(^, к), и получившееся дифференциальное уравнение может быть
решено численно. Идея состоит в том, чтобы выбрать свободные
параметры а VL Р таким образом, чтобы B.7) было асимптотически
устойчивым дифференциальным уравнением, например, ^3 = а и а>0.
Следовательно, в отличие от B.6), функции 9{q(t)) и G[q(i))u[i)
экспоненциально убывают. Трудность этого подхода заключается в хорошем
выборе а. При малых значениях а затухание будет недостаточно
сильным, а при больших ос получившееся дифференциальное
уравнение становится жестким, и явные методы будут уже не эффективны.
Ашер, Чин и Райх A994) детально исследовали вопрос о выборе а.
Стабилизация с помощью проекции
Рассмотрим теперь другой способ избежать неустойчивости в
предыдущем примере, а именно, повторное проецирование численного
решения на многообразие решений.
Згщэни шщекса 2. Рассмотрим систему A.14а,Ь) и предположим,
что (j/n-iJ'^n-i) — приближение к решению в момент <„_i, которое
удовлетворяет уравнениям ^(Уп-i) = О и 5'y(yn-i)/B/n-i»^n-i) = О-
Применение одношагового численного метода (метод пространства
состояний, разд. VI. 1) с этими значениями к системе индекса 1 A.14а,с)
даст приближение y^j^n» которое, вообще говоря, не удовлетворяет
уравнению связи A.14Ь). Естественный способ проецирования
приближения Уп и^ многообразие решений М A17) — проекция вдоль
образа матрицы Д (см. также о проецированных методах Рунге—
Кутты в разд. VII.4). Поэтому мы определим у^ как решение системы
y-yn^fziVn^^Jf^^ 9{У)=0 B.8)
и затем подправим г^, решая уравнение 9у{Уп)/{Упу^п) ==0.
Применение упрощенных итераций по Ньютону к нелинейной системе B.8)
требует декомпозиции матрицы
Применяя блочный вариант метода исключения, мы видим, что
обратимость матрицы B.9) вытекает из условия A.10) и что декомпозиции
подлежит лишь матрица у^ Д . Эта декомпозиция обычно уже
делается в процессе применения численного метода, так что проецирование
B.8) не требует дополнительных вычислительных затрат.
( I
\9у{Уп)
VI1.2. Методы понижения индекса 517
Возникает естественный вопрос: не разрушает ли процедура
проецирования свойства сходимости используемого метода? Для одно-
шагового метода порядка р локальная погрешность имеет
величину 0{hP'^^). Так как проходящее через точку (x/n-i'-^n-i) Решение
A.14а,с) удовлетворяет уравнению 9{y{t)) = 0y то 9(yn) = (^{f^^^^)-
Таким образом, для решения B.8) справедливы равенства /i = 0(h^'^^),
у^^у^ = 0{h^'^^) и г„ — z„ = C?(/i^"*"^). Согласно теореме о неявной
функции это решение зависит гладким образом от (Уп^^п)^ ^^^ ^^^
отображение (Уп-и -^n-i) "^ (Уп» ^^п) представляет одношаговый метод
порядка р для задачи A.14а,с). А тогда сходимость порядка р
вытекает из стандартной теории (см. разделы VI. 1 и П.З). Это
доказательство применимо и для многошаговых методов.
Механические системы со связями. Для рассмотренной выше
системы индекса 3 B.4а,Ь,с) ситуация несколько сложнее. Пусть
моменту t^^i соответствуют согласованные значения {Яп-iy^n-i^^n-i) у ^
мы, применив одношаговый метод к системе B.4а), B.5) индекса 1,
получим {q^,u^). Поскольку координатная связь B.4с) зависит только
от q, проекции для q и и можно выполнить последовательно.
Проекция на координатную связь. Определим q^ как решение
нелинейной системы
M{g„)(g„-9j + G''(9„)/i = 0,
5(?„) = 0.
Проекция на скоростную связь. Используя полученное в
предыдущей проекции значение q^, определим и^ как решение системы
M(g„)K-«„) + G^(g„)/z = 0,
G(9„K = 0.
Проецирование такого рода предложил Любих A991) на том
основании, что «оно инвариантно относительно аффинных преобразований
координат». Заметим, что система B.11) линейна, тогда как B.10)
— нелинейна, и ее надо решать методом Ньютона с помощью
итераций (упрощенных). То обстоятельство, что задача имеет индекс 3,
предполагает обратимость матрицы в уравнении B.5), откуда следует
существование проецированных значений q^ и и^ (по крайней мере,
при достаточно малой длине шага). Допустимо небольшое изменение
аргументов матриц М и С^ в верхних строках формул B.10) и B.11)
или решение системы B.11) итерациями, если это дает преимущества
с вычислительной точки зрения. Сходимость этого метода
доказывается точно так же, как и в случае индекса 2.
Стабнлизахщя по скоростям. Из B.6) видно, что погрешности в
скоростной связи G{q)u = О более критичны для численного решения,
чем погрешности в координатной связи g(q) =0. Поэтому
представляет интерес исследовать метод, в котором численное решение про-
518 Гл. VII. Дифференциально-алгебраические задачи высших индексов
.004
.003
.0011-
На КООрДИНгП^НуЮ связь л :r^ ;]\'
М I'U^ V: U без проецирования
.0021- л М/; V
j\j;\/| ' на скоростную СВЯЗЬ ,
!Mi
лЛЛ
на коорд. и скор, связи
О 25 50 75 100
Рис. 2.2. Глобальная погрешность при разных вариантах
проецирования (программа DOPRI5, Atol = Rtol = 10"^).
ецируется только на скоростную связь. Алишенас и Олафссон A994)
пришли к выводу, что «проецирование на скоростную связь является
наиболее эффективной проекцией с точки зрения улучшения
численного интегрирования».
Мы использовали программу D0PRI5, чтобы решить уравнение
маятника B.1) в формулировке с индексом 1 в четырех разных
вариантах: (i) стандартное применение без использования проекций,
(ii) проецирование только на координатную связь, (iii) проецирование
только на скоростную связь, (iv) последовательное проецирование на
координатную и скоростную связи. Изменение глобальной
погрешности (координат и скоростей) в ходе интегрирования показано на
рис. 2.2. Отсюда мы делаем вывод, что проекция на координатную
связь без проецирования на скоростную связь не уменьшает
глобальную погрешность (в нашем примере она стаида даже больше). С другой
стороны, стабилизация по скоростям столь же эффективна, как и
полная проекция (для координат и скоростей): на рис. 2.2 разницы почти
не видно.
Дифференциальные уравнения с инвариантами
С описанной выше методикой тесно связано численное решение
дифференциальных уравнений с инвариантами. Рассмотрим
начальную задачу
у' = Пу), у@)=Уо- B12)
Пусть известно, что существует инвариант
У(У)=0. B.13)
Например, дифференциальное уравнение A.46а,е) для (д, и) имеет
инварианты A.46с) и A.46d). Законы сохранения (полной энергии и др.)
тоже могут быть записаны в виде B.13). Инвариант B.13) называется
первым интегралом, если в окрестности решения <Py(y)f{y) =0.
Линейные первые интегралы вида <р{у) = с-\'dTу сохраняются
точно большинством методов численного интегрирования (например,
методами Рунге—Кутты и многошаговыми). Квадратичные первые
VI 1.2. Методы понижения индекса 519
явный метод Эйлера, h = 0.01 явный метод Эйлера, h = 0.01
с проекцией на Я = Const
симплектич. метод Эйлера, h = 0.01 симплектич. метод Эйлера, h = 0.01
Рис. 2.3. Исследование проекции на многообразие H(p,q) = H(po,qo).
интегралы сохраняются точно симплектическими методами Рунге—
Кутты (см. теорему 11.16.7). Более сложные инварианты в общем
случае не сохраняются.
Описанную выше технику проецирования можно приспособить для
решения задачи B.12-13) (см. Шампайн 1986; Айх 1993; Ашер, Чин и
Райх 1994). Численный метод применяется к уравнению B.12), и
выполняется проецирование (ортогональное или какое-либо иное)
численного решения на многообразие, определяемое уравнением B.13).
Как было показано выше, эта процедура сохраняет порядок
сходимости основного метода.
520 Гл. VII. Дифференциально-алгебраические задачи высших индексов
Гамильтоновы системы. Дифференциальные уравнения вида
p'i = ~ip,q), Я'i = ^^ip,яh i=l,...,n, B.14)
где Я : М^" -> М — гладкая функция, всегда имеют первый
интеграл H{p,q) = Const. Представляется заманчивым использовать эту
информацию и проецировать численное решение на многообразие
^(Ру я) = ^(РоуЯо) ' В качестве примера рассмотрим возмущенную
задачу Кеплера с гамильтонианом
гг/ ч Pi+Pi 1 0.005 ,. _,
и начальными значениями ^^(О) = 1 — е, gjCO) = 0> Pi@) = О» РгС^) =
= ^A +€)/(! — е) (эксцентриситет е = 0.6). На рис. 2.3 вверху
показаны численные решения, полученные явным методом Эйлера с длиной
шага Л = 0.01, слева — без проецирования, справа — с проекцией на
Н = Const. Видно заметное улучшение, но численное решение все же
не отражает геометрической структуры точного решения
(инвариантный тор). Мы получили также решение с помощью симплектического
метода Эйлера (см. уравнение A6.54) в разд. 11.16). Здесь видно, что
численное решение (без проецирования) качественно правильно
передает поведение решения (это можно объяснить на основе обратного
анализа погрешностей, см. разд. 11.16), тогда как проецирование на
Н = Const разрушает это свойство. Для исправления ситуации
можно предложить следующее: решать задачу симплектическим методом,
проецировать численное решение на Я = Const ^ но продолжать
интегрирование с непроецированными значениями.
Методы, использующие представления
в локальном пространстве состояний
Эти методы известны также как
дифференциально-геометрический подход (Потра и Рейнболдт 1990). Идея состоит в том, чтобы
рассматривать дифференциальна-алгебраическую систему как
дифференциальное уравнение на многообразии (см. разд. VII.1) и решать
уравнение в этом многообразии, введя подходящие локальные
координаты.
Проиллюстрируем этот подход на примере маятника. Записанные
в декартовых координатах уравнения были приведены в начале этого
раздела. Многообразием решений является
М= {(ar,2/,ti,v) I х^-|-у^ = 1, xti + 2/t; = 0}
(ср. с уравнением A.22)). Это двумерное многообразие в М"*. Его
можно параметризовать, введя координаты {<р^г}) следующим
образом:
. ' ^ B.16)
2/ = siny>, i; = iycosy?.
VI 1.2. Методы понижения индекса 521
Несложные вычисления показывают, что запись системы B.1а,Ь),
B.3) в новых координатах приводит к хорошо известному уравнению
у?'= 7?, •q'^-costp. B17)
Это дифференцигипьное уравнение не представляет трудностей для
численного решения. Численное приближение в исходных
координатах можно затем получить с помощью B.16). Очевидно, что уравнения
связи для координат и скоростей удовлетворяются точно.
Хотя этот пример хорошо иллюстрирует основную идею, он
может ввести в заблуждение. Прежде всего, в типичных прикладных
задачах оказывается невозможным использовать одну и ту же
параметризацию на всем интервале интегрирования. Во-вторых, выбор
координат обычно нетривиален, и преобразованное
дифференциальное уравнение может оказаться гораздо сложнее, чем исходное (см.,
например, Алишенас 1992).
Представление в локальном пространстве состояний.
Предположим, что дифференциально-алгебраическая система, которую мы
хотим решить, может быть записана в виде дифференциального
уравнения
y=v[y), уем B.18)
на гладком с?-мерном многообразии М С М'^. Рассмотрим
координатную функцию а;: С/ —)• V (дифференцируемую достаточное число раз,
биективную, с матрицей а;'(г/) полного ранга), которая отображает
открытое множество С/СМ^на КС-М,и обозначим ?;GМ^ координаты
в и. Преобразование y = uj{ri) переводит уравнение B.18) в
uj'ir,)r,'z=v{ujGj)). B.19)
Так как v(y) ЕТуЛ4 для всех у ? М (см.A.19)), то существует т;'
такое, что уравнение B.19) выполняется. Более того, ту' единственно,
потому что матрица и;*{г]) имеет полный ранг. Вводя обозначение
о;'G7)+ = (u;'G/)^u;'(r;)) (^^{т])^ Д-^я псевдообратной к uj'(r]) матрицы,
мы получим
rj' = u;'(tj)+v{u>(r,)). B.20)
Это — обыкновенное дифференциальное уравнение в М^; принято
говорить, что оно является представлением (формой записи) уравнения
B.18) в локальном пространстве состояний. Заметим, что
различные координатные функции приводят к разным формам записи в
пространстве состояний.
Процедура численного решения уравнения B.18) такова.
Предположим, что для y(tk) известно приближение у^ ? М. Выберем
некоторую координатную функцию и применим какой-либо
стандартный метод (например, метод Рунге—Кутты) с начальным значением
7]i^ =а;~^ (у^^) к уравнению, записанному в пространстве состояний, т.е.
522 Гл. VII. Дифференциально-алгебраические задачи высших индексов
к B.20). Это даст приближение г/^^^^, соответствующее моменту
времени tf^^^. Наконец, положим jJi^^i ^^i'Hk+i)' ^^ определению этого
процесса, численное приближение j/^^^j снова лежит в М.
Если используется одна и та же форма уравнения в
локальном пространстве состояний (как в примере с маятником, уравнение
B.17)), то свойства сходимости для B.20) переносятся на B.18)
непосредственно с помощью координатной функции у = и)(т]). В более
сложных ситуациях может оказаться необходимым изменение выбора
координат несколько раз, а с вычислительной точки зрения может
быть даже выгодно изменять его на каждом шаге интегрирования.
Теорема 2.2. В рассмотренной выше процедуре численного
решения B.18) обозначим у = uJi^{t]) преобразование координат на к-м
шаге. Если в окрестности (jj^^(у 1^) матрицы cjj^(г;) я u;j^(r7)+ равномерно
ограничены по к, то свойства сходимости для стандартных
обыкновенных дифференциальных уравнений переносятся на задачу B.18)
на многообразии М.
Доказательство. В случае одношаговых методов имеем
Ук+1 =^л(^лЧул) + лф^(^;^(у^.л)),
где Ф^(г),к) — функция приращения метода при применении его к
уравнению B.20), в котором и заменено на w^^. Благодаря
предположению о регулярности uji^(t)) эту формулу можно переписать в виде
У/с+1 = 2/л + ЛФ^^(Ул.'*)>
так что она будет иметь стандартный для одношагового метода вид.
Предположения теоремы гарантируют, что существует единая
постоянная Липшица у всех функций Ф^^ относительно первого
аргумента. Поэтому остаются в силе доказательства сходимости из разд. П.З.
Для многошаговых методов ситуация аналогична. П
Выбор локальных координат. Поясним два выбора для
механической системы со связью B.4), многообразие решений которой имеет
вид
M = {{q.u)\g{q)=0, G(q)u = 0}. B.21)
Здесь g, гх G М'* — обобщенные координаты, g{q) G М"^ и G{q) = gg{q).
Изложенное ниже более или менее непосредственно переносится и на
другие дифференциально-алгебраические системы с известными
многообразиями решений.
Разделение обобщенных координат (Уихидж и Хауг 1982). В
предположении, что строки матрицы Якоби G(q) линейно независимы,
существует разделение q = (?/, т?) такое, что матрица g^irj,^) обратима
(?7GlR"""'", ^GM'"). Согласно теореме о неявной функции
уравнение связи g(q) =iO может быть разрешено относительно fj в
окрестности согласованного значения ^q = (%»%)• Следовательно,
существует функция fj=: h(r)) (определенная для rj близких к t}q) такая, что
VI 1.2. Методы понижения индекса 523
д(г}, h(rj)) = 0. При соответствующем разделении и = (г/, ?) уравнение
связи для скоростей примет вид д^ (rj, г^и-^-д^ (rj, fj)i/ = О, что позволяет
выразить V как функцию г/, г/, т.е. V = k(T),i/). Таким образом, будет
задана координатная функция и;(г], i/) = (G7, /1G7)), (г/, к{т], i/))), и
дифференциальное уравнение в этих локальных координатах запишется
так:
rj' = i,^ i/' = i/'(u;(r;,^)), B.22)
где i/^(q,u) объединяет t/-компоненты решения u'(q,u) линейной
системы A.38е). Подчеркнем, что для численной реализации нет
надобности знать аналитический вид уравнения B.22). Однако надо решать
нелинейную систему каждый раз при вычислении правой части
уравнения B.22).
Параметризация касательного пространства (Потра и Рейнболдт
1991; Йен 1993). Вместо разделения компонент дни будем
расщеплять векторы q — q^ и u — Uq следующим образом:
где столбцы Qq образуют базис касательного к многообразию g{q) = О
пространства {v \ G(qQ)v =¦ 0} , который дополняется столбцами Q^ до
базиса во всем пространстве. Условие g{q) = О вместе с первым
соотношением B.23) определяет (локально) q и fj как функции г/.
Подобным же образом условие G{q)u = О и второе соотношение B.23)
определяют и и V как функции i/ и q. Обозначив полученные
зависимости т] = h{r)) и i/ = к{г]у I/), мы получим формально ту же
координатную функцию, что и в предыдущем примере, и в представлении в
пространстве состояний уравнение примет вид
7;' = 1/, i/' = g+u'(u;(r;,^)), B.24)
где Qq = (QoQq)~^Qo — матрица, являющаяся псевдообратной для
Qqj а u^(q,u) обозначает решение линейной системы B.5).
Для вычисления Л (ту) требуется решить нелинейную систему,
матрица Якоби которой имеет вид
( ^ -^л
Это наводит на мысль взять —Q^ =G^(gfo) или, что еще лучше, -Q^ =
= Л/"" ^ {Яо)^^(Яо)» чтобы итерации в упрощенном методе Ньютона
приводили к линейным системам с матрицей, которая уже появилась
в B.5). Линейная система для вычисления k(rj,i/) имеет такую же
структуру.
Из-за того, что вычисление правой части в B.24) требует решения
нелинейной системы, авторы этого подхода предпочли использование
многошаговых методов, которые, вообще говоря, требуют меньше
вычислений правой части, чем одношаговые методы. В связи с методами
Рунге—Кутты Потра A995) предложил использовать определенные
524 Гл. VII. Дифференциально-алгебргшческие задачи высших индексов
предсказанные значения вместо точных решений этих нелинейных
систем, а также ограничиться требованием, чтобы на многообразии М
лежало только приближенное значение, получаемое в конце
каждого шага. Тогда полученный алгоритм эквивалентен решению задачи
индекса 1 в сочетании с проецированием на Л< в конце каждого шага.
Переопределенные
дифференциально-алгебраические уравнения
В противоположность описанному в начале этого раздела
подходу, в котором уравнение связи заменяется продифференцированным
один или несколько раз уравнением связи, мы будем здесь
рассматривать как единое целое исходную систему уравнений, дополненную
одной или большим числом производных уравнения связи. Например,
уравнения движения механической системы со связью примут вид:
q' = tz, B.25а)
M[q)u' = /(g, и) - G^((/)A, B.25b)
0 = i7((/), B.25c)
0 = G(g)w, B.25d)
0 = 9,,{ч){и. и) + G[q)M{q)-\f{q, и) - G^(<?)A). B.25e)
Эта система переопределена: в ней больше уравнений, чем
неизвестных. Тем не менее, она имеет единственное решение, если
выполняется условие A.47) и заданы согласованные начальные значения.
Для примера рассмотрим численное решение системы B.25)
методом ФДН. Формальное его применение (см. разд. VI.2) дает:
Як " Я" ^1'^к = О, B.2ба)
M[q^)[u, - G) - /i7(/((/,, и,) - G^{q^)\,) = О, B.26b)
9(Як)=0. B.26с)
G{q,)u, = 0, B.26d)
9яяiЯk){Ч^u,)-^G{q,)M{q,r'{f{q,,u,)-G^(q,)\,)=0. B.26е)
где 7 = /?;,/а^, q= (E?Jo ^гЯд/^^к и й= (Efjo <^1ЩI^к — известные
величины. Система B.26) переопределена и в общем случае не имеет
решения. Поэтому естественно искать решение B.26) методом
наименьших квадратов (Фюрер 1988). Для этого существуют различные
способы. Можно рассматривать разные нормы. Можно потребовать,
чтобы некоторые уравнения выполнялись точно, а остальные решать
методом наименьших квадратов. Фюрер и Леймкулер A991)
накладывали все связи B.26c,d,e), а остальные уравнения решали с
использованием специальной псевдообратной матрицы. Это можно сделать
с помощью введения множителей Лагранжа /i/f, т;/^ в первые два
уравнения B.26) следующим образом:
M(<?fc)(9fc-?-/.7"fe) + ft7(G''(<7feK+(G,(<7k)«fc)'''?fc) =0, B.27а)
VI 1.2. Методы понижения индекса 525
МШ{Ч - й) - ЫПЯк - «J - G''iq,)X,) + fijG'^(q,)nk = 0. B.27b)
При достаточно малых Л система уравнений B.27а,Ь) и B.26c,d,e)
имеет локально единственное решение, если выполнено условие A.47).
Связь с формулировкой ГГЛ (см. с. 510). Если опустить
уравнение связи для ускорений B.26е), то надобность в двух множителях
Лагранжа отпадает и можно положить г;^ =0. Получающаяся
система уравн^гний B.27а,Ь) и B.26c,d) — не что иное, как стандартная
дискретизация методом ФДН системы A.48).
Бесструктурные задачи старших индексов
Рассмотрим дифференциально-алгебраическую систему общего
вида
F(i/',tz) = 0. B.28)
Для численного решения ее мы построим «лежащее в ее основе ОДУ»
(см. определение 1.2) и решим его с помощью какого-либо метода
интегрирования. Этот подход развил в нескольких своих работах Камп-
белл A989, 1993). Основную идею мы поясним, следуя изложению
Кампбелла и Мура A995).
Опираясь на определение индекса дифференцирования,
рассмотрим «уравнения массива производных»
которые мы будем записывать в компактном виде как
G(u\w,u) = 0, B.29)
где It; = {и'\ и'",..., w(*^+^)) объединяет старшие производные и. В
уравнении B.29) мы будем рассматривать гу,и, а также и' как
независимые переменные. Кроме обычных предположений о дифферен-
цируемости, предположим еще, что
(А1) матрица [G^,,G^) является 1-полной относительно и' (это
означает, что соотношение 0^,^и' -f G^Aw = О влечет Аи' ===0);
(А2) матрица (G^^i.G^^j) имеет постоянный ранг;
(A3) матрица {G^i,G^^^yG^) имеет полный ранг по строкам,
Потребуем, чтобы эти предположения выполнялись в окрестности
конкретного решения системы B.28). Построение «лежащего в основе
ОДУ» опирается на следующую лемму и ее доказательство.
Лемма 2.3 (Кампбелл и Мур 1995). Рассмотрим достаточно
гладкую задачу B.28) и предположим, что условия (А1), (А2) и (A3)
выполнены. Тогда существуют разделения координат w = {w^,w^),
и= (гХд, Uf^) (а также и' = (г/'^, и[) с тем же разделением, что и для
и) такие, что уравнения массива производных B.29) эквивалентны
526 Гл. VII. Дифференциально-алгебраические задачи высших индексов
системе
К = 1а(ч)^ ^а = V^2(^6^ "ь)> ^2 30)
В окрестности согласованного начального значения (uq,Wq,Uq) .
Доказательство. Рассмотрим матрицу (G^,,G^,G^^),
вычисленную в точке (uq, и^о, Wq) , и выполним QR-факторизацию, в которой
перестановки столбцов ограничены компонентами, лежащими в
пределах векторов u',w,u и. Это дает
Q^(G„„G„„GJP =
S,
0
0
с,
Сг
0
с.
с.
0
D,
Оз
Db
D,
D,
De
B.31)
где B^,C^,D^ — неособенные матрицы в силу предположения (A3),
Q — ортогонгипьная матрица и Р = diag (Pj, Pji ^з) ^ подходящими
матрицами перестановок Pi,P2»^3- Зафиксировав матрицу
перестановок Р, выполним такую же факторизацию матрицы (G^,,G^^G^),
вычисленной в некоторой произвольной, но близкой к (wq, Wq.Uq)
точке (u\w,u). В силу предположения (А2) мы получим разложение
вида B.31) с гладкими матрицами Q,B^,C^ и Д-. Разложение B.31)
определяет разделения w = {w^,w^^) и u=:(w^,w^,). Первый, второй
и четвертый блочные столбцы в B.31) образуют обратимую
матрицу. Следовательно, согласно теореме о неявной функции уравнение
B.29) может быть разрешено относительно u',it;^,u^, и мы получим
эквивалентную систему
Надо еще показать, что функции (р^ и (р^ не зависят от Wf^. По
определению V?,- имеем:
Дифференцирование по w^ лает
Умножая это соотношение на Q^ и используя B.31), мы видим, что
D^(d(p^/dw^) = 0. Но так как D^ — неособенная матрица, отсюда
следует, что (d(p^/dw^) = О, т.е., <^з "^ зависит от Wf^. Теперь из
B.32) вытекает, в силу предположения (А1), что и (д^р^/дио^^) равно
нулю. Этим заканчивается доказательство леммы. П
Предположим, что нам известно, как вычислить fa(ub)^ /ь(^ь) ^
9?з("б) Д^^ данного значения и^. Тогда из B.30) мы получаем
обыкновенное дифференциальное уравнение для и^, которое можно решить
любым методом численного интегрирования (методом Рунге—Кутты
VI 1.2. Методы понижения индекса 527
или многошаговым, явным или неявным и т.д.), а остальные
компоненты задаются уравнением w^ = <^з(^б) • Следовательно, такой способ
численного решения сохраняет все связи (в том числе и скрытые).
Вычисление значений fa(Uf^), fi,{u^) и <^з(^ь)- ^^
предположения (A3) следует, что соотношение (G^^/,G^, G^^)^G = О эквивалентно
равенству G = О. Поэтому можно использовать любой метод
нахождения точки минимума (w',it;,u^) функции G^G при заданном щ.
Кампбелл и Мур A995) предлагают использовать итерации методом
Гаусса—Ньютона.
Замечание. Весьма близкий алгоритм предложили Кункель и
Мерман A996). Вместо извлечения из уравнений массива
производных обыкновенного дифференциального уравнения для всех
переменных, они извлекают эквивалентную задачу индекса 1 и решают ее
стандартными методами интегрирования, В этой модификации число
дифференцирований исходной системы B.28) обычно сокращается на
единицу.
Упралснения
1. Повторите эксперимент, представленный на рис. 2.1, с другими
численными методами (явный метод Эйлера, многошаговые методы,
с постоянной и переменной длинами шага и пр.). Вы увидите, что
в некоторых ситуациях погрешность в giq^) растет только
линейно, а погрешность в G{q^)u^ остается ограниченной. Попытайтесь
объяснить свое наблюдение.
2. а) Докажите, что матрица в B.5) является 1-полной относительно
и' в том и только в том случае, если сужение М на ядро G
является инъективным. (Это как раз является необходимым условием
применимости методов, рассмотренных в этом разделе.)
Ь) Покажите на примерах, что для удовлетворения условия из
части (а) этого упражнения не требуется ни чтобы М была
неособенной матрицей, ни чтобы G имела полный ранг.
VII.3. Многошаговые методы
для ДАУ иццекса 2
«Метод ФДН столь прекрасен, что трудно представить
себе что-либо лучшее».
(Л. Петзолд, в 1988 г. (со слов П. Дойфлхарда))
Получить результаты о сходимости многошаговых методов для
задач индекса 2 и выше труднее, чем для полуявных задач индекса 1
(см. разд. VI.2). Первые результаты по сходимости для схем ФДН,
справедливые для линейных ДАУ с постоянными коэффициентами,
но произвольного индекса, получили Синковец, Эрисман, Йип и
Элтон A981). Позже сходимость методов ФДН для нелинейных систем
ДАУ изучали Гир, Гупта и Леймкулер A985), Лётстедт и Петзолд
A986), а также Бренан и Энгквист A988). Другой, независимый
вариант анализа сходимости был развит в работах Грипентрога и Мерц
A986) и Мерц A990). В них рассматривались общие линейные
многошаговые методы и задачи, в которых дифференциальные и
алгебраические уравнения (и/или переменные) не разделены явно.
Существует несколько реализаций схем ФДН для
дифференциально-алгебраических систем. Наиболее широко используется
программа DASSL, которую написала Петзолд A982). Она подробно описана
в книге (Бренан, Кампбелл и Петзолд 1989). Позже появились
программы LSODI (Хайндмарш 1980) и SPRINT (Берзинс и Ферзеланд
1985).
В этом ргизделе мы рассмотрим пол у явные задачи
У'-^^У^'^' C.1)
В предположении, что /ид дифференцируемы достаточное число
рг13 и что матрица
9y{y)fz (j/i ^) обратима C.2)
в окрестности решения, так что задача имеет индекс 2. Линейный
многошаговый метод для C.1) имеет вид:
к к
Т^^гУп^г = лХ!АЛ2/„+.-.^п+.). C.3а)
0 = <7(y„+fc). C.3b)
Это не единственное возможное определение многошагового метода
VI 1.3. Многошаговые методы для ДАУ индекса 2 529
для задачи C.1). Можно заменить (З.ЗЬ), скажем, уравнением
к
o = J2f^i^iУrг+i)' C-4)
1=0
которое получается, если в (VI.2.1) положить е = 0. Нижеследующие
результаты без труда переносятся и на второй подход. Впрочем, для
методов ФДН оба определения эквивалентны, потому что у этих схем
/?о = --- = 4-1=0.
Полученные в этом разделе результаты о сходимости
справедливы и для систем индекса 2 вида г/ = f(y, z), О = д(у, z) при условии,
что последние могут быть преобразованы к виду C.1) без
использования дифференцирований (см. обсуждение вопроса в тексте после
уравнения A.14)). Это вытекает из инвариантности метода C.3)
относительно таких преобразований. То же справедливо и для задач
вида М(и)и^ = (р(и), если многошаговый метод определен
уравнениями
к к
j=0 1=0
Существование и единственность
численного решения
Уравнения C.3) образуют нелинейную систему для y^^f^.z^^f^.
Имеется следующий результат относительно существования ее
решения:
Теорема 3.1. Пусть стартовые значения для решения y(x),z(x)
системы C.1) удовлетворяют требованиям
yj-y(xj)=0{h), zj-z{xj)=0{h), g{yj)=0(h') C.6)
при j = о,..., Ar — 1 и Xj = XQ-\-jh. Если в окрестности этого решения
выполняется условие C.2) и /?^^ ^ О, то нелинейная система
к к
^а,у, = Л^;/?,/(г/,.г,), C.7а)
t=0 1=0
0 = д{у,) C.7Ь)
имеет решение при /i < /iq . Это решение локально единственное, и
для него справедливы оценки
yk-yi^k) = 0(h), z,-z{x,) = 0{h). C.8)
Доказательство. Положим
к-\ /с-1 ^
V-=-'?^yi + hY^^f(y,,z,) C.9)
t=0 *^ »=0
530 Гл. VII. Дифференциально-алгебраические задачи высших индексов
и определим С как величину, близкую к z(Xf^), причем д(т])/(т]Х) = 0.
Далее, определим величину к(C,^/а^) как новую длину шага, которую
мы опять обозначим h. Тогда система C.7) будет эквивалентна
системе
yk=V-\-hf{y,,,Zf^), C.10а)
0 = РB/,), (З.ЮЬ)
которая представляет просто неявный метод Эйлера. Покажем
теперь, что
r)-y(Xk) = 0(h), С-Фк)=0(Л), 9(ri) = 0(h'). C.11)
Первое из этих соотношений следует из того, что yj —y(Xj) = 0(h)
и Yli=o^i — ^' Второе является следствием определения С и
условия C.2). Справедливость последнего соотношения C.11) можно
усмотреть следующим образом. Заменим в C.9) все /(у,,-г,) на
f(y(Xf^),z(xi^)), что внесет в г/ погрешность порядка 0(h'^). Тогда
v-yM = -J2^(yi-yi'^k))'^''(J2^)fЫ^^l
,=0 f" ^.=0 ^^
с учетом A.14Ь,с) отсюда вытекает, что
9i^)^'-I1^9y{yM){yi-y{x,))-^0(h^). C.12)
1=0 ^
Теперь последнее равенство в C.11) следует из требований C.6) и из
того, что 9у{у(х^))(у^ - y{Xf^)) = д(у^) -^ O(h^).
Для доказательства существования локально единственного
решения системы C.10) можно адаптировать применительно к неявному
методу Эйлера доказательство «Теоремы 4.1» из работы ХЛР89. Но
вместо этого мы переформулируем систему C.10) так, чтобы можно
было применить теорему о неявной функции. Запишем (З.ЮЬ) в таком
виде:
0 = д{у,)=9(у,)-9{ф))+9{Ф)) = C.13)
= l\y{v{h) + T{y,-r,{h)))dT.{y,-rj{h))+g{r,(h)).
Здесь мы указали явно зависимость г; от Л. Множитель у;^ - 77(Л)
согласно C.10а) заменим на hf{yf^,Zj^), разделим на Л и получим
систему
г/*-'?(Л)-Л/(Ук.2^ = 0, C.14а)
^ <7у('?(Л) + г(у,-,,(Л)))^г./(У*,гЛ-^И'г(Л))=0, C.14Ь)
которая является дискретным аналогом системы A.14а,с). При Л = О
значения у^^ =^@) и Zf^ = С@) удовлетворяют уравнениям C.14), по-
VI 1.3. Многошаговые методы для ДАУ индекса 2 531
тому что 9(rj(h)) = 0(h^) и 9у(т])/{лХ) = ^' Далее, производные
функций C.14) по переменным (y^.z,^) имеют вид
fl + 0{h) 0(h) \
\ Oil) (9yh)(ri,0 + O{h))' C.15)
И при /г < /io эта матрица имеет ограниченную обратную. Поэтому
теорема о неявной функции (Ортега и Рейнболдт 1970, р. 128)
гарантирует существование локально единственного решения системы C.14),
а следовательно, и систем C.10) и C.7). П
Влияние возмущений
Следующая теорема рассматривает влияние возмущений в
многошаговой формуле C.3) на численное решение.
Теорема 3.2. Пусть y^^Zf^ определяются системой C.7);
рассмотрим возмущенные значения yf^y^i^, удовлетворяющие системе
к к
Y,cc,y, = hY,PJ{y,,z,)^h8, C.16а)
1=0 1=0
0 = <?(j/fc) + e. C.16b)
Пусть выполнены условия теоремы 3.1 и, кроме того,
yj-yj=0(h^), zj-zj=0(h), S = 0{h), e = 0(h') iZ.n)
при j = о,..., fc — 1. Тогда при Л < /iq справедливы оценки
\\yk-yk\\<c{\\Yo-Y,\\ + h\\Z,-Z,\\ + h\\S\\ + \\e\\),
\\^lc-^Л<тdhy^У^^^^УJ-УJЯ+l'\\Уo-Уo\\+ C.18)
"St^'
+ Л||^о-^о|| + Л||<$|| + |И|),
где Уо - Vq = (yfc-i - J/fc-i. • • •. Уо - УоР . Н^о - '^'оН = o<'^<Y_i И^О' " ^iИ'
а также аналогичные оценки для г-компоненты.
Доказательство. По аналогии с доказательством теоремы 3.1
положим
1=0 '* 1=0 '^
и переопределим масштабы и обозначения Л и (J, так что C.16) примет
вид
У/^=^+Л/(У)кД/с) + ^, C.19а)
0 = 9{Ук) + 0. C.19Ь)
532 Гл. VII. Дифференциги1ьно-алгебраические задачи высших индексов
Рассуждая, как в доказательстве теоремы 3.1, из C.17) можно
вывести, что yf^ — fj= 0(h) и Zi^—C = 0{h), где С удовлетворяет
равенству gy{fj)f(fjX) =0- Ориентируясь на аналогию с C.14), перепишем
C.19Ь) в виде
0 = ^ ^y(^+^(yit-^))dr.(/(y,JJ + ^) + ^G(J7) + ^e. C.20)
Теперь это дискретный аналог уравнения A.29). Вычтем C.20) из
C.14Ь) и воспользуемся обратимостью матрицы ^'уЛ • Мь1 получим
оценку
\\?k-'k\\<c{\\%-yu\\Hn-l\\HS\\ + l\\9{fi)-9in)\\ + lm\)- C.21)
Вычтем теперь C.14а) из C.19а) и воспользуемся условием Липшица
для /. Получим оценку
\\y,-yk\\<\\fi-v\\ + hL{\\y,-y,\\ + \\z,-z,\\) + h\\S\\.
Комбинация двух последних оценок дает
\\k-yk\\<C{\\ri-r,\\ + h\\S\\ + \\e\\),
\\z,-z,\\<ji\\9y{fi)ifi-ri)\\ + h\\v-r,\\ + h\\S\\ + m\). ^^'^^^
Утверждение теоремы следует теперь из определений т; и С и из того,
что у^-7}= 0(h). П
Замечание 3.3. а) Из приведенного выше доказательства видно,
что постоянная С в C.18) зависит от оценок определенных
производных функций / и 5^» но не зависит от констант, входящих в члены
вида 0{...) в C.17) (если h достаточно мало). Это обстоятельство
будет использовано ниже при доказательстве сходимости,
Ь) Для одношаговых методов (например, неявного метода
Эйлера, метода трапеций) член || YIjZq 9y{yk){yj - У^)|| в C.18) можно
опустить, если потребовать, чтобы д(у^) =^(Уо) ~ 0. Действительно, из
Ух =Уо-^0{к) следует ду(У1)(Уо-Уо)=9у{Уо){Уо-Уо)-^0(к\\уо-у^\\).
Дгшее,
9у{Уо)(Уо'-Уо)-9{Уо)-'9{Уо)'^0{\\у^^-Уо\\^).
Таким образом, при достаточно малых h обсуждаемый член имеет
оценку 0(к\\у^-у^\\).
Локальная погрешность
Пусть стартовые значения у^- = y{xj), г = '2г(х ) (j = О,..., А: — 1)
лежат на точном решении задачи C.1). Разности у;^ — y(xi^), Zj^ — z{xi^),
получающиеся после однократного применения многошаговой
формулы C.7), называют локальными погрешностями метода.
VI 1.3. Многошаговые методы для ДАУ индекса 2 533
Лемма 3.4. Пусть ДАУ C.1) удовлетворяет условию C.2), а
многошаговый метод C.7) имеет порядок р (в смысле, определенном
в разд.111.2). Тогда локальная погрешность метода удовлетворяет
оценкам
у, - j/K) = ОСЛР+М, Ч - z{x,) = 0{kn. C.23)
Доказательство. Положим у = у(^1) > ?j = ^i^j) "Р** i = О,..., Ar.
Эти величины удовлетворяют уравнениям C.16) с S = 0{h^) и 0 = 0.
Поскольку yj = yj и Zj = Zj при j < к, утверждение леммы вытекает
непосредственно из теоремы 3.2. П
Сходимость методов, использующих ФДН
Исследование сходимости для схем, основанных на ФДН, проще,
чем для общих многошаговых методов, потому что y^^i^ зависит
только от у„,..., Уг1+/с-1 и "^ зависит от 2^,..., -г:^^^^^..^ благодаря
равенствам /?о = ... = /?;j_i = 0. Нижеследующий результат был получен
рядом авторов (Гир, Гупта и Леймкулер 1985; Лётстедт и Петзолд
1986; Бренан и Энгквист 1988).
Теорема 3.5. Рассмотрим задачу C.1) индекса 2,
удовлетворяющую условию C.2). Тогда к-шаговая ФДН-схема (HI. 1.22') при к <6
сходится с порядком р=: ку т.е.
Уп - 2/(^п) = от, z^ - г(х J = от при x^ = nh< Const,
C.24)
если стартовые значения удовлетворяют условиям
у. - y{xj) = 0{hP-^') при j = 0,...,k-l. C.25)
Замечание. Условие C.25) можно заменить более слабым условием
у — y(Xj) = O(h^) при А: > 3 (но не при /: = 1, см. упр. 1).
Доказательство. Мы соединим идею доказательства сходимости
для методов Рунге—Кутты (теорема 4.4 из ХЛР89) с методикой,
использованной в разд. П1.4. Сначала в части (а) доказательства,
опираясь на образ «веера леди Уиндермир», мы исследуем
распространение локальных погрешностей и их накопление на всем отрезке для
у-компоненты. В части (Ь) мы рассмотрим г-компоненту, а в части
(с) некоторые технические детали.
а) Наряду с численным решением {у„,2:„}, которое далее
будем обозначать также {y^j-^^}, будем рассматривать другие
решения {Уп,г^] (?=1,2,...), получаемые многошаговым методом для
j = ?-l,...,?-f/: — 2 со стартовыми значениями yj = y(xj), Zj=z{Xj),
взятыми на точном решении. Нашей первой целью является
получение оценок yii — уп^^ у выраженных через локальные погрешности
У^^к--! "/^+1-1 {^^^^ стартовые погрешности, если i = 0). Для
простоты опустим верхний индекс, и рассмотрим два соседних многошаговых
534 Гл. VII. Дифференциально-алгебраические задачи высших индексов
решения {у„,?„} и {Уп^^п}- Чтобы иметь возможность применить
теорему 3.2, зафиксируем три достаточно большие константы Cq, С^ , С2
и предположим, что при nh < Const
\\yn-yM\\<Coh, ||У„-У„||<С,Л2, ||?„-^(xJ||<CA C.26)
Обоснование этому будет дано ниже, в части (с) доказательства.
Обозначим А2/„ = у„-у„, Дг„ =?„-?„ и ДУ„ = (Ду„^^,_1,...,Ау„)^.
Так как в случае ФДН-схем у^^^ , z^^f^ не зависят от г„,..., ^„^-/c-i'
то из теоремы 3.2 при J = О и ^ = О мы получим оценки
\\Ay„^,\\<C\\AYJ, C.27а)
1|А^„+*11 < f (Ё ЫУп+1с)^Уп^Л + Л||ДП,1|) • C.27Ь)
Здесь С не зависит от выбора Cq, С^, С2, если h достаточно мало (см.
замечание 3.3а). Из нашего предположения C.26) и из C.27) следует,
что ^Уп^к = O(h^) и Az^^f^ = 0(h). Поэтому можно линеаризовать
многошаговую формулу:
к
5^а,Ду„+, = /i/?,/,(j7„+„?„+fc)Az„+, + (9(Л||ДУ„||), C.28а)
»=0
о = <7„(j/„+J Ду„+, + 0{h\\AYJ). C.28b)
Воспользуемся теперь операторами проектирования
Qn = {fA9yf^r'9y)(yn+kX+k), Pn = i-Qu C.29)
(см. также определение 4.3 ниже), для которых справедливы
соотношения
Р„2 = Р„, Ql = Q^, P„Q„ = g„P„ = 0, g„+i = Q„ + C?(A). C.30)
Последнее из них вытекает из C.26) и гладкости решения y(x),z{x).
Умножим теперь C.28а) на Р^^^ ("Р^ этом будет исключено Az^^f^),
а C.28Ь) — на f^iOylz)'^ • ^ учетом C.30) мы получим
к
2а,Р„+,Ду„+, = 0(Л||ДУ„||), д„^,Ду„+, = 0(Л||ДУЛ). C.31)
»=0
Введем векторы
Un = (Pn+k-Ayn+k-v ¦ • -.Л.АУп)^,
к = [Qn+k-Ayn+k-K- ¦ • .<?„Ду„)^-
Тогда ДУ„ = U„ + V^, а. соотношения C.31) примут вид
t^n+i = И ® IWn + 0{h\\UJ + /4IK.II). C.32а)
К.+1 = (N®I)V„+ 0(h\\UJ\ + h\\VJ), C.32b)
VI 1.3. Многошаговые методы для ДАУ индекса 2
535
где
А =
1
-Q, -Qn
О
О
Я =
/О
1
\
о 0\
о о
C.33)
10/ \ 10/
и q' = oiJa^. В соответствии с леммой III.4.4 выберем теперь норму
\\и\\ так, чтобы ЦЛ®/)! < 1. Затем выберем норму ||V|| (возможно,
иную), для которой ||Л^® /|| </><!• При этом из C.32) будет
следовать, что
/Гп+ilh ./1 + 0(Л) 0{h) \(\\и„\\\
VIK+illZ-V 0{h) p^o{h))\\\v^\\)-
C.34)
Приведем матрицу в C.34) к диагональному виду, как это делалось в
доказательстве леммы VI.3.9. Тогда мы получим
||Ay„||<Con5<i(l|f^nll + IIK,ll)<
< Const^iWU^W + ip'^ + h)\\Vo\\), C.35а)
||V„|| < Сопв1^{ЩЩ\\ + (р'^ ^h)\\V,\\) . C.35b)
Векторы Uq и Vq состоят из локальных погрешностей у-компоненты
или погрешностей стартовых значений; согласно C.23) и C.25) они
имеют порядок величины 0{hP'^^). Поэтому из C.35) следует, что
для распространяющихся погрешностей справедливы оценки
1|Аг/„||<СзЛ'"+^,
IK(j/„+*)A2/„+ill < QCp" + hW^' при i = О,..., fc - 1.
Суммирование дает искомую оценку для у-компоненты:
\\уп-уМ\\< Е Нуп-у^^'II <QЛ^
Ь) Поскольку z^ зависит только от y„_jt» • • •»Уп-1 ^ "^ зависит
от предыдущих значений г, можно применить теорему 3.2, положив
у. = у{х-), ?• = z{x-), S = O(h^) и ^ = 0. При этом получим
\K-^n)\\<^i2\\9y{yM){yn-j-y(^n-M + 0{hn. C.38)
j = l
Используя C.36) и равенство у^ = y{x^)'\-0{h^), следующее из C.37),
найдем, что
1К(у(^п))iVn-j - yi^n.jM = II Е 5уЫ^п)) (Упч - yt'j)
C.36)
C.37)
г=о
n-fc+l
< Е {hy(y^n){yLj-yit))\\+o(h'^^')) = o(h''^')
1=0
536 Гл. VII. Дифференциально-алгебраические задачи высших индексов
и, следовательно,
lk„-^WII<Q/"'. C.39)
с) Вообще говоря, постоянные С^,С^ и С^ будут зависеть от
Co,Ci,C2, входящих в наши предположения C.26). При р>2 мы
можем ограничить длину шага Л так, чтобы
и тогда численные решения на рассматриваемом интервале всегда
будут удовлетворять условиям C.26).
При р=1 (неявный метод Эйлера) согласно замечанию З.ЗЬ оценку
C.27Ь) можно заменить на
\\Az„^,\\<C\\AY„\\. C.40)
Поэтому вместо C.28а) мы получаем непосредственно
Ay„^,-Ay„ = Oih\\AyJ\), C.41)
где соответствующая члену 0(...) константа не зависит от Cq, С^ ,
6*2, если Л достаточно мало. После этого сходимость доказывается
стандартным способом, без привлечения проекторов C.29). П
Используя идеи, развитые в разд. П1.5, изложенное выше
доказательство можно распространить на случай переменных длин шага.
Первоначально доказательство сходимости в таком виде дали Гир,
Гупта и Леймкулер A985).
Общие многошаговые методы
Для сходимости многошагового метода общего вида C.3) с
производящими многочленами
к к
1=0 t=0
получен следующий результат.
Теорема 3.6. Рассмотрим задачу C.1) индекса 2,
удовлетворяющую условию C.2). Предположим у что многошаговый метод устойчив
(определение 1П.3.2) и строго устойчив на бесконечности (нули a(Q
лежат внутри единичного круга |С| < 1 j. Если порядок метода р > 2,
то для глобальной погрешности справедливы оценки
Уп - У(^п) = От^ ^п " Фп) = 0{hn для x^ = nh< Const
при условии J что стартовые значения (при j = 0,...,/:—Ij
удовлетворяют условиям
yj - y(xj) = 0{hP+'), z^ - z(xj) = 0(hn. C.42)
Доказательство. Доказательство, в основном, такое же, как и для
схем ФДН. Но так как у^^^ > ^п+л зависят не только от У„, • • •, Уп+/с-11
но u от 2у,,..., z^^i^__i, необходимы следующие изменения.
VI 1.3. Многошаговые методы для ДАУ индекса 2 537
В дополнение к C.26) предположим еще, что ||?^ —-nil ^ C^h. Из
теоремы 3.2 вместо C.27) получим
\\Ay,^,\\<C(\\AYJ + h\\AZJ),
\\Az„^,\\<j(t^\\9y(yn+,)Ay„+j\\ + h\\AYJ-i.h\\AZj\
и C.28) примет вид
к к
;^а,Ду„+, = л5]/?,Л(У„+.-?„+*)Аг„^.+0(Л||ДУ„|| + /12||Д2Л),
1=0 1=0
0 = 9y{y„+,)Ay„^,+O{h\\AY„\\ + h'\\AZJ). C.43)
Рекурсия для А^:^^ получается следующим образом. Умножим
верхнюю строку C.43) на {{9у/г)-'^ду)(Уп-^к^^п+к)у что дает
к к
hY^t^i Az^^i = J2^i {(9у1г)~^9у)(Уп+к>^п-^к) ^Уп^г-^
Используя проекторы Р„, Q„ из C.29) и векторы U^.V^, мы получим
равенства C.32) с дополнительным членом 0(/i2||AZ^||). Из C.44)
получаем
1=0 1=0
u2|
hAZ,^, = {B^I)hAZ,-^o[h\\UJ-^\KHh'\\AZj)^
где
В =
1 0 0
\ 10
и C'- = pjp^. Для этого уравнения возьмем норму, для которой
||5 0/|| < /с < 1. Это возможно, потому что метод строго устойчив
на бесконечности. В итоге мы получим неравенства
/ ll^n+ill \ /1 + 0(Л) 0{h) 0{h) \ 1 \\IQ\
\\Vn+x\\ < 0{h) p + 0{h) 0(h) \\VJ
\Л||Д^„+1||/ V 0(h) Oil) K + 0{h)J \h\\AZJ,
C.45)
которые решаются так же, как в доказательстве предыдущей
теоремы, что дает
\\AyJ<C^h^^\ ||Д.-„||<C7(p" + к" + Л)ft^
\\9y{yn+k)Ay„+j\\<C,(p" + K" + h)hP+' np«j = 0,...,k-l.
538 Гл. VII. Дифференциально-алгебраические задачи высших индексов
Суммируя распространяющиеся погрешности, как в C.37), мы
получим желаемые оценки для у- и 2-компонент. П
Решение нелинейной системы
упрощенным методом Ньютона
Нелинейную систему C.3) обычно решают упрощенным методом
Ньютона. Интересно исследовать сходимость итераций. Как и в
доказательстве теоремы 3.1, введем г/ по формуле C.9) и
перемасштабируем Л, так что нелинейная система примет вид
y-r,-hf(y,z)=0,
9(У) = 0
(мы опустили индексы). Мы получили не что иное как неявный метод
Эйлера, и можно воспользоваться его обсуждением в работе ХЛР89,
гл. 7. Матрица Якоби нелинейной системы C.47) имеет вид
а обратная к ней —
/ P + 0(h) fA9j.)-^+0{h)\
где P = I — fz{9yfz)''^9y — оператор проектирования из C.29).
Рассмотрим теперь упрощенный метод Ньютона как простые итерации
для функции
Ф(у,г)=(^)-^(^-''-^((^'^)). C.50)
Индекс О у Jq указывает, что в качестве аргументов производных
в C.48) взято некоторое фиксированное приближенное решение [rjX)
системы C.47). Будем использовать обозначение {Д}о Д^я fy(fj,0,
и т.п. Прямое вычисление Ф'(у, г) дает
( {/г(9у/г)-Чоа9у}о-9у)+0{к) h{P]of,-\-0{h^) \
\h-Hi9yL)-'}o({9y}o-9y)+0(l) {{9yL)-'9y}oi{f.}o-h)+0(h))'
Если предположить, что (fjX) аппроксимирует неподвижную точку
функции C.50) с погрешностью 0(h), то в этой неподвижной точке
мы имеем
VI 1.3. Многошаговые методы для ДАУ индекса 2 539
Введем масштабирующую матрицу D = diag (I,hl) (это соответствует
умножению г-переменных на Л). Тогда \\ОФ'(уу z)D''^\\ = 0(h).
Поэтому, используя норму ||j/|| H-/i||2:||, мы выигрываем множитель h в
каждой итерации упрощенным методом Ньютона.
Замечание. Приведенный анализ остается в силе, если в Jq
матрицу / полностью или частично заменить нулями. Для механических
задач такой алгоритм предложили Гир, Гупта и Леймкулер A985).
Упралснения
1. Покажите, что предположение g(yj) = O(h^) (j = О,..., А: — 1) в
теореме 3.1 нельзя опустить.
Контрпример. Рассмотрите систему х' = 1, t/ = Аг(г), О = у — а:, где
k(z) = (е^~^ -h 1)/2. Примените неявный метод Эйлера с
начальными значениями Xq = О, y^^h, Zq = 1.
2. (Гир, Хсу и Петзолд 1981; Гир и Петзолд 1984.) Рассмотрите
задачу
(;,°)(r.Li.'A)@=as)- '"^'
a) Докажите, что система C.52) имеет индекс 2 при любых
значениях Г).
b) Покажите, что ^-компонента точного решения имеет вид z[x) =
= g{x)-f'(x).
c) Убедитесь, что неявный метод Эйлера, будучи применен
очевидным способом к C.52), порождает рекурсию
'"^'=lT-n'^^^'тh,{^^""^'^
h )
Следовательно, метод сходится при г; > —1/2, но неустойчив при
У] < —1/2. При ;;= — 1 численное решение не существует.
VII.4. Методы Рунге—Кутты
для ДАУ индекса 2
«РК-методы оказались популярными на конференции ИМА
по численному решению ОДУ».
(Берн и Хайндмарш, SIAM News, март 1990 г.)
Этот раздел посвящен исследованию сходимости неявных методов
Рунге—Кутты для полуявных систем C.1) индекса 2,
удовлетворяющих условию C.2). Метод е-вложения из разд. VI.1 определяет
численное решение посредством уравнений
S S
Уп+1 =Уn + f^^ fc.'fn.. ^n+i = 2„ + Л 5Z ''i^ni' D1а)
t=i 1=1
где
*„, = /(y„,,Z„,), 0 = 5(У„.), D.1b)
а внутренние стадии определяются уравнениями
S S
Ущ = Vn^hY^ai^Ky ^т = ^n-^hJ^^iAj' D.1с)
j=i i=i
(Метод пространства состояний (VI. 1.12) здесь не имеет смысла,
поскольку алгебраические условия не зависят от г.)
Первые результаты о сходимости в этой ситуации получила Пет-
золд A986).. Они сформулированы для задач общего вида F(y', у) = О
в предположении «однородности индекса один». Поскольку система
C.1) становится «однородной индекса один», если z заменить на и'
(Гир 1988; см. также упр. 1), результаты Петзолд применимы и к
уравнениям C.1). Бренан и Петзолд A989) продолжили
исследование для полуявной системы C.1). Их основной результат состоит в
том, что для D.1) глобальная погрешность у-компоненты — порядка
0(/i^"*"^), в то время как для г-компоненты она порядка O(h^), где
q — стадийный порядок метода. Этот результат был улучшен в
работе ХЛР89^^, в которой использовался другой подход (локальная и
глобальная погрешности исследовались отдельно).
Нелинейная система
Сначала мы исследуем существование, единственность и влияние
возмущений на решение нелинейной системы D.1). Для упрощения
обозначений мы будем писать (г}Х) вместо (у^,^^^), считая эти
величины зависящими от h; мы опустим также индекс п в таких
обозначениях, как Y^- и т.п. Тогда нелинейная система примет вид
См. примечание на стр. 503. — Прим. ред.
VI 1.4. Методы Рунге—Кутты для ДАУ индекса 2 541
j=i ) i=l,...,s. D.2)
0 = 9{Y,),
Если решение системы D.2) известно, то из D.1с) можно вычислить
величины ^„, (при условии, что (а,^) — обратимая матрица), а затем
найти у„+1,^п+1 **з D.1а).
Теорема 4.1 (ХЛР89, р. 31). Предположим, что {т},С)
удовлетворяет требованиям
9{n) = 0(h^), 9y{ri)f{riX)=0{h) D.3)
И условие C.2) выполняется в окрестности (г]Х)- Если матрица
{a^j) метода Рунге—Аутты обратима, то нелинейная система D.2)
при /i < /iq обладает локально единственным решением, для которого
справедливы соотношения
Y,-r,=:0(h), Z,-C = 0(h). D.4)
Замечание. Условия D.3) выражают предположение о близости
{rjX) к согласованным начальным значениям. В то же время из D.2)
видно, что решение (У^, Z,) этой системы не зависит от С-
Величина С в D.3) только конкретизирует ту ветвь решения уравнения
9у{у)/{Уу z) =0, к которой близко численное решение.
Доказательство теоремы 4.1 для неявного метода Эйлера было
дано в разд. VII.3 (теорема 3.1). Если заменить C.14) на
S
Yi - ф) - h Y, aijf{Yj,Zj) = О, D.5а)
l\y{r,(h) + r{Y,-r,(h)))dr-^a,jf(Yj,Zj) + lg{v(h))=0, D.5b)
TO OHO непосредственно переносится на методы Рунге—Кутты общего
вида. П
Влияние возмущений. Наряду с D.2) будем рассматривать также
возмущенную систему^
Yi = fi+hJ2aijf{Yj,Zj) + hSi,]
0 = 9{Yi) + e,,
Исследуем теперь влияние возмущений J, и в^ па численное решение.
Теорема 4.2 (ХЛР89, р. 33). Пусть У^, Z^ представляет решение
системы D.2), а возмущенные величины Yi/Z^ удовлетворяют системе
D.6). К условиям теоремы 4.1 добавим еще следующие
предположения:
fj-rj = 0{h^), Z,-C = 0(/i), S, = 0(h), e, = 0(h^). D.7)
1 = 1,. ..,5. D.6)
542 Гл. VII. Дифференциально-алгебраические задачи высших индексов
Тогда при /г < /iq справедливы оценки
\\yi-YM<c{\\fi-r,\\ + hm\ + \\e\\), D.8а)
\\Zi - Z,\\ < ^ {\\9,(r,){fi-v)\\ + h\\ii- vll + Л||<5|| + ll^ll), D.8b)
где \\S\\ = max,- \\S^\\ и \\в\\ = max, ||^J|. Если начальные значения
удовлетворяют условиям д{г]) =0 и g{fj) = О, то справедлива более
сильная оценка:
ll^i-^.ll<f (л||^-'7|| + ад| + 1И|)- D.9)
Постоянная С в D.8) и D.9) зависит только от величин,
ограничивающих значения определенных производных функций f и д, но она не
зависит от констант, входящих в члены вида 0{...) в D.3) и D.7).
Доказательство. Оценки D.8) получаются распространением
доказательства теоремы 3.2. Если оба начальных значения т] и fj
лежат на многообразии д(у) = О, то из разложения Тейлора получаем
0 = g{fi)'-g{r})=gy(ri)(fi-T))i-\-O{\\fi-T]\\^). При этом член gy(T])(fj-r))
в D.8Ь) — порядка С?(Л^||^—^||), и им можно пренебречь. П
Оценка локальной погрешности
Начнем с определения двух операторов проектирования, имеющих
важное значение при исследовании локальных погрешностей в
задачах C.1) индекса 2.
Определение 4.3. Для значений Pq.Zq, при которых матрица
(9у/г){Уоу^о) обратима, мы определим проекторы Q и Р равенствами
«=(/Л5„Л)"Ч)(г'о-^о). P = i-Q. D.10)
Геометрическая интерпретация. Пусть многообразие К
определено как и = {у;д{у) = 0} и пусть T^^U = кет(ду(у^)) —его касательное
пространство в точке у^^Ы. Далее, пусть V= {f(yQ^z) ; z любое}
и Ty^V = 1т(Д (t/oj -2:0)) — его касательное пространство в точке /q =
= f(yoyZQ). Здесь Zq — то значение г, для которого /(Уо^-^^о) «^ежит
в Ту^и, т.е. для которого выполнено условие ду{УоI{Уо1^о) = 0 (см.
A.14с)). На рис.4.1 стрелки изображают поведение f(yo,z) при
изменении z\ можно сказать, что пространство Tj^V содержит те
направления, вдоль которых управляющие переменные z приводят решение
к многообразию U. В силу C.2) эти два пространства трансверсаль-
ны, и их прямая сумма порождает у-пространство. Из D.10) следует,
что проектор Р проецирует на Ty^U параллельно Tj^V, а Q
проецирует на Tf^V параллельно Ty^U.
Рассмотрим теперь начальные значения уц = У{^) i ^0 ^ ^(^)' ^^^"
тые на точном решении, и обозначим yi.z^ численное решение мето-
VI 1.4. Методы Рунге—Кутты для ДАУ индекса 2 543
Рис.4.1. Проекторы Р и Q.
дом Рунге—Кутты D.1). Локальную погрешность
<5Ул(^) = У1-у(^ + Л), Sz^(x) = z^-z(x^h) D.11)
можно оценить следующим образом:
Лемма 4.4 (ХЛР89, р. 34). Пусть метод Рунге—Кутты с обратимой
матрицей коэ4х})ИЦиентов (а^) удовлетворяет условиям В(р) и C(q)
из разд.IV.5, причем р> q. Тогда
Sz,{x) = 0{h''),
где Р{х) — проектор D.10), вычисленный при (у(х), z(x)). Если,
кроме того, метод Рунге—Кутты жестко точный (а,, = 6, для всех г), то
(J2/Jx) = 0(/i"^'"(P+^'^+2)). D.13)
Доказательство. Точные значения решения rj = у(х), Vj = у(х-\-
4-c,/i), Z, = z(x-bc^h) удовлетворяют системе D.6) с б,- = О и
j = l
Поэтому разность решений точного и численного (удовлетворяющего
системе D.2) с г; = у(х)) можно оценить с помощью теоремы 4.2. Это
дает
у;. - у(х -f c,/i) = 0(/i^+M. ^i - Ф + Cih) = 0(/i^). D.14)
Так как квадратурная формула {6,,с,} имеет порядок р, то
у(х -f Л) - у(х) ^hJ2 fri/Ы^ + ^tЛ), z(x + c,h)) = 0(h^-^').
1=1
Вычитание этой формулы из D.1а) дает
3
У1-г/(х + Л) = Л/Лг/(х),г(х)M^6,(^,-а(х + с,Л))+0(Л''+1)+0(/1'+2).
1=1
Поскольку P(x)f^{y(x),z(x)) = 0, этим доказана оценка D.12) для
544 Гл. VII. Дифференциально-г1лгебраические задачи высших индексов
у-компоненты. Оценка для 2:-компоненты следует из соотношений
5
Z, - г(х Ч- Л) = ^ 6,0;,^. [Z^ - z(x -f c^h)) + 0{h^^')
(cm. A.28)) и D.14).
Если предполагается, что а,, = 6, для всех i, то givi) = О и
разложение Тейлора имеет вид
Q=9{yi)-9{y{x + h))=^9^(y{x))8y,,(x) + 0(h\\Sy^[x)\\). D.15)
Тогда Q[x)Syf^[x) = (9(Л||(?г/^(х)||), и оценка D.13) следует из D.12) и
D.10). D
Для некоторых важных методов Рунге—Кутты (таких, как Радо
ПА и Лобатто IIIC) оценки леммы 4.4 не являются оптимальными.
Точные оценки будут даны в теореме 4.9 для коллокационных методов
и в разд. VII.5 для методов Рунге—Кутты общего вида.
Сходимость для у-компоненты
Определяемое системой D.1) численное решение {у^} не зависит
от {z^]. Следовательно, сходимость для у-компоненты можно
рассматривать независимо от оценок для г-компоненты.
Теорема 4.5 (ХЛР89, р. 36). Пусть условие C.2) выполнено в
окрестности решения (у(х),г(х)) уравнения C.1) и начальные
значения согласованы. Предположим далее, что матрица метода Рунге—
Кутты (а,.^.) обратима, выполнено условие |Л(оо)|< 1 (см. (Vl.l.lle))
и локальная погрешность удовлетворяет условиям
5у^{х) = 0(НП, P{xNy,ix) = 0(h'+'), D.16)
где Р(х) — тот же проектор, что и в лемме 4.4. Тогда метод D.1)
сходится с порядком г J т.е.
2/„ - у(х^) = 0(h'') при х„ - Xq = пЛ < Const.
Если, кроме того, 6у^^{х) = С?(Л''+^), то д(Уп) = 0{h^'^^).
Доказательство. Полное доказательство этого результата
приведено в работе ХЛР89, pp. 36-39. Здесь мы ограничимся его
изложением для жестко точных методов (у которых а,, = 6, для всех г).
Некоторые части докгьзательства при этом значительно упрощаются, и
все же этот случай охватывает многие важные методы Рунге—Кутты
(такие, как Радо ПА, Лобатто IIIC и метод ОДНРК (IV.6.16)). Из
предположения а^- = Ь- {для всех г) следует, что д{Уп) = О при любом
п и, как следствие D.15) и D.16), что
Sy,ix) = 0(h^^'). D.17)
Нижеследующее доказательство аналогично доказательству
теоремы 3.5; в нем снова используется образ «веера леди Уиндермир»,
рис.11.3.2.
VI 1.4. Методы Рунге—Кутты для ДАУ индекса 2 545
Кроме численного решения {у„, ^„ } , обозначаемого также {у^' -^п } »
мы будем рассматривать также решения {у^,^^}, даваемые методом
Рунге—Кутты для начальных значений у^ = y(^t) j ^i = ^i^i)^ взятых
на точном решении. Получим сначала оценку у^ — Уп"*"^ при п > ^-f 1,
выраженную через локальную погрешность 6у^^(х^) = у^^^ ""l/^+i • Д-^^
упрощения обозначений будем обозначать {у„} и {у^} два соседних
решения методом Рунге—Кутты и Ау„ = у^-у^ их разность.
Допустим, что
\\Уг,-У(^п)\\<Со1г, \\AyJ<C,h' D.18)
(ниже это допущение будет обосновано). Тогда применение теоремы
4.2 с rf,. = О и ^,- = О дает:
\\Упг - Ут\\ < С||АУпН, ll^ni - Kill < СЦАуЛ, D.19)
где С — некоторая константа, не зависящая от Cq и Cj. Из условия
Липшица для f(y,z) следует, что
S
l|Ay„+,||<||Ay„|| + /»X^|6,|(i,||y„,-yj| + L2ll^„.-^„,||).
t = l
Подставляя сюда D.19), получим ЦАу^^^Л < (H-/iL)||Ayyj||, а
следовательно, и
УДУпП < С'зНАуоЦ при nh < Const D.20)
Для нашей ситуации в «веере леди Уиндермир» использование D.17)
дает
\\yi-yi^^\\<C2\\Syh{^i)\\<Csh'-^^ при п>^+1 и nh< Const.
Суммируя, мы получаем желаемую оценку:
\\Уп-уМ\\ < Е 112/п -2/п^'11 < C,h' при nh < Const,
1=0
Поскольку Cg и 6*4 не зависят от Cq или С^ (при достаточно малых
Л), то предположение D.18) может быть докгьзано индукцией по п при
условии, что постоянные Cq и С^ выбраны достаточно большими. D
Сходимость для Z-компоненты
Теорема 4.6 (ХЛР89, р. 40). Рассмотрим задачу C.1)-C.2)
индекса 2 с согласованными начальными условиями и предположим^ что
матрица (а, ) метода Рунге—Кутты обратима и |Я(оо)| < 1. Если
глобальная погрешность у-компоненты является величиной порядка
O(h^), д(Уп) = 0{h^^^) и локальная погрешность z-компоненты —
величина порядка 0{h^), то глобальная погрешность z-компоненты
z^ — z(x^) = 0{h^) при 2Гу^ — Xq = пЛ < Const.
546 Гл. VII. Дифференциально-алгебраические задачи высших индексов
Замечание. Если кроме условия обратимости (а, ) и |Я(ос)| < 1
выполнены также условия B{q) и C[q), то z^— z(x^) = 0[h^) (см.
лемму 4.4).
Доказательство. Запишем глобальную погрешность в виде
^п + 1 - ^(-^n + l) = ^п + 1 - ?п + 1 +<^^/|(^п)' D.21)
где (Ууг+1)^п+1) — численное решение, получаемое при начальных
значениях {y[x^),z[x^)), а 5z^[x^) — локальная погрешность. Из
(VI. 1.1 Id) мы имеем
S
^п+1 - ?п+1 = Л(оо) (г„ ~z(xj) + Y. bi^iji^nj-^nj)' D.22)
Из условия ^(y„) = 0(/i*'"^^) следует, что ^j^(y„)(y„-l/(ar„)) = 0(/i''+^);
с учетом условия у„ — у(х„) = O(h^), на основании теоремы 4.2 мы
приходим к выводу, что Z^j — Z^j =0(h^). Подставив D.22) в D.21),
получим
^„+1 - Фп+i) = Я(^) (г„ - z{x„)) + 0{h^),
что и доказывает теорему. П
Коллокационные методы
Коллокационные методы, введенные в разд. II.7, составляют
важный подкласс неявных методов Рунге—Кутты. Для задачи C.1)
индекса 2 они могут быть определены следующим образом.
Определение 4.7. Пусть с^,..., с, — s различных вещественных
чисел. Обозначим u(x),v(x) многочлены степени s (коллокационные
многочлены), которые удовлетворяют условиям
Фо) = Уо^ ^(^о) = ^0' D.23а)
u'(xo + c./i) = /(w(xo + c,./i),i;(xo + c,./i)),l .
> г = 1,...,5. D.23Ь)
0 = g{u(x, + c,h)), J
Тогда численное решение определяется формулами
У1 =: w(xo-h/i), z^=v(xQ-\-h). D.23с)
Непосредственное распространение теорем П.7.7 и II.7.8 на задачи
индекса 2 показывает, что D.23) эквивалентно 5-стадийному методу
Рунге—Кутты D.1), коэффициенты которого определяются
условиями B{s) и C(s) (их определение см. в разд. IV.5). Эта
эквивалентность позволяет вывести из теоремы 4.1 существование и локальную
единственность коллокационных многочленов при условии, что
матрица соответствующего метода Рунге—Кутты обратима. Поэтому
далее мы будем предполагать, что с, ф^О для всех г. Случай
сингулярной матрицы метода Рунге—Кутты рассмотрен в упражнениях 2
иЗ.
VI 1.4. Методы Рунге—Кутты для ДАУ индекса 2 547
Качество аппроксимации y{x),z(x) многочленами u(x),v(x)
описывается следующей теоремой, расширяющей теорему II.7.10.
Теорема 4.8. Рассмотрим коллокационный метод D.23), у которого
все с^фО. Тогда для А: = 0,1,..., 5 я х G [xq, Xq + /i] имеем
||г/('^)(x)-2/('^)(x)||<C/г*^^-^
\\v^^)(x)-z^^^x)\\<Ch'-''.
Доказательство. Воспользуемся тем, что u{xQ-\-c-h) = У-^ ^(^о"*"
-fc,/i) = Z, являются внутренними стадиями метода Рунге—Кутты
D.1). Следовательно, коллокационные многочлены можно записать
в виде
S
w(xo + //i)=yo^o@-f^>;-A@, D.24а)
1=1
S
v(xo + th) = zo ioit) + Y^ Z, e,{t), D.24b)
t=l
где i^(t) — многочлены Лагранжа, определяемые равенствами
Из известных оценок погрешности интерполяции вытекает, что точное
решение у{х) удовлетворяет равенству
5
2/(хо+<Л) = Уо^о@ + Е2/К + ^.Л)^.@ + 0(Л^^М. D.25)
1=1
Множитель /i*"^^ в погрешности интерполяции появляется из (s-f 1)-й
производной y(xQ-\-th) по t. Очевидно, что погрешность
интерполяции можно дифференцировать столько же раз, сколько и функцию
у(х). Если продифференцировать D.25) к раз, то согласно теореме
Ролля разность
/1*у(*)(хо + <Л)- (уо^^'''(<) + Еу(^о + с.ЛК|'"(<)) D.25')
« = 1
обращается в нуль не менее чем в s -f 1 — Аг точках.
Следовательно, в D.25') многочлен в скобках можно интерпретировать как
интерполяционный многочлен степени s — к для функции Н^у^^Цх^-\-1к).
Поэтому его погрешность тоже порядка 0(Л*"*"^). Вычитая D.25) из
D.24а) и дифференцируя результат к раз, получим
h''{u^''Hxo+th)-y^''\x, + th)) = Y{Y,-y(x, + c,h))e'^\t) + 0(h'+').
548 Гл. VII. Дифференциально-алгебраические задачи высших индексов
Аналогичная формула получается и для г-компоненты. Заключение
теоремы следует теперь из D.14) при q = s. П
Сверхсходимость коллокационных методов
Теперь естественно поинтересоваться, существует ли при XqH-/i
сверхсходимость, имеющая место в случае обыкновенных
дифференциальных уравнений (см. теорему II.7.9). Ответ будет
утвердительным, если метод — жестко точный, т.е. если с, = 1.
Теорема 4.9. Если с,- ф О для всех г я с, = 1, то у-компонента
локальной погрешности коллокационного метода D.23) удовлетворяет
равенству
yi-y(xo + h) = 0(hP+'),
где р — порядок квадратурной формулы, положенной в основу
метода.
Доказательство, Подставим коллокационные многочлены в
дифференциально-алгебраическую задачу и определим невязку
равенствами
u'{x) = f{u{x),v{x))-^S(x), D.26а)
0=:д{и{х))+в{х). D.26Ь)
Согласно определению 4.7
S{xo -f Cih) = О, в{х^) = О, в{хо + Cih) = 0. D.27)
Продифференцируем теперь D.26Ь) по х и с учетом D.26а) получим:
0 = 9у{и{х)){/(и(х),у{х))+6{х))+в'{х). D.28)
Этот результат является мотивировкой использования уравнения
о = 9^(и) (/(«, V) + S{x)) + в'{х) D.29)
ДЛЯ произвольных (и, г;) в окрестности решения задачи C.1).
Благодаря условию C.2), уравнение D.29) можно разрешить относительно
V и переписать это уравнение в виде
v = G{u,S{x),e\x)). D.30)
Подставляя это выражение в D.26а) и в C.1), получим
u'(a:) = /(u(x),G(tx(x),E(x),e'(x)))+J(x), D.31а)
j/'(x) = /(y(x),GB/(x),0,0)). D.31b)
Теперь, чтобы вычислить и{х) — у(х), применим нелинейную
формулу вариации постоянной (теорема 1.14.5). Это требует вычисления
невязки и(х), подставленной в D.31b):
u'(x)-f[u(x),G{u(x),0,0)) =
= f(u(x),G{u{x),Six),в'(х))) + Six) -f(u{x),G{u(x),0,0)) =
= Ф(а;,1)-Ф(а;,0L-*(х), D.32)
VII.4. Методы Рунге—Кутты для ДАУ индекса 2 549
где
Ф(х, г) = /(гг(х), G{u{x), т • S(x), т• в'{х))) .
Формула Ф(х, 1) — Ф(х, 0) = /q дФ/дт (х, г) с/г показывает, что невязку
D.32) можно записать в виде
Q,(x)S(x) + Q^(x)e'(x). D.32')
Подставим это выражение в уравнение A.14.18) и получим
и(х) — у(х) = I [резольвента(х, t)] • [невязка(^)] dt =
J Xq
= nS,{x,t)S{t) + S^{x,t)9'{t))dt.
J Xq
Интегрируя второй член по частям, получим (с учетом того, что
tf(xo) = 0)
y^-^y{x^^h) = J i^S,{x,-^h,tM{t)--^(x,-^h,t)e{t))dt-^
+ S^ixo + Л, Хо + h) e(xQ + h). D.33)
Из условия с, = 1 следует, что ^(хд + Л) = О, поэтому последний член
в D.33) исчезнет. Теперь основная идея состоит в том, чтобы
вычислить интеграл в D.33) с помощью квадратурной формулы {6,-, с,}
(см. также доказательство теоремы П.7.9). Используя обозначение
ait) = S, (хо + h, t) S{t) - ^{х, + h, t) e(t), D.34)
-y(a^o + ^)= / (т@Л = Л^6,.сг(хо + с,./1)-}-егг(а-). D.35)
^Xn .'^l
МЫ получим
лхо + Л
Vi
Благодаря равенствам D.27) мы имеем G(xq-f c,/i) = 0 для всех г, и
погрешность квадратуры оценивается неравенством
\\егг{ст)\\ < ChP-^^ max 1^(^^@11. D.36)
t^[xo,XQ-\-h]
Производная сг(<) порядка р содержит производные /, ^ и S[x), в[х).
Согласно теореме 4.8 они равномерно ограничены при Л < Лц .
Следовательно, у^ — y(xQ -}- Л) = егг(сг) = 0(/i^"'"^), что и доказывает теорему.
П
Проецированные методы Рунге—Кутты
Для коллокационных методов, не являющихся жестко точными,
сверхсходимость (как в теореме 4.9) доказывается в случае, когда
метод комбинируется с определенной проекцией. Мы начнем с более
тщательного исследования локальной погрешности у-компоненты в
D.33).
550 Гл. VII. Дифференциально-алгебраические задачи высших индексов
Лемма 4.10. Если с, ф О для всех г, то у-компонента локальной
погрешности коллокационного метода D.23) представима в виде
D.37)
где в — невязка J определяемая уравнением D.26Ь), ар — порядок
квадратурной формулы^ положенной в основу метода.
Доказательство. В ходе доказательства теоремы 4.9 было
выяснено, что локальная погрешность может быть представлена в виде
2/1 - у(хо + /i) = 52(^0 + Л, хо -I- h) в(х^ + Л) -h 0{hP-^^)
(см. уравнение D.33)). Поэтому нам остается лишь вычислить
52(х, х). Поскольку всякая резольвента равна единичной матрице,
когда ее аргументы равны, то из определения S2(x,t) и формулы D.32')
следует, что
S^{x, х)=1 Л (и(х), G{u{x),tS{x), тв'(х))) ^ (и(х), tS(x), тв'{х)) dr.
Дифференцируя D.30) по в', получим
Далее, из D.27) следует, что S(x) = 0{h^) и S'(x) = 0(/i*), когда
X = Xq -h /i. В силу теоремы 4.8 и{х) — у(х) = 0(h''^^), и при х = Xq + H
мы получаем
S^(x,x)=(f,{9j,)-'){y(x),z(x))+0(h').
Утверждение леммы следует теперь из того, что р < 2s и в(х^ -\-h) =
= 0(Л*+1). П
Можно дать следующую геометрическую интерпретацию леммы
4.10. Если расщепить локальную погрешность (Ууд(хо) в соответствии
с проекциями, изображенными на рис. 4.1, то при этом
компонента Q(xQ'\-h)Syf^(xQ) имеет порядок величины С?(Л*"*"^), а
компонента P(xQ-|-/i)rfy^(xo) — порядка 0(h^'^^). Это наводит на следующую
мысль: численное решение, получаемое методом Рунге—Кутты,
проецировать после каждого шага на многообразие д{у) =0 с помощью
проектора P{xq -\- h).
Определение 4.11 (Ашер и Петзолд 1991). Пусть Ух^г^ —
численное решение, полученное неявным методом Рунге—Кутты D.1).
Определим у^, Л как решение системы
0 = 5(j/i).
Если значение у^ (и z^) используется для пошагового интегрирования
задачи C.1), то эту процедуру мы будем называть проецированным
методом Рунге—Кутты.
VI 1.4. Методы Рунге—Кутты для ДАУ индекса 2 551
Замечания. 1) Если g(yi) достаточно мало, то нелинейная система
D.38) имеет локально единственное решение. Итерации
ньютоновского типа с начальными значениями у{ —Ух, А(°) = О будут сходиться к
этому решению. Это сразу следует из теоремы Ньютона-Канторовича
(Ортега и Рейнболдт 1970), потому что матрица Якоби системы D.38),
вычисленная при начгипьных значениях:
{ I -л(J'l.^l)^
имеет ограниченную обратную в силу условия C.2).
2) Для жестко точных методов Рунге—Кутты (у которых а^- = Ь-
для всех г) проецированный и непроецированный методы совпадают.
3) Из доказательства следующей теоремы видно, что аргумент в
fziVi' ^i) может быть заменен какой-либо другой аппроксимацией
величин y(xQ -1- h), z(xq + h), погрешность которой не превышает O(h').
В следующей теореме доказывается сверхсходимость
проецированных коллокационных методов и в том случае, если соответствующий
метод Рунге—Кутты не является жестко точным. Результаты,
касающиеся сверхсходимости общих методов Рунге—Кутты, представлены
в разд. VI.8.
Теорема 4.12 (Ашер и Петзолд 1991). Если с- ф О для всех г, то
для у-компоненты локальной погрешности проецированного колло-
кационного метода D.23), D.38) справедливо равенство
У1-г/(хо + л) = 0(Л''+М,
где р — порядок квадратурной формулы, положенной в основу
метода.
Доказательство. Введем обозначения е^ = ^j — y(xQ -h Л), Cj = г/^ —
—2/(^0 4- h) для локальных погрешностей и
Q={fA9yLr'9y)(yi,h), P=I-Q
ДЛЯ проекторов из определения 4.3. Идея состоит в том, чтобы
расщепить Cj согласно
е^ =Pe^+gej D.39)
и оценить каждую компоненту отдельно. Первая формула в D.38)
вместе с D.37) и ^(xq -{- h) = 0(h^'^^) имеет следствием
P€,=Pe,=0{hP-^')'{-0(h'-^'\\e,\\). D.40)
Далее, имеем: О = д(ух) -д{у(х^-^ h)) = 9y(yi)€x+0(\\€x\\^), откуда
Qe,=0(\\e,f). D.41)
Подстановка D.40) и D.41) в D.39) дает:
e,=0(h''^') + 0(h'-''\\e,\\)+0{\\e,f).
Отсюда непосредственно следует утверждение теоремы. П
552 Гл. VII. Дифференциально-алгебраические задачи высших индексов
Для проецированных коллокационных методов глобальная
сходимость с порядком 0{h^) выводится точно так же, как в
доказательстве теоремы 4.5. Заметим, что численное решение всегда остается на
многообразии д{у) = О, так что применима оценка D.9).
Сводка результатов по сходимости
В табл. 4.1 собраны оптимальные оценки погрешностей для
некоторых важных методов Рунге—Кутты при их применении к задаче C.1)-
C.2), имеющей индекс 2. Оценки локальных погрешностей можно
получить следующим образом: для методов Гаусса, Радо IA и ОДНРК
— по лемме 4.4, Радо ПА — по теореме 4.9, Лобатто IIIC — по теореме
5.10 (см. ниже) и Лобатто IIIA — с помощью упр. 4. Для
проецированных методов оценки получаются из теоремы 4.12 и соображений,
приведенных в разд. VII.5. Мы не представили здесь результатов по
сходимости для Z-компоненты решения, потому что существуют
разные способы ее численного определения. Результаты по глобальной
сходимости для методов Радо IA, Радо ПА, Лобатто IIIC и ОДНРК
вытекают из теорем 4.5 и 4.6; для остальных же методов (Гаусса и
Лобатто IIIА) их получить несколько труднее, потому что их функция
устойчивости удовлетворяет лишь условию |Д(оо)| = 1. Подробное
обсуждение этих методов можно найти в работах ХЛР89 и Жэ A993).
Упражнения
1. Рассмотрим задачу ]/ = f(y,z), 0 = д{у) индекса 2. Если положить
г = ti', v = (t/, li)^, то задача примет вид:
^<"»=('"л) "'')="¦
Докажите, что если существует [gyfz)"^, то тогда пучок матриц
F^ -h AF^/ имеет индекс 1.
Указание. Рассмотрите преобразование
(J ;)(i^. + AF„,)(i 5), D.42)
где а и 6 выбраны так, чтобы верхний правый блок матрицы D.42)
обратился в нуль: а = fyfAdyfz)"^» * = Л •
2. Рассмотрите методы Рунге—Кутты, коэффициенты которых
удовлетворяют требованиям
а^,. = О для всех i и матрица (a,j),j>2 обратима.
(Примеры — кол локационные методы, у которых с^ = О, как у
метода Лобатто IIIA.)
Если ^(т;) = О, то нелинейная система D.2) имеет локально
единственное решение, для которого У^ = ту, Z^ = С •
VI 1.4. Методы Рунге—Кутты для ДАУ индекса 2 553
Таблицд 4.1. Оценки погрешностей для задачи C.1)-C.2) индекса 2
Метод
Гаусса
проецировалный
Гаусса
Радо IA
проецировсшный
Радо IA
Радо НА
Лобатто IIIA
Лобатто II 1С
ОДНРК (IV.6.16)
ОДНРК (IV.6.18)
число
стадий
г 3 нечетное
t 5 четное
5
3
3
3
( 3 нечетное
t 5 четное
3
5
3 j
локальная
погрешность
У
/,5 + 1
^25 + 1
h'
д2,-1
^25
^2,-1
^2,-1
h^
h"
г
h'
h'-'
h'
h'
h'-'
h'
h'
глобгитьная
пофешность
У z
h^'
h' h'-^
д2,-2
h^'-' h'
''-' [Г
^2,-2 f^,-l
h" h'
/.2 /,1
3. Пусть Ci = 0, C2,..., с, — s различных действительных чисел.
Тогда существуют единственные многочлены и(х) и v{x) (degu = s,
deg г; = 5 - 1), для которых выполняются равенства D.23а,Ь).
Указание. Воспользуйтесь идеями доказательства теоремы П.7.7
и упр. 2.
4. Справедливы ли заключения теорем 4.8 и 4.9, когда с^ == О ?
5. (Вычисление алгебраической переменной z с помощью кусочно
разрывной интерполяции, см. Ашер 1989.) Изменим
определение z„^i в методе Рунге—Кутты D.1) следующим образом: пусть
v(x) — многочлен степени s—1, для которого v{x^-\-c^h) = Z^^
для всех г; определим г^^^ = ^(^п + Л) • В случае коллокационных
методов D.23) это определение снимает условие v(xq) = Zq и в то
же время понижает степень v{x) на единицу.
a) Проверьте, что z^^j не зависит от z^ , даже если функция
устойчивости метода не обращается в нуль на бесконечности.
b) Докажите, что для проецированных коллокационных методов,
у которых с- фО для всех г, справедлива оценка Zj^ — z(x^) = 0{h'^).
c) Для проецированных методов Гаусса сравните этот результат с
тем, что получается при стандартном подходе.
6. Теорема 4.8 остается в силе, если опустить условие v(xq) = Zq ъ
определении 4.7 и считать v(x) многочленом степени 5 — 1.
VII.5. Условия порядка ддя ДАУ
индекса 2
Для приложений полученного в предыдущем разделе результата
о сходимости (теоремы 4.5) желательно знать оптимальные значения
г в D.16). Сравнивая разложения Тейлора для точного и численного
решений, мы выведем условия на с,,а, ,6 , которые эквивгипентны
D.16). Для коллокационных методов мы получим снова результат
теоремы 4.9. Для других методов (таких, как Лобатто IIIC) оценки
леммы 4.4 будут значительно улучшены.
В этом разделе излагается теория, развитая в работе ХЛР89^)
(раздел V), но в несколько ином варианте, полностью
аналогичном выводу условий порядка для задач индекса 1, приведенному в
разд. VI.4. Полученные в этом разделе результаты здесь
применяются только к методам Рунге—Кутты; Рош A988) приводит
аналогичные формулы для методов Розенброка. А. Квернё A990) провела
независимое исследование для задачи f(y, z') = 0, z = д{у) индекса 2
и получила те же самые условия порядка для методов Рунге—Кутты.
Производные точного решения
Рассмотрим задачу индекса 2
y' = f(y,z), E.1а)
0 = д(у) E.1Ь)
И предположим, что начальные значения Vq^Zq согласованы. Первая
производная решения у(х) выражается формулой E.1а).
Дифференцируя это равенство, получаем
y" = fy(y,z)y' + fAy,z)z'. E.2)
Чтобы вычислить 2:', продифференцируем E.lb) дважды:
0 = 9у(у)у', E.3а)
0 = 9уу{у)(у',у')+ду(у)у" E.3b)
и подставим сюда E.1а) и E.2). Это дает
0 = 9yy(f,f)+9yfyf + 9yf^'=' E.4)
(очевидные аргументы функций опущены), или, что эквивалентно,
^' = {-9yf,r'9yy(fJ) + {-9yLr'9yfyf- E.5)
Здесь мы использовали входящее в определение задачи индекса 2
предположение C.2) о том, что матрица д f^ обратима в окрестности
решения. Продифференцируем теперь E.1а) и E.5) по х и заменим
^ См. примечание на стр. 503. — Прим. ред.
VI1.5. Условия порядка для ДАУ индекса 2 555
появляющиеся при этом у' и z' выражениями E.1а) и E.5).
Используя формулу
^ (-</,/.)-'«= E.6)
= i-9yfX'[9yy{h{-9yf^)-'^J)+9yf.y{(-9yf,)-'u,f) +
+ 9yhz{i-9yh)~'»A-9yf,)~^9yy(fJ) + {-9yfz)~4yfyf)),
где вектор и — постоянный (ср. формулу (VI.4.7)), мы получим
У' = /у1-Ь/Л-9у/гГ'9уу{/.Л + /г(-9у/гГ'9у/у/. E-7)
z''={-9yfгr'9yyyifJJ)'^Ч-9yfгr'9yy{fJyf)'^ E-8)
+ 4-9yfzr'9yy{fJz(-9yfz)'''9yy{fJ))-\-
^Ч'-9у1гУ^9уу{иг{-9у1гУ^9у1у!)^{-'9у1гУ^9у1уу[и)^
-^^{-9у1гГ'9у/уг{/Л-9у/гГ'9уу{/.Л) +
^'^{-9у!гУ^9у1уг{1Л-9у1гУ'9у!у1)^{-9у1гУ^9у1у1у1Л-
+ {-9у/гГ'9у/у/г(-9у1гГ^9уу(/,Л'^
+ (-9yfzr^9yfyfzi-9yfz)~^9yfyf'^
-^{-9у/гГ'9у/гг{{-9у1гГ'9уу{и)Л-9у/гГ'9уу{/.Л) +
-^А-9у/гГ'9у1гг{(-9у/гГ'9уу{и)Л-9у/гГ'9у1у/)-^
-^(-9yfz)~^9yfzz{i-9yfz)''^9yfyfA-9yfzr^9yfyf) '
Очевидно, что графическое представление этих выражений будет
весьма полезным.
Деревья и элементарные дифференциалы
Как и в разд. VI.4, мы отождествим каждое появление / с
вершиной-точкой («тонкой» вершиной), каждое дифференцирование / — с
выходящим из этой вершины вверх ребром, выражение (—9yfz)^^9 —
с вершиной-кружком («толстой» вершиной), а дифференцирования д
в этом выражении — тоже с выходящими вверх ребрами. Графы,
соответствующие выражениям для у', z', у"^ z" в формулах E.1а), E.5),
E.7) и E.8), представлены на рис.5.1.
Производные у характеризуются деревьями, у которых корень
(самая нижняя вершина) — точка. Эти деревья мы будем обозначать t
или <,, а дерево, состоящее только из корня (соответствующее у')
обозначим т. Производным Z соответствуют деревья, у которых корень
— кружок. Их мы будем обозначать и или и,.
Определение 5.1. Обозначим DAT2 = DAT^^U DAT22 множество
дифференциально-алгебраических деревьев индекса 2, которые
определяются рекурсивно следующим образом:
556 Гл. VII. Дифференциально-алгебралгческие задачи высших индексов
Рис. 5.1. Графическое представление первых и вторых производных.
a) теОАТ2^',
b) [<1,...,<^,гг1,...г/„]^еШГ2^,
если t^,,..,t^eDAT2^ и и^,.. .u^eDAT2^\
c) [<1,...,иг^^^^2, ,если <i,...,t^G^T2j^
и либо m > 1, либо m = 1 и ^^ ^ [w]^^, где и G 1)ЛТ2^.
Определение 5.2. Порядком jiepebSi t G DAT2 или ti G /)ЛТ2^
(обозначается /9(<) или p(w)) будем называть число вершин-точек минус
число вершин-кружков.
Определение 5.3. Элементарные дифференциалы F(t) (или F(u)),
соответствующие деревьям из DAT2, определяются так:
а) F(T) = f;
^) ^<<^)=-^^^{^(^^'>-'-^^^^^
если < = [<!,...,<^, u^,...,u^]yeDAT2y\
с) F{u) = {--gJ,)'^^{F(t,)^...,F{tj)^
если W = [<!,...,<J,G^T2,.
Разлолсение Тейлора для точного решения
Чтобы продолжить процесс, который привел к E.7) и E.8), надо
дифференцировать элементарные дифференциалы F{t) и F(u). Это
описывается следующими правилами:
i) к каждой вершине добавляется ветвь с т (дифференцирование /
или 5^ по у и добавление множителя г/ = f)\
VI 1.5. Условия порядка для ДАУ индекса 2 557
ii) к каждой вершине-точке добавляется ветвь с [г, г]^; к каждой
вершине-точке добавляется ветвь с [[t]J^ (это дает два дерева
и соответствует дифференцированию f по z и добавлению
множителей (-9yf^)~'^9yy(fJ) и (-9yfz)''^9yfyf из E.5));
iii) каждая вершина-кружок расщепляется на две новых вершины-
кружка, лежащие друг над другом и соединенные ребрами через
новую вершину-точку. Затем строятся четыре новых дерева: к
нижней из этих вершин-кружков добавляется ветвь с г, а к
новой вершине-точке добавляется ветвь с г, или [г, г]_^, или [[г] ]^
(это соответствует дифференцированию (—9yfz)^^ и вытекает
непосредственно из формулы E.6)).
Некоторые из элементарных дифференциалов в E.8) появляются
более одного раза. Чтобы понять, сколько раз появляется такое
выражение (или соответствующее дерево) в производных у или z, мы
будем указывать порядок порождения вершин следующим образом
(см. рис.5.2). Для деревьев порядка 1, т.е. для г, [т,т]^ и [[rJJ^,
добавляем метку 1 к вершине-точке так, что
за каждой вершиной-кргрюком следует по крайней мере , ^.
одна непомеченная вершина-тонка. ^ ' '
Всякий раз при «дифференцировании» некоторого дерева по
сформулированным выше правилам мы присоединяем к нему новое дерево
(порядка 1) с новой меткой так, чтобы условие E.9) выполнялось.
Очевидно, что при этом вдоль каждой ветви метки будут идти в
возрастающем порядке.
V
Рис. 5.2. Примеры монотонно помеченных деревьев.
Определение 5.4. Дерево t G DAT2y (или uG DAT22), у которого
помечены p{t) (или р[и)) из вершин-точек в монотонно
возрастающем вдоль каждой ветви порядке так, чтобы выполнялось условие
E.9), называют монотонно помеченным деревом. Множества таких
монотонно помеченных деревьев обозначаются LDAT2 , LDAT22 и
LDAT2.
Описанный выше процесс дифференцирования деревьев
порождает все элементы LDAT2, причем каждый из них — только по одному
разу. Каждое дифференцирование увеличивает порядок деревьев на
единицу. Таким образом, мы получили следующий результат:
Теорема 5.5 (ХЛР89, р. 58). Для точного решения системы E.1)
справедливы формулы
558 Гл. VII. Дифферегадаально-алгебраические задачи высших индексов
teLDAT2y,p{t)zzq teDAT2y,p{t)=q
^^'Чч)= Е ^(«)(l/o.^o)= Е o(u)F(u){y„z,).
ueLDAT2t,p{u)=q u?DAT2t ,p{u)=q
Целые коэффициенты a(t) и a (и) указывают число возможных
монотонных разметок соответствующего дерева. П
Производные численного решения
Запишем один шаг методом Рунге—Кутты для задачи E.1) с
согласованными начальными значениями (Vq^Zq) в следующем виде:
S S
yi=yo + J2'>i''i' ^i=-o + E^-^.- (^-1°^)
«=i 1=1
где
k, = hf(Y„Z,), 0 = giYi) E.10b)
И
5 S
Использовавшиеся в формуле D.1) величины hk^^^hi^^ мы здесь
переобозначили через Аг,,^,. Это несущественное изменение позволяет
сделать вывод условий порядка согласованным с материалом,
изложенным в разд. VI.4. Поскольку приведенный там вывод условий
порядка очень близок к нижеследующему, мы ограничимся здесь только
основными идеями.
Будем рассматривать у^г^, к^,?-, Y^^Z^ как функции h и
вычислим их производные при Л = 0. Из E.10а) мы получим
у1"@) = ЕЬ.-*1"@). E.11)
t = l
а ИЗ E.10Ь)
k\'\Q) = q(f(Y,^Z,)) '' I 0= (givS) ' I . E.12)
Полные производные функций /(Y^.Z^) и g(Yi) можно вычислить по
формуле Фаа ди Бруно (см. (VI.4.14) и (VI.4.15)). Это дает
(/m.^.))"^"=E'^;;I^:^^H>^^^'^-^^^^^^'^^^'¦¦¦^^^^')^
E.13)
где /i, + ... + //^ + ^1 4 ... + J^n = ? - 1. и
{^^y.)Г = E^(y."" у.'-') E")
VI 1.5. Условия порядка для ДАУ индекса 2 559
(а здесь /Xj -\-.. . + fi^ =я)- Суммы в E.13) и E.14) берутся по
множествам «специальных помеченных деревьев». Подставим теперь
^^"" = Е«0*]''^ E.15)
В E.13) и E.14); тогда из E.12) получим
^¦1^)@) = , ^ ^"'llit:.'^^ (Е °о^1"'@), ¦ ¦ • ¦ ^1"'@), • • ¦) E.16)
и
1 — 1 ггъъо ^ ^i — ^ /
7{Я-1)(
Подставляя E.16) в первый член E.17) и вычитая Zj ^@), мы
получим
S
(-?уЛ)(г/о-''о)Е«и^]'"''@) = E18)
= t'.j Е ^>^""'i:it''°\tbM->m г<"'@),...)+
j = l (m,n)?f@,l) ^ ^/=1 ^
^ m>2 ^ V==l
Эта формула позволяет нам вычислить ZJ^" ^, если матрицы (gyf^)
и (а- ) обратимы. Обозначим элементы матрицы, обратной к (а,,),
через LV-J:
K) = ("ij)-'- E.19)
Тогда из E.16) и E.18) с помощью индукции по q можно вывести
следующий результат:
Теорема 5.6 (ХЛР89). Для производных Аг, и Z, справедливы
формулы
^!"@)= J2 7(ОФ.(<)^^(<)(г/о.~-о).
t?LDAT2y,p[t)=q
u^LDAT2^,p[u)-q
560 Гл. VII. Дифференциально-алгебраические задачи высших индексов
где коэффициенты Ф^(t) и Ф^(и) определяются рекурсиями
если < = [<!,...,<^,til,...,wjj^,
если w=[<i,...,<^]^,
а рациональные коэффициенты 7@ '^ 7(^) — посредством рекурсий
7(г) = 1,
7@=P@7(^i)---7(<mO(tii)...7K)^ если <=[<!,..., <^,Ui,...,uJj,,
Теперь производные численного решения у^ можно получить из
E.11), а чтобы найти производные z^, вычислим i^ из E.10с) и
подставим в E.10а), что дает
z,=z,-^J^b,u;,j{Zj^z,) E.20)
и для производных
^i'^@)=E^^O-^i'^@)- (^-21)
Таким образом, мы получили следующий результат:
Теорема 5.7. Для численного решения E.10) справедливы
формулы
teLDAT2y,p{t)=q t = l
5
где коэффициенты j и Ф,- определяются в теореме 5.6. П
Условия порядка
Сопоставление теоремы 5.7 с теоремой 5.5 приводит к следующему
результату:
Теорема 5.8 (ХЛР89). Для метода Рунге—Кутты E.10)
справедливы формулы
VII.5. Условия порядка для ДАУ индекса 2 561
y(xQ-{- h) — у^ = 0(h^'^^) тогда и только тогда, когда
^2ь,Ф,A) = щдлягеплт2^, p(t)<P.
z{xq -\- h) - z^ = 0(h^'^^) тогда и только тогда, когда
* 1
J2 ^4i^i(«) = -j-y для ие DAT2^, р(и) < q,
где коэффициенты 7 и Ф, определяются в теореме 5.6, а и;, • —
формулой E.19). П
Замечание 5.9. Пусть P[xq) = I - [1,[ду!,)-^ду)[у^,г^)
—проектор, введенный в определении 4.3. Так как P(xQ)f2(yQ, Zq) = 0, то
^'(^o)^(')(yo.^o) = 0 E.22)
ДЛЯ всех деревьев / G DAT2 вида t = [и] , где и G DAT2^.
Следовательно, при построении методов Рунге—Кутты порядка р такие
деревья порядка р рассматривать не надо (ср. теорему 4.5).
Повторно применяя определение Ф,, данное в теореме 5.6, мы
получим следующий алгоритм формирования условия порядка,
соответствующего данному дереву:
Каждой вершине ставится в соответствие один индекс
суммирования. Если корень является вершиной-кружком, то ему
сопоставляются три индекса. Левая часть условия порядка будет представлена
суммой (по всем индексам) произведений следующих множителей:
6,, если г — индекс корня-точки,
b-uj^j(jjjf^, если i,j, к — три индекса корня-кружка,
а,-, если j — вершина-точка, расположенная
непосредственно над вершиной г,
о;, •, если j — вершина-кружок, расположенная
непосредственно над вершиной г.
В табл. 5.1 собраны условия порядка для некоторых деревьев из
DAT2. Мы не включили сюда деревья, имеющие только вершины-
точки, потому что им соответствуют точно те же условия порядка,
что и в разд. II.2 (табл. 2.2). Несколько деревьев из DAT2 приводят
к одному и тому же условию порядка (см. упр. 2). Заметим также,
что некоторые из условий порядка для деревьев [и] , где и G DAT2^,
идентичны таковым для задач индекса 1 (см. упр. 1 в разд. VI.4).
Упрощающие предпололсения
Для построения неявных методов Рунге—Кутты важную роль
играют упрощающие предположения В(р), С(т]) и D(^) из разд. IV.5.
562 Гл. VII. Дифференциально-алгебраические задачи высших индексов
Таблица 5.1. Деревья и условия порядка
Р@
2
3
3
3
3
рН
1
2
2
2
граф
Y
•у
XX
граф
V
условие порядка
j:biu,ijc]=i
Y^biWijCjOjkCk = k
V^ L 2 2 4
условие порядка
^biu;,ju^j/fC^ = 2
Yj^i^ij^jkcl =3
Y^biLUijiVjkCkQkeCl = §
Следующий результат является распространением теоремы IV.5.1 на
задачи индекса 2.
Теорема 5.10 (ХЛР89, р. 67). Пусть матрица (а-Л метода Рунге—
Кутты обратима и Ь- = а^^ для i = 1,... ,5. Тогда при
выполнении предположений В(р), С(т]) и D(() с р<2г] ир<т]-{-^-\-1 для
у-компоненты локальной погрешности метода E.1) справедливо
равенство
Доказательство. Здесь мы обрисуем только основные идеи
доказательства; его детали можно найти в работе (ХЛР89, pp. 64-67).
Сначала упростим условия порядка с помощью С(т)), как это
делалось в разд. II.7 (см. рис. II.7.1). Если выполнено предположение
0A]), то больше не надо учитывать деревья, у которых есть ветвь,
оканчивающаяся на [г,..., г] с числом деревьев г, равным А: — 1,
где к <т]. Перепишем теперь условие C(ri) в таком виде:
u,-c*=A-c^^
при А: = 1,...,?;.
E.23)
Теперь легко видеть, что возможна также редакция деревьев,
оканчивающихся ветвью [г,..., г],, если в ней число деревьев г составляет
от 1 до г/.
VI 1.5. Условия порядка для ДАУ индекса 2 563
Упрощающее условие D(^) позволяет нам удалить также деревья
[г,..., г, t]y, у которых число т не превосходит ^ и t Е DAT у .
Записывая D(^) в виде
S S
Е^i'i^'iJ = Е *i^u - ^h'j~' "Р« ^ = 1- • >^^ E-24)
t=i »=1
мы видим, что можно удалить и деревья [г,..., г, w] с и ? DAT^
и1<Аг<^ [к — число т). Так как по условию теоремы р <2т)
и p<^4-^-hl, то после этих редукций останутся только деревья—
«кусты» [г,..., т] , для которых условия порядка удовлетворяются
в силу В(р), а также деревья вида [и]у с w G DAT^. Но благодаря
предположению 6, = а„ мы имеем
1 = 1 ^
О при j = l,...,s-l,
при j = s ,
так что и эти деревья можно свести к деревьям—«кустам». П
Замечание. Если функция / в E.1а) линейна по z:
f(y,z) = fo{y) + fAy)^, E.26)
ТО элементарные дифференциалы, соответствующие деревьям вида
[<J,..., ^yyj, t/j,..., и^]у с n > 2, тождественно равны нулю, и
соответствующие условия порядка рассматривать не надо. В этой ситуации
условие р <2rj можно ослабить, заменив его на р<2г)+1. Важным
классом задач, удовлетворяющих условию E.26), являются
механические системы со связью при формулировке их как задач индекса 2,
т.е. в виде уравнений A.46a,b,d).
Чтобы проиллюстрировать применение теоремы 5.10, рассмотрим
методы ЛобаттоШС. Они удовлетворяют условиям В(р),С(т}) и D(^)
с p=2s —2, rj = s—l и ^ = s—1 (см. табл. IV.5.13), а также условию
а^- = Ь-. Следовательно, для этих методов локальная погрешность
может быть оценена по теорюме 5.10 как 6у^^(х) = 0{h^'~^).
Следующий результат показывает, что для методов, не
удовлетворяющих условию а^,- = 6,, оценки леммы 4.4 вряд ли могут быть
улучшены.
Лемма 5.11. Пусть р — наибольшее целое число, для которого
у-компонента локальной погрешности удовлетворяет условию
Sy,(x)=0(h'>-'').
Если матрица метода Рунге—Кутты обратима и с^фХ для всех i, то
p<s\
где S* — количество различных отличных от нуля чисел среди
Cj ,..., с^.
564 Гл. VII. Дифферешдаально-алгебргшческие задачи высших индексов
Доказательство. Из условий порядка для деревьев [ [г,..., т]^]^
следует, что
Т biU>ij f ' q(t)dt = f q(t)dt
,% Чо Jo
E.27)
ДЛЯ любых многочленов q{t) степени < р— 1. Положим теперь q(t) =
= d'{t), где d{t) — многочлен минимальной степени, принимающий
значения rf(c,.) = О для всех г, d@) = О и d(l) ф 0. Этот многочлен
q(i) не удовлетворяет условию E.27). Его степень равна s*. Отсюда
и следует неравенство р < s*. D
Проецированные методы Рунге—Кутты
Интересно, конечно, исследовать порядок сходимости и тех
проецированных методов Рунге—Кутты (см. определение 4.11),
которые еще не охвачены теоремой 4.12. Основным инструментом
нашего анализа будет следз^ющая интерпретация проецированных методов
Рунге—Кутты.
Таблиид 5.2. Исходный и расширенный методы Рунге—Кутты
с
1 + е
А
Ь^
Ь^
0
е
е
Лемма 5.12 (Любих 1991). Рассмотрим s-стадийный метод Рунге—
Кутты с обратимой матрицей коэффициентов Л и определенный в
табл. 5.2 расширенный (s -h 1)-стадийный метод. Обозначим
соответствующие численные решения после одного шага у^ и у\,
предполагая, что начальное значение у^ удовлетворяет уравнению д(у^) = 0.
Если функция f в уравнении E.1а) линейна по z, т.е. имеет вид
E.26), то для численного решения у^, даваемого проецированным
методом Рунге—Кутты D.1), D.38), справедлива формула
yi-yl^Oihe), E.28)
где h достаточно мало и е —^0.
Доказательство. Последняя стадия расширенного (s-f- 1)-стадий-
ного метода Рунге—Кутты имеет вид
o = </(n+i). ^ ¦
И МЫ получаем у\ =У^_^^ (заметьте, что это — результат, который
даст один шаг неявного метода Эйлера с длиной шага h€ и начальным
VI 1.5. Условия порядка для ДАУ индекса 2 565
значением у^). Используя линейность / относительно z и полагая
Л = heZy^^, мы получим
у1=У1+Ле/о(у!) + /Лу!)А,
0 = 9{у{).
Сравним теперь E.30) с D.38). Справедливость равенства E.28) при
достаточно малых h и е вытекает из теоремы о неявной функции. П
Применение теоремы о неявной функции к E.30) показывает
также, что у\ столько же раз дифференцируема по /i и ?, сколько и
правая часть задачи E.1). Следовательно, разложение Тейлора yf
по степеням h имеет коэффициенты, сходящиеся к конечному
пределу при ?• -> О.
Таким образом, можно получить условия порядка для
проецированного метода Рунге—Кутты (примененного к задаче E.1), E.26)),
рассматривая предельный переход е -> О в условиях порядка для
расширенного метода Рунге—Кутты (см. упр. 5). Мы продемонстрируем
это, распространив утверждение теоремы 5.10 на проецированные
методы Рунге—Кутты.
Теорема 5.13 (Любих 1991). Пусть матрица метода Рунге—Кутты
А обратима^ и задача индекса 2 удовлетворяет условию E.26). Тогда
при выполнении условий В(р), C{ri) и D(() с p<2rj-\-l и p<rj-\-^-\'l
для локальной погрешности проецированного метода Рунге—Кутты
выполняется равенство
yj-j/(xo + /i) = 0(ftP+i). E.31)
Если, кроме того, р <2т], то E.31) имеет место и при нелинейной
зависимости f от z.
Доказательство. Надо проверить, что условия В(р), С(г}) и D(^),
а также E.23), E.24) и E.25) в пределе ?-> О выполняются также
и для расширенного метода из табл. 5.2. Покажем это для условия
E.23). Матрица, обратная к матрице расширенного метода Рунге—
Кутты, имеет вид
[ьт е) "^[-е-ЧТА-' в"')' ^^'^^^
Отсюда видно, что E.23) выполняется для г = 1,..., 5. При г = s -|-1
получаем
5 + 1 5
J2^s+i,jc'; = -e-' X! b.u^.jc'j+e-'il + e)". E.33)
i=i »,j=i
Используя условие E.23) при г < 5 и условие В(р), находим, что
выражение в правой части E.33) равно —б"-^ -\-е''^A-\-б)'^ ,и оно стремится
к к при е-^0. Следовательно, в пределе при е—^0 условие E.23)
выполняется также и для i = s-^l. Отсюда для случая, когда f(y,z)
566 Гл. VII. Дифференциально-алгебраические задачи высших индексов
линейно зависит от z, утверждение теоремы выводится так же, как
и в доказательстве теоремы 5.10 (см. также замечание, следующее за
доказательством теоремы 5.10).
Обобщение теоремы на нелинейные задачи можно доказать, вводя
возмущение. Пусть z[x) — точное решение задачи E.1); рассмотрим
задачу
0 = д(и)
в переменных г/ и А (Любих 1991). Эта новая задача, тоже имеющая
индекс 2, имеет очевидное решение и(х) = у{х) и Х{х) = 0.
Поскольку система E.34) линейна относительно алгебраической переменной
А, то к ней применима уже доказанная часть нашей теоремы, и для
решения проецированным методом Рунге—Кутты мы получаем
21-фо + Л) = 0(Л^+^). E.35)
Но надо еще оценить у^—и^. Это можно сделать с помощью
теоремы 4.2. Наряду с нелинейной системой D.2) (с г; = Уо) рассмотрим
результат применения метода к задаче E.34):
t^. = % + л Е a,j [f{Uj, z(xo + cjh)) + Д {Uj, z(x, + Cjh)) Л.),
Здесь первую строку можно записать в виде
E.36)
U, = yo + hY,aijf{Uj,z(x,-^Cjh)-^Aj)+0{h\\A\\'),
где ||Л|| = тах^. ЦЛ^-Ц. Тогда по теореме 4.2
\\Ui-Yi\\<Ch\\\f, E.37а)
||Л, + г(хо + c,ft) - Z,|| < С\\А\\\ E.37b)
Поскольку выполнено условие C(rj), оценки D.14) и E.37b)
показывают, что А- = O(h^). С помощью E.37) отсюда получаем, что
у^ — u^=C?(/i2''+^), и тогда равенство у^ — 2^ =0(h'^^'^^) является
следствием того, что Zj — z(xq -\-h) = 0{h^). П
Примеры. 1) Коллокационные методы удовлетворяют условиям
В(р), C(s) и D(p — s), где s — число стадий, ар — порядок
квадратурной формулы, положенной в основу метода (см. лемму IV.5.4).
Поэтому вышеизложенное является альтернативным доказательством
теоремы 4.12.
2) Проецированный 5-стадийный метод Радо IA (см. табл. IV.5.13)
имеет для линейных по z задач порядок 25 — 1, а для нелинейных
задач индекса 2 общего вида — порядок 25 — 2.
VI1.5. Условия порядка для ДАУ индекса 2 567
Упралснения
1. Обозначим г наибольшее число, при котором для локальной
погрешности z-компоненты справедливо соотношение Szf^{x)=0(h^).
Для неявных методов Рунге—Кутты, у которых матрица
коэффициентов обратима, Щоо) = О и с^ < 1 для всех j, докажите, что
Г<5*,
где S* — число различных не равных нулю чисел среди с^,..., с,.
Указание. Из условий порядка для деревьев—«кустов» [т,.. .ут]^
следует, что для всех многочленов q(t) степени < г — 1
^b,u;,ju;j, f\{t)dt = q(l),
2. Пусть некоторое дерево из множества DAT2 удовлетворяет
одному из двух условий:
a) из вершины-кружка (не корня) выходит одно ребро;
b) за вершиной-точкой (не корнем) с одним исходящим ребром
следует вершина-кружок.
Тогда соответствующее условие порядка эквивалентно таковому
для дерева с тем же порядком, но меньшим числом вершин-
кружков. Значит, при построении методов Рунге—Кутты не надо
рассматривать деревья, удовлетворяющие условиям (а) или (Ь).
3. Пусть функция f(y,z) в E.1) линейна по г. Охарактеризуйте
деревья из DAT2, для которых элементарные дифференциалы
тождественно равны нулю.
4. Дайте новое (алгебраическое) доказательство теоремы 4.9,
используя теорему 5.10 и лемму IV.5.4.
5. (Любих 1991.) Рассмотрите проецированный метод Рунге—Кутты
для линейных по z задач индекса 2 и докажите, что в этом
случае у^ — y(xQ -h /г) = 0(/г'*) тогда и только тогда, когда выполнено
условие
^6,(l-c,)u;,,c2 = i
в дополнение к тем четырем условиям порядка, которые
необходимы уже для обыкновенных дифференциальных уравнений.
VII. 6. Полуявные методы дня систем
иццекса 2
Методы, рассмотренные в разделах VII.3 и VII.4, не используют
полуявную структуру дифференциально-алребраического уравнения
y' = f{y,z), 0 = <,(у) F.1)
(у € М'*, Z G М"*), и они могут применяться также в более общих
ситуациях. В этом разделе мы покажем, как можно использовать
полуявную структуру ДАУ для вывода новых, более эффективных методов
интегрирования. Основная идея заключается в том, чтобы дискрети-
зировать дифференциальную переменную у явным образом, а
алгебраическую переменную z — неявным.
Самый простой метод этого типа — полуявный метод Эйлера:
Ух =yo'^hf{yQ,ZQ), F.2а)
0 = 9{Уг). F.2Ь)
Подстановка F.2а) в F.2Ь) дает для Zq систему О = g{yQ -\- hf{yQ, Zq))
(нелинейную), имеюи^ую локально единственное решение, если
9y{y)fzB/' ^) — обратимая матрица F.3)
в точке (уо, -2:0). После того как Zq вычислено, значение у^
определяется по явной формуле F.2а).
На этом примере можно видеть некоторые интересные черты
полуявных методов. Здесь возможна более эффективная реализация, чем
при дискретизации с помощью неявного метода Эйлера, потому что
размерность нелинейной системы меньше (т вместо п-\-т). По
сравнению с явным методом Эйлера в его варианте «понижение индекса
и проецирование» (см. разд. УП.2), в полуявном методе не требуется
точное вычисление производной ^^(t/). Численное приближение у^
зависит только от начального значения у-компоненты, как и точное
решение F.1).
В этом разделе мы рассмотрим полуявные методы Рунге—Кутты,
а также экстраполяционные и многошаговые методы. Они очень
эффективны, в частности, для механических систем со связью, когда
используется формулировка в виде задачи индекса 2, потому что в
этом случае нелинейные системы просто не возникают (см. ниже).
Полуявные методы Рунге—Кутты
В работе ХЛР89 ^) предложено следующее расширение метода F.2)
до явных методов Рунге—Кутты:
1-1
>;=% + ftE«0^>S'^i)' г=1,...,5, F.4а)
^' См. примечание на стр.503. — Прим. ред.
VI 1.6. Полуявные методы для систем индекса 2 569
о = (?(у;.), (б.4Ь)
S
г/l = Уo + лE^•M•'^i)- (б.4с)
» = 1
0 = 9{Уг)- F.4d)
Так как У^ = i/q , уравнение F.4Ь) при г = 1 выполняется
автоматически, потому что начальное значение предполагается согласованным.
Далее подставляем Уз из F.4а) в F.4Ь) и получаем нелинейное
уравнение для Z^, которое имеет (локально) единственное решение, если
0217^0 и выполнено обычное для задач индекса 2 предположение F.3).
Таким образом, найдены Z^ и У2. Следующий шаг позволяет
вычислить ^2 и Уд и т.д.
Локальная погрешность и свойства сходимости метода F.4)
были исследованы в работе ХЛР89 (см. также Бразей и Хайрер 1993).
Оказывается, коэффициенты а,,,^, должны удовлетворять
дополнительным условиям порядка. Вследствие этого для метода 5-го
порядка нужно 8 стадий (Бразей 1992), тогда как для классических
методов Рунге—Кутты — только 6 стадий (см. разд. П.5). Арнольд
A995) и Муруа A995) независимо предложили модификацию,
которая упрощает условия порядка и делает этот подход более
эффективным. Сущность их идеи — ввести явную стадию У^ = j/q , Z^ = Zq ,
y2 = yo + ha2if(yo,ZQ) и отказаться от условия д{У2) = 0 на второй
стадии. Здесь мы изложим подход Муруа A995), который носит
несколько более общий характер. При согласованных начальных значениях
{Уо^^о) определим:
У1=Уо, Zi=Zq, F.5а)
Yi=yo + h'^a,jf(Yj,Zj), i = 2,...,s, F.5b)
»
Yi = yo + hJ^aijf(Yj,Zj), 0 = </(!;.), t = 2,...,5, F.5c)
y,=Y,. F.5d)
Значение z^ может быть вычислено либо из уравнения скрытой связи
9у[У\I{У\) -s^i) = О, либо с помощью дополнительной стадии
П+1 =2/o + '^E^^+ij/(^i'^i)' 0 = G(y,^i) F.5е)
как 2J = Z^^Y- ^Ь1 положили здесь У,^1 = 2/1, так что значение
fiXaj^i' ^«+i) может быть снова использовано в качестве /(Уо> ^о) ^^^
следующего шага. Существенное отличие от первоначального подхода
F.4) состоит в том, что численное решение [y^.z^) зависит от обоих
начальных значений [у^ и Zq).
570 Гл. VII. Дифференцис1Льно-алгебраические задачи высших индексов
Существование численного решения. Предположим, что
начальные значения удовлетворяют равенствам д(уо) = О и 5'у(Уо)/B/о' ^о) =
= 0(S) с некоторым достаточно малым S >0 (мы должны допустить
мгипые возмущения в уравнении скрытой связи, так как, вообще
говоря, приближение z^, получаемое из F.5е), не удовлетворяет
равенству gy(yi)f(yi ,z^) = 0). Рассуждая методом индукции, допустим, что
значения (У , Z ) уже известны для j = 1,..., г — 1 и удовлетворяют
равенствам Yj = yQ-\-0(h), Zj = ZQ-\-0{h-\-S). Тогда У^
определяется по явной формуле F.5Ь), так что У^ = Уо^'^С^)- Запишем теперь
условие 0 = д(У^) в виде
0= / 9y{yo + r(Y,-y,))dT-J2%fiyj,Zj),
•^0 j=i
F.6)
как мы это делали в C.13). Здесь У, надо заменить выражением
F.5с). Мы получили нелинейное уравнение вида F(Z,,/i)=:0. Так
как F(zq,0) = O{S) и
dF
—(^0,0) = aii-gy(yQ)f^(yQ,ZQ),
то по теореме о неявной функции уравнение F.6) имеет локально
единственное решение при выполнении условий F.3) и
2,^:^0 для всех г. F.7)
Кроме того, Z,- = -^о -f 0{h -f- S).
Распространение погрешности и сходимость. Если начальные
значения не согласованы, то заменим нелинейное уравнение в F.5с) на
g(Y^) =^(t/o), так что метод остается корректным во всей окрестности
многообразия решений; заметим, что полученное выше заключение о
единственности численного решения остается в силе. Преимущество
такого обобщения состоит в возможности дифференцирования по
начальным значениям. Тогда метод F.5) с z^, определяемым из F.5е),
можно переписать в такой форме:
2/п+1=Уп+ЛФB/„,г„,/1),
^п + 1=ФB/п^^п^Л),
где Ф и Ф — гладкие функции. При исследовании сходимости и, в
частности, условий порядка важную роль будет играть следующая
треугольная матрица:
; _ \"
F.9)
"*+i,;.+i/
VI 1.6. Полуявные методы для систем индекса 2 571
Лемма 6.1. Предположим, что метод F.5), удовлетворяющий
условию F.7), записан в форме F.8). Если д(у^) =0 и 9у(Уо)/{Уо, Zq) =
= 0{h), то справедливы соотношения
дФ 5Ф
-д^{Уо^ ^0. h) = 0{h), —(уо, Zq, h) = и;,^1д • / + 0(/i),
где w;,^ii определено формулой F.9).
Доказательство. Из F.5Ь) следует, что dYJdzQ = 0(h). Поэтому,
дифференцируя F.5с) по Zq , получим
8Y * dZ
j=i
'о
.dY, ^,.2,
0 = 9у{Уо)оГ + 0{Н'). (б.ЮЬ)
Подстановка F.10а) в F.10b) и умножение на матрицу, обратную к
9y{УQ)fz{Уo^^o)^ дает соотношение
22%-^ = 0(h) для 1 = 2,...,5+1.
j=i
о
Утверждение леммы следует из того, что Z^=Zq , т.е. dZ^/dzQ=I. П
Рассмотрим две пары начальных значений (Уо^-^^о) ^ (i/o'^o)' УД^
влетворяющих условиям д{у^) = О, д(у^) = 0, 5'у(Уо)/(Уо'^о) = ^(Л),
9у{Уо)/{Уоу^о) ^ ^W- ^^ леммы 6.1 следует, что для разностей
At/Q = Уо ~ Уо ' • • • справедлива рекурсия
[\\Az,\\)^[ 0{1) \w,^г^HO{h))[\\Az,\\)¦ ^^'^^^
Локальная погрешность метода F.5) определяется как обычно.
Обозначим ее <Jy/,(x) = У1-2/(хЧ-Л), Szf^(x) = z^-z{x-^h), где {yi,z^)
— численное приближение, полученное с начальными значениями
(у(х), z(x)), которые взяты на точном решении задачи F.1).
Теорема 6.2 (Муруа 1995). Рассмотрим задачу F.1) с
согласованными начальными значениями. Пусть выполнено условие F.7) и
K+i,il<l. F.12)
где w^_^ii определяется формулой F.9). Если локальная
погрешность удовлетворяет оценкам
rfy,(x)=0(ft^+i), Sz,ix) = 0{h'"), F.13)
ТО при х^ — Xq< Const имеют место оценки
у„ - у(х„) = 0(ft"""('-'"+i)), z„ - z{x„) = С7(Л'"'"(^-"')).
572 Гл. VII. Дифференциально-алгебраические задачи высших индексов
Доказательство. Рекурсия F.11) позволяет применить лемму
VI.3.9, положив е = Л2 и а = |г/;,^1 д! -1-0(Л), откуда видно, что вклад
локальной погрешности в точке х,- в глобальную погрешность при х^
для J/- и г-компоненты ограничен соответственно величинами
Утверждение теоремы доказывается суммированием этих вкладов. П
Условия пордцда. Условия порядка для метода F.5) можно
вывести тем же способом, что и для методов Рунге—Кутты в
предыдущем разделе. Единственное отличие в том, что в некоторых
местах коэффициенты а,- надо заменять на а,^ . Условия порядка для
г-компоненты можно получить непосредственно из теоремы 5.6, так
как Zj =^,4-1 • ^ результате получается следующий алгоритм
формирования условия порядка, соответствующего данному дереву:
Каждой вершине ставится в соответствие один индекс
суммирования. Левая часть условия порядка представляет собой сумму (по
всем индексам) произведений следующих множителей:
а,,, если i — индекс корня-точки,
^«+1 f» если г — индекс корня-кружка,
а,-, если j — вершина-точка, расположенная непосредственно
над вершиной-точкой г,
2,- , если j — вершина-точка, расположенная непосредственно
над вершиной-кружком г,
w^jy если j — вершина-кружок, лежащая непосредственно
над вершиной-точкой г.
В правой части условия порядка стоит единица, деленная на
рациональное число 7> которое определено в теореме 5.6.
Чтобы выполнялись условия F.13) теоремы сходимости, условия
порядка должны удовлетворяться для деревьев t G DAT2y с p{t) <r
и для деревьев и G DAT22 с р(и) < m — 1.
Конструирование методов. Деревья из разд. П.2 составляют
подмножество «деревьев индекса 2», которые мы здесь будем
рассматривать. Из описанного выше принципа конструирования ясно, что
коэффициенты a-j и 6,- := 3^, должны удовлетворять классическим
условиям порядка, описанным в разд. II.2. Поэтому естественно взять
известный явный метод Рунге—Кутты определенного порядка и
определить a^j таким образом, чтобы удовлетворялись остальные условия
порядка. Арнольд A995) и Муруа A995) показали, как можно
сконструировать полуявные методы, основанные на паре вложенных
методов Дорман да и Принса (табл. П.5.2). Мы обрисуем здесь основную
идею этого построения.
VI 1.6. Полуявные методы для систем ршдекса 2 573
Можно получить существенное упрощение условий порядка, если
потребовать, чтобы
i ^q
J2^ij^r' = - "Р« г=1,...,5 + 1, F.14)
j=i ^
где с, = ^ а-J и с, = ^• а,^. При г = 1 соотношение F.14) выполняется
автоматически, потому что а^ =0. При г> 1 ему можно
удовлетворить при g = 1 (определение с,), q = 2 и ^ = 3. Упрощение условий
порядка подобно тому, что показано на рис. П.5.2. Согласно
определению матрицы W соотношения F.14) эквивалентны следующим:
i
Y^'^ijCj =qc^i'^ при г = 1,.. .,5-1-1. F.15)
i=i
Это имеет следствием дальнейшую редукцию множества условий
порядка, а немногие оставшиеся можно рассмотреть непосредственно.
Дальнейшие подробности и коэффициенты получившегося метода
можно найти в оригинальной работе Муруа A995). Эти
коэффициенты использованы в программе РНЕМ56 (см. разд. VH.T).
Приложение к механическим системам со связью. Рассмотрим
систему
q' = u, F.16а)
M[q)u' = f{q,u)-G^[q)K F.16b)
0 = ^((?), F.16с)
где G{q) = д (q). Дифференцирование уравнения связи F.16с) дает
0 = G(q)u. F.16d)
Если матрица M(q) обратима, то система F.16a,b,d) имеет вид F.1)
с y=[q^u) и z = X. Предположение F.3) эквивалентно A.47).
К этой конкретной системе метод F.5) можно применить
следующим образом. Предположим, что для j = 1,..,, г — 1 уже известны
Qj, Uj, Aj и U; = М[Qj)-^{f(QJ,Uj)-GT(Q.)Aj), и положпи
i-l t-l
j=i i=i
Вычислим теперь Л,, U- из системы уравнений
(^,1,'Т')(л!)=№')' '-'
где Qi = qo + hjyj=ia,jUj и Я, =-С(д,)(«о + ЛЕ^;1Ч^^])/(ЧЛ -
известные величины. Следовательно, нам надо будет решать
только линейные системы типа F.17). Это и делает полуявные методы
574 Гл. VII. Дифференциально-с1лгебраические задачи высших индексов
очень привлекательными для численного решения механических
систем со связями. Если необходимо, этот метод можно комбинировать
с проецированием, как это объяснено в разд. VII.2, так что численное
приближение будет удовлетворять и уравнению связи для координат.
Заметим, что в методах, которые предложил Арнольд A995), Q, =
= Qi^i при г > 2, что позволяет несколько сэкономить на вычислениях
G при расчете матрицы в F.17).
Экстраполяционные методы
Для нежестких обыкновенных дифференциальных уравнений
наиболее эффективным экстраполяционным алгоритмом является метод
ГБШ (см. разд.П.9). Любих A989) распространил этот метод на
дифференциально-алгебраические уравнения индекса 2.
Рассмотрим начальное значение jjq , удовлетворяющее уравнению
^(уд)=0. Тогда аппроксимация Sf^(x) значения у{х) (где х=х^-^2тк)
определяется так:
y^=yo + hf{yQ,ZQ), д(у^) = 0, F.18а)
2/.+i=y,_i+2/i/(t/,.,z,.), G(y,>i) = 0, г=1,...,2т, F.18b)
•5/»W = (y2m-l+22/2mH-2/2m+l)/4. (б.18с)
Стартовый шаг здесь такой же, как и для полуявного метода Эйлера,
рассмотренного в начале этого раздела. Он неявный по Zq и явный
по У1. Для случая, когда уравнение F.1) линейно по z, т.е. когда
/(у,г)=/оЫ + Л(у)г, F.19)
МЫ далее покажем, что для численных аппроксимаций 5/j(xQ-f-2m/i) и
Z2m существует /i^-разложение. Следовательно, эти величины можно
использовать в качестве базиса экстраполяционного метода.
Реализация этого метода в виде программы совершенно аналогична
таковой для метода ГБШ (выбор последовательности числа шагов,
управление порядком и длиной шага, плотная выдача и т.п.).
Поскольку экстраполированные значения не удовлетворяют уравнению связи
д(у) =0, рекомендуется проецировать их на это многообразие (как
разъяснено в разд. VII.2) после каждого принятого шага.
Предположение F.19) выполняется для многих интересных задач,
например, для механической системы со связью F.16a,b,d), где z = X
играет роль множителя Лагранжа.
Теорема 6.3 (Любих 1989). Если условия F.3) и F.19) выполнены^
то численное решение, даваемое методом F.18)у имеет
асимптотическое h"^-разложение
а также h^-разложение для погрешности Sf^(x2m)^
VI 1.6. Полуявные методы для систем индекса 2 575
Численное решение {у,} в методе F.18) лежит на многообразии,
которое определяется уравнением д(у) = 0. Чтобы иметь возможность
применить результаты и идеи, развитые в разделах П.8 и II.9, обобщим
метод F.18) на случай, когда начальные значения произвольны:
Ух =Уо + '*/B/о'-о)' 9(У1) = 9(Уо)^ F.20а)
2/,>1=2/,-1+2Л/(у,,г,), G(y,+i)=^(y,_i), г = 1,..., 2m. F.20b)
Исключим теперь переменные z. С помощью тождества
9{yi+i)-9(yi-i) = J^ 9y[-^^ ^"^^ / 4 /
уравнение F.20b) можно переписать в виде
0 = J ^9y(J'^''^^'~' +<rhf(y„z,))dcT.f(y,,z,). F.21)
В силу предположения F.3) и теоремы о неявной функции уравнение
F.21) может быть разрешено относительно г,, поскольку 2, —
гладкая функция величин (yi^i -|-y,_i)/2, у, и Л. Подставив это решение
в F.20Ь), мы получим рекуррентное соотношение вида
2/.>1=2/.-1+2/1ФB/,,(у,>1+У,-1)/2,Л). F.22)
Подобным же образом можно переписать и стартовый шаг F.20а).
Рассмотрим более общую систему
w = v-\-hf(u, z), g(w) = g(v), F.23)
где w, V и h — известные величины. Ее можно переписать в
эквивалентной форме
^= f 9y{v-^rhf{u,z))dT^f(u,z)
Jo
и выразить отсюда z как гладкую функцию и, v и h (опять же
опираясь на теорему о неявной функции). Следовательно, решение F.23)
можно записать так:
w = v + hФQ(u,v,h), F.24)
и стартовый шаг F.20а) примет вид
У1 = 1/0 + ЛФо(уо> Уо' ^)- (в.25)
Решающее значение в этих переформулировках имеет то
обстоятельство, что двухшаговая схема F.22) и стартовый шаг F.25) определены
не только на многообразии р(у) = О, но и в его открытой окрестности.
Поэтому применима стандартная теория, рг1звитая для
обыкновенных дифференциальных уравнений. Полученные для метода F.22),
F.25) результаты справедливы и для метода F.18), потому что эти
методы совпадают, когда начальные значения удовлетворяют условию
^(Уо)=0.
576 Гл. VII. Дифференциально-алгебраические задачи высших индексов
Асимптотическое разложение для симметричных двухшаговых
методов. Имея в виду описанные выше переформулировки, рассмотрим
теперь метод
2/1 = Уо + ^Ф^(уо,у^,к), F.26а)
2/,>1=2/.-1+2ЛФB/,,B/,>1+2/,_1)/2,Л). F.26Ь)
Предположим, что функции приращения Фо и Ф здесь —
произвольные гладкие функции, для которых выполнены условия Фо(у, ?/, 0) =
= Ф(У) У J 0) = f(y)) так что обе схемы согласованы с обыкновенным
дифференциальным уравнением у' = f[y). Для получения
Л^-разложения погрешности надо, чтобы стартовый шаг F.2ба) был совмести.м
с F.26Ь) в следующем смысле: три величины
У2/С-1 •= ^к - ЛФо(^Л' ^/с' -Л)' У2к '•= Ч^ ,g 27)
У2к^1 :=У^'{'НФ^(и^,У1^,к)
должны удовлетворять рекуррентному соотношению F.26Ь) при
произвольных и^ и Vf^.
Теорема 6.4. Если метод F.26) удовлетворяет условиям
совместимости F.27), то численные аппроксимации
У2т^ (У2т+1+У2т-1)/2
имеют асимптотическое разложение по четным степеням h.
Доказательство. Приняв за образец доказательство теоремы
П.9.2, которое предложил Штеттер, положим w^^ := Уз/с > ^ пусть г;;^
— решение уравнения
У2к+\ '= Ч + ЛФо(^^к, V;,, Л). F.28)
При этом мы получим одношаговый метод удвоенной размерности:
где Л* = 2/1, а У2/с+1 определяется формулой F.28). Вследствие
предположения F.27) этот одношаговый метод будет симметричным.
Поэтому 2/2т ^ '^т ^ '^т имеют асимптотическое Л2-разложение (см.
теорему П.8.10). Из равенства
(У2т+1 + У2т-1)/2 = У2т + H^i^m^ ^т^ ^) " ^oi^m^^m^ "М)
следует, что то же верно и для (t/2m+i + У2т-1)/2- ^
Доказательство теоремы 6.3. Как мы уже видели, метод F.20)
может быть записан в форме F.26). Поэтому осталось только
проверить условие совместимости F.27). Из определения Фо(и,г;,/г), в
силу эквивалентности уравнений F.25) и F.23), мы имеем:
y2k^i=4-hf(Uk.z-), 9{У2к-1)=9М.
У2к+1=^к-^^1{4>^'^)^ 9{У2к^1)=9{^к)-
VI 1.6. Полуявные методы для систем индекса 2 577
Поскольку / линейна по z, отсюда следует F.20Ь) с Zj/j = {z" -f- г"*" )/2.
Поэтому существование асимптотического Л^-разложения для У2т и
Sf^{x2m) вытекает из теоремы 6.4, а из F.21) видно, что и z^m имеет
/i 2-разложение. П
/3-блоковые многошаговые методы
Проведенный в разд. УП.З анализ сходимости показывает, что для
сходимости многошагового метода с порядком р необходимо, чтобы
все корни его о*-многочлена лежали внутри единичного круга. Это —
серьезное ограничение. Оно исключает, например, все явные и
неявные методы Адамса. Аревало, Фюрер и Сёдерлинд A996) предложили
модификацию, допускающую использование «нежестких»
многошаговых методов. Их идея состоит в применении к разным частям задачи
различных дискретизаций.
Для задачи индекса 2
2/' = /оЫ + Л(г/)^. о = 5Ы. F-29)
где /(у, z) = /0B/) + fz [y)z зависит линейно от z, рассмотрим
дискретизацию
к к к
II»i2/n+i = ^1] A/B/n+i' ^п+,) - ^/zB/n+J Zl7,-^n+i F.30)
1=0 j=0 1=0
и для ее производящих многочленов введем обозначения
к к к
Ж)=Е «.<'• '^(о=Е-^.^'- ^@=Е^.<'-
»=0 »=0 »=0
Теорема 6.5 (Аревало, Фюрер и Сёдерлинд 1996). Пусть для
задачи F.29) индекса 2 выполнено условие F.3). Предположим, что
многошаговый метод (р, <т) устойчив и имеет порядок р (р= к или
p^k-^-l), что г(С) = 7/с(С-l)'^ ^ ^"^о все корни <т(С) - т(С) лежат
внутри единичного круга |С| < 1 • Тогда глобальная погрешность при
х^ — Xq< Const удовлетворяет равенствам
у„-у{х„) = От, z„-zix„) = 0(h').
Доказательство. Конкретный вид г(С) в условии теоремы
эквивалентен условию
к
1=0
так что добавленный в F.30) член мал. Кроме того, этот член
содержит множитель /^ (Уп^к)' '^^^ ^'^^ локальная погрешность
удовлетворяет равенствам
Sy,(x) = 0(/i*+>), P(x)Sy,(x) = 0(hf+'),
где P{x) — введенный в определении 4.3 проектор.
Доказательство сходимости проводится с учетом сказанного выше
по той же схеме, что и доказательство теоремы 3.6, Единственное
578 Гл. VII. Дифференциально-алгебраические задачи высших индексов
отличие состоит в том, что в уравнениях C.43) и C.44) коэффициенты
0- надо заменить на /?• — 7» • П
В принципе, можно взять любой сходящийся многошаговый метод
(р, а) порядка р=к или р= к-\-1 и попытаться оптимизировать
параметр 7/с в г(С) так, чтобы корни (t[Q — t[Q стали малыми. Для
неявных методов Адамса результат оказался довольно
неутешительным: сходящиеся /^-блоковые методы Адамса можно получить только
для к <Ъ (Аревало, Фюрер и Сёдерлинд 1996; см. также упр. 3).
Метод ФДН с корректированной разностью. Рассмотрим теперь
(Ar-f-1)-шаговый метод ФДН, определенный уравнением (III.1.22'), и
заменим V^+^y^^i на У'^Д^!. При этом получается так называемый
метод ФДН с корректированной разностью:
il]^'yn^x=h{u,-^^^4n^?j^ F-31)
который предложил Сёдерлинд A989). Метод F.31) — это А:-шаговый
метод порядка р = А: -Ь 1. Его /9-многочлен такой же, как и у метода
ФДН, но <т[0 = С'^ - (С - 1)V(^ + 1). При г(С) = -(С - 1)V(^ + 1) все
корни разности (t{Q — г(С) равны нулю. Именно поэтому данный
метод является идеальным кандидатом в методы типа F.30).
Упралснения
1. Постройте все полуявные методы F.5) третьего порядка (г = m = 3
в уравнении F.13)) с числом стадий 5 = 3.8 качестве свободных
параметров можно взять Cj, Сд, а, с^, С4.
Указание. Начните с классического метода Рунге—Кутты
третьего порядка (см. упр. 4 в разд. П.1) и покажите, что из условий
порядка следует F.14) с ^ = 2.
2. Покажите, что метод (IV.9.15), который предложили Бадер и
Дойфлхард A983), имеет вид F.26), где
Ф(и, V, h) = f(u) - Ju -h Jv,
Фо(«, V, h) = (I- hjy^ {f(u) -Ju-^ Jv).
Проверьте условие F.27).
3. Пусть [Pk^cTk) —производящие многочлены Ar-шагового неявного
метода Адамса (см. разд.III.1). Для А: =1,2,..., 10 исследуйте
численно функцию
Я;рG) :=тах{|С*| ; С* — корень уравнения ^/^(С) -7(С - l)'^ =0}.
Для каких значений к можно найти 7 такое, что Rk(^) < 1?
VII. 7. Расчет многозвенных механизмов
«Динамика многозвенных систем имеет важное значение
в таких областях, как робототехника, биомехгшика,
управление космическими кораблями, проектирование
дорожных и рельсовых экипажей и динамика машин».
(В. Шилен 1990)
После того как мы рассмотрели несколько ргизличных подходов к
численному решению механических систем со связями, интересно
посмотреть их эффективность при приложении к конкретной ситуации.
Мы рассмотрим два конкретных многозвенных механизма, один —
нежесткий, а другой — жесткий. По общим вопросам расчета
механических систем мы отсылаем читателя к следующим работам: Хауг
A989); Робертсон и Швертассек A988).
Описание модели
Мы рассмотрим сначала «сжимающий механизм Андрьюса»,
получивший широкую известность как «пробный камень» для программ
численного интегрирования благодаря работам Джилса A978) и Ман-
нинга A981) (см. также Ормрод и Андрьюс 1986). Этот механизм
состоит из семи абсолютно твердых тел, соединенных шарнирами и
движущихся в одной плоскости. Он представлен на рис. 7.1,
заимствованном (с разрешения автора) из книги Шилена A990). Численные
значения констант, заимствованные оттуда же, приведены в
таблицах 7.1 и 7.2. Стрелки на чертежах в правой части рис. 7.1 исходят
из центров тяжести Ср...,Су. В табл.7.1 коэффициент упругости
пружины между точками D и С обозначен через Cq , а ее длина в
нерастянутом состоянии — через ?q . Предположим, что механизм
приводится в действие мотором, расположенным в точке О и
создающим постоянный крутящий момент mom = 0.033. В качестве начгипа
координат выбрана точка О на рис. 7.1, а координаты остальных
неподвижных точек А, В и С таковы:
fxa\_ /-0.06934^
00227 у
tH
-0.03635
0.03273
^ [^Л _ /0.014\
)' [ycj-\0.072j-
G.1)
Таблица 7.1. Геометрические
d = 0.028
еа = 0.01421
гг= 0.007
50 = 0.01874
sd= 0.02
tb = 0.00916
ub = 0.00449
rfa = 0.0115
2f= 0.02
ra = 0.00092
56 = 0.01043
zt= 0.04
и = 0.04
CO = 4530
параметры
e = 0.02
/a = 0.01421
ss = 0.035
5C = 0.018
ta = 0.02308
«0 = 0,01228
^0 = 0.07785
580 Гл. VII. Дифференциально-алгебраические задачи высших индексов
Рис. 7.1. Семизвенный механизм
(из книги Шилена A990), с разрешения автора).
№
1
2
3
4
5
6
7
Таблица 7.2. Параметры семи тел
массы mi,..., my
0.04325
0.00365
0.02373
0.00706
0.07050
0.00706
0.05498
моменты инерции /i,.
2.194.10"^
4.410 10"^
5.255-10"^
5.667.10"^
1.169-10"-^
5.667.10'^
1.912 10"^
.,/7
При выводе уравнений движения мы будем использовать
следующие углы (см. рис. 7.1)
9i = P^ ^2 = 0' ^3 = 7, ^4 = Ф> Яъ = ^^ Яб = ^^ Я7 = ^ G.2)
в качестве обобщенных координат механической системы.
Обозначим (Xj^yA декартовы координаты центра тяжести С j-ro тела
(j = 1,..., 7). Тогда кинетическая энергия нашей системы из семи
тел равна
7 i? . ^2 7 -2
VI 1.7. Расчет многозвенных механизмов 581
где (jjj — полный угол поворота j-ro тела; массы тел m и их моменты
инерции Ij приведены в табл.7.2. Величины Xj, yj, ij-f 2/j и ljj
могут быть выражены через углы G.2) из простых геометрических
соображений (см. рис. 7.1):
С^ : ^1 = га-cos/3,
У1 = га- sin /?,
i^,-\-yl = ra^'P\
^1 = /?;
С2 : Х2 = rr-cos/?—rfa-cos(/? +6),
У2 = rr-sin^-- c(a-sin(/?-h6),
xl-\-yl = {ri^ -'2'da-rr-cos0 + da^) • /?^ +
+ 2. (-ГГ. da cos 0 4-rfa^) ^3-0-|-cfa^ • 0^,
C3 : X3 = x6H-5a-sin7 + 56cos7,
y^=: yb— sa- cos7 -f 56• sin7,
^3 = 7;
C4 : X^ =• xa-{- zt • cos J -f (e — ea) • sin(Ф -f 8),
y^ = ya + zt' sin (J — (e — ea) • cos(Ф -f J),
i2 + 2/4 = (e - ea)^ • ф2 H- 2 • ((e - ea)^ + г^ (e ~ ea) • sin Ф) • Ф • <j -f
+ (z^ -h 2 • z^ (e - ea) • sin Ф -f (e - ea)^) • rf^,
0^4 = Ф + <У;
C5 : Xg = xa+^a-cos<J—f6sinJ,
y^ = ya-\- ta- sin (J -|- ^6 • cos <J,
cJ5 = J;
Q : 2?6 = xa-f-i« sine-h (z/-/a) •cos(Q-|-6:),
у^ = ya — u ' cose+ {zf—fa) •sin(n-h6:),
x2-fr/2 = (z/-/aJ.n2 + 2.((z/~/aJ-u.(z/-/a)sinfi).n.5-f
+ {Ы-faf - 2 • li • {zf-fa). sin Q + u^) • i^,
и;. = й + е;
582 Гл. VII. Дифференциально-алгебраические задачи высших индексов
С7 : Xj = ха+иа-sine — иЬ'cose,
у^ z= уа— иа 'cosе — иЬ-sinе,
х^ + у^ = (ua^-htit^) е^.
Потенциальная энергия системы обязана своим происхождением
мотору в начале координат и пружине, соединяющей точки D и С.
Согласно закону Гука она равна
(?— t V-
U = ^mom-/3-^c^^—^, G.4)
где ? — расстояние между точками D и С:
е= y/ixd- хсУ + (yd- усУ,
xd=: хЬ-^ SC' sin 'У -{- sd- cos 7,
yd= уЬ— SC' cos7 -h 5c/• sin7.
Наконец, мы должны составить алгебраические уравнения связи.
Механизм содержит три контура. Первый контур соединяет О с В через
К^, А'з, А'з; другие два соединяют О с А, один — через К^, Л'о, А'4, A'g ,
а другой — через А'^, A'j, A'g, А'7. Для каждого контура мы получим
два алгебраических соотношения:
гг' cos 1З — d' cos(y^ -f- 0) — 55 • sin 7 = ^^,
rr-sin/? — d • sin(l3 -\- Q) + 55-cos 7 = yb;
rr' cos /3 — d • cos(в -\- Q) — e •sin(Ф^-(^) — zt-cos S = xa,
G.5)
rr-sin/? — d'sin(l3-\-Q) -\-e ^cos(Ф-\-S) — zt-sinS = ya\
rrcos/? —rf •cos(/?-|-6) - zf • cos[Q-\-e) — usme = xa,
rr-sin/? — rf-sin(/?-|-0) — z/-sin(n + 6') + и -cose = ya.
Уравнения G.5) представляют уравнение связи g{q) = О, где q —
обобщенные координаты G.2) и ^ : R^ -^ IR^. Поскольку L = Т — U—
~^\3\ — . •. — Ag^g и кинетическая энергия Т задана формулой G.3),
а потенцигьльная энергия U — формулой G.4), то уравнения
движения A.46) теперь полностью определены.
Подпрограммы на Фортране
Для удобства читателя мы включили в текст существенные
части подпрограмм на Фортране, описывающих эту дифференциально-
алгебраическую задачу. Уравнения движения имеют вид
M(q)q = f{q.q)-G'^{q)\, G.6а)
0=<;(9), G.6Ь)
где q G К^ — вектор, определенный в G.2), и Л G IF-^. В
нижеследующем описании переменые Q(l),.. .,QG) соответствуют углам
VI1.7. Расчет многозвенных механизмов 583
/i,. . .,?: (в точности, как в G.2)), aQP(l),.. .,QPG) — их производным
/?,..., ^. Во всех подпрограм.мах мы использовали сокращения
SIBE = SII (Q(l)) СОВЕ = COS (Q(l))
SITH = SII (QB)) COTH = COS (QB))
SIGA = SII (QC)) COGA = COS (QC))
SIPH = SII (QD)) COPH = COS (QD))
SIDE = SII (QE)) CODE = COS (Q(S))
SIOM = SII (QF)) COOH = COS (QF))
SIEP = SII (QG)) COEP = COS (QG))
SIBETH = SII (Q(l)+QB)) COBETH = COS (Q(l)+QB))
SIPHDE = SII (QD)+Q(S)) COPHDE = COS (qD)+QE))
SIOMEP = SII (QF)+QG)) COOHEP = COS (QF)+QG))
ВЕР = QPA) THP = QPB)
PHP = qPD) DEP = QP(S)
OMP = QPF) EPP = QPG)
Остальные параметры XA,YA, ... ,D,DA,E,EA,.. .,M1,I1,M2, ...
определены в формулах G.1) и в таблицах 7.1 и 7.2. Обычно они
помещаются в COMMON блоке. Элементы матрицы M(q) из G.6) определяются
так:
_ д^Ь _ д^Т
Эта матрица симметричная и (благодаря специальному упорядочению
координат) трехдиагональная. Ее ненулевые элементы (на диагонали
и под нею):
НA,1) = H1*RA**2 + M2*(RR**2-2*DA*RR*C0TH+DA**2) +11+12
НB,1) = H2*(DA**2-DA*RR*C0TH) + 12
МB,2) = H2*DA**2 + 12
МC,3) = H3*(SA**2+SB**2) + 13
НD,4) = М4*(Е-ЕА)**2 + 14
НE,4) == M4«((E-EA)**2+ZT*(E-EA)*SIPH) + 14
M(S,S) = M4*(ZT**2+2*ZT*(E-EA)*SIPH+(E-EA)**2) + М5*(ТА**2+ТВ**2)
+ +14+15
М(б,6) = M6*(ZF-FA)«*2 + 16
ИG,6) = M6«((ZF-FA)**2-U*(ZF-FA)*SI0H) + 16
МG,7) = M6*((ZF-FA)**2-2*U*(ZF-FA)*SI0H+U**2) + M7*(UA**2+UB**2)
+ +16+17
Для функции / В G.6) ее ?-я компонента определяется формулой
,. .. д(т-и) 'дцт-ц) .
Записав ее в операторах Фортрана, мы получаем
XD = SD*COGA + SC*SIGA + ХВ
YD = SD*SIGA - SC*COGA + YB
LAIG = SQRT ((XD-XC)**2 + (YD-YC)**2)
FORCE = - CO * (LAIG - LO)/LAIG
FX = FORCE * (XD-XC)
FY = FORCE * (YD-YC)
F(l) = MOM - M2*DA*RR*THP*(THP+2*BEP)*SITH
584 Гл. VII. Дифференциально-алгебралческие задачи высших индексов
FB) = H2*DA*RR*BEP«*2*SITH
FC) = FX*(SC*COGA - SD*SIGA) + FY*(SD*COGA + SC*SIGA)
FD) = H4*ZT*(E-EA)«DEP«*2*C0PH
FE) = - H4*ZT*(E-EA)*PHP«(PHP-»-2*DEP)*C0PH
FF) = - H6«U*(ZF-FA)«EPP«*2*C00H
FG) = M6*U*(ZF-FA)*0MP*(OHP+2*EPP)*C00H
Следующие шесть операторов определяют алгебраическое уравнение
связи g(q) = О (см. G.5)):
G(l) = RR*COBE - D*CGBETH - SS*SIGA - ХВ
GB) » RR*SIBE - D«SIBETH ¦»• SS*COGA - YB
GC) = RR*COBE - D*COBETH - E^SIPHDE - ZT^CODE - XA
GD) « RR*SIBE - D*SIBETH + E*COPHDE - ZT*SIDE - YA
GE) « RR*COBE - D*COBETH - ZF*COGMEP - U*SIEP - XA
GF) = RR*SIBE - D^SIBETH - ZF*SIOMEP + U*COEP - YA
Приведем здесь также матрицу Якоби G(q) = д (q). Ненулевые
элементы массива размерности 6x7 таковы:
GQA,1) « - RR*SIBE + D^SIBETH
Gq(l,2) * D*SIBETH
GQA.3) » - SS*COGA
GQB,1) » RR^COBE - D«COBETH
GQB,2) = - D*COBETH
GQB,3) = - SS*SIGA
GqC,l) s - RR«SIBE -b DfSIBETH
GQC,2) = D«SIBETH
GQC.4) » - E«COPHDE
GQC,5) = - E*COPHDE + ZT*SIDE
GQD,1) s RR*COBE - D*COBETH
GQD,2) =
GQD,4) =
GQD,5) =
GQE,1) =
GQE,2) =
GQE,6) =
GQE,7) =
GQF,1) =
GQF,2) =
GQF,6) »
GQF,7) «
- D^COBETH
- E«SIPHDE
- E*SIPHDE - ZT*CODE
- RR^SIBE + D*SIBETH
D*SIBETH
ZF*SIOHEP
ZF*SIOHEP - U*COEP
RR^COBE - D*COBETH
- D*COBETH
- ZF*COOHEP
- ZF^COOHEP - U*SIEP
Для применения численного метода к системе, когда используется
формулировка в виде задачи индекса 1, нам потребуется также
выражение gqq{q){q,q)- Вот оно:
D«C0BETH*(VA)+VB))*«2 +
D«SIBETH*(VA)+VB))*«2 -
GQQd) = - RR*C0BE*VA)**2 +
+ SS*SIGA*VC)**2
GQQB). « - RR«SIBE*VA)**2 +
¦ SS«C0GA*VC)*«2
GQQC) » - RR*C0BE«VA)**2 + D*C0BETH*(VA)+VB))**2
+ E*SIPHDE*(VD)+VE))**2 + ZT«C0DE*VE)*«2
GQQD) » - RR*SIBE«VA)**2 + D*SIBETH*(VA)+VB))**2
f E*C0PHDE*(VD)+VE))**2 + n*SlDE*4(S)**2
GQQE) « - RR*C0BE«VA)*«2 -»¦ D«C0BETH*(VA)+VB))**2
f ZF*C00HEP*(VF)+VG))««2 + U*SIEP*VG)*«2
GQQF) » - RR*SIBE*VA)«*2 + D*SIBETH*(VA)+VB))*«2
f ZF*SI0HEP*(VF)+VG))*«2 - U*C0EP«VG)**2
Вычисление согласованных начальных значений
Вычислим сначала решение системы g(q) = 0. Так как эта система
содержит шесть ур^авнений для семи неизвестных, одну из них
можно задать произвольно, скажем, 0@) = О, а остальные координаты
VI1.7. Расчет многозвенных механизмов
585
Рис. 7.2. Решение задачи о семизвенном механизме.
G.7)
вычислить с помощью итераций по методу Ньютона. Это дает
/3@) = -0.0617138900142764496358948458001,
7@)= 0.455279819163070380255912382449,
Ф@)= 0.222668390165885884674473185609,
E@) = 0.487364979543842550225598953530,
П@) = -0.222668390165885884674473185609,
е{0) = 1.23054744454982119249735015568.
Условие G(q)q = О будет выполнено, если положить
0@) = ё@) = 7@) = Ф@) = (J@) = П@) = ё@) = 0.
Тогда значения А@) и д@) будут однозначно определяться из
уравнения G.6а) и дважды продифференцированного уравнения связи
О = 9gg{q)(q, q) + G{q)q. Надо только решить линейную систему с ма-
G.8)
трицей
(M(q) Grriq)\
[G{q) О ;
G.9)
Заметим, что д^^ вычислять не требуется, потому что ^@) = 0.
Благодаря выбору 0@) = О большинство компонент А@) и q@) равны
нулю, и только первые две компоненты отличны от нуля:
^@) = 14222.4439199541138705911625887,
0@) = -10666.8329399655854029433719415,
Ai@) = 98.5668703962410896057654982170,
Л2@) = -6.12268834425566265503114393122.
Графики решения (по mod 27г) для этого семизвенного механизма
приведены на рис.7.2 для 0<t < 0.03 .
G.10)
586 Гл. VII. Дифференциально-алгебраические задачи высших индексов
Численные расчеты
Преобразуем сначала систему G.6) в систему уравнений первого
порядка, введя новую переменную v = q. Наши программы
применимы только к задачам, в которых вектор производных умножен на
постоянную матрицу. Поэтому будем рассматривать w = q тоже как
переменную, так что G.6а) становится алгебраическим соотношением.
Различные формулировки задачи, которые обсуждались в разд. VH.l,
теперь будут выглядеть так:
Формулировка в виде задачи индекса 3. Если положить v — q 1л
W = q, то систему G.6) можно переписать в таком виде:
q = v, G.11а)
v = u\ G.11b)
0 = M{q)w-^f(q,v)-^G''(q)X, G.11с)
0 = 9(q). G.11d)
Формулировка в виде задачи индекса 2. Если
продифференцировать уравнение О = g(q) один раз и заменить G.lid) на
0 = G(q)v, G.Не)
то мы получим задачу индекса 2, математически эквивалентную G.6).
Формулировка в виде задачи индекса 1. Еще одно
дифференцирование уравнения G.11е) дает
0 = <7„(9)(r,v) + G(<?)«;, G.11f)
И уравнения G.11a,b,c,f) составляют задачу индекса 1.
К этим формулировкам мы применили несколько программ, меняя
допускаемую погрешность от 10"^ до 10~^°. Результаты показаны на
рис. 7.3 в двойном логарифмическом масштабе. Здесь по оси ординат
отложено время счета (на рабочей станции SUN Spark 20), а по оси
абсцисс — погрешность [q, г;)-компонент при х^^^ = 0.03.
Явные методы Рунге—Кутты. Формулировка в виде задачи
индекса 1 допускает применение явных методов, реализованных, например,
в программах DOPRI5 или DOP853, которые описаны в первом томе.
Для нашей задачи мы написали подпрограмму вычисления функций,
которая при каждом вызове решает линейную систему G.11c,f) для w
и Л и результат подставляет в уравнения G.11а,Ь). Поскольку
полученное дифференциальное уравнение для (д, v) не является жестким,
неудивительно, что программы, основанные на явных методах,
работают очень эффективно (см. рис. 7.3).
Чтобы избежать явления сноса (см. разд.VII.2), мы применили
также комбинацию этого метода с проецированием на многообразие
VI 1.7. Расчет многозвенных механизмов
587
10°
0-^
(
сек
DASSL
" RADAU5 5"
: \ ^^^
Pl^^
LuuiiiJuiiiu i..Juiuii
JTv^PHF.MS^X У^ ,;^^^
у"-;:>Мс:^^\^ мЕхх
^C^J^ DOP853_VEL
тлллрот^ X/'CJ
U\Jrt\lJ_ V tL,
погрешность
1 liiiiii 1 Liiiii liiiim 1 Liiiii Uiiiiii liu Liiiiii 1 lumii
IQO 10-^ 10-^ 10-9
Рис. 7.3. Диаграмма «объем вычислений — точность».
решений. Это можно реализовать программно с помощью
подпрограммы SOLOUT, которую вызывает D0PRI5 после каждого успешного
шага (чтобы указать, что численное приближение было изменено,
задайте IRTRN = 2). Для получения графика, обозначенного DOPRI5_VEL
на рис. 7.3, использовалась только стабилизация по скоростям.
Полное проецирование — на уровне координат G.1 Id) и скоростей G.Не)
— обходится несколько дороже, но улучшения результата не дает.
На рис. 7.4 слева вверху показаны результаты трех различных
реализаций: первый подход — «стандарт» — без всякого проецирования,
«скорость» — выполнялась только стабилизация по скоростям,
«позиция» — делались последовательные проекции на уровне координат
и скоростей. Видно, что стабилизация по скоростям дает наилучший
результат в отношении достигнутой точности и времени счета.
Полуявные методы. Эти методы, обсуждавшиеся в разд. VII.6,
особенно подходят для численного решения (нежестких) механических
систем со связями. Приходится решать только линейные системы с
матрицей G.9), в остальном же эти методы явные. Поскольку они
применяются непосредственно к формулировке с индексом 2, уравнение
связи для скоростей G.Не) удовлетворяется автоматически, и нет
надобности в использовании подпрограммы для вычисления ggg(q)(v, v).
Экстраполяционная программа МЕХХ, которую разработал Лю-
бих A989) (см. также Любих, Новак, Пеле и Энгстлер 1992),
реализует полуявное правило средней точки F.18). Применение
экстраполяции обосновано существованием Л^-разложения (теорема 6.3) и
588 Гл. VII. Дифференциально-алгебраические задачи высших индексов
поэтому дает методы сколь угодно высокого порядка.
Неудивительно, что эта программа дает отличные результаты при вычислениях с
высокой точностью.
Бразей A994) разработал программу НЕМ5 — первую
программу, реализующую полуявные методы Рунге—Кутты. Ее
модифицировали и улучшили Арнольд A995, программа НЕХ5) и Муруа A995,
программа РНЕМ56). На рис. 7.3 показаны также результаты,
полученные с помощью последней из этих программ. В нашем
конкретном примере, где вычисление 5'gg(9)(v,v) не требует больших затрат,
она слегка уступает в эффективности D0PRI5_VEL. Однако Арнольд
A995) и Муруа A995) сообщают об экспериментах, в которых
вычисление gqq{q)(VyV) требовало больших затрат и полуявные методы
показали свое преимущество перед явными методами Рунге—Кутты
с проецированием на уровне скоростей.
Метощл ФДН. Петзолд A982) разработала знаменитую программу
DASSL, которая реализует многошаговые методы, основанные на
формуле дифференцирования назад — ФДН (см. также Бренан, Камп-
белл и Петзолд 1989). Эта программа написана для задач общего вида
F(t/, ti', х) = О, поэтому нет надобности вводить q в качестве новой
переменной в G.6). Мы использовали эту программу с принятыми по
умолчанию значениями всех параметров, за исключением тех,
которые определяют оценку погрешности. Мы задали INF0B)=1 и
ATOL(I)=RTOL(I) = (^''' ^^^ 1=1....,14,
il.ODO для 1>15.
Это означает, что мы управляем точностью q и г, но не лагранже-
вых множителей А. В расчетах, результаты которых представлены на
рисунках 7.3 (в формулировке с индексом 2) и 7.4, мы использовали
полную матрицу Якоби задачи, полученную численным
дифференцированием. Это оказалось более эффективным, чем заготовка
аналитического приближения, в котором пренебрегается производными /,
М и G.
Неявные методЦ|1 Рунге—Кутты. Наша программа RADAU5
написана для задач вида By* = /(х, у) с постоянной матрицей В, которая
может быть и сингулярной. Поэтому ее можно применять к любой из
трех приведенных выше формулировок задачи. Сходимость
гарантируется теоремой VI. 1.1 в случае формулировки с индексом 1,
теоремами 4.5 и 4.6 для формулировки с индексом 2 и результатами работы
ХЛР89 — в случае индекса 3. Однако чем выше индекс, тем труднее
решать нелинейные уравнения в методе Рунге—Кутты. Мы
применяли эту программу с опциями IWORK E) = 14, IW0RKF) = 0hIW0RKG)
= 13, а для формулировки с индексом 3 — с опциями IW0RKE) = 7 и
IWORKF) = 7, так что при оценке погрешностей ускорение w и
множитель Лагранжа А учитывались с весом Л^. Это гарантирует сходи-
VI 1.7. Раигчет многозвенных механизмов
589
10°
сек
h
[ О стандарт
г м скорость
Г Д позиция
Г .^
"д^ии biiii bull Lmi
D0PRI5 2^^
Р" DOP853
погрешность
kmj..Liiii JMim Uuiii LiiiiImiiI
10°
г ^«« DASSL //
V- о индекс 1 X^^
Г М индекс 2 f^f^
I ife погрешность
Liiiiii Lmii.t.kuiii 1 biiii biiiiii Liiim biiiij-Luii
J
10°
10-
10-^
10-»
10°
10-
10-^
RADAU5
ю^Ь
о индекс 1
м индекс 2
Д индекс 3
погрешность
кит kiim kiiiii kiin i kimii Ltiiiii Lmiii kiiiii hum i У
10° 10-3 io-<^
{QPV-
RADAU5
M стандарт
H улучш. ЛИН. aLnre6pa
погрешность
Liiii Uiiiit Lull Lull IdiMn I limn I Ц
10-3 io-<^
Рис. 7.4. Диаграммы «объем вычислений — точность».
мость упрощенных итераций по Ньютону (обоснование дано в работе
ХЛР89, гл. 7). Далее, мы воспользовались специальной структурой
q = v, V = w нашей системы, задав IW0RK(9) = 14 и IWORK(IO) = 7.
Это ускоряет вычисление получающихся линейных систем.
Результаты показаны на рис. 7.3 (для формулировки с индексом 2) и для всех
трех формулировок задачи — на рис. 7.4 слева внизу. Мы
использовали аналитическое приближение для матрицы Якоби (пренебрегая
производными /, М и G) и не применяли проецирование на
многообразие решений.
Экономия в линейной алгебре. Если задача нежесткая, то для
решения нелинейных уравнений метода можно использовать
упрощенную матрицу Якоби. Если пренебречь производными /, М и G (что
590 Гл. VII. Дифференциально-алгебраические задачи высших индексов
мы и сделали в описанных выше расчетах), то в случае с индексом 2
мы получим линейную систему вида
/-а/ / О О \ /^Я\ /а\
О О Л/ G^ А^ р с ' (^^^^
\ О G О О / \ДА/ \d/
где а = (h^)"^, h — длина шага и 7 — собственное значение
матрицы метода Рунге—Кутты. Вычисление матрицы в G.12) не
требует дополнительных затрат, потому что M(q) и G(q) все равно
надо вычислить для правых частей уравнений дифференциально-
алгебраической системы. Исключение переменной Дг; в последней
строке G.12) дает меньшую систему
такого же типа, как для явных методов. После того как решение G.13)
найдено, значения Av и Aq легко получаются из первых двух строк
G.12). Заметим, что матрица в G.13) не зависит от а = (/17)""^ •
Следовательно, на каждом шаге требуется только одно LU-разложение,
независимо от числа различных собственных значений матрицы
метода Рунге—Кутты. Реализация этой идеи значительно уменьшила
вычислительные затраты на решение нелинейных систем, что видно
на рис. 7.4 внизу справа.
Впервые подобную экономию линейно-алгебраических вычислений
предложили Гир, Гупта и Леймкулер A985) для схем ФДН.
Изложенная выше идея не ограничена случаем индекса 2, она
непосредственно распространяется и на случаи с индексами 1 и 3. Заметим,
наконец, что имеется еще возможность сохранять разложение
матрицы из G.13) на протяжении нескольких шагов, даже если длина шага
изменилась.
Жесткая механическая система
Введем теперь некую «жесткость» в рассмотренную выше
механическую систему. Для этого примем во внимание упругость одного из
составляющих ее звеньев (проще всего, по-видимому, выбрать /\g) и
заменим его пружиной с очень большим коэффициентом упругости
с^. Тогда длина этой пружины станет еще одной неизвестной
переменной qg. Пусть длина пружины в нерастянутом состоянии равна zf
(см. табл. 7.1), а ее центр тяжести С^ остается на постоянном
расстоянии fa от верхнего шарнира (см. рис. 7.1). Кроме того, мы упростим
задачу, полагая, что момент инерции этого тела остается
постоянным. Очевидно, что алгебраические уравнения связей G.5) останутся
прежними, в них надо только заменить постоянную zf новой
переменной ^8 • Соответственно должна быть изменена матрица производных
G(q) = g'(q). Теперь она имеет размерность 6x8.
VI1.7. Расчет многозвенных механизмов 591
Уравнения движения для этой измененной задачи выводятся
следующим образом. В кинетической энергии G.3) изменяется только
вклад от шестого тела — новой пружины. Теперь будет
Cq'. Xq = ха-^ и-sine-\-(qg—fa)' cos(n -f e),
Уб = ya-U'Cose + (qg-fa)s\n(Q-\-e),
il-^yl = (gs-faf'П^-\-2{{д^-fa)^-u{qg^ fa) •sinQ)'Qi-^
+ ((^8 -fa)^-2u- (q^ - fa) • sin П -f w^) • бЧ
-I- 2 • U • cos fi • ^ • ^8 "^ ^8 '
В потенциальной энергии надо добавить член, соответствующий
новой пружине. Поэтому вместо G.4) мы теперь получим
и = -тот- fi + CQ hc^ , G.14)
причем коэффициент упругости новой пружины с^ велик.
Получившаяся система опять имеет вид G.6), только теперь q ЕШ^.
Начальные значения G.7), G.8), G.10) будут согласованными и для новой
задачи, если мы дополнительно потребуем, чтобы
4siO) = zf, <?8@) = 0, G.15)
а отсюда следует и %{0) = 0. К этой жесткой механической системе
мы применили основанные на неявных методах программы RADAU5 и
DASSL, взяв значение с^ = 10^^. Поведение этих методов было почти
такое же, как и для первоначальной задачи (рис. 7.4), так что не было
надобности приводить еще один рисунок. Однако использующие
явные методы программы D0PRI5, РНЕМ56 и МЕХХ здесь, разумеется,
непригодны.
Следует отметить, что эффективность программ, основанных на
неявных методах, внезапно снижается, когда То1 < l/cj. Это
происходит потому, что точное решение задачи (с начальными значениями,
описанными выше) очень быстро осциллирует с частотой 0{у/с[) и
амплитудой 0(\/с^) около гладкого решения. Кр. Любих A993)
разработал общую теорию для подобных случаев. При очень высоких
требованиях к допустимой погрешности любая программа
вынуждена отслеживать колебания, и длина шага становится малой.
Упралснения
1. Рассмотрите дифференциальное уравнение
/ jjTf \ (-^ О \тт1 \ тт1 \ ( COSX sina!\
y=U{x)[^^ _y^jU{x)y, ?^W=(^_sinr cosxj
G.16)
(так называемая «задача Крайсса»). Примените к этой жесткой
задаче программу RADAU5, основанную на методе Рунге—Кутты.
592 Гл. VII. Дифференциально-алгебраические задачи высших индексов
Вы увидите, что при фиксированной допустимой погрешности
число вычислений функций возрастает при уменьшении е>0. Затем
примените метод к эквивалентной системе
y' = z, 0=(^Q ^j(/(x)z + f/(x)y G.17)
и покажите, что число вычислений функций не возрастает при
a) Объясните это явление, исследовав сходимость упрощенных
итераций по Ньютону.
b) Докажите, что индекс системы G.17) с б: = О равен 2.
VII.8. Симплектические методы ддя
гамильтоновых систем со связями
Для численного решения гамильтоновых систем со связями
могут быть, в принципе, использованы все подходы, обсуждавшиеся в
разд. VII.2. Как будет показано ниже, недостаток этих методов
понижения индекса состоит в том, что при дискретизации разрушается
симплектическая структура потока.
В разд. 1.6 мы видели, что уравнения движения консервативных
механических систем могут быть записаны либо в координатах
положение — скорость (формулировка Лагранжа), либо в координатах
положение — импульс (формулировка Гамильтона). Точно так же
обстоит дело и для механических систем со связями. В этом разделе
мы рассмотрим гамильтонов формализм:
?' = Яр(р,<?), (8.1а)
p' = -H^(p,q)-G^(q)\, (8.1b)
0 = g{q). (8.1с)
Здесь Н : М" х М" —>R — функция Гамильтона, Н и Я обозначают
ее частные производные, д :R^ -> R^ (где т<п) — уравнение
связи, и G{q) = g^[q). Если T'(^,g) = ^q'^M(q)q (с обратимой матрицей
^(я)) — кинетическая энергия механической системы и U(q) — ее
потенциальная энергия, то мы получим р= M(q)q и
Hip,q)=\p''M(q)-'p+U{g), (8.2)
(см. уравнение A.6.26)), тогда как функция Лагранжа определяется
формулой C(q,q) = T[q^ q) — U[q). Если M(q) = I (единичная
матрица), то p = g, и обе формулировки — A46) и (8.1) — тождественны.
Если M(q) действительно зависит от д, то с вычислительной
точки зрения формулировка (8.1) может оказаться более выгодной, чем
A.46) (см. упр. 1).
Дифференцируя два раза уравнение связи в (8.1), мы получим
0 = С(9)Яр(р,д), (8.3а)
О = ^ (С(<?)Яр(р, <,)) Hpip, q)-G{q)H^^{p, q) [н^(р, q)+G^{q)x).(S.3b)
Видно, что А можно выразить через р я q, если матрица
G(q)Hj,pip,q)G^{g) обратима (8.4)
594 Гл. VII. Дифференциально-алгебраические задачи высших индексов
в окрестности рассматриваемого решения. Поэтому (8.1) является
дифференциально-алгебраической системой индекса 3. Если H(p,q)
задана формулой (8.2), то условие (8.4) совпадает с A.47).
Свойства гамильтонова фазового потока
Любое решение системы (8.1) удовлетворяет уравнениям (8.1с) и
(8.3а). Поэтому оно лежит на многообргизии
Л^={(Р,9)| </(<?) = о, С(д)Яр(р,9) = 0}. (8.5)
Если выразить Л из уравнения (8.3b) — что возможно, если
выполнено условие (8.4) — и подставить получившееся выражение в (8.lb),
то мы получим дифференциальное уравнение на многообразии М.
Ситуация здесь точно та же, что и в случае A.22) в разд. VII.1.
Симплектическая структура. Нашей ближайшей целью будет
обобщение теоремы 1.14.12 на гамильтоновы системы со связью.
Рассмотрим дифференциальную 2-форму
п
u;^ = Y^dp^ Adq^, (8.6)
1=1
где р^ и д^ обозначают, соответственно, компоненты векторов р и q.
Обозначим v?e фазовый поток системы (8.1), ставящий в соответствие
начальному значению (Ро,Яо)?М. значение {p(t),q(t))?M . Для
дифференцируемой функции д:М—>М мы далее будем обозначать через
^*cj2 дифференциальную 2-форму, определяемую равенством
(</*«')(^1,^2) = '^^{9'{Р, яК,. «/'(р. 9)^2).
которое формально совпадает с определением 1.14.11, но здесь нас
интересует только случай, когда векторы ^^ и ^2 лежат в касательном
пространстве к многообразию (8.5)
T^,,,)M = {(u,v)\G(q)v=0, ^{G(q)H^(p,q))v + G(q)H^^(p,q)u = 0].
Теорема 8.1. Фазовый поток (р^ : М -? М системы (8.1) является
преобразованием у сохраняющим симплектическую структуру на М,
т.е.
ДЛЯ всех ty для всех (p,q) и для любых векторов ^1,^2» лежащих в
касательном пространстве Т^^^^^М.
VI 1.8. Симплектические методы для гамильтоновых систем 595
Доказательство, Для произвольного ^ G Т/ >.М касательный
вектор ^^ = (р[(р, д)^ € '^{p{t),q{t))^ является решением уравнения в
вариациях
где JA^ (Л' = 1,..., m) получаются при дифференцировании (8.3b).
Вычислим теперь производную по времени от (^^(^[.^l)- ^^
зависящие от Л или SX члены взаимно уничтожаются, как было показано
при доказательстве теоремы 1.14.12. Поэтому мы получим
"" '•'" (8.7)
+ Е''*''ЧЕ^^))к!,й).
К=:1
Stt ^9
Первая сумма в правой части равенства (8.7) обращается в нуль
вследствие симметрии вторых частных производных. Второе выражение
тоже обращается в нуль, потому что ^2 лежит в касательном
пространстве ^(p(t) <7(П)-^- Следовательно, tc;2(^{,^2) — постоянная, что
и доказывает теорему. П
Сохранение фуш^щи Гамильтона. Дифференцирование функции
Гамильтона H(p{t),q{t)) по времени дает выражение
-^р Hq- HpG А -h Я^ Яр,
где все величины берутся в точке {p[t), q[t)) - Здесь первый член
взаимно уничтожается с последним, а оставшийся член равен нулю
потому, что на многообразии решений G[q)H [р, д) = 0. Таким образом,
функция Гамильтона постоянна вдоль решений системы (8.1).
Симплектический метод первого порядка
Обсудим теперь несколько подробнее осуществимость, сходимость
и симплектичность одного простого метода первого порядка.
Рассматриваемые здесь идеи будут полезны для лучшего понимания методов
более высокого порядка, которые будут обсужпаться в дальнейшем.
596 Гл. VII. Дифференциально-алгебраические задачи высших индексов
Взяв за основу уравнения A1.16.54), рассмотрим следующую
дискретизацию системы (8.1):
Р1=Ро-/1(Я,(р1,(/о) + С^(<7о)А1), (8.8а)
?1=(/о + /1Яр(р1,9о), (8.8Ь)
0 = <7(9i). (8-8с)
Численное приближение (Pi,9i) будет удовлетворять уравнению
связи (8.1с), но не удовлетворяет (8.3а). Поэтому добавим еще проекцию
Pi=Pi-hG'^iq,)fi, (8.8d)
0 = С(91)Яр(р1,91), (8.8е)
И тогда метод (8.8а-е) должен давать приближения, остающиеся на
многообразии Л4 (8.5).
Существование численного решения. Рассмотрим систему
несколько более общую, чем (8.8). Если начальные значения не согласованы,
заменим соотношения (8.8с) и (8.8е) на
^(^i) = 9{Яо) + hG(qo)Hp{po,qo), (8.9а)
G(q^)H,(p,,q,) = G{qo)H^{Po. (/о)- («ЭЬ)
Покажем, что нелинейная система (8.8а,Ь), (8.9а) имеет локально
единственное решение. Подобно тому, как это делалось в
доказательстве теоремы 3.1, запишем
9{qi)-9{Qo)= / 9g{Яo-^^'{Яl'-Яo))dт'{ql-qo).
Jo
Подставляя сюда g{qi) из (8.9а) и q^ из (8.8Ь) и разделив на Л,
получим
G{qo)Hp(Po.qo)= I 9g{qo + r{q,^ q^)) dr H^ip^.q^). (8.10)
Jo
Используя (8.8a), напишем разложение Hp(p^,qQ) в виде
Нр{Р1.яд = Н [p^.q^-hj Н {pQ-\-a(p^'-Pf),q^d(T{H {p^,q^-{-G'^(qo)\i)
Jo
и, подставляя его в (8.10) и интегрируя по частям, найдем, что (8.9а)
эквивалентно соотношению
0= / {l-T)9^,{qo + Tiqi-qo))dT.{Hp{Po,qo),Hp{p,,qo))- (8.11)
Jo
- / 9д{Яо-^'^{Я1-'Яо))^'^ I ^pp(Po+^(Pi-Po)'9o)^^(^<7(Pii^o)+G^(9o)'^i)-
Jo Jo
Это линейная система алгебраических уравнений относительно Л^,
откуда может быть найдено выражение Л^ как гладкой функции Pi^q^
VI 1.8. Симплектические методы для гамильтоновых систем 597
и начальных значений Pq.Qq. Это выражение для А^ подставляем в
(8.8а), и тогда (8.8а,Ь) превращается в нелинейную систему
уравнений для Pi,9i, которая согласно теореме о неявной функции имеет
при достаточно малых h единственное решение, близкое к Ро'^о- ^""
тересно, что при Л —>• О величина Л^ из (8.11) сходится не к значению
Л@), которое определяется из (8.3b), а к решению Xq уравнения
о = ^</„(Яр, Яр) - GH^p(H^ + G^Ao),
В котором все функции вычислены при начальных значениях (pq, ^о) •
Существование решения (р^,//) системы (8.8d), (8.9b) следует из
теоремы Ньютона—Канторовича (см. Ортега и Рейнболдт 1970) с
начальным приближением р^ := р^ и /i = 0; тот же результат можно
получить и с помощью теоремы о неявной функции.
Итак, мы не только доказали существование локально
единственного решения у системы (8.8), но и показали, что замена (8.8с,е) на
(8.9) расширяет определение метода на случай произвольных
начальных значений (близких к Af). Таким образом, мы нашли одношаго-
вый метод
В IR^", который на многообразии М сводится к методу (8.8). При
гладких функциях д и Н функция Ф тоже будет гладкой, и к
этому методу применима классическая теория (сходимость,
асимптотические разложения и т.д.).
Сходимость с поряцком 1. Нам достаточно показать, что
локальная погрешность имеет порядок величины 0(h'^). Тогда сходимость
доказывается применением теоремы П.3.6 к методу (8.12). Из
проведенного выше исследования существования численного решения мы
знаем, что Pi = Po-\-0(h), qi = qo'?0(h) и Х^= XQ-^O(h). Поэтому
из (8.8а,Ь) следует, что
q, = q{to -f Л) + 0(/i2), р, = p{to + Л) - hG^iqo) ^^ + 0(h^)^ (8-13)
где SX = Xq — Х{1^). Возмущающий член hG'^(qQ)SX исключается с
помощью проекции (8.8d,e). В самом деле, из (8.13) и (8.8d) получаем
р^ = p[tQ + Л) - G'^{qQ)u^O{h'^), так что
G{q{U^h))H^{p{iQ^h)-G'^{qQ)u,q{tQ^h))=0[h^).
В силу условия (8.4) и теоремы о неявной функции отсюда следует,
что i/=zO{h^), и локальная погрешность обеих компонент (р и q)
имеет порядок 0(/l^).
598 Гл. VII. Дифференциально-алгебраические задачи высших индексов
Симплектичность. Дифференцирование соотношений (8.8а,Ь)
показывает, что
/\=1 J—1 к — 1
J I J I L \~^ д H .^ \j^j L \~^ д H ^ \i J
dqi =dqo-\-h2^ ^^j^^j (p^, q^)dp^ + ^ 2^ g^/g^j (Pi> ^o)^^o
(здесь верхние индексы указывают компоненты). Если взять внешние
произведения первой формулы и dqQ, а также второй формулы и dp{,
то некоторые члены уничтожатся (как в доказательстве теоремы 8.1),
и мы получим
п п п Q2fj
Y^dp( Adqli=^dpl^Adql-h ^ j{Pi,qo)dpi Adqf^,
/=i /=i /,J=i ^ P
n n n Q2JJ
J2dp{^dq{ = Y^dp(Adqi-\-h ^ ^rr.j(Puqo)dp(Adq^,
1=1 1=1 I,J=l P ^
Складывая обе формулы, получим
п п
J2 dpi Adq{ = Y^ dp', Л dq',. (8.14)
1=1 1=1
Это и доказывает, что метод (8.8а-с) сохраняет симплектическую
структуру. Покажем теперь, что и проецирование (8.8с1,е)
сохраняет симплектическую структуру. Вычислим
к—1 J—1 /v=l
Используя равенство (/(^i) = О, мы получим, как и выше, что
п п
^dp(Ad(/( = ^cfp/Ad(?[. (8.15)
1=1 1=1
Уравнения (8.14) и (8.15) вместе показывают, что в целом вся
процедура (8.8а-е) сохраняет симплектическую структуру.
SHAKE и RATTLE
Эти алгоритмы были сконструированы для задач, у которых в
функции Гамильтона переменные разделены:
H(p.q)=\p'^M-'p-^U{q) (8.16)
VI 1.8. Симплектические методы для гамильтоновых систем 599
(матрица М — постоянная). Они пользуются большой
популярностью при моделировании в молекулярной динамике. Отметим, что
при такой функции Гамильтона задача (8.1) принимает вид
дифференциального уравнения второго порядка Mq" = —UAq) — С^(д)Х со
связью (8.1с).
SHAKE. Этот метод, который предложили Рюккерт, Чиккотти и
Берендсен A977), определяется уравнениями
9„+1 - 29„ + <?„_! = -h'M-' ([/,(?„) + G^(q„)X„), (8.17а)
О = </(<?„+!). (8.17Ь)
При отсутствии связей он идентичен методу Штёрмера,
рассмотренному в разд. III. 10, на который в прикладных работах по
молекулярной динамике часто ссылаются как на метод Верле (Верле 1967).
Формула р^ = M(g„^i — g„_i)/2/i служит для аппроксимации р-компо-
нент. При программной реализации этого двухшагового метода
рекомендуется использовать его стабилизированную версию (см. конец
разд. III. 10).
RATTLE. Если обозначить р^^,^^ :=р^ ~ (Л/2)(С/,(G„) + G^(GjAJ,
то алгоритм SHAKE можно переписать в такой форме:
Pn+i/2=Pn-^(t^,('7n) + <7^(<7n)\). (818а)
<7„+1='?п + ''Л/-Ч+1/2. (818Ь)
0 = </(9„+i). (8.18с)
Как и в методе SHAKE, для определения p^^i надо знать qn-\-2'
Чтобы избежать этой трудности, Андерсен A983) предложил определять
Pn^i из соотношений
Pn+l=Pn+l/2-^(t^,(Wl) + <^'"(9n+lK). (818d)
0 = G(<7„+i)M-V„+i. (8.18е)
так что при этом удовлетворяется и уравнение скрытой связи (8.3а).
Уравнения (8.18d,e) представляют линейную систему уравнений для
iPn + l^^n)'
Распространение на функщт Гамильтона общего ыща. Жэ A994)
заметил, что алгоритм RATTLE может быть распространен на
функции Гамильтона общего вида следующим образом. Для
согласованных значений (р^,7„) ЕМ определим величины
600 Гл. VII. Дифференциально-алгебраические задачи высших индексов
Р„+1/2 = Рп - 2 (^,(Рп+1/2- 9п) + С^{Яп)К), (819а)
9п+1 =9п+2(^p(Pn+i/2'9n) + ^p(Pn+i/2.9n+i))- (819b)
0 = i/(g„+i), (8.19с)
Pn+i =Pn+i/2- 2(^9(Pn+i/2.9n+i) + G'^(9n+iK). (8-19d)
0 = G(9„+i) Яр (p„+i, ?„+,). (8.19e)
Это — частный случай s = 2 пары Лобатто III А—IIIB, которую мы
рассмотрим ниже.
Уравнения (8.19а-с) составляют нелинейную систему для
неизвестных Prx^i/2^ 9n+i ^ ^п' ^^^ ж^ способом, что был использован
для метода (8.8), уравнение (8.19с) может быть переформулировано
так, чтобы Ayj можно было выразить как гладкую функцию р„, д^,
Pn^i/2i Яп-^1 ^ ^^• Следовательно, численное решение существует,
локально единственно и зависит гладким образом от Л и начальных
значений (р„,9„). То же самое справедливо и для системы (8.19d,e).
Если уравнения (8.19с,е) заменить уравнениями (8.9), то мы получим
гладкое расширение метода (8.19), определенное в окрестности М в
Теорема 8.2. Численный метод (8.19) является симметричным^ он
сходится с порядком 2 и сохраняет симплектическую структуру.
Доказательство, а) Мы рассмотрим более общую ситуацию, когда
уравнения (8.19с,е) заменены уравнениями (8.9). Заменив теперь h на
—Л и обменяв местами (Рп^Яп) ^ (Pn+i'^n+i)» ^ также А„ и /i^^, мы
получим
Яп = Яп-^1 - 2 [^р(Рп-^1/2^ Яп + l) + ^р(Рп + 1/2^ Яп)) )
9{Яп) = 9(Яп+1) " f^G{q^^^)Hp(p^_^^,q^^^),
Рп = Рп + 1/2 + 2 (^g(^n + l/2' Яп) + О'^(ЯпЖ) >
С(Яп)^р{Рп^Яп) = С(д,+1)^р{Рп+1^Яп+1)'
Но это в точности те же уравнения, что и (8.19a,b,d) и (8.9). Это
доказывает, что даже расширение метода на окрестность М является
симметричным.
Ь) Рассмотрим метод (8.19) как отображение (р„, д„) •-> (p„-|_i, Яп+х)
на многообразии М (8.5). Те же рассуждения, что и для метода
(8.8), показывают, что порядок метода (8.19) не меньше единицы. Но
VI 1.8. Симплектические методы для гамильтоновых систем 601
так как это симметричный метод, его порядок должен быть четным
(разд. 11,8). Это и доказывает, что (8.19) — метод, сходящийся с
порядком 2.
с) То, что метод (8.19) определяет на М преобразование,
сохраняющее симплектическую структуру, может быть докг1зано тем же
способом, что и для метода (8.8). Леймкулер и Скил A994) сделали
это для случая функции Гамильтона (8.16) с разделяющимися
переменными. Мы не будем здесь останавливаться на подробностях,
поскольку симплектичность метода (8.19) следует также из теоремы
8.5, доказанной ниже. П
Замечание 8.3. При применении метода (8.19) для пошагового
интегрирования можно избежать проецирования (8.19d,e) в тех точках,
где не требуется выдачи значения p^^i. В самом деле, начиная со
второго шага, (8.19а) можно заменить на
не изменяя при этом численных аппроксимаций q^ и Pn^i/2' Такой
же прием возможен и для метода (8.8).
Пара Лобатто IIIA—IIIB
Разделенные методы Рунге—Кутты хороши для гамильтоновых
систем без связей (см. разд. 11.16). Здесь мы исследуем вопрос о
распространении этих методов на систему (8.1) со связью. Рассмотрим
разделенный метод
S S
л- = Ро Н- л Х^ aijkj, Q, = go + ^ ^^^З,/^-, (8.20а)
5 S
Pi = Ро + Л X) ^^i' 9i = 9о + Л Y^i^i' (^•^oь)
»=1 1=1
ki = -^iPi'Qi) -С^(«.)Л,. A = ^(Л.Qil (8-20C)
где 6,.,a,- и 6,,2,- — коэффициенты двух схем Рунге—Кутты (ср.
уравнения A1.16.26)). Не конкретизированные пока величины Л,
(г = 1,...,5) можно задать различными способами. Можно
положить Л,- = А(Р,,Q,), где А(р, д) — функция, определяемая
уравнением (8.3b), или же определить Л, неявным образом, добавив условие
G{Qi)Hp(P„Q,) = О или giQ,) = 0.
Нас интересуют схемы, сохраняющие симплектическую
структуру. Поэтому естественно рассматривать методы, удовлетворяющие
условиям теоремы 11.16.10.
602 Гл. VII. Дифференциально-алгебраические задачи высших индексов
Лемма 8.4. Если коэффициенты метода (8.20) удовлетворяют
условиям
6. =6., г=1,...,5, (8.21)
6,3,.^. -^bjaji - b^bj =0, г, i = 1,..., 5, (8.22)
то выражения J входящие в формулы (8.20), связывает соотношение
п п 5 m п Q IV-
/=1 1=1 »=1 К=1 1=1 ^
Если переменные в функции Гамильтона разделяются, т.е. H(p,q) =
= Т{р) -\-U(q), то для справедливости этого соотношения достаточно
одного условия (8.22).
Доказательство. Тем же способом, как в доказательстве
теоремы 11.16.6, вычислим выражение D = Y^j dp{ Л dq{ — J2j ^Ро ^ ^Яо (см.
также доказательство теоремы 11.16.10). Тогда все члены исчезнут,
кроме тех, которые обязаны своим происхождением члену G'^{Q^)A-
в уравнении (8.20с). Мы получим
S т п ло 1^ ^ г\ К
D=-hY,b,Y,{^fY.ik^ШdQi^dQl^¦Y,'j-J¦{QMf^^^dQ^^|.
%=\ к=\
j%^^'^^''" ' ' fr{99^
Ввиду симметрии второй производной д^ член, содержащий 2-форму
dQf Л dQf, тождественно равен нулю. Лемма доказана. П
Для нас представляют интерес разделенные методы Рунге—Кут-
ты, обладающие следующими свойствами:
• численное решение остается на многообразии М (8.5);
• «численный» поток (Ро^^о) ^ (Рг^Ях) является преобразованием
на М, сохраняющим симплектическую структуру;
• порядок сходимости выше второго.
Если величины Л,- определяются из условия
9(Qi) = 0 для г = 1,...,5, (8.23)
то Y!,i ^9^ 1^Я^{Ях)^Я\ = о, и из леммы 8.4 следует, что метод (8.20)
сохраняет симплектическую структуру, если выполняются условия
(8.21) и (8.22). Таким образом, имеет место второе из
перечисленных свойств. Отсюда видно, насколько важны условия (8.23). Если
решать симплектическим методом систему с пониженным индексом
(8.1а,Ь), (8.3b), то в общем случае мы не получим симплектический
«численный» поток на М.
Как достичь выполнения первого свойства, в частности,
выполнения условия g[q^) =0? Можно потребовать , чтобы метод 6,',3. был
VI 1.8. Симплектические методы для гамильтоновых систем 603
жестко точным, т.е. чтобы
a,j=lj для j = l,...,s. (8.24)
В этом случае q^=Q^, и равенство ^'(^i) = О выполняется
автоматически при выполнении условий (8.23). Из условий (8.24) и (8.22)
следует, что
а,, = О для г=1,...,5 (8.25)
(предполагая 6, отличными от нуля), и тогда нелинейная система
(8.20а,с), (8.23) больше не зависит от Л,. Однако этот параметр через
kg появляется в определении р^ в уравнении (8.20Ь). Там его можно
использовать для того, чтобы наложить связь G(qi)H (pi,q^) = 0.
Из-за условия (8.25) возникает новая трудность. Если
рассматривать (8.20Ь,с) как определение величин Pi,9i,^,-,^,-, то
остальные уравнения (8.20а) и (8.23) образуют нелинейную систему для
Pj,..., Р,, Qi,..., Q,, Л^,..., Л,_ 1. Подсчитав число уравнений этой
системы {2sn'\-sm) и число неизвестных {2sn-\-{s — 1)т), нетрудно
убедиться, что эта нелинейная система в общем случае не имеет
решений. Жэ A994; 1996) предложил потребовать,чтобы
Sij. = 0 для j=:l,...,s. (8.26)
Тогда Qi=qQyVi условие (8.23) автоматически выполняется при г = 1
(всегда предполагается, что начальные значения согласованы). В
силу (8.22) отсюда следует (при ненулевых 6,), что
a-^ = bi для г = 1,...,5. (8.27)
Обе матрицы А и А метода Рунге—Кутты — особенные. Пусть Aq
— подматрица размерности E— 1) х 5, которая получается из А
после удаления первой строки, и Aq — подматрица Л, образованная ее
первыми 5—1 столбцами. Доказать существование численного
решения системы (8.20), (8.23) можно, если потребовать выполнения такого
условия: матрица размерности (« — 1) х (s — 1)
AqAq обратима. (8.28)
Распространим теперь метод на случай произвольных начальных
значений. Для этого заменим условие (8.23) условием
9{Qi) = 9{Яо) + CihG{qQ)Hp(pQ,qQ) для г = 1,..., 5
(где с, = J2j a^j ), а условие G(q^)Hp{pi,q^) = 0 — условием (8.9b). По
аналогии с уравнением (8.10) воспользуемся соотношением
9{Qi)-9{Qo)=h f 9,iqo + r(Q,-qo))dT.f2^,jH^(PpQj) (8-29)
•'О , = 1
604 Гл. VII. Дифференциально-алгебраические задачи высших индексов
и подставим в него разложение
Я^(Р^.,(?,.) = Яр(Ро>«,)-
Мы получим систему линейных уравнений для Л^,..., A,_i,
подобную (8.11), которая при Л = 0 (и, соответственно, Л^ = Л°) принимает
вид
о = |</„(Я,, Яр) + {E^ijCj)GH^,H, -
j = l
г=1 j=l
где все функции берутся в точке (Ро»9о)- Благодаря условиям (8.28)
и (8.4) эта система разрешима относительно Л°. Тогда теорема о
неявной функции гарантирует существование локально единственного
решения уравнений метода (8.20), (8.23) и, тем самым, существование
гладкого расширения на окрестность М.
Следующий вопрос — существуют ли методы высокого порядка,
обладающие всеми этими свойствами?
Теорема 8.5. Яара s-стадийных методов Лобатто IIIА—Я/Б, в
которой роль метода 6,-,3,j играет Лобатто IIIА и роль метода Ь^^а^л
— Лобатто IIIB (определение этих методов см. в разд. IV. 5)
удовлетворяет всем требованиям (8.21), (8.22), (8.24), (8.25), (8.26), (8.27) и
(8.28).
Доказательство. Свойства (8.21), (8.24), (8.25), (8.26) и (8.27)
следуют непосредственно из определения этих методов. Условие сим-
плектичности (8.22) впервые доказал Сун Чжень A993). Положим
d,j = 6,a,j + ^^j^ji ~ ^^i^^j • тогда при к = 1,.. .,s прямое вычисление
дает
j; ,..,-1 = 6.4 + ^A-с?)-6,1 = 0.
Здесь использован тот факт, что метод Лобатто IIIА удовлетворяет
условиям C{s), а Лобатто IIIB - условиям D(s) (см. табл.IV.5.13).
Поскольку абсциссы с^,..., с, квадратурной формулы Лобатто
различны, полученная система уравнений с матрицей Вандермонда имеет
единственное решение d-j = О, что и доказывает выполнение условия
(8.22).
VI 1.8. Симплектические методы для гамильтоновых систем 605
Покажем теперь, что
5-1
пЯ
E(E2vS0^r^ = -7-^ Д-^я г,(У = 2,...,5. (8.30)
Это означает, что Aq^qK = W, где V и W — неособенные
матрицы типа Вандермонда, откуда с очевидностью вытекает (8.28).
При g = 2,..., 5 — 1 уравнение (8.30) следует из того факта, что
методы Лобатто П1А и ПШ удовлетворяют соответственно условиям
C{s) и C(s — 2). Остается только показать, что коэффициенты S- :=
:= Y2k Z^j ^ij^jk^k~^ ~ ^i/^i^ ~ 1) обращаются в нуль для всех г. Из
(8.26) и Cj = О имеем 6^ = 0. Поскольку 2^^ = bj = 6^ и с, = 1, условие
Sg=0 есть не что иное, как условие порядка (для порядка s), которое
выполнено (см. разд.IV.5). Кроме того, методы Лобатто П1А и ПШ
удовлетворяют, соответственно, условиям D{$-'2) и D(s). Поэтому
равенство Yli^^i^T^^^i = ^ выполняется при т= 1,...,5 — 2, откуда
следует, что Jj» • • •>^e-i тоже равны нулю. Таким образом, все
соотношения (8.30) доказаны. П
Осталось еще обсудить порядок сходимости пары Лобатто П1А—
П1В. Так как нам удалось показать, что этот метод является
вложенным в одношаговый метод, который определен во всей
окрестности М , то здесь применима теория сходимости, развитая в разд. П.З.
Надо только исследовать локальную погрешность метода. Каждый
из методов имеет классический порядок 25 — 2 (разд. IV.5), и из
результата упражнения 4 следует, что эта пара, рассматриваемая как
разделенный метод Рунге—Кутты, тоже имеет порядок 25 — 2. Жэ
A994) показал, что наличие связи (8.1с) не уменьшает порядок. Это
доказательство сверхсходимости громоздко и очень сложно
технически, поэтому мы его здесь не воспроизводим.
Композитные методы
Другая возможность получения симплектических методов
высокого порядка для системы (8.1) — это композиция методов низкого
порядка. Эта идея восходит к работе Иошиды A990), а Райх A996)
распространил ее на системы со связями.
Рассмотрим симметричный метод второго порядка (8.19) и
обозначим его расширение на окрестность М через Фд . Мы исследуем
следующую композицию:
Фс,л<>Фс.л^Фс.л. (8.31)
Метод (8.31) представляет собой одношаговый метод, определенный в
окрестности М. Если начальные значения лежат на wM, то
численное решение остается на М. Более того, композиция (8.31) является
606 Гл. VII. Дифферешщально-алгебраические задачи высших индексов
симплектической и симметричной. Отметим, что при реализации
этого метода можно обойтись без проекций (8.19d,e) (см. замечание 8.3).
Порядок такого метода определяет следующая
Теорема 8.6. Пусть отображение (Ро^Яо) ^ (Pi, ^i) определено
формулами (8.19). Если
2ci-fC2 = l, 2c?-hc^ = 0, (8.32)
то композитный метод (8.31) имеет порядок 4.
Если Фf^ представляет симметричный одношаговый метод порядка
р = 2к, определенный в некоторой окрестности Mj то из соотношений
2ci +С2 = 1, 2с?+Чс5+^ = О (8.33)
следует, что порядок композитного метода (8.31) равен p-f 2.
Доказательство. Положим Уо = {РоуЯо)^ и y(t) = {p{t)yq(t)) .
Локальная погрешность метода (8.19) удовлетворяет соотношению
Так как базовый метод имеет вид Ф^{Уо) = Уо "•" ЛФ(Уо) '^l' ^о
у(<о + Bс1+С2)/1)-Фе.лоФс,АоФс.лA/о) = Bс? + с^)%о)ЛЧС7(Л^).
Тогда из условий (8.32) следует, что порядок метода (8.32) не ниже
третьего, а так как он симметричный, то его порядок должен быть 4.
Приведенное доказательство легко распространить и на случай более
высокого порядка. D
Уравнения (8.32) имеют решение
1 </2
откуда видно, что промежуточный шаг в композиции (8.31) — это
«шаг назад» (с отрицательной длиной шага CjA).
Теорема 8.6 позволяет строить симплектические интеграторы для
системы (8.1) любого четного порядка. Однако получающийся при
этом метод порядка р = 2к требует З'^"^ обращений к базовому методу
(8.19).
Для случая гамильтоновых систем без связей известно, что
композиции вида
Фс,Л ^ ^c,h ^ • • • <^ ^с.гН ^ Фс.Л ^ ^с.^гН ^ • ' • ^ ^сЛ ^ ^c,h (8-34)
дают лучшие методы (Иошида 1990; Маклахлан 1995; Санс-Серна и
Кальво 1994). Райх A996) исследовал возможность распространения
этих методов на гамильтоновы системы со связями и нашел, что при
этом необходимы дополнительные условия порядка. Его
исследование опирается на «обратный анализ погрешностей» для интеграторов
на многообразиях.
VI 1.8. Симплектические методы для гамильтоновых систем 607
Обратный анализ погрешностей (для ОДУ)
¦Хотя обратный анализ — совершенно простое понятие,
имеются серьезные основания думать, что тот, кто
обучался классическое^ математике, остается не готовым
принять его». (Дж.Х. Уилкинсон, NAG Newsletter 2/85)
В разд. 11.16 мы коротко пояснили идею обратного анализа
погрешностей для симплектического метода Эйлера. Здесь мы
распространим этот анализ на произвольные одношаговые методы. Рассмотрим
задачу
У' = /Ы, у{0) = Уо (8.35)
и произвольный одношаговый метод t/Q »-> у^ для этой задачи.
Предположим, что функция f{y) и определяемые методом функции
дифференцируемы достаточное число раз, так что локальная погрешность
может быть представлена в виде разложения Тейлора вида
У1-у(Л) = ^р+1(г,о)Л''+Ч...+^д,ыл^ + 0(л^+»). (8.36)
Теорема 8.7. Рассмотрим одношаговый метод порядка р, и пусть
его локальная погрешность представима в виде (8,36). Тогда
существуют функции fj(у) (j = Pi-. yN) такие, что
y,-y{h) = 0{h''*'), (8.37)
где y[t) — решение возмущенного дифференциального уравнения
Г = /(У) + Л%E0+ .. + Л^-7^-1(у). т = Уо' (8.38)
Замечание. Если функция f(y) -f Л''/рB/) + ... -h А^~ Vn-iB/)
Удовлетворяет условию Липшица, то из доказательства теоремы П.3.4
видно, что на ограниченных отрезках Уп—у{пк) = 0(к^). Отсюда
следует, что численное приближение у„ гораздо ближе к решению
задачи (8.38), чем задачи (8.35). Поэтому исследование системы (8.38)
проливает новый свет на поведение численного решения.
Доказательство. На основании нелинейной формулы вариации
постоянных (теорема 1.14.5) мы имеем
y{h) = y{h)+l ^{h,s,y{s)).[h'>f,ms)) + ... + h^f^{y{s)))ds,
где 2/(^,^0'2/о) обозначает решение задачи (8.35), соответствующее
начальным значениям t/(<o) = Уо • Разлагая здесь интеграл в ряд
Тейлора, получим
у(Л)-у(Л) = л''+1/р(Уо) + л''+'(/р+1 + ^/;/+5/'/р)(г'о) + -- • (8¦3^)
608 Гл. VII. Дифференциально-алгебраические задачи высших индексов
Из условия (8.37) следует, что коэффициенты в (8.39) должны
совпадать с коэффициентами в (8.36) до определенного порядка. Отсюда
имеем: /р(у) = rfp+i(y), /p+i(y) =dp+2(y)-(/;(у)/Ы + /'Ы/рЫ)/2,
И т.д. Существенно, что коэффициент при Л^+^ в (8.39) содержит
fj{y) в качестве линейного члена, а остальные выражения зависят
только от /,- (у) с i < j. Следовательно, сопоставление
коэффициентов позволяет определить функции fj(y) рекуррентным образом. П
Пример 8.8. Для иллюстрации этой теоремы рассмотрим
дифференциальное уравнение Вольтерры—Лотки:
u' = u{v-l), v' = vB-u). (8.40)
Эта система имеет первый интеграл
/(ti, v) = 2lnu — u-\-lnv — v, (8.41)
откуда следует, что все ее решения — периодические. Некоторые из
них показаны на рис. 8.1 слева вверху.
К этому дифференциальному уравнению мы применили три
различных численных метода. Первый из них — хорошо известный
явный метод Эйлера y„^i = j/„ + Л/(у„). На рис. 8.1 справа вверху
показаны численное решение и точное решение (сплошная кривая) при
начальных значениях Uq = 2.725, Vq = 1. Кроме того, здесь же
показаны решения возмущенного дифференциального уравнения (8.38) при
N = 1 (штрих-пунктирная кривая) и ЛГ = 2 (пунктирная кривая). В
случае явного метода Эйлера уравнение (8.38) принимает вид
!/' = /(y)-f(/7)(y) + Y^(/"(/,/)+4/77)(y)- (8.42)
На рисунке ясно видно хорошее согласие численного решения с
точным решением возмущенной системы, несмотря на довольно большую
длину шага Л = 0.12.
На том же рисунке слева внизу показаны результаты такого же
эксперимента с неявным методом Эйлера у^^^ = у^ H-A/(y„^.i).
Возмущенное дифференциальное уравнение получается из (8.42) заменой
Л на —Л (потому что явный и неявный методы Эйлера являются
сопряженными).
Третий метод — симплектический метод Эйлера (см. ниже
уравнение (8.45)), который для задачи (8.40) принимает вид
«n+i = «n + ^tz„(^n+i-l)) ^n+i=^n+ftv„^iB-ti„).
Первый член возмущенного дифференциального уравнения таков:
и* = u{v- 1) - hu(uv-4v-\'V^ -h 1)/2,
о (о.4о)
v' = Ц2-и)-\-кЦш)-Ьи-\-и^-\-4)/2.
Качественное поведение этого метода совершенно иное, нежели у двух
предыдущих. Можно показать, что система (8.43) имеет первый ин-
VI 1.8. Симплектические методы для гамильтоновых систем
609
V
4
3
2
1
г /^ """*^\неявный м. Эйлера
[- / N. Л = 0.12
2 4 6" 1
I V
4
3
2
1
- симплектич. м. Эйлера
- //^^^"^^Х Л = 0.12
2 4 6 «
Рис. 8.1. Решение возмущенного дифференциального уравнения
различными методами.
теграл, близкий к I{ujv) (упр. 5). Следовательно, решения ее будут
периодическими, как и в случае исходной невозмущенной системы.
Пример 8.9. Для гамильтоновой системы без связей
9' = Яр(р,<?), p' = -H^ip,q) (8.44)
метод (8.8) принимает вид
^1 = ^0 + ЛЯ^,(р1, до), Pi = Ро - ЛЯд(р1, ^о)- (8.45)
Аналогичный метод (но неявный относительно q и явный
относительно р) рассматривался в разд. 11.16 (формула A1.16.54)). Там были
вычислены первые члены возмущенного дифференциального уравнения
(8.38), и мы с удивлением отметили, что оно тоже является
гамильтоновой системой. Такое же вычисление можно провести и здесь. Для
системы (8.45) возмущенное дифференциальное уравнение имеет вид
r = H,{p,q), p' = -H^(p,q), (8.46)
где (при N = 2)
Для удобства обозначений мы предполагали, что р и q — скаляры.
Однако при соответствующей интерпретации возникающих
выражений эта формула справедлива и для задач с более чем одной степенью
свободы.
610 Гл. VII. Дифференциально-алгебраические задачи высших индексов
Пример 8.10. Метод второго порядка (8.19) при применении его к
системе без связей (8.44) принимает вид
Г (8.47)
где Pi/2 =Pq — (Л/2)Я^(Р1/2» ^о) • Вычислив главный член его
локальной погрешности, мы найдем, что возмущенное дифференциальное
уравнение (8.38) при N = 2 имеет вид
г = Я,(р, д) + ^ (-ЯрррЯ,^ + 2Я,„Я,Я, + 2Н^^Х +
+ 2Яр,Я„Яр + 4Н^рН^^Н^) (р, q),
р' = -Я,(р, я) + ^ {Н^,,Н1 - W^^^H^H^ - 2Я,„Я2 -
- 2Н^,Н^^Н^ + 2ЯррЯ„Я, - 6Н^,Н^^Н^) (р, 9).
Легко проверить, что это гамильтонова система вида (8.46) с
^ = ^ + 5i {'^^"""'Р - "^r>Hl + 2Я„Я,Я,).
Краткий обзор дальнейших результатов. Дальнейшая разработка
обратного анализа погрешностей для обыкновенных
дифференциальных уравнений выходит за рамки вопросов, рассматриваемых в
настоящей главе. Поэтому мы приведем здесь некоторые интересные
результаты, не вдаваясь в подробности.
Прежде всего, мистерия предыдущих примеров перестала быть
таинственной. В случае, когда дифференциальное уравнение (8.35)
является гамильтоновой системой, и к ней применяется симплекти-
ческий метод интегрирования, возмущенная система (8.38) будет
снова гамильтоновой при любых N. Этот результат доказан в работе
Хайрера A994), в которой приведены явные формулы, выражающие
функции fj{y) через элементарные дифференциалы, и дана явная
формула для возмущенной функции Гамильтона. Эта явная
формула гарантирует однозначность определения Н[р, q) в тех областях,
где определена Я(р, q). Другие доказательства этого результата дали
Райх A996), а также Бенеттин и Джорджилли A994).
Если функция / бесконечно дифференцируема, то показатель А^,
на котором обрывается разложение в теореме 8.7, произволен. В
общем случае ряд (8.38) при N —^оо расходится, и постоянные,
спрятанные в оценке (!?(Л^+^) в формуле (8.37), стремятся к бесконечности
вместе с Л^, даже если / — аналитическая функция. Поэтому
интересно найти строгие оценки для t/j — y[h) при оптимально выбранном
N. Такие результаты получили независимо Бенеттин и Джорджилли
VI1.8. Симплектические методы для гамильтоновых систем 611
A994) и Хайрер и Любих A996). Опираясь на них, можно показать,
что при симплектическом интегрировании функция Гамильтона
остается ограниченной (с погрешностью порядка 0{h^)) на
экспоненциально больших отрезках времени. Кроме того, теория КАМ^) может
быть полезна для лучшего понимания, как ведут себя
симплектические численные схемы на больших интервалах интегрирования.
Обратный анализ погрешностей на многообразиях
Рассмотрим гамильтонову систему со связью (8.1) и численный
одношаговый метод, который дает аппроксимацию (Рп^Яп) >
остающуюся на многообразии М (8.5). Можно ли распространить описанный
выше обратный анализ погрешностей для ОДУ на этот случай?
Прийти к этой цели можно, по крайней мере, двумя путями.
Первый — это ввести локальные координаты, чтобы получилась гамиль-
тонова система без связи. Тогда можно применить обратный анализ
погрешностей для ОДУ к одношаговому методу, записанному в
локальных координатах.
Второй подход позволяет конструировать возмущенную функцию
Гамильтона прямо в исходных координатах. Для частного случая
функции Гамильтона с разделенными переменными этот подход
развил Райх A996). Мы поясним его на примерах методов первого и
второго порядков (8.8) и (8.19).
Обратный анализ погрешностей для метсща (8.8). Рассмотрим
сначала подсистему (8.8а-с). Этап проекции (8.8d,e) будет рассмотрен
позже. Из уравнения (8.11) значение А^ может быть выражено через
Pi)^i>Po>9oj Дзже если начальные значения не согласованы. После
' подстановки этих функций в (8.8а) уравнения (8.8а,Ь) представляют
собой два соотношения, связывающих переменные Pi,^i,Po»9o ^ '^•
Согласно теореме о неявной функции эти два соотношения
позволяют выразить (Poj^i) через (р^^о) ^ ^' Следовательно, решение А^
уравнения (8.11) может быть записано как функция (Piyqo.h).
Обозначим эту функцию
А1=А(р„?о,Л)- (8.48)
Тогда система (8.8а,Ь) примет вид
Р1=Ро-Л(Я,(Р1,до) + С;^(до)'^(Р1.9о1Л)),
Ях = 9o + '^^p(Pi'9o)»
и уравнение связи (8.9а) выполняется автоматически, в силу
определения X{pi, Яо, h). Рассмотрим теперь функцию Гамильтона
П(р, q) = Н(р, q)+9(qfX(p, q, Л), (8.50)
^' Теория Колмогорова—Арнольда—Мозера о сохранении инвариантных
торов при возмущениях интегрируемых гамильтоновых систем (см.
Арнольд 1974, €.365). — Прим. ред.
612 Гл. VII. Дифференциально-алгебраические задачи высших индексов
где А(р, g,/i) — функция, определенная формулой (8.48).
Соответствующая гамильтонова система имеет вид
д' = Я^(р, q)-^9{qf\p(p^ (/, Л),
p' = -H^{p.q)-^G^{q)\{p,q,h)^g(qf\^(p,q,h).
Здесь важно заметить, что при начальных значениях,
удовлетворяющих условию ^(^о) = 0) численное решение (Pi.qi) системы (8.49) в
точности совпадает с численным решением, которое получается при
применении симплектического метода Эйлера (8.45) к гамильтоновой
системе (8.51) (без связи). Таким образом, пример 8.9 показывает, что
численное решение {Pi^qi) с точностью до 0{h^) близко к точному
решению системы (8.46), в которой в определении функции Я надо
заменить Н па И из (8.50).
Подобным же образом можно рассмотреть и этап проецирования
(8.8d,e). Решение // системы (8.8d), (8.9b) зависит от р^, g^ и /i
(зависимость от Ро'^о можно опустить, поскольку соотношения (8.8а,Ь)
позволяют выразить эти величины через р^, q^ и h). Соотношение
(8.8d) позволяет нам также рассматривать /г как функцию р^, q^ и
h. Рассмотрим теперь функцию Гамильтона
Q{p.q) = 9{qf^.q.h) (8.52)
и соответствующую гамильтонову систему
Р' = -G^{q)^{P^ q. h) - 9{qYp.q{p, q, h).
Если g{qi) = 0, то численное приближение p^, найденное с помощью
(8.8d), а именно, р^=р^— hG'^{qi)fi{pi, ^i, Л), совпадает с тем
численным решением системы (8.43) с начальными значениями (р^ ? 9i) >
которое дает метод (8.45). И опять пример 8.9 показывает, что численное
решение (Pi,gi) с точностью до О (Л"*) близко к точному решению
системы (8.46), в которой в определении функции Я надо заменить Я
на Q из (8.52). Полученные результаты подытоживает
Теорема 8.11. Рассмотрим одношаговый метод (8.8) и
предположим у что начальные значения согласованы, т.е. (Ро^^о) ^М. Тогда
справедливы оценки
р,-р(л)=о(л'), я1-т=о{к'),
где p{t),q(t) — решение гамильтоновой системы (8.46), в которой
H = H + G+f^{H,G} + ^{{H,{H,G}} + {G,{G,H}})
И
^ — У ^УрУд ' To хУрР^Ч ^qq^p ' ^ypqyp^q J »
VI 1.8. Симплектические методы для гамильтоновых систем 613
причем 7i и Q задаются, соответственно, формулами (8.50) и (8.52).
Здесь скобка Пуассона {HyG} двух функций Я,С:М"хМ"—^Е
определяется так: {Я, G} := Я^С^ - Я^С^ (ср, формулу (П.16.65)).
Доказательство. Будем рассматривать одношаговый метод как
композицию отображений {pq,(/q) ^ (Pi,9i) и (РхуЯх)^ (Pi,Ях). Если
пренебречь членами порядка 0{h^), то оба отображения можно
интерпретировать как Л-поток гамильтоновых систем. А тогда
утверждение теоремы следует из формулы Кампбелла—Бейкера—Хаус-
дорфа A1.16.83). П
Обратный анализ погрешностей для метода (8.19). Будем
рассматривать решение Xq системы (8.19а,Ь), (8.9а) как функцию
переменных Р1/2уЯо и /i, т.е. Aq = A(pi/2»9o''*)> а решение р,^ системы (8.19d),
(8.9b) — как функцию переменных р^, q^ и Л, т.е. /Xq =/^(Pi,^!,^).
Тогда метод (8.19) можно представить как композицию из
Pi/2 = Ро - 2 {^q(Pi/2y Яо) + С'^(д^)Х{рх/2^ Яо, Л) j,
9i = 9о + 2 (^р(^1/2' ^о) + ^p(Pi/2> ^i)). (8-54)
Pi = Pl/2 - 2 {^qiPl/2^ 9l) + (^^{Я1)^{Р1/2^ Я^^У)
С этапом проекции
Pi = Pi - 2^^(^i)^(Pi'^1' ^)^ (^•^^)
где «^(Pd^i, Л) =/i(Pi,9i,/i) — A(pi/2,gi,/i). Мы видим, что при
согласованных начальных значениях (Ро,^о) ^ -^ метод (8.54) совпадает с
методом (8.47) при замене Н(руя) на
Щр, я) = Н[р, я) 4-9[Я?\[Р. Я. Л), (8.56)
а этап проекции (8.55) можно интерпретировать как метод (8.45) с
функцией Гамильтона
а(Р,9) = ^</(9)Мр.9.Л). (8.57)
Тем же путем, что и для метода первого порядка, мы получаем
следующую теорему:
Теорема 8.12. Рассмотрим метод (8.19) и предположим, что
начальные значения согласованы, т.е. (рд, Яо) ^ М - Тогда справедливы
оценки
где p{t),я{^) — решение гамильтоновой системы (8.46), в которой
н = н+6+^{н,д} + ^{{н,{н,д}} + {д,{д,н}})
614 Гл. VII. Дифференциально-алгебраические задачи высших индексов
^ У ^Ур^я То \ рр я ^яя р ^Уря^рУя)'
причем % и G задаются у соответственно ^ формулами (8.56) и (8.57).
П
Последние две теоремы показывают, что даваемое
рассмотренными методами при согласованных начальных значениях численное
решение совпадает (с точностью до определенного порядка) с точным
решением возмущенной гамильтоновой системы без связей.
Возмущенная функция Гамильтона определена в окрестности
многообразия, так что в полной мере применимы результаты обратного анализа
погрешностей для ОДУ.
Упражнения
1. (Жэ 1995.) Система A.46) эквивалентна следующей:
g' = u,
(М(д)иУ = M^{q)(u, и) -f /((/, и) - G^^A, (8.58)
0 = g{q).
Для случая, когда система A.46) получается из функции Лагран-
жа ?(д, q) = ^q^M{q)q — U{q), покажите, что /(g, и) всегда
содержит член —М (g)(ti,i/) (кориолисовы силы), который таким
образом компенсируется в формулировке (8.58).
2. Покажите, что пример B.1а-с) имеет вид (8.1а-с) с функцией
Гамильтона
Я(р,д) = (р?4-р2)/2-Ьд2.
Если вычислить А из B.3) и подставить в B.1а-с), то
получившееся дифференциальное уравнение уже не будет гамильтоновым.
3. Дайте другое доказательство теоремы 8.1, применив на этот раз
теорему 1.14.12.
Указание (Райх 1996). Пусть А = А(р, д) определено из уравнения
(8.3b); рассмотрите гамильтонову систему без связей с функцией
Гамильтона
Я(р,д) + G(G)^А(р,G).
Соответствующий поток сводится к потоку системы (8.1) вдоль
многообразия связи М.
VI 1.8. Симплектические методы для гамильтоновых систем
615
4. Рассмотрим разделенный метод Рунге—Кутты и применим его
к разделенному обыкновенному дифференциальному уравнению
(без связей). Предположим, что оба метода основаны на одной
и той же квадратурной формуле порядка р, причем первый
метод удовлетворяет условиям C{rj), D{^), а второй — условиям
C(fj), D{^). Докажите, что эта пара имеет порядок
min(ру 2 minG7, fj) -h 2, minG;, rj) -f min(^, ^) -f- 2, min(?/-h^, ^H-f) H-1 j.
Покажите, что пара Лобатто П1А—П1В имеет порядок 25 — 2.
Указание. Используйте идеи доказательства теоремы П.7.4 для
проверки условий порядка (разд. П. 15).
5. Вычислите первый интеграл для дифференциального уравнения
(8.43). Какова причина существования такого инварианта?
Указание, Преобразование и^е^ , v = е^ приводит к гамильтоно-
вой системе.
Ответ. 7(гх, г;) = 1{и, v) + h{(u-\' v)^ - lOti - Sv -f 8 In iz + 2 In v)/4.
tso (leht alles zu Ende allhicr:
Feder, Tince, Tobak und auch wir.
Zum IcRcenmal wird eingetunkt,
Dann kommc dcr grofie
schwarze
О
(W. Busch, Bilder zur Jobsiade 1872)
Конец имеет всё под небесами —
Перо, табак, чернила и мы сами.
Последняя заканчивается строчка,
А дальше — черная большая Ф
(В. Буш, Картинки к «Иобсиаде», 1872)
Приложение. Программы на Фортране
Во время подготовки этой книги было разработано несколько
программ для решения жестких и дифференциально-алгебраических
задач вида
My' = f(x,y), у{хо) = Уо^ (АЛ)
где М — постоянная квадратная матрица. Если М — сингулярная
матрица, то задача дифференциально-алгебраическая. В этом случае
начальные значения должны быть согласованными.
Реализующая неявный метод Рунге—Кутты программа RADAU5
и ее расширение RADAUP могут применяться и к задачам высших
индексов (> 2), тогда как программа ROD AS, основанная на методе
Розенброка, а также использующая экстраполяционный метод
программа SEULEX подходят только для жестких дифференциальных
уравнений явного вида (т.е. разрешенных относительно производных)
и задач индекса 1. Программы SDIRK4, R0S4 и SODEX по-прежнему
доступны, но они не обновлялись.
В том случае, когда М — не постоянная матрица, подходящими
преобразованиями и/или введением новых переменных любое неявное
дифференциальное уравнение можно привести к виду (А.1). Если
первоначальная задача имеет одну из форм
ВШ = П=^,У), У" = /(^.У,У'), B{y)i/'=f(x,y,y')
ИЛИ подобную им, то эффективность программы может быть
повышена посредством установки определенных параметров, что будет
объяснено в этом приложении далее.
Связь с программой в процессе интегрирования может быть
установлена с помощью подпрограммы SOLOUT, которую пишет
пользователь. Это проиллюстрировано ниже в управляющей программе
— драйвере. Другие применения этой подпрограммы обсуждаются в
конце приложения.
Мы будем рады приветствовать любые опыты со всеми нашими
программами, которые можно получить^)
— через anonymous ftp (с "ftp.unige.ch'', каталог "pub/doc/math"),
— или через "http://www.unige.ch/math/",
— или непосредственно от авторов (если вы пришлете дискету),
Адрес: Section de Mathematiques, Case postale 240, CH-1211 Geneve 24,
Switzerland
E-mail: hairer@divsun.unige.ch wanner@divsun.unige.ch
^ В этом приложении полные тексты программ не приводятся ввиду их
большого объема. О том как получить некоторые другие программы см. в
конце разд. V.5. — Прим. ред.
Приложение. Программы на Фортране 617
Драйвер для программы RADAU5
«Задача решения уравнения Ван-дер-Поля настолько
труднее всех остальных...»
(Л.Ф. Шампайн 1987)
На отрезке [О, 2] решается уравнение Ван-дер-Поля
У2 = (A - У1)У2 - 2/i) А, 2/2@) = -0.66
с е = 10"^. Подпрограммы FVPOL, JVPOL вычисляют правую часть
дифференциального уравнения и его матрицу Якоби. Подпрограмма
SOLOUT используется для печати решения в равноотстоящих точках.
с
с link driver radauS decsol dc-decsol or
С link driver radauS lapack lapackc dc-lapack
С
IHPLICIT REAL*8 (A-H,0-Z)
С PARAMETERS FOR RADAUS (FULL JACOBIAI)
PARAMETER A0=2,LW0RK=4«ID*ID+12*ID+20,LItf0RK=3*ID+20)
DIMEISIOI Y(ID),VORK(LUORK),IUORK(LIWORK)
EXTERIAL FVPOL,JVPOL.SOLOUT
С — PARAMETER II THE DIFFEREITIAL EQUATIOI
RPAR=1.0D-6
С — DIMEISIOI OF THE SYSTEM
1=2
С — COMPUTE THE JACOBIAI AIALYTICALLY
IJAC=1
С — JACOBIAI IS A FULL MATRIX
MLJAC=I
С DIFFEREITIAL EQUATIOI IS II EXPLICIT FORM
IMAS*0
С — OUTPUT ROUTIIE IS USED DURIIG IITEGRATIOI
I0UT»1
С — IIITIAL VALUES
X=O.ODO
YA)=2.0D0
YB)=-0.66D0
с — EIDPOIIT OF IITEGRATIOI
XEID»2.0D0
с — REQUIRED TOLERAICE
RTOL=1.0D-4
AT0L=i.ODO*RT0L
IT0L=O
с — IIITIAL STEP SIZE
H=1.0D-6
С — SET DEFAULT VALUES
DO 1=1,20
IWORK(I)=0
W0RK(I)=O.DO
EID DO
С — CALL OF THE SUBROUTIIE RADAUS
CALL RADAUS(I,FVPOL,X,Y,XEID,H,
+ RTOL,ATOL,ITOL,
+ JVPOL,IJAC,MLJAC,MUJAC.
* FVPOL,IMAS,MLMAS,MUMAS,
+ SOLOUT.IOUT,
•t- WORK ,LWORK, lUORK ,LIUORK ,RPAR, IPAR, IDID)
618 Приложение. Программы на Фортране
с — PRIIT FI1AL SOLUTIOI
HRITE F,99) X,YA),YB)
99 F0RMATAX,>X =',F5.2,' Y=',2E18.10)
С —- PRIIT STATISTICS
WRITE F,90) RTOL
90 FORMATS rtol=',D8 2)
HRITE F,91) (IW0RK(J),J=14,2O)
91 FORMATC fcn=M5,' jac=',I4,' step=M4,' accpt=M4,
+ ' rejct=\I3,' dec=',I4,' sol=\I5)
STOP
EID
С
SUBROUTIIE SOLOUT (IR,XOLD,X,Y,COIT,LRC,I,RPAR,IPAR,IRTRI)
С — PRIITS SOLUTIOI AT EQUIDISTAIT OUTPUT-POIITS BY USIIG "COITRS"
IMPLICIT REAL*8 (A-H,0-Z)
DIMEISIOI Y(I),C0IT(LRC)
COHHOI /IITERI/XOUT
IF (IR.EQ.l) THEI
HRITE F,99) X,YA),YB),IR-1
X0UT=O.2D0
ELSE
10 CQITIIUE
IF (X.GE.XOUT) THEI
С — COITIIUOUS OUTPUT FOR RADAU5
HRITE F,99) X0UT,C0ITR5A,X0UT,C0IT,LRC),
+ C0ITR5B,X0UT,C0IT,LRC),IR-1
XOUT=XOUT+0.2D0
GOTO 10
EID IF
EID IF
99 F0RHATAX,'X =^F5.2,' Y=\2E18.10,' ISTEP=\I4)
RETURI
EID
С
SUBROUTIIE FVPOL(I,X,Y,F,RPAR,IPAR)
С —- RIGHT-HAID SIDE OF VAI DER POL'S EQUATIOI
IMPLICIT REAL*8 (A-H,0-Z)
DIMEISIOI Y(I),F(I)
FA)=YB)
FB)=(A-YA)**2)*YB)-YA))/RPAR
RETURI
EID
С
SUBROUTIIE JVPOLd ,X ,Y ,DFY ,LDFY ,RPAR, IPAR)
С — JACOBIAI OF VAI DER POL'S EQUATIOI
IMPLICIT REAL*8 (A-H,0-Z)
DIMEISIOI Y(I),DFY(LDFY,I)
DFYA,1)=0.0D0
DFYA,2)=1.0D0
DFYB,1)=(-2.0D0*YA)*YB)-1.0D0)/RPAR
DFYB,2)=A.0D0-YA)**2)/RPAR
RETURI
EID
Приведем результат решения задачи на машине Sun SPARKstation 20
2000000000Е+01 -О 6600000000Е+00
1858210825Е+01 -О 7575052373Е+00
1693217727Е+01 -О.9068995621Е+00
1484573110Е+01 -О,1233017457Е+01
1083921362Е+01 -О.6195010714Е+01
18636412S6E+01 0.7535196392Е+00
X = 0.00
X = 0.20
X = 0.40
X = 0.60
X = 0.80
X = 1.00
Y =
Y =
Y =
Y =
Y =
Y =
0
0
0
0
0
-0
ISTEP
ISTEP
ISTEP
ISTEP
ISTEP
ISTEP
s
=
=
s=
=
=
0
10
11
13
21
144
Приложение. Программы на Фортране 619
X = 1.20 Y = -0.1699715970Е+01 О.8997232240Е+00 ISTEP = 145
X = 1.40 Y * -0.1493380698Е+01 О.1213958018Е+01 ISTEP = 147
X = 1.60 Y = -0.1120822309Е+01 0.4373266499Е+01 ISTEP =153
X = 1.80 Y = 0.1869064482Е+01 -0.7496053261Е+00 ISTEP = 275
X = 2.00 Y = 0.1706171005Е+01 -О.8928020961Е+00 ISTEP = 276
X = 2.00 Y = 0.1706171005Е+01 -О.8928020961Е+00
rtol=0.10D-03
fcn= 2263 jac= 182 steps 293 accpt= 276 rejct= 9 dec= 251 sol= 662
Подпрограмма RADAU5
Эта программа использует неявный метод Рунге—Кутты, а
именно, трехстадийный метод Радо ПА, приведенный в табл. IV.5.6.
Детали его реализации описаны в разд. IV.8.
SUBROUTIIE RADAU5(I,FCI,X,Y,XEID,H,
+ RTOL,ATOL,ITOL,
+ JAC ,IJAC,HLJAC,ffiJJAC,
+ HAS ,INAS,NLNAS,NUNAS,
+ SOLOUT,IOUT,
+ UORK,LUORK,IWORK»LIWORK»RPAR,IPAR,IDID)
С
С lUNERICAL SOLUTIOI OF A STIFF (OR DIFFEREITIAL ALGEBRAIC)
С SYSTEK OF FIRST ORDER ORDIIARY DIFFEREITIAL EQUATIOIS
С H*Y'=F(X,Y).
С THE SYSTEH CAI BE (LIIEARLY) IMPLICIT (NASS-HATRIX H .IE. I)
С OR EXPLICIT (M=I).
С THE METHOD USED IS AI IMPLICIT RUIGE-KUTTA METHOD (RADAU IIA)
С OF ORDER 5 WITH STEP SIZE COITROL AID COITIIUOUS OUTPUT.
С C.F. SECTIOI IV.8
С
С AUTHORS: E. HAIRER AID G. WAIIER
С UIIVERSITE DE GEIEVE, DEPT. DE MATHEMATIQUES
С CH-1211 GEIEVE 24, SWITZERLAID
С E-MAIL: HAIREReDIVSUI.UIIGE.CH, UAIIEReDIVSUI.UIIGE.CH
С
С THIS CODE IS PART OF THE BOOK:
С E. HAIRER AID G. WAIIER, SOLVIIG ORDIIARY DIFFEREITIAL
С EQUATIOIS II. STIFF AID DIFFEREITIAL-ALGEBRAIC PROBLEMS.
С SPRIIGER SERIES II COMPUTATIOIAL MATHEMATICS 14,
С SPRIIGER-VERLAG 1991, SECOID EDITIOI 1996.
С
С VERSIOI OF SEPTEMBER 30, 1995
С
С IIPUT PARAMETERS
С
С I DIMEISIOI OF THE SYSTEM
С
С FCf lAME (EXTERIAL) OF SUBROUTIIE COMPUTIIG THE
С VALUE OF F(X,Y):
С SUBROUTIIE FCI(I,X,Y,F,RPAR,IPAR)
С REAL*8 X,Y(I),F(I)
С F(l)=... ETC.
С RPAR, IPAR (SEE BELOW)
С
С X IIITIAL X-VALUE
С
С Yd) IIITIAL VALUES FOR Y
С
С XEID FIIAL X-VALUE (XEID-X MAY BE POSITIVE OR lEGATIVE)
С
С Н IIITIAL STEP SIZE GUESS;
620 Приложение. Программы на Фортрале
с FOR STIFF EQUATIOIS WITH IIITIAL TRAISIEiT,
С H=1.D0/(I0RM OF F'), USUALLY l.D-3 OR l.D-5, IS GOOD.
С THIS CHOICE IS lOT VERY IHPORTAIT, THE STEP SIZE IS
С QUICKLY ADAPTED. (IF H=O.DO, THE CODE PUTS H=l.D-6).
С
С RTOL»ATOL RELATIVE AID ABSOLUTE ERROR TOLERAICES. THEY
С CAI BE BOTH SCALARS OR ELSE BOTH VECTORS OF LEIGTH I.
С
С ITOL SWITCH FOR RTOL AID ATOL:
С IT0L«O: BOTH RTOL AID ATOL ARE SCALARS.
С THE CODE KEEPS, ROUGHLY, THE LOCAL ERROR OF
С Yd) BELOW RTOL*ABS(Y(I))+ATOL
С IT0L=1: BOTH RTOL AID ATOL ARE VECTORS.
С THE CODE KEEPS THE LOCAL ERROR OF Y(I) BELOW
С RTOL(I)*ABS(Y(I))+ATOL(I).
С
С JAC lANE (EXTERIAL) OF THE SUBROUTIIE WHICH COMPUTES
С THE PARTIAL DERIVATIVES OF F(X,Y) WITH RESPECT TO Y
С (THIS ROUTIIE IS OILY CALLED IF IJAC^l; SUPPLY
С A DUMMY SUBROUTIIE II THE CASE IJAC^O).
С FOR IJAC»1, THIS SUBROUTIIE MUST HAVE THE FORM
С SUBROUTIIE JAC(I,X,Y,DFY,LDFY,RPAR,IPAR)
С REAL*8 X,Y(I).DFY(LDFY,I)
С DFYA,1)« ...
С LDFY, THE COLUMI-LEIGTH OF THE ARRAY, IS
С FURIISHED BY THE CALLIIG PROGRAM.
С IF (MLJAC.EQ.I) THE JACOBIAI IS SUPPOSED TO
С BE FULL AID THE PARTIAL DERIVATIVES ARE
С STORED II DFY AS
С DFY(I,J) = PARTIAL F(I) / PARTIAL Y(J)
С ELSE, THE JACOBIAI IS TAKEI AS BAIDED AID
С THE PARTIAL DERIVATIVES ARE STORED
С DIAGOIAL-WISE AS
С DFY(I-J+MUJAC+1,J) = PARTIAL F(I) / PARTIAL Y(J).
С
С IJAC SWITCH FOR THE COMPUTATIOI OF THE JACOBIAI:
С IJAC^O: JACOBIAI IS COMPUTED IITERIALLY BY FIIITE
С DIFFEREICES, SUBROUTIIE "JAC" IS lEVER CALLED.
С IJAC=1: JACOBIAI IS SUPPLIED BY SUBROUTIIE JAC.
С
С MLJAC SWITCH FOR THE BAIDED STRUCTURE OF THE JACOBIAI:
С MLJAC^I: JACOBIAI IS A FULL MATRIX. THE LIIEAR
С ALGEBRA IS DOIE BY FULL-MATRIX GAUSS-ELIMIIATIOI.
С 0<»MLJAC<I: MLJAC IS THE LOWER BAIDWITH OF JACOBIAI
С MATRIX (>» lUMBER OF lOI-ZERO DIAGOIALS BELOW
С THE МАИ DIAGOIAL).
С
С MUJAC UPPER BAIDWITH OF JACOBIAI MATRIX (>= lUMBER OF lOI-
C ZERO DIAGOIALS ABOVE THE МАИ DIAGOIAL).
С lEED lOT BE DEFIIED IF MLJAC^I.
С
С MAS,IMAS,MLMAS, AID MUMAS HAVE AIALOG MEAIIIGS
С FOR THE "MASS MATRIX" (THE MATRIX "M" OF SECTIOI IV.8): -
С
С MAS lAME (EXTERIAL) OF SUBROUTIIE COMPUTIIG THE MASS-
C MATRIX M.
С IF IMAS=0, THIS MATRIX IS ASSUMED TO BE THE IDEITITY
С MATRIX AID lEEDS lOT TO BE DEFIIED;
С SUPPLY A DUMMY SUBROUTIIE II THIS CASE.
С IF IMAS=1, THE SUBROUTIIE MAS IS OF THE FORM
С SUBROUTIIE HAS(I,AM,LMAS,RPAR,IPAR)
С REALMS AM(LMAS,I)
С AMA,1)»
С IF (MLMAS.EQ.I) THE MASS-MATRIX IS STORED
Приложение. Программы на Фортране 621
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
AS FULL HATRIX LIKE
AH(I,J) = H(I,J)
ELSE, THE MATRIX IS TAKEI AS BAIDED AID STORED
DIAGOIAL-UISE AS
AH(I-J+NUHAS+1,J) « M(I,J).
INAS GIVES IIFORRATIOI 01 THE NASS-KATRIX:
IHAS=0: H IS SUPPOSED TO BE THE IDEITITY
MATRIX» MAS IS lEVER CALLED.
IMAS=1: MASS-MATRIX IS SUPPLIED.
MLMAS SWITCH FOR THE BAIDED STRUCTURE OF THE MASS-MATRIX:
MLMAS-I: THE FULL MATRIX CASE. THE LIIEAR
Ч ALGEBRA IS DOIE BY FULL-MATRIX GAUSS-ELIMIIATIOI.
. 0<»MLMAS<I: MLMAS IS THE LOWER BAIDWITH OF THE
MATRIX (>« lUMBER OF lOI-ZERO DIAGOIALS BELOW
THE МАИ DIAGOIAL).
MLMAS IS SUPPOSED TO BE .LE. MLJAC.
MUMAS UPPER BAIDWITH OF MASS-MATRIX (>» lUMBER OF lOI-
ZERO DIAGOIALS ABOVE THE МАИ DIAGOIAL).
lEED lOT BE DEFIIED IF MLMASM.
MUMAS IS SUPPOSED TO BE .LE. MUJAC.
SOLOUT lAME (EXTERIAL) OF SUBROUTIIE PROVIDIIG THE
lUMERICAL SOLUTIOI DURIIG IITEGRATIOI.
IF I0UT=1, IT IS CALLED AFTER EVERY SUCCESSFUL STEP.
SUPPLY A DUMMY SUBROUTIIE IF I0UT=O.
IT MUST HAVE THE FORM
SUBROUTIIE SOLOUT (IR,XOLD,X.Y,COIT»LRC,I,
RPAR,IPAR,IRTRI)
REAL*8 X»Y(I),COIT(LRC)
SOLOUT FURIISHES THE SOLUTIOI "Y" AT THE IR-TH
GRID-POIIT "X" (THEREBY THE IIITIAL VALUE IS
THE FIRST GRID-POIIT).
"XOLD" IS THE PRECEEDIIG GRID-POIIT.
••IRTRI" SERVES TO IITERRUPT THE IITEGRATIOI. IF IRTRI
IS SET <0, RADAU5 RETURIS TO THE CALLIIG PROGRAM.
COITIIUOUS OUTPUT:
DURIIG CALLS TO "SOLOUT^*, A COITIIUOUS SOLUTIOI
FOR THE IITERVAL [XOLD^] IS AVAILABLE THROUGH
THE FUICTIOI
>» C0ITR5(I,S,C0IT,LRC) <«
WHICH PROVIDES AI APPROXIMATIOI TO THE I-TH
COMPOIEIT OF THE SOLUTIOI AT THE POUT S. THE VALUE
S SHOULD LIE II THE IITERVAL [XOLDД].
DO lOT CHAIGE THE EITRIES OF COIT(LRC), IF THE
DEISE OUTPUT FUICTIOI IS USED.
lOUT SWITCH FOR CALLIIG THE SUBROUTIIE SOLOUT:
IOUT-0: SUBROUTIIE IS lEVER CALLED
I0UT=1: SUBROUTIIE IS AVAILABLE FOR OUTPUT.
WORK ARRAY OF WORKIIG SPACE OF LEIGTH ••LWORK".
WORK(l), W0RKB),.., W0RKBO) SERVE AS PARAMETERS
FOR THE CODE. FOR STAIDARD USE OF THE CODE
WORKd),.. ,W0RKBO) MUST BE SET TO ZERO BEFORE
CALLIIG. SEE BELOW FOR A MORE SOPHISTICATED USE.
W0RKB1),..,WORK(LWORK) SERVE AS WORKIIG SPACE
FOR ALL VECTORS AID MATRICES.
••LWORK" MUST BE AT LEAST
I*(LJAC+LMAS+3*LE+12)+20
622 Приложение. Программы на Фортране
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с ¦
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
WHERE
LJAC=I
LJAC=MLJAC+HUJAC+1
AID
LMAS=0
LNAS»!
LNAS-HLnAS-f-NUNAS'^l
AID
LE^I
IF HLJAC=I (FULL JACOBIAI)
IF HLJAC<I (BAIDED JAC.)
IF IIIAS=0
IF IHAS=1 AID HLNAS=I (FULL)
IF RLNAS<I (BAIDED NASS-N.)
IF HLJAC=I (FULL JACOBIAI)
LE=2*HLJAC+HUJAC+1 IF MLJAC<I (BAIDED JAC.)
II THE USUAL CASE WHERE THE JACOBIAI IS FULL AID THE
HASS-HATRIX IS THE IIDEITITY (IHAS=0), THE HIIIMUH
STORAGE REQUIRENEIT IS
LWORK = 4*I«I+12*I+20.
IF IW0RK(9)=«1>0 THEI "LWORK" HUST BE AT LEAST
I*(LJAC+12)+(I-Hl)*(LHAS+3*LE)+20
WHERE II THE DEFIIITIOIS OF LJAC, LNAS AID LE THE
lUNBER I CAI BE REPLACED BY I-Nl.
LWORK DECLARED LEIGHT OF ARRAY "WORK".
IWORK IITEGER WORKIIG SPACE OF LEIGHT "LIWORK".
IWORK(l)»IW0RKB),...»IW0RKB0) SERVE AS PARAMETERS
FOR THE CODE. FOR STAIDARD USE, SET IWORKA),..,
IWORKB0) TO ZERO BEFORE CALLIIG.
IW0RKB1),...»IWORK(LIWORK) SERVE AS WORKIIG AREA.
"LIWORK" HUST BE AT LEAST 3*1+20.
LIWORK DECLARED LEIGHT OF ARRAY "IWORK".
RPAR, IPAR REAL AID IITEGER PARAMETERS (OR PARAMETER ARRAYS) WHICH
CAI BE USED FOR COMMUIICATIOI BETWEEI YOUR CALLIIG
PROGRAM AID THE FCI, JAC, MAS, SOLOUT SUBROUTIIES.
SOPHISTICATED SETTIIG OF PARAMETERS
SEVERAL PARAMETERS OF THE CODE ARE TUIED TO MAKE IT WORK
WELL. THEY MAY BE DEFIIED BY SETTIIG WORK(l),...
AS WELL AS IWORK(l),.. . DIFFEREIT FROM ZERO.
FOR ZERO IIPUT, THE CODE CHOOSES DEFAULT VALUES:
IWORK(l) IF IWORKA).IE.O, THE CODE TRAISFORMS THE JACOBIAI
MATRIX TO HESSEIBERG FORM. THIS IS PARTICULARLY
ADVAITAGEOUS FOR LARGE SYSTEMS WITH FULL JACOBIAI.
IT DOES lOT WORK FOR BAIDED JACOBIAI (MLJAC<I)
AID lOT FOR IMPLICIT SYSTEMS (IMAS=1).
IW0RKB) THIS IS THE MAXIMAL lUMBER OF ALLOWED STEPS.
THE DEFAULT VALUE (FOR IW0RKB)=O) IS 100000.
IWORKO) THE MAXIMUM lUMBER OF lEWTOI ITERATIOIS FOR THE
SOLUTIOI OF THE IMPLICIT SYSTEM II EACH STEP.
THE DEFAULT VALUE (FOR IWORKC)=0) IS 7.
IW0RKD) IF IW0RKD).EQ.O THE EXTRAPOLATED COLLOCATIOI SOLUTIOI
IS TAKEI AS STARTIIG VALUE FOR lEWTOI'S METHOD.
IF IW0RKD).IE.O ZERO STARTIIG VALUES ARE USED.
THE LATTER IS RECOMMEIDED IF lEWTOI'S METHOD HAS
DIFFICULTIES WITH COIVERGEICE (THIS IS THE CASE WHEI
¦STEP IS LARGER THAI lACCPT + IREJCT; SEE OUTPUT PARAM.).
DEFAULT IS IW0RKD)=O.
Приложение. Программы на Фортране 623
с
с THE FOLLOWIIG 3 PARAMETERS ARE IHPORTAIT FOR
С DIFFEREITIAL-ALGEBRAIC SYSTEMS OF IIDEX > 1.
С THE FUICTIOI-SUBROUTIIE SHOULD BE WRITTEI SUCH THAT
С THE IIDEX 1,2»3 VARIABLES APPEAR II THIS ORDER.
С II ESTIMATIIG THE ERROR THE IIDEX 2 VARIABLES ARE
С MULTIPLIED BY H. THE IIDEX 3 VARIABLES BY H**2.
С
С IU0RKE) DINEISIOI OF THE IIDEX 1 VARIABLES (MUST BE > 0). FOR
С ODE'S THIS EQUALS THE DIMEISIOI OF THE SYSTEM.
С DEFAULT IW0RKE)=I.
С
С IU0RKF) DIMEISIOI OF THE IIDEX 2 VARIABLES. DEFAULT IW0RKF)=O
С
С IW0RKG) DIMEISIOI OF THE IIDEX 3 VARIABLES. DEFAULT Il*0RKG)=O.
С
С IW0RK(8) SWITCH FOR STEP SIZE STRATEGY
С IF IH0RK(8).Eq.l MOD. PREDICTIVE COITROLLER (GUSTAFSSOI)
С IF IU0RK(8).EQ.2 CLASSICAL STEP SIZE COITROL
С THE DEFAULT VALUE (FOR IW0RK(8)=0) IS IH0RK(8)=1.
С THE CHOICE IU0RK(8).EQ.l SEEMS TO PRODUCE SAFER RESULTS;
С FOR SIMPLE PROBLEMS, THE CHOICE IU0RK(8).Eq.2 PRODUCES
С OFTEI SLIGHTLY FASTER RUIS
С
С IF THE DIFFEREITIAL SYSTEM HAS THE SPECIAL STRUCTURE THAT
С Yd)» = Y(I+M2) FOR 1=1,...,M1,
С WITH Ml A MULTIPLE OF M2, A SUBSTAITIAL GAII II COMPUTERTIME
С CAI BE ACHIEVED BY SETTIIG THE PARAMETERS IW0RK(9) AID IWORK(IO).
С E.G., FOR SECOID ORDER SYSTEMS P'=V, V'sG(P,V), WHERE P AID V ARE
С VECTORS OF DIMEISIOI 1/2, OIE HAS TO PUT Nl=M2=I/2.
С FOR M1>0 SOME OF THE IIPUT PARAMETERS HAVE DIFFEREIT MEAIIIGS:
С - JAC: OILY THE ELEMEITS OF THE lOI-TRIVIAL PART OF THE
С JACOBIAI HAVE TO BE STORED
С IF (MLJAC.EQ.I-Ml) THE JACOBIAI IS SUPPOSED TO BE FULL
С DFY(I,J) = PARTIAL F(I+M1) / PARTIAL Y(J)
С FOR I=1,I-M1 AID J=1,I.
С ELSE, THE JACOBIAI IS BAIDED ( Ml = M2 ¦ MM )
С DFY(I-J+MUJAC+1,J+K*M2) = PARTIAL F(I+M1) / PARTIAL Y(J+K*M2)
С FOR I=1,MLJAC+MUJAC+1 AID J=1,M2 AID K=0,MM.
С - MLJAC: MLJAC=I-M1: IF THE lOI-TRIVIAL PART OF THE JACOBIAI IS FULL
С 0<=MLJAC<I-M1: IF THE (MM+1) SUBMATRICES (FOR K=0,MH)
С PARTIAL F(I+M1) / PARTIAL Y(J+K*M2), I,J=1,M2
С ARE BAIDED, MLJAC IS THE MAXIMAL LOWER BAIDWIDTH
С OF THESE MM+1 SUBMATRICES
С - MUJAC: MAXIMAL UPPER BAIDWIDTH OF THESE MM+1 SUBMATRICES
С lEED lOT BE DEFIIED IF MLJAC=I-M1
С - MAS: IF IMAS^O THIS MATRIX IS ASSUMED TO BE THE IDEITITY AID
С lEED lOT BE DEFIIED. SUPPLY A DUMMY SUBROUTIIE II THIS CASE.
С IT IS ASSUMED THAT OILY THE ELEMEITS OF RIGHT LOWER BLOCK
С OF DIMEISIOI I-Hl DIFFER FROM THAT OF THE IDEITITY MATRIX.
С IF (MLMAS.EQ.I-Ml) THIS SUBMATRIX IS SUPPOSED TO BE FULL
С AM(I,J) = M(I+M1,J+M1) FOR I=1,I-M1 AID J=1,I-M1.
С ELSE, THE MASS MATRIX IS BAIDED
С AM(I-J+MUMAS+1,J) = M(I+M1,J+M1)
С - MLMAS: MLMAS=I-M1: IF THE lOI-TRIVIAL PART OF M IS FULL
С 0<=MLMAS<I-M1: LOWER BAIDWIDTH OF THE MASS MATRIX
С " MUMAS: UPPER BAIDWIDTH OF THE MASS MATRIX
С lEED lOT BE DEFIIED IF MLMAS=I-H1
С
С IWORKO) THE VALUE OF Ml. DEFAULT M1=0.
С
С IWORK(IO) THE VALUE OF M2. DEFAULT M2=M1.
С
С
624 Приложение. Программы на Фортране
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с—
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с—
WORK(l) UROUID, THE ROUIDIIG UIIT, DEFAULT i.D-16.
W0RKB) THE SAFETY FACTOR II STEP SIZE PREDICTIOI,
DEFAULT 0.9D0.
W0RKC) DECIDES WHETHER THE JACOBIAI SHOULD BE RECOMPUTED;
IICREASE W0RKC), TO 0.1 SAY, WHEI JACOBIAI EVALUATIOIS
ARE COSTLY. FOR SMALL SYSTEMS W0RKC) SHOULD BE SMALLER
(O.OOIDO, SAY). lEGATIV W0RK<3) FORCES THE CODE TO
COMPUTE THE JACOBIAI AFTER EVERY ACCEPTED STEP.
DEFAULT O.OOIDO.
W0RKD) STOPPIIG CRITERIOI FOR lEWTOI'S METHOD, USUALLY CHOSE! <1.
SMALLER VALUES OP WORKD) MAKE THE CODE SLOWER, BUT SAFER.
DEFAULT 0.03D0.
W0RKE) AID W0RKF) : IF W0RKE) < HIEW/HOLD < W0RKF), THEI THE
STEP SIZE IS lOT CHAIGED. THIS SAVES, TOGETHER WITH A
LARGE W0RK<3), LU-DECOMPOSITIOIS AID COMPUTIIG TIME FOR
LARGE SYSTEMS. FOR SMALL SYSTEMS OIE MAY HAVE
W0RKE)>1.D0, W0RKF)=1.2DO, FOR LARGE FULL SYSTEMS
W0RKE)»0.99D0, W0RKF)>2.DO MIGHT BE GOOD.
DEFAULTS W0RKE)=l.DO, W0RKF)=1.2D0 .
W0RKG) MAXIMAL STEP SIZE, DEFAULT XEID-X.
W0RK(8), W0RK(9) PARAMETERS FOR STEP SIZE SELECTIOI
THE lEW STEP SIZE IS CHOSEI SUBJECT TO THE RESTRICTI01
W0RK(8) <« HIEW/HOLD <> W0RK(9)
DEFAULT VALUES: W0RK(8)>0.2D0, W0RK(9)>8.DO
OUTPUT PARAMETERS
Yd)
H
IDID
IW0RKA4)
IWORKdS)
IW0RKA6)
IW0RKA7)
IWORKdS)
IW0RKA9)
IW0RKB0)
X-VALUE FOR WHICH THE SOLUTIOI HAS BEEI. COMPUTED
(AFTER SUCCESSFUL RETURI X«XEID).
lUMERICAL SOLUTIOI AT X
PREDICTED STEP SIZE OF THE LAST ACCEPTED STEP
REPORTS 01 SUCCESSFULIESS UPOI RETURI:
IDID» 1 COMPUTATIOI SUCCESSFUL,
IDID= 2 COMPUT. SUCCESSFUL (IITERRUPTED BY SOLOUT)
IDID»-1 IIPUT IS lOT COISISTEIT,
IDID--2 LARGER IMAX IS lEEDED,
ЮЮа^-З STEP SIZE BECOMES TOO SMALL,
IDIDs-4 MATRIX IS REPEATEDLY SIIGULAR.
IFCI lUMBER OF FUICTIOI EVALUATIOIS (THOSE FOR lUMERICAL
EVALUATIOI OF THE JACOBIAI ARE lOT COUITED)
IJAC lUMBER OF JACOBIAI EVALUATIOIS (EITHER AIALYTICALLY
OR lUMERICALLY)
ISTEP lUMBER OF COMPUTED STEPS
lACCPT lUMBER OF ACCEPTED STEPS
IREJCT lUMBER OF REJECTED STEPS (DUE TO ERROR TEST),
(STEP REJECTIOIS II THE FIRST STEP ARE lOT COUITED)
IDEC lUMBER OF LU-DECOMPOSITIOIS OF BOTH MATRICES
ISOL lUMBER OF FORWARD-BACKWARD SUBSTITUTIOIS, OF BOTH
SYSTEMS; THE ISTEP FORWARD-BACKWARD SUBSTITUTIOIS,
lEEDED FOR STEP SIZE SELECTIOI, ARE lOT COUITED
Приложение. Программы на Фортране 625
Подпрограмма RADAUP
Если задать опцию iwork(ii) = з, эта программа математически
эквивгипентна RADAU5. Единственное отличие состоит в том, что
явно расписанное суммирование в ней заменено выполнением циклов, а
коэффициенты метода помещены в массивы. Это делает программу
чуть более медленной (особенно на малых задачах), но имеет то
преимущество, что коэффициенты метода легко заменяемы. В настоящее
время в ней доступны коэффициенты методов Радо ПА порядков 5, 9
и 13 посредством задания значений iwork (и) равных соответственно
3, 5 или 7. Список параметров у этой программы такой же, как у
RADAU5:
SUBROUTIIE RADAUPd,FCI,X,Y,XEID,H,
+ RTOL,ATOL,ITOL,
+ JAC ,IJAC,HLJAC,HUJAC,
-I- MAS ,IHAS,NLNAS»NUNAS,
+ SOLOUT,IOUT.
+ UORK,LWORKJWORK,LIVORK,RPAR,IPAR,IDID)
Подпрограмма RODAS
Эта программа реализует метод Розенброка, который был описан
в разд. VI.4. Метод удовлетворяет также «алгебраическим»
условиям порядка и поэтому применим и для решения дифференциально-
алгебраических задач индекса 1. Приведем здесь список параметров
этой программы:
SUBROUTIIE RODAS(I,FCIJFCI,X,Y,XEiD,H,
+ RTOL,ATOL,ITOL,
+ JAC ,IJAC,HLJAC,HUJAC,DFX,ILFX,
+ HAS »INAS,HLNAS,NUHAS,
+ SOLOUT,IOUT,
•i- WORK,LUORKJUORK»LIVORK,RPAR,IPAR,IDID)
По сравнению с RADAU5 здесь добавлено три параметра. Значение
IFCI указывает, зависит или нет от х правая часть f(x^y) уравнения
(А1). Если / зависит от х, программе требуется частная
производная df/dx. Она может находиться численным способом (для этого
надо задать idfx = о и подпрограмму-пустышку в качестве dfx) или
аналитически. В последнем случае надо задать idfx = i и написать
подпрограмму, вычисляющую df/dx. Параметры work и iwork здесь
означают, конечно, не всегда то же самое, что в RADAU5. Они
описаны в комментариях программы.
626 Приложение. Программы на Фортране
Подпрограмма SEULEX
Это экстраполяционная программа, основанная на линейно
неявном методе Эйлера (см. разделы IV.9 и VI.5). Плотная выдача была
включена в сотрудничестве с А. Остерманом. Входные параметры
имеют тот же смысл, что и в RODAS. Параметры work и iwork описаны
в комментариях программы.
SUBROUTIIE SEULEX(I.FCI,IFCI,X,Y,XEID,H,
+ RTOL,ATOL,ITOL,
+ JAC ,IJAC,MLJAC,MUJAC,
+ HAS ,IMAS,HLHAS,MUHAS,
+ SOLOUT,IOUT,
+ WORK,LHORK,IWORK,LIWORK,RPAR,IPAR,IDID)
Задачи, имеющие особую структуру
Если первые т^ уравнений системы (А.1) имеют вид
yi=yi+m2^ гда z = l,...,mi (А.2)
и mj — целое кратное т2, а остальные уравнения не зависят
явно от у^ ^^,..., у^ , рекомендуется установить значения параметров
IWORKO) и iwoRK(io) равными соответственно т^ и т2. Это
обусловит более эффективную обработку возникающих линейных систем и
выгодно, в частности, когда значение т^ велико.
Если задано ненулевое значение iworkO), надо обратить внимание
на аккуратность определения подпрограмм jag и mas. Вычисляться и
храниться в массиве размерности (п — т^) х п должна только
нетривиальная часть матрицы Якоби, т. е. строки с индексами т^ -h 1,..., п.
Аналогично, только правый нижний блок (размерности п — т^)
матрицы М должен определяться в подпрограмме mas. Однако
подпрограмма FCH должна содержать определение всех компонент f[x,y), в
частности, оператор F(i) = Y(i+M2) для i=i,... ,Mi. Остается и
возможность задания опций для описания ленточной структуры. Приведем
примеры типичных ситуаций, когда возникают уравнения вида (А.2).
2/" = /(^9 2/9 2/') • После введения новой переменной z = y' система
принимает вид
У -Z, z' = f(x,y,z),
соответствующий (А.1). Если уЕМ"^, то оба параметра iworkO) и
iwoRK(io) надо задать равными т. Задающие ленточную структуру
опции можно использовать, если обе матрицы df/dy и df/dy'
ленточные.
Приложение. Программы на Фортране 627
С(х^у)у^ = f{x^y). Опять вводим Z = г/, и задача становится
эквивалентной дифференциально-алгебраической задаче вида (А.1):
у'= 2, 0 = C(x,y)z-f(x,y).
Оба параметра iworkO) и iwork(io) надо задать равными размерности
у. Если на не постоянные коэффициенты умножаются лишь
немногие компоненты у*, то более эффективным может оказаться введение
новых переменных только для этих компонент.
С!{х^у)у^^ = f{x^y^y^) . С новыми переменными 2: = у' и u = z^ =
= у" эту задачу можно записать в форме (А.1) так:
у' = г, z' = u, 0 = C{x,y)u-f(x,y,z).
Здесь т^ =2т2, а mj равно размерности у.
Использование SOLOUT и плотной выдачи
Подпрограмма SOLOUT, которую задает пользователь,
вызывается после каждого принятого шага и позволяет получить решение в
любой точке этого шага (плотная выдача). Эта возможность может быть
использована для табуляции решения в предписанных точках вывода
(см. описанный выше драйвер для RADAU5) или для графического
представления решения. Приведем еще два возможных применения
SOLOUT.
Локализация события. Предположим, что мы хотим определить
значение х, при котором д{х,у{х)) =0, где у{х) — решение
задачи (А.1). Во время интегрирования в подпрограмме SOLOUT можно
проверять, имеют ли значения ^(a^,_i, У,_1) и ^(ж,-,у,) разные
знаки. Когда это произойдет, плотную выдачу (доступную во всех
наших программах) можно использовать для локализации нуля
функции у(х,у(х)). Эта процедура очень полезна для задач с разрывной
правой частью (см. разд.П.6).
Проецирование. Эффективный способ решения дифференциально-
алгебраических уравнений высших индексов состоит в понижении
индекса в сочетании с проецированием. Если «жесткая» (или
«нежесткая») программа напрямую применяется к задаче с
пониженным индексом, получаемое решение будет страдать от так
называемого «явления сноса». Чтобы избежать этого «сноса», рекомендуется
после каждого шага проецировать численное решение на
многообразие решений задачи. Это удобно делать с помощью подпрограммы
SOLOUT.
Литература
Список литературы содержит работы, на которые имеются
ссылки в тексте. После каждой работы курсивными цифрами в
квадратных скобках указаны разделы, в которых на данную работу имеются
ссылки.
Абрагам, Марсден и Ратью (R. Abraham, J.E. Marsden & Т. Ratiu)
A983): Manifolds, Tensor Analysis, and Applications. Applied Mathematical
Series vol. 75, Springer-Verlag 1983; second edition 1988, 654 pp. [VII. 1]
Абрамович и Стиган (M. Abramowitz & I.A. Stegun)
A964): Handbook of mathematical functions. Dover, 1000 pages.
[Имеется перевод: Справочник по специальным функциям с формулами,
графиками и математическими таблицами, под ред. М. А. Абрамовица и
И. Стиган. — М.: Наука, 1979.] [IV.2], [IV.4], [IV. 12], [IV.13], [IV.Ц]
Аддисон (С.A. Addison)
A979): Implementing a stiff method based upon the second derivative
formulas. Techn. Rep. 130/79, Dept. of Comput. Sc, Univ. of Toronto,
Canada. [V.3], [V.5]
Айх (E. Eich)
A993): Convergence results for a coordinate projection method applied
to mechanical systems with algebraic constraints. SIAM J. Numer. Anal.,
vol. 30, pp. 1467-1482. [VII.2]
Акилов, см. Канторович и Акилов
Аксельссон (О Axelsson)
A969): A class of Л-stable methods. BIT, vol. 9, pp. 185-199. [IV.3], [IV.5]
A972): A note on a class of strongly Л-stable methods. BIT, vol. 12, pp. 1-4.
frv.sj
Александер (R. Alexander)
A977): Diagonally implicit Runge-Kutta methods for stiff O.D.E.'s. SIAM
J. Numer. Anal., vol. 14, pp. IOO6-I92I. [IV.3], [IV.6]
A997): Reliability of software for stiff initial value problems. To appear in
SIAM J. Sci. Comput. [IV. 10]
Алишенас (Т. Alishenas)
A992): Zur numerischen Behandlung, Stabilisierung durch Projektion und
Modellierung mechanischer Systeme mit Nebenbedingungen und Invariant en.
Dissertation, Stockholm, TRITA-NA-9202. [VII.2]
Алишенас и Олафссон (Т. Alishenas & 6. Olafsson)
A994): Modeling and velocity stabilization of constrained mechanical
systems. BIT, vol. 34, pp. 455-483. [VII.2]
Альт (R. Alt)
A971): Methodes A-stables pour Integration de systemes differentiels mal
conditionnes. These, Univ. Paris VI. [IV.6]
Андерсен (H.C. Andersen)
A983): Rattle: a "velocity" version of the Shake algorithm for molecular
dynamics calculations. J. Comput. Phys., vol. 52, pp. 24-34. [VII.8]
Андрьюс, см. Ормрод и Андрьюс
Литература 629
Аревало, Фюрер и Сёдерлинд (С. Arevalo, С. Fuhrer & G. Soderlind)
A996): Stabilized multistep methods for index 2 Euler-Lagrange DAEs. BIT,
vol. 36, pp. 1-13. [VII.6]
Арнольд В. И. (V.I. Arnol'd)
A979): Математические методы классической механики. — М.: Наука,
1974; 1979 B-е изд.). English translation: Springer-Verlag 1984, 1989. [VILl]
Арнольд M. (M. Arnold)
A993): Stability of numerical methods for differential-algebraic equations of
higher index. Applied Numerical Mathematics, vol. 13, pp. 5-14. [VILl]
A995): Half-explicit Runge-Kutta methods with explicit stages for
differential-algebraic systems of index 2. Submitted for publication. [VII.6], [VILl]
Арнольда (W.E. Arnoldi)
A951): The principle of minimized iterations in the solution of the matrix
eigenvalue problem. Quart. Appl. Math., vol. 9, pp. 17-29. [IV. 10]
Атанс и Фалб (M. Athans & P.L. Falb)
A966): Optimal Control. McGraw-Hill Book Company, New York, 879pp.
[VILl]
Ауцингер, Франк и Мачек (W. Auzinger, R. Frank, & F. Macsek)
A990): Asymptotic error expansions for stiff equations: the implicit Euler
scheme. SIAM J. Numer. Anal., vol. 27, pp. 67-104. [VI.5]
Ашер (U. Ascher)
A989): On numerical differential algebraic problems with application to
semiconductor device simulation. SIAM J. Numer. Anal., vol. 26, pp. 517-
538. [VIL4]
Ашер и Бадер (U. Ascher & G. Bader)
A986): Stability of collocation at Gaussian points. SIAM J. Numer. Anal.,
vol. 23, pp. 412-422. [IV.13]
Ашер и Петзолд (U. Ascher & L.R. Petzold)
A991): Projected implicit Runge-Kutta methods for differential-algebraic
equations. SIAM J. Numer. Anal., vol. 28, pp. 1097-1120. [VIL4]
Ашер, Чин и Райх (U.M. Ascher, H. Chin & S. Reich}
A994): Stabilization of DAEs and invariant manifolds. Numer. Math., vol. 67,
pp. 131-149. [VIL2]
Бадер и Дойфлхард (G. Bader & P. Deuflhard)
A983): A semi-implicit mid-point rule for stiff systems of ordinary differential
equations. Numer. Math., vol. 41, pp. 373-398. [IV.9], [IV. 10], [VII.6]
Бадер, см. также Ашер и Бадер; Хайрер, Бадер и Любих
Байокки и Крузе (С. Baiocchi & М. Crouzeix)
A989): On the equivalence of Л-stability and G-stability. Appl. Numer.
Math., vol.5, pp. 19-22. [V.6]
Баккер (M. Bakker)
A971): Analytical aspects of a minimax problem (Dutch), Technical Note
TN 62, Mathematical Centre, Amsterdam.
Баркер, Берман и Племмонс (G.P. Barker, A. Berman & R.J. Plemmons)
A978): Positive diagonal solutions to the Lyapunov equations. Linear and
Multilinear Algebra, vol. 5, pp. 249-256. [IVЛ A]
Баумгарте (J. Baumgarte)
A972): Stabilization of constraints and integrals of motion in dynamical
systems. Comp. Meth. Appl. Mech. Eng., vol. 1, pp. 11-16. [VI 1.2]
Бейлс, Каракашьян и Сербии (L.A. Bales, О.A. Karakashian & S.M. Serbin)
A988): On the Aq -acceptability of rational approximations to the exponential
function with only real poles. BIT, vol. 28, pp. 70-79. [IV.4]
630 Литература
Бенеттин и Джорджилли (G. Benettin & A. Giorgilli)
A994): On the Hamiltonian interpolation of near to the identity symplectic
mappings with application to symplectic integration algorithms. J. Statist.
Phys., vol. 74, pp. 1117-1143. [VII.8]
Берендсен, см. Рюккерт, Чиккотти и Берендсен
Берзинс и Ферзеланд (М. Berzins & R.M. Furzeland)
A985): A user's manual for SPRINT - a versatile software package for solving
systems of algebraic, ordinary and partial differential equations: part 1 -
algebraic and ordinary differential equations. Thornton Research Centre, Shell
Research Ltd. TNER.85.058. [V.5], [VII.3]
Берман, см. Баркер, Берм an и Племмонс
Берн и Хайндмарш (G.D. Byrne & А.С. Hindmarsh)
A975): A polyalgorithm for the numerical solution of ordinary differential
equations. ACM Trans. Math. Software, vol. 1, pp. 71-96. [V.5]
A987): Stiff ODE solvers: a review of current and coming attractions. J. of
Comput. Physics, vol. 70, pp. 1-62. [IV. 10]
Берн, см. также Браун, Берн и Хайндмарш
Бернштейн (S. Bernstein)
A914): Sur la definition et les proprietes des fonctions analytiques d'une
variable reelle. Math. Annalen, vol. 75, pp. 449-468. [IV. 11]
A928): Sur les fonctions absolument monotones. Acta Mathematica, vol. 51,
pp. 1-66. [IV. 11]
Берридж (К. Burrage)
A978): A special family of Runge-Kutta methods for solving stiff differential
equations. BIT, vol. 18, pp. 22-41. [IV.5], [IV.6], [IV.8]
A978): High order algebraically stable Runge-Kutta methods. BIT, vol. 18,
pp. 373-383. [IV.5], [IV. 13]
A982): Efficiently implementable algebraically stable Runge-Kutta methods.
SIAM J. Numer. Anal., vol. 19, pp. 245-258. [IV.13]
A987): High order algebraically stable multistep Runge-Kutta methods.
SIAM J. Numer. Anal., vol. 24, pp. 106-115. [V.9]
A988): Order properties of implicit multivalue methods for ordinary
differential equations. IMA J. Numer. Anal., vol. 8, pp. 43-69. [V.9]
Берридж и Бутчер (К. Burrage & J.С. Butcher)
A979): Stability criteria for implicit Runge-Kutta methods. SIAM J. Numer.
Anal., vol. 16, pp. 46-57. [IV. 12]
A980): Non-linear stability of a general class of differential equation methods.
BIT, vol. 20, pp. 185-203. [IV.12], [V.9]
Берридж, Бутчер и Чипман (К. Burrage, J.С. Butcher & F.H. Chipman)
A980): An implementation of singly-implicit Runge-Kutta methods. BIT,
vol. 20, pp. 326-340. [IV.8]
Берридж и Хундсдорфер (К. Burrage & W.H. Hundsdorfer)
A987): The order of В-convergence of algebraically stable Runge-Kutta
methods. BIT, vol. 27, pp. 62-71. [IV.15]
Биккарт (Т.A. Bickart)
A977): An efficient solution process for implicit Runge-Kutta methods. SIAM
J. Numer. Anal., vol. 14, 1022-1027. [IV.8]
Биккарт и Рубин (Т.A. Bickart & W.B. Rubin)
A974): Composite multistep methods and stiff stability. In: Stiff Differential
Systems, R.A. Willoughby (ed.), Plenum Press, New York. [V.3]
Биккарт, см. также Слоат и Биккарт
Биркхофф и Варга (G. Birkhoff & R.S. Varga)
A965): Discretization errors for well-set Cauchy problems, I. J. Math. Phys.,
vol. 44, pp. 1-23. [IV.5]
Литература 631
Болле и Крузе (С. Bolley & М. Crouzeix)
A978): Conservation de la positivite lors de la discretisation des problemes
d'evolution paraboliques. R.A.I.R.O. Analyse numerique, vol. 12, pp. 237-
245. [IV. 11]
Болтянский, см. Понтрягин, Болтянский, Гамкрелидзе и Мищенко
Бразей (V. Brasey)
A992): A half-explicit Runge-Kutta method of order 5 for solving constrained
mechanical systems. Computing, vol. 48, pp. 191-201. [VII.6]
A994): Half-explicit method for semi-explicit differential-algebraic equations
of index 2. These № 2664, Sect. Math., Univ. de Geneve. [VII.7]
Бразей и Хайрер (V. Brasey & E. Hairer)
A993): Half-explicit Runge-Kutta metnods for differential-algebraic systems
of index 2. SIAM J. Numer. Anal., vol. 30, pp. 538-552. [VII.6]
Браун, Берн и Хайндмарш (P.N. Brown, G.D. Byrne & A.C. Hindmarsh)
A989): VODE: a variable coefficient ODE solver. SIAM J. Sci. Stat. Comput.,
vol. 10, pp. 1039-1051. [V.5]
Бренан (К.Е. Вгеnаn)
A983): Stability and convergence of difference approximations for higher-
index differential-algebraic systems with applications in trajectory control.
Doctoral thesis, Dep. Math., Univ. of California, Los Angeles. [VII. 1]
Бренан, Кампбелл и Петзолд (К.Е. Вгеnаn, S.L. Campbell & L.R. Petzold)
A989): Numerical solution of initial-value problems in differential-algebraic
equations. North HoUand, New York, 210pp. [VII. 1], [VII.3], [VII.7]
Бренан и Петзолд (К.Е. Вгеnаn & L.R. Petzold)
A989): The numerical solution of higher index differential/algebraic
equations by implicit Runge-Kutta methods. SIAM J. Numer. Anal., vol. 26,
pp. 976-996. [VII.4]
Бренан и Энгквист (К.Е. Brenan & L.R. Engquist)
A988): Backward differentiation approximations of nonlinear differential
/algebraic equations, and Supplement. Math. Comp., vol. 51, pp. 659-676,
pp. S7-S16. [VI 1.3]
Буй, см. Kaпс, Пун и Буй
Бутчер (J.С. Butcher)
A964): Implicit Runge-Kutta processes. Math. Comput., vol. 18, pp. 50-64.
irv4
A964): Integration processes based on Radau quadrature formulas. Math.
Comput., vol. 18, pp. 233-244. [IV.5]
A975): A stability property of implicit Runge-Kutta methods. BIT, vol. 15,
pp. 358-361. [IV. 12]
A976): On the implementation of implicit Runge-Kutta methods. BIT,
vol. 16, pp. 237-240. [IV.8]
A977): On Л-stable implicit Runge-Kutta methods. BIT, vol. 17, pp. 375-
378. [IV.5]
A979): A transformed implicit Runge-Kutta method. J. Assoc. Comput.
Mach., vol. 26, pp. 731-738. [IV.8]
A981): A generalization of singly-implicit methods. BIT, vol. 21, pp. 175-
189. [V.3]
A982): A short proof concerning B-stability. BIT, vol. 22, pp. 528-529.
[IV. 12]
A987): Linear and non-linear stability for general linear methods. BIT,
vol. 27, pp. 182T189. [V.9]
A987): The equivalence of algebraic stability and AN-stability. BIT, vol. 27,
pp. 510-533. [V.9]
632 Литература
A987): The numerical analysis of ordinary differential equations. Runge-
Kutta and general linear methods. John Wiley & Sons, 512pp. [IV. 12]
A990): Order, stepsize and stiffness switching. Computing, vol 44, p. 209-
220. [IV.2]
Бутчер, см. также Берридж и Бутчер; Берридж, Бутчер и Чипман
Бьёрк (A. Bjorck)
A983): A block CjR algorithm for partitioning stiff differential systems. BIT,
vol. 23, pp. 329-345. [IV. 10]
A984): Some methods for separating stiff components in initial value
problems. In: Numerical Analysis, Dundee 1983, D.F. Griffiths, ed., Lecture Notes
in Math. 1066, Springer Verlag, pp. 30-43. [IV.10]
Бюргерс (J.M. Burgers)
A948): A mathematical model illustrating the theory of turbulence. Advances
in appl. mech., vol. 1, pp. 171-199. [V.8], [VI.6]
Вазов (W. Wasow)
A965): Asymptotic expansions for ordinary differential equations. Intersci-
ence, John Wiley & Sons, New York, 263pp. [Имеется перевод: Вазов В.
Асимптотические разложения решений дифференциальных уравнений.
— М.: Мир, 1968.] [VI.3]
Вайнер, см. Штремель и Вайнер
Вал Лоун, см. Голуб и Ван Лоун
Вал-дер-Поль (В. van der Pol)
A926): On "Relaxation Oscillations". Phil. Mag., vol. 2, pp. 978-992;
reproduced in: B. van der Pol, Selected Scientific Papers, vol. I, North-Holland
Publ. Comp. Amsterdam)
(I960). [VIA]
Ванзелов (R. Vanselow)
A979): Stabilities-und Fehleruntersuchungen bei numerischen Verfahren zur
Losung steifer nichtlinearer Anfangswertprobleme. Diplomarbeit, Sektion
Mathematik, TU-Dresden. [IV.12]
Ваннер (G. Wanner)
A976): A short proof on nonlinear Л-stability. BIT, vol. 16, pp. 226-227.
pv.it]
A980): Characterization of all A -stable methods of order 2m — 4. BIT,
vol. 20, pp. 367-374. [IV.5]
Ваннер, Хайрер и Нёрсетт (G. Wanner, E. Hairer & S.P. Norsett)
A978): Order stars and stability theorems. BIT, vol. 18, pp. 475-489. [IV.Ah
)lV.6h [V.A]
A978): When /-stability implies Л-stability. BIT, vol. 18, p. 503. [IV.A]
Ваннер, см. также Капс и Ваннер; Нёрсетт и Ваннер; Соттас и Ваннер;
Хайрер и Ваннер
Вара (J.M. Varah)
A979): On the efficient implementation of implicit Runge-Kutta methods.
Math. Comp., vol. 33, pp. 557-561. [IV.8]
Варга, см. Биркхофф и Варга
Васильева А. Б. (А.B. Vasil'eva)
A963): Асимптотика решений некоторых задач для обыкновенных
нелинейных дифференциальных уравнений с малым параметром при
старших производных. Усп. матем. наук, т. 18, вып.З, с. 15-87. English
translation: Russian Math. Surveys, vol.18, Nr. 3, pp. 13-84. [VI.3]
Васильева, см. также Тихонов, Васильева и Свешников
Литература 633
Вейерштрасс (К. Weierstrass)
A868): Zur Theorie der bilinearen und quadratischen Formen. Akad. der
Wiss. Berlin 18. Mai. 1868, Werke vol. II, pp. 19-44. [VII.1]
Верле (L. Verlet)
A967): Computer "experiments" on classical fluids. I. Thermodynamical
properties of Lennard-Jones molecules. Physical Review, vol. 159, pp. 98-
103. [VII.8]
Видлунд (O.B. Widlund)
A967): A note on unconditionally stable linear multistep methods. BIT,
vol. 7, pp. 65-70. [IV.3], [V.l], [V.2]
Вольфбрандт (A. Wolfbrandt)
A977): A study of Rosenbrock processes with respect to order conditions and
stiff stability. Thesis, Chalmers Univ. of Techn., Goteborg, Sweden. [IV.4],
[IV.7J
Вольфбрандт, см. также Нёрсетт и Вольфбрандт; Штайхауг и Вольфбрандт
Галеркин Б. Г. (B.G. Galerkin)
A915): Разложения в ряды для некоторых случаев равновесия пластин
и балок. Вестник инженеров, Петроград, вып. 10. [IV. 10]
Галлун, см. Фенг, Холланд и Галлун
Гамкрелидзе, см. Понтрягин, Болтянский, Гамкрелидзе и Мищенко
Гантмахер Ф. P. (F.R. Gantmacher)
A954): Теория матриц. — М.: ГИТТЛ, 1953 (т.1), !954 (т.2); изд. 3-е — М.:
Наука, 1967; translations: Chelsea NY 1959, Interscience NY and London
1959, D. Verl. d. Wiss. Berlin 1958/59, Dunod Paris 1966. [VII.1]
Гекелер (E. Gekeler)
A979): Uniform stability of linear multistep methods in Galerkin prodecures
for parabolic problems. J. Math. Sciences, vol. 2, pp. 651-667. [V.l]
A984): Discretization Methods for Stable Initial Value Problems. Lecture
Notes in Math., No. 1044, Springer Verlag. [V.l]
Гийу и Лаго (A. Guillou & В. Lago)
A961): Domaine de stabilite associe aux formules d'integration numerique
cVequations differentielles, a pas separes et a pas lies. Recherche de formules
a grand rayon de stabilite. ler Congr. Assoc. Fran. Calcul, AFCAL, Grenoble,
Sept. 1960, pp. 43-56. [IV.2]
Гийу и Суле (A. Guillou &; J.L. Soule)
A969): La resolution numerique des problemes differentiels aux conditions
initiales par des methodes de collocation. R.I.R.O., vol. R-3, pp. 17-44. [V.3]
Гир (C.W. Gear)
A971): Numerical initial value problems in ordinary differential equations,
Prentice Hall, 253 pp. [V.2], [V.5]
A971): Simultaneous numerical solution of differential-algebraic equations.
IEEE Trans. Circuit Theory, vol. CT-18, pp. 89-95. [VI.2]
A982): Automatic detection and treatment of oscillatory and/or stiff ordinary
differential equations. In: Numerical integration of differential equations,
Lecture Notes in Math., vol. 968, pp. 190-206. [IV. 1]
A988): Differential-algebraic equation index transformations. SI AM J. Sci.
Stat. Comput., vol. 9, pp. 39-47. [VII.4]
A990): Differential-algebraic equations, indices, and integral algebraic
equations. SIAM J. Numer. Anal., vol. 27. [VII. 1]
Гир, Гупта и Леймкулер (C.W. Gear, G.K. Gupta &; B. Leimkuhler)
A985): Automatic integration of Euler-Lagrange equations with constraints.
J. Соmp. Appl. Math., vol. 12&13, pp. 77-90. [VII.1], [VII.3], [VIL1]
634 Литература
Гир и Петзолд (C.W. Gear & L.R. Petzold)
A983): Differential/algebraic systems and matrix pencils. In: Matrix Pencils,
Ё. Kagstrom к A. Rune (eds.), Lecture Notes in Math. 973, Springer Verlag,
pp. 75-89. [VII. ll
1984): ODE methods for the solution of differential/algebraic systems. SI AM
. Numer. Anal., vol. 21, pp. 716-728. [VII. 1], [VII.3]
Гир и Саад (C.W. Gear к Y. Saad)
1983): Iterative solution of linear equations in ODE codes. SIAM J. Sci.
tat. Comput., vol. 4, pp. 583-601. [IV.10]
Гир, Xcy и Петзолд (C.W. Gear, H.H. Hsu & L. Petzold)
A981): Differential-algebraic equations revisited. Proc. Numerical Methods
for Solving Stiff Initial Value Problems, Oberwolfach, BRD. [VII.3]
Гир, см. также Кампбелл и Гир
Голуб и Ван Лоун (G.H. Golub & C.F. Van Loan)
A989): Matrix Computations. Second edition, John Hopkins Univ. Press,
Baltimore and London. [Имеется перевод: Голуб Дж., Ван Лоун Ч.
Матричные вычисления. — М.: Мир, 1999.] [VIIЛ]
Готтвальд (В.A. Gottwald)
A977): MISS — Ein einfaches Simulations-System fur biologische und che-
mische Prozesse, EDV in Medizin und Biologie, vol. 3, pp. 85-90. [IV.10]
Григориефф (R.D. Grigorieff)
A977): Numerik gewohnlicher Differentialgleichungen, Bd. 2, Mehrschritt-
verfahren. Teubner Studienbiicher, 411 Seiten umit 49 Figuren, 32 Tabellen
und zahlreichen Beispielen". [V.l]
Григориефф и Шролль (R.D. Grigorieff к J. Schroll)
A978): Uber Л (a)-stabile Verfahren hoher Konsistenzordnung. Computing,
vol. 20, pp. 343-350. [V.2]
Гринд, ван де, и Крайевангер (J.A. van de Griend к J.F.B.M. Kraaijevanger)
A986): Absolute monotonicity of rational fonctions occuring in the numerical
study of initial value problems. Numer. Math., vol. 49, pp. 413-424. [IV. 11]
Грипентрог и Мерц (E. Griepentrog к R. Marz)
A986): Differential-algebraic equations and their numerical treatment.
Teubner Texte zur Math., Band 88. [VI.l], [VII. 1], [VII.3]
Гупта, см. Гир, Гупта и Леймкулер
Гурвиц и Курант (A. Hurwitz к R. Courant)
A925): Funktionentheorie. 2. Aufl., Verlag von Julius Springer, Berlin.
[Имеется перевод: Гурвиц А. и Курант Р. Теория функций. — М.: Наука,
1968.] [V.4]
Гурлей ГA.R. Gourlay)
A970): A note on trapezoidal methods for the solution of initial value
problems. Math, of Comp., vol. 24, pp. 629-633. [IV.3]
Густафссон (К. Gustafsson)
A991): Control theoretic techniques for stepsize selection in explicit Runge-
Kutta methods. ACM Trans. Math. Soft., vol. 17, pp. 533-554. [IV.2]
A994): Control-theoretic techniques for stepsize selection in implicit Runge-
Kutta methods. ACM Trans. Math. Soft., vol. 20, pp. 496-517. [IV.8]
Густафссон, Лунд и Сёдерлинд (К. Gustafsson, М. Lundh к G. Soderlind)
A988): A PI stepsize control for the numerical solution of ordinary
differential equations. BIT, vol. 28, pp. 270-287. [IV.2]
Литература 635
Далквист (G. Dahlquist)
A951): Fehlerabschatzungen bei Differenzenmethoden zur numerischen
Integration gewohnlicher Differentialgleichungen. ZAMM, vol. 31, pp. 239-240.
[VI]
A956): Convergence and stability in the numerical integration of ordinary
differential equations. Math. Scand., vol. 4, pp. 33-53. [V.7]
A963): A special stability problem for linear multistep methods. BIT, vol. 3,
pp. 27-43. [IV.3], tIV.9], [IV.12], [VlJ, [V.6]
A975): Error analysis for a class of methods for stiff nonlinear initial
value problems. Numerical Analysis, Dundee 1975, Lecture Notes in Math.,
No. 506, pp. 60-74. [IV.12], [V.6]
A978): G -stability is equivalent to Л-stability. BIT, vol. 18, pp. 384-401.
)IV.1S]9IV.61
A978): Positive functions and some applications to stability questions for
numerical methods. In: Recent Advances in Numerical Analysis, C. de Boor
& G.H. Golub (eds.), Academic Press, New York, pp. 1-19. [IV.5]
A983): On one-leg multistep methods. SI AM J. Numer. Anal., vol. 20,
pp. 1130-1138. [V.6], [V.7], [V.9]
Далквист и Йелч (G. Dahlquist & R. Jeltsch)
A979): Generalized disks of contractivity for explicit and implicit Runge-
Kutta methods. TRITA-NA Report 7906. [IV.12], [IV. 13]
A987): Reducibility and contractivity of Runge-Kutta methods revisited.
Report Nr. 46, Inst. f. Geometrie u. Prakt. Math., RWTH Aachen. [IV.12]
Далквист, Миндью и Левек (G. Dahlquist, H. Mingyou & R. LeVeque)
A983): On the uniform power-boundedness of a family of matrices and the
applications to one-leg and linear multistep methods. Numer. Math., vol. 42,
pp. 1-13. [V.7]
Далквист и Сёдерлинд (G. Dahlquist & G. Soderlind)
A982): Some problems related to stiff nonlinear differential systems. In:
Computing Methods in Applied Sciences and Engineering, V.R. Glowinski &
J.L. Lions (eds.), North-Holland, INRIA [V.7]
Далквист, см. также Сёдерлинд и Далквист
Даниел и Мур (J.W. Daniel & R.E. Moore)
A970); Computation and theory in ordinary differential equations, W.H.
Freeman and Company, 172 pp. [V.4]
Дейвис (P.J. Davis)
A963): Interpolation and approximation. Blaisdell 1963; Dover 1975. [V.3]
Деккер (К. Dekker)
A981): Stability of linear multistep methods on the imaginary axis. BIT,
vol. 21, pp. 66-79. [V.4]
A982): On the iteration error in algebraically stable Runge-Kutta methods.
Report NW 138/82, Math. Centrum, Amsterdam. [IV.14]
A984): Error bounds for the solution to the algebraic equations in Runge-
Kutta methods. BIT, vol. 24, pp. 347-356. [IV. 14]
Деккер, Крайевангер, Шнайд (K.Dekker, J.F.B.M. Kraaijevanger & J. Schneid)
A990): On the relation between algebraic stability and В -convergence for
Runge-Kutta methods. Numer. Math., vol. 57, pp.249-262. [IV.15]
Деккер и Фервер (К. Dekker &; J.G. Verwer)
A984): Stability of Runge-Kutta methods for stiff nonlinear differential
equations. North-Holland, Amsterdam-New-York-Oxford. [Имеется
перевод: Деккер К., Вервер Я. Устойчивость методов Рунге—Кутты для
жестких нелинейных дифференциальных уравнений. — М.: Мир, 1988.]
[IV.1S], [IV.14], [IV.1S]
636 Литература
Деккер и Хайрер (К. Dekker & Е. Hairer)
A985): A necessary condition for BSI-stability. BIT, vol. 25, pp. 285-288.
[IV.14J
Деккер, см. также Лю, Деккер и Спейкер
Джиле (D.R.A. Giles)
A978): A comparison of three problem-oriented simulation programs for
dynamic mechanical systems. Thesis, Univ. Waterloo, Ontario. [VII. 7]
Джорджилли, см. Бенеттин и Джоджилли
Дзеннаро, см. Хайрер и Дзеннаро
Ди Марцо (G.A. Di Marzo)
A992): KODAS5D), methodes de Rosenbrock d'ordre 5D) adaptees aux
problemes differentiels-algebriques. Memoire de diplome en Mathematiques,
Universite de Geneve 1992. [IV. 10], [VI.4]
Дойфлхард (P. Deuflhard)
A983): Order and stepsize control in extrapolation methods. Numer. Math.,
vol. 41, pp. 399-422. [IV.9]
A985): Recent progress in extrapolation methods for ordinary differential
equations. SI AM Review, vol. 27, pp. 505-535. [IV.9]
Дойфлхард и Новак (P. Deuflhard & U. Nowak)
A987): Extrapolation integrators for quasilinear implicit ODEs. In P.
Deuflhard & B. Engquist (eds.j, Large-Scale Scientific Computing. Birkhauser,
Boston. [VI. 5], [VI. 6]
Дойфлхард, Хайрер и Цугк (P. Deuflhard, E. Hairer & J. Zugck)
A987): One-step and extrapolation methods for differential-algebraic
systems. Numer. Math., vol. 51, pp. 501-516. [VI.5]
Дойфлхард, см. также Бадер и Дойфлхард
Дорманд и Принс (J.R. Dormand & P.J. Prince)
A980): A family of embedded Runge-Kutta formulae. J. Comp. Appl. Math.,
vol. 6, pp. 19-26. [IV.2]
Дородницын A. A. (A.A. Dorodnicyn)
A947): Асимптотическое решение уравнений Ван-дер-Поля. Прикл. ма-
тем. и мех., т. 11, с. 313-328. [VI.1]
Дункан, см. Карр, Дункан и Уолшо
Женен (Y. Genin)
A974): An algebraic approach to Л-stable linear multistep-multiderivative
integration formulas. BIT, vol. 14, pp. 382-406. [V.4]
Жэ (L. Jay)
A993): Convergence of a class of Runge-Kutta methods for differential-
algebraic systems of index 2, BIT, vol. 33, pp. 137-150. [VII.4]
A994): Runge-Kutta type methods for index three differential-algebraic
equations with applications to Hamiltonian systems. Thesis No. 2658, Univ.
Geneve. [VII. 8]
A995): Structure-preserving integrators. Submitted for publication. [VII.8]
A996): Symplectic partitioned Runge-Kutta methods for constrained
Hamiltonian systems. SIAM J. Numer. Anal., vol. 33, pp. 368-387. [VII.8]
Зиман (E.C. Zeeman)
A972): Differential equations for the heartbeat and nerve impulse. Published
in Towards a theoretical biology (Edited C.H. Waddington) Edinburgh
University Press, Volume 4, pp. 8-67. Reprinted in Catastrophe theory, Selected
papers 1972-1977, Addison-Wesley 1977, pp. 81-140. [IV.10]
Литература 637
Зоммерфельд (A. Sommerfeld)
A942): Vorlesungen iiber theoretische Physik. Bd.l., Mechanik; translated
from the 4th german ed.: Acad. Press. {Имеется перевод: Зоммерфельд A.
Механика. — M.: ИЛ, 1947.] [IV.1], [VII.1]
Зоннефельд и вал Лер (P. Sonneveld & В. van Leer)
A985): A minimax problem along the imaginary axis. Nieuw Archief V. Wis-
kunde D), vol. 3, pp. 19-22. [IV.2]
Иберхубер, см. Франк, Шнайд и Иберхубер
Изерлес (A. Iserles)
A981): Generalized order star theory, in : Pade approximations and its
applications. Amsterdam 1980, ed. M.G. de Bruin &: H. van Rossum, Lecture
Notes in Math. #888. [IV4]
Изерлес и Нёрсетт (A. Iserles & S,P. Norsett)
A984): A proof of the first Dahlquist barrier by order stars. BIT, vol. 24,
pp. 529-537. [V.4]
Изерлес и Странг (A. Iserles & G. Strang)
A983): The optimal accuracy of difference schemes. Trans. Am. Math. Soc,
vol. 277, pp. 779-803. [IV4]
Изерлес и Уилльямсон (A. Iserles & R.A Williamson)
A983): Stability and accuracy of semi-discretized finite difference methods.
IMA J. Numer. Anal., vol. 4, pp. 289-307. [IV.4]
Ил (B.L. Ehle)
A968) :High order Л-stable methods for the numerical solution of systems
of DEs. BIT, vol. 8, pp. 276-278. [IV.3], [IV.4], [IV.5]
A969) :On Pade approximations to the exponential function and Л-stable
methods for the numerical solution of initial value problems. Research Report
CSRR 2010, Dept. AACS, Univ. of Waterloo, Ontario, Canada. [IV.3], [IV.5/
A973): Л-stable methods and Pade approximations to the exponential.
SIAM J. Math. Anal., vol. 4, pp. 671-680. [IV.4], [IV.5]
Ил и Пайсел (B.L. Ehle & Z. Picel)
A975): Two-parameter, arbitrary order, exponential approximations for stiff
equations. Math. Comput., vol. 29, pp.501-511. [IV.5]
Ингланд (R. England)
A982): Some hybrid implicit stiffly stable methods for ordinary differential
equations. In: Numerical Analysis, Proc. Mexico, (ed. J.P. Hennart), Lecture
Notes in Math., No. 909, Springer Verlag, pp. 147-158. [V.3]
Иошида (H. Yoshida)
A990): Construction of higher order symplectic integrators. Phys. Lett. A,
Vol.150, p.262-268. [VII.8]
Йелч (R. Jeltsch)
A976): Stiff stability and its relation to A0- and Л@)-stability, SIAM J.
Numer. Anal., vol. 13, pp. 8-17. [V.2]
A976): Note on Л-stability of multistep multiderivative methods. BIT,
vol. 16, pp. 74-78. [V.4]
A978): Stability on the imaginary axis and A-stability of linear multistep
methods. BIT, vol. 18, pp. 170-174. [V.4]
A988): Order barriers for difference schemes for linear and nonlinear
hyperbolic problems. In: Numerical Analysis 1987, D.F. Griffiths & G.A. Watson
(eds.), Pitman Research Notes in Math., No. 170, pp. 157-175. [IV.4]
Йелч и Неванлинна (R. Jeltsch & О. Nevanlinna)
A978): Largest disk of stability of explicit Runge-Kutta methods. BIT,
vol. 18, pp. 500-502. [IV.4]
638 Литература
A981): Stability of explicit time discretizations for solving initial value
problems. Numer. Math., vol. 37, pp. 61-91; Corrigendum: Numer. Math., vol. 39,
p. 155. [IV.4]
A982): Stability and accuracy of time discretizations for initial value
problems. Numer. Math., vol. 40, pp. 245-296. [IV.4], [V.2], [V.4]
Йелч, см. также Далквист и Йелч
Йен (J. Yen)
A993): Constrained equations of motion in multibody dynamics as ODEs on
manifolds. SIAM J. Numer. Anal., vol. 30, pp. 553-568. [VII.2]
Йип, см. Синковец, Эрисман, Йип и Эптон
Калахан (D.A. Calahan)
A968): A stable, accurate method of numerical integration for nonlinear
systems. Proc. IEEE, vol. 56, p. 744. [IV.7]
Каллендер, Хартри и Портер (A. Callender, D.R. Hartree & A. Porter)
A936): Time-lag in a control system. Phil. Trans, of the Royal Society
London), Series A, vol. 235, pp. 415-444. [IV.2]
Кальво, см. Санс-Серна и Кальво
Камел, см. Энрайт и Камел
Кампбелл (S.L. Campbell)
A982): Singular Systems of Differential Equations II. Pitman, London.
iVI1'}
A989): A computational method for general higher index singular systems
of differential equations. IMACS Transactions Scientific Computing, vol. 1.2,
pp. 555-560. [VII.2]
A993): Least squares completions for nonlinear differential algebraic
equations. Numer. Math., vol. 65, pp. 77-94. [VII.2]
A995): High index differential algebraic equations. J. Mech. Struct. &
Machines, vol. 23, pp. 199-222. [VII.1]
Кампбелл и Гир (S.L. Campbell &; С.W. Gear)
A995): The index of general nonlinear DAEs. Numer. Math., vol. 72, pp. 173-
196. [VII. 1]
Кампбелл и Myp (S.L. Campbell & E. Moore)
A995): Constraint preserving integrators for general nonlinear higher index
DAEs. Numer. Math., vol. 69, pp. 383-399. [VII.2]
Кампбелл, см. также Бренан, Кампбелл и Петзолд
Канторович Л. В. и Акилов Г. П. (L. Kantorovich & G. Akilov)
A959): Функциональный анализ в нормированных пространствах. — М.:
Физматгиз, 1959; изд. 2-е и 3-е: Функциональный анализ. — М.: Наука,
1977 и 1984. (German translation: Akademic-Verlag, Berlin, 1964). [VI.3]
Капс (P. Kaps)
A977): Modifizierte Rosenbrockmethoden der Ordnungen 4,5 und 6 zur
numerischen Integration steifer Differentialgleichungen. Dissertation, Univ.
Innsbruck. [IV.7]
Капс и Ваннер (P. Kaps & G. Wanner)
A981): A study of Rosenbrock-type methods of high order. Numer. Math.,
vol. 38, pp. 279-298. [IV.7]
Капс и Остерман (P. Kaps & A. Ostermann)
A989): Rosenbrock methods using few LU-decompositions. IMA J. Numer.
Anal., vol. 9, pp. 15-27. [IV.7]
A990): L(a)-stable variable order Rosenbrock-methods. in: K. Strehmel, ed.,
Numerical treatment of differential equations, Teubner Texte zur Mathema-
tik, Band 121, p. 80-91. [IV.7]
Литература 639
Капс, Пун и Буй (P. Kaps, S.W.H. Poon & T.D. Bui)
A985): Rosenbrock methods for stiff ODEs: a comparison of Richardson
extrapolation and embedding technique. Computing, vol. 34, pp. 17-40.
[IV. 7]
Капс и Рентроп (P. Kaps & P. Rentrop)
A979): Generalized Runge-Kutta methods of order four with stepsize control
for stiff ordinary differential equations. Numer. Math., vol. 33, pp. 55-68.
[IV.7]
Каракашьян, см. Бейлс, Каракашьян и Сербии
Карр, Дункан и Уолшо (J. Carr, D.B. Duncan & С.Н. Walshaw)
A995): Numerical approximation of a metastable system. IMA J. Numer.
Anal., vol. 15, pp. 505-521. [IV. 10]
Като (Т. Kato)
A960): Estimation of iterated matrices, with application to the von Neumann
condition. Numer. Math., vol. 2, pp. 22-29. [V.7]
A966): Perturbation Theory for Linear Operators. Grudlehren der math.
Wissenschaften, Bd. 132, Springer Verlag, Berlin. [Имеется перевод: Като Т.
Теория возмущений линейных операторов. — М.: Мир, 1972.] [V.7]
Като, см. также Фудзита и Като
Каш (J.R. Cash)
A976): Semi-implicit Runge-Kutta procedures with error estimates for the
numerical integration of stiff systems of ordinary differential equations.
J ACM, vol. 23, pp. 455-460. [IV.7]
A979): Diagonally implicit Runge-Kutta formulae with error estimates. J.
Inst. Math. Applies, vol. 24, pp. 293-301. [IV.6]
A979): Stable recursions, with applications to the numerical solution of stiff
systems. Academic Press, 223 pp. [V.2]
A980): On the integration of stiff systems of O.D.E.s using extended backward
differentiation formulae. Numer. Math., vol. 34, pp. 235-246. [V.Sl
A981): Second derivative extended backward differentiation formulas for the
numerical integration of of stiff systems. SI AM J. Numer. Anal. vol. 18,
pp. 21-36. [V.3]
A983): The integration of stiff initial value problems in ODEs using modified
extended backward differentiation formulas. Comp. &: Maths, with Appls.,
vol. 9, No. 5, pp. 645-657. [V.3], [V.5]
Каш и Консидайн (J.R. Cash & S. Considine)
A992): An MEBDF code for stiff initial value problems. ACM Tans. Math.
Software, vol. 18, No. 2, pp. 142-158. [V.5]
Квернё (A. Kvaerno)
A990): Runge-Kutta methods applied to fully implicit differential-algebraic
equations of index 1. Math. Comp., vol. 54, pp. 583-625. [VII.5]
Кертис A.P. (A.R. Curtis)
A983): Jacobian matrix properties and their impact on choice of software for
stiff ODE systems. IMA J. Numer. Anal., vol. 3, pp. 397-415. [IV.10]
Кертисс Ч.Ф. и Хиршфельдер (C.F. Curtiss & J.О. Hirschfelder)
A952): Integration of stiff equations. Proc. Nat. Acad. Sci., vol. 38, pp.235-
243. [IV. 1]
Килинг (S.L. Keeling)
A989): On implicit Runge-Kutta methods with a stability function having
distinct real poles. BIT, vol. 29, pp. 91-109. [IV4]
Киршбраун (M.D. Kirszbraun)
A934): Ueberdie zusammenziehenden und Lipschitzschen Transformationen.
Fund. Math., vol. 23, pp. 77-108. [IV.12]
640 Литература
Кларк (К. Clark)
A988): A structural form for higher index semistate equations I: Theory
and applications to circuit and control theory. Linear Alg. Appl., vol. 98,
pp. 169-197. [VII. 1]
Клопфенштайн, см. Крейн и Клопфенштайн
Коллатц (L. Collatz)
A950): Numerische Behandlung von Differentialgleichungen. Grundlehren,
Springer Verlag, Band LX (later editions and translations). [Имеется
перевод: Коллатц Л. Численные методы решения дифференциальных
уравнений. — М.: ИЛ, 1953.] [IV.10], [IV.15]
Коллет, Экман, Эпштайн и Штуббе (P. Collet, J.-P. Eckmann, Н. Epstein &
J. Stubbe)
A993): Analyticity for the Kuramoto-Sivashinsky equation. Physica D, v. 67,
pp. 321-326. [IV. 10]
Конг, см. Скил и Конг
Консидайн, см. Каш и Консидайн
Крайевангер (J.F.B.M. Kraaijevanger)
A985): В-convergence of the implicit midpoint rule and the trapezoidal rule.
BIT, vol. 25, pp. 652-666. [IV.15]
A986): Absolute monotomcity of polynomials occuring in the numerical
solution of initial value problems. Numer. Math., vol. 48, pp. 303-322. [IV. 11]
A991): A characterization of Lyapunov diagonal stability using Hadamard
products. Linear Alg. Appl., vol. 151, pp. 245-254. [IV.Ц]
Крайевангер и Шнайд (J.F.B.M. Kraaijevanger & J. Schneid)
A991): On the unique solvability of the Runge-Kutta equations. Numer.
Math., vol. 59, pp. 129-157. [IV.14], [IV.15]
Крайевангер, см. также ван де Гринд и Крайевангер; Деккер, Крайевангер
и Шнайд; Лю и Крайевангер
Крайер (C.W. Cryer)
A973): А new class of highly stable methods. A$ -stable methods. BIT,
vol. 13, pp.153-159. [V.2]
Крайсс (H.O. Kreiss)
A962): Uber die Stabititatsdefinition fur Differenzengleichungen die partielle
Differentialgleichungen approximieren. BIT, vol. 2, pp. 153-181. [V.7]
Крамер (G. Cramer)
J 1750): Introduction aTanalyse des lignes courbes algebriques. Geneve, 1750.
IV.3)
Крейн и Клопфенштайн (R.L. Crane & R.W. Klopfenstein)
A965): A predictor-corrector algorithm with an increased range of absolute
stability. J. ACM, vol. 12, pp.227-241. . [V.l]
Кронекер (L. Kronecker)
A874): Uber Schaaren von quadratischen und bilinearen Formen. Akad. der
Wiss. Berlin 19. Jan. 1874, Werke vol. I, pp. 351-413. [VII.1]
A890): Algebraische Reduction der Schaaren bilinearer Formen. Akad. der
Wiss. Berlin 27. Nov. 1890, Werke vol. Ill2, pp. 141-155. [VII.1]
Kpox (F.T. Krogh)
A966): Predictor-Corrector methods of high order with improved stability
characteristics. J. Assoc. Comput. Mach., vol. 13, pp. 374-385. [V.l]
Крузе (M. Crouzeix)
A975): Sur Tapproximation des equations differentielles operationnelles line-
aires par de methodes de Runge-Kutta. These, Univ. Paris VI. [IV.6]
A979): Sur la B-stabilite des methodes de Runge-Kutta. Numer. Math.,
vol. 32, pp. 75-82. [IV.12]
Литература 641
Крузе и Равьяр (М. Crouzeix & RA. Raviart)
A976): Approximation des equations devolution lineaires par des methodes
a pas multiples. С R. Acad. Sc. Paris, Ser. A 283, pp. 367-370. [V.7]
A980): Approximation des problemes devolution. Unpublished Lecture
Notes, Universite de Rennes. [IV.6], [IV.Ц], [V.7]
Крузе и Рюамп (M. Crouzeix & F. Ruamps)
A977): On rational approximations to the exponential. R.A.I.R.O. Analyse
Numerique, vol. 11, pp. 241-243. [IV.4]
Крузе, Хундсдорфер и Спейкер (М. Crouzeix, W.H. Hundsdorfer & M.N.
Spijker)
A983): On the existence of solutions to the algebraic equations in implicit
Runge-Kutta methods. BIT, vol. 23, pp. 84-91. [IV. Ц]
Крузе, см. также Байокки и Крузе; Болле и Крузе
Крылов В. И. (V.I. Krylov)
A959): Приближенное вычисление интегралов. — М.: Физматгиз, 1959;
изд. 2-е — М.: Наука, 1967. English translation: Approximate calculation
of integrals. Macmillan, New York, 1962. [V.3]
Кункель и Мерман (P. Kunkel & V. Mehrmann)
A995): Canonical forms for linear differential-algebraic equations with
variable coefficients. J. Comp. Appi. Math., vol. 56, pp. 225-251. [VII. 1]
A996): Regular solutions of nonlinear differential-algebraic equations and
their numerical determination. Preprint, TU Chemnitz-Zwickau. [VII.2]
Купер (G.J. Cooper)
A985): Reducible Runge-Kutta methods. BIT, vol. 25, pp. 675-680. [IV.12]
A986): On the existence of solutions for algebraically stable Runge-Kutta
methods. IMA J. Numer. Anal., vol. 6, pp. 325-330. [IV. 14]
Купер и Сейфи (G.J. Cooper & A. Sayfy)
A979): Semiexplicit Л-stable Runge-Kutta methods. Math, of Comp., vol. 33,
pp. 541-556. [IV.6]
A983): Additive Runge-Kutta methods for stiff ordinary differential
equations. Math, of Comp., vol. 40, pp. 207-218. [IV.1]
Курант, Фридрихс и Леви (R. Courant, К. Friedrichs & H. Lewy)
A928): Ueber die partiellen Differenzengleichungen der mathematischen Phy-
sik. Math. Ann., vol. 100, pp. 32-74. [Имеется перевод: Курант P.,
Фридрихс К. и Леви Г. О разностных уравнениях математической физики.
Усп. матем. наук, 1940, вып. 8, с. 125-160.] [IV.2]
Курант, см. также Гурвиц и Курант
Курди (М.А. Kurdi)
A974): Stable high order methods for time discretization of stiff differential
equations. Thesis, Univ. of California. [IV.6]
Лаго, см. Гийу и Лаго
Лагранж (J.L. Lagrange)
1776): Sur l'usage des fractions continues dans le calcul integral. Nouv. Mem.
e Г Acad, royale du Sc. et Belles-Lett res de Berlin, Oeuvres Tome quatrieme,
pp. 301-332. [IV.3]
A788): Mechanique analitique. Paris, chez la Veuve Desaint, Libraire,
MDCCLXXXVIII, avec approbation et privilege du Roi. Oeuvres vol. 11 et
12. [Имеется перевод: Лагранж Ж. Аналитическая механика, тт. 1,2. —
М.-Л.: ГИТТЛ, 1950.] [IV.1]
Ланг (S. Lang)
A962): Introduction to differentiable manifolds. John Wiley. [Имеется
перевод: Ленг С. Введение в теорию дифференцируемых многообразий. —
642 Литература
М.: Мир, 1967.] Third and enlarged edition: Differential and Riemannian
manifolds. Graduate Texts in Mathematics, Springer 1995. [VII. 1]
Лебедев В. И. (V.I. Lebedev)
A989): Explicit difference schemes with time-variable steps for solving stiff
systems of Equations. Sov. J. Numer. Anal. Math. Modelling 1989, vol. 4,
№ 2, pp. 111-135. [IV.2]
A994): Как решать явными методами жесткие системы
дифференциальных уравнений. — Вычислительные процессы и системы, вып.8, под
ред. Г.И. Марчука. — М.: Наука, 1991, с. 237-291. English translation in:
Numerical methods and applications, ed. by G.I. Marchuk, pp. 45-80, CRC
Press 1994. [IV.2]
A995): Extremal polynomials with restrictions and optimal algorithms.
Advanced Mathematics: Computations and Applications. A.S. Alekseev and
N.S. Bakhvalov, eds., Proc. Int. Conf. AMCA-95. — Novosibirsk: NCC
Publishers, 1995, pp. 491-502. [IV.2]
A996): Explicit difference schemes with variable time steps for solving stiff
systems of equations. In: Numerical Analysis and Its Applications, Rousse
1996, L. Vulkov, J. Wasniewski & P. Yalamov, eds., Lecture Notes in
Computer Sci. 1196, Springer-Verlag, pp. 274-283. [IV.2]
Лебедев В. И. и Медовиков A. A. (V.I. Lebedev & A.A. Medovikov)
A994): Явный метод второго порядка точности для решения жестких
систем обыкновенных дифференциальных уравнений. Известия ВУЗ, сер.
Матем., 1998, № 9D36), с. 55-63. Manuscript, Russian Academy of Science,
Moscow, 1994. [IV.2]
Лебедев В. И. и Финогенов С. A. (V.I. Lebedev & S.A. Finogenov)
A976): Об использовании упорядоченных чебышевских параметров в
итерационных методах. ЖВМ и МФ, 1976, т. 16, № 4, с. 895-907. [IV.2]
Левек и Трефетен (R.J. LeVeque & L.N. Trefethen)
A984): On the resolvent condition in the Kreiss matrix theorem. BIT, vol. 24,
pp. 584-591. [V.7]
Левек, см. также Далквист, Миндью и Левек
Леви, см. Курант, Фридрихс и Леви
Леймкулер и Скил (B.J. Leimkuhler &; R.D. Skeel)
A994): Symplectic numerical integrators in constrained Hamiltonian
systems. J. Comput. Phys., vol. 112, pp. 117-125. [VII.8]
Леймкулер, см. также Гир, Гупта и Леймкулер; Фюрер и Леймкулер
Лер, ван, см. Зоннефельд и ван Лер
Леру (M.-N. Le Roux)
A980): Methodes multipas pour des equations paraboliques non lineaires.
Numer. Math., vol. 35, pp. 143-162. [V.8]
Лётстедт (P. Lotstedt)
A985): Discretization of singular perturbation problems by BDF methods.
Report No.99, Uppsala Univ., Dept. of Comp. Sci. [VI.2]
A985): On the relation between singular perturbation problems and
differential-algebraic equations. Report No. 100, Uppsala Univ., Dept. of Comp. Sci.
[VI.2]
Лётстедт и Петзолд (P. Lotstedt &: L. Petzold)
A986): Numerical solution of nonlinear differential equations with
algebraic constraints I: Convergence results for backward differentiation formulas.
Math. Comput., vol 46, pp. 491-516. [VII.3]
Ли (I. Lie)
A990): The stability function for multistep collocation methods. Numer.
Math., vol. 57, pp. 779-787. [V.3]
Литература 643
Ли и Нёрсетт (I. Lie & S.P. Norsett)
A989): Superconvergence for multistep collocation. Math, of Comput., vol. 52,
pp. 65-79. [V.3]
Линдберг (В. Lindberg)
A971): On smoothing and extrapolation for the trapezoidal rule. BIT, vol. 11,
pp. 29-52. [IV.9]
A972): A simple interpolation algorithm for improvement of the numerical
solution of a differential equation. SIAM J. Numer. Anal., vol. 9, pp. 662-668.
[VLSI
A974): On a dangerous property of methods for stiff differential equations.
BIT, vol. 14, pp. 430-436. [IV.3]
Линдберг, см, также Энрайт, Халл и Линдберг
Линигер (W. Liniger)
A956): Zur Stabilitat der numerischen Integrationsmethoden fur Differen-
tialgleichungen. These, Universite de Lausanne, 95 p. [V.6]
Линигер и Уиллоуби (W. Liniger & R.A. Willoughby)
A970): Efficient integration methods for stiff systems of ordinary differential
equations. SIAM J. Numer. Anal., vol. 7, pp. 47-66. [IV.8]
Линигер, см. также Неванлинна и Линигер; Одех и Линигер
Лоун, Ван, см. Голуб и Ван Лоун
Лопес и Триджианте (L. Lopez &: D. Trigiante)
A989): A projection method for the numerical solution of linear systems
in separable stiff differential equations. Intern. J. Computer Math., vol. 30,
pp. 191-206. [IV.10]
Лосон (J.D. Lawson)
A967): Generalized Runge-Kutta processes for stable systems with large
Lipschitz constants. SIAM J. Numer. Anal., vol. 4, pp. 372-380. [IV.9]
Лунд, см. Густафссон, Лунд и Сёдерлинд
Лю, Деккер и Спейкер (M.Z. Liu, К. Dekker &: M.N. Spijker)
A987): Suitability of Runge-Kutta methods. J. Comp. Appl. Math., vol. 91,
pp. 53-63. [IV. 14]
Лю и Крайевангер (M.Z. Liu &; J.F.B.M. Kraaijevanger)
A988): On the solvability of the systems of equations arising in implicit
Runge-Kutta methods. BIT, vol. 28, pp. 825-838. [IV. Ц]
Любих (Ch. Lubich)
A988): Convolution quadrature and discretized operational calculus I.
Numer. Math., vol. 52, pp. 129-145. [V.7]
A989): Linearly implicit extrapolation methods for differential-algebraic
systems. Numer. Math., vol. 55, pp. 197-211. [VI.6] [VII.l]
A989): h2-extrapolation methods for differential-algebraic systems of index
2. Impact Comput. Sc. Eng., vol. 1, pp. 260-268. [VII.l], [VII.6]
A991): On the convergence of multistep methods for nonlinear stiff
differential equations. Numer. Math., vol. 58, pp. 839-853, and Erratum (Numer.
Math., vol. 61, pp. 277-279) [V.7], [V.8], [VI.2]
A991): Extrapolation integrators for constrained multibody systems. Impact
Comp. Sci. Eng., vol. 3, pp. 213-234. [VII.2]
A991): On projected Runge-Kutta methods for differential-algebraic
equations. BIT, vol. 31, pp. 545-550. [VII.5]
A993): Integration of stiff mechanical systems by Runge-Kutta methods.
ZAMP, vol. 44, pp. 1022-1053. [VII.7]
644 Литература
Любих, Новак, Пеле и Энгстлер (Ch. Lubich, U. Nowak, U. Pohle & Ch. Engst-
ler)
A992): MEXX — numerical software for the integration of constrained
mechanical multibody systems. Preprint SC 92-12, Konrad-Zuse-Zentrum,
Berlin. [VI.7]
Любих и Остерман (Ch. Lubich & A. Ostermann)
A993): Runge-Kutta methods for parabolic equations and convolution
quadrature. Math. Comp., vol. 60, pp. 105-131. [V.8]
Любих и Рош (Ch. Lubich & M. Roche)
A990): Rosenbrock methods for differential-algebraic systems with solution-
dependent singular matrix multiplying the derivative. Computing, vol. 43,
pp. 325-342. [VI.6]
Любих, см. также Хайрер, Бадер и Любих; Хайрер и Любих; Хайрер, Любих
и Рош
Маклахлан (R.I. McLachlan)
A995): On the numerical integration of ordinary differential equations by
symmetric composition methods. SIAM J. Sci. Comput., vol. 16, pp. 151—
168. [VII.8]
Маннинг (D.W. Manning)
A981): A computer technique for simulating dynamic multibody systems
based on dynamic formalism. Thesis, Univ. Waterloo, Ontario. [VII.7]
Марден (M. Marden)
A966): Geometry of polynomials. Mathematical Surveys, American
Mathematical Society, Providence, Rhode Island, 2nd edition, 243 p. [V.7]
Марков A. A. (A.A. Markov)
A890): Об одном вопросе Д. И. Менделеева. Записки Акад. Наук, СПб,
1890, т. 62, с. 1-24; см. Марков А. А. Избранные труды по теории
непрерывных дробей и теории функций наименее уклоняющихся от нуля. —
М.-Л.: ГИТТЛ, 1948, с. 51-75. [IV.2]
Марсден, см. Абрагам, Марсден и Ратью
Масси (W.S. Massey)
A980): Singular homology theory. Graduate Texts in Mathematics 70,
Springer Verlag, 265 pp. [IV.4]
Мачек, см. Ауцингер, Франк и Мачек
Медовиков, см. Лебедев В. И. и Медовиков А. А.
Мерман, см. Кункель и Мерман
Мерц (R. Marz)
A989): Index-2 differential-algebraic equations. Results in Mathematics,
vol. 15, pp. 149-171. [VII. 1]
A990): Higher index differential-algebraic equations: Analysis and numerical
treatment. Banach Center Publ., 24, Numer. Anal, and Math. Modelling,
pp. 199-222. [VII.1], [VII.3]
Мерц, см. также Грипентрог и Мерц
Микельсен (M.L. Michelsen)
A976): Semi-implicit Runge-Kutta methods for stiff systems, program
description and application examples. Inst. f. Kemiteknik, Danmarks tekniske
H0jskole, Lyngby. [VI.4]
Миллер К. и Миллер Р.Н. (К. Miller & R.N. Miller)
A981): Moving finite elements. I. SIAM J. Numer. Anal., vol. 18, pp. 1019-
1032. [VI.6]
Миндью, см. Далквист, Миндью и Левек
Литература 645
Минти (G.J. Minty)
A962): On a simultaneous solution of a certain system of linear inequalities.
Proc. Amer. Math. Soc, vol. 13, pp. 11-12. [IV.12]
Мищенко, см. Понтрягин, Болтянский, Гамкрелидзе и Мищенко
Монтихано (J.I. Montijano)
A983): Estudio de los metodos SIRK para la resolucion numerica de ecuaci-
ones diferenciales de tipo stiff. Thesis, Univ. Zaragoza. [IV. 14]
Мортон, см. Рихтмайер и Мортон
Мур Р.Э., см. Даниел и Мур
Мур Э., см. Кампбелл и Мур
Муруа (A. Murua)
A995): Partitioned half-explicit Runge-Kutta methods for
differential-algebraic systems of index 2. Submitted for publication. [VII. 6], [VII. 7]
Мюллер, Проль, Раннахер и Турек (S. Miiller, A. Prohl, R. Rannacher &
S. Turek)
A994): Implicit time-discretization of the nonstationary incompressible Na-
vier-Stokes equations. Proc. 10th GAMM-Workshop, Kiel, W. Hackbusch &
G. Wittum eds., Vieweg. [IV.3]
Мюльтай (H.N. Multhei)
A982): Maximale Konvergenzordnung bei der numerischen Losung von An-
tangswertproblemen mit Splines. Numer. Math., vol. 39, pp. 449-463. [V.3]
A982): A-stabile Kollokationsverfahren mit mehrfachen Knoten. Computing,
vol. 29, pp. 51-61. [V.3]
Навье (C.L. Navier)
A823): Memoire sur les lois du mouvement des fluides (lu а Г Acad, le 18 mars
1822). Paris, Mem. de l'Acad. Royale des Sciences, Tome VI, pp. 389-440.
[V.8]
Неванлинна (О. Nevanlinna)
A976): On the logarithmic norms of a matrix. Report HTKK-MAT-A94,
Helsinki Univ. of Tech. [VLSI
A976): On error bounds for G-stable methods. BIT, vol. 16, pp. 79-84. [V.6]
A977): On the numerical integration of nonlinear initial value problems by
linear multistep methods. BIT, vol. 17, pp. 58-71. [V.8]
A985): Matrix valued versions of a result of von Neumann with an application
to time discretization. J. Comput. Appl. Math., vol. 12& 13, pp. 475-489.
[V.7]
Неванлинна и Линигер (О. Nevanlinna & W. Liniger)
A978): Contractive methods for stiff differential equations, I. BIT, vol. 18,
pp. 457-474. [V.7]
A979): Contractive methods for stiff differential equations, II. BIT, vol. 19,
pp. 53-72. [V.7]
Неванлинна и Одех (О. Nevanlinna & F. Odeh)
A981): Multiplier techniques for linear multistep methods. Numer. Funct.
Anal. Optim., vol. 3, pp. 377-423. [V.8]
Неванлинна, см. также Йелч и Неванлинна
Нейман, фон (J. von Neumann)
A951): Eine Spektraltheorie fur allgemeine Operatoren eines unitaren Raum-
es. Math. Nachrichten, vol. 4, pp. 258-281. [IV.11]
Нёрсетт (S.P. N0rsett)
A974): Multiple Pade approximations to the exponential function. Report
No. 4/74, Dept. of Math., Univ. of Trondheim, Norway. [IV.4]
646 Литература
A974): Semi-explicit Runge-Kutta methods. Report No. 6/74, Dept. of
Math., Univ. of Trondheim, Norway. [IV.6]
A975): Runge-Kutta methods with coefficients depending on the Jacobian.
Report No. 1/75, Dept. of Math., Univ. of Trondheim, Norway. [IV\7l
A975): C-polynomials for rational approximations to the exponential
function. Numer. Math., vol. 25, pp.39-56. [IV.3]
A976): Runge-Kutta methods with a multiple real eigenvalue only. BIT,
vol. 16, pp. 388-393. [IV.8]
Нёрсетт и Ваннер (S.P. Norsett &: G. Wanner]
A979): The real-pole sandwich for rational approximations and oscillation
equations. BIT, vol. 19, pp. 79-94. [IV.3], [IV.4]
A981): Perturbed collocation and Runge-Kutta methods. Numer. Math.,
vol. 38, pp. 193-208. [IV.5], [IV. 13]
Нёрсетт и Вольфбрандт (S.P. Norsett Sz A. Wolfbrandt)
A977): Attainable order of rational approximations to the exponential
function with only real poles. BIT, vol. 17, pp. 200-208. [IV.4]
A979): Order conditions for Rosenbrock types methods. Numer. Math.,
vol. 32, pp. 1-15. [IV.7]
Нёрсетт, см. также Ваннер, Хайрер и Нёрсетт; Изерлес и Нёрсетт; Ли и
Нёрсетт
Нипп и Штоффер (К. Nipp & D. Stoffer)
A995): Invariant manifolds and global error estimates of numerical
integration schemes applied to stiff systems of singular perturbation type - Part I:
RK-methods. Numer. Math., vol. 70, pp. 245-257. [VI.3]
Новак, см. Дойфлхард и Новак; Любих, Новак, Пеле и Энгстлер
Нойес, см. Филд и Нойес
Одех и Линигер (F. Odeh &; W. Liniger)
A977): Non-linear fixed-h stability of linear multistep formulae. J. Math.
Anal. Appl., vol. 61, pp. 691-712. [V.8]
Одех, см. также Неванлинна и Одех
Олафссон, см. Алишенас и Олафссон
О'Малли (R.E. O'Malley)
1974): Introduction to Singular Perturbations. Academic Press, New York.
VI.3]
Ормрод и Андрьюс (M.K. Ormrod & G.C. Andrews)
A986): Advent: a simulation program for constrained planar kinematic and
dynamic systems. Publications of the Amer. Soc. of Mech. Eng., 86-DET-97.
[VII.7]
Ортега и Рейнболдт (J.M. Ortega & W.C. Rheinboldt)
A970): Iterative Solution of Nonlinear Equations in Several Variables.
Academic Press, New York. [Имеется перевод: Ортега Дж., Рейнболдт В.
Итерационные методы решения систем уравнений с многими неизвестными.
— М.: Мир, 1975.] [VI.3], [VII.3], [VII.4], [VII.8]
Остерман (A. Ostermann)
A988): Ueber die Wahl geeigneter Approximationen an die Jacobimatrix
bei linear-impliziten Runge-Kutta-Verfahren. Dissertation, Univ. Innsbruck,
pp. 66. [IV. 11]
A990): Continuous extensions of Rosenbrock-type methods. Computing, vol.
44, pp. 59-68. [VI.4]
Остерман, см. также Капс и Остерман; Любих и Остерман; Хайрер и
Остерман
Литература 647
Паде (Н. Pade)
A892): Sur la representation approchee d'une fonction par des fractions
rationnelles. Premiere These ("A Monsieur Hermite"), Ann. Ec. Norm. Sup.
C), vol. 9, Supp. 3-93, Oeuvres pp. 72-165. [IV.3]
A899): Memoire sur les developpements en fractions continues de la fonction
exponentielle pouvant servir d'introduction a la theorie des fractions continues
algebriques. Ann. Ec. Norm. Sup. C), vol. 16, pp. 395-426; Oeuvres pp. 231-
262. [IV.3]
Пайсел, см. Ил и Пайсел
Парсеваль (М.А. Parseval)
A799): Private communication to S.F. Lacroix. See: Lacroix, Traite des
differences et des series, Paris 1800, p. 377, or Traite du calcul diff. et du
calcul int., 2e ed, vol. 3, p. 394, Paris 1819. Also published in Paris Memoires
presentes par divers savants a l'acad. d. sc, vol 1,)
A806), p. 639.
Пеерсторфер (F. Peherstorfer)
A981): Characterization of positive quadrature formulas. SI AM J. Math.
Anal., vol. 12, pp. 935-942. [IV. 13]
Пейзи (A. Pazy)
A983): Semigroups of Linear Operators and Applications to Partial
Differential Equations. Appl. Math. Sciences 44, Springer Verlag. [V.7]
Перрон (O. Perron)
A913): Die Lehre von den Kettenbruchen. Teubner, 520 pp., 3rd ed., repr.
1977. [IV. 13]
Петзолд (L.R. Petzold)
A982): A description of DASSL: A Differential/Algebraic System Solver.
Proceedings of IMACS World Congress, Montreal, Canada. [VII.3], [VII.7]
A983): Automatic selection of methods for solving stiff and nonstiff systems
of orainary differential equations. SIAM J. Sci. Stat. Comp., vol. 4, pp. 136-
148. [IV.2]
A986): Order results for implicit Runge-Kutta methods applied to
differential/algebraic systems. SIAM J. Numer. Anal., vol. 23, pp. 837-852. [VI. 1],
[VII-4]
Петзолд, см. также Ашер и Петзолд; Бренан, Кампбелл и Петзолд; Бренан
и Петзолд; Гир и Петзолд; Гир, Хсу и Петзолд; Лётстедт и Петзолд
Пеле, см. Любих, Новак, Пеле и Энгстлер
Племмонс, см. Баркер, Берман и Племмонс
Пойа и Сегё (G. Polyа &: G. Szego)
A925): Aufgaben und Lehrsatze aus der Analysis. Two volumes, Grundlehren
Band XX, Springer Verlag, many later editions and translations. [Имеется
перевод: Полиа Г. и Сеге Г. Задачи и теоремы из анализа, в 2 частях. —
М.: Наука, 1978 (изд. 3-е).] [IV.4]
Понтрягин, Болтянский, Гамкрелидзе и Мищенко (L.S. Pontryagin, V.G. Bol-
tyanskij, R.V. Gamkrelidze & E.F. Mishchenko)
A961): Математическая теория оптимальных процессов. — М.: Физмат-
гиз, 1961. English translations: Wiley 1962, Pergamon Press 1964. German
translation: Oldenbourg 1964. [VII. 1]
Портер, см. Каллендер, Хартри и Портер
Потра (F.A. Potra)
A995): Runge-Kutta integrators for multibody dynamics. Mechanics of
Structures and Machines, vol. 23, pp. 181-197. [VII.2]
648 Литература
Потра и Рейнболдт (F.A. Potra & W.C. Rheinboldt)
A990): Differential-geometric techniques for solving differential algebraic
equations. In E.J. Haug & R.C. Deyo, eds, Real-Time Integration of
Mechanical System Simulation, Springer-Verlag, Berlin, pp. 155-191. fVII.2]
A991): On the numerical solution of Euler-Lagrange equations. Mech. Struct.
b Mech., vol. 19A), pp. 1-18. [VII.2]
Пресс, Фланнери, Теукольски и Веттерлинг (W.H. Press, В.P. Flannery,
S.A. Teukolsky & W.T. Vetterling)
A986,1989): Numerical Recipes, the art of scientific computing (FORTRAN
version). Cambridgre University Press, 702 pp. [IV. 10]
Принс, см. Дорманд и Принс
Проль, см. Мюллер, Проль, Раннахер и Турек
Протеро и Робинсон (A. Prothero & A. Robinson)
A974): On the stability and accuracy of one-step methods for solving stiff
systems of ordinary differential equations. Math, of Comput., vol. 28, pp. 145-
162. [IV.3], [IV. 15]
Пун, см. Капс, Пун и Буй
Пюизё (V. Puiseux)
A850): Recherches sur les fonctions algebriques. Journal de Math, vol 15, pp.
365-480. [V.4]
Равьяр, см. Крузе и Равьяр
Раймер (М. Reimer)
A967): Zur Theorie der linearen Differenzenformeln. Math. Zeitschr., vol. 95,
pp. 373-402. [V.4]
Райт (К. Wright)
A970): Some relationships between implicit Runge-Kutta, collocation and
Lanczos r methods, and their stability properties. BIT, vol. 10, pp.217-227.
[IV.3]
Райх (S. Reich)
A996): Symplectic integration of constrained Hamiltonian systems by
composition methods. SIAM J. Numer. Anal., vol. 33, pp. 475-491. [VII.8]
A996): On higher-order semi-explicit symplectic partitioned Runge-Kutta
methods for constrained Hamiltonian systems. Numer. Math [VII.8]
Райх, см. также Ашер, Чин и Райх
Раннахер, см. Мюллер, Проль, Раннахер и Турек
Ратью, см. Абрагам, Марсден и Ратью
Реймонд (J.D. Reymond)
A989): Implementation des methodes Radau IIA d'ordre 7 et 9. Diploma
thesis, Univ. Geneva. [IV. 10]
Рейнболдт (W.C. Rheinboldt)
A984): Differential-algebraic systems as differential equations on manifolds.
Math. Comp., vol. 43, pp. 473-482. [VII.l]
Рейнболдт, см. также Ортега и Рейнболдт; Потра и Рейнболдт
Ремез Е. Я. (E.Ya. Remez)
A957): Оощие вычислительные методы чебышевского приближения.
Задачи с линейно входящими вещественными параметрами. — Киев: Изд-
во АН УССР, 1957. [IV.2]
Рентроп, Рош и Штайнебах (P. Rentrop, М. Roche & G. Steinebach)
A989): The application of Rosenbrock-Wanner type methods witn stepsize
control in differential-algebraic equations. Numer. Math., vol. 55, pp. 545-
563. [VI.l], [VI.4]
Рентроп, см. также Капс и Рентроп
Литература 649
Риман (В. Riemann)
A857): Allgemeine Voraussetzungen und Hulfsmittel fur die Untersuchung
von Functionen unbeschrankt veranderlicher Grofien. J. f. d. r. u. angew.
Math., vol. 54, pp. 101-104; Werke pp. 81-84. [Имеется перевод: Риман Б.
Сочинения. — М.-Л.: ГИТТЛ, 1948, с. 88-90.] [V.4]
Рихтмайер и Мортон (R.D. Richtmyer к K.W. Morton)
A967): Difference Methods for Initial-Value Problems. Wiley-Interscience.
[Имеется перевод: Рихтмайер P., Мортон К. Разностные методы решения
краевых задач. — М.: Мир, 1972.] [V.7]
Роберсон и Швертассек (R.E. Roberson & R. Schwertassek)
A988): Dynamics of Multibody Systems. Springer Verlag. [VII.7]
Робертсон Б.Ч. (B.C. Robertson)
A987): Detecting stiffness with explicit Runge-Kutta formulas. Rep. 193/87,
Dept. Comp. Sci., University of Toronto. [IV.2]
Робертсон X.X. (H.H. Robertson)
A966): The solution of a set of reaction rate equations. In: J. Walsh ed.:
Numer. Anal., an Introduction, Academ. Press, pp. 178-182. [IV.1], [IV. 10]
Робинсон, см. Протеро и Робинсон
Розенброк (H.H. Rosenbrock)
A962/63): Some general implicit processes for the numerical solution of
differential equations. Computer J., vol. 5, pp. 329-330. [IV.7]
Рош (M. Roche)
A988): Rosenbrock methods for differential algebraic equations. Numer.
Math., vol. 52, pp. 45-63. [VI.4]
A988): Runge-Kutta and Rosenbrock methods for differential-algebraic
equations and stiff ODEs. Doctoral thesis, Universite de Geneve. [VII. 5]
A989): Runge-Kutta methods for differential algebraic equations. SI AM J.
Numer. Anal., vol. 26, pp. 963-975. [VI.4]
Рош, см. также Любих и Рош; Рентроп, Рош и Штайнебах; Хайрер, Любих
и Рош
Рубин, см. Биккарт и Рубин
Рюамп, см. Крузе и Рюамп
Рюккерт, Чиккотти и Берендсен (J.-P. Ryckaert, G. Ciccotti & H.J.С. Berend-
sen)
A977): Numerical integration of the cartesian equations of motion of a system
with constraints: molecular dynamics of n-alkanes. J. Comput. Phys., vol. 23,
pp. 327-341. [VII.8]
Саад (Y. Saad)
A981): Krylov subspace methods for solving large unsymmetric linear
systems. Math. Comp., vol. 37, pp. 105-126. [IV.10]
A982): The Lanczos biorthogonalization algorithm and other oblique
projection methods for solving large unsymmetric systems. SI AM J. Numer. Anal.,
vol. 19, pp. 485-506. [IV. 10]
Саад, см. также Гир и Саад
Сандберг и Сичман (I.W. Sandberg & Н. Sichman)
A968): Numerical integration of systems of stiff nonlinear differential
equations. The Bell System Technical Journal, vol. 47, pp. 511-527. [IV.12]
Санс-Серна и Кальво (J.M. Sanz-Serna & M.P. Calvo)
A994): Numerical Hamiltonian Problems. Appl. Math, and Math. Comput.
7, Chapman & Hall, 207pp. [VII.8]
Саульев В. К. (V.K. Saul'ev)
A960): Интегрирование уравнений параболического типа методом сеток.
— М.: Физматгиз, 1960. [IV.2]
650 Литература
Свешников, см. Тихонов, Васильева и Свешников
Сегё (G. Szego)
A939): Orthogonal Polynomials. AMS Coll. PubL, vol. XXIII, 403pp.
[Имеется перевод: Сегё Г. Ортогональные многочлены. — М.: Физматгиз.
1962.] [IV.13]
Сегё, см. также Пойа и Сегё
Сейфи, см. Купер и Сейфи
Сербии, см. Бейлс, Каракашьян и Сербии
Сёдерлинд (G. Soderlind)
A981): On the efficient solution of nonlinear equations in numerical methods
for stiff differential systems. Report TRITA-NA-8114, Royal Inst, of Tech.,
Stockholm. [IV. 10]
A989): A multi-purpose system for the numerical integration of ODEs. Appl.
Math. Comp., vol. 31, pp. 346-360. [VII.6]
Сёдерлинд и Далквист (G. Soderlind & G. Dahlquist)
A981): Error propagation and stiff differential systems of singular
perturbation type. Rep. TRITA-NA-8108, Royal Inst, of Tech., Stockholm. [VI.2]
Сёдерлинд, см. также Аревало, Фюрер и Сёдерлинд; Густафссон, Лунд и
Сёдерлинд; Далквист и Сёдерлинд
Синковец, Эрисман, Йип и Эптон (R.F. Sincovec, A.M. Erisman, E.L. Yip &
M.A. Epton)
A981): Analysis of descriptor systems using numerical algorithms. IEEE
Trans. Aut. Control, AC-26, pp. 139-147. [VII.3]
Сичман, см. Сандберг и Сичман
Скил и Конг (R.D. Skeel & А.К. Kong)
A977): Blended linear multistep methods. ACM TOMS, vol. 3, pp. 326-343.
]V.2], [V.3], [V.5]
Скил, см. также Леймкулер и Скил
Слоат и Биккарт (Н.М. Sloate & Т.A. Bickart)
A973): Л-stable composite multistep methods. J. ACM, vol. 20, pp. 7-26.
)v.s]
Соболевский П. E. (P.E. Sobolevskii)
(l959): О нестационарных уравнениях гидродинамики вязкой жидкости,
{окл. АН СССР, т. 128, № 1, с. 45-48. [V.8]
Соммейер (В.P. Sommeijer)
A991): RKC, a nearly-stiff ODE solver. Available from netlib@ornl.gov, send
rkc.f from ode. [IV.2], [IV.10]
Соммейер и Фервер (В.P. Sommeijer & J.G. VerwerJ
A980): A performance evaluation of a class of Runge-Kutta-Chebyshev
methods for solving semi-discrete parabolic differential equations. Report
NW91/80, Mathematisch Centrum, Amsterdam. [IV.2]
Соммейер, см. также Фервер, Хундсдорфер и Соммейер; ван дер Хаувен и
Соммейер
Соттас (G. Sottas)
A984): Dynamic adaptive selection between explicit and implicit methods
when solving ODE's. Report, Sect, de math., Univ. Geneve. [IV.2]
Соттас и Ваннер (G. Sottas & G. Wanner)
A982): The number of positive weights of a quadrature formula. BIT, vol. 22,
pp. 339-352. [IV.13]
Суле, см. Гийу и Суле
Спейкер (M.N. Spijker)
A983): Contractivity in the numerical solution of initial value problems. Nu-
mer. Math., vol. 42, pp. 271-290. [IV.11]
Литература 651
A985): Feasibility and contractivity in implicit Runge-Kutta methods. J.
Comp. Appl. Math., vol. 12 et 13, pp. 563-578. [IV.Ц]
A985): Stepsize restrictions for stability of one-step methods in the numerical
solution of initial value problems. Math. Comp., vol. 45, pp. 377-392. [IV. 11]
A986): The relevance of algebraic stability in implicit Runge-Kutta methods.
Teubner Texte zur Mathematik 82 (K. Strehmel, ed.), pp. 158-164. [IV.15]
A991): On a conjecture by LeVeque and Trefethen related to the Kreiss
matrix theorem. BIT, vol. 31, pp. 551-555. [V.7]
Спейкер, см. также Крузе, Хундсдорфер и Спейкер; Лю, Деккер и Спейкер;
Хундсдорфер и Спейкер
Стеклов В. А. (V. Steklov)
A916): О приближенном вычислении определенных интегралов при
помощи формул механических квадратур. Сходимость формул
механических квадратур (сообщение первое). — Петроград, Изв. Акад. наук,
серия 6, 1916, т. 10, № 3, с. 169-186; Sur Г approximation des fonctions a Taide
des polynomes de TchebychefT et sur les quadratures (note II) — там же,
1917, т. 11, № 8, с. 535-566. [IV.13]
Стиган, см. Абрамовиц и Стиган
Стилтьес (T.J. Stieltjes)
A884): Quelques recherches sur la Theorie des quadrature dites mecaniques.
Annales Scientif. de TEcole Norm. Sup., troisieme serie, tome I, pp. 409-426.
[IV.12]
Стокс (G.G. Stokes)
A845): On the theories of the internal friction of fluids in motion, and the
equilibrium and motion of elastic solids. Cambr. Phil. Soc. Trans., vol. 8.
Republished in: G.G. Stokes, Mathematical and Physical Papers, vol. 1,
Cambridge 1880. [V.8]
Странг, см. Изерлес и Странг
Стьюарт (G.W. Stewart)
A972): On the sensitivity of the eigenvalue problem Ax=XBx. SIAM J. Nu-
mer. Anal., vol. 9, pp. 669-686. [VII. 1]
Сун Чжень (Sun Geng)
A993): Symplectic partitioned Runge-Kutta methods. J. Comput. Math.,
vol. 11, pp. 365-372. [VII.8]
Тадмор (E. Tadmor)
A981): The equivalence of L2-stability, the resolvent condition, and strict
H-stability. Lin. Alg. and its Applies., vol. 41, pp. 151-159. [V.7]
Тихонов A. H. (A.N. Tikhonov)
A952): Системы дифференциальных уравнений, содержащие малые
параметры при производных. Матем. сборник, 1952, т. 31G3):3, с. 575-586.
[VI.3]
Тихонов А. Н., Васильева А. Б. и Свешников А. Г. (A.N. Tikhonov, А.В.
Vasil'eva & A.G. Sveshnikov)
A985): Дифференциальные уравнения. — М.: Наука, 1980.
Differential Equations. Trans, from the Russian by A.B. Sossinskij. Springer-Verlag,
238pp. [VI.3]
Трефетен, см. Левек и Трефетен
Триджианте, см. Лопес и Триджианте
Турек, см. Мюллер, Проль, Раннахер и Турек
Тюрке, см. Хайрер и Тюрке
652 Литература
Уиддер (D.V. Widder)
A946): The Laplace Transform. Princeton University Press, London. [IV. 11]
Уилкинсон (J.H. Wilkinson)
A965): The Algebraic Eigenvalue Problem. Clarendon Press, Oxford, 662
p. [Имеется перевод: Уилкинсон Дж. X. Алгебраическая проблема
собственных значений. — М.: Наука, 1970.] [IV.2]
Уиллоуби (R.A. Willoughby (ed.))
A974): Stiff Differential Systems. Plenum Press, New York. [IV. 1]
Уиллоуби, см. также Линигер и Уиллоуби
Уилльямсон, см. Изерлес и Уилльямсон
Уихидж и Хауг (R.A. Wehage & E.J. Haug)
A982): Generalized coordinate partitioning for dimension reduction in
analysis of constrained dynamic systems. J. Mechanical Design, vol. 104, pp. 247-
255. [VII.2]
Уоккер (P.P. Wakker)
A985): Extending monotone and non-expansive mappings by optimization.
Cahiers du C.E.R.O., vol. 27, pp. 141-149. [IV.12]
Уолшо, см. Kapp, Дункан и Уолшо
Уоткинс и Хансон-Смит (D.S. Watkins & R.W. HansonSmith)
A983): The numerical solution of sparably stiff systems by precise
partitioning. ACM trans. Math. Soft., vol. 9, pp. 293-301. [IV.10]
Уоттс, см. Шампайн и Уоттс
Фалб, см. Атанс и Фалб
Фейер (L. Fejer)
A933): Mechanische Quadraturen mit positiven Coteschen Zahlen. Math.
Zeitschrift, vol. 37, pp. 287-309. [IV.13]
Фельдхёйзен, ван (M.V. van Veldhuizen)
A984): Z?-stability and Kaps-Rentrop methods. Computing vol. 32, pp. 229-
237. [IV.7], [VI.4]
Фенг, Холланд и Галлун (A. Feng, CD. Holland & S.E. Gallun)
A984): Development and comparison of a generalized semi-implicit Runge-
Kutta method with Gear's method for systems of coupled differential and
algebraic equations. Comp. & Chem. Eng., vol. 8, pp. 51-59. [VI.4]
Фервер (J.G. Verwer)
A980): On generalized Runge-Kutta methods using an exact Jacobian at a
non-step point. ZAMM, vol. 60, pp. 263-265. [IV. 7]
A996): Explicit Runge-Kutta methods for parabolic partial differential
equations. To appear in Applied Numerical Mathematics. [IV.2]
Фервер, Хундсдорфер и Соммейер (J.G. Verwer, W.H. Hundsdorfer &
B.P. Sommeijer)
A990): Convergence properties of the Runge-Kutta-Chebyshev method. Nu-
mer. Math., vol. 57, pp. 157-178. [IV.2]
Фервер и Шольц (J.G. Verwer &: S. Scholz)
A983): Rosenbrock methods and time-lagged Jacobian matrices. Beitrage zur
Numer. Math., vol. 11, pp. 173-183. [IV.1]
Фервер, см. также Деккер и Фервер
Ферзеланд, см. Берзинс и Ферзеланд
Филд и Нойес (J. Field & R.M. Noyes)
A974); Oscillations in chemical systems. IV: Limit cycle behavior in a model
of a real chemical reaction. J. Chem. Phys., vol. 60, pp. 1877-1884. [IV. 10]
Финогенов, см. Лебедев В. И. и Финогенов С. А.
Литература 653
Франк, Шнайд и Иберхубер (R. Frank, J. Schneid & C.W. Ueberhuber)
A981): The concept of В -convergence. SIAM J. Numer. Anal., vol. 18,
pp. 753-780. [IV. 15]
A985): Stability properties of implicit Runge-Kutta methods. SIAM J.
Numer. Anal., vol. 22, pp. 497-514. [IV.14], fIV. 15]
A985): Order results for implicit Runge-Kutta methods applied to stiff
systems. SIAM J. Numer. Anal., vol. 22, pp. 515-534. [IV.14], [IV.15]
Франк, см. также Ауцингер, Франк и Мачек
Франклин (J.N. Franklin)
A959): Numerical stability in digital and analogue computation for diffusion
problems. J. Math. Phys., vol 37, pp. 305-315. [IV.2]
Фридли (A. Friedli)
A978): Verallgemeinerte Runge-Kutta Verfahren zur Losung steifer Differen-
tialgleichungssysteme. Oberwolfach Conference 1976, Lecture Notes in Math.
631, pp. 35-50. [IV. 11]
Фридрихс, см. Курант, Фридрихс и Леви
Фюрер (С. Fuhrer)
A988): Differential-algebraische Gleichungssysteme in mechanischen Mehr-
korpersystemen: Theorie, numerische Ansatze und Anwendungen. Doctoral
thesis, Technische Universitat Mvinchen [VII.2].
Фюрер и Леймкулер (С. Fuhrer & B.J. Leimkuhler)
A991): Numerical solution of differential-algebraic equations for constrained
mechanical motion. Numer. Math., vol. 59, pp. 55-69. [VII.2]
Фюрер, см. также Аревало, Фюрер и Сёдерлинд
Фудзита и Като (Н. Fujita & Т. Kato)
A964): On the Navier-Stokes initial value problem. I. Arch. Rat. Mech. Anal.,
vol. 16, pp. 269-315. [V.8]
Хайам (D.J. Higham)
A989): Analysis of the Enright-Kamel partitioning method for stiff ordinary
aifferential equations. IMA J. Numer. Anal., vol. 9, pp. 1-14. [IV.10]
Хайам и Холл (D.J. Higham & G. Hall)
A990): Embedded Runge-Kutta formulae with stable equilibrium states. J.
of Comp. and Appl. Math., vol. 29, pp. 25-33. [IV.2]
Хайам, см. также Холл и Хайам
Хайндмарш (А.С. Hindmarsh)
A980): LSODE and LSODI, two new initial value ordinary differential
equation solvers. ACM-SIGNUM Newsletter 15, pp. 10-11. [IV. 10], [V.5],
[VII.3]
A983): ODEPACK, a systematized collection of ode solvers. In Scientific
Computing, R.S. Stepleman et al. (eds.), North-Holland, Amsterdam, pp. 55-
64. [V.5]
Хайндмарш, см. также Берн и Хайндмарш; Браун, Берн и Хайндмарш
Хайрер (Е. Hairer)
A980: Highest possible order of algebraically stable diagonally implicit
Runge-Kutta methods. BIT, vol. 20, pp. 254-256. [IV. 13]
A982): Constructive characterization of Л-stable approximations to expz
and its connection with pp. 247-258. IIV.5]
A986): A- and Б-stability for Runge-Kutta methods - characterizations and
equivalence. Numer. Math., vol. 48, pp. 383-389. [IV.13]
A994): Backward analysis of numerical integrators and symplectic methods.
Annals of Numer. Math., vol. 1, pp. 107-132. [VII.8]
654 Литература
Хайрер, Бадер и Любих (Е. Hairer, G. Bader & Ch. Lubich)
A982): On the stability of semi-implicit methods for ordinary differential
equations. BIT, vol. 22, pp. 211-232. [IV.9], [IV. 11]
Хайрер и Ваннер (E. Hairer & G. Wanner)
A981): Algebraically stable and implementable Runge-Kutta methods of
high order. SIAM J. Numer. Anal., vol. 18, pp. 1098-1108. [IV.5], [IV.13]
A982): Characterization of non-linearly stable implicit Runge-Kutta
methods. In: Numerical integration of differential equations, Lecture Notes in
Math., vol. 968, pp. 207-219. [IV.5J, [IV.13]
A995): Analysis by its history. Undergraduate Texts in Mathematics,
Springer-Verlag New York. [IV.4],
A996): On a generalization of a theorem of von Neumann. To appear in
ZAMM. [IV. 12]
Хайрер и Дзеннаро (E. Hairer & M. Zennaro)
A996): On error growth functions of Runge-Kutta methods. To appear in
Appl. Numer. Math. [IV. 11], [IV. 12]
Хайрер и Любих (E. Hairer & Ch. Lubich)
A988): Extrapolation at stiff differential equations. Numer. Math., vol. 52,
pp. 377-400. [VI. 5]
A988b): On extrapolation methods for stiff and differential-algebraic
equations. Teubner Texte zur Mathematik, Band 104, Teubner, Leipzig, pp. 64-73.
[VLSI
A996): The life -span of backward error analysis for numerical integrators.
Numer. Math. [VII.8]
Хайрер, Любих и Рош (Е. Hairer, Ch. Lubich & M. Roche)
A988): Error of Runge-Kutta methods for stiff problems studied via
differential algebraic equations. BIT, vol. 28, pp. 678-700. [VI.3]
A989): Error of Rosenbrock methods for stiff problems studied via
differential algebraic equations. BIT, vol. 29, pp. 77-90. [VI.3]
A989) [сокр. ХЛР89]: The numerical solution of differential-algebraic
systems by Runge-Kutta methods. Lecture Notes in Math. 1409, Springer
Verlag. [VI.l], [VILl]t [VU-S], [VllAl [VII.5], [VI17]
Хайрер и Остерман (E. Hairer & A. Ostermann)
A990): Dense output for extrapolation methods. Numer. Math., vol. 58,
pp. 419-439. [VI.5]
Хайрер и Тюрке (E. Hairer & H. Turke)
A984): The equivalence of В-stability and Л-stability. BIT, vol. 24, pp. 520-
528. [IV.5], [IV. 13]
Хайрер, см. также Бразей и Хайрер; Ваннер, Хайрер и Нёрсетт; Деккер и
Хайрер; Дойфлхард, Хайрер и Цугк
Халл, см. Энрайт и Халл; Энрайт, Халл и Линдберг
Хамминг (R.W.Hamming)
A959): Stable predictor-corrector methods for ordinary differential equations.
J. ACM, vol. 6, pp. 37-47. [V.l]
Хансон-Смит, см. Уоткинс и Хансон-Смит
Хартри, см. Каллендер, Хартри и Портер
Хаувен, ван дер (P.J. van der Houwen)
A968): Finite difference methods for solving partial differential equations.
MC Tract 20, Math. Centrum, Amsterdam. fIV.2]
A973): One-step methods with adaptive stability functions for the integration
of differential equations. Lecture Notes in Mathematics No. 333, Springer-
Verlag, Berlin, pp. 164-174. [IV.7]
A977): Construction of integration formulas for initial value problems. North
Holland series in Applied Math, and Mech., 269 pp. [IV.2], [IV.11]
Литература 655
Хаувен, ван дер, и Соммейер (P.J. van der Houwen & В.P. Sommeijer)
A980): On the internal stability of explicit, m-stage Runge-Kutta methods
lor large m-values. Z. Angew. Math. Mech., vol. 60, pp. 479-485. [IV.2]
Хауг (E.J. Haug)
A989): Computer-aided Kinematics and Dynamics of Mechanical Systems.
Allyn & Bacon, Boston. [VIL7]
Хауг, см. также Уихидж и Хауг
Хаусдорф (F. Hausdorff)
A921): Summationsmethoden und Momentfolgen. Math. Zeitschrift, vol. 9,
pp. 74-109 and pp. 280-299. [IV. 11]
Хенри (D. Henry)
A981): Geometric Theory of Semilinear Parabolic Equations. Springer
Lecture Notes in Mathematics 840. [Имеется перевод: Хенри Дж.
Геометрическая теория полулинейных параболических уравнений. — М.: Мир,
1985.] [V.8J
Хенричи (P. Henrici)
A962): Discrete Variable Methods in Ordinary Differential Equations. Wiley,
New York. [V.7]
Хиберт, см. Шампайн и Хиберт
Хиршфельдер, см. Кертисс и Хиршфельдер
Холл (G. Hall)
A985): Equilibrium states of Runge-Kutta schemes. ACM Trans. Math.
Software, vol. 11, pp. 289-301. [IV. 1], [IV.2]
A986): Equilibrium states of Kunge-Kutta schemes, part II. ACM TVans.
Math. Software, vol. 12, pp. 183-192. [IV.2]
Холл и Хайам (G. Hall & D.J. Higham)
A988): Analysis of stepsize selection schemes for Runge-Kutta codes. IMA
J. Numer. Anal., vol. 8, pp. 305-310. [IV.2]
Холл, см. также Хайам и Холл
Холланд, см. Фенг, Холланд и Галлун
Хопф (Е. Hopf)
A950): The partial differential equation щ + uux = puXx • Comm. on Pure
and Appl. Math., vol. 3, pp. 201-230. [VI.5], [VI.6]
Хофер (E. Hofer)
A976J: A partially implicit method for large stiff systems of ODE's with
only few equations introducing small time-constants. SI AM J. Numer. Anal.,
vol. 13, pp. 645-663. [IV.10]
Xcy, см. Гир, Xcy и Петзолд
Хундсдорфер (W.H. Hundsdorfer)
A985): The numerical solution of nonlinear stiff initial value problems: an
analysis of one step methods. CWI Tract, Nr. 12, Mathematisch Centrum,
Amsterdam. 7lV.ll], [IV.12], [IV.14]
A986): Stability and В-convergence of linearly implicit Runge-Kutta
methods. Numer. Math., vol. 50, pp. 83-95. [IV.15]
Хундсдорфер и Спейкер (vV.H. Hundsdorfer & M.N. Spijker)
A981): A note on В-stability of Runge-Kutta methods. Numer. Math.,
vol. 36, pp. 319-331. [IV.12]
A987): On the algebraic equations in implicit Runge-Kutta methods. SI AM
J. Numer. Anal., vol. 24, pp. 583-594. [IV.Ц]
Хундсдорфер и Штайнингер (W.H. Hundsdorfer & B.I. SteiningerJ
A991): Convergence of linear multistep and one-leg methods for stiff nonlinear
initial value problems. BIT vol. 31, p.124-143. [V.6], [V.7]
656 Литература
Хундсдорфер, см. также Берридж и Хундсдорфер; Крузе, Хундсдорфер и
Спейкер; Фервер, Хундсдорфер и Соммейер
Цугк, см. Дойфлхард, Хайрер и Цугк
Чебышев П. Л. (P.L. Chebyshev (Tchebychef))
A854): Theorie des mecanismes connus sous le nom de parallelogrammes.
Mem. de Г Acad. Imp. St.-Petersbourg, tome VII A854), pp.539-568; Oeuvres
Tome I, pp. 111-143. [Имеется перевод: Теория механизмов, известных
под названием параллелограмов. Чебышев П. Л. Избранные труды. —
М.: Изд-во АН СССР, 1955, с. 611-648.] [IV.2]
Чейс (Р.Е. Chase)
A962): Stability properties of Predictor-Corrector methods for ordinary
differential equations, J. Assoc. Comput. Mach., vol. 9, pp.457-468. [V.lJ
Чиккотти, см. Рюккерт, Чиккотти и Берендсен
Чин, см. Ашер, Чин и Райх
Чипман (F.H. Chipman)
A971): Л-stable Runge-Kutta processes. BIT, vol. 11, pp. 384-388. [IV.5]
A976): A note on implicit Л-stable RK methods with parameters. BIT,
vol. 16, pp. 223-227. [IV. 5]
Чипман, см. также Берридж, Бутчер и Чипман
Шампайн (L.F. Shampine)
A977): Stiffness and nonstiff differential equation solvers, II: detecting
stiffness with Runge-Kutta methods. ACM TOMS, vol. 3, pp. 44-53. [IV.2]
A980): Implementation of implicit formulas for the solution of ODEs. SIAM
J. Sci. Stat. Comput., vol. 1, pp. 103-118. [IV.8]
A981): Evaluation of a test set for stiff ODE solvers. ACM Trans. Math.
Soft., vol. 7, pp. 409-420. JIV.lOj
A982): Implementation of Rosenbrock methods. ACM Trans. Math. Soft.,
vol. 8, pp. 93-113. [IV. 7]
A986): Conservation laws and the numerical solution of ODEs. Comp. Maths.
Appls., vol. 12B., pp. 1287-1296. [VII.2]
A987): Control of step size and order in extrapolation codes. J. Comp. Appl.
Math., vol. 18, pp. 3-16. [IV.9]
Шампайн и Уоттс (L.F. Shampine & H.A. Watts)
A979): DEPAC — design of a user oriented package of ODE solvers. Report
SAND-79-2374, Sandia Nat. Lab., Albuquerque, New Mexico. [V.5]
Шампайн и Хиберт (L.F. Shampine & K.L. Hiebert)
A977): Detecting stiffness with the Fehlberg D,5) formulas. Comp. & Maths.
with Appls., vol. 3, pp. 41-46. [IV.2]
Швертассек, см. Роберсон и Швертассек
Шерер (R. Scherer)
A979): A necessary condition for B-stability. BIT, vol. 19, pp. 111-115.
[IV.3], [IV.12]
Шефер (E. Schafer)
A975): A new approach to explain the "High Irradiance Responses" of
photomorphogenesis on the basis of phytochrome. J. of Math. Biology, vol. 2,
pp. 41-56. [IV. 10]
Шёнберг (I.J. Schoenberg)
A953): On a Theorem of Kirszbraun and Valentine. Amer. Math. Monthly,
vol. 60, pp. 620-622. [IV. 12]
Литература 657
Шилен (W. Schiehlen, ed.)
A990): Multibody systems handbook. Springer Verlag, Berlin. [VII.7]
Шнайд (J. Schneid)
A987): В -convergence of Lobatto 111С formulas. Numer. Math., vol. 51,
pp. 229-235. [IV. 15]
Шнайд, см. также Деккер, Крайевангер и Шнайд; Крайевангер и Шнайд;
Франк, Шнайд и Иберхубер
Шнайдер (С. Schneider)
A991): ROW-methods adapted to differential-algebraic systems. Math.
Comp., vol. 56, pp. 201-213. [VI. Al
A991b): Private communication. [VI.Ц
A993): Analysis of the linearly implicit mid-point rule for differential-
algebraic equations. Electronic Transactions on Numerical Analysis, vol. 1,
pp. 1-10. [VI.5]
Шольц (S. Scholz)
A989): Order barriers for the Б-convergence of ROW methods. Computing,
vol. 41, pp. 219-235. [IV.15]
Шольц, см. также Фервер и Шольц
Шролль, см. Григориефф и Шролль
Штайнебах (G. Steinebach)
A995): Order-reduction of ROW-methods for DAEs and method of lines
applications. Preprint, TH Darmstadt. [VI.4]
Штайнебах, см. также Рентроп, Рош и Штайнебах
Штайнингер, см. Хундсдорфер и Штайнингер
Штайхауг и Вольфбрандт (Т. Steihaug & A. Wolfbrandt)
A979): An attempt to avoid exact Jacobian and nonlinear equations in
the numerical solution of stiff differential equations. Math. Comp., vol. 33,
pp. 521-534. [IV.1]
Штеттер (H.J. Stetter)
A968): Improved absolute stability of predictor-corrector schemes.
Computing, vol. 3, pp. 286-296. [V.l]
A973): Analysis of discretization methods for ordinary differential equations.
Springer, Berlin. [Имеется перевод: Штеттер X. Анализ методов
дискретизации для обыкновенных дифференциальных уравнений. — М.: Мир,
1978.] [IV.3], [IV.9], [IV.12]
Штоффер, см. Нипп и Штоффер
Штремель и Вайнер (К. Strehmel & R. Weiner)
A982): Behandlung steifer Anfangswertprobleme gewohnlicher Differential-
gleichungen mit adaptiven Runge-Kutta Methoden. Computing, vol. 29, pp.
153-165. [IV. 11]
A987): Б-convergence results for linearly implicit one step methods. BIT,
vol. 27, pp. 264-281. [IV. 11], [IV. 15]
Штуббе, см. Коллет, Экман, Эпштайн и Штуббе
Шур (J. Schur)
A918): Uber Potenzreihen, die im Innern des Einheitskreises beschrankt sind.
J. Reme u. angew. Math., vol. 147, pp. 205-232. [V.3]
Эйкен (R.C. Aiken ed.)
1985): Stiff computation. Oxford, Univ. Press, 462pp. [IV. 1], [IV.3], [IV.8],
V.5]
Эйлер Л. (L. Euler)
A737): De fractionibus continuis dissertatio. Comm. acad. sc. Petrop., vol. 9,
pp. 98-137; Opera Omnia vol. XIV, pp. 187-215 (vide §7). [Имеется перевод:
658 Литература
Эйлер Л. Введение в анализ бесконечных, т. I (изд. 2-е). — М.: Физмат-
гиз, 1961. — Гл. XVIII. О непрерывных дробях, с. 269-286J [IV.13)
A752): Elementa doctrinae solidorum. Nov. comm. acad. sci. Petropohtanae
vol. 4, p. 109-140; Opera Omnia vol. XXVI, pp. 71-93. [IV.i]
Экман, см. Кол лет, Экман, Эпштайн и Штуббе
Энгквист, см. Бренан и Энгквист
Энгстлер, см. Любих, Новак, Пеле и Энгстлер
Энрайт (W.H. Enright)
A974): Optimal second derivative methods for stiff systems. In: Stiff
Differential Systems, ed. by R.A. Willoughby, Plenum Press, New York.
A974): Second derivative multistep methods for stiff ordinary differential
equations, SIAM J. Numer. Anal., vol. 11, pp. 321-331. [V.3]
A978): Improving the efficiency of matrix operations in the numerical solution
of stiff ordinary differential equations. ACM Trans, on Math. Software, vol. 4,
pp. 127-136. [IV.8]
Энрайт и Камел (W.H. Enright & M.S. Kamel)
A979): Automatic partitioning of stiff systems and exploiting the resulting
structure. ACM TOMS, vol. 5, pp. 374-385. [IV.10]
Энрайт и Халл (W.H. Enright & Т.Е. Hull)
A976): Comparing numerical methods for the solution of stiff systems of
ODEs arising in chemistry. In: Numerical methods for differential systems,
recent developments in algorithms, software and applications, L. Lapidus &
W.E. Schiesser, Eds., Academic Press, New York, 1976, pp. 45-66. [IV.10]
Энрайт, Халл и Линдберг (W.H. Enright, Т.Е. Hull & В. Lindberg)
A975): Comparing numerical methods for stiff systems of ODEs. BIT, vol. 15,
pp. 10-48. [IV. 10]
Эптон, см. Синковец, Эрисман, Йип и Эптон
Эпштайн, см. Коллет, Экман, Эпштайн и Штуббе
Эрисман, см. Синковец, Эрисман, Йип и Эптон
Эрмит (Ch. Hermite)
A873): Sur la fonction exponentielle. Comptes rendus de Г Acad. Sciences,
vol. 77, pp. 18-24, 74-79, 226-233, 285-293. (Euvres, tome III, pp. 150-181.
[IV.3]
Юань Чжао-дин (Yuan Chzao Din)
A958): Некоторые разностные схемы решения первой краевой задачи
для линейных дифференциальных уравнений с частными
производными. Диссертация, МГУ, 1958.
Якоби (C.G.J. Jacobi)
A826): Ueber Gauss' neue Methode die Werthe der Integrate naherungsweise
zu finden. Journ. f. reine u. angew. Math., vol. I, pp. 301-308; Werke
Vol. VI A981), pp. 1-11. [IV.5]
Указатель обозначений
А порядковая звезда 65 , 321
Л® J тензорное (прямое) произведение 246 , 371
В относительная порядковая звезда 73 , 83 , 324
В(р) упрощающее предположение 87 , 406
С константа погрешности 56 , 281 , 296
C(rj) упрощающее предположение 87 , 406
С+ положительная полуплоскость 66
С~ отрицательная полуплоскость 70
С{р) сопутствующая матрица 363
DAT , DAT2 , DATy , DAT2y , DATz1 DAT2Z —множества
дифференциально-алгебраических деревьев 452 , 555
D(?) упрощающее предположение 87
?*л@ упрощающее предположение 406
&в@ упрощающее предположение 406
di индекс дифференцирования 499
Dr диск (круг) радиуса г 287
Е(у) многочлен Е 56 , 115
E(z) погрешность 32
F(t) элементарный дифференциал 125 , 453 , 556
/(?) преобразование Фурье 288
Н{р , я) функция Гамильтона 593
Kq(s) ядро Пеано 288
K(Z) функця устойчивости для уравнения у'=\(х)у 212
LDAT , LDAT2 , LDATyy LDAT2y , LDATZ , LDAT22 —множества
дифференциально-алгебраических деревьев 454 , 557
^{t) многочлен Лагранжа 547
L(q , q) функция Лагранжа 22 , 508
La(x) полином Лагерра 114
LT множество помеченных деревьев порядка q 125
Р проектор 542
pD порядок дифференцирования 354
pi индекс возмущений 504
Pj порядок интерполяции 354
Р^{х) сдвинутый полином Лежандра 95 , 231
660 Указатель обозначений
Q проектор 542
Q(/i , C) характеристический многочлен 318 , 328
Rkj{z) аппроксимация Паде 62
R(z) функция устойчивости 26 , 54 , 126 , 154
гАр , ) коэффициент дискретной резольвенты 373 , 394 , 428
г(? , /г) дискретная резольвента 373 , 394
5 область устойчивости 26 , 273
gscal нормированная область устойчивости 74
S(Z) матрица устойчивости 401
Sa сектор Л (а)-устойчивости 283
S(p) матрица устойчивости 328
Т кинетическая энергия 508 , 580
Т множество деревьев 136
Tm(z) многочлен Чебышева 43
TW множество деревьев для W -методов 135
Г(т7 , С) свойство Т 98
U потенциальная энергия 508 , 582
\\u\\D норма 249
\\\u\\\D норма в прямом произведении пространств 246 , 249
|||и|||G норма в прямом произведении пространств 371
||v||G норма , порождаемая скалярным произведением 347 , 398
X преобразованная матрица метода Рунге—Кутты 95 , 98 ,
211 и д.
aD(A~l) коэффициент коэрцитивности 245
а0(А~1) коэффициент коэрцитивности 245
SD (х) погрешность дифференцирования 353
Sh(x) локальная погрешность 257 , 258 , 259 , 363
6j(x) погрешность интерполяции 354
SLM(x) погрешность линейного многошагового метода 362
SOL(x) погрешность одноопорного метода 353
/х(Л) логарифмическая норма 194
//(С) множитель 384
и односторонняя константа Липшица 207 , 245 , 344 , 380
р пороговый коэффициент 203
p(t) порядок дерева 453 , 556
р(С) производящий многочлен 272
<т(С) производящий многочлен 272
^в(^) функция роста погрешности 220
<Pr{x) функция роста погрешности для линейных задач 195
V оператор конечной разности назад 275
Предметный указатель1
Автоматическое обнаружение
жесткости (automatic stiffness detection)
31
Адамса методы (Adams methods) 14 ,
273 , 275 и д. , 282 , 287 , 300 , 326 , 578
, кривые локуса корней (root
locus curves for ~ ~) 275
Алгебраическая устойчивость
методов общих линейных (algebraic
stability of general linear methods) 400
PK (~~ ofRK ~) 209 ид. ,
236 , 263
многошаговых (~ ~ of
multistep ~ ~) 409 и д.
Алгебраические уравнения связи
(algebraic constraints) 582
Алгебраический критерий В
-устойчивости (algebraic criterion for
instability) 209
Андрьюса сжимающий механизм
(Andrews' squeezer mechanism)
579 и д.
Арнольди процесс (Arnoldi process)
187
Бадера—Дойфлхарда метод (Bader-
Deuflhard method) 156 ид.
Баккера многочлены (Bakker
polynomials) 47 , 52
Баумгарте стабилизация (Baumgar-
te stabilization) 515
Беккера—Дёринга модель (Becker-
Doring model) 173 и д.
Белоусова—Жаботинского реакция
(Belousov-Zhabotinskii reaction) 168
Бернштейна неравенство (Bernstein
inequality) 365
— теорема (~'s theorem) 365
Брюсселятор (Brusselator) 14 , 29 ,
171 , 175
Бюргерса уравнение (Burgers
equation) 391 , 488 , 494
Ван-дер-Поля уравнение (van der Pol
equation) 12 , 33 , 146 , 163 , 167 , 414 ,
446 , 449 , 481 , 617
, асимптотическое решение
(asymptotic solution of ~ ~ ~ ~)
414
Ван дер Хаувена и Соммейера
подход (van der Houwen & Sommeijer's
approach) 47
Вандермонда матрица (Vandermonde
matrix) 94 , 236
«Beep леди Уиндермир» (Lady
Windermere's Fan) 533 , 544
Вейерштрасса—Кронекера теорема
(Weierstrass-Kronecker theorem)
497
Векторное поле на многообразии
(vector field on manifold) 502
Верле метод (Verlet method) 599
Висящая веревка (hanging rope)
22 и д. , 50
Вольтерры интегральное уравнение
(Volterra integral equation) 396
Вольтерры—Лотки уравнение
(Volterra-Lotka equation) 608
Гамильтона принцип (Hamilton
principle) 18
— функция , гамильтониан (Hamilto-
nian function) 519 , 593 и д.
— функция , сохранение
(preservation of ~) 595 и д.
Гамильтоновы системы (~ systems)
520 и д.
со связями (constrained ~ ~)
593 и д.
Гаусса квадратурные формулы
(Gaussian quadrature formulas) 231 ,
408
— методы (~ methods) 87 , 211 , 226 ,
229 , 250 , 258 , 552 и д.
ГБШ методы (GBS methods) 27 , 29 ,
156
ГЛ/7-формулировка механической
системы (GGL formulation of
mechanical system) 510 , 525
Гибридные многошаговые методы
(hybrid multistep methods) 302
Гиперболические задачи (hyperbolic
problems) 49
— разностные схемы (~ difference
schemes) 65
Гира—Саада метод (GBS method)
187 и д.
' В конце Предметного указателя приведены термины , начинающиеся с
латинских и греческих букв , а также названия программ , задач и методов
в виде сокращений латинскими буквами. — Прим. ред.
662 Предметный указатель
Главный корень (principal root) 322
— лист (~ sheet) 322 , 330
«Горб» (hump) 133 , 145 , 448
«Греко-латинское» преобразование
(Graeco-Roman transformation) 288
Грина функция (Green's function) 18
Гронуолла лемма (Gronwall lemma)
504
Далквиста барьер второй (Dahl-
quist's second barrier) 65 , 280 , 288 ,
323 , 335 , 337
первый (~ first *v) 336
— тестовое уравнение (~ test
equation) 26 , 272
Даниела—Мура гипотеза (Daniel-
Moore conjecture) 65 , 323 , 333 , 336 ,
407
ДАУ (DAE) 415 , 495
— индекса 1 (~ of index 1) 417
— индекса 2 (~ of index 2) 528 , 540 ,
555
Движущиеся конечные элементы
(moving finite elements) 487 и д.
Демпфирование (damping) 45 и д. ,
58 , 293
Деревья для ДАУ индекса 1 (trees
for index 1 DAE) 452 и д.
— для ДАУ индекса 2 (~ for index
2 DAE) 555
— для ОДУ (~ for ODE) 110 и д. ,
124 и д.
— для W-методов (~ for W-
methods) 135
— монотонно помеченные (monoton-
ically labelled ~) 454 , 557
— помеченные (~ ~) 124
Диагонально неявные методы РК
(diagonally implicit RK methods) ,
см. ДНРК
Диаграмма «объем вычислений —
точность» (work-precision diagram)
178 и д. , 184 и д. , 340 и д. , 587 , 589
Дини производная (Dini derivative)
435
Диполи (dipoles) 83
Дискретная резольвента (discrete
resolvent) 373
— формула вариации постоянных
(~ variation of constants formula)
372 , 389 и д.
Дискриминант (discriminant) 318
Дифференциальная 2-форма
(differential 2-form) 594
Дифференциально-алгебраические
уравнения (differential-algebraic
equations) , см. ДАУ
переопределенные (~ *%* overde-
termined) 524
Дифференциально-геометрический
подход (differential-geometric
approach) 520
Дифференциальные уравнения
возмущенные (perturbed differential
equations ) 607 и д.
второго порядка (~ ~ of second
order) 626 и д.
— — на многообразиях (~ ~ on
manifolds) 502 , 520 и д. , 594
с инвариантами (~ ~ with
invariants) 518 ид.
Диффузия (diffusion) 14 , 29 , 175
ДНРК (DIRK) 82 , 109 и д.
Дойфлхарда и Новака метод (method
of Deuflhard & Novak) 492
Доминантное инвариантное
подпространство (dominant invariant sub-
space) 186
Дорманда и Принса методы (Dor-
mand & Prince methods) 27 , 31 , 34 ,
38
Дородницына асимптотическая
формула (Dorodnicyn's asymptotic
formula) 416
Единственность решений для
методов РК (uniqueness of RK solutions)
250 , 440
для многошаговых методов (~
of multistep solutions) 345 и д. , 529
Жесткая механическая система
(stiff mechanical system) 590
— устойчивость многошаговых
методов (~ stability of multistep
methods) 283
Жесткие собственные значения (~
eigenvalues) 186
векторы (~ eigenvectors) 186
— уравнения (~ equations) 9 и д.
Жестко точные методы (stiffly
accurate methods) 59 , 111 и д. , 259 , 418 ,
462 ид. , 603
ОДНРК (~~ SDIRK ~)
111 ид.
Жесткость (stiffness) 175
— , обнаружение (~ detection) 31
Забегающая вперед точка
(super-future point) 302
Предметный указатель 663
Задачи оптимального управления
(optimal control problems) 506 и д.
Звезды порядковые (order stars) , см.
Порядковые звезды
Золотарева аппроксимация (Zolota-
rev approximation) 47
— многочлен (~ polynomial) 48
Инварианты (invariants) 518
Индекс (index) 496 и д.
— возмущений (perturbation ~) 503
— дифференцирования
(differentiation ~) 498 и д. , 525
— нильпотентности (~ of nilpoten-
су) 498 , 512
Йелча—Неванлинны теорема
(Jeltsch-Nevanlinna theorem) 75 ,
326
КАМ теория (КAM theory) 611
Карта (chart) 502
Катастрофа «сборки» (cusp
catastrophe) 170
Каша алгоритм (Cash's algorithm)
303
Каша расширенные многошаговые
методы (extended multistep
methods of Cash) 302
Квазилинейные дифференциальные
уравнения (quasilinear differential
equations) 487 , 627
Кинетическая энергия (kinetic
energy) 17 и д. , 508 , 580 , 591
Кирхгоф фа закон (Kirchhoff's law)
419
Колебания высокочастотные (high
oscillations) 20 , 21 , 60
Коллокационные методы
возмущенные (perturbed collocation methods)
95
для ДАУ индекса 2 (~ ~ for
index 2 DAE) 546 и д.
многошаговые (multi-step ~ ~)
305 и д. , 312 , 403
однократно неявные (singly
implicit ~ **) 151
одноопорные (one-leg ~ ~) 359
одношаговые (one-step ~ ~) 61 ,
63 , 87 , 94 , 208 , 236
проецированные (projected ~
~) 549
Коллокационный многочлен
(collocation polynomial) 306
Композитные многошаговые методы
(composite multistep methods) 302
Композиция методов (composition of
methods) 64 , 605 и д.
Консервативная система
(conservative system) 508
Константа погрешности (error
constant) 280 ид. , 294
для методов ФДНВП (~ ~ for
SDBDF methods) 299
Энрайта (~ ~ for Enright
~) 296 и д.
для рациональных
аппроксимаций (~ ~ of rational
approximations) 56 , 67 , 76 , 82
Контрактивность (contractivity)
193 и д.
Контрпримеры для определений
индекса (counter-examples for index
definitions) 506 и д.
— для свойств устойчивости (~ for
stability properties) 227
— для существования (~ for
existence) 247
Конфлюентные методы РК
(confluent RK methods) 214
— узлы (~ nodes) 233
Корень дерева (root of a tree) 452
Коши интегральная формула
(Cauchy's integral formula) 430
Коэрцитивность (coercivity) 245
Коэффициенты коэрцитивности
(coercivity coefficients) 245 и д.
Крайсса задача (Kreiss problem) 591
Крайсса матричная теорема (Kreiss
matrix theorem) 363 и д.
«Красно-черная» редукция (red-
black reduction) 191
Кратные вещественные полюсы
(multiple real poles) 82 , 116 ид.
Кривая локуса корней (root locus
curve) 274 и д.
для методов Адамса (~ ~ ~
for Adams methods) 275
— — — — — Милна—Симпсона
(^ ~ ~ for Milne-Simpson ~) 278
Нюстрёма (~ ~ ~ for
Nystrom ~) 278
ФДН (~ ~ ~ for BDF
~) 279 , 387
ФДНВП (~ for
SDBDF ~) 300
Энрайта (~ ~ ~ for
Enright ~) 297
модифицированная
(modified ~ ~ ~) 386
Кристоффеля—Дарбу формула
(Christonel-Darboux formula) 152
664 Предметный указатель
Критерий G-устойчивости (criterion
for G-stability) 348
— остановки (stopping ~) 141 , 190 ,
192
Крылова подпространство (Krylov
subspace) 187
Кунцмана—Бутчера методы (Kuntz-
mann-Butcher methods) 54 , 57 , 87
Курамото—Сивашинского
уравнение (Kuramoto-Sivashinsky
equation) 172
Кэли преобразование (Cayley
transform) 272
Кэри Гранта пробор (Сагу Grant's
part) 77 , 80 , 82
Лагерра полиномы (Laguerre
polynomials) 86 , 114 , 152
Лагранжа—Гамильтона принцип
(Lagrange-Hamilton principle) 508
Лагранжа многочлены (Lagrange
polynomials) 547
— множители (~ multipliers)
223 и д. , 509 , 524
— теория (~ theory) 17 , 22
— функция (~ function) 22 , 223 , 508 ,
593
Лебедева реализация (Lebedev's
realization) 45
Лежандра полиномы сдвинутые или
смещенные (shifted Legendre
polynomials) 87 , 95 , 106 , 231
Линейно неявное правило средней
точки (linearly implicit midpoint
rule) 156 и д. , 166 , 485
— неявный метод РК (~ ~ RK
method) 121
Липшица постоянная , оценка
(estimation of Lipschitz constant) 33 , 34
односторонняя (one-sided ~ ~)
207
— условие одностороннее (~ ~
condition) 207 и д. , 245 , 344 , 380 , 398
Лобатто IIIА методы (Lobatto IIIA
methods) 54 , 57 , 91 и д. , 213 , 241 ,
252 , 258 , 552
— IIIA-IIIB пара (~ IIIA-IIIB pair)
601 и д. , 615
— 11 IB методы (~ 11 IB methods)
91 и д. , 213 , 241 , 252 , 258
— IIIC методы (~ IIIC ~) 91 и д. ,
211 , 226 , 250 и д. , 253 , 258 , 446 и д. ,
552
Логарифмическая норма
(logarithmic norm) 194 , 433
Локальное пространство состояний
(local state space) 521
Локальные координаты (~
coordinates) 522
Локуса корней кривая , см. Кривая
локуса корней
Лосона преобразование (Lawson's
transformation) 156
Маятник (pendulum) 509 , 514 , 520
Межузельная вязкость (internodal
viscosity) 488
Метастабильность (metastability)
174
Метод е -вложения (е -embedding
method) 416 , 425 , 437 , 450 , 492 , 540
— пространства состояний (state
space form ~) 418 , 426
Механические системы (mechanical
systems) 508 и д.
со связями (constrained ~ ~)
509 , 515 , 524 , 573 , 579 и д. , 593
Мёбиуса преобразование (Mobius
transformation) 365
Милна—Симпсона методы (Milne-
Simpson methods) 278 , 282 , 326
, кривая локуса корней (root
locus curve for ~ ~) 278
Многообразие (manifold) 501
Многочлен E(y) (polynomial E(y))
56 , 85 , 115 и д.
Многочлен M(x) (polynomial М(х))
61 , 108 , 231 и д.
Многошаговые методы (mult 1st ер
methods) 271 и д.
/3 -блоковые (/3 -blocked ~~)
577
для задач индекса 1 (~ ~ for
index 1) 425 и д.
для задач индекса 2 (~ ~ for
index 2) 528 и д.
для квазилинейных ДАУ (~ ~
for quasilinear DAE) 492
ко л локационные (~ collocation
methods) 305 и д. , 312 , 402
обобщенные (generalized ~ ~)
295 и д.
общие (general ~ ~) 272 , 536
смешанные (blended ~ ~) 300 ,
341
со второй производной (second
derivative ~ ~) 295
— — со старшими производными
(multiderivative ~~K18
Многошаговый двойник одноопорно-
го метода (multistep twin of one-leg
Предметный указатель 665
method) 345
Множество
дифференциально-алгебраических корневых деревьев (set
of differential algebraic rooted trees)
452
Множители (multipliers) 383 и д. ,
387 ид. ,
МРФДН-методы (MEBDF methods)
304
Навъе—Стокса уравнение (Navier-
Stokes equation) 392
Начальные значения для итерации
методом Ньютона (starting values
for Newton iteration) 141
— — согласованные (consistent
initial values) , см. Согласованные
начальные значения
Неавтономные задачи
(non-autonomous problems) 122 , 132 , 163 , 451
Непрерывное численное решение
(continuous numerical solution)) , см.
Плотная выдача
Непрерывные дроби (continued
fractions) 64 , 102 , 230 и д. , 241 , 243 и д.
, связанные с квадратурными
формулами (~ ~ related to
quadrature formulas) 230 и д. , 241 , 243 и д.
Неприводимые методы РК
(irreducible RK methods) 215
Несогласованные начальные
значения (inconsistent initial values)
466 и д.
Неявные дифференциальные
уравнения (implicit differential
equations) 122 , 132 , 149 , 164
F(u' , и) = 0 496 , 504 , 525
Mti' = y>(ti) 122 , 149 , 164 ,
420 , 451 , 470
M(u)u'=ip(u) 487 , 506 , 627
HPK (IRK) , см. Рунге—Кутты
методы неявные
НРК(ДАУ) [IRK(DAE)] 418
Ньютона метод упрощенный
(simplified Newton) 140 и д. , 538
Ньютона—Канторовича теорема
(theorem of Newton-Kantorovich)
440
Нюстрёма методы (Nystrom
methods) 278
, кривая локуса корней (root
locus curve for ~ ~) 278
Область устойчивости (stability
domain , ~ region) 26 , 273
абсолютной (region of absolute
stability) 273
— — крестообразная (cross-shaped
stability domain) 52
методов Адамса (~ ~ of Adams
methods) 275
Дорманда—Принса (~ ~ for
DOPRI ~) 28
— — — Рунге—Кутты неявных
(~~ of IRK ~) 55
Рунге—Кутты явных (~ ~
of ERK ~) 28
Милна—Симпсона (~~ of
Milne-Simpson ~) 278 и д.
МРФДН (--of MEBDF ~)
304
Нюстрёма (~ — of Nystrom
~) 278
ФДН (~ ~ of BDF ~) 279
Чебышева (— — of Cheby-
shev —) 44 и д.
— — — Энрайта (— — of Enright
methods) 297
неявного метода Эйлера (~ ~
of implicit Euler ~) 53 , 279
нормированная (scaled — —) 74
схем предиктор-корректор (~
~ of predictor-corrector schemes)
277
управления длиной шага
(region of step-control stability) 37 , 42
экстраполированного линейно
неявного правила средней точки
(stability — of extrapolated linearly
implicit mid-point rule) 160
— — экстраполированного метода
Эйлера (— — of extrapolated Euler)
161
экстраполированного правила
трапеций (— ~ of extrapolated
trapezoidal rule) 155
— — экстраполяционных методов
ГБШ (~ ~ of GBS extrapolation
methods) 29
Обратная связь дифференциальная
(derivative feedback) 40
интегральная (integral ~) 40
пропорциональная
(proportional ~) 40
Общие линейные методы (general
linear methods) 328 и д.
, алгебраическая
устойчивость (algebraic stability of ~ ~ ~)
398 и д.
Одноопорные многошаговые методы
(one-leg multistep ~) 345 и д.
666 Предметный указатель
, оценки погрешностей (error
bounds for ~ ~ ~) 353
ОДНРК (SDIRK) , см. Рунге-Кут-
ты методы однократно
диагонально неявные
ОДНРК программа (SDIRK-code)
149
ОДУ (ODE) , обыкновенные
дифференциальные уравнения (ordinary
differential equations) , см.
Дифференциальные уравнения
ОДУ , лежащее в основе ДАУ
(underlying ODE) 499 , 525
ОНРК (SIRK) , см. Рунге—Кутты
методы однократно неявные
Оптимального управления задачи
(optimal control problems) 506 и д. ,
513
Орегонатор (Oregonator) 22 , 168
Отделимо жесткая система
(separably stiff system) 186
Отключение вершин дерева (short-
circuiting tree) 111 ид.
Относительное разделение (relative
separation) 186
Паде аппроксимации для ег (Pade
approximations to ez ) 62 и д. , 85 ,
196
диагональные (diagonal ~ ~)
63 , 92
, области устойчивости(stability
domains for ~ ~) 66
Параболические ДУЧП (parabolic
PDE) 43 , 390 и д.
— разностные схемы (~ difference
schemes) 65
Параллельные процессоры (parallel
processors) 150
Параметризация касательного
пространства (tangent space paramet-
rization) 523
Парсеваля равенство (Parseval
identity) 289 , 293
Пеано ядро (Peano kernel) 288 , 293
Первый интеграл (first integral) 518
Переходная фаза (transient phase)
10 , 13 , 58 , 186 , 432
ПИД-управление (PID control) 39
Плотная выдача (dense output) 627
в методах Розенброка для ДАУ
(~ ~ of DAE Rosenbrock methods)
466
Энрайта (~ ~ of Enright
~) 298 и д.
ОДНРК порядка 4 (~ ~
of SDIRK4 ~) 118
в многошаговых коллокацион-
ных методах (~ ~ of multistep
collocation ~) 307
в экстраполяционных методах
для ДАУ (~~ of DAE
extrapolation ~) 161 , 483 ид.
Пограничный слой (boundary layer)
424 , 432
Погрешностей обратный анализ
(backward error analysis) 607 и д. ,
611 ид.
Погрешность глобальная (global
error) 257 и д. , 361 , 362 , 368 , 442 ,
446 и д.
— дифференцирования
(differentiation ~) 353
— допустимая (tolerance) 16 , 17 , 19 ,
41 , 60 , 142
— интерполяции (interpolation ~)
354
— локальная (local ~) 133 , 148 ,
257 и д. , 448 , 532 , 542 и д.
Положительные квадратурные
формулы (~ quadrature formulas) 210 ,
230 ид. , 234 ид.
— рациональные функции (positive
rational functions) 104 ид. , 107 , 352
Полулинейные задачи (semi-linear
problems) 198
Полуявная форма ОДУ (semi-explicit
form of ODE) 491
Полуявные методы (half-explicit
methods) 568 и д.
Понтрягина принцип минимума
(Pontryagin minimum principle) 508
Пороговый коэффициент (threshold
factor) 203 , 207
Порядки
ди4х})еренциально-алгебраические (differential-algebraic
orders) 476
Порядковые барьеры для ДНРК и
ОДНРК (order barriers for DIRK
and SDIRK) 237
Порядковые звезды (order stars)
65 и д. , 315 и д.
двойственные (dual ~ ~) 333 ,
337
для аппроксимаций Паде (~ ~
for Pade approximations) 67
для методов многошаговых (~
~ for multistep ~) 321 ид.
одношаговых (~ ~ for
one-step ~) 65
Предметный указатель 667
ОДНРК (~ ~ for SDIRK
~) 70 , 120
для ФДН-метода 2-го порядка
(~~ for BDF2) 322
относительные (relative ~ ~)
73 , 84 , 324
Порядок В -сходимости (order of В-
convergence) 262
— дерева (~ of a tree) 453 , 556
— квадратурной формулы (~ of а
quadrature formula) 231
— погрешности
дифференцирования (differentiation error ~) 354 ,
358 и д.
интерполяции (interpolation ~
~) 354 , 358 ид.
Последовательность числа шагов
(step number sequence) 154 , 475
Потенциальная энергия (potential
energy) 17 , 508 , 582 , 591
Правило средней точки неявное
(implicit midpoint rule) 153 , 345
— — — пол у явное (half-explicit ~
~) 587
явное (explicit ~ ~) 278 , 282
Правило трапеций (trapezoidal ~)
54 , 58 , 64 , 153 , 212 , 265 , 280 , 345 ,
399
Предиктор-корректор схемы
(predictor-corrector schemes) 276 и д.
Предсогласованность (preconsisten-
су) 401
Приведенная система (reduced
system) 414 , 416 , 431
Присоединенное дифференциальное
уравнение (adjoint differential
equation) 507 , 512
Пробные задачи (test problems)
167 и д.
Проектирования операторы ,
проекторы (projections) 534 , 542 и д.
Проекционные методы (projection
methods) 186
Проекция (projection) , см.
Проецирование
Проецирование (projection) 516 ид. ,
519 и д. , 627
Проецированные кол локационные
методы (projected collocation
methods) 551
— методы Рунге—Кутты (~ Runge-
Kutta ~) 549 и д. , 564 и д.
Производящие многочлены р и <т
(generating polynomials) 272
Протеро—Робинсона задача
(Prothero-Robinson problem) 180 ,
256 , 361 , 368
Псевдоспектральный метод (pseudo-
spectral method) 172
Пуассона скобка (Poisson bracket)
613
Пучок матриц регулярный (regular
matrix pencil) 496 , 511
Радо IA (Radau IA) 88 и д. , 211 ,
250 и д. , 258 , 446 и д. , 552
— НА (~ НА) 54 , 57 , 88 и д. , 139 ,
166 , 211 , 225 , 250 и д. , 258 , 446 и д. ,
552 , 625
— методы многошагового типа (~
methods of multistep type) 308
Разделение жесткой системы
(partitioning of a stiff system) 186
— обобщенных координат
(generalized coordinate ~) 522 , 525 и д.
Разделяющиеся методы Розенброка
(partitioned Rosenbrock methods)
469
Разложение решений СВЗ (expansion
of SPP solutions) 431 и д.
Распространение погрешности (error
propagation) 229
Расширенные методы ФДН
(extended BDF methods) 267
— многошаговые методы (~ multi-
step ~) 267 и д.
Рауса критерий (Routh criterion) 107
Рациональные аппроксимации ez
(rational approximations to ez 56 ,
62
— — с вещественными полюсами
(~ ~ with real poles) 76 , 82 , 116 и д.
Реализация Лебедева (Lebedev's
realization) 45
— методов НРК (implementation of
IRK methods) 139 и д.
— методов Розенброка (~ of Rosen-
brock ~) 131
— экстраполяционных схем (~ of
extrapolation schemes) 162 и д.
Регулярные пучки матриц (regular
matrix pencils) 496 , 511
Резольвента дискретная (discrete
resolvent) 373
Рейнольдса число (Reynolds number)
488
Римана поверхности (Riemann
surfaces) 317 и д.
РК (RK) , см. Рунге—Кутты
методы
Робертсона реакция (Robertson
reaction; 11 , 28 , 167 , 186
668 Предметный указатель
Розенброка методы (Rosenbrock
methods) 121 и д. , 166 , 184 и д. ,
199 и д.
для ДАУ (~ ~ for DAE)
450 и д. , 492
г жестко точные (stiffly accurate
~ ~) 462 и д.
разделяющиеся (partitioned ~
~) 469
— — с неточной матрицей Якоби
(~ ~ with inexact Jacobian) 134
, снижение порядка (~ ~ , order
reduction) 267 и д.
» функция устойчивости (~~ ,
stability function) 126
Руте—Кутты методы (Runge-Kut-
ta methods)
аддитивные (additive ~ ~) 121 ,
137
диагонально неявные , ДНРК
(diagonally implicit ~ ~ , DIRK) 76 ,
109 ид. , 237 ид. , 252
для ДАУ индекса 1 (~ ~ for
index 1 problems) 418 ид.
для ДАУ индекса 2 (~ ~ for
index 2 DAE) 540 и д.
для ДАУ квазилинейных (~ ~
for quasilinear DAE) 492 и д.
для СВЗ (~ ~ for SPP) 418 и д. ,
436 и д.
жестко точные (stiffly accurate
~~) 59 , 418
линейно неявные (linearly
implicit ) 121
многошаговые (multistep ~ ~)
317 , 404 и д.
неявные , НРК (implicit ~ ~ ,
IRK) 53 и д. , 87 и д.
однократно диагонально
неявные , ОДНРК (singly diagonally
implicit ~ ~ , SDIRK) 54 , 57 , 109 и д. ,
210 , 237 и д. , 446 и д. , 552 и д.
неявные , ОНРК (singly
implicit , SIRK) 150 и д.
полуявные (half-explicit ~ ~)
568 , 588
проецированные (projected ~
~) 549 и д. , 564 и д.
разделенные (partitioned ~ ~)
602 ид. , 615
стабилизированные явные
(stabilized explicit ~ ~) 43 и д.
явные , ЯРК (explicit ~ ~ ,
ERK) 26 , 586
РФДН (EBDF) , см. Каша
расширенные многошаговые методы
Сверхпоказательная функция (su-
perexponential function) 197 , 222
Сверхсходимости точка (superconver-
gence point) 120 , 335
Сверхсходимость (superconvergence)
548 , 605
СВЗ (SPP) , см. Сингулярно
возмущенные задачи
Свойство С (property С) 326 и д.
— Т(~Т) 98 и д.
Сглаживающий шаг для
экстраполяции (smoothing step for
extrapolation) 154 ид.
Симметричные методы (symmetric
methods) 153 , 237 , 576
Симплектическая структура , симпле
тичность (symplecticity)
594 , 598
Симплектические методы (symplec-
tic methods) 593 и д.
Сингулярно возмущенные задачи
(singular perturbation problems)
413 и д. , 477
Скрытая связь (hidden constraint)
500
Скрытое ОДУ (underlying ODE) , см.
ОДУ , лежащее в основе ДАУ
— подмногообразие (hidden subman-
ifold) 498
Слабая ЛУУ-устойчивость (weak
AN-stability) 402
— неустойчивость (~ instability) 278
Снижение порядка (order reduction)
256 и д. , 267 , 424 , 495
Согласованные начальные значения
для ДАУ индекса 1 (consistent
initial values for index 1) 415 , 420
для ДАУ индекса 2 (~ ~ ~
for index 2) 500
для механических систем
(rsj ~ ~ for mechanical systems) 584
Сопутствующая матрица (companion
matrix) 363
Стабилизация (stabilization) 515 и д.
Стабилизированные явные методы
РК (stabilized explicit RK methods)
43 и д.
Стадийный порядок (stage order)
257 , 411 , 423
«Сэндвич» с вещественными
полюсами (real-pole sandwich) 77 и д.
Таблица порядков экстраполяцион-
ных методов для ДАУ (order
tableau for DAE extrapolation
methods) 475 и д. , 486
Предметный указатель 669
Тейлора разложение (Taylor
expansion)
для решения ДАУ методом
Розенброка (~ ~ of DAE Rosenbrock
solution) 455 и д.
— — для точного решения ДАУ
(~ ~ of DAE exact solution) 453 ,
556
Тейлора рядов метод (Taylor series
method) 295
Теорема о диске (disc theorem) 73 ,
287
Точки подгонки к экспоненте
(exponential fitting points) 70
Транзисторный усилитель
(transistor amplifier) 419 и д. , 422
Управление (control) , см. Функция
управления
— длиной шага (step size ~) 35 ид. ,
145 и д.
Упрощающие предположения
(simplifying assumptions) 87 , 96 и д. ,
211 , 236 и д. , 363
для ДАУ индекса 2 (~ ~ for
index 2 DAE) 561
для методов Розенброка (~ ~
for Rosenbrock methods) 130
для многошаговых методов РК
(~ ~ for multistep RK methods)
405 и д.
Упругий стержень (elastic beam)
17 и д. , 22 , 30 , 170
Уравнение в пространстве
состояний (state space form ordinary
differential equation) 416
Уравнение связей (constraints)
509 и д.
Уравнения массива производных
(derivative array equations) 525
Условие Т(г7 , С) (condition T(rj , ?))
98 и д.
Условия порядка для ДАУ индекса
2 (order conditions for index 2 DAE)
554 , 560 и д. , 565
для методов многошаговых со
второй производной (~ ~ for
second derivative multistep methods)
295
ОДНРК (~ ~ for SDIRK
~) 110
— — — — Розенброка (~ ~ for
Rosenbrock ~) 123 и д.
для ДАУ (~ ~ ~ ~ ~
for DAE) 458 , 464
для несогласованных
начальных значений (~ ~ for inconsistent
initial values) 468
для общих линейных методов
(~ ~ for general linear methods) 329
— — для полуявных методов РК
(~~ for half-explicit RK methods)
572
— — для W-методов (~ ~ for W-
methods) 135
Устойчивость управления длиной
шага (step-control stability) 35 и д.
для методов Дорманда—
Принса (~ ~ for Dormand & Prince
methods) 37
ФДНВП (SDBDF) , см. ФДН-методы
со второй производной
ФДН-методы (BDF methods) 10 , 11 ,
166 , 271 , 279 , 293 , 299 , 300 , 316 , 321 ,
333 и д. , 347 , 524 , 528 , 533 , 578 , 588
— с корректированной разностью
(difference-corrected ~ ~) 578
— со второй производной (second
derivative ~~) 299 , 312
Фельберга метод (Fehlberg's method)
35
Фон Неймана теорема (theorem of
von Neumann) 194 , 371
Формулы дифференцирования назад
(backward differentiation formulas) ,
см. ФДН-методы
Фробениуса норма (Frobenius norm)
191
Функционал цены (cost functional)
506 , 513
Функция абсолютно монотонная
(absolutely monotonic function) 204
— роста погрешности (error growth
~) 195 ид. , 220 ид. , 228
сверхпоказательная (~ ~ ~
superexponential) 197 , 222
— управления (control) 506 и д.
— устойчивости (stability ~) 26 и д.
внутренняя (internal ~ ~ 200
методов ДНРК (~ ~ of DIRK
methods) 76 , 114
— — — коллокационных (~ ~ of
collocation ~) 60 и д.
HPK(~~ofIRK ~) 53 ид. ,
101 и д.
для уравнения у' = \(х)у
(~~~~~ for у' = А(:г)у) 212 ид.
ОДНРК (~ ~ of SDIRK ~)
114
670 Предметный указатель
Розенброка (~ ~ of Rosen-
brock ~) 126
Чебышева (~ ~ of
Chebyshev ~) 44 и д.
экстраполяционных (~ ~ of
extrapolation ~) 154 и д.
Фурье преобразование (Fourier
transform) 173 , 288
быстрое (fast (FFT)) 173 ,
182
Хайама и Холла метод (method of
Higham & Hall) 37 и д.
Хаммера—Холлингсуорта метод
(Hammer-Hollingsworth method)
54 и д. , 57
Характеристика алгебраически
устойчивых методов
(characterization of algebraically stable methods)
238
— положительных квадратурных
формул (~ of positive quadrature
formulas) 234
Характеристическое свойство
Л-устойчивых методов РК
(characterization of Л -stable RK methods)
106
— уравнение для линейных
многошаговых методов (characteristic
equation for linear multistep ~) 272
для многошаговых методов РК
(~~ for multistep RK ~) 318
для общих линейных методов
(~ ~ for general linear ~) 328
для схем предиктор-корректор
(~ for predictor-corrector schemes)
276
Хессенберга форма матрицы (Hes-
senberg form of a matrix) 144 , 188
Химические реакции (chemical
reactions) 11 , 167 и д.
ХЛР89 (HLR89) 503 и д.
Чебышева методы (Chebyshev
methods) , см. Стабилизированные
явные методы РК
второго порядка (~ ~ of second
order) 46 , 48
— многочлены (~ polynomials)
43 и д. , 52
смещенные (shifted ~ ~) 44 и д.
— функции устойчивости
демпфированные (damped ~ stability
functions) 44
Численные эксперименты (numerical
experiments) 166 и д. , 338 и д. ,
446 и д. , 586 и д.
Число вращений (rotation number)
233
Шермана—Моррисона—Вудбери
формула
(Sherman-Morrison-Woodbury formula) 189
Штёрмера метод(Stormer's method)
599
Штурма алгоритм (Sturm's
algorithm) 235
Шура блочное разложение (block-
Schur decomposition) 189
— критерий (Schur's criterion) 314
Шура—Кона критерий (Schur-Cohn
~) 282
Эйлера метод линейно неявный
(linearly implicit Euler method)
157 , 160 и д. , 164 , 166 , 470 , 493
— — — — для ДАУ индекса 1
(~ ~ ~ ~ for index 1 DAE) 470 и д.
для ДАУ квазилинейных
(~ ~ ~ ^ for quasilinear DAE) 493
неявный (implicit ~~) 10 , 11 ,
21 , 53 , 54 , 58 , 160 , 196 , 279 , 483 , 530 ,
539 , 608 и д.
полуявный (half-explicit ~ ~)
568 , 574
— — симплектический (symplectic
~~) 519 , 595 , 608 , 612
экстраполированный
(extrapolated ~~) 161
явный (explicit ~ ~) 10 , 25 , 73 ,
519 , 608
— уравнения (Euler equations) 508
— формула для многогранников
(Euler's polyhedral formula) 72
ЭКБУХ метод (EKBWH-method)
188 и д.
Эквивалентность понятий
устойчивости (equivalence between stability
concepts) 214 , 216 , 220 , 241 , 349
Экономия в линейной алгебре
(savings in linear algebra) 589
Экстраполяционная таблица
(extrapolation tableau) 154
Экстраполяционные методы
(extrapolation methods) 16 , 27 , 153 и д. ,
470 и д. , 492 , 574
для ДАУ индекса 1 (~ ~ for
index 1 DAE] 470 и д.
для ДАУ индекса 2 (~ ~ for
index 2 DAE) 574 и д.
квазилинейных (~ ~ for
quasilinear DAE) 492
Предметный указатель 671
ГБШ (~ ~ GBS) 27 , 136
Элементарные дифференциалы
(elementary differentials) 125
для ДАУ индекса 1 (~ ~ for
index 1 DAE) 452 и д.
для ДАУ индекса 2 (~ ~ for
index 2 DAE) 556
— — для W-методов (~ ~ for W-
methods) 136
Энрайта и Камела метод (Enright &
Kamel method) 189 и д.
Энрайта методы (Enright methods)
295 и д. , 301 , 312
, кривая локуса корней (root
locus curve for ~ ~) 297
Эрмита интерполяционная задача
(Hermite interpolation problem) 306
Эрмита квадратурная формула
(Hermitian quadrature formula) 244
Явление сноса (drift-off phenomenon)
515 , 586
Якоби матрица (Jacobian) 25 , 28 , 29 ,
31 , 426
— — запаздывающая (time-lagged
~) 138
неточная (inexact ~) 134
А-допустимая аппроксимация (Л-
acceptable approximation) 56
Л-контрактивный метод
(Л-contractive method) 378
Л-устойчивость (Л-stability) 53
Л-устойчивость аппроксимаций Па-
де (Л-stability of Pade
approximations) 72
рациональных (~ of rational
~) 70 и д.
— и положительные функции (~ via
positive functions) 104 и д.
— методов многошаговых (~ of mul-
tistep methods) 273
одношаговых (~ of one-step ~)
56 и д.
ОДНРК (~ of SDIRK ~) 115
Л-устойчивость сильная (strong ~)
64
, 4-устойчивость (A-stability) 284
Л о-устойчивость (Ло -stability) 284
Л @)-устойчивость (Л@)-stability)
283
Л (а)-устойчивость (Л (а)-stability)
59
— методов многошаговых (~ of mul-
tistep methods) 283
Радо (~ of multistep Radau
~) 311 и д.
МРФДН (~ of MEBDF ~)
304 и д.
смешанных (~ of blended ~)
301
ФДН (~ of BDF -1 284
ФДНВП (~ of SDBDF ~) 299
экстраполяционных (~ of
extrapolation ~) 160 , 162
Энрайта (~ of Enright ~) 297
A N-устойчивость методов общих
линейных (Л TV-stability of general
linear methods) 402
PK (~ of RK ~) 212 и д. ,
227 и д.
В-сходимость (В-convergence)
256 и д.
— G -устойчивых одноопорных
методов (~ of G -stable one-leg
methods) 356
— методов многошаговых (~ of
multistep methods) 411 ид.
PK (~ of RK ~) 256 и д.
— порядка г (~ of order г) 262
— правила трапеций (~ of
trapezoidal rule) 265
— при переменной длине шага (~
for variable step sizes) 261
В -устойчивость (В-stability) 208 ,
216 , 227 и д. , 230
В TV-устойчивость (В TV-stability)
220
DJ-приводимые методы PK (DJ-
reducible RK methods) 214
G-устойчивость (G-stability)
347 ид. , 398
/-устойчивость (/-stability) 56 , 66 ,
82 , 325
Х-устойчивость (L-stability) 57 ,
117 и д.
S-приводимые методы PK
E-reducible RK. methods) 215
SC -устойчивость (SC -stability) 36
V-преобразование (V-
transformation) 94 и д.
672 Предметный указатель
W-методы (W-methods) 134 ид. ,
158 и д.
W-преобразование (W-
transformation) 94 и д. , 210 и д.
/3 -блоковые многошаговые методы
(/?-blocked multistep methods) 577
?-вложения метод (е -embedding
method) 416 ид.
е -разложения для СВЗ (е
-expansions for SPP) 431 ид.
в -метод @-method) 54 , 64
BEAM 170 , 179 и д. , 184 и д. , 338 и д.
BECKDO 173 и д. , 176 , 179 , 181 и д.
BRUSS 171 , 179 , 181 , 184 и д. , 338 и д.
BRUSS-2D 175 и д. , 179 , 182 , 185
CUSP 171 , 338 и д.
DASSL 528 , 588 и д.
DEABM 13 , 14
DEBDF 339 и д.
DEPAC 339
DIRK 109
DOP853 20 и д. , 27 и д. , 31 , 37 ,
41 и д. , 586 и д.
DOPRI5 11 , 29 , 33 и д. , 41 и д. , 167 ,
177 и д. , 514 , 518 , 586 и д.
DUMKA 46 , 47
DUMKA3 185
EBDF 302
EPISODE 339
EPISODEB 339
EULSIM 163 , 185
Е5 168 , 176 и д. , 338 и д.
FFT 173
GRK4A 129
GRK4T 129 , 133
НЕМ5 588
НЕХ5 588
HIHA5 37 , 38 , 42
HIRES 168 и д. , 176 и д. , 184 и д. ,
338 и д.
IRK(DAE) 418
KS 172 и д. , 338 и д.
LADAMS 340 и д. , 343
LIMEX 493
LSODE 166 , 177 и д. , 338 и д.
LSODI 528
MEBDF 304 , 342 и д.
METAN1 162
МЕХХ 587
ODEX 15 , 16 , 28 , 162
OREGO 168 , 176 и д. , 184 , 338 и д.
РЕСЕ 277
РНЕМ56 588
PLATE 169 , 176 и д. , 338 и д.
RADAU5 12 и д. , 59 и д. , 139 и д. ,
166 , 177 и д. , 422 , 588 , 619 и д.
RADAUP 183 и д. , 625
RATTLE 599
REALFT 173
RKC 48 и д. , 167 , 177 и д.
RKF4E) 37 , 42
RKF5D) 35 , 37 , 42
ROBER 167 , 176 и д. , 184 , 338 и д.
RODAS 166 , 177 и д. , 184 и д. ,
463 ид. , 625
RODAS5 166 , 184 и д. , 466
ROS4 166
SBLEND 341
SDBDF 299
SDIRK , см. ОДНРК
SDIRK4 166 , 183 и д.
SECDER 342
SEULEX 162 , 166 , 177 и д. , 185 , 626
SHAKE 599
SODEX 162 , 166 , 185
SOLOUT 587 , 627
SPRINT 339 и д. , 528
STIFF-DETEST 167
STRIDE 150
VDPOL 167 , 177 и д. , 184 , 338 и д.
VODE 339 и д.
Дополнение
Содержание первого тома
Для удобства читателей мы решили привести здесь перевод
оглавления 2-го английского издания первого тома этой книги. Новый или
существенно переработанный по сравнению с первым изданием
материал отмечен знаком *. Это позволит читателям лучше
ориентироваться в имеющихся в тексте ссылках на разделы , теоремы и
формулы глав I—III.
Из предисловия к первому изданию
Предисловие ко второму изданию
Глава I. Классическая математическая теория
1.1. Терминология
1.2. Наиболее ранние дифференциальные уравнения
Ньютон
* Лейбниц и братья Вернулли
* Вариационное исчисление
Клеро
* Упражнения
1.3. Элементарные методы интегрирования
Уравнения первого порядка
Уравнения второго порядка
* Упражнения
1.4. Линейные дифференциальные уравнения
Уравнения с постоянными коэффициентами
Вариация постоянных
Упражнения
1.5. Уравнения со слабыми особенностями
* Линейные уравнения
Нелинейные уравнения
Упражнения
1.6. Системы уравнений
Колеблющаяся струна и распространение звука
Фурье
* Лагранжева механика
* Гамильтонова механика
* Упражнения
1.7. Общая теорема существования
Сходимость метода Эйлера
Теорема существования Пеано
Упражнения
1.8. Теория существования решения , основанная на итерационных
методах и рядах Тейлора
Метод последовательных приближений Пикара—Линделёфа
Метод рядов Тейлора
Рекурсивное вычисление коэффициентов ряда Тейлора
Упражнения
674 Дополнение
1.9. Теория существования решения для систем уравнений
Векторные обозначения
* Подчиненные матричные нормы
Упражнения
1.10. Дифференциальные неравенства
Введение
Фундаментальные теоремы
Оценки с использованием односторонних условий Липшица
* Упражнения
1.11. Системы линейных дифференциальных уравнений
Резольвента и вронскиан
Неоднородные линейные уравнения
Тождество Абеля—Лиувилля—Якоби—Остроградского
Упражнения
1.12. Системы с постоянными коэффициентами
Линеаризация
Приведение к диагональному виду
Разложение Шура
Численные расчеты
* Каноническая форма Жордана
Геометрическое представление
Упражнения
1.13. Устойчивость
Введение
Критерий Рауса—Гурвица
Вопросы численной реализации
Функции Ляпунова
Устойчивость нелинейных систем
Устойчивость неавтономных систем
Упражнения
1.14. Производные по параметрам и начальным значениям
Производная по параметру
Производные по начальным значениям
Нелинейная формула вариации постоянных
* Потоки и сохраняющие объем потоки
* Канонические уравнения и симплектические отображения
Упражнения
1.15. Краевые задачи и задачи на собственные значения
Краевые задачи
Задачи Штурма—Лиувилля на собственные значения
Упражнения
1.16. Периодические решения , предельные циклы , странные
аттракторы
Уравнение Ван-дер-Поля
Химические реакции
Предельные циклы в системах большой размерности ,
бифуркация Хопфа
* Странные аттракторы
* Взлеты и падения в модели Лоренца
Каскады Фейгенбаума
Упражнения
Содержание первого тома 675
Глава П. Методы Рунге—Кутты и экстраполиционные методы
11.1. Первые методы Рунге—Кутты
Общая формулировка методов Рунге—Кутты
Обсуждение методов порядка 4
«Оптимальные» формулы
* Численный пример
Упражнения
11.2. Условия порядка для методов Рунге—Кутты
Производные точного решения
Условия для порядка 3
Деревья и элементарные дифференциалы
Разложение Тейлора для точного решения
Формула Фаа ди Бруно
Производные численного решения
Условия порядка
Упражнения
Н.З. Оценка погрешности и сходимость методов Рунге—Кутты
Строгие оценки погрешности
Главный член погрешности
Оценка глобальной погрешности
Упражнения
11.4. Практическая оценка погрешности и выбор длины шага
Экстраполяция по Ричардсону
Вложенные формулы Рунге—Кутты
* Автоматическое управление длиной шага
* Длина начального шага
* Численные эксперименты
* Упражнения
11.5. Явные методы Рунге—Кутты высших порядков
Барьеры Бутчера
Шестистадийные процессы пятого порядка
Вложенные формулы пятого порядка
* Процессы более высоких порядков
* Вложенные формулы высоких порядков
* Вложенный метод восьмого порядка
* Упражнения
* II.6. Плотная выдача , уравнения с разрывами , вычисление
производных
* Плотная выдача
* Непрерывные пары Дорманда и Принса
* Плотная выдача для DOP853
* Локализация событий
* Уравнения с разрывными производными
* Численное определение производных по начальным условиям
и параметрам
* Упражнения
II.7. Неявные методы Рунге—Кутты
Существование численного решения
* Методы Кунцмана и Бутчера порядка 2s
НРК-методы , основанные на квадратурной формуле Лобатто
* Коллокационные методы
* Упражнения
676 Дополнение
11.8. Асимптотическое разложение глобальной погрешности
Глобальная погрешность
Переменная длина шага
Отрицательные значения h
Свойства присоединенного метода
* Симметричные методы
Упражнения
11.9. Экстраполяционные методы
Определение метода
* Алгоритм Эйткена—Невилля
* Метод Грагга , или ГБШ
Асимптотическое разложение для нечетных индексов
Существование явных методов Рунге—Кутты произвольного
порядка
Управление порядком и длиной шага
* Плотная выдача для метода ГБШ
* Управление погрешностью интерполяции
* Упражнения
* 11.10. Сравнение вычислительных качеств
* Задачи
* Поведение программ
* «Растянутая» оценка погрешности для DOP853
* Влияние последовательности чисел шагов в ODEX
* 11.11. Параллельные методы
* Параллельные методы Рунге—Кутты
* Параллельные итерированные методы Рунге—Кутты
* Экстраполяционные методы
* Повышение надежности
* Упражнения
11.12. Композиция В-рядов
Композиция методов Рунге—Кутты
В-ряды
Условия порядка для методов Рунге—Кутты
* «Эффективный порядок» Бутчера
* Упражнения
11.13. Методы , использующие старшие производные
Коллокационные методы
Методы Эрмита—Обрешкова
Методы Фельберга
Общая теория условий порядка
Упражнения
11.14. Численные методы для дифференциальных уравнении
второго порядка
* Методы Нюстрёма
Производные точного решения
Производные численного решения
Условия порядка
* О конструировании методов Нюстрёма
* Экстраполяционный метод для уравнения у" = /(# , у)
* Задачи для численных сравнений
* Поведение программ
* Упражнения
Содержание первого тома 677
Р-ряды для разделяющихся дифференциальных уравнений
Производные точного решения , Р-деревья
Р-ряды
Условия порядка для разделяющихся методов Рунге—Кутты
Дальнейшие приложения Р-рядов
Упражнения
Симплектические методы интегрирования
Симплектические методы Рунге—Кутты
Пример из динамики галактик
Разделяющиеся методы Рунге—Кутты
Симплектические методы Нюстрёма
Сохранение гамильтониана; обратный анализ
Упражнения
Дифференциальные уравнения с запаздывающим аргументом
Существование
Методы с постоянной длиной шага для постоянного запаздывания
Методы с переменной длиной шага
Устойчивость
Пример из динамики популяций
Моделирование эпидемии
Пример из кинетики ферментативных реакций
Одна математическая модель в иммунологии
Интегро-дифференциальные уравнения
Упражнения
Глава III. Многошаговые методы и общие линейные методы
II 1.1. Классические линейные многошаговые формулы
Явные методы Адамса
Неявные методы Адамса
* Численный эксперимент
Явные методы Нюстрёма
Методы Милна—Симпсона
Методы , основанные на дифференцировании (ФДН)
Упражнения
III.2. Локальная погрешность и условия порядка
Локальная погрешность многошагового метода
Порядок многошагового метода
Константа погрешности
Неприводимые методы
Ядро Пеано многошагового метода
Упражнения
II 1.3. Устойчивость и первый барьер Далквиста
Устойчивость формул дифференцирования назад
Наивысший достижимый порядок устойчивых многошаговых
методов
Упражнения
II 1.4. Сходимость многошаговых методов
Представление в виде одношагового метода
Доказательство сходимости
Упражнения
II 1.5. Многошаговые методы с переменным шагом
Методы Адамса с переменным шагом
678 Дополнение
Рекуррентные соотношения для 9j(n)y $j(n) и Ф!(п)
Методы ФДН с переменным шагом
Методы общего вида с переменным шагом и их порядки
Устойчивость
Сходимость
Упражнения
II 1.6. Методы Нордсика
Эквивалентность многошаговым методам
Неявные методы Адамса
ФДН-методы
Упражнения
II 1.7. Реализация и численное сравнение
Выбор шага и порядка
* Некоторые доступные программы
* Сравнение численных результатов
II 1.8. Общие линейные методы
Общая процедура интегрирования
Устойчивость и порядок
Сходимость
Условия порядка для общих линейных методов
Построение общих линейных методов
* Упражнения
III.9. Асимптотическое разложение глобальной погрешности
Поучительный пример
Асимптотическое разложение для строго устойчивых
методов (8.4)
Слабо устойчивые методы
Сопряженный метод
Симметричные методы
Упражнения
II 1.10. Многошаговые методы для дифференциальных уравнений
второго порядка
Явные методы Штёрмера
Неявные методы Штёрмера
Численный пример
* Общая формулировка
* Сходимость
Асимптотическая формула для глобальной погрешности
* Погрешности округления
Упражнения
* Приложение. Программы на Фортране
* Драйвер для программы DOPRI5
* Подпрограмма DOPRI5
* Подпрограмма DOP853
* Подпрограмма ODEX
* Подпрограмма ODEX2
* Драйвер для программы RETARD
* Подпрограмма RETARD
Литература
Указатель обозначений
Предметный указатель
Оглавление1)
От редактора перевода 5
Из предисловия к первому изданию 6
Предисловие ко второму изданию 7
Предисловие к русскому изданию 8
Глава IV. Жесткие задачи — одношаговые методы 9
IV.1. Примеры жестких уравнений 10
Системы , описывающие химические реакции 11
Электрические схемы 12
Диффузия 14
«Жесткий» стержень 17
Высокочастотные колебания 21
Упражнения 21
IV.2. Анализ устойчивости для явных методов Рунге—Кутты 25
Анализ устойчивости для метода Эйлера 25
Явные методы Рунге—Кутты 26
Экстраполяционные методы 27
Анализ примеров из IV. 1 28
Автоматическое обнаружение жесткости 31
Устойчивость управления длиной шага 35
ПИ-управление длиной шага 39
Стабилизированные явные методы Рунге—Кутты 43
Упражнения 49
IV.3. Функция устойчивости неявных методов Рунге—Кутты 53
Функция устойчивости 53
А -устойчивость 56
L -устойчивость и А (а) -устойчивость 57
Численные результаты 59
Функции'устойчивости порядка > з 60
Аппроксимации Паде для показательной функции 62
Упражнения 63
IV.4. Порядковые звезды 65
Введение 65
Порядок и устойчивость для рациональных аппроксимаций ... 70
Устойчивость аппроксимаций Паде 72
Сравнение областей устойчивости 73
Рациональные аппроксимации с вещественными полюсами 76
«Сэндвич» с вещественными полюсами 77
Аппроксимации с кратным вещественным полюсом 82
Упражнения 85
Перевод выполнили Е.Л. Старостин (гл. IV) , И.А. Кульчицкая (гл. V) ,
А.В. Тыглиян (гл. VI) и С.С. Филиппов (гл. VII). — Прим. ред.
680 Оглавление
IV.5. Конструирование неявных методов Рунге—Кутты 87
Гауссовы методы 87
Методы Радо IA и Радо НА 88
Методы Лобатто ША , ШВ и НЮ 91
W -преобразование 94
Конструирование неявных методов Рунге—Кутты 100
Функция устойчивости 101
Положительные функции 103
Упражнения 106
IV.6. Диагонально неявные методы Рунге—Кутты 109
Условия порядка 109
Жестко точные методы ОДНРК 111
Функция устойчивости 114
Аппроксимации с кратным вещественным полюсом
и с Я(оо)=0 116
Выбор метода 118
Упражнения 119
IV.7. Методы типа Розенброка 121
Вывод метода 121
Условия порядка 123
Функция устойчивости 126
Конструирование методов 4-го порядка 127
Методы высших порядков 130
Реализация методов типа Розенброка 131
¦Горб» 133
Методы с неточной матрицей Якоби (И^-методы) 134
Упражнения 137
IV.8. Реализация неявных методов Рунге—Кутты 139
Иная запись нелинейной системы 139
Упрощенные итерации Ньютона 140
Линейная система 143
Выбор длины шага 144
Неявные дифференциальные уравнения 149
Программа ОДНРК 149
Методы ОНРК 150
Упражнения 152
IV.9. Экстраполяцконные методы 153
Экстраполяция симметричных методов 153
Сглаживание 154
Линейно неявное правило средней точки 156
Неявный и линейно неявный метод Эйлера 160
Реализация 162
Упражнения 164
IV.10. Численные эксперименты 166
Использованные программы 166
Двенадцать задач-тестов 167
Обсуждение результатов 176
Разделение и проекционные методы 186
Упражнения 191
IV.11. Контрактивность для линейных задач 193
Евклидовы нормы (теорема фон Неймана) 194
Функция роста погрешности для линейных задач 195
Малые нелинейные возмущения 198
Контрактивность в нормах || • ||оо и || • ||i 201
Оглавление
681
Исследование порогового коэффициента 203
Абсолютно монотонные функции 204
Упражнения 206
IV.12. В -устойчивость и контрактивность 207
Одностороннее условие Липшица 207
Б-устойчивость и алгебраическая устойчивость 208
Некоторые алгебраически устойчивые НРК методы 210
А N -устойчивость 212
Приводимые методы Рунге—Кутты 214
Теорема об эквивалентности для 5-неприводимых методов 216
Функция роста погрешности 220
Вычисление у>в (х) 223
Упражнения 227
IV.13. Положительные квадратурные формулы и Б-устойчивые
методы Рунге—Кутты 230
Квадратурные формулы и соответствующие непрерывные
дроби 230
Число лоложительных весов 233
Характеристика положительных квадратурных формул 234
Необходимые условия алгебраической устойчивости 236
Характеристика алгебраически устойчивых методов 238
«Эквивалентность» А- и В -устойчивости 241
Упражнения 243
IV.14. Существование и единственность решений НРК 245
Существование 245
Контрпример 247
Влияние возмущений и единственность 248
Вычисление Qo(A~1) 250
Методы с вырожденной матрицей А 252
Методы Лобатто IIIC 253
Упражнения 254
IV.15. 5-сходимость 256
Феномен снижения порядка 256
Локальная погрешность 259
Распространение погрешности 261
^-сходимость при переменной длине шага 261
В -сходимость влечет алгебраическую устойчивость 263
Правило трапеций 266
Снижение порядка для методов Розенброка 267
Упражнения 269
Глава V. Многошаговые методы для жестких задач 271
V.I. Устойчивость многошаговых методов 272
Область устойчивости 272
Методы Адамса 275
Схемы предиктор-корректор 276
Методы Нюстрёма 277
Методы ФДН 279
Второй барьер Далквиста 280
Упражнения 282
V.2. «Почти» Л-устойчивые многошаговые методы 283
А (а) -устойчивость и жесткая устойчивость 283
А(а) -устойчивые методы высоких порядков 284
Приближение методов низкого порядка методами высокого
682 Оглавление
порядка 286
Теорема о диске 287
Барьеры точности для линейных многошаговых методов 288
Упражнения 292
V.3. Обобщенные многошаговые методы 295
Многошаговые методы Энрайта со второй производной 295
Методы ФДН со второй производной 299
Смешанные многошаговые методы 300
Расширенные многошаговые методы Каша 302
Многошаговые коллокационные методы 305
Методы «типа Радо» 308
Упражнения 312
V.4. Порядковые звезды на поверхностях Римана 315
Поверхности Римана 315
Полюсы характеризуют вычислительные затраты 319
Порядок и порядковые звезды 321
«Догадка Даниела—Мура» 323
Методы со «Свойством С» 325
Общие линейные методы 328
Двойственные порядковые звезды 333
Упражнения 335
V.5. Эксперименты с многошаговыми программами 338
Использованные программы 338
Упражнения 343
V.6. Одноопорные методы и G-устойчивость 344
Одноопорные (многошаговые) методы 344
Существование и единственность 345
G -устойчивость 346
Алгебраический критерий 348
Эквивалентность Л-устойчивости и G -устойчивости 349
Критерий для положительных функций 352
Оценки погрешности одноопорных методов 353
Сходимость Л-устойчивых многошаговых методов 357
Упражнения 358
V.7. Сходимость для линейных задач 361
Разностные уравнения для глобальной погрешности 361
Матричная теорема Крайсса 363
Некоторые применения матричной теоремы Крайсса 366
Глобальная погрешность для задачи Протеро—Робинсона 368
Сходимость для линейных систем с постоянными
коэффициентами 369
Матричный вариант теоремы фон Неймана 371
Дискретная формула вариации постоянных 372
Упражнения 378
V.8. Сходимость для нелинейных задач 380
Задачи , удовлетворяющие одностороннему условию Липшица .. 380
Метод множителей 383
Множители и нелинейности 387
Дискретная вариация постоянных и возмущения 389
Сходимость для нелинейных параболических задач 390
Упражнения 396
V.9. Алгебраическая устойчивость общих линейных методов 398
G-устойчивость 398
Алгебраическая устойчивость 399
Оглавление 683
А N -устойчивость и эквивалентность различных определений
устойчивости 401
Многошаговые методы Рунге—Кутты 404
Упрощающие предположения 405
Квадратурные формулы 407
Алгебраически устойчивые методы порядка 2s 409
В-сходимость 411
Упражнения 412
Глава VI. Сингулярно возмущенные задачи и задачи индекса 1 ... 413
VI.1. Решение задач индекса 1 414
Асимптотическое решение уравнения Ван-дер-Поля 414
Метод ?-вложения для задач индекса 1 416
Метод пространства состояний 418
Транзисторный усилитель 419
Задачи вида Мм'=<р(и) 420
Сходимость методов Рунге—Кутты 422
Упражнения 424
VI.2. Многошаговые методы 425
Методы для задач индекса 1 425
Сходимость для сингулярно возмущенных задач 426
Упражнения 430
VI.3. Эпсилон-разложения для точных решении и для РК-решений 431
Разложение гладкого решения 431
Разложения , включающие члены пограничного слбя 432
Оценка остаточного члена 434
Разложение решения метода Рунге—Кутты 436
Сходимость РК-методов для дифференциально-алгебраических
систем 437
Существование и единственность решения метода Рунге—Кутты 440
Влияние возмущений 441
Оценка остаточного члена в численном решении 442
Численное подтверждение 446
Возмущение начальных значений 446
Упражнения 449
VI.4. Методы Розенброка г 450
Определение метода 450
Производные точного решения 451
Деревья и элементарные дифференциалы 452
Разложение Тейлора для точного решения 453
Разложение Тейлора для численного решения 455
Условия порядка 458
Сходимость 460
Жестко точные методы Розенброка 462
Построение ROD AS — жестко точного вложенного метода 463
Несогласованные начальные значения 466
Упражнения 468
VI.5. Экстраполяционные методы 470
Дискретизация с помощью линейно неявного метода Эйлера 470
Возмущенное асимптотическое разложение 472
Таблица порядков 475
Разложение погрешности для сингулярно возмущенных задач .. 477
Плотная выдача 483
Упражнения 485
684 Оглавление
VI.6. Квазилинейные задачи 487
Пример; движущиеся конечные элементы 487
Задачи индекса один 490
Численное решение уравнения С(у)у' = /(у) 491
Экстраполяционные методы 492
Упражнения 494
Глава VII. Дифференциально-алгебраические задачи
высших индексов 495
VII.1. Понятие индекса и различные примеры 496
Линейные уравнения с постоянными коэффициентами 496
Индекс дифференцирования 498
Дифференциальные уравнения на многообразиях 501
Индекс возмущений 503
Задачи теории управления 506
Механические системы 508
Упражнения 511
VII.2. Методы понижения индекса 514
Понижение индекса дифференцированием 514
Стабилизация с помощью проекции 516
Ди4>ференциальные уравнения с инвариантами 518
Методы , использующие представления в локальном
пространстве состояний 520
Переопределенные дифференциально-алгебраические
уравнения 524
Бесструктурные задачи старших индексов 525
Упражнения 527
VII.3. Многошаговые методы для ДАУ индекса 2 528
Существование и единственность численного решения 529
Влияние возмущений 531
Локальная погрешность 532
Сходимость методов , использующих ФДН 533
Общие многошаговые методы 536
Решение нелинейной системы упрощенным методом Ньютона ... 538
Упражнения 539
VII.4. Методы Рунге—Кутты для ДАУ индекса 2 540
Нелинейная система 540
Оценка локальной погрешности 542
Сходимость для у-компоненты 544
Сходимость для z-компоненты 545
Кол локационные методы 546
Сверхсходимость коллокационных методов 548
Проецированные методы Рунге—Кутты 549
Сводка результатов по сходимости 552
Упражнения 552
VII.5. Условия порядка для ДАУ индекса 2 554
Производные точного решения 554
Деревья и элементарные дифференциалы 555
Разложение Тейлора для точного решения 556
Производные численного решения 558
Условия порядка 560
Упрощающие предположения 561
Проецированные методы Рунге—Кутты 564
Упражнения 567
Оглавление
685
VII.6. Полуявные методы для систем индекса 2 568
Полуявные методы Рунге—Кутты 568
Экстраполяционные методы 574
/3-блоковые многошаговые методы 577
Упражнения 578
VII.7. Расчет многозвенных механизмов 579
Описание модели 579
Подпрограммы на Фортране 582
Вычисление согласованных начальных значений 584
Численные расчеты 586
Жесткая механическая система 590
Упражнения 591
VII.8. Симплектические методы для гамильтоновых систем со связями .. 593
Свойства гамильтонова фазового потока 594
Симплектический метод первого порядка 595
SHAKE и RATTLE 598
Пара Лобатто IIIA-IIIB 601
Композитные методы 605
Обратный анализ погрешностей (для ОДУ) 607
Обратный анализ погрешностей на многообразиях 611
Упражнения 614
Приложение. Программы на Фортране 616
Драйвер для программы RADAU5 617
Подпрограмма RADAU5 619
Подпрограмма RADAUP 625
Подпрограмма RODAS 625
Подпрограмма SEULEX 626
Задачи , имеющие особую структуру 626
Использование SOLOUT и плотной выдачи 627
Литература 628
Указатель обозначений 659
Предметный указатель > 661
Дополнение. Содержание первого тома 673
Научное издание
Эрнст Хайрер , Герхард Ваннер
РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Жесткие и дифференциально-алгебраические задачи
Заведующий редакцией академик В. И. Арнольд
Зам. зав. редакцией А. С. Попов
Ведущий редактор И. В. Ритус
Художественный редактор Н. В. Зотова
Оригинал-макет подготовлен С. С. Филипповым в пакете Plain-T^X
с использованием кириллических шрифтов ,
разработанных в редакции АИП издательства «Мир»
Лицензия ЛР № 010174 от 20.05.97 г.
Подписано к печати 20.08.99. Формат 60 х ЭО1/^ • Бумага офсетная N» 1.
Печать офсетная. Объем бум. л. 21 , 50. Усл. печ л. 43 , 00. Уч.-изд. л. 36 , 79.
Изд. № 1/9566. Тираж 1000 экз. Заказ 3359
Издательство «Мир »
Министерства РФ по делам печати , телерадиовещания
и средств массовых коммуникаций
129820 , ГСП , Москва , 1-й Рижский пер. , 2.
Отпечатано в Производственно-издательском комбинате ВИНИТИ ,
140010 , г. Люберцы , Московской обл , Октябрьский пр-т , 403
Тел 554-21-86
ISBN 5-03-003117-0