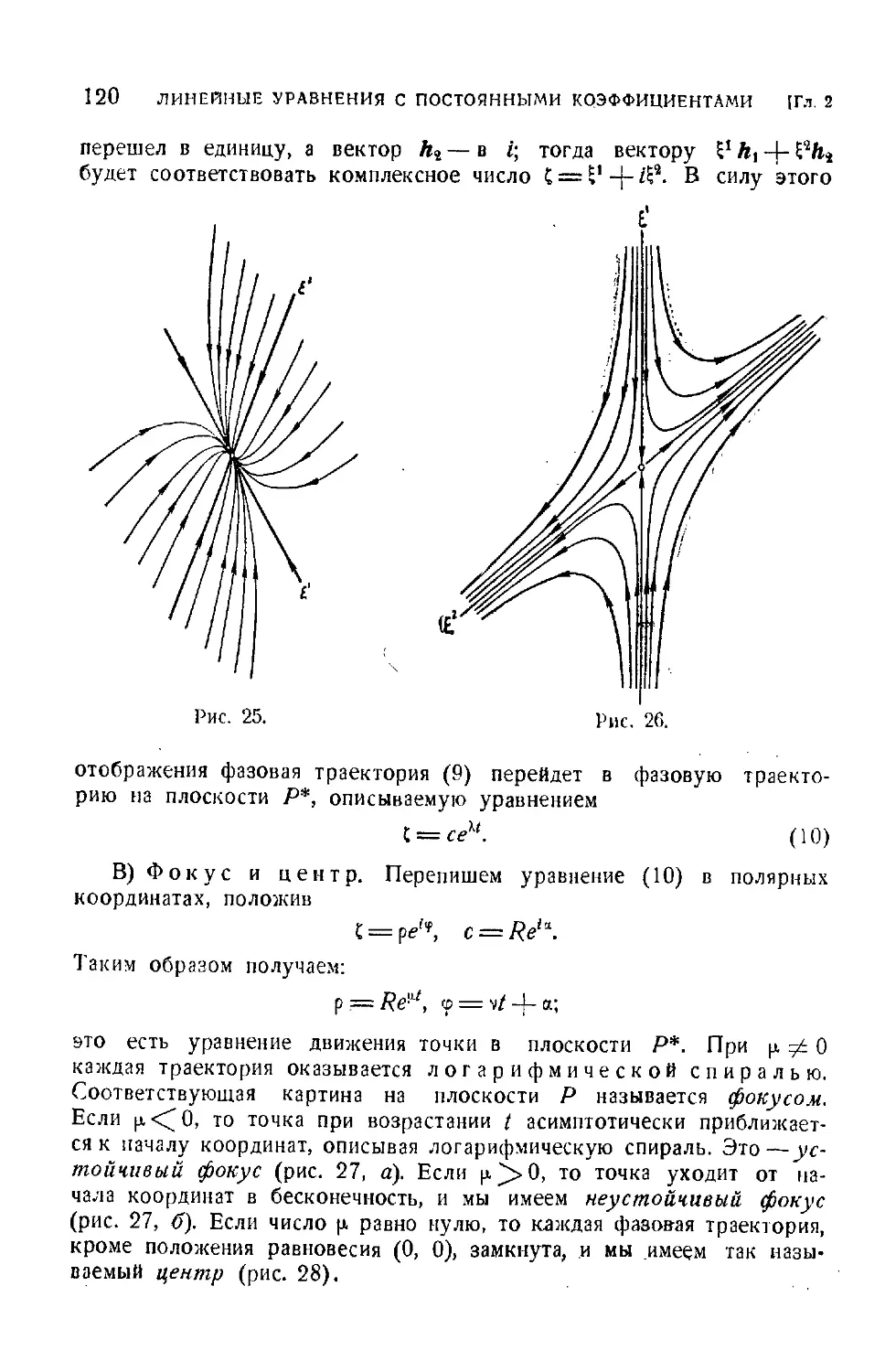
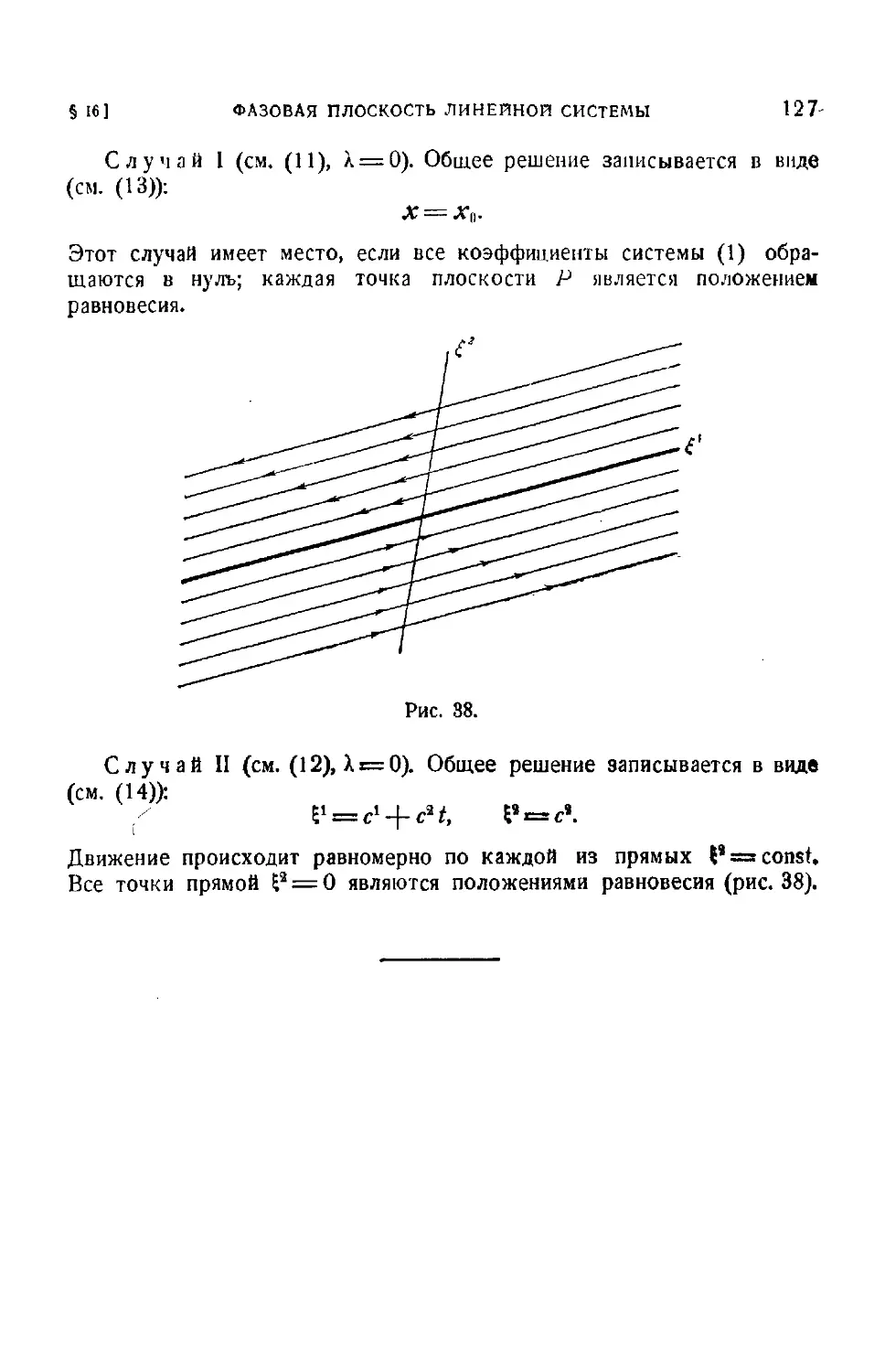
Текст
Л. С. ПОНТРЯГИН
ОБЫКНОВЕННЫЕ
ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ
ИЗДАНИЕ ЧЕТВЕРТОЕ
Д о п у и (е н о Министерством
высшего и ср>‘<)чесо специального обои ’-оваичр СССР
в качестве учебники
Оля студеитов учиверсае'ив
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1974
22.161.6
П 56
УДК 517.9
УЧЕБНИК УДОСТОЕН ГОСУДАРСТВЕННОЙ ПРЕМИИ СССР
ЗА 1975 г.
1702050000—155
П 053 (02)-82
82-83
СОДЕРЖАНИЕ
От автора ................................................. / 5
Глава первая. Введение........................................... 7
§ 1. Дифференциальное уравнение первого порядка ............. 7
§ 2. Некоторые элементарные методы интегрирования........... 13
§ 3. Формулировка теоремы существования и единственности ... 21
§ 4. Сведение общей системы дифференциальных уравнений к
нормальной.................................................. 25
§ 5. Комплексные дифференциальные уравнения................. И
§ 6. Некоторые сведения о линейных дифференциальных уравне-
ниях ........................................................ И
Глава вторая. Линейные уравнения с постоянными коэффи-
циентами ...................................................... 41
§ 7. Линейное однородное уравнение с постоянными коэффици-
ентами (случай простых корней) .............................. 42
§ 8. Линейное однородное уравнение с постоянными коэффициен-
тами (случай -кратных корней) ............................. 60
§ 9. Устойчивые многочлены ................................ 50
§ 10. Линейное неоднородное уравнение с постоянными коэффици-
ентами ................................................ 62
§ 11. Метод исключения ...................................... 67
§ 12. Метод комплексных амплитуд ............................ 75
§ 13. Электрические цепи .................................... 80
§ 14. Нормальная линейная однородная система с постоянными ко-
эффициентами ................................................. 93
§ 15. Автономные системы дифференциальных уравнений и их фа-
зовые пространства .......................................... 10В
§ 16. Фазовая плоскость линейной однородной системы с постоян-
ными коэффициентами .......................................... ИЗ
Глава третья. Линейные уравнения с переменными коэффи-
циентами ....................................................• 523
§ 17. Нормальная система линейных уравнений ................ 123
§ 18. Линейное уравнение n-го порядка ...................... 133
§ 19. Нормальная линейная однородная система с периодическими
коэффициентами............................................... 143
Глава четвертая. Теоремы существования ...................... 1)2
§ 20. Доказательство теоремы существования и единственности для
одного уравнения ............................................ 152
§ 21. Доказательство теоремы существования и единственности для
нормальной системы уравнений................................. 164
1
4
СОДЕРЖАНИЕ
§ 22. Непродолжаемые решения ............................. 173
§ 23. Непрерывная зависимость решения от начальных значений н
параметров ............................................... 178
§ 24. Дифференцируемость решения по начальным значениям я
параметрам ............................................... 185
§ 25. Первые интегралы ................................... 196
Глава пятая. Устойчивость ................................ 204
§ 26. Теорема Ляпунова ................................... 205
§ 27. Центробежный регулятор (ясследованяя Вышнеградского) 218
§ 28. Предельные циклы.................................... 224
§ 29. Ламповый генератор.................................. 244
§ 30. Положения равновесия автономной системы второго порядка 251
§ 31. Устойчивость периодических решений ................. 268
Д о б а р л е н и е I, Некоторые вопросы анализа ........... 284
§ 32. Топологические свойства евклидовых пространств...... 284
§ 33. Теоремы о неявных функциях ......................... 298
Добавление 11. Линейная алгебра .........................* . 309
§ 34. Минимальный аннулирующий многочлен.................. 309
§ 35. Функции матриц .................................... 316
§ 36. Жорданова форма матрицы ............................ 323
Предметный указатель ........................................329
ОТ АВТОРА
Эта книга написана на основе лекций, которые я в течение ря-
да лет читал на механико-математическом факультете Московского
государственного университета. При составлении программы лекций
я, исходил из уверенности, что выбор материала не должен быть
случайным и не должен опираться исключительно на сложившиеся
традиции. Наиболее важные и интересные применения обыкновенные
дифференциальные уравнения находят в теории колебаний и в теории
автоматического управления. Эти применения и послужили руковод-
ством при выборе материала для моих лекций. Теория колебаний
и теория автоматического управления, несомненно, играют очень важ-
ную роль в развитии всей современной материальной культуры,
и потому я считаю, что такой подход к выбору материала для
курса лекций является, если и не единственно возможным, то во
всяком случае разумным. Стремясь дать студентам не только чисто
математическое орудие, пригодное для применений в технике, но
также продемонстрировать и сами применения, я включил в лекции
некоторые технические вопросы. В книге они изложены в § 13, 27,
29. Эти вопросы составляют неотъемлемую органическую часть
моего курса лекций и, соответственно, этой книги.
Кроме материала, излагавшегося на лекциях, в книгу включены
некоторые более трудные вопросы, разбиравшиеся на студенческих
семинарах. Они содержатся в § 19, 31 книги. Материал, ^держа-
щийся в § 14, 22, 23, 24, 25, 30, излагался на лекциях частично
и не каждый год.
Для удобства читателя в конце книги приведены два добавления,
которые содержат материал, не входящий в курс обыкновенных
дифференциальных уравнений, но существенным образом использую-
щийся в нем. В первом добавлении (отсутствовавшем в предыдущем
издании) изложены основные топологические свойства множеств
6
ОТ АВТОРА
расположенных в эвклидовом пространстве, и дано доказательство
теорем о неявных функциях; второе добавление посвящено линейной
алгебре.
В этом, втором издании по новому изложены теоремы о непре-
рывной зависимости решений от начальных значений’ и параметров,
а также о дифференцируемости решений по этим величинам. Сдела-
ны также многие более мелкие исправления.
В заключение я хочу выразить благодарность моим ученикам
и ближайшим товарищам по работе В. Г. Болтянскому, Р. В. Гам-
крелидзе и Е. Ф. Мищенко, помогавшим мне при подготовке и чте-
нии лекций, а также при написании и редактировании этой книги.
Мне хочется также отметить решающее влияние на мои научные
интересы, оказанное выдающимся советским специалистом в области
теории колебаний и теории автоматического управления Александ-
ром Александровичем Андроновым, с которым меня связывали долго-
летние дружеские отношения. Его влияние существенно сказалось на
характере и направленности этой книги*
Л. С. Понтрягин
ГЛАВА ПЕРВАЯ
ВВЕДЕНИЕ
Эта глава посвящена в первую очередь определению тех понятий,
которые будут изучаться в дальнейшем. Что такое система обыкно-
венных дифференциальных уравнений, что называется ее решением
и как много этих решений существует — таковы главные вопросы, на
которые дается ответ в этой главе. Количество решений определяется
теоремами существования и единственности, которые здесь не дока-
зываются, а только формулируются. Доказательство этих и ряда дру-
гих теорем того же типа дается в четвертой главе, а до этого сфор-
мулированные в первой главе теоремы многократно используются, чем
выясняется их значение. Кроме этих основных сведений, в первой
главе приводятся решения дифференциальных уравнений нескольких
простейших типов. В конце главы рассматриваются комплексные диф-
ференциальные уравнения и их комплексные решения и приводятся
простейшие замечания относительно систем линейных дифференциаль-
ных уравнений.
§ 1. Дифференциальное уравнение первого порядка
Дифференциальными уравнениями называются такие уравнения,
в которых неизвестными являются функции одного ?или нескольких
переменных, причем в уравнения входят не только сами функции, но
и их производные. Если неизвестными функциями являются функции
многих переменных, то уравнения называются уравнениями в частных
производных, в противном случае, т. е. при рассмотрении функций
только одного независимого переменного, уравнения называются
сбыкновенными дифференциальными уравнениями. В дальнейшем мы
будем иметь дело только с последними.
Так как в ряде физических применений независимым переменным,
от которого зависят неизвестные искомые функции, является время,
которое принято обозначать через t, то всюду в дальнейшем неза-
висимое переменное будет обозначаться через Неизвестные функции
будут обозначаться через х, у, 2 и т. д. Производные функций по t
8
ВВЕДЕНИЕ
(Гл. t
. л . dx п d2x
будут, как правило, обозначаться точками: х= ~, х—-^ и т. д.
В тех случаях, когда это неудобно или невозможно, мы будем указы-
вать порядок производной верхним индексом в скобках; например,
dtn *
В первую очередь мы займемся рассмотрением одного диф-
ференциального уравнения первого порядка, т. е.
уравнения, в которое входит лишь первая производная неизвестной
функции. Уравнение это может быть записано в виде:
F(ft х, х)=0. (1)
Здесь t—независимое переменное, х—его неизвестная функция,
. dx „ ' .
х = м—ее производная, а г — заданная функция трех переменных.
Функция F может быть задана не для всех значений ее аргументов;
поэтому говорят об области В задания функции F. Здесь имеется
в виду множество В точек координатного пространства трех пере-
менных t, х, Решением уравнения (1) называется такая функ-
ция x = cp(f) независимого переменного tt определенная на некотором
интервале rj<^f<^ra (случаи 1\ =— оо, гв = -ф"°° не исключаются),
что при подстановке ее вместо х в соотношение (1) мы получаем
тождество на всем интервале Интервал назы-
вается интервалом определения решения <p(f). Очевидно, что под-
становка х = ср(/) в соотношение (1) возможна лишь тогда, когда
функция <p(f) на всем интервале имеет первую производ-
ную (и, в частности, непрерывна). Для того чтобы подстановка х=ср(О
в соотношение (1) была возможна, необходимо также, чтобы при
произвольном значении переменного t из интервала точка
с координатами (f, cp(Z), $(/)) принадлежала множеству В, на котором
определена функция F.
Соотношение (1) связывает три переменные величины f, х, Л. В не-
которых случаях оно определяет переменное St как однозначную
неявную функцию независимых переменных х. В этом случае диф-
ференциальное уравнение (1) равносильно дифференциальному урав-
нению вида
Я = /(t х). (2)
Дифференциальное уравнение (2) называется разрешенным относи-
тельно производной; оно в некоторых отношениях более доступно
для изучения, чем общее дифференциальное уравнение (1). Именно
уравнения, разрешенные относительно производной, мы и будем те-
перь рассматривать. Мы не будем уже считать, что соотношение (2)
получено в результате разрешения относительно Л уравнения вида (1),
а будем исходить из функции /(/, х) как из заданной функции двух
независимых переменных х.
$ л ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ПЕРВОГО ПОРЯДКА
9
Для того чтобы пользоваться наглядными геометрическими пред-
ставлениями, мы введем в рассмотрение координатную плоскость Р
переменных t и х. При этом t как независимое переменное мы бу-
дем откладывать по оси абсцисс, а х как зависимое переменное —
по оси ординат. Функция /, определяющая дифференциальное урав
некие (2), может быть задана не
для всех значений своих аргумен-
тов t и х, или, говоря геометри-
ческим языком, не во всех точках
плоскости Pt а лишь в точках не-
которого множества Г плоскости Р
(рис. 1). Относительно множества Г
мы в дальнейшем всегда будем
предполагать, что оно является от-
крытым, Это значит, что наряду
с каждой точкой р в Г входит и
некоторый круг положительного
радиуса с центром в р (см. § 32).
Относительно функции f будет
предполагаться, что как она сама, так и ее частная производная
df , ,
являются непрерывными функциями пары переменных t, х на всем
множестве Г, Решение х=ср(/) уравнения (2) будем геометрически
изображать в плоскости Р в виде кривой с уравнением х=*<р(/)*
Кривая эта в каждой точке имеет касательную и полностью прохо-
дит в открытом множестве Г; она называется интегральной кривой
дифференциального уравнения (2).
Теорема существования и единственности
Известно, какую большую роль в алгебре играют теоремы, отве-
чающие на вопрос о том, сколько решений имеет та или другая си-
стема алгебраических уравнений. Такова, например, основная тео-
рема алгебры, утверждающая, что многочлен л-й степени всегдв
имеет ровно п корней (считая с их кратностями). Точно так же в
теории дифференциальных уравнений важным теоретическим вопросом
является вопрос о том, насколько много решений имеет дифферен-
циальное уравнение. Оказывается, что каждое дифференциальное
уравнение имеет бесконечное множество решений, и потому при-
ходится ставить вопрос не о числе решений, а о том, как можно
описать совокупность всех решений данного дифференциального урав-
нения. Ответ на этот вопрос дает теорема существования
единственности (теорема 1), которая в этом параграфе приво-
дится без доказательства. Доказательство будет дано значительно
позже (см. § 20).
10
ВВЕДЕНИЕ
[Гл. t
Теорема 1. Пусть
(3)
— дифференциальное уравнение. Будем предполагать, что функция
f(t, х) задана на некотором открытом множестве V плоскости
Р переменных t, х. Относительно функции f будем предполагать,
A df
что она сама и ее частная производная являются непре-
рывными функциями на всем открытом множестве Г. Теорема
утверждает, что:
1) для всякой точки (/0, х0) множества Г найдется решение
х = ? (/) уравнения (3), удовлетворяющее условию
'p(U=x«; (4)
2) если два решения х = ф(/) и x==^(t) уравнения (3) совпа-
дают хотя бы для одного значения t = tQ1 т. е. если
<p(U=z(4),
то решения эти тождественно равны для всех тех значений
переменного t, для которых они оба определены.
Числа /0, _г0 называются начальными значениями для решения
х = ?(/), а соотношение (4) — начальным условием для этого реше-
ния. Говорят также, что решение х = ср(/) удовлетворяет начально-
му условию (4) или же что оно имеет начальные значения tQt х0.
Утверждение, что решение удовлетворяет начальному усло-
вию (4) (или имеет начальные значения f0, х0), предполагает,
что интервал определения решения x = cp(f) содержит
точку
Таким образом, теорема 1 утверждает, что координаты любой
точки (^, х0) множества Г являются начальными значениями для не-
которого решения, уравнения (3) и что дза решения с общими началь-
ными значениями^ совпадают. х
Геометрическое содержание теоремы ^заключается в том, что
через каждую точку (1$, _г0) множества Г проходит одна и толь-
ко одна интегральная кривая уравнения (3) (см. рис. 1).
Говоря, что через каждую точку (/0, лг0) множества Г проходит
столько одна» интегральная кривая, мы допускаем некоторую неточ-
ность. В самом деле, решением уравнения (3) называется функция
x = y(t), заданная на вполне определенном интервале
Наряду с этой функцией может существовать функция х = ф(О>
также удовлетворяющая уравнению (3) и имеющая те же начальные
значения f0, _г0, но заданная на другом интервале Вто-
рая часть теоремы 1 утверждает лишь, что функции ср(/) и ф(£) сов-
падают там, где они обе определены, но вовсе не утверждает, что
интервалы их определения и Sy<^t<^Si одинаковы.
§ I] ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ПЕРВОГО ПОРЯДКА 11
Если один из интервалов, например полностью содер-
жит другой, то мы будем говорить, что решение х = ф(/), заданное
на интервале является продолжением решения х = <р(0*
Естественно сосредоточить все внимание на тех решениях, которые
нельзя продолжить ни вправо, ни влево. Такие решения мы будем
называть не продолжаемыми, Нетрудно доказать (но это будет сде-
лано позднее, см. § 22), что каждое решение может быть продол-
жено до непродолжаемого и при-
том единственным способом. Если
теперь подразумевать под интег-
ральной кривой график непродолжа-
емого решения, то утверждение
о том, что через каждую точ-
ку (*о> хо) проходит единственная
интегральная кривая, становится
точным.
Каждое решение х = <р(О урав-
нения (3) мы интерпретировали
геометрически в виде графика функ-
ции ср(^). Дадим теперь геометри-
ческую интерпретацию самого уравнения (3). Через каждую точку
(t, х) множества Г проведем прямую /Рх с угловым коэффициентом
/(/, х), Мы получаем поле направлений, соответствующее уравнению
(3), что и дает геометрическую интерпретацию этого уравнения.
Связь между геометрической интерпретацией уравнения и гео-
метрической интерпретацией его решений заключается в том (рис. 2),
что любая интегральная кривая х = ср(/) в каждой своей
точке (Л <р(0) касается прямой l^^y
Примеры
1. Для того чтобы проиллюстрировать значение теоремы 1
(в данном случае второй ее части), решим дифференциальное ура-
внение
х = а х, (5)
где а — действительное число. Здесь
/ (t, х) = а х,
так что функция / в действительности зависит лишь от перемен-
ного х. Множество точек, на котором определена функция /, в дан-
ном случае совпадает со всей плоскостью Р. Как сама функция
f(t,x)~ax, так и ее производная являются непрерыв-
ными функциями переменных t и х во всей плоскости Р. Таким
образом, теорема 1 к уравнению (о) применима. Непосредственной
12
ВВЕДЕНИЕ
[Гл. t
подстановкой в уравнение (5) проверяется, что каждая функция
х — се**> (6)
где с — произвольное действительное число, является решением
уравнения (5). Решение это непродолжаемо, так как оно задано
уже на всей прямой — оо<^/<^оо. Покажем» что, придавая все-
возможные значения числу су мы получим все решения уравнения
(5). Пусть x = cp(f) — произвольное решение этого уравнения. По-
кажем, что при надлежащем выборе числа с мы имеем ср (t) — ceai.
Пусть tQ—некоторая точка интервала существования решения ср(/)
и х0 = ср(£0). Положим с = х0<?~аЧ Тогда решения x==cp(f)
и х — се** = уравнения (5) имеют одинаковые начальные
значения (f0, х0) и потому в силу второй части теоремы 1 совпадают. Таким
образом, формула (6) исчерпывает совокупность всех решений диф-
ференциального уравнения (5).
2. Дадим математическое описание процесса распада ра-
диоактивного вещества. Количество вещества, еще не распавшегося
к моменту времени t, обозначим через х(£). Из физических сообра-
жений следует, что (если нет условий для возникновения цепной
реакции) скорость распада, т. е. производная i (t), пропорциональна
имеющемуся количеству нераспавшегося радиоактивного вещества:
г
Здесь р—постоянный положительный коэффициент пропорциональ-
ности, зависящий от свойств радиоактивного вещества, а знак ми-
нус в правой части означает, что x(t) убывает. Мы видим, что
функция х (I) удовлетворяет простейшему дифференциальному ура-
внению, рассмотренному в примере 1, так что
х (0 = се~^.
Для определения константы с достаточно указать какие-либо
начальные значения. Если, например, известно, что в момент времени
t = Q имелось количество вещества х0, то с — х^ и мы имеем:
x(f) =
Скорость распада выражается здесь величиной £ размерности \)сек.
Часто вместо величины £ скорость распада характеризуют так на-
виваемым периодом полураспада, т. е. временем, за которое распа-
дается половина имеющегося запаса вещества. Обозначим период
полураспада через Т и установим связь между величинами £ и Т.
Мы имеем:
откуда
Т = У1п2.
р
§2] НЕКОТОРЫЕ ЭЛЕМЕНТАРНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ 13
§ 2. Некоторые влементарные методы интегрирования
Главной задачей, возникающей перед нами, когда мы имеем дело
с дифференциальным уравнением, является задача отыскания его
решений. В теории дифференциальных уравнений, так же как
в алгебре, вопрос о том, что значит найти решение уравнения, можно
понимать по-разному. В алгебре первоначально стремились найти
общую формулу с применением радикалов для решения уравнений
каждой степени. Таковы были: формула для решения квадратного
уравнения, формула Кардана для решения кубического уравнения
и формула Феррари для решения уравнения четвертой степени.
Позже было установлено, что для уравнений выше четвертой степени
общей формулы решения в радикалах не существует. Осталась
возможность приближенного решения уравнений с числовыми коэф-
фициентами, а также возможность исследования зависимости корней
уравнений от его коэффициентов. Примерно такова же была эволю-
ция понятия решения в теории дифференциальных уравнений. Перво-
начально стремились решать, или, как говорят, «интегрировать диф-
ференциальные уравнения в квадратурах», т. е. пытались записать
решение при помощи элементарных функций и интегралов от них.
Позже, когда выяснилось, что решение в этом смысле существует
лишь для очень немногих типов уравнений, центр тяжести теории
^ыл перенесен на изучение общих закономерностей поведения решений.
В этом параграфе будут приведены методы интегрирования
в квадратурах некоторых простейших уравнений первого порядка.
А) (Уравнение в полных дифференциалах). Решим
уравнение
правая часть которого представлена в виде отношения функций
g(tjX) и Предполагается, что функции g(t, х) и h(t, х) опре-
делены и непрерывны на некотором открытом множестве Г плоскости
Р переменных tt х, причем внаменатель h(t,x) не обращается в нуль
ни в одной точке этого множества, а выражение h(t9 x)dx —
— х)Л представляет собой полный дифференциал на всем мно-
жестве * Г. Последнее означает, что существует функция х),
определенная на множестве Г и удовлетворяющая на всем этом мно-
жестве условиям
dF{t,x) ,,, ч dF(t, х) z. ч
= х), - ! = — х). (2)
Уравнение (1) условимся символически записывать в виде ура-
внения
h(tf x)dx — gif, x)dt = Qt
14
ВВЕДЕНИЕ
[Гл I
левая часть которого является полным дифференциалом. Оказывается,
что для каждого решения х = ср(t) уравнения (1) справедливо тождество
ср (t)) = const
Обратно, каждая функция х = ср(^), заданная на некотором интер-
вале и определяемая как неявная функция из уравнения
F(f,x) — c . (3)
(с произвольной константой с), является решением дифференциаль-
ного уравнения (1).
Докажем предложение А). Пусть х = ср (f)—решение дифферен-
циального уравнения (1), определенное на интервале Г1<^<СГ'Ь
Тогда для всех точек этого интервала мы имеем:
__
й(М(0)’
откуда получаем:
hit, ?(0)=0.
Левая часть этого равенства, в силу (2), представляет собой полную
производную по t функции cp(f)), так что
т((»=о ,
на всем интервале В силу известной теоремы анализа,
функция F(t ср (t)) есть константа на всем этом интервале.
Обратно, пусть x = y(t) есть решение уравнения (3), рассматри-
ваемое на некотором интервале, так что
F(t,
Дифференцируя это тождество по t мы в силу (2), получаем:
h(t, ?(0)?(0-£(Л?(0) = 0,
откуда видно, что х = ср(/) есть решение дифференциального уравне-
ния (1).
Итак, предложение А) доказано.
Результату, сформулированному в предложении А), можно дать
следующее геометрическое истолкование. Каждая интегральная кри-
вая дифференциального уравнения (1) расположена целиком на неко-
торой линии уровня функции F(t> х), т. е определяется уравне-
нием (3). Обратно, каждая связная часть линии уровня (т. е, гра-
фик решения уравнения (3), рассматриваемого на некотором ин-
тервале представляет собой интегральную кривую.
Так как линия уровня функции F (t, х) может состоять из нес-
кольких отдельных кусков, то в этом случае целая линия уровня не
«21 НЕКОТОРЫЕ ЭЛЕМЕНТАРНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ 15
является одной интегральной кривой, а распадается на несколько
интегральных кривых. Иными словами, одна константа с может,
в силу неявного уравнения (3), определять несколько (я даже беско-
нечно много, см. пример 3) различных непродолжаемых решений.
Б) (Линейные уравнения). Решим уравнение
x~a(t)x-\-b(t)t (4)
где a(t) и b(t) определены и непрерывны на некотором интервале
ri<^t<Zr2 (случаи Г1 = — оо и гг=-|~со не исключаются). Таким
образом, открытое множество Г в плоскости Р определяется усло-
виями Г[ t т*2, налагаемыми на t при произвольном х. Это мно-
жество представляет собой полосу, если г\ и г2 конечны; полупло-
скость, если конечна только одна из величин rlt rit и плоскость,
если бесконечны обе величины гь г%. Правая часть уравнения (4) непре-
рывна вместе со своей частной производной по х на всем множестве
Г, так что для уравнения (4) выполнены условия теоремы 1. Пусть
tQ— некоторая точка интервала ri<O<Cr* Положим:
t
A(t)-=^a (т)dt. (5)
Го
Функция A(t) определена на всем интервале <^7^. Оказывается,
что совокупность всех решений уравнения (4) записывается формулой
где х0— произвольная константа. Каждое из этих решений опреде-
лено на всем интервале и потому непродолжаемо (так
как за пределами этого интервала не определена правая часть уравне-
ния (4)).
Для доказательства предложения Б) заметим прежде всего, что
функция х, заданная соотношением (6), является решением уравнения
(4). Это непосредственно проверяется путем подстановки.
Докажем, что формула (6) содержит все решения. Пусть
x = —некоторое решение уравнения (4), определенное на ин-
тервале Этот интервал должен содержаться в интервале
rj<^f <V2, так как правая часть уравнения (4) определена только
на этом последнем интервале. Пусть т0, £0 — начальные значения ре-
шения х = <р(0- Докажем, что можно так подобрать число х0 в фор-
муле (6), чтобы определяемое этой формулой решение имело своими
начальными значениями т0, £0, т. е. удовлетворяло условию
(т° \
xt + 5 е~ А (г) b (т) dx I еА (То) — (7)
4) '
16 ВВЕДЕНИЕ [Гл I
Этим будет доказано (см. теорему 1), что решение х = <р(/) совпа-
дает с решением (6) на всем интервале
Соотношение (7) является уравнением первой степени относи-
тельно неизвестной величины х0, причем коэффициент еЛ(т°> при
отличен от нуля. Следовательно, уравнение (7) разрешимо относи-
тельно неизвестной величины х0.
Итак, предложение Б) доказано.
Для сравнения приведем другой (принятый в большинстве учебни-
ков) вывод формулы (6), облегчающий ее запоминание. Прежде всего
рассматривается однородное уравнение
y>=a(t)y. (8)
Это — уравнение в полных дифференциалах (см. А)). В самом де-
ле, символически его можно записать в виде
— a(t)dt = O.
Соответствующая функция F(tt у) задается формулой
F(t, j/) = lnW-A(O,
и потому, в силу А), решения однородного уравнения (8) определя-
ются как неявные функции из соотношения
In [у| — A (t) = cu
Отсюда получаем [у| = £Л^+С1 или, иначе,
где с может принимать любые действительные значения. (Этот вывод
содержит неточность, поскольку функция h(tt у)=у может обра-
щаться в нуль, так что условие 1) предложения А) не выполнено;
неточность легко может быть устранена, но мы этого делать не бу-
дем, так как формула (9) является частным случаем формулы (6),
которая выше была полностью доказана.)
Для получения с помощью формулы (9) решения неоднород-
ного уравнения (4) применяется так называемый метод вариации
постоянной. Именно, решение уравнения (4) ищется в виде (9), где
с уже не константа, а некоторая неизвестная функция переменного Л
Подставляя это предполагаемое решение в уравнение (4), получаем:
сеА (0 еА (0 = a (t) сеА (0 + b (0 *
или, что то же,
'ceAW = b(t).
$21
НЕКОТОРЫЕ ЭЛЕМЕНТАРНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
17
Отсюда находим:
с = $ е~b (t) dt — х0 -|- $ е ~Л(Т) b (т) dxt
/о
где х0— константа интегрирования.
Примеры
1. Решим уравнение
X=f{t)g(x),
называемое уравнением с ющи миг я—переменными, Будем
предполагать, что функция f(t) определена и непрерывна на интер-
вале а функция g(x) определена, непрерывна и не об-
ращается в нуль на интервале qi<Zx<^q<i. Рассматриваемое уравне-
ние есть уравнение в полных дифференциалах. Именно, оно может
быть записано символически в виде:
Соответствующая функция F(t> х) задается формулой
х t
P{t, x) = J-A- C/(x)rfx.
Xq /о
Здесь xn принадлежит интервалу а х изменяется на
том же интервале; f0 принадлежит интервалу a t изменя-
ется на том же интервале. В силу предложения А), все решения
нашего уравнения получаются как неявные функции из соотношения
*0 Zo
2. Решим уравнение
• 1 ! х \
х = h I -- j,
в котором правая часть зависит лишь от отношения переменных
х и t. Уравнение это называется однородным.
Будем предполагать, что функция h(y) определена и непрерывна
на интервале <j/<^а.2 и что на этом интервале функция h (у) — у
не обращается в нуль. Наше уравнение решается путем замены пе-
ременных. Именно, вместо неизвестной функции х мы введем неизвест-
ную функцию у, положив x=yt. Производя эту подстановку, мы
18
ВВЕДЕНИЕ
[Гл. I
получаем для повой неизвестной функции у уравнение
S>t+y = hty)
или, что то же,
л_ *(>)—У
3 Г
Полученное уравнение с разделяющимися переменными решается
по способу, указанному в примере 1.
3. Решим уравнение
x = x2cos/ (10)
с разделяющимися переменными. Множеством Г для него является
вся плоскость (/, х). При х^>0 и при х< 0 уравнение это можно ре-
шать по способу, указанному в примере 1. Для каждой из этих
полуплоскостей мы имеем:
или, иначе»
1 /
-------------------------------= sinr— с.
х
Таким образом, получаем:
Кроме решений, описываемых этой формулой, мы имеем очевидное
решение
х=0. (12)
Покажем, что формулы (11) и (12) охватывают совокупность всех
решений уравнения (10). Пусть (f0, х0) — произвольные начальные
впачения. Если хо = 0, то решение (12) имеет эти начальные значения.
Если же х0 0, то указанные начальные значения имеет решение (11) при
. . . I
c = sni f0 + — •
ло
Решение (12) определено па интервале (— оо, -f-оо) и пбтому не-
продолжаемо. Точно так же при |с|^>1 формула (И) определяет
©дно непродолжаемое решение, заданное на интервале (— оо, -|- оо).
При фиксированной константе с, удовлетворяющей неравенству | с j 1,
формула (И) задает не одно решение, а бесконечное мно-
жество решений. Каждое отдельное решение в этом случае
определено на интервале где !\ и г3 — два соседних нуля
функции sin/ — с (рис. 3).
4. Покажем, что если правая часть уравнения не имеет непре-
рывной производной, то вторая часть теоремы I (единственность)
$ 21
НЕКОТОРЫЕ ЭЛЕМЕНТАРНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
19
может не иметь места. Рассмотрим уравнение
£
х = Зх
(13)
Правая часть уравнения (13) определена и непрерывна для всех
_ 2
з
значений х, но ее производная 2х терпит разрыв при х = 0. Если
Рис. 3.
принять за Г множество всех точек плоскости Р, удовлетворяющих
неравенству х ф 0, то к уравнению (13) применима теорема 1, и в
каждой из полуплоскостей х^>0, х<^0 уравнение (13) можно
20
ВВЕДЕНИЕ
[Гл. t
решать по способу, указанному в примере 2. Решая уравнение (13)
2
з
этим способом, мы получаем: х = t— с. или
x = (t~ с)8. (14)
Часть графика функции (14) (при t<^c) проходит в полуплоскости
х<^0, часть же (при t^>c)— в полуплоскости х^>0. Непосредст-
венно проверяется, однако, что функция (14) является решением
уравнения (13) при всех значениях / на интервале — ооt4~ оо.
В то же время №0 также является решением уравнения (13).
Таким образом, через каждую точку л; = 0, t^c прямой х = 0
проходят уже два решения (рис. 4): решение (14) и решение х = 0.
Мы видим, что вторая часть теоремы 1 (единственность) не имеет
места для уравнения (13).
§3| ФОРМУЛИРОВКА ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ 21
§ 3. Формулировка теоремы существования
и единственности
В § 1 было рассмотрено одно дифференциальное уравнение пер-
вого порядка, причем была сформулирована теорема существования
и единственности для этого уравнения. Теория обыкновенных диф-
ференциальных уравнений имеет дело и с более общими системами
уравнений. Обычно система обыкновенных дифференциальных уравне-
ний состоит из стольких уравнений, сколько в нее входит неизвест-
ных функций; при этом все неизвестные функции являются функциями
одного и того же независимого переменного. Во всех случаях те-
орема существования и единственности является основным теорети-
ческим положением, дающим возможность подойти к изучению дан-
ной системы дифференциальных уравнений.
Теорема существования и единственности формулируется и до-
казывается применительно к системе уравнений, по внешнему виду
имеющей несколько частный тип. В действительности же к этой си-
стеме уравнений сводятся системы сравнительно общего типа. Систе-
мы дифференциальных уравнений того частного типа, о котором
здесь идет речь, мы будем называть в дальнейшем нормальными.
Система
х1, х3, . . . , х”); /= 1, . . . , и, (1)
обыкновенных дифференциальных уравнений называется нормальной.
В этой системе t — независимое переменное, х1,..., хп — неизвестные
функции этого переменного, а ,..., fn — функции от п 1 перемен-
ных, заданные на некотором открытом множестве Г пространства
размерности в котором координатами точки являются числа tt
х\...,хп. В дальнейшем всегда будет предполагаться, что функции
f(t, X1, х\..., хп), П, (2)
непрерывны на открытом множестве Г; точно так же'.будет пред-
полагаться, что и*их частные производные
существуют и непрерывны на множестве Г. Следует заметить, что
частные производные (3), непрерывность которых предполагается,
берутся только по переменным х1,..., хп, а не по независимому
переменному t.
Решением системы уравнений (1) называется система непрерыв-
ных функций
xl = f(t), (4)
определенных на некотором интервале и удовлетворя-
ющих системе (1). Интервал называется интервалом
22
ВВЕДЕНИЕ
[Гл !
определения решения (4) (случаи rt = — со, г2 = -[- со не исключаются).
Считается, что система функций (4) удовлетворяет системе уравнений
(1), если при подстановке в соотношение (1) вместо х\хп
функций (4) соотношения (1) превращаются в тождества по t на всем
интервале Для возможности этой подстановки необходимо,
чтобы функции (4) имели производные в каждой точке интервала
и чтобы правые части уравнений (1) были определены
для всех подставляемых в них значений аргументов. Таким образом,
точка с координатами
t, ?'(0...?я(0
должна принадлежать множеству Г для всех значений t на интервале
Дадим теперь формулировку теоремы существования и единствен-
ности для нормальной системы (1). (Доказательство будет приведено
в § 21.)
Теорема 2. Пусть (1) — нормальная система обыкновенных
дифференциальных уравнений. Здесь правые части уравнений (1)
определены на некотором открытом множестве Г, а функции
(2) и (3) непрерывны на этом множестве. Оказывается, что
для каждой точки
tv .........-v?, (5)
множества Г существует решение
x; = cpf(0, л, (6)
системы (1), определенное на некотором интервале, содержащем
точку tb, и удовлетворяющее условиям:
'pf(Q=^; /=1.....«• (7)
Далее, оказывается, что если имеются два каких-либо решения
х*’ = /(/), Z=l,..., п, J U
системы (1), удовлетворяющих условиям
<Р'(^) = Х‘(<о) = ^> п, (9)
причем каждое решение определено на своем собственном ин-
тервале значений переменного t, содержащем точку t^, то ре-
шения эти совпадают всюду, где они оба определены.
Значения (5) называются начальными для решения (6), а соот-
ношения (7) называются начальными условиями для этого реше-
ния. Мы будем говорить в дальнейшем, что решение (6) имеет на-
чальные значения (5) или удовлетворяет начальным условиям (7).
I 31 ФОРМУЛИРОВКА ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ 23
Таким образом, теорему существования и единственности для нор-
мальной системы кратко можно формулировать так:
Каковы бы ни были начальные значения (5), всегда сущест-
вует решение системы (1) с этими начальными значениями, опре-
деленное на некотором интервале, содержащем точку t$. Далее,
если имеются два решения с одинаковыми начальными значе-
ниями (5), каждое из которых определено на своем интервале,
содержащем tQi то эти решения совпадают на общей части этих
интервалов.
Совершенно так же, как в § 2, введем здесь понятие непродол-
жаемого решения.
А) Пусть
= Z=l,..., п, (1U)
— решение системы уравнений (1), определеннее на интервале
= 1 — \,...,п, (11)
— решение той же системы уравнений (1), определенное на интер-
вале Мы будем говорить, что решение (И) является
продолжением решения (10), если интервал содержит
интервал (т. е. и решение (10) совпадает
с решением (11) на интервале >4 <^<>2- В частности, мы будем
считать, что решение (И) является продолжением решения (10) и
в том случае, когда оба решения полностью совпадают, т. е. 5! = ^,
г4 = $.. Решение (10) будем называть непродолжаемым, если не
существует никакого отличного от него решения, являющегося его
"^Продолжением.
Нетрудно доказать (но это будет сделано позднее, см. § 22, А)),
что каждое решение может быть продолжено до непродолжаемого
и притом единственным способом.
Формулируем теперь еще одну теорему существования, доказа-
тельство которой будет приведено в § 21.
Теорема 3. Пусть
х>b‘(t\,
п
I = 1, ..., п,
(12)
—нормальная линейная система уравнений. Здесь коэффициенты
alj(t) и свободные члены bl (t) являются непрерывными функци-
ями независимого переменного Z, определенными на некотором
интервале qi<^t<^q*. Оказывается, что для любых начальных
значений
?! ^4 q*
(13)
24
ВВЕДЕНИЕ
[Гл. I
существует решение системы (12) с этими начальными значе-
ниями, определенное на всем интервале
В частности, если коэффициенты и свободные члены системы (12)
определены на всей прямой, т. е. если — оо, ^а=-|-со, то для
любых начальных значений существует решение системы (12), опре-
деленное на всем бесконечном интервале —оо<^<^4“°°*
Решения нормальной системы (1) интерпретируются геометри-
чески в виде интегральных кривых в (я4~ 0'меРном прост-
ранстве с координатами t> х1, .хп (ср. § 1). Уравнения интеграль-
ной кривой имеют вид:
= /==1, п, (14)
где (14) есть решение системы.
Сама система (1) интерпретируется с помощью поля направлений
в (п 1)-мерном пространстве (ср. § 1).
Примеры
1. Решим нормальную линейную систему уравнений
X = — <оу, J? = (д)Х. (15)
Множеством Г для нее является все трехмерное пространство с коор-
динатами t, х, у. Непосредственно проверяется, что система функций
х = сх cos (о>/ y=qsin(u>f-|-^)» (16)
где ct и —произвольные постоянные, представляет собой реше-
ние системы (15). Для того чтобы показать, что, выбирая надлежа-
щим образом постоянные сЛ и с^ можно получить по формуле (16)
произвольное решение, зададимся начальными значениями tQt х0, у$
и покажем, что среди решений (16) имеется решение с этими на-
чальными значениями. Мы получаем для постоянных сх и условия
с, cos («)/0 4“ с«) = Ci sin (u)^0 4- с%)=Уо. (17)
Пусть р и ?—полярные координаты точки (х0, <р0), так что
х0 = р cos ср, Уо = р sin ср.
Тогда уравнения (17) переписываются в виде:
Ci cos (со/0 4“ с4) = р cos ср, с{ sin (o>f0 4~ <л) = Р sin
Полагая
Cj = р, = ср —
мы, очевидно, выполним условия (17). Таким образом, через каждую
точку (/0, х0, у0) проходит решение, задаваемое формулой (16).
§ 4] СВЕДЕНИЕ ОБЩЕЙ СИСТЕМЫ УРАВНЕНИЙ К НОРМАЛЬНОЙ 25
В силу теоремы 2 (единственность) формула (16) охватывает сово-
купность всех решений.
2. Покажем, что если правые части (2) системы уравнений (1)
k раз непрерывно дифференцируемы, т. е. имеют непрерывные про-
изводные порядка k (включая смешанные) по всем переменным it
х1, х”, то (А4-1)"я производная решения (4) системы (1) сущест-
вует и непрерывна.
В самом деле, для решения (4) имеет место тождество:
Ф‘‘(0=/(*> ... ?л(0)> i= ь ...» О8)
Если правые части (2) имеют непрерывные первые производные, то
правая часть тождества (18) имеет непрерывную производную по
и потому функция ф*(0 существует и непрерывна. Дифференцируя
написанное тождество (18) k раз, мы последовательно убедимся в су-
ществовании и непрерывности всех производных порядков 2, 3,..., А-]- 1
функций ^(t).
§ 4. Сведение общей системы дифференциальных уравнений
к нормальной
В предыдущем параграфе была сформулирована теорема суще-
ствования и единственности для нормальной системы дифференци-
альных уравнений. Здесь будет показано, каким образом весьма
общие системы дифференциальных уравнений сводятся к нормальным
системам дифференциальных уравнений, и тем самым будет установ-
лена теорема существования и единственности для этих общих си-
стем уравнений.
Дадим сначала понятие о системе дифференциальных уравнений
в общем виде.
В случае одной неизвестной функции х независимого перемен-
ного t обычно рассматривается одно уравнение, которое можно запи-
сать в виде:
F(t, х, Я....х(п)) = 0. (1)
Здесь t — независимое переменное, х — его неизвестная функция, а
F—заданная функция я-{-2 переменных. Функция F может быть
задана не для всех значений ее аргументов, поэтому говорят об
области В задания функции Л. Здесь имеется в виду открытое
множество В координатного пространства размерности п-1- 2, в ко-
тором координатами точки являются переменные t, xt Jf, х<л).
Если максимальный порядок производной, входящей в дифференци-
альное уравнение, равен я, то говорят, что имеется уравнение п-го
порядка. Решением уравнения (1) называется такая непрерывная функ-
ция x = cp(f) независимого переменного t, определенная на некото-
ром интервале Г1<О<СГ*’ 410 ПРИ подстановке ее вместо х в урав-
26
ВВЕДЕНИЕ
(Гл I
нение (1) мы получаем тождество по t на интервале rt t
Очевидно, что подстановка х = ср(0 в соотношение (1) возможна
лишь тогда, когда функция ср (t) на всем интервале своего существо-
вания имеет производные до порядка п включительно.
Для того чтобы подстановка x = cp(Q в соотношение (1) была воз-
можна, необходимо также, чтобы точка, имеющая координаты {£, ср(0,
ф(0» ..о принадлежала множеству В определения функции Р
при произвольном t из интервала rt<^f<^r9.
Если имеются две неизвестные функции одного независимого
переменного, то рассматриваются два дифференциальных уравнения,
вместе образующих систему уравнений. Система эта может быть
записана в виде:
F(t, х, Л, x'm), y,S>, ,/")) = 0, 1
Q(t, х, Л.....х(ш), у, J>.._y(n)) = 0. J
Здесь t—независимое переменное, х и у — две его неизвестные
функции, a F и Q — две функции, каждая от/п-|~п-[“3 переменных,
заданные в некотором открытом множестве В. Если максимальный
порядок производной функции х, входящей в систему (2), равен т,
а максимальный порядок производной функции _у, входящей в си-
стему (2), равен п, то число т называется порядком системы (2)
относительно х, число п— порядком системы (2) относительно у,
а число т-\-п называется порядком системы (2). Решением си-
стемы (2) называется пара непрерывных функций x = cp(f) и ^ = ф(^),
заданных па некотором интервале и обладающих тем
свойством, что при подстановке их в соотношения (2) мы приходим
К тождествам по t на всем интервале i\<^t ^ак и в случае од-
ного уравнения, предполагаются выполненными условия, дающие воз-
можность делать подстановку х = ср(£), _у = ф(?) в систему (2).
Аналогично определяются системы дифференциальных уравнений
с тремя и большим числом неизвестных функций от одного незави-
симого переменного. Если неизвестными функциями системы диф-
ференциальных уравнений являются функции х1, ..., х”, а наивыс-
ший порядок производной функции х*, входящей в систему, ра-
вен qi, /=1, п, то число qi называется порядком системы
относительно х1, а число q = qt^~ q.2~f- ... ~\~qn называется поряд-
ком системы. Таким образом, нормальная система (1) § 3 имеет
порядок п.
Если соотношение (1) может быть разрешено относительно xtn),
то уравнение (1) переписывается в виде:
хя=/а, х, х, х(п-°). (3)
Точно так же, если система (2) может быть разрешена относительно
§
СВЕДЕНИЕ ОБЩЕЙ СИСТЕМЫ УРАВНЕНИЙ К НОРМАЛЬНОЙ
27
величин х(т) и у(Гь), то эта система может быть переписана в виде.
x{m^—f(tt х, х, ...» х^т~1\ у, Jr, ..., у(п-1)),
y(n) = g(tt х, х, у, _р, ..., у("~1}).
Уравнение (3) и система (4) называются разрешенными относитель-
но высших производных. Аналогично определяются разрешенные от-
носительно высших производных системы с произвольным числом не-
известных функций. В частности, нормальная система (1) § 3 является
разрешенной относительно высших производных. В дальнейшем мы
будем заниматься почти исключительно системами, разрешенными» от-
носительно высших производных.
Покажем теперь, что всякая имеющая порядок п система диффе-
ренциальных уравнений, разрешенная относительно высших производ-
ных, сводится к нормальной системе порядка п. Для начала покажем,
как одно уравнение порядка п сводится к нормальной системе по-
рядка п.
А) Пусть
у, .....у'""1’) (5)
(4)
— одно дифференциальное уравнение порядка п, разрешенное отно-
сительно высшей производной. Здесь t—независимое переменное,
у — неизвестная функция переменного t. Далее, /(/, у, j>, у(п-1))
есть заданная функция и-|-1 переменных t, у, j>, ..., y(n_I), опреде-
ленная в некотором открытом множестве Г координатного прост-
ранства размерности n-j- 1. Относительно функции f(t, у, у, ..., у(п-,))
мы будем предполагать, что она непрерывна на множестве Г и что
ее частные производные
dfit’y'^yxy'n,y>. а=о, 1.1
(где предполагается, что у(0)=у) также непрерывны на множестве Г.
Для замены уравнения (5) нормальной системой уравнений вводятся
новые неизвестные функции №, х2, ..., хп независимого перемен-
ного t при помощи равенств
х1 = у, х*=у\ ..., хп = у(п1\ (6)
Оказывается, что уравнение (5) эквивалентно системе
х',-1 = хп,
xn = f(f, х1, х*, хп).
Из этого в силу теоремы 2 следует, что для каждой точки f0,
у0> Л» •••> Уо(л множества Г существует решение y = <J>(f)
28
ВВЕДЕНИВ
(Гл. I
уравнения (5), удовлетворяющее начальным условиям
* = 0, 1, .... п-1,
или, как говорят, решение с начальными значениями
Ь- Уо> Л> •••• У"-1’- (8)
Далее, любые два решения с начальными значениями (8) совпада-
ют на общей части их интервалов определения. Если уравнение (5)
линейно, т. е. функция f линейна относительно переменных у, ...
..., а коэффициенты ее определены и непрерывны на интер-
вале q{<^t<^q^ то для любых начальных значений f0, ...
r^e имеется решение у = ф(£), определенное
на всем интервале qi<^t<^.
Докажем, что уравнение (5) эквивалентно системе (7). Допустим,
что функция у удовлетворяет уравнению (5), и докажем, что функции
х1, .... хп> определенные соотношениями (6), удовлетворяют систе-
ме (7). Дифференцируя соотношения (6), вводящие новые неиз-
вестные функции х1, ..., х", получаем:
£=1, п—I, (9)
у(п)_ (Ю)
Заменяя правые части соотношений (9) на основе соотношений (6),
а правую часть соотношения (10) на основании уравнения (5), кото-
рому функция у удовлетворяет, мы получаем систему (7). Допустим,
что, наоборот, функции х1, ..., х” удовлетворяют системе (7); при-
мем тогда х1 за у и покажем, что функция у удовлетворяет уравне-
нию (5). Полагая в первом из уравнений системы (7) х1 =у, полу-
чаем x2=j>. Заменяя во втором из уравнений (7) х2 через полу-
чаем x3=JJ. Продолжая это построение дальше, мы приходим к со-
отношениям (6). Наконец, заменяя в последнем из уравнений системы
(7) каждую функцию х1, хп в силу формул (6), получаем урав-
нение (о) для у.
Так как функция f определена на множестве Г, то правые части
системы (7) также определены на множестве Г при условии замены
координат по формулам (6). Для системы (7) выполнены условия
теоремы 2 на множестве Г. Таким образом, можно произвольно
выбрать начальные значения xj, х*, х" в множестве Г. Эш
начальные значения в силу замены (6) превращаются в начальные
значения
— t, у0> •••>
для уравнения (5).
Если уравнение (о) линейно, то система (7) также линейна. Из
этого в силу теоремы 3 вытекает заключительная часть предло-
жения Л).
$ 41 СВЕДЕНИЕ ОБЩЕЙ СИСТЕМЫ УРАВНЕНИЙ К НОРМАЛЬНОЙ 29
Таким образом, предложение А) доказано.
Прием, описанный в предложении А), дает возможность привести
к нормальной системе произвольную систему дифференциальных
уравнений, разрешенную относительно высших производных. Для
того чтобы не загромождать изложения формулами, рассмотрим
в нижеследующем предложении Б) систему четвертого порядка, со-
стоящую из двух уравнений.
Б) Пусть
й=/(/, и, й. V, )
? (И)
V = g(tt и, й, v> v) )
— система двух уравнений второго порядка. Здесь t—независимое
переменное, а и и v — его неизвестные функции. Сведем систему (11)
к нормальной системе, введя новые неизвестные функции х1, х9, х*,
х4, по следующим формулам:
х1 = и, х9 = й, х8 = и, х4 = й.
При этой замене система (И) переходит в систему
х1 = х9,
х1, Xе, х8, х4), pg)
х3 = х4,
xl — gft, X1, Xе, X8, X4).
Если предположить, что функции f и g, стоящие в правых частях
уравнений (11), определены в некотором открытом множестве Г пя-
тимерного пространства, где координатами точки служат tt и, й, vt
причем функции эти непрерывны и имеют непрерывные частные про*
изводные первого порядка по переменным и, й, vt v, то система (12)
нормальна и удовлетворяет условиям теоремы 2 на множестве Г»
Отсюда легко следует, что для произвольной точки ив, й0,
множества Г существует решение и = ср(£), т> = ф (t) системы (11)ь
удовлетворяющее начальным условиям
?(<«)=»(>> ?(Q = *e>
<Ж) = *0-
Кроме того, всякие решения с одинаковыми начальными условиям»
совпадают на общей части их интервалов существования.
Доказательство предложения Б) проводится точно так же, кам
и доказательство предложения А).
Если одно уравнение и-го порядка задано в форме
F(t, у} J), Уя))=0, (1В>
не разрешенной относительно высшей производной у(я) неизвестной фу»,
кции, то прежде всего возникает вопрос о возможности разрешен»»
3tt ВВЕДЕНИЙ [Гл. 1
его относительно этот вопрос можно считать ве относящимся
к области дифференциальных уравнений, он относится скорее к об-
ласти теории функций. Здесь, однако, имеются некоторые вопросы,
которые разбираются в теории дифференциальных уравнений. Они
носят следующий характер. Допустим, что уравнение (13) является
квадратным относительно переменного Тогда оно определяет
двузначную функцию остальных переменных. Там, где два зна-
чения действительно различны, мы приходим в сущности к двум
различным уравнениям вида (5), но там, где два значения перемен-
ного определяемые уравнением (13), сливаются, расщепление
на два уравнения вида (5) невозможно и приходится рассматривать
уравнение (13). Изучение таких уравнений приводит к понятию об
особых решениях дифференциального уравнения и к рассмотрению
уравнений на поверхностях. Эти вопросы, однако, в книге рассмат-
риваться не будут.
Примеры
1. Решим уравнение
X -J- иРх — 0, (14)
где со — положительная константа.
Непосредственно проверяется, что функция
х — г cos (о)/ а)> г^О, (15)
где г и а — постоянные, удовлетворяет этому уравнению. Покажем,
что формула (15) охватывает совокупность всех решений. Пусть
х = ?(0—произвольное решение уравнения (14). В силу теоремы 3
(см. конец предложения А)) можно считать, что решение x=y(t)
определено для всех значений t Положим <р(0) = ф(О) = х0. Не-
посредственно проверяется, что можно подобрать постоянные г и а
таким образом, чтобы имели место равенства rcosa = x0, —no sin a —
= х0. Если эти равенства выполнены, то решения (15) и <p(f) имеют
одинаковые начальные значения 0, х0, и потому совпадают (см.
предложение А)).
Функция (15) описывает гармонический колебательный процесс.
Положительная константа г называется амплитудой колебания (15),
а a — его начальной фазой или просто фазой. Уравнение (14) на-
зывается уравнением гармонических колебаний. Число о> называется
частотой колебаний, хотя в действительности число колебаний
в секунду определяется формулой
со
2^'
2. Рассмотрим движение точки р массы т по горизонтальной
прямой I под действием силы F, притягивающей ее к точке о на
$4] СВЕДЕНИЕ ОБЩЕЙ СИСТЕМЫ УРАВНЕНИЙ К НОРМАЛЬНОЙ 31
той же прямой и пропорциональной расстоянию между точками р и о.
Для составления уравнения движения точки р введем на прямой I
координату, приняв за начало точку о. Переменную координату
точки р обозначим через х = х(1). Тогда в силу второго закона
Ньютона уравнение движения точки р будет иметь вид:
тх = F= —kx.
Это уравнение обычно записывается в виде:
тх kx — 0.
(16)
Физически сила F может быть осуществлена какой-либо пружиной
(рис. 5). Число k называется коэффициентом упругости этой пру-
жины. Согласно формуле (15) решение уравнения (16) имеет вид:
х — г cos (1/
\ К m Г
Таким образом, частота колебаний w = у точки р определя-
ется ее массой т и упругостью пружины k\ она не зависит от на-
чальных условий. От начальных условий, т. е. от положения точ-
ки р и ее скорости Д в момент f = 0, зависят амплитуда г коле-
бания и его начальная фаза а.
Рис. 5.
3. Составим и решим приближенно уравнение математического
маятника. Математический маятник представляет собой точку р
массы т, которая под действием силы тяжести движется по окруж-
ности К радиуса /, лежащей в вертикальной плоскости. Величина Z
называется длиной маятника. На окружности К введем угловую ко-
ординату, приняв за начало координат самую нижнюю точку о ок-
ружности К (рис. 6). Переменную координату точки р обозначим
через cp = cp(Z). Точка р находится под действием силы тяжести
P=mg, направленной вертикально вниз. Составляющая этой силы,
направленная по нормали к окружности, уравновешивается благодаря
реакции связи (окружности или нити, заставляющей точку двигаться
по окружности); составляющая, направленная по касательной к ок-
ружности в точке р, равна — mg sin ср (если за положительное
32
ВВЕДЕНИЕ
[Гл I
направление на касательной принять направление, соответствующее
возрастанию угла ср). Таким образом, уравнение движения точки р
имеет вид:
/и/ф = —mg sin ср
или, иначе,
/?4-gsin<p = 0. (17)
Уравнение это нелинейно, и его решение представляет большие
трудности. Если предположить, что координата tp точки р в процессе
движения мало отклоняется
от нуля, то приближенно в
уравнении (17) можно заме-
нить sin tp через <р, и мы по-
лучим «приближенное» ли-
нейное уравнение маятника:
Zq5-]-g-<p=O.
Его решение имеет вид (см.
(15)):
Таким образом, частота «ма-
лых колебаний» маятника
определяется формулой о> =
Число v малых колебаний маятника
в секунду определяется фор-
мулой
Например, длина секундного маятника, т. е. маятника, совершаю-
щего одно колебание в секунду (у=\[сек), определяется формулой
1= -гтсек* As; 0,25 м,
4яа
§ 5. Комплексные дифференциальные уравнения
До сих пор мы рассматривали лишь действительные уравнения
и их действительные решения. В некоторых случаях, однако, напри-
мер при решении линейных уравнений с постоянными коэффициен-
тами, бывает легче найти сначала комплексные решения дей-
ствительного уравнения, а затем уже выделить из них действитель-
ные решения. Для изложения этого подхода мы должны ввести
$5] КОМПЛЕКСНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 33
понятия комплексной' функции действительного переменного и комп-
лексной системы дифференциальных уравнений.
А) Говорят, что задана комплексная функция x(t) действитель-
ного переменного t, если на некотором интервале каж-
дому значению переменного t поставлено в соответствие комплексное
число
x(0=?(04-W
где ср (0 и ф(£) являются действительными функциями действитель-
ного переменного t, Функция <p(f) называется действительной ча-
стью комплексной функции ^(0, а функция ф(0 называется мнимой
частью комплексной функции x(Q. Комплексная функция х (0 назы-
вается непрерывной, если функции' у (0 и ф(0 непрерывны. Точно
так же комплексная функция /(£) называется дифференцируемой»
если, дифференцируемы функции <p(f) и ф(£); производная х(0 комп-
лексной функции х(0 определяется формулой
х(0 = ?(04-W)-
Непосредственно проверяется, что имеют место обычные правила
дифференцирования суммы, произведения и частного двух комплекс-
ных функций действительного переменного.
Б) Пусть
? = //((,?...zn)-, /=1......п (1)
— нормальная система дифференциальных уравнений. Относительно
функций h1 (t, z1, ..., zn), стоящих в правых частях уравнений, мы
предположим, что они определены для комплексных значений пере-
менных z1, ..., zn. Мы можем ограничиться, например, случаем,
когда функции эти являются многочленами относительно перемен-
ных zl, ..., zn с коэффициентами, являющимися действительными
или комплексными непрерывными функциями действительного пере-
менного tr определенными и непрерывными на интервале Qi<Z^
При ..этих условиях вполне законна постановка вопроса об отыскании
комплексных решений системы (1). Систему
^х'Ю; /=1, ...» п, (2)
комплексных функций действительного переменного t, заданных на
некотором интервале будем называть решением системы
(1), если при замене переменных zz функциями переменного t по,
формулам (2), мы получим систему тождеств по t на этом интервале.
Так как по предположению, правые части уравнений (1) являются
многочленами относительно zl, ..., zn, то они определены для всех
значений этих переменных. Оказывается, что имеет место следующая
теорема существования и единственности для системы (1). Пусть
/
*0» *'(j> • • • f -*0
2 Понтрягин Л. С.
34
ВВЕДЕНИЕ
(Гл. I
— произвольная система начальных значений. Здесь z', z"—про-
извольные комплексные числа, a /0— произвольное действительное
число, удовлетворяющее условию qi<^tQ<^q^ Тогда существует ре-
шение
^=x'(0;
системы (1), удовлетворяющее начальным условиям
x'(Q=^; /=ь ......
Всякие два решения с одинаковыми начальными условиями совпадают
на общей части их интервалов определения. Если система (1) ли-
нейна, т. е. многочлены hJ имеют степень 1, то для любых началь-
ных значений существует решение уравнения (1), определенное на
всем интервале
Эта теорема существования и единственности для нормальной си-
стемы комплексных уравнений непосредственно вытекает из тео-
ремы 2 после расщепления каждой комплексной неизвестной функ-
ции zJ на ее действительную и мнимую части. В самом деле, по-
ложим:
^ = х^-}-1у*; у*=1, я, (3)
и заменим переменные г7; 7=1, л, в системе (1) по форму-
лам (3); тогда будем иметь:
xJ =fJ (t> х\ ...» xn, у1, ...,yn) +
x1, xnt y\ y"), (4)
где f и g1 — действительные функции действительных аргументов,
удовлетворяющие соотношениям
f(t, х\ хп, у, ...» х1, хп, у1, уп) —
= (t, х* -f- 6Л < • •» х” -|- /у”).
Из (4) следует:
xi=f(tt х1, .хп, у1, ...» у"), 7 = 1> •••» rt’ 1
У = У(/, X1, Xя, у1, ...» уП), 7=1, п. J
Таким образом, нормальная система (1) комплексных уравнений за-
менилась нормальной системой (5) действительных уравнений. Так
как правые части уравнений (1) являются многочленами относи-
тельно г1, znt то правые части уравнений (5) являются многочле-
нами относительно х1, x,lt у1, у*. Так как коэффициенты
многочленов h} являются непрерывными функциями переменного t
на интервале q\<Zt<Zq* то на том же интервале и коэффициенты
многочленов f и g1 являются непрерывными функциями. Таким об-
разом, правые части системы (5) определены и удовлетворяют усло-
виям теоремы 2 в открытом множестве Г, определяемом единствен-
*5] КОМПЛЕКСНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ' 35
ним условием налагаемым на tf в то время как осталь-
ные переменные х1, ...» хп и у\ ...» уп остаются произвольными.
Полагая
Z7(0 = ?; (0 + ^(0, 7=1,
мы приходим к задаче отыскания
ных условиях
решения системы (5) при иачаль-
Н^=у1’
7=1.
7=1.
Л,
п.
В силу теоремы 2 решение это существует; всякие два решения
с одинаковыми начальными условиями совпадают на обшей час!»
их интервалов определения.
Если система (1) линейна, то система (5) также линейна, и по-
тому заключительная часть предложения Б) вытекает из теоремы 3.
Следует отметить, что система (1), в правых частях которой
стоят многочлены относительно переменных z1, .znt может быть
действительной, т. е. коэффициенты этих многочленов могут
быть действительными функциями переменного t; тем не менее мы
можем и в этом случае рассматривать систему (1) как комплексную,
именно искать ее комплексные решения, считая, что функции z1, ...,2*
комплексны. Этот подход к действительным уравнениям применяется
потому, что в некоторых случаях легче найти комплексные решения
действительных уравнений, чем их действительные решения. В этом
случае находят сначала комплексные решения действительной системы
уравнений, затем из комплексных решений выделяют действительные
решения, т. е. рассматривают только такие комплексные решения,
мнимая часть которых обращается в нуль. Именно таким приемом
будут в дальнейшем решаться линейные уравнения с постоянными
коэффициентами.
Так же, как в действительном случае, и в комплексном случае к
нормальной системе можно свести довольно общие системы диффе-
ренциальных уравнений. Таким образом, мы имеем в комплексном
случае предложения, аналогичные предложениям А), Б) § 4. Здесь
дадим только формулировку теоремы существования для одного
уравнения л-го порядка.
В) Пусть
z, £, z'"-1)) (6)
— уравнение порядка л, в котором правая часть является многочле-
ном относительно переменных z, Д ..., z(n-n с коэффициентами,
являющимися непрерывными действительными или комплексными
функциями переменного t, определенными на интервале q\<^t
Если теперь z0, — произвольные начальные значения,
2*
36
ВВЕДЕНИЕ
[Гл. Т
где zQ, 20, 2'0(л”|> — произвольные комплексные числа, а7в^—дей-
ствительное число, удовлетворяющее . неравенствам то
существует решение 2 = ср(0 уравнения (6), удовлетворяющее началь-
ным условиям
<р(ta)=za, ф(/,0)=г0,(<(,)=/«-'>.
Всякие два решения с одинаковыми начальными условиями совпа-
дают на общей части их интервалов определения. Если уравнение (6)
линейно, т. е. многочлен f имеет степень 1, то для любых началь-
ных значений существует решение, определенное на всем интерв;а-
ле -
В § 7 и далее важную роль будет играть комплексная функ-
ция еи действительного переменного tt где X — комплексное число.
Дадим здесь определение этой функции и докажем некоторые её
свойства.
Г) Пусть w = uJyi'u— произвольное комплексное число; положим:
£w = £w(cosv-|-f sin v). (7)
Легко видеть, что имеет место соотношение
е® = е™*
Ниже будет доказана формула
(8)
Из (7) непосредственно следуют известные формулы Эйлера:
cos v =-----, sin v =---------ту.-.
z zi
Пусть X = p.-J-h есть комплексное число. В силу формулы (7) мы
имеем:
(cos'd -f- / sin ^).
Мы покажем, что для комплексных значений X имеет место следую-
щая формула дифференцирования:
— = (9)
хорошо известная для действительных значений параметра X.
Формула (7), принятая здесь за определение функции ew
комплексного переменного w> может быть доказана, если фун-
кцию ew определить с помощью ряда
е *=1+да+_+_+...+__+<...
Мы, однако, будем считать, что функция ew определяется формулсй (7).
§5] КОМПЛЕКСНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 37
Докажем формулу (8). Пусть
Тогда имеем:
eWl eWi — eUl (cos -ф- * sin vj eUi (cos / sin иД —
_ e«i + “a (CQS l s[n +
Докажем теперь формулу (9). Рассмотрим сначала случай чисто мни-
мого числа k = h. Мы имеем:
— еы = ~ (cos vf 4-1 sin vf) = — v sin vt -k h cos vt =
at at '
= h (cos v/ + sin vf) = he1**.
Далее, для произвольного k = в силу формулы дифференци-
рования произведения имеем:
£ = А . е-‘) = ± (^) еы + (?’') =
= еы -|-еы =(р. 4- h) = кеи.
Примеры
1. Рассмотрим комплексное уравнение
£ = U (10)
где z = x-\-ly есть комплексная неизвестная функция действитель-
ного переменного t, а Х = р,—|—Zv — комплексное число. Из (9) сле-
дует, что
z = ceu (11)
есть решение уравнения (10) при произвольной комплексной посто-
янной с. Покажем, что формула (11) охватывает совокупность всех
решений. Для этого, как и в примере 1 § 1, можно было бы вос-
пользоваться теоремой единственности, но мы используем здесь и тео-
рему 3, для того чтобы показать, как при ее помощи можно несколько
упростить вычисления. В данном случае эти упрощения очень незна-
чительны, но в дальнейшем аналогичный прием может дать более
существенные результаты. Итак, пусть г = /(/) —произвольное ре-
шение уравнения (10). В силу теоремы 3 (см. заключительную часть
предложения В)) можно считать, что решение эго определено для всех
значений t. Полагая y(O) = zo, мы видим, что решение z —у (0 имеет
своими начальными значениями числа 0, zfl. Те же начальные значе-
ния имеет, очевидно, и решение
получаемое из (11) при c = z0.
38 ВВЕДЕНИЕ (Гл I
Если положить c = reia, где г^О и а — действительные числа,
то решение (11) записывается в форме
z = reu*ia. (12)
Расщепим теперь уравнение (10) на действительную и мнимую части.
Мы имеем:
х + ZP = (н+ ь) (-V н- 1у) = (И* — ЧУ) + i + НУ)>
ИЛИ
I (13)
^=^4-|лу. J
Таким образом, система (13) двух действительных уравнений равно-
сильна одному комплексному уравнению (10), и потому произвольное
решение x = <p(0, J = <p(O системы (13) связано с произвольным ре-
шением (12) уравнения (10) соотношением
? (0 + (0 = reU + г“ = г (еи/ cos (yt а) + Z sin (vf -j- а)).
Отсюда получаем:
х = y(t) = re^ cos (v/ a), 1
у = ф (/) = re^ sin (vtf 4- a). J
Итак, пользуясь комплексными функциями и уравнениями, мы нашли
решение (14) системы (13) действительных уравнений.
2. Дадим еще один пример расщепления комплексного уравнения
па два действительных. Пусть
^ = га4-/г
— комплексное уравнение, где z — x-^ly есть комплексная неиз-
вестная функция действительного переменного /. Мы имеем:
X 4- 1у = (х 4- iy? ~Н (X + iy) = (х*-у* — у)-[-1 (2ху -f- х)
и потому
| £ = — у* — у,
( $ = 2ху 4* х.
§ 6. Некоторые сведения о линейных дифференциальных
уравнениях
Система дифференциальных уравнений называется линейной если
все неизвестные функции и их производные, вместе взятые, входят
в уравнения системы линейно. Таким образом, система линейных
§ 5 J НЕКОТОРЫЕ СВЕДЕНИЯ О ЛИНЕЙНЫХ УРАВНЕНИЯХ 39
уравнений самого общего вида может быть записана в форме
/=1, (1)
/. *
Здесь х1, ...» хп — неизвестные функции независимого переменного tr
а коэффициенты и свободные члены ^ (/) уравнений являются
функциями t. Если все свободные члены системы (1) тождественно
равны нулю, то система называется однородной. Каждой линейной
системе соответствует однородная линейная система, получающаяся
из нее отбрасыванием свободных членов. Таким образом, линейной
системе (1) соответствует линейная однородная система
Z=l......п. (2)
/.ft
Отметим несколько непосредственно проверяемых свойств линей-
ных систем. При их формулировке будет предполагаться, что все
коэффициенты и свободные члены линейной системы определен^
и непрерывны на интервале все рассматриваемые реше-
ния будут предполагаться заданными на всем интервале Ях^^^Яъ*
А) Если у1 = ср' (t) и у1 — ф' (£); /= 1, п — два решения ли-
нейной однородной системы (2), a и — два произвольных числа,
то система функций
у1 — <ч<ре (О 4- ^ф' (0- < =1.....
также представляет собой решение однородной системы (2). Анало-
гичное утверждение справедливо также для трех и большего числа
решений однородной системы (2).
Б) Если х' = ф‘(/) и — /=1, л, — два решения ли-
нейной системы (1), то система функций
? = х'Ю-Ф'Ю; *=1..............«.
представляет собой решение системы однородных уравнений (2). Да-
лее, если y = (pf(/)t Z=l, п, есть решение однородной системы
уравнений (2), a xl = ty'(t)\ л, есть решение линейной
системы (1), то система функций
х1 = ф1'(t)(/); /=1, л,
представляет собой решение линейной системы (1).
В) Допустим, что свободные члены системы линейных уравне-
ний (1) представлены в виде сумм:
40 ВВЕДЕНИЕ [Гл. 1
рассмотрим наряду с системой (1) две системы уравнений:
S^(0(^)u, + q(0 = 0; /=1, ..о и, (3)
Л*
S at}b (0(/»(Л) + dt (0 =» 0j I = 1, ..., п. (4)
Л Л
Если х* = ф*(0, /=1» ...э л, есть решение системы (3), а х* — у^(/)>
/=1, л, есть решение системы (4), то система функций
xi = аф* (0 + ₽/ (0, 2=Ь...,Я> .
представляет собой решение системы (1).
Г ЛА ВА ВТОРА Я
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ
КОЭФФИЦИЕНТАМИ
Системы обыкновенных дифференциальных уравнений с постоян-
ными коэффициентами представляют собой большой и важный класс
обыкновенных дифференциальных уравнений, решающихся до конца
при помощи элементарных функций. Ввиду того, что решение этих
уравнений принципиально не представляет больших трудностей, часто
считают, что они не имеют сколько-нибудь значительного интереса
для теории, и в учебниках им обычно отводят место простого при-
мера к общей теории линейных уравнений. Между тем линейные урав-
нения с постоянными коэффициентами имеют многочисленные техни-
ческие применения, так как работа весьма многих технических объектов
достаточно адэкватным образом описывается этими уравнениями. Именно
технические применения выдвигают ряд новых задач теоретического ха-
рактера в теории линейных уравнений с постоянными коэффициентами.
Решению этих теоретических задач посвящено немало работ, имеющих
прикладную направленность, и некоторые из них нашли отражение в
настоящей главе. Так, в этой главе используются обычные для ин-
женерной практики операционные обозначения, которые
очень удобны для решения систем уравнений методом исключения.
Рассматривается вопрос об устойчивости решений систем
линейных уравнений, очень важный в теории автоматического управ-
ления. Далее, излагается так называемый метод комплексной
амплитуды, представляющий собой удобный способ нахождения
частных установившихся решений и широко применяемый в электро-
технике.
Не ограничиваясь решением чисто математических задач, порож-
денных практикой, я привожу здесь в очень краткой догматической
форме изложение теории электрических цепей. Расчет электрических
цепей дает хорошую и важную с технической точки зрения иллю-
страцию развитых в этой главе математических методов.
Кроме того, в настоящую главу включено исследование фазовой
плоскости линейных систем второго порядка, которому предшест-
вует самое начальное изучение фазовых пространств автономных
42 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ (Гл. 2
(вообще говоря, нелинейных) систем. Фазовые пространства авто-
номных систем также находят важные приложения в технике.
Благодаря всему сказанному глава о линейных уравнениях с
постоянными коэффициентами занимает в этой книге значительно
больше места, чем это обычно бывает в учебниках по теории обык-
новенных дифференциальных уравнений. Изложение всего материала
настоящей главы очень элементарно, за исключением лишь § 14,
где используется жорданова форма матриц. Все сделанное при по-
мощи жордановой формы в дальнейшем не употребляется и может
быть пропущено, как это подробно указано в § 14.
§ 7. Линейное однородное уравнение с постоянными
коэффициентами (случай простых корней)
В этом и следующем параграфах будет решено линейное одно-
родное уравнение с постоянными коэффициентами порядка п, т. е.
уравнение
z<n)4-«i*(n’n+ ... + (1)
где z есть неизвестная функция независимого переменного Д а. ко-
эффициенты ah ..., ая суть постоянные числа (действительные или
комплексные). Сначала будут найдены все комплексные решения
этргр уравнения, а затем (в случае, когда коэффициенты ап
действительны) из них будут выделены действительные решения.
Уравнение (1) можно записать в виде:
г(п) _ — — ,.. — & — anzt (2)
так что к нему применима теорема существования и единственности
(см. предложение В) § 5). В дальнейшем будет использована лишь
единственность, так как решения уравнения (2) будут найдены явно
и тем самым существование их будет установлено; единственность
же будет использована для доказательства того, что найдены все ре-
шения.
В инженерных применениях обыкновенных дифференциальных
уравнений с постоянными коэффициентами важную роль играет опе-
рационное исчисление. Мы используем здесь символические
(или, иначе, операционные) обозначения, лежащие в основе опера-
ционного исчисления. Суть этих обозначений заключается в том, что
производная по времени t от произвольной функции z — z(t) обоз-
d Л
начается не через — г, а через рг, так что буква р, стоящая сле-
ва от функции, является символом дифференцирования
по L Если позволить себе применить к символу дифференцирова-
ния р некоторые алгебраические действия, то мы приходим к
in
СЛУЧАИ ПРОСТЫХ КОРНЕЙ
43
обозначению
k
~^Z=PZ-
Пользуясь этим обозначением, мы можем написать
авг1л) 4- a1z(n-1) +... + ал_1^ + anz =
= a^z 4- a^ 'z 4-... 4 ап^г 4- a„z.
Если теперь в правой части последнего равенства позволить себе
вынести за скобку функцию г, то мы получаем равенство
сог" 4- а/"'1’ 4-... 4- a„_t2 4- anz ==
= (a<Z 4- aiPn~> 4- •4- аи-iP 4- a«)z-
Таким образом, мы приходим к формальному определению.
А) Пусть
L (Р) = V 4- а>рн~' + • • + “n-iP + ап
— произвольный многочлен относительно символа р с постоянными
коэффициентами (действительными или комплексными) и z— некото-
рая действительная или комплексная функция действительного пере-
менного t Положим:
ЦрУг—а^ 4-aIz("-|,4-...4-an_1^4-an2. (3)
Если L(p) и М(р) суть два произвольных многочлена относительно
символа р (или, как говорят, оператора дифференцирования р\
а z, функции переменного t> то, как легко видеть, мы имеем
тождества
L (р) (*1 + *,) = £. (р) 214- /. (р)г„
(L (р) 4- М (р)) z — I. (р) z 4- М (р) z,
• L(p)(M(p)z) = (L(p)M(p))z.
В силу введенных обозначений уравнение (1) может быть запи-
сано в виде:
L(p)2 = 0, (4)
где
L (р) = РЯ 4- а<РП "1 + • • • + °п-\Р + ап-
Б) Пусть L (р)—произвольный многочлен относительно символа р»
Тогда
L(p)e)J = L('k)e>J. (5)
Докажем формулу (5). Мы имеем
ре^ —
44 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
(см. формулу (9) § 5). Из этого следует, что ркеи = Kkekt. Отсюда
формула (5) вытекает непосредственно (см. (3)).
Из формулы (5) следует, что функция еи тогда и только тогда
является решением уравнения (4), когда число X есть корень много-
члена L(p). Многочлен L(p) называется характеристическим много-
членом уравнения (4). В том случае, когда он не имеет кратных
корней, совокупность всех решений уравнения (4) описывается следу-
ющей теоремой.
Теорема 4. Предположим, что характеристический много-
член L (р) уравнения
L(p)z = 0 (6)
(см. (1) и (4)) не имеет кратных корней, и обозначим его корни
через
, Хл.
Положим:
г1 = е^, гг = е^‘..z„ = eV. (7)
Тогда при любых комплексных постоянных с1, с\ .сп функция
Z — с1 q 4- с* z2 4- ... 4- cnzn (8)
является решением уравнения (6). Решение это является общим
в том смысле, что каждое решение уравнения (6) может быть
получено по формуле (5) при надлежащем выборе констант
с1, с\ При этом константы с1, с2, ..., сп (называемые
постоянными. интегрирования) однозначно определяются для
каждого данного решения г.
Заметим, что функции (7) определены на всей числовой пря*.
МОЙ — ОС t 4- ОО.
Доказательство. Из формулы (5) следует, что каждая функ-
ция системы (7) является решением уравнения (6), а из того, что
уравнение (6) линейно и однородно, вытекает (см. § 6, А)), что при
произвольных комплексных константах с1, с2, сп формула (8) дз-
ет решение уравнения (6). Покажем, что если z* = z*(t) есть произ-
вольное решение уравнения (6), то оно может быть записано в виде (8).
В силу предложения В) § 5 мы можем считать, что решение z*
определено на всей прямой —oo<^f<^oo. Положим:
^(О) = го, гД0) = 2#, г<»-Ь(0)==4»-''.
Покажем теперь, что константы q, q, ..., сп можно выбрать так,
чтобы и решение z(t), определяемое формулой (8), удовлетворяло
тем же начальным условиям
г(О) = го, ^(0) = го...... ?n-I>(0)=z»-’. (9)
Подставляя функцию z из формулы (8) в уравнения (9), получаем:
; ' р’4я(0) + ...+ с"г^(0) = ^); s—0, 1, я — 1. (Ю).
§ 71
СЛУЧАЙ ПРОСТЫХ КОРНЕЙ
43
Соотношения (10) представляют собой систему из п уравнений отно-
сительно неизвестных с1, с*, ...» сп. Для того чтобы система (10)
была разрешима, достаточно, чтобы детерминант матрицы
/Z, (0) (0) г, (0) г'Г‘>) г»(0) ^(0) г2(0) г^2)(0) z^n-”(0) ... г„(0) \ ... М°) ... 2„(0) - <п_,,(0)/ (П)
не обращался в нуль. Непосредственно в и дно, /1 что матрица (11) и 1 ... 1 Х4 ... Хя х22 ... X2 1 п меет вид:
А2 • С/
и потому ее детерминант (детерминант Вандермонда) отличен от нуля,
так как все числа Хп Х4...Хга попарно различны. Однако мы дадим
другое (непосредственное) доказательство того, что детерминант мат-
рицы (11) отличен от нуля. Доказательство это в дальнейшем будет
обобщено и на случай кратных корней.
Если бы детерминант матрицы (И) обращался в нуль, то суще-
ствовала бы линейная зависимость между ее строками. Допустим#,
что эта линейная зависимость имеет место. Это значит, что суще-
ствуют такие числа bn_it Ьп_^, ..., bQt не обращающиеся одновременно
в нуль, что, умножая на них строки матрицы (11) и складывая, полу-
чаем нулевую строку. Выписывая £-й член этой нулевой строки, пблу-
чаём:
(0)+(0) +... + (0) + ^п-” (0)=0. (12)
Если обозначить через М (р) многочлен Ь$п~х +
то соотношение (12) можно записать в виде;
М (р) zk I (_0 = о.
В силу формул (5) и (7), отсюда получаем:
Ж(ХА)=0,
а это невозможно, так как степень многочлена М(р) не превосхо-
дит п — 1, потому он не может иметь п различных корней
46
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ (Гл 2
Х|> ...» ...» ^л- Полученное противоречие показывает, что детер-
минант системы (10) отличен от нуля, и потому константы с1, ,сп
можно (и притом однозначно) выбрать так, чтобы решения гф(£) и
z(t) удовлетворяли одинаковым начальным условиям. При таком
(и только при таком) выборе этих констант решение (8) совпадает
с заданным решением z1!s(f).
Итак, теорема 4 доказана.
Если коэффициенты многочлена L(p), входящего в уравнение (б),
действительны, то возникает вопрос о выделении действительных
решений из совокупности (8) всех комплексных решений.
Решение этого вопроса опирается на предложение Г), при форму-
лировке и доказательстве которого мы будем пользоваться вектор-
ными обозначениями. Напомним их здесь.
В) Вектором п-.мерного пространства будем называть последо-
вательность, состоящую из п чисел:
и = (их, и\ ип).
Здесь и — вектор, a w1, и2, ..., и*— числа, называемые его коорди-
натами Векторы всегда будем обозначать жирными буквами. Если
координаты вектора — действительные числа, то вектор считается
действительным, если же координаты его комплексны, то и сам
вектор считается комплексным. Вектор и, комплексно сопряженный
с вектором и, определяется равенством
и = (и1, ип).
Очевидно, что вектор и тогда и только тогда является действитель-
ным, когда
а = и.
Произведение вектора д = (п’, ип) на действительное или
комплексное число а определяется формулой
ай = на = (ап1, azz2, ..., ап").
Сумма векторов
и = (и\ I?, ...» и") и ©=(и1, ...» и")
определяется формулой
а-f- ^ — (п1•••» ип“Ьг,п)'
Нулевым вектором называется вектор 0, все координаты которого
равны нулю.
Пусть
#2, ..., иг
— конечная система векторов. Соотношение
-j— + • • • + (t>rur 0,
§71
СЛУЧАИ ПРОСТЫХ КОРНЕИ
47
где аь аг.....а, — числа, среди которых имеются не равные нулю,
называется линейной зависимостью между векторами йь й2. иг.
Если между векторами не существует линейной зависимости, то они
называются линейно независимыми. Пусть
«; = (“}> И], .... llj),
Числа и1, образуют матрицу (rzj); I— 1, ..., л; J= 1, г. Если
считать, что верхний индекс I указывает номер строки, а нижний
J—номер столбца, то матрица (пр имеет высоту п и ширину г.
Таким образом, вектору й; в матрице (up соответствует /-й столбец
(состоящий из координат этого вектора). Отсюда видно, что линей-
ной зависимости векторов ut, й2, йг соответствует линейная
зависимость столбцов матрицы (up. В случае г = п матрица (up квад-
ратна, и векторы йи й2, ...» йп тогда и только тогда линейно неза-
висимы, когда детерминант |и‘| этой матрицы отличен от нуля.
Г) Пусть
Zt, Zit ..., zn (13)
— система из п линейно независимых комплексных векторов в л-мёр-
ном пространстве. Допустим, что система (13) вместе с каждым
вектором содержит сопряженный ему вектор. При этих предположе-
ниях вектор г, определяемый формулой
г = с,г1 (14)
тогда и только тогда действителен, когда коэффициенты, стоящие
при сопряженных векторах, сопряжены, а коэффициенты, стоящие
при действительных векторах, действительны.
Докажем это. Будем предполагать для определенности, чго выпол-
нены соотношения
Zj = Zj\ у = 2^4~1, п- J
Тогда вектор z согласно (14) имеет вид:
Z — ClZt 4- C!Zi + . .. + 4- с2АНг4й+, 4- • • •+ (1V
а вектор z—вид:
z = c*zt 4- c'Zi 4-.. .4- C2A22a„14- C^'Zik 4- c‘iA+l2.2ft+14-... 4- Cn zn. (16)
Если
= c™-' = c^> cn = c\ (17)
то из равенств (15) и (16) следует, что z = z} т. е. что вектор е
действителен. Если, наоборот, предположить, что вектор z дей-
48
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
ствителен, т. е. что z = z, то равенства (15) и (16) дают (в силу
линейной независимости векторов (13)) систему соотношений (17).
Итак, предложение Г) доказано.
Нижеследующее предложение Д) дает способ выделения дей-
ствительных решений из совокупности всех комплексных решений
уравнения (6) в случае, когда коэффициенты многочлена L (р) дей-
ствительны.
Д) Допустим, что коэффициенты многочлена L(p) действительны;
тогда наряду с каждым комплексным корнем X многочлен L (р) имеет
сопряженный с ним корень X. Решения и еу уравнения (6) сопря-
жены между собой (см. § 5,Г)). Если же корень X действителен, то реше-
ние eKt действительно. Таким образом, наряду с каждым решением в
системе решений (7) имеется также комплексно сопряженное с ним
решение. Для того чтобы решение (8) уравнения (6) было действи-
тельным, необходимо и достаточно, чтобы коэффициенты, стоящие при
комплексно сопряженных решениях, были сопряжены, а коэффициенты
при действительных решениях действительны.
Для доказательства обозначим через zk вектор с координатами
{гА(0), £А(0),., г("“2)(0), (0)} и через z — вектор с координа-
тами {г0, £0,4я”1)}- Тогда соотношения (10) принимают вид:
cizJ 4~ +... + cnzn = z.
Векторы zt, zn линейно независимы, так как детерминант мат-
рицы (11) отличен от нуля. Таким образом, необходимость приведен-
ного в Д) условия следует непосредственно из Г). С другой стороны,
если это условие выполнено, то решение (8) действительно. В самом
деле, если Xt и Х2 — два комплексно сопряженных корня, а с1 и с* —
две комплексно сопряженные константы, то функции и
комплексно сопряжены, а следовательно, их сумма действительна.
Итак^'предложение Д) доказано.
Примеры
1. Найдем все комплексные решения уравнения
Г —3^4-9^+ 13z = 0.
Его можно записать в виде (6), где
Z.(rt = /-3/ + 9^+13.
Непосредственно проверяется, что р = —1 есть корень характера
стического многочлена L (р). Разделив Л(р)на получаем:
Цр) = (р+1)(р'-4р+1У),
откуда находим еще два корня 2 4^3/. Таким образом, корнями
§71
СЛУЧАЙ ПРОСТЫХ КОРНЕЙ
49
многочлена L (р) являются числа
X1==2-|-3Zf Х2 = 2 —3Z, Х3 = — 1.
В силу теоремы 4 общее комплексное решение рассматриваемого
уравнения имеет вид:
z = 4- Л*(2“з0' + с3<?<
В нижеследующих примерах 2 и 3 даются два общих правила
выделения действительных решений. Правила эти непосредственно
вытекают из предложения Д).
2. Будем считать, что система решений (7) удовлетворяет условиям
»Z'Zfe -i= ^л+1==:v • ••tZn = zn9 (18)
и положим:
2г1 = д:1-|-(У1> = xk 4" (Ул»
где ..., xk, yit — действительные функции. Будем, далее,
считать, что числа с1, с , сп удовлетворяют условиям (17) и по-
ложим:
с1 = 1-(а' — lb1), , сгк 1 = ^(ак — 1Ьк),
где а1, а*, 61, bk — действительные числа. При этих обозна-
чениях общее действительное решение уравнения (6) записывается в
виде:
Z = а]Х! + blyi 4-... 4-aftx* +bkyk -j-cik+izik+i 4-... +cnzn,
где
а\ t1,..., Ь\ ..., сп
суть произвольные действительные числа.
3. Опять будем считать, что решения (7) удовлетворяют условиям
(18); положим:
X1 = p,i4"^i> ..•> ^ал-1 = 4"
В предположении, что числа с1, с®, ...» сп удовлетворяют условиям
(17), мы можем положить:
с1 =4 р/1*............= g-p***1*’
В этих обозначениях каждое действительное решение г записывается
в виде:
2=?^ cos (v,f (Xj) ... cos 4-а*)4-
+ 4-... 4-Л’М.
Здесь рп pft, оц, аА, с2А+1, .,.,слсуть произвольные действи-
тельные константы. Из последней записи видно, что каждая мнимая
60
ЛИНЕПНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
часть vy ф 0 корпя Ху придает решению колебательный характер
частоты vy, а каждая действительная часть р.у корня Ху дает ему
либо рост (при р.у>0), либо убывание (при р.у0).
4. Используя результаты примеров 2 и 3, мы можем записать все
действительные решения уравнения, рассмотренного в примере 1,
в двух следующих формах:
z ~ а1е* cos bxev sin 3£
z = cos(3/-|-a])+
§ 8. Линейное однородное уравнение с постоянными
коэффициентами (случай кратных корней)
Если характеристический многочлен
L (р) =рп + «iP'1'1 + • • • + an-iP 4* ая
уравнения
Л(р)г = 0 (1)
(см. § 7, А)) имеет кратные корни, то среди функций вида еи нельзя
найти п различных решений уравнения (1). Для нахождения в этом
случае решений другого вида можно воспользоваться следующим на-
водящим соображением. Пусть Xt и X,— два различных действитель-
ных корня характеристического многочлена L (р); тогда функция
—г----является решением уравнения (1). Если теперь предполо-
л,
жить, что при изменении коэффициентов многочлена L (р) число Ха
стремится к Хр то это решение переходит (в пределе) в функцию
о которой естественно предположить, что она является реше-
нием уравнения (1) в случае, если X, есть двукратный корень мно-
гочлена L(p). Аналогично мы приходим к догадке, что если X есть
^-кратный корень характеристического многочлена L(p), то решениями
уравнения (1) являются все функции:
eytt teht, tk~xext.
Распространяя эту догадку на случай комплексных кратных корней,
мы приходим к предположению о справедливости нижеследующей
теоремы (являющейся обобщением теоремы 4):
Теорема 5. Пусть
L(p)z=0 (2)
— линейное однородное уравнение порядка п с постоянными коэф-
фициентами, Пусть, далее, Хр Хт—совокупность всех по-
парно различных корней характеристического многочлена L(p)
уравнения (2), причем корень Ху имеет кратность kj, так что
5 *1
СЛУЧАЙ КРАТНЫХ КОРНЕЙ
51
A’j + + • • • + — П' Положим:
гх = е^, z^ = tey^9 =ffrr!exi';
г^=е^, zkl¥2 = te4........... zftl+fcj =
(э)
zn = tl'm~>e'm‘.
Тогда все функции (3) являются решениями уравнения (2), так
что при любых комплексных постоянных с1, с3, .сп функция
z = с1'1 + • + cnzn (4)
также является решением этого уравнения. Решение это явля-
ется общим в том смысле, что каждое решение уравнения (2)
может быть получено по формуле (4) при надлежащем выборе
констант с1, ...» сп. При этом константы с\ .сп однозначно
определяются для каждого данного решения z.
Заметим, что функции (3) определены на всей числовой прямой
— оо t оо.
Доказательству теоремы 5 предпошлем доказательство формулы
смещения.
А) Пустб L (р)—произвольный многочлен, X — произвольное ком-
плексное число и f{t) — произвольная достаточное число раз диффе-
ренцируемая функция. Тогда имеет место следующая важная формула:
А(р)(^7(О) = ^^(р + А)/(о. (5)
Докажем формулу (5). Проверим ее сначала для случая Л (р) — р.
Мы имеем:
Р = X e»f(t) + euf(t) = е11 (р + X)/(Q.
Теперь формулу (5) легко проверить для произвольного многочлена
первой степени L(p) = qp-\- Ь. Мы имеем:
0Р+О(^/(О)=^(ех7(О) + ^х7(О=
= (Р + 4/(0 + beuf{t) = еи\а(р-\- X) + fr] f(t).
Доказательство формулы (5) в общем случае проведем индуктивно
по степени п многочлена L(p). Для л=1 формула, как мы видели,
верна. Допустим, что она справедлива для многочлена степени
п — 1 («^2), и докажем ее для многочлена L(p) степени п. Для
этого многочлен L(p) степени п разложим на два множителя L(p) =
— L<t(p)> где Ц(р) имеет степень 1, а Л2(р) имеет степень
п—1. Так как для каждого из многочленов Z-i(p) и Л2(р) формула
(5) справедлива, то мы имеем (см. § 7, А)):
L (р)(eltf(t)) = Lt(p) (Л2 (р) (ew/(0)) = L,(p) (р + X)/(Q) =
= еи L, (р + X) Lt (р + X)f (0=ellL (р + X) f(t).
52 ЛИНЕПНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
Таким образом, формула (5) доказана.
Докажем теперь предложение Б), в котором теорема 5 почти пол-
ностью содержится.
Б) Пусть L (р) — произвольный многочлен относительно символа р
и пусть функция wr(0 действительного переменного t определяется
формулой -
u>r(0 = i(p)^',
где X—комплексное число. Оказывается, что если X есть Л-кратный
корень многочлена L(p), то функции о>0(Y), .тождественно
равны нулю. С другой стороны, оказывается, что если функции w0(O>
Wj(/), ..., равны нулю хотя бы для одного значения t = t9i
т. е. имеют место равенства
% W = Ш1 (^о)“ • •= (^о)= 0, (6)
то.Х есть корень многочлена L(p) и кратность этого корня не меньше k.
Докажем предложение Б).
В силу формулы смещения (см. (5)) имеем:
= (7)
Допустим сначала, что X есть Л-кратный корень многочлена L(p)>
т. е. что
L(p) = M(p)(p-X)k.
Заменив в этом тождестве р через р-\-Ъ получим:
= (8)
Из формул (7) и (8) получаем:
.ш/.(0 = еХгЛ4(рН“^)(Р*О= 0 при г = 0, 1, ...» k—1,
так как pktr = 0 при r<^k. Таким образом, первая часть предложе-
ния Б) доказана.
Допустим теперь, что имеют место соотношения (6). Разлагая
L (р -|- X) по степеням р, получаем:
L (р X) = Ь9 4~... 4" Ьп_1рп~* 4“ ЬпРп- (9)
Из соотношений (7) и (9) получаем;
“о (t«) = еиоЬв,
а это в силу (6) дает
*о = О.
Допустим теперь, что имеют место равенства
b^bl^...= br^ = o, r^k—1, (10)
§ 81
СЛУЧАЯ КРАТНЫХ КОРНЕИ
53
и докажем, что Ьг = 0. В силу (7), (9) и (10) имеем:
шг [t9) = eu<>r\br.
В силу (6) из этого следует
Ьг = 0.
Таким образом, Ь§ ~ Ьх = ... = bk_x = 0, и многочлен L(p-(-l) имеет
вид:
L (Р + X) = bkpk +... + Ь^ = 4-... + vfe)/ = мх (р)р\
Заменяя в этом тождестве р через р — \> получаем:
а это показывает, что К есть корень многочлена L(p), причем крат-
ность его не меньше k.
.Таким образом, предложение Б) доказано.
Доказательство теоремы 5. Из первой части предложе-
ний Б) непосредственно следует, что функции (3), указанные в фор-
мулировке теоремы 5, являются решениями уравнения (2). Докажем,
что, выбирая надлежащим образом константы с1, сп, мы можем
получить по формуле (4) произвольное решение z* уравнения (2)
(при этом, в отличие от того, что было сделано при доказательстве
теоремы. 4, мы здесь не будем пользоваться теоремой 3).
Пусть z* — произвольное решение уравнения (2), определенное
на некотором интервале Г1<^<Уз, и пусть ^ — некоторое число
из этого интервала. Положим:
z*(M=z^ ...» 4/i”u(Q=4n”,)-
Теперь будем искать такие константы с1, ..., сл, чтобы решение z
уравнения (2), определяемое формулой (4), удовлетворяло тем. же
начальным условиям, что и заданное решение z*. Тогда будем иметь
z = z* (на интервале Г|<4<^Га) в силу теоремы единственности.
Для определения констант с1, сп мы получаем систему уравнений
c’4s) (tn) + сЧ? &) +... 4- cnz(? (ta) = 44 s = О, 1, ..., п - 1. (11)
Для того чтобы система (11) была разрешима, достаточно, чтобы
детерминант матрицы
pi zs(4) ... zn(t№)
4f,(Q ... (t0) (12)
К'Ж) 4'*~,)(U ...
был отличен от нуля. Покажем, что этот детерминант не равен нулю.
Для этого покажем, что строки матрицы (12) линейно независимы.
54 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ (Гл. 2
Допустим противоположное» и пусть Ьп_ь Ьп_ч,Ь%— те константы,
не обращающиеся одновременно в нуль, на которые следует умно-
жить первую, вторую и так далее строки матрицы, для того чтобы
сумма их была равна нулю. Выписывая сумму элементов /-го столбца,
получаем равенство
+ ... 4-frn^(/e)+^_^(Q=о,
которое можно переписать в виде:
=°> (13)
где A4(p)=Z?0pn"14-ft1pn-a4- ... + Полученное равен-
ство (13) для у = 1, ..., дает, что Xj есть по меньшей мере Агкрат-
ный корень многочлена М(р) (см. предложение Б)). Точно так же
для 7 = Ai4"b ...» *1 + ^ полученное равенство дает, что Х^ есть
по меньшей мере Агкратный корень многочлена М(р). Совокупность
всех равенств (13) приводит нас к выводу, что (с учетом кратностей)
многочлен М(р) имеет не менее п корней, а это невозможно, так
как его степень не выше, чем п — 1. Итак, предположение о равенстве
нулю детерминанта матрицы (12) привело нас к противоречию, а это
значит, что система (11) разрешима (и притом однозначно) относи-
тельно неизвестных
с1» с®, сп.
Таким образом, теорема 5 полностью доказана.
Отметим одно очевидное следствие теоремы 5.
В) Каждое решение z(t) уравнения (2) может быть записано
в виде:
г(0=/,(0^+Л(0^'+ ... +/w(0e4
где Д (0 есть многочлен степени, не превосходящей числа kj—1,
7=1, т. При этом многочлены fm(t) определены
однозначно решением z(f)t так как их коэффициенты являются
константами интегрирования с1, с2, сп, которые в силу теоремы 5
определены решением z(t) однозначно.
Если коэффициенты уравнения (2) действительны, то перед нами
стоит задача выделения из совокупности комплексных решений урав-
нения (2) его действительных решений.
Г) Будем считать, что коэффициенты характеристического много-
члена L (р) уравнения (2) действительны. Пусть X — некоторый корень
многочлена L (р) кратности k\ тогда при r=0, 1,..., k—1 функ-
ция treu является решением уравнения (2). Если корень X действи-
тельный, то функция Геи действительна, если же корень X комплекс-
ный, то наряду с решением treu имеется комплексно-сопряженное
ему решение так как X есть корень кратности k многочлена L(p).
Таким образом, в системе решений (3) наряду с каждым комплексным
§8] СЛУЧАИ КРАТНЫХ КОРНЕИ 55
решением имеется сопряженное с ним решение. Для того чтобы ре-
шение (4) было действительным, необходимо и достаточно, чтобы
коэффициенты при действительных решениях были действительными,
а коэффициенты у попарно сопряженных комплексных решений были
попарно сопряжены.
Доказательство предложения Г) проводится точно так же, как и
доказательство предложения Д) § 7 на основе предложения Г) § 7.
Примеры
1. Решим уравнение
zv + 3ziv + + =
Уравнение это может быть записано в виде (2), где характеристиче-
ский многочлен L(p) имеет вид:
Корнями этого многочлена служат числа
Х1 = О, Х2 = --1,
имеющие кратности At = 2, = 3. Поэтому в силу теоремы 5
система решений (3) для рассматриваемого уравнения имеет вид:
= 1, t zi = e~it z^ = te~ft = fe"1.
Общее решение дается формулой
z = (с1 сЧ) -|- (с3 -|- сЧ -|- сЧ*) е~*.
2. Решим уравнение
ziv + 2z" + z = 0.
Характеристический многочлен равен L (р) = (р* -|-1)2; его корнями
(двукратными) являются числа kj = Z, Х2 = —L Общее решение рас-
сматриваемого уравнения записывается в виде:
z = (с‘ 4~ + (f3 + е~л*
Нижеследующие два примера дают общие правила выделения
действительных решений, непосредственно вытекающие из предложе-
ния Г). Примеры 3 и 4 вполне аналогичны примерам 2 и 3 § 7.
3. В примере 2 § 7 не учитывался конкретный вид решений,
а было лишь предположено, что система решений zn состоит
из попарно сопряженных решений и действительных решений. По-
этому те же рассуждения показывают, что и в случае кратных кор-
ней, мы имеем следующее общее правило. В системе (3) следует
каждую пару комплексно-сопряженных решений заменить действитель-
ной и мнимой частями одного из этих решений. Полученная таким
56 ЛИНЕЙНЫЕ УРАВНЕНИЯ' С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ (Гл Ж
образом система функций обладает тем свойством» что любое дейст-
вительное решение является их линейной комбинацией с действитель-
ными коэффициентами.
4. Пусть _
few, treu
— два комплексно сопряженных решения из системы (3). В случае
действительного решения z часть суммы (4), соответствующая этим
решениям, может быть записана в виде:
z = ctre{iL¥i4]t
Положим:
1 /а
Тогда мы будем иметь:
z = ptre^ cos (yi -|- а). (14)
Этим способом можно каждую пару комплексно-сопряженных реше-
ний,. входящих в сумму (4), заменить действительной функцией вида
(14), содержащей две произвольные действительные константы р и а.
Здесь вновь, как и в примере 3 § 7, видно, что наличие мнимой
части v 0 корня X придает решению колебательный характер, а
наличие действительной части у. 0 корня X вызывает либо возра-
стание решения (при у, 0), либо его убывание (при у,<^0). Нако-
нец, кратность корня X вызывает появление множителя Г, который
также влечет возрастание решения, однако при Г— оо и при у,<^0
возрастание решения, вызванное множителем f, гораздо меньше, чем
убывание, вызванное множителем так что при у-<^0 (и любой
кратности корня) решение стремится к нулю при возрастании t.
5. Используя результаты примеров 3 и 4, мы можем записать
все действительные решения уравнения, рассмотренного в примере ‘2,
в двух следующих формах:
z = (а1 4" cos 4“ № 4" ^*0sin
z = pj cos (t 4- оц) 4- cos (i 4- 04).
§ 9. Устойчивые многочлены
Пусть
L(p)z=0 (1)
— линейное однородное уравнение с постоянными коэффициентами.
Вопрос о том, как ведут себя решения этого уравнения при
/ —4~°° (стремятся ли они к нулю, остаются ограниченными или
неограниченно возрастают), играет очень важную роль в целом ряде
приложений теории обыкновенных дифференциальных уравнений.
10]
УСТОЙЧИВЫЕ МНОГОЧЛЕНЫ
67
В примерах 3 § 7 и 4 § 8 уже отмечалось, что этот вопрос о по-
ведении решений уравнения (1) связан с тем, каковы действительные
части корней многочлена L (р). Формулируем теперь эту связь более
точно:
А) Многочлен L (р) называется устойчивым, если все его корни
имеют отрицательные действительные части или, говоря геометриче-
ским языком, лежат по левую сторону от мнимой оси плоскости
комплексного переменного. Пусть
/=1.....т
— все корни многочлена L(p). Если многочлен этот устойчив, то
существует такое положительное число а, что
Р7< —а, / = 1, (2)
Мы покажем, что для каждого решения ср (t) уравнения (1) в (&том
случае найдется такое положительное число М что
| ср (01 М при t 0. (3)
Эта формула не только показывает, что каждое решение уравнения (1)
стремится к нулю при со, но и оценивает, насколько быстро
это стремление к нулю происходит.
: Докажем s = 1, ...» и, Мы имеем: формулу (3) сначала для произвольного решения Z& уравнения (1), входящего в систему функций (3) § 8. ,г М 4Г СИЛ*)* zs = teJ, откуда =t e J
Так как число + а в силу (2) отрицательно, то функция fe
стремится к нулю при t —>оо и потому ограничена при Таким
образом, мы имеем:
<Л4, при / S3 0,
или, что то же,
I | <С ^se at ПРИ t О’
Если теперь
<Р (0 = <^1 + + . . . + Cnza
— произвольное решение уравнения (1), то при t^>0 имеем:
|?(0|< (|с’| м, + |с’| .^4-...+ |.Aln)e^ = ^e-"z.
Таким образом, неравенство (3) доказано. Следует отметить, что
если хотя бы один из корней X,- многочлена L (р) имеет положитель-
ную действительную часть то существует решение е урав-
нения (1), неограниченно возрастающее при /~*оо.
58 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ (Гл. 2
Нахождению различных, по возможности удобных для практи-
ческого применения условий устойчивости многочленов до сих пор
посвящаются многие исследования математиков. Для многочлена вто-
рой степени условие устойчивости непосредственно выводится из
формулы решения квадратного уравнения (см. Б)). Вопрос об устой-
чивости многочлена произвольной степени п был решен в несколько
различных формах математиками Раусом и Гурвицем. Условия Ра-
уса — Гурвица, однако, мало удобны для вычислительной практики,
м потому продолжают до сих пор отыскивать новые формулировки
условий устойчивости. Здесь будет приведено доказательство крите-
рия Рауса — Гурвица для п = 3 и без доказательства будет дано
условие устойчивости для произвольной степени п в форме Гурвица.
Б) Многочлен второй степени L(p) = p*-]-ap-]-b с действитель-
ными коэффициентами а и b тогда и только тогда устойчив, когда
коэффициенты его положительны.
Это утверждение легко проверяется при помощи формулы реше*
ния квадратного уравнения.
В) Если многочлен L (р)=рп -|- а^рп^ 4" ... 4-ая с действитель-
ными коэффициентами устойчив, то все его коэффициенты положи-
тельны.
Для доказательства разложим многочлен L(p) на действительные
множители первой и второй степени, т. е. на множители вида р-]-с
и р* -]-ар Ь. Так как многочлен L(p) устойчив, то и каждый мно-
житель указанного вида, входящий в его состав, также устойчив.
Для устойчивости множителя р-]-с необходимо, чтобы число с было
положительно, а для устойчивости множителя р*-\-ар-]-Ь необхо-
димо, чтобы оба числа а, b были положительными. Из положитель-
ности коэффициентов множителей легко следует положительность
коэффициентов произведения.
Нижеследующая теорема дает критерий устойчивости для много-
членов 3-й степени.
Теорема 6. Многочлен
L(p) = a9p3-[-aipi-]-atp-]-a3, ав>0
с действительными коэффициентами тогда и только тогда устой-
чив, когда числа аь аъ а3 положительны и, сверх того, выпол-
нено неравенство
Доказательство. При доказательстве будем рассматривать
многочлен
L (р)=Р3 + аР* + Ьр 4- с; (4)
случай общего многочлена L(p) легко сводится к этому. В силу предло-
жения В) нам достаточно доказать, что многочлен (4) с положи-
тельными коэффициентами а, Ь> с тогда и только тогда устойчив,
§9}
УСТОЙЧИВЫЕ МНОГОЧЛЕНЫ
59
когда имеет место неравенство
ab с. (5)
При доказательстве мы воспользуемся тем, что корпи многочлена
являются непрерывными функциями его коэффициентов.
Выясним прежде всего, при каких условиях многочлен (4) имеет
чисто мнимые корни, в частности, корень р = 0, который также сле-
дует считать чисто мнимым, так как он лежит на мнимой осп. Мы
имеем:
L(p) = (pJs-a)(pi-Jt-b)—ab-^c. (6)
Если многочлен L(p) имеет корень 0, то с = 0, а это по предполо-
жению исключено, так как с^>0. Допустим, что корнем многочле-
на L(p) является число /о), где ю Ф 0. Если предположить при этом,
что число —о>3 -1- b отлично от нуля, то число (/ш-ф-а)(—w2-|-Z>)
имеет отличную от нуля мнимую часть и не может взаимно уничто-
жаться о действительным числом —ab -|- с. Таким образом, число /о>
лишь тогда может быть корнем многочлена L (р), когда—ц?-}-# = 0;
в этом случае мы имеем равенство
L = — ab -j- с — 0.
Обратно, если ab = c> то в силу (6) многочлен L (р) имеет чисто мни-
мые корни р = -ь-1\^Ь. Таким образом, многочлен L(p) (с положи-
тельными коэффициентами) тогда и только тогда имеет чисто мнимые
корни, когда ab = c. В частности, при непрерывном изменении поло-
жительных коэффициентов а, Ь, с корень многочлена L(p) только
тогда может пересечь мнимую ось, когда выполнено равенство ab — с.
Допустим, что неравенство (5) не выполняется. Тогда либо ab = ct
либо ab<c. В первом случае многочлен L (р) имеет чисто мнимые
корни и, следовательно, неустойчив. Покажем, что во втором случае,
т. е. при выполнении неравенства
ab <>, (7)
многочлен L(p) также неустойчив. Будем менять непрерывно коэф-
фициенты а и оставляя их положительными, так, чтобы они стре-
мились к нулю и чтобы при этом неравенство (7) не нарушалось.
При этом изменении ни один корень не перейдет с одной стороны
мнимой оси на другую, и, следовательно, свойство многочлена быть
устойчивым или неустойчивым не изменится. При а = /? = 0 получаем
многочлен р3-}-с, который имеет корни с fcos у ± I sin yj, лежа-
щие по правую сторону мнимой оси. В силу непрерывности зависи-
мости корней от коэффициентов, неустойчивость (наличие корней
справа от мнимой оси) сохраняется и при достаточно малых поло:
жительных а и Ь>
60 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
Допустим теперь, что неравенство (5) выполнено, и покажем, что
многочлен L (р) устойчив. Для этого будем менять коэффициент с
так, чтобы он стремился к нулю, оставаясь положительным, и чтобы
неравенство (5) при этом не нарушалось. При с = 0 мы получаем
многочлен
Цр) = Р(Р* + ар + Ь),
имеющий один нулевой корень и два корня с отрицательными дей-
ствительными частями. При малом положительном с эти два кйрня
мало изменятся, так что произведение их останется положительным,
а нулевой корень перейдет в малый положительный или отрицательный.
Так как произведение всех трех корней равно отрицательному чис-
лу — с, то корень, близкий к нулю, будет отрицателен.
Итак, теорема 6 доказана.
Для того чтобы формулировать необходимые и достаточные усло-
вия устойчивости любого многочлена с действительными коэффици-
ентами, условимся сначала о терминологии. Пусть
/ Ри Ра ••• Pin \
- / Pei Ра • • • Pin 1
\ Pni Pni • • • Рпп /
— произвольная квадратная матрица порядка л. Будем называть ее
главным k-м минором детерминант матрицы
/Ри Ри ... PiA
I Ра Ра • • • Put I
\Рт Рю •••Pkn/
минор этот мы будем обозначать через АДР). Таким образом, детер-
минант АДР) составлен из элементов матрицы Р, входящих в пер-
вые k столбцов и строк.
Теорема 7. Пусть
a<>Pn + a^~iJr ••• +a«> а«>0 (8)
— произвольный многочлен степени п с действительными коэф-
фициентами. Для того чтобы выяснить вопрос о его устойчи-
вости, составляют матрицу
1а' «3 а8 • • • 0 к
а» а* ... 0
Q = 0 . • • •
^0 ...... ап]
§9]
УСТОЙЧИВЫЕ МНОГОЧЛЕНЫ
61
порядка н. Оказывается, что многочлен (8) устойчив тогда а
только тогда, когда все главные миноры Aa(Q), &=1, Jt
матрицы. Q положительны.
ТеОрема 7 в этой книге доказана не будет. Доказательство ев
можно найти, например, в книге: Н. Г. Чета ев, Устойчивость дви-
жения, Гостехиздат, М., 1956 (см. стр. 79 — 83).
Во избежание недоразумений опишем матрицу Q. Столбец номера
k матрицы Q имеет вид:
• •• а*+1 икак_гак_^
где элемент ak стоит на главной диагонали; при этом элемент
индекс k -\-j которого отрицателен или больше п, считается рав-
ным нулю.
Примеры
1. Выведем из теоремы 7 теорему 6. В случае п — 3 матрица Q
имеет вид:
/а> а8 0 \
( а0 аа О
\0 at а8у
Ее три главных минора имеют значения
Mfi)=A> MQ)=aias —аваз> MQ) = «»-М<Э)-
Условие их положительности вместе с условием положительности
коэффициента а0 равносильны условиям:
а0^>0, а, 0, а8^>0,
Из совокупности этих условий вытекает, как легко видеть, положи-
тельность коэффициента аа. Таким образом, в случае п = 3 теорема 7
превращается в теорему 6.
1 2. В случае п = 4 матрица Q имеет вид:
/а, а3 0 0 \
„_______________________/ ао а4 0 |
I О а3 О I.
\0 а^ а<2 a^j
Ее главные миноры имеют следующие значения:
Д1 (Q) = ад MQ)= ai— ао ад
А3 (Q) = а3 Да (Q) — а* а4; Д4 (Q) = а4 • Д3 (Q).
Условие положительности этих миноров вместе с условием а0^>0
эквивалентно, как легко видеть, условиям
а0^>0, аг 0, а3^>0, а4^>0,
дз (Q)= ai «8 «3 ~ «в а, — < «4 > 0.
62
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ (Гл. 2
§ 10* Линейное неоднородное уравнение с постоянными
коэфф и циентам и
Здесь будет дано решение линейного уравнения с постоянными
коэффициентами со свободным членом специального вида, являющимся
так называемым квазимногочленом.
А) Квазимногочленом будем называть всякую функцию F(t\
которую можно записать в виде:
... (1)
где Хп Х2, , \т суть некоторые комплексные числа, а /1(/),
f2(/), ••• > /«(0—многочлены от /. Из предложения В) § 8 следует,
что каждое решение линейного однородного уравнения с постоянными
коэффициентами является квазимногочленом. Можно доказать, что и
обратно, каждый квазимногочлен является решением некоторого
линейного однородного уравнения с постоянными коэффициентами.
Если какие-нибудь два числа последовательности Хь Х2, , Хт сов-
падают между,собой, например, если Х, = Х2, то члены суммы (I),
соответствующие этим числам, можно объединить и заменить чле-
ном Таким образом, запись (1) всегда можно при-
вести к такому виду, что числа Хп Х^ , Хт, входящие в нее, по-
парно различны. Отметим, что сумма и произведение двух произ-
вольных квазимногочленов также есть квазимногочлен; далее, если
к произвольному квазимногочлену применить произвольный опе-
ратор L(p), то мы вновь получим квазимногочлен.
Таким образом, в настоящем параграфе будет рассматриваться
уравнение -
L(p)z = F(f), (2)
где F(t) есть некоторый квазимногочлен. Наряду с уравнением (2)
рассмотрим соответствующее однородное уравнение
L(p)u — 0. (3)
Нижеследующее предложение непосредственно вытекает из заме-
чания Б) § 6.
Б) Если z есть некоторое решение уравнения (2), то произволь-
ное решение z того же уравнения может быть записано в виде:
z = z zz,
где zz есть некоторое решение уравнения (3).
Так как произвольное решение однородного уравнения мы оты-
скивать уже умеем, то дело сводится, таким образом, к отысканию
одного решения или, как говорят, частного решения уравнения (2)
в случае, когда F{t} есть квазимногочлен. Так как, далее, каждый
квазимногочлен записывается в виде (1), то в силу замечания В) § 6
§ 10 ]
ЛИНЕЙНОЕ НЕОДНОРОДНОЕ УРАВНЕНИЕ
63
дело сводится к отысканию частного решения уравнения (2) в слу-
чае, когда F(0=/(06’W> где/(f) —многочлен. Для этого случая
решение отыскивается в нижеследующей теореме.
Во избежание недоразумений отметим, что в дальнейшем под
многочленом степени г мы будем понимать функцию вида
4~«i^"~14- . л ап не предполагая непременно, что стар-
ший коэффициент а0 отличен от нуля.
Теорема 8. Рассмотрим неоднородное уравнение
L(p)z=f(t)e\ (4)
в котором f(t) есть многочлен степени г относительно t, а X—
комплексное число. Пусть /г = 0, если L(X)^ 0, и k — кратность
корня X, если L(X)=O. Оказывается, что существует частное
решение уравнения (4), имеющее вид:
z = tkg(t)e\ (5)
где g(ty есть многочлен степени г относительно t. Коэффициенты
много члена g (t) можно на й ти методом неопределенных коэф-
фициентов.
Доказательство. Положим:
/(0 = авГ+Л(0 (6)
и будем искать многочлен g{t) в виде:
g(0 = ^of + g*(0, (7)
где многочлены /*(0 и g*(t) имеют степень г—1. Далее, в силу
выбора числа k мы имеем:
L(p) = M(p)(p~\)k, (8)
где А1(Х)^:0. Для того чтобы функция (5) являлась решением урав-
нения (4), должно быть выполнено условие (см. § 8, А))
L (р) etJ tk g(t) = etJ L (р + К) t* g(t) = euf(t),
г. е. многочлен g(t) должен удовлетворять условию:
L(p + ^g(t)=f(i). (9)
Многочлен Л4(р—}—л) имеет своим свободным членом число Л4(Х) 0
и потому может быть записан в виде:
м (р 4- X)=м (X) 4- м* (р) р, м (X) о. (Ю)
Принимая во внимание соотношения (6), (7), (8) и (10), мы можем
теперь условие (9), налагаемое на многочлен g(t), записать в виде:
ba М (\)рк tk^r-Y-b0М* (Р) pk+Чк+г-\- L (р 4- X) t* g* (t) = а» f 4-/* (0.
(ID
64 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл, 2
Приравнивая члены, содержащие tr в равенстве (11), получаем соот-
ношение
(12)
из которого коэффициент Ь9 искомого многочлена g(t) определяется
(ибо Ж(Х)^О) и притом однозначно. Будем считать теперь, что
коэффициент Ь9 уже выбран, так что соотношение (12) выполнено;
тогда соотношение (11) принимает вид:
L(p + l)tkg*(f)==f*(t) — (13)
где в правой части равенства стоит известный многочлен степени
г—1, а слева — неизвестный многочлен g*(0 степени г—1. Урав-
нение (13) отличается от уравнения (9) только степенью вхо-
дящих в него многочленов, которая понизилась на единицу. Повто-
ряя для уравнения (13) вычисления, проведенные ранее для уравне-
ния (9), мы вычислим коэффициент bi при высшей, т. е. (г— 1)-й
степени t многочлена g*(0. Продолжая этот процесс дальше, мы
вычислим все коэффициенты b9, bit , br многочлена g(t) таким
образом, чтобы он удовлетворял условию (9), и тем самым найдем
решение вида (5) уравнения (4).
Можно было бы подставить решение вида (5) прямо в уравне-
ние (4) и, считая коэффициенты многочлена g(t) неизвестными, по-
лучить для этих коэффициентов систему линейных уравнений путем
приравнивания коэффициентов при одинаковых членах в правой и
левой частях соотношения (4). Проведенные выше вычисления по-
казывают, что система уравнений, получаемая для коэффициентов
многочлена g(t) разрешима.
Таким образом, теорема 8 доказана.
Замечание. Полученная система для определения коэффици-
ентов многочлена g(t) является системой линейных уравнений с тре-
угольной матрицей: при приравнивании коэффициентов у членов
tr еи- мы получаем уравнение, содержащее только при приравнива-
нии коэффициентов у членов tr~{eu мы получаем уравнение, содер-
жащее только Ь9 и Ьь и т. д.
Установим одно важное свойство квазимногочленов.
В) Если квазимногочлен
Р(0=Л(0А'+Л(0А' + . . . +/m(0eV,
где Хт —попарно различные числа, тождественно равен
нулю на некотором интервале все многочлены j\(t\
. . .> /т(0 тождественно равны нулю, а следовательно, и все
коэффициенты квазимногочлена F(t) равны нулю. Из этого непос-
редственно следует, что если два квазимногочлена F(t) и F*(t) тож-
дественно равны между собой на некотором интервале
то их соответственные коэффициенты совпадают.
I 10] ЛИНЕЙНОЕ НЕОДНОРОДНОЕ УРАВНЕНИЕ G5
Предложение В) будем доказывать индуктивно по числу т, ко-
торое будем здесь называть порядком квазимиогочлена F(t). При
т— 1 оно справедливо, так как в этом случае равенства /’’(/) =
= /1 (0 = 0 и = 0 эквивалентны. Проведем теперь индуктив-
ный переход от т— 1 к т(дг^2). Если квазимногочлен F(t) тож-
дественно равен нулю на интервале rt<^t <^г%, то это же имеет мес-
то и для квазимногочлена
G(f) = pl+l
где р — оператор дифференцирования, а I—степень многочлена
В силу предложения А) § 8 мы имеем:
G(0 = ^i(/)^VX,,,)/ + ^(0^VXm)r + - • + &п-|(0е(Х'п-1-Х'<
где
&(0=(НА-V+1A(0-
Квазимногочлен О(/) имеет порядок т — 1 и так как он тождествен-
но равен нулю на интервале то в силу предположения
индукции все многочлены , gm_\ (0 тождественно равны нулю.
Предположим, что какой-либо из многочленов ^(Z),. . ., /тЛ({) не
равен нулю, например и приведем это предположение к
противоречию. Допустим, что многочлен (0 имеет степень kt т. е.
= причем ф 0. Непосредственно про-
веряется, что
Sv (/)=(р + >4 - ^)'+*Л (/)=(Ч - ^)г+* % tk +. ..,
а так как многочлен gi(0 тождественно равен нулю на интервале
Г!</<г2, то мы имеем:
(X, - Xm)z+1 й0 = 0.
Так как числа Xj и Хт различны, то из этого следует, что а0 = 0.
Полученное противоречие доказывает, что все коэффициенты мно-
гочленов /](/), . . равны нулю, т. е. F(t)=fm(i)e ,п . От-
сюда мы заключаем, что и все коэффициенты многочлена fm(t) так-
же равны пулю.
Случай тождественного равенства двух квазимногочленов F (Г) и
F*(t) на интервале ri<^t<^r9 сводится к рассмотренному путе?.1 об-
разования квазимногочлена F(t) — F*(t).
Итак, предложение В) доказано.
Примеры
1. Найдем частное решение уравнения
z z = t cos t = у / е,е 4- .у t е~\ (14)
3 Понтрягин Л. С.
68 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл, 2
Решим отдельно уравнения
2 + г==Ье« (15)
S-j-z (16)
Очевидно, что если z есть решение уравнения (15), то г есть реше-
ние уравнения (16). Таким образом, достаточно решить лишь урав-
нение (15). Для него г=1, X = Z, Л=1. Поэтому частное решение
следует искать в виде:
t (с1 elt*
Соотношение (9) принимает вид:
1(р4-024-1](Л4-Л2)=р>
ИЛИ
(р’-|-2/р)(Л + Лг) = р.
Это дает:
откуда с3 = — ~= = Таким образом, частное решение
уравнения (15) имеет вид:
г = (™ t --i*\ elt
а решение уравнения (14) оказывается равным
г + г = ~t (ё* <г‘7) + Т (е < _ е~ и) = ~ cos t + £ sin t.
2. Рассмотрим функцию
f (t) = cos 2t • cos 3t • г4Л
Так как каждый множитель cos2f, cos3/, представляет собой ква-
зимногочлен, то и их произведение f(t) также есть квазимногочлен.
Приведем этот квазимногочлен к виду (1):
о/ it e2it + e~3it ц
cos 21 • cos 36 ev = -—------------ev =
__ I. . I 1 + i)t 1 L W j_ L ed-^t
4 т 4 '4 '4
Приведение квазимногочленов к виду (1) полезно при решении
неоднородных уравнений на основе теоремы 8.
§11] МЕТОД ИСКЛЮЧЕНИЯ 67
§ 11. Метод исключения
До сих пор мы занимались решением одного линейного уравне-
ния с постоянными коэффициентами. Оказывается, однако, что весьма
общую систему линейных уравнений с постоянными коэффициентами
можно в некотором смысле свести к одному уравнению. Сведение
это осуществляется методом исключения, аналогичным тому,
который употребляется в теории линейных алгебраических (не диф-
ференциальных) уравнений. Здесь будет дано изложение этого метода
и сделаны некоторые выводы из него.
Мы будем рассматривать систему уравнений
л
Sz»xW(0, (1)
5=1
здесь х1, . . хп— неизвестные функции независимого переменного
t, a P(f), . . (t)—заданные функции времени L Каждый символ
LJs(p) представляет собой многочлен с постоянными коэффициентами
относительно оператора дифференцирования р, так что один член
(р) Xs представляет собой линейную комбинацию с постоянными
коэффициентами относительно функции Xs и ее производных. Число
уравнений системы (1) равно числу неизвестных функций.
Порядок системы (1) относительно неизвестной функции Xs обоз-
начим через qs, так что общий порядок системы (I) определяется
формулой q = + * * • +?л* Ставя задачу решения системы
(1), мы, естественно, должны предполагать, что каждая неиз-
вестная функция Xs имеет все производные до порядка qs включи-
тельно; предположение о существовании производных более высоких
порядков не вытекает из постановки задачи.
Применяя к системе (1) метод исключения, мы будем предпо-
лагать, что каждая из неизвестных функций Xs имеет достаточное
число производных, точно так же, как и каждая из функций f (/).
Делая эти допущения, мы, с одной стороны, сужаем класс рассмат-
риваемых решений (предположение о достаточной дифференцируемос-
ти неизвестных функций), а, с другой стороны, сужаем класс рас-
сматриваемых уравнений (предположение о достаточной дифференци-
руемости функций f (Q). Первое из этих ограничений можно снять,
доказав, что если хп есть решение системы (I) и если
правые части fJ (t) имеют достаточное число производных, то каждая из
функций Xs имеет достаточное число производных (см. примеры 3 и 4).
Перейдем к изложению метода исключения.
А) Рассмотрим матрицу
(L\(p). . .L}t(P)\
............... ел
\Llkp). . .Lna(p)]
3*
68
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
системы уравнений (1). Каждый элемент матрицы (2) есть мно-
гочлен относительно р. Таким образом, можно вычислить детерми-
нант D(p) матрицы (2) и ее миноры. Алгебраическое дополнение
элемента LJs(p) матрицы (2) (т. е. минор этого элемента, взятый с
надлежащим знаком) обозначим через М*(р). Из курса высшей ал-
гебры известно, что имеет место тождество:
л
(р)/.'(,) = &'£)(р), (3)
где Ц есть так называемый символ Кронекера:
S*=1, &$ = 0 при i^s.
Умножая уравнение (1) на многочлен AlJ(p) (т. е. производя ряд
дифференцирований, умножений на числа и сложений) и суммируя
затем по /, мы получаем равенство
п
Е = (/>)//(/). (4)
(При переходе от равенств (1) к равенству (4) мы использовали
существование достаточно большого числа производных у функ-
ций Xs и /(/).) ® силу GO равенство (4) можно переписать в виде
= (?)/'(/). (5)
f
!
Полученная нами система уравнений (5) (Z== 1,...,??) обладает тем
свойством, что каждая неизвестная функция х* входит лишь в одно
уравнение (5). Мы доказали, таким образом, что если система функ-
ций х1,..., хп представляет собой решение системы (1), то каждая
отдельная функция х1 является решением уравнения (5).
Не следует думать, однако, что если для каждого номера i вы-
брать произвольным образом решение х* уравнения (5) и затем со-
ставить систему функций х1,...,хл, то полученная система функций
будет решением системы (1). Для того чтобы найти общее решение
системы (1), нужно найти общее решение х1 каждого
уравнения (5),/= составить систему функций х1,...^" и
затем выяснить, при каких условиях (при каких соотношениях между
постоянными интегрирования) эта система функций удовлетворяет
системе уравнений (1).
Сделаем теперь некоторые выводы из метода исключения. Форму-
лируем прежде всего результат, полученный в предложении А), для
случая однородной системы уравнений
п
= /=1,(6)
$= 1
§ П1
МЕТОД ИСКЛЮЧЕНИЯ
69
Б) Если система функций х^.^х* представляет собой решение
системы (6), то каждая отдельная функция х\ входящая в это ре-
шение, удовлетворяет уравнению
О(р)х* = Ъ>
где D(p) — детерминант матрицы (Ц(р)) системы (6). Из этого,
в частности, следует, что если детерминант D(p) есть устойчивый
многочлен (см. § 9, А)), то каждое решение х1,...,хп системы (6)
удовлетворяет неравенству
при (7)
где а есть положительная константа, зависящая от системы (6), а
R— константа, зависящая от решения х1, ...jX*.
Неравенство (7) непосредственно следует из неравенства (3) § 9.
Покажем теперь, как, пользуясь методом исключения, следует ре-
шать однородную систему уравнений (6).
Систему (6) перепишем в векторной форме
L(p)x = Ot (8)
где L(p) = (Us(p))— матрица системы (6), а х=(х1,...,хп).
В) Допустим, что детерминант D(p) системы (6) не обращается
тождественно в нуль, и пусть X — корень многочлена D(p), имеющий
кратность А. Будем искать решение уравнения (8), имеющее вид:
x = g(t)e“, (9)
где (/) = (g\t),,.., gn (/)) — вектор, компоненты
(Ю)
которого являются многочленами степени k—1 относительно t
с неопределенными коэффициентами. Каждое решение вида (9) уравне-
ния (8) мы будем называть соответствующим корню X.
Подставляя предполагаемое решение (9) в уравнение (8), мы по-
лучим (см, § 8, А)):
Q = L(p)g[t}eu = euL{p-\-^g{t),
После сокращения на еи это дает:
Hp + W)=o. (U)
Таким образом, вектор (9) тогда и только тогда является решением
уравнения (8), когда многочлены (10) удовлетворяют условию (11).
Переписывая векторное уравнение (11) в координатной форме,
получим п соотношений:
+ = /=1..................(12)
70 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. ?
Левая часть каждого соотношения (12) представляет собой много-
член степени k—1 относительно коэффициенты которого явля-
ются линейными однородными функциями коэффициентов многочле-
нов (10). Приравнивая нулю коэффициент при каждой степени t
в каждом из соотношений (12), мы получим систему линейных одно-
родных уравнений относительно коэффициентов многочленов (10).
Эта система эквивалентна уравнению (11).
Таким образом, изложенный метод сводит задачу отыскания ре-
шений вида (9) к решению некоторой линейной однородной системы
алгебраических уравнений. Из сказанного видно, что решения вида
(9) определены на всем бесконечном интервале —оо<-j-оо.
Вопрос о том, как отыскивать все решения уравнения (8), ре-
шается нижеследующей теоремой:
Теорема 9. Допустим, что детерминант D(p) системы (6)
не обращается тождественно в нуль, и пусть
— совокупность всех различных корней многочлена D(p). Тогда
произвольное решение х уравнения (8) может быть записано
в виде:
х = Xj хП1, (13)
где Xi — некоторое решение уравнения (8), соответствующее кор-
ню Xf (см. В)). Отсюда, в частности, следует, что каждое ре-
шение уравнения (8), определено для всех значений Л
Доказательство. Допустим, что х — (х1,,..,^/1)—некоторое
решение уравнения (8) определенное на интервале пока-
жем, что па этом интервале оно может быть записано в виде (13).
В силу предложения Б), каждая функция Xs, 5=1,...,п, на интер-
вале удовлетворяет уравнению
О(^)х5=0,
и потому в силу предложения В) § 8 может быть записана на этом
шпервале в виде:
т
5=1,...,я. (14)
i = l
Здесь gst (/) есть многочлен степени k-t — 1, где kt — кратность корня kf.
Таким образом, каждое решение х уравнения (8) на интервале
своего определения Г1<^<^тв записывается в виде:
X = (15)
где gi(t) — вектор, компоненты которого являются многочленами
степени —1. Для доказательства теоремы 9 нам достаточно пока-
зать теперь, что каждое слагаемое gi(t)e*** в правой части равен-
§ 111
МЕТОД ИСКЛЮЧЕНИЯ
71
ства (15) есть решение уравнения (8). Для доказательства этого под-
ставим решение (15) в уравнение (8). Мы получим:
о = L (р) (gl (0 . + gm (0 ?">') =
= ?*' L (р + X,) gr, (0 4-... 4- е>т‘ L{p + xm) gm (0. (16)
Так как числа Х^.^Д^ попарно различны, то, в силу предложения
В) § 10, из равенства (16) следует:
е'1< L(p-\-\i)gi{t') — Q,
или, иначе,
= Q,
Но это и значит, что xi = gpi(0^Xi/ есть решение уравнения (8),
Итак, теорема 9 доказана.
Примеры
L Решим методом исключения систему уравнений
х1х1х'2 = 0, 1
х1 — + = J
Перепишем ее в символической форме:
(р + })х'-[-рх* = 0, )
(^-i)x‘4-(^4-i)x4 = o. J
Детерминант системы, как легко видеть, равен 2р -f- 1; он име-
ет двукратный корень Х =—1. Согласно теореме 9 решение систе-
мы следует искать в виде:
Xх = (at + b) е~*, |
xi — (ct-]rd)e~t, J
Подстановка этих функций в первое уравнение дает (после сокра-
щения на е~^.
а г — ct — d—0f
откуда
с = 0, |
a — d.)
Те же соотношения для коэффициентов получаются и при подста-
новке во второе уравнение системы. Таким образом, общее решение а
72
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ (Гл. 2
рассматриваемой системы записывается в виде:
л4 = (а£-|- Ь) е~*, 1
х* = ае~*, )
где а и b — произвольные постоянные.
2. Применим метод исключения к нормальной системе линейных
однородных уравнений с постоянными коэффициентами:
^=^6^, /=1, .... п (17)
s= I
(более полно такая система будет изучена в § 14). Перепишем систе-
му (17), пользуясь символическими обозначениями
pxJ='^1 a's Xs, /= 1, .... п,
5=1
или, иначе
/=1,(is)
5=1
где В' —символ Кронекера. Система (18) является частным случаем
общей системы (6), причем
L's (р) — aJs— рЦ
и детерминант £)(/?) в данном случае оказывается характеристическим
детерминантом матрицы (а4) системы (17). Решение системы (18)
следует теперь искать методом неопределенных коэффициентов, изло-
женным в предложении В) и теореме 9.
Систему (17) можно записать в векторной форме:
х — Ах, (19)
где Лг=(а0, х = (х\ ..., хл). В частном случае, когда все корни
Ар ..„ Хл характеристического многочлена D(p) попарно различны
и потому просты, решение уравнения (19), соответствующее собствен-
ному значению Az> имеет вид:
Xl=gieil, (20)
где компоненты вектора являются многочленами нулевой степени,
т. е. числами.
Подставляя решение (20) в уравнение (19), получаем:
- Agie .
§ н]
МЕТОД ИСКЛЮЧЕНИЯ
73
После сокращения на е 1 находим:
Agi = \gt,
а это значит, что gi есть собственный вектор матрицы А с соб-
ственным значением Так как в случае различных собственных
значений все собственные векторы с заданным собственным значением
коллинеарны между собой, то, выбирая для собственного значения Xf
некоторый фиксированный собственный вектор hif мы получим gi~
=zclhif где с1 — произвольная константа. Таким образом, если все
собственные значения матрицы Л различны, то произвольное решение
х уравнения (19) записывается в виде:
х = 4- ... (21)
где с1, ...» сп — произвольные константы.
3. Рассмотрим линейную систему
п
L's(p) Xs (t), /=1.......п, (22)
s=l
с постоянными коэффициентами (см. (1)), и пусть — ее порядок
относительно неизвестной функции а
1 Ч~ #2 ”Н • < 4“
— порядок системы (22). Пусть, далее,
!ь\(р) ... £>)\
.................................. (23)
V>) ••• зд/
— матрица системы (22), a D(p)— ее детерминант. Мы покажем, что
степень многочлена D(p) не превосходит числа q. Если эта степень
равна q, то систему (22) мы будем называть нормализуемой. В этом
случае ее можно разрешить относительно высших производных
(х1/^, ..., (хп^п\ (24)
н потому7 опа может быть сведена к нормальной системе (см. § 4, Б)).
По предположению, степень многочлена L's(p) не превосходит
числа qs, так что мы можем написать
= (25)
где многоточием обозначены члены меньшей, чем qs, степени. Вычис-
ляя детерминант D(p) матрицы (23) с учетом формулы (25), легко
убеждаемся, что
74
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
где Д есть детерминант матрицы (а^). В этой формуле опущены члены
меньшей, чем q, степени. Таким образом, установлено, что максималь-
ная возможная степень многочлена D(p) есть q, и если эта степень
равна 7, то А 0. Выделяя в системе (22) члены со старшими про-
изводными (24), мы приходим к системе
£ aJs{xs)(^ (26)
Таким образом, если система (22) нормализуема, то Д^О, и си-
стема (26) разрешима относительно высших производных (24).
Так как нормализуемая система (22) сводится к нормальной,
то согласно сказанному в примере 2 § 3 каждое решение нормали-
зуемой системы (22) имеет любое наперед заданное число производ-
ных, если только правые части fJ(t) системы (22) достаточное число
раз дифференцируемы.
4. Рассмотрим теперь случай, когда детерминант D(p) системы (22)
не равен тождественно нулю, но степень многочлена D(p) меньше
порядка q системы (22). Мы покажем, что и в этом случае всякое
решение системы (22) имеет любое заданное число производных,
если только правые части достаточное число раз дифференци-
руемы.
Согласно предположению степень многочлена D(p) меньше q, и
потому детерминант Д равен нулю. Таким образом, между столбцами
матрицы (ау) имеется линейная зависимость; пусть Ь\ Ьп—коэф-
фициенты, осуществляющие эту зависимость. Среди чисел Ь1, Ьп
могут оказаться равные нулю. Мы изменим нумерацию функций
х1, ..., хп таким образом, чтобы имели место соотношения
Ь' =^0, ^^0, Z?m+1 = ...= Z>rt = O; (27)
Яъ Q\ 7з> • • > 7i 7m-
Так как в силу (27) имеем Ь[ ф 0, то мы можем считать, что ZP = 1.
Введем теперь вместо неизвестных функций х1, ...» х” новые
неизвестные функции у1, .у", положив:
х1 = у1; х* = у* + blpq^~qiyxt 1=2, ...» т\
х*=у', Z = /n-|-l, п. (28)
Соотношения (28) могут быть разрешены относительно новых
неизвестных функций у1, у"; именно мы имеем:
у1 = х1; у1 =х1—Ь*ря'~91х\ 1 = 2, т;
у1 = х1, 1 = ...» п. (29)
Подставляя вместо неизвестных функций х1, ..., хп новые неизвест-
ные функции у1, ,уп в систему (22), мы получим новую систему
$ 12) МЕТОД КОМПЛЕКСНЫХ АМПЛИТУД ’Л 75
уравнений
" * А
^Ц(р)У!=Г(0, /=1, (30)
Непосредственно видно, что порядок q* системы (30) относительно
функции у1 меньше qlr а порядки ее относительно остальных неиз-
вестных у4, у” равны соответственно q.2t qn. Таким образом,
порядок q* системы (30) меньше порядка q системы (‘22).
Если рассматривать преобразования (28) и (29) как линейные
преобразования переменных уп в переменные х1, ...» х31 и
обратно с коэффициентами, являющимися многочленами относительно р,
то видно, что детерминант каждого из линейных преобразований (28)
и (29) равен Из &того следует, что детерминант £)* (р) си-
стемы (30) равен детерминанту D(p} системы (22). Таким образом,
разность между порядком и степенью детерминанта в системе (30)
меньше, чем в системе (22)? применяя описанное преобразование ко-
нечное число раз, мы придем к нормализуемой системе.
Пусть теперь
х* = /(f), (31)
— некоторое решение системы (22). Так как порядок системы (22)
относительно неизвестной функции х1 равен qit то функция / (0
предполагается qt раз дифференцируемой. В силу преобразования (29)
решению (31) системы (22) соответствует решение
У = /'(/), и, (32)
системы (30). Из соотношения (32) видно, что функция /(f) диффе-
ренцируема qt раз. Из сказанного следует, что из каждого решения (31)
системы (22) мы получаем некоторое решение (32) системы (30),
так что при переходе от системы (22) к системе (30) пи одно ре-
шение не теряется. Так как в результате ряда преобразований мы
приходим к нормализуемой системе, решения которой имеют любое
заданное число производных, то из преобразования (28) видно, что
и решение (31) системы (22) имеет любое заданное число производных.
§ 12. Метод комплексных амплитуд
В различных разделах техники и физики, в которых имеют дело
с колебательными процессами, важную роль играют гармонические
колебания. Математически гармоническое колебание задается функцией
• г cos (wf а), г^О. (1)
Здесь г—амплитуда колебания, а — его начальная фаза, а число w
определяет частоту колебания и обычно называется частотой. Мы
76 ЛИНЕПНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
уже видели (см. пример 1 § 4), что уравнение
je-l-u)*x=o (2)
имеет в качестве своего общего решения гармоническую функцию (1)
частоты ш с произвольными амплитудой и фазой. Уравнение (2) назы-
вается уравнением гармонического осциллятора.
При изучении гармонических колебаний нередко приходится иметь
дело с уравнением
L (р) х = г cos (<ot -ф- а), (3)
где в правой части стоит гармоническая функция. Уравнение (3) легко
решить, пользуясь способом, изложенным в теореме 8, так как гар-
моническая функция является квазимногочленом. В случае, когда
коэффициенты многочлена L (р) действительны, можно использовать
теорему 8 несколько иным способом. Способ этот называется в электро-
технике методом комплексных амплитуд и заключается в сле-
дующем.
А) Наряду с действительной гармонической функцией (1) рас-
смотрим соответствующую ей комплексную гармоническую функцию
(4)
где
'р = ге'Л (5)
Функция (4) обладает тем свойством, чю ее действительная часть
Совпадает с функцией (1):
— re1 =r cos (<«/ -|- а) + /г sin (art -ф- а).
Комплексное число (5) называется комплексной амплитудой ком-
плексной гармонической функции (4); оно объединяет в себе дейст-
вительную амплитуду г и начальную фазу а. Отметим, что
В случае, если коэффициенты многочлена L(p) действительны, для
решения уравнения (3) решают предварительно уравнение
L(p)2 = pe‘w. (6)
Непосредственно видно, что если г = х-\-1у есть решение уравне-
ния (6), то х есть решение уравнения (3). Предполагая, что Zw не есть
корень многочлена L (р)\
(7)
ищем (см. теорему 8) решение уравнения (6) в виде комплексной
гармонической функции г = ае'^ с комплексной амплитудой a =
§ 12] МЕТОД КОМПЛЕКСНЫХ АМПЛИТУД 77
Подставляя функцию z = ae1^ в уравнение (6), получаем:
(см. § 7,Б)). Таким образом, решение уравнения (3) находится в виде
функции
X = 5 COS ₽); (9)
амплитуда s и начальная фаза р этого решения определяются из
формулы
(см. (8)). В частности, s = J с I = . Если многочлен L (р) устой-
чив, то соотношение (7), очевидно, выполнено. В этом случае любое
решение уравнения (3) имеет вид:
х = и -J- 5 cos (<ot 4- Р), (10)
где и есть решение однородного уравнения L(p)u = Q. Решение «
этого однородного уравнения стремится к нулю при t—*оо, и потому
любое решение уравнения (3) стремится к решению (9). Решение (9)
называется установившимся} оно соответствует установившемуся
процессу, в то время как решение (10) описывает переходный про-
цесс. Установившееся решение (9) является единственным периодиче-
ским решением среди всех решений (10).
При применении метода комплексных амплитуд обычно не рас-
сматривают решений действительного уравнения (3), а сразу исходят
из комплексного уравнения (6).
Изложим теперь метод комплексных амплитуд в применении к
системе уравнений. Речь идег об отыскании частного решения системы
уравнений
=r;cosM + a^), /=1, ...» /г (И)
I
с действительными коэффициентами, в правых частях которой стоят
гармонические колебания одной и той же частоты ю.
Б) Предположим, что детерминант D(p) системы (11) (см. § И, А))
не обращается в пуль при р = 1<о. Для отыскания решения системы (И)
будем искать сначала решение системы уравнений
п
= /=1, ...» п, (12)
Й=1
где
78 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
Так как коэффициенты всех многочленов [Jh (р) действительны, то
из всякого решения г1, z* системы (12) мы получаем решение
x* = Rez\ А=1, л,
системы (11). Решение системы (12) ищем в виде;
? = *=1, п. (13)
Подстановка функций (13) в систему (12) дает (после сокращения
на elV)i) систему уравнений
которая однозначно разрешима относительно неизвестных akt так
как детерминант ее £)(Zw) по предположению отличен от нуля. Найдем
решение этой системы и положим:
тогда в силу (13) мы находим решение
xft = sftcos(«^4’?ft)> А=1, п, (14)
системы (11). Если детерминант D(p) системы (11) есть устойчивый
многочлен, то неравенство 2) (Zin) О выполнено, и, сверх того,
каждое решение системы (И) отличается от решения (14) слагаемым,
стремящимся к нулю при Z — -фоо (см. § 11, Б)). Таким образом,
в случае устойчивого многочлена D(p) решение (14) системы (11)
не только является одним из частных решений, но представляет
собой установившееся решение.
Пример
Решим уравнение
х -ф- офх = г cos (wf 4- а) (15)
гармонического осциллятора, находящегося под воздействием внешней
гармонической силы. Вместо уравнения (15) рассмотрим соответствую-
щее комплексное уравнение
5 = (16)
Если to zfi ф|, то уравнение (16) имеет решение вида 2 = причем
в силу формулы (8)
п?'«
° о?—«а •
1
§
МЕТОД КОМПЛЕКСНЫХ АМПЛИТУД
79
Таким образом, уравнение (15) имеет решение
г
СО*------------------------- СО2
1
где Р = а при «1 » и ^ = a^-ic при Формула (17) дает
вынужденные колебания осциллятора под воздействием гармониче-
ской внешней силы. Здесь важно отметать явление резонанса, заклю-
чающееся в том, что амплитуда
вынужденного колебания возрастает с убыванием разности
((J&J — (о|. Интересно также отметить, что фаза £ колебания (17) совпа-
дает с фазой а вынуждающей силы при и противоположна
ей при Общее решение уравнения (15) записывается в виде:
х = г, COS (<*>^ + a.) + J „Л-.р cos (art + Р),
где и = rx cos (а)^ + оц) есть решение соответствующего однородного
уравнения. Слагаемое и называется собственным колебанием осцил-
лятора.
Если = то формула (17) теряет смысл. В этом случае ре-
шение уравнения (16) следует искать в виде:
z = pteiajt,
где р — комплексное число (см. теорему 8). Согласно формуле (9)
§ 10 имеем:
[(/? /ц))2 + О)2] pf = r/“,
откуда
Гг'«
? 21(Л
Таким образом, частное решение уравнения (16) имеет (при = ш)
вид:
г„'Н-т)
2t<ij 2ca ’
а решение уравнения (15) оказывается равным
rt / . . тс \ rt . , , . ч
х = X— COS wt -4- a — -х- = тг- sin (wr -f- a).
2u \ ‘ z) z« 1
Таким образом, при co = wJ явление резонанса заключается в том>
rt
что амплитуда становится переменной и неограниченно возрастает
с течением времени. В реальных приборах это явление не наблюдается
ввиду наличия <трения».
80
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
§ 13. Электрические цепи
Теория обыкновенных дифференциальных уравнений находит свои
применения в различных областях техники; она применяется в электро-
технике и, в частности, радиотехнике. При некоторой идеализации
работа радиоприбора может быть математически описана системой
обыкновенных дифференциальных уравнений, причем неизвестными
функциями времени в этой системе являются величины токов, про-
ходящих через различные детали прибора, или падения напряжения
между отдельными узлами прибора. Радиоприборы дают очень бога-
тый материал, иллюстрирующий применения теории обыкновенных
дифференциальных уравнений, гораздо более богатый, чем, например,
задачи механики. Богатство это характеризуется, в частности, тем,
что систему обыкновенных дифференциальных уравнений, возникшую
из какой-нибудь технической задачи, часто удается смоделировать
электрическим прибором, т. е. сконструировать такой электрический
прибор, работа которого описывается той же системой уравнений,
что и интересующий нас технический объект. Такой моделирующий
электроприбор может до некоторой степени помочь в решении систе-
мы уравнений, так как, наблюдая за его работой, мы тем самым
наблюдаем за поведением неизвестных функций, удовлетворяющих
системе уравнений. Физические законы, управляющие работой электро-
приборов, формулируются настолько просто, что они легко могут
быть сообщены даже человеку, почти незнакомому с физикой. Здесь
в несколько догматической форме дается изложение простейших
законов электротехники и приводится несколько примеров примене-
ния дифференциальных уравнений к изучению работы электроприборов
Элементы электрических цепей
К числу важнейших деталей, из которых конструируются электро-
приборы. принадлежат сопротивление, индуктивность (самоиндук-
ция) и емкость (конденсатор). Каждая из этих деталей является
двухполюсником, т. е. обладает двумя контактами, которые при монти-
ровании электроприбора присоединяются к полюсам других деталей.
Во время работы электроприбора через двухполюсник, вмонтирован-
ный в этот прибор, проходит электрический ток, и при этом электри-
ческое состояние двухполюсника характеризуется в каждый момент
времени t двумя величинами: силой тока идущего от полюса а
к полюсу b двухполюсника ab, и падением напряжения Uab(t) от
полюса а к полюсу Ь. Сила тока Iab(t) может принимать как поло-
жительные, так и отрицательные значения; если ток «течет.» от по-
люса а к полюсу b (имеется в виду так называемое техническое
направление тока), то число Iab(t) положительно; в противном случае
оно отрицательно. Падение напряжения Uab(t) от полюса а к по-
§ 13 1
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
81
люсу b представляет собой разностьVa(t)— V*(0 потенциалов в по-
люсе а и полюсе Ь. Таким образом, обе величины и
характеризующие состояние двухполюсника ab в момент времени t,
зависят от того, какой из полюсов поставлен на первом месте и ка-
кой на втором. При перемене порядка полюсов каждая из величин 1аЬ (t)t
Uab(t)> очевидно, меняет знак, так что мы имеем соотношения:
^«(0 = — . (1)
= (2)
Для каждого двухполюсника ab функции и вре-
мени t не независимы, а связаны некоторым соотношением, представ-
ляющим собой физический закон, управляющий работой двухполюс-
ника. Для сопротивления, самоиндукции и емкости физические за-
коны, управляющие их работой, даются нижеследующим предложе-
нием.
А) Для двухполюсника ab, представляющего собой сопротивле-
ние, имеет место соотношение (закон Ома):
Uab(t) = RM (3)
здесь Rab — положительный коэффициент, называемый сопротивле-
нием и могущий для различных двухполюсников принимать различ-
ные значения, но постоянный для каждого данного двухполюсника;
при этом мы имеем всегда
Rb. = R^ (4)
Для двухполюсника ab> представляющего собой индуктивность, имеет
место соотношение:
Uab^ = Lab^lab(tyt (5)
здесь Lab есть положительный коэффициент, называемый индуктив-
ностью и могущий для различных двухполюсников принимать раз-
личные значения, но постоянный для каждого данного двухполюсника.
При этом
(6)
Для двухполюсника ab, являющегося емкостью (конденсатором), имеет
место соотношение
IaAt)=Cab^Uat>(t), (7)
где СаЬ есть положительный коэффициент, называемый емкостью
и могущий принимать различные значения для различных двухпо-
люсников, но имеющий для данного двухполюсника вполне опреде-
ленное значение; при этом мы имеем:
СаЬ = СЬа. (8)
82 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
Интегрируя соотношение (7), мы получаем:
t
uab (t) = Uab (t0) + Л ( (О л- (9)
*0
Функция
QaAL) = CabUab(t)
представляет собой физическую величину, связанную с состоянием
конденсатора в данный момент времени и называемую зарядом кон-
денсатора ab. Соотношение (9) часто пишут в виде:
^ab- J
где под ^Iab(t)dt подразумевают заряд конденсатора-
Соотношение (4) вытекает из (1), (2) и (3):
Rablab (!) = Uab (t) = - Uba (t) = - RbJba (t) = Rba Iba (i)) =
= RbcJab (0-
Аналогично устанавливаются соотношения (6) и (8).
Важную роль в работе электрических приборов играет явление
взаимоиндукции между двумя индуктивностями.
Б) Две индуктивности афх и а^2 с величинами Lab — Lx и
La^ = L% могут находиться в состоянии взаимоиндукции, характери-
зующемся коэффициентом взаимоиндукции /И = Л4дг> аЬ В этом
случае падение напряжения UQlbi (0 = U\ (0 на двухполюснике аф1
связано не только с током /а^ (Q = /t (/), но также и с током
la^ — (t). Точно так же напряжение = ^4(0 на двух-
полюснике а.фч связано не только с током //(f), но и с током /](/).
Соотношения, которые имеют здесь место, даются формулами
+ (Ю)
= + (И)
СлЬ U t
При этом для коэффициента Ма взаимоиндукции выполнены
равенства *
а.2Ъ, — Ь&9
кроме того, для него имеет место неравенство
Чем больше «взаимодействие» двух индуктивностей, тем более коэф-
фициент взаимоиндукции М приближается по величине к значе-
нию LiLfr
§ 13] ЭЛЕКТРИЧЕСКИЕ ЦЕПИ 83
Описанные в предложении А) двухполюсники называются пассив-
ными} сами они не могут вызвать появления в приборе электричес-
ких явлений. Непосредственной причиной появления в приборе элек-
трических токов служат активные двухполюсники — источники на-
пряжения и источники тока.
В) Для двухполюсника ab> представляющего собой источник на-
пряжения, имеет место соотношение
Uab{t)=u{t), (12)
где U(t) — заданная функция времени /, характеризующая источник
напряжения. Соотношение (12) можно рассматривать как связываю-
щее функции Uab(t) и lab(t\ только связь эта такова, что функция
Iab(t) в нее не входит. Для источника тока ab аналогично имеет
место соотношение
/„(0=7(0,
где I(t) — заданная функция от t, характеризующая источник тока.
Наиболее часто рассматриваются источники напряжения и источники
тока, для которых функции U(t) и I(t) являются либо константами,
либо периодическими функциями вида
г COS (a>t а).
Таковы главнейшие и в то же время простейшие детали, из ко-
торых монтируются электроприборы. Сами приборы называются
электрическими цепями, а детали, из которых они монтиру-
ются,— их элементами. Следует отметить, что существуют эле-
менты, отличные от описанных выше, в частности существуют много-
полюсные элементы. Примером трехполю с и ого элемента служит
электронная лампа (триод), работа которой будет разобрана
в дальнейшем (см. § 29).
Законы Кирхгофа
Перейдем теперь к формулировке законов Кирхгофа, управ-
ляющих работой электрических цепей.
Г) Электрической цепью ’называется конечная совокупность эле-
ментов (в частности, двухполюсников вышеописанных видов), полюсы
которых соединены в так называемые узлы цепи, так что в каждом
узле соединяются два или большее число полюсов различных элемен-
тов цепи. Первый закон Кирхгофа утверждает, что сумма
всех токов, втекающих в каждый узел цепи из всех элементов*
примыкающих к этому узлу, равна нулю. Второй закон Кирх-
гофа вытекает из предположения, что в каждом узле а цепи име-
ется электрический потенциал Уа(0» а падение напряжения
84
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
от узла а к узлу b представляет собой разность потенциалов, имею-
щихся в узлах а и Ь, так что Uab(t) — ЦД/)— Vb(t). Из этого пред-
положения вытекает, что если a, bt с, Л, k есть некоторая по-
следовательность узлов электрической цепи, то имеет место
соотношение
иаъ (о+ад)+• • •+(0+и.а (о=о,
которое и представляет собой второй закон Кирхгофа. Его формули-
руют следующим образом: сумма падений напряжения вдоль всяко-
го замкнутого контура цепи равна нулю. (В этих формулировках
законов Кирхгофа не предполагается, что элементами цепи явля-
ются двухполюсники.) Дадим теперь более четкую формулировку
законов Кирхгофа применительно к цепям, составленным из двухпо-
люсников.
Д) Пусть 5-—некоторая электрическая цепь, составленная из
двухполюсников. Первый закон Кирхгофа утверждает, что если а
есть произвольный узел цепи S, a t^a, Ь.га,.,,, bqa — совокупность
всех двухполюсников, примыкающих к узлу а (рис. 7), то
^а(0 + ^а(0 + ...+ ^а(0 = 0.
Второй закон Кирхгофа утверждает, что если abt bc,„.,hk, ka— не-
которая последовательность двухполюсников, входящих в цепь S
(каждый следующий двухполюсник начинается в том узле, в котором
кончается предыдущий, рис. 8), то
иаь (0 + ад)+...+uhk (t)+ика (о=о.
Рассчитать работу электрической цепи, составленной из двухпо-
люсников,— это значит найти ток и напряжение, соответствующие
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
85
§ И]
каждому двухполюснику, входящему в цепь; таким образом, если
цепь состоит из п двухполюсников, то перед нами стоит задача
отыскания 2л функций времени. Закон, управляющий работой каждого
отдельного двухполюсника, дает одно соотношение между искомыми
функциями, так что для 2л искомых функций мы уже получаем л
соотношений. Остальные л соотношений дают законы Кирхгофа.
Тот факт, что законы Кирхгофа дают именно л независимых между
собой соотношений, можно доказать, но здесь мы этого делать не
будем. В результате использования всех соотношений мы получаем
систему из 2л уравнений для 2л искомых функций. Уравнения эти
частично дифференциальные, частично конечные (алгебраические).
Законы Кирхгофа дают конечные уравнения и ими прежде всего
нужно воспользоваться для исключения части неизвестных функций.
При этом обычно пользуются одним из следующих двух путей.
Можно за основные неизвестные функции принять токи и выразить
через них напряжения. В этом случае нужно прежде всего восполь-
зоваться первым законом Кирхгофа: выразить все токи через мини-
мальное число независимых (в силу этого закона). Независимые токи
называются контурными. После этого следует воспользоваться
вторым законом Кирхгофа, заменяя в нем каждое напряжение его
выражением через соответствующий ток. Этот способ называется
методом контурных токов. Второй способ заключается в том,
что за основные неизвестные функции принимают напряжения на
двухполюсниках, а токи выражают через напряжения (при помощи
законов, управляющих работой каждого двухполюсника). В этом
случае нужно при помощи второго закона Кирхгофа выразить все
напряжения через минимальное число независимых (в силу этого
закона). Независимые напряжения называются узловыми. Затем нужно
использовать первый закон Кирхгофа, заменяя в нем каждый ток его
выражением через соответствующее напряжение. Этот способ назы-
вается методом узловых напряжений.
Операционное сопротивление двухполюсника
Прежде чем перейти к разбору примеров расчета электрических
цепей, запишем соотношения (3), (5), (9), (10), (И), т. е. законы,
управляющие работой двухполюсников, при помощи символических
обозначений.
Е) Пусть ab — двухполюсник, представляющий собой сопротив-
ление, индуктивность или емкость. Положим: f
U(0 = '(0, Rat, = R> = ц СаЬ = С.
Если в дополнение к употреблявшимся ранее символическим обо-
значениям (см. стр. 42, § 7, А)) ввести естественное обозначение
86 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
—f(f)= f(y)dx, то соотношения (3), (5), (9) можно записать
одной формулой
U(t) = Z(p)I(i) (13)
(рис. 9), где, соответственно, Z(p) = R, Z(p) — Lp, Z(p) — — .
ср
Функция Z(p) называется операционным сопротивлением двухполюс-
ника ab. Для емкости она не является
собой рациональную функцию
£/(0 = ^/(0- (14)
многочленом, а представляет
Соотношение (14) после умножения
на Ср приобретает привычный вид
l(t) — CpU(t), где имеется лишь
многочлен от р. Если положить
*
—I ।— еопротиблеяие
L
— индуктивность
- 2L
^/С бзоимаиндупция
-----1------ емкость
Q^— Z(p) ’
то соотношение (13) приобретает вид.
Рис. 9.
источники
напряжения-
постоянного
гармонического
и произболького
переменного
Условные обозначения
некоторых элементов
электрических испей
Рис. 10.
Функция Q(p) называется операционной проводимостью двухполюсника
ab и имеет соответственно вид:
G(P) = ~, О(р) = -У-, G(p) = Cp.
Соотношения (10), (И) в операционных обозначениях получают вид:
^(0 = 1^ (04-АШ0>
U1(t)=LipIi(t)^MpIi(ty
Перейдем к разбору примеров. Для наглядности электрические
цепи изображают графически, ставя в соответствие каждому узлу
точку, а каждому двухполюснику — отрезок или кривую, соединя-
ющую соответствующие узлы; на каждом таком отрезке изобража-
ется условное обозначение соответствующего двухполюсника (рис. 10).
§ 13]
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
87
Примеры
1 (Колебательный контур). Пусть S—электрическая цепь
с четырьмя узлами a, b, с, d, состоящая из четырех двухполюс-
ников ab, be, cd, da (рис. И). Двухполюсник ab— индуктивность А»
двухполюсник Ьс — сопротивление
двухполюсник cd — емкость С; наконец,
двухполюсник ad—источник напряже-
ния Uad(f) = U(t). Для расчета исполь-
зуем метод контурных токов. Приме-
няя первый закон Кирхгофа к узлу Ь,
получаем /вд(0~Ь = или, иначе,
7ай(0 = /йс(0- Так обстоит дело всегда,
когда к одному узлу примыкают ровно
два двухполюсника. Таким образом,
мы имеем:
lab (0 = (0 = (0 = U (0 = / (О-
Здесь 1(f) есть контурный ток.
Далее, выписывая для каждого двухполюсника закон, управляющий
его работой, получаем:
(15)
Uab (f) = Lpl(t), =
uc<t (0 = / ОХ Uda (0=- /7 (О-
Второй закон Кирхгофа дает:
иаЬ (О + Ubc (О + Ucd (О + Uda (0 = 0, (16)
Из соотношений (15) и (16) получаем:
(^+«4—^-)/(/)= 77 (О- (17)
Можно умножить обе части соотношения (17) на р (что означает
почленное дифференцирование); тогда мы получим:
(^ + ^+4-)1 V=PU (0- 08)
Таково дифференциальное уравнение рассматриваемой цепи.
Если изъять из цепи двухполюсник ad, то мы получим так на-
зываемую разомкнутую цепь, состоящую из трех пассивных
двухполюсников ab, be, cd. Эту цепь (всю целиком) можно рас-
сматривать как двухполюсник с полюсами а и d (рис. 12). Для
такого двухполюсника закон, управляющий его работой, дается
соотношением (17), аналогичным соотношению (13). Здесь функ-
88
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
ция Z(p) = Lp-\-R-\-^~
'-'Р
в л ением, а обратная
является операционным сопроти-
ей
величина
ляется операционной проводи-
мостью.
Если положить (/(/) = О, то это
будет равносильно предположению, что
а
Рис. 12. Рис. 13.
°(Р^— LCp"RCpI
в нашей цепи отсутствует активный двухполюсник ad, и цепь со-
стоит из трех пассивных двухполюсников ab, be, cd, причем узлы
а и d совпадают (рис. 13). Уравнение, описывающее работу этой пас-
сивной электрической цепи S*, имеет вид:
+ + -!)/(/) = о. (19)
Как уже отмечалось раньше, в пассивной электрической цепи элек-
трические явления сами по себе не возникают, и это отражается
в том, что частным решением уравнения (19) является функция
/(0 = 0. Можно, однако, рассмотреть работу электрической цепи S*,
считая, что ток в ней уже имеется, и выяснить, как этот ток будет
изменяться со временем. Пусть X] и Х2— корни многочлена
/у -\-Rp 4-1. (20)
Так как числа /_, С больше нуля (см. А)), то действительные
части корней Xj и Х2 отрицательны, и потому электрический про-
цесс в цепи S* затухает со временем (см. § 9,А)). Затухание это
может проходить, однако, различными способами; если корни Xj и Х2
комплексны, то всякое ненулевое решение уравнения (19) имеет ко-
лебательный характер (см. пример 3 § 7); если же корни Х( и Х2
действительны, то затухание происходит апериодически, именно вся-
кое решение уравнения (19) становится, начиная с некоторого мо-
мента времени, монотонным. Вопрос о том, будут ли корил X, и Х2
комплексны или действительны, решается тем, какой знак имеет число
д = Ш2_______Ь
27 / LC9
§ П]
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
89
если Д<^0, то решения уравнения (19) имеют колебательный харак-
тер, если же Aj>0, то они апериодичны.
Особый интерес представляет колебательный контур 5* в том
случае, когда в нем вовсе отсутствует сопротивление /?. В этом
случае наша цепь состоит лишь из двух пассивных элементов ab и
ed, причем b — c, a — d (рис. 14). При этом предположении уравне-
ние электрической цепи получает вид: _________________
(р’+£4)ад=о. J
Общее решение этого уравнения запись»- с —
вается в виде: > "
1(f) = s cos (о^ + р), S
где Таким образом, при
отсутствии сопротивления в пассивном
колебательном контуре происходят незатухающие колебания ча-
стоты
1
(0. — -=- .
Vic
Величина называется собственной частотой колебательного
V LC
контура 5 в общем случае.
Вернемся теперь к рассмотрению колебательного контура 5 и
рассмотрим случай гармонического источника напряжения U (/).
Так как корни многочлена (20) имеют отрицательные действи-
тельные части, то можно рассматривать в цепи 5 установившийся
процесс. Решение будем искать по способу комплексных амплитуд
(см. § 12). Пусть U(f) — reiU>t— комплексное гармоническое колеба-
ние с действительной амплитудой г^>0. Тогда правая часть уравне-
ния (18) имеет вид:
pU(t) — р (ге1Ы) = 1г<яеы.
Мы имеем:
причем комплексная амплитуда а тока /уст(0 определяется формулой
г
° — / 1 \ / 1 \
+ + тj Я4-1 [и - )
(см. § 12, А)). Отсюда для действительной амплитуды получаем:
90
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
Из этой формулы видно, что при заданной амплитуде г источника
напряжения амплитуда 5 силы тока достигает своего максимума при
собственной частоте to = контура S. При этой частоте
г
амплитуды 5 и г связаны соотношением 5 = ~п> т. е- кон-
г\
тур при этой частоте ведет себя так, как будто в нем имеется
лишь сопротивление. Для остальных частот амплитуда 5 тока имеет
меньшее значение, чем Это явление называется резонансом
г\
(ср. § 12, пример). Колебательный контур L, R, С резонирует
на свою собственную частоту — -
2 (Трансформатор). Трансформатор состоит из двух обмоток,
первичной и вторичной, помешенных на одной катушке.
К первичной обмотке подключается источник переменного напряже-
ния, ко вторичной — нагрузка, например внешнее сопротивление.
Каждая обмотка имеет индуктивность и сопротивление (внутреннее).
Между обмотками имеется взаимоиндукция. Таким образом, транс-
форматор можно рассматривать как электрическую цепь, состоящую
из двух раздельных контуров, связанных индуктивно. Первый контур
состоит из трех двухполюсников: —индуктивность b^ —
внутреннее сопротивление ахсх — источник напряжения UaiC =
Второй контур состоит также из трех двухполюсников: — ин-
дуктивность Л2; #2с2—внутреннее сопротивление /?2; — сопро-
тивление нагрузки R. Кроме того, имеется взаимоиндукция М>1ь1.а.!г>а =
— М (рис. 15). В силу 1-го закона Кирхгофа имеем:
Таким образом, мы имеем два контурных тока Ztr /$. Применяя вто-
рой закон Кирхгофа, получаем:
Цр1^ Mph + Rih-Z/(0 = 0,
Lpl, ^-Mpli + R^ + Rr* =0,
§ 13)
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
91
или иначе
Мр 11 -}- (^2р "4" ^?2 “1“ R) L = 0.
Детерминант D (р) этой системы имеет вид:
D (р) = (ЦЦ - АР) р* + (Ц R. + LiR + L&) p + R> (R, + ₽).
В силу предложения Б) § 9 этот многочлен устойчив (так как LxLi —
— 7И2^>0). Рассмотрим работу трансформатора в случае, когда нап-
ряжение U(/) изменяется гармонически, и будем искать установив-
шееся решение по способу § 12, Б). Положим:
U{t) = u^,
где Wj — действительное положительное число (амплитуда напряжения,
поданного на первичную обмотку). Неизвестные функции /р /.2 будем
искать в форме
= /а = а/^,
где о.2— комплексные амплитуды токов.
Наибольший теоретический интерес представляет идеальный тран-
сформатор, т. е. такой трансформатор, в котором величины R^
и LjLa — М2 малы. Пренебрегая этими величинами в уравнениях для
определения величин и о2, получаем:
L। • Zojoj /И * Ztooj —— и J,
М • /ада! -|- (Li - Zw —|— R)ai = 0.
Так как M^VLxL^ то, вычитая из второго уравнения первое, умно-
женное на j/~^, ыы получим:
л»,=
Таким образом, амплитуда u$ — R\c*\ падения напряжения на нагруз-
ке R оказывается равной
величина называется коэффициентом трансформации. Таким
образом, если L^>Lb то мы имеем трансформатор, повышающий
напряжение
1-
при мы получаем трансформатор, понижающий напряжение
«2 < 1
«1
92
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ (Гл. 2
3 (Электрический фильтр). Рассмотрим электрическую цепь
с четырьмя узлами a, b, ct d и пятью двухполюсниками (рис. 16):
Рис. 16.
ab — индуктивность £,
Ьс — индуктивность той же величины L,
bd — емкость С,
ad — источник напряжения Uad(t)= U(t),
cb — сопротивление нагрузки
Положим:
lab == I Ъс ===
Тогда в силу 1-го закона Кирхгофа имеем;
Ibd — li —l& ha = А*
На основании 2-го закона Кирхгофа получаем:
Uab + Ube + Ucd + Uda =
Ubc 4“ Ucd + Udb —
или
Lph + Lplt + RI%— U(t) = 0,
^ + /?Л + -^(/2-Л) = о.
Умножив второе уравнение на р, получим следующую систему;
ip/» 4-(£.р4-/?)/в = ^/(0,
-Т/, + ^ + ^ + 1^ = 0.
Детерминант этой системы имеет вид:
D (р) = LV + LRp1 4- .
Согласно теореме б многочлен D(p) устойчив. Будем теперь считать,
что U—beia>it где b — действительная амплитуда напряжения (см.
§ 14]
НОРМАЛЬНАЯ ЛИНЕЙНАЯ ОДНОРОДНАЯ СИСТЕМА
93
§ 12). Неизвестные функции Ц и /3 будем искать в форме
Ц = а1ем, Ц = аге!и>(, „4
где и — комплексные амплитуды токов, т. е. ограничимся
отысканием установившегося режима.
Поставим задачу об определении падения напряжения Ucd = RI^
на нагрузке. Мы имеем:
b
— с
— / Р \ / 9 / \ ’
+/<0 — £V)
\ G / \ G /
откуда находим амплитуду а = | 1 R напряжения Uca\
bR
U | 4X0 I 4 \ « ,i п । •
T-f Л 1
При малых значениях частоты ад мы имеем: у ^1; иначе говоря, на-
пряжения малой частоты легко передаются через фильтр, почти не
меняя амплитуды. При больших значениях частоты мы имеем:
а R
b ~ CLW9
так что напряжения высокой частоты почти не проходят, «фильтру-
ются».
§ 14. Нормальная линейная однородная система
с постоянными коэффициентами
В этом параграфе решается система уравнений
/ п . ,
х' = У axJ\ /=1, п, (1)
. . zrj/. -- \
постоянными коэффициентами. 3)та система может быть решена
методом исключения (см. § 11 и, в частности, пример 2 в §11).
(Здесь она решается путем приведения матрицы Д = (а*) к жордано-
вой форме. В случае, когда все собственные "значения”"матрицы Л
различны, возможность приведения ее к жордэновой, т. е, в данном
случае диагональной, форме представляет собой весьма элементарный
алгебраический факт. В общем случае возможность приведения ма-
трицы А к жордановой форме относится к наиболее сложным резуль-
татам курса линейной алгебры. В дальнейшем в этой книге исполь-
зуются лишь те результаты настоящего параграфа, которые опира-
94
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
ются на приведение матрицы _К . диагональному„виду н случае
различных ее собственных значений. Результаты, использующие воз-
можность приведения матрицы А к жордановой форме в общем слу-
чае (предложения В), Г), Ж)), в дальнейшем не применяются и при
чтении могут быть пропущены.
Обычно приведение матрицы А к жордановой форме для реше-
ния системы (1) используется путем линейного преобразования неиз-
вестных функций х\ хп. Этот способ изложен в конце настоя-
щего параграфа под заголовком «Преобразование переменных». Дру-
гой способ, по существу также опирающийся на приведение матри-
цы А к жордановой форме, изложен в первой части параграфа.
В этом параграфе мы не будем делать различия между матрицей
А и соответствующим ей преобразованием А в пространстве векто-
ров х = (№, ...» хп), так как базис меняться не будет. Исключе-
ние составляет лишь доказательство предложения Е).
Случай простых корней характеристического
уравнения
А) Система дифференциальных уравнений (1) в векторной форме
переписывается в виде:
х=Ах. (2)
Здесь A=(aJ), а вместо системы х1, . . хп неизвестных функций
введен неизвестный вектор
х = (х!, . . хп);
под производной х вектора х понимается вектор (^1, . . £п). Ес-
ли h есть собственный вектор матрицы А с собственным значением
X т. е. если
Ah = lh
(см. § 34, Б)), то векторная функция х, определяемая соотношением
х = heu9
является решением уравнения (2).
Последнее утверждение проверяется путем подстановки x = heu в
соотношение (2).
Теорема 10. Пусть
х = Ах (3)
— такая система дифференциальных уравнений (см. А)), что соб*
стенные значения /Ф . . \п матрицы А попарно различны, и
пуст ь
hu . . Л„
§ 14] НОРМАЛЬНАЯ ЛИНЕЙНАЯ ОДНОРОДНАЯ СИСТЕМА
95
— соответствующие собственные векторы этой матрицы. По-
ложим:
Xi^hie^, /=1, . . п. (4)
Тогда векторная функция
X = c1Xt-|-. . (5)
где с1, . . сп— константы, является решением уравнения (3),
и всякое решение уравнения (3) задается этой формулой.
Доказательство. В силу предложения А) каждая функция Xi
представляет собой решение уравнения (3), и потому в силу пред-
ложения А) § 6 формула (5) всегда дает решение уравнения (3). До-
кажем теперь, что всякое решение уравнения (3) может быть запи-
сано в виде (5). Пусть <р(/)— произвольное решение уравнения (3).
В силу теоремы 3 решение ф(£) можно считать заданным на всей
бесконечной прямой —оо<^£<^оо. Таким образом, решение это оп-
ределено и при / = 0. Положим ф(О) = хо- Пусть
Jfo = С1 fti + • . +cnhn
— разложение вектора Хо по векторам базиса hi, . . hn (векторы
hit . . hn образуют базис в силу предложения В) § 34). Тогда
решение х> определяемое формулой (5), очевидно, удовлетворяет на-
чальным условиям
Х(О) = хо.
Тем же начальным условиям ф(О) = Хо удовлетворяет и решение
Ф(/); таким образом, в силу теоремы единственности (см. теорему 2),
Х = ф(0.
Итак, теорема 10 доказана.
В случае, если матрица (а}), задающая уравнение (3), действи-
тельна, перед нами встает задача выделения из всех решений (5)
действительных реп^ний. /
Б) Будем считать, что матрица (а^/задающая уравнение (3), дей-
ствительна, и выберем Ъекторы hrf. . ., hfl таким образом, чтобы
действительным собственник значениям соответствовали действитель-
ные векторы, а комплексно сЪрряженным — комплексно сопряженные.
Тогда в системе решений (4^/каХдому действительному собственному
значению будет соответствовать ^действительное решение, а каж-
дым двум комплексно Аопряженным\ собственным значениям будут
соответствовать комп^ксно сопряженньГ^ решения. Оказывается, что
решение (5) тогда м только тогда действительно, когда константы,
стоящие при действительных решениях, действительны, а константы,
стоящие при комплексно сопряженных решениях, сопряжены.
Правильность предложения Б) непосредственно вытекает из пред-
ложения Г) 4 7.
96
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ (Гл. 2
Общий случай
Перейдем теперь к решению системы (1) в общем случае (матри-
ца (л-) может иметь кратные собственные значения). Разбор этого
случая опирается на весьма нетривиальную и сложно доказываемую
алгебраическую теорему о приведении матрицы к жордановой фор-
ме (см. § 36),
В) Запишем систему (1) в векторной форме
х = Дх (6)
й пусть
ftp ...» Aft
— некоторая серия с собственным значением X (см. § 36, А)) отно-
сительно матрицы А, так что выполнены соотношения
= AА2== -ф-Ар ... > Ahjt=='khj{~\-
Введем последовательность векторных функций, положив:
/г-1 /r-i
®г(0 = (^Г)1Л1 + (^2)!^+ Л-Пг, г=Ъ (7)
Оказывается тогда, что векторные функции
хг = (0еи. г=1, ... , ft, (8)
являются решениями уравнения (6), причем
хг(0) = Аг. (9)
Таким образом, каждой серии из ft векторов соответствует система
из ft решений.
Для доказательства того, что векторные функции (8) являются
решениями уравнения (6), укажем два тождества относительно век-
торных функций (7). Тождества эти следующие:
(dr(0 = <dr-l(0> Г= 1, , ft,
A(Or (0 = AO)r(0 + ®r.i(0» г=Ь...» ft.
В этих соотношениях принято (O0(/) = 0. Оба они проверяются
непосредственно путем проведения элементарных вычислений. При
помощи этих тождеств непосредственно проверяется, что функции
(8) являются решениями уравнения (6). Действительно, мы имеем:
xr (t) = (0 еи + X®, (0 еи = (®г_, (О + X®, (0) еи =
= А(ЯГ (t)eu= Axr(t).
Перейдем теперь к формулировке и доказательству теоремы,
дающей решение системы (1) в общем случае.
§ MJ
НОРМАЛЬНАЯ ЛИНЕЙНАЯ ОДНОРОДНАЯ СИСТЕМА
97
Теорема И. Пусть
х=Ах (10)
— векторная запись системы (1). В силу теоремы 30 (см. § 36)
существует базис
Ль h„
состоящий из серий относительно матрицы А. Для определен-
ности будем считать, что h{i , hkt есть серия с собственным
значением hk^i, hkt-\-k2 есть серия с собственным зна-
чением X*, и т. д. В силу предложения В) каждой из серий соот-
ветствует система решений, так что мы можем выписать
следующие решения уравнения (10):
/ А-1 \
x1 = ft1ex‘z, ... , t)! fti+ •••
xftl + i = fefcl + iex^, ^x*1+fta= (11)
= i)! ft*i+1 + • • + ft*i+*»)eUt’
Оказывается, что формула
X — С1 Х{ -}— ... сп хп,
(12)
где с1, ... , сп — константы, всегда дает решение уравнения (10)
и что каждое решение уравнения (10) описывается формулой (12).
Доказательство. Так как функции Xi, ... , Хп являются
решениями уравнения (10) (см. В)), то в силу предложения А) § 6‘
формула (12) всегда дает решение уравнения (10). Покажем, что вся-
кое решение уравнения (10) при надлежащем подборе констант
с1, ... , сп записывается в виде (12). Пусть <р(£) — произвольное ре-
шение уравнения (10). В силу теоремы 3 решение (р(0 можно счи-
тать заданным на всей прямой —оо<^£<^со, и потому вектор
ф(0) = х0 определен. Разложим этот вектор по базису Лр ... ,
х0 = е1 hi 4~ ... -\~cnhn.
Если теперь подставить найденные константы с1, ... , сп в соот-
ношение (12), то мы получим решение х(0, удовлетворяющее на-
чальным условиям
х(0) = ? х1(0)+ ... 4-спХп(0) = с|/114* ... —
(см- (9)). Таким образом, решения ср(£) и х(0 имеют общие началь-
ные значения и потому совпадают.
Итак, теорема И доказана. Щ
Теперь нам осталось выделить из решений, заданных формулой
(12), действительные решения в случае, когда матрица (aj) действи-
4 Понтрягин Л. С.
98
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
тельна. Делается это совершенно так же, как и в случае простых
корней характеристического уравнения.
Г) Предположим, что матрица (а*), определяклцяя уравнение (10),
действительна Выберем в этом случае базис hn по способу,
предусмотренному в теореме 30 (см. § 36) для/случая, когда матрица
(а*) действительная При таком выборе бааИса среди решений (И),
построенных в теореме 11, будут, с одной стороны, действительные,
с другой же стороньк— попарно комплексно сопряженные. Оказы-
вается, что решение (124 тогда и только тогда действительно, когда
константы, стоящие при действительных решениях, действительны, а
константы, стоящие при к'тшл^гксно сопряженных решениях, ком-
плексно сопряжены.
Предложение Г) непосредственно вытекает из предложения Г) § 7.
В заключение следует «П'метитК что изложенные выше результаты
настоящего параграфа те/но связаньк с результатами § 7, 8. В па-
раграфах 7, 8 было рассмотрено одно однородное уравнение п-го
порядка с постоянными коэффициентами^По методу § 4 это урав-
нение может быть/записано в виде порма\ной системы из п уравне-
ний. Таким образом, результаты § 7, 8 можЬр было бы вывести из
результатов ^стоящего параграфа. При этом оказывается, что харак-
теристический многочлен полученной нормальной системы совпадает
с характеристическим многочленом исходного уравнения.
Преобразование переменных
Д) В системе уравнений (1), определяемой постоянной матрицей
Д=(а*.), вместо неизвестных функций
х1, ...,хя (13)
введем новые неизвестные функции
yi,...,yn, (14)
положив
п
У^^з’Л, (15)
/=1
где —постоянные коэффициенты, образующие невырожденную мат-
рицу 5 = (£). В новых неизвестных наша система запишется в виде:
п
? = (16)
§14] НОРМАЛЬНАЯ ЛИНЕЙНАЯ ОДНОРОДНАЯ СИСТЕМА ' 99
где матрица B = (bj) получается из матрицы А по формуле
5 = (17)
Докажем это. Дифференцируя соотношение^^) по t, получаем
У == J — «« (18)
i==T\ yr
Таким образом, компоненты вектора = (х1,... ,_£п) преобразуются
так же, как компоненты векто^а/х = (х1,..Xя). Из этого уже
следует формула (17) (см. § 34, А^Проведем, однако, доказательство,
данное там, заново. В матричной форме соотношения (15) и (18)
переписываются в виде: / \
v^Sx, jfAsx;
и мы имеем таким образом \
A— Sx—SAx — SA-
Этим формула ДЛ^) доказана.
Подбирая должным образом матрицу 5, мы можем добиться того,
чтобы матрица В получила наиболее простой вид. Так как преобра-
зование (17) матрицы А в матрицу В есть трансформация матрицей 5,
то мы можем достичь того, чтобы матрица В имела жорданову форму
(см. § 36, Б)).
Е) Если собственные значения
, Хл
матрицы А системы (1) все различны между собой, то линейное
преобразование (15) можно выбрать так, что система (16) полу-
чает вид:
У = Х*у*, я. (19)
Если, сверх того, матрица А действительна, так что в последо-
вательности ХЬ...,ХЯ, наряду с каждым комплексным собствен-
ным значением ХА, имеется комплексно сопряженное ему значение
= а переменные (13) действительны, то преобразование (15)
можно выбрать так, чтобы каждому действительному собственному
значению Ху, соответствовало действительное переменное У, а паре
комплексно сопряженных собственных значений Xft и X, — ком-
плексно сопряженные переменные yk и Таким образом,
сопряженным собственным значениям соответствуют сопряжен-
ные уравнения
/ = 7 = (20)
4*
100 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ (Гл. 2
Пусть
4 = ^ + ^. у*=В‘ + й)* (21)
где р^, £*, т)А — действительные величины. Тогда пару сопряжен-
ных между собой уравнений (20) можно заменить парой действитель-
ных уравнений
7)fc = 4- (22)
Производя такую замену для каждой пары комплексно-сопряженных
собственных значений, мы сможем заменить систему действительных
переменных (13) новой системой действительных переменных, причем
уравнения для них частично имеют вид (19) (для действительных
значений Ху), а частично — вид (22) (для пар комплексно-сопряженных
собственных значений).
Для доказательства предложения Е) в пространстве 7? векторов
Х = (№, х") поставим матрице А в соответствие линейное пре-
образование А (см. § 34) и обозначим через hk собственный вектор
преобразования А с собственным значением Xft. Примем теперь за ба-
зис в R векторы
/11, hn, (23)
и соответствующие этому базису координаты вектора х обозначим
через у1, уп. Мы получим таким образом линейное преобразова-
ние (15). В новой системе координат преобразованию А соответствует
матрица В, имеющая, как легко видеть, диагональный вид, причем
на диагонали стоят числа Xv ..., Хл. Таким образом, система (16) по-
лучает вид (19).
Если теперь матрица А действительна, то каждому действитель-
ному собственному значению Ху поставим в соответствие действитель-
ный вектор fty, а паре комплексно сопряженных собственных значе-
ний Xft и XZ = XA— пару комплексно сопряженных собственных век-
торов hk и = Произвольный вектор х в новых координатах
записывается в виде:
п
(24)
/=1
и если он действителен, то коэффициенты при действительных век-
торах должны быть действительны, а коэффициенты при комплексно
сопряженных векторах должны быть комплексно сопряжены (см. § 7, Г)).
Таким образом, каждому действительному собственному значению Ху
соответствует действительное переменное у7, а паре комплексно со-
пряженных собственных значений ХА и Xz = Xft соответствуют комп-
k 1 ~k
лексно сопряженные величины у и у =у .
§ 14] НОРМАЛЬНАЯ ЛИНЕЙНАЯ ОДНОРОДНАЯ СИСТЕМА 101
Для перехода от пары комплексно-сопряженных уравнений (20)
к паре действительных уравнений (22) запишем уравнение (20), под-
ставив в пего значения ХА и yk из (21); мы получим тогда
+цk=+hk)=иг? - v?+1 +tW)-
Приравнивая отдельно действительные и мнимые части этого соотно-
шения, получаем систему уравнений (22).
Итак, предложение Е) доказано.
Система уравнений (19) имеет очевидное решение
yk = ckeKkti k—\t , п,
но для того, чтобы получить решение исходной системы (3), нужно
произвести переход от неизвестных (14) к неизвестным (13), а для
этого нужно знать собственные векторы (23) матрицы А (см. (24)).
Таким образом, пд^ложеше, Е1_р„а^нрсильно.х€Ор£мв-Д0«. - ----- -
71ля ^ре ш ен и я системы (1) в общем случае можно использовать
приведение матрицы А к жордановой форме; получаемое здесь пред-
ложение Ж) равносильно теореме 11.
Ж) Пусть матрЬча А системы (1) произвол1д«гя. Выберем преоб-
разование (15) таким"бЦразом> чтобы мау-рйца В имела жордапову
форму (см. § 36). Пусть X-Xq/iho из собственных значений матрицы А
и k — размер одной нз жордайодых/йлеток матрицы В с собствен-
ным значением X. Будем считат^/^чГто эта клетка занимает первые k
строк. Соответствующая это>''клетке система уравнений имеет вид:
у1 = Ху1 у^~ Ху2 -I- у\ ,yk~l =_yA = Xyft.
Каждой другой жордановой клетке матрицы В соответствует ана-
логичная система уравнений, которую легко решить.
X
Примеры
1, Применение метода, изложенного в этом параграфе, к реше-
нию системы (1) требует отыскания базиса
hi, . . . , hn
векторного пространству составленного из серий (см. теорему 11).
Это отыскание само по cfeQe представляет некоторую алгебраическую
задачу. Покажем, как, пользуясь результатами этого параграфа, мож-
но решить систему (1) м е т о д о'о еопреде ленных коэффици-
ентов, не отыскивая базиса, состаКдюнного из серий. Пусть X — неко-
торое собственное значение матрицы (а^Этому собственному значению
вообще говоря, соответствует песколькбХсерий, входящих в базис
ftp • • • > пусть k будет наибольшая из длин серий, соответ-
102 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
ствующих собственному значению к. В силу теоремы 11 каждое из
решений, соответствующих собственному значению к, может быть за-
писано в виде:
х'=/'(0еи, Z=l, л, (25)
где /r(f) есть многочлен степени —1. Таким образом, подстав-
ляя в систему (1) решение в виде (25) и считая, что коэффициенты
многочленов /=1, п, суть неизвестные константы, мы,
пользуясь методом неопределенных коэффициентов, найдем все реше-
ния системы (1), соответствующие собственному значению к. При
таком способе решения системы (1) не нужно знать серий, соответ-
ствующих собственному значению к, а нужно знать лишь длины
этих серий. Отыскание длин представляет собой более простую алгеб-
раическую задачу, чем приведение к жордановой форме; задача эта
решается теорией элементарных делителей матриц, относящейся
к линейной алгебре. Теория элементарных делителей нигде в этой
книге не используется.
2. Покажем теперь, как решить систему (1) методом исключения,
изложенным в § 11. Для применения метода исключения запишем
систему (I) в виде:
л
/«1
где
Детерминант D (р) матрицы (Llj(p)) в данном случае представляет со-
бой характеристический многочлен матрицы (а*). Пусть к — некото-
рый корень многочлена D(p)t или, что то же, собственное значение
матрицы (а.). Кратность корня к обозначим здесь через I. В силу
предложения В) § 11 всякое решение системы (1), соответствующее
корню к, следует искать в виде:
xi — gt(t)eu, i=\, nt
где степень многочлена g* (t) не превосходит числа I— 1. Если срав-
нить метод, излагаемый в этом примере, с методом, данным в при-
мере 1, то мы видим, что вся разница заключается в определении
максимальной степени многочленов. Метод примера 1 дает более
точное определение степени многочленов, так как число Л, вообще
говоря, меньше числа I. В самом деле, сумма всех длин серий,
соответствующих собственному значению к, равна Z. Таким образом,
равенство k — l может иметь место лишь в случае, когда есть
только одна серия, соответствующая собственному значению к.
§ 15 1
АВТОНОМНЫЕ СИСТЕМЫ
ЮЗ
§ 15. Автономные системы дифференциальных уравнений
и их фазовые пространства
Здесь будет дана геометрическая интерпретация автономной
системы уравнений в виде фазового пространства этой системы.
Эта интерпретация существенно отличается от геометрической интер-
претации системы уравнений, указанной в §§ 1, 3 и правильнее дол-
жна называться не геометрической, а кинематической, так как в этой
гнгерпретации каждому решению системы уравнений ставится в соот-
ветствие не кривая в пространстве, а движение точки по кривой.
Кинематическая интерпретация (фазовое пространство) в некоторых
отношениях более выразительна, чем геометрическая (система интег-
ральных кривых).
Автономные системы
Система обыкновенных дифференциальных уравнений называется
автономной, если в нее явно не входит независимое переменное
(или, как мы будем говорить, время) t. Это значит, что закон из-
менения неизвестных функций, описываемый системой уравнений
не меняется с течением времени, как это обычно и бывает с физи-*
ческими законами. Очень легко доказывается, что если
х1 = ср((£), 1 =
есть решение некоторой автономной системы уравнений, то
Xs = <?* (О = <?' G + с)>
где с — константа, также есть решение той же автономной системы
уравнений. Проведем доказательство этого факта на примере нор-
мальной автономной системы уравнений.
А) Пусть
j£i=fl(xl,...,xn), 1=1, (1)
— автономная нормальная система уравнений порядка п и
х=/(х)
— векторная ее запись. Автономность системы (1) заключается в том,
что функции Г (х1,...,хл), 2=1,. ..,и, являются функциями пере-
менных х1,,..,хп и не зависят от времени t. Относительно функ-
ций f (х1,.хл) мы будем предполагать, что они определены на
некотором открытом множестве А пространства размерности п, где
координатами точки являются переменные х1, ...,хя. Мы будем пред-
полагать, что функции fl (х1,..., хя) и их частные производные пер-
вого порядка непрерывны на множестве А. Оказывается, что если
х' = </(0, (2)
104 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
— решение уравнения (1), то
(0=?' С + 4 /=1, (3)
также есть решение системы (1).
Из правила дифференцирования сложной функции вытекает соот-
ношение
4(0—(г + 4 1=1.....« (4)
Действительно,
Н (') = 4 ?(0=i т1V+о = ?'« + о • -
— Ф’ <? + О • (* + 4
Докажем теперь, что (3) есть решение системы (1). Так как (2)
есть решение, то мы имеем тождества
?'(0=/‘(?1(0 ?"(0)> /=1......п.
Заменяя в этих тождествах t через мы получаем:
$Ч' + О=7/(?Ч* + <), ...» ?"(* + ')), z=L л.
Из этого в силу (4) и (3) вытекает
4 (0 ==?'(' +О =/! (?*(* +4 <р"+ 4=fl(4(0> 4(0)-
Перейдем теперь к кинематической интерпретации решений системы
(1). Формально речь будет идти об интерпретации в л-мерно-м про-
странстве, но для наглядности разумно представлять себе случай
плоскости (п = 2).
Б) Каждому решению
х1 (f), 1= 1, .п (5)
автономной системы (1) поставим в соответствие движение точки в
л-мерном пространстве, задаваемое уравнениями (5), где х1, хп —
координаты точки в пространстве, a t — время. В процессе своего
движения точка описывает некоторую кривую — траекторию дви-
жения. Если сопоставить решению (5) не процесс движения, а траек-
торию движения точки, то мы получим менее полное представление
о решении, поэтому желательно на траектории указать хотя бы на-
правление движения. Оказывается, что если наряду с решением (5)
имеется другое решение
X1 = (/), 1=1, ...» л, (6)
то траектории, соответствующие этим решениям, либо не пересека-
ются в пространстве, либо совпадают. Именно, если траектории име-
ют хотя бы одну общую точку, т. е. >
Я, (7)
§ 151
АВТОНОМНЫЕ СИСТЕМЫ
105
то
Ф1' (0 = (* + 4 где с = t, — t* (8)
Последние равенства показывают, что траектории, описываемые пер-
вым и вторым решениями, совпадают между собой, но первое ре-
шение описывает ту же самую траекторию, что и второе, с «запоз-
данием» на время с. Если точка, соответствующая первому решению,
достигла некоторого положения на траектории в момент времени
то точка, соответствующая второму решению, уже побывала в
этом положении в момент времени t.
Для того чтобы вывести из равенства (7) тождество (8), рассмот-
рим наряду с решением (5) решение
<р£(о=/а+0 (9)
(см. А)). Из равенства (7) при с = Ц—t* следует равенство
?И^) = ?'(^ + С) = ?^1)==О«), /=1,п.
Таким образом, решения (6) и (9) системы (1) имеют общие началь-
ные условия (а именно, значения в момент времени f2) и потому в
силу теоремы единственности совпадают, так что мы имеем:
^40=<pU0==<p‘(z + c)> / = •••>«•
Положения равновесия и замкнутые траектории
Поставим вопрос о том, может ли траектория, изображающая
решение системы; пересекать себя.
В) Пусть
= (10)
— некоторое решение системы (1). Допустим, что имеет место ра-
венство
№=<рШ ^/2, (п)
где числа и /2, конечно, принадлежат интервалу П<^<>2 опре-
деления решения (10). Оказывается, что при этом условии решение
(10) может быть продолжено на весь бесконечный интервал —оо<^
<^<^-|-оо. Поэтому мы сразу будем считать, что само решение (10)
определено на этом интервале —оо t -|- оо. Оказывается далее,
что возможны два следующих взаимно исключающих случая.
1) Для всех значений t имеет место равенство
у1 (t) — а\ I — 1,..., п,
где (а1,...,#*) есть точка множества Д, не зависящая от t Таким
образом, в этом случае точка (ср1 (f),tp"(O) в действительности
не движется при изменении /, а стоит на месте... Само решение (10)
106 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
и точка (а1,..., а") в этом случае называются положением равнове-
сия системы (1).
2) Существует такое положительное число Т, что при произвольном
t имеют место равенства
но при |Х| — хотя бы для одного 1=1, п имеет место
неравенство
'р'Сч)?* т'Сч)-
В этом случае решение (10) называется периодическим с перио-
дом Г, а траектория, описываемая решением (10), называется замкну-
той траекторией, или циклом.
Докажем предложение В). Как было отмечено в предложении Б),
из равенства (11) следуют тождества
?г(^ + с) = ?'(0, п, с = ^-^. (12)
При этом функции tp1 (t -j- с), .tpn (t с) также представляют реше-
ние системы (1) (см. А)). Это решение и первоначальное решение (10)
совпадают там, где они оба определены (теорема 2). Если объеди-
нить эти два решения, мы получим новое решение с ббльшим интер-
валом существования, чем исходное, а именно, с интервалом т\— с
при с^>0 и ri<O<Va — с при с<^0. Так как и
равноправны, то знак величины с можно изменить, так что решение
можно продолжить на интервал !\—| с | t <^г3 +1 с |. Так как,
кроме того, для продолженного решения равенство (11) по-прежнему
выполнено, то к нему опять можно применить указанный способ
расширения интервала существования, и потому мы можем продол-
жить решение (10) на всю бесконечную прямую с сохранением для
него тождества (12).
Каждое число с, для которого выполнено тождество (12), будем
называть периодом решения (10); множество всех периодов реше-
ния (10) обозначим через F. Множество F есть некоторое множество
чисел. Установим некоторые его свойства. Заменяя в соотношении (12)
t через t — с, получаем <?* (/) = <?* (t — с). Таким образом, если с
есть период, то —с также есть период. Допустим, что и — пе-
риоды, т. е.
(t + сд = (0> (* + (0>
1 = 1, п.
Тогда
?1'((^ + ^) + О = ?'Д + ^) = '?'(0> * = 1. .... «•
Таким образом, если сх и с2 суть периоды, то ct-|-ca также есть
период. Допустим, что съ ..., ст, ... есть последовательность
§ 15 1
АВТОНОМНЫЕ СИСТЕМЫ
107
периодов, сходящаяся к некоторому числу с0; тогда мы имеем
+ Z=l, tn — 1, 2, ..,
Так как функции <р* (/) непрерывны, то при <p;C + co) = ?i(O> m оо мы получаем:
т. е. мы видим, что с0 также есть период, так что множество F
вамкнуто.
Так как число с в равенстве (12) отлично от нуля (^ ^ то
множество F содержит числа, отличные от нуля. Из установленных
свойств множества F легко выводится, что для него есть только
две возможности; 1) множество F совпадает с множеством всех дей-
ствительных чисел; 2) в множестве F имеется минимальное положи-
тельное число 7} и тогда F состоит из всех целочисленных кратных
числа Т. Докажем, что действительно имеются только эти две возмож-
ности. Так как множество F вместе с каждым числом с содержит
число — си так как в F имеются числа, отличные от нуля, то в F
имеются положительные числа.
Допустим, что в множестве F нет наименьшего положительного
числа, т. е. что для произвольного положительного числа г имеется
положительный период с<^е. Из доказанных свойств множества F
следует (так как с есть период), что все числа гпс, где гп — целое,
также являются периодами. Так как с<^е, то для произвольного
действительного числа се можно подобрать такое целое /?г, что
|с0 — /пс|<^е. Таким образом, произвольное число является пре-
дельным для множества F, и потому, ввиду замкнутости множества F,
это множество совпадает с множеством всех действительных чисел.
Допустим теперь, что F не есть множество всех действительных
чисел. В силу доказанного, в F имеется тогда наименьшее положи-
тельное число Т. Пусть с — произвольный период. Можно тогда выб-
рать такое целое число ni, что | с — гп7'\<^Т. Допустим, что
тогда | с— шТ\ есть отличный от нуля период, а это невозможно,
так как |с — шТ\<^Т, что противоречит минимальности числа 7'.
Итак, доказано, что каждое число с из F может быть записано в виде
с = тТ\ где пг— целое число.
Теперь уже легко проверить, что если F есть множество всех
действительных чисел, то имеет место случай 1), а если F не есть
множество действительных чисел, то имеет место случай 2). Таким
образом, предложение В) доказано.
Кратко предложение В) можно сформулировать, сказав, что име-
ется три сорта траекторий: 1) положение равновесия; 2) периодичес-
кие траектории (циклы); 3) траектории без самопересечений. Естест-
венно считать, что последний случай является «наиболее общим».
Из теоремы 2 следует, что через каждую точку области Д зада-
ния системы (1) проходит траектория, изображающая решение системы.
108 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ (Гл. 2
Таким образом, вся область Д заполнена траекториями, причем, сог-
ласно Б), траектории эти попарно не пересекаются. Среди всех траек-
торий особо выделяются самопересекающиеся, которые являются
либо положениями равновесия, либо циклами. Эти два сорта траекто-
рий имеют весьма важное значение.
Такова кинематическая интерпретация решений автономной си-
стемы уравнений. Сама система уравнений также допускает геомет-
рическую интерпретацию.
Фазовые пространства
Г) Поскольку автономная система уравнений (1) определена на
открытом множестве Д, каждой точке (xj, х*) множества Д по-
ставлена в соответствие последовательность из п чисел, именно по-
следовательность:
с(*:.....х").....fn(xj,х").
Эти числа можно рассматривать как компоненты вектора/(xj, х"),
проведенного в «-мерном пространстве и выходящего из точки
(xj, х"). Таким образом, автономной системе ставится в соот-
ветствие геометрический образ — векторное поле, заданное на
открытом множестве Д. В каждой точке (xj, х") множества Д'
определен вектор /(xt*, xj), выходящий из этой точки. Связь
между геометрической интерпретацией решений и геометрической
интерпретацией самой системы уравнений заключается в следующем?
Пусть (х*, х")—произвольная точка множества Д. В силу гео-
метрической интерпретации системы уравнений этой точке поставлен
в соответствие выходящий из нее вектор/(xj, xj). Далее, в
силу теоремы 2 существует решение х* = <?*(£) системы (1), удов-
летворяющее начальным условиям
В силу кинематической интерпретации решению х* = tp1 (f) соответст-
вует в пространстве движение точки, описывающее траекторию,
причем в момент времени t = t$ движущаяся точка проходит через
положение (xj, xj) в пространстве. Оказывается, что вектор-
ная скорость точки, описывающей решение х1 — ^1^), в момент ее
прохождения через положение (xj, xj) совпадает с вектором
/(xj, ..xj). Именно это совпадение и выражается системой уравне-
ний (1) при
xz = x*, Z=h «; / = /0.
Пространство размерности п, в котором интерпретируются реше-
ния автономной системы (1) в виде траекторий и сама автономная
система (1) в виде векторного поля, называется фазовым прост-
§ 15]
АВТОНОМНЫЕ СИСТЕМЫ
109
ранством системы (1). Траектории называются фазовыми траек-
ториями, векторы /(xj, ...» xj) называются фазовыми скоростями.
Связь между обеими интерпретациями заключается в том, что ско-
рость движения точки по траектории в каждый момент времени со-
впадает с фазовой скоростью, заданной в том месте пространства,
где в этот момент находится движущаяся точка.
Рассмотрим теперь положения равновесия с точки зрения фазовых
скоростей.
Д) Для того чтобы точка (а1, ..., ап) множества А была положе-
нием равновесия системы (1), т. е. чтобы имелось решение xr = tp' (/)
системы, для которого
/ = 1, п, (13)
необходимо и достаточно, чтобы фазовая скорость /(а1, ..., а”) в
точке (а1, ...» а”) была равна нулю. Таким образом, для отыскания
всех положений равновесия системы (1) нужно решить систему урав-
нений
ап)=0, 1=1, п.
Эта система представляет собой не систему дифференциальных урав-
нений, а, как говорят, систему конечных уравнений (производные
в нее не входят).
Для доказательства утверждения Д) допустим, что (а1, .а”)
есть положение равновесия, т. е. что имеется решение xl = <pr (X),
для которого выполнены соотношения (13), и подставим в систему (1)
это решение. Так как производная постоянной равна нулю, то под-
становка дает
.... ?'(() = 4а' = 0-
Таким образом, вектор/(а1, .ап) фазовой скорости действительно
обращается в пуль в точке а1, ...» ап. Допустим, что, обратно, век-
тор/(а1, ...» ал) фазовой скорости обращается в нуль в точке
(а1, а71), т. е. что /'(а1, .ал) = 0, / = 1, .п, и покажем,
что в этом случае равенства (13) определяют решение системы (1).
Подстановка дает
ф* (t)=fl (а1, а71), /=1, ..., п\
равенства эти выполнены, так как слева стоит производная константы,
а справа — нуль.
Е) Геометрическая интерпретация решения (2) системы уравнений
(1), указанная в § 3, ставит в соответствие этому решению кривую К
в (п + 1)-мерном пространстве переменных t, х1, ..., хп, определя-
емую системой уравнений (2). Здесь t является одной из координат
в пространстве Переход к интерпретации в n-мерном фазовом
НО ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ (Гл. 2
пространстве S переменных х1, хп заключается в том, что мы
перестаем считать величину i координатой точки, а считаем ее па-
раметром. Таким образом, фазовая траектория L получается из кри-
вой К в результате проектирования пространства 7? на про-
странство 5 в направлении оси £
Геометрическую наглядность это проектирование приобретает
при п = 2. В этом случае пространство 7? трехмерно, а простран-
ство 5 представляет собой плоскость (см. пример 4).
Примеры
1. Рассмотрим автономное дифференциальное уравнение
х=/(х) (14)
первого порядка, правая часть которого непрерывна и имеет непре-
рывную производную на всей прямой Р изменения переменного х.
Предположим дополнительно, что нули функции f(x) или, что то
же самое, положения равновесия уравнения (14), не имеют предель-
ных точек. В этом предположении положения равновесия разбивают
прямую Р на систему Е интервалов. Каждый интервал (а, Ь) системы
Е обладает тем свойством, что на нем функция f (x) не обращается
в нуль, а каждый конец а или b его является либо нулем функции
/(х), либо равен ±оо. Таким образом, система Е состоит из конеч-
ного или счетного числа конечных интервалов и не более чем двух
d
е
Рис. 17.
полубесконечных интервалов или же содержит только один беско-
нечный в обе стороны интервал (—оо, -|-оо). Пусть (а, Ь)—неко-
торый интервал системы Е, х0— точка этого интервала и x = tp(£),
— непродолжаемое решение уравнения (14) с начальными
значениями 0, х0. Допустим для определенности, что тог-
да оказывается, что
при Г1<^<СГ«’
(15)
lim tp(0 = a, lim <р (t) = b,
* — г 1 t —
(16)
Далее, если число а, или соответственно Ь, конечно, то число гх
или соответственно г2, бесконечно. Таким образом (рис. 17), каждый
интервал (а, Ь) представляет собой одну-единственную фазовую тра-
екторию уравнения (14).
§ 15] АВТОНОМНЫЕ СИСТЕМЫ 111
Докажем соотношения (15), (16). Из предположения /*(х0)^>0 сле-
дует, что на интервале (а, Ь) функция /(х) положительна и потому
каждая точка этого интервала, описывая фазовую траекторию, дви-
жется слева направо. Таким образом, при возрастающем t точка ср (/)
может покинуть интервал (а, 6), лишь перейдя его правый конец Ь.
Допустим, что это происходит при некотором = тогда при t — tt
имеем ср(^) = 5, а это значит, что две различные траектории x=y(t)
и х—Ь пересекаются, что невозможно. Точно так же доказывается,
что точка ср(/) не может покинуть интервал (а, Ь) при убывающем £
Таким образом, соотношение (15) доказано.
Допустим теперь, что Нт ср(/) = < и пусть <p(f) —решение
t -» Го
уравнения (14) с начальными значениями 0, с. Так как /(с)^>0, то
при некотором отрицательном значении имеем а это зна-
чит, что две различные траектории ср (0 и ty(t) пересекаются, что не-
возможно. Таким образом, доказано, что lim <р(/)= 6. Точно так же
t — rs
доказывается и соотношение
lim <р (0 = а. "—2---------°>
„ . ___о_______Ъ______ с Л>
Допустим, наконец, что о<^оо, и щ
покажем, что тогда гв = 4-с<^ Допустим
противоположное, именно, чго г.2<^оо. ___о_______ ь____ с
Определим тогда функцию ^(/), положив '
2(Z) = cp(0 при Г[ t г8 и x(t) = b при Рис. 18.
Очевидно, что функция х(0 не"
прерывна и удовлетворяет уравнению (14), а это невозможно, так
как тогда пересекаются две различные траектории х — */(/) и х — Ь.
Полученное противоречие показываем что r^— -j-оо. Точно так же
доказывается, что при а — со имеем гх — — со.
Пусть Ь — произвольное положение равновесия уравнения (14),
а (а, Ь) и (Ь, с) — два интервала системы £, примыкающие к нему
(соответственно слева и справа). Каждый из интервалов (а, 5), (&, с)
представляет собой одну траекторию. Если обе точки, описывающие
траектории (с, Ь) и (/>, с), приближаются (при возрастании О
к положению равновесия Ь, то положение равновесия b называется
устойчивым (рис. 18, а). Если обе точки, описывающие траектории
(а, Ь) и (/>, с), удаляются от точки Ь, то положение равновесия
b называется неустойчивым (рис 18, б). Если по одной из траекторий
точка приближается, а по другой удаляется, то положение равнове-
сия Ь называется полуустойчивым (рис. 18, в). Для того чтобы
положение равновесия b было устойчивым, необходимо и достаточно,
чтобы функция f(x) была положительна на интервале (а, Ь) и отри-
цательна на интервале (Ь, с). Для того чтобы положение равновесия
Ь было неустойчивым, необходимо и достаточно, чтобы функция
112 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл 2
/(х) была отрицательна на интервале (а, Ь) и положительна на ип-
тервале (Ь, с). Для того чтобы положение равновесия b было полу-
устойчиво, необходимо и достаточно, чтобы функция /(х) имела
один и тот же знак в на обоих интервалах (а, Ь) и (bt с).
Допустим, что /(£)^0; тогда знак функции /(х) вблизи точ-
ки b совпадает со знаком величины Отсюда следует,
что при /(£)<^0 положение равновесия b уравнения (14) устойчиво,
а при /(А)^>0 оно неустойчиво.
2. Рассмотрим уравнение
•*=/(*), (17)
где /(х) есть периодическая функция с непрерывной первой про-
изводной. Для определенности будем считать, что период ее
равен 2к. Все сказанное в примере 1 относительно уравнения (14)
остается правильным и для уравнения (17), так как уравнение
(17) является частным случаем уравнения (14). Однако, для того
чтобы учесть специфику уравнения (17) (периодичность функции
/(х)) разумно считать, что фазовым пространством уравнения (17)
является не прямая, а окружность К радиуса единица, на
которой выбрано некоторое начало отсчета 0 и направление обхода
(например, против часовой стрелки). Каждому числу х поставим
в соответствие точку $ окружности К, отложив от начала отсчета
против часовой стрелки дугу длины х (рис. 19). При этом всем
числам x-|~2£z (k — целое число) будет соответствовать на окруж-
ности одна и та же точка 5. Так как /(х -|- 2Атс)=/(х), то можно
положить /($)=/(х), и функция f оказывается заданной на
окружности Д'. Уравнение (17) задает теперь движение точки ;
по окружности К- Если х(0 есть некоторое решение уравнения (17),
то соответствующая числу x(t) точка ?(£) движется по окружно-
сти /С Если а — такая точка на окружности К, что /(а) = 0, то
существует такое решение х(0 уравнения (17), что $(f) = a, и х
АВТОНОМНЫЕ СИСТЕМЫ
НЗ
§ 151
есть положение равновесия уравнения (17). Допустим для просто-
ты, что положения равновесия уравнения (17) на окружности К
не имеют предельных точек; тогда их имеется лишь конечное
число или нет вовсе (рис. 20). Положения равновесия разбивают
окружность на конечную систему Е интервалов. Если положений
равновесия вовсе нет, то система Е содержит лишь один «интер-
вал» (окружность). Если имеется лишь одно положение равнове-
сия а, то система Е также содержит лишь один интервал,
состоящий из всех точек окружности К за исключением точки а.
В первом случае интервал вовсе не имеет концов, во втором оба
его конца совпадают. Пусть 1—некоторый интервал системы Е
, и x(t)— некоторое решение уравнения (17) с начальными значе-
ниями 0, х0, где % есть точка интервала /. Решение x(t) всегда
определено для всех значений t, и точка 5(f) принадлежит интер-
валу L Если интервал / имеет концы (один или два), то точка
пробегает интервал I в определенном направлении, причем каж-
дая точка интервала / проходится решением 5(f) один раз. Если
интервал / совпадает со всей окружностью, то, отправившись из
положения 50, точка через некоторое время Т вернется в нее, так
что'5(О) = 5(Г). В этом случае 1(f) периодически зависит от числа
t с периодом Т. Соответствующее движению 5(f) числовое решение
x(f) уравнения (17) удовлетворяет условию
х (t -f- Т) = х (f) к 2тс.
Из этого примера видно, что фазовым пространством системы
уравнений не всегда целесообразно считать эвклидово координат-
ное пространство, а иногда приходится считать более сложное гео-
метрическое образование. Ниже, в примере 3, мы столкнемся с этим
обстоятельством в более сложной обстановке, чем в этом примере.
3. Рассмотрим систему уравнений
х1=/*(х\ х2), f=l, 2, (18)
где функции /'(х1, х2) являются периодическими относительно обоих
аргументов с периодами 2тс:
//(х14-2^тс, х24-2/т:)=/|‘(х,,х2), /=1, 2.
Как всегда, будем предполагать, что функции /f(x!, х2) непрерывны
и имеют непрерывные частные производные первого порядка. Ввиду
периодичности функций fl(x\ х2) разумно считать, что фазовым
пространством системы (18) является не плоскость, а более сложное
геометрическое образование, именно, поверхность тора или, как го-
ворят, тор (рис. 21). Опишем эту поверхность.
В трехмерном эвклидовом пространстве с декартовыми координа-
тами х, у, z выберем в плоскости х, z окружность К радиуса еди-
ница с центром в точке (2, 0, 0). Примем на этой окружности зз
114 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
начало отсчета точку с координатами (3, 0, 0). Тогда каждому числу
х1 будет поставлена в соответствие точка окружности К (см. при-
мер 2). Будем теперь вращать плоскость (х, z) в пространстве (х,д/, z)
вокруг оси z. Описываемая при этом вращении окружностью К по-
верхность Р представляет собой тор. Пусть V — некоторая точка
Рис. 21.
окружности /С. В результате поворота плоскости (х, z) на угол х2,
исчисляемый в радианах, точка перейдет в некоторую точку р тора
Р (рис. 21). Если сделать поворот не на угол х2, а на угол х2-|-2Атс,
то мы придем к той же точке р тора Р. Таким образом, точка р
тора Р однозначно определяется двумя циклическими координатами
Е1, Е2, и каждой паре циклических координат I1, £2 соответствует на
торе одна вполне определенная точка. Мы видим, таким образом, что
функции /^(х1, х2) можно считать заданными не на плоскости, а на
поверхности тора Р:
/(V, Е2)=/(х\ х2).
Пусть теперь х1 (0, х2(£)—некоторое решение системы (18). Ставя
в соответствие каждому из чисел х1 (t) и х2(0 циклические координаты
E*(f) и $2(0* мы получаем точку Е1 (/), Е2(0 тора Р. Таким образом,
каждое решение х’(/), х2(0 системы (18) может быть изображено
движением точки по тору, причем закон движения в каждый момент
времени определяется той точкой V(t), ^(t) тора, через которую
траектория в этот момент проходит. Это объясняется тем, что функ-
ции (5\ Е2) заданы на торе. Таким образом, весь тор Р оказывается
покрытым траекториями, каждые две из которых либо не пересекаются,
либо совпадают. В частности, если траектория пересекает самое себя,
то она либо замкнута, либо является положением равновесия.
Изображение 'фазовых траекторий системы (18) не на плоскости,
а на поверхности тора отражает специфическое свойство системы
(18) (периодичность функций /') и удобно при ее изучении.
§ 161
ФАЗОВАЯ ПЛОСКОСТЬ ЛИНЕЙНОЙ СИСТЕМЫ
115
4. Каждое решение автономной системы уравнений
х = — toy, j? = ых
записывается в виде:
x = r cos(W-}~a)> >' = г sin а), (19)
где г и а — константы. Система уравнений (19) определяет в трех-
мерном пространстве /? переменных х, у винтовую спираль при
г Ф 0 и прямую линию (именно, ось t) при г = 0.
В фазовой плоскости 5 переменных х и у та же система уравне-
ний (19) определяет окружность при г# 0 и точку (положение равно-
весия) при гх=О. Переход от кривых в пространстве /? к кривым
на плоскости 5 осуществляется проектированием в направлении оси
t на координатную плоскость ху.
5. Каждое решение неавтономной системы уравнений
х = 1, $ = t
записывается в виде:
х = t а, у — -j- Ь, (20)
где а и b — константы. Из общей теории известно (единственность
решения), что в трехмерном пространстве /? переменных t, xt у две
кривые, определяемые системой уравнений (20), либо не пересекаются,
либо совпадают. Для того, чтобы получить проекцию кривой, опреде-
ляемой системой (20), на плоскость 5 переменных х, у, следует из
системы (20) исключить t Производя это исключение, получаем:
y.= l(x —
Это уравнение определяет на плоскости ху параболу с осью, напра-
вленной вдоль положительной полуоси х и вершиной в точке (а, Ь).
Две такие параболы: одна с вершиной в точке (alf bi), а другая
с вершиной в точке (о^, Ь%)—не пересекаются лишь в случае, если
ах — аъ bt # Ь2. Если же # о* то соответствующие параболы пе-
ресекаются (в одной точке). Пересечение траекторий происходит по-
тому, что исходная система дифференциальных уравнений неавто-
номна. Поэтому изображение решений на плоскости ху в случае
неавтономной системы нецелесообразно.
§ 16. Фазовая плоскость линейной однородной системы
с постоянными коэффициентами
Здесь будут построены фазовые траектории на фазовой плоскости
системы
х1 =а\х1 )
• 2 112 2 1
X = а*Х 4” аах » )
116 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
или в векторной форме
Х=Ах (2)
с постоянными действительными коэффициентами а.. При этом нам
придется разобрать несколько различных случаев, так как фазовая
картина траекторий системы существенно зависит от значений коэф-
фициентов.
Следует заметить, что начало координат (точка (0, 0)) всегда
является положением равновесия системы (1). Это положение равно-
весия тогда и только тогда является единственным, когда детерми-
нант матрицы (а*) отличен от нуля, или, что то же, оба собственных
значения этой матрицы отличны от нуля.
Допустим, что собственные значения матрицы А действительны,
различны и отличны от нуля. Тогда, как это следует из результатов
§ 14 (теорема 10) произвольное действительное решение уравнения (2)
можно записать в виде:
x = c'hle1' (3)
Здесь ht и hi — действительные линейно независимые собственные
векторы матрицы Д; Xj и Х2 — его действительные собственные зна-
чения, а с1 и с2 — действительные константы. Решение (3) разложим
по базису (ftj, ftj, положив
л (4)
тогда мы будем иметь:
¥ = = (5)
Координаты V, 5® на фазовой плоскости Р системы (1), вообще говоря,
не являются прямоугольными, поэтому отобразим аффинно фазовую
плоскость Р на вспомогательную плоскость Р* таким образом, чтобы
при этом векторы перешли во взаимно ортогональные еди-
ничные векторы плоскости Р*, направленные соответственно по оси
абсцисс и оси ординат (рис. 22). Точка х=Е,Л1 + Е2Л2 плоскости Р
перейдет при этом отображении в точку с декартовыми прямоуголь-
ными координатами Е2 в плоскости Р*. Таким образом, траектория,
заданная параметрическими уравнениями (5) в плоскости Р перейдет
в траекторию (которую мы также назовем фазовой), заданную теми
же уравнениями в прямоугольных координатах плоскости Р*. Мы
начертим сперва траектории, заданные уравнениями (5) в плоскости Р*,
п затем отобразим их обратно в плоскость Р.
Наряду с фазовой траекторией (5) в плоскости Р* имеется траек-
тория, задаваемая уравнениями
V = (6)
§ 16 J
ФАЗОВАЯ ПЛОСКОСТЬ ЛИНЕЙНОЙ СИСТЕМЫ
117
а также траектория, задаваемая уравнениями
£* = — 5’2 = ЛХа/. (?)
Траектория (6) получается из траектории (5) зеркальным отражением
относительно оси абсцисс, а траектория (7) — относительно оси орди-
нат. Таким образохм, указанные два зеркальных отображения оставляют
картину траекторий на плоскости Р* инвариантной. Из этого видно,
что если вычертить траектории в первом квадранте, то уже легко
представить себе всю фазовую картину в плоскости Р*.
Заметим, что при с1 = с’2 = 0 мы получаем движение точки, опи-
сывающее положение равновесия (0, 0). При с2 — 0, е1 ^>0 получаем
движение, описывающее положительную полуось абсцисс, при Р = 0,
с2^>0 получаем движение, описывающее положительную полуось
ординат. Если Xj 0, то движение, описывающее положительную
полуось абсцисс, протекает в направлении к началу координат,
если же ^^>0, то движение это имеет противоположное направле-
ние— от начала координат. В первом случае точка движется,
неограниченно приближаясь к началу координат, во втором — неогра-
ниченно удаляясь в бесконечность. То же справедливо и относительно
движения, описывающего положительную полуось ординат. Если с1
и с2 положительны, то движение точки протекает в первой четверти,
не выходя на ее границу.
Дальнейшее, более детальное описание фазовой плоскости прове-
дем отдельно для нескольких случаев — в зависимости от знаков
чисел
А) Узел. Допустим, что оба числа Xj и отличны от нуля
и имеют один знак, причем
(8)
118 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
Разберем сперва случай, когда
*i<0,
<0.
При этих предположениях движение по положительной полуоси
абсцисс направлено к началу координат, точно так же, как движе-
ние по положительной полуоси ординат. Далее, движение по произ-
вольной траектории внутри первого квадранта состоит в асимптоти-
ческом приближении точки к началу координат, причем траекто-
рия при этом касается оси абсцисс в начале координат. При /, стре-
мящемся к —со, точка движется так, что абсцисса и ордината ее
бесконечно возрастают, но возрастание ординаты сильнее, чем воз-
растание абсциссы, т. е. движение идет в направлении оси ординат.
Эта фазовая картина называется устойчивым узлом (рис, 23, а).
Если наряду с неравенством (8) выполнены неравенства
Х>>0, Х2>0,
то траектории остаются прежними, но движение по ним направлено
в противоположном направлении. Мы имеем неустойчивый узел
(рис. 23, б).
Б) Седло. Допустим, что числа Хг и имеют противоположные
знаки. Для определенности предположим, что
*1<0<Х2.
В этом случае движение по положительной полуоси абсцисс идет к
началу координат, а движение по положительной полуоси ординат —
§ IS1
ФАЗОВАЯ ПЛОСКОСТЬ ЛИНЕЙНОЙ СИСТЕМЫ
~ П9
от начала координат. Траектории, лежащие внутри первого квадран-
та, напоминают по своему виду гиперболы, а движения по ним про-
исходят в направлении к началу вдоль оси абсцисс, и в направлении
от начала вдоль оси ординат. Эта
фазовая картина называется сед-
лом (рис. 24).
Рисунки 23, й, б и 24 дают
картину траекторий на вспомога-
тельной фазовой плоскости Р*.
Расположение траекторий на фа-
зовой плоскости Р получается из
этого с помощью аффинного пре-
образования и зависят от положе-
ния собственных векторов (см.,
например, рис. 25 и 26).
Рассмотрим теперь случай,
когда собственные значения мат-
рицы А комплексны. В этом слу-
чае они комплексно сопряжены и
могут быть обозначены через
X = (jl-[-Zv и k =[1 — /м, причем
м Ф 0. Собственные векторы матрицы
пряженными, так что их можно обо:
А могут быть выбраны со-
,ачить через h и h. Положим:
Л = (Й1 — Iht),
где h[ и — действительные векторы. Векторы ht и линейно
независимы, так как в случае линейной зависимости между ними мы
имели бы линейную зависимость между huh. Итак, векторы h\ и h*
можно принять за базис фазовой плоскости Р уравнения (2).
Произвольное действительное решение уравнения (2) можно запи-
сать в виде:
X — cheu che^t (9)
где с — комплексная константа. Пусть
С = $’-]-£» = Г?*;
тогда мы имеем:
x = Vhi +
Отобразим аффинно фазовую плоскость Р на вспомогательную
плоскость Р* комплексного переменного С так, чтобы вектор h\
120 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
перешел в единицу, а вектор й4—в /; тогда вектору +
будет соответствовать комплексное число С = 5’ 4~^3- В силу этого
отображения фазовая траектория (9) перейдет в фазовую траекто-
рию на плоскости Р*, описываемую уравнением
С = сеи, (10)
В) Фокус и центр. Перепишем уравнение (10) в полярных
координатах, положив
С = ре% c = №fa.
Таким образом получаем:
р = ф = у/ а;
это есть уравнение движения точки в плоскости Р*. При р- # 0
каждая траектория оказывается логарифмической спиралью.
Соответствующая картина на плоскости Р называется фокусом.
Если р,<^0, то точка при возрастании t асимптотически приближает-
ся к началу координат, описывая логарифмическую спираль. Это—ус-
тойчивый фокус (рис. 27, а). Если р. j>0, то точка уходит от на-
чала координат в бесконечность, и мы имеем неустойчивый фокус
(рис. 27, б). Если число р. равно нулю, то каждая фазовая траектория,
кроме положения равновесия (0, 0), замкнута, и мы имеем так назы-
ваемый центр (рис. 28).
§16] ФАЗбВАЯ ПЛОСКОСТЬ ЛИНЕЙНОЙ СИСТЕМЫ 121
Рисунки 27 и 28 дают картину во вспомогательной фазовой пло-
скости; в плоскости Р картина аффинно искажается (см., например,
рис. 29 и 30).
Рис. 27.
Выше мы рассматривали так называемые невырожденные
случаи: корни Xj и различны и отличны от нуля. Малое
изменение элементов матрицы (ар не меняет в этих предположениях
общего характера поведения фазовых траекторий. Исключение состав-
ляет случай центра: при малом изменении элементов матрицы (ар
122 ЛИНЕПНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ {Гл. 1
равенство р = 0 может нарушиться, и центр перейдет в устойчивый
или неустойчивый фокус. Включение этого вырожденного случая
(центра) в основной текст па-
/ раграфа объясняется его важ-
ностью. Остальные вырожден-
ные случаи будут рассмотрены
] в примерах 1 и 3.
//////у) / / / / / £' Примеры
/ / ( ( {Вырожденный узел).
1 I Если матрица А системы (1)
к имеет лишь одно собственное
значение X, то возможны два
существенно различных слу-
Рис. 30. чая, при описании которых
мы будем обозначать через А
преобразование, соответствующее матрице А.
Случай I. Существует в плоскости А базис состоящий
из двух собственных векторов преобразования А:
Ah{ = Ahi = Х^. (11)
Случай 11. Существует в плоскости Р такой базис hv hb что
Ahj= Хйь Ahi== ~Лр (1 ^)
Существование базиса одного из видов (11), (12) непосредственно
г.ытекает из теоремы 30, но здесь мы докажем этот факт непосред-
ственно. Пусть hi — собственный вектор преобразования А и h2 —
произвольный вектор, не коллинеарный вектору h^ Тогда мы имеем:
Ahj = Xftj, Ah$ —= aft[рЛ-з-
Из этого видно, что преобразование А имеет в базисе hb hi матрицу
/X оь\
1'0 р/
так что его собственными значениями являются X и р, и потому
Р = X. Если а = 0, то для базиса hb ft2 выполнены соотношения (11).
Если же а 0, то, заменив вектор hL коллинеарным ему вектором ahb
мы получим базис, удовлетворяющий условию (12).
Непосредственно проверяется, что в случае I общее решение
уравнения (2) записывается в виде:
X = cyhieu = Х$еи. (13)
§ 16]
ФАЗОВАЯ ПЛОСКОСТЬ ЛИНЕЙНОЙ СИСТЕМЫ
123.
Написанное решение имеет начальное значение (0, х0). При Х^О
каждое решение описывает полупрямую, выходящую из начала коор-
динат. При Х<^0 движение происходит в направлении к началу ко-
ординат (рис. 31, а), при Х^>0— от начала координат (рис. 31, б);
относительно случая Х = 0 см. пример 3.
Непосредственно проверяется также, что в случае 11 произвольное
решение уравнения (2) имеет вид:
х = c{hxeu 4" с2 {hxt fcj) еи.
Разлагая это решение по базису hy в виде х = 4~ по-
лучаем уравнение траекторий в плоскости Р относительно базиса /г1} /|4:
5* — (с1 -J- cH)eut = (14)
Аффинное отображение фазовой плоскости Р, переводящее векторы
hx и hi в единичные ортогональные векторы, направленные по осям
координат плоскости Р*, переводит траектории плоскости Р в траек-
тории плоскости Р*, в которой уравнения (14) дают траектории уже
в прямоугольных координатах.
Разберем случай X О (случай Х = 0 см. в примере 3). Пусть
сначала Х<^0. Рассмотрим траектории, заполняющие плоскость Р*,
в этом случае. Прежде всего из уравнений (14) видно, что, меняя
одновременно знаки у с1 и с2, мы получим симметрию плоскости Р*
относительно начала координат, при которой траектории переходят
в траектории. Таким образом, достаточно рассмотреть заполнение
траекториями верхней полуплоскости. При с2 = 0, с1 0 получаем
две траектории: одну при 0, другую—при < 0. Первая совпа-
дает с положительной полуосью абсцисс, вторая — с отрицательной
полуосью абсцисс; движение по обеим направлено к началу координат.
Рассмотрим, далее, траекторию с, = 0, с4^>0. Мы имеем:
= c*teu, = с2еи. (15)
124 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 2
При £ = 0 получаем точку (0, с*) на оси ординат. При t, возра-
стающем от нуля, точка сначала движется направо, затем налево,
все время опускаясь вниз к началу координат, к которому она под-
ходит по траектории, касающейся положительного направления оси
Рис. 32.
абсцисс. При t, убывающем от нуля до —оо, точка движется налево,
одновременно поднимаясь вверх, однако налево быстрее, чем вверх,
так что общая тенденция ее движения — в отрицательном направлении
вдоль оси абсцисс. Если в уравнениях (15) придавать константе
Рис. 33.
все положительные значения, то описанные таким образом траектории
заполняют всю верхнюю полуплоскость (рис. 32, а). Мы имеем здесь ус-
тойчивый вырожденный узел. Если X 0, то траектории полу-
чаются из описанных путем зеркального отражения плоскости относи-
тельно оси ординат (рис. 32, б), а движение по ним идет в противо-
положном направлении, т. е. от начала координат. Эго — неустойчивый
§ 16] ФАЗОВАЯ ПЛОСКОСТЬ ЛИНЕЙНОЙ СИСТЕМЫ - 125
вырожденный узел. На рис. 33, а, б показаны фазовые траектории
в плоскости Р.
2. Рассмотрим линейное однородное уравнение второго порядка
с постоянными коэффициентами
+ = (16)
Заменяя это уравнение нормальной системой по способу, изложенному
в § 4, получаем:
х — у,
• А I О7)
у = — Ьх — ау. }
Фазовую плоскость системы (17) считают фазовой плоскостью урав-
нения (16). Непосредственно проверяется, что характеристический
многочлен системы (17) совпадает с характеристическим многочленом
уравнения (16), т. е. равен
р^-\-ар-\-Ь. (18)
Таким образом, если корни многочлена (18) комплексны, то фазовая
плоскость уравнения (16) представляет собой фокус или центр. Рас-
смотрим фазовую плоскость в случае действительных различных и
отличных от нуля корней многочлена (18).
Пусть X — корень многочлена (18) и ft = (/i\ й3)— соответствую-
щий ему собственный вектор. Мы имеем тогда (учитывая вид системы
Таким образом, собственное направление, соответствующее собствен-
ному значению X, определяется прямой линией, имеющей уравнение
у = Хх;
мы будем называть ее собственной прямой.
Если корни Xi и Х3 отрицательны, то мы имеем устойчивый узел
(см. А)). В этом случае обе собственные прямые проходят во второй
и четвертой четвертях; траектории вблизи начала координат касаются
той из них, которая расположена ближе к оси абсцисс (рис. 34).
Если корни Xi и Х2 положительны, то мы имеем неустойчивый
узел (см. А)). Обе собственные прямые проходят в первой и третьей
четвертях; вблизи начала координат траектории касаются той из них,
которая расположена ближе к оси абсцисс (рис. 35).
Если корни Xj и Х2 имеют разные знаки, то мы имеем седло;
одна собственная прямая проходит во второй и четвертой четвертях,
а другая—-в первой и третьей. В направлении первой из этих пря-
мых траектории приближаются к началу координат, а в направлении
второй — отходят от него (рис. 36).
126 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ (Гл. 2
3. Рассмотрим, наконец, случай, когда хотя бы одно из собствен-
ных значений матрицы А обращается в нуль.
Рис. 35.
Случай I. В нуль обращается лишь одно собственное значение:
Xj О, Х2 = 0.
В этом случае решение можно записать в виде (4), где tp и ?
даются формулами (5). Так как Х2 = 0, то £2 = const, и движение про-
исходит по прямым £2 = const в направлении к прямой Е1 = 0 или от
нее в зависимости от знака числа ХР Все точки прямой ^=0
являются положениями равновесия (рис. 37).
Если же имеется единственное собственное значение Х1 = Х2 = 0,
то могут представиться два случая, рассмотренные в примере 1.
** «а
€Й
s*^.r- •;
w« .»,„
Й
ss
&^&Як
HOt^a
'BdQo yhou ,.^
(0
3
’^is^
^Ifi
S
J^Uep A — a-
r!t'd^9d 3
П^“= Uou “° r«
"“too,,,,
•u
•W/y ^OggB(I
'"’'! HEh^^tn
^e
^ivu
1 lJ *^)
[»i s
ГЛАВА ТРЕТЬЯ
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПЕРЕМЕННЫМИ
КОЭФФИЦИЕНТАМИ
В этой главе излагается теория линейных уравнений, сперва для нор-
мальной системы л-го порядка, а затем для одного уравнения я-го по-
рядка, причем почти все результаты, относящиеся к одному уравне-
нию, выводятся из соответствующих результатов о нормальной си-
стеме. Третий параграф главы посвящен нормальным линейным одно-
родным системам с периодическими коэффициентами. Главным
результатом здесь является теорема Ляпунова о возможности линей-
ным периодическим преобразованием переменных перевести нормаль-
ную систему с периодическими коэффициентами в нормальную систе-
му с постоянными коэффициентами. В дальнейшем этот результат
находит важное применение в теории устойчивости. Доказательство
его очень просто, но опирается на сравнительно неэлементарную те-
орию функций от матриц. Эта теория, не являющаяся частью теории
обыкновенных дифференциальных уравнений, излагается для удобства
читателей в добавлении II. Таким образом, третий параграф этой главы
(§ 19) является неэлементарным благодаря используемому в нем мат-
ричному исчислению.
§ 17. Нормальная система линейных уравнений
Здесь будет рассмотрена нормальная система линейных уравнений
с переменными коэффициентами
п
Z=l, . . .,п. (1)
Напомним, что если есть интервал существования и не-
прерывности коэффициентов а*.(1) и свободных членов bl(t) системы
(1), то, в силу теоремы 3, каждое решение может быть продолжено
па весь интервал 7 г- В дальнейшем мы будем считать, что
каждое рассматриваемое решение задано на этом интервале и каждое
рассматриваемое значение t принадлежит ему.
$ 17]
НОРМАЛЬНАЯ СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ
129
Фундаментальная система решений
В первую очередь будет рассматриваться однородная система
уравнений
= 2 /=С ...» я, (2)
/«I
или, в векторной записи,
х=Д(0х. (3)
А) Установим простейшие свойства уравнения (3).
а) Если х = ф(О есть решение уравнения (3), обращающееся в
нуль при некотором значении
ф(*о)=О, (4)
то решение это тождественно равно нулю
ф(0 = 0, <7100*
6) Если
<М0, ф*(0> ...» <Рг(О
— решения уравнения (3), то векторная функция
ф(О==С1ф1(О+ ... + <<фг(0»
где с1, ...» — константы, также является решением уравнения (3).
Свойство б) проверяется непосредственно. Свойство а) вытекает
из;того, что вектор х = 0, тождественно равный нулю, очевидно,
является решением уравнения (3), а потому решение Ф(0» предусмотрен-
ное в а)г как имеющее с этим решением общее начальное условие (4),
должно с ним совпадать.
Б) Пусть
Ф1 (0, фг(0, ..., фг(0 (5)
— система решений уравнения (3), Она называется линейно зависи-
мо^ если существуют такие константы с1, с2, crt не все рав-
ные нулю, что .
cl4>i(04-cV(0+ ••• +сГФг(0=°-
В противном случае система (5) решений уравнения (3) называется
Линейно независимой. Оказывается, что если хотя бы для одного
Значения t = t9 векторы
Ф1 (М. фзСо). .... 47 Go) (G)
5 Понтрягин Л. С.
130
Глава 7
РИС. 7.13. Перколяционный кластер и его остов (черный цвет) по результатам
моделирования на квадратной решетке размером 147 х 147 при рс — 0,593 [168].
перерезать одну обособленную связь. Вытесняющая жидкость (вода) не
может проникнуть в обособленные ветви, потому что запертому там
маслу просто некуда деться.
Остов включает все узлы, лежащие на всех возможных траекториях
несамопересекающегося случайного блуждания, начинающихся в узле
(узлах) впрыскивания и заканчивающихся на границе области. Несамо-
пересекающееся случайное блуждание не может привести в обособлен-
ную ветвь, потому что иначе для возвращения на остов пришлось бы
дважды побывать в том единственном узле, связывающем с ним эту
ветвь.
Конкретная реализация перколяционного кластера и его остова
показана на рис. 7.13 для перколяции по узлам квадратной решетки на
пороге протекания. Остов связывает узел, находящийся в центре квад-
ратной решетки размером 147 х 147, с узлами на ее границе. Перколи-
рующий кластер содержит 6261 узел, в то время как в остове всего 3341
узел.
Мы изготовили лабораторную модель перколяционного кластера,
показанного на рис. 7.13 [168]. Модель сделана из эпоксидной смолы и
имеет цилиндрические поры диаметром 1,1 мм и высотой 0,7 мм. Поры
связаны каналами шириной 0,7 мм. Модель заполнялась вязким под-
крашенным глицерином. Обычный эксперимент по вытеснению состоял
в том, что в центре объема впрыскивался воздух, который вытеснял
ЯП
НОРМАЛЬНАЯ СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЯ
131
векторного пространства, то они составляют его базис» и потому
вектор <p(Q может быть записан в виде:
<p(Q = c1<fi(U + --- + c"<P«(^)> (9)
где с1,...»с" — надлежащим образом выбранные числа. Решения
ф(0 и г,<р1(0 + -- + ^"фп(0 имеют общее начальное условие
(см. (9)) и потому совпадают, так что имеет место равенство (8).
Перейдем теперь к координатному описанию полученных фактов
и к. установлению некоторых других результатов.
ЛГ) Пусть
j «МО (10)
/-некоторая система решений уравнения (3). Решение ф*(0 в коор-
динатной форме запишем, положив
Ф*(0=(?*(<)» ?*(0>-••»?*(<))•
Составим теперь матрицу
/ф1(0 - ?1(0 - ?А(0\
<?*(*) ... ... т*(0 \
шо ••• ?:(О/
|Л-м столбцом которой служит решение фА(/) системы (2) или, тсч-
(нее, его координаты. Детерминант этой матрицы обозначим через
ttZ(Z); он называется детерминантом Вронского системы решений (10).
/Очевидно, что если решения (10) линейно независимы, то детерминант
j Вронского W(t) не обращается в нуль пи при одном значении t\
I в этом случае система (10) является фундаментальной системой ре-
шений. Далее, если система (10) линейно зависима, то детерминант
i Вронского тождественно равен нулю. В случае, когда система (10)
i является фундаментальной, мы будем называть матрицу (11)
[^мент альной.
Докажем теперь, что произвольно заданная квадратная матрица
порядка л, составленная из функций переменного t и удовлетворя-
ющая некоторым естественным условиям, является фундаментальной
для некоторой системы уравнений вида (2).
Д) Будем считать, что матрица (11) есть произвольно заданная
матрица функций переменного t, непрерывно дифференцируемых
на интервале с детерминантом, нигде не обращающимся
в нуль на этом интервале. Оказывается, что эта матрица (И) явля-
ется фундаментальной для некоторой (одной-единственной) систе-
мы (2), определенной на интервале
Для доказательства этого запишем в формулах предположение,
i что векторная функция фд. (0, координаты которой составляют
б’
132 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ [Гл. J
А-й сюлбец матрицы (11), является решением уравнения (3). Мы
имеем
п
t,k=i,...,n. (12)
7=1
Если в этом соотношении зафиксировать индекс I, а считать меня-
ющимся только индекс А, то систему полученных соотношений можно
рассматривать как систему линейных алгебраических уравнений отно-
сительно неизвестных Ц](0,<4(0- Система эта однозначно раз-
решима, так как матрица ее получается из матрицы (11) транспони-
рованием и потому детерминант ее отличен от нуля. Таким образом,
функции a*(t) при каждом фиксированном / однозначно находятся
из соотнсшений (12), и притом оказываются непрерывными функ-
циями, так как функции (0 и (0 непрерывны.
ФормулаЛиувилля
При доказательстве предложения Ж) нам понадобится правило
дифференцирования детерминанта. Дадим его здесь.
E)(JlyCTb (<pf (О) —квадратная .матрица порядка л, элементы кото-
рой являются Дифференцируемыми функциями переменного и пусть
W(0 — детерминант этой матрицы. Производную W7 (0 этого детер-
минанта можно вычислять по следующей формуле:
= (0 + -..+ (13)
^Слагаемое 1^(0, стоящее на /-м месте в правой части равенства,
определяется следующим образом.' В матрице дифференцируют
по t все члены /-й строки, а .остальные строки оставляют без измене-
ния; детерминант. полученной .матрицы и есть 1У<(0. Очевидно, что
роли строк и столбцов можно поменять., .
Для доказательства формулы (13) рассмотрим сперва детерминант
U квадратной матрицы (п‘) порядка п, как функцию всех элементов
(/,/=1,...) л, этой матрицы, считая, что элементы эти явля-
ются независимыми переменными. Вычислим частную производную
dU
К
функции U по переменному zzj; здесь г и л фиксированы. Алгебраи-
ческое дополнение элемента и/ в матрице (iij) обозначим через у/,
так что
п
(И)
§ m
НОРМАЛЬНАЯ СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ 233
Формула эта дает разложение детерминанта U по элементам г-й
строки. Алгебраическое дополнение 14 не ’зависит от переменного urs
и потому, дифференцируя равенство (14) по zzj, получаем:
Если положить Ui=¥j(t), то мы имеем Дифференцируя
IV(t) как сложную функцию, мы получаем в силу формулы (15):
г J
Так< как, очевидно,
/=1
то формула (13) доказана.
Перейдем теперь к доказательству так называемой формулы
Лиувиллял*
Ж) £Пусть W(t)~ детерминант Вронского фундаментальной
системы решений" ypaSHeimtr (2)7тотаЗ”ймеет место формула
... . - * .
... , |5(т)</т
I W(t)=W(t„)e‘a
(16)
/где 5(0 — след (т. е. сумма диагональных членов) матрицы A(t)
.......................... »
-г-. -" 5.(0=а\ (0 + «К0 +
к [ Для доказательства^_ф_ррмудьг_Д16)_внедек. дифференциальное
s уравнйшё',“кот^ому удовлетворяет детерминант Вронского.
Вычислим производную IV_этого Детерминанта, _ пользуясь
формулой (13).' Для того чтобы провести вычисления более обо-
зрймым^ббраЗом,7-будем считать строки матрицы (11J ...ректорами,
именно положим:
х' (0 = (<р/ СО, •... >_<£ (0)-. i =.Ь. п.
Соотношение (12) можно теперь записать в виде:
X' (0=«! (0 X* (0 +... + 4(0 х" (О- (17)
' Соотношение это показывает, что производная f-й строки матрицы
(11) является линейной комбинацией строк той же матрицы. Таким
образом, при вычислении детерминанта !V(-{7) мы должны f-ю строку
/детерминанта W(t) заменить линейной комбинацией (17) строк того
: же детерминанта. Так как от прибавления кратных других строк
' к данной строке детерминант не меняется, то детерминант
134 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ (Гл. 3
получается из детерминанта W(t) умножением его Z-й строки на
и по/ому мы имеем:
Таким образом, в силу формулы (13) получаем:
Единственным решением этого уравнения с начальным условием
^(0k = (o= W(tt)
является (16). Таким образом, формула Лиувилля доказана.
Метод вариации постоянных
Перейдем теперь к изучению неоднородных систем.
Пусть
у= A(t)y-{-b(t) (18)
— векторная запись неоднородной системы (1) и пусть >у = ф(/) —
некоторое решение этого уравнения. Наряду с уравнением (18) рас-
смотрим соответствующее однородное уравнение (3). Из замечаний
§ 6 непосредственно следует, что произвольное решение уравнения
(18) может быть записано в виде:
J = <f(0 -f-4(0>
где q)(0 есть произвольное решение уравнения (3).
Таким образом, решение неоднородного уравнения (18) сводится
к решению однородного и к отысканию частного решения неодно-
родного уравнения. Покажем, каким образом, зная фундаментальную
систему решений однородного уравнения (3), можно (при помощи
квадратур) найти частное решение неоднородного уравнения.
3) (Метод вариации постоянных.) Пусть
<pi(0> •••> ч>я(0
— фундаментальная система решений однородного уравнения (3). Бу-
дем искать решение уравнения (18) в виде
j=c,(o<p1(o+-..+^(o<fn(a (19)
где коэффициентами являются неизвестные функции от t. Подставляя
это значение у в уравнение (18), получаем:
t-’ (0 ф> (0+•«• -Г ? (0 ярл (0+(t) ф, (0+...+Сп (0 ф; (t)=
= А (0 (с1 (0 <р, (О +...+сп (О Ф„ (О) + ь (О,
к,
$ 17 J НОРМАЛЬНАЯ СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ 135
откуда» принимая во внимание, что <pi(0> • ••><Рп(О— решения урав-
нения (3), получаем:
С1 (0 <f 1 (0 + • • • + сп (/) Ф„ (0 = ь (0. (20)
Так как^р! (/),..., <prt(0 — линейно независимые векторы в каждой точке
то из соотношения (20) величины с1^), ...» гл(0 определяются одно-
значно, и потому величины с1^),.cn(t) можно найти при помощи
квадратур. Уравнение (20) относительно сп(0, записанное в
координатной форме, имеет вид
п
^(tyc'^b^t), 1=1.....п. (21)
/-1
И) Пусть Ф (£) = (Чр* (£))— фундаментальная матрица уравнения (3\
обращающаяся при t = t9 в единичную матрицу. Тогда решение не-
однородного уравнёния(18) с начальными значениями t9tу9 записывает-
ся в виде:
> = Ф(0(уо + $ф-*(О*(ОЛ)> (22)
где Ф~*(0— матрица, обратная матрице Ф(£).
Непосредственно проверяется, что при t = t9 формула (22) дает
у=у0. Точно так же можно было бы непосредственной подстанов-
кой в уравнение (18) проверить, что формула (22) дает решение урав-
нения (18). Можно также вывести формулу (22) методом вариации
постоянных. В самом деле, формула (21) в векторной форме перепи-
сывается следующим образом:
ф(/) с {ty = b{ty.
Отсюда находим:
с (0 = Ф"1 (!) b (0, или с (0 = Ф 1 (0 Ь (!) dt. (23)
Далее, формула (19) может быть переписана в виде:
п
/ю=2 п,
или в векторной форме
у = Ф(/)с(0.
Подставляя в эту формулу значение c(t) из соотношения (23),
получаем:
у = Ф(0| ф_,(0 b(tydt. (24)
Таким образом, формула (24) (а потому и формула (22), являющаяся
ее частным случаем) дает решение уравнения (18).
136 ЛИНЕЙНЫЕ УРАВНЕНИЯ С-ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 3
Матричная з а пи сь си ст е м линейных уравнений.;
В ряде случаев удобно бывает записывать уравнение (3) в мат-
ричной форме, при которой неизвестной величиной является
фундаментальная матрица уравнения (3). Дадим здесь эту запись.
К) Пусть (7) — фундаментальная система решений уравнения (3);
тогда
• п
ф'(0= 5 а‘а (*)<?' (О-
- а = I
В матричной форме это соотношение принимает вид:
Ф(0=Д(0ф(0> <25)
где Ф(0 — производная фундаментальной матрицы Ф (£) = (ср* (/)) по
времени t, т. е. Ф (t) = (<ру- (/)). Таким образом, фундаментальная мат-
рица Ф(/) уравнения (3) удовлетворяет матричному уравнению (25);
более того, каждое решение матричного уравнения
X=A(t)X, (26)
' • » л 4
где X — неизвестная матрица, является фундаментальной матрицей
уравнения (3), если только детерминант матрицы X отличен от нуля.
В дальнейшем под решением уравнения (26) будем подразумевать
лишь такую матрицу X, удовлетворяющую уравнению (26), детер-
минант которой отличен от нуля. Очевидно, что отыскание одного
решения матричного уравнения (26) равносильно отысканию .всех ре-
шений уравнения (3). Отметим, что если Х = Ф(О иЛ = Ф (/)—г два
решения матричного уравнения (26), то существует такая постоянное
матрица Р, что
Ф(/) = Ф(/)Р- (27)
Докажем последнее соотношение. Пусть
Ф(О=(<р'(0)- ф(О = (?/(0). /
(О = (<?И0, . • •, у (0). Ф, (0 == (?) (0.(0);,
тогда
<Pi(0> . . <prt(0 (28)
есть фундаментальная. система решений уравнения (3), а так как
<р7(() также есть решение уравнения (3), то оно может , быть выра-
жено через фундаментальную систему (28), так что мы имеем:
л
47(0=S^<Fu(0-
а—I
§ 17] НОРМАЛЬНАЯ СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ 137
Переписывая это соотношение в скалярной форме, получаем:
л
?J(0=.S <р«(0Д/- (29>
а=1
Соотношение (27) представляет собой матричную запись соотноше-
ния (29) при P —
Л) В уравнении (3) введехМ новое векторное неизвестное у при
помощи преобразования
y = S(0x, (30)
где S (0 = (5/(0) — невырожденная матрица, зависящая от t. Урав-
нение для новой неизвестной векторной функции у имеет вид:
(31)
т. е. вновь является уравнением типа (3). Преобразованию (30) век-
торного переменного соответствует преобразование
Y—S(t)X (32)
матричного переменного (см. К)).
Выведем сначала уравнение (31) для неизвестного у. Мы имеем:-
y=-^S(t)x) = S(t)x-\-S(t)x =
= (5(0 + 5(0 А (0) х=( 5(0 + 5(0 А (0) 5-1 (0у.
Для того чтобы установить, что преобразованию (30) векторного
неизвестного соответствует преобразование (32) матричного неиз-
вестного, перепишем преобразование (30) в скалярной форме
п
а — I
Вектору Ф/(О = ((Р/1 (О’ •••» Ф/(0) фундаментальной системы уравне-
ния (3) преобразование (30) ставит в соответствие вектор ф;(0 =
= (ф] (0, ..., ф" (0 ) по формуле
fl
Ф‘(0 = 25'^?И0.
а— 1
Таким образом, фундаментальной матрице Ф(0 уравнения (3) соот-
ветствует фундаментальная матрица 47(0 уравнения (31) по формуле
Ф(0 = £(0Ф(0>
а это и значит, что матричное неизвестное преобразуется по фор-
муле (32).
138 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ (Гл. 3
П ример
Из предложения В) видно, что для нахождения всех решений
уравнения (3) достаточно найти его фундаментальную систему реше-
ний, т. е. п линейно независимых решений. Покажем, что, зная одно
нетривиальное решение системы (2), можно на единицу снизить поря-
док системы (2), т. е. свести ее к решению линейной системы по-
рядка п — 1.
Пусть
<Р(0=^(0, фя(0)
— решение уравнения (3) или, что то же, системы (2), Будем искать
решение уравнения (3) в виде:
JC=«q>(O+j. (33)
где и — неизвестная функция, а у — неизвестный вектор, о котором
мы будем предполагать, что первая его компонента равна нулю:
У = (0,/....Уп).
Подстановка вектора х из формулы (33) в уравнение (3) дает
«ч> (0+«ч> (0 + Jл (О («Ф (0 +л
Учитывая тот факт, что <р (0 есть решение уравнения (3), получаем
отсюда
Выпишем это уравнение в координатной форме, выделив при этом
первое из получаемых уравнений:
*?1(0=S«;(0J'/> (34)
= nq>f(0, / = 2, ...» п. (35)
/“2
Определяя й из уравнения (34) и подставляя полученное значение
в соотношения (35), получаем:
п
....(36)
/ = 2
где
Следует помнить, что подстановка значения й из (34) в (35) возможна
лишь на том интервале, где функция <р> (0 не обращается в нуль.
Если теперь ф(0 = {ф2(0, ф"(0} — какое-либо решение системы
§ 18]
ЛИНЕЙНОЕ УРАВНЕНИЕ л-ro ПОРЯДКА
139
(36), то, определяя функцию и из соотношения
п
й<р‘(О = £Ж)ф'(0
/=2
при помощи квадратуры, получаем решение исходной системы (2)
в виде:
х = и<р(04-^(0-
§ 18. Линейное уравнение л-го порядка
Здесь будет рассмотрено линейное уравнение порядка л:
у{п} + «I (О У"-0 + (t)y = ь (0, (1)
коэффициенты a^t) и свободный член b(t) которого мы будем пред-
полагать определенными и непрерывными на интервале
Исследование уравнения (1) будет производиться здесь путем его
сведения к нормальной системе линейных уравнений по методу, ука-
занному в § 4.
Фундаментальная система решений
А) Для сведения уравнения (1) к нормальной линейной системе
введем новые неизвестные функции
х1=у, x*=J>, хл=Уп-1).
Эти новые неизвестные функции х1, ...эХ" удовлетворяют линейной
системе (см. § 4, А)):
Хп 1 = х",
хп = — ап (t) х1 — an_I (0 х2 —... — (О хп -|- b (t).
Полученную систему в векторной форме запишем в виде;
х=А(0х + *(0> (2)
где матрица А (/) имеет вид: 0 1 0 ... 0 \ 0 0 1 ... 0 0 0 0 - 0 : (3)
0 0 0 ... 1 \ — an(t) —апЛ(1) — a^t) ... — в,(0/
140 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 3
а вектор b(t) определяется формулой
*(0 = (0, 0,..., b(t)\
Уравнения (1) и (2) эквивалентны между собой; именно, каждому
решению j/ = <|>(Z) уравнения (1) соответствует решение
х = ф(0 = ('И0. Ш ....
уравнения (2), и наоборот, каждому решению
х = ф(0 = (?*(<). <р’(0. .... ?"(0)
уравнения (2) соответствует решение
уравнения (1), причем соответствие это взаимно однозначно. Если
решения <p(f) уравнения (1) и <р(0 уравнения (2) соответствуют
в указанном смысле друг другу, то мы будем писать
Ф(О^<р(О-
Из эквивалентности уравнений (1) и (2), в частности, следует, что
любое решение уравнения (1) может быть продолжено на весь интер-
вал (см. теорему 3), так что в дальнейшем мы будем
считать, что каждое рассматриваемое решение уравнения (1) задано
на этом интервале и каждое рассматриваемое значение t принадле-
жит ему.
‘ В первую очередь изучим однородное уравнение ..
+ + = ' (4)
Пусть
Х=Д(0х \ (5)
— соответствующая ему система уравнений, данная в векторной
записи, где матрица A (t) определяется формулой (3).
Б) Пусть
Ф1(О> MX ...> ФАО (6)
—-некоторая система решений уравнения (4). Непосредственно про*
вернется, что функция
ф(/)=с1<|>|(04- ... 4-</<}»,(0.
где с1, ... , сг — константы, является решением уравнения (4). Си-
стема решений (6) называется линейно зависимой, если существуют
такие константы с1, ..., сг, не обращающиеся одновременно в нуль,
что
с*Ф,(0+...-Нгфг(О=о. , (7)
§ 18] ЛИНЕЙНОЕ УРАВНЕНИЕ л-го ПОРЯДКА 141-'
Оказывается, что если
<мо> .... <М0 (8)
— решения уравнения (5), соответствующие решениям (6):
Ф,-(0^ф/(0> г=1, ...,г
(см. А)), то решения (8) линейно зависимы (см. § 17, Б)) тогда и
только тогда, когда линейно зависимы решения (6).
Докажем это. Допустим, что решения (6) линейно зависимы, т. е.
имеет место соотношение (7). Выписывая соотношение (7) и те соот-
ношения, которые получаются из него путем дифференцирования,
получаем:
г'Ф,(О+ ... -Н'<МО=о,
С1ф1(0+ ..Н-‘%(0 = 0, /04
/'ф'Г"(/)-]- ... +^фг,я-п(0 = о.
Принимая во внимание, что
Ф/(0 = (ф/(0. <М0.....Ф/Л_,,(О),
мы ' видим, что соотношения (9) в векторной записи имеют вид:
1 . . + ... (Ю)
так что имеет место линейная зависимость и между решениями (8)
Допустим, наоборот, что решения . (8) линейно зависимы, т. е. что
.имеют место соотношения (10). Ставя в соотношение (10) вместо
каждого вектора <₽,(() его первую компоненту, получаем соотноше-
ние (7), так что решения (6) линейно зависимы.
' ’ В) Система решений
...... 'ЫО.....фд(0 (11)
уравнения (4) называется фундаментальной, если она линейно неза-
висима (обозначениями предусмотрено, что число решений системы
(11) равно порядку уравнения (4)). Оказывается, что фундаменталь-
ные системы решений уравнения (4) существуют и что если система
(II) является фундаментальной, то каждое решение уравнения (4)
может быть записано в виде:
о(0-г ... -Нл'Ы0>
где с\ ...» сп— константы. Из сказанного видно, что для нахожде-
ния всех решений уравнения (4) достаточно найти его фундаменталь-
ную систему решений. (Для линейного однородного уравнения с по-
стоянными коэффициентами фундаментальная система решений была
построена в § 7, 8.)
142 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 3
Покажем прежде всего, что фундаментальная система решений
уравнения (4) существует. Для этого воспользуемся фактом сущест-
вования фундаментальной системы решений уравнения (5) (см. § 17, В)).
Пусть
ФИО, •••. Ф»(0 (12)
*—фундаментальная система решений уравнения (5) и пусть
.... фя(0 (13)
— соответствующие решениям (12) решения уравнения (4):
Ф;(О#Фг(О. /=1, ...,л
(см. А)). Так как решения (12) линейно независимы, то в силу Б)
линейно независимы и решения (13), и потому они составляют фун-
даментальную систему. Допустим теперь, что система (И) является
фундаментальной для уравнения (4) и пусть решения (12) соответ-
ствуют решениям (11). Пусть, далее, ф(£)— произвольное решение
уравнения (4) и <р(/)—соответствующее ему решение уравнения (5).
Так как система (11) по предположению фундаментальна, т. е. ли-
нейно независима, то соответствующая ей система (12) также линей-
но независима, т. е. фундаментальна. Таким образом, в силу предло-
жения В) § 17, получаем:
Ф(0=^ф|(0+ ••• + ^ф«(0-
Заменяя в этом соотношении каждый вектор его первой компонен-
той, получаем:
Ф(О=^Ф1 (04- ... +^ф«(0.
Таким образом, предложение В) доказано.
Г) Детерминантом Вронского системы решений (11) уравнения
(4) называется детерминант:
о,(О ... б„(0
ф, (0 - - • (О
«7(0 =
^(я-"(0 ... ФГ‘*(О
Если решения (12) уравнения (5) соответствуют решениям (И) (см. А)),
то детерминант Вронского (см. § 17, Г)) системы решений (12) урав-
нения (5) совпадает с детерминантом (14); это видно непосредственно.
Таким образом, то, что верно для детерминанта Вронского системы
(12), верно и для детерминанта (14). Отсюда в силу предложения Г)
§17 заключаем, что детерминант (14) или не обращается в нуль ни в
одной точке, или равен нулю тождественно; для того чтобы система
решений (11) была линейно независимой, т. е. фундаментальной, не-
обходимо и достаточно, чтобы детерминант (14) не обращался в
§ Ш1
ДИНЕЙНОЕ УРАВНЕНИЕ л-го ПОРЯДКА
143
нуль. Из предложения Ж) § 17 следует формула Лиувилля для
детерминанта (14):
t
—J «1 (T)rft
W(f)=W(tt)e '° . (15)
Она получается из формулы (16) §. 17, если учесть, что след, т. е.
сумма диагональных членов матрицы (3), равен —Ниже, в при-
мере 2, будет дано более простое непосредственное доказательство
формулы (15).
Д) Пусть
... -\-0a(t)2=b(t) (16)
— неоднородное уравнение и пусть
... +an(t)y = O (17)
— соответствующее ему однородное уравнение. Из предложений
§ 6 непосредственно следует, что если у0 (?) есть частное решение
уравнения (16), то произвольное решение уравнения (16) имеет вид:
г = Ф(О + Хо(О,
где ф(0—решение урав-непия (17).
Метод вариации постоянных
Е) Пусть
М), ’МО 08)
— какая-либо фундаментальная система решений уравнения (17).
Тогда решение уравнения (16) может быть получено в виде:
... И-с”(0Фп(0, (19)
где функции
(20)
получаются как решения системы алгебраических уравнений:
М)И(0+ ... -I(/)?(/)=о,
Ф1(Ос1(0+ +М)<я(0=о,
(21)
... + -2W”(0 = 0,
n (0 с' (0 + •. • + $ ' ° (0 > (0=ь (f).
144 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 3
Так как детерминант системы уравнений (21) относительно неизвест-
пых величин (20) есть детерминант Вронского системы решений (18),
то в силу предложения Г) он не обращается в нуль ни при одном
значении t и потому из системы уравнений (21) можно определить
величины (20), а по ним определяются квадратурами и нужные нам
функции
^(0.....*л(0-
Доказательство предложения Е) вытекает из предложения 3) § 17.
Можно также провести его и непосредственно. Сделаем это. Предпо-
лагая, что на величины (20) наложены условия (21), мы получаем
из формулы (19) путем дифференцирования следующие соотношения:
г = ^(0ф,(0 + ... +^(Пф„(О.
г=^(0ф1(0Ц- ... +^(0^(0,
= ...
... + сп (0 ф£” (I) +
+ ?(0Ф,1я-1,(0+ ... +?(0ф<,"-,’(0=
=с*(0ф}я) (0+ ... +ся(0ф^(0+^(0.
Подставляя эти выражения в уравнение (16), получаем тождество.
Таким образом, если функции с*(0> • ••> удовлетворяют соотпо-
тениям (21), то функция (19) является решением уравнения (16).
Примеры
1. Если известно нетривиальное (не равное тождественно пулю)
решение ф(0 уравнения (4), то порядок этого уравнения можно
снизить на единицу, т. е. свести его решение к решению линейпоСо
уравнения порядка я—1. Для этого произведем замену
У = ф(О*, (22)
где v — новая неизвестная функция. Мы покажем сейчас, что резуль-
тат подстановки (22) в левую часть уравнения (4) приводит вас £
уравнению
+ bn.l(f)t>-\-b.(t)v = O ~ (23)
для v, причем
М0 = Ж Й„(0 = О. (24)
Так как все наше исследование справедливо для уравнения п-г&
порядка, коэффициент при n-й производной у которого равен едини-
це, то соотношение (23) приходится делить на b0 (t) = ф (Q, и потому
| 18] ЛИНЕЙНОЕ УРАВНЕНИЕ я-го. ПОРЯДКА 145
сведение уравнения (4) к уравнению (23) имеет место лишь на таком
интервале, где ф(7) не обращается в нуль. Полагая
и заменяя неизвестную функцию v новой неизвестной функцией
мы приходим к уравнению
w(n~1> (tj 4" • • • + 4-i (7) = О
порядка п—1. Если имеется решение х(0 этого уравнения, то ре-
шение v уравнения (23) получаем квадратурой:
v = ^(t)dt,
а решение у уравнения (4) получается подстановкой найденной функ-
ции v в (22).
Докажем, что подстановка (22) приводит уравнение (4) к виду
(23), причем выполнены соотношения (24). Дифференцируя соотноше-
ния (22), получаем:
у{1е> = Ф + • • • •
где не выписаны члены, содержащие производные от v порядков,
меньших чем k. Из этого следует, что уравнение (4) принимает вид
(23), причем bQ(t) = ф(7). Так как ф(7) есть решение уравнения (4),
то v — 1 есть решение уравнения (23). Подставляя решение т>=1
в (23), получаем bn(t) — O. Таким образом, соотношения (24) доказаны.
2. Приведем доказательство формулы Лиувилля (15) для одного
уравнения /г-го порядка, не опирающееся на формулу Лиувилля для
Системы (см. формулу (16) § 17). При этом мы будем пользоваться
правилом дифференцирования детерминанта, данным в § 17 (см. § 17»
Е)). В силу этого правила дифференцирования мы получаем из (14):
IF (t) = uz, (0+... + (0 4-... + wn (О,
где (t) есть определитель Вронского Wz(7)> в котором продиффе-
ренцирована Z-я строка. Если 1<^п, то в результате дифференциро-
вания 7-й строки мы получаем строку, совпадающую с (7 -р 1)-й стро-
кой определителя W(7), и потому мы имеем:
^(7)= Г,(0 = . ••= ^п-|(0=0.
При дифференцировании и-й строки мы получаем строку
ф^(7),...,ф^(7),
которая в силу уравнения (4) является линейной комбинацией строк
определителя W(7), причем л-я строка берется с коэффициентом
146 ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ [Гл, 3
— В силу наличия в определителе Wn(t) строк определителя
Вронского с номерами 1, ...,л—1> эти строки в линейной комбина-
ции можно отбросить» и остается лишь д-я строка с коэффициентом
— Таким образом, для определителя Вронского получаем диф-
ференциальное уравнение
Г(О=_в1(ОГ(0.
Решая его, получаем формулу Лиувилля (15).
§ 19. Нормальная линейная однородная система
с периодическими коэффициентами
Среди линейных уравнений с переменными коэффициентами осо-
бенно важную роль играют уравнения с периодическими коэф-
фициентами. Настоящий параграф посвящается изложению некоторых
свойств нормальных линейных однородных систем дифференциальных
уравнений с периодическими коэффициентами. Из приводимых здесь
свойств этих систем центральным является теорема Ляпунова. При-
веденное здесь доказательство теоремы Ляпунова менее элементарно,
чем все предыдущее изложение книги. Оно опирается на матрич-
ное исчисление, необходимые сведения из которого излагаются
в добавлении II.
Пусть
X=A(t)X (1)
— нормальная линейная однородная система уравнений, записанная
в матричной форме (см. § 17, К)). Мы будем предполагать, что
коэффициенты этой системы являются периодическими функциями
времени t с периодом т, т. е. матрица A (t) удовлетворяет условию
А (Г|-Ч =
А) Для всякого (матричного) решения
Х = Ф(О (2)
уравнения (1) (см. § 17, К)) найдется такая постоянная (невырожден-
ная) матрица С, что
Ф (/-’-т) = Ф (£) С.
Матрицу С мы буде>< называть основной для решения (2). Если
Х = Ф(0—какое-либо другое решение уравнения (1), а С—его
основная матрица, то мы имеем:
С=Р ЛСР, (3)
где Р — некоторая невырожденная постоянная матрица.
? 191 СИСТЕМА С ПЕРИОДИЧЕСКИМИ КОЭФФИЦИЕНТАМИ 147
Для доказательства существования матрицы С заметим, что, наря-
ду с решением (2), решением уравнения (1) является и матрица
В самом деле,
ф(^ + т)=А(^4-1:)Ф(^ + 1:)=А(0Ф(^ + х).
Таким образом, в силу формулы (27) § 17 имеем:
Ф(*4-т)=Ф(0С,
где С — постоянная матрица.
Для доказательства формулы (3) также воспользуемся формулой
(27) § 17. Так как Ф(0 есть решение уравнения (1), то в силу упо-
мянутой формулы имеем:
Ф(0 = Ф(ОР.
Отсюда
Ф (t -f- т) = Ф (t 4- т) Р=Ф (t) СР = Ф (О Р 'СР,
что и дает соотношение (3).
Б) Уравнение (1) и уравнение
Y=B(t)Y (4)
с периодической матрицей В (t) того же периода т, что и матрица
A (t), называются эквивалентными, если существует линейное пре-
образование
Y = S(t)X
(см. § 17, Л)) с периодической матрицей S(f) периода т, переводя-
щее уравнение (1) в уравнение (4). Оказывается, что уравнения (I)
и (4) тогда и только тогда эквивалентны, когда существуют решения
Х = Ф(0 и У=Ф(^) этих [уравнений с одной и той же основной
матрицей.
Докажем это утверждение. Допустим сначала, что уравнения (1)
и (4) эквивалентны. Пусть А' = Ф(^) — произвольное решение урав-
нения (1) с основной матрицей С; тогда Y = (t) = S{t) Ф (0 есть
решение уравнения (4), и мы имеем:
Ф(^ + т) = 5(/ + т)Ф(^ + т) = 5(0Фр -Н)=5(0Ф(0С = Ф‘(0
Таким образом, основная матрица С решения Ф(/) является основной
и для решения Ф (О-
Допустим теперь, что существуют решения X — Ф(/) и
уравнений (1) и (4) с одной и той же основной матрицей С; тогда
мы имеем:
> Ф (/ + г) = Ф (/) С, Ч (t 4- г) = (О С. .
Т48 ЛИНЕЙНЫЕ УРАВНЕНИЯ' с ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ [Гл. 3
Деля второе из этих соотношений справа на первое, получаем:
Ф (t -j- х) Ф-1 (f 4- = ЧГ (О Ф"1 (О-
Таким образом, матрица
S(0= Т (О Ф’1 (О
является периодической с периодом х, и мы имеем:
Ф(0 = 5(0Ф(0- (5)
Так как каждое из решений Ф(£) и Ф (t) однозначно определяет свое
уравнение (см. § 17, Д)), то из (5) следует, что уравнение (4) полу-
чается из уравнения (Г) путем преобразования с матрицей 5(0-
Как видно из предложений А) и Б), каждому уравнению вида (1),
рассматриваемому с точностью до эквивалентности (см. Б)), соответ-
ствует матрица С, определенная с точностью до трансформации
(см. (3)). Более того, совокупность всех инвариантов матрицы С
относительно преобразований вида (3) составляет полную с й-
стему инвариантов уравнения (1), определенного с точностью
до эквивалентности.
. Следует заметить, что все сказанное в предложениях А) и Б)
верно как в случае, когда рассматриваются только действительные
матрицы, так и в случае, когда . рассматриваются комплексные мат-
рицы. В нижеследующей важной теореме Ляпунова (теорема 12)
мы будем различать действительный и комплексный случаи.
Теорема 12. Всякое уравнение (1) эквивалентно (см. Б))
уравнению
Y=BY,
где В—постоянная матрица. (Матрица В. вообще говоря, комп-
лексна.) Если в уравнении (1) матрица A(t) периода х действи-
тельна, то это уравнение, рассматриваемое как периодическое,
с-, периодом 2т, эквивалентно уравнению
Y—BXY,
где матрица Вх постоянна и действительна, причем матрица
перехода S(t) от уравнения (/) к уравнению Y—B^Y также дейст-
вительна.
Доказательству теоремы 12 предпошлем следующее предложение.
В) Пусть
У = 13 У (6)
— система линейных одноро/дпых уравнений с постоянными коэффи-
циентами, записанная в матричной форме. Матрица В здесь постоянна.
Оказывается, что матрица
У=е'“ (7)
(см. § 35, Г)) является решением уравнения (6).
s 191 СИСТЕМА С ПЕРИОДИЧЕСКИМИ КОЭФФИЦИЕНТАМИ 149.
Для доказательства того, что (7) есть решение уравнения (6),
выпишем функцию etB в явном виде. Мы имеем:
#8 /3
= е + + + ... .
Отсюда для производной ~ etB получаем:
=в . ) = Ве'в.
Доказательство теоремы 12. Пусть С—основная матрица
некоторого решения Л' = Ф(^) уравнения (J), В силу предложения
Г) § 35 существует матрица В, удовлетворяющая условию
ехВ =С.
Докажем, что уравнения (1) и 1
Y=BY (8)
эквивалентны. Действительно, в силу предложения В) матрица
Y=efB является решением уравнения (8), Таким образом, если
уравнение (8) рассматривать как уравнение с периодическими коэф-
фициентами с периодом т, то основная матрица решения
есть Су именно (см. формулу (20) § 35): 4
eu+^B^etBe'B^etBC -
Так как основные матрицы рассматриваемых решений уравнения (1)
« уравнения (8) совпадают, то эти уравнения эквивалентны (см? В)).
“ ’ Таким образом, первая часть теоремы 12 доказана.
1 Будем считать теперь, что A (t) — действительная матрица, Ф(^)-*
— некоторое действительное решение уравнения (1) и С—основная
матрица этого решения, так что
Ф^4-т) = Ф(0С. 1 (9)
Так как Ф (I) — действительная матрица, то С—также действительная
матрица. Из (9) следует, что
ф^4-2т)=Ф(«?-}-т)С=Ф(0Са. ' (10)
В силу предложения Г) § 35 существует действительная матрица Ви
удовлетворяющая условию
Докажем, что уравнение (1) и уравнение
r=S,K, (1.1)
150 ЛИНЕЙНЫЕ УРАВНЕНИЯ в ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ 1Гл. 3
рассматриваемые как уравнения с периодом 2т, эквивалентны. Дей-
ствительно, матрица является решением уравнения (11). Таким
образом, если уравнение (11) рассматривать как уравнение с пери-
одическими коэффициентами периода 2т, то основная матрица реше-
ния Y=etBi есть С2. Так как основные матрицы рассматриваемых
решений уравнений (1) и (11) (см. (10)) совпадают, то эти уравнения
эквивалентны.
Итак, теорема 12 доказана.
Г) Пусть С—произвольная квадратная матрица порядка п, моду-
ли всех собственных значений которой меньше некоторого положи-
тельного числа р. Элементы матрицы Ст, где т — натуральное число,
обозначим через тс;, так что Cm = (mcij). Тогда существует такое
положительное число г, не зависящее от J, т, что
|%'|<грт. (12)
Отсюда, в частности, следует, что для произвольного вектора х
имеет место неравенство
| Стх | п*г?т | х |. (13)
Для доказательства оценки (12) рассмотрим ряд
* 9^ 2^
/(z)=l+| + -^+ .
радиус сходимости которого, очевидно, равен р. Из теоремы 29
(см. § 35) следует, что матричный ряд
/(О=£ + -^ + Ь+... +
сходится и, в частности, сходится числовой ряд
Так как ряд этот сходится, то все его члены не превосходят
некоторого числа г, причем число г можно выбрать общим для всех
пар чисел (/, j). Таким образом, Оценка (12) имеет место.
Д) Пусть
x = A(t)x (14)
— векторная запись матричного уравнения (1) и С—основная
матрица некоторого решения Ф(£) уравнения (1). Собственное
значение X кратности k матрицы С называется характеристиче-
ским числом кратности k уравнения (1) и уравнения (14). Так
как с точностью до трансформации матрица С не зависит от слу-
чайности выбора решения Ф(^) уравнения (1) (см. А)), то харак-
теристические числа уравнения (14) и их кратности определены
здесь инвариантно. Если X есть характеристическое число краг-
§ 191
СИСТЕМА С ПЕРИОДИЧЕСКИМИ КОЭФФИЦИЕНТАМИ
•151
ности k уравнения (14), то число — Ink называется характеристи-
ческим показателем кратности k уравнения (14). Допустим, что
все действительные части характеристических показателей уравнения
(14) меньше некоторого числа у; тогда существует такое положи-
тельное число что для всякого решения ф(0 уравнения (14)
имеет место оценка
I ф (О I R1 ф (0) I ПРЙ * 0* (15)
Докажем неравенство (15). Пусть Ф(£) — решение уравнения (1)
с начальным условием Ф(0)=С; тогда любое решение ф(0 уравне-
ния (14) записывается в виде:
ф(0=Ф(0ф(0). (16)
Это проверяется подстановкой вектора (16) в уравнение (14).
Далее мы имеем:
Ф(^Х)=Ф(ОС, Ф(/4-2г) = Ф(/)<Л . . . , Ф£+/яг) =
= Ф<0Сг ... (17)
Так как на отрезке элементы матрицы Ф(^) ограни-
чены, то существует такое положительное число <з, что
IФ (^t) ЖI а I при (18)
Так как, далее, все собственные значения матрицы С по модулю
меньше числа е11, то в силу (13) для произвольного вектора х
имеет место оценка
| Стх | ntre™11 х |. (19)
Пусть теперь t—произвольное положительное число; найдем тогда
такое целое неотрицательное число т, что
£ = zn-t1, .
В силу (16) и (17) мы имеем:
Ф (0 = Ф Q Ф (0) = Ф (Q С™ ф (0).
Отсюда согласно (18) и (19) получаем:
|ф(0|^сп^^Чф(0)(.
Так как число при не меньше некоторой константы
с^>0, то последнее неравенство можно записать в виде:
Таким образом, оценка (15) доказана.
ГЛАВА ЧЕТВЕРТАЯ
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
Здесь в первую очередь доказываются уже формулированные
ранее теоремы 1, 2, 3 существования и единственности. Далее, рас-
сматривается вопрос о зависимости решения от начальных значений
и параметров, если последние входят в уравнения. В первую оче-
редь разбирается зависимость решения с фиксированными начальными
вначениями от параметров, а затем весьма простым приемом началь-
ные значения превращаются в параметры, и, таким образом, дело
сводится к вопросу о зависимости решения от параметров. Как
в случае начальных значений, так и в случае параметров доказы-
ваются непрерывная зависимость решения от этих переменных и диф-
ференцируемость решения по ним.
В том и другом случае здесь приводятся только так называемые
интегральные теоремы, а нередко упоминаемые в учебниках «локаль-
ные» теоремы вообще не приведены. Объясняется это тем, что как
в самой теории, так и в ее приложениях важны именно интеграль-
ные теоремы; локальные же теоремы в лучшем случае служат средст-
вом доказательства интегральных и не заслуживают специального
внимания. Слово «интегральные», употребленное здесь, никакого
отношения к операции интегрирования не имеет. Оно означает лишь,
что решения рассматриваются не на малых интервалах врёмеПи,1' а
«интегрально», «в целом», т. е. рассматриваются н е п р о д о л ж а е м ы е
решения (см. § 3, А)). В связи с этим изучению непродолжаемых ре-
шений посвящен здесь специальный параграф (§ 22).
Кроме этого материала, в настоящую главу включен Параграф
о первых интегралах системы обыкновенных дифференциальных урав-
нений и примыкающее к понятию первого интеграла исследование
линейного уравнения в частных производных.результаты этого па-
раграфа в дальнейшем изложении нигде не используются.
§ 20. Доказательство теоремы существования и единственности
для одного уравнения
В этом параграфе будет дано доказательство сформулировайпОй
в § 1 теоремы 1 существования и единственности для одного урав-
нения первого порядка
х),
(1)
§ 20] СЛУЧАЙ ОДНОГО УРАВНЕНИЯ ЛвЗ
правая часть которого определена и непрерывна вместе со своей
частной производной на некотором открытом множестве Г пло-
скости Р переменных t, х. Доказательство теоремы 2, приводимое
в следующем параграфе, представляет собой усложнение доказатель-
ства теоремы 1 и содержит его как частный случай. Приводя дока-
зательство сначала для случая одного уравнения, я имею целью
выявить основные идеи этого доказательства, которые в общем
случае загромождаются второстепенными деталями. Доказательство
теорем 1 и 2 проводится в этой книге методом последователь-
ных приближений) принадлежащим Пикару и применяемым в анализе
при доказательстве многих теорем существования. Этот метод яв-
ляется одновременно методом приближенного вычисления решения и
потому имеет большую практическую ценность. В некоторых случаях
метод последовательных приближений может быть истолкован как
метод сжатых отображений. Здесь я провожу доказательство
таким образом, чтобы показать близость этих двух методов. Различие
же этих методов выявится при доказательстве теоремы 3.
Основные идеи доказательства
Первым шагом при доказательстве теоремы 1 методом последо-
вательных приближений является переход от дифференциального урав-
нения к интегральному) который мы формулируем в виде отдель-
ного предложения.
А) Пусть х — ср (^) — некоторое решение уравнения (1), определен-
ное на интервале г«, так что выполнено тождество
(2)
и пусть
<p(Q = x0 (3)
— некоторое начальное условие, которому это решение удовлетво-
ряет. Оказывается, что тогда для функции ср(/) на всем интервале
rj<^/<^r2 выполнено интегральное тождество
<Р (0 = *0 + / (% Т СО) dx, (4)
Обратно, если для некоторой непрерывной функции y(t) на интер-
вале выполнено тождество (4), то функция x — диф-
ференцируема, является решением уравнения (I) н удовлетворяет
начальному условию (3). Кратко говоря, интегральное уравнение (4)
эквивалентно дифференциальному уравнению (2) вместе с началь-
ным условием (3).
154 ТЕОРЕМЫ СУЩЕСТВОВАНИЯ (Гл. ♦
Докажем это. Допустим сначала, что выполнено соотношение (4).
Заменяя в нем переменное t его значением t9, получаем: ^(^)=х0.
Таким образом, из (4) вытекает (3). Далее, правая часть тождества (4)
очевидно дифференцируема по t, а потому дифференцируема по
t и левая его часть. В результате дифференцирования тождества (4),
получаем тождество (2).
Допустим теперь, что выполнены соотношения (2) и (3). Инте-
грируя соотношение (2) в пределах от до t, получаем:
? (i) — ¥ (4) = $/(^ ¥ (’')) rf't-
В силу соотношения (3) из последнего равенства получаем (4).
Таким образом, предложение А) доказано.
Введем теперь некоторые обозначения, используемые ниже при до-
казательстве теоремы 1.
Б) Пусть х = ср (/) — такая непрерывная функция, определенная
на некотором отрезке что ее график целиком располо-
жен в открытом множестве Г, и — некоторая точка отрезка
Тогда, пользуясь правой частью тождества (4), можно
функции <р(/) поставить в соответствие функцию определенную
также на отрезке ПРИ помощи равенства
<р* (0 = -р $/(т, ср (т)) dt (5)
/о
(график функции ср* (£), конечно, уже может не проходить в мно-
жестве?). Таким образом, правую часть тождества (4) можно рассматри-
вать как оператор, ставящий в соответствие функции ср функцию ср*.
Обозначая этот оператор одной буквой А, мы запишем соотноше-
ние (5) в виде формулы
<р* = .4'?. (6)
Пользуясь оператором А, интегральное уравнение (4) можно записать
в виде:
(7)
В) Пусть <?(/)—некоторая непрерывная функция, определенная на
отрезке Нормой этой функции называется макси-
мум ее модуля
)1<Н= шах |<р(01-
Если и y(f) — две непрерывные функции, заданные на отрезке
<га, то норма ||ф — хII их разности <|>(0 —Х(0 является не-
« 20]
СЛУЧАЙ ОДНОГО УРАВНЕНИЯ
155
отрицательным числом, оценивающим, насколько сильно отличаются
эти функции друг от друга. Если число ||ф— Х|| мало, то функции
ф и х «близки» друг к другу. Равенство ||ф— хИ = 0 имеет место
тогда и только тогда, когда функции ф и х тождественно совпадают.
Пользуясь понятием нормы, легко можно формулировать известное
из курса анализа условие равномерной сходимости последователь-
ности непрерывных функций. Пусть
<Ро(Д .... <Р.Ю> ... " (8)
— последовательность непрерывных функций, заданных на отрезке
rj t г2. Последовательность (8) равномерно сходится к функции
ст, определенной на том же отрезке если
lim || ср — срг ||=0.
Для того, чтобы последовательность (8) равномерно сходилась, доста-
точно, чтобы имели место неравенства
hi+i —
где числа л0> а{} ...» aif ... образуют сходящийся ряд.
Прежде чем перейти к детальному проведению доказательства
теоремы 1, изложим кратко суть метода последовательных прибли-
жений, применяемого для решения уравнения (7). Строится после-
довательность
?0. <Р1> •••> ?i. ... (9)
непрерывных функций, определенных на некотором отрезке
который содержит внутри себя точку t$. Каждая функция по-
следовательности (9) определяется через предыдущую ври помощи
равенства
Т/+1=Л?/, Z = 0, 1, 2, ... (10)
Если график функции <рг проходит в множестве Г, то функция срг+1
равенством (10) определяется, но для того, чтобы могла быть опре-
делена следующая функция ср;+а, нужно, чтобы и график функции
проходил в множестве Г. Этого, как мы покажем, удается до-
стичь, выбрав отрезок достаточно коротким. Далее, также
за счет уменьшения длины отрезка можно достичь того,
чтобы для последовательности (9) выполнялись неравенства
hi+i — — Vi-ill. z=1> 2.............. (и)
где 0<^Л<И. Из неравенств (И) следуют неравенства
hi+1 — Till — ?оМ‘> /=1, 2, ....
и, таким образом, последовательность (9) равномерно сходится (см. В)).
156
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
[Гл. 4
Далее уже легко устанавливается, что предел ф последовательности (9)
удовлетворяет уравнению (7). •
Ту же конструкцию можно описать-несколько иным способом —
— в форме метода сжатых отображений. Выберем некоторое семей-
ство 2 функций, заданных на отрезке п г2 (причем П<Оо<С
<^г2), так, чтобы графики этих функций проходили в множестве Г.
Допустим еще, что в отношении оператора А семейство 2 удовлет-
воряет следующим двум условиям: 1) применяя оператор А к любой
функции семейства 2; мы вновь получаем функцию семейства 2;
2) существует такое число kt
что для двух про-
извольных функций ф и х се-
мейства 2 выполнено неравен-
ство
W — — хГ •
J
В этом смысле отображение
А является сжатым (правиль-
нее было бы сказать «сжимаю-
щим*). '
Легко видеть, что если для
семейства 2 выполнены форму-
лированные условия, то, исходя
из произвольной его функции ср0, мы по индуктивной формуле (10)
получим бесконечную последовательность (9), удовлетворяющую усло-
вию (11), и, как было отмечено выше, равномерно сходящуюся
к решению уравнения (7).
Перейдем теперь к доказательству теоремы 1 па основе изло-
женных соображений.
Доказательство теоремы 1
Начальные значения н искомого решения уравнения (I) яв-
ляются координатами точки (£0, х0), лежащей в множестве Г. Выбе-
рем прежде всего какой-либо прямоугольник П с центром в точке
(f0, х0) со сторонами, параллельными осям, целиком вместе со своей
границей содержащийся в множестве Г (рис. 39). Длину горизонталь-
ной (параллельной оси t) стороны прямоугольника - П обозначим
через 2</, а длину вертикальной стороны — через 2а. Таким образом,
точка (t, х) тогда. и только тогда принадлежит прямоугольнику П,
когда выполнены неравенства:
И — ^•<'7. I* — *•!==£«• . .(12)
Так как прямоугольник П есть замкнутое множество, содержа-
щееся в Г, то непрерывные на нем функции /(г, х) и —— ог-
§ 20]
СЛУЧАЙ ОДНОГО УРАВНЕНИЯ
157
раничены, и потому существуют такие положительные числа М и К,
что для t и х, удовлетворяющих условиям (12), выполнены не-
равенства
(13)
Наряду с прямоугольником П будем рассматривать более «узкий»
прямоугольник Пг, определяемый неравенствами
Р — /о I G | х — а,
где
(14)
(см.* рис. 39). Более точно число г. определим далее. Обозначим
через 2Г семейство всех непрерывных функций, заданных на отрезке
— /0|^г, графики которых проходят в прямоугольнике Пг. Таким
образом, функция ср, определенная на отрезке 1 г, тогда и
только тогда принадлежит семейству 2Г, когда для любого t при-
надлежащего этому отрезку, выполнено неравенство
|<Р(0 — *ol^e- (15)
Постараемся теперь выбрать число г таким образом, чтобы были
выполнены следующие два условия:
а) Если функция ср принадлежит семейству 2Г, то функция
ср* = Дер (см. (5), (6)) также принадлежит семейству 2Г.
б) Существует такое число k, что для любых двух
функций ф и х семейства 2Г имеет место нергвенство
| Д<|> — Дх||^||ф- Х||. (16)
Рассмотрим условие а). Для того чтобы функция у* = Дер при-
надлежала семейству 2Г, необходимо и достаточно, чтобы при
- /0|=^г было выполнено неравенство
|<Р*(0 —хв]<а.
* В силу (5) и (13) мы имеем:
t
1т*(0 —= ?(О)I<Mr.
Из этого видно, что при
условие а) выполнено.
168 ТЕОРЕМЫ СУЩЕСТВОВАНИЯ [Гл. 4
Рассмотрим теперь условие б). Мы имеем:
Ф* (/) = Хо 4- $/(т, ф (т)) йЬ,
Х*(0 = *• + $/(''» х (x))rfx.
Вычитая второе равенство из первого, получаем:
|ф*(О-х*(О| = |$(/(т, ф(т))-/(т, Х(х)))^|<
*0
t
ФСО)—f^, хО))Н- (18)
Оценим теперь последнее подынтегральное выражение, пользуясь
формулой Лагранжа и вторым из неравенств (13):
|/(т, ф(т))—/(т, х(т))|= -^^-(ФСО—хСО) ^АНФСО—х(т)|;
(19)
здесь 0 — число, заключенное-между ф(т) и у (т) и, следовательно,
удовлетворяющее неравенству |9 — лг0| Из (18) и (19) следует:
II Аф-Ах11 = НФ* -X* И^/СгНф-хН.
Таким образом, условие б) выполнено, если число k — Kr меньше
единицы, т. е. если
г<-1-. (20)
Итак, если число г удовлетворяет неравенствам (14), (17) и (20), то
для семейства выполнены условия а) и б), В дальнейшем будем
считать число г выбранным таким образом, что неравенства (14), (17)
и (20) для него выполнены.
Построим теперь последовательность
То, П •••> ?;> ••• (21)
функций, определенных на отрезке г, положив:
сро(£) = лго, (22)
= / = 0, 1, 2, ... (23)
Так как функция (22) принадлежит семейству 2Г, то и все функ-
ции ^последовательности (21) принадлежат этому же семейству (см.
§20/
СЛУЧАЙ ОДНОГО УРАВНЕНИЯ
159
условие а)). Далее, мы имеем (см. (15)):
|| ?i — <P»II= тах |<Р1 —
В силу (16) получаем:
II <РШ — fi II = II Аъ — A<?i-i II k II <Fi — <р/-1 II >
откуда
IlVi+t — ?<|l<^'. 1 = 0, 1, 2, ...
Таким образом, в силу В), последовательность (21) равномерно схо-
дится на отрезке к некоторой непрерывной функции <р.
Так как все функции последовательности (21) принадлежат семей-
ству 2Г, то и функция ср принадлежит ему (см. (15)). Покажем, что
функция ср удовлетворяет уравнению (7). Для этого заметим, что по-
следовательность
А<?0, Дур Лсрг, ...
равномерно сходится к функции А^р; действительно, мы имеем: |
Переходя в соотношении (23) к пределу при /—>оо, получаем:
ср= А ср.
Итак, существование решения x — cp(t) уравнения (l)f удовлет-
воряющего начальному условию (3), доказано; при этом уста-
новлено, что решение x — <p(t) определено на интервале 11 — г,
где г — произвольное число, удовлетворяющее неравенствам (14),
(17) и (20).
Перейдем теперь к доказательству единственности. Пусть х = ф(/)
и x = /(t)— два решения уравнения (1) с общими начальными
значениями х0 и гх<^К^Гъ— интервал, являющийся пересечением
интервалов существования решений <|> и очевидно, что Г1<^о<Сгв-
Покажем, что если решения ф(£) и %(t) совпадают в некоторой
точке интервала то они совпадают и на некотором
интервале Ц — | г, где г — достаточно малое положительное
число. Положим х{ = ф(^i) = £(^); тогда величины tu могут
быть приняты за начальные значения обоих решений х = ф(/) и
x = В этом смысле точка (£„ л^) ничем не отличается от точки
(£0, х0), и поэтому мы сохраним за точкой (^, xj обозначение (^0, х0):
это позволит нам сохранить и другие прежние обозначения. Переходя
от дифференциального уравнения (1) к интегральному уравнению (4),
мы получаем для обеих функций ф(/) и ^(0 интегральные равенства,
которые в операторной форме могут быть записаны в виде:
<|» = Л<|», Х = ЛХ- (24)
160
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
(Гл. 4
Выберем теперь, как и прежде, в открытом множестве Г прямо*
угольник П с центром в точке (£0, хв), а затем прямоугольник Пг
таким образом, чтобы число г кроме неравенств (14), (17), (20)
удовлетворяло еще тому условию, что при 11 — | г функции ф
и / определены и удовлетворяют неравенствам
|<Н0~ Хо|<а, |х(0 — *о|<а.
Это возможно, так как функции <p(Q и /(0 непрерывны. Тогда
функции ф(0 и х(0> рассматриваемые на отрезке — £0|^г, входят
в семейство 2Г, и, следовательно, в силу неравенства (16) и соотнО?
шений (24) получаем:
h —Х|) = ИФ — W —xi
а это возможно только тогда, когда Цф— ^|=0,т.е. когда функции ф
и у совпадают на отрезке | г.
Докажем теперь, что функции ф(0 и y(t) совпадают на всем
интервале Г|<^< Допустим противоположное, именно, что су-
ществует точка t* интервала для которой ф (£*)?£
Ясно, что /♦ 7^ tQ. Для определенности будем считать, что
Обозначим через W множество всех тех точек t отрезка
для которых ф(£) = ^(0, и докажем, что множество W замкнуто.
В самом деле, пусть . — последовательность точек множества М
сходящаяся к некоторой точке т. Тогда ф(т/) = ^(т/), и потому, в
силу непрерывности функций ф и
ф(т) = lim b(T1.) = limx(Tj) = xW»
<—ОО ОО
т. е. точка т также принадлежит множеству ЛЛ
Обозначим через точную верхнюю грань множества ЛЛ Так как
N замкнуто, то принадлежит этому множеству, т. е. ф(М = х(М*>
следовательно, £*. Но тогда, в силу ранее доказанного, функции
ф(£) и Х(0 должны совпадать па некотором интервале \t — | г,
и точка tt не может быть точной верхней гранью множества ЛЛ
Таким образом, мы пришли к противоречию.
Итак, теорема I доказана.
Пример
Для весьма простого уравнения
найдем решение методом последовательных приближений. Решение
будем искать с начальными значениями
§ 21 J СЛУЧАЙ НОРМАЛЬНОЙ СИСТЕМЫ УРАВНЕНИЙ 161'
Соответствующее интегральное уравнение запишется в виде:
<р(0=1 4-
О
Будем строить теперь последовательность
?о> -о ...
Мы имеем:
?о(0=Ь
?! (О — I + 5 = I “Ь
О
(О = 1 4“ J (1 4“г) = 1 4~ 2Г
о
?9(0=14-|(1+т+-2! = i + f + +
о х
?„(0— 1 +* + 4 f3 + i ^+--- + ^я>
Пределом этой последовательности (равномерно сходящейся на лю-
бом отрезке числовой оси) является функция ср (6 = е*.
§ 21. Доказательство теоремы существования и единственности
для нормальной системы уравнений
Здесь будет доказана сформулированная в § 3 теорема 2 суще-
ствования и единственности для нормальной системы уравнений
х1=р(1> х\ х'\ ... , х”), /=1, ... , л, (1)
правые части /'(/, х1, х'\ ...» хп) которой вместе с их частными
др (t, л1, ... , хп) . » <
производными = ... , п, определены и
непрерывны на некотором открытом множестве Г пространства пере-
менных t, х1, ... , хп. Полагая
х = (х*, , хп), (2)
f(t, *) = (/’(t x),/s(<, х), ... , fn(t. X)).
мы перепишем систему (1) в векторной форме (ср. § 14, А)):
X=f(t, X).
(3)
6 Понтрягин Л. С.
162
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
[Гл. 4
Доказательство будет проводиться в векторной форме методом по-
следовательных приближений и будет представлять собой почти
буквальное повторение доказательства теоремы 1, данного в преды-
дущем параграфе. Кроме доказательства' теоремы 2 здесь будет дано
доказательство теоремы 3, также методом последовательных при-
ближений, но несколько видоизмененным по сравнению с доказатель-
ством теоремы 2.
Вспомогательные предложения
Для того чтобы непринужденно пользоваться векторными обозна-
чениями, установим прежде всего некоторые естественные определе-
ния и простые неравенства для векторов и векторных функций.
Длина или модуль |х| вектора (2), как известно, определяется
формулой
IX| = + 4- ••• +(*Т
Известно и без труда доказывается, что если х и у суть два век-
тора, то имеет место неравенство
Из этого неравенства следует аналогичное неравенство и для про-
извольного числа векторов Xi, ... , Xt, именно:
|лгг-|- ... |Х||4- ... -j-|xj. (4)
Пусть ф(/) = (ср|(/), , срл(О) — непрерывная векторная функция
действительного переменного t, т. е. вектор, координаты которого
являются непрерывными функциями переменного Л Если функция ср(/)
определена на интервале Г[<4<^г2, то при Г1<^и<^Га на том же
интервале можно определить векторную функцию
/
ч>(о=5 ч’С'И’'»
/о
задав компоненты ф*(/), ... , фл(0 вектора ф(£) формулами
t
Ф* (o=S
при этом имеет место неравенство
t t
15 <p(T)rfxl^!5
to to
(5)
§ 2t 1
СЛУЧАЯ нордильноп СИСТЕМЫ УРАВНЕНИЯ
163
Для доказательства этого неравенства разобьем отрезок интегриро
вания на tn равных частей, положив:
Д = *~~-к АД, Л=1, ... , т
in ’ - v 1
(число Д будет положительным при и отрицательным пр*
Тогда согласно определению интеграла от векторной функ-
ции и в силу (4), мы имеем:
t т т
I $ <р (т)аС-с I = ! lim 2ч)(^>Л|< lim S 1ч>О-|л1 =
= |$ I<РСО! |*
/о
Установим еще одно неравенство для векторной функции
g{x) = {gx(x\ ... , хп), ... , g'lx1, ... , хп))
векторного переменного X, заданной на выпуклом множестве Д про-
странства переменных х\ ...» Xя. Предположим, что имеют место
неравенства:
dgt (х1, ... , х")I г
дГ/
где К—положительное число. Оказывается тогда, что для двух лю-
бых точек х и у множества Д выполнены неравенства-
|^(Х)-£(У)| ^п*к\X— у\. (6)
Для доказательства неравенства (6) введем в рассмотрение отре-
зок, соединяющий точки х и у, именно положим:
«(i)=j + s(x-y).
Когда s пробегает значения 1, точка .?($) пробегает отрезок,
соединяющий точки х и и, ввиду выпуклости множества Д, вса
время остается в нем. Мы получаем (применяя формулу Лагранжа):
g* (X) - (У) = ? (*(1)) - (* (0)) = |s=e •
Вычисляя производную по формуле производной от сложной
функции, получаем:
tig1 (z (s)) dgi (z1 ($), ... , zrt (а)) _
ds ds
__ у dg‘ (Z1 (s), , z" (s)) dz“ (s) Xdgl(z'(s), ... , t
jU (>Afe ds_dxk ' У
л=1
164 ТЕОРЕМЫ СУЩЕСТВОВАНИЯ (Гл. 4
Таким образом,
п п
— /С|х—.у|.
fr=I fe=l
Возводя последнее неравенство в квадрат, суммируя его по /, и из-
влекая корень, получаем:
Так же, как при доказательстве теоремы 1, от дифференциаль-
ного уравнения (3) перейдем к интегральному.
А) Пусть дт = <р(О—некоторое решение дифференциального
, уравнения (3), так что выполнено тождество
q>(o=/a> ф(0)> (7)
и пусть
<Р (<о) = х0 (8)
— начальное условие, которому это решение удовлетворяет. Оказы-
вается, что совокупность соотношений (7) и (8) эквивалентна одному
соотношению
i
<р (0 = *0 + $/ (t, <F СО) dt. (9)
h
Докажем это. Допустим, что выполнено интегральное тождество
(9). Подставляя в него £=£0, получаем равенство (8), а дифферен-
цируя его по t, получаем тождество (7). Допустим теперь, что вы-
полнены соотношения (7) и (8). Интегрируя соотношение (7) в пре-
делах от до t и принимая во внимание соотношение (8), мы полу-
чаем соотношение (9).
Б) Пользуясь правой частью тождества (9), каждой векторной
функции <p(t), график которой проходит в множестве Г, поставим
в соответствие функцию ср*(/), положив:
t
Ф* (О = Хо-г \f(?, Ч-Ь)Ж (10)
Кратко, в операторной форме то же соотношение запишем в виде:
<р* = Лф. (11)
Уравнение (9) теперь может быть записано в виде:
<р=Лф- (12)
В) Пусть <р(£)—непрерывная векторная функция, заданная на от-
резке Определим норму jj<p || этой функции, положив:
М = шах [<р(0|.
§ 21] СЛУЧАЙ НОРМАЛЬНОЙ СИСТЕМЫ УРАВНЕНИЙ " ' 165
Пользуясь понятием нормы, можно формулировать определение равно-
мерной сходимости последовательности
Фо, <Рь ф/> ...
(13)
непрерывных векторных функций, заданных на отрезке rt t
Последовательность (13) векторных функций равномерно сходится
к непрерывной функции ср, заданной на том же отрезке r\^t
если
lim ||ф — <pf Ц = 0.
/-*00
Для того чтобы последовательность (13) равномерно сходилась, дос-
таточно, чтобы были выполнены неравенства
ЙФ.Ч1—
где числа а0, аь .ait ... образуют сходящийся ряд.
Перейдем теперь к доказательству теоремы 2.
Доказательство теоремы 2
Так как точка (£0, х0) = (^> х?, ...» х") принадлежит откры-
тому множеству Г, то существуют такие положительные числа q и а,
что все точки (6 X), удовлетворяющие условиям
|Z —Z0|sC<7, |Х — Хо|<а,
(14)
лежат в множестве Г. Так как множество П, состоящее из всех то-
чек (Л х), удовлетворяющих условиям (14), замкнуто и ограничено
(рис. 40), то непрерывные функции
|/(t х)| И 1^7^
' (JX
п,
ограничены на нем, т. е. существуют такие положительные числа Л1
и К> что
\f(t, х)\^М,
I дх'
I.
п> (15)
на множестве П,
Наряду с множеством П рассмотрим содержащееся в нем мно-
жество Пг, определяемое неравенствами
11 — tfi I г, |х — Хо I а,
где
r^q (16)’
166
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
[Гл. 4
(рис. 40). Обозначим через 2Г семейство всех непрерывных вектор-
ных функций, заданных на отрезке |f — f0|^r, графики которых
проходят в Пг. Таким образом, функция <р, определенная на отрезке
\t — £oj^r, тогда и только тогда принадлежит семейству 2Г, ксгда
для любого t> принадлежащего этому отрезку, выполнено неравенство
|ф(0 — Хо|<«. (17)
Постараемся выбрать теперь число г таким образом, чтобы были
выполнены следующие два условия:
а) Если функция ф принадлежит семейству то функция ф* =
= Дф (см. (10), (И)) также принадлежит семейству 2Г.
б) Существует такое число k, 0<^А<^1, что для любых двух
функций ф н х семейства имеет место неравенство
ДхИ^Н-Х!!- (18)
Рассмотрим условие а). Для того чтобы функция ф* — Дф при-
надлежала семейству Qri необходимо и достаточно, чтобы при
ft — было выполнено неравенство:
| <р* (0 — х01 < а.
В силу (10), (5) и (15) мы имеем:
t t
I Ф:;: (0 — X.; = j ф (0) dz | | $ \f(x, Ф (т)) I tZt ] < Mr.
to ' h
Из этого видно, что при
условие а) выполнено.
§ 21 ] СЛУЧАЙ НОРМАЛЬНОЙ СИСТЕМЫ УРАВНЕНИЙ 167
Рассмотрим теперь условие б). Мы имеем:
It* (0 - х* (О I = | {(/(^ Ф W) - х «)) I
to
t
< | $ \f(?, t «) - X (0) I dz |. (20)
/о
Оценим теперь последнее подынтегральное выражение, пользуясь не-
равенствами (6) и (15):
1/(т, ф (т)) - /е, х (т» к лч । w - х <*) I. (21)
Из (20) и (21) следует
II At — Ayr || =||t* — X* II =sS пгКг || ф — х ||
Таким образом, условие б) выполнено, если
' ' ' 'Ч^ц. (22)
где 1.
Итак, если число г удовлетворяет неравенствам (16), (19), (22)
(которые мы в дальнейшем будем считать выполненными), то для
семейства выполнены условия а) и б).
Построим теперь последовательность векторных функций
ф0(О = Хо, <pt(0, ..., <Pf(O, ...» (23)
определенных на отрезке |Z— Zo | г, положив
Ф»и = Лфг, Z=0, 1, ... (24)
Так как функция ф0 принадлежит семейству 2Г, то и все функции
последовательности (23) принадлежат этому же семейству (см. усло-
вие а)). Далее, мы имеем (см. (17)):
||ф1 —фо11= max |ф!(0 —X0|sga.
11 - Л) I < г
В силу (18) получаем:
Ифм -ф<11=М% — Аф;..11!^Мф/ — ф/-! II >
откуда
II Фм — Ф(11<йАг. .. (25)
Таким образом, в силу В) последовательность (23) равномерно схо-
дится к некоторой непрерывной функции ф, принадлежащей семей-
ству 2Г. Покажем, что функция ф удовлетворяет уравнению (12).
Для этого заметим, что последовательность
Лф0, Афр Лф^ ...
168
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
|Гл. 4
равномерно сходится к функции Лф; действительно, мы имеем
(см. (18)):
|| Лф - Лф/ !? k || ф - (fj || .
Переходя в соотношении (24) к пределу при I—*оо, получаем:
Ф=Лф.
Итак, существование решения х = ф(0 уравнения (3), удо-
влетворяющего начальному условию (8), доказано; при этом
установлено, что решение х = ф(0 определено на интервале
|/— I г» г$е г—произвольное число, удовлетворяющее неравен-
ствам (16), (19), (22).
Перейдем теперь к доказательству единственности. Пусть х — ф (О
и х = Х(0 — Ава Решения уравнения (3) с общими начальными зна-
чениями /0, л*0 н — интервал, являющийся пересечением
интервалов существования решений ф н у: очевидно, что г2.
Покажем, что если решения ф(/) и уд/) совпадают в некоторой точ-
ке /j интервала Г] <Д'й* 70 01111 совпадают и на некотором интер-
вале \i— /] |<^г, где г — достаточно малое положительное число.
Положим х|=^ф(/1) = у(/>); тогда величины Х\ могут быть при-
няты за начальные значения обоих решений х— ф(/) и х = у(/).
В этом смысле почка (/Е, ХЕ) ничем не отличается от точки (/у. лг0)
и потому мы сохраним за точкой (/Е, ХЕ) обозначение (tt)> ,г0); это
позволит нам сохранить и другие прежние обозначения. Переходя
от диффсреинналыюго уравнения (3) к интегральному уравнению (9),
мы получаем для обеих функции ф(?) и у(/) интегральные равенства,
которые tt операiорнон (Ьорме могут быть записаны в виде:
ф = Дф, у — Лу. (26)
Выберем теперь, как н прежде, в множестве Г множество II с цент-
ром в точке (/п, х0) (см. неравенства (Н)), содержащееся в Г,
а затем множество Пг таким образом, чтобы число г, кроме не-
равенств (16), (19), (22), удовлетворяло еще тому условию, что
при \t — /о''-уг функции ф и у определены и удовлетворяют нера-
венствам:
14(0 —А'о lz(0 — A-Ol<rt.
Это возможно, так как функции ф(/) и у(/) непрерывны. Тогда
функции ф(/) и /(/), рассматриваемые на отрезке 11 — вхо-
дят в семейство S2r н, следователи но, в силу неравенства (18) и
соотношений (26), получаем:
ГФ-хММЧ’- хО,
а это возможно только тогда, ког/ia |jф — у 1| = 0, т. е. когда
функции ф и у совладеют на отрезке |/—
§ 2Г1 СЛУЧАЙ НОРМАЛЬНОЙ СИСТЕМЫ'УРАВНЕНИЙ , - -169
Докажем теперь, что функции ф(£) и %(/) совпадают на всем
интервале Г1<^<^Г2. Допустим противоположное, именно, что суще-
ствует точка t* интервала <^г2, для которой ф(£*) #х(Н-
Ясно, что t* £0. Для определенности будем считать, что
Обозначим через N множество всех тех точек t отрезка
для которых ,ф(О —Х(0> и докажем, что множество N замкнуто.
В самом деле, пусть ть т2, ...—-последовательность точек множества
А/, сходящаяся к некоторой точке t. Тогда ф (т/) = х(т»)> и потому, в
ейлу непрерывности функций ф и /,
т|?(т)= Пт^(тг) = Ит х(^) = Х(тЬ
i —> со /—>оо
т. е. точка т также принадлежит множеству N.
Обозначим через ty точную верхнюю грань множества N, Так
как /V замкнуто, то принадлежит этому множеству, т. е. ф(^) =
= X(G); следовательно, 71 Но тогда, в силу ранее доказанного,
функции ф(0 и х(0 должны совпадать на некотором интервале
| / — | <^г, и точка G не может быть точной верхней гранью мно-
жества N. Таким образом, мы пришли к противоречию.
' Итак, теорема 2 доказана.
Выделим теперь в виде отдельного предложения некоторые фак-
ты, установленные при доказательстве теоремы 2 и нужные в дальнейшем:
Г) Предположим, что правые части системы (1) (или, в вектор-
ной форме, уравнения (3)) определены и непрерывны вместе со свои-
п гг
ми частными производными на открытом множестве 1. Пусть
(£0, ху)— некоторая точка множества Г, a q и а — такие положитель-
ные числа, что множество П, состоящее из всех точек, удовлетворя-
ющих неравенствам (14), содержится в Г. Пусть, далее, Л1 и К—та-
кие положительные числа, что для всех точек (t х), удовлетворяю-
щих неравенствам (14), выполнены неравенства (15). Пусть, наконец,
г—какое-либо положительное число, удовлетворяющее неравенствам
(16), (19), (22). Тогда решение уравнения (3) с начальными значения-
ми (tQf х0) определено на интервале \t —^0|<^г. Более того, оно ыа
отрезке \t — ^0|^г получается как предел последовательности функ-
ций (23), индуктивно заданных соотношением (24), причем для этих
функций выполнено неравенство (25).
Доказательство теоремы 3
Перейдем к доказательству теоремы 3, утверждающей, что для
нормальной линейной системы
п
' /=!,..„и, (27)
170 ТЕОРЕМЫ СУЩЕСТВОВАНИЯ (Гл. 4
коэффициенты aj(t) и свободные члены b'(t) которой определены и
непрерывны на интервале существует решение с произ-
вольными начальными значениями
^АД), *0» (28)
определенное па всем интервале Мы покажем, что тот
же самый оператор А (см. (10), (И)), применявшийся при доказатель-
стве теоремы 2, но построенный теперь при помощи правых частей
системы (27), порождает последовательность векторных функций
<Ро(О> Ф1(0> ф.(0> (29)
сходящуюся на всем интервале причем равномерно на
любом отрезке, содержащемся в этом интервале. При этом за <ро(0
можно принять произвольную непрерывную векторную функцию, за-
данную на интервале <?2- Для проведения метода последова-
тельных приближений нам здесь потребуется более точно оценить
числа — ф*II» / = 0, 1,2, ... При этом будет видно, что в
рассматриваемом случае метод последовательных приближений не ук-
ладывается в рамки метода сжатых отображений.
Пусть А— оператор, определенный соотношениями (10) и (И),
исходя из системы (27) дифференциальных уравнений и начальных
значений (28). Оператор А применим, очевидно, к любой непрерыв-
ной функции <p(f), определенной на интервале q\<^tИз пред-
ложения А) следует, что система (27) с начальными условиями (28)
равносильна операторному уравнению
ф = Дф, (30)
для которого мы и найдем решение, определенное на всем интервале
Функции последовательности (29), заданной индуктивным
соотпошен нем
ф.,1=Аф., / = 0, 1,2,..., (31)
определены на интервале q}<^t <^q^
Пусть — произвольный отрезок, содержащий внутри
себя точку и содержащийся в интервале так что
<7i <П<^<г‘2<72-
Покажем, что последовательность (29) равномерно сходится на отрез-
ке к решению уравнения (30). Для правых частей урав-
нений (27) мы имеем:
§211 СЛУЧАИ НОРМАЛЬНОЙ СИСТЕМЫ УРАВНЕНИИ ' 171
и потому при имеют место неравенства
'•/=’....
где К—некоторое положительное число. Так как функции ф,)(0 и
(pi (О ограничены на отрезке то на этом отрезке имеет
место неравенство
|ф1(0— ч>о
где С—некоторая константа. Далее, на том же отрезке мы полу-
чаем последовательно (см. (5) и (6)):
,|ф4(0 —Ф1(О|= ^(/(Х>Ф1(Х))~/(Х>Фо(Х)))Йт <
|/('с>ф1('с))— М;
I фз (0 — Ф-2 (0 I = ф2 W) — /(МР1 (т)))({х <
А» =с | j \f(.^ ф4 0)) —/(х< Ф1 (т)) 1dz ^0 к-1.11
t
1 ф<+1 (0 — Ф» (01 = J (/(ъф£ W) —/(х>Ф.-1 С)))й
^0 < | j |/(^. ф,- (*)) ф;-1 (0) 1d' ^0 1 f h 1 •
Отсюда получаем:
- п.-/> (п*К(г2-г^1 _
IIФ/+1 Ф/ II £ i
Так как числа С ~.г^ образуют сходящийся ряд, то по-
следовательность (29) равномерно сходится на отрезке к
некоторой непрерывной функции <р (t). Для этой функции мы имеем:
t
||Аф—Лф||^ max f |/(ъф,(х))— /(т> ф("))1л1^
^1г?К(Гъ — гОЦф,- — ф||
172 ТЕОРЕМЫ СУЩЕСТВОВАНИЯ [Гл. 4
так что последовательность функций
Аф1, ...» А<р;, ...
равномерно сходится к функции Aq> на отрезке Перехо-
дя к пределу в соотношении (31), мы получаем:
Так как есть произвольный отрезок, содержащий точ-
ку и содержащийся в интервале последовательность
(29) сходится в каждой точке интервала и потому функ-
ция q)(/) определена на всем интервале Qi<^t <^Qt и на всем этом ин-
тервале является решением уравнения (30).
Итак, теорема 3 доказана.
Пользуясь методом доказательства теоремы 3, установим нижесле-
дующее важное для дальнейшего предложение:
Д) Допустим, что заданная па отрезке непрерывная
(скалярная) функция и (t) удовлетворяет интегральному неравенству
t
и (/) $ (х и (т)-|- fl) dxt а^>0, Р^>0; (32)
to
оказывается тогда, что она удовлетворяет неравенству
п(/)^ — 1). (33)
Для доказательства предложения Д) рассмотрим наряду с интег-
ральным неравенство^^ (32) интегральное уравнение
t
v(i) = fav(i)-[-$)dx (34)
to
и покажем, что имеет место неравенство Для этого будем
решать интегральное уравнение (34) методом последовательных приб-
лижений. Так как подынтегральное выражение в (34) линейно относи-
тельно функции v(t), то последовательность приближений равномерно
сходится на всем отрезке (см. доказательство теоремы 3).
За исходную функцию при построении последовательных приближе-
ний примем функцию (£) = и (I). Далее положим:
?, 4 f (О = J (’ Л' (') + ?) (35)
to
Мы докажем индукцией по 1У что каждая функция и4-(^) удовлетворяет
интегральному неравенству
(0 Vi + Р) dx‘ Об)
to
§22] НЕПРОДОЛЖАЕМЫЕ РЕШЕНИЯ . 173
При / = 0 это неравенство верно, так как v9(t) = u(f) (см. (32)).
Допустим, что оно справедливо для функции ^-(0, и докажем его для
функции ^+|(0. В силу предположения индукции, мы имеем:
’ t
Vt+1 (О = (*) + ?) dz Vi (/).
Таким образом,
pi + 1(0^^(0- (37)
Поэтому, ввиду положительности числа а, мы получаем из (35):
t
+ Vi+, (t) + р) dx.
tn
Проведенная индукция доказывает неравенство (36); одновременно
установлено неравенство (37). Из этого следует, что предел v(tj
последовательности (/) = и (t)} хц(0, ..., (0» • • не меньше каждой из
функций Vi (0, и в частности v(t)^ u(t).
Теперь для завершения доказательства предложения Д) достаточно
Показать, что решение и(0 интегрального уравнения (34) совпадает
с правой частью неравенства (33). В силу предложения А) § 20
решение v (t) уравнения (34) совпадает с решением дифференциального
уравнения
. у (0 = a v (0 ?
при начальном условии р(/о) = О, т. е. с правой частью неравен-
ства (33), Таким образом, предложение Д) доказано.
§ 22. Непродолжаемые решения
В § 3 было введено понятие непродолжаемого решения (см. § 3, А)).
Зйёсь при помощи совершенно элементарных соображений из теоре-
mj»i 2 будет выведено, что каждое решение может быть продолжено до
решения, далее непродолжаемого (см. А)). В этом смысле непродол-
Жа'емые решения исчерпывают совокупность всех решений. Далее,
в''предложениях Б) и В) будет установлено одно важное свойство
пёпродолжаемых решений, которое найдет свои применения в следу-
ющих параграфах этой главы.
Пусть
'-1 X=f(t> X) (1)
— векторная запись нормальной системы уравнений (см. § 21, (1),
(&)), правые части которой определены и непрерывны вместе со сво-
df* ft х)
ими частными производными - на некотором открытом мно-
жестве Г пространства /? переменных х1, хп.
174 ТЕОРЕМЫ СУЩЕСТВОВАНИЯ [Гл. 4
А) 1) Существует непродолжаемое решение уравнения (1) с про-
извольными начальными значениями из Г.
2) Если некоторое непродолжаемое решение уравнения (I) сов-
падает с некоторым другим решением уравнения (I) хотя бы при
одном значении t, то оно является продолжением этого решения.
3) Если два непродолжаемых решения уравнения (1) совпадают
между собой хотя бы для одного значения t, то они полностью
совпадают, т. е. имеют один и тот же интервал определения и равны
на нем.
Докажем предложение А).
Пусть. (f0, Хо)— произвольная точка из Г. Построим такое ре-
шение х = <р(0 уравнения (1) с начальными значениями х0, что
оно является продолжением любого решения уравнения (1) с началь-
ными значениями х0.
Каждому решению уравнения (I) с начальными значениями х0
соответствует свой интервал определения. Множество всех правых
концов этих интервалов обозначим через а множество всех их
левых концов — через Точную верхнюю грань множества /?3
обозначим через тп% (в частности, может оказаться, что w2==oo), а
точную нижнюю грань множества обозначим через (в частнос-
ти, может оказаться, что Шу =— оо). Построим решение х = ф(£)
с начальными значениями /0, х0, определенное на интер-
вале nty t /п2. Пусть t* — произвольная точка этого интервала.
Допустим для определенности, что Так как есть точная
верхняя грань множества то существует решение х = 'ф(0 урав-
нения (1) с начальными значениями £0, х0, интервал определения ко-
торого содержит точку и мы положим ф(^*) = ф(£*). Получен-
ное значение функции ф в точке t* не зависит от случайно выбранного
решения х = ’ф(/). Действительно, если бы вместо решения х = ф(0
мы взяли решение х = %(0 с начальными значениями f0, и ин-
тервалом определения, также содержащим точку £*, то, в силу един-
ственности (см. теорему 2), мы имели бы ф(£*) = х(^*). Таким обра-
зом, функция ф(/) однозначно определена на всем интервале /И[<^
В то же время она является решением уравнения (1) с
начальными значениями t$, х0, так как вблизи каждой точки t* ин-
тервала ту t функция ф(£) совпадает, по построению, с не-
которым решением уравнения (I).
Пусть теперь х = ф(0—некоторое решение уравнения (1) с на-
чальными значениями tQ, х0, определенное на интервале
Тогда Гу — элемент множества а г2— элемент множества /?2, и
потому /TZi^ri, т. е. интервал Г1<^<^г2 содержится в ин-
тервале т{<^1 Так как решения ф(^) и ф(£) имеют одни и те
же начальные значения, то, в силу теоремы 2, они совпадают всюду,
§22] НЕПРОДО.ПЖЛПМЫЕ РЕШЕНИЯ 175
где они оба определены, т. е. на интервале t г2, а это и зна-
чит, что решение ф(0 является продолжением решения ф(/).
Построенное решение ф(/), очевидно, непродолжаемо. В самом
деле, пусть решение ф(0 является продолжением решения ф(/). Тогда
Zo, -^о можно Припять за начальные значения решения и, в силу
доказанного выше, решение ф(0 есть продолжение решения а
это значит, что решения <р(/) и ф(/) полностью совпадают. Из таких
же соображении следует, что q>(Z) есть единственное пепродолжаемое
решение с начальными значениями tQi х0.
Допустим теперь, что непродолжаемое решение ф(/) совпадает
с некоторым другим решением ф(Л хотя бы при одном значении I.
Обозначим это значение t через и положим ф(^) = ЛГо* Тогда
являются начальными значениями для непродолжаемого решения
9(0 и для решения ф(/). В силу доказанного выше, решение <р(/)
есть продолжение решения ф(/). Если решение ф(/) непродолжаемо,
то, в силу тех же соображений, оно является продолжением решения
ф(£), и потому решения ф(£) и ф(£) полностью совпадают.
Итак, предложение А) доказано.
Б) Пусть Е— замкнутое ограниченное множество пространства /?,
содержащееся в открытом множестве Г, и х = <р(0— некоторое ненро-
должаемое решение (см. А)) уравнения (1), определенное на интер-
вале Тогда существуют такие числа г{ и г2,
что точка (/, ф(0) пространства R находятся вне мно-
жества Е, когда t не принадлежит отрезку
Мы докажем лишь существование такого числа что при
г,<^t <^лт-> точка (/, ф(0) не принадлежит множеству Е. Существо-
вание числа Г1 доказывается аналогично. Если пг2 = оо, то существо-
вание числа г2 очевидно, так как при t, возрастающем до бесконеч-
ности, точка (/, ф(0), первая координата которой равна t} обязательно
должна покинуть ограниченное множество Е.
Будем считать поэтому, что /л2<^оо, и докажем существование
числа г?. При этом мы используем опенку числа г, данную в предло-
жен! hi Г) § 21. В пространстве R введем евклидову метрику. Так как
множество Е замкнуто и ограничено, а дополнение к открытому мно-
жеству 1' замкнуто, то расстояние р между множеством Е и допол-
нением к множеству Г (см. § 32, пример 3) положительно. Пусть
Е*— множество всех точек пространства R, расстояние которых до
мпожеС1ва Е не превосходит числа -1р. Тогда Е*— замкнутое огра-
ниченное множество, содержащееся в Г, так что правые части системы
(1) и их производные по /~1, ..., /г, определены на множестве
Е* и ограничены па нем. Таким образом, для любой точки (t7 X) из
176
•ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
[Гл. 1
£* выполнены неравенства
\f(t, x)|sSAi)|^JE)|5S/f( it 7—1,2, п, (2)
где М и Д'—некоторые положительные числа. Выберем два таких
положительных числа q и а, что Если (4, Хо)—неко-
торая точка множества Е и П — множество всех точек (t, X), удов-
летворяющих неравенствам I-V — Хо а, то, очевидно,
множество П содержится в Е*, и потому для всех точек (t> х) мно-
жества П выполнены неравенства (2)- Таким образом, если число г
удовлетворяет неравенствам (16), (19/, (22) § 21, то существует ре-
шение х = ф(0 уравнения (1) с начальными значениями t0, х0, опре-
деленное на интервале |£ — 4КГ- Здесь важно лишь то, что найден-
ное число г является одним и тем же для всех точек (4>; Хп)
множества Е. Покажем, что за г4 можно принять число — г. До-
пустим противное, т. е. что при некотором 4^>/zzs— г точка (4, ф(4))
лежит в множестве Е. Тогда мы можем принять величины 4 и ф(4)
за начальные значения решения х = ф(0 и, в силу сказанного выше,
интервал р — 4|<СГ должен содержаться в интервале пгх <^t т.^
Но это противоречит неравенству 4^>,zzi— г- Таким образом, пред-
ложение Б) доказано.
Для автономной системы имеет место предложение В), анало-
гичное предложению Б) и непосредственно из него вытекающее. Пусть
X=f(X) (3)
— векторная запись автономной системы уравнений, правые части
которых непрерывны вместе с их частными производными но х1, .хп
в некотором открытом множестве А пространства S переменных
х\ ..., хп.
В) Пусть F—замкнутое ограниченное множество пространства
целиком расположенное в А, и х = ф(О—некоторое пснродолжае-
мое решение уравнения (3) с интервалом определения
Если <сю, то существует такое число гъ чго при 4
принадлежащем интервалу r^<^t точка ф(/) находится вне
множества F. Точно так же, если — оо, то существует такое
число гь <^Ti что при 4 принадлежащем интервалу
<^П, точка ф(0 находится вне множества F.
При доказательстве предложения В) будем рассматривать лишь
случай т.г сю и установим существование числа г2. В пространстве R
всех точек (4 X), где х — точка из S, определим открытое множе-
ство Г, состоящее из всех точек (4 х), где t—произвольное число,
а X — точка множества А. Далее, пусть w — некоторое число, удов-
летворяющее условию //?1 т /«г. Обозначим через Е множество,
§22]
НЕП^ОДОЛЖАЕМЫЕ РЕШЕНИЯ
177
состоящее из веек точек (?, X), где а х—точка множе-
ства F. Очевидно, множество Е замкнуто, ограничено и содержится
б Г. В силу предложения Б), существует такое число что при t,
принадлежащем интервалу г.2 t /п.>, точка (t, ф(0) не принадле-
жит множеству Е. Очевидно, мы можем выбрать число г3 так, чтобы
Это условие выполнялось и чтобы, кроме того, было /?г<^г2. Тогда
при выполнены неравенства и, следовательно,
точка (t, q> (/))> У которой r$<^t <^//z.2, может не принадлежать мно-
жеству Е лишь благодаря тому, что точка q>(f) не принадлежит мно-
жеству F. Таким образом, предложение В) доказано.
Примеры
1. Для иллюстрации результатов этого параграфа рассмотрим
автономное уравнение первого порядка:
где f(x)— многочлен, все корни которого действительные и простые.
Пусть аъ аъ .ап—их запись в возрастающем порядке. Фазовым
пространством уравнения (4) является прямая Р, а открытым мно-
жеством Д для него служит совокупность всех точек прямой Р, за
исключением ..., atv так как в них правая часть уравнения (4)
обращается в бесконечность. Положим:
X
О
Тогда совокупность всех решений уравнения (4) описывается соотно-
шением
F (x)~t А- с.
Так как в автономном уравнении сдвиг времени на константу не ме-
няет траектории, то совокупность всех траекторий уравнения (4)
гкмесге с описанием движения по ним точки х(/) дается соотношением
/•(Л-) = t.
Рассмотрим движение точки x(t) по интервалу <\v <^а2. Так как
f(x) сохраняет знак на интервале Л|<^х<^а2, то F(at) ф F(a^), Для
определенности будем считать, что
= F (а2Х uh — Р («Д
Легко видеть, что в то время, когда t пробегает интервал
точка x(t) пробегает интервал Отсюда видно, что х(7)
есть непродолжаемое решение с интервалом определения
Здесь оба конца этого интервала конечны; это объясняется тем, что
17(8 ТЕОРГ.МЫ СУЩЕСТВОВАНИЯ IT.-!. 4
при подходе к концам интервала времени тг <^1 //г2 точка х{1)
подходит к граничным точкам области А.
2. Предложение Б) в некотором смысле отвечает на вопрос, по-
чему интервал определения продолжаемого решения может оказаться
ограниченным справа ил?; слеш. Последим за поведением иепродол-
жаемого решения X—- .у(/), ограничиваясь для простоты случаем,
когда множество Г огпшшчено. Границу множества Г обозначим че-
рез (7.
Пусть //Zj<^/7?2 •—интервал определения непродолжаемого ре-
шешгя х~ф(/). Так как множество Г ограничено, то оба числа
и ///-2 отличны от -но?. Покажем, что при t -н> т* расстояние точки
(t, (р (0) от множества О стремится к нулю. Пусть s—произвольное
положительное число и Et— совокупность всех точек множества Г,
расстояние которых до множества G больше или равно е. Легко до-
казывается, что множество /\ замкнуто в R и ограничено. В силу
предложения Б) существует такое число что при r$<^t
точка (f, <р(0) не принадлежит множеству Et и, следовательно, ее
расстояние до множества G меньше е. Таким образом, при
расстояние точки (t <р(0) ДО множества G стремится к нулю. При-
ближение точки (t <р(0) при f—>7/7.2 к границе О множества Г н
является причиной того, что решение х = <р(0 не может быть про-
должено га правый конец /?л2 интервала его определения.
§ 23. Непрерывная зависимость решения от начальных
значений и параметров
Учитывая зависимость решения заданной системы уравнений от
начальных значений этого решения, мы приходим к решению как
функции от независимого переменного и начальных значений. Различ-
ные свойства этой функция многих переменных имеют важное значе-
ние. Здесь будет доказана непрерывность этой функция ио сово-
купности переменных. Доказательство непрерывной зависимости реше-
ния от начальных значений будет сведено к теореме о непрерывной
зависимости решения при фиксированных начальных значениях от
параметров, непрерывно входящих в правые части системы. Эта
теорема будет доказана в первую очередь.
Непрерывная зависимость решения
от параметров
Мы будем рассматривать нормальную систему уравнений:
xl —fl (t, A'1, ..., хп, u1, ..., р/), I — 1, ..., и, (1)
правые части шдсрых зависят от параметров р.1, ..., р/ и определе-
ны в некотором открытом множестве Г пространства R переменных
§ 23]
НЕПРЕРЫВНАЯ ЗАВИСИМОСТЬ ОТ НАЧАЛЬНЫХ ЗНАЧЕНИИ
.179
Л х1, ...» х", pi1, ...» рЛ Будет предполагаться, что правые части
системы (1) и их частные производные
-да. W-1.............». т
по переменным х1, ..., х71 являются в Г непрерывными функциями со-
вокупности всех переменных. Полагая
Х = (х‘, ..., х"); p = .... п/>.
f(t, X, X, JLl), X, р)),
мы запишем систему (!) в векторной форме:
X=f(t> X, р).
(3)
А) Точку. пространства R будем обозначать через (/, х, р). За-
фиксируем начальные значения Zo, х0 и обозначим через /И совокуп-
ность всех таких р, что точка (/0, х0, р) принадлежит множеству Г*
Очевидно, что М является открытым множеством в пространстве
переменных р1, рЛ Каждой точке р множества Л1 соответствует
непродолжаемое решение <р(0 р) с начальными значениями /0, х0 урав-
нения (3), определенное на интервале т} (р) I /д.> (р) (см. § 22, А)),
который, очевидно, может зависеть от р, что и выражено в обо-
значениях. Множество Т всех пар t, р> для которых функция ф(/, р)
определена, описывается, очевидно, условиями; точка р принадлежит
множеству Л4, а число t удовлетворяет при этом неравенствам Wi(p)<\
t ЯЦ (р).
Теорема 13. Множество Т всех пар /, р, на которых опре-
делена функция ф(С р), являющаяся при каждом фиксированном р
непродолжаемым решением уравнения (3) с начальными значения-
ми Хо, представляет собой открытое множество прост-
ранства переменных Z, р1, ..., р/. Далее оказывается, что функ-
ция ф(С р) есть непрерывная функция пары переменных р на
множестве Т.
Следует обратить внимание на нетривиальнссть и важность того
факта, что множество Т является открытым.
Доказательство. Пусть /*, р*— произвольная точка мно-
жества Т. Докажем, что точка t, р, достаточно близкая к точке /*, р*,
принадлежит множеству Т и что разность ф(/, р)— ф(/*, р*) мала.
Этим теорема будет доказана.
Сначала мы будем считать, что t*^t^ Так как решение ф(С р*)
определено при t = t*, то /*<^яг3(р*), и потому существует такое
число г2, что г*<^г2<^/л2(р*), так что решение ф(С р*) определено
л частности на всем отрезке tQ Когда число t пробегает
отрезок точка (t, ф(£, р.*), р*) описывает в пространстве
180
„ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
[Гл. 4
R некоторую кривую Q. Пусть а и b — два положительных числа.
Обозначим через П совокупность всех точек (t, х> ц) пространства
R, удовлетворяющих условиям:
|х — <р(£, !н — (4)
Из того, что Q представляет собой замкнутое ограниченное множе-
ство, содержащееся в открытом множестве Г, следует существование
таких положительных чисел а и Z?, что множество П также содер-
жится в: Г. В дальнейшем мы будем считать, что числа а и b удовлет-
воряют этому условию. Так как производные (2) непрерывны и по-
тому ограничены по модулю некоторым числом К на множестве
II, то, в силу неравенства (6) § 21, для точек (t Хъ fl), {7, х$, И)
множества П выполнено соотношение
J/(i, Х.2, Х|, Ю1 =<П^|Х4 — Х,|. (5)
Далее, из равномерной непрерывности (см. § 32, И)) функции f(t} х, р)
па множестве 11 следует существование такой монотонной положи-
тельной функции р2(е) положительного переменного е, стремящейся
к нулю вместе с е, что для точек (Л х, ц*), (Z, х, ц) множества П
выполнено соотношение
\f(t, х, Н)— f(t, х, Ц*)><р4|м, —ц*|)- (6)
Пусть теперь х = <р(/, ц), | ц - - ц* | b — решение уравнения (3)
с начальными значениями (f0, х0). В силу предложения Б) § 22 точка
(I, <р(/, |д), ц) должна покинуть замкнутое множество II при t -> 7?л2(|и).
Через мы обозначим то значение 1> при котором точка (t> <р(/, ц), ц)
впервые достигает границы множества П. Очевидно, что до-
дадим оценку разности |<р(£, ц)—<р(£, ц*)! на отрезке
Для этого запишем уравнение (3) в интегральной форме (см. § 21, А))
для значений параметра ц и g* и вычтем второе интегральное со-
отношение из первого; мы получим:
t
y(t, ц) —<р(Г, Ц*) = $(/(т, ц), ю—7(т, <р(т, ц*)> Н*))<Л
to
Оценим разность, стоящую справа под знаком интеграла. Мы имеем:
1Л< Ф(т, ц), ц)—/(т, <р(т, ц*)( ц*)| < |/(т, q>(t, и), Н) —
—f^> н*)> юж/е, ж i1*)- н)— /(^ <₽е> н*)> н*)|.
Первое из слагаемых, стоящих в правой части, оценивается в силу
неравенства (5), рторое — в силу неравенства. (б); объединяя эгн
§ 23]
НЕПРЕРЫВНАЯ ЗАВИСИМОСТЬ ОТ НАЧАЛЬНЫХ ЗНАЧЕНИИ
Ш
олешси, получаем:
t
1ф(*> Ц) — ф(£, Ц*)| Ю —<р(т, Ц*)1+МН —
h
Полагая и (0 = | ф (t, р) — ф(б р*)|, мы, в силу предложения Д) § 21,
получаем при t t
|ф«, р)-ф(f, («««-'•> - 0^
< ?’li^y'l' i - l) = c,₽,(| Ц - (< I, (7)
Пусть р2 — положительное число, удовлетворяющее неравенствам*
[>^Ь, (8)
^М?2)<«- (9)
В Дальнейшем будем считать, что р удовлетворяет неравенству
|н — |**|<р4, • (Ю)
и покажем, что f2 = r2, так что решение ф(£, ц) определено на всем
отрезке
Так как точка ц), р), по предположению, лежит на гра-
нице множества П, то для этой точки одно из неравенств (4) должно
переходить в точное равенство. В силу неравенств (8), (10), имеем
| р ,— p:i:|<^- Далее, в силу неравенств (\10), (9) и (7), имеем
|ф(Л2, р)—ф(£2, Ц*)1<СЯ- Так как, наконец, то из всех пе-
равенств (4) в равенство может переходить лишь неравенство
п потому мы имеем /2 = г2.
Таким образом, доказано, что при существуют такое чис-
ло и такое положительное число р.2, что при t{} <zt га и
|p— Ц*|<СРй точка Ц) принадлежит множеству Т и выполнено
неравенство (7).
Аналогично доказывается, что при существуют такое чис-
ло г. О* и такое положительное число ph что при Г\^1-^Лъ и
| р— pi точка (t, р) принадлежит множеству Т и выполнено
неравенство
1ф(^> и)—<p(t к’Ч), (п)
аналогичное неравенству (7).
Из сказанного следует, что если точка (/*, р*) принадлежит мно-
жеству Ту то, каково бы ни было расположение точки t* относитель-
но t0, всегда существуют такие положительные числа г и р, что при
|^-f*|<r, |р-р*|<.р, (12)
точка (/, р) принадлежит множеству Т и имеет место неравенство
|ф(С ц) — ф(6 Н*)|<сР(|ц — м*1)- (13>
182
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
[Гл. 4
Так как совокупность всех точек (t, g), удовлетворяющих условию (12),
составляет окрестность точки (£*, р,*), то Т есть открытое множество.
Докажем теперь, что функция ф(£, р) непрерывна в точке р:|:).
Для этого оценим разность <р (Л р) — ф(£*, [!*). Мы имеем:
1ф(6 ц) —Ф(^, р*) I^|<p(t, ц) —ф(*> Р*)| +
+ l«p(f. Ю —ф(^*> р,*)!-
Первое из слагаемых, стоящих в правой части, мало, когда мало
число |р — р*| (см. (13)). Второе из слагаемых мало, когда малым
является число \t — i* |, в силу непрерывности функции <р(£» р*)
переменного t. Таким образом, ф(/, р) есть непрерывная функция
пары переменных Л р.
Итак, теорема 13 доказана.
Непрерывная зависимость решения
от начальных значений
Теперь мы будем рассматривать нормальную систему уравнений:
хг=/'(^, х!, ..., х”), /=1, ...» л, (14)
правые части которых определены и непрерывны вместе со своими
частными производными
4^., I, /=1.........п, (15)
dxJ* ’ J ’ ’ ’ 1 ’
на некотором открытом множестве Г пространства переменных
t, х!, хп. Пусть
X=f(t, X) (16)
— векторная запись системы (14).
Б) Каждой точке ('с, g) множества Г соответствует непродолжаемсе
решение <p(G т, g) уравнения (16) с начальными значениями ^=г,
х0 = g, определенное на интервале /л1 (т, g) t /л2 (х> I) (см- § 22, А)),
который зависит от начальных значений т, g. Множество S всех то-
чек (/, т, |) пространства переменных Л т, 51, для которых
функция ф(/, т, g) определена, описывается, очевидно, условиями:
точка g принадлежит множеству Г, а число t удовлетворяет при
эю.м неравенствам Ш|(", gX/<Cj^(-:, !)•
Теорема 14. Множество S всех точек (tf ч, g), на кото-
рых определена функция ф(Л т, g), являющаяся непродолжаемым
решением уравнения (16) с начальными значениями т, g, есть откры-
тое множество в пространстве переменных Л т, \п. Далее
оказывается, что функция (p(t, т, g) непрерывна по совокупности
всех своих аргументов на множестве S.
§ 23 J НЕПРЕРЫВНАЯ ЗАВИСИМОСТЬ ОТ НАЧАЛЬНЫХ ЗНАЧЕНИЙ 183,
Конструкция, излагаемая в нижеследующем предложении В), де-
лает эту теорему непосредственным следствием теоремы 13.
В) Пусть (т, g)—произвольная точка множества Г. Вместо не-
зависимого переменного t, имеющегося в уравнении (16), введем
новое независимое переменное 5 по формуле
f = T + (17)
Вместо неизвестной векторной функции х, имеющейся в уравнении
(16), введем новую неизвестную векторную функцию у по формуле
х=Ч+у (18)
В новых переменных уравнение (16) запишется следующим образом:
аз)
Так как функция f(t, х) переменных t, х определена на открытом
множестве Г, то функция
g(s, У, !)=/(<: 4-3, g-4-.у) (20)
переменных s, у, т, g определена при условии, что точка (т-^s, g-j-jr)
принадлежит множеству Г. Это условие, как легко видеть, выделяет
в пространстве R переменных s, у т, g некоторое открытое мно-
жество Г, и на этом множестве векторная функция (20) непрерывна,
а ее компоненты имеют непрерывные частные производные по пе-
ременным у\ Будем считать, что величины т, g являются
параметрами в уравнении (19), и пусть
-У = 44- t, g) (21)
— непродолжаемое решение уравнения (19) (см. § 22, А)) с фикси-
рованными начальными значениями s — 0, у = 0, т. е. решение, удов-
летворяющее начальным условиям
Ш t, |)=0. ' (22)
Переходя к старым переменным по формулам (17) и (18), мы полу-
чим функцию
х=ф(^, t, = г g), (23)
являющуюся, как показывает непосредственная проверка, решением
уравнения (16), удовлетворяющим начальному условию
<р(т, т, £) = |.
Из того, что решение (21) непродолжаемо, следует, что решение (23)
также непродолжаемо, так как если бы решение (23) можно было
продолжить, то можно было бы продолжить и решение (21).
184 ТЕОРЕМЫ СУЩЕСТВОВАНИЯ (Гл. 4
Доказательство теоремы 14. Предложение В) сводит изу-
чение зависимости решения от начальных значений к изучению зави-
симости решения (при фиксированных начальных значениях)
от параметров, входящих в правую часть уравнения. Это изучение
было осуществлено в теореме 13. В силу этой теоремы, непродол-
жаемое решение у = ф($, т, |) уравнения (19), содержащего в правой
части параметры т, взятое при фиксированных начальных значениях
s0 = 0, = 0, определено на некотором открытом множестве Т в прост-
ранстве переменных s, т, | и непрерывно на этом множестве по
совокупности всех своих аргументов. Непродолжаемое решение
х = ф(/, т, |) уравнения (16) с начальными значениями т, | выра-
жается через решение у — ф($, т, |) по формуле (23). Переход от
аргументов $, т, £ функции ф к аргументам t, т, | функции ф осу-
ществляется формулами
/ = т, т=т, | = (24)
Это преобразование пространства переменных s, т, | в пространство
переменных /, т, | является аффинным и потому переводит открытое
множество 7, на котором определена функция ф, в некоторое открытое
множество на котором определена функция <р (см. § 32, пример 1).
Таким образом, множество S всех точек (t, т, |), на котором опре-
делена функция ф, является открытым в пространстве переменных
т, Непрерывность функции ф следует из непрерывности функции ф,
в силу формулы перехода (23). Таким образом, теорема 14 доказана.
Теоремы 13 и 14 могут быть объединены в одну:
Теорема 15. Пусть х = ф(£, т, jw) — непродолжаемое ре-
шение уравнения (3) с начальными значениями т, Тогда функция
ф(/, т. р.) определена на некотором открытом множестве
пространства переменных /, т, |, р. и непрерывна на нем.
Эта теорема доказывается так же, как теорема 14,— путем заме-
ны переменных (17), (18) и последующей ссылки на теорему 13.
Следствия теорем 13 и 14
Теоремы 13 и 14 представляют собой несколько необычно сфор-
мулированные интегральные теоремы непрерывности.
Приведенные здесь формулировки интегральных теорем непрерыв-
ности (теоремы 13 и 14) являются новыми; они существенно отличаются
от формулировок, имевшихся до сих пор в математической литера-
туре. Нижеследующие предложения Г) и Д) являются прямыми след-
ствиями теорем 13 и 14. Эти предложения по своим формулиров-
кам ближе к обычным формулировкам интегральных теорем непре-
рывности. Следует, однако, отметить, что формулировки теорем 13
и 14 наиболее полно охватывают факты, относящиеся к Непрерывной
зависимости решений от параметров и начальных значений. Предло-
жение Г) по существу было установлено в процессе доказательства
§ ,2(1.1 ДИФФЕРЕНЦИРУЕМОСТЬ ПО НАЧАЛЬНЫМ ЗНАЧЕНИЯМ - 185
теоремы 13, но здесь оно выводится из самой теоремы 13, чтобы
подчеркнуть полноту ее содержания.
Г) Если решение <р (Л р) уравнения (1) с начальными значениями
А'о при р = р* определено на отрезке содержащем
(это означает, что отрезок содержится в интервале опреде-
ления решения <р (Л р*)), то существует такое положительное число
р, что при !р— р*|<^р непродолжаемое решение ф (t, р) с началь-
ными условиями tQl Xq также определено на отрезке Далее,
для всякого положительного е найдется такое положительное £<^р,
что при |р— р* имеем |ф(7, р)— ф(£, р*)|<^£.
При доказательстве этого предложения используем теорему 13.
Так как множество Т всех пар t, р, на котором определена функция
ф (t, р), огкрыто, а точки (гь р*) и (г2, р*) принадлежат ему, то
существует настолько малое положительное число р, что при
| р — р* | р точки.(гьр) и (г2, р) принадлежат множеству 7’. Это
'значит, что интервал определения непродолжаемого решения ф (/, р)
содержит весь отрезок т. е. решение ф (/, р) определено
на этом отрезке. Множество Р всех точек (f, р), для которых
| р—р* | р, замкнуто, ограничено и расположено в 7'.
Так как Р содержится в 7', а функция ф (/, р) непрерывна на 7, то
сна равномерно непрерывна на Р. Отсюда непосредственно вытекает
правильность второй части предложения Г).
Д) Если решение ф (t, |) = ф (t, f0, |) уравнения (16) с началь-
ными значениями f0, | при | = определено на отрезке
содержащем то существует такое положительное число р, что при
|| —Xol^Cp непродолжаемое решение ф (t, |) также определено на
отрезке Далее, для всякого положительного е найдется
такое положительное 8<^р, что при Г1^^^г2 || — имеем:
1чД, I) — <ЦЛ -Vo) |<е.
Предложение Д) выводится из теоремы 14 точно так же, как
предложение Г) из теоремы 13.
§ 24. Дифференцируемость решения по начальным
значениям и параметрам
В предыдущем параграфе была доказана непрерывность решения
по начальным значениям и параметрам. Здесь будет установлено, что
в некоторых предположениях решение дифференцируемо по началь-
ным значениям и параметрам.
Так же как в предыдущем параграфе, сначала мы рассмотрим
дифференцируемость решения по параметрам, а затем на основе по-
лученных результатов при помощи конструкции, данной в предло-
жении В) § 23, докажем дифференцируемость решения по начальным
значениям..
186
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
[Гл. 4
Дифференцируемость по параметрам
Мы будем рассматривать такую же систему дифференциальных
уравнений
х1,..., хл, Ji1,..,,|?), (1)
как и в § 23; правые части ее определены и непрерывны вместе
dfl
с их частными производными в некотором открытом множестве
Г пространства 7? переменных t> х1,..., хл, р.1,..., рА Пусть
х, н) (2)
— векторная запись системы (1).
Доказательство дифференцируемости решений по параметрам
р1,р* будет проведено в предположении, что правые части си-
стемы (1) непрерывно дифференцируемы по этим параметрам в от-
крытом множестве Г.
Доказательству дифференцируемости мы предпошлем предложе-
ние А), называемое обычно леммой Адамара.
А) Пусть g tp, zz1,..., п9) — функция p-\-q переменных,
определенная в области А пространства этих переменных, выпуклой
относительно переменных zz1,zz9. Полагая
ip), « = (!?„..., ZZ9),
мы сможем записать ее как функцию g(tt и) двух векторов. Будем
предполагать, что во всей области своего определения функция
g(tt и) и ее частные производные , у=1,..., q, непрерывны.
Оказывается тогда, что для любой пары точек (£, (/, с оди-
наковой координатой t из области А имеет место соотношение
я
g{t> Ut) — g(t, 5 hj(t} «.,)(«/—z;{), (3)
7=1
где функции hj(tt д2), у = 1,определены и непрерывны для
всех указанных значений аргументов t, ul9 д2 (в частности, и при
совпадении «, = «3), причем hj(t9 и, и) = ^ g(tt и).
Для доказательства предложения А) положим:
&($) = Hl 4~ «1), (4)
Мы имеем тогда
1
g(t, u^—gif, u^ = g(t, w(l)) — gif, w(0)) = ^ git, w(.<?)) ds.
0
§ 24] ДИФФЕРЕНЦИРУЕМОСТЬ ПО НАЧАЛЬНЫМ ЗНАЧЕНИЯМ 187 '
Вычислим теперь производную (s)); мы имеем:
U о
fsg(t,w GO) = ~ g(t, W1 (S),..., w'1 ($)) ==
2dg(t,w(s)) dwJ (s)
dwJ ds
Так как, в силу (4), очевидно, имеем:
то, полагая еще
О
мы получаем формулу (3). Так как, по предположению, функции
непрерывны, то функции hj (f, й2) также непрерывны.
Таким образом, предложение А) доказано.
Теорема 16. В силу теоремы 13 непродолжаемое решение
ф(/,= ц),<?”(tp.)) уравнения (2) при фиксированных
начальных значениях t9, х0 определено на некотором открытом
множестве Т пространства переменных t, р.1,р/ и является
непрерывной функцией всех своих аргументов. Оказывается,
что если частные производные правых частей системы (1)
по аргументам а1, ...,р/ определены и непрерывны в открытом
множестве Г, то частные производные
Z= А=1..............ц
определены и непрерывны на всем открытом множестве Т.
Кроме того, смешанные частные производные
-&Г »'<*.»* 1=1............»;*=!....I.
определены, непрерывны и не зависят от порядка дифференци-
рования на всем множестве Т.
Доказательство. Для нахождения производной мы вы-
числим разность ср' ft, ц2) — ср' (/, jij). Так как функция ф(£, ц) удо-
влетворяет уравнению (2), то вычисление этой разности естественно
связано с вычислением разности
Pl)-
188
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
[Гл 4
Последнюю разность мы вычислим с помощью леммы Адамара, счи-
тая при этом, что
f = U = (X, р.), g(t, U)=f(t, Xt Jl).
Для того чтобы применить лемму Адамара к этому случаю, прежде
всего подходящим образом выделим открытое множество А в про-
странстве переменных (Л — х, р), выпуклое по паре перемен-
ных х, р. При этом мы будем иметь своей целью доказательство
существования и непрерывности производных в окрестности произ-
вольной точки (l*t р,*) множества Т. Перейдем к построению откры-
того множества А.
Так как решение ф(/, р*) определено при t = t*, то существу-
ет такой отрезок содержащий числа и t* внутри себя
(т. е. что решение ф(/, р*) определено
па этом отрезке. Когда t пробегает отрезок точка
(£, ф(/, р*), р*) описывает в открытом множестве Г непрерывную
кривую. Пусть а и b — два таких положительных числа, что множе-
ство всех точек (f, х, pj, удовлетворяющих условиям ,
|х — <p(i, Р*)|<а, |ц —(5)
целиком содержится в открытом множестве Г. В силу предложения
О § 23 существует такое положительное число р, что 2р<^£
и при , р— Ц*|<С2р решение ф (t, р) определено нт всем отрезке
и па том же отрезке выполнено неравенство | ф (/, р) —
— Ф (t И*) I <С а- Открытое множество А определим теперь как сово-
купность всех т)чек (t, х, р), удовлетворяющих условиям
Г1<3<4>, I-V—<р(^>
|Р — Ц*|<2р.
Очевидно, что открытое множество А выпукло по ларе переменных (х, |д).
Для вычисления производной —j- обозначим через еь единичный
вектор /-мерного пространства, направленный по /г-й оси. Пусть pt—
некоторый вектор, удовлетворяющий условию ' ит —
число, удовлетворяющее условию Положим р2 = -j- xeft.
Тогда оба вектора р[ и р3 удовлетворяют условию
I — J1* | < 2 р, | — Ц* | < 2 р.
Поэтому па всем отрезке Г]^/^г2 имеют место неравенства
|q>(t Ц1) — <p(f, |л*)|<а, |<р(6 ц2) — ф(Л р*)|<Л
Таким образом, когда t пробегает интервал точки
(/, ф(/, Р(), рО и (/, ф(/, р2), р2) описывают кривые, целиком располо-
женное в открытом множестве А. Применяя лемму Адамара к раз-
ности
/'С Ч>С> ЦД Рг)— /'С- ф((. Ц1)< 14).
I 24.1
ДИФФЕРЕНЦИРУЕМОСТЬ ПО НАЧАЛЬНЫМ ЗНАЧЕНИЯМ
189
мы получим:
Гр, <р(/, Цй), Ий)—/(t ф(*> И1)> И1) =
п
=2 т) (</(*> ^)—И1)) +
j= I
i
+ S А п + * <*’ т) — !л*>- (6)
А = 1
Здесь функции Л*, у=1, л-|-Д непрерывно зависят в силу лем-
мы Адамара от величин t, ф(/, Hi)> Нь Ф(А На), На и, следовательно,
в конечном итоге, от величин /, Иь т (так как Цй = М'1Ч“тел> а ве-
личины yij) и <р(Л и2) непрерывно зависят от Л fij и /, цй;
см. теорему 13).
Для вычисления производной
ду1
~д^
нужно,
очевидно, составить
предварительное частное
(f, И1) = 0(
и перейти в нем к пределу при т—>0.
Подставляя в систему (1) ее решения х = ф(£, Hi) и Х = ф(/, цй)
й вычитая первое соотношение из второго, мы получаем, в силу (6):
п
у hj (t И1 И1 t)4.
(✓6 Jtaw
/ = I
л44-Л(^, F*!, т), 1=1, (7)
Эти соотношения верны при
Г1<*<Г2, |Р1 — H*i<p, |т|<р, t^O.
Таким образом, функции
<Р‘(6 ц1; т), (/, ftp т) (8)
при т ф 0 удовлетворяют линейной системе дифференциальных урав-
нений
’ п
= + И1, ^) (9)
/=1
с начальными условиями
ф‘До> Ц1> т) = Иг)—у'(<<" М1) — ~-x” = 0.
В то время как функции ф'(6 ц1? т), определены
лишь при х 0, сама система уравнений (9) определена и при т = 0,
190 ТЕОРЕМЫ СУЩЕСТВОВАНИЯ [Гл. 4
причем правые части ее заданы и непрерывны на открытом множе-
стве, которое описывается неравенствами
|Ц1 — и*|<р, |х|<р. (10)
Так как система (9) линейна, то в силу теорем 3 и 13 эта система
имеет решение
М'ь 4 •••> y"=xn(t> Pi> ’) (И)
с начальными значениями 0, определенное и непрерывное на всем
открытом множестве (10). Согласно теореме единственности (теорема 2),
па всем открытом множестве (10) при т^0 справедливы равенства
Y(t, р„ т) = /(Л ц1( Т), л.
Но правые части равенств (11) определены и непрерывны на всем
открытом множестве (10), включая и значения т —0. Поэтому, пере-
ходя в равенствах (И) к пределу при т->0, мы получаем:
.^‘(Л Р() T)=Iimz.^t Ц1( Х) = х«(^ ц1; 0). (12)
О/л* т—»0 т->0
Так как правая часть этого равенства определена и непрерывна на
открытом множестве
П<^<г2, |И1 —P-*i<P> (13)
dv' (tt р.])
то на всем этом открытом множестве частная производная т * г •
определена и непрерывна. В частности, она определена и непрерывна
в некоторой окрестности точки (Р, р.*).
Так как, далее, функции у1=2£1(1} 0), /=1, л, удовлет-
воряют системе дифференциальных уравнений (9) при т = 0, то этой
же системе уравнений удовлетворяют и функции
z п
у ад '
Таким образом, все эти функции на открытом множестве (13) обла-
дают непрерывными частными производными по t. Иначе говоря, на
открытом множестве (13) существует и непрерывна смешанная про-
изводная
Подставляя в систему (1) ее решение xl = r/(f, цД Z = nf
заведомо определеннее на открытом множестве (13), мы получаем:
R). (15)
§ 24] ДИФФЕРЕНЦИРУЕМОСТЬ ПО НАЧАЛЬНЫМ ЗНАЧЕНИЯМ 191
Так как функции ^(f,j%i), 7=1,...,л, в силу доказанного имеют не-
прерывные частные производные по |л* на всем открытом множе-
стве (13), а правые части системы (1) имеют непрерывные производ-
ные по переменным х1, ..., хп, у.1, р/, то правые части соотноше-
ний (15) имеют непрерывные частные производные по р.* на всем,
открытом множестве (13). Таким образом, и левые части соотноше-
ний (15) имеют непрерывные частные производные
д
ф*
\ di j
• (16)
на открытом множестве (13).
Итак, обе частные производные (14) и (16) непрерывны на откры-
том множестве (13), а потому в силу известной теоремы анализа они
совпадают между собой на этом множестве.
Так как точка (£*, ц*) принадлежит открытому множеству (13),
то доказательство теоремы 16 этим полностью завершено.
Дифференцируемость по начальным значениям
Мы будем рассматривать ту же самую систему дифференциальных
уравнений
х1, хл), /=1, л, (17)
что и в § 23 (см. § 23, формула (14)), правые части которой опреде-
лены и непрерывны вместе с их частными производными на неко-
тором открытом множестве Г пространства переменных tt х1, хп.
Пусть
X =f{t, X) (18)
— векторная запись системы (17).
В отличие от § 23, мы будем считать переменным лишь начальное
значение £ неизвестной функции х, а начальное значение т перемен-
ного t зафиксируем, положив т = £0. Дифференцируемость решения
по т в дальнейшем не используется, а для того, чтобы она имела место,
система (17) должна удовлетворять дополнительным условиям (непре-
рывная дифференцируемость правых частей по t).
Теорема 17. Пусть
q (t, t* £)=<p (t, I)=(?'(t, I),..., <?n (t, £))
— не продолжав мое решение уравнения (18) с начальными значе-
ниями tQj £. Из теоремы 14 непосредственно следует, что
функция <р (t, £) определена и непрерывна на некотором откры-
том множестве Sf в пространстве переменных t1, ..., £n.
192
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
[Гл. 4
Оказывается, что на всем множестве S' существуют и непре-
рывны частные производные
fe'OL.- i /—1 п.
кроме того, на этом множестве непрерывны и не зависят от
порядка дифференцирования смешанные частные производные
Доказательство. Конструкция, данная в предложении В)
§ 23, сводит доказательство к теореме 16. Так как правая часть
уравнения (19) § 23 имеет непрерывные частные производные по
всем переменным у\ ...» уп, Е1, то, в силу теоремы 16, част-
ные производные
функций ф1 (см. § 23, В)) определены и непрерывны на всем откры-
том множестве 5' и на нем же непрерывны и не зависят от порядка
дифференцирования смешанные частные производные
Далее, так как решение ф(/, £) = ф(6^о, 1) определяется через ре-
шение ф(/, |) по формуле (23) § 23 при т = то из найденных
свойств функции (/, t{], |) вытекают соответствующие свойства
функций (/, |), указанные в формулировке теоремы 17.
Теоремы 16 и 17 могут быть объединены в одну:
Теорема 18. Предположим, что правые части системы (1)
на всем открытом множестве Г имеют непрерывные производ-
ные по параметрам. рД Д. Пусть
ф</. i .“)=(?'и, I. м). .... I- н))
— непродояжаемое решение уравнения (2) с начальными зна-
чениями |. Тогда функция ф (t, р) определена на неко-
тором открытом множестве Г пространства переменных t,
р и непрерывна на нем (см. теорему 15). Оказывается, что част-
ные производные
я/—- — /, у—1, и, л—1,
определены и непрерывны на всем открытом множестве Г. Кроме
того, смешанные частные производные
д~^(Т I, р) d-f(t, р)
dt dg/ ’ dt d[j.k
§24] ДИФФЕРЕНЦИРУЕМОСТЬ ПО НАЧАЛЬНЫМ ЗНАЧЕНИЯМ ' 193
определены, непрерывны и не зависят от порядка дифференциро-
вания на всем множестве Г.
Эта теорема доказывается так же, как теорема 17,— путем за-
мены переменных (17), (18) § 23 (при т = г0) и последующей ссылки
на теорему 16.
Уравнения в вариациях
Иногда бывает нужно получить некоторые сведения о производ-
ных решения <р(/, р,) уравнения (2) по параметрам р? при фиксиро-
ванном значении р, = рА Оказывается, что для этого нет надобности
искать решение ф(£, Ji) уравнения (2) при переменном р, и затем
дифференцировать его по р?, а можно получить эти сведения из рас-
смотрения некоторой системы линейных дифференциальных уравне-
ний. Аналогично обстоит дело и с изучением производных решения
ф& Б) уравнения (18) по начальным значениям при фиксирован-
ном | = Хо.
Б) Пусть р) = (ср’(^ р,)> .cp"(f, р,)) — непродолжаемое ре-
шение уравнения (2) с начальными значениями tQ, xQt и пусть
— интервал его определения при фиксированном вйаче-
df*
нии р=р*. Если частные производные правых частей системы
(1) непрерывны в области Г, то, в силу теоремы 16, частные произ-
водные
вычисленные при р = р*, определены и непрерывны как функции t
на всем интервале пц t т* Положим:
/«о, х, и); /;(0=/;(^. <рФ ц*). цч
g‘k(t, X, ц*), Ц*)_
В силу теоремы 13, функции /((/) и g'k (t) переменного t определены
и непрерывны на всем интервале m^<^t <^т^. Система линейных
уравнений
п
+ (19)
j=1
определенная на интервале называется системой урав-
нений в вариациях (по параметрам) для системы (1) при
р. = |ц*. Оказывается, что система функций
/ = ф'(0> .... / = Ф-?Ф (20)
7 Понтрягин Л. С.'
194
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
(Гл. 4
является решением системы уравнений (19) при начальных усло-
виях
^(Q = 0. (21)
Для доказательства предложения Б) подставим в систему (1) ее
решение x^(p(Z, g). Мы получим тождество
Ф('- rtM). (22)
В силу теоремы 16 обе части этого тождества имеют производную
по у? при ц = JA*, определенную на всем интервале тх<^1
причем
д ду* (it ц) д (t, ц)
d(ift dt dt d\j.k
Дифференцируя тождество (22) по у? при g = мы, в силу
сказанного, видим, что функции (20) составляют решения системы (19).
Для получения начального условия (21) достаточно продифференци-
ровать по |хЛ начальные условия
<Р*(Ч» g) = xj.
Таким образом, предложение Б) доказано.
В) Пусть <р (£, |) = (<р! (/, £),..., <рп(/, £))—пепродолжаемое ре-
шение уравнения (18) с начальными значениями g и ntx t /тг2 —
интервал его определения при фиксированном значении g = x0. В силу
теоремы 17 частные производные
АГ0)= ф'(0.
вычисленные при g = x0, определены и непрерывны как функции t
на всем интервале тх <Z t <Z Mi- Положим
f‘(t, = Ф(л x„)).
J IMJ J '
Функции/<(0 переменного t определены на всем интервале wi<3<C//z2-
Система линейных уравнений
п
У1= X (23)
j -- 1
определенная на интервале тх t пгъ называется системой
уравнений в вариациях (по начальным значениям) для си-
стемы (17) при начальных значениях ti)t xti. Оказывается, что система
функций
У1-?)(<).... yn = ^(t) (24)
$ 241 ДИФФЕРЕНЦИРУЕМОСТЬ ПО НАЧАЛЬНЫМ ЗНАЧЕНИЯМ 195
является решением системы уравнений (23) при начальных условиях
Ф)(Ы = 8', (25)
где В* = 0 при z /, a 8j= 1.
Тот факт, что система функций (24) составляет решение линей-
ной системы (23), доказывается точно так же, как в предложении Б), —
и последую-
Нячальные
путеда подстановки в систему (17) решения х = ф(£, |) i
п его дифференцирования полученного тождества по
условия (25) получаются из
дифференцированием их по
начальных условий
с.
Примеры
1. Пусть
я1 = /' (X1,
xn)=f‘(x), 1 = 1,
(2в)
— автономная система дифференциальных уравнений и
Х=/(Х)
(27)
— ее векторная запись. Пусть, далее, а = (а\ .ап) — положение
равновесия этой системы (см. § 15), так что — 0 и система
функций х1=а11 хп = ап составляет решение системы (26), Ре-
шение уравнения (27) с начальными значениями 0, £ обозначим через
ф(/, ® = |)).
Вычислим производные
а) = Ц(1) (28)
от функций с/ (t, |), вычисленные при | = п, пользуясь предложе-
нием В).
Функции
' A1’ dxf ai
являются в этом случае константами. Таким образом, система урав-
нений в вариациях (23) в данном случае есть линейная однородная
синема с постоянными коэффициентами
п
У = 2 «'Z (29)
/ = |
и производные (28), являющиеся решениями системы (29), легко мо-
гут быть найдены в то время как решение ф(/, |) при переменном
найти, вообще говоря, трудно.
7*
198 ТЕОРЕМЫ СУЩЕСТВОВАНИЯ ГГл. 4
Система уравнений в вариациях (29) играет важную роль для
мучения поведения решений уравнения (27) вблизи положения рав-
новесия а, как это мы увидим в следующей главе. Там, однако, си-
стема (29) появляется не как система уравнений в вариациях, а как
линеаризация системы (26) вблизи положения равновесия а, Линеари-
вация системы (26) осуществляется следующим образом: вместо не-
известных функций х1, хп вводятся новые неизвестные функции
8хх, ..., 6хл
по формулам
х1 = а1 + 8х*, г=1, п. (ВО)
Производя в системе (26) замену переменных (30) и разлагая правые
части в ряды Тейлора по новым неизвестным функциям 8х\ .Sx71,
мы получим:
А8^=/‘(а)+£ ^8x'+... = S ар-к'Н--... (81)
/«I ;=1
где не выписаны члены второго порядка малости относительно вели-
чины 8хг.
Линеаризуя систему (31), т. е. сохраняя в ней лишь линейные
члены, мы получим систему уравнений, совпадающую с системой (29).
§ 25. Первые интегралы
Здесь будет дано понятие о первых интегралах и решена краевая
вадача для линейных уравнений в частных производных.
Первые интегралы
Пусть
х1=Р(х\ х71), i=\t пу (1)
—нормальная автономная система уравнений, правые части которой
вместе с нх частными производными определены и непрерывны на
некотором открытом множестве А пространства переменных х1,... , xnt
и пусть
x=f(x) (2)
— векторная запись этой системы.
А) Функция
и(х\ хп) = и(х),
определенная и непрерывная вместе со своими частными производ-
ными на некотором открытом множестве О, содержащемся в А, на-
вывается первым интегралом системы (1), если при подстановке в
$25]
ПЕРВЫЕ ИНТЕГРАЛЫ
-197
нее произвольного решения х=ф(/) уравнения (2), траектория ко-
торого целиком расположена в множестве G, мы получаем постоян-
ную относительно t величину, т. е. функция п(ф(0) зависит только
от выбора решения ф (£), но не от переменной t. Оказывается, что
любой первый интеграл и(х) системы (1) удовлетворяет условию
п
i = I
ди (х)
дх*
f‘(x) = 0
(3)
и что, обратно, всякая функция и (х), удовлетворяющая условию (3),
является первым интегралом системы (1).
Докажем, что первый интеграл и(х) системы (1) удовлетворяет
условию (3). Пусть | — произвольная точка множества G и х = ф (/, —
решение уравнения (2) с начальными значениями 0, Мы имеем;
п
о=-/,»«р«. 8»|,_0=2s>7'®
f = I
так как £ — произвольная точка из G, то соотношение (3) выполнено
на множестве G.
Допустим теперь, что для функции п(х) выполнено соотноше-
ние (3), и пусть х — ф(0 — произвольнее решение уравнения (2),
траектория которого лежит в Q. Подставляя х — ф(/) в функцию
zz(x), мы получим некоторую функцию
тф) = и(ф (0)-
Днффе; енцируя эту функцию по t, получаем:
п
т=2 /«(<>)=о.
i = 1
Таким образом, «(ф(0) не зависит от t.
В дальнейшем изучение первых интегралов системы (1) будет
проводиться чисто локально в некоторой окрестности точки а от-
крытого множества Д, не являющейся положением равновесия си-
стемы (1):
(4)
Б) Первые интегралы
г/1 (х), ...» uk(x)
системы (1), определенные в некоторой окрестности точки а (см. (4)),
называются независк/.:ыми в точке а или просто независимыми,
если функциональная матрица
198
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
(Гл. 4
имеет ранг k. Оказывается, что в некоторой окрестности точен а
(см. (4)) существуют л—1 независимых первых интегралов системы
уравиедай (Ц
Докажем это. Так как вектор/(а) отличен от нуля, то отлична
©г муля хотя бы одна из его компонент. Будем считать, что
/Ча)^0.
ПУСТЬ £ (V, ...,ГЛ в») — точка, близкая к точке а, и х = ф(Ц) —
решение уравнения (2) с начальными значениями 0, В координат-
мой форме решение это можно записать в виде:
д«=<р'(<л‘,е"-1), /=1, (б)
Будем рассматривать эту систему сооотношений как систему уравне-
ний относительно неизвестных
t. (6)
При = I — 1, п, эта система уравнений имеет очевидное
решение V = a1, $rt~1 = art~1, £ = 0, и функциональный опреде-
литель системы (5) отличен от пуля в этой точке.
В самом деле,
Т*’(0, V, 5Л-1) = ^, z = l, ...» п~ 1,
(О, V, £Л’1) = аЛ,
ж потому
„<У (0..Л1. -u gn~') = ?/ I = 1
д& P * *
•^V(0, a\ .... a'1-1) =fn (а) Ф 0.
n\ j= 1, ..., n— 1;
(7)
Отсюда видно, что интересующий нас функциональный определитель
Отличен от нуля. Таким образом, существует такая окрестность Q
точки а, что при х, принадлежащих О, система уравнений (5) разре-
шима относитеаьпо неизвестных (6) (см. § 33) и решение записывается
в виде:
V—-д’ (х), = цп~1 (х), t — v(x). (8)
Покажем, что функции
iP (х), ..., ип~1 (х), (9)
входящие в эти соотношения, являются первыми интегралами систе-
мы (1), и притом независимыми в точке а. Функциональная матрица
системы (5) найдена (см. (7)); из ее вида легко следует, что функ-
ш.чщльная .’кпрцна
I 25}
ПЕРВЫЕ ИНТЕГРАЛЫ
199
является единичной, и потому функции (9) независимы. Покажем,
что они являются первыми интегралами системы (1). Для этого до-
статочно доказать, что при подстановке в функция (9) любого ре-
шения х = ф(£) уравнения (2) они превращаются в величины, но за-
висящие от t. Так как система (8) является обращением системы (В),
то функции (9) удовлетворяют тождествам
«'(<₽(^)) = V, (10)
(см. § 33, пример 1). Таким образом, при подстановке в функция (9)
решения х = ф(^, £) мы получаем величины, не зависящие от £
Пусть теперь х = ф(/)— произвольное решение уравнения (1),
проходящее в окрестности О. Пусть tQt xQ — его начальные значения,
причем х0 принадлежит G. Так как система (5) разрешима при Х^=Х^
то существует решение х = ф(^> |0), проходящее через точку х* и
потому решение ф (/) может быть записано в виде:
<р(0 = ф(г-Н> Ь),
где с—константа (см. § 15, Б)). Таким образом, при подстановке
х— ф(/) в функцию и1 (х) получаем, в силу (10):
п'(<₽(0)= «'(?('-К &,)) = !•', Z=1...... п~\.
Итак, предложение Б) доказано.
В) Пусть
н1 (х), .пл”! (х) (11)
— независимые в точке а первые интегралы системы уравнений (1),
причем
и1 (а) = bl, I = 1, ..п — 1; Ь = (Ь\ ..., Ьп~1)}
и пусть w(x) — некоторый первый интеграл системы (1), опреде-
ленный в окрестности точки а. Существует тогда такая функция
Wfy1, •••> определенная на некоторой окрестности точки b
пространства переменных у1, .у*1’1, что имеет место тождество
w(x)= (х), ип~' (х)) (12)
на некоторой окрестности точки а.
Докажем это. В силу А), первые интегралы п1(х), ...» гС”1 (х),
w(x) удовлетворяют соотношениям
V^g<l/'« = 0, /=|.......»-1;
Таким образом, эти первые интегралы зависимы (см. (4)). В то же
время первые интегралы (11) независимы. Отсюда, в силу известной
200
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
(Гл. 4
теоремы анализа (см. § 33, пример 2), следует существование функ-
ции Wz, для которой выполнено соотношение (12).
Если нам известны некоторые первые интегралы системы (1), то
тем самым решение системы (1) облегчается. Точно это обстоятель-
ство формулируется в нижеследующем предложении:
Г) Пусть
п'г11 (х), ...» п"(х) (13)
— система из п — k независимых в точке а (см. Б)) первых инте-
гралов автономной системы уравнений (1). Пользуясь функциями (13),
можно понизить порядок системы уравнений (1) на п — k единиц,
т. е. заменить ее автономной системой порядка А; в частности, когда
имеется максимальное число п—1 независимых первых интегралов,
порядок автономной системы (1) можно свести до первого и, следо-
вательно (см. § 2, пример 1), решить ее в квадратурах.
Докажем предложение Г)- Так как первые интегралы (13) незави-
симы, то в функциональной матрице
• г ! 1 .1
—г—Д i = k 4- I, ..., п: 1 = 1, ..., п.
\ dxj ) ’
имеется квадратная матрица порядка п — k с отличным от нуля де-
терминантом. Будем считать для определенности, что отличен от нуля
детерминант матрицы
Uo- I, J = k-y\, п.
Пользуясь этим, введем в окрестности точки а новые координаты
у‘.....уп 0 4)
вместо прежних
X1, ..., хп,
положив
/ = Ух* = г?+1(х), уп = Пп(х). (15)
Этими формулами действительно вводятся новые координаты j*1, ..., уп,
так как функциональный определитель системы соотношений (15)
отличен от нуля в окрестности точки а (см. § 33). В повой системе
переменных (14) система (1) примет вид:
у'= i>l(yl, ..., уп), i=l, п. (16)
Но так как каждая функция (13) удовлетворяет условию (3), то мы
будем иметь при l = k-4 1, ..., п\
п
, d i< i V ди1 (X) г ( ,
у = и' (х1, ..., х") = ' - 7 (xj = 0.
- /Ж UAJ
/ — I
§ 23] ПЕРВЫЕ ИНТЕГРАЛЫ 201
Таким образом,
?+,Су)=о, ^(j) = 0.
Ввиду этого система (16) фактически оказывается автономной систе-
мой порядка k.
Линейное уравнение в частных производных
первого порядка
Соотношение (3) можно рассматривать как уравнение в частных
производных относительно неизвестной функции и (х) переменных
х1, .х\ В предложениях Б) и В) установлено, что при /(а)^0
в окрестности точки а существуют п— 1 независимых решений этого
уравнения и что, имея п—1 независимых решений его, можно полу*
чить всякое другое при помощи формулы (12). При этом ясно, что
всякая функция, задаваемая формулой (12), является решением урав-
нения (3). В этом смысле'можно считать, что уравнение (3) решенц
именно, показано, что, умея решать систему (1), мы тем самым умеем
решать и уравнение (3). Можно, однако, подойти к решению урав-
нения (3) с другой точки зрения, а именно можно поставить и решить
краевую задачу для уравнения (3) и даже для уравнения, более общего
чем (3).
Д) Пусть
п
2(x) SF (х-п) (17)
— уравнение в частных производных относительно неизвестной функ-
ции и(х), где F (Ху и)— некоторая заданная функция, имеющая не-
прерывные производные первого порядка по всем своим аргументам.
Пусть, далее,
x = .... (18)
— заданная в векторной форме параметрическая запись некоторой
поверхности размерности п—1, проходящей через точку а при
t* =.,. = tn~l = 0, так что
|(0, 0) = а.
Мы будем предполагать, что поверхность (18) дифференцируема и в
точке а не касается вектора f (а), т. е. векторы
....(19)
линейно независимы. Пусть, наконец,
М'1. .... tn i) (20)
202
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
[Гл. 4
— некоторая функция, заданная на поверхности (18). Оказывается,
что в окрестности точки а существует, и притом единственное, реше-
ние п(х) уравнения (17), совпадающее на поверхности (18) с заданной
функцией (20), так что
^)) = М^ ...»tn~l>
Для нахождения решения и(х) используются траектории системы (1),
начинающиеся на поверхности (18). Эти траектории называются харак-
теристиками уравнения (17).
Докажем предложение Д). Для этого введем в окрестности точки а
фазового пространства системы (1) новые координаты вместо коорди-
нат х1, хп. Пусть х = ср(£, ..., /л“!) — решение уравнения (2),
начинающееся в точке |(Р, ..., f1’1) поверхности (18), т, е. решение
с начальными значениями 0, £(Д, ..., f1’1).
Мы имеем тогда систему соотношений
= t\ tn '\ i = l, n, (21)
правые части которых имеют непрерывные частные производные по
переменным t, t\ ..., f1-1 (см. теорему 17). Если считать в ней не-
известными величинами переменные
t, ...» tn~\ (22)
то система эта при х — а имеет очевидное решение
и функциональный определитель ее не обращается в нуль в этой
точке, как это следует из линейной независимости векторов (19).
В самом деле, ср(0, ..., 1п 1) = £(/1, tn ’), и потому частит!
производная ср (0, .
> 0) равна -^1 (0, .
., 0); далее, гр (0,..., 0)--
—f(a). Таким образом, система соотношений (21) дает возможность
ввести в некоторой окрестности точки а вместо координат лл, ..., хп
новые координаты (22) (см. § 33). В этих новых координатах урав-
нение (17) записывается особенно просто, и легко может быть решена
поставленная в предложении Д) краевая задача. Пусть и(х)— неко-
торая функция, определенная в окрестности точки а. Подставим в пей
вместо переменных лл, ,хп переменные (22) по формулам (21);
тогда мы получим функцию
v (t, /*, tn '):=u(q(t, Г'1)).
Мы имеем:
tl, ...,
ct
yi ди (x) н
dxt '
ПЕРВЫЕ ИНТЕГРАЛЫ
203 '
§ 25]
где х = ср(7, /л-1). Таким образом, в переменных (22) уравне-
ние (17) получает вид:
dv(t, =F(ф (<> ti, " v(t> ti""t (23)
Так как поверхность (18) в координатах (22) задается уравнением
t = 0, то нам следует найти решение уравнения (23), обращающееся
в заданную функцию п0(^, •••> tn~x) при # = 0. Для нахождения та-
кого решения следует решить уравнение (23), считая его обыкновен-
ным дифференциальным уравнением с независимым переменным t, а
переменные 1\ ..., tn^ — параметрами. При этом следует искать реше-
ния с начальными значениями
О, п0(Л Г"’).
Получающаяся функция v(tf t\ .f1-1), в силу теоремы 18, имеет
непрерывные производные по всем переменным.
Этим краевая задача, поставленная в Д), решена.
Замечание. Пусть
xl=fl(ty хл) (24)
— неавтономная система дифференциальных уравнений. Для того чтобы
ввести понятие первого интеграла этой системы, преобразуем ее в авто-
номную систему, введя дополнительную неизвестную функцию
xn^ = t.
Тогда система (24), дополненная уравнением
xTi'ri — 1,
будет автономной; ее первые интегралы считают первыми интегралами
системы (24).
П р и у е р
Пусть
Н= Н(х\ Xй; У* ...» Уп) = АЯх, У) (25)
— функция двух систем нерешенных. Система обыкновенных диффе-
ренциальных уравнений:
х^Щх,у), ?.И(х Л (2б)
называется гамильтоновой системой, а функция Н(х, у)— гамиль-
тоновой функцией этой системы. Непосредственно проверяется, что
функция (25) является первым интегралом системы (26).
ГЛАВА ПЯТАЯ
УСТОЙЧИВОСТЬ
Работа очень многих механических, электрических и другого типа
устройств (машин, приборов и т. п.) описывается системами обыкно-
венных дифференциальных уравнений. Система обыкновенных диффе-
ренциальных уравнений имеет всегда бесконечное множество решений,
и для задания одного определенного решения нужно указать его на-
чальные значения. Между тем употребляемые в практике устройства
обычно работают на вполне определенном режиме, и в их работе, во
всяком случае на первый взгляд, невозможно обнаружить наличия бес-
конечного множества режимов работы, соответствующих различным
решениям системы уравнений. Это может объясниться либо тем, что
начальные значения решения при запуске устройства выбираются
каким-то определенным образом, либо тем, что начальные значения при
продолжительной работе прибора утрачивают свое влияние, и устрой-
ство само стабилизирует свою работу на стационарном решении.
С последним явлением мы уже сталкивались, когда разбирали работу
электрических цепей. Приведем еще один пример. Стенные часы идут
с совершенно определенным размахом маятника, хотя при запуске их
маятник можно отклонить от вертикального положения более или
менее сильно. Если при запуске часов маятник отклонить не доста-
точно сильно, то после небольшого числа колебаний он остановится.
Если же отклонение достаточно велико, то через короткое время
амплитуда колебаний маятника станет вполне определенной, и часы
будут идти с этой амплитудой колебаний неопределенно долго, прак-
тически бесконечно долго. Таким образом, у системы уравнений, описы-
вающей работу часов, имеются два стационарных решения: положение
равновесия, соответствующее отсутствию хода, и периодическое реше-
ние, соответствующее нормальному ходу часов. Всякое другое решение,
а этих решений, несомненно, имеется бесконечное множество, очень
быстро приближается к одному из этих двух стационарных и по исте-
чении некоторого времени становится практически не отличимым от
него. Каждое из отмеченных двух стационарных решений является
§ 26] ТЕОРЕМА ЛЯПУНОВА 205
в некотором смысле устойчивым. Это значит, что если мы берем не
стационарное решение, а решение, отклоняющееся от стационарного
в начальный момент и притом не слишком сильно, то взятое нестацио-
нарное решение приближается к стационарному. Таково не вполне
точно формулированное определение устойчивости решения. На этом
же примере видно, что фазовое пространство системы уравнений, опи-
сывающей работу часов, распадается на две области притяжения.
Если взять начальное значение в одной из областей, то решение будет
стремиться к положению равновесия; если взять начальные значения
в другой области, то решение будет стремиться к периодическому
решению.
Из сказанного уже видно, что для полного понимания работы
какого-либо устройства желательно иметь хорошее представление
о фазовом пространстве системы уравнений, описывающей работу
этого устройства. При этом важнее всего знать все устойчивые
решения этой системы уравнений.
Из теоремы о непрерывной зависимости решения от начальных
значений (см. § 23) мы уже знаем, что если задаться определенным
конечным промежутком времени, то при достаточно малом откло-
нении начальных значений решение отклонится мало на всем заданном
промежутке времени, но это свойство решения вовсе не означает
устойчивости. Когда речь идет об устойчивости, отклонение на не-
определенно большом отрезке времени должно быть малым,
если только отклонение начальных значений мало.
Настоящая глава в основном посвящена проблеме устойчивости
положений равновесия и периодических решений.
В нее включены также два важных приложения к техническим
задачам: излагаются исследование Вышнеградского о работе паровой
машины с регулятором Уатта и исследование Андропова о работе
лампового генератора электрических незатухающих колебаний. Пер-
вое из ^этих исследований явилось основополагающим в теории ав-
томатического регулирования, второе — в теории нелинейных ко-
лебаний.
В § 30 проводится исследование поведения траекторий вблизи
положений равновесия автономной системы второго порядка, что не
толпе относится к проблеме устойчивости. Этот параграф по своей
трудности несколько превосходит средний уровень книги. Еше более
трудным по своему содержанию является последний параграф этой
главы (§ 31).
§ 26. Теорема Ляпунова
Здесь будут даны понятие устойчивости по Ляпунову и достаточ-
ные условия устойчивости применительно к положению равновесия
автономной системы (см. § 15).
208
устотмвость
tn 5
Устойчивость положения равновесия
Пусть
..., Хп), 1=*Л.........................п (1)
— нормальная автономная система, и
x=f(x) (2)
— ее векторная запись. Относительно функций
/‘(х1, ..., Xя), I— 1, ..., п (3)
мы будем предполагать, что они определены и имеют непрерывные
частные производные первого порядка па некотором открытом мно-
жестве А пространства переменных х1, .хп. В дальнейшем при уста-
новлении критерия устойчивости требования дифференцируемости
будут усилены: именно, будет предполагаться, что функции (3) имеют
на множестве А непрерывные частные производные второго порядка.
Не давая формального определения устойчивости по Ляпунову,
постараюсь прежде всего выразить идею устойчивости. Положение
равновесия а = (а\ ..., ап) уравнения (2) следует считать устой-
чивым, если всякое решение уравнения (2), исходящее при£ = 0 из
точки, достаточно ^близкой к а, остается в течение всего дальнейшего
своего изменения (т. е. при ^^>0) вблизи точки а. Физический смысл
устойчивости ясен. Физический объект (например, какая-либо машина),
движения которого управляются уравнением (2), может находиться
в положении равновесия а лишь тогда, когда это положение равно-
весия устойчиво, так как в противном случае ничтожное отклонение
от положения равновесия, вызванное случайным толчком, может повлечь
уход объекта далеко от положения равновесия.
Ниже через <р |) будет обозначаться решение уравнения (2)
с начальными значениями i — 0, х = так что ф(/, §) есть векторная
функция скалярного переменного t и векторного переменного |, удовле-
творяющая условию
(4)
Определение. Положение равновесия а уравнения (2) назы-
вается устойчивым по Ляпунову, если 1) существует настолько малое
положительное число р, что при || — а | р решение ср (^, |) уравне-
ния (2) определено для всех положительных t\ 2) для всякого поло-
жительного числа г найдется такое положительное число В<^р, что
при i | ид:еем |Ч>(А при всех *>0. Устойчивое
по /Ляпунову положение равновесия а уравнения (2) называется асимп-
§ 26] ТЕОРЕМА ЛЯПУНОВА 207
тотпчески устойчивым, если 3) существует настолько малое поло-
жительное число о<^р, что при 1g — а|<^« имеем:
lim I cp(t, — а| = 0.
/ —► 4" СО
Дадим прежде всего достаточные условия устойчивости положена»
равновесия для линейной однородной системы с постоянными коэф-
фициентами:
А) Пусть
Я— Ах (в)
— линейное однородное уравнение с постоянными коэффициентами,
взятое в векторной записи. Решение его с начальными значениями
О, g обозначим через ф(/, £). Если все собственные значения матрицы А
имеют отрицательные действительные части, то существуют така*
положительные числа а и г, что выполнено неравенство
IW (в)
Из неравенства (6) непосредственно следует, что положение равно-
весия х = 0 уравнения (5) является устойчивым по Ляпунову и асимп-
тотически устойчивым.
Докажем неравенство (6). Положим:
Л=(ар; L (р) = (а' — р8‘).
Тогда, пользуясь символом дифференцирования р (см. § 7), урав-
нение (о) в скалярной форме можно записать в виде системы
п
^lL‘(p)x) = 0, Z=1.......п. (7)
/ = I
Пусть ЛЦ(р) — минор элемента и.(р) матрицы L(p), взятый с надле-
жащим знаком, так что выполнено тождество
л
2 M^p)L‘(p) = ^D(p),
i ® 1
где D(p)— детерминант матрицы L(p). Умножая соотношение (7) на
многочлен М%(р) и суммируя полученное соотношение по /, получаеж
;; п п
О — 2 2 M’:(p)L’(p)xJ^ V V.D(p)x
i -- I / I / = 1
Таким образом, если
208
УСТОЙЧИВОСТЬ
[Пт. 5
— некоторое решение уравнения (5), то каждая функция х* удовле-
творяет дифференциальному уравнению
D (р) х! = 0.
Так как все корни многочлена D(p) по предположению имеют отри-
цательные действительные части, то (см. § 9, А)) для функции х1
выполнено неравенство
\х*\^е~а‘> Z= 1, п;
где R и а — положительные числа, не зависящие от номера L Из этого
неравенства следует неравенство
Re~at (f^O).
Последнее неравенство уже было доказано ранее (см. § И, Б)) в более
общих предположениях; здесь это доказательство проведено заново.
Пусть — единичный координатный вектор номера Z, так что
е£ = (0, 1, 0),
где единица стоит на Z-м месте. Пусть, далее, (^)— решение уравне-
ния (5) с начальным значением так что
фх(0) = ^, /=1, т
Тогда решение *ф(/, |) уравнения (5) с начальным значением
1 = ......П
очевидно, запишется в виде:
п
£)=£*ч>г(о. (8)
i = I
Так как для каждого решения фДО выполнено неравенство
Re^
то для решения ф(^, |), очевидно, выполнено неравенство (6).
Устойчивость по Ляпунову положения равновесия х = 0 непосред-
ственно вытекает из неравенства (6). Действительно, если в — заданное
положительное число, то достаточно принять за В число ™. Асимп-
тотическая устойчивость также вытекает нз неравенства (6),
Функция Ляпунова
При установлении критерия устойчивости положения равновесия
нелинейной системы (1) пользуются так называемым дифферен-
цированием в силу системы уравнений; дифференцирование это
находит применения не только при доказательстве теоремы Ляпунова.
§ 26]
ТЕОРЕМА ЛЯПУНОВА
'209
Б) Пусть
F(x\ xn) — F(x)
— некоторая дифференцируемая функция переменных х1,...» xnt опре-
деленная на множестве А, Ее производная по t в силу системы урав-
нений (1) в точке х = (х\ .хп) определяется следующим образом.
Пусть <р(/) — решение уравнения (2), удовлетворяющее при некотором
значении t = t§ начальному условию:
<Р(*о)=Х-
Производная
Л1, w
в силу системы (1) определяется формулой
или в силу формулы полной производной
п
i = I
Из формулы (9) видно, что (х) не зависит от решения <р(0»
а однозначно определяется выбором точки х.
Докажем теперь одно свойство автономной системы.
В) Решение автономного уравнения (2) с начальными значениями
0, £ по-прежнему будем обозначать через <р (£> £). Оказывается, что
функция ср (/» удовлетворяет тождеству
ф(/, Ш|)) = <р(^, I). (10)
Докажем формулу (10). Положим:
П = I), (Н)
где s — фиксированное число, и рассмотрим решение
<Р1 (0 = <р(^ П)
уравнения (2). Так как <р(£, |) есть решение уравнения (2), то в силу
автономности этого уравнения (см, § 15, А)) решением является и
функция <р2(0, определяемая соотношением:
фз (t) = ф (t 4- s, g).
Мы имеем, таким образом, два решения cpj (t) и q>2(f) уравнения (2),
Далее,
<Р1(0) = Ф(0, п) = 1]
210
УСТОЙЧИВОСТЬ
[Гл. 8
(см. (4)),
<p2(0) = <p(s, =
(см. (И)). Таким образом, решения <pt (t) и (t) имеют общие началь-
ные значения и потому совпадают, а это и означает, что соотноше-
ние (10) выполнено.
В доказательстве теоремы Ляпунова основную роль играет неко-
торая положительно определенная квадратичная форма, называемая
функцией Ляпунова. Отметим сначала некоторые свойства положи-
тельно определенных квадратичных форм (см. Г)), а затем построим
и самую функцию Ляпунова (см. Д)).
Г) Пусть
х = (х\ х") (12)
— переменный вектор n-мерпого пространства. Квадратичной формой
от вектора х называется его функция IF(x), определяемая формулой
IF (х) =
i, / = 1
где Wjj — zoji — действительные числа. Квадратичная форма IF (х)
называется положительно определенной, если при х 0 имеем:
IF (х) > 0.
Оказывается, что для любой положительно определенной квадратичной
формы IF(x) всегда можно подобрать два таких положительных
числа р, v, чго для произвольного вектора х имеют место неравенства
|x|x|2<lF(xX\|x|a. (13)
Из -’того следует, что для произвольного х (см. (12)) имеет место
неравенство
(14)
Докажем существование чисел р и v. Для этого рассмотрим значе-
ния функции VZ(|), когда вектор | принадлежит единичной сфере,
т. е. удовлетворяет условию
Ш=1. (15)
Так как сфера (15) представляет собой замкнутое ограниченное мно-
жество, а функция IF(|) непрерывна, то на сфере (15) она достигает
своего минимума р н своего максимума v. Так как все векторы
сферы (15) отличны от пуля, то числа ;л и v положительны. Пусть х —
произвольный вектор; тогда мы имеем х = Х£, где вектор Е при-
1
ТЕОРЕМА ЛЯПУНОВА
2 И.
надлежит сфере (15), я потому для вектора § выполнены неравенства
Умножая это неравенство на X2, получаем неравенства (13).
Перейдем теперь к построению функции Ляпунова.
Д) Пусть
х‘= £ а’х1, /=1, п (16)
/= 1 }
— линейная однородная система уравнений с постоянными коэффи-
циентами, причем все собственные значения матрицы Д = (ар имеют
отрицательные действительные части. Существует тогда положительно
определенная квадратичная форма W(х), производная которой в силу
системы (16) (см. Б)) удовлетворяет неравенству
(in
где х — произвольный вектор, ар — положительное число, не завися-
щее от вектора х.
Построим форму U/(x). Будем считать, что система (16) есть
скалярная запись векторного уравнения (5). Решение уравнения (5)
с начальными значениями 0, | будем, как н в предложении А), обо-
значать через ф(/, |); тогда мы имеем:
п
2^4(0 (18)
i = 1
(см. (8)). Положим теперь
со
U7(g) = ) I’M*, IW-. (19)
о
Мы имеем в силу (18)
п 00
17' (£)= S (2М)
1, ; = I О
Так как каждая функция (/) удовлетворяет неравенству (6), то
каждый несобственный интеграл, стоящий в правой части равенства (20),
сходится, и потому UZ(x) есть квадратичная форма относительно
вектора Эта квадратичная форма является положительно определен-
ной, так как при £ # 0 подынтегральное выражение в формуле (19)
положительно, и, следовательно, U7(^)^>0. Вычислим теперь произ-
водную (g) функции IT (g) в силу системы (16). Для этого,
согласно предложению Б), мы проведем через точку | решение ф (Г,
212
устойчивость
П’п. 5
и затем вычислим производную при t = 0 от функции W(ф (£, $)),
Заметим предварительно, что в силу В)
’Ж £))='$('44 I),
так что
w (W 1Ш Ш £))12сЬ =
О
= $ ItCX’- g)l2<fc = $ |Ч>4
0 4
Таким образом, мы имеем:
00
W(<, = ^’Ц-» =
= -1Ш ОТ = о = -ИГ.
Итак, мы получили равенство
^(16>(ё)=— I ёР,
по в силу второго из неравенств (13) имеем:
и потому получаем:
^(16)
Таким образом, неравенство (17) доказано.
Теорема Ляпунова
Перейдем, наконец, к формулировке и доказательству теоремы
Ляпунова.
Пусть
а = (а1, ..., ап)
— положение равновесия автономной системы (1). Положим:
х1 — а1 -ф-Дх\ i= 1, 2, nt (21)
и примем за новые неизвестные функции величины
Дх1, Дхл. (22)
Производя подстановку (21) в системе (1) и разлагая правые части
в ряд Тейлора по переменным (22), получаем:
Д^ V + (23)
/X1
ТЕОРЕМА ЛЯПУНОВА
213
где Я* — член второго порядка малости относительно неизвестных (22).
Так как а есть положение равновесия системы (И. «»
/Да) = 0;
далее, полагая
(24)
(25)
мы можем записать систему (23) в виде:
tzjАх'-1-R1, Z=l, л.
/=1 7
Теорема 19. Если все собственные значения матрицы А = (aj)
(см. (24)) имеют отрицательные действительные части, то поло*
жение равновесия а системы (1) асимптотически устойчиво; болев
полно, существует настолько малое положительное число а, что
при |1 — flK° имеет место неравенство
|q>(t |)-а|<г|&-а|еЛ (26)
где г и а — положительные числа, не зависящие от g.
Доказательство. Будем считать, что положение равновесия а
системы (1) совпадает с началом координат, т. е. что а = 0. Этого
всегда можно достичь, произведя параллельный перенос системы коор-
динат; при этом матрица А не изменится. Предполагая, что а = 0, мы
имеем:
Дх; = х1,
и потому система (25) записывается в виде:
+ 1=1, ..„п,, (27)
где
_ 1 VI dsf^x) / ь
К —2 L х •
л * = 1
Пусть теперь №(х) — функция Ляпунова (см. Д)) для линейной
системы
х1=^а^.х\ п, (28)
получаемой из системы (27) линеаризацией, т. е. отбрасыванием
остаточных членов Вычислим производную ^^(х) функции IF(x)
214
УСТОЙЧИВОСТЬ
в силу системы (27). Мы имеем:
п п
2 d-W+2^«'=
i, /-=1 i = l
и
= UZ(28)(x)+ V
1 = 1
Так как функция U7(x) удовлетворяет условию (17), то мы имеем:
п
(X) < - R (X) + 2 R1 *-
1=1
Выберем теперь настолько малое положительное число Ь, чтобы при
W(x)^b (29)
вектор х принадлежал множеству А (такое число b существует
в силу (13)). Вторые производные > будучи непрерывными
функциями, ограничены в эллипсоиде (29) и потому в этом эллипсоиде
| R1 I < k IX I3 * * * < W(x),
, П dW(x)
где k — некоторая константа. Далее, так как - - есть линейная
форма относительно xft, то
I (/Л
где I—некоторая константа (см. (14)). Таким образом, существует
такое положительное число qt что при W(x)^b мы имеем:
п
дх' 7 v 7
i=i
Выберем теперь положительное число с таким образом, чтобы было
Cs^b, q]Sc
Тогда мы будем иметь:
UWx^-l^x),
если только выполнено неравенство
U"(х) ==^с (30)
§ 26]
ТЕОРЕМА ЛЯПУНОВА
210
Полагая a = -j, получаем неравенство
^(27) (Х)^ — 2а№(х),
справедливое, если для х выполнено неравенство (30).
Пусть £ — внутренняя точка эллипсоида (30), т. е. точка, удо-
влетворяющая неравенству
W)O (81>
Решение системы (27) с начальными значениями 0? как и раньше,
обозначим через <р(£, |) и положим:
I)).
Функция U'(i) определена для всех тех значений ^^0, для кото-
рых определено решение (р(tt g), и в силу Б) она удовлетворяет
условию
w (t) — 2aw (/) (32)
до тех пор, пока для нее выполнено неравенство
(33)
Если бы решение ср (/, |) существовало не для всех положительным
значений t, то точка ,г = ф(£, g) непременно должна была бы при
возрастающем t покинуть эллипсоид (30) (см. § Э2> В), Допустим,
что точка х = (р(^|) покидает этот эллипсоид и пусть f^>0 —те
значение t, при котором она впервые попадает на его границу. Тогда
на отрезке точка ф(£, £) принадлежит эллипсоиду (30), и
потому выполнено неравенство (32), так что w (i) неположительна.
Следовательно, с = w(t') w (0) с, что противоречиво.
Таким образом, решение <р(/, |), а вместе с ним и функция w(/)
определены для всех положнтел: пых значений I и для всех этих зна-
чений выполнено неравенство (32). Если £ 0, то w(0^>0» и мы
можем произвести следующие выкладки, исходя из неравенства (32)
t
—2 а; 2?.t при 0;
v,yt) - ’ и
о
In w (0 — In (0) — 2а t.
Последнее неравенство дает:
Г(Ф(г, ЮХ W<X'.
Из э’юго неравенства, используя неравенства (13), мы получаем:
1фО g)|Xyl ifX, (34)
причем это верно, если только для g выполнено неравенство (31).
216
УСТОЙЧИВОСТЬ
[Гл. S
В силу второго из неравенств (13), из соотношения
1§К<’ = ]/-7 (Зв)
следует неравенство (81). Таким образом, если выполнено неравен-
ство (85), то верно неравенство (34). Извлекая из него квадратный
корень, получаем неравенство:
|<ра, £)1<1Л-1£|е-”'; ^0,
Г
которое совпадает с неравенством (26), причем г="|/Г—, а а = 0.
Итак, теорема 19 доказана.
Нижеследующее предложение Е) описывает случай, в некотором
смысле противоположный рассмотренному в теореме 19.
Е) Положение равновесия а уравнения (2) будем называть вполне
неустойчивым, если существует такое положительное число с, что
всякое решение <р(Л |) уравнения (2), начинающееся в точке | а
шара — а|<3 обязательно покидает этот шар и больше в него
уже не возвращается, т. е. найдется такое положительное число Т= Г(§),
что при t = Т решение (t, g) определено, и для всех значений Т,
для которых это решение определено, оно удовлетворяет неравен-
ству (<₽(/, £) — а Оказывается, что если все собственные зна-
чения матрицы имеют положительные действительные части,
то положение равновесия а уравнения (2) является вполне неустой-
чивым.
Для доказательства предложения Е) используем некоторые резуль-
таты, установленные в процессе доказательства теоремы 19; при этом,
как и раньше, будем считать, что а = 0. Для этого, наряду с урав-
нением (2), для которого по - предположению все собственные значе-
ния матрицы имеют положительные действительные части, рас-
смотрим уравнение
х = ~/(х), (36)
для которого точка 0, очевидно, удовлетворяет условиям теоремы 19.
В силу конструкции, данной при доказательстве теоремы 19, для
уравнения (36) существует функция Ляпунова W (х), удовлетворяющая
неравенству
(Х)^ — 2aU7(x)
при условии (30). Выписывая левую часть этого неравенства в явном
виде (см. (9)), получаем;
п
(X) = 2 Г - 2аГ W’
i = l
§ 261
ТЕОРЕМА ЛЯПУНОВА
217
или, иначе,
^(1) (х)^2аГ(х).
Это неравенство заведомо верно, когда выполнено неравенство (30).
Пусть теперь £— некоторая внутренняя точка эллипсоида (30)
(см. (31)). Положим:
w(/)=U7(q)(?, §)).
Для функции w(£) выполнено неравенство
w(/)^ 2aW(Z), (37)
когда для нее имеет место неравенство
w (t) с.
Так как Ej ф 0, то w(Q^>0, и можно произвести следующие выкладки,
исходя из неравенства (37):
t
—— 2a; I при
w(t) J w(t) *
о
w(/)^^(0)^a'; U7((p(/> £))^ U/(£)e2a'.
Из последнего неравенства следует, что при росте t точка х = <р(^, |)
непременно выйдет на границу эллипсоида (30) и, следовательно,
покинет его внутренность. Покажем, что после этого она уже не
вернется внутрь эллипсоида (30). Допустим противоположное; тогда
найдется такое положительное значение f, что ^(f) = c, а при всех
положительных достаточно малых значениях At выполнено неравен-
ство w(f -J- Из последних двух соотношений следует, что
w(f)^0, а это противоречит неравенству (37), которое верно при
/ = так как w(f)=c.
Таким образом, доказано, что траектория х — ф (/, |), где 0 —
внутренняя точка эллипсоида (30), обязательно уходит из эллип-
соида (30) и больше в него уже не возвращается. В силу второго
из неравенств (13), из неравенств (35) следует неравенство (31), так
что шар (35) содержится в эллипсоиде (30). Ввиду этого из дока-
занного следует правильность утверждения Е).
Пример
В дополнение к предложению А) покажем, что если матрица А
имеет собственное значение X с положительной действительной частью,
то положение равновесия х = 0 уравнения (5) уже не является устой-
чивым по Ляпунову. Действительно, в силу предложения А) § 14
решением уравнения (5) является векторная функция x—chelty где
с — произвольная действительная константа, a h — собственный
218
УСТОЙЧИВОСТЬ
[Гл 5
вектор матрицы А с собственным значением X. Если X — действительное
число, то при достаточно малом с указанное решение начинается
в точке сЛ, сколь угодно близкой к положению равновесия х = 0,
но с течением времени становится сколь угодно большим по модулю.
Если же X — комплексное число, то тем же свойством обладает ре-
шение c(heu 4- heu) уравнения (5).
§ 27. Центробежный регулятор (исследования Вышнеградского)
В современной технике благодаря изобилию приборов автомати-
ческого управления чрезвычайно большую роль играет теория
автоматического регулирования. Одним из важнейших
вопросов, возникающих перед кон-
структором автоматического регу-
лятора, является вопрос об устой-
чивости работы системы ма-
шина — регулятор. Этот вопрос во
многих случаях может быть решен
на основании теоремы Ляпунова
(см. § 26).
Наиболее дайно существующей
системой автоматического регули-
рования является система паровая
машина — центробежный регулятор
Уатта. Центробежный регулятор,
вполне хорошо справлявшийся со
своей задачей в конце XVIII и в
первой половине XIX века, в се-
редине XIX века ввиду его кон-
структивных изменений стал работать
ненадежно. Широкие круги теоре-
тиков и инженеров искали выхода
из возникшего кризиса. Вопрос с полной ясностью и простотой был
решен выдающимся русским инженером Вышнеградским, основателем
теории автоматического регулирования. Работой Вышнеградского
<0 регуляторах прямого действия» (1876 г.) начинается теория регу-
лирования машин, отвечающая на вопросы промышленной практики.
В настоящем параграфе в упрощенном виде излагается исследование
Вышнеградского.
Центробежный регулятор (рис. 41) представляет собой верти-
кальный стержень могущий вращаться вокруг своей вертикаль-
ной оси, в верхнем конце которого на шарнирах прикреплены два
одинаковых стержня и с одинаковыми грузами на концах.
Стержни Li и скреплены дополнительными шарнирами, гак что
отклоняться от своего вертикального положения они могут лишь
§ 27]
ЦЕНТРОБЕЖНЫЙ РЕГУЛЯТОР
219
Рис. 42.
одновременно на один и тот же угол находясь в одной и той же
гертикальной плоскости, неподвижно связанной со стержнем 5. Когда
стержни Lj и отклоняются от своего вертикального положенжй
на угол <р, они при помощи шарниров приводят в движение специальную
муфту уИ, надетую на стержень 5, так что расстояние этой муфты
до верхнего конца стержня S пропорционально cos <р. Длину верти-
кальных . стержней Lt и £, примем эа единицу, а массу каждого ив
грузов, прикрепленных на их концах, обозначим через т. Если стер-
жень S вращается с угловой скоростью 6, а стержни 1Л и откло-
нены от вертикального положения на
угол ср, то на каждый из грувов дейст-
вует центробежная сила
т№ sin ср. (1)
Одновременно на каждый груз действует
сила тяжести, равная
mg. (2)
Так как в направлении стержня Ц силы,
действующие на груз, уравновешиваются
реакцией стержня то для расчета силы,
действующей на груз, следует разложить
обе упомянутые силы по осям, первая из
которых направлена вдоль стержня, а вторая — в перпендикулярном
направлении, в сторону возрастания угла <р. Непосредственно видно
(рис. 42), что составляющая силы (1) в направлении возрастания
угла ф равна
sin р cos ср, (3)
а составляющая силы тяжести (2) в том же направлении равна
— mg sin ф. (4)
Таким образом, равнодействующая обеих сил (3) и (4) задается
формулой
in№ sin ф cos ср — mg sin ср. (5)
Упрощенное объяснение работы центробежного регулятора заклю-
чается в том, что при заданной угловой скорости 6 стержни L1 и
отклоняются под действием сил (1), (2) на угол у, определяемый ив
равенства
sin ср cos ср — mg sin <р = 0, (6)
т. е. путем приравнивания нулю силы (5). Из соотношения (6) угол ф
определяется как однозначная монотонно возрастающая функция ско*
! ости 9; в l-tom смысле регулятор Уатта может рассматриваться как
измеритель скорости вращения. Это есть так называемое ci ати-
920
УСТОЙЧИВОСТЬ
(Гл. В
ческое рассмотрение регулятора. В действительности мы имеем здесь
динамическое явление. Масса /п, находясь под воздействием
силы (5), совершает движение, описываемое дифференциальным урав-
нением. Кроме силы (5), на массу т действует при ее движении сила
трения в сочленениях шарниров. Сила эта весьма сложным образом
зависит от происходящего движения. Существенно упрощая имеющуюся
здесь сложность, мы будем считать, что сила трения пропорциональна
скорости ф движения массы т и имеет знак, противоположный этой
скорости, т. е. имеет величину
—
где Ь — постоянная. Таким образом, если принять <р за координату,
определяющую положение массы zn, то мы получим для <р дифферен-
циальное уравнение:
— tr№ sin ср cos ср — mg sin ср — bfy (7)
(Расчет силы (5) проведен здесь в предположении, *что 0 и <р посто-
янны. При меняющихся 6 и ср возникают добавочные силы, которые,
однако, уравновешиваются реакциями стержней и шарниров, заставля-
ющих стержни двигаться в одной плоскости. Таким образом, уравне-
ние (7) оказывается справедливым.)
Паровая машина представляет собой маховое колесо с моментом
инерции J, приводимое во вращательное движение силой пара и спо-
собное совершать полезную работу, например поднимать клеть из
шахты. Дифференциальное уравнение паровой машины может быть,
таким образом, записано в виде:
= /->! —Р, (8)
где со —угловая скорость вращения маховика, Рх — момент силы
действия пара, Р—момент силы воздействия на маховик тяжести
клети. Момент силы воздействия пара РА зависит от того, насколько
приоткрыта заслонка, подающая пар в цилиндры паровой машины,
а момент Р зависит от загруженности клети.
Центробежный регулятор присоединяется к паровой машине
с целью поддержать равномерность ее хода. Он «измеряет» ско-
рость вращения махового колеса и, если опа оказывается слишком
большой, уменьшает подачу пара, а если она оказывается слишком
малой — увеличивает подачу пара. Для осуществления этой цели махо-
вое колесо паровой машины связывается при помощи зубчатой пере-
дачи с вертикальным стержнем регулятора (рис. 41), так что между
угловыми скоростями со и 0 возникает постоянная связь:
О пы, (9)
где п— так называемое передаточное число. Таково воздействие
машины на регулятор, в результате которого осуществляется
$ 27 ]
ЦЕНТРОБЕЖНЫЙ РЕГУЛЯТОР
221
измерение скорости вращения маховика. С другой стороны, муфта Л4
регулятора связана с заслонкой, подающей пар, так что
pi — pl~[~ Л (cos ср— cos <р*), (10)
где <р* — некоторое «среднее» значение ср, вблизи которого должно
поддерживаться значение регулируемой величины ср, р\ — значение
силы воздействия пара Рх при ф = ф* а — постоянный коэф-
фициент пропорциональности.
Как видно из (10), обратное воздействие регулятора
на паровую машину осуществляется таким образом, что при
увеличении угла ср подача пара (а вместе с ней и сила воздействия
пара Рх) уменьшается. В результате описанных взаимодействий маши-
ны и регулятора, последний, казалось бы, полностью осуществляет
поставленную перед ним задачу, увеличивая подачу пара при умень-
шении скорости вращения маховика и уменьшая подачу пара при
увеличении скорости. В связи с этим естественно ожидать, что ско-
рость вращения маховика будет стабилизироваться. Это и наблюда-
лось в паровых машинах, строившихся до середины XIX столетия.
Для того чтобы выяснить причины начавшего наблюдаться после середи-
ны XIX столетия нарушения работы регулятора, необходимо было
точно изучить динамику работы системы машина — регулятор и
исследовать ее устойчивость, что и было сделано Вышнеградским.
Как видно из соотношений (7)—(10), система машина—регу-
лятор описывается двумя дифференциальными уравнениями:
ту = /плМ sin ф cos ср — mg sin ср — by,
Jib = k COS Cp — Ff
(11)
где F — P— Fi q- k cos cp* — величина, зависящая от нагрузки. Перво®
из этих урапений имеет второй порядок. Для приведения системы
к нормальному виду введем новое переменное ср, положив:
Тогда система (11) запишется в нормальной форме:
Ср = ф,
i — /fW sin ср cos со — g sin ср — - ф,
т Y 1 5 г тг’ } (12)
k F
= у COS Ср — у.
J J
Правильная работа паровой машины заключается в том, что
угловая скорость со вращения ее маховика остается постоянной при
неизменной нагрузке Р, т. е. при постоянном F, а заслонка, подаю-
щая пар, неподвижна. Последнее означает, что угол <р остается
222
УСТОЙЧИВОСТЬ
(Гл. 5
неизменным. Таким образом, речь идет об отыскании такого решения
системы (12), которое имеет вид:
? = 9 = 0, о) =
т. е. об отыскании положения равновесия этой системы. Задача заклю-
чается в том, чтобы, найдя положение равновесия системы (12), иссле-
довать его устойчивость.
Приравнивая пулю правые части соотношений (12) и решая
получающиеся уравнения, найдем координаты положения равновесия:
фо = О,
cos?0 = ^> (13)-
Положим:
cp = onJ--Acp, ф = ф0-|-Дф, <о = со0 —Дох
В результате такой замены и линеаризации* уравнений (12), мы
получаем систему:
Дф == Дф,
Дф = cos 2<р0Д<р sin 2ф0Дсп — g cos ?0Д? — Дф,
k
Деи = — j sin ср0Дф.
Подставляя во второе из этих уравнений значение величины
из (13), получаем после простых вычислений:
Дф = _ si" Д» д,, _ 1 Дф + дю.
Т cos ф0 ' т т 1 <оо
Характеристический ний для Дт>, Дф, До) многочлен полученной линейной системы уравне- равеи:
— Р g cos ?0 k . — -J sin 7o 1 b n tn '' ' 0 0 2# sin <p0 w.) — P >
или, после вычисления определителя и умножения на — I,
vr/ г 1 иг 1 COS Фо { J<00
Все коэффициенты этого многочлена положительны, и потому необ-
ходимым и достаточным условием его устойчивости является (в силу
§ 27 1
центробежный регулятор
223
теоремы 6) выполнение неравенства
* . $ sin2% \ j . W sin2 <?0
in COS Фо Jo)0
или, иначе, неравенства
bj 2k cos 2F
% “о
(14)
(см. (13)). Соотношение (14) представляет собой, в силу теоремы
Ляпунова (теорема 19), до с т а т о ч н о е условие устойчивости
системы машина — регулятор.
Для того чтобы выяснить смысл правой части последнего нера-
венства, введем играющее важную роль в технике понятие неравно-
мерности хода паровой машины. Из соотношений (13) видно, что
при изменении величины F — P — Fx k cos ср* (т. е. при изменении
нагрузки Р) меняется стабильная скорость w0. Величина харак-
теризует скорость изменения величины при изменении нагрузки
ее абсолютная величина = (как мы сейчас увидим, производ-
ная ~~ отрицательна) и называется неравномерностью хода паро-
вой машины. Мы имеем в силу (13):
Ftoy = const,
и потому, дифференцируя, получаем:
dF~ 2F'
Таким образом,
и условие устойчивости
(14) переписывается окончательно в виде:
(15)
Из формулы (15) Вышпеградским были сделаны следующие
выводы:
1. Увеличение массы т шаров вредно влияет на устойчивость.
2. Уменьшение коэффициента трения b вредно влияет на устой-
чивость.
3. Уменьшение моментов инерции J маховика вредно влияет на
устойчивость.
4. Уменьшение неравномерности v вредно влияет на устойчивость.
Чтобы сделать свои выводы доступными для инженеров и при-
влечь внимание к наиболее важным из них, Вышнеградский формули-
рует в конце работы свои знаменитые «тезисы».
224
УСТОЙЧИВОСТЬ
[Гл. 5
Первый тезис: Катаракт (трение) есть существенная принад-
лежность чувствительного и правильно действующего регулятора,
короче: «без катаракта нет регулятора».
Второй тезис: астатические регуляторы (т. е. регуляторы
с нулевой неравномерностью) даже и с катарактом не должны быть
употребляемы, короче: «без неравномерности нет регулятора».
Нарушения работы регуляторов в середине XIX столетия объяс-
няются тем, что благодаря развитию техники все четыре величины,
входящие в соотношение (15), стали изменяться в направлении, ухуд-
шающем устойчивость. Именно, ввиду увеличения веса заслонок
(связанного с возрастанием мощности машин) стали применяться все
более тяжелые шары. Совершенствование обработки поверхностей
деталей приводило к уменьшению трения. Увеличение рабочей ско-
рости машин сделало необходимым уменьшение момента инерции J
маховика. Наконец, стремление уменьшить зависимость скорости от
нагрузки приводило к уменьшению неравномерности хода.
Уяснив неблагоприятное влияние всех указанных факторов, Вышне-
градский в своих тезисах рекомендует искусственное увеличение тре-
ния (при помощи специального устройства — катаракта) и увеличение
неравномерности хода (за счет изменения чисел п и k, зависящих от
конструкции машины).
§ 28. Предельные циклы
В этом параграфе будет определено и до некоторой степени изу-
чено понятие предельного цикла, введенное великим француз-
ским математиком Пуанкаре, а также дан один критерий, позволяющий
в некоторых случаях установить существование предельного цикла.
Понятие предельного цикла играет важнейшую роль как в самой
теории обыкновенных дифференциальных уравнений, так и в ее при-
ложениях к технике.
Мы будем рассматривать нормальную автономную (см. § 15)
систему уравнений
xl=fl(x\ хп), I— 1, ..., //, (1)
правые части которых определены и имеют непрерывные частные
ЭР Л л.
производные на некотором открытом множестве А фазового про-
странства R переменных х1, .хп. Мы будем пользоваться также
векторной записью этой системы:
x = f(x). (2)
Все наиболее существенные построения этого параграфа будут отно-
ситься к случаю п — 2. Чтобы подчеркнуть двумерность, мы будем
говорить о фазовой плоскости Р системы (1), а не о ее фазо-
$ 28)
ПРЕДЕЛЬНЫЕ ЦИКЛЫ
225
вом пространстве R. При рассмотрении фазовой плоскости будут
играть существенную роль геометрические построения, обладаю-
щие большой наглядностью. Случай, когда открытое множество Д
совпадает со всей фазовой плоскостью Р, отнюдь не является три-
виальным, и для простоты можно сосредоточить все внимание на нем.
Предельный цикл и поведение траекторий
вблизи него
Предельным циклом уравнения (2) (zz = 2) называется изолиро-
ванное периодическое решение этого уравнения. Более полно, пусть
Хп=ф(£) — периодическое решение уравнения (2) и К — описываемая
этим решением замкнутая кривая в плоскости Р, Решение х = <р(0
(а также траектория К) считается изолированным периодическим
решением и называется предельным циклом, если существует такое
положительное число р, что, какова бы ни была точка | плоскости Р,
находящаяся от кривой К на положительном расстоянии, меньшем
чем р, решение уравнения (2), проходящее через точку не является
периодическим.
Сказанное означает геометрически, что в фазовой картине урав-
нения (2) на плоскости Р вблизи замкнутой траектории К не про-
ходит других замкнутых траекторий этого уравнения. Вопрос о том,
как ведут себя траектории уравнения (2) вблизи предельного цикла К*
решается следующей теоремой.
Теорема 20. Пусть х = <р (0 — предельный цикл уравнения (2)
(п=2) и К—замкнутая траектория, описываемая этим реше-
нием на плоскости Р. Замкнутая кривая, как известно, разби-
вает плоскость на две области: внутреннюю и внешнюю,
а так как траектории уравнения (2) не могут между собой
пересекаться, то каждая отличная от К траектория является
внутренней или внешней по отношению к траектории К, Оказы-
вается, что как для внешних, так и для внутренних траекто-
рий имеются две взаимно исключающие друг друга возможности
поведения вблизи К- Именно, все внутренние траектории, начи-
нающиеся вблизи К, наматываются на К, как спирали, либо при.
(Рис- 43, а), либо при t-> —со (рис. 43,6). То же самое
имеет место и для внешних траекторий (рис. 43, а, б).
Если все траектории (как внешние, так и внутренние), начинаю-
щиеся вблизи К, наматываются на К при то предельный
цикл называется устойчивым (рис. 43, а). Если все траектории, начи-
нающиеся вблизи К, наматываются на К при —оо, то предель-
ный цикл К называется вполне неустойчивым (рис. 43, б), в двух
других случаях, (т. е. если внутренние траектории наматываются на К
при — рр, а внешние—при или наоборот) предельный
цикл К называется полуустойчивым (рис. 43, в).
8 Понтрягин Л. С.
226
УСТОЙЧИВОСТЬ
[Гл. 5
Как само доказательство теоремы 20, так и более полное описа-
ние «наматывания» траекторий на предельный цикл опираются на
понятие функции последования. Эта функция имеет наглядный гео-
метрический смысл и без детального доказательства ее свойств может
быть описана сравнительно коротко.
Дадим это описание. Пусть К — замкнутая кривая на фазовой пло-
скости Р, соответствующая периодическому решению с периодом ъ
Рис. 13.
Пусть, далее, L — прямолинейный отрезок в плоскости Р, пересекаю-
щий кривую К, не касаясь ее, в единственной точке а, внутренней
для отрезка L. На отрезке L (точнее, тта прямой, содержащей этот
отрезок) обычным образом введем числовую координату. Координату
точки а обозначим через н0. Через точку р отрезка L с координа-
той и проведем траекторию уравнения (2) и будем двигаться по ней
в направлении возрастания времени t.
Геометрически ясно, что если точка р близка к а, то мы будем
двигаться вблизи кривой /С, и потому вновь и вновь будем встречать
отрезок L. Первая встреча произойдет через время, близкое к т,
в некоторой точке q (рис. 44), координату которой мы обозначим
I 28]
ПРЕДЕЛЬНЫЕ ПИКЛЫ
227
.через Xi (??)- Точно так же, если мы будем двигаться из точки р по
траектории в направлении убывания времени, то через время, близ-
кое к т, мы впервые встретим отрезок L в некоторой точке г, коор-
динату которой обозначим через X-i GO- Обе функции и непре-
рывны и взаимно обратны, т. е.
X 1 (Zj («)) = "> Xi (X -1 (»)) = "•
Действительно, если двигаться из точки q в направлении убывания
времени, то мы
впервые встретим отрезок L в точке р, так чю
X i(^i(n)) = w- Точно так же, при дви-
жения из точки г в направлении воз-
растания времени мы впервые встре-
тим отрезок L в точке р, т. е.
Xi(X J (")) = «* Функция х = Х1 назы-
вается функцией последования; для
дальнейшего существенно, что она не-
прерывна и имеет непрерывную обрат-
пую функцию x”1:=X-i-
В действительности функции и
/ 1 имеют непрерывные производные
(см. В)), по это их свойство не будет
использовано при доказательстве тео-
ремы 20.
Приведенные здесь геометрические
соображения наглядно достаточно убе-
дительны. Читатель, склонный удовольствоваться ими, может озна-
комиться с доказательством теоремы 20, не читая предложений Л)
и Б), в которых существование и свойства функции последования
доказываются строго.
Л) Обозначим через <р(/, решение уравнения (2) с начальными
значениями 0, g. Пусть L—прямолинейный отрезок на фазовой пло-
скости Р уравнения (2), на котором введена числовая координата -и,
так что в параметрической форме отрезок задается линейным урав-
пением:
x = g(v).
Допустим, что траектория <р (/, пересекает отрезок L в его внут-
ренней точке а с координатой v0 в момент времени £0» так чт0
<P(X0, =
причем траектория qj(f, |0) в момент времени f0 не касается отрезка Л.
Существуют тогда такие положительные числа 5 и а, что: 1) при
определены непрерывные функции £(£) и г»(|), удовлет-
воряющие условиям
<К'Ф> 5) = £KI)); i(Ы = = (3)
в*
228
УСТОЙЧИВОСТЬ
(Гл. 8
2) имеет место единственность; именно, если при || — £о! <С V
j/—^)i<C2 и.меет место равенство
I) —£fa) = 0, (4)
то величины t, v удовлетворяют условиям:
* = *(£), v = v(g). (5)
Сказанное означает геометрически, что траектория, выходящая
в момент времени f = 0 из точки близкой к §0, пересекает отре-
зок L в точке с координатой ^(|)> близкой к т>0, в момент вре-
мени f(|), близкий к /о, причем пересечение это является единствен-
ным на некотором интервале времени — f0|<^e, а функции t (£)
и v(§) непрерывны.
Следует заметить, что траектория <р(Л £0) может пересекать от-
резок L не только в момент времени /0, но и в некоторый другой
момент времени tu причем точка пересечения может даже совпасть
с а (этот случай имеет место, если <р (t, §0) — периодическое реше-
ние), но функция f(|) (а возможно и v(|)), получаемая из рассмотре-
ния пересечения в момент времени tb будет, очевидно, отличаться
от функции, получаемой из рассмотрения пересечения в момент вре-
мени
Доказательство предложения А) почти непосредственно вытекает
из теоремы о неявных функциях (см. § 33), примененной к уравне-
нию (4), в котором £ считается независимой переменной величиной,
a i и v~~ ее неявными функциями. При | = |0 уравнение (4) имеет
очевидное решение = Для доказательства того, что функ-
циональный определитель левой части уравнения (4) отличен от нуля
в точке (|(>, v0), запишем уравнение (4) в скалярной форме:
= Z=l, 2. (6)
Производные от левых частей этих соотношений по t в точке
(|о, *>о) Дают компоненты вектора ф(/0) |0); производные от левых
частей этих соотношений по v в той же точке дают компоненты
fan) о
вектора------~ • Экторы эти линейно независимы, так как тра-
ектория <р(/, |0) в момент f0 не касается отрезка L, Следовательно,
функциональный определитель системы (6) отличен от нуля в точке
(|о> *>о)- Таким образом, теорема о неявных функциях к уравне-
нию (4) применима, и существует его непрерывное решение ^(^), г»(§),
определенное на некоторой окрестности 111 а и обращающееся
В to, Vo при |=|0.
В силу второй части теоремы существования неявных функций,
найдется такая окрестность U точки (|0, f0, ud) tf пространстве пере-
менных v, что всякая точка (|, t, v) из этой окрестности, удов-
летворяющая уравнению (4), удовлетворяет и уравнениям (5).
§ 28]
ПРЕДЕЛЬНЫЕ ЦИКЛЫ
229
В отличие от того, что содержится в формулировке предложения
А), эта единственность, в силу теоремы 27, имеет место, когда малы
не только величины || — £0| и \t — |, но также величина | о—ф0|.
Для того, чтобы доказать единственность при малости только двух
первых из указанных величин, покажем, что если эти две величины
малы и точка (§, t, v) удовлетворяет условию (4), то величина
|ф—I также мала. Окрестность Ц в которой имеет место един-
ственность в силу теоремы 27, можно задать неравенствами
I © — ©о I
Из предложения Г) § 23 следует, что при достаточно малом В на
всем интервале времени \t—^(<^е имеет место неравенство
IЧР (А I)—ф(^ Io) I 1> где Т — наперед заданное малое число. Таким
образом, точка пересечения траектории ф(А |) с отрезком L при
||— In |<А №—*olO лежит тем ближе к отрезку траектории
ф(7, Io) (i^—^о|<Се)’ чем меньше 8, и потому малость координаты »
этого пересечения обеспечивается достаточной малостью числа 8.
Таким образом, предложение А) доказано.
Б) Пусть ф(б |) — решение уравнения (2) с начальными значени-
ями 0, пусть, далее, ф(А а) — периодическое решение с периодом ч
К— замкнутая кривая на фазовой плоскости Р, соответствующая реше-
нию ф(7, а), и L — прямолинейный отрезок, пересекающий кривую К
без касания в единственной точке а, лежащей внутри него. На
отрезке L введем числовую координату, так что№=^(г») есть пара-
метрическое уравнение отрезка Ц заданное при помощи этой коор-
динаты, и пусть v~u0—координата точки а. Оказывается, что при
достаточно малом а^>0 траектория ф(/, g (г?)) = ф (б и), где
| и — п0|<^а, пересекает отрезок L как при положительных значе-
ниях так и при отрицательных его значениях. Обозначим через
tx (и) минимальное положительное значение t, при котором траекто-
рия ф (7, и) пересекается с L, и через Xi (п)—координату этой точки
пересечения на отрезке L. Точно так же обозначим через Li(w)
минимальное по модулю отрицательное значение при котором тра-
ектория ф(/, и) пересекается с А, и через x_i(?O — координату этой
точки пересечения на отрезке L. Оказывается, далее, что если а доста-
точно мало, то при | и—п0|<^а все четыре построенные функции
Ь(«)> XiOO. t-\ («). х-1(н)
непрерывны и удовлетворяют условиям
Ь(”о) = т> Xi («о) = “о, t-1 (Wo) = •— Х-1 («»)“«►
Кроме того, функции Xi и X-t взаимно обратны при достаточно
230
УСТОЙЧИВОСТЬ
|Гл. 6
малом и, т. е.
х । (xi 00) = Xi (х -100)=
Функция / = */j называется функцией, последования.
Для доказательства предложения Б) используем предложение А),
считая, что = — tQ = k~.f где k—произвольное целое
число, (В действительности мы используем лишь значения k ——1,
О, +1.) В силу предложения А), существуют непрерывные функции
(w) = (# 00) и Хл00 = г;л(йг(г0)> удовлетворяющие условиям:
ф(Юг0- §(»)) = ^(»о) = ^> Zft(»o) = "o> (7)
причем, в силу единственности, функции, удовлетворяющие этим
условиям, определены однозначно. В частности, ^(и) = и.
Докажем, что
X* (Хг (")) = Х*+/(")- (8)
Пользуясь соотношением (7) и предложением В) § 26, получаем:
е (х* (xz («)))=ф Ю (Xi («))> s Ot (°))) —
= Ф Ю (Xz ("))> Ф (^(н)> S («))) = ф (Xz 00) + h (н), g (.zz)),
причем выполнены условия
h (7л O?o)) O?o) — h (uo) + h (Ilo) — ~r 0 T;
7j? (7j O'o)) = ??0.
С другой стороны, мы имеем:
g(^!i(it)) = <(^M(^ g(n)l .
причем
Z.A’-Ч (»fl) =
0;+/(^) = (M- O'-
В силу единственности функций, удовлетворяющих условиям (7), мы
получаем:
Xk (Xi («)) = ь+/ («)•
Таким образом, соотношение (8) доказано.
В частных случаях, когда k = ~~ 1,/—и = 1==—
получаем:
X-i(Xi (»))=Хо 00 = п,
Xi (х-i GO)=zo («) = »•
Таким образом, функции и Z1 — Z-i взаимно обратны.
Докажем теперь, что при достаточно малом I и — щ | траектория
w) первый раз пересекается с L при возрастании t в момент
§ 23 1
ПРЕДЕЛЬНЫЕ ЦИКЛЫ
231
времени ^(и), а при убывании t — в момент времени Из един-
ственности пересечения (см. А)) следует, что на каждом из интерва-
лов \t — (—х) | а, 111 в, if — J е траектория ф (i, и) пересе-
кается с отрезком L в единственной точке.
Других пересечений с отрезком L траектория ф(/, и) при
|/|<^04“х) и достаточно малом |п— и& | вообще не имеет по сле-
дующим соображениям.
Часть К* траектории /<, описываемая точкой (p(f, а\ когда
£ t <-~1 (х— е) или —(“ — s) t — s, (9)
является замкнутым множеством, которое не пересекается с замкну-
тым множеством L и потому расстояние р между множествами /С* и
L положительно. Далее, в силу предложения Г) § 23, расстояние
между точками <p(f, а) и ф(£, zz), когда t принадлежит множеству
(9), меньше р, если только величина — zz01 достаточно мала.
Таким образом, и траектория ф (f, и), когда I принадлежит мно-
жеству (9), не пересекается с отрезком L,
Итак, предложение Б) доказано.
Доказательство теоремы 20. Выберем на фазовой пло-
скости Р прямолинейный отрезок А, пересекающий кривую /б, не ка-
саясь ее, в единственной точке а, внутренней для отрезка L. Введем
на отрезке L числовую координату и обозначим через zz0 координату
точки а. Для определенности будем считать, что точкам отрезка L,
лежащим вне кривой К, соответствуют координаты, большие zz0,
а точкам, лежащим внутри К, — координаты, меньшие zz0. Через X
обозначим функцию последования, соответствующую отрезку L (см. Б)).
Таким образом, для всех чисел достаточно малого интервала
|н—г-ги iа траектория уравнения (2), начинающаяся на отрезке L
в точке р с координатой и, при возрастании времени впервые пере-
секает отрезок А в точке q с координатой ^(?z) = ih
Мы имеем, очевидно:
Z(wa)=u#.
Далее, если для числа и выполнено равенство
X (If) = it,
(10)
то траектория, начинающаяся в точке р с координатой н, замкнута.
Так как, по предположению, траектория К является изолированной
замкнутой траекторией, то существует настолько малое положитель-
нее число а, что при |м— «o|<J уравнение (10) имеет единственное
решение zz = zz0. Из этого следует, что для всех точек интервала
имеет место одно из неравенств:
Z (»)<«. (11)
X (")>«• (12)
232
УСТОЙЧИВОСТЬ
(Гл. 5
В самом деле, если бы для некоторых точек этого интервала имело
место неравенство (11), а для некоторых — неравенство (12), то, в силу
непрерывности функции на том же интервале нашлась бы точка и%
для которой выполняется равенство (10), что невозможно. Так как
траектория, начинающаяся в точке р с координатой и, принадлежащей
интервалу w0 и п0 -ф- а, не может пересечь траектории ТС, то обе
точки р и q лежат по одну сторону кривой К (а именно, вне ТС),
так что
X («) > "о-
(13)
Рассмотрим теперь случай, когда для всех точек интервала
ne<^w<jz04-a имеет место неравенство (И). Пусть — произволь-
ное число этого интервала. Определим индуктивно последовательность
чисел иь положив:
”i+i = X(“i), 1=1,2,...
(14)
В силу неравенств (И) и (13) эти числа расположены на интервале
пв и щ -ф- а и образуют убывающую последовательность. Следо-
вательно, они имеют некоторый предел п*. Переходя в равенстве (14)
к пределу при Z->oo, получаем x(IZ*) = M*> а так как точка п*
принадлежит интервалу | и — то, в силу единственности реше-
ния уравнения (10) на этом интервале, zz*=zz0. Итак, lim izf = zz0.
i -* оо
Обозначая через pi точку отрезка L с координатой щ, мы видим, что
последовательные точки рь р.ь... пересечения траектории, начина-
ющейся в рь с отрезком L сходятся к точке а, лежащей на траек-
тории 7<. Так как время перехода по нашей траектории от точки
до точки р/+1 близко к периоду т предельного цикла К (и, в частно-
сти, ограничено), то при росте i весь отрезок траектории от точки pL
до точки прижимается к траектории К (см. § 23, Г)). Это и
значит, что траектория, начинающаяся в точке рь спирально наматы-
вается па траекторию К при Z—Таким образом, доказано, что
при выполнении неравенства (11) траектория, начинающаяся в любой
точке отрезка L с координатой zz, принадлежащей интервалу n0<^zz<^
<^zz0-|-a, спирально наматывается на К при Z—
Если на интервале и0 <ф и щ -ф- а имеет место неравенство (12),
то для обратной к х функции х~* на некотором интервале zz0<^*d<4
<С Щ + Р имеет место неравенство
х
Исходя из пего, мы точно так же покажем, что в этом случае любая
траектория, начинающаяся в точке отрезка L с координатой v, при-
надлежащей интервалу zz0 <4 v -ф-Р» спирально наматывается на
траекторию К при I -> — со.
§ 281
ПРЕДЕЛЬНЫЕ ЦИКЛЫ
233
Аналогично исследуется поведение траекторий, начинающихся на
отрезке L в точках с координатами и, из достаточно малого интер-
вала w0^>h^>w0 — 7.
Так как каждая траектория, проходящая достаточно близко от
траектории Д', пересекает отрезок L в точке с координатой, доста-
точно близкой к zz0, то мы разобрали поведение всех траекторий,
близких к предельному циклу.
Таким образом, теорема 20 полностью доказана.
Замечание. Для того чтобы объединить в одной формули-
ровке связь между поведением функции ^(w) вблизи zz0 с поведением
как внешних, так и внутренних траекторий, мы рассмотрим нера-
венства
1х(н) — и0|<|и —и0Ц
. - ( ( (15)
1х(») —«о1>1« —«о1- J
Если в полуокрестности линии К (внешней или внутренней) выпол-
нено первое из этих неравенств, то точка q находится на линии L
ближе к а, чем р, и потому в этой полуокрестности траектории
спирально наматываются на Д'при Если же в полуокрестно-
сти выполнено второе из неравенств (15), то в этой полуокрестности
траектории спирально наматываются на К при t —>— 00.
В) Функция последования x = Xi и ее обратная функция
(см. Б)) имеют непрерывные производные.
Для доказательства напомним, что функция (zz), А = ±1, опре-
деляется из уравнения (7):
Ч>(^. £(")) —№) = 0, (16)
где zz является независимым переменным, a tk и Xfc определяются
как неявные функции переменного и. Так как функция <р (/, §) имеет
непрерывные частные производные по компонентам вектора | (см.
теорему 17), а функция | = ^(zz), являющаяся линейной относительно ft,
имеет непрерывную производную по zz, то левая часть соотноше-
ния (16) имеет непрерывную производную по и. Поэтому, в силу
теоремы 28, неявные функции tk(u) и ХлОО, определяемые уравне-
нием (16), имеют непрерывные производные по и.
Таким образом, предложение В) доказано. .
Большую привлекательность имеет геометрическое изучение функ-
ции последования х СО- Изобразим ее в виде графика уравнения
®=х00 (17)
в плоскости переменных zz, vt считая при этом для удобства, что
zzo^>O. Для того чтобы изучить решение уравнения (10), мы рас-
смотрим наряду с кривой (17) биссектрису первого координатного
угла
v—u
(18)
234
УСТОЙЧИВОСТЬ
[Гл. 5
(рис. 45). Для нахождения всех решений уравнения (10) следует
найти все точки пересечения линий (17) и (18). Для того чтобы
замкнутая траектория /С была предельным циклом, необходимо и доста-
выполнено второе из неравенств
цикл К вполне неустойчив.
точно, чтобы точка (wfl, н0) являлась
изолированной точкой пересечения
графиков (17) и (18). Если эти
графики не касаются друг друга
в точке (и& rzft), т. е. если у' (л0) 1,
то точка (w0, п0) их пересечения
обязательно изолированная. В этом
случае траектория К называется
грубым предельным циклом. При
X (см. Рис- 45) в обеих
полуокрестностях очевидно выпол-
нено первое из неравенств (15)» и,
следовательно, предельный цикл К
устойчив. При у (zz0) 1 (рис. 46)
(15), и, следовательно, предельный
Если графики (17) и (18) касаются друг друга в точке (нв, н0)»
но кривая (17) переходит с одной стороны биссектрисы (18) на
другую, то предельный цикл К является либо устойчивым, либо вполне
неустойчивым. Если же кривая (17), касаясь биссектрисы (18), нахо-
дится по одну ее сторону (рис. 47), то соответствующий предельный
цикл является полуустойчивым.
Критерий существования предельного цикла
Г) Пусть <р(£) — некоторое решение уравнения (2) (л произвольно),
определенное для всех значений и остающееся для этих зна-
чений t в замкнутом ограниченном множестве F, расположенном в А.
§ 28 1 ПРЕДЕЛЬНЫЕ ЦИКЛЫ 235
Точка р пространства /? называется ^-предельной точкой решения
ф(^), если существует такая неограниченно возрастающая последова-
тельность значений (больших Q
Л, 1Ь tky ...; lim^ = oo,
Л-юо
ЧТО
Пт<р(у=/>.
/г—* со
Совокупность 2 всех w-предельных точек решения <р(£) называется
его ^-предельным множеством. Оказывается, что множество 2
непусто, замкнуто, ограничено и состоит из целых траекторий; последнее
означает, что если точка | принадлежит 2, то решение <р (ty с началь-
ными значениями (0, |) определено для всех значений t, и вся траек-
тория <р (£, |) входит в множество 2. Очевидно, что ш-предельное
множество траектории <р(£, |) целиком содержится в 2.
Докажем предложение Г). Из замкнутости и ограниченности мно-
жества F следует, что множество 2 (очевидно, содержащееся в F)
непусто и ограничено. Покажем, что оно замкнуто. Пусть
— некоторая последовательность точек множества 2, сходящаяся
к некоторой точке р множества F; докажем, что р принадлежит 2.
Пусть £„ е2, ..., £й, ... и s2, ..., ... —две такие последователь-
ности положительных чисел, что
lim £Л, — 0; lim sk — со.
k ОО k —* GO
Так как точка рк принадлежит 2, то найдется такое значение Л.
что расстояние между точками pk и <р(.\) меньше еЛ. Для выбранных
значений
Л» ^2> •••> Пт/А = оо
А’-юо
мы получаем
lim ф (¥*)=/>,
А?-*оо
а это значит, что точка р входит в 2.
Покажем теперь, что множество 2 состоит из целых траекторий.
Пусть g—произвольная точка множества 2 и <р (t, g)— решение с началь-
ными значениями (0, |). Пусть, далее, Т—такое значение перемен-
ного t (оно может быть и отрицательно), для которого решение <р (ty |)
определено, так что точка <р(7’, |) существует. Так как точка | при-
надлежит 2, то найдется такая неограниченно возрастающая последо-
вательность
Z i1 im
' k -> (JO
236
УСТОЙЧИВОСТЬ
[Гл. 3
что
lim ф(/А) = |. (19)
k сю
Так как решение ф(0 определено для всех достаточно больших зна-
чений t, то при заданном Т определены (начиная с некоторого Л)
точки
ф(^+п=<₽(т; фо
(см. § 26, В)). Из формулы (19) в силу теоремы 14 мы имеем:
Н m q> (tk + Т) = li m Ф (Т, Ф (t/t)) = Ф ( Г, |),
k —► сю k -♦ сю
а из этого следует, что точка ф(7', |) принадлежит множеству 2,
а следовательно, и множеству F. Таким образом, траектория ф (t, g)
не может покинуть множества F ни при t возрастающем, ни при t
убывающем, а потому в силу предложения В) § 22 она определена
для всех значений t.
Итак, предложение Г) доказано.
Рассмотрим некоторые частные случаи io-предельного множества.
Если решение ф(/) (см. Г)) есть положение равновесия, т. е. ф(£) = „г.?,
то ш-предельнсе множество решения ф(£) состоит, очевидно, из одн й
точки хп. Если ф(^) есть периодическое решение, описывающее замкну-
тую траекторию К, то ш-предельное множество решения ф(/), очевидно,
совпадает с К. Наконец, если К есть периодическое решение, а ф(^) —
спирально навертывающаяся на пего при траектория, то К
есть со-предельное множество решения ф(/).
Докажем теперь теорему, дающую возможность установить в неко-
торых случаях существование периодического решения. В случае анали-
тических правых частей системы (1) это периодическое решение будет
либо предельным циклом, либо будет содержаться внутри семейства
периодических траекторий (см. пример 3).
Теорема 21. Пусть ф(£)—решение уравнения (2) (п = 2),
определенное для всех значений и остающееся при этих
значениях t в замкнутом ограниченном множестве F, содержа-
щемся в А, и пусть 2 есть ^-предельное множество решения ф(0.
Если множество 2 не содержит положений равновесия, то оно
состоит из одной замкнутой траектории К. При этом воз-
можны два случая: 1) ф(0 есть периодическое решение, а К—опи-
сываемая им траектория, 2) траектория, описываемая реше-
нием ф(£), при ^->4“°° наматывается на траекторию К, как
спираль.
Доказательство. Если ф(£) — периодическое решение, то
множество 2 состоит из единственной периодической траектории К,
описываемой решением ф(7), и утверждение теоремы очевидно (слу-
§ 28)
ПРЕДЕЛЬНЫЕ ЦИКЛЫ
237
чай 1). Допустим, что решение q>(t) не является периодическим и
пусть b — произвольная точка множества 2. Через точку b проведем
прямолинейный отрезок А, не коллинеарный вектору f(b) фазовой
скорости, выходящему из точки b (f(b) 0, так как, по предположе-
нию, точка b множества 2 не является поло-
жением равновесия), и выберем этот отрезок
настолько коротким, чтобы все траектории,
проходящие через точки этого отрезка, пере-
секали его (не касаясь) в том же направлении,
что и траектория, проходящая через b (рис. 48).
Так как точка b является оьпредельной для
траектории ф (£), а последняя не является зам-
кнутой, то эта траектория должна, очевидно,
бесчисленное множество раз пересечь отрезок
L и притом в различных точках (см. А)). Пусть
д1 = ф(/1) и «2 = ф(/2) —две следующие друг за другом во времени
(Z,<^) точки пересечения траектории ф(£) с отрезком L. Кусок
траектории ф (t), обозначим через Вместе с отрезком
он
на две
образует замкнутую кривую Q, которая разбивает плоскость
области G| и й2. Пусть h — малое положительное число.
Геометрически очевидно (рис. 49),
что точки ф (1\ — h) и ф (f2 -р ле-
жат по разные стороны кривой Q;
будем считать, что первая принад-
лежит области а вторая — об-
Рпс. 49.
ласти 0$. Через отрезок а}а2 все
траектории входят из области в
область 0%. Таким образом, ни одна
траектория не может выйти из об-
ласти С.2 через этот отрезок. Войти
или выйти в область 0.2 через кри-
вую М никакая траектория также
не может, так как М есть кусок
траектории, а траектории не могут
пересекаться между собой. Так
как кусок /И траектории ф(£) пе-
ресекается с отрезком L только в своих концах, то концы от-
резка L лежат по разные стороны кривой Q. Обозначим через а
тот конец отрезка А, который лежит в области G2. Траектория ф(£),
начиная с вся протекает в области <?2 и не может пере-
секать отрезок поэтому точка b не принадлежит отрезку
(см. А)), и, следовательно, она должна лежать на отрезке аа.г. Если
теперь а3 = ф(^3)—следующая (во времени) после а.2 точка пересе-
чения траектории <p(f) с отрезком L, то из аналогичных соображений
238
УСТОЙЧИВОСТЬ
[Гл. 5
видно, чю она лежит на отрезке Ьа$ (рис. 49). Обозначая через
а*==Ф(^)> .... а* = Ч>(^), ...
следующие друг за другом (во времени) точки пересечения траекто-
рии ф(/) с отрезком А, мы убедимся, что они образуют на отрезке L
монотонную последовательность точек, идущих в направлении от аг
к Ь. Покажем, что предел У последовательности аь а* ..., akt ...
совпадает с Ь>
Для этого мы, прежде всего, докажем, что последовательность
..., tk1 ... неограниченно возрастает. Допустим, что 1пп/Л=з
= т<4-оо. Тогда ф (т) = д' и /(&') = <р (т) = Иш а это
невозможно, так как вектор <p(t)—<p(/ft) направлен вдоль отрезка А,
а вектор f(b') не коллинеарен этому отрезку. Таким образом, должно
быть выполнено соотношение Пт/Л = Ц-оо, и потому вся траекто-
рия ф (t) при пересекается с L лишь в точках а]( ait ..., aki ...
Следовательно, эта траектория имеет на отрезке L лишь одну ш-пре-
дельную точку Ь' (см. А)), так что V = д. Отметим, что в проведенном
доказательстве было пока использовано лишь то, что сама точка/?
не является положением равновесия.
Покажем теперь, что траектория <р(/) не может входить в w-npe-
дельное множество для какой-либо другой траектории *ф(/). Допустим
противоположное. Тогда каждая точка траектории <p(f) является
(«-предельной для *ф(/) (см. Г)); в частности, таковой будет точка а{.
Так как точка не является положением равновесия, то в силу
доказанного выше последовательные точки
..., •••
пересечения траектории с отрезком L образуют монотонную
последовательность, сходящуюся к ait и других ^-предельных точек
траектории if(/) на отрезке L не существует. Но это противоречит
тому, что все точки а2, а3, ..., лежащие на траектории ф(/), являются
ю-пр сдельны ми точками траектории яр(/)*
Итак, доказано, что незамкнутая траектория, среди ил-предель-
ных точек которой нет положений равновесия, не может быть
сама ил-предельной.
Так как траектория К содержится в («-предельном множестве 2
траектории <р(/), а это множество замкнуто (см. Г)), то все («-пре-
дельные точки траектории К содержатся в 2 и потому не являются
положениями равновесия. Таким образом, к траектории К можно
применить доказанное выше предложение, так что траектория К должна
§ 28]
ПРЕДЕЛЬНЫЕ ЦИКЛЫ
239
быть замкнутой. Из всего построения видно, что траектория <р(0
наматывается на К, как спираль, и потому множество 2 состоит лишь
из замкнутой траектории К, проходящей через точку Ь.
Таким образом, теорема 21 доказана.
При м е р ы
I. Дадим пример системы уравнений вида (1) (и = 2), имеющей
периодические решения различного типа, в частности предельные
циклы различных видов. Первоначально мы зададим ее в полярных
координатах ср, р, а затем уже преобразуем в декартовы координаты х, у.
Имея в виду последующее преобразование к декартовым координатам,
!..ы зададим ее в виде:
?= 1; Р —Р£(Р?)> (20)
где g(zz)—непрерывно дифференцируемая функция своего аргумента,
определенная для всех неотрицательных его значений. При рассмо-
трении в полярных координатах мы будем использовать лишь поло-
жительные значения для р.
Множество всех положительных значении р, для которых g(p“) — 0,
обозначим через 7V, а его дополнение в множестве положительных
чисел — через Z). Каждому числу zza из N соответствует, очевидно,
решение
? = I, р == пи
уравнения (20); соответствующая траектория Ktt(i замкнута: она является
окружностью в плоскости Р с центром в начале координат и радиу-
сом Иц, Так как множество N замкнуто в совокупности всех поло-
жительных чисел, то I) открыто и состоит из конечного или счетного
числа интервалов, попарно друг друга не пересекающих. Пусть
р zz2—один из конечных интервалов. Тогда замкнутые
траектории Klfi и Ки2 ограничивают в плоскости Р кольцо Q. Для
всех чисел р интервала z/j р <4 функция £(р2) сохраняет знак,
так что на всем интервале имеет место одно нз неравенств:
е(р*)<0; £(р*)>0. (21)
Пусть
Р-Р О «) (22)
•—решение системы (20) с начальными значениями £ = 0, <р=0, р = zz,
где В силу доказанного в примере 1 § 15 функция р(£, п)
определена для всех значений t и при приближается к одному
из концов интервала а при — 00 — к другому. Из
этого следует, что траектория (22) при >4-о° и —оо нама-
тывается, как еппоаль па окружности K1!v KUn. Именно, если выполнено
первое из неравенств (21), то траектория (22) представляет собой
240
УСТОЙЧИВОСТЬ
[Гл. 3
спираль, наматывающуюся на при оо и на при — оо
(рис. 50). Если выполнено второе из неравенств (21), то решение (22)
представляет собой спираль, наматывающуюся на Kfll при t —> — оо
и на при t —>4~°° (рис. 51). Таким образом, кольцо Q заполнено
однотипными спиралями одного из двух видов в зависимости от того,
какое из неравенств (21) выполняется на интервале «1<^Р<Сгг2- Если
множество 2V ограничено и п*— его верхняя грань, то на бесконечном
интервале траектории (22) в одну сторону наматыва-
ются на окружность /<н«, а в другую сторону уходят в бесконечность.
Рис. 50.
Если точка и0 множества /V является его изолированной точкой,
то замкнутая траектория является предельным циклом, вид кото-
рого зависит от типа спиралей, заполняющих кольца, примыкающие
к траектории KUQ. Если точка ив множества 2V не является его изоли-
рованной точкой, то периодическое решение Ка<3 не является пре-
дельным циклом. Если при этом в /V содержится целый интервал
с центром в п0, то периодическое решение Кц<3 содержится внутри
целого семейства периодических решений, составляющих совокупность
концентрических окружностей с общим центром в начале координат.
Если к числу и0 с одной стороны примыкает целый отрезок чисел
множества N, а с другой — интервал из D, то траектория /Qo является
крайней в семействе замкнутых траекторий, примыкающих к ней
с одной стороны, а с другой стороны на нее наматывается семейство
спиральных траекторий. Возможны, однако, и более сложные случаи
примыкания замкнутых траекторий к периодическому решению /Сао.
Их легко себе представить; например, N может быть канторовым
совершенным множеством.
Запишем теперь систему (20) в декартовых координатах, положив:
A- = pcoS!?, j/ = psinp. (23)
§ 28}
ПРЕДЕЛЬНЫЕ ЦИКЛЫ
241
Дифференцируя соотношения (23), мы получаем:
Х = Р cos <р —sin <p = pg(ps). — P'T-^-vgG^ + y1)— у; 1
х (24)
_Р = р sin <р+ pep cos ? = pg(p2)-у + р- L=yg^ 4- уа) 4-х. j
Итак, в декартовых координатах система (20) записывается в виде:
jf = xg(xa-h/)— у\ _p=j,g(x94-/) + x. (25)
(Здесь сможет быть, например, произвольным многочленом.) Система (25)
имеет в начале координат положение равновесия.
2. Пусть
x'=fx(x\ р); х3=/9(х1, х2 р)
— нормальная автономная система второго порядка, правые частя
которой зависят от числового параметра р и обладают непрерывными
частными производными первого порядка по всем своим аргументам х\
х2, р. Пусть, далее,
х=/(х, р) (26)
— векторная запись этой системы. Решение уравнения (26) с началь-
ными значениями 0, § обозначим через q> (£, р); предположим, что
<p(f, р0) есть периодическое решение уравнения (26) при (р = р0)
периода Т. Выясним вопрос о том, что происходит с этим решением
при изменении параметра р вблизи значения р0.
Решения уравнения (26) будем изображать в одной и той ж®
плоскости Р независимо от значения параметра р. Пусть К — замкну-
тая траектория, соответствующая решению ф(£, |0, р0) и L — гладкая
кривая, заданная в плоскости Р параметрическим векторным уравнением
X = Ф (zz),
которая пересекается с траекторией К в единственной точке
1о = Ф(О, Ро)=Ф(А Ро) = Ф(«о)> (27)
не касаясь ее. Рассмотрим векторное уравнение:
<Р (*, 'Ф(и), Ю— "ФОО-О, (28)
в котором независимыми переменными будем считать р, и, а неизве-
стными функциями t и v. Независимые переменные пусть меняются:
и вблизи zz0, р вблизи р0. Решения будем искать при tr близком к 1\
vt близком к Uq. При и = п0, р=-ро имеется очевидное решение
уравнения (28): t—T, v = u^ (см. (27)), и функциональный опреде-
литель, соответствующей системы уравнений при этих значениях пере-
менных отличен от нуля, так как векторы/(§0> р0) и ф' (м0) незави-
симы. При р = ро уравнение (28) определяет функцию последования
242
УСТОЙЧИВОСТЬ
(ГЛ. 5
v = y(ic u0) уравнения (26) (р. = р,в) вблизи замкнутой траектории К-
При [1, близком к [i0, функция v~yjy, р) также определяется из
уравнения (28) и может считаться функцией последования уравне-
ния (26) вблизи периодического решения Д'. Однако уравнение (26)
при может и не иметь периодического решения. Для отыска-
ния периодического решения уравнения (26) при р., близком к р,0,
}ассмотрим уравнение
7. (г6 !х) — и — 0 (29)
относительно неизвестной функции и (и) переменного р. Если произ-
водная левой части уравнения (29) по переменному и при и = ие,
р, = р,0 отлична от нуля, т. е. если
X ("о> P-о) 1, (30)
то уравнение (29) заведомо имеет дифференцируемое решение и (и),
н тогда уравнение (26) имеет при р., близком к р.3, единственное
периодическое решение, гладко влг’сяшое от р н превращающееся
в К при р. = :0. Условие (30) означает предположение грубости
цикла К. В полученном результате заключается оправдание термина
«грубый». Грубый предельный цикл не исчезает (и остается гру-
бым) при малых изменениях правых частей системы, он «прочен» при
этих изменениях.
Если график уравнения
?’ = ХО. р.) (31)
в плоскости переменных и, v при р = ро касается в точке (zzp, zz0)
биссектрисы
(32)
с порядком касания единица (рис. 52,6), то кривая (31) при р. = рв
лежит по одну сторону биссектрисы (32), и предельный цикл К является
§ 281
ПРЕДЕЛЬНЫЕ ЦИКЛЫ
243
гюлуустойчивым (рис. 53, б). При изменениях параметра р. вблизи
наиболее естественное поведение графика (31) заключается в том, что
при значениях р., лежащих по одну сторону от р,0, точка пересечения
графиков (31) и (32) вовсе исчезает (рис. 52, а), а при значениях р,,
лежащих по другую сторону, появляются две точки пересечения этих
графиков (рис. 52, в), так что у уравнения (26) появляются два гру-
бых предельных цикла, близких к К (рис. 53, в). Таким образом,
при прохождении параметра р. через значение р.о мы сначала не имеем
предельного цикла (рис. 53, а), далее при р. = р.о появляется один
полуустойчивый цикл, и при дальнейшем изменении параметра р. он
распадается на два грубых предельных цикла, близких к Д'. Описан-
ное явление принято называть «рождением» предельных циклов урав-
нения (26) при изменении его правой части.
3. Отметим некоторые очень важные свойства периодического
решения К уравнения (2) в случае аналитических правых частей. Здесь
мы без доказательства используем тот факт, что решение ср (У, |)
уравнения (2) является в этом случае аналитической функцией пере-
менных t и Е1, Е*2. При построении функции последования будем счи-
тать, что кривая L задается аналитическим уравнением. В этих пред-
положениях функция последования х (м) оказывается аналитической,
будучи решением аналитического уравнения.
Так как нулям функции х 00—и соответствуют периодические
решения уравнения (2), то ввиду аналитичности функции х (и) воз-
можны лишь два взаимно исключающих друг друга случая: 1) К есть
предельный цикл — случай, когда щ есть изолированный нуль функ-
ции х (п) — п; 2) Периодическое решение К содержится внутри семейства
периодических решений — случай, когда функция х(м) —и тожде-
ственно равна нулю. Если на траекторию К спирально наворачивается
какая-либо другая траектория, то К не содержится внутри семейства
периодических решений и, следовательно, является предельным
циклом. Таким образом, при аналитических правых частях в слу-
чае 2) теоремы 21 периодическое решение К является предельным
циклом.
244
УСТОЙЧИВОСТЬ
[Гл. 5
§ 29. Ламповый генератор
Здесь схематически будет описано устройство простейшего лампо-
вого генератора — прибора, являющегося источником периодических
(незатухающих) электрических колебаний. Будет дана качественная
математическая теория работы генератора. Урав-
нение, описывающее работу лампового генера-
тора, нелинейно. Его предельный цикл и соот-
ветствует периодическим колебаниям, возбуждае-
мым генератором. Адэкватность математического
понятия предельного цикла и физического понятия
незатухающего колебания, возбуждаемого ламповым
генератором, была впервые установлена выдающим-
ся советским ученым А. А. Андроновым. До ис-
следований Андронова работу лампового генератора
пытались объяснить при помощи линейных диффе-
ренциальных уравнений, что не могло дать правиль-
ной математической картины работы генератора.
А) Триод (один из видов электронной лампы) представляет собой
трехполюсник aks. Условное изображение триода показано на рис. 54.
Здесь а — анод, k — катод, s — сетка. Между полюсами s* и k подается
разность напряжений Us (сеточное напряжение), однако ток между
полюсами s и k отсутствует; от полюса а к полюсу /г через лампу
течет ток 1а (анодный ток). Закон, управляющий работой триода,
записывается формулой
la=f(Us).
(1)
Функция / называется характеристикой триода. Мы будем считать,
что она является монотонно возрастающей и положительной и удовлет-
воряет условиям:
lim /(£/,) = О,
lim =
где In — ток насыщения
триода (рис. 55). Обычно
предполагают также, что
максимум функции /'(£Д)
достигается в точке 6^ = 0.
Описанный в А) под на-
званием триода трехполюс-
ник в действительности включает в себя, кроме электронной лампы,
еще анодную батарею, батарею сеточного смещения и батарею нака-
ливания катода.
§ 29]
ЛАМПОВЫЙ ГЕНЕРАТОР
245
Б) Ламповый генератор с колебательным контуром в анодной
цепи имеет следующее устройство (рис. 56). Он имеет четыре узла а,
ky sy b и состоит из триода aks (см. А)) с характеристикой f(Us),
конденсатора ak с емкостью С, сопротивления ab величины /?, индук-
тивности bk величины L и еще одной индуктивности sky величина
которой не имеет значения.
Индуктивности kb и связа-
ны отрицательной взаимоин-
дукцией —714 (7И 0), которая
осуществляет так называемую
обратную связь в ламповом ге-
нераторе. Если обозначить че-
рез J силу тока, идущего через
сопротивление Ьау или, что
то же самое, через индуктив-
ность kb:
Рис. 56.
J— ^ba
то оказывается, что величина J, как функция времени ty удовлетворяет
следующему дифференциальному уравнению:
= (2)
Выведем уравнение
имеем:
где 1ка — ток, идущий
свойств триода имеем:
(2). В силу первого закона Кирхгофа
d ~I- ?ka — а*
МЫ
(3)
через конденсатор ka. Кроме того, в силу
Л/г---- 0-
(4)
Применяя второй закон Кирхгофа к колебательному контуру kbaky
получаем (см. (4)):
L1kb~\-RIba~\~ ak di — 0.
Дифференцируя это соотношение, получаем:
Lfkb "F RJba "F ~C^ak — 0- (5)
В силу взаимоиндукции между индуктивностями kb и ks получаем
(см. (4), а также § 13, Б)):
= (6)
Таким образом, из соотношений (1), (3), (5), (6) следует (2).
246
УСТОЙЧИВОСТЬ
(Гл. 5
В) Уравнение (2) в фазовой плоскости переменных / J имеет
единственное положение равновесия с координатами:
У=/(0), /=0. (7)
Это положение равновесия асимптотически устойчиво, если
Я>^/'(0), (8)
и вполне неустойчиво (см. § 26, Е)), если
«<-^/'(0). (9)
Бесконечно удаленная точка плоскости переменных J, J во всех слу-
чаях вполне неустойчива. Это значит, что существует настолько боль-
шой круг К в плоскости J, J, что всякая траектория уравнения (2),
начиная с некоторого момента времени, приходит в этот круг и остается
в нем. При выполнении неравенства (9) положение равновесия (7)
также вполне неустойчиво. Таким образом, в силу теоремы 21
(см. § 28) (о-нредельное множество любой траектории, отличной от
положения равновесия (7), представляет собой замкнутую траекто-
рию. Итак, в случае выполнения неравенства (9), ламповый генератор
является источником периодических незатухающих электрических
колебаний.
Замечание. При надлежащем выборе характеристики f урав-
нение (2) имеет единственный предельный цикл, а все осталь-
ные траектории уравнения (2), отличные от положения равновесия (7),
наматываются на него. Одна из характеристик, обладающих этим
свойством, будет указана в примере.
Для доказательства предложения В) введем вместо неизвестной
функции J новую неизвестную функцию х, положив:
-V 4-/(0) (10)
с тем, чтобы точке (7) соответствовало начало координат плоско-
сти X, X.
Сделав подстановку (10), получаем из уравнения (2) уравнение
?+TJf + /Jc^=rcl/(^)-/(°)]- (И)
Функцию переменного х, стоящую в правой части этого уравнения,
обозначим через g’(x). Непосредственно видно, что функция g
является ограниченной, монотонно возрастающей и обращается в нуль
лишь при нулевом значении аргумента (рис. 57). Полагая сверх того,
$ 29 ]
ЛАМПОВЫЙ ГЕНЕРАТОР
247
мы запишем уравнение (11) в виде:
х 2ох о?х = /т
Вводя новее переменное у = х> мы из этого уравнения получаем
нормальную систему:
( х — у,
| — — м-х — 2бу - J- g (у). 12)
Для отыскания положений равновесия системы (12) приравниваем ее
правые част нулю:
I У = о, . ____________________________________
| — с<гх — 26y -J- g (у) = 0.
Полученная система имеет------------------------------------------ £
единственное решение
х=0, у=0. -
Таким образом, начало ко-
ординат является единствен- Рис, 57.
ным положением равновесия
системы (12), а из этого следует, что единственным положением
равновесия уравнения (2) является точка (7).
Выясним теперь условия устойчивости положения равновесия (0, 0)
системы (12), для чего линеаризуем эту систему в точке (0, 0). Мы
Получаем систему:
х—у,
у = — oAv — 28у g (0) у.
(13)
Легкие вычисления дают характеристический многочлен
Ха + (28 — £'(0)П + о>*
Линейной системы (13). В новых обозначениях условия (8) и (9) со-
ответственно принимают вид: 28^>g'(0), 28<^g'(O)- Таким образом,
при выполнении условия (8) положение равновесия (0, 0) асимптоти-
чески устойчиво (см. теорему 19 и § 9, Б)), а при выполнении усло-
вия (9) оно вполне неустойчиво (см. § 26, Е)).
Для выяснения поведения траекторий системы (12) в далеких
частях фазовой плоскости х, у рассмотрим линейную систему:
( х=у,
| j) = — (оах — 28у,
полученную из системы (12) отбрасыванием ограниченного во всей
плоскости члена g(y). Легкие вычисления дают характеристический
(14)
248
УСТОЙЧИВОСТЬ
[Гл. 8
многочлен системы (14):
к3 4-2814-о»3; (15)
так как числа 28 и о>3 положительны, то его корни имеют отрица-
тельные действительные части. Таким образом, в силу предложе-
ния Д) § 26 для линейной системы (14) существует функция Ляпу-
нова U7(x, у), удовлетворяющая условию:
W'(ii) (х, у) — piF(х, у). (16)
Вычислим теперь производную (х, у) функции №(х, у) в силу
системы (12). Мы имеем:
1Г(12)(х, y) = Ww(x, (17)
Так как функция g(y) ограничена, то имеет место неравенство
dW^y • g(y) /^(х77) (18)
(см. формулу (14) § 26), где у — некоторая положительная кон-
станта.
Полагая теперь
мы из (16), (17) и (18) получаем неравенство
(х, у)^ — 2а№(х, у) при 1Г(х, (19)
Уравнение
У7(х, у) = са (20)
определяет в плоскости х, у эллипс. Из неравенства (19) непосред-
ственно следует, что в точке (х, у), принадлежащей эллипсу (20)
функция lF(x, у) убывает вдоль траектории системы (12), проходя-
щей через точку (х, у). Таким образом, все траектории системы (12),
пересекая эллипс (20), входят внутрь этого эллипса. Если
х = ср(О, У = Ф(О (21)
— решение системы (12), начинающееся в точке (£, ^) вне эллипса
(20), то, полагая
w(0=^(?(0, Ф(0),
мы для функции w(i) получаем неравенство
— 2aw(/), (22)
верное при условии
& (О с3.
ламповый генератор
249
§ 29 1
Интегрируя неравенство (22), получаем:
Г(?(0, ri)e~2af.
Из этого следует, что траектория (21) обязательно входит в эллипс
(20). При этом ни одна траектория не может выйти из этого эллипса,
так как в его граничных точках все траектории входят внутрь.
Пусть теперь К—некоторая окружность в плоскости содер-
жащая эллипс (20). Из доказанного следует, что всякая траектория
системы (12), отличная от положения равновесия (0, 0), обязательно
входит в окружность Д' и остается в ней. Так как точка (0, 0) вполне
неустойчива, то траектория эта не может иметь ее в числе своих
со-предельных точек и потому в силу теоремы 21 (см. § 28) она
есть либо спираль, наматывающаяся на периодическое решение, либо
периодическое решение.
Итак, предложение В) доказано.
Пример
А. А. Андронов, который впервые составил для лампового гене-
ратора нелинейное уравнение (2), рассмотрел случай, когда характе-
ристика f триода имеет особо простой вид, а именно она равна
нулю при отрицательных значениях аргумента и равна положитель-
ной константе b при положительных значениях аргумента. Считая,
что /(0) = -|- и производя замену переменных (10), мы придем к си-
стеме (12), в которой функция g(y) определяется условием:
( — при у 0,
| при у 0,
где а = ~. Система (12) с выбранной таким образом разрывной
функцией g(j) записывается при у 0, т. е. в верхнем полупло-
скости, в виде:
( Х=у,
( — 28у о>% ^4)
а при ><0, т. е. в нижней полуплоскости, в виде:
х=у,
у = — оАс — 23у — w2a. (2^)
Мы будем считать, что корни многочлена (15) комплексные. Таким
образом, положение равновесия (0, 0) системы (14) представляет
собой устойчивый фокус (см. § 16, В)); системы же (24) и (25) отли-
чаются от системы (14) только сдвигом: их положения равновесия
помещены не в начале координат, как у системы (14), а в точке (а, 0)
250
УСТОЙЧИВОСТЬ
| Гл 1
у системы (24) и в точке (—ау 0) у системы (25). Заметим, чю
спирали линейной системы (14) наматываются на положение равно-
весия (0, 0) по часовой стрелке и что при прохождении полу-
витка спирали фазовая точка приближается к началу координат,
так что ее первоначальное расстояние от начала координат умно-
жается на некоторое число Х<^1, не зависящее от начального поло-
жения точки (см. § 16, В)).
Для того чтобы представить себе фазовую плоскость системы (12)
в случае, когда функция £(у) определяется условиями (23), нужно
верхнюю полуплоскость заполнить полувитками спиральных траекто-
рий системы (24), а нижнюю — полувитками спиральных траекторий
системы (25); при переходе же через прямую у — 0 следует непре-
рывно переходить с одних траекторий на другие. Исходя из этого
описания фазовой картины системы (12) (см. (23)), будем искать ее
замкнутые траектории.
Рассмотрим траекторию системы (12) (см. (23)), начинающуюся
на оси абсцисс в точке с координатой $^>0. Так как движение
в фазовой плоскости системы (12) происходит по часовой стрелке,
то из выбранной точки траектория пойдет в нижнюю полуплоскость
и, следовательно, будет управляться системой (25). После прохожде-
ния полувитка спирали в нижней полуплоскости фазовая точка вновь
понадает на ось абсцисс в точку с координатой
— (а (а 4“ £))• (26)
Это следует из того, что при прохождении полувитка спирали рас-
стояние фазовой точки от положения равновесия (—а, 0) умножается
на X. Точка с координатой (26), лежащая на оси абсцисс, будит
затем двигаться в силу системы (24) и, после прохождения полу-
витка спирали в верхней полуплоскости, придет на ось абсцисс
в точку с координатой:
а 4- X (2а 4- к (а + 4). (27)
Таким образом, траектория, начинающаяся в точке с координатой
на положительной части оси абсцисс, после полного обхода
вновь попадает па положительную часть оси абсцисс, но уже в точку
с координатой (27), и мы получаем отображение / положительной
полуоси абсцисс в себя, определяемое соотношением
X (4 = а 4- 2Ха 4~ X3iz 4~
Функция у (с) есть функция последования для системы (12) (см. (23)).
Имеется лишь одно значение 6, удовлетворяющее условию
Х(0=Л
й этому значению £ соответствует предельный цикл системы (12),
й иритом грубый и устойчивый, так как х'(£) = л2<^1 (см. § 28).
§ '0] ПОЛОЖЕНИЯ РАВНОВЕСИЯ'АВТОНОМНОЙ СИСТЕМЫ 251
§ 30. Положения равновесия автономной системы
второго порядка
Здесь будут классифицированы и изучены невырожденные поло-
жения равновесия нормальной автономной системы уравнений вто-
рого порядка:
х=/(х, у),
ч (О
У = у),
причем будет предполагаться, что правые части дважды непрерывно
дифференцируемы, а в теореме 23 — что они трижды непрерывно
дифференцируемы.
Невырожденные положения равновесия
Так как положение равновесия всегда можно принять за начало
координат, то мы будем предполагать, что подлежащее изучению по-
ложение равновесия системы (1) есть начало координат. Линеаризуя
систему (1) в точке (0, 0), т. е. разлагая правые части системы (1)
в ряды Тейлора по х и у и отбрасывая члены второго порядка, по-
лучаем линейную систему:
х — а\х -I- о-.у,
: - (2)
у = щх -ф- а2у.
Пусть X и — собственные значения матрицы (ар. Положение равно-
весия (0, 0) системы (1) называется невырожденным, если числа X
и р не равны между собой и их действительные части отличны от
пуля. Поведение траекторий линейной системы (2) было детально
изучено в § 16. Здесь будет показано, что для невырожденного по-
ложения равновесия поведение траекторий вблизи положения равно-
весия (0, 0) системы (1) в существенном совпадает с поведением
траекторий вблизи положения равновесия (0. 0) системы (2).
За положением равновесия (0, 0) системы (1) сохраняется наиме-
нование, данное в § 16. Если числа X и р оба действительны и отри-
цательны, то положение равновесия называется устойчивым узлом.
Если числа X и р оба действительны и положительны, то положение
равновесия называется неустойчивым узлом. Если числа X и р ком-
плексно-сопряжены и имеют отрицательную действительную часть, то
положение равновесия называется устойчивым фокусом. Если числа X
и р комплексно-сопряжены и имеют положительную действительную
часть, то положение равновесия называется неустойчивым фокусом.
Наконец, если числа X и р действительны и имеют различные знаки,
то положение равновесия называется седлом.
252
УСТОЙЧИВОСТЬ
(Гл 5
Наиболее простые свойства поведения траекторий вблизи поло-
жений равновесия можно установить, непосредственно опираясь на
теорему Ляпунова (теорема 19) и предложение Е) § 26. Таким обра-
зом, мы получаем предложение:
А) Устойчивый узел и устойчивый фокус являются асимптотически
устойчивыми положениями равновесия. Неустойчивый узел и неустой-
чивый фокус являются вполне неустойчивыми положениями равно-
весия.
Это предложение в значительной степени уже решает вопрос
о поведении траекторий вблизи узла и фокуса. Действительно, если
известно, что данное положение равновесия является асимптотически
устойчивым, то с точки зрения приложений уже часто бывает не
важно, каким именно способом стремятся к нему траектории. То же
самое относится и ко вполне неустойчивому положению равновесия.
Совсем другую роль играет седло: зная поведение траекторий вблизи
него, можно высказать ценные суждения о поведении траекторий на
всей плоскости. В то же время теорема о поведении траекторий
вблизи седла доказывается значительно труднее, чем соответствующие
теоремы относительно узла и фокуса.
Произведем теперь в фазовой плоскости системы (1) линейное
преобразование координат, с тем, чтобы придать ей наиболее про-
стой вид:
Б) Разлагая правые части системы (1) в ряды Тейлора по х и у
с точностью до членов второго порядка, получим:
[ X = а\х 4- а[у + г (х, у),
| — а\х a'iy 4- $ (х, _у),
где остаточные члены г (х, у) и s(x, j/) в точке х = 0, j = 0 обра-
щаются в нуль вместе со своими первыми производными по х и у
и могут быть записаны в виде:
г У) — гнх" +
S (х, у) — s1 iX* 4- 2stixy 4- з.г,у'\
причем коэффициенты rtj и sif- этих «квадратичных форм» являются
функциями переменных х> у, ограниченными вблизи начала коорди-
нат. Оказывается, что, производя действительное линейное преобра-
зование величин х, у в величины 5, ц, можно привести систему (3)
к простому виду, причем следует различать два случая: 1) Если соб-
ственные значения X, [л матрицы (ар действительны и различны, то
система уравнений для $ и записывается в виде:
1 = + 7)), т) = (хт)4-а(£, ф. (5)
2) Если собственные значения матрицы (а() комплексно-сопряжены,
т. е. имеют вид и Iх — т0 система уравнений для $ и
1301
ПОЛОЖЕНИЯ РАВНОВЕСИЯ АВТОНОМНОЙ СИСТЕМЫ
253
записывается в виде;
S = — ^)> ^ = ^4-р.7)4-о(Е, 7)). (6)
В обоих случаях остаточные члены р(Е, tj) и а($, у) обладают теми
свойствами, которые были отмечены выше для функций г (х, j)
и s(x, 7). В первом случае система принимает вид (5), если принять
ва оси направления собственных векторов матрицы (др.
Для доказательства предложения Б) достаточно найти такое ли-
нейное преобразование координат х, у в координаты Е, т;, чтобы
линейная система (2) приобрела простой вид. Такое преобразование
уже было найдено (см. § 14, Е)). Применяя то же преобразование
к системе (3), мы получим систему (5) или, соответственно, систему (6).
Поведение траекторий вблизи седла
Теорема 22. Предположим, что положение равновесия
О=(0, 0) системы (1) является седлом. Пусть Р — прямая, про-
ходящая через точку О в направлении собственного вектора
матрицы (др с отрицатель-
ным собственным значением,
a Q — прямая, проходящая
через точку О в направлении
собственного вектора мат-
рицы (др с положительным
собственным значением. Тогда
(рис. 58) существуют росно
две траектории U\ и Z/2 си-
стемы (1), которые при
t __> _i_ оо асимптотически
приближаются к точке О.
Рис. 53.
Эти траектории вместе с точкой О образуют непрерывную
дифференцируемую кривую U, касающуюся прямой Р в точ-
ке О. Точно так же существуют ровно две траектории V\
и системы (1), которые при t—*— оо асимптотически при-
ближаются к точке О; эти траектории вместе с точкой О
образуют непрерывную дифференцируемую кривую V, касающуюся
прямой Q в точке О, Остальные траектории системы (1), про-
ходящие вблизи точки О, ведут себя, в общем, так же, как
в случае линейного уравнения (см. § 16).
Траектории и U% называются устойчивыми усами седла О,
а траектории и называются неустойчивыми усами седла О.
Доказательство. Прежде всего примем прямую Р за ось
абсцисс, а прямую Q — за ось ординат; тогда система (1) запишется
в виде (5). Переходя снова к обозначениям х и у вместо 5 и tj, мы
254
УСТОЙЧИВОСТЬ
!Гл. 5
получим систему ypacneirHi
( x^f(x, у)^=ах4-г(х, у),
I J’ — S (•*> V) = ИУ + 5 (х> у)>
(7)
где г(х, у) и s(.r, у) имеют гид (4); здесь X 0, и^>0. Отметим
для дальнейшего, что в последующем доказательстве будут исполь-
зованы лишь следующие свойства правых частей системы (7): непре-
рывная дифференцируемость правых частей по х и у и ограничен-
ность функций rj п s4. (см. (4)) вблизи начала координат.
Доказательство распадается на две гласные части: а) доказатель-
ство существования уса Ub подходящего к точке О вдоль положи-
тельной части оси абсцисс при убывании координаты х; б) доказа-
тельство его единственности. Существование и единственность уса М3
доказываются аналогично. Для рассмотрения усов V, и ^достаточно
изменить знак времени Г: при
этом устойчивые усы перейдут в
неустойчивые и наоборот.
Перейдем к доказательству
существования уса (Д. Для этого
положим:
w (х, у)~у — ах8 (а 0)
и рассмотрим в плоскости (х, у)
параболу, определяемую уравне-
нием
у)(х, у) = 0. (8)
Парабола (8) разбивает, плоскость
на две части: положительную, со-
держащую положительную полу-
ось ординат, и отрицательную. По-
рспней для параболы. Покажем прежде
веете, что, если а — достаточно большое положительное число, а х
достаточно мало (| х | О» то все траектории системы (7) (за исклю-
чением положения равновесия О), пересекающие участок | х | а
параболы (8), переходят с отрицательной стороны на положитель-
ную, т. е. снаружи внутрь (рис. 59). Для этого вычислим производ-
ную (х, у) функции ю(х, у), В силу системы (7) в точках пара-
болы (8) мы имеем:
d)(7) (х, ах2) =у — 2ахх = а (р, — 2Х) х* -ф- $пх2 +. * •
(здесь невыписанныс члены содержат х по крайней мере в 3-й сте-
пени). Число а 2Х положительно, а функция ограничена в
окрестности начала координат; поэтому можно выбрать настолько
§30) ПОЛОЖЕНИЯ РАВНОВЕСИЯ АВТОНОМНОЙ СИСТЕМЫ 255
большое число а, что
а (р. — 2Х) — | $и | >> 8, 8 (к
Опущенные члены выражения для ю(7) (х, ах2) имеют, по крайней
мере, третий порядок малости по х, и потому существует такое по-
ложительное е, что при | х | £ мы имеем:
у)(7)(х, ах2)^0,
причем равенство имеет место лишь при х = 0, т. е. в точке О. Из
доказанного следует, что все траектории системы (1), за исключением
положения равновесия О, пересекают рассмотренный участок пара-
болы (8) в направлении роста функции <л(х, у), т. е. снаружи внутрь.
Точно так же доказывается, что участок | х | е параболы
у ах2 = 0 (9)
пересекается всеми траекториями системы (7), за исключением поло-
жения равновесия О, снаружи внутрь (внутренняя часть параболы (9)
содержит отрицательную полуось ординат, рис. 60).
Пусть а и b — точки, в которых прямая х = г пересекает соот-
ветственно параболы (8) и (9). Рассмотрим треугольник [О, а, £],
составленный из двух кусков парабол (8) и (9) и прямолинейного
отрезка [а, Ь]. Если е достаточно мало, то все траектории системы (1),
проходящие в треугольнике [О, а, Ь}, идут справа налево (рис. 61),
в частности пересекают отрезок [а, Ь] справа налево, входя в тре-
угольник [О, а, Ь]. Это следует из того, что выражение
х = Хх -|- г (х, у)
(см. (7)) при 0<^х^£, | у | <Г ах2 отрицательно, так как Х<^0, а
256
УСТОЙЧИВОСТЬ
{Гл. 8
г(х, у) есть «квадратичная форма» по х и у с ограниченными коэф-
фициентами.
Пусть <р (Л р)— траектория системы (7), начинающаяся при 2 = 0
в некоторой точке р интервала (а, Ь). Эта траектория входит в тре-
угольник [О, а, /;] через сторону [а, Ь]. Она может при возрастании t
либо выйти из треугольника через дуги парабол Оа, ОЬ, либо вовсе
не выйти из треугольника. В последнем случае траектория при t —* оо
асимптотически приближается к точке О. Геометрически видно, что
если траектория <р (£» р) выходит из треугольника через дугу Оа, то
и траектория ф(£, р'), где р' есть точка интервала (a, р), также выхо-
дит из треугольника через дугу Оа (рис. 61). Далее, если траектория
<р (t, р) выходит из треугольника через дугу Оа, то, в силу теоремы
о непрерывной зависимости решения от начальных значений (тео-
рема 14 и предложение Д) § 23), траектория ф(£, р₽), где р* — точка,
достаточно близкая к рг, также выходит через дугу Оа. Таким обра-
зом, совокупность всех таких точек р интервала (а, Ь), для которых
траектория <p(f, р) выходит из треугольника через дугу Оа, состав-
ляет некоторый интервал (а, а'), (Этот интервал непуст, т. е. аг^а,
ибо траектории, начинающиеся в точках р, достаточно близких к а,
очевидно, пересекают дугу Оа.) Точно так же совокупность всех
таких точек р, для которых траектория <р(£, р) выходит из треуголь-
ника через сторону ОЬ, составляет интервал (Ь, Ь'). Интервалы (а, а')
и (Ь, Ь') не могут пересекаться, так что точка а' лежит выше точки Ь’
или, в крайнем случае, совпадает с ней. (В действительности имеет
место совпадение, по это требует еще сравнительно сложного дока-
зательства.) Таким образом, отрезок [У, Ь'\ содержит хотя бы одну
точку, и потому существует траектория ф(/, р0), начинающаяся на
отрезке }а', Ь'] и асимптотически приближающаяся к точке О.
Касательная к траектории <р(£, р0) в точке (х, у/) имеет угловой
коэффициент
k(x у)—^ + s-^ У)
1 ’ >}"“Хх + г(х, у)’
Так как точка (х, у) траектории ф(£, р0) принадлежит треугольнику
[О, а, &], то
| у | ах2, 0<^х<^е, (10)
а из этого следует, что число k(x, Достается конечным и при х—Л)
стремится к нулю. С другой стороны, угловой коэффициент I (х, у)
секущей, проведенной из точки О в точку (х, у) траектории ф (t, />0),
равен у, а так как имеют место неравенства (10), то при х—>0
имеем /(х, у/)—-0. Таким образом, кривая <р(£, р0), упирающаяся
в точку О, имеет в точке О непрерывную производную и касается
оси абсцисс. Траектория q»(t, /?0) представляет собой ус U\> Ус U*
подходящий к точке О вдоль отрицательной части оси абсцисс, также
§301
ПОЛОЖЕНИЯ РАВНОВЕСИЯ АВТОНОМНОЙ СИСТЕМЫ
257
касается в точке О оси абсцисс; оба эти уса составляют вместе кри-
вую U с уравнением
У = иХх), (11)
где н’(х) есть непрерывная и непрерывно дифференцируемая функция
переменного х, причем и' (0) = 0.
Итак, существование устойчивых усов Ui и Ц, составляющих
вместе с точкой О кривую 7/, определяемую уравнением (11), дока-
зано. Докажем теперь единственность этих усов. Для этого преобра-
зуем в окрестности начала координат плоскости (х, у) систему
координат так, чтобы кривая (11) стала, осью абсцисс. Мы добьемся
этой цели, введя вместо неизвестной функции у новую неизвестную
функцию z по формуле
у=«(х) + г. (12)
Произведя в системе (7) замену (12), получаем новую систему урав-
нений
( x=f{x, u(x) + z} = F(x, z),
| i — g(x, и (x) z) — к' (x) f (x, a (x)-\-z)=G (x, z),
где неизвестными функциями являются х и г. Так как функция ц(х)
имеет непрерывную производную, то функция Л(х, z) имеет непре-
рывные производные по обеим переменным х и г, а функция О(х, z)
непрерывна по х и имеет непрерывную производную по z. Однако
существование непрерывной производной функции G(x, z) по х не
установлено. Таким образом, не установлено, что для системы (13)
выполнены обычные наши предположения о непрерывной дифферен-
цируемости правых частей по всем переменным, являющимся неизвест-
ными функциями. Очевидно, однако, что каждому решению системы (13)
соответствует в силу (12) решение системы (7) и обратно. Таким
образом, по поведению траекторий системы (13) можно судить о по-
ведении траекторий системы (7).
Устойчивые усы ил и Т/8 системы (7) перешли в отрезки оси
абсцисс плоскости (х, г), и потому система (13) имеет решения,
в которых функция х некоторым образом монотонно меняется,
асимптотически приближаясь к нулю, а функция z тождественно
равна нулю. Из этого следует, что
О(х, 0) = 0.
Ниже будет показано (см. В)), что функция О(х, z) может быть
записана в виде:
G(x, z)~zH(xt z), (14)
где /7 (х, z) — непрерывная функция переменных х и z. Из соот-
*/48 Понтрягин Л. С.
268
устойчивость
[Гл. 5
ношения (14) в силу непрерывности функции Я(х, z) мы получаем:
*)1 =Ит С(0^)-С(0л0)^Иш G(O,a) =
jZo '"*° g^Q *
= lim/7(0, z) — H(0> 0).
ж-*0
Но в силу (7) и (13) мы имеем =р> так что
Ж«-4)
Я(0, 0) = [1.
Таким образом, второе из уравнений системы (13) имеет вид:
2 = zH(x, z),
где Н(х, z) близко к р. в окрестности начала координат к, следо-
вательно, положительно. Из этого следует, что в окрестности начала
координат вдоль каждой траектории, отличной от усов U\ к {/8,
координата z сохраняет знак и по модулю увеличивается при увели-
чении t. Таким образом, ни одна траектория, протекающая вне оси
абсцисс плоскости (х, z), не может асимптотически приближаться
к точке О, и единственность устойчивых усов {Д и £78 доказана.
Теперь доказано, что на интервале (в, 6) существует лишь одна
такая точка р0, что выходящая из нее траектория системы (7) при
*оо асимптотически приближается к точке О, образуя ус t7v
Если точка р лежит на интервале (а, р0)> то выходящая из нее
траектория пересекает дугу Оа, а если точка р лежит на интер-
вале (Ь, р0), то выходящая из нее траектория пересекает дугу ОЬ.
Исходя из парабол
х — ау2 = 0, (15)
х4“<ху9 = 0 (16)
н прямой
У = «
(рис. 62), можно построить треугольник [О, с, rf], обладающий свой-
ствами, аналогичными свойствам треугольника [О, а, Й]. Существует
лишь одна такая точка q$ на интервале (с, d), что выходящая из нее
траектория при убывающем t асимптотически приближается к точке О
я образует неустойчивый ус V\. Если точка q лежит на интервале
(с, £о), то выходящая из нее при убывающем t траектория пересе-
кает дугу Ос, а если точка q лежит на интервале (^ <0, то выхо-
дящая из нее при убывающем t траектория пересекает дугу OtZ.
Рассмотрим теперь кривую
/(х, у) = 0 (17)
(см. (7)). Легко видеть, что она касается оси ординат в точке О.
5 30]
ПОЛОЖЕНИЯ РАВНОВЕСИЯ АВТОНОМНОЙ СИСТЕМЫ
259
Так как функция f(x, у) имеет вторые непрерывные производные,
и потому кривая (17) имеет в точке О определенный, радиус кри-
визны, то число а можно выбрать настолько большим, а число в —
настолько малым, что на отрезке кривая (17) проходит между
Рис. 62.
параболами (15) и (16) (рис. 63). Справа от кривой (17) функция
/(х, у) отрицательна, и потому векторы фазовой скорости в точках,
лежащих справа от кривой (17), направлены налево. Проведем из
точки с вертикальный отрезок [се],
нижний конец е которого лежит
на усе t/р Пусть р*- -точка интер-
вала (а, р0). Если точка р доста-
точно близка к точке р0, то, в
силу теоремы о непрерывной зави-
симости решения от начальных зна-
чений (теорема 14 и предложение Д)
§ 23), точка, вышедшая из р, прой-
дет достаточно близко к началу
координат и потому пересечет от-
резок [с, е]. При дальнейшем дви-
жении она обязательно пересечет
дугу Ос. В самом деле, если дви-
жущаяся точка пересекает линию
(17), то она обязательно пересе-
кает перед «этим дугу Ос. Если
же движущая точка не пересекает
линии (17), то она перемещается все время налево, а расстояние ж
от этой точки до линии (11), измеряемо^ по вертикали, растет;
таким образом, и в этом случае траектория пересекает дугу Ос.
260
устойчивость
(Гл. 5
Таким образом, рассматриваемая траектория входит в треугольник
[О, г, d\. После этого траектория уже должна будет пересечь интер-
вал (с, qQ) в некоторой точке q. Если, наоборот, пустить из точки q
интервала (с, ^0) траекторию в направлении убывания t, то при
х = z = 0 и обладающая
достаточной близости точек q и £0
эта траектория, пройдя вблизи начала
координат, пересечет интервал (а, р0)
в некоторой точке р' (рис. 64). Сопо-
ставляя эти два обстоятельства, легко
прийти к выводу, что при
имеем Это дает полное каче-
ственное представление о поведении
траекторий вблизи седла.
Таким образом, теорема 22 доказана.
Докажем теперь свойство (14) функ-
ции О(х, г).
В) Пусть О(х, г) — непрерывная
функция, определенная вблизи значений
непрерывной производной g~O(x, z). Если
O(xt 0) = 0,
то
Q(x, z) = zH(xt z),
где Н(х, z)—непрерывная функция
Для доказательства предложения В) определим функцию Н(х> Z),
положив:
//(х, z) = - при
д Z <18>
Н(х, z) = ^G(x, z) при z=0
и покажем, что определенная таким образом функция непрерывна.
При z=^0 функция, определенная соотношениями (18), очевидно,
непрерывна. Докажем, что она непрерывна в точке (х0, 0). Мы
имеем:
О(х, z) = G(x, z) — О(х, 0) = z£- G(xt 0z)t
где 0^9^ 1. Так как функция ~ O(xt z) непрерывна, то при
С72
х—>х0, z-O(z^O) имеем - = ~G (х, flz) — G(x0, 0).
Таким образом, предложение В) доказано.
| Ю] ПОЛОЖЕНИЯ РАВНОВЕСИЯ АВТОНОМНОЙ СИСТЕМЫ 261
Поведение траекторий вблизи узла и фокуса
Изучение узла и фокуса значительно проще, чем изучение седла.
При этом достаточно рассмотреть лишь случай устойчивости, так как
неустойчивые узлы и фокусы получаются из устойчивых переменой
направления течения времени. Основным приемом при исследовании
узла и. фокуса является введение полярных координат.
Теорема 23. Пусть 0=(0, 0) —устойчивый узел системы (1)
с собственными значениями к и р., причем |1<^Х<^0. В напра-
влении собственного вектора с собственным значением X проведем
через О прямую Р, а в направлении собственного вектора с соб-
ственным значением р — прямую Q. Оказывается, что каждая
траектория, начинающаяся достаточно близко к точке О, асимп-
тотически приближается к О и имеет в точке О касательную.
При этом только две траектории касаются прямой Q, подходя
к точке О с противоположных сторон, остальные же все каса-
ются прямой Р. В случае неустойчивого узла (0<^Х<^) пове-
дение траекторий при t—> — оо аналогично.
Доказательство будет проведено в предположении трех-
кратной дифференцируемости правых частей системы (1). В силу
предложения Б) система (1) может быть записана в виде (5); обо-
значая переменные Е и tj вновь через х и у, получаем систему
f х =f(x, у) = Хх 4- Г (X, у),
I Р = g(x, у) — ру 4- 3 (х, у).
При этом функции г(х,у) и s(x, у) трижды непрерывно дифферен-
цируемы и в точке О обращаются в нуль вместе со своими первыми
производными по х и у.
Введем теперь полярные координаты, т. е. положим:
х = р cos <р, у = р sin ср. (20)
Дифференцируя соотношения (20) и подставляя их в систему (19),
получаем:
( р cos ср — рф sin ср = Хр cos ср 4* г (р cos ср, р sin Ср),
( р sin Ср 4~ рф COS ср = р.р sin ср $ (р COS ср, р sin Ср).
Разрешая полученные соотношения относительно риф, получаем:
( P==p(Xcos,<p + (i.sin4<p)4-/7(p, ф),
| рф === (|* — X) р sin ср cos <р 4- G (р, ср),
где функции
Р(р, ср) = cos ср * г (р cos ф, р sin ф) -f- sin ср • з (р cos ср, рв1Пф),
G(p> ф) =—sin ср. r(p cos ф, р sin ф) 4" cos ф* s(p cos ф, р sin ф)
9 Цонтрягиа Л. О.
262
УСТОЙЧИВОСТЬ
[Гл. 5
периодичны по <р с периодом 2я, трижды непрерывно дифференци-
руемы по р и и при р = 0 обращаются в нуль вместе со своими
первыми частными производными по р:
F( 0, <?) = 0(0, <?) = =-^-Й = 0. (22)
В силу приводимого ниже предложения Г) функция О(р, <?) может
быть записана в виде:
О(р. ?) = р^(р. ?)
где /7(р, <р)—дважды непрерывно дифференцируемая* по р и ср
функция, обращающаяся в нуль при р = 0 (и любом ср, см. (31)
и (22)):
Я (О, <р) = 0, (23)
так что
^=0. М
Деля второе из соотношений (21) на р, мы получаем си’стему
р = Р (X cos’ <р 4-sin’ ?) 4-F (р, <р),
I ф = (р. — X) sin <р cos ср 4~ н (р, <р).
Систему (25) будем рассматривать на фазовой плоскости перемен-
ных р и ср, откладывая ср по оси абсцисс, а р — по оси ординат.
Системы (19) и (25) отнюдь не эквивалентны друг другу, так как
преобразование (20) плоскости (х, у) в плоскость (р, <р) не взаимно
однозначно; тем не менее из поведения траекторий системы (25)
можно делать выводы о поведении траекторий системы (19). Пове-
дение траекторий системы (25) мы будем рассматривать только
в полосе | р | <^ е.
Найдем прежде всего положения равновесия системы (25). Из
первого уравнения (25) видно, что при достаточно малом р ф О
величина р отлична от нуля (см. (22)), и потому в полосе |р|<^е все
положения равновесия лежат на оси р = 0. После этого из второго
уравнения (25) находим все положения равновесия (см. (23))
р = 0, А = 0, ±1, ±2,...
Линеаризуя систему (25) в точке р = 0, <р= у, получаем (см. (22)
и (24)):
( Др = р,АДр,
I Дф = (|А —X) •(— !)* Дср + а,, др,
где рь (равное X при k четном и ц при k иечстном) есть отрица-
§30] ПОЛОЖЕНИЯ РАВНОВЕСИЯ АВТОНОМНОЙ СИСТЕМЫ 263
тельное число. Таким образом, точка р = 0, ф = ту есть устойчивый
узел системы (25) при четном к и седдо при нечетном k (рис. 65).
Неустойчивые усы седла при этом направлены по оси <р, а устой-
чивые— по кривым, приближающимся к седлу сверху и снизу (см.
теорему 22).
Покажем теперь, что при достаточно малом положительном е
каждое решение системы (25), начинающееся в полосе |р (<^е, либо
является устойчивым усом одного из седел системы (25), либо, не
выходя из полосы [р | <^8, асимптотически приближается к одному из
узлов системы (25).
Каждому положению равновесия р==гО, = поставим в соот-
ветствие
kn
его окрестность определяемую
8, где 8 — положительное число.
неравенствами | р |<^8,
Если k четно, то рас-
сматриваемое положение равновесия является устойчивым узлом, и
в силу его асимптотической устойчивости существует настолько
малое положительное число 8, что каждое решение, начинающееся
в окрестности Ukt асимптотически приближается к узлу. Если k
нечетно, то соответствующее положение равновесия есть седло, и
существует настолько малое положительное число 8, что отличное от
положения равновесия решение, нгчинающееся в U& либо описывает
устойчивый ус седла, либо покидает окрестность Uk (см. теорему 22).
Так как правые части системы (25) периодичны по f, то можно
выбрать положительное 8, общее для всех окрестностей £/ft. Теперь
можно выбрать настолько малое положительнее число е 8, что
в полосе | р | е правая часть первого из уравнений (25) имеет знак,
противоположный знаку р, так что на каждом решении, начинающем-
ся в этой полосе, величина | р | убывает. Далее, при фиксирован-
ном 8 можно выбрать настолько малое положительное число е, что в
264
УСТОЙЧИВОСТЬ
[Гл. 5
прямоугольнике
11^ Лж , ь (k 4-1) ж ь
1рК«> + ---8
правая часть второго из уравнений (25) сохраняет знак и по модулю
превосходит некоторое положительное число а, так что решение,
начинающееся в этом прямоугольнике, покидает его через время, не
превосходящее числа и входит в ту из окрестностей Uk или
Uk+U которая соответствует устойчивому узлу. В силу периодичности
системы (25) по <р число е можно считать общим для всех прямо-
угольников рассматриваемого вида.
Мы видим теперь, что при выбранном е каждое решение, начи-
нающееся в полосе |р|<С®> либо пробегает устойчивый ус седла,
либо асимптотически приближается к устойчивому узлу.
Каждому решению системы (25), начинающемуся в полосе |р|<Се»
соответствует решение системы (19), начинающееся на расстоянии,
меньшем чем е, от устойчивого узла О этой системы. Для того чтобы
получить все такие решения системы (19), достаточно рассматривать
лишь решения системы (25), начинающиеся при О^р<^в. В силу
периодичности системы (25) по <р и периодичности преобразования (20)
существуют лишь два решения системы (19), соответствующие устой-
чивым усам седел системы (25), проходящим при р^>0, и эти реше-
ния системы (19) асимптотически приближаются к положению равно-
весия О, касаясь прямой Q и подходя к О с противоположных
сторон. Решениям системы (25), стремящимся к устойчивым узлам,
соответствуют решения системы (19), стремящиеся к положению
равновесия О и касающиеся при подходе к О прямой Р.
Таким образом, теорема 23 доказана.
Теорема 24. Допустим, что начало хоординат О системы (1)
представляет собой фокус, т. е. собственные значения мат-
рицы (а*) являются комплексно сопряженными числами
X = р, -|- iv, X = р — iv,
причем р. ф 0, v ф 0. Оказывается, что если р.<^0, то при t—>co
все траектории, проходящие вблизи точки О, наматываются на
начало координат О как спирали; если же р^>0, то при —оо
все траектории, проходящие вблизи точки О, наматываются на
начало координат О, как спирали.
Доказательство. Для доказательства воспользуемся канони-
ческим видом (6), переименовав в нем переменные Е и iq в перемен-
ные х и у. Таким образом, нам следует изучить систему уравнений
X =f (X, у) = рХ — vy 4- Г (X, у),
/ = = у).
§30] ПОЛОЖЕНИЯ РАВНОВЕСИЯ АВТОНОМНОЙ СИСТЕМЫ 265
Введем полярные координаты, т. е. Положим]
X = р СОЗ Ф,
и г (27)
у = р sin <р.
Дифференцируя соотношения (27) и подставляя полученные выраже-
ния в систему (26), получаем:
р cos (р — р^ sin ср — [Ар cos ср — vp sin <р -|- г (р cos ср, р sin ср),
р sin рф cos ср = vp cos <р р,р sin ср s (р cos<p, р sintp).
Решая полученную систему уравнений относительно риф, получаем
( Р = !^Р + (Р. ?). ,„йч
< (лэ)
I ? = * +р-?(р. ?).
где р(р, <р) и у(р, ср) — функции, ограниченные при малых р и перио-
дические по ср с периодом 2я. Будем для определенности считать,
что [А<^0. Рассмотрим траекторию системы (28), начинающуюся
в точке (ро, <р0), где О<уро<\ а а—достатрчно малое число. Из
уравнений (28) следует, что траектория эта асимптотически прибли-
жается к оси р = 0, причем ср стремится либо к -|-оо, либо —
к —оо в зависимости от того, положительно число или отрица-
тельно. Из этого следует, что соответствующая траектория в плоско-
сти (х, j>) навертывается, как спираль, на начало координат.
Таким образом, теорема 24 доказана. Нижеследующее предло-
жение Г), являющееся существенным обобщением доказанного выше
предложения В), используется только при доказательстве теоре-
мы 23.
Г) Пусть G(p, ср) — функция, определенная в области U7, заданной
неравенствами |р|<Л, удовлетворяющая условию
G(0, ср) = О (29)
и обладающая тем свойством, что функция
дб (р> ?)
др
существует и имеет непрерывные частные производные до порядка г
включительно* Тогда функция G(p, ср) в области W может быть
записана в виде:
G(P> = ?).
где функция 77(р, ср) определяется равенствами
Н(р, ?) = G (р -- ПРИ Р7^ °>
//(О, =
(30)
(31)
9 Понтрягин Л. С.
266
УСТОЙЧИВОСТЬ
[Гл. S
и имеет в области U7 непрерывные частные производные до порядка г
включительно. (При г=0 доказываемое предложение Г) превра-
щается в предложение В).)
Для доказательства предложения Г) рассмотрим функцию
К(М>=^.
О 5 Г.
(32)
Эта функция обладает в области IF непрерывными частными про-
изводными по р до порядка s —|— 1 включительно и удовлетворяет
условию
К (0, ?)==0 (33)
(см. (29)). Докажем, что при р & 0 имеет место равенство
/К(р, у)\_ у , у)
\ р / **
м
О А з,
(34)
где числа 7<, ... , 7* при каждом фиксированном А не завися! от
функции О(р, у) и удовлетворяют условию
Те + 71+ +l>“£Tpp (35)
а числа 0*, 0t, 0Л удовлетворяют неравенствам
Z = 0, L А.
(36)
Вычисляя
лучаем:
производную п0 Ф°РмУле Лейбница, по-
t))=tL
dp* \ p ХГ T/y pfr+1 tr
ab ak при каждом фиксированном k не за-
функций
(37)
где числа а0>
висят от функции О(р, <р). Разлагая каждую из
1 — 0, 1, k в ряд Тэйлора по р, получаем:
Жр,у) дОС(О,у) , £ д£+дК(0, у) 1
Эр Эр ~ I! држ
, Р*~‘ ^(0, у) . р*~ж
(А—01 * д/ * (Й-/+ 1)1
Далее, подставляя выражения (38) и (37), мы получаем в силу (33)
k k
' Гу b,; W^ + yT/P^^(^t)] ,39]
ЭрА \ p / p*+l “ д/ dp**1 J1 ' •
ngf ’>. (38)
0рЯ+1 ' '
§30j
ПОЛОЖЕНИЯ РАВНОВЕСИЯ АВТОНОМНОЙ СИСТЕМЫ
267
где bt и 7;-* константы, не зависящие (при каждом фиксированном k)
от выбора функции О(р, <р).
Для доказательства соотношения (34) достаточно теперь устано-
вить, что константы Ьь bk равны нулю, а константы у* Tv-» 7*
удовлетворяют условию (35). Так как перечисленные константы не
зависят от выбора функции G(p, <р), то указанные их свойства доста-
точно установить для функций О(р, <р) какого-либо спецнального
вида. Рассмотрим случай, когда Q (р, <р) является многочленом:
<«»
В силу (32) находим:
( #(Р> У) )_ «а-н /4П
р / *,+ 1* 1 f
С другой стороны, равенство (39) для многочлена (40) имеет вид:
А А
* ( лйл )=+2 4 да
i=! /=о
Правые части равенств (41) и (42) должны совпадать при |р|<%
р ф 0, а так как числа at, .ал+1 произвольны, то из этого
вытекает равенство нулю чисел Ьь ..., bk и соотношение (35).
Таким образом, формула (34) доказана.
Введем в рассмотрение функцию £*(р> срХ £=0> 1» ...» по-
ложив:
(р. ?)=ПРИ р * °>
? ' (43)
/ /п «О- ’ д К®'
t*(0. ?) —ЯП—5^—•
Из равенств (34) и (35) следует, что А*(р, <р) есть непрерывная
функция пары переменных р, ср во всей области W. Очевидно, что
при р ф 0 выполнены равенства
Ui(P, ?)=^’Л), Г,...» s —1. (44)
Докажем, что эти равенства справедливы и при р = 0. Пусть
0<^р0<^8, 0<^р<^в; тогда мы имеем:
Мр> ?)=МРо> <Р)+$ ^+t(5, ?)<#• (45)
Ро
Так как функции, стоящие в левой и правой частях этого равен-
ства, непрерывны, то равенство это справедливо и при р = 0, так
9*
268
УСТОЙЧИВОСТЬ
(Гл. 5
что мы имеем:
о
£а(0, ф)=1а(Ро, ?)+ J ?)<&
Ро
(46)
Вычитая соотношение (46) из (45) и деля результат на р, находим:
1*(р» ?) — <р)
\ Ьа-и (5, т) (%
о
Р
(Р>0).
Р
Переходя к пределу при р->0, мы видим, что правая производная
функции Lk(p, <?) по р в точк§ р = 0 существует и равна 4+t (0. ?)•
Точно так же доказывается, что и левая производная равна (0> ?)•
Таким образом, равенство (44) справедливо во всей области Wt
. Из соотношений (43), (32) при k = Q, s — r следуют равенства
(30), (31), а из соотношений (44) и (32) следует, что функция /7(р, 0
обладает непрерывной производной
О s, 0 s г,
а это и значит, что функция /7(р, ср) обладает всеми непрерывными
частными производными до порядка г включительно.
Итак, предложение Г) доказано.
§ 81. Устойчивость периодических решений
В этом параграфе будет рассматриваться вопрос об устойчивости
периодических решений автономных систем, а также систем с перио-
дическими правыми частями.
Понятие устойчивости
В параграфе 26 уже было дано определение устойчивости по
Ляпунову положения равновесия автономной системы. Здесь мы, прежде
всего, дадим определение устойчивости по Ляпунову решения произ-
вольной системы уравнений.
Пусть
X=f(t, X) (1)
гвекторная запись произвольной нормальной системы уравнений
порядка nt правые части которой вместе с их производными
определены и непрерывны на некотором открытом множестве Г про-
странства переменных t, х- Решение уравнения (1) с начальными
значениями 0, | обозначим через (р (t, 6, §).
§31] УСТОЙЧИВОСТЬ'ПЕРИОДИЧЕСКИХ РЕШЕНИИ 269
Определение. Решение ф(£) уравнения (1) с начальными зна-
чениями tQ, х9 называется устойчивым по Ляпунову, если выполнены
условия: 1) Существует такое положительное число р, что при
решение ф (£, tQ> jq) определено для в^х значений
t^t9, в частности и само решение ф(0 определено для всех
2) Для всякого положительного числа е можно подобрать такое поло-
жительное число 8 р, что при [Xj — х01 <8 выполнено неравенство
|ф(/, ^о» -*i)— ф(О|<С® при Устойчивое по Ляпунову реше-
ние ф(0 уравнения (1) с начальными значениями t9t х0 называется асим-
птотически устойчивым, если найдется такое положительное чи-
сло -о^р, что при | xt — х01 а имеем:
|ф(6 tQf хД—~ ф(0|“*0 при f->oo.
Приведенные здесь определения устойчивости по Ляпунову и
асимптотической устойчивости^инвариантны относительно случайного
выбора начальных значений ху решения ф(^). Это легко может
быть выведено из предложения Д) § 23.
В частном случае, когда система (1) автономна, а решение ф(£) есть
положение равновесия, приведенные здесь определения устойчивости
совпадают с данными в § 26.
Ниже будут рассмотрены системы (1), правые части которых
зависят от t периодически с периодом г
x)=f(t,x), (2)
а также системы (1), являющиеся автономными:
f(t,x)=f(x). (3)
В том и другом случае будет исследоваться вопрос об устойчивости
периодического решения ф(^) периода -с:
ф(<4-т) = ф(0, (4)
которое в случае автономной системы будет предполагаться отличным
от положения равновесия. В случае периодической системы (см. (2))
будут даны достаточные условия асимптотической устойчивости реше-
ния (4) периода -с. Автономная система является частным случаем
периодической, и потому можно было бы ожидать, что эти условия
применимы и для периодического решения автономной системы. Ока-
зывается, однако, что для нее они невыполнимы (периодическое реше-
ние автономной системы не может быть асимптотически устойчивым),
и потому для устойчивости по Ляпунову периодического решения
автономной системы даются другие, более слабые условия.
А) Для того чтобы изучить поведение решений уравнения (1) вблизи
решения ф(0> введем новую неизвестную векторную функцию у,
положив:
х=ф(о-Ьз'.
(5)
270
УСТОЙЧИВОСТЬ
(Гл. S
В дальнейшем мы будем считать, что правые части системы (1) имеют
на множестве Г вторые непрерывные производные по координатам
вектора х. Произведя в системе (1) замену переменных (5), принимая
во внимание, что ф(0 есть решение уравнения (1), и разлагая пра-
вые части по у, получаем:
J
Линеаризуя эту систему, т. е. отбрасывая члены г1 второго порядка
малости относительно у, получаем линейную систему;
(7)
*
где А (/) — матрица с элементами
д,-т_ V(t))
аЛ1>— дх!
Будем считать теперь, что правая часть уравнения (1) — периодиче-
ская периода т по t (см. (2)) и что решение ф(0 — также периоди-
ческое периода т. При этих предположениях линейная система (7)
является периодической периода т:
в’(/-Н) = а'(0,
так что можно говорить о ее характеристических числах (см. § 19, Д)).
Оказывается, что в случае, когда система (1) автономна (см. (3)),
а ее периодическое решение ф(0 отлично от положения равновесия,
линейная система (7) обязательно имеет одно характеристическое число
равным единице.
Докажем последнее утверждение. Пусть Ф (0 — матрица, удовлет-
воряющая матричному уравнению
Ф=,4(0Ф
с начальным условием
«(U = ^ (8)
и пусть С—основная матрица решения Ф (0 (см. 19, А)), так что
Ф(/ + т) = Ф(0С. (9)
Непосредственно проверяется, что всякое решение ф(0 векторного
уравнения (7) записывается в виде:
(0=Ф (0 (/о)-
Из этого и из соотношений (8) и (9) следует
$(А»4-т) = Сф(/в). (10)
Примем теперь во внимание, что система (1) автономна. Мы имеем
(см. (3)):
<i (0=/(<Н0);
5 Ч 1 УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ 271
дифференцируя это соотношение no t, получаем:
Ф(0 = А(0ф(0.
Таким образом, векторная функция ф(<) удовлетворяет векторному
уравнению (7). Но векторная функция ф(0 является периодической
с периодом т; таким образом, из (10) получаем:
ф(#е) = ф(#о + *) = Сф(*Д (11)
а так как ф(^о)^О (ибо ^p(f) не есть положение равновесия), то из
этого следует, что матрица С имеет собственное значение, равное
единице, и, следовательно, одно из характеристических чисел уравне-
ния (7) равно единице.
Теоремы Ляпунова и Андронова — Витта
Теперь мы можем формулировать достаточные условия устойчи-
вости периодического решения <p(t) для случаи, когда система (1) пе-
риодична, и для случая, когда она автономна.
Теорема 25. Пусть уравнение (1) периодично по t с периодом
т (см. (2)) и <p(f) — его периодическое решение также периода т
(см. (4)). Если все характеристические числа уравнения (7) (см.
§ 19, Д)) по модулю меньше единицы, то решение <р(0 асимпто-
тически устойчиво; более того, существует такое число <з^>0,
что при [ X,—Хо К а имеет место оценка:
I ф {tx if X,) —ф (1) 1 IА-Хо |. г > (12)
где г и а—Ъва положительных числа, не зависящих от
Теорема 26. Пусть уравнение (1) автономно, и <р(/)— его
периодическое решение периода х, отличное от положения равно-
весия. Если характеристическое число уравнения (7), равное еди-
нице, имеет кратность единица, а все остальные характеристи-
ческие числа уравнения (7) по модулю меньше единицы, то реше-
ние <p(f) устойчиво по Ляпунову.
Теорема 25 принадлежит Ляпунову. Теорема 26 принадлежит Андро-
нову и Витту, которые получили ее как довольно простое следствие
одной весьма тонкой теоремы Ляпунова. Здесь дается другое дока-
зательство теоремы 26, опиракщееся на метод Ляпунова.
Доказательствам теорем 25 и 26 предпошлем построения, нужные
в обоих случаях.
В § 26 было дано определение производной некоторой функции
в силу автономной системы уравнений. Дадим его здесь для случая
неавтономной системы.
Б) Пусть
F(x)=P(xt, хп)
272
УСТОЙЧИВОСТЬ
(Гл. б
— некоторая скалярная функция векторного переменного X. Произ-
водную *о) этой функции в силу системы (1) в точке tn, х0
определим следующим образом. Пусть <р(0.— решение уравнения (1)
с начальными вначениями -^о- Положим:
X0) = ^F(q>(O)|/ = Ze.
Осуществляя указанное справа дифференцирование, получаем:
п
'гт«. *>= 2 *>
В случае, если система (1) автономна, производная х) функ-
ции f (х) в силу системы (1) в точке t, х не зависит от t
В) Пусть
£ = &? + />(/, г) (J3)
— нормальная система дифференциальных уравнений в векторной за-
писи, где В = (Ь^ — постоянная матрица, все собственные значения
которой имеют отрицательные действительные части, a p(tt z)—
остаточный член, определенный при t^tQi |г|<^с (с^>0) и допу-
скающий оценку
|р(/, 2)|<p|z|4, {14)
где р — положительное число. Оказывается, что решение z — 0 урав-
нения (13) асимптотически устойчиво; более того, для решения
2 = Zi) с начальными значениями /0, zb || ct с имеет место
оценка
!х(*> ° »z (15)
где г, а — положительные числа, не зависящие от zv
Предложение В) доказывается совершенно так же, как теорема
Ляпунова (см. § 26). Проведем это доказательство без излишней дета-
лизации.
Пусть W(z) — функция Ляпунова для линейной системы
z = Bz (16)
с постоянными коэффициентами (см. § 26, Д)), так что выполнено
неравенство
Ш = 2 < - W (г) (₽ > 0).
«, /
Из этого неравенства в силу опенки (14) получаем при
W (я) с»
« зп
УСТОЙЧИВОСТЬ^ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ
273
неравенство
i,J i
где а<^р и са—некоторые положительные числа. Положим:
w(0 = ^(X(*» zj), где
Для функции w(/), выполнено неравенство
w (О — 2а®> (О» (17)
если только для нее имеет место соотношение
w (t) с4.
Из (17) следует, что пока имеет место неравенство ф(1)^съ функ-
ция w (t) убывает, точнее не возрастает, а так как в начальный мо-
мент t = t$ выполнено неравенство то точка x(t *1) не
может покинуть замкнутого множества F, определяемого неравенст-
вом U7(£)^c2, и потому решение %(tt определено для всех зна-
чений (ср. § 22, Б), В)) и для всех этих значений имеет место
неравенство (17). Считая теперь, что Zj 0, мы можем произвести
следующие выкладки, исходя из неравенства (17):
или, интегрируя, получаем:
In w (t) — In w(/о) — 2a (t —• /0),
а из этого следует:
W(i)^w(Qe-2att~h\
или, что то же,
Из этой оценки непосредственно вытекает оценка (15).
Таким образом, предложение В) доказано.
Доказательство теоремы 25
В силу теоремы 12 существует преобразование
y=T(t)z, (18)
где матрица T(t) действительна и имеет период 2т, при котором
уравнение (7) переходит в уравнение
i = Bz
274
УСТОЙЧИВОСТЬ
[Гл. 5
с постоянной действительной матрицей В. Решением уравнения
z — Bz является матрица etB (см. § 19, В)), и потому матрица е2гВ
является основной для этого уравнения, а значит, и для уравнения (7).
Таким образом, в силу предположений теоремы 25 все собственные
значения матрицы е2хВ по модулю меньше единицы. Но согласно тео-
реме 29 собственные значения матрицы еъв имеют вид е2т\ где к
пробегает все собственные значения матрицы В. Таким образом,
|е9хХ|<^1, и потому все собственные значения матрицы В имеют от-
рицательные действительные части. Применяя преобразование пере-
менных (18) к уравнению (6), мы приводим его к виду (13), и для
его решения z = x(^» ^t) получаем оценку (15). Ив этой оценки
в силу невырожденности матрицы T(t) получается оценка (12).
Таким образом, теорема 25 доказана.
Доказательство теоремы 26
Исходя ив предположения, что уравнение (7) имеет характеристи-
ческое число единица кратности один, а все остальные его характе-
ристические числа по модулю меньше единицы, покажем, что суще-
ствует такое преобразование:
(19)
с действительной матрицей Т(t) периода 2т, переводящее уравне-
ние (7) в уравнение
z — Bz (20)
с постоянной матрицей Bt которая имеет вид:
/В*\0\
В —..;•••• ,
\ о jo/
(21)
где £?*— квадратная матрица порядка п—1, все собственные значе-
ния которой имеют отрицательные действительные части.
Пусть С—основная матрица некоторого решения матричного урав-
нения (см. (7))
Г=А(0К (22)
Так как матрица С имеет собственное значение единицу кратности
один, то в некотором базисе она имеет вид:
С*; О
о'П
(23)
где С* — действительная квадратная матрица порядка п — I, все собст-
венные значения которой по модулю меньше единицы (см. § 34, Ж), 3)).
§ 31] УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ 275
Так как матрица С и матрица (23) получаются друг из друга транс-
формацией, то матрица (23) является основной для некоторого реше-
ния уравнения (22); мы будем считать, что С совпадает с матрицей (23).
В силу предложения Г) § 35 существует действительная матрица В*,
удовлетворяющая условию:
причем в силу теоремы 29 все собственные значения матрицы В*
имеют отрицательные действительные части» Очевидно, что матрица В
(см. (21)) удовлетворяет условии:
Лв=с’
(см. (23)). Таким образом (ср. доказательство теоремы 12), сущест-
вует преобразование (19), переводящее уравнение (7) в уравнение (20).
Выясним теперь, каким условиям должна удовлетворять мат-
рица T(t)t для того чтобы преобразование (19) переводило уравне-
ние (7) в уравнение (20). Дифференцируя соотношение (19), получаем:
> = /(/)*+ T(t)z = T(t)Bz.
Заменяя в этом соотношении z по формуле Г~1 (/)у, получаем:
^ = (Г(0+ Г-' (t)y.
Так как это уравнение совпадает с уравнением (7), то мы имеем:
и, умножая это соотношение справа на матрицу Г(0, получаем:
T(t)+T(t)B==A(t)T(t). (24)
Это условие, налагаемое па матрицу Т(1), является необходимым и
достаточным для того, чтобы преобразование (19) переводило урав-
нение (7) в уравнение (20). Расщепим соотношение (24) на два, пред-
ставив матрицу T(t) в виде:
Т(0=(Г*(0» t(t)\
где матрица T*(t) имеет п строк и п— 1 столбцов, а матрица t(t)
представляет собой последний столбец матрицы Т(/) и потому яв-
ляется отличным от нуля вектором. Мы имеем (см. (21));
Г* (0+ Г* (0 Я* = A (t) Т* (0, (25)
Г(0=Д(0Ч^ (26)
Из последнего соотношения видно, что t(t) есть периодическое ре-
шение периода 2т уравнения (7) и потому для него выполнено
279
УСТОЙЧИВОСТЬ
[Гл. 5
условие (ср. (10))?
Таким -образом» вектор £(f0) есть собственный вектор матрицы С*
с собственным значением единица. Так как матрица
, /с*8*о\
\ О Ц/
имеет единицу собственным значением кратности один, и уже известен
один вектор ф(^о)т^0 с этим собственным значением у матрицы С*
(см. (11)), то мы имеем:
*(/0) = т<р(А>)
и потому
*(0 = 1<р(0
(ибо обе векторные функции t(t)t <p(f) являются решениями уравне-
ния (7)). Из этого видно, что если в матрице Т(t) заменить ее послед-
ний столбец £(0, вектором ф(0> то вновь полученная матрица
(Г* (О, Ф(0) будет удовлетворять условиям (25) и (26). Поэтому мы
будем считать, что
Т(0=(Т*(0, Ф(0). (27)
Исходя из полученных соотношений (25), (27), преобразуем'неиз-
вестную функцию х уравнения (1) в автономном случае (см/(3))
в новые неизвестные функции 2*, 5, где2* = (21, ..., zn ’) есть век-
тор размерности п—1, который в дальнейшем мы будем рассматри-
вать как матрицу с одним столбцом, а 5 — новое скалярное перемен-
ное. Для этого положим:
х= 7'*(^)^*-(-<р(5)—^(2* S), (28)
Это преобразование периодично по 5 с периодом 2т. Каждой паре г*,
5 при достаточно малом 12* | соотношение (28) ставит в соответствие
точку х, близкую к точке <р (s) периодической траектории ЛГ, опре-
деляемой решением х = ср(£). Вблизи каждой пары ^* = 0, s = s(1
отображение (28) взаимно однозначно, так как функциональный опре-
делитель этого отображения в точке £* = 0, s = равен детерми-
нанту матрицы 7'(s(() (см. (27)) и потому отличен от нуля. Коорди-
нату $ пары (г*, s) будем считать циклической координатой периода 2т,
т. е. будем отождествлять пары (z*> 5) и (2*, s-|~2T)- Так как
пары (0, sft) и (0, преобразованием (28) переводятся в одну
и ту же точку <р(л'о) траектории К, то некоторые окрестности пар (0, $0)
и (0, $о~гт) отображаются взаимно однозначно на одну и ту же
окрестность точки <p(s0) линии К- Таким образом, отображение (28)
двуслойно накладывает множество всех пар (г*, $) (при достаточно
I 31] УСТОЙЧИВОСТЬ-ПЕРИОДИЧЕСКИХ РЕШЕНИИ 277
малых | z* |) на некоторую окрестность линии Д'. При этом замкнутая
кривая, состоящая из всех пар (0, s), 2т, дважды наклады-
вается на линию К>
Заменим теперь в уравнении (1) (см. (3)) неизвестный вектор х по
формуле (28). Подстановка в левую часть дает:
х = 7*' (5) z*s + 7* (5) z* + ф' (5) & (29)
Подстановка в правую часть дает:
/W=/(<P(s))+ (s) t*(s)2*+R(s, z*)t (30)
где остаточный член R (5, &*) периодичен по s с периодом 2т и имеет
второй порядок малости относительно вектора z*t Приравнивая правые
части соотношений (29) и (3Q),. получаем:
7* (5) z* 4- <р' (5) $ 4- Т*' (5) 2*s =/(ф (5)) + A ($) 7* (5) z* + R (s, z*).
Заменяя матрицу Д($)7*($) по формуле (25) и заменяя /(ф(з))
через ф' (5), получаем:
т* (s) z* 4~ <р ($) $ + ?*'(s) —
= <₽' (5) + (г*' (s) + 7* (s) £?*) z* + R (S, z*)>
откуда
7*(s)(z* — Я*г*)4-(ф'($)4- 7'*'(s)z*)(i-l) = /?(5, г*). (31)
Введем теперь в рассмотрение новые вспомогательные переменные:
вектор д* = (и\ ,и”’1) и скаляр и" В л-мерном пространстве
переменных («*, ия) = (н\ и2, ц”) рассмотрим линейное преобра-
зование М зависящее от параметров 5 и z*, положив:
7И («*, ил) = 7* (5) а* 4- (ф' (s) 4- Г*’ (s) z*) к*.
При г* = 0 преобразование Л1 превращается в 7(s), и потому при z*,
близком к нулю, преобразование М невырожденно. Таким образом,
уравнение
Л4(«*, и*) — R(s, 2*)
однозначно разрешимо (при 2*, близком к нулю) относительно неиз-
вестных и*, unt и его решение
tt* = Q*(5, z*)>
un = q(s, z*)
периодично по 5 с периодом 2т и имеет второй порядок малости
относительно вектора z*. Так как соотношение (31) можно переписать
в виде:
М(2*~ В*2*, S—1) = R(S, z*),
то мы получаем:
— д* 5 — ] — q
278
УСТОЙЧИВОСТЬ
[Гл. S
Итак, в пространстве переменных z*. s уравнение (1) записывается
в виде
Z* = Z?*Z* 4* Q* (S, z*), (32)
5=1 +9(5, z*). (33)
Существует теперь такое положительное числов, что при |z*|<^e
остаточный член 9(5, z*) удовлетворяет неравенству | q (5, z*)|<^I.
При выполнении этого неравенства на каждом решении z* = z*(f),
5 = 5(f) за независимое переменное можно вместо t принять и
уравнения (32), (33) перепишутся тогда в виде:
dz*___ B*z* + 9* (s, 2*)
ds 1 + 9 (5» 2*) ’
________________________________________
ds i + 9 (s, z*) 1
или иначе:
~ = z*), (34)
g = 14-*(sF z*), (35)
где остаточные члены ft*(s, z*) и £(s, z*) периодичны no 5 с перио-
дом 2т и имеют второй порядок малости относительно вектора z*.
В системе (34), (35) независимым переменным является s, a z* и t
рассматриваются как неизвестные функции от 5. Уравнение (34) не
содержит неизвестной функции f, и его можно решать отдельно.
Таким образом, для того чтобы найти решение системы (32), (33)
с начальными значениями f0, z*, следует сначала найти решение
z* (s, z* $j) уравнения (34) с начальными значениями z*, которое
в силу предложения В) при достаточно малом | z* [ определено для
всех значений и имеет оценку
|z*(5, z*, 501 < г J z* | е-а\ (36)
После этого следует найти решение уравнения (35) с начальными
значениями f0, z*, Л'(; это решение дается очевидной формулой:
t = tQ + $ (1 + k (5, Z* (5, Z*, $0)) —
si
= t0 — S| + 5 + (5, Z* (5, z?, $0) ds. (37)
Последнее уравнение можно разрешить относительно $, если только
| z* [ достаточно мало, так что мы получаем:
5 = 5 (f, Z*> $0- (38)
§ 31J УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ 279
Подставляя это выражение для s в решение 2*(s, х*, 5t) уравне-
ния (34), получаем:
Х*(0 = Х*(«(6 ъ), 2*, st). (39)
Формулы (38) и (39) вместе дают решение системы (32), (33) с на-
чальными значениями tQ, z*, st. Из (37) следует, что при мы
имеем:
|s(f, x* (40)
где I — некоторая положительная константа. В частном случае, когда
х* = 0, $1 = ^ решение (38), (39) имеет вид:
£*(/) —0, S(t)=t.
Из оценок (36) и (40) следует, что это решение системы (32), (33)
устойчиво по Ляпунову,
Подставляя решение (38), (39) в формулу преобразования (28), мы
получим решение х = ф(2, xj уравнения (1) с начальными значе-
ниями t = tv x = xl = g(z*, $i). Так как отображение (28) взаимно
однозначно на некоторой окрестности пары z* = 0, s = tf0, то любое
решение ф(£, Xj) уравнения (1) с начальными значениями t99 Х\ при
достаточно малом | Xi — х0| может быть получено таким способом из
некоторого решения (38), (39) системы (32), (33). При этом решение
Х = ф(0 получается из решения z* = 0, s = t Теперь из устойчи-
вости по Ляпунову решения z* = 0, s=t вытекает (в силу равно-
мерной непрерывности отображения (28)) устойчивость по Ляпунову
исходного периодического решения х = ф(Г).
Таким образом, теорема 26 доказана.
Применим полученные здесь результаты к случаю предельного
цикла.
Г) Будем считать, что автономная система (1) (см. (3)) имеет вто-
рой порядок;
*'=/(*'» *8) =f‘(x\ 1=1, 2,
и пусть
АГ = ф(О
— ее периодическое решение с периодом т. Система (7) имеет здесь
вид:
У —дх^......У 1~ ’’ 2-
В силу предложения А) одно характеристическое число этой системы
равно единице; второе обозначим через к. Оказывается, что
f (дР \ а
J \ Vxi ‘Г’ ох* )
Х = (41)
280
УСТОЙЧИВОСТЬ
[Гл. 5
Таким образом, если
С^/Чф(0) , ^(Ф(О)
А \ дх1 "Г” дх*
о
то периодическое решение х = ф(0 устойчиво по Ляпунову. В дей-
ствительности (см. пример) существует функция последования /(и)
периодического решения х = ф(0 (см. § 28), для которой
Х' («о) = (42)
так что при X 1 периодическое решение х = ф(0 является грубым
предельным циклом. Он устойчив при Х<^1 и неустойчив приХ^>1..
Докажем неравенство (41). Основная матрица С решения У = Чг(0
уравнения F = 4(f)F с Начальным значением Т(0) = £* (см. А))
задается равенством
С = Т(т).
В силу формулы Лиувилля мы имеем:
t
Det ЧГ (t) = Det W(0)e»
где
S(0 = a|W + W = ^ + ^
(см. § 17, Ж)). В нашем случае, когда матрица С имеет второй поря-
док и одно ее собственное значение равно единице, а другое равно X,
имеем:
С/*/1 (? (Л) ,
J ) at
X = DetC = e°
Пример
Пусть ф(0 — периодическое решение автономной системы (1)
(см. (3)) периода т с начальными значениями f0, х0. Решение этой
системы с начальными значениями f0, £ будем обозначать через ф(£, |).
Построим для решения ф(0 аналог функции последования (см. § 28),
который будет здесь отображением (п—1)-мерного пространства пе-
ременных ип~} в себя.
Пусть
x=g(u); и — (и\ ип 1) (43)
— уравнение поверхности, пересекающей траекторию ф(0 в единствен-
ной точке
Хв = Ч>а(>. х0) = §(«„) (44)
$31] УСТОЙЧИВОСТЬ-ПЕРИОДИЧЕСКИХ РЕШЕНИЙ 281
и не касающейся в этой точке траектории <р(0, так что векторы
w <«>
линейно независимы. Найдем пересечение траектории <p(f, g(a)) с по-
верхностью (43) при t близком к tQ т, считая, что | и — ий | мало.
Пусть g(v)— точка пересечения; тогда справедливо соотношение:
фО, £(«)) —£(®) = 0. (46)
При а = д0 мы имеем очевидное решение уравнения (16):
< = ^o + s « = «о
(см. (4) и (44)). Здесь мы считаем и независимым переменным, a t9
U—неизвестными величинами. Так как функциональный определитель
системы (46) при t = t& +*ч я = «0, ф = й0 по неизвестным функ-
циям t и ф не равен нулю в силу линейной независимости векто-
ров (45), то при малом | и — и01 существует решение
системы (46) с малыми \t(u) — (^0 + т)1 и lx(tt) — й01* Отображение
Х(й) пространства переменных-и1, .ип~1 в себя (определенное при
малом | и — я01) будем называть отображением последования.
Каждому решению и~и{ уравнения
Х(и) — «=>0 (47)
соответствует г периодическое решение <р(/, g(Ui)) автономного урав-
нения (1) (см. (3)) с периодом, близким к т; в частности, решению
и = соответствует исходное периодическое решение <р (f) =
= g(ttQy)- Если функциональная матрица
\ ди/ / v ' J ’ ' ’
не имеет собственных значений, равных единице, то решение я = йе
уравнения (47) является изолированным. В самом деле, функциональ-
ная матрица уравнения (47) при « = д0 равна
/И — £*.
Для того чтобы детерминант этой матрицы не обращался в нуль,
необходимо и достаточно, чтобы матрица Л4 не имела собственного
значения, равного единице.
Выясним теперь вопрос о том, всякая ли периодическая траекто-
рия Ку проходящая вблизи траектории К, описываемой решением <р(0,
описывается решением <р(£, ^(kJ), где есть некоторое решение
уравнения (47). Именно так обстояло дело в плоском случае (п = 2).
Оказывается, что при дело обстоит уже не так. Разберем этот
282
УСТОЙЧИВОСТЬ
{Гл. -5
вопрос. Будем считать, что т есть минимальный период решения (р (/),
т. е. что равенство
<₽ (*0 Н-О=«₽ (Хо)
может иметь место лишь при условии, что t = kxt где k — целое
число (см. § 15, В)). Если траектория близка к траектории К>
то она пересекается с поверхностью (43) в некоторой точке g(a&
причем | — й01 близко к нулю. Положим:
«2 = Х(«1Х «з = Х(««)....... «,+1 = Х(«Д •••
Так как траектория Ki — замкнутая, то в этой последовательности
найдется точка, совпадающая с точкой пусть им будет первая
из них. Тогда траектория описывается решением ф (f, ^(«q)), при-
чем минимальный ее период близок к числу Ат; решение <р(Л g(Ui))
замыкается только после того, как оно k раз обойдет вдоль траек-
тории ф(0. В плоском случае возможен лишь случай А = 1. Будем
называть число k кратностью траектории К\> Для отыскания дву-
кратных траекторий нужно решать не уравнение (47), а уравнение
х(х(«)) —«==о;
для отыскания трехкратных траекторий нужно решать уравнение;
(«))] — й = 0
и т. д. Функции %(%(«)), Х[Х(Х(Й))1» ••• называются итерациями
функции ^-кратную итерацию обозначим через Х*(й)- Таким
образом, для нахождения всех А-кратных периодических решений,
близких к решению ф (f), следует решать уравнение
Х*(«) —а = (48)
но из всех решений уравнения (48) следует брать лишь те, которые
не являются решениями уравнений предшествующих кратностей; ре-
шение а = й0 уравнения (47) является решением и всякого уравне-
ния (48). Функциональная матрица уравнения (48) при й = д0 равна,
очевидно, Mk — Е*\ таким образом, для того чтобы уравнение (48)
имело лишь одно решение и = и^ близкое к достаточно, чтобы
детерминант матрицы — Е* был отличен от нуля, или, что тоже,
чтобы матрица Mk не имела собственных значений, равных единице,
или, наконец, чтобы матрица М не имела собственных значений, рав-
ных k/1. Таким образом, для того чтобы вблизи траектории К не
было периодических траекторий данной кратности А, достаточно,
чтобы матрица М не имела собственных значений, равных 1.
В частности, таких собственных значений у матрицы М нет, если все
ее собственные значения по модулю меньше единицы.
Из сказанного видно, какую важную роль играет матрица М
в изучении траекторий автономного уравнения (1) (см. (3)), близких
§ 31] УСТОЙЧИВОСТЬ-ПЕРИОДИЧЕСКИХ РЕШЕНИЙ 283
к периодическому решению <р(0* Покажем теперь, что если уравне-
ние (7) имеет характеристическое число единица кратности единица,
то при некотором выборе поверхности (43) матрица Л1 совпадает
с матрицей С* (см. (23)). Положим:
В силу предложения В) §24, мы имеем:
Ф (0 = А (О Ф(0, (49)
причем выполнено начальное условие:
Таким образом, матрица ЧТ (Q представляет собой решение матричного
уравнения (49), являющегося матричной записью уравнения (7), и
потому
чг(<в+т)=с.
Так как матрица С имеет собственное значение единица кратности
единица, то в пространстве векторов у (см. А)) можно выбрать такой
базис, что матрица С запишется в виде (23). Выберем теперь за коор-
динаты в фазовом пространстве уравнения (1) (см. (3)) компоненты
вектора у, положив:
X = q>(Q H-jr
(ср- (5)). Полученные таким образом в фазовом пространстве коорди-
наты вновь обозначим через х1, .хп и поверхность (43) зададим
уравнениями:
х1 = п1, ..., xn~i = un~it хп = 0.
Дифференцируя соотношение (46) по и1, ип~1 при я = 0, t =
—|—х, ф = 0 в предположении, что t — t(u) и ф = ^(й) — функции
переменных и1, ип~\ получим равенство
С*=М (50)
В случае, когда п = 2, матрица С* есть скаляр X, и соотноше-
ние (50) дает равенство (42).
Если все собственные значения матрицы С* по модулю меньше
единицы, то вблизи траектории К нет периодических решений никакой
кратности. Это следует из оценки (36).
ДОБАВЛЕНИЕ I
НЕКОТОРЫЕ ВОПРОСЫ АНАЛИЗА
Это добавление содержит два параграфа, посвященных двум со-
вершенно различным вопросам анализа.
В § 32 приведены основные факты, относящиеся к понятию непре-
рывности в пространстве многих переменных; важное место в этом
параграфе - занимает понятие открытого множества. Я придаю суще-
ственное значение тому,, что правые части дифференциальных уравне-
ний считаются заданными на открытых множествах. Точно так же
я считаю существенным, что решение, зависящее от параметров, ока-
зывается естественным образом определенным на открытом мно-
жестве (см. теорему 13). В связи с этим четкое понимание того, что
представляет собой открытое множество, совершенно необходимо для
понимания теорем существования решений обыкновенных дифферен-
циальных уравнений.
В § 33 приведено доказательство теорем существования неявных
функций и некоторые их применения.
Вопросы, затронутые в этих двух параграфах, не всегда с доста-
точной точностью и полнотой освещаются в курсе анализа, и потому
я позволил себе включить их в эту книгу.
§ 32. Топологические свойства евклидовых пространств
В анализе важную роль играет геометрическое изображение или,
как говорят, геометрическая интерпретация аналитических соотноше-
ний, т. е. формул. Геометрическая интерпретация дает возможность
установить связь между формулами и геометрическими образами и тем
самым на помощь анализу привлекает геометрическую интуицию.
Образец такой связи между формулами и геометрическими образами
дает аналитическая геометрия. В прямом смысле слова геометрические
образы могут рассматриваться на плоскости и в трехмерном простран-
стве, но анализ, имеющий дело с многими переменными, пользуется
геометрическим языком и в многомерных пространствах. Здесь мы
§ 32] ТОПОЛОГИЧЕСКИЕ СВОЙСТВА ЕВКЛИДОВЫХ ПРОСТРАНСТВ 285
будем рассматривать многомерные евклидовы пространства, представ-
ляя их себе одновременно как векторные. Важнейшими геометриче-
скими свойствами геометрических образов являются топологические
свойства; на простейших ий них мы здесь и остановимся.
Евклидовы пространства
Напомним прежде всего понятие л-мерного евклидова векторного
пространства.
А) Будем называть п-мерным вектором последовательность из п
действительных чисел; числа эти называются координатами вектора.
Их мы, как правило, будем обозначать одной и той же буквой с но-
мерами в виде индексов наверху, например через х1, х4, ...» Xя; сам
вектор будем обозначать той же буквой, только жирной, в данном
случае — буквой х. Формулой это запишем в виде:
X — (X1, X4, . .. , Xя).
Совокупность всех л-мерных векторов будем называть п-мерным век-
торным пространством и обозначать одной большой буквой, напри-
мер через R. Сумма и разность двух векторов
х = (х1, х4 ..., х”), у = (у1, у/4, .... уя)
определяются формулами: *
x-|-wy = (x1 +/1, ...» х71-]—jvn); х—j = (xl—у, хп—уп).
Произведение вектора х на действительное число а определяется фор-
мулой
ах = (ах1, ..., ах*).
Особую роль в векторном пространстве играет нулевой вектор 0, все
координаты которого равны нулю. Таким образом, в векторном про-
странстве определены алгебраические операции сложения и вычитания
векторов и умножения вектора на число. В евклидовом векторном
пространстве определена, кроме того, операция скалярного произве-
дения двух векторов. Именно, если х иу — два произвольных век-
тора, то в соответствие им ставится число (х, j), называемое их ска-
лярным произведением и определяемое формулой
(х, j) = xiy -j- ,.. хпуа.
Если вектор j совпадает с вектором х, то мы получаем скалярный
квадрат (х, х) = х4 этого вектора, который всегда неотрицателен и
обращается в нуль только при х = 0. Длина, или модуль, вектора х
определяется формулой
В дальнейшем мы часто будем векторы называть также точками
28в
ДОБАВЛЕНИЕ Г. НЕКОТОРЫЕ ВОПРОСЫ АНАЛИЗА
евклидова пространства За расстояние между двумя точками х и у
принимается модуль разности векторов х и у, т, е. число |х— ji.
Установим теперь некоторые основные неравенства для скалярного
произведения и расстояния в евклидовом пространстве.
Б) Для любых двух векторов х и у евклидова векторного про-
странства имеют место неравенства:
(х, (О
+ (2)
Далее, для любых трех точек а, д, € евклидова пространства имеет
место неравенство
(3)
Для доказательства первого неравенства рассмотрим вектор ax-|-j,
где a — произвольное действительное число, и составим скалярный
квадрат этого вектора. Мы имеем:
(ax -|- j)* — а2х4 + 2а (х, у) 4'У3*
Так как скалярный квадрат вектора не может быть отрицательным,
то величина, стоящая в правой части последнего равенства, ни при
каком значении а не может принимать отрицательного значения, и
потому квадратное уравнение
a‘2x* + 2а (X, j)-)~y4==0
относительно неизвестной величины а не может иметь двух различных
действительных корней. Отсюда следует, что дискриминант этого ква-
дратного уравнения, т. е. получаемое при его решении подкоренное
выражение (х, j)2— x2j2, неположителен, а это и значит, что выпол-
нено неравенство (1).
Для доказательства неравенства (2) возведем в квадрат его левую
часть; мы будем иметь:
IX у Г2 = (х + J)4 = х4 + 2 (X, J) + J4,
а это, в силу неравенства (1), дает:
I х-\- у I4 -С | X i4 4- 2 IX11 у I 1 у I4 = (| X i 4- I J» i)4.
Из этого непосредственно следует неравенство (2) (так как оба числа
| х |, |j| неотрицательны).
Наконец, для доказательства неравенства (3) достаточно в нера-
венстве (2) положить х = а Ь, у — Ь — с.
Итак, предложение Б) доказано.
§ 32]
ТОПОЛОГИЧЕСКИЕ. СВОЙСТВА ЕВКЛИДОВЫХ ПРОСТРАНСТВ
287
Открытые, замкнутые и ограниченные подмножества
евклидова пространства
Напомним определения операций объединения и пересечения мно-
жеств — в данном случае множеств, расположенных в евклидовом
пространстве R. Пусть
(4)
— произвольная конечная система множеств пространства /?. Опреде-
лим множество S, считая, что точка х из R тогда и только тогда
принадлежит 5, когда она принадлежит хотя бы одному из мно-
жеств (4). Множество 5 называется объединением множеств (4). Опре-
делим, далее, множество Р, считая, что точка х из R тогда и только
тогда принадлежит множеству Р, когда она принадлежит каждому
из множеств (4). Множество Р называется пересечением множеств (4).
Пусть М — произвольное множество из R. Определим множество D,
считая, что точка х из R тогда и только тогда принадлежит множе-
ству £>, когда она не принадлежит множеству М Множество D назы-
вается дополнением множества М Очевидно, что дополнение множе-
ства D совпадает с М
Пусть
Оь ..., Dk (5)
— система множеств, дополнительных к множествам (4), так что Di
является дополнением множества Легко усмотреть, что дополне-
ние к объединению множеств (4) является пересечением мно-
жеств (5) и, наоборот, дополнение к пересечению множеств (4)
является объединением множеств (5).
Перейдем теперь к установлению некоторых простейших тополо-
гических свойств множеств, расположенных в евклидовом простран-
стве. Эти свойства, в основном, связаны с определением понятий
открытого и замкнутого множеств в евклидовом пространстве R.
В) Пусть а — произвольная точка евклидова пространства R и
г — произвольное положительное число. Множество всех точек из R,
расстояние которых до точки а меньше г, называется шаром ради-
уса г с центром в а. Всякий шар с центром в а называется окре-
стностью точки а (ниже — см. пример 3—понятие окрестности
будет расширено). Множество Q точек пространства R называется
открытым, если для всякой точки а из Q существует ее окрестность,
целиком содержащаяся в множестве G. Пусть Л4 — произвольное мно-
жество из R. Точка а из R называется предельной для множества Л4,
если каждая окрестность точки а содержит точку множества М,
отличную от а. В этом случае каждая окрестность точки а обяза-
тельно содержит бесконечное множество точек из М. Множество F
точек из R называется замкнутым, если каждая его предельная
288
ДОБАВЛЕНИЕ 1. НЕКОТОРЫЕ ВОПРОСЫ АНАЛИЗА
точка принадлежит ему. Оказывается, что дополнение к любому
открытому множеству замкнуто, а дополнение к любому замкнутому
множеству открыто.
Докажем предложение В). Покажем прежде всего, что если-каждая
окрестность точки а содержит хотя бы одну точку множества /И,
отличную от а, то опа содержит бесконечное множество точек мно-
жества 7И. Пусть Ui — произвольная окрестность точки а и — ее
радиус. Пусть далее Xi — отличная от а точка множества 7И, содер-
жащаяся в U\. Так как xt а, то | Xi — а | = 0. Шар ради-
уса с центром в точке а не содержит точки х(, но он содержит
некоторую точку х2 множества 7И, отличную от а. Продолжая этот
процесс дальше, мы получим бесконечную последовательность хр.
хь ... попарно различных точек множества 7И, содержащихся в U\.
Докажем последнее утверждение предложения В). Пусть G—не-
которое множество из R и F — его дополнение. Допустим что G—
открытое множество, и докажем, что F—замкнутое. Пусть а — пре-
дельная точка множества F; покажем, что опа принадлежит множеству F,
т. е. не принадлежит множеству G. Допустим противоположное, т. е.
что точка а принадлежит G. Тогда, в силу предположенной откры-
тости множества G, существует окрестность точки а, целиком содер-
жащаяся в О и, следовательно, не содержащая точек из F, а это
вначит, что точка а не является предельной для F.
Допустим теперь, что множество F замкнуто, и докажем, что
множество О открыто. Пусть а — произвольная точка из G Так как
опа не принадлежит множеству F, то в силу замкнутости она не
является его предельной точкой и потому существует окрестность
точки а, не содержащая отличных от а точек из F; но а также не
принадлежит F, и потому вся эта окрестность содержится в G Тем
самым доказано, что множество О открыто.
Таким образом, предложение В) доказано.
Очевидно, что все пространство R является одновременно откры-
тым я замкнутым. Далее, каждое конечное множество F из R
замкнуто. В самом деле, множество F вообще не имеет предельных
точек и потому содержит их все, т. е. замкнуто. -
В случае, когда размерность векторного пространства R равна
единице, это пространство совпадает с множеством всех действитель-
ных чисел, и алгебраические операции над векторами превращаются
в обычные операции над действительными числами, а модуль совпа-
дает с модулем числа. Расстояние между двумя точками а и b в этом
случае равно модулю \а—Ь\ их разности. Непосредственно видно,
что в пространстве действительных чисел множество всех точек х,
удовлетворяющих неравенству х<^а или неравенству х^>а, где а —
фиксированное число, является открытым. Дополнение к этому мно-
жеству, определяемое неравенством или неравенством х^ а,
вамкнуто.
$ 32] ТОПОЛОГИЧЕСКИЕ СВОЙСТВА ЕВКЛИДОВЫХ ПРОСТРАНСТВ 289
' Г) Объединение и пересечение конечного числа открытых мно-
жеств евклидова пространства R открыты. Объединение и пересече-
ние конечного числа замкнутых множеств пространства R замкнуты *).
Докажем это. Пусть
01, О*..., G* (6)
— конечная совокупность открытых множеств пространства R. Дока-
жем, что их объединение открыто. Пусть а — произвольная точка,
принадлежащая этому объединению; тогда она принадлежит хотя бы
одному из множеств (6), например, множеству Ог. Так как множество 0(
открыто, то существует окрестность точки а, содержащаяся в Of, но
тогда эта окрестность содержится и в объединении' множеств (6).
Докажем, что пересечение множеств (6) открыто. Пусть а — про-
извольная точка из этого пересечения; тогда она принадлежит каж-
дому множеству 0( системы (6). Так как множество G; открыто, то
существует шар радиуса с центром в а, содержащийся в Gi: Пусть
г—минимальное из чисел гь га, .rk; тогда шар радиуса г с цен-
тром в а содержится в каждом из множеств системы (6) и, следова-
тельно, принадлежит их пересечению. Таким образом установлено, что
пересечение множеств (6) открыто.
Переходя от открытых множеств (6) к их дополнениям, мы полу-
чим соответствующие результаты относительно замкнутых множеств
(см. В)).
Таким образом, предложение Г) доказано.
Д) Пусть R — езклидово пространство,
Я1> 4*2» ...» flfe, ... (7)
— некоторая бесконечная последовательность точек из R и М — не-
которое множество точек из R. Заметим, что последовательность
отличается от множества не только тем, что ее точки занумерованы,
но также тем, что точки с различными номерами могут совпадать между
собой. Поэтому множество всех точек, входящих в бесконечную по-
следовательность, существенно отличается от самой последователь-
ности; в частности, оно может быть конечным. Последовательность (7)
называется ограниченной, если существует такое число г, что для
каждой точки ak последовательности (7) выполнено неравенство
Точно так же, множество 7И называется ограниченным, если
существует такое число г, что для каждой точки х из 7И выполнено
неравенство | х | г. Говорят, что последовательность (7) сходится
к точке а из R, если имеет место соотношение
Jim |afe — а | = 0. (8)
k -• оо
♦) Нетрудно доказать, что всегда объединение любой системы (не обя-
зательно конечной) открытых множеств открыто, а пересечение любой
системы замкнутых множеств замкнуто. Нам эти факты не понадобятся.
290
ДОБАВЛЕНИЕ I. НЕКОТОРЫЕ ВОПРОСЫ АНАЛИЗА
Если при этом последовательность (7) содержит бесконечное множе-
ство различных точек, то точка а является предельной для мно-
жества всех точек последовательности (7) и притом единственной
предельной точкой этого множества. Оказывается, что из ограниченной
последовательности точек всегда можно выделить сходящуюся под-
последовательность точек. Из этого непосредственно следует, что всякое
ограниченное бесконечное множество М имеет предельную точку.
Докажем предложение Д), Допустим, что имеет место соотноше-
ние (8) и что множество А всех точек последовательности (7) бес-
конечно. Из соотношения (8) следует, что каждый шар с центром а
содержит все точки последовательности (7), за исключением конеч-
ного числа. Так как множество А бесконечно, то из сказанного сле-
дует, что каждая окрестность точки а содержит бесконечное множе-
ство точек из Л. Следовательно, каждая окрестность точки а содер-
жит точки, отличные от а, а это и значит, что точка а является
предельной для Д.
Покажем, что точка b а не может быть предельной для Д.
Расстояние от а до Ь обозначим через 2р; так как а bt то р^>0.
Шары Р и Q с центрами в точках а и b радиуса р не пересекаются.
Это следует из неравенства (3). Так как шар Р, по доказанному,
содержит все точки множества Д, за исключением конечного числа,
то шар Q может содержать лишь конечное число точек множества А
и потому точка b не является предельной для множества А.
Допустим теперь, что последовательность (7) ограничена, и выбе-
рем из нее сходящуюся подпоследовательность. При доказательстве
мы используем тот факт, что для числовых подпоследовательностей
это возможно. Перейдем к координатной записи точек последователь-
ности (7), положив:
аь — (а\, al, a"), k—\, 2, ...
Так как последовательность (7) ограничена, то существует -такое
число г, что | ak | г, а отсюда следует, что
[ | <г, Z= 1, 2, А=1, 2,
Таким образом, последовательность чисел
а\, <$, .... al, ... (9)
ограничена и потому из нее можно выбрать сходящуюся подпосле-
довательность. Для того чтобы не менять обозначений, мы будем
считать, что эта выбранная подпоследовательность есть сама после*
довательность (9), так что имеет место соотношение
Нт а* — а1,
k 0Q
§ 32] ТОПОЛОГИЧЕСКИЕ СВОЙСТВА ЕВКЛИДОВЫХ ПРОСТРАНСТВ 291
где а1 — некоторое число. Теперь из последовательности
at al, ...» 4, ... (10)
ввиду ее ограниченности можно выбрать сходящуюся подпоследова-
тельность. Для того чтобы не менять обозначений, мы вновь будем
считать, что эта выбранная подпоследовательность есть сама после-
довательность (10). Продолжая этот процесс по всем номерам
1, 2, ..., п координат, мы выделим такую подпоследовательность
6b Ьъ ...» blt ... (11)
последовательности (7), что для координат точек этой подпоследова-
тельности имеют место соотношения
lim bl = a\ i=l, 2, ..., nt (12)
i -»co
где a1 — некоторое число.
Положим a = (a1, ..., art). Из соотношения (12) непосредственно
следует, что
Нтп | Ьг — а | = 0.
/ -»со
Таким образом, из последовательности (7) выбрана сходящаяся под-
последовательность (11).
Покажем, наконец, что всякое бесконечное ограниченное множе-
ство М имеет предельную точку. Так как множество М бесконечно,
то из него можно выбрать бесконечную последовательность
а ь ..., • • •,
все точки которой попарно различны. В силу уже доказанного, из этой
последовательности ввиду ее ограниченности можно выбрать беско-
нечную подпоследовательность
G, ь* 03)
сходящуюся к некоторой точке а. Так как все точки последователь-
ности (13) попарно различны, то точка а является предельной для
множества всех точек последовательности (13) и, следовательно, пре-
дельной для множества М.
Итак, предложение Д) доказано.
В некоторых вопросах играют важную роль замкнутые ограни-
ченные подмножества евклидовых пространств. Докажем одно харак-
теристическое свойство таких подмножеств; оно называется компакт-
ностью,
Е) Множество Л4 точек евклидова пространства R называется
компактным, если каждое его бесконечное подмножество имеет пре-
дельную точку, принадлежащую множеству М Оказывается, что
292 ДОБАВЛЕНИЕ I. некоторые вопросы анализа'
множество М тогда и только тогда компактно, когда оно одновре-
менно замкнуто и ограничено.
Докажем предложение Е).
Допустим сначала, что множество F замкнуто и ограничено, и
пусть М — его произвольное бесконечное подмножество. В силу пред-
ложения Д) множество Ж имеет некоторую предельную точку а. Эта
точка является предельной и для множества F. В силу замкнутости F,
точка а принадлежит F. Таким образом, всякое бесконечное подмно-
жество М множества F обязательно имеет предельную точку, при-
надлежащую F> так что F компактно.
Допустим теперь, что множество F компактно. Докажем, что оно
ограничено. Допустим противоположное; тогда из F можно выбрать
такую последовательность
аь ..., ак, ... (14)
попарно различных точек, что
| ak | > k, A = 2, ...
Пусть а — произвольная точка из R. В силу неравенства (2), мы имеем
— a| + |a|> откуда
I «л — а | k — | а |.
Это значит, что расстояние от точки а до точки ak неограниченно
возрастает с ростом kt и потому любая окрестность точки а содер-
жит лишь конечное число точек множества (14). Таким образом, бес-
конечное подмножество (14) множества F не имеет предельной точки,
что противоречит компактности множества F.
Докажем, наконец, что компактное множество F замкнуто. Пусть
с — его предельная точка. Так как каждая окрестность точки с содер-
жит точку множества F, отличную от с, то из F можно выбрать
последовательность
сь .... clt ... (15)
попарно различных точек, сходящуюся к с. В силу Д) единственной
предельной точкой точек последовательности множества (15) является г,
а так как, по предположению компактности, это множество должно
иметь предельную точку, принадлежащую F, то точка с принадле-
жит F. Итак, каждая предельная точка с множества F принадлежит
ему и, следовательно, множество F замкнуто.
Таким образом, предложение Е) доказано.
Непрерывные отображения
Пусть А и В — два произвольные множества. Говорят, что задано
отображение f множества А в множество В (или, иначе, функция f
на множестве А со значениями в множестве В), если каждой точке х
§ 321 ТОПОЛОГИЧЕСКИЕ СВОЙСТВА ЕВКЛИДОВЫХ ПРОСТРАНСТВ 293
из Ая поставлена в соответствие вполне определенная точка j=/(x)
множества В. Если С—некоторое множество точек из А, то образом
f(C) множества С при отображении f называется множество всех
точек. вида где х — произвольная точка из С. Если D —
некоторое множество точек из В, то прообразом X"1 (£)) множества D
при отображении f называется совокупность всех таких точек х
из Л, что точка /(х) принадлежит D.
Ж) Пусть и S — два евклидовых векторных пространства,
М — некоторое множество точек из R и /—отображение множе-
ства Л1 в пространство 5. Отображение (или, что то же самое, функ-
ция) / называется непрерывным в точке а множества Л4, если для
каждого [положительного числа в существует такое положительное
число 8, что при |х —а|<[8 (где х — точка из М) мы имеем
|/(х)—/(а) [<['£. Функция f считается непрерывной на всем множе-
стве /И, если она непрерывна в каждой точке а этого множества.
Функция / называется равномерно непрерывной, если для всякого
положительного числа е существует такое положительное число 8,
что при | Xj — х2|<^8 (где xt и х2— точки из 7И) мы имеем
|/(xt)—f (Х2) | <[ Очевидно, что равномерно непрерывная функция
является непрерывной. Перейдем от векторных обозначений к скаляр-
ным. Именно, положим
* = (X1....хО; Г(х) = а1(х), ...» Л(Х)),
где р и q—размерности евклидовых пространств /? и S соответ-
ственно. Тогда вместо одной векторной функции f векторного пере-
менного х мы получим q скалярных функций от р скалярных пере-
менных, именно:
fJ(x)=f}(x\ х”), 7=1......q. (16)
Легко доказывается, что непрерывность векторной функции /(х) век-
тора х равносильна непрерывности всех функций (16) по совокуп-
ности переменных х1, .хр. То же относится к равномерной непре-
рывности. Здесь это доказываться не будет.
3) Пусть /? и 5 — два евклидовых векторных пространства и
f—непрерывное отображение некоторого открытого множества О
из R в пространство 5. Оказывается, что прообраз / 1 (И) любого
открытого множества Н пространства S является открытым множе-
ством пространства R.
Докажем это. Пусть Н—произвольное открытое множество ;из 5
и а— точка множества Так как Н—открытое множество и
точка д=/(а) принадлежит ему, то существует окрестность V
точки Ь, содержащаяся в /7. Окрестность V есть шар некоторого
положительного радиуса е с центром в Ь. В силу непрерывности ото-
бражения / существует такое положительное число 8, что при
|х—• .а.|<О (здесь х —точка из О) имеем |/(х)—/(а)|<[£. Так как
294
ДОБАВЛЕНИЕ I, НЕКОТОРЫЕ ВОПРОСЫ АНАЛИЗА
а — точка открытого множества Q то существует шар с центром
в а некоторого радиуса г, содержащийся в О. Пусть 5 — наименьшее
из чисел Виг; тогда шар радиуса а е центром в а, очевидно, содер-
жится в множестве /_| (//). Следовательно, это множество открыто.
И) Пусть и 5 — два евклидовых векторных пространства,
F— замкнутое и ограниченное (т. е. компактное) множество из R и
/—непрерывное отображение множества F з пространство 5. Ока-
зывается тогда, что отображение f равномерно непрерывно, а множе-
ство f(F) является замкнутым и ограниченным (т. е. компактным).
Ив последнего вытекает, в частности, что непрерывная числовая функ-
ция /, определенная на компактном множестве F, имеет максимум и
минимум.
Докажем прежде всего, что отображение / равномерно непрерывно.
Допустим противоположное; тогдз существует такое положительное
число а, что при любом положительном 8 найдутся две точки а и х
из Р, для которых |х— а К В, а |/(х)—Пользуясь этим,
можно построить бесконечную последовательность пар точек
Хь а* х* .akt хл; ...,
для которых выполнены условия
l/(*J-/(«*) *=1,2,...; (17)
lim | л:* — аА| = 0. (18)
к -> оо
Так как последовательность аь .... содержится в замкнутом
ограниченном множестве F, то из нее можно выбрать подпоследова-
тельность, сходящуюся к некоторой точке а из F. Для того чтобы
не менять обозначений, будем считать, что сама последовательность
а1г ...» ak, ... сходится к а.
Так Как функция f непрерывна в точке а, то существует такое поло-
жительное число 8, что при | х — a j <^8 мы имеем |/(х) —f(a) | <С у*
Ввиду того, что последовательность аь ..., ak, ... сходится к а и
имеет место соотношение (18), найдется настолько большой номер А,
что |а* —а|<^8» |х* —а|<^8 (см. (3)). Для такого k мы имеем
I/(X.) -f(ak) I < |/(х4) -/ (а) I + |/(ал) - f(a) | < 2 • |,
что противоречит неравенству (17).
Докажем теперь, что множество f(F) компактно. Пусть /И™ про-
извольное бесконечное множество точек из f(F), Из множества М
можно выбрать бесконечную последовательность попарно различ-
ных точек
bi, ..., bk, ... (19)
Для каждой точки bk этой последовательности выберем такую точку
§ 32] ТОПОЛОГИЧЕСКИЕ СВОЙСТВА ЕВКЛИДОВЫХ ПРОСТРАНСТВ 29в
ak из F, что f(ak) — bk, 6—1, 2, ... Точки alf ... , а#... попарно
различны и потому имеют предельную точку а в множестве F. По-
кажем, что точка b=f(a) является предельной для множества (19).
Пусть V—произвольная окрестность точки Ь, т. е. шар некоторого
радиуса е^>0 с центром в Ь. Так как функция / непрерывна
в точке а, то существует такое положительное число 8, что при
| х — а | В (здесь х — точка из Р) \f(x) — f(a) I <С е- Так как точка а
является предельной для множества точек аь ..., akt ... , то в шаре
U радиуса В с центром а найдутся, по крайней мере, две различные
точки ak и az этого множества. Точки bk и принадлежат шару. К
и так как они различны, то, по крайней мере, одна из них не совпа:
дает с точкой Ь. Таким образом, произвольная окрестность Уточки Ь
содержит хотя бы одну точку множества (19), отличную от Ь. Сле?-
довательно, b является предельной точкой для множества (J?x
а потому и для множества М. Таким образом, множество f(P) ком-
пактно.
Если размерность пространства 5 равна I, то f—f есть число-
вая функция. В этом случае множество /(F) есть замкнутое ограни-
ченное множество действительных чисел. Точные верхняя и нижняя
грани множества f(P) конечны и принадлежат ему. Точная верхняя
грань множества f(P) есть максимум функции /, а точная нижняя
грань — ее минимум.
Таким образом, предложение И) доказано.
Примеры
Рассмотрим некоторые примеры непрерывных функций.
L Пусть R и 5—два евклидовых пространства. Каждой точке
... , хр) пространства поставим в соответствие точку
= , yq) пространства S, положив
У'= Za^-Ь^ . .... Я-
Здесь aj—некоторые числа, составляющие матрицу Д = (ар, а &—
числа, составляющие вектор Ь = (Ь\ , bq). Система скалярных
соотношений (20) в векторной форме записывается в виде:
у — Ах-\-Ь.
(21)
Соотношение (21) определяет так называемое аффинное отображение
пространства R в пространство S.
Докажем, что аффинное отображение непрерывно. Для краткости
обозначим его одной буквой /. Пусть Xj и х3 — две точки из /?,
расстояние между которыми | — х» | 8. Оценим расстояние между
298
ДОБАВЛЕНИЕ I. НЕКОТОРЫЕ ВОПРОСЫ АНАЛИЗА
точками y1=f(xl) и ^2—/(хй) в пространстве 5. Мы имеем:
У1— У* = А C*i — хД
или в скалярной форме
р
У1—у!=£а/(х‘ — х'), (22)
i= 1
Пусть -[ — максимальное из чисел | aj |, так что |а^|^удля всех/, у.
Так как [х!— х21 8, то |х* — х^|<^8. Из этих неравенств, в силу
соотношения (22), получаем:
IX— XI < Л8»
Возводя это соотношение в квадрат, суммируя по у и извлекая затем
квадратный корень, получим |yj —у1 j/q. Таким образом,
чтобы было выполнено неравенство |у—достаточно взять
6 <5—Мы видим, что аффинное отображение не только непре-
РШ
рывно, но и равномерно непрерывно.
Из доказанного следует (см. 3)), что если Н—некоторое
открытое множество пространства 5, то его прообраз (Н) п0и
аффинном отображении f есть открытое множество в R.
Если матрица А—квадратная (т. е. p = q) и невырожденная
(т. е. детерминант ее отличен от нуля), то система соотношений (20)
может быть разрешена относительно неизвестных х1, ... , хр, так
что вектор х однозначно выражается через вектор у
х=Су + d.
Это значит, что аффинное отображение f имеет в этом случае
обратное ему отображение у*1, также являющееся аффинным. При
этом открытые множества пространства R переходят в открытые
множества пространства 5; то же самое имеет место и для их допол-
нений, т. е. для замкнутых множеств. Если невырожденное аффинное
отображение f пространства R на пространство 5 трактовать как
преобразование координат в пространстве R, при котором меняется
понятие о расстоянии, то мы видим, что топологические свойства
(открытость и замкнутость множеств) не зависят от системы
координат, через которую определяется расстояние между точ-
ками.
2. Пусть — евклидово пространство и а — некоторый его вектор,
отличный от нуля. Каждому вектору х из R поставим в соответствие
число у=/(х), положив
У = & х).
Функция /, очевидно, является аффинным отображением пространства
R в пространство действительных чисел и потому непрерывна. Таким
§ 32] ТОПОЛОГИЧЕСКИЕ СВОЙСТВА ЕВКЛИДОВЫХ ПРОС1*РАНСТВ 2©7
образом, прообраз любого открытого множества действйтёльйых чисел
является открытым. Множество всех действительных чисел w удовле-
творяющих неравенству у<^а или у^>а, открыто. Прообраз этого
множества 'в пространстве R определяется неравенсивем^^в,
или (а, х)^>а. Эти неравенства Определяют в пространней
крытые полупространства, на которые < пространство R разбивается
гиперплоскостью (а, х)=а. Дополнения к этим открытии ^полупро-
странствам определяются неравенствами (о, х)^а и (а, £)<& Эти
полупространства замкнуты,* так как являются дополнениями к от-
крытым.
Конечная система неравенств
(аи х)<а1( , (аА> х)<аА>
где air ... , а*— векторы, аь , аА — числа, определяет в про-
странстве R от^рытый ^пук^й (дообще говоря, неограниченный)
многогранник. Он является, рткрытым - м^ожеством, поскольку полу-
чен как пересечение нескольких открытых по^пр(>стран^.?Точцо
так же конечная система неравенств
(ар х)^а1э ... , (akt Х)<ал
определяет в пространстве R выпуклый замкну тыймнвгогранник; он
является замкнутым множеством как пересечение замкнутых полупро-
странств.
3. Пусть R — евклидово ^пространство, a L и М—два^ф'ТЙЩ-
множества. Расстоянием 'между .множествами L и, М наЗДваёйО<^-
ная нижняя грань всех чПсеЯ'] Af—yj, гдех— произвольная ¥бчка
из А, а у — произвольная точка из М Если множество L содержит
лишь одну точку х, то мы получаем расстояние /(х) точки х до
множества М, которое является числовой функцией точки х про-
странства R.
Легко видеть, что расстояние /(х) точки х до множества М об-
ращается в нуль только тогда, когда точка х либо принадлежит
множеству /И, либо является предельной для него. Таким образом,
в случае замкнутого множества Л1 из соотношения f(x) = 0 следует,
что х принадлежит /И.
Докажем, что расстояние /(х) точки х до множества М есть не-
прерывная функция. Пусть х и у — две точки из R, расстояние Между
которыми меньше е: |х—у|<^£, и а— произвольная точка из М,
тогда мы имеем, в силу неравенства (3):
f(x)^\x — а|^|х— jI + Ij — 4
Так как это неравенство справедливо для любой точки а множе-
ства М, то оно останется справедливым, если мы заменим в нем
правую часть ее точной нижней гранью (когда точка а пробегает
298 ДОБАВЛЕНИЕ Г. НЕКОТОРЫЕ ВОПРОСЫ АНАЛИЗА
все множество 7И):
У(хХ | х — у 14-/0>) <е +/ Су).
Таким образом, f(х)— /(у)<^а. Точно так же доказывается, что
/(у) — /(х) е. Из этих двух неравенств следует, что | /(х) — f(y) |<^е.
Таким образом, из неравенства |х—у|<^е вытекает, что
|/(х)—/(у) а это значит, что функция /(х) не только непре-
рывна, но и равномерно непрерывна.
Так как расстояние f (х) точки х до множества М есть непре-
рывная функция, то неравенства /(х)<^а и /(х)^>а определяют в
пространстве /? открытые множества (см. 3)). Дополнительные мно-
жества определяются неравенствами /(х)^а и /(х)^а. Таким об-
разом, определяемые этими неравенствами множества замкнуты. В
частности, множество Л1, определяемое неравенством /(х)=сО, замк-
нуто. Множество М получается из М присоединением к нему всех
его предельных точек и называется замыканием множества М Если
множество М ограничено, то множество, определяемое неравенством
/(х)=Са, не только замкнуто, но, как легко видеть, и ограничено.
Если'замкнутое ограниченное множество F не пересекается с зам-
кнутым множеством М, то расстояние между этими множествами по-
ложительно. Для доказательства обозначим вновь через /(х) рассто-
яние точки х до множества М Так как функция /(х) непрерывна,
то на замкнутом ограниченном множестве F она имеет минимум т.
Легко видеть, что т и есть расстояние между множествами F и М
.Покажем, что /п^>0. Пусть а — такая точка из F, что /(а) = яг.
Если бы было яг = 0, то точка а принадлежала бы множеству М
(ввиду его замкнутости), а это невозможно, так как множества F и
М не пересекаются.
Так как расстояние /(х) точки х до произвольного множества
М есть непрерывная функция, то, в частности, расстояние |х— а|
точки х до точки а является непрерывной функцией от х. Из этого
следует, что всякий шар (см. В)) есть открытое множество. В пред-
ложении В) окрестностью точки а был назван произвольный шар
с центром в точке а. В ряде случаев бывает удобно считать окре-
стностью точки а произвольное открытое множество, содержащее
а. При таком расширении понятия окрестности определение предель-
ной точки не меняется.
§ 33. Теоремы о неявных функциях
В этом параграфе доказываются известные теоремы анализа о су-
ществовании и дифференцируемости неявных функций. Эти теоремы
имеют многочисленные применения и, в частности, употребляются
в этой книге. Доказательство теоремы существования неявных фун-
$ 33)
ТЕОРЕМЫ О НЕЯВНЫХ ФУНКЦИЯХ
299
кций проводится здесь тем же методом последовательных приближе-
ний (или сжатых отображений), который используется в § 20 и 21,
а доказательство дифференцируемости неявных функций использует
лемму Адамара (см. § 24, А)).
Таким образом, все содержание этого параграфа очень ’ Йлй^ко
примыкает к методам четвертой главы и хорошо их иллюстрирует.
Мы будем рассматривать систему уравнений д'
f (t\ ... , х1, v. , хя) = 0, 2=1, ... , л, (1)
относительно неизвестных х\ . Xя, считая 21, ... , tk независимыми
переменными. В дальнейшем будем предполагать, 4то левые части
уравнений (1), т. е. функции
f ... , tkt х\ ... , хя), i=l, ... , л, (2)
определены и непрерывны на некотором открытом множестве Г про-
странства 2? переменных 2\ А, х1, ., х* вместе с их частными
производными
... , п. (3)
Полагая t = {t\ ... , 2й); х = (х1, . . , Xя);
f(t, x) = (/1ft л), ...,/*(*, X)),
мы можем записать систему уравнений (1) в векторной форме
f& *) = 0. (4)
Решением уравнения (4) будем называть всякую непрерывную
векторную функцию х=ф($) векторного аргумента ^«определенную
на некотором открытом множестве Q пространства Т переменных
21, ... , 2й, которая при подстановке в уравнение (4) превращает его
в тождество
/ft ф(*)) = 0> (5)
выполненное для всех точек t открытого множества Q.
Теорема 27. Предположим, что функциональный опреде-
лителъ
W, *) |
1ТН |
отличен от нуля в каждой точке (£ х) открытого множества
Г. Тогда для каждой точки (20, х0) открытого множества Г,
удовлетворяющей условию
f(t9j хо) = О, (6)
существует непрерывное решение х = ф(2) уравнения {^ удовле-
творяющее условию
ГР
<Р(<о) = *в-
300
ДОБАВЛЕНИЕ I. НЕКОТОРЫЕ ВОПРОСЫ АНАЛИЗА
Далее, имеет место единственность. Именно, существует такое
открытое множество U в пространстве R, содержащее точку
х0), что каждая точка (t, х) множества U, удовлетворяющая
уравнению (4), удовлетворяет также уравнению х = <р(У). Иными
словами, вблизи точки (t9, х0) нет ни одной точки, удовлетво-
ряющей уравнению (4) и не принадлежащей графику функции
*=ф(0-
При доказательстве этой теоремы мы используем равномерную
сходимость последовательности векторных функций векторного пере-
менного. В § 20 и 21 рассматривались лишь последовательности
функций скалярного переменного; поэтому мы повторим здесь отно-
сящиеся сюда понятия для случая векторного переменного (ср. § 21, В)).
А) Пусть F— замкнутое ограниченное множество точек про-
странства Т. Нормой ]| <р|| непрерывной векторной функции х = <р(£),
заданной на множестве F, будем называть максимум ее модуля:
||ф|| = шах |ф(<)|.
Пользуясь понятием нормы, можно формулировать определение равно-
мерной сходимости последовательности
Фв> <₽!>..•> ... (8)
непрерывных векторных функций векторного аргумента, заданных на
множестве F\ последовательность (8) равномерно сходится к непре-
рывной функции ф(£), заданной на том же множестве F, если
lim ||ф— фг|| = 0.
Для того чтобы последовательность (8) равномерно сходилась к не-
которой непрерывной функции, достаточно, чтобы были выполнены
неравенства
II ф(+1—Фг II < «о
где числа а0, , af, ... образуют сходящийся ряд.
Доказательство теоремы 27. Для того чтобы применить
к уравнению (4) метод последовательных приближений, перепишем
это уравнение в несколько измененном виде. Для этого положим
b'=£j f X*), l,j=\.......П. (9)
Так как функциональный определитель
dxi
отличен от нуля в каждой точке (А х) открытого множества Г, то
матрица В=(Ь§ имеет обратную матрицу 2Г1. Систему уравнений (1)
§ 33] ТЕОРЕМЫ О НЕЯВНЫХ ФУНКЦИЯХ 301
перепишем теперь в виде:
= х), 1=1, ... , п. (io)
/ /
Правую часть соотношения (10) обозначим через h'(tf х). В силу
соотношения (9) мы имеем, очевидно:
х0) = О, (11)
В векторной форме уравнение (10) можно записать в виде:
Bx — h(tt х). (12)
Применяя к этому соотношению матрицу В~\ получим эквивалентное
ему соотношение
x = g(t, х), (13)
где g(t, x) = (gi(it х), ...» gn(tt x)) = B~ih(tt х). Из соотноше-
ний (11) следует: .
хо) = О. (14)
Так как, кроме того, уравнение (13) эквивалентно уравнению (4), а
точка (£0, х0) удовлетворяет уравнению (4), то она удовлетворяет я
уравнению (13), т, е.
g(fa Хо) = хо. (15)
К уравнению (13), удовлетворяющему условиям (14) и (15), мы я
применим метод последовательных приближений. Именно, мы поста-
вим в соответствие векторной каждой функции х = ф(£) векторного
переменного t функцию ф* (£), положив
ф*(0=^(Л фф). (16)
Мы будем писать (используя «операторные» обозначения)
ф* = Д ф. (17)
Мы перейдем теперь к построению такого семейства □ непре-
рывных функций ф(0, что оператор А переводит каждую функцию
семейства 2 в функцию, также принадлежащую этому семейству, я
является сжатым на семействе 2.
Выберем два таких положительных числа q и а, что при
\t — t*\^q, |х —x0|=sSa (18)
точка (£, х) принадлежит открытому множеству Г и для нее выпол-
нены неравенства
а 1 ь
/,/=1......п, (19)
ю Понтрягин Л. С.
302
ДОБАВЛЕНИЕ I. НЕКОТОРЫЕ ВОПРОСЫ АНАЛИЗА
где /г — некоторое число, удовлетворяющее условию 0<^£<^1. Это
возможно, так как множество Г открыто, а производная —
непрерывна и обращается в нуль в точке (/0, х0) (см. (14)). В силу
формулы (6) § 21 для любых двух точек (ft х) и (ft у) множества
(18) выполнено неравенство
\g(t, X) — g(t, у)|^£|х — (20)
(ср. (19)). Далее, так как функция g(t, х) непрерывна, то сущест-
вует настолько малое положительное число что
\g(t, x^ — gtffi, х0)| < (1 — k)a при — (21)
Полагая в неравенстве (20) j = x0, мы получаем из (20) и (21) (при
|х — xf(|=C«, |Z —Г0|^г):
I g (t, X) — х01 = I g (t, X) — g (t{}, x(1) I
^\g(t, x) — g(t, Xo)| -f- |^(ft Xp) — g(tat x0)|=^
<£|x — x0|4-(l — k)a.
Таким образом,
|^(f, x) — x0|^a (22)
при условии, что
I f — to | sS Г, I x — xB I «5 a. (23)
Так как r^qy то для любых двух точек (ft х) и (ft .у) множества
(23) выполнены оба неравенства (20) и (22).
К семейству 2 причислим каждую определенную на замкнутом
шаре — ftj^r непрерывную фун* 1йю <₽(/), удовлетворяющую на
нем условию |<р(0 — х0|=^«. Из неравенства (22) следует, что каж-
дая функция семейства 2 переводится оператором А в функцию того
же семейства, а из неравенства (20) следует, что оператор А является
на семействе 2 сжатым:
||Д 1р — А <р II sS k II ip — <р ||
для любых двух функций ф, ф семейства 2.
Из этого следует (ср. стр. 167—168), что в семействе 2 сущест-
вует единственная функция ср, удовлетворяющая условию
ф=Лф (24)
или, иначе, тождеству
Ф (*) = £(*> ф(0)> (25)
которое эквивалентно тождеству (5).
Докажем теперь, что если точка (ft х) принадлежит множеству (23)
и удовлетворяет уравнению (4) (или, что то же, уравнению (13)), то
$ 33] ТЕОРЕМЫ О НЕЯВНЫХ ФУНКЦИЯХ 303
она удовлетворяет и уравнению
х = <р(0. (26)
В самом деле, в силу (20) мы имеем:
|X—<₽(f)l = U(*> x)~g(t, <р(О)|<Х:|х —<p(f)|.
Но так как Л<^1, то это возможно лишь в случае, если х==<р(/).
В частности, так как точка (/0, х0) удовлетворяет условию (6), то
она удовлетворяет и условию (7).
Итак, мы построили решение х = «р(/) уравнения (4), определен-
ное на открытом множестве О, определяемом неравенством \t —
и открытое множество Ц, содержащее точку (^, хв), определяемое
неравенствами |/—|х — х0|<^«, для которого имеет место
единственность.
Таким образом, теорема 27 доказана.
Теорема 28. Так же как в теореме 21, предположим, что
функциональный определитель
х))
I дх? I
отличен от нуля в каждой точке (£, х) открытого множест-
ва Г; кроме того, предположим, что частные производные
р=<......41='........."
также определены и непрерывны на всём множеств# Г. Оказы-
вается тогда, что любое решение х=<р(£) = (Ф*(0, .... 4р"<0)
Л д®* (/)
уравнения (4) имеет непрерывные частные производные , р =
= 1, ...» k, i— 1, .п, на всем открытом множестве О опре-
деления этого решения.
Доказательство. Пусть — произвольная точка открытого
множества G, на котором определено решение х = <р(/) уравнения (4)
и х0 = (р(^0). Покажем, что в некоторой окрестности точки tQ частные
производные существуют и непрерывны.
Пусть а и q~ такие положительные числа, что при
11 — to | --G q, I x — x01 tfC a (27)
точка (t, x) принадлежит открытому множеству Г, точка t принад-
лежит открытому множеству G, г функция ф(£) удовлетворяет условию
|<р(0 —Хо!<а.
Л f
Для вычисления производной обозначим через ер единичный
вектор /г-мерного векторного пространства Т, направленный по
10*
304
ДОБАВЛЕНИЕ I. НЕКОТОРЫЕ ВОПРОСЫ АНАЛИЗА
оси, и положим = 11 J- xepi где t\—вектор пространства 7, а т —
действительное число. Тогда мы имеем:
lim У(О-?г(Л)ч (28)
Таким образом, функция
т) = тЧ*»)—^ (*.).„ (29)
является предварительным частным при вычислении производной ^-р.
Выберем настолько малое положительное число г, что при
|Л~ векторы и h удовлетворяют условию
|*1~*о1<Л> |*2~ *0|<?-
Множество (27) выпукло, и потому к разности
/'(*2> Ф(*2))-/‘(*Ь ф(*1)).
которая равна нулю, мы можем применить лемму Адамара. Именно,
мы имеем:
Г (t* <р (М)—(^i>
= S Щ (h, т) (4 - /0 + 2 М (tb т) (/,)) = о, (30)
z=i /=1
где Ц\ (tb т) и т) определены и непрерывны при
| т |<^г. Так как
/<(*0, 0) = -А7/‘ (^ х0),
а функциональный определитель
(-^-/‘(*0. •*(,)
отличен от нуля, то при достаточно малом г определитель |АЛг’(£ъ т)|
отличен от нуля. Считая, что т ^6 0, и деля соотношение (30) на т,
получаем:
2 ^(Л, ^(*1- = г). (31)
J = I
Эта система уравнений относительно функций <[/ (^, *с) разрешима, и
мы получаем:
= (32)
где функция (/ъ т) непрерывна и определена при условии \t —
111 rt не исключая значения -с = 0, так как коэффициенты и пра-
$ 33]
ТЕОРЕМЫ О НЕЯВНЫХ ФУНКЦИЯХ
305
вне части системы (31) определены для этих значений и определитель
этой системы отличен от нуля. Соотношение (32), где слева стоит функция,
определенная лишь при т =£ 0, а справа — функция, определенная и не-
прерывная при произвольном | т | г, при переходе к пределу дает:
lim ф'(гь — 0). (33)
т —* 0
Соотношения (28), (29) и (33) показывают, что производная
существует и непрерывна при |
Таким образом, теорема 28 доказана.
Примеры
1. Пусть /? — пространство переменных х\ ...» хп, а — некото-
рая точка из R и
uf(x) = uj(x\ ...» Xя), л, (34)
— система функций, определенных на некоторой окрестности точки а.
Мы будем предполагать, что эти функции, так же как их частные
производные —непрерывны и что определитель функцио-
нальной матрицы (- I отличен от нуля прих = а. 1огда в силу
непрерывности он отличен от нуля и в некоторой окрестности точ-
ки а. Пользуясь функциями (34), мы можем в некоторой окрестности
точки а вместо координат х1, .хп точки х ввести новые коор-
динаты у\ уп той же точки, положив
ys = и1 (х', ..., хп), .....п, (35)
или в векторной форме
У = «(х). (Зв)
Действительно, в силу теоремы 27, систему скалярных уравне-
ний (35) или, что то же самое, векторное уравнение (3G) можно раз-
решить относительно х- Именно, можно получить векторное реше-
ние
x — v(y), (37)
определенное в некоторой окрестности точки b — и (а) переменного
у, удовлетворяющее тождеству
y = u(v(y)) (38)
по переменному причем Ф(Ь) = а. В силу теоремы 28 компоненты
^(у)» •••» vn(y) вектора ф(у) имеют непрерывные производные пр
переменным у\ ..., уп.
306
ДОБАВЛЕНИЕ I. НЕКОТОРЫЕ ВОПРОСЫ АНАЛИЗА
Докажем, что наряду с тождеством (38) имеет место тождество
х = *п(гг(х)) (39)
по переменному х. Для этого рассмотрим уравнение
u(x) — h(z) (40)
относительно неизвестного вектора z-—(zl, ...» zn). Мы имеем оче-
видное решение z — х этого уравнения. Подставим теперь в тождество
(38) вместо у функцию тг (х); тогда мы получим тождество по х:
н(х) — и (Ф (а (х))),
которое показывает, что решением уравнения (40) является функция
z = zr(u(x)). Но, в силу единственности, это решение должно совпа-
дать с ранее указанным решением z — x, и потому мы имеем х =
= zi(u(x)). Таким образом, тождество (39) имеет место.
Тождества (38) и (39) и показывают, что преобразования (36) и
(37) являются взаимно обратными и могут служить для дифферен-
цируемого преобразования координат х\ хп в координаты
и обратно в некоторой окрестности точки а простран-
ства R.
2. Пусть R—пространство переменных х\ .хп, а — некото-
рая точка этого пространства и
ц\х)^и\х'.......хп)> k (41)
— система функций, определенных на некоторой окрестности точки а.
Мы будем предполагать, что функции (41), так же как их частные
duJ (х)
производные > непрерывны.
В функциональной матрице
/ди ' (х) \
\ дх£ Г
1, .... п,
(42)
будем считать, что индекс j указывает номер строки, а I— номер
столбца, так что матрица (42) имеет k строк и п столбцов. Заметим,
что у-я строка
[да’(х) dui(x)\
\ 6л1 ’ * “ ’ $ля /
представляет собой градиент функции и} (х). Если ранг этой матрицы
в точке а равен k, то, в силу непрерывности, он равен k и в неко-
торой окрестности точки а. В этом случае функции (41) называются
независимыми. В случае, если ранг матрицы (42) меньше k на не-
которой окрестности точки а, функции (41) называются зависимыми.
§ 33] ТЕОРЕМЫ О НЕЯВНЫХ функциях 307
Если k<^n и система функций (41) независима, то ее можно
дополнить функциями и*+1(х), ..., ип(х) до независимой система
функций
п1 (х), .... п*(х), ип(х), (43)
В самом деле, матрица (42) при х==а постоянна и строки ее ли-
нейно независимы. Эту матрицу можно дополнить постоянными стро-
ками до квадратной невырожденной. Добавленные строки можно
считать градиентами линейных функций w*+l (х), .ип (х).
Докажем теперь нижеследующее важное предложение: допустим,
что функции (41) независимы, а функция w(x) такова, что си-
стема функций
их (х), ..., и* (х), w (х) (44)
уже зависима. Тогда существует такая функция W (у1, yk)
с непрерывными производными, что выполнено тождество
w (х) = U7 (и1 (х), ..., и* (х)) . (45)
по переменному х. Иначе говоря, функция w(x) выражается
через функции (41).
Для доказательства этого предложения дополним независимую
систему (41) до независимой системы (43) и введем при помощи нее
новые координаты по формуле (36) примера 1, положив
Пусть х — Ф(у) — обращение этого соотношения (см. (37)). Положим
IV(j) = w(©(j)). (46)
Определенная таким образом функция W(у) = V7(у1, уп) в дейст-
вительности зависит только от переменных у\ ..., yk (это мы дока-
жем ниже) и является искомой функцией W (у1, ..., yk). В самом
деле, подставляя в соотношение (46) у = и(х\ мы, в силу тождества
(39), получим:
IV (и1 (х), ..., пк (х)) = w (х),
что совпадает с доказываемым соотношением (45).
Остается доказать, что функция (46) не зависит от переменных
ум, .... уп. Для доказательства обозначим через уг одну из этих
переменных и докажем, что
^> = 0. (47)
дуг 4
Мы имеем:
dW(y) _ VI dw(x) dv‘(у) , я
ду м dxi дуг * ' '
808
ДОБАВЛЕНИЕ !. НЕКОТОРЫЕ ВОПРОСЫ АНАЛИЗА
Так как система (41) независима, а.система (44) зависима, то градиент
функции w линейно выражается через градиенты функций (41), т. е.
дю(х)_ ди*(х) । . дик(х)
~д!‘ —а' +
i — 1,
л, (49)
где
на
, ak—некоторые функции от х. Умножая соотношения (49)
и суммируя по Z, получаем:
...
dvl (у)
дуг
^(У)_, V ди' (х) dv‘ (у) , . у ди»(х) до1 (у)
дуг 1 дх1 ду ’ * *' к 2т дх* ду ’ '
Но мы имеем, очевидно,
У dus (х) dv1 (у)__dys__п
Z dxi ’ дуг
(ибо г^>£). Таким образом, правая часть
нулю и соотношение (47) доказано.
соотношения (50) равна
ДОБАВЛЕНИЕ П
ЛИНЕЙНАЯ АЛГЕБРА
В этом добавлении излагаются те результаты линейной алгебру
которые используются в некоторых, наименее элементарных парагра-
фах книги. Следует отметить, что § 36 опирается только на резуль-
таты § 34 и совсем не использует результатов § 35.
§ 34. Минимальный аннулирующий многочлен
Собственные значения и собственные векторы
А) Каждой квадратной матрице
А = (aj), Z, / = 1, 2, ..., п,
порядка л, элементами которой являются действительные или комп-
лексные числа, соответствует линейное преобразование А векторного
координатного пространства /? размерности л; именно: вектору
х — (х1, ..., хп)
пространства R ставится в соответствие вектор
Ах=у = (у\ у'1),
определяемый соотношением
/
Пулевой матрице 0 (все элементы которой равны нулю) соответствует
при этом нулевое преобразование О, переводящее каждый вектор в
нуль. Единичной матрице
Е=т («=1° "р" i*/'|
J \ 7 (1 при I=j /
соответствует единичное, или тождественное преобразование Е про-
странства /?:
Ех = х.
310
ДОБАВЛЕНИЕ II. ЛИНЕЙНАЯ АЛГЕБРА
Если в пространстве Ц введены новые координаты ..., х'п, свя-
занные со старыми координатами х1, .л?1 формулами перехода
Х,} — 2 six<>
или в матричной зап-иси
У = Sx,
то преобразованию А в новой системе координат будет соответство-
вать матрица
A' = SASl. (1)
Докажем соотношение (1). Мы имеем:
У = Sy = 5 Ах — S AS~'xf.
Б) Пусть А — линейное преобразование и А — матрица, соот-
ветствующая преобразованию А в некоторой системе координат.
Отличный от нуля вектор h называется собственным вектором пре-
образования А, а число X — собственным значением этого преобра-
зования, соответствующим вектору ft, если выполнено соотношение
Ah — Xft. (2)
Детерминант матрицы (а*— zBy):
О(г) = |а1у-г8,у|=|Д — zE\
называется характеристическим многочленом матрицы А. Оказы-
вается, что коэффициенты многочлена D(z) не зависят от выбора
системы координат, а полностью определяются преобразованием А.
Поэтому многочлен D(z) называется также характеристическим мно-
гочленом преобразования А. Далее, число X тогда и только тогда
является собственным значением преобразования А, когда оно есть
корень многочлена D(z).
Докажем независимость многочлена D(z) от выбора системы коор-
динат. В новой системе координат преобразованию А соответствует
матрица SAS \ где S ~ некоторая невырожденная матрица (см. (1)).
Мы имеем:
| S AS“’ — zE] = | S AS"’ — -sSES’1 | = | S(A — zE) S' | =
= |S|-| A ™zE|.|S-!| = |5|-|A — zEI-ISr^l А — zE\.
Запишем теперь в координатной форме соотношение (А — ХЕ) h = 0,
равносильное соотношению (2):
у (а; — Х8у) М= О, I = 1, ..., п.
j-'
Эта систем.а однородных уравнений тогда и только тогда допускает
ненулевое решение /г1, hnt когда детерминант £)(Х) этой системы
§ 34] МИНИМАЛЬНЫЙ АННУЛИРУЮЩИЙ МНОГОЧЛЕН 311
равен нулю. Таким образом, каждый корень X многочлена D(z) яв-
ляется собственным значением преобразования А и обратно.
В) Если собственные значения Хь ..., преобразования А попарно
различны, то соответствующие им собственные векторы hk
линейно независимы.
Доказательство индуктивное—по числу k. При k=\ это
утверждение очевидно. Допустим, что оно верно для k — 1 вектора,
и докажем его для k векторов. Допустим, чтоа^-Р —
Применяя к этому соотношению преобразование А, получил!:
с другой стороны,
Составляя разность найденных соотношений, получаем:
а\ (М — М л» Ч~ • • • 4" ak-\ Q'k-x — М kfe-i -О-1
Отсюда, по предположению индукции,следует, что Cj= ... =0^ = 0,
и исходное соотношение сводится к akhk — fy откуда аА = 0.
Таким образом, если все корни характеристического многочлен»
D(z) различны между собой, то мы можем принять за базис про-
странства /? собственные векторы Ль hn преобразования А,
В этом базисе преобразованию А соответствует диагональная матрица.
В общем случае приведение матрицы преобразования к диагональной
форме невозможно, и возникает необходимость построения сравни-
тельно сложной теории, к изложению которой мы и переходим.
Минимальный аннулирующий многочлен
Г) Квадратные матрицы порядка п по известным правилам могут
складываться и перемножаться между собой, а также умножаться на
числа; этим операциям над матрицами соответствуют те же операции
над преобразованиями. Таким образом, если
/(г) = a§zm 1 -р ... -j- ат
— многочлен с действительными или комплексными коэффициентами
относительно переменной z, то, подставляя вместо z в этот много-
член матрицу А, мы получаем матрицу
f(A) = М” + + • • + атЕ,
являющуюся многочленом от матрицы А. Аналогично определяется
многочлен /(А) от преобразования А. Если /(z)^0, а матрица
f (А) является нулевой (в этом случае преобразование/(А) также, оче-
видно, является нулевым), то многочлен /(а) называется аннули-
рующим матрицу А и преобразование А. Оказывается, что характе-
312 ДОБАВЛЕНИЕ И. ЛИНЕЙНАЯ АЛГЕБРА
ристический многочлен D(z) матрицы А аннулирует матрицу А:
D(4) = 0.
Для доказательства рассмотрим «-мерное векторное пространство
7? с базисом
... , еп
и рассмотрим соответствующую этому базису координатную систему,
так что
— ... , I, ...» 0),
где координата 1 стоит на /-м месте. Обозначим через А преобра- .
зование, которому в выбранном базисе соответствует матрица А.
Тогда мы имеем:
Aej = £ a'es
s
или, что то же,
2(а;£-8;Д)е, = 0. (3)
S
Положим:
Ls. (г) = as. —
Здесь U. (г) есть многочлен относительно z степени нуль или
единица, а
(^(0)
— матрица, составленная из многочленов. Алгебраическое дополнение
элемента А/(г) в этой матрице обозначим через Mfs (г), так что имеет
место соотношение
= (4)
Умножая соотношение (3) слева на многочлен Л1!(А) и суммируя
полученное соотношение по /, получаем, согласно (4):
s Mi (А) (а*Е - $А) es = £ Mi (A) LSj (Л) es = £ 8/ D (Л) es =
J s, J s
= D(A) ^ = 0.
Таким образом, преобразование D(A) переводит все базисные векторы
пространства R в нуль и потому является нулевым, а значит и соот-
ветствующая преобразованию Ь(А) матрица D(A) также является
нулевой:
П(4) = 0.
Д) В множестве всех многочленов, аннулирующих матрицу А
(или преобразование А), имеется единственный, с точностью до чис-
§34] МИНИМАЛЬНЫЙ'АННУЛИРУЮЩИЙ МНОГОЧЛЕН 313
левого множителя, многочлен А (г) минимальной степени; этот много-
член А (г) является делителем всех остальных многочленов, аннули-
рующих матрицу А; он называется минимальным многочленом, анну-
лирующим матрицу А. В дальнейшем будет предполагаться, что коэф-
фициент при старшей степени многочлена А (г) равен едйнице. В слу-
чае, если матрица А действительна, многочлен А (г) действителен.
Для доказательства предложения Д) напомним, что если /(г) и
^(г) — два произвольных многочлена, a d(z)—их общий наиболь-
ший делитель, то имеет место тождество:
б/(г) = /? (г)/(г) + 9(г)5(г), (5)
где p(z) и q(z) — подходящим образом выбранные многочлены.
Существование тождества (5) доказывается при помощи алгоритма
деления многочленов. Из соотношения (5) следует, что если много-
члены f(z) и g(z) аннулируют матрицу А, то их общий наибольший
делитель d(z) также аннулирует матрицу А. Из Г) следует, что мно-
гочлены, аннулирующие матрицу А, существуют. Пусть теперь А(д)—
многочлен минимальной степени, аннулирующей матрицу А, и f(zj —
произвольный многочлен, также аннулирующий матрицу А. Если бы
многочлен /(г) не делился на многочлен А (г), то общий; наибольший
делитель этих многочленов имел бы степень, меньшую чем много-
член А (г), и также аннулировал бы матрицу А, а. это по предполо-
жению невозможно. Пусть теперь матрица А-действительна; тогда
0= А (А) = А (А)= А (А).
Таким образом, многочлен А (г) аннулирует матрицу А и потому
делится на A(z), а это возможно лйшь при Д(г) = А(г). Таким обра-
зом, предложение Д) доказано.
Е) Пусть А (г) — минимальный аннулирующий многочлен матрицы А.
Число X тогда и только тогда является собственным значением
матрицы А, когда оно есть корень многочлена А (г).
•Для доказательства обозначим через А преобразование и-мерного
координатного векторного пространства, соответствующее матрице А.
Заметим, что если f (г)—произвольный многочлен, то
из Ah = kh следует /(A) ft =/(/)&. (6)
В самом деле, мы имеем:
Eh = h, Ah=lh, A*h = Alh = Wi> . , Amh = Xmh.
Умножая эти соотношения на коэффициенты многочлена f (2)
и складывая их, получаем соотношение (6).
Допустим, что X есть собственное значение матрицы А; тогда
существует такой вектор Л 7^ 0, что Aft = Xft, и из (6) следует
Д(А)Л = Д(Х)Л; но так как Д(А) = 0, то Д(Х) = О. Обратно,
314
ДОБАВЛЕНИЕ I!. ЛИНЕЙНАЯ АЛГЕБРА
пусть X — корень многочлена А (г); тогда А(г) = (г— Х)Г(г). Так
как А (г) есть минимальный аннулирующий многочлен матрицы А,
то многочлен Г (г) не является для нее аннулирующим и потому
матрица Г (А), а следовательно, и преобразование Г (А), отличны
от нуля. Таким образом, существует вектор х, для которого
Г (A)x = fc'^O, и мы имеем 0 = А (А)х=(А —ХЕ) Г (А)х =
=(А— ХЕ) ft', и, следовательно, АЛ' = ХЬ', так что X есть собст-
венное значение матрицы А.
Итак, предложение Е) доказано.
Координатное векторное пространство R, смотря по надобности,
может рассматриваться как действительное, когда в нем берутся
только векторы с действительными координатами, или как комплек-
сное, когда в нем берутся векторы с комплексными координатами.
Если х=(х\ , .. , хп) есть вектор комплексного пространства R,
то х = (х\ . . . , 5й) есть вектор, комплексно сопряженный с X.
Если S есть подпространство комплексного пространства Л, го
подпространство S, составленное из всех векторов, комплексно
сопряженных с векторами из S, считается комплексно сопряженным
с подпространством 5.
Комплексное (или действительное) пространство R считается
разложенным в прямую сумму своих подпространств Si и S^, если
каждый вектор х из R может быть, и притом единственным спосо-
бом, записан в виде суммы:
X — X, + х.ь
где вектор xt принадлежит подпространству Sif /=1, 2.
Ж) Пусть А(г) = А, (г) А.Дг) — разложение минимального анну-
лирующего матрицу А многочлена на два взаимно простых мно-
жителя. Обозначим через S; (/=1, 2) линейное подпространство
пространства R, состоящее из всех векторов х из R, удовлетворяю-
щих условию А;(А)х = 0, где А — преобразование с матрицей А.
Оказывается, что пространство R распадается в прямую сумму своих
подпространств Si и S3. (Если матрица А комплексна, то в форму-
лированном здесь утверждении пространство R следует считать ком-
плексным.) Допустим теперь, что матрица А действительна; тогда
следует отметить два важных случая. 1) Множители А1(г) и А3(г)
действительны; тогда пространство R и его подпространства St и S3
можно считать действительными. 2) Множители А}(г) и А2(г) ком-
плексно сопряжены между собой; тогда пространство R следуег счи-
тать комплексным, а его подпространства Si и S2 оказываются ком-
плексно сопряженными.,
Докажем предложение Ж). Так как множители Aj(z) и А3(г)
взаимно просты, то имеет место тождество
1 = pt (г) Д, (г) 4- р-i (г) Да (z), (7)
§ 34] МИНИМАЛЬНЫЙ АННУЛИРУЮЩИЙ МНОГОЧЛЕН 815
где pi(z) и р$(2)—надлежащим образом подобранные многочлены
(см. (5)). Заметим, что если множители At(z) и A^(z) действительны,
то многочлены pi(z) и р^(г) могут быть выбраны действительными,
так как они получаются при помощи алгоритма деления из много-
членов At(z) и A2(z). Пусть теперь х — произвольный вектор из R;
в силу (7) имеем:
x=pl(A)Al(A)x+pi(A)Ai(A)x.
Полагая
-*1 = Pi (Л) А.2 (4) х; х*—рх (A) At (А) х,
мы получаем разложение x=xt4~-^2> причем
Ai(A)x, = A((A)p2(A)A2 (А)х = /?2(А) А (А)х = 0,
Д4(А)х2 = А2(А)р1(А)А1(А)х=А (А)А(А)х = 0,
так что вектор х, принадлежит подпространству 6j. Если теперь
x=xi 4“ — какое-либо разложение вектора х в сумму, в которой
x't принадлежит 5^ (7—1, 2), то в силу (7) мы имеем:
xi =/>i (A) At (A) xi 4-р3 (А) Д2 (А) х[ = р2 (A) At (A) (xi 4- Хз) = х»
точно так же хз^х* и единственность разложения доказана.
Если матрица А действительна и множители Aj(z) и As(z) дей-
ствительны, то, исходя из действительного вектора хг мы получаем
действительные векторы Xi и х«. Если же матрица А действительна,
а множители Aj(z) и Д4(г) комплексно сопряжены, то векторные под-
пространства 6*1 и 6*2 в силу самого своего определения комплексно
сопряжены.
Таким образом, предложение Ж) доказано.
3) Пусть А — линейное преобразование п-мерного пространства /?,
Хц . и К
— совокупность всех собственных значений этого преобразования,
Д (г)=(z — Xj)*! (г — Х,)*2... (г — Хг)*г
— минимальный аннулирующий многочлен преобразования А и
D (г) = ( -1)" (г - (г - . (z - Х^ (8)
— характеристический многочлен преобразования А. Так как многочлен
D(z) делится на многочлен A (z), то
Я i i=lt • ••> Г-
В силу предложения Ж) пространство R разлагаете* в прямую
сумму своих подпространств 6*ь 6*2, ...» 5*г> где состоит из всех
векторов х( удовлетворяющих условию
(Л — Х^/'х = &.
816
ДОБАВЛЕНИЕ Н. ЛИНЕЙНАЯ АЛГЕБРА
Оказывается, что размерность пространства 8} равна Число
называется кратностью собственного значения Х£.
Докажем, что размерность пространства равна qt. Про-
странство инвариантно относительно преобразования А, т. е.
содержится в Таким образом, если в пространстве 6*г
выбран некоторый базис, то преобразованию А, рассматриваемому
на соответствует некоторая матрица At порядка pif где pt — раз-
мерность пространства St. Если базис пространства составить
из базисов всех пространств то в полученном базисе преобразо-
ванию А будет соответствовать матрица 4, состоящая из матриц
Ар .Аг, расположенных вдоль диагонали матрицы А. Из этого
видно, что характеристический многочлен преобразования А проел -
ранства R будет равен произведению
... Dr(z)t
где Di(z) — характеристический многочлен преобразования А, рас-
сматриваемого на подпространстве Так как Д4 (г) = (г — XJ*/ есть
аннулирующий многочлен преобразования А на подпространстве Sit
то преобразование А на имеет лишь одно собственное значение Хо
и потому характеристический многочлен D^z) имеет вид
(—l)pt(z— ибо степень его равна порядку матрицы Аь т. е.
размерности р{ пространства Следовательно, мы имеем D(z)~
= (— “ МР1 •• (г — и потому pi = qi (см. (8)).
Таким образом, предложение 3) доказано.
§ 35. Функции матриц
В этом параграфе мы не будем делать различия между преобра-
зованием А и соответствующей матрицей А, так как система коор-
динат не будет меняться. Кроме того, в этом параграфе будут исполь-
зованы некоторые сведения из теории функций комплексного пере-
менного (см., например, И. И. Привалов, Введение в теорию
функций комплексного переменного, Флзматгиз, I960).
Матричные степенные ряды
А) Пусть
Д(г)==(г_Х1)^(г_х/3...(г-Хг)Ч (I)
I — 1, г, 4~4~...4-kr =
— минимальный аннулирующий многочлен матрицы А, причем
Хр Х2, ..., Хг (2)
— его попарно различные корни. В силу предложения Е) § 34 числа
(2) составляют совокупность всех собственных значений матрицы А.
§ 35]
ФУНКЦИИ МАТРИЦ
317
Говорят, что на спектре матрицы А задана функция UZ, если
каждому собственному значению матрицы А поставлена в соответ-
ствие последовательность чисел
^(1)(М> •••> /=Ъ ...» г. (3)
Если U7 (г) — некоторая функция комплексного переменного г, голо-
морфная в точках Х(-, то, понимая под числами (3) значение самой
функции и ее производных до порядка ki — 1 в точке мы полу-
чаем функцию, заданную на спектре матрицы А. Если для двух
функций комплексного переменного z значения (3) соответственно
совпадают, то говорят, что эти две функции совпадают на спект~
ре матрицы А. Оказывается, что два многочлена f (г) и g(z) тогда
и только тогда совпадают на спектре матрицы А, когда /(A) = g(A).
Далее оказывается, что, каковы бы ни были произвольно заданные
числа (3), всегда существует единственный многочлен <р (г) степени
— 1, значения которого на спектре матрицы А совпадают с чис-
лами (3), т. е.
?(/)(М = ^(/)(М> J = o, .... ^-1, (4)
При этом коэффициенты многочлена ср (г) являются линейными функ-
циями величин (3) и потому непрерывно зависят от них.
Докажем эти утверждения. Положим h(z)=f(z)— g(z)* Если
f(A) = g(A), то h (А) = 0. Далее, если значения многочленов f(z)
и g(z) на спектре матрицы А совпадают, то функция h(z) на спек-
тре матрицы А обращается в нуль. Таким образом, чтобы доказать
ту часть утверждения А), которая относится к многочленам f (z) и
g(z), достаточно доказать, что многочлен h(z) тогда и только тогда
аннулирует матрицу А, когда он обращается в нуль на спектре этой
матрицы. Докажем это. Допустим, что многочлен h(z) аннулирует
матрицу А; тогда в силу предложения Д) § 34 он делится на много-
член A(z) и потому имеет число Х£ своим корнем кратности не
меньше /г, (см. (1)), а из этого следует, что он обращается в пуль
па спектре матрицы А. Если многочлен /z(z) обращается в нуль
на спектре матрицы А, то он имеет число Л£ своим корнем крат-
ности не меньше и потому делится на многочлен A(z) (см. (1)),
откуда следует, что Л(А) = 0.
Докажем теперь ту часть предложения А), которая относится к
функции ф (г). Совокупность соотношений (4) можно рассматривать
как систему линейных уравнений относительно коэффициентов мно-
гочлена ф (г); система эта имеет k уравнений и k неизвестных. Для
доказательства утверждения А) достаточно установить, что детерми-
нант этой системы отличен от нуля, а для этого в свою очередь
достаточно доказать, что в случае обращения в нуль правых частей
этих уравнений имеется лишь нулевой многочлен <р (г), удовлетворя-
ющий условиям (4). В случае обращения в нуль правых частей
818 ДОБАВЛЕНИЕ II. ЛИНЕЙНАЯ АЛГЕБРА
уравнений (4) многочлен <р (г) обращается в нуль на спектре матрицы А
в потому в силу ранее доказанного делится на многочлен Д(г), а
Так как он имеет степень не выше k—1, то он тождественно равен
нулю.
Таким образом, предложение А) доказано.
Б) Пусть А—действительная матрица; тогда минимальный анну-.
лирующий ее многочлен Д (г) действителен (см. § 34, Д)) и потому
наряду с каждым его корнем (см. (1)) имеется комплексно сопря-
женный ему корень той же кратности. Оказывается, что если чис-
ла (3) удовлетворяют условиям:
/ = 0, kt— 1, i= 1, г, (5>
то многочлен ср (г), определенный соотношениями (4), действителен, и
потому матрица ср (А) также действительна.
Для доказательства предложения Б) обозначим коэффициенты
многочлена ср (г) через ср1, ..., ср*. Систему уравнений (4) относитель-
но неизвестных ср1, ,ср* можно, не вникая в подробности, записать
теперь в виде:
k
= а=1, (6)
f;=i ‘
Система эта в силу условий (5) обладает тем свойством, что наряду
с каждым ее уравнением в ней имеется и комплексно сопряженное
ему уравнение, т. е. уравнение
k__ _
?₽=^-
0=1
Перейдем теперь от равенств (6) к сопряженным им равенствам
k____________________________ _
т
Совокупность соотношений (7) представляет собой систему линейных
уравнений относительно неизвестных ср1, .ср*. Однако ввиду фор-
мулированного свойства системы (6), система уравнений (7) совпада-
ет с ней, отличаясь, быть может, лишь порядком нумерации уравне-
ний, Так как система (6) имеет отличный от нуля детерминант,
то два ее решения ср1, ..., срА и ср1, ср* совпадают между собой:
сра=гсра, а=1, А, а это и означает, что числа ср1, ..., ?* дей-
ствительны. Таким образом, предложение Б) доказано.
Пусть
/и) = а«-Га12 + ^г:-|- ••• -Нтг'"+ ••• (8)
§ 35|
ФУНКЦИИ МАТРИЦ
3W
— аналитическая функция комплексного переменного z, заданная ря-
дом (8) с радиусом сходимости р, так что при |z|<^p ряд (8) схо-
дится, а при 1г|^>р он расходится.
Для дальнейшего напомним, что ряд
f(z) = at-[-2a2z-|- ... + татzml4- ....
получаемый из ряда (8) путем формального дифференцирования, име-
ет тот же радиус сходимости, что и ряд (8), и сходится внутря
круга сходимости к производной f (z) функции f{z).
Может случиться, что, подставляя вместо z в ряд (8) матрицу 4,
мы получим сходящийся матричный ряд
/(Л) = а0£4-а1Л+ ... ат Ат — (9)
(Матричный ряд называется сходящимся, если числовой ряд, состав-
ленный из элементов, стоящих в /-й строке и у-м столбце, сходится
при любых z, /= 1, .л.) В этом случае говорят, что функция f(z)
определена на матрице А,
Теорема 29. Сохраним обозначения предложения А). Если
все собственные значения матрицы А лежат внутри круга схо-
димости ряда (8), т. е.
|\-|<Р> Z=l, ...» г,
то матричный ряд (9) сходится, так что матрица f(A) опре-
делена. Числа
Ж), /=1, ..., г, (10)
среди которых, возможно, есть совпадающие, составляют сово-
купность всех собственных значений матрицы f(A). Далее, если
собственные значения матрицы А лежат и в круге сходимос-
ти ряда, определяющего некоторую функцию g(z), так что матри-
ца g(A) определена, то для совпадения матриц f(A) и g (А) не-
обходимо и достаточно, чтобы функции f (z) и g(z) совпадали
на спектре матрицы А.
Доказательство. Составим частичную сумму
/m(*) = ao + ai*+ +amzm
ряда (8); тогда при | z | р мы имеем:
/(/)(z) = lim /$(*).
т-*со
Пусть, далее, ym(z) — многочлен степени k — 1, совпадающий с
многочленом /го(г)на спектре матрицы А (см. А)). Так как собствен-
ные значения (2) матрицы А удовлетворяют условию |^|<^р,
/=1, то мы имеем:
lim / = 0, —1, г.
«1—00
820
ДОБАВЛЕНИЕ И. ЛИНЕЙНАЯ АЛГЕБРА
Из этого в силу предложения А) следует, что последовательность
многочленов <?m(z) покоэффициентно сходится к некоторому много-
члену ф (г) степени — 1, причем многочлен ср (?) и функция f(z)
совпадают на спектре матрицы А. Так как многочлены cpm (z) и fm(z)
совпадают на спектре матрицы А, то мы имеем;
fm(A) = cpm(4);
при /п->оо правая часть стремится к <р(А), а это значит, что и ле-
вая часть при /?г-> со сходится. Таким образом, ряд (9) сходится
к матрице f (А) — ср (А).
Докажем теперь, что многочлен
Г(г) = [г~ЦХ,)]*' [г-Ж)|"2 ••• [г-Ж)]*'
аннулирует матрицу f(A). Для этого рассмотрим многочлен
(г) = [?т (г) - <рт (М)Г‘ W (О]*3 • •
•••[?«(*)-<Р,Ж)]*Г (11)
и покажем, что он аннулирует матрицу А. Многочлен cpm(z) — <pm(Xx)
обращается в нуль при z = Xf и потому он делится на двучлен
ж — Хр Таким образом, многочлен (11) может быть записан в виде:
Фт(г) = Фда(г)Д(г)
и потому многочлен Фт(?) аннулирует матрицу А, т. е.
[?и (А) - <fm (X,) Еf * [?m(А) - (Х2) £]"J ...
••• [?т(Д)- ?m(Xr) /:|"^о.
Переходя в этом соотношении к пределу при zzz—>оо, получаем:
KM)-/(X,)Z:M/(A)-/(X2)Z:]^ ... [/(A)-/(XJЕ\кг = 0,
а вто и значит, что многочлен Г (?) аннулирует матрицу f (А).
Ив доказанного, в частности, следует, что все собственные зна-
чения матрицы /(А) содержатся среди чисел (10) (см. § 34, Е)).
Докажем, что каждое число (10) является собственным значением
матрицы/(А). Пусть hi — собственный вектор матрицы А, соответ-
ствующий собственному значению дх-, так что
Ahj = ХД.
В силу формулы (6) § 34 из этого следует:
/т(А)Л,.=/т(Х,)Л(.
Переходя в этом соотношении к пределу при т—>оо, получаем:
/(A)^=/(Mftf.
Таким образом, число /(Хг) есть собственное значение матрицы /(А).
ФУНКЦИИ МАТРИЦ
321
$ 351
Допустим теперь, что круг сходимости функции g(z) также со-
держит все собственные значения матрицы А. Тогда в силу дока-
занного матрица ^(А) определена и существует многочлен ф (г) сте-
пени —1, совпадающий с функцией g(z) на спектре матрицы А,
причем ф(А) = £(А). Если теперь /(А) = ^(А), то <р(А) = ф(А), и в
силу предложения А) многочлены ср (г) и ф(г) совпадают на спект-
ре матрицы А, а следовательно, и функции /(г) и ^(г) совпадают на
спектре матрицы А. Обратно, если функции f(z) и g(z) совпадают
на спектре матрицы А, то многочлены ср (г) и ф(г) также совпа-
дают на спектре матрицы А, и потому в силу А) <р(А) = ф(А), но
тогда и /(A) = g*(A). Таким образом, теорема 29 доказана.
Неявные функции матриц
Пусть F (г, w) — функция двух комплексных переменных, задан-
ная рядом
F (z, w) — а -|- bz -|- cw + dz* -|- ezw -j- fw* . (12)
При перемене порядка сомножителей в членах этого ряда (например»
при замене произведения zav^ на функция F(zt w) не меняется.
Поэтому при подстановке в ряд (12) матриц А и В вместо его
аргументов z, w естественно ограничиться случаем, когд^а матрицы А и В
перестановочны между собой. Если ряд (12) сходится при любых
значениях переменных z, w, то можно доказать, что, подставляя в этот
ряд вместо z и w любые перестановочные матрицы А и В, мы по-
лучим сходящийся матричный ряд, который определит некоторую
матрицу, обозначаемую через F (А, В). Однако доказывать сходимость
этого ряда в общем случае мы не будем, так как ниже рассматри-
ваются лишь такие частные случаи, в которых имеется конечное
число членов, зависящих от z, так что фактически речь идет о схо-
дящихся рядах одного комплексного переменного w.
В) Пусть F (z> w) — аналитическая функция двух переменных»
определенная рядом (12), сходящимся при всех значениях z, w9
и А—заданная матрица. Пусть, далее, каждому собственному значе-
нию X; матрицы А поставлено в соответствие число удовлетво-
ряющее условиям
М = °. <=1......г. (13)
Тогда существует перестановочная с А матрица В, удовлетворяющая
условию
F(A, В) = 0. (14)
Далее, если коэффициенты ряда (12) и матрица А действительны
и если для каждых двух комплексно сопряженных собственных
822
ДОБАВЛЕНИЕ IT. ЛИНЕЙНАЯ АЛГЕБРА
впачений Х; и ку= матрицы А соответствующие числа и |ху- также
комплексно сопряжены: = то существует действительная пере-
становочная с А матрица В, удовлетворяющая условию (14).
Докажем предложение В). Из соотношений (13) в силу теоремы
о неявных функциях комплексного переменного следует, что для лю-
бого Z=l,..., г существует функция IT (z) = (z), определенная
для значений z, близких к \iy и удовлетворяющая условиям
F(z, U7(z)) = 0, (15)
= Z=l,..., г. (16)
Для нахождения производных (Xf) функции W(z) в точке z~li
нужно последовательно дифференцировать соотношение (15) по zt
подставляя в нем затем z — Х;:
^Л(г, U7(r))U(==o. (17)
Из этих соотношений можно последовательно определить числа
1И’(Хг), kt— 1, Z=l,..., г. (18)
Исходя из чисел (16), (18), построим многочлен (z), удовлетворяю-
щий условиям (4). Покажем, что матрица /? = <р(А), очевидно, пере-
становочная с А, удовлетворяет условию (14).
Для доказательства подставим в ряд (12) значение w = (z). Мы
получим тогда функцию O(z)~F(z', o(z)) переменного z. Для дока-
вательства равенства (14) достаточно установить, что функция Ф (z) равна
нулю на спектре матрицы А (см. теорему 29). При вычислении
производных (Х/) функции Ф(г) в точке Xf,/ = 0, 1,..., kt—1,
мы можем многочлен <p(z) заменить функцией W (z), так как у этих
функций производные порядков 0, 1,..., /г,—1 в точке Х; соответ-
ственно равны. Но при замене в F(z> y(z)) многочлена <p(z) функ-
цией IT(z), определенной вблизи Xf, мы получаем тождественный
нуль (см. (15)). Таким образом, функция Ф(г) обращается в нуль па
спектре матрицы А.
Докажем теперь, что если коэффициенты ряда (12) и матрица А
действительны, а числа удовлетворяют условиям сопряженности,
т. е.
U7(ГТ) = WTxT), Z=l, .... Г,
то многочлен cp(z), а следовательно, и матрица В = =р(Л) действи-
тельны. В самом деле, при этих предположениях числз
вычисляемые из условий (17), удовлетворяют условиям (5), и по-
тому многочлен ср (г) действителен (см. Б)).
Итак, предложение В) доказано.
5 36]
ЖОРДАНОВА ФОРМА МАТРИЦЫ
323
Г) Аналитическая функция е* комплексного переменного ж
определяется рядом
«771
е*= 1 +г + зг+ ••• + ^]+ (19)
который сходится при всех значениях переменного z. Как известно^
для двух произвольных комплексных чисел z и w имеет место
тождество ez + w — е?-е™, вытекающее из свойств ряда (18). Отсюда
следует, что для двух перестановочных между собой квадратных
матриц А и В имеет место тождество
еА + в = еА • ев. (20)
Оказывается, что для любой невырожденной матрицы А существует
перестановочная с А матрица Bt удовлетворяющая условию
ев—А. (21)
Далее оказывается, что для любой действительной невырожденной
матрицы А существует действительная матрица By irrprolffODOinia
с А и удовлетворяющая условию
А\ (22)
Для доказательства разрешимости уравнения (21) относительно
В достаточно применить предложение В) к функции F(z,w)^ev— ж.
В самом деле, так как матрица А невырождена, то все ее собствен-
ные значения Х; отличны от нуля, и потому существуют числа р»
удовлетворяющие условию е^ —к£=0 (см. первое из соотношений
(13)), причем второе из соотношений (13) адесь, очевидно, выполнено.
Для доказательства существования действительной матрицы В*
удовлетворяющей условию (22), достаточно к функции F(zt w)e
= ew — z2 применить вторую часть предложения В). В самом делеь
если Xz есть действительное, положительное или отрицательной
число, то положим |1/ = 1пХ/, взяв действительную ветвь логарифму
Если же Х(- — комплексное число, то за И^ХД и UZ(Xz) можно при-
нять комплексно сопряженные числа.
Итак, предложение Г) доказано.
§ 36. Жорданова форма матрицы
А) Последовательность векторов
hm (1)
пространства R называется серией с собственным значением X отно-
сительно преобразования А, если выполнены соотношения
Oj A h±;— Х/т^, Ahi ~~~ Xh^ hy .»., *4”
324
ДОБАВЛЕНИЕ И. ЛИНЕЙНАЯ АЛГЕБРА
Если матрица Л преобразования А действительна, то последователь-
ность
h„ .... hm, (2)
очевидно, образует серию с собственным значением X. Серии (1)
и (2) будем называть комплексно сопряженными. Если число X и
векторы (1) действительны, то серия считается действительной.
Теорема 30. Существует базис пространства /?, состоящий
из всех векторов одной или нескольких серий относительно пре-
образования А. Если матрица А действительна, то серии, состав-
ляющие базис, можно выбрать так, чтобы серии с действитель-
ными собственными значениями были действительными, а серии
с - комплексными собственными значениями были попарно сопря-
жены.
Доказательство. Пусть
Д (z) = (г-)..)** ... (г-ХгЛ (3)
— минимальный аннулирующий матрицу А многочлен, где
Xj, Хг
— попарно различные собственные значения матрицы А В силу
предложения Ж) § 34 пространство /? можно разбить в прямую
сумму его подпространств соответствующих множителям (3),
так что пространство состоит из всех векторов х, удовлетворяю-
щих условию (4 — X/E)*ix = 0. Это значит, что аннулирующим мно-
гочленом преобразования А, рассматриваемого па пространстве
является многочлен (z—Х,)\ Легко видеть, что этот многочлен явля-
ется минимальным.
Допустим, что матрица А действительна. Объединим сначала все
множители из (3) с действительными Xi в множитель Aj (z), а все
остальные — в множитель A2(z). Тогда А (г) — А] (.г) Д.» (z) есть раз-
ложение на действительные взаимно простые множители, и соответ-
ствующее разложение пространства /? в прямую сумму подпространств
и можно считать действительным. Пространство разобьем теперь
в прямую сумму действительных слагаемых, соответствующих действи-
тельным собственным значениям Х;, и в этих действительных прямых
слагаемых мы в дальнейшем построим базисы, состоящие из действи-
тельных серий. Пространство R% разобьем на попарно комплексно
сопряженные прямые слагаемые, соответствующие комплексно сопря-
женным собственным значениям, и в этих комплексно сопряженных про-
странствах мы в дальнейшем построим базисы, состоящие из комплексно
сопряженных серий; при этом достаточно построить базис из серий в од-
ном из двух комплексно сопряженных пространств, а во втором
взять комплексно сопряженный базис.
§ 36] ЖОРДАНОВА ФОРМА МАТРИЦЫ 325
Итак, нам достаточно доказать, что если линейное преобразова-
ние At действующее в векторном пространстве S’, имеет минималь-
ный аннулирующий многочлен (г — X)*, то в этом пространстве можно
выбрать базис, состоящий из серий относительно преобразования А,
причем из серий действительных, если пространство S, матрица Д и
число X действительны.
Перейдем к доказательству этого утверждения. Для краткости по-
ложим С = А—ХЕ и обозначим через совокупность всех векто-
ров х из S, удовлетворяющих условию
С'х = 0.
Мы имеем тогда
Пусть
h\, hi (2=1, .... Л)
— система векторов из Т1, линейно независимых относительно про-
странства это значит, что вектор
4" • • • “f~ ar^i
может принадлежать пространству Т1"1 лишь при условии
а1 = ... = йг = 0.
Покажем, что при фиксированных I и j векторы
= (J<i) (4)
принадлежат пространству 7}_}- и линейно независимы относительно
пространства Мы имеем:
с; -jhf- j = C'ft = о (а = 1. г),
и, следовательно, векторы (4) принадлежат пространству 7}_у. До-
пустим теперь, что вектор
+... + аХ-/ = х
принадлежит пространству Тогда имеем:
O==C'-/-‘jr=C’-1(aJftJ+ ... 4-агл:),
а это значит, что вектор ••• Ч~аг^ принадлежит простран-
ству 7}_! и потому числа alt ...» аг равны нулю.
Выберем теперь максимальную систему векторов
... > (5)
326
ДОБАВЛЕНИЕ И. ЛИНЕЙНАЯ АЛГЕБРА
пространства Tk, линейно независимых относительно пространства
По доказанному векторы
Л;_!=С^ (а= 1, , г,) (6)
принадлежат пространству Tk_x и линейно независимы относительно
пространства таким образом, систему (6) можно дополнить до
максимальной системы
Ч-........^-7 (7)
векторов пространства Tk_b линейно независимых относительно про- .
странства Т Продолжая этот процесс дальше, мы построим в
пространстве 7}(/^>0) максимальную систему векторов
h\, ... , h'i, (8)
линейно независимых относительно пространства причем будут
выполнены соотношения
/r=Cft;+1 (<х=|......ri + l; r(^ri + t).
Докажем теперь, что совокупность У у всех векторов, принадле-
жащих всем системам (8), l=j, j— 1, ... , 1, составляет базис про-
странства Т у. Доказательство будем вести индуктивно по числу у.
Для У=1 система совпадает с системой (8) при J~~] и потому
является базисом пространства 7'}(Го = О). Допустим, что наше ут-
верждение доказано для системы £у, и докажем его для системы
Ij/h г Допустим, что имеет место соотношение
+ ... + ar h /+1 Д- bi br ftrj + ... =0 (9)
J -Т 1 J ±1 J h' J ] J
J
Применяя к соотношению (9) преобразование В}, получаем:
Oi 4~ • • “4 === о,
а это возможно лишь при условии аг = ... =ar0; таким об-
разом, в соотношение (9) могут входить лишь векторы системы
и, следовательно, по предположению индукции, соотношение (9) три-
виально. Пусть теперь х—произвольный вектор пространства +
Так как система (8) при z=y*4-l есть максимальная линейно неза-
висимая система относительно пространства Ту, то существует такой
вектор
4~ ... 4-й ft /-Н,
/+1
что вектор Х — у принадлежит пространству 7) и в силу предложе-
§ ЗС ] ЖОРДАНОВА ФОРМА МАТРИЦЫ Mft.
ния индукции выражается линейно через векторы системы 2}/* a art.
значит» что вектор X выражается линейно через векторы системы
Итак, доказано, что система У}А. есть базис пространства
Если пространство S, матрица Л и число X действительны, тоь
выбирая векторы системы (5) действительными, мы получаем дейст-
вительную систему (6), которую можно дополнить до действительно!
системы (7). Продолжая таким образом, мы получаем действе*
тельную систему
Покажем теперь, что система состоит из серий. Именно, по*
кажем, что векторы /i®, /г®, ... образуют серию с собственным зна-
чением X. Мы имеем:
О = Ch] = (А — ХЕ) h],
так что Ак] — )Л1]\ далее,
/»® = СЯ® = (Л —ХЕ)
так что Ah* = ХЛ® -ф- h]t и т. д.
Итак, теорема 30 доказана. \ * . v i ,, ’ 1 . ..
В построенном согласно теореме 30 базисе преобразованию А
соответствует уже не исходная матрица А*==(а^ алйоторая но-
вая матрица B = (blpt имеющая особо простую форму, называемую
жордановой. Таким образом, теорема 30 является теоремой о при-
ведении матрицы к жордановой форме. Разберем этот вопрос
подробнее.,
Б) Жордановой клеткой порядка т с собственным значением X
называется квадратная матрица (g\) порядка mt определяемая соот-
ношениями
g\ — K i — 1, ... , т\ g' + I = 1, z = 1, ...» in — 1;
£•'=0 при j—z<^0 и при ; — z^>l,
а. е. матрица
/X 1 0 ... 0 0\
0 X 1 ... 0 01
о о х ... о о
О О О ... X 1 /
\о о о ... о х/
Оказывается, что для каждой квадратной матрицы А порядка п
можно подобрать такую невырожденную квадратную матрицу что
матрица E=<S,HS-1, получаемая из матрицы А путем трансформации
матрицей 6*, имеет жорданову форму, т. е. состоит из одной
328
ДОБАВЛЕНИЕ II. ЛИНЕЙНАЯ АЛГЕБРА
или нескольких жордановых клеток, расположенных по ее главной
диагонали, в то время как все элементы ее, не входящие в жорда-
новы клетки, равны нулю.
Докажем это. Пусть — координатное векторное пространство
размерности п и А — линейное преобразование, соответствующее (в
некоторой системе координат) матрице А. Пусть теперь/ь —
базис пространства /?, составленный из серий (см. теорему 30). Мы
предположим векторы/ь ..., fn расположенными в таком порядке,
что векторы каждой серии идут в последовательности /ь ...,Д
один за другим. Обозначим через В = (Ь1^ матрицу преобразования А
в базисе ...» /л. Пусть
• • •’ ~fm
— первая серия, входящая в последовательность flt ..., fn и X — соот-
ветствующее собственное значение. Тогда, как это непосредственно
следует из определения серии, мы имеем:
b‘ = k, 1=1, ь\ =1; 2=1, т~ 1;
/Л=0 при и при
Таким образом, первой серии последовательности /h .fn соответ^
ствует первая жорданова клетка в матрице В. Точно так же второй
серии базиса будет соответствовать вторая жорданова
клетка в матрице В, и т. д. Так как переход от матрицы А к мат-
рице В осуществляется при помощи трансформации (см. § 34, А)),
то В — SAS'1.
Таким образом, предложение Б) доказано.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автоматического регулирования теория 218
Автономные системы уравнений 103, 108, 251,
279
Ацлмара лемма 186
Амплитуда гармонического колебания 30, 75
-------комплексная 76
Андронов 244,, 249
Андронова — Витта теорема 271
Аннулирующий многочлен матрицы 309, 311,
312
—------минимальный 309, 313, 314, 315
Анодный ток триода 244
Асимптотическая устойчивость 205, 213, 252,
269, 272
Вариации постоянных метод 16, 134, 143
Вектор 46, 285
— действительный 46
— комплексный 46
Векторные функции векторного переменного
ДфЗ
Векторы, комплексно сопряженные 46 •
В таимоиндукцйя 82
Вполне неустойчивое положение равновесия
2)6, 252
Вронского детерминант 131, 142, 145
Вышпеградский 218, 219, 223
Выпшеградского тезисы 224
Гамильтонова система 203
Генератор ламповый 244, 245, 246, 249
Грубый предельный цикл 234, 212
Двухполюсник 80
— активный 83
— пассивный 83
Действительные решения линейных уравнений
48, 54, 55, 56, 95, 98, 99
Детерминант Вронского 131, 142, 145
Дифференциальное уравнение см. Уравнение
дифференциальное
Дифференцирование векторных функций 94
— комплексных функций 33
— функции в силу системы уравнений 208,
209, 271
Дифференцируемость неявных функций 303
— решений 25, 186, 187, 191, 192
Длина вектора 285 “
Дополнение к множеству 287
Емкость 81
Жорданова клетка 101. 327
— форма матрицы 101, 323, 327
Зависимость решений от параметров я яачмь»
пых условий 178, 179, 182. 184 185 ИС
187, 191, 192
— функции 306, 307
Замена координат 305
Заряд конденсатора 82
Значения начальные 10, 22, 28, 34
Инвариантное подпространство 316
Индуктивность 81
Интеграл первый 196
Интегральная кривая 9. 10^ 11, 14, 24
Интегральное уравнение, эквивалентное хяЪ*
ференцнальному 153, 16<
Интегрирование уравнений в квадратурах 11
Интервал определения решена» 8, 21
Интерпретация решения геометрическая 9. II,
— — дифференциального уравнения 11, 24
Исключения метод 67
Источник напряжения 83
— тока 83 „
Квадратичная форма 210
---положительно определенная 210
Квазимногочлен 62
Кирхгофа закон второй 83, 84
---первый 83, 84
Колебания вынужденные 79
— гармонические 30, 75
— собственные 79
Колебательный контур 87
Комплексная амплитуда 76
Контурные токи 85, 87
Координаты вектора 46
Коэффициент взаимоиндукции 82
— трансформации 9J
— упругости 31
Краевая задача для уравнений в частных про-
изводных 201
Кратность собственного значения 316
Кронскера символ 68
Лампа электронная 244
Линейная зависимость векторов 47
---решений 129, 140
— система см. Система уравнений линейная
Линейное уравнение см. Уравнение линейное
Линня уровня 14
Лнувилля формула 132, 133, 143, 145, 280
. Ляпунова, теоремы 148, 205, 212, 213. 271
- — функция 2U8, 210, 211. 213, 2^0, 2/2
Малые колебания маятника 32
М:ирица основная 146
— фундаментальная 131, 135
>80
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Матрицы жорданова форма 323, 327
Матричная запись систем линейных уравнений
136, 146
Матричное исчисление 146
Матричные ряды степенные 150, 316, 319, 321
Маятник математический 31
Метод вариации постоянных 16, 134, 143
— исключения 67, 102
— комплексных амплитуд 76, 77
Юнтурных токов 85
• неопределенных коэффициентов 101
— последовательных приближений 153, 170,
299
— сжатых отображений 153, 170, 299
— узловых напряжений 85
Многогранник выпуклый 297
Многочдеи аннулирующий 309, 311, 312
— — мвннмадьный 302, 313. 311, 315
— устойчивый 57, 58, 60, 61
— характеристический 44, 310
Множество ш-пределыюс 235, 236
— замкнутое 287
— компактное 291
— ограниченное 289
— открытое 287
Модуль вектора 162, 285
Напряжения узловые 85
Начальная фаза гармонического колебания 30,
75
Начальные значения, начальные условия 10,
22, 28, 34
Неопределенных коэффициентов метод 101
Неравенства интегральные 172
Неравномерность кода паровой машины 223
Норма векторной функции 164 , 300
— функция 154
Нормальная система дифференциальных урав-
нений 21
Область задания 8, 9, 21, 25, 26, 27, 29 173,
178, 182, 136, 187, 191, 192
Обратная связь 245
Объединение множеств 287 , 289
Окрестность точки 287, 298
Операционные (символические) обозначения
42, 43
Основная матрица решения 146
Отображение последования 231.
— аффинное 295
— непрерывное 293
— равномерно непрерывное 293, 294
О[резок 163
Падение напряжения 80
Паровая машина 213, 220
Первые интегралы 196
— — , независимые в точке 197, 198, 199, 200
Передаточное число 220
Пересечение множеств 287, 289
Переходный процесс 77
Период 106
Периодическое решение 106, 268, 271, 279, 280
Плоскость фазовая 115, 224
II жаэатель характеристический 151
II ,ле направлений 11, 24
Положение равновесия 105, 106, 109
---автономной системы второго порядка
119, 231
— —------------невырожденное 119, 251
---неустойчивое 111. 216, 217, 261
— — полуустойчивое III
Положение равновесия устойчивое III 206,
252, 261
Полупространство замкнутое 297
— открытое 297
Порядок квазимногочлена 65
— системы дифференциальных уравнений 26
--------- относительно одного неизвестного
26
Последовательность ограниченная 289
Последовательных приближений метод 153.
170, 299
Постоянные интегрирования 44
Предельный цикл 224, 225, 234, 236, 244 246.
ЭТО
---грубый 234, 242, 280
---неустойчивый 225, 234, 280
---полуустойчнвый 225
---устойчивый 225, 234, 280
Проводимость операционная (двухполюсника)
86
Продолжение решения II, 23
Прообраз множества при отображении 293
Пространство векторное 285
— евклидово 285
Процесс переходный 77
— установившийся 77
Прямая собственная 125
Радиоактивный распад 12
расстояние межДу множествами 29Т
— от точки до множества 297
Регулятор центробежный 218, 219, 220
Резонанс 79, 90
Решение комплексное 32, 33, 35
— матричного уравнения 136
— пспродолжаемое 11, 18, 23, 173, 174 175
176, 178, 179, 182, 184
— особое 30
— уравнения и системы уравнений 8, 21 25,
26, 33, 35
— установившееся 77, 78
— устойчивое 205
— частное линейного неоднородного уравне-
ния 62, G3, 143
Рождение предельных циклов 212. 213
Ряды матричные 150, 316, 319, 321
Свойства топологические 284, 296
Седло 118, 119, 125, 251, 253
Серия векторов относительно матрицы 96 97»
102, 323
Сжатых отображений метод 153, 170, 299
Сила тока 80
Символические обозначения 42, 43
Система гамильтонова 203
— решений фундаментальная 129, 130, 139, 141
— уравнений 21, 26, 27 , 29, 38, 73, 93, 94. 97
98, 103, 108, 128. 146, 251
— — автономная 103. 108, 251, 279
---в вариациях 193, 194, 195, 196
---линейная 38, 39, 67, 69, 70, 72, 73, 74, 93,
94, 97, 98. 128, 146
— — нормализуемая 73
---нормальная 21. 9), 94, 97 , 98, 103, 128, 146
------- автономная 103
-------линейная 23, 93, 94, 97, 98, 128, 146
---------однородная с периодическими коэф-
фициентами 146
---------с переменными коэффициентами
128
---, разрешенная относительно высших про*
изводиых 27
Скалярное произведение векторов 285
Скалярный квадрат 285
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Скорость фазовая 109
Смешения формула 51
Снижение порядка линейного уравнения 114
— — системы 138, 200
Собственная прямая 125
— частота контура 89
Собственные векторы и собственные значения
309, 310
Сопротивление 81
— операционное (двухполюсника) 85, 86
Спектр матрицы 317
Сходимость последовательности 289
— равномерная 155, 165, 300
Тезисы Вышпеградского 221
Теоремы о непрерывности и дифференцируе-
мости решений 152, 184, 186, 187, 191, 192
— — неявных функциях 298, 299, 303
— существования и единственности 10, 22, 23,
27. 29, 33, 35, 152
Ток анодный триода 214
— контурный 85, 87
Тор 113
Точка <о-прсдельная 235
Траектория 104
— замкнутая 104, 105, 106
— фазовая 109, 116
Трансформатор 90
— идеальный 91
Триод 244
Узел 117, 118, 251, 261
— вырожденный 122, 124, 125
— неустойчивый 118, 124, 125, 251. 231
— устойчивый 118, 124, 125, 251, 2G1
У зловые напряжения 85
Уравнение гармонического осциллятора 76, 78
— дифференциальное 7
---в частных производных 7, 201
------------ линейное первого порядка 291
— линейное 15, 28, 42, 44. 50, 62, 63, 136
---с переменными коэффициентами 15, 139
— — — постоянными коэффициентами 42, 44,
50, 62, 63
— неоднородное 62. 63
— — — однородное 42, 41, 50
— матричное’136, 116
— первого порядка 8
-------в полных дифференциалах 13
------- линейное 15
------- однородное 17
-------, разрешенное относительно производ-
ной 8
-------с разделвющнмися переменными 17
— , разрешенное относи (ельно высшей про-
изводной 27
— с периодическими коэффициентами 146, 148
Уравнения в вариациях 193, 194, 195, 196
Условия начальные 10, 22, 28, 34
Установившийся процесс 77
Устойчивость асимптотическая 206, 213, 252
269, 271
— многочленов 57, 58, 60, 61
— периодических решений 268, 271, 280
— положения равновесия 206, 207, 213, 251
Устойчивость по Ляпунову 206, 208, 269, 271
— предельного цикла 225, 231
— произвольного решения 26), 272
Устойчивые многочлены 57, 58
Усы седла 253
--- неустойчивые 253
--- устойчивые 253
Фаза начальная гармонического колебав**
30, 75
Фазовая плоскость 115, 224
— — линейной системы с постоянными коэ^Ь
фициентами 115
— скорость 109
— траектория 104, 109, ПО, 116
Фазовое пространство автономной системы
103, 108. 113
Фильтр электрический 92
Фокус 120 , 251, 261, 261
— неустойчивый 120, 251
— устойчивый 120, 251
Форма квадратичная 219
— — положительно определенная 210
Формула Лиувилля 132, 133, 143, 145, 280
— смещения 51
Формулы Эйлера 36
Фундаментальная матрица 131 135
— система решений 129, 130, 139, 141
Функции матриц 316, 319
— — неявные 321
— , совпадающие на спектре матрицы 317.31Э
Функция, заданная на спектре матрицы 317
- Ляпунова 208, 210, 211, 213, 216, 272
— последования 226, 227, 230, 233, 242, 280
Характеристика триода 211
Характеристики 202
Характеристический многочлен 44. 310
— показатель уравнения с периодическим*
коэффициентами 151
Характеристическое число 150
Центр 120
Центробежный регулятор 218, 219, 220
J (спи электрические 80, 83
Цикл 106
Циклы предельные см. Предельный цикл
Частное решение 62, 63 143
Частота колебаний 30, 75
— собственная колебательного контура МЭ
Число передаточное 220
— характеристическое 150
Шар 287
Эйлера формулы 36
Эквивалентность уравнений с периодическим
коэффициентами 147, 148
Электрическая цепь 80, 83
Электрический фильтр 92
Электронная лампа (триод) 244