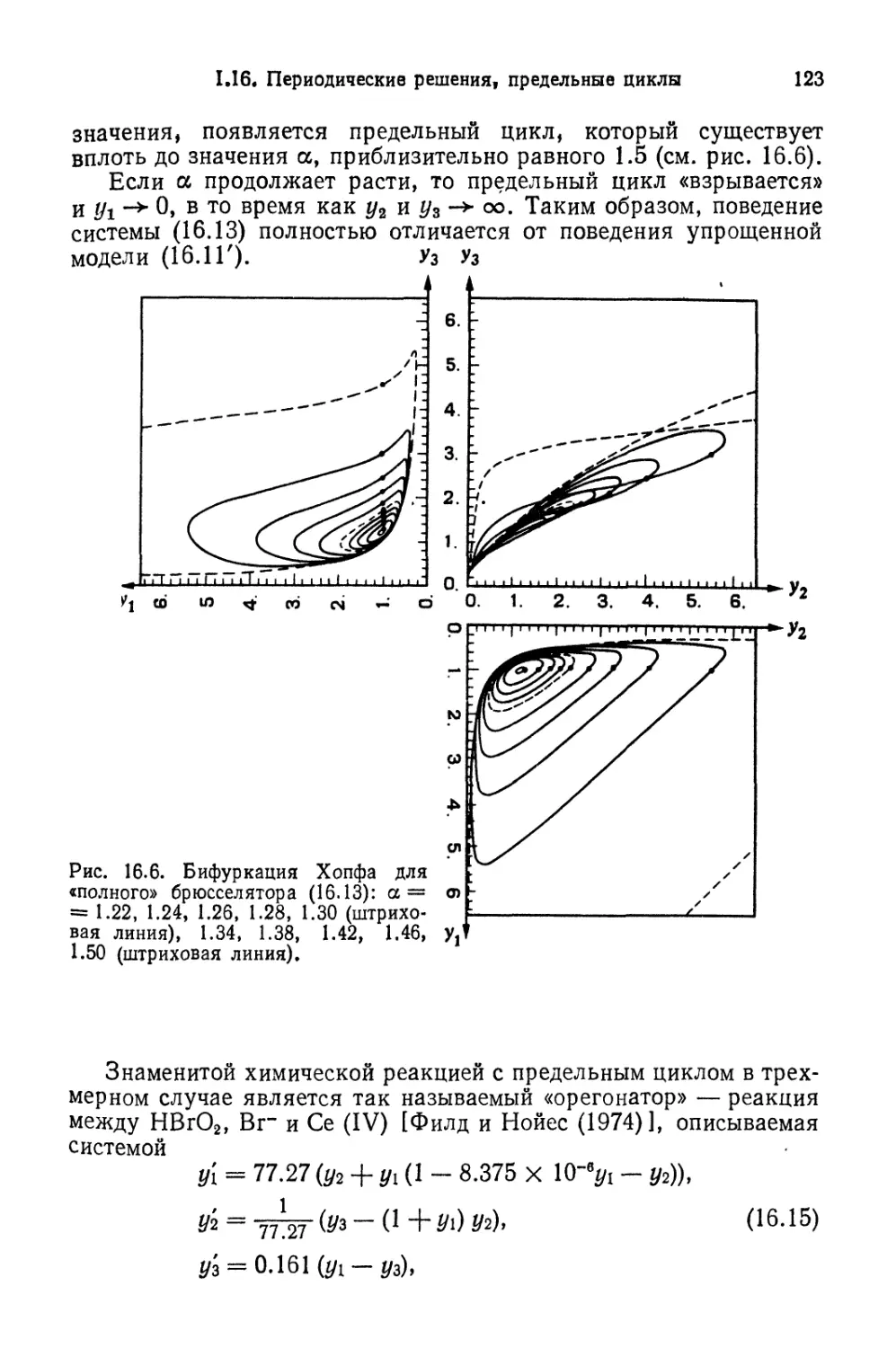
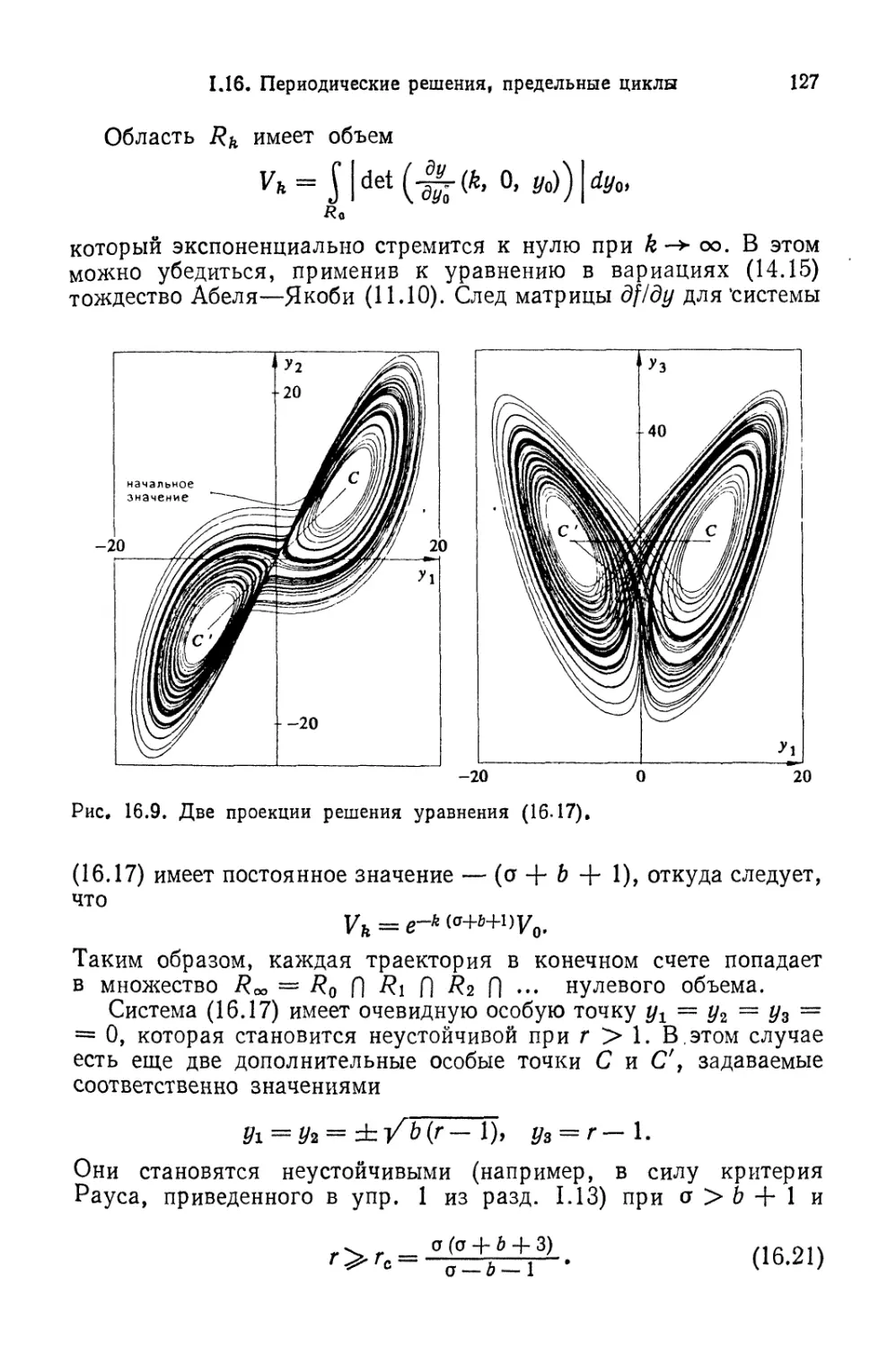
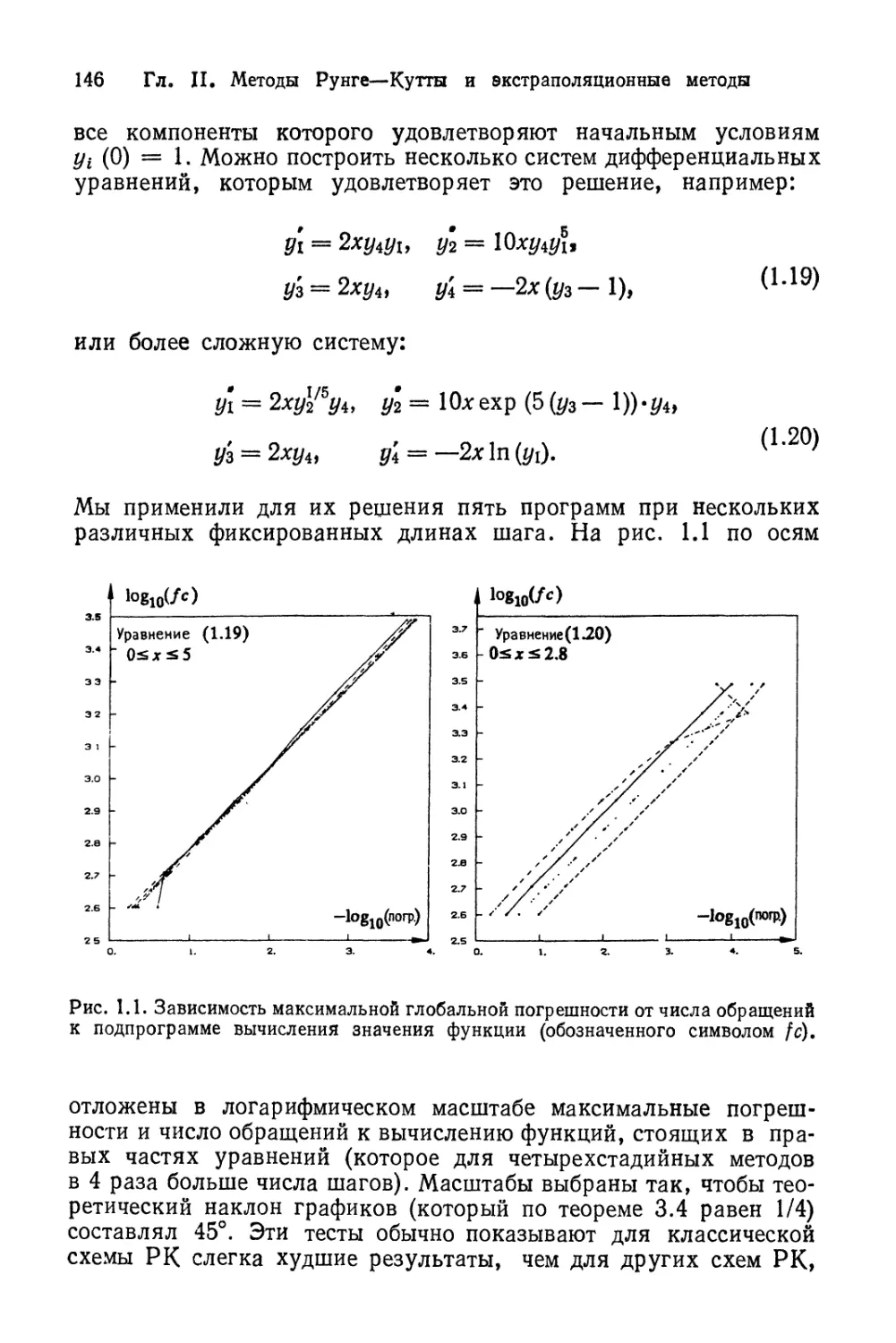
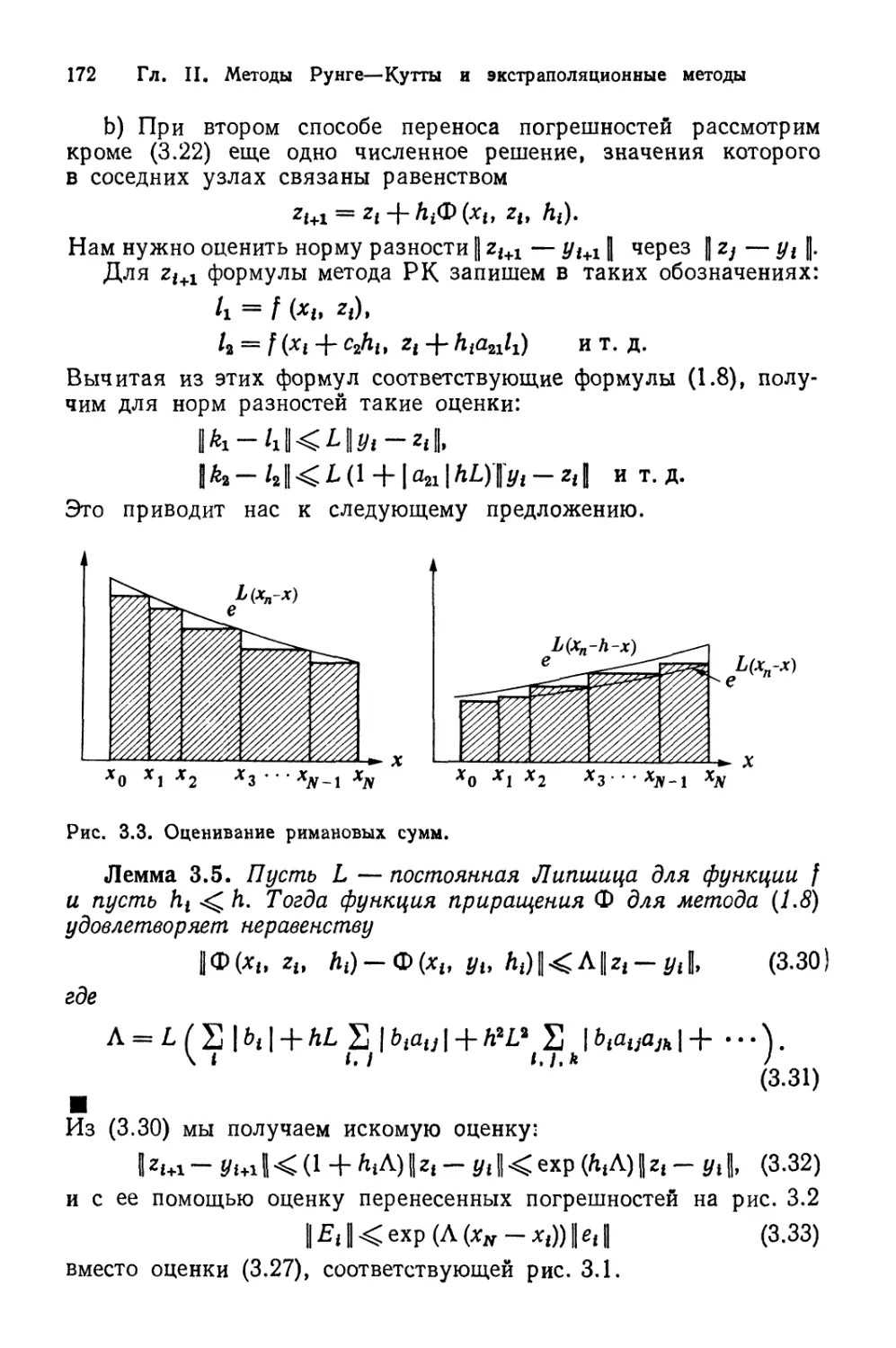
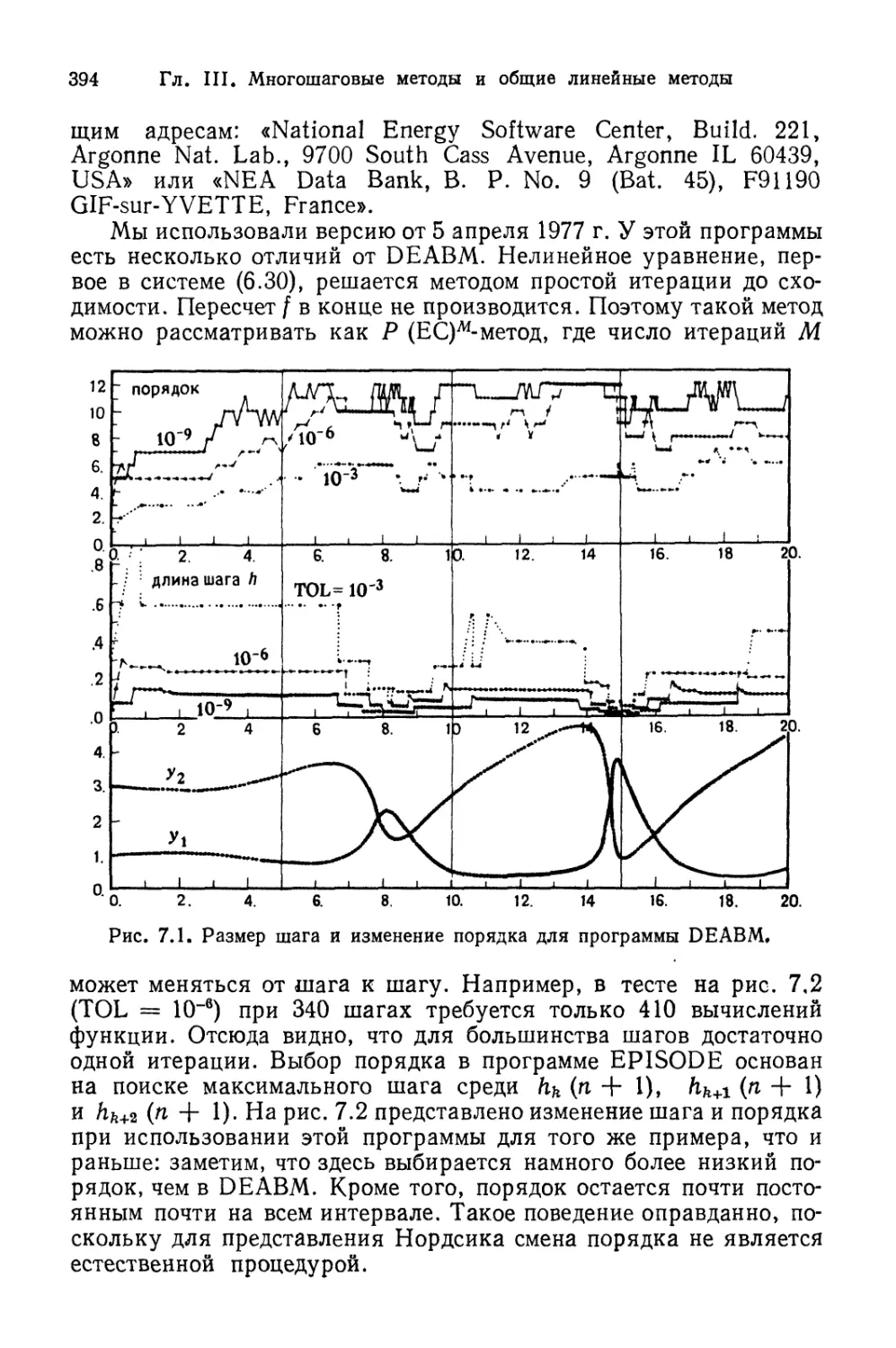
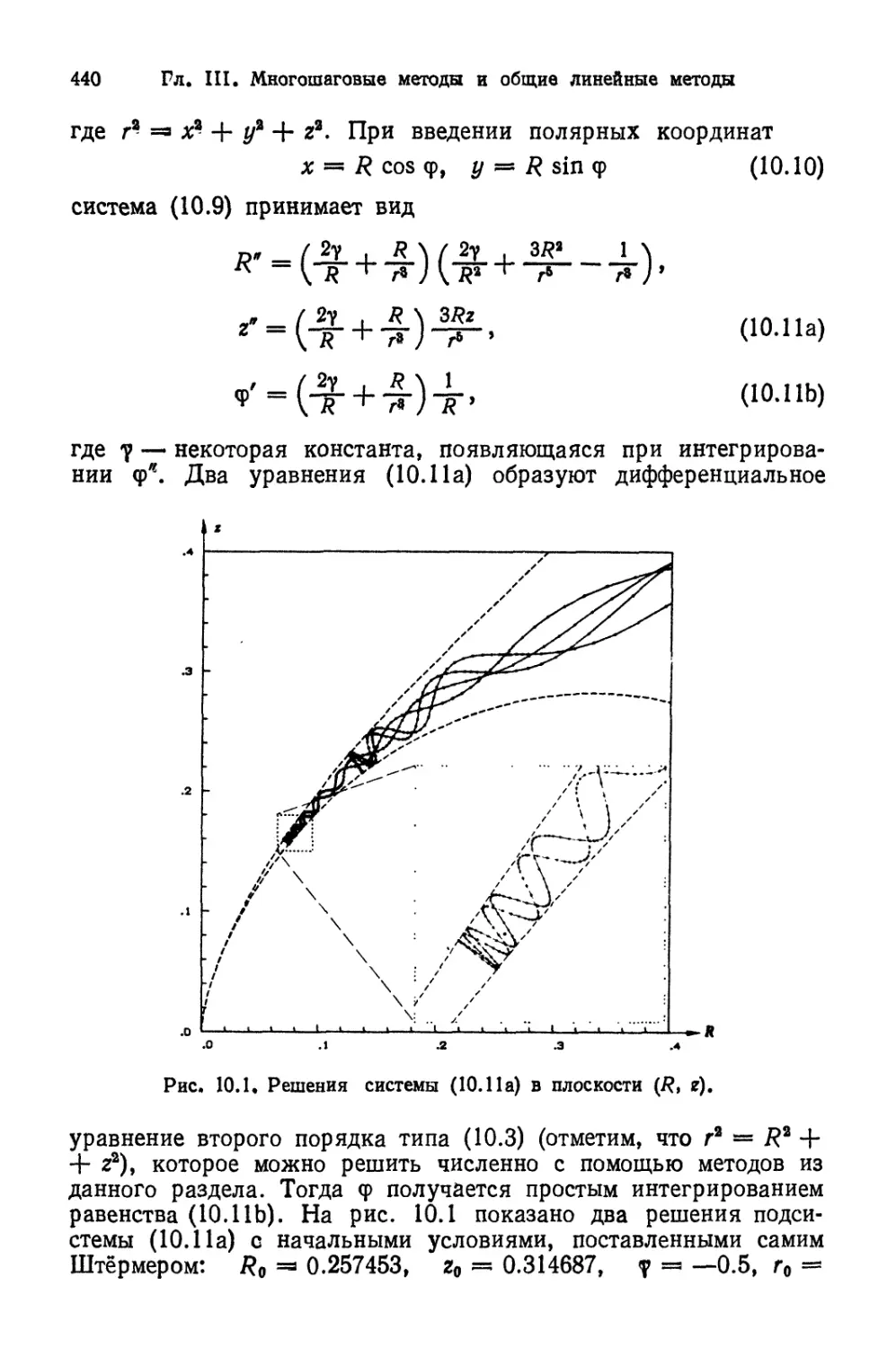
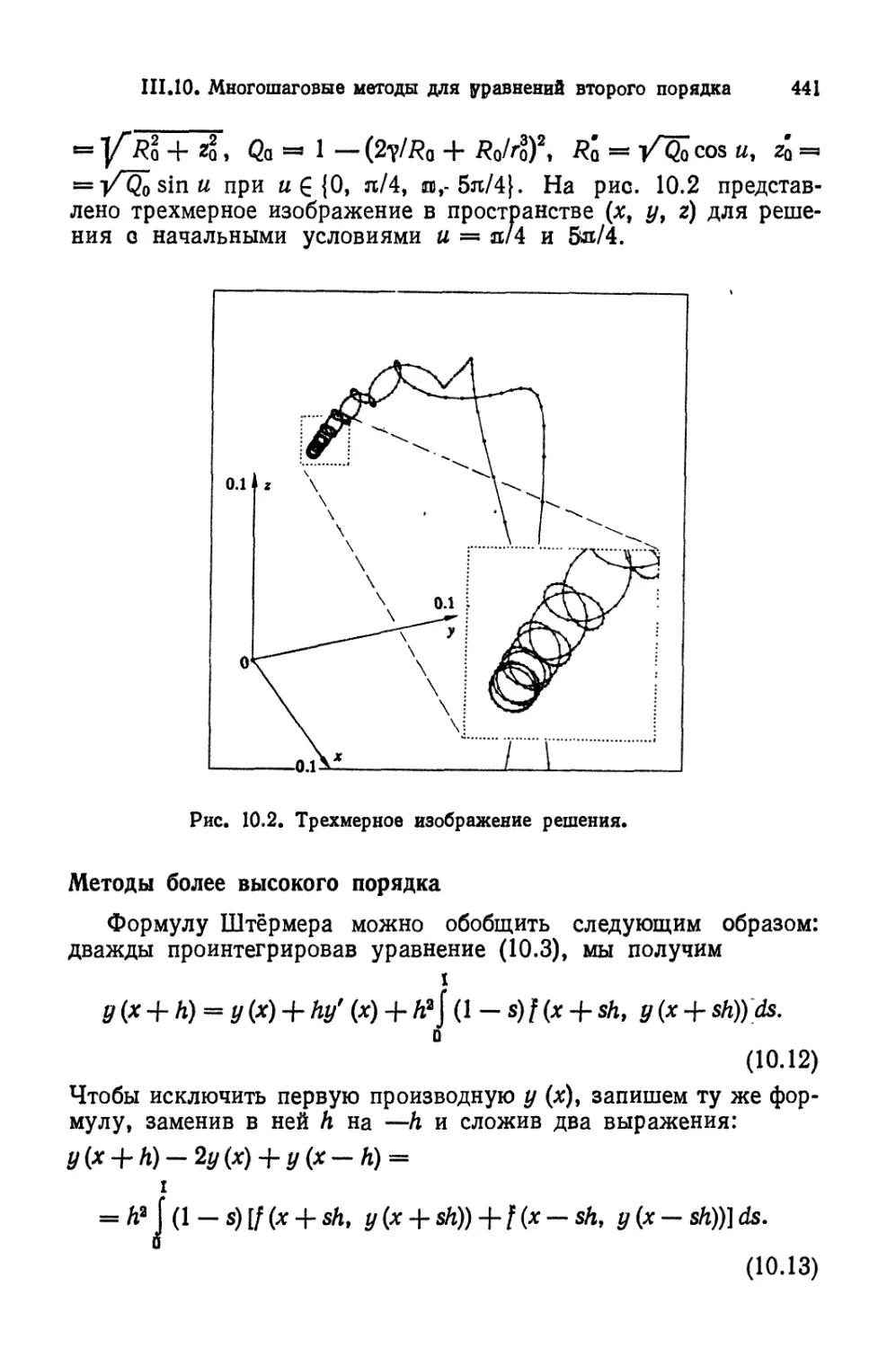
Решение обыкновенных дифференциальных уравнений. Нежесткие задачи - Хайрер Э., Ваннер Г., Нерсетт С.

Автор: Хайрер Э. Ваннер Г. Нерсетт С.
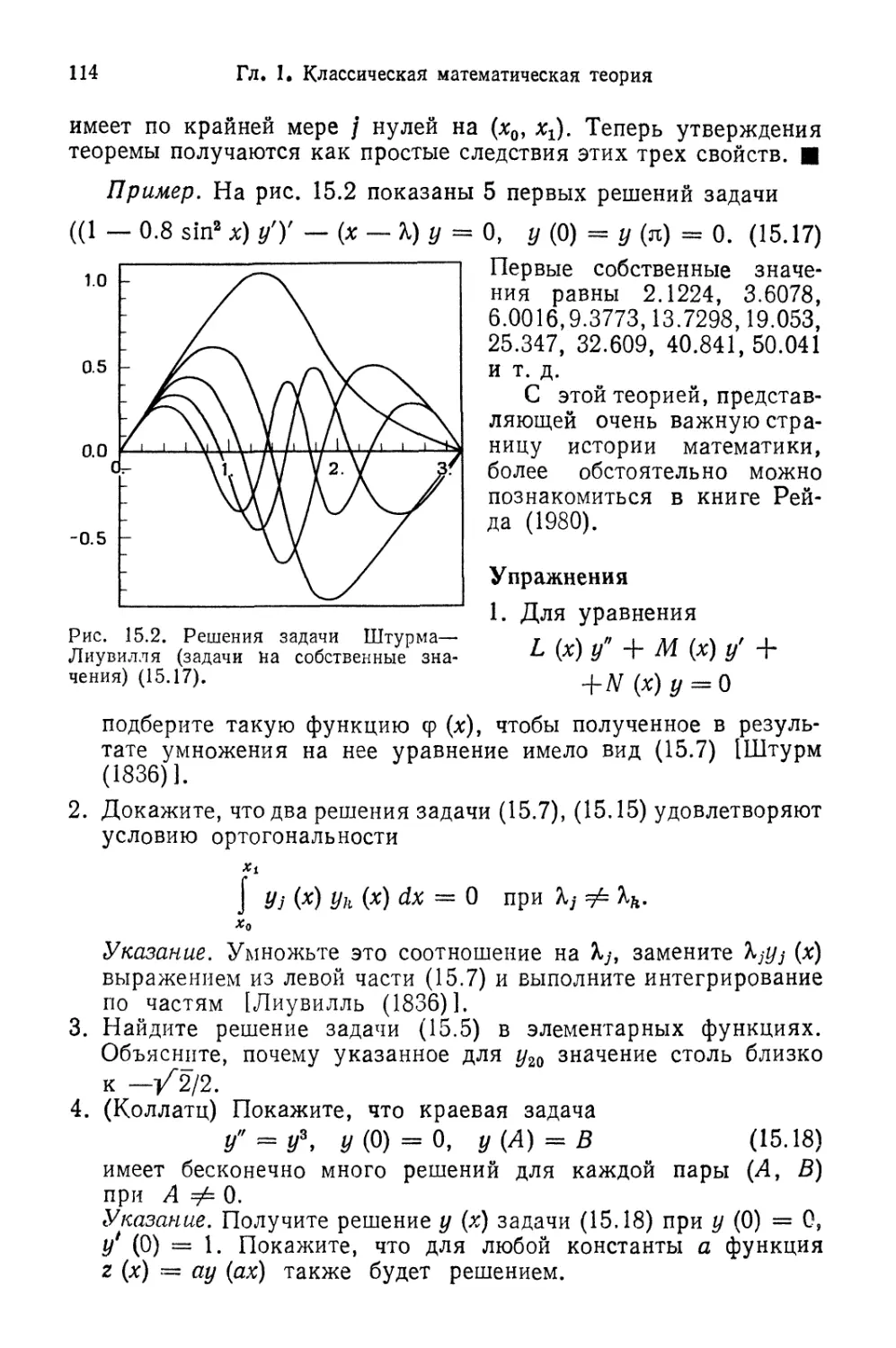
Теги: дифференциальные, интегральные и другие функциональные уравнения конечные разности вариационное исчисление функциональный анализ математика дифференциальные уравнения практика примеры
ISBN: 5-03-001179-Х
Год: 1990
Похожие
Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи
Лекции по теории обыкновенных дифференциальных уравнений
Обыкновенные дифференциальные уравнения.
Обыкновенные дифференциальные уравнения
Текст
                    Э. Хайрер
С. Нёрсетт
Г. Ваннер
Решение
обыкновенных
дифференциальных
уравнений
Нежесткие задачи
Перевод с английского
И. А. Кульчицкой и С. С. Филиппова
под редакцией С. С. Филиппова
Москва «Мир» 1990

ББК 22.193 + 22.161.6
Х15
УДК 517.91
Хайрер Э., Нёрсетт С, Ваннер Г.
Х15 Решение обыкновенных дифференциальных уравнений.
Нежесткие задачи: Пер. с англ. —М.: Мир, 1990. —512 с,
ил.
5-03-001179-Х
Книга известных математиков (Швейцария, Норвегия), дающая кар-
картину современного состояния теории и практики численного решения
обыкновенных дифференциальных уравнений. Изложены основные теорети-
теоретические результаты, приведены наиболее употребительные численные ме-
методы, дано большое число примеров практических применений в физике
и прикладных науках. Представлены тексты программ на Фортране.
Для математиков-прикладников и всех, кто в своей работе встречается
с решением дифференциальных уравнений, для аспирантов и студентов
вузов.
ББК
Редакция литературы по математическая наукам
18В N 5-03-001179-Х (русск.) © 5рг1П^ег-Уег1а^ ВегНп НеМеШег^ 1987.
Е 3-540-17145-2 (англ.) АИ п&Ыз гезепгес!. АиШогаеб {гапзЫюп
Ггот Еп&Нзп 1ап^иа^е ебШоп риЬ-
НбЬес! Ьу 5рг1П^ег-Уег1аб ВегНп Не1-
бе1Ъег& №тс Уогк Токуо
© перевод на русский язык, «Мир», 1990

Предисловие к русскому изданию
Первые численные методы решения обыкновенных дифферен-
дифференциальных уравнений изобрели еще Ньютон и Эйлер. К началу
XX века были уже известны ставшие теперь классическими ме-
методы Адамса и Рунге—Кутты. Текущий период характерен бур-
бурным развитием вычислительной техники и усиленным примене-
применением ЭВМ и численных методов для решения резко расширя-
расширяющегося круга задач. Изменение требований породило новую
волну конструирования и исследования численных методов интег-
интегрирования обыкновенных дифференциальных уравнений, не
ослабевшую и сегодня. Ранее известные методы были детально
изучены и обобщены, построены новые классы методов, созданы
методы, ориентированные на решение задач со специальными
свойствами, например, так называемых жестких систем. Большой
прогресс достигнут и в разработке удобных для пользователей,
эффективных и надежных программ.
За последние 20—25 лет этим вопросам посвящено огромное
число журнальных публикаций, множество монографий, как
узкоспециальных, так и общего характера, а также учебных
пособий (некоторые из них включены авторами в список литера-
литературы в конце книги). Однако почти все они изданы за рубежом.
На русский язык были переведены лишь рассчитанная на матема-
математиков-профессионалов монография Штеттера A973) и сборник
обзорных лекций, прочитанных на летней школе в Англии (ре-
(редакторы Холл и Уатт A976) 1}), да еще две-три книги по весьма
частным вопросам. Важнейшие сведения о численных методах
решения задачи Коши для обыкновенных дифференциальных
уравнений можно, конечно, найти в любом учебном пособии по
численным методам. Но систематического и доступного широкому
кругу читателей изложения названных выше вопросов на русском
языке до сих пор не было.
Предлагаемая вниманию читателей книга призвана восполнить
этот пробел. Написана она специалистами, которые внесли зна-
значительный вклад в развитие излагаемых в книге вопросов и имеют
большой педагогический опыт. Книга доступна студентам уни-
университетов и других вузов, специализирующимся в области при-
прикладной математики, и она, несомненно, будет полезна широкому
кругу специалистов, работающих в области численных методов,
а также всем лицам, занимающимся приложением этих методов.
Н. С. Бахвалов
1) См. в конце книги список литературы, добавленной редактором перевода.

Предисловие
«Насколько я помню, я никогда не встречал авторского
предисловия, которое имело бы какую-то иную
цель, кроме одной — оправдать публикацию Книги.»
(Марк Твен)
«Афоризм Гаусса: «Когда здание закончено, никто не
должен заметить какие-либо следы строительных ле-
лесов», — часто используется математиками для оправ-
оправдания того, что они не уделяют внимания мотивировке
своей работы и истории той области, в которой они
работают. К счастью, крепнет противоположное отно-
отношение, и многочисленные авторские отступления в этом
очерке показывают, на чьей стороне мои симпатии.»
(Б. Б. Мандельброт, 1982)
«Это дает нам хороший повод закончить большую
часть книги до нового года.»
(из письма авторов в издательство Шпрингер, дати-
датированного 29 октября 1980 г.)
Книга в двух томах: в законченном сейчас первом томе рас-
рассматриваются нежесткие уравнения, а жесткие — в готовящемся
втором. Первый том содержит три главы, одна посвящена класси-
классической математической теории, вторая — методам Рунге—Кутты
и экстраполяционным, третья — многошаговым методам. Прило-
Приложение содержит несколько программ на фортране, написанных
нами для расчетов примеров, приведенных в кдаге.
Каждая глава делится на разделы, и нумерация формул,
теорем, таблиц и рисунков в каждом разделе своя; она включает
также номер раздела, но не главы. Ссылки на другие главы редки,
они специально оговариваются. Конец каждого доказательства
обозначен буквами «С^ИЗ» ^иой ега! йетопзкапйит — что и тре-
требовалось доказать (лат.)). Поскольку это выглядит довольно
нелепо, когда доказательство отсутствует, либо оно предшествует
теореме, то мы писали «ЫЕБ» (шЬП ега! Aетоп51гапс1ит) в таких
случаях 1}. Библиографические ссылки даются указанием автора
и (в скобках) года. Список литературы не претендует на полноту,
он содержит, в основном, работы, которые обсуждаются в тексте.
В заключение мы хотим поблагодарить всех, кто нам помогал
и поддерживал при подготовке этой книги. Первый импульс
к написанию этой книги дал чудесный «минисимпозиум», который
1) В русском переводе «(ЗЕБ» и <МЕБ» в конце доказательств шли формули-
формулировок теорем заменены значком ■» — Прим. ред.

Предисловие 7
Г. Далквист организовал в Стокгольме в 1979 г. Всю рукопись
очень тщательно прочли И. Стайниг и Хр. Любих, которым мы
обязаны чрезвычайно ценными» математическими и лингвистиче-
лингвистическими советами. Мы благодарны также И. П. Экманну за пре-
превосходные программные средства, с помощью которых оконча-
окончательно редактировалась и печаталась рукопись. На более ранней
стадии мы пользовались программами для работы с текстами,
которые написал Р. А1енк. Благодарим за помощь также*персонал
Женевского вычислительного центра. Все компьютерные графики
были сделаны на их великолепном прецизионном плоттере. И пос-
последнее, хотя не менее важное обстоятельство — это приятное
сотрудничество с группой планирования и выпуска издательства
Шпрингер, которой мы хотим выразить свою признательность.
29 октября 1986 г. Авторы

Глава I
Классическая математическая
теория
«... ЬаНе кЬ ез 1ттег Шг Ъеззег, тсЫ тИ йет Ап!ап(*
апгиГап&еп, с!ег 1ттег йаз 5сЬ\^ег$1е 1$Ь.
«...я всегда считал, что лучше начинать не с начала,
так как оно самое трудное».
(Выписка из Ф. Шиллера в записной книжке Б. Ри-
мана)
Первая глава посвящена классической теории дифференциаль-
дифференциальных уравнений, которую мы считаем полезной и необходимой
для глубокого понимания численных процессов и явлений. Кроме
того, по ходу изложения удобно привести интересные примеры
дифференциальных уравнений и их свойств.
Вначале в разд. 1.2—1.6 мы проследим историческое развитие
классических методов интегрирования с помощью разложения
в ряд, квадратур и элементарных функций с самого их зарожде-
зарождения (Ньютон и Лейбниц) и до эпохи Эйлера и Лагранжа. Затем
(разд. 1.7—1.14) речь пойдет о теоретических свойствах суще-
существования, единственности, устойчивости, непрерывности
и дифференцируемости решений. Начало этой теории положил
Коши в 1824 г., а завершенный вид она приобрела в основном
за последующие 100 лет. В конце главы мы дадим краткий обзор
еще нескольких тем: краевых задач, периодических решений,
предельных циклов и странных аттракторов (разд. 1.15 и 1.16).

1.1. Терминология
Дифференциальное уравнение первого порядка — это уравнение
вида
У''=*Г(х, У) A.1)
с заданной функцией / (х, у). Функция у (х) называется решением
этого уравнения, если при всех х выполняется равенство
У* (х) =* Пх, у (х)). A.2)
Еще Ньютон, Лейбниц и Эйлер заметили, что решение обычно
содержит свободный параметр и поэтому определяется единствен-
единственным образом только тогда, когда задано начальное значение
В разд. 1.7 мы рассмотрим принадлежащее Коши доказательство
существования и единственности такого решения. Дифферен-
Дифференциальные уравнения возникают во многих приложениях.
В разд. 1.2 мы увидим, как первые такие уравнения появились
в механике, а в разд. 1.3 будет показано, как некоторые из них
можно решить в явном виде.
Дифференциальное уравнение второго порядка для у имеет вид
У* = Г(х,У,Уг). A.4)
Здесь решение обычно содержит два параметра и определяется
однозначно только по двум начальным значениям: .
У(хо)=*Уо, У'Ы^Уп- A.6)
Уравнения второго порядка редко допускают решение в явном
виде (см. 1.3). Как при их численном решении, так и в теорети-
теоретических исследованиях обычно вводят переменные уг (*):= у (х),
Уг (х)'— У' (х) и приводят уравнение A.4) к системе
Ух == У2, Уг (х<>) = у о,
, Уи Уг), № (*о) = У о-
Это пример системы дифференциальных уравнений первого по-
рядка размерности п (см. разд. 1.6 и 1.9):
у{ = Д (X, уи ..., уп), Ух (Х0) — #ю,
Уп =* !п (х, Уи •••> Уп)> Уп (хо) ^ У

10 Гл. 1. Классическая математическая теория
Большая часть этой книги посвящена теории решения задачи
Коши для системы A.6). В конце XIX века [Пеано A890)] стало
обычным введение векторных обозначений
У = (Уг, • • •, Уп)Т> I = (к, • • • > [п)т>
при которых A.6) принимает вид у' = / (х, у), что совпадает
с A.1), но теперь под у и / понимаются векторы.
Для уравнения второго порядка A.4), помимо преобразования
его к системе A.4'), существует и другая возможность — постро-
построение методов, специально приспособленных к уравнениям второго
порядка (методы Нюстрёма). Этому будут посвящены специаль-
специальные разделы книги. Конечно, ничто не мешает нам рассматривать
A.4) как систему уравнений второго порядка размерности /г,
интерпретируя //и/в A.4) как векторы.
•Если же начальные условия A.5) заменены условиями типа
У (хо) ~ а> У (хг) — ^> т- е- когда не все условия, определяющие
частное решение, заданы в одной и той же точке х0, то говорят
о краевой задаче, В этом случае теория существования решения
и его численное нахождение значительно усложняются.
В разд. 1.15 мы приведем ряд соответствующих примеров.
В заключение определим уравнение в частных производных
как задачу типа
т-'('«
для неизвестной функции и (I, х) двух независимых переменных.
Можно также рассматривать уравнения в частных производных
более высокого порядка, задачи с тремя и четырьмя независимыми
переменными или системы уравнений в частных производных.
Очень часто задачу Коши для таких уравнений удобно привести
к системе обыкновенных дифференциальных уравнений, напри-
например, используя конечные разности или конечные элементы для
приближения по переменной х. Таким образом, уравнение
ди о д2и
а2
дг дх*
приняло бы вид
йщ а2 , о .
-— _ 111 —. /11 I 4 1
иг Ахл ч 4+А 1 ' 1~
Данная процедура называется «методом прямых», или «методом
частичной дискретизации» (по пространственной переменной).
В разд. 1.6 мы увидим, что эта и обратная ей процедура весьма
часто употребляется, начиная с работ Лагранжа и Фурье. Анало-
Аналогичная идея лежит и в основе «метода дискретизации по вре-
времени» [Роте A930I.

1.2. Наиболее ранние дифференциальные уравнения
«...Такова, например, задача обратного метода каса-
касательных; Декарт тоже признавался, что не смог одолеть
ее». (Лейбниц, 27 августа 1676 г.)
«...а, как известно, все другие Изобретатели не имеют
права на Изобретение.» (Ньютон, 29 мая 1716 г.)
«Вовсе не очевидно, что г-н Ньютон раньше, чем я,
получил характеристику и алгоритм для бесконечно
малых...» (Лейбниц)
«И этим он признал, что еще не нашел способа, кан
свести задачи к дифференциальным уравнениям.»
(Ньютон)
Ньютон
Дифференциальные уравнения так же стары, как дифферен-
дифференциальное исчисление. Ньютон рассмотрел их в своем труде о диф-
дифференциальном исчислении [Ньютон A671)] и исследовал их
решение с помощью интегрирования и разложения в ряд. Среди
изученных Ньютоном уравнений первого порядка одним из самых
1111111 \'т1 /]/////
/////////
111111111
11111////
11111////
11111////
11111/11/
шин'/,
II //
111/
I///
/ / / /
/ / /
/ /У
/ /'
/У.
\\\\ *\Л \
\ \ \ \
>.\\Ч\ \ \ \ \ \
\\\\ \\ \ \ \ \
\ \ \ \ \ \ \
\\\\\\\\
\\ \ \ \ \ \ \ \ \
\ \ \ \
\ \ \ \
\ \ \ \
\\\\
\ \ \ \
Ш!
чч>\_\\\\\
\\\ \\\\
\\\ \ \ \ \
ч\\\\ \\\\\ .
ч\\ \ \ \ \\\ \\
ч\\\\\ \ \\\\ .
\\\ \ \ \ \ \ \ \ \ \
!!!
III
Ь)
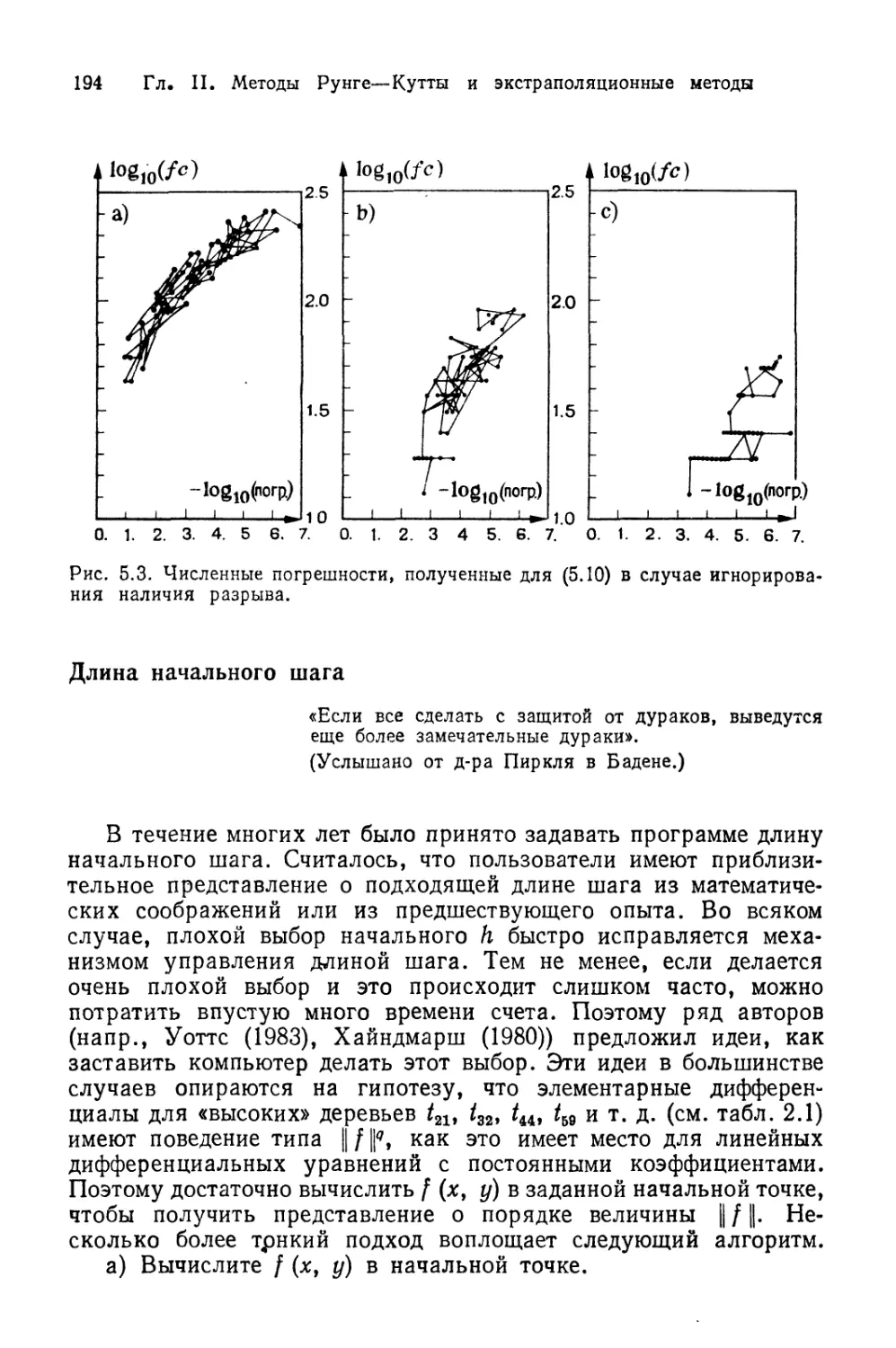
Рис. 2.1. а) Точное решение и приближенное решение; б) векторное поле; в) раз-
, личные кривые, служащие решениями уравнения B.1).
ранних был пример [см. работу Ньютона A671), проблема II,
решение второго случая II, пример I]
/ 1 О I I О I /Г\ Л \
у — 1 — ох -\- у -\- х -+■ хд. \^'Ч
Каждому значению х и у такое уравнение ставит в соответствие
производную решений у'. Поэтому мы получаем векторное поле,
которое для данного конкретного уравнения изображено на
рис. 2.1. Итак, вопреки распространенному мнению, векторные

12 Гл. 1. Классическая математическая теория
поля существовали задолго до Ван Гога. Решением являются
кривые, которые всюду отвечают этим заданным направлениям.
Ньютон исследовал решение данного уравнения с помощью
бесконечного ряда, члены которого он получал рекурсивно
(«...и они кидаются к рядам, где г-н Ньютон без труда опередил
меня; но...», Лейбниц). Первый член — это начальное значение
при х = 0:
д — 0 + ....
Подставляя его в дифференциальное уравнение B.1), получим
У1 - 1 + ...,
что при интегрировании дает
Теперь, снова используя B.1), придем к соотношению
у''' = 1 —. Зх + х + ... га 1 — 2х + ...,
интегрируя которое, получим
У '—' X -"—" Х^ "-]■" ••• •
На следующем этапе
Продолжая этот процесс, мы в итоге придем к приближенному
решению
д = X XX —| тт"" X 2г- л —р ' «л X ' — дг ' X И Т. Д.,
3 6 ' 30
график которого (при отбрасывании членов более высокого по-
порядка) дан на рис. 2.1 вместе с точным решением. На графике
можно увидеть, что приближенное решение близко к точному
только при малых значениях х. Другие примеры приведены
в упр. 11—13 из разд. 1.3.
Лейбниц
Второй изобретатель дифференциального исчисления, Лейб-
Лейбниц, пришел к дифференциальным уравнениям около 1676 г.
при рассмотрении геометрических задач, таких как обратная
задача о касательной [Лейбниц A693)]: найти кривую у (х) по
заданной длине касательной АВ, например, если она всюду равна
постоянной а (рис. 2.2). Такая постановка приводит к дифферен-
дифференциальному уравнению первого порядка:
■»__Л
Ь ~~

1.2. Наиболее ранние дифференциальные уравнения
13
Лейбниц натолкнулся на эту задачу благодаря серебряным кар-
карманным часам («Ього1о§1о рогШШ зиае 1Ьесае аг§еп1ае») Б, кото-
которые тянут по столу за цепочку АВ длины а. При этом он с гор-
гордостью заметил, что ни один из лучших ученых не мог раньше
решить эту задачу. Отметим интересный факт: для обоснования
В
А4 А2 А3
+ А
Рис. 2.2 и 2.3, Иллюстрации из работ Лейбница и Ковалевского.
ввоего дифференциального уравнения B.3) для карманных часов
Лейбниц представил их движение прямолинейным на очень малых
участках (рис. 2.3), что сегодня можно интерпретировать как метод
Эйлера для численного решения задачи B.3). В истории часто
встречается такое любопытное явление, как с дифференциальными
уравнениями, которые первоначально были получены с помощью
процедуры, «обратной» к «ломаным Эйлера». Другим примером
этого явления служит вариационное исчисление.
Вариационное исчисление
В 1696 г. Иоганн Бернулли предложил самым выдающимся
математикам мира («Рго!ипс1юп5 т рппиз Ма1Ьезоз сиНоп, 5а1и-
1ет!») решить задачу о брахистохроне (задачу наискорейшего
спуска), в основном с целью посрамить своего брата Якоба, реше-
решение которого, как он ожидал, будет неверным. Задача состоит
в нахождении кривой у (х), соединяющей две точки Ро и Ръ такой,
что точка, скользящая по ней под действием силы тяжести, до-
достигнет Рх за возможно кратчайшее время. Для решения этой
задачи Йог. Бернулли A697Ь) воспользовался оптической ана-
аналогией: он представил себе стопку тонких слоев однородных
материалов; он знал, что луч света, распространяющийся со
скоростью у, проходит такую стопку за кратчайшее время, если

14
Гл. 1. Классическая математическая теория
выполняется закон Снеллиуса
31П а »
(принцип Ферма). Поскольку скорость • пропорциональна корню
квадратному из потери высоты, при переходе ко все более тонким
слоям он получил дифференциальное уравнение первого порядка
зШ а
У1+У
/2
B.4)
Можно показать, что решениями этого уравнения являются
циклоиды (см. упр. 7 из разд. 1.3). Якоб в своем ответе также
Рьд. I .
Н
Б
Н I К Ь М N О Р
Рис. 2.4. Решения вариационной задачи (Иоганн Бернулли, Якоб Бернулли,
Эйлер),
представил решение, значительно уступающее в изяществе, но
при этом, к сожалению, правильное, и теперь уже сам предложил
своему брату Иоганну решить пару новых задач. Метод Якоба
(см. рис. 2.4) напоминает обращение современного метода «конеч-
«конечных элементов». Он привел к появлению знаменитой работы
Эйлера A744), где общее решение задачи
*1
) !(х, д, д)ах = тш
дано с помощью дифференциального уравнения второго порядка
и»у>У" + 1гуУ' + !гх -1у = 0 B.5)
и подробно рассмотрены 100 вариационных задач. В частном
случае, когда / не зависит от #, проинтегрировав уравнение B.5),

1.2. Наиболее ранние дифференциальные уравнения
15
мы получим
/ - 1гУ' - К. B.6)
В своем доказательстве для вывода уравнения B.5) Эйлер исполь-
использовал ломаные. И только идеи, высказанные в 1755 г. 19-летним
Лагранжем, позволили получить доказательство, которое в на-
настоящее время является общепринятым [Функ A962), Голдстайн
A980K. Тогда Эйлер A756) в честь Лагранжа назвал'всю эту
область исследований «вариационным исчислением» ("...1атеп
§1опа рптае туепИотз аси11351то Оеоте1гае Таиппегш Ьа
Огап§е ега! гезегуа!а").
Клеро
Клеро открыл новый класс уравнений с интересными свой-
свойствами [см. работу Клеро A734), задача III]. Изучая движение
прямого угла (см. рис. 2.5),'Клеро получил дифференциальные
уравнения вида
У
- 0. B.7)
Это были первые неявные
дифференциальные уравне-
уравнено'2*п7Й"?люстрация И3 работы Рис' 2-6' Рвения дифференциального
Клеро A734). уравнения Клеро.
ния. Их особенность состоит в том, что решениями служат не
только прямые семейства у = Сх — ?(С), но также и огибаю-
щие это семейство кривые (см. упр. 10 из разд. 1.3). На рис. 2.6
показан пример с функцией / (С) = 5 (С3 — С)/2.
Поскольку уравнение имеет третью степень по у', заданное
начальное значение допускает три разных решения. Кроме того,
в точке, где прямая касается огибающей, решение можно про-
продолжить либо по прямой, либо по огибающей. Это дает огромное
разнообразие кривых решения. Ныне мы объясняем это любо-
любопытное явление тем, что в этих точках не выполняется условие
Липшица [см. также Айне A944)].

1.3. Уравнения, разрешимые в квадратурах
и элементарных функциях
Рассмотрим теперь некоторые простейшие типы уравнений,
которые можно решить с помощью вычисления интегралов.
Уравнение с разделяющимися переменными
У =* Г (х) 8 (У).
Поделив его на § (у) и проинтегрировав, получим решение
(Лейбниц, 1691, из письма Гюйгенсу.)
Частным случаем является линейное уравнение у' = / (х) у с ре-
решением
у (х) = СК (*), К (х) = ехр (|/ (х) их).
Неоднородное линейное уравнение
У^ГЫУ + В (*)• C.2)
Здесь подстановка у (х) = с (х) /? (х) приводит к уравнению
с' (х) = § (ХУ% (х) [Йог. Бернулли A697)]. Таким образом, полу-
получим решение
AЩAз+с\. C.3)
Уравнения в полных дифференциалах
Уравнение вида
Р {*, У)+ <2 (х, У) У' = 0 C.4)
можно, оказывается, сразу решить, если оно удовлетворяет усло-
условию
дР __ д(±
Для этого с помощью интегрирования находят такую функцию
Р (*> У), что
Е--Р дР -
дх ~ г> ду ~~

1.3. Уравнения, разрешимые в квадратурах 17
Тогда C.4) преобразуется в уравнение — Р(х, у (х)) = 0, реше-
решения которого выражаются формулой Р (х, у (х)) = С. В случае
когда C.5) не выполняется, Клеро и Эйлер исследовали способ,
который с помощью умножения C.4) на подходящий множитель
М (х, у) (интегрирующий множитель) позволяет иногда получить
уравнение МР + М&у' = 0, удовлетворяющее условщо C.5).
Уравнения второго порядка
Уравнения второго порядка допускают решение с помощью
интегрирования намного реже, чем уравнения первого порядка.
Оно возможно в случае линейных уравнений с постоянными
коэффициентами, что было известно еще Ньютону (для уравнений
второго порядка). Кроме того существует несколько приемов
понижения порядка, например следующий.
В линейное уравнение
=*а (х) у' + Ь(х)у
подставим
у = ехр у р (х) их]. C.6)
Производные этой функции содержат только производные р
более низких порядков:
у' = р.ехр (| р (х) йх\ у" = (р2 + р') ехр (\ р (х) йх\
а поэтому, подставив их в дифференциальное уравнение, после
деления на у получим уравнение более низкого порядка
р* + р* = а (х) р + Ь (х), C.7)
которое, однако, является нелинейным [Риккати A723), Эйлер
A728)].
Если уравнение не зависит от у, т. е. имеет вид у" = / (х, у'),
то естественно взять у' = V и перейти к уравнению V' == / (х, V).
Важный случай представляют уравнения, не зависящие от х:
У" = / (У, У').
Здесь мы будем рассматривать у' как функцию от у: у' = р (у).
Тогда по цепному правилу (дифференцирования сложной функ-
функции) придем к уравнению первого порядка у" = р'р = / (у, р).
После того как функция р (у) найдена, остается проинтегрировать
уравнение у' = р (у), относящееся к типу C.1) (Риккати A712):
«Рег НЬегаге 1а ргетезза 1огти1а с1а11е зесопйе сПНегепге, ...,
сЫато р 1а зиппогта1е ВР ...», см. также работу Эйлера A769),
задача 96).

18 Гл. 1# Классическая математическая теория
Эйлер положил начало изучению всего класса дифференциаль-
дифференциальных уравнений, допускающих интегрирование аналитическими
методами. Эти результаты занимают более 800 страниц
в томах XXII и XXIII его труда Орега Отша. Более современное
изложение можно найти в работе Айнса A944). Незаменимым
источником по этой теме является книга Камке A942). Помимо
описания методов решения и общих свойств решений, в ней со-
содержится систематически упорядоченный перечень более 1500
дифференциальных уравнений с решениями и ссылками на лите-
литературу.
Часто даже для простых на вид уравнений вычисления ока-
оказываются очень сложными, и весьма скоро стало ясно, что не
всегда можно получить элементарное решение. Лиувилль A841)
первым доказал, что некоторые уравнения, как, например, у' =*
*= #2 + у2, нельзя решить с помощью элементарных функций.
Поэтому в XIX веке математиков стали все более интересовать
общие теоремы существования и численные методы нахождения
решений.
Упражнения
1. Найдите с помощью предложенного Ньютоном метода другие
решения уравнения B.1), например при у @) =* 0.1, у @) =я
— 0.2, у @) =5 0.3, и начертите их графики.
2. Решите уравнение Ньютона B.1) в квадратурах.
3. Решите уравнение Лейбница B.3) в терминах элементарных
функций.
Указание. Вычисление интеграла по у может вызвать затруд-
затруднения. Воспользуйтесь заменой а2 —у1 = и2, —уйу = ийи.
4. Решите уравнение у' — \ (у), где
/ (у) = УТ7\>
и начертите график решения.
5. Решите задачу о хозяине и собаке: собака бежит со скоростью хв>
к хозяину, идущему со скоростью V вдоль оси у. Задача сво-
сводится к дифференциальному уравнению
6. Решите уравнение ту* = —к/у2у описывающее падение тела
в соответствии с законом всемирного тяготения Ньютона.
7. Проверьте, что циклоида
X — Хо = К (Т — 51П Т), у — Н=Н A — СО5 Т),

1.3. Уравнения, разрешимые в квадратурах 19
удовлетворяет дифференциальному уравнению B.4) из задачи
о брахистохроне. Решая задачу B.4) прямым способом, после
некоторых упрощений мы придем к интегралу
1/2
который вычисляется с помощью замены у = (зт IJ.,
8. Покажите, что дифференциальное уравнение
* + уу' = у' V*2 + у2 —
имеет решение 2ау = а2 + 1 — л;2 при любом а. Начертите
эти кривые и найдите другое решение (данный пример привел
Лагранж A774) для объяснения «явления Клеро»).
9. Приведите «уравнение Бернулли» [Як. Бернулли A695)]
У' + / (х) У = 8 (х) уп с помощью, преобразования координат
г(х) = (у (х))<* с соответствующим выбором ц к линейному
уравнению [Лейбниц, Ас1а Ешй. A696), Йог. Бернулли
A697)].
10. Проверьте, что огибающую решений у = Сх — / (С) уравне-
уравнения Клеро B.7) можно задать параметрически:
х (Р) = Г
Покажите, что эта огибающая также является решением
B.7), и найдите ее при I (С) = б (С3 — С)/2 (см. рис. 2.6).
11. [Ньютон A671), «РгоЫета II, 5о1и1ю раг11си1аге»]. Решите
уравнение в полных дифференциалах:
Зх2 — 2ах + ау — Зу2у' + аху' ~ 0.
Ньютон указал решение х3 — ах2 + аху — у9 = 0. Отметим,
что он пропустил произвольную константу интегрирова-
интегрирования С.
12. [Ньютон A671)]. Решите уравнения
п' —
У - 1г + ^ + гг +
б) у' *= —Зх + Зху + у2 — ху2 + у3 — ху3 4
— ху* + 6х2у — 6х2 + 8х3у — 8х3
— 10л;4 + ... .
Ньютон получил следующие результаты:
У - х
Л Л
2а ^ 2а2 ^ 2а* ^ 2а*
_ _ 3 2 0 з 25 * 91 б 111 б 367 7
у — -^-х — гх ^-г 2о~х нГх зь~х^

20
Гл. !. Классическая математическая теория
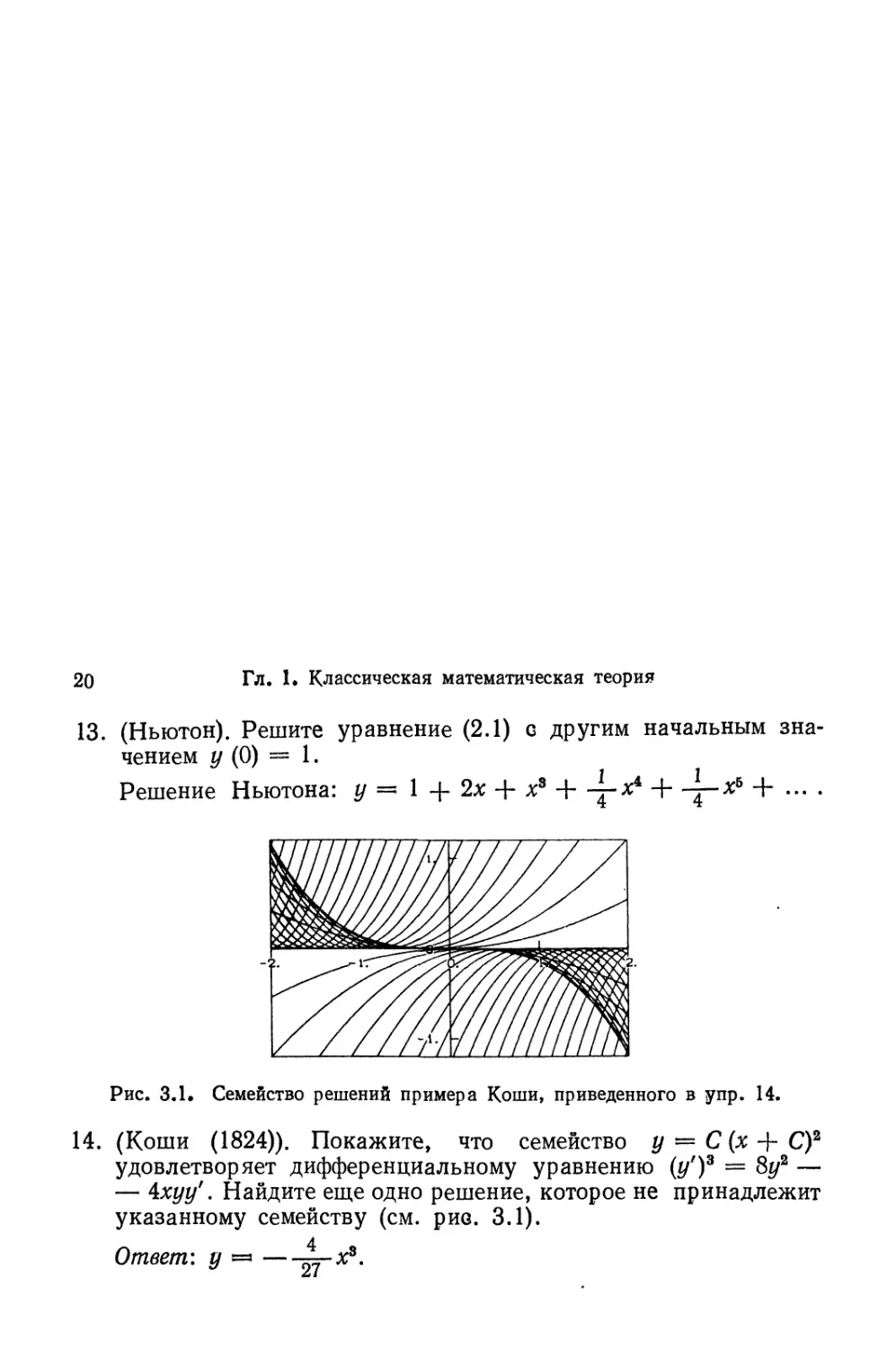
13. (Ньютон). Решите уравнение B.1) с другим начальным зна-
значением у @) = 1.
у ()
Решение Ньютона: у = 1 + 2х + х3 + -|-х4 +
хь + ...
Рис. 3.1. Семейство решений примера Коши, приведенного в упр. 14.
14. (Коши A824)). Покажите, что семейство у = С (х + СJ
удовлетворяет дифференциальному уравнению (у1K = 8у2 —
— Ьхуу'. Найдите еще одно решение, которое не принадлежит
указанному семейству (см. рис. 3.1).
Ответ: у « —

1.4. Линейные дифференциальные уравнения
Еи1ег, Нзе7 Ри1ег, с'ез1 по!ге таНь А гл;?»,
«Читайте Эйлера, читай!е Эйлера, он учитель ?.ля
всех нас.»
(Лаплас)
Следуя за Эйлером A743), мы хотим изучить общее решение
линейного дифференциального уравнения гюрялкя п. Урэгление
(у): - а0 (х) у("> + ах (х) у<"- *> -|- ... -! - а, (х) у - 0 D,1
с заданными функциями а0 (х), ..., а.п (х) называется однородным
Если известно п решений их {х)> ..., ип (х) уравнения D.1), ^о
любая линейная комбинация
у (х) =* Схщ (х) + Спип (х) D,2)
в постоянными коэффициентами С\, ..., Сп также булет решением,
поскольку все производные у входят в D,1) только линейно.
Уравнения с постоянными коэффициентами
Сначала рассмотрим частный случай
у(») (х) - 0. D.3)
После однократного интегрирования получим у(п~ п (х) ■- 6\,
после двухкратного ^е»--2) (х) = Сгх + С2 и т. д. Заменив проич-
вольные константы Сг на новые, в итоге придем к формуле
у (х) - Схх?-г + С\х»-2 + ... + Сп.
Таким образом, в «общее решение» уравнения D.3) входит п «сво-
«свободных параметров». Рассмотрев еще ряд примеров, Эйлер инту-
интуитивно предположил, что этот же результат верен и для уравнения
общего вида D.1). Однако данный вопрос был полностью выяснен
лишь много лет спустя.
Рассмотрим теперь уравнение общего вида с постоянными
коэффициентами:
У{п) + Аху(п-*) + ... + Апу ~ 0. D.4)
Нам нужно найти базис, состоящий из п линейно независимых
решений их (х), ..., ип (х). Для этой пели Эйлер взял за основу
преобразование C.6), C.7): если а (х) и Ь (х) — постоянные вели-

22 Гл. 1. Классическая математическая теория
чины, предположим, что в C.7) р также является константой
и, следовательно, р' равно нулю, откуда получим квадратное
уравнение р2 =?= ар + Ь. Тогда для любого корня этого уравнения
выражение C.6) принимает вид у = ерх. Таким образом, в общем
случае мы предположим, что у = ерх, где р — неизвестная кон-
' станта. Поэтому от D.4) мы придем к характеристическому урав-
уравнению
рп + А1рп-1 + ... + дп = о. D.5)
Если его корни р^ ..., рп различны, то все решения уравнения
D.4) даются формулой
у (х) = Сгер*х + ... + Сперп\ D.6)
Интересно отметить, что «самые выдающиеся математики мира»
многие десятилетия бились над нахождением этого решения,
которое современным студентам кажется столь тривиальным.
Сложности при поиске решения D.6) возникают в том случае,
когда D.5) не имеет п различных корней. Рассмотрим пример,
предложенный Эйлером:
у* - 2ду' + д*у - 0. D.7)
В нем р — ц — это двукратный корень соответствующего харак-
характеристического уравнения. Если мы предположим, что
* у = е**и, D.8)
то D.7) примет вид и* = 0, и мы вернемся к уравнению D.3).
Следовательно, общее решение D.7) имеет вид у (х) == &* (Сгх + С2)
(см. также упр. 5 ниже). После нескольких дополнительных
примеров такого типа становится ясно, что преобразование D.8)
производит сдвиг характеристического многочлена, так что в том
случае, когда ц — корень кратности &, для и получается уравне-
уравнение, оканчивающееся членами ... + 5и^+1) + Си^ ~ 0. По-
Поэтому выражение
-1 + ... +
дает нам к независимых решений.
И наконец, для пары комплексных корней р = а ± ф реше-
решения е<°и-'Р)*, е^а~1^х можно заменить вещественными функ-
функциями
еах (Сг СО5 Р# + С2 5111 Р#).
Изучение неоднородного уравнения
Ь (У) = / (х) D.9)
было начато в работе Эйлера A750). Приведем из нее случай, когда
/ (х) является многочленом, как, например, в уравнении
Ау* + Ву' + Су = ах2 + Ьх + о. D.10)

1.4 Линейные дифференциальные уравнения 2>
Здесь Эйлер представляет решение в виде у (х) = Ех1 + Рх
-\- 0 + V (х). Подставляв '~то ьыражепие в D.И»), из условг^
обращения в нуль всех встречающихся степеней х получим
СП - а, С Г + 2ВЕ = Ь, СО + #/7 -> *
Ли" + Яг/ + Су = 0.
Отсюда при условии, что С отлично о г мул и, V:.,] можем 1тнпти /;\
/^ и С. Мы видрм, что общее решении >и<^ч'1оподт,го уу^тинг
равно сумме его частного решения и общее*, > <~"к'иия епппв г(->;;'.^;-
ющего однородного уравнения. Это угверх (• яорно ти в с/>»л,,.
случае, что можно проверить с пп^- ^, ч ■ р^сгей'ллх приеме?
линейной алгебры.
Описанный метод поиска частного ре- 'Я с помощью не-
неизвестных коэффициентов работает иодобгнм <)бь-ач;;м и в 'ю:-.
случае, когда } (х) состоит из-экспонеш, епг^сов и косииух>15.
Его часто называют «быстрым методом». Приятно отмешть, 4|\>
именно этот метод исторически был открыт первым.
Вариация постоянных
Исследование общего случая неоднородного уравнения
ап(х)у ■-/(%) D.11)
является заслугой Лагранжа A775) («...с помоат,Ь)О нового мето^1,
простого, как можно только мечтать.» — См. чакже работу 4/1аг-
ранжа A788), вторая часть, разд. V). Пусть нгг- изяеепгд п /ьт>
нейно независимых решений щ (л), ..., ип (х) оЦ-н^рэоппго ур*;в
нения. Тогда, распространяя на этот случай метод, яримс'.ч и -ь■"?
к уравнению C.2), представим решение в виде [вместо D.2)]
у (х) ■=■' с1 (х) их (х) + ... •{ сп (х) ип (х), D \ -;
где сх (х) ~- неизвестные функции («метоц вариации посто^нг^л.^).
Нам надо подставить выражение D.12) в D.11). Для этого -;ьг-
числим первую производную
У = Ъ С1Ыг 4- 1, Сгп1.
Если мы будем слепо продолжать дифференцирование, то скоро
получим громоздкие и бесполезные формулы. Здесь Лагранж
проявил проницательность, потребовав обращения в нуль первой
суммы, т. е. выполнения равенств
с(и\1} ~ 0 при / --- 0, а затем при / =-= 1,. . ., п — 2. D.13)
Далее, повторяя лифференцирорш-ие // и исключая каждт.п

24
Гл« 1. Классическая математическая теория
нежелательные члены D.13), мы придем к формулам
У == 2^ С\\Х\^ • • • 9 у =
У ^ ^ сA
Если подставить их в D.11), то произойдет замечательное взаим-
взаимное сокращение членов благодаря тому, что щ (х) удовлетворяют
однородному уравнению. И с учетом D.13) мы окончательно полу-
получим линейнук) систему
щ ..
их
I)
I)
С2
т
Сп
О
О
О
(х)/а0 (х)
D.14)
Ее определитель называется «определителем Вронского», а реше-
решением являются величины с{ (х)у ..., с'п (х)у проинтегрировав кото-
которые, мы найдем сх (х), ..., сп (х). Разд. 1.11 позволит намного
глубже понять эту формулу.
Упражнения
1. Найдите решение «Ьшиз, аеяиа1юп15 йШегепИаНз яиагН §га-
йиз» (уравнений четвертого порядка) а4#<4) + У — О» ^4У{4) —
— У = 0;
решите уравнение «зерИни §гайиз» у^ + #E) + У(А) + У{Ъ) +
+ у =5 0 [Эйлер A743), примеры 4, 5, 6].
2. Решите с помощью предложенного Эйлером метода уравнения
у" — Зу' — 4у = соз х, у" -\- у = соз х.
Указание. В первом случае частное решение можно искать
в виде Е соз х + Р 51п х. Однако во втором случае это пред-
представление непригодно из-за резонанса. Тогда надо использо-
использовать выражение Ех соз х + Рх 51п к, как при решении урав-
уравнения D.7).
3. Найдите решение уравнения
соз,
0
0
1
при условии у @) 8=5 #' @) г= 0:

1.5. Уравнения со слабыми особенностями
25
а) используя решение из упр. 2;
б) методом Лагранжа (вариации постоянных).
4. (Понижение порядка при одном известном решении). Пред-
Предположим, что нам известно ненулевое решение их (х) урав-
уравнения
у'1 + сц (х) у6 + а2 (х) у « 0.
иг (х) = еР**9 и2 (х) = Ит
Покажите, что второе линейно независимое решение можно
найти с помощью представления и2 (х) = с (х) иг (х).
5. Исследуйте случай кратных характеристических корней урав-
уравнения D.7), рассматривая их как предельный случай р2 -> Р1
и используя решения
и т. д.
(Даламбер A748): «И наконец, если значения р и р' равны,
мы вместо этого будем считать, что р = а + а, р' ~ а — а,
где а — бесконечно малая величина...».)
1.5. Уравнения со слабыми особенностями
Многие -встречающиеся в приложениях уравнения имеют
особенности, т. е. точки, в которых функция / (#, у) в дифферен-
дифференциальном уравнении обращается в бесконечность. Мы изучим
1.-1=
Рис. 5.1. Решения уравнения E.1) при 6=1, ц = 3/2, ц = 1/2, ц = —1/2.
некоторые вопросы классической теории таких уравнений, по-
поскольку численные методы, о которых дальше пойдет речь, часто
отказывают в особых точках и плохо работают вблизи от них.
В качестве первого примера рассмотрим уравнение
у =
Ь%
у>
E.1)

Гл. I
с особой топкой при х -■= П. Поп)ч^,' го решелие с помощью
метода разделения переменных C.1):
у (х) = С**ей* = С (х* 4- б***1 +...). E,2)
! ре^пл>ия изображены на рис, 5 1 для разных значений д.
В их поведении наблюдаются фундаментальные различия, завися-
[цие от д.
Линейные уравнения
Эллер положил начало систематическому изучению уравнений
■ особепнос-гями. Он поставил допрос: какой тип уравнений вто-
второю порядка удобно решать с помощью рядов, как в случае
'5.2)? IЭйлер A769), РгоЫета 122, р. 177 «.,.с]иаз согптойе
1»ег .^епез гезоКеге Псе!... .»] Он нашел ураиление
х* (а -'г Ьх) у" Ч- х (с -г гх) у' + (/ + ^) у - 0. E.3)
Прчм_гл'?л:)жнм> что у имеет вид
оо
У= 2 Л^», Л0^=0, E.4)
и подставим эту формулу в E.3), что напоминает процедуру
Ньютона B.2). Мы обнаружим, что степенные множители х2 и х
и\:п у" и г/"' соответственно в точности восстанавливают то, что
УГ[ч:чено в результате дифференцирования, и получим соотно-
соотношения
Я (Я — 1)аЧ-?с + / = 0, E.5а)
+ 0 (я + « — 1) а + (д + I) с + Л Аг -
{(д + I - 1) (д + 1-2) Ь + (д+1 — 1)е + д] Аи, E.5Ь)
где I = 1, 2, 3 Уравнение E,5а) называется индексным и при
и, отличном от нуля, определяет два характеристических корня дг
и ог (расположенных в порядке убывания). Для каждого из них
ир !л произвольном Л о соотношение E.5Ь) позволяет рекурсивно
вычислять Аг, А2 и т. д. Радиус сходимости полученного ряда
определяется далее в упр. 8, Таким образом, мы находим два
л пней но независимых решения иг (х) и и2 (х) дифференциального
у ранения» что нам и требоналось (см. 1.4). Однако существует
ситуация, когда определение второго решении вызывает затруд-
затруднения, а именно: когда коэффициент Аг в E.5Ь) при некотором I
обращается в нуль, т. е. если дЛ —д% есть целое число («РгоЬ-
1еша 123»). В этом случае в результате ряда акробатических
приемов [Эйлер A769): «...яиоё х°10 аеяш'уа1еа1 1рз1 1о8^...»1
З^йлер пришел к мысли, что второе решение надо искать с помощью

1.5. Уравнения со слабыми особенностями 27
представления
оо
и2 (х) = иг (х) 1о§ х + Ц А\2)х"*+1. E.6)
Подставив эту формулу в E.3), он сумел вычислить коэффициенты
А[2). Пример такой ситуации приведен в упр. 1.
Позднее Эйлер A778) заметил, что рекуррентная формула
E.5Ь) становится особенно изящной, если вместо E.3) брать
в качестве исходного дифференциальное уравнение
х A — х) у* + (о — (а + Ь + 1) х) у' — аЪу « 0. E.7)
Тогда описанный метод дает соотношения
Я (Я— 1) + сц = 0, цх = 0, цг = 1 — с, E.8)
А ПРИ <71==°- E>9)
Полученные решения, названные позднее гипергеометрическими
функциями, стали особенно знаменитыми в XIX веке в связи
с работой Гаусса A812).
Указанный метод применим и в более общем случае диффе-
дифференциального уравнения
х2у" + ха (х) у' + Ь(х)у = 0, E.10)
где а (х) и Ь (х) — регулярные аналитические функции. Тогда
говорят, что 0 является регулярной (или слабой) особой точкой.
Аналогично об уравнении (х — х0J у" + (х — х0) а (х) у' +
+ Ъ (х) у = 0 говорят, что оно обладает регулярной особой точ-
точкой х0. В этом случае решения можно получить, используя алге-
алгебраические особенности (х — хоу.
В завершение мы хотим еще изучить поведение решения на
бесконечности для уравнения вида
а (х) у" + Ь(х)уг + с (х) у = 0. E.10а)
Для этого проведем замену переменных I = Их, г {I) = у (х),
при которой уравнение примет вид
Ра D-) 2" + (^а (-)-) - 14 D)) г' + с (±-) г = 0; 'E.10Ь)
оо называется регулярной особой точкой уравнения E.10а),
если 0 является регулярной особой точкой для E.10Ь). Соответ-
Соответствующие примеры приведены в упр. 9.

28 Гл. I. Классическая математическая теория
уравнения
оЬпесНез Ье1т Аи!1ге!.еп
уоп ь^^иЬшеп БкеПеп &с^еЬепепЫЬ ЫсЫ хи ЬеИеп».
«11 & ли встречаются особенности, математик все равно
«м'но >меет справляться с ними в каждом случае».
(К. Хойн, 1900)
Описанный ьыше метод позволяет иногда получать и для
решений нелинейных уравнений если не весь ряд, то по крайней
меро 1пру рго
Примгр. Посмотрим, чго произойдет, если мы попытаемся
решить классическую задачу о брахистохроне B.4) с помощью
представления решения в виде ряда. Пусть к = 0 и начальное
значение у @) -~ 0. Запишем уравнение следующим образом.
1 ълду + д Ь. E.11)
В начальной точке у @) == 0, а / обращается в бесконечность
В этом случае большинство численных методов потерпело бы
неудачу. Будем искать решение в виде у = Аох^. Подставив эту
формулу в E.11), придем к уравнению ц^А\у?я~~'1 + А0х9 = Ь.
Из начального условия следует, что у (х) становится пренебре-
пренебрежимо малым при малых значениях х. Поэтому положим первый
член раышм Ь и получим равенства Зд — 2 = 0 и фА\ = Ь.
Такт(м образом, формула
2 1/з
задает первое приближение к решению. Теперь идея состоит
ч исноль ювании E.12) для того, чтобы отойти от начальной точки
на малую величину х, а чат>-м п[)одолжить решение с помощью
одной из численных пошаговых процедур, описанных в следу-
следующих главах.
Попытаемся более точно аппроксимировать решение о по-
помощью представления у = Аох^ + Аххя±г. Подставив его в E.11),
получим уравнение
^ЛоУ7 + ц (З? + 2г) А\А{х3д+г~2 + Аохд + ... = I.
Используем второй член для нейтрализации третьего, что даст
нам равенства 3<7 + г — 2 = ц, или г = ц = 2/3, и 2АА
= —1. Таким образом, функция
1/з
лучше аппроксимирует решение. Сравнение следующих численных
результатов с точным решением у (х) из 1.3, упр. 7 при Ь = 2,

1.5. Уравнения со слабыми особенностями 29
показывает, что аппроксимации E.12) и E.13| являются полез-
полезными:
л = 0.10 у (*) = 0.342839 и (х) = 0.355689 V D = 0.343038
х = 0.01 у (х) = 0.076042 и (х) = 0.076631 V (х) = 0.076044.
Упражнения
1. Найдите общее решение уравнения х2уп + хуг + §хпу = 0
с постоянной § [Эйлер A769), РгоЫета 123, ЕхетрЫт 1]
2. Примените разработанный Эйлером метод к уравнению Бесселя
х2у" + ху' + (х2 — ё2) У ^ 0. Начертите решения, полученные
при § = 2/3 и §• = 10/3.
3. Найдите решения уравнений л;2^ — 2^' + У = 0, д;^" —
— 3;п/' + 4у = 0. Уравнения такого типа часто называют ура-
уравнениями Эйлера или Коши'. Однако еще Йог. Бернулли было
известно их решение*
4. [Эйлер A769), РгоЫета 123, Ехетр1ит 2]. Периметр эллипса
с осями 1 и х < 1 равен
2Я
у (х) = ] E1П2 5 + X2 СО82 5I/2 дз.
0
а) Проверьте, что у (х) удовлетворяет дифференциальному урав-
уравнению
х A - х2) у' — A+ х2) у' + ху = 0. E.14)
б) Найдите решения этого уравнения.
в) Покажите, что замена переменных х2 = I, у (х) = г {I) пре-
преобразует E.14) в гипергеометрическое уравнение E.7).
Указание, В а) расчеты приводят к интегралу
— 2 СО52 5 + ?2 СО54 5
Г 1 — 2 С
3 A-
о
Надо показать, что он равен нулю. Разложите его в ряд по
степеням а
5. Попытайтесь решить уравнение
х2уп + (Зх - 1) / + у - 0
с помощью ряда E.4) и изучите его сходимость.
6. Найдите ряд вида
у = А&<* + А^8 + А2х<*+2в

30 Гл. 1. Классическая математическая теория
который в окрестности точки х = 0 служит решением нелиней"
ного «уравнения Эмдена — Фаулера» из астрофизики: (х2у'У +
2Ц2 = о.
7. Аппроксимируйте решение уравнения Лейбница B.3) в окре-
окрестности сингулярного начального значения у @) = а с по-
помощью функции вида у (х) — а — Схя. Сравните результат
с точным решением, полученным в упр. 3 из разд. 1.3.
8. Покажите, что радиус сходимости ряда E.4) с коэффициентами,
заданными в E.5) и E.9), равен соответственно
1) Г = -у ; 11) Г=1.
9. Покажите, что для гипергеометрического уравнения E.7)
оо является регулярной особой точкой, а для уравнения Бес-
Бесселя из упр. 2 не является.
10. Рассмотрим задачу Коши
Т E.15)
а) Докажите, что для X <; 0 задача E.15) имеет единственное
решение при х ^> 0.
б) Если & (х) дифференцируема к раз и % <! 0, то решение
у (х) при х 1> 0 дифференцируемо к + 1 раз и выполняет-
выполняется равенство
УИ) @) = A - А-) *(/-« @), /=1,2,....

1.6. Системы уравнений
Лагранж
Первые системы уравнений появились в работе Лагранжа
A759). Одним из вопросов, интересовавших его в самом, начале,
было распространение звука. Считая подход Ньютона недостаточ-
недостаточным, Лагранж попытался объяснить это явление с помощью
известных результатов теории упругости. Если мы будем рассма-
рассматривать среду как последовательность материальных точек и
обозначим через уг (I), у2 (^), уъ (/), ... их отклонения от положения
У///////
'Л
"X
/,
>1
У
Уз-
-У 4
Рис. 6.1. Модели распространения звука, колеблющейся и висящей струны
равновесия (рис. 6.1), то по закону Гуна из теории упругости
получим
у\ = Ю (-2У1 + у2),
У1 = К" & — 2у2 + уд, F.1]
• • •
Уп = К2 (Уп-л — 2уп).
Это система п линейных дифференциальных уравнений. В данном
разделе мы будем обозначать через I независимую переменную
(время), чтобы не перепутать ее с пространственной переменной х
в соответствующем уравнении в частных производных. Лагранж
заметил, что такие же уравнения получаются из уравнения Далам-
бера A748)
д2и
д*2
д2и
дх*

32 Рл, 1. Классическая математическая теория
для колеблющейся струны (согсНз уфгагШЬиз), если ее моделиро-
моделировать с помощью конечного числа материальных точек, располо-
расположенных на струне, не имеющей массы (рис. 6.1).
В качестве другого примера Лагранж [A762), № 36] рассмо-
рассмотрел материальные точки, присоединенные к висящей струне
(рис. 6.1). В этом случае натяжение увеличивается в верхней части
струны, и мы имеем следующие уравнения движения:
у{ = К2 (-ух + г/2),
у1 = К2 (ух - зУ2 + 2г/3)\
Уз = К2 Bу2 - Ьуг + Зу4), F.2)
Уп = К2 ((л - 1) уп-1 - Bл - 1) уп).
Конечно, во всех этих примерах предполагается, что отклонения у%
«бесконечно» малы, и поэтому линейные модели реалистичны.
Используя обозначения, которые получили распространение
лишь веком позже, запишем эти уравнения в виде
п
У"( = .2 Щ)у} A = 1, .... я). F.3)
Данные формулы представляют систему линейных уравнений
2-го порядка с постоянными коэффициентами. Лагранж решил
систему F.3) с помощью подстановки уг = сгер1\ которая приводит
к уравнениям
п
, ..., п). F.4)
Таким образом, р2 должно быть собственным значением матрицы
Л, а с = (с1$ ..., сп)Т —соответствующим собственным вектором.
Здесь, как мы видим, впервые появляется задача на собственные
значения; впервые используется также «метод прямых» для волно-
волнового уравнения.
Лагранж [A762), №30] объясняет, что для решения F.4)
из п — 1 уравнений вычисляются величины с%!съ ..., сп!сг как
функции от р, а затем полученный результат подставляется в пос-
последнее уравнение. Это приводит нас к многочлену степени п
для величины р2 (характеристическому многочлену), для которого
надо найти п различных корней. Таким образом, мы получаем
2/г решений у[Н = с</> ехр (±ру0 и общее решение как их линей-
линейную комбинацию.
Ситуация усложняется, если характеристический многочлен
имеет кратные корни. В этом случае Лагранж в своей знаменитой
«Аналитической Механике» [A788), вторая часть, разд. VI, № 7]
утверждает, что в решение входят «вековые» члены, аналогичные

1.6. Системы уравнений 33
тем, которые получаются из формулы D.8). Однако веком позже
стало понятно, что это не совсем верно. (См., например, работу
Вейерштрасса A858): «...воспользуюсь случаем, чтобы устранить
недоразумение, содержащееся в лагранжевой теории малых коле-
колебаний и во всех известных мне более поздних изложениях послед-
последней».) Поэтому отложим выяснение данного вопроса до разд. 1.12.
В завершение раздела рассмотрим подробное решение уравне-
уравнений FЛ), так как полученные при этом результаты чрезвычайно
важны [Лагранж A759I. Соответствующая задача на собственные
значения F.4) принимает в этом случае вид р2сг = /С2 (—2сг +
+ са), р% = К2 (сг-г — 2сг + с1+1) при * = 2, ..., п — 1 и р2сп =
= К2 (сп_г — 2сп). Введем обозначение р2/К2 + 2 = ц. Тогда
= О, сп+1 = 0. F.5)
Это означает, что с% являются решениями разностного уравнения,
а поэтому 1} с/ = Аа* + ВЫ, где а и Ъ — корни соответствующего
характеристического уравнения г2 — цг + 1 = 0, и, следова-
следовательно, для них выполняются равенства
а + Ь = <7, аЬ = 1. F.6)
Условие с0 = 0 из F.5), приводящее к равенству А + В = О,
показывает, что с, = А (а^ — Ы) при А Ф 0. Из второго условия
сп+1 = 0 или эквивалентного ему условия (а/Ь)п+1 = 1 с учетом
соотношения аЬ = 1 оцедует, что
где к может иметь любое из значений к = 1, ..., п. Таким образом,
получим
тек
л, F.7а)
2. (б.7Ь)
И наконец, формула Эйлера, открытая им в 1740 г., е1х — г'*=
= 2ь 51п х («...такая привычная сегодня для геометров»), дает
для собственных векторов (при А = —И2) значения
5^г, /, *=1, .... п. F.8)
Поскольку рк — чисто мнимые величины, мы используем «при-
«привычную» формулу также и для ехр (±рьЬ и получим, наконец.
1) См., например: Н. С. Бахвалов, Численные методы. —М.: Наука, 1973,
гл. II., § 7. — Прим. ред.
2 Хайрер Э. и др.

34 Гл. 1. Классическая математическая теория
общее решение
п
у* Н) = > 51П ' , , (пъ СО5 Гъ1 + Ьъ ЗШ Гъ(), Гъ —
F.9)
В результате длительных расчетов Лагранж получил, что зна-
значения
п
2 X1 • Щя
п
31П ——-Г ^// @)
п + 1
определяются начальными положениями и скоростями материаль-
материальных точек. В настоящее время эти выражения получают с помощью
соотношений ортогональности
О , / Ф К
п
п + 1 — п + 1
/1+1
У, К — X у •••} **•
Он изучил также случай, когда число материальных точек п
стремится к бесконечности (при этом в формуле для гк можно
заменить зт х на х)> и, опередив на 50 лет Фурье, оказался у по-
порога открытия теории рядов Фурье. «Первую часть этого иссле-
исследования он провел с большим умением, применяя много искусных
аналитических приемов, однако переход от конечных сумм к бес-
бесконечным оставляет желать много лучшего...» [Риман A854)]#
Фурье
«,Ра}ои1ега1 ^ие 1е Нуге Aе Роипег а ипе 1трог1апсе
сарНа1е с1ап$ ГЫ$1о1ге с1е$ таШётаЩиез».
«Добавлю, что книга Фурье имеет основополагающее
значение в истории математики».
(А. Пуанкаре, 1893)
Первые системы первого порядка появились благодаря задаче
о теплопроводности [Био A804), Фурье A807)]. Фурье представил
стержень последовательностью молекул, температуру которых
мы обозначим через уг, и вывел из закона Ньютона, что энергия,
передаваемая данной частицей соседним, пропорциональна раз-

1.6. Системы уравнений 35
ности их температур, т. е. у^г — уг для левой пары и у1+1 — уг —
для правой. («Поскольку две молекулы одного тела расположены
чрезвычайно близко друг к другу и имеют разные температуры,
более разогретая молекула сообщает менее разогретой количество
тепла, которое точно выражается через произведение, образован-
образованное длительностью промежутка времени, очень малой разницей
температур и некоторой функцией расстояния между молеку-
молекулами».) На языке формул эта длинная фраза означает, что'полное
приращение энергии молекулы I выражается следующим образом:
FЛ0)
или, в более общем виде — системой первого порядка с постоян-
постоянными коэффициентами:
п
= И <*иУи I = Ь .. •* л. F.11)
/1
Подставив теперь выражение уг = с^р', получим задачу на
собственные значения
п
рсг = 2] ацс^ I = 1* ..., п. F.12)
Если предположить, что стержень охлажден на обоих концах
до нуля (г/0 = уп+1 = 0), то можно использовать введенные выше
собственные векторы Лагранжа, с помощью которых мы получим
решение
п
{I) = ^ 81пТТТаь ехР (-»*0. »* = 4/(а (зш-д^у)8. F.13)

Неограниченно увеличивая п (и тем самым обращая «метод пря-
прямых»), Фурье от F.10) пришел к своему знаменитому уравнению
теплопроводности
дх*
Так было положено начало теории рядов Фурье.
Упражнения
1. Проверьте, что для функции и (#), дифференцируемой доста-
достаточное число раз, выполняется равенство
и(х — 6) — 2и(х) + и(х + 6) _ „ , , , б2ц4 (х) ,
= и (х)-\ ^2~—г
Указание. Используйте разложение в ряд Тейлора для и (х +
+ б) и и (х — 6). Это соотношение устанавливает связь между
F.10) и F.14), а также между F.1) и волновым уравнением.
2*

36 Гл. 1. Классическая математическая теория
2. Решите уравнение F.2) при п = 2 и п = 3, следуя описанной
выше схеме Лагранжа A762). При этом естественным образом
возникает характеристический многочлен матрицы.
3. Решите систему первого порядка F.11) с начальными значе-
значениями уг @) == (—1)' и той же матрицей Л, что и в упр. 2,
и начертите решения. Физически такое уравнение могло бы
описывать струну с грузами, висящую, например, в мёде.
4. Найдите первые члены разложения в особой точке х = 0 для
следующей системы нелинейных уравнений:
*У + 2хуг = 2уг* + %х*у (у2 - 1), у @) - 0,
х2г" == г (г2 — 1) + х2у% г @) = 1, F.15)
с постоянным параметром X. Это уравнение Эйлера для вари-
вариационной задачи
( +4х*(^- IJ) ах,
у(оо) = 1, 2(оо) = 0,
о массе «монополя» из ядерной физики [см. работу Хуфта
A974I.

1.7. Общая теорема существования
. СаисЬу аппопсе, ^ие, роиг зе сопЬгтег аи уоеи йп
СопзеП, И пе з'аНасЬега р1из а сктпег, сотте П а ?аЦ
]1^и'а ргёзеп!, ёез Aётопз1га11опз рагЫ1етеп* п&ои-
геизез». (СопзеП AЧпз1гисиоп с!е ГЕсо1е ро1у!есЬг^ие,
24 поу. 1825)
«Г-н Коши объявляет о том, что, выполняя положение
Совета, он больше не будет стремиться давать совер-
совершенно строгие доказательства, как он это делал до
сих пор».
(Совет по обучению Политехнической школы, 24
ноября 1825 г.)
«У всех вас профессиональная деформация сознания;
эдесь сходимость совершенно не важна...»
(П. Хенричи, 1985)
Теперь мы вступаем в новую эру развития предмета нашей
книги, более теоретическую, чем предыдущая. Ее открывают
исследования Коши, который не был столь очарован долгими
численными расчетами, как, например, Эйлер, зато фанатично
добивался безупречной математической строгости и точности. Он
критиковал своих предшественников за использование в работе
бесконечных рядов и других бесконечных процессов без должного
внимания к оценкам погрешности или результатам о сходимости.
Около 1820 г. Коши сформулировал теорему сходимости для ме-
метода ломаных Эйлера, а лет через 15 — для метода степенных
рядов Ньютона (см. разд. 1.8). Кроме оценки погрешности эти
результаты позволяют также получить общие теоремы существо-
существования решений произвольных дифференциальных уравнений («лю-
(«любого дифференциального уравнения»), для которых решения были
известны только в весьма немногих случаях. Другим важным
следствием стала возможность судить о единственности решения,
позволяющей делать вывод о том, что только найденное нами
(численно или аналитически) решение отвечает данному началь-
начальному значению и других таких решений не существует. Лишь
в этом случае мы вправе сказать, что решили задачу.
Самое первое доказательство Коши было недавно найдено
в отрывочных заметках [Коши A824)], которые никогда при его
жизни не публиковались (может быть, эти заметки не удовлетво-
удовлетворили министра образования: «...что второй профессор г-н Коши
представил только отдельные листки, которые не могли удовлет-
удовлетворить^ комиссию, и что до сих пор было невозможно заставить его
подчиниться требованию Совета и выполнить постановление ми-
министра»).

38 Гл. 1, Классическая математическая теория
Сходимость метода Эйлера
Приступим теперь, «обнажив голову и преклонив колени»,
к изложению идей этого исторического доказательства. Сформу-
Сформулируем его так, чтобы оно допускало прямое обобщение на си-
системы большей размерности.
Начнем со скалярного дифференциального уравнения
= /(*.»). »(*а) = »о. */(*) = ? G.1)
и воспользуемся методом, который описан Эйлером A768) в пос-
последнем разделе его работы «ЫзШиШпез Са1сиН 1п1е§гаП5» (Са-
(Сари! VII), т. е. рассмотрим разбиение отрезка интегрирования
и на каждом отрезке заменим решение первым членом его ряда
Тейлора:
У г — У о = (Ч — хо)
У2 — У* = (*1 — *Д ! (*ь Уг), G.3)
Уп — Уп-1 — (Хп — *п-1) /
/
Для указанного разбиения будем использовать также обозначение
а ~ (г10, й1э ..., /1п-1)>
где Нг = хг+1 — хг. Если соединить у0 и уи уги у2и т. д. прямыми,
то получится ломаная Эйлера
Ун (х) = Уг + (х — хг) / {хи уг) при хг < х < *|+1. G.3а)
Лемма 7.1. Предположим, что \[\ ве превосходит А на мно-
множестве
О = К*. У) I *о < х < X, | у - у01< 6}.
Если X — х0 <! Ь/А, то заданное формулами G.3) численное реше-
решение (хг, уь) останется в В при любом разбиении G.2) и будут
выполняться неравества
\Уъ(х) — Уо\<А-\х — хо\, G.4)
I Ун (х) - (г/о + (х - х0) ! (х0У г/0)) |< е | х - х01, G.5)
(х, у) — / (х0, Уо) К е на ^.
Доказательство. Оба неравенства получаются в результате
суммирования строк G.3) и использования неравенства треуголь-
треугольника. Из G.4) сразу следует, что при А (х — х0) -< Ь ломаная
остается в п. Ш
Наша следующая задача состоит в оценке изменения ун (х)
при изменении у0. Возьмем другое начальное значение г0 и вы-

1.7. Общая теория существования 39
числим для него
= (Хг — Хо) / (ХО, 20). G.6)
г»
Нам надо оценить | гх — уг\. Вычитая G.6) из первой формулы
в G.3), получим
Ч — Уг = 20 — у0 + (хг — х0) (/ (х0, г0) — / (х0, г/о)).
Отсюда видно, что нам нужна оценка для / (х0, г0)—/ (х0, у0).
Если предположить, что
\!(х, г) ~Цх, у)\<Ь\г-у\, G.7)
то мы придем к неравенству
Лемма 7.2. Пусть при фиксированном разбиении Н начальным
значениям у0 и г0 отвечают ломаные- Эйлера у^ (х) и гн (х) соот-
соответственно. Если в выпуклой области, содержащей (х, ун (х))
и (х, гн (х)) при всех х0 <! х << X, выполняется соотношение
то
гн (х) - ун (х)\ < * <*-*.> | аг0 — г/01. G.10)
Доказательство. Из G.9) следует G.7), из G.7) — G.8), а из
G.8) — неравенство
Если повторить те же рассуждения для г2 — у2л г3 — у3 и так да-
далее, то в итоге мы получим G.10). ■
Замечание. Условие G.7) называется «условием Липшица».
Именно Липшиц A876) заново открыл эту теорию (примечание
к статье Липшица: «Автор, очевидно, не знаком с работами Коши...»)
и отстаивал использование условия G.7) вместо более сильного
предположения G.9). Доказательство Липшица излагается также
в классическом труде Пикара [A891—1896), том II, гл. XI,
разд. I].
При переходе ко все более мелкому разбиению G.2), т. е. при
= тах й*->0,
?=о, ..., п—г
мы надеемся, что ломаная Эйлера сойдется к решению задачи
G.1). И действительно, мы имеем следующий результат.
Теорема 7.3. Пусть на множестве

40 Рл. 1. Классическая математическая теория
/ (х, у) — непрерывная функция, | /1 не превосходит А и удовлет-
удовлетворено условие Липшица G.7). Если X — х0 <; Ь/Л, то:
а) при | Н | -*• 0 ломаные Эйлера уъ (х) сходятся равномерно
к непрерывной функции ф (х)\
Ь) ф (х) непрерывно дифференцируема и является решением задачи
G.1) на отрезке [х0, Х]\
с) при х0 < х < X задача G.1) не имеет других решений.
Доказательство, а) Выберем е > 0. Поскольку / равномерно
ограничена на компактном множестве Э% существует б > 0,
такое что из условий
б и [ х)г — а2 К А6
следует неравенство
1/@1, ^-/(, <>2)|<е. G.11);
Теперь преположим, что разбиение G.3) отвечает условию
т. е. |Л|<6. G.12)
Сначала изучим, что произойдет при добавлении точек сетки.
На первом шаге рассмотрим разбиение к A), которое получается
при добавлении новых точек только в первому отрезку разбие-
разбиения. Из неравенства G.5) (относящегося к этому первому отрезку)
следует, что для нового уточненного решения уъ ц) (х\) выполняется
оценка | ун A} (х\) — уь (хг) \ <; г \ Х\ — Хо \. Поскольку раз-
разбиения Н и Н A) совпадают на отрезке хг <; х <; X, мы можем
применить лемму 7.2, с помощью которой получим неравенство
Уь со (х) — ун (*) | < еь <*-**> (хг — х0) е при хг < х < X.
Затем добавим дополнительные точки на интервале (х19 х2) и обо-
обозначим новое разбиение через Н B). Тем же способом придем к оцен-
оценкам
\УЫ) М ^ц) ()||- хг
и
| Ун B) (х) — ун (I) (х) | < еь <дг~^) (х2 — Хг) г при х2 < х < X.
Полностью вся ситуация представлена на рис. 7.1. Обозначив
А
через А окончательное разбиение, при х% ^ х <! Хг+ъ мы получим
IУ к (х) — уь (х) | <
в(^<*-*!> &_*„)+...+ еь 1-*й (хг - *„)) + е(х- дг«)<
X
в ^ ^ <*-«> Й5 = -2- (ей <*-*•> - 1). G.13)

1.7. Общая теория существования
41
Теперь, если мы имеем два различных разбиения Л и Я и они оба
удовлетворяют условию G.12), введем третье разбиение /г, ко-
которое получается измельчением каждого из них (как это обычно
делается при доказательстве существования интеграла Римана),
и дважды применим G.13). Тогда из неравенства треугольника
и из G.13) следует, что
Ук{х)-ук ^
При достаточно малых в > О эта величина становится сколь угодно
малой, что говорит о равномерной сходимости ломаных Эйлера
к некоторой непрерывной функции ф (х).
Рис. 7.К Веер леди Уиндермир |О. Уайльд A892)].
Ь) Введем модуль непрерывности
е (б): = вир {| / (и19 V!) - / (и2,
Если х принадлежит разбиению А, то из G.5) [заменив (х0, у0)
на (х, ун (х)) и х на х + б ] мы получим
Ы* + в) - Уь(х) - б/(х, уп(х))|<е(б)б. G.14)
Переходя к пределу при | К \ -*• 0, мы придем к соотношению
I Ф (х + 6) - Ф (х) - б/ (х, Ф (х))} <
< е (б) б. G.15)

42 Гл. 1. Классическая математическая теория
Поскольку 8 (б) -> 0 при б -* 0, отсюда следует, что ф (х) диффе-
дифференцируема и ср' (х) = / (х, ф (я)).
с) Предположим, что задача G.1) имеет второе решение \|) (я),
и пусть разбиение Л отвечает условию G.12). Обозначим через
у{ь1) (х) ломаную Эйлера при начальном значении (я*, г|) (хс)) (она
определена при хг <; х -< X). Из соотношения
<*
,[/(*.
и G.11) следует, что
(*) — У^ (х) 1 ^ е I х — XI | при
Используя лемму 7.2, мы тем же способом, что и в части а), вы-
выведем оценку
(х)|<±-(^ (—О « 1). G.16)
Переходя к пределу при | А | -► 0 и в -► 0, получим неравенство
| г|) (х) — ф (х) | <! 0, доказывающее единственность. ■
Теорема 7.3 о существовании и единственности решения —
это локальный результат. Однако если рассматривать конечную
точку решения как новое начальное значение, то можно снова
применить теорему 7.3 и продолжить решение. Повторяя эту
процедуру, мы придем к следующему результату.
Теорема 7.4. Пусть V является открытым множеством в К2,
а\ид\1ду непрерывны в I/. Тогда для любой точки (х0, у0) (= V
существует единственное решение задачи G.1), которое можно
продолжить до границы V (в обоих направлениях).
Доказательство. Теорему 7.3, очевидно, можно переписать
так, чтобы она утверждала существование и единственность реше-
решения для интервала (X, х0) слева от х0. Остальное следует из того
факта, что любая точка в Ц имеет окрестность, удовлетворяющую
условиям теоремы 7.3. ■
Интересно упомянуть о том, что формула G.13) при
0 дает оценку погрешности
для ломаной Эйлера (|А| <! б). Здесь у (х) означает точное ре-
решение задачи G.1). Следующая теорема уточняет приведенные
выше оценки в случае, когда / (х, у) является также дифференци-
дифференцируемой по х.

Ь7. Общая теория существования 43
Теорема 7.5, Предположим, что в окрестности решения вы-
полняются неравенства
дх
Тогда для ломаных Эйлера при достаточно малых \Н\ справедлива
следующая оценка погрешности:
-1)-|Л|. G.18)
Доказательство. При \иг — и2 \ *< | Н | и | ^ — VI]
А \Н\ в силу дифференцируемости / мы получим вместо
G.11) оценку
I / (ии Щ) — / (> ^г) | < (Л4 + АЬ) | Н \.
Подставив эту величину в качестве е в G.16), мы придем к требуе-
требуемому результату. ■
Оценка G.18) показывает, что глобальная погрешность метода
Эйлера пропорциональна максимальной длине шага \Н\. Тогда
для достижения точности, например, в три десятичных знака нам
понадобилось бы порядка тысячи шагов; точность в шесть десятич-
десятичных знаков требует, как правило, миллиона шагов и т. д. Таким
образом, мы видим, что данный метод нельзя рекомендовать для
расчетов о высокой точностью. Поиск методов, которые сходятся
быстрее, составит основное содержание гл. II.
Теорема существования Пеано
«51 а ез1 ип сотр!ехе <Гогс1ге я, е! Ь ип потЪге гёе1,
а1огз оп реи1 с1ё1егттег Ь1 е! /, ой Ь' е51 ипе ^иапШё
р1из ^гапёе ^ие Ь, е! / ез! ип 51^пе Aе ЬпсИоп ^и^
а сЬацие потЬге 4е 1'1п1егуа11е ее Ь а Ь' \ьМ соггезроп-
с1ге ип согар1ехе (еп с!' аи!ге5 то1з, Ц ез! ип сотр1ехе
!опсИоп с!е 1а уаг1аЫе гёеИе I, йёНте роиг 1ои1е5 1ез
уа1еигз Aе 1Чп1егуа11е (Ь, Ъ9))\ 1а уа!еиге Aе // роиг
г~Ь ез! а; е! дапз 1ои1 1Чп1;егуа11е F, Ь') сеИе ЬпсИоп
\1 8а11з!а11 а Гё^иа^^оп сШГёгепНеПе йоппёе».
«Если а — комплексное число порядка я, а 6 — ве-
вещественное, тогда можно определить Ъ' и /, где Ъ' —
величина, превосходящая 6, а / обозначает функцию,
которая каждому числу из интервала от Ь до Ъ' ставит
в соответствие комплексное число (другими словами,
Ц — это комплексная функция вещественной пере-
переменной г, определенная для всех величин из интервала
(Ьу Ь')); значение (( при г = Ь равно а, и на всем ин-
интервале (Ьу Ь') эта функция Ц удовлетворяет заданному
дифференциальному уравнению».
(Первоначальная формулировка теоремы Пеано)

44
Гл. 1. Классическая математическая теория
Условие Липшица G.7) — это решающее средство при доказа-
доказательстве соотношения G.10), а в итоге и теоремы сходимости.
Если мы полностью откажемся от условия G.7) и потребуем только
непрерывности / (х, у), то уже нельзя будет гарантировать сходи-
сходимость ломаных Эйлера.
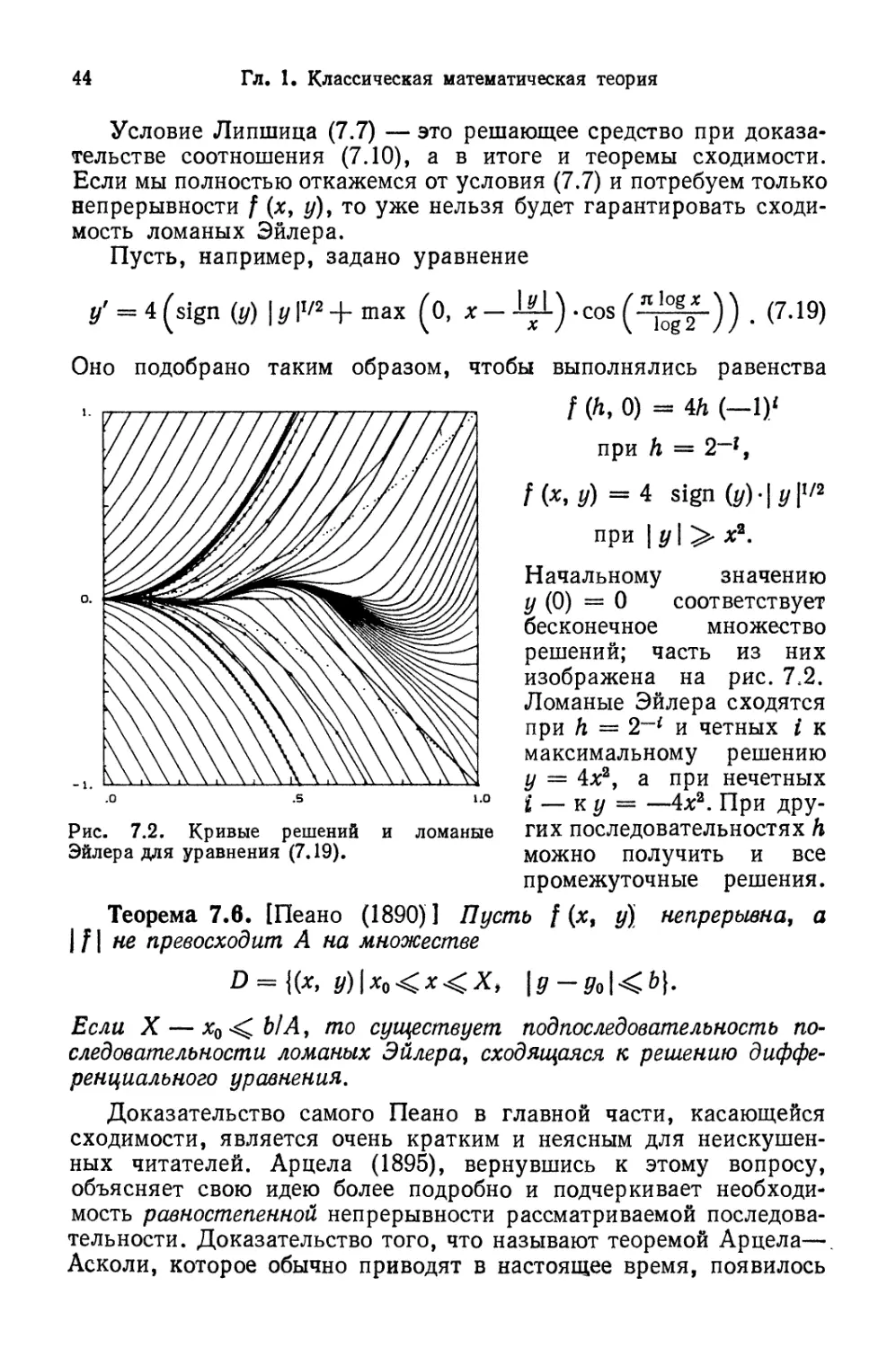
Пусть, например, задано уравнение
(у)
(о, х-
соз
. G.19)
о.
■** 1 •
Оно подобрано таким образом, чтобы выполнялись равенства
/ (А, 0) =» 4А (
при А =
*, У) =4 51§п
при |#| >
Рис. 7.2. Кривые решений
Эйлера для уравнения G.19).
1.0
и ломаные
Начальному значению
г/ @) = 0 соответствует
бесконечное множество
решений; часть из них
изображена на рис. 7,2.
Ломаные Эйлера сходятся
при А = 2~1 и четных г к
максимальному решению
у — 4л;2, а при нечетных
I — к у = —4г*. При дру-
других последовательностях А
можно получить и все
промежуточные решения.
Теорема 7.6. [Пеано A890)] Пусть / (х9 у) непрерывна, а
/1 не превосходит А на множестве
О = \(х, У)\*о<х<Х, \у-уо\<Ь\.
Если X — л:0<;б/Л, то существует подпоследовательность по-
последовательности ломаных Эйлера, сходящаяся к решению диффе-
дифференциального уравнения.
Доказательство самого Пеано в главной части, касающейся
сходимости, является очень кратким и неясным для неискушен-
неискушенных читателей. Арцела A895), вернувшись к этому вопросу,
объясняет свою идею более подробно и подчеркивает необходи-
необходимость равностепенной непрерывности рассматриваемой последова-
последовательности. Доказательство того, что называют теоремой Арцела—
Асколи, которое обычно приводят в настоящее время, появилось

1*7. Общая теория существования 45
лишь позднее (см., например, работы Перрона A918), Хана
A921)). Вкратце его можно изложить следующим образом.
Доказательство. Рассмотрим последовательность ломаных Эй-
Эйлера при уменьшении длины шага:
V! (*), 0а (х), а3 (х) G.20)
Из G.4) следует, что при фиксированном х она ограничена. Вы-
Выберем последовательность чисел г1э г2, г3, ..., плотную на интер-
интервале (х0, X). Тогда в G.20) существует последовательность, сходя-
сходящаяся при х = Гд (Больцано—Вейерштрасс). Обозначим ее
через
°|!)(*). °$1}(*). 4г)(х), .... G.21)
Далее выберем из G.21) подпоследовательность, сходящуюся
при х = га:
»{2) (*), <42) М, 42) (х), . ... G.22)
и т. д. Затем возьмем «диагональную» последовательность
, V^3\X), . . ., G.23)
которая, за исключением конечного числа членов, является под-
подпоследовательностью всех этих последовательностей и поэтому
сходится при всех г/. В завершение с помощью оценки
| <п) (х) - о<я) (п) \<А\х-
[см. G.4I, которая выражает равностепенную непрерывность по-
последовательности, мы получим
(X) — Ът (X)
(х) - <п) (П) | +1 № {п)
}т (гп — ит (х) I <
X —
Для фиксированного в^>0 мы выберем из {гх, га, ...} конечное
подмножество /?, отвечающее условию Ш1П \\х — 011 О Л
х <! X} <; е/Л, а затем выберем такое #, что
(г/) -- ^т) (г/) | < е при л, /тге# и
Это неравенство указывает на равномерную сходимость G.23).
Таким же способом, как и в части Ь) доказательства теоремы
7.3, мы придем к выводу, что получаемая в пределе функция —
это решение задачи G.1). Надо только добавить в G.14) член
О (|Л|), если х не является точкой разбиения. ■

46 Гл. 1. Классическая математическая теория
Упражнения
1. Примените метод Эйлера о постоянным шагом хм — хг =
= \1п к дифференциальному уравнению у' = ку, у @) = 1
и получите классическую аппроксимацию решения у A) =
= ек. Оцените погрешность.
2. Примените метод Эйлера о постоянным шагом к задачам
@) = о,
С помощью теоремы 7.5 дайте строгие оценки погрешности
и сравните их с истинными погрешностями. Основная труд-
трудность состоит в нахождении нужной области, в которой вы-
выполнялись бы оценки теоремы 7.5 и при этом постоянные Л,
Ь и М не были бы слишком большими, но в то же время гаран-
гарантировали, что графики решений останутся внутри области
(см. также 1.8, упр. 3).
3. Докажите следующий результат: если дифференциальное урав-
уравнение у' = / (х, у), у (х0) = у0 с непрерывной функцией /
имеет единственное решение, то ломаные Эйлера сходятся
к нему.
4. «Существует элементарное доказательство теоремы существо-
существования Пеано» [Уолтер A971I. Предположим, что |/| не пре-
превосходит Л. Тогда последовательность
Ум = 01 + й шах {/ (х, у) | хг < х <хм, ^ — ЗЛА < # < дг + АН]
сходится для всех непрерывных ^ к (максимальному) решению.
Попытайтесь доказать это. К сожалению, такое доказательство
нельзя распространить на системы уравнений, если они не
являются «квазимонотонными» (см. разд. 1.10, упр. 3).

1.8. Теория существования решения, основанная
на итерационных методах и рядах Тейлора
Возможен и другой подход к теории существования решения —
на основе итерационного уточнения приближенных решений.
К этой мысли пришли уже очень давно. В частности, много при-
примеров такого типа можно найти в работе Лагранжа, главным об-
образом в его астрономических расчетах. В качестве иллюстрации
рассмотрим уравнение Риккати
У' = х2 + У + 0Лу*, у@) = 0. (8.1)
Оно не имеет элементарного решения из-за вхождения в правую
часть квадратичного члена. Поэтому совершенно естественно
возникает мысль пренебречь данным членом, который действи-
действительно вначале очень мал, и решать пока задачу
(8.2)
С помощью формулы C.3) мы получим отсюда первое решение
уг (х) = 2е* — (х2 + 2х + 2). (8.3)
Благодаря ему мы теперь больше знаем о члене 0.1 у2, которым
первоначально пренебрегли: он будет близок к 0.1 у\. Поэтому
напрашивается мысль о том, чтобы данное решение снова подста-
подставить в (8.1) и решать уже дифференциальное уравнение
(У1 (х))\ у2 @) = 0. (8.4)
Можно еще раз использовать формулу C.3), и после некоторых
вычислений мы получим выражение
) + ^е>*--1.<*(*» +з* +6*-64)-
(* + 8х* + 32*2 + 72* + 76).
Оно уже намного ближе к точному решению, что видно из сравне-
сравнения погрешностей е1 = у (х) — уг (х) и е2 (х) = у (х) — у2 (х):
я = 0.2 ех = 0.228 Х10-07 е2 = 0.233 X Ю2
х = 0.4 ег = 0.327 X Ю5 е2 = 0.566 X Ю9
х = 0.8 ег = 0.534Х10-08 е2 = 0.165 х 10-°б.
Продолжение данного процесса выглядит многообещающим, но
расчеты вскоре становятся чрезвычайно утомительными.

48 Гл. 1, Классическая математическая теория
Метод последовательных приближений Пикара
Общая формулировка этого метода заключается в следующем:
мы попытаемся, если это возможно, таким образом расщепить
функцию / (х, у) из дифференциального уравнения
У* = / (*, У) = /1 (*• у) + /2 (х, у); у (х0) = у0, (8.5)
чтобы любое дифференциальное уравнение вида уг = \х (х, у)
+ § (х) можно было решить аналитически, а /2 (х, у) была мала.
Тогда мы начнем с первого приближения у0 (х) и, решая уравне-
уравнения
= ?г (X, У1+1) + /2 (X, уг (*)), ^+1 (д:0) = Г/0, (8.6)
вычислим последовательно ух (х), у2 (х), ... . Самая примитивная
разновидность этого процесса получается при выборе /х = О,
/2 ^ /* тогда, проинтегрировав (8.6), мы сразу придем к формуле
х
У иг (х) = Уо + \ ! (^ Ух E)) Лв. (8.7)
Она называется методом последовательных приближений Пикара.
Этот метод появлялся в литературе несколько раз, в частности
в работах Лиувилля A838), Коши, Пеано A888), Линделёфа
A894), Бендикссона A893). Пикар A890) считал его лишь побоч-
побочным продуктом аналогичного процесса для уравнений в частных
производных и досконально проанализировал его в своем знамени-
знаменитом трактате [Пикар A891—96), том Ц, гл. XI, разд. III].
Основной практический недостаток метода состоит в необходи-
необходимости многократного вычисления интегралов, что обычно не очень
удобно, если вообще возможно, и что быстро становится чрезвы-
чрезвычайно утомительным занятием. С другой стороны, метод является
хорошим инструментом для теоретических исследований.
Легко увидеть его быструю сходимость при малых | х — хо\:
если мы вычтем из (8.7) такую же формулу, но с заменой ь на I — 1,
то придем к выражению
X
Ум (х) - у г (х) = I (! E, у, E))- ! (8У уы E))) дв. (8.8)
Теперь, применив условие Липшица G.7) и неравенство треуголь-
треугольника, получим
х
\ Ум (х) -9Лх)\<ь\\у1 E) - т-х (з) I Л- (8-9)
«О

1.8. Террия существования решения 49
Положив у0 (х) = Уо и применив неравенство треугольника к фор-
формуле (8.7) с индексом / = 0, выведем оценку
где Л, как и в разд. 1.7, ограничивает |/|. Далее, подставляя
это выражение в правую часть (8.9) и многократно повторяя эту
подстановку, окончательно придем к оценке
I У г (х) - »,-! (х) | < Аи -' 1*=**1. (8.10)
Ее правая часть — это (с точностью до постоянного множителя
А1Ь) член ряда Тейлора для еИ*—*о1э сходящегося при всех х.
Отсюда следует, что | уг+к — уг | становится сколь угодно ма-
малым при больших I. Погрешность ограничена остаточным членом
данного ряда. Поэтому последовательность уг (х) равномерно схо-
сходится к решению у (х). Например, если Ь\х — х01 <! 1/10
и постоянная А невелика (порядка 1. — Ред.), то 10 итераций
дали бы численное решение примерно с 17 правильными знаками.
Метод рядов Тейлора
•»
«Аргё$ аусмг топЪгё ИпзиШзапсе с1е$ тёШос1е$ AЧп^ё-
^гаНоп [опйёез зиг 1е Aёуе1орретеп1 еп 5ёг1е$, 11 те
ге$1е а (Иге еп реи с!е то!з се ^и'оп реи! 1еиг зиЬзИ-
1иег».
«После того как я показал недостаточность методов ин-
интегрирования, основанных на разложении в ряд, мне
остается кратко сказать, чем их можно заменить».
(Коши)
При доказательстве существования решения возможен и тре-
третий способ — на основе изучения сходимости рядов Тейлора для
решений. О нем упоминает в примечании Лиувилль A836), а свое
окончательное развитие этот способ получил в работе Коши
A839—1842).
^ Мы уже встречались с рекурсивным вычислением коэффи-
коэффициентов ряда Тейлора в исследованиях Ньютона (см. разд. 1.2).
Позднее Эйлер A768) сформулировал общую процедуру для стар-
старших производных решения задачи
У' = /(*, У), УМ = Уо, (8-11)
которые получаются последовательным дифференцированием:
уГ = Л. + Ш = /* + У> ,я
и т. д. Тогда решение имеет вид

50 Гл. 1. Классическая математическая теория
Формулы (8.12) для старших производных быстро становятся
очень сложными. Поэтому Эйлер предложил использовать только
несколько членов этого ряда при достаточно малом Н и повторить
вычисления от точки хъ = х0 + й («аналитическое продолжение»).
Доказательство сходимости
Теперь мы наметим основные этапы принадлежащего Коши
доказательства сходимости ряда (8.13). Предположим, что / (х, у)
является аналитической в окрестности начального значения х0,
г/0, которое для простоты обозначений поместим в начало коорди-
координат х0 = у0 = 0:
!(х, У)=
г, /
где аи — кратные частных производных, входящих в (8.12).
Если предположить, что ряд (8.14) сходится при |#|<г,
| у | <! г, то неравенства Коши из классического комплексного
анализа дают оценку
\аи\<-Ш> где М = тах |/(*, д)\. (8.15)
Теперь идея состоит в следующем: поскольку в (8.12) все знаки
положительны, мы получим наихудший из возможных результа-
результатов, если заменим в (8.14) все ац на наибольшие возможные зна-
значения (8.15) («метод мажорант»):
^
A—х/г)A—у/г) •
А мажорирующее дифференциальное уравнение
,
9 - A_*/г)A_у/г
легко интегрируется с помощью разделения переменных (см.
разд. 1.3) и имеет решение
1/П (8.16)
Это решение представляется степенным рядом, сходящимся при
всех х, таких, что | 2М 1о§ A — х1г) | <3 1. Поэтому ряд (8.13)
также сходится, по крайней мере при всех
— ехр(—1/2 М)). Ш

1.8. Теория существования решения 51
Рекуррентное вычисление коэффициентов
ряда Тейлора
«...сНезез УегТапгеп ргакИзп теп* т Рга&е коттеп
капп».
«...об этом способе практически не может быть и речи».
(Рунге—Кёниг, 1924)
«Если мы используем правильный подход,.то верным
будет в точности обратное...».
(Р. Е. Мур, 1979)
«Правильный подход» в действительности является развитием
подхода Ньютона. Его открывали заново несколько раз [см.,
например, работу Стеффенсена A956)], а программная реализа-
реализация его общей формы была осуществлена Гиббонсом A960) и
Муром A966). Более широко библиография представлена в ра-
работе Ваннера A969).
Идея подхода состоит в следующем: пусть величины
У (*)))<" I *=*. (8-17)
обозначают коэффициенты ряда Тейлора для у (х) и / (х, у (х)).
Тогда (8.13) примет вид
оо
Из (8.11) получим равенство
(8-18)
Теперь предположим, что / (х, у) состоит из последовательности
алгебраических операций и элементарных функций. Это приводит
нас к последовательности элементов
#> У'> Р* Чу г* ••• и> наконец, /. (8.19)
Для каждого из них найдем формулы для определения 1-то коэф-
коэффициента ряда Тейлора по предыдущим:
а] г = р ± ц\
Кх = Р% ± <2и I = 0, 1, . .., (8.20а)
г
Л|= ЦРАг-и «=0, 1# ..., (8.20Ь)
/«о
(произведение Коши).

52 Гл. 1. Классическая математическая теория
с) г == р/</: запишем р = гд, используем формулу Ь) и раз
решим ее относительно
( 11 \
-\Рг - У. Я,BМ , * = 0, 1 (8.20с)
Такие формулы существуют и для многих элементарных функций
(по той причине, что в действительности эти функции сами яв-
являются решениями рациональных дифференциальных уравне-
уравнений). Примеры:
с1) г = ехр (р): используем равенство г' = р'г и применим
(8.20Ь). Отсюда получим (при I == 1, 2, ...|
= ехр (Ро), Кг = 1^ С - /) /?/^Ы. (8.20Й)
/=о
е)' г = 1о§ (р): представим формулу как р = ехр (г] и прове-
проведем перестановку в й), откуда следует, что
Л (8.20е)
I) г = ре9 с Ф 1 — постоянная. Используем соотношение
г# = срс~1рй, т. е. рг* = сгр', и применим (8.20Ь):
,1-1
° \/-о
г == соз (р)\ 5 = 51П (р): как и в ё), получим:
= соз Р09 1 ^

/Г' (8.20Й
Попеременное использование (8.20) и (8.18) позволяет нам
очень экономичным способом вычислить коэффициенты ряда
Тейлора для (8.17) до любого требуемого порядка. Нетрудно на-
написать для приведенных формул подпрограммы, к которым надо
обращаться в том же порядке, в каком элементарные операции
входят в дифференциальное уравнение (8.11)\ Существуют и та-
такие программы, которые для / (х, у) «компилируют» операторы
Фортрана в список вызовов подпрограмм. Одну из них написали
Т. Шиманский и Дж. X. Грей [см. работу Кнаппа—Ваннера
A969I.

1.8. Теория существования решения 53
Пример. Дифференциальное уравнение уг = х2 + у2 приво-
приводит к рекуррентным соотношениям
(Р + 2 ^Д 1 01У = у @),
= 7ТТ
где Рг = 1 при I = 2 и Рг = 0 при I Ф 2 — коэффициенты для х2.
Можно представить, насколько это проще, чем формулы (8.12).
Важное свойство данного подхода состоит в том, что его можно
применять в интервальном анализе и получать с помощью остаточ-
остаточного члена ряда Тейлора в форме Лагранжа надежные оценки
погрешности. Более подробно этот вопрос изложен в книгах
Р. Е. Мура A966) и A979).
* «
Упражнения
1. Получите из (8.10) оценку
и объясните, почему этот результат похож на соотношение
G.16).
2. Примените метод Пикара к задаче у' = Ку> у @) = 1.
3. Выполните три последовательных приближения Пикара для
задачи у' = х2 + у2, у @) = 0, у A/2)= ? и дайте строгую оценку
погрешности. Сравните результат с точным решением у A/2) =
= 0.041791146154681863220768806849179.
4. Найдите с помощью метода последовательных приближений
решение задачи
Обратите внимание, что метод может хорошо работать и для
тех уравнений, которые у других методов вызывают серьезные
затруднения. Еще большее различие возникает при решении
уравнений
= 0 и ^
5. Определим / (х, у) следующим образом:
0 при я<!0,
2х при х>0, у<0у
х при
— 2х при х > 0, х2 < у.

54 Гл. 1. Классическая математическая теория
а) Покажите, что / (х, у) непрерывна, но не удовлетворяет
условию Липшица.
б) Покажите, что для задачи у' = / (я, у), у @) = 0 метод по-
последовательных приближений не сходится.
в) Покажите, что существует единственное решение и метод
ломаных Эйлера сходится.
6. Используйте метод последовательных приближений Пикара
для доказательства следующего утверждения:
если / (я, у) непрерывна и удовлетворяет условию Липшица
G.7) в бесконечной полосе п = {(х, у)\ х0 <! х <; X}, то за-
задача Коши у' = / (ху у), у (д;0) = у0 имеет единственное ре-
решение при х0 -< х •< X.
Сравните этот общий результат с теоремой 7.3.
7. Определим функцию у (х) (обратную «интегралу ошибок»)
соотношением
о
Покажите, что она удовлетворяет дифференциальному урав-
уравнению
^ до-
дополучите рекуррентные формулы для ее коэффициентов ряда
Тейлора.

1.9. Теория существования решения
для систем уравнений
Первое обращение к теории существования решений диффе-
дифференциальных уравнений, рассматриваемых совместно, содержится
на последних сохранившихся страницах работы Коши A824).
Используя индексные обозначения, которые еще не были приняты
в те времена, мы запишем уравнения в виде
у[ = /1 (х> Уъ • • -I Уп), Ух (*о) = */ю> У\ С*) =
(9.1)
Уп = /л (X, Г/1, : . ., уп), Уп (хо) = УпО> Уп (X) = ?
и поставим вопрос о существовании п решений уг (х), ..., уп(х).
Поскольку любым заданным функциям ух, ..., уп уравнения (9.1)
ставят в соответствие производные этих функций, естественно
снова рассмотреть по аналогии с G.3) метод Эйлера
Ук, 1+1 = Уы + (Хиг — хг)-?к (хгу у11у ..., упг) (9.2)
Здесь подразумевается, что ук1 аппроксимируют ук (хг), где
х0 < хг < х2 < ... — разбиение отрезка интегрирования, такое,
как в G.2).
Теперь попытаемся перенести все, что мы сделали в разд. 1.7,
на новую ситуацию. Хотя при обобщении оценки G.4) не возни-
возникает проблем, и мы получаем
— хо\, если |/Л(х, д19 . . ., уп)\<Аку (9.3)
но положение несколько осложняется для G.7). Нам надо оценить
. . .> 2п) —}к(х, Ух% . . ч Уп) =
(9.4)
где производные д[к/дуг взяты в подходящих промежуточных точ-
точках. Здесь Коши использовал неравенство, которое он открыл
незадолго до этого и которое теперь называют неравенством
Коши—Шварца 1}. («И наконец, из формулы A3) 11-го урока
по дифференциальному исчислению следует ...».) С его помощью
1} Или неравенством Коши—Буняковского.—Прим. ред.

56 Гл. 1. Классическая математическая теория
получается соотношение
|/ь(х, гъ . .., гп) — !к(ху уъ . .., г/п)|< (9.5)
< (Ш+-+ШТ «* -*»■+••■+<*» - «■>«•■
На этом этапе уже чувствуется, что для дальнейшего развития
теории целесообразно ввести векторные обозначения.
Векторные обозначения
В интересующей нас области эти обозначения были введены
в работах Пеано A888) и A890). Как он сам говорил, на него ока-
оказали влияние знаменитый трактат Грассмана «Учение о протяжен-
протяженности» и исследования Гамильтона, Кели и Сильвестра. Введем
векторы (Пеано называл их «комплексами»)
У=(Уь ...» Уп)т> Уг = (Уи, ■ ■ •> Уш)т> * = («и . - .# *п)т и т- Д'
При этом мы надеемся, что читатель не будет путать компоненты уг
вектора у с векторами, помеченными индексом. Рассмотрим «век-
«векторную функцию» / (х, у) = (/х (х, у), ..., /п (х, у))т1 тогда урав-
уравнения (9.1) примут вид
Уг = / (х, у), у (х0) = г/о, У (X) = ?, (9.Г)
а метод Эйлера (9.2) будет задан формулой
^Уг + (*м — *г)!(х1> Уг)> 1 = 0> 1, 2 и т. д. (9.2')
Теперь обозначения ничем не отличаются от одномерных случаев
G.1) и G.3).
Принимая во внимание оценку (9.5), введем для вектора у =
^ (уи •••> Уп)т норму (в оригинале «модуль»)
\\у1=:(у1+...+у1У<\ (9.6)
которая удовлетворяет всем обычным свойствам нормы, в част-
частности неравенству треугольника
пг
2 Уг
пг
(9-7)
Теперь мы можем записать оценки (9.3) и (9.5) вполне аналогично
G.4) и G.7).
Теорема 9.1. Предположим, что || / (х, у) || <^ А\ тогда для
определенного с помощью {9.2') вектора уг выполняется оценка
\\У1-Уо\\<А\х1-хо\. (9.8)

Если
1.9. Теория существования решения для систем уравнений 57
-< <7ьг» то
(9.9)
где Ь = (ХЯк{У"- (9.10)
Доказательство, Оценка (9.9) получается в результате
возведения в квадрат неравенства (9.5) и суммирования по к =
Оценка (9.9) называется «теоремой о среднем» х). Ее можно
найти во многих книгах по математическому анализу.
Евклидова норма (9Л5) — это не единственная возможная
норма, мы будем также использовать норму
|»| = тах(|й|, ..., \уп\). (9.60
» «
(«Можно было бы также определить тх — наибольшее из абсо-
абсолютных значений элементов х; для него свойства модулей почти
очевидны» (Пеано).) В этом случае, чтобы установить соотноше-
соотношение (9.9), мы оценим (9.4) следующим образом:
Поэтому теорема 9.1 остается справедливой, если заменить (9.10)
выражением
^2). (9.10')
И наконец, если мы хотим использовать норму
то в теореме 9.1 вместо (9.10) надо подставить
Во всех трех случаях мы установили полную аналогию с G.5)
и G.7) из разд. 1.7. Остается только еще раз перечитать разд. 1.7
и 1.8: теоремы 7.2, 7.3, 7.4, 7.5 и 7.6 вместе с доказательствами
и оценки G.10), G.13), G.15), G.16), G.17) и G.18) переносятся
на более общий случай с единственным изменением —вместо аб-
абсолютных величин надо подставить нормы.
1) В русскоязычной математической литературе этот термин используется
в ином смысле, а соотношение (9.9) называют условием Липшица. — Прим, ред.

58 Гл. К Классическая математическая теория
Подчиненные матричные нормы
Обозначим через B матрицу с элементами <7ь*- Определенная
в (9.10') константа, которую мы теперь обозначим через
(9.1 Г)
называется матричной нормой, подчиненной векторной норме
(9.6'). Это наименьшее число, при котором для всех векторов у
справедлива оценка
Ш<№1Ы (9-12)
или, другими словами,
Л <913)
Аналогично в (9.10") входит матричная норма, подчиненная
норме (9.6"), т. е.
(Х! ) (9.11")
Однако выражение (9.10) (которое называется «нормой Шура»)
не подчинено норме (9.6), так как оно, хотя и удовлетворяет (9.12),
но не является наименьшей возможной оценкой, т. е. точной верх-
верхней гранью. В этом случае подчиненная норма задается форму-
формулой
(9.11)
где Хшах — максимальное собственное значение произведения
матриц BТС}. Это можно усмотреть из равенства
так как BТ0, всегда можно привести к диагональному виду с по-
помощью ортогонального преобразования.
Все указанные формулы остаются справедливыми и для ком-
комплексных матриц. Надо только заменить ($Т на ф* (транспониро-
(транспонированная и комплексно сопряженная матрица). Об этом можно
прочитать, например, в книгах Уилкинсона A965) или Бахва-
лова A973), гл. VI, § 3.
Последовательные приближения Пикара для систем
Метод последовательных приближений Пикара также распро-
распространяется на системы, если в (8.7) у1+1 (х), у0 и / E, уь {з)) интер-
интерпретировать как векторы, интегрируемые покомпонентно. Ре-
Результат о сходимости с оценкой (8.10) тоже остается в силе; для

1.9. Теория существования решения для систем уравнений 59
его доказательства надо использовать после (8.8) и перед (8.9)
неравенство
I ь ъ
(9.14)
для векторной функции § (х) = {§г (х), ..., §п (х))т. Соотноше-
Соотношение (9.14) доказывается применением неравенства треугольника
(9.7) к частичным суммам Римана, определяющим оба интеграла.
Метод рядов Тейлора, доказательство сходимости и рекур-
рекуррентное вычисление коэффициентов ряда Тейлора также непосред-
непосредственно обобщаются на системы уравнений.
Упражнения
1. Решите систему
01 = —02, 01@)=- 1,
02 = + 01, 02 @) = 0
методами Эйлера и Пикара, установите точные оценки погреш-
погрешности во всех трех упоминавшихся нормах. Проверьте резуль-
результаты, используя точное решение ух (х) = соз х, у2 (х) = зт х.
2. Рассмотрим дифференциальные уравнения
Г/2 = 01 - ЮОг/2, у2 @) - 0, у2 A) -
а) Найдите точное решение у (х) с помощью метода, изложен-
изложенного в разд. 1.6.
Ь) С помощью G.10) найдите оценку погрешности для
\\г{х) —у (х) ||, где г (х) = 0.
с) Примените к этому уравнению метод Эйлера с шагом Н =
= 1/10.
б) Примените метод последовательных приближений Пикара.
3. Вычислите решение в виде ряда Тейлора для системы с постоян-
постоянными коэффициентами уг = Ау> у @) = у0. Докажите, что
этот ряд сходится при всех х. Используйте его для уравнения
из упр. 1.
Ответ:
00 л
у (*) = 2 тг а'уо = '• еАху°-
1=0

1.10. Дифференциальные неравенства
Дифференциальные неравенства — это изящный инструмент,
который позволяет совершенно по-новому взглянуть на урав-
уравнения G.10), G.17) и лучше понять их. И в этой области начало
исследованиям положила работа Пеано A890), а затем они были
продолжены Перроном A915), Мюллером A926), Камке A930).
Классическим трудом по этому предмету является книга Валь-
Вальтера A970).
Введение
Основная идея состоит в следующем: обозначим через V (х)
ломаную Эйлера, определенную в G.3) или в (9.2); тогда
= /(**> Уг) при хг<х<хм. A0.1)
В произвольно выбранной норме исследуем погрешность
т(х) =№(х)—у(х)\ A0.2)
как функцию от х и, естественно, попытаемся оценить ее рост.
К сожалению, т (х) не обязательно будет дифференцируемой
из-за угловых точек, которые, во-первых, содержатся в ломаной
Эйлера, а во-вторых, порождены нормами, особенно (9.6') и
(9.6"). Поэтому рассмотрим так называемые производные Дини,
определенные следующим образом:
/ ч 1 • т(х + к)—т(х)
(х) = 1ип вир ——[—т —
&>о п
г\ / \ 1 • пг(х -\-Н) — т (х)
О~т (х) = Ьт зир —^—!—г —,
й<0
Н
гч / \ 1 • • г тп (х + к) — т (х)
О+т (х) = Ьт 1п1 —^—^ —
/ \ 1 • - г т (х + Н) — т (х)
„т (х) = Ьт 1п! —1 ^ ' К-+-\
см., например, работы Шеффера A884), Хобсона A921), гл. V,
§ 260, § 280. Свойства
\-\и>(х)[<1ш>(х + к)-»(х)\

1.10. Дифференциальные неравенства 61
являются простым следствием неравенства - треугольника (9.7).
Разделив A0.3) на Н > 0, мы получим оценки
A0.4)
где ю'(х) — правая производная вектор-функции ш (х). Если мы
применим их к т (х) из A0.2), то придем к соотношению
О+т (х) < || V' (х) - у' (х) | = | о' (х) - [ (х, V (х)) + / (х, о (*)),-
- / (х, д (х)) I
из которого, применяя неравенство треугольника и условие
Липшица (9.9), получим, что
И+т (х) < б (*) + Ьт (х). A0.5)
Здесь мы ввели функцию
б (*) = |о'(*) - / (*, * (*))Ь A0.6)
» •
которая называется дефектом г) приближенного решения V (х)-
Эта фундаментальная величина служит мерой того, насколько
функция V (х) не удовлетворяет исходному дифференциальному
уравнению. Неравенство G.11) совместно с A0.1) указывает на,
то, что б (#)<; е, а поэтому мы можем продолжить оценку A0.5).
Я+т (х) < Ьт (х) + 8, т (х0) = 0. A0.7)
Соотношение A0.7) [или A0.5)] называется дифференциальным
неравенством. Вопрос заключается в том, допускается ли замена
знака «О на «=», т. е. можно ли вместо A0.7) решить уравнение
и' = Ьи + е, и (х0) = 0, A0.8)
и сделать вывод, что т (х) <; и (х)? С учетом формул из разд. 1.3
или 1.5 это означало бы, что
т (г\ <? -— (рь (*—*о) П ПО СП
41 ^Л1 <^ Г\ /• \ )
Таким образом, мы получили бы оценку погрешности G.17) есте"
ственным способом и, кроме того, открыли бы изящное и мощное
средство для новых оценок различного рода.
Фундаментальные теоремы
Общая теорема типа
(*> т(х))\
"(Х) A0.10)
при
и(х0)
В отечественной литературе б (*) принято называть нормой невязки исход-
исходного дифференциального уравнения (9.1') для функции V (х). — Прим. ред.

62 Гл. 1. Классическая математическая теория
не может быть верна. Контрпримером может служить любое диф-
дифференциальное уравнение с неединственным решением, скажем
у' — ц (х, у) = у^у, для которого
т(х) = ^-, м(лг)=О. A0.11)
Пеано и Перрон сделали важное наблюдение, позволяющее нам
преодолеть эту трудность. Оно заключается в том, что одно из
первых двух неравенств надо сделать строгим (см. работу Пеано
A890), § 3, лемма 1).
Теорема 10.1. Предположим, что функции т (х) и и (х) не-
непрерывны и при х0 <[ х <! X удовлетворяют условиям
а) п+т (х) < д (х, т (х)),
Ь) О+и(х)Ъ>е(х,и(х)), A0.12)
с) т (х0) < и (х0).
Тогда
т (х) < и (х) при х0 < х < X. A0.13]
Это утверждение справедливо и в том случае, если в а) и Ъ) п+
заменить на О+.
Доказательство. Чтобы можно было сравнивать производные
й+т и О+и в A0.12), рассмотрим точки, в которых т (х) = и {х).
В этом состоит основная идея доказательства.
Если бы A0.13) не выполнялось, мы могли бы выбрать точку х2,
в которой т (х2) > и (х2), и искать первую слева от х2 точку хх%
такую что т (хх) = и (хх). Тогда при малых Н г> 0 будет выпол-
выполняться неравенство
т(хг + Н) — т (хг) и (хг + Ь) — и (хг)
Переходя в нем к пределу, получим соотношение И+т (хх) !>
> п+и (хх). Однако оно противоречит условиям а) и Ь), в силу
которых
п+т {хх) < § (хх, т (хх)) =
Эту теорему можно сформулировать многими способами, на-
например с использованием левых производных Дини [Вальтер
A970), гл. II, § 8, теорема V]. Опираясь на рассуждения из вве-
введения, мы придем к следующему результату.
Теорема 10.2. («Фундаментальная лемма».) Предположим, что
V (х) — приближенное реи> чие системы дифференциальных у рае-

1.10. Дифференциальные неравенства 63
нений у' = / (я, у), у (хд) = у0, которое удовлетворяет следующим
условиям:
а) |V (х0) ~ у (хоу|<р,
Ь) IIV (х) - / (х, V (х)) I < 8,
с) |/(*,о)-/(*,4г)|</.|о-у|.
Тогда при х ^ х0 справедлива оценка погрешности
^ - 1).
Замечание. Два члена в A0.14) выражают влияние на погреш-
погрешность приближенного решения погрешности р в начальных зна-
значениях и невязки е соответственно. Это соотношение означает
непрерывную зависимость погрешности от обеих величин и един-
единственность решения, поскольку у (х) = V (х) при р = е = 0.
Доказательство. Положив " т (х)'= \\ у (х) — V (х) ||, как и
в A0.7), получим
п+т (х) <; Ьт (х) + е, т (#0) <; р.
Попытаемся сравнить это неравенство с дифференциальным урав-
уравнением
и' = Ьи + е, и (;0) = р. A0.15)
Теорему 10.1 непосредственно применить к этому случаю нельзя.
Поэтому в A0.15) заменим 8на8 + ц,д>0и решим другое урав-
уравнение:
и' = Ьи + е + Л > 1-й + е, и (х0) = р.
Теперь теорема 10.1 дает оценку A0.14), где вместо г стоит е + т].
Поскольку эта оценка справедлива при всех а *> 0, она выпол-
выполняется и для я = 0. ■
Другая формулировка теоремы 10.2. Из условий
а) || V (х0) — у (х0) || < р,
ь) КМ-/(*.*(*))!<«(*),
следует, что при х ^ х0 имеет место оценка
II У(х)-г>
(з)
= | / E)
Доказательство. Достаточно применить формулы C.3). ■
Теорема 10.3. Если функция § (х9 у) непрерывна и удовлетво-
удовлетворяет условию Липшица, то импликация A0.10) справедлива для
непрерывных функций т (х) и и {х).

64 Гл. 1. Классическая математическая теория
Доказательство, Определим функции хюп (х), ип (х) как ре-
решения начальных задач
®'п (х) = § (х, тп (х)) + —, шп (х0) = т (хо)у
К (х) = б" (х, 0П (х)) - -р 0П (х0) = и (*0).
Тогда по теореме 10.1
т(х)<шп(х), Vп(x)^и(x) при хо<х<Х. A0.16)
Из теоремы 10.2 следует, что функции хюп (х) и Vп (х) сходятся
при п->оо к решениям уравнений
™' {А = ё (х, су (х)), т (х0) = т
о' (х) = ё (*, о (х)), у (хь) = и
так как дефект равен ±\1п. И наконец, вследствие неравенства
т (Хо) <^ и (^о) и единственности решений мы придем к соотно-
соотношению до (х) < у (х). Переходя в A0.16) к пределу при п-> оо,
мы получим, что т (х) ^С и (х). Ш
Можно еще больше обобщить теорему 10.2, если заменить
условие Липшица Ь) некоторым нелинейным выражением типа
, у)\<а(х9 №-
Тогда дифференциальное неравенство для догрешности т (х)
надо сравнивать с решением уравнения
и' = со (х, и) + 6 (х) + а, и (х0) = р, я > 0.
Более подробно этот вопрос изложен в работе Вальтера A970),
гл. Ц, § 11.
Оценки с использованием односторонних условий
Липшица
В упр. 2 из разд. 1.9 мы уже отметили давно известный факт,
что при использовании в оценках G.16), G.17) или G.18) положи-
положительных констант Липшица Ь (например (9.10), (9.10'), (9.10"))
можно упустить мне)го информации о погрешностях. Все оценки
растут экспоненциально по х9 даже если решения и погрешности
затухают. Поэтому было предпринято много усилий для улучше-
улучшения оценок погрешности, как, например, в статьях Эльтерманна
A955), Ульманна A957), Далквиста A959) и в работах, на которые
ссылаются эти авторы. Мы с большим удовольствием будем сле-
следовать особо ясному изложению этого вопроса в работе Далк-
Далквиста.

1.10. Дифференциальные неравенства 65
Оценим производную функции т (х) = | V (х) — у (х) \\ бо-
более тщательно по сравнению с A0.5): при к > 0 с использованием
A0.6) и (9.7) мы получим
-/(*, у(х)))
Теперь, применив к функции у Л- к] (х, у) формулу Коши для ко-
нечных приращений, придем к неравенству
:* 0)
из которого окончательно получим д#я к > 0
т (х + к) — т (х) ^ / + Л -^ (*, п) — 1
1 у тах •
+ 0 (к). ~ A0.18)
Выражение в правой части A0.18) приводит нас к следующему
определению.
Определение 10.4. Пусть 0. является квадратной матрицей.
Назовем выражение
-*0, Л>0 Л
логарифмической нормой С}.
Приведем далее формулы для ее вычисления [Далквист A959),
Эльтерманн A955)].
Теорема 10.5. Логарифмическая норма A0.19) получается по
следующим формулам: для евклидовой нормы (9.6)
у (О) = ХтйХ = наибольшее собственное значение матрицы
(<2г+<2) A0.20)
Для тах-нормы (9.6')
ц (<2) = тах ('^ + I] | дк1 \) # A0.20')
Для нормы (9.6я)
@) - тах ^и + а2 19м 1). (Ю.20#)
3 Хайрвр 9. и др.

66 Рл, 1, Классическая математическая теория
Доказательство. Соотношения A0.20') и A0.20") являются
почти тривиальным следствием формул (9.1 Г), (9.1 Г) и опреде-
определения A0.19). Дело в том, что присутствие единичной матрицы /
подавляет при достаточно малых Н абсолютные величины диаго-
диагональных элементов. A0.20) следует из того факта, что собственные
значения матрицы
(/ + кЦУ (I + НО) = I + И @Т +0) + к^тЯ
при к ->• 0 сходятся к 1 + ЬХ^ где %1 — собственные значения
матрицы О7 + ф. ■
Замечание. Для комплекснозначных матриц приведенные выше
формулы принимают вид:
[х (B) = наибольшее собственное значение матрицы у {0* + 0),
1ФН
Яы\).
)
С помощью неравенства A0.18) можно весьма существенно уси
лить теорему 10.2.
Теорема 10,6. Предположим, что справедливы оценки
(^ ) при г\$[у(х), V(x)]
и
К (*)-/(*, у(х))||<6(х), №(хо)-у(хо)\\<Ср. A0.21)
Тогда при х > х0 выполняется соотношение
р + |е-*<'>6(з)&), (Ю.22)
X
где Ь (х) = / E) д&.
Доказательство. Поскольку при фиксированном х отрезок
[с; (л;), у (х) ] является компактным, величина
К = тах тах -р-
конечна. Тогда (см. доказательство теоремы 10.5) выполняется
соотношение
, и)) + <2 (Л),

1.10. Дифференциальные неравенства 67
где член О (К) равномерно ограничен по г). (Для норм (9.6') и
(9.6") этот член в действительности равен нулю при К < 1/К-)
Таким образом, подстановка условия A0.21) в A0.18) дает нера-
неравенство
й+т (х) -< / (х) т (х) + б (х).
Теперь оценка A0.22) получается тем же способом, что и в тео-
теореме 10.2.
Упражнения
1. Примените теорему 10.5 к примеру из упр. 2 в разд. 1.9. Обра-
Обратите внимание на значительное улучшение оценок.
2. Докажите следующее утверждение (одна из формулировок
знаменитой «леммы Гронуолла», Гронуолл A919)): предполо-
предположим, что положительная функция т (х) удовлетворяет нера-
неравенству
х
[ т ($) (к=1 хл)(х). A0.23)
Тогда имеет место оценка
т (х) < ре** <*-**> + -- (г1 <*-*•> - 1). A0.24)
Примените при доказательстве:
а) прямой способ, вычитая из A0.23) равенство
х
и (х) = р + в (х — л:0) + ^ \ и E) <&\
Ъ) дифференцирование т (х) в A0.23) и теорему 10.1.
с) Докажите теорему 10.2 с помощью приведенной выше леммы
Гронуолла. Такие же взаимосвязи имеются, конечно, и в бо-
более общих случаях.
3. Воспользовавшись примером
Ух = #2, у'ч — —уи
установите, что распространение теоремы 10.1 на системы
дифференциальных уравнений первого порядка при покомпо-
покомпонентной интерпретации неравенств в общем случае неверно
[Мюллер -A926)]. Однако такого рода обобщение теоремы
10.1 можно доказать при дополнительном предположении
о квазимонотонности функций $г (х, уъ ..., уп), т. е. при ус-
условии
, Уъ • • •» Уз, • • -» УпЖёг (х> Уг> • • •> гз> • • •> Уп)>
если у} < 2у при всех / Ф I.

68 Гл. I. Классическая математическая теория
Попытайтесь доказать это.
Важно отметить, что многие системы, полученные из пара-
параболических дифференциальных уравнений, вроде F.10), дей-
действительно квазимонотонны. Поэтому изложенные в данном
разделе идеи допускают много интересных применений [см.
работу Вальтера A970), гл. IV].
4. Докажите следующие свойства логарифмической нормы:
а) \1 (а<2) = а\х (<?) при а >- 0,
б) ~
в)
г)
5. Для евклидовой нормы \1 (О) A0.20) является наименьшим
числом, удовлетворяющим неравенству
Данное свойство справедливо для всех норм, порожденных
скалярным произведением. Докажите это.
6. Покажите, что для эвклидовой нормы условие A0.21) экви-
эквивалентно неравенству

1.11. Системы линейных дифференциальных
уравнений
Приобретенные знания о существовании и единственности ре-
решений и сведения из линейной алгебры помогут нам, как и мате-
математикам XIX века, лучше понять многие вопросы, касающиеся
линейных дифференциальных уравнений высокого порядка, ко-
которые остались не вполне выясненными в разд. 1.4 и 1.6.
Уравнение D.9) в результате деления на ао(х) (Оо(х)ф0
вне особых точек) принимает вид
A1.1)
У™ + аг (х
...+ап{х)у = 1 (х).
Вводя переменные у = уъ у' = у29 ...,
чим
/Уг\ ( 0 1
О О
: 1
■ • . *
\Уп/
\—ап(х) —ап_1(х) ... —ап{х))
Уг
\Уп/
уп, мы полу-
полу/ о \
о
о
V/ (*)/
A1.1')
Как и в разд. 1.9, обозначим через у вектор (у19 ..., уп)т', а через
( (х) — неоднородную часть. Тогда A1.1') будет частным случаем
системы линейных дифференциальных уравнений общего вида
A1.2)
у' = А (х) у + ! (х),
А(х) = (аи(х)), / (*) = (М*))> I, /=1
К ней можно непосредственно применить теоремы из разд. 1.9
и 1.10. Поскольку частные производные правой части A1.2)
по уг равны ам (х), выполняется оценка Липшица (см. условие (с)
из второй формулировки теоремы 10.2), где / (х) = || А (х) \\
в любой подчиненной матричной норме [(9.11), (9.1 Г), (9.1 Г)].
Применим теорему 7.4 и вторую формулировку теоремы 10.2,
где в качестве «приближенного решения» возьмем V (х) — 0.
Мы можем также выбрать / (х) = \х (А (х)) [см. A0.22), A0.22'),
A0.22")] и использовать теорему 10.6.
Теорема 11.1. Пусть А (х) непрерывна на отрезке [х0> Х\.
Тогда при любых начальных значениях у0 = (у10, ..., уп0)Т су-
существует единственное решение системы A1.2) для всех х0 •<

70 Гл. I. Классическая математическая теория
х < X, и оно удовлетворяет оценке
У
X
A1.3)
или / (х) - у (А (х)).
При / (х) = 0 решение у (х) линейно зависит от начальных зна-
значений, т. е. существует матрица К (х> х0) («резольвента»), та-
такая что
у (х) = К (х, х0) у0. A1.4)
Доказательство. Поскольку / (х) непрерывна и поэтому огра-
ограничена на любом компактном отрезке [хОу X], оценка A1.3)
показывает, что решение можно продолжить до конца отрезка.
Линейная зависимость следует из того факта, что при / = 0
линейные комбинации решений снова будут решениями, и из
единственности решения. ■
В силу единственности решения с начальными условиями у0
в х0 и уг = /? (х1у х0) у0 в хх должны совпадать. Поэтому при
х0 < хх <; х2 справедливо равенство
# (*2> *о) = ^ (^2» хх) ^ {х19 х0). (П.5)
*
И наконец, проинтегрировав назад от хъ ух, т. е. выполнив пре-
преобразование координат х = хг — I, 0 <; I <; хх — х0, мы должны
прийти, снова вследствие единственности, к начальным значе-
значениям. Таким образом,
Я (*0,*1) = (Я (*1, *о))-\ (П.6)
так что A1.5) справедливо и в общем случае.
Матрица Вронского (вронскиан)
Рассмотрим ух (х) = (уи (х), ..., уп1 (х))Т (I = 1, ..., п) — мно-
множество п решений однородного дифференциального уравнения
У' =А(х)у9 A1.7)
которые в точке х = х0 являются линейно независимыми (т. е.
образуют фундаментальную систему). Составим матрицу Врон-
Вронского [Вронский A810)]
Уи (*) • • • Ут (х)\
УтМ (X) ... Упп (X)/

1.11. Системы линейных дифференциальных уравнений 71
Тогда
ТГ (х) = А (х) МУ (х),
а любое решение можно записать в виде
(х) Н ЬСпУп(х) = V? (х)-с, где с = (сг, ..., спO'. A1.8)
Если это решение должно удовлетворять начальным условиям
У (#о) = */о> т0 мы получим с = И?" (х0) */0 и формулу
(П.9)
Таким образом, если найдено п линейно независимых решений,
то и все решения известны. Однако в общем случае при непостоян-
непостоянной матрице А (х) почти ничего не известно о том, как их построить.
Тождество Абеля —Лиувилля —Якоби —Остроградского
Из A1.6) уже видно, что 47 (х) остается регулярным при всех х.
Теперь покажем, что определитель № (х) можно задать явно сле-
следующим соотношением:
(х) = ае* {У? (х0)).ехр И Тг (А
Тг (Л (х)) = а1Х (х) + а22 (х) + ... +
+ апп(х), A1.10)
которое связывает определитель У7 (х) со следом матрицы А
[Абель A827), Лиувилль A838), Якоби A845), § 17].
Для доказательства (см. также упр. 2) мы найдем производ-
производную -зрйе! (И? (х)). Поскольку йе! (№ (х)) — полилинейная форма,
ее производная (по правилу Лейбница) является суммой п членов,
первый из которых равен
/Уп Ум
. , У 21 У 22
х = аех
\Уп1 Уп2
Подставим сюда у'и = ацуи + ... + а\пУп1 в соответствии
с A1.7). Члены а12у2г9 ..., а1пупг исчезают, так как они кратны
строкам со 2-й по л-ю. Поэтому 7\ = ап йе! (ЧУ (х)). Сложив
все Тгу мы окончательно получим формулу
(х)) = (ап(х)+ ... +апп(х)).йе1(]Р (х)), A1.11)
проинтегрировав которую, придем к A1.10).

72 Гл. 1. Классическая математическая теория
Неоднородные линейные уравнения
Обобщив идеи Йог. Бернулли для C.2) и Лагранжа для
D.9), мы теперь найдем решение неоднородного уравнения A1.2)
посредством «вариации» постоянной с, т. е. сделав с «переменной»
в «общем решении» A1.8) однородного уравнения у (х) = № (х)Х
X с (х) [Лиувилль A838)]. Точно так же, как в разд. 1.3 для
C.2), из A1.2) и A1.7) с помощью дифференцирования мы полу-
получим
Следовательно, сг = Ц?"*1/- В результате интегрирования, взяв
постоянные интегрирования с, мы придем к равенству
Из начальных условий у (х0) == д0 определим о = ЧУ*1 (х0) у0.
Итак, мы получили следующий результат.
Теорема 11.2. («Формула вариации постоянных».) Пусть А (х)
и ? (х) являются непрерывными. Тогда отвечающее начальным ус-
условиям у (х0) = у0 решение неоднородного дифференциального
уравнения у' = А (х) у + / (х) вычисляется по формуле
Уо
+1 V-1 (в) I E)
хо)уо+ ^К(х, $)!{8)с1з. A1.12)
Упражнения
1, Найдите резольвентную матрицу /? (х, х0) для систем
а) у[ = уи Ь) У1 = у2,
у 2 = 3^2, у 2 = — т
и проверьте справедливость соотношений A1.5), A1.6), а
также A1.10).
2. Восстановите оригинальное доказательство Абеля для A1.10),
которое относилось к случаю
Ух + РУ\ + ЯУ\ = 0,
для этого надо умножить уравнения на у« и ух соответственно
и вычесть одно из другого, чтобы исключить д. Затем проин-

1.И. Системы линейных дифференциальных уравнений 73
тегрируйте полученное равенство и используйте результат
для вывода тождества, связывающего два интеграла,
СО ОО
(а) = ^е0*-*9*1-1 ах и у2 (а) -
о о
каждый из которых удовлетворяет уравнению
Указание. Для проверки A1.13) проинтегрируйте от нуля до
бесконечности выражение -^ (ехр {ах — х2) ха) [Абель A827),
случай IV].
3. [Куммер A839I Покажите, что общее решение уравнения
(*) = *ту (*) A1.14)
можно получить в квадратурах.
Указание. Дифференцирование A1.14) дает
Для нахождения рекуррентного соотношения предположим
что общее решение уравнения
(хи), A1.16)
уже известно. Покажите, что тогда функция
ОО
а
является общим решением уравнения A1.15), а при некоторых
условиях на параметры — и A1.14). Для того чтобы упростить
расчеты, рассмотрите функцию
найдите производную по и, умножьте ее на хт—1 и проинтегри-
проинтегрируйте от 0 до бесконечности.
4. (Слабые особенности в системах.) Покажите, что линейная
система
1 A1.17)

74
Гл. 1« Классическая математическая теория
имеет решения вида
у (х) =
V1x
V2x
A1.18)
где 0О, юъ ... — векторы. Определите сначала р и я0, а затем
рекурсивно х>г9 V2 и т. д. (Убедитесь, что существует п неза-
независимых решений вида A1.18), если собственные значения Ао
удовлетворяют условию Х{ Ф \/ ш0& (^У1) [Фукс A866)].)
5. Найдите общее решение систем со слабой особенностью
\
1 мУ и г/'= !
■амн
4
1
■им*
X
\
4
1
4
3
4
1
\
1
4
1
•«■мам
4
Указание. Первую систему легко решить на основании упр. 4,
а для второй требуются дополнительные приемы (см. формулу
E.6)). Возможен и другой способ: использовать преобразова-
преобразование х == е\ у (х) = г (г) и применить методы из разд. 1.12.
х) Т. е. разность Х$ —- X/ не равна целому числу. — Прим. ред.

1.12. Системы с постоянными коэффициентами
«Техника интегрирования линейных дифференциаль-
дифференциальных уравнений с постоянными коэффициентами развита
здесь на самом высоком уровне.»
(Примечание Ф. Клейна в книге Рауса A898))
Линеаризация
Системы линейных дифференциальных уравнений с постоян-
постоянными коэффициентами образуют класс уравнений, для которых
резольвенту 7? (х, х0) можно вычислить явно. Обычно они встре-
встречаются при линеаризации независящих от времени (т. е. авто-
автономных, или перманентных) нелинейных дифференциальных урав-
уравнений
#* = Ы*/ъ --->Уп) или у1^!ь{уъ ччУп) A2.1)
в окрестности стационарной точки [Лагранж A788), см. также
работы Рауса A860), гл. IX, Томсона и Тейта A879I. Выберем
координаты таким образом, чтобы эта стационарная точка попала
в начало координат, т. е. выполнялось равенство /* @, ...,0) == 0.
Затем разложим /* в ряд Тейлора, пренебрегая всеми нели-
нелинейными членами:
ж или
к к
Эта система уравнений с постоянными коэффициентами, введен-
введенная в разд. 1.6 (см. F.3), F.11)):
у' = Ау или у" = Ау. A2.1")
Автономные системы инвариантны относительно сдвига х-*х + С.
Поэтому мы всегда можем предполагать, что х0 = 0. Для произ-
произвольного х0 резольвента задается формулой
И (*, х0) = /? (х — х0, 0). A2.2)
Приведение к диагональному виду
В разд. 1.6 мы уже видели, что из предположения у (х) =
= пе следует равенство
АV = XV или Аь = А,20, A2.3)
и поэтому V Ф 0 должен быть собственным вектором А, а X —
соответствующим собственным числом (в первом случае, а во вто-

76 Гл. 1. Классическая математическая теория
ром случае, который мы больше не будем рассматривать, — ква-
квадратным корнем из собственного числа). Из A2.3) следует, что
такой вектор V Ф О существует тогда и только тогда, когда опре-
определитель, который называется характеристическим многочленом
матрицы Л, равен нулю:
%А (X): = с1е1 (XI - А) =
= (X — Хг) (X — Х2) ... (X — Хп) = 0. A2.4)
Теперь предположим, что для п собственных значений Хг
можно выбрать п линейно независимых собственных векторов я*.
Тогда из A2.3) мы получим равенство
А (#102 • • • уп) == 0^2 • • • Уп) сИа§ (Хг, Х2, ..., Хп),
или
если через Т обозначить матрицу, столбцами которой являются
собственные векторы А. При сравнении A2.5) с A2.Г') мы видим,
что дифференциальное уравнение значительно упрощается за
счет использования преобразования координат
д (х) = Тг (х), д' (х) = Тг' (х), A2.6)
которое приводит систему к виду
г' (х) = сНа§ (Хъ Х2, ..., Хп) г (х). A2.7)
Таким образом, исходная система дифференциальных уравнений
распадается на п скалярных уравнений, для которых легко найти
решение
г(х) = сНа^(ехр {Ххх), ехр {Х2х)> ..., ехр (Хпх)) г^
откуда с помощью A2.6) определяется
у (х) == Т сНа§ (ехр (Хгх), ехр (Х2х), ...,
ехр \Л'Пх)) *х у$. \1^1,о)
Разложение Шура
«Бег Ве^е!з !з1 1е!сЫ ги
«Это легко доказать.»
(Шур, 1909)
Предыдущая теория, какой бы красивой она ни казалась,
имеет несколько недостатков:
а) не все яхя-матрицы имеют п линейно независимых соб-
собственных векторов;
Ь) даже если исходная матрица обратима, матрица Т может
иметь очень плохое поведение (см. упр. 1).

1.12. Системы с постоянными коэффициентами
77
Однако, как утверждает классическая теория, симметричные
матрицы А всегда можно привести к диагональному виду с по-
помощью ортогональных преобравований. Следуя работе Шура
A909), обобщим эту классическую теорию на несимметричные
матрицы. Вещественная матрица ^ называется ортогональной,
если ее столбцы являются попарно ортогональными векторами
с нормой 1, т. е. если С}Т0. = / или BТ = О.—1. Комплексная ма-
матрица ^ называется унитарной, если ($*С} = / или С* = С},
где B* — сопряженная матрица для B, т. е. транспонированная
и комплексно сопряженная.
Теорема 12.1.
а) (Шур) Для каждой комплексной матрицы А существует
унитарная матрица 0., такая что
X
X . • •
X ..
X >
X
\
A2.9)
Ь) [Уинтнер—Мурнаган A931I Для вещественной матрицы А
можно выбрать вещественную и ортогональную матрицу ф,
если для каждой пары комплексно сопряженных собственных зна-
значений %Л Л = а ± ф можно заменить блок
% Х\ /XX
на
\Х X
Доказательство, а) Матрица А имеет по крайней мере один
собственный вектор с собственным значением %г. Используем этот
нормированный вектор в качестве первого столба матрицы AХ.
Ее остальные столбцы выбираются произвольно среди векторов,
дополняющих первый столбец до ортонормированного базиса.
Тогда
A2.10)
к (п — 1)-мерной матрице А и
Далее применим тот же прием
придем к соотношению
!
0
\
X ... X \
X ... X
XV

78
Гл. 1. Классическая математическая теория
С помощью унитарной матрицы
/ПО
\
получим
М х
/\ . . .
/\ » • .
/\ . . .
Л • • •
X
X
X
X
Продолжение этого процесса в итоге приведет нас к треугольной
матрице типа A2.9), причем ф = ^1^2 ... фп_х.
Ь) Пусть А — вещественная матрица. Если Хх — веществен-
вещественное число, то в качестве (^ можно выбрать вещественную и орто-
ортогональную матрицу. Теперь предположим, что Хх = а + *Р (Р ф
Ф 0) — невещественное собственное число с соответствующим
собственным вектором и + ш, т. е.
А (и± IV) = (а ± ф) (и ± ш) A2.11)
или
, Аи == $и + аи. A2.1Г)
Поскольку Р Ф О, и и V линейно независимы. Выберем ортого-
ортогональный базис й, б в подпространстве, натянутом на и и V, и возь-
возьмем йи йв качестве первых двух столбцов ортогональной матрицы
Тогда из A2.1 Г) следует, что
X ... Х\
X X
X X
\
о
X
X
А
Сам Шур не придавал большого значения «своему» разложе-
разложению, он просто вывел его как средство для доказательства ин-
интересных свойств собственных значений (см., например, упр. 2).
Ясно, что при вещественной и симметричной А матрица 07АО.
тоже будет симметричной, а поэтому диагональной (см. также
упр. 3).
Численные расчеты
Приведенное выше теоретическое доказательство не слишком
полезно практически: оно требует знания собственных значений,
а их вычисление из характеристического многочлена является

1.12. Системы с постоянными коэффициентами
79
одной из хорошо известных глупостей в численном анализе.
При разумном применении численного анализа идут по другому
пути:, вещественную матрицу А сразу приводят сначала к форме
Хессенберга, а затем с помощью последовательности ортогональ-
ортогональных преобразований — вещественной форме Шура, предложен-
предложенной Уинтнером — Мурнаганом ((ЗК-алгоритм Фрэнсиса, реализо-
реализованный в виде программы Мартином, Петерсом и Уилкинсоном,
алгоритм II/14 в книге Уилкинсона—Райнша A970)). Тогда соб-
ствецные значения получаются без дополнительных усилий.
Однако программа, названная «Н(ЗК2», не дает форму Шура для Л,
так как она продолжает работу до нахождения собственных
векторов. Поэтому надо произвести некоторые действия, чтобы
прервать программу в нужный момент (например, в версии Н<ЗК2
на Фортране из сборника Эйспак A974) в операторе с меткой 60
надо заменить «340» на «1001»). Счастливые обладатели пакета
«МаИаЬ» просто вызывают процедуру ЗСНиК.
Когда форма Шура найдена, преобразование у (х) = фг (х),
у'(х) = 0.г'(х) [см. A2.6I приводит к системе
гп
п-1, п
I
A2.12)
Для ее последнего уравнения г'п = Х^п можно найти решение
гп = ехр (Хпх) гп0. Далее, уравнение для гПшт1 имеет вид
A2.12')
где гп известно. Это линейное уравнение (неоднородное, если
п_ип Ф 0), которое можно решить с помощью метода Эйлера,
изложенного в разд. 1.4. Здесь возможны два случая:
а) если %п_1 Ф Хп, то представим гп-1 в виде гп-\ =
{Х) Р (к) A2')
п р п
= Е ехр {Хп-гх) + Р ехр (кпх), подставим эту формулу в A2.12')
и сравним коэффициенты. В результате получим: Р =
= &П-1, п^поКК — К-г) и Е == 2п-1,0 — Р*
Ь) Если Хд.1 == Хп, то будем искать гп„\ в виде гп^ = (Е +
+ Рх) ехр (Хпх) и получим Р == Ьп_1уПгп0 и Е = гп.1>0.
На следующем этапе, действуя по той же схеме, найдем гп_2
и т. д. Для элементов резольвенты в случае 'к1 Ф К]- можно полу-

80
Гл. 1. Классическая /математическая теория
чить простые рекуррентные формулы [Парлетт A976)]. Предполо-
Предположим, что
п
*| (*) = 2 Ег] ехр (^х),
и подставим это выражение в A2.12). Из сравнения коэффициен-
коэффициентов мы получим для г = п, п — 1, п — 2 и т. д. следующие зна-
значения:
Н =21,0 —
Каноническая форма Жордана
«Проще, чем вы думали». (Американский математи-
математический журнал, 1980)
Если мы, как и многие математики, не будем чураться плохо
обусловленных матриц (см. упр. 1), то полученную выше форму
Шура мы сможем и дальше преобразовать к знаменитой жорда-
новой канонической форме.
Теорема 12.2. [Жордан A870), книга вторая, § 5 и 6] Для
любой матрицы А существует невырожденная матрица Т, такая9
что
1\
1
К)
1
, A2.14)
(Блоки могут иметь разную размерность, а *кг не обязательно
различны.)
Доказательство. [Флетчер—Соренсен A983)] Мы можем счи-
считать, что матрица уже имеет форму Шура. Можно, конечно, также
считать, что одинаковые собственные значения располагаются
рядом на главной диагонали.
Следующий шаг состоит в том, чтобы убрать все ненулевые
элементы, не принадлежащие верхним треугольным блокам,

1.12. Системы с постоянными коэффициентами
81
содержащим одинаковые собственные значения. Продемонстри-
Продемонстрируем эту процедуру на следующем примере: пусть Хг Ф Х2 и
А =
V
Наша задача — найти такую матрицу преобразования, чтобы
исчезли Ь, с, Л и е. Будем искать ее в виде
К а \
Ь с
й е
К!
Л/2
/
0
Р <7'
г $
\ А
—
/
•
0
р я'
г з.
I
4
%! а
1
! о о "
0 0
К !
К)
Все элементы сц этих матриц уже совпадают, за исключением
правого верхнего блока 2x2 (I = 1, 2 и / = 3, 4). Перемножая
матрицы, получим Ххр + аг + Ь = к2р, %гг + А == Х2г и анало-
аналогичные уравнения для ди5. Матрицы этих систем имеют треуголь-
треугольную структуру, и, поскольку Хг Ф Х2у легко найти гир, а затем
5 и ц. Теперь ясно, что нужно делать в более общей ситуации (по-
(попытайтесь построить пример!).
На последующих шагах мы обрабатываем оставшиеся блоки
раздельно. Таким образом, мы предполагаем, что все диагональ-
диагональные элементы блока равны, и рекурсивно преобразуем блок
к форме, указанной в утверждении теоремы.
Будем считать, что матрица А имеет вид
А
I а
О I
и в качестве индуктивного предположения примем, что Аг можно
привести к жордановой форме с помощью матрицы 7\. Тогда
выполняется равенство
\Тг.
о
о
к 1
X

82
Гл. 1, Классическая математическая теория
где вектор Ъ имеет значение Ь =? Т\ а. Затем стоящую справа
матрицу можно упростить следующим образом:
\х\
0
0
:|
X 1
X
1
с?3» • •
X..
1
К о
1
1
1°
/
1
Ь2 0
1
1
0'
/
ч
0
0
•
•
&! 0
X 1
X
X...
Здесь мы будем различать два случая:
а) Ь{ = 0. Тогда мы поменяем местами первую пару (блочных)
строк и столбцов и снова получим индуктивное предположение.
Ь) Ъг Ф 0. В этом случае для замены Ъг на 1 используем масшта-
масштабирующую диагональную матрицу (упр. 4). Наша последняя
задача — убрать 68» &4> ••• • Эти члены выталкиваются вправо
следующим образом:
X 1
X 1
3
/
0
-ь,
0
1
0
0
-Л
0
0
1
/
0
-ь,
0
1
0
0
0
0
1
X
1
X
1
X
X
Ьв
1
X
и т. д. Чтобы с помощью такой процедуры окончательно изба-
избавиться от всех Ъи мы должны предположить, что первый блок не
меньше последующих. Это упорядочение надо провести в начале
с помощью перестановок*

1.12. Системы с постоянными коэффициентами
83
Произведением матриц всех этих преобразований и будет
матрица Т из A2.14). ■
Следствие 12.3. Для любой матрицы А и любого числа е Ф О
существует невырожденная матрица Т (зависящая от е), такая что
Т~гАТ =
(К
л
8 \
. 8
К/
К е\
К)
A2.14')
Доказательство. Умножьте уравнение A2.14) справа на ма-
матрицу Э = сНа§ A, е, е2, е3, ...), а слева — на Ь. ■
Численные трудности, возникающие при определении жорда-
новой канонической формы, описаны в работе Голуба—Уилкин-
сона A976). Для этой цели создано несколько программ, например
программа, описанная в статье Когстрёма—Руэ A980).
Когда матрица А приведена к жордановой канонической
форме A2.14), решение дифференциального уравнения у' = Ау
можно вычислить с помощью метода, изложенного в связи
с A2.12'), случай Ь):
у (х) = ТОТ^уо, A2.15)
где О — блочно-диагональная матрица с блоками вида
к I
Это обобщение формулы A2.8).
Геометрическое представление
На рис. 12.1 представлены геометрические формы решений
системы у' = Ау размерности п = 2. Они изображены в виде
траекторий в фазовом пространстве (у19 у^). Случаи а), Ь), с) и е)
относятся к уравнениям, полученным при линеаризации A2.16)
в четырех критических точках (см. рис. 12.2).
Многое в их структуре сохраняется и для нелинейных систем
A2.1) в окрестности точек равновесия. Исключение могут состав-
составлять «структурно неустойчивые» случаи, как, например, при

84
Гл. 1. Классическая математическая теория
а)
1
0
г
1
0
1
2
0
1
Ь)
1
0
1/3
1
1
1 у
1/3
0
^
с)
А)
Рис. 12.1. Решения линейная двумерны» систем.
1/3
2
1/6
2
-1/3
0
-1/3
-1/6
Рис. 12.2. Потон решений системы A2.16).

1.12. Системы с постоянными коэффициентами
85
наличии комплексных собственных значений, у которых а =
= Ке (к) = 0. По этому вопросу написано много статей, где
обсуждаются «критические» или «особые» точки (см., например,
знаменитый труд Пуанкаре A881, 1882, 1885)).
На рис. 12.2 мы показали решения квадратичной системы
у!
У2 =
У2)(Л — У1—У2),
у2),
A2.16)
которая имеет четыре критические точки всех четырех возможных
структурно устойчивых типов (упр. 4).
Упражнения
1. а) С помощью решения уравнений (А —%,г1) VI ~ 0 найдите
собственные векторы матрицы
А
—1 20
—2 20
—3 20
19 20
—20
A2.17)
Ответ, ч - A, 0, ...)Г> о, - A, —1/20, 0, ...)Г, о3 — A,
—2/20, 2/400, 0, ...)Г, о4 = A, —3/20, 6/400, —6/8000, 0, ...)г
и т. д.
Ь) Численно найдите матрицу, обратную кГ = (ю19 02> •••> °п)»
и определите ее наибольший элемент (ответ: 4.5Х1012). Таким
образом, матрица Т очень плохо обусловлена.
с) Найдите численно или аналитически из A2.13) решения
системы
Ау, у% @) « 1, I « 1, ..., 20.
A2.18)
Обратите внимание на наличие «горба» [Молер и ван Лоан
1978I: хотя все собственные значения А отрицательны, реше-
решения сначала очень сильно растут и только после этого зату-
затухают, стремясь к нулю. Это типично для несимметричных
матриц и связано с плохой обусловленностью Г. (См. рис. 12.3,
где решения показаны в логарифмическом масштабе (!).)

86
Гл* !• Классическая математическая теория
Ответ.
л—20*
— е
19
,й- A + 20) 20*§
18 1
17 !
Рис. 12.3. Решения уравнения A2.18) с мат-
матрицей A2.17).
2. (Шур.) Докажите, что собственные значения матрицы А удо
влетворяют оценке
2
и равенство выполняется тогда и только тогда, когда А при-
приводится к диагональному виду с помощью ортогонального
преобразования (см. также упр. 3).
Указание. 2 1аг/|2~ это слеД матрицы Л*Л, т. е. инвариант
унитарных преобразований
3. Покажите, что разложение Шура 5 = <2*Л<3 имеет диагональ-
диагональный вид тогда и только тогда, когда А*А — АА*. Такие ма-
матрицы называются нормальными.
Указание. Это условие эквивалентно равенству 5*5 = 55*.
Покажите, что кососимметричные матрицы являются нор-
нормальными.

1.12. Системы с постоянными коэффициентами
87
4. Пусть задано Ь Ф 0. Определите такое а, при котором выпол
няется равенство
X Ь\ /1 0\ /1 0\ /X 1
[ [ [
5. Найдите четыре критические точки системы A2.16) и для
каждой из них — собственные значения и векторы матрицы
д[/ду. Сравните свои результаты с рис. 12.2 и 12.1.
6. Определите разложение Шура и жорданову каноническую
форму матрицы
/14 4 2\
Л = -1-2 20 1
\—4 -4 20/
Ответ. Жорданова каноническая форма имеет вид
/2 1 \
2
V
7. Приведите матрицы
А =
а
1
%
Ь
1
й
1
V
, л =
А
\
1
X
6
0
й
1
к жордановой канонической форме. Во втором случае рассмо-
рассмотрите две возможности: & + с? = 0 и Ь + А Ф 0.

1.13* Устойчивость
р конкурса извещает о том, что Премия 1877
года будет присуждаться за исследование по теме:
Критерий динамической устойчивости.*
(С. Дж. Фир (вице-председатель), Дж. Каллис,
Дж. Дж. Стоке, Дж. Клерк Максвелл)
Введение
«Чтобы проиллюстрировать значение данного вопроса, пред-
представим частицу, скользящую вниз внутри гладкого наклонного
цилиндра вдоль его нижней образующей либо по внешней стороне
цилиндра вдоль верхней образующей. В первом случае слабое
нарушение движения вызвало бы лишь осцилляции частицы около
образующей, а во втором случае частица совсем удалилась бы от
образующей. В первом случае движение было бы устойчивым
в смысле поставленного вопроса, а во втором — неустойчивым...
желательно найти условие, позволяющее нам судить, когда дви-
движение системы, возможное с точки зрения динамики, отвечает
требованию: при слабом нарушении движения оно продолжится
лишь с малыми отклонениями». («Жюри конкурса» в книге Рауса
A877)).
Всякий раз, когда аналитическое решение задачи неизвестно,
численные решения можно получить только для заданных началь-
начальных значений. Но часто нам нужна информация об устойчивости
решений при всех начальных значениях в окрестности некоторой
точки равновесия. Как и в разд. 1.12, мы поместим точку равнове-
равновесия в начало координат и дадим следующее определение.
Определение 13.1. Пусть имеется система уравнений
\ = и (Уи ..., уп), г ■= 1, ..., п, A3.1)
в которой $г (О, ..., 0) = 0, I а= 1, ..., п. Тогда точка 0 (начало
координат) называется устойчивой по Ляпунову, если для любого
е > 0 существует б > 0, такое, что для всех решений системы из
неравенства \у (хо)\\ < б следует, что*||у {х)\ < е при всех х > х0.
В своей знаменитой работе, получившей премию Адамса,
Раус A877) сделал первый шаг: он исследовал устойчивость
линеаризованного уравнения
^ A3.2)

1.13. Устойчивость 89
(«Будем говорить, что величины хл уу г и т. д. малы, если можно
пренебречь их квадратами.») Из вида полученного в разд. 1.12
общего решения A3.2) непосредственно вытекает следующий ре-
результат.
Теорема 13.1. Линеаризованное уравнение A3.2) устойчиво по
Ляпунову тогда и только тогда, когда все корни характеристиче-
характеристического уравнения
Ы (XI - А) = а0Хп + агХп~* + • • • + ап_хХ + ап = 0 A3.3)
удовлетворяют условию Ке (X) <; 0, а для кратных корней, поро-
порождающих жордановы клетки, выполняется неравенство Ке (X) < 0.
Доказательство. Непосредственно усматривается из A2.12)
и A2.15). Для жордановых клеток «вековой» член [т. е. Е + Рх
в решении уравнения A2.12), случай Ь)], стремящийся к беско-
бесконечности с ростом х, должен быть «"убит» с помощью экспоненты
со строго отрицательным показателем. ■
Критерий Рауса — Гурвица
Следующим шагом, который привел к знаменитому критерию
Рауса—Гурвица, была проверка условий Ке (X) < 0 прям-' по
коэффициентам уравнения A3.3) без вычисления его корней.
Для решения данной задачи Раус объединил две известные идеи;
первая — это принцип аргумента (Коши), согласно которому
число корней многочлена р (г) = и (г) + IV (г) внутри замкнутого
контура равно числу (положительных) оборотов вектора (и (г),
V (г)) при обходе переменной г границы в положительном направле-
направлении (см., например, книгу Хенричи A974)).1} На рис. 13.1 пред-
представлен пример для многочлена
2е + б25 + 1624 + 25*8 + 242а + 142 + 4 в
(г + 1) (г + 2) (г2 + г + 1) (г2 + 2г + 2). A3.4)
На полуокружности г в Ке'е (я/2 <0 < Зя/2, /? достаточно
велико) аргумент р (г) благодаря доминирующему члену гп делает
/г/2 положительных оборотов. Чтобы все нули р принадлежали
отрицательной полуплоскости, дополнительно требуется /г/2 поло-
положительных оборотов вдоль мнимой оси. Отсюда вытекает
Лемма 13.2. Пусть р (г) является многочленом степени п и
пусть р (гу) Ф 0 при у ^ К. В этом случае все корни р (г) лежат
х> На русском языке см., например, М. А. Лаврентьев и Б. В. Шабат, Ме-
Методы теории функций комплексного переменного (изд. 3-е) — М.: Наука, 1965,
с. 88. — Прим. ред.

90
Гл. 1. Классическая математическая теория
в отрицательной полуплоскости тогда и только тогда, когда
вдоль мнимой оси аг§ (р {ьу)) делает /г/2 положительных оборотов
при уу изменяющемся от —оо до +оо. ■
Вторая идея состоит в использовании теоремы Штурма [Штурм
A829)], которая тесно связана с алгоритмом Евклида для много-
многочленов. Штурм сделал открытие, что при делении многочлена
Рис. 13.1. Векторное поле функции аг& (р (г)) для
многочлена р(г)> определенного формулой A3.4).
-1 (У) на Рь (у) остаток ри1 (у) лучше брать с отрицательным
знаком:
Л-1 (У) = Рг (У) Яг {У) — Рм (У)- A3-5)
Тогда в силу свойства «системы Штурма», состоящего в том, что
(ри1 (у)) ф 81еп 0*1-1 (у)), если рг (у) = 0, A3.6)
величина
и* (у) — число перемен знака в ряду чисел
(Ро (</), Р1 (У), .... Рт (У))
A3.7)
не меняется в нулях многочленов рг (у), ..., рт^ (у). Из этого
вытекает следующий результат.

1.13. Устойчивость
91
Лемма 13.3. Предположим, что система вещественных мно-
многочленов р0 (у)у рг (у)у ..., рт (у) удовлетворяет условиям:
&Ч (р0) > Aе§ (рх);
Ро (у) и Рг (у) не обращаются одновременно в нуль;
Рт (У) Ф 0 при всех у $ К;
IV) выполняется свойство A3.6) системы Штурма.
Тогда величина
до (оо) — до (—оо)
A3.8)
равна отсчитываемому в положительном направлении числу обо-
оборотов вектора (р0 (у), р1 (у)) при у, стремящемся от —оо к + °о.
Доказательство. В силу свойства системы Штурма хю (у) не
меняется в нулях рх (у), ..., рт„г (у). По предположению 111),
\/
л
А ро
\/
+ + о-~ __о + + + + о - - ~ - о + +
Рис. 13.2. Повороты вектора (р0 {у), р% (у)) и соответствую-
соответствующая функция од.
Рт (у) также не оказывает влияния. Поэтому хю (у) может изме-
изменяться только в нулях р0 (у). Если 1Ю (у) в точке # возрастает
на единицу, то /?0 (у) либо изменяет знак с «+» на «—» и рг (у) > О,
либо с «—» на «+» и р! (у) < 0 (по условию И) равенство рх ($) =
~ 0 невозможно). В обоих случаях вектор (р0 (у), Рг (у)), повора-
поворачиваясь, пересекает мнимую ось в положительном направлении
(см. рис. 13.2). Если хю (у) уменьшается на единицу, то этот вектор
пересекает мнимую ось в отрицательном направлении. Утвержде-
Утверждение теоремы следует теперь из условия 1), так как вектор (р0 (у),
Рг (У)) направлен горизонтально при у -> —оо и у-> +оо. ■
Объединение двух предыдущих лемм дает нам требуемый
критерий устойчивости: пусть задан характеристический много-
многочлен A3.3)
р (г) = а&п + ах2п~х -| + ап = 0, а0 > 0.
Разделим р (ьу) на 1п и отделим вещественную и мнимую части:
ТГ- = а0У"
Ро(у)
л—4
± ....
A3.9)
- • • • •

92 Гл. 1. Классическая математическая теория
Благодаря специальной структуре этих многочленов алгоритм
Евклида A3.5) для них чрезвычайно прост: запишем многочлен
Рг (У) = сгоу"-< + сг1у»-'-* + с12у»-*-* + ..., A3.10)
и для частного в A3.5) имеем формулу цх (у) = (с(_х> о/сьо).у,
при условии, что с10 Ф 0. Теперь, подставив A3.10) в A3.5),
придем к следующим рекуррентным формулам для вычисления
коэффициентов
~1° ~*и \ч, о ч, и! /
A3.11)
Если при некотором Л с10 = 0, то частное цг (у) будет многочленом
степени выше первой и алгоритм Евклида будет оканчиваться на
Рт (У)у где т <п.
Очевидно, что полученная таким способом система многочле-
нов (Рг (у)) удовлетворяет условиям 1) и IV) леммы 13.3. Условие
и) эквивалентно неравенству р {1у) Ф 0 при у ^ К, а 111) следует
из и), так как рт (у) — это наибольший общий делитель много-
многочленов р0 {у) и рг {у).
Теорема 13.4. [Раус A877)] Все корни вещественного много-
многочлена A3.3) с коэффициентом а0 > 0 лежат в отрицательной
полуплоскости Це X < 0 тогда и только тогда, когда
сго > 0 при 2 = 0, 1, 2, ..., п. A3.12)
Замечание. Благодаря условию сг0 > 0 деление на с10 в фор-
формуле A3.11) можно опустить (общий положительный множитель
в рм (*/)), откуда следует та же теорема [Раус A877I: «...таким
образом, вспомнив это простое правило перекрестного умноже-
умножения, мы можем записать...»). Однако при больших п это не ре-
рекомендуется из-за возможного переполнения.
Доказательство. Системы координат (р0, рг) и (Ке (/?), 1т (р))
имеют противоположную ориентацию. Поэтому п/2 положитель-
положительных оборотов р (ьу) соответствуют п!2 отрицательным оборотам
(ро (*/)> Р\ (у))- Если все корни р (X) лежат в отрицательной полу-
полуплоскости КеЯ < 0, то из лемм 13.2 и 13.3 следует равенство
т (оо) — ш (—оо) = —/г, которое возможно только в том случае,
когда т (оо) = 0, хю (—оо) = п. Это означает, что у всех много-
многочленов рг (у) коэффициенты при старших членах положительны.
С другой стороны, если выполнено условие A3.12), то рп (у) =
= сп0. Следовательно, многочлены р0 (у) и р1 (у) не могут иметь
общих множителей и р (X) ф 0 на мнимой оси. Теперь, снова
применяя леммы 13.2 и 13.3, мы придем к утверждению теоремы. ■

1,13. Устойчивость
93
Эту теорему МОЖНО ДОКа- Таблица 13.1. Таблица Рауса для A3.4)
зать и по-другому, исполь-
используя «положительные функ-
функции» (см. том II).
Пример 1. В табл. 13.1
приведена таблица коэффи-
коэффициентов Рауса A3.11) для
многочлена A3.4). Ясно, что
он удовлетворяет условиям
устойчивости.
Пример 2. [Раус A877)] Выразим условия устойчивости для
уравнения четвертой степени
г4 + рг3 + </г2 + тг + 5 *= 0. A3.13)
Значения си (без деления) приведены в табл. 13.2.
Таблица 13.2. Таблица Рауса для A3.13)
* = 0
1= 1
1= 2
1= 3
1 = 4
* = 5
» о
1 — О
1
6
11.
14.
11.
7.
4
: 0
83
01
56
12
/ =
— 16
—25
—21
—И
4
1
.67
.97
/ = 2 / = 3
24 —4
14
4
г
?
0
1
2
3
4
1
/==о
- г
- Г) Г — р28
— Г) Г — р28) Р$
—Ц 8
Л О
Мы имеем устойчивость тогда и только тогда, когда выполня-
выполняются неравенства
Р > 0, ря — г > 0, (р? — г) г — ра5 > 0, 5 > 0.
Вопросы численной реализации
Несмотря на большое историческое значение и математиче-
математическое изящество критерия Рауса, при больших размерностях
для его применения в вычислительной практике в настоящее
время существует два препятствия:
1) для больших матриц нелегко вычислить характеристиче-
характеристический многочлен;
2) этот многочлен очень опасно использовать при наличии
погрешностей округления.
Таким образом, если мы не занимаемся точными символьными
преобразованиями или не производим приближенные расчеты
с высокой степенью точности, рекомендуется избегать харак-
характеристических многочленов и использовать численно устойчивые
алгоритмы для задачи на собственные значения (см., например,
книгу Эйспака A974)).

94
Гл. 1. Классическая математическая теория
Численные эксперименты. 1. Матрица
—0.5
•
1 .
•
•
—0.5
•
п
I
•
—0.5
■
•
—п
•
—0.5
имеет характеристический многочлен
п
р (г) = П (г2 + 0Л2 + /2 + 0.0025).
Мы вычислили коэффициенты р с двойной точностью, а затем
применили алгоритм Рауса с обычной точностью (которая у нашей
машины равна 1.5х10~8). Результаты вычислений указывают
на устойчивость только при п -< 15, а при п ^> 16 она не обна-
обнаружена, хотя собственные числа матрицы —0.05 ± Ы всегда
лежат в отрицательной полуплоскости, С другой стороны, при
прямом вычислении собственных значений А с помощью под-
подпрограмм Эйспака осложнения не возникали ни при каких /г.
2. Мы испытывали алгоритм Рауса также и на (масштабиро-
(масштабированных) числителях диагональных аппроксимаций Паде для
ехр (г),
I
Г
я(я
2)
•>
Bя)Bд— 1) 2! ' Bл) Bя— 1)Bл — 2) 3 1
A3.14)
у которых, как известно, все собственные значения принадле-
принадлежат С". В этом примере результаты были правильными лишь при
п<;21, а при больших м — неверными из-за погрешностей
округления.
Функции Ляпунова
Продолжим рассмотрение вопроса об устойчивости нелиней-
нелинейной системы A3.1): «можно ли ее действительно определить, изу-
изучая только члены первого порядка?» [Раус A877), гл. VII].
Начало этой теории положили Раус и Пуанкаре, а свое завершение
она получила в знаменитой работе Ляпунова A892). В качестве
общей ссылки на обширную теорию, которая была разработана
с тех пор, приведем книги Руша, Хабетса и Лалуа A977) и В. Хана
A967).

1.13. Устойчивость
95
Ляпунову (и Раусу) основным инструментом служили так
называемые функции Ляпунова V (у19 ..., уп), которые должны
удовлетворять условиям
V (Уи .... Уп) >Л
V (Уи •••» Уп) = 0 тогда и только тогда,
когда у{ — ... ~ уп = 0, A3.15)
и на решениях задачи A3.1)
^ A3.16)
Обычно при малых у функция V (у) имеет квадратичное пове-
поведение, и условие A3.15) означает, что
с\\у?<У(у)<С\\у\^ С>с>0. A3.17)
Существование такой функции Ляпунова является достаточным
условием устойчивости начала координат.
Начнем с построения функций Ляпунова в линейном случае:
У' =Ау.' A3.18)
Лучше всего это делать в базисе, который естественно задается
собственными векторами (или жордановыми цепочками векторов)
матрицы А. Поэтому введем преобразование у = Тг, г = Т~гу,
которое приводит А к жордановой канонической форме A2.14')
^ = Т~гАТ, а систему A3.18) к виду
*' = /г. A3.19)
Если мы положим
У0'(г) = И2 и V (у) - Уо (Т^у) = V, (г), A3.20)
то производная V (у (х)) будет вычисляться по формулам
= 2 Ке (г (х), /г (х)) < 2ц (У) У (у (х)). A3.21)
Согласно формуле A0.20) для логарифмической нормы,
2р> (У) = наибольшее собственное значение матрицы / + /*.
Матрица / + У* является блочно-диагональной и состоит из
трехдиагональных блоков:
в
2 Ке ^
в
A3.22)

96 Гл. 1. Классическая математическая теория
Вычтя диагональ и применив формулу F.7а), мы увидим, что
собственные значения матрицы A3.22) размера т X т равны
, *=1, ..., т. A3.23)
Используя эту формулу или с помощью упр. 4 мы получим сле-
следующую лемму.
Лемма 13.5. Если все собственные значения А удовлетворяют
условию Ке Х1 <—р < 0, то для уравнения A3.18) существует
квадратичная функция Ляпунова, удовлетворяющая неравенству
Последнее дифференциальное неравенство приводит к оценке
(теорема 10.1)
V (у (х)) < V (уо)- ехр (-р (х - х0))
и обеспечивает выполнение соотношения Нт||#(х)|| — 0, т.е.
асимптотическую устойчивость.
Устойчивость нелинейных систем
Теперь легко распространить те же идеи на нелинейные урав-
уравнения. Примером служит следующая теорема.
Теорема 13.6. Пусть задана нелинейная система
(х9 у), A3.25)
у которой все собственные значения матрицы А отвечают условию
Ке Хг < —р < 0. Предположим далее, что для любого в > 0
существует такое б > 0, что
1ё(х, #)|1<е[|г/|| при Ы|<6, х>х0. A3.26)
Тогда начало координат асимптотически устойчиво по Ляпу
нову.
Доказательство. Используя построенную в лемме 13.5 функ
цию Ляпунова V (у), из A3.25) получим
. A3.27)

1.13. Устойчивость 97
Из неравенства Коши с учетом A3.26) следует, что
4гУ<У (*Ж(-Р-Ц Т НТ-Ч е) V (У (*»• A3.28)
При достаточно малых 8 выражение в правой части отрицательно,
и мы получим асимптотическую устойчивость. ■
Мы видим, что для нелинейных систем устойчивость обеспе-
обеспечивается только в окрестности начала координат. Это можно
также заметить и на рис. 12.2. Другое отличие состоит в том, что
может быть нарушена устойчивость для собственных значений,
лежащих на мнимой оси. Примером служит система [Раус A877)]
01 = —02 + 01, 02 = 01- A3.29)
Здесь, взяв функцию Ляпунова V = (у\ + у1)/2, мы получим
производную V = у\9 которая положительна при у\Ф 0. По-
Поэтому все решения с ненулевыми начальными значениями воз-
возрастают. В работе Ваннера A983) дан обзор по этому вопросу
(«проблема центра» и ее связь с предельными циклами).
Устойчивость неавтономных систем
Если коэффициенты системы
У' =А(х)у A3.30)
не являются постоянными, проверка условия устойчивости для
собственных значений А при каждом значении х становится не-
недостаточной для утверждения об устойчивости.
Примеры: 1. [Раус A877)] Системе
= 02, 02 = — 3Г01 A3.31)
удовлетворяет функция ух (х) = а -\Лс.
2. Пример со строго отрицательными собственными значе-
значениями: начнем с задачи
—1 0
4 _
Рассмотрение производной функции V = {у\ + 0г)/2 показывает,
что V возрастает в секторе
2 + УЗ
4 Хайрер Э. я др.

98
Гл. 1. Классическая математическая теория
Идея состоит в том, чтобы взять начальные значения из этой
области и с ростом х поворачивать систему координат с той же
скоростью, с которой вращается решение:
.соз ах —$1паху
Т(х) =
в\п ах соз ах
A3.32)
При у @) = A, \)т подходит выбор а ~ 2, и A3.32) имеет решение
у (Х) = ((соз 2х — 51п 2х) е*$ (соз 2х + зШ 2х) е*)т. A3.33)
Ясно, что оно неустойчиво, хотя при всех х величина —1 остается
двукратным собственным значением матрицы А (х).
Третий пример можно найти в приведенном ниже упр. 6.
Мы видим, что для неавтономных систем теория устойчивости
является более сложной. Отметим два частных случая, когда
устойчивость может быть установлена:
1. ап (х) < 0 и А (х) отвечает условию диагонального доми-
доминирования; тогда у (Л (х)) <; 0, и устойчивость следует из тео-
теоремы 10.5.
2. А (х) = В + С (х), где В — постоянная матрица, собствен-
собственные значения которой отвечают неравенствам Ке^ <—р < 0,
а || С (х)|| < 8, причем 8 настолько мало, что можно применить до-
доказательство теоремы 13.6.
Упражнения
1. Напишите условия устойчивости для многочленов
22 I «7 г а _- и и г3 4- юг2 4- аг 4- г = 0
Ответ, а) р > 0 и ? > 0; б) г > 0 и ^ — г>0.
2. [Гурвиц A895)] Проверьте, что условие A3.12) эквивалентно
положительности главных миноров матрицы
а3
Ш, /-1
(ак = 0 при к < 0 и к > /г). Убедитесь, что алгоритм Рауса
A3.11) — это разновидность метода исключения Гаусса, пре-
преобразующего Н к треугольной форме.

1.13. Устойчивость 99
3. Многочлен
5.4.3-2.1 25 5.4.3.2 г* ■ 5-4.3 г* . 5-4 г2 .5 , 1
"Т 1Л.П.Й.7 Л\ I 1Л.О.Я 41 » 1П.О 01 "Г 1П * I *
10-9.8.7.6 5! ^ 10.9.8-7 41 ' 10-9.8 31 ' 10-9 21 » 10
является числителем аппроксимации Паде 5—5 для ехр 2,
Проверьте, что все его корни удовлетворяют условию Ке г < 0.
Попытайтесь установить этот результат для произвольных п
(см., например, работу Биркхофа и Варги A965), лемма 7).
4. (Гершгорин) Докажите, что собственные значения матрицы
А ~ (аи) лежат в объединении кругов
[
г\ |г
Указание. Запишите формулу Ах = кх в координатах
перенесите диагональные элементы в правую часть и выбе
рите такое I, чтобы \хг\ был максимальным.
5. Определите устойчивость начала координат для системы
У\ = — 92 ~ У\
У 2 = У\ + 2уф.
Указание. Исходя из выражения V —(у] + у1)/2 + ..., най-
найдите такую функцию Ляпунова 4-й степени, чтобы выполнялось
равенство V' = К{у\ + у1У + ..., и определите знак К.
6. (Дж. Ламберт, 1986). Рассмотрите систему
у' = А(х)-у, где А(х)
4х
A3.34)
а) Покажите,- что оба собственных значения матрицы А (х)
при всех х > 0 удовлетворяют условию Ке % < 0.
Ь) Вычислите р> (А) по формуле A0.20) и покажите, что \1 (А) <;
< 0 тогда и только тогда, когда т/5 — 1 <; х <^ •/!> + 1.
с) Найдите общее решение системы A3.34).
Указание. Введите новые функции
*2 (х) = У2 (х)у гг (х) = хуг (х)9
с помощью которых вы придете ко второму уравнению из
A1.19) (упр. 5 в разд. 1.11).
4*

100
Гл. I. Классическая математическая теория
Решение:
уг (х)
A3.35)
ё) Определите такие а и 6, чтобы функция \\у (х)||1 была воз-
растающей при 0 < х < |/5— 1.
Г/ V
><*
Л**
< V* *
Рис. 13.3. Регулятор скорости паровой машины
Джеймса Уатта.
е) Определите такие^ аи 6, чтобы функция \\у (д:) Ц1 была воз-
растающей при )/5 + 1 < л: < со.
Ответы: Ь = 1.8116035а для с!) и
6 = 0.2462015а для е).
7. Помогите Джеймсу Уатту (см. копию оригинального чертежа
1788 г. на рис. 13.3) решить задачу устойчивости для регуля-

1.13. Устойчивость 101
тора его паровой машины: если о — угловая скорость вращения
вала двигателя, его ускорение зависит от подачи пара и внеш-
внешней работы следующим образом:
со' = (к со5 (ф + а) — Р), к, Р > 0.
Здесь ф и а — углы, показанные на рис. 13.3. Вторая произ-
производная ф определяется через центробежную силу, вес *и трение
по следующей формуле:
ф" = оJ 51П ф СО5 ф — § 51П ф — Ьф', §", Ь > 0.
Найдите точку равновесия ф" = ф( = со' = 0 и определите,
при каких условиях она устойчива (решение упрощается при
а = 0).
Правильные решения следует посылать по адресу: Джеймсу
Уатту, знаменитому изобретателю паровой машины, Вестмин-
Вестминстерское аббатство, 6НC, 1РХ, Лондон.
Замечание. Статья Гурвица A895) появилась благодаря
изучению похожей практической задачи, а именно о «...ре-
«...регулировании турбин курорта на водах Давос».

1.14 Производные по параметрам
и начальным значениям
«Для одного уравнения д-р Ритт решил указанную
в заголовке задачу очень простым прямым методом...
Доказательство д-ра Ритта нельзя непосредственно
обобщить на системы уравнений»*
(Т. X. Гронуолл A919))
В данном разделе мы рассмотрим вопрос о том, являются ли
решения дифференциальных уравнений дифференцируемыми!
а) по начальным значениям!
б) по постоянным параметрам, входящим в уравнение,
и о том, как вычислить эти производные. Оба вопроса, конечно,
чрезвычайно важны: если для заданных начальных значений
решение уже найдено (численно), часто требуется узнать, как
повлияют на него малые изменения этих начальных значений.
Такой вопрос встает, например, в том случае, когда некоторые
начальные значения не известны точно и должны быть опреде-
определены из других условий, таких как фиксированные граничные
условия. Кроме того, начальные значения могут содержать по-
погрешности, влияние которых требуется изучить. Те же задачи
возникают в том случае, когда в дифференциальные уравнения
входят неизвестные или содержащие погрешности постоянные
параметры.
Задачи а) и б) эквивалентны: пусть система дифференциальных
уравнений
У' =/(*, У', р), У(х0) = */„ (ИЛ)
содержит параметр р (или несколько параметров). Мы можем
расширить исходную систему:
Р)\ У(хо) = д
) A4Л)
Тогда параметр станет начальным значением для уравнения р' —
= 0. И обратно: для системы
У' = ! {х, У), У (*0) = Уо (Н.2)
можно записать равенство у (х) = г (х) + у0, из которого получим
= Р (х, г, уо)9 г (*0) = 0. A4.2')

1.14. Производные по параметрам и начальным значениям 103
В этом случае начальное значение становится параметром. По-
Поэтому из двух задач а) и б) выберем сначала б) (как это сделал
Гронуолл), так как она нам кажется более простой.
Производная по параметру
Обычно задача содержит несколько параметров. Но Поскольку
нас интересуют частные производные, мы можем рассматривать
параметры по очереди, сохраняя остальные фиксированными.
Поэтому в излагаемой теории достаточно считать, что / (х, у, р)
зависит только от одного скалярного параметра р.
Заменив параметр р в A4.1) на цу мы получим другое решение.
Обозначим его через г (х)\
*' = ! (х, г, ?), г (х0) = у0. A4.3)
Тогда будет естественным вычесть A4.1) из A4.3) и линеаризовать
разность!
г' — у' = / (х, г, ?) — / (х, у, р)
, У, Р) (г—у)
> Р) (Я-Р) + Р2 (Я -
Если ввести обозначение (г (х) — у (х))/(<7 — р) = Ф (х) и от
бросить остаточные члены, то мы придем к уравнению вида
(*' У{Х)>
Оно является ключевым при решении поставленной задачи.
Чтобы это уравнение имело смысл, нам необходимо сделать пред-
предположения о существовании входящих в него производных.
Теорема 14.1. [Гронуолл A919)] Предположим, что при х0
X частные производные
ду др
существуют и являются непрерывными в окрестности решения
у {х). Тогда существуют частные производные
причем они непрерывны и удовлетворяют дифференциальному
уравнению A4.5).

104
Гл. 1. Классическая математическая теория
Доказательство. Эта теорема породила знаменитую лемму
Гронуолла (см. 1.10, упр. 2). Докажем ее здесь с помощью экви-
эквивалентной теоремы 10.2. Введем обозначения
Ь = шах
К
А = шах
К.
др
A4.6)
где шах взят по всей рассматриваемой области. Если считать
г (х) приближенным решением задачи A4.1), то, используя пер-
первый раз теорему 10.2, мы получим для нормы невязки соотношение
'-'М-1(х9 г(х), р)| = [/(*, *(*), <?) — /(*, г(х), р)||<
из которого следует оценка
IIг(х) - у (х)||< 4 IЯ - РI
<»-*•>
1).
(Н.7)
Поэтому при достаточно малом значении \д — р\ и #0 << л; << X
мы можем сделать ||г (х) — у (х)\\ сколь угодно малой. По опреде-
определению дифференцируемости и в силу оценки A4.7) для любого
е > 0 существует такое б, при котором для остаточных членов
в A4.4) выполняется неравенство
\р1(г — у) + Р%(Ч — рЦ<*\Я — р\> если |<7-/?|<6. A4.8)
(В действительности ситуация несколько сложнее: для оценок
Ц р! || < е и ||р2|| < 8 величина б может зависеть от х, но в силу
компактности и непрерывности ее можно заменить равномерной
оценкой. Это небольшое препятствие можно было бы преодолеть
и другим способом — ограничив вторые производные. Но почему
мы должны заботиться о таких деталях? Сам Гронуолл их не
упоминает.)
Рассмотрим теперь выражение (г (х) — у (я))/(<7 — р) как при-
приближенное решение задачи A4.5) и применим теорему 10.2 во
второй раз. В силу A4.8) и A4.4) норма невязки уравнения A4.5)
ограничена величиной 8, а константа Липшица линейного диффе-
дифференциального уравнения A4.5) также равна Ь (см. A1.2)). По-
Поэтому из A0.14) мы получим оценку
(X) — у (X)
Я — Р
8
которую можно сделать сколь угодно малой; этим доказывается
тот факт, что г|) (х) — производная функции у (х) по р.
Непрерывность. Частные производные ду/др = "ф (х) являются
решениями дифференциального уравнения A4.5), которое мы
запишем в виде
= ё (*, Ф, Р),

1.14, Производные по параметрам и начальным значениям 105
где по предположению # непрерывно зависит от р. Поэтому не-
непрерывная зависимость \|) от р снова следует из теоремы 10.2. ■
Теорема 14.2. Пусть у (х) является решением уравнения A4.1);
рассмотрим матрицу Якоби
А(х)=-^~(х,д(х), р). A4.9)
Предположим, что К (х, х0) является резольвентой уравнения
у' = А (х) у (см. A1.4)). Тогда решение уравнения A4.3) со
слабо возмущенным параметром ц задается формулой
X
A4.10)
Доказательство. Это соотношение — формула вариации по-
постоянных A1.12), примененная к A4.5). ■
Итак, мы видим, что чувствительность решений к изменениям
параметров зависит, во-первых, от частных производных дЦдр
(что вполне естественно), а во-вторых, от величины Я (х, $),
т. е. от устойчивости дифференциального уравнения с матрицей
A4.9).
Производные по начальным значениям
Обозначения. Обозначим через у (х, х0, у0) решение у (х)
в точке х, удовлетворяющее начальным значениям у (х0) = у0.
Мы надеемся, что использование одной и той же буквы у для двух
различных функций не вызовет никаких недоразумений.
Следующие тождества являются тривиальными следствиями
определения или вытекают из соображений единственности, как
в случае A1.6):
д1Л A4.11)
У(х0, *о, Уо) = Уо> A4.12)
У (*2, *1> У (*ъ х0, Уо)) = У (ха, х0, у0). A4.13)
Теорема 14.3. Предположим, что частная производная I по у
существует и непрерывна. Тогда решения у (ху х0, у0) дифферен-
дифференцируемы по у0, и производная задается матрицей
A4Л4)

106 Гл, 1. Классическая математическая теория
где К — решение так называемого «уравнения в вариациях»
*'
A4.15)
Доказательство. Формулы A4.2) и A4.2') показывают, что
обе производные дР/дг и дР/ду0 равны д}/ду, а поэтому в силу
теоремы 14.1 производная ду/ду0 существует. Чтобы получить
формулу A4.15), нам надо продифференцировать A4.11) и A4.12)
по у0. Ш
В завершение мы вычислим производную у(х9 х0, у0) по х0.
Теорема 14.4. При условиях теоремы 14.3 решения дифферен-
дифференцируемы также и по х0, а производная вычисляется по формуле
ду
Доказательство. Продифференцируем по х0 тождество
У (*1, *о> У (х0, х19 ух)) = у19
которое следует из A4.13), и применим A4.14) и A4.11) (см.
упр. 3). ■
Нелинейная формула вариации постоянных
Завершим данный раздел обобщением теоремы 11.2 на системы
нелинейных дифференциальных уравнений.
Теорема 14.5. [Алексеев A961), Грёбнер A960)] Обозначим
через у и г решения систем
У' = / (х, У), У (*о) = Уо» A4.17а)
г ' = / (х, г) + § (х, г), г {х0) - у0 A4.17Ь)
соответственно и предположим, что д}/ду существует и является
непрерывной. Тогда решения уравнения A4.17а) и возмущенного
уравнения A4.17Ь) связаны соотношением
|, 5, г(з))§($, г(з))с1з. A4.18)
Х0
Доказательство. Выберем разбиение х0 = 50< 5г < 52 < ...
... < 5^ = л: (см. рис. 14.1). Ниспадающие кривые представляют
решения невозмущенного уравнения A4.17а) с начальными зна-
значениями 5*, г E;). Разности й$, возникающие вследствие различных
наклонов г (з) и у (з) [из A4.17Ь) надо вычесть A4.17а)], равны
— ё ($1> г (^))'^1 + о (А^). Эта «погрешность» в точке 5*

1.14. Производные по параметрам и начальным значениям
107
«переносится» затем на конечное значение х> составляя в точке х
величину, определенную теоремой 14.3. В итоге имеем
ду
A4.19)
Поскольку
N
*) = 2 V»
к—*
в результате подстановки A4.19) и перехода к пределу
мы получим интеграл в A4.18). ■
0
Рис. 14.1. Веер леди Уиндермир, действие второе.
Если нам нужно учесть также возможное различие в началь-
начальных значениях, мы можем сформулировать
Следствие 14.6. Пусть у (х) иг (х) являются решениями урав
нений
У' = / (*> У), У (*о) = Уо>
г' —}(х9г) + е (х9 г), г (х0) = г0.
Тогда выполняется соотношение
I
0
> г (з)) Оз.
X,
A4.20)

108 Гл. 1. Классическая математическая теория
Эти две теоремы позволяют получить множество оценок устой-
устойчивости общих нелинейных систем. В случае линейных систем
х, 5, г) не зависит от г, и формулы A4.20), A4.17) сводятся
к формуле вариации постоянных A1.12). Кроме того, оценивая
сверху тривиальным образом интегралы в A4.20), мы придем
к фундаментальной лемме A0.14), а также ко второй формулировке
теоремы 10.2.
Упражнения
1. Изучите зависимость от начальных значений в задаче
/ = у\ хо = О, г/0 = 1, X = 0.999. A4.21)
2. Решите численно уравнение A4.21), используя 999 шагов
метода Эйлера G.3) при Хг+1 — Х[ =0.001. Оцените влияние на
конечный результат погрешности на первом шаге (равной 10~6)
и объясните низкую точность.
3. Докажите следующую лемму элементарного анализа, применен-
примененную в доказательстве теоремы 14.4. Если для функции Р (х, у)
существует дР/ду, а у (х) дифференцируема и отвечает условию
Р (*> У (*)) = с°пз1, A4.22)
то в точке (х, у (х)) существует производная дР/дх> которая
вычисляется по формуле
Указание. Из A4.22) выведите тождество
1. У (%)) — Р (*0. У (*1)) = Р (*0. У (*о)) — Р (*0. У (*!))•

1Л5. Краевые задачи
и задачи на собственные значения
Хотя наша книга в основном посвящена задачам с начальными
условиями, или задачам Коши, мы хотим в этой первой главе
осветить также некоторые свойства краевых задач и задач на
собственные значения.
Краевые задачи
Такие задачи возникают в системах дифференциальных урав-
уравнений, например!
Ух = !ч (х, уи У2), ' /1С1Ч
, ч A0.1)
У2 = Н (х, у и У2),
когда нет начальной точки х0, в которой были бы известны одно-
одновременно уг (х0) и у2 (х0). В этом случае вопросы существования
и единственности становятся намного сложнее.
Пример 1. Рассмотрим дифференциальное уравнение
у" = ехр (у) или у{ = г/2, у& = ехр (у{) A5.2а)
с граничными условиями
Уг @) = ^ уг A) = Ь. A5.2Ь)
Чтобы применить доказанные нами теоремы существования или
провести численные расчеты [например, с помощью метода Эйлера
G.3)], мы можем поступить следующим образом: предположим,
что недостающее начальное значение равно у20- Тогда можно
вычислить решение и проверить, равно ли найденное значение
для уг A) числу Ъ. Таким образом, наша задача состоит в том,
чтобы определить, есть ли нуль у функции одной переменной
Р (У2оJ = Уг A) - Ь. A5.3)
Уравнение A5.2а) является квазимонотонным, что означает
монотонную зависимость Р (у20) от у20 (рис. 15.1а, см. упр. 3
в разд. 1.10). Кроме того, при очень малых или очень больших
значениях у20 величина уг A) сколь угодно мала или велика или
даже обращается в бесконечность. Поэтому A5.2) при всех ау Ь
имеет единственное решение (см. рис. 15.1Ь).
Корень уравнения Р (у20) — 0 можно вычислить итерационным
методом (методом деления отрезка пополам, методом ложного
положения и т. д.; а если производную уг A) по у20 найти из тео-

по
Рл. К Классическая математическая теория
ремы 14.3 или определить численно с помощью конечных раз-
разностей, то также методом Ньютона). Тогда задачу Коши нужно
решать несколько раз. Для небольших задач, таких, как в при-
приведенном выше примере, это можно просто сделать на компьютере
в диалоговом режиме. Более сложные задачи с большим числом
неизвестных начальных значений требуют более высокой техники
программирования. Описанный метод принадлежит к наиболее
широко распространенным методам и называется методом
стрельбы (или пристрелки).
2.
Рис. 15.1. а) Решения уравнения A5.2а) при различных начальных значениях
17 04
Ь) Единственное решение уравнения A5.2а) при а= 1, Ь = 2, #2о в
= —0.476984656.
с) Решения уравнения A5.4а) при у @) == 1 и г/2о ^ 1> 2, ..., 8.
6) Два решения уравнения A5.4а), у @) = 1, у A) = 0.5, у2о = 7.93719,
у20 = 0.97084.
Пример 2. Для дифференциального уравнения
У = — ехр {у) или у[ = у2, г/2 = — ехр (у{) A5.4а)
с граничными условиями
Уг@) = а9 угA) = Ь. A5.4Ь)
Р (у20) уже не удовлетворяет требованию монотонности, что
осложняет ситуацию: на рис. 15.1с изображены решения при
а = 1 и различных начальных значениях у20. Из рисунка можно
увидеть, что если Ь расположено выше некоторого значения (рав-
(равного 1.499719998), то задача совсем не имеет решений, а при мень-
меньших Ь существует два решения (рис. 15. Ы).
Пример 3.
Ух = У2У У2 = У\, Ух @) = 1, Ух A00) = 2.
A5.5)

1.15. Краевые задачи и задачи на собственные значения 111
Это уравнение похоже на A5.2), и для него справедливо то же,
что и прежде, утверждение о существовании и единственности
решения. Однако если мы попытаемся найти решения методом
стрельбы, то окажемся в затруднении из-за длины интервала:
решение почти никогда не существует на всем интервале. В дей-
действительности правильное решение равно у20 = —0.70710616655.
Но уже при у20 = —0.7071061 уг (х) стремится к +оо при х ->•
->- 98.2. С другой стороны, при у20 = —0.70711 мы имеем гД (94.1) =
= —оо. Таким образом, область существования Р (у20) из A5.3)
по длине меньше чем 4хЮ~6.
В подобных случаях используют метод параллельной стрельбы:
отрезок разбивают на несколько подотрезков, на каждом из кото-
которых находят решение при хорошем выборе начальных значений.
В конечных точках подотрезков производится согласование ре-
решений. Таким образом, уравнение A5.3) превращается в систему
большей размерности. Параллельной стрельбе посвящено мно-
множество публикаций. В качестве общей ссылки назовем работу
Дойфлхарда A980).
Задачи Штурма — Лиувилля на собственные значения
Начало изучению данного вопроса положила замечательная
статья Штурма [Штурм A836)] в журнале, незадолго до этого
основанном Лиувиллем. Ее продолжил ряд статей Лиувилля
и Штурма, опубликованных в последующих номерах. В настоящее
время эти работы считаются отправной точкой «геометрической
теории», где главные усилия направлены не на интегрирование
уравнения, а только на получение прямо из дифференциального
уравнения геометрических свойств решения, таких как его форма,
осцилляции, изменения знака, нули, существование максимумов
и минимумов и т. д. («Однако к этой цели можно прийти, рассма-
рассматривая лишь сами дифференциальные уравнения, и нет никакой
необходимости их интегрировать».)
Физические задачи, которые привели к такой постановке
проблемы, как и в разд. 1.6, связаны с изучением теплоты и малых
колебаний упругой среды. Рассмотрим уравнение теплопровод-
теплопроводности с переменным коэффициентом теплопроводности:
С^ О I 1 I \ ММ \ 1 / \ / / \ ^ /\ /«г Г»\
_____ . I Н I VI I / I V 1// Ъ /VI ^"^- М I I К Г» 1
^/ дх \ х ' дх / \ / > \ / -^ > \ ;
которое подробно изучено в «Теории теплоты» Пуассона. Этот
автор предположил, что и (х9 () = у (х) е~и. Тогда A5.6) прини-
принимает вид

112 Гл. 1. Классическая математическая теория
Перепишем A5.7) в виде
(к (х) у')' + О(х)у = 0 A5.8)
и сформулируем теорему сравнения Штурма.
Теорема 15.1. Рассмотрим дополнительно к A5.8) дифферен-
дифференциальное уравнение
A5.9)
и предположим, что к, к дифференцируемы, О, 0 непрерывны и
и при всех х выполняются соотношения
О <%(х)<к(х), О(х)>О(х). A5.10)
Пусть у (х), р (х) являются линейно независимыми решениями
уравнений A5.8) и A5.9) соответственно. Тогда между любыми
двумя нулями у (х) находится по крайней мере один нуль 1) (х),
т. е. если у (хх) = у (х2) = 0 и хх < х2, то на открытом интер-
интервале (хъ х2) существует такое х3, что $ (хг) = 0.
Доказательство. Доказательство самого Штурма основано на
отношении
а (Х) =
4 к }
к (х) у'
которое равно тангенсу угла наклона прямой, соединяющей
начало координат с точкой решений на плоскости (ку\ у), и удо-
удовлетворяет дифференциальному уравнению первого порядка.
Чтобы избежать сингулярностей, вызванных обращением у' (х)
в нуль, мы предпочтем пользоваться полярными координатами
[Прюфер A926I:
к (х) у' (х) = р (х) со5 ф (х), у (х) = р (х) $1П ф (х). A5.11)
Дифференцируя A5.11), мы придем к следующему дифференци-
дифференциальному уравнению для ф:
<р' = -1-. соз2 ф + С (х) зш2 ф. A5.12)
Тем же способом мы введем функции р (х) и ф (х) для второго
дифференциального уравнения A5.9) и получим
Ф' = Д-соз2ф + 0(х)81п2ф. A5.13)
Теперь предположим, что хх, х2 — два последовательных нуля
у (х). Тогда ф (хг) и ф (х2) должны быть кратны я, так как р (х)
всегда отлична от нуля (единственность в задаче Коши). В силу

1.15. Краевые задачи и задачи на собственные значения 113
A5.12) ср' (х) положительна в хг и х2. Поэтому мы можем счи-
считать, что
Ф (хг) = 0> Ф (*г) = л> ф (*г) € [0, я). A5.14)
Вследствие того, что уравнения A5.12) и A5.13) имеют первый
порядок, а также в силу неравенств A5.10) можно применить
теорему 10.3, которая приведет к соотношению
Ф (х) > Ф (*) при хг < х < х2.
Равенство ф (х) = ф (х) не может выполняться всюду, так как
в силу A5.12) и A5.13) мы получили бы тогда соотношения
к (х) = к (х), О (х) = О (х) и линейную зависимость решений
У (х)> # (х)- Следовательно, существует такое х0 б (х19 х2), при
котором ф (х0) > ф (я0). В этом случае <р (х) > ф (х) при всех
^ ^> ^о» чт0 обеспечивает существование точки х3 ё (хх> л:2), в кото-
которой ф (^3) = я). ■
Следующая теорема показывает, что у нашей задачи на соб-
собственные значения имеется бесконечное множество решений. Доба-
Добавим к A5.7) граничные условия
У(х*) = У(*1) = 0. A5.15)
Теорема 15.2. Задана на собственные значения A5.7), A5.15)
имеет бесконечную последовательность собственных значений Ъ,г <
< %г < А,3 < ..., которым отвечают решения у% (х) («собственные
функции») с 0, 1,2, ... нулями соответственно внутри интервала
(х0, хх). Нули уз (х) разделяются нулями у]+1 (х). Если 0 < /Сх
! к (х) <; /С2 и Ьх<*С I (х) <! Ь2, то справедливо соотношение
Доказательство. Пусть у (х> X) является решением A5.7)
с начальными значениями у (х0) = 0, у' (х0) = 1. Из теоремы 15.1
(при к (х) = к (х), О (х) = О (х) + кХ) следует, что с ростом X
нули у (х, X) перемещаются к х0, а поэтому число нулей на (х0, хх)
представляет собой неубывающую функцию от X.
Сравнивая теперь A5.7) с решением
5Ш {-/(X — ЬгУКг (х — х0))
Уравнения Кхуп + (X — Ьх) у = 0 при (X > 1Х), мы увидим, что
У (х, X) при X < Ьг + К1]2"^1(х1 — х0J имеет на (х0, хх\ не более
/ — 1 нулей. Подобным образом, сравнение у (х, X) с функцией
51П (V (X - Ь2)/К2 (X - Х0)),
которая служит решением уравнения К2у" + (X — Ь«) у = О,
показывает, что при X > Ь2 + К2]2л2/(х1 — х0J функция у [х, X)

114
Гл. 1. Классическая математическая теория
имеет по крайней мере / нулей на (*0, хг). Теперь утверждения
теоремы получаются как простые следствия этих трех свойств. ■
Пример. На рис. 15.2 показаны 5 первых решений задачи
(A — 0.8 51П2 х) у')' — (х — X) у = 0, у @) = у (л) = 0. A5.17)
Первые собственные значе-
значения равны 2.1224, 3.6078,
6.0016,9.3773,13.7298,19.053,
25.347, 32.609, 40.841,50.041
и т. д.
С этой теорией, представ-
представляющей очень важную стра-
страницу истории математики,
более обстоятельно можно
познакомиться в книге Рей-
-о.вь Лу / даA980>-
\ А /
Упражнения
1. Для уравнения
Рис. 15.2. Решения задачи Штурма— т / \ " \ м ( \
Лиувилля (задачи на собственные зна- *- Vе) У "Т М (X)
чения) A5.17). , ц /^\ __
подберите такую функцию <р (х), чтобы полученное в резуль-
результате умножения на нее уравнение имело вид A5.7) Штурм
A836)].
2. Докажите, что два решения задачи A5.7), A5.15) удовлетворяют
условию ортогональности
XI
\
х0
У] (х) Ун
0
при
Указание. Умножьте это соотношение на %], замените Х^у^ (х)
выражением из левой части A5.7) и выполните интегрирование
по частям [Лиувилль A836)].
3. Найдите решение задачи A5.5) в элементарных функциях.
Объясните, почему указанное для у20 значение столь близко
к —/2/2.
4. (Коллатц) Покажите, что краевая задача
У" = У\ #@) = 0, у (Л) = 5 A5.18)
имеет бесконечно много решений для каждой пары (А, В)
при А Ф 0.
Указание. Получите решение у (х) задачи A5.18) при у @) = 0,
У @) = 1. Покажите, что для любой константы а функция
г (х) = ау (ах) также будет решением.

1.16. Периодические решения,
предельные циклы, странные
аттракторы
Явление предельных циклов впервые было теоретически опи-
описано Пуанкаре A882) и Бендикссоном A901) и с тех пор нашло
много применений в физике, химии и биологии.
Уравнение Ван-дер-Поля
«У меня есть теория: если вы хотите какой-то метод
скомпрометировать—ищите решение уравнения Ван-
дер-Пол я».
(П. Э. Задунайский, 1982)
Первые примеры такого типа из практики были изучены Ре-
леем A883), а позднее Ван-дер-Полем A920—1926) в серии статей
по нелинейным осцилляциям: решения уравнения
У" + Щ' + У = 0
являются затухающими при а > 0 и неустойчивыми при а < 0.
Идея состоит в изменении а (например, с помощью включенного
в цепь триода) таким образом, чтобы при малых у выполнялось
а < 0, а при больших у — неравенство а > 0. В качестве про-
простейшего выражения, описывающего физическую ситуацию в не-
несколько идеализированной форме, можно взять а = е (у2 — 1),
е > 0. Тогда данное уравнение примет вид
A6.1)
или, если записать его как систему,
е>0.
В этом уравнении малые колебания усиливаются, а большие —
затухают. Поэтому можно ожидать, что существует устойчивое
периодическое решение, к которому сходятся все остальные ре-
решения. Его называют предельным циклом. Иллюстрации из статьи
Ван-дер-Поля в их первоначальном виде воспроизведены на
рис. 16.1.

116
Гл. 1. Классическая математическая теория
-2-1 о 1 г-* и
Рис. 16.1. Иллюстрации из работы Ван-дер-Поля A926).
Доказательство существования
Существование предельных циклов изучается с помощью ме-
метода сечений Пуанкаре. Его идея состоит в том, чтобы пересечь
решения гиперплоскостью Р и при начальном значении у0 ^ Р
рассмотреть первую точку Ф (у0), в которой решение снова пере-
пересекает Р в том же направлении.
Для нашего примера A6.2) выберем в качестве Р луч уг = О,
Ух > 0 и исследуем знаки производных у{ и #2 в A6.2). Знак у'2
меняется на кривой

1.16. Периодические решения, предельные циклы
117
которая на рис. 16.2 изображена штриховой линией. Отсюда
следует (см. рис. 16.2), что Ф (у0) существует для всех у0 $ Р.
Поскольку два различных решения не могут пересекаться вслед-
вследствие единственности, отображение Ф является монотонным.
Кроме того, Ф ограничено [например, любым решением, начинаю-
начинающимся на кривой A6.3)],
а поэтому Ф (у0) < */0 при
больших у0. И наконец, в
силу неустойчивости нача-
начала координат Ф (у0) > у0
при малых у0. Следова-
Следовательно, должна существо-
существовать неподвижная точка
отображения Ф (уо)у т. е.
предельный цикл. ■
Замечание. На самом
деле предельный цикл
является единственным.
Этот факт доказывается
сложнее; идею доказа-
доказательства мы укажем ниже,
в упр. 8 [Льенар A928)].
С помощью подобных
рассуждений доказывается Рис* 16О2- Отображение Пуанкаре для урав-
п„п ' о ? нения Ван-дер-Поля, 6 = I.
следующий общий резуль- *
тат.
Теорема 16.1. [Пуанкаре A882), Бендикссон A901I Любое
ограниченное решение системы размерности 2
Ух = А [Уи У2), Уг = Н {уи У$ • A6.4)
должно:
\) либо стремиться к критической точке /х = /2 = 0 для
бесконечного множества точек хг ->- оо;
И) либо быть периодическим;
Ш) либо стремиться к предельному циклу. Ш
Замечание. Приводимое ниже упр. 1 объясняет, почему пер-
первая возможность записана в несколько более сложной форме,
чем это кажется необходимым.
Стационарные приближения при больших г
Стационарные приближения представляют собой важное сред-
средство упрощения сложных нелинейных систем. Рассмотрим A6.2)
при очень большом е. Тогда в окрестности кривой /2 (у19 у2) = 0
производная у'2 = /2 по у2 имеет очень большое по модулю отри-

118
Гл. I. Классическая математическая теория
дательное значение. Поэтому решение будет очень быстро при-
приближаться к положению равновесия в окрестности кривой у'2 =
— /^(УьУг) ^ 0» которая в нашем примере задана формулой A6.3).
Эту формулу можно подставить в A6.2), что даст нам уравнение
более низкой размерности
= Т(Т^г- A6-5)
50
Рис. 16.3. Решение уравнения Ван-дер-Поля при е
нарными приближениями*
60 70 80
10 в сравнении со стацио-
Оно легко решается с помощью формул из разд. 1.3, и в резуль-
результате мы получаем
1о§
4
+ сопз*.
Эти кривые показаны пунктиром на рис. 16.3 из работы Ван-
дер-Поля, где они соответствуют значению е = 10 и дают, как
видно, хорошее приближение к решению.
Асимптотические решения при малых 8
Основы метода вычисления периодических решений при малых
параметрах заложили астрономы, в частности Ньюкомб и Линд-
стедт, а в работе Пуанкаре A893) он был доведен до совершенства.
Продемонстрируем метод малого параметра на примере уравнения
Ван-дер-Поля A6.1). Идея состоит в том, чтобы искать решение
в виде ряда по степеням е. Поскольку период также будет изме-
изменяться, сделаем замену переменной
1 = хA +угг + у2е2 + ...) A6.6)
и положим
у(х) = г @ = г0 @ + гг, (/) + г\ (I) + ... . A6.7)
Теперь, подставив в A6.1) у' (х) = г' {I) A + ухъ + ...), у" (х) =
= г" (/) A + ухе + -..J> мы получим уравнение
(го
Bу
...)
= 0.
A6.8)

1.16. Периодические решения, предельные циклы 119
Сравнивая коэффициенты при е°, получим уравнение
го + 2о = О. A6.8; О)
Фиксируем произвольно начальное значение г' @) = 0, тогда
20 == А соз I. Далее, для коэффициентов при е получим
г\ + *1 = —2у1го — (го — 1) г0 =
~$^пЗ^. A6.8; 1)
Главная идея здесь в том, что, поскольку мы ищем периодические
решения, из правой части A6.8; 1) надо удалить члены, содержа-
содержащие соз I и 51П /, чтобы избежать появления в гх (I) членов вида
/•соз г и /-51П г («...и таким образом убрать члены, называемые ве-
вековыми...»). Отсюда мы получим значения уг — 0 и А = 2. Тогда
можно найти решение A6.8; 1), которое при начальном условии
г{ @) = 0 равно
*! = В СОЗ / + -|- 81П / — -~ ЗШ Ы. A6.9)
Теперь ясно, как следует продолжить этот процесс: после подста-
подстановки A6.9) и упрощения члены при е2 в A6.8) дают уравнение
A6-8*> 2)
3 5
—2~ соз 3/ + -^ соз 5/.
Чтобы избежать вековых членов, надо взять В = 0 и у2
и тогда
3 5
г2 = С соз I + -^р соз Ы <^~ соз Ы.
На следующем этапе будут определены значения С = —1/8
и Уа — 0» и т. д. В итоге мы придем к следующему результату:
периодическая траектория уравнения Ван-дер-Поля A6.1) при
малых е задается формулами
у (х) = г (*), / = х A — б2/8 + ...),
*(/) = 2со5 / + е (д- 51п/ - -|- 5Ш 3/) + A6.10)
СО5
82 (
П + ...
и имеет период 2к (I + е2/8 + ...).

120 Гл. 1. Классическая математическая теория
Химические реакции
Законы химической кинетики порождают дифференциальные
уравнения, которые для реакций с участием двух и более молекул
становятся нелинейными и обладают интересными свойствами.
Некоторые из этих уравнений имеют периодические решения
(например, в случае реакции Белоусова—Жаботинского), они
находят также важные применения для объяснения биологиче-
биологических явлений (см., например, работу Пригожина, Лефевера A969)).
Рассмотрим подробно модель Лефевера и Николиса A971),
так называемый «брюсселятор»: предположим, что шесть веществ,
Л, В, I), Е9 X, У\ участвуют в следующих реакциях*
A6.11)
В + X -> У + &* (бимолекулярная реакция)
*|
2Х + У -»- ЗХ, (автокаталитическая трехмолекулярная реакция)
Х-+Е.
Если обозначить через А (х), В (х)> ... концентрации веществ Л,
В, ... как функции времени х, то реакции A6.11), согласно закону
действующих масс, описываются следующими дифференциаль-
дифференциальными уравнениями:
А' = — М|
В = —к2ВХ$
Б' = к2ВХ,
Е = к±Х>
X' - кгА — к2ВХ + к3Х2У — к^Х,
У = кгВХ — к3Х2У.
Теперь упростим эту систему: исключим из рассмотрения уравне-
уравнения для О и Е, так как они не влияют на остальные; предполо-
предположим, что Л и В поддерживаются постоянными (положительными)
и возьмем все скорости реакций кг равными единице./ Далее, вве-
введем обозначения X (х) ~\ ух (х), У (х) =; й М и в результате
получим систему
2 A6.11)
уху2.
Она имеет одну особую точку у[ = у\ = 0 при У\ = Л, у2 = В/А.
В окрестности этой точки линеаризованное уравнение неустой-
неустойчиво тогда и только тогда, когда В > Л2 + 1- Далее, изучая об-

1Л6. Периодические решения, предельные циклы
121
ласти, где у{, у'ъ или {у\ + у2У положительны или отрицательны,
мы придем к выводу, что все решения остаются ограниченными.
Таким образом, при В > Л2 +• 1 должен существовать предель-
предельный цикл, который, как видно из численных расчетов, является
единственным (рис. 16.4).
Когда В приближается к
Л2 + 1, наблюдается интересное
явление (бифуркация Хопфа).
Оно состоит в том, что предель-
предельный цикл становится все меньше
и меньше и, наконец, исчезает в
критическую точку. Другой при-
пример такого типа приведен в упр. 2.
Предельные циклы в системах
больших размерностей
бифуркация Хопфа
Теорема Пуанкаре—Бендикс-
сона, очевидно, верна только
в том случае, когда размерность
системы равна двум. Контрпри-
Контрпримером при большей размерности
может служить почти каждое
механическое движение без трения, как, например, сферический
маятник (рис. 16.5), к изучению которого обращались многие
ученые прошлого (см., например, работу Лагранжа A788), вто-
вторая часть, разд. VIII, гл. И, § 1). В этом случае уравнения дви-
движения в сферических координатах принимают вид
,* • , , / '\2 • , A6.12)
ф = 51П ф СО5 \|) (ф J — 51П \|), ч
Рис. 16.4. Решения уравнений <;брюс
селятора», Л = 1, 5 = 3.
а кривая решения представлена на рис. 16.5. Если увеличение
ф/Bл) за одну осцилляцию — иррациональное число, то решение
не является периодическим и не стремится к периодическому или
стационарному решению.
Поэтому в случае больших размерностей предельные циклы
обычно находят с помощью численного исследования определен-
определенного выше отображения Пуанкаре Ф в методе сечений. Периоди-
Периодическое решение (т. е. неподвижная точка отображения Ф) называ-
называется аттрактором, если все собственные значения Ф' (у0) по мо-
модулю меньше 1. Все решения, начинающиеся в окрестности аттрак-
аттрактора, будут стремиться к нему.
Однако существует одна ситуация, в которой предельные
Циклы возникают совершенно естественно [Хопф A942) ], а именно,

122
Гл, 1. Классическая математическая теория
когда в особой точке системы у' = / (*/), у, / ^ К", все собствен-
собственные значения /' (у0) имеют строго отрицательную вещественную
часть, за исключением одной пары, пересекающей мнимую ось.
При этом подпространство, натянутое на собственные векторы,
отвечающие устойчивым собственным значениям, продолжается
в двумерное аналитическое многообразие, внутри которого появ-
появляется предельный цикл. Это явление называется «бифуркацией
Хопфа». Доказательство этого факта аналогично методу Пуан-
Пуанкаре разложения по малому параметру A6.7) [см. ниже упр. 6
и 7], и поэтому Хопф даже сомневался, стоит ли его публиковать
(«...мне трудно поверить, что в приведенном выше предложении
содержится что-либо существенно новое...»).
а)
•
Рис. 16.5. Одно из решений для сферического маятника:
а) 0 < х < 20, Ь) 0 < х < 100,
В качестве примера рассмотрим «полный брюсселятор» A6.11):
мы больше не будем считать В постоянным, а предположим, что В
добавляется к смеси с постоянной скоростью а. Введем обозна-
обозначение В (х) =: у3 (х) и вместо A6.11') (при А = 1) получим систему
A6.13)
Уз = —уф + а-
Она имеет особую точку уг = 1, у2 == у3 = а с производной
1 —1\
1
A6.14)
—ее —1
—а 0
Характеристический многочлен этой матрицы равен А,3 + C —
— а) X2 + C — 2а) Я + 1 = 0 и удовлетворяет условию устой-
устойчивости (см. 1.13, упр. 1) тогда и только тогда, когда а < (9 —
= 1.21922. Поэтому, если а возрастает сверх этого

1.16. Периодические решения, предельные циклы
123
значения, появляется предельный цикл, который существует
вплоть до значения а, приблизительно равного 1.5 (см. рис. 16.6).
Если а продолжает расти, то предельный цикл «взрывается»
и Уг -* 0, в то время как у2 и у3 -> ею. Таким образом, поведение
системы A6.13) полностью отличается от поведения упрощенной
модели A6.1 Г). Уз Уз
ГГТ Г*1 I I ГТ I I I I I I
*
Рис. 16.6. Бифуркация Хопфа для
«полного» брюсселятора A6.13): а= ш
= 1.22, 1.24, 1.26, 1.28, 1.30 (штрихо-
(штриховая линия), 1.34, 1.38, 1.42, 1.46, у,
1.50 (штриховая линия).
Знаменитой химической реакцией с предельным циклом в трех-
трехмерном случае является так называемый «орегонатор» — реакция
между НВгО2, Вг"" и Се (IV) [Филд и Нойес A974)], описываемая
системой
у{ - 77.27 (у2 + УЛ1- 8.375 X 10^ - у2)),
(A+)) A6Л5)
з = 0.161

124
Гл. 1. Классическая математическая теория
решения которой показаны на рис. 16.7. Это пример «жесткого»
дифференциального уравнения, решения которого быстро изме-
изменяются по величине на много порядков. Поэтому данный пример
служит серьезным испытанием для программ численного интегри-
интегрирования, и мы обратимся к нему еще раз во II томе нашей книги.
-3. -2. -1. 0. 1
(
3.
2.
1.
0.
1.
2.
3
-
-
0.
-
200.
1 1 ^"Ч
200.
400. X
1
400.
-3. -2. -1.
200
400.
Рис. 16.7. Предельный цикл «орегонатора».
Следующий пример мы взяли из теории сверхпроводимости:
два перехода Джозефсона с емкостной связью между ними. Полу-
Получаемые в этом случае уравнения имеют вид [см., например, работу
Джиованнини—Вайса—Ульриха A978) ]:
с (Уг - ау5) = к - 81п (ух) — у'и /1С 1С.
//ч . / ч / A0.10)
с (у2 — ау{) = 12— зш [у2) — У2.
Здесь ух и у2 — углы («разности квантовых фаз на переходах»),
рассматриваемые по модулю 2я. Таким образом, уравнение

1.16. Периодические решения, предельные циклы
125
A6.16) представляет собой систему на торе Т2 для (у1у у2) и в К2
для разностей потенциалов (у[, у$. Из численных расчетов видно,
что система A6.16) имеет притягивающий предельный цикл, кото-
который описывает явление «запирания фаз» (см. рис. 16.8).
5.
О.
5.
1.
У\
о.
о.
Рис. 16.8. Переходе Джозефсона A6.16) при с =2, а = 0.5, г± « 1.11, г2 =
= 1.08.
Странные аттракторы
«Г-н Далквист, когда наступит весна?» «Завтра в два
часа».
(Прогноз погоды, Стокгольм, 1955)
«Мы были так наивны...»
(X. О. Крайс, Стокгольм, 1985)
Когда речь идет об открытии знаменитой «модели Лоренца»,
лучше всего процитировать самого автора [Лоренц A979)]:
«К середине 1950-х годов, несмотря на весьма низкое качество
получаемых результатов, вошло в моду «численное предсказание
погоды», т. е. прогноз на основании численного интегрирования
доступных для обработки приближений к уравнениям, описываю-
описывающим атмосферу. Маленькая, но решительная группа ученых под-
поддерживала статистическое предсказание (...), вероятно, вследствие
неправильного истолкования одной статьи Винера (...). Я скеп-
скептически относился к этой идее и решил проверить ее, применив
статистический метод к множеству искусственных данных, полу-
полученных при численном решении некоторой системы уравнений (...).
Первая задача состояла в нахождении подходящей для решения
системы (...). Требовалось, чтобы она была достаточно простой
и имела непериодическое общее решение, так как при выявлении
периодичности статистическое предсказание периодического ряда

126 Гл. 1» Классическая математическая теория
стало бы тривиальным делом. Возможность соединения этих
условий была далеко не очевидной (...). Прорыв наступил во время
моего посещения д-ра Барри Зальцмана, работающего теперь
в Йельском университете. Во время наших бесед он показал мне
одну работу по тепловой конвекции, где им использована система
из семи обыкновенных дифференциальных уравнений. Большин-
Большинство полученных им численных решений быстро приобретало перио-
периодический характер, но одно решение отказывалось устанавли-
устанавливаться. Кроме того, оказалось, что в этом решении четыре пере-
переменных приближаются к нулю. Можно было предположить, что
уравнения, которые управляют остальными тремя неизвестными,
при исключении из них членов, содержащих первые четыре пере-
переменные, также будут иметь непериодические решения. По воз-
возвращении я решил эти три уравнения на нашем компьютере и под-
подтвердил непериодичность, на которую указывал Зальцман. В конце
концов дело пошло».
В измененных обозначениях три уравнения с непериодическими
решениями имеют вид:
где
К3
а, г
У1 =
У 2 =
Уз =
= — ЯУ\
= У\Уч -
~ТаУ2»
'з + гу\ ~
- Ъуъ%
•У2,
и Ь — положительные константы.
отображение
Фх
Ы =
: У (X, 0,
A6.17)
Обозначим через фх:
A6.18)
которое является фазовым потоком дифференциального уравнения.
Поскольку A6.17) —автономная система, выбор х0 = 0 не огра-
ограничивает общности, и тождество A4.13) принимает вид
Ф*+*. = Ф*1 ° Ф*,. A6.19)
Из A6.17) следует, что
{^^)) {^ ^) A6.20)
Поэтому шар
#о = {(уи У2, уз) | у\ + у\ + (у* - о - гJ < с )
отображается потоком фх в себя при условии, что с достаточно
велико, так что #0 полностью содержит эллипсоид, определяемый
приравниванием нулю правой части A6.20). Следовательно, если х
принимает возрастающие значения 1, 2, 3, ..., то #0 отображается
в области Ях = фх (#0), Я2 = Фг (#о) = Ф1 (#0 1в силу A6.19)]
и т. д., причем /? /? # /?

1.16. Периодические решения, предельные циклы
127
Область
имеет объем
который экспоненциально стремится к нулю при &-> оо. В этом
можно убедиться, применив к уравнению в вариациях A4.15)
тождество Абеля—Якоби (НЛО). След матрицы д[/ду для 'системы
начальное
значение
-20 О
Рис. 16.9. Две проекции решения уравнения A6-17),
A6.17) имеет постоянное значение — (а + Ь + 1), откуда следует,
что
Таким образом, каждая траектория в конечном счете попадает
в множество Яоо = ^0 П #1 Л &2 П ••• нулевого объема.
Система A6.17) имеет очевидную особую точку ух = у2 = у3 =
= 0, которая становится неустойчивой при г > 1. В.этом случае
есть еще две дополнительные особые точки С и С, задаваемые
соответственно значениями
Уг
1)
Они становятся неустойчивыми (например, в силу критерия
Рауса, приведенного в упр. 1 из разд. 1.13) при о > Ь + 1 и
а (а + Ъ + 3)
0 — # —
A6.21)

128
Гл. К Классическая математическая теория
В первом примере мы используем значения Зальцмана Ь = 8/3,
а = 10 и г = 28. («Здесь мы отметим еще одно счастливое обстоя-
обстоятельство: Зальцман использовал а = 10 в качестве грубого при-
приближения числа Прандтля (около 6) для воды. Если бы он выбрал
для изучения воздух, то, вероятно, взял бы а = 1, и непериодич-
ипиипинтипяпягчпиипи
пкиптипииигигтттпип
питании:::
«»#.*
иитатитг.иинтниипнк
питпкияикпт
4 С С С
Рис. 16.10. Отображение Пуанкаре для уравнения A6.17).
ность не была бы открыта» [Лоренц A979) ].) На рис. 16.9 представ-
представлена кривая решения системы A6.17) с начальными значениями
ух = —8, у2 = 8, у3 = г — 1, которая действительно выглядит
довольно хаотической.
Чтобы яснее понять, что происходит, отметим следующий
факт: любое решение, начинающееся на плоскости у3 == г — 1
между двумя особыми точками, окружает одну из них и возвраща-
возвращается с обратной стороны. Поэтому выберем указанную плоскость П

1.16. Периодические решения, предельные циклы 129
в качестве сечения и рассмотрим отображение Пуанкаре Р\
П -> П. Численное изучение данного отображения показывает,
что существует критическая линяя, выше которой решения идут
вправо, а ниже — влево. Следовательно, образ Р (П) состоит из
двух множеств, как показано на рис. 16.10. Отсюда вытекает, что
образ Р2 включает 4 слоя, образ Р3 — 8 слоев и т. д., причем слои
размещаются все ближе друг к другу. Поэтому аттрактор состоит
из бесконечного множества листов, расположенных наподобие
точек канторова совершенного множества. Такие аттракторы на-
называют теперь странными аттракторами. («Следовательно, ат-
аттрактор описанного типа нельзя отбрасывать как частный патоло-
патологический случай». — Рюэлль—Такенс A971).)
Каскады Фейгенбаума
Хотя начало статьи Лоренца A9.79) написано очень хорошо,
утверждения последнего ее раздела верны лишь отчасти. Следуя
Лоренцу, будем теперь изменять в A6.17) параметр Ь, полагая
одновременно г = гс (см. A6.21)) и
а = Ь + 1 + /2(Ь+1)(Ь + 2). A6.22)
При таком значении о параметр гс достигает минимума. Численное
интегрирование показывает, что при очень малых Ь (точнее,
Ь <; 0.139) решения A6.17), очевидно, сходятся к устойчивому
предельному циклу, который дважды пересекает сечение Пуанкаре
Уз = т — 1 в двух различных местах и окружает обе критические
точки С и С. При больших Ь (например, Ь = 8/3) коэффициенты а
и г слабо отличаются от изученного выше случая и существует
странный аттрактор. Но что происходит внутри интервала изме-
изменения 6? Мы вычислили решения модели Лоренца A6.17) для 687
промежуточных значений Ъ, расположенных от 0.138 до 0.148.
Для каждого из них мы рассчитали 800 пересечений сечения Пуан-
Пуанкаре. На рис. 16.11 представлены значения уъ при которых
решение пересекает плоскость Пуанкаре ув = г — 1. При этом
после каждого изменения Ь первые 40 итераций не показаны на
рисунке, так что виден только аттрактор.
Для малых Ь существует одна периодическая траектория;
потом при Ь = Ь± = 0.1397 она неожиданно расщепляется на
траекторию с периодом два, которая в свою очередь расщепляется
при Ь = Ь2 = 0.1433 на траекторию с периодом четыре, затем
восемь и т. д. Существует точка &«>, после которой движение ста-
становится хаотическим. Но и за этим значением снова и снова
встречаются интервалы устойчивых аттракторов периодов 5, 3, ...
и т. д. Полная картина напоминает результат вычислений по ре-
рекуррентной формуле
хп+1 = а(хп — х2п)9 A6.23)
5 Хайрер Э. и др.

130
Гл. 1. Классическая математическая теория
которая рассматривалась во многих статьях [см., например,
Мей A976), Фейгенбаум A978), Колле—Экманн A980)].
<^08
-0.09
1
"К.
0.140
1
>1Ь,
#я и
период 5 |^Ч-Ц
период 3
0.145
II
II
1!
I
II
11
*
Рис. 16.11. Значения у± сечений Пуанкаре для уравнения
A6.17) в зависимости от Ь.
-0.09
-0.09
Рис. 16.12. Отображение Пуанкаре эллипса A6.24)-
-0.08
Но отчего возникает это сходство? С помощью рис. 16.12
изучим отображение Пуанкаре для системы A6.17) со значением
Ь = 0.146. Мы выбрали эллипс
Уг = —0.084 + (и —V) -0.7071,
= -0.077 + {и + V) -0.7071, A6'24)

1.16. Периодические решения, предельные циклы 131
где и = 0.012 сов ф, V = 0.0015 зт ср, 0 < ф <; 2л. Что проис-
происходит с этим эллипсом после одной итерации? Он сожмется в тон-
тонкую линию, изогнутую в форме, буквы I) и отображающуюся в
себя.
Таким образом, отображение Пуанкаре—это, по существу,
отображение отрезка [0, 1] в себя, подобное тому, которое опи-
описывается соотношением A6.23). Замечательное открытие Фейген-
баума состоит в том, что для всех отображений подобной формы
всегда наблюдаются одни и те же явления, и, в частности, величина
Цш Iй ~~ \г = 4.6692016091029906715...
является универсальной константой — числом Фейгенбаума. По-
Повторяющиеся удвоения периодов при значениях Ьъ Ъ%, ЪЬ} ...
называются каскадами Фейгенбаума.
Упражнения
1. Уравнение Ван-дер-Поля A6.2) при е = 1 имеет предельный
цикл с периодом Т = 6.6632868593231301896996820305, про-
проходящий через у2 = 0, уг = Л, где
А = 2.00861986087484313650940188.
Теперь замените A6,2) системой
у = у2 (А - ух),
У2 = (A - у\) У2 - Ух) (А - ух),
у которой на предельном цикле появилась стационарная
точка. Изучите поведение решения, начинающегося внутри
него, например, со значения у10 = 1, г/20 = 0.
2. [Фроммер A934)] Рассмотрите систему
У\ = #2 + 2у1#2 — г/2, у1 = уг + A + е) у\ + 2у\у* — уЬ A6.25)
Исследуя устойчивость, как в упр. 5 из разд. 1.13, либо с по-
помощью численных расчетов покажите, что при е > 0 система
A6.25) имеет предельный цикл асимптотического радиуса г ==
= У 6е/7. (См. также статью Ваннера A983) и разд. 1.13, упр. 5.)
3. Решите 16-ю проблему Гильберта: какое максимальное число
предельных циклов может иметь квадратичная система
У\ = + + # + \ + УУ + ау1
Уг = Ро
Математическая общественность ждет Вас: более 80 лет никому
не удается решить эту задачу. В настоящее время наибольшее
5*

132 Гл. I. Классическая математическая теория
известное число равно 4, как, например, для системы
У\ = Цг — У2— Ыу\ + E + в) угу2 + у1%
У2 = Ух + у\ + (—25 + 8е — 96) угу2,
в = —10-", е = — Ю-», Л, = — Ю-200
(См. работы Ши Сонглина A980), Ваннера A983), Перко
A984).)
4. Найдите замену координат, при которой уравнение
ту" + (-А + В (уУ) у1 + ку = 0
становится уравнением Ван-дер-Поля A6.2), см. книгу Кры-
Крылова—Боголюбова A947).
5. Примените к уравнению математического маятника
...=0,
0@) = 8, 0@) = 0
метод асимптотических разложений A6.6) и A6.7) и изучите
период как функцию от 8.
Ответ, Период равен 2я A + еа/16 + ...).
6. Вычислите предельный цикл (бифуркацию Хопфа) для урав-
уравнения
у" + у = *У - (у'Г, у7 @) = о
при малых е, используя для этого метод Пуанкаре A6.6),
A6.7) со значением г0 (/) = 0.
7. Аналогичным способом (как в упр. 6) изучите брюсселятор
F.1 Г) при А = \ и В = 2 + е2.
Указание. Для упрощения расчетов перенесите особую точку
A,2) в начало координат, а затем выберите новые координаты,
используя собственные векторы линеаризованного уравнения
(см. A2.22) и A2.23)). В результате получится уравнение
у" + у = _е2 {у' - 1) - (уУ (у + у') + 2уу'.
Ответ, г (/) = е B/^3) со$ I + ..., I = х A — е2/18 + .. .)§
а поэтому период асимптотически равен 2я A + е2/18 + ...).
8. [Льенар A928)] Докажите, что предельный цикл уравнения
Ван-дер-Поля A6.1) для каждого е > 0 является единственным.
Указание. Тождество
подсказывает выбор координатной системы уг (х) — у )
У% (х) — У* + е (#3/3 —у). Запишите соответствующую си-
систему первого порядка, исследуйте знаки у[9 у'ч и рост функции

1.16. Периодические решения, предельные циклы 133
«энергии» V (х) = (у\ + у1)/2. Кроме того, обобщите результат
на уравнение вида у" + / (у) у' + § (у) = 0. Подробнее этот
вопрос изложен, например, в книге Симмонса A972).
9. [Рэлей A883)]. При малых и и Я найдите периодическое ре-
решение уравнения
уя + щг + X (уУ + п*у = 0.
Ответ, у = А 51п (пх) + (кпА3/32) соз (Зпх), где значение А
определяется из формулы и + C/4) %-п2А2 = 0.
Ю. [Бендикссон A901)]. Если в некоторой области й на пло-
плоскости выражение
всегда отрицательно или всегда положительно, система A6.4)
не может иметь замкнутых решений в О
Указание, Примените формулу Грина

Глава II
Методы Рунге — Кутты
и экстраполяционные методы
Численные методы для обыкновенных дифференциальных урав-
уравнений естественным образом разделяются на два класса. В один
из них входят методы, использующие одно стартовое значение на
каждом шаге («одношаговые методы»), а другой образуют методы,
опирающиеся на несколько значений решения («многошаговые
методы»). В этой главе изучаются одношаговые методы, а много-
многошаговые методы рассмотрены в гл. III. Обе главы в значительной
мере независимы, и каждую из них можно читать, по крайней
мере их начальные разделы, не зная содержания другой.
Глава начинается с изложения теории методов Рунге—Кутты*
включая вывод (с помощью помеченных деревьев) условий, опре-
определяющих порядок аппроксимации, оценки погрешностей, дока-
доказательства сходимости, вопросы программной реализации, методы
высших порядков. В разд. 11.7 вводятся неявные методы Рунге—
Кутты. Им будет уделено больше внимания во втором томе, пос-
посвященном жестким дифференциальным уравнениям. Следующие
несколько разделов посвящены элегантной идее экстраполяции
(Ричардсон, Ромберг и др.) и ее использованию для построения
программ, интегрирующих с высоким порядком точности. Затем
рассматривается алгебраическая теория композиции методов,
на основании которой в дальнейших главах будут изучены свой-
свойства порядка аппроксимации для многих общих классов методов.
Глава заканчивается специальными методами для дифференциаль-
дифференциальных уравнений второго порядка у" = / (х, у) и для дифференци-
дифференциальных уравнений с запаздывающим аргументом.
Для иллюстрации работы методов, описанных в этой главе,
мы выбрали пример из небесной механики — ограниченную задачу
трех тел. Рассматриваются два тела с массами 1 — [х и [х, участ-
участвующие в совместном круговом движении в некоторой плоскости,
и движущееся вблизи них в той же плоскости третье тело пренебре-
пренебрежимо малой массы. Уравнения имеют вид
» I о ' ' У\ -г М- #1 — М<
VI = Ц\ + ^#2 — М> —г; М» —гч—
у1K/2> я2 = @/1 - у
= 0.012277471, у.' = 1 —

II. 0. Введение
135
тщательно определили начальные условия!
дх @) = 0.994, у[ @) = 0, у2 @) = 0,
у'2ф) == —2,00158510637908252240537862224,
Хепй = 17.0652165601579625588917206249,
чтобы решение получилось периодическим с периодом ХепЛ.
Такие периодические решения много десятилетий привлекали
начальное
значение
-* РК-решение
75 шагов И0РК15
(полигональное и интер-
интерполирующее решение)
Рис. 0.1. Орбита Аренсторфа, вычисленная эквидистант-
эквидистантным методом Эйлера, эквидистантным методом Рунге —
Кутты и методом Дормана и Принса с переменной длиной
шага.
внимание астрономов и математиков (Пуанкаре). Теперь их часто
называют «орбитами Аренсторфа» (см. Аренсторф A963); этот
автор также провел много расчетов на «быстродействующих элект-
электронных вычислительных машинах»). Задача принадлежит классу С°°
(т. е, решения бесконечно дифференцируемы), за исключением двух
особых точек: уг= —\х и уг = 1 — |и, уг = 0. Поэтому, как мы
знаем из разд. 1.7, метод ломаных Эйлера сходится к решению.
Но будет ли он действительно полезным для вычислений в нашем
случае? Мы провели вычисления, взяв 24000 шагов длины

136 Гл. И, Методы Рунге—Кутты и экстр апелляционные методы
к — Хеш2/24000, и построили орбиту, приведенную на рис. 0.1.
Результат нельзя назвать замечательным.
Метод Рунге—Кутты (приведенный в табл. 1.2 слева) работает
уже гораздо лучше, он быстрее сходится к решению. Мы взяли
6000 шагов длины ХеЫ/6000, чтобы объем вычислительной работы
остался прежним. Ясно» что точность теряется больше всего в тех
частях орбиты, которые близки к особой точке. Поэтому про-
программы с автоматическим выбором длины шага, описанные
в разд. 11.4, работают гораздо лучше, и программа БОРК15
(табл. 4.6) вычисляет орбиту с точностью до 10 за 75 шагов. На
некоторых участках длина шага становится очень большой, и
графическое представление результата в виде ломаной, соединяю-
соединяющей точки решения, становится неудовлетворительным. Сплошная
кривая на рис. 0.1 —интерполированное решение E.7), точное
и для всех промежуточных значений. Оно полезно также во мно-
многих других случаях, например при решении дифференциальных
уравнений с запаздывающим аргументом, для вывода результатов
в большом числе промежуточных точек («плотная выдача») или
в точке, заранее не известной («неявная выдача»).
Для достижения еще более высокой точности нужны методы
более высокого порядка. Например, программа БОРК18
(табл. 6.4) вычисляет орбиту быстрее, чем ВОРК15, и при более
строгих ограничениях на допустимую погрешность (скажем, не
превосходящую 10~6). Наивысший порядок точности достигается
применением экстраполяционных методов (разд. П.9). Программа
СЮЕХ (при /Стах = 15) вычисляет орбиту с точностью до 10~30,
делая около 25000 вычислений функций, стоящих в правых ча-
частях уравнений — как раз тот объем вычислений, что и в упомя-
упомянутом выше решении методом Эйлера.

11.1. Первые методы Рунге — Кутты
«Численное определение какого-то решения заданного
дифференциального уравнения, аналитическое реше-
решение которого неизвестно, кажется, до сих пор мало
занимало внимание математиков.,.»
(К. Рунге, 1895)
Метод Эйлера для решения начальной задачи
У' = /(*, У)> У(*о) = Уо A-1)
был описан Эйлером A768) в его «Интегральном исчислении»
(раздел второй, гл. VII). Метод прост для понимания и програм-
программирования. Мы подробно исследовали его сходимость в разд. 1.7
и убедились, что глобальная погрешность имеет вид Ск, где С —
постоянная, зависящая от задачи, и к— максимальная длина шага.
Если желательно, скажем, получить 6 точных десятичных знаков,
то требуется, следовательно, порядка миллиона шагов, что не
слишком удовлетворительно. С другой стороны, еще со времен
Ньютона известно, что можно найти гораздо более точные методы,
если [ в A.1) не зависит от у, т. е. если мы имеем задачу
решаемую квадратурой!
1. A.2)
1
В качестве примера рассмотрим «правило средней точки» (или
первую квадратурную формулу Гаусса)!
д (X) « У = у^
где кг = хг+1 — хг и х0, хг> ..., хп-19 хп = X — граничные точки
подынтервалов, на которые разбит интервал интегрирования.
Известно, что оценка глобальной погрешности этой формулы
У (X) — У имеет вид Ск2, Таким образом, если желаемая точность
составляет 6 десятичных знаков, ее обычно можно получить при-
приблизительно за тысячу шагов, т. е. этот метод в тысячу раз бы-
быстрее. Поэтому Рунге A895) поставил следующий вопрос: нельзя ли
распространить метод A.3') и на задачу A.1)? Первый шаг длины
Ь = к0 должен иметь вид
( ^ ()) A.3)

138 Рл. II, Методы Рунге—Кутты и экстраполяционные методы
Но какое значение взять для у (х0 + к/2)? За неимением лучшего
естественно использовать один малый шаг метода Эйлера длины
к/2. Тогда из A.3) получим
К = / (я* Уо)>
+ к^ A.4)
Уг = Уо
Может показаться странным, что для вычисления к2 мы предла-
предлагаем сделать шаг методом Эйлера, о неэффективности которого
говорилось полстраницей выше. Однако решающим обстоятель-
обстоятельством является умножение к2 в третьем выражении на Я, в резуль-
результате чего влияние погрешности становится менее существенным.
Точнее говоря, вычислим для уг в A.4) разложение Тейлора
по степеням кг
*о + -2-> 0о+ "/о) = A-5)
= 9о + Ы (*о. Уо) + ~2" Их + У) (*о. «/о) +
Его можно сравнить с рядом Тейлора для точного решения, кото-
который получается из A.1) повторным дифференцированием с заме-
заменой у' на / каждый раз, когда оно появляется [(Эйлер A768),
задача 86, пар. 656; см. также формулы (8.12) гл. I]:
У (*о + ^ = Уо + Ы (ХО, Уо) + -2" (/» + Ы) {*о> Уо) +
... • A.6)
Вычитая из последнего равенства предыдущее, получим для по-
погрешности первого шага выражение
уо)+ ... . A.7)
Таким образом, если все частные производные [ второго порядка
ограничены, то | у (х0 + к) — ух \ < 7(Я3.
Чтобы получить приближенное значение решения задачи
A.1) в конечной точке X, будем применять формулы A.4) после-
последовательно к интервалам (х0, хг), (хх, х2), ..., (хп_1у X), подобно
тому как применялся метод Эйлера в разд. 1.7. По аналогии с до-
доказательством сходимости в разд. 1.7, мы покажем в разд. II.3,
что, как и в случае задачи A.1'), погрешность численного решения
ограничена величиной вида СН2 (к — максимальная длина шага).

11.1. Первые методы Рунге—Кутты 139
Таким образом, A.4) является усовершенствованием метода Эйлера.
Для вычислений с высокой точностью надо найти еще лучшие ме-
методы, и этим мы будем заниматься главным образом в следующих
разделах.
Общая формулировка методов Рунге — Кутты
Рунге A895) и Хойн A900) построили новые методы, включив
в A.4) один или два добавочных шага по Эйлеру. Но именно Кутта
A901) сформулировал общую схему того, что теперь называется
методом Рунге—Кутты.
Определение 1.1. Пусть 5 — целое положительное число
(«число стадий», или «этапов») и а%ъ а31, а32, ..., а8Ъ а82, я8,з-1> •••>
ъ ..., Ь8, с2у ..., с$ — вещественные коэффициенты. Тогда метод
1 — / (*о, Уо),
— ! (*о + Ыг, у о +
*3 ~ / (*0 + Ф, у о + к @81*1 + 082*2))»
A.8)
Уо + к (а81кг + ... + ов, з-А^)),
+ ... + Ь8к8)
называется 8-стадийным E-этапным) явным методом Рунге—
Кутты (ЯМРК) для задачи A.1).
Обычно коэффициенты с% удовлетворяют условиям
С2 == а2и СЬ — аВ1 ~Ь С32# • • • > ^3 ^^ аз1 Н~ • • • 4" а8, 3-1
или, короче,
01= 23 ау- A.9')
Эти условия были приняты Куттой без каких-либо комментариев.
Смысл их в том, что все точки, в которых вычисляется/, являются
приближениями первого порядка к решению. Эти условия сильно
упрощают вывод условий, определяющих порядок аппроксимации
для методов высокого порядка. Однако для методов низких по-
порядков эти предположения не являются необходимыми (см.
упр. 6).
Определение 1.2. Метод Рунге—Кутты A.8) имеет порядок
если для достаточно гладких задач A.1)
(*о+ *)-& К КЛ^1, A.10)
т. е. если ряды Тейлора для точного решения у (х0 + к) и для
совпадают до члена кр включительно.

140 Гл. II. Методщ Рунге—Кутты и экстр апелляционные методы
После статьи Бутчера A964Ь) вошло в обычай символически
представлять метод A.8) посредством следующей таблицы:
О
«32
A.8')
• • #3,3-1
&! Ь2 . . .
Примеры. Рассмотренный выше метод Рунге, а также методы
Рунге и Хойна порядка 3 приведены в табл. 1.1.
Таблица 1.1. Методы Рунге—Кутты низших порядков
Рунге, порядок 2
0
0
Рунге, порядок 3
0
1_
2
1
1
2
О 1
О О
1
1
1 о
6 3 6
Хойн, порядок 3
0
1
3
2
3
1
3
0
1
4
2
3
о А
4
Обсуждение методов порядка 4
«Из более новых методов я считаю наилучшим сле-
следующий, предложенный г-ном Куттой».
(К. Рунге, 1905)
Займемся теперь определением 4-стадийных методов Рунге—
Кутты A.8) с таким расчетом, чтобы они имели порядок 4. Выше
мы видели, что надо делать: вычислить производные порядков 1,
2, 3 и 4 от уг = ух (К) при к = 0 и сравнить их с производными
точного решения. Теоретически при известных правилах диффе-
дифференциального исчисления это совершенно тривиальная задача.
С использованием A.9) получаются следующие условия:
A.11а)
A.11Ь)

11.1. Первые метода Рунге—Кутты 141
4
A.11с)
4"'
= Ьвад2с2 + Ь4 (а^с2 + а&съ) = -§> A.1Ы)
A.1
_ 1
~72"'
, /
и и 1 л им
Уъ&Ц&ЗъСъ.^ 04^43^32^2 ==: пд • A.11П^
Эти вычисления, не приведенные в статье Кутты (они даны, од-
однако, в работе Хойна A900)), очень утомительны. И громозд-
громоздкость их очень быстро растет для более высоких порядков.
В разд. 11,2 мы увидим, что при использовании соответствующих
обозначений они могут стать очень изящными.
Кутта дал общее решение уравнений A.11) без объяснений.
Ясное изложение вывода решений приведено в книге Рунге и
Кёнига A924). Здесь мы будем следовать идеям Дж. К. Бутчера,
которые проясняют роль так называемых упрощающих предпо-
предположений и применимы также в случае более высоких порядков.
Лемма 1.3. Если
и 1( л) / A.12)
то уравнения д)> §) и Ъ) в A.11) являются следствиями остальных.
Доказательство, Покажем это для §). С помощью уравнений с)
и е) получим:
2
Для уравнений д) и Ь) процедура аналогична. ■
А теперь мы покажем, что в нашем случае условие A.12) яв-
является и необходимым.
Лемма 1.4. При 8 =» 4 A,12) следует из уравнений A.11) и
При доказательстве этой леммы используется следующая

142 Гл. II. Методе Рунге—Кутты и экстраполяционные методы
а
с
0
Ь
й
0
0\
0
о)
(
Ъ
&
Лемма 1.5. Пусть I) и V суть ЗхЗ-матрицы, такие, что
A.13)
Тогда либо Уеъ = 0, либо 1/Те3 — 0, где еъ — (О, О, 1)г.
Доказательство леммы 1.5. Если с1е! V Ф 0, то из 1}Уеъ — О
следует Уев — 0. Если же йе! V = 0, то существует вектор х =
= (хъ х2, х3)Тф0, такой, что 1/тх = 0, и поэтому Ут11тх= 0.
Но тогда из AЛЗ) следует, что х должен быть пропорционален
вектору е3. ■
Доказательство леммы 1.4. Введем величины
I] Ь%пц — Ь;A
для / = 1, ...» 4.
Итак, надо доказать, что й] — 0. Введем теперь матрицы
V
( Ъ Ь Ь \
ьХ Ь*с3 ьХ 1
, У =
2 ^ С\
02 02 /. ^2/^/ — ' л
^3 ^3 у | **Ъ\0\ ~~~ " г>
2 V *|
1^4 1«'4 X | 4/^'/ л
A.14)
Перемножение этих матриц с использованием условий A.11)
дает
1 1 Л
2
1
■там
3
0
3
0
0
0
, причем
/ 1
2
1
\ 3
1 N
3
1
4 .
Далее, последний столбец У не может быть нулевым, так как из
того, что сг = 0, следует
2__
/
в силу условия Ь). Таким образом, из леммы 1.5 следует, что й2 =
= &ъ = й4 = 0. Последнее тождество ^ = 0 вытекает из равен-
равенства йг + й2 + ^з + ^4 = 0» которое является следствием
A.11а, Ь) и A.9). ■
Из лемм 1.3 и 1.4 получается следующая

11.1. Первые методы Рунге—Кутты 143
Теорема 1.6. Если выполнены предположения A.9), то уравне-
уравнения A*11) эквивалентны следующим:
&\ 1 \ 1 \ 1 1 /1 1 Г* \
1 + с?2 + с?3 + С?4 ^ 1| AЛ5а)
Ъ2с2 + Ь3с3 + Ь±сА = -у, (IЛ 5Ь)
«« 2 , * 2 1 ' /1 1С \
0з<?з + 04^4 = т> AЛос)
С?з^3^32^2 ~| ^4^4 (^42^2 "Т" ^43^3/ — "о" 9 A • 101^
л . ^ 1-/1 \ /1 1 С *\
М4з = Ъг(\ — с3), AЛ5])
» •
— и /1 />\ /1 1 К1г\
— Од \х —" 64^, ^1.1ОК^
Доказательство очевидно. ■
Из A.15]) и AЛ1Ь) следует, что
с2(\— с3)ф0. AЛ6)
Отсюда, в частности, вытекает, что в силу AЛ5к) с4 = 1.
Решение уравнений A.15). Уравнения а)—е) и к) выражают
тот факт, что коэффициенты Ьг и сг являются весами и узлами
квадратурной формулы четвертого порядка при с1 = 0 и с4 = 1.
В силу A.16) возможны следующие четыре случая:
I) с2~и, с3 = V> причем ифь> иф-?г^ и и ъ
A.17)
Тогда уравнения а)—е) образуют невырожденную линейную си-
систему для определения Ъъ Ь2> ^3, Ь±. Эта система имеет решение
1 — 2и
12« A — и) (у — и) ' 3 12оA — о) (о —и) '
3 — 4м — 40
~ 12A-и)
Остальные три случая с двойными узлами основаны на правиле
Симпсона:
1 1
4) с2 = 1, ^8 = ~2"> Ь^ = ифО9 Ь2 = -^

144 Гл. II. Методы Рунге—Кутты и экстраполяционные методы
После того как выбраны Ьг и сг, получаем а43 из уравнения ]
и тогда два уравнения I) и 1) образуют линейную систему для
определения а32 и а42. Определитель этой системы
(С&
согласно A.16), не равен нулю. Наконец, из A.9) находим а2
аЪ1 и а41-
Особенно популярными стали два варианта, которые выбрал
КуттаA901). Это случай3) прим = 2/6и случай 1) при и = 1/3,
V = 2/3. Они приведены в табл. 1.2. Оба метода обобщают класси-
классические квадратурные формулы, сохраняя их порядок. Первый
из них более популярен, второй более точен («Мы будем рассмат-
рассматривать это приближение как лучшее в общем случае...» —Кутта).
Таблица 1.2. Методы Кутты
«Классический»
метод Рунге—•
Кутты
Правило 3/8
0
1
2
1
2
1
1
2
0
0
1
6
1
2
0
2
6
1
2
6
1
6
0
1
3
2
3
1
1
3
1
~" 3
1
1
8
1
1
3
8
1
3
8
1
8
«Оптимальные» формулы
Предпринималось много исследований, чтобы выбрать воз-
возможно «лучшие» из множества различных формул РК 4-го по-
порядка.
Первой попыткой в этом направлении был очень популярный
метод, который предложил Гилл A951). Он преследовал цель
уменьшить, насколько возможно, количество требуемой машин-
машинной памяти («регистров»). Этот метод широко использовался на
первых компьютерах в пятидесятых годах и представляет поэтому
исторический интерес. Гилл заметил, что больше всего машинной
памяти нужно при вычислении к3, когда «требуются регистры для
хранения в какой-либо форме» величин
1 +
У 0 + ЯЗ]Л&1 + #32^2, У 0 +
Уо

П.1. Первые методы Рунге—Кутты 145
«Ясно, что для третьей стадии будет достаточно трех регистров,
если подлежащие хранению величины линейно зависимы, т. е.
если»
A «31 «32
1 аа «42 1 = 0.
1 Ьг Ь2
Гилл заметил, что это условие удовлетворяется для методов типа 3),
если и = A +|/0,5)/3. Получающийся метод можно тогда пере-
переформулировать следующим образом («Каждая вычисленная вели-
величина засылается в регистр, ранее содержавший соответствующую
величину предыдущей стадии, больше не нужную»):
у: = начальное значение, к: = Щ(у), у: = у-\-О.Ьк, <7: = к,
:=* Ы (у), у:~ у+{\- /05) {к - ?),
:=* B — /2) к + (—2 + 3 /05) ?,
(&--<7), (Ы8)
B + /2) к + (—2 - 3/05) <7,
к:= НЦу)> д:= 9 + -$ 1-> §-+ переход к следующему шагу).
Ныне на больших компьютерах о высокой скоростью счета этот
метод больше не употребляется, но он может все же представлять
интерес для систем уравнений очень высокой размерности.
Делались и другие попытки: для случая 1) подобрать и и V
в A.17) так, чтобы погрешность (члены порядка Л6, см. разд. П.З)
стала, насколько возможно, малой. Мы обсудим этот вопрос в
разд. П.З.
Численный пример
дгоззеп ОешсМ даг! тап па1йгНсЬ зоЬЬеп Ве1$-
р1е1еп шсМ ЬеПе^еп...»
«Конечно, таким примерам нельзя придавать слишком
большого веса...»
(В, Кутта, 1901)
Сравним результаты применения пяти различных методов
к двум системам уравнений, которые возьмем в качестве тестов.
Выберем решение вида
{ = ехр E1П (*2)), у2 = ехр Eз1п (#
уг = 81П (х2) + 1, #4 = соз (л:2),

146 Гл. П. Методы Рунге—Кутга и экстр апелляционные методы
все компоненты которого удовлетворяют начальным условиям
уь @) = 1. Можно построить несколько систем дифференциальных
уравнений, которым удовлетворяет это решение, например:
у\ = 2ху4уи у 2 =
0з = 2x04, 04 = —2х @з — 1),
A.19)
или более сложную систему:
.1/5
ух = 2ху2' 04, 02 = Юх ехр E {у3 — 1)) -04,
0з =
у\ = —2х 1п
A.20)
Мы применили для их решения пять программ при нескольких
различных фиксированных длинах шага. На рис. 1.1 по осям
Э.5
Э.4
ЭЭ Ц
32 -
3 1
3.0
2.9
2.8
2.7
2.6
Уравнение A.19)
25
-1°810(погр.)
О.
3.
Рис. 1.1. Зависимость максимальной глобальной погрешности от числа обращений
к подпрограмме вычисления значения функции (обозначенного символом }с).
отложены в логарифмическом масштабе максимальные погреш-
погрешности и число обращений к вычислению функций, стоящих в пра-
правых частях уравнений (которое для четырехстадийных методов
в 4 раза больше числа шагов). Масштабы выбраны так, чтобы тео-
теоретический наклон графиков (который по теореме 3.4 равен 1/4)
составлял 45°. Эти тесты обычно показывают для классической
схемы РК слегка худшие результаты, чем для других схем РК,

11.1. Первые методы Рунге—Кутты
147
но различия оказываются очень малыми. Здесь сравнивались сле-
следующие методы:
. классический метод РК (в табл. 1.2 —
левая таблица)
правило 3/8 Кутты (в табл. 1.2 — правая
таблица)
— —■ ,—•—, — _-, — оптимальная формула (см. упр. За из
разд. П.З), и = 0.3587, V = 0.6346
_._._._,_._._._ Ральстон A962), Халл A967), и = 0.4,
V = 0.45
—..—..—..—..—..—. .формула Гилла A.18)
Упражнения
1. Покажите, что любой 5-стадийный явный метод РК порядка 5
при применении к задаче у' *= ку (к — комплексная постоян-
постоянная) дает
9 7
/а
Указание, Покажите сначала, что отношение уг/у0 должно
быть многочленом степени 5 от г, а затем определите его коэф-
коэффициенты, сравнивая производные уг по Н с производными
точного решения.
2. [Рунге A895); см. также введение к методам Адамса
в разд. III.1.] Теоретическая форма капель жидкости опре-
определяется дифференциальным уравнением Лапласа A805):
= а
2
A.21)
где а — постоянная, (Кг + К2)/% — средняя кривизна и г —
высота (см. рис. 1.2). Если подставим сюда 1/Кг = г/ът ф и
(кривизну меридиональной кривой), то получим
A.22)
где мы положим а =* 1. Добавив уравнения
= —зт<р,
A.22')
получим систему трех дифференциальных уравнений для ф E),
г (з)у г E), где 5 — длина дуги. С помощью метода Рунге A.4)
вычислите и постройте различные кривые, соответствующие
начальным значениям Ф @) == 0, г @) = 0 и г @) = 20 (г0 <
0 для лежащих капель; рассчитайте также форму висящих

148
Гл. II. Методы Рунге—Кутты и экстраполяциокные методы
капель, изменив соответствующим образом знаки в A.22)).
Проделайте вычисления с различными длинами шага и сравните
результаты.
Указание. Не забудьте про особенность в начале: из A.22) и
A.22') при малых 5 имеем г « 5, <р — А$, где —А = г0, откуда
E1П ф)/г -> —20.
Рис. 1.2. Формы капель.
3. Найдите условия, при которых двухстадийный явный метод
РК должен иметь порядок два, и определите все такие методы
(«...моги еше тсеИеге Егог1египб гисЬ1 теЬг пбНб 1зЬ(Ки11а))х).
4. Найдите все трехстадийные методы порядка три (т. е. решите
уравнения A.11, а—й) при Ь4 = 0).
Ответ. с2 = и, с3 = у, а32 == V (V — иI(и B — За)),
Ь2 = B — Зо)/Fи (и — ^)), Ь3 = B — )
[КуттаA901)].
5. Постройте все методы порядка 2 вида
О
са
О с3
0 0 1
«... далее обсуждать здесь больше нечего» (Кутта). — Нем.

IIЛ. Первые методы Рунге—Кутты 149
Такие методы «имеют свойство, заключающееся в том, что соот-
соответствующий процесс Рунге—Кутты требует относительно
мало памяти в компьютере» [Ван дер Хаувен A977), § 2.7.2].
Примените эти методы к уравнению ус — ку и сравните о ре-
результатом упр. 1.
6. Определите условия, при которых двухстадийные методы РК,
не удовлетворяющие условиям A.9):
— / (х0 + сгН} уо),
у о + а
Ь2к2),
будут иметь порядок два. Обсудите возможности использовать
эту дополнительную свободу выбора сх и с2 [Оливер A975)].

11.2. Условия порядка для методов Рунге—Кутты
«...я слышал сообщение Мерсона...».
(первое знакомство Дж. Бутчера с методами
Рунге—Кутты)
В этом разделе мы изучим общую структуру условий, опреде-
определяющих порядок метода, или условий порядка, как их называют
для краткости [Мерсон A957), Бутчер A963)]. Со времени появ-
появления этих первых работ способ вывода условий порядка прошел
большую эволюцию. Он совершенствовался главным образом под
влиянием более поздних работ Бутчера, с которым авторы много
раз обсуждали эти вопросы. В нашем изложении использовано,
кроме того, доказательство «теоремы 6» из работы Хайрера и
Ваннера A974); мы опирались также на наш опыт преподавания.
В разд. 11.11 мы увидим, что те же самые идеи позволяют доказать
общую теорему о композиции методов (В-рядов), открывающую
подход к условиям порядка для гораздо более широкого класса
методов.
Для упрощения вывода целесообразно преобразовать урав-
уравнение A.1) к автономной форме путем добавления х к зависимым
переменным:
B.1)
Основная трудность вывода условий порядка состоит в уяс-
уяснении связи между формулами и соответствующими корневыми
помеченными деревьями. Эта связь выявляется наиболее есте-
естественным образом, если воспользоваться удачно выбранной си-
системой индексных и тензорных обозначений [как в работах Гилла
A951), Хенричи A962), Гира A971)]. Как это принято в тензор-
тензорной нотации, мы будем обозначать компоненты векторов верх-
верхними индексами, причем, чтобы избежать путаницы, будем исполь-
использовать для этих индексов заглавные буквы. Тогда автономную
систему общего вида можно записать так:
..., Уп), ■/- 1, ..., п. B.2)
Перепишем прежде всего формулы метода A.8) для автономного
дифференциального уравнения B.2). Чтобы сделать запись всех

11.2. Условия порядка для методов Рунге—Кутты 151
формул A.8) более симметричной, мы перейдем от функций кь =
?я / (§г) к их аргументам &. Тогда формулы A.8) примут вид
1-1
= у& + Е
7 . B.3)
' = уо + 2 ЗД7(ёЬ • •-, в?)-
В частности, если система B.2) происходит из B.1), то при 1 = 1
Второе равенство вытекает из условия A.9), которое, как видим,
становится вполне естественным. Если оно удовлетворено, то
для вывода условий порядка достаточно рассмотреть только авто-
автономное уравнение B.2).
Как указывалось в разд. 11.1, нам надо сравнить ряды Тейлора
для у( и для точного решения. Для этой цели вычислим сначала
значения производных у{ и ^ по й при к — 0. Ввиду сходства
обеих формул достаточно проделать это для §{. В правые части
формул B.3) входят выражения вида Лф (Л), и мы воспользуемся
формулой Лейбница:
м. B.4)
Теперь приглашаем читателя сделать глубокий вдох, вспомнить
основные правила дифференциального исчисления, взять пяток
листов машинных распечаток и на оборотной стороне их присту-
приступить к следующим вычислениям;
ц =5 0: согласно B.3),
B.5; 0)
Я — 1: из B.3) и B.4) получим
Е^и0. B.5; 1)
Ц = 2: чтобы применить формулу B.4), нам понадобится первая
производная от \3 )
ГЬШП B-6; 1)
где, как это принято, /^ означает д^/дуК. Подставим сюда выра-
выражение для (ё?){1) из формулы B.5; 1), заменив в ней индексы *,
и *? на /, к, /С. Применяя теперь формулу B.4) к правой части

152 Гл. II. Методы Рунге—Кутти и экстр апелляционные методы
равенства B.3), найдем, что
(§1У2) |»-о = 2 Ц аAа1к 2 Ш* ]«=».- B.5; 2)
[, к к
Ъ = 3: сначала продифференцируем выражение B.6; 1), чтобы
найти
(8,)У2) - 2 ГЬ (а) • Ш1} №)т + Е Й (в/) (в?)(8). B-6; 2)
К, 1> Я
Подставим сюда значения производных (§*У1) и (§?У2) при Л = О,
которые уже найдены (формулы B.5; 1) и B.5; 2)), затем опять
из B.3) с помощью B.4) получим
3 2 /№%Е
3-2 Ц а//а/4а« 2 /#2/ь|«.- B.5; 3)
2, Аг. * Я, Ь
Для величин (у(){я) |л==а (^ » 1, 2, 3) справедливы те же фор-
формулы B.5; 1—3), если в них заменить ац на Ь;.
Производные точного решения
Производные точного решения получить гораздо легче. Для
этого надо взять уравнение B.2):
= Р (У)
и просто дифференцировать его, подставляя вместо производных
правые части B.2). Для второй производной получим
2 /* (у) • (/)A) - 2 &1м) !к {у). B.7; 2)
Дифференцируя B.7; 2) еще раз, найдем
(/)C) = 2 1'кь (у) /к (у) !ь (у) + 2 !к (у) $ (у) I1 (у). B.7; 3)
К, Ь К| Ь
Условия для порядка 3
Чтобы порядок метода был равен 3, производные, определяе-
определяемые выражениями B.5; 1—3) с заменой а^ на Ь^, должны быть
равны производным B.7; 1—3), причем для любого дифференци-

П.2. Условия порядка для методов Рунге—Кутты 153
ального уравнения. Сопоставляя соответствующие выражения,
убеждаемся, что имеет место
Теорема 2.1. Метод Рунге—Кутты B.3) [или A.8)] имеет
порядок 3 тогда и только тогда] если выполнены следующие равен-
равенства:
B.8)
Эти выражения можно еще более упростить, подставив в них
а1к = с] согласно A.9), что приводит к формулам A.11а — 6).
Деревья и элементарные дифференциалы
Теоретически ясно, как продолжать этот процесс, но на прак-
практике он скоро приводит к очень сложным формулам. Поэтому
целесообразно перейти к графическому представлению. Для этого
заметим, что в каждом члене формулы B.5; 3) индексы /, к, I
связаны в пары в качестве нижних индексов в а^, ап> аки и
точно таким же образом индексы «/, К, Ь связаны попарно в ка-
качестве верхних и нижних индексов в выражениях
Графически представить эти связи можно так:
31 = \/
<32= *
/
(для первого и второго члена соответственно). Назовем эти объекты
«помеченными деревьями», потому что это связные графы (деревья),
вершины которых помечены индексами суммирования. Их можно

154 Гл. II, Методы Рунге—Кутты и экстр апелляционные методы
представить и как отображения. Например, помеченным дере-
деревьям ^1 и ^зг соответствуют отображения
I _ /, к -* / и 1-»к, к-»}. B.9')
Эти отображения каждой вершине графа (кроме одной) ставят
в соответствие другую вершину, связанную с ней направленным
вниз ребром.
Определение 2.2. Пусть А — упорядоченное множество индек-
индексов: Л = {/<й</<т< ...}» и Лд — его подмножество, со-
состоящее из первых д индексов. Назовем (корневым) помеченным
деревом порядка ц($^> 1) отображение
и
такое, что I (г) < г для всех г € Ая — {/}. Множество 'всех поме-
помеченных деревьев порядка ц обозначается ЬТЯ. Будем называть
г «сыном» I (г), а I (г) — «отцом» г (г — отображение «сыновей»
на «отцов»). Вершина / («праотец» всей «династии») называется
корнем I. Порядок ц помеченного дерева равен числу всех его вер-
вершин и обычно обозначается р (/).
Определение 2.3, Назовем выражение
к, ь..
..
элементарным дифференциалом, соответствующим помеченному
дереву I ^ ЬТЯ. Здесь суммирование производится по ц —I
индексам /С, />, ..., (которые соответствуют множеству Ая —
— {/}), и каждое слагаемое является произведением ц символов /,
верхние индексы которых пробегают все множество Ач вершин /,
а нижние индексы — множество соответствующих «сыновей».
Если множество Ая записано в виде
B.10)
то определение Р (/) можно переписать следующим образом:
- Е , Д/Й.Ю), B.11)
поскольку «сыновья» индекса составляют его полный прообраз
при отображении I.

П.2. Условия порядка для методов Рунге—Кутты 155
Примерами элементарных дифференциалов являются
1КЦ I И Ь 1К1Ц у
К, I К, Ь
соответствующие помеченным деревьям /31 и /82 B.9). Эти выраже-
выражения входят в формулы B.5; 3) и B.7; 3).
Следующие три помеченных дерева
\/
У
имеют одинаковую топологическую "структуру; более того, их
элементарные дифференциалы
т
V
/ к
\/
т
\
к 1
\/
•
1км[ и! у Ь 1кц Ш у Ь 1ьк1 1м1 B.12)
К, Ь, М Я, I, М К, Ь, М
совпадают, поскольку они отличаются лишь обозначениями ин-
индексов суммирования. Этот пример подсказывает дать следующее.
Определение 2.4. Два помеченных дерева I и и назовем экви-
эквивалентными, если они имеют одинаковый порядок ц и существует
подстановка а: Ая -> Лд, такая, что о (/) = / и 1а = аи на мно-
множестве Лд — {/}.
Легко видеть, что этим мы определили отношение эквивалент-
эквивалентности на множестве ЬТд.
Определение 2.5. Класс эквивалентности помеченных дере-
деревьев порядка ц называют (корневым) деревом порядка ^. Множество
всех деревьев порядка ц обозначается Тч. Порядок дерева опре-
определяется как порядок его представителя из ЬТЧ и тоже обозна-
обозначается р @- Обозначим, далее, через а [I) (для 1$ Гд) число
элементов в классе эквивалентности I, т. е. число различных воз-
возможных монотонных индексаций 1У)
Геометрически дерево отличается от помеченного дерева тем,
что у него опущены все индексы. Часто бывает целесообразно
включить в рассмотрение пустое дерево 0 как единственное дерево
порядка 0. Единственное дерево порядка 1 обозначают т. Пред-
Представители всех деревьев порядка <<5 приведены в табл. 2.1. Число
деревьев для порядков 1, 2, ..., 10 представлено в табл. 2.2.
) Речь идет о таких расстановках индексов, при которых сохраняется отно-
отношение порядка, заданное на множестве Ая, т. е. по существу о монотонных (изо-
тонных) отображениях. — Прим. ред.

156 Гл. II. Методы Рунге—Кутты и экстраполяционные методы
Таблица 2.1. Деревья и элементарные дифференциалы вплоть
до порядка пять
я
0
1
2
3
4
5
1
0
т
'21
'31
'32
'41
'42
'43
'44
'51
'52
'53
'54
'55
'56
'57
'58
'59
граф
0
ч
/к
1 к
V
)
т 1 к
у /
'г*.
^ •
\/* /
7 Р \ь
р\ 1 ;
• рт 1
7@
1
1
2
3
6
4
8
12
24
5
10
15
30
20
20
40
60
120
а@
1
1
1
1
1
1
3
1
1
1
6
4
4
3
1
3
1
1
У
V4 *У * К ~1^ *М
К ,Ь ,М
у ^.У гК.Ь ,А/
V У К Ь М Р
^кр^^м^М^Р
>^ /*//" //
^-^У VI 1 У \лЗ V У
Ф/0
1
А ,/
2 а1как1а]т
к ,1 ,т
2 а]как1акт
к ,1,т
2 а]как1п1т
к ,/»т
у* к/ у/л ур
^■^ /* к/ Ас/п ур
^а]как1а1та)р
^а]-как1арпатр
2-Д «««*-%
Таблица 2.2. Число деревьев
я
сагё (Тд)
1
1
до
2
1
10-го порядка
3 4 5
2 4 9
6
20
7
48
8
115
е
286
10
719

II.2. Условия порядка для методов Рунге—Кутты 157
Разложение Тейлора для точного решения
Теперь мы можем для ^-й производной точного решения сфор-
сформулировать результат в общем- виде.
Теорема 2.6. Для точного решения уравнения B.2) справедлива
формула
(/)'" |*=*. = Е Р1 (О Ы = Е «(О Р1 @ (Уо).' B.7; я)
Доказательство. Теорема справедлива при ^ = 1, 2, 3 [см.
формулы B.7; 1—3I. Чтобы вычислить, например, четвертую
1 B7 ;
I '
, * B.7
/ ч \
\/ * ^/ * B.7-3)

Рис. 2.1. Производные точного решения.
производную, надо продифференцировать формулу B.7; 3), в ко-
которой два члена соответствуют двум деревьям B.9) и каждый из
них содержит три множителя /..., отвечающие трем вершинам
этих деревьев. Дифференцирование этих членов по правилу Лейб-
Лейбница и подстановка правой части уравнения B.2) вместо произ-
производных у' геометрически интерпретируется как добавление к каж-
каждой вершине нового ребра с вершиной, помеченной новым индек-
индексом суммирования (рис. 2.1).
Очевидно, что в этом процессе для ^-й производной появляются
все помеченные деревья порядка <7> и каждое из них только один
раз.
Если сгруппировать теперь все члены с одинаковыми элемен-
элементарными дифференциалами, мы получим второе выражение в фор-
формуле B.7; д). Ш

158
Гл. II. Методы Рунге—Кутты и экстраполяционные методы
Формула Фаа ди Бруно
Займемся теперь вычислением ^-й производной численного
решения уг и величин §^, Для этого надо сначала получить обоб-
обобщение формул B.6; 1) («цепного правила») и B.6; 2) на случай
<7-й производной от суперпозиции двух функций. На рис. 2.2
приведено представление этих формул в виде графов.
B.б;2)
Рис. 2.2, Производные функции I<?
Формула B.6; 2) состоит из двух членов, причем первый член
содержит три множителя, а второй —только два, так что в его
графе индекс / — «пустой», в формуле он отсутствует, его назна-
назначение — показать, что надо взять вторую производную. Следо-
Следовательно, дифференцируя выражение B.6; 2), мы получим пять
членов, которые выпишем здесь для удобства читателя (и невзи-
невзирая на неудобства при их наборе!..):
/С, 1>, М
К, М
B-6;3)

11.2. Условия порядка для методов Рунге—Кутты 159
Соответствующие деревья изображены в третьем ряду рис. 2.2.
При каждом дифференцировании мы производим следующие
операции.'
1) дифференцируем первый множитель /я...* т- е- добавляем
к дереву новую ветвь, идущую от корня /;
2) увеличиваем на единицу порядок производной каждого из
множителей §, что графически представляется удлинением соот-
соответствующей ветви.
Каждый раз мы добавляем новый индекс. Все получаемые
при этом деревья имеют «специальный» вид: разветвления у них
возможны только у корня.
Определение 2.7. Обозначим ЬЗд множество специальных по-
меченных деревьев порядка <?, т. е. таких помеченных деревьев,
у которых разветвления встречаются только у корня.
Лемма 2.8 (формула Фаа ди Бруно). При ц^>\ справедлива
формула
= 2 гх„
Кг Кт
B.6; G-1)
Для каждого и^ ЬЗд здесь т — число выходящих из корня вет-
ветвей, 61э ..., 6ТО — числа вершин на этих ветвях, так что ц = 1
б + б
Замечание. Здесь отсутствуют привычные коэффициенты, ука-
указывающие кратности членов, поскольку мы пользуемся поме-
помеченными деревьями.
Производные численного решения
«Трудно сохранить хладнокровие, когда обсуждаешь
различные производные...» (С. Гилл, 1956)
Чтобы обобщить формулы B.5; 1—3), нам потребуются сле-
следующие определения;
Определение 2.9. Пусть I — помеченное дерево с корнем /.
Введем величину
Ф;(/)== И
где суммирование производится по ц — 1 индексам к, 1У ... (как
в определении 2.3), каждое слагаемое является произведением
Я — 1 коэффициентов а, у каждого из которых индексы соста-

160 Гл, II. Методы Рунге—Кутты и экстраполяционные методы
вляют одну из пар «отец» —«сын» дерева I, Если множество Ая
записано в виде B.10), то
%г @ = 2 *(/,,. /,.. .а, (/ )# у B.13)
Определение 2.10. Для каждого 1^ЬТA определим вели-
величину у @ как произведение р (I) на порядки всех деревьев, кото-
которые получаются из I, если последовательно удалять их корни
[вместе с инцидентными им ребрами, см. рис. 2.3 или форму-
формулу B.17)].
* 9 -2-6 . 4 =432
Рис. 2.3. Пример определения величины у (/)•
Обе введенные величины, разумеется, не зависят от индек-
индексации, поэтому как Ф7- ({), так и у (I) имеют смысл и для I ^ Тч.
Примеры приведены в табл. 2.1.
Теорема 2.11. Для производных §/ имеет место равенство
Для производных определяемого методом B.3) численного решения
у{ справедлива формула
? @ Е *А @ *'@ (№) =
= 2 *AI®1}Ь,Ф1ЮР'(*)Ы- BЛ4)
Доказательство. Благодаря сходству выражений B.3) для у±
и §1 достаточно доказать первое равенство. Мы докажем его
индукцией по <7, следуя тем же путем, на котором были получены
равенства B.5; 1—3). Сначала применим к B.3) формулу Лейб-
Лейбница B.4), что дает
м = Я 2 аи V Ш"~Х) \у=у, B-15)
Далее воспользуемся'формулой Фаа ди Бруно (лемма 2.8). Нако-
Наконец, используем индуктивное предположение о справедливости

11.2. Условия порядка для методов Рунге—Кутты 161
формул B.5; 1)—B.5; д—1) и подставим соответствующие выра-
выражения в формулу B.6; ц—1) вместо производных (§/ 8)( , при-
приняв во внимание, что всегда б3 < ц. После несложных преобразо-
преобразований, изменив порядок суммирования, получим
2 ••■
X 2 аи Ц а^ФыУг)... 2 ЪкФкит) X
B.16)
Теперь мы подошли к самому трудному месту доказательства:
надо уяснить себе, что каждой совокупности деревьев
A1 / /1 Г*ТТО 11 С 1 V Т С Т Г/'
соответствует определенное I ^ ^Т*д, такое, что
у (I) = 9.7 (/х) ... у (*т), B.17)
Это помеченное дерево I получается заменой ветвей и деревьями
1ъ •••> ^т» и соответствующие индексы переносятся с и на I в есте-
естественном порядке, т. е. сохраняется их упорядоченность (при-
(примеры приведены на рис. 2.4). Таким способом оказываются по-
построенными все деревья г ^ ЬТд, причем каждое возникает
только один раз. Итак, после подстановки B.17), B.18) и B.19)
в формулу B.16) последняя перейдет в формулу B.5; ^). ■
Описанное выше построение I можно использовать также для
индуктивного определения деревьев. Заметим сначала, что класс
эквивалентности I зависит только от классов эквивалентности
гъ ..., 1т (это видно на рис. 2.4).
Определение 2.12. Будем обозначать
^= [*!,...,*«] B.20)
Дерево, после удаления корня которого (вместе с инцидентными
ему ребрами) останутся деревья 1Ъ ..., 1т (рис. 2.5).
С помощью B.20) все деревья могут быть выражены в конеч-
конечном счете через х. Например, г21 = [т], *31 = [г, г], /82 = Их]],
и т.д.
6 Хайрер Э. в др.

162 Гл. II. Методы Рунге—Кутты и экстраполяционные методы
V
\
т
V
т
л
т
п
т
и
Рис. 2.4. Пример взаимно однозначного соответствия {и, 1и ...,
Рис. 2,5, Рекурсивное определение деревьев.
Условия порядка
Теперь, сопоставляя теоремы 2.6 и 2.11, мы получим оконча-
окончательный результат:
Теорема 2.13. Чтобы метод Рунге—Кутты A.8) имел поря-
порядок р, необходимо и достаточно выполнения равенств
1
2 ъ&; (О
7@
B.21)
для всех деревьев I порядка, меньшего или равного р.
Доказательство. Достаточность вытекает из проведенных выше
рассуждений. Для доказательства необходимости нужно, чтобы

11.2. Условия порядка для методов Рунге—Кутты 163
элементарные дифференциалы, соответствующие различным де-
деревьям, были действительно независимыми (см. ниже упр. 3 и 4). ■
Эта теорема позволяет легко Сосчитать число условий порядка
для любого р. Результаты подсчета, сделанного с помощью
табл. 2.2, приведены в табл. 2.3. Читателю, наверно, теперь
понятно, что конструирование формул Рунге—Кутты высоких
порядков — нелегкая задача.
Таблица 2.3. Число условий порядка
Порядок р
Число условий
12 3 4
12 4 8
5
17
6 7
37
8
85
9
200
10
486
•
1205
Пример. Для дерева ^42 из табл. 2.1 имеем
^Х
(второе выражение получено с помощью условия A.9)). Получи-
Получилась как раз формула A.Ш). Все остальные условия A.11)
соответствуют другим деревьям, у которых порядок р ^ 4.
Упражнения
1. Найдите все деревья порядка 6 и порядка 7.
Указание. Рассмотрите все представления р — 1 в виде суммы
положительных целых чисел и подставьте вместо каждого
члена этих сумм все известные деревья соответствующих
низших порядков. Вы можете также написать программу
для произвольного порядка р и воспользоваться компьютером.
2. Обозначим число деревьев порядка д через ат Докажите, что
Сравните результат с табл. 2.2.
3. Вычислите элементарные дифференциалы из табл. 2.1 для
случая скалярного неавтономного уравнения первого по-
порядка, т. е. уравнения B.1), где /х = 1 и Р = / (я, у). Это
поможет вам понять трудности, с которыми встретились пер-
первые авторы (Кутта, Нюстрём, Гута) при поисках условий для
высших порядков. Обратите внимание, что р этом случае
выражения для гы и 1Ь1 совпадают, так что здесь условие тео-
теоремы 2.13 для порядка 5 является достаточным, но не необ-
необходимым.
6*

164
Гл. II. Методы Рунге—Кутты и экстраполяционные методы
Указание. Для 1Ы, к примеру, мы имеем ненулевые производ-
производные, если только К = Ь = 2. Заставляя индексы М и Р про-
пробегать значения от 1 до 2, получим тогда
4 V*/ — Ч/ ов г^ 11 у) \1 ух \ II уу/1У
(см. также Бутчер A963а)).
4. Покажите, что для любого I $ Тя существует дифференциаль-
дифференциальная система, такая, что для нее Р1 (() (у0) = 1, а для всех
остальных деревьев и выполняется равенство Р1 (и) (у0) == 0.
Указание. Для дерева 1Ы такой системой будет
== уз, у'ъ =
у\
со всеми начальными значениями, равными нулю,
себе этот факт, а также общую формулу
Уясните
— 11 г/
«сыновей»»
5. Кутта A901) утверждал, что схема, приведенная в табл. 2.4,
имеет порядок 5. Был ли он прав? Попытайтесь исправить
приведенные значения.
Таблица 2.4. Один из методов Кутты
0
1
3
2
5
•
1
2
3
4
5
1
3
4
25
1
4
6
81
7
30
48
192
6
25
—3
90
81
18
30
0
15
4
50
~~ 81
5
~~ 30
125
192
8
81
4
30 °
81 100
0 192 192
Ответ. Значения коэффициентов аЬ) (/ = 1, ..., 5) должны
быть F, 36, 10, 8, 0)/75; правильные значения коэффициентов
Ъ} равны B3, 0, 125, 0, —81, 125)/192 [Нюстрем A925I.
6. Проверьте равенство
2]
—1I

11.2, Условия порядка для методов Рунге—Кутты 165
7. Докажите, что при применении метода РК к линейной системе
у' = А (х) у + ё (х) B.22)
локальная погрешность у (х0 + К) — уг будет величиной
О {Нр+1) в том и только том случае, если
2
Ь}с]-1арсгГ1 = (Я + Г)г для
и к

и т. д.
Указание. Запишите систему B.22) в автономной форме и
исследуйте, какие элементарные дифференциалы равны нулю
тождественно. [См. также Крузё A975)].

Н.З. Оценка погрешности и сходимость
методов Рунге~Кутты
«Ез !еЬН тёеззеп посЬ с1ег Ве\уе15 йазз сНезе ШЬешп^з—
УегГаЬгеп сопуег^еп! 51П<3 ойег, \уаз ргакИзсЬ шсЫл^ег
1з1, ез !еЬН ет КгНегшгп, игл ги егтИЫп, ше к1ет
(Не ЗсЬгШе ^етасЫ \уегс1еп тйззеп, ит ете уог&езсЬ-
пеЬепе Сепаш&кек гм еггекЬеп».
«Между тем еще нет доказательства, что эти прибли-
приближенные методы сходятся, или, что практически важ-
важнее, нет критерия, определяющего, сколь малыми
надо сделать шаги, чтобы достичь предписанной точ-
точности».
(Рунге, 1905).
Со времен работы Лагранжа A797) и особенно Коши всякий
установленный численно результат принято сопровождать на-
надежной оценкой погрешности («...Геггеиг сотгшзе $ега тГёпеиге
а...») х). Лагранж дал известные оценки погрешности много-
многочленов Тейлора, а Коши вывел оценки для погрешности метода
ломаных Эйлера (см. разд. 1.7). Через несколько лет после пер-
первых успехов методов Рунге—Кутты Рунге A905) также пришел
к заключению, что для' этих методов нужны оценки погреш-
погрешностей.
Строгие оценки погрешности
Способ, которым Рунге получил оценку погрешности, делае-
делаемой на одном шаге («локальной погрешности»), может быть опи-
описан в нескольких строках (далее следует свободный перевод):
«Для метода порядка р рассмотрим локальную погрешность
е (А) = У (х0 + к) - уг C.1)
и воспользуемся ее тейлоровским разложением»
е (Л) = е @) + Не' @) + • • • + ^- е<« (Эй), C.2)
где 0 < 9 < 1 и е @) = е' @) = ... = е<"> @) = 0.
Явное вычисление е(р> (к) дает выражение вида
е<"> (к) = Ех (к) + кЕг (к), C.3)
*} «... совершаемая ошибка была бы меньше, чем ...». — Франц.

П.З. Оценка погрешности и сходимость методов Рунге—-Кутты 167
где Ег (к) и Е2 (к) содержат частные производные / до порядков
р — 1 и р соответственно. Далее, поскольку е^ @) = 0, имеем
Е± @) = 0. Таким образом, если ограничены все частные произ-
производные I до порядка р включительно, имеем Ег (к) = О (к) и
Е2 (к) — О (I). Следовательно, существует постоянная С, такая
что | ем (к) | < Ск и
^1.» ' C.4)
Бибербах A923, разд. 1-й, гл. II, § 7) использовал несколько
иной подход [более подробное объяснение см. Бибербах A951)].
Запишем
C.5)
и воспользуемся тейлоровскими разложениями
у (у0+Ь) = уо+у'Ш ь+у" (х0) -й- + • • • + у{р+1) (Щ
к (А) = к( @) + к\ @) й + ... + &!р) (9,Л) -^-. C.6)
Для векторных функций эти формулы справедливы покомпонентно
(возможно, с различными 0). В силу условий порядка первые
члены разложения C.5) по степеням к обращаются в нуль. Таким
образом, справедлива
Теорема 3.1. Если метод Рунге—Кутты A.8) имеет порядок
р и если все частные производные / (х, у) до порядка р включи-
включительно существуют (и непрерывны), то локальная погрешность
метода A.8) допускает следующую строгую оценку:
или
Продемонстрируем этот результат, применяя к скалярному
дифференциальному уравнению первый метод Рунге A.4), кото-
который имеет порядок р = 2. Дифференцируя A.1), получим
УC} (х) = ([хх + 2/ху/ + и2 + /„</« + Ш (х, У (х)). C.9)

168 Гл. II. Методы Рунге—Кутты и экстраполяционние методы
(К
хо + -о">
имеет вид
C.10)
(здесь /0 означает / (х0, уо))« Если условия теоремы 3.1 выпол-
выполнены, то легко видеть, что выражения C.9) и C.10) ограничены
постоянной, которая не зависит от А, что и дает оценку C.8).
Главный член погрешности
Для методов высших порядков строгие оценки погрешностей,
подобные C.7), становятся очень непрактичными. Поэтому го-
гораздо более реалистично рассматривать первый ненулевой член
в тейлоровском разложении погрешности. Для автономных систем
уравнений B.2) член погрешности проще всего получить, вычи-
вычитая друг из друга ряды Тейлора и пользуясь формулами B.14)
и B.7; </).
Теорема 3.2. Если метод Рунге—Кутты имеет порядок р
и если [ непрерывно дифференцируема р + 1 Р#з> то для главного
члена погрешности имеем:
2
ъ^ГЩ 2 C.18)
где
е (I) = 1 - V @ Ц Ь]®} (*). ■ C.19)
По поводу величин 7 @ и Ф^ (I) см. определения 2.9 и 2.10, а
также формулы B.17) и B.19). Выражения е (I) называются
коэффициентами погрешности.
Пример 3.3. Для двухпараметрического семейства методов РК
A.17) 4-го порядка коэффициенты погрешности для девяти де-
деревьев из табл. 2.1 таковы (с2 = и, с8 = Ь):
= — 4"+ 12 (" + )
в
1446,4.
е (У =
е (<„) = —4е

Н.З. Оценка погрешности и сходимость методов Рунге—Кутты 169
Доказательство. Последние четыре формулы следуют из A.12).
Выражение для еAЬ9) тривиально, а выражения для е (/Б8) и е AЪ1)
следуют из A.11Ь). Далее,
р а \ •—~ 5 1/^/ —— 1 ^ (I —— и\
о
выражает погрешность квадратуры. Для е (^б5) удобнее^ всего
ввести величину с\ = 2/аО'с/» тогда е (^55) = 1 — 20 "~ '
Теперь из A.1 Ы, Г) получаем:
1 , , 3—4у
= 24A-р) > Ь*С4 д 24 G-Л) '
Для «классического» метода 4-го порядка (табл. 1.2а) эти
коэффициенты погрешности нашел Кутта A901) [см. также Лот-
кин A951)]:
1 11 1 2 11 1
24~' 24"*' "иГ' ~~' ~~Т' Т' ~Т' ~ 4
Кутта отметил, что для второго метода (табл. 1.2Ь) коэффици-
коэффициенты погрешности
1_ _1_ \_ 1^ 1^ _2_ 1^ ^ -\
64 ' 36 ' 24 ' 4 ' 9 ' 27 ' 9 ' 6 ' )
таковы, что, за исключением 4-го и 9-го коэффициентов, все они
меньше, чем у предыдущего метода («А1з Ьеззег посЬ епуе1з1
51сЬ...» х)). Для определения оптимальных коэффициентов A.17)
Ральстоном A962) (и многими другими авторами) были прове-
проведены весьма кропотливые вычисления. Решения, минимизиру-
минимизирующие константы C.20), рассматриваются в упр. 3 ниже.
Оценка глобальной погрешности
аисЬ ете аи!ге^еп<1е 2еН...»
«Да, это было волнующее время...»
(П. Хенричи, 1983)
Глобальной (накопленной) погрешностью называется погреш-
погрешность численного решения после выполнения нескольких шагов.
Пусть мы имеем некоторый одношаговый метод, с помощью ко-
которого при заданных начальных данных (х0, у0) и длине шага Н
мы определяем численное решение уъ аппроксимирующее у (#0 +
+ И). Воспользуемся обозначениями Хенричи для этого процесса:
Уг = Уо + йФ (% Уо> й), C.21)
и назовем Ф функцией приращения для данного метода.
«Но еще лучше оказывается .,.». — Нем.

170 Гл. П. Методы Рунге—Кутты и экстраполяционные методы
Тогда численное решение в точке X > х0 получается с по-
помощью пошаговой процедуры
Ум = Уг + ЬФ (*|, Уь Ьг), Нг = хм - хь хк = X, C.22)
и наша задача состоит в оценке глобальной погрешности
C.23)
Эта оценка находится простым способом, очень похожим на дан-
данное Коши доказательство теоремы сходимости (теорема 7.3 из
гл. I): локальные погрешности переносятся в конечную точку
точные решения
метод _
C.22)
точное решение
" ■ **-1
Рис. 3.1. Оценивание глобальной
погрешности, метод а).
Рис. 3.2. Оценивание глобальной по-
погрешности, метод Ь).
и затем складываются. Этот «перенос погрешностей» можно вы-
выполнить двумя разными способами:
а) перенося погрешности вдоль кривых точных решений
(см. рис. 3.1); этот способ может дать хорошие результаты, если
известны хорошие оценки распространения погрешности для
точных решений, например из теоремы 10.6 из гл. I, использу-
использующей понятие логарифмической нормы |д. (д[/ду)\
Ь) перенося погрешность г-го шага посредством выполнения
N — I шагов численного метода (см. рис. 3.2); этот способ исполь-
использовали в своих доказательствах Коши A824) и Рунге A905),
он легко обобщается на многошаговые методы (см. гл. III) и будет
для нас важным инструментом при доказательстве существования
асимптотических разложений (см. разд. 11.8).
В обоих случаях оценим сначала с помощью теоремы 3.1
локальные погрешности:
C.24)

П.З» Оценка погрешности и сходимость методов Рунге—Кутты 171
Предупреждение: величины ег на рис. 3.1 и 3.2 при I
не совпадают, но они допускают сходные оценки.
Займемся теперь оценкой перенесенных погрешностей Ег.
а) При первом способе переноса мы воспользуемся извест-
известными результатами из гл. I, в частности теоремами 1.10.6 и 1.10.2
или формулой A.7.17).
Теорема 3.4. Обозначим V окрестность точки {(*, у (х)) | х0 <;
<^ х ^С X}, где у (х) — точное решение уравнения B.2). Пусть
в V справедливы оценки локальных погрешностей C.24) и выпол-
выполнено одно из условий:
д! -' или Л #Л<1. C.25)
ду
Тогда имеет место следующая оценка глобальной погрешности
C.23):
Е К НР 41 (ехр (Ь \х„ - х0)) - 1), C.26)
( С при Ь ^> 0,
где Н = тах Ни
С —
{ С ехр (— Щ при Ь < 0,
и Н достаточно мало для того, чтобы численное решение остава-
оставалось в V\
Замечание. При Ь ->• 0 оценка C.26) переходит в НрС (х^ — ^0)-
Доказательство. Из теоремы 1.10.2 (при 8 = 0) или теоремы
1.10.6 (при б = 0) получаем
| Ег ||< ехр A(х*-хОЛ е%|. C.27)
Подставляя в неравенство
выражение C.27) с учетом C.24) и принимая во внимание, что
1 ^ НР'Ни приходим к такому неравенству:
Е||<Ь?С[Ноехр (Ь (х„ - хх)) + Нгехр (Ь (хк- х2)) + *••]•
Выражение в квадратных скобках мажорируется следующими
интегралами:
— х))йх при 1>0, C.28)
I при 1<0 C.29)
(см. рис. 3.3). Отсюда и получается оценка C.26). ■

172 Гл. II. Методы Рунге—Кутты и экстраполяционные методы
Ь) При втором способе переноса погрешностей рассмотрим
кроме C.22) еще одно численное решение, значения которого
в соседних узлах связаны равенством
Нам нужно оценить норму разности || гм — уих | через \г} —уг |.
Для ги1 формулы метода РК запишем в таких обозначениях:
к = / (*1 + Фи *1 + МгА) и т. д.
Вычитая из этих формул соответствующие формулы A.8), полу-
получим для норм разностей такие оценки:
-2|| и
Это приводит нас к следующему предложению
Ь(хп-Н-х)
Ь(хп-х)
о
Рис. 3.3. Оценивание римановых сумм.
Лемма 3.5. Пусть Ь — постоянная Липшица для функции /
и пусть Нг ^ Н, Тогда функция приращения Ф для метода A,8)
удовлетворяет неравенству
| Ф (*ь ги А,) - Ф (хи у и А,) 1 < Л || 2| - у, I, C.30)
1в1 М>Л C.31)
■
Из C.30) мы получаем искомую оценку:
|г«+1-У|+1КA + Л|А)|г«-»«|<ехр(А|Л)|г|-»1|, C.32)
и с ее помощью оценку перенесенных погрешностей на рис. 3.2
|^||<ехр(Л(х|Г-дг,))|в|| C.33)
вместо оценки C.27), соответствующей рис. 3.1.

II.3. Оценка погрешности и сходимость методов Рунге—Кутты 173
Повторяя доказательство теоремы 3.4, придем к следующему
результату.
Теорема 3.6. Предположим, что для начальных значений, ле-
лежащих на точном решении, локальная погрешность удовлетворяет
оценке
\у(х+Н)-у (х) - ЛФ (х, у (х), К) || < СйН-1 § C.34)
и что в окрестности решения функция приращения Ф удовлетво-
удовлетворяет неравенству
\\Ф(х, г, й)-Ф(х, у, Л)|<Л|2-у|. C.35)
Тогда для глобальной погрешности C.23) справедлива следующая
оценка:
IIЕ || < Нр 4 (ехр (Л (*„-*„)) - 1), C.36)
где Н = тах Нг. ■ •
Упражнения
1. [Рунге A905)] Покажите, что для явных методов Рунге—
Кутты порядка р = $, у которых Ьь ^ 0, аи ^ 0 (для всех
I, /), постоянная Л для Ф удовлетворяет неравенству
< ехр (НЬ)
и что оценка C.36) останется справедливой, если Л заменить
на Ь.
2. Покажите, что формула C.20) для е ((ъь) после подстановки
выражений для Ьд и Ь4, приведенных ниже формулы A.17),
примет вид
2 — 15о + 9) — и Fс/а — 42у + 27) — и2 B6у — 18)
12A—
3. Определите значения и и V в A.17) так, чтобы в формулах
C.20) было:
9
а) тах \е({ь1)\ = тт, Ь) 2 I^(^бО 1 = т1п,
*=5, 6, 7. 8 *«1
9
с) тах а({)\е Aъг) \ = тт, д) 2 а (/) | в (^5г) 1 = тт.
?=5, 6, 7, 8 <=1
а) и = 0.3587, с; = 0.6346, тт = 0.1033;
Ъ) и = 0.3995, V = 0.6, тт = 1.55;
с) и = 0.3501, с; = 0.5839, тт = 0.1248;
й) и = 0.3716, у = 0.6, тт в 2.53.

174 Гл. II. Методы Рунге—Кутты и экстраполяционные методы
4. Примените какой-либо явный метод Рунге—Кутты к задаче
У' = / (*, У), У @) = 0, где
/(*,
Г *" ' 'А при дг>0,
12@) при * = 0,
причем 1<0 и § (х)—функция, дифференцируемая доста-
достаточное число раз (см. упр. 10 в разд. 1.5).
а) Покажите, что погрешность после первого шага имеет вид
где С2 — постоянная, зависящая от коэффициентов метода.
Вообще говоря, С2 Ф 0 и для методов высших порядков.
Ь) Вычислите С2 для классического метода 4-го порядка (см.
табл. 1.2).

11.4. Практическая оценка погрешности
и выбор длины шага
«1сЬ ^1аиЬе тйеззеп, <1а55 ет ргакШсЬег Кесппег
51сЬ те1$1еп8 тН <1ег §епп§егеп ЗкпегпеК Ье^пй^еп
\У1гс1> (Не ег аиз <1ег 11еЪегетз1;1ттип^ зетег КезиИа1е
Гиг ^гбззеге ип<1 кктеге ЗсЬпИе
«Между тем я верю, что вычислитель-практик в боль-
большинстве случаев будет довольствоваться меньшими
гарантиями, которые он извлекает из совпадения
своих результатов при больших и меньших шагах».
(К. Рунге, 1895)
Даже упрощенные оценки погрешностей из разд. Н.З, которые
довольствуются лишь главным членом погрешности, не пред-
представляют практического интереса, потому что они требуют вычи-
вычисления и оценивания верхних границ ряда частных производных
высоких порядков. Между тем главное преимущество методов
Рунге—Кутты по сравнению с методом ряда Тейлора как раз
в том и состоит, что они не требуют вычисления этих производ-
производных. Для практики, однако, оценки погрешностей необходимы, —
с одной стороны, чтобы обеспечить длину шага Ни достаточно
малую для достижения требуемой точности вычисляемых резуль-
результатов, а с другой стороны — чтобы гарантировать достаточно
большую длину шага во избежание бесполезной вычислительной
работы. Поэтому мы обсудим теперь альтернативные методы
оценивания погрешностей.
Самый старый способ, который использовал Рунге в своих
численных примерах, состоит в повторении вычислений с умень-
уменьшенной вдвое длиной шага и сравнении результатов*, те десятич-
десятичные знаки, которые не изменились, считаются правильными
1сЬ зсЬНеззеп ги йпг1еп §1аиЬе...»*)).
Экстраполяция по Ричардсону
«...ее полезность при практических вычислениях вряд
ли может быть переоценена».
(Г. Биркгофф—Г. К. Рота)
Идея Ричардсона, которая была опубликована в его класси-
классической работе [Ричардсон A910)], посвященной главным образом
дифференциальным уравнениям в частных производных, и разъ-
разъяснена во всех подробностях в более поздней работе [Ричард-
1) «... я надеюсь, что отсюда можно заключить ...». — Нем,

176 Гл. II. Методы Рунге— Кутты и экстр апелляционные методы
сон A927I, состоит в более осторожном использовании извест-
известного поведения погрешности как функции Л.
Предположим, что, пользуясь некоторым определенным мето-
методом Рунге—Кутты порядка р и исходя из заданной начальной
точки (х0, у0), мы провели расчет для двух шагов при длине шага А
и получили при этом численные результаты уг и у2. Исходя из
той же начальной точки (х0, у0), сделаем теперь расчет для одного
большого шага длины 2А и обозначим полученное численное ре-
решение до. Как мы знаем из теоремы 3.2, погрешность ух предста-
вима в виде
ег = У (*в + А)" - Уг = С-АИ* + О (ЙЖ), D.1)
где С выражается через коэффициенты погрешности метода и эле"
ментарные дифференциалы Р3 {I) (у0) порядка р + 1. Погрешность
у2 состоит из двух частей: из перенесенной погрешности первого
шага, имеющей вид
и локальной погрешности второго шага, тоже выражаемой фор-
формулой D.1), но с элементарными дифференциалами, вычисленными
при уг = у0 + О (Л). Таким образом, получаем, что
+ О (Л)) к*>+1 + О (А*-*), D.2)
откуда
р = 9Г*/?Н-* А- О
.По аналогии с D.1) для большого шага имеем
у (х0 + 2А) — ни = С BА)"+Г + О (А^+2). D.3}
Если пренебречь членами О (Ар+2), формулы D.2) и D.3) позво-
позволяют исключить неизвестную постоянную С и «экстраполировать»
значение у2, лучше аппроксимирующее у (х0 + 2А). Итак, мы
получили следующий результат.
Теорема 4.1. Пусть некоторым методом РК порядка р в ре-
результате выполнения двух шагов длины А найдено численное зна-
значение у2, а в результате выполнения одного большого шага длины
2Н получено значение ш. Тогда погрешность у2 может быть оце-
оценена по формуле
У
а выражение
аппроксимирует величину у (х0 + 2Н) с порядком р + 1.

11.4. Практическая оценка погрешности и выбор длины шага 177
Формула D.4) дает очень простой способ оценки погреш-
погрешности, а D.5) позволяет дополнительно увеличить точность на
один порядок1). «... Развиваемая в следующих разделах улуч-
улучшенная теория сложна и наводит на мысль, что практика может
быть столь же сложной, тогда как в действительности она проста».
(Ричардсон.)
I
Автоматическое управление длиной шага
, оп зе соп!еп1е <1е ггшШрПег ои с!е (Ну15ег
раг 2 1а уа1еиг с!и раз...»
«Обычно довольствуются умножением или делением
длины шага на 2...»
(Ческино, 1961)
Мы хотим теперь написать программу, которая автоматически
подбирала бы длину шага так, чтобы локальная погрешность не
превышала предписанной допустимой величины (допуска).
Если начальная длина шага была выбрана равной й, про-
программа выполняет вычисление двух шагов длины к и одного шага
длины 2Л, как описано выше. Затем на основе формулы D.4)
вычисляется погрешность:
тах |У2'*ГШ*' . D.6)
1 п *1
Часто используют и другие нормы, например евклидову. В D.6)
&х — масштабируюи&ш множитель. Для вычисления абсолютной
погрешности полагают йг = 1, а для относительной йг = | у2у * |.
Часто используют и смешанное масштабирование типа
, \уОу1\9 1), или й% = тах(\у%,|, \уОшй\
или что-нибудь еще в этом роде. Затем величина егг сравнивается
с заданной величиной допустимой погрешности Ы, что позво-
позволяет, зная зависимость погрешности от длины шага Скр+1, вычи-
вычислить оптимальную длину шага («...1е ргосёйё соппи», СезсЫпо
A961)) 2)
D.7)
) В отечественной литературе по численному анализу эти формулы рас-
рассматриваются как частный случай правила Рунге [см., напр., Бахвалов A975)].—
Прим. ред.
а) «Известный прием» Ческино A961). — Франц.

178 Гл. II. Методы Рунге—Кутты и экстраполяционные методы
Далее, для получения хорошей программы требуется известная
осторожность. Умножим D.7) на гарантийный фактор [ас. Обычно
выбирают [ас равным 0.8, 0.9, @.2ЪУ'1р+1) или (О.ЗвI'^*1), чтобы
в ближайшее время погрешность была приемлемой с высокой
вероятностью. Кроме того, нельзя допускать, чтобы длина шага Н
возрастала или убывала слишком быстро. Для этого можно
выбирать новую длину шага, например следующим образом:
= Н*тт(}астах9 тах([аст1П, [ас*Aо1/еггI/(р+1))). D.7')
Тогда, если егг <; Ы, два вычисленных шага считаются при-
пятыми, и решение продолжается исходя из у% или у2 (в послед-
последнем случае говорят о методе «локальной экстраполяции»), при-
причем в качестве длины нового шага берется Нпехо. В противном
случае оба шага отбрасываются, и вычисления повторяются
с новой длиной шага кпет. Максимальный коэффициент увели-
увеличения шага [астах обычно выбирают между 1.5 и 5. Он пред-
предотвращает слишком сильное увеличение длины шага программой
и способствует ее надежности. Понятно, что, если его выбрать
слишком малым, это может привести и к излишнему увеличению
вычислительной работы. Наконец, для шагов, выполняемых
непосредственно после отбрасывания забракованных шагов, реко-
рекомендуется положить [астах~ 1 [Шампайн и Уотте A979)].
Вложенные формулы Рунге—Кутты
«Мне потребовалось много времени, чтобы понять это,
но объяснение с трудом поддается описанию»,
(Мерсон, 1957)
«Скрейтон правильно критикует процесс Мерсона: неко-
некоторые ожидали от него очень многого, хотя сам Мер-
Мерсон не претендовал на это».
(Р. Ингланд, 1969)
Идея их состоит в том, чтобы вместо пользования экстраполя-
экстраполяцией Ричардсона построить такие формулы РК, которые сами
содержали бы кроме численного приближенного значения ух
некоторое выражение у1 более высокого порядка (или каким-
либо иным образом более точное, чем у±). Последнее могло бы
тогда служить для управления погрешностью и длиной шага на
каждом шаге. В частности, это удешевило бы выбраковку шагов.

11.4. Практическая оценка погрешности и выбор длины шага 179
Итак, нам надо найти такую таблицу коэффициентов (см.
A.8'))
0
с*
ап
Ьх Ъ%
Ь ь2
... 6,-1
... 6..х
6.
6.
D.8)
чтобы величина
У1== Уо + к{ЬА + ••• +
имела порядок р, а
л = Уо + ь ФА + — + М8)
— порядок д (обычно д-р — 1 или д — р + 1).
D.9)
D.9')
Согласно теореме 2.13, мы должны удовлетворить условиям
= —т^т- для всех деревьев порядка </? D.10)
и
@ =
ттг
деревьев порядка
D.10')
Первые методы такого типа предложили Мерсон A957), Ческино
A962) и Зонневельд A963) (см. табл. 4.1, 4.2 и 4.3, в которых
заголовок вида «фамилия р (д)» ука-
указывает, ЧТО порядок Ух равен р, а ПО-
рядок «оценщика погрешности» уг ра-
равен ц.
Однако эти методы еще не пол-
полностью удовлетворяют сформулирован-
сформулированным нами выше требованиям. У Мер-
сона уг имеет порядок 5 только для
линейных уравнений с постоянными
коэффициентами. Поэтому этот метод
переоценивает погрешность при малых
Л, но все же работает вполне хорошо и
применяется весьма широко, особенно
пользователями библиотеки МАО («команда, приносящая резуль-
таты»). Точно так же у Зонневельда уг оценивает не погреш-
погрешность аппроксимации, а «последний учтенный член». Метод
Таблица 4
0
1
4
1
2
1
Ух
.1.
1
■■«•1И
4
0
1
1
1
6
Ческино 2
1
2
2
2
- 0
2
2
4
6
D)
0
1
6

180
Гл. II. Методы Рунге— Кутты и экстргполяционные методы
Таблица 4.2. Мерсон 4(«5»)
0
1
3
1
3
1
2
1
У±
$1
1
3
1
6
1
8
1
2
1
2
1
6
1
6
0
0
0
0
3
8
3
~~~2"
3
"~ 2
0
2
2
2
3
0
1
6
Таблица 4.3. Зонневельд
0
1
2
1
2
1
3
4
Ух
6г
1
2
0
0
5
32
1
6
1
— 2
1
2
0
7
32
1
3
7
3
1
13
32
1
3
7
3
4C)
1
~~ 32
13 16
6 """ 3
Ческино не экономичен, потому что он оценивает погрешность
со слишком высокой точностью (см. ниже упр. 1—3).
Формулы, которые удовлетворяют условиям D.10) и D.10'),
вывели Сарафян A966), Иигланд A969) и Фельберг A968, 1969).
Продемонстрируем вывод формулы Фельберга второго порядка:
0
с*
031 а32
Согласно D.10) и D.10'), должны удовлетворяться уравнения
_ 1 DЛ2)
~ 3 '
1
Выбрав с2 = 1 и Ь3 = 0, из первых двух уравнений получим
Ъг = Ьг = 1/2. Осталось 4 уравнения с 5 неизвестными. Если
положить с3 = 1/2, то Ъг = х/6, б2 = х/6, Ъ3 = 4/6 оказываются
коэффициентами правила Симпсона и, наконец, а32 = 1/4- Полу-
Получившийся метод приведен в табл. 4.4. Второй метод из табл. 4.4
тоже предложил Фельберг A969). Он содержит одну дополни-

11.4. Практическая оценка погрешности и выбор длины шага 181
тельную стадию, но коэффициенты выбраны так, что а^ — Ъь
для всех /, поэтому вычисленное последним значение / на теку-
текущем шаге может быть снова использовано, так как оно совпадает
с первым значением /, которое надо вычислить на следующем
шаге. Поскольку коэффициенты погрешности для ух у метода
ККР2 C)В в сто с лишним раз меньше, последний претендует на
лучшее качество, чем метод ККР2 C) (ниже мы увидим,» что это,
конечно, не совсем верно).
Таблица 4.4. Вложенные методы Рунге—Кутты
ККР2C)
0
1
1
2
У\
1
1
1
4
1
2
1
6
1
4
1
2
1
6
0
4
6
0
1
4
27
«
1
У\
Л
ККР
1
4
189
"-"800
214
891
214
891
533
2106
2C)В
729
800
1
33
1
33
о
650
891
650 0
891
800 1
1053 78
Фельберг вывел много других формул различных порядков.
В табл. 4.5 Приведен метод 4-го порядка с 6 стадиями — один из
наиболее используемых в настоящее время.
Таблица 4
0
1
4
оо со
12
13
1
1
1
2
11л
У1
.5. Фельберг 4E)
1
4
3
32
1932
2197
439
216
8
27
25
216
16
135
9
32
7296
2197
о
—о
о
о
0
3680
513
3544
2565
1408
2565
6656
12825
845
4104
1859
4104
2197
4104 "
28561
56430 *
11
40
1 0
5
9 2
50 55

182
Гл. II. Методы Рунге—Кутты и экстраполяционные методы
Формула Дормана и Принса
Возникает естественный вопрос: а почему бы не использовать
лучшее из полученных значений, т. е. выражение старшего по-
порядка рь в качестве численного результата и начального зна-
значения для следующего шага? Естественно ответить на этот вопрос
так: но тогда наша «оценка погрешности» $г — уг уже не будет
оценивать погрешность, а ведь мы хотим оценивать погрешности,
не так ли? Однако на такой ответ имеются два естественных
возражения:
а) поскольку обычно свойства устойчивости или неустойчи-
неустойчивости решаемой дифференциальной системы неизвестны, локаль-
локальные погрешности обычно имеют мало общего с глобальными по-
погрешностями;
Ь) Фельберг, чтобы сделать свои методы оптимальными,
пытался минимизировать коэффициенты погрешности для резуль-
результата низшего порядка уг. Как следствие этого возникает опас-
опасность, что разность уг — рь состоящая главным образом из ми-
минимизированных коэффициентов погрешности, недооценивает ло-
локальную погрешность.
Поэтому интересно вывести методы, у которых члены по-
погрешности для результата старшего порядка были бы минимизи-
минимизированы, а результат младшего порядка вычислялся бы только
для использования в механизме управления длиной шага. Такой
Габлица
0
1
5
3
10
4
5
8
9
1
1
1
А
п
4.6. Дорман—Принс 5D) (ЭОРК15)
1
5
3
40
44
45
19372
6561
9017
3168
35
384
35
384
5179
57600
9
40
56
15
25360
2187
355
33
0
0
32
9
64448
6561
46732
5247
500
1113
500
1113
7571
16695
212
729
49
176
125
192
125
192
393
640
5103
18656
2187
6784
2187
6784
92097
339200
И
84
11 0
84
187 1
2100 40

П.4. Практическая оценка погрешности и выбор длины шага 183
метод, в котором к тому же аз1 — Ьи так что результат последнего
вычисления производной может снова использоваться на следу-
следующем шаге, построили Дорман'и Принс A980). Он дает велико-
великолепные результаты. Коэффициенты этого метода приведены
в табл. 4.6.
Численное исследование механизма управления
длиной шага
На рис. 4.1 и 4.2 представлены результаты действия описан-
описанного выше механизма управления длиной шага D.7'). В качестве
примера мы выбрали модель брюсселятсра (см. разд. 1.16)
У2
.3 -
.2 &-
.1 -
глобальная
- погрешность
/локальная \
1 (^погрешность/
длина ,
шага А
■ ' ' 1 ' ' I I 1 3 1 I 1 I
'■'''''''
Рис. 4.1. Метод ККР2C) с управлением дли-
длиной шага, Ы = 5 X 10, 178 шагов + 5 от-
отброшенных.

184 Гл. II. Методы Рунге—Кутты и экстраполяционные методы
с начальными значениями ух @) = 1.01, у2 @) = 3, очень близ-
близкими к особой точке; интервал интегрирования взят 0 <1 х «< 20.
На этих рисунках представлены следующие графики:
1) внизу — решение уг (х) и у2 (х) со всеми принятыми ша-
шагами интегрирования*;
.2
.1
.0
7.
6.
5.
4.
Э.
2.
1.
О.
5 *
.0
4.
э.
глобальная
погрешность.
6. 10.
погрешность/
I ■ ,
5.
длина шага И
\Ь.
о.
5.
10.
15.
15.
15.
2 )
2 )
1 I I 1
20.
Рис. 4.2. Метод ККР2C)В с управлением длиной
шага, Ш = 3 X ЮЛ 101 шаг + 12 отброшен-
отброшенных,
2) выше — все длины шагов, как принятых, так и отброшен-
отброшенных;
3) третий снизу график показывает оцененную погрешность
§ (егг); желаемая точность (допуск погрешности М) показана
прерывистой горизонтальной линией;
4) вверху рисунков изображены глобальные погрешности обеих
компонент численного решения. Видно, что из-за неустойчивости
решений относительно возмущений начальных значений появ-

11.4» Практическая оценка погрешности и выбор длины шага 185
ляются довольно большие глобальные погрешности, хотя допу-
допускаемые локальные погрешности всюду малы.
Мы сравнивали здесь две формулы Фельберга ККР2C) и
ККР2C)В из табл. 4.4. Можно заметить, что вторая формула
требует много меньшего допуска на локальные погрешности,
чтобы получаемые в действительности глобальные погрешности
были сравнимыми. Этот метод с его малыми коэффициентами по-
погрешности для уг недооценивает действительные погрешности.
Можно заметить также, что гарантийный фактор в форму-
формуле D.7') (здесь выбран ]ас = 0.8) обычно хорошо поддерживает
локальную погрешность ниже желаемого уровня.
Численное сравнение методов 4-го порядка
Интересно посмотреть, как ведут себя различные методы 4-го
порядка с управлением длийой шага. Следующий пример мы
выбрали из отчета Фельберга A968):
у{ = 2хуг 1п (тах (#2, Ю")), дг @) = 1,
D.16)
д'2 = _ 2ху21п (тах (уи 10~3)), у2 @) = е,
правильный* решением которого является уг = ехр ($т (л:2)), у2 =
= ехр (соз (л:2)). В серии расчетов мы изменяли допустимую
погрешность от 10"~3 до 10"! причем каждое следующее значение
было в У^Ю раз меньше предыдущего. Интегрирование произво-
производилось на интервале 0 <^ х ^ 5. Все полученные результаты
представлены на рис. 4.3, где по оси абсцисс отложены (со знаком
минус) десятичные логарифмы максимальной глобальной погреш-
погрешности («точность»), а по оси ординат — десятичные логарифмы
количества обращений к вычиглению функций («работа»). Исполь-
Использовались те же методы, что и представленные на рис. 1.1, и им
соответствуют такие же линии. К ним добавлены здесь метод
Фельберга (табл. 4.5), метод Дормана и Принса (табл. 4.6) и ме-
метод Бутчера шестого порядка (табл. 6.1). Метод Фельберга
ККР4E) оказался лучше, чем классический без локальной экстра-
экстраполяции. Однако имеющееся в работе Фельберга A968) утвержде-
утверждение, что его метод якобы «...экономит от 40 до 60% машинного
времени...», вряд ли правомерно. Как видим, и этот метод недо-
недооценивает локальную погрешность. Кроме того, применение
локальной экстраполяции в значительной степени лишает метод
ККР4E) его преимущества.
Лучшим из всех этих методов, несомненно, является метод,
использующий набор коэффициентов, предложенный Дорманом
и Принсом.

186
Гл. II. Методы Рунге—Кутты и экстраполяционные методы
3.5
3.4
3.3
32
3.1
3.0
2.9
2.8
2.7
2.6
2.5
24
2.3
3.5
34
3.3
3.2
3.1
3.0
29
2.8
2.7
2.6
2.5
2.4
2.3
- без локальной экстраполяции
Бутчер
Дорман- Принс
Фелберг
1.
2.
4.
5.
с локальной экстраполяцией
Бутчер
Дорман-Принс
Фелберг _
1
2.
5.
Рис. 4.3. Диаграмма «точность — объем вычислений»
(последний оценивается числом обращений к подпро-
подпрограмме вычисления функции).

11.4. Практическая оценка погрешности и выбор длины шага
187
Упражнения
1. Покажите, что метод Рунге D.4) можно интерпретировать как
два шага методом Эйлера (длины /1/2), сопровождаемые экстра-
экстраполяцией по Ричардсону.
2. Постройте вложенные формулы КК1B) с двумя и тремя ста-
стадиями, удовлетворяющие условию а8г = Ьг. (Фельберг: «Оег
Уо11$1апсН§ке1{ Ьа1Ьег зе1 посЬ ег^аЬп1...» х).) Примеры при-
приведены в табл. 4.7 (второй из методов определяется, конечно,
неоднозначно).
Таблица 4.7. Вложенные методы низкого порядка
ККР1B)
0
1
"Ч
01
1
1
1
2
0
1
2
ККР1B)В
0
'1
2
1
91
*
• 1
2
1
256
1
256
1
512
255
256
255
256
255
256
0
1
512
1) «Ради полноты следует еще упомянуть...» — Нем.*

11.5. Дальнейшие вопросы практических
вычислений
Плотная выдача
Механизм управления длиной шага, описанный в разд. 11.4,
выбирает точки, в которых вычисляется решение, в соответствии
с требованиями к допустимой локальной погрешности. Часто,
однако, требуется вычислить и выдать решение в заданных точ-
точках, которые к тому же могут быть расположены достаточно
плотно. Одна из возможностей получения решения в таких задан-
заданных точках состоит в уменьшении длины шага всякий раз, когда
это нужно. Такое повторное уменьшение длины шага от почти
оптимальной величины нарушает управление длиной шага и
может привести к очень сильному росту времени счета и погреш-
погрешностей округления (Шампайн, Уотте и Давенпорт A976)). Поэтому
представляет интерес вывод таких методов РК, которые были бы
способны выдавать значения решения во всех промежуточных
точках х* = х0 + 6Л, где 0 < 9 <! 1 (так называемые непрерыв-
непрерывные методы РК). Разумеется, такие непрерывные методы пред-
представляют особенный интерес, если их коэффициенты а^ не зави-
зависят от 0: это позволяет на каждом шаге интегрирования вычи-
вычислить решение в сотнях точек без особых дополнительных затрат.
Пример 5.1. В случае трехстадийного непрерывного метода
РК третьего порядка условия порядка примут следующий вид:
Ьг + Ь2 + 63 = В,
_±_ ь _ 9а
2 I ^3С3 — ""пГ >
E.1)
+ "зСз = -у ,
93
Это следует из теоремы 2.1, если у (х0 + К) заменить на у (х0
+ Эй). Простые вычисления показывают, что эти уравнения
неразрешимы, если требовать независимости <?2> <?з и а32 от 9.
Поэтому ослабим наше требование. Так как непрерывная формула
используется только один раз для каждой выдаваемой величины,
мы будем требовать, чтобы ее точность соответствовала глобаль-
глобальной погрешности формулы третьего порядка, а она является ве-
величиной О (Л3). Итак, мы требуем второго порядка при всех 8
и третьего — при 8 = 1. Выбрав с2 = 1/2, с3 = 1 и решая пер-

11.5. Дальнейшие вопросы практических вычислений
189
вые три уравнения при произвольном 9, а последнее — при
6 = 1, мы получим схему (табл. 5.1), которая является расши-
расширением одного из методов Кутты A901).
Таблица 5.1. Непрерывный метод. Рунге—Кутты
0
1
2
1
1
э2
-| в)
В
2
Пример 5.2. Однако существует простой и элегантный способ
интерполяции третьего порядка, если добавить вычисление функ-
функции /х = / (*о + А, Уг)» которая все равно будет нужна на сле-
следующем шаге. Мы имеем тогда два значения функции г/0, уг и
два значения производной /0 = к19 /х и можем, следовательно,
сделать кубическую интерполяцию. Для этого случая схема
с разделенными1 разностями примет следующий вид:
Хх
Уо
Уо
Ух
Ух
I
А
(А - П)/Н
№
/о)/#
E.2)
где
= (Ух —
и интерполяционная формула Ньютона дает
у {хо + Щ = Уо + ле [/0 + в(Л — /о) +
+ 6F-1)^-24 +/0)] E.3)
(см. также Абрамовиц и Стиган A964), формула 25.2.26).
Пример 5.3. Предыдущая идея допускает красивое расшире-
расширение, если выполнить ричардсоновскую экстраполяцию на двух
шагах, как описано в теореме 4.1. Для большей точности вос-
воспользуемся экстраполированным значением у2: = //2 и сделаем
вычисление производной /2 = / (#0 + 2Л, у2)9 которая исполь-
используется на следующем шаге. Далее, поскольку постоянная С

190
Гл. II. Методы Рунге—Кутты и экстраполяционные методы
в D.1) определяется из D.3) и D.4), мы можем найти экстраполя-
экстраполяцией лучшее значение и для уг:
Уг' = Уг + ,У»~~^ • E.4)
Однако без дополнительного вычисления в нашем распоряжении
нет производной при новом значении уг. Существует две возмож-
возможности для увеличения точности:
А) воспользоваться интерполяционным многочленом четвер-
четвертой степени, опираясь на значения у0, /0, уи у2, /2;
В) использовать в качестве /х производную при значении уг
до экстраполяции и интерполировать при помощи многочлена
пятой степени, опирающегося на значения уо,!о>Уг> /ь #2» /г (проб-
(пробные вычисления показали, что дополнительное вычисление функ-
функции при новом значении ух — это бесполезная трата сил).
Если обозначить д.х = (уг — уо)/Н и Л2 = (у2 — Уг)/к, то ана-
аналогичная E.3) интерполяционная формула Ньютона для слу-
случая А) дает
у
Щ =
а для случая В):
У (х0 + Щ = у0
+ (в
+ (в
е
2/0)/4
е - 2) (/2 -
— А, + (е —
их -
E.5)
6 (^
1) (№ - 4/х +
2) B/0 —
F -
- 2/0)/4 +
E.6)
Численный пример. Для уравнений D.16) с начальными значе-
значениями уг C) = ехр E1П (9)), у2 C) = ехр (соз (9)) мы произвели
сравнение двух предыдущих методов. Мы рассчитали решение
на 10 двойных шагах при Н = 0.05 с помощью классического
.0003
0000
-.0003
Рис. 5.1. Погрешность интерполяции формулы E.5)
на 10 двойных шагах РК-метода четвертого поряд-
порядка для уравнения D.16) (квадратиками обозначены
вычисленные РК-методом точки).

11.5. Дальнейшие вопросы практических вычислений
191
метода Рунге—Кутты и затем для каждого двойного шага произ
вели интерполяцию 10 промежуточных значений. Полученные
погрешности представлены графиками на рис. 5.1 и 5.2, Отчет-
Отчетливо видно, что формула E.6) предпочтительнее. Формула E.5)
достаточна только для методов третьего порядка.
.0003
.0000
-оооз
Рис. 5.2. Погрешность интерполяции формулы E.6) в
сочетаний с классическим РК-методом четвертого по-
порядка для примера D,16),
Непрерывные вложенные формулы
Непрерывные расширения методов Рунге—Кутты построили
Хорн A983) и Энрайт, Джексон, Нёрсетт и Томсен A985). Хорн
нашел, что формулу Фельберга (табл. 4.5) можно приспособить
для получения глобального решения 4-го порядка точности,
если добавить еще одно вычисление функции (правой части урав-
уравнения).
Для предпочтительного метода Дормана и Принса (табл„ 4.6)
непрерывное расширение 4-го порядка возможно даже без допол-
дополнительного вычисления функции. Это решение, при 0 -- 1 пере-
переходящее в решение уг пятого порядка точности, определяется
следующими формулами:
Ьг @) = 0 A + 0 (—1337/480 + 8 A039/360 + 9 (—1163/1152)))),
Ь2 (9) - О,
Ьг @) = ЮО02 A054/9275 + 0 (—4682/27825 + 9 C79/5565)))/3,
64 @) « —502 B7/40 + 0 (—9/5 + 0 (83/96)))/2,
Ъь @) = 1822502 (—3/250 + 0 B2/375 + 0 (—37/600)))/848,
&в (9) = —2292 (—3/10 + 0 B9/30 + 0 (—17/24)))/7,
б
у [х, + 8А) « и, + й Ц Ъ} (8) кР E.7)
Эти формулы вместе с коэффициентами из табл. 4.6 дают отлич-
отличный инструмент для плотной выдачи результатов, графического
представления решения, для решения уравнений с запаздыва-
запаздывающим аргументом (см. разд. 11,15), для «неявной» выдачи и т. п.

192 Гл. II. Методы Рунге—Кутты и экстраполяционные методы
«Неявная» выдача
Нередко значение хеп4, для которого желательно вычислить
и выдать решение, заранее не известно: оно зависит от вычи-
вычисляемого решения неявным образом. Такие ситуации встречаются
очень часто. Примером может служить отыскание периодических
решений и предельных циклов, обсуждавшихся в разд. 1.16:
нам надо было узнать, когда решение достигнет сечения Пуанкаре
в первый раз.
Такие задачи очень легко решаются методом Ньютона; произ-
производные решения по х известны из дифференциального уравне-
уравнения. Пусть мы хотим определить х% которое удовлетворяет урав-
уравнению
Р (х, У (*)) = 0. E.8)
Алгоритм 5.4. Вычисляйте решение дифференциального урав-
уравнения шаг за шагом, пока знак Р (хиъ у1+1) не станет отличным
от знака Р {хи уг) [это, однако, не вполне надежно, так как Р
может изменить знак дважды на интервале интегрирования;
для повышения надежности можно использовать формулы E.3),
E.5) или E.6)]. Затем делайте итерации по Ньютону для отыска-
отыскания решения уравнения E.8):
у
где
После этого новое значение уг вычисляется с помощью одного
шага методом РК с положительным или отрицательным значе-
значением Н. Все численные примеры в разд. 1.16 были рассчитаны
этим способом.
Решение уравнения E.8) можно рассчитать также с помощью
непрерывного метода РК. В случае метода 5-го порядка, предло-
предложенного Дорманом и Принсом, это делается с помощью фор-
формул E.7).
Уравнения с разрывными производными
«Если вы пишете программу, не рассчитанную на
любые ситуации, то рано или поздно найдется кто-
нибудь, кто станет решать задачу с разрывами. Вам
следует это учесть...»
(А. Р. Кертис, 1986)
Функции, стоящие в правых частях дифференциальных урав"
нений, нередко бывают не аналитическими; они могут быть до-
достаточно гладкими всюду, кроме некоторых поверхностей, на

11.5. Дальнейшие вопросы практических вычислений 193
которых терпят разрыв /2 (х, у) или их производные. Если раз-
разрывна сама /, задача Коши может вообще не иметь решения.
Например, решение уравнения -
У
(У<0)
E.9)
перестает существовать после достижения оси х9 уак что началь-
начальная задача при у @) = 0 не имеет решения.
Однако обычно существует решение, которое удовлетворяет
дифференциальному уравнению во всех точках непрерывности /.
Возможны следующие подходы к решению таких задач:
Способ 1. На поверхности разрыва остановить вычисление
решения (используя алгоритм" 5.4, если необходимо) и возобно-
возобновить его далее уже с новыми значениями /.
Способ 2. Игнорировать наличие разрыва и применять алго-
алгоритм с контролем локальной погрешности, автоматически упра-
управляющий длиной шага. Нет надобности говорить, что это может
приводить к большим затратам времени счета и не дает особо
надежных результатов.
Численный пример. Мы применили способ 2 с алгоритмом
ЭОРК15, описанным в разд. 11.4, к следующему примеру:
У =
если О
а) 1
Ь) 1/3
I с) E - у)/9 \
, если 2<Су
E.10)
{у @) = 1, у E) = ?). Правильные ответы таковы:
а) 4.5; Ь) 17/6; с) 5 — 3 ехр (—5/18).
Для каждого случая мы провели расчет 81 раз, изменяя допусти-
допустимую погрешность A0""8 ^ Ы ^ 10~7), и результаты представили
на рис. 5.3. По осям в логарифмических масштабах отложены
погрешности вычисленных значений у E) и число обращений
к вычислению /.
Как видим, при изменении М результаты ведут себя совер-
совершенно хаотично. Как правило, точность снижается на один —
Два десятичных знака, а число шагов очень велико. Другой при-
пример подобного рода будет рассмотрен в разд. 11.9 и 11.10.
• Хайрер Э. и др.

194 Гл. II. Методы Рунге—Кутты и экстраполяционные методы
-1ой10(погр)
1 I
I I
10
-с)
1.0
-1обю(логр.)
I I
0. 1. 2. 3. 4. 5 6. 7. 0. 1. 2. 3 4 5. 6. 7. О. 1. 2. 3. 4. 5. 6. 7.
Рис. 5.3. Численные погрешности, полученные для E.10) в случае игнорирова-
игнорирования наличия разрыва.
Длина начального шага
«Если все сделать с защитой от дураков, выведутся
еще более замечательные дураки».
(Услышано от д-ра Пиркля в Бадене.)
В течение многих лет было принято задавать программе длину
начального шага. Считалось, что пользователи имеют приблизи-
приблизительное представление о подходящей длине шага из математиче-
математических соображений или из предшествующего опыта. Во всяком
случае, плохой выбор начального к быстро исправляется меха-
механизмом управления длиной шага. Тем не менее, если делается
очень плохой выбор и это происходит слишком часто, можно
потратить впустую много времени счета. Поэтому ряд авторов
(напр., Уотте A983), Хайндмарш A980)) предложил идеи, как
заставить компьютер делать этот выбор. Эти идеи в большинстве
случаев опираются на гипотезу, что элементарные дифферен-
дифференциалы для «высоких» деревьев 12Ъ 1Ъ2, /44, /б9 и т. д. (см. табл. 2.1)
имеют поведение типа || / Ц*7, как это имеет место для линейных
дифференциальных уравнений с постоянными коэффициентами.
Поэтому достаточно вычислить / (х, у) в заданной начальной точке,
чтобы получить представление о порядке величины || /1|. Не-
Несколько более трнкий подход воплощает следующий алгоритм.
а) Вычислите / (х, у) в начальной точке.

П.5. Дальнейшие вопросы практических вычислений 195
Ь) Положите
где р — порядок метода,
с) Положите
Очень часто, однако, начальные условия находятся в особом
положении, где большинство компонент /^ может оказаться ну-
нулями. Поэтому добавим еще два шага к нашему алгоритму:
6) Сделайте один шаг методом Эйлера с длиной шага А, полу-
полученной в с). ,
е) Повторите шаги а) — с) о новым начальным значением и
выберите меньшую из двух полученных длин шага.
Алгоритм типя приведенного или другой, подобный ему,
обычно хорошо угадывает длину начального шага или, по край-
крайней мере, предотвращает очень плохой выбор его. Лишь в неко-
некоторых случаях имеется дополнительная информация для выбора
начального А, например из предыдущего опыта или решения
аналогичных задач.
Численное определение производных по начальным
условиям и параметрам
Для эффективного решения краевых задач методом стрельбы,
о котором говорилось в разд. 1.15, нужны производные решений
по (недостающим) начальным условиям. Аналогично, если мы
хотим подобрать неизвестные параметры по имеющимся данным,
скажем с помощью метода наименьших квадратов в нелинейном
случае, нужны производные решений по параметрам, входящим
в дифференциальное уравнение.
Однако результат численного определения этих производных
ни в коем случае не будет гладкой функцией начальных условий
или параметров из-за действия механизма управления погреш-
погрешностью с его операторами условных переходов AР ... ТНЕЫ ...)
и отбрасыванием забракованных шагов.
Пример. Для модели брюсселятора
\
@) = 1.3, ^
у 2 = Вуг — у\уъ, у 2 @) = В
мы рассчитали численное решение при х = 20 как функцию
от В при 2.9 < В < 3.1 с шагом ДВ = 0.0001. Использовался
метод Дормана и Принса с допустимой локальной погрешностью
7*

196
Гл. II. Методы Рунге—Кутты и экстраполяционные методы
1о1 = 3 X 10. Графики разделенных разностей для дуг/дВ
и ду2/дВ при х = 20 представлены на рис. 5.4а и ясно показы-
показывают отсутствие гладкости.
Простой способ преодоления этой трудности состоит в замо-
замораживании всей последовательности длин шагов: выбранные про-
1.0 -
.0
2 9
-1.0
Рис. 5.4. Разделенные разности для численного решения системы E.11): а) без
замораживания длин шагов; Ь) с замораживанием длин шагов,
граммой в расчете с первым значением параметра В длины шагов
заносятся в память и вновь используются во втором расчете для
В + ДВ. Разделенные разности результатов таких двух расчетов
будут гораздо лучше аппроксимировать ду/дВ. Эта процедура
при очень малых ДВ идентична тому, что называют «внутренним
дифференцированием», но программируется она намного проще.
Результаты, полученные для задачи E.11) с замораживанием
длин шагов, показаны на рис. 5.4Ь.
Упражнения
1. (Бутчер.) Испытайте вашу любимую
ющем примере:
Уг = А (Уи {/2), Ух @)
У2 = и {Уи У2), У2 @)
где / определяется так:
программу на следу-
следу= 1,
= О,
к = 0, /а = 81§П (ух)
е1зе
/2 = 0, /д = —81§П (у2)
еш! Иш

И.5. Дальнейшие вопросы практических вычислений
197
Вычислите ух (8), у2 (8). Покажите, что точное решение пе-
периодично.
2. Решите численно задачу у' =ь / (у), у @) = 1, у C) = ?, где
если О
2,
а) 1
Ь) 4
с) —4
если 2
Замечание. Правильный ответ: а) 4.5; Ь) 12$ с) ехр A0) + 1.
3. Рассмотрите 5-стадийный метод Рунге—Кутты. Обозначьте 5*
число различных значений сг. Докажите, что порядок любого
непрерывного расширения не превосходит 5*.
Указание. Пусть д (х) — мйогочлён степени 5*, удовлетворя-
удовлетворяющий условиям ц (сг) = 0 при I = 1, ..., 5. Исследуйте выра-
выражение 24й| @) д

11.6. Явные методы Рунге—Кутты
высших порядков
*Мы теперь конструируем формулу РК 10-го порядка
(Дж. Бутчер, 1969)
••*
Барьеры Бутчера
Для методов порядка 5 надо удовлетворить 17 условиям по-
порядка (см. табл. 2.3). Выбрав 5 = 5, мы должны определить
15 параметров. Уже Кутта поднимал вопрос о том, что решение,
возможно, все-таки существует, но он не надеялся на это и обра-
обратился прямо к случаю 5 = 6 (см. разд. П.2, упр. 5). Вопрос,
поставленный Куттой, оставался открытым в течение более 60 лет.
Около 1963 года ответ на него был найден независимо в трех
работах (Ческино, Кунцман A963), ШанксA966), Бутчер A964Ь,
1965Ь)). Работы Бутчера являются наиболее глубокими, и в нашем
изложении мы будем следовать в основном его идеям.
Теорема 6.1. При р^-Ь не существует явных методов РК
порядка р с числом стадий з = р.
Доказательство. Рассмотрим сначала случай 5 == р = 5. Вве-
Введем C, 3)-матрицы V и V:
- 8%
ёз
8а
—- 2
где
1.1
З/2
-й/2
2
2 \3 Яз/0/ — Сз/2
2
/<
с^/2
F.1)
F.2)

П.6. Явные методы Рунге—Кутты высших порядков
199
Из условий порядка для порядка 5 следует, что
6 12
1 1
12
О
о
о
20
о о
F.3)
С помощью леммы 1.5 получаем отсюда, что ё = 0 и» следова-
следовательно, с4 == 1, как в лемме 1.4. Положим теперь в F.1)
8] = [ 21 Ьгаи - Ь} A
{сз
F.4)
Тривиальными вычислениями можно проверить, что матрица VГУ
имеет снова вид F.3). На этот раз отсюда следует, что с4 = съ,
т. е. съ = 1. Следовательно, выражение
^ &1 (Г—с^й^а^с^ F.5)
должно быть равно нулю (потому что 2 <! к < / < *')• Однако,
выполнив умножение под знаком суммы, т. е. представив ее как
разность двух сумм, и применяя к каждой соответствующее усло-
условие порядка (определяемое из табл. 2.1), найдем, что выраже-
выражение F.5) должно быть равно 1/120. Получилось противоречие.
Для случая р = 5 = 6 надо рассмотреть все «одноногие» де-
деревья, т. е. деревья, у которых корню инцидентно только одно
ребро, на которое «привиты» деревья пятого порядка. Соответ-
Соответствующие условия порядка имеют вид
.... выражения для порядка 5) = —^-.
Если положить Ь) = 2] г Ьга^, эти условия будут иметь ту же
структуру, что и в случае р = 5 = 5, и можно снова воспользо-
воспользоваться теми же идеями, что и выше. Но значения у @ будут здесь
уже другими, и поэтому произведение У У вместо F.3) будет равно
г- 1!
2!
2)
-1)!
3!
0"
0
0_
E = 6)
F.3')
— 1)! 5!
0 0
Далее, для р = 5 = 7 будем использовать деревья-«аисты», у ко-
которых условия порядка вида
Ььа^а^ (акт„... выражения для порядка 5) =
V % /» ...
и будем полагать Ь\ == 2л>; &гвив/*» и т-Д- Мы надеемся, что
общий случай р = 5 ^ 5 теперь ясен. ■

200 Гл. II, Методы Рунге—Кутты и экстраполяционные методы
Шестистадийные процессы пятого порядка
Мы продемонстрируем во всех подробностях, как конструи"
руются такие процессы, следуя при этом идеям, которые позво-
позволили Бутчеру A964Ь) построить 7-стадийные формулы 6-го по-
порядка. Такие же предположения, все более и более усложняясь,
использовались потом во всех последующих построениях явных
методов Рунге—Кутты (ЯРК) высоких порядков.
«Разыскивая такие процессы, мы, руководствуясь анализом,
проведенным в предыдущем разделе, сделаем следующие пред-
предположения:»
б
2 Ьгаи = Ь^A — с/), / = 1, ..., 6, F.6)
/=1
Ь2 = 0. F.8)
С выгодами, которые дает условие F.6), мы познакомились уже
в разд. 11.1 (см. лемму 1.3): оно позволяет пренебречь всеми
«одноногими» деревьями, кроме 121.
Использование условия F.7) вместе с условием F.8) дает
аналогичный эффект. Например, равенства
Ь' )Ц 7 7^ {Ь*^ Ъ Ь Ъ —~ г» /-> л 9
* ^^^ щи *1. х . т?
г. к
ЬА = 4-
становятся эквивалентными. Каждая отходящая от корня ветвь,
состоящая из двух ребер и двух вершин, заменяется двумя вет-
ветвями, несущими по одной вершине каждая. Условие F.7) не
может выполняться для всех *', потому что при г = 2 оно выгля-
выглядит так: 021^1 = с\12, откуда следует, что Сг = 0, а тогда и все
остальные с* будут равны нулю.
После описанного выше приведения останутся только деревья,
соответствующие квадратурным условиям порядка
, ?= 1, 2, 3, 4, 5 F.9)
(которые выражают условия того, что квадратурная формула
с-весами Ьг и узлами сгу аппроксимирующая интеграл по отрезку

II.6. Явные методы Рунге—Кутты высших порядков 201
[0, 1I, будет точной для многочленов меньше пятой степени)
и еще двум уравнениям:
2 1
2 1
Ь{С^ацС\ = - . ~ • (б-П)
Вычитая последнее уравнение из предыдущего, получим
1.1
В силу F.7) выражение в скобках не обращается в нуль только
при / = 2, откуда
\^ 1,'Л Л 'Л /С 1О"\
^« ^%С%а12 == 1ы1. ^О.1^ьу
Упрощение можно продолжить. Из F.6) следует, что св = 1.
Рассмотрим теперь условия порядка, аналогичные F.10) и F.11),
но без сг в левой части, и проделаем с ними те же операции, ко-
которые мы выполнили над F.10) и F.11), а из результата вычтем
равенство F.12). Мы получим уравнение
И &|A-с,)аа = 0, . F.12')
где отличны от нуля только три члена суммы. Сделаем последнее
упрощение. Вычитая и складывая F.11) с другими условиями
порядка, мы придем к равенству
Ьг A — а) аисл (с3 - съ) = -^ |р. F.13)
(Здесь берется разность условий порядка, соответствующих
деревьям ^43 и 1ЬЪ из табл. 2.1, и из нее вычитается умноженная на
с3 разность условий, соответствующих деревьям г32 и 1^. — Прим.
ред.) При этом опять число членов в сумме слева уменьшилось.
Результатом проведенного рассмотрения является
Теорема 6.2. Следующий алгоритм дает 6-стадийные явные
методы РК порядка 5 с пятью свободными параметрами:
1. с2, с3, с4, сь могут быть выбраны в качестве свободных па-
параметров, подчиненных лишь некоторым очевидным ограничениям.
2. св = 1, что следует из F.6) при \ = 6.
3. Ъъ Ь3, Ь4, &5, Ьв определяются из линейной системы
а Ь2 =* 0.
4. а32 находим из F.7) при I = 3, а±2 = X выбираем произ-
произвольно, а48 определяем из F.7) при I* = 4.

202
Гл. II. Методы Рунге—Кутты и экстраполяционные методы
5. аЪ2 находим из F.12'), аи — из F.13).
6. аъз находим из F.7) при I = 5.
7. а63, а64, а65 определяем из линейной системы, образованной
уравнениями F.6) при ] = 3, 4, 5.
8. а62 находим из F.7) при I = 6.
9. аи (/ = 2, ..., 6) находятся из A.9). Ш
Примерами таких процессов являются метод Кутты—Ню-
стрёма (разд. П.2, упр. 5), формула Фельберга (табл. 4.5) и фор-
формула пятого порядка Дормана—Принса (табл. 4.6). Возможен
и иной выбор свободных параметров (см. упр. 1).
Семистадийные процессы шестого порядка
Такие процессы вывел Бутчер A964Ь), следуя описанным выше
путем. На этот раз, кроме уравнений F.6)—F.11), надо допол-
дополнительно учесть еще шесть уравнений, так что вычисления ста-
становятся более сложными. Бутчер пришел к алгоритму, где с2,
^3» сб> св являются свободными параметрами. Среди множества
возможных примеров мы выбрали метод, представленный в
табл. 6.1, потому что он обладает положительными весами Ъи
Таблица 6.1. Метод Бутчера 6-го порядка
0
1
2
2
3
1
3
5
6
1
6
1
1
1
2
2
9
7
36
35
~~ 144
1
~ 360
41
260
13
200
4
9
2
9
55
~~ 36
11
~~ 36
22
13
0
1
— 12
35
48
1
"" 8
43
156
11
40 '
15
8
1
2
118
39
11
40
1
10
32
195
4
25
80
39
4 13
25 200
Дальнейшие барьеры Бутчера
Обратимся теперь к методам 7-го порядка. Оказывается, что
существование таких методов с восемью стадиями невозможно —
этому препятствует следующий барьер:

П.6. Явные методы Рунге—Кутты высших порядков 203
Теорема 6.3. [Бутчер A9655)] При /? >• 7 не существует
явных методов РК порядка р, имеющих 8 = р + 1 стадию. Ш
Мы не воспроизводим здесь доказательства, поскольку оно
намного сложнее, чем у теоремы 6.1.
Что касается методов порядка 8, то Кёртис A970), а также
Купер и Вернер A972) построили такие процессы с 5 = 11. Дол-
Долгое время оставался открытым вопрос, существуют ли т*акие ме-
методы с 10 стадиями. Мечте Джона Бутчера разрешить этот труд-
трудный вопрос до своего 50-летия не суждено было осуществиться.
Но в конце концов ему удалось доказать, что такие методы не
существуют, к 60-летию Далквиста.
Теорема 6.4. [Бутчер A985Ь) ]. При р >- 8 не существует
явных методов РК порядка /?, имеющих 8 = р + 2 стадии. Ш
Доказательство этой теоремы еще более сложно, и мы снова
отошлем читателя к оригинальной статье Бутчера.
Формула десятого порядка
Наивысший порядок, фактически достигнутый для явно по-
построенных ЯРК-методов, равен десяти (Книга рекордов Гин-
Гиннесса, с. 333). Кёртис A975) сконструировал 18-стадийный метод
порядка 10. Его построение было основано только на упроща-
упрощающих предположениях типа F.7), F.8) и их расширениях. Позже
Хайрер A978) сконструировал 17-стадийный метод, используя
полный арсенал идей упрощения. Коэффициенты не являются
рациональными числами, поскольку они построены на базе ква-
квадратурной формулы Лобатто 10-го порядка. Как мы увидим
далее, этот метод может быть полезен, если требуется точность
выше чем примерно 10~15. Поэтому мы не воспроизводим здесь
коэффициентов метода в виде десятичных дробей [они приведены
о 21 десятичным знаком в работе Хайрера A978)]. Вместо этого
мы представим их здесь в виде решений последовательности ли-
линейных уравнений, откуда их можно получить с любой желаемой
точностью (далее с. п. = свободный параметр):
= ^16 = /2 (С. П.), С
С1з = 0.766654 (с. п.),
- —Г1 -г7-2>т11/21 с -±Г1 -Г7+2УН1/21
сп = I — Сд> С1о = 1 — С12 (четыре узла квадратурной фор-
формулы Лобатто),
6A—с13)—4A—

204 Рл. II. Методы Рунге—Кутты в экстраполяционные методы
2 3
= си, A — с1Б) = — A — с14), с8 = сш с4 = -2- с8,
_ 4с4-3с,
20с6с7
15с9(с6 + с7)
Ьп =
п
0.13 (о. п.), Ьи = 0.18 (о. п.), Ь16 = 0.12 (с. п.),
Ь1в = 1/30 (с. п.),
0* = 0, Ьъ = О, Ь8 =0, Ьа + Ь1в = О,
Ь3 + Ь1Ъ = О, Ь9 + Ь13 = 0, 67 + 614 = О,
60
(веса квадратурной формулы Лобатто)'.
Вычисление ненулевых коэффициентов ац производится затем
в четыре этапа, как показано в табл. 6.2.
Таблица в.2.
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
1
1
1
1
1
1
1
1
1
4
4
4
4
3
3
4
1
0
0
0
0
0
0
0
0
0
0
0
3
0
3
1
1
0
0
0
0
0
0
0
0
0
0
3
3
1
1
1
0
0
0
0
0
3
3
0
0
0
1
1
1
0
0
0
0
3
3
0
0
0
1
1
1
1
4
4
4
4
3
0
4
1
1
1
4
4
4
4
3
0
4
1
1
4
4
4
4
0
0
4
1
4
4
4
4
0
0
4
4
4
4
4
0
0
4
2
2
2
0
0
2
2
2
0
0
2
2
2 2
0 0
2
2 2 2 2
8 9 10 11 12 13 14 15 16

II.6. Явные методы Рунге—Кутты высших порядков 205
Этап 1. Используются уравнения
г-1
2 Д^ = си I = 2, ..., 17,
г-1 2
= Т"' * = 3 14, 17,
1-1 ^3
= -~, / = 4, ..., 14, 17,
FЛ4)
2 у
2

12 6 13 6
2 «13,7^/ = 2 а6|2 с/, 2 «н.ус/ = 2
для ^ <; 10. При 2 = 2 имеется единственное условие 02,1
При 2 = 3 имеем уже два условия:
_ з
Из этой линейной системы определяются Оз, 1 и а3.2. Аналогичным
образом все ненулевые я^ при / <[ 10 вычисляются путем реше-
решения линейных систем с матрицами типа Вандермонда.
Этап 2. Здесь используются условия
17
2 Ьгаи=^Ь](\ — с^ /=П, 12, 13, 14, 15, 16,
17
2 Ь*^<«« = -4" Ь/ A — с/), /= И, 12, 13, 14, 15,
17
2 2 1 / 3\
Ь^ац = -^- Ь/ A — с/), / = 11, 12, 13, 14,
»-/+х F.15)
17
-с}), / = 11, 12.

206 Гл. II. Методы Рунге—Кутты и экстр апелляционные методы
При / = 16 имеется единственное условие, которое дает
#17,1в = -у5- A —* си)-
Два условия при / = 15 дают коэффициенты а16, 1б и а11у 1б, и т. д.
Здесь опять приходится решать линейные системы с матрицей
типа Вандермонда.
Этап 3.
#15, в = #15, 13» #15, 7 ==: #15, 14 > #1в, 8 = #1в, 15» #17, 2 = #17, 1в»
#17, 8 ^ #17, 15» #13,4 = #б, 4» #13, 5 == #б, 5» #14. 4 == #7, 4»
#14, 5 = #7, 5 #15, 2 = #3, 2-
Значения #1б, 1 и а1в, г вычисляются из первого уравнения F.14)
при / = 15 и I = 16 соответственно.
Этап 4. Введем величины
1-Х
г = Н, 12, 13, 14, 17, F.16)
и вычислим щ, решая систему пяти уравнений
1—1

2 ЬС 2
«:=1Г, 12, 13, 14, 17 ?=6, 7, 9, 10 /==1
где к = 0, 1, 2, 3, 4 (к = 4 добавлено произвольно). Затем вос-
воспользуемся уравнениями F.16) вместе с F.14) при I = 11, 12, 13,
14, 17, чтобы для этих значений I вычислить а^ с / = 6, ..., 10.
Наконец, для вычисления оставшихся аг1 воспользуемся первым
уравнением F.14).
Читателя, желающего глубже разобраться в проверке усло-
условий порядка, мы отошлем к оригинальной статье Хайрера A978).
Дальнейшее повышение порядка методов теряет смысл, если
нет особой нужды в них как в инструменте для вычислений с очень
высокой точностью. Получение формул еще более высокого по-
порядка превращается в сложную проблему, бросающую вызов
математикам. Трудности растут быстрее, чем по экспоненте,
а методы становятся громадными монстрами и делают к тому же
управление длиной шага все более и более трудным.
Вложенные формулы высоких порядков
Фельбергу — гению манипуляций с формулами — по суще-
существу первому удалось построить вложенные формулы высоких
порядков. Его крупнейшим успехом была формула 7-го порядка
с оценкой погрешности с помощью формулы 8-го порядка. Этот
его метод часто используется во всех вычислениях, требующих
высокой точности, например в астрономии. Мы с большим удо-
удовольствием воспроизводим в табл. 6.3 оригинал страницы из

II.6. Явные методы Рунге—Кутты высших порядков
207
00,
1
Си
О
с
03
Си
►Я
е
со
СО
=г
5
о
*
а
т-Н
1-Н
О
т-Н
О
00
г-
СО
ю
со
см
т-Н
о
о
840
о
Й
О г~*
ч
О О О
см
1-Н
г-Н
1-Н
00 й
СО
со
1-Н
1
см о о
см ю
см
1 г-Ч
СМ СО •чГ
СО
ю
о
г-Н
1
1-Н
1-Н
Ю
О
О
,-н
О
см
•-И см
— \
ю
со
■
125
СО
125
см
1
108
о
о
ю
801 ,
со
со
1-Н
<м
1-Н
СО
006
225
О
о
о
г-Н
СО
300
о
со
см
со
[^
107
704
о
о»
ел
ю
со
1
о
о
со
оо
а:
о
со
г-Н
1>
1-Н
а»
г-Н
• 311
СО
1—
СЛ
й
см
1-Н
СО
о
СО
ю
135
108
О
о
г-Н
т-\
801
а
о
1-Н
840
00
1-Н
2133
301
4496
341
■-1
164
со
4100
со
1
1025
со
т-Н
1
о
о
2383
4100
о
1—1
<—<
840
1
О
со
со
со
со
СО
г-Н
г-Н
т-Н
1
205
т-Н
о
о
о
о
со
205
о
г-Н
г-Н
т~>
840
О
СМ
со
со
1С
2193
289
4496
341
т~>
164
00
4100
00
1
1025
со
1
о
о
1777
о
о
т~>
1
г—*
см
1—1

О
00
Таблица 6.4. Метод Дормана—Принса 8G) (БОРН18)
?
18
_1_
12
8
_5
16
_3_
8
59
400
93
200
5490023248
9719169821
13
20
1201146811
1299019798
1
1
ч
_1_
18
_1_
48
32
_5
16
_3
80
29443841
614563906
16016141
946692911
39632708
573591083
246121993
1340847787
-1028468189
846180014
185892177
718116043
403363854
491063109
16
0 -^
0 --13- 12-
0
0
_3
32
75
64
0
о
0
75_
64
_3
16
77736538
692538347
61564180
158732637
_3
20
-28693883
1125000000
22789713
633445777
23124283
1800000000
545815736
2771057229
-433636366 -421739975 100302831
683701615 2616292301 723423059
0 -37695042795 -309121744 -12992083
15268766246 1061227803 490766935
- 180193667
1043307555
790204164
839813087
6005943493
2108947869
800635310
3783071287
393006217 123872331
1396673457 1001029789
8478235783 1311729495 -10304129995 -48777925059 15336726248 -45442868181
508512852 1432422823 1701304382 3047939560
0 -3185094517 -477755414 - 703635378 5731566787
667107341 1098053517 230739211 1027545527
0 -5068492393 -411421997 652783627 11173962825
434740067 543043805 914296604 925320556
1032824649
5232866602
850066563
13158990841
6184727034
3398467696
4093664535
808688257
3936647629
1978049680
3065993473
597172653
3962137247
1805957418
-160528059
65686358
487910083
248638103
685178525 1413531060
14005451
335480064
0
0
0
13451932
455O6623
0
0
0
со
о
1
с?
ч
т
-59238493
1068277825
181606767
758867731
561292985
797845732
-808719846
976000145
1757004468
5645159321
656045339
265891186
- 1041891430 -3867574721
1371343529 1518517206
760417239 465885868
1151165299 322736535
118820643
751138087
-528747749
2220607170
±
А
53011238
667516719
45
Я
Ф
«
со
а
О
(О

11.6. Явные методы Рунге—Кутты высших порядков 209
отчета Фельберга A968), тем более что более поздняя журнальная
публикация содержит опечатку.
Методы Фельберга страдают» двумя недостатками:
1) как уже упоминалось, они задуманы для продолжения
интегрирования по формуле р-го порядка с минимизирова-
минимизированными коэффициентами погрешности и поэтому имеют тен-
тенденцию недооценивать погрешность;
2) для задач вида у' = / (х), сводящихся к квадра-
квадратурам, они дают оценки погрешностей, тождественно
равные нулю.
Первые вложенные формулы высших порядков, свободные от
второго недостатка, построил Вернер A978). Его метод порядков
8 (9) включен нами в число тестируемых в приведенном ниже
численном примере.
Прекрасные численные результаты дает метод порядков 8 G),
который предложил Принс и Дорман A981), приложившие много
усилий, чтобы минимизировать коэффициенты погрешности для
аппроксимации 8-го порядка. Коэффициенты их формулы вос-
воспроизведены в табл. 6.4 (с разрешения авторов).
Реализующая этот метод подпрограмма ВОРК18, написанная
на Фортране, включена в приложение к этой книге. В ней осу-
осуществлена минимизация требований к объему памяти (см. упр. 5).
Численный пример
Все упомянутые выше методы были запрограммированы с не-
несколько более сложным управлением длиной шага. Их испытание
проводилось на ЭВМ Ш1уас 1100/60 (машинная точность =
= 1.73 X 10~18). Решался пример D.16) при задании допустимой
погрешности в интервале 10~8 ^ Ы ^ 10"*17. Метод Бутчера 6-го
порядка, который на рис. 4.3 был методом самого высокого по-
порядка, здесь сравнивался с методами еще более высоких порядков.
Из рис. 6.1 опять ясно, что формула Фельберга недооценивает
погрешность. Отчетливо видно превосходство метода Дормана—
Принса при Ш >- 10~13; далее его превосходит метод 10-го
порядка.
Коэффициенты в БОРК18 не являются точными рациональ-
рациональными числами: это лишь аппроксимации непрерывными дробями
с точностью до 18 десятичных знаков. Поэтому программа<
ЭОРК18 не должна использоваться при слишком высоких тре-
требованиях к точности (при Ш < 10*~16). На рис. 6.2 показаны
результаты, которые получены на дающей высокую точность
машине СБС для задачи у\ = г/г/6, у\ = —у\у\1Ыу у\ D) = 2,
у2 D) = 1.5, точное решение которой уг (9) = 3, у2 (9) = 1.

210 Гл. II. Методы Рунге—-Кутты и экстраполяционныв методы
3. 4.
6. 7. 8. 9. 10. 11. 12. 13. 14. 15.
Рис. 6.1. Число обращений к подпрограмме вычисления функции (/с) в зависи-
зависимости от глобальной погрешности для значений допустимой погрешности от
10~е до Ю*. Сплошная линия — без локальной экстраполяции, штриховая —
с локальной экстраполяцией; квадраты — метод Хайрера 10-го порядка, табл. 6.2;
треугольники — метод Бутчера б-го порядка, табл. 6.1; прямые крестики —
метод Фельберга 7 (8), табл. 6.3; косые крестики — метод Вернера 8 (9), A978);
штрих-пунктирная линия — программа БОРШ8, табл. 6.4.
5.
Э. -
2. -
1.
•10"*
10
-21
10
-20
10
-18
ж-
к 1_1П~16
10"
1(Г12
-1об10(погр)
8. 9. 10. 11 12. 13 14. 15. 16 V/. 18.
Рис. 6.2. Результаты для
метода Дормана — Прин-
са G) 8 при малых зна-
значениях допустимой пог-
погрешности.

11.6. Явные методы Рунге—Кутты высших порядков 211
Упражнения
1. Найдите условия, которым надо подчинить свободные коэф-
коэффициенты, чтобы метод, описанный в теореме 6.2, мог быть
снабжен вложенной формулой 4-го порядка для оценки по-
погрешности. Как выбрать коэффициенты, чтобы все Ь% были
неотрицательны? Чтобы коэффициенты погрешности для 6-го
порядка были минимальны?
2. Постройте 6-стадийную формулу 5-го порядка, у которой
съ = 1/3, с4 = 1/2, съ = 2/3.
3. (Бутчер) Покажите, что для любого метода РК порядка 5
с]
242
(следовательно, не существует методов ЯРК 5-го порядка,
у которых все Ь-х > 0).
Указание. Раскройте скобки и воспользуйтесь условиями
порядка.
4. Напишите (или возьмите) программу с методом РК высокого
порядка и рассчитайте орбиту Аренсторфа для ограниченной
задачи трех тел @.1) (см. введение к этой главе) с начальными
условиями
Л@) = 0.994, у[@) = У2@) = 0у
у'2 @) = —2.0317326295573368357302057924,
}д> = 0.012277471, у/ = 1 — у>.
Вычислите решение при
хепй = 11.124340337266085134999734047.
Начальные условия выбраны так, чтобы решение было пери-
периодическим (с такой точностью). Если начертить орбиту, соот-
соответствующую решению, на ней будет на одну петлю меньше,
чем на той, что приведена во введении (рис. 0.1).
5. (Шампайн, 1979.) Покажите, что метод Дормана—Принса 8 G)
(табл. 6.4) можно реализовать в программе таким образом,
чтобы требуемая память зависела от размера п системы как 9п.
Указание, а) Воспользуйтесь расположением нулей в таблице
коэффициентов. Ь) (Метод III): вычислив величины къ 62, ,,м
к9 [см. A.8)], подсчитайте суммы
9 9 9
2 аикл для /= И, 12, 13, 2 Ъ*ки 2 Ь*ки
/1 /1 /1
/ / /
Тогда освободится место в памяти, занятое величинами к2,
к3, ... и т. д., которые больше не нужны. См. программу
ООРК18 в приложении.

И-7- Неявные методы Рунге—- Кутты
«Было традицией рассматривать только явные про-
процессы».
(Дж. К- Бутчер, 1964)
«Быстродействующие вычислительные машины сде-
сделали возможным использование преимуществ сложных
методов».
(П, К. Хаммер и Дж, У. Холлингсуорт, 1955)
Введение
Первые неявные методы РК использовал Коши A824) для ...
(вы правильно угадали!) оценки погрешностей («МёШойез сНуегзез
^ш реиуеп! ё1ге етр1оуёез аи Са1си1 питёпяие...» х), см. упр. 6).
Коши применил теорему о среднем значении к интегралу, рассмо-
рассмотренному в разд. 1.8 и XI 1
У {*й = У 1
«о
и получил формулу
Ух = Уо + Ч (*в + 0Л1 Уо
где 0 < 9, в < 1 (так называемый «0-метод»). Предельными слу
чаями ее являются 0 = 6 = 0 (явный метод Эйлера) и 0 = в = 1
= Уо + Щ
Эту формулу называют неявным методом Эйлера.
Для повышения эффективности вычислительного процесса
применим, как это мы сделали в разд. 11.1, «правило средней
точки» @ = 6= 1/2) и, положив к± = (у± — Уо)/к$ получим
из G.2) формулу
G.4)
Этот метод называют неявным правилом средней точки.
1) «Различные методы, которые могут быть использованы в численных рас-
расчетах...» — Франц»

II.7, Неявные методы Рунге—Кутты 213
Есть еще и другая возможность: аппроксимируя интеграл G.1)
по правилу трапеций, получим
Уг = Уо + \ Ц (*о. Уо) + / (*1. Уг) Ь G-5)
Рассмотрим еще квадратурную формулу Радо:
*0
Здесь надо как-то аппроксимировать значение у (х0 + 2Л/3). Одна
из возможностей состоит в использовании квадратичной интер-
интерполяции по значениям у0, у'о и у (х\):
Получающийся при этом метод предложили Хаммер и Холлинг-
суорт A955):
з~ К у0 +
G.6)
—
Схемы G.4) и G.6) имеют такой же вид, как формулы A.8), если
суммирование в аргументах / распространить до «5».
Определение 7.1. Пусть Ьи аи (I, / = 1, ..., 5) — веществен-
вещественные числа. Метод
% ЬА1 1 5,
называется з-стадийным методом Рунге—Кутты. Если % = 0
при ^ •</, имеем явный метод (ЯРК). Если а^ = 0 при *>/
и хотя бы одно ап ф 0, имеем диагонально неявный метод РК
(ДНРК). Если, кроме того, все диагональные коэффициенты оди-
одинаковы, ан = 7 (^ = 1, ..., 5), мы говорим об однократно диаго-
диагонально неявном методе РК (ОДНРК-методе). Во всех остальных

214 Гл, II, Методы Рунге—Куттш и экстраполяционные методы
случаях мы говорим о неявных методах Рунге—Кутты (НРК-ме-
тодах)!>. ■
Использованную выше запись коэффициентов ЯРК-методов
в виде таблицы легко распространить на все случаи, включая
в таблицу все ненулевые аг^ в том числе лежащие на диагонали
и выше. Такая запись для методов G.4) и G.6) приведена
в табл. 7.1.
Таблица 7.1. Неявные методы Рунге—Кутты
^Неявное правило Метод Хаммера—Холлингсуорта
средней точки»
1
2
1
2
0
2
3
0
1
3
1
4
0
1
3
3
4
Интерес к неявным методам РК возобновился и даже вырос
в связи с проблемой жестких дифференциальных уравнений
(см. том II).
Существование численного решения
Для неявных методов значения кг уже нельзя вычислять по-
последовательно, так как G.7) в этом случае представляет собой
систему уравнений, определяющих величины кг неявным образом.
В случае методов ДНРК имеем последовательность систем раз-
размерности п: для кг, затем для к2 и т. д. Для полностью неявных
методов все $п неизвестных {ки ь = 1, ..., 5, и каждый вектор кг
имеет размерность п) должны определяться одновременно, что
еще более увеличивает трудность задачи. В связи с этим есте-
естествен вопрос: а имеют ли вообще решение уравнения G.7)? (На
этом основании редакция журнала возвратила Бутчеру первую
версию его статьи A964а).)
Теорема 7,2, Пусть / — непрерывная и удовлетворяющая усло-
условию Липшица с постоянной Ь функция в некоторой окрестности
начальных условий. Если выполнено неравенство
Ь<~ ^ .. G.8)
I шах 2] I о I
1 1
1) В иностранной литературе стали традиционными следующие аббревиа-
аббревиатуры: ЕКК, ЭШК, ЗЭЩК, ШК| которые соответствуют приведенным в опре-
определении ЯРК, ДНРК, ОДНРК, НРК- — Прим. ред.

П.7. Неявные методы Рунге—Кутты 915
то существует единственное решение уравнений G.7), которое
может быть получено итерированием. Если / (х, у) р раз не-
непрерывно дифференцируема, то* все кг как функции Н тоже при-
принадлежат множеству Ср.
Доказательство. Существование решения G.7) будем доказы-
доказывать с помощью итераций:
(«...оп 1а гёзоийга ГасПетеп1 раг йез 2р;я-ох1та1юп5 зиссеззь
уез...» (СаисЬу A824)х). Определим К (Е К5Л как К = (къ ..., к8)Т
и введем норму || К || = тах (| кг [). Тогда G.7) можно записать
в виде К = Р (К) у где
С помощью условия Липшица, повторно используя неравенство
треугольника, легко показать, что
1Р (Кг) - Р (Кг)К Н1 тах 2 | аи |-Ц Кг - К
Отсюда в силу G.8) следует, что Р (К) — сжимающее отображение.
Принцип сжимающих отображений обеспечивает тогда существо-
существование и единственность решения, а также сходимость последова-
последовательных приближений к неподвижной точке.
Доказательство дифференцируемое™ опирается на теорему
о неявных функциях из классического анализа. Запишем G.7)
в виде
Ф (Л, К) = К - Р (К) - 0.
Матрица частных производных дФ/дК при А = 0 является еди-
единичной матрицей. Поэтому решение уравнения Ф (Л, К) — 0,
которое при Л = 0 переходит в кг = / (х0, у0), непрерывно диффе-
дифференцируемо в окрестности точки Н = 0. ■
Для жестких дифференциальных уравнений (у которых /,
очень велико) неравенство G.8) дает весьма сильное ограничение
длины шага, неприемлемое на практике. Мы вернемся к этому
вопросу во втором томе.
Определение порядка остается таким же, как и для явных
методов, и условия, определяющие порядок метода («условия
порядка»), выводятся точно тем же путем, что и в разд. 11.2.
) «... легко разрешить с помощью последовательных приближений ...»
(Коши A824)). — Франц.

216 Гл. II. Методы Рунге—Кутты н экстр апелляционные методы
Пример 7.3. Рассмотрим неявные двухстадийные методы по-
рядка 3. Условия порядка принимают следующий вид (см. тео-
теорему 2.1):
г + Ь2 = 1,
Ь2с2 = -^-,
Ь2С2 = -у ,
а12с2) + Ь2 {а21сг + а22с2) = -^-. G.9]
Из первых трех уравнений вытекает следующее условие орто-
ортогональности (оно встречается в теории квадратурных формул
Гаусса):
1
| (* — сг) {х — с2) ^д:=0, откуда с2 = 3 Г ^ > GЛ0)
о
а также
^ ^ 1/2,
В четвертое уравнение подставим а21 = с2 — ^ а1г = сг — а12
и будем рассматривать а12 и с% как свободные параметры. Это дает
1/6 —
а =
Положив а12 — 0, мы получим однопараметрическое семейство
методов ДНРК порядка 3. Метод ОДНРК получится, если по-
потребовать еще ап = а22 [Нёрсетт A974), см. табл. 7.2].
Таблица 7.2. ОДНРК-метод порядка 3
V
1-7
V
1 —27
1
2
0
V
1
2
з=ь Уз
6

11.7. Неявные методы Рунге—Кутты
217
Коэффициенты методов четвертого порядка должны удовлет-
удовлетворять еще четырем условиям, хотя осталось только два свобод-
свободных параметра. Тем не менее в Этом случае существует единствен-
единственное решение, приведенное в табл. 7.3.
Таблица 7.3. Метод Хаммера—Холлингсуорта порядка 4
1
2
1
2
Уз"
6
1 6
1
4
1
4
1
1
1
2
Уз"
6
■
1
4
1
4
1
2
Уз
6
Методы Кунцмана и Бутчера порядка 2з
Ясно, что формула G.4) и метод, приведенный в табл. 7.3,
являются обобщениями соответственно одноточечной и двух-
ч-
Рис, 7.1, Редукция с С
Рис. 7.2. Редукция с Б (д)>
точечной квадратурных формул Гаусса. Кунцман A961) [см.
также Ческино и Кунцман A963)] и Бутчер A964а) открыли, что
при всех 5 существуют НРК-методы порядка 2$. Главным инстру-
инструментом доказательства этого являются следующие упрощающие
предположения:
С (Л):
Я. GЛ2)
(эти предположения аналогичны предположениям F.7) и позво-
позволяют производить редукцию условий порядка, соответствующих
тем или иным деревьям, как схематически показано на рис. 7.1),

218
Гл. II, Методы Рунге—Кутты и экстраполяционные методы
а также
F): 2&^ГЧ = -у-0~^ / = 1. ...»я. ?=1. .... Б.
G.13)
(ср. с предположениями F.6) и леммой 1.3); эти предположения
делают возможной окончательную редукцию всех деревьев, как
показано на рис. 7.2 (попробуйте сделать это на каком-нибудь
примере).
В результате, если т) и | достаточно велики, все деревья при-
приводятся к деревьям, соответствующим квадратурным условиям
порядка (ср. F.9))
В(р):
G.14)
Итак, установлена
Теорема 7,4 (Бутчер) Если удовлетворяются равенства G.12),
G.13) и G.14), причем р < $ + Г) + 1, Р < 2т) + 2, то метод
имеет порядок р. Ш
Для получения формул порядка 2$ Бутчер принял условия
G.14) с р = 25 (т. е. что сг и Ъг являются узлами и весами квадра-
квадратурной формулы Гаусса) и G.12) с г\ = 5. Как можно показать,
тогда G.13) тоже выполняется с | = 5. Тогда применима теорема
7.4 с р = 2§. (Ниже будет дано простое объяснение полученного
для порядка результата с помощью идеи коллокации.) Методы,
соответствующие 5 = 3 и 4, приведены в табл. 7.4 и 7.5. При
5 = 5 коэффициенты метода могут быть еще выражены в радика-
радикалах. Они приведены в работе Бутчера A964а). Первое сообщение
о впечатляющих численных результатах, даваемых этими мето-
методами, появилось в диссертации Зоммера A965) из области небес-
небесной механики.
Таблица 7.4. Метод Кунцмана—Бутчера порядка б
1
2
1
2
1
2
1
г
1/15
10
УТб
10
5
36
5
36
5
36
- 4-
■. 1 —
- -}- —
5
18
УТъ
24
УТ5
30
2
9
2
9
2
9
1
4
9
УТб
15'
УТб
15
5
36
5
36
5
36
5
18
УТ5
30
У75
24

11.7. Неявные методы Рунге—Кутты
219
Таблица 7.5. Метод Кунцмана—Бутчера порядка 8
1
2
1
'2
©I
©4 ©1 —
>1 + ©з + ©4
©I + ©5
©1
©б
я
©1 + ©з
1 + ©3 + ©4 ©1 + ©3 ~ ©4
2щ
Узо
144
+ 2*1/30
2©!
2©;
8
2©!
1/2
со.
D
= ©«
35
Узо
24
5 УЗО
168
-2©8,
_ 1 / 15
УЗО
144 '
— 2^30
1/2
35
^з
0J V 21
©; == ©2 —
24
5 УЗО
168
2©3.
НРК-методы, основанные на квадратурной
формуле Лобатто
Квадратурные правила Лобатто [Лобатто A852), Радо A880I
являются модификацией идеи квадратур Гаусса: они требуют,
чтобы, первый и последний узлы совпадали с концами интервала
интегрирования* т. е. сг ~ 0, с8 = 1. С этими узлами удобнее
обращаться, а в пошаговой процедуре их можно использовать
дважды. Остальные с% выбираются затем так, чтобы оптимизиро-
оптимизировать квадратурную формулу. Для интервала интегрирования
I—1, 1] они являются нулями ортогональных многочленов Якоби
Р^Л* (х) или производных многочленов Лежандра Р^г (х) (см.,
напр., Абрамовиц и Стиган A964), 25.4.32). В результате полу-
получаются квадратурные формулы порядка 2$ — 2. Бутчер A964а, с)
обнаружил, что квадратурные правила Лобатто можно распро-
распространить на НРК-методы, у которых первая строка и последний
столбец матрицы коэффициентов состоят из нулей. При этом пер-
первая и последняя стадии становятся явными, число неявных стадий
понижается до 5 — 2, тогда как порядок метода остается равным
2§ — 2. Эти методы характеризуются условиями 5B§—2) и
С E—1) [см. G.12)* G.14I. Коэффициенты методов с 5 = 3 и 4
даны в табл. 7.6.

220 Гл. 11. Методы Рунге—Кутты и экстраполяционные методы
Таблица 7.6. Полученные Бутчером формулы Лобатто порядков 4 и б
0
1
2
1
0
1
4
0
1
б
0
1
4
1
2
3
0
0
0
1
б
0
5-Т/Г
10
10
1
5
5
0
+ 1/5"
60
-Т/Т
60
1
б
1
12
15
5
0
1
6
+ 7Уб"
60
-Т/5"
12
15
5
0
-7Т/5*
60
1
б
+ у г
12
ТУ
0
о
о
о
"ТГ
Во втором томе будет показано, что эти методы, хотя и имеют
преимущества с точки зрения соотношения между порядком
и числом неявных стадий, но для жестких дифференциальных
уравнений недостаточно устойчивы.
НРК как коллокационные методы
«Ез 151 ег$1аипПсЬ, йазз сНе МеШо<1е 1го1г Шгег Рп-
тНшШ щи! ёег ^епп^еп КесЬепагЪеН т У1е1еп Ра1-
1еп... зо^аг &и*е Бг^еЪтззе Не!егЬ.
«Удивительно, что этот метод, несмотря на свою при-
примитивность и малые вычислительные затраты, во мно-
многих случаях... дает даже хорошие результаты».
(Коллатц, 1951)
После 1970 года появилась серия работ [Райт A970), Хулм
A972), де Боор и Шварц A973), Нёрсетт и Ваннер A979I, кото-
которые мало-помалу выяснили, что многие методы НРК некоторым
образом эквивалентны коллокационным методам и что свойства
их порядков совершенно естественны. Позже, в главе о жестких
уравнениях, мы познакомимся с обобщением этой идеи (так на-
называемая «возмущенная коллокация»), которое охватывает все
методы Рунге—Кутты.
Понятие коллокации является старым и общеупотребительным
в численном анализе [см., например, многие страницы у Кол-
латца A960), или отчет Фрейзера, Джонса и Скана A937I. Для
обыкновенных дифференциальных уравнений оно состоит в оты-
отыскании многочлена степени 5, у которого в 5 заданных точках
производные совпадают («коллоцируют») с векторным полем диф-
дифференциального уравнения.
Определение 7.5. Пусть 5 — положительное целое число и
•••, с8 — вещественные числа (как правило, выбираемые на

11.7. Неявные методы Рунге—Кутты 221
интервале [0, 1]). Определим коллокационный многочлен и (х)
степени 5 следующим образом:
ы (*о) ^ Уо (начальное условие)^ G.18а)
и' (х0 + СгН) = { (х0 + ФУ и (хь + с%к)), I = 1, ..., 5. G.18Ь)
Численное решение дифференциального уравнения задается при
этом выражением
Ух = « (хо +А}- G.18с)
Если некоторые из узлов с% совпадают, условие коллокации
G.18Ь) будет содержать старшие производные. Тогда оно приводит
к методам, использующим старшие производные (см. разд. 11.12).
Поэтому мы будем пока считать все узлы различными.
Теорема 7.6. Коллокационный метод G.18) эквивалентен ^-ста-
^-стадийному методу НРК, у которого •
аи = (
о
= [ 1^A)(И (I, ] = 1, ..., 5), G.19)
о
где I; E) являются многочленами Лагранжа
(*) « П (I - Ск) IП (с, - Ск). G.20)
^2 / к*1
Доказательство. Обозначим и'(х0 + с^Н) = А2, тогда
5
и' (хо + Нг) = 2 А|•/;(/) (Лагранж).
Теперь проинтегрируем это выражение:
| /й)
о
и подставим в G.18Ь), учитывая также G.19). При этом получается
НРК-метод G.7). ■
Теорема 7,7, НРК-метод, у которого все с% различны и порядок
больше или равен 5, является коллокационным методом тогда
и только тогда, если предположения G-12) выполнены для т) = 5.
Доказательство. Условия G.12) однозначно определяют коэф-
коэффициенты ац. Запишем их в виде равенства
G.21)

222 Гл. II. Методы Рунге—Кутты и экстраполяционные методы
справедливого для всех многочленов р степени, меньшей чем §.
Даваемые формулой G.19) а^ удовлетворяют этому соотношению:
подставив G.19) в G.21), мы получим интерполяционную формулу
Лагранжа. ■
5
Теорема 7.8, Пусть М(х) = П (х — сг) и М ортогональна
многочленам степени г— 1> т. е.
I
\ М E) з*~1 из = 0, ц = 1, ..., г. G.22)
о
Тогда метод G.18) имеет порядок р = з + г-
Доказательство. Предлагаемое доказательство использует
формулу Грёбнера—Алексеева, которая позволяет хорошо понять
подоплеку результата. Другое доказательство указано ниже,
в упр. 7. Соотношение G.22) означает, что квадратурная формула
Х0+Ь 5
[ 8 (з) (Ь = Н ^ Ь,в (*о + с/1) + еп (ё) G.23)
имеет порядок 5 + г = р, и для ее погрешности справедлива
оценка
егг (§) | < СкР+1-т*х | в{р) (х) \. G.24)
Далее основная идея доказательства состоит в следующем. Будем
рассматривать равенство
и' (х) = / (х, и (х)) + {и'{х) - ? (х, и (х)))
как возмущенное уравнение
и применим квадратурную формулу G.23) для приближенного
интегрирования ф°РмУлы Грёбнера—Алексеева A.14.18). Со-
Согласно G.18Ь), результат тождественно равен нулю, так как в точ-
точках коллокации возмущение обращается в нуль. Таким образом,
из G.23) и G.24) следует оценка
II У(х)-и (х) || = || егг (ё) |< С ■ АИ-* ■ тах | ^ E) ||, G.25)
где
В (з) = О3у [ху 5, и (в)У(и {$) - [ (з\ и (з)))
и О3 — символ частной производной по третьему аргументу у,
т. е. по начальному условию и (з). Итак, мы видим, что локальная
погрешность ведет себя как О (к*>+1).
Остается, однако, маленькая техническая деталь: показать,
что производные § (х) остаются ограниченными при к -*• 0. Эти

1К7. Неявные методы Рунге—Кутты 223
производные выражаются через частные производные / (х, у)
и производные и (х). Эти последние остаются ограниченными при
& -> 0, как показывает следующая теорема. ■
Теорема 7.9. [Хулм A972)] Коллокационный многочлен и(х)
порождает непрерывный НРК-метод порядка 8, т. е. для всех х,
х0 < х < х0 + (г имеем
Ых)-и(*ЖСА«+1. ' G.26)
Более того, и для производных и (х) справедливы оценки
..., 5. G.27)
Доказательство. Точное решение у (х) удовлетворяет усло-
условиям коллокации всюду, следовательно, также и в точках х0 +
+ аН. Поэтому, точно так же, как это делалось при доказатель-
доказательстве теоремы 7.6, применим 'Интерполяционную формулу Лаг-
ранжа к {/' (х):
5
у' (х) = 2 / (*о + еД у (х0 + с3Н)) 13 (I) + ц (х), х = хй + <Л,
где погрешность интерполяции ^ (х) = О (й8), если у (х) достаточно
гладкая. Учитывая, что х = х0 + Л, и интегрируя эту формулу,
получим
/-1 о
где /? (х) = О (Л5*1). Вычтем отсюда соответствующее выражение
для и (х)\
№ \ 13 E) 08 + /? (х). G.28)
о
Далее наша задача сводится к очевидным оценкам. Положим
Во = тах
'О
О
= тах 21 '}А"!) (О I Для А = 1, 2,'...
а воспользуемся условием Липшица для /. Для величины
М= тах

224
Гл. И. Методы Рунге—Кутты и экстраполяционные методы
получается неравенство
М < НЬВ0М + шах 1 # (х) ||.
Из него следует оценка G.26). Дифференцируя G.28) к раз и делая
оценки с учетом того, что К{к) (х) = 0 (А5+1-й), получим
*),
тах 1 уЮ (х) - и <*> (х) 1 < Ь>~к1ВКМ + О
откуда следует G.27), потому что М = 0 (к&+1).
Упражнения
1. Постройте одноточечный коллокационный метод E = 1) с сг
= 0 и сравните его с формулой G.2). Определите его порядок
в зависимости от 9.
2. Рассчитайте все коллокационные методы второго порядка
с 5 = 2 при произвольных сг и с2-
3. Рассмотрите методы из упр. 2, соответствующие выбору сг =
= 1/3, с2 = 1, а также сг = 0, с2 = 2/3. Определите порядки
полученных методов и объясните результат.
4. Интерпретируйте неявное правило средней точки G.4) и явный
метод Эйлера как коллокационные методы. Является ли метод
G.5) коллокационным? А метод G.6)?
5. Определите порядки методов из табл. 7.7.
Таблица 7.7. Методы Эле
Метод Эле Цд, порядок 5
Метод Эле
порядок 4
4-
4 -
- Уб
10
10
1
88-
296 -
16
16
-7Уб~
360
{- 169 Уб
1800
36
~Уб
36
296-
88
16
16
- 169 Уб
1800
360
36
+ Уб"
36
2 л- 3
225
225
9
1
9
Уб"
Уе"
0
I
2
•
1
0
5
24 '
1
6
1
6
0
1
3
2
3
2
3
0
1
24
1
6
1
6
Указание. Воспользуйтесь теоремами 7.7 и 7.8.
Обобщите на произвольные 5 [Эле A968)].
6. [Коши A824)]. Из уравнения G.2) найдите условия, которым
следует подчинить функцию /*(х, у), чтобы для скалярного
дифференциального уравнения выполнялись неравенства

11.7. Неявные методы Рунге—Кутты
225
Уг (ЯЭ) > у {хг) > уг (НЭ), где уг (ЯЭ) (у± (НЭ)) означает чис-
ленное решение, полученное на одном шаге с помощью явного
(неявного) метода Эйлера. Для эадачи
у' =
@1= О,
рассчитайте обоими методами пять шагов с к = 0.2, чтоби
оценить верхнюю и нижнюю границы решения у A).
Результат Коши: 0.9659 <; у A) < 0.9810. Для одного шага
с К = 1 он получил 0.926 < у A) < 1.
Вычислите точное решение элементарным интегрированием
уравнения.
7. [Бутчер A964а)] Дайте алгебраическое доказательство тео-
теоремы 7.8.
Указание. Из теоремы 7.7 следует GЛ2) для п = 5. Далее,
условия G.14) с р = 8+г (теория квадратурных формул
Гаусса) имеют следствием G.13) для 5 = г. Чтобы убедиться
в этом, умножьте два вектора щ = 2 А^?"^/ и ^/ = Ь/ A —
= Ь •••* 5) на матрицу Вандермонда
V =
Г 1 1
1
'3
5—1 5—
С1 С2
,5—1
Наконец, примените теорему 7.4.
8 Хайрер Э. и др.

И.8. Асимптотическое разложение
глобальной погрешности
«Мет УеггкЫ аи! Йаз Кез^Нес! тоаг
«Мой отказ от остаточного члена был легкомыслен-
легкомысленным ...»
(В. Ромберр, 1979)
Нашей следующей целью будет усовершенствование ричардсо-
новского метода экстраполяции (см. разд. 11.4) посредством вы-
выполнения повторных экстраполяции и исключения все большего
числа членов СЪР+к погрешности. Хорошую теоретическую основу
для этой процедура дает изучение асимптотического поведения
глобальной погрешности. Для задач типа у' = / (х)> сводящихся
к интегрированию функций, решение этой проблемы дает формула
Эйлера—Маклорена* и дальнейшее развитие связано с работами
Ромберга A955) и его последователей. Первые строгие результаты
для дифференциальных уравнений связаны с именами Хенричи
A962) и Грэгга A964) [см. также Штеттер A973)]. Последователь-
Последовательное исключение членов погрешности мы изложим здесь* следуя
работе Хайрера и Любиха A984L которая допускает обобщение
и на многошаговые методы.
Локальная погрешность
Пусть имеется одношаговый метод, который мы запишем
в виде
0п+1 = дп + ЬФ (*», ды Ь). (8.1)
Если метод имеет порядок р, то в каждой точке решения он обла-
обладает локальной погрешностью вида
У(х + Ь} — у (х] — НФ (х, у (х), Щ =
= <*Р+1 (х) №+* + ... + йы (х) Л"-И + О (Н* +2), (8.2)
если правая часть дифференциального уравнения дифференци-
дифференцируема достаточное число раз. Для методов Рунге—Кутты первые
члены погрешности были вычислены в разд. II.3 (см. теорему 3.2)#
Глобальная погрешность
Численное решение в точке х = х0 + пН обозначим теперь
Уп~: Ун М- Из теоремы 3.6 известно, что глобальная погрешность
ведет себя как Ьр. Мы будем искать функцию гр (я) такую, что
Уъ (х) -У(х) = ер (х) Нр + о (Ьр). (8.3)

II.8. Асимптотическое разложение глобальной погрешности 227
Основная идея состоит в том* чтобы рассматривать величину
Уь(х)-ер{х)НР = :дь(х) (8.4)
как численное решение, даваемое другим методом:
Вп+1 = Уп + ЬФ(хП9 дп, к).
Сравнивая с (8.1), мы видим^ что функция приращения этого
нового метода есть
Ф(х, д, 6) = Ф(х, у+ер(х)ЬР,к)-(е1?(х + к)-ер(х))кР-К
(8.5)
Наша задача состоит в нахождении такой функции ер (х) с усло-
условием ер (х0) = 0? чтобы метод с функцией приращения Ф имел
порядок р + I.
Разлагая локальную погрешность одношагового метода Ф
по степеням А, мы получим
(х}-кФ (х, у {хЪ к} =
) . (8.6)
Здесь использовано равенство
д, 0) = ^г(х,д). (8.7)
Член, содержащий кр+х$ исчезнет3 если определить ер (х) кан
решение задачи Коши
Применяя теорему 3.6 к методу Ф} имеем теперь
№ (х) -д(х) = ер (х) к' + О (ЙИ-1). (8.9)
Первый член искомого асимптотического разложения определен.
Повторим теперь эту процедуру, отправляясь от метода с функ-
функцией приращения Ф. Этот метод имеет порядок р + 1, и равенство
(8.7) тоже удовлетворяется. В конечном результате на этом пути
получается следующая
Теорема 8.1. [Грэгг A964)] Пусть имеется метод с доста-
достаточно гладкой функцией приращения Ф, удовлетворяющий условию
согласованности Ф (х, у, 0) = / (#, у) и обладающий разложением
(8.2) для локальной погрешности. Тогда глобальная погрешность
имеет асимптотическое разложение вида

228 Гл. II. Методы Рунге—Кутты и экстраполяционные методы
где е$ (х) — решения неоднородных дифференциальных уравнений
вида (8.8) с начальными условиями е$ (х0) = Ъ^ а Е^ (х) ограничена
при х0 < х < хепЛ и 0 < К < Но. Ш
Свойства дифференцируемое™ функций е] (х) зависят от глад-
гладкости / и Ф (см. (8.8) и (8.2)). Разложение (8.10) будет служить
теоретическим основанием во всех обсуждениях экстраполя-
ционных методов.
Примеры
1. Для уравнения у' — у, у @) = 1 и метода Эйлера при
к = \[п и х = 1 с помощью биномиальной теоремы получим:
п А п/31
Отсюда, раскрывая скобки, можно получить
2]
/=1
где 5[/} — числа Стирлинга первого рода [1730 г.; см. Абрамовиц
и Стиган A964), разд. 24.1.3]. Мы получили, очевидно, ряд Тей-
Тейлора для функции
•••/•
Радиус сходимости этого ряда равен единице.
2. Для дифференциального уравнения у' = } (х) и правила
трапеции G.5) разложение (8.10) примет вид известной формулы
Эйлера—Маклорена A736):
A) - ^ / (х) их - ^ Ш1В>ъ (/BА"П @ - 1{2к~1) (°)) + Егг-
При N -> оо ряд обычно расходится из-за быстрого роста чисел
Бернулли при больших к. Однако формула может быть полезна
при небольших значениях ^.Формулы такого рода называют асим
птотическими разложениями [Пуанкаре A893)].

Н.8, Асимптотическое разложение глобальной погрешности 229
Переменная длина шага
Теорема 8.1 справедлива не только при постоянной длине
шага. Для случая переменной длины шага разумно предположить,
что существует функция 17 (х) > 0, такая что длины шагов зависят
от параметра к следующим образом:
хп+1— *п = «(*п)*. . (8.11)
Тогда разложение локальной погрешности (8.2) примет вид
у (х + ч! (х) к\ — у (х) — к% (х) Ф (х, у (х)9 ч! (х) А)'=»
= ЛР+1 (X) %Р+1 (X)
а вместо (8.5) получим
, У, *(х)к) = Ф(х, у + ер(х)кр, 4}(х)к) —
Поэтому вместо (8.6) разложение локальной погрешности нового
метода будет иметь вид
41 (х) к) — у (х) — к% (х) Ф (х9 у {х], « (х) к) =
= «(х) [*Р+1 (х) *р (х) --^-(х, у (х)) ер (х) + е'р (х)] ЪР+* + О
и доказательство обобщенной теоремы 8.1 требует лишь неболь-
небольших изменений.
Отрицательные значения Ъ
Наиболее важные экстраполяционные алгоритмы используют
асимптотические разложения с четными степенями А. Чтобы дать
теоретическое обоснование для этих методов, надо объяснить
смысл уК (х) при к отрицательных.
Обоснование. Запишем (8.1) в виде
Ун (х + к) = ун (х) + кФ (х, ун (х]9 к} (8.Г)
и заменим к на —к:
У-н (х — к) = у_п (х) — кФ (х9 У-п (х)9 —к).
Теперь заменим здесь х на х + к:
у-н (х) = у+ (х + к) -кФ (х + к, у_н (х + к), -к). (8.12)
Для определения у_н (х + к) мы получили уравнение, которое
при достаточно малых к имеет единственное решение (по теореме
о неявных функциях). Запишем это решение в виде
У-ь (х + к) = у* (х) + ЛФ* (х9 у-н (х)9 к). (8Л3)

230 Рл. II. Методы Рунге—Кутты и экстраполяционные методы
Сравнивая (8.12) и (8.13) и обозначая А = у_п (х + Ь], 5 =
= у_ь (х)9 мы приходим к следующему определению.
Определение. Пусть Ф (х, у, К) — функция приращения не-
некоторого метода. Определим тогда функцию приращения Ф* (х,
уг Н\ присоединенного метода следующей парой формул:
5 = А — ЬФ(х + Ь, А, —Ь],
(8.14)
А = В + НФ* (х, В, к].
Пример: Для явного метода Эйлера присоединенным методом
является неявный метод Эйлера.
Теорема 8,2. Пусть Ф — метод Рунге—Кутты {77) с коэф-
коэффициентами аи, Ь7-, а (*, / = 1, ..., з). Тогда присоединенный
метод Ф* эквивалентен ^-стадийному методу Рунге—Кутты
о коэффициентами
с* = 1 —
Доказательство. Формулы (8.14) показывают, что для опре-
определения присоединенного метода надо в G.7) поменять местами у0
и Уи Л и —Ь и затем вместо х0 подставить х0 + Ь. В результате
получается
Чтобы сохранить упорядоченность си •••! о8 (обычно естествен-
естественную), сделаем перестановку значений кг в обратном порядке,
для чего заменим все индексы г на § + 1 — I. ■
Свойства присоединенного метода
Теорема 8.3. Ф** = Ф.
Доказательство. Это свойство (давшее повод к названию
«присоединенный») доказывается заменой Н на —Ь и ватем х на
х + Н, В на А и А на В в формулах (8.14). ■
Теорема 8.4. Присоединенный метод имеет тот же порядок,
что и исходный. Его главный член погрешности отличается от
главного члена погрешности исходного метода множителем (—1)^#
Доказательство. Заменим в (8.2) Н на —й, затем подставим
х 4- Ь вместо х и упорядочим заново члены по степеням Ь. При

11.8* Асимптотическое разложение глобальной погрешности 231
этом получается
д (х) + ар+1 (х) ЛН-» (-1У + О №+*) -
Щ-кФ{х + Ь, у(х + к), -к}.
(Здесь учтено, что Ар+1 (х + к) = <1р+1 (х) + О (Л).) Теперь обо-
обозначим 5 левую часть этого тождества, положим А == у (х ^г к)
и применим {8-Щ. Это приводит к равенству
[ж) + йр+1 (х) АЖ (- 1у> + ЙФ* (х9 д (х)$ к)
выражающему утверждение теоремы. ■
Теорема 8.5. Присоединенный метод имеет такое же асимпто
тическое разложение глобальной погрешности (8.10K что и исход
ный методу но о заменой к на —й.
Доказательство. Повторим о отрицательным й ту процедуру8
которая привела к доказательству теоремы 8-1. Первый отделен-
отделенный член3 соответствующий (8.9), будет
9-ъ (х) -В(х) = ер (х) (- и)' + О (ЙР-Н]. (8.9')
Справедливость этого выражения вытекает из того факта, что
решение (8.8) при начальном условии ер (х0) = 0 изменяет знак
вместе с неоднородным членом с1р+1 (х). Итйк} первый член раз-
разложения установлен. Чтобы иметь возможность продолжить
процедуру определения дальнейших членов разложения, надо
показать, что преобразование (8.4) перестановочно с операцией
перехода к присоединенному методу, т. е. что имеет место равен-
равенство
= (Ф*Г. (8.15)
Для доказательства (8.15] заметим! что из (8.4] и определения Ф
вытекает равенство
= Уь (х) - ер (х) к* + кФ (х9 уи (х) - ер (х) кР> к).
Здесь опять подставим —й вместо й, а затем заменим х на х + к.
Наконец, положив В = у_К (х) — ер (х) (—к)? и А = у_ь (х +
+ к) — ер (х + к) (—к)р, применим (8.14) и получим
-ер(х)(-кУ + кФ*(х, д-ъ{х)-еР1х){-НУ, к). (8.16)
С другой стороны, если выполнить преобразование
= У-ь (х) - ер (х) (- ЪУ 18.40

232 Гл. II. Методы Рунге—Кутты и экстр апелляционные методы
(см. теорему 8.4) и подставить в (8.13)\ мы получим опять равен-
равенство (8.16), но на этот раз с (Ф*)~ вместо Ф*, что и доказывает
формулу (8.15). ■
Симметричные методы
Определение 8.6. Метод называют симметричным, если Ф =
= Ф*.
Пример. Правило трапеции G.5) и неявное правило средней
точки G.4) симметричны: перестановки уг «-* у0, Н +-+ —к их0^
«-► х0 + к оставляют эти методы инвариантными.
Следующие две теоремы принадлежат Ваннеру A973).
Теорема 8.7. Если
Яз-И-Г* 8-7+1 + аП = ^5-7+1 = Ь[> (8Л7)
то соответствующий метод РК симметричен.
Доказательство: см. теорему 8.2. Условие с* == 1 — с8+\^ про-
проверяется суммированием равенств (8.17) по / от 1 до 5. ■
Теорема 8.8. Коллокационный метод о симметрично распре-
распределенными точками коллокаций симметричен.
Доказательство. Если а = 1—с«+1-*, то многочлены Лаг-
ранжа обладают свойством 1г ({) = 1$+1^ A — 0- Условия (8.17)
тогда легко получаются из G.19). ■
Эти результаты позволяют теперь доказать следующее важное
свойство симметричных методов, подмеченное уже давно:
Теорема 8.9. Если метод симметричен и выполнены условия
теоремы 8.1, то асимптотическое разложение (8.10) содержит
только четные степени Ь:
Ун (*1 -*(*) = е2я (х) № + ^2,+2 (дг) /12*+2 + • • • 18.18)
= 0.
Доказательство. Если Ф* = Ф, то в силу (8.13) у„ъ (х) =
= Ун (х) и утверждение следует из теоремы 8.5. ■
Пример. Самый старый пример такого разложения —формула
Эйлера—Маклорена.
Упражнения
1. Пусть одношаговый метод (8.1) имеет порядок р>2 и кроме
условия Ф (х, у, 0) = / (х, у) выполняется еще равенство
У)+ •%-(*> УУПх, У))- (8.19)'

П.8, Асимптотическое разложение глобальной погрешности
233
Покажите» что тогда главный член локальной погрешности
метода Ф, определяемого формулой (8.5), будет иметь вид
(X) - -у 4'р+1 (X).
(X, у (х))
Проверьте, что (8.19) выполняется для всех методов РК ср
2. Рассмотрите применение метода второго порядка
2.
0
1
1
1
2
1
2
у, у @) = 1., Покажите, что
к задаче у'
(х) = "б"
3. Рассмотрите метод второго порядка
(х) = -24~ е», е2 (х) =
хех9
(х) =
8
0
1
2
1
1
2
0
1
4
1
1
2
1
4
Покажите, что для этого метода
4
+
- 4-р
(обозначения соответствуют табл. 2.1). Покажите, что отсюда
вытекают равенства
*) = 0ие8 (я) = 0,
4.
так что один шаг экстраполяции по Ричардсону повышает
порядок метода на 2. (Установите связь между этим методом
и алгоритмом ГБШ из разд. 11.9.)
Обсудите симметрию других классов методов НРК из разд. 11.7.
{Ответ: они не симметричны.)

11.9. Экстраполяционные методы
«Следующий метод аппроксимации можно считать или
не считать новым, но я считаю, что он важен для
практики...»
(С- А. Кори, 1906)
«Открытие Д2-экстраполяции было навеяно теорией»
подсказавшей арифметические эксперименты, которые
дали желаемые результаты»,
(Л. Ф. Ричардсон, 1927)
«Экстраполяция является мощным средством...» (Р. Бу-
лирш — И. Штёр, 1966)
«Экстраполяция, по-видимому, не является особенно
эффективным способом ..., наши исследования поста-
поставили вопрос, есть ли вообще смысл заниматься ею
как отдельным методом».
(Л, Ф. Шампайн и Л, С, Бака, 1984}
Определение метода
Пусть имеется задача Коши у' = / (я, у), у (д:0) = у0. Задав-
Задавшись базовой длиной шага Н > 0, выберем последовательность
положительных целых чисел
< пь < ... (9.1]
и определим соответствующие длины шагов Нг > Н2 > Н3
как Нг = Н/пг. Возьмем теперь численный метод порядка р и,
выполняя щ шагов длины Ни вычислим приближенное решение
нашей начальной задачи
Щ (*о + Щ = I Ти I (9.2)
(это установившееся обозначение; первоначально буква Т симво-
символизировала правило трапеций). Выполнив вычисления для ряда
последовательных значений 1% исключим из асимптотического
разложения (8.10) возможно большее число членов, вычисляя
интерполирующий многочлен
= е0 + ерН*> + *р*АР+" + • • • + ер+*-2Йр+*-2, (9.3)

11,9. Экстр апелляционные методы
235
для которого
рAн) = Ти1, Я — /,-/— 1, ...,/-*+1. (9.4)
И в заключение сделаем «экстраполяцию к пределу» Ь -^ О* т. е.
будем рассматривать значение
Р @1 = *о =■'*** (9.51
как численное решение$ даваемое методом экстраполяции.
Условия (9.4) дают систему к линейных уравнений для опре-
определения к неизвестных е0, ер, ...9
Пример. Для к = 2, пг = 1, /12 — 2 приведенное выше опре-
определение совпадает с процедурой, описанной в начале разд. 11.4.
Теорема 9.1. Точность аппроксимации решения задачи Коши
величиной Т'; к соответствует численному методу порядка р
й1
Доказательство. Сравним (9.3), (9.4) с асимптотическим раз
ложением (8.10), которое перепишем в форме
Я)
(9.4')
где взято N = р + к — 1 и
Я) ЬЦ
% д) И^ = О
(потому чтоер+к^г (х0) = 0пкг ^ Н). Формула (9.4') представляет
линейную систему уравнений с неизвестными у (х0 + Я),
+ Я), ..., Нр+к-2ер+^2 (х0 + Я) и с матрицей
1
1
1
„Р+к-2
п1-Ь+\
похожей на матрицу Вандермонда. Она отличается от (9.4) только
возмущающим членом Аг в правой части, имеющим порядок
О (Нр+к). Матрица А обратима (см. упр. 6). Вычтя эти формулы
друг из друга, легко получить, в частности, оценку
у (х0 + Я) -е01<||А-Ц^тах| А,| = О(№+*). ■

236 Гл. П. Методы Рунге—Кугга и экстраполяционные методы
Замечание. Случай р = 1 (а также р — 2 для разложений по
степеням к2) можно рассмотреть и иначе, интерпретируя разность
у (х0 + Я) —е0 как погрешность интерполяции [см. (9.21I.
Большое достоинство рассматриваемого метода состоит в том,
что он дает полную таблицу результатов вычислений
т т
1 21 1 22
<* 31 *82 *
которые образуют последовательность вложенных методов и поз-
позволяют легко оценить локальную погрешность и выбрать страте-
стратегии для методов переменного порядка.
Несколько числовых последовательностей используются в ка-
качестве (9.1):
«последовательность Ромбергаъ [Ромберг A955) ]з
1, 2, 4, 8, 16, 32, ... (9.6)
«последовательность Булиршаъ (также упомянутую Ромбергом
A955)):
1, 2, 3, 4, 6, 8, 12, 16, 24, 32, ... (9.7)
в которой чередуются степени 2 с 1.5x2*. Для этой последователь-
последовательности в высших порядках требуется меньшее число вычислений
функции, чем для предыдущей, и она стала известной благодаря
успеху «алгоритма Грэгга—Булирша—Штёра [Булирш—Штёр
A966)].
Приведенные выше последовательности обладают тем свой-
свойством, что при интегрировании задачи у' — [ (х) многие значения
функции можно запомнить и заново использовать для меньших Нг.
Кроме того, Нт т{ (пм/пг) для этих последовательностей удо-
удовлетворяет «условию Теплица», т. е. он строго больше единицы,
что позволяет доказывать сходимость при / == к -> оо [Бауэр,
Рутисхаузер, Штифель A963)]. Однако при работе с дифферен-
дифференциальными уравнениями с фиксированным или ограниченным
порядком, как показал Дойфлхард A983), наиболее экономичной
является «гармоническая последовательность»
1, 2, 3, 4, 5, 6, 7, ... (9.8)

П.9, Экстраполяционные методы 237
Алгоритм Эйткена—Невилла
При р = 1 формулы (9.3) и- (9.4) переходят в классическую
задачу интерполяции, и можно экономно вычислять значения Т^ &,
пользуясь классическими методами. Поскольку нам нужны зна-
значения интерполяционных многочленов только при к = 0, наи-
наиболее экономичным будет основанный на идеях Жордаца A928)
«алгоритм Эйткена—Невилла» [Эйткен A932), Невилл A934)],
который приводит к формуле
& * ./-1» к
Рациональная экстраполяция
Многие авторы в 60-х годах считали, что вместо полиномов
в (9.3) лучше использовать рациональные функции. В этом случае
формулу (9.9) нужно заменить другой:
П)
[Булирш и Штёр A964)], где
9 о = 0
В случае систем дифференциальных уравнений деление векторных
величин следует понимать покомпонентно.
Позже численные эксперименты [Дойфлхард A983)] пока-
показали, что рациональная экстраполяция почти никогда не является
более выгодной, чем полиномиальная.
Вычислительный пример
Мы решали задачу
(9.11)
о точным решением у (х) = 1/соз х. Использовался метод Эйлера,
был взят базовый шаг Н = 0.2. На рис. 9.1 для трех последова-
последовательностей чисел шагов (9.6), (9.7) и (9.8) сопоставлены в двойном
логарифмическом масштабе объем вычислительной работы 1§ A +
+ П) — 1 + п*х — 1 + ... + Я/-ь+1 — 1) и получаемая точность
-1ё(\Пу{х + Н)\)

238
Гл. II. Методы Рунге—Кутты и экстраполяционные методы
2.
1.
10,1
88
66
• •.-'■:•■» ' 33
: ■•;' '22 ,
(9.8)
1
I
I
9. 11.. 13. 15.
I 1 I
(9.7)
-1о810(погр)
13. 15.
77
(9.6)
9. 11. 13. 15.
Рис. 9.1. Точность экстраполя-
экстраполяции метода Эйлера для примера
(9Л1). Вверху — гармоническая
последовательность, посереди-
посередине — последовательность Бу-
лирша, внизу — последователь-
последовательность Ромберга.
Экстраполяция с помощью симметричных методов
Если опорный метод является симметричным, то, как мы знаем,
он имеет асимптотическое разложение по степеням к2 (теорема 8.9),
и каждая экстраполяция исключает две степени к. Поэтому мы
можем просто заменить в (9.3) к на кг и для р = 2 [т. е. ц = 1
в формуле (8.18)] тоже воспользоваться алгоритмом Эйткена—
Невилла с такой модификацией. Вместо формулы (9.9) мы по-
получим
Вычислительный пример. На этот раз мы решали задачу (9.11)
с помощью неявного правила средней точки G.4). Хотя этот метод
неявный, но благодаря простой структуре дифференциального
уравнения его применение требует решения лишь квадратного
уравнения. Мы использовали ту же длину базового шага Н = 0.2
и те же последовательности чисел шагов (9.6), (9.7) и (9.8), что

11.9. Экстр апелляционные методы
239
Рис. 9.2. Точность экстра-
экстраполяции неявного правила
средней точки. Вверху —
гармоническая последова-
последовательность, посередине — по-
последовательность Булирша,
внизу — последовательность
Ромберга,
2.
1.
о.
2.
1.
О.
2.
1.
I ■ I
(9.8)
-1о810(погр)
I I
3. 5. 7. 9. 11. 13.
*.'»;;;: •'•'•^•;,.: \ :':у*:у.:-*~"
15. 17.
21 ^•■■
33
(9.7)
22
3.
5.
7.
V*"' .••■'.'•■ .••■■.•'.'
г :.'■■:■.■ т
. г 1 22
1 I 1.1 1 1 1 ■ 1
(9.6)
1ов10(погр)
1.
3.
5.
7.
1 1
13. 15.
17.
и выше. Аналогичным образом представлены и погрешности на
рис. 9.2.
Метод Грэгга, или ГБШ
«Будучи полностью явным, алгоритм Грэгга столь
идеально приспособлен в качестве опорного для экстра-
экстраполяции по Ричардсону, что никакой другой симме-
симметричный двухшаговый алгоритм не может конкури-
конкурировать с ним». (X. И. Штеттер, 1970)
Здесь лучше всего привести цитату из работы Штеттера A970I
«Разложения по степеням Н2 крайне важны для эффективного
применения ричардсоновской экстраполяции. Поэтому, когда
Грэгг доказал в 1963 р.* что величина 5Ь (х), получаемая с по-
помощью алгоритма
Ум = Ум + Щ (хи
= 1. 2, ..., 2л, (9.13Ь)

240 Гл. II, Методы Рунге—Кутты и экстраполяционные методы
4
(9.13с)
где х = х0 + 2яА, ^| = д:0 + Й, обладает асимптотическим раз-
разложением по четным степеням А и имеет удовлетворительные
свойства устойчивости, это явилось большим достижением. Это
>2*-1
тг т>>
'*+!
Рис, 9.3. Симметричность метода Грэгга,
привело к построению очень мощного экстраполяционного алго-
алгоритма ГБШ (Грэгга—Булирша—Штёра) *) ...»
Данное Грэггом доказательство этого свойства было очень
длинным и сложным, и опять-таки «большим достижением» яви-
явилась элегантная идея Штеттера интерпретировать (9.13Ь) как
одношаговый алгоритм, для чего переписать (9.13), введя нечетные
и четные индексы. Введем для этого следующие величины;
Н* = 2А, х% =
V*. = У2к+1 — Ы (Х2к> У2к) = "о" (У2к+1
(9.14)
Тогда метод (9.13) можно переписать в виде (см. рис. 9.3)
к*
\ Уй+1 /
(9.15)
Как видно из рис. 9.3, этот метод, отображающий пару (ик, )
в (ик+1, уй+1), является симметричным. Симметрию можно проверить
*) В иностранной литературе принята аббревиатура ОВ5
НгзсЬ — 51оег). — Прим. ред.
В и-

11.9. Экстраполяционные метода 241
и аналитически (см. определение 8.6), сделав перестановки
Пк+г *~* иь* °*+х «■* Уь* Ь* «-* —Л*, х\ «-* х% + Л*. Простые вы-
вычисления показывают, что при этом формула (9.15) не изменяется.
Метод (9.15) согласован с дифференциальным уравнением (си-
(системой!)
и9 = }(х^)> и(х0) = у09
V' = I (X, II), V (ХО) = у0
(это видно, если в функции приращения устремить Л* к нулю).
Точным решением этой системы является просто и (х) = V (х) =
= у (х). Поэтому из теоремы 8.9 следует4 что
д (х) - иь* (х) = 2 я/ (х) ФУ1 + (Л*J/+2 А (х, Н% (9.17а)
I
д(х) - VЬ. (х) = 2 Ь^х) {НУ1 + (НТ+2В (х, Н9) (9.17Ь)
11
и п] {х^ = Ъ) (д;0) = 0. Мы видим из (9.14), что ун {х) обладает
разложением по четным степеням к при условии, что число ша-
шагов — четное.
Сглаживающий шаг
«Предупреждаем читателя о возможной неустойчивости,
особенно при применении формул 25.5.2...» (Дж.П. Дэ-
вис и И. Полански в «Справочнике» под ред. Абрамо-
вица и Стиган)
«Явное правило средней точки» (9.13Ь), использованное в рас-
рассмотренной выше конструкции, имеет все же плохую репутацию
«слабо неустойчивого». Мы обсудим подробно это свойство во
введении к гл. IV (том II). Зигзагообразное поведение погрешности
подсказало идею заменить у2п взвешенным средним из трех ве-
величин
2лА) = -~ (йп-! + 2у2п + у2п+1) = \ (и»
(см. (9.13с) и (9.14)). Теперь из (9.17) вытекает следующий ре-
результат, полученный Грэггом.
Теорема 9.2. Пусть / (я, у) $ С2'+2. Тогда численное решение,
определяемое формулами {9.13), обладает асимптотическим раз-
разложением вида
I
У (х) - 8к (х) = 2] в] (х) № + Л2'+2С (х, Л), (9.18)
/1
где е1 (х0) = 0, а С (я, К) ограничена при х0 <; х << 0 и 0 <! Н <!

242
Рл, II. Методы Рунге—Кутты и экстраполяционные методы
Доказательство. Разложение (9.18) получится, если сложить
равенства (9.17а) и (9.17Ь) и подставить й* = 2й, причем в] (х) =
= (я; (*) + Ь, (х)) 2»*-». Я
Вычислительный алгоритм и пример
Итак, этот метод может быть использован для ричардсоновской
экстраполяции тем же способом, что и рассмотренные выше сим-
симметричные методы. Последовательности чисел шагов выбираются,
однако, с условием, что щ должны быть четными, т. е.
(9.6')
(9.7')
(9.8')
2, 4, 8, 16, 32, 64, ...8
2, 4, 6, 8, 12, 16, ...,
2, 4, 6, 8, 10, 12, ..., .
Далее полагаем
и вычисляем основанные на разложении по степеням Аа экстрапо-
экстраполированные значения Ти^ по формуле Эйткена—Невилла (9.12).
Пример вычислений.
Мы применили этот ал-
алгоритм опять к задаче
(9.11), взяли длину ба-
базового шага Н = 0.2
и, вычислив погрешнос-
погрешности, сопоставили их о
объемом вычислитель-
вычислительной работы (измеряемой
количеством вычислений
значений /\ которое рав-
равно теперь 1 +
О.
2.
из-за дополнительного
вычисления функции
для сглаживающего
шага). Результаты по-
показаны на рис. 9.4.
Эти результаты поч-
почти такие же, как для
неявного правила сред-
Рис, 9.4. Точность экстра-
экстраполяции метода Грэгга для
примера (9.11).
О.
2.
1.
'91
*?''Т-.
22
И
зз
I I I I I I I 1 I
(9.80
3.
5.
7.
9. 11. 13. 15.
17.
Р'
И
33
22
(9.Г)
I I I I I I I I 1 ■ I
з.
5.
7.
9.
■-:>.
л-'-
/ ■ ■ .*•
зз
•'■■
I I I I
22
1. 3. 5. 7. 9. 11. 13. 15. 17. .

11,9, Экстраполяционные методы 243
ней точки, но теперь опорный метод — явный, и это намного
ценнее. Для всех трех последовательностей ясно видно превос-
превосходство над экстраполяцией, опирающейся на метод Эйлера,
особенно в диагональных Ткк для больших значений к.
Асимптотическое разложение для нечетных индексов
Для полноты мы хотим еще вывести из (9.17Ь) существование
разложения по степеням А2 у у2к+19 хотя эт0 не имеет практиче-
практического значения для описанного выше вычислительного алгоритма.
Теорема 9,3, (Грэгг) Для х = х0 + B& + 1)А имеет место
разложение
У (х) - уь (х) = 2 ^ (*) А2' + А2/+2Я (х, А), (9.19)
где коэффициенты б;, вообще говоря, отличны от соответству-
соответствующих коэффициентов для четных индексов и Ъ$ (х0) Ф 0.
Доказательство. Значение */2й+1 можно вычислить (см. рис. 9.3)
либо делая шаг вперед от Vк, либо шаг назад от Vк+1. Для сим-
симметрии возьмем среднее из этих двух выражений и запишем
1 Ь
№ + V) + -у (! (Хк, ик) — / {Хь+ь И/Н-1))- (9-20)
Вычитая отсюда точное решение, мы получим
2 (Уь (х) - у (х)) == ю2Ь (х—Н)—у(х—Н)
Ц(х — к, и2Н (х — К)) — / (х + К и2Н (х + А))].
Все полученное выражение симметрично по А благодаря симме-
симметрии и2и(х) (и2ьA) = и„2Н (|)) и ь2Ь> (х). Поэтому асимптотическое
разложение для у2к+1 не содержит нечетных степеней А. ■
Оба выражения, как для четных индексов, так и для нечетных,
можно по-прежнему скомбинировать в одну формулу (см. упр. 2).
Существование явных методов Рунге—Кутты
произвольного порядка
Легко видеть, что каждое из выражений 7\ к представляет
некоторый явный метод РК (см. упр. 1). Если применить к (9.18)
известную формулу для погрешности полиномиальной интер-
интерполяции (см., например, Абрамовиц и Стиган A964), формула
25.2.27), мы получим
у (х0 + Н) - Г;, к = 2 (~У ек (х0 + Н) Н>* + О (№*+*). (9.21)
п1 *# # п[

244 Гл. II. Методы Рунге—Кутты и экстр апелляционные методы
Так как ек (х0) = 0, то
2 У
П1 '# # П1-
е\ (х0) #2*+1 + О (Н2к+2). (9.22)
Это показывает, что Ти к представляет некоторый метод ЯРК
порядка 2к.
В качестве приложения этого результата может быть указана
Теорема 9.4, (Грэгг.) Для четных р существуют явные методы
РК порядка р, имеющие 8 = р2/4 + 1 стадию.
Доказательство. Этот результат получается путем подсчета
числа вычислений функции /, необходимых в алгоритме ГБШ
при использовании гармонической последовательности и без за-
завершающего сглаживающего шага. ■
Замечание. Экстраполяция, опирающаяся на метод Эйлера,
приводит к ЯРК-методам с 8 = р (р — 1)/2 + 1 стадиями. Это
лишний раз показывает важность разложения по степеням Н2.
Управление порядком и длиной шага
Экстраполяционные методы имеют то преимущество, что у них
на каждом шаге можно менять не только длину шага, но и по-
порядок метода (т. е. число столбцов в таблице Т]9 к). Благодаря
этой двойной свободе их оптимальная практическая реализация
в виде программы более сложна, чем для методов РК фиксиро-
фиксированного порядка. Первые программы были разработаны Булир-
шем и Штёром A966) и их студентами. Очень успешные экстра-
экстраполяционные программы, разработанные П. Дойфлхардом и его
сотрудниками, описаны в работе Дойфлхарда A983).
Выбор длины шага может быть сделан точно таким же спосо-
способом, как и для вложенных методов фиксированного порядка
(см. разд. II.4). Если вычислены первые к строк экстраполяцион-
ной таблицы, то мы имеем Ткк в качестве аппроксимации наи-
наивысшего порядка (согласно (9.22), равного 2к) и, кроме того,
Т^ ь-1 порядка 2к — 2. Поэтому для управления длиной шага
естественно использовать выражение
еггк = \Тъ,ъл-Тък\. (9.23)
Как в разд. П.4, для оптимальной длины шага получаем формулу
Нк = Я.0.94.@.65/о//^ггАI/BА-1). (9.24)
Заметим, что здесь гарантийный фактор отчасти зависит от по-
порядка.
Для выбора оптимального порядка нам необходима мера вы-
вычислительной работы, которая позволила бы сравнивать различ-

II.9, Экстраполяционные методы 245
ные методы. Работа, затрачиваемая на вычисление Ткк9 может
измеряться числом Ак вычислений функции /. Для алгоритма
ГБШ это число определяется рекуррентной формулой
(9.25)
Однако большое число вычислений функции может быть компен-
компенсировано большой длиной шага Нк, даваемой формулой (9.24).
Поэтому рассмотрим в качестве меры вычислительной работы
работу на единичный шаг:
(9.26)
Теперь идея оптимального выбора порядка (т. е. индекса к) со-
состоит в том, чтобы минимизировать №к.
Опишем теперь комбинированное управление выбором порядка
и длины шага несколько подробнее. Допустим, что в некоторой
точке интегрирования длина шага Н и индекс к {к > 2) уже вы-
выбраны. Тогда шаг реализуется следующим образом. Сначала
вычисляется к — 1 строка экстраполяционной таблицы, а также
величины #ь_2, №ь_2, еггк_19 Нк_ъ М7к_г.
а) Сходимость в строке к — 1. Если еггк^1<^Ы, то значе-
значение Тк_1$ к_г принимается в качестве вычисленного результата,
и интегрирование продолжается с новыми значениями
ку если
к— I иначе;
(9.27)
Г "к _
г/ ^ ппеа>9
ппехо | -г
если
(Ак[Ак^> если /г,^ = к.
В (9.27) единственная нетривиальная формула —это выбор длины
шага Нпет в случае увеличения порядка (кпе^ = к). В этом
случае мы хотим избежать вычисления еттк, так что Нк и Ч7к
остаются неизвестными. Но так как мы предположили, что зна-
значение к близко к оптимальному, то имеем \7к « У?ь-ъ что и ведет
к предлагаемой формуле увеличения длины шага.
Ь) Монитор сходимости. Если еггк_г > Ы, надо сначала
решить, можно ли ожидать сходимости по крайней мере в строке
к + 1. Из равенства (9.22) следует, что в асимптотическом пре-
пределе
м - Тк, м II « (^"J еггы (9.28)

246 Рл. II. Методы Рунге—Куттш и энстраполяционные методы
где егтк„г вычисляется по формуле (9.23). К сожалению, еггк
нельзя сравнить с (9.28), так как в асимптотической формуле
сказывается влияние различных факторов, зависящих от реша-
решаемого дифференциального уравнения (ср. (9.22)). Если же тем
не менее предположить, что еттк в (гц/п^J раз меньше чем (9.28),
то мы получим, что еттк ж (пг/пкJ еггк_ъ. Поэтому уже на данном
этапе шаг отбрасывается, если
^У <9-29>
и пересчитывается заново с кпеао < к — 1 и Япеш в соответствии
с (9.27). Если же выполнено противоположное (9.29) неравенство,
то рассчитывается следующая строка экстраполяционной та-
таблицы, т. е. Тк9 к> еггк, Нк, №*.
с) Сходимость в строке к. Если еггк <; Ы, то значение Ткк
принимается в качестве вычисленного решения, и интегрирование
продолжается с новыми значениями к и Н\
виз
**пет —
, если
к + 1» если 47к < 0.9*1Рм> (9.30)
к во всех других случаях;
еСЛИ
если кпехв = к + 1.
д) Второй монитор сходимости. Если еггь > Ы, то, как
и в пункте Ь), проверяется соотношение
п1
(9.31)
Если оно удовлетворено, то шаг отбрасывается и пересчитывается
заново с кпш <^ и #пеш из (9.30). В противном случае продол-
продолжаем счет:
е) В надежде на сходимость в строке к + 1 вычисляются
Тк+1, н+ъ еггк+и Нк+и №к+1. Если еггк+1 < Ы, то значение
^л+1, к+1 принимается в качестве вычисленного решения, и интег-
интегрирование продолжается после нового выбора порядка:
0.9-№ь) кж-^к-и (9.32)

11.9. Экстраполяционные методы 247
Если еггк+1 > Ы, то шаг отбрасывается и пересчитывается заново
с кпех» < & и Нпет выбранным по формуле (9.24).
Рекомендуются следующие "небольшие изменения приведен-
приведенного алгоритма;
1) Ограниченность памяти машины приводит к ограничению
максимального числа столбцов йшах экстраполяционной таблицы
(например, ктах = 9). Поэтому на вновь назначаемый индекс
кпет надо наложить ограничения 2 <; кпехо <; &тах— 1. Это
обеспечивает возможность активизации пункта е) на каждом
шаге.
2) После отбрасывания шага ни длина шага, ни порядок не
должны увеличиваться.
3) Норму в (9.23) следует понимать, как масштабированную
норму (ср. D.6)). Например, компоненты погрешности могут быть
отнесены к б(?льшей из двух величин: 10~в (к примеру) и 1-й ком-
компоненты численного решения в начале и конце рассматриваемого
интервала.
Численное исследование комбинированного
управления длиной шага и порядком
В нижеследующих примерах мы покажем, как изменяются
длина шага и порядок для приведенного выше алгоритма. Для
этой цели нами была написана на Фортране подпрограмма СЮЕХ,
текст которой приведен в приложении.
В качестве первого примера снова возьмем модель брюсселя-
тора D.15). В нижней части рис. 9.5 показаны обе компоненты
решения (ср. рис. 4.1 и 4.2 в разд. II.4). В средней и верхней
части рисунка приведены графики изменения длин шагов (Яшах =
= 1.7) и порядков при трех значениях Ы: 10~8 (пунктир), 10"
(штриховая линия) и 10~9 (сплошная линия). Легко заметить, что
программа СЮЕХ автоматически выбирает подходящий порядок
(который существенно зависит от значения Ш). Вертикальные
участки на графиках длин шагов указывают на отбраковку и пере-
пересчет соответствующего шага.
Рассмотрим теперь поведение механизма управления порядком
метода вблизи разрывов. В следующем примере!
(9.33)
имеется разрыв первой производной у (х) при х = 0 и два разрыва
второй производной (при х = ±1). Результаты расчетов показаны
на рис. 9.6. При вычислениях с 1о1 = 10 разрывы при х = ±1
не были распознаны. В остальных случаях видно, как порядок

248 Гл. II, Методы Рунге—Кутты и экстраполяциокные методы
ДЛИНА ШАГАЯ
0. 2. 4.
16. 18. 20
О.
2.
8. 10 12. 14 16. 18. 20
Рис. 9.5. Решение, изменения длины шага и порядка для подпрограммы
понижается до 4-го (наименьшего возможного) в окрестности
точек разрыва, так что эти точки проходятся довольно эффек-
эффективно.
Упражнения
1. Покажите, что экстраполированные методы Эйлера дд, 3#,
Т3у3 [с последовательностью чисел шагов (9.8)] эквивалентны
методам Рунге—Кутты из табл. 9.1. Найдите также схемы РК,
соответствующие первым элементам алгоритма ГБШ.

П.9, Экстраполяционные методы
249
2.
5 1||||'
-2.
*.
0.
1.
2.
Рис. 9.6. Решение, изменения длины шага и порядка для подпрограммы ООЕХ,
полученные на примере с разрывной функцией (9.33).
2. Комбинируя формулы (9.17а) и (9.19), получите формулу
г
в (*) - Л = 2г [а, (х) + (-1)* р, (х)] № + Н*Ч*Е„ (х9 к)
для асимптотического разложения, соответствующего методу
Грэгга в той его части, которая определяется формулами
(9.13а и Ь).

250 Гл. II. Методы Рунге—Кутты и экстраполяционнше методы
Таблица 9.1. Экстраполяционные методы
как методы Рунге—Кутты
порядка 1 7*3,2 порядка 2
Т9%3 порядка 3
0
I
3
2
3
I
3
1
3
1
3
1
3
1
3
1
3
0
1
2
1
3
2
3
1
2
1
3
1
3
0
0
0
1
3
1 1
0
1
2
1
3
2
3
1
2
1
3
1
3
0
0
0
—2
I
3
3
2
3
2
3. [Штеттер A970)]. Докажите, что для любого вещественного Ь
(обычно заключенного между 0 и 1) метод
+ Ь [Ь! (*о, Уо) + A—Ь)! (*1§ уг)]9
[A — Ь) / (**-1, Уг-г) + Щ (хи уг) +
+ A — Ь){(хии у1+1)], I = 1, 2, ...,
У иг = И-
обладает разложением по степеням Н2. Покажите, что это
свойство сохраняется и для сглаживающего шага
(х) =
+ У2п-1 + А A — Ь) I
^) + ЬЬ{ (х2й, д2п)].
4. [Штеттер A970)]. Является ли шаг методом Эйлера (9.13а)
существенным для существования разложения по степеням й2?
Докажите, что если заменить (9.13а) стартовой процедурой
У% = Уо + АФ (х0, у0, Н)
первого порядка, то разложение по степеням Н2 получится
при условии, что величины у_г = у0 —НФ (а:0, у0, —К), у0 и у±
удовлетворяют (9.13Ь) при ь = 0.
Указание. Штеттер в своем доказательстве опирался на сообра-
соображения о возмущении начальных условий. Более естественная
возможность состоит в замене шагов по Эйлеру в (9.15) новой
стартовой процедурой.
5. Получите численные решения системы дифференциальных урав-
уравнений
= 2, у @) = 30,
гг = 0.032— 0.4*2, г @) = 0

11.9. Экстраполяционные методы
251
при длинах шагов Н = 0.5 и Н = 0.25, пользуясь методом
из упр. 3 разд. 11.8. Вычислите погрешности решения и экстра-
экстраполированного результата. Проверьте вычислениями утвер-
утверждение, содержащееся в указанном упражнении.
Замечание. Точное решение имеет вид*
у (х) - 30 + 2.51а (сЬ ("/0.0128 х))*
г (х) = /(Ш 1Ь (/(Ш28*)-
6. Покажите, что определитель матрицы
А =
1
1
пР
1
при 0 < ач < а2 < ... < ап строго положителен.
Указание. Вычтите из столбца п столбец п — 1, умноженный
на аъ затем из столбца п — 1 столбец п — 2, умноженный на аг>
и т. д. и, наконец, вычтите из столбца 2 столбец 1, умноженный
на а?. Затем вынесите положительные множители (а2 — аг),
(а3 —ах), ... (ап —аг) и покажите, что определитель А можно
представить в виде суммы определителей аналогичных матриц
меньшей размерности, умноженных на положительные коэф-
коэффициенты.

НЛО. Сравнение вычислительных качеств
*По-видимому, программа Б1РЕХ1 является вопло-
воплощением современного состояния экстраполяционных
методов...»
(Л. Ф. Шампайн, Л. С, Бака, 1984}
Теперь уместно представить некоторые результаты сравнения
вычислительных качеств описанных выше программ СЮЕХ (метод
экстраполяции) и ВОРИ8 (метод Дормана и Принса порядка 8).
Тексты обеих программ приведены в приложении. Мы сочли
интересным включить в число сравниваемых еще и широко изве-
известную программу О1РЕХ1 [Дойфлхард A983)]. Хотя эта про-
программа воплощает точно тот же математический метод, что и
СЮЕХ, она отличается многими деталями стратегии выбора по-
порядка, основанной на некоторой информационно-теоретической
модели.
Из большого числа использованных нами для тестирования
примеров дифференциальных уравнений мы отобрали здесь сле-
следующие шесть систем [первый пример приобрел известность
благодаря статье Булирша и Штёра A966), а следующие два
взяты из знаменитого набора Ое1ез1 5е1, Халл, Энрайт, Феллен
и Седжвик A972)].
ЛАСВ: дифференциальные уравнения для эллиптических функ-
функций Якоби [см. Абрамовиц и Стиган A964), 16.16]:
Уг = У2Уз> Уг @) = 0,
У2 = —УгУг> У2 @) = 1,
Уз = —О.Ыу1у2> Уз @) = 1,
0 < х < 20.
Т\УОВ: уравнения задачи двух тел:
У г = У г* Уг @) = 0.5,
У2 = Уь У2 @) = 0,
0 < х < 20.

НЛО, Сравнение вычислительных качеств 253
уравнение Ван-дер-Поля (см. разд. 1.16):
Уг = У2, т Уг @) = 2,
У2 = A — у\) У2 — Уи У2 @) = О,
О < х < 20.
«брюсселятор» (см. разд. 1.16):
Уг = 2 + у\у2 — 9.533уь уг @) = 1,
у\ = 8.533уг — у?у2, у2 @) = 4.2665,
О < х < 20.
: уравнение Лагранжа для висящей струны (уравнение
F.2) из разд. 1.6 при п = 10', К = 1). Начальные условия: все
У% @) = 0» за исключением у8 @) = 1. Интервал интегрирования:
О .< х < 10.
РЬЕ1: задача небесной механики, которую мы назвали «Пле-
«Плеяды»: семь звезд с координатами хь уг и массами т1 = ь (ь =
= 1, ..., 7) движутся в одной плоскости:
01= ЪЩ {У1 - У()/Гф
11
1Ф1
где
\ и 1 = и .. .17
Начальные условия:
@) = 3, ^@) = з, ж8@) = —1, д:4@)==—3,
@) = 2, хв @) = -2, д:7 @) = 2,
@) = -3, у,@) = 2, г/4 @) = 0,
@) = —4, у7@) = 4,
^ @) — \>\ @) ^ 0 Для всех ^> за исключением*
х'6 @) = 1.75; хв7 @) = -1.5; ^ @) = -1.25; уь @) = 1
Интервал интегрирования [0, 3].
Точные решения этих задач представлены графиками на
рис. ЮЛ как функции х. Исключение сделано для задачи РЬЕ1^
решение которой представлено в виде траекторий в плоскости х9 у.

254 Гл. II. Методы Рунге—Кутты и экстр апол яционные методы
мсв
ВК178
УОРЬ
10. -
5.
о
■■/,
| 1 Р1 ! 1 '1' 1
0. 5
ЬАОК
10.
15.
20.
Рис. 10.1. Численные решения приведенных выше шести задач.

НЛО. Сравнение вычислительный качеств
255
Чтобы дать лучшее представление о вычислительных труд-
трудностях, встретившихся в задаче РЬЕ1, мы привели на рис. 10.2
графики решений х%, у% и их производных х'и у'% как функции
независимой переменной.
ю. -
5. -
-
: У1'|
|>3
к
ух
1ЦЙ.»
I \
^ «_
\
г
3*
Рис. 10.2. Точные решения задачи РЬЕ1.
Результаты расчетов
Каждый из указанных выше примеров решался со следу-
следующими значениями допусков локальной погрешности* Ы = 10~3,
10~в, 10~9, 102 и 10~15. На конце интервала интегрирования
вычисленное решение сравнивалось с точным решением (которое
вычислялось на компьютере СЭС с Ы — 10~22). В качестве меры
эффективности мы сопоставляем на графиках рис. 10.3 в двойном
логарифмическом масштабе полученную точность — 1§ (| егг |)
и число обращений к вычислению функций. Видно, что обе экстра-
поляционные программы (СЮЕХ и О1РЕХ1) дают почти равно-
равноценные результаты. Программа ООРК18 с ее фиксированным по-
порядком точности явно превосходит их при 10 < Ы < Ю-12,
и только при самых высоких требованиях к точности начинает ска-
сказываться высокий порядок точности экстраполяционных программ.

256 Гло Ив Методы Рунгв—Кутты и экстр аполяционныв методы
ТИТОВ
ООРК18
-1о8)О(логр)
I 1 I I
0. а 6. 9. 12 15
4.
БОРЯ18
-1об10(погр.)
I ■ I I , ■ I . I I , I I
е. э.
15
вяш
3.
У.'
оЬех
I I I I I I
3. 6. 9. 12. 15.
ЬАСК
О 3 6 91 12. 15
РЬЕ1
Б1РЕХ1
ОЭЕХ
I I I I
■ I I I
О. 3 6 9. 12. 15.
Рис. 10.3. Диаграммы «точность — объем вычислений» для приведенных выше
примеров.
Пример с негладким решением
Уравнение (9.33) содержит в интервале интегрирования три
точки, в которых терпят разрыв первая или вторая производные.
В этом случае получаемая точность — вопрос удачи: как рас-
расположатся границы шагов интегрирования относительно точек
разрыва. Этот пример мы решили для очень большого числа зна-
значений допустимой погрешности (Ы = К)-3-'/10, I = 0, 1, ...,90).
Полученные значения погрешностей и числа обращений к вы-
вычислению функций ведут себя совершенно хаотически. Для всех
трех сравниваемых программ они представлены на рис. 10.4.

НЛО. Сравнение вычислительных качеств
257
10
-12
ОРЕХ
■1об10(погр)
35
30
25
20
Р1РЕХ1
10-3 -1ов,0(поф)
3.5
30
25
20
10
-12
РОРШ8
-1од10(погр)
1 2 3 4 5 6 7 8 9 10 11 12 13 1 2 3. 4 5 6 7 8 9 10.1112 13 1 2 3 4 5 6 7. 8 9.10.11.12 13
Рис. 10.4. Диаграммы «точность — объем вычислений» для уравнения (9.33).
Можно заметить, что Э1РЕХ1 делает приблизительно вдвое
больше вычислений функции, чем две другие программы, из
которых (ЮЕХ слегка выигрывает благодаря понижению по-
порядка в окрестности точек нарушения гладкости.
Заключение
Для гладких задач и допустимой локальной погрешности
от 10~3 до 102 предпочтительнее программа ООРК18, имеющая
фиксированный порядок точности. Экстраполяционные программы
превосходят ее при очень малых значениях допустимой погреш-
погрешности благодаря автоматическому увеличению порядка точности.
Программа ОбЕХ превосходит две другие при решении задач
с негладкой функцией благодаря предусмотренному в ней авто-
автоматическому понижению порядка.
9 Хайрер Э. и др.

11.11. Композиция В-рядов
Теперь мы установим центральную теорему о композиции
объектов, которые мы назвали В-рядами (в честь Бутчера). Эта
т.еорема будет иметь много приложений к более общим методам,
например к методам со старшими производными (разд. 11.12),
методам Розенброка (том II) и др. Она заменит также теорию
условий порядка, развитую в разд. П.2.
Композиция методов РК
Пятистадийных методов ЯРК пятого порядка не существует
(см. разд. 11.6). Бутчеру A969) принадлежит идея подыскать
такие различные пятистадииные методы, определенная композиция
которых давала бы результат пятого порядка точности («эффектив-
(«эффективный порядок»). Это послужило отправной точкой очень красивой
алгебраической теории численных методов, хотя сама идея боль-
большого практического интереса не представляет, главным образом
из-за проблемы изменения длины шага.
Пусть имеется два метода, например трехстадийных»
О
'2
'3
О
«31 "
32
«2Х
#31 #32
A1.1)
Ъ
3
Отправляясь от начального условия у0, применим их один за
другим, сделав по одному шагу одинаковой длины Н (ср. формулы
B.3)):
ёг = Уо + Н 23 йц! Ш> Уг = Уо + Н1> Ч Ш, A1.2)
'| = Й+АЕ Я ^ ('Л Уг = Уг + Н 2 Ь$ (/,). A1.3)
Если подставить уг из A1.2) в A1.3) и собрать все §г, 1Ь вместе,
то легко видеть, что композицию можно интерпретировать как
большой метод РК с коэффициентами
2ь>с;
*
п
'21
!31
32
0
С2
С3
С4
С5
С6
«21
«31
«41
«51
«61
*1
«32
«42
«52
«62
ь2
«43
«53
«63
ь3
«54
«64
*4
A1.4)
«65
*5 66

11.11. Композиция В-рядов 259
Теперь интересно посмотреть условия порядка нового метода.
Для этого надо вычислить выражения
2 Ъ^ 2 2 Ь^}, 3 2"^с?» 6 2 Ь1пцС1 и т. д.
(см. табл. 2.1). Если подставить сюда выражения из первой таб-
таблицы A1.4), то не слишком трудные для низких порядков вы-
вычисления показывают, что эти величины могут быть выражены
через соответствующие величины для двух методов A1.1). Для
первого метода мы обозначим эти выражения а (*), для второго
метода Ь (/), а для композитного метода — через аЬ (/):
а (т) = 2 Ь» а (/20 = 2^ Ъфи а (/а) = 3-2 &Д ... A1.5а)
Ь(т) = 2 Ьи Ь(/я) = 22 Ь&9 Ь(/30 = 3-2 5/2?, ... A1.5Ь)
аЬ{%) = 2 &** аЬ(*21) = 22 Ь*с,, аЬ('зО = 3-2 Ьс*9 ... A1.5с)
Здесь ф, {ц—деревья из табл. 2.1.-В этих обозначениях упомя-
упомянутые формулы будут иметь такой вид!
аЬ (/21) = а (/21) + 2Ь (т) а (т) + Ь (/„),
аЬ ((Ь1) - а (*„) + ЗЬ (г) а (гJ + ЗЬ D0 а (г) + Ь (*„), (И '
аЬ (/32) = а (/32) + ЗЬ (т) а (/21) + ЗЬ (/21) а (т) + Ь (/32)
и т. д.
Интересно, конечно, понять теперь общую структуру этих
формул для произвольных деревьев. Однако, пользуясь старыми
средствами, это сделать нелегко («...громоздкие, утомительные
вычисления показывают., что...»). Наряду с этим существует
проблема идентификации различных методов, дающих одинаковые
численные результаты (см. упр. 1 ниже). Кроме того, мы хотим,
чтобы теория включала процессы более общие, чем методы Рунге—
Кутты, например точное решение или методы со старшими про-
производными.
В-ряды
Разрешить все эти проблемы можно, непосредственно рассма-
рассматривая композицию рядов Тейлора из разд. II.2. Определим
множество всех деревьев
в которое включено и «пустое» дерево 0 порядка О, представляю-
представляющее начальные условия; соответствующим ему элементарным диф-
дифференциалом является тождественное отображение: Р @) (у) =
= у. Аналогично определим множество всех помеченных деревьев:

260
Гл. II, Методы Рунге—Кутты и экстраполяционные методы
Определение 11.1. [Хайрер и Ваннер A974)] Пусть а @),
а СО,, а у21)9 а (/31), ... — последовательность вещественных коэф-
коэффициентов, определенных для всех деревьев, т. е. а: Т -> К.
Назовем В-рядом следующий ряд:
а @) / + /га (г) /' (у) + -^- а (*21) $ (у) /* (у) + ...
A1.7)
(см. определения 2.2, 2.3 и теорему 2.11).
Согласно теореме 2.11, приближенное (численное) решение,
даваемое методом РК, является В-рядом, а в силу теоремы 2.6
это верно и для точного решения, у которого все коэффициенты
В-ряда равны единице.
Обычно представляет интерес только конечное число членов
таких рядов, не превосходящее порядков рассматриваемых мето-
методов или степени гладкости функции (. Поэтому все наши даль-
дальнейшие результаты будут верны с точностью до членов погреш-
погрешности О (кк+х).
Определение 11.2. Пусть I ^ ЬТ — какое-то помеченное де-
дерево порядка ц = р (г), и фиксировано некоторое целое число ь
@ <; I <; д). Обозначим тогда 5^ (^) = 5 субдерево, образованное
первыми I индексами, и с1г (г) множество субдеревьев, образован-
образованных индексами х + 1, ..., ц {разностное множество). На графах
мы будем выделять субдерево 5, обозначая его вершины круж-
кружками, а ребра — двойными линиями.
Пример 11.3.
ао=0
«И был свет» (Гайдн).

ИЛ1. Композиция Б-рядов
261
Определение 11.4. Пусть аг
следовательности коэффициентов, такие что а @) =
тогда для дерева I порядка ц = р ($) композицию
суть две по-
по1. Определим
П
а (г)
A1.8)
где первая сумма берется по всем а (I) различным возможным
индексациям дерева } (см. определение 2.5).
Пример 11.5. Легко видеть, что формулы A1.6) являются
частными случаями A1.8). Дерево I из примера 11.3 допускает
шесть различных индексаций, что дает в результате
аЬ (/и) = Ь @) а (/„) + 5Ь (т) а (тJ а
+ 10
+ 10
5
{кг) а (х) а {1г1) +
а {кх) + -§-ь
(хK ] +
+ |- Ь
(хJ]
4
Ь (/4х) а (т) + -у Ь (/42) а (т) +
A1.9)
(обозначения деревьев соответствуют табл. 2.1).
Докажем теперь основную теорему этого раздела.
Теорема 11.6. [Хайрер и Ваннер A974)] Пусть, как и выше,
а: Т -> К и Ь: 71 -> К — две последовательности коэффициентов,
такие что а @) = 1. Тогда композиция двух соответствующих
им В-рядов является тоже В-рядом:
В(Ъ, В (а, у)) = В(аЬ, у), A1.10)
где «произведение» аЬ: Г -> К приведено в определении 11.4.
Доказательство. Введем следующее обозначение для внутрен-
внутреннего ряда-
В (а, у) =§ (к). A1.11)
Тогда доказательство становится очень похожим на рассуждения,
приведенные в разд. 11.2 (см. рис. 2.2), с той лишь разницей|
что вместо р (§) мы отправляемся теперь от
гь<8>р
и должны вычислить производные этой функции. Выберем для
примера член 5 = (В2 из этого ряда!
ЗГ Ь ^ /* &) & (В) 1М (§)- A1.13)

262 Гл. II. Методы Рунге—Кутты и экстраполяционные методы
По формуле Лейбница ^-я производная этого выражения при И = О
равна
) Ь 082) [# (§) 1м (ё) !М (§)У^3) |д-о. A1.14)
3
Пользуясь классическими правилами дифференциального исчис-
исчисления, вычислим теперь, как это делалось в лемме 2.8, производ-
производные выражения
A1-15)
Для первой производной это дает
Ы!
и т. д. Воспользуемся опять графическим представлением этого
процесса дифференцирования (рис. 11.1).
т
I
т т
к
Р т
п
Рис. 11.1. Производные формулы A1.15),
Мы видим, что получаются деревья и порядка д, у которых
$з (и) — 5 (где 3 = р E)) и элементы множеств с13 (и) не имеют
разветвлений. Соответствующие выражения аналогичны выраже-
выражениям B.6; ц — 1) из леммы 2.8. Наконец, надо подставить выра-
выражения для производных §" (см. A1.11)) и произвести перегруппи-
перегруппировку членов. Тогда, как и на рис. 2.3, длинные ветви из с13 (и)
заменятся деревьями г порядка б, умноженными на а (г). Таким
образом, для каждого данного дерева I получаются как раз коэф-
коэффициенты, описываемые формулой A1.8).

11.11. Композиция В-рядов 263
Множитель 1/а (^) обязан своим происхождением тому обстоя-
обстоятельству, что в В (аЬ, у) член с аЬ (О Т7 @ появляется а (I) раз. ■
Поскольку к\ (у) = В (Ь, у\ является Б-рядом частного вида,
у которого Ь (т) = 1, а все остальные Ь (I) = 0, то из доказанной
теоремы вытекает
Следствие 11.7. Если а: Т -> К — последовательность коэф-
коэффициентов, такая, что а @) = 1, то
Щ (В (а, у)) = В (а',
а'(т)=1,
= Р (<) а и) ... а(и, (П.16)
означаещ, что с1± (/) = {1Ъ 12, ..., ^т[ (см.
определение 2.12).
Доказательство. Формулы A1.16) получаются из A1.8) при
1=1, ц = р @ с учетом того факта, что выражение в скобках
не зависит от индексации дерева
Условия порйдка для методов Рунге—Кутты
В качестве приложения следствия 11.7 продемонстрируем
вывод условий порядка. Запишем метод РК B.3) в виде
8* = Уо + 2 аф» кь = кЦвд. (П.17)
Допустим, что §г и кг являются В-рядами, коэффициенты которых
обозначим
Тогда следствие 11.7 позволяет нам непосредственно переписать
формулы A1.17) в виде
@ = 23 *Л (О,
к, @ =
откуда легко получаются формулы B.17), B.19) и теорема 2.11.
Аналогично, если мы положим у (к) — В (у, у0) для точного
решения дифференциального уравнения и сравним (умноженную
на к) производную ку' (к) ряда A1.7) с выражением к} (у) из след-
следствия 11.7, мы сразу же получим, что у (^) = 1 для всех I, так что
теорема 2.13 становится ненужной.

264 Гл. П. Методы Рунге—Кутты и экстраполяционные методы
сЭффективный порядок» Бутчера
Разобравшись в том, что такое композиция методов, будем
теперь искать такие методы а и A, что Aа = ед вплоть до членов,
соответствующих порядку 5 (здесь е — некоторый метод пятого
порядка). Кроме того, построим еще методы Ь и с, такие, что
Рис. 11.3.
Рис. 11.2.
ег<\ = Ь и йс — е2, где вх и е2 —тоже методы пятого порядка
(см. рис. 11.2). Тогда композиция методов Ьа*-2с по своим вы-
вычислительным свойствам соответствует результату выполнения
к шагов методом пятого порядка (рис. 11.3). Один из возможных
наборов коэффициентов, вычисленный Бутчером A969), приведен
в табл. 11.1.
Таблица 11.1 Метод Бутчера с эффективным порядком 5. Вверху слева — ме-
метод а, справа — метод Ь, внизу — метод с.
0
1
5
2
5
1
2
1
1
5
0
3
16.
1
4
1
6
2
5
о
0
0
5
16
5
4
0
2
2 1
3 6
0
1
5
2
5
3
4
1
1
5
0
75
64
37
36
19
144
2
5
9.
4
7
3
о
117
64
3
4
25
48
4
9
2 1
9 8
0
1
5
2
5
3
4
1
1
5
0
161
192
27
28
7
48
2
5
19
12
19
7
о
287
192
291
196
475
1008
36
49
2 7
7 72

11.11. Композиция В -рядов
265
Упражнения
1. Покажите, что пары методой, приведенные в табл. 11.2—11.4,
дают идентичные численные результаты (по крайней мере для
достаточно малых к).
Ответ. Эквивалентность методов а) очевидна, если в одном из
них переставить стадии; в случае Ь) достаточно отбросить
лишние стадии [Далквист
И Йелч A979)]; В с) надо Таблица 11.2. Эквивалентные методы а)
отождествить равные ста-
стадии [Штеттер A973), Хун-
дсдорфер иСпейкерA981) ].
См. также обзор Бутчера
A984) о «пространстве Рун-
ге—Кутты».
2. Продолжите формулы A1.6), вычислив композицию аЬ
для всех деревьев порядков 4 и 5.
3. Проверьте, что методы, приведенные в табл. 11.1, действи-
действительно удовлетворяют свойствам точности, о которых гово-
говорилось выше.
Таблица 11.3 Эквивалентные методы Ь)
0
1
0
1
1
4
0
3
4
1
0
0
0
3
4
1
0
1
4
1
3
7
2
2
0
0
1
1
2
0
1
3
0
0
0
2
4
0
0
—1
0
0
1
1
2
1
2
2
1
1
2
1
1
1
2
Таблица 11.4. Эквивалентные методы с)
1
1
1
\
1
2
—1
1
1
4
1
2
\
2
1
4
1
1
5
1
1
4
2
2
2
з
1
4
1
\
3
2
3
4
2
з
1
4
4. Докажите, что множество
= {а: Г->К; а@) =
с законом композиции из определения 11.4 является группой
(некоммутативной).
Указание. Воспользуйтесь теоремой 11.6.

11.12. Методы, использующие старшие производные
В разд. 1.8 уже рассматривалось вычисление старших произ-
производных решений дифференциального уравнения
(УТ = /'(*. У1> ••> Уп)> /=1, ...» я. A2.1)
«Цепное правило» (правило дифференцирования суперпозиции
функций) дает
Поэтому введем дифференциальный оператор й, действие кото
рого на функцию >Р (л:, у) определяется равенством
Поскольку Ву3 = р, формулы, обобщающие A2.2), будут иметь
вид:
(*/')«> = (ДV) (х, у), / = 0, 1, 2, A2.3)
Эти обозначения удобны для определения нового класса методов,
сочетающих в себе черты как методов Рунге—Кутты, так и мето-
методов, использующих ряды Тейлора.
Определение 12.1. Пусть заданы вещественные коэффициенты
Метод, определяемый формулами
2 2ЬГ*]Г). A2.4)
называют ъ-стадийным, методом РК с использованием производных
ц-го порядка, явным, если все а^ равны нулю при *' ^ /, и неяв-
неявным — в противном случае.

11.12. Методы, использующие старшие производные 267
Так как их = 1, й1х = 0 (/ ^ 2), то естественным обобщением
условий A.9) здесь будет
^-2ай}. A2.5)
Определение 12.1 взято из работы Кастлюнгера и Ваннера A972),
но конкретные методы этого типа публиковались и ранее. В част-
частности, такую структуру имеют очень удачные методы Фельберга
A958, 1964).
Коллокационные методы
Естественным способом получения 5-стадийных методов с про-
производными до <7-го порядка является использование идеи коллока-
ции с кратными узлами. Другими словами, соотношение G.18Ь)
надо заменить на
о + сгН) = (О1 у) (х0 + сгН, и (х0 + сгН)), 1=1, ... ■> 5,
/=1, ..., Ць A2.6)
где и (х) —это многочлен степени цх + Цг + ••• + <7«> а заданные
целые числа цъ ..., д3 —«кратности» узлов сг, ..., с$. Например,
при^х = /п, цг = ... = дв = 1 получаются методы типа Фельберга.
Для обобщения результатов и идей разд. 11.7 надо заменить
использованную в теореме 7.6 интерполяцию по Лагранжу ин-
интерполированием с кратными узлами [Эрмит A878): «Ле те зшз
ргорозё йе Ьготгег ип ро1употе...» *)]. Дело в том, что формулу
A2.6) можно интерпретировать как обычное условие коллокации,
где узлы собраны в 5 групп, причем 1-я группа содержит цг «бес-
«бесконечно» близких друг к другу узлов (теорема Ролля). Запишем
формулу для интерполяционного многочлена Эрмита р (/) сте-
степени 2 Й1 — * в так°м виде:
2
Здесь «базисные» многочлены /;> (I) степени ^д; — 1 должны
удовлетворять условиям
г1, если 1 = 1 и к = г — 1,
' 1 A2.8)
0 в остальных случаях.
Их лучше всего получать из интерполяционной формулы Ньютона
(с кратными узлами) 2). Как и в разд. 11.7, применим теперь
1) «Я поставил себе целью найти многочлен...».—Франц.
2) См., например, Бахвалов A975), гл. П. § б. — Прим, ред.

268 Гл. II, Методы Рунге—Кутты и экстр апелляционные методы
к многочлену р @ = Ни' (х0 + Иг) нашу интерполяционную фор-
формулу:
8
Ни(хй + 1Н) = I] 2 //г (/) й|г), A2.9)
где
^г) = ~ргг(г)(^а + ^). A2.10)
Подставляя в A2.6) выражение
Н
о
о учетом A2.9), легко убедиться, что доказана
Теорема 12.2. Коллокационный метод A2.6) эквивалентен НРК
методу A2.4) с 8 стадиями и использованием ц-х производных,
у которого
а$ = \ 11гA)&и Ъ\г) = \ //г@ сИ. Ш A2.11)
Теоремы 7.7, 7.8 и 7.9 непосредственно обобщаются на случай
«конфлюентных» (т. е. с совпадающими узлами) квадратурных
формул. Таким образом, метод РК с ^-ми производными имеет
такой же порядок, как и соответствующая ему квадратурная
формула
«Алгебраическое» доказательство этого результата более сложно
(ср. упр. 7 из разд. 11.7). Для случая ц$ = ц оно дано у Кастлюн-
гера и Ваннера A972Ь).
Предположениям G.12) ч соответствуют теперь следующие
формулы:
Р=1, 2,...,2и- <12Л2>

После того как выбраны си эти уравнения однозначно определяют
значения а{ц]у так как они образуют линейную систему с «кон-
флюентной» матрицей Вандермонда [см., например, Гаучи A962)].
Формула A2.12) получается, если в A2.7) положить р (I) =
а затем проинтегрировать от 0 до сг.

11.12. Методы, использующие старшие производные 269
Примеры методов. Квадратурные формулы «гауссовского»
типа с кратными узлами существуют при нечетных ц [Струд и
Станку A965)]. Им соответствуют неявные методы Рунге—Кутты
с использованием производных ц-тъ порядка [Кастлюнгер и
Ваннер A972Ь)]. При 5=1, конечно, сг = 1/2, что дает
Ь[2к) = 0, Ь[2к+1) = 2~2к, а$ = - (—1)* 7Гк. %
Приведем также коэффициенты для случая 5 = 2 и цх = Цъ — 3-
Узлы С1 и веса Ъ\к) нашли Струд и Станку. Метод имеет восьмой
порядок!
= 0.185394435825045, с2 = 1 — съ
0.5,
Ь[2)/2\ = 0.0240729420844974,
Ь[3)/3\ = 0.00366264960671727, *43) - б{3).
0.201854115831005 —0.0164596800059598 \
0.516459680005959 0.298145884168994 /'
B)ч /—0.0223466569080541 0.00868878773082417 \
\а1к ) = ^ 0.0568346718998190 —0.0704925410770490 / '
C /0.0116739668400997 —0.00215351251065784 \
^'*^ = \ 0.0241294101509615 0.0103019308002039 / *
Методы Обрешкова
Мы рассмотрим теперь частный случай коллокационных ме-
методов с 5 = 2, сг = 0, с2 — 1. Эти методы называются методами
Обрешкова. Их коэффициенты могут быть получены в замкнутой
форме посредством повторного интегрирования по частям [Нёр-
сетт A974а)].
Лемма 12.3. Пусть задано целое положительное число т и
многочлен Р (I) степени /п. Тогда равенство
т т
I] Ы (Ыу) (х19 ух) Р<т-п @) = Ц А' фу) (лг0, Уо) Р{т-п A) A2.13)
определяет метод со старшими производными, имеющий поря-
порядок т.
Доказательство. Обозначив у (х) точное решение дифферен-
дифференциального уравнения, будем исходить из соотношения
I

270 Гл. П. Методы Рунге—Кутты и экстраполяционные методы
Преобразуем этот интеграл, применяя повторно интегрирование
по частям до тех пор, пока не будут использованы все производ-
производные многочлена Р A — I). Мы получим
т т
2 ^Уи) (*0 Р{тЧ) @) = 2 Л^(/) (*о) ^(т~7) A) + О (Нт+г).
у=о /=а
Вычитая это равенство из A2.13), мы найдем, что разность левых
частей —величина порядка О (кт+1). В силу теоремы о неявной
функции это показывает, что равенство A2.13) определяет зна-
значение уг с таким порядком точности, если (постоянное) значе-
значение р(т) отлично от нуля. ■
Замечание. Мы взяли здесь для Р аргумент 1 — I (вместо
более естественного /), чтобы избежать чередования знаков.
При удачном выборе многочлена Р {I) большинство его про-
производных при г = 0 и \ = 1 должно, конечно, обращаться в нуль.
Тогда метод A2.13), сохраняя порядок /тг, будет наиболее эконо-
экономичным. Взяв
(к+ 1I '
мы получим методы, имеющие порядок т = к + I, которые обычно
и называют методами Обреижова:
---- A2Л4)
Здесь после члена /-й степени в левой части и после члена /г-й сте-
степени — в правой все коэффициенты автоматически обращаются
в нуль. Частными случаями этих методов являются:
к — 1, / == 0 — явный метод Эйлера,
к = 0, / = 1 — неявный метод Эйлера,
/ = 1 — правило трапеций.
Методы Фельберга
Другой класс методов с высшими производными предложил
Фельберг A958, 1964). Его идея состояла в том, чтобы из решения
задачи у' = / (х, у), у (х0) = у0 вычесть т членов ряда Тейлора
(см. разд. 1.8)
A2.15)

IIЛ2. Методы, использующие старшие производные 271
и получившееся дифференциальное уравнение О' (х) = ? (х, Р (х)),
где
т \ т
х,6+ЦГг(х- хоу - 2 Уг1 (х-Хо)*-*, A2.16)
решать методом Рунге—Кутты. Зная, что решение уравнения
A2.16) и его первые т производных обращаются в нуль при на-
начальных условиях, можно надеяться достичь более высоких по-
порядков.
Постараемся пояснить эту идею. Для упрощения обозначений
уберем шляпки над буквами и будем считать, что преобразование
A2.15) выполнено заранее. Разложим в ряд Тейлора решение не-
неавтономного уравнения, как это сделано в разд. 11.1. Тогда из
A.6) мы получим, что
/ = О,
и + у = о,
}хх + Уху! + !уУР + !У (!л + У) = 0 И Т. Д.
(см. также упр. 3 из разд. П.2). Из этих формул следует, в свою
очередь, что / = О, /Я = 0, ..., дт-х11дхт~1 = 0. Поэтому обра-
обращаются в нуль все элементарные дифференциалы порядков <лг
и большинство из них для более высоких порядков. Соответствую-
Соответствующие условия порядка могут быть опущены. Первыми ненулевыми
членами будут
г\ТП. е
• для порядка та + 1,
дх
и Ъ'Ц? для п°Рядка
и т. д. Им соответствуют условия порядка!
5
2 Ь'с" = 1ГТТ
— для порядка т + 1,
^+1 ^г и
— для порядка т + 2, и т. д.
Условие 2 ац = си которое обычно позволяет сгруппиро-
сгруппировать некоторые члены в A.6), становится ненужным, потому
что все эти члены равны нулю.

272 Гл. II. Методы Рунге—Кутты и экстраполяционные методы
Для полного понимания вопроса надо рассмотреть его с точки
зрения применения разделяющегося метода к разделяющейся си-
системе уравнений у' = / (х, у)> х' = 1. Эти понятия разъясняются
в разд. 11.14 (см. рис. 14.4).
Пример 12.4. Для 3-стадийного метода решение системы урав-
уравнений, образованной четырьмя условиями для порядка т + 3,
указал Фельберг A964). Выбор сг = с3 = 1 максимально упро-
упрощает вычисление выражения A2.16); при этом остальные коэффи-
коэффициенты определяются однозначно (см. табл. 12.1).
Таблица 12.1, Метод Фельберга порядка ш+ 3
1
8
1
8
т + 3
т+3
1
т
(т
т + 3
О
т
(т + 2) 29
В этой же работе Фельберга A964) был выведен вложенный
метод с двумя добавочными стадиями порядков т + 3 (т + 4).
Все эти методы широко применялись для проведения научных
расчетов в 60-х годах.
Общая теория условий порядка
Из тех же соображений, что и в разд. П.2, мы предположим,
что система A2.1) является автономной. Общая форма условий
порядка для метода A2.4) была найдена в диссертации Кастлюн-
гера [Кастлюнгер и Ваннер A972)]. Позже она была получена
как простое следствие теоремы о композиции В-рядов [Хайрер и
Ваннер A974)]. Суть здесь в том, что, согласно теореме 2.6, вы-
выражение
Р'у) Ы 2 тг р № ы = в
является В-рядом с коэффициентами
1, если
(
A2.18)
0 в остальных случаях.
Таким образом, мы получим обобщение следствия 11.7
$ (В (а, №)) = В (а«>, Уо), A2.19)

11.12. Методщ, использующие старшие производные 273
где, согласно формуле A1.8) о ц = р (/),
, A2.20)
(здесь сумма берется по всем а (!) различным индексациям де-
дерева I). Это дает нам рекуррентные формулы для вычисления
коэффициентов В-рядов, появляющихся в A2.4).
Рис. 12.1. Различные способы индексации дерева На-
Например 12.5. Изображенное на рис. 12.1 дерево 1& допускает
три различные индексации, из которых две порождают одно и то же
разностное множество й2 (I), так что формула A2.20) принимает вид
а" (/42) = 2 B (а (т}J + а (*„)). A2.21)
Для всех остальных деревьев до четвертого порядка включи-
включительно а @ = 1. Итак, для вторых производных с помощью
формулы A2.20) можно составить следующую таблицу:
а" (т) = 0,
а" (*31) = За (т),
а" (*в) = За (т),
а" (*«) = 6 (а (
а" (/«) = 4 (а (т))а + 2а
а* (<«) = 6 (а (т)J,
а" (и = 6а (<и) A2.22)
(обозначения деревьев см. в табл. 2.1).

274 Гл. II. Методы Рунге—Кутты и экстраполяционные методы
Итак, пусть вид выражений а(*' (/) установлен. Перепишем
теперь формулы A2.4) в виде
1 1Л
и предположим, что выражения к\1\ §%, у% являются В-рядами1
к\1) = В (к\1\ у0), В1 = В (&, до), У1 = В (уи до).
Тогда коэффициенты этих рядов определяются по рекуррентным
формулам;
(9 = Р @ в* СО ... &(*«), к1гЧт) = 1 (см. A1.17')),
1 (см. A2.22)),
(см. упр. 1 или упр. 2), и т.д.;
а @ = Е Ё а!?кГ (о
Ид наконец,
У1 @ = 2 РГ
Метод A2.4), удовлетворяющий условиям A2.5), имеет порядок р,
если, как обычно,
Ух @ = 1 для всех /, у которых р (I) <; р.
Дальнейшие подробности и конкретные методы приведены
в статье Кастлюнгера и Ваннера A972); см. также упр. 3.
Упражнения
1. Обобщите пример 12.5 и получите формулы для аC) (I) для всех
деревьев до четвертого порядка включительно.
2. (Кастлюнгер.) Докажите следующий вариант формулы A2.20),
который позволяет обобщить соотношения A1.17') более не-

11.12. Методы, использующие старшие производные 275
посредственным образом, а также может быть использован
для получения формул из примера 12.5:
@ = -
*»2» . ..« пгпг
если I = [/х, ..., 1т\.
Указание: см. статью Хайрера и Ваннера A973), раздел 5.
3. Покажите, что следующие условия:
Ъ(Р = 1,
где
обеспечивают третий порядок метода A2.4).
4. [Цурмюль A952), Альбрехт A955)]. Продифференцируйте си-
систему дифференциальных уравнений первого порядка у' =
= ! Iх> У)- Вы придете к задаче Коши
у" = ф2у) (х, у), у (х0) = у09 у' (х0) = Д,.
Примените к этой задаче специальный метод для систем диф-
дифференциальных уравнений высших порядков (см. следующий
раздел). Вы получите метод, использующий высшие произ-
производные. Покажите, что нижеследующий метод имеет шестой,
порядок:
К = №§ (*о, Уо)>
Здесь
, у).

П. 13. Численные методы для дифференциальных
уравнений второго порядка
«Ми1а1юпет то1из ргорог!юпа1ет еззе
1трге55ае».
«Изменение движения пропорционально приложен-
приложенной силе».
(Ньютон, 1687)
Многие встречающиеся на практике дифференциальные урав-
уравнения представляют собой системы уравнений второго порядка:
У* = Их, у, у*). A3.1)
Главным образом это связано с тем, что силы пропорциональны
ускорениям, т. е. вторым производным. Как уже упоминалось
в разд. 1.1, такая система может быть преобразована в систему
дифференциальных уравнений первого порядка, но удвоенной
размерности; для этого в качестве новой зависимой переменной
рассматривают вектор (г/, у')Т\
У) \!(х, У> У) Г у(*о) = Уо.
Чтобы получить численное решение уравнения A3.1), можно
применить, например, метод Рунге—Кутты к системе A3.2).
Это дает
= У о + к Е а ц к} у
/
(*о + ак, уо + к^ ацк1у у'о + к Ц ацк)\
Ух = Уо +
' A3.3)
Подставив первую формулу A3.3) в остальные, мы получим
Уо + Ъку'о + к2
ьл,
ц} у +
A3.4)
где
2 Ц A3.5)

П.13. Методы для дифференциальных уравнений второго порядка 277
Для программирования представление A3.4) предпочтительнее,
чем A3.3), потому что оно требует почти вдвое меньше машинной
памяти. Это может оказаться важным преимуществом, в частности
если система уравнений A3.1) имеет большую размерность.
Методы Нюстрёма
Р. X. Мерсон: <к.,.Я не видел статьи Нюстрёма. Была
она на английском?»
Дж. Беннетт: «Нет, нет, не на финском, а на немец-
немецком».
A957)
Э. И. Нюстрём A925) был первым, кто рассмотрел методы
вида A3.4), в которых коэффициенты не обязательно удовлетво-
удовлетворяют соотношениям A3.5) («Ва Ыз^'еШ сПе (ИгеЫе Апшепс1ип§
с!ег Кип§езсЬеп Ме1Ьос1е аи! с!еп дасЬИ§еп Ра11 уоп ОШегепИаЬ
§1е1сЬип§еп г^/еНег Огс1пип§ шсЫ ЬеЬапдеН ^аг, ...» Ыуз1гот,
1925.) *) Прямые методы подобного рода получили название мето-
методов Нюстрёма.
Определение 13.1. Метод Нюстрёма A3.4) имеет порядок р,
если для достаточно гладких задач вида A3.1)
У
A3.6)
A3.7)
Пример метода Нюстрёма, где условия A3.5) не выполняются,
приведен в табл. 13.1. Нюстрём утверждал, что этот метод при-
применять проще, чем «метод Рунге—Кутты», и что он уменьшает
Таблица 13.1. Метод Нюстрёма четвертого порядка
0
1
2
1
1
8
1
8
0
1
6
0
0
1
6
1
2
1 0
" °
1
2
0
0
1
6
1
2
0
2
6
-<-
1
2
6
\
ТГ ^~ 1
х) «Так как до сих пор прямое применение метода Рунге к важному случаю
Дифференциальных уравнений второго порядка не рассматривалось ...». — Ню-
Нюстрём, 1925. — Нем.

278 Гл. II. Методы Рунге—Кутты и экстраполяционные методы
объем вычислений примерно на 25 %. Это, конечно, неверно, если
метод Рунге—Кутты применяется в виде A3.4) (см. также упр. 2).
Действительное улучшение может быть получено в том случае,
когда правая часть уравнения A3.1) не зависит от у'\
У" = / (х, У)-
A3.8)
Тогда метод Нюстрёма принимает вид
Ух
Уп + Л^а + Л21]
A3.9)
у1 = уЬ+ь
и коэффициенты а^ больше не нужны. Примеры приведены
в табл. 13.2. Обратите внимание, что метод пятого порядка здесь
Таблица 13.2. Методы для уравнения
Нюстрём, порядок 4
= /(*, в)
Нюстрём, порядок 5
0
сг 1
2
1
1
1
8
0
1
6
1
6
1
2
1
3
4
6
0
1
6
0
1
5
2
3
1
Л,
1
50
—1
27
3
10
14
336
14
336
7
27
—2
35
100
336
125
336
9
35
54
336
162
336
0
35
336
требует только четырех вычислений /. Это — существенное улуч-
улучшение по сравнению с методами Рунге—Кутты, которые требуют
не менее шести вычислений / (теорема 6.1).
Нашей ближайшей целью будет вывод условий порядка для
методов Нюстрёма. Для этого мы обобщим теорию, развитую
в разд. 11.2, на дифференциальные уравнения второго порядка
[Хайрер и Ваннер A976)].

11.13. Методы для дифференциальных уравнений второго порядка 279
Производные точного решения
Как и для уравнений первого-порядка, мы можем ограничиться
системами автономных дифференциальных уравнений
№' = !'№> ...* Уп> У'\ ...I УП) A3.11)
(добавив, если надо, уравнение хп = 0). Верхний индекс / обо-
обозначает /-ю компоненту соответствующего вектора. Вычислим
теперь производные точного решения уравнения A3.11). Вторую
производную дает само уравнение A3.11):
(У'У2) = 1'(У> У\ A3.12; 2)
Повторное дифференцирование этого уравнения о использованием
A3.11) дает
ёш «(У> А 03.12; 3)
т у
= 2 1&^{^ У')*У'Ш*У'Ь+ A3.12; 4)
« ь у у
. ь
К. й у
2
к» ь
0» 91 ^-(9, У)!й(9, У).
К$ Ь
Продолжение этого процесса становится еще более сложным, чем
Для дифференциальных уравнений первого порядка. Поэтому
графическое представление приведенных выше формул будет
очень полезным. Чтобы различать производные по у и по у\
нам понадобятся два рода вершин: «тонкие» и «толстые». На
рис. 13.1 показаны графы, соответствующие приведенным выше
формулам.
Дадим теперь точное определение этих графов.

280 Гл. И. Методы Рунге—Кутты и экстраполяциочные методы
Определение 13.2. Помеченным N-деревом порядка ц назовем
пару (/, /'), состоящую из помеченного дерева
(: Ад {/} ->■ Лд
(см. определение 2.2) и отображения
1'\ Ад ->• {«тонкая», «толстая» (вершина)},
которая удовлетворяет следующим условиям:
а) корень I — всегда «толстая» вершина, т. е.
V (/) = «толстая»;
к I к I Р1 к I к 1 , / /
уу< у у К<
у у
3 3 3 3
A3.12;3)
к I т к I т мт шгп к 1 т
V
к I т к I т мт шг
Рис. 13.1. Производные точного решения.
Ь) любая «тонкая» вершина может иметь не более одного «сына»,
который должен быть «толстым».
Множество всех помеченных 1\[-деревьев порядка ц будем
обозначать ЬЫТд.
Условие Ь) в определении 13.2 мотивируется тем, что все
производные функции § (у, у') = у' тождественно обращаются
в нуль, за исключением первой производной по уг.
В дальнейшем мы будем называть конечной вершиной всякую
вершину, не имеющую «сыновей», и там, где не может возникнуть
недоразумения, будем обозначать помеченное Ы-дерево просто I
вместо (I, I').
Определение 13.3. Для помеченного 1\[-дерева { будем обо-
обозначать через
Р* @ О/. У)
выражение, которое представляет собой сумму по всем индексам
«толстых» вершин 1У кроме / (индекса корня), и по всем индексам
«тонких» конечных вершин. Общий член этой суммы является
произведением выражений
, м
ду1 ... ду'м ...
(у, у') и
.

11.13. Методы для дифференциальных уравнений второго порядка 281
Множитель первого типа соответствует каждой толстой вер-
вершине к> толстые «сыновья» которой имеют индексы т, ..., а ин-
индексы /, ... принадлежат либо „ее тонким «сыновьям» (если они
являются конечными вершинами), либо (толстым) «сыновьям»
этих тонких «сыновей» вершины к (и тогда индекс промежуточной
тонкой вершины исчезает из формулы); случаю г = О соответ-
соответствуют, очевидно, конечные толстые вершины. Множитель у'К
соответствует тонкой конечной вершине с индексом к. Вектор
Р (О (Уу У*) мы опять будем называть элементарным дифферен-
дифференциалом.
Примеры можно найти в табл. 13.3. Еще раз подчеркнем, что
индексы тонких вершин, не являющихся конечными, не играют
никакой роли в предыдущем определении. Далее, по аналогии
с определением 2.4 дадим
Таблица 13.3. БЫ-деревья, элементарные дифференциалы и условия порядка
/
'1
'2
'з
'4
'5
'л
Ч
'8
'9
'10
'и
'12
'13
1
•У
ч.
^
к 1
к 1 т
1 т
к<^,1
т }
*^
к 1 тр
У р
^^ АО
/ /Л ^
р@
1
2
3
3
4
4
4
5
5
5
5
5
5
а(г)
1
1
1
1
1
3
1
1
6
3
4
1
1
7@
1
2
3
6
4
8
24
5
10
20
30
60
120
?'(')(У,У')
^кУ'К
к
2 !'кшУ'Ку'1'у'М
К ,ь ,М
2 /кшрУ У У У
К ,1 & ,Р
2 /1мрУ'1У'М*Р
V *' г1у'Му'Р
2 Мру'му'р
♦/0
1
СУ
2
/
3
т
2сл«|

282 Гл. П. Методы Рунге—Кутты и экстр апелляционные методы
Определение 13.4. Два помеченных И-дерева (I, V) и {и, ит)
эквивалентны, если они отличаются только перестановкой их
индексов, т. е. если они имеют одинаковый порядок ц, и суще-
существует взаимно однозначное отображение а: Ап-+АA, такое что
(/) / 1 = ои на Ая — Ш и *'сг = и'.
Например, второе и четвертое помеченные 1\[-деревья в фор-
формуле A3.12; 4) на рис. 13.1 эквивалентны; эквивалентны также
второе и пятое деревья в формуле A3.12; 5).
Определение 13.5. Класс эквивалентности помеченных Ы-де-
ревьев <7-го порядка называется ^-деревом порядка ц. Множество
всех И-деревьев порядка ц обозначается ЫТд. Далее, будем обо-
обозначать через а (/) число элементов в классе эквивалентности /,
т. е. число различных возможных монотонных индексаций \
(ср. определение 2.5).
Представители 1^-деревьев до пятого порядка включительно
приведены в табл. 13.3. Теперь мы в состоянии записать в замкну-
замкнутом виде формулу для производных точного решения системы
A3.11).
Теорема 13.6. Для точного решения уравнения A3.11) спра-
справедлива формула
Р{г) (У, У ) = 2 ее (О Р @ (у, у'). A3.12; ц)
Доказательство. Общая формула здесь получается, как и
в разд. 11.2, путем продолжения вычислений, которые привели
к формулам A3.12; 2—4). ■
Производные численного решения
Запишем формулы метода A3.4) несколько иначе!
ё\ = Уа + И аиМ {ей в1)>
'1 V. A3ЛЗ)
91 = + % + Ъ 5№1 ( )
Теперь уравнения для промежуточных величин ^, ц\ имеют та-
такой же вид, как и для уь у{. В A3.13) входят выражения вида
&2Ф (К) и /гф (Н). Поэтохму, кроме формулы B.4), нам понадобится
еще формула
=а = Я (Я - 1) (Ф (Н))^2) |*-а. A3.14)

11.13. Методы для дифференциальных уравнений второго порядка 283
Будем теперь последовательным дифференцированием вычислять
значения производных %{ и §'{ при Н = 0:
A3.15;
|»0,,? A3.16; 1)
=а = 2 2 З,//' |„о. ^. (-13.15; 2)
Теперь для дальнейшего дифференцирования нужна формула
* (а. л))A)-
к
A3.17)
с помощью которой получаем
К
з.22
*
Чтобы записать общую формулу, нам потребуется
Определение 13.7. Для помеченного Ы-дерева I обозначим
через Ф^ (^) выражение, являющееся суммой по индексам всех
толстых вершин I, кроме / (индекса корня); общий член этой
суммы представляет собой произведение множителей следующего
вида:
акЬ если толстая вершина к имеет толстого «сына» /;
ак1, если толстая вершина к соединена с / через своего тон-
тонкого «сына», и
с™, если толстая вершина к соединена с т тонкими конечными
вершинами.
Теорема 13.8. Для производных функций §(, §\ из формул
метода A3.13) имеют место равенства
1^0 = {д + 1) Ц V @ I] 3*/Ф/ @ Р* @ (Уо, Уо),
A3.15;

284 Гл. II. Методы Рунге—Кутты и экстр апелляционные методы
и-а = 2 Т С) 2 Ф/ (О Р' (О (Уо, Уо), A3.16; д)
где величина у (^) вычисляется согласно определению 2.10.
Доказательство. Для небольших значений ц эти формулы
получены выше; в общем случае они доказываются, как в тео-
теореме 2.11. Система уравнений A3.2) является частным случаем
так называемых разделяющихся систем (см. разд. 11.14, где тео-
теорема 13.8 получает новое освещение). ■
Ввиду подобия формул для г/ь у[ формулам для §1, &\ справед-
справедлива также следующая
Теорема 13.9. Производные определяемого методом A3.13) чис-
численного решения ух, у{ удовлетворяют следующим равенствам:
Шд) ко = д 2 т (9 2 6,ф, @ р* @ (г/о, у0), A3.18; я)
Aзлэ; 9-
Условия порядка
Порядок метода Нюстрёма (определение 13.1) исследуется
путем сравнения разложений Тейлора для у\, у[ с такими же
разложениями для точного решения у (х0 + к), у' (х0 + к
Теорема 13.10. Чтобы метод Нюстрёма A3.4) имел поря-
порядок р, необходимы и достаточны следующие условия:
2
(р@
(I)<р-1, A3.20)
I. у) = -±— для Ы-деревьев 1с р (I) < р. A3.21)
р (^) обозначает порядок Ы-дерева I, величина Фг (I) задана
определением 13.7, а у ({) —формулой B.17).
Доказательство. Достаточность вытекает непосредственно из
теорем 13.6 и 13.9. Необходимость может быть доказана тем же
способом, что и для уравнений первого порядка (ср. упр. 4 из
разд. II.2). ■
Обсудим вкратце вопрос, может ли дополнительная свобода
выбора параметров метода A3.4) (полученная отказом от предпо-
предположений A3.5)) привести к его существенному улучшению. По-
Поскольку условия порядка для методов РК (теорема 2.13) являются
подмножеством условий A3.21) (см. ниже упр. 3), то увеличить

IIЛ3, Методы для дифференциальный уравнений второго порядка 285
порядок метода эта дополнительная свобода не позволяет. Можно
лишь уменьшить некоторые (но не все) коэффициенты погреш-
погрешности. Поэтому мы обратимся к методам Нюстрёма A3.9) для диф-
дифференциальных уравнений второго порядка специального вида
A3.8).
Чтобы исследовать условия порядка для методов A3.9), за-
запишем уравнение A3.8) в автономной форме!
У" = ! {У)- A3.22)
Специальный вид этого уравнения имеет следствием тождествен-
тождественное обращение в нуль тех элементарных дифференциалов, кото-
которые содержат производные по у'. Следовательно, надо рассмотреть
лишь подмножество И-деревьев, имеющих следующий специаль-
специальный ВИД!
Определение 13.11. М-дерево /'называется специальным Ы-
деревом (ЗК-деревом), если его толстые вершины имеют только
тонких «сыновей».
Теорема 13.12. Метод Нюстрёма A3.9) для дифференциаль-
дифференциального уравнения специального вида A3.8) имеет порядок р в том и
только том случае, если
2 б*Ф> Ю = (Р (о + 1) V (/) для ЗЫ-деревьев I с р @<р-1, A3.23)
2ЬгФг @ = —— для 8Ы-деревьев I с р (*) < р. A3.24)
Все 51М-деревья до пятого порядка включительно вместе
с соответствующими элементарными дифференциалами, а также
необходимыми для записи условий порядка выражениями Ф7-
и значениями р, а и у представлены в табл. 13.3.
О конструировании методов Нюстрёма
При конструировании методов Нюстрёма полезно использо-
использовать рассмотренные ниже упрощающие предположения.
Лемма 13.13. Условие A3.23) становится следствием A3.24),
если предположить, что выполнены равенства
6, = 6,A -сг), /= 1, ..., 5. A3.25)
Доказательство. Пусть I является 5М-деревом порядка не
выше р — 1. Обозначим и 5Л^-дерево порядка р (I) + 1, которое

286 Гл. II. Методы Рунге—Кутты и экстраполяционныв методы
получается из I добавлением новой ветви с тонкой вершиной, ис-
исходящей от корня г. Согласно определению 13.7, Фг (и) = сгФг (/),
а из формулы B.17) следует, что <у (и) = (р (*) + 1) У (*Ур(О-
Заключение леммы следует из того, что
где мы воспользовались предположением A3.25). ■
Лемма 13.14. Пусть I и и—два 8 N-дерева, изображенные
на рис. 13.2 (предполагается, что очерченные кругами их части
идентичны). Условия порядка для I и и одинаковы, если предполо-
предположить выполнение равенств
„2
..., 5. A3.26)
и —
Рис. 13.2. Деревья из леммы 13.14.
Доказательство. Из определения 13.7 и формулы A3.26)
следует, что Фг У) = Ф* (и)/2, а из формулы B.17) получаем, что
у (^) = 2у (и). Таким образом, условия порядка для /ии совпа-
совпадают. ■
Условия A3.25) позволяют нам освободиться от уравнений
A3.23), а роль условий A3.26) аналогична той роли, которую
условия A.9) играли для методов Рунге—Кутты. Условия A3.26)
выражают то обстоятельство, что величины §( в формулах A3.13)
аппроксимируют у (х0 + сгН) с точностью до членов О (№). Из
леммы 13.14 следует, что могут быть опущены все 5Ы-деревья,
имеющие хотя бы одну толстую конечную вершину (т. е. деревья
^4» ^в» *9» ^ю> ч.з в таол. 1о.о).
С помощью упрощающих предположений A3.25) и A3.26)
теперь легко построить явные методы Нюстрёма пятого порядка
при 5 = 4. Условия порядка для деревьев 1Ъ 12, 1В, 1Ь и 1% показы-
показывают, что квадратурная формула с узлами сг = 0, с2, с3, с4 и
весами Ь19 Ь2, Ьг, Ь4 имеет пятый порядок. Следовательно, узлы
должны удовлетворять соотношению ортогональности
I
] х (х — с2) (х — с3) (х — с4) их == 0,
о
I
]
о

11.13. Методы для дифференциальных уравнений второго порядка 287
и мы видим, что при выборе квадратурной формулы все еще оста-
остаются две степени свободы. После этого выбора коэффициенты аи
определяются уже однозначно, и их можно вычислить следующим
образом. Значение а21 определяется из A3.26) при I = 2. Условия
порядка для G и <и образуют систему из двух линейных уравнений
о неизвестными
^ И 2
I I
Затем с помощью A3.26) при I = 3 находим а31 и а32. Наконец,
условие порядка для /12 позволяет определить величину 1л#4/С/,
и оставшиеся коэффициенты а41, а42, а43 могут быть вычислены из
линейной системы уравнений с матрицей типа матрицы Вандер-
монда. Метод из табл. 13.2 был получен именно таким путем.
При конструировании методов еще более высоких порядков
полезно использовать дальнейшие упрощающие предположения,
например равенство
которое при ц = 0 сводится к A3.26), а также равенство
которое можно рассматривать как обобщение условия A.12).
Дальнейшие подробности читатель найдет в ряде работ, где пред-
представлены методы Нюстрёма высших порядков [Хайрер и Ваннер
A976), а также Альбрехт A955), Баттин A976), Беентьес и Гер-
ритсен A976), Хайрер A977, 1982)].
Глобальная сходимость
Вводя переменную гп = (уп, у'п)ту метод Нюстрёма A3.4)
можно записать в такой форме:
A3.29)
где
Формула A3.29) представляет специальный одношаговыи метод
для дифференциального уравнения A3.2). Для метода Нюстрёма

288 Гл. II. Методы Рунге—Кутты и экстраполяционные методы
р-го порядка локальная погрешность (у (х0 -Ь Ь) — ди уг (х0 +
+ Ь) — у[)т может быть оценена сверху величиной СНР+Х (см.
определение 13.1), что согласуется с формулой C.24). Следова-
Следовательно, теоремы о сходимости из разд. П.З, а также полученные
в разд. П.8 результаты об асимптотических разложениях гло-
глобальной погрешности и здесь остаются в силе.
Программная реализация методов Нюстрема
Для того, чтобы программа была эффективной, необходим
механизм управления длиной шага. Его можно организовать
так же, как и для методов РК (см. разд. П.4). Для оценки ло-
локальной погрешности можно применять экстраполяцию по Ри-
Ричардсону или конструировать вложенные методы Нюстрема.
Ряд вложенных методов Нюстрема построил Фельберг A972).
В этих методах для управления длиной шага используется аппро-
аппроксимация у (х0 + К) с (р + 1)-м порядком точности. Аппроксима-
Аппроксимация у' (х0 + к) с точностью до (р + 1)-го порядка не требуется,
так как для пошагового продолжения решения применяется
аппроксимация более низкого порядка.
Как и для дифференциальных уравнений первого порядка,
здесь оказалась лучше другая стратегия — использовать аппро-
аппроксимацию более высокого порядка для пошагового продолжения
решения. Дорман и Принс A978) сконструировали метод порядков
7 F), коэффициенты которого приведены в табл. 13.4. Методы
такого же типа, но более высоких порядков опубликовали не-
недавно Филиппи и Грэф A986).
Экстраполяционный метод для уравнения д" = I (х, д).
Ьез са1си1з оп&таих, согпргепап! егтгоп! 3.000 р&
т-!оПо ауес 358 &гапс1ез р1апсЬез, е{ епсоге 3.800 ра&ез
с1е Aёуе1орретеп1з таШётаИчиез соггезропс1апЬ, ар-
рагИеппеп! гпат1епап! а 1а со11ес1юп Йе гпапизспЬ
с1е 1а В^ЫюШё^ие йе Г11туег5И:ё, СЬпзИаша.
Оригинальные вычисления, содержащие около 3000
страниц ин-фолио с 358 большими таблицами, и еще
3800 страниц соответствующих математических вы-
выкладок принадлежат теперь коллекции рукописей
библиотеки университета Христиании.
(Штёрмер, 1921)
Переписав дифференциальное уравнение A3.8) в виде системы
уравнений первого порядка -
кг.* ■ и )<*•>=и )• A3ЭД

X
ы
•о
СО
■о
Таблица 13.4. Метод Дормана—Принса порядка 7 F)
а
1/
10
2
8
т
1
200
1
150
171
8192
5
288
75
45
4096
25
528
7-уТ1 1003-205^/21 -25
14 12348 9О552(
7 + ^/27 793+187^/17 -25
14
12348
C31
90552х
+ 11 Зд/21)
378
2772
1
0
0
315
8192
25
672
25
43218
25
F24
693
-128
237699C61
-79л/2Г)
3411 —745у/2Т
24696
128
•A044 •
43218^ 9745659
14885
127у^Т)
24696
+ 247 у/г\) + 3779^21)
-A57-Зу/2П 25A43 —Юд/гТ) -25
3969
0
(8?6
1280
596673(9П
+ 18у/2~П
0
4428
1722
A77?
377УПУ
20
О
О
О
45
Ш(т
8
4Т
360
7E-уТГ)
36
7G-у/П) 0
360
о
2_
20
О
О
О
45
360
360
-1
20
О
О
О
45
49
180
49
180
20
О
п>
1Г
09
а
н
о
я
•8
ю
00
со

290 Гл. II. Методы Рунге—Купы и экстраполяционные методы
можно применить алгоритм ГБШ (9.13) прямо к системе A3.30),
что дает
, A3.31а)
, A3.31Ь)
у'1+1 = У1-1 + Щ (**> уг), 1=1, 2, . . ., 2/1,
Л (х) = (у**.! + 2у2п + */2п+1)/4, A3.31с)
ь (X) =
Здесь 5Л (х) и 5& (я) аппроксимируют у (х) и у' (а:) при х = х0
+ Я, причем Я = 2пН и хг = х0 + Иг. Сделаем теперь следующее
важное замечание: для вычисления значений у0, у2, у±, ..., у2п
(с четными индексами) и у[, уз, ..., У2п+\ (с нечетными индексами)
нужно вычислить только значения функции / (х0, у0), / (х2, у2),...
..., / (х2п, У*п)- Мы знаем, далее, что как у2п, так и (*/2л-1 + У2п+г)/2
обладают асимптотическими разложениями погрешности по чет-
четным степеням к (см. формулы (9.17)). Поэтому понятно, что фор-
формулы A3.31с) следует заменить на
5/1 (х) = у2п,
8'ь (X) = (у'2п-1 + У2п+1)/2 A3.3 1С')
[Грэгг A965I. При использовании этого конечного шага число
вычислений функции уменьшается в два раза. Вычисленные
приближенные значения можно теперь использовать для экстра-
экстраполяции. Взяв гармоническую последовательность (9.8Г), положим
и рассчитаем экстраполированные выражения Тг$ ^ и Т\%\ с по-
помощью формулы Эйткена—Невилла (9.12).
Замечание. Исключая в A3.31Ь) значения у}, мы получим
эквивалентную формулу
Уш - 2*/* + Уг-2 = BкJ / (х„ уг), A3.32)
часто называемую правилом Штермера. Но для программирова-
программирования предпочтительнее формулировка A3.31Ь), потому что она
более устойчива по отношению к погрешностям округления (см.
разд. ШЛО).
Численные эксперименты
Этот раздел мы завершим сравнением вычислительных свойств
разных методов, для чего нами написаны следующие три про-
программы:

11.13. Методы для дифференциальных уравнений второго порядка 291
ОЭЕХ2 — программа, основанная на описанном выше экстра-
поляционном методе. Она организована так же, как и СЮЕХ
(экстраполяционная программа для дифференциальных уравне-
уравнений первого порядка). В частности, стратегия выбора порядка и
длины шага описана в разд. 11.9.
БОРКШ основана на вложенных методах Нюстрёма фиксиро-
фиксированного порядка с коэффициентами из табл. 13.4. Выбор длины
шага делается как в программе БОРК18 и был описан в разд. П.4.
Р1ЬОК9 использует вложенные методы Нюстрёма порядков
9(8), которые предложили Филиппи и Грэф A986). Она органи-
организована так же, как и БОРКШ.
4.0
I I I I I I I 1 I I I I I I I
40
3.5
пьак
СЮЕХ2
-Ю§10(погр)
0. 4 8. 12. 16. 0. 4. 8 12. 16. 0. 4 8. 12. 16.
Рис. 13.3. Диаграммы «точность — объем вычислений» для приведенных выше
примеров.
Листинги программ ОБЕХ2 и БОРКШ приведены в прило-
приложении.
С помощью этих программ решались три системы дифферен-
дифференциальных уравнений вида у" = / (х, у) из разд. 11.10 (задачи
ТМУОВ, ЬАОК и РЬЕ1). Каждая из задач решалась при следую-
следующих задаваемых значениях допустимой локальной погрешности!
1о1 = Ю-3, Ю-6, Ю-9, Ю-12, 10-16. На рис. 13.3, как и ранее, по
осям отложены в логарифмических масштабах точность (величина
погрешности егг) и число /с вызовов подпрограммы вычисления
функции. Чтобы продемонстрировать превосходство специальных
методов для уравнения у" = / (х9 у)У мы включили также резуль-
результаты расчетов по программе ОЭЕХ, предназначенной для решения
дифференциальных уравнений первого порядка (см. разд. 11.9).
Видно, что ОЭЕХ2 действительно считает лучше, чем ОЭЕХ.
Эта программа считает почти вдвое быстрее, в согласии с теоре-
теоретическими соображениями. При больших требованиях к точности
(Ш < 10~10) она дает наилучшие результаты. Действительно,
экстраполяционная программа позволяет доходить до очень вы-
высоких порядков точности. При требованиях к точности 10~3"
10*

292 Гл. II. Методы Рунге—Кутты и экстраподяционные методы
Ы ^ 10~8 более предпочтительны программы ЭОРК^ и
Р1ЬОК9, использующие методы фиксированных порядков. Однако
при решении этих задач не заметно их преимуществ перед про-
программой ООРК18, рассчитанной на системы уравнений первого
порядка (ср. рис. 10.3).
Испытывалась также программа Б1РЕХ2, написанная Дойфл-
хардом и Бауэром (см. Дойфлхард A985)). Она показала резуль-
результаты, аналогичные полученным для ОЭЕХ2.
Системы высших порядков
Обобщение идей этого раздела на системы уравнений более
высоких порядков
У{п) ={(х,У,У'> ...,У<*-1)) A3.33)
представляется теперь более или менее непосредственным. И в этом
случае действительное улучшение возможно только когда правая
часть уравнения A3.33) зависит лишь от х и у. Этой теме посвятил
свою замечательную работу Цурмюль A948). Таблицы условий
порядка и методов приведены у Хебзаккера A982)»
Упражнения
1. Убедитесь, что методы из табл. 13.2 имеют, соответственно,
четвертый и пятый порядки.
2. Коэффициенты погрешности метода Нюстрёма р-го порядка
определяются формулами
в (/) = 1 — (р @ +1O (О 23 6,Ф, (I) для р (I) = /7,
' A3.34)
в' @ = 1 - т @ 2 ЬА @ для р (*) = р+ 1.
а) Покажите, что упрощающее предположение A3.25) имеет
следствием соотношение
е (I) = _р (/) е' (и) при р (*) = р,
где Ы- дерево и получается из I добавлением ветви о тонкой
вершиной, исходящей из корня I.
Ъ) Для метода Нюстрёма из табл. 13.1 вычислите коэффициенты
погрешности и сравните их с таковыми для классического ме-
метода Рунге—Кутты.
3. Покажите, что условия порядка для методов РК (теорема 2.13)
составляют подмножество условий A3.21). Они соответствуют
тем ЛЛ-деревьям, у которых все вершины толстые.

11.13. Методы для дифференциальных уравнений второго порядка 293
4. Иногда порядок р метода Нюстрёма A3.9) определяют смягчен-
смягченными требованиями
(см. Нюстрём A925)). Покажите, что условия A3.35) не до-
достаточны для получения глобальной сходимости порядка р.
Указание. Исследуйте асимптотическое'разложение глобальной
погрешности с помощью теоремы 8.1 и формулы (8.8).
5. Покажите, что вычисляемые описанным в этом разделе экстра-
поляционным методом приближения Ткк и Т'ъь эквивалентны
приближенным решениям, которые дает некоторый метод
Нюстрёма порядка р = 2й, имеющий 5 = -^- + -~- + 1 стадий.

11.14. Р-ряды для разделяющихся обыкновенных
дифференциальных уравнений
БМс1е и! ге^пез
Разделяй и властвуй
(Макиавелли)
В разд. П.2 и 11.11 мы развили теорию В-рядов, позволяющую
найти условия порядка для методов Рунге—Кутты, ориентиро-
ориентированных на решение автономных дифференциальных уравнений.
Это предполагает, что интегрирование х и у производится оди-
одинаковым образом, т. е. что выполнены условия A.9). Мы уже
встречались, однако, с некоторыми ситуациями, в которых эта
теория оказывалась недостаточной.
1) Если л: и у интегрируются различным образом, т. е. усло-
условия A.9) не выполнены, то, как мы видели (см. упр. 6 в разд. 11.1),
возникают дополнительные условия порядка. Чтобы разобраться
в их структуре, надо обобщить теорию В-рядов на разделяющееся
обыкновенное дифференциальное уравнение B.1).
2) Рассмотренный в разд. 11.12 подход Фельберга требует
изучения методов РК, не удовлетворяющих условию A.9), причем
в точке (хОу у0) производные /, }Ху !ХХУ ... равны нулю.
3) В разд. 11.13 рассматривались прямые методы для диффе-
дифференциального уравнения второго порядка у" = / (у, у'). Чтобы
найти общую структуру условий порядка для этих методов, мы
обобщили теорию В-рядов на разделяющееся обыкновенное диф-
дифференциальное уравнение
II /ч/- A4Л)
!(у> у)
Для таких ситуаций желательно, конечно, иметь единую
теорию. С этой целью Хайрер A981) предложил обобщение тео-
теории В-рядов на общий случай разделяющегося обыкновенного
дифференциального уравнения:
A4.2)
который включает все перечисленные выше ситуации, так что
для них условия порядка получаются как частные случаи.
Другие важные приложения этой теории встретятся при
изучении условий порядка для методов, в которых к разным

11.14. Р-ряды для разделяющихся ОДУ .!-а
частям системы обыкновенных дифференциальных уравнений
применяются различные вычислительные схемы. Такими час1>л.1>$
могут быть, например, линейная и нелинейная части (на згу
ситуацию ориентированы И?-методы, см. том II), или «нежесткая,*
и «жесткая» компоненты дифференциального уравнения (состгнгг-
стзующие методы называют разделяющимися, или составными).
Для простоты обозначений мы будем рассматривать систему
A4.2) как разделяющуюся на две компоненты. Обобщение на
большее число компонент не представляет трудностей. Чтобы
лучше понять, как должны быть в этом случае определены эле-
элементарные дифференциалы и соответствующие им деревья, мы
рассмотрим сначала производные точного решения уравнения
A4.2).
Производные точного решения; Р-деревья
Чтобы не выписывать суммы и лишние индексы, предположим,
что уа и уъ в (.14.2) являются скалярными величинами. Все даль-
дальнейшие формулы останутся справедливыми и для векторов,
если производные интерпретировать как полилинейные отобра-
отображения. Дифференцируя A4.2) и подставляя вместо производных
снова A4.2), для первой компоненты, т. е. уа, получим;
B) = ^а_ I + д[а_ г A4.3.2)
* а дуа1а ' дуь 1Ьу \ /
Уа д2 \1а> 1а)^Г дуЬдуа VV I а) Т
д О[а г I д [а
дуадуь
Аналогичные формулы получаются и для производных уъ.
Для графического представления этих формул нам потре-
потребуются вершины двух сортов. Как и в разд. 11.13, мы будем поль-
пользоваться «тонкими» и «толстыми» вершинами, отвечающими /а
и /ь, соответственно. Тогда формулы A4.3) можно графически
представить так, как показано на рис. 14.1.
Дадим теперь формальное определение этих графов.
Определение 14.1. Помеченным Р-деревом порядка ц назовем
пару (I, I'), где I — помеченное дерево
1\ Ад {/} —►■ Ад
(см. определение 2.2) и I' — отображение
I': Ад -> {«тонкая», «толстая» (вершина)}.

296 Гл. II, Методы Рунге—Кутты и экстраполяционные методы
Обозначим ЬТРд множество всех помеченных Р-деревьев порядка
с «тонким» корнем (т. е. V (/) = «тонкая»). Аналогично, ЬТРЬЯ —
множество всех помеченных Р-деревьев ^-го порядка с «толстым»
корнем.
A4.3.1)
к
\
к I к I / /* к I к I
V V "\ '< V V
Рис. 14.1. Производные точного решения да
В A4.3.3) второй и пятый члены равны. В связи с этим дадим
Определение 14.2. Два помеченных Р-дерева 9-го порядка
(У I') и {и, и!) эквивалентны, если существует такое взаимно
однозначное отображение а: Ла->-Лд, что а (/)==/ и выпол-
выполняются перестановочные соотношения, представленные следую-
следующей диаграммой:
1
E 0 {„тонкий", „толстый"}
Определение 14.3. Класс эквивалентности помеченных Р-де-
Р-деревьев ц-го порядка называется ^-деревом, порядка ц. Множество
всех Р-деревьев порядка ц с «тонким» корнем обозначается ТР%
а с «толстым» корнем — ТРьд. Порядок Р-дерева I будем обозна-
обозначать через р @, а число элементов в классе эквивалентности
через а {I).
Ниже, в табл. 14.1, приведены примеры Р-деревьев и числа
р {I) и а {I) для них. Мы обсудим сначала рекурсивное пред-
представление Р-деревьев, играющее фундаментальную роль в изла-
излагаемой теории (оно обобщает индуктивное определение деревьев
2.12).

11.14. Р-ряды для разделяющихся ОДУ 297
V
V
Рис. 14.2. Рекуррентное определение Р-деревьев.
Определение 14.4. Пусть 1Х, ..., 1т — Р-деревья. Будем обо-
обозначать
(И.4)
(единственное) Р-дерево с «тонким»- корнем, такое что после уда-
удаления корня и инцидентных ему ребер остаются Р-деревья
11у ..., (т. Совершенно аналогично обозначим через Ъ[1Ъ ..., 1т]
Р-дерево, получаемое объединением 1Ъ ..., 1т на одном новом «тол-
«толстом» корне. Наконец, введем обозначения %а и %ь для «тонкого»
и «толстого» Р-деревьев порядка 1. Рис. 14.2 иллюстрирует это
определение.
Займемся теперь уточнением связи между Р-деревьями и
отдельными членами в формулах A4.3). Введем еще обозначение
С
1
а, если корень I «тонкий»,
и 4 - A4.5)
Ъ, если корень г «толстый». 7
Определение 14.5. Элементарные дифференциалы, соответ-
соответствующие системе A4.2), определяются индуктивно следующим
образом:
(Уа) (У) = !а (У),
Ы (у) = !ъ (у)
И
дт? (и)
Р (О (У) = ^
где у = (уа, уь) и / = а[^, ..., ^т] или I = ь[/ь ..., /т].
Элементарные дифференциалы для Р-деревьев до третьего
порядка включительно выписаны в табл. 14.1.
Вернемся теперь к началу раздела и продолжим дифференци-
дифференцирование формул A4.3). Легко видеть, что в терминах помеченных
Р-деревьев дифференцирование Р {I) (уа> Уь) можно интерпре-
интерпретировать как добавление новой ветви с «тонкой» или «толстой»
вершиной и новым индексом суммирования поочередно к каждой

Гл* II. Методы Рунге—Кутты и экстраполяционные методы
Таблица 14.1. Р-деревья и их элементарные дифференциалы
Р-дерево
\
\
V
V
<
<
<
<
Ч
\
A4.4)
.1.1*»]]
.икп
Пт.]
»!'»]
р(')
1
2
2
3
3
3
3
3
3
1
2
2
а(|)
1
1
1
1
о
л.
1
1
1
1
1
1
1
1
элементарный
дифференциал
К
д *а
2 \1 а '*а'
ду
в2/а
(( /" \
2 ЧЬ*1ъ>
дУь
* Ь
т
дУь вУь к
п
из вершин помеченного Р-дерева I. Тем же способом, каким мы
доказывали теорему 2.6 для неразделяющихся дифференциаль-
дифференциальных уравнений, может быть доказана
Теорема 14.6. Производные точного решения уравнения {14.2)
выражаются формулами
/(О (У'а, Уь)= % а* V) Р (*) (Уа, Уб)>
Р @ (Уа, Уь)= 13 а (О Р @ («/а, */ь). ■
Я 1 Ъ* гд
A4.3.С])

11.14. Р-ряды для разделяющихся ОДУ 299
Р-ряды
Мы уже видели в разд. 11.11, какую важную роль играет
ключевая лемма — следствие 11.7 — при выводе условий порядка
для методов Рунге—Кутты. Поэтому обобщим данный результат
и на разделяющиеся обыкновенные дифференциальные уравнения.
Прежде всего, удобно ввести два новых Р-дерева 0а и 0Ъ
порядка 0, которым соответствуют элементарные дифференциалы
@а) (У) = Уа и Р @Ь) (у) = Уъ- Далее, положим
ТРа={0а}{]ТРа1[)ТРа2[)...,
Ь = \0Ь\[)ТР\[)ТРЬ2\)...,
1ТРЬ = \0Ь\ \]ЦГР\\]ЦГР\\] ... .
Определение 14.7. Пусть с @а)', с @Ь), с (та), с (ть), ... —
система вещественных коэффициентов, определенных для всех
Р-деревьев: с; ТРа II ТРЬ ~> К.
Тогда ряд
Р (^ У) = (Ра (С, У), РЬ (С, У))Т>
где
Ра (С ) ^

, у) 2

называется Р-рядом.
Теорема 14.6 просто утверждает, что точное решение уравне-
уравнения A4.2) является Р-рядом
(Уа (*о + Л), Уь (*о + ЩТ = Р (У» (Уа (Хо), Уь (*о))).
у которого у (г) = 1 для всех Р-деревьев
Теорема 14.8. Пусть с: ТРа [] ТРЬ ->■ Р — такая последо-
последовательность коэффициентов, у которой с @а) = с @Ъ) = 1.
Тогда
гае
С @О) = С @Ь) = О,
с'(та) = с'(ть)=1, A4.8)
с' @ = р @ с {к) ... с Aт),
если I = о[/ь ..., 1т] или I = ^к, ..., 1т].

300 Гл, II, Методы Рунге—Кутты и экстраполяционные методы
Доказательство этой теоремы родственно доказательству тео-
теоремы 11.6, Более подробно оно приведено в работе Хайрера
A981). ■
Применим теперь теорему 14.8 к случаям, указанным в начале
этого раздела.
Методы РК с нарушением условия A.9)
Рассмотрим применение метода РК A.8) к неавтономному
дифференциальному уравнению у' = I (х, у). Мы не предполагаем
условие A.9) выполненным, так что х- и у- компоненты интегри-
интегрируются по-разному. Поэтому добавим к нашему дифференциаль-
дифференциальному уравнению еще уравнение х' = 1 и получим систему
Она имеет вид A4.2), если положить уа = у, уь = х, /а (уа, уь) =
== / (*> У) и !ь (Уа, Уь) = 1. Поскольку 1Ь — постоянная, все
содержащие производные /$ элементарные дифференциалы тожде-
тождественно обращаются в нуль. Следовательно, те Р-деревья, у ко-
которых хотя бы одна толстая вершина не является конечной,
рассматривать не надо. Остается рассмотреть множество
Та = \( $ ТРа\ все толстые вершины конечные}. A4.10)
Для вывода условий порядка метода РК
г=Н! (х0
И
Уг = 9о + 2
мб! предположим, что кг и %1 являются первыми компонентами
Р-рядов:
&1 = Ра (Ъь (Уо> *о))| 81 = Ра (&> (Уо> Хо)).
Кроме того, положим
так что %г @Ь) = 1, %г (%) = ог и %г (/) = 0 для остальных
Р-деревьев с «толстым» корнем. Теперь из A4.11) на основе тео-
теоремы 14.8 получаем, что для всех I $ ТЛ
A4Л2)
а«к, @-

11.14. Я-ряды для разделяющихся ОДУ 301
Мы получили рекуррентные соотношения для определения коэф-
коэффициентов к^ [I). Условия того, что метод будет иметь порядок р,
принимают вид
2 Ьгк( (() = 1 при 1$ТХ, р @ < р. A4.13)
Мы видим, что обычные условия порядка, (типа A.11)) исчезают,
за тем исключением, что для толстых вершин вместо ^а^ под-
подставляются С\.
На рис. 14.3 представлены первые элементы множества Тх.
. \ \ V V V
< < ч, V V
Рис, 14.3, Элементы множества, Тж.
Пример. Условие A4.13) для пятого, восьмого и последнего
деревьев рис, 14.3 принимает соответственно вид
3 2 Ьгсгаи= 1,
I, 1
3-2
Методы Фельберга
Если для точного решения уравнения д' = ^ (д:, ^) значения
9 (А:)» у' (*). •-» ^'1 ^ (х) обращаются в нуль при я = х0, то и
/, 5//5д:, ..., дП1~{Цдхт~-1 равны нулю в точке (х0, у0) (см. разд. 11.12,
т
т т 4-1 -— т
т
Рис. 14.4. Р-деревья, которые следует рассмотреть для метода ФельберГа
(разд. 11.12),
методы Фельберга). Для этого случая на рис. 14.4 мы привели
элементы множества Тя, для которых элементарные дифферен-
дифференциалы в общем случае не обращаются в нуль в точке (д:0, у0).

302 Гл. II. Методы Рунге—Кутты и экстраполяционные методы
Методы Нюстрёма
В качестве последнего приложения теоремы 14.8 представим
новый вывод условий порядка для методов Нюстрёма (разд. 11.13).
Дифференциальное уравнение второго порядка у" = / (у, у') мо-
может быть записано в форме разделяющейся системы:
A4и)
В обозначениях A4.2) мы имеем уа = уу уь = у\ /а (уау уь) = Уь,
1ъ (Уа> Уь) = / (Уа, Уъ)- Вследствие специального вида )а должны
быть рассмотрены только те Р-деревья, которые удовлетворяют
условию
«тонкие вершины могут иметь не более одного
сына, который должен быть толстым» A4.15)
(см. определение 13.2). Следовательно, существенными Р-де-
ревьями являются
ТЫ* = {( 6 ТРад; г удовлетворяет A4.15)},
ТЫд = {(€ ТРьд\ I удовлетворяет A4.15)}.
Отсюда вытекает, что каждый элемент ТЫ*+1 может быть записан
в виде I = а[и], где и € ТЫьд. Поэтому существует взаимно одно-
значное отображение ТЫд+1 на ТЫд, которое не изменяет элемен-
элементарные дифференциалы:
Р Ш) (Уа, Уъ) = ^'Р (и) {Уа, Уъ) = Р {и) (уа, уь).
Из этого свойства следует, что
НРЪ (с, (уа, Уъ)) = Ра (с', (?«, Уъ)), A4.16)
где с' @ = р @ с (и), если * = а[и]. A4.17)
Эти обозначения согласуются с A4.8).
Условия порядка для метода A3.13) можно теперь вывести
следующим образом. Предположим, что цг и ц\ представляют
Р-ряд:
В1 = Ра (С|, (У0, Уо)), В1 = РЪ (С|, (г/0, #6)).
Тогда из теоремы 14.8 следует, что
ЫЦМи Й) = Рь(сь (Уо, уо)). A4.18)
Умножив это соотношение на Л, с помощью A4.16) получим:
/, (Уо, уо)). A4.19)

11.14. Р-ряды для разделяющихся ОДУ
303
Здесь с[ =
, т. е.
@ = 0 для / = 0а и I = <га,
Если подставить выражения A4.18) и A4.19) в A3.13), мы по-
получим, как обычно, рекуррентные соотношения
@ — 2] я*,7'с2 @» если корень «тонкий»,
@ = 2] пцс] ((), если корень «толстый».
Точно таким же способом получают и условия порядка (для р-го
порядка)
Ц @ = 1 для 1$ Т№д) ? = 2,...э р;
ь A4.20)
=1 для I € Г< ? = 1, ..., р.
Упражнения
1. Обозначим через <хд число элементов множества ТР" (число
Р-деревьев порядка ц с «тонким» корнем, см. табл. 14.2). Дока-
Докажите, что
Таблица 14.2. Число элементов
х
множества ТРа
X A--
я
1
2
3
4
5
1
2
7
26
107
я
6
7
8
9
10
ад
458
2 058
9 498
44 947
216 598
Вычислите несколько пер-
первых чисел ад и сравните их с
числами
ад = сагс! (Тч) из табл. 2.2.
2. Докажите, что не сущест-
существует явного 4-стадийного
метода РК порядка 4, который не удовлетворял бы усло-
условию A.9).
Указание. Воспользуйтесь техникой доказательства леммы 1.4.
3. Покажите, что условия порядка A4.20) совпадают с теми,
которые дает теорема 13.10.

И. 15. Дифференциальные уравнения
с запаздывающим аргументом
«Детальное изучение реального мира вынуждает нас
принимать в расчет, хотя и с неохотой, тот факт, что
скорость изменения физических систем зависит не
только от их состояния в настоящий момент, но также
и от их истории в прошлом.»
(Беллман и Кук, 1963)
Дифференциальные уравнения с запаздывающим аргументом —
это такие уравнения, как
у' (х) = ! (х, у (*), у (* - «)), A5.1)
или
У' (х) =» ! (х, у (*), у (х — «х), у(х — *2)), A5.2)
или даже еще более общего вида. Здесь производная решения
зависит также от его значений в предыдущих точках.
Запаздывание встречается во многих моделях прикладной
математики. Запаздывание (в более общем случае—отклонения
аргумента) может быть также источником интересных математи-
математических явлений, таких как неустойчивости, предельные циклы»
периодический характер решений.
Существование
Для уравнений типа A5.1) или A5.2), если величина запазды-
запаздывания 17 ограничена снизу положительной постоянной, вопрос
о существовании решения решается легко. Предположим, что на
отрезке х0 — <с <; х <! х0 решение известно:
У (х) = Ф (х).
Тогда на отрезке х0 <! х <! х0 + т функция у ,(х -г т) является
известной функцией х и A5.1) становится обыкновенным диффе-
дифференциальным уравнением, к которому зррименимы известные
теоремы существования. Определив у {х) при х0 <] х •< х0 + «в,
мы можем затем перейти к вычислению решения при х0 + т? <!
< х •< х0 + 2т и т. д. Этот «метод шагов», таким образом, для
всех х позволяет получить результаты о существовании и един-
единственности решения. Заинтересованному читателю мы рекомен-

11.15. Дифференциальные уравнения с запаздывающим аргументом 305
дуем книги Беллмана и Кука A963) и Драйвера A977, особенно
гл. V)х).
Пример 1. Рассмотрим уравнение
у' (х) = — у (х — 1), у (х) = 1 при — 1 < х < 0. A5.3)
Применяя описанный выше «метод шагов», получим
у (х) = 1 — х при 0 < х
2!
при 1 < х < 2,
при2<х<3,
и т. д. Решение представлено на рис: 15.1. Заметим, что решение
имеет разрывные производные, несмотря на то, что правая часть
Рис. 15.1. Решение уравнения A5.3).
дифференциального уравнения и начальная функция принадле-
принадлежат классу С°°. Это происходит оттого, что начальная функция
не удовлетворяет дифференциальному уравнению. Однако с каж-
каждым шагом <с эти разрывы все более сглаживаются.
Пример 2. Этот пример ясно показывает, что решения урав-
уравнения с запаздывающим аргументом зависят не только от началь-
начального условия, но и от всей истории процесса от х0 — тг до х0.
A5.4)
а) ф (х) = 0.8
Ь) ф (х) = 0.8 + х
с) ф (х) = 0.8 + 2х
при —1 •< х •< 0,
при — 1 < х < 0,
при —1 < х < 0.
х) На русском языке можно рекомендовать книги Эльсгольца A951) и Эльс-
гольца и Норкина A963), указанные в списке дополнительной литературы в конце
книги. — Прим. ред.

306
Гл. II. Методы Рунге—Кутты и экстраполяционные методы
Решения показаны на рис. 15.2. Объяснение колебательного по-
поведения решений будет дано ниже.
Рис. 15.2. Решения задач A5.4).
Методы с постоянной длиной шага
для постоянного запаздывания
Применяя метод Рунге—Кутты A.8) к уравнению о запазды-
запаздывающим аргументом A5.1), мы получим
в\п) =
аи! {хп + с3к, ёТ\ 9 (хп
п\ д (хп
I
к И Ь$ (хп
I
Сразу возникает вопрос, как задавать значения у (хп + с^г — ч).
Но если запаздывание постоянное и длина шага выбрана так, что
41 == кку где к — некоторое целое число, то естественно использо-
использовать уже вычисленные к шагов назад значения решения:
ё\
\п)
а„Т [хп
A5.5а)
где
(я) =
сг<.п—к)
6/ а
если
если
к.
■ к.
A5.5Ь)
A5.5с;

11.15. Дифференциальные уравнения с запаздывающим аргументом 307
Это можно интерпретировать как последовательное решение
уравнения
У' (*) = / (*> У {*). Ф (* — *)) A5.1а)
для интервала [х0, х0 + %), затем уравнений
у' (х) = /(*, у(х), г(х)),
/ (х) = / (х — <с, г (*), ф (х — 2т)) , • A^ Ь)
для интервала 1х0 + <с, л:0 + 2т], затем
У (*), г (х))9
г' (х) =1(х — % г (х), V (х)),
& (х) = I (х — 2т, у (л:), ф (д; — Зт)) A5.1с)
для интервала [х0 + 217, д;0 + Зт], и т. д. Это точный численный
аналог упомянутого выше «метода шагов».
Теорема 15.1. Если Си а^, Ъ} — коэффициенты метода
Рунге—Кутты р-го порядка, то процесс A5.5) сходится с поряд-
порядком р.
Доказательство. Последовательность A5.1а), A5.1Ь), ... —это
последовательность систем обыкновенных дифференциальных
уравнений, нормально решаемых методом РК р-го порядка. По-
Поэтому результат непосредственно вытекает из теоремы 3.6. ■
Замечание. Для коллокационного метода, основанного на
гауссовой квадратурной формуле, из теоремы 15.1 вытекает
сверхсходимость — результат, который получил Беллен A984).
Численный пример. Мы интегрировали уравнение A5.12)
(см. ниже) на интервале 0 <! х •< 10 при а = 1.4 с начальными
условиями у (х) = 0 при — 1 < х < 0 и у @) = 0.1, взяв сле-
следующие длины шага: Н = 1, 1/2, 1/4, 1/8, ... Использовался
метод Бутчера шестого порядка (см. табл. 6.1). Результаты вы-
вычислений представлены в табл. 15.1. Хорошо виден 6-й порядок
сходимости.
Таблица 15.1. Результаты расчетов для метода A5.5)
1
1/2
1/4
1/8
1/16
1/32
1/64
число
шагов
10
20
40
80
160
320
640
число вычисле-
вычислений функции
70
140
.280
560
1120
2240
4480
максимальная
погрешность
1.69Х 10"а
4.76Х 10
4.76Х 10"в
7.80X10-9
8.90Х 100
2.14Х10-11
3.41 Х10'13

308 Гл. II. Методы Рунге—Кутты и экстраполяционные методы
Методы с переменной длиной шага
К сожалению, метод A5.5) не позволяет произвольно менять
длину шага, и применение его к уравнениям с переменной вели-
величиной запаздывания не столь просто. Если мы желаем достичь
полной гибкости, нам необходима глобальная аппроксимация ре-
решения. Бесполезно иметь приближения только на некоторой
последовательности точек. Поэтому подходящими методами для
таких задач являются многошаговые методы типа Адамса или
ФДН (см. разд. III. 1), или же непрерывные методы Рунге—Кутты.
Ввиду легкости программирования мы выбрали метод Дормана
и Принса порядка 5 D), присоединив к нему формулы E.7) из
разд. 11.5. Превосходство этой процедуры над многими другими
интерполяционными методами показал Готтвальд A985), проведя
обширное численное тестирование их. Для каждого интервала
интегрирования решение в целом представляется многочленом
4-й степени. Поэтому после каждого успешного шага интегриро-
интегрирования подпрограмма КЕТАКО (незначительная модификация
подпрограммы ООРК15) вызывает подпрограмму 5ТОКЕ, кото-
которая записывает в память (в общий блок СОЕР) коэффициенты
этцх многочленов вместе о соответствующими значениями х.
Тогда при вызове вещественной функции УЬАО (I, X) произ-
производится поиск нужного интервала для х и вычисляется соответ-
соответствующий многочлен для 1-го решения. Поэтому, чтобы подпро-
подпрограмма КЕТАКО решала уравнение с запаздывающим аргумен-
аргументом, скажем A5.4), надо, чтобы подпрограмма РСИ включала
такой оператор:
Р A) = —1.4 * УЬАО A, X — 1., РН1).
Тексты подпрограмм КЕТАКО, 5ТОКЕ и УЬАО вместе о при-
примером вызывающей программы приведены в приложении. С их
помощью были получены результаты, представленные на рис. 15.1
и 15.2.
Как мы видели, решение имеет разрывы производных в неко-
некоторых точках, например, для уравнения A5.1) в точках х0 + я,
х0 + 21/, х0 + Зт7, ... и т. д. Поэтому точность улучшится, а время
счета сократится, если эти точки выделить и возобновлять в них
вызов подпрограммы КЕТАКО.
При конструировании усложненных программ для решения
дифференциальных уравнений с запаздывающим аргументом бо-
более общего чем A5.1) вида возникает ряд трудностей, в частности,
нахождение всех точек разрыва производных до определенного
порядка, а также экономное распоряжение памятью для хране-
хранения всех коэффициентов, представляющих запомненное решение,
и своевременное освобождение от того, что больше не понадо-
понадобится.

11.15. Дифференциальные уравнения с запаздывающим аргументом 309
Характеристические значения экспоненциальных
решений
На рис. 15.1 и 15.2 можно заметить, что решения после на-
начальной фазы как будто приближаются к функциям, похожим на
е?х со5 Р (х — 6). Попытаемся определить значения аир. Рас-
Рассмотрим уравнение
A5.6)
Выбор запаздывания и = 1 не означает потери общности, так
как любое запаздывание <с Ф 1 можно свести к <и=1 заменой
переменных.
Будем искать решение вида
9 (х) = &*ш ь где у = а, + ф. A5.7)
Подставляя A5.7) в уравнение A5.6), получим следующее «ха-
«характеристическое уравнение» для
_ ^-т = о. A5.8)
При р Ф 0 оно имеет бесконечное множество решений. В самом
деле, если |?| становится большим, то из A5.8) видно, что ре-?
тоже должно быть большим, поскольку А, фиксировано!
V « \1<г*. A5.8')
Отсюда вытекает, что у = а + ф расположено вблизи мнимой
оси. Следовательно, | <р | « | р |, а из A5.8') находим, что
| Р | « | (л | ег*.
Поэтому корни уравнения A5.8) асимптотически располагаются
на кривых —а = 1п | Р | — 1п | р |. Из A5.8') видно также, что
характеристическое уравнение имеет корень, когда аргумент
выражения \кег1$ близок к я/2 (при р > 0), т. е. когда
Р « аг§ [л — -^- + 2&гс, к = 1, 2,
Таким образом, имеется две последовательности характеристи-
характеристических значений, уходящих в бесконечность по логарифмическим
кривым слева от мнимой оси, и расстояние между двумя последо-
последовательными значениями асимптотически приближается к 2л>.
Итак, «общее решение» уравнения A5.6) — это похожая на
ряд Фурье суперпозиция решений типа A5.7) [Райт A946), см.
также Беллман и Кук A963), гл. 4]. Чем меньше величина Ке 7,
тем быстрее эти решения затухают при х -*- оо. Поэтому домини-

310 Гл. II. Методы Рунге—Кутты и экстраполяционные методы
рующими решениями (при условии, что соответствующие коэф-
коэффициенты не равны нулю) являются те, у которых наибольшие
значения Ке у, т. е. наиболее близкие к началу координат. Урав-
Уравнению A5.3) соответствует характеристическое уравнение у +
+ ^-7 = 0 с решением у = —0.31813 ± 1.33724*', а для A5.4)
характеристическое уравнение у + \Ае~^ = 0 имеет решение
<р = —0.08170 ± 1.51699*'. Это очень хорошо объясняет асимпто-
асимптотическое поведение решений на рис. 15.1 и 15.2.
Для случая матричных уравнений
у' (х) = Ау (х) + Ву(х— 1),
где матрицы Л и В не приводятся одновременно к диагональному
виду, полагаем у (х) = Vе^x, где V Ф 0 — некоторый постоянный
вектор, И| подставляя в уравнение, получаем
Это уравнение имеет нетривиальные решения только при усло-
условии, что 7 удовлетворяет характеристическому уравнению для
этого более общего случая:
ее* (у1 — А — Ве-У) = 0. A5.8")
Решения уравнения A5.8") расположены в комплексной плоскости
подобно решениям уравнения A5.8), только теперь в каждой
полосе шириною 2я) вместо одной точки будут находиться г =
= гапк (В) точек.
Устойчивость
Все решения уравнения A5.6) устойчивы при #->оо, если
все характеристические корни уравнения A5.8) имеют отрица-
отрицательную вещественную часть. Этот результат можно получить
как из указанной выше теоремы о разложении, так и из теории
преобразования Лапласа 1см., например, Беллман и Кук A963),
гл. 1], между которыми, впрочем, имеется тесная связь.
Чтобы найти границу области устойчивости, будем искать
такие значения (X, ц,), при которых первое решение у переходит
через мнимую ось, т. е. у = 1*9, где 9 вещественно. Подставляя
в A5.8), получим
при 9 = 0 (вещественное у)
% = Ш — у<г**9 при 9 ф 0.
Во втором случае, разделяя вещественную и мнимую части, для
вещественных ^ и [л имеем!
8соз9 9
е * у

11.15. Дифференциальные уравнения с запаздывающим аргументом 311
Эти линии нанесены на рис. 15.3. Они разделяют плоскость (X, |ш)
на область устойчивости и область неустойчивости решений урав-
уравнения A5.6). Этот результат получил Хейес A950).
Рис. 15.3. Область устойчивости для уравнения
Положив 0 = я/2, мы найдем, что решения уравнения у' (х) =
\ху (х — 1) будут устойчивыми при
п
и неустойчивыми при
п
9- и при II >0.
A5.9а)
A5.9Ь)
Пример из динамики популяций
«Лорд Черуэлл привлек мое внимание к одному урав-
уравнению, эквивалентному уравнению (8) [здесь урав-
уравнение A5.12)] с а — 1п 2, которое он встретил, зани-
занимаясь приложением вероятностных методов к задаче
о распределении простых чисел. Я признателен ему
за то, что таким образом он познакомил меня с инте-
интересной проблемой.»
(Э. М. Райт, 1945)
Мы хотим теперь продемонстрировать обсуждавшиеся выше
явления, а также возможности наших программ на нескольких
примерах прикладных задач. Впечатляющий список различных

312 Гл. II, Методы Рунге—Кутты и экстраполяционные методы
приложений дифференциальных уравнений с запаздывающим
аргументом во всевозможных областях науки приведен в книге
Драйвера A977).
Пусть у (х) представляет численность популяции некоторого
вида, и рассматривается ее изменение во времени. Простейшая
модель неограниченного экспоненциального роста у' =^= %у была
уже давно заменена гипотезой, что темп роста уменьшается с уве-
увеличением количества особей у из-за болезней и недостатка пищи
и места, что приводит к следующей модели:
У'(х) =к(а-у(х))-у(х} A5.10)
[Верхюльст A845), Перл A922)]. «Ыоиз йоппегопз 1е пот 1о§1-
зЩие а 1а соигЬе сагас!ёп5ёе раг ГёдиаИоп ргёсёйеп1е» *) (Вер-
хюльст). Это уравнение решается в элементарных функциях
(упр. 1). Все решения с начальными условиями у0 ►> 0 при х ->• со
асимптотически стремятся к а. Если предположить, что скорость
роста зависит от численности предыдущего поколения, уравнение
A5.10) переходит в уравнение с запаздывающим аргументом:
' (Д) в к (а - у (х - ч))-у (х) A5.11)
[Каннингем A954), Райт A955), Какутани и Маркус A958)].
Подставляя в A5.11) новую функцию г (х) = кту (%х) и после
преобразований переобозначив снова г через у и ка% через а,
получим уравнение
A5.12)
Оно имеет точку равновесия у (х) = а. Подстановкой у (х) =
= а + г (х) и последующей линеаризацией можно получить
уравнение г' (х) = —аг (х — 1), и условие A5.9) показывает, что
эта точка равновесия локально устойчива при 0 < а •< я/2,
Следовательно, характеристическое уравнение (в данном случае
7 + ае—ч = 0) имеет два вещественных решения тогда и только
тогда, если а < 1/е = 0,368. При этом возможны монотонные
решения уравнения A5.12); в противном случае они носят коле-
колебательный характер. При а ?> я/2 равновесное решение неустой-
неустойчиво: рождается периодический предельный цикл.
Представленные на рис. 15.4 решения рассчитаны тоже с по-
помощью приведенных в приложении программ КЕТАКЭ, 5ТОКЕ,
УЬАО с подпрограммой РСИ вида
РA) =(А —УЬАОA, X —1., РН1))*У A)
для значений А =0.35, 0.5, 1., 1.4 и 1.6.
х)«Мы назвали логистической кривую, характеризуемую предыдущим уравне-
уравнением». — Франц.

IIЛ5. Дифференциальные уравнения с запаздывающим аргументом 313
Рис, 15.4. Решение задачи популяционной динамики A5.12),
Моделирование эпидемии
«Бе 1оиз сеих дш оп! 1таИе сеИе таиНё, с'ез{ 8апз
соп*гес1И: М. йе 1а Сопйагмпе яш 1'а ГаН ауес р1из
Aе зиссёз. II ез! Щг уепи а Ъои{ <1е регзиа<3ег 1а теП-
1еиге рагНе с1и тогк!е тзоппаЫе с!е 1а &гапс1 и1Ш1ё
с!е Гшоси1аBоп: ^иап^ аих аи1гез, 11 зега11 тиШ
уоиЫг етрЬуег 1а га1зоп ауес еих: ри15диЧ1з п'^
раз раг рппарез. II !аи41ез сопсИшге сотте Aез еп!ап!з
уегз 1еиг
«Из всех, кто занимался этим предметом, наиболь-
наибольшего успеха, бесспорно, добился г-н де ля Кондамин.
Он уже окончательно убедил большинство здраво-
здравомыслящих людей в большой пользе прививок; что до
остальных, то бесполезно надеяться повлиять на них
доводами рассудка, потому что они в принципе не-
непоколебимы. Их следует, как детей, вести к их благу.;.*
(Даниил Бернулли, 1760)
Даниил Бернулли («Оос{еиг еп тесНсте, РгоГеззеиг йе РЬу-
д еп Шшуегзйё Че Ва1е, Аззоаё ёЬап^ег Йе ГАсайепне Йез
5с1епсез»1)) был первым, кто применил дифференциальное ис-
исчисление для моделирования развития инфекционных заболева-
заболеваний в своей статье о вакцинации против оспы A760). В начале
нашего столетия математическое моделирование эпидемий вновь
привлекло интерес ученых. В конечном счете это привело к появ-
появлению классической модели Кермака—Макендрика A927). Пусть
Ух (х) является мерой восприимчивой части населения, у2 (х) —
*> «Доктор медицины, профессор физики Базельского университета, ино-
странный член Академии наук» — Франц.

314 Гл. II. Методы Рунге—Кутты и экстр апелляционные методы
зараженной, и у3 (х) — невосприимчивой (например, приобретшей
иммунитет) части. Естественно предположить, что число вновь
заражаемых в единицу времени людей пропорционально произве-
произведению ух (х) у2 (х)у как в бимолекулярных химических реакциях
(см. разд. 1.16). Если, кроме того, предположить, что скорость
роста числа невоспримчивых людей пропорциональна числу за-
зараженных, мы придем к следующей модели:
У\ = —
2/2 = У\У2 — */2, УЗ = У%
A5.13)
(для простоты мы выбрали все константы скоростей равными
единице). Эту систему можно проинтегрировать элементарными
/ Уз (невосприимчивые)
-г— У} (восприимчивые)
—• —•—
у2 (зараженные)
5.
10.
15.
20
Рис, 15.5, Решение модели Кермака—Макендрика A5.13).
методами (разделите второе уравнение на первое и решите Ауг\Лух =*
= —1 + 1/Уг)* На рис. 15.5 показано численное решение с на-
начальными условиями #1@) =5, у2 @) =0.1, уъ @) =0. Видно,
как вспыхивает и разражается эпидемия, но в конце концов
каждый приобретает иммунитет, и далее ничего не происходит,
Но если допустить, что приобретенный иммунитет через оп-
определенное время 17 теряется, и люди становятся вновь восприим-
восприимчивыми к заболеванию, мы получим периодические вспышки
болезни. Если ввести еще инкубационный период т2, то вместе:
A5.13) мы получим следующую модель:
у{ (Х) = —ух (х) Г/2 (X - 1) + № (X
г/2 (х) = ух (х) у2 (х — 1) — у2 (*),
Уз (х) = у2 (х) —у2(х— 10)
Ю),
A5.14)
(здесь взято и = 10, <с2 = !)• Решение системы A5.14) для началь-
начальных значений уг (х) = 5, у2 (х) = 0.1, уъ (х) = 1 при х <! 0 пока-
показано на рис. 15.6 и описывает периодические вспышки болезни.

11.15. Дифференциальные уравнения с запаздывающим аргументом 315
О.
5.
10.
Рис 15.6. Периодические вспышки ваболевания, модель A5,14).
Пример из кинетики ферментативных реакций
Следующий пример более сложен, чем предыдущие. Он опи-
описывает кинетику реакций, где катализатором служит фермент
(энзим) [Окамото и Хаяси A984)]. Рассмотрим следующую це-
цепочку реакций:
У
1 2
к2 3
I
У
4 к.
A5.15)
Здесь I — внешний субстрат, запас которого поддерживается
постоянным; совместное действие п молекул конечного продукта У4
ингибирует стадию реакции У1 -> Уъ так что ее константа ско-
скорости имеет вид
к
* 1+а(уй(х))п '
Обычно считают, что молекула ингибитора должна перемещаться
в место нахождения регулирующего энзима посредством таких
процессов, как диффузия или активный перенос. Рассматривая
эти медленные процессы как причину запаздывания по времени,
можно получить следующую модель:
A5.16)
у'з (х) = т (х) —
У*(х) = Уз(х)-
1
уз (х),
0.5^/4 (х),
1 + 0.0005
—4))
»

316 Гл.II. Методы Рунге—Кутты и экстраполяционные методы
Эта система имеет точку равновесия гуг = у2 = у8 = 0.5#4 = /.
Линеаризация ее в окрестности равновесной точки дает
у{ {х) = — схух (х) + с2у* (х - 4),
У2 (х) = схух (х) — у2 (х) — с2у* (х — 4),
Уг (х) = у2 (х) - уз (х),
У* (х) = Уз (х) — 0.5у4 (х).
A5.17)
Здесь введено обозначение сг: = уг = / A + 0.004/8) для равно-
равновесного значения уг и положено с2 = сг-Р-0.006. Подставляя
о
20
40.
Рис. 15.7. Решения задачи ферментативной кинетики A5.16), /= 10.5. Началь-
Начальные значения близки к равновесному состоянию.
сюда вектор у (х) ~V^еVx, мы придем к характеристическому
уравнению (см. уравнение A5.8я)), которое после некоторых
преобразований примет вид
Т) 0
Т)
-4*= 0.
A5.18)
Как и в статье Окамото—Хаяси, положим / = 10.5. Тогда урав-
уравнение A5.18) имеет одну пару комплексных корней, лежащих
в С+, а именно,
= 0.04246 ± 0.47666?,
и равновесное решение неустойчиво (см. рис. 15.7). Период ко-
колебаний решения линеаризованного уравнения равен, таким
образом, Т =2я/0.47666 =13.18. Поэтому решения уравнения
A5Л6) стремятся к предельному циклу с приблизительно тем же
периодом.

11.15. Дифференциальные уравнения с запаздывающим аргументом 317
Одна математическая модель в иммунологии
Нашу серию примеров мы завершим рассмотрением модели,
которую предложил Марчук A975) для описания борьбы виру-
вирусов V (*)• антител Р (/) и плазматических клеток С @ в человече-
человеческом организме, пораженном вирусным заболеванием. Уравне-
Уравнения модели таковы:
= 6 И ЬР (* - яг) V {I - %) - кь (С - 1), A5.19)
Первое уравнение — такое же, как в модели Лотки—Вольтерры
для системы хищник—жертва.' Второе уравнение описывает рож-
рождение новых плазматических клеток с запаздыванием по вре-
времени, вызванное инфекцией, в отсутствие которой второй член
порождает равновесие при С =1. Третье уравнение моделирует
синтез антител плазматическими клетками (Н^С) и их убыль в ре-
результате старения (—Н^Р) и в результате связывания антигенов
(—Н8РУ). Наконец, множитель \ (т) имеет вид
1» если т<!0.1,
A — /п)-д-, если 0.1 «<т<, 1
и выражает факт замедления процесса образования плазматиче-
плазматических клеток, когда организм ослаблен вирусной инфекцией.
Характеристика степени ослабления т (I) определяется четвер-
четвертым уравнением
= ЬвУ — й7/я,
где первый член выражает ослабление, а второй — восстанов-
восстановление.
Эта модель позволяет, меняя коэффициенты йх, Нъ ..., А8,
моделировать все состояния организма: устойчивое здоровье,
неустойчивое здоровье, острые формы заболевания, хронические
формы и т. д. (подробнее см. гл. 2 в книге Марчука A983)). На
рис. 15.8 показаны решения, рассчитанные нами по этой модели
Для следующих значений параметров: % = 0.5, Нг = 2, А2 = 0.8,
Л3 = 104, А4 = 0.17, Нь = 0.5, Л7 = 0.12, Л8 = 8 и при начальных
Условиях V @ = шах @, I + 10"в), если I < 0, С @) = 1,
Р @ =1, если I <; 0, т @) = 0. Получаемая картина зависит от

318 Гл. II. Методы Рунге—Кутты и экстраполяционные методы
величины Нв. При Нв = 10 мы видим полное выздоровление (оп-
(определяемое условием V (I) < 10~1в), а при Лв =300 наблюдаются
периодические вспышки болезни, связанные с ослаблением орга-
организма: т (/) достигает значений, близких к единице.
о.
о.
10- 20. 30. 40. 50Т
Рис. 15.8. Решения иммунологической модели Марчука*
60
Интегро-дифференциальные уравнения
Нередко оказывается, что предполагать поведение системы
в момент х зависящим от ее состояния в какой-то определенный
предыдущий момент х — % не очень реалистично: правильней было
бы считать, что система испытывает влияние предшествующих
состояний, имевших место в течение некоторого периода времени.
В таком случае уравнение A5.1) следует заменить, например,
уравнением
( Г ^
У' (х) = /Ь (*), ) К (х, I, у (I)) сЦ\. A5.20)
Численное решение таких задач обходится намного дороже.
Если К (х, I, у) обращается в нуль в окрестности диагонали
х = I, то можно, в конце концов, использовать программу
КЕТА1Ш, где при каждом обращении к вычислению функции
придется вызывать подпрограмму, вычисляющую интеграл.

11.15. Дифференциальные уравнения с запаздывающим аргументом 319
К счастью, многие интегро-дифференциальные уравнения
удается свести к обыкновенным дифференциальным уравнениям
или к дифференциальным уравнениям с запаздывающим аргумен-
аргументом, вводя вместо интеграла новые переменные.
Пример. [Вольтерра A934)] Рассмотрим уравнение
У' (х) = (г-ау (х) - \у Ц) к (х- 1)<%\у (*), A5.21)
описывающее динамику популяции. Здесь интегральный член
описывает уменьшение скорости размножения вследствие загряз-
загрязнения среды. Пусть теперь, например, к (х) = с. Тогда, положив
X
| У F) Я = *(*), *(*) = »'(*).
о
мы получим обыкновенное дифференциальное уравнение
V" (Х) = [в — Ш>' (X) — СО (X) ] V' (X).
Такой же метод можно применить и к уравнению A5.20)
с «вырожденным ядром», т. е. когда
т
К (х, I, у) = 2 «I (х) Ьг (I, у). A5.22)
к 1
Подставляя A5.22) в A5.20) и вводя
X
VI (х) = I Ьг E, у (I)) <%, A5.23)
мы получим дифференциальное уравнение с запаздывающим ар-
аргументом:
т
у' (х) = ?(х, у (х), 2 аг (х) V, (х)),
1=1
Щ (х) = Ъг (х, у (х)) - Ьг(х — % у(х — %)), A5.20')
X = 1, ..., 171.
Упражнения
1. Найдите решение уравнения Верхюльста—Пёрла A5.10).
2. Найдите точки равновесия для уравнения Марчука A5.19)'
и исследуйте их устойчивость.
3. Пусть ядро к (х) в уравнении Вольтерры "A5.21) имеет вид
к (*) = р (х\ е~**9

320 Гл. II, Методы Рунге—Кутты и экстраполяционныв методы
где р (х) — некоторый многочлен. Покажите, что эта задача
может быть преобразована в обыкновенное дифференциальное
уравнение.
4. Рассмотрите интегро-дифференциальное уравнение
У' (х) = !\х9д (х), ] К (х, |, д (I)) сц) A5,24)
и покажите, что:
а) Для вырожденного ядра A5.22) задача A5.24) эквивалентна
обыкновенному дифференциальному уравнению
У' (х) = / ((х, у (х)9 Д ал (х) V^ (*)), A5 25)
Щ (х) = Ь3 (х, у (х)).
Ъ) Применение явного метода Рунге—Кутты р-го порядка
к задаче A5.25) приводит к формулам
/=1 '
1-1
и\п) = рп [хп + С1Н) + н 2 анК [хп + с%К хп + с{К
где
[X) — У,
, хп
(эти формулы получил Пузе A963)).
с) При применении метода A5.26) к задаче A5.24) сходимость
порядка р получается и в том случае, если ядро не удовлетво-
удовлетворяет требованию A5.22).
Указание. Аппроксимируйте ядро вырожденным ядром.
5. [Дзеннаро A986)]. Для дифференциального уравнения с за-
запаздывающим аргументом A5.1) рассмотрите метод A5.5),
в котором формула A5.5с) заменена на
Г
Ф (^д + Ф - %), если п < к,
Яп-к (Ъ)> если п >

Гл. II. Методы Рунге—Кутты и экстраполяционные методы 321
где <7П (8) — многочлен, даваемый непрерывным методом
Рунге—Кутты (см. разд. 11.5):
п (в) = уп + Н 21 Ь, (9) / (хп + СД ё)п\ у\п >).
/1
Докажите, что:
а) Из условий ортогональности
= 0 A5.27)
при ? + р @ < р
следует сходимость порядка р, если исходный метод Рунге—
Кутты имеет порядок р для обыкновенных дифференциальных
уравнений.
Указание. Воспользуйтесь теорией В-рядов и формулой Грёб-
нера—Алексеева A4.18) из разд. 1.14.
Ь) Если для данного метода Рунге—Кутты многочлены Ь3 (9)
степени не выше [{р + 1)/2] таковы, что
I
9<-% (в) <Ю = -у 6, A - с)) A5.28)
о
при д = 1, ..., [(р- 1)/2] и Ь, @) = 0, Ь, A) = Ь,,
то условия A5.27) удовлетворяются. Кроме того, имеют место
условия порядка
2 ^ @)ф^ О = -71Г при р
с) Условия A5.28) однозначно определяют вид многочленов
6,(9) степени [(р + 1)/2].
6. Решите уравнение Вольтерры A5.21) с к (х) =с и сравните
решение с решением задачи «без загрязнения среды» A5.10).
Какой популяции живется лучше: при наличии загрязнения
или без него?
Ц Хайрер Э. в др.

Глава III
Многошаговые методы и общие
линейные методы
Эта глава посвящена изучению многошаговых и общих много-
многозначных методов. После прослеживания их исторического раз-
развития (Адаме, Нюстрём, Милн, БДФ) мы изучаем в последующих
разделах порядок, устойчивость и свойства сходимости этих мето-
методов. Сходимость наиболее удобно исследовать в форме одношаго-
вых методов в пространствах высших размерностей. Разделы
111.5 и III.6 посвящены методам с переменной длиной шага и ме-
методам Нордсика. Затем мы обсуждаем различные имеющиеся
программы и сравниваем их характеристики на численных при-
примерах из разд. НЛО, а также на некоторых уравнениях высокой
размерности. Прежде чем закончить главу разделом о специаль-
специальных методах для уравнений второго порядка, мы обсудим две
темы, для которых развита обширная теория: первая из них —
общие линейные методы, включая методы Рунге—Кутты, много-
многошаговые методы и многие их обобщения, а другая — асимптоти-
асимптотическое разложение глобальной погрешности таких методов.

III. 1. Классические линейные
многошаговые формулы
«... и если бы я располагал только своими собственными
возможностями, то мне пришлось бы прервать начатое.
Но в этот момент профессор Дж. К. Адаме предоста-
предоставил мне вполне удовлетворительный метод решения
с помощью квадратур дифференциального уравнения
Лапласа, теоретически описывающего формы капель
жидкости...»
(Ф. Башфорт, 1883)
Еще раньше, чем методы Рунге—Кутты, был рассмотрен
другой способ усовершенствования метода Эйлера — методы
Адамса. Джон Куч Адаме разработал их для решения задачи,
с которой столкнулся Ф. Башфорт при исследовании капиллярных
процессов. И задача, и схемы численного интегрирования опубли-
опубликованы в работе Башфорта A883). В действительности появление
этих методов должно датироваться не позднее чем 1855 годом,
так как в этом году Ф. Башфорт обратился в Королевское общество
с просьбой о предоставлении государственной субсидии. Он
писал: «...но я обязан г-ну Адамсу, предложившему метод реше-
решения дифференциального уравнения
ййг
представленного в виде
поскольку это уравнение описывает теоретическую форму капли
с точностью, превосходящей наиболее тонкие измерения».
В отличие от одношаговых методов, в которых численное
решение получают только из дифференциального уравнения и на-
начального условия, алгоритм Адамса состоит из двух частей:
первая из них — это стартовая процедура для определения
Уъ ••., Ук-г (приближенных значений точного решения в точ-
точках х0 + к, ..., х0 + (к — 1) А), а вторая — многошаговая формула
Для получения приближенного значения точного решения
У (*о + Щ- Затем эта формула применяется рекурсивно для того,
чтобы по численному решению на к последовательных шагах
вычислить у (х0 + (к + 1) к) и т. д.
11*

324 Гл. III* Многошаговые методы и общие линейные методы
Стартовые значения можно получить несколькими способами.
Дж. К. Адаме вычислял их с помощью разложения точного ре-
решения в ряд Тейлора (как описано в разд. 1.8, см. также упр. 2).
Другой способ состоит в использовании какого-либо одношагового
метода, например метода Рунге—Кутты (см. гл. II). Стартовые
значения часто также вычисляют методами Адамса низкого по-
порядка с очень малым шагом.
Явные методы Адамса
Теперь тем же способом, что и Адаме, выведем первую группу
явных многошаговых формул. Для точек сетки введем обозначе-
обозначение хг = х0 + 1к и предположим, что нам известны численные
приближенные значения уп, уп~ь •••> Уп-к+1 точного решения
у (хп), ..., у (хп„к+1) дифференциального уравнения
Уг =/(*. У)у #(*о) = #о-
Адаме рассматривает A.1) в интегральной форме:
0 (*п+1) = 0 (*п) + ) пи »@)л. а.2)
*п
В правую часть A.2) входит искомое решение у (х). Но поскольку
нам известны его приближенные значения #п-л+1> •••» Уп> то мы
располагаем также и величинами
и = / (*ь &) при * = я — й + 1, ..., я, A.3)
а поэтому естественно заменить функцию / (/, г/ (/)) в A.2) интер-
интерполяционным многочленом, проходящим через точки \{хи /^) | ь =
= я — & + 1, ..., я}. Его можно выразить через разности назад
вида
следующим образом:
Р @ = Р (*п + Л) = Д (-1У ( ^ ) У;/п A.4)
[интерполяционная формула Ньютона; см., например, работу
ленричи A962)]. Тогда численный аналог A.2) задается формулой
хп
или после подстановки A.4)
й—I
Уп+1 = Уп+Ъ2> УЯ^п* A-5)

II 1.1. Классические линейные многошаговые формулы 325
где коэффициенты у^ удовлетворяют равенству
-5
о
(-1)/Д $^0з A.6)
(их числовые значения см. в табл. 1.1). Далее для этих коэффи-
коэффициентов будет выведено простое рекуррентное соотношение (фор-
(формула A.11)).
Таблица 1.1. Коэффициенты явных методов Адамса
/
0
1
1
1
2
2
5
12
3
3
8
4
251
720
б
95
288
19
60
б
087
.480
7
5257
17 280
1
3
8
070
628
017
800
Частные случаи A.5). Для 6=1, 2, 3, 4, выразив разности
назад через /п_у, получим следующие формулы:
= 2: уп+1 = уп + Н [-у-/и — -у '»■*]' п
к = 3: уп+1 = #п + й I 2~2 'п ПГ ' 71~1 ' Г2~ ' п~2 I'
л_ ^ Г 55 ^ 59 ; л_ 37 I? 9 ?
Уп~г п I "^4~' п 24~' 71~1 ' 24~' п~а 24~ 'п""8
Замечание. Для & = 1 мы имеем явный метод Эйлера.
Неявные методы Адамса
Формулы A.5) получены при интегрировании интерполяцион-
интерполяционного многочлена A.4) от хп до хп+ъ т. е. вне интервала интерполя-
интерполяции (хп_к+ъ хп). Хорошо известно, что вне этого интервала интер-
интерполяционный многочлен обычно дает довольно плохое прибли-
приближение. Таким образом, явные методы Адамса не очень точны.
Поэтому Адаме исследовал также методы, где A.4) заменен на
интерполяционный многочлен, дополнительно использующий
точку (хп+1, 1п+1), т. е. на
Р* @ = />• (*» + Л) - 2 (-1)/

326 Гл. III. Многошаговые методы и общие линейные методы
Подставляя этот многочлен в A.2), получим следующий неявный
метод:
к
уп+1 = ?п+йЕ V/У7/«+ь A.8)
где коэффициенты у/ удовлетворяют равенству
7
A.9)
а для / <^ 8 приведены в табл. 1.2. Для этих коэффициентов
также можно вывести простое рекуррентное соотношение (упр. 3).
Таблица
/
у?
1.2. Коэффициенты
0
1
1
1
2
2
—I
12
3
1
24
4
—19
720
неявных
б
—3
160
методов
6
—863
60 480
Адамса
7
—275
24 192
3
8
-33
628
953
800
Полученные таким образом формулы имеют общий вид:
#71+1 — У» + А [Рй/п+1 + • • • + Ро/п-Л+1]. A -8')
Первые из них суть
= 0:
A.8')
= 2: УП+1 = #п Т" Л I |~2™" / П+1 Н [2~ /71 [у / 71-1 I 5
= уп + Л I ~2^* /п+1 Н 24~'п 24~ 'п"*1 ' 24~ 'п I'
В частных случаях к = 0 и к = 1 мы имеем неявный метод Эй-
Эйлера и правило трапеций соответственно. В действительности это
одношаговые методы, и они уже рассмотрены в гл. 11.7.
Вся группа методов A.8) более точно, чем A.5), аппроксими-
аппроксимирует решение дифференциального уравнения. Мы подробно оста-
остановимся на этом вопросе после введения понятий порядка й кон-
константы погрешности (разд. III.2). Повышение точности получено
за счет того, что формула A.8) определяет уп+1 только неявно.
Таким образом, в общем случае на каждом шаге требуется ре-
решать нелинейное уравнение. Это можно сделать с помощью ые-

III.!. Классические линейные многошаговые формулы 327
тода простой итерации. Пусть у(п%1 аппроксимирует дп+1\ опреде-
определим
Тогда, если шар к достаточно мал, то при Г-> оо у<^ сходится
к численному решению A.8) уп+\. На практике в качестве у(п%1
используют значение, полученное по явной формуле A.5) («пре-
(«предиктор»), а затем выполняют одну итерацию формулы A.10)
(«корректор»). Этот метод использован в работах Мултона A926)
и Милна A926). Дж. К. Адаме решал неявное уравнение A.8)
методом Ньютона, как это принято теперь в случае жестких урав-
уравнений (см. т. II).
Замечание. Формулу A.5) часто приписывают Адамсу и Баш-
форту, а A.8) — Адамсу и Мултону [Мултон A926)]. В действи-
действительности обе формулы принадлежат Адамсу.
Рекуррентные соотношения для уг
Используя эйлеров метод производящих функций [см., напри-
например, работу Хенричи A962)], можно вывести простые рекур-
рекуррентные соотношения для уг. Обозначим через 0 (О ряд
оо
о (о = 2
Из определения у;- и биномиальной теоремы получим

1=0 о \ / / о /=
A_/Iо8A-0
о
Это равенство можно записать в виде
или
Сравнивая коэффициенты при 1т, получим требуемое рекуррент
ное соотношение
Аналогичная формула для неявных методов Адамса рассматри
вается в упр. 3.

328 Гл. III. Многошаговые методы и общие линейные методы
Явные методы Нюстрёма
сПриближенное интегрирование нашло, особенно в пос-
последнее время, обширную область применения в точ*
ных науках и в технике».
(Е. Дж. Нюстрём, 1925)
В своей обзорной статье по численному интегрированию диф-
дифференциальных уравнений (на которую мы уже ссылались в
в разд. 11.13) Нюстрём A925) также представил новый класс
многошаговых методов. Вместо A.2) он рассматривает интеграль-
интегральное уравнение
ХП+1
У (хп+г) = У (Хп-г) + I IV, У @) Л. A.12)
Точно так же, как Адаме, он заменяет неизвестную функцию
! {и У @) многочленом р (/), заданным с помощью A.4), и полу-
получает формулу
к—1
Уп+1 = Уп-1 + к Ц Х^'/п A-13)
с коэффициентами
х - -и и~$
Первые шесть из этих коэффициентов приведены в табл. 1.3.
Е. Дж. Нюстрём рекомендовал формулы A.13) по той причине,
что коэффициенты И/ больше подходили ему для расчетов, чем у^
из A.5). Этот, несомненно, разумный при ручном счете совет те-
теряет смысл в случае вычислений на ЭВМ.
Таблица 1.3. Коэффициенты явных методов Нюстрёма
/
0
2
1
о
2
1
3
3
1
3
4
29
90
6
14
45
6
1139
3780
Частные случаи. При к = 1 имеем формулу
. A.13')
Этот простейший двухшаговый метод называется правилом сред-
средней точки. Его симметричность оказалась крайне полезным свой-

III.К Классические линейные многошаговые формулы 329
ством для экстраполяционных схем из разд. 11.9. Случай к = 2
не дает ничего нового, поскольку щ = 0. Для к = 3 получим
==: Уп-1
Методы Милна—Симпсона
1 П
Снова рассмотрим интегральное уравнение A.12). Но теперь
заменим подынтегральное выражение на многочлен р* (/) из A.7),
в котором дополнительно к /п, ..., Дг-ь+1 при интерполяции ис-
используется также значение /п+1. Действуя, как обычно, получим
на этот раз неявные формулы
к
Коэффициенты х% определяются формулой
A.16)
а числовые значения для первых из них приведены в табл. 1.4.
Таблица 1.4. Коэффициенты методов Милна—Симпсона
/
X*
0
2
1
2
2
1
3
3
о
4
—1
90
8
—1
90
в
—37
3780
Запишем методы для нескольких значений к, выразив разности
назад в A.15) через /„_/
= 0:
=1: Уп+г^Уп-г
== 2: #п+1 = Уд^ -{- Л I ~з" /п+1 "Г ~3~'Л » "з" /п-1 ^ >
п \~1с1о~1п+1 "г "^о~'Л ' "9оГ*п-1 '
90 'п~а 90
В частном случае к = 0 мы имеем в точности неявный метод
Эйлера с шагом 2Л. Для к = 1 получим выведенное ранее правило
средней точки. Частный случай к «2 дает интересный метод,

330 Гл. III. Многошаговые методы и общие линейные методы
известный как метод Милна [см. работы Милна A926), A970)].
Это прямое обобщение правила Симпсона.
Было исследовано и много других подобных методов. Все
они основаны на интегральном уравнении вида
ХП+1
У (Хп*г) = У (хп-г) + | / (<• У @)
*п-\
в котором / (?, у {I)) заменяется интерполяционным многочле-
многочленом р (I) [формула A.4)] или р* (I) [формула A.7)]. Например,
для 1=3 получим
Данную формулу Милн A926) использовал в качестве «предик-
«предиктора» для своего метода: для решения неявного уравнения A.15')
он применяет одну или две итерации метода простой итерации
о начальным приближением, вычисленным по формуле A.18).
Методы, основанные на дифференцировании
«Моя фамилия Сеаг. — Как? — Сеаг, сЫш, И, ау,
аге. — Леа?»
(В парижской гостинице.)
Все рассмотренные до сих пор многошаговые формулы осно-
основаны на численном интегрировании, т. е. интеграл в A.17) ап-
аппроксимируется с помощью какой-либо квадратурной формулы.
Теперь перейдем к многошаговым методам, воплотившим совсем
другую идею — численного дифференцирования искомой функ-
функции.
Предположим, что известны приближенные значения Уп-к+ъ •••
уп решения дифференциального уравнения A.1). Чтобы вывести
формулу для уп+1, рассмотрим интерполяционный многочлен ц (х)у
проходящий через точки \(хь уг) | I = п — к + 1, ..., п + 1}. Как и
многочлен A.7), его можно выразить через разности назад, а
именно
= д (хп + зН) = Д (-1)' ( ** * ) у'Уп+1- A-19)
Определим теперь неизвестное значение уп+1 таким образом,
чтобы многочлен ц (х) удовлетворял дифференциальному уравне-
уравнению по крайней мере в одном узле сетки, т. е.
' (*п+1-г) =

II 1.1. Классические линейные многошаговые формулы 331
дЛя г = 1 получим явные формулы. При к = 1 и к =2 они экви-
эквивалентны явному методу Эйлера и правилу средней точки соот-
соответственно. В случае к = 3 формула имеет вид
"З" 071+1 + ~2~ 071 — 071-1 + X 071-2 = Ып- 0-21)
Однако она неустойчива, как и все остальные формулы при к > 3
(см. разд. III.3), и поэтому непригодна для расчетов.
Значительно интереснее формулы, получаемые из A.20) при
г = 0. Это неявные формулы
к
/} О/ у'0/1-1-1 == щ л-1-1 A.4&)
с коэффициентами
г ч ' A$ \ ]
которые после дифференцирования биномиального коэффициента
приводятся к виду
65 = 0, 8/ =-у- при />1. A.23)
Поэтому A.22) сводится к формуле
к
Эти многошаговые методы, известные как формулы дифференци-
дифференцирования назад (ФДН- или ЕШР-методы), широко используются
для интегрирования жестких дифференциальных уравнений (см.
т. II). Они введены в работе Кёртиса и Хиршфельдера A952);
Митчелл и Крэггс A953) называют их «стандартными пошаговыми
методами».
Для полноты изложения приведем эти формулы, выразив
в них разности назад через
""«Г* 071+1 ^071 Н 2~ 0П-1 == Щп+1*
«
= 4: -у^- г/п+1 — 4уп + Зг/д-х — -у- 0п-2 + -у- 0п-з = Ы

332
Гл. III. Многошаговые методы и общие линейные методы
= 5:
137
60
10 5
п-1 з"Уп-2 +
(\
147
60
15
20
5" #71-4
, 15
п~2 ~* 4~~
"/
71+1 >
6 ,
5~ ^п~4 •
1
При & > 6 ЕШР-методы неустойчивы (см. разд. III.3).
Упражнения
1. Пусть заданы дифференциальное уравнение у' =у2, у @) = 1
и точные стартовые значения ух = 1/A —хг) при { = 0, 1, ...
Рис. 1.1. Решение дифференциального уравнения A.24) и иллюстрация из книги
Башфорта.
;.., к — 1. Применить методы Адамса и изучить выражение
у (хк) — уъ при малых шагах.
2. Рассмотрим дифференциальное уравнение из начала данного
раздела. Оно описывает форму капли и может быть задано
в виде [Ф. Башфорт A883); та же задача, что и в упр. 2 из
разд. 11.1, но в другой системе координат]
их
р СО5 ф,
йг
= р зш
A.24)
где
_1_
Р
A.25)
Можно считать р функцией координат х и г и понимать под
ней радиус кривизны. Через ф обозначен угол между нормалью
к кривой и осью г (рис. 1.1). Заданы следующие начальные ус-

III. 1. Классические линейные многошаговые формулы 333
ловия: х @) = 0, г @) = 0, р @) = 1. Решить это уравнение
с помощью предложенного Адамсом способа:
а) Предположим, что р можно представить в виде
р = 1 + Ь2ф2 + Ь4Ф4 + ... .
Подставив это выражение в A.24), в результате интегриро-
интегрирования получим первые члены разложения х (ф) и г{ф) в ряд
Тейлора о коэффициентами, зависящими от Ь2> &4> •••> и т. д.
Эти параметры можно вычислить из A.25), приравняв коэффи-
коэффициенты при ф. Таким образом, получают решение при малых
значениях ф (стартовые значения).
Ь) с помощью одной из предложенных многошаговых формул
вычислить решение для заданного C (например, Р = 3) на интер-
интервале [0, я].
3. Доказать, что определенные в A.9) коэффициенты у] удовлет-
удовлетворяют соотношениям
т5
—
4. Пусть коэффициенты К;, х*, у;, у* определены в A.14), A.16),
A.6), A.9) соответственно. Показать, что выполняются равен-
равенства
/ = 2у] — 7/-1 при / > 0
(где 7-1 =7-1 =0).
Указание: разбив интеграл в A.14) на два слагаемых, можно
установить равенство х7- = у^ -\- у*. Соотношение 7/ ^ V,/ —
— 77-1 получается с помощью известного тождества для бино-
биномиальных коэффициентов.

III.2. Локальная погрешность
и условия порядка
«Вы знаете, я ведь многошаговый человек... и никому
не говорите, что моей первой программой для первой
шведской ЭВМ была реализация метода Рунге—
Кутты...»
(Г. Далквист, 1982, после нескольких бокалов вина;
печатается с его разрешения)
Исследования Далквиста A956, 1959) положили начало об-
общей теории многошаговых методов, а широкую известность она
приобрела благодаря книге Хенричи A962). Для всех многошаго-
многошаговых формул из предыдущего раздела общим является линейное
вхождение в них значений численного решения уь а также /
Поэтому рассмотрим разностное уравнение общего вида
<*к9п+к + <*к-1Уп+к-1 + • • • + аоУп = Л (Ръ1п+к + • • • + Ро/п)» BЛ)
включающее все эти формулы как частные случаи. В B.1) пара-
параметры <Х|, $г — вещественные числа, А обозначает величину
шага, а
В этой главе мы будем считать, что выполнены следующие усло-
условия:
а*=^0, КЖРо|>О. B.2)
Первое предположение означает, что неявное уравнение B.1)
разрешимо относительно уп+к по крайней мере при достаточно
малых Л. Второе соотношение из B.2) всегда можно получить,
уменьшив при необходимости индекс к.
Формула B.1) называется линейным многошаговым, а точнее,
линейным к-шаговым методом. Будем различать явные ($к = 0)
и неявные фЛ Ф 0) многошаговые методы.
Локальная погрешность многошагового метода
Поскольку численное решение, полученное многошаговым
методом, зависит не только от задачи Коши A.1), но и от выбора
стартовых значений, определение локальной погрешности в этом
случае будет не таким простым, как для одношаговых методов
(сравнить с разд. 11.2 и II.3).

III,2. Локальная погрешность и условия порядка 335
Определение 2.1. Локальной погрешностью многошагового ме-
метода B.1) называется величина
У Ш — ук9
где у {х) — точное решение задачи у' = I (х, у), у (х0) = у0,
а У к — численное решение, полученное по формуле B.1) при точ-
точных стартовых значениях уг = у (хг), I = О, 1, ..., к — 1.
Т I I I I I
*0 Х1 Х2 '" хк-1 хк
Рис. 2.1. Иллюстрация локальной погрешности.
В случае к = 1 это определение совпадает с определением
локальной погрешности для одношаговых методов. Чтобы пока-
показать связь с другими ее возможными определениями, сопоставим
формуле B.1) линейный разностный оператор
к
(У, х, к) = Е [а1У (х + 1Н) - АРУ (х + Щ. B.3)
Здесь у (х) — какая-либо дифференцируемая функция, которая
задана на интервале, включающем значения х + *"А, I = 0, 1, ..., к.
Лемма 2.2. Рассмотрим дифференциальное уравнение A.1)
с непрерывно дифференцируемой функцией I (я, у) и решением у {х).
Тогда для локальной погрешности выполняется равенство
У Ш -Ук= («*/ ~ /хрь ~- {хкУ т]))~Г I (у, х0, К).
Здесь т] в скалярном случае является некоторым промежуточным
значением между у (хк) и ук. Если / — векторная функция, то
(хк> л) — матрица Якоби, строки которой вычислены, воз-
возможно, при разных значениях, принадлежащих отрезку между
У (**) и ук.
Доказательство. По определению 2.1, ук задается в неявном
виде уравнением
~ ЛР|/ (хи у (хг))] + акук — АрА/ (хк, ук) = 0.

336 Гл. III. Многошаговые методы и общие линейные методы
Подставляя в него B.3), получим
(У, х0, Н) = ак [у (хк) — ук] — к$к [/ (хк, у (хк)) - / (хк, ук)],
откуда по теореме о среднем следует утверждение леммы. ■
Эта лемма показывает равенство локальной погрешности и
главного члена выражения <хЦ1Ь (у, х0, А), которое иногда также
называют локальной погрешностью (Далквист 1956, 1959). Для
явных методов оба определения совпадают.
Порядок многошагового метода
Определив локальную погрешность многошагового метода,
для него таким же образом, как для одношаговых методов, можно
ввести понятие порядка.
Определение 2.3. Говорят, что многошаговый метод B.1)
имеет порядок р, если выполняется одно из следующих двух
условий:
1) Ь {у, х, Н) = О (Ар+1) для всех достаточно гладких функ-
функций у (х)\
Н) локальная погрешность формулы B.1) равна О (Нр+1) для
всех достаточно гладких дифференциальных уравнений A.1).
Отметим, что по лемме 2.2 условия 1) и и) эквивалентны.
Следующая хнаша задача — выразить порядок многошагового
метода через'его свободные параметры аг и E$. Далквист A956)
первым указал на фундаментальную роль многочленов
Р (С) = *С + А-1Б + ... + о,
* (С) = РС* + РС*- ++Р ( '
Назовем их производящими многочленами многошагового метода
B-1).
Теорема 2.4. Многошаговый метод B.1) имеет порядок р
тогда и только тогда, когда выполняется одно из следующих
эквивалентных условий:
к к к
1) Ц аг = 0 и Ц а,** = я Ц Р^-1 при G=1, ..., Р\
*1 *0 *0
11) р (ен) - На (ен) = О (А**1) при к -> 0;
— а (С) = О (« — 1H приС->1.
Доказательство. Подставляя в B.3) разложение в ряд Тейлора
(при необходимости усеченное) для у (х + Иг) и у' (х + *А), по-

III.2. Локальная погрешность и условия порядка
337
лучим
(у. х, Н) =
,« ^Лы (г+1)
Г1 ^ Т\ *
г>0
B.5)
откуда следует эквивалентность условия 1) равенству Ь (г/, я, А) =
= О (Нр+1) для всех достаточно гладких функций у (я).
Остается доказать эквивалентность всех трех условий тео-
теоремы 2.4. Эквивалентность условий 1) и И) следует из тождества
1(ехр, 0, Л)\=р(^1 — Ла (*»)',
в котором через ехр обозначена экспоненциальная функция,
и полученного из B.5) равенства
I (ехр, 0, Н) -
+
Т
"к
2 °^ ^
С помощью преобразования ^ = ен (или А = 1о§ ^) условие 11)
можно записать в виде
Р (С) - Ь8 ^ (С) = О (Aов 0р+1) при С -> 1,
что эквивалентно условию 111), поскольку
1ов С = (С - 1) + О ((С - IJ) при 5 -* 1. ■
Замечание. Для многошаговых методов условия первого по-
порядка, называемые обычно условиями согласованности, можно
также записать в виде
=0,
=0A).
B.6)
Если читателю понятно доказательство приведенных выше ус-
условий порядка, то и более общий случай неравномерных сеток
не представит для него трудностей [см. разд. II 1.5 и книгу Штет-
тера A973)].
Пример 2.5. Порядок явных методов Адамса. Сначала опреде-
определим, для каких дифференциальных уравнений явные методы
Адамса теоретически дают точное решение. Это происходит в том
случае, когда многочлен р ({) в A.4) равен / A, у (()). Предполо-
Предположим теперь, что / (/, у) = / A) не зависит от у и является много-
многочленом, степень которого меньше к. Тогда с помощью явных ме-

338 Гл. III. Многошаговые методы и общие линейные методы
тодов Адамса получается точное решение дифференциальных
уравнений
у' = цх<*-~1 при <7 = 0, 1, ..., к.
Это означает, что локальная погрешность равна нулю, а, следова-
следовательно, по лемме 2.2
= 1 (х«, 0, Ь)
Г к
при д = 0, ...
Эти равенства совпадают с условием 1) из теоремы 2.4 при р = к,
а поэтому явные методы Адамса имеют порядок не ниже к. Да-
Далее показано, что он и не превосходит к (пример 2.7).
Пример 2.6. В неявных методах Адамса вместо р (I) исполь-
используется многочлен р* @, заданный в A.7). Поскольку степень р* (()
на единицу выше, чем у р (I), такие же, как в примере 2.5, рассу-
рассуждения показывают, что неявные методы Адамса имеют порядок
не ниже к + 1.
Аналогично можно рассмотреть все остальные методы из
разд. III.1 (см. упр. 2 и табл. 2.1).
Константа погрешности многошаговых методов
Порядок многошагового метода показывает, насколько бы-
быстро погрешность стремится к нулю при к -> 0. Однако методы
одного порядка могут иметь разные погрешности; они различаются
константой погрешности. Из формулы B.5) видно, что разност-
разностный оператор ^ соответствующий многошаговому методу порядка
р, для всех достаточно гладких функций у (х) удовлетворяет
равенству
I {у, х, К) = Ср+1/1'+У+1> (х) + О (АР+а), B.7)
где константа Ср+1 вычисляется по формуле
к к
1
Су Т1 I 1 ==
B.8)
Эта константа не подходит в качестве меры точности, поскольку
для нее можно получить любое числовое значение, умножив фор-
формулу B.1) на соответствующую постоянную, что не изменит чис-
численного решения \уп). Для этого больше подошла бы константа
а^хСр+1, так как локальная погрешность многошагового метода
удовлетворяет соотношению (см. лемму 2.2 и формулу B.7))
у (хк) -ук = аТ1Ср+1Нр+1у(р+1) (х0) + О {НР+2У B.9)

III.2. Локальная погрешность и условия порядка 33 9
Но такое определение тоже не может нас удовлетворить по не-
нескольким причинам, которые станут понятны из следующего объ-
объяснения. Обозначим через еп глобальную погрешность, масштаби-
масштабированную на Нр:
вп~ нр
Вычитая B.1) из B.3) и учитывая B.7), получим
к к
23 «а»* = ь1~р 23 ?! (/ (*п+«, уп+д -! (*п+1. у
/ 0
Теперь, чтобы в B.10) ртносящийся к погрешности член внести
под знак суммы с коэффициентами р^, используем равенство
к
2
Ьг 2 BЛ
Линеаризуем выражение
у (хп+ь)) = ^ (хп+е, у (дт^О) А^п+е + О (Н2?)
и подставим его, а также B.11), в B.10). Пренебрегая членами
О (А2) и О (Н2р)9 мы можем рассматривать полученную формулу
как многошаговый метод, примененный к задаче
еГ (х) = -|- (х, у (х)) е (х) - С^) (х), в (хв) = 0, B.12)
где
^ B.13)
является естественной мерой глобальной погрешности и поэтому
называется константой погрешности.
Другой вывод определения B.13) будет указан в разделе,
посвященном глобальной сходимости (см. упр. 2 из разд. II 1.4).
Кроме того, решение задачи B.12) дает первый член асимптоти-
асимптотического разложения глобальной погрешности (см. разд. III.9).
Пример 2.7. Константа погрешности явных методов Адамса.
Рассмотрим дифференциальное уравнение у' = / (а:) с функцией
! (х) == (к + 1) хк и точным решением у (х) ~хк+1. Поскольку
это уравнение интегрируется точно явным методом Адамса (см.
пример 2.5), имеет место равенство
к
У (хк) - У (Хк-г) = Ь 2

340
Гл. III. Многошаговые методы и общие линейные методы
Поэтому локальную погрешность ^-шагового явного метода Адамса
A.5) можно записать в виде
У (*к) -Ун = Лъу*/*-! = Ьк+Ыт (*о) = к*+*уьу*+" (*0).
В силу неравенства ук Ф 0 из этой формулы следует, что порядок
^-шагового метода не превосходит к (сравните с примером 2.5).
Кроме того, учитывая, что ак = 1, при сопоставлении последнего
соотношения с формулой B.9) придем к равенству Ск+1 = ук.
И наконец, для методов Адамса р (!;) = {;* — %к—1 и р' A) =1,
а поэтому с помощью B.6) получим значение константы погреш-
погрешности С =ук.
В табл. 2.1 приведены константы погрешности всех рассмо-
рассмотренных выше многошаговых методов (отметим, что для явного
метода Нюстрёма и метода Милна—Симпсона а A) =2).
Таблица 2.1. Порядок и константа погрешности
многошаговых методов
Метод
явный Адамса
неявный Адамса
правило средней точки
Нюстрёма, к > 2
Милна, к = 2
Милна—Симпсона, к> 3
ФДН
Номер
формулы
A.5)
A.8)
A.13')
A.13)
A.15')
A.15)
A.22')
Порядок
к
к + 1
2
к
4
к+ 1
к
Константа
погрешности
Ук
Ук+1
1/6
кк/2
— 1/180
— II(к 4- 1)
Неприводимые методы
Пусть производящие многочлены р (^) и от (^) метода B.1)
заданы формулами B.4), и предположим, что они имеют общий
множитель ф (^). Тогда определим многочлены
* (П -
~ Ф(О ' а
которые являются производящими многочленами нового, более
простого многошагового метода. С помощью оператора сдвига Л,
заданного соотношением
Еуп = Уп+% или Еу (х) = у (х + к),
этот многошаговый метод можно записать в компактной форме
р* {Е) уп = ко* (Е) /п.
Умножив обе части формулы на ф (Е), мы увидим, что любое
ее решение {уп\ будет также и решением исходного метода

III.2. Локальная погрешность и условия порядка 341
р (Е) уп = ко (Е) /п. Таким образом, оба метода в сущности сов-
совпадают. Обозначим через Ь* разностный оператор, сопоставлен-
сопоставленный новому приведенному метЪду, а через Ср+\ — его константу
из B.7). Из равенства
I (*/, х, к) - Ф (Е) I* (у, х, К) - С;+1Н»+*<р (Е) */«>+'> (х) + О
A) ЛН-у+О (Х) + О
сразу получим Ср+\ = ф A) С^, и поэтому также выполняется
соотношение Ср+\/а A) = Ср+ио* A). Итак, оба метода имеют
одинаковые константы погрешности.
Проведенный анализ показывает, что многошаговые методы,
у которых производящие многочлены имеют общий множитель,
не представляют интереса. Поэтому обычно мы будем предпола-
предполагать, что
и о (У не имеют общих множителей. B.13)
Многошаговые методы, удовлетворяющие этому свойству, назы-
называются неприводимыми.
Ядро Пеано многошаговых методов
Порядок и константа погрешности не дают полного описания
погрешности, так как в ее разложении последующие члены ряда
могут значительно превосходить Ср+1. Поэтому было предпринято
несколько попыток — первоначально для квадратурных формул —
получить полное описание погрешности. Следующие результаты
опираются на идеи Пеано A913):
Теорема 2.8. Пусть многошаговый метод B.1) имеет поря-
порядок р, а ц — некоторое целое число A <! ц <! р). Тогда для любой
функции у (х)у непрерывно дифференцируемой ц + 1 раз, выпол-
выполняется равенство
Ь (у, х, к) = к«+х \ Кя E) у«+" (х + зк) Оз. B.14)
о
где
называется ц-м ядром Пеано многошагового метода B.1).
Замечание. В определении ядра Пеано использовано обозна-
обозначение
A — 8)г при I— 5>0,
О при * — $<0.

342 Гл. III. Многошаговые методы и общие линейные методы
Поэтому Кя (з) является кусочно-полиномиальной функцией и
удовлетворяет равенству
B.15)
Доказательство. По теореме Тейлора с интегральным представ-
представлением остаточного члена
(х\ -4- А*7"* \ — #/@-И) (х 4- 5/Л ^5.
*) Ч *
г=0 О
(У
г=0 О
Подставив эти два выражения в B.3), с помощью таких же рас-
рассуждений, как в доказательстве теоремы 2.4, получим, что при
ц <[ р стоящие перед интегралом многочлены сокращаются. Тогда
из равенства
г н
о о
следует утверждение теоремы. ■
Кроме представления B.15), ядро Пеано Кд (з) обладает сле-
следующими свойствами:
Кд(з) = 0 при 5^(— оо, 0I([6, оо)
и ц = 1, ..., р\ B.16)
Кя (з) — непрерывно дифференцируемая ц — 2 раза функция
и К'я E) = —Кд-1 (з) при <7 = 2, ..., р (при G = 2 в обобщен-
обобщенном смысле)- B.17)
Кг (§) — кусочно-линейная функция с разрывами в точках О,
1, ...,&. В точке / она имеет скачок Р;, а на интервале
(/ — 1» /) ее угловой коэффициент равен — (а/ + <^иг +••• +
+ а*); B.18)
константа Ср+1 из B.8) вычисляется по формуле
к
Ср+1= \ Кр(8)Aз. B.19)
о
Приведем доказательство утверждений B.16) и B.19). Равен-
Равенство Кя (з) == 0 при 5 ^ к и д <! р вытекает прямо из определе-

III.2. Локальная погрешность и условия порядка
343
ния ядра Пеано. Чтобы доказать это равенство и для 5 < 0, рас-
рассмотрим многочлен у (х) — (х — 5)?, где 5 является параметром.
Тогда из теоремы 2.8 следует, что
Ну, о, 1)=
-*)*-1^ при
1.
-1.
2.
1.
1
-1.
_ К
).
-
1.
>
2.
1
3.
Рис. 2.2. Ядра Пеано трехшагового метода Нюстрёма.
а поэтому Кя (8) = 0 при 5 < 0, что и завершает доказательство
свойства B.16). Соотношение B.17) устанавливается о помощью
интегрирования по частям выражения B.14). В качестве примера
на рис. 2.2 изображены ядра Пеано для 3-шагового метода Ню-
Нюстрёма A.13*).
Упражнения
1
Построение многошаговых методов.
а) Для любого многочлена р (^) степени к, удовлетворяющего
условию р A) = 0, существует единственный многочлен а (^),
степень которого не превосходит &, такой что соответствующий
многошаговый метод имеет порядок не ниже к + 1;
Ь) При условии а) существует единственный многочлен а (^)
степени </г, такой что соответствующий многошаговый метод
(который в этом случае будет явным) имеет порядок не ниже к.
Указание. Используйте условие 111) из теоремы 2.4.
Найдите многошаговый метод вида
#71+2 + «1^71+1 + а0Уп =
имеющий максимально возможный порядок. Изучите получен-
полученную формулу на примере у' = у, у @) = 1, Н = 0.1.
3. Проверьте приведенные в табл. 2.1 значения порядка и кон-
константы погрешности для формул дифференцирования назад.
4. Покажите, что в явных и неявных методах Адамса, а также
в формулах дифференцирования назад ядро Пеано Кр (з)

344 Рл. III. Многошаговые методы и общие линейные методы
не меняет знака. Выведите из этого свойства соотношение
Ь(У, х, А) =
где 2 ^ (я, х + Щ, а Ср+ц —> константа из B.8).
б. Пусть у (х) — точное решение уравнения у' = / (х, у), а стар-
стартовые значения равны уг = у (хг), 2 = 0, 1, ..., к — 1. Пред-
Предположим, что } непрерывна и удовлетворяет условию Лип-
Липшица по у (необязательно, чтобы / была дифференцируемой).
Докажите, что для локальной погрешности согласованного
многошагового метода (для которого верны равенства B.6))
выполняется соотношение
У Ы - й | < А» (А),
где со [Щ -> 0 при Ь -* 0.

Ш.З. Устойчивость и первый барьер Далквиста
«... с тех пор автору не раз приходилось встречаться
с такими методами численного интегрирования диф-
дифференциальных уравнений, которые обладали подку-
пающе малой погрешностью аппроксимации, но тем
не менее таили в себе большую опасность вычисли-
вычислительной неустойчивости».
(X. Рутисхаузер, 1952)
В своей знаменитой статье Рутисхаузер отметил, что высокого
порядка и малой локальной погрешности еще недостаточно для
того, чтобы многошаговый метод был пригодным для практиче-
практических расчетов. Численное решение может быть «неустойчивым»
даже при очень малом шаге А. На этот же факт указал Тодд A950),
применив ряд разностных методов к дифференциальным уравне-
уравнениям второго порядка. При изложении мы будем опираться в ос-
основном на работу Далквиста A956), в которой этот эффект изу-
изучен систематически. История развития понятий численной устой-
устойчивости интересно представлена в статье Далквиста A985) «33
года численной неустойчивости, часть I».
Начнем с примера из работы Далквиста A956) (см. упр. 2
из разд. 1П.2). Среди всех явных 2-шаговых методов выберем
формулу максимально возможного порядка. С помощью теоремы
2.4 легко определить, что это метод 3-го порядка, имеющий вид
- Ьуп = к D/п+1 + 2/п). C.1)
Его применение к дифференциальной задаче
У' = У, У @) = 1 C.2)
дает линейное разностное уравнение
-Л) уп+1 - E + 2/х) уп = 0. C.3)
В качестве стартовых возьмем значения точного решения у0 = 1
и Уг — ехР (Л). На рис. 3.1 изображены точное решение ехр (х)
и численное решение для шагов к == 1/10, к = 1/20, к = 1/40
и т. д. Несмотря на малую локальную погрешность, результаты
являются неудовлетворительными. Из рис. 3.1 видно, что с умень-
уменьшением шага они все ухудшаются.
Этот факт легко объяснить. Подставим в C.3) у; = Р» как это
обычно делается для линейных разностных уравнений [Ла-

346
Гл. III. Многошаговые метода и общие линейные методы
гранж A775I. В результате получим характеристическое урав-
уравнение
C.4]
Общее решение C.3)' вычисляется по формуле
C.5)
где
(А)I = 1 + Л + О (А1),
= -5
— корни уравнения C.4), а коэффициенты А и В определяются
по стартовым значениям у0 и ух. Поскольку 1,х (И) аппроксимирует
з.
2. -
1.
Рис. 3.1. Численное решение, полученное неустой-
неустойчивым методом C.1).
ехр (к)> первый член в C.5) аппроксимирует значение точного
решения ехр (х) в точке х — пк. Возмущение в наш ме*год вносит
второй член из C.5), называемый часто паразитным решением:
так как при к -> 0 ^2 (к) по абсолютному значению превосходит
единицу, это паразитное решение с ростом п становится очень
большим и начинает преобладать в решении уп.
Теперь обратимся к вопросу об устойчивости метода общего
вида B.1). Важную роль играет поведение решения при п -> со
(или к -> 0) и фиксированном пк. Очевидно, что B.1) при к -> 0
сводится к формуле
п = 0.
C.6)
Ее можно рассматривать как численный метод B.1), примененный
к решению дифференциального уравнения
Уг = 0.
C.7)

III.3. Устойчивость и первый барьер Далквиста 347
Подставив в формулу C.6) у^ = ^ и разделив ее на %п, получим,
что 2 должно быть корнем уравнения
Р (С) = «*С* + «ь-1^1 Н + а0 = 0. C.8)
Как и в разд. 1.5, здесь снова возникают трудности, когда C.8)
имеет корень кратности т>1. В этом случае [Лаграрж A792),
см. далее упр. 1] решениями C,6) являются величины уп =
—. п1—\%п ц _. 1^ ^ т^ и суперпозиция приводит к следующему
результату.
Лемма 3.1. Пусть многочлен р (%) имеет корни ^19 ..., &
кратностей тъ ..., тг соответственно. Тогда общее решение
C.6) задается формулой
> C.9)
где р} (п) — многочлены степеней т$ — 1. ■
Из формулы C.9) видно, что для ограниченности уп при п ->
-> со требуется, чтобы корни C.8) лежали в круге единичного
радиуса, а корни, принадлежащие единичной окружности, были
простыми.
Определение 3.2. Многошаговый метод B.1) называется
устойчивым, если его производящий многочлен р (^) [формула
C.8) ] удовлетворяет корневому условию, т. е.
1) корни р (^) лежат на (или внутри) единичной окружности;
и) корни, принадлежащие единичной окружности, являются
простыми.
Замечание. Чтобы отличать это понятие устойчивости от осталь-
остальных, его иногда называют нуль-устойчивостью или п-устойчиво-
стью в честь Далквиста.
Примеры. Для явного и неявного методов Адамса р @ =
= 2* — С*"- Кроме простого корня, равного 1, этот многочлен
имеет нулевой корень кратности к — 1. Поэтому методы Адамса
устойчивы.
Это утверждение верно также для явного метода Нюстрёма
и методов Милна—Симпсона, для которых р (<У .= С* — С*"-
Заметим, что в этом случае имеется еще простой корень — 1,
который может представлять опасность при решении некоторых
дифференциальных уравнений (см. т. II).
Устойчивость формул дифференцирования назад
Для ФДН-формул исследовать устойчивость сложнее. Посколь-
Поскольку характеристический многочлен выражения V' уь+п == 0 Ра*
вен С*""' (С— 11' ^ 0» из представления A.22'} следует, что эти

348
Гл. III. Многошаговые методы и общие линейные методы
методы имеют производящий многочлен р (^) вида
C.10)
При изучении его нулей удобнее рассматривать многочлен
* ,1
C.11)
полученный с помощью преобразования ^ = 1/A —г). Он равен
к-й частичной сумме ряда Тейлора для функции — 1о§ A —г).
Рис. 3.2. Корни многочлена р (г), определенного формулой C.11).
Поскольку корни р {г) и р (С) связаны указанным преобразова-
преобразованием, выполняется следующая лемма.
Лемма 3.3. к-шаговая ФДН-формула A.22') устойчива тогда
и только тогда, когда все корни многочлена C.11) лежат вне круга
\г\ \г — 1 | <; 1}, а корни на его границе являются простыми. Ш
Корни многочлена C.11) для различных значений к изобра-
изображены на рис. 3.2.
Теорема 3.4. к-шаговая ФДН-формула A.22') устойчива при
4<б а неустойчива при к ^ 7.
Доказательство. Первое утверждение легко проверить про-
простым перебором конечного числа случаев [см. рис. 3.2. Впервые
это отметили Митчелл и Крэггс A953)]. Однако вторую часть

III.3. Устойчивость и первый барьер Далквиста
349
теоремы доказать Сложнее, так как она относится к бесконечному
числу случаев. Ее первое полное доказательство содержится
в техническом отчете Крайера,. A971), а сокращенный вариант
опубликован в его же статье A972). Другое доказательство, осно-
основанное на критерии Шура—Кона, дано в работе Кридона и Мил-
Миллера A975) [см. также книгу Григорьева A977I. Схема этого
доказательства приведена ниже в упр. 4. Мы изложим доказатель-
доказательство из статьи Хайрера и Ваннера A983), где используется пред-
представление
р (г) =
в котором
0
Ф E) &, C.12)
ле
1 — зе1
Разобьем комплексную плоскость на к секторов:
О, 1,
1
1 .
На лучах, ограничивающих 57-, выполняется равенство еш
= —1, а поэтому C.12) сводится к интегралу
о
о положительной весовой
р (г) всегда принадлежит
Ф (§), т. е. углу между е**
и еш = —\а Таким обра-
образом, на этих лучах аг& (р(г))
не может совершить
полный оборот, а по-
поскольку аг§ (гк) делает
один полный оборот на
бесконечности между Э =
==2я(/— 1/2)/й и 9 =
= 2я (/ + 1/2)/й, то в
силу принципа аргумента
[см., например, книгу
Рис. 3.3. Аргумент многочлена
р (г), определенного формулой
C.11).
функцией. Следовательно, аргумент
углу, который покрывает функция
///•/•//••/•//
••////////••//•/

350
Гл. III. Многошаговые методы и общие линейные методы
Хенричи A974I каждому сектору 5^ (/ = 1, ..., к — 1, случай
/ = 0 исключается) принадлежит ровно один корень р (г)
(см. рис. 3.3).
Для завершения доказательства нам остается только ограни-
ограничить область, где расположены нули р (г). Сделаем это следующим
образом. Заметим, что в C.12) член 5* становится большим при
5 > 1. Поэтому разобьем C.12) на два интеграла: р (г) = /х — /а,
где
г 1 г
с с с
г = 1 ф E) 08 — I е4ЛО5*ф E) О5, /2 = е1*® I 5яф E)
О 0 1
Из неравенства | Ф («) | < В (8), в котором
1 при -у<в< л,
получим оценку
Затем из положительности 8к выведем соотношение
/а =
где Ф принадлежит выпуклой оболочке множества {ф E); 1
5 <; г}. Любой ее элемент можно представить в виде
где 5 = а52 + A — а) 51? 0 < а < 1, 1 < 51э 52 < г. Поскольку
Ф («) | монотонно убывает при 5 ;> 1, выполняется неравенство
Ф | ;> | ф (г) |. Элементарные геометрические соображения при-
приводят к соотношению | Ф | >- 1/2/*, и в результате получим оценку
Из C.13) и C.14) следует, что при
г> Я (в) = (B* + 4) В F) + 1I/<*-П C.15)
верно соотношение | /а | > | 1г |, а поэтому р (г) не может
обращаться в нуль. Кривая К @), также нанесенная на рис. 3.2,
отделяет от секторов 5^ область, которую мы назовем «пирогом
с сыром мадам Имхоф». Каждый его кусок (при / Ф 0) должен
содержать корень многочлена р (г). Как показывает простой ана-
анализ, принадлежащая 5Х часть «пирога» при к = 12 настолько
мала, что обеспечивает наличие нулей р (г) внутри круга \г*

III.3. Устойчивость и первый барьер Далквиста 351
| г — 1 | <! 1}. Поскольку К (9) при фиксированном Э монотонно
убывает с ростом к, как и К (п!к), то же утверждение верно для
всех к ^ 12. При 6 < к << 12 на неустойчивость методов указы-
указывают и численные расчеты (см. рис. 3.2 или упр. 4). ■
Наивысший достижимый порядок устойчивых
многошаговых методов
Вполне естественно возникает вопрос об устойчивости много-
многошаговых методов максимально возможного порядка. Далквист
A956) провел его исследование, результатом которого стал зна-
знаменитый «первый барьер Далквиста».
Как следует из подсчета условий порядка (теорема 2.4), для
того чтобы линейный многошаговый метод имел порядок р, его
параметры должны удовлетворять р + 1 линейным уравнением.
Поскольку метод содержит 2к + 1 .свободных параметров (без
ограничения общности можно считать ак = 1), его наивысший
достижимый порядок равен 2к. Это утверждение можно действи-
действительно проверить (см. упр. 5). Однако, как показывает следующая
теорема, такие методы не имеют практического значения.
Теорема 3.5. (Первый барьер Далквиста) Порядок р устойчи-
устойчивого линейного к-шагового метода подчиняется следующим ограни-
ограничениям
р <^ к + 2 при четных к,
р <; к + 1 при нечетных
р <; к при $ь/а,к <; 0 (в частности, для явных методов).
Отложим доказательство теоремы, чтобы дать ряд необходи-
необходимых для него обозначений и лемм. Сначала введем «греко-рим-
«греко-римское преобразование»
= т=т или г==т=т- (ЗЛ6)
Оно отображает круг | ^ | < 1 в полуплоскость Ке г <3 О,
верхнюю полуплоскость 1т г > 0 — в нижнюю, окружность
)^| = 1 — в мнимую ось, точку 5= 1 в 2=оо, а ^ = —1
в 2 = 0. Теперь рассмотрим многочлены
V С3-17)

352 Гл. III. Многошаговые методы и общие линейные методы
Поскольку нули /? (г) и р (О связаны преобразованием C.16),
условие устойчивости многошагового метода можно выразить
в терминах 7? (г) следующим образом: все нули /? (г) лежат в ле-
левой полуплоскости Ке г <; 0, и на мнимой оси нет кратных нулей.
Лемма 3.6. Пусть многошаговый метод является устойчивым
и имеет по крайней мере нулевой порядок. Тогда
1)а, = 0« Яь-1 = 2*-*р' A) ф 0;
п) все ненулевые коэффициенты К (г) имеют один и тот же
знак.
Доказательство. Разделив формулу C.17) на гк и подставив
в нее г = оо, найдем значение коэффициента ак = 2~*р A). Это
выражение должно быть равным нулю вследствие условия нуле-
нулевого порядка. Тем же способом получим коэффициент ак„х =
= 21~~/ер/ A), который отличен от нуля, так как в силу устойчиво-
устойчивости корень 1 многочлена р (^) не может быть кратным. Второе
утверждение леммы доказывается с помощью разложения на
множители
(г) = а*_! П (г + *,) П ((г + щJ + о/2),
где —X] — вещественные корни, а —«/ ± ^V^ — пары комплексно
сопряженных корней. По условию устойчивости ^>0и Щ^ 0,
откуда следует, что все коэффициенты 7? (г) имеют один и тот же
знак. ■
Далее выразим условия порядка из теоремы 2.4 в терминах
многочленов Я (г) и 5 (г).
Лемма 3.7. Многошаговый метод имеет порядок р тогда и
только тогда, когда выполняется равенство
5 (*) = Ср+1 () + О (()
при г-^оо. C.18)
Доказательство. Сначала заметим, что член О ((^ — 1)р) в ус-
условии 111) теоремы 2.4 по формуле B.7) равен С«+1 B; — 1)*
+ О ((I — 1)р+1). Применяя преобразование C.16), получим
C.18), так как С — 1 = 21 (г — 1) = 2/г + О (B/гJ) при г-+ оо
Лемма 3.8. Для коэффициентов разложения в ряд Лорана
при всех ] !> 0 выполняется неравенство [г2у+1 > 0.
Доказательство. Рассмотрим ту ветвь функции 1о§ 2;, которая
является аналитической на комплексной плоскости ^ с разрезом
вдоль отрицательной части вещественной оси и удовлетворяет

II 1.3. Устойчивость и первый барьер Далквиста 353
равенству 1о§ 1=0. Преобразование C.16) отображает этот раз-
разрез в отрезок вещественной оси [—1, +1]. Поэтому функция
1о§ ((г + 1)/(г — 1)) — аналитическая на комплексной плоскости
с разрезом вдоль этого отрезка (см. рис. 3.4). Формула
2+1 2
показывает существование разложения' C.19). Чтобы доказать
с л Ъ
-1
Рис. 3.4. Разрез на плоскости г с кривой у.
положительность его коэффициентов, используем формулу Коши
для коэффициентов функции / (г) = 2 ап (г — го)п:
а = ! Г !{г)
они в данном случае имеют вид
V
[Коши A831), см. также работу Бенке—Зоммера A962I. Здесь
р — произвольная кривая вокруг отрезка [—1, 11, например,
такая, как на рис. 3.4.
Заметим, что 1ов ((г + 1)/(г — 1)) = 1оё (A + хI{\ — х)) —
—Ы, если г стремится к вещественному значению х € (—1, 1)
сверху, и 1о§ ((г + 1)/(г — 1)) = \оц (A + хI{\ — х)) + 1п9 если г
стремится к х снизу. Отсюда следует, что
-^1
Другое доказательство этой леммы, без использования тео
рии функций комплексного переменного, описано в упр. 10.
12 Хайрер Э. и др.

354 Гл. III. Многошаговые методы и общие линейные методы
Доказательство теоремы 3.5. Подставив в C.18) ряд C.19],
получим
= многочлен (г) + йгГ1 + <!&-* + О (г~3), C.21)
где
их = —\лга0 — р8а2 — Рба4 —• ...
<*а = —IV*! — М^з — РЛ — ... C.22)
Из леммы 3.6 и положительности [д>;- (лемма 3.8) следует, что в фор-
формулах для йг и Л2 все слагаемые имеют один и тот же знак. По-
Поскольку пъ-х Ф О, для четных к выполняется неравенство Лг Ф О,
а для к нечетных йх Ф 0. Тогда первые два ограничения теоремы
3.5 — это прямое следствие формулы C.18).
И наконец, при $к/ак < 0 докажем неравенство р < к: пред-
предположим противное, т. е. что порядок больше к. Тогда по формуле
C.18) многочлен «5 (г) равен главному члену разложения # (г)х
X Aо§ ((г + 1)/(г — I))), что можно записать (подставив р; = 0
при четных /) в виде соотношения
т-2 2

При г = 1 получим
C-23)
В силу формулы C.17) и равенств 5 A) = рь, Я A) = ак доста-
достаточно доказать, что 5 A)_/К A)|> 0. Формула C.19) при 2->1
дает соотношение
оо
а поэтому первое слагаемое в C.23) строго положительно. Не-
Неотрицательность второго слагаемого следует из лемм 3.6 и 3.8. ■
Устойчивые многошаговые методы, достигающие максимально
возможного порядка к + 2, имеют особую структуру.
Теорема 3.9. Устойчивые многошаговые (к-шаговые} методы
порядка к + 2 являются симметричными, т. е.
*$ = — а*-* Р; = Р*-л лри всех ]. C.24)
Замечание. Для симметричных многошаговых методов из оп-
определения следует равенство р @ = — БЛр A/Б). Поскольку ве-

III.3. Устойчивость и первый барьер Далквйста 355
личина 1/& — нуль многочлена р (&), как и &, все корни устой-
устойчивых симметричных многошаговых методов лежат на единичной
окружности и являются простыми.
Доказательство. При сравнении формул C.18) и C.21) видно,
что йг = О — необходимое условие порядка к + 2. При предпо-
предположении об устойчивости метода из леммы 3.6 следует, что все
четные коэффициенты # (г) равны нулю. Поэтому к четйо, а # (г)
удовлетворяет соотношению 7? (г) = —7? (—г). По определению
Я (г) оно эквивалентно равенству р (^) = —&р A/^), которое и
дает первое условие из C.24). С помощью указанного соотноше-
соотношения для # (г) из формулы C.18) получим равенство 5 (г) —
— 5 (—г) = О (B/гJ), которое означает, что 5 (г) = 5 (—г). Пре-
Преобразовав последнее соотношение к эквивалентному виду в тер-
терминах а (&), придем ко второму условию из C.24). ■
Упражнения
1. Рассмотрим линейное разностное уравнение C.6) с характери-
характеристическим многочленом
Пусть р (I) имеет различные корни ^, ..., &, а /П/ >- 1 — крат-
кратность корня С;. Покажите, что при 1 •</<!/, 1 •< I <1 Щ — 1
последовательности
п>0
образуют систему к линейно независимых решений уравнения
C.6).
2. Покажите, что все корни многочлена р (г), заданного формулой
C.11), за исключением простого нулевого корня, принадле-
принадлежат кольцу
Указание. Используйте лемму, которую можно найти в работе
Мардена A966): если все коэффициенты многочлена акгк +
+ ^а-1^" + ...+ а0 — вещественные и положительные, то
его корни лежат в кольце рх <! | г \ -< ра, где
(/) а р2= тах (/)
3. Примените лемму из предыдущего примера к многочлену
р (С)/(& — 1) и покажите, что ФДН-формулы устойчивы при
к = 1, 2, 3, 4.
12*

356
Гл. III. Многошаговые методы и общие линейные методы
4. Дайте отличное от приведенного выше доказательство теоремы
3.4, применив к многочлену
C-25)
критерий Шура—Кона [см., например, книгу Мардена A966),
гл. XI. Для заданного многочлена с вещественными коэффи-
коэффициентами
/ (г) = ао + агг + ... + акгк
рассмотрим коэффициенты а\*\ определяемые формулами
а также произведения
Рг =
_| при
, ..., к,
= 0, ..., /г — / —
C.26)
при /=1, ..., *—1; C.27)
Затем обозначим через л число отрицательных, а через р — по-
положительных элементов среди Ри ..., Рк. Тогда /(г) имеет
не менее п нулей внутри круга единичного радиуса и не ме-
менее р нулей вне этого круга.
а) Докажите следующие формулы для коэффициентов много-
многочлена C.25):
к
21 ь(к— 1)
—* аг = —Ь$ 02= 4 '
*в1 C.28)
и (и п *
1
Ь) Проверьте, что коэффициенты а<*> из C.26) имеют такие знаки,
как в табл. 3.1. Для к < 13 эти громоздкие расчеты можно вы-
Таблица 3.1. Знаки а
к
1-
1 =
/=
1
з
4
б
2
0
3
+
0
4
+
0
8
+
-|.
0
б
+
+
7
+
8
+
—*
0 10 11 12 13 >13
+ + + + + +
4* + + + —• —*

III.3. Устойчивость и первый барьер Далквиста 357
полнить на ЭВМ, используя при этом язык символьных пре-
преобразований, чтобы избежать погрешностей округления. Для
всех к > 2 легко проверить неравенства ао1) > 0 и Оо2) > 0.
Чтобы установить соотношение а^3) = (ао2)J — (^~гJ < 0 для
к ^ 13 рассмотрите выражение
-1)Ч222 = а{01) [а\ -а\ -а01ак„21 + а21а*|] -
— |а^! |(а0-Ыа |)(|а^ | + <и),
которое можно записать в виде (а0 + | ак |) ф (к), где
ф(А) = (яо — \аиI) (яо — аь — ао]ак-2\ + а2\ак\) —
3 2 / к . 1 ^ 1
~ Я0 - а0 ^ + +
к—\ (^-
к*
Покажите, что <р A3) < 0, а с ростом к (к^ 13) ф монотонно
убывает (заметим, что а0 = а0 (к) действительно зависит от к
и а0 (к + 1) = а0 (&) + 1/(й + 1)). И наконец, из отрицатель-
отрицательности C.29) выведите неравенство а{03) <0 при й>13.
с) Используйте табл. 3.1 и критерий Шура—Кона для про-
проверки теоремы 3.4.
5. (Многошаговые методы максимального порядка.] Проверьте
следующие утверждения:
а) не существует й-шаговых методов порядка 2к + 1;
Ь) существует единственный (неявный)- ^-шаговый метод по-
порядка 2к\
с) существует единственный явный й-шаговый метод порядка
2к—\.
6. Докажите, что симметричные многошаговые методы всегда
имеют четный порядок. Уточним формулировку: если сим-
симметричный многошаговый метод имеет порядок 25 — 1, то
в действительности это также метод порядка 25.
7. Покажите, что следующие многочлены описывают все устойчи-
устойчивые 4-шаговые методы 6-го порядка:
Р (9 = (Р - 1) (Р + 2|хС + 1$, ||»|< 1,
-1- (8 + 38ц) С2.

358 Гл. III. Многошаговые методы и общие линейные методы
Подсчитайте константу погрешности и убедитесь3 что ее нельзя
сделать произвольно малой.
Ответ. С = — A6 — 5ц,)/G560 A + [*)).
8. Докажите следующие оценки для константы погрешности:
а) для устойчивых методов порядка к + 2
Ь) для устойчивых методов порядка к + 1 при нечетных к
С < - 2-*щ;
с) для устойчивых явных методов порядка к ((Лу = 0 при
четных /)
Покажите, что все эти оценки оптимальны.
Указание. Сравните формулы C.18) и C.21) и используйте
соотношение а A) = 2к^1акт.1 из леммы 3.6.
9. Коэффициенты \^^>^ из формулы C.19) удовлетворяют рекур-
рекуррентному соотношению
—1^ + + Р
Первые из этих коэффициентов имеют следующие числовые
значения:
I 2 ,22 214
~~ 14175 # .
10. Другой способ доказательства леммы 3.8. Умножив равенство
C.30) на B/ + 3) и вычитая из него такую же формулу, но
с заменой / на / — 19 получим
B/ + 3)
Покажите, что выражение в скобках является отрицатель-
отрицательным, и по индукции докажите утверждение леммы 3.8.

Ш.4. Сходимость многошаговых методов
«...Метод Адамса значительно превосходит любой
другой метод. И если применение его не стало в до-
достаточной мере всеобщим (особенно в Германии, где
более популярны методы, которые развили Рунге,
Хойн и Кутта), то причина этого, возможно, в том,
что до сих пор отсутствовало дельное исследование
точности интегрирования по Адамсу. Этот пробел
мы хотим здесь восполнить...»
(Р. фон Мизес, 1930)
Сходимость методов Адамса исследована фон Мизесом A930)
в его основополагающей статье, за которой последовал целый
поток публикаций, где улучшались оценки погрешности или из-
изложенные в этой статье идеи применялись к другим отдельным мно-
многошаговым методам, как, например, в работах Толлмина A938),
Фрике A949), Вайсингера A950), Виториса A953). Однако в общем
случае сходимость методов B.1) первым доказал Далквист A956),
сформулировав ее необходимые и достаточные условия. Подлин-
Подлинное изящество внесли в доказательство идеи Бутчера A966),
основанные на представлении многошаговых методов в форме
одношаговых, но в пространстве большей размерности. Кроме того,
такое представление можно легко распространить на более об-
общий класс методов численного интегрирования (см. разд. III.8).
Мы не-можем надеяться на разумные результаты по сходимости
численных методов, если задача
У' = /(*, </), У(*о) = Уо D.1)
не будет иметь единственное решение. Поэтому сделаем следую-
следующие предположения, естественные в нашем случае, как это видно
из разд. 1.7 и 1.9:
функция / непрерывна на множестве
# = \(х, У); *€ [*0. Н \У(х) — у\)
где через у (х) обозначено точное решение задачи D.1),
а Ь — некоторое положительное число. D.2а)
Кроме того, / удовлетворяет условию Липшица | / (х, у) —
- / (х, г) ||< 11| у - г 1 при (*, у), (*, г)$й. D.2Ь)
Если мы применим к-задаче D.1) многошаговый метод B.1)
с шагом к, то получим последовательность \уг\. Для заданных х

360 Гл. III. Многошаговые методы и общие линейные методы
и А, таких что (х — хо)/Н = п — целое число, введем следующее
обозначение численного решения:
Уь (*) = Упу если х — х0 = пН. D.3)
Предполагается, что многошаговый метод — «хороший» в смысле
сходимости численного решения ун (х) к точному решению у (х)
при к -> 0. Кроме того, мы надеемся на быструю сходимость
в случае, когда функция / является более гладкой, чем преду-
предусмотрено условиями D.2).
Определение 4.1. (Сходимость)
1) Линейный многошаговый метод B.1) называется сходящимся,
если для всех задач Коши D.1), удовлетворяющих требованиям
D.2),
У (х) — Уь (х) -> 0 при к -> 0, х $ [х0, к ],
при условии, что для стартовых значений выполняется соотно-
соотношение
У (х0 + 1к) — ун (х0 + Щ -> 0 при А -> 0, I = 0, 1, ..., к — 1.
и) Метод B.1) сходится с порядком р, если для любой задачи
D.1) с достаточно гладкой функцией / существует положительное Но$
такое, что
\в(х)-Вь(х)\<СН' при
и стартовых значениях, отвечающих неравенству
В (х0 + Щ - ук (х0 + й}|< С
при к < й0, 1 = 0, 1, ..., к — 1.
Очевидно, что в этом определении мы предполагаем существование
решения задачи D.1) на [х0, Л].
В данном разделе мы ставим цель доказать, что устойчивость
совместно с согласованностью являются необходимым и достаточ-
достаточным условием сходимости многошагового метода. Это выражается
знаменитой формулой
сходимость = устойчивость + согласованность
[сравните также с работой Лакса—Рихтмайера A956I. Начнем
с изучения необходимых условий сходимости.
Теорема 4.2. Если многошаговый метод B.1) сходится, то
он обязательно является:
V) устойчивым и
и) согласованным (т. е. имеет первый порядок:
р A) = 0, р* A) = а A)).

III.4. Сходимость многошаговых методов 361
Доказательство. Применение многошагового метода B.1) к
дифференциальному уравнению у' = 0, у @) = 0 дает разностное
уравнение C.6). Предположим противное, т. е, что р (?) имеет
корень Еь модуль которого |?х|>1, или кратный корень &2
на единичной окружности. Тогда 1Ц и пХя будут расходящимися
решениями C.6). Умножив стартовые значения на >/71,,мы добь-
добьемся их сходимости к у0 = 0 при Н -> 0. Решения уп (х) = у^Н^***
и Уь (*)=(*/У^) %2/Ь останутся при этом расходящимися при лю-
любом фиксированном х, что противоречит предположению о схо-
сходимости. Поэтому метод B.1) должен быть устойчивым.
Теперь рассмотрим задачу Коши у' = 0, у @) = 1 с точным
решением у {х) = 1. Ей также соответствует разностное уравнение
C.6), которое в новых обозначениях имеет вид
Щ + а^уь(х + (Л - 1)й) + ... +<*оУк(х) = 0.
При подстановке Н -> 0 из сходимости сразу следует, что р A) = 0.
И наконец, применим метод B.1) к задаче у' = 1, у @) == 0.
Ее точное решение у {х) = х. Поскольку мы уже установили
равенство р A) = 0, легко проверить, что частное решение раз-
разностного уравнения имеет вид уп = пНК, или ун (х) = хК, где
К = о A)/р' A). Для сходимости необходимо, чтобы выполнялось
равенство К = 1. ■
Примечательно, что, хотя теорема 4.2 доказывается с помощью
почти тривиальных дифференциальных уравнений, условия 1)
и и) окажутся не только необходимыми, но и достаточными для
сходимости.
Представление в виде одношагового метода
Для дальнейшего изложения полезно переписать многошаго-
многошаговый метод как одношаговый, но в пространстве большей размер-
размерности [см. работы Бутчера A966),Скила A976)]. Для этого введем
величину ф = ф (хи уь ..., уг+к^19 А), неявно определяемую урав-
уравнением
♦ = 2 Р// & + \К У1+1) + Р^ хг + кН, Щ - 2 щу1М , D.4)
где а) = а//ай, р/ = Р//ал. Тогда многошаговую формулу B.1)
можно представить в виде
= — 2

362
Гл. III. Многошаговые методы и общие линейные методы
Введем векторы размерности тк (т
ференциальных уравнений)
размерность системы диф-
дифО,
D.6)
и
1
—2 • • •
0 ...
1
1
0
0
0
. ех =
1
0
0
0
D.7)
и, добавив ряд тривиальных тождеств, запишем многошаговый
метод D.5) в компактной форме
где
Ум = (Л ® /) Уг + НФ (хи Ги А), I > 0, D.8)
Ф(хь Уи к) = (ег ® /)*(дг„ Г„ К). D.8а)
Здесь через Л ® / обозначено тензорное произведение Кронекера,
т. е. блочная матрица размерности тк, с (т, т)-блоками а^/.
Читатели, не знакомые с обозначением и свойствами этого произ-
произведения, могут для простоты считать D.1) скалярным уравнением
(т = 1) и Л ® / = Л.
Следующие леммы показывают, как в этих новых обозначениях
выражаются понятия порядка и устойчивости.
Лемма 4.3. Пусть у {х) — точное решение задачи {4.1). Для
г = 0, 1, ... определим вектор У1+1 численного решения после
одного шага
?м = (Л ® /) У (хг) + НФ (*„ Г (*,), К)
с точными стартовыми значениями
I) 5сла многошаговый метод B.1) имеет первый порядок, а /
удовлетворяет условиям D.2), то существует /г0 > 0, такое что
для Н <; Ао
I К (**+!) - ?|+11| < Лео (Л), 0 < I < Л/А -
где со (Л) -> 0 пры Л -> 0.
II) 5слм многошаговый метод B.1) имеет порядок р, а / ф
ференцируема достаточное число раз, то существует постоянная
М, такая что для всех достаточно малых Н
0

IIIА. Сходимость многошаговых методов
363
Доказательство. По определению 2.1 первая компонента век-
тора У (х1+1) — У иг и является локальной погрешностью. По-
Поскольку остальные компоненты равны нулю, из упражнения 5
в разд. III.2 и определения 2.3 следует утверждение теоремы. ■
Лемма 4.4. Предположим, что многошаговый метод B.1) ус-
тойчив. Тогда существует векторная норма (в Рт*)? такая что
матрица А из D.7) удовлетворяет соотношению
в подчиненной матричной норме.
Доказательство. Если % — корень многочлена р (^), то
(Л^1, %к~2> ..., 1) является собственным вектором матрицы А}
соответствующим собственному числу %. Поэтому собственные чи-
числа матрицы А (т. е. корни р (%)) удовлетворяют корневому ус-
условию из определения 3.2. Следовательно, ее каноническая жорда-
нова форма имеет вид (см. разд. 1.12):
о
О
4-1
D.9)
где %ъ ..., %1—собственные числа, которые равны по модулю
единице и должны быть простыми. Теперь, умножив столбцы
матрицы Т на соответствующие числа, установим, что | е^ | <
< 1 — | %; | при / = / + 1, ..., к — 1. Тогда в силу (9.1Г)
из гл. I выполняется неравенство | У ® /]«><! 1. С помощью
преобразования Т из D.9) определим норму \х\: = \(Т-г ® /) х
Итак, получим
П(А <Ъ\ 1\ у II II (Т~1 ^ /\ (Л ^ Л у II \\{ 1 &\ 1\ ^Т-1
^/1 у^у I ) Л — || ^1 ^ I I ^/1 У^У I ) Л ||оо — | ^*» ^у 2 ) \1
а следовательно, | А ® /1|<; 1.
Доказательство сходимости
Теперь можно доказать теорему о сходимости Многошаговых
методов.
Теорема 4.5. Если многошаговый метод B.1) устойчив и имеет
первый порядок, то он сходится. Если метод B.1) устойчив и
имеет порядок р9 то он сходится с порядком р.

364
Гл. III. Многошаговые методы и общие линейные методы
Доказательство. Как и в теореме о сходимости одношаговых
методов (разд. II.3), мы можем считать без ограничения общности,
что функция / (л:, у) определена для всех у ^ Кт, х а [х0, Л] и
удовлетворяет на этом множестве (глобальному) условию Лип-
Липшица. Отсюда следует, что при достаточно малых Н для функций
\|) (хг, У и Н) и Ф (хи Угу К) выполняется условие Липшица по
второму аргументу (с константой Липшица /,*). Поэтому для С —
Рис. 4.1. Веер леди Уиндермир для многошаговых методов.
функции перехода от вектора Уь к Уии заданной формулой D.8),
из леммы 4.4 получим
|С(У^) — 0B^)||^A +НЬ*)\\У1 — 2г|. D.10)
Далее доказательство проводится так же, как для одношаговых
методов, а его иллюстрация представлена на рис. 4.1. Здесь стрел-
стрелки указывают на действие С. Из леммы 4.3 известно, что || У (хг+1 —
— С (У (л^)) || <! Лео (к). Это соотношение совместно с D.10) по-
показывает, что локальная погрешность У {хи1) — О (У (я*)) этапа
1+1 на этапе т дает погрешность, не превосходящую Лоо (к) X
X A + Л1*)™-Н-1. Таким образом,
(Л) [A
У (*<>) — У о || ехр (ткЬ*) + ^' (ехр (ткЬ*) — 1).
D.11)
Сходимость метода B.1) является прямым следствием формулы
D.11). Если многошаговый метод имеет порядок р, то сходимость
с порядком р доказывается точно так же, но с заменой со (к) на
МкР. Ш

II 1.4. Сходимость многошаговых методов
365
Упражнения
1. Рассмотрим функцию (при х ]> 0)
!(*, У) =
2х -,
0<у<х2,
— 2х, у > х2.
а) Покажите, что у (х) = х2/3 — единственное решение задачи
у' = / (я, у), у @) = 0, хотя / и не удовлетворяет условию
Липшица в окрестности начала координат.
Ь) Примените к этой задаче правило средней точки B.2') со
стартовыми значениями у0 = 0, у1 = —к2 и проверьте, что чис-
численное решение в точке х = пН имеет вид уь {х) = (—1)пх2
(см. книгу Григорьева A977)). '
2. Другое обоснование выбора константы погрешности: предполо-
предположим, что 1 — единственное собственное значение матрицы А
из D.7), равное по модулю единице. Покажите, что ему соответ-
соответствуют правый собственный вектор A, 1, ..., 1)г и левый соб-
собственный вектор A, 1 + а^-ь 1 + с4_г + О Т
глобальный вклад локальной погрешности
числа шагов равен
^-г, -О- Тогда
после большого
г>
п \
1
D.12)
Умножив это уравнение слева на левый собственный вектор,
покажите, что с учетом B.6) С будет константой погрешности,
определенной с помощью B.13).
Замечание. Для многошаговых методов с несколькими собствен-
собственными значениями, равными по модулю 1,э формула D.12) также
верна, но с заменой А°° на Е (см. разд. Ш.8).

III.5. Многошаговые методы с переменным шагом
«Это был крепкий орешек ...1
(Тирольское присловье)
Из разд. П.4 становится понятно, что в эффективной программе
численного интегрирования должно быть предусмотрено изменение
величины шага. Однако в случае многошаговых методов эта про-
процедура вызывает затруднения, так как формулы из предыдущих
разделов требуют значений численного решения в равноотстоящих
точках. Принципиально существуют две возможности преодоле-
преодоления этого затруднения:
О воспроизведение стартовых значений на новой (равномер-
(равномерной) сетке с помощью интерполяции многочленами;
И) построение методов, приведенных в соответствие узлам не-
неравномерной сетки.
Данный раздел посвящен второму подходу. Исследуем для этого
согласованность, устойчивость и сходимость. Его современная
реализация (стратегия выбора порядка и шага)" будет рассмотрена
в разд. 111.7.
Методы Адамса с переменным шагом
Вероятно, Ф. Ческино A961) первым предложил «гладкий»
переход от шага к к новому шагу еьН. Его идеи развили Форринг-
тон A961), а позднее Крох A969): рассмотрим произвольную сетку
(хп) и обозначим величины шагов через Нп = хп+1 — хп. Будем
считать величины у^ аппроксимирующие у (*у), известными при
/ = л — й + 1, ..., я и введем обозначение }3 = / {х^ У}). Точно
так же, как в разд. III.1, обозначим через р (*) интерполяционный
многочлен, проходящий через точки (Х]9 /;), / = п — к + 1, ..., п.
Используя интерполяционную формулу Ньютона, запишем
E.1)
где разделенные разности I 1хп ..., хп^\ определяются рекур-
рекурсивно:
1 = ^ E.2)
^*П> * * *' Хп~1+1^ — ^ 1хП-1* • • • 9 *п-

111,5. Многошаговые методы с переменным шагом 367
Для практических расчетов формулу E.1) удобно переписать в виде
[см. статью Кроха A969)]
- 2 П ^Х, Ф/ С). E-1')
где
7-1
^1 \п) — 1Х Ип+1 — хп-0 11/*п> • • •» ^п-Я» Ч0*'3;
Теперь определим значение, приближающее у (л:п+1):
*П+1
E.4)
Подставляя в E.4} формулу E.4'), получим
*= Ря + Ля 2 Й (л) Ф/ (л), E.5)
где
E.6)
Л,
71
Формула E.5) — это обобщение явного метода Адамса A.5) на
случай переменного шага. Отметим, что при постоянном шаге
приведенные выше выражения сводятся к следующим (упр. 1):
Подобным образом можно вывести неявные методы Адамса с пере-
переменным шагом. По аналогии с разд. III. 1 обозначим через р* (/)
интерполяционный многочлен степени к, проходящий через точки
(хь /у)» / = л — А ■+• 1, ..., /г, п + 1. (Значение /п+1 =
= / (*п+ь Уп+г) содержит неизвестное решение уп+1-) Снова ис-
используя интерполяционную формулу Ньютона, получим:
' Р* @ = Р @ + П (I — хп^) I [лгп+1, хП9...9 хп-к+1].
Численное решение, определяемое формулой
теперь можно представить в виде
Уп+1 =* Рп+1 + ЛП^А (Л) Фк (П + 1). E.7)

368 Гл. III. Многошаговые методы и общие линейные методы
Здесь рп+1 — приближенное значение решения, полученное с по
мощью явного метода Адамса
Л-1
Ри+1 ^Уп + НпЯё! (П) Ф/ (Л),
/0
а
E-8)
Рекуррентные соотношения для #/ (я), Ф/ (я) и Фу (п)
сЕсли допустить произвольное изменение шага, то
наибольшим недостатком будут затраты на подсчет
коэффициентов метода интегрирования».
(Ф. Т. Крох, 1973)
Значения Ф* (п) (/ = 0, ..., к — 1) и Фк (п + 1) можно эф-
эффективно вычислять с помощью рекуррентных соотношений
Фо (п) = Ф5 (п) = /„,
Фж (п) = Фу (п) - Ф} (л - 1), E.9)
ф; (п) = ру (л) Фу (л),
которые сразу следуют из определений E.3) и E.8). Коэффициент
1=0
можно вычислить по формулам
*П+1 *П-
Х-п Хп—1
Сложнее подсчитать коэффициенты {*] {п) [Ф. Т. Крох A974)].
Введем ц-кратный интеграл
П хп *п
и заметим, что

III.5. Многошаговые методы с переменным шагом 369
Лемма 5.1. Верны следующие равенства:
"" Я '
-1, 9+1
1
Доказательство. Первые два соотношения следуют непосред-
непосредственно из E.10). Для доказательства рекуррентного соотношения
введем разность
Ясно, что ^<о (хп) = 0 при 1 = 0, 1, ..., ц—1. Кроме того,
равна нулю ц-я производная д. (х), так как по правилу Лейбница
хп+1 - хп.ш
Итак, выполняется тождество й (х) = 0, и, подставив в него
* = хп+1, мы придем к утверждению леммы. ■
С помощью последнего рекуррентного соотношения можно
последовательно вычислять с2<? (хп+1) при ^=1, ..., к— 1;
Сзд(хп+1) при ц= 1, ..., & —2;...; сйд (л:п+1) при д= 1. Эта
процедура позволяет эффективно определять коэффициенты
(л) = сп (хп+1) методов Адамса.
Формулы дифференцирования назад
с переменным шагом
ФДН-формулы A.22) также можно обобщить естественным
образом на случай переменного шага. Обозначим через ц (г) ин-
интерполяционный многочлен степени к, проходящий через точки
(хг> Уду I — п + 1, л, ..., п — к + 1. Его можно выразить через
разделенные разности
_<)у[дгп+1, хП9 ..., х^и1]. E.11)

370 Гл. III. Многошаговые методы и общие линейные методы
Требование
Я* (хп+г) = / (хп+г> 0п+1)
сразу приводит к ФДН-формуле о переменным шагом
к 7-1
2 К П (хп+1 — хп+1_г)д[хп+1, ..., хпЧ+1] = Нп!(хп+1, дп+1). E.12)
Вычисление ее коэффициентов намного проще, чем в методах
Адамса.
Многошаговые методы общего вида с переменным шагом
и их порядок согласованности
В теоретических исследованиях методов удобно использовать
их форму записи с линейным вхождением Ц] и /;. Например,
неявный метод Адамса E.7) принимает вид
(C + 2шп) /„+! +
E.13)
где для отношения шагов введено обозначение а>п = л
Или 2-шаговую ФДН-формулу E.12) можно записать в форме
©п)а
1+2юп 9п + 1+2й)п
Чтобы дать единую теорию для всех этих многошаговых методов
с переменным шагом, рассмотрим формулы следующего вида:
к-1 к
9п+к + 2 ^п9п+] = Лп+а-1 И Рм/п+;. E.15)
Коэффициенты а;-п и р^п в действительности зависят от отношений
<йг == Ъц1Н%тЛ% г — п + 1, ..., м + & — 1. По аналогии со слу-
случаем постоянного шага дадим следующее определение.
Определение 5.2. Метод E.15) согласован с порядком р, если
для всех многочленов ц (я), степень которых не превосходит р,
и всех сеток (х^ выполняется равенство
*-1 к
Ц (*п+к) + 23 ауп<7 (^п+у) = Лп+А-1 23 Р./*?' (^71+^).
/М) /=0
По определению явный метод Адамса E.5) имеет порядок к,
неявный метод Адамса E.7) — порядок к + 1, а ФДН-формула
E.12) — порядок к.
Понятие согласованности надо, конечно, связать с локальной
погрешностью. Действительно, если метод имеет порядок р, от-

II 1.5. Многошаговые методы с переменным шагом 371
ношения Н^Нп ограничены при /=л+1|.-.|л + Л — 1 и
коэффициенты
аЗп> Руп ограничены, E.16)
то для достаточно гладких функций у (х) разложение в ряд Тей-
Тейлора приводит к соотношению
Л—I к
у (хп+к) + 2] а!пу (хп+д - Лп+л-1 I] р/я0' (*„+/) - О (Лй+Г). (Б. 17)
/«о /=о
Считая у {х) решением дифференциального уравнения, из триви-
тривиального обобщения леммы 2.2 на переменный шаг получим, что
локальная погрешность в точке хп+к (см. определение 2.1) также
равна 0(крп+{).
По этой причине необходимо изучить условие E.16). Очевидно,
что методы E.13) и E.14) удовлетворяют ему всегда, когда от-
отношение шагов Лп/Лп_1 ограничено' сверху. В общем случае мы
имеем следующий результат.
Лемма 5.3. Для явных и неявных методов Адамса, а также
для ФДН-формул коэффициенты а;п и р^л ограничены, если для
некоторого й выполняется соотношение
К1К-1 <
Доказательство. Приведем доказательство только для явных
методов Адамса. Для остальных методов оно мало отличается от
данного, и поэтому опустим его. Из формулы E.5) видно, что коэф-
коэффициенты <Х;П не зависят от м, а поэтому ограничены. Значения Р;п
состоят из произведений &] (п) на коэффициенты выражения Ф* (м),
записанного в виде линейной комбинации величин /п, ..., /п_/.
Из формулы E.6) следует соотношение I &] {п) \ <^ 1. В силу не-
неравенства хп+1 — хп„и1 < шах A, Й>) (хп — хп„з) по индукции
получим, что коэффициенты выражения Ф/ (я) также ограничены.
Поэтому и р;-п ограничены, что и доказывает лемму. ■
Условие йп/Лп-1 <! й — это вполне разумное требование,
которое легко предусмотреть в программе.
Устойчивость
«Это так просто...»
(Р. Д. Григорьев, семинар в Халле, 1983)
Для методов с переменным шагом изучение устойчивости было
Начато в статьях Гира—Ту A974) и Гира—Ватанабе A974).
Дальнейшие исследования проведены Григорьевым A983) и Крузе
— Лисбоной A984).

372 Гл. III. Многошаговые методы и общие линейные методы
В разд. III. 3 мы увидели, что на равномерных сетках устой-
устойчивость эквивалентна ограниченности численного решения, по-
полученного для скалярного дифференциального уравнения у' = 0.
Сделаем и теперь то же самое, но для более общего случая. При-
Применение метода E.15) к задаче у' = 0 дает разностное уравнение
с переменными коэффициентами
Вводя вектор Уп = (Уп+ь-г •••> Уп)Т) перейдем к эквивалентному
уравнению
сопровождающей матрицей
&П-1, и — а1, п — аО,п
1 0 ... О О
1 О О
1 О
E.18)
Определение 5.4. Метод E.15) называется устойчивым, если
для всех л и />0 выполняется неравенство
^ ..Ап+1Ап ||<М. E.19)
Отметим, что в общем случае Ап зависит от^ отношений шагов
•••> ®п+ь-1- Поэтому условие E.19) обычно будет приводить
к ограничениям на эти величины.
Поскольку у методов Адамса E.5) и E.7) коэффициенты О/Л
не зависят от я, они устойчивы при любой последовательности
шагов.
В следующих трех теоремах мы представим результаты об
устойчивости методов общего вида с переменным шагом. Первая
теорема взята из работы Крузе—Лисбоны A984) и основана на
теории возмущений:, метод с переменным шагом считается воз-
возмущением сильно устойчивого метода с фиксированным шагом.
Теорема 5.5. Пусть метод E.15) обладает следующими свой-
свойствами:
а] порядок р > 0, т. е. 1 + 2] а]п = 0/
Ь) коэффициенты а^п = а,] (а>п+1, ..., (оп+ъ„1) — непрерывные
в окрестности точки A, ..., 1) функции;

III.5. Многошаговые методы с переменным шагом
373
с) соответствующая формула с постоянным шагом сильно устой
чива, т. е. все корни многочлена
к—1
. ■■- 1) С' — О
лежат в открытом круге единичного радиуса | ^ | < 1/ за исклю-
исключением корня ^1=1.
Тогда существуют вещественные числа ©, О (© < 1 < О), такие
что при выполнении условия
метод устойчив.
при всех п
E.20)
Доказательство. Пусть А — сопровождающая матрица фор-
формулы с постоянным шагом. .Как и в доказательстве леммы 4.4,
приведем к канонической жордановой форме
Т-1АТ =
\
где по предположению с) | А |х < 1. Отметим, что стоящий в по-
последнем столбце матрицы Т собственный вектор матрицы А,
соответствующий ее собственному числу 1, равен 1к = A, ..., 1)г.
Из предположения а) следует, что /& является также собственным
вектором и для всех матриц ЛЛ. Поэтому верно равенство
0\
о
"МПГ = Ап
и в силу непрерывности || Ап \г <; 1 при достаточно близких к 1
значениях соп+1, ..., а>п+ь-1- Теперь устойчивость следует из соот-
соотношения
которое приводит к неравенству
Следующий результат [Григорьев A983I основан на сокраще-
сокращении размера матриц Ап на единицу. Идея заключается в исполь-

374
Гл. III. Многошаговые методы и общие линейные методы
зовании преобразования
1 1 1 ... Г
1 1 ... 1
1 ... 1
Т =
0
т-г =
1 —1
1 —1
1 ...
О ... —1
1
Отметим, что в последнем столбце матрицы Т стоит вектор
из предыдущего доказательства. С помощью простых вычислений
получим
... о
г-мпт = | -
1
Здесь бй—в = @, ..., О, 1), а матрица А*п имеет вид
♦ ♦
— &к—24 п — &к—3# п
1
0
1
о
о
о
E.21)
где
*_2# л = 1
.1§ п ~ а^ь п == а^/, „ при / = 2, ..., к — 1.
Заметим, что а*, п совпадают с коэффициентами многочлена, опре-
определяемого следующей формулой:
(С* + а*-Ь "Б*-*4 + • • • + «I. «С + «О, п) =
- (С - 1) (С*-1 + а*_8. пС*-2 + • • • + аГ. «С + «о#. »).
Теорема 5.6. Пусть метод E.15) имеет порядок р > 0.
В ^/пол( случае метод устойчив тогда и только тогда, когда для
всех п и I ^> 0 выполняются условия
а) \\А*п+1 ...
п
Доказательство. С помощью индукции легко показать, что
г-чп+/...лпг =
. . . Ля
о
1
где
Оп%1 =
т ™ " А\.

II 1.5. Многошаговые методы с переменным шагом 375
Поскольку в данной теореме размер рассматриваемых матриц
уменьшается на единицу, она особенно полезна для исследования
устойчивости двухшаговых методов.
Пример. Рассмотрим двухшагдвый ФДН-метод E.14). Здесь
Матрица E.21) в этом случае имеет вид
Л • I * \ л» * _
+ 2<»П+1 *
При | а5л | < ц < 1 выполняются условия теоремы 5.6, из кото-
которых следует устойчивость. Данное соотношение верно, если
имеет место неравенство
Интересным следствием сформулированной теоремы является не-
неустойчивость двухшаговых ФДН-формул в случае, когда величина
шага растет не медленнее, чем определено соотношением
К > 1 + /2.
Исследовать устойчивость Л-шаговых (к ;> 3) методов значи-
значительно сложнее, так как в них входит несколько отношений шагов
Для ФДН-методов высокого порядка Григорьев A983) нашел
следующие оценки вида E.20), обеспечивающие устойчивость:
Таблица 5.1. Оценки E.20) для ^-шаговых
ФДН-формул
к
ш
п
2
0
2.414
0.
1.
3
836
127
4
0.979
1.019
5
0.997
1.003
Эти ограничения, конечно, нереалистичны, так как они включают
все патологические изменения шага.
Менее пессимистичные оценки можно получить, предположив,
что шаг изменяется более гладко [Гир—Ту A974)]: известно, что
локальная погрешность имеет вид д. (хп) Л«+1 + О (Ап+2)> где
й (х) — ее главный член. С помощью управления величиной
шага эта погрешность сохраняется равной значению ТОЬ.
Поэтому, если к (х) находится вне некоторой окрестности нуля,
то выполняется равенство
Ая = IТОЬ/4 (хп) !>/("+») + О (Лп),

376 Гл. III. Многошаговые методы и общие линейные методы
из которого следует (при условии Нп+1Г/Нп ^ О), что
КЛК = I л (хп)/а {хп+1) \^»+1> + о (Нп}.
Если д, (х) дифференцируема, то получим
| К*1К - 11 < СНп. E.22)
На этом предположении основано несколько результатов Гира—Ту
об устойчивости. («Следовательно, мы можем рассчитывать, что
метод будет устойчивым, если устойчив метод с фиксированным
шагом ...»). Суммируя неравенства E.22), получим условие
п+1
Е | **+!№*-1 К С (*-
У
содержащее только отношения шагов. Имеем следующую теорему.
Теорема 5.7. Пусть коэффициенты а}п метода E.15) являются
непрерывно дифференцируемыми функциями от ©п+ь •••» ®п+к-1
в окрестности {(©п+1, ..., ©„+&_!); © < ©^ <С &}, и предположим,
что метод устойчив при постоянных шагах (т. е. при ©; = 1).
Тогда из условия
п+1
Е IЪигШ; — 11<С при всех п и />0 E.23)
совместно с © <^ Лу+1/Л/ ^ Й следует условие устойчивости E.19).
Доказательство. Как и в доказательстве теоремы 5.5, обозна-
обозначим через А сопровождающую матрицу формулы с постоянным
шагом, а через Т соответствующее преобразование, такое что
|| 71-1 А Т | = 1. Применяя теорему о среднем к выражению
а;-(©п+1, ...? ©п+ь-1) — а./0> •••! 1)> придем к соотношению
п+Ь—I
/=+1
Следовательно,
Из этого неравенства выведем, что
Сходимость
Для методов Адамса с переменным шагом сходимость впервые
изучил Пиотровски A969). Для доказательства сходимости в об-
общем виде введем вектор Уп = (уп+к^ ..., уп+1, уп)т> По ана-
аналогии с D.8) метод E.15) приводится к эквивалентному виду:
Уп+1 = (Ап ®1)Уп + К+ъ-1®п (*п, Уп, А»), E.24)

111,5. Многошаговые методы с переменным шагом 377
где матрица Ап задана в E.18), а
Значение 4е = Чп (хп, Уп, Нп) неявно задается соотношением
Л—I / Л—I
Далее обозначим через
У (*п) = (У (*п+м)| • • •> У
точные значения, аппроксимируемые вектором Уп. Теперь теорему
о сходимости можно сформулировать следующим образом.
Теорема 5.8. Предположим, что
а) метод E.15) устойчив, имеет порядок р, а его коэффициенты
Рм ограничены;
Ъ\ для стартовых значений' выполняется условие
с) отношения шагов ограничены ( )
Тогда метод сходится с порядком р, т. е. для любого дифферен
циального уравнения у' = / (х, у), у (х0) = у0 с достаточно глад
кой функцией / глобальная погрешность удовлетворяет соотноше
нию
\\\ при
где Ь = тах
Доказательство. Поскольку метод имеет порядок р, а коэф-
коэффициенты и отношения шагов ограничены, из формулы E.17) видно,
что для локальной погрешности
бп+1 = У (*п+1) - (Ап ®1)У (Хп) - Лп+^Фп (Хп> У (Хп)> К) E.25)
верно соотношение
бЛ+1 = О (А^1). E.26)
Вычитая E.24) из E.25), придем к равенству
У (хп+г) -Уп- (Ап ® /) (У (хп) - Уп)
+ Нп+к-1 \Фп (*п,
откуда по индукции следует
У (хп+1) - Уп+1 = ((Ап... Л о) ® /) (У (х0) - Го) +
п
+ И Ним((Ап...Аи1) ® I)\Ф3(х,, У (х,)> Н,)-
/
/«о
п
, к5)} + 2 ((Ап... Аи1)

378 Гл. III. Многошаговые методы и общие линейные методы
Как и в доказательстве теоремы 4.5, получим, что Фп удовлетво
ряет равномерному условию Липшица по Уп. С учетом устойчи
вости и равенства E.26) выведем отсюда оценку
IУ (*п+1) - Уп+11 < Е Ниъ-гЬ IУ (*/) -У$\ + Схк>.
/О
Для решения этого неравенства введем последовательность \еп}$
определенную следующим образом:
E.27)
= И
По индукции легко показать, что
1И*п)-^п1<еп. E.28)
Из E.27) при п ^ 1 получим соотношение
еп+1 = еп + /гл+А-1^8п < ехр (Нп^^Ь) еп>
а поэтому и неравенство
еп < ехр ((Л — *0) ^) 8х =*
= ехр ((Л - х0) Ц
которое совместно с E.28) и завершает доказательство теоремы
5.8. ■
Упражнения
1. Докажите, что при постоянном шаге выражения #/ (п) и Ф/ (п)
[формулы E.3) и E.6)] сводятся к виду
ё! (п) = 7/, Ф/ (п) = V'/».
где у; определены в A.6).
2. [Григорьев A983I. Для й-шаговых ФДН-методов рассмотрим
сетки с постоянным отношением шагов ®, т. е. Нп = сйА^
при всех п. В этом случае элементы матрицы А*п (см. E.21))
не зависят от п. Покажите с помощью численных расчетов,
что все собственные значения А*п по модулю меньше единицы
при 0 < со < #ку где Кк имеют следующие значения:
к
2 ,
2.414
1
3
.618
I
4
.280
1.
5
127
1
6
.044

III.6. Методы Нордсика
Важные результаты представлены в статье Нордсика A962),
где для обыкновенных дифференциальных уравнений рассматри-
рассматривается класс методов, позволяющих изменять шаг удобным спо-
способом (см. разд. III.7). Уже сам автор указал на то, что его методы
эквивалентны в некотором смысле неявным методам Адамса.
Сначала мы изложим его вывод методов, а затем изучим их связь
с линейными многошаговыми методами.
Нордсик A962) отметил, что «...все методы численного интегри-
интегрирования эквивалентны нахождению многочлена, аппроксимирую-
аппроксимирующего */(*)...». Его идея состоит в том, чтобы представить этот
многочлен через производные от нулевого до к-го порядка вклю-
включительно, т. е. е помощью вектора («вектора Нордсика*)
Величины у{Р имеют смысл приближенных значений для уИ) (хп),
где у (х) — точное решение дифференциального уравнения
У' в / (*, у). F.2)
Чтобы определить процедуру интегрирования, необходимо задать
правило нахождения гп+1 по известным гп и дифференциальному
уравнению F.2). При использовании разложения в ряд Тейлора
(например, при к = 3) такое правило имеет вид
куп+1 = Нуп + 2 -^т-уп + 3-^-т-уп + 4-гтв,
21 31 41 F.3)
1 ;
где значение е выбирается таким образом, чтобы выполнялось ра-
равенство
F.4)
Подставляя F.4) во второе соотношение из F.3), получим
4 -ц- е — к (/ (д:п+1, ^„+0 — /2), F.5)

380
Гл. III. Многошаговые методы и общие линейные метода
Н* т
где
Н!Рп = Нуп + 2^Гуяп + 3^
С учетом этого выражения для е метод принимает вид
к9 » , I /г / ч *р\
Л*
к*
3 ур уп + Л (/ (хя+ь
(б.б)
ил ш. о.
л + А (/ (-^л+Ь Ул+0 — /л).
31
Первое уравнение — неявное относительно уп+1, а остальные —
явные. Отметим, что если величины у]!* достаточно точно аппрок-
аппроксимируют уМ (хп), то значение е [формула F.5I аппроксимирует
У[А) (хп)- С точки зрения точности это свойство выглядит привле-
привлекательно. Но, к сожалению, метод F.6) является неустойчивым.
Чтобы показать это, подставим в F.6) / (я, у) = 0. В этом слу-
случае метод обращается в линейное преобразование
2 « = М? (К 7)
с матрицей
@ 1 2 3).
/1
0
0
1
1
0
0
1
2
1
0
1\
3
3
V
/174\
1 ! 1
- 3/2
Видно, что собственные значения М равны 1, 0, — B + */3) и
—1/B + у^З), откуда следует неустойчивость метода F.6), а
поэтому и его практическая непригодность. С часто встречающим-
встречающимся явлением неустойчивости методов высокой точности мы уже
столкнулись в разд. III.3.
Чтобы преодолеть указанную трудность, Нордсик предложил
заменить постоянные 1/4, 1, 3/2, 1, стоящие в F.6) перед скобками,
на произвольные значения (/0, 1и /а, /8) и использовать эту до-
дополнительную степень свободы для достижения устойчивости.
Такую модификацию можно записать в компактной форме:
= (Р ® /) гп + (I ® /) (А/ (х„+ь Уп+г) - (вхР ® /) *„). F.8)
Здесь гп задано в F.1), Р — треугольная матрица Паскаля, опре-

Ш.6. Методы Нордсика 381
деляемая формулой
в противном случае,
I = (А>> к, •••* 1н)т> а е1 — @» 1, 0,....* 0)г. Отметим, что ин-
индексы векторов и матриц начинаются с нуля.
Для простоты обозначений в следующих теоремах будем далее
рассматривать только скалярные дифференциальные уравнения,
для которых метод F.8) принимает вид
= Р*п + I Шп+1 - е\Ргп\ F.8')
Конечно, все результаты остаются верными и для систем уравне-
уравнений. Условие F.4), связывающее этот метод с дифференциальным
уравнением, фиксирует значение .
*1=1. F.9)
Анализируя описанным выше способом устойчивость метода об-
общего вида F.8), мы придем к разностному уравнению F.7) с мат-
матрицей
М = Р — 1етР F \0)
Например, при к = 3 эта матрица имеет вид
/1 1-/0 1 — 2/0 1-3/0\
0 0 0 0
0 —12 1 — 2/3 3-3/а
\0 —18 — 2/8 1 —3/3/
Заметим, что 1 и 0 являются собственными значениями матрицы
Му а ее характеристический многочлен не зависит от /0. Нордсик
определил /2, ...} 1к таким образом, чтобы остальные собственные
значения М были равны нулю. В случае к = 3 это выполняется
при /2 = 3/4, /3 = 1/6- Коэффициент /0 можно выбрать из условия
обращения в нуль константы погрешности метода (см. далее тео-
теорему 6.2). В нашем случае получается /0 = 3/8, а весь метод зада-
задается вектором
-(± 1 ±
- V 8 •1э 4
» б; •
Интересно отметить, что этот метод эквивалентен неявному 3-ша-
говому методу Адамса. Действительно, исключая с помощью
формулы F.8) с уменьшенными индексами члены (й3/31) у"п и
(Н2121) у"п, придем к методу [см. формулу A.8*)]
24
* №уп+1 +19уп— 5#;_1 + Уп-й- F.

382 Гл. III. Многошаговые методы и общие линейные методы
Эквивалентность многошаговым методам
Работы Деклу A963), Осборна A966) и Скила A978) позволяют
глубже понять связь между методами Нордсика и многошаговыми
методами. Следующие две теоремы показывают, что любой метод
Нордсика эквивалентен некоторой многошаговой формуле и имеет
порядок не ниже к.
Теорема 6.1. Рассмотрим метод Нордсика F.8) с коэффициен-
коэффициентом 1г = 1. Тогда первые две компоненты вектора гп удовлетворяют
линейной многошаговой формуле (при п ^> 0)
к к
Е «0П+1 - А Е Р|/ь+1. FЛ2)
^0 ^0
где производящие многочлены имеют вид
р (О » A4 (у - Р) е[ {II
о (С) = Ы (С/ - Р) е\ (Ц - Р) /.
Доказательство. Приведенное в самих указанных статьях
доказательство значительно упрощается при использовании произ-
производящих функций (дискретное преобразование Лапласа):
(С) = 2
Умножив формулу F.8') на ^п+1 и проведя суммирование, получим
1 @ = ЪР2 (I) + I (НР @ - е\Р12 @) + (г0 - Й/о). F.14)
Подобным образом линейный многошаговый метод можно перепи-
переписать в виде
р (?) У (С) = Нб (С) Р (I) + ръ-г Ш, F.15)
где
р (?) = 1к9 A/0, & (С) = С*а A/0, F.16)
а Рй_х — многочлен степени к — 1, зависящий от стартовых зна-
значений. Для доказательства теоремы надо показать, что первые две
компоненты 2 (&) удовлетворяют соотношению вида F.15). Сна-
Сначала перепишем уравнение F.14):
' 2 @ = (/ - ЪРУ* I {НР (I) - е[РЦ (I)) +
+ (/ - СР)-1 (г0 - /А/о),
При этом первые две компоненты 2 (^) примут вид
V (I) = е\ A - ^Р)-1 / (А/7 (С) - еГР^ @) + е1 (/ - ^Р) (г0
нр к) = ^ (/ - ^р)-1 / {нр «) - «гр» (о)+*г

II 1.6. Методы Нордсика
383
Теперь, сокращая стоящие в скобках члены и умножая равенство
на Aе1 (/—?Р), мы придем к формуле F.15) с многочленами
б (С) =
F.17)
С помощью F.16) мы сразу получим формулы F.13). Итак, оста-
остается показать, что многочлен рк_г в F.17) имеет степень к— 1.
Поскольку Р — матрица размера (к + 1) X {к + 1), многочлен
Рк-г *при | ^ | —>- оо ведет себя как ^к'1. И наконец, из соотноше-
соотношения F.15) следует, что ряд Лорана для рА-1 не может содержать
членов с отрицательными степенями. ■
Подставляя в F.13) (^/ —Р)"*1/ = и и применяя к линейной
системе (^/ — Р) и = / правило Крамера, из F.13) получим изящ-
изящное выражение
Р @ = Aе*
— 1 г0
О 1г
о /а
— 1
—2
— 1
— 11
1 К
о E) =
о к о
/ 1 1
Б-1 -2
С-1
F.13а)
1
*
и о
о
F.13Ь)
Заметим, что р (^) не зависит от 10. Кроме того, ^0 = 1 является
простым корнем р (С) тогда и только тогда, когда 1ъ Ф 0. Вы-
Выполняется соотношение
р' A) = о A) = к\ 1к. F.18)
Условие F.9) эквивалентно равенству ак = 1.
Теорема 6.2. Пусть 1к Ф 0. Определенный в F.13) многошаго-
многошаговый метод имеет порядок не ниже й, а его константа погрешности

384 Гл. III. Многошаговые методы и общие линейные методы
(см. B.13)) вычисляется по формуле
Здесь компоненты вектора
ЬТ = (Во, &ъ •••> Вк) = A» 2"! -§-» 0, —25", 0, -^-, ... 1
являются числами Бернулли.
Доказательство. По теореме 2.4 порядок равен к тогда и только
тогда, когда
С учетом равенства ее* (С/ — Р) = (С — 1)*+1 это условие эк-
эквивалентно условию
е! (С/ - РГ11 - \оё С • еоГ Й/ - -Р) * - См + О ((С - 1)),
а в силу F.18) достаточно показать, что
(\о&^е1 - вГ) (С/~ РГ1 = Ьг + О(« ~ 1)). F.19)
Обозначив левую часть равенства F.19) через ЬТ (^), получим
(V - Р)ТЪ (I) - Aо§ $.е0 - ег). F.20)
В этой системе ^-е уравнение (ц >- 2)
эквивалентно уравнению
(О V ^ (СI
которое является произведением Коши. Поэтому формулу F.20)
можно переписать в виде
откуда следует, что
У^Ь (Г)

Если в эту формулу подставить С в 1» то получим равенство

Ш.6. Методы Нордсика 385
которое означает, что Ья A) = Вч, где Вя — <7"е число Бернулли
(см. книгу Абрамовица и Стиган, гл. 23).
Таким образом, мы показали, что любому методу Нордсика
F.8) соответствует линейный многошаговый метод, имеющий
порядок не ниже к. Следующая наша задача — установить соот-
соответствие в обратном направлении.
Теорема 6.3. Пусть (р, а) являются производящими много-
многочленами к-шагового метода F.12), имеющего порядок не ниже й,
и предположим, что ак = 1. Тогда:
а) существует единственный вектор I, такой что р и о опреде-
определяются формулами F.13);
Ь) если, кроме того, многошаговый метод неприводим, то сущест-
существует невырожденное преобразование Т, при котором решения си-
систем F.8') и F.12) связаны соотношением
гп - Т-Чп, F.21)
где /-я компонента вектора ип вычисляется по формулам
( У
1шЛ х^к-З+гУп+Ь *ФЬ-./+*/п+и При V -^ / -^ К 1| ,« ооч
Ып При / = &.
Доказательство, а) Для любого многошагового метода порядка
к многочлен р (^) однозначно определяется по о (%) (см. теорему
2.4). Разлагая определитель из F.13Ь) по первому столбцу, по-
получим
где Г; (^) — многочлен степени /\ отвечающий условию Гу A) Ф 0.
Следовательно, / можно найти из о (^).
Ь) Пусть у0, ..., #ь-1 и /0, ..., /ь_1 заданы. Тогда многочлен
Рк-г Ш в F.15) удовлетворяет равенству
С другой стороны, если для метода Нордсика известен стартовый
вектор 20, вычисленный при значении / из утверждения а), то
Рк-г @ определяется формулой F.17). Приравнивая оба выра-
выражения, получим
{№ = (Р @ *Ъ - * (I) е\) (I - &Г1 г0. F.23)
т
Теперь обозначим через </ (/ = 0, ...» к — 1) коэффициенты век-
векторного многочлена
(р (С) е1 - д (С) е\) (I - &Г1 = 2 № F.24)
/о
2
/«о
13 Хайрер Э- и др.

386
Гл. III. Многошаговые методы и общие линейные методы
т т
и возьмем 1ь = е\. Затем выберем в качестве Т квадратную мат-
рицу, у которой /-й столбец равен 1\, а поэтому и0 = Тг0 вслед-
вслед() Н} к П /
п,
ствие F.23) и Н!п = Ну к. Проводя для уп, ..., уп+к-г и /7
..., 1п+к-1 те же рассуждения, что и для у0, ..., укшт1, придем к ра-
равенству ип = Тгп для всех п.
Для завершения доказательства остается лишь проверить
невырожденность Т. Пусть вектор V = (о0, ух, ..., оЛ)г отличен
от нулевого и удовлетворяет равенству Ть = 0. По определению II
имеет место равенство ьх = 0, и из F.24) следует (с учетом пре-
преобразования F.16)), что
Р @ *о (9 = о (С) ф1 (С), F.25)
где 1?| (С) = йе! (^/ — Р) е] (Ц — Р)*~гю — многочлены, степень
которых не превосходит к. Более того, из правила Крамера сле-
следует, что степень %г (I) не превосходит к— 1, V! = 0. Поэтому
в силу F.25) по крайней мере один из корней р (^) должен быть кор-
корнем а (^), что противоречит предположению о неприводимости ме-
метода.
В таблицах 6.1 и 6.2 даны векторы I, соответствующие неяв-
неявным методам Адамса и ФДН-методам. Для этих двух классов ме-
методов мы более подробно исследуем их эквивалентность.
Таблица 6.1. Коэффициенты /у 6-шаговых
неявных методов Адамса
к = 1
гС ~~~ О
к= 4
к = 5
и а
к — О
/о
1/2
5/12
3/8
251/720
95/288
19 087/60 480
к
1
1
1
1
1
1
и
1/2
3/4
11/12
25/24
137/120
и
1/6
1/3
35/72
5/8
и
1/24
5/48
17/96
и
1/120
1/40
и
1/720
Таблица 6.2. Коэффициенты /^
к= 1
к == 2
и о
к — о
к= 4
к= 6
/о
1
2/3
6/11
12/25
60/137
20/49
1
1
1
1
1
1
/я
1/3
6/11
7/10
225/274
58/63
«-шаговых ФДН-методов
и
1/11
1/5
85/274
5/12
и
1/50
15/274
25/252
/в
1/274
1/84
и
1/1764

Ш.6. Методы Нордсика 387
Неявные методы Адамса
Следующие результаты принадлежат Бирну и Хайндмаршу
A975). Поскольку их «эффективный пакет» ЕР15ОВЕ основан на
представлении Нордсика для методов с переменным шагом, мы
включили в рассмотрение и этот случай. Методы Адамса естествен-
естественным образом определяют многочлен, аппроксимирующий неиз-
неизвестное решение уравнения F.2), а именно: при заданных уп
и /п» •••> !п-ш й-шаговый метод Адамса эквивалентен построе-
построению многочлена рп+х (х) степени к + 1» удовлетворяющего сле-
следующим условиям:
Рп+1 (хп) = Ут Рп+1 (хп+г) = Уп+и .д 9
при / = я — к+и п+1 * # '
Условие F.26) определяет уп+1 неявно. Заметим, что разность
между двумя последовательными многочленами рп+1 (х) — рп (х)
обращается в нуль в точке хп, а ее производная — в точках
•••» Хп- Поэтому, вводя обозначение еп+1 = уп+1 —
п (Хп+г), мы можем записать эту "разность в.виде
- рп (х) - Л (|^^) еп+и F.27)
где Л — единственный многочлен степени к + 1, определяемый
следующими условиями:
Л@) = 1, Л (—1) — О,
F'28)
- 0 при / = /г - & + 1, ..., п.
Подставив в производную выражения F.27) значение х = хп+1,
мы увидим, что при Нп = #п+1 — хп выполняется соотношение
Лп/п+1 ~ Кр'п (хп+г) = Л' @) еп+1.
Если ввести вектор Нордсика
+
\)\Рп
и коэффициенты Г/!
- 2 Г^, F.29)
/О
то F.27) становится эквивалентным формуле
5п+1 = РК + ГГГ1 [Л/Л+1 - е\Ргп], F.30)
в которой Г = (Го, Гх, ..., 1ъ+1)т. Это метод вида F.8'). Однако
он имеет размерность к + 2, а не А + 1, как следовало ожидать
13*

388 Гл. III. Многошаговые методы и общие линейные методы
на основании теоремы 6.3. Причина этого заключается в следующем:
пусть многошаговый метод, соответствующий методу F.30), имеет
производящие многочлены р Щ и а (^). Тогда из условий Л(—1) =
= 0 и Л' (—1) = 0 следуют равенства а @) = р @) = 0, означаю-
означающие, что метод приводим. Тем не менее метод F.30) применим на
практике, так как последнюю компоненту вектора гп можно ис-
использовать для контроля величины шага.
Замечание. При к ^> 2 определенные в F.29) коэффициенты Г/
зависят от отношений шагов Н]/Н^1у / = п — к + 2, ..., д. Их
можно вычислить из формулы
г к
[
в которой 1} = (#п-/+1 — #п+1)/(#п+1 — хп) (см. также упр. 1).
ФДН-методы
Один шаг ^-шагового ФДН-метода заключается в построении
многочлена дп+1 (х) степени ку удовлетворяющего условиям
<7п+1 (*;) = У] при / = п - к + 1, ...| п + 1,
• / ч ( F.32)
Чп+1 (Хп+1) = /п+1#
и в нахождении значения уп+ъ при котором это возможно. Как
и для методов Адамса, в данном случае верно равенство
Яп+1 (X) - Яп (X) - Л (|^Г~) • (Уп*1 - Яп (ХпЛ), F.33)
где Л (() — многочлен степени к, определяемый условиями
=О при / = п —Л+1, ...,/г,
Л@)=1.
Вводя вектор
= [Яп (хп), НпЯп (хп), ..., -~д{пк) (хп)\
и коэффициенты Г^, задаваемые формулой
к
Л @ - 2 ГА
/0

II 1.6. Методы Нордсика 389
преобразуем F.33) к виду
= Ргп + ГГГ! [А/п+1 - етхРгп]. F.34)
Вектор Г = (Го, Гь ..., 1к)т можно вычислить из формулы
в которой I] = (хп^+1 — ^п+1)/(^п+1 — хп)- При постоянном шаге
формула F.34) соответствует формуле из теоремы 6.3, а коэффи-
коэффициенты I] = Г//?! совпадают с приведенными в табл. 6.2.
Упражнения
1. Пусть 1)к) (/ = 0, ..., к) являются коэффициентами Норд-
Нордсика для й-шаговых неявных методов Адамса (они определены
с помощью теоремы 6.3, а их числовые значения даны втабл. 6.1).
Обозначим через 1\к) (/ = 0, ..., к ■+- 1) коэффициенты, вве-
введенные с помощью F.29) и F.31), в случае постоянного шага.
Покажите, что выполняются соотношения
при
при / = 1, ..., к-\-1.
Используйте их для проверки табл. 6.1.
2. а) Найдите матрицу Т из теоремы 6.3 для 3-шагового неяв-
неявного метода Адамса.
Ответ:
/10 0 3/8\
0 0 0 1
0 6 6 3/4
\0 4 12 1/6/
Покажите, что вектор Нордсика гп имеет вид
б) Вектор гп для двухшагового неявного метода Адамса F.30)
(при постоянном шаге) также задается формулой
но теперь уп менее точно аппроксимирует у (хп).

III.7. Реализация и численное сравнение
При реализации многошаговых методов существует большая
свобода выбора (даже если ограничиться рассмотрением методов
Адамса). Можно непосредственно использовать методы с перемен-
переменным шагом из разд. III.5 либо применять метод с постоянным ша-
шагом, определяя при этом с помощью интерполяции значения вне
узлов сетки, необходимые при изменении шага. Кроме того, воз-
возможен выбор между формулировкой в разделенных разностях
E.7) и представлением Нордсика F.30).
Исторически первый подход состоял в использовании формулы
A.8), дополненной интерполяцией (Дж. С. Адаме A883): «Конечно,
мы всегда можем изменить значение со (величину шага), если
большая или меньшая скорость убывания последовательных раз-
разностей указывает на целесообразность увеличения или уменьшения
интервала. Только при этом необходимо, выбрав одно из уже вы-
вычисленных значений или применив интерполяцию через них,
найти координаты нескольких новых значений ср, разделенных
новым интервалом»). Сточки зрения теории метод E.7) с перемен-
переменным шагом выглядит более подходящим и красивым. Для обоих
подходов изменение шага является достаточно дорогой проце-
процедурой, тогда как изменить порядок очень просто — надо только
прибавить следующий член разложения A.8). Если же реализу-
реализуется представление Нордсика F.30), то мы имеем обратную ситуа-
ситуацию. Теперь изменение порядка не является таким же естествен-
естественным, как прежде, зато можно легко изменить шаг, умножив
вектор Нордсика F.1) на диагональную матрицу сНа§A, со, со2, ...),
где со = кпт1к014 — отношение шагов. Это и послужило основной
причиной введения такого представления.
Выбор шага и порядка
В литературе 60-х годов многое было сделано по вопросу
о начале многошаговых вычислений и необходимости для этого ме-
методов Рунге—Кутты [см., например, работу Ралстона A962)].
В настоящее время основанные на многошаговых методах про-
программы в начале счета просто используют методы первого порядка
и очень малый шаг и поэтому являются самостоятельно стартую-
ющими.
Теперь предположим, что до точки хп численное интегриро-
интегрирование протекало успешно, а для нахождения уп+ъ аппроксимирую-
щего у (хп+1), мы выбрали величину шага Нп и порядок к + 1.
Чтобы решить, подходит ли г/п+ь мы должны иметь оценку локаль-

II 1.7. Реализация и численное сравнение 391
ной погрешности обрывания ряда. Такую оценку дает, например,
формула
&*+1 (л + 1) = Уп+1 — Уп+и
где значение у*п+\ вычислено по неявной формуле Адамса порядка
к + 2. Вычитая формулу E.7) из нее же, но с заменой к на к + 1,
получим
л + 1) = К (вш (п) - ёи (п)) Фк+1 (п+1). G.1)
Главный член этого выражения не изменится, если вместо
Ф (л + 1) мы поставим
к
(л + 1) = П (хп+1 - хп„ь) р [хп+1, хп, ..., хк]. G.2)
Верхний индекс р у / обозначает- замену /п+1 = / (л:п+1, /^^)
на / (^п+1> Рп+1) при образовании разделенных разностей. Если
решать неявное уравнение E.7) итерационным методом с началь-
начальным приближением рп+и то Ф*+1 (п+1) придется вычислять
в любом случае. Поэтому единственной затратой при подсчете
оценки
(л + 1) = К (вь+г {п)-ёк (п)) Ф1+1 (п + 1) G.3)
будет нахождение §"&+! (п). После того как вычислено выражение
G.3), мы требуем выполнения (в некоторой подходящей норме)
неравенства
G.4)
означающего, что данный шаг был успешным.
Если вместо E.7) рассматривать представление Нордсика F.30)
то оценка локальной погрешности будет уже не такой простой,
так как векторы / в F.30) полностью различаются при разных
порядках. Одну из возможных оценок погрешности можно найти
в статье Бирна—Хиндмарша A975).
Предположим теперь, что значение уп+1 принято. Далее мы
должны выбрать новые шаг и порядок. Идея выбора шага состоит
в нахождении наибольшего кп+1, при котором предсказанная ло-
локальная погрешность является допустимой, т. е. выполняется
соотношение
1)
Однако эта процедура на практике не используется из-за сложной
зависимости величин & (п + 1) и Ф/н-1 (п + 2) от шага Нп+1.
Кроме того, слишком дорого обходится подсчет коэффициентов
ёк+1 (п + 1) и §к (п + 1). Чтобы преодолеть эту трудность, пред-

392 Гл. III. Многошаговые методы и общие линейные методы
положим, что сетка равномерная (это необоснованное предполо-
предположение, но из него следует простая формула для нового шага).
Тогда локальная погрешность (для метода порядка к + 1) имеет
вид С (хп+2) Нк+2 + О {Нк+% где С — гладкая функция от х.
Поэтому локальную погрешность в точке хп+2 можно приблизить
ее значением в хп+ъ и так же, как в случае одношаговых методов
(см. формулу D.7) из разд. 11.4), мы получим в качестве оптималь-
оптимальной величину шага
1/<*+2)
Локальная погрешность ЬЕк+1 (п + 1) вычисляется по формуле
G.3) или, снова при предположении о равномерности сетки, по
формуле
ЬЕк+г (п + 1) = Ьу1+№ц (* + 1). G.6)
где значения 7*4-1 приведены в таблице 1.2 (см. упр. 1 из разд.
III.5 и упр. 4 из разд. III.1).
Теперь опишем, как можно определить оптимальный порядок.
Поскольку при всех порядках необходимо одинаковое количество
вычислений функции, для выбора нового порядка в основном при-
применяются две стратегии. Можно выбирать порядок к + 1 из усло-
условия либо минимальности оценки локальной погрешности, либо
максимальности нового оптимального шага. Эти две стратегии не
всегда эквивалентны, так как в формулу G.5) входит показатель
степени 1/(к + 2). Более подробно этот вопрос будет рассмотрен
ниже при описании программы ОЕАВМ. Необходимо отметить,
что в каждой из реализаций методов Адамса — а их существует
множество — описанный алгоритм усовершенствован и дополнен
еще рядом процедур. Например, шаг сохраняется постоянным,
если отношение Ь,пш1коы близко к 1, что упрощает вычисления
коэффициентов §; (л).
Некоторые распространенные программы
Для демонстрации стратегий выбора порядка и шага в мно-
многошаговых методах мы выбрали три программы: ОЕАВМ,
ЕР15СЮЕ и ЬЗСЮЕ.
ОЕАВМ — это модификация программы ЭЕ, описанной в книге
Шампайна—Гордона A975). Она датируется 1980 годом, а ее ав-
авторы — Шампайн и Уаттс. При численном тестировании мы при-
применяли переработанную версию программы, относящуюся к фев-
февралю 1984 г. Европейские пользователи могут ее получить по
адресу «КесЬепгеп1гит йег К^ТН АасЬеп, ЗеКегйег №её 23,
— 5100 АасЬеп,

1П.7, Реализация и численное сравнение 393
В этой программе реализовано представление E.7) в разделен-
разделенных разностях для формул Адамса о переменным шагом. При
решении уравнения E.7), нелинейного относительно уп+и в ка-
качестве предиктора (Р) принимают значение рп+1, затем вычис-
вычисляется (Е), }п+1 = / (хп+1, Рп+г) и выполняется одна итерация
корректора (С), которая и определяет уп+1. В конце, если шаг
оказался успешным, то вычисляется значение }п+1 = / (хп+1, уп+1)
для следующего шага. В этой реализации РЕСЕ на каждом успеш-
успешном шаге требуется дважды вычислять значение функции. Теперь
кратко опишем стратегию выбора порядка из этой программы!
после выполнения шага методом к + 1-го порядка с помощью
несколько модифицированной формулы G.6) вычисляются
ЬЕь-х (п + 1), ЬЕк (п + 1) и ЬЕк+г (п + 1). Затем, если верно
неравенство
шах (| ЬЕы (л + 1) ||, 1 ЬЕк (п + 1) ||) < | ЬЕМ (п + 1)|, G.7)
то порядок понижается на единицу. Повышение порядка рассмат-
рассматривается только в том случае, когда принят результат последнего
шага, не нарушено соотношение G.7) и примененный метод соот-
соответствовал сетке с постоянным шагом. Тогда вычисляется оценка
ЬЕк+2 (п + 1) = Л?!+2Ф*+2 (п + 1),
в которой используется новое значение /п+1 == / (#п+1*
и, если имеет место неравенство
порядок увеличивается на единицу. На рис. 7.1 показано изме-
изменение шага и порядка для примера из разд. П.4 (см. рис. 4.1,
а также рис. 9.5 из разд. П.9). На графике нанесены решение,
шаг и порядок для уровней точности 10~3, 10~в и 10~9. По поведе-
поведению выбираемой величины порядка видно сильное отличие от
основанной на экстраполяции программы СЮЕХ (разд. 11.9).
На участках наиболее быстрого изменения решения значительно
меняется только шаг, но не порядок. Отметим также, что на боль-
больших интервалах шаг остается постоянным, а порядок меняется
довольно часто (особенно при ТОЬ = 10~9). Это согласуется с за-
замечанием из книги Шампайна—Гордона A975): «... слабое умень-
уменьшение оцениваемой погрешности может вызвать колебания порядка,
что в свою очередь помогает программе продолжать счет с по-
постоянным шагом».
ЕР15СЮЕ при значении параметра МР = 10 реализует пред-
представление Нордсика F.30) переменного порядка для методов
Адамса. Авторами этой программы являются Бирн и Хайнд-
марш A975), а для ее получения следует обратиться по следую-

394
Гл. III. Многошаговые методы и общие линейные методы
щим адресам: «Ма1юпа1 Епег^у ЗоН^аге Сеп{ег\ ВшЫ. 221,
Аг§оппе №1. ЬаЬ., 9700 5ои1Ь Сазз Ауегше, Аг§оппе 1Ь 60439,
118А» или «ЫЕА Оа1а Вапк, В. Р. Ыо. 9 (Ва1. 45), Р91190
СНР-зиг-УУЕТТЕ, Ргапсе».
Мы использовали версию от 5 апреля 1977 г. У этой программы
есть несколько отличий от ОЕАВМ. Нелинейное уравнение, пер-
первое в системе F.30), решается методом простой итерации до схо-
сходимости. Пересчет / в конце не производится. Поэтому такой метод
можно рассматривать как Р (ЕС^-метод, где число итераций М
- / длина шага Ь
0. 2. 4. 6. 8. 10. 12. 14 16. 18. 20.
Рис. 7.1. Размер шага и изменение порядка для программы БЕАВМ,
может меняться от шага к шагу. Например, в тесте на рис. 7,2
(ТОЬ = 10~6) при 340 шагах требуется только 410 вычислений
функции. Отсюда видно, что для большинства шагов достаточно
одной итерации. Выбор порядка в программе ЕР15СЮЕ основан
на поиске максимального шага среди Нь {п + 1), Нк+1 (п + 1)
и къ+2 (п + 1). На рис. 7.2 представлено изменение шага и порядка
при использовании этой программы для того же примера, что и
раньше: заметим, что здесь выбирается намного более низкий по-
порядок, чем в ОЕАВМ. Кроме того, порядок остается почти посто-
постоянным почти на всем интервале. Такое поведение оправданно, по-
поскольку для представления Нордсика смена порядка не является
естественной процедурой.

Ш.7. Реализация и численное сравнение
395
0 2. 4 6. 8. 10, 12. 14. 16. 18, 20.
Рис. 7.2. Размер шага и изменение порядка для программы ЕР15ООЕ.
длина шага Ь
0. 2. 4 б. 8. Ю. 12. 14. 16. 18. 20.
Рис. 7.3. Размер шага и изменение порядка для программы ЬЗСЮЕ.

396 Гл. III. Многошаговые методы и общие линейные методы
ЬЗСЮЕ (с параметром МР = 10) — это еще одна реализация
методов Адамса. Ее предшественником является программа ОЕАК
(Хайндмарш, 1972), которая в свою очередь представляет модер-
модернизированный и улучшенный вариант на основе программы
О1Р5иВ (Гир, 1971). Мы использовали версию от 17 июня 1980 г.
Ее можно получить из тех же источников, что и ЕР15СЮЕ. ЬЗСЮЕ
основана на представлении Нордсика для методов Адамса с по-
постоянным шагом. По алгоритму изменения шага и порядка она
близка к программе ЕР15СЮЕ (см. рис. 7.3).
Сравнение численных результатов
«...Среди трех семейств методов метод Рунге—Кутты
постоянного порядка наиболее прост, понятен в ряде
аспектов и наименее эффективен».
(Шампайн и Гордон, 1975)
Интересной проблемой является, конечно, сравнение разных
реализаций одного и того же численного метода. Помимо про-
программ ОЕАВМ, ЕР15СЮЕ и ЬЗСЮЕ мы рассмотрим подпрограмму
Б02САР из библиотеки ИАО (библиотека ЫАО, Магк 10), кото-
которая представляет собой версию программы Хайндмарша ОЕАК.
Еще мы включили в сравнение результаты счета по программе
ООРК18, основанной на методе Рунге—Кутты фиксированного
порядка (разд. 11.6), чтобы показать различие в поведении одно-
шаговых и многошаговых методов.
Таблица 7.1. Используемые при сравнении программы
Название
программы
БЕАВМ
ЕР15СЮЕ
ЬЗСЮЕ
ЭО2САР
БОРК18
Линия на рисунке
~т—т • « | • • —— • • ■■■—» • • ~т—т
«
Объем памяти
при больших N
22- N
18-Л
17-N
19-N
9-#
Все эти методы мы применили к численному решению шести
задач из разд. 11.10: 1АСВ, ШОВ, УЭРЬ, ВКШ, ЬАОК, РЬЕ1
(при пяти уровнях точности 10, 10, 10"9, 10~12, 10~15). На рис. 7.4
нанесена в двойной логарифмической шкале зависимость числа
вызовов функции от достигнутой точности. ОЕАВМ кажется
лучше других программ (по крайней мере при ТОЬ <С 10).
ООРК18 и ЕР15ООЕ требуют наибольшего количества вычисле-
вычислений функции. Авторы программы ЕР15СЮЕ рекомендуют при-
применять ее «для задач, у которых сильно изменяется характер по-
поведения решения». Основанная на методе Рунге—Кутты программа
требует намного меньших дополнительных затрат (вре-

1П.7, Реализация и численное сравнение
397
мсв
ЕР18ООЕ
ЭЕАВМ
-1о§10(погр.)
I I I I . I I I I I I I I I . I
-2. О. 2. 4. 6. 8. Ю. 12. 14.
3.
. В1Ш8
ЕР18СЮЕ
I I 1 I I I
-1об,0(погр)
■ I I 1 I I
О.
6 8. 10. 12. 14.
БОРК18
I I I I I I I |_ I I I I I
4.
3.
ЬАОК
БЁАВМ
I I I I !
-2. О. 2. 4. 6 8. Ю 12. 14. -2. О 2 4 6 8 10 12. 14
3.
_ УЭРЬ
ЁР18СШЕ
РЁАВМ
I I I I I I 1 I I I I
- РЬЕН
ш
БОРК18
02СА*
•1
У ^Ь8ООЕ
\ 1 I I I 1 1
I I I I I I
-2. 0. 2 4 6. 8. 10. 12 14. -2. 0. 2. 4 6 8 10. 12 14
Рис. 7.4. Число обращений к подпрограммам вычисления функций (\с) для раз-
различных программ при решении для шести задач из раздела 11.10-

398
Гл. III. Многошаговые методы и общие линейные методы
2.
-1.
ДАСВ
ЕР18СЮЕ / ж--">-' ~х"
■ I
-2. 0. 2. 4. 6. 8. 10. 12. 14.
2.
I
1о$ю(время)
1.
-1
ВК11&
-ЕР15СШЕ
~1о810(погр)
■ 1 ■ ■ I ■ I I I I I I I I I
-2. О. 2. 4. 6. 8. 10. 12 14.
I.
-1.
тмгов
ЕР150ОЕ
I I I 1 I I 1 I I I I I
ПОРШ8
-Ю810(погр.)
-2. О. 2. 4. 6. 8 10. 12. 14.
3.
2.
1.
ЬАОЯ
ЕР18СШЕ
I I I I I I I I
Р0РК18
Ч0810(погр)
-2. 0. 2. 4. 6. 8. 10. 12. 14.
2.
0.
-1.
УОРЬ
ЕР18СШЕ
1 I I I I I I I I I 1 I I I • I
-2. О. 2. 4. 6. 8. 10. 12, 14.
3.
2. -
1. -
0.
РЬЁ1
- л
1$СШЕ.
.я
~1о810(погр.)
-2. 0. 2. 4. 6. 8. 10. 12. 14.
Рис. 7.6. Время работы центрального процессора (в секундах) для различных
программ при решении шести задач из раздела 11.10.

II 1.7. Реализация и численное сравнение 399
мени счета на операции, не входящие в подпрограмму вычисления
функции) по сравнению с многошаговыми методами. Это видно
из рис. 7.5, на котором для тех же шести задач указана зависимость
времени счета (на ЭВМ 1Ж1УАС 1100/60) от достигнутой точности
(в двойной логарифмической шкале).
Отметим, что в задачах, где вычисление функции обходится
дешево (как в первых пяти примерах), программа с методов Рунге—■
Кутты затрачивает намного меньше времени, чем основанная на
многошаговых методах, хотя в общем она должна повторить эти
вычисления большее число раз. Для задачи РЬЕ1, в которой вы-
вычисление правой части достаточно дорого, эта разница уже не
столь велика.
Теперь обратимся к изучению случая, когда задача имеет очень
большую размерность, а отдельные ее компоненты не очень сложны.
Уравнения в частных производных.
Рассмотрим уравнение реакции о диффузией (брюсселятор
в диффузией)
ди 1 1 2
_ _ 1 } и ю*ли г а
дЪ
при 0 <! я < 1, 0 < # < 1, ?>0, сь = 2« 10~8 совместно о гра-
граничными условиями Неймана
2а. - о 2°. - о
дп ~"и» дп "~и
и начальными условиями
и(х, д, 0) =0.5 + 0,
V (х, у, 0) - 1 + 5х. { '
С помощью метода прямых (см. разд. 1.6) эту задачу можно при-
привести к системе обыкновенных дифференциальных уравнений.
Введем обозначения
и определим функции
Дискретизация в G.8) производных по пространственным пере-
переменным дает систему ОДУ размерности 2Ы2, состоящую из урав-
уравнений
а

400 Гл. III. Многошаговые методы и общие линейные методы
У ч
/=0.5
/«1
е!с.
/=11.5
Рис. 7,6. Решение а (х, у, 0 для *=> 0, 0.5, ..., 11.5.

III.7. Реализация и численное сравнение
401
/-0.5
/=1.5
е(с.
ч__——■
4 —. — -•""■"
#—11-5
Рис. 7.7. Решение V (х, у, 0 для /= 0, 0.5, •♦„ 11.5.

402
Гл. III. Многошаговые методы и общие линейные методы
Уц = 3.41/„ - 1Я,Уи + а (Ы - IJ
+ У и ^ +
где I, / = 1, ..., #. В G.12) еще не определены значения ^
^+1,л Ум> ••• • В силу граничных условий G.9) их надо выби-
выбирать следующим образом:
и N+1
, N-1-
То же относится и к величинам ц
Решение системы G.12) как функция от (хг, у^ (при Л^ = 21)
представлено на рис. 7.6 и 7.7 через равные промежутки времени!
I = 0, 0.5, Ь 1.5, ..., 11.5.
3.4
32
24
о
6.
8.
Рис. 7.8. Число вызовов функций /с и время работы центрального процессора
для задачи G.12) при N — 21 в зависимости от достигнутого уровня точности.
По оси абсцисс отложен взятый с обратным знаком десятичный логарифм допу-
допустимой погрешности.
Применим теперь различные программы и задаче G.12) при
N = 21. Ее размерность уже равна 882. Как и при сравнении ре-
результатов счета предыдущих задач, на рис. 7.8 показана зависи-
зависимость количества обращений к вычислению правой части и вре-
времени счета от достигнутой точности. Мы использовали уровни
точности 10~2, 10~4, 10~8 для всех методов, за исключением ЭЕАВМ,
для которого они равны 10°, 10", 10". Это необходимо из-за
применения в программах разных норм. Из сопоставления двух
графиков на рис. 7.8 видно, что основанная на экстраполяционных
методах программа СЮЕХ (разд. 11.9) вычисляет функцию наи-
наибольшее число раз, но при этом требует наименьших дополнитель-
дополнительных затрат и сравнима по времени счета с программой БОРК18.

III.8. Общие линейные методы
«...методы, достаточно общие для того, чтобы включить
как частные случаи линейные многошаговые методы
и методы Рунге—Кутты...»
(К« Барридж и Дж. С. Бутчер, 1980)
В примечательно короткое время A964—1966) независимо
друг от друга появилось множество работ, где предприняты
попытки обобщить либо методы Рунге—Кутты в направлении
многошаговых, либо, наоборот, последние в направлении первых.
Это вызвано стремлением сделать преимущества многошаговых
методов доступными для методов Рунге—Кутты либо «разрушить
барьер Далквиста», модифицируя многошаговые формулы. Грэгг
и Штеттер A964) ввели «обобщенные многошаговые методы»,
Бутчер A965а) — «модифицированные многошаговые методы», и
в том же году появилась работа Гира A965) по «гибридным ме-
методам». Годом позже Бирн и Ламберт A966) опубликовали работу
по «псевдометодам Рунге—Кутты». Все эти методы входят в класс
«общих линейных методов», которому и посвящен данный раздел.
Приведем пример такого метода [Бутчер A965а), порядок
равен пяти 11
дп+1/2 = #п~ +
Вп+1 - 4гC2#п - дп_г) + ^ F4Гл+1/2 + \51п+1 +12/»
Теперь можно сделать выбор, для каких методов развивать тео-
теорию — для «обобщенных» многошаговых или «обобщенных» ме-
методов Руиге—Кутты. На основании разд. III.4, где показано,
что теория сходимости становится красивее, если многошаговые
методы рассматривать как одношаговые в пространстве большей
размерности, мы выберем вторую возможность: поскольку в фор-
формуле (8.1) предыдущая информация представлена значениями
Уп> Уп-ь введем вектор ип = (уп> уп-т)т и преобразуем последнюю
строку в (8.1) к виду
64
93
л
15
93
0
12
93
0
1
93
0
НУп)

404 Гл. III. Многошаговые методы и общие линейные методы
которая теперь будет иметь форму
Ип+1 = 5ап + АФ (хПУ ип, к). (8.2)
Свойства таких общих методов исследованы в работах Бутчера
A966), Хайрера—Ваннера A973), Скила A976), Купера A978)
и других авторов. Очевидно, что ничто нам не мешает считать
5 и Ф произвольными или по-другому интерпретировать ип.
Общая процедура интегрирования
Рассмотрим систему
У' = / % У)> У (*о) = Во* (8.3)
где / удовлетворяет условию регулярности D.2). Пусть система
дифференциальных уравнений (8.3) имеет размерность т, а раз-
разностное уравнение (8.2) — размерность ц^ ту и хп = х0 + пН
являются точками разбиения равномерной сетки. Рассматривае-
Рассматриваемый метод состоит из трех частей:
(I) процедура продвижения на шаг, т. е. формула (8.2), где
квадратная матрица 5 не зависит от задачи (8.3);
(II) функция точных значений г (ху К), которая служит для
интерпретации величины ип; ип должно быть приближенным
значением гп = г (хПУ Л), и тогда глобальная погрешность
будет вычисляться как разность ип — гп. Предполагается, что
по г (х, К) можно восстановить точное решение у (х) задачи
(8.3);
(III) стартовая процедура ср (Л), которая определяет старто-
стартовое значение и0 = ср (Л), ср (Л) приближает величину г0 = г (х0, К).
Таким образом, соответствующая (8.3) дискретная задача
описывается формулами
= ф (Л), (8.4а)
— $ип + АФ (хп> "п, А), /1 = 0, 1, 2, ..., (8.4Ь)
которые дают численное решение а0> иъ а2, ... . Отметим, что
функция приращения Ф (х, и, Л), стартовая процедура ср (Л)
и функция точных значений г (х, К) зависят от дифференциального
уравнения (8.3), хотя это явно и не указано.
Примеры метода (8.4)
Пример 8.1. Наиболее простой случай представляют одно-
шаговые методы. Их характерная особенность состоит в том, что
размерности дифференциальной и разностной задач совпадают
(т. е. т = д), а 5 — единичная матрица. Кроме того, ф (А) = у0
и г (х, А) = у (х). Эти методы уже изучены в гл. II.
Пример 8.2. В разд. III.4 показано, что линейные много-
многошаговые методы также относятся к классу (8.4). Для ^-шаговых

III.8. Общие линейные методы 405
методов размерность разностной задачи равна д = кт, а про-
процедура продвижения на шаг задается формулой D.8). Стартовая
процедура определяет вектор" ср (к) = (ук-1у ..., уъ уо)Т, и, на-
наконец, функция точных значений имеет вид г (х, к) = {у (х +
(*1)Л)( Л) ())Т
Наиболее распространенный способ реализации неявного мно-
многошагового метода — это процесс предиктор — корректор [срав-
[сравнить с A.10) и разд. 111.71: у(п+ь — приближенное значение для
Уп+н — «предсказывают» с помощью явного многошагового ме-
метода, скажем,
У
(8.5;Р)
а затем «исправляют» (обычно один или два раза):
(хп+к, уЦ^), (8.5;Е)
акУп+к
= А $*/„+* + р^п+л-1 Н 1- роМ- (8.5;С)
Если итерации (8.5) выполняются до сходимости, то этот процесс
совпадает с примером 8.2. Однако на практике проводится лишь
фиксированное число итераций (пусть их число равно М), и тео-
теоретически метод уже не является «чисто» многошаговым. Мы
различаем два вида методов предиктор—корректор (РС) в зави-
зависимости от того, оканчивается ли шаг коррекцией (8.5; С). Пер-
Первый алгоритм символически обозначается Р (ЕС)М, а второй,
когда /п+ь дополнительно вычисляется еще один раз для даль-
дальнейшего использования на последующих шагах, как Р (ЕС)МЕ.
Теперь рассмотрим, как эти две процедуры можно выразить
в форме методов (8.4).
Пример 8.2а. Р (ЕС)МЕ-методы. Стартовая процедура и функ-
функция точных значений остаются теми же, что и для многошаговых
методов, и так же ц = кт. Кроме того, 5 = А ® /, где матрица А
задана в D.7), а / — единичная матрица размера тхт. Заметим,
что 5 зависит только от формулы корректора и не зависит от фор-
формулы предиктора. Функция приращения имеет вид
Ф (х, а, А) = (ег ® /) г|? (х, и, А),
где ех = A, 0, ..., 0)Г. Для вектора и = (а1, ..., ик)Т, у кото-
которого компоненты и/ € Рт, функция г|? (х, и, А) определяется
следующим образом!
(х, и, А) = аГ1 (М (х + кк, уШ)) +
,/ (х + (к - 1) Л, и1) + ... + р0/ (х, ик)),

406
Гл. III. Многошаговые методы и общие линейные методы
где значение у<я> вычисляется из формул
= Ь(Н^! (х + (к- 1)к, и1) + .•. + р# (*, и*))
аои* = к
(при 1=1, ..., М).
Пример 8.2Ь. Для Р (ЕС)м-методов формулировка в виде ме-
метода типа (8.4) усложняется, так как информация, которую
следует перенести на следующий шаг, определяется не только
значениями уп-и+ъ •••> Уп> но зависит еще и от Л/п+ь-1, ...» Ыт
где к[п+1 = к\ (хп+], у1!+11)). Таким образом, размерность раз-
разностной задачи становится равной ц = 2кт. Обычная стартовая
процедура (как для многошаговых методов) дает
ф(й) = (Ук-ъ ••.. Уо> к!(хк„ъ дк_д* —» Ы(хо> Уо))Т-
Если определить функцию точных значений как
г (х, к) = (у (х + (к — 1) к), ..., # (я),
куг
то процедура продвижения на шаг будет задана следующим
образом!
5 =
А
0
0
1
•
0
0.
0.
*
0
в
.0
. 0
.
1
0
0
.
0
Ф (х, а, К) =
Р*1
о
и> к).
1
0
Здесь А — матрица из D.7), а В — матрица размера кх к, ранг
которой равен единице:
Для и = (и1, ..., ик, кЬ1, ..., №к)т функция ф (х, щ к)
имеет вид
\|э (х, и, к) = / (х + кк>
где д<я~1) определяется из соотношений
^Р#/@) , р I , , р к и
- й
+ АЛ, у<'-1>) + Р^1 + • • • + Ро»*)-

II 1.8. Общие линейные методы 407
Еще раз отметим, что 5 зависит только от формулы коррек-
корректора.
Пример 8.3. Методы Нордсика также относятся к типу (8.4).
Это следует непосредственно из представления F.8). В этом
случае функция точных значений
г(х,Н)= (у{х),ку' {х),^у"{х), ..., ^У(к)(*))
состоит не только из значений точного решения, но содержит
также и его производные.
Пример 8.4. Циклические многошаговые методы. Донельсон
и Хансен A971) исследовали возможность построения схемы дис-
дискретизации на основе нескольких отличных друг от друга &-шаго-
&-шаговых методов, используемых циклически. Пусть 8У- и Ф7- опреде-
определяют процедуру продвижения на шаг для /-го многошагового
метода; тогда численное решение и0, иъ ... вычисляется по сле-
следующим формулам!
Щ = Ф (Л),
ап+1 = 3^ап + ЛФ7- (хП9 иП9 Л), если п = (/ — 1) той т.
Чтобы получить метод (8.4) с не зависящей от номера шага ма-
матрицей 8, рассмотрим один цикл как один шаг нового метода
(8.6)
- 8и*п + Н*Ф (х*п, а2, к*)
с шагом Л* = тН. Здесь х*п = х0 + пк*> 5 = 5т ... 525Ь а Ф
выбирается соответственно. Например, в случае т = 2
Ф (х*, и*, Л*) = 4" 5*Ф1 (х*> и*>
к
*
Интересно отметить, что на основе циклически используемых
к-шаговых методов можно получить сходящиеся методы порядка
2к — 1 (или 2к при четных к). Таким способом можно разрушить
«первый барьер Далквиста» (теорема 3.5). Для более подробного
ознакомления см. книгу Штеттера A973) и упр. 2.

408 Гл. III. Многошаговые методы и общие линейные метода
Пример 8,5. Общие линейные методы.
«Следуя совету Аристотеля...» (оригинал на гре-
греческом языке можно найти в работе Бутчера)
«...мы ищем наилучшее кан среднее между крайно-
крайностями».
(Дж. С Бутчер, 1985а)
Эти методы введены в работе Барриджа—Бутчера A980) и яв-
являются настолько общими, что включают все предыдущие при-
примеры как частные случаи, но в то же время в них функция при-
приращения выражается явно через дифференциальное уравнение
и несколько свободных параметров. Методы задаются формулами
и\п+1) = 2 агЖп) + к 2 ЬиГ (хп + сД ю\п))> I = 1, ..., к> (8.7а)
/1 /1
*\п) = И аии\п) + Н 2 Ы (хп + с3к, VI*), * = 1,..., 5. (8.7Ь)
/1 /1
Этапы {и\п\ I = 1, ..., к) называются внешними этапами, так как
они содержат всю необходимую информацию с предыдущего шага,
которая используется при выполнении текущего шага. Этапы
{о\п\ г = 1, ..., з) являются внутренними и остаются в «черном
ящике» текущего шага. Очень часто некоторые внутренние этапы
совпадают с внешними, как, например, в методе (8.1), где
Одношаговые методы Рунге—Кутты характеризуются условием
к = 1. В конце данного раздела мы обсудим алгебраические усло-
условия, при которых линейные методы имеют порядок р.
Пример 8.6. Покажем, что проведенный в данном разделе
анализ применим не только к численным методам дискретизации
дифференциальных уравнений первого порядка. Для этого рас-
рассмотрим задачу Коши второго порядка
У" = ё (х, У)> У (*о) = 0о> У' (*о) = Уа> (Щ
которую, очевидно, можно также записать и как систему первого
порядка (8.3). Заменив у" (х) центральной разностной производ-
производной, получим метод
Уп+1 - %Уп + 071-1 = Л2# (*71, Уп)>
который при введении дополнительной переменной
Пуп = Уп+1 — Уп
можно представить в виде
(Уп+г\ /1 0\/Ь
\д'п+1) \0 )

III.8. Общие линейные метода 409
Теперь он имеет форму (8.4) о функцией точных значений
г (х, к) = {у (х), (у(х + Н) — у (х))/к)т. Здесь у (х) обозначает точное
решение задачи (8.8).
Все методы Нюстрёма (разд. 11.13), конечно, попадают в этот
класс, как и многошаговые методы для дифференциальных урав-
уравнений второго порядка. Более подробно они будут изучены в
разд. ШЛО.
Пример 8.7. Многошаговые многоэтапные методы со стар-
старшими производными представляют, видимо, наиболее широкий
класс задаваемых в явном виде линейных методов и являются
обобщением методов из разд. 11.12. В обозначениях данного раз-
раздела их можно записать следующим образом!
иГ1)=2 °»а'п>+2 тг 2
4п) - 2 М"+2 тг 2
Такие методы изучены в работе Хайрера—Ваннера A973).
Устойчивость и порядок
Далее при изучении устойчивости, порядка и сходимости мы
в основном будем опираться на работу Скила A976). Для устой-
устойчивости численного метода требуется, чтобы полученное с его
помощью решение оставалось ограниченным при к ->- 0. Этим
обосновано следующее определение.
Определение 8.8. Метод (8.4) называется устойчивым, если
матрица 5" равномерно ограничена при всех п ;> 0.
Локальная погрешность метода (8.4) определяется точно
так же, как для одношаговых (разд. II.3) и многошаговых
(разд. II 1.2) методов»
Определение 8.9. Пусть г (х, к) является функцией точных
значений метода (8.4) и гп = г (хПУ к). Тогда локальная погреш-
погрешность имеет вид (см. рис. 8.1)
(89)
== 2п+1 — 8гп — АФ (хП9 гп, Л), п = 0, 1, ....
Порядок нельзя определить столь же просто. Требование,
чтобы локальная погрешность имела величину О (А"*1) (как

410
Гл. III, Многошаговые методы и общие линейные методы
для одношаговых и многошаговых методов), оказывается доста-
достаточным, но в общем случае .не является необходимым для сходи-
сходимости порядка р. Для формулировки соответствующего опре-
определения нам потребуется спектральное разложение матри-
матрицы 5.
Во-первых, отметим, что если локальная погрешность (8.9)
стремится к нулю при Н ->- 0 (и фиксированном пН = х — х0),
то выполняется равенство
0 = г (*, 0) — 8г (х, 0),
(8.10)
и поэтому 1 является собственным значением матрицы 5, а
г (х7 0) — соответствующим собственным вектором. Кроме того,
локальная погрешность
гп+1
Метод (8.4)
л
Рис. 8.1, Определение локальной погрешности,
вследствие устойчивости 5 не может иметь собственных значений
вне единичной окружности, а собственные значения, равные по
модулю единице, не могут порождать жордановы цепочки. Обо-
Обозначим собственные значения, равные по модулю единице, через
^г(=1), ^2,...,^. Тогда жорданова каноническая форма 5
(см. A.12.14)) будет блочно-диагональной матрицей:
[/1 N
7 (Н
Л
/
\
V
С
Ч
\
Т'\

III.8. Общие линейные методы 411
Если мы разложим ее на члены, соответствующие единичным соб-
собственным значениям, то получим
(8.11)
где
Е = Т <Ш§ {/, 0, 0, ...} Т~\
, О, .. \
• • •
= Т(Иаё{0, О, 0, ...? 7} Г-1.
Теперь все готово для следующего определения.
Определение 8.10. Метод (8.4) имеет порядок р (согласован
с порядком р), если для всех задач (8.3) с функцией /, непрерывно
дифференцируемой р раз, локальная погрешность удовлетворяет
соотношениям
4> = О (кр)>
Е (й0 4- 4 4- ... + Лп) + <*п+1 = О (Н")
при 0 < пН < сопз*. (8.13)
Замечание. В работе Скила A976) это свойство названо ква-
квазисогласованностью порядка р.
Если правая часть дифференциального уравнения (8.3) р раз
непрерывно дифференцируема, то в общем случае ф (к), Ф (ху и, к)
и г (х, к) также являются гладкими, а поэтому локальную
погрешность (8.9) можно разложить в ряд Тейлора по степе-
степеням к:
= Ъ + ТхЛ + • • • + Тр-хЛ*-1 + О (к%
(хп) к + * • * + ар (хп) к* + о (л*+1) (а< 4}
Тогда функции й] (х) непрерывно дифференцируемы р — / + 1
раз. Следующая лемма дает более практичное описание порядка
методов (8.4).
Лемма 8.11. Пусть локальная погрешность метода (8.4) удов-
удовлетворяет соотношениям (8.14) с непрерывными функциями ^ (х).
В этом случае метод имеет порядок р тогда и только тогда,
когда
йп = О (Нр) при 0 < пН < СОП5* и Ейр (х) •= 0. (8Л5)
Доказательство. Условие (8.15) эквивалентно равенствам
4 = 0 (Н% Ейп+1 = О (кР+х) при 0 < пк < сопз1, (8 Л б)
которые, очевидно, являются достаточными для порядка р. Пока-
Покажем теперь, что они также и необходимы. Поскольку Е2 = Е

412 Гл. III. Многошаговые методы и общие линейные методы
[см. (8.12I, из условий порядка р следует, что
тг = О (А"), Е (йх + ... + йп) = О (к?) при 0 < пк < сопз*. (8.17)
Лучше всего это видно при умножении (8.13) на Е. Рассмотрим
теперь пары (п, Л), для которых пк = х — х0 при некотором
фиксированном х. Подставим (8.14) (заметим, что йп = О (кр))
в выражение Е (йх-\- ...-{- йп) и аппроксимируем полученную
сумму с помощью соответствующего интеграла Римана:
п
2 ^р (*/-1) + О (кр) =
/-1
\ар(8)Aз-\-О(Нр).
я
Из (8.17) следует равенство Е ] с1р ($) с1з = 0, при дифференци-
ровании которого придем к соотношению Е йр (х) = 0. ■
Сходимость
В дополнение к численному решению, заданному форму-
формулами (8.4), рассмотрим возмущенное численное решение (йп), т. е.
й0 = Ф (Л) + г0,
п, йп, К) + ^+1, ц = 0,
при некотором возмущении ,?? = (г0, гх, ..., г^). Например, «точ-
«точное» решение гп = г (хП1 к) можно считать возмущенным при
возмущении, равном локальной погрешности. Следующая лемма
дает наилучшую из возможных качественных оценок разности
«п — йп, выраженную через возмущение 7?. Нам надо предполо-
предположить, что функция приращения Ф (х, к, к) удовлетворяет усло-
условию Липшица по и (в компактной окрестности решения). Это
выполняется для всех разумных методов.
Лемма 8.12. Предположим, что метод (8.4) устойчив, а
последовательности (ип) и (йп) заданы формулами (8.4) и (8.18)
соответственно. Тогда существуют положительные постоянные
с и С, такие что при любом возмущении К и НЫ <; сопз!
где
п
= тах 2

III.8. Общие линейные методы 413
Замечание. Норма | Я ||5 задана в р^+г)<7. Ее положитель-
положительность объясняется следующим образом: если ЦТ? ||5 = 0, то при
п = 0, 1, 2, ... мы получим последовательно г0 = 0, гг = 0,
и т. д.
Доказательство. Введем обозначение бп = йп — ип. Тогда
ба+1 = 5бп + Н1п + гп+1, . (8.19)
где
К , Н) — Ф (хп, яв, А).
По предположению существует константа Ь, такая что || 5П || ^
^<1||бп|. Решая разностное уравнение (8.19), придем к равен-
равенствам б0 = г0 и
п
. 2 5Л+1"?о. (8.20)
2а
В силу устойчивости существует постоянная 5? для которой
||5/1||1<В при всех п > 0. (8.21)
Таким образом, из (8.20) следует соотношение
С помощью индукции по п получим
I вп I ^ A + Л5)п || /? |в ^ ехр (сопз1 • В)
что и доказывает второе неравенство леммы. Из (8.20) и (8.21)
п
шах
1=о
а поэтому при Л^Л <! с опз1 выполняется соотношение
|Ь шах \\йп — ип\\. Ш
Замечание. Норму, которая, подобно || • ||5, позволяет оценить
сверху и снизу через возмущение величину шах | ип — йп ||,
называют минимальным функционалом устойчивости для метода.
Эти идеи более подробно изложены в работах Спейкера A971)
и Штеттера A973).
С помощью данной леммы можно доказать следующую теорему.
Теорема 8.13. Рассмотрим устойчивый метод (8.4) и пред-
предположим, что -его локальная погрешность удовлетворяет соот-
соотношению (8.14) с непрерывно дифференцируемой функцией AР (х).

414
Гл, III. Многошаговые методы и общие линейные методы
В этом случае метод сходится с порядком р, т. е. для его глобаль-
глобальной погрешности ип — гп выполняется равенство
Мп — гп^О (Лр) при О •< пН < сопз1
тогда и только тогда, когда он согласован с порядком р.
Доказательство. В силу равенства ЕЗ = Е [см. (8.11) и (8.12)]
выполняется тождество
= 2
Е(й0 + - • + 4) +
/=о
- E - Е) 2 5-' ^
из которого следует, что при п <! N — 1 и й
ЦЕ (й0 + ... + 4) + 4+1К О + II5 - ЕI) || В \\а. (8.22)
Оценка снизу из леммы (8.12), но с заменой гп и йп на 4 и гп
соответственно доказывает вторую часть утверждения, т. е.
«только тогда».
Для доказательства первой части утверждения, т. е. «тогда»,
используем оценку сверху из этой же леммы. Нам надо показать,
что из согласованности порядка р следует соотношение
п
тах
(8.23)
В силу (8.11) и (8.12) выполняется тождество
ЗпЧ = Е + $ЧЕ2 + •. • + %~]ЕХ + ,
которое вместе с леммой (8.11) приводит к равенству
21Г1
/
2 $л-/ ь =
/=0
а • •
п
г 2 Ъ
/=0
Последний член этого выражения равен О (Нр), так как в соот-
соответствующей норме 1 Ё || < 1, а поэтому
п
/=о
=-• тах |^1.
п
Остальное следует из того, что сумма 2 ЪпЧ& (^/-О равномерно
/1
ограничена по п, если \\1,\\ = I, I Ф I и й имеет ограниченную
вариацию. Проще всего это увидеть при суммировании по частям
[Абель A826)]:
п
п
.

III.8. Общие линейные методы 415
Условия порядка для общих линейных методов
Условия (8.15) не очень удббны для построения общего ли-
линейного метода (8.7) порядка р. Вместо них нам хотелось бы
иметь алгебраические условия на свободные параметры, как в слу-
случае методов Рунге—Кутты. Мы покажем, как этого можно до-
добиться с помощью теории В-рядов из разд. 11.11 (см. также ра-
работу Барриджа и Мосса, 1980). Чтобы избежать тензорных про-
произведений, в дальнейшем будем считать рассматриваемое диф-
дифференциальное уравнение скалярным. При этом все результаты
верны и для систем. Далее предположим, что дифференциальное
уравнение является автономным, а поэтому можно прямо при-
применить теорию из разд. 11.11. Это будет обосновано ниже в заме-
замечании 8.17.
Теперь предположим, что компоненты функции точных зна-
значений г (х, к) = (гг (х, к), ...5 гк (#, Н))т можно разложить в В-ряд
гг (*, к) = В {гь у (*)),
и тогда, введя обозначение г (I) = (хг (/), ..., гк У))т3 запишем
г (х, к) = х@)у (х) + кг (у) / {у (х)) + • • ■. (8.24)
Прежде чем вывести условия порядка, отметим, что соотношение
(8.7Ь) имеет смысл, только если ю\п) -> у (хп) при к -> 0. В про-
противном случае нельзя определить / (о/п))« Поскольку и)п) аппрок-
аппроксимирует 2} (хп, Л), мы приходим к условию 2 аг] 2;- @) = 1.
Совместно о (8.10) оно дает так называемые условия предсогласо-
ванностш
Аг{0)=е. (8.25)
Здесь А я А — матрицы с элементами а^ и а^ соответственно, а
е = A, ..., 1)Т. Напомним, что локальная погрешность (8.9)
для общего линейного метода (8.7) задается формулой
= гх (хп + К к) - 2 ад (хП9 к) - 2 Ьик} (^), (8.26а)
где
VI = Е Я,Л (хп, к) + 2 ЬиЫ Ы- (8.26Ь)
Чтобы вывести условия порядка, запишем о* и й\п+1) в виде
В- рядов:
ог = В (V,, у (*.)), й\п+1) = В (Аи у (хп)).

416 Гл. III. Многошаговые методы и общие линейные метода
По теореме о композиции В-рядов и по формуле A1.10) из
разд. 11.11 получим
2| (хп + Л, Н) = В (гг, у (хп + Л)) = 5 (ги В (р, у (*„))) =
= В(рг„ у(хп)).
Подставив все эти ряды в (8.26) и приравняв коэффициенты,
придем к соотношениям
@ = (р*|) @ - 2 (им (О - 2 ад @
/ . ' (8.27)
(о = 2 а|Л (о + 2 бау, (о.
/1 /1
Применение леммы (8.11) дает следующий результат.
Теорема 8.14. Рассмотрим вектор й (г) = (йг @, ..., йг (
с компонентами йг (<), заданными формулой (8.27). Общий линей-
линейный метод (8.7) имеет порядок р тогда и только тогда, когда
(*) = 0 при 1$ Г, р (I) < р - 1,
@ = 0 при ($Т, р @ = р.
[Матрица Е определена в (8.12)].
Следствие 8.15. Условия
й @ = 0 при * 6 Т, р @ < Р (8.29)
являются достаточными для того, чтобы общий линейный метод
имел порядок р. И
Замечание 8.16. Выражение (ргг) (г) в (8.27) можно найти
с помощью формулы (П.8) из разд. 11.11. Поскольку р (/) = 1
для всех деревьев г, имеет место равенство
(Р, )-ггЬг2ж'(^(*»' (8'30)
где вторая сумма взята по всем возможным индексациям поме-
помеченного дерева I. Эта довольно сложная формула значительно
упрощается при предположении, что все коэффициенты г{ (I)
функции точных значений зависят только от порядка I, т. е.
гь (I) = XI (и), если р У) = р (и). (8.31)
В этом случае формула (8.30) принимает вид

III.8. Общие линейные методы 417
Здесь %1 представляет некоторое дерево порядка /, например,
= 0. (8.33)
Обычно компоненты г (х> к) состоят из у (х), у (х + /А), Ну' (х),
Н2у" {х), ..., а в этом случае предположение (8.31) выполняется.
Замечание 8Л7. Покажем, как надо определить в (8.7) коэф-
коэффициенты си чтобы результаты, полученные выше для автоном-
автономных систем, были верны и в общем случае. Для дифференциаль-
дифференциального уравнения хг = 1 формула (8.7Ь) принимает вид
юп = А ип + кВе.
Предполагая, что уравнение х' = 1 интегрируется точно, т. е.
«п = г @) хп + кг (т), мы получим 0П = хпе + кс, где вектор
о = (рх, ..., с8)г задается формулой
о « Аг (т) + Ве. (8.34)
При таком определении сг численные результаты для задачи
у' = / (х, у) и для расширенной автономной системы дифферен-
дифференциальных уравнений совпадают.
В заключение приведем в табл. 8.1 условия порядка до треть-
третьего включительно [при предположении (8.31)]. Заметим, что
условия (8.25) всегда считаются выполненными, а с задано в (8.34).
Через с* обозначен вектор (с{, ..., с{)т.
Построение общих линейных методов
Покажем на примере, как можно построить методы низкого
порядка: возьмем к = 5 = 2 и фиксируем функцию точных зна-
значений
г(х, к) = (у (х), у (х — к))т.
Этот выбор удовлетворяет условиям (8.24) и (8.31) при
Поскольку вторая компонента в г (х + А, Л) равна первой в г (х,
А), вполне естественно искать методы с матрицами
(ап а12\ ^ /Ьп Ь12
\ 1 о ;• \о о
Кроме того, наложим требование, чтобы матрица В имела вид
В=\бп О
и, следовательно, метод был явным.
14 Хайрер Э. н др.

418
Гл. III. Многошаговые методы и общие линейные методы
Условие предсогласованности (8.25), формула (8.34) и условия
порядка из табл. 8.1 дают следующие уравнения!
(8.35а)
(8.35Ь)
= Яш С2 в ^21 #221
Х2 * XX * Х2 #
хсг -+- 612^2) = Ь
^12 Т^ ^ \^11^12 » У12 \а22 • **{'Ъи'\)) "" * •
(8.35с)
(8.35с1)
(8.35е)
(8.351)
(8.358)
Таблица 8.1. Условия порядка для общих линейных методов
т
та
т8
[т2]
1
2
3
3
Аг
Аг
Аг
Аг
где
(т«).
0(-С
• Ве — г (т)
4- ЗВс2 = 2
■Ь ЗВо (т2) =
г»/
») = Аг (т2)
Условие
+ 2@)
Та) + 22 (Т)
(т3) 4- 32 (т2
= 2 (Т8) + 32
4- 2Ве
порядка
4-2@)
) 4- 32 (х)
(х2) 4- 32
4-
го
2@)
+ 2 @),
Система содержит 9 уравнений и 11 неизвестных. Выбрав в ка-
качестве свободных параметров сг и са, мы получим решение сле-
следующим образом: найдем о^, ЬХ1 и Ь12 из линейной системы (8.35A,
е, I), затем й1а, 222 и б21 из (8.35с, §), и, наконец, ап, ап и й21
из (8.35а, Ь).
Частное решение при сг = 1/2, с2 = —2/5 имеет вид
А =
16/11 —5/11
1 О
3/2 —1/2
3/2 -1/2
Г^0
в
104/99 — 50/99\
0 0 ]
0 0
— 9/10 0
(8.36)
Этот устойчивый явный 2-шаговый, 2-этапный метод 3-го порядка
принадлежит Бутчеру A984).
Построение методов более высокого порядка быстро становится
очень сложным, и в этом случае большую помощь окажет исполь-
использование упрощающих предположений.
Теорема 8.18. Пусть для функции точных значений выпол-
выполняется условие (8.31). Тогда из упрощающих предположений
(8.37)
Аг (%1) + /ЯсЫ = сК / = 1, ..., р

II 1.8. Общие линейные методы 419
вместе с соотношениями предсогласованности (8.25) и условиями
порядка для «разветвленных деревьев»
й (т') = 0, / = 1, ..., р,
следует, что метод E.7) имеет порядок р.
Доказательство. Используя формулы (8.27), по индукции
получим:
V (I) = V (т/) при р 0) -/,/=. 1, ...# р - 1
и, следовательно,
а @ = й (т/) при р (/) - /, / = 1, ..., р. ■
Упрощающие предположения (8.37) допускают интересную
интерпретацию: они эквивалентны тому, что внутренние этапы
ь^ совпадают до порядка р — 1 включительно с точным реше-
решением в точках хп + сгк, т. е.
) - У (хп + сгН) = О (Нр).
В случае методов Рунге—Кутты (8.37) сводится к условиям G.12)
из разд. 11.7.
Другие примеры общих линейных методов, удовлетворяющих
соотношениям (8.37), можно найти в работах Барриджа—Мосса
A980) и Бутчера A981). Советуем посмотреть также более поздние
статьи Барриджа A985) и Бутчера A985а).
Упражнения
1. Рассмотрите композиции (см. пример 8.5)з
а) явного и неявного методов Эйлера}
б) неявного и явного методов Эйлера.
Каким методам они эквивалентны? Какой порядок имеют эти
составные методы?
2. а) Предположим, что каждый из т многошаговых методов
(рь <*д> / = 1, ..., т, имеет порядок р. Докажите, что поря-
порядок соответствующего циклического метода не ниже р.
б) Постройте устойчивый 2-циклический, 3-шаговый линей-
линейный многошаговый метод 5-го порядка: сначала найдите одно-
параметрическое семейство линейных 3-шаговых методов 5-го
порядка (которые обязательно будут неустойчивыми).
Ответ.
V
14

420 Гл. III. Многошаговые методы и общие линейные методы
Затем определите сг и с2, при которых собственные значения
матрицы 5 составного метода будут равны 1, 0, 0.
3. Докажите, что композиция двух разных общих линейных
методов (с одной и той же функцией точных значений) снова
даст общий линейный метод. Вследствие этого циклические
методы из примера 8.4 относятся к общим линейным.
4. Предположим, что все собственные значения 5 (за исключе-
исключением ^1 = 1) лежат внутри единичной окружности. Тогда
минимальный функционал устойчивости равен
л—I
= шах
5. Проверьте для линейных многошаговых методов, что условия
согласованности B.6) эквивалентны согласованности первого
порядка в смысле леммы 8.11.
6. Запишите метод (8.1) в виде общего линейного метода (8.7)
и определите его порядок (ответ: р = 5).

Ш.9. Асимптотическое разложение глобальной
погрешности
Асимптотическое разложение глобальной погрешности мно-
многошаговых методов изучено в знаменитой диссертации' Грэгга
A964). Там приведено очень громоздкое доказательство, которое
в измененном варианте можно найти также в книге Штеттера
A973). Скил A976) высказал предположение о существовании
асимптотических разложений для общих линейных методов.
Ниже мы дадим доказательство (Хайрер и Любич A984)), осно-
основанное на идеях из разд. 11.8.
Поучительный пример
Чтобы понять, каким может быть ожидаемое асимптотическое
разложение, начнем с примера. Рассмотрим простое дифферен-
дифференциальное уравнение
у' =~У> У@) = 1,
выберем постоянный шаг к и применим 3-шаговую формулу диф-
дифференцирования назад A.22) с одной из следующих трех стар-
стартовых процедур:
Уо = 1, Уг = ехр (—к), у2 = ехр (—2к) (точные значения); (9.1а)
й12/ + 2/2^; (9ЛЬ)
р . (9Лс)
Три левых графика на рис. 9Л (расположенные в том же порядке,
что и соответствующие стартовые процедуры) показывают гло-
глобальную погрешность, деленную на к3, при пяти величинах шага:
к = 1/5, 1/10, 1/20, 1/40, 1/80.
Для первых двух стартовых процедур можно отметить равно-
равномерную сходимость к функции е3 (х) = хе~х/4; [см. формулу B.12) ],
а поэтому соотношение
Уп-У(хп) = ег(хп)к* + О(к*) (9.2)
выполняется равномерно при 0 <С пк <! сопз!. В третьем случае
имеет место сходимость к е3 (х) = (9 + х) е~х/4 (упр. 2), но она
уже не является равномерной. Поэтому (9.2) выполняется только
для значений хПу расположенных на некотором расстоянии от
нуля, т. е. при 0 < а <С пк •< соп$1. На трех правых графиках
рис. 9Л нанесены функции
(Уп-у(хп)-е3(хп)к*)/к\ (9.3)

422 Гл. III. Многошаговые методы и общие линейные методы
.1
-.1 -
.0
-.5
-1.0
-1.5
[ 1 1 1
-
• (9Ла)
1 I
.4
Л =0.2
1 1
.6
1 ,
.В -1.
-.1
.0
-.5
-1.0
-1.5
к 1 ^
Б>\ .2
1\
\ \
:1\ \о.о5
1
\
.1
к
У
н
\
.4
«0.2
1 1
.6
1 ,
.6 1
(9.1Ь)
2.0 -
1.0
Х>
10.0
.0
-10.0 -
-20.0 -
Рис. 9.1. Значения величин (уп —у (хп))/к* (слева) и (уп~у (хп) — е3 (хп) к*)/Н*
(справа) для трехшагового ФДН-метода и для трех различных стартовых про-
процедур.

1П.9, Асимптотическое разложение глобальной погрешности 423
Сходимость к функции е4 (х) можно наблюдать во всех случаях.
Поскольку для третьей стартовой процедуры (9.1с) ег (х0) Ф О,
последовательность (9.3) в этом случае, очевидно, расходится
как О A/А).
Из этого примера следует вывод о том, что для линейных
многошаговых методов в общем случае не существует асимпто-
асимптотического разложения вида
Уп = У (*п) = *р (*п) ЬР + ер+1 (хп) к*>+1 + • • •,
которое было бы равномерным при 0 <; пк <; соп$1. В него необ-
необходимо еще добавить отвечающие возмущению члены
Вп-У (*») = («р (*») + «9 ЛР + (еР+1 (*») + *Р1) НР+1 + • • •, (9.4)
которые будут компенсировать нерегулярность вблизи х0. Если
возмущения е« затухают экспоненциально (при п -> оо), то на
некотором расстоянии от х0 они не влияют на асимптотическое
разложение в хп.
Асимптотическое разложение для сильно устойчивых
методов (8.4)
Для распространения методики из разд. 11.8 на многошаговые
методы полезно записать их как «одношаговый» метод в про-
пространстве большей размерности 1см. D.8) и пример (8.2)]. Это
означает, что мы изучаем асимптотическое разложение сразу для
общего метода (8.4). Поскольку в (9.4) входят члены бди', при
итерационном доказательстве приведенной далее теоремы 9.1
мы придем к функциям приращения, которые также зависят от
п и имеют вид
Фп (х, и,к) = Ф (*, и + Нап (Л), Л) + рп (Л). (9.5)
Поэтому рассмотрим на равномерной сетке (хп) следующую чи-
численную процедуру:
Щ =* Ф (Л),
«
л.
где Фп задана формулой (9.5), а функция точных значений снова
обозначена через г (х, к). Изучение асимптотического разложе-
разложения упрощается при дополнительных предположениях:
А1) Метод (9.6) сильно устойчив, т. е. он устойчив (опреде-
(определение 8.8) и 1 является единственным собственным значением 5,
равным по модулю единице. В этом случае спектральный радиус
матрицы 5—Е (см. формулу (8.11)) меньше единицы;
А2) ап (к) и рп (к) — многочлены, коэффициенты которых
при п ->• оо экспоненциально убывают как О (р5). Здесь р0 обо-

424 Рл« III♦ Многошаговые методы и общие линейные методы
значает некоторое число между спектральным радиусом 5—Е
и единицей, т. е. р E—Е) < р0 < 1;
АЗ) функции ф, г и Ф дифференцируемы достаточное число
раз.
Предположение АЗ позволяет нам разложить локальную
погрешность, заданную формулами (8.9), в ряд Тейлора!
= * {хп + Л, к) - 5г (хп, к) - ЛФ {хп, г (хп9 к) +
+ кап (к), к) - Щп (к) =
Ж (*•• * (хп, 0), 0) ап (к) - • • • - ЙРП (й) + О
Выражения, содержащие ап (к), можно еще больше упростить.
Действительно, для гладкой функции О {х) выполняется равенство
О (хп) ап (к) = О (*о) «тг (Л) + НО' (*0) пап (к) + • • • + к"+1Я (п9 к).
Отметим, что п1<хп (к) снова является многочленом по Л, а его
коэффициенты затухают как О (рл), где р удовлетворяет усло-
условию р0 < р < 1. С помощью тех же рассуждений можно показать
ограниченность остаточного члена ^ (п, к) при 0 <; пк •< сопз!.
Вследствие этого запишем локальную погрешность в виде
= D» (хп) + Ьп) + • • • + (Лы (хп) + 8™) к"*1 + О
при 0 < пк < сопз1. (9.7)
Функции и* (х) являются гладкими, а возмущения Ь*п отвечают
условию &п =я О (рп). Разложение (9.7) единственно, так как
6^ ->• 0 при п -> оо.
Метод (9.6) называется согласованным с порядком /?, если
локальная погрешность (9.7) удовлетворяет соотношениям (лем-
(лемма 8.11)
йп = О{кр) при 0<яЛ<соп${ и Ейр(х) = О. (9.8)
Отметим, что в силу этого определения возмущения б« должны
равняться нулю при / = 0, ...,/?—1, но на б« не наложено
никаких условий. Из экспоненциального убывания этих членов
следует, что по-прежнему в согласии с определением 8.10,
^па + Е (йп + ... + 4) = О {кр) при 0 < пк < сош*.
Теперь можно легко проверить, что для метода (8.6) остаются
справедливыми лемма (8.12) (Фп удовлетворяет условию Лип-
Липшица с той же константой, что и Ф) и теорема сходимости (8.13).

111,9. Асимптотическое разложение глобальной погрешности 425
В следующей теореме мы используем то же обозначение, что и для
одношаговых методов, а именно ин (х) = ип при х = хп.
Теорема 9.1. (Хайрер, Любий, 1984) Пусть для метода (9.6)
выполняются предположения А1—АЗ и он согласован с порядком р
(р ^ 1). Тогда глобальная погрешность имеет асимптотическое
разложение вида
н (х) - г (х, Н) = ер(х)Н»+...+ е1Г (х) Н" + Е (х, К) Н»+1, (9.9)
где величины г$ (х) даны в доказательстве (см. формулу (9.18)),
а Е (х, Н) равномерно ограничена по Н $ [О, Но] при значениях х
из компактных отрезков, не содержащих х0. Имеет место более
точный, чем (9.9), результат:
ип-гп = (ер(хп) + грп)Нр + «.« + {еы(хп) + е%)к" + Ё(п, к)к"+\
(9.10)
где е« =8 О (рл), р E — Е) < р < 1 и Ё (п, к) ограничена при
0 <] пк <; сопз1.
Замечание. Из (9.10) и (9.9) получается формула
Е (хп, к) = Ё (л, к) + /Гге? + /Г2^-1 + . •. + Г'
а поэтому остаточный член Е (х, к) в общем случае не является
равномерно ограниченным по к при значениях х из отрезка [х0, х ].
Однако если х находится на некотором расстоянии от х0, напри-
например х >- х0 + б (б > 0 фиксировано), то последовательность е!п
стремится к нулю быстрее, чем любая степень Ып <; к.
Доказательство, а) Как и в случае одношаговых методов (см.
доказательство теоремы 8.1 из гл. II), построим новый метод,
который для заданных гладкой функции е (х) и последователь-
последовательности еп, отвечающей условию вп =* О (рп), имеет численное
решение
ип-ип^(е(хп) + гп)кР. (9.11)
Такой метод определяется формулами
и0 =* © (А),
^ \! ^ ^ (9.12)
= Зип + кФп (хП1 ип, к),
где ф (к) =5 ф (к) — (е (х0) + е0) к*> и
и, к) = Фп(х, и + (е(х) + гп)кР, к) —
- 8е (х)) ЪГ* - (вп+1 -
Поскольку Фп, а также Фп имеют вид (9.5), локальную погреш-
погрешность можно разложить в ряд (9.7). Определим теперь е (х) и

426 Гл. III. Многошаговые методы и общие линейные методы
еп таким образом, чтобы метод (9.12) был согласован с поряд
ком р + 1.
б) Локальную погрешность йп метода (9.12) можно разло
жить следующим образом:
йо = (Ъ + е (х0) + во) Ы> + О (ЙИ-1),
- НФп (хп, гп> к) =
- 5) г (хп) + (8п+1 - 5еп)) Л
(-0 (хп) (е (хп) + гп) + г' (хп)) Л*Н + О
Здесь функция
в силу (9.5) не зависит от п. Метод (9.12) согласован с поряд-
порядком р, если [см. (9.8I
1) е0 - — То — е (х0),
и) йр(х) + (I — 3)е(х) + 5Рп + еп+1-8гп = 0 при х и хп,
111) Ее' (х) « ЯС (х) в (х) — Я^р+1 (х).
В настоящий момент предположим, что систему A) — A11) можно
решить относительно е (х) я вп. В части г) доказательства будет
показано, что это действительно так. По теореме сходимости 8.13
метод (9.12) сходится с порядком р + 1. Следовательно, равенство
&п — 2П == О (кр+1) выполняется равномерно
при 0 <; пк <; сопз1,
откуда следует утверждение (9.10) при N = р.
в) Метод (9.12) удовлетворяет предположениям теоремы с за-
заменой р на р + 1 и р0 на р. Как и в теореме 8.1 (разд. П.8),
с помощью индукции мы придем к утверждению теоремы.
г) Остается найти решение системы @—(ш). Условие (И)
выполняется, если для некоторой константы о
На) йр (х) - E - /) (е (х) + с),
НЬ) еп+1 — о = 5 (в„ — с) — 62.
С помощью соотношения (/ — 5 + Е) (/ — 5) == / — Е, кото-
которое следует из равенств 55 = Е2 = Е [см. (8.11)], формула (па)
приводится к эквивалентному виду
(/ - 5 + ЕУ1 йр (х) =*-A-Е)(е (х) + с). (9.13)
Из A) мы получим е0 — о » — тр — (е (х0) + с), а поэтому в
силу (9.13)
A-Е) (в0 -с) - - (/ -Е) Тр + (/ - 5 + Е)-Чр(х0).

Ш.9. Асимптотическое разложение глобальной погрешности 427
Поскольку Ейр (х0) =* 0, это соотношение выполняется, в част-
частности при условии
е0 _ с =* - (/ - Е) ур + (I - 8 + Е)~ЧР (х0). (9Л4)
Числа еп — с определяются теперь рекуррентно соотношением
(НЬ):
е„ - с = 5" (80 - с) - 2
5
= Е(ва-с) + C- Е)п(*а-с)- Е 5 6? + Е 5 8? -
/а 1
-1: E - Е)"-г ьи>
/1
при выводе которого использовано равенство 5Л *=* Е + (8 — Е)п.
Если выбрать
' 00
то указанная выше последовательность |еп} будет отвечать усло-
условию гп = О (рл), так как в силу (9.14) Е (е0 — с) = 0 и б« =
(Р)
Для нахождения е (х) определим
V (х) = Ее (х).
С помощью формул (9.15) и (9.13) мы можем по V (х) восстано-
восстановить е (х):
е (Х) =* V (х) — (I — 8 + Е)-Хйр (х). (9.16)
Теперь перепишем уравнение A11) как дифференциальное
о' (х) « ЕО (х) {V (х)-A-8 + Е)-1 йр (х)) - Ейр+1 (х), (9.17)
а условие A) дает для него начальное значение V (х0) == —Е (ур
+ е0). Такую задачу Коши можно решить относительно V (х),
а затем с помощью (9.16) получить из него е (х). Эта функция и
определенное выше вп являются решением системы A) — (ш). ■
Замечания, а) Из (9.15)—(9.17) следует, что для главного члена
погрешности выполняются соотношения
^ (дг) = ЕО(х)ер(х) - Е^р+1 (д) _ (/ - 5 + Е)-1 ^(дг)
5р (*о) = -ЯТр - Е 2 б/р - (/ - 5 + ЕГ1 Ар (х0).
б) Поскольку функция ер+1 (д:) — это и есть главный член по-
погрешности для метода (9.12), она удовлетворяет дифференциаль-

428 Гл. III. Многошаговые методы и общие линейные методы
ному уравнению (9.18) с заменой и; на #;-+1. Поэтому по индукции
для у >< р мы получаем
е) (х) — ЕО (х) е\ (х) + неоднородная функция (х).
Слабо устойчивые методы
Теперь изучим асимптотическое разложение для устойчивых
методов, которые не обладают сильной устойчивостью. К этому
типу относится, например, явное правило средней точки A.13'),
к которому мы обратились в связи с <ЗВ5-алгоритмом (разд. 11.9).
Как и в начале данного раздела, применим правило средней
точки к задаче у' = —г/, у @) — 1 и рассмотрим следующие три
стартовые процедуры:
У о — 1, Уг = ехр (—А), (9.19а)
(9Л9Ь)
(9.19с)
На рис. 9.2 на трех левых графиках представлена глобальная
погрешность, деленная на А2. Для первых двух стартовых процедур
мы имеем сходимость к функции хе~х/6, а для (9.19с) отношение
погрешности к А2, т. е. (уп — у (хп))/к2, сходится к
— 3 е \
) при четных п
ех \
^ )
е~х ( —^ 1- -~-) при нечетных п.
Теперь вычтем из глобальной погрешности члены порядка А2
и разделим остаток на А3 в случае (9.19а) и на А4 для Ь) и с). Ре-
Результат показан в правой части рис. 9.2.
Приведенный пример прекрасно иллюстрирует тот факт,
что асимптотического разложения вида (9.9) или (9.10) больше
нет, но оно существует, если рассматривать хп только с четными п,
а при нечетных п оно тоже существует, но будет уже другим
(см. также упр. 2 из разд. 11.9). Далее мы получим подобный
результат для более общих методов.
Будем говорить, что метод вида (8.4) слабо устойчив, если он
устойчив, но матрица 5 кроме ^ = 1 имеет и другие собственные
значения, равные по модулю 1; обозначим их через ^ ^
Тогда 5 можно представить в виде [см. (8.11)]
5 - СА + &Е2 + ... + 1гЕх + К, (9.19)

Ш.9. Асимптотическое разложение глобальной погрешности 429
4 8 16
1.00
.50 -
.00
-.50
-1.00
.1 -
.0
-.1
-.2 -
.0
*- 1 —
• 1
-2 -
1 О
5 -
О
- 5 -
-1.0
Рис. 9.2. Асимптотическое разложение правила средней (точки три различные
стартовые процедуры).

430 Гл. III. Многошаговые методы и общие линейные методы
где Е] — проекторы (соответствующие собственным значениям /
а спектральный радиус /? удовлетворяет неравенству р (#) < 1.
При последующем изложении мы ограничимся случаем, когда
все Б; (/ = 1» •••» I) являются корнями из единицы. Это позволяет
просто доказать существование асимптотического разложения
и в то же время представляет наиболее важный частный случай.
Общая ситуация рассмотрена в работе Хайрера и Любича A984).
Теорема 9.2. Пусть метод (9.6) с не зависящей от п функ-
функцией Фп является устойчивым, согласованным с порядком р и
удовлетворяет условию АЗ. Если для всех собственных значений
(матрицы 3), равных по модулю единице, при некотором поло-
жительном целом ц выполняется равенство С/ = 1 (/= 1, ...,/),
то существует асимптотическое разложение вида (со = ш/
ип~*п = 2 со"8 (ер8 (хп) ЬР+...+екш (хп) Н») + Е (л,
5=0
(9.20)
где е/з (х) — гладкие функции, а Е (/г, Н) равномерно ограничена
при 0 < б < пН < соп${.
Доказательство. Основная идея доказательства состоит в том,
чтобы рассматривать д последовательных шагов метода (9.6)
как один метод с большим шагом. Введем обозначения йп ==
^ ипя+1 @ < * <^ <7 — 1> * фиксировано), Я = цН, хп == хг + пЯ.
Тогда метод примет вид
«тг+1 = 8'ип + НФ C?П1 ия9 .Л), (9.21)
где функция Ф подобрана соответствующим образом. Например,
при 9 =
Ф(дг, и, к) = \5Ф(х, и,±)+±-Ф(х+±, За
Из предположения о собственных значениях следует равенство
- Б1 + ... + Е1 + Я",
из которого видно, что метод (9.21) сильно устойчив. Прямой
подсчет дает для локальной погрешности метода (9.21) формулы
(Хя)

III.9. Асимптотическое разложение глобальной погрешности 431
С помощью подстановки (9.19) и равенства $ =* 1 при Ё~
— Ег + ... + Е\ получим выражение
которое в силу (8.15) равно нулю. Следовательно, метод (9.21)
также согласован с порядком р. Таким образом, мы проверили,
что метод (9.21) отвечает всем предположениям теоремы 9.1.
Поэтому получим
п, А) к*+\
где Е% (/г, к) обладает требуемыми свойствами ограниченности.
Если мы определим в/, (х) к^к решение системы Вандермонда
2 / (ДГ) = ё„ (X),
5=0
то придем н (9.20). ■
Сопряженный метод
Для метода (8.4) функция точных значений г (х, Л), стартовая
процедура ф (Л) и функция приращения Ф (х, и, к) обычно опре-
определяются и при отрицательных к (см. примеры из разд. Ш.8).
Как и в случае одношаговых методов (разд*. 11.8), мы укажем
точный смысл численного решения ин (х) при отрицательных Л.
Это естественным образом приводит нас к изучению асимптотиче-
асимптотических разложений по четным степеням А.
Введем обозначение ин (х) = ип при х = х0 + пк (к > 0).
Тогда метод (8.4) примет вид
ик (х0) - Ф (Л),
+ Л) = 5«Л (*) + ЛФ (л:, ин (*), Л) при л: » д;0 + «Л
Сначала в (9.22) заменим Л на —к:
и-ь (х0) « ф (—Л),
и-л (дг — к) = 5и«л (х) — АФ (х, и„ъ (х), —Л),
а затем х на х + А, что даст нам формулы
«-л (*о) в Ф (—А),
-ъ (х + Л) — АФ (х + А, и^ (х + А), —А).

432 Гл. III. Многошаговые методы и общие линейные методы
При достаточно малых к это уравнение можно решить относительно
й_ь (х + к) (теорема о неявной функции). Тогда мы получим
«-л (*о) = Ф (—Л),
«-Л (х + к) - 8~Ч_Н (х) + ЙФ* (х, и_н (х), к). (9'23)
Метод (9.23), который снова относится к типу (8.4), называется
сопряженным методом для (9.22). Его функция точных значений
равна г* (х, к) = г (х, —к). Отметим, что при заданных 5 и Ф
новая функция приращения Ф* определяется парой формул
V = 8и — кФ (х + к, и, — к),
и = 5"Ч> + АФ* (х, V, Л), (9'24)
Пример 9.3. Рассмотрим линейный многошаговый метод с про-
производящими функциями
= 2«
Тогда
/=0
о __
• • •
1
0
1
О
О
1 О
/ 1 \
О
Ф (х, и, к) =
где г|> — г|) (х, и, к) — решение уравнения (и = («й-1> •••> ио)Т
Прямо из формулы (9.24) получается, что
О 1
О О
/=о
1
Ф* (*, о, Л) =
/О
О Ь|>*(*. о, Л),

Ш.9. Асимптотическое разложение глобальной погрешности 433
где \|)* = \|)* (х, о, к) (при о — (я0, ..., ок^)т) задается следу-
следующим образом:
Отсюда видно, что сопряженный метод снова является линей-
линейным многошаговым. Его производящие многочлены равны
9* (С) = -Ък9 (у), а* (С) « С*ст (|) . (9.25)
Нашей следующей целью будет доказательство того факта,
что сопряженный метод имеет точно такое же асимптотическое
разложение, что и исходный метод, но с заменой к на —Л. Для
этого необходимо, чтобы матрица 5 также была устойчивой.
Поэтому все собственные значения 5 должны лежать на еди-
единичной окружности.
Теорема 9.4. Пусть метод (9.22) является устойчивым, со-
согласованным с порядком р, и предположим, что для всех собствен-
собственных значений 8 при некотором целом положительном ц выпол-
выполняется равенство Ц = 1. Тогда глобальная погрешность имеет
асимптотическое разложение вида (со = е2п(/д)
Ч (хп) - г (хП9 К) = 2 ®П8 (еРв (хп) ^+...+ет (хп) Л") +
0
Е(хп, К)Н»+\ (9.26)
которое справедливо и для положительных, и для отрицательных /г.
Остаточный член Е (х, к) равномерно ограничен при \к
Доказательство. Как и в доказательстве теоремы 9.2, рассмо-
рассмотрим ц последовательных шагов метода (9.22) в качестве одного
нового метода. Из предположения о собственных значениях
следует, что 5* = / = единичной матрице. Поэтому новый метод
по существу является одношаговым. Единственное отличие со-
состоит в том, что его стартовая процедура и функция точных зна-
значений могут зависеть от Л. Простое распространение на этот
случай теоремы 8.5 из гл. II (упр. 3) дает существование раз-
разложения
к) = ёр1 (хпя+г) ЬР+ ...

434 Гл. III. Многошаговые методы и общие линейные методы
Оно справедливо и для положительных, и для отрицательных /г,
а остаточный член Ег {х, к) ограничен при | к |<Л0 и х0 < *<;Л.
Те же рассуждения, что и при доказательстве теоремы 9.2, при-
приводят нас к требуемому разложению. ■
Симметричные методы
Для общих линейных методов определить симметрию не
так просто, как в случае одношаговых методов. В примере 9.3
мы увидели, что компоненты численного решения сопряженного
метода имеют обратный порядок. Поэтому требования ф (к) =
= ф (—Л), 5 — 5 и Ф — Ф* являются слишком ограничитель-
ограничительными.
Однако во многих методах, представляющих практический
интерес, функция точных значений удовлетворяет отношению
симметрии вида
г (х, к) ~С1г{х + цК% —к) (9.27)
где ф — квадратная матрица, а ; — целое число. Оно выпол-
выполняется, например, в случае линейных многошаговых методов,
у которых функция точных значений равна
г (х, к) «■ (у (х + (к — 1) Л), ..., у (х))Т;
такие методы отвечают условию (9.27) при
1\
)
и <7 = *-1- (9-28)
Определение 9.5. Пусть функция точных значений удовлетво-
удовлетворяет условию (9.27). Метод (9.22) называется симметричным
[относительно (9.27) 1, если для численного решения выполняется
условие, аналогичное (9.27):
иь (х) =* <3и_ь (х + цН). (9.29)
Пример 9.6. Рассмотрим линейный многошаговый метод и
предположим, что для производящих многочленов сопряженного
метода (9.25) справедливо равенство
р*(О-Р(О. а* (С)-а (С). (9.30)
Это эквивалентно требованию [см. C.24I
Прямой подсчет (с использованием формул из примера 9.3) пока-
показывает, что если отношение симметрии (9.29) выполняется при

III.9. Асимптотическое разложение глобальной погрешности 435
х =* х0, то оно справедливо и для всех х = х0 + пк. Это налагает
дополнительное условие на стартовую процедуру ср (к).
В завершение продемонстрируем, как можно использовать
теорему 9.4 для доказательства асимптотических разложений
по четным степеням Л. Обозначим через и{ (х) у-ю компоненту
ин (х). Из отношения симметрии (9.29) для многошаговых мето-
методов следует
(х) = и\ (х — (к— 1) к).
Кроме того, для любого многошагового метода
а поэтому для симметричных методов выполняется равенство
и
Если многошаговый метод симметричен в смысле определения 9.5,
то, как следует из теоремы 9.4, в асимптотическое разложение
глобальной погрешности входят только четные степени к.
Упражнения
1. Рассмотрим сильно устойчивый линейный многошаговый метод
порядка р, записанный в форме (9.6) (см. пример 9.3), и вве-
введем обозначение
а) Докажите равенство
где матрица Е взята из формулы (8.11), а 1 = A, ..., )
Ь) Покажите, что в разложении (9.9) функция ер (х) = 1ёр (х),
где
а С — константа погрешности [см. B.13I. Определите также
2. Найдите функцию еъ (х) и возмущения (г3п)п>о в разложе-
разложении (9.4) при использовании 3-шагового ФДН-метода для
решения задачи у' = —у, у @) = 1 со стартовой процедурой
(9.1 с). Сравните ваш результат с рис. 9Л.

436 Гл. III. Многошаговые методы и общие линейные методы
3. Рассмотрим метод
и0
(9 31)
ЛФ (*п, 2П, к) }
с функцией точных значений г (х, к).
а) Докажите, что глобальная погрешность имеет асимптоти-
асимптотическое разложение вида
(дгп) И + ^ (хп,
где ^ (х, /г) равномерно ограничена при 0 < к < /г0 и л:0 <
<*< Л.
Ь) Покажите, что для метода (9.31) остается справедливой
теорема 8.5 из гл. II.
4. Пусть многочлены р* (I) и а* (I) заданы с помощью (9.25).
При предположении
р* (С) - Ср @, а* (С) = Са (О
отношение симметрии (9.29) выполняется для всех х = #0
+ яЛ, если оно верно при я = #0- По какой причине в (9.30)
С =- 1?

ШЛО. Многошаговые методы для дифференциальных
уравнений второго порядка
«В 1904 г. мне потребовался подобный метод для вы-
вычисления траекторий заряженных частиц в, магнитном
поле; перепробовав различные уже известные методы
и не найдя среди них удобного для моей задачи, я сам
разработал достаточно простой метод, которым сразу
и воспользовался».
(С. Штёрмер, 1921)
Дифференциальные уравнения второго порядка заслуживают
дополнительного внимания вследствие своей значимости. В разд.
IIЛ3 мы уже видели, что для отдельных дифференциальных
уравнений второго порядка прямое' применение некоторых одно-
шаговых методов более эффективно, чем использование класси-
классических методов Рунге—Кутты. Исследуем теперь, сохраняется ли
эта ситуация и в случае многошаговых методов.
Рассмотрим дифференциальное уравнение второго порядка
= /(*, У, У')> (ЮЛ)
где у может быть вектором. Обычным способом перепишем A0.1)
в виде системы первого порядка и применим многошаговый метод
к к
2 агуп+1 = Н 2 Чиу'п+и A0.2)
2=0 *=0
к к
2
Если правая часть дифференциального уравнения не зависит
от у\
то естественно обратиться к численным методам, не содержащим
первой производной у'. Исключая {у'п\ из уравнений A0.2),
получим
2 а,уп+| = л1 2 к
А
где новые коэффициенты аи рг определяются из формул
2к (к \2 1к

438 Гл, III. Многошаговые методы и общие линейные методы
Далее мы исследуем методы A0.4), коэффициенты которых не
обязательно удовлетворяют A0.5). При этом мы надеемся добиться
того же порядка при меньшем числе шагов.
Первые методы
«Мш сосчитали более 120 различных траекторий; эта
огромная работа потребовала более 4500 часов...»
(С. Штёрмер, 1907)
«Кроме того, его доклад довольно сух и скучен...»
(Мнение Б, Римана об Энке, 1847)
Поскольку большинство дифференциальных уравнений небес-
небесной механики имеет вид A0.3), неудивительно, что первые по-
попытки построения специальных методов для таких уравнений
были сделаны астрономами.
В своем трактате о северном сиянии С. Штёрмер A907) вывел
дифференциальное уравнение второго порядка, описывающее
движение заряженных частиц в магнитном поле Земли. Для
обширных численных расчетов этих траекторий (см. приведенную
выше цитату!) он построил точный и простой метод: сложив ряды
Тейлора для у (хп + к) и у (хп—Л), мы получим
У (Хп + Щ-2У (хп) + У(Хп-Ь) = &У (хп)
-4- /|F) /у \±
■ 360 У \лпO-
Подставив сюда у* (хп) из дифференциального уравнения A0.3)
и пренебрегая членами более высокого порядка, придем к формуле
Уп-1 =
которая дает первый простой и точный метод, называемый иногда
методом Штёрмера или Энке. Чтобы увеличить точность, заме-
заменим производные у более высокого порядка на центральные
разности /
(хп) =
(хп) » Д*/^ + ...;
получим формулу
Она пока не очень практична, поскольку разделенные разности
в правой части содержат неизвестные значения /п+1 и /Л+2- Пре-
Пренебрегая разностями пятого порядка (т. е. полагая А4/п-2 *=

ШЛО. Многошаговые метода для уравнений второго порядка 439
— Д4/п_4 и А2/„_1 = А2/„_2 + Д3/„-8 + А*/п-4). придем к фор-
формуле («...формула, которая лежит в основе нашего метода...»,
Штёрмер, 1907)
Уп+1 — %Уп + Уп-1 =
[А7 + А7 + А*/ А4/](Ю.7)

«Если бы Очерки Астрономического общества были
полностью свободны от грубых численных ошибок...»
(П. X. Кауэлл и А. С. Д. Кроммелин, 1910)
Через несколько лет Кауэлл и Кроммелин A910) использо-
использовали те же идеи для исследования движения кометы Галлея.
Они рассмотрели один дополнительный член в разложении A0.6),
а именно:
60 480 Д ^п"8 ^ 195Г
Прямое использование формулы A0.6) в ее варианте четвертого
порядка
обосновал Е. Нумеров A924, 1927): вместо того, чтобы заменить
А2/п-1 на какое-то явное выражение, он попытался решить прямо
это неявное нелинейное уравнение относительно уп+1.
Задача Штёрмера
«При достаточном навыке вычисляют около трех
точек (ку г) в час».
(С. Штёрмер, 1907)
Предположим, что элементарный магнит помещен в начало
координат, а его ось соответствует оси г. Тогда траектория (х («),
у (з)9 г (з)) заряженной частицы в этом магнитном поле является
решением системы (Штёрмер, 1907)
((Зг* - г2) *' - ЗдйяО, (Ю.9)
—

440
Гл. III. Многошаговые метода и общие линейнне методы
где га =* #а + г/а + 2а. При введении полярных координат
х ~ К соз ф, у да # 31П ф A0.10)
система A0.9) принимает вид
A0.11а)
A0.11Ь)
-И
ЗКг
Ф
3
к
где 7 — некоторая константа, появляющаяся при интегрирова-
интегрировании ф\ Два уравнения A0.11а) образуют дифференциальное
.4
.2
11111
.О
.1
.4
Рис, 10.К Решения системы A0.11а) в плоскости (/?, г).
уравнение второго порядка типа A0.3) (отметим, что г2 = К2 +
+ г2), которое можно решить численно с помощью методов из
данного раздела. Тогда ф получается простым интегрированием
равенства (Ю.НЬ). На рис. 10.1 показано два решения подси-
подсистемы A0.11а) с начальными условиями, поставленными самим
Штёрмером: По => 0.257453, *0 « 0.314687, <р я —0.5, г0 =*

ШЛО. Многошаговые методы для уравнений второго порядка
441
До + *о■ Оа — 1 — B?/Да + #сАоJ, Да « /& соз и,
/^зшй при а^{0, я'4» я.-бя/4}. На рис. 10.2 представ

лено трехмерное изображение в пространстве (х, у, г) для реше
ния с начальными условиями и « я/4 и 5п/4.
Рис. 10.2. Трехмерное изображение решения.
Методы более высокого порядка
Формулу Штёрмера можно обобщить следующим образом:
дважды проинтегрировав уравнение A0.3), мы получим
х
у (х + Л) = у (х) + Ну' (х) + А21 A — 5) / (х -\- $Н, у(х + $к))д&.
A0.12)
Чтобы исключить первую производную у (х)у запишем ту же фор-
формулу, заменив в ней Л на —Л и сложив два выражения:
= Ла Г
у(х-зН))]й8.
A0.13)

442
Гл« III. Многошаговые методы и общие линейные методы
Так же как при выводе формул Адамса (разд. III. 1), заменим
неизвестную функцию / ((> у (I)) интерполяционным многочле-
многочленом р @, заданным формулой A.4). Это даст нам явный метод
к—1
Уп+1- %Уп + Уп-г = А2 Е <^ Щп (Ю.14)
с коэффициентами
^=(-1)^A-а) (~1) + E) *. (Ю.15)
Их числовые значения даны в табл. 10.1, а способ вычисления
описан в упр. 2.
Таблица 10.1. Коэффициенты метода A0.14)
0
1
1
0
2
1
12
3
1
12
4
19
240
5
3
40
6
863
12 096
7
275
4032
Приведем частные случаи формулы A0.14):
к = 2: уп+1 — 2уп + уп„г = А2/п,
3: уп+1 - 2уп + */п_х = Л2 [-^ /п — -
4:
Т2 ^п-2] * A0Л4')
п-1 == А I -^- /п |2" /п-1 ~Г "д" /п-2 |2* /п-3 I •
При й = 5 метод A0.14) эквивалентен формуле A0.7), которая
задает метод, использованный Штёрмером A907, 1921), а при
к = 6 получается метод из работы Кауэлла и Кроммелина A910).
Простейший из этих методов (к — 1) был успешно применен
в качестве основы при построении экстраполяционного метода
(разд. 11.13, формула A3.32)).
Для повышения точности можно также использовать интер-
интерполяционный многочлен р* {I) из A.7), который проходит через
дополнительную точку (#п+1, /„+!.). Заменив в A0.13) / (?, у (/))
на р* (г)у мы придем к неявному методу:
к
уп+1 - 2уп + у п-1 = й2 2 а/
Коэффициенты а/ определяются формулой
а] = (-1I1 [(
A0.16)
A0.17)
а их числовые значения для / <; 6 приведены в табл. 10.2.

ШЛО. Многошаговые методы для уравнений второго порядка 443
Таблица 10.2.
1
_ ^^
0
1
Коэффициенты
1 2
, 1
12
неявного
я*
3
о
4
—1
240
метода
8
—1
240
A0.16)
6
—221
60 480
7
-19
6048
При к — 2 (а также к « 3) получается интересный метод
10 , . 1
который обычно приписывают Нумерову.
Используя идеи Нюстрёма и Милна для уравнений первого
порядка, можно вывести и другие методы. При заменах й-► 2&,
25 -* в и х-*х— Ь формула A0Л3) примет вид
у (х + Ь) — 2у(х — Ь) + у(х — Зй) « У | B — 5),
+ E- 1) Ь, у (х + (в- 1) А)) + (Ю.18)
+ 1(х-(8+1)Н,д(х-(8+ 1) А))] А.
Замена / (<, г/ (<)) на многочлен р (*) (или р* (/))'даст нам новые
классы явных и неявных методов.
Общая формулировка
Следующая наша цель — изучить устойчивость, согласован-
согласованность и сходимость общих линейных многошаговых методов для
задачи A0.3). Запишем их в виде
к к
Л ЪУп+1 = А2 2
Производящие многочлены с коэффициентами аг и фг снова обо-
обозначим через
РЮ-ЕоцЛ ст(С)=2]р^. A0.20)
Если метод A0.19) применить к задаче Коши
, у (хь) «
то будет естественно потребовать согласованности стартовых
значений с обоими начальными условиями, т. е.
прий^о, « = 0, 1, ..., *— 1. A0.22)

444 Гл. III. Многошаговые методы и общие линейные методы
Условие устойчивости
Чтобы получить представление о том, какое условие устой-
устойчивости необходимо для сходимости, рассмотрим простую задачу:
/ = 0, у0 = 0, у'о = 0.
Ее численное решение удовлетворяет линейному разностному
уравнению с характеристическим многочленом р (^). Те же рас-
рассуждения, что и при доказательстве теоремы 4.2, показывают,
что необходимым для сходимости является следующее условие.
Определение 10.1. Метод A0.19) называется устойчивым, если
для производящего многочлена р (Ъ) выполняются условия:
1) Корни р (С) лежат на (или внутри) единичной окружности;
и) Кратность корней на единичной окружности не превос-
превосходит двух.
Одношаговое представление метода A0.19)
Для рассматриваемых методов можно построить теорию по
аналогии с разд. 111.2—III.4. Такой подход разработан Далкви-
стом A959) и описан также в книге Хенричи A962). Мы предпочи-
предпочитаем переписать A0.19) в форме (8.4) и прямо применить резуль-
результаты из разд. III.8 и III.9 (см. пример 8.7). Для этого мы могли
бы ввести вектор ип = {уп+к-1, •••> Уп)Т, что кажется вполне
естественным. Но тогда соответствующая матрица 5 не будет
удовлетворять условию устойчивости из определения 8.8 из-за
двукратных корней, равных по модулю единице. Чтобы преодо-
преодолеть это препятствие, мы отделим такие корни. Представим ха-
характеристический многочлен в виде произведения
Р(О = Р1(О-Р.(О (Ю.23)
так, чтобы каждый из многочленов
/ т
Р1 (Б) = Е Ъ&, Р2«) = Е *«С A + т = к) A0.24)
4=0 1=0
имел только простые корни с модулем 1. Без ограничения общно-
общности в дальнейшем будем считать, что т ^ I и ак = уь = кт = 1.
С помощью оператора сдвига Е, определенного в B.10), метод
A0.19) можно записать в виде
р (Е) Уп = &а (Е) Гп.
Основная идея заключается в том, чтобы ввести новую перемен-
переменную р2 (Е) уп (обозначим ее через Ьл)п). Тогда многошаговая фор-
формула будет эквивалентна системе
Р1 (Е) ьп = На (Е) /п, р2 (Е) уп - /шп. A0.25)

ШЛО. Многошаговый методы для уравнений второго порядка
445
Если ввести вектор
ип = (Уп+г-1» • • •» ®п> Уп+т-ъ • • • > Уп) >
то формулу A0.25) можно записать в виде
ип+1 = 5ип + кФ (хп, ип, к),
где
A0.26а)
О 0
0 К
"
п.
о
о
V
п
о
о
. A0.27)
Матрицы С и К являются сопровождающими:
—71-1 —Тг-2 ... —То
О
1
0
1
0
О
1 О
К =
1
О
1
—Не
О
О
1 О
а ф = Ф (#п, «п, й) задается неявно формулой
к-\ I
\|) = ^ Р/ (Хп + /Л, ^п+<7-) + Рь/ I ^п + «Л> кг^ —
A0.28)
В ней я)) записана как функция от хп, {уп+ь-1> .-•> Уп) и к. Но
из второго соотношения в A0.25) видно, что каждое из значе-
значений Уп+и-и ...» Уп+т можно выразить в виде линейной комбина-
комбинации элементов ип. Поэтому в действительности \|з является функ-
функцией переменных (хП9 ип, к).
Формула A0.26) задает процедуру продвижения на шаг. Соот-
Соответствующая стартовая процедура имеет вид
Ф(А) = @1-ъ ..., о0, Ут-ъ ..., УоУ A0.26Ь)
и в силу A0.25) определяется по значениям (ук^и ..., уо)т един-
единственным образом. Функцией точных значений является
г(х, Н)=
(х),
. A0.26с)

446 Гл. III. Многошаговые методы и общие линейные методы
При нашем выборе многочленов рх (?) и р2 (?) (оба имеют только
простые корни с модулем 1) матрицы О и К ограничены при возве-
возведении в любую степень. Следовательно, это справедливо также и
для 5, и метод A0.26) устойчив в смысле определения 8.8.
Согласованность и сходимость
Найдем условия на параметры а* и Рь при которых метод
A0.26) согласован с порядком р (в смысле леммы 8.11). Начнем
с погрешности в начальных условиях:
й0 = 2 (#0, к) — ф (к).
Первые / компонент этого вектора имеют вид
т
а последние т компонент равны
У(Ъ) — Уз> / = 0, ..., т— 1.
Мы видим, что условие, достаточное для выполнения соотноше-
соотношения <20 = О (кр), состоит в следующем:
У(Х])-У* = О(ЬР+1) при / = 0, 1, ..., *-1. A0.29)
Затем рассмотрим локальную погрешность в точке хп,
йп+1 = г(хп + к, к) — 8г (хП9 к) — ЛФ (*п, г (хп, Л), к).
Она имеет все нулевые компоненты, за исключением первой, ко-
которая равна
ьп, г{хп, к), к).
Так же, как в разд. 111.2, введем линейный разностный оператор
, х, к) - р (Е) у (х) - к2о (Е) у" (х) =
к
(х + гк) - к%у" (х + ьк)).
Используя формулу A0.28), по теореме о среднем получим
= \1 {у, хп, к) + Л2Р/(*„+*, т|).<#|1, (Ю.30)
где XI имеет то же значение, что и в лемме 2.2. Отсюда следует, что
4+1 = О (АИ-1) <=> I (у, Хп, к) - О (й*+2).
Применяя теперь теорему сходимости 8.13, придем к следующему
результату.

ШЛО, Многошаговые методы для уравнений второго порядка 447
Теорема 10.2. Предположим, что метод A0.19) устойчив, стар-
стартовые значения отвечают условию A0.29) и для всех достаточно
гладких функций у (х) выполняется равенство
Ь(у, х% Ь\=*О{ЬР+*\. A0.31)
Тогда метод A0.19) сходится с порядком р, т. е.
IIУ (*п) — Уп К СНР при 0<мЛ<сопз!. ■
Следующая теорема дает полезный критерий для проверки соот-
соотношения A0.31).
Теорема 10.3. Многошаговый метод A0.19) удовлетворяет ра-
равенству A0.31) тогда и только тогда, когда выполняются эквива-
эквивалентные условия:
к к\
1) Ц щ = 0, 2 1Щ = 0
1й
к к
и Е а4р = ц (ц — 1) 2 Н11^ при ц = 2, ..., р,
щ р (е*) _ &О И = О (Л^2) при Ь -+ 0,
ш)
Доказательство опускается, так как оно повторяет доказа-
доказательство теоремы 2.4. ■
Замечания. 1. Многочлен р (С) обязательно имеет двукратный
корень ^ = 1. Поэтому многочлены р1э р2 из A0.24) отвечают ра-
равенствам рг A) = 0 и р2 A) == 0. Таким образом, функция точных
значений г (х, Н) имеет предел при Ь -> 0.
2. Как и в случае методов Адамса, легко проверить, что ме-
метод A0.14) имеет порядок &, а A0.16) — порядок к + 1.
Асимптотическая формула для глобальной погрешности
Предположим, что метод A0.19) устойчив и согласован о по-
порядком р. Тогда локальная погрешность для A0.26) равна
р (хп) + О (ЛР+*), A0.32)
где
к
2 (а*Р+2 (Р + 2) (Р


448 Гл. III. Многошаговые методы и общие линейные методы
Формулу A0.32) можно проверить, разложив в A0.30) Ь (у, хп, к)
в ряд Тейлора. Применяя теорему 9.1 (если среди корней р (^)
только один имеет модуль 1) или теорему 9.2, получим, что глобаль-
глобальная погрешность метода A0.26) имеет вид
ин (х) ~г{х, к) = е (х)
где е (х) — решение уравнения
гш (х) = Е ^~ (х, г(х, 0), 0) е (х) - Еег.Ср+2у«>+Ъ (х). A0.33)
Здесь Е — это матрица, определенная в (8.12). Поскольку в ло-
локальной погрешности A0.32) нет членов порядка кр9 из (9.16) сле-
следует равенство е (х) = Ее (х). Тогда (см. упр. 4а) эту функцию
можно записать в виде
/ у (х) I \
4 ' \н(х) 1/
Вычислив -у- (ху г (я, 0), 0) и Еег (подробное описание см.
в упр. 4), мы увидим, что A0.33) преобразуется в эквивалентную
систему
?' (х) = -^- -|- (х, у (х)) х (х) - -^ уЧ>+*> (х), A0.34а)
(Ю.34Ь)
Дифференцируя A0.34Ь) и подставляя в полученное уравнение
V' (х) из A0.34а), мы, наконец, придем к уравнению
х" (х) = -§-(*> У (*))« (*) ~ О/<р+2> (х), A0.35)
ду
где
A0-36)
Здесь мы использовали соотношение о A) = р! A)-рг A), которое
является прямым следствием равенства A0.23) и предположения
о том, что порядок метода не ниже первого. Постоянная С в A0.35)
называется константой погрешности метода A0.19). Она играет
ту же роль, что и B.13) для уравнений первого порядка.
Поскольку последняя компонента вектора ип равна уп> мы
приходим к требуемому результату
Уп-У (*п) = * (*п) ЬР + О (к*+1),

ШЛО» Многошаговые методы для уравнений второго порядка 449
где к {х) отвечает A0.35). Применяя результаты из разд. Ш.9,
можно получить и последующие члены асимптотического разло-
разложения глобальной погрешности^
Порядковый барьер для устойчивых методов A0.19)
Вполне естественно встает вопрос о поиске среди устойчивых
многошаговых методов A0.19) метода максимально возможного
порядка.
Теорема 10.4. Порядок р устойчивого линейного многоша-
многошагового метода A0.19) удовлетворяет ограничениям:
р <! к + 2 при четных к,
Р < к + \ при нечетных к.
Теорема 10.5. Устойчивый многошаговый метод A0.19) по-
порядка к + 2 является симметричным, т. е.
а* = «*-./> Р^ = Ры при всех /.
Эти две теоремы доказываются подобно теореме 3.5 и 3.9.
Здесь мы опускаем доказательства, которые читатель может найти
в оригинальной статье Далквиста A959) или в книге Хенричи
A962).
Погрешности округления
Обсудим кратко еще одно преимущество представления A0.26).
Среди множества способов реализации многошагового метода
остановимся на следующих двух:
1) хранение значений (уп+к-и • • -I Уп) и вычисление уп+ъ
прямо по формуле A0.19);
и) хранение ип и использование формулы A0.26). Назовем
это стабилизацией A0.19).
Оба процесса математически эквивалентны. Однако о вычисли-
вычислительной точки зрения они различаются. При малых к рекуррент-
рекуррентное соотношение A0.19) неустойчиво (из-за двукратных корней
на единичной окружности), а рекуррентная формула A0.26) устой-
устойчива (матрица 5 ограничена при возведении в любую степень).
Чтобы проиллюстрировать эту разницу, применим формулу Штёр-
мера A0.14'), отвечающую значению 4 = 4, к задаче у" = —у
с точным решением у (х) = зт х. В качестве стартовых возьмем
значения точного решения и выберем шаг Ь = 0.01, чтобы погреш-
15Хайрер Э. в др.

450 Гл, 1П# Многошаговые методы и общие линейные методы
ность обрывания ряда сохранялась меньшей, чем погрешности
округления (одинарная точность при ЕР8МАСН = 1.5В — 8).
На рис. 10.3 показано абсолютное значение глобальной погреш-
-3.0
-4.0 -
-5.0 -
-6.0 -
-7.0 -
-8.0
непосредственное вычисление
.о
1.О 2.О
З.О
4.0 5.0
6.О
7.0
8.0
Рис. 10.3. Погрешности округления для двух реализаций фор-
формулы Штермера A0.14') при & = 4,
ности для обеих реализаций. Видно, что погрешность стабилизи-
стабилизированного варианта меньше в 100 раз. Направленные вниз пики
соответствуют смене знака глобальной погрешности.
Упражнения
1. Найдите решение задачи Штермера A0.11а)] с помощью одного
из методов данного раздела.
2. а) Покажите, что производящие функции коэффициентов
и в[ [определенных в A0.15) и A0.17)]
оо
оо
5 @ = Ц
удовлетворяют формулам
5* @ = 2 <*№
2а
Ь) Подсчитайте коэффициенты й; ряда
оо
2 ^ -
/
и выведите рекуррентное соотношение для О[ и о}
с) Докажите равенство
1

ШЛО. Многошаговые методы для уравнений второго порядка
451
3. Пусть р B) является многочленом степени к с двукратным кор-
корнем 1. Тогда существует единственный многочлен о '"
такой что соответствующий* метод имеет порядок к + 1.
4. Рассмотрим метод A0.26) и для простоты предположим, что
дифференциальное уравнение является скалярным.
а) Для любого вектора пи С К* его образ Епи о матрицей Е
из (8.12) удовлетворяет равенству
Т
х!1'
где у, х — вещественные числа, а 1 — вектор, у которого все
элементы равны 1. Векторы *у! и х1 имеют размерности / и т
соответственно.
Ь) Проверьте, что при ех = A, 0, ..., 0)г справедливо соот-
соотношение
/ с* \ _ / (а/р! A)) 1 \
\ Р* / ~ V(Р/РНП) 1/'
с) Покажите, что
0)
Указание. Если ввести Уп == (уп+й-1» •••> Уп)г> то по формуле
A0.28) г{) можно представить функцией от (хп, Уп, К). Век-
Векторы Уп и ип связаны соотношением
КУп =
(А),
где
*т
Хт» • •
"т
1
1
, л-» —
о
1
0
1
Для вычисления -^- (л:, г (*, 0), 0) используйте цепное пра-
правило (дифференцирования сложной функции). См. также
упр. 2 из разд. Ш.4 и упр. 1 из разд. Ш.9.
5. Определите константу погрешности A0.36) для методов A0.14)
и A0.16).
Ответ, а* и Оь+г соответственно.
15*

Приложение. Программы на Фортране
... но программные продукты находятся на разных
стадиях разработки, от экспериментальных (эвфемизм
для плохо написанных) до того, что мы можем на-
назвать ...
(Ч. Гир, 1985)
Следующие программы на Фортране были разработаны для
наших численных расчетов. Они могут быть получены от авторов
Eес11оп йе ЛЫкёта^иез, Сазе Роз1а1е 240, СН—1211 Оепёуе 24,
5то1&ег1апA) на дискете фирмы ИБМ. Пожалуйста, пришлите 15
швейцарских франков.
Это программа явного метода Рунге—Кутты, основанная на
формулах Дормана и Принса (см. табл. 4.6 в разд. П.4) с авто-
автоматическим управлением длиной шага. Наилучший метод, если
допустима невысокая точность (от КИ до 10~7).
БОРН15 A*, ГС1*, X , У, ХЕМ , ЕР5 , НМАХ , Н)
Л«
С 1ШМВВ1СЛ1, ЗОШТКШ ОТ А 5У5ТЕМ ОТ К1Н5Т ОНОЕН
С ОН01ИАНУ 01*ТВНВНТ1ЛЬ В011АТЮК5 У'=Г(Х,У).
С ТН15 18 АИ ЕМВЕОБЕО НиКОЕ-КИТТА МЕТНОО ОТ ОНБВН DM
С д\1Е ТО ООНМАИБ & РНШСВ (И1ТН 5ТВР512В СОИТНОЬ) .
С С.Г. 8ВСТЮК 11.4
С
С 1ИРЦТ РАНАМВТЕН5
С N 01МВН8ЮН ОК ТНВ 8У8ТВМ (И.ЬВ.51)
С ГСИ ИАМВ (ВХТВНКАЬ) ОТ В\}ЪПО\Л1НЕ СОМРЦТ1КС ТНВ
С ПНЗТ БВН1УАТ1УВ Р(Х,У):
с зивноцикв рскск.х.у,^)
С НВАЬ*4 Х,У(Ы),Р(М)
С ГA)=... ВТС.
С X 1ШТ1АЬ Х-УАЬЦВ
С ХВИБ ПЫАЬ Х-УАШВ (ХВКЭ-Х Р051Т1УВ ОН КВСАТ1УВ)
С У(Я) 1М1Т1АЬ УАЬЦВЗ ГОН V
С ВР8 ЮСМ ТОЬВНАНСВ
С НМАХ МАХГМАЬ 5ТЕР512Е
С Н ГШИАЬ 8ТВР812В СЦЕВВ
С
С ОЦТРЦТ РАНАМВТВНЗ
С У(И) 80Ы1ТЮМ АТ ХВКО
С
С ВХТВККА1 ЗиВНОЦТ^Е (ТО ВВ ЗЦРРЫВО ВУ ТНЕ 118ВН)
С 30Ю118 ТН13 511ВНО11Т™Б 18 САЫВО АГТВН ВУВКУ
с зцссвззкиыу сомритво зтвр (акб тнв
С 1ШТ1А1, УАШВ):
С 811ВНО1П1КВ 80ЮЦ8 (КН.Х.У^)
С НВАЬ*4 Х,У(Ю
С ГиНМ5НВ5 ТНВ 8ОЬЦТЮК У АТ ТНВ ИН-ТН
С аН1Б-РОШТ X (ТНВ 1К1Т1АЬ УАЬЦВ 18 СОИ-
С 8ЮВВВ0 А8 ТНВ Г1Н5Т СНЮ-РОГИТ).
С ЗЦРРЬУ А БЦММУ 8ЦВНОиТ1КВ, 1Г ТНВ ЗОШТЮИ
С 18 N01 РВ81НЕБ АТ ТНВ 11*ТВВМВ01АТВ Р01КТ5.

Приложение. Программы на Фортране 453
НВАЬ*4 К1E1).К2E1),КЗE1),К4E1),К5E1),У1E1),У(Ю
ЬОСЮАЬ НВЛВСТ
С СОММОЙ 8ТАТ САЫ ВВ Ц8В0 ГОН 8ТАТ18Т1С8
С ЯГСМ Ш1МВВН ОГ РШГСТКЖ ВУАШАТ10К8
С М8ТЕР И11МВВН О? СОМРЦТЕО 8ТВР8
С ЫАССРТ 1ШМВВН ОГ АССВРТВБ 8ТВР8
С ЯНВЛСТ 1ШМВЕН ОГ НВЛВСТВО 8ТВР8
ОАТА МАХ/3000/, 1ЛЮ1ЖБ/5.В-8/
С МАХ МАХ1МАЬ М1МВВН ОГ 8ТЕР8
С ШКХтО 8МАЫВ8Т 1ШМВВН 8АТ18ГУ1ИС 1
С (ТО ВВ АОАРТВБ ВУ ТНВ Ц8ВН)
с — иаиль рнвранатюкз
НМАХ=АВ8(НМАХ)
Н=АМ1К1(АМАХ1A.В-4,АВ5(Н)),НМАХ)
Н=81СН(Н,Р08ЫВС)
= АМАХ1(ЕР8,7.*ШгО1Ш0)
КАССРТ=0
NНЕ^СТ=О
САЫ
САЫ
С ВА81С 1МТВаНАТЮН 8ТВР
1 1Г(К8ТВР.аТ.ЫМАХ.ОН.Х+.1*Н.ВО.Х)СОТО 79
С ТНВ ПН8Т 6 8ТАОВ8
НО 22 1=1,N
22 У1A)=УA)+Н*.2*К1A)
САЫ РСН(Н,Х+.2*Н,У1.
00 23 1=1,N
23 У1A)=УA)+Н*(C./40.)*К1A)+(9./40.)*К2A))
САЫ РСК(Н,Х+.3*Н,У1>КЗ)
ПО 24 1=1,N
24 У1A)=УA)+Н*(D4./45.)*К1(I)-E6./15.)*К2(I)+C2./9.)*КЗA))
САЫ ГСГ*(Н,Х+.8*Н,У1,К4)
00 25 1=1,N
25 У1A)=УA)+Н*(A9372./6561.)*К1(I)-B5360./2187.)*К2A)
& +F4448./6661.)*КЗA)-B12./729.)*К4A))
САЬЬ ГС№(Ы,Х+(8./9.)*Н,У1,К5)
00 26 1=1,N
26 У1A)=УA)+Н*((9017./3168.)*К1(I)-C55./33.)*К2(I)
& +D6732./5247.)*КЗ(I)+D9./176.)*К4(I)-E103./18656.)*К5A))
ХРН=Х+Н
САЫ ГСКСИ.ХРН, У1.К2)
ЪО 27 1=1,N
27 У1A)=УA)+Н*(C5./384.)*К1A)+E00./1113.)*КЗ(I)
& +A25./192.)*К4A)-B187./6784.)*К5A)+A1./84.)*К2A))
С С0МР11ТЕ 1КТЕКМВ01АТЕ 8ЦМ ТО 8АУВ МВМОНУ
00 61 1=1,Ы
61 К2A)=G1./57600.)*К1(I)-G1./16695.)*КЗA)
& +G1./1920.)*К4A)-A7253./339200.)*К5(I)+B2./525.)*К2A)
С ТНВ ЬА8Т 8ТАСВ
САН ГС!4(*1,ХРН,У1»КЗ)
00 28 1=1,N
28 К4A)=(К2A)-A./40.)*КЗA))*Н
С ВИНОЙ ВЗТ1МАТЮМ
ЕНН=О.
00 41 1=1,N
0ВГ*ОМ=АМАХ1A.Е-5, АВ8 (У1 (I) ) , АВ8 ( У( I) ) , 2 .
41 ВНВ = ВВН+(К4A)/0В1<ОМ)**2
ВКК=80НТ(ВКК/РЮАТ(К) )

454 Приложение. Программн на Фортране
с — сомрутатюи ог ныви
С ИВ НВО1ЛНВ .2<=НКВН/Н<=10.
ГАС = АМАХ1(. 1, АМ1ИК5. , (ВНН/ВРЗ)**A./5. )/.9))
ННВЧ-Н/ТкС
1Г(ВНН.ЬВ.ВР5)ТНВМ
С ЗТВР 18 АССЕРТВБ
44 1=1,N
К1A)=КЗA)
44 УA)=У1A)
Х = ХРН
САЬЬ
, АВ8(Н))
вьзв
5ТЙР 18 НВЛВСТВО
= ТН11В
аото 1
С — ТАИ ВХ1Т
79 ИН1ТВF,979)Х
979 ГОНМАТС ВХ1Т ОТ 0ОРН15 АТ Х=\В11.4)
ЕЫО
НЕАЬ*4
ивт
ВNО
Это программа явного метода Рунге—Кугга, основанная на
формулах Дорманда и Принса с автоматическим управлением
длиной шага (табл. 4.6 из раздела 11.6). Она написана для расче-
расчетов с двойной точностью и предпочтительна, если допустимая по-
погрешность находится в пределах примерно от 10~* до 10~13. Не
применяйте ее, если нужна точность выше 106.
, ГСН, X, V, ХВКБ, ВР5, НМАХ, Н)
л»
С 1ШМВН1СА1, 80ШТ10М ОТ А ЗУЗТВМ ОТ ПНЗТ ОНОВН
С ОНО1КАНУ О1РТВНВОТ1АЬ В0ЦАТЮК8 У=Г(Х,У)-
С ТН18 13 АИ ВМВВБОВО ВиИСВ-КиТТА МВТНОО ОТ ОНОВК G)8
С П\}В ТО СОНМАМ & РЙ1КСВ (Н1ТН 8ТВР312В СОКТНОЬ) .
С СТ. ЗВСТЮМ 11.6
С
С 1ЫР11Т РАНАМЕТВНЗ
с
С N 01МВК510И ОГ ТНВ 8У8ТВМ (М.ЬВ.51)
с геи ыамв (вхтвныаь) ор зивкоитгкв сомритгис тнв
С Р1НЗТ БВН1УАТ1УВ Г(Х,У):
с зивноитгив гсм(м,х,у,г)
С НЕАЬ*8 Х|У(Ы)|Р(Н)
С ТA)=... КТС.
С X 1ШТ1АЬ Х-УАЬЦВ
С ХВИО Р1МАЬ Х-УАЬИВ (ХВИБ-Х РО31Т1УВ ОН
С У(Ы) 1К1Т1АЬ УАЬЦВЗ РОН V
С ВРЗ ЬОСАЬ ТОЬБНАМСБ
С НМАХ МАХХМАЬ 8ТВР312В
С Н 1М1Т1АЬ 8ТВР812В О11В55
С

Приложение. Программы на Фортране 455
С СШТР11Т РАНАМВТВН5
С
С У(Ю 80ШЮМ АТ
с
с вхтвниаь зивноццив (то вв зцррыво ву тнв цзвн)
с
С 8О1О11Т ТН13 311ВН0иТ1МВ 13 САЫВО АРТВН ВУВНУ
с зцссвззрцыу сомрцтво зтвр (ам тнв
С Ш1Т1А1. УАШВ):
С 511ВН01ЛIN8 ЗОЬОЦТ (НВ,Х,У,!1)
С НВАЬ*8 Х,У(Ю
с ршинзнвз тнв зоитол у ат тнв ян-тн
С ОШБ-РОШТ X (ТНВ 1М1Т1А1. УАШВ 13 СОЛ-
С ЗЮВНВО АЗ ТНВ Р1Н5Т СНЮ-РО1ЫТ) .
с зыррьу а эмму зивноитгив, 1Г тнв зоштюы
С 13 ИОТ 0В31НЕ0 АТ ТНВ 1МТВКМВО1АТВ РО1ЫТЗ.
С
1МР1ЛС1Т КЕАЬ*8 (А-Н.О-2)
КВАЬ*8 К1E1),К2E1),КЗE1),К4E1),К5E1),К6E1),К7E1)
Г()У1(б1)
ьосюаь нв^вст
С0ММ0N/ЗТАТ/N^СN,NЗТВР,NАССРТ,NНВ^СТ
С СОММОЙ 8ТАТ САЫ ВВ Ц8В0 ГОН ЗТАТ18Т1СЗ
с — лгсы ыимвкн ог риыстюм
с — изтвр нцмввн от сомритво зтврз
С МАССРТ КИМвВН ОР АССВРТВО ЗТВРЗ
с — мнвлст кимввв ор нвлвство зтврз
СОММОК/СОВР/С2,СЗ,С4,С5,С6,С7,С8,С9,С10,С11,С12,С13,
1А21,АЗ 1, А32 , А41,А43,А51,А53,А54,А61,А64,А65,А71,А74,А75,А76,
1А81,А84,А85,А86,А87,А91,А94,А95,А96,А97,А98,А101,А104,А105 , А1Об,
8.А107,А108, А109, А111, А114, А115, А116, А117, А118, А119, АНЮ, А121,
ЛА124,А125,А126,А127,А128,А129,А1210,А1211,А131,А134,А135,А136,
&А137.А138, А139,А1310,А1311,В1,В6,В7,В8,В9,В10,В11,В12,В13,
ЬВН1,ВН6,ВН7,ВН8,ВН9,ВН1О,ВН11,ВН12
ОАТА ММАХ/2000/.11НО11Ы0/1.73Р-18/
С ЫМАХ МАХ1МАЬ ИиМвВН ОР 5ТВР5
С 1ШО1Ш0 ЗМАЫВЗТ ИиМВВН 8АТ13РУ1МС 1. П0 + иНО11МО> 1. ПО
С (ТО ВВ АРАРТВО ВУ ТНВ ЦЗВН)
САЫ СОВРЗТ
РО8№а = 051СК( 1. 00 , ХБЫО-Х)
с — иатгАЬ рйвранатюиз
НМАХ=БАВ5(НМАХ)
1.0-10,0АВ5(Н)) ,НМАХ)
^.ГАЬЗЕ.
=О
Nвв^ст=о
САЬЬ
С ВА31С ГИТВСНАТЮМ ЗТВР
1 1Р(К5ТВР.аТ.КМАХ.ОН.Х+.0300*Н.В0.Х)аОТО 79
(()
1Р ( (Х+Н-ХВ^ ) «РОЗНВС . ОТ . О . БО)Н=ХВИО-Х
САЫ
2
С ТНВ Р1НЗТ 9 ЗТАСВ5
00 22 1 = 1,11
22 У1A)=УA)+Н«А21*К1A)
САЫ, РСК(К,Х+С2*Н,У1
ПО 23 1=1,Л'
23 У1A)=УA)+Н*(А31*К1A)+А32*К2A))
САЫ РСН(М,Х+СЗ*Н,У1,КЗ)
НО 24 1*1,N
24 У1A)=УA)+Н*(А41*К1A)+А43*КЗA))

456 Приложение. Программы на Фортране
САЫ ГСМ(М,Х+С4*Н,У1,К4)
БО 25 1=1,N
25 У1A)=УA)+Н*(А51*К1A)+А53*КЗA)+А54*К4A))
САЫ ГСЛ(М,Х+С5*Н,У1.К5)
БО 26 1*1,N
26 У1A)=УA)+Н*(А61*К1A)+А64*К4A)+А65*К5A))
САЫ ГСМ(М,Х+С6*Н,У1.К6)
ПО 27 1*1,N
27 У1A)=УA)+Н*(А71*К1A)+А74*К4A)+А75*К5A)+А76*К6A))
САЫ ГСМ(Ы,Х+С7*Н,У1,К7)
00 28 1=1,N
28 У1A)=УA)+Н*(А81*К1A)+А84*К4A)+А85*К5A)+А86*К6A)+А87*К7A))
САЫ ГСМ(Ы,Х+С8*Н, У1.К2)
БО 29 1=1,N
29 У1A)=УA)+Н*(А91*К1A)+А94*К4A)+А95*К5A)+А96*К6A)+А97*К7A)
& +А98*К2A))
САЫ ГСЫ(М,Х+С9*Н,У1,КЗ)
00 30 1=1,N
30 У1A)=УA)+Н*(А1О1*К1A)+А1О4*К4A)+А1О5*К5A)+А1О6*К6A)
& +А107*К7A)+А108*К2A)+А109*КЗA))
С СОМРИТВ 1ЯТВКМВВ1АТВ ЗиМЗ ТО 8АУВ МВМОНУ
НО 61 1=1,N
У113 = А111*К1A)-»-А114*К4A)+А115*К5A)+А116*К6A)-»-А117*К7A)
& +А118*К2A)+А119*КЗA)
У123=А121*К1A)+А124*К4A)+А125*КбA)+А126*К6A)+А127*К7A)
& +А128*К2A)+А129*КЗA)
К4A)=А131*К1A)+А134*К4A)+А135*К5A)+А136*К6A)+А137*К7A)
& +А138*К2A)+А139*КЗA)
К5A)=В1*К1A)+В6*К6A)+В7*К7A)+В8*К2A)+В9*КЗA)
К6A)=ВН1*К1A)+ВН6*К6A)^ВН7*К7A)+ВН8*К2A)+ВН9*КЗA)
К2A)=У113
61 КЗA)=У123
С ТНВ ЬА5Т 4 ЗТАСВЗ
САЫ РСЫ(М,Х + С10*Н,У1.К7)
ПО 31 1=1,N
31 У1A)=УA)+Н*(К2A)+А1110*К7A))
САЫ ГСМ(М,Х+С11*Н,У1,К2)
ХРН=Х+Н
ПО 32 1=1,N
32 У1A)=УA)+Н*(КЗA)+А1210*К7A)+А1211*К2A))
САЫ РСЫС^ХРИ, VI,КЗ)
ПО 33 1=1,N
33 У1A)=УA) + Н*(К4A)+А1310*К7A)+А1311*К2(П)
САЬЬ
00 35 1 = 1,N
К5A)=УA)+Н*(К5A)+В10*К7A)+В11*К2A)+В12*КЗA)+В13#К4A))
35 К6A)=УA)+Н*(К6A)+ВН10*К7A)+ВН11*К2A)+ВН12*КЗA))
С ВННОН ВЗТ1МАТЮМ
ВНН=0.00
00 41 1=1,N
0В1<ОМ = 0МАХ1A.0-6,0АВ8(К5A)) ,0АВЗ(УA)) ,2
41 ВНК = ВНВ+((К5A)-К6A))/0В!<ОМ)**2
ВНН=03ОКТ(ВНН/0ГЬОАТ(К))
С СОМР11ТАТЮМ О?
С ИВ НВ01ЛНВ .33 /
ГАС=0МАХ1(A.00/6.00),0М1М1C.00,(ВВН/ВР5)**A.00/8.00)/.900))
НИВУ^Н/ГАС
1Г(ВНН.СТ.ВР8)С0Т0 51
С 5ТВР 13 АССВРТВО
00 44 1=1,N
44 УA)=К5A)
САЫ
1Р@
IР(КВ^ВСТ)НNВМ=РО8NВ^*^МIN1(^АВ5(НNВVУ),^АВ$(Н))

Приложение. Программы на Фортране 457
НВЛВСТ=.РАЬ5В.
СОТО 1
С 5ТВР 13 КВЛВСТВО
51
СОТО 2
С ГАИ ВХ1Т
79 НН1ТВF,979)Х
979 РОНМАТС ВХ1Т ОГ 0ОРЙ18 АТ Х=',016.7)
соврзт
с тн15 зивноццыв звт5 тнв с0вгг1с1влтз рок тнв оонмаыо-рн1ясв
с мвтноо ор оновн 8 н1тн вннон в5т1матон ор ойовн 7 а№ 13 8тасвз
1мрь1с1т кваь*8 (а-н.о-2)
соммом/совр/с2,сз,с4,с5,с6,с7,с8,с9,с10,с11,с12,с13,
ь а21, а31, а32 , а41, а43 , а51, а53 , а54 ^а61 , а64 , а65 , а71, а74 , а75 , а76,
& а81,а84,а85,а86,а87,а91,а94,а95,а96,а97,а98,а101,а104,а105,а106,
8. а107, а108.а109, ан 1, а114 , а115 , а116, а117 , а118, а119, а1110, а121,
& а124,а125,а126,а127,а128,а129,а1210,а1211,а131,а134,а135,а136,
& а137,а138,а139,а1310,а1311,в1,в6,в7,в8,в9,в10,в11,в12,в13,
& вн1(вн6,ви7,вн8,вн9,вн10,вн11,вн12
С2=1.00/18.00
03=1.00/12.00
С4=1.00/8.00
05=5.00/16.00
06=3.00/8.00
07=59.00/400.00
€8=93.00/200.00
09=5490023248.00/9719169821.00
010=13.00/20.00 ^
011=1201146811.00/1299019798.00
012=1.00
013=1.00
А21=С2
А31=1.00/48.НО
А32=1.00/16.НО
А41=1.00/32.00
А43=3.00/32.00
А51=5.00/16.ПО
А53=-75.00/64.00
А54=-А53
А61=3.00/80.00
А64=3.00/16.00
А65=3.00/20.00
А71 = 29443841.00/614563906. 00
А74 = 77736538.00/692538347. 00
А75 = -28693883.00/1125. 06
А76=23124283.00/18.08
А81 = 16016141.00/946692911. 00
А84=61564180.00/158732637.00
А85 = 22789713.00/633445777. 00
А86=545815736.00/2771057229.00
А87=-180193667.00/1043307555.00
А91=39632708.00/573591083.00
А94 = -433636366.00/683701615. 00
А95=-421739975.00/2616292301.00
А96=100302831.00/723423059.00
А97=790204164.00/839813087.00
А98=800635310.00/3783071287.00
А101 = 246121993.00/1340847787. ЪО
А104=-37695042795.00/15268766246.00
А105=-309121744.00/1061227803. 00

458 Приложение. Программы на Фортране
А106=-12992083.00/490766935.00
А107 = 6005943493.00/2108947869. 00
А108=393006217.00/139667 3457.00
А109=123872331.00/1001029789.00
АН 1 = -1028468189. 00/846180014. 00
А114 = 8478235783.00/508512852. 00
А116=1311729495.00/1432422823.00
А116 =-10304129995.00/1701304382.00
А117=-48777925059.00/304 7939560.0 0
А118=15336726248.00/103282464 9.00
А119=-45442868181.00/3398467696.00
АН 10 = 3065993473. 00/597172653. 0 0
А121 = 185892177.00/718116043. 00
А124=-3185094517.00/667107341.00
А125=-477755414.00/1098053517.00
А126 =-703635378.00/230739211.00
А127 = 5731566787.00/1027545527.00
А128=5232866602.00/850066563.00
А129 =-4093664535.00/808688257.00
А1210=3962137247.ВО/1805957418.00
А1211 = 65686358.00/487910083. 00
А131 = 403863854.00/4 91063109.00
А134 = -5068492393.00/4 34740067.00
А135=-411421997.00/54304 3805.00
А136=652783627.00/914296604.00
А137=11173962825.00/925320556.00
А138=-13158990841.00/6184727034.00
А139=3936647629.00/197804 9680.00
А1310=-160528059.00/685178525!00
А1311=248638103.00/1413531060.00
В 1=14005451.00/335480064.00
В6=-69238493.00/1068277825.00
В7=181606767.00/758867731.00
В8^561292985.00/797845732.00
В9=-1041891430.00/1371343529.00
В10 = 760417239.00/1151165299.00
В11=118820643.00/751138087.00
В12 =-528747749.00/2220607170.00
В13=1.00/4.00
ВН1=13451932.00/45517662 3.00
ВН6=-808719846.00/97600014 5.00
ВН7=1757004468.00/5645159321.00
ВН8=656045339.00/265891186.00
ВН9=-386757472^1. 00/15 18517206» 00
ВН10=465885868.00/322 736535.00
ВН11=530112 38.00/667516719.00
ВН12=2.00/45.00
НВТШМ
зоьоцт^зтбр.х.у.Ю
1мрыс1т осшвьв рнес15юм (а-н.0-2)
нвтинм
3. Ойех
Программа основана на методе экстраполяции (см. разд. II.9)
о переменным порядком и переменной длиной шага. Хороша
при всех уровнях точности, превосходна для очень высокой
точности (например, 10~20 или 10"0).

Приложение. Программы на Фортране
459
ООВХ (К,ГСМ|ХьУ,ХВК0,ВР5,НМАХ,Н)
с
С
С
С
С
С
С
С
С
с
С
с
С
с
С
С
с
С
С
С
С
С
С
С
с
С
с
с
с
с
с
С
с
С
с
С
С
С
С
С
с
с
С
с
М1Л4ВН1СА1
ОН01ИАНУ 0
ТН18 18 АН
ВХРЫС1Т ,М
АИО ОНБВН
ЗО1Л)Т1ОМ О? А ЗУ5ТВМ ОР Р1Н5Т ОНВВН
1*ТВВВЫТ1АЬ ВОЦАТЮИЗ У*=Г
ВХТВАРОЬАТЮН-АЬООВГТНМ, В
ЮР01ИТ\ Н1Л.В (Н1ТН 8ТВР312Е
ЗВХВСТ1ОИ).
С.Г. ЗВСТЮЫ 11.9
1ИРЦТ РАВАМВТВК8
N
ГСИ
X
хвив
У(Ю
ВР8
НМАХ
Н
01МВН8ЮИ ОГ ТНЕ 8У8ТЕМ (
(Х,У).
А5К0 ОИ ТНВ
СОИТНОГ,
1
И.ЬВ.51)
иамв (ВХТВНЫА1) ог зиввоитгкв сомрцт^с тнв
К1ВЗТ 0ВВ1УАТ1УВ Г(Х,У):
зивноит1мв гси(м,х.у.г
ПИАЬ Х-УАЬЦВ (ХЕИО.СТ.Х)
ХП1 1 1ЛЬ Т Ли^ии Г \/ Л I
ЮСАЬ ТОЬВНАИСВ
МАХ1МАЬ 8ТЕР812Е \
гишаь ЗТВР812В оивзз
О11ТР11Т РАВАМВТВВЗ
У(М)
ВХТВНИАЬ 3
зоьоит
зоьитюн ат хвно
иввоитгмв (то вв зиррыво в
ТН13 зивноитгив 18 саыео
)
-^ /О М Т>
У ТНВ ЦЗВВ)
АГТВВ ВУВНУ
зцеевззгиыу сомритво зтвр (аио тнв
1МТ1АЬ УАЬЦВ):
зцввоитгмв зоюцт (ин,
НВАЬ*8 Х,У(И)
РиВК13НВ8 ТНВ ЗОШТЮИ У
^СВЮ-Р01М^ X (ТНВ 1ШТ1А1
5ЮБКВБ АЗ ТНВ ПВЗТ ОВЮ
зиррьу а оцмму зивкоит1ив
15 ЫОТ 0В51НВ0 АТ ТНВ ^[ИТ
X,У,И)
АТ ТНЕ ЫН-ТН
УАИ)В 13 СОИ-
-РО1ИТ).
, 1Р ТНВ ЗОЩТЮИ
ВНМВ01АТВ РО1ИТЗ.
О
\
1МРЫС1Т НВАЬ*8 (А-Н.0-2)
ЮС1САЬ НВЛВСТ,ЬА5Т
СОММОЙ /ЗТАТ/NГСN,NЗТВР,NАССРТ,NНЕ^СТ
СОММОЫ ЗТАТ САЫ ВВ ЦЗВБ ГОН ЗТАТ13Т1СЗ
N^'СN лимввн ог гикстюи еуаьца
ызтвр ицмввн ог сомритво зтврз
ИАССРТ КЦМВВН ОГ АССВРТВБ ЗТВРЗ
ЫНВ.1СТ мимввн ог нвлвство зтврз
СОММОЫ /ВХТАВЬ/ Б2E1),Т(9,61),ЫЛ(9),НН(9),N(9).ВНК.ГАС,
С
С
БАТА N.1/2,4,6,8,10,12,14,16,18/
ЭАТА А/3.00,7.00,13.00,21.00,31.00,43.00,57.00,73.ЛО,91.00/
ОАТА NМАX/800/,КМ/9^^НО^N^/1.730-18/
NМАX МАХ1МАЬ ИиМВЕН ОТ ЗТВРЗ
N^МВЕВ ЗАТ15ГУ1ЫС 1. 00 + ЦНОМО> 1. 00

460 ' Приложение. Программы на Фортране
С (ТО ВВ АОАРТВЭ ВУ ТНВ Ц5ЕН)
БАТА РАС1/2.0-2/,РАС2/4.00/,РАСЗ/.900/,РАС4/.800/
ЭАТА ЗАРВ1/.6500/.5АРВ2/.9400/
С 1ШТ1АЬ РНВРАНАТIОN5
ВР304=ВРЗ*5АРВ1
ИАССРТ=0
Н = 0Мт(Н,НМАХ, ( ХВМ -X ) /2 . 00)
САЫ 50Ю11Т (МАССРТ+1,Х,У,Ю
ВНН=0.00
ИA)=0.00
НВЛВСТ=.РАЬЗВ.
ЬАЗТ=.РАЬ5Е.
С 18 ХВЫй НВАСНВО 1М ТНВ ЫВХТ ЗТВР?
10 Н1=ХВКБ-Х
гг (Н1.^в.^но^N^) ао то но
Н = 0М1т(Н,Н1,НМАХ)
1Р (
саы
С ТНВ ПНЗТ АN^ ЬАЗТ ЗТВР
1Р (ЫЗТВР.ВО.О.ОВ.ЬАЗТ) ТЫВЫ
г, НО 20 ^1,К
[ кс=^
САЫ МЮВХи.Х, У.Н.НМАХ.К,
20 1Р (Л.СТ.1.АМ0.ВВК.ЬЕ.ЕРЗ) 00 ТО 60
СО ТО 55
В№ 1Р
С ВА51С 1ЫТВСНАТЮМ ЗТВР
30 С0МТ1МУВ
Ы5ТВР=М5ТВР+1
1Р (№ТЕР.ОВ.ММАХ) 00 ТО 120
КС=К-1
00 40 Д=1,КС
40 САЫ МЮЕХ(.1,Х, У.Н.НМЛХ.Л.ГСГ*,)
С СОNVВНаВNСВ МОШТОН
1Г (К.ЕО.г.ОКДНЁ'аВСТ1) СО ТО 50
1Г (ВНН.ЬВ.ВРЗ) СО ТО 60
1Г (ВНН/ВР5.СТ. (г>?ЬОКТ(Ги(К+1)*НЛК))/4.Ъ0)**2) СО ТО 100
50 САЫ МЮЕХ(К,Х,У,Н,НМАХ,К, РСЮ
кс=к
I? (ВНН.ЬЕ.ЕРЗ) СО ТО 60
С НОРВ РОН СОМУВНСВМСВ 1Ы ЫИВ К+1
55 1Р (ВНН/ВР5.СТ.(^^^ОАТ(N^(К+1))/2.БО)**2) СО ТО 100
КС=К+1
САЫ М10ВХ(КС,Х,У.Н,НМАХ^
1Р (ВНН.СТ.ВРЗ) СО ТО 100
С ЗТВР 18 АССВРТВО
60 Х=Х+Н
БО 70 1=1,N
70 УA)=ТA,1)
САЫ ЗОЬОЦТ (МАССРТ+1,Х,У,М)
С СОМРЦТВ ОРТ1МАЬ ОНБВН
1Г (КС.ВО.2) ТНВЫ
К0РТ=3
1Р ([НВ^ВСТ]) КОРТ = 2
СО ТО 80
ВИО 1Р
1Р (КС.ЬВ.К) ТНЕЫ
КОРТ=КС
1Р (»У(КС-1).ЬТ.»У(КС)*РАСЗ) К0РТ = КС-1
1Р (»У(КС).ЬТ.»У(КС-1)*РАСЗ) КОРТ=М1М0(КС+1, КМ-1)

Приложение. Программы на Фортране 461
вьзв
КОРТ=КС-1
I? (КС.ОТ.З.АМ.1У(КС-2).1.Т.1У(КС-1)*ГАСЗ), КОРТ = КС-2
1Г (Н(КС).ЬТ.1У(КОРТ)*ГАСЗ) КОРТ=МIN0 (КС , КМ-1)
В№ 1Р
с — Агтвн а нв^ствб зтвр
1
л
{ 80
К=М1М0(КОРТ,КС)
1ДВ\1ВСТ=.ГАЬ5В.1
ао то То
С СОМРЦТВ 8ТЕР312В ГОй ЫВХТ 5ТВР
1Г (КОРТ.ЬВ.КС) ТИВЫ
Н=НН(КОРТ)
ВЬ5В
1Г (КС.ЬТ.К.АИО.»У(КС) . 1Т. Н(КС-1) *ГАС4 ) ТНВЫ
Н=НН(КС)*А(К0РТ+1)/А(КС)
ВЬЗВ
Н=НН(КС)*А(КОРТ)/А(КС)
К=КОРТ
00 ТО 10
С ЗТВР 15
100 К=М1М0(К,КС)
1Р (К.аТ.2.АК0.**(К-1).ЬТ.»У(К)*ГАСЗ) К = К-
NНв^ст=Nнв^ст+1
Н=НН(К)
нв^вст=.тн^в.
СО ТО 30
С ЗОНДОМ ВХ1Т
110
С ТКИ ВХ1Т
120 КН1ТВ F,*) ' МОЙВ ТНАИ \ПНКХ,' ЗТЕРЗ
с
зиВН011Т1НВ МЮВХи.Х.У.Н.НМАХ.Л.РСМ)
с --- тн1з зивноцтгкв сомрцтвз тнв .1-тн елыв ог тнв
С ВХТНАРОЬАТЮЫ ТАВЬВ АИБ РНОУЮВЗ АЫ Е5Т1МАТЮН
С ОГ ТНВ ОРТ1МАЬ 8ТВР312В
1МРЫС1Т КВАЬ*8 (А-Н.О-2)
ЕХТВИИЛЬ РСИ
ВВАЬ*8 У(М),ПУE1),УН1E1),УН2E1)
РПММЛМ /СТАТ /НРРМ НСТРР МДГ*РРТ МОРТРТ
СОММОЙ /ВХТАВЬ/ 02E1),Т(9,51),ИД(9),НН(9),Н(9),ВНН,РАС,
1 А(9) ,ВР804,1Л10иМО,ГАС1,РАС2,5АРВ2
С --- ВШВН 5ТАКТ1М0 ЗТВР
НО 30 1=1,М
УН1A)=УA)
30 УН2A)=УA)+НЛ*02A)
С . ХРЫС1Т МЮР01ИТ
НО 35 ММ=1,М
САЫ РСМ(К,Х + НД*0ГЬОАТ(ММ) ,УН2.БУ)
ПО 35 1=1,N
УЗ=УН1A)
УН1A)=УН2A)
35 УН2A)=У5 + 2.П0*Н.1*0УA)
С ПИАЬ ЗМ00ТН1М0 ЗТВР
САЬЬ ГСМ(К,Х+Н,УН2,0У)
ПО 40 1=1,N
40 Т(.1,1) = (УН1A)+УН2A)+1и*0УA))/2.В0
NРСN=NРСN+N^(^)

462 Приложение. Программы на Фортране
РОЬУГ*ОМ1АЬ ЕХТНАРОЬАНСШ
1Р (Л.ВОЛ)
00 60 Ь=Л,2,-1
=(
60 1 =
Т(Ь-1,1)
60 ССШТИШЕ
ВНН=0.00
НО 65 1 = 1, N
С ВСАИЫС
а'САЬ = 0МАХ1@АВ5(УA)),0АВ5(ТA,1))
65 внн=внн+((тA,1)-тB,1))/5саь)**2
внн=озонт(внн/орьоат(Ю)
с сомрцтв 0рт1ма1. 5твр512в5
вхр0=1.00/0рюатB*л-1)
расм1ы=тас1*«вхр0 {
рас = 0м1н1(рас2/расм1и,0мах1(расмш,(внн/кр504)**кхр0/загв2
РАС=1.00/РАС
НН(Л)=0М1М(Н*РАС,НМАХ)
вно
зоьоит (
1МРЫС1Т НВАЬ*^ (А-Н.0-2)
НВАЬ*8 У(Ы)
4. О<1ех2
Программа основана на методе экстраполяции (см. разд. 11.13)
с переменным порядком и переменной длиной шага. Предназначена
для интегрирования дифференциальных систем второго порядка
вида у" = / (х, у). Хороша для всех уровней точности.
0БВХ2 (Л, ГСЯ, X , У , УР, ХВМ , ВР8 , НМАХ , Н)
с
с
с
с
с
с
р
с
р
с
с
с
с
с
с
с
с
с
с
с
с
с
р
с
р
с
с
с
ШЖВНЮАЬ
ОН01ЫАНУ
зоьитюи ор а зузтвм ор звсоыб онбвн
О1РРВНВМТ1АЬ ВОЦАТЮМЗ УН*Р(Х,У).
ТН13 15 АЛ ВХТНАРОЬАТЮЛ-АЬаОНГТНМ, ВАЗВБ ОЛ ТНВ
ВХРЫС1Т
АЫБ ОНОВН
МЮР01М Н1ЛВ (К1ТН 5ТВР512В СОКТНОЬ
ЗВЬЕСТЮИ).
СР. ЗВСТЮИ II. 13
1ИРЦТ РАНАМВТВКЗ
N
РСЫ
X
хвыо
У(И)
УР(Ы)
ВРЗ
НМАХ
н
ШИВИЗЮИ ОР ТНВ ЗУЗТЕМ (N.16.51)
камв (вхтвнкаь) ор зивноитгмв сомрипыс тн
ЗВСОИП БВН1УАТ1УВ Р(Х,У):
СТТООЛ1Т*РТЪ10 Р^4 Ъ1 ^ Ы V V Р\
оиОпии 1 1П& г Чу П ^ П | Л | I % Г }
НВАЬ*8 Х.УСИ),Р(Ы)
РA)=... ВТС.
1Н1Т1АЬ Х-УАЬиВ
Г1ИА1, Х-УАЬЦВ (ХВМО.ОТ.Х)
1Н1Т1АЬ УАЬЦВЗ РОН У
1Ы1Т1А1 УАШВЗ РОН У1
ЮСАЬ ТОЬВНАМСВ
МАХ1МАЬ 5ТВР312В
щтАь ЗТВР312В ацвзз
ОЦТРЦТ РАНАМВТВНЗ
у(М)
УР(М)
зоьитюы ат хвм
ОВК1УАТ1УВ ОР ЗОЛИТЮМ АТ ХЕМ

Приложение. Программы на Фортране.
463
с
с
С
С
С
С
С
С
С
С
С
С
с
С
с
С
С
с
ехтеним
5 О ИЛ 2
(то вв зыррыво ву тнв
ТН13 ЗиВНОиПИЕ 18 СКЫЕд АРТВН ВУВНУ
ЗиССЕЗЗШЬЬУ СОМРЫТЕО 5ТВР (Айв ТНЕ
1)<1Т1АЬ УАЬОЕ):
зиВНОЦИМЕ 5ОИЛ2 (ЫН.Х.У.УР.М)
НВАЬ*8 X,V(N),VР(N)
Р1ШК15НЕ5 ТНЕ 5О^^ТIОN (У,УР) АТ ТНЕ ЛН-ТН
СНЮ-РОГЫТ X (ТНВ 1МТ1АЬ УАИ1В 15
ЗЮЕНВО АЗ ТНВ ПВЗТ СНЮ-РО1НТ).
811РРЬУ А Б1ЖМУ ЗЫВНОЦТ^В, 1Г ТНВ
15 N01 0В81НВ0 АТ ТНЕ 1МТЕНМЕ01АТЕ Р01ЫТ5.
1МРЫС1Т НВАЬ$8 (А-Н.0-2)
Ь0С1САЬ НЕ^СТ.ЬАЗТ
НЕАЬ»8 У(N),VР(N)
&ТВР5
5ТЕР5
зтврз
(9),НН(9),К(9),ВНН,ГАС,
С
С
С
С
СОММОЙ /ЗТАТ/N^'СN,N5ТВР,NАССРТ,NНВ^СТ
СОММОЫ ЗТАТ САИ ВВ Ц5Е0 ГОН ЗТАТ15Т1С5
ыгсы нимввн ог рцкстюк
МЗТВР N^МВВН ОР СОМРИТВО
МССРТ Ы1;МВВН ОГ АССВРТЕО
Nнв^ст К1ЖВВН ог нвавство
СОММОМ /ЕХТАВЬ/ ЫF1),Т(9,61),ТР(9,51),
А(9),ВР504,ЦНОиМО,ГАС1,ГАС2.8АГЕ2
БАТА КЛ/2,4,6,8,10,12,14,16,18/
ОАТА А/2.00,4.00,7.00,11.00,16.00,22.00,29.00,37.00,46.00/
ЭАТА ИМАХ/800/, КМ/9/, 11Н01ШБ/1.730-18/
^АХ МАХ1МАЬ N^МВВН ОГ ЗТВРЗ
1Ш01ШР 5МАЫЕ5Т КиМВВН 8АТ18ГУ1КС 1. 00>иНОиИ0> 1. 00
(ТО ВВ АОАРТЕО ВУ ТНЕ ЦЗВН)
БАТА ГАС1/2.0-2/,ГАС2/4.00/,ГАСЗ/.900/,ГАС4/.800/
ОАТА ЗАГВ1/.6500/,5АГЕ2/.9400/
1М1Т1АЬ РНВРАНАТI0NЗ
ВР804=ЕР5*8АГВ1
N5ТЕР=0
ИАССРТ=О
К = МАX0C,МIN0(8,1ИТ(-ОЬОС10(ВРЗ)*.600+1.500 )))
н=омт(н,нмАХ, (xвN^-x)/2.^0)
САЫ ЗОЬЦТ2 (NАССРТ+1,X,V,УР,N)
ВНН=0.00
С
10
ТНВ
СО ТО НО
С
нв^вст=.ГА^зЕ.
ЬАЗТ-.ГАЬЗЕ.
13 ХВМ НВАСНВО
Н1=ХВЫ0-Х
1Г (Н1.ЬВ
Н = 0М1Ш(Н,Н1,НМАХ)
1г (Н.ав.н1-^но^N^)
САЫ ГСМ(Н,Х,У,02)
NГСN=NГСN+1
ТНВ Р1Н5Т АИО ЬАЗТ 5ТВР
1Г (МЗТВР.ВО.О.ОН.ЬАЗТ)
5ТЕР?
20
С
30
00 20 Л=1,К
кс=^
САЫ 8Т0ВНМ(Л,Х,У, VР,Н,НМАX,N,ГСN)
1Г (Л.аТЛ.АКО.ВВВ.ЬВ.ВРЗ) СО ТО 60
СО ТО 55
ВЫО 1Г
ВА31С ^ТВСНАТЮМ ЗТВР
С0МТ1КЦЕ
N5ТВР=NЗТЕР-Ц
1Г (МЗТВР.ОВ.ММАХ) СО ТО 120
КС=К-1
00 40 ^1

464 Приложение. Программы на Фортране
40 СА1Ь .Л..
С СОМУВНСВМСВ М0М1Т0Н
1Г (К.В0.2.0Н.НВЛВСТ) 00 ТО 50
1Г (ЕНН ЬЕ ЕР8) СО ТО 60
1г (внн/врз.ст. (ог1.оат(м.1(к+1)*млк))/4.оо)**2) ,со то юо
\ 50 САЫ. 5Т0ВНМ(К,Х, V, УР, Н, НМАХ, N. ГСЮ
КС = К
1Г (ЕНН.ЬВ.ВРЗ) СО ТО 60
С НОРВ РОВ СОМУВНОВИСВ 1Ы ЫИВ К+1
55 1г (кнн/врз.ст. (б*1ьоат(м.ик+1))/2.оо)**2) со то юо
КС=К+1
САЫ, 5Т0ВНМ(КС, X, V, УР,Н,НМАХ,К,
1Г (ВЙН.0Т.ВР5) 00 ТО 100
С ЗТВР 13 АССВРТВБ
60 Х=Х+Н
ВО 70 1=1,М
70 УA)=ТA,1)
NАССРТ=NАССРТ+1
СКЫ ЗОЬЦТ2
С СОМРЫТВ ОРТГМАЬ
1Г (КС.ВО.2) ТНВК
К0РТ=3
1Г (НВЛВСТ) К0РТ=2
СО ТО 8.0
ЕМ 1Р
1Р (КС.1В.К) ТНВИ
КОРТ=КС
1Г (**(КС-1).ЬТ.И(КС)*ГАСЗ) К0РТ=КС-1
1Р (Н(КС).ЬТ.Н(КС-1)*КАСЗ) КОРТ=М1М0(КС+1,КМ-1)
ВЬЗВ
К0РТ=КС-1
1Г (КС.СТ.З.АК0.1У(КС-2) .ЬТ.У*(КС-1)*РАСЗ) К0РТ=КС-2
1Р (К(КС) . ЬТ.И(КОРТ)*ГАСЗ) КОРТ = М^0( КС , КМ-1)
с — агтвн а нв^вств^ зтвр
80 1Р (НЕЛВСТ) ТНЕЫ
К=М1К0(КОРТ,КС)
Н=0М1М(Н,НН(К))
НВЛВСТ=.РАЬЗВ.
СО ТО 10
С СОМР1ЛВ ЗТЕРЫ^В ГОВ ЫВХТ ЗТВР
1Р (КОРТ.ЬВ.КС) ТНКМ
Н=НН(КОРТ)
ВЬЗЕ
1Р (КС.ЬТ.К. АN^.^У(КС) .ЬТ.И(КС-1)*РАС4) ТНВN
Н=НН(КС)*А(К0РТ+1)/А(КС)
В ЬЗВ
Н=НН(КС)*А(КОРТ)/А(КС)
К=КОРТ
СО ТО 10
С ЗТВР 15
100 К=МШ0(К,КС)
Nнв^ст=NНв^ст+1
Н=НН(К)
нв^вст=.тн^в.
ао то зо
С ЗОЬЦТЮЫ ВХ1Т
110 С0ЛТ11ШВ
С РА1Ь ВХ1Т
120 ИН1ТВ F,*) * МОНЕ ТНАN '^МАХ,* ЗТВРЗ

Приложение. Программы иа Фортране 465
311ВНО11Т1М 5ТОВНМ( ^ , X, V, УР» Н^ НМАХ,Я,
с — тн1з зивноот^в сомрцтвз тнв з-тн им ор тнв
С ВХТКАРОЬАТЮЫ ТАВЪВ АИО РНОУЮВЗ АN ВЗТ1МАТ10Ы
С --- ОГ ТНВ ОРПМАЬ ЗТВР512В
1МРЫС1Т ВВАЬ*8 (А-Н,О-2)
ВХТВНЫАЬ ГСЫ
НВАЬ*8 У(Ю.УРСИ),0УE1),УН1E1),2Н1E1)
СОММОЙ /ВХТАВЬ/ 02E1)>Т(9,51)>ТР(9>51),N^(9),НН(9),N(9),ВИН,ГАС,
1 А(9) ,ВР504,ШгО1Ш0,ГАС1,ГАС2,8АГЕ2
С В1Л.ВК ЗТАКТ1ЫС ЗТВР
ВО 30 1=1, N
УН1A)=УA)
30 2Н1A)=УРA)+Н.1*02A)
С ВХРЫС1Т МЮРО1ЫТ EТ0ВНМВН) НЫЬВ
м=N^(^)/2-1
1Г (Л.ВОЛ) 00 ТО 37
00 36 ММ=1,М
БО 33 1=1,N
33 УН1A)=УН1A)+!и2*2Н1A)
саьь РСN(N,x+н^2*^^^^оАТ(мм) ,
БО 35 1=1,М
36 2Н1A)=2Н1A)+На2*0УA)
С ПЫАЬ ЗТВР
37 С0КТ1НЦВ
00 40 1=1,N
40 УН1A)=УН1A)+НЛ2*2Н1A)
САЫ РСК(М,
00 43 1 = 1, М
43 ТР(.1,1)=2Н1A)+Н.1*0УA)
С Р0ЬУЯ0М1АЬ ВXТНАРО^АТIОN
1р (^.в^. 1) ввтшгм
ЙО 60 Ь=Л,2,-1
РАС=(^^>^ОАТ(N^(^))/^р^ОАТ(N^(^-1)))**2-1.^о
60 1=1,N
ТР(Ь-1,1)=ТР(Ь,1)+(ТР(Ь,1)-ТР(Ь-1,1))/ГАС
60 С0ЫТ1КЦВ
ВНК=0.00
00 65 1=1,N
С ЗСАЬ1Ыа
ЗСАЬ=0МАХ1(ПАВЗ(УA)),ОАВ5(ТA,1)),1.0-6,
ЗСАЬР=0МАХ1@АВЗ(УРA)),0АВЗ(ТРA.1)), 1. 0-6 ,11НО1Ж0/ВР504)
65 ВНй=ВНН+((ТA,1)-ТB,1))/ЗСАЬ)**2+((ТРA,1)-ТРB,1))/ЗСАЬР)**2
ВйН=05ОНТ(ВЯН/0ГЬОАТ(К*2))
С СОМРиТВ 0РТ1МАЬ ЗТВР312ВЗ
ВХРО=1.00/0ГЬОАТB*Д-1)
РАСМ1И=РАС1**ВХР0
РАС=0М1М1(РАС2/РАСМ1К,0МАХ1(РАСМ1М,(ВНН/ВРЗВ4)**ВХР0/8АРВ2))
РАС=1.00/РАС
^♦(^)=А(^)/нн(^)
(ЫКРИТЗ, Х,У,УР,К)
1МРЫС1Т КВАЬ*8 (А-Н.0-2)
ЯВАЬ*8
нвтинн
вио

466 Приложение. Программы на Фортране
5. ЭорНп
Программа явного метода Рунге—Кутты—Нюстрёма, основан-
основанная на формулах Дормана и Принса о автоматическим управ-
управлением длиной шага. Предназначена для интегрирования
(см. табл. 13.4 из разд. 2.13) дифференциальных систем вида
У' = / (*. У),
ООРНШСН, ГСМ.Х» V, УР.ХВИО.ВРЗ.НМАХ.Н)
С МЦМВН1СА1, ЗОННОЙ ОГ А 5УЗТВМ ОР 5ВСОИ0 ОНОВН
С ОН01КАНУ П1РГВНВ1*Т1АЬ ВСШАТЮИЗ УИ=Г(Х,У).
С ТН13 18 АИ ВМВВООВО ЫУ5ТН0ВМ МВТНОЭ ОР ОНОВН FO
С 0\)В ТО СОНМАМ & РНШСВ (И1ТН ЗТВР512В СОИТНОЮ
С С.Г. ЗВСТЮМ 11.13
с
С 1ИР11Т РАНАМВТВНЗ
с
С N 01МВМ5ЮК ОР ТЫВ ЗУЗТЕМ (N.16.51)
с рсы иамв (вхтвныаь) ор зывноитхив сомритгиа тнв
С ЗВСОИО ОВН1УАТ1УВ Г(Х,У):
с зивноинив гсм(м,х,у,г)
С НЕАЬ*8 Х,У(Н),Р(Н)
С ГA)=... ВТС.
С X 1Н1Т1АЬ Х-УАШВ
С ХВМЭ ПМАЬ Х-УАЬЦВ (ХВМ.аТ.Х)
С У(И) 1К1Т1АЬ УАЬЦВЗ ГОН V
С УР(Ы) .1Ы1Т1АЬ УАШВ5 РОН У
С ВРЗ ЬОСАЬ ТОЬВНАКСВ
С НМАХ МАХ1МАЬ ЗТВР812В
С Н 1И1Т1А1 ЗТВР312В 01}В85
С
С ОЦТРиТ РАНАМВТВНЗ
Л» _____ _______
С У(Ы) 80ЬЦТЮК АТ ХВИО
С УР(Ы) ОВН1УАТ1УЕ ОР ЗОЬиТЮЫ АТ ХЕ№
С
с вхтвннаь 511вно1ткв (то вв зирриео ву тнв извн)
с
С 50ШТ2 ТН13 ЗиВН0иТ1КВ 13 САЫВО АРТВН БУБНУ
С 811ССВ85Р1Л1.У СОМРЫТВО ЗТЕР (АЫО ТНВ
С 1К1Т1АЬ УАЬЫВ):
С 8ЦВНОЦТ1МВ 8ОЬЫТ2 (МН,X,V,УР,Ю
С НВАЬ*8 Х,У(И),УР(М)
С РЦНЫ18НВ8 ТНВ 80ШТ10И (У.УР) АТ ТНВ ЫН-ТН
С аНЮ-РОГИТ X (ТНВ 1МТ1АЬ УАЬЦВ 13
С 5ЮВНВ0 АЗ ТНВ Р1НЗТ ОНЮ-РОГИТ) .
с зирръу а юимму з^вно^ТINВ, 1Р тнв
С 18 ИОТ 0Е31НВ0 АТ ТНВ 1КТВНМВО1АТВ РО1ИТ5.
1МРИС1Т НВАЬ*8 (А-Н.О-2)
НВАЬ*8 К0E1),К1E1),К2E1),КЗE1),К4E1),У1E1),У(М),УР(Н)
ЬОСЮМ НВЛВСТ
С СОММОЙ 5ТАТ САИ ВВ ЦЗВО РОН ЗТАТ13Т1СЗ
с — ырси иимввн ор риыстюн
С ЫЗТВР МиМВВН ОР СОМР11ТВО 8ТВРЗ
С ИАССРТ 1ШМВВН ОР АССВРТВО ЗТВРЗ
с — мнвдет кцмввн ор нв^вств^ зтврз
ОАТА КМАХ/2000/,иНОЦМ0/1.73Э-18/
с — имах махгмаь мимввн ор зтерз
С иНОЦИП 8МАЫВЗТ 1ШМВВН ЗАТ13РУ1На 1
С (ТО ВВ АЭАРТВО ВУ ТНВ ЦЗВН)
АЬРН1=.Ю0
АЬРН2=.2ОО

Приложение. Программы на Фортране 467
АЬРНЗ=3.00/8.00
АЬРН4=.5ОО
3021=ОЗОНТB1.00)
АЬРН5=G.00-3021)/14.00
АЬРН6=G.00+3021)/14.00
С0=.05О0
С4=16.00/45.00
С5=49.00/180.00
010=1.00/200.00
020=1.00/150.00
021=1.00/75.00
030=171.00/8192.00
031=45.00/4096.00
032=315.00/8192.00
040=5.00/288.00
041=25.00/528.00
042=25.00/672.00
043=16.00/693.00
050=A003.00-205.00*3021)/12348.00
051=(-18775.00+4325.00*3021)/90552.00
052= A5600. 00-3425'. 00*5021) /43218. 00
053=(-46208.00+10112.00*3021)/237699.00
054=C411.00-745.00*5021)/24696.00
060=G93.00+187.00*5021)/12348.00
061=(-8275.00-2825.00*8021)/90552.00
062=B6100.00+6175.00*5021)/43218.00
С63=-A905280.00+483712.00*3021)/9745659.00
064=C327.00+797.00*3021)/24696.00
065=-E81.00+127.00*3021)/1722.00
070=(-157.00+3.00*3021)/378.00
071=C575.00-250.00*5021)/2772.ЪО
072=-B1900.00+1375.00*3021)/3969.00
073=A168640.00+23040.00*5021)/596673.00
074=-A353.00+26.00*5021)/2268.00
075=A2439.00+2639.00*8021)/4428.00
076=C5.00-7.00*5021)/36.00
080=.0500
084=8.00/45.00
085=D9.00+7.00*3021)/360.дО
086=D9.00-7.00*3021)/360.00
С 1ШТ1АЬ РНВРАНАТЮК5
НМАХ=0АВ5(НМАХ)
Н = ОМ1М1(ОМАХ 1A.0-8,ОАВЗ(Н)),НМАХ)
= 0МАХ1(ЕР5,9.00*11НО1Ш0)
СТ=.
МАССРТ=О
САН, 5ОИЛ2(КАССРТ+1,Х,У»УР,М)
САЫ ГСЫ(М,Х,У,КО)
С ВА31С 1КТВОНАТЮН 5ТВР
1 1Г(М5ТВР.ОТ.ММАХ.ОН.Х+.0500*Н.ЕО.Х)СОТО 79
I^((x-xвN^)*Р05NЕО+^но^N^.ст.о.^о)
НР2=Н*Н
М5ТВР=Ы5ТВР+1
С ТНВ Г1Н5Т 5 5ТАОВ5
00 21 1=1,N
21 У1A)=УA)+АЬРН1*Н*УРA)+НР2*О10*К0A)
САЬЬ ГСМ(М,Х+АЬРН1*Н,У1,К1)
00 22 1=1,N
22 У1A) = УA)+А1.РН2*Н*УРA) + НР2*(С20*К0A)+С21*К1A))
САЫ ГСМ(М,
00 23 1 = 1,N

468 Приложение. Программы на Фортране
23 У1A)=УA)+АЬРНЗ*Н*УРA)+НР2*(СЗО*К0A)+а31*К1A)+С32*К2A) )
САЫ ГСМ(Ы,Х + АЬРНЗ*Н,У1,КЗ)
00 24 1-1,N
24 У1A)=УA)+АЬРН4*Н*УРA)+НР2*(С40*К0A)+О41*К1A)+С42*К2A)+
& С43*КЗA))
САЬЬ ГСН(Г*,Х + АЬРН4*Н,У1,К4)
00 25 1=1,N
25 У1A)=УA)+АЬРН5*Н*УРA)+НР2*(С50*К0A)+С51*К1A)+С52*К2A)+
& С53*КЗA)+С54*К4A))
С СОМРЫТВ 1МКНМК01АТЕ ЗИМ ТО 5АУВ МВМОНУ
00 61 1=1,N
У13=С60*КОA)+061*К1A)+С62*К2A)+С63*КЗA)+С64*К4A)
КЗA)=С70*К0A)+С71*К1A)+С72*К2( I)+ 07 3*1C (I)+074*К4(I)
61 К2A)=У15
С ТНВ ЬАЗТ 4 5ТАСВ5
САН. КСМ(И,Х+АЬРН5*Н,У1.К1)
00 26 1=1,N
26 У1A)=УA)+АЬРН6*Н*УРA)+НР2*(К2A)+С65*К1A))
САЫ КСМ(М,Х+АЬРН6*Н,У1,К2)
00 27 1=1,N
27 У1A)=УA)+Н*УРA)+НР2*(КЗA)+С75*К1A)+С76*К2A))
ХРН=Х+Н
САЫ ГСМ(Г*,ХРН, VI,КЗ)
00 28 1=1,N
28 У1A)=УA)+Н*УРA)+НР2*(С80*К0A)+С84*К4A)+С85*К1A)+С86*К2A))
НО 30 1=1,N
30 К4A)=УРA)+Н*(С0*(К0A)+КЗA))+С4*К4A)+С5*(К1A)+К2A)))
САЫ ГСМ(М,ХРН,У1,К1)
00 33 1=1,N
33 К2A)=НР2*(К1A)-КЗA))/20.00
С ВННОН ВЗТIМАТIОN
ЕНН=0.00
00 41 1=1,N
^ЕNОМ= ОМ АХ 1 A.0-6,0 АВ5 (У1( I) ) ,0АВЗ(УA) ) , 2 .
41 ЕКН=ВНН>(К2A)/ОЕМОМ)**2
ВНН=05ОНТ(ВНН/0ГЬОАТ(Ю)
С СОМРЦТАТЮМ ОР НМЕ**
С НЕ НЕ01ЛНВ .2< = НNБ^У/Н< = 10.
РАС=0МАХ1(.100,ОМ1К1E.00,(ЕНН/ЕР5)**A.00/7.00)/.900))
1Г(ЕНН.ЬЕ.ЕРЗ)ТНЕМ
С ЗТЕР 15 АССЕРТЕО
МАССРТ=ЫАССРТ+1
00 44 1=1,N
УРA)=К4A)
К0A)=К1A)
44 УA)=У1A)
Х = ХРН
САЫ 5ОЬиТ2(МАССРТ+1,Х, V, УР.Ю
1Г@АВ5(НМВИ).СТ.НМАХ)НМЕМ-Р03МЕС*НМАХ
IГ(НЕ^ЕСТ)НNЕИ=Р05NЕа♦^МIN1(^АВЗ(НNЕМ),0АВ5(Н)
НЕЛЕСТ=.ГАЬ5Е.
ВЬЗЕ
С ЗТЕР 15 НЕЛВСТВО
1Г(МАССРТ.СВ.1)NНВ^СТ=NНВ^СТ+1
СОТО 1
С ГАИ ВХ1Т
79 ИН1ТВF,979)Х
979 ГОНМАТ(' ВХ1Т ОГ 0ОРН1Ы АТ Х=',016.7)

Приложение. Программы на Фортране 469
ЗОИ1Т2 (ИНРМБ.Х, V, УР.Ю
1МРЫС1Т КВАЬ*8 (А-Н.О-2)
НВАЬ*8 У(М)
в. Ке1аг<1
Модификация программы БОРК15 для дифференциальных
уравнений с запаздывающим аргументом (см. разд. 11.15). Вклю-
Включен пример головной программы, вызывающей КЕТАГф. Подпро-
Подпрограммы 5ТОКЕ и УЬАО также полезны для сплотного» вывода
и построения графиков.
С 8АМР1.В САЫЛЫа РНОСНАМ ГОН НЕТАНО --
С ЗОЬУГЫа РНОВЬВМ A5.12) Н1ТН 5АМВ 1ШТ1АЬ СОМЮ1Т1О№
С А8 ГОН ТАВЬВ 15.1.
ВХТВНЫАЬ
хо=о.
ЬА8Т=0
Н = 0.5
УA)=0.1
= П.0АТA-1)
ВРЗ=1.В-6
НМАХ=1.
СкЫ НВТАНОA.РСМ,Х,У,ХВЫ0,ВР5,НМАХ,Н)
ИН1ТВF,*)Х,У(П
1*Н1ТВ.F,«) ' СОММОN ЗТАТ: ' , ИКСЫ, Ы5ТВР , ЫАССРТ, ЛНВ.ТСТ
ЗТОР
01МВЫ810Ы ,()
ВХТЕНМАЬ РН1
А=1.4
РA)=(А-УЬАСA,Х-1.,РН1))*УA)
ВЫО
НВАЬ ^^NСТIОN РН1A,Х)
1ГA.В0.1)РН1=0.
КЕТ1ШН
нвтано(ы,рек,х,у>хвыо,врз,нмах,н)
С ЦЦМВН1СА1, ЗОШТЮЫ ОР А ЗУ5ТВМ ОР Р1НЗТ ОНОВН
С НВТАНОВО ОГРРВНВИТГАЬ ВОЦАТЮИЗ V ' =Р ( X , У( X ), У ( Х-ТАЦ ),..).
С ТН13 18 ВАЗВО ОЫ АИ ЕМВЕООЕЭ НЦКСВ-КиТТА МЕТНОБ ОР ОНЭЕН DM
С ОИВ ТО ООНМАЫО & РН1ЫСВ '(И1ТН ЗТЕР312В СОЫТНОЬ).
С СР. ЗВСТЮЫЗ 11.5 АЫО 11.15
С
С 1ЫРЦТ РАНАМВТВНЗ
С N 01МВМЗЮЫ ОР ТНВ ЗУ8ТВМ (Ы.ЬВ.51)
С РСИ ЫАМВ (ВХТВНКАЬ) ОР 511ВК0иТ1МБ С0МРЦТ1ЫС ТНВ
С Р1НЗТ 0ВН1УАТ1УВ Р(Х,У):
с зивноиныв с
С НВАЬ*4 Х,У(М
С ВХТВНИАЬ РН1

470 Приложение. Программы на Фортране
С РA)=-УЬАСA,Х-1.,РН1)+...
С РB)=... ВТС.
С ЯНЕКЕ "РН1" 18 ТНЕ (ВХТВНЫАЮ ЫАМВ ОР
С А ВЕА1 Г1ШСТ1ОМ СОМРЦТ1ЫС ТНЕ
С 1-ТН СОМРОИВКТ ОР ТНВ 1Ы1Т1АЬ Р1ШСТ1ОИ РН1(Х)
С НВАЬ Р1ШСТЮМ РН1A,Х)
С 1Р A.ВО.1) РН1=... ВТС.
С X 1ШТ1А1, Х-УАИ1В
С ХВИО Р1ИА1. Х-УАШВ (ХЕИЬ>Х)
С У(Ю 1И1Т1А1 УАШВ8 РОВ У
С ВР8 ЬОСАЬ ТОЬВНАЫСВ
С НМАХ МАХГМАЬ 8ТВР 812В
С Н 1Ы1Т1А1 8ТВР 812В С11В58
С
С ОиТРЧТ РАВАМВТВНЗ
с
С У(Ю 8О1Л1Т1ОИ АТ ХВ№
НВАЬ*4 К1E1),К2E1),КЗE1),К4E1),К5E1),К6E1),К7E1)
ЬООЮАЬ НВДВСТ.018С
СОММОН/РО81Т8/1Р1В8Т,ЬА8Т,Х0,Х1А8Т,1РО5,018С
С МВАМ1НО ОР ТНВ8В УАВ1АВЬЕ8:
С 1Р1В8Т ЮМВ8Т 8ТВР МиМВВН 8ТИЬ 1И МВМОКУ СОВР;
С 1А8Т А00НВ88 ОР ЬА8Т БАТА МН1ТТВН ВУ 8Т0КЕ ОЫ СОММОЙ ВЫСК СОВР
С Ми5Т ВВ 8ВТ ТО О 1И ТНВ САЫЛЫС РВООНАМ
С ВВРОНВ ТНВ Р1В8Т САЫ.
С Х0 1И1Т1А1. РО1ИТ, МЦ8Т ВВ 8ВТ 1М ТНВ СМЫНО РНООКАМ
С ВВРОНВ ТНВ Р1Я8Т САЬЬ.
С Х1А8Т =Х+Н ОР 1.А8Т МН1ТТВМ 8ТВР;
С 1РО8 Р081ТЮМ ОР ЬА8Т 8иССВ88РЦЬ ЗВАНСН 1М РЦИСТЮМ
С Б18С ЬОСЮАЬ УАК1АВЬВ, ЫВСВ88АНУ РОК ТНВ 015Т1НСТЮМ
С ОР К7 АИБ К1 ОР ТНЕ Р0Ы.0Н1ЫС ЗТВР 1И ТНВ САЗВ
С ИНЕЙ У(Х0) 18 01РРВНВМТ РНОМ РН1(Х0).
С СОММОЙ 8ТАТ СОМТА1Ы8 8ТАТI8ТIС^^
с — ирси иимвЕК ор тысиом
с — И8ТВР иимвЕВ ор сомритво зтврз
С ИАССРТ ЫЦМВВВ ОР АССВРТВО 8ТВРЗ
С 11К8.7СТ ИиМВЕК ОР НВДЕСТВО 8ТЕР8
С 1Ш01Ж0 ЗМА1ЬВ8Т МиМВВН 8АТ18РУ1ИС 1.+11КО1Ш0>1.
С (ТО ВВ АБАРТВО ВУ ТНВ Ц8ВН)
ОАТА 1ШО1ШО/5.В-8/
БАТА ИМАХ/3000/
С ИМАХ МАХ1МАЬ ИиМВВК ОР 8ТЕР8
С 1ШТ1А1, РИВРАНАТЮИЗ
НМАХ=АВ5(НМАХ)
Н = АМ1Га (АМАХ1A.В-4,АВЗ(Н)),НМАХ)
Н=$1С[<(Н,1.)
ВР8=АМАХ1(ВР$,7.*иНО1Ш0)
ВВДВСТ^.РАЬЗВ.
МНВЛСТ=0
МРСМ=1
И8ТЕР-0
САН ТСН(Н,Х,\,И)
1Р (.ЫОТ.013С) САЫ РСИСМ, X, V, К1)
С ВА31С ГИТВСНАТЮИ ЗТВР
1Р(НЗТВР.ОТ.ЯМАХ.ОН.Х>.1*Н.ВО.Х)СОТО 79
1Р((х-хвыо)+оноимо..
1Р((Х+Н-ХВЫО).аТ.О.
С ТНВ 7 ЯМОВ-КИТТА ЗТАОВ8
00 22 1=1,N
22 У1A)=УA)+Н*.2*К1A)
СКЫ РСМ(К,Х+.2*Н,У1,К2)
00 23 1=1,N
23 У1A)=УA)+Н*(C./40.)*К1A)+(9./40.)*К2A))
САЬЬ ГСМ(Ы,Х+.3*Н,У1.КЗ)

Приложение. Программы на Фортране 471
00 24 1=1,N
24 У1A)=УA)+Н*(D4./45.)*К1A)-E6./Л5.)*К2A)+C2./9.)*КЗA))
САЬЬ ГСЫ(^Х+8*НУ1К4)
ПО 25 1=1,N
25 УК I)=УA)+Н*(A9372./6561.)*К1A)-B5360./2187.)*К2A)
I +F4448./6561.)*КЗA)-B12./729.)*К4A))
САЫ, ГСК(Ы,Х+(8./9.)*Н,У1,Кб)
00 26 1=1,N
26 У1A)-ТA)+Н«((9017./3168.)*К1A)-C55./33.)*К2A)
& +D6732./6247.)*КЗA)+D9./176.)*К4A)-E103./18656.)*К5A))
ХРН=Х+Н
САЫ. ?СМ(М, ХРН, VI. Кб)
00 27 1=1,N
27 У1A)=УA)+Н*(C5./384.)*К1A)+E00./1113.)*КЗ(I)
Ь +A25./192.)*К4A)-B187./6784.)*К5A)+A1./84.)*К6A))
САЫ РСМ(М,ХРН,У1,К7)
00 28 1=1,N
28 К2(I)=(G1./57600.)*К1(I)-G1./16695.)*КЗ(I)+G1./1920.)*К4A)
& -A7253./339200.)*К5A)+B2./526.)*К6(I)-A./40.)*К7(I))*Н
С ЕЯКОВ В8Т1МАТЮМ
ВКН=О.
00 41 1=1,N
0В11ОМ=АМАХ1A.В-5,АВЗ(У1A))»АВЗ(ГA)),2.«Ш1О1Ш0/ВРЗ)
41 ВНН=ВНН+(К2A)/0ВМОМ)**2
ВНН=30НТ(ВНН/Р1.0АТ(Ю)
С СОМРЦТАТЮМ ОР
С — ИВ НВО1ЛНВ .2
ГАС=АМАХ1(.1,АМ1Н1E.,(ЕНН/ВР5)♦*A./5.)/.9))
1Р(ВНН.ЬВ.ВР8)ТВВЫ
С 8ТВР 18 АССВРТВБ
ЫАССРТ=МАССРТ+1
САН 8Т0ВВ(Х,ХРН,У,Н,К1,КЗ,К4,К5,К6)
00 44 1 = 1, N
11A)=17A)
44 УA)=У1A)
С НВСОМРЦТВ II 1И ТНВ СА8В ОР 018СОНТ1Ыиои8 1Ы1Т1АЬ РНА8В
1Г(.ИОТ.018С) САЬЬ РСЫ(М,ХРН,У,К1)
Х = ХРН
1Р(АВЗ(Н№*П .аТ.НМАХ)НЫВМ=НМАХ
1Г(НВДВСТ)НМВМ=АМ1М1(АВ8(ННВМ),АВ8(Н))
НВЛВСТ=.РАЬ8В.
ВЬ8В
С 8ТВР 18 НВЛВСТЕО
НВЛЕСТ=.Т1ШВ.
1Р(ИАССРТ.аВ.1)МНВЛСТ=МВВЛСТ+1
ВИО 1Р
Н=НИВН
аото 1
С — РАН ВХ1Т
79 МН1ТВF,979)Х
979 РОНМАТС ВХ1Т ОР НВТАВО АТ Х=',В11.4)
НВТ11ВМ
ВИО
8Т0НВ(X,ХРН,V,N,РО1,РОЗ,РО4,РС5,РС6)
РАНАМВТВВ (МИ=4,МХ8Т=800)
СОММОМ/С0ВР/Х8Т0ЖМХ8Т) , У5Т0Н(NN,МХЗТ),
& С1 (М,МХЗТ),С2(N11,МХЗТ),СЗ(М,МХЗТ) ,С4(№,МХЗТ)
С С0ВРР1С1ВЫТ8 РОН (ИОЪАЬ ВОЫЛЮН АНЕ 8ТОКВ0 1М СОВР
СОММОМ/Р081ТЗ/1Р1Н8Т,ЬА8Т,ХО,Х1А8Т,1Р08.018С
ЬАЗТ=ЬАЗТ+1
1Р1НЗТ=МАХ0A,ЬАЗТ-МХЗТ+1)
1А0Н=МО0(ЬАЗТ-1,МХЗТ)+1
ХЬА8Т=ХРН
Х8ТОКAА0В)=Х
00 2 1=1,NN
У8Т0НA,1А0В)=УA)
С1A,1А0Н)=РС1A)

472 Приложение. Программы на Фортране
С2A,1АПН)=-A337./480.)*РС1(I)+A05400./27825.)*РСЗ(I)-
4 A35./80.)*РО4A)-E4675./212000.)*РС5A)+F6./70.)*РС6A)
СЗA,1А0Н)=A039./360.)*РО1(I)-D68200./83475.)*Р03A)+
& (9./2.)*РО4A)+D00950./318000.)*РС5A)-F38./210.)*РС6A)
С4A,1А0Н)=-A163./1162.)*РС1(I)+C7900./16695.)*РаЗA)-
& D15./192.)*РС4(I)-F74325./508800.)*РС5A)+C74./168.)*РС6A)
СОИНЫЦВ
выо
НВАЬ Р1ШСТ1ОЫ УЬАСA,Х.РН1)
РАНАМВТВН (ЫМ=4,МХЗТ=800)
1.001СА1. 018С
С0ММ0М/С0ВР/Х8Т0Н(МХ8Т),УЗТ0Н(ЫЫ,МХ8Т) ,
С1(МИ,МХ5Т) ,С2(М,МХ5Т) ,СЗ(ЫН,МХЗТ) ,С4(ЫЫ,МХЗТ)
СОММОЫ/РО81Т8/1Р1Н8Т,ЬАЗТ,Х0,ХЬАЗТ,1РО8,013С
С 1Ы1Т1АЬ РНАЗВ
1Р @13С) ТЫВЫ
1Р(АВЗ(Х-Х0).ЬВ.C.«иНОиЫ0*АВ5(Х))H15С=.ГАЬЗЕ
1Р(Х.1В.Х0)ТНВН
УЬАС=РН1A,Х)
ВNО 1Р
1Р
С СОМРЦТВ ТНВ РО31ТЮЫ ОР X
1Р (Х.ЬТ.ХЗТ0НAР1НЗТ)) ТНВЫ
МВ1ТВ F,*) ' МВМОНУ Р1Л.1., МХ8Т = '.МХ8Т
ЗТОР
В№ 1Р
1РОЗ=МАХ0AР1НЗТ,М1Ы0(ЬАЗТ,1РО8))
1 1А0Н-МО0AРО8-1,МХ8Т)+1
1Р (Х.ЬТ.ХЗТОНAА0Н).АЫ0.1РОЗ.СТ.1Р1НЗТ)
1Р03=1Р03-1
аото 1
ВИО. 1Р
2 1А0Н=МО0AРО8,МХЗТ)+1
1Р AР03.ЬТ.ЬАЗТ) ТНВЫ
1Р (Х.ОТ.Х5ТОЙAА0Н)) ТНВЫ
1Р03=1Р03+1
СОТО 2
ВИО 1Р
ВЫО 1Р
С СОМР1ЛЕ ТНВ 0В81НВ0 АРРНОХ1МАТЮЫ
1А0Н=МО0AРО5-1,МХЗТ)+1
1Р AР08.В0.ЬА8Т) ТНВЫ
И=Х1А8Т-Х8ТОЙAА0Н)
ВЬ5В
Н=Х8ТОН(МО0AРОЗ,МХЗТ)+1)-ХЗТОНAА0Н)
ВКО 1Г
3=(Х-ХЗТОВAА0Н))/Н
УЬАA=УЗТ0НA,1РОЗ)+Н*3*(С1A,1РОЗ)+3*(С2A,1РО8)
4 +3*(СЗA,1Р08)+8*С4A,1Р03))))
выо

Литература
Абель (И. Н. АЬе1)
A826): 1Мег$исЬип8еп ОЬег <Не КеШе:
/я т(/я--1)
СгеИе I. !. A. г. и. апде^у. МаШ. Aп 2^апд1озеп НеКеп), уо1. 1, р.311—339.
A827): 11еЬег еЫ^е ЪезИтт1е Ше^гаЬ/СгеПе ДЛ. й. г. и. ап^е^. МаШ.,
уо1. 2, р. 22—30.
Абрамовиц, Стиган (М.. АЬгаточагНг апс! I, А. $1е^ип)
A964): НашНюок о! таШета11са1 {ипсНопз, Ооуег, 1000 радез. Шмеется
перевод: Справочник по специальным функциям с формулами, графиками
и математическими таблицами, под ред. М. А» Абрамовица и И. Стиган* —
М.: Наука, 1979. — 832 с.1
Адаме C. С. Ас1ат$)
A883): см. Башфорт A883).
Айне (Е. Ь. 1псе)
A944): ОгсНпагу дШетеппг! е^иа^^опз, Ооуег РиЬНсаИопз, Ые^ Уогк, 558 рр,
{Имеется перевод предыдущего издания: Айне Э. Л. Обыкновенные диффе-
дифференциальные уравнения. — Харьков: Гостехиздат Украины, 1939. — 717 с]
Алексеев В. М. A961): Об одной оценке возмущений решений обыкновенных
дифференциальных уравнений. — Вестниы МГУ, серия I (математика,
механика), № 2, с. 28—36.
Альбрехт (Л. А1ЪгесМ)
A955): Вейга^е гит Кипде-Кииа-Уег?апгеп, 2АММ, уо1. 35, р. 100—110.
Аренсторф (К. Р. АгепзЬг!)
A963): РепосНс зоЬКопз о! Ше гезШс1ес1 Шгее Ьос1у ргоЫет гергезепИпд
апа1у1лс сопИпиа{1опз о! Кер1ег1ап еШр^к тоНопз, Атег. Д. МаШ., уо1.
ЬХХХУ, р. 27—35,
Ар цела (С. Агге1а)
A895): 5и11е Ыпг'ют 61 Нпее, МетоНе Aе11. К* Ассас!. Aе11е Зс. сИ Во1о§па,
5е зепе, уо1. V, р. 225—244, зее а1зо: уо1. V, р. 257—270, уо1, VI, A896),
р. 131—140,
Барридж (К. Виггаде)
A985): Огс1ег ап^ з1аЫ1Йу ргорегИез о! ехрНсК тиШиуаЫе теШойз. Арр1.
Ыитег. Апа1., уо1. 1; рр. 363—379.
Барридж, Бутчер (К. Вшта&е апс! 3. С. ВикЬег)
A980: Ыоп-Нпеаг з1аЪШ1у о! а депега1 с1азз о! с!Шегегй1а1 е^иа^^оп теШос!8,
В1Т, уо1. 20, рр. 185—203.
Барридж, Мосс (К. Виггаде апс! Р. Мозз)
A980): 51трШут§[ аззитр11опз !ог Ше огйег о! рагШ1опе<1 шиШуа1ие те-
1Ьос1з. В1Т, уо1. 20, рр. 452—465.
Баттин (К. Н. ВаШп)
A976): НезоЫиоп о! Кипде-Ки^1а-Ыуз!г6т сопсИНоп
1МЬ огс!ег, А1АА Д., уо1. 14, рр* 1012—1021.

474 Литература
Бауэр, Рутисхаузер, Штифель (Р. Ь. Ваиег, Н. НиШпаизег апс! Е. 5ие!е1)
A963): Ые^ азрес^з т питепса1 ^иаа'^а^иге. Ргос. о! 5утроз1а 1п АррК
АЫЬ. уо1. 15, р. 199—218, Ат. Ма*Ь. 5ос.
Бахвалов Н. С. Численные методы. — М.: Наука, 1973 и 1975.
Башфорт (Р. ВазЫогШ)
A883): Ап аНетр! 1о 1ез1: 1Ье Шеопез о! сарШагу асИоп Ьу сотраппд Ше
1Ьеоге11са1 апс! теазигео* !огтз о! йгорз о! Пшй. Ч\ПШ ап ехрЫпаИоп о! Шете-
(Ьос! о! 1п1е§га1юп етрЬуес! т сопз1гис1тд Ше 1аЫез чуЫсп §1уе Ше Шеоге-
*1са1 ?огт о! зисЬ с!горз, Ьу ,1. С. Ас1атз, СатЬпйде 11ту. Ргезз.
Беентьес, Герритсен (Р. А. Вееп^ез апд V/. <1. Оеггйзеп)
A976): Шфет огйег Нипде-КиНа теШойз !ог 1Ье питепса1 зоЫНоп о!
зесопс! огйег Й1Яегепиа1 еяиаИопз ^1Шои1 Пгз! с1епуа11уе5, Еерог! Ы^ 34/76,
Ма1Ь. Сеп^гит, Атз1егс1ат.
Беллен (А. Ве11еп)
A984): Опе-з^ер соИосаНоп !ог а*е1ау бШетеппа! е^иа^^опз, I. Сотри!. АррЬ
Ма1Ь. Уо1. 10, р. 275—283.
Беллман, Кук (Н. ВеИтап апс! К. Ь. Сооке)
A963): ОшегепШЬОШегепсе е^иаиопз, Асайет1С Ргезз, 482 р. [Имеется
перевод: Беллман Р., Кук К. Л. Дифференциально-разностные уравне-
уравнения. — М.: Мир, 1967.]
Бендикссон (I. ВепсНхзоп)
A893): 5иг 1е са1си1 с!ез 1п1ёдга1ез й'ип зуз1;ёте 6'ёциаИопв Й1!!ёгепие11е8
раг с!ез арргох1та11опз зиссезз1уез, 51оск. Акас1. РогЬ., Уо1. 51, р. 599^612.
A901): 5иг 1ез соигЬез йёНтез раг с!ез ёяиаНопз с11![ёгеп11е11ез, Ас!а Ма1Ье-
та1;1са, уо1. 24, р. 1—88.
Бенке, Зоммер (Н. ВеЬпке апс! Р. Зоттег)
A962): ТЬеог1е с!ег апа1у1;13сЬеп Рипк1:1опеп е1пег котр1ехеп УегапйегНсЬеп.
2ътеНе АиЛа^е. Зрппдег Уег1ад, ВегНп-ОбШп§[еп-Не1с1е1Ьег§[.
Бернулли Даниил (О. Вегпои1Н)
A760): Езза1 й'ипе поиуеПе апа1узе с!е 1а тог1аН1ё саизёе раг 1а реШе уёго1е,
е! с!ез ауап1адез с!е Г1поси1а11оп роиг 1а ргёуешг, Шз!. еГМёт. с!е ГАсас!.
Коу. 5с1епсез, Раг1з, 1760, р. 1—45; №егке Вапс! 2, р. 235—267.
Бернулли Иоганн (ЗоЪ. Вегпои1Н)
A696): РгоЫета поуит Ма1Ьета11С13 ргороз1^огит. Ас1а Егис1. Ь1рз
МОСХСУ1, р. 269, Орега Отп1а уо1. 1, р. 161 апс! 165, Ьаизаппае & Ое-
пеуае 1742.
A697): Эе Сопо1сИЬиз е( 5рЬаего1с11Ьиз диаейат. 5о1и1ю апа1у1;1са Ас^иа•'
иоп13 т АсШ А. 1695, рад. 553 ргорозИае, Ас1а Егис1. Ырз., АЮСХСУИ,
р. 113—118.
A697Ь): ЗоЫНояие РгоЫета11з а зе т Ас1Ь 1696, р. 269, ргорозй, с!е
1пуеп1епс1а Ыпеа ВгасЬуз^осЬгопа, Ас^а Егис1. Ь1рз.МОСХСУН, р. 206, Орега
Отша уо1. 1, р. 187—193.
Бернулли Якоб рас. ВегпоиШ)
A695): ЕхрИсаИопез, Аппо*а11опез & АсМШопез ас! еа, циае т Ас113 зир.
апш йеСигуа ЕкзИса, 1зосЬгопа Рагасеп1пса, & Уе1апа, Ыпс тс!е тетога1а,
&рагит соп1гоуегза 1е^ипс!иг: иЫ йе Ь1пеа тесИагит сИгесНопит, аШз^ив
ПОУ15, Ас1а ЕтибИ. Ь1рз1ае, Аппо АЮСХСУ, р. 537—553.
A697): 5о1и1ю РгоЫета1ит Рга1егпогит, РесиНап Ргодгатта^е Са1. ^ап.
1697 Огошпдае, пес поп Ас^огит Ь1рз. тепзе ,1ип. & 5ес. 1696, & РеЬг.
1697 ргорозИогит: ипа сит РгорозШопе гес1ргоса аНогит. Ас^а Егис1.
Ырз. АЮСХСУИ; р. 211—217.
Бибербах (Ь. В1еЬегЬасЬ)
A923): ТЬеопе <1ег О1ГГегепиа1^1е1сЬипбеп, ОгипсИеЬгеп ВA. VI, ЗрИп^ег-
Уег1ад.
A951): Оп №е гетатйег о! Ше Нипде-КиНа !огти1а Ш 1Ье Шеогу о! огс11-
пагу с11[!егеп11а1 аяиа11опз, 2еИзсЪт. апде^. МаШ. РЬуз. BАМР), уо1. 2,
р. 233—248.

Литература 475
Биркгофф, Варга (О. ЬНгкЬо!! апс! К. 3. Уагда)
A965): О15сге112а11оп еггогз !ог туеН-зе! СаисЬу ргоЫетз I, 1оигпа1 о! МаШ.
апс! РЬузкз, уо1. ХПУ, р. 1—23.
Бирн, Ламберт (О. О, Вугпе апс! К. 3. ЬатЬег!)
A966): Рзеис1о-Кипбе-Ки!!а теШоо18 шуо1шп§[ Ь/о рот!з, I. Аззос. Сотри!.
МасЬ., уо1. 13, р. 114—123.
Бирн, Хайндмарш (О. О. Вугпе апс! А. С. НтйтагзЬ)
П975): А ро1уа1§[опШт !ог Ше питепса1 зо1и!юп о! огсНпагу сШ-
!егепИа1 е^иа!^оп$, АСМ Тгапз. оп МаШ. Зо!!тоаге, уо1. 1; Ыо. 1, р.
71—96.
де Боор, Шварц (С. бе Воог апс! В. Б^агЧх)
A973): СоНосаНоп а! Саиззгап рот!з, 31АМ I. Ыитег. Апа1. уо1.10, р. 582—
606.
Булирш, Штёр (К. ВиНгзсЬ апб ,1. 51оег)
A964): РеЫегаЬзсЬа1;2ипдеп ипс! Ех1гаро1а1юп т1^ гаНопакп Рипк11опеп
Ье1 Уег!аЬгеп уот НкЬаг^зоп-Туриз, Ыит. Ма1Ь. Уо1. 6, р. 413—427.
A966): Китепса1 1геа1теп1 о! опЛпагу с11!!егеп11а1 ециа11опз Ьу ех!гаро1а-
1юп те!Ьос!з, Ыит. МаШ, уо1, 8, р. 1—13.
Бутчер у. С. ВикЬег)
A963): СоеШаегйз Ьг {Ье з!ис!у о! Нгтде-КиИа 1п1е^гаиоп ргосеззез, Д.
Аиз1га1. МаШ. Зое, уо1. 3, р. 185—201.
A963а): Оп Ше 1п1ебгаиоп ргосезз о! А. Ни1а, 2# Аиз1га1. МаШ, Зое. уо1. 3,
р. 202—206.
A964а): 1трНсН Нипде-КиНа Ргосеззез. МаШ. Сотри^. уо1. 18, р. 50—64.
A964Ь): Оп Нипде-КиЙа ргосеззез о! ЫдЬ огс!ег, Д. Аиз1га1. МаШ. Зое. уо1, IV,
Раг! 2, р. 179—194.
A964с): Ше^гаНоп ргосеззез Ьазей оп Кас1аи ^иас1^а^и^е 1огти1аз, МаШ.
Сотри!., Уо1. 18, р. 233—244.
A965а): А тосШей тиШз1ер теШос! !ог Ше питепса1 1п1едгаиоп о! огс!1пагу
с11^егеп11а1 едиаНопз. ^. АСМ, уо1. 12, р. 124—135.
A965Б): Оп Ше а1:ЫпаЫе огс!ег о! Нип^е-КиНа теШойз, МаШ. о! Сотр.
уо1. 19, р. 408—417.
A966): Оп Ше сопуег§[епсе о! питепса1 зо1ииопз 1о огсНпату й1ИегепИа1
едиа!1опз, МаШ. Сотри!., уо1. 20, р. 1—10.
A967): А тиШз!ег ^пегаНхаИоп о! Нипде-КиНа теШойз ч/НЪ. Ьиг ог !1уе
з!адез. ^. АСМ, уо1. 14, р. 84—99.
A969): ТЬе еГГес^уе огс!ег оГ Нип^е-КиЙа теШос!з, 1п: Соп!егепсе оп Ше
питепса1 зо1иИоп о! с11!!егеп!1а1 едиа^опз, Ьес1иге по!ез 1П МаШ., УоК 109,
р. 133—139.
A972): Ап а1&еЪга1с !Ьеогу о! т!едга11оп теШойз, МаШ. Сотри!., Уо1. 26,
р. 79—106.
A975): Ап огс!ег Ьоипс! !ог 1^ипде-Ки!!а теШос!з, 31АМ I, Г\[ит. Апа1. уо1. 12,
р. 304—315.
A981): А депегаНгаКоп о! зт^у-ипрНсй теШойз, В1Т, уо1. 21, р. 175—189,
A984): Ап аррНсаНоп оГ Ше 1^ипде-Ки!!а зрасе, В1Т, уо1. 24, р. 425—440.
A985а): Сепега1 Нпеаг теШос!: а зигуеу, Арр1. Ыит. МаШ., уоЬ 1, р. 273—
284.
A985Ь): ТЬе поп-ех1з!епсе о! !еп 8!а^е е^ЬШ сгс!ег
теШойз, В1Т, уо1. 25, р. 521—540.
Вайсингер C. д)
A950): Е1пе уегзсЬаг!!е РеЫегаЬзсЬа!2ипд гит Ех!гаро1а!1опзуегГа11геп
уоп Ас1атз, 2АММ, уо1. 30, р. 356—363,
Ван-дер-Поль (В. Уап с!ег Ро1)
A926): Оп «Не1аха!1оп Озс111а!1опз», РЫ1. Мад., уо1. 2, р. 978—992; герго-
с!исес! 1п: В. уап с!ег Ро1, 5е1ес!ес1 Зс1еп!1Пс Рарегз, уо1. 1, КогШ-Но11апс1
РиЫ. Сотр. Атз!егс1ат A960).
Ваннер (О. ^)

476 Литература
A969): ШедгаИоп %еч/6ЪпИсЪег ОШегеп11а1§1е1с1шп§[еп, 1л'е КеШеп,
Ки11а-МеШос1еп, В1 МаппЫт Н(Ь. 831/831а, 182 р.
A973): Кип&е-КиНа теШойз ч/НЪ. ехрапзюпз т еуеп ро\уег8 о! А, Сотри-
ип§ уо1. И, р. 81—85.
A983): Оп 5Ы'з соип!ег ехатр1е !ог Ше 16Ш НПЪег* ргоЫет, 1п1егпа1 Нер.
5ес*. с!еМаШ., 11шу. Сепёуе. 1982; 1П дегтап т: ^ЬгЬисЬ ОеЬегЬНске МаШе-
таИк 1983, ес1. СЬа((ег]19 Репуб, КиНзсЬ, Ьаидчуйх, ЫесП, В1 МаппЬеш,
р. 9—24.
Вейерштрасс (К. ^е1ег81газ$)
A858): 11еЬег ет (Не Ьото^епеп Рипс^1опеп г^геНеп Огарев Ье1ге![епс1е8 ТЬео-
гет, пеЬз^ Ашуепйипд йеззеШеп аи! сИе ТЬеопе с1ег к1е1пеп 5сЬ\У1пдип§еп,
Мопа1зЬег. с!ег Кбш^. Ака^. ^ег ^1зз., 4. Магг 1858, ^егке Вс1. 1, р. 233—
246.
Вернер C. Н. Уегпег)
A978): ЕхрНс1( Нипде-Ки^^а теШойз чгНЪ. ез11та1ез о! 1Ье 1оса1 1гипсаНоп
еггог, 51АМ Л. Ыитег. Апа1., уо1. 15, р. 772—790.
Верхюльст (Р. Р. УегЬи1з1)
A845): НесЬегсЬез таШёта^иез зиг 1а 1о1 с1'ассго1ззетеп1 с!е 1а рори1а^1оп,
Ыиоу. Мет. Асас1. Ноу. ВгихеИез, уо1. 18, р. 3—38.
Вольтерра (V. УоИегга)
A934): Нетагяиез зиг 1а Ко1е с!е М. Рё^шег е* М-11е ЬатЬ1П. С. Н. Асас1.5с.
{. СХС1Х, р. 1682. 5ее а1зо: V. УоИегга — II. с1«Апсопа, Ьез аззоааиопз
Ь1о1од1яиез аи рот! с!е уие таШёта1;1дие, Рапз 1935.
Вронский (Н. \^гопзк1)
A810): Ргениег рппС1ре йез тё1Ьос!ез а1§о^^^Ьт^^иез сотте Базе с!е 1а 1е-
сЬшдие а1до^^^11т^^ие, риЬНсаиоп геГизес! Ьу Ше Асас1. ее Рапз (!ог тоге
(ЫаПз зее: 5. О1скз1е1п, 1п1. МаШ. Соп^гезз 1904, р. 517).
Гаусс (С. Р. Саизз)
A812): О18дшзШопе8 депега1ез С1гса зеНет тНпйат
2)
уо1. 3, р. 123—162.
Гаучи (VI. Оаи^сЫ)
A962): Оп туегзез о! Уапс1егтопс1е апс! соп!1иеп! Уапс1егтопс1е
Ыитег. МаШ. уо1. 4, р. 117—123.
Гиббоне (А. СИЬЬопз)
A960): А ргодгат !ог Ше аи^ота!1с ШекгаНоп о! Й1!!егеп11а1 е^иа^^оп8
Ше теШос! о! Тау1ог зепез, Сотри*ег ^. уо1. 3, р. 108—111.
Гилл E. ОШ)
A951): А ргосезз !ог Ше з^ер-Ьу-з^ер ЫедгаМоп о! с!1!!егепиа1 е^иа^^оп8 1п
ап аи1отаис сИ^Иа1 сотриНп^ тасЫпе, Ргос. СатЬп^^е РЬ11оз. 5ос, уоК
47 9518
47, р. 95—108.
Гир (С. ЧУ. Сеаг)
A965): НуЬпс! теШойз !ог 1П1*1а1 уа1ие ргоЫетз 1П огсНпагу сИ!!егеп!1а1
еяиаНопз, 51АМ ^. Ыитег. Апа1. зег. В, Уо1. 2, р. 69—86.
A971): Ыитепса1 1пШа1 уа1ие ргоЫетз 1п оЫ1пагу (Н!!егеп{1а1 е^иа^^оп8,
Ргеписе-На11, 253 р.
Гир, Ватанабе (С. \У. Оеаг апс! Э. 5. \Уа1апаЬе)
A974): 81аЫШу впй сопуегдепсе о! уаг1аЫе огс!ег тиШзЬр теШойз, 31АМ
^. Ыит. Апа1. И, р. 1044—1058.
Гир, Ту (С. \У. Сеаг апс! К. №. Ти)
A974): ТЬе еЯес!з о! уаг1аЫе тезЬ 812еоп Ше з!аЬШ1у о! ти111з1ер теШос!з,
31АМ I. Ыит. Апа1. 11, р. 1025—1043.

Литература 477
Гобсон (Е. №. НоЬзоп)
A921): ТЬе Шеогу о! !ипс1юпз о! а геа1 уапаЫе, уо1. 1, СатЬпс^е, 670 р.
Голдстайн (Н. Н. СоЫзИпе)
A980): А ЬШогу о! Ше Са1си1из о!- УапаИопз, $рпп§ег-Уег1а&, 410 р.
Голуб, Уилкинсон (С. Н. Оо1иЬ апс! ,1. Н. \\Шктзоп)
A976): Ш-сопAШопес1 е1§епзу$1:ет5 апй 1Ье сотри!аиоп о! Ше ,1огс!ап сапо-
тса1 !огт, 51АМ Кеу1е\у, уо1. 18, р. 578—619.
Готтвальд (В. А. СоИ^аЫ)
A985): 2иг Мос1еШегип§[ геЙуеггодегЧег Ыо1о§15сЬег Ргогеззе, МоттаИк
РасНЪепсМе, уо1. 109, р. 350—354, 5рпп&ег-Уег1а§.
Грёбнер (№. СгбЬпег)
A960): О1е ЫегеШеп ипс! Шге Апчуепйипдеп, Э. Уег1. с1. \У18$. ВегНп, 2пс1 еск
1967.
Григориефф (К. О. ОтщопеН)
A977): Йитепк дечуоЬпПсЬег ВШетепИа^ЫсЪип^еп 2. ТеиЬпег 51ис!1еп-
ЬйсНег, 51:иидаг1:.
A983): 51аЫШу о! тиИ1з^ер-те111ос1з оп уапаЫе §[пс15! Ыитег. Ма1Ь., 42,
р. 359—377.
Гронуолл (Т. Н. ОгогшаН)
A919): Ко^е оп 1Ье с1епуа11уез ш!п гезрес! 1о а рагате!ег о! 1Ье зо1и!1опз
о! а зуз1ет о^ 61НетепИа\ е^иаиопз, Апп. Ма*Ь. Уо1. 20, р. 292—296.
Грэгг (№. В. От&т)
A964): Нереа1ес1 ех1гаро1а^оп 1о 1Ье Нт11 1П 1Ье питепса1 зо1иНоп о? огсИ-
пагу A1!!егеп^1а1 еяиаНопз, ТЬез^з, Ошу.о! СаН!огп1а;зее а1$о 51АМ Л. Ыитег.
Апа1. уо1. 2, р. 384—403 A965)
A965): Оп ех1гаро1а1юп а1^опШтз !ог огс11'пагу 1П1иа1 уа1ие ргоЫетз, 51АМ
^. Мит. Апа1. зег. В, уо1. 2, р. 384—403.
Грэгг, Штеггер (№. В. Сга^ апс! Н. ^. 51е11ег)
A964): ОепегаНгес! тиШз1ер ргес!1с1ог-соггес1ог теНюсЬ. !• АСМ, уо1. 11;
р. 188—209.
Гурвиц (А. Ниг^Их)
A895): 11еЬег сИе ВесИпдип^еп, ип!ег \уекЬеп е1пе С1е1сЬип§ пиг \^игге1п
тЙ педа^уеп гее1еп ТЬеНеп Ьез1Ы. Ма1Ь. Апп., уо1. 46, р. 273—284; Шегке
уо1. 2, р. 533!!.
Даламбер C. 1е Копе! сГА1етЪег1)
A748): ЗиНе с1ез гесЬегсЬез зиг 1е са!си1 1п1ёдга1, ^иа^^^ете рагИе: МёШосЗез
роиг 1п1ё^гег ^ие1^иез ё^иа^^оп5 сИНёгепиеИез, Н1з1. Асай. ВегНп, Тот IV,
р. 275—291.
Далквист (О. ОаЬ^шз*)
A956): Сопуегдепсе апс! з1аЬ1Н1у 1П 1Ье питепса1 1п1е^га1;1оп о! огс!1пагу
с11!!егеп1;1а1 е^иа1^оп5, Ма1Ь. Зсапс!., уо1. 4, р. 33—53.
A959): З^аЫШу апс! еггог Ьоипс1з 1П 1Ье питепса1 1п1е^га1;1оп о! огс!1пагу
сШ!егеп11а1 е^иаиопз. Тгапз. о! 1Ье Ноуа1 1пз1. о! ТесЬп., 51оскЬо1т, 5шес1еп,
Ыг. 130, 87 р.
A985): 33 уеагз о! питепса1 тз1аЫШу, раг! 1, В1Т,уо1.25, р. 188—204.
Далквист, Йелч (О. ОаЬЦи1з1 апс! 1^. ^еИзсЬ)
A979): ОепегаНгес! сНзкз о! соп^гас11У11;у !ог ехрНс11 апс! 1трПс11 Нип^е-
Ки11а теШойз. Керог! Т^ИА-КА-7906, ЫАИА, Ноу. 1пз1. ТесЬп. 51оск-
Ьо1т.
Деклу C. ОезсЬих)
A963): А по!е оп а рарег Ьу А. Могс1з1еск, Керог* N0. 131, Иер1. о! Сотр.
5а.,.11шу. о! 1Шпо1з а^ 11гЬапа-СЬатра1§п.
Джованнини, Вейсс-Пармеджиани, Ульрих (В. ОНоуапшш, Ь. \^е1зз-Рагте^д1ап1
апс! В. Т. ШпсЬ)
A978): РЬазе 1оск1П§ 1п соир1ес! «ТозерЬзоп \^еак Нпкз, Не1уе1. РЬуз1са Ас1а,
1 уо1. 51, р. 69—74.

478 Литература
Дзеннаро (М. 2еппаго)
A986): Ыа1ига1 согШпиоиз ех*епзюпз о! Кип^е—КиМа теШойз. МаШ. Сот-
Сотри*. Уо1. 46, р. 119—133.
Дойфлхард (Р. ОеиНЬагс!)
A980): Кесеп! айуапсез 1п тиШр1е зЬооИпд {есЬт^иез. 1п: СотриЫюпа!
{есЬшяиез !ог огсНпагу с!Шегепиа1 е^иа^^оп8 (СПасЬуеН-Зауегз, ее!.), 5ес1юп 10,
р. 217—272, Асас1ет1С Ргезз.
A983): Огс1ег апс! з1ерз12е соп*го1 т ех!гаро1аИоп теШойз, Мит. Ма(Ь.
уо1. 41, р. 399—422.
A985): Несеп! ргодгезз !п ех^гароЫюп теНюск !ог огсИпагу сШ!егепиа1
еяиаНопз, 51АМ Кеу., уо1. 27, р. 505—535.
Дойфлхард, Бадер (Р. Оеи!Шагс1 апс! О. Вас1ег)
A982): Ми111р1е зЬооНпд 1есЬп1яиез геу1$йес1, РгерНп* Мг. 163, Ш1у. НеЫеЬ
Ьегд, 1пз1. Апде\у. Ма1Ь., Э-6900 Не1с1е1Ьегд 1, Зиттагу риЬНзЬес! т:
Р. ЭеиШагс!, Е. Ншгег, A983) р. 74—94.
Дойфлхард, Хайрер (Р. ОеиПЬагс! апс! Е. На1гег ее!.)
A983): Китепса11геа1теп1 оГ туегзе ргоЫетз 1п с11!!егеп^1а1 апс! 1п1едга1
е^иа^^опз, В1гкЬаизег, Воз1оп, Вазе1, 357 р.
Донельсон, Хансен ^. Оопе1зоп апс! Е. Напзеп)
A971): СусНс сотроз11е ти1из*ер ргесИс!ог-соггес1огте!Ьос!з, 51АМ Д. Ыи-
тег. Апа1., уо1. 8, р. 137—157,
Дорман, Принс C. К. Оогтапс!, апс! Р. I. Рппсе)
A978): Ке\у Цище-КиИа еАцотИЪтв !ог питепса1 з1ти1а1юп 1п с!упат1са1
аз^гопоту, Се1езИа1 МесЬашсз, уо1. 18, р. 223—232.
A980): А !атПу о! етЬес!с1ес1 ^ипде-Ки{1а !огти1ае, Д. Сотр. Арр1. МаШ.
уоЬ 6, р. 19—26.
Драйвер (К. О. Опуег)
A977): ОгсНпагу апс! с!е1ау сИ!!егеп11а1 еяиа^1опз, АррНес! Ма^Ь. Заепсез 20,
Зрппдег Уег1ад, 501 р.
Жор дан (С. Догйап)
A870): Тга11ё аез 5иЬзи1иНопз е| с!ез ёяиаиопз а1^ёЬпяиез, Рапз, 667 р.
A928): 5игипе?огти1есГт1егро1а1:юп, АШ Сопегеззо ВоЬепа, уо1. 6, р. 157—
177.
Зоммер (р. Зоттег)
A965): КитепзсЬе кпч/епйипц 1трИгИег Нип§е-Ки*1а-Рогте1п, 2АММ,
уо1. 45. ЗопйегЬеП, р. Т77—Т79.
Зонневельд (Д. А. 2оппеуе1с1)
A963): Аи1отаAс Ме^гаИоп о! огс!1пагу сИ!!егеп^1а1 едиаНопз, Нерог! Н743,
МаШетаИзсЬ Сеп1гит, Роз1Ьиз 4079, 1009АВ Атз1егёат. Арреагес! т Ьоок
!огт 1964.
Ингланд (К- Еп&1апс1)
A969): Еггог ез1;1та1;ез !ог Нипде-Ки11а 1урезо1и^1опз (о зуз^етз о* опИ-
пагу с!1!!егепиа1 едиаНолз: ТЬе Сотри1ег Д. уо1. 12, р. 166—170.
Йосс, Джозеф (О. 1оо83 апс1 р. О. .УозерЪ)
A980): Е1етеп1агу з*аЫШу апс! Ы!игса*юп Шеогу, $рппдег-Уег1а§, 286 р.
(зее сЬарЬг VII).
[Имеется перевод: Йосс Ж., Джозеф Д. Элементарная теория устойчивости
и бифуркаций. —М.: Мир, 1983.]
Какутани, Маркус E. Каки1аш апс! Ь. Магсиз)
A958): Оп 1Ье поп-Нпеаг с11!!егепсе-сИГГегеп11а1 едиа^оп у' (*) = [Л — В X
X у (/ — т)] у (/), т: СопМЬиНопз 1о Ше Шеогу о! попНпеаг озс1Лаиопз.
Ес1. Ьу 5. Ье!зсЬе12, РппсеЬп, уо1. IV, р. 1—18.
Камке (Е. Катке)
A930): 1ГеЬег (Не е1пс!еииде ВезиттШеЙ с1ег 1п1е^га1е уоп О1Г!егепНа1-
§1е1сЬипдеп Н,5Й2.Вег. НеЫеШег^ Акас1. ^1зз. Ма1Ь. Ка1ипу. К1., 17. АЬ-
ЬапсП., зее а1зо МаШ. 2еИзсЬг., уо1. 32, р. 101—107.

Литература 479
A942): 0Шегепиа1д1е1сЬипдеп, Ьбзип&зтеШойеп ипс! Ьбзип^еп, Вескег &
Ег1ег, Ье1р21§, 642 р.
[Имеется перевод: Камке Э. Справочник по обыкновенным дифференциаль-
дифференциальным уравнениям. — М.: ИЛ. 1951.^-828 с, а также перевод б-го немец-
немецкого издания A959): изд. 2-е, — М»: Физматгиз, 1961; изд. 3-е, 4-е, 5-е. —
М.: Наука,1965, 1971, 1976.]
Каннингэм (№. ,1. Сипшп^Ьат)
A954): А попНпеаг сШГегегШаЬсШГегепсе ециапоп о! §[готуШ, Ргос. МаШ#
Асай. 5а., ША, уо1. 40, р. 708—713.
Кастлюнгер, Ваннер (К. Н. КазНипдег апс! С \Уаппег)
A972): Кип^е-Кииаргосеззезш^Ь тиШркподез, Сотри1шдуо1. 9, р. 9—24
A972Ъ): Оп Тигап 1уре 1трНсЦ Кип^е-КиНа те1Ьос15, СотриПп^ уо1. 9,
р. 317—325.
Кауэлл, Кроммелин (Р. Н. Со^еИ апс! А. С. О. СготтеНп)
A910): ЬуевИдаНоп о! 1Ье тоНоп о! НаИеу'з соте! !гот 1759 1о 1910.
АррепсНх 1о СгеешласЬ ОЪзегуаиопз 1от 1909, ЕсИпЬигдЬ, р, 1—84.
Кейли (А. Сау1еу)
A858): А тетсмг оп Ше Шеогу о! таШсез, РЫ1. Тгапз. о! Коуа1 5ос. о1 Ьоп-
<1оп, уо1. СХЬУШ, р. 17—37, МаШета11са1 Рарегз уо1. 2, Ыг. 152, р. 475.
Келлер (Н. В. Ке11ег)
A968): Китепса1 теШойз !ог 1:\уо-рот1 Ьоипс1агу-уа1ие ргоЫетз, В1а1зсЗе11
РиЫ. Сотр., 184 р. (зее зесИоп 2.4).
Кермак, Макендрик (\У. О. Кегтаск апс! А. С МсКепс1г1ск)
A927): Соп1г1Ьи11ОП5 1о Ше та1Ьета11са1 1Ьеогу о! ерЫегшсз (Раг! 1), Ргос,
Ноу. Зое, А., уоЬ 115, р. 700—721,
Кертис (А. Н. СигИз)
A970): Ап е1^Ы;11 огйег Нип^е-КиНа ргосезз ш1Ъ. е1еуеп !ипс11о
рег з!ер, Ыитег. АЫЬ. Уо1. 16, р. 268—277.
A975): НщЬ-огс1ег ехрИсИ Нип^е-КиНа !огти1ае, 11шг изез, апс!
Иопз, .1. 1пз1. МаШз. АррПсз, уо1. 16, р. 35—55.
Кертис, Хиршфельдер (С. Р. Сиг1;1зз апс! .1. О. Н1гзсЬ!е1с1ег)
A952): 1п1е^гапоп о! зИ!! е^иа1;^опз, Ргос. о! 1Ье ЫаИопа1 Асас1ету о! 5с1еп-
сез о! II. 5., уо1. 38, р. 235—243,
Кинг (К. Кгщ)
A966): Кип^е-КиНа те!Ьос1з шИЬ сопз!га1пеA т1штит еггог ЬоиЫз, МаШ*
Сотри!., уо1. 20, р. 386—391.
Клеро (А. С. СШгаи!)
A734): 5о1и^1оп с1е р1из1еигз ргоЫётезой II &'а%Н бе 1гоиуег с!ез соигЬез 6оп1
1а ргорпё(ё сопз1з1е бапз ипе сегЫпе ге1а11оп еп1ге 1еигз ЬгапсЬез, ехрптёе
раг ипе Е^иа^:^оп с!оппёе. Мётокез с!е МаШ. е! с!е РЬуз. с!е ГАсас!. Ноуак
с1ез Заепсез, Рапз, Аппёе МОССХХХ1У, р. 196—215.
Кнапп, Ваннер (Н. Кпарр апс! С. \Уаппег)
A969): ЫЕ5Е II, А рго&гат Ьг огсИпагу с!Шегепиа1 еяиаНопз из1п§ Ые-
зепез, МНС Керог! N0. 1008, МаШ. НезеагсЬ Сеп1ег, 1]тчч ^{зеопзхп. Ма-
сНзоп, \^1зс. 53706.
Ковалевский (О. Ко\уа1е\узк1)
A908): см.1 Лейбниц A693).
Когстрем, Руэ (В. Као§з1гбт апс! А. КиЬе)
A980): Ап а1допШт Ьг питег1са1 сотри1;а11оп о! 1Ье ,1огс1ап погта1 Ьгт
сотр1ех та!пх: АСМ Тгапз. Ма1Ь. $ой\^аге, уо1. 6, р. 398—419 (К
Мау 1975, геу1зес1 Аид. 1977, ассер!ес1 Мау 1979).
Коллатц (Ь. Со11а1г)
A951): КитепзсЬе ВеЬапсИипд уоп ЭШегепИа^екпип^еп, ОгипA1еЬгеп
Вапс! IX, Зрпп^ег Уег1ад, 458 р., зесопс! е&Нюп. 1955; 1Ыгс1 ебШоп апс!
епдПзЬ 1гапз1а1юп 1960.
[Имеется перевод: Коллатц Л. Численные методы решения дифференциаль-
дифференциальных уравнений. — М.: ИЛ, 1953.]

480 Литература
Коллег, Экманн (Р. Со11е1 апй 3, Р. Ескшапп)
A980): ИегаЫ таре оп Ше т*егуа1 аз Aупат1са1 зуз*ет5. В^кЬаизег, 248 р.
Кори E. А. Согеу)
A906): А теШос! о! арргохкпаиоп, Атег* МаШ- МопШ1у УоК 15, р. 137—140.
Кош и (А. Ь. СаисЬу)
A824): Кёзитё ЗезЬесопз Йоппёез а ГЕсо1е Коуа1е Ро1у1есЬш'яие. ЗиИе с!и
Са1си1 1пНт1ёз1та1; риЬНзЬед: ЕяиаНопз <Шёгеп11е11ез огёпшгез, ей. СЬг.
СШат, ЛоЬпзоп 1981.
П831): 5иг 1а тесание се1ез*е е{ зиг ип поиуеаи са1си1 арре1ё са1си1 йез
НтИез, 1и а Гасай. йе Типп 1е И ос!. 1831; а1зо: ехегс. с!*апа1. е* ее рЬу-
31Яие та(Ь., 2, Рапз 1841; Оеиугез B), 12.
A839—42): 5еуега1 ай!с1е8 т Сотр1ез Кепйиз бе ГАсас!. с!ез Заепсез Aв
Рапз. (Аид. 5. Ыоу. 21, 1839. Липе 29, Ос*. 26, 1840, ек).
Крайер (С. №. Сгуег)
A971): А ргоо! о! Ше 1пз1аЪ1Н*у о! Ьас1гогагс1-с1Шегепсе тиН15*ер теШойз
1ог Ше питепса1 1п1едгаAоп о! огсAпагу <Ш!егеп11а1 е^иа^^оп8. ТесЬ. К ер.
N0. 117. Сотр. 5сЬ Оер*., 1Гп1у. о! ^зсопзт, р. 1—52.
A972): Оп Ше 1пз1аЫШу о! ЫдЬ огдег Ьаск^аг4-A1!!егепсе тиШ$1ер теШоёз,
В1Т, уо1. 12, р. 17-25.
Кридон, Миллер (В. М. Сгеейоп апс! 3. 3. Н. МШег)
A975): ТЬе $1аЬ1И1у ргорегИез о! я*з!ер Ьаск^агс1-<1Шегепсе зсЬетез, В1Т,
уо1. 15, р. 244—249.
Крох (Р. Т. КгодЬ)
A969): А уапаЫе з!ер уаНаЫе огйег тиШзЫр теШос! гот 1Ье питеНса1 зо-
1и11оп о! огсНпагу A!пегепAа1 е^иа^^опз, 1пГоппаИоп Ргосез81п§ 68, ЫогШ-
Но11апс1, Атз1егйат, р. 194—199.
A973): А1допШтз !ог сЬап^пб Ше з*ер вгге. 51АМ 2. Ыит. АпаЬ, 10,
р. 949—965.
A974): СЬап^тд з!ер з!2е 1п Ше 1п1едгаИоп о! (Ш!егегШа1 е^иа^^опз из1п^
тодШеб сИу!с1еЗ сПпегепсез. Ргосеес11пдз о! *Ье Соп!егепсе оп (Ье Ыит. 5о1.
о! ООЕ, Ьес1иге Ыо1ез 1п МаШ. N0.362, Зрппдег-УеНа^, Ые\у Уогк, р. 22—71.
Крузе (М, Сгоигегх)
A975): 5иг Гарргох1та*1оп йез ^иа*1опз с!1!!ёгеп11е11е8 орега^оппеИез Н-
пёа1гез раг с!ез тёШойез с!е Кип^е-Ки^а, ТЬёзе ё'ё^а!, 11шу. Рапз 6, 192 р.
Крузе, Лисбона (М. Сгоиге1х апс! Р. Л. ЫзЬопа)
A984): ТЬе сопуегдепсе о! уапаЫе-з{ерз12е, уаНаЫе 1огти1а, тиШз1ер
теШойз, 51АМ ^. Ыит. Апа1. 21, р. 512—534.
Крылов Н. М., Боголюбов Н. Н. Введение в нелинейную механику. — Киев:
Изд-во АН УССР, 1937.
Куммер (Е. Е. Киттег)
A839): Ыо1е зиг Пп*ё8га«оп AеГёяиа«оп йпу1<1хп ~ хт у раг 4ез 1п16§га1е$
ёёНшез.СгеПе Л.!. (!. г. и. ап§етлг. МаШ. уо1. 19, р. 286—288.
Кунцманн C. Кигйгтапп)
A959): Оеих Ьгти1ез орита1ез 6и (уре Ае Кип^е-Ки^^а, СЬШгез, уо1. 2,
р. 21—26.
A961): Ыеиеге ЕпЬлг1ске1ип§еп Йег МеШойе уоп Кипбе-Ки^^а, 2АММ, уо1. 41,
р. 28—31.
Купер (О. ,1. Соорег)
A978): ТЬе огс!ег о! сопуег^епсе о! депега1 Нпеаг теШо^з !ог ог^хпагу с11!!е-
геп^1а! е^иа^^опз. 51АМ Л. Ыитег. Апа1., уо1. 15, р. 643—661.
Купер, Вернер (С 3. Соорег апс! Л. Н. Уегпег)
A972): 5оте ехрИсй 1<ипде-Ки1*а теШойз о! Ыф. огс!ег, 51АМ Л. Ыитег,
Апа!., уо1. 9, р. 389—405.
Кутта (\^. КиПа)
A901): Ве1*гад гит паЬегип&з^зеп 1п1едга^1оп 1о*а1ег
, 2е51зсЬг. !йг МаШ. и. РЬуз., уо1. 46, р. 435—453.

Литература 481
Лагранж (<1. Ь. с!е Ьа&гап&е)
A759); КесЬегсЬез зиг 1а па!иге е^ 1а ргорадаМоп би зоп, М1зсе11. Таиппеп-
31а 1. I, Оеиугез 1. 1, р. 39—148.
A762): Зо1и1юп бе бШёгегйз ргоЫётез бе Са1си1 1п1ёбга1, МлзсеИ. ТаиН-
пепза, 1. III, Оеиугез 1. 1, р. 471—668.
A774): 5иг 1ез 1п1ё^га1е$ рагИсиНёгез с!ез Е^иа^^оп5 сИГГёгепНеНез, Осиугез,
1от. 4, р. 5—108.
A775); КесЬегспе риг 1ез ЗиИез Нёсиггеп1ез, Ыоиуеаих Мет. бе 1/Асаб. гоуа1е
без Заепсез е{ ВеПез-ЬеНгез, ВегНп, Оеиугез уо1. 4, р. 159.
A788): Мёсашяие апа\у1'щие, Рапз, Оеиугез 1. 11, е! 12
[Имеется перевод: Лагранж Ж- Аналитическая механика. — М.—Л.: Гос-
техиздат, 1950, т. 1 и 2.]
A792): Мётсаге зиг Гехргеззюп би 1егте ^ёпега1 с!ез зёпез гёсиггеп1ез, 1огз-
аие ГёяиаНоп &ёпёга!псе а без гас1пез ёдаТез. Ыоиу. Мёга. бе ГАсас!. гоуа1е
аез $с!епсе$ с(е ВегПп, Оеиугез I. 5, р. 627—641.
A797): ТЬёопе с!ез ГопсИопз апа1у!1диез, соп!епап1 1ез рппс!рез с!и са)си1
ш!!ёгеп11е1, бёдадёз с!е 1ои1е сопз1с!ёга1юп сГтПштеп! реШз, с!'ёуапои13зап1з,
с!е НтИез е! с(е !1их1опз, е! гёйиНз а 1'апа1узе а1^еЬг^^ие без ^иапШёз Птез,
Рапз, 1797, поиу. еб. 1813, Оеиугез Тоте 9.
Лаке, Рихтмайер (Р. В. Ьах апб К- О. К1сЬ*туег)
A956): Зигуеу о! Ше з1аЬ1Шу о( Ппеаг Нтйе сA1!егепсе едиа^1оп$. Сотт.
Риге Арр1. МаШ., уо1. 9, р. 267—293.
Лаплас (Р. 5. Ьар1асе)
(Ап XIII = 1805): 5ирр1ётеп( аи сНх1ёте Нуге би ТгаИё бе тёсаг^ие сё-
1ез1е зиг Гас1юп сар111а1ге, Раг1з сЬег Соигс1ег, 65+ 78 р.
Лейбниц (О. №. Ье\Ътг)
A691): МеШобиз, ^иа тпиттегагит Нпеагит сопз1гис^1оп ех ба^а ргорпе-
1а1е 1ап^еп11ит зеи аеяиа^1о т!ег аЬзс15зат е1 огб1па1ат ех ба!о уо1оге
зиЬ1ап^еп!1аПз, ехЬ1Ье!иг. ЬеНег 1о Ниудепз, т: С. I. СегЬагб1, ЬеШшгепз
таШ. ЗсЬпПеп, 1850, Вапб II, р. 116—121.
A693): (Со1Ьо*гесН Ои1Нг1т1 ЬегЪпИги): 5ирр1етеп1ит реотеЫае О1теп-
зопае $еи^епегаНзз1та отп1ит 1е1га дошзтогит е!!есНо рег то!ит: 51-
гшШегдие тиШр1ех соп$1гис11о Нпеа ех с!а*а ЬпдепИит сопб111опе, Ас1а
ВгибИогит; Ыр$1ае, р. 385—392; &егтап (гап$1а1юп: О. Ко^ак^зк!, Ье1Ь-
Ш2 йЬег б1е Апа1уз13 без ШепсШсЕеп, ОзЫаНз К1азз1кег, Ыг. 162 A908),
р. 24—34.
Лефевер, Николис (Н. Ье!еуег апб О. ЫкоНз)
A971): СЬегшса11пз1аЬШНез апб зиз^атеб озсШаНопз, I» Шеог. В1о1.> уо1. 30,
р. 267—284.
Линделёф (Е. Ыпс1е1о!)
A894): 5иг ГаррИсаНоп без тё!Ьобе б'арргох1та^1оп зиссезз1уез а Гё^ибе
без Ыё&гакз гёеНез без щиаИопв бШёгепаеИез огб1па1ге8, I. бе МаШ., 4е зёпе
уо1. 10; р. 117—128.
Липшиц (Н. Ь1рзсЫ12)
A876): 5иг 1а розз!ЫШё бЧп1ёёгег сотр1е!етеп1 ип зуз1ёте боппё б'ёяиа-
11опз б1![ёгеп11е11ез, ВиПеПп без 5с1епсез МаШ. е1 Аз1г., Рапз, уо1. 10,
р. 149—159.
Лиувилль (Л. ЬлоиуШе)
A836): Зиг 1е бёуе1орретеп^ без !опсAопз ои рагНез бе !опс^1опз ел зёпез
боп! 1ез бгуегз 1егтез зоп! азз^ёиз а заНз^аке § ипе тете ёяиаКоп бШё-
гепЬ'еИе би зесопб огбге, соп1епап^ ип рагатё!ге уапаЫе, Лоигп. бе МаШ.
ригез е! арр1., уо1. 1, р. 253—265.
A838): Зиг 1а ТЬёопе бе 1а уапаНоп без сопз*ап1ез агЫ1га1гез, ЫоиуШе
3. бе МаШ. уо1. 3, р. 342—349.
A841): Нетагяиез поиуеНез зиг ГёдиаИоп бе Н^ссаи, Л. без МаШ. ригез
е* арр!., уо1. 6, р. 1—13.
15 Хайрер Э. и др.

482 Литература
Лобатто (К. ЬоЬаНо)
A852): Ьеззеп оуег ОШегепНа1- еп 1п*е§гаа1-Кекеп1п§(, 2 уоК, Ьа Науе 1851—
1852.
Лоренц (Е. N. Ьогепг)
A979): Оп Ше ргеуа1епсе о! ареНосНсИу гп 51тр1е зуз^етз, О1оЬа1 Апа1уз!з,
Салагу 1978, ей. Ьу М. 0гте1а апс! I, Е. МаЫеп, ЬесЫге Йо1ез т МаШе-
та&сз, уо1. 755, р. 53—75.
Лоткин (М. ЬоОДн)
A951): Оп Ше ассигасу о! Кип&е-Кийа теШойз, МТАС уо1. 5, р. 128—
132.
Льенар (А. М. 1лёпагс1)
A928): Е*ис1е с!е$ озсШаИопз еп!ге*епие5, Кеуие дёпёга1е а*е ГЕ1ео*г1сЙё,
1оте XXIII, р. 901—912, е* 946—954.
Ляпунов (А. М. Ьларипоу)
A892): РгоЫёте &ёпёга1 с!е 1а 8{аЪШ1ё ди тоиуетеп!, гизв. *гас1. еп !гап-
са1з 1907 (Аппа1ез с!е 1а РасиНё с1ез БЫепсез с!е Тои1оизе), герпп!ес1 1947
Рппсе1оп Ошу. Ргезз, 474 р«
Ляпунов А. М.
A892): Общая проблема устойчивости движения. — В кн.: Собрание со-
сочинений, т. II, с, 7—263. —М.—Л.: Изд-во АН СССР.
Марден (М. Магйеп)
A966): Оеоте1гу о! ро1>пот1а1з, Атепсап Ма1петаиса1 $0С1е1у, Ргоу1-
йепсе, 1^Ьос1е 1з1апс1, 2пс1 ес11Иоп
Марсден, Мак-Кракен (Л. Е. Магзбеп апс! М. МсСгаскеп)
A976): ТЬе Нор! Ы!игсаИоп апс! 11з аррПсаИопз, Зрппдег, Ие^ Уогк, р. 408.
[Имеется перевод: Марсден Дж., Мак-Кракен М. Бифуркация рождения
цикла и ее приложения.—М.: Мир, 1980.]
Марчук Г. И.
A975): Простейшая математическая модель вирусного заболевания.—
Новосибирск, ВЦ СО АН СССР, препринт.
A980): Математические модели в иммунологии. — М.: Наука.
Мерсон (К. Н. Мегзоп)
A957): Ап орега!юпа1 теШос! !ог 1Ье з1ис1у о! Ме^гаИоп ргосеззез, Ргос.
5утр. Эа1а Ргосеззтд;, ^еаропз ^езеагсЬ Ез1аЬН5Ьтеп1, ЗаНзЬигу, Аиз1га-
На, р. ПО—1 1о 110—25.
Мизес, фон (К. уоп М1зез)
A930): 2иг питепзсЬеп 1п1е^таИоп уоп ОШегепиа1д1е1сЬипдеп, 2АММ,
уо1. 10, р. 81—92.
Милн (№. Е. МПпе)
A926): Митепса1 Ше&таНоп о! огсНпагу сИ!!егеп^1а1 еяиа^1оп, Атег. МаШ.
МопШу, уо1. 33, р. 455—460.
A970): Митепса1 зо1иИоп о! сИ!!егепиа1 е^иаиопз. Эоуег РиЬНсаНопз,
1пс. Ые^ Уогк, зесопй ес!Шоп. [Имеется перевод первого издания: Милн В. Э.
Численное решение дифференциальных уравнений. — М.: ИЛ, 1955.]
Митчелл, Крэггс (А. Н. МйспеИ апс! ^. №. Сга^з)
A953): З^аЫШу о! с!Шегепсе ге1аЦопз 1п Ше зоЫ:1оп о! опНпагу AШегеп1;1а1
е^иа1^оп5, МаШ. ТаЫез А1с1з Сотри!., уо1. 7, р. 127—129.
Молер, ван Лоан (С. Мо1ег апс! С. Уап Ьоап)
A978): Н1пе1ееп йиЫоиз ^ауз *о сотрите Ше ехропепНа1 о! а таМх: 51АМ
НеУ1е^, Уо1. 20, р. 801—836.
Мултон (Р. К. МоиНоп)
A926): Ие\у теШос!з гп ех!ег!ог Ьа1Нз^1сз. ЦЫу. СЫсадо Ргезз
Мур (И. Е. Мооге)
A966): 1п1егуа1 Апа1у$15, Ргеп^1се-На11, 1пс, 145 р.
A979): МеШодз апс! аррНсаНопз о! 1п1егуа1 апа1у51з, 51АМ 51и(Не$ 1п Арр1.
МаШ., р. 190.

Литература 483
Мюллер (М. МШ1ег)
A926): ОеЬег баз РипйатегйаШЬеогет 1п сЗег ТЬеог1е йег §е^бЬпНсЬеп
ВШегепИа1фе1сЪищеп, МаШ. ЯейзсЬг., уо1. 26, р. 619—645. (Кар. III).
Мэй (К. М. Мау)
A976): 51тр1е таШетаНса1 пЫеЬ ту11Ь уегу сотрНсаЫ с!упат1с8, Ыа-
1иге, уо1. 261, р. 459—467.
Невилл (Е. Н. КеуШе)
A934): ИегаНуе ЫегроЫюп, Ш. МаШ. Зое. I. Уо1. 20, р. 87—120.
Нёрсетт E. Р. КогзеК)
A974а): Опе-з1ер теШойз о! Негшйе Шре !ог питеНса1 ЫедгаИоп о! $Ш!
8у$1ет5, В1Т, уо1, 14, р. 63—77.
A974Ь): 8ет1 ехрНсИ Кип^е-КиКа теШойз, Керог* N0. 6/74, 18ВМ
82-7151-009-6, Оер*. МаШ. Ш1у. ТгопсИшт, Ыошау, 68+ 7рр.
Нёрсетт, Ваннер E. Р. Ыогзеи апс! О. Шаппег)
A979): ТЬе геа!-ро1е вапсМсЪ !ог гаНопа1 арргох!та11оп8 апс! озсШаНоп
еяиаНопз, ВТТ уо1. 19, р. 79—94»
Нордсик (А. ЫогсЫесЖ)
A962): Оп питепса1 1п*едгаиоп о! огсНпагу A1!!егепиа1 е^иаиопз, МаШ.
Сотр., уо1. 16, р. 22—49.
Нумеров (В. Ыитегоу (В. V. Коитегош))
A924): А теШос! о! ех^гаро1а^1оп о! регШгЬаИопз. МопШ1у по^сез о! Ше
Коуа1 Аз1гопот1са1 5ос1е1у о! A2х/<Н2 в | (х, () А$1гоп, КасЬг1сЫеп, уо1. 230,
р. 359—364.
Ньютон (I. Ые\у1оп)
A671): МеШойиз Р1их1опит е* БеНепит 1пПп1*агит, есШа ЬопсИп! 1736,
Оризси1а та!ЬетаИса уо1. 1. ТгайиИ: еп !гапса15 раг М. бе ВиНоп, Рапз
МОССХЬ. [Имеется перевод: Ньютон И. Математические работы. — М.—Л.:
Объединенное научно-техническое издательство НКТП СССР, Главная ре-
редакция технико-теоретической литературы, 1937, с. 25—166} Метод
флюксий и бесконечных рядов.]
A687): РЬПозорЫае паЬгаНз рппс1р1а таШетаМса, 1трг!та!иг 8. Реруз,
Кед. Бос. Ргаезез, ]иН1 5, 1686, ЬопсНш аппо МОСЬХХХУП. [Имеется
перевод: Ис. Ньютон, Математические начала натуральной философии/Пере-
философии/Перевод с латинского с примечаниями и пояснениями А. Н. Крылова. — В кн.:
Собрание трудов академика А. Н. Крылова, т. VII, — М,—Л.; Изд-во
АН СССР, 1936.]
Нюстрём (Н. Л. Ыу51гот)
A925): 11еЬег (Не питеН$сЬе 1п1е^гаИоп уоп ОШегепИа^екЬипдеп, Ас1а
Бос. Бс1. Репп., уо1. 50, N0. 13, р. 1—54.
Окамото, Хаяси (М. Окато1о апс! К. Науаз111)
A984): Р^е^иепсу сопуешоп тесЬап1зт 1п епгута11с !еес!Ьаск зуз^етз,
I. ТЬеог. В1оЬ, уо1. 108, р. 529—537,
Оливер р. ОНуег)
A975): А сипохНу о! 1оту-оп1ег ехрНсН Еип§е-Кииа теШос!$, Ма1Ь. Сотр.,
уо1. 29, р. 1032—1036.
Осборя (М. К. ОзЬогпе}
A966): Оп КогсЫеск 5 теШос! !ог Ше питег!са1 $о1ииоп о! огс1тагу сШ!е-
геп^1а1 еяиа^опз, ВТТ, уо1. 6, р. 51—57.
Парлетт (В. N. РаНеП)
A976): А гесиггепсе атопд 1Ъе е1етеп1:з о! !ипс!1опз о! 1г1апди1аг та1г!сез,
Ыпеаг А1деЬга Арр1., уо1. 14, р. 117—121.
Пеано (О. Реапо)
A888): 1п1ё^га^1оп раг зёНез йез ёдиаНопз бШётепИеИев 1тёа1гез, Ма№. Ап-
па1еп, уо1. 32, р. 450—456.
A890): Оётопз*гаиоп бе УЫё%таЫШё\ с!ез ёяиа!1опз с11!!ёгвпие11ез огсНпак-ез,
МаШ. Аппа1еп уо1.37, р. 182—228; зее а1зо 1Ье дегтап {гапзЫюп апб сот-
теп*а«оп: О. М1е, МаШ. Аппа1еп уо1. 43 A893), р. 553—568.
16*

484 Литература
A913): Кез1о пе11е ?оптш1е сН ^иа(^га^ига, езргеззо сап ип Ые^гак йеНпНо
АШ Ое11а Кеа1е Ассай. Ое1 1лпсе1, КепсИсогШ, уо1. 22, № 9, р. 562—569»
Кота.
Перл, Рид (К- Реаг1 апс! Ь. I. Кееа*)
A922): А ?игШег по*е оп Ше таШетаИса1 Шеогу о! рори1аНоп ^гочуШ, Рго-
сеесНп&з о! Ше №Нопа1 Асас1. о! Заепсез, уо1. 8, N0. 12, р. 365—368.
Перко (Ь. М. Регко)
A984): ЫтН сус1ез о! циадтаИс 8уз1етз 1п Ше р1апе, Коску МоипШп
о! МаШ., уо1. 14, р. 619—645.
Перрон (О. Реггоп)
A915): Ет пеиег Ех1$1епгЬе\уе1з !йг (Не 1п1е§га1е бег
у' = {(х, у), МаШ. Аппа1еп, уо1, 76. р. 471—484.
A918): гиг 2еН 1п РеЫе): Е1п пеиег Ех181еп2Ье^е18 !йг сИе 1п^е§га1е етеп
5уз1етз ^е^оЬНсЬег 01[Гегеп11а1^Ье1сЬип^еп, Ма1Ь. Аппа1еп, уо1. 78, р. 378.
A929): ОеЬег 51аЬ1Ша1 ипс! азутр1о115сЬез УегЬаНеп бет 1п*-е^га^е Vоп ^^^'
!егеп11а1^1е1сЬип^ззуз1етеп, Ма1Ь. 2., уо1. 29, р. 129—160 (зее раг. 3).
Пикар (Е. Р'юатй)
A890): Методе зиг 1а Шёопе Йез ^иаНопз аих с!ёпуёез рагИеНез е1 1а
тёШос!е с1ез арргох1таИопз зиссезз1уез, Д. бе МаШ. ригез е{ арр1., 4е зёпе,
уо1. 6, р. 145—210.
A891—1896): ТгаИё сГАпа1узе, 3 уо1з, Раг1з.
Пиотровски (Р. РЫго^зку)
A969): 51аЬШ1у, сопз1з1епсу апс! сопуегдепсе о! уаНаЫе А5-з1ер теШойз
гог питепса1 1П^е^га11оп о[ 1аг&е зуз1етз о! огсИпагу бШетепНа! е^иа^^опз,
ЬесЫге Ыо^ез т МаШ. 109, Оипс1ее 1969, р. 221—227.
Пригожин, Лефевер и др. (I. Рг1^о§1пе, К. Ье!еуег, А. ОоЫЬеЬг, М. НегзсЬ-
A969): Ыа^иге, уо1. 223, р. 913.
Принс, Дорман (Р. I. Рппсе апс! ^. К. Оогтапс!)
A981): Н1^Ь отбет етЬеййес! Кипде-Кииа Гогти1ае, I. Сотр. Арр1. МаШм
уо1. 7, р. 67—75.
Прюфер (Н. РгйГег)
A926): Ыеие НегкНипд; с1ег 5^игт-Ыоиу111зсЬеп
РипкИопеп. МаШ. Аппа1еп уо1. 95, р. 489—518.
Пуанкаре (Н. Ротсагё)
A881, 82, 85): Зиг 1ез соигЬез Aё1т1ез раг 1ез ёциаНопв сШ1ёгепие11ез, I.
бе МаШ., Зезёпе, I. 7, р. 375—422, *. 8, р. 251—296, 4е зёпе, 1. 1, р. 167—
244. [Имеется перевод: Пуанкаре А. О. кривых, определяемых дифферен-
дифференциальными уравнениями.—М.—Л.: Гостехиздат, 1947.]
A893): Ьез тёШойез поиуеИез 6е\а тёсаг^ие сё1ез!е, Тоте II, 480 р., Оаи-
(Ыег-УШагз Рапз. [Имеется перевод: Пуанкаре А. Избранные труды, т. I,
II. — М.: Наука, 1971.]
Пуассон ($.0. Ро1$зоп)
A835): ТЬеопе таШёта^ие с1е 1а сЬа1еиг, Рапз, ВисЬеИег, 532 р. $ирр1е-
теп1: 1837, р. 72.
Пузе (Р. Роиге!)
A963): Е*ис1е еп уие с!е 1еиг каНетеп! питё^^^ие с!ез ё^иа1:^опз т{ё§га1е$
йе 1уре УоИегга. Кеу. Ргапса1з ТгаНетеп! 1п!огтаиоп (СЫ!!гез), уо1. 6,
р. 79—112.
Радо (К. Кайаи)
A880): Е1ийе зиг 1ез !огтез с1'арргох1та^1оп ^и^ зегуеп! к са1си1ег 1а уа1еиг
питёпяие с!'ипе т!ё&га1е сИПпИе, ЫоУ111е ^. с!е МаШёт. ригез е! арр1.,
2езег., 1оте VI, р. 283—336. (Уо1Г р. 307).
Райт Э. (Е. М. ЧУпдЫ)
A945); Оп а зециепсе йеНпес! Ьу а поп-Нпеаг гесиггепсе !огти1а, I. о! Ьопс1оп
МаШ. 5ос, уо1. 20, р. 68—73.

Литература 485
A946): ТЬе поп-Нпеаг с1Шегепсе-с1Шегепиа1 еаиаиоп, (Эиаг*. Л. о! МаШ.,
уо1. 17, р. 245—252.
A955): А поп-Нпеаг с1Шегепсе-с1Шегепиа1 ^иаНоп, I. !• с1.г. и. апдету. МаШ.»
уо1. 194, р. 66—87.
Райт К. (К. ШщМ)
A970): $оте геЫюпззЫрз ЪеЫееп 1трНсИ: Нип&е-КиНа соНосаНоп апс!
Ьапсгозз т теШо^з, апд Ше1Г з1аЫШу ргорегИез, ВТТ уо1. 10, р. 217—227.
Ральстон (А. На1з1оп)
A962): Нип^е-Ки^а теШойз \*аШ гшштит еггог Ьоипйз, МаШ. Сотри*.
уо1. 16, р. 431—437, согг. уо1. 17, р. 488.
Раус (Н. .1. НоиШ)
A877): А ТгеаИзе оп Ше з1аЫШу о! а &1Уеп зЫе о! тоНопз, Ъе\щ Ше еззау
1о ъгЫсЪ Ше Ас1атз рпге \^аз ас1]'ис1деЗ 1п 1877, 1п 1Ье 11п1уегз11у о! Сат-
Ьпс1^е, Ьопс1оп, р. 108.
A884): А ТгеаНзе оп Ше йупагшсз о! а зуз1ет о! т'щ[6 ЬосНез, раг! А апс! II,
4Ш е^1Иоп A з! е<3. 1860, 6Ш ес1. 1897, ^егтап 1гап51аИоп VIШ гетагкз о!
Р. К1е1п 1898). [Имеется перевод: Раус Э, Дж. Динамика системы твердых
тел. — М.: Наука, 1983. — т. I, II.]
Рейд (Ш. Т. Нес!) .
A980): 51иггп1ап Шеогу !ог огсНпагу сИ!!егеп1:1а1 е^иа^^опз, 8рпп§ег-Уег1аб,
Арр1. МаШ., 5епе 31, р. 559.
Риккати C. К1сса^1)
A712): 5о11шопе ^епега1е с!е1 РгоЫета туегзо 1п1огпо а га^ О8с!1а1ог! ...
с!е1егттаг 1а сигуа, а сш сопзеп^з ипа 1аГезрге$з1Опе, С1огпа1е йе'ЬеНегаИ
й'ИаНа, уо1. Н, р. 204—220.
A723): Аштайуешопез 1п ае^иа^^опез Й1Г1егеп11а1ез зесипсН ^гасНиз, Ас^а
Егис1. Ырз, аппо МЭССХХШ, р. 502—510.
Риман (В. Шетапп)
A854): ОеЬег 6'ге ИаЫеИЪагЬей е1пег РипсНоп с!игсЬ е1пе {п&опотеШзсЬе
Йе^Ье, уоп Aет УегГаззег ЪеЬиГз $е1пег НаЬШ^а11оп ап с!ег игиуеЫШ ги
СоШп^еп с!ег рЫ1озорЬ15сЬеп РасиНаЧ е1п§еге1сЬ^; со11ес1ес! ^огкз, р. 227—
265. [Имеется перевод: Риман Б. Сочинения. — М.—Л.: Гостехиздат, 1948,
с. 225—261: О возможности представления функции посредством тригоно-
тригонометрического ряда.]
Ричардсон (Ь. Р. ШспапЗзоп)
A910): ТЬе арргох1та!е агИпте{1'са1 зоЫМоп Ьу ?тйе йШегепсез оГ рЬу-
З1са1 ргоЫетз 1пс1ис11п^ с11[[егепИа1 е^иаиопз, ш!Ь ап аррНсаНоп 1о Ше
з1ге5зез 1П а тазопгу с!ат, РЫ1. Тгапз., А, уо1. 210, р. 307—357.
A927): ТЬе о*е!еггес1 арргоасп 1о Ше ИтН, РЫ1. Тгапз., А, уо1. 226, р. 299—
349.
Ромберг (XV. КотЬег^)
A955): Уеге1пГасЫе питепзсЬе 1п{едга*юп, Котке У1с1. 5е1зк РогЬс11, уо1. 28,
р. 30—36.
Роте (Е. Ко*Ье)
A930): 2^е1сИтепз{опа1е рагаЬоНзсЬе КапсЬуег1аи{&аЪеп а1з Сгепг!а11 е1псЛ-
теп51опа1ег Капс1уег1аи!8аЬеп, МаШ. Аппа1еп, уо1. 102; р. 650—670.
Рунге (С. Кип^е)
A895): ОеЬег сИе питепзсЬе АиИозип^ уоп В1!!егеп1:1а1^1е1сЬип^еп, МаШ.
Апп., уо1. 46, р. 167—178.
A905): ОеЬег сИе питепзсЬе Аи!16зип§ 1о1а1ег В1!!егепиа1^1е1сЬип§еп, ОбШп-
^ег МасЬг., р. 252—257.
Рунге» Кёниг (С. Кип&е апс! Н. Кбп!^)
A924): УоНезип^еп йЬег питепзсЬез НесЬпеп, СгипсИеЬгеп XI, Зрппдег-
Уег1а§, р. 372.
Рутисхаузер (Н. НиНзНаизег)
A952): ОеЬег сИе тз1аЬШШ уоп Ме1Ьос1еп гиг Iп^ед^а^^оп ^бЬпЬ'сЬег
ОШ^Ы, 2АМР, уо1. 3, р. 65—74.

486 Литература
Руш, Абетс, Лалуа (К. КоисЬе, Р. НаЬе*з ала* М. Ьа1оу)
A977): 81аЬШ1у 1пеогу Ьу Ыарипоу'з бгт&Л теШос!, АррЬ МагЪ. 5сЬ, 22,
5рпп&ег-Уег1а§, р. 396. {Имеется перевод: Руш Н., Абетс П., Лалуа М.
Прямой метод Ляпунова в теории устойчивости. — М.: Мир, 1980.1
Рэлей (Ьогс! Нау1е!дЬ)
A883): Оп татЫпес! уШгаНопз, РЫК Ма&. Бег, б, уоК 16, р. 229—235.
Рюэль, Такенс (О. Кие11е апй Р. Такепз)
A971): Оп 1Ье па1иге о! 1игЬи1епсе, Соттип. ЛЫЬ. РЬуз1с8, уо1. 20, р. 167—
192.
Сарафян (О. 8ага!уап)
A966): Еггог езИтаИоп 1ог Кип&е-Кииа теШодз ШгоидЬ рзеиЙо-ИегаЦуе
югти1аз; ТесЬп. Кер. N0.14, Ьоиз1апа$Ые 11шу., Мету ОНеапз, Мау 1966,
Симмонс (Б. Р. 51тропз)
A972): ОШегепНа! ециапопз ыНЪ аррНсаНопз впб Ы$1ог1са\ по!ез,
НШ, р. 456.
Скил (Н. 5кее1)
A976): Апа1уз*$ о! Нхес!-5^ерз12в те^Ьойз, 51АМ I. Штег. АпаЬ, уо1.
р. 664—685.
A978): Еяшуа1еп* !огтз о! тиШз^ег !огти1аз, КероН К-78—940,
о! Сотр. 5с1., уту. о! 1Шпо1з а! Ш)апа-СЬатра1§п
Спейкер (М. N. ЗрЦкег)
A971): Оп 1Ье з^гис^иге о! еггог езита1езГог НпНе бШетепсе теШо^з; Ыитег.
МШ., уо1. 18, р. 73—100.
^ 5!!
, , р
Стеффенсен ^. р. 51е!!епзеп)
A956): Оп 1Ье гез^псес! ргоЫеш о! 1пгее ЬосЛез, К. Йапзкв У1с1епзк. 5е1зк#,
МаМуз. Мес1с1. 30 №. 18.
Струд, Станку (А. Н. 51гоис1 апй Б. Б. 31апси)
A965): <Эиас1га*иге !огти1ез чгИЪ ти1ир1в Оаизз!ап пос!ез, 51АМ I. Ыитег.
Апа1., зег. В, уо1. 2, р. 129—143.
Тодд C. Тос1с!)
A950): Ыо1ез оп тос!егп питеНса1 апа1уз!з, I, Ма1Ь. ТаЫез А1йз Сотри!.,
уо1. 4, р. 39—44.
Толлмин (\^. То11т!еп)
A938): ОеЬег (Не РеЫе аЬзсЬйиипд Ье1т АAатззсЬеп Уег!аЬгеп гиг 1п1едга-
Поп ^е^оЬпйЬег ОШегегШа1§1е1сЬипдеп, 2АММ, уо1. 18, р. 83—90.
Томсон, Тэйт (№. Тотзоп (Ьогс! КеМп апс! Р. О. ТаИ)
A879): Тгеа11зе оп паЬга1 рЬ11озорЬу (Уо1. 1, Раг1 I), СатЬгЫде; N6^ есН-
Поп 1890, р. 508,
Уайльд (О. \*Шс1е)
A892): Ьа<3у \^1пс1егтеге'з Рап, Сотес1у 1п !оиг ас^з Шмеется перевод: Оскар
Уайльд, Избранные произведения в двух томах. — М.: ГИХЛ, 1960. —
т. 2, с. 7—68; Веер леди Уиндермир.|
Уилкинсон (Л. Н. ^ЛШктзоп)
A965): ТЬе е1^еЬга1с С1^епуа1ие ргоЫет, Мопо^гарЬз оп питеНса1 апа1уз!з,
Ох!огс1, р. 662. [Имеется перевод: Уилкинсон Дж. X. Алгебраическая про-
проблема собственных значении. — М.: Наука, 1970.]
Уилкинсон, Райнш (Л. Н. "МШктзоп апс! С. КетзсЬ)
П970): Ыпеаг А1^еЬга, СгипсИеЬгеп Вале! 186, 5рНп^ег-Уег1а§, р. 439.
[Имеется перевод: Уилкинсон, Райнш. Справочник алгоритмов на языке
АЛГОЛ. Линейная алгебра. — М.: Машиностроение, 1976.]
Уинтнер, Мурнаган (А. А^Ыпег апс! Р. Э. МигпадЬап)
A931): А сапошса1 [огт !ог геа1 таМсез йпс!ег огШодопа1 1гапз!оггааиоп8,
Ргос. N8*. Асас1. БЫ. 11.3.А., уо1. 17, р. 417—420.
Ульманн (№. 1]Ытпапп)
A957): РеЫегаЬзсЬгИгипдеп Ье1 Ап!ап^з^ег1аи!даЬеп де^бЬпйсЬег ОШегеп-
11а1д1е1сЬипдззу51ете I. Огс1пипд, 2АММ BеЙ5спг. Апдету. МаШ. МесЬ.)
уо1. 37, р. 88—99.

Литература 487
Уолтер (№. ЧуаИег)
A970): ОШегепНа! апс! Ые^га! 1^иаШие$, 5рг1пбег-Уег1аб р. 352, §егтап
есШюп 1964.
A971): ТЬеге 13 ап е1етеп*агу ргоо! о! Реапо'з Шеогет, Атег. МаШ. МопШ1у,
уо1. 78, р. 170—173.
Уоттс (Н. А. ^3**3)
A983): 51агип§ з!ерз12е !ог ап ОЭЕ зо1уег, I. Сотр. Арр1. МаШ. уо1. 9,
р. 177—191.
Фейгенбаум (М. Ре1§епЬаит)
A978): СЗиапШаЦуе ишуегзаШу 1ог а с1аз5 о! попНпеаг 1гапз?огта1юп5,
3. 51а1. РЬуз. уо1. 19, р. 25—52, уо1. 21 A979), р. 669—706.
Фельберг (Е. РеЫЬегд)
A958): Ете МеШос!е гиг РеЫегуегк1етегип§ Ье!п Кипее-КиМа Уег!аЬгеп,
2АММ, уо1. 38, р. 421—426.
A964): Ие^ Ы&Ь-огс!ег Кип&е-КиМа !огти1аз чгНЪ $1ер $1ге соп1го1 !ог зу-
з1ет8 о! Ягз! апс! зесопй огЭег д1Яегепиа1 е^иаиоп8, 2АММ, уо1. 44, 5оп-
бетЪеП Т17-Т19.
A968): С1аз81са1 гШЪ-, 31х1Ь-, зеуегйЬ-* апс! ещМЪ огбег Нип§е-Ки11а !ог-
ти1аз т1Ъ з1;ер 312е соп*го1; ЫА5А ТесЬп1са1 НероН 287 A968); ех1гас! риЬ-
НзЬес! т СотриНпб уо1. 4., р. 93—106 A969).
A969): Ьо^-огс1ег с1а551са1 Нип^е-Кийа Гогти1аз ч/НЪ з!ер 312е соп1;го1 апс!
Ше1Г аррПсаНоп 1о зоте1 Ьеа1 1гапзГег ргоЫетз, ИА5А ТесЬп1са1 Керог! 315
A969), ех^гас! риЬНзЬес! ш СотриПп^ уо1. 6, р. 61—71 A970).
A972): С1азз1са1 е1^ЬШ-апс! 1о^ег-огс1ег Нип^е-КиНа-Куз^гбт Гогти1аз шШ
з1ерз12е соп!го1 !ог зрес1а1 зесопс!-огс1ег сИ1!егеп11а1 е^иа^^опз, ЫА5А ТесЬп!-
саЬНерог^ Н-381.
Филд, Нойес C. Н. ПеЫ апс! К. М. Ыоуез)
A974): ОзсШаИопз 1П сЬеш1са1 зуз1етз. IV, 1Лтй сус1е ЬеЬау1ог !п а тос!е1
о? а геа1 сЬет1са1 геасНоп, ^. СЬет. РЬуз1С8, уо1. 60, р. 1877—1884.
Филиппи, Грэф E. РШрр! апс! .1. Сга!)
A986): Ые^ Кипбе- Ки*1а-Куз1гбт Гогти1а-ра1гз о! огс!ег 8G), 9(8), 10(9)
апс! 11 A0) гот (ЗШегепКа! е^иа^^опз о! Ше !огт у" = I (х, у), 3. Сотри!.
апс! АррНес! МаШ., уо1. 14, р. 361—370.
Фиторис (Ь. У1е^опз)
A953): Иег Н1сЫип^з!еЬ1ег етег с!игсЬ с!аз Ас!атззсЬе 1п^егро1а^юпзуег[аЬгеп
^е^оппепеп ШЬегип^зЮзип^ е1пег С1е1сЬип^- у' = / (х, у). Оез1егг. Акас!.
^153., Ма1Ь.-па*ипу. К1., АЫ. Па, уо1. 162, р. 157—167 апс! р. 293—299.
Флетчер, Соренсен (К. Р1екпег апс! ^. С. Зогепзеп)
A983): Ап а1^огИЬт1с с!епуаИоп о! Ше Логс!ап сапопка1 {огт, Атег. МаШ.
МопШ1у, уо1. 90, N0. 1, р. 12—16.
Форрингтон (С. V. Э. Рогпп^оп)
A961—1962): Ех^епзюпз о! 1Ъе ргес!1с1ог-соггес1ог теШос! !ог Ше зо1и11оп
о! зуз^етз оГ огсЛпагу сЛГ!егеп11а1 еяиа^1опз, Сотри!. I. 4, р. 80—84.
Франческини (V. РгапсезсЫш)
A980): Ре^епЬаит зе^иепсе оГ Ь1Гигсаиопз т Ше Ьогепх тос!е1, ^. 5Ш.
РЬуз., уо1. 22, р. 397—406.
Фрейзер, Джонс, Скан (К. А. Ргапгег, \У. Р. ^опез апс! 5. \У. 5кап)
A937): АррпштаНопз 1о !ипсиопз апс! 1о Ше зоЫюпз о! сИ!!егепНа1 ециа-
1юпз, Нерог1$ апс! Метогапс!а Ыг. 1799 B913): Аегопаи11са1 КезеагсЬ Сотт11-
1ее, р. 33.
Фрике (А. Риске)
A949): ОеЬег сИе РеЫегаЬзсЬй12ип§ с!ез АйатззсЬеп Уег!аЬгепз гиг 1п1едга-
иоп ее^оЬпПсЬег БШегепИа^ЫсЬипбеп егз!ег Огйпип^, 2АММ, уо1. 29,
р. 165—178.
Фроммер (М. Рготтег)
A934): ОеЬег с!аз Аи!1ге!еп уоп ^1гЬе1п ипс! 51гис!е1п (^езсЫоззепег .ипс!
Н 1п1едга1кигуеп) тс!ег ОтдеЬипд гаИопа1ег иЬи1Ь11111

488 Литература
МаШ. Апп., уо1. 109, р. 395—424.
Фукс (Ь. РисЬз)
A866): 2иг ТЬеопе бет Нпеагеп иШетепИа^ЫсЪип^еп тН уегапйегНсЬеп
СоеШаегйеп, СгеИе Л. !. 6. г. и. ап^ечу. МаШ., уо1. 66., р. 121—160. (рге-
риЬП$Ьес1 Ы аРгодгатт с!ег зШизсЬеп ОечуегЬезсШе гп ВегНп, Оз1егп
1865»)
Функ (Р. Рипк)
A962): УапаНопзгесЬттд ипс1 Шге Агшепйипд т РЬуз1к ипс! ТесЬшк, 5рпп-
дег-Уег1ад, СгипсНеЬгеп Вс1. 94, 676 р.
Фурье C. В. ^. Роипег)
A807): 5иг 1а ргора&а!юп с!е 1а сЬа1еиг, иприЬНзЬес! тапи$спр{; риЬНзЬес!:
Ьа Шёопе апа1у1-цие бе 1а сЬа1еиг, Рапз 1822.
Хайндмарш (А. С. НтйтагзЬ)
A972): ОЕА^: огс11пагу с11Г!егепИа1 е^иа^^оп зуз1ет зо1уег ОСШ-30001,
Кеу. 2, ЬЬЬ, Ыуегтоге, СаШ.
A980): ЬЗОЭЕ апб Ь5ОБ1, 1^о пе^у тШа1 уа1ие огсИпагу с11!Гегеп^а1 е^иаиоп
5о1уегз, АСМ 51дпит Ые^з1еиег 15, 4,
Хайрер (Е. На1гег)
A977): МёШойез с!е Ыуз1гбт роиг ГёяиаНоп сННёгегШеПв у9 = (? (д?,
Иитег. Ма1Ь., уо1. 27, р. 283—300.
A978): А Кипее-КиНа теШоб о! огбет 10, ^. 1пз1. МаШз. АррНсз, уо1.
р. 47—59.
A981): Огс1ег сопс!Шоп5 1от питепса1 теШос!з !ог раг1:1Нопес1 огсНпагу
гепИа1 е^иа^юпз, Ыитег. МаШ., уо1. 36, р. 431—445
A982): А опе—з!ер теШос! о! огс!ег 10 !ог у = | (* у)
^ р
A982): А опе—з!ер теШос! о! огс!ег 10 !ог у = | (*, у), 1МА Д» Ыит. АпаК,
уо1. 2, р. 83—94.
Хайрер, Ваннер (Н. На1гег апс! С \Уаппег)
A973): МиН1з1:ер-тиШ81а2е-тиШс1егуа11уе теШобз !ог огсИпагу с!Шегеп-
^а1 еяиаНопз, Сотри1т&, Уо1. 11, р. 287—303.
A974): Оп Ше ВикЬег дгоир апс! Оепега1 тиШ-уа1ие теШойз, СотриНпд
Уо1. 13, р. 1—15.
A976): А Шеогу !ог Муз1гбт теШойз, Ыитег. МаШ. уо1. 25, р. 383—400.
A983): Оп Ше т51аЫШу о! Ше ВОР 1огти1аз, 51АМI. Ыитег. Апа1., уо1. 20,
N0. 6, р. 1206—1209.
Хайрер, Любих (Е. На1гег апс! СЬ. ЬиЫсЬ)
A984): Азутр1оис ехрапзхопз о! Ше §[1оЬа1 еггог о! Пхес! $1ер$12в теШо^з,
Ыитег. МаШ., уо1. 45, р. 345—360.
Халл (Т. Н. Ни11)
A967): А зеагсЬ !ог орИтит теШойз !ог Ше питепса1 Ме^тМоп о! огсИ-
огсИпагу с1ШегепНа1 едиаНопз, 51АМ Кеу., уо1. 9., р. 647—654.
Халл, Джонстон (Т. Н. Ни11 апс! К- Ь. ^оЬп5^оп)
A964): Оритит Кип^е-Кииа теШос!з, МаШ. СотриЬ, уо1. 18, р. 306—310.
Халл, Энрайт и др. (Т. Е. Ни11, №. Н. ЕппдМ, В. М. Ре11еп апс! А. Е. 8ес1д-
шск)
A972): СотриИщ питепса1 теШос1з ^оп огсИпагу сИГ!егепиа1 е^иа^^опз, 51АМ,
^. Ыитег. Апа1., уо1. 9, р. 603—637.
Хаммер, Холлингсуорт (Р. С. Наттег апс! *1. ^. НоШп§з\уогШ)
A955): Тгаре2О1с1а1 теШойз о! арргох1таИпд зоШНопз о! сИ!!егепиа1 е^иа-
Нопз, МТАС-уо1. 9, р. 92—96.
Хан В. (^. НаЬп)
A967): 51аЫШу о! тоНоп, Зрппдег, Уег1ад, р. 446.
Хан Г. (Н. НаЬп)
A921): ТЬеог1е с1ег гееИеп РипкИопеп, 5рНпдег-Уег1ад, ВегНп, р. 600.
Хаувен, ван дер (Р. .1. уап с1ег Нои^еп)
A977): СогЫгисИоп о! 1п1е§[гаиоп !огти1аз !ог ШИа! уа1ие ргоЫетз,
Но11апс1 Ат51егс1ат, р. 269.

Литература 489
Хебзаккер (Н. М. НеЬзаскег)
A982): СопсШюпз Гог Ше соеШаеп1з о! Кигц*е-Кииа теШой /ог зуз^етз
о! п-Ш огйег с1ШегегШа1 ециа1юпз, .1. Сотри!. Арр1. МаШ., уо1. 8, р. 3—14.
Хейес ДО. Э. Науез)
A950): Коо1з о! Ше 1гапз2епс1еп1а1 едиаНоп аззос1а1ес1 шШ а сег!ат с!Ше-
гепсе 6ШетепИа\ е^иа^^оп, .1. о! Ьопс1оп МаШ. 5ос, уо1. 25, р. 226—232.
Хенричи (Р. Непг1С1)
A962): О1зсге{е уапаЫе теШойз & огсНпагу сШ!егегШа1 е^иа^^оп$, .ТоЬп
Ш\еу & Зопз, 1пс, Ыето Ургк-Ьопйоп-Зудпеу.
A974): АррПес! апс! сотри1а1юпа1 сотр1ех апа1уз1з, Уо1ите I, .ТоЬп \^1-
1еу & Зопз, №\у Уогк, р. 682.
Хирш, Смейл (М. \^. Н1ГзсЬ апс! 3. Зта1е)
A974): О1ГГегепиа1 е^иаиоп5, с1упат1са1 зуз^етз апб Нпеаг а1деЪга, Асас1,
Ргезз, р. 358.
Хобсон (Е. ^. НоЬзоп)
A921): ТЬе Шеогу о! ГипсИопз о! а геа1 ушаЫе, уо1. I, СатЬНс1де, 670 рр.
Хойн (К. Неип)
A900): №иеМеШос!е гиг арргох1таиуеп 1п1е^га11оп с!ег О1!!егепиа1^1е1сЬип-
§еп е1пег ипаЬЬап^1деп УегйпйегНсЬеп, * 2еИзсЬг. !йг МаШ. и. РЬуз., уо1. 45,
р. 23—38.
Хуфт (ОЛ НооП)
A974): Ма^пеНс топоро1ез 1п ипШед §аиде Шеопез, Мис1. РЬуз. уоЬ В79,
р. 276—284.
Хопф (В. НорГ)
A942): АЬ2^е1*&ип& е1пег репос!18сЬеп Ьозипд уоп е1пег з1а11опагеп Ьбзип-
^е1пез ОШегепиа1зу51еп15, Вег. таШ. рЬуз1к. КЬ. Акас!, а. ТОзз. Ье1р21§,
Вс1. ХС1У, р. 3—22.
Хорн (М. К. Нот)
A983): РоигШ апй ШШ-огс1ег зсаЫ Нип^е-КиНа а1^опШтз 1ог 1геа11пд с!епсе
ои*ри1, 51АМ ^. Иитег. Апа1. уо1. 20, р. 558—568.
Хулм (В Ь. Ни1те)
A972): Опе-з1ер р1есе\^1зе ро1упот1а1 Оа1егк1п теШойз !ог ШИа! уа1ие
ргоЫетз, МаШ. о! Сотри!, уо!. 26, р. 415—426.
Хундсдорфер, Спейкер (XV. Н. НипдзсЭог^ег апс! М. N. Зр^кег)
A981): А по!е оп В-з1аЫШу о! Кип^е-КиНа теШойз, Ыит. МаШ. Уо1. 36,
р. 319—331.
Цурмюль (К. 2игтйЫ)
A948): Кип^е-КиНа Уег!аЬгеп гиг питепзсЬеп 1п1е^га11оп уоп О1!!егеп-
иа1§1е1сЬип&еп п-1ег Огбпип^, 2АММ, уо1. 28, р. 173—182.
A952): Нип^е-КиНа УегГаЬгеп ип!ег Уепуепйип^ ЬбЬегег АЫеНип^еп, 2.ап&ету.
МаШ. МесЬ., уо1. 32, р. 153—154.
Ческино (Р. СезсЫпо)
A961): Мос1Шса{юп с!е 1а 1оп^иеиг с!и раз с1апз Г1п1ё^гаиоп питег^^ие раг
1ез тёШобез а раз Нез, СЬ1Ягез 2, р. 101—106.
A962): Еуа1иа11оп с!е Геггеиграграз с!апз 1ез ргоЫетез
уо1. 5, р. 223—229.
Ческино, Кунцман (Р. СезсЫпо апс! ^. Кип12тапп)
A963): РгоЫетез (Ш!егепНе1з дъ соп^Шопз тШа1з (тёШойез
Бипоб Рапз, р. 372.
A963): РгоЫетез сШГегегШеЬ с!е сопс!Шопз 1П111а1ез, Оипос! Рапз;
1гапз1а11оп: Ыитепса1 зоЫНопз оГ 1пШа1 уа1ие ргоЫетз, Ргеп11се На11,
1966.
Шампайн (Ь. Р. 5Ьатр1пе)
A979): 31ога§е гебисИоп !ог Кипее-Кииа сос!е8, АСМ Тгапв. МаШ.
Уо1. 5, р. 245—250.

490 Литература
Шампайн, Бака (Ь« Р, ЗЬатрте апс! Ь. 8. В аса)
A984): Р1хес1 уегзиз уапаЫе огс1ег Кип^-КиМа, К ер*. 5АШ)84-1410, ЗапсНа
N314 ЬаЬз., АШияие^ие, Ые^ Мех1со, р, 57. зее а1зо АСМ Тгапз. Ма1Ь,
ЗоГЬл, уо1. 12. рр. 1—23, 1986.
Шампайн, Гордон (Ь. Р. ЗЬатрше апс! М. К. СогсЬп)
A975): Сотри1ег ЗоМюп о! ОпНпагу ОШегеп11а1 Е^иа^^оп5, ТЬе 1п!11а1
Уа1ие РгоЫет, Ргеетап апс! Сотрапу, Зап Ргапазсо, р. 318.
Шампайн, Уотгс (Ь. Р. ЗЬатрте апс! Н. А. А^аШ)
A979): ТЬе аг! о! чгпШпц а Кип&е-Ки11а сос!е, II, Арр1. Ма1Ь. Сотри!.,
уо1., 5, р. 93—121.
Шампайн, Уотгс, Давенпорт (Ь. Р. ЗЬатрте, Н. А. \УаШ апс! 5. М. Оауепрог!)
A976): 5о1ут& попзШ! ог^1пагу с1Шегепиа1 е^иа^^опз — ТНе 81а1е о! Ше
аг1, 51АМ Неу., уо1. 18, р. 376—410.
Шанкс (Н. В. ЗЬапкз)
A966): 5о1и1юпз о! Ог!Гегеп1!а1 е^иа1:^опз Ьу еуа1иа1юп8 о! !ипсиопз,МаШ.
оГ Сотр., уо1. 20, р. 21—38.
Шеффер (Ь. ЗсЬеГГег)
A884): 2иг ТЪеопе с1ег 81еИ§еп РипкНопеп е1пег гееИеп Уегап^егНсЬеп, Ас1а
Ма1Ьета11са, уо1. 5, р. 183—194.
Ши Сонлин (ЗЫ 5оп&1т&)
A980): А сопсге!е ехатр1е о! Ше ех1з1епсе оГ Гоиг Пт11 сус!ез !ог р1апе
га!1С зу$1ет5, За 51П1са, уо1. 23, р. 153—158.
Штёр, Булирш C. 31оег апс! Н. ВиПгзсЬ)
A973): Ет!йЬгип§ т Й1е питег1зсЬе МаШета^к, Зрг1п§ег Уег1а&, 1
1973, Еп^ИзЬ 1гапз1аНоп 1980 (зее зес^оп 7.3.5.).
A980): 1п^гос(исиоп 1о Ыитепса1 Апа1у51з, 5рГ1п^ег-Уег1а§, 609 р,,
ейШоп 1973.
Штёрмер (С. 31бгтег (С. 51оегтег)
A907): 5иг 1ез 1га)ес1о1гез с1ез согризсикз ёксМзёз. АгсЬ. зсЬ рЬуз. па!.,
Оепёуе, уо1. 24, р. 5—18, 113—156, 221—247.
A921): МёШо^ез сГЫё^гаИоп питёпцие с1ез ^иаНопз йхГГегпИеПез огс!1-
па1гез. С. К. соп^г. т1егп. таШ., 31газЬоиг§, р. 243—257.
Штеттер (Н. .1. 31еПег)
A970): 5утте1;пс 1\уо-з1ер а1^опШтз !ог огсИпагу с11!Гегепиа1 едиаНопз,
СотриИп& уо1. 5, р. 267—280.
A973): Апа1у51*8 о! (ИзстеИхаИоп теШойз Гог огсИпагу с11[Гегеп11а1 е^иа^юп5,
5рГ1п^ег-Уег1а^, ВегНп—Не1с1е1Ьег2—Ые^у Уогк. [Имеется перевод: Штет-
Штеттер X. Анализ методов дискретизации для обыкновенных дифференциальных
уравнений. — М.: Мир., 1978. — 451 с]
Штурм (СЬ. 51игт)
A829): ВиИеПп с1ез 5с1епсез с1е Рёгиззас, 1оте XI, р. 419, зее а1$о: А1^Ьге
бе СЬо^ие^ е* Мауег A832).
A836): Зиг 1ез ёяиа^опз сИ[Гёгеп11е11ез Нпёагез с1и зесопс! огс1ге, ^ои^па1 с1е
Ма1Ь., ригез е* арр1. (ЬюиуШе), уоК 1, р. 106—186. (зее а1$о р. 253, р. 269,
р. 373 оГ Ш15 уо1ите).
Шур (Ь. ЗсЬиг)
A909): ОеЬег (Не сЬагас^епзизсЬеп ^агге1п етег Ипеагеп ЗиЬзШиИоп тН
е1пег Ап^епйипб аи! сНе ТЬеоНе с1ег 1п1е^га1д1е1сЬип§еп, МаШ. Апп., уо1. 66,
р. 488—510.
Эйлер (Ь. Еи1ег)
A728): Ыоуа теШойиз тпитегаЪПез ас^иа^^опз с11[!егепиа1ез зесипб1
гейисепсН дЛ аециа11опез с!1Йегеп1;1'а1ез рг1т1 §гас!из, Сотт. асас!.
Ре1гор. уо1. 3. р. 124—137.; Орега Отша уо1. XXII, р. 1—14.
A743): Ое 1п1едга^опе ае^иа1^опит сИНегепиаПит аШогит ^гайиит, М1з-
сеИапеа ВегоПпепз1а уо1. 7, р. 193—242; Орега Отша уо1. XXII, р. 108—
149. Зее а1зо: ЬеНег Ггот Еи1ег 1о ^оЬ. ВегпоиШ, 15, 5ер*. 1739.

Литература 491
A744): МеШойиз 1пуеп!епсН Нпеаз сигуаз тах1т! тЫетпуе ргорг!еЫе &аис1еп«
1ез..., Ьаизаппае & Сепеуае, Орега Отша Aп1;г. Ьу Сага1Ьеос!огу) уо1. XXIV,
р. 1—308. [Имеется перевод: Эйлер Л. Метод нахождения кривых линий,
обладающих свойствами максимума либо минимума.—М.—Л.: Гостех-
издат, 1934, 600 с]
A750): МеШойиз ае^иа^^опе$ сНГГегепИакз аШогит ^гасНит т1е&гапсН
иИепиз ргото!а, ЫоУ1 Соттеп!. асас!. заеп!. Ре1:гор. уо1. 3, р. 3—35; Орега
Отша уо1. XXII, р. 181—213.
A756): Е1етеп1а сакиН уапаиопит, рге$еп1ес! Зер1етЬег 16, 1756 а.1 1Ье
Асас1. о! Заепсе, ВегНп; рппЫ 1766, Орега Отша уо1. XXV. р. 141—176.
A768): 1пзШиИопит СакиН 1п1е§гаПз, Vо1итеп РНтит, Орега Отша
уо1. XI. [Имеется перевод: Эйлер Л. Интегральное исчисление, т. I. —М.:
Гостехиздат, 1956, 415 с]
A769): 1п5Ши1югшт СакиН 1п1е§гаНз, Vо1итеп 5есапс1ит, Орега Отп!а
уо1. XII. [Имеется перевод: Эйлер Л. Интегральное исчисление, т. II. —
М.: Гостехиздат, 1957, 368 с]
A778): Зреатеп {гапзГогтаиошз зт&и1ап$ зепепит, Иоуа ас*а. асас!. Ре1*
гор., уо1. 12 A794): р. 58—70, Орега Отша уо1. XVI, р. 41—55.
Эйспак (И. Р. Е1зраск)
A974): В. Т. 5тйЬ, 3. М. Воу1е, В. §. ОагЬо^, У. ЛсеЬе, V. С. К1ета,
С. В. Мо1ег: Ма1пх Е1^епезуз1ет Нои^1пез, (Рог1гап1гапз1а11опз о! а1^опШт8
риЬПзЬес! 1П КетзсЬ апс! \^11к1пзоп), Ьес^иге Ио^ез т Сотри1ег 5с1епсе,
уо1. 6, Зргт&егЛ/ег1а§[.
Эйткен (А. С. АНкеп)
A932): Оп 1п1егро1а^1оп Ьу {^егаНоп оГ ргорог11опа1 раг!з, ^11Ьои1: 1Ье изе
о? сИ[!егепсез; Ргос. Ес11пЬигдЬ МаШ. 5ос. Зесопс! зег. V©!. 3, р. 56—76.
Эле (В. I. ЕЫе)
A968): Ш&Н огс!ег А-з1:аЫв теШос1з !ог 1Ье питег1са1 зо1и^1оп о! зуз^етз
о! ^. Е.'з В1Т уо1. 8, р. 276—278.
Эльтерманн (Н. ЕИегтапп)
A955): РеЫегаЬзсЬаЧгип^ Ье1 паЬегип^з^е1зег Ьбзищ* уоп Зуз1;етеп уоп
ВШегепИа1%\е1сЪип%еп егз^ег Огс!пип^ МаШ. 2е1*$сЬг. уо1. 62, р. 469—501.
Энрайт, Халл, Линдберг (VI. Н. Епп^Ы, Т. Е. Ни11 апс! В. ЫпйЬег^)
A975): СотриИп^ питепса1 те^Ьойз !ог зШ? зуз!етз о! О. 8. О. О. Е. з,
В1Т, уо1. 15, р. 10—48.
Энрайт и др. (\^. Н. Епп^Ы, К. К. ^скзоп, 8. Р. Могзей апб Р. С. ТЬотзоп)
A985): 1п1егро1ап1:з !ог Кип^е-Кииа ?огти!аз, Тесщ-пса1 Нерог* 180/85,
Ьер1. Сотри!. Зсхепсе, Тогоп1о, Сапас1а М55 1А5, р. 36.
Эрмит (СЬ. Негтйе)
A878): Ех1гаН й'ипе 1е11ге Йв М. СЬ. НегтИе а М. ВогсЬапИ зиг 1а ГогтиЬ
а1п1егро1аИоп с!е Ьадгапде, 1. с!е СгеПе, уо1. 84, р» 70; Осиугез, 1оте III,
р. 432—443.
Якоби (С. О. 3, ЗасоЫ)
A845): ТЬеопа поу! тиИ1рИса!ог!з зуз1етаИ асяиаЬ'опит EШегепНа1ит
уи1^аг1ит аррНсапсИ, СгеПе 1.1. с1. г. и. ап^е^. МаШ., уо1. 29, р. 213—279,
333—376.

Дополнительная литература *)
Бахвалов Н, С.
A955): Некоторые замечания к вопросу о численном интегрировании диф-
дифференциальных уравнений методом конечных разностей. Доклады АН СССР,
т. 104, № 6, с. 805—808.
Бахвалов Н. С, Жидков Н. П., Кобельков Г. М.
A987): Численные методы.—М.: Наука. — 600 с.
Бордовицина Т. В.
A984): Современные численные методы в задачах небесной механики. —
М.: Наука. — 136 с.
Бутчер (Л. СЬ. ВикЬег)
A987): ТЬе пшпепса1 апа1уз1з о! огсНпагу (ШГегепШ! щиаНопв: Кипде—
КиИа апс! &епега1 Нпеаг те{Ъос15, №Пеу, СЫсЬез1ег, 512 рр.
Горбунов А. Д.
A967): Разностные уравнения и разностные методы решения задачи Коши
для систем обыкновенных дифференциальных уравнений. — М.: Изд. ВЦ
МГУ.
Крылов В. И., Бобков В. В., Монастырный П. И.
A982): Начала теории вычислительных методов. Дифференциальные урав-
уравнения. — Минск: Наука и техника. — 286 с.
Лаврентьев М. А., Шабат Б. В.
A973): Методы теории функций комплексного переменного. —М.: Наука. —
736 с.
Ламберт C. ^. ЬатЪег!)
A973): СотриЫюпа1 теШойз т огсНпагу сШГегеп{1а1 е^иа^^опз, №Пеу,
Ьопдоп—№чу Уогк—ЗМпеу—Тогоп^о, 278 рр.
Лапидус, Зайнфельд (Ь. ЬарМиз, ^. Н. 5ет!е1й)
A971): Ыитег1са1 зоШНоп о! огсНпагу сНГГегеп11а1 е^иа^^оп$, Асас1ет1с Ргезз,
Ые^ Уогк—Ьопёоп, 299 рр.
Максвелл Д. К., Вышнеградский И. А., Стодола А.
A949): Теория автоматического регулирования.—М.: Гостехиздат.
Самарский А. А., Гулин А. В.
A989): численные методы.—М.: Наука.—432 с.
Холл, Уатт (С На11 апс! .1. М. ТМап, есШогз)
A976): Мос1егп пшпепса1 те!Ьос1з [ог огё1пагу сН!!егеп^а1 е^иа^;^оп5, С1а-
гепёоп Нгезз, Ох^огс!. [Имеется перевод: Современные численные методы
решения обыкновенных дифференциальных уравнений, редакторы Дж. Холл
и Дж. Уатт. — М.: Мир, 1979. — 312 с]
Эльсгольц Л. Э., Норкин С. Б.
A971): Введение в теорию дифференциальных уравнений с отклоняющимся
аргументом. —М.: Наука. — 296 с.
1) Литература, добавленная редактором перевода.

Указатель обозначений
А ® I тензорное произведение 362
а (*) коэффициенты 23-ряда 259, 260
Яу (а, у) В- ряд 260
В (р) квадратурные условия поряда 218
@) непрерывный метод 191
а^, Ъ} коэффициенты метода РК 139, 213
С константа погрешности 339, 383, 448
Ср+1 константа локальной погрешности 338
С (г)) упрощающие предположения 217
В дифференциальный оператор 266
В |т (х) производные Дини 60
В (^) упрощающие предположения 218
йг \г) разностное множество 260
Е главная часть 5 411
ер {х) коэффициенты разложения глобальной по-
погрешности 226, 227
/ [хп> ..., хп—г] разделенные разности 336
Р1 {I) {у) элементарный дифференциал 154, 156, 280,
281, 297
&] (п) коэффициенты методов Адамса с переменным
шагом 367
Н длина шага 135, 136
E) ядро Пеано 341
= (А» 1ъ •••) коэффициенты Нордсика 380, 386
Ь постоянная Липшица 39, 57
Ь (у, я, к) линейный разностный оператор 335, 446
ЬЙТд помеченные Ы-деревья 280
Ь8д специальные помеченные деревья 159
ЬТд, ЬТ помеченные деревья 154, 259
ЬТРад, ЬТРа помеченные Р-деревья 296, 299
ЫТд М-деревья 282
Р (с, у) Я-ряд 299
Р (ЕС)М предиктор—корректор 394, 406
Р (ЕС)МЕ предиктор—корректор 393, 405
\\0\\ матричная норма 58
]? (х9 х0) резольвента 70
5 матрица общего линейного метода 404
(() субдерево 260

494 Указатель обозначений
••• деревья 156
Тд, Т корневые деревья 155, 259
71*, 1» Т], ь экстраполяционная таблица 234, 235, 290
ТР*, ТРа Р-деревья 296, 299
У (Уи •••> У) функция Ляпунова 95
№ (х) матрица Вронского 70
|| у || норма вектора 56
уп (х) ломаная Эйлера 38
У (х, #о> У о) решение задачи Коши 105
гп = г (хп, к) функция точных значений 404
а/, $^ коэффициенты многошагового метода 334, 370
а (^) число элементов в классе эквивалентности
155, 156, 281,282,298
(п) коэффициенты методов Адамса с переменным
шагом 368
(/) произведения порядков деревьев 156, 160,
281
коэффициенты явных, неявных методов Адам-
Адамса 325, 326
Ц разности назад 324
р (<2) логарифмическая норма 65
Ф (Н) стартовая процедура 404
Ф (/) весовые коэффициенты 156, 159, 281, 283
^ (п) разделенные разности 368
Ф/ (п) разделенные разности 367
Ф (л:0, у0, Н) функция приращения 169, 362, 404
Ф* (*» У* й) функция приращения сопряженного метода
230
р (() порядок дерева 154, 155, 281, 296, 298.
Р (С)> сг B1 производящие многочлены 336
ф, Фа деревья порядка 1 155, 156, 297

Предметный указатель
Абеля—Лиувилля—Якоби—Остроград-
Абеля—Лиувилля—Якоби—Остроградского тождество (АЬе!—1ло1ш11е—
^соЫ—Оз1го^гас1зк12 1с1епШу) 71
Автоматическое управление длиной ша-
шага (аи!ота11с з!ер З12е соп!го1) 177
Автономные системы (аи!опотоиз зуз-
1етз) 75, 150
Адамса методы (Айатз теИюйз) 323
неявные AтрНс11 ~ ~) 325
с переменным шагом (уапаЫе
з*ер 512е ) 366
в представлении Нордсика (~ ~
аз ЫогсЫеск теШойз) 379, 381, 386,
387
, рекуррентные соотношения для
коэффициентов (~~, гесштепсе-ге-
1аИопз Ьг Ше уг) 327, 333
явные (ехрНсИ — ~) 324
Алгоритм ГБШ (СВЗа^опШт) 240,
290
— Евклида (ЕисИсГз —) 90, 92
— Рауса (КоиШ —) 94, 98
— Эйткена—Невилла (АНкеп—NеV^^-
1е —) 237
Аренсторфа орбиты (Агепз1ог! огЬ11з)
135,211
Аргумента запаздывание A1те 1а^з, ге-
1аг<1ес1 аг^итеп1з) 304
— принцип (рппс1р1е о1 1Ье аг^итеп1)
89, 349
Арцела—Асколи теорема AЬеогет о!
Аггек—АзсоН) 44
Асимптотическая устойчивость (азут-
р!оНс з*аЫШу) 96
Асимптотические решения при ма-
малых 8 ^ зо1и!2опз !ог зта11 рагате-
1егз) 118
Асимптотическое разложение глобаль-
глобальной погрешности (~ ехрапз1оп о! 1Ье
-11--1 еггог) 226, 288, 421, 447
— симметричного метода
~-"—', зутте^пс теМюс!) 232
— сопряженного метода
~~'~, ас1]*о1п1 ~) 231
— по четным степеням Н
( ъ~ 1П /12) 232, 238, 435
локальной погрешности^^' о!
1Ье 1оса1 еггог) 226
Барьеры порядковые Бутчера (огйег
Ьагпегз о! ВиЬсЪег) 198, 202
Далквиста (~~ о! ИаЫдшз!)
351, 449
Бернулли уравнение (ВегпоиШ е^иа-
Иоп) 19
— числа (— питЬегз) 228, 384
Бесселя уравнения (Веззе1 едиа11оп) 29
Бифуркация рождения цикла (НорГ
Ы!игса11оп) 121
Брахистохрона (ЬгасЬузЬсЬгопе) 13,
19,28
Брюсселятор (Вгиззе1а1ог) 120, 132,
183, 253
— с диффузией (— ^21Ь с1Ши51оп) 399
— «полный» (Ги11 —) 122
Булирша последовательность (ВиНгзсЬ
зеяиепсе) 236
Бутчера барьеры (Ви^сЬер Ьагг1егз)
198, 202
— метод 6-го порядка (~'з 6-1Ь огйер
теШой) 202
— методы порядка 2$ (~*$ те!Ьос!з
о! огйег 25) 217
— ряды E-зепез) 258
— формулы Лобатто (Ви1сЬег'з Ьо-
Ьа11о !огти1аз) 220
Ван-дер-Поля уравнение (Уап с!ег РоГз
еяиаИоп) 115, 131, 132, 253
Вариационная задача (уаг1аИопа1 рго-
Ыет) 14, 36
Вариационное исчисление (^ са1си1из)
13
— уравнение ^ щшИоп) 106
Вариация постоянных (уаг1а12оп ог соп-
з!ап1з) 23, 72
нелинейная (попПпеаг~~) 106
Веер леди Уиндермир (Ьас1у \^1пс1ег-
теге'з Гап) 41, 107, 170,364
Вековые члены («зеси1аг» 1егтз) 32, 119
Вектор Нордсика (ЫогсЫеск уес!ог)
379, 387, 389
Векторное поле (~ Не1с1) 11
Векторные обозначения (~ по1аНоп)
10,56
Верхюльста—Перла уравнение (Уег-
Ьи1з1—Реаг1 едиаНоп) 312
Вершина конечная (епс!-уег1ех) 280
— толстая, тонкая («[аЬ>, «теа^ге» —)
279
Висящая струна (Ьап^т& з1г1П^) 32
Вложенные формулы (етЬес!с1ес1 !огти-
1аз) 178, 206
Вольтерры уравнение (УоНегга'з е^иа-
Иоп) 319, 321
Вронского матрица (вронскиан) (Шгоп-
зк1ап) 70
— определитель (—) 24

496
Предметный указатель
Выбор порядка (огйег зе1есAоп) 390
Выдача неявная AтрНс11 ои!ри!) 192
— плотная (йепзе~) 188, 191, 469
Вырожденное ядро (йе^епега!е кегпе1)
319, 320
Вычислительные примеры (питепса1
ехатркз)
, методы РК 4-го порядка
41Ь огйег К К теШойз) 145, 185
высших порядков
Ы%Ъ. огйег теШойз) 209
, многошаговые методы ('
тиШз1ер теШойз) 396
, сравнение программ (~ ~, сот-
рапзопз оГ сойез) 252, 396
, уравнения 2-го порядка
2пй огйег еяиаНопз) 290
, экстр аполяционные методы
■, ех!гаро1а1юп теШойз) 237
Гармоническая последовательность
(Ьагтошс зеяиепсе) 237
Гаусса квадратурные формулы (Оаиз-
З1ап ^иа^^а^и^е Гоптш1аз) 137, 217
ГБШ-алгоритм (СВ5 а^опШт) 240, 290
Гершгорина теорема (СегзсЬ&опп'з
1Ьеогет) 99
Гилла метод (ОНГз теШой) 145
Гильберта 16-я проблема (ННЬегСз
161п ргоЫет) 131
Гипергеометрические функции (Ьурег-
§еоте1пс ГипсИопз) 27
Главный член погрешности (рппс1ра1
еггог 1егт) 168
Глобальная погрешность (§1оЬа1 еггог)
169, 226, 421
Граничные условия (Ьоипйагу сопсН-
Иопз) ПО
Графы (^гарЬз) 153
Грёбнера—Алексеева теорема (формула)
(ОгбЬпег—А1екзееу 1Ьеогет (Гогти-
1а)) 106,222
Греко-латинское преобразование
(Сгеек-Котап (гапзГогтаНоп) 351
Грина формула (Сгееп'з Гогти1а) 133
Гронуолла лемма (Сгоп^аИ 1етта) 67
Грзгга метод (Сга^'з те!Ьос!) 239
Даламбера уравнение (сГА1етЪег1*8
щиаИоп) 31
Далквиста барьеры (ВаЬ^гЛз* Ьаг-
Г1егз) 351, 449
Дерево Aгее) 155
— помеченное AаЪе11ес1 —) 154
— специальное (зрес1а1 —^ 159
Дефект (см. тж. норма невязки) Fв-
Гес1) 61, 64
Джозефсона переходы (.ТозерЬзоп
]ипс11опз) 124, 125
Диаграммы «точность—объем вычисле-
вычислений» (\\югк—ргес131оп Й1а§гатз) 146,
186, 194, 210, 238, 239, 242, 256, 257,
291,397,398, 402
Динамика популяций (рориЫюп йу-
пагшсз) 311, 319
Дини производные {р\п\ йепуаНуез) 60
Дискретное преобразование Лапласа
(Й1зсге1е Ьар1асе 1гапзГогта11оп) 362
Дифференциальные неравенства (йШе-
гепИа1 1педиа1Шез) 60, 96
для систем (— ~ !ог зуз1етз) 67
— уравнения (йШегеп11а1 е^иа^^опз)
второго порядка (зесопй огйер
) 9, 17,276, 437
жесткие (зШГ ) 124, 214, 331
с запаздывающим аргументом
линейные (Нпеаг ~~) 16, 17,
21,26,69,75
неявные AтрИс11 ~~) 15
первого порядка (Пгз! огйег — ^
9
в частных производных (раг-
На1 ) 10,399
ДНРК (ОЩК) 213
Дормана—Принса метод фогтапй апй
Рг1псе теШой) 182
—, непрерывное расширение
~^~у сопИпиоиз ех1епз1оп) 191
для. уравнения 2-го порядка
■^ ~ Гог 2пй огйег еаиаНопз) 289
Евклида алгоритм (ЕисИсГз а1богНЬт)
90, 92
Жесткие дифференциальные уравнения
(зНН (Н!!егепНа1 едиаНопз) 124, 214,
331
Жорданова каноническая форма
сапоп1са1 Гогт) 80, 87, 95
— клетка (~ Ьюск) 89
— цепочка векторов (~ сЬа!п) 95
Задача о брахистохроне (Ьгаспузк)-
сЬгопе ргоЫет) 13, 19, 28
— двух тел A^о Ьойу ^ 252
— о касательной обратная (шуегзе
1ап^еп1 —) 12
— Коши AпШа1 уа1ие —) 10, 109
— краевая (Ьоипйагу уа1ие'—') 10, 109
~ начальная (с начальными условия-
условиями) 0пШа1 уа!ие ~) 10, 109
на собственные значения (е1депуа-
) 32,93, Ш

Предметный указатель
497
— трех тел ограниченная (гез1пс1ес1
Шгее Ьос1у ~) 134
— Штурма—Лиувилля E1игт—Ыои-
уШе е1&епуа1ие ~) 111
Замораживание длин шагов (з1ер З1ге
Ггееге) 196
Запаздывающий аргумент A1 те 1ад,
ге1агсЫ аг^итеп!) 304
Зонневельда метод Bоппеуе1сР5 теНюс!)
180
Иммунология Aттипо1оду) 317
Интегрирующий множитель (?ас!ог
М (х, у)) 17
Интегро-дифференциальные уравнения
Aп1е^го-с11[[егеп11а1 е^иа^^опз) 318,
320
Интервальный анализ (т!егуа1 апа1у-
813) 53
Интерполяционная формула Лагранжа'
(Ьадгапде т1егро1а1юп Гогти1а) 222
Ньютона (№\у!оп'з ~ —) 324,
366
у— с кратными узлами (^ ~ ~
чуНЬ тиШр1е пос!е$) 267
Интерполяционный многочлен Эрмита
(НеггшЧе'з ~ ро1упогша1) 267
Каноническая форма Жордана
сапошса1 Гогт) 80, 87, 95
Капли (Лгорз) 147, 323, 332
Кауэлла—Кроммелина метод (СочуеП
апс! СготтеНп'з теНЫ) 439, 442
Квадратурные формулы Гаусса (Саиз-
31ап ^иас1^а^и^е Ьгти1аз) 137, 217
Лобатто (ЬоЬаНо ) 219
Радо (Нас1аи — —) 213
Квазимонотонность (яиаз1топо1опе) 46,
47, 109
Кинетика ферментативных реакций (еп-
гуте ЫпеИсз) 315
— химическая (сЬегтса1 ^ 120
Классический метод Рунге—Кутты
(«ТЬе» Кипде— КиЙа те1Ьос!) 144
Клеро уравнение (С1а1гаи1 сИГГегеп11а1
е^иа^^оп) 15, 19
Коллокация (со11оса1юп) 220
— с кратными узлами (~ ш1Ъ ти1Нр1е
пойез) 267
Комбинированное управление выбором
порядка и длины шага (сотЫпес!
огаег- апс! з1ер З12е соп!го1) 245, 247
Композиция методов (сотрозШоп о(
К К те1Ьос!5) 258
— Б-рядов (~ о1 5-зег1ез) 261
Константа погрешности методов Норд-
сика (еггог соп81ап! о! г4огдз1еск
1Ь!) 383
многошаговых методов (~ ~ о1
тиШз!ер теШойз) 338, 339
. для уравнений 2-го поряд-
порядка (~ — [ог 2пс1 огйег еяиаНопз) 448
Корень дерева (гоо! оГ а 1гее) 154
Корневое условие ^ сопс!Шоп) 347
Корни характеристического уравнения
(гоо1з о! сЬагас1ег1зис е^иа^^оп) 22
кратные (тиШр1е ~%~ —') 25
Корректор (соггес!ог) 327, 393, 405
Коши—Буняковского—Шварца нера-
неравенство (СаисЬу—5сЬ\\гаг2 шеаиаН-
1у) 55
Коши задача AшМа1 уа1ие ргоЫет)
10, 109
— произведение (СаисЬу рго^исЦ 51,
384
Коэффициенты погрешности (еггог сое!-
Нс}еп*з) 168
Краевая задача (Ьоипс1агу уа1ие рго-
ргоЫет) 10, 109
Кратные характеристические корни
(тиШр1е сЬага^епзИс уа1иез) 25
— узлы интерполяционной формулы
(~ пойез о! 1п1:егро1а1:1оп !огти1а) 267
Критерий Рауса—Гурвща (Кои1Ь—
Нигш(г сгИег1оп) 89
— Шура—Кона (ЗсЬиг—СоЬп —) 356
Критические точки (сгШса1 рот1з) 83,
85, 87, 117
Кронекера тензорное произведение
(Кгопескег 1епзог ргойис!) 362
Кунцмана методы порядка 2з (Кип1г-
тапп'з те!Ьос!з оГ огйег 2з) 217, 218,
219
Кутты методы (КиНа'з—) 144
Лагранжа интерполяционная формула
(Ьа^гапде 1п1егро1аИоп Гогти1а) 222
— метод (вариации постоянных) (те-
Шос1 о! ~ (уаг1аИоп о! сопз1ап18) 23,
25
— многочлены (~ ро1упот1а1з) 221
Лапласа дискретное преобразование
(с11зсге1е Ьар асе ЬапзГогтаНоп) 382
— уравнение (формы капель) (с!Шегеп-
На1 едиаНоп оГ — (Гогтз оГ Йгорз))
147, 323
Лейбница формула (ЬеНэгПг* !огти1а)
151
Лемма Гронуолла (ОготуаП 1етта) 67
— фундаментальная ({ипс1атеп1а1 —)
62, 108
Линеаризация (НпеатаНоп) 75
Линейные дифференциальные уравне-
уравнения (Нпеаг сШ1егепНа1 е^иаиопз) 16,
17,21

498
Предметный указатель
неоднородные (тЬотодепеоиз
~ ) 16,22, 72
однородные (Ьотодепеоиз
~ ) 16,21
с постоянными коэффициента-
коэффициентами (~~— \уЦп сопз1ап! соеГП-
С1еп1з) 21, 75
со слабыми особенностями
лу11Ь \уеак 5тди1агШез) 26
многошаговые (^-шаговые) методы
тиШз1ер (&-з1ер) теИюйз 334
формулы (~~ [опгш1аз) 323
, сходимость порядка р
(~ ^' ~, сопуег&епсе о! огйег р) 360
Липшица условие (ЫрзсЬНг сопс!Шоп)
15, 39, 57, 359
одностороннее (опе-з1с1ес1 ~ ~)
64
Лобатто квадратурные формулы (Ьо-
Ьа11о ^иас1^а^и^е Гогти1аз) 219
Логарифмическая норма Aодап1Ьгшс
погт) 65, 68, 95
Логистическая кривая Aа соигЬе 1о-
^з^ие) 312
Локальная погрешность Aоса1 еггог)
170, 226, 334, 409
— экстраполяция (~ ех1гаро1а11оп)
210
Лоренца модель (Ьогепг тос!е1) 125
Ляпунова функции (Ыарипоу !ипс1юпз)
94,99
Марчука модель (МагсЬик'з тос!е1) 317,
318
Матрица Вронского (вронскиан) (\^гоп-
зИап) 70
— комплексная (сотр1ех тагпх) 58, 77
— нормальная (погта1 ~) 86
— ортогональная (ог!Ьо&опа1 —) 77
— симметричная (зутте1г1С ~) 77
— сопряженная (асЦот! —) 77
— унитарная (ипйагу ~) 77
— Якоби расоЫап) 105
Маятник математический (репсМит)
132
— сферический EрЬепса1 —) 122
Мерсона метод (Мегзоп'з те!Ьос!) 180
Метод (теНюс!)
— вариации постоянных ^ о! уаг1а-
Ноп оГ сопз1ап15) 23, 25
— Гилла (ОИГз-) 145
— Грэгга (Ога^'з —) 239
— дискретизации по времени (~ оГ
с115сге11га11оп т 11те) 10
— Дормана—Принса фогтапс! апс!
Ргтсе —) 182
, непрерывное расширение
(~~, сопНпиоиз ех1епз!оп) 191
для уравнений 2-го порядка
(~ ^^ ^^ [ог 2пс1 огйег е^иа^^опз) 289
— Зонневельда Bоппеуе1сГ5 —) 180
— Кауэлла—Кроммелина (Со^еИ апс!
СготтеНп'з —) 439, Ш
— композитный (сотрозНе ~) 259
— Лагранжа (~ оГ Ьа&гап^е) 23, 25
— мажорант (таргап! ~) 50
— малого параметра (Ые\усотЬ—Ьтс1-
з!ес11—Ротсагё —) 118
— Мерсона (Мегзог^з —) 180
— Милна (МИпе —) 330
— Нумерова (Ыитегоу'з ^ 439, 443
— Ньютона (Ые\у(оп'з —) 192
— опорный (Ьаз1с ~) 238
— параллельной стрельбы (тиШр1е
з1юо1т& 1есЬп1яие) 111
— последовательных приближений
Пикара (Ркагс! 11ега11оп —) 48, 58
— Принса—Дормана (Рппсе апс! Г>оп-
тапсГз —) 208, 210
— прямых (~ оГ Нпез) 10, 32, 399
— разделяющийся (рагНПопей ~) 272
— рядов Тейлора (ТауЬг зег1ез —) 49
— сечений Пуанкаре (~ оГ Ротсагё
зес1юпз) 116
— симметричный (зуттеЫс ~) 232,
434
— сопряженный (аф'от! ^ 230, 431
— стрельбы (пристрелки) (зпооищ
110
— Хойна (Неип'з~) 140
— частичной дискретизации (~ ог И-
пез, ог ^^ оГ с11зсге112аиоп 1П зрасе)
10
— Ческино (СезсЫпо'з те!Ьос!) 179
— Эйлера (Еи1ег'з —) 13, 38, 56, 135,
137, 325
неявный AтрНа1 (Ьаск^агс!)
— —) 212, 326
, оценка погрешности (еггог езН-
та!е !ог ) 42, 43
, сходимость (сопуег&епсеоГ~~)
38
— Энке (Епске'з —) 438
Методы (те!Ьос15)
— Адамса (Айатз ~) 323
неявные AтрПс11 ~ ~) 325
с переменным шагом (уаг1аЫе
з!ер 51ге ~ ~) 366
в представлении Нордсика (~ ~
аз^Ногс1з1еск те!Ьос!з) 379, 381, 386,
387
явные (ехрПсй ~~) 324
— Бутчера (Ви1сЬег'з~) 202, 217, 220
— гибридные (ЬуЬпс! ~) 403

Предметный указатель
499
— для уравнений 2-го порядка (~ !ог
2п6 огйег еаиа1юпз) 276, 277, 288,
437
— кол локационные (соПосаНоп ~)
220, 267
— Кунцмана (КипЬтапп'з —) 217,
218, 219
— Кутты (КиНа'з —) 144
— линейные многошаговые (Л-шаго-
вые) (Ыпеаг тиШз1ер (#-з!ер) ~) 334
— Милна—Симпсона (МПпе—51тр-
зоп ~) 329
— многошаговые (тиШз!ер ~ (!огти-
1аз)) 134, 322
как общие линейные методы
(~~ аз депега1 Нпеаг те1пос15) 404
многоэтапные со старшими про:
изводными (ти1Н-з1ер тиШ-з1аде
тиШ-с1епуа11уе ~) 409
модифицированные (тосИНеД
) 403
неприводимые Aггес1ис1Ые ~ —)
340
обобщенные (депегаНгес! ~ ~)
403
, паразитные решения (рагазШс
зоЫюпз оГ ~ ~) 346
симметричные (зутте1Нс ~ —)
354
с переменным шагом (уаНаЫе
з1ер З12е ~ ~) 366
, устойчивость (з!аЫШу о! ~ ~)
345, 347
, характеристическое уравнение
(сЬагас1епз11с еаиаИоп о! а ~~)
346
циклические (сусНс ~ ~) 407
, ядро Пеано (Реапо кегпе1 о! а
) 341
— непрерывные (сопНпиоиз ~) 188,
308, 321
— неприводимые рггес1ис1Ые ^ 340
— Нордсика (Ыогс*51еск ^ 379
как общие линейные методы
(~ ~ а8 ^епега1 Нпеаг те1Ьо^з) 407
, эквивалентность многошаговым
методам (~~, е^и^Vа1епсе т1Ъ
тиШз!ер те!Ьо^з) 382
— Нюстрёма (Ыуз1гбт —) 277, 328
как общие линейные методы
'— аз депега1 Ппеаг те1Ьос!з) 409
, конструирование (сопз!гисИоп о!
— —) 285
многошаговые явные (ехрНсМ
тиШз1ер — —) 328
, сходимость (сопуегеепсе о!^—
287
, условия порядка (огйег сопсИ
«опз !ог ) 284, 302
— Обрешкова (ОЬгезсЬкоГГ ~) 269
— общие линейные (депега1 11пеаг
403, 408
— одношаговые (опе-з1ер ^ 134, 226
— предиктор—корректор (ргесНс^ог—
соггес!ог ргосезз) 405
— РК (см. методы Ринге—Кутты)
да к)
— Рунге—-Кутты (Кипде-—Ки11а те-
1Ьо^з) 134, 139, 213
вложенные
—) 178,206
диагонально неявные
па1 1трИс!1 ——) 213
для уравнений с запаздыва-
запаздывающим аргументом ( ^"^' !ог <1е1ау
ё^иа^^оп) 306
непрерывные (сопИпиоиз *^
) 188,308, 321
неявные ртрНсИ <^ ~ —)
212, 214
однократно диагонально не-
неявные (з1пд1у Шадопа1 1трНсИ ^^ ~
—) 213
с нарушением условия A.9)
( уЫаНпе A.9)) 300
со старшими производными
^ег1УаИуе ~~~) 266
явные (ехрНсИ ~~~) 139,
151, 213
4-го порядка D1Ь огйег
*■** ^^ ^^ ^^ \ 40
— сильно устойчивые (з!пс11у з1аЫе
—) 423
— симметричные (зутте1пс ^ 232,
354, 434
— слабо устойчивые (\уеак1у з1аЫе
428
— ФДН (ВЭР- —) 308, 331
в представлении Нордсика
аз Ыогс1з1еск те!Ьо^з) 386, 388
с переменным шагом (уаНаЫе
з1ер З1ге ) 369, 375, 378
, устойчивость (з!аЫШу о1 ~ ~)
347
•— Фельберга (РеЫЬегд'з~) 181, 207
с высшими производными (ти1-
НДеНуаНуе ) 270, 301
— Хаммера—Холлингсуорта (Наттер
ап^ НоШпдз^ог^'з —) 213, 214, 217
—- Ш тёр мера E1оегтег'з ~) 438, 439,
442
— экстр аполяционные (ех!гаро1аМоп
—), 234, 288
как ЯРК-мвтоды (~~ аз ЕКК

500
Предметный указатель
) 243, 250
— Эле (ЕЫе'з ~) 224
Милна метод (МПпе тпепюб) 330
Милна—Симпсона методы (МПпе—
51тр5оп те1пос1з) 329
Многочлен интерполяционный Эрмита
(НегтИе т1егро1а11оп ро1упогша1)
267
— коллокационный (со11оса1юп ~) 221
— характеристический (сЬагас1еп-
8«с ~) 22, 32, 76, 91, 93, 122
Многочлены Лагранжа (Ьа^гап^е ро1у-
погша1з) 221
— производящие (^епегаИпд —) 336
Моделирование эпидемии (тГесИоиз
сНзеазе тойеШпз) 313
Модель Лоренца (Ьогепг тос!е1) 125
Монитор сходимости (сопуег&епсе то-
пйог) 245
Начального шага длина (з1аг1тд з!ер
51ге) 194
Начальное условие (значение) BпШа1
уа1ие) 9, 109
Невязка (йеГес!) 61, 63
Нелинейная формула вариации по-
постоянных (попНпеаг уапа1юп-оГ-соп-
з1ап1з Гогти1а) 106
Неоднородное линейное уравнение (т-
Ьото&епеоиз Нпеаг е^иа^^оп) 16, 22,
72
Непрерывные вложенные формулы
(сопИпиоиз етЬес!с1ес1 !опгш1аз) 191
— методы РК (~ КК теИЫз) 188,
308, 321
Неприводимые методы Bггес1ис1Ые те-
НЫз) 340
Неравенства дифференциальные (сНГГе-
гепИа1 1педиа11иез) 60, 96
для систем (~'— Гог зуз1етз) 67
Неустойчивость численная (питег1са1
тз*аЫШу) 345
Неявные методы Адамса AтрПс11
Айатз теШойз) 325
в представлении Нордсика ^
аз ЫогсЫеск теШойз) 379, 381,
386, 387
Рунге—Кутты (~ К К —) 212
как коллокационные мето-
методы ( аз со11оса11оп —) 220
основанные на квадратур-
квадратурной формуле Гаусса (~~~ Ьазес!
оп Оаизз1ап Гогти1аз) 217
Лобатто (~
.^ ЬоЬайо ^иас1а^и^е) 219
, существование решения
(ех1з1епсе о? $о1иAоп о! ~ ~ ~) 214
Нордсика вектор (Ыогс!з1еск уес!ог)
379, 387, 389
— методы (~ теШойз) 379, 382,. 407
Норма вектора (уес^ог погт) 56, 57
евклидова (ЕисПйеап ^^ ^ 56, 65
— матричная (та1пх ^ 58
логарифмическая Aодап1пгшс
—) 65, 68, 95
подчиненная (зиЬогсИпа1е ~
58
— невязки (с!еГес!) 61
— Шура (ЗсЬиг погт) 58
Нормальные матрицы (погта1 та!г1-
сез) 86
НРК AКК) 214
Нуль-устойчивость (гего-з^аЬШ^у) 347
Нумерова метод (Ыитегоу'з теШос!)
439, 443
Ньютона интерполяционная формула
(Ые\у1оп'з ЫегроЫюп Гогти1а) 324,
366
с кратными узлами (~ ~ ~
"чуйп ти111р!е пойез) 267
— метод (~ те!Ьос!) 192
Нюстрёма методы (Ыуз1гбт те!Ьос!з)
277, 328
как общие линейные методы
(~~ аз &епега1 Нпеаг теИюйз) 409
, конструирование (сопз1гисИоп о!
) 285
многошаговые явные (ехрНсй
ти111з1ер ) 328
, сходимость (сопуег&епсе о! ~ ~)
287
, условия порядка (огйер сопсН-
Нопз !ог ^ —) 284, 302
Обратная задача о касательной (шуегзе
1ап&еп1 ргоЫет) 12
Обрешкова методы (ОЬгезсЬко!! те-
1Ьос1з) 269
Общие линейные методы (депега1 Н-
пеаг —) 403, 408
Ограниченная задача трех тел (гез1пс-
1ес1 1Ьгее Ьос1у ргоЫет) 134
Одностороннее условие Липшица (опе-
З1с1ес1 Ь1рзсЬ112 сопс!Шоп) 67
ОДНРК EБ1КК) 213
Оптимальная длина шага (орИта1 з!ер
31ге) 177
Оптимальные формулы (орИта1 !ог-
ти1аз) 144
Оптимальный порядок многошагового
метода (орИта1 огйег (тиШз!ер)) 392
экстр аполяционного метода (
(ех!гаро1аиоп)) 244
Орегонатор (Огедопа1ог) 123, 124

Предметный указатель
501
Ортогональная матрица (ойЬо&опа1
та!пх) 77
Ортогональное преобразование (-—'
(гапзГогта{юп) 77
Особая точка (сгШса1 рот!) 122
регулярная (слабая) (ге^и1аг
(\уеак) зт&и1аг рот1) 27
Особенность уравнения (зт&и^агйу) 25
«Отец» («ГаШег») 154
Отношение симметрии (зутте1гу ге1а-
Коп) 434
— шагов (з!ер з12е таНо) 371, 390
Отображение Пуанкаре (Ротсагё тар")
117, 121, 129, 131
— «сыновей» на «отцов» (зоп-Га^Ьег
таррт&) 154
Оценка погрешности (еггог езИта^е) 60
для ломаной Эйлера (~ ~ Гог
Еи1ег ро1у&оп) 42, 43
надежная (геНаЫе еггог
53
строгая (пдогоиз ~~) 166
Ладе аппроксимация экспоненты (Рас1ё
аррпштаМоп 1о ехр (г)) 94, 99
Паразитные решения (рагазШс зо1и-
Нопз) 346
Пеано теорема существования (ех1з1еп-
се {Ьеогет оГ Реапо) 43, 46, 56
— ядро (Реапо кегпе!) 341
Периметр эллипса (репте!ег оГ 1Ье
еШрзе) 29
Периодические решения (репосНс зо1и-
Нопз) 118, 133, 135
Пикара метод последовательных при-
приближений (Р1сагс! ИегаНоп те1Ьос1)
48, 53, 58
дЛЯ систем (— ~ ~ Гог
зуз1етз) 58
«Пирог с сыром мадам Имхоф» (Мас1ат
1тЬоГз сЬеезе р1е) 350
«Плеяды» («1Ье Р1е1ас1е5») 253
Плотная выдача (йепзе ои!ри!) 136,
188, 191, 469
Погрешность глобальная (накоплен-
(накопленная) (&1оЪа1 еггог) 169, 226, 421
— локальная Aоса1 —) 170, 226, 334,
409
, численная оценка (пшпепса1 ез-
НтаНоп о! ) 390, 391
— округления (гоипсНп^ ~) 449
Погрешности главный член (рппара1
— 1егт) 168
— константа (~ соп$1ап!) 338, 339,
383, 448
— коэффициенты (^ сое!!1С1еп^з) 168
— оценка (~ ез^та^е) 63, 166
для метода Эйлера (~ ~ о!
Еи1ег'з теШос!) 42, 43
практическая (ргас1ка1 ^^^
175, 390
Помеченное дерево AаЪе1Ы 1гее) 153,
154
специальное (зрес1а1 ~~) 159
— //-дерево (— N—) 280
— Р-дерево (~ Р—) 295
Порядок дерева (огйег ог а 1гее) 155
помеченного (~ о! а 1аЬе11ес1 ~)
154
— методов Адамса (— о! Айатз те-
1Ьос15) 337, 338
многошаговых (~ о! тиШзЫр^
336
с переменным шагом (— о!
уапаЫе з!ер 31ге ) 370
общих линейных (— оГ ^епега1
Нпеаг —) 411
Рунге—Кутты (~ оГ К К —) 139
экстраполяционных (~ о! ех!га-
ро1а11оп —) 235
— оптимальный (орИта1 ~) 244, 392
— эффективный (еГГесНуе ^ 264
Последовательность Булирша (Ви-
ПгзсЬ зедиепсе) 236
— гармоническая (Ьагтошс ^ 236
— Ромберга (НотЬег^ —) 236
Правило «3/8» C/8-ш1е) 144
— Симпсона E1трзоп —) 143
— средней точки (гшс!рот!—) 137, 328
неявное AтрПс11 ~~) 212,
214
— трапеций Aгарего1с1а1—) 213, 326
— цепное (спат ~) 17
— Штёрмера (ЗЬегтег'з —) 290
Предельный цикл (Нтй сус1е) 115, 131
Предиктор (ргесИс!ог) 327, 393, 405
Предсогласованности условия (ргесоп-
31з1епсу сопс!Шопз) 415
Преобразование «греко-латинское»
(Огеек-Нотап 1гапз!огтаиоп) 351
— Лапласа дискретное (сНзсге1е Ьар1а-
се —) 362
— ортогональное (ог!по&опа1 ~) 77
Приведение матрицы к диагональному
виду (с11а^опаН2а11оп) 75
Примеры вычислений (питег1са1 ехат-
р1ез)
, методы РК 4-го порядка (—
4Ш огйег КК теШойз) 145, 185
высших порядков (~,
ЪщЪ ) 209
, многошаговые методы
тиШз!ер те!Ьос!5) 396
, сравнение программ (~ ~, сот-

502
Предметный указатель
рапзопз о! сойез) 252, 396
, уравнения 2-ро порядка (
2пс1 отйет е^иа1^оп5) 290
, экстр аполяционные методы (
~, ех1гаро1аAоп те!Ьос15) 237
Принса—Дормйна метод (Рппсе апс1
ОогтапсГз те(Ьос!) 208, 210
Принцип аргумента (рппс1р1е о! 1Ье
агдитеп!) 89, 349
Произведение Коши (СаисЬу ргойис!)
51, 384
— Кронекера (тензорное) (Кгопескег
1епзог ргойис!) 362
Производные Дини (От! йепуаНуез) 60
— по начальным значениям (~ ш{Ъ.
гезрес! (о шШа1 уа1иез) 105
— по параметру (^ ~~~ рагате-
1егз) 103
, численное определение (пи-
тепса1 сотриЫюп о! ~ —)
195
Производящие многочлены многошаго-
многошагового метода (§епега!т§ ро1упо1ша1з
оГ а тиШз1ер теНюф 336
— функции коэффициентов методов
Адамса (~ {ипсМопз !ог ^е у() 327
Процедура продвижения на шаг (!ог-
чгагй з!ер ргосейиге) 404
— стартовая (зЫгИп^ —) 323, 404
Процесс предиктор—корректор (рге-
(Нс1ог—соггес!ог ргосезз) 405
Псевдометоды Рунге—Кутпгы (рзеисЬ
Кипде—Ки11а те1Ьо^з) 403
Пуанкаре—Бендикссона теорема AЬео-
гет о! Ротсагё—ВепсИхзоп) 117, 121
— отображение (~ тар) 117, 121, 129,
131
— метод малого параметра (те1Ьос1
оГ~ Ьг е зта11) 118, 132
сечений {~~~ зесИопз) 116,
129, 192
Равностепенная непрерывность (е^и^-
согШпийу) 44, 45
Радо квадратурная формула
зсЬете) 213
Разделенные разности (с1МAе<1
гепсез) 366, 390, 393
Разделяющаяся система уравнений
(рагШюпес! 5уз1ет) 272, 294
Разделяющийся метод (~ те!Ьос!) 272
Разложение Тейлора точного решения
(Тау1ог ехрапз1оп оГ ехас! зо1и11оп)
138, 157
решения методом РК (
К К —) 138
Разности назад (Ьаскчагагс! сШГегепсез)
324
— разделенные (сНуМес! —) 366, 390,
393
Разностное уравнение (сШГегепсе е^иа-
1юп) 33
Распространение звука (ргорада^оп
оГ зоипс!) 31
Рауса алгоритм (Кои1Ь а1дог11Ьт) 94,
98
— таблица (— 1аЫеаи) 93
Рауса—Гурвица критерий (~—Ниг-
^11г сгИег1оп) 89
Рациональная экстраполяция (гаНопа1
ех!гаро1а11оп) 237
Реализация многошаговых методов Aт-
р1етеп1аИоп о1 тиШз!ер те1Ьос!з)
390
Регулярная особая точка (геди1аг зШ-
ди1аг ро1п!) 27
Регулятор паровой машины (з!еат
еп^1пе доуегпог) 100, 101
Резольвента (гезо1уеп1) 70, 72, 75, 79,
105
Решение с помощью разложения в ряд
(зоШюп Ьу зепез ехрапзюп) И
— паразитное (рагазШс —) 346
Риккати уравнение (ШссаН е^иа1^оп)
17, 47
Ричардсоновская экстраполяция (Ш-
сЬагс!зоп еx1^аро1а^^оп) 175, 189, 233
РК (К К) — см. Рунге—Кутты методы
Ромберга последовательность (НотЬегд
5е^иепсе) 236
Рунге методы (Кипде'з теИюйз) 140
— правило 177
Рунге—Кутты методы (Нипде—Ки11а
те!ЬоA5) 134, 139, 213
вложенные (етЬесИес!
—) 178, 206
диагонально неявные
па1 ипрПсй — ) 213
для уравнений с запаздыва-
запаздывающим аргументом (~ ~ ~ 1от с!е1ау
е^иа^^оп5) 306
непрерывные (сопИпиоиз
) 188, 191,308,321
неявные ОтрНсЙ ~~
212,214
однократно диагонально не-
неявные (з1п§1у A1адопа1 ~~~~)
213
с нарушением условия A.9)
( У1о1а«п8 A.9)) 300 ,
— со старшими производными
(ЫЬг с1ег1уа11уез ~~~) 266
эквивалентные ^1

Предметный указатель
503
) 265
явные (ехрПсН ~ ~ ~I39,
151, 198, 213, 228, 243
4-го порядка D1Ь огйег
) 140
псевдометоды (р$еис!о~<~-'~) 403
Сечения Пуанкаре (Ротсагё зесИопз)
116, 129
Сильно устойчивые методы (з1пс*1у
з!аЫе теНюйз) 423
Симметричные методы (зутте1пс ~)
232, 354, 434
Симпсона правило (Зшрзол ги!е) 143
Система автономная (аи1опотоиз зу-
з!ет) 75
— дифференциальных уравнений
1-го порядка (Пгз! огйег ~ о! йШе-
гегШа1 е^иа^^опз) 9, 34
2-го порядка (зесопс! ~ ~ ~
) 10,276
квазимонотонная (циаз1топо-
1опе ~ — ~ —) 46, 67
линейных 1-го порядка Aз1 ог-
огйег Нпеаг ~ ~) 34, 69, 75
} геометрическое пред-
представление ('— ~ ~ ~ ~ ~ ~$ део-
теШс гергезегйаНол) 83
2-го порядка Bпс1 ~ ~ ~
~ ) 32
— разделяющаяся (рагШюпей ~) 272,
294
— многочленов Штурма E1игт зе-
^иепсе) 90
Слабая особая точка (чагеак зтди1аг
ро!п1) 27
Слабые особенности (~ з1пди1агШе8)
25
в системах (~ ~ !ог зуз1етз) 73
Слабо устойчивые методы (^еак1у з!аЬ-
1е теШойз) 428
След матрицы Aгасе о! а таМх) 71
Собственная функция (е1деп[ипс11оп)
113
Собственное значение (число) (ещепча-
1ие) 32, 75, 86, 99
устойчивое (з!аЫе —) 122
Собственный вектор (ешепуес1ог) 32,
75,95
Согласованность (сопз15*епсу) 337, 411,
446
Соотношения ортогональности (ог!Ьо-
допаН'су ге1аНоп$) 34
Специальное помеченное дерево (зре-
Ыа! 1аЬе11ес1 1гее) 159
Сравнение вычислительных свойств ме-
методов и программ (гштепса! сотра-
Нзопз о! те^Ьойз апй сойез) 145 185
209,237,252,290,396
Стабилизация (81аЪШ2аНоп) 449
Стартовая процедура (з1аг11Пй ргосейи-
ге) 323, 404
Стационарная точка (зШюпагу ро1пЦ
75
Стационарные приближения при боль-
больших е (з1еас!у-51а1е арргох1та1юпз
Гог 8 1агде) 117
Странные аттракторы (з1гап§е а11гас-
1огз) 125
Струна (з1г1П§) 32
Существование решения дифференци-
дифференциального уравнения (ех1з1епсе о! а
$о1и1юп оГ а AШегепиа1 ециаНоп)
37, 47, 55
численного (~ оГ а гштег1са1—)
214
Сферический маятник (зрЬепса1 репйи-
1ит) 122
Сходимость метода Эйлера (сопуегдепсе
оГ Еи1ег'з теШос!) 38
— в строке (экстраполяционного ме-
метода (~ т Нпе к) 245
— методов многошаговых (~ о! ти1-
11з1ер те!Ьос15) 359
для уравнений 2-го порядка
— ~~ ^ог 2п6. огйег е^иа^^опз)
446
с переменным шагом (
уаг1аЫе з!ер 512е ) 376
Нюстрёма (~ ~ Ыуз1гбт
287
общих линейных ^ ~ ^епега1
Нпеаг—) 412
Рунге—Кутты ( Нип^е—
Ки11а —) 166
«Сын» («зоп») 154
Тейлора ряд (Тау1ог зег1ез) 49, 138, 151
, доказательство сходимости (~ ~
сопуегдепсе ргоо!) 50
, рекуррентное вычисление коэф-
коэффициентов (гесишуе сотриЫюп ог
Тау1ог сое!!1с1еп15) 51
Тензорное произведение Кронекера
(Кгопескег 1епзог ргойис!) 362
Теорема Арцела—Асколи AЬеогет о1
Аг2е1а—АзсоН) 44
— Гершгорина (СегзсЬдопп'з —) 99
— Грёбнера—Алексеева (ОгбЬпег—
А1екзееу ~) 106
— о среднем («теап уа1ие ~») 57
— Пуанкаре—Бендикссона (— оГ Ро1П-
сагё—ВепЙ1Х5оп) 117, 121
— сравнения Штурма E1игт'з сотра-

504
Предметный указатель
Нзоп —) 112
— существования общая (§епега1 ех1-
з!епсе —) 37
Пеано (— ~ о\ Реапо) 43
для систем уравнений (~ ~ !ог
зуз1етз оГ е^иа^^опз) 55
, доказательство методом Пикара
ргооГ из1п§ Р1сагс1Йега1юп) 48
, рядов Тейлора (~ ~
ТауЬг зепез) 49
— Штурма E1игт'з —) 90
Точка критическая (сгШса1 рот!) 83,
85, 117, 121
— особая (З1пди1аг ~, з!п§и1агНу)
26,85
регулярная (слабая) (геди1аг
к)) 27
равновесия ^шНЬгшт ~) 83
— стационарная (зЫюпагу ~) 75
Уатта регулятор (\Уа1Гз з1еат епдте
доуегпог) 100
Унитарная матрица (ипйагу та1пх) 77
Управление длиной шага для методов
многошаговых (з1ер 81хе соп1го1 !ог
тиШз1ер теНюск) 390
руНге—Кутты (~ ~
— КиПа ~) 177, 183
экстр аполяц ионных (
ех1гаро1а1юп —^) 244, 245,
247
многошаговых
те1Ьос!з)
— порядком методов
(огаег соп1го1 Гор
390
экстраполяционных ^
ех!гаро1а11оп —) 244, 247, 248
Упрощающие предположения (з1трН-
Гутд аз8итр!юп8) 141, 217, 418
Уравнение Бернулли (ВегпоиШ е^иа-
Ноп) 19
— Бесселя (Ве$зе1 —) 29
— Бан-дер-Поля (Уап с1ег РоГз^ 115,
131, 132,253
— в вариациях (вариационное) (уапа-
1юпа1 —) 106
— Волыперры (УоНегга'з —) 319, 321
— гипер геометрическое (Ьурегдеоте-
1г1с —) 27, 29
— Даламбера (<ГА1етЬегГз —) 31
— индексное Aпс1ех ~) 26
— Клеро (С1а1гаи1 —) 15, 19
— колеблющейся стуны (~ Гор 1Ье
У1Ьга(шд з1г1п§) 32
— Лапласа (формы капель) (сШГегеп-
Иа\ ~ о\ Ьар1асе (с!езсг1Ыпд 1Ье
Гогт оГ йгорз)) 147, 323
— математического маятника
1ит ~) 132
— неоднородное линейное (тЬотоде-
пеоиз Ппеаг ~) 16, 22, 72
— разностное (сШГегепсе ~) 33
— Риккати (К1сса11 ~) 17, 47
— теплопроводности (Ьеа! —) 35, 111
— характеристическое (сЬагас!еп-
зНс ~) 22, 33, 89, 309, 346
— Эйлера для вариационной задачи
(Еи1ег — !ор а уапа!юпа1 ргоЫет)
14,36
Уравнения автономные (аи!опотоиз
е^иа1^опз) 75
— в полных дифференциалах AоЫ
— в частных производных (рагИа!
) 10, 399
— второго порядка (зесопс! огйер —) 9,
10, 17
не зависящие от х
1пс1ерепс1еп1 оГ х) 17
— дифференциальные, см. Дифферен-
Дифференциальные уравнения (с!ШегепМа1
е^иа^^опз)
с запаздывающим аргументом
(с!е1ау ) 304
— жесткие (з!Ш ) 124, 214, 331
— интегро-дифференциальные (т1е-
2го ) 318, 320
— линейные, см. Линейные дифферен-
дифференциальные уравнения (Ппеаг ~ ~)
— перманентные (регтапеп! ~) 75
— с особенностями (~ "^ИЬ З1пди1аг1-
иез) 25
— с разделяющимися переменными
(~~ зерагаЫе уапаЫез) 16
— с разрывными производными (сИз-
соп{1пиоиз —) 192, 197, 247
— Эйлера (Еи1ег'з —) 29
Условие корневое (гоо! сопсШюп) 347
— Липшица (ЫрзсЫЪг —) 15, 39, 57,
359
одностороннее (опе-зЫес! ~ ~)
64
— ортогональности (огИю^опаШу ге-
1а11оп) 114
Условия граничные (Ьоипйагу сопсИ-
1юпз) ПО
— начальные (шШа1 уа1ие) 9, 109
— предсогласованности (ргесопз1з1еп-
су сопсНМопз) 415
— согласованности (сопз1з1епсу ~) 337
для уравнений 2-го порядка
( Ьт 2пс1 огйег е^иа^^опз) 446
общих линейных методов (~ ~
!ог депега1 Нпеаг те1Ьос!з) 411
— порядка методов многошаговых (ор-

Предметный указатель
505
с1ег ~ !ог тиШ81ер теНюйз) 334, 336
Нюстрёма (~ Ь
~) 281,284
общих линейных
пега1 Нпеаг ~) 415
Рунге—Кутты (~ ~ ~ Кип-
де—КиНа—) 150, 152, 162, 163, 263
с0 старшими производ-
производными ( — тиШйепуаНуе —)
272
Устойчивость асимптотическая (азутр-
1о11с з1аЬШ1у) 96
— дифференциального уравнения
(см. — решений) (з1аЫШу оГ а (Ш!е-
гепИа1 едиаИоп)
— линеаризованного уравнения (~ о!
а Нпеавдей —) 88
'— многошаговых методов (~~ ти1-
. Из 1ер" !огти1аз) 347
для уравнений 2-го порядка
(~ ~ ^— {ог 2п6. й Н)
444
с переменным шагом
уапаЫе з!ер З1ге ~~) 371
— неавтономных систем (—— поп-
аи 1опотои$ зуз1ет$) 97
— нелинейных систем (~~ попИ-
пеаг ~) 96
— общих линейных методов (<—'~ се-
сенега! Нпеаг теШойз) 409
— по Ляпунову (~ 1П 1Ье вепзе о! 1Ла-
рипоу) 88
— сильная (з!пс1 ^^) 423
— слабая (\уеак —) 428
— решении дифференциального урав-
уравнения (— о! а (ШГегепНа! е^иаиоп)
88, 105
с запаздывающим аргумен-
аргументом (— ~ с!е1ау ^^ —) 310
— формул дифференцирования назад
(~~ 1Ье ВОР-Гогти1аз) 347
— численная (пшпег1са1 ~) 93, 345
Фаа ди Бруно формула (Раа сИ Вгипо'з
Гогти1а) 159
Фазовое пространство (рпазе-зрасе) 83
Фазовый поток (Ио\у оГ 1Ье сНИегепНа!
е^иа1^оп) 126
ФДН-методы (формулы) (ВОР-те1Ьос1з
(-!огти1аз)) 308, 331
в представлении Нордсика (~ ~
аз ЫогЙ51еск те1Ьос1$) 386, 388
с переменным шагом (~ уаг1аЫе
з1ер 312е —) 369, 375, 378
, устойчивость (з1аЬШ1у о!
ВОР-!огти1аз) 347
Фейгенбаума каскады (Ре1§епЬаит саз-
сайез) 129
-г- число (~ питЬег) 131
Фельберга методы (РеЫЬегд'з
181,207
с высшими производными
(~ шиШс1ег1уаиуе —) 270, 301
Форма капель (Гогт ог йгорз) 147, 323,
332
Формула вариации постоянных (уа-
Г1а11оп о? соп81ап!з !огти1а) 72, 105,
108
нелинейная (попНпеаг
) 106
— Грёбнера—Алексеева (ОгбЬпег
Аккзееу —) 106, 222
— Грина (Огееп'з —) 133
— десятого порядка A0-1п огйег
203 •
— Дормана—Принса (Эогтапс! апс1
Рппсе—) 182
— интерполяционная Лагранжа (Ьад-
гапде т1егро1а!юп ^-) 222
Ньютона (Ые>у1оп'з ) 324,
366
с кратными узлами ( ~
туйЬ тиШр!е пойез) 267
— Лейбница (Ье1Ьшг' ^ 151
— Эйлера (Еи1ег'з —) 33
— Эйлера—Маклорена (Еи1ег—Мас-
1аиг1п —) 228, 232
Формулы вложенные высоких поряд-
порядков (етЬесЫес! Ьгти1аз о! Ь
огйег) 206
непрерывные (согйтиоиз
191
Рунге—Кутты (~ К К —) 178
— дифференцирования назад, см.
ФДН-методы (ЬасЬуагс! <ИНегеп11а-
11ОП —)
— квадратурные Гаусса (Оаизз1ап
Яиас1га1иге —) 137, 217
Лобатто (ЬоЬа11о ~ ~) 219
Радо (Найаи ) 213
— линейные многошаговые (Нпеаг ти1-
1!з1ер —) 323
— оптимальные (ор1лта1 ~) 144
— Пузе (Роиге! —) 320
— Фельберга (РеЫЬег^ ~) 180, 206
Фундаментальная лемма (!ипс!атеп1а1
1етта) 62, 108
— система решений (~ зуз1ет о! зо-
ЫИопз) 70
Функции гипергеометрические (Ьурег-
деоте!г1с Гипс^1опз) 27
— Ляпунова (ЫарипоУ ~) 94, 99
— собственные (е1депГипс{юп5) 113
— Якоби эллиптические ^асоЫап е1-

506
Предметный указатель
с ГипсМопз) 252
Функция приращения (тсгетеп* Гипс-
Поп) 169
общих линейных методов (
!ог депега1 Нпеаг теШойз) 404
— точных значений (соггес! уа1ие
404
Фурье ряды (Роипег зепез) 34, 35
Хаммера—Холлингсуорта метод (Нат-
тег апс! НоШп§5тоог1Ь'$ те1ЬоA) 213,
214,217
Характеристические значения (сЬагас-
1еп5Нс уа1иез) 309
Характеристический многочлен (— ро-
1упош1а1) 22, 32, 76, 91, 93, 122
Характеристическое уравнение (~
еяиа^оп) 22, 33, 89, 309, 346
Химическая кинетика (спет1са1 к!пе-
«С5) 120
Хойна метод (Неип'з теНюс!) 140
Хопфа бифуркация (Нор Г ЫГигсаНоп)
121
Цепное правило (сЬат ги1е) 17, 158
Цикл предельный (ПтЦ сус1е) 115, 131
Циклические многошаговые методы
(сусНс тиШз1ер те1Ьос!з) 407
Ческино метод (СезсЫпо'з теНюс!) 179
Числа Бернулли (ВегпоиШ питЬегз)
228, 384
— Стирлинга (ЗНгНпб ~) 228
Численные примеры, см. Вычислитель-
Вычислительные примеры (гштепса1 ехатрЬ)
Число деревьев (гштЬег о1 1геез) 156
— условий порядка (~~ отбет соп-
(ИНопз) 163
— Фейгенбаума (Ре1§епЬаит ~) 131
Чувствительность решений (зепзШуйу
о! Ше зоЫюпз) 105
Штпёрмера методы E1оегтег'з
438, 439, 442
— правило (— ш1е) 290
Штурма—Лиувилля задача E1игт—
ЫошпПе е1депуа1ие ргоЫет) 111
— система многочленов E1игт зе-
^иепсе) 90
— теорема E1игт'з 1Ьеогет) 90
сравнения (~ сотраг1зоп ^ 112
Шура—Кона критерий (ЗсЬиг—СоЬп
сг11ег1оп) 356
— норма' (ЗсЬиг погт) 58
— разложение (~ йесотрозШоп) 76,
87
— форма матрицы (— !огт) 79
Эйлера ломаная (Еи1ег ро1удоп) 13, 38
— метод (~'$ те^Ьос!) 13, 38, 56, 135,
137, 325
неявный (!трИсН (Ьаск^агд) ^*
—) 212, 326
, оценка погрешности (еггог езН-
та1е о! ~ ~) 42, 43
, сходимость (сопуег^епсе о1 ~ ^
38
— уравнение для вариационной зада-
задачи (~ е^иа^^оп !ог а уаг1аиопа1 ргоЬ-
1ет) 14,36
— уравнения (—'в е^иа^:^оп8) 29
— формула (~*з !огти1а) 33
Эйлера—Маклорена формула (Еи1ег—
Мас1аипп —) 228, 232
Эйткена—Невилла алгоритм (Айкеп—
ЫеуШе а1доп1Ьт) 237
Эквивалентность методов РК
1епсе оГ НК теШойз) 265
— помеченных деревьев (~~ 1аЬе11ес1
^геез) 155
Л/'-деревьев (~ ~ — ЛГ-1гее5) 282
Р-деревьев (— ~ ~ Р-1гее$) 296
Эксперименты численные 290 (см. тж.
Вычислительные примеры)
Экстраполяционные методы (ех1гаро1а-
11оп теШодз) 234
для уравнений 2-го порядка
(— ~ [Ог 2пс1 огйег е^иа1^опз) 288
Экстраполяция к пределу Н -»- 0 (~ 1о
1Ье НтИ К -+ 0) 234
— локальная Aоса1 ^ 210
— по Ричардсону (Шсйагйзоп ~) 175,
189, 233
— рациональная (га1юпа1 ^ 237
Эле методы (ЕЫе'з теШобз) 224
Элементарный дифференциал (е1етеп-
1агу (ШГегепИа1) 154, 156, 281, 297,
298
Эмдена—Фаулера уравнение (Етйеп—
Ро^1ег е^иа^:^оп) 30
Энке метод (Епске'з те1Ьос!) 438
Эпидемии моделирование (Ыес1юиз
сИзеазе тоде1Ппд) 313
Эрмита интерполяционный многочлен
(Негтйе'з ЫегроЫюп ро1упот1а1)
267
Этапы внешние, внутренние (ех!егпа1,
1п1егпа1 з1а^ез) 408
Ядро вырожденное (с1е0епега1е кегпе1)
319, 320
— Пеано (Реапо ~) 341
Якоби матрица расоЫап) 105
— эллиптические функции (— еШрИс
ГипсНопз) 252
ЯРК (ЕНК) 139,213

Оглавление
Предисловие в русскому изданию 5
Предисловие 6
Глава I. Классическая математическая теория 8
1.1. Терминология 9
1.2. Наиболее ранние дифференциальные уравнения 11
Ньютон 11
Лейбниц 12
Вариационное исчисление 13
Клеро 15
1.3. Уравнения, разрешимые в квадратурах и элементарных функ-
функциях 16
Уравнение с разделяющимися переменными 16
Неоднородное линейное уравнение 16
Уравнения в полных дифференциалах 16
Уравнения второго порядка 17
Упражнения 18
1.4. Линейные дифференциальные уравнения 21
Уравнения с постоянными коэффициентами 21
Вариация постоянных 23
Упражнения 24
1.6. Уравнения со слабыми особенностями 25
Линейные уравнения 26
Нелинейные уравнения 28
Упражнения 29
1.6. Системы уравнений 31
Лагранж 31
Фурье 34
Упражнения 35
1.7. Общая теорема существования 37
Сходимость метода Эйлера , 38
Теорема существования Пеано 43
Упражнения 46
1.8. Теория существования решения, основанная на итерационных
методах и рядах Тейлора 47
Метод последовательных приближений Пикара 48
Метод рядов Тейлора 49
Доказательство сходимости 60
Рекурсивное вычисление коэффициентов ряда Тейлора. . . 51
Упражнения 53
1.9. Теория существования решения для систем уравнений. ... 55
Векторные обозначения 56
Подчиненные матричные нормы 58
Последовательные приближения Пикара для систем 58
Упражнения 59
1.10. Дифференциальные неравенства 60
Введение 60
Фундаментальные теоремы 61
Оценки с использованием односторонних условий Липшица 64
Упражнения 67

508 Оглавление
1.11. Системы линейных дифференциальных уравнений 69
Матрица Вронского (вронскиан) 70
Тождество Абеля—Лиувилля—Якоби—Острогр адского 71
Неоднородные линейные уравнения 72
Упражнения 72
1.12. Системы с постоянными коэффициентами 75
Линеаризация 75
Приведение к диагональному виду 76
Разложение Шура 76
Численные расчеты 78
Каноническая форма Жордана 80
Геометрическое представление 83
Упражнения 85
1.13. Устойчивость 1 88
Введение 88
Критерий Рауса—Гурвица 89
Вопросы численной реализации 93
Функции Ляпунова 94
Устойчивость нелинейных систем 96
Устойчивость неавтономных систем 97
Упражнения 98
1.14. Производные по параметрам и начальным значениям. . . . 102
Производная по параметру 103
Производные по начальным значениям 105
Нелинейная формула вариации постоянных 106
Упражнения 108
1.15. Краевые задачи и задачи на собственные значения 109
Краевые задачи 109
Задачи Штурма—Лиувилля на собственные значения .... 111
Упражнения 114
1.16. Периодические решения, дредельные циклы, странные аттрак-
аттракторы 115
Доказательство существования 116
Стационарные приближения при 8 117
Асимптотические решения при малых 8 118
Химические реакции 120
Предельные циклы в системах больших размерностей, бифур-
бифуркация 121
Хопфа 121
Странные аттракторы 125
Каскады Фейгенбаума 129
Упражнения 131
Глава II. Методы Рунге—Кутты и экстраполяционные методы .... 134
11.1. Первые методы Рунге—Кутты 137
Метод Эйлера для решения начальной задачи 137
Общая формулировка методов Рунге—Кутты 139
Обсуждение методов порядка 4 140
«Оптимальные» формулы 144
Численный пример 145
Упражнения 147
П.2. Условия порядка для методов Рунге—Кутты 150
Производные точного решения 152
Условия для порядка 3 152
Деревья и элементарные дифференциалы 153
Разложение Тейлора для точного решения 157
Формула Фаа ди Бруно 158

Оглавление 609
Производные численного решения 159
Условия порядка 162
Упражнения 163
И.З. Оценка погрешности и сходимость методов Рунге—Кутты. . 166
Строгие оценки погрешности 166
Главный член погрешности 168
Оценка глобальной погрешности 169
Упражнения 173
11.4. Практическая оценка погрешности и выбор длины шага. . . 175
Экстраполяция по Ричардсону 175
; Автоматическое управление длиной шага 177
Вложение формулы Рунге—Кутты 178
Формула Дормана и Принса 182
Численное исследование механизма управления длиной
шага 183
Численное сравнение методов 4-го порядка 185
Упражнения 187
11.5. Дальнейшие вопросы практических вычислений 188
Плотная выдача 188
Непрерывные вложенные формулы 191
«Неявная» выдача 192
Уравнения с разрывными производными 192
Длина начального шага 194
Численное определение производных по начальным условиям
и параметрам 195
Упражнения 196
11.6. Явные методы Рунге—Кутты высших порядков 198
Барьеры Бутчера 198
Шестистадийные процессы пятого порядка 200
Семистадийные процессы шестого порядка 202
Дальнейшие барьеры Бутчера 202
Формула десятого порядка 203
Вложенные формулы высоких порядков 206
Численный пример 209
Упражнения 211
11.7. Неявные методы Рунге—Кутты 212
Введение 212
Существование численного решения 214
Методы Кунцмана и Бутчера порядка 2з 217
НРК-методы, основанные на квадратурной формуле Лобатто 219
НРК как коллокационные методы 220
Упражнения 224
11.8. Асимптотическое разложение глобальной погрешности. . . 226
Локальная погрешность 226
Глобальная погрешность 226
Примеры 228
Переменная длина шага 229
Отрицательные значения Н 229
Свойства присоединенного метода 230
Симметричные методы 232
Упражнения 232
11.9. Экстраполяционные методы 234
Определение методы 234
Алгоритм Эйткена—Невилла 237
Рациональная экстраполяция 237
Вычислительный пример 237

510 Оглавление
Экстраполяция с помощью симметричных методов 238
Метод Грэгга, или ГБШ 239
Сглаживающий шаг 241
Вычислительный алгоритм и пример 242
Асимптотическое разложение для нечетных индексов 243
Существование явных методов Рунге—Кутты произвольного
порядка 243
Управление порядком и длиной шага 244
Численное исследование комбинированного управления дли*
ной шага и порядком 247
Упражнения 248
11.10. Сравнение вычислительных качеств 252
Результаты расчетов 255
Пример с негладким решением 256
Заключение 257
11.11. Композиция В-рядов 258
Композиция методов Рунге—Кутты 258
В-ряды 259
Условия порядка для методов Рунге—Кутты 263
«Эффектный порядок» Бутчера 264
Упражнения 265
11.12. Методы, использующие старшие произврдные 266
Коллокационные методы 267
Методы Фельберга 270
Общая теория условий порядка 272
Упражнения 274
11.13. Численные методы для дифференциальных уравнений второго
порядка 276
Методы Нюстрема 277
Производные точного решения 279
Производные численного решения 282
Условия порядка 284
• О конструировании методов Нюстрема 285
Глобальная сходимость 287
Программная реализация методов Нюстрема 288
Численные эксперименты 290
Система высших порядков 292
Упражнения 292
11.14. Р-ряды для разделяющихся обыкновенных дифференциальных
уравнений 294
Производные точного решения; Р-деревья 295
Р-ряды 299
Методы Рунге—Кутты с нарушением условия A.9). . . . 300
Методы Фельберна 301
Методы Нюстрема 302
Упражнения 303
11.15. Дифференциальные уравнения с запаздывающим аргументом 304
Существование 304
Методы с постоянной длиной шага для постоянного запазды-
запаздывания 306
Методы с переменной длиной шага 308
Характеристические значения экспоненциальных решений 309
Устойчивость 310
Пример из динамики популяций 311
Моделирование эпидемии 313
Пример из кинетики ферментативных реакций 315
Одна математическая модель в иммунологии 317

Оглавление 511
Интегро-дифференциальные уравнения 318
Упражнения , 319
Глава III. Многошаговые методы и общие линейные методы 322
III. 1. Классические линейные многошаговые формулы 323
Явные методы Адамса 324
Неявные методы Адамса 325
Рекуррентные соотношения для ^ 327
Явные методы Нютрема 328
Методы Милна—Симпсона 329
Методы, основанные на дифференцировании 330
Упражнения 332
II 1.2. Локальная погрешность и условия порядка 334
Локальная погрешность многошагового метода 334
Порядок многошагового метода 336
Константа погрешности многошаговых методов 338
Неприводимые методы 340
Ядро Пеано многошаговых методов 341
Упражнения 343
III.3. Устойчивость и первый барьер Далквиста 345
Устойчивость формул дифференцирования назад 347
Наивысший достижимый порядок устойчивых многошаговых
методов 351
Упражнения 355
II 1.4. Сходимость многошаговых методов 359
Представление в виде одношагового метода 361
Доказательство сходимости 363
Упражнения 365
111.5. Многошаговые методы с переменным шагом 366
Методы Адамса с переменным шагом 366
Рекуррентные соотношения для ц% (я), Ф; (п) и Ф/ (п). . . . 368
Формулы дифференцирования назад с переменным шагом. . . 369
Многошаговые методы общего вида с переменным шагом и их
порядок согласованности 370
Устойчивость 371
Сходимость 376
Упражнения 378
111.6. Методы Нордсика 379
Эквивалентность многошаговым методом 382
Неявные методы Адамса 387
ФДН-методы 388
Упражнения 389
111.7. Реализация и численное сравнение 390
Выбор шага и порядка 390
Некоторые распространенные программы 392
Сравнение численных результатов 396
Уравнения в частных производных 399
111.8. Общие линейные методы 403
Общая процедура интегрирования 404
Примеры метода (8.4) 404
Устойчивость и порядон 409
Сходимость 412
Условия порядка для общих линейных методов 415
Построение общих линейных методов 417
Упражнения 419
с 111.9. Асимптотическое разложение глобальной погрешности. . . 421
Поучительный пример 421

512 . Оглавление
Асимптотическое разложение для сильно устойчивых мето-
методов (8.4) 423
Слабо устойчивые методы 428
Сопряженный метод 431
Симметричные методы 434
Упражнения 435
ШЛО. Многошаговые методы для дифференциальных уравнений вто-
второго порядка 437
Первые методы 438
Задача Штермера 439
Методы более высокого порядка 441
Общая формулировка 443
Условия устойчивости 444
Одношаговое представление метода A0.19) 444
"Согласованность и сходимость 446
Асимптотическая формула для глобальной погрешности. . . 447
Порядковый барьер для устойчивых методов A0.19) 449
Погрешности округления 449
Упражнения 450
Приложение. Программы на Фортране 452
Литература 473
Дополнительная литература 492
Указатель обозначений 493
Предметный указатель 495
Научное издание
Эрнст Хайрер, Снверт Пауль Нёрсетт, Герхард Ваннер
РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Заведующий редакцией чл.-корр. АН СССР В. И. Арнольд
Зам. зав. редакцией А. С. Попов
Научн. редактор С. В. Чудов
Мл. научн. редактор Т. Ю. Дехтярева
Художник Г. М. Чеховский
Художественный редактор В. И. Шаповалов
Технический редактор А. Л. Гулина
Корректор Т. И. Стифеева
ИБ Я» 7025
Сдано в набор 20.02.89. Подписано к печати 16.11.89.
Формат 60Х90*/1в. Бумага офсетная № 2. Печать
офсетная. Гарнитура литературная. Объем бум. л. 16,00.
Усл. печ. л. 32,00. Усл. кр.-отт. 32,00. Уч.-изд. л. 27,38.
Изд. № 1/6445. Тираж 14 000 экз. Зак. 736. Цена 2 р. 20 к.
Издательство «Мир»
В/О кСовэкспорткнига» Государственного комитета СССР
по печати,
129820, ГСП, Москва, 1-й Рижский пер., 2.
Типография № 6 ордена Трудового Красного Знамени издательства «Машиностроение»
при Государственном комитете СССР по печати,
193144, г. Ленинград, ул. Моисеенко, 10.