Ю.С. ОЧАМ
м етоды
мдтемдтической
ФИЗИКИ

Ю. С. ОМАН
МЕТОДЫ
МАТЕМАТИЧЕСКОЙ
Ф И 3 И н И
Допущено
Министерством высшего и среднего
специального образования СССР
в качестве учебного пособия для студентов
физико-математических факультетов
педагогических вузов
ИЗДАТЕЛЬСТВО
«ВЫСШАЯ ШКОЛА»
М ОС КВ А —1966

ЧАСТЬ I
ВЕКТОРНЫЙ АНАЛИЗ
(математическая теория поля)
§ /. Скалярные и векторные поля
Математическая теория поля изучает скалярные и векторные
поля. Говорят, что в области V задано поле, если каждой точке
этой области соответствует определенное значение некоторой
величины — числовой или векторной.
Если в каждой точке рассматриваемой области задана вели-
чина, принимающая числовые значения, то поле называется скаля-
рным, если же в каждой точке области задан вектор, то поле
называется векторным.
Примеры. 1. Рассмотрим распределение температуры внутри
некоторого помещения. Эта температура может оказаться различ-
ной в различных точках (например, высокой в тех точках, кото-
рые находятся вблизи от источников тепла, и более низкой вдали
от них). Распределение температуры внутри помещения является
примером скалярного поля. В каждой точке здесь задана ска-
лярная величина — температура в этой точке.
2.	Рассмотрим неоднородное твердое тело. Если в каждой
его точке определена плотность*, то внутри тела V задано ска-
лярное поле. Величиной, определенной в каждой точке поля»
является плотность.
3.	Рассмотрим поле сил тяготения, образованное некоторым
притягивающим телом.
* Плотностью тела в данной точке М называется предел, к которому
стремится отношение массы небольшой области, окружающей точку Му
к объему этой области; предел берется при стремлении диаметра этой об-
ласти к нулю: в точке М плотность равна lim — (рис. 1).
diam ©-*0 V
Если плотность тела во всех точках одинакова, то тело называется од-
нородным, если же различна — неоднородным.
1*
4
Часть J
Пусть в начале координат помещено некоторое тело массы m
(будем считать его материальной точкой массы tn). Тогда еди-
ничная масса, помещенная в произвольной точке пространства,
будет притягиваться к началу координат с силой, равной —
(где 7 — гравитационная постоянная, а г — расстояние от единич-
ной массы до начала координат; рис. 2). Таким образом, в каждой
точке С, лежащей вне притягивающей массы, определен некоторый
вектор силы F, направленный к началу координат и численно
равный В этом случае имеет место векторное поле; оно
задано во всем пространстве, кроме начала координат (в начале
координат вектор F не определен).
4.	Рассмотрим еще один пример векторного поля.
Пусть некоторая часть пространства (например, русло реки)
заполнена движущейся жидкостью. Тогда в каждой точке прост-
ранства определен вектор скорости той частицы жидкости, ко-
торая попала в эту точку. Этот вектор может зависеть от време-
ни (иными словами, может оказаться, что скорость одной частицы,
попавшей в эту точку, отличается от скорости другой частицы,
позднее попавшей в ту же точку). Тогда говорят, что наше поле
является нестационарным. Если же скорость в каждой точке
зависит только от положения этой точки, но не зависит от того,
какая частица жидкости попала в эту точку (иными словами,
скорость в данной точке не изменяется с течением времени), то
говорят, что поле является стационарным.
Вообще скалярное или векторное поле называется стацио-
нарным, если рассматриваемая величина зависит только от поло-
жения точки в пространстве (но не зависит от времени). Если
же рассматриваемая величина зависит также и от времени, то
поле называется нестационарным.
В дальнейшем мы будем изучать только стационарные поля.
Заметим, однако, что если дано нестационарное поле, то, рас-
MaUausgk
знание без границ W «Ь
§1	5
сматривая его в какой-нибудь определенный момент времени,
мы получаем как бы моментальный фотографический снимок
этого поля. Это будет стационарное поле.
Стационарное поле обозначается так: и = f (М) (или и =
— <? (М), и = ф (М) и т. д.). Здесь М — переменная точка прост-
ранства, и — число (значение скалярного поля в точке М). Век-
торное поле мы будем обозначать А = А (М), где, как и раньше,
М — переменная точка, а А — вектор (значение векторного поля
в точке М).
Как же задать стационарное поле аналитически?
Если это поле является скалярным, то задание поля равно-
сильно заданию обыкновенной функции трех переменных:
u = f(x, у, z).	(1)
Действительно, здесь каждой точке* М. (х, у, z) из области оп-
ределения функции f соответствует определенное числовое зна-
чение переменной и, а это и означает, что в этой области задано
стационарное скалярное поле.
Если поле является векторным, то для того, чтобы его за-
дать, надо знать все три проекции переменного вектора на оси
координат. Так как эти проекции, в свою очередь, зависят
от положения точки в пространстве (т. е. от координат х, у, г),
то векторное поле может быть задано равенством:
Л = Р(х, у, z)7 + Q(x, у, z)j + R(x, у, z)k,
(2)
где Р, Q, R — скалярные функции от трех переменных х, у, г.
Рассмотрим в качестве примера поле сил тяготения (см. стр.
3, пример 3) и попытаемся задать его аналитически. Сила ?,
приложенная к точке С единичной массы, направлена по радиус-
вектору R (в сторону, противоположную радиус-вектору) и чи-
сленно равна 7 • —. Поэтому
т R___________fmR
1Я|а ’ 1Я1 “ TtfF
здесь взято произведение численной величины силы на единич-
ный
вектор
R
\R\'
направленный вдоль вектора
Р;
указывает на то, что векторы F и R направлены
знак «минус»
в противопо-
* Буквами х, у, г обозначены декартовы координаты точки М. Мы
предполагаем, что в пространстве задана декартова система координат Охуг.
6
Часть I
ложные стороны). Переходя к координатам и учитывая, что
R = xi 4- yj + гЪ, | /? | = У х2 4- z/2 4- г2 , получим
F - yn(xi+ yj 4?£)
г ~	3_
(х2 4 у2 4 г2)2
Рассмотрим специальные виды полей.
Скалярное поле называется плоскопараллельным, если в
пространстве можно выбрать декартову систему координат так,
чтобы величина, задаваемая этим полем, не зависела от одной из
координат (например, от z). Скалярное плоскопараллельное поле
можно задать формулой и = f(x, у).
Векторное поле называется плоскопараллельным, если в
пространстве можно выбрать декартову систему координат так,
чтобы вектор поля не зависел от одной из координат (например,
от г) и был расположен в плоскости, где эта координата постоянна
(т. е. в плоскости z — const). Векторное плоскопараллельное по-
ле можно задать формулой А -=Р(х, у) i \Q(x, у) /.
Всякое плоскопараллельное поле можно изучать только на
плоскости Оху (так как в любой плоскости, параллельной пло-
скости Оху, картина будет одна и та же). Поэтому плоско-
параллельное поле называют также плоским полем.
Среди скалярных полей следует выделить также, как част-
ный случай, сферические поля.
Скалярное поле называется сферическим, если скалярная
величина, определяемая полем, зависит только от расстояния меж-
ду точкой и началом координат. Такая величина постоянна на каж-
дой сфере с центром в начале координат.
Скалярное сферическое поле задается формулой
и - f ( р л-2 f у2 J- z2 ).
Так, например, модуль силы притяжения точки М{х, у, z)
единичной массы к точечной массе т, расположенной в начале
координат, является сферическим полем:
|F| ______И!___.
*2 + у2 4 z2
Введем понятие непрерывного поля.
Скалярное поле n — f называется непрерысным в точке
Мо, если разность / (М) — /(Мо) стремится к нулю при стремле-
нии точки М к Л40. Точнее говоря, это поле непрерывно в точке Л40,
если для любого числа е > 0 можно найти такую окрестность
знание без ераниц	“ w
точки Мо, что для всех М, принадлежащих этой окрестности,
выполнено неравенство
|/(М)-/(М0)|<е.
Если скалярное поле задано аналитически в декартовой
системе координат:
u = f(x, у, z),
то непрерывность этого поля в точке Л10(х0, у0, z0) равносильна
непрерывности функции f(x, у, г) в этой точке.
Аналогично определяется непрерывность векторного поля
А (Л1) в точке Мо: это поле непрерывно в точке Мо, если для
любого е > 0 можно подобрать окрестность точки Мо такую,
что для всех точек М, попавших в эту окрестность, имеет место
неравенство
|Л(Л1) - Л(М0)|< е.
Если векторное поле задано аналитически:
A=Pl+Qj+Rk,
то непрерывность этого поля равносильна непрерывности всех
трех функций: Р(х, у, z), Q(x, у, z), R(x, у, z).
Так, например, поле сил тяготения (см. стр. 5) непрерывно
всюду, кроме начала координат.
Следует заметить, что, изучая поля в математической тео-
рии поля, мы не придаем конкретного физического смысла той
величине, которая задана в этом поле. Иными словами, здесь
рассматриваются только самые общие свойства полей — такие,
которые присущи любому скалярному (или любому векторному)
полю. Результаты, полученные в общей (математической) теории
поля, затем, в физике, применяются к конкретным физическим
полям, например к электромагнитному полю, или к полю темпе-
ратур и т. д. Такие конкретные поля изучаются различными
разделами физики: к тем общим свойствам полей, которые рас-
сматриваются в векторном анализе, добавляются свойства, ха-
рактерные только для того или иного конкретного поля.
§ 2. Скалярное поле. Поверхности уровня.
Производная по дуге
Рассмотрим скалярное поле
w = / (х, у, z).
Геометрическое место тех точек, для которых величина и
принимает одно и то же числовое значение С, называется по-
верхностью уросня, соответствующей числу С.
8
Часть I
Например, для поля
и = х4- у-\-г
поверхностью уровня, соответствующей значению 1, будет пло-
скость
*4- у + z=l,
поверхностью уровня для значения 2— плоскость
• x4-f/4-z = 2
и т. д.
Для любого сферического скалярного поля поверхностями
уровня являются сферы с центром в начале координат; напри-
мер, для поля
i
и~ *’4-£/*4-Л
поверхностью уровня и = 4 служит сфера
1	— 4
x’4r0a4-z’
или
Ха 4- У* 4- 2я =	.
Рассмотрим теперь какую-либо точку М(х, у, г), в которой
определено скалярное поле. Если из этой точки переместиться
в другую точку УИ, (xlt yt, Zi), то значение функции может из-
мениться— увеличиться или уменьшиться. Совершенно ясно, что
при перемещении точки вдоль различных кривых скорость этого
изменения будет различной. Так, например, если точка движется
вдоль кривой, лежащей на поверхности уровня, то функция не
будет изменять своего значения. Если же двигаться вдоль кри-
вой, соединяющей точки на различных поверхностях уровня, то
значение функции будет изменяться с той или иной быстротой.
Для того чтобы оценить скорость изменения функции при пере-
мещении точки вдоль некоторой кривой, введем понятие произ-
водной от функции вдоль кривой.
Средней скоростью изменения функции вдоль дуги Л4Л11 на-
зывается отношение приращения функции (при переходе от М к
к длине дуги ММГ.
Средняя скорость равна
^alallauswk
знание без границ «
Однако средняя скорость еще не вполне характеризует бы-
строту изменения функции: на отдельных участках дуги ММ}
эта скорость мала, на других — велика. Беря среднюю скорость,
мы не можем оценить поведение функции вблизи какой-либо
точки М. Для того чтобы сделать это, будем брать все более и
более короткие участки дуги MMV Переходя затем к пределу
(заставляя Мх двигаться вдоль данной кривой, неограниченно
приближаясь к М), получим истинную скорость изменения функ-
ции в точке М (по данной дуге) или,
иными словами, производную по дуге	———
в точке М.	--------
Дадим теперь точное ©пределе- '"'<7
ние производной по дуге. Для этого
предварительно введем понятие на-	рис. 3
правленной кривой.
Пусть задана кривая L, проходящая через точку Л1, и на
этой кривой выбрано некоторое направление движения (напри-
мер, то направление, которое указано стрелкой на рис. 3). Кри-
вая с выбранным на ней направлением называется направленной
кривой. В дальнейшем под словом «кривая» или «дуга» мы бу-
дем подразумевать только направленную кривую.
Если L — направленная кривая, а Л4 и Мх— две точки на
этой кривой, то под символом о ММА понимают длину дуги
MMlt взятую со знаком «плюс», если точка М{ следует после
точки М (в соответствии с выбранным направлением на кривой),
или со знаком «минус», если точка Мх предшествует точке М.
Производной по дуге L в точке М называется предел, к ко-
торому стремится отношение
^ММ}
когда точка Му двигаясь вдоль дуги L, стремится к точке М
(рис. 3).
Поставим перед собой задачу вычисления производной
по дуге.
Обозначим производную по дуге L через ~.
Тогда
df
dL
= Пт IW-HM)
mJ m
вдоль L
В числителе этой дроби стоит приращение функции трех пере-
менных. Если считать, что функция /(М) дифференцируема, то
приращение функции можно заменить приближенно полным диф-
Часть I
10
ференциалом. Совершаемая при этом ошибка В является беско-
нечно малой более высокого порядка, чем р (где р — расстояние
от точки до М). Поэтому
df . , _д£
df .. д:
-Л- = lim-----------------
dL MX-*M
вдоль L
Найдем пределы дробей —
Рассмотрим, например,
ределенности, что точка
выбранным направлением
ложительна*:
df
(1)
Az
оЛ1Л41
^мм (рис. 4), считая, для оп-
Ьх
ММ1 ’
lim
Мх-М
Mj следует после М (в соответствии с
по кривой), т.
Ьу
*
Ьу
e. что дуга MMr по-

&У
м^м\ММг\
by
lim
в
| AfAli |
Второй сомножитель
этом произведении яв-
ляется отношением длины
хорды | ММ11 к дуге, ко-
торую стягивает эта хорда.
Как известно из анализа,
это отношение стремится
к единице (при условии,
что касательная сущест-
вует и непрерывна** на
участке Af/HJ. А отноше-
Ди
ние ; .... - является коси-
I ММ[ |
нусом угла plt составлен-
ным хордой AfAfj с осью
Оу. Предел этого отноше-
ния, следовательно, равен косинусу угла р между касательной к L
(в точке М) и осью Оу (точнее косинусу угла между касатель-
ным вектором к L в точке М и положительным направлением
оси Оу)’.
lim —= *im гетт ’ ’ Ммм ' = cosp • 1 = cosp.
мх-м	мх^м\ммЛ ^мм1
* Читатель может легко проверить, что окончательный результат не
изменится, если точку приближать к точке М с другой стороны.
•* Говорят, что касательная непрерывна в точке М' дуги L, если угол
между касательными в точках М' и М" стремится к нулю при М"-+М' (вдоль
дуги L). Если кривая всюду на участке АВ имеет непрерывную касательную,
то эта кривая называется гладкой на участке АВ. Если же дугу АВ можно
разбить наконечное число гладких участков, то эта дуга называется кусочно-
гладкой.
flafaHauslul
знание Без границ ’ *
§ 2	 1 1
v	v Дх
Аналогично найдем lim —tttz- = cosa,
M,-Af V/WM1
.. Az
^Л^ммг=COS1-
Далее
Д'™	- J,™ । мм, ।
| MMi I _
В самом деле, В есть бесконечно малая более
малости, чем р (т. е. чем |	|), и поэтому
равенстве (1), получим
df
Переходя к пределу в
df	df
= ~7Г~ cos
oL	дх
df
высокого порядка
___*___> О
| MMi |
(2)
где частные производные	взяты в точке М,
а а, р, 7 — углы, составленные с осями координат касательным
вектором к направленной кривой L в точке М.
Из этой формулы вытекает следующий
результат:	/ / 2
Производная по дуге L в точке М не	/ /
зависит от вида дуги, а зависит только от
направления касательного вектора к L в	----
точке М.	*
Или, иными словами, если кривые Lx и
L2, проходящие через точку М, имеют в Рис. 5
этой точке один и тот же касательный век-
тор, то производная в этой точке по дуге равна производ-
ной по дуге Lt (рис. 5).
Доказательство этого непосредственно следует из формулы (2).
В силу сказанного можно в дальнейшем говорить не о про-
изводной по дуге, а о производной по направлению:
Производной по направлению вектора т в точке М называ-
ется производная по любой дуге L, проходящей через точку М
и касающейся вектора т.
Заметим в заключение, что частным случаем производных
по направлению являются частные производные:	— произ-
водная по направлению вектора i (т. е. по направлению оси Ох),
du	— ди
-----производная по направлению вектора /,	----производ-
ная по направлению вектора k.
12
Часть I
§ 3. Градиент скалярного поля
Рассмотрим скалярное поле
u = f(x, у, z)
и найдем производную от и в направлении вектора т, где т =
= ai 4- bj + ck. Для этого сначала найдем направляющие косину-
сы вектора т:
с os а = —	; cos р = —.........—; cos 7 =---------  — .
/а» 4- са	Ka’4-fe24^c’	Vа* 4- Ьа 4- с»
Следовательно,
ди . ди ,, ди
ди ______________________ дх а ду дг С
д~	У aa4-fea + ca
В числителе этой дроби стоит скалярное произведение двух
векторов: вектора т и вектора, составляющие которого равны
ди ди ди	«
частным производным скалярного поля	в данной
точке М. Обозначим этот вектор символом grad и (читается:
градиент и); тогда по определению имеем
, ди : . ди - , ди т
grad и = -^,+	—	(2)
Следовательно,
ди _ grad и • т
дт	| т |
Учитывая, что скалярное произведение двух векторов равно
произведению их численных значений на косинус угла между
ними, мы можем переписать последнее равенство следующим об-
разом:
ди Igradu | • I х | • cos (grad и, х) .	, .	.	,	-
—= —--------—’•	~ | grad и I • cos (grad и, т), (3)
дх	х I
где правая часть равенства есть проекция градиента на направ-
ление т.
Итак, производная в направлении т равна проекции градиен'
та на это направление. Отсюда ясно, что производная в точ"
WatatiausiSl
знание без границ * *
§3
13
ке М будет наибольшей в направлении градиента, и в этом слу-
чае она равна численному значению градиента. Таким образом,
нами вскрыт смысл градиента: это — вектор, в направлении
которого функция будет расти с наибольшей скоростью.
Заметим, что в направлении, прямо противоположном на-
правлению градиента, функция будет быстрее всего убывать.
Градиент имеет вполне определенное значение (по величине
и по направлению) в каждой точке данного поля. Следовательно,
сам градиент образует новое поле, но уже векторное.
Пример. Дано скалярное поле и =	. В каком направ-
лении функция будет возрастать быстрее всего, если исходить
из точки Л4(1; 2; 1)?
Решение. Найдем сначала градиент в произвольной точке:
а ди Т ।	ди - ди т	Зх3у* — .	2хау -	хауа	т
grad u =	1 + -X- / + -д— k — —— I 3----- I----k.
ь	дх 1	ду 1 1 dz z ' z 1 z1
Затем найдем grada в точке Af:
grad и |м = 12i + 4/ — 4k.
Это и будет то направление, в котором функция растет быстрее
всего (если исходить из точки М). Производная в направлении
/ ди \
градиента, т. е. (—, равна модулю градиента:
\ От /щах
/ ди \	г--------------- г------
—=-	= /122+ 4’+ (—4)2 = ]/176 » 13,3.
\ 0х /шах
Теорема. Пусть градиент функции и = f(x, у, z) в точке М
отличен от нуля. Тогда он перпендикулярен к любой линии,
проходящей через точку М и
лежащей на поверхности уров-
ня*'.
Доказательство. Про-
ведем через точку М линию /,
лежащую на поверхности уров-
ня (рис. 6). Так как функция
не изменяет своего значения,
когда точка движется по кри-
вой /, то = 0. Но произ-
водная по дуге равна производ-
ной по направлению вектора
Рис. 6
* Говоря, что вектор перпендикулярен к линии в точке М, мы под-
разумеваем, что он перпендикулярен к ее касательной, проведенной в точке М.
14
Часть 1
касательной т; поэтому —= также равна нулю. Воспользуемся
di
теперь формулой (3):
Qu	_
—= |gradu|-cos (grad и, т).
di
Так как -^-= О и gradu=#0 (по условию), то cos(t, grad и) =0,
di
т. е. угол между векторами т и grad и равен 90°. Теорема до-
казана.
Из этой теоремы вытекает, что все касательные, проведен-
ные в точке Л1 к кривым, лежащим на поверхности уровня, рас-
положены в одной плоскости (если grad и =£ 0 в точке М).
Действительно, все эти касательные проходят через точку М и
перпендикулярны одному и тому же вектору — градиенту и. Зна-
чит, они все лежат в одной плоскости.
Геометрическое место касательных, проведенных в точке М
к линиям, лежащим на поверхности уровня, называется каса-
тельной плоскостью к этой поверхности в точке М. Уравнение
этой плоскости легко написать. Если точка М имеет координа-
ты х0, у0, z0, то вектор, перпендикулярный касательной плоско-
сти,— градиент — запишется следующим образом:
du \ у . / du
dy L ,, , ' ' I dz
v /*<>• yB, z0 \
I k.
xo< Vo> To
8га<1и1м = (4г)
Зная точку, через которую проходит искомая плоскость, и зная
вектор, перпендикулярный плоскости, можно написать уравнение
касательной плоскости:
du
dx
| (х — хй) +
Хв, У о • го
(-^-) (У-Уо) + (
\ у /Хо, ув, гв	\
du
dz
I (z—2о)-О-
XB, Uo* zo
(4)
До сих пор мы рассматривали касательную плоскость толь-
ко к поверхности уровня. Если же нам дана произвольная по-
верхность уравнением f (х, у, г) — 0, то ее можно считать поверх-
ностью уровня для функции и = f (х, у, г), и, следовательно,
уравнение касательной плоскости к этой поверхности получится
также по формуле (4).
Пример 1. Написать уравнение касательной плоскости к па-
раболоиду 2 = х2 + у2 в точке М (2; 1; 5).
Решение. Заданную поверхность можно рассматривать,
как поверхность уровня для функции и = г — х2 — у2 (действи-
тельно, геометрическое место тех точек, где и = 0 совпадает с
ftatailausA
знание без границ Ч "Ь
§2_________________________________________________________________________________________ 15
поверхностью г — х2_—у* = 0, или z = x* + y2). Так как grada=
= — 2xi — 2yj+l-k,no
grad и	= — 4i — 2/ + k,
а уравнение касательной плоскости к данному параболоиду в
точке /И примет вид:
—4 (х —2) —2 (г/—1)4- 1 .(z-5) = 0,
или, после упрощений:
—4х — 2у + z 4- 5 — 0.
Пример 2. Имеет ли коническая поверхность х2 4- У2 — z2=0
касательную плоскость в точке М (0; 0; 0)?
Решение. Эта поверхность слу-
жит поверхностью уровня для функции
и =х2 + У2 — 22. Заметим, что grad и =
— 0. Следовательно, ни теорема, ни
следствие из нее к данному случаю
неприменимы: нельзя утверждать, что
все касательные, проведенные в точке
М к линиям, лежащим на этой поверх-
ности, образуют плоскость. И дей-
ствительно, геометрическое место этих
касательных совпадает с самой кони-
ческой поверхностью. Значит, коничес-
кая поверхность не имеет касательной
плоскости в вершине (рис. 7).
Приведенный пример показывает,
что далеко не всякая поверхность имеет касательную плоскость.
Если поверхность S имеет во всех своих точках касательную
плоскость и эта плоскость изменяется непрерывным образом при
перемещении точки по поверхности, то поверхность называется
гладкой. Точнее говоря, для гладкой поверхности двугранный
угол между касательными плоскостями в точках М и М' стре-
мится к нулю при стремлении точки М' к М (по любому пути,
лежащему на этой поверхности).
Если поверхность задана уравнением F (х, у, z) = 0, то для
ее гладкости достаточно, чтобы во всех ее точках существовали
dF
непрерывные частные производные
dF dF к
не обращаю-
щиеся одновременно в нуль; это следует из того, что уравнение
касательной плоскости в точке М (х0, у0, z0) таково:

Если поверхность S может быть разбита простыми дугами
16
Часть I
на конечное число гладких поверхностей, то S называется ку-
сочно-гладкой поверхностью.
Так, например, сфера, параболоид, плоскость являются
гладкими поверхностями. Поверхность куба, поверхность конеч-
ного кругового цилиндра — кусочно-гладкие поверхности.
Вернемся теперь к градиенту функции трех переменных.
Доказанная выше теорема утверждает, что градиент перпенди-
кулярен к касательной плоскости поверхности уровня. Этого и
следовало ожидать: функция трех переменных будет возрастать
быстрее всего, если от точки М двигаться по нормали* к по-
верхности уровня. Докажем теорему, которая является в неко-
тором смысле обратной к этой теореме.
Теорема. Если S — гладкая связная** поверхность, и
f (х,у, г)—функция с непрерывными частными производными такая,
что grad f перпендикулярен к S во всех точках S, то S являет-
ся поверхностью уровня для f(x, у, z).
Доказательство. Зафиксируем на S некоторую точку А
и докажем, что
f(M) = f(A)
для любой точки /И на поверхности S. Соединим точки М и А
спрямляемой гладкой дугой L, лежащей на S (это возможно в силу
связности и гладкости S). Так как grad f перпендикулярен к
поверхности S, то он, в частности, всюду перпендикулярен к ка-
сательному , вектору дуги L. Но тогда s= 0 всюду на L.
Запишем параметрические уравнения кривой L, приняв в
качестве параметра длину дуги I, отсчитываемую от точки А:
х = х(I), y=y(l), z = z(l). Тогда началу дуги соответствует
значение параметра / = 0, концу дуги — значение / = (где
li — длина всей дуги L). Подставив в функцию / (х, у, г)
вместо х, у, z их выражения через I, мы получим функцию од-
ного переменного I, т. е. f[x(l), у (Г), z(/)J; обозначим ее для
краткости <$>(/); тогда
/(7И)-/(Л) = <р(/1)-<р(О);
применив к последней разности теорему Лагранжа, получим
f (М) - f (Л) = «р (11) — <р (0) = (11 - 0) <?' (/ср),
где 0 < /ср <
Но производная от <р(/) совпадает с производной от
f(x, у, ?) по дуге L (что вытекает из определения производной
* Нормалью к поверхности в точке М называется перпендикуляр к
касательной плоскости, проведенной в этой точке.
•• Поверхность S называется связной, если любые две точки поверхно-
сти S можно соединить непрерывной спрямляемой линией, целиком лежащей
на этой поверхности.
ftalaHausiifa
знание без границ “ w
§± 17
по дуге). Мы доказали раньше, что •— = 0; следовательно, и
/(/)==0; в частности, <р'(4р) = 0, откуда f^M) — /(Л) = 0, или
/(Л4) = /(Д). Так как это равенство справедливо для любой
точки М на S, то функция f(x, у, z) всюду равна f(A), т. е.
постоянна. А это и означает, что S является поверхностью уро-
вня для функции f(x, у, z).
В заключение сформулируем некоторые свойства градиента:
1)	градиент постоянной функции равен нулю;
2)	градиент суммы двух функций равен сумме их градиен-
тов:
grad (и + и) = grad и + grad v\
3) градиент
формуле
произведения двух функций вычисляется по
grad uv — grade; 4- tbgrad.u;
4)	градиент частного от деления двух функций вычисляется
по формуле
, и	v-gradu—и-grad v	, _
grad — — —-------------, если v =£ 0.
Для доказательства всех этих утверждений достаточно вос-
пользоваться определением градиента.
§ 4. Интеграл по поверхности
Для рассмотрения векторного поля нам понадобится одно
новое понятие — понятие интеграла по поверхности. В настоя-
щем параграфе будет определен и изучен интеграл по поверх-
ности.
Пусть нам дана ограниченная поверхность S, во всех точ-
ках которой задана функция и = f (х, у, г). Иными словами область
определения функции f (х, у, z) либо
совпадает с S, либо содержит S.
Разобьем S на несколько малых
частей: AS,, AS2,,.. ASn (элемен-
тарных площадок) и внутри каждой
из них выберем произвольно точку:
М|, /И2,.... Л7Я (рис. 8). Тогда сле-
дующая сумма*
F (М J A	4* f (M2) A S2 4-... 4-
п
+ / (Л4„)Д$„= S/(Mt)AS4

* Здесь и всюду в дальнейшем символами ASlt AS2, ASs, .. . , ASn мы
,,,(>зпачаем не только сами поверхности, но и их площади.
18
Часть 1
называется интегральной суммой для функции f (х, у, г). Пре-
дел интегральной суммы (при стремлении максимального диа-
метра элементарных площадок AS* к нулю), если он сущест-
вует, называется интегралом по поверхности S от функции
f(x, у, г); он обозначается /А г) Таким образом, по оп-
ределению
/ (х, у, z) dS = lim S f (M*) A S*.
dfam Л S^-0 *_j
Сформулируем принимаемую нами без доказательства тео-
рему существования интеграла по поверхности.
Пусть S — ограниченная, гладкая или кусочно-гладкая
поверхность, имеющая конечную площадь. Если функция
f(x,y,z) непрерывна во всех точках поверхности S и ограни-
чена на этой поверхности, то предел интегральной суммы
S f(Mk)&Sk (при стремлении максимального диаметра ASa к ну-
лю) существует. Иными словами, при этих условиях сущест-
вует интеграл от функции f(x,y,z) по поверхности S.
В дальнейшем мы будем считать, что все рассматриваемые
поверхности являются ограниченными и гладкими (или кусоч-
но-гладкими), и что они имеют конечную площадь.
Рассмотрим, какие физические задачи могут привести нас к
понятию интеграла по поверхности.
1.	Пусть в каждой точке материальной поверхности S зада-
на поверхностная плотность f(х, у, г) (под поверхностной плот-
ностью в точке М, подразумевается предел, к которому стремит-
ся отношение где AS — площадь небольшой части поверх-
ности, охватывающей точку М, а А т — масса этой части поверх-
ности; предел берется при стягивании площадки AS к точке М).
Поставим перед собой задачу о вычислении массы всей по-
верхности S. Для этого вычислим ее сначала приближенно.
Разобьем S на несколько мелких площадок: ASt, AS2,... ASn.
Если диаметры этих площадок малы, а плотность f(x,y,z) яв-
ляется непрерывной функцией, то можно считать, что плотность
во всех точках площадки А5Л одинакова; за эту плотность мож-
но принять, например, /(МД, где Mk — какая-либо точка пло-
щадки ASa. Тогда масса ASa приближенно равна f(Mk)ASk, а
масса всей поверхности приближенно равна 2j/(Ma)AS*. Оче-
*=1
видно, чем мельче брать плсщадки ASa, тем точнее эта сумма
19
даст величину массы. Точное значение массы можно получить,
взяв предел этой суммы
п
т = lim S f (Mk) Д Sk.
diam ДЗ^—О
Но этот предел равен интегралу по поверхности.
Итак,
т = W (х, У> z) dS>
т.	е. масса материальной поверхности S равна интегралу по
этой поверхности от поверхностной плотности.
2.	Рассмотрим задачу о вычислении площади поверхности S.
п
Очевидно, S = Ед S*.
Л=1
Переходя в этом равенстве к пределу (при diam Д Sk -> 0),
получим
Л
S = lim S &Sk.
diam Д S^-0 j
Но в правой части этого равенства стоит предел интегральной
суммы (построенной для функции f(x,y,z) = 1).
Итак,
If 1 ds,
S
т. е. площадь поверхности равна интегралу по этой поверх-
ности от функции, тождественно равной единице.
Другие примеры приложения интеграла по поверхности бу-
дут рассмотрены в теории векторного поля.
Отметим некоторые свойства интеграла по поверхности:
1)	интеграл от суммы двух функций равен сумме интегралов
от каждой функции в отдельности:
I/ (х, У, z) + 9 (х, У, г)] dS = JJ f (х, y,z) dS + JU (x, y, z)
dS-t
2)	постоянный множитель можно выносить за знак интегра-
ла по поверхности:
ф/(х, у, z) dS = a^f (х, у, z) dS;
3)	если поверхность S разбита на две части Si и S2, при-
чем эти части не имеют общих точек, то
20
Часть I
§?(*>У> г)
dS = ^f(x,y,z) dS + ^f(x,y,z) dS.
Замечание к свойствам 1), 2), 3). Из существования
интегралов в правых частях равенств вытекает существование
интегралов в левых частях.
4.	Теорема о среднем. Пусть S — ограниченная, гладкая
или кусочно-гладкая поверхность, имеющая конечную площадь;
если функция f(x,y,z) непрерывна и ограничена на S, то на по-
верхности S найдется такая точка х0, yQ, z0, для которой имеет
место равенство:
П / (х> у, z) dS = f (х0, у0, z0)-S.
Доказательство всех
z
Рис. 9
приближенно каждую площадку
этих свойств производится
дословно так же, как и до-
казательство аналогичных
свойств для двойных интег-
ралов.
Выведем формулу для
вычисления интеграла по по-
верхности. Пусть поверх-
ность S задана уравнением
2 = <р (х, у) и проектируется
на плоскость Оху в плоскую
область о (рис. 9). Разобьем
область S на мелкие части
Д5Р Д52,..., Д5Л и рас-
смотрим проекции этих час-
тей на плоскость Оху: Дар
Да2,.... Дал. Будем считать
Д5а плоской (например, Д5Л
заменим соответствующей частью касательной плоскости, прове-
денной в какой-либо точке Mk, где Mk — точка, лежащая на Д5А).
Тогда между площадями Д5А и Дал имеет место следующее соот-
ношение:
Д^ = ASfc.cos
где — острый двугранный угол между плоскостью Оху и ка-
сательной плоскостью в точке Mk. Этот угол равен острому уг-
лу между осью Ог и нормалью к поверхности в точке Mk. Итак,
ДЗА,=
COSfk 
Следовательно,
NataHausiSk
знание без грани» “ w
21
j ff (х, у, z) dS = lim S f (xk, yk, zk) ASk =
5	diamAS^-O A=l
= J!m .
diamAa.-»O &=|	t-ubIA
Под знаком предела оказалась интегральная сумма от функции
двух переменных х и у (заметим, что угол у можно также рас-
сматривать, как функцию от х и у). Ее предел равен двойному
интегралу по области а. Следовательно,
JJ	= flx,y,<p(x,y)] ~-r	(1>
Таким образом, нами выведена формула для вычисления интег-
рала по поверхности. Ее можно сделать более удобной для при-
менения, если подставить в нее значение cosy. Для того, чтобы най-
ти cos 7, заметим, что поверхность г— <р(х, у) является поверхностью
уровня для функции и — z — ?(х, у). Поэтому нормаль к поверх-
ности будет направлена вдоль градиента и, т. е. вдоль вектора
gradu=_^i-_^/+l.fc.
Косинус угла, составленного этим вектором с осью Oz, равен:
COST=/(£)*+(<+>•* <2>
Подставляя найденное значение cosy в равенство (1), получим
.fl f (х, у, z) dS—\jf [х, у, ср (х, у,)] j/	da. (3)
Замечание. Укажем на одно следствие из формулы (1),
которое нам понадобится в дальнейшем.
Рассмотрим интеграл по поверхности S от функции
дх
* Заметим для дальнейшего, что cosa= —	  —--
ИС?ф\2	/ С®\2
-£) +Ы+1
д<р
Г	&У
COS р = -- -------
22
Часть I
Ф (х, у, z) cos у, где 7 — острый угол между осью Oz и нормалью
к поверхности S. Тогда по формуле (1) имеем:
НФС*. У> г) cos у dS = JJФ [х, у, <р(х, z/)] cos у =
S	a	COS у
= ДОФ[*, у)] da,
а
где 2 = ч>(х,у) — уравнение поверхности S. Итак,
П ФI*. У, <? (х, г/)] da = [[ф (х, у, г) cos 7 dS.	(4)
a	S
Пример. Вычислить массу поверхности конуса г = + V*2 + У2 >
ограниченной сверху плоскостью z = h, если поверхностная плот-
ность в каждой точке пропорциональна расстоянию от этой точ-
ки до начала координат (с коэффициентом пропорциональности С).
Решение. Согласно условию, плотность f (х, у, г) =
и поэтому масса конической поверхности
может быть вычислена по формуле
пг — С ]/ х2 + У2 + г2 dS.
Поверхность конуса задана уравнением
г = }/ х2 -f- у2 ; она проектируется на плос-
кость Оху в круг а; уравнение контура
этого круга имеет вид х2 -j- у2 = h2 (рис. 10).
Рис. 10 Итак, в соответствии с формулой (3),
Получившийся двойной интеграл легко вычислить, если перейти
2л Л3	т.
к полярным координатам; он равен —х- . Итак,
О
о „ 2nhs 4nCh3
m=2C' —= -r-.
$ <5. Формула Гаусса-Оспгроградского
В настоящем параграфе мы выведем формулу, позволяющую
выразить в некоторых случаях поверхностный интеграл через
тройной (формула Гаусса-Оспгроградского).
ftaiailauSfVii
знание без ераниц * *
§5 23
Теорема. Пусть V — некоторая область в пространстве,
a S — граница этой области. Если функции P(x,y,z),
Q(x,y,z), R(x,y,z) непрерывны и имеют непрерывные част-
ные производные во всех точках области V (включая грани-
цу), то для них справедливо следующее равенство:
1!Ж+^
V
[Р cos а 4- Q cos р + R cos у] dS,
S
где а — угол между внешней нормалью к поверхности S и
осью Ох, р — угол между внешней нормалью и осью Оу, у —
угол между внешней нормалью и осью Ог.
Для доказательства рассмотрим сначала интеграл
I.P
Считая, что тело V ограничено снизу поверхностью z = <f>(x, у),
а сверху — поверхностью z — ф (х, у), и что егб проекцией на плос-
кость Оху является область о (рис. 11)*, запишем этот тройной
интеграл следующим образом:
* Мы наложим пока следующее ограничение на поверхность £:если тело V
проектируется на плоскость Оху в область а, то каждая прямая, параллель-
ная оси Ог и проходящая через внутреннюю точку области а, прокалывает
поверхность S только в двух точках (точке входа и точке выхода); анало-
Ч1чное условие должно иметь место и при проектировании тела V на плос-
кости Oxz и Оуг.
Это ограничение впоследствии будет нами снято (когда мы выясним век-
торпый смысл формулы Гаусса-Остроградского).
Часть /
<И*. у) ,
J
V	О <f(X, у)
Интеграл, стоящий в квадратных скобках, можно непосредствен-
но вычислить:
Ф (х. У)
\ ^dz==R(x>y^(х>у)) — Я (х> У> ?<х>У))-
<₽ (X.yj
Поэтому
№ dv== Л * у' у^do ~~ ff я	у'9 у^da'
V	о	а
Полученные двойные интегралы легко свести к интегралам по
поверхности. Так, например, для того чтобы свести первый из
этих интегралов к интегралу по поверхности S2 (где S2 — верх-
няя часть поверхности 5), достаточно применить формулу (4) из
предыдущего параграфа:
ДОЯ (х> У> Ф (х. У)) da = Л Я (х« У>z) cosb dS-
Здесь у2 — острый угол между нормалью к S2 и осью Oz.
Совершенно аналогично доказывается, что
П Я (*, У, t (х, у,)) da = Д Я (х, у, z) cos ь dS,
а	од
где тх — острый угол между нормалью к поверхности Sj и осью
Oz.
Подставив в равенство (1) вместо двойных интегралов соот-
ветствующие поверхностные, получим
ш
V
f (j R(X,y.z)
St
cos
dS.
cos 7i
Заметим, что острый угол у2 в первом из этих интегралов сов-
падает с углом у, составленным внешней нормалью с осью Oz\
острый угол во втором интеграле равен 180° — у, где у—угол
между внешней нормалью и осью Oz (рис. 12). Выражая в обоих
интегралах у2 и через у, мы будем иметь:
fj’f	Я(х, у, г) cos у dS — Jy?(x, y,z) cos(180° — y)dS=
s,	st
= JJ Я(х,г/,г) cos 7 dS 4-	Я (x, y, z) cos 7 dS.
NaiuHausieik
знание без границ “
§ 6
25
Учитывая теперь, что и Sa вместе составляют всю поверх-
ность S, получим:
Ш %dv =
(2)
Г	S
Аналогично равенству (2), могут быть выведены следующие ра-
венства:
cos a dS,
(3)
s
V
ш %
V	S
(4)
Складывая почленно равенства (2), (3), (4), получим

cos а + Q cos р 4- R cos у] dS.
s
Это и есть формула Гаусса - Остроградского, которую нам тре-
бовалось вывести.
§ 6.	Векторное поле. Векторные линии.
Векторные трубки
Перейдем к изучению векторного поля. В § 1 были даны
определение и примеры векторных полей. Напомним эти примеры.
1.	Поле сил тяготения, образованное притягивающей мате-
риальной точкой массы т, расположенной в начале координат.
В данном случае мы имеем векторное поле F, где F — вектор си-
лы, с которой единичная масса в точке С (x,y,z) притягивается
к началу координат. Мы знаем, что
F |7?13 -
V™ у	упу Т— ____________У™ Ь
= — ------------у 1----------------у 1	J
2	(x24-//24-z8) 2	(x24-£/*4-z2) 2
Здесь R = xi + yj 4- zk.
2.	Поле скоростей в стационарном течении жидкости.
3.	Если и — f (х, у, г) — скалярное поле, то А — grad и обра-
зует векторное поле.
26
Часть I
Одним из важных понятий, связанных с векторным полем,
является понятие векторной линии.
Векторной линией стационарного векторного поля на-
зывается такая линия, у которой касательная в каждой
точке направлена вдоль заданного в этой точке вектора
поля (рис. 13).
Приведем примеры векторных линий.
1.	Если векторное поле явля-
~	ется полем сил тяготения, рас-
смотренным выше (см. пример 1),
то векторными линиями являют-
ся лучи, сходящиеся к началу
s	координат (заметим, что если за-
данное поле является полем сил,
s'	то векторные линии этого поля
рис- 13	называются силовыми линиями).
2.	В поле скоростей при
стационарном течении жидкости векторными линиями являются
траектории движущихся частиц жидкости.
3.	В поле градиента A =gradw векторная линия — это та
линия, при движении вдоль которой скалярная величина и рас-
тет с наибольшей скоростью (так как скорость рссга функции в
каждой данной точке будет наибольшей в направлении градиен-
та). Эта линия называется линией наибыстрейшего возраста-
ния функции и.
Для того чтобы найти векторную линию поля
А = Р (х, у, z) Т + Q (х, у, г) 7+ R (х, у, г) k,
поступают следующим образом. Пусть параметрические уравне-
ния искомой векторной линии таковы: х = х(/),у =y(t), z —
Тогда вектор касательной в произвольной точке этой линии имеет
вид:
— dx—. . by- , dz т
Х ~ dtl+ dt ~dtk'
В силу определения векторной линии, этот вектор колинеарен
вектору поля в точке (х, у, г). Поэтому одноименные проекции
этих векторов пропорциональны:
dx	dy	dz
dt	__ dt	_ dt
P(x,y,z) ~~ Q(x,y,z) ~ R(x,y.z) ’	* '
Обозначим численную величину этих отношений одной буквой Ф.
Заметим, что численное значение этих отношений может зави-
ftaiatiausifi',
знание без границ * *
*6	27
сеть от координат точки х, у, г, а также от значения параметра
I в этой точке. Поэтому, вообще говоря, Ф зависит от х, у, z, t.
Зависимость Ф от x,y,z,t может быть выбрана совершенно про-
извольно. Приравнивая каждое из отношений (3) к произвольно
заданной функции Ф (х, у, г, 0, получим систему трех уравнений
с тремя неизвестными функциями х (0,1/(0, г (0:
~ Ф (х, у, z, t) Р (х, у, г);	- Ф (х, у, z, t) Q (х, у, z)\
Ф(х,у,г, t) R(x, у, z).
(4)
Решив эту систему, мы найдем искомые функции х (0, у (0, z (t).
Гот факт, что функция Ф выбрана произвольно, не отразится на
окончательном результате. Замена функции Ф какой-либо другой
функцией приведет только к изменению тех параметрических
уравнений, которые задают искомую векторную линию.
Пример 1. Найти векторные линии ноля тяготения, образо-
ванного материальной точкой, находящейся в начале координат.
Р е ш е н и е. Так как в этом ноле
унх {	упу	(/иг
-	у
(*Ч-у* +-Z2) 2	(X2 Ч/Ч za) 2	2
(см. первый пример в начале этого параграфа), то уравнения век-
торных линий найдутся из пропорции
dx
dT________
у/их
з
(х2+^-|
dy	dz
(U	dt
yny	ynz
~3	"	'_3
(x« f УЧ-z2) 2	(X2 I УЧ-z2) 2
Приравняем эти отношения к функции Ф (х, у, z, t) —
3
(Х2-|- U2-|-z2) 2
----------—------- (функцию Ф (х, у, z, t) выбираем так, чтобы после
сокращений система уравнений получилась по возможности бо-
не простой):
dx
~dt _____
-упх
(х2 I У‘ I z2) 2
dy_
dt__________
VW
_3
(x2-!-//2 |-z2) 2
dz
dt________
tmz
_3
(x2 ( ty2 ( z2) 2
28	•	Часть I
_	(xa4-f/2-H2)2
\mt *
Откуда	dx _ х , dy______у_, dz z
dt t ’ dt t ’ dt t *
Интегрируя эту систему уравнений, получим
х = Cit; у = C2t\ z = Cat.
Это—семейство векторных линий. В данном случае они образуют
семейство прямых, проходящих через начало координат; точнее
говоря, векторными линиями здесь являются полупрямые, иду-
щие от начала координат в бесконечность (само начало коор-
динат не принадлежит ни одной из векторных линий: в начале
координат векторное поле не определено).
Для того, чтобы из семейства всех векторных линий выде-
лить одну, надо задать точку Мо (х0,у0,г0), через которую эта
векторная линия должна проходить, и по координатам заданной
точки определить Ср С2, Са. Пусть, например, Мо имеет коорди-
наты 3; 5; 6; тогда уравнение векторной линии, проходящей че-
рез Мо, можно записать в виде х — 3/, у — 5t, z6/. Здесь точ-
ка Мо получается при значении параметра t = 1.
Пример 2. Найти линии наибыстрейшего возрастания функ-
ции и = и (х, у, г).
Решение. Эти линии являются векторными линиями поля
градиента, т. е. поля
- j	dur . dur . 5ur
grad и =	(5)
Следовательно, дифференциальные уравнения, определяющие
семейство векторных линий поля (5), таковы:
•	I	9
Л = Л =
ди	ди	ди ‘
дх	ду	dz
Решая эту систему уравнений, найдем искомое семейство линий
наибыстрейшего возрастания функции и (х, у, z).
Введем еще одно важное понятие — векторной трубки.
Пусть нам задана некоторая площадка а, расположенная в
векторном поле. Через каждую точку этой площадки проходит
векторная линия.
Часть пространства, заполненная векторными линиями,
проходящими через точки площадки а, называется вектор-
ной трубкой, соответствующей этой площадке.
WataHausA
знание без границ - *
£7 29
Пример 3. Рассмотрим поле тяготения, образованное мате-
риальной точкой, расположенной в начале координат.
Здесь векторными линиями являются прямолинейные лучи,
выходящие из начала координат (см. пример 1). Поэтому любая
Рис. 14
векторная трубка в этом поле имеет форму конуса с вершиной в
начале координат (рис. 14).
§ 7. Поток векторного поля через поверхность
Рассмотрим гладкую ограниченную поверхность S, располо-
женную в некотором непрерывном векторном поле А. Выберем
па этой поверхности определенную сторону*, которую назовем
положительной стороной; противоположную сторону поверхности
назовем отрицательной. Будем говорить, что такая поверхность,
у которой выбраны положительная и отрицательная стороны,
ориентирована. Буквой п обозначим единичный вектор норма-
ли в точке М к поверхности S, причем этот вектор направлен
* Здесь и всюду в дальнейшем мы будем рассматривать только двусто-
ронние поверхности, т. е. поверхности, обладающие тем свойством, что если точ-
ка М перемещается вдоль замкнутой кривой на этой поверхности, то вектор нор-
м.члн п после обхода замкнутой кривой, возвращается в исходное положение.
Заметим, что далеко не всякая гладкая поверхность является двусторонней,
‘‘•"’смотрим, например, лист Мебиуса, получающийся от склеивания «крест-
||.1крест» противоположных сторон АВ и CD прямоугольника ABCD (точка А
"pii склеивании должна совпасть с С, а В — с D: см. рис. 15) Здесь при
"'[’смещении точки М вдоль пунктирной линии, исходя из точки Мо, вектор
п возвращается в точку Af0 в перевернутом виде, т. е. не в свое исходное
"'’ложение (см. рис. 16).
30
Часть I
от отрицательной к положительной стороне поверхности; ясно,
что положение вектора п зависит от положения точки М на
поверхности.
Рассмотрим следующую функцию: f (М) (Л п); она опреде-
лена во всех точках поверхности S. Если А - Pi 4- Qj ] Pk, а на-
правляющие углы векторам равны, соответственно а, [3,у (т. е.
п ~ cos 1 i -|- cos [5 • j • cos 7 -k), то f (M) Pcosa. | Qcosp | /?cosy.
Puc. 15	Puc. 16
Эта функция непрерывна на поверхности S. Следовательно, су-
ществует интеграл от f (Л4) по поверхности S. Этот интеграл
называется потоком векторного поля через поверхность S (в
выбранном направлении) и обозначается символом II (или Ils):
И - |j (An)dS-f| (P cos a \Q cos [4 | P cos y) dS. (1)
’s	s	__
Итак, потоком векторного поля А через ориентирован-
ную поверхность S называется поверхностный интеграл по
поверхности S от скалярного произведения (Ап), где п — еди-
ничный вектор нормали к поверхности S, направленный от
отрицательной стороны поверхности к положительной.
Заметим, что, изменяя ориентировку поверхности S, мы изме-
ним знак потока, не изменив его абсолютной величины.
Здесь определение потока дано для случая гладкой поверх-
ности. Если же ориентированная поверхность S является кусоч-
но-гладкой, то под потоком векторного поля через поверхность
S подразумевается алгебраическая сумма потоков через каждую
гладкую часть поверхности S.
Если поверхность S является замкнутой, то ее обычно ориен-
тируют следующим образом: внешнюю сторону поверхности счи-
тают положительной, а внутреннюю — отрицательной. Поэтому,
говоря о потоке векторного поля через замкнутую поверхность,
будем считать, что она ориентирована так, как об этом сказано
выше. Таким образом, под п (в случае замкнутой поверхности
S) подразумевается единичный вектор внешней нормали.
Выясним физический смысл потока векторного поля в слу-
чае гидродинамической интерпретации этого поля.
^ialatiaus^ii.
знание без границ “ *
31
Пусть А (М) — Pi 4- Qi 4- Rk — скорость движущейся
жидкости в точке М. Рассмотрим поток этого поля через неко-
торую поверхность S в данном направлении:
П = J] (Л л) dS = lim 2(Л п)лч Д^.
8	dluinASg->0 /_|
Каждое слагаемое (Л п)м{ приближенно равно объему
того количества жидкости, которое прошло через площадку AS/
в выбранном направлении за единицу времени. Действительно,
считая приближенно площадку плоской, заметим, что объем
жидкости, прошедшей через эту площадку за весьма малый про-
межуток времени Д/, равен объему цилиндра, основание которого
равно а образующая направлена по вектору ЛСвточкеЛ^)
и численно равна |Л|Д/:
V/.д/ — | Л |-Д/«Д5гсо$ф,
где ф — угол между вектором Л и нормалью п (рис. 17)*; учи-
тывая, что | Л | • cos ф = (Л n)wi, можно записать:
У/.дг = (A rijjHi-bSiM.
Для того чтобы подсчитать количество жидкости Vlf протек
шей через площадку Д5/ за единицу времени, разобьем мыслен
но эту единицу времени на мел-
кие части Д/„ Д/2..... Мт.	Тог-
да количество жидкости за всю
единицу времени равно объему,
протекшему за время Д tit плюс
объем, протекший за время Д/2 и
т. д.
Vf = (Л n)Mib S^t^-V
+ (Ап)М1 Д5,ДГ,4- ... +
4-_(Лп)л<1Д5,Д/от=
i 4- Д it 4" • • • 4
Д/От) = (Ari)MlbSt.
* Мы считаем, что угол ф— острый, т. е. что вектор поля направлен
ту же сторону, что и нормаль к поверхности. Если бы угол ф был тупым,
т е. если бы нормаль была направлена в обратную сторону, то это отрази-
сь бы на знаке произведения.
32
Часть I
Итак, количество жидкости, протекшей за единицу времени
через площадку ASP равно (An)Mi &St; следовательно, количест-
во жидкости, протекшее за единицу времени через всю поверх-
ность S, равно
л
(An)Mi&St:
i—i
п
Vs	(2)
/-1
Это равенство является приближенным: при его выводе мы счи-
тали площадки AS,—плоскими, а вектор п—постоянным на каждой
площадке ASr Равенство (2) становится тем точнее, чем меньше диа-
метры площадок AS,; в пределе (при di am -+ 0) оно переходит
в точное:	_
Г = £(Лл) dS.
Итак, в случае гидродинамической интерпретации вектор-
ного поля, поток через ориентированную поверхность S равен ко-
личеству жидкости, протекшей за единицу времени через эту
поверхность (в направлении от отрицательной к положительной
стороне поверхности). Заметим, что если жидкость протекает в
противоположном направлении ориентированной поверхности S,
то поток будет отрицателен. Наконец, может оказаться, что че-
рез часть поверхности <$ жидкость течет в одном направлении,
а через другую часть—в противоположном. Тогда поток вектор-
ного поля через всю поверхность равен алгебраической сумме
потоков через части этой поверхности.
Рассмотрим особо случай замкнутой поверхности S. Если
в этом случае поток через S положителен, то это означает, что
из той части пространства, которая ограничена поверхностью S,
вытекает больше жидкости, чем втекает в нее. В этом случае го-
ворят, что внутри S имеются источники, постоянно выделяющие
жидкость. Напротив, если поток отрицателен, то внутрь S вте-.
кает больше жидкости, чем вытекает из нее. В этом случае
говорят, что внутри S имеются стоки, поглощающие жидкость.
Пример 1. Дано векторное поле А = (х 4- y)i + (у — х) j 4-
4 z k. Вычислить поток этого поля через поверхность сферы ра-
диуса 1 с центром в начале координат.
Решение. В данном случае нормаль к поверхности в кажч
дой точке направлена по радиус-вектору этой точки. Поэтому
единичный вектор нормали легко вычислить по следующей фор-
муле:
§ 8
Сп'циальнйСпя
JValaHaasatJ
знание без границ * w
33
п = -А- = “ + yl±lJL ^Т + y~i+zk,
|/?|	^x’-h^-l-z2
так как Ух2 + у2 -|-г8 = 1 для любой точки, лежащей на поверх-
ности данной сферы. Итак,
[А п) = (х-\-у)х -1- (л — у) у + ZZ = х2 4- у2 + г2.
Поэтому поток равен:
j f (J п) dS = JJ (x2 I- if I- z=)dS = J'J 1 dS = S = 4».
Здесь мы воспользовались тем, что всюду на поверхности сферы
имеет место равенство х2 4- у2 г2 — 1.
Пример 2. Вычислить поток поля сил тяготения А =-----* — -
И8
через сферу радиуса а с центром в начале координат.
Решение. Здесь п —	; следовательно,
и
§ 8. Дивергенция векторного поля
Поток векторного поля через замкнутую поверхность S
иногда называют производительностью той части пространства
V, которая ограничена поверхностью S. Это объясняется тем,
что если данное векторное поле рассматривать как поле скоро-
стей движущейся жидкости, то поток через S равен количеству
жидкости, «произведенной» внутри V.
Взяв отношение потока через S к величине объема V, полу-
чим среднюю производительность области V. Однако средняя
производительность еще недостаточно характеризует интенсивность
векторного поля в окрестности каждой точки данной области:
одни участки области могут оказаться гораздо интенсивнее,
«производительнее» других. Поэтому для того чтобы оценить
2 Ю. С. Очан
34
Часть /
производительность вблизи какой-либо точки М, лежащей внут-
ри области V, мы должны вычислять среднюю производитель-
ность во все меньших и меньших областях, окружающих точ-
ку М. Переходя к пределу (при стягивании области к точке Л1),
получим число, достаточно хорошо характеризующее «произво-
дительность» векторного поля в окрестности точки М. Это число
называется дивергенцией поля в точке М.
Дивергенцией векторного поля А в точке М называется
предел, к которому стремится отношение потока через замкну-
тую поверхность, окружающую точку М, к объему области,
ограниченной этой поверхностью. Предел берется при стягива-
нии поверхности к точке М:
Z
е	_
5	div>4=lim——у-------
v-м у
ХалТхКЛ/	Те точки векторного поля, в
которых дивергенция поло-
жительна, называются источ-
v	никами. Этот термин объяс-
_____________________________ _ няется тем, что если описать
yjj “_____________у около такой точки достаточно
/	малую замкнутую поверх-
ность, то поток через эту
/	поверхность окажется поло-
х	жительным(и, следовательно.
Рис. 18,	если- истолковывать наше
векторное поле гидродинами-
чески, то через эту поверхность жидкость вытекает наружу).
Те точки, в которых дивергенция отрицательна, называются сто-
ками.
Пусть векторное поле задано аналитически: А = Pi 4- Q7 4-
4- Rk, где Р, Q, R — скалярные функции, имеющие непрерывные
производные первого и второго порядков. Попытаемся найти ана-
литическое выражение для дивергенции в точке М. Опишем для
этого около точки М произвольную замкнутую поверхность я
обозначим через V ту часть пространства, которая ограничена
этой поверхностью (рис. 18). Тогда
JT (Л n) dS JJ (Р cos a -f- Q cos Р 4х R cos l) dS
div A =lim -—г-----— lim ------------п------------»
v-м v v-m	v
где a, p, 7— направляющие углы внешней нормали. Преобразу
'Naldliaus^
знаниеВезераниц 'w
$8  35
ем полученный поверхностный интеграл к тройному по формуле
Гаусса-Остроградского:
div А = lim----------п-----------
у.м	у
и применим к тройному интегралу теорему о среднем; в силу
этой теоремы, внутри области V найдется точка Мср такая, что
fff/aP dQ dR\.v_ v(dP _.dQ,dR\
jjj + fc) dV - 4^ + <>У +
Поэтому
div A =lim
V-M
dQ dR\
-
dP dQ dR
dx dy dz
у
Когда объем V стягивается к точке М, тогда и всякая ^его внут-
ренняя точка (в частности, Мср) стремится к М. Но тогда, в си-
.	dp , dQ , dR
лу непрерывности функции 4-	• ее значение в точке
Мср стремится к ее значению в точке М. Поэтому
div А == ~
dx
dQ . дЯ
dy ' dz*
(i;
где все частные производные вычисляются в точке М. Это и
есть искомая формула для вычисления дивергенции векторного
поля.
Равенство (1) позволяет записать в векторной форме дока-
занную ранее теорему Гаусса-Остроградского. Если учесть, что
(Р cos a -J- Q cos р + /? cos у) dS является потоком векторного
поля А = Pl + Qj Rk через поверхность S, а
является дивергенцией этого поля, то равенство
s

2*
36	Часть I
может быть переписано следующим образом:
S	V
Итак, поток, векторного поля А через замкнутую поверхность равен
тройному интегралу от дивергенции div А по той области, ко-
торая ограничена этой поверхностью. Конечно, это равенство
справедливо лишь в том случае, когда div А непрерывна всюду
внутри области V.
Пример 1. Вычислить поток векторного поля А = (x-f- y)i
-[-(у— x)j-\-zk через поверхность единичного радиуса с центром
в начале координат.
Решение. Ранее мы решали эту задачу, вычисляя поток
непосредственно, исходя из его определения (см. пример 1 в § 7).
Решим снова эту задачу — на этот раз с помощью теоремы
Гаусса*Остроградского; для этого_вычислим сначала div А:
дх ' ду 1 oz
Итак,
П = П = ф div^V = ф 3dV - 3V = 34 к = 4к.
Пример 2. Вычислить поток поля сил тяготения
А
(я)3
через поверхность сферы с центром в начале координат радиуса
а с помощью теоремы Гаусса-Остроградского невозможно, так
как дивергенция разрывна при х = 0, у — 0, г = 0.
Заметим, что если бы мы попробовали, несмотря на это,
применить теорему Гаусса-Остроградского, то получили бы за-
ведомо неверный результат: в данном случае* div А — 0 (всюду,
* Для вычисления дивергенции данного поля в произвольной точке,
отличной от (0; 0; 0), надо записать это поле аналитически (в декартовой
системе координат):	_
_ ут ( xi + yj -Ь zk )
А----	з >
(х2 4- у2 + г2) 2
и применить формулу (1).
$8  37
Natalia и still.
кроме точки (0, 0, 0)). Поэтому мы получили бы n=fffdiv AdV—
= JJJOdV =0, что неверно, так как на самом деле П — —
(см. пример 2 на стр. 33).
Расхождение в результатах объясняется тем, что при вычис-
лении по теореме Гаусса-Остроградского мы не обратили внима-
ния на разрывность подинтегральной функции внутри области V;
следовательно, применять эту теорему в данном случае мы не
имели права.
Замечание. Формула Гаусса-Остроградского была выве-
дена нами в предположении, что граница области V (поверхность S)
удовлетворяет некоторым дополнительным условиям (см. сноску
на стр. 23). Теперь, используя векторный смысл формулы Гаусса-
Остроградского, можно освобо-
диться от этих ограничений (и тем
самым доказать, что теорема Га-
усса-Остроградского имеет место
при гораздо более широких усло-
виях).
а)	Пусть V — произвольная
область, ограниченная одной зам-
кнутой поверхностью S; допустим,
что область V можно разбить на
конечное число областей Vlt У2,..,
Vk, границы которых удовлетво-
ряют условиям, при которых была
доказана теорема; для определен-
ности будем считать, что область
V может быть разбита на две та-
кие области Vj и У2, ограниченные поверхностями Si и S2 (см.
рис. 19)., К каждой из этих областей теорема Гаусса-Остроград-
ского применима. Поэтому
Ш div Л dv = (л й) rfS; Iff div лау=	(Я л) dS.
vt	St	V2	-St
Поверхность Si состоит из двух кусков: So— общая граница
областей и У2 и S/— остальная часть поверхности Sx; анало-
гично разбивается поверхность 32 (на So и S2). Поэтому
JJ (An)dS = JJ (An)dS + JJ (An) dS,
S1	s+	с'
50	\
J J (А п)	= J J (А /г) rfS Ч- J j* (A n) dS.
Sq	s2
(2)
(3)
Часть I
Интегралы по поверхности So в равенствах (2) и (3) берутся в
разных направлениях (чтобы подчеркнуть это, мы обозначили
один из этих интегралов через J J, а другой — через JJ); эти
S0	-$0
интегралы равны друг другу по модулю, но противоположны по
знаку, поэтому при сложении они взаимно уничтожатся. Итак,
окончательно
JJJdivH dV = JJJ div>W7+ f jj dhMdV = Jf (Л n) dS
+ JJ =	JJ (4n)dS +JJ (An)dS +
Si	So	s;	So
+ Jf (Л n) dS = f f (ЛЙ) dS + fj pn) dS = J J (Л n) dS.
< < < ' '
Здесь мы учли, что поверхности Si и S2 в сумме составляют всю
поверхность S, ограничивающую область V.
Итак, формула
V	S
доказана для произвольной области, ограниченной одной поверх-
ностью.
б)	Теорема Гаусса-Остроградского допускает еще и дальней-
шее обобщение. Пусть область V ограничена несколькими поверх-
ностями— одной внешней поверхностью So и несколькими по-
Рис. 21
Рис. 20
знание без границ
$8
39
верхностями Slt S2,..., S„, ограничивающими область V изнутри
(рис. 20). Покажем, что теорема Гаусса-Остроградского остается
в силе и в этом случае.
Будем считать, для определенности, что область V ограни-
чена снаружи одной поверхностью So и изнутри — тоже одной
поверхностью Sj (рис. 21). Рассечем область V поверхностью 2
на две области и Г2. При этом область ограничена одной
замкнутой поверхностью, Составленной из поверхности So (часть
поверхности So), поверхности Si (часть поверхности SJ и поверх-
ности 2. Область V2 ограничена также одной замкнутой поверх-
ностью, составленной из So, Si и 2. Применяя формулу Гаус-
са-Остроградского отдельно к Vj и V2 получим:
JJJ divA/V = JJ(J5n)dS + Ц(Яп)а5 + Д(Лп)</5,	(4)
1	s0	-s'l
J f J div ЛГИ = JJ(^n)dS + JJ(^n)dS +jJ(Zn)dS. (5)
Sq	S|	e
Интегралы по поверхности 2 в равенствах (4) и (5) берутся при
различной ориентации поверхности 2, поэтому они равны по мо-
дулю, но противоположны по знаку. Складывая почленно ра-
венства (4) и (5) и учитывая, что интегралы по поверхности 2
сокращаются, получим:
И div AdV = И (4й)dS+ И ds-
V	So	St
где оба потока (по So и по S J берутся в направлении внешней
нормали к области V; заметим, что внешняя нормаль к области
V на поверхности S, направлена внутрь самой поверхности Sv
Обобщая полученный результат на произвольную область V,
ограниченную снаружи поверхностью So, а изнутри каким угод-
но числом поверхностей Slt S2,..., Sn, можно так переписать
формулу Гаусса-Остроградского:
Jjfdiv4dV =
=Jf (Лй)48 + JJ(^S)dS + jJ(^4)dS + ...+ (((Лп)йЗ.
So	St	S,	Sn
При этом следует помнить о том, что при вычислении потоков
по всем поверхностям So, Slt..., Sn следует брать направление
40	Часть I
нормали, внешней по отношению к области V (для поверхностей
SIt S2,..., Sn эта нормаль направлена во внутрь соответствую-
щих поверхностей).
§ 9. Соленопдальные поля
Если во всех точках некоторой области G дивергенция век-
торного поля (заданного в области G) равна нулю, то говорят,
что поле соленоидально в этой области.
Пример. Поле тяготения F — —соленоидально в любой об-
1Я|3
ласти G, не включающей начала координат. Действительно,
Р	7™* . Г ЧтУ 7 ynz Т.
Г —	з * 1	3	’ J	з * к>
(x2+t/2+z2)2	(x24-t/2+z2) 2	(x2+f/24-z2)2
непосредственным вычислением устанавливается, что
div F = 0
в любой точке, отличной от начала координат. С другой сторо-
ны, дивергенция в начале координат бесконечна. Это можно
установить, если воспользоваться определением дивергенции:
поток через сферическую поверхность радиуса а равен — Акутт,
отношение потока к объему шара, заключенного внутри этой
поверхности, равно ~	Переходя к пределу при
—3~ ла3
а -> 0, найдем дивергенцию в точке (0; 0; 0):
(divF)o,o,o=	= — оо.
д->0 и
Пусть область G такова, что любая замкнутая поверхность S,
лежащая в этой области, содержит внутри себя только точки
области G.
Таким свойством обладает, в частности, все пространство;
этим свойством обладает внутренность шара, внутренность эллип-
соида и т. д. Однако этим свойством не обладает, например,
область G, представляющая собой все пространство с одной вы-
колотой точкой: сферическая поверхность S с центром в этой
точке принадлежит области G, однако не все точки, лежащие
внутри поверхности S, принадлежат области G.
знание без ерениц
§10	41
Если область G обладает указанным свойством, то для того,
чтобы векторное поле, заданное в G, было соленоидальным, не-
обходимо и достаточно, чтобы поток через любую замкнутую
поверхность, принадлежащую к G, равнялся нулю.
Достаточность этого условия вытекает из самого определе-
ния дивергенции, а необходимость — из теоремы Гаусса-Остро-
градского.
В заключение рассмотрим один важный пример соленоидаль-
ного поля.
Жидкость называется несжимаемой, если объем, занимаемый
каким-либо количеством жидкости, не изменяется при переме-
щении этого количества жидкости. Иными словами, однородная
жидкость несжимаема, если ее плотность не изменяется с тече-
нием времени.
Всякая реальная жидкость (например, вода) практически
несжимаема (конечно, при условии сохранения постоянной тем-
пературы и при небольших давлениях).
Рассмотрим теперь стационарное движение несжимаемой
жидкости и докажем, что поле скоростей в этом случае солено-
идально. Для доказательства возьмем произвольную замкнутую
поверхйость S, расположенную в этом поле. В силу условия не- к
сжимаемости, количество жидкости, поступающей внутрь поверх-
ности S за единицу времени, равно количеству жидкости, уда-
ляющейся за то же время из области, ограниченной этой поверх-
ностью. Следовательно, поток через произвольную замкнутую
поверхность в этом поле равен нулю, а это означает, что дивер-
генция поля равна нулю во всех точках.
Итак, стационарное поле скоростей движущейся несжимае-
мой жидкости является соленоидальным полем.
§ 10, Циркуляция векторного поля по контуру
Рассмотрим векторное поле А — Pi + Qj -f- Rk и замкнутый
контур Z, расположенный в этом поле. Криволинейный интеграл
J Pdx 4- Qdy + Rdz называется циркуляцией векторного поля А по
контуру I.
Разумеется, циркуляция зависит не только от А и Z, но и
от направления обхода, принятого на контуре Z: изменив направ-
ление обхода, мы изменим и знак циркуляции.
Напомним известное из курса анализа определение криволи-
нейного интеграла: разбивая кривую Z на элементарные дуги
Д/ь Д/2,..., Д/л (дуги следуют друг за другом в направлении
обхода кривой Z), выбираем на каждой из них произвольным
42
Часть Т
образом по точке: М1г
следующую сумму, коч
Рис. 22
кций Р, Q, R по кривой
М2,...,» Mn (рис. 22). Затем образуем
рую назовем интегральной суммой'.
п
2 (Л (М*) 47*);
Л-1
здесь A (Mk) — значение вектора поля
в точке Мk, Д/д, — вектор, геометричес-
ки совпадающий с хордой, соединяю-
щей концы дуги Д/Л, причем направле-
ние этого вектора совпадает с выбран-
ном направлением вдоль кривой /.
Предел построенной интегральной
суммы при шах Д/д, -> 0 называется
криволинейным интегралом от фун-
/, или интегралом векторного поля А
по кривой /. Этот предел обозначается J Pdx+Qdy + Rdz, или
,f Adi. Таким образом,
Jah = lim 2й(7иЛ)д/;).
I max Д ^-*-0 Л=1
Если / является замкнутой кривой, то ^Adl называется цирку-
ляцией векторного поля А по контуру /.
Циркуляция векторного поля по контуру имеет простой фи-
зический смысл. Пусть векторное поле А является силовым по-
лем, и в этом силовом поле движется точка М по контуру /.
Вычислим работу, совершаемую точкой М при ее движении.
Для этого прежде всего заметим, что вся работа составляется
как сумма элементарных работ ЬТ1г ..., йТп, совершаемых
при перемещении вдоль элементарных дуг Д/х, Д/2,.. -,Мп. Каж-
дую же элементарную работу нетрудно вычислить, считая при-
ближенно отрезок Д/А прямолинейным, а силу вдоль этого от-
резка постоянной и равной ее значению в точке Л4Л. Тогда
ДТ*==|Л(М4)| • |д£|.соз(Л(Л1*), Д/,) = (A
Следовательно, вся работа может быть вычислена с помощью
следующего приближенного равенства:
7’=2дг*«2Р<Л1‘>-д7‘)-
Л=1	k= 1
flalattausin!.
знание без границ * w
_____________________________________________ 43
Это равенство будет тем точнее, чем меньше элементарные ду-
ги Д/А. При Д/й->0 оно переходит в точное равенство:
Т= ПтУ(Л(Л14).д74),
Д/.-+0
к k—0
т. ё.
Т = J Adi.
Итак, если А — силовое поле, то циркуляция поля по конту-
ру I равна работе, совершаемой при перемещении точки в этом
силовом поле вдоль контура I.
В анализе дается следующий метод вычисления криволи-
нейного интеграла J Pdx 4- Qdy -f- Rdz: пусть кривая I задана па-
раметрическими уравнениями: х = <?(/); у = <]>(/); з = х(0» гДе
/0 < t < Т; если направление обхода по кривой / соответствует
возрастанию параметра от t0 до Т, то
J Pdx -|- Qdy+Rdz=
i
= f№(0. Ш x(0) •?'(«) + <31? w. 9(0. x(01-9'(0 +
+ Я[<Р(0, Ф(0> X(01 • X' (0} di.
(1)
Если кривая / — замкнутая,
то криволинейный интеграл от
Pdx + Qdy 4- Rdz является цир-
куляцией^ векторного поля А=
—Pi 4- Qj 4~ Rk вдоль контура I
и тогда формулу (1) можно рас-
сматривать как формулу для
вычисления циркуляции.
Пример. Рассмотрим твер-
дое тело, вращающееся с по-
стоянной угловой скоростью <0
вокруг некоторой оси, напри-
мер вокруг оси Oz (рис. 23).
z
Скорость А каждой [точки вращающегося тела зависит от
положения этой точки. Исследуем векторное поле скоростей.
Обозначим через to — вектор, численно равный угловой ско-
рости ш и направленный по оси вращения в ту сторону, откуда
Часть I
вращение кажется совершающимся против часовой стрелки.
Тогда o) = (w-^. Вектор скорости А в любой точке М(х, y,z)
перпендикулярен к о и к вектору R — /?0, где R — радиус-век-
тор точки, Rq — радиус-вектор центра окружности, по которой
происходит вращение точки М\ вектор А численно равен <в • | R — Ro |-
Следовательно, вектор А равен векторному произведению векторов
и R — Ro:
(Здесь учтено, что =0, так как векторы <в и Ro распо-
ложены на одной прямой.)
Таким образом, Л = [шТ?] =
i j k	-	-
00 (О = — Ш'У •* + “-я
Вычислим циркуляцию поля А по следующей окружности С
радиуса а, лежащей в плоскости Оху.
' х — a cos ©,
у = a sin 0,
z = 0.
►
При этом направление обхода по окружности выберем так, чтобы
оно совпадало с направлением вращения (т. е. при обходе по
окружности параметр 0 возрастает от 0 до 2тг).
J A dl = J (— wydx	tnxdy) ~
с	с
2-гс
= У [—G)-asin6-(—a sin©)-]- <o-acos0-ncos0]dQ —
о
= 2<» • а2~ = 2<й • S,
где S — площадь круга.
Заметим, что циркуляция по любой окружности, лежащей в
плоскости Оху,также равна 2<oS (даже если центр этой окружно-
сти не лежит в начале координат). ..
С другой стороны, циркуляция по любой окружности, лежа-
щей в вертикальной плоскости, равна нулю; так, например,
циркуляция по окружности Cj
x = acos©, y~b, z = asin©
вычисляется следующим образом:
2п
У A dl — У (— <nydx + wcdy) = У — <о • b • (— a sin 0) dQ = 0.
c, ct	о
^alaHausX
знание без границ У *
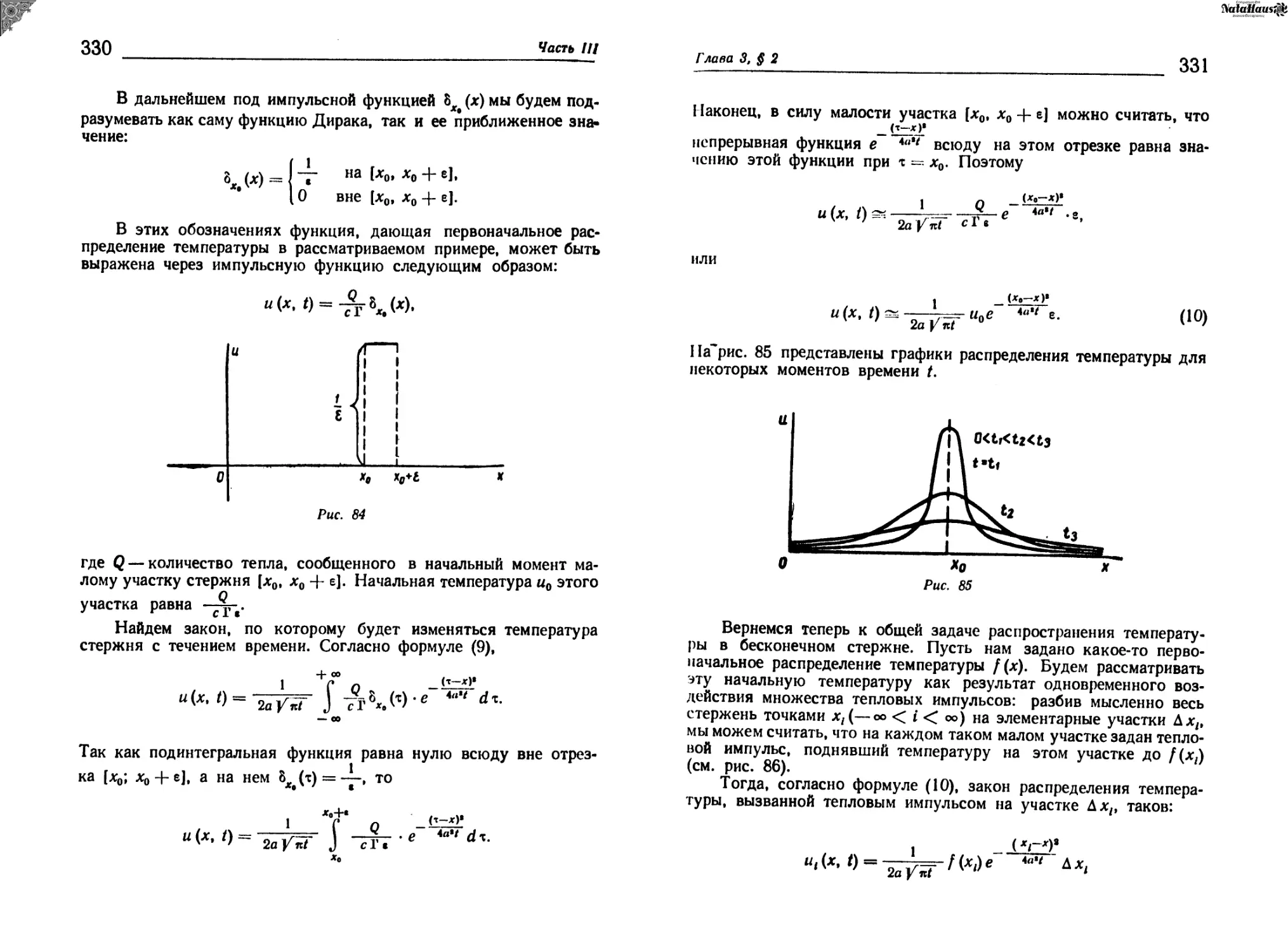
______________________________________ 45
$ 11. Формула Грина-Остроградского и теорема
Стокса
Рассмотрим плоский замкнутый контур I (расположенный,
например, в плоскости Оху) и область а, ограниченную этим
контуром. Пусть векторное поле А плоскопараллельно: любой
вектор поля параллелен плоскости Оху и не зависит от г, т. е.
А = Р (х, у) • i Q (х, у)' j, где Р и Q — непрерывные функции с
непрерывными частными производными первого порядка (всюду
в области о и на ее границе). Тогда циркуляция векторного по-
ля А по контуру I может быть выражена через двойной интег-
рал по области о:
I	<3 L	v J
(1)
Здесь интегрирование по контуру I совершается в положи-
тельном направлении, т. е. так, что при обходе по контуру в
этом направленнии область а остается сле-
ва от контура.
Формула (1), известная из курса ана-
лиза, называется формулой Грина (или фор-
мулой Грина-Остроградского). Докажем ее.
Предположим сначала, что область а
обладает следующим свойством: каждая
вертикальная и каждая горизонтальная пря-
мая, проходящая через какую-либо внутрен- ------1-------15--х
нюю точку области о, пересекает границу рис 24
области только в двух точках (см., напри-
мер, рис. 24). Такую область будем называть правильной. Пусть,
например, область а ограничена снизу линией у == ф (х), сверху—
линией у = ср (х), и пусть ее проекцией на ось Ох служит отрезок
[а; 6]. Вычислим интеграл da. Согласно правилу вы-
числения двойного интеграла, имеем:
„ „ _ b <f(x)	b	Аг=<р(л) —
И ара=И dydx =	У)] \ dx =
°	а <И*)	а	У=ф(х)
b	Ъ
= J Р (х, ср (х)) dx— J Р (х, ф (х)) dx.
а	а
(2)
Часть /
46
Ь
Интеграл J Р (х, <р (х)) dx равен криволинейному интегралу
а
J Р (х, y)dx, взятому по дуге АВ; это следует из формулы вы-
АВ
числения криволинейного интеграла (см. формулу (1) из § 10)
и из того, что уравнения х = х, у ~ (х) можно рассматривать,
как параметрические уравнения дуги АВ, где роль параметра
играет абсцисса х (причем а<х<6). Итак,
ь
f Р (х, <р (х)) dx = Г Р (х, у) dx.
а		АВ
Аналогично
ь
J Р(х, ф (х)) dx = у Р (х, у) dx.
Учитывая эти формулы, перепишем равенство (2) следующим
образом:
Заметим далее, что криволинейные интегралы от Р (х, y)dx,
взятые по вертикальным отрезкам ВГВ и AAV равны нулю. По-
этому написанное выше равенство можно переписать так:

изменив теперь направление движения вдоль АВ на обратное,
получим
УУ da = — И Pdx + У Pdx-}- У Pdx-}- J Pdx\ = — У Pdx,
С У	[вл	АА1	AtBi	В\В J Z
так как линии BA, AAlt AtBt и BJ3 образуют в совокупности
всю границу /, проходимую в положительном направлении.
Допустим теперь, что область а не является правильной, но
может быть разбита на конечное число правильных областей
^aldlfausiek
знание без ераниц W *
47
(например, на две правильные области; рис. 25). Покажем, что
равенство
= <3>
сохраняется и в этом случае. Действитель-
но,
°	°1	о»
 Применим к интегралам по правильным
областям и о2 выведенную формулу
(учитывая при этом, что граница об-
ласти состоит из дуги tr и отрезка
MN, а граница области с2 — из дуги /2
И отрезка NM):
Pdx — f Pdx;
MN
Складывая почленно эти равенства и замечая, что при этом ин-
тегралы по MN и по NM взаимно уничтожаются, получим
а	ад
da = — f Pdx — J Pdx =
Итак, равенство (3) справедливо не только для любой правиль-
ной области, но и для любой области а, которая может быть
разбита на конечное число правильных.
Совершенно аналогичным путем выводится формула
Л-a?do=J	и)
a	I
также справедливая для любой такой области с, которую можно
разбить на конечное число правильных областей.
Вычитая почленно из равенства (4) равенство (3), получим
формулу Грина-Остроградского
И[й-‘£]Ни'+‘>"'
Формула Стокса. Обобщим формулу Грина-Остроградского на
тот случай, когда I — произвольный замкнутый контур (а не только
плоский) и поле А — также произвольное (а не обязательно пло-
скопараллельное).
48
Часть I
Выведем, так называемую формулу Стокса, которая позво-
ляет свести вычисление циркуляции векторного поля А =
= Р(х, у,_ z) i -J- Q(x, у, z)j -pR(x, у, z)k по пространственному
контуру Z к вычислению интеграла по поверхности S, натяну-
той на этот контур.
Предположим, что контур
нение которой
может быть
26, то при
Z натянут на поверхность, урав-
записано следующим образом:
z — f {х, у). Обозначим эту по-
верхность через S, а ее проек-
цию на плоскость Оху — через
с. Очевидно, границей области
о служит замкнутая кривая к,
получающаяся при проектиро-
вании кривой Z на плоскость
Оху (рис. 26). Выберем опре-
деленное направление обхода
контура и проведем нормаль
п в какой-либо точке поверх-
ности, причем направим эту
нормаль в ту сторону, откуда
обход контура Z кажется совер-
шающимся против часовой
стрелки*. Если выбрать направ-
ление обхода контура так, как
проектировании на плоскость Оху
указано на рис.
обход по контуру X будет происходить в положительном направ-
лении (т. е. при обходе по контуру X область а будет оставать-
ся слева от контура). _
Пусть А = Р14- Q7+ Rk — векторное поле, заданное во всех
точках поверхности S. Будем считать, что Р, Q, R — непрерыв-
ные функции с непрерывными частными производными первого
порядка. Для того чтобы вычислить циркуляцию векторного по-
ля А вдоль контура Z, надо вычислить три криволинейных ин-
теграла:
f Ad i — f Pdx-[- Qdy + Rdz = J Pdx + J Qdy -f- J Rdz.
i	i	i	i	i
Рассмотрим, например, первый из этих интегралов; для этого
разобьем контур I на т малых дуг AZn AZ2,..., AZm и предста-
вим наш интеграл как предел интегральной суммы:
* Мы говорим в этом случае, что направление нормали п согласовано
с направлением обхода контура I.
NdtaHausfM
знание без границ
49
т
С (х, у, г) dx = lim £Р(хк, у„, z„)bxt =
Г	"*’» 4-1
т	*
= lim J P(xk, yk, f(xk, yk))bxk.
д^° k=l
(3)
После замены zk на f(xk, yk), под знаком предела оказалась ин-
тегральная сумма для функции двух переменных
Р(х, у, f(x, у)).
При этом точка (х, у) пробегает контур X (когда точка в прост-
ранстве (х, у, z) пробегает контур Z). Предел интегральной сум-
мы равен криволинейному интегралу от этой функции двух пе-
ременных по контуру X:
т
lim X P[xk, yk, f(xk, yk)]Axk = [P(x, y, f(x, y))dx.
ft=i	xJ
Следовательно, в силу равенства (3),
J Р (х, у, z)dx = § Р (х, у, f (х, у)) dx.
I	X
(4)
Применим к интегралу по плоскому контуру X формулу Грина-
Остроградского (см. (1)):
Jp (х, У, f (X, y)dx = — J J ~ P	(*’ y)1 d a. (5)
Производная, стоящая под знаком интеграла, является полной
производной. При ее вычислении следует учитывать не только
то, что Р непосредственно зависит от у, но и то, что Р зависит
от у через посредство z (где z — f (х, у). Поэтому по формуле
для полной производной имеем:
дР[х, у, f{x, у)] дР(х, у, z) । дР(х, у, z) ,
ду	ду	дг у
(6)
Заметим, что производная фигурирующая в правой части этого
равенства, берется только по у, входящему явно (т. е. при вы-
числении этой производной мы не принимаем во внимание зави-
5Q	Часть f
симость P от у через посредство z). Итак, учитывая (4), (5) в
(6), получим:
ШдР др ,
ду "Г dz 'Zy
da.
Перейдем теперь от интеграла по области а к интегралу по по-
верхности S. Для этого воспользуемся формулой (4) из § 4:
da ~
I
~dz2y IcosydS =
s
dP	dP ,	] ,c
---4-cos г	4- z cos 7 aS.
dy ‘	dz v ‘J
S
Учитывая (см. формулу (2) из § 4 и сноску к этой формуле), что
cos 7 =
1
zy
; cos p = —
получим: cos р =—2^-0057. Поэтому, заменяя в последнем ин-
теграле — 2у cos 7 на cos р, будем иметь:
kdj'=yj[-'^cosK+-^cos₽]‘is- <7>
I	I
Это равенство выведено нами в пред-
положении, что поверхность пересе-
л,2	кается каждой вертикальной прямой
не более, чем в одной точке. Одна-
/ s2 \ ко оно остается в силе и для лю-
хх7 бой поверхности, разбиваемой на
конечное число поверхностей ука-
занного вида.
Действительно, пусть, например,
I,	S разбивается на поверхности и
Sa линией /0, причем поверхности Sj
У и S2 пересекаются каждой вертикаль-
ной прямой только в одной точке (см.
рис. 27). Обозначим через / весь кон-
Рис. 27	тур поверхности S, а через 1Х и /2 —
^lalaHaustM
знание без границ *
те части I, которые примыкают, соответственно, к Sj и S2. Тогда
получим:	.
f Pdx = Н [“ Vos 4+₽]dS-
Zj+Zo	S,
f Pdx = ff [~^ cos 1 + 4?cos ₽] dS-
lt+l0	st
Направление обхода показано стрелками на рисунке.
При почленном сложении этих равенств криволинейные
интегралы по /0* взаимно уничтожаются (так как интегралы по /0
берутся в противоположных направлениях); интегралы по и
по /2 в сумме дадут интеграл по всему контуру /. Поэтому
+ (7)
Z	S
Итак, формула (7) справедлива для любой поверхности.
Аналогично этому можно вывести формулы, позволяющие
свести J Qdy и J* Rdz к поверхностным интегралам:
J Qdy = JJ [—	cos а+	cos 7 ]dS,	(8)
i	s
f№=ff[_^cosp+^cosa]ds- (9)
I	s
Почленно складывая равенства (7), (8), (9), получим формулу
Стокса:
JPdx + Qdy + Rdz = JJ{[-^ - -g]cosa +
z	s
dP _
dz	dx j
cosp 4-
-Д- cos T
nil I • I
(10)
Заметим, что формула Грина-Остроградского действитель-
но является частным случаем этой формулы: она получается из
формулы Стокса, если область является плоской областью, рас-
положенной в плоскости Оху. В этом случае § Rdz = 0, cosa=0,
z
52
Часть I
cosp = 0, cos7 = l и, следовательно, равенство (10) переходит
в равенство
I	s
т. e. в формулу Грина-Остроградского.
Пример. Рассмотрим поле скоростей точек твердого тела,,
вращающегося с постоянной угловой скоростью <оо вокруг оси Ог:
А = [<о /?] — — uQyi + <t)ox/
(см. пример на стр. 43—44). Вычислим циркуляцию поля А по про-
извольной замкнутой кривой /, лежащей в -плоскости, перпенди-
кулярной к оси вращения (т. е. в плоскости Оху или в плоскости^
ей параллельной):
J Adi = J — <оо ydx + ^xdy.
i	i
Применим к вычислению этого интеграла теорему Стокса, при-
няв в качестве S плоскую область, ограниченную кривой I (тогда
вектор нормали к поверхности равен k и поэтому cos а = cos р = 0,
cosy = 1). Следовательно,
J Adi = J — ^oydx 4- io0xdy=
i	i
=П ds=2ш« Пds=2“»s-
s	S
Этот результат уже получен ранее (см. пример на стр. 43—44)
для того случая, когда I являлась окружностью, лежащей в плос-
кости Оху.
Точно таким же путем можно установить, что если / — зам-
кнутый контур, лежащий в плоскости, параллельной оси враще-
ния, то J AdT~ 0.
§ 12. Плотность циркуляции векторного поля.
Ротор
Рассмотрим векторное поле А = Pi + Qj + № гДе P,Q,R и
их частные производные 1-го порядка непрерывны в точке Мо
и в ее окрестности.
____________________________________________ 53
знание без границ
Проведем через точку Л10 какую-либо поверхность S и на
этой поверхности построим замкнутый контур /, окружающий Мо
(рис. 28). Выбрав определенное направление на этом контуре,
вычислим циркуляцию
Ясно, что величина этого ин-
теграла зависит от контура
/ и, вообще говоря, стремится
к нулю при стягивании кон-
тура к точке Л10.
Отношение циркуляции
по контуру I к площади о
той части поверхности S, ко-
торая ограничена данным
контуром, называется средней
плотностью циркуляции.
Рис. 28
^Adl
Средняя плотность циркуляции равна —--
Если контур I стягивать к точке Л1о (так, чтобы при этом
контур все время оставался бы на поверхности S), то площадь о
стремится к нулю. Предел, к которому стремится при этом сред-
няя плотность циркуляции, называется плотностью циркуляции
в точке по поверхности S. '
§ Adi
Плотность циркуляции равна lim —------
1-М0	°
О)
Для вычисления плотности циркуляции в точке Л40 преобразуем
криволинейный интеграл в поверхностный (по теореме Стокса)
и затем применим теорему о среднем.
J Adi
Плотность циркуляции в точке Л10 равна lim —----------
/-л/0	°
J Pdx + Qdy -j- Rdz
= lim —--------------
54
Часть I
fnr^-^lcosa+Г^-^
J J НФ/ dz] l_dz dx
= Jim 1----------------------
..	л	Q
diama-^0
— cos 7)
Ф/J ‘J
----------da =
cosp 4-
== lim -		дЯ — dQ' _ ду dz _	cos a 4-	dP _ дЯ dz dx	cos p	dQ_ dP дх dy	cosy	^cp * ®
diama-*0
Здесь a, p, 7— направляющие углы вектора нормали к поверх-
ности S (направление нормали выбрано так, чтобы оно было со-
гласовано с направлением обхода контура /; см. сноску на стр. 48),
а Л1ср— некоторая промежуточная точка области о. При стягива-
нии площадки о точка Л4ср стремится к точке 7И0. При этом зна-
чение функции
Г дЯ dQ] । Г дР d/Я D . Г dQ dP]
--------cos а -Н -3-----*д~ cos В 4-	----5- cos 7
|_ ду dz J	[_ dz dx J г 1 L dx dy] 1
в точке Л4СР стремится к значению этой же функции в точке Л1о;
дЯ dQ
это следует из того, что, по условию, производные —,	...
непрерывны в точке Af0, а также из того, что направляющие
косинусы (cos a, cosp, cos 7) являются непрерывными функциями
точки М (мы предполагаем, что поверхность S является гладкой
в некоторой окрестности точки Л10).
Итак, плотность циркуляции в точке Мо равна
/ dR	dQ\	. ( дР	дЯ\ о .	( dQ	дР\	/оч
л----згЧ cos a	4-	---д— Icosp4-	-5^---cos 7.	(2)
\ ду	дг ]	1	\ dz	дх / r '	\ dx	ду/ *	4 '
Выведенная формула показывает, что плотность циркуляции
в точке Мо зависит:
от заданного векторного поля А = Pi + Qi 4~ Rk (в выраже-
дя dQ
ние для плотности циркуляции входят производные	...
UZ 4
в точке Л1о);
от вектора нормали п к поверхности S в точке Л40 (в вы-
ражение для плотности циркуляции входят направляющие коси-
нусы вектора нормали: cos a, cosp, cos 7).
Вместе с тем формула (2) показывает, что плотность цирку-
ляции в точке Л40 не зависит от поверхности S, а только от век-
тора нормали к этой поверхности. Иными словами, если через
точку Мо провести две различные поверхности Sj и S2, имеющие
один и тот же вектор нормали в этой точке, то плотность цир-
^alaHausA
знание без границ Ч
§ 12
55
куляции в точке Мо по каждой из поверхностей будет одна и
та же. Поэтому можно говорить не о плотности циркуляции по
поверхности S, а о плотности циркуляции в направлении векто-
ра п.	_
Плотностью циркуляции векторного поля А в точке Мо в на-
правлении вектора п называется плотность циркуляции в этой
точке по любой поверхности S, имеющей в качестве нормали
(в точке Мо) вектор п.	_
Итак, если А — Pi 4- Qj + Rk, п = cos а • i -f- cosp • /4-cos т-k,
то плотность циркуляции в точке Мо в направлении п равняется:
/ dR	dQ\	. / дР	др\	о । ( dQ	&Р\	/Q4
(-5---5^1 COS a-k 1-Х-5- COS В -к Нт* ч- COSY. (3)
\ ду	dz /	1 \ дг	дх )	г 1 \ дх	ду)	*	' *
Заметим, что выражение, стоящее в правой части равенства,
представляет собой скалярное произведение двух векторов: век-
тора i-cosa 4- J-cosp 4-^-cos y (это единичный вектор, направлен-
ный вдоль нормали п; обозначим его п0) и вектора
(dR __ г ( дР __ 0/^ - (dQ _ дР\ g
\ду dzj'\dz dx)l'\dx ду) ’
который зависит только от заданного поля А. Обозначим этот вектор
символом rot А (читается так: ротор векторного поля Д). С по-
мощью понятия ротора можно следующим образом переписать
формулу (3) для вычисления плотности циркуляции:
плотность циркуляции в точке Мо в направлении п равна
(rot А-п0 ).
Итак, плотность циркуляции в точке 7И0 в направлении п
। -I г -Л~ \
равна^ j rot Д | cos (rot Д, л0),аэто—проекция ротора на направле-
ние п. Следовательно, плотность циркуляции в направлении п
равна проекции ротора на это направление.
Отсюда ясно, что плотность циркуляции в точке Мо будет
наибольшей в направлении ротора, и в этом случае она равна
численному значению ротора. Таким образом, нами вскрыт смысл
ротора', это — вектор, в направлении которого плотность цир-
куляции в данной точке является наибольшей. Численно ротор
в данной точке равен наибольшей плотности циркуляции в этой
точке.
Ротор поля А
rotA = (w_^V+(aP_8R\7+(aQ_ эр\5 (4)
\ ду дг) \дг дх )• 1 \дх ду)	' '
56
Часть I
имеет вполне определенное значение (по величине и по направ-
лению) в каждой точке данного поля. Следовательно, сам ротор
образует новое векторное поле.
Пример 1. Вычислить ротор векторного поля А, заданного
равенством
А = (х2 + £/2) F+ + г2) / + (г2 + х2)Л.
Здесь
Р = х2 + у2, Q = уг + г2, /? = г2 + х2;
поэтому, по формуле (4), получаем:
rot А = (—2г) i + (— 2х) / + (— 2у) k.
В частности, в точке (0; 0; 1)
rot Л = — 21.
Значит, в этой точке плотность циркуляции является наибольшей
в направлении вектора — 21 (т. е. плотность является максималь-
ной, если циркуляцию вычислять по контурам, лежащим в плос-
кости Oyz\ иными словами, если брать различные контуры, ок-
ружающие точку (0; 0; 1), то, при одинаковых размерах площа-
док, ограниченных этими контурами, циркуляция окажется наи-
большей для контура, помещенного на плоскости Oyz).
Пример 2. Рассмотрим поле скоростей точек твердого тела,
вращающегося с постоянной угловой скоростью <»0 вокруг оси Oz
(см. пример 1 предыдущего параграфа). Как мы видели, это поле
задается формулой
А =— <»о^ + а>оХ/.
Следовательно, в любой точке
rot А = ((й0+«0) k = 2w0& = 2«.
Итак, ротор скоростей вращающегося твердого тела направлен
по вектору угловой скорости. Этого и следовало ожидать: в лю-
бой точке пространства циркуляция будет наибольшей по тем
контурам, которые лежат в плоскости вращения (т. е. в плоскости,
параллельной плоскости Оху).
Пример 3. Рассмотрим стационарное поле скоростей движу-
щейся жидкости.
Движение частиц жидкости, расположенных внутри некото-
рого малого объема, за небольшой промежуток времени можно
ftalatiauswk.
знание Вез границ “ ш
? 12 57
рассматривать приближенно как вращение твердого тела с по-
стоянной угловой скоростью. В самом деле, при вращении твер-
дого тела с постоянной угловой скоростью выполняются следую-
щие условия:
1)	расстояние между двумя фиксированными точками не ме-
няется с течением времени;
2)	траектории всех точек — окружности;
3)	движение по каждой такой траектории является равно-
мерным.
При произвольном стационарном движении жидкости эти ус-
ловия, вообще говоря, не выполняются. Однако за малый про-
межуток времени две близкие точки не смогут далеко отойти друг
от друга: за малый промежуток времени расстояние между ними
почти не изменится.
На небольшом участке пути траекторию любой частицы жид-
кости можно приближенно считать круговой.
За малый промежуток времени модуль скорости изменяется
лишь незначительно; поэтому в течение этого промежутка вре-
мени можно считать скорость постоянной по модулю.
Учитывая все сказанное выше, мы можем приближенно
считать движение жидкости в окрестности каждой ее частицы
круговым движением твердого тела. Поэтому с каждой точкой
той области, где происходит движение жидкости, можно связать
определенный вектор, численно равный угловой скорости в дан-
ной точке и направленный по оси вращения; этот вектор назы-
вают вектором угловой скорости в данной точке.
Дадим точное определение вектора угловой скорости.
Вектором со угловой скорости в точке М стационарного* поля
скоростей v движущейся жидкости называется вектор, равный
у rot v.
4 - 1
со = rot v.
At
Для частного случая, когда жидкость движется, как твердое
тело, вращающееся с постоянной угловой скоростью, это опре-
деление совпадает с обычным определением угловой скорости
вращающегося тела. Но и для произвольного стационарного дви-
жения жидкости понятие угловой скорости в точке также имеет
физический смысл: если в точку М поместить маленькую турбин-
* Можно говорить о векторе « угловой скорости и в том случае, когда
движение жидкости является нестационарным; однако, в этом случае вектор
<» зависит не только от положения точки М, но и от момента времени.
Вектор угловой скорости в точке М в момент времени t Называется вектором
мгновенной угловой скорости.
58
Часть I
I er
ку *, ось которой направлена по вектору со, то эта турбинка бу-
дет вращаться с угловой скоростью, численно равной <о (т. е. с
угловой скоростью, равной по модулю — | rot v |). Если же эту
турбинку поместить в той же точке М, но направить ось вдоль
какого-либо другого вектора п, то она тоже будет вращаться,
но с угловой скоростью, равной половине проекции ротора на п
(т. е. с угловой скоростью, равной половине плотности циркуля-
ции в точке М в направлении вектора п).
Не следует думать, что вектор угловой скорости в точке
обязательно должен быть перпендикулярен вектору линейной ско-
рости в этой точке. Так, например, если v = i-\-zj, то roto =—i,
-	1	7
о = rot v = — -х- и, следовательно, в данном случае вектор
«> не перпендикулярен v.
Однако в том случае, когда пЬле скоростей v является плос-
копараллельным (например, если вектор v всегда параллелен
плоскости Оху и не зависит ни по величине, ни по направлению
от z), то rot v перпендикулярен v и, значит, «> I v. Действитель-
но, если v = Р(х, «/)•?+ Q(x, у)-], то rot Б =	k, отку-
да следует, что rot v I v и, следовательно, w I v.
Если поле скоростей v плоскопараллельно и если, кроме того,
жидкость движется вдоль каждой траектории с постоянной по моду-
лю линейной скоростью (т. е. если | v | имеет одно и то же числовое
значение во всех точках траектории), то по виду траектории можно
судить о направлении и величине ротора. Так, например, если
при выполнении указанных условий одна из траекторий имеет вид,
изображенный на рис. 30, причем жидкость течет в направлении,
указанном стрелкой, то в точке вектор w (MJ перпендикулярен
плоскости чертежа и направлен к читателю; следовательно, так
же расположен и ротор в точке Mv В точке /И2 вектор о (MJ
направлен в противоположную сторону; это же верно и для rot v
в точке М2- Заметим, кроме того, что угловая скорость в точке М3
больше, чем в точке М1г поэтому
lrot'iL.>lrot‘'L-
• Под турбинкой мы подразумеваем совокупность нескольких плоских
лопастей, проходящих через одну и ту же ось и прочно закрепленных на
этой оси (см. рис. 29).
%г1ай<га$Ж
знание без границ * *
§12 59
Приведенный пример показывает, что в случае плоскопараллель-
ного движения с линейной скоростью, постоянной по модулю
вдоль каждой траектории, ротор велик там, где кривизна векторной
линии велика (например, в точке М2), и мал там, где кривизна мала
(например, в точке ЛД). Этим и объясняется название ротора
(от латинского слова rotare — вращать); этим же объясняется и
другое, часто применяемое название ротора — «вихрь поля».
Рис. 29
Следует заметить, что приведенные рассуждения остаются в
силе только для плоскопараллельного поля с постоянной по модулю
(вдоль каждой траектории) линейной скоростью. В случае же, если
эти условия нарушены, ротор поля может быть отличен от нуля и
там, где кривизна векторных линий равна нулю (например, там, где
векторные линии прямые). Так, например, если поле А задано ра-
венством: A — z(xi 4- yj-\~ zk), то все векторные линии этого поля
прямые, однако ротор отличен от нуля: rot Л — — y-i 4-х-/ =£ 0.
С другой стороны, существуют такие векторные поля, у которых
ротор во всех точках равен нулю, хотя векторные линии и не
являются прямыми (например, поле А — Zxy-i 4- х2-/).
Теорема Стокса в векторной форме. После того, как введено
понятие ротора векторного поля, можно сформулировать теорему
Стокса в более удобной форме. Для этого заметим, что в левой
части формулы Стокса стоит циркуляция векторного поля
А = Pi + Qj + Rk по контуру /, а в правой — под знаком по-
верхностного интеграла — скалярное произведение вектора
(dR dQ\7 . / дР дР\- . ( dQ дР\т .
I Sy -	+ Ь? ~ аГ/1 + (1? - 1)У)к (т-е- РотоРа векторного
поля) на единичный вектор нормали к поверхности S:
п = cos а • i + cos р •/-]- cos 7-k.
60
Часть I
Поэтому формула Стокса может быть записана так:
Adl^ JJ rot-MS,
s
где rot- А — проекция вектора rot А на нормаль к поверхности S.
Выражение в правой части равенства (5) является потоком
ротора. Поэтому формула Стокса может быть прочитана следую-
щим образом:
Циркуляция векторного ' поля по замкнутому контуру I
равна потоку ротора этого поля через поверхность, натянутую
на контур I.
При этом, конечно, направление обхода по контуру / и на-
правление нормали на поверхности должны быть согласованы
друг с другом.
£ 13. Правила действия над дивергенцией и ро-
тором
Дивергенция и ротор являются дифференциальными опера-
циями, аналогичными операции вычисления производной от функ-
ции одной переменной. Приведем основные правила действий
с этими операциями.
1.	Дивергенция и ротор постоянного вектора равны нулю.
Действительно, если А ~ ai + bj + ck, где а, b, с — постоян-
ные числа, то div Л =	4- 4- + 4- = 0. Аналогично проверяет-
ся ot/ oz	г
ся, что rot А = 0.
2.	Дивергенция и ротор обладают свойством линейности',
это значит, что если С = аА + ЬВ, где А и В — векторные по-
ля, а а и b — постоянные числа, то
divC = а • div А + b • div В;
rotC = a-rot А + b-rotB.
Проверим, например, первую формулу. Пусть А =	+
+ Qj + R& В = Р27 + Qj-f- R2k. Тогда С = (аРх + 6Р2) i +
+ («Qi + %) / + (a#i + bRJk, и
diV С = 4 (аР, + bPJ + ± (aQ, + Ы?2) + 4 («Я, + W2) =
\ дх 'ду ' дг J '	\ дх ' ду дг /
NatalfausMi
знание без границ * *
$ 14
61
3.	Рассмотрим, как вычисляется дифференциальная операция
от произведения двух функций, скалярных или векторных.
а)	Пусть и и v — два скалярных поля. Тогда поле uv также
является скалярным. В скалярном поле мы знаем только одну
дифференциальную операцию — градиент. Градиент произведения
мы уже вычисляли (см. выше, стр. 17).
grad uv ~ и • grad о + v • grad и.
б)	Пусть и — скалярное поле, А — векторное. Тогда произ-
ведение и-А является векторным полем. Можно говорить о ди-
вергенции и о роторе этого поля. Имеют место следующие фор-
мулы:
div и-Л = (gradw- Л) -|-M-div^;
rotu-Д = [grad и- Я] + u-rotA
Эти формулы можно проверить, предварительно представив А
в виде: А — Pi -|- Qj -]- Rk.
в)	Пусть Л и В — векторные поля. Тогда их произведение
можно образовать двояко: взяв скалярное произведение, мы по-
лучим скалярное поле (ДВ); взяв векторное произведение, по-
лучим векторное роле [Д-В]. Таким образом, можно говорить
о следующих дифференциальных операциях над произведением
двух векторных полей:
grad (ЛВ), rot [Вй], div [ЛВ].
Первые две из этих операций не могут быть выражены через
дифференциальные операции над каждым полем в отдельности
(т. е. для них не существует формулы, аналогичной формуле
для _производной от произведения). Что же касается операции
div [ДВ], то для нее имеет место формула
div [ДВ] = (B-rotД) — (Д-rotВ),
которая может быть легко проверена читателем.
£ 14, Безвихревое поле
Векторное поле, ротор которого тождественно равен нулю,
называется безвихревым.
Прежде чем сформулировать условия, необходимые и доста-
точные для того, чтобы поле было безвихревым, дадим одно оп-
ределение.
Часть I
Р
Рис. 31
Область V называется односвязной, если на любой замкну-
тый контур, расположенный в области V, можно натянуть по-
верхность а, целиком лежащую в области V.
Примеры. Все пространство, внутренность шара, шар с до-
бавленными точками границы, все пространство, из которого вы-
колота одна точка, — являются односвязными областями.
Пространство,- из которого исклю-
чены все точки, лежащие на некото-
рой прямой (например, исключена ось
/ д) является неодносвязной областью,
(rot к) м0 *ракже неодносвязной областью являет-
ся внутренность тора («бублик»).
Докажем следующую теорему.
Теорема Г. Для того чтобы по-
ле, заданное в односвязной области
V, было безвихревым, необходимо и дос- '
таточно, чтобы циркуляция по любо-
му контуру, лежащему в этой области,,
равнялась нулю.
Доказательство
чность. Пусть j
z
контуру I, лежащему в V. Докажем, что
Достато-
AdT = 0 по лю-
бому замкнутому
rot А — 0 в любой точке области V.
Допустим противное. Предположим, что нашлась точка Мо,.
в которой rot Л отличен от нуля. Обозначим модуль ротора в
этой точке через а; так как ротор в этой точке не равен нулю,
то а > 0.
Проведем плоскость Р через точку 7И0 перпендикулярно к
вектору (rotH)Mo (рис. 31). Обозначим через и нормаль к плос-
кости Р, а через rot—Л — проекцию ротора на эту нормаль:
rot—Л — скалярная функция, определенная в точке Мо и в ее
окрестности; очевидно, что в самой точке Л40 имеет место ра-
венство:
(го^л)м. = 1го‘лк = а-
Если считать rot Л непрерывной векторной функцией*, то и
rot- Л — непрерывная функция. Поэтому около точки Л40 мож-
* А это так, если А=Р i -b QTRk, где Р, Q, R имеют непрерыв-
ные частные производные 1-го порядка.
^ataHausrik
знание без границ “ *
$ 14
63
но описать такую окрестность а (на плоскости Р), что всюду в
этой окрестности значения функции rot—А отличаются от значе-
ния этой же функции в точке Л40 менее чем на ; но тогда
всюду в этой окрестности будет rot— 4>-|-.
Пусть / — контур этой окрестности. Применим к циркуля-
ции вектора по этому контуру теорему Стокса (в векторной фор-
ме):
j Z = JJrot-Л do >-|-а > О,
I	G
где а — область, ограниченная контуром /.
Таким образом, предположив, что rot А 0 хотя бы в од-
ной точке, мы пришли к противоречию (нашелся контур /, цир-
куляция по которому отлична от нуля, что противоречит усло-
вию);
Итак, если J Adi = 0 по любому контуру /, то rot Л = О
всюду в области V.
Необходимость. Пусты rot 4 = 0 всюду в области V.
Рассмотрим произвольный замкнутый контур L, лежащий в
области V, и докажем, что
j*4d/ = O.
L
Для этого натянем на L поверхность S; в силу односвязности
области V, это можно сделать так, чтобы поверхность S цели-
ком принадлежала области V.
Применим теорему Стокса в векторной форме:
Adi = JJrot-4dS = 0;
последнее равенство основано на том, что по условию rot 4=0,
а следовательно, и проекция ротора на п тождественно равна
нулю.
Итак, если rot 4 = 0, то Ad 1 — 0 для любого замкну-
того контура L. Теорема доказана.
Независимость криволинейного интеграла от пути интегри-
рования. До сих пор мы рассматривали интеграл f 4 dlтолько
64
Часть I
по замкнутым контурам L. Откажемся от этого ограничения и
изучим некоторые вопросы, связанные с интегралами по произ-
вольному (не обязательно замкнутому) пути интегрирования^
Пусть задано векторное поле А. Будем говорить, что СЛ d I
L
не зависит от пути интегрирования, если, каковы бы ни были
две точки ТИх и М2 (расположенные в поле), величина интегра-
ла по дуге оМх М2 не зависит от вида этой дуги (но, конечно,
зависит от точек и М2).
Выясним необходимые и достаточные условия независимос-
ти криволинейного интеграла J A dl от пути интегрирования.
Теорема 2. Пусть векторное поле А задано в односвязной
области. Для того чтобы интеграл J Adi не зависел от пути
L
интегрирования, необходимо и достаточно, чтобы поле А было
безвихревым.	
Доказательство. Достаточность. Пусть rot А = 0. Тог-
да J A d7 — 0 для любого замкнутого контура (см. теорему 1).
Возьмем две произвольные точки ТИх и М2 и проведем две ду-
ги MxPM2 и	(рис. 32). Если обоз-
, л	начи?ь через L весь замкнутый контур
MjQM2PMlt то получим
// J	JZd/ = O;
L
Mi	J Adi + J ЛЛГ=0. (1)
M2QM2	M2PMt
Puc. 32
Ho
J Adl=— J Adi.
M2PMt	MtPM2
Поэтому равенство (1) можно переписать так:
J Ad7 — J AdI—0,
MiQM2	mjpm2
или
f AdT = f AdT.
MtQM2
M2PM2
Таким образом, доказана независимость интеграла от пути.
Необходимость. Пусть интеграл \AdТ не зависит от пути.
L
Тогда интеграл по любому замкнутому контуру С равен нулю;
это легко проверить, если взять на контуре С какие-либо две
точки и М2 (рис. 33); по условию, j Ad
MtAMs
куда следует, что§AdT — 0. Но если интеграл
с
по любому замкнутому контуру равен нулю,
то rot Л = 0 (см. теорему 1).
Итак, теорема 2 доказана полностью.
Пример 1. Поле А = (3x2^2z + Зх2 )i -|-
+ 2x3^z7+(xV + 3z2)Ai,
MtBMi
н
8
Рис. 33
определенное во всех точках пространства Oxyz, является без-
вихревым (легко проверить, что rot А = 0). Следовательно,
J A d I = 0 по любому замкнутому контуру L. Если же вычис-
лять этот интеграл по незамкнутым контурам, то он, вообще
говоря, не равен нулю, но от вида пути интегрирования не за-
висит (а зависит только от начальной и конечной точек этого
пути).
Пример 2. Поле сил тяготения, порожденное точечной при-
тягивающей массой, помещенной, например,.в начале координат,
(Х2+^2+22)3/г
является безвихревым полем, что легко проверяется вычислени-
ем. Поэтому циркуляция этого поля по любому замкнутому
контуру L равна нулю:
J A d I = 0.
L
Но циркуляция силового поля по замкнутому контуру равна
работе, совершаемой этим полем (при перемещении точки еди-
ничной массы по контуру £); следовательно, работа силового
поля тяготения по любому замкнутому контуру равна нулю.
Следует заметить, что это утверждение остается верным не
только для поля тяготения, образованного притягивающей то-
3 Ю. С. Очан
66
Часть I
Ж'-
iw' ’
чечной массой, но и для любого поля тяготения в односвяз-
ной области V (даже если это поле порождено не точечной мас-
сой, а какой угодно притягивающей массой, расположенной вне
области V).
§ /5. Потенциальное поле
Пусть векторное поле А является полем градиентов для не-
которого скалярного поля <р:
А = grad ср.
Скалярное поле называется потенциалом векторного поля А.
Возникает вопрос: всякое ли векторное поле А является
полем градиентов некоторого скалярного поля? Иными словами,
всякое ли векторное поле Л имеет потенциал? Как будет показа-
но позднее, ответ на этот вопрос отрицателен. Если векторное
поле А имеет потенциал, то оно называется потенциальным. До-
кажем теорему, дающую условия потенциальности векторного
поля A=Pi	(где Р, Q, R — непрерывные функции с
непрерывными частными производными_первого порядка).
Теорема 1. Для того, чтобы поле А было попгенциальным, Л
необходимо и достаточно, чтобы оно было безвихревым.
Доказательство. Необходимость. Пусть А = grad <р =
=	’ -J- |“/+	. Непосредственно вычисляя rot А и учитывая
при этом известную из анализа теорему о равенстве смешанных
rntT— /д8<р а8<р I f д8Ф d8<p \J . / ds<p д2<р Q
ГО1 л -	^[дхдг dzdx J J [дудх . дхду.) к
Итак, если А — grad ср, то rot А = 0; иными словами rot grad ср=О.
Достаточность. Пусть rot А — 0. Тогда \Adl не зависит
от пути интегрирования L. Закрепим начало дуги L (в качест-
* По условию, все составляющие вектора А имеют непрерывные част-
д2<р д2<р
ные производные; следовательно^ все смешанные производные , дудх
н т. д. непрерывны.
NalaHausiisk
знание без границ “ *
§15	''.............	. ;, ...	. - *........................... -	67
ве начала этой дуги примем какую-либо фиксированную точку
ЛТ0(х0, у0, г0), лежащую В данном поле, например, начало коор-
динат). Тогда интеграл J Л сП будет зависеть только от второго
L
конца дуги £; пусть этот второй конец дуги находится в точ-
ке М(Х, Y, Z)*. Запишем интеграл следующим образом:;
х, Y, Z
§AdT= J Р dx + Qdy -|- Rdz.
L	x0,y0,z0	!
Обозначим величину этого интеграла через <р(Х, У, Z):
X, Y, Z
<P (X, У, Z) = J Pdx 4- Qdy + Rdz,
Xo,yo,zo
и докажем, что grad<p = 71.
Для этого вычислим сначала
оХ
д<Р _ lim <p(X4-ft,y,Z)-<p(X,y,Z) _
дХ ~ J™	h
X+h,Y,Z	X, Y,Z
J Pdx 4- Qdy^- Rdz— J Pdx + Qdy 4- Rdz
_ Ijin	. *<h #<м Зе
A->0-	h
Так как эти интегралы не зависят от пути, то в первом из
/ X-\-h,Y ,Z\
них
в каче стве пути можновзять.. путь интегрирова -
,z0 /	'	’	'	- - 		 tSj ‘	.
ния второго интеграла с добавлением ^прямолинейного отрезка,
соединяющего точки 7И(Х, У, Z) и Mi(X + h, У, Z) (рис. 34).
Поэтому	? : , i
X,Y,Z X+h,Y,Z X.Y.Z
d<? _	^o.Zo X,Y,Z x0, ye,za
dx ~ J/™.	—T	—
X+h, Y,Z	' -
= lim	--
h~0	h
* Координаты точки М (конца пути интегрирования) обозначим пропис-
ными буквами, чтобы не смешивать с текущими координатами переменной
точки на кривой L.	
3*
68	Часть I
Для того чтобы подсчитать последний интеграл, напишем пара-
метрические уравнения отрезка ММ^.
х = х, y=Y, z =Z,
причем переменный параметр х пробегает значения от X до
X + Л; величины у и z вдоль отрезка ММ± постоянны.
Рис. 34
Применяя способ вычисления криволинейного интеграла,
получим
X+h, Y, Z	X+h
j Pdx 4- Qdy + Pdz= J P (x, Y, Z) dx.
X,Y,Z	X
X+h-
J P(x, Y, Z)dx
Поэтому | =	------Л-------•
Применяя к последнему интегралу теорему о среднем и перехо-
дя к пределу при h -> 0, получим
= lim Р (S.y.Z)KX + ft)-Xl = iim р у, Z) = р (X, Y, Z).
ол h->0	п	Л-0
Здесь £ заключено между X и X 4- h и, следовательно, стре-
.мится к X при h -> 0. При переходе к пределу мы учли непре-
рывность функции Р.
sjs 69
знание без границ
Итак, А = Р (X, Y, Z); аналогично доказывается, что
^- = <2(X,y,Z); А=Я(Х,У,2).
Следовательно,
grad 9=^-Г +	+ ^-k = Pl+Q~j + Rk = A.
Таким образом, мы доказали, что поле А является потенциа-
льным. Одновременно мы нашли способ построения потенциала
поля А: если А = Pi + Qj + Rk (причем rot Д = 0), то потенци-
ал вектора А вычисляется с помощью следующего криволиней-
ного интеграла:
х, у, z
<р(Х, Y, Z) = J Pdx + Qdy + Rdz,	(1)
%<>t Mot zo
где (x0, y0, z0)— произвольная фиксированная точка. Ясно, что
точку (х0, у0, z0) можно выбирать по-разному; таким образом,
мы получим различные функции <p(X,Y,Z). Однако все они
отличаются друг от друга только постоянным слагаемым.
С вопросом о разыскании потенциала векторного поля тес-
но связан вопрос о восстановлении функции трех переменных
по ее полному дифференциалу.
Пусть дано дифференциальное выражение Pdx + Qdy + Rdz,
где Р, Q, R — непрерывные функции трех переменных с непре-
рывными частными производными. Из предыдущей теоремы сра-
зу вытекает следующий результат:
Теорема 2. Для того чтобы выражение Pdx 4- Qdy + Rdz
было полным дифференциалом некоторой функции <р(х, у, г),
необходимо и достаточно, чтобы ротор векторного поля Pi-{-
Qi Rk был тождественно равен нулю.
Доказательство этой теоремы основано на том утверждении,
что если dq — Pdx-}- Qdy -g Rdz, то grad 9 = Pi Qj Rk, и, об-
ратно, если grad 9 = Pi -g Qj 4- Rk, to J9 = Pdx Qdy -j- Rdz.
Отсюда виден и способ восстановления функции по ее пол-
ному дифференциалу: для того чтобы найти <р(х, у, г), доста-
точно применить выведенную выше формулу (1).
Заметим, что формула (1) дает нам простой способ вычис-
ления криволинейного интеграла от полного дифференциала
Pdx + Qdy + Rdz в том случае, когда известна функция 9 (х, у, г),
дифференциал которой равен Pdx -j- Qdy 4- Rdz.
70
Часть I
Пусть надо вычислить
Хг, У1, Z,
J Pdx + Qdy 4- Rdz.
Xt. У1, Z,
Так как, по условию, функция <р(х, у, г) является потенциалом
векторного поля Pi 4- Q j + Rk, то она может отличаться только на
постоянное слагаемое от функции
J Pdx + Qdy + Rdz:
xt, ух,2х
x, у, 2
cp(x, у, z)-\-C— J Pdx 4- Qdy 4- Rdz.
'	xx, Vi, ZM
Определить С легко, если в качестве точки (х, у, г) взять
(*i. Уъ 21):
хх, ух, Zi
<р (xi. У1> 21) 4- С = J Pdx 4- Qdy 4- Rdz = 0,
Xi, У1, Zi
откуда C = — <p(xi, ylt z^.
Итак, для всех точек (х, у, z) справедливо равенство:
х, у, г
<р(х, у, г) —ср (Xi, ylt zt) = j Pdx 4- Qdy 4- Rdz.
Xi, yx, zt
Оно остается верным, если в качестве (х, у, z) взять точку
(^2> У^1 2г)*	,
Xt, Уг, 2Х
У Pdx 4- Qdy 4- Rdz = ср (х2, у2, г2) — ср (хи ylt zY).
Xi, Vi, Zi
i
Мы получили формулу, которая является аналогом извест-
ной формулы Ньютона-Лейбница.
Интеграл в границах от точки М± до точки М2 от пол-
ного дифференциала функции ср(х, у, г) равен разности значе-
ний этой функции в точках М2 и Mv
В заключение рассмотрим физический смысл теорем, дока-
занных в этом параграфе.
Как мы видели, работа (см. пример 2 на стр. 65), совер-
шенная полем сил тяготения при перемещении точки по замкнутому
'________	71
МаИашЖ
знание без границ - *
контуру в односвязной области, равна нулю. Аналогичным
свойством обладают также некоторые другие силовые поля (нап-
ример, электростатическое поле). Такие силовые поля обладают
тем свойством, что их ротор ра-
вен нулю (см. § 14). Каждое из
таких полей является полем гра-
диентов для некоторого скаляр-
ного поля <р(х, у, z) (определен-
ного однозначно с точностью до
постоянного слагаемого). Это ска-
лярное поле и будет потенци-
алом данного силового поля. Раз-
ность значений потенциала в точ-
ках Л43 и дает величину работы,
совершаемой силами поля при
перемещении точки единичной
массы из Afx в Л12 (физики назы-
вают разность значений потенци-
ала <p(M2) — ф(Л11) коротко «раз-
У
ностью потенциалов»).
Пример 1. Найти потенциал векторного поля
А = (Зх2 + 2ху) i 4- (х2 + 2у + 2)/ + (у + 3z*) k.
Легко проверить, что это поле является безвихревым (rotA=0).
Следовательно, оно имеет Потенциал <р. Для того чтобы его
найти, достаточно вычислить криволинейный интеграл:
х, y, z
<Р (X, У, Z) = J (Зх2 + 2ху) dx 4- (х2 4- 2у 4- z) dy + (//+Зг2) dz,
взяв в качестве точки (х0, уй, 20), например, начало координат,
а в качестве пути интегрирования — любую линию, соединяю-
щую точки (0, 0, 0) и (X, У, Z), например прямолинейный от-
резок или ломаную, изображенную на рис. 35 (напомним, что
этот интеграл не -зависит от пути интегрирования). Вычисляя
интеграл, находим
<р(Х, У, Z) = Xs 4- Х2У 4- У2 4- ZY + Z3.
Итак, потенциалом поля А является функция <р = х3 4- xsy 4-
4~ У2 4~ гУ 4- z3, а также любая функция семейства
9 = х3 4- х2у 4- у3 4- zy 4- z3 4- С.
72
Часть I
Заметим, что для вычисления потенциала по его градиенту нет
необходимости прибегать к криволинейному интегралу. Покажем
это на нашем примере.
Так как,для искомой функции?, grad? = А, то
%=3х‘ + 2ху; ^=^ + 2</ + г;|? = г/+ЗЛ (2)
Проинтегрируем почленно по х первое из этих равенств:
Это интегрирование мы должны провести по переменной х, счи-
тая у и z постоянными. Поэтому интеграл найдется с точностью
до слагаемого, не зависящего от х; однако, это слагаемое —
постоянная интегрирования — может зависеть от у и г. Обозна-
чая его z), получим
9 = х3 4- х*у + <]> (у, г).
(3)
Чтобы найти ф(г/, г), возьмем частную производную от ? по у
из равенства (3) и приравняем ее к из равенств (2):
= у2 1 ^(у, г)
ду	ду
= х2 + 2у + г»
откуда z^-- = 2y + z.
Интегрируя по у и учитывая,
что
постоянная и тегрирования не зависит от у, но может зависеть
от z, получим
О/. 2) = J (21/ + Z)dy = у2 + zy + X (2),
где х(г)~ пока неизвестная функция от z.
Подставляя ^(у, г) в равенство (3), получим:
Ф = х3 + х2у + у2 + гу + х (2).
(4>
Остается найти х(г)* Для этого находим^ из равенства (4) и
приравниваем к из равенств (2):
# + x'(z) = */ + 32!2,
откуда х (z) — z3 4- С.
ftatattausw.
знаниебезфаниц У *
Sis 73
Итак, окончательно
<Р(Х, у, г) = х3 + х2у + у2 + zy + z3 + С.
Пример 2. Найти функцию <р по ее полному дифференциа-
лу:
dy = (3x2?/2z 4- Зх2) i + 2x3yz j 4- (х3 у2 4- 3z2) k.
Выражение в правой части этого равенства является полным
дифференциалом некоторой функции. Действуя так же, как и в
предыдущем примере, находим:
= х3 + x3y2z + z3 С.
Пример 3. Дано поле сил тяготения, образованное точечной*
массой т0, расположенной в начале координат. Найти работу,
совершенную в этом поле при перемещении точки М единичной
массы из положения (х„ ylt zj в положение М2 (х2, у2, z2).
Поле сил тяготения, образованное точечной массой т0, на-
ходящейся в начале координат, может быть аналитически зада-
но следующим равенством (см. стр. 6):
(х2 4- 1/2-р Z2) 2
Это — потенциальное поле. Работа Т, совершенная на пути от
точки ЛМ*1, Уи г1) к точке М2(х2, у2, z2), равна следующему
интегралу:
(х„ yt, z,)
т— С	xdx + ydy-±zdz
1 — J — 7	-----------з~ *
(Xt, yt, 20	у
(х24-1/в 4- z2)х
Подинтегральное выражение является полным дифференциалом
функции --------——, что видно непосредственно. Поэтому,
(xa4-i/2 za)2
согласно обобщенной формуле Ньютона-Лейбница, имеем:
х,. yt, г,
7*_____________________________7fz7o___	_
1	J_
(х2+«/24-г2)2
74
Часть I
где ра и pj — расстояния точек М2 и от начала координат.
Функция <р ------——j— = является потенциалом
(ЛН’ + г>)Т |Л|
данного силового поля. Разность ее значений в точках М2 и
Mi дает величину работы при переходе от Afx к М2.
§ 16.	Криволинейные координаты
До сих пор, желая задать аналитически скалярное или век-
торное поле, мы пользовались декартовой системой координат.
Так, например, скалярное поле мы задавали с помощью функ-
ции трех переменных; этими переменными были абсцисса, орди-
ната и аппликата переменной точки пространства. Однако ясно,
что задание абсциссы, ординаты и аппликаты точки является не
единственным способом определения положения точки в прост-
ранстве. Это можно сделать и иным способом, например, с по-
мощью криволинейных координат.
Пусть по некоторому, вполне определенному, правилу каж-
дой точке М пространства однозначно соответствует некоторая
тройка чисел (qlt q2, qa), причем различным точкам соответствуй
ют различные тройки чисел. Тогда говорят, что в пространстве
задана система координат; числа qt, q2, qa, которые соответст-
вуют точке М, назовем координатами (или криволинейными ко-
ординатами) этой точки.
В зависимости от того правила, по которому тройка чисел
fai, q2, qa) ставится в соответствие точке пространства, говорят
о той или иной системе координат.
Если хотят отметить, что в данной системе координат по-
ложение точки М определяется числами qv q2, qa, то это запи-
сывают так: M(qt, q2, qa).
Пример 1. Пусть в пространстве отмечена некоторая фик-
сированная точка О (начало координат) и через нее проведены
три взаимно перпендикулярные оси с выбранным на них мас-
штабом (оси Ох, Оу, Ог). Тройке чисел х, у, г поставим в соот-
ветствие такую точку М, что проекции ее радиус-вектора ОМ
на оси Ох, Оу, Ог равны, соответственно, числам х, у, г. Такой
способ установления зависимости между тройками чисел (х, у,
г) и точками М приводит нас к хорошо известной декартовой
системе координат.
Легко видеть, что в случае декартовой системы координат
не только каждой тройке чисел отвечает определенная точка
пространства, но и, обратно, каждой точке пространства соот-
ветствует определенная тройка координат.
^alaliausjSk
знание без ераниц W
§16 75
Пример 2. Пусть в пространстве снова проведены три оси
Ох, Оу, Ог, проходящие через фиксированную точку О (начало
координат).
Рассмотрим тройку чисел г, ср, г, где г > 0, 0<<?<2 тс, и по-
ставим в соответствие этой тройке чисел точку М такую, что ее
аппликата равна г, а ее про-
екция на плоскость Оху имеет
полярные координаты г и ф
(рис. 36). Ясно, что здесь каж-
дой тройке чисел г, ср, г соот-
ветствует определенная точка
М и, обратно, каждой точке М
отвечает определенная тройка
чиселг, ср, г, где г > 0, 0 < ср <
<2тг, — со < » < -f- со (за ис-
ключением того случая, когда
точка М лежит на оси Ог: в
этом случае гиг определены
однозначно, а углу ср можно
приписать любое значение).
Числа г, ср, z называются
цилиндрическими координата-
ми точки М.
Рис. 36
Легко установить связь между цилиндрическими и декар-
товыми координатами точки:
x=rcoscp, y = rslncp, z — z	(1)
и г = V х2 4- у2 ; ср = arctg г = г.	(2)
Пример 3. Введем сферическую систему координат.
Зададим три числа р, 0, ср, характеризующие положение
точки М в пространстве, следующим образом: р— расстояние
от начала координат до точки М (длина радиус-вектора), 0 —
угол между положительным направлением оси Ог и радиус-век-
тором ОМ (широта точки М), ср — угол между положительным
направлением оси Ох и проекцией радиус-вектора на плоскость
Оху (долгота точки М).
у
♦ Строго говоря, ф — arctg — только, если у > 0; х > 0. Если х < 0
Л
у
(при любом z), то ф = я -р- arctg —; если же х > 0, у <0, то ф = 2я -р
У	У
-р arctg —— . Впрочем, во всех случаях tgф = — .
X	X
76
Часть I
Ясно, что и в этом случае не только каждой точке со-
ответствует определенная тройка чисел р, 0, у, где р > 0, 0<0<тг,
О < <р < 2к, но и обратно, каждой такой тройке чисел отвечает
определенная точка пространства (снова за исключением точек
оси Ог, где эта однозначность нарушается).
Легко найти связь между сферическими и декартовыми
координатами точки (рис. 37):
x = psinOcosy, у = р sin Osin <р, z = pcosO	(3)
и р= Ух2 + у2 4 z2; 0 — arccos г --------------; ср — arctg . * (4)
Вернемся к произвольной системе координат (qlf q2, qa).
Будем считать, что не только каждой точке пространства отве-
чает определенная тройка чисел (glt q2, qa), но и, обратно, каж-
дой тройке чисел отвечает определенная точка пространства
(при этом, как мы видели на примерах, область изменения чи-
сел Vi. Яз иногда приходится ограничивать; например, в сфе-
рических координатах р принимает не всевозможные значения,
а только такие, что р > 0; широта 0 — не всевозможные значе-
ния, а только ограниченные неравенством 0 < 0 < к, и т. д.).
Введем понятие координатных поверхностей и координат-
ных линий.
• См. предыдущую сноску,
Специально Оля	_
МДаНаиэЖ.
знание Сез ераниц * *
SJ6 77
Множество тех точек, для которых координата qt постоян-
на, называется координатной поверхностью qx. Аналогично
определяются координатные поверхности qa и qa (рис. 38).
Очевидно, что если точка М имеет координаты С2, Ся,
то в этой точке пересекаются координатные поверхности:
Qi — Cii Яг — С2, q» ~ Оа»
Множество тех точек, вдоль которых изменяется только
координата qx (а остальные две координаты q2 и qa остаются
неизменными), называется координатной линией qa. Очевидно,
что всякая координатная линия qt является линией пересечения
координатных плоскостей q2 и qa. Аналогично определяются
координатные линии q2 и qa.
Пример 1. Координатными поверхностями (по координате х)
в декартовой системе координат являются все плоскости х =
= const (они параллельны плоскости Oyz). Аналогично определя-
ются координатные поверхности по координатам у и z.
Координатная х-линия — это прямая, параллельная оси Ох\
координатная #-линия (z-линия) — прямая, параллельная оси Оу
(оси Ог).
Пример 2. Координатными поверхностями в цилиндричес-
кой системе являются любая плоскость, параллельная плоскос-
ти Оху (координатная поверхность г — const), поверхность кру-
гового цилиндра, ось которого направлена по оси Ог (коорди-
натная поверхность г const) и полуплоскость, ограниченная
осью Ог (координатная поверхность у =. const) (рис. 39).
Название «цилиндрическая система координат» объясняется
тем, что среди ее координатных поверхностей имеются цилинд-
рические поверхности.
Координатными линиями в этой системе являются г-линия —
прямая, параллельная оси 0г\ <р-линия — окружность, лежащая
в горизонтальной плоскости с центром на оси 0г\ г-линия —
луч, выходящий из произвольной точки на оси Ог, параллель-
ный плоскости Оху.
Пример 3. Координатными поверхностями в сферической
системе координат служат сферы с центром в начале коорди-
нат (поверхность р = const), полуплоскости, ограниченные осью
Ог (поверхности <р — const) и конические поверхности с образую-
щими, составляющими постоянный угол с положительным на-
правлением оси Ог (поверхности О ~ const) (рис. 40).
Так как среди координатных поверхностей имеются сферы,
то эту систему координат называют сферической.
Координатные линии здесь таковы: р-линия — луч, выходя-
щий из начала координат, 0-линия — полуокружность с центром
78
Часть I
в начале координат, соединяющая две точки на оси Oz; у -ли-
ния — окружность, лежащая в горизонтальной плоскости, с цен-
тром на оси Oz.
Во всех рассмотренных выше примерах координатные ли-
нии, проходящие через какую-либо точку, ортогональны друг
другу. Это бывает далеко не во всякой системе координат. Од-
нако мы ограничимся «изучением только таких систем координат,
для которых это имеет место; такие системы координат назы-
ваются ортогональными.
Система координат (ft, q2, qa) называется ортогональной,
если в каждой точке М координатные линии, проходящие через
эту точку, пересекаются под прямым углом.
Рассмотрим теперь какую-нибудь точку М и проведем еди-
ничные векторы ft, е2 и е9, касающиеся в этой точке
соответствующих координатных линий и направленные в сторо-
ну возрастания соответствующей координаты. Если эти векторы
в каждой точке образуют правую тройку, то мы говорим, что
нам задана правая система координат. Так, например, декарто-
NalatiauslSi
знание без границ \ *
$ 16  79
ва система координат х, у, z (при обычном расположении осей)
является правой (см. рис. 41, а). Также являются правыми ци-
линдрическая система координат г, ф, z (но именно при. этом по-
рядке координат; если изменить порядок следования координат,
взяв, например, г, г, ф, мы ужр не получим правой системы);
(см. рис. 41, б).
Сферическая система координат также является правой (ес-
ли установить такой порядок следования координат: р, 0, ф);
см. рис. 41, в.
Рис. 41
Заметим, что в декартовой системе координат направление
вектора ех не зависит от того, в какой точке М мы проводим
этот вектор; то же самое справедливо и относительно 'векторов
еу и е/. Иное мы наблюдаем в криволинейных системах коор-
динат: так, например, в цилиндрической системе координат век-
торы е<р в точке М и в какой-либо другой точке Мх уже вовсе
не обязаны быть параллельными друг другу. То же относится и
* Обычно тройку ортогональных единичных векторов в декартовой сис-
теме координат ех, еу, ег обозначают через i, ~j, k. Этими обозначения-
ми мы уже пользовались неоднократно.
Часть I
80
к вектору ег (в разных точках он имеет, вообще говоря, разные
направления).
Таким образом, тройка единичных ортогональных векторов
q, е2, е3 в криволинейной системе координат зависит от поло-
жения точки М, в которой эти векторы рассматриваются. Трой-
ка единичных ортогональных векторов et, е2, е3 называется по-
движным репером, а сами эти векторы — единичными ортами
(или просто ортами).
Коэффициенты Ламе. Рассмотрим точку М с координатами
qlt Яг> Яз и соседнюю с ней точку	Д^, q2, q3). Обе эти
точки лежат на одной и той же координатной ^|-линии. Рас-
смотрим отношение длины дуги о/ИМ, этой линии* к прира-
щению координаты qt
ношение имеет предел
коэффициентом Ламе
значается через Нр
о Д4Л11
(т. е. к числу Д^): -	. Если это от-
при Д^! -> 0, то этот предел называется
для координаты qt в точке М\ он обо-

= lim
Д41
где М (qlt q2, qa), Мх (qx + Lqv q2, q3). Ясно, что коэффициент
Ламе, вообще говоря, зависит от положения точки М. Поэто-
му мы будем его обозначать иногда следующим образом:
0/1» Яъ> Яз)-
Точно так же определяется в точке М
для 2-й координаты:
коэффициент Ламе
Н2 ~ lim
Mi ’0
^ММ2
Д?Э
где M(qlt q2, q3), M2(qlt q2 + &q2,q3) и дуга MM2 берется
координатной линии q2.
Аналогично этому коэффициент Ламе определяется
третьей координаты:
ВДОЛЬ
и для
Н, = lim .
* Координатная фрлиния является направленной кривой (направление
на этой линии выбирается в сторону возрастания координаты qd. Поэтому,
в соответствии с соглашением, принятым ранее (см. стр. 9), будем считать
дугу oMMi положительной, если точка следует за точкой М (т. е. ес-
ли Д<?1 > 0), или отрицательной, если точка Mj предшествует точке М (т. е.
если Д<?1 < 0).
Аналогичное замечание о знаке дуги имеет место и для дуг, лежащих
на координатных ^-линиях и ^-линиях.
^atattausiVii
знание без ераниц * *
§ 16 81
Зная коэффициенты Ламе, можно приближенно подсчитать
длины дуг координатных линий при небольших приращениях ко-
ординат. Действительно, если Д^, &q2, hq3 малы, то из опреде-
ления коэффициентов Ламе вытекают следующие приближенные
равенства:
„ ~	_ ^ММ2 „ _ оЛ1Л13
Д91 ’	2	^2 ’	3	’
откуда
^MM2~H2-bq2\	- Н3<Дд8, (1)
где значения коэффициентов Ламе Hv Н2, Н3 берутся в точке М.
Выясним, чему равны коэффициенты Ламе в различных
конкретных системах координат.
1.	В декартовой системе координат все коэффициенты Ламе
(Нх, Ну, Н2) в любой точке равны единице. Действительно, ес-
ли, например, придать х приращение Дх, то величина направ-
ленного отрезка координатной линии, заключенного между точ-
ками М (х, у, г) и (х -|- Дх, у, z), равна Дх. Поэтому
Hr = lim = lim — 1. Аналогично находим И., и Н2.
Дх-.О йХ Дж -0 йХ	у
Итак,	Нх = 1; Ну = 1; Н2 = 1.	(2)
2.	В цилиндрической системе координат коэффициенты Ламе
таковы:
Hr = 1; Н9 = г; Нг = 1.
Убедимся в этом, например, для Нг (рис. 42) *:
= lim	аг .
Г Дг-»0 Дл
Аналогично для Hv :
Hv = lim
v д^о д?
= lim .
дг-0 Дл
= lim =
д^о д<?
(3)
Таким же путем убеждаемся, что Н2 = 1.
* Для определенности на рисунках 42 и 43 мы придаем координатам
положительные приращения; однако ясно, что это не ограничивает общности:
изменив знак, например, у Дг, мы изменим знак и у	но в таком случае
знак отношения —-А—— не изменится.
82
Часть I
3.	В сферической системе координат коэффициенты Ламе
таковы:
Hf = 1; Н» = р; = р sin 6.	(4)
^ММ
Действительно, Hv = lim—т—но = psin 0Д<р
д<р-о а<Р
(рис. 43). Поэтому
и .. psin0-A<p .
= lim -—т—1 — psin 0.
*	Д-Р-.0 А? Г
Далее
Др
= lim -7-
Др-0 Ар
Н. = lim —т—-
Р Др->0 Ар
§ 17. Скалярные и векторные поля
в криволинейных координатах. Вычисление
градиента с помощью криволинейных
координат
Если в пространстве задана система координат qv q» qa, то
всякое скалярное поле можно представить аналитически с по-
мощью функции трех переменных
w=/(<71,	<7з)-	(О
ftataHauswl'
знаниебезграниц ч*
9 17	83
Для того чтобы представить аналитически векторное поле И в
том же пространстве, надо задать в каждой точке пространства
проекции вектора А на единичные орты elt е* ёа. Но вектор Л
зависит от положения точки М (qv q2, <?8); следовательно, от ко-
ординат этой точки зависят и проекции вектора Л; иными сло-
вами, каждая из этих проекций является функцией от трех пе-
ременных qlt q2, qa:
проекция	Л на et	равна	(qlt	q2,	qa)',
проекция	Л на са	равна	Л2	(qlt	q2,	qa);
проекция	Л на еа	равна	Л8	(qlt	q2,	qa).
Поэтому
Л = Л1 (qlt q2, qa) + Л2 (qlt q2, qa) ea + Aa (qlt q2, qa) ea. (2)
Следует заметить, что здесь не только числовые коэффици-
енты Ль Л2, Л8 зависят от положения переменной точки
М (qv qa, qa), но и направления ортов е2, еа зависят от точки М.
Градиент в криволинейных координатах. Пусть скалярное
поле задано равенством (1). Поставим задачу о вычислении гра-
диента этого поля в любой точке M(qlt q2, qa).
Прежде всего найдем проекцию градиента на вектор ev
Как известно, проекция градиента на какое-либо направление
равна производной в этом направлении; поэтому
, г df
пр^ grad / =	.
*	det
С другой стороны, известно, что производная по направлению
равна производной по любой дуге, касающейся этого направле-
ния; в частности, производная по направлению et равна произ-
водной по дуге / координатной <?глинии (если направление на
дуге выбрать в сторону возрастания координаты q^; итак,
пр- grad f =	= -2-.
Но производная по дуге, по определению, равна следующе-
му пределу (рис. 44):
dl
= lim
AG-M
вдоль I
MMi
84
Часть I
откуда
д/ li'm И<714-А<71, <7г. <7з) —/(<71. <7а. <7»)
Ы ~ д
Умножая и деля последнюю дробь на Д^ и учитывая, что
lim ^*1. _ /ур получим
df i:~. /(<714- Д<71. <72. <7») —/(<71. <72. <7з)	д<71	_ df 1 /Q4
dl ~	д<71	' о ММ, “ dq, Нх ’
делания
Рис. 44
Следовательно,
. с	1 df
проекция gra d f на равна .
Аналогично:
. с	1 df
проекция grad / на с2 равна тт—/—,
** 2	^?2
1 г	I df
проекция grad / на са равна	.
Итак,
. .	1 df - . 1 df - .	1 df -
®rad f = 77? ^e‘ + 77?	+ 7Г, A/,'’'
(3)
Если, в частности, поле задано в декартовой системе ко-
ординат: u~f(x, у, г), то (так как Нх — Ну = Нг = 1)
grad и — i 4-	/ 4- ~г~	(За)
ь	Ох 1 dy 1 ' dz	' '
Если поле задано в цилиндрической системе координат:
и = f (г, ср, z), то, учитывая выведенные ранее значения коэф-
фициентов Ламе Нг, , Нг, получим
. df - , 1 df - . df -
grad и ~ —г~ e. 4----------V- ev 4- —r- ez.
b	dr r 1 r dtp v 1 dz z
(36)
NataHausjisb
знание без ераниц * *
§ 18  85
Если же поле задано в сферической системе координат, то
. df - . 1 df - .	1 df - ч
grad и =	<?₽ H----H-----------л------ev . (Зв)
b	dp p 1 p d0	p-smB dtp *	' '
Если нам надо вычислить производную скалярного поля
u = f(qltqit qa) в точке М в направлении некоторого вектора
s = Ci + а2с2 + аз(,з> достаточно спроектировать градиент на
направление $:
сц du а2 du a3 du
du __ (grad u-s) Hi dqi H2 ’ dq2 Л/8 8дя ,
ds Is I	|/ a* a* +°*
Читатель может самостоятельно выписать частные случаи этой
формулы в конкретных системах криволинейных координат.
Замечание. Если дано скалярное поле и, то его аналити-
ческая запись в различных системах координат будет различна;
различными будут и аналитические записи для градиента. Од-
нако все эти различные формулы для градиента задают одно
и то же векторное поле: ведь grad и в каждой точке простран-
ства определен однозначно и не зависит от способа аналити-
ческой записи исходного поля и. Это свойство градиента назы-
вают инвариантностью градиента относительно выбора системы
координат.
§ 18. Интегральные и дифференциальные
операции над векторным полем
в криволинейных координатах
Пусть векторное поле А задано в криволинейных коорди-
натах:
А = Ai (qt, q2, qa) ct + Д2 (qt, q2, qa) e2 + Д3 (glt q2, qa) ea. (1)
Над этим полем можно произвести дифференциальные операции—
операции нахождения дивергенции и ротора — и интегральные
операции — вычисление криволинейного интеграла (в частности,
вычисление циркуляции), вычисление потока и нахождение по-
тенциала поля (в случае, если rot А -- 0).
Начнем с вычисления интегральных операций.
Вычисление криволинейного интеграла векторного поля. Мы
ограничимся тем случаем, когда путь интегрирования совпадает
86
Часть I
с некоторым участком координатной линии. Пусть, например,
нам надо вычислить
pTd7,
где вектор Л задан равенством (1), аг линия /—-участок коор-
динатной ^-линии, причем на этом участке координата qx меня-
ется в границах от а до Ь.
Для вычисления интеграла разобьем дугу / точками
Мя,..., обозначим, кроме того, начальную и конечную
точки дуги через Мо и Мп; тогда
_ _	п— 1 __	_
ГЛЛ_= lim AWM,,
I	maxp/J-O />e0
где A/z = MtMl+x. Заметим, что так как все точки Mz лежат на
координатной ^рлинии, то эти точки будут отличаться друг от
друга только значениями первой координаты qx, значения же
координат q2 и q3 остаются неизменными вдоль всей линии /.
Поэтому можно записать координаты точек Mt следующим об-
разом:	q2, q3). Разность первых координат в точках
и о означим Д q\,i. Далее, векторы MtMi+i можно счи-
тать направленными по касательной к координатной линии I в
точке Mf, поэтому
Д/, =	-ё.а ё,.
Следовательно,
Т(М,) • ДI, = [Л, (М,) ёг + А, (М,) ё, + Л, (М,) ё,| • И, (М,)Д91,, ё, =
л-1
и	(Л(М)<И= lim £л(Л1,)Д/“ =
/	max|A/z|- о /=0
л-1
= lim Ел,(А1,)Я,(М,)Д9м =
max|MIZ|->°z„0
л—1
= lim YiA1(ql,l,qi,q3)‘Hl(qlti,qi,qa)^qi,i.
тах|д vi ,/|~°
Под знаком предела стоит интегральная сумма для функции
одного переменного qx (две остальные координаты q2 и q3 по-
ftatatlauswk
знание без границ ч *
§ is 87
стоянны). Предел этой интегральной суммы равен определенно-
му интегралу по переменному (в границах от а до Ь). Итак,
ь
fЛ(М) dl = J Ах (qlt q2, q3) Щ (qlt q2, q3)dqt.	(2)
l	a
Рис. 45
Это и есть формула для вычисления криволинейного интеграла, если
путь интегрирования— некоторый участок координатной ^-линии.
Аналогично записываются
формулы и в том случае, когда
путями интегрирования слу-
жат участки координатной
да-линии или ^3-линии.
Если же надо вычислить
циркуляцию по замкнутому
контуру, составленному из
дуг координатных линий, то
мы разбиваем весь контур на
участки, вдоль которых из-
меняется только одна из
координат, вычисляем интег-
ралы по этим участкам и
затем складываем резуль-
таты.
Поток векторного поля
через поверхность. Здесь мы
ограничимся вычислением потока П через поверхность S, являю-
щуюся частью координатной поверхности (например, частью
^-поверхности). Общего случая произвольной поверхности S мы
рассматривать не будем.
По определению потока, он равен JJ (А п) dS. В данном
случае, единичный вектор нормали к поверхности S совпадает с
± е3 (так как, по условию, S лежит на ^-поверхности). Выбе-
рем перед е3 знак плюс (т. е. будем вычислять поток в направ-
лении вектора е3). Тогда
(А п) = (А^ + Ая е2 + А3 е3) • е3 = А3.1
Поэтому
П = (A n)dS = A3(qlt q2, q3) dS.
Для того., чтобы вычислить последний интеграл, разобьем повер-
хность S на элементарные площадки сетью координатных линий
88
Часть I
(рис. 45). Тогда, переходя к интегральной сумме (и учитывая,
что на поверхности S координата q3 постоянна), получим
П = JJ>43(<71»	Чз)dS = lim \ Ла(Mi.k) AS/.*.	(3)
5	diani jf-*0 i I,
Здесь Mi,k — точка пересечения двух координатных линий: t-ой
дглинии и &-ой <?2-линии. Символом AS/,* обозначен криволиней-
ный прямоугольник, стороны которого лежат на координатных
линиях, а вершины находятся в точках Mi,k\ М/-н,*; М/,*+ь
ЛТ/4-1. Л4-1 .
Обозначим координаты /И/.* так: Mi,k (q\,i, qz.k, Чз)> а при-
ращения координат и q2 при переходе от Mi,k к соседней вер-
шине элементарной площадки AS/,* обозначим Aq\,i и Д^2.*-
Далее, заметим, что AS/,* является (с точностью до беско-
нечно малых более высокого порядка) прямоугольником со сто-
ронами: Mt,k М/_|-1,* и М/,* /И/,*4-|. Длина каждой из сторон
легко вычисляется с помощью коэффициентов Ламе:
Mi,k Mi,k+\ ~	bq\,i = Hl(q\,i, q-i,k, Чз)^Ч^,1
Mi,k M/+i,* ' H2(q\ti, q~i,k, <7з)А<?2,л«
Поэтому
AS/,* = H^qij, q2.k, Чз) ^2 (Ч\,ь 42.k, Чз) fyi.i ^42,k-
Подставляя это выражение в (3), получим
П = lim ^A3(qi,i, qt.k, Чз) #i(<7i,b 42.k, Чз) X
lk
max ^0
X Я2(<7!./, 42,k, g3)A<7i,/А72.*.
В правой части этого равенства стоит интегральная сумма для
функции двух переменных (qt и q2); ее предел равен двойно-
му интегралу по этим переменным. Для того чтобы расставить
границы интегрирования в этом интеграле, надо знать, как из-
меняются координаты qt и q2, когда переменная точка пробега-
ет область S. Пусть, например, при постоянном qt координата
q2 пробегает все значения от 9(7,) до ф (<7f); пусть, кроме того,
полное изменение q{ будет от а до b (рис. 46). Тогда, в соответ-
ствии с теорией двойного интеграла, мы можем написать:
Ь
п = j У Л(<71.	Чз)Н1(Ч1> Ч2> 9аЖ(<71. Чг> 4s)dqidql. (4)
a f(fli)
^ataHauswk
знание без араниц W *
$18	89
Формула (4) несколько упрощается, если область S ограничена
координатными линиями; так, например, если q2 изменяется от
с до d при любом (рис. 47), то
ь d
п = j J Л(71. Я*> Яз)^1(Яь Яг. Яз) (71. 72. 7з) dq2dqv (4')
a с
Аналогично формуле (4) (или формуле 4') вычисляется поток
через часть (/^поверхности или через часть ^-поверхности.
Пример. Вычислить поток векторного поля А=р20(?р+ре2н(?н
через верхнюю полусферу S с центром в начале координат ра-
диуса а (в направлении внешней нормали сферы).
Рис. 46
Здесь поверхность S является частью координатной р-по-
верхности (в сферических координатах). На S координата 0 ме-
няется от 0 до (при любом <р), а полное изменение <р — от
О до 2г. Поэтому, если учесть, что И» -= р, — р sin0 и что
на поверхности S имеет место р = const (р а), получим
II
2п 2
ApdS = f J a20-a-asin0d0d<p =
оо
2к	к	2тг
= а4 [ (— 0 cos 0 + sin0Jo2 dy — а4 |	— 2га4.
Вычисление дивергенции векторного поля. Для того чтобы под-
считать дивергенцию векторного поля
^1 (71. 7г»7я)^1	(71. 7г» 7з)^2“Ь Aa(^I, q2, Яз)^з. (0
90
Часть I
воспользуемся ее определением:
SS(An)ds
div А — lim ——v—
v-м v
где V — область, включающая точку М, a S — поверхность, ог-
раничивающая
м0
Рис. 48
эту область; предел берется при стягивании об-
ласти V к точке М. Так как этот предел
не зависит от формы области V (лишь
бы эта область включала точку М), вы-
берем ее наиболее удобным для вычисле-
ний способом. Для этого проведем коор-
динатные линии через точку М и на этих
линиях отложим (в сторону возрастания
соответствующей координаты) дуги MMit
ММ2, ММ3. Затем на этих дугах построим
криволинейный параллелепипед («ребра-
ми» которого являются дуги координат-
ных линий, а «гранями» — куски коорди-
натных поверхностей, рис. 48). Если дуги
ММЪ ММ2 и ММ3 достаточно малы, то
их можно приближенно считать отрезками прямых. Поэтому, в
силу ортогональности координатной системы,
V ММХ • ЛШа • Л1М8.
Подсчитаем теперь, чему равны ребра этого параллелепипеда. Ес-
ли координаты точки М таковы: M(Qlt д2, 7з). то точки Mlt М2,
Ma определяются следующими координатами:
М1(71 + д71. 7г. <7э).	(71» 7г + д7а. 7з). ЛМ71. 7г. 7з+д7з)-
Поэтому (см. формулы (1) на стр, 81)
ММj =* H^qlt ММ2 H2bq2, ММ3 ss Н3Ьд3 *.
Итак,
V ~'Н&Н^д^Ьд*
Вычислим поток векторного поля через поверхность S (границу
области V). Поток П через всю поверхность является суммой
потоков через 6 «граней» параллелепипеда; вычислим эти потоки.
• Мы пишем Aft, а не |Д<71|, так как Д<71 >0 (дугу ММХ мы от-
кладывали на координатной линии в сторону возрастания координаты <7i).
Аналогично для &q2 и Д<?8.
§J8	91
IXalattaus',
Вычислим сначала поток через пару противоположных гра-
ней MMi М\ Ма и Ма/И0М0 М'2. Для этого применим форму-
лу для вычисления потока, выведенную выше (стр. 89):
П,= JJ (An)dS= —
ММ,м\ Mt
<7»+д9» 0»+д<71
<?•	91
Чз> Яз) Н j О/i Яз Яз) X
х H3(qlt q2, q3)dqidqa,
___	9.+д9» 9i+^9i
П2 = И n)dS= J J A2(qlt q2 + &q2, q3) X
4* Vl
X Н^Яз + A^2. Яз) H3(qi> Яз + ^43)d4i dqa.
Знак «минус» в первом из этих интегралов поставлен потому,
что поток через поверхность ММХ М\ Ма берется не в направ-
лении вектора е2, а в противоположном (так как внешняя нор-
маль всюду на этой поверхности равна — е2). Заметим, кроме
того, что на каждой из этих поверхностей вторая координата
постоянна (на поверхности ММХМ\М3 она равна q2, а на по-
верхности М2М0М0М2 она равна q2 + Д(?2). Сложим вычислен-
ные потоки (т. е. найдем поток через пару площадок MMt М\Ма
и М2 Мо М0М2):
9.+д9.9|+д91
J J	• ^2dqtdq3.
Здесь мы применили под интегралом теорему Лагранжа о ко-
нечных приращениях к функции А2 Нх На (по переменной q2).
Для того чтобы завершить вычисление П2 + Щ, проще все-
го было бы применить теорему о среднем к полученному двой-
ному интегралу; однако этого делать нельзя, так как
в подинтегральную функцию, кроме qt и qa, входит также q2> ко-
торое уже не постоянно, а зависит от qlt q3. Поэтому приме-
ним следующий прием. Пусть функция (А2Н1Н3) (которая
предполагается непрерывной) достигает в нашем прямоугольном
92
Часть /
параллелепипеде наибольшего значения р и наименьшего т. Тогда
наш двойной интеграл заключен между интегралами:
9.+д9« 91+д91
9»	91
mbq2 dqx dq3 и
91+^91 91+^91
J	J	dqt dq3,
Ч»	9i
т. е. между числами
mbqi bq2 bqa и р.д<71 д?2 д«7э-
Иными словами,
т- Aft Д^2 Д<7з < П2 + П,’ < ц-Д?! Д^2 д<7з.
или
па + и;
д<71 Дq2 &q9
Так как т — наименьшее, а у.—наибольшее значение непрерыв-
ной функции в параллелепипеде, то в этом параллелепипеде найдет-
ся точка Л4ср, такая, что в ней эта функция в точности равна
промежуточному числу
щ-ьп;
Д(71 Д<7Я Д<78 ’
т. е.
4-(AMtws)
(ty2 ' 2	1 Мер
па + п;
Д^Д^Ддз ’
П, + п;= (А я, И,)	 д?1 д<?2 д?,.
иуа	Мер
Аналогично вычисляются потоки через другие пары противопо-
ложных граней:
Hi + 111 ~ (А Нз) йср • д<71 Д<7и Д<7з.
П3 + П3 —	(Л8 Н£ Н2) = • Д^1 Д^2 д9з»
Мер
где Мср и МСр — какие-то точки, лежащие внутри параллелепипеда.
Итак, весь поток через замкнутую поверхность, ограничивающую
параллелепипед, таков:
п = и (А «1 ад |яр + -к н°> к
+ ^г(4а//1Н2)|Яр}д<71Д?,Д<7,.
§ 18	 93
знание без границ Ч’Ь
Беря отношение этого потока к объему параллелепипеда и затем
устремляя Aft, Д^2» к нулю, получим дивергенцию в точке М:
div А ==
^-(А,НгН.) -	+	+ ±(А,Н,Н,)\- |а91Дд,Д?,
oqi_________™cp дд2_______________дда_______________ImcpJ________
Hi Н2 Я8-Д<71Л<72Д<7»
Д<7,-0
д^.-о
Итак,
=	1 р (AiH2Ha) д (А2 На) д (Л8 Hi Н2) |
Hi Н2 На I dgi ' дда ' дда J
где все частные производные и коэффициенты Ламе вычисляют-
ся в точке М. Это и есть формула для вычисления дивергенции
в произвольной системе координат.
В частности, если поле задано в декартовой системе коор-
динат:
А = АЛ (х, у, z)-i + Ау (х, у, z) -j 4- Аг(х, у, z) • k,
то
div А = “ +
дх 1
, дАг
ду ' dz '
(5а)
Если поле задано в цилиндрической системе координат:
Л = Л, (г, <р, г) ег + Л9 (г, <₽, z)+ Аг(г, ?, г) ёг,
то (учитывая, что Hr = 1, Hv = г, Нг = 1) получим
div А =	+ Г ^.1.	(56)
г | дг 1 dtp 1 dz J	' '
Если поле задано в сферической системе:
А = АР (р, 0 ,<р) ер + Лн (р, 0, ср) ён + Av (р, 0, <р) ,
то (так как Hf = 1, Ян = р, Н? ~ psinB)
А Г-Л 1	РЦ>-Р3). ni <SillH) ,	1
div Л = -д- . „а {-------sin 0 Н-----------р -4--р } • (5в)
р1 sin Н ( др	1 дв 1 ' д<р 1 J
Пример 1. Вычислить дивергенцию векторного поля сил тяго-
тения, созданного массой т, расположенной в начале координат.
94
Часть I
Мы уже рассматривали это поле и выяснили, что его мож-
но аналитически записать следующим образом (см. стр. 5—6):
7/п (х i + yl 4- zk)
з •
(х*+ »•+«•)2
или
т/п R
1₽18
(6)
(6)
Первый способ аналитической записи данного поля позволяет,
конечно, найти его дивергенцию в любой точке. Однако, как
мы видели (см. стр. 36), это приводит к громоздким вычисле-
ниям.
Запишем это же поле с помощью сферических координат,
учитывая, что ef направлен вдоль радиус-вектора R, и что по-
этому
Я = рер, а |/?| = р:
R Т m Р - _ тт ~
И’ “	9 ~	₽• р’
Применяя к этому полю формулу (5в), получим
1 * (-4 • р’)
divF——а J-ь •	• sin6= pasine----—£-----— sin 0 = 0.
ра sin 0 др	Р 81ПО др
Итак, мы пришли к тому же результату, который мы получили
ранее другим способом: дивергенция поля тяготения, образован-
ного массой т, равна нулю (всюду, кроме той точки, где рас-
положена масса т).
Пример 2. Вычислить дивергенцию поля сил скоростей Л точек
твердого тела, вращающегося с постоянной угловой скоростью
<оо вокруг неподвижной оси.
Мы уже изучали это поле (см. выше, стр. 43) и нашли, что
оно равно [ш Я], где ш — вектор угловой скорости (направлен-
ный по оси вращения и численно равный <оо), a R — радиус-
вектор точки.
Рассматривая это поле в цилиндрической системе коорди-
нат и принимая ось 0z за ось вращения, получим:
А = <оо г • ev .
ftalattauswli
знание без границ * *
________________________________________________________________________________________________ 95
Это равенство можно получить, если учесть, что скорость вра-
щающегося тела в каждой точке направлена по вектору ev и
численно равна шог.
Найдем теперь div А (используя формулу 56):
div Л = div |w0 г ej = -7-—^—.= О,
.так как ш0 г не зависит от у.
Итак, данное поле является соленоидальным.
Ротор в криволинейных координатах. Для того чтобы вы-
числить ротор векторного поля
= ^1(V1« V2» Vs) + ^2,(V1» V2» Vs) ^2 4“ Aj(Vl- V2» Vs) ^8 »
достаточно найти его проекции на орты е1г ё2, ёа." Найдем," на-
пример, проекцию ротора в точке М на вектор еа. Как известно,
проекция ротора на какое-либо направ-
ление равна плотности циркуляции по-	М2
ля Л в данном направлении. Для под- ^х***^><
счета плотности циркуляции в направ- уг	у.
лении еа вычислим отношение цирку- /	\
ляции по малому замкнутому контуру,
окружающему точку /И, к площади у.
области а, ограниченной этим контуром.
При этом область а должна быть рас-
положена на поверхности, нормаль к
которой_в точке М направлена вдоль	рис. 49
вектора еа.
В качестве этой поверхности удобнее всего принять коор-
динатную поверхность q3 — const, проходящую через М, а в ка-
честве области а — область ММг NM2, ограниченную координат-
ными линиями (рис. 49).
Если координаты точек М, Mlt N, М2 таковы:
M(Vt»V2. Vs); ЛМ^ + Д^, q2, q3)\ N(qi + bqu q2,+^q2t qa)\
^^(Vl» Vs 4" ^V2> Vs)>
то площадь области о приближенно вычисляется по формуле:
о	• ММ2 ~ /^Д^ • H2bq2 = Н2 bqx bq2,
где коэффициенты Ламе Нх и Н2 вычислены в точке М.
96
Часть /
Вычислим теперь циркуляцию по контуру MMt NM2M (на-
правление обхода контура выбирается так, чтобы оно было со-
гласовано с направлением нормали):
NM,	М,М
MM,NM,M
Все интегралы в правой части равенства взяты по дугам коор-
динатных линий. Поэтому их можно вычислить по формулам
(2) (см. выше, стр. 87). Вычислим, например, интегралы по ду-
гам и ММ2,
<ь+д<ь
= j Av(qx, qit q3) Hi(qt, q2, q3)dqlt
MM,	g.
Adi = — J A(7i.<72 + д72. 7s) #i(7i. 7г + ^q^dqx.
В процессе интегрирования в обоих этих интегралах вторая и
третья координаты постоянны. Знак «минус» перед вторым ин-
тегралом объясняется тем, что при движении по дуге NM3 ко-
ордината qy убывает.
Сложим почленно эти два равенства:
Adi =
<7»+д<7»
J
-А.Н
dqi =
«I» Q, +
<7j. «•. 4t
dq2
<7|. 4 ’,4t
^q2dqt.
Здесь мы применили формулу Лагранжа.
Далее, оценивая этот интеграл (так же, как мы это делали
при вычислении дивергенции), найдем
f Adi +
Д71 Д<?2.
мм.
мм, Nht	/2 "ср '
где Мср — некоторая точка на площадке MMXNM2 М.
^ataHauswk
знание без границ “ w
$ /в	97
Аналогично находим сумму интегралов по дугам MXN и
Л4а М:
( Adi + f Adi = д(Л,Н,) I_ -Д^-Др,,
MiN	М»М	I Мср
где Мср— какая-то точка площадки ММХ NM2M. Итак, вся
циркуляция по замкнутому контуру такова:
I Adi =
MMiNMtM
(д(А2Н2)
I dqi
Мер
Мср
•Д(71 Д<72-

Взяв отношение этой циркуляции к площади ММХ NM2 М
и перейдя к пределу при Ддх -> О, Д(?2 -> 0, мы получим плот-
ность циркуляции в направлении вектора е3.
Плотность циркуляции в направлении е3 равна
f Adi
.. MMt NMt Ul
hm -------------------------=
(а(Ланг) | atA.HQi ) .	.
= lim I а<1‘ 1яср~ U =
a<7i-o	Я1//а-Д<71-Дда
Д<71’0
=	1	_ dWh)}
H\H2 |	J *
Здесь частные производные и коэффициенты Ламе вычисляются
в точке М.
Это и будет проекция rot А на F3.
Аналогично находятся проекции rot А на остальные орты:
проекция rotA naq = —l— Р(^а^а) _ д(ЛаНа)1
яа	dq2	dq3 )'
проекция rotA на ~ег = гДу- Й-У(1) _ д(Л8Н8))
пъП\Л dq3	dqi J
Поэтому
rot А -	1	7 .
г01 л ~ H,Ht [ dq3 ~д^~J 61 +
4-	1 Гд(Л1Я1) _ d(>W] " ,	1 Га<ЛаА/а)	д(АхНМ -	/Q.
Нзнх [ dq3 дЯ1 J 4 Ч" /АЯа [ дЧ1 д^~] *3-	(В)
4 Ю. С. Оман
98
Часть /
Это и есть формула для вычисления ротора в произвольной ор-
тогональной системе координат.
В частности, в декартовой системе координат:
А = A~i + Ау / + Aje,
М,  dAz \ . . /дАу  дАх \ .
dz дх 'у дх	ду )
(8а)
В цилиндрической системе координат для поля А = Arer+Av е? -|-
+ А^г ротор вычисляется по формуле:
rot Л = -L - *М| ё, +	- ^1 ё, +
г [ dtp dz j ' Г [ dz dr J T '
, 1 р(Дуг) d4r-|-	(86)
r [ dr de Jг'
Здесь учтено, что Hr = 1, Н<? = г, Нг = 1.
Наконец, в сферической системе координат
А = Ар ер 4“ Ау еу 4~ Azet
и поэтому (если учесть, что Нр = 1, Ну — р, Н9 — psin©)
~я 1 [d(4<ppsinH) 5(Днр)]- ,
Г01 71 - p»sin«[ де ~~д^~] р **	(8в)
I 1 ГдЛр _ d (Ар psin 0) ] - , 1 [d (А н Р) _ ddp 1 -
р sin в [d ф	dp J н ' р [ dp де J
Пример 1. Вычислить ротор поля сил тяготения (см. выше,
стр. 94)
Применяя формулу (8в) и учитывая, что здесь проекции
вектора? на орты таковы: Fp =----Fy = 0; Fv = 0, полу-
чим, что rot? = 0. Итак, поле F является потенциальным.
Пример 2. Вычислить ротор поля скоростей А точек твер-
дого тела, вращающегося с постоянной угловой скоростью w0
вокруг неподвижной оси.
Эту задачу мы уже решали с помощью декартовых коорди-
нат (см. пример 2 на стр. 56). Если использовать цилиндричес-
кие координаты, вычисления проводятся проще.
ftatattausM.
знание Вез границ * *
§ 18'	 99
В данном случае А = и/е^см. стр. 94). Поэтому (если
учесть, что Аг = О, Ле = О, Лт = о»/) получим с помощью фор-
мулы (86):
rot Л =	• ее = 2w0‘iz — 2<о,
т. е. ротор равен удвоенному вектору угловой скорости.
Следует заметить, что скалярное поле div Л и векторное
поле rot Л инвариантны относительно выбора системы координат.
Это надо понимать следующим образом: хотя аналитические
формулы, позволяющие вычислить div Л, различны в различ-
ных системах координат, однако все они определяют одно и
то же скалярное поле: ведь значение дивергенции в каждой
точке пространства определяется однозначно по заданному ис-
ход ному полю Л.
Аналогичное замечание имеет место и в отношении ротора
поля Л.
Восстановление потенциала векторного поля. Если векторное
поле Л = А& 4- А2е2 + AgCa потенциально (т. е. rot Л =е 0), то
естественно возникает задача восстановления его потенциала
u(qlt <7я)- Это легко сделать, если учесть, что
..	1 ди - I ди —	1 ди -
grad и — тт~ — Сз 4~ п— з—^2 4~ п—л—^’з-
ь	Hi dqi 1 1 Н9 dq2 21 Н9 dq9 »
Приравнивая составляющие этого вектора одноименным состав-
ляющим вектора Л, получим
1 ди _ д .	1 ди __ д	1 ди _ А
Hi dqi Л1’ Н9 dq9 ~ Л«;	7h~d^ ~ Д«’
откуда
< “ А//.. < = АгН„ %- . л,//,.
Интегрируя эти уравнения (так же, как мы это делали при вос-
становлении потенциала в декартовых координатах), получим и,
как функцию от qlt q9, qa (с точностью до постоянного слагае-
мого).
Пример. Восстановить потенциал поля
Л = 2р cos <р cos 0 ер — р cos <р sin 0 4-
+ (— psin<pctge + -^-£^’V
\	р Sin Ь j г
100
Часть /
Применяя формулу (8в), найдем, что rot А = 0. Следовательно,
поле потенциально. Обозначив его потенциал буквой и и при-
равняв одноименные составляющие вектора А и вектора
„ . du — .	1 du
grad и = ер 4------------
&	др р 1	р дН
1 ди -
р sin Н ~dqT ’
получим
= 2р cos ? cos 0;	— — р2 cos ? sin 0;
ди
д<р
— psin? ctg0+
aa cos <р'
р sin 6
psin0.
Из первого уравнения находим и = р2cos?cos0 4-/(0, ?). Да-
лее, дифференцируя и по 0 и приравнивая результат к
—p’cos? sin 0, найдем-|^- =0, откуда следует, что f не зависит от 0
(т. е. /(?, 0)==Л (?)). Далее, учитывая выражение для 4^-,
найдем, что Д (?) = a* sin ? 4- С. Итак, окончательно
и = р* cos ? cos 0 4- a2 sin ? 4- С.
§ 19. Дифференциальные операции второго
порядка
Вычисляя градиент скалярного поля, мы производим над этим
полем дифференциальную операцию первого порядка. Аналогич-
но этому можно говорить о дифференциальных операциях пер-
вого порядка над векторным полем (это операции взятия дивер-
генции и взятия ротора). Каждая операция первого порядка
приводит к новому полю — векторному или скалярному. Если
над ним произвести снова операцию первого порядка, то над ис-
ходным полем будет произведена операция второго порядка.
Изучим, какие возможны операции второго порядка.
Пусть исходное поле было скалярным (поле и). Над ним
возможно произвести лишь одну дифференциальную операцию
grad и. Новое поле оказалось векторным. Над ним можно про-
извести одну из двух операций: взять дивергенцию или ротор.
Итак, над скалярным полем и можно произвести следующие две
различные операции второго порядка:
div grad и и rot grad и.
^alatfaus',
знание Вез границ
I» 101
Исследуем каждую из них:
1) rot grad u = 0. Это следует из доказанной ранее теоремы
о том, что поле grad и является безвихревым (см. § 14);
2) div grad и\ эта операция приводит, вообще говоря, к но-
вому скалярному полю. Операция второго порядка div grad и
называется «оператором Лапласа» или «лапласианом», и обозна-
чается коротко /п и’.
/л\и = div grad и
(букву «л» внутри А мы поставили для того, чтобы не смеши-
вать с обозначением для приращения функции. Однако обычно
ее не ставят в обозначении лапласиана, записывая его так:
А и. В большинстве случаев по смыслу бывает ясно, что под-
разумевается под Ди — лапласиан или приращение).
Вычислим лапласиан скалярного поля и при задании поля
в различных системах координат.
а) В декартовой системе координат: и=и(х, у, г),
ди	-г	।	ди - .	ди т
grad	и — —ч—	i	-J-	-з— /	—з— k,
ь	дх	1	ду 1 1	dz ’
«.	_	.	д /	ди	\	.	д f ди	\	, д	/	ди	\
div	grad и	=	-ч-	)	4-	—г— -ч—)	-|- -ч— I	-ч—	],
ь	дх у	дх	j	1	ду \ду	j	' dz	I	dz	j
т. e.
d*u
dy*
d*u
dzr ’
(la)
б) В цилиндрической системе координат: u = u(r, <р, z).
о	j	ди - .	1 du - . ди —
Ьмхь grad и =	- е, + — ег +
Беря дивергенцию этого векторного поля, находим лапласиан w:
в) В сферической системе координат н = н(р, 0, <р). Прово-
дя аналогичные вычисления, находим
/	1 Г • о д [ ди «\ , д / ди .	,	1 д'и 1	.
/л =	."Б S1H0 -ч- -ч- Р’ + -чп" чп Sin 0 4----н-п-з-« •	(1В)
--- рб) * 8 sinB[ фу dp j 1 дН	) 1 sin6 dtp8J ' '
Наконец, в общем случае, в произвольной ортогональной систе-
ме координат, лапласиан поля u = u(qlt q2, q3) можно вычислить
по следующей формуле:
д tH9H9 ди \ д !НГН9 ди \ д (HtH9 ди
Ф1\	dqi j ' д<7а у Я, dq9 J ' dq9\ H9 dq9
(1)
102
Часть I
Отсюда, как частные случаи, легко могут быть получены все
выведенные выше формулы для лапласиана в конкретных коор-
динатных системах.
Скалярное поле, лапласиан которого в некоторой области
тождественно равен нулю, называется гармонической функцией.
Примеры гармонических функций:
1. и = г. .... .=— ; в том, что эта функция является
V х2 -Р у2 4- z2
гармонической, можно убедиться, непосредственно вычисляя лапла-
сиан, в декартовой системе координат; однако здесь проще вычис-
лить лапласиан, предварительно записав это поле с помощью сфери-
1 т,	ди
ческих координат: и = —. Тогда
I	л.
-г и, в силу фор-
Г
мулы (1в), получаем сразу /д\ и = 0.
2. Любая линейная функция от декартовых координат:
и = Ах + By -|~ Cz + D является гармонической.
Следует заметить, что термин «гармоническая функция» не
совсем точен. Правильнее было бы говорить «гармоническое
скалярное поле» или «гармоническая функция точки». Если го-
ворить не о функции точки, а о функции трех независимых пе-
ременных, то она может оказаться гармонической при одном
истолковании этих переменных и не гармонической—при другом.
Так, например, функция трех переменных и = aq} ф- bq2 + cq3
(где а, Ь, с — постоянные числа) является гармонической, если
91» 9г» 9я — декартовы координаты точки; но эта же функция не
является гармонической, если q2, q3 — сферические координа-
ты точки, т. е. если = р, q2 — &, q3 — (в том, что функция
и — ар ф- Ь® + сер не является гармонической, легко убедиться
непосредственной подстановкой в выражение для лапласиана 1 в).
Итак, говоря в дальнейшем, что та или иная функция яв-
ляется гармонической, мы будем подразумевать, что скалярное
поле, задаваемое этой функцией, является гармоническим (т. е.
что лапласиан этого поля тождественно равен нулю).
Гармонические функции очень важны в приложениях. Не-
которые общие свойства гармонических функций будут изучены
позднее (часть 3, глава 4).
Рассмотрим теперь дифференциальные операции второго по-
рядка в векторном поле А.
Операций первого порядка здесь две: div А и rot А.
Над скалярным полем div А можно произвести только
операцию взятия градиента. Это приводит нас к операции вто-
рого порядка grad div А.
ftalaHausTM
fJ9 103
Над векторным полем rot А можно произвести операции div
и rot; это приводит нас еще к двум операциям второго поряд-
ка: div rot А и rot rot А.
Операция div rot А приводит к тождественному нулю, ка-
ково бы ни было векторное поле А, лишь бы составляющие
вектора А (при разложении А по ортам) были достаточное чис-
ло раз дифференцируемы. Проверить
это можно непосредственным вычисле-
нием, записав А в какой-либо системе
координат, например в декартовой, и
подсчитав div rot А. Однако убедиться
в том, что div rot А = 0, можно и
без вычислений, следующим образом.
Докажем сначала, что поток век-
тора rot Л через любую замкнутую по-
верхность S равен нулю (рис. 50). Это
следует сразу из теоремы Стокса:
JJ rot Л • ndS = JJ rot Л • п -dS+ JJ rot Л • ndS =
s	Si
= J Ad~l+ \Ad~l = 0.
i+	i-
Здесь мы разбили поверхность S на части и S2 (с помощью
линии /), и к потоку через каждую часть применили теорему Сток-
са. При этом мы учли, что интеграл по Sj равен криволиней-
ному интегралу по кривой Z, взятому в направлении, указанном
стрелкой, а интеграл по S2 равен криволинейному интегралу по
Z, взятому в обратном направлении (это отмечено так: J/+ и J;-).
Ясно, что сумма этих интегралов равна нулю.
Для того чтобы вычислить теперь div rot Л в точке М, до-
статочно вспомнить определение дивергенции:
J J rot Л • п • dS
div rot Л L= lim —------------- = 0.
V-Af	V
Здесь учтено, что числитель дроби, стоящей под знаком преде-
ла, тождественно равен нулю.
Последних двух операций второго порядка (rot rot Л и graddiv А)
мы не будем подробно рассматривать. Укажем только, что они, во-
обще говоря, не приводят к тождественному нулю.
Между этими операциями существует тесная связь. Она мо-
жет быть записана с помощью следующей формулы: если поле
104
Часть I
А задано в декартовой системе координат:
А = Axi -f- Ayj -f- Agk,
то
grad div A = rot rot A + A,	(2)
где под Л\Л подразумевается следующий вектор:
Ул\Л == /л \ Ax-i 4-	х Ау • / + Ул s Аг  k.
В справедливости формулы (2) читатель может убедиться
непосредственным вычислением (в декартовой системе координат).
NalaUausinj.
знание без границ	* ш
ЧАСТЬ II
КРАЕВЫЕ ЗАДАЧИ.
ОРТОГОНАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ
§ 1. Краевые задачи для обыкновенных
дифференциальных уравнений второго
порядка. Собственные решения
Рассмотрим линейное однородное уравнение второго порядка
а^у" + <hy' + а2у = О,
(1)
где а0,	а2—непрерывные на интервале (а; Ь) функции, причем
а0 не обращается в нуль внутри этого интервала.
Как известно, в этом случае общее решение имеет вид:
у = Сх (х) + С2 ф (х),
(2)
где ср(х) и ф(х)— два частных решения, образующие фундамен-
тальную систему (т. е. такие решения, для которых определи-
тель Вронского
w(x) =
?(х) ф(х)
?'(*) ф '(X)
отличен от нуля всюду на интервале (а; 6); это равносильно то-
му, что ср(х) и ф(х) непропорциональны друг другу).
Для того, чтобы из семейства (2) выделить определенное част-
ное решение, надо задать начальные условия Коши:
У |х-х,= Уо> у' |х-=хв = Уо,
где х0 — какая-либо внутренняя точка интервала (а, Ь), a yQ и
y'Q— заданные числа.
Однако часто для выделения определенного частного реше-
ния задают другие условия, отличные от начальных условий
106
Часть II
Коши. Важным типом таких условий являются так называемые
краевые или граничные условия, заключающиеся в том, что на
обоих концах интервала (а; Ь) задаются значения искомого ре-
шения или значения производной от искомого решения и т. д.
Приведем примеры граничных условий:
1)	у(р) = А, у[Ь\—В, где А и В — заданные числа*;
2)	У'(а) = A, yf(b) = В\
3)	функция у = у(х) (искомое решение уравнения) ограни-
чена при х->а + 0 и при х^Ь — 0.
Заметим, что наряду с этими условиями могут быть заданы
и различные их комбинации. Например, можно потребовать,
чтобы функция у(х) была ограничена при х-+Ь— 0, а значение
этой функции при х = а равнялось А.
Задача нахождения того решения, которое удовлетворяет
заданным краевым условиям, называется краевой (или граничной)
задачей.
Далеко не при всяких граничных условиях существует ре-
шение уравнения, удовлетворяющее этим условиям. Так, напри-
мер, не существует решения уравнения у" + у = 0, удовлетво-
ряющего граничным условиям: //(0) =0, г/(2~) == 7. В самом деле,
общее решение этого уравнения имеет вид:
у = CjCos х + С2 sin х.
Для того чтобы удовлетворялись заданные граничные условия,
надо, чтобы одновременно выполнялись два равенства:
Cj cos 0 + С2 sin 0 = 0,
Ct cos 2гс 4- С2 sin 2к = 7,
противоречащие друг другу (первое выполняется только при
Сх — 0, а второе — при Сх = 7). Следовательно, нет решения,
удовлетворяющего этим краевым условиям.
С другой стороны, может оказаться, что данным краевым
условиям удовлетворяет бесконечное множество решений; так,
например, краевым условиям у(0) = 0, у(~) = 0 удовлетворяют
все решения уравнения у" = имеющие вид: y = Csinx.
Среди большого разнообразия краевых условий особо вы-
деляют так называемые однородные краевые условия.
• Если функция f(x) определена на интервале (а; Ь) и имеет конечный
предел А при х-*-а4-0, то мы это будем записывать так: f(a) = А. Поэтому,
когда мы пишем равенства у(а) = А, у'(а) = А, мы подразумеваем, что
lim у(х) = А, или lim у'(х) = А.
х-а+0	х-д + 0
Аналогичный смысл имеют записи: f(b) = В, у(Ь) = В, у'(Ь)=В.
Указанного здесь соглашения мы будем придерживаться на протяжении
всей книги.
ftataHausW.
знание без границ * ш
£/ 107
Краевые условия называются однородными, если из того,
что некоторые функции <pt(x), <р2(х)»---»<Рл(*) удовлетворяют этим
условиям, следует, что любая линейная комбинация этих функ-
ций + ... + Cn<f>n(x)[Cl,...,Сп — постоянные) также удовле-
творяет этим условиям. Приведем наиболее важные типы одно-
родных краевых условий:
1)	У(а) ~ 0, у(Ь) = 0 (краевые условия 1-го типа);
2)	у'(ci) = 0, у'(Ь)=О (краевые условия 2-го типа);
3)	у(х) ограничено при х-+а + 0 и при х^Ь — 0 (краевые
условия 3-го типа).
Кроме перечисленных, однородные краевые условия могут
быть смешанного типа, например, у(х) ограничена при + О,
у(х) — 0 при х = Ь.
Заметим, что если в некоторой окрестности точки а все коэффи-
циенты уравнения (а0, ах, а2) непрерывны, причем то ста-
вить третье краевое условие (т. е. требовать ограниченности
частного решения при х->а + 0) не имеет смысла: в этом слу-
чае любое решение ограничено в окрестности точки а. Условие
ограниченности решения при х-+а + 0 имеет смысл ставить лишь
тогда, когда какая-либо из функций а0, alt а2 терпит разрыв при
х = а, или тогда, когда а0 — 0 при х — а.
Аналогичное замечание имеет место и для правого конца ин-
тервала (а; Ъ).
Каково бы ни было однородное уравнение (1) и каковы бы
ни были однородные граничные условия, им всегда удовлетво-
ряет тривиальное решение у = 0.
Если существует функция <р(х), отличная от тождественного
нуля и удовлетворяющая данному дифференциальному уравне-
нию и данным однородным краевым условиям, то говорят, что
f(x) является собственным решением заданной краевой задачи.
Пример 1. Найти собственные решения уравнения у" + у —О,
удовлетворяющие краевым условиям: у(0) = 0; г/(тг) = О.
Собственным решением этой краевой задачи является функ-
ция t/ = sinx, а также все функции вида t/ = C-sinx (где С =
= const, Су^О).
Пример 2. Краевая задача у" -J- у = 0, где у(0) = О,
= 0, не имеет ни одного собственного решения. Действитель-
но, общее решение таково:
у = Ct cos х + С2 sin х;
подставляя сюда граничные условия, получим: Сх = О, С2 = 0.
Следовательно, единственной функцией, удовлетворяющей этой
краевой задаче, является тривиальное решение у = 0.
108
Часть 11
Прежде чем переходить к изучению вопросов, связанных с
краевыми задачами, рассмотрим некоторые общие теоремы о ли-
нейных дифференциальных уравнениях второго порядка.
§ 2. Самосопряженное уравнение второго
порядка
Линейное однородное уравнение второго порядка, записан-
ное в следующем виде:
1А(х) • у'\ — <?(*) • У = 0.	(О
называется самосопряженным уравнением. Здесь /С(х) и q(x)—
непрерывные функции на (а; Ь), причем А(х), кроме того, имеет
непрерывную производную на (а; Ь).
Докажем, что всякое линейное однородное уравнение
+ агу' + а2у = 0
(2)
(где Oq, at, а2 непрерывны на (а; Ь), причем гао^=О) может
быть приведено к самосопряженному виду (1). Для этого доста-
точно умножить обе части уравнения (2) на функцию у. (х), ко-
торую подбираем так, чтобы выполнялись равенства:
а0 р (х) — К(х) и ах р (х) = К'(х), т. е. чтобы имело место
[о0 н (х)]' = ах р (х).
Отсюда находим р(х):
К и (x)F _ _£i_
а0 р (*) ао ’
и, следовательно,
In (п0 р (х)) = I — dx + In С,
J ао
f — dx
а0 р (х) = С е J а°
откуда
И(*) = е
ао
^-dx
(3)
MaHausik
знание без границ * *
$2 109
А теперь приведем уравнение (2) к самосопряженному виду,
умножив все члены этого уравнения на найденное выражение
для |х(х) (приняв, например, С = 1):
+у'~-‘
ао
a ~dx
+ у,^.е^. =0,
ИЛИ
dx L	J «0
Уравнение приведено к виду (1): здесь
I
=	, q(x) = --^e
Докажем некоторые теоремы о решениях самосопряженных
уравнений.
Теорема 1. Пусть К(х) обращается в нуль в точке х — а,
причем К(х) = (х — а)~(х), где т(а)=£0. Тогда, если одно из
решений уравнения (1) может быть представлено в виде
yt=(x—a)nz(x), где z (а)	0, п>0*, то другое решение, линейно
независимое с ним, стремится к бесконечности при х-+а + 0.
Доказательство. Пусть ух(х) и у2(х)—линейно независи-
мые решения уравнения (1), причем yt(x) = (х — a)n-z(x). Подстаь-
ляя эти решения в уравнение (1), получим следующие тождества:
iKy'i] — УУ! = 0;
(Kt/d —<7^2 = 0.
Умножая первое из них на у2, а второе—на уг и затем вычитая
одно из другого, получим
Уг^уЦ'-у^Ку^О;
добавим и вычтем Ку^у*.
yi[Kyjy + у2 Ку\ —yt [Ky’jy ~ j
— Уi. \Ky']y — У\ Ку 2 = 0.
Это можно переписать так:
[Ку'1У*У — [КУ2У1]' = 0,
Число п может быть^и не целым.
110
Часть II
или
[К( У\Уъ—
т. е.
ШУ\У* — У2У1) = С,	.	(4)
где С — некоторая постоянная; она отлична от нуля, потому, что
К^О по условию, а у\у2— y'2yt = У*. У\ 0, так как решения
^2 У\
уу и у2 линейно независимы, и их определитель Вронского отли-
чен от нуля.
Выберем теперь столь малую правую полуокрестность (а;а+е)
точки а, чтобы в этой полуокрестности было всюду z(x)^0.
Тогда всюду на (а; а 4-е) функция у^х) также отлична от нуля.
Учитывая это, перепишем тождество (4) следующим образом:
у\Уг — У2У1
У\
=
yJ
С
~ К-У2
— С
К‘у\
или
4	»		<----
о*х° «Ч
Рис. 51
Интегрируя это тождество в границах от х до х0, где х0— не-
которая фиксированная точка интервала (а; а 4- е), а х — произ-
вольная точка, лежащая между а и х0 (рис. 51), получим*
*о
t/2(xn) _ уг(х) = Г —С
УМ у^х) J К У*
х
Обозначим
Учитывая далее,
= Сд. Тогда
Г С dt 1
У2(х) — У1(х)	4“ С J Ку* J ’
что yt(x) =» (х— а)п г(х) и что К(х) = (х —
получим
х0
Уг{х) = (х~ а)пг(х) [ сх 4- С J	((_ а)аП[2(/)j .
* Переменную интегрирования мы обозначили через t.
?>ialatlaus№k
знание без ераниц Ч
111
Применим теперь к полученному интегралу теорему о среднем*
*•
У2(х) = (х — a)nz(x) [ Ci + С Я(Т).[2(Х)|2 J (/_a)2n+i ] »	(5)
X
где х < т < х0.
Вычисляя последний интеграл, найдем при п > О
УМ = (х — a)nz(x) [Cj — 2/m(T)[z(T)]« ((х0—а)ал	(х—а)ал )] ’
или
. .	. \п t \	C'z(x)-(x — a)n _________________C'z(x)_______
yt(x) - Сх(х — a) z(x) 2пк(т)[2(т)]2(х0 —a)2« + 2лк(т).[г(т)]а-(х — a)n ’
Здесь первые два слагаемых стремятся к нулю при х -+а + 0, а
последнее — к бесконечности**. Следовательно, у2(х) -> со при
х -* а + 0.
Мы рассмотрели случай п>0. Если же п=0, то равенство (5)
перепишется следующим образом:
£/я(х) = z(x)[C! 4- iu(t)[z(t)]« 1п(*° ~	k(t)[z(t)]> ln ~~	’
откуда снова вытекает, что у2(х) -> «> при*-* а 4- 0. Теорема дока-
зана.
•	Напомним формулировку теоремы о среднем: «если две функции f(t)
и ф(/) непрерывны на la; fe], причем ф(0у=О, то внутри [а; 6] найдется
ь	ь
точка т такая, что имеет место равенство: J ф(0• |(0dt — <р(т) J^(/)d/>.
а	а
В данном случае эта теорема применима, так как функции ф(/) = ^__Jph+i
И *(O [z(0]a непРеРывны на Iх; xob причем ф(0 #= 0.
•	* Если lim п(х) • [z(x)]8 = В =#= 0, то мы можем подобрать х0 так, чтобы на
х-»а+о
(а; х0) функция *(x)[z(x)]a была заключена между “2 и -g" . Тогда дробь
будет оставаться (при х->а 4- 0) по модулю ограниченной чис-
2
Следовательно, ее произведение на (х — а)п стремится к
1
нулю, а ее произведение на _______а^п стремится к бесконечности при
х-4- а 4- 0.
к(х).[г(х)]а
2
ламп н
112
Часть II
Легко видеть, что аналогичная теорема справедлива и для пра-
вого конца интервала (а; Ь) (т. е. при х-+ b — 0).
Пример 1. Уравнение
х*у" + ху' — у = 0
легко может быть приведено к самосопряженному виду умноже-
1 .
нием на —:
X
ху" + У' —^У = 0,
или
(*/)' —7 • У = 0.
На интервале (0; +«>) функция /C(x)=x отлична от нуля, при-
чем К(х)->0 при х^> + 0- Одно из решений этого уравнения
ух{х) = х ограничено при х -> 4- 0; его можно представить в виде
У1=(х — 0)-1. Другое решение, в соответствии с теоремой 1,
должно быть неограниченным при 4- 0. Это действительно
. 1
так: легко проверить, что функция уг = — удовлетворяет урав-
X
нению и стремится к со при 4- 0.
Теорема 2. Пусть К(х) обращается в нуль при х = а, при-
чем К(х) = (х — а)т:(х), где я(а)>0, a q(x) либо ограничена при
х-*• а + 0, либо стремится к 4~ 00 при х->а+0. Тогда для любого,
ограниченного при х->аЦ-0, решения у(х) уравнения (1) имеет
место
lim К(х)у'(х) = 0.
х-»а+0
Докажем эту теорему для того случая, когда q(x) ограничена
при х -> а + 0 (доказательство для того случая, когда q(x) + со
при х^а + 0, значительно сложнее, и мы его опускаем).
Подставим у(х) в уравнение (1) и проинтегрируем получен-
ное тождество в границах от х х0, где х и х0 — некоторые точки
интервала (а; Ь)’.
(К (Х)У(Х)] - <Хх)1/(л) S 0,	(6)
К(х0)(/(*о) — К(х)у'(х)— J q(t)y(t)dt = 0.
X
Следовательно,
*о
К(х)у'(х) = К(х0)у'(х0) — J q(t)y(t)dt.	(7)
11________________________________________________ 113
Первое слагаемое постоянно; второе (интеграл) имеет конеч-
ный предел при х-+а + 0; этот предел равен несобственному ин-
х.
тегралу J q(t)y(t) dt*.
а
Обозначим функцию от х, стоящую в правой части равенст-
ва (7), через Q(x), а ее предел при х->а + 0 — через М\ докажем,
что М = 0.
д X *7
Рис. 52
Пусть М =£0. Опишем около а такую полуокрестность (а;д-г)
(рис. 52), что для всех х из этой полуокрестности
I Q(*) I 1 I М
I л(х) 1^ 2 |п(а)
(что возможно, так как lim	0). Перепишем теперь
тождество (7) в следующем виде:
WW = Q(x),
или
* w “ К(х) ~ (х—а)п(х) ’
и проинтегрируем его в границах от х до xv:
х.
J «Лио dt-
X
Применяя к этому интегралу теорему о среднем, получим:
I уМ - уМ I = IГ „ <*> dt =	L"- *’ >
IJ (/ —а)к(/)	л(т) J t — а
X	X
> 4  |^) | •|пТ=1	+ “(при х^ а + 0).
* Существование этого несобственного интеграла вытекает из непрерыв-
ности и ограниченности подинтегральной функции q(t)y(t) на интервале
(а; х0).
*♦ т — некоторая точка на интервале (х; Xj); следовательно, х принад-
лежит интервалу (a; Xj), а, значит,
114
Часть //
Но тогда у (хх) — у(х) -> со, а, следовательно, t/(x)->oo, что
противоречит условию ограниченности решения у(х) при x-^a-f-O.
Итак, предположение, что М =/= 0, было неверным; значит,
М = 0, т. е. lim К (х) у'(х) = 0. Теорема доказана.
х-а+0
Аналогичная теорема справедлива и для правого конца ин-
тервала (а; Ъ) (при х-^Ь — 0).
Пример 2. Уравнение ху” + у' — у = 0 может быть за-
писано так:-^ (ху') — ~у = 0. Здесь q(x) =~ -+ + со при
х -> + 0. Одно из решений есть у ~ У х; оно ограничено в пра-
вой полуокрестности точки х = 0. Производная от этой функ-
ции у' ——неограничена при х-> + 0, однако, в соответствии
X
с теоремой, произведение К(х) у'(х) /т. е. х- —7=) стремится
\	2у х )
к нулю при X 0.
Пример 3. Рассмотрим уравнение (ху') 4- у • у = 0. Его
решение у — sin In х ограничено при х-> + 0; однако ху' не стре-
мится к нулю при х -> + и (здесь у = ------—
это выражение не имеет предела при х->4-0).
Кажущееся противоречие с теоремой 2 объясняется тем, что
здесь не выполнены условия этой теоремы: здесь q(x) = —— и,
следовательно, функция q(x) не является ни ограниченной, ни
стремящейся к + 00 при х -► + 0.
Из этого примера видно, что условия, наложенные на q(x),
и ху' — eosin х;
существенны.
§3. Собственные числа и собственные функции
В § 1 нами была рассмотрена задача о решении линейного
однородного уравнения при заданных краевых условиях.
В настоящем параграфе мы вернемся к этой задаче.
Рассмотрим уравнение
(КуУ — ЧУ + ЧУ = 0,	(1)
где К — постоянное число, К(х), q(x), р(х) непрерывные на (а; Ь)
функции, причем К(х) имеет непрерывную производную. Будем
считать, кроме того, что во всех точках этого интервала К(х)>0,
р(х) > 0, q(x)^G\ при этом р(х) ограничена на (а; Ь). Уравнение
(1) называется уравнением Штурма-Лиувилля.
$2
115
Ясно, что уравнение Штурма-Лиубилля является частным
случаем самосопряженного уравнения (1), рассмотренного в пре-
дыдущем параграфе; только вместо q(x) из уравнения (1), § 2,
здесь подставлена разность q(x)—kp(x).
Пусть нам заданы какие-либо однородные краевые условия
(вроде тех, которые были рассмотрены в § 1). Те значения К,
при которых уравнение (1) имеет нетривиальное решение, удов-
летворяющее заданным краевым условиям, называются собст-
венными числами (или собственными значениями) данной крае-
вой задачи, а нетривиальные решения, отвечающие этим к, —
собственными решениями (или собственными функциями).
Пример. Дифференциальное уравнение
У' + ^=0
(2)
является частным случаем уравнения (1): здесь К = 1, р = 1,
<7 = 0. Зададим следующие граничные условия на интервале
(0; /): г/(0) = 0; </(/) = 0.
Общее решение данного уравнения (2) таково:
у = CiCos x]/k~+ С2 sinx)/T (при К >0),
у =	+ С2 х (при К — 0),
у = CxexV~x + С2 е ~xV^ (при К < 0).
При К = 0 данным краевым условиям удовлетворяет только
функция г/^0 (действительно, подставляя в общее решение у=
= Сх + С2х сперва х = 0, у = 0, а затем х — I, у = 0, найдем:
Сх = 0, С2 = 0). Итак, К = 0 не является собственным числом
данной краевой задачи.
Также не являются собственными числами ни одно к<0:
подставляя в общее решение данные краевые условия, получим
Cj = С2 = 0, откуда у = 0.
Пусть теперь К > 0. Подставляя краевые условия в общее
решение у = Cicosx]/к + С2 sinp^T, получимСх=0, C2sin
= 0. Эта система допускает, кроме тривиального решения Ct=0,
С2 = 0, также следующие нетривиальные решения: Q = 0,
С2у= 0,/}/1Г=/гк, где k — произвольное целое положительное
число. Итак, все числа к = являются собственными
I*
числами данной краевой задачи, а функции у = sin-^-—собст-
венными решениями или собственными функциями (собственное
решение здесь определяется с точностью до постоянного мно-
жителя— в данном случае с точностью до множителя С2; мы
116
Часть II
приняли в качестве собственного решения ту функцию, которая
соответствует значению С2 = 1).
Укажем некоторые свойства полученной системы собствен-
ных значений:
1 _ 1 _ 2а«а. . 1
р ’ Л2 р »•••»	р
и собственных функций:
. пх	. 2кх	. knx
Уь = sin—; y2 == sin -j-;...; yk = sin—;...
1.	Собственных чисел имеется бесконечно много; все собст-
венные числа могут быть расположены в виде возрастающей
последовательности, члены которой занумерованы натуральными
числами.
2.	Все собственные числа неотрицательны.
3.	Каждому собственному числу соответствует только од-
на (с точностью до числового множителя) собственная функцияyk.
4.	Каждой собственной функции соответствует только одно
собственное число.
5.	Собственные функции, соответствующие различным номе-
рам, ортогональны друг другу на участке (0; /); это значит, что
интеграл от произведения двух таких функций в границах от 0
до I равен нулю:
z
С . kitx . mnx ,
I sin — sin — dx ='0 .
о
Проверить это равенство легко непосредственным интегрирова-
нием (для этого надо сначала представить произведение сину-
сов в виде алгебраической суммы с помощью следующей фор-
мулы тригонометрии: sin a- sin 0 = ~ cos (а — 0)—g-cos(a 4- 0)) .
Все эти свойства собственных чисел и собственных функций
рассмотренной здесь краевой задачи могут быть обобщены на кра-
евые задачи очень широкого класса.
Прежде чем формулировать общую теорему, условимся, ка-
кие краевые задачи будем ставить.
а. Краевая задача 1-го типа: у(а) = 0 будет нами ставить-
ся только в том случае, если функции К(х),	q(x), р(х) не-
прерывны не только на интервале (а; Ь), но и в точке а и ее
окрестности, причем К(а) =/= 0.
0. Краевая задача 2-го типа: у'(а) = 0 будет ставиться так-
же только в том случае, если К(х), К'(х), q(x), р(х) непрерывны
а точке а и ее окрестности, причем К(а) 0.
NalallauS'
знание без границ
§2  117
7. Краевая задача 3-го типа: у(х) ограничена при х -► a +0,
будет ставиться только в том случае, если К(х)->0при
х -+ a + 0 (см. замечание на стр. 107). Кроме того, мы будем считать,
что в этом случае К(х) представима в виде К(х) = (х— а)к(х),
где ~(а) =/= 0, a q(x) либо ограничена, либо стремится к + 00 при
х^> а + 0.
Аналогичные краевые условия (при соответствующих требо-
ваниях к функциям К(х), q(x), р(х)) задаются и в правом конце
интервала (а; Ь) (при этом, конечно, не обязательно, чтобы кра-
евое условие на правом конце было того же типа, что и краевое
условие на левом конце).
Задача нахождения собственных чисел и собственных функ-
ций уравнения Штурма-Лиувилля при краевых условиях 1, 2
или 3 типов на концах интервала называется задачей Штурма-
Лиувилля.
Докажем сначала следующую лемму.
Лемма. Пусть функции с?(х) и (х) удовлетворяют уравне-
нию (1) и краевым условиям одного и того же типа в точке а.
Тогда имеет место следующее равенство.
lim K(x)<p(x)-7'W = 0.
x-»a+0
Доказательство. 1. Йусть в точке а задано краевое
условие 1-го типа. Так как при этом К(х), q(x), К'(х) непрерыв-
ны в точке айв некоторой ее окрестности и К(а) 0, то
всякое решение уравнения (1) (в частности, <р(х) и <р(х))
определено не только на участке(а; Ь), но и на несколько большем
участке (а — е; Ь)\ эти решения непрерывны и имеют непреры-
вные производные всюду на (а — е; Ь). Согласно краевому усло-
вию, <р(а) = 0. Следовательно,
lim К(х)ср(х) <р'(х) = К(а)ср(а)^(а) = О
х-а+0
(К(а) — конечное число по условию; ср'(а) — конечное число в силу
существования непрерывной производной <р'(х) всюду на (а—е; Ь)).
2. Пусть в а задано краевое условие 2-го типа. Тогда те же
рассуждения показывают, что <р(а)—конечное число. Так как,
по условию <р'(°) = 0, то
lim К (х)<р(х)<р'(х) = К (а)<р(а)/(а) = 0.
х-«а+0
_ 3. Пусть в а задано краевое условие 3-го типа (т. е. <р(х)
и <р(х) ограничены при х->а + 0). Так как мы договорились
118
Часть 11
ставить это краевое условие только при К (х) = (х — о) к (х) (где
к (а) 0), то, согласно теореме 2 (§ 2), имеет место:
lim К(х)?(х)=0.
х-*а+0
Кроме того, по условию <р (х) ограничена при х -> а 4- 0. Поэтому
lim [<р(х) К(х)?(х)] =0.
х-*а+0
Лемма доказана.
Сформулируем и докажем теперь следующую общую тео-
рему.
Теорема. Пусть задано уравнение
(К'У'У — q*y + Хр!/== о	(1)
и краевые условия], 2 или 3 типов. Пусть функции К (х), К' (х),
q(x) и р(х) непрерывны на интервале (а; Ь), причем всюду на
этом интервале К (х) > 0, q (х)	0, р (х) > о и р (х) ограничена.
Кроме того, пусть на концах интервала эти функции удовлет-
воряют требованиям а), р) или 7) (в зависимости от типа краево-
го условия на соответствующем конце интервала; см. стр. 116).
Иными словами, пусть задана- краевая задача Штурма-Лиувилля.
Собственные числа и собственные функции этой краевой
задачи обладают следующими свойствами'.
1)	собственных чисел бесконечно много; все собственные
числа могут быть расположены в виде возрастающей последова-
тельности, члены которой занумерованы натуральными числами:
Xj <^2	•••	< ••• ’
2)	все собственные числа неотрицательны;
3)	каждому собственному числу соответствует только
одна (с точностью до числового множителя) собственная функ-
ция;
4)	каждой собственной функции соответствует только
одно собственное число;
5)	собственные функции, соответствующие различным но-
мерам k и т, ортогональны друг другу с весом р (х); это значит,
что для любых k и т, таких, что k-^ m имеет место равенство*
ъ
j <Pm (•*)<₽*(*) р(*)^ = 0‘
а
Доказательства первого свойства собственных чисел
мы здесь давать не будем: это доказательство основывается на
теории интегральных уравнений и далеко выходит за рамки дан-
ной книги.
ftatattauswk
знание без ерании * *
П 119
Докажем второе свойство собственных чисел. Пусть
— некоторое собственное число, а <рЛ (х) — соответствующая соб-
ственная функция. Докажем, что > 0.
Так как <рЛ(х) является решением уравнения (1) при Х = ХЛ,
То имеет место следующее тождество:
[ К (х) (*)]' — <7 (*) (х) + р (х) <рЛ (х) = 0.	(2)
Умножим все члены ^того тождества на <рЛ(х) и проинтегрируем
его в границах от 5 до ?], где 5 и т) — какие-либо числа между а и b
a <5 < т) < Ь*:
(х) [X (х) (*)] 'dx— (х) [<рЛ (х)]я dx +
ч
+ f Р (х) [<РЛ (X)]’ dx = 0.
Найдем отсюда
-----------------
) р-(?л)я dx
Применим ко второму интегралу, стоящему в числителе, прави-
ло интегрирования по частям (приняв и — <рЛ, dv = (К<р'кУ dx):
р(уЛ)’4х — [тл-п-кГ I- f K-(n)*dx
Ч = -------------,---------1--------. О)
Устремим 5 к а + 0, tj к b — 0. Тогда все интегралы в формуле
(3) устремятся к соответствующим несобственным интегралам
• Мы интегрируем тождество (2) в границах от 6 до т). Могло бы по-
казаться, что проще было бы провести доказательство, интегрируя его сразу
в границах от а до Ь. Но это было бы возможно только в том случае, если
бы мы были уверены, что все произведения (х)• [к(х)' и т. д. инте-
грируемы на [а; Ь]. В границах же от 6 до т) все эти функции наверняка
интегрируемы, так как они непрерывны на сегменте [$, ц].
120
Часть U
(в границах от а до 6)*. А выражение	устремится к
нулю; действительно,
a lim ^4(т1)<р'(т,)К(-ф = 0, lim (S) ?'(S) X (5) = 0,
т^Ь-0	*	6-а+0	«
в силу леммы.	*
Итак,
ь
J [ <7 (Фл)я + К-(<Рл)2] dx
h = -------i,------------,
J p (<рЛ)а dx
a
откуда (в силу того, что > 0, К > 0, р > 0) следует, что ХЛ>0.
Докажем теперь третье утверждение теоремы, т. е.
докажем, что каждому собственному числу ХЛ соответствует
только одна (с точностью до числового множителя) функция
<М*)-
Пусть некоторому собственному числу ХЛ соответствуют две
различные собственные функции <р(х) и <р(х). Подставляя эти
функции в уравнение (1), получим два тождества:
(А ф')' —	+ Хр<р 0,
(К<?У —qy +	0,
или
(К<рУ^(ч-Ц)9,
(Л?)' (q -ХР)9.
Умножим обе части первого равенства на <р, а второго — на <р
и вычтем из первого второе:
Ф (К 9')' - <Р (* ?)' - 0.
Прибавим к левой части равенства выражение Л и вычтем
его:
? (W ~ MW + <P'(W)]^O.
• Эти интегралы наверняка существуют (конечные или бесконечные),
в силу неотрицательности на (а; Ь) подинтегральных функций; заметим, что
предел интеграла, стоящего в знаменателе, наверняка конечен, так как
функция р (ф^)8 ограничена на (а; Ь).
^alatiausi^i
знание без границ “ w
_____________________________________________________________________________________________ 121
Последнее тождество можно переписать так:
(W^r-(W)'^o,
или
(К<р'<р — Kw'Y = 0,
откуда
Кф'ф — Кср<р' = с,
где С — некоторая постоянная величина.
Найдем С; для этого заметим, что, согласно лемме,
lim К (х) ср' (х) <р(х) = 0, lim К (х) ср(х)ср' (х) = 0. Поэтому
ж-»а+0	х-»а+0
lim [ Кер'ср —К<р<р' 1 ~ 0.
х-а+0
Но выражение в скобках постоянно; следовательно, оно
дественно равно нулю:
Кер'ср — Ксрср' = 0,
откуда (так как К (х) 0)
ф'<р _ (р<р' = о,
тож-
или
= 0.
<р <р
Ф ср
Таким образом, доказано, что определитель Вронского для двух
решений ер и ср тождественно равен нулю, откуда следует про-
порциональность функций ер и ср:
?(х) = а.<р(х).
Итак, две собственные*функции, отвечающие одному и тому же
собственному числу X, могут отличаться только постоянным
множителем.
Четвертое свойство доказывается совсем просто: если
бы двум различным собственным числам Хл и Хш (Хл =£ Хот) соот-
ветствовала одна и та же собственная функция <р(х), то име-
ли бы место тождества:
НК (х) ер' (х)Г — q (х) ер (х) + Хл. р (х) ср (х) = 0,
I [К (х) ер' (х)]' — q (х) ер (х) + Хт . р (х) ср (х) = 0.
122
Часть 11
Вычитая их почленно, получим
(хл~ Кп)р(х)<Р(*) = 0,
что невозможно, так как p(x)>0,	и ф(х) отлично от
тождественного нуля.
Докажем пятое свойство собственных функций — их
ортогональность с весом р(х).
Пусть <рт(х) и <рЛ(х) —две собственные функции, отвечаю-
щие различным собственным числам Хте и ХЛ. Тогда имеют место
следующие тождества:
(А” (х) (х)]' — q (х) tpk (х) 4- ХЛ р (х) <рЛ (х) = О,
1* (х) <pm (X)]' — q (х)	(х) + Xm Р (х) <pm (х) s 0.
Умножим обе части первого из этих тождеств на <рот(х), а вто-
рого— на <pk(x) и затем вычтем из первого второе:
Проинтегрируем все члены этого тождества в границах от $ до
т], где а < I < 7} < Ь:
f [^(x)<p;(x)]'^(x)dx-f [K(x)<p^(x)]'<pjx)dx +
+ (Ч —М f р(х)9л(х)9т(х)^х = 0.	(4)
К первым двум интегралам применяем процесс интегрирования
по частям:
J	= [К(х)ф;(х)<Р,п(х)]^ -^(x)-(f>'k(x)<pm(x)dx-,
?	• ъ ?
\ [К W <,(*)]' W dx = [X w w ъ w]t -J W*1-
Вычитая почленно эти равенства, получим
ч	3
= [к (*)	w <tm w]’ - [к «9га«?»(*)]’ •
ftataHausIM
знание без границ
И 123
Выражения [К (х) yi (х) ут(х)] ’ и [Л(х) <рт (х)%(х)]’ стремятся
к нулю при В -> а 4- О, т) -► 6 — 0 (это следует из леммы). По-
этому разность двух первых интегралов в формуле (4) также
стремится к нулю при $->а + 0,	— 0. Но тогда к нулю
стремится и третье слагаемое в левой части равенства (4), т. е.
(ХЛ — М J Р (х) ?*(*) <Рт (Х) dx = 0.
т)-»Ь—0	Е
или, так как	то
7
Jim J p(x)yk(x)<?m(x)dx = 0.
Е-а+Ог
i) .ft—0 *
Следовательно,
b
$?(*)?M<f>m(x)dx==0.
Таким образом, ортогональность функций <рЛ(х) и <рт(х) с весом
р(х) доказана.
Выше мы рассмотрели (см. стр. 115) одну задачу на нахож-
дение собственных чисел и собственных функций и убедились
на этом примере, что собственные числа и собственные функции
обладают свойствами, сформулированными в доказанной теореме.
В следующих параграфах будут рассмотрены еще несколько
примеров краевых задач, важных для применений.
§ 4, Уравнение Бесселя
Уравнением Бесселя р-го порядка (где р —заданное целое
неотрицательное число) называется следующее дифференциаль-
ное уравнение*
хV 4- ху' 4- (х8 — р2) у = 0.	(1)
Это уравнение легко привести к самосопряженному виду, раз-
делив все его члены на х:
(ху'У 4-
х---—)*/ = 0.
х ]
(2)
• Часто приходится иметь дело с уравнением Бесселя и при р нецелом.
Однако мы этого случая рассматривать не будем.
124
Часть П
Попытаемся найти решение этого уравнения в виде суммы
степенного ряда по степеням х:
р = б04Ах4-М94-... +МЯ + —	(3)
Для удобства дальнейших вычислений изменим обозначения:
обозначим буквой а0 первый из коэффициентов ряда (3), отличный от
нуля, а буквами ах, а2, а3...— все последующие коэффициенты.
Конечно, может случиться, что уже Ьо 0; тогда Ь0~а0, Ьх =
= «j.... Если же b0 ~ = ... = bm_i = 0, bm^= 0, то обозначаем
bm = а0, bm+i = ах, bm+2 = о2 и т. д. Итак, в общем случае
у = aQxm + аххт^ -Ь a2xm+94- ... + оях'л+л 4- ... ,	(4)
где /72 > 0, а0 0.
Почленно дифференцируя ряд (4), найдем у'\ затем, умно-
жая ряд для у' на х и еще раз дифференцируя, получим
(ху')* = а3т2хт~х + (т 4-1)8*"1 4- а2 (т 4- 2)8xm+14-...
... 4- ап(т 4- п)8х'я+л"1 4- ... .
Подставляя выражение для (ху')' и для у в уравнение (2), будем
иметь следующее тождество:
a0m2xm“’ 4- ах (т 4- l)9xw 4- о2 (т 4- 2)9xm+1 4- ...
... 4- ап(т 4- п)8х'л+л~1 4-... — а0р2хт~1 — ахр2хт — а^х"** —...
... — апр2хт*п~1 —... 4- o0^m+1 4-... 4- оя_2хт+л"1 4-... 0.
Приравняв нулю сумму коэффициентов при каждой степени х,
составим бесконечную систему уравнений для определения коэф-
фициентов:
п0 (т2 — р2) = 0,
п1[(/п4- I)2 — р9] = 0,
а2 [(/л 4- 2)9 — р2] 4- а0 = 0,
а3 [(т + З)8 — р2] 4-01=0,
оя [(ю 4- и)2 — р8] 4 а„_2 = 0,
Из первого уравнения системы находим, что т* — р9 = 0 (так
как а0 ф 0 по условию). Следовательно, т — р (напомним, что т—
неотрицательное число; следовательно, т ф— р).
ftataMausiSk
знание без границ * *
§4 125
Из остальных уравнений находим аь а2, а8,..., ая,...; одна-
ко, для облегчения вычислений, преобразуем сначала выражения
в квадратных скобках (учтя, что т — р):
<h 1(Р + I)8 - Р*] = О,
а, «Р + 2)’ - Р2| + а„ = 0,
о. 1(р + 3)® - р‘1 + а, = О,
я„[(р + ")!—Р’1 + а„.,= О,
или
flx-(2p 4-1) = О,
а2-2-(2р4-2) = — а0,
а8-3-(2р 4~ 3) = — ар
а<-4- (2р + 4) = — а2,
ай-л-(2р + п) = —а„_2
Отсюда видно, что ах = аа = аь — ... = а2Л+1 = ... = О,
п —.	аО . п —_________а2 __ __________ао_________ .
2	2 (2р 4-2) ’ ы< 4 (2р 4- 4)	24-(2р 4-2) (2р 4-4) ’
__	—«4	_ —а0
® ~ 6 (2р + 6) “ 2-4-6- (2р + 2) (2р 4-4) (2р 4 6) И Т< Д<
о к	М“О*
Вообще, °2Л —'2-4 ...2Л-(2р4 2)-(2р4 4) ... (2р4 2А) ~
М-Р*	_ «о-рЧ-Р* »
2*. Л! 2*(р+“1) (р 4- 2)... (р 4- k) 2»*- Л! (р 4 А)! ‘
Подставляя найденные коэффициенты в ряд (4) и учитывая, что
т = р, получим:
= а0 [хр--------------xP+i 4- ---------------хр*л
2«-1!(р4-1)!	2«-2!(р4-2)1
4- р] (—О*	4- 1
2»*Л!(Р4Л)!
* Для того чтобы эти формулы оставались справедливы и ппи n-=n
или Л = 0, полагают, как обычно, 01=1.	Р Р и
126
Часть II
Для упрощения этого ряда вынесем за скобки р!; кроме того,
разделим все члены ряда на 2Р и умножим на 2р всю сумму
ряда:
у = afipp\
'[_х_\р	(JL\P"
\ 2 /	\ 2 )
L pi	ii(p-h i)i
/_х\р+«
\ 2 /
2! (Р + 2)!
/ х \р+»Л.
Ряд, стоящий в квадратных скобках, абсолютно сходится для
всех значений х (это легко проверить с помощью признака
Даламбера). Сумма этого ряда называется функцией Бесселя
порядка р и обозначается Jp(x):
( х \р / х Vм 3	/ х у’К
pW pl • И(p-h 1)1 ' 21 <Р4-2)1 “* "*
/ х \p+aft
+<-')‘Uiur+ •	(5)
Решением нашего уравнения является любая функция вида
Л-/р(х) (буквой А обозначено число а0-2/,-р!; поскольку а0 мо-
жет принимать любые значения, то и Л может принимать любое
постоянное значение).
Функция Jp (х) ограничена при х -> + 0; действительно,
Jp (х) непрерывна для всех х (как сумма сходящегося степенного
ряда) и, следовательно, ограничена в окрестности любой точки —
в частности, в окрестности нуля.
Для того чтобы исследовать вопрос о втором частном ре-
шении, линейно независимом с Jp (х), воспользуемся теоремой 1
из § 2. В данном случае роль К (х) в дифференциальном урав-
нении Бесселя играет функция х (т. е. ?((х) = (х— 0)-1). Най-
денное нами частное решение Jo (х) может быть записано в виде:
JD(x) = xp
Г _J_____________ха
[ р\2р 11 (р 4-1)12/’+»
или Jp(x) ----- (х — ОУ’-г(х), причем z(0)^0. Следовательно, в
данном случае применима указанная теорема 1. Из нее вытека-
ет, что второе частное решение, линейно независимое с Jp(x),
неограничено в окрестности нуля. Обозначая одно из решений,
линейно независимых с Jp(x), через Np (х) (эта функция называ-
ftalaUauslik
знание без границ ' *
94 127
ется функцией Неймана), запишем общее решение уравнения
следующим образом:
y = CvJp(x)+Ct-Np(x).
Функция Неймана Np (х) неограничена при х -► + 0.
Укажем на некоторые свойства функций Бесселя:
1)	функции Бесселя четного порядка являются четными
функциями (так как в их разложении в ряд содержатся только
четные степени аргумента). Функции Бесселя нечетного порядка—
нечетные функции; -
2)	все функции Бесселя определены и непрерывны на всей
числовой прямой и имеют производные любого порядка; это
следует из того, что любая функция Бесселя разложима в
степенной ряд, сходящийся для всех значений х, а сумма сте-
пенного ряда, как известно, является непрерывной функцией,
имеющей производные всех порядков;
3)	каждая функция Бесселя имеет бесконечное множество
вещественных корней. Корни, расположенные на положительной
полуоси, могут быть занумерованы натуральными числами в по-
рядке возрастания (как мы увидим впоследствии, это будет
вытекать из одного общего свойства собственных чисел);
4)	имеют место следующие формулы дифференцирования:
J„^(x), р = 0, 1, 2,...	(6а)
(х), р = 1, 2, 3............. (66)
Доказываются эти формулы непосредственным дифференцирова-
нием соответствующих рядов (т. е. тех рядов, которые полу-
чаются в результате деления или умножения степенного ряда для
Jp (х) на хр). Проверку этих равенств мы предоставляем читателю.
В частности
-^-У0(х)=-Л(х),	(7а)
-fr(*AW) = *A(*);	(76)
5)	имеет место следующее «ассимптотическое равенство»:
. , .	1 / 2 I pit п \
(•*) = у cos 2 J;	(8)
с возрастанием х точность этого приближенного равенства быстро
повышается. Погрешность, получающаяся при замене Jp(x) правой
128
Часть II
частью равенства (8), очень мала при больших значениях х
__з
и имеет порядок малости тот же, что их 2 .
Приближенного равенства (8) мы не доказываем.
Из равенства (8), в частности, вытекает, что функция Jp(x)
имеет корни, близкие (для больших значений х) корням урав-
(pit	п \
х------------; что разность между двумя соседни-
2	4 /
ми корнями функции Jp(x) стремится к к (при удалении этих
Рис. 53
корней в бесконечность); что график функции Jp(x) при удале-
нии от начала координат имеет вид кривой, изображающей за-
тухающие колебания; длина полуволны этой кривой почти
постоянна (близка к к), а амплитуда убывает обратно пропорцио-
нально квадратному корню из х;
6) построим графики функций Бесселя нулевого, первого и
’второго порядков (рис. 53) и приведем таблицу нескольких
первых корней этих функций.
flalattausl
знание без границ
§5 129
Положительные корни функций Jo (х),	(х), J2(x).
Корень Функция	Pi	Ра	р»	р*	р»
	2,4048	5,5201	8,6537	11,7915	14,9309
AU)	3,8317	7,0156	10,1735	13,3237	16,4706
AU)	5,136	8,417	11,620	14,796	17,960
Последующие корни этих функций могут быть найдены с по-
мощью приближенной формулы: рп+1 « рл + г; так, например,
для функции А(х)
Ре »	+ к ~ 14,9309 4- 3,1416 = 18,0725;
|л7«|лв + тг« 18,0725 + 3,1416 = 21,2141, и т. д.
Функции Бесселя называются также цилиндрическими
функциями; это объясняется тем, что многие физические задачи,
связанные с бесконечным цилиндром (например, задача о рас-
пространении тепла внутри бесконечного кругового цилиндра),
приводят к функциям Бесселя.
§ б. Краевая задача, приводящая к функциям
Бесселя. Ортогональность функций Бесселя.
Рассмотрим следующую краевую задачу: найти нетривиаль-
ные решения уравнения
xV + ху' + (Хх8 — р2) у = 0,	(1)
или, в самосопряженном виде,
{ху')'-£-у + 1ху=>0,	(2)
при следующих краевых условиях на интервале (0, /):
у (х) ограничена при х -> + 0;
«/(0 = 0.	(3)
При этом мы считаем р>0— фиксированным целым числом.
Уравнение (2) принадлежит к классу тех уравнений, кото-
рые в общем виде были рассмотрены в § 3. Следовательно, к
этому уравнению применимы и все те результаты, которые были
там получены. В частности, мы можем утверждать, что задача
имеет нетривиальные решения только для неотрицательных собст-
5 Ю. С. Очан
130
Часть II
венных значений X и что все собственные значения могут быть
расположены в виде возрастающей последовательности:
0 -С Ч < Ч < ••• < Ч < ••• •
Найдем все эти собственные числа.
Заметим сначала, что 0 не является собственным числом.
Действительно, при Х = 0 уравнение (1) принимает вид:
х*у" А- ху' — р2у = 0,
которое имеет следующее общее решение*:
при р — 0:	при р > 0
у = Сд -|- С2 In х	У~Сххр-\- С^х-р.
В обоих случаях из условия ограниченности решения при х->-Ь0
следует, что С2 — 0, а из условия у (/) = 0 следует, что Сд — 0.
Значит, при X — 0 наша краевая задача имеет только тривиаль-
ное решение, т. е. X = 0 не является собственным числом.
Итак, все собственные числа данной задачи положительны.
Обозначим их X = v’ где v > 0, и перепишем уравнения (1) и (2)
в следующем виде:
х'у" 4- ху' 4-(v»xa- р«) у = 0,	(1а)
или
(ху')' —~ у 4- V8 ху = 0.	(2а)
Эти уравнения легко привести к уравнению Бесселя с помощью
замены переменных vx = t. Тогда у’х — yt‘t'x = y't-v\ Ухх~(Ух)х~
^(У,-)',^ Уц-'t, = У1г*‘-
Таким образом, уравнение (1а) приводится к виду
(—У Ун-*а + (—) у;•v+~Р*)У = °’
\ v J	\ v /
т. е.
t*yH + ^ + ^ — Р2)У = ^
* Это—уравнение Эйлера. Вообще, уравнением Эйлера второго порядка
называется всякое уравнение вида
аох*у" 4- ахху' + a9y^f (х),
где а0, ах, ая — постоянные числа. Оно сводится к уравнению с постоянны-
ми коэффициентами с помощью замены независимой переменной J х = ef.
^alatidusmii
знание без границ “ *
о 131
а это — уравнение Бесселя. Его общее решение:
^=^(0 + ^(0.
Следовательно, общее решение уравнения (1а) (и (2а)) имеет
вид
!/ = C1Jp(vx)+Ca^(vx).	(3)
Определим Ci, С2, v из краевых условий. Условие ограничен-
ности решения при х -> + 0 приводит к тому, что С2 = 0. Если
бы было С2^0, то функция (3) была бы неограничена (в силу
неограниченности функции Np).
Условие 1/(0 = 0 приводит нас к равенству
<4(v/) = o.
Так как С\ 0 (при Сх = 0 мы получили бы тривиальное ре-
шение), то Jp(vl) = 0. Это означает, что v/ является корнем
уравнения Jp(x) = 0; следовательно,	(где р.ь ^.... — по-
ложительные корни бесселевой функции Jp(x)). Итак, v= -у~;
k = v8 =	. Следовательно, все собственные числа урав-
нения (1) или (2) таковы*:
2	2	2
1	_ 1< 2 .	. > _	.
• [Ъ »	*4 р » ••• »	 ^9	» ••• ♦
а собственные функции:
!/i = JP . y^=JP (-у- ; ...; Уь =	; -
(собственные функции мы нашли из равенства (3), учтя, что
Са = 0, v = -у- ; в ка честве С\ можно принять любое, отлич-
ное от нуля, число; здесь взято Ct = 1).
Укажем на некоторые свойства этих собственных решений
(они сразу следуют из общей теоремы, рассмотренной в § 3):
|Л?
1) каждому собственному числу кЛ=—соответствует (с точ-
ностью до постоянного множителя) только одна собственная
функция (в данном случае, Jp^-~-x^) ;
• Отсюда, в частности, следует, что функция Jp(x) имеет бесконечное
множество корней; действительно, каждый корень р. удовлетворяет равенству
|i =с I у X , а собственных чисел X, как известно, бесконечно много (см. те-
орему в § 3).
5*
132
Часть 11
2) любые две собственные функции из последовательности:
J	......(4)
\ * / \ * / \ • /
ортогональны друг другу с весом х на отрезке (0, /). Это значит,
что для любых k и	справедливо равенство
j’H^) У,(^)хЛг = 0.	(5)
О
Естественно поставить вопрос: а чему равен интеграл (5) при
k = /? Докажем, что имеет место равенство
(6)
6
Равенство (6) нам понадобится впоследствии (в теории рядов
Фурье).
Выведем сначала формулу (6) для того частного случая,
когда I = 1, т. е. докажем равенство
f IЛ (!Ал*)]аxdX = 4-[*С (нл)]а-
6
(6')
Для его доказательства рассмотрим уравнение (2), которому
удовлетворяет любая функция Jp(vx):
(ху'У 4- (v*x--—} у = 0.
\ ^* /
Подставляя в это уравнение функцию Jp (vx), получим тождество
[ х 4- J, («) 1' + (у>х----------------J„ («) 0.	(70
I dx р J \	* /
Беря, в частности, v = у.Л, будем иметь
[х -£ Л (IM)]' + ( Ф - -7-) Jp М = 0.	(7.)
Умножая все члены равенства (72) на Jp(yx) и все члены равен-
ства (7j) на Jp(\Lkx) и затем вычитая их почленно, получим
pf /pH)] H-
+ (Нл — v’) xJP M JP M = °-
^alaitaus^k
знание без границ * *
52__________________________________________________ 1зз
Проинтегрируем это тождество в границах от 0 до +1, и к пер-
вым двум интегралам применим интегрирование по частям; тог-
да, после сокращений, получим:
k,(vx) x-Ljp (Илх) — Jp (р.Лх) х	Jр (vx)l’ =
t	QX	UX	Jq
1
= (v« — |12 ) j xJp (|ХЛХ) Jp (yxdx),
или
[J, (vx) X JP (|1A.X) • — Jp (|1Лх) X Jp(yx) . v] ’ =
1
= (v’~hJ) f x-Jp(y.kx)Jp(yx) dx.
0
Подставляя границы 0 и +1 в левую часть равенства и учиты-
вая, что —корень функции Jp(x), перепишем это равенство
следующим образом:
1
нЛ Wp (Нл) = (— Й) J xJp (р.Лх) Jp (vx) dx,
или
I
J xJpMJp^ dx —
wt-JpW'pM
va___,.2
(8)
Если теперь устремить v к |лЛ, то мы получим искомый интеграл
(неопределенность типа 2- в правой части равенства (8) раскроем
по правилу Лопиталя):
= lim
i	1
I *PP(l1*x)l’dx =	\xJP(^kx)Jp^x)dx=
о
Vk‘JpWp Ы _ ,.m	(ha-) __ , r r,
= lim
v->^	2v
1
Итак, j *)laxdx =-|-[/р(|хл)1а; равенство (6') доказано.
Для того чтобы теперь вывести формулу (6) в общем виде
134
Часть II
(т. е. для любого / > 0), сделаем в интеграле
xdx за-
мену переменной ~ = г. Тогда
х dx = Г j [Jp(i^z)]9zdz =4"[ J'p^ ]2’
о	*
Таким образом, вы-
вод формулы (6) завер-
шен.
Заметим попутно,
что, если в равенство
(8) подставить X = р,
(Г/Л), то мы получим
1
У*«Мил*)А>(нх) ^х = 0,
о
откуда следует доказанная ранее орто-
гональность функций Бесселя.
В заключение укажем на некото-
рую аналогию между совокупностью
собственных решений тригонометричес-
кого уравнения У'4-Х у = 0 (при краевых
условиях у (0) ~ 0, у (/) — 0; см. § 3, стр.
115-116) и совокупностью собственных
решений уравнения (2) (при краевых ус-
ловиях (3)) из настоящего параграфа.
Обозначим через < р2 < ... по-
ложительные корни уравнения sinx=0
(т. е. рЛ = Лк). Тогда собственные ре-
шения краевой задачи для уравнения
У" + У — 0 могут быть записаны так:
sin —j~ х;...; sin-^-x;...
»	I
Графики всех этих функций получаются из графика функции
jy=sin х сжатием вдоль оси Ох так, что отрезки (0; pj, (0; р2),...,
(0; рЛ)... переходят в отрезок (0; /) оси Ох; для наглядности
начертим график функции у = sin* и графики трех пер-
вых собственных функций (ясно, что собственные функции
надо строить только на интересующем нас отрезке (0; /)) (рис. 54.)
WalatiauSfl^!.
знание без границ ’ w
М 135
Теперь построим несколько последовательных собственных
решений уравнения (х у')'---— 4-kxt/ = 0. Их графики также
X
получаются из графика функции у = Jp (х) сжатием вдоль оси
Ох так, чтобы отрезки (0; р.,); (0; р-2);...; (0; р.Л);... перешли в от-
резок (0; /); здесь — положительные корни функции Jp (х).
Построим график функции у = Jp (х) и графики трех первых соб-
ственных решений данной краевой задачи (на рис. 55 построение
проведено для случая
Р = D-
Функции Бесселя,
рассмотренные в § 4 и
§ 5, являются первым
примером специальных
функций, т. е. таких
функций, которые яв-
ляются решениями ли-
нейных дифференциаль-
ных уравнений 2-го по-
рядка с переменными
коэффициентами. С дру-
гими примерами специ-
альных функций мы
познакомимся в следу-
ющих параграфах.
Часто термин «спе-
циальные функции» по-
нимается в более широ-
ком смысле; а именно,
специальной функцией
называют всякую функ-
цию, представимую в
виде суммы степенного
ряда и не являющуюся
элементарной. С этой,
более широкой, точки
зрения специальными
функциями являются
также, например, функ-
ции у = Erf х (см. ниже, часть
х	\
т. е. функция у — J —dt I
о	*	/
3, стр. 234), интегральный синус
и многие другие.
136
Часть //
§6. Уравнение Лежандра нулевого порядка.
Полиномы Лежандра
Уравнением Лежандра порядка п называется .уравнение вида
«/"(!-**)- 2ху' + у (х-г^?) = 0.
(1)
Здесь п — заданное целое неотрицательное число.
В частности, при п = 0 получим уравнение Лежандра нуле-
вого порядка:
Г(1~
ха) — 2ху' -|- X у = 0.
(2)
Если привести это уравнение к самосопряженному виду, то оно
перепишется так:
[r/'(l-x2)]' + Xi/ = 0.
(3)
Это уравнение удовлетворяет на интервале (—1;1) всем тем
требованиям, которые предъявлялись к общему уравнению
Штурма-Лиувилля (см. § 3):
(К(х)у'У — q(x) г/ + Хр(х) # —0.
В данном случае К(х) \—х9, q(x)~ 0, р(х)~1; все эти
функции непрерывны и неотрицательны на( — 1 ; 1).
Так как К (х) = 0 на обоих концах интервала (—Г, 1), то ес-
тественно поставить следующую краевую задачу:
у(х) ограничена при 1 + О и при 1 —0.
Согласно общей теории, для этой краевой задачи существует
возрастающая последовательность собственных чисел:
Убедимся, прежде всего, что все числа вида X —/п(т4~1) (где
m > 0, целое) являются собственными числами. Впоследствии
(в § 13) будет доказано, что других собственных чисел эта за-
дача не имеет.
Итак, пусть X = m (пг + 1 )• Для того чтобы доказать, что X
является собственным числом, достаточно убедиться, что урав-
нение
у"(\ — Xs) — 2ху' 4- m (m + 1)# =0
(4)
имеет нетривиальное ограниченное решение на интервале (—1; 1).
Прежде всего убедимся, что X = 0 является собственным
числом; в самом деле, в этом случае уравнение (4) приводится
к виду
у"(\ — х9) — 2ху' = 0.
SVatofiaus;^!
знание без границ * w
ff 137
Это уравнение имеет очевидное ограниченное решение у=С (другое,
1 I х
линейно независимое с ним решение у = С2 In у _ *	неограни-
чен) на (—1; 1)).
Рассмотрим теперь к = т(т 4-1), где т > 1, целое. Убедимся,
что в этом случае уравнение (4) имеет в качестве решения сле-
дующий многочлен m-ой степени:
Для этого рассмотрим сначала функцию и — (хя — 1)т и най-
дем ее производную:
и' = т(х? — l)m"l-2x;
умножив обе части этого равенства на хя—1, получим следую-
щее тождество:
или
и' (х2 — 1) == 2 тх (хя — 1)ш,
и' (хя — 1) == и • 2 тх.
Возьмем производные порядка т 4- 1 от обеих частей этого тож-
дества; применяя формулу Лейбница для дифференцирования
произведения*, получим:
[«')<" + " (х’— 1) + Ст +1	• 2х + Й. + 1	-2 =
su<m + " • 2mx + Cj,+ iu('"’-2m,
ИЛИ
„<т + Ч (А. _ ,) + (т + 1)иИ + I). 2х+ ('"-НИ u<m) . 2
•= и,т + ” • 2 тх + (т + 1) и,т> -2 т.
Приводя подобные члены, сведем это тождество к виду
u<m+2,(l—х") —2х u<m + ” +m(m+ 1) u<m’ = 0,
•Приведем формулу Лейбница, известную из курса анализа:
(UV)<k} == Uk V 4-	° V 4- Cl U<k “2) V" -b . ..
... 4- Ci “ Z) V(/) 4».. .. ф. Ckk ~ 1 U’ И* ~ ’> 4- U V{k) ;
здесь Ci — биномиальные коэффициенты, C^ =	0 ♦» • (т/4^ 1) 4
138
Часть II
ИЛИ
[u<n,]'-(l— *") — 2*4	+О • u<m’®0,
откуда сразу видно, что функция является решением урав-
нения (4). Но
dm
Следовательно, многочлен /л-ой степени	(** — 1)т, а также
любой многочлен вида
р = С-^-(**-1)”	(5)
является решением уравнения (4). Из общей теории следует,
что не существует других решений, линейно независимых с (5),
которые удовлетворяли бы нашим краевым условиям; иными
словами, всякое решение уравнения (4), отличное от (5), неогра-
ничен© на (—1; 1).
Легко подобрать коэффициент С так, чтобы многочлен (5)
принимал значение, равное 1 при х=1. Для этого перепишем
многочлен (5) в следующем виде:
dm
» = Css-(*-l)"(* + I)™,
и применим формулу Лейбница:
i/ = C([(*-l)m),m)(* + l)m +С1, [(*-!)” )<га-1,[(*+!)”]'+
. ф- (* — !)“•[(*+ l)mJ(n”| = C(ml(*+ 1)” +
-J- m-m ! (х — 1 )• m(x 4- 1 )от-14-... 4- (х — 1 )mпг! ).
Отсюда видно, что
У L_i = С • m ! 2” у |л и , = С • (- 1Г tn ! 2m.
Следовательно, при С = 	" имеет место

Многочлен (5) при С — - называется многочленом Лежандра
NalaHausIM
знание без границ ’ *
_________________________________________________ 139
(или полиномом Лежандра) т-ойстепени и обозначается Рт(х)-
Рт (х) =	"dx”-	~ 1)т •
Кроме того, полиномом Лежандра степени 0 называется функция,
тождественно равная 1:
Ро(*)^1.
Таким образом, собственными числами рассмотренной краевой
задачи являются Хо = 0; К, ==1-2; Хя = 2-3; Ха = 3-4; Х4 = 4-5;
Хв = 5«6;..., а соответствующими собственными функциями:
P0(X)sl, Р,(х) = х, P,(x)=-^rJ-,
₽,(*) = :5л‘у3л , Pt (X) =	+ 3,
D /	63хь — 70х‘ + 15х
'ъ \х) —	g	» • • •
Из общей теории (§3) следует, что:
1) каждому собственному числу Х = /и(/и+1) соответствует
только одно (с точностью до постоянного множителя) решение
Рт(х), ограниченное на ( —1; 1);
2) два различных полинома Лежандра ортогональны друг
другу на отрезке (— Г, 1) (с весом равным 1):
1
J Р/ (х) Pj(x)dx = 0 при j.	(6)
-I
Отметим, кроме того, следующее свойство полиномов Лежандра:
jy^x^dx^^A-	(7)
при любом /п > 0. Доказательство формулы (7) основано на по-
следовательном интегрировании по частям. Для того чтобы про-
вести это интегрирование, введем следующие обозначения:
W = jhW (*• - ‘ )";	- О";
......................;
140
Часть I!
Очевидно, что Рт ° (х), Р(т 2> (х),...., Р{т "° (х) являются по-
следовательными первообразными от полинома Лежандра Рт(х).
Заметим, что Р{тт\х), Р{тт+'} (х),...,	(х) обращаются в
нуль в точках — 1 и 4- !*•
Рассмотрим теперь искомый интеграл
1
J [Pm(x)]»dx
-1
1	I
= j 'Pm« Pm(x)’dx~Pm (x) P(m-'>(x) I -
-1	-1
1
- f P„(x)P!^,> (x)dx= —
-1
1
f P„(x)P£"(x)dx =
—1
1	1	1
=-P’m(x)P^(x) I + f Pm(x)P£2'(x) dx = J Pm(x)P£2'(x)dx.
—-1 — 1	—I
Здесь мы дважды применили интегрирование по частям (приняв в
первый раз и = Рт (х), dv = Рт (x)dx, v = P!7u (х) ; во второй раз
и = Рт(х), dv = P!^n(x) dx, v = Р{т2}(х). При интегрировании
учтено, что Pt" (1) = 0, Pt"(- 1) = 0, Pt2> (1) = Pt" (-1)= 0.
Применяя таким же способом интегрирование по частям еще
несколько раз (в общей сложности т раз), в конце концов по-
лучим
1	1
f [Pm(x)fdx = (-\r {p^\x}-p^my(x)dx.	(8)
—I	—1
Заметим теперь, что
p(m> /и _	1 Г (ха 1 У71]— —-— Г (х2 — 1 улТ2™) —
_	1 Г хЪп _ тх*т-* _1_	1(2"° =__1__(2 т) I •
учитывая, кроме того, что Р(^т} (х) = ^2^(х3 — 1)ш, перепишем ра-
венство (8) следующим образом:
* Это следует из того, что 4- I и — 1 являются /«-кратными корнями
для функции р{~т)(х) = - I g-fft (х2— 1)т; следовательно, все производные
от этой функции до (т—1)-го порядка включительно также обращаются в
нуль при х = -ф- 1 и при х = — 1 .
*6	141
J '	  —	—  —....................................... —	-
1\а1(гНаи$Ж
знание без границ	’ *
А	/__1 )т ( 2/п )1 г
J [Pm(x)]adx = т(2т''т\2” J (ха—l)mdx-
-1 -1
(2m)l г
= (m!)»2«m J U — х ) dx-
(9)
Последний интеграл легко вычисляется по частям. Обозначим
1
1т = J (1 — x2)mdx и примем и = (1 — х2)т, dv — dx.
—1
Тогда
11 с
/т = х (1 — х*)т | — J х • т (1 — х3)т~1 (— 2х) dx =
—1 —1
1	1
— 2т J х«(1 — xa)m-Idx = 2т J [ 1 —(1 — ха)]( 1 — xa)m~I dx'—
-i	-i
i	।
— 2т j (1—x8)OT-ldx — 2m J (1 — x2)mdx = 2m(Jm_x — Im).
—1	—1
Из равенства Im = 2m(Im_x — Im)получаем Im == Im.x.
Применяя эту формулу должное число раз, сведем /т к /0:
г _ 2т .	_ 2т 2т — 2 .
т~ 2т + 1 ‘ т~1 ~ 2т 4.1 ’ 2m — 1 7"»-» “ • • • =
—	^,п'	— 2 %гп— *	2	.
2т -f- 1 2т — 1 2т — 3 ’ ’ * ~1~ 0
2т 2т — 2 2m — 4	2	~
= 2 т > 1 ’ 2m — 1 ’ 2m —3 ’ * ’'' V ’ 2 ’
i
так как /0 = J dx = 2. Подставляя теперь найденное значение 1т
— 1
в равенство (9), получим окончательно
f . D , Ч13.	(2ffl)]	2m- (2m —2), , .4  2_
J I * m Wi “x {m!)’ 2am ’ (2m	1) • (2m — 1)... 3- 1 ’ Z
— 1
__	(2m) I 2m • m\	Q	(2m) I 2
“ (ml )2 2tm • (2m + 1) (2m — 1)... 3-1 *Z~ rnl2m-l-3 • 5~. .. (2m 4- 1) =
(2m) 1-2	2
(2m	1)1 ~ 2m 4^1 *
142
Часть 11
Таким образом, формула (7) доказана.
Докажем еще одно свойство полиномов Лежандра.
Полином Рт (х) имеет, т различных действительных корней',
все они расположены на интервале (—1; 1).
Рассмотрим функцию Рт"т>(х) = 2т тГ (х9 — 1)"‘; она имеет два
корня — 1 и + 1; следовательно, по теореме Ролля, производная
от этой функции (т. е. функция	(х)) имеет корень а, за-
Рис. 56
ключенный между — 1 и 1. Кроме того, как было замечено рань-
ше, функция	(х) имеет корни — 1 и + 1. Поэтому про-
изводная от Мг'” + 1) (х) (т. е. функция Р{т~т + 2} (х)) имеет кор-
ни:	заключенный между — 1 и а, и р2 — между а и + 1. Кроме
того, р!п“'п + 2> (х) имеет корни—1 и 4- 1. Продолжая аналогич-
ные рассуждения, придем к тому, что Рт~т+3} (х) имеет три
корня между —1 и 1, Р{т~т + 4) (х) — четыре корня и т. д. и, на-
конец, Рт(х) имеет т различных корней между—1 и 1.
Используя доказанные свойства полиномов Лежандра, а так-
же учитывая, что полином Рт (х) является четной функцией при
ftalattausW.
знание без границ “ *
§7 143
т четном и нечетной функцией и при tn нечетном, можно по-
строить графики нескольких первых полиномов Лежандра
(рис. 56).
$7. Уравнение Лежандра п-го порядка
Рассмотрим теперь общее уравнение Лежандра
y"(l-x’)-2*j/'+!/(x-r^5 Uo,	(1)
или, в самосопряженном виде,
(/(1	+	(2)
Поставим краевую задачу; найти на интервале (—1; 1) то реше-
ние этого уравнения, которое ограничено при х->— 14-0 и при
х->1—0. Поскольку эта задача является частным случаем за-
дачи Штурма-Лиувилля (см. § 3), о ней можно высказать сле-
дующие утверждения.
Все собственные числа не отрицательны; собственные реше-
ния, отвечающие различным собственным числам, ортогональны
друг Другу (с весом 1), т. е.
1
У (x)y^(x)dx = o,
И т. д.
Будем считать, что п — заданное целое положительное чис-
ло, и докажем, что все числа вида \= т(т-\- 1) (где т = п,
п 4- 1, п,-\- 2,....) являются собственными числами. Для этого
перепишем уравнение (1), подставив 1 =	1):
у"(\ — х*) — 2ху' + у[ т{т+ 1)—	= 0 ,	(3)
и сделаем в нем замену переменной:
п
У = (Д—^)2 г.
Найдя из этого равенства у' и у" и подставив в (3), после
преобразований получим:
z" (1 — х2) — 2 (п 4- 1)хг' 4- [т(т 4- 1) — п(п 4- l)]z — 0. (4)
Этому уравнению удовлетворяет, в частности, функция [Рт(х)]<л>
144
Часть II
т е. n-ая производная полинома Лежандр а). В этом можно убе-
диться следующим образом: функция Рт (х) удовлетворяет урав-
нению
/'(1 — х«) — 2 ху' + т (т + 1)«/ = 0.
Следовательно, имеет место тождество:
[ Рт (х) Г (1 -	- 2х [ Рт (х) Г -f- т (т + 1) Рт (х) s 0.
Продифференцировав это тождество п раз и пользуясь при этом
формулой Лейбница (см. выше, стр. 137), получим
iPmW 1<л + 2’(1-*•) + "[₽„ (•*)!'"+ 1,(-2х)+
+ л(п-П [Рт(х)Г(-2) + 1Рга(х)](п+,)(-2х) +
л»
+ HP„(«)IW (— 2) + m(m + 1)[ Pm(x)l<n| — 0.
После очевидных преобразований это тождество приведется к
следующему виду:
+ [m(m + 1) —n(n+1)) [/’„(л-)]1"1 вО.
Но последнее тождество представляет собой результат подста-
новки функции [Рот(х)](п) в уравнение (4). Следовательно, функ-
ция
*=[ р„ (*) 1*”
является решением уравнения (4).
Возвращаясь к уравнению (3) (и вспоминая, что
п
у = (1 — Xs)2 • z), получим следующее решение уравнения (3), ог-
раниченное на интервале (—1; 1):
_£1	(5)
Функция (5) дает нетривиальное, ограниченное на (—1; 1) реше-
ние уравнения (1) при 1 = т(т+1), где т > п (легко видеть,
что при /п<п решение (5) является тождествен ным нулем).
ftalaflauswil
знание без ераниц ч *
g 7  145
Функции (5) называются присоединенными функциями Ле-
жандра', мы их будем обозначать * Р^(х):
п
(6)
(здесь п > 0 фиксировано; т > п).
Итак, задача разыскания ограниченного на (—1;1) решения
уравнения (1) имеет следующие собственные числа:
n(n+ 1); (п+ 1)(п + 2); (и 4- 2) (п + 3);....	(7)
и соответствующие им собственные функции:
Р"(х); Рпп + х(х)', Р" + 2(х);....	(8)
Можно доказать, что никаких собственных чисел, кроме тех, ко-
торые перечислены в последовательности (7), данная задача не
имеет.
Из общей теории (см. §3) следует, что каждому собственно-
му числу соответствует только одна (с точностью до постоян-
ного множителя) собственная функция; таким образом, функции,
входящие в последовательность (8), исчерпывают все собствен-
ные решения.
Два собственных решения уравнения (1), соответствующие
двум различным собственным числам, ортогональны друг другу
(с весом 1) на интервале (—1;4-1). Поэтому справедливы сле-
дующие равенства:
j P"m(x)-Pt(x)dx = 0,
—I
где
m^k, т> п , k> п.
Эти равенства можно переписать так:
1
У [Р„(х) 1<л) [ Р„(х)|<">(!-хГ dx — 0,
-1
где т k, т> п, k> п.
•Индекс вверху мы пишем без скобок, чтобы не смешивать с обозна-
чением производной. Заметим, что в литературе существуют и другие обоз-
начения для присоединенных функций Лежандра; так, например, иногда
функция Р1^ (х) обозначается так: Р%} (х) (см., например, Тихонов и Самар-
ский, «Уравнения математической физики», стр. 630). Такая символика для
обозначения присоединенной функции неудобна (символ Р\^ (х) напоминает
символ производной). Поэтому мы будем всюду в дальнейшем придержи-
ваться принятых нами обозначений.
146
Часть II
В случае, если k = tn, эти интегралы уже не равны нулю.
Можно доказать (тем же путем, как это было сделано для по-
линомов Лежандра), что при любом т, т > п справедливо ра-
венство:
-1
2 (m 4- л) I
(2/П-4- I) Он — л)1
или, что то же самое,
С Г dn г, /	1’,.	.	2(m + «)l
J [ dxn Рт (х ) J (1 X )п dx — (2 /и + 1) (т — л)1
Выпишем несколько первых присоединенных функций Ле-
жандра Рт (х) порядка л = 1:
Pi (х) = (1 - х^  [ Pt (х)]' = (1 - х^;
Р,(х)= (1 -x’)v- [Ps( х)]' = (1 - х*)~- Зх;
Pj(x) = (l — х9)2 • [Р8 (*))' = (1 — х9)2 • ("у-*’—4" ). ИТ- д-
Несколько первйЗ? присоединенных функций Р2т (х) порядка
л = 2:
Pl (х) = (1 - х’) [Ра (Х)Г = (1 - х!) • 3;
Р| (х) = (1 -х‘) [ Рэ(X)]" = (1 -х*) • 15х;
PJ (х) = (1 -х«)(Р4(х))" = <1 — ж«)(-*°®-х»-£-1 и т. д.
$ 8. Краевые задачи, приводящие к тригономет-
рическим функциям
1. В § 3 мы рассмотрели задачу: найти собственные числа и
собственные функции уравнения у" + X у = 0 при краевых условиях
t^(0) = 0, ^/(/)—0. Тогда было выяснено, что единственными
собственными числами этой задачи являются:
ч _ яа ф ч 2ал®	, __ Лая2
— —р , . . . ,	, . . . J
'bdtatlauswl!.
знание без границ * w
§8
147
им соответствуют следующие собственные функции:
. «х	. 2тсх	. knx
У1 « sin -J— ; e/a = sin —7—; • •.; yk = sin —j—
2. Рассмотрим теперь то же уравнение, но с другими крае-
выми условиями: у" + К у 0, у' (0) = 0, у' (Z) = 0. Соглавно об-
щей теории, Хне может быть отрицательным. Поэтому ограни-
чимся изучением двух случаев: а) X == 0; б) X > 0.
а)	Если X — 0, то общее решение уравнения имеет вид:
//— Cj х -}- Са.
Так как по условию у' |х = о^О, у' |х«./ = 0, то Ct = 0. Однако на-
ши краевые условия не накладывают никаких ограничений на С2.
Поэтому любая функция у = С2 (в частности, у^ 1) является
решением нашей задачи при X = 0. Итак, X = 0 является соб-
ственным числом, а функция у = 1 — соответствующей соб-
ственной функцией.
б)	Пусть X > 0; обозначим X = v®. Тогда общее решение урав-
нения будет у = cos v х + C2sin vx. Подставив в выражение
для производной у' — — Сх v sin v х + С2 v cos v х данные краевые
условия, получим:
С2 v = 0; — Cj v sin v I -f- Ca v cos v I = 0,
откуда Ca = 0, v I — k -к (k — любое натуральное число). Собствен-
ными функциями, отвечающими числам v = *	, являются
у— Сх cos -”* . Принимая Сг = 1 и учитывая, что X == v®, полу-
чим следующие собственные числа и собственные функции на-
шей краевой задачи (учитывая также найденное ранее собствен-
ное число X = 0):
х-о х -	• х - 22 7:3 X -
Лд — и ,	—	—J— , Ла — —р-, . . . ,	— —р—....
.	пх	2ях	knx
Уо=^ 1; 1/1 = COS —; у2 = cos —у—;...; yk = cos —— ;...
Все эти функции ортогональны друг другу (с весом 1) на уча-
стке (0; Z).
3. Рассмотрим то же уравнение у” Ч-Xt/ = 0, задав на кон-
цах интервала (—Z; Z) следующие однородные краевые условия:
*/( — /) = 1/(0; y'(-i) = y'(D-
148
Часть И
Эти краевые условия отличны от тех, которые были рассмотре-
ны в общей теореме из § 3. Следовательно, результаты этой тео-
ремы в данном случае неприменимы. В частности, пока нельзя
гарантировать, что все собственные числа неотрицательны. Поэ-
тому нам придется рассмотреть все три возможных случая —
а) X < 0; б) X = 0; в) X > 0.
а)	Пусть X < 0; обозначим Х = — v®. Тогда уравнение перепи-
шется в виде у" — »*у = 0. Его общее решение имеет вид:
у = Cjevx + С2 ; следовательно, у' ех — Са v е~'х.
Подставим краевые условия:
С, e~h + C,eh = С, eh + С, г1’;
С, v «-'* — С2 = С, ve'* — С2 ve-'*
откуда находим (учитывая, что >#(), е1' Фе ь):
С, = 0, С2 = 0.
Итак, никакое X < 0 не является собственным числом.
б)	Пусть X = 0. Тогда уравнение приводится к виду у” — 0;
его о^щее решение у = Ctx С2. Подстановка краевых условий
приводит к уравнениям:
— Ci I 4~ С2 — Ci I - С2 *,
Ci = сг,
откуда видно, что С2 — произвольно, а Сх = 0. Итак, при X = 0 за-
дача имеет нетривиальные решения ул=С2(в частности, у=1).
Значит, X = 0 — собственное число.
в)	Пусть X > 0. Обозначая X = v®, приведем уравнение к виду:
у" + v8 У = 0; его общее решение таково: у = Сх cos v х 4- С2 sin v х.
Подставляя краевые условия, получим:
j Cr cos v I — Ся sin v/ = Ci cos v / + Ca sin v /,
( —Ci v sin v I -f- C2 v cos v I — Ci v sin v I 4- C2 v cos v /,
или, после упрощений и сокращения на v,
C2sinv/ = 0; Clsinv/ = 0.
Если sin v I ф 0, то Ci — 0 и Са — 0; решение тривиально. Наша
краевая задача имеет нетривиальные решения только при sin v/= 0,
откуда v/ = k к, и, значит v = —— (k = 1,2,3,...).
^ataHaus,^!.
знание Вез границ У w
§9 149
Следовательно, собственные числа (кроме ранее найденного чис-
ла X = 0) таковы:
' __ л® » ______ 2ала , _________ Л® Л®
р » Л2 — р » • • • »	— р » • • •
А® л®
Каждому такому собственному числу —— отвечают две линей-
но независимые функции: cos -	и sin -k . Действитель-
но, при v = любое решение уравнения y'f -f- ( j у — 0
удовлетворяет поставленным краевым условиям, а, значит, в
.	knx . kлX
частности, им удовлетворяют функции cos—z— и sin—z—.
Кажущееся противоречие с общей теоремой о собственных
значениях объясняется тем, что последняя была доказана только
для трех типов краевых условий. В данном же случае мы имеем
краевые условия, отличные от тех, которые были там рассмот-
рены; следовательно, к данному случаю эта теорема не приме-
нима (рассмотренная здесь задача не является задачей Штурма-
Лиувилля).
Выпишем все собственные числа и собственные функции
данной краевой задачи:
*o = O	X — p	2®те» Aa	-p	• • •	fe®7T® — p	 • •
Уо - 1	nx Vi— cos l nx У1- sin z	2nx y2 — cos 2nx y2 — sin l	• • •  • •	knx Ук - cos z knx Vk - sin z	• • • • • •
Все эти собственные функции ортогональны друг другу с весом 1 на
интервале (—/, /) (даже если они соответствуют одному и тому
же ХЛ). Это, конечно, не вытекает из общей теоремы, но может
быть доказано непосредственным интегрированием.
$ 9. Ряды по ортогональным системам функций
В предыдущих параграфах мы рассмотрели различные после-
довательности ортогональных функций. Такими были, например:
1)	последовательность тригонометрических функций:
. тех . 2ях	knx
Sin —j— ; sin —7— ; . . .; sin —— ;...
*	i *	*
150
Часть //
Эта система ортогональна на отрезке (0; /) с весом 7 = 1;
2)	последовательность функций Бесселя:
г ( Н* \ J ( ^2* \	/ / V-kX
р \ 1 / р \ 1 /...............Jp \ ~~1
(где р > 0 — фиксированное целое число, н < Р-2 <* • • • • <
<	< ... — все положительные корни функции Jp (х)). Эта си-
стема ортогональна на (0; /) с весом 7 (х) = х;
3)	последовательность полиномов Лежандра
Р0(х),	Р2(х)....Рт(х),...
ортогональна на (—1; 1) с весом 7=1;
4)	последовательность присоединенных функций Лежандра
Рп(х), Р^ + ^х).....Рт(х),...
(п > 0 фиксированное целое число) ортогональна с весом 7 = 1
на отрезке (—1; 1).
Вообще, если дана задача Штурма-Лиувилля, т. е. уравнение
IК (х) у' J — q (х) у + X р (х) у = 0
и соответствующие краевые условия на интервале (а, Ь), то си-
стема собственных функций этой краевой задачи:
<?»(*). ?2(*)....
ортогональна на (а; Ь) с весом 7 = р(х), где р(х)>0 на (а; Ь).
Пусть нам дана некоторая ортогональная на (а; Ь) с весом
7 (х) > 0 последовательность функций:
<?1(х), <р2(х)..................................(1)
Рядом по системе (1) называется всякий ряд вида:
Ci <Pi(x) + с2%(х) + ... + сл<р„(х) + • • •	(2)
(где q. с2,... — числовые коэффициенты).
Пусть теперь ф(х)— какая-либо функция*, заданная на (а; Ь).
* Для определенности, читатель может считать функции <pt (х) , <р2(х)> • • •»
фл(х), . . . ,а также ф (х) и 7 (х)— непрерывными на [a; 6J. Однако боль-
шая часть дальнейших рассуждений остается в силе и для любых, интегри-
руемых на [а; Ь) функций, например для функций, ограниченных на (а; Ь)
и имеющих лишь конечное число точек разрыва.
^alaliausA
знание без границ * *
$9 151
Допустим, что функция ф(х) может быть разложена в ряд
(2) и что этот ряд равномерно сходится на отрезке (а, Ь). В этом
случае коэффициенты ряда (2) можно легко найти. Для этого
умножим обе части равенства
Ф (*) = Ci <Pi (х) + с2 <р2 (х) 4- •.. + Ck (х) 4-...
на <р*(х)?(х) (при фиксированном k). Тогда
Ф W ф* W К (*) = q <р, (дг) (х) у (х) + с, <рг (х) (х) у (х) + ... +
+ с* feW)’7 (•*)+•••	(3)
Если ряд (2) равномерно сходился, то также равномерно будет
сходиться и ряд (3) (после умножения всех членов ряда на огра-
ниченную функцию, его равномерная сходимость не нарушит-
ся). Проинтегрировав почленно равенство (3) в границах от а до
ь
Ь, получим (учитывая, что j <?, (х) qk (х) у (х) dx = 0 при i^k):
а
b	b
J <? (*) <f>k (X) 7 (х) dx = ск J [<рЛ (x)l’ 7 (x) dx,
a	a
откуда
b
J Ф (*) (x) 7 (x)dx
J l<P* (x)]a7(x)dx
a
(4)
Числа сл называются коэффициентами Фурье функции ф (х) по
ортогональной системе {<pft(x) а ряд (2) с этими коэффициента-
ми— рядом Фурье функции ф(х) (по системе {<Р*(х)}).
При выводе формул для вычисления коэффициентов Фурье
мы заранее предположили, что функция ф (х) может быть разло-
жена в ряд (2) и что этот ряд равномерно сходится на (а; Ь). Одна-
ко проверить, выполняются ли эти условия для функции ф(х),
мы, вообще говоря, не можем. Поэтому поступим следующим
образом: построим формально по данной функции ф(х) ряд (2)
(вычислив его коэффициенты по формулам (4)) и выясним, стре-
мятся ли частные суммы Sn(x) этого ряда к ф(х) (при и-* оо).
Но тут мы сталкиваемся со следующей трудностью: оказы-
вается, даже для таких простых систем ортогональных функций,
как тригонометрические системы или система полиномов Лежан-
дра, модуль разности | ф (х) — Sn (х) | не обязательно стремится
В
152	Часть II
к нулю во всех точках основного интервала; так, например, если
дана система
sinx, sin2x......sin их...
на отрезке (0, т:), то можно построить такую непрерывную функ-
цию ф(х), что ее ряд Фурье по этой системе расходится на бес-
конечном множестве точек.
Поэтому мы несколько видоизменим задачу: вместо того,
чтобы оценивать модуль разности | ф (х) — Sn(x) |, оценим интег-
рал от этого выражения:
ь

(5)
Если этот интеграл стремится к нулю при п -> оо, то мы скажем,
что ряд Фурье сходится в среднем, к Ф(х). Геометрически этооз-
Рис. 57
начает, что площадь об-
ласти, заключенной между
линиями у = Sn (х) н
у — ф (х), стремится к ну-
лю при п -> со (рис. 57).
При оценке интеграла
(5) нам придется иметь
дело с интегралом от мо-
дуля; а модуль, даже от
элементарной функции,
является слишком слож-
3 ной функцией и трудно
поддается исследованию
(в частности, вычисление
и исследование интеграла
от модуля функции является нелегким делом). Поэтому вместо мо-
дуля разности будем рассматривать квадрат разности: ясно, что
квадрат некоторой величины мал тогда и только тогда, когда ее
модуль мал; в то же время ясно и то, что квадрат функции
проще и легче поддается исследованию, чем модуль функции.
Итак, выясним, стремится ли к нулю интеграл
ь
J [ф(х)~ S„(x)]’dx.
а
(6)
Если да, то говорят, что ряд Фурье сходится в среднем квадра-
тичном к ф(х).
В тех случаях, когда семейство функций (х), <р2(х),....
^lalaHausii^i
знание без границ “ w
§9 153
Фл(х),... ортогонально с весом 7 (х), мы будем оценивать интеграл
от квадрата разности с весом 7 (х), т. е. интеграл
ь
[ф(х) — Sn (x)j’T(x)dx;
(7)
если он стремится к нулю (при п->со), то говорят, что ряд
Фурье сходится к ф(х) в среднем квадратичном с весом 7(х).
Итак, оценим интеграл (7), учитывая при этом, что
ь
J Ф (х) Фл (х) I (х) dx
Sn (х) == ct <pi (х) Ч-... -I сп ч>п (х), и что ck -----------.
J 1фл (х)]а 7 (х) dx
а
Квадратный корень из интеграла (7) называется квадратичным
отклонением функций ф(х) и Sn(x) и обозначается &т(ф, 5Л).
Поэтому интеграл (7) равен квадрату этого отклонения:
ь
[ (Ф. £«)]’ j IФ (*) “ Sn (*) 1’ 7 (*)dx =
а
бг	л
= j Ф(*)— ^ck^(x) y(x)dx =
aL	^=*1
n
" Ck <f>k
b	n	b	b
= J ^ydx —	J* Ф ФлТ dx "I- j
a	k=*l a	a
3
ydx.
n
Возводя в квадрат сумму YiCkcf>k и учитывая, что интегралы
Л=1
от произведений <Р/ Т (при i Л/) равны нулю, получим
b	п b	п b
[ МФ» S«)?= .[ Ф’ ldx~ Я^С/. J ф у dx |	7 dx.
а	Л=1 а	Л = 1 а
b
j Ф <fk 1 dx
Принимая во внимание, чтосЛ = -—Т1----------- и, следовательно,
.Гфл 7 dx
а
154	Часть II
Ь	ь
j* ф 9л 7 dx = ck j* 9л I dx, бУДем иметь:
a	a
b	n	b	n b
[МФ> 5л)],= ^ ^idx — 2E Ск-ск У<р*7</х4- ScJJ<p2 ydx
a	A=1	а	A=ol a
откуда
b	n	b
[МФ» sn)]'= $^dx —	7 dx.	(8)
a	Л—1 a
Равенство (8) имеет фундаментальное значение в теории рядов
Фурье. Из него вытекает ряд важных следствий:
а)	так как [ В7(ф, Sn)]’> О, то для любой ортогональной си-
стемы {<рЛ} и для любой функции ф имеет место неравенство
b	п b
j ф2 7 dx — £ c2k J <f>2 7 dx > 0,
а	A=1 a
ИЛИ
n b	b
ijcJ J*Pa ldx< j фа7*/х;	(9)
A=«l a	a
б)	из неравенства (9) следует, что частные суммы ряда с
ОО ft
неотрицательными членами £ c2k J 7 dx ограничены числом
А=»1 а
b
j ф’ 7 dx. Следовательно, этот ряд сходится, и его сумма не
а
Ъ
превосходит числа
а
оо b	b
£ с\ J 9л 7 dx < $ ФЯ 7 dx.	(10)
Az-l а	а
Неравенство (10), справедливое для любых ортогональных (с
весом 7) систем (<рл(х)} и для любой функции ф(х), называется
неравенством Бесселя',
в)	если ряд Фурье сходится в среднем квадратичном (с ве-
сом 7 (х)) к функции ф (х), то, по определению, это означает, что
&т(ф, S„)->0 (при п-+ со). Но тогда, в силу равенства (8),
ft	п b
j фа 7 dx — £ c2k jj tp2 7 dx -> 0 при n -> oo,
a	a
________________________________________________ 155
Dlaiattaи$;Ж
знание Без границ “ ш
или
л b	Ь
lim ScJ J SP* Тdx —	J ф®ydx.	(11)
л->оо	a	a
oo b
Предел этой суммы равен сумме ряда ]£ c2k J <f>2k 7 dx (этот
a
ряд сходится, как было доказано выше). Следовательно, для
сходимости в среднем квадратичном (с весом у) ряда Фурье к
функции ф(х) необходимо и достаточно выполнение следующего
равенства:
со	ь	ь
Е 4 J 9*' Т dx = j* Ф8 Т dx-	(12)
Л=»1 а	а
Это равенство, равносильное равенству (11), называется равен-
ством Парсеваля.
Замкнутые системы функций. Назовем классом С' семейство
всех функций ф(х), ограниченных на отрезке [а; 61 и имеющих
на этом отрезке не более конечного числа точек разрыва*.
При этом принято считать тождественно равными друг другу
две функции из класса С', отличающиеся друг от друга лишь
для конечного числа значений независимого переменного. В част-
ности, функцию, отличную от нуля лишь в конечном числе то-
чек, мы будем считать тождественно равной нулю.
Пусть задана некоторая последовательность не равных тож-
дественно нулю функций из класса С':
9i(*),	(13)
ортогональная на [а, 6] с весом 7. Эта система называется зам-
кнутой в классе С', если равенство Парсеваля выполняется для
любой функции ф(х) из С'. Иными словами, система (13) замкну-
та в классе С', если ряд Фурье
Ci 91 (*) + са <р2 (х) + ... 4- сп <?п (х) Н..
для любой функции ф (х) из С' сходится в среднем квадратичном
(с весом у) к самой этой функции.
Рассмотрим (без доказательства) одну общую теорему, даю-
щую достаточные условия замкнутости системы функций.
* Обычно символам С обозначают семейство всех функций, непрерыв-
ных на сегменте [а; Ь]; рассмотренное нами семейство С' значительно шире,
чем семейство С.
Функция, заданная на отрезке [а; Ь] и имеющая на нем не более ко-
нечного числа точек разрыва, называется кусочно-непрерывной на этом от-
резке. Таким образом, можно сказать, что С' — это семейство всех функций,
ограниченных и кусочно-непрерывных на [а; Ь].
156
Часть II
Пусть дана задача Штурма-Лиубилля: уравнение
1К(х)у']'— q(x) у-\- к р(х) г/ = 0
с соответствующими краевыми условиями на интервале (а, Ь).
Как известно, эта задача имеет бесконечно много собственных
чисел:
О Х2 <С Хд < ... < Х^ < ...,
и бесконечно много собственных функций, причем каждому соб-
ственному числу Хл соответствует одна (и, с точностью до по-
стоянного множителя, только одна) собственная функция <рл(х).
Семейство всех собственных функций
•PiW. <р8
является ортогональной системой на [a, Ь] с весом р(х). Можно
доказать, что эта система является замкнутой в классе С'.
Теорема. Система всех собственных функций задачи Штурма-
Лиувилля замкнута в классе С'.
Таким образом, каждая ограниченная функция ф(х) с конеч-
ным числом точек разрыва разложима в ряд Фурье по ортого-
нальной системе собственных функций задачи Штурма-Лиувилля:
<Pi (х) + с2 <?2 (х) + ... + ck (х) 4-... .
Этот ряд сходится в среднем квадратичном на интервале (а; Ь)
(с весом 7(х)) к функции ф(х).
Полные системы функций. Система ортогональных (с весом
7 (х)) функций <jpj (х), (х),..., <рл (х),...	называется полной в
классе С', если не существует отличной от нуля функции из это-
го класса, ортогональной (с весом 7 (х) )ко всем функциям <pk (х).
Теорема. Если система {<рл (х)} замкнута в классе С', то
она полна в этом классе.
Доказательство. Допустим, что данная замкнутая си-
стема не полна. Тогда найдется функция ф(х) из класса С'
ь
такая, что j ф (х) <рл (х) 7 (х) dx = 0 для Л= 1, 2, 3.;	следова-
а
тельно, все коэффициенты Фурье функции ф(х) равны нулю; но
тогда, в силу равенства Парсеваля (система ведь замкнута по
условию!), имеет место:
ь
J [ф (х))в 7 (х) dx = 0.
а
§9 157
знание без границ	' w
А если интеграл от неотрицательной функции равен нулю, то
сама эта функция тождественно равна нулю* *•. Значит [ф (х)]® 7 (х)=0,
откуда ф (х) = 0. Итак, не существует отличной от нуля функции
класса С', ортогональной одновременно ко всем функциям
<Р1 (х), <ря (х),...; следовательно, система (х), t <р2 (х),... полная.
Из доказанной теоремы вытекает, в частности, следующее
свойство замкнутых систем:
Если из замкнутой ортогональной системы исключить хо-
тя бы одну функцию, то оставшаяся система уже незамкнута.
В заключение параграфа остановимся еще на одном свойстве
рядов Фурье — так называемом экстремальном свойстве частных
сумм ряда Фурье.
Пусть ф (х) — какая-либо функция из класса С', а <р2..—
данная ортогональная (с весом 7) система. Зададим число п и
постараемся подобрать коэффициенты ар а2......ап так, чтобы
линейная комбинация из п первых функций нашей ортогональ-
ной системы
«19100 4-...+ %?„(*)
по возможности меньше отличалась от функции ф(х). Это надо
понимать так, что квадратичное отклонение (ф, Ln) должно быть
минимальным по сравнению с квадратичным отклонением функ-
ции ф от любой другой линейной комбинации ₽i <Pi (х) + . • • +
+ РлФлОО (при том же п).
Разыскание коэффициентов ар а2,..., ая, удовлетворяющих
условию минимальности отклонения (ф, Ln), проводится пример-
но тем же методом, что и вывод формулы (8).
* Докажем это утверждение.
Если функция /(х) > 0 непрерывна, то оно почти очевидно; в самом
деле, если бы нашлась хотя бы одна точка х0, в которой /(х)^0 (например,
f (х0) — m > 0), то, в силу непрерывности, неравенство f (х) > -у-имело бы
место	в	некоторой окрестности	этой точки	(например, на	интервале	(а;	₽)).
Ь	а	р	ь	р
Но тогда было	бы J f (х)	dx =	J	f (х) dx 4-	J	f (x) dx 4.	J f (x) dx	>-	[ f (x)	dx >
а	а	а	в	a
b
> -тс- (P — a) > 0, что противоречит тому, что J f (х) dx = 0.
*•	a
Если же функция f(x) является какой-либо функцией из С' (не обяза-
тельно непрерывной), то точно таким же путем доказывается, что в точках
непрерывности этой функции она должна равняться нулю. В точках же раз-
рыва функция f(x) может отличаться от нуля, но таких точек лишь конеч-
ное число. А функцию, отличную от нуля лишь в конечном числе точек,
мы считаем тождественно равной нулю (см. стр. 155).
158
Часть 11
Пусть аь а2,..., ап — произвольные числа. Тогда
Ь Г п	1>
[МФ. £„)]’= j !<*« =
а	*-1
b	п	b	п Ъ
= j ф9	7 dx —	2 £ аА f	ф <рЛ 7 dx	S а* j <j£	7 dx.
a	Asal	a	A«i а
В этом можно убедиться, раскрывая скобки под знаком интег-
ь
рала и учитывая, что J<pz ^dx = 0 при i=£j.
а
b
J Ф <Рл 7 dx
Принимая во внимание, что ——-------------=сЛ(гдесА—коэф-
H'&'ldx
а
фициент Фурье) и что, следовательно,
ь	?
Уф 7 dx = ck j <РА 7dx,
а	а
получим
b	п b	п b
[ МФ’ £л)]2= У ф9 7 d* —2 £ ak ck У <рА 7 dx+ £<4У<рА ^dx.
а	А=1 а	Л=1 а
п Ь
VI 2 f 2 j
Прибавим и вычтем из правой части равенства Дск]<рА 7 ах;
*=1 а
тогда, после очевидных преобразований, будем иметь:
[MW1 =
b	п	b	п b
У ф* 7 dx + S (аА — сЛ)9 У <РА 7 dx — 2 с\ У <р£ т dx.
а	Л=1	а	а
В выражении, стоящем в правой части этого равенства, от
п	b
чисел «1, «2» • • •»ап зависит только (ctA — ck)9 У dx. Эта сум-
*=1	а
ма достигает наименьшего значения тогда и только тогда, когда
otj = q, а, = са,..., ал = сп. Итак, минимальное значение откло-
нения МФ» ^п) будет достигаться тогда, когда Ln является
n-ой частной суммой ряда Фурье. Следовательно, каковы бы ни
Natatlauswk
знание без границ * *
§ Ю 159
были коэффициенты ах, а2,..., ая в линейной комбин ации Ln =
— «1 ?i + • • • + «л<РЛ» всегда имеет место неравенство:
МФ- «»)< МФ- £„),
(14)
где S„ = q ft 4- сп <р„ — n-ая частная сумма ряда Фурье.
При этом, если хотя бы один из аЛ отличен от соответствующего
коэффициента Фурье, то неравенство (14) превращается в строгое
неравенство:
МФ- «л)<МФ- Ьл).
£ 10. Тригонометрические ряды Фурье
Пусть нам дана какая-либо из следующих трех ортогональ-
ных (с весом 7=1) систем функций:
на
на
теле . 2nx • knx
sin—j-; sin-y-; ...; sin—p
интервале (О, Z) (система синусов)',
. лх	2nx	knx
1; cos —; cos ——;...; cos ——
интервале (0; I) (система косинусов)’,
.	__ 7ГХ „ 2пх	knx
1; cos —; cos —j—;...; cos —j—
nx . 2kx	kn x
sin —-—; sin ——;...; sin ——
(1)
(2)
(3)
I
на интервале (— I, l) (общая тригонометрическая система).
Ортогональные системы (1), (2), (3) называются тригоно-
метрическими системами функций, а ряд Фурье по любой из
этих систем — тригонометрическим рядом Фурье.
Каждая из этих систем замкнута в классе С' (на соответ-
ствующем интервале). Это будет доказано в § 13. Заметим, по-
путно, что замкнутость первых двух систем вытекает также из
общей теоремы о замкнутости системы собственных функций
задачи Штурма-Лиувилля (известно, что система синусов яв-
ляется системой собственных функций краевой задачи у" -|- \у =0,
У (0) — У (0 = 0» а система косинусов — краевой задачи у" -j-X у =0,
у’ (0) — У' (0 = 0). Замкнутость же третьей из рассмат-
160
Часть II
риваемых систем не вытекает непосредственно из общей теоре-
мы, так как краевая задача, для которой эта ортогональная си-
стема служит системой собственных функций, не является
задачей Штурма-Лиувилля.
Рассмотрим подробнее ряды Фурье по каждой из тригоно-
метрических систем.
1. Ряд Фурье по системе {sin k—\\ 2; 3;..., на-
зывается рядом Фурье по синусам. Коэффициенты этого ряда для
функции ф(х) вычисляются по формулам:
j ф (x) sin A ”*. dx
= i	»
Jsin» dx
о
откуда
i
Ьк— -j- j ф (x) sin -k * x- dx.
6
(4)
Если функция ф(х) принадлежит классу С', то ряд Фурье с
коэффициентами, вычисленными по формулам (4), сходится в
среднем квадратичном к ф(х). Это записывают с помощью
равенства:
, . .	,	. пх . .	. 2пх .	. , knx .	/еч
ф (х) = bt sin — 1- b2 sin — 1- ... 4- bk sin —J 1-...	(5)
Пример 1. Разложить в ряд Фурье по синусам на интервале
(0; к) функцию ф (х) = х к.
Вычислим коэффициенты этого ряда:
“Я
,	2 Р .	. ч . knx ,	2 — 4cos k п
Ьb = — I (X - - n) sin---------dx —----------г------
K П I '	П	R
o
откуда
x 4- г: = 6 sin x — sin 2x 4- — sin 3x-A sin 4x 4- -y sin5x—... (6)
Это равенство следует понимать в том смысле, что ряд (6)
сходится в среднем квадратичном к функции х -|-т на интер-
вале (0; я).
§ 10
161
п Г» л	। пх 2пх	knx
2. Ряд Фурье по системе 1; cos-p-; cos—у—;.. .;cos ——
называется рядом Фурье по косинусам. Если записать этот ряд
в виде
Л.	nx .	2пх .	,	knx
4- ах cos ~y~ 4- аа cos —--|-... 4- ak cos ——
то его коэффициенты для функции ф (х) вычисляются по формулам:
I
Г ф(х) • I • dx t
А =-----7-------- = Т | Ф (х)
fladx	о
,	knx
ф (х) cos —— dx l
1	2 f,. . knx .
-7-------------= — J <|>(*)cos-7— a*-
Обозначая свободный член A = (таким образом, а0 = 2Л),
получим:
i	i
«о = j- | Ф (*)dx' °* = “Г J Ф № cos	dx‘
о	о
Ряд Фурье с такими коэффициентами сходится в среднем
квадратичном на интервале (0; /) к функции ф(х); это записы-
вается так:
, / . «at	пх . 2тгх. ,	knx .
Ф(*) = -f- 4- Qi cos—j— 4- g2cos—— 4-... 4- akcos -j- + ... (8)
Пример 2. Функция ф(х) = х4-к разлагается в ряд Фурье
по косинусам на интервале (0; тс) следующим образом:
3	4	4
х 4- я = -к- ------cos х — -7Г- cos Зх — ...
Z	Л	УК
•••	(9 b л. cos(2^4-1)x •••	(9)
Этот ряд сходится в среднем квадратичном к функции х 4- тс на
интервале (0; г).
Ряды (6) и (9) различны, но на интервале (0; к) они сходят-
ся (в среднем квадратичном) к одной и той же функции.
6 ю. С. Очан
162
Часть 11
3.	Рассмотрим ряд Фурье по общей тригонометрической
системе на интервале (— Z; I). Если этот ряд записать в следую-
щем виде:*
-у- + (a, cos -|- б, sin + ... + cos +
+ Мп-^) + ...,	(Ю)
то, согласно общим формулам для коэффициентов ряда Фурье,
коэффициенты данного ряда вычислятся по формулам:
/	р	kn х
j ф (х) • I • dx	I Ф (х) cos —j—dx
«о _ ~l_________.	„ —I________________.
2 — i	’ ak — i
с .	C knx
J la dx	j cos’ —j— dx
i
J.	. knx
ф (x) sin —j— dx
-i
откуда
i	i
(x) dx\ ak = ~ J ф (x) cos dx\
-i
i
bk =	dx.	(H)
—i
Если функция ф(х) принадлежит классу С' (на интервале
(—Z; /)), то ряд (10) с коэффициентами, вычисленными по фор-
мулам (11), сходится в среднем квадратичном к ф(х) (что вы-
текает из замкнутости общей тригонометрической системы).
Замечание. Разложение в ряд по общей тригонометриче-
ской системе несколько упрощается, если функция ф(х) являет-
ся четной или нечетной на интервале (—Z; Z).
* Как и в случае ряда по косинусам, мы обозначили свободный член
Со
через ~2~.
NatatiausTisk
знание без границ * *
§ ю 163
а)	Пусть функция ф(х)— нечетная функция, заданная на
(— /; /). Докажем, что соответствующий ей ряд Фурье по общей
тригонометрической системе не содержит свободного члена и
членов с косинусами, а коэффициенты при синусах имеют вид:
i
b„= -f-J+Wsin-^-dx.	(12)
О
Действительно, если ф (х) — нечетная функция, то произведение
ф (х) cos -** х- является также нечетной функцией, а произведение
ф (х) sin — четной. Поэтому
/	i
а° = -]- J Ф(х)= А	= ~Г J Ф W cos dx = 0;
-I	-I
i	i
bk = -J-J ^(x)sin-^~- dx =	( ф(х)зт -”*-dx.*
—I	0
* Здесь использованы следующие свойства четных и нечетных функций:
а) если /(х) — четная функция, заданная на (—Г, 0, то J / (х) dx «
I	~* 1
2 J f (х) dx;
I
б) если f (х)— нечетная функция, заданная на (—/; 0, то j f (x)dx = 0.
Докажем свойство а). Пусть /(х) — четная функция. Представим интег-
рал J / (х) dx в виде суммы двух интегралов:
—/
I	о	1
f f (х) dx = J f (х) dx 4- f f (x) dx;
-l	-i	6
сделав в первом из этих интегралов замену переменных х = —/и учтя, что
/(—0 = /(/), получим
I	0	III
J /(х) dx = f f (_ 0 (_ I) dt 4- f / (X) dx =ff(t)dl+ (7(x) dx.
—I'l	0	0	0
I	l.	l.	l.
Ho J f (0 dt = I’ f (x) dx. Поэтому I f (x) dx — 2 I f (x) dx.
0	0	-I	0
Аналогично доказывается и свойство б).
Рассмотренные свойства могут быть наглядно проиллюстрированы на
рнс. 58.
6*
164
Часть 11
Таким образом, при разложении нечетной функции ф(х) в ряд
по общей тригонометрической системе на интервале (—/; /) мы
получим ряд, составленный из одних синусов:
ф(х) = djsin + b2sin 4-bksin —— -| ...
Рис. 58.
б)	Пусть ф(х)—четная функция, заданная на (—Z, Z). При
ее разложении в ряд по общей тригонометрической системе ока-
зывается, что все bk равны нулю, а п0 и ak могут быть вычисле-
ны по формулам:
i
2
«о = — ] Ф (*) dx'>
I
2 f , . . kitх ,
ak = -j-\ty(x) cos —j— ax\
6
таким образом, при разложении четной функции на интервале
(— /; /) мы получим ряд, состоящий из одних косинусов:
, . . д0	it х .	2 it х ,	.	kit х
4>(х) = -£- 4- cos — 4- С2 cos —---------------Ь • • • 4 ak cos -у— у ...
Пример 3. Разложить по общей
на отрезке (—1, 1) функцию
тригонометрической системе
Ф (*)=--
х при 0 < х< 1,
1 при — 1 < х < 0.
Функция ф(х) задается
ниями на разных участках
различными аналитическими выраже-
интервала (—1; 1). Поэтому для вы-
ftaiaiLauswk
знаниеСез границ “ *
§ to 165
числения интегралов, содержащих эту функцию, представим их
в виде суммы двух интегралов: от — 1 до 0 и от 0 до 1;
J	°.	1
an = — j ф (х) cos n ” х dx — J ф (х) cos пях dx 4- j* ф (х) cos rntxdx =
-1	-1	о
0	1.
~ J 1 • cos n~xdx 4- j xcosnirxdx;
-i	о
вычисляя эти интегралы, получим:
О при п четном (п Ф 0),
а
2
—при п нечетном.
3	I
Аналогично вычисляются а0 и Ьп: аа ~ -я-; Ь„ —------
U П о 2 ’ п	пп
Поэтому
3/2	1	\	1
Ф U) = т +-г cos тех-sin ях I-й— sin 2 ях 4-
* ' '	4 I я’	я / 2я	1
/2	1	\
+-----55—2~ cos Зях-sin Зкх)...
1 I 3я яа	Зя	/
Этот ряд сходится в среднем квадратичном к ф(х) на интер-
вале (— 1; 1).
Пример 4. Разложить в ряд Фурье по общей тригонометри-
ческой системе на интервале (—я; тс) функцию ф(х) = х.
Эта функция является нечетной; поэтому все ап и а0 равны
нулю; что же касается Ьп, то для их вычисления можно вос-
пользоваться формулой (12):
,	2 f	,	(— 1)я+» • 2
Ьп — — I х sin п х dx — ---------------------
л я J	п
о
Итак,
2	2	2
х — 2sin х-----н- sin 2х 4- -.-sin Зх----т sin4x4~. •.
kS	О
Этот ряд сходится в среднем квадратичном к функции
ф(х) -- х на интервале (—я; я); следовательно, здесь имеет место
166
Часть 11
равенство Парсеваля (см. § 9, формула (12)). В данном случае
оно примет следующий вид:
оо	1,
У] b2n J sin® nxdx =
Л«"1 —К
It
j x'dx.
—It
(остальных коэффициентов Фурье мы не пишем, так как они
равны нулю). Вычисляя фигурирующие здесь интегралы и под-
оо
,	/	,чя+1	2	V 4	2п8
ставляя Ьп = (— 1)л+1 • —, получим к = “3“’ 0ТКУДа
л—1
оо
S1 _ п»
п» ~ "6“’
п-1
т. е. сумма ряда, составленного из обратных величин квадратов
я8
натуральных чисел, равна -g-:
Аналогично, разлагая в ряд Фурье на (—к; л) функцию
ф(х) = х‘ и затем, применяя к полученному ряду равенство Пар-
севаля, можно найти сумму другого числового ряда:
. J_. JL + +-L+ = —
2<	3* ' • • • ~ п* ' ’ • •	90 
Эти примеры показывают, что с помощью тригонометриче-
ских рядов Фурье можно находить суммы некоторых числовых
рядов. Однако основное значение рядов Фурье заключается да-
леко не в этом: главное значение рядов Фурье заключается
в том, что на них основан важный метод решения уравнений
математической физики — метод Фурье или метод разделения
переменных. Он будет подробно рассмотрен в третьей части.
Теорема Дирихле. До сих пор, говоря о сходимости триго-
нометрических рядов Фурье, мы рассматривали только вопрос
об их сходимости в среднем квадратичном. Естественно, возни-
кает вопрос: имеет ли место для этих рядов сходимость в обыч-
ном смысле слова? Для каких функций ф(х) и для каких точек
х ряд Фурье сходится в обычном смысле и имеет суммой ф(х)?
Ответ на этот вопрос достаточно труден. Даже среди непрерыв-
ных функций имеются такие, для которых тригонометрический
ряд Фурье расходится в отдельных точках. Однако некоторые
^iataiiaus&k.
знание без границ “
____________________________________________________ 167
соображения, связанные с вопросом о сходимости тригонометри-
ческих рядов Фурье, все же можно изложить.
Для этого введем понятие кусочно-монотонной функции.
Функция f(x) называется кусочно-монотонной на интервале
(а, Ь), если этот интервал можно разбить на конечное число ин-
тервалов (a; xt), (хх; х2), (х2; х3),..., (хя_р Ь), внутри каждого из
которых функция монотонна*.
Заметим, что если функция f(x) кусочно-монотонна и огра-
ничена на (а; Ь), то всякая ее точка разрыва является точкой
разрыва первого рода (т. е. в этой точке существуют предел функ-
ции слева и предел функции справа). Действительно, если точка
С является точкой разрыва, то она либо разделяет два интервала
монотонности функции, либо является внутренней точкой такого
интервала. В обоих случаях около С найдется левая полуокрест-
ность (а; С) и правая полуокрестность (С; р), в каждой из которых
функция монотонна. Но тогда в силу монотонности и ограничен-
ности на каждой из этих полуокрестностей функция имеет пре-
делы при х -*• С — 0 и при х -> С 4- 0 (т. е. С является точкой раз-
рыва первого рода). Напомним, что пределы функции слева и
справа в точке разрыва принято обозначать символами /(С —0)
и /(С+ 0).
Теперь сформулируем (без доказательства) теорему Дирихле,
дающую достаточные условия сходимости тригонометрического
ряда Фурье во всех точках основного интервала.
Теорема Дирихле. Если функция ф(х) из класса С' на интер-
вале (0; /) является кусочно-монотонной на этом интервале, то
се ряд Фурье по синусам (а также ее ряд Фурье по косинусам)
сходится во всех точках интервала (0; /). Сумма этого ряда
равна ф(х) во всех точках непрерывности этой функции, лежа-
щих внутри интервала (0; /); в точках же разрыва, лежащих
внутри этого интервала, сумма ряда равна ft--~
Аналогичная теорема справедлива и для ряда Фурье по об-
щей тригонометрической системе-, однако в этом случае вместо
интервала (0; I) надо брать интервал (— I; /).
Замечание. В приведенной теореме ничего не сказано о
сходимости тригонометрического ряда Фурье на концах основ-
ного интервала. Рассмотрим, как ведет себя сумма ряда Фурье
па концах интервала.
На концах основного интервала тригонометрический ряд
Фурье сходится для любой кусочно-монотонной функции из клас-
са С'. Однако сумма ряда на концах основного интервала ведет
* В частном случае, на некоторых нз этих интервалов функция может
оказаться и постоянной.
168
Часть II
себя по-разному для различных типов тригонометрических рядов:
а) сумма ряда по синусам равна нулю на концах интервала
(0; /) для любой кусочно-монотонной функции из класса С'\
б) сумма ряда по косинусам для кусочно-монотонной функ-
ции ф(х) из класса С' на (0; /) равна: в точке х = 0 — числу
ф(0-|-0), а в точке х ~ I — числу ф(/ — 0);
в) сумма ряда по общей тригонометрической системе для
кусочно-монотонной функции ф(х) из класса С' на (—/; /) рав-
,	.	0) + Ф(/ —0)
на в точках I и — I одному и тому же числу — т >----------
Вернемся теперь к рассмотренным в этом параграфе четырем
примерам на разложение в ряд Фурье. Так как все функции,
приведенные в этих примерах, кусочно-монотонны на основном
интервале, то их ряды Фурье сходятся во всех внутренних точ-
ках основного интервала; в каждой из этих точек сумма ряда
равна значению соответствующей функции (кроме функции ф(х)
из третьего примера: в точке разрыва х0 = 0 сумма ряда равна
. На концах основного интервала сум-
ма ряда для функций из 1 и 4 примеров равна нулю,.для функ-
ции из 3 примера — единице, а для функции из второго примера:
к — в левом конце интервала и 2к — в правом.
ф(0-0) + ф(04-0) _ 1 \
2	2 )
§ 11. Ряды Фурье-Бесселя
Пусть нам задана система функций
J
р
(1)
ортогональная с весом х на интервале (0; /) (здесь р>0 — фик-
сированное целое число, р1 < р2 <.. .< рЛ < ...— все положитель-
ные корни функции Jf,(x)). Ряд Фурье для функции ф(х)поэтой
ортогональной системе называется рядом Фурье-Бесселя функ-
ции ср (х). Коэффициенты этого ряда вычисляются согласно общей
теории (см. § 9) по формулам
^lalattaus^
знание без границ Ч
§ " 169
Интеграл, стоящий в знаменателе, был нами вычислен рань-
ше (см. формулу (6) из § 5):

Итак, формулы для коэффициентов ряда Фурье-Бесселя мож-
но привести к следующему виду:
i
с„ = ". "I ?-тт (’ X ф (х) УIdx.	(2')
o
Ряд Фурье-Бесселя для функции ф(х) имеет вид:
=	+ (^) + ••• + СЛ(Т) + ”-’ <3>
где коэффициенты ck вычислены по формуле (2'). Равенство (3)
надо понимать в том смысле, что последовательность частных
сумм ряда (3) сходится на интервале (0; /) в среднем квадратич-
ном к <р(х) (с весом х), т. е. что
/
j (ф(х) —5Я (х)]2х</х->0
о
при П -> оо.
Это имеет место для любой функции <р(х) из класса кусочно-
непрерывных ограниченных функций, так как ортогональная си-
стема (1) замкнута в классе С' (см. общую теорему о замкну-
тости системы собственных функций, стр. 156).
Пример. Разложить в ряд по функциям
*^0 (Нт**)» ^0 (Н*2 *^)> ’ • > о *^)» ’ • •
функцию ф(х) == 1 —х на интервале (0, 1) (здесь < р,2 < ... —
положительные корни функции J0(x)).
Искомый ряд будет иметь вид:
1 —х = ctJ0^ х) 4- с2 /0([г2 х) -J- ...,
(4)
где коэффициенты вычисляются по формулам:

1
Jx (1 — х) Ji)([j.kx)dx,
о
170
Часть II
или, после замены переменной p-*x = z,
— zV0(z)dz
б
Для упрощения этого выражения используем формулы (7а) и (76)
из § 4 и вытекающее из них равенство fzJ0(z)dz= zA(z) 4- С.
Применяя эти формулы (и интегрируя при этом второй интег-
рал дважды по частям), получим после упрощений:
2	>
ck — f j . Г । 'о (2)
{Л (иА)]« •	J
Подсчитаем, в частности, ct и с2. Используя таблицы для Jt(x)
v-k
и вычисляя J J0(z)dz с помощью разложения функции J0(z) в
степенной ряд,* получим:
ct = 0,984 ...; ся = 0,666...
Следовательно, первые два члена искомого ряда Фурье таковы:
1 — х - 0,984 Jo (2,4048 х) + 0,666 70 (5,5200 х) 4- ...
§ 12.	Ряды Фурье-Лежандра
а)	Система функций
PM, PJx), Р2(х),..., Рот(х),....
(где Рт(х)— полиномы Лежандра) ортогональна с весом 1 на
интервале (—1; 1). Эта ортогональная система замкнута в се-
мействе кусочно-непрерывных ограниченных функций. Следова-
тельно, любую такую функцию ф(х) можно разложить в ряд
Фурье-Лежандра:
Ф (х) = с0Р0 (х) 4- с1Р1 (х) + ... 4- стРт (х) 4- ...,
• Прием приближенного вычисления интегралов с помощью степенных
рядов можно было бы применить сразу к интегралам (5) без их предваритель-
ного преобразования по формулам (7а, б). Однако это привело бы к более
громоздким вычислениям.
KatallausWlk
знание Вез границ	' *
§ П 171
коэффициенты которого вычисляются по формулам:
J Ф (х) Рт (х) dx	L
«Я=-=П--------------=~2- '\fMPMdx.
-I
-I
Пример 1. Разложить функцию
ф(х)==
— 1 для — 1 < х < О,
1 для 0< х < 1
в ряд Фурье по полиномам Лежандра (на интервале (—1; 1)).
Здесь легко вычисляются коэффициенты Фурье:
I	о	I
с0 = 4’ J Ф (х) ро (х)dx = J (— 0 ’ 1 dx+ 4" J 1 ’ 1 dx = 0;
— I	—1	о
1	0	1
й=4" fмwdx = ~2 J xdx+4"J
xdx =
1
С2 = J Ф <Х) Р* (х)dx = 0;
1
7 Р	7	Q
C« = "2*J ф(х)Р8(х)</х= — -g-; с< = 0; св = -^-,...
— 1
Таким образом, первые члены разложения данной функции в
ряд Фурье-Лежандра таковы:
ф (•»)=4 р> 4 • р> w+4 р> +—
_ 3 „	7	5?-Зх , 9	63х670хя4 15х ,
~ 2 Х 8 ’	2 ф 16	8	Ь • • • •
Пример 2. Разложить функцию (х) = —.......... —	(и —
У1 — 2их 4- и*
фиксированное число, по модулю меньшее, чем 1) в ряд Фурье-
Лежандра на (—1; 1).
172
Часть 11
Эта функция непрерывна и ограничена на (—1; 1); следо-
вательно, она разложима в ряд Фурье:
--J___=^с0Р0 (х) + cj\ (х)+с2р2 (Х)4-....
/1 — 2их -I и2
1
Коэффициенты cm = —i ——1- -......— Рт (х) dx.
z iiKl— 2«х + «»
He произ-
водя всех выкладок, укажем без доказательства, что для лю-
бого tn > 0 имеет место ст = ит. Следовательно, ряд Фурье-
Лежандра приобретает вид:
—---------= Ро (х) iuPi (х) ч- и2Р2 (х) -Ь ... 4- итРт (х) + .. .
/1 — 2их и2
Функция двух переменных ф (х, и) ~ —	• — называется
К1 — 2их ч- и2
производящей функцией для полиномов Лежандра: если ее раз-
ложить в степенной ряд по степеням и, то коэффициенты этого ряда
совпадают с соответствующими полиномами Лежандра.
б)	Система функций
Рпп (х), Pnn+i (х), Рпп+2 (х),...» Р£ (х),...
(n-ые присоединенные функции Лежандра) также образует орто-
гональную на (—1; 1) систему. Так как эти функции составля-
ют семейство всех собственных функций задачи Штурма-
Лиувилля, то они образуют замкнутую систему в классе кусоч-
но-непрерывных ограниченных функций. Следовательно, любая
функция этого класса может быть разложена в ряд Фурье по
присоединенным функциям Лежандра (п > О— фиксированное
число):
ф (х) = ап Рп (х) -hani iPn+i (х) 4-... + атР^ (х\	,
где коэффициенты ат(т>п) вычисляются по формулам:
-1
— 1
1
= ^(x)P"(x)dx.
2(от4-л)1 I ’	’ ,n ’
— 1
MaHausWV
знание без границ W ч»
* 12 173
в)	Рассмотрим еще одну ортогональную систему функций,
связанную с функциями Лежандра. Пусть п — фиксированное
целое число (п > 0). Система функций
Рп (cos 0), Pn+i (cos0),..., P”(cos0),...	(1)
ортогональна на участке [0; тс] с весом sin©. Действительно,
Г
( Р'‘(cos 0) • Рп (cos 0) sin 0d0 = — f P* (z) Pn. (z) dz —
J *	*	«J •	J
0	1
= (р;'(г)р;(г)* = о
-1
(при i =/- j). Заметим, кроме того, что если i = /, то этот интег-
рал также может быть легко вычислен:
([Fucose)]2 sin еда = j!
0	•— 1
(см. формулу (9) в § 7); в частности, при п = 0:
f lP„(cose)i!sinede =
LUI тр* д
о
Всякая кусочно-непрерывная, ограниченная на [0; тс] функция
/(0) может быть разложена в ряд Фурье по ортогональной си-
стеме (1):
/ (Н) = спРп (cos 0) | cni, P„+i (cos0)	4- cmP?n (cos 0)4-...	(2)
Коэффициенты этого ряда вычисляются по общим формулам те-
ории рядов Фурье:
откуда
f / (Я) Рп (cos Н) sin В dH
---------------------------
т	г.
j [ Р”Дсо$8) j2 sin BdH
b
174
Часть 11
или, в частности, при п = 0:
/(6)P’n(cose)sinede,
О
У f<е>р”(cos e>sin ede-
о
(3)
(3')
Если функция /(0) ограничена и кусочно-непрерывна на
участке [0; тс], то ряд (2) с коэффициентами, вычисленными по
формулам (3) (или, при п = 0, по формулам (3')), сходится в
среднем квадратичном к /(0); иными словами, ортогональная
система (1) замкнута в классе кусочно-непрерывных ограничен-
ных функций. Это вытекает сразу из замкнутости системы по-
линомов Лежандра (или, при n > 1, из замкнутости системы
присоединенных функций Лежандра). Действительно, пусть /(0)
ограничена и кусочно-непрерывна при 0 < 0< к; тогда функция
/(arccosx), как функция от х, также ограничена и кусочно-не-
прерывна при — 1 < х < 1. Ее ряд Фурье по функциям Рт (х)
сходится в среднем квадратичном к функции f(arccosx) (в силу
замкнутости системы Р«(х), т — п, п -f-1,...):
f (arccos х) = спРп (х) + слиР"+1 (х) -f-... + стРпт (*)+•.. (4)
Коэффициенты этого ряда равны соответствующим коэффициен-
там ряда Фурье функции /^0) при разложении по функциям
P£(cos0). Заменяя теперь в равенстве (4) х на cos0, мы при-
ходим к равенству (2), которое следует понимать в том смысле,
что частные суммы ряда (2) сходятся в среднем квадратичном с
весом sin0 к функции /(0).
Итак, из замкнутости системы Рт(х) (п. — фиксировано)
вытекает замкнутость системы P«(cos0) на участке [0; тс].
§ 13.	О замкнутости системы
тригонометрических функций и системы
полиномов Лежандра
В § 9 (стр. 156) было высказано утверждение о том, что си-
стема всех собственных функций краевой задачи Штурма-Лиу-
вилля замкнута в классе кусочно-непрерывных ограниченных
§ IS
175
DlalaUauslVii
функций. Из этой теоремы вытекает замкнутость любой из тех
систем, которые были рассмотрены нами выше*.
Однако это общее утверждение не было нами доказано, да
и не может быть доказано в рамках данной книги. Здесь мы
ограничимся доказательством замкнутости только для некото-
рых конкретных систем функций.
В основу доказательства теорем замкнутости мы положим
теоремы Вейерштрасса о приближении непрерывной функции
многочленами (или тригонометрическими многочленами). Дока-
зательства этих теорем известны из курса анализа. Здесь мы
ограничимся их формулировками.
Первая теорема Вейерштрасса. Если f(x) — непрерывная на
[а; Ь] функция, то для любого в > 0 существует многочлен
Qn = а0 + щх 4- а2ха 4-... 4- апхп,
такой, что для всех х из отрезка, [а; Ь] имеет место нера-
венство’.
|/(x)-Q„(x)|<«.
Вторая теорема Вейерштрасса. Если f (х) — непрерывная на
J— it; it] функция, удовлетворяющая условию: /(тс) = / (—тс)**, то
для любого в > 0 существует тригонометрический многочлен
Тп (х) =	-j- (at cos х 4- sin x) 4- (Oj cos 2x 4-
4- b2 sin 2x) 4-... 4- (an cos nx 4- bn sin nx),
такой, что для всех х из отрезка [—тс; тс] имеет место нера-
венство

Эти теоремы означают, что любую непрерывную на отрезке
функцию можно приблизить с любой степенью точности много-
членом (или тригонометрическим многочленом, если f(— тс) =
— / 00) • При этом многочлен (или тригонометрический многочлен)
* За исключением общей тригонометрической системы
(. nx т.х	k~x kr.x )
j 1;	cos —,	sin —;	. . . ; cos —j—,	sin -y—;	.. .>	на интервале (—/; /);
она также замкнута, но ее замкнутость не вытекает из общей теоремы, так
как эта система не является системой собственных функций задачи Штур-
ма-Лиувилля.
** Это, в частности, выполняется для любой периодической функции с
периодом 2к.
176
Часть 11
будет близок к функции f(x) во всех точках данного отрезка;
в этом случае говорят, что многочлен Qn(x) (или Тп(х)) равно-
мерно приближает с точностью до в функцию f(x) на данном
отрезке.
Из теорем Вейерштрасса вытекают следующие теоремы:
Следствие 1. Если f (х) — кусочно-непрерывная ограниченная
функция на (а; Ы, то для любого е > О существует многочлен
Q„(x), такой, что имеет место неравенство:
J Щ*) — Qn (х)]Мх<е.
а
Следствие 2. Если f (х) — кусочно-непрерывная ограниченная
функция на [—я; «], то для любого е > О существует тригоно-
метрический многочлен Тп(х), такой, что имеет место не-
равенство:	____________
< е.
Эти следствия из теоремы Вейерштрасса означают, что лю-
бую ограниченную кусочно-непрерывную на отрезке функцию
можно приблизить в среднем квадратичном к многочлену с лю-
бой степенью точности (или тригонометрическому многочлену);
иначе говоря, можно найти Qn(x) (или Тп(х)) так, чтобы среднее
квадратичное отклонение данной функции от Qn(x) (или от Тп(х))
было меньше любого, наперед заданного, положительного числа е.
Доказательство обоих следствий проводится почти одинако-
во. Ограничимся, например, доказательством второго следствия.
Пусть /(л) терпит разрывы в точках х, < х2 < • • • < хт_!
отрезка [ — к; «]. Обозначим, для единства записи, через х0 точ-
ку — я и через хт— точку я. Пусть, кроме того, | f (х) | < А
всюду на [—я; я].
Опишем около каждой точки х0, xlt х2,..., хт_}, хт непе-
ресекающиеся окрестности радиуса В, где 6— какое-либо положи-
тельное, достаточно малое, число, и определим новую вспомога-
тельную функцию f(x) следующим образом:
a) f(x) — f(x) всюду на отрезке [—я; п] за пределами этих ок-
рестностей’, <
б)}(-я) = 0; }(я) = 0;
в) на отрезках |х0, х0 4- 8|, [х, — В; xt 4- 8], [х2 — В; х2 4- В],....,
[хт — 8; хт] функция f(x) линейна.
Тогда функция f (х) будет непрерывной функцией, принима-
ющей равные значения на концах интервала [ — я; я] и мало от-
Слециально Олп	-
DlatattausX
знание без границ	Ч *
§ is 177
личающейся от /(х) (рис. 59). Последнее надо понимать
в том смысле, что квадратичное отклонение функций /(х) и
/(х) будет очень мало (и может быть сделано сколь угодно ма-
лым для достаточно малого б). В самом деле:
1/ J !/(*) —=
г —г
х0-Н *t—* xt+8 xf-«	хт	_
У + У + J +.1'	J	|/(x)-/(z)]’d* =
хв х0-|-8	х,-8
/ Хо+« х,4-8 х,4-6	х,п	__
I/ j 4- .( Ч- J’ +•••-!- J' И(х) — /(x)]adx<
г хе	х,—6 х,-8	хт—6
/х„|-6	Х|]-6	х.4-8	хт
У + У + У +•••+ У (2Л)Мх =
х0 х,-б х,—г	х/л-6
х«-ьб
Здесь мы разбили участок интегрирования на несколько участ-
ков и учли, что f (х) = f (х) на участках (х0 + б, х, — б),
(Х| -J- б, х2 — б),..., (хт^ б, хт — б), и, следовательно, соответст-
вующие интегралы равны нулю. Остальные интегралы мы оценили,
учтя, что в них подинтегральная функция [/(х) — /(х)]а не превос-
ходит числа (2Л)а.
178
Часть 1Г
Если выбрать число Й так, чтобы было 2Л ]/28т<то
J f(*)-f(x)]‘dx<±-
Воспользуемся теперь второй теоремой Вейерштрасса и най-
дем такой тригонометрический многочлен Тп(х), что
| ~f(x)~ Т„(х)|
В
Такой тригонометрический многочлен существует, так как f(x)
непрерывна и / (я) = / (— я) (следовательно, условия теоремы Вей-
ерштрасса выполнены). Заметим, что квадратичное откло-
нение функций f (х) и Тп (х) не превосходит числа

Теперь рассмотрим квадратичное отклонение функций /(х) и
Тп(х)-.
« (А Т„) = 1/ j |/ (х) - Т„ w dx < 1/ J |/ (х) - / (х))* dx +
F —к	F	—л
• Это неравенство вытекает из следующего утверждения: для любых
двух функций и (х) и и (х) из семейства С' имеет место:
(и 4* v)’ dx
(1>
ь
Докажем неравенство (1). Прежде всего заметим, что j (и — cv)\dx> 0 при
а
любом с; следовательно,
ь	ь	ь
J нМх — 2с
а	а	а
Если квадратный многочлен (относительно с) неотрицателен для всех значе-
[ uvdx 4- с* f v*dx > 0.
NalaHauslM
знание без границ *
§ 13 179
Итак, найдется тригонометрический многочлен, среднее квадра-
тичное отклонение которого от функции f(x) меньше, чем е.
Следствие 2 доказано.
Перейдем к доказательству замкнутости конкретных систем
функций.
Теорема 1. Общая система тригонометрических функций
11; sin х; соз х; sin 2х; cos 2х;...; sin nx; cos их;... ) замкну-
та на [—к; к] в классе кусочно-непрерывных ограниченных
функций.
Доказательство. Пусть /(х) — кусочно-непрерывная ог-
раниченная функция на (—я; nJ и
-у- 4 (ах cos х -| - sin х)4-(аа cos 2x4-Ьа sin 2х) 4-... 4-
4- (ап cos nx 4- bn sin nx) 4-...
— ее ряд Фурье. Возьмем произвольное е > 0 и подберем триго-
нометрический многочлен Tn (х) так, чтобы его квадратичное
отклонение от /(х) было меньше е:
ний с, то его дискриминант < 0. Поэтому
b b
b -]« ь ь
J uvdx — j u*dx  | v*dx <: 0;
a a
откуда
b
J uvdx
l'vfdx .
Это — неравенство Коши. Умножая обе его части на 2 и затем прибавляя к
ним J u2dx 4- | v*dx, получим:
а	а
b	bbb	ГЪ	ГЪ Ъ
J u'dx 4- 2 j uvdx 4- J vadx < J u*dx 4- 2 1/ | u*dx • 1/ f v*dx 4- f u’dx,
a	a
f (u + v)1 dx C
vldx
Извлекая квадратный корень из обеих частей этого неравенства, получим не-
равенство (1). Из неравенства (1) сразу следует неравенство в тексте, если
положить и = f (х) — f (х); v = f (х) — Тп (х), а = — я, Ь=п.
180
Часть II
[f (x) — T N(x)]* dx
e.
Возьмем частную сумму Sn(x) ряда Фурье; так как частная
сумма ряда Фурье дает наименьшее квадратичное отклонение от
/(х) (по сравнению с другими тригонометрическими многочлена-
ми того же порядка; см. § 9, стр. 157—159), то
[/(%) — SN(x)\*dx <
J If (х) - TN (х)\2 dx ,
—к
откуда	______________________
/к
8 (/, ЗД == 1/ J [f (х) — Sjv (х)]а dx < е.
V —к
Но для всех п> N имеет место неравенство
Ч/. 5Я)<8(/, S„)
(так как квадратичное отклонение 6(/, S,,) монотонно убывает с
возрастанием номера л; это сразу вытекает из формулы (8)
на стр. 154). Следовательно, 8(/, Sn) < е для всех n>N.
Итак, квадратичное отклонение частной суммы S„(x) ряда
Фурье от функции f (х) может быть сделано сколь угодно малым
(для всех, достаточно больших п), т. е. это отклонение стре-
мится к нулю при л-> оо. Поскольку это имеет место для лю-
бой кусочно-непрерывной ограниченной функции — общая триго-
нометрическая система замкнута в классе С'.
Теорема 2. Система тригонометрических функций
{sin х; sin 2х;...; sin лх;... | замкнута на [0; тс| в классе кусочно-
непрерывных ограниченных функций.
Доказательство. Пусть f (х) — кусочно-непрерывная, ог-
раниченная функция на |0; тс). Продолжим ее нечетно на [—к; к],
т. е. построим вспомогательную нечетную функцию /(х), совпа-
дающую с /(х) на (0; к). Эта функция также кусочно-непрерыв-
на и ограничена (на [—тс; тс|). Ее ряд Фурье по общей тригоно-
метрической системе совпадает с рядом Фурье по синусам для
функции f(x) на (0; к); действительно,*
1 к-
ап = — j f (х) cos nxdx = 0,
— к
* Через ап. Ьп обозначены коэффициенты ряда Фурье функции f (х)
при ее разложении по общей тригонометрической системе {1, sinx, cosx,
sin2x, cos2x, . . через bn обозначены коэффициенты ряда Фурье функции
[(х) по синусам.
ri\ataUau$WV.
знание без границ “ *
._________________________________________ 181
так как /(x)cos пх — нечетная функция;
-	1 г -	1 Р -
bn= —-1 /(х) sin nxdx — — • 2 I f (x) sin nxdx —
—к	0
2 p
== — 1 /(x)sin nxdx — bn.
о
Здесь учтено, что f (x) sin nx — четная функция и что на (0; те]
имеет место f (х) ~ f (х).
В силу предыдущей теоремы, квадратичное отклонение
Sn(x) от f (х) стремится к нулю на [— тс; nJ при со.
Оценим теперь квадратичное отклонение Sn(x) от /(х) на
10; тс]:
8 (/• S„) = 1/ .1' 1/	S„ (X)l’ dx =
Г о
—>0 при	со.
=]/4- h/w-s„w]!</x
Итак, lim 1/ |[/(х)—Sn(x)]2dx = 0, а это и означает (в силу
л V о
произвольности /(х)), что система {sinx, sin2x,...] замкнута в
классе кусочно-непрерывных ограниченных функций на {0; тс].
Теорема 3. Система тригонометрических функций |1; cosx;
cos2x;...; cosnx;...} замкнута на [0; тс] в классе кусочно-не-
прерывных, ограниченных функций.
Доказательство этой теоремы проводится так же, как и до-
казательство теоремы 2.
Из замкнутости этих систем вытекает, что все эти системы
полны в классе ограниченных кусочно-непрерывных функций на со-
ответствующих отрезках (см. стр. 156). Так, например, не существует
ограниченной кусочно-непрерывной функции, отличной от нуля,
которая была бы ортогональна одновременно всем функциям
'sinx; sin2x;...; sinnx;...) на отрезке ]0; я].
Теоремы 1—3 доказаны для отрезков |—я; я] и [0; я]. Ана-
логичные теоремы имеют место и для тригонометрических систем
на отрезках {—/; /] и (0; /]; доказательство теорем для этого,
более общего, случая проводится аналогично.
* Здесь учтено, что ]/ (л) — Sn (х)]2—четная функция.
182
Часть 11
Перейдем к доказательству теоремы о замкнутости семейства
полиномов Лежандра.
Теорема 4. Система полиномов Лежандра
РМ, Р^х), Р2(х).........Рт(х),...
замкнута на отрезке [—1; 1] в классе ограниченных кусочно-
непрерывных функций.
Доказательство. Заметим, прежде всего, что любой
многочлен Qn(x) может быть представлен как линейная комби-
нация полиномов Лежандра. Для этого прежде всего докажем,
что все функции х°, х1, х\,.., хп,... представимы как линейные
комбинации полиномов Лежандра.
Для х°, х1, х2 это очевидно: х° — 1 • Р0(х); х1 = 1 • РДх);
х2 — у Р2(х) +у Р0(х). Допустим теперь, что это доказано для
всех степеней х до л-ой степени включительно, и докажем, что
хя+1 такЖе представима как линейная комбинация полиномов
Лежандра. Для этого заметим, что РП+А (х) — сохяН + с\хп + ••• +
4-^+1, где со/0; поэтому xn+l = ~РпП (х) — ~-хп —... —
1-0	«-О
— ——; заменяя в этом выражении степени хп, Xя"1,... и т. д.
О)
линейными комбинациями полиномов Лежандра (что возможно
по предположению), получим и хл+1 представленным в виде та-
кой линейной комбинации.
Итак, доказано, что любая степень хп представима в виде
линейной комбинации полиномов Лежандра. Но тогда это же
справедливо и для любого многочлена Qn (х). Таким образом,
всякий многочлен Qn (х) может быть записан следующим образом:
Qn (х) = ао ро (х) 4" “1 pi (х) 4- • • • 4- алРя (х),
где а0, ар ...., ал — какие-то числа.
Перейдем теперь к доказательству теоремы. Пусть /(х) —
ограниченная кусочно-непрерывная функция на [—1; 1] и
с0Р0 4- qPi (х) 4- саРа (х) + ... + спРп (х) 4-...
— ее ряд Фурье по полиномам Лежандра. Возьмем произвольное
е > 0 и подберем многочлен Qn (х) так, чтобы его среднее квад-
ратичное отклонение от /(х) было меньше чем е:
|/" I/ (*) — Qn (*)!’dx < <•
Это возможно в силу 1-го следствия из теоремы Вейерштрасса.
Многочлен Qn можно представить, как линейную комбинацию
полиномов Лежандра:
S'3 183
Qn (x) s aoPo +	(x) 4- ... + aNPN (x).
Далее возьмем частную сумму Sn ряда Фурье; так как частная
сумма Фурье дает наименьшее квадратичное отклонение от f(x)
по сравнению с другими линейными комбинациями полиномов
Лежандра порядков < W (см. § 9, стр. 157—159), то
SN (x)Jadx
— 1
J [f (x) — Qn (x)]Mx ,
-i
откуда
5 (/. SN) =	(x) — SN (x)]8 dx < e.
Но для всех n>N имеет место неравенство 5(/, Sn)<5(/, SN).
Следовательно, 6 (/, Sn) < а для всех п> N.
Итак, квадратичное отклонение частной суммы Sn(x)
ряда Фурье (по полиномам Лежандра) может быть сделано сколь
угодно малым (для достаточно больших п), т. е. это отклонение
стремится к нулю при оо.
Поскольку это имеет место для любой кусочно-непрерывной
ограниченной функции, система полиномов Лежандра замкнута
в этом классе функций.
Вернемся теперь к краевой задаче для уравнения Лежандра,
рассмотренной в § 6. Там было доказано, что все числа вида
т(т + 1) (где т ~ 0, 1, 2,....) являются собственными числа-
ми этой краевой задачи. Однако там был оставлен без доказа-
тельства тот факт, что эта краевая задача не имеет других соб-
ственных чисел. Теперь же это можно доказать.
Теорема 5. Задача разыскания ограниченного на (—1; 1)
решения уравнения (1 — х8) у" — 2ху' -]-1у — О не имеет других
собственных чисел, кроме чисел Xm = m(m4-1) (т — 0, 1, 2,..).
Доказательство. Допустим, что, кроме чисел Хо, Xlt Х2,...,
эта задача имеет еще некоторое собственное число р (отличное
от всех Хт). Тогда ему соответствовала бы некоторая собствен-
ная функция <р(х) (отличная от тождественного нуля, ограни-
ченная на (—1; 1) и непрерывная во всех внутренних точках
этого интервала). По свойству собственных функций она должна
была бы быть ортогональна всем остальным собственным функ-
циям; следовательно, она была бы ортогональна всем полиномам
Лежандра, а это невозможно, так как система полиномов Ле-
жандра полна (полнота системы полиномов Лежандра вытекает
из се замкнутости; см. выше, § 9, стр. 156).
184	Часть II
Итак, эта краевая задача не имеет никаких собственных
чисел, кроме чисел вида = m(m + 1).
Теоремы 4 и 5 легко обобщить на ортогональные системы
присоединенных функций Лежандра любого фиксированного по-
рядка п и на совокупность собственных чисел соответствующей
краевой задачи. Формулировку и доказательство этих теорем
мы представляем читателю.
^alaHaustik
знание без границ Ч
ЧАСТЬ III
УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
ГЛАВА I
ВЫВОД НЕКОТОРЫХ УРАВНЕНИЙ МАТЕМАТИЧЕСКОЙ
ФИЗИКИ
Для решения многих физических задач требуется найти ту
или иную функциональную зависимость—например, зависимость
какой-либо физической величины от времени, от координат точ-
ки и т. д. Непосредственно найти искомую зависимость обычно
бывает трудно или даже невозможно; в таком случае мы ста-
вим перед собой задачу: найти связь между искомой функцией
и ее производными, т. е. составить дифференциальное уравнение,
которому удовлетворяет эта функция.
Если искомая функция зависит только от одной независи-
мой переменной (у = /(*)), то дифференциальное уравнение, кото-
рому удовлетворяет эта функция, называется обыкновенным диф-
ференциальным уравнением. Такие уравнения мы изучали в курсе
анализа.
Если же искомая функция зависит от двух или большего
числа независимых переменных (например, z = f(x, у)), то диф-
ференциальное уравнение содержит, кроме самой неизвестной
,	/ dz dz
функции, также ее частные производные по х и у	,
d2z d2z	\ гр
-^2 , и т. Д J • Такое уравнение называется уравнением
в частных производных.
В этой главе мы рассмотрим несколько физических задач,
которые приводят к уравнениям в частных производных.
§1. Уравнение колебания струны
Рассмотрим струну, т. е. тонкую натянутую нить (для оп-
ределенности расположим ее вдоль оси Ох). Будем считать ее
186
Часть 111
однородной (линейная плотность равна Г), упругой, туго натя-
нутой. Кроме того, будем считать, что ее отклонения очень ма-
лы; иными словами, мы будем рассматривать только малые ко-
.лебания струны. Чтобы придать этому термину точный матема-
тический смысл, условимся считать угловой коэффициент струны
в любой момент времени столь малым, что его квадратом можно
пренебречь, когда он стоит в качестве слагаемого рядом с еди-
ницей (коротко это выражают словами: квадрат углового коэф-
фициента ничтожно мал по сравнению с единицей).
Условимся, кроме того, рассматривать только плоские по-
перечные колебания струны, т. е. такие колебания, при которых
струна все время остается в одной плоскости (назовем ее пло-
скостью Охи) и каждая точка струны перемещается только по
перпендикуляру к оси Ох. Это значит, что точка струны, имею-
щая в положении равновесия абсциссу х, сохраняет ту же абс-
циссу в процессе колебания; ордината же этой точки и изменя-
ется с течением времени; таким образом, она зависит от t
(а также, разумеется, от х: законы колебания различных точек
струны, вообще говоря, различны). Для того чтобы описать ма-
тематически закон колебания струны, надо найти эту зависимость
и от х и t, т. е. найти функцию двух переменных и = и(х, t).
Зная эту функцию, мы сможем найти положение любой точки х
в любой момент времени t. Зная эту функцию, мы сможем найти
форму, которую принимает струна в любой момент времени t = t0
(для этого достаточно в функции и = и(х, t) закрепить / = /0;
тогда получится функция одного переменного и = и(х, t0), графи-
ком которой служит струна в момент t0). Наконец, зная функ-
цию и = и (х, t), мы можем определить закон колебания каждой
конкретной точки (с абсциссой х0): и = и (х0, t).
Для того чтобы найти функцию и = и (х, t), составим
дифференциальное уравнение, которому эта функция удовле-
творяет.
Рассмотрим некоторую точку струны с абсциссой х и другую,
близкую к ней, точку х + Дх (рис. 60). Согласно второму закону
Ньютона, сумма всех сил, действующих на малый участок стру-
ны, равнс по величине и по направлению вектору ускорения
этого участка, умноженному на его массу. Рассчитаем все силы,
действующие на участок АВ. Это, прежде всего, силы натяже-
ния, действующие на концах этого участка, и направленные по
касательным к дуге в соответствующих точках. Они равны друг
другу по своей численной величине, что вытекает из малости
колебаний и из того, что равнодействующая этих сил вызывает
только вертикальные перемещения и, следовательно, сама на-
^alaHausA
знание без границ Ч
Глава 1,§ 1
187
правлена по вертикали*. Обозначая численную величину силы
натяжения в любой точке через 7, а углы наклона касательной
к оси абсцисс в точках А и В — через 04 и а2, получим, что
вертикальная составляющая сил натяжения равна
Tsina2 — Tsinap
Кроме сил натяжения, на струну могут действовать и дру-
гие силы (например, вес струны). Равнодействующая всех сил,
приложенных к какому-либо участку струны и отличных от сил
натяжения, называется внешней силой на этом участке. Обозначим
через <р(х, /) тот предел, к которому стремится отношение вне-
шней силы, действующей на участок АВ, к массе этого участка
(при Дх -> 0). Эта величина называется плотностью внешней силы',
она может зависеть и от точки х, и от момента времени t. Если
плотность внешней силы известна, то вся внешняя сила, дей-
* Докажем, что из этого вытекает численное равенство сил натяжения
в точках Л и В; пусть сила натяжения равна Ту в точке А и Т2 — в точке В.
Если углы наклона касательной к оси абсцисс в этих точках равны, соот-
ветственно , «1 и а2, то из равенства нулю горизонтальной составляющей сле-
дует, что
Ту cos ai — Тг cos at = 0;
Ту _ cosaa _ -и Л -fr tg»g1
T, — cos gj “ r 14-tga«2 *
Отбрасывая квадраты угловых коэффициентов, являющиеся слагаемыми при
единице, получаем:
у, — 1; Ту — Т2.
1 2
188
Часть HI
ствующая на малый участок АВ, равна <р(х, /)-Г-Дх*, где Г —
линейная плотность струны (в силу однородности струны Г по-
стоянна). Так как, по условию, каждая точка струны может дви-
гаться только по вертикали, то и внешнюю силу мы должны считать
направленной по вертикали. Обозначая, для краткости, равно-
действующую всех сил, приложенных к участку АВ (т. е. сил
натяжения и внешней силы) через FAB, получим
= Т (sin а2 — sin ах) 4- ср (х, /) • Г • Дх.
Подсчитаем теперь разность sina2— sinaP Учитывая, что
а = а (х) = arctg их, перепишем эту разность следующим образом:
sin а2 — sinax = sin а (х 4~ Дх) — sin а (х) = -г- sin а (х)
• Дх.
хср
Здесь мы применили формулу Лагранжа; хср — некоторая
точка, заключенная между х и х + Ах.
Вычислим производную от sina(x):
~ sin a (х) = cos a (х) • a' (х) = —	1	- • (arctg и' =
dx	/14-tg2«(x)
д2и
'дх2'
Итак,
откуда
sin ах — sin а2
• Дх,
хср
F хТ
1 АВ
д2и\
д*2 / хср
• Дх 4- ср (х, /) Г Дх.
(О
С другой стороны, сила, действующая на материальную
точку, равна произведению массы этой точки на ускорение; счи-
• Строго говоря, внешняя сила, действующая на участок АВ, равна
<р(х, /)-Г«|ЛВ|, где | АВ | — длина дуги АВ. Но, в силу условия малости
X + Дх _________
колебаний, I АВ I ж Дх. Действительно, | АВ I — j* ]/1-j-( их)2 dx
X
X + ДХ
ж j dx = Дх; здесь учтено, что величиной (нх)2 можно пренебречь, если
X
она стоит в качестве слагаемого рядом с единицей.
MdaHausA
знание Вез границ ’ *
Глава 1, § 1
189
тая (при достаточно малом Дх) отрезок АВ материальной точкой,
получим
Приравняем это к выражению для FAB из формулы (1):
^.Г.Дх = 7.(^)^Дх + ?(х, 0-Г.Дх.
Деля все члены этого равенства на Дх и затем переходя к
пределу при Дх -► 0 (т. е. при В -> Л), получим в пределе:
=	+	(2)
Это равенство справедливо в любой точке А струны (т. е.
при любом х, 0 < х < /) и в любой момент времени t. Следова-
тельно, равенство (2) является дифференциальным уравнением,
которому удовлетворяет искомая функция и(х, /). Это уравнение
можно привести к виду
д2и „ д2и .	.<	о
° “Ь (•*• 0»	(3)
Т
где через а2 обозначено частное у. Легко заметить, что раз-
/а
мерность коэффициента а2 равна у, где / — длина, / — время;
JM2 *
в частности, в системе единиц СИ, [а2] = —. Это следует из
того, что [7] = —у ,[!] = — , у = —. Отсюда вытека-
vcrV	Jn	J. J vc/v
ет, что [a] =	(т. e. а имеет размерность скорости).
В случае отсутствия внешней возмущающей силы <р(х, /)
(или в том случае, когда она столь мала по сравнению с силой
натяжения, что ею практически можно пренебречь)** уравнение
(3) упрощается:
• Символом |/г] обозначается размерность величины k.
** Строго говоря, надо сравнивать с силой натяжения Т не <р(х, /),
а | ср (к, 0I'dx; дело в том, что ср (х, /) не имеет размерности силы, и, следова-
b
тельно, величины ср (х, t) и Т не могут сравниваться друге другом. Внешняя
сила, действующая на участок Дх, равна <р(х,/)ГДх, а следовательно, вся
I
внешняя сила, действующая на струну в момент t, равна ( ср(х, t)Vdx. Ее
о
и надо сравнивать с силой натяжения. В частности, если единственная внеш-
няя сила, действующая на струну,—ее вес и если этот вес очень мал по
сравнению с силой натяжения, им пренебрегают, и струну называют не-
весомой.
190
Часть ///
д*и _ а д*и
dt* ~а дх* ‘
(4)
Это уравнение называется уравнением свободных, колебаний
струны.
Начальные и граничные условия. После того, как составлено
уравнение колебания струны, естественно попытаться его решить,
т. е. найти ту функцию u(x, t), которая удовлетворяет этому
уравнению. Заметим, что если, например, уравнение (4) имеет
решение, то оно далеко не единственно (например, вместе с
функцией и(х, /) этому же уравнению удовлетворяет функция
C‘U(X, t) при любом постоянном с, функция и(х, /) + Ьх + ct +
+ d — при любых постоянных Ь, с и d и ряд других функций).
Задача состоит не в том, чтобы найти множество различных ре-
шений уравнения (4), а в том, чтобы найти одно определенное
решение — а именно то, которое дает закон колебания данной
конкретной струны. Для того чтобы из множества всевозмож-
ных решений выделить одно определенное — искомое — решение,
надо наложить на него ряд дополнительных условий, которые
вытекают из физических соображений и характеризуют данную
конкретную струну. Эти дополнительные условия должны удов-
летворять следующим требованиям:
1)	они должны быть непротиворечивы-, это значит, что су-
ществует хотя бы одна функция и (х, t), удовлетворяющая дан-
ному уравнению и всем данным дополнительным условиям;
2)	они должны гарантировать единственность решения; это
значит, что не может быть двух различных функций, одновре-
менно удовлетворяющих данному уравнению и всем данным до-
полнительным условиям;
3)	они должны гарантировать устойчивость решения; это
означает, что незначительное изменение дополнительных условий
или коэффициентов дифференциального уравнения приведет лишь
к незначительному изменению решения уравнения. В этом слу-
чае говорят также, что решение уравнения непрерывно зависит
от дополнительных условий и от коэффициентов уравнения.
Обычно, исходя только из физического смысла дополнитель-
ных условий, мы можем установить, что существует единствен-
ное решение уравнения, удовлетворяющее этим условиям, и что
решение устойчиво. Однако иногда кажущаяся физическая оче-
видность может подвести; поэтому, строго говоря, задавая
дополнительные условия, надо всегда математически доказать
существование, единственность и устойчивость решения, удовле-
творяющего этим условиям.
Дополнительные условия в уравнениях математической фи-
зики разбиваются на два типа:
WataHauslM
знание без границ ’ w
Глава 1,§1	191
а)	начальные условия, характеризующие искомую величину
в начальный момент времени;
б)	граничные или краевые условия, характеризующие пове-
дение искомой величины на границе рассматриваемой области
(в любой момент времени t).
В частности, для того чтобы найти закон колебания стру-
ны, можно задать следующие краевые и начальные условия:
1.	Если струна имеет конечную длину I (например, она рас-
положена на отрезке [0; I] оси Ох) и закреплена на концах, то
граничные условия таковы:
и (0, t) — 0; и (I, 0 = 0
(в любой момент t).
Однако заданием только этих граничных условий закон ко-
лебания не определяется однозначно. Он будет зависеть еще и
от начальной формы струны, и от начальной скорости струны
в каждой точке. Итак, кроме граничных, должны быть заданы
следующие начальные условия:
и(х, /)|/=о = ?(х); и'((х, 0|/=о = ф(х),
или, в более короткой записи,
и (х, 0) = у (х), ut (х, 0) = ф (х).
Здесь <р(х) и ф (х) — известные, заранее заданные функции:
первая из них в качестве графика имеет форму струны в началь-
ный момент, вторая указывает, какова в начальный момент ско-
рость каждой точки струны.
Из физических соображений ясно, что, придав некоторое
начальное положение и некоторую начальную скорость каждой
точке струны, а затем отпустив струну, мы вызовем вполне опре-
деленное движение точек струны; следовательно, задание гра-
ничных и начальных условий однозначно определяет некоторый
закон колебания струны.
Задача заключается в том, чтобы найти этот закон (это будет
сделано в главе 2, § 1 и 4) и чтобы строго доказать его един-
ственность— при заданных граничных и начальных условиях
(это будет сделано в главе 2, § 3). Кроме того, следовало бы
доказать устойчивость этого решения, но мы этого делать не
будем, так как само определение устойчивости дано нами не
вполне точно; в этом определении остается неясным, какой точ-
192
Часть II!
ный смысл надо придать выражениям: «незначительное измене-
ние начальных условий», «незначительное изменение решения»
и т. д. Математически строго доказать какое-либо утверждение
можно пытаться только тогда, когда это утверждение точно
сформулировано. Точная же формулировка этих понятий увела
бы нас слишком далеко. Поэтому ограничимся приведенным вы-
ше полуинтуитивным и неточным определением устойчивости, и
попросим читателя принять на веру, что все граничные и началь-
ные условия, которые будут в дальнейшем задаваться, обеспечи-
вают устойчивость решения.
2.	Пусть конечная струна расположена на отрезке (0; /).
Если концы струны (или один из них) не закреплены в точках
х — 0 и х = 1, а движутся по некоторому заданному закону*, то
мы получим граничные условия другого вида, отличные от рассмот-
ренных выше. Так, например, если левый конец (х = 0) движет-
ся по закону и(0, /) = a (t), а правый конец—по закону =
= р(/), где a(t) и р(/) — заданные функции от t (в частном слу-
чае постоянные), то эти условия, наложенные на концы струны,
являются более общими, чем приведенные в предыдущем пункте;
они уже не являются однородными (если два решения удовлет-
воряют этим новым граничным условиям, то сумма этих реше-
ний не обязана им удовлетворять). Решение уравнения колеба-
ния струны при неоднородных граничных условиях будет дано
в главе 2, § 5.
3.	Граничные условия на концах струны могут быть и дру-
гой природы. Можно наложить определенные требования не на
ординату и того или иного конца струны, а на угловой коэффи-
циент струны в точке х = 0 или в точке х = I.
Если в левом конце струны касательная все время остается
горизонтальной (т. е. их(0, /) = 0) или в правом конце касатель-
ная всегда горизонтальна (т. е. ux(l, t) = 0), то граничные ус-
ловия являются однородными (в соответствующем конце струны).
Если же и'х(0,	= или и'х(1, /)==3(/) (где а (/) или
р (/) — заданная функция от t, отличная от тождественного нуля),
то эти граничные условия являются неоднородными.
4.	Если струна является бесконечной (т. е. оба ее конца
столь далеки от интересующего нас участка струны, что практи-
чески струну можно считать бесконечной), то говорить о гра-
ничных условиях не имеет смысла: бесконечная струна не имеет
* Напомним, что поскольку мы рассматриваем только поперечные ко-
лебания струны, то и концы струны должны двигаться только по направле-
нию, перпендикулярному к оси абсцисс (т. е. абсциссы концов должны оста-
ваться постоянными).
^ataMaus<Mt
знание без границ -
Глава 1,§ 2 193
границ. Однако по-прежнему должны быть даны начальные
условия:
«(х, 0) = <р (х), ut (х, 0) = ф (х),
где <р(х) и ф(х) — функции, заданные для всех значений х.
Решение уравнения колебания бесконечной струны будет да-
но в главе 5, § 3.
§ 2. Уравнение колебания мембраны
Мембраной называют тонкую плоскую пластинку (для оп-
ределенности, расположим ее на плоскости Оху). Будем считать
ее однородной (поверхностная плотность равна Г), упругой, туго
натянутой. Как и в случае струны, мы будем рассматривать
только малые колебания мембраны; чтобы уточнить это требова-
ние, условимся считать тангенс двугранного угла, образованного
касательной плоскостью к мембране и плоскостью Оху (в любой
точке и в любой момент времени), столь малым, что квадратом
этого тангенса можно пренебречь, когда он стоит рядом с еди-
ницей в качестве слагаемого.
Попытаемся расшифровать -это условие. Пусть уравнение
мембраны (т. е. уравнение той поверхности, форму которой при-
няла мембрана) в некоторый момент времени будет u = f(x, у)
(ось Ои перпендикулярна плоскости Оху). Тогда уравнение каса-
тельной плоскости в точке (х, у, и) примет вид: U — и=*
~ № —х) 4- 'Jy (У — а слеД°вательно, вектор нормали за-
пишется так:
-	ди -	ди
П =---5-1------5-
дх ду
Двугранный угол 7 между касательной_ плоскостью и плоскостью
Оху равен углу ме жду векторами п и k. Поэтому " cos 7 =
= -  1	• а «81 = Г1~СО5‘7 = 1 /(W+7W •
Г1+(«;)2+(<)2	с°н V [дх> W
Следовательно, если tg2 7 ничтожно мал по сравнению с еди-
...	-	1 । (V । (ди \а
ницеи, то в сумме 1 4-	} 4- j можно пренебречь слагае-
[ ди \2	/ ди \2
мыми Hs- и 4- .
\ дх I \ду /
Далее, условимся рассматривать только поперечные колебания
мембраны; это значит, что если точка мембраны имеет в поло-
жении равновесия абсциссу х и ординату у, то она имеет те же
7 Ю. С. Очар
194
Часть III
абсциссу и ординату во всем процессе колебания: меняется толь-
ко аппликата и.
Наша задача заключается в том, чтобы найти закон колеба-
ния мембраны, т. е. найти функцию и — и (х, у, t), дающую от-
клонение и любой точки мембраны (с координатами х, у) в лю-
бой момент времени t.
Для того чтобы найти эту функцию, составим дифференциаль-
ное уравнение, которому она удовлетворяет.
Докажем предварительно две леммы.
Лемма 1. Если функция f(x, у, г) непрерывна всюду на
поверхности S и
у, z)dS = 0
s
для любого куска s поверхности S, то f (х, у, z) = О (во всех
точках поверхности).
Доказательство. Допустим, что на поверхности на-
шлась точка Мо, в которой наша функция отлична от нуля;
например, / (Мо) = а > 0. В силу непрерывности функции можно
описать такую окрестность вокруг точки Мо, что всюду в этой
окрестности
у, z)>
Обозначим через s0 ту часть поверхности S, которая попала
Ьнутрь данной окрестности, и оценим интеграл по поверхности s0:
Jf/(*, t/, z)dS>-|-s0>0.
So
Итак, на поверхности S нашлась такая ее часть s0, что интеграл
по s0 отличен от нуля, а это противоречит условию. Следова-
тельно, допущение о том, что существует точка на 5, где функ-
ция отлична от нуля, неверно. Значит f(x, у, z) = 0 всюду на S.
Замечание. Доказанная лемма справедлива не только для
поверхностных, но и для тройных, двойных и определенных
(одномерных) интегралов. Так, например, для тройных интегра-
лов она читается следующим образом: «Если функция /(х, у, z)
непрерывна в области V и если для всякой области v, заключенной
в V, имеет место	У- г)^ = о. то f (х, у, г) = 0 всюду
v
в V». Доказательство этой леммы для тройных, двойных и оп-
ределенных интегралов ничем не отличается от приведенного до-
казательства для поверхностных интегралов.
Nalaliausitik
знание без границ * *
Г лава 1, § 2
19S
Лемма 2. Пусть функция f(x, у, z) и ее частные производ-
ные первого порядка непрерывны на гладкой поверхности S.
Если для любой замкнутой кривой /, лежащей на S, имеют место
равенства:
J / (х, у, z)dx = 0;	J/(x, у, z)dy = 0,
i	i
то f (x, у, z) = const всюду на S.
Доказательство. Пусть s — произвольный кусок поверх-
ности S, а / — его граница. По условию,
[ f (х, у, z) dx = 0,	f/(x, у, z)dy = G.
/	I
Применив к каждому из этих интегралов теорему Стокса, получим:
£[(•* cosP--^cosf)dS = °.
—~ cos а	~~ cos 7 j dS = 0.
dz 1 дх • }
Так как эти равенства имеют место для любого куска по-
верхности S, то, по лемме 1, имеют место тождества:
df a df	л
~~ cos В —~ cos 7 == 0,
dz 1 ду •	’
df , df	л
•--COS а 4- ~ COS 7 == 0,
dz	дх 1	’
(и куда
а/ д/ д/
дх _ ду __ dz
cos a cos fl cos 7 ’
г. e. составляющие градиента функции f пропорциональны сос-
тавляющим единичного вектора нормали к S. Но в таком слу-
чае градиент во всех точках поверхности S сам направлен по
нормали к S, а это возможно только тогда, когда ‘S является
поверхностью уровня для функции f(x, у, z) (см. стр. 16). Сле-
довательно, /(х, у, г) постоянна на S.
Выведем теперь дифференциальное уравнение колебания мем-
браны.
Рассмотрим какой-либо участок мембраны; пусть в состоянии
равновесия этот участок занимает область о (на плоскости Оху),.
7*
196
Часть III
а в некоторый момент t он принимает форму S (рис. 61). Так
как, по условию, колебания являются поперечными, то S проек-
тируется на плоскость Оху в область а.
Рассчитаем все силы, действующие на поверхность S.
Это прежде всего силы натяжения, действующие на поверх-
ность S и приложенные к ее границе. Обозначим через Т (х, у, и)
численную величину силы натяжения на единицу длины контура
вблизи точки (х, у, и). Точнее говоря, Т (х, у, и) определяется
Iaf I
как предел, к которому стремится отношение • при
М, где точки М (х, у, и) и Mt берутся на некоторой линии I,
а Д/^—вся сила натяжения, приложенная к участку ли-
нии I. Величина Т(х, у, и) называется плотностью сил натяже-
ния в точке (х, у, и)*.
Для того чтобы подсчитать всю силу натяжения, действую-
щую на S (приложенную к контуру /), разобьем / на ряд ма-
леньких элементарных дуг. Вектор силы натяжения, приложен-
ный к элементарной дуге AZ, перпендикулярен к этой дуге (точ-
нее, к ее касательной) и расположен в касательной плоскости к
поверхности S; следовательно, он перпендикулярен к единичному
вектору п нормали поверхности S (см. рис. 61). Так как вектор
* Здесь рассматривается только тот случай, когда натяжение в каждой
точке не зависит от направления линии I, прохолящей через эту точку
(т. е. натяжение одинаково во всех направлениях). Конечно, может оказать-
ся, что конкретная мембрана в одном направлении сильнее натянута, чем
в другом, но мы этого, более общего, случая не рассматриваем.
^atailausA
знание без границ * *
Глава 1,§ 2 197
натяжения численно равен Т|д/| и перпендикулярен векторам
д7 и п, то .он равен их векторному произведению:
ДГ= [ТД/.л],
или
ДГ = Т [Д/ • л].
Суммируя эти элементарные силы натяжения по всем Д/ ,
получим всю силу натяжения, действующую на S. При этом
проекции суммарной силы натяжения на оси Ох и Оу равны ну-
лю (так как, по условию, все точки мембраны перемещаются
только в вертикальном направлении), а проекция на ось Ои (чис-
ленно равная всей силе натяжения) вызывает перемещение пло-
щадки S.
Подсчитаем указанные проекции. Проекция элементарной
силы ДГ на ось Ох равна скалярному произведению этой силы
на орт i:
ДГ -i = Т- [д7 • п ] • i.
В правой части этого равенства стоит смешанное, или трой-
ное, произведение векторов Д7, л, i . По свойству смешанно-
го произведения круговая перестановка сомножителей не изме-
няет произведения. Поэтому
ДГ • i — Т • [ л г] • ДС
Суммируя по всем Д/ и затем переходя к пределу при
шах |Д/| -> 0, получим проекцию Fx всей силы натяжения на ось Ох:
Fx = lim kF • i = lim 2 Лл • »1 Д / =
max I Д/|-() ду	тах1д/|-°дГ
= [ T • [л i 1 dl.
i
(1)
Проекции силы натяжения на оси Оу и Ои (т. е. Г и Г )
равны таким же криволинейным интегралам:	У
Fy = [Лл/И/,
I
Fu = J T[nk]dT.
I
(2)
(3)
198
Часть 111
Для того чтобы упростить эти интегралы, выразим вектор
- ди ди
п че₽ез di иal-
Уравнение поверхности S (в момент t) будет и = и(х, у, t)
(здесь t фиксировано). Следовательно, уравнение касательной
плоскости в точке (х, у, и) имеет вид:
U — u=
а вектор нормали равен
дх 6у'+	'
Чтобы получить единичный вектор нормали, надо найден-
ный вектор разделить на его длину:
ди - ди - -
~dx'l~dy'l+k
п = ----------------.
2
Но, по условию, слагаемыми
но пренебречь. Поэтому
ди\*
дх)
'ди\а
ду)
при единице мож-
и
-	ди	ди	- . т
П — —	-х—		I	-х- • / -4- k.
дх	ду	7 1
Найдем векторные	произведения	[n-t], [п- /], [п-Л]:
k
In • i] =
i
__ди
дх
/
__ди
ду
О
дн т
ду
О
- ди ~,
I — -г- • k\
дх ’
-	-j-. ди
I" • Ч = -57,
ди
Поэтому интегралы (1), (2), (3) можно переписать следую
щим образом:
F^jrdy + T^du,
(1
Глава 1, § 2
199
Tdx — Td£du,
С ггди ,	. rr ди ,
I — Т л dx + 7\- dy.
J dy 1 dx v
(2')
(3')
В интегралах (Г) и (2') вторые слагаемые могут быть опу-
щены, так как они являются величинами второго порядка ма-
йи du
лости по сравнению с частными производными и ; дейст-
вительно, например
ди ,	rrdu (ди . . ди , \ гг(ди\2, , ди ди ,
т^- du = Т з- < dx 4- ч- dy — T H- dx 4- Тг д- dy,
1 дх	дхудх * ду а )	\дх) 1 1 дх ду
тди , „,ди ди ,	.	гг (ди\2 .
аналогично Т х- du = Т^~ д- dx 4- Т д- dy.
дх	ду	дх	1	\ду1	у
Итак,
F, = fTdy, Fy = -{Tdx.
Так как F, = 0, F = 0, то
•*	л
Tdy —0, ^Tdx — 0.
i
Эти равенства имеют место для любого замкнутого конту-
ра I на S. Следовательно, по лемме 2, всюду на 3 имеем: Т =
~ const. Итак, доказано, что в условиях нашей задачи плот-
ность натяжения во всех точках мембраны одинакова.
Рассмотрим теперь проекцию суммарной силы натяжения
на ось Ои:
Fu-j-Tdrydx + T^dy = T^-a(idx+ % dy.
Так как подинтегральная функция содержит переменные х
и у, но не содержит и (в частности, и также выражены
только через х и у), то интегрирование по контуру I можно за-
менить интегрированием по его проекции X, а затем к этому
интегралу применить формулу Грина-Остроградского (см. рис.
61, стр. 196).
200
Часть 111
Кроме сил натяжения, на мембрану могут действовать и
другие силы (например, вес). Равнодействующая всех сил, при-
ложенных к какому-либо участку мембраны и отличных от сил
натяжения, называется внешней силой на этом участке. Обозна-
чим через <р(х, у, t) тот предел, к которому стремится отноше-
ние внешней силы, действующей на элементарную площадку Да
в момент времени t, к массе этой площадки при стягивании До
к точке (х, у). Функция ср (х, у, 1) называется плотностью внеш-
ней силы. Так как каждая точка мембраны может двигаться
только по направлению оси и, то и внешняя сила в каждой
точке параллельна оси Ои. Для того чтобы найти теперь всю
внешнюю силу, действующую на а (или, что то же самое, на
S), надо разбить а на элементарные площадки Да; внешняя си-
ла, действующая на каждую элементарную площадку, рав-
на ср(х, у, /)-Г-До, а следовательно, вся внешняя сила
равна
У> 0г^°-	(5)
а
Итак, окончательно, вся сила Ф, действующая на S, нап-
равлена по оси Ои и численно равна сумме выражений (4) и (5):
•-f.w+5)+-’h
Применяя теорему о среднем, получим
где Мср—некоторая промежуточная точка площадки с.
С другой стороны, сила, действующая на материальную
точку, равна произведению массы этой точки на ускорение;
считая (при достаточно малом диаметре S) площадку S мате-
риальной точкой, получим
ф — г S
dt2 ’
или, так как колебания мембраны малы, то* S~o, и поэтому
Действительно, S
здесь мы уч-
а	о
ли , что величинами (и'х)2 и (и'у)2 можно пренебречь, если они являются слагае-
мыми рядом с единицей.
^lataHaustVi’
знание без границ Ч **
Г лава 1, § 2	201

Приравнивая это к выражению для Ф из формулы (6), по-
лучим, после сокращения на а:
Г т (— _±_ .и ffirl — д*и г
[1	+ ду2) * ]мср~ dt2 ‘
Стягивая теперь площадку а к точке М(х, у) (и устремляя
при этом Л1ср к М), получим в пределе:
m /д2и . д2и\ . г д*и г
T^ + a?) + <Pr = 5F г
Это равенство выполняется в любой точке (х, у) области* 2
и в любой момент времени t. Оно и является искомым урав-
нением, которому удовлетворяет функция и (х, у, t). Для его
Т
упрощения разделим все его члены на Г и обозначим у через
а* (легко проверить, что а имеет размерность м/сек):
д2и 21	• дли \ .	.	..
~dt2 ~ а ( дх» + ~ду2) +
В случае отсутствия внешней возмущающей силы или в
том случае, когда она столь мала, что ею можно пренебречь,
уравнение (7) упрощается:
д2и _ 2 ( д2и dau
~di* ~ а + Ip';*-
Это — уравнение свободных колебаний мембраны.
Рассмотрим вопрос о начальных и граничных условиях.
1.	Если мембрана является ограниченной (т. е. ее диаметр
равен конечному числу) и ее граница закреплена на плоскости
Оху, то граничное условие будет: и (х, у, /) = 0 в любой мо-
мент времени t для всех тех точек (х, у), которые принадлежат
границе мембраны. Здесь граничное условие записано словесно;
его можно было бы записать и с помощью формул, но способ
этой записи зависит от формы мембраны. В главе 2 мы рас-
смотрим случаи прямоугольной и круглой мембран; там и бу-
дет выяснен вопрос о том, как записать с помощью формул
наше граничное условие в каждом конкретном случае.
Кроме граничного, естественно задать начальные условия.
В данном случае они имеют вид:
У» OUo =/(х» У)’
Буквой 2 обозначена проекция всей мембраны на плоскость Оху.
202
Часть III
ди(х, у, t)
dt
или, в более короткой записи,
=	у),
о
и(х, у, 0) = /(х, у)\ u't(x, у, 0) = ф(х, у).
Здесь f(x, ^ — заданная функция, определенная всюду в
области 2. Она дает начальное отклонение мембраны в каждой
точке.
Функция <р(х, у) также задана в области 2; она дает на-
чальную скорость в каждой точке мембраны.
Из физических соображений ясно, что эти условия гаран-
тируют единственное решение (действительно, при заданном на-
чальном отклонении и заданной начальной скорости мембрана,
закрепленная на границах, будет колебаться по вполне опреде-
ленному закону). В главе 2 будет найдено это решение (для
частных случаев прямоугольной и круглой мембран). Доказа-
тельства же единственности и устойчивости решения мы прово-
дить не будем.
2.	Если мембрана не закреплена в точках ее границы, то
граничные условия будут иметь другой вид (они могут стать
неоднородными); например, точки границы могут двигаться по
некоторому определенному, заданному закону (при этом, разу-
меется, каждая точка границы должна двигаться только в вер-
тикальном направлении, так как, по условию, колебания мем-
браны являются поперечными).
В дальнейшем, изучая закон колебания мембраны, мы огра-
ничимся только тем случаем, когда мембрана закреплена в точ-
ках ее границы.
3.	Если мембрана бесконечна и совпадает со всей плоскос-
тью Оху, то здесь не имеет смысла говорить о граничных усло-
виях; в этом случае закон колебания мембраны вполне опреде-
ляется заданием начальных условий:
и(х, у, O) = f(x, у)- и\(х, у, 0) = ф(х, у),
где f(x, у) и ф (х, #) —функции, заданные на всей плоскости.
4.	Интересен случай стационарного уравнения мембраны,
т. е. тот случай, когда мембрана находится в состоянии покоя:
отклонение каждой ее точки от плоскости Оху не зависит от
времени t, а зависит только от абсциссы и ординаты этой точки:
и = и (х, у). Ясно, что эта задача легко решается, если контур,
вдоль которого закреплена мембрана, расположен на плоскости
Оху\ в этом случае и сама мембрана целиком расположится на
этой плоскости. Если же контур мембраны не лежит в плоскос-
ти Оху, а является некоторой замкнутой пространственной кри-
вой I (рис. 62), то задача сводится к решению уравнения
Г лава 1, § 3
203
дяи . дяи _____л
+ дуя ~
при граничном условии
“(*. У)|наХ = Н*. у)-
(9)
(10)
Здесь X — проекция кривой I на плоскость Оху, а функция
f (х, у) задает величину отклонения точек контура / от плоскости
Оху.
Найдя функцию и(х, у), удовлетворяющую уравнению (9)
и граничному условию (10), мы получим уравнение поверхности S,
по которой расположится мембрана,
натянутая на контур I (такую фор-
му примет, например, мыльная плен-
ка, натянутая на проволочный кар-
кас /).
Уравнение (9) называется урав-
нением Лапласа для функции двух
переменных. Его решениями являют-
ся гармонические функции. Следова-
тельно, наша задача сводится к то-
му, чтобы найти гармоническую
функцию и (х, у), определенную в
области а (см. рис. 62) и принимаю-
щую на ее границе заданные зна-
чения. Проблема отыскания такой
гармонической функции называется
плоской задачей Дирихле. К этой за-
if
Рис. 62
даче мы еще вернемся впоследствии
(в связи с решением стационарного уравнения теплопроводности) •
§ 3. Вывод уравнения теплопроводности
Рассмотрим однородное и изотропное* тело V. Если различ-
ные точки этого тела имеют различную температуру, то внутри
тела будет происходить естественный процесс передачи тепла от
участков более нагретых к участкам менее нагретым. Задача,
которая при этом возникает, заключается в том, чтобы описать
этот процесс математически. Эта задача будет решена, если мы
найдем функцию и(х, у, z, t), дающую температуру и в любой
точке (х, у, г), расположенной внутри данного тела, и в любой
* Тело называется изотропным в тепловом отношении, если его тепло-
вые свойства (например, свойство передавать тепло) одинаковы во всех точ-
ках и по всем направлениям.
204
Часть ///
момент времени t. Зная эту функцию, мы сможем найти распреде-
ление температуры внутри тела в любой данный момент време-
ни t\ для этого достаточно зафиксировать t в функции и(х, у, z,t).
Эта функция позволит также проследить, как изменяется с те-
чением времени температура в каждой конкретной точке; для
этого достаточно зафиксировать координаты точки и проследить
за тем, как изменяется и с изменением t.
Для того чтобы найти функцию и(х, у, z, t), надо составить
дифференциальное уравнение, которому удовлетворяет эта
функция.
Пусть G — произвольная область, лежащая внутри данного
тела V, и S — граница этой области (рис. 63). Через поверхность
S за время t из области G выделяется некоторое количество тепла *.
Рис. 63
Подсчитаем его двумя различными способами. Приравняв затем
результаты вычисления, получим искомое дифференциальное урав-
нение.
Из физики известен следующий, экспериментально установ-
ленный закон (рис. 64): «если даны две равные, расположенные
параллельно друг другу, площадки, каждая из которых имеет
свою температуру, то количество тепла Д</, переходящего за ма-
лый промежуток времени Д/ от более нагретой площадки к ме-
нее нагретой, пропорционально разности температур площадок
(А«). их площади (Д5), времени (Д0 и обратно пропорционально
расстоянию между площадками (п)». Если обозначить коэффициент
пропорциональности через k (он зависит от теплопроводных свойств
среды и называется коэффициентом теплопроводности), то
^q = -k — .Д5-Д/.
’	п
• Если через поверхность S тепло не уходит из области G, а поступает
в нее, то будем говорить, что выделение тепла через S отрицательно.
NahrHauswk
знание без ераниц ' «Ь
Глава 1, § 3 205
Знак минус поставлен потому, что Ды и Дд имеют разные
знаки: если температура второй площадки выше, чем температура
первой (т. е. Lu > 0), то тепло переходит от второй к первой
(т. е. Lq <0), и наоборот.
В приведенной здесь формулировке этот закон является
только приближенным: он верен лишь для малых Lt и п и тем
точнее, чем меньше Lt и п.
Используя этот закон, мы можем подсчитать количество тепла,
выделяющегося из G через элементарную площадку* ** AS, распо-
ложенную на границе области G. Для этого проведем мысленно
параллельно AS (за пределами об-
ласти на расстоянии п) другую пло-
щадку A S'; если эти площадки дос-
таточно близки, то можно считать,
что все тепло, выделяющееся через
AS, попадает на AS' (рис. 65).
Поэтому
Д<7==—£•—-AS-A/ =
v	п
п
Рис. 65
где М — какая-либо точка на A S, а ЛГ — проекция точки М на
A S'. В пределе (при п -> 0) отношение ц ~ u перейдет в
производную от и по направлению внешней нормали п. Итак,
Lq = —k~-LS-Lt.
дп
Разобьем теперь всю границу S области G на элементарные
площадки AS/f и на каждой элементарной площадке выберем
по точке М/. Тогда количество тепла, выделяющегося из G через
AS/, равно:
Д<7/«—-AS/-Lt,
1 \дп )Mt 1
и, следовательно, все тепло, выделяющееся (за время A f) через S,
равно:
.д5/..
I	I	I
* Элементарную площадку AS можно приближенно считать плоской.
** Коэффициент теплопроводности k постоянен во всех точках данного
тела (так как тело, по условию, однородно и изотропно).
206
Часть III
Переходя к пределу при max diam Д5£ -> 0, получим
’—'к®
или, так как производная по направлению равна проекции гра-
диента на данное направление,
<7 = —(gradu-n0)dS;
здесь «о— единичный вектор внешней нормали.
Применим теперь к полученному поверхностному интегралу
теорему Гаусса-Остроградского:
q = — k-M-J J J div grad u-dV.
О
Под знаком тройного интеграла стоит лапласиан и. Поэтому
окончательно
? = —&-Д/-УУУ /n\u-dV.	(1)
о
Вычислим теперь то же количество тепла q иным способом.
Разобьем область G на ряд элемен-
тарных областей Д vk и подсчитаем коли-
чество тепла Д^, выделяющегося из Дрл
за время Д/ (рис. 66). Очевидно, количество
тепла, выделяющегося за то же время из
всей области G, равно сумме всех Д qk.
Из физики известно, что количество
тепла, отданное в окружающее простран-
ство некоторым телом за время Д/, про-
порционально массе этого тела и пони-
жению температуры этого тела за время
Д t. Коэффициент пропорциональности на-
зывается коэффициентом теплоемкости и обозначается через с.
Применить этот закон непосредственно к телу G мы не мо-
жем: различные точки этого тела имеют различную температуру
и поэтому нельзя говорить о том, чему равно понижение темпе-
ратуры тела за время Д/. Однако этот закон можно применить
к каждой элементарной области ДиА в отдельности: если диаметр
этой области достаточно мал, то можно считать, что во всех ее
точках в данный момент температура одна и та же.
Итак,
A<4 = — c-mk^tu,
(2)
^alaHausA
знание без границ Ч
Глава 1, § 3
207
где mk — масса области Аоа (она равна Г-ДиД а А,и — частное
приращение функции и (обусловленное изменением только одной
переменной /). Знак «минус» мы поставили потому, что А^'диА^м
имеют разные знаки: если тело остыло за время А/, т. е. А/и< О,
то тело отдало некоторое тепло и, следовательно, А(/Л>0; если
же тело нагрелось за время A t, то А, и > 0, но A q'k < 0, так как
тело не отдало, а получило тепло.
Заметим, далее, что а* иГ Поэтому мы можем заменить А, и
на u't&t. Таким образом, равенство (2) можно переписать сле-
дующим образом:
Д^а-с-Г-Д^и^-Д/,
где Mk — какая-либо точка внутри области bvk.
Суммируя теперь все A q'k, получим общее количество тепла,
выделившегося из G за время А/:
9 = Хд?;^-с-Г.Д/-Х(^)м -Д«А.
k	k
Сумма, стоящая в правой части этого равенства, является
интегральной суммой. Переходя к пределу (при diam ДоА-► 0),
получим
, = _с.Г.дьД|^У.	(3>
о
Таково количество тепла, выделяющегося из тела G за время
в результате свободного теплообмена, в предположении, что
внутри V нет дополнительных источников тепла. Если же такие
источники существуют, то к выражению из формулы (3) следует
добавить тепло, доставляемое этими источниками.
Рассмотрим количество тепла, возникающего благодаря этим
источникам в малой области, окружающей точку (х, у, г) за время
от момента t до момента t + A t. Предел, к которому стремится
отношение этого количества тепла к массе области А/n и к А/,
при стягивании области к точке (х, у, г) и при A t -> 0 называется
плотностью источников тепла в точке (х, у, z) в момент време-
ни t и обозначается Л(х, у, z, t). Если в некоторой точке в ка-
кой-то момент времени А > 0, то в этой точке имеется источник
тепла; если же при некоторых х, у, z, t величина А отрицательна,
то в этой точке в данный момент времени действует поглотитель
тепла. Ясно, что количество тепла, которое выделяется из Аоа бла-
208
Часть III
годаря наличию источников тепла, равно A (xk, yk, zk, 0ГАиЛА0
а все количество тепла, выделяемого из G благодаря наличию
источников, равно S A (xk, yk, zk, /)ГД vkL t или в пределе (при
k
diam A vk -> 0),
Г A t J J j* А (х, у, z, f)dV.
о
Складывая это с тем количеством тепла, которое было най-
дено в формуле (3), получим окончательно
<4>
о	о
Формула (4) дает общее количество тепла, выделившегося из те-
ла G за время А/. В силу закона сохранения энергии (в данном
случае — тепловой энергии), оба способа подсчета количества тепла,
выделившегося из G, должны дать один и тот же результат, так
как все изменение количества тепла в G может произойти только
за счет выделения тепла через поверхность S. Итак, мы можем
приравнять общее количество тепла, выделившегося через поверх-
ность S за время А / (см. фомулу (1)), к тому количеству тепла,
которое найдено по формуле (4):
-k^/^u.dV= -cVLt
О	о
+r^Adv-
о
сокращая на А/ и перенося все члены в одну часть равенства,
получим:
4-ГЛ ]dV = 0.	(5)
Равенство (5) имеет место для любой области G, принадлежа-
щей V. Следовательно, подинтегральная функция тождественно
равна нулю (см. замечание к лемме 1 из предыдущего параграфа).
Итак,
fez л\ и — с Г ~ + ГА (х, у, z, t) = 0.
(6)
Это и есть искомое дифференциальное уравнение для опре-
деления функции и (х, у, г, 0. Здесь fe, с, Г — известные величи-
NataHauswk
знание без ераниц * *
Глава 1, § 3
209
ны, а А (х, у, z, t) — известная функция, дающая плотность рас-
пределения источников тепла и предполагаемая непрерывной.
Если Л =£ 0, то уравнение называется уравнением несвобод-
ного теплообмена.
При А = 0 уравнение (6) становится однородным линейным
уравнением. Это — уравнение свободного теплообмена. Его можно
записать следующим образом (если обозначить -р- = а8):
у	С А	/
£=»>•&«.	(7)
или
0U
—--- = От
dt
д2и d2u
dx2 + 7)у2
д2и
dz2
(7')
Коэффициент а2 имеет размерность .
Частным случаем рассматриваемой задачи является изучение
стационарного распределения температуры внутри тела; вопрос
ставится так: каково должно быть распределение температуры
внутри тела, чтобы дальнейшего теплообмена не происходило?
Очевидно, в этом случае и не зависит от /; следовательно, и есть
функция только координат точки. Уравнение стационарного рас-
пределения температуры получится из уравнения (7) или (7'),
ди л
если учесть, что в этом случае = 0; выпишем получившееся
уравнение:
(8)
или
д2и . д2и	д2и  
~дх* + 'ду2	~д^ ~
(8')
Итак, стационарное распределение температуры осуществляется
с помощью гармонической функции и (х, у, г) (напомним, что гар-
монической называется всякая функция с непрерывными вторыми
производными, удовлетворяющая уравнению \ и = 0).
У читателя может возникнуть недоумение: разве может при-
остановиться свободный теплообмен внутри тела, различные точки
которого имеют различную температуру (ведь гармоническая функ-
ция в общем случае непостоянна)? Да, может, если на границе
области V поддерживать искусственно постоянную температуру
(различную в различных точках границы). Но это уже связано
с вопросом о граничных и начальных условиях, к которому мы
и переходим.
210
Часть III
Граничные и начальные условия. 1. Трехмерная задача тепло»
проводности. Пусть V — заданное ограниченное тело и S — его
граница. Для того чтобы найти закон распределения температуры
внутри V, надо знать распределение температуры в начальный
момент:
и (х, у, z, O) = F (х, у, z),
где F (х, у, z) — заданная, определенная внутри V функция ♦. Кроме
того, надо знать температуру окружающей среды. Эта температура
не обязана быть одинаковой во всех точках границы S, она мо-
жет меняться с течением времени, но она должна быть известной.
Таким образом, кроме приведенного выше начального условия,
должно быть задано граничное условие:
й(х, у, z, t)KaS = f(x, у, z, 0,
где f(x, у, z, t) — заданная функция, определенная во всех точ-
ках на поверхности S и для всех моментов времени t.
Можно доказать, что существует, и притом единственное,
решение уравнения (7) или (7'), удовлетворяющее этим начальным
и граничным условиям.
Если распределение температуры внутри V стационарно, то
говорить о начальных условиях не имеет смысла: в начальный
и во все последующие моменты времени распределение темпера-
туры одно и то же; оно не может быть произвольно задано —
оно должно быть найдено. Что же касается граничных условий,
то они задаются так же, как и в случае нестационарной задачи
(только распределение температуры на границе, в данном случае,
не может зависеть от /):
М*. У> z)Ls = f(x> У> гУ
где Дх, у, z) — функция, заданная на S.
Задача разыскания гармонической внутри V функции и (х, у, г),
принимающей на границе области заданные значения, называется
задачей Дирихле. К задаче Дирихле сводится разыскание закона
стационарного распределения температуры.
Эта задача нами будет решена в том частном случае, когда
область V является шаром (глава 2, § 15); в случае же произ-
* В дальнейшем (в этом и следующем параграфах) мы будем предпола-
гать, не оговаривая этого особо, что все заданные функции удовлетворяют
следующим условиям: а) они ограничены в своей области задания; б) они не-
прерывны или кусочно-непрерывны в этой области; последнее означает, что
область задания можно разбить на конечное число областей, внутри каждой
из которых данная функция непрерывна.
WalaHauslik
знание без границ “ w
Г лава 1, § 3
211
вольной области V мы ограничимся тем, что выясним, к какой
задаче сводится наша проблема (см. главу 4, § 2).
Там же (в четвертой главе) будет доказана единственность
решения задачи Дирихле.
2. Плоская (двумерная) задача теплопроводности. Пусть об-
ластью V является бесконечный цилиндр (рис. 67) с образующими,
параллельными оси Oz. Если при этом
граничные и начальные условия не
зависят от z, то, очевидно, и реше-
ние также не зависит от z. В этом
случае уравнение (7') приведется к
виду
ди _ 2	। д8ц\
dt ~а + ду2)'
а начальное и граничное условия —
к виду:
«(*» У> 01/и0 = П*. У),
“(Х> У> 0 Las У' *)•
Название «плоская задача» объясняет-
ся тем, что в сечении а тела V пло-
скостью Оху будет такая же картина
распределения температуры, как и в
любом параллельном сечении; поэто-
му для того чтобы знать распределение температуры в V, дос-
таточно знать распределение температуры в плоской области о.
Если распределение температуры внутри цилиндра V стацио-
нарно, то искомая функция и зависит только от двух перемен-
ных х и у. Она удовлетворяет уравнению
dau . д2и __
дх2 + ~ду2 ~
(9)
и граничному условию
0)LaS = /(*« У\
Задача решения уравнения (9) при граничном условии, не зави-
сящем от z, называется плоской задачей Дирихле*.
К рассмотренным в этом пункте математическим задачам
приводит также следующая физическая задача.
Пусть область V представляет собой тонкую материальную
пластинку а, лежащую на плоскости Оху и изолированную (в тепло-
* С плоской задачей Дирихле читатель уже встречался при рассмотре-
нии стационарного уравнения мембраны (см. стр. 202—203).
212
Часть III
вом отношении) сверху и снизу от окружающей среды: сообще-
ние с внешней средой производится только через контур пластин-
ки. Тогда искомая функция — распределение температуры внутри
пластинки — зависит только от х, у, t\ уравнение, которому удо-
влетворяет эта функция, таково:
ди __ 2 / даи , д2и \
~di ~а + "ду2)'
а начальные и граничные условия имеют вид:
и (х, у, О |,_0 = F (х, у); и (х, у, t) |на х = f (х, у, 0,
где функция F (х, у) дает распределение температуры внутри
пластинки в начальный момент, a f(x, у, t) дает распределение
температуры на контуре X в любой момент
Если же распределение температуры в области стационарно,
то мы снова возвращаемся к плоской задаче Дирихле: найти реше-
ние уравнения -f-	= 0 при заданных значениях функции
и(х, у) на контуре X области а:
и(х> S/)lHax = f(x> У)-
Впоследствии мы решим плоскую задачу Дирихле для того случая,
когда а является кругом (глава 2, § 9).
3. Линейная (однэмерная) задача теплопроводности. Пусть тело V
есть часть пространства, ограниченная двумя параллельными плоско-
стями (для определенности будем считать их перпендикулярными
оси Ох и пересекающими эту ось в точках с абсциссами а и р). Если
начальные и граничные условия не зависят от у и z, то, очевидно,
и решение уравнения не зависит от у и z. Поэтому искомая функ-
ция и(х, t) удовлетворяет уравнению
ди 2 д2и
dt дх2
которое можно получить из уравнения (7'), если учесть, что в данном
д2и п д2и п т,
случае = 0 и = 0. Начальное и граничное условия запи-
шутся так:
и (a,	u(P, 0 = /2(О»
где F (х) — заданное начальное распределение температуры, а Д (0
и Д(0— температуры, поддерживаемые на боковых стенках об-
ласти.
^alattausihi
знание без границ “ w
Глава 1, § 3
213
Если распределение стационарно, то искомая функция зави-
сит уже только от одного переменного х; она удовлетворяет
уравнению
и граничным условиям:
и(а) = А, и($) = В,
где А и В — постоянные числа (температура, поддерживаемая на
стенках). Эта задача (линейная задача Дирихле) очень легко ре-
шается: решением уравнения является функция и = Схх + С2, где
Сх и С2 подбираются так, чтобы удовлетворялись данные гранич-
ные условия. Итак, решениями одномерной задачи Дирихле яв-
ляются только линейные функции.
К тем же уравнениям, которые рассмотрены в этом пункте,
приводит и другая физическая задача.
Пусть область V представляет собой тонкий однородный стер-
ень; будем, для определенности, считать его расположенным
на оси Ох между точками х = а и х ~ р. Пусть его размеры
в направлении осей Оу и Oz столь малы, что ими можно пре-
небречь. Если стержень изолирован в тепловом отношении от
окружающей среды всюду, кроме своих концов, то распределение
температуры в нем удовлетворяет уравнению
ди „ д2и
— = а*-----
dt и dx2 ’
а также начальному и граничным условиям:
и(х, t)\t_0 = F(x); и (а, 0 = w(p, /)==А(0,
где F (х)— начальное распределение температуры в стержне (на
участке (а, р]), а /1 (/) и /2 (t) — температуры, поддерживаемые на
концах стержня (температура может зависеть от времени /).
Задача о распределении тепла в стержне нами будет рассмот-
рена в § 6 главы 2 (для случая конечного стержня) и в § 2 главы 3
(для случая бесконечного стержня).
Если в стержне установилась стационарная температура, то
ее распределение внутри стержня будет уже функцией только
одного переменного; эта функция и (х), удовлетворяет уравнению
^ = 0
дх*
и граничным условиям:
и (а) = Д; и (Р) = В
214
Часть III
(Д — постоянная температура, поддерживаемая на левом конце
стержня, В —на правом). Как мы видели выше, единственная
функция, удовлетворяющая этому уравнению и данным граничным
условиям, —линейная.
£ 4. Вывод основного уравнения гидродинамики
Рассмотрим некоторую область V, заполненную движущейся
однородной жидкостью, плотность которой в процессе движения
остается неизменной (напомним, что такую жидкость называют
несжимаемой: объем, занимаемый каким-либо количеством жид-
кости, не изменяется при перемещении этого количества жид-
кости). Если движение жидкости является стационарным (т. е.
ее скорость v(x, у, г) зависит только от координат точки, но в
каждой данной точке не меняется с течением времени), то, как
мы видели (см. стр. 41), векторное поле является соленоидальным:
divt> = 0.	(1)
Это уравнение называется уравнением движения несжимаемой
жидкости. Оно еще не дает возможности определить скорость
v: ведь для того, чтобы найти v, надо знать три составляющих
вектора v, т. е. три скалярные функции, а уравнение для их оп-
ределения у нас только одно. В гидродинамике выводятся из фи-
зических соображений еще несколько уравнений, и из этой систе-
мы уравнений находятся все составляющие вектора v. Мы не бу-
дем составлять этих уравнений; вместо этого наложим на движе-
ние жидкости некоторое дополнительное требование — и тогда,
в этом частном случае, нам удастся обойтись одним уравнением (1).
Назовем стационарное движение жидкости потенциальным,
если его скорость v образует потенциальное поле (т. е. rot v » 0).
Конечно, не всякое движение жидкости является потенциальным;
так, например, вращение жидкости вокруг неподвижной оси (с
постоянной угловой скоростью) не является потенциальным: ротор
скорости здесь не равен нулю. Мы же ограничимся изучением
только потенциального движения жидкости*.
Если rot v = 0, то векторное поле имеет потенциал, т. е. су-
ществует такое скалярное поле и, что grad и — v. Очевидно, доста-
точно найти потенциал и, чтобы знать векторное поле v.
• Движение реальной жидкости является потенциальным, если действие
сил вязкости ничтожно мало по сравнению с действиями сил давления, и если
в рассматриваемой области нет завихрений, обусловленных срывом частиц
жидкости со стенок пограничного слоя или резкими колебаниями температуры.
Глава /, § 4
215
Для того чтобы составить дифференциальное уравнение для
потенциала и, достаточно в уравнение (1) вместо v подставить
grad и; тогда получим
div grad и = О,
или
/\ и = 0.	(2)
В декартовых координатах это уравнение выглядит так:
дх» + ду* + dz*
Итак, нами выведено уравнение для потенциала и (х, у, г).
Если потенциал будет найден, то скорость v определится из ра-
венства
v — grad и.
Как мы видим, потенциал скорости в потенциальном стационар-
ном движении жидкости является гармонической функцией.
Граничные условия. Так как, по условию, рассматриваемое
движение жидкости стационарно, то говорить о начальных ус-
ловиях не имеет смысла: в начальный и во все последующие
моменты времени распределение скоростей одно и то же. Сле-
довательно, может идти речь только о граничных условиях.
Совершенно ясно, что ставить здесь задачу Дирихле не име-
ет физического смысла: лам не могут быть известны значения
потенциала скорости на границе области V.
Однако мы можем знать, чему равна сама скорость на гра-
нице области V или_ (что в данном случае важнее) чему равна
проекция скорости v на внешнюю нормаль п к поверхности.
Пусть величина этой проекции задана в каждой точке по-
верхности S (здесь S — граница области V), например
проекция v на п — f(x,y,z),
где f(x, у, z), определена всюду на S. Тогда это условие
можно сформулировать так:
проекция grad и на п ~ f (х, у, z), или *
ди
дп
= / (х, у, г).	(3)
на S
•Напомним, что проекция градиента на какое-либо направление равна
производной в этом направлении.
216
Часть III
Итак, окончательно задача может быть сформулирована сле-
дующим образом.
Найти функцию и (х, у, г), удовлетворяющую всюду в об-
ласти V уравнению
д2 и , д2 и । д2 и _ Л
~д72 + ~дуГ + dz2~U
и на границе области условию -Й- = f (х, у, z) .
дп
Задача отыскания функции, гармонической в области V, если
на границе этой области задана нормальная производная иско-
мой функции, называется задачей Неймана.
В отличие от рассмотренных ранее задач, задача Неймана не
всегда имеет решение.
Для того чтобы в этом убедиться, заметим следующее: так
как, по условию, жидкость несжимаема, то поток поля скоро-
стей через любую замкнутую поверхность равен нулю. В част-
ности, равен нулю и поток через поверхность S, ограничиваю-
щую область V:
JJ (vn) dS = 0.
s
Но, по условию,
( v п) = проекции v на п = f (х, у, г).
Следовательно,
f f f(x,y,z)dS = 0.	(4)
Таким образом, ставить задачу Неймана имеет смысл только
тогда, когда заданная на границе области функция f(x,y,z)
удовлетворяет равенству (4) ( иначе говоря, когда J J -- dS = о) .
Это условие является необходимым для разрешимости задачи
Неймана. Вместе с тем оно и достаточно: можно доказать, что
если оно выполнено (и если поверхность S является гладкой или
кусочно-гладкой), то задача Неймана имеет решение.
Решение этой задачи единственно с точностью до постоянно-
го слагаемого; это значит, что различные решения отличаются
друг от друга только постоянным слагаемым. Заметим, однако,
что, хотя потенциал и (х, у, г) определяется только с точностью
до постоянного слагаемого, скорость v определяется совершенно
однозначно: ведь две скалярные функции, отличающиеся посто-
янным слагаемым, имеют один и тот же градиент.
^alaHaus^
знание без границ Ч *
Г лава 1, § 4
217
Плоская задача гидродинамики. Если областью V является
бесконечный цилиндр с образующими, параллельными оси Ог,
а граничное условие (значение нормальной составляющей ско-
рости на границе области) не зависит от z и, наконец, если из-
вестно, что вектор скорости в каждой точке области V паралле-
лен плоскости Оху, то очевидно,
что распределение скорости внутри
V не зависит от г:
v = v(x, у).
Но тогда и потенциал скорости
зависит только от х и у:
и = и (х, у).
Он удовлетворяет уравнению
Рис. 68
д2и	д2и
дх2	ду2
н граничному условию
у),
дп
Так как поле и(х, у) имеет совершенно одинаковую картину во
всех сечениях цилиндра, параллельных плоскости Оху, то в этом
случае можно ограничиться решением задачи на плоскости Оху\
найти в плоской области а (где а — сечение области V плоскостью
Олт/) функцию и (х, у), удовлетворяющую внутри области а урав-
д2 и . д2 и Л	Л
нению —-т-а—|—s-j- = 0, и на контуре области — условию
С/Л	иу
ди	_
— f (х,у), где п — внешняя нормаль к контуру области а
(рис. 68).
Эта задача называется плоской задачей Неймана.
Так же, как и в случае пространственной задачи Неймана,
функция f (х, у) не может быть задана совершенно произвольно:
она должна удовлетворять условию
J / (х, г/)	= О,	(5)
i
где Z — контур области а. Здесь под интегралом по дуге / пони-
мается предел интегральной суммы
218
Часть III
f (xk* Ул)
h
где Д— длины элементарных дуг, на которые разбита кривая /,
a (xk, ук) — произвольная точка на соответствующей элементар-
ной дуге; предел берется при шах Д /Л -> О*.
При выполнении условия (5) (и, конечно, при условии глад-
кости или кусочной гладкости контура /) плоская задача Ней-
мана всегда имеет решение, причем единственное с точностью
до постоянного слагаемого.
ГЛАВА 2
РЕШЕНИЕ УРАВНЕНИЙ МЕТОДОМ ФУРЬЕ
(метод разделения переменных)
В предыдущей главе мы вывели дифференциальные уравнения
для решения некоторых физических задач. В настоящей главе
мы изложим метод, с помощью которого можно будет решить
эти уравнения (т. е. для каждого уравнения найти то решение,
которое удовлетворяет заданным начальным и граничным усло-
виям). Существует несколько различных методов решения урав-
нений с частными производными; с важнейшим из них — мето-
дом Фурье — мы познакомимся в этой главе (а также — с нес-
колько иной точки зрения — в главе 3). В главах 4 и 5 будут
рассмотрены еще два метода решения уравнений в частных про-
изводных (метод функции Грина и метод характеристик).
•Не следует смешивать криволинейный интеграл ^f(x,y)dl —
I
= lim У f (xk Ук) Д Ik от скалярной функции f(x, у) с криволинейным интег-
k
ралом от векторной функции J Adi, изученным в 1-й части. Это — совер-
I
шенно различные интегралы, хотя и родственные друг другу: легко видеть,
что интеграл от векторной функции может быть приведен к криволинейному
интегралу от скалярной функции: J Adl= J | А | cos <р dl, где 9 —угол меж-
/7
ду вектором А и вектором касательной к / (этот угол зависит от точки на
кривой).
Аа1аНаи$Ж
знание без границ * *
Глава 2, § 1 219
§ /. Решение уравнения свободных колебаний стру-
ны методом Фурье
Пусть нам задана конечная однородная струна, закрепленная
на концах (в точках х — 0 и х — I). Если на нее не действуют
внешние силы, то функция u(xtt), дающая закон колебания
струны, должна удовлетворять уравнению
д*и , д2и	.. .
граничным условиям:
н (0,0-0, ^ (/,/) = 0
(2)
и начальным условиям:
и (X, t) I/. о - <Р (х)- Ut (х, t) |/ « о == Ф (х) ,
(3)
где '?(х) и ф(х) — заданные функции (см. главу 1, §1).
В данном случае как само линейное уравнение (1), так и
граничные условия (2), однородны, а следовательно, если неко-
торые функции удовлетворяют уравнению (1) и условиям (2), то
и любая их линейная комбинация также удовлетворяет этому
уравнению и этим условиям. На этом и основан метод Фурье.
Суть его заключается в том, что на первом этапе мы находим
некоторый запас функций, удовлетворяющих уравнению (1) и ус-
ловиям (2); пусть это будут функции и2(х, t), u.2(xt t),...,
ип(х, 0,.... На втором этапе строится линейная комбинация* из
этих функций:
и (х, t) = Ci их (х, 0 + с2«а (х, t) 4-... + сп ип (х, t) 4- ...;
в силу однородности уравнения и однородности граничных усло-
вий, эта сумма также удовлетворяет и уравнению, и граничным
условиям при любых значениях коэффициентов ряда; остается
подобрать эти коэффициенты так, чтобы функция и(х, t) удовле-
творяла не только граничным, но и начальным условиям (3).
Для того чтобы осуществить этот план, попытаемся найти
такие решения, которые представимы в виде произведения двух
• Здесь «линейная комбинация» толкуется в несколько расширенном
смысле; под «линейной комбинацией» подразумевается не только конечная
сумма, но и сумма бесконечного ряда.
220
Часть HI
функций, одна из которых зависит только от х (обозначим ее
Х(х)), а другая — только от t(обозначим ее Т(/)):
ц(х,О = Х(л)Т(0.	(4)
Если функция (4) является решением данного уравнения (1),
то в результате ее подстановки в уравнение получим тождество:
[Х(х) Т(/)йа’|Х(х) Т (QU,
или
Х(х) T"(t) = a*X"(x)T(t).
Разделим переменные в этом тождестве:
JT (0 _ X" (х)_,	,,,
asT(/)~ Х(х)	'°'
Выражения, стоящие в обеих частях тождества (5), не зави-
сят ни от х, ни от t. Действительно, левая часть равенства
не зависит от х; так как это равенство является тождеством, то
и правая часть его не может зависеть от х. Далее, правая часть
равенства не зависит от /; следовательно, не зависит от t и ле-
вая часть. Обозначив обе части этого равенства через — |х (где
р. = const)*, получим
Т"(П == X" (%) _
аяГ(/)~ Х(х) ‘ ’
откуда
Г'(/) + |Аа87,(0 = 0,	(6)
Х"(х) +|хХ(л) = 0.	(7)
Подберем jx так, чтобы выполнялись граничные условия;
очевидно, что условие и (0. /) — 0 равносильно тому, что X (0) — 0,
а « (/,/) = 0 равносильно тому, что X (/) = 0. Следовательно, дело
сводится к тому, чтобы ргшить следующую краевую задачу: «найти
нетривиальные решения уравнения (7) при граничных условиях
* Знак «минус» перед |х ставится только для удобства дальнейшей запи-
си. Ои еще не означает, что константа «—у» отрицательна. Знак этой кон-
станты выяснится только впоследствии (когда мы убедимся, что у.>0и, сле-
довательно , — у. < 0).
Специально Оля	*
5Уа1айа<мЖ
знание Без границ	* *
Глава 2, § / 221
X (0) = 0, X (/) = 0 ». Эту краевую задачу мы уже решали (см.
часть 2, §3) и нашли ее собственные числа:
я1	28 я’
"/Г > На — ~~р
и соответствующие им собственные функции:
(х) = sin-р-; X2(x)=sin рА;...; Х„(х) = sin Ар;...
Ни при каких других значениях р. эта краевая задача не имеет
нетривиальных решений.
Найдем T2(t),..., ТЛ (/), ..., соответствующие найден-
ным значениям ji. Подставляя в равенство (6) вместо р число
k* Л8
РЛ = —, приведем это равенство к виду:
Г;(О + а’^-Т»(0 = О,
Т/л	ak л t	1 п •	ak л t	л pj
Л(0 = Ak cos	—--h Bk sin	—j— ,,	где Ал	и Bk — две
произвольные постоянные.
Подставляя найденные Хк(х) и Tk(t) в равенство (4). получим
всевозможные нетривиальные решения уравнения (1), представи-
мые в виде произведения функций одного переменного и удов-
летворяющие данным граничным условиям:
Ul (х, О = ХМ Tdt) = sin р (At cos -р- -1.. в, sin ;
и, (х, t) = X, (х) Т2 (0 = sin ~ р2 cos Ар. + В2 sin Ар j;
и„ (х, t) = Xk (х) Т„ (/) = sin Ар (Л, cos Ар + В„ sin -Ар);
Теперь перейдем ко второму этапу решения задачи. Возьмем
сумму всех uk(x, t) (k = 1,2, 3 ...). При любых значениях коэф-
фициентов Д, А2......В{ В2,... сумма этих функций удовле-
творяет как данному уравнению, так и граничным условиям*.
♦При условии, что ряд сходится и что его можно дважды почленно диф-
ференцировать (как по переменной х, так и по переменной /).
222
Часть III
Остается подобрать эти коэффициенты так, чтобы сумма удов-
летворяла также и начальным условиям.
Итак, пусть
Vi knx
и (х, t) = 2. sin —f-
k ™ i
(я	kant . o . kant \
Ak cos —-----h Bk sin —j— ;
«	[	> к	I I
(8>
подставим сюда t = 0. Тогда
и (x, 0) = Ak sin .
k— i
С другой стороны, согласно первому из начальных условий,
ц(х,0) = <?(х).
Поэтому для всех х из (0; /) должно выполняться равенство
<р(х)- ^4sin-^.
*=1
Пусть <р(л)— кусочно-монотонная ограниченная функция;
тогда это равенство будет выполняться, если в качестве Ak при-
нять коэффициенты Фурье (при разложении <р(х) в ряд Фурье по
синусам):
2 г	k я к
Л Л = — \ <Р (*) sin ~Т~ dx.	(9)
Аналогично найдутся и Bk: продифференцируем почленно
равенство (8) по t (при этом допускается, что такое дифферен-
цирование ряда возможно):
,	Т’ч I Л kon . kant . D ka-K kant\ . k*x
u, (x, t) = £ (- Л — Sln + B“ ~T cos ~) Sln ~T
k — 1
и подставим сюда t — 0. Тогда
CO
'/	Vo kan . kitx
ut (x, 0) = ^Bk -j— sin -j— .
Л-1
С Другой стороны, согласно второму начальному условию,
и / (х, 0) = ф (х).
^alaHausA
знание без границ Ч
Глава 2, § 1
223
Поэтому
00
,. ч V d ban . knx
Ф(*) = 2j В„ -j- sin -у— .
A-l
Мы получили разложение ф(х) в ряд Фурье по синусам;
следовательно, коэффициенты этого ряда равны коэффициентам
Фурье:
i
D kait 2	. knx ,
— = у J Ф (*) sin — dx,
О
откуда
i
Bi'=-^r^(x>sin^rt,x-	(10)
о
Итак, коэффициенты Ак и Вк подобраны с таким расчетом, что-
бы сумма (8) удовлетворяла заданным начальным условиям. Под-
ставляя ЛЛ и Вк (из равенств (9) и (10)) в формулу (8), получим
искомое решение дифференциального уравнения, удовлетворяю-
щее заданным начальным и граничным условиям.
Возникает вопрос: не существует ли другого решения этой
задачи? Однозначно ли определяется закон колебания струны
заданием дифференциального уравнения и начальных и гранич-
ных условий? Положительный ответ на это будет дан в § 3, где
доказывается единственность найденного решения.
Принимая пока без доказательства, что других решений за-
дача не имеет, исследуем полученное решение.
Формула (8) дает нам решение, записанное в форме беско-
нечного ряда. Его первый член
Щ(х, t) = ^Av cos	Sin	(8X)
называется основным тоном колебания, определяемого форму-
лой (8).
Если бы все остальные члены ряда отсутствовали и коле-
бание происходило бы по закону (8j), то струна в любой мо-
мент времени имела бы форму синусоиды Ki sin где буквой
Ki обозначено выражение cos -|- Z^sin^-; величина коэф-
фициента Ki меняется со временем, и его максимальное значе-
224
Часть HI
ние равно V Л? + В? (на рис. 69 изображены крайние и несколь-
ко промежуточных положений струны, колеблющейся по закону
(в^.Число V A2i + В? называется амплитудой основного тона
колебания. Если струна колеблется по закону, заданному фор-
мулой (8J, то каждая точка струны колеблется с частотой —
= — колебаний в единицу времени; действительно, если за-
фиксировать х, то и(х, i) представляет собой периодическую
функцию от t с периодом — = —; следовательно, в единицу
~Т
времени каждая точка совершает -кг = -кт колебаний. Наряду с
а
частотой, нередко рассматривается так называемая круговая час-
тота u>lt которая равна произведению частоты на число 2я;
в данном случае со1 =	.
Рассмотрим второй член ряда (8) (второй член ряда (8) на-
зывается первым обертоном колебания):
/	(л %ап1 । п • 2ant \ . 2пх	/о ч
м2 (*» 0 = I Acos —---1- Ва sin—j—I si n—— .	(8a)
Если бы колебание происходило по закону (8а), то струна
в любой момент времени t имела бы форму синусоиды
7<а(/) sin где Ка(/) = А2 cos + Ва sin^^ (рис. 70). На участке
(0; /) помещались бы две полуволны этой синусоиды; точка
х — остающаяся в покое в процессе колебания, называется
^laiaHausi^i
знание без границ “ w
Глава 2, § 1 225
узлом-, максимальное значение коэффициента Л8(/) равно УА*+В£:
это — амплитуда первого обертона. Частота колебания первого
обертона в каждой точке равна /я =-|р круговая частота <оа =
“ I *
Третий член ряда (8)
/	(л Зап/ . D . Зап/ \ . Зпх	.
и3(х, t) = (^8COS-J--h Basin—y-jsin——	(88)
называется вторым обертоном. и
Амплитуда второго обертона
равна ]/~	4- В|, частота
, За
/з = 22~, круговая частота
Зпа	- „	__
(,,з = “ I струна в любой мо- _ х------------------*
мент принимает форму синусо- ° э у '
иды, полуволны которой имеют
длину узлов уже два,
они помещаются в точках
х-уидг=-у- (рис. 71).	Рис' 71
Вообще Л-ый член ряда (8)
а (л । п • kant\ . knx	,Q .
(х, t) = (Aftcos —-1- Bftsin -y- j sin -у—	(8Л)
называется k— 1-ым обертоном; амплитуда k — 1-го обертона рав-
на J/AJ . частота fk —	, круговая частота <«Л => у^-.
Формула (8) дает не только закон колебания струны — она
вместе с тем позволяет разложить сложное колебание на ряд
простейших — синусоидальных колебаний (они называются сто-
ячими волнами). В синусоидальном колебании амплитуда характе-
ризует силу, громкость звука, а частота колебания—высоту
звука. Если амплитуды стоячих волн, т. е. числа У A^-j- В[,
убывают с ростом номера k, то основной тон звучит громче всех
обертонов и ухо легко улавливает его и выделяет среди осталь-
ных звуков. Обертоны в этом случае будут звучать значительно
слабее; они придают колорит, «окраску» звуку, издаваемому
струной.
Пример. Найти закон свободного колебания струны длиной
1 м, закрепленной в концах, если известно, что ее натяжение
8 Ю. с. Очан
226
Часть 1П
Т и линейная плотность Г таковы, что а = 1/	= 100 — . В
Г Г	сек
начальный момент струна оттянута в середине на высоту 0,01 м,
а затем отпущена без начальной скорости.
В данном случае дифференциальное уравнение колебания
струны имеет вид:
д/« ~ 1и дх* •
Граничные условия (если струну расположить на оси абс-
цисс, между точками х = 0 и х~. 1) запишутся следующим об-
разом:
ц(0, 0 = 0, ц(1, /) = 0,
и
о	0,5
Рис. 72
а начальные условия:
при 0 < х <_ 0,5,
u(xt t) |/_.о =
—Л 4-0,02 при0,5<л<1,
Ои
(9)
0 |/-о= °-
Первое из этих начальных условий мы получим, если запишем
уравнение ломаной (см. рис. 72), вдоль которой расположилась стру-
на в начальный момент; второе начальное условие означает, что
начальная скорость во всех точках равна нулю.
В соответствии с намеченной схемой ищем сначала решения
в виде
ц(х, о = ад-ло.
удовлетворяющие данным граничным условиям. Это приводит
к уравнениям:*
Х"4-ИХ = О,	(10)
• Для сокращения записи мы опускаем обозначения независимых перемен**
ных у функций Х(х), Т(0- Штрихи около функции обозначают дифференци-
рование по той переменной, от которой эта функция зависит (например,
X" означает вторую производную от Х(х) по х).
^alaUaus^it.
знание без границ * ш
Глава X, $ I	227
Т" + 10*р.Т = О,	(11)
и граничным условиям Х(0) = 0; Х(1) = 0.
Решая уравнение (10) при заданных граничных условиях,
получим:
Н* =	, Хл(х) = sin kк х (k = 1, 2,...).
Подставляя найденные в равенство (11) и решая полу-
ченные уравнения, найдем
Тк — Akcos ЮОЛк/ + BAsin 100 Лк/.
Следовательно,
ик(х, /) = (ДЛсоз 100 Лк/ Bftsin 100 Лк/) sin Лкх.
Суммируя все uk(x, /), получим решение нашей задачи в виде
суммы ряда:
и(х, t) = L(H*cos 100 Лк/ 4- Bftsin 100 Лк/) sin Лкх. (12)
h
Подставим / — 0 и учтем первое начальное условие:
<р(л) = S Ак sin Лкх.
А
Здесь через <р(х) обозначена функция (9). Разлагая ее в ряд
Фурье по синусам, получим
1	0.5
2	С	х
ЛЛ = р	] <р(х) sin Лкх dx — 2 1	т-д sin kivcdx 4-
о	о
1
+ 2 J 4- 0,02 ) sin kvxdx = sin ~ .
0.5 '
В частности,
л 0,08 я л А 0,08 л п я 0,08
, , А2 — 0, А$ — —9^'а •	— 0, Дв 25я# ’ "
Чтобы найти Вд, продифференцируем (12) по /:
(х, /) = S (—Л** ЮОЛкsin 100 Лк/ 4- Вл- ЮОЛкcos ЮОЛк/)sin Лкх
А
к*
228
Часть ill
Подставляя сюда t — 0 и учитывая второе начальное усло-
вие, получим
О ~ У Bk- lOOfor-sin kn:x.
k
Числа £?л«100#7г являются коэффициентами Фурье функции,
тождественно равной нулю:
1
Bk- 100А?к -р J0-sin knxdx —О,
о
откуда следует, что все Bk равны нулю.
Итак, окончательно, искомым решением является сумма
следующего ряда:
,	..	0,08	.	0,08	п .
и (х, t) — —cos WOizt • sin кх-----cos ЗООк/ • sin Зкл +
cos 500я/ • sin 5тгх —...
25л’
Функция (х, t) = — ’0—cos 100к/ sin пх является основным тоном
колебания; это — колебание с частотой /\ —	• — 50 и с амп-
литудой —0,008 м. Первым обертоном будет функция
^з(х> 0	“^7l'«“cos ЗООтт/sin Зкх*. имеющая в девять раз меньшую
амплитуду и втрое большую частоту колебаний. Еще меньшую
амплитуду и еще большую частоту имеет второй обертон и т. д.
Если приближенно считать, что закон колебания струны
дается основным тоном, то
и (х, /) ~ cos ЮОк/sin кх.
§ 2, Интегралы, зависящие от параметра, и их
приложения
Настоящий параграф имеет вспомогательное значение: ре-
зультаты этого параграфа будут использованы в § 3 при дока-
зательстве единственности решения задачи о колебании струны,
а также в других местах книги (в частности, в главе 3).
Пусть функция двух переменных f (х, I) определена и не-
прерывна в некотором прямоугольнике а<х<£; а</<£
(рис. 73). Интеграл от этой функции по переменной х (при фик-
• Функция ut(x, t) тождественно равна нулю, и поэтому мы ее не
принимаем во внимание.
^lakMauswk
знание без границ ч *
229
Глава 2, § 2
сированном t) в границах от а до b зависит, вообще говоря, от /;
обозначим эту функцию от t через <р(0:
ь
?(0 = J f(x> 0 Же.	(1)
Интеграл, стоящий в правой ча-
сти этого равенства, называется ин-
тегралом, зависящим от парамет-
ра t. Естественно поставить такой
вопрос: при каких условиях, нало-
женных на под интегральную фун-
кцию f(x, t), функция <р(0 будет
непрерывной, дифференцируемой и
т. д.? Имеет место следующая
теорема:
Теорема 1. Если функция
f(x, t) непрерывна и ограничена
вместе со своей производной по t
и имеет ограниченную вторую производную по t в прямоугольни-
ке а< х <Ь, а </ <0, то для всех t из интервала (а, й) интег-
рал (/) представляет собой дифференцируемую функцию, причем
ь
= t)dx.	(2)
а
Здесь предполагается, что а и b — конечные числа.
Мы не будем доказывать эту теорему, так как она вытекает,
как частный случай, из следующей, более общей теоремы.
Теорема 2. Если функция f(x, t) непрерывна и ограничена
вместе со своей первой производной по t и имеет ограниченную
вторую производную по t в прямоугольнике а < х < b, а < t < р,
и если функция Ф(х) непрерывна и абсолютно интегрируема*
на (а’, Ь), то интеграл
ь
?(0 = J t)<b(x)dx	(3)
а
b
* Функция Ф (х) называется абсолютно интегрируемой, если J | Ф (х) | dx
а
существует. Если а и b — конечные числа, то абсолютно интегрируемой
будет всякая непрерывная ограниченная функция от х; если же а = —оо
ь
или Ь = -|-со, то j |Ф (х)| dx является уже несобственным интегралом,
а
который существует далеко не для всякой непрерывной функции Ф (х).
230
часть in
является дифференцируемой функцией от t, причем
ъ
<?'(*) = J ft (х> t)®(x)dx.
а
(4)
Здесь а — конечное число или — <х>\Ь — конечное число или
4* ОО .
ь
Замечание. Существование интеграла J f (х, t) Ф (х) dx
а
вытекает из того, что f(x, /) —ограничена и непрерывна, а
Ф(х) — абсолютно интегрируема; действительно, если |/(х, 0 |
всюду на (а; Ь), то \f(x, 0Ф(х)|<К-|Ф(х)|; так как /С-|Ф(х)|
интегрируема на (а; о), то и функция f(x, /)Ф (лг) | (а следо-
вательно, и /(х, 0Ф(х)) тоже интегрируема на (а; Ь).
Аналогично проверяется и существование интеграла
р;(^. t)^(x)dx.
а
Доказательство. Для того чтобы доказать дифферен-
цируемость функции 9(0 и равенство (4), достаточно доказать, что
ь
lim Т(' +	= f f (х, t) Ф(х)dx,
Л-0 Л	J
а
т. е. разность
ь
=	+	f f (Xt
h	j
a
стремится к нулю при Л->0. Оценим эту разность, учитывая,
ъ	ь
что <p(t) == р(х, t)®(x)dx, 9(t + А) = р(x^t + Л)Ф(x)dx:
а	а
|₽1 =
у(/4-Л)—9(f)
h
ъ
— J ft (х, t)®(x)dx
а
NataHauSfini
знаниебезграниц
Глава 2, § 2	231
ь	ъ
p*<+20AW-MM)»wd,r f(x< ^(х}Лх
J	л	J
а	а
b
У ф (Х)	_ ft (X, t) ] dx |.
a
Применим теперь к разности f(x, t + Л) — f (x, f) теорему
Лагранжа о конечных приращениях:
ь
1*1 = | j ф W [/;(«. т) -(х, 0] dx |.
а
Здесь т заключено между t и t + h. Применим снова теорему
Лагранжа (на этот раз к разности, стоящей в квадратных
скобках)
ь
l*l = | j® 5)(t-0dx |.
а
Здесь 6 заключено между t и т. Оценим теперь получив-
шийся интеграл, учитывая, что, по условию, f(t (х, t) ограничена
(например, | ftt (х> I) | <М) и что |т — /| < |А|:
ь
|/?| = |	5)(т — tjdx |<
а
Ъ	Ъ
< j |ф(х)|	-=Л-|Л|- j|O(x)|dx.
а	а
Последнее, выражение стремится к 0 при Л-*0; следова-
тельно, и R 0 при h 0, т. е.
ь
Нт .	= f f (x у ф(x)dx.
h-o	h	J '	'	'
a
Таким образом, функция ?(/) имеет производную, и эта
ь
производная равна С f't(x, t)Q(x)dx, что и требовалось доказать.
Из этой теоремы сразу вытекает теорема 1. Действительно,
232
Часть ///
если а и Ь —конечные числа, то функция Ф(х) = 1 абсолютно
интегрируема на (а; Ь). Подставляя в равенства (3) и (4) вместо
Ф (х) единицу, получим утверждение, содержащееся в теореме 1.
В качестве одного из приложений доказанных теорем вы-
числим два несобственных интеграла. Эти интегралы не могут
быть вычислены непосредственно (неопределенные интегралы не
могут быть выражены через элементарные функции).
«о
1. Вычислим интеграл | е~х* dx.
По определению несобствен-
ного интеграла,
с
е~х'dx = lim |
С-*оо Д
Обозначим
Цс)=\ e~x'dx.
Рассмотрим теперь вспомогательную функцию от двух пе-
ременных	и подсчитаем двойной интеграл от этой функ-
ции по областям о(, оа, о3, где а3 — четверть круга (с центром
в начале координат и радиусом с), расположенная в 1-ом квад-
ранте, Oj — четверть такого же круга, но радиусом с У 2 , а а2 —
квадрат, ограниченный прямыми х = 0, х — с, у = 0, у~с.
Так как область а3 содержится в оа, а аа в Oj (рис. 74) и так
как е > 0, то имеют место следующие неравенства:
И < j j e-^da < Д e~^do.	(5)
°» °« °1
Крайние интегралы могут быть вычислены с помощью по-
лярных координат:
2 с/2
УУе-‘,-‘',Л>= j f е~'“rdrdtf =(I — ё~и‘).
а,	0	0
ftalaftaustik
233
Глава 2, § 2
Что же касается интеграла по области а8, то он легко
может быть выражен через / (с):
J ё~х*~у*da = J J е~х* е~у*dxdy = f е~у* [ J ё~х* dx] dy =
og	0 0	о о
= J ё~у' 1 (с) dy — 1 (с) j е~у' dy = I (с)1 (с) = [/ (с)]1.
Подставляя найденные выражения для двойных интегра-
лов в неравенство (5), получим:
откуда
Крайние члены этих неравенств стремятся к одному и то-
У п ~
му же пределу — к числу . Следовательно, к тому же пре-
делу стремится и средний член:
lim / (с) = —	,
т. е.
lim f е~х* dx = —%— .
с-»оо V
Таким образом,
( e~x'dx =	(6)
V	*
о
Формула (6) может быть обобщена. Пусть а > 0. Тогда для вы-
•В
числения интеграла е~ах* dx сделаем в нем замену переменной
v р а = г:
234
Часть Ш
Итак,
со
(ба)
Интегралы (6) и (6а) широко применяются в теории вероят-
ностей; поэтому часто их называют «интегралами вероятностей».
С интегралами вероятностей тесно связана некоторая функ-
ция Erfx, которую называют «функцией ошибок»*. Она задается
следующим равенством:
X
Erf х = -Д=- С e-“dt.
V « J
о
Легко видеть, что эта функция определена для всех значе-
ний х, монотонно возрастает (ее производная по х равна
2	-X» ох
е > 0), непрерывна и принимает всевозможные значения
от —1 до 1. При этом Erf0=0, lim Erf х = — 1, lim Erfx = 1.
—©о	x-*-|~co
График этой функции приведен на рис. 75.
00
2. Вычислим интеграл [ е~ах* cosp xdx, где а>0. Если
о
в предыдущем примере можно было обойтись без теорем об
интегралах, зависящих от параметра, то здесь эти теоремы
будут существенно использованы.
• Обозначение функции Erf происходит от английских слов error function
(функция ошибок). Эта функция широко применяется в теории вероятностей;
она дает интегральный закон распределения случайных ошибок измерения.
^alattausi
знание без границ
Глава 2, § 2	235
Будем рассматривать наш интеграл, как функцию от р
(считая а фиксированным, положительным числом):
?(₽) =
со
J e-ax*cospxdx.
о
Под интегралом стоит произведение двух функций: cospx—
функция от двух переменных р и х и е~ах* — функция от х,
абсолютно интегрируемая на участке (0; Ч-оо). Однако непосред-
ственно к этому интегралу применить теорему 2 нельзя, так как
вторая производная по р от cospx (она равна —j^cospx) неогра-
ничена на участке (0; Чг«>). Поэтому разобьем данный интеграл
на сумму двух интегралов, а затем преобразуем второй из этих
интегралов:
1	4-СО
9 (Р) = J е-™' cos рл dx + J е~ах* cos рх dx =
о	1
= fe-“-cos₽xdx+
О	1
К первому интегралу непосредственно применима теорема
2, так как -д-s-cospx = — x’cospx ограничена на участке 0
< 1 (при любых Р). Ко второму интегралу эта теорема также
применима:	функция х2е~ах* абсолютно интегрируема на
участке (1; +<») (в чем легко убедиться, дважды проинтегрировав
СО
по частям интеграл | x2e-ox,dx; он сводится к интегралу
00
j е~ах* dx, сходимость которого доказана). Второй же сомножи-
।
тель под знаком интеграла — функция — непрерывен всюду
на (1; Ч~ °°) и имеет ограниченную вторую производную по р.
Итак,
1	со
?' (₽) = Г (- X sin ₽х) dx + Г х‘е-1Х‘ (-	dx =
О	I
х sin рх dx.
о
236
Часть 111
К последнему интегралу применим интегрирование по частям,
ОО
приняв и = sin px, dv = — J e~ax*xdx. Тогда,
о
<?' (?) = ( —е-0*’ х sin рх dx =
со со
е~ах*
—— Pcos рх dx =
со
—J е~ах*cos $xdx = —? №)•
о
p—ax1	(
~ sinpx—x— — I
r	2a	J
0	0
Решая полученное дифференциальное уравнение
<р' (Р) = — -L- <р(р), найдем ф(Р):
V—4-*»
Л—ь,<и--4- + 1"С:
3*
<р(р) = Се 4“ .
Постоянная С не зависит от Р; мы ее найдем, положив р = 0:
<р(0) = С.е°=С.
С другой стороны,
<р (0) =« f е “ * • cos 0 • dx = f е ах* dx — — 1/^—
J	J	2га
0	О
(см. формулу (6а)).
Следовательно, С =
?(₽) =
и
₽•
^alaHausA
знаниебезграниц Ч4*
Глава 2, § S 237
Итак,
со	___
J cos ftxdx =	е 4и
о
(7)
где а > 0, р — любое число.
$ 3. Доказательство единственности решения
задачи о колебании струны
Теорема. Если уравнение
д/S С ^х8 “Ь f С*» О	(О
имеет решение, удовлетворяющее начальным условиям:
и (х, 0) = <р (х); и' (х, 0) = ф (х),	(2)
и граничным условиям:
и (0, 0 ен 0; и (I, 0 0,	(3)
то такое решение будет только одно.
Замечание. Мы проведем доказательство только для того
случая, когда решение и (х, t) имеет ограниченные частные про-
изводные до третьего порядка включительно на участке 0<х</,
0</</о (/0— какой-либо фиксированный момент времени).
Точнее говоря, мы докажем, что среди функций и (х, 0, имеющих
ограниченные производные до третьего порядка включительно,
не найдется двух различных, которые одновременно удовлетво-
ряют уравнению (1) и условиям (2), (3). Следует заметить, что
теорема единственности имеет место и для более широкого
класса функций (даже для таких, для которых и'х(х, t) не су-
ществует в отдельных точках), однако доказательства для более
общего случая мы проводить не будем.
Доказательство. Допустим, что наша задача имеет
два решения: щ (х, t) и u2(xt t)\ докажем, что они тождествен-
но равны друг другу.
Рассмотрим разность и(х, t) = u1(x, t)— u2(x,ty, так как щ
и и9 удовлетворяют уравнению (1), то справедливы тождества:
d’u, (х, 0 _ о дЧ (%, 0 . .. Л.
dt2	~ дх2	"И
= а2 -^-а- ° + f(x, t).
ot2	дх2 • ' ’ ’
г
238 Часть 111
Почленно вычитая их друг из друга, получим:
Qft 1^1	0	^2 (^> 0J = дх*~
или
д'и(х, t) = 2 д*и(х, t)	z4v
dt* ~а дх* •	{ '
Итак, и (х, t) удовлетворяет уравнению u(t = а2ы'х; легко
проверить также, что и (х, t) удовлетворяет начальным условиям:
и(х, 0)==0, ut(x, 0) =0,	(5)
и граничным условиям:
и (0, 0=0, и (I, t) = 0.	(3)
Докажем, что и (х, t) = 0.
Умножим обе части тождества (4) нап^(х, 0 и затем про-
интегрируем их по х в границах от 0 до /:
я г	9 я •
и... -U. = Сги •UA
tt t	хх t’
I	I
J uttu'( dx == a2 J uxxu'tdx.	(6)
о	о
Исследуем каждый из этих интегралов в отдельности:
i	i	i
bo	о	'
Здесь мы использовали первую теорему о дифференцировании
интеграла по параметру; в данном случае она применима, так
как вторая производная по t от подинтегральной функции
(uj)8 существует и ограничена (это следует из существования и
ограниченности всех частных производных до третьего порядка
включительно от функции и(х, /); см. замечание перед доказа-
тельством теоремы на стр. 237);
2) к интегралу, стоящему в правой части равенства (6), при-
меним интегрирование по частям:
I	I	Х=1 I
f uxxu'idx = J u'td(u'x) = ut(x,t) u'x(x, t) l-^uxu’xdx =
0	0	x=0 0
/
= «; ('. 0 < (I. 0 - u, (0, 0 < (0, t) —L C.2. (u^dx. (8)
*17	*
0
^atallaus^k
знание без границ \ *
Глава 2, § 3	239
Легко проверить, что оба слагаемые, стоящие перед ин-
тегралом, равны нулю. Действительно, так как, в силу гранич-
ных условий, п(0, /) == О при любом /, то и и, (0, /) = 0 при
любом t. Аналогично проверяется, что u't (I, /) == 0. К по-
следнему же интегралу J (и'х)2 dx применим теорему 1 из
предыдущего параграфа (она здесь применима, так как вторая
производная от (и'х)2 ограничена):
Итак, равенство (8) можно записать так:
i	i
f и „и, dx = —Г J (uj'dx J.	(9)
о	о	*
Учитывая теперь равенства (7) и (9), перепишем тождество
(6) следующим образом:
i
о
или.
Отсюда следует, что интеграл, стоящий в фигурных скобках,
не зависит от /; от х он тоже не зависит (х — переменная ин-
тегрирования в этом определенном интеграле). Следовательно,
i
J [(«;)•+ «)’] dx с.
о
(Ю)
Докажем, что эта константа С равна нулю. Для этого убе-
димся, что интеграл равен нулю при t = 0; а так как, по до-
казанному, этот интеграл не зависит от t, то он равен нулю тож-
дественно.
240
Часть ///
При t — 0 левая часть равенства (10) примет следующий вид:
i
f [ («; (х, О))2 + а\их (х, О))2 ] dx.	(11)
6
Выражение u't(x, 0) равно нулю при любом х в силу вто-
рого из начальных условий (5). Кроме того, в силу первого из
этих условий, и (х, 0) se 0; дифференцируя по х это тождество,
получим: их(х, 0) ~ 0.
Итак, подинтегральное выражение в (11) равно тождествен-
но нулю; следовательно, интеграл (11) равен нулю. Но в таком
случае, и интеграл (10) равен нулю при любом t:
i
С [(«у + а* («!/]<*-°-
о
Под знаком этого интеграла стоит неотрицательная непре-
рывная функция. Если определенный интеграл от такой функции
равен нулю, то сама подинтегральная функция должна тождест-
венно равняться нулю (доказательство этого утверждения см. в
сноске к стр. 155).
Таким образом,
(w;)2 + fl2(«;)2^o,
откуда
ut (х, /) = 0, их (х, t) = 0,
т. е. и(х, t) не зависит ни от х, ни от t:
и (х, /) = const.
Но при t = 0, и (х, 0) = 0.
Следовательно,
и (х, f) ~ 0.
Вспоминая теперь, что и(х, t) = ur(x, t) — u2(x, /), заклю-
чаем, что
W1(x, /) = м2(х, t).
Итак, любые два решения данного уравнения (1), удовлетво-
ряющие условиям (2) и (3), должны Сыть равны друг другу
(т. е. эта задача не может иметь двух различных решений).
Теорема единственности решения для задачи о колебании
струны доказана.
^ataHausilk
знание без арениц Ч*
Глава 2, § 4	241
£ 4. Общие замечания о методе Фурье
В § 1 уравнение свободных колебаний струны было решено
методом Фурье. Уже на этом примере ясна схема применения
этого метода.
В настоящем параграфе излагается в общем виде сущность
метода Фурье для линейных дифференциальных уравнений.
Дифференциальное уравнение называется линейным, если
его можно свести к такому уравнению, в левой части которого
стоит многочлен, линейный относительно неизвестной функции
и ее производных, а в правой части — выражение, не содержа-
щее ни неизвестной функции, ни ее производных.
Не вдаваясь в физический смысл неизвестной функции и (он
различен для различных конкретных задач) и независимых пе-
ременных (обозначим их х и у), мы можем записать линейное
уравнение второго порядка в общем виде следующим образом
(для случая, когда неизвестная функция зависит от двух пере-
менных):
+ 2fc% + си'т + du'x + еи'у +f“ = g-
Здесь a, b, с, d, е, f, g— заданные функции двух пере-
менных х и у, или, в частном случае, постоянные числа.
Если в линейном уравнении правая часть g тождественно
равна нулю, то уравнение называется однородным. Очевидно,
что, если функции ult и2..ип являются решениями линейного
однородного уравнения, то любая их линейная комбинация
7,^ -|- ос2^2 + ... + а-пип также является его решением.
Все уравнения, выведенные нами в первой главе, являются
линейными уравнениями второго порядка. Некоторые из них
(например, уравнения свободных колебаний струны или мембра-
ны) являются однородными, другие (например, уравнение вы-
нужденных колебаний)— неоднородными.
Метод Фурье для однородных уравнений. При изложении
сущности метода Фурье для однородного уравнения ограничимся
тем случаем, когда в уравнении отсутствует смешанная произ-
водная* и когда все коэффициенты уравнения постоянны. Тогда
уравнение запишется в виде:
аи'хх + cu"uv + du'x + euy+fu = 0,	(1)
* Метод Фурье (или «метод разделения переменных») применим не толь-
ко к уравнениям с постоянными коэффициентами, но и к некоторым (однако
далеко не к любым) линейным уравнениям с переменными коэффициентами.
Примеры применения метода Фурье к уравнениям с переменными коэффи-
циентами приведены ниже (см., например, решение задачи колебания круг-
лой мембраны, стационарной задачи теплопроводности для сферы и др.).
242
Часть III
где a, с, d, е, f — заданные числа. Для однозначного определе-
ния функции и(х, у) на нее должны быть наложены некоторые
дополнительные условия (граничные или начальные). Некоторые
из этих условий являются однородными (например, в рассмот-
ренной нами задаче о свободных колебаниях струны, однородны-
ми являлись граничные условия), другие — неоднородными (на-
пример, в указанной задаче неоднородными являлись начальные
условия).
На первом этапе ищем такие решения уравнения (1), кото-
рые представимы в виде произведения нескольких функций
одного переменного и удовлетворяют заданным однородным усло-
виям:
ц(х, y) = X(x)Y(y).	(2)
Подставляя произведение (2) в уравнение (1), получим
aX"Y + cXY" + dX'Y + eXY' + fXY = 0
(где X', X" означают производные по х, a Y', Y" — производ-
ные по у). Разделяя переменные, перепишем это равенство сле-
дующим образом:
aX" + dX'+fX — cY"—eY'
X	~ Y
Приравнивая оба эти отношения постоянной — л, получаем урав-
нения для определения X и Y:
aX" + dX' + fX + ХХ = 0;	(1а)
— cY” — еГ' + ХУ = 0.	(16)
Для того чтобы определить К, используем заданные одно-
родные условия; из однородных условий, наложенных на и (х, у),
вытекают некоторые однородные (как правило, граничные) усло-
вия на одну из новых искомых функций, например на Х(х).
Таким образом, для определения функции Х(х) мы приходим к
краевой задаче, аналогичной тем, которые рассматривались во
второй части книги; чаще всего (хотя и не всегда) это приводит
к краевой задаче Штурма-Лиувилля. Задаче Штурма-Лиувил-
ля отвечает счетное множество собственных чисел k2,..., Хл,...
и счетное множество функций Xt (х), Х2 (х).Xk (х),...; кроме
того, для каждого найдется два линейно независимых реше-
ния уравнения (16) или одно (если с — 0). Для определенности
будем считать, что каждому \k соответствует только одно Yk(y).
Тогда решениями исходного уравнения (1), представимыми в виде
4\alaHausnik
знание без границ Ч *
Г лава 2, § 4	 243
произведения двух функций одного переменного, будут всевоз-
можные функции вида:
uk(x,y) = Xk(x) Yk(y).	(3)
Все эти функции удовлетворяют заданному однородному
уравнению (1) и заданным однородным дополнительным условиям.
Перейдем теперь ко второму этапу решения задачи методом
Фурье: взяв линейную комбинацию* функций (3) с произволь-
ными коэффициентами сЛ:
и (х, y) = !Lck Xk (х) Yk (у),	(4)
k
подберем эти коэффициенты так, чтобы функция и (х, у) удовле-
творяла бы не только данному уравнению (1) и заданным одно-
родным условиям (это будет выполнено при любых коэффициен-
тах сА), но и заданным неоднородным условиям. Делается это
следующим образом: если, например, неоднородное условие сво-
дится к тому, что
и(х, г/) Ь=о = <?(*)	(5)
(где <р(х) — известная функция), то, подставляя в равенство (4)
у - 0, получим
<р (х) = S ck • Yk (0) • Xk (х).	(6)
k
Равенство (6) можно рассматривать как разложение функ-
ции <р(х) в ряд Фурье по ортогональной системе Xk(x). Следо-
вательно, коэффициенты ряда (6):
ck • ГЛ(Э),
можно вычислить по формулам для коэффициентов Фурье, откуда
найдутся все числа ck.
Подставив найденные ck в ряд (4), мы найдем искомое решение
нашей задачи: функция, представленная в виде ряда (4) с най-
денными коэффициентами, удовлетворяет как данному уравнению
(1), так и заданным дополнительным (однородным и неоднород-
ным) условиям.
Рассмотренная нами схема решения однородного уравнения
методом Фурье может несколько усложниться в различных слу-
чаях. Например, если искомая функция зависит не от двух, а
от трех или большего числа переменных, то эту функцию надо
* Под «линейной комбинацией» подразумевается не только линейная
комбинация конечного числа членов, но и бесконечный сходящийся ряд из
Функций вида (3) с произвольными постоянными коэффициентами.
244
Часть III
искать в форме произведения не двух, а большего числа функ-
ций одного переменного. Далее, коэффициенты уравнения (1) не
обязаны быть постоянными: они могут быть заданными непре-
рывными функциями от х и у. Наконец, неоднородные условия
могут оказаться более сложными, чем рассмотренные выше.
Однако все это лишь несколько усложнит выкладки, не изменив
сущности метода.
Впрочем, следует иметь в виду, что далеко не для всякого
линейного однородного уравнения может быть осуществлено
разделение переменных. Не приводя здесь условий применимости
метода Фурье, укажем только, что для весьма многих, практи-
чески важных случаев этот метод приводит к цели.
Метод Фурье для неоднородного уравнения. Пусть перед на-
ми стоит задача решения неоднородного линейного уравнения
а"« + си'ю +	+ си,+ fu=g (х, у).
(7)
где g (х, у) — заданная функция, отличная от тождественного ну-
ля; как и в случае однородного уравнения, будем считать, что
член, содержащий смешанную производную, отсутствует и все
коэффициенты а, с, d, е, f постоянны.
Пусть на искомую функцию наложены некоторые дополни-
тельные (однородные и неоднородные) условия.
Для того чтобы найти искомую функцию, поступаем следую-
щим образом: на первом этапе рассматриваем соответствующее
однородное уравнение.
аи'хХ + си'уу + du'x + еи'у + fu = О
и заданные однородные условия; действуя так же, как и ранее,
находим семейство собственных функций Хк(х), отвечающих,
соответствующей краевой задаче Штурма-Лиувилля. После
этого возвращаемся к нашему неоднородному уравнению (7); бу-
дем искать его решение в форме ряда, разложенного по собствен-
ным функциям:
и (х, у) ='S (у) Хк (X),	(8)
k
где (У) — пока не известные функции от у, их надо подобрать
с таким расчетом, чтобы функция, определяемая рядом (8), удов-
летворяла заданному неоднородному уравнению и заданным не-
однородным условиям (однородным же условиям ряд (8) удовлет-
воряет при любых (у)— это объясняется выбором функций Хк (х)).
Для того чтобы найти все $к(у), подставим ряд (8) в урав-
^alatldusA
знание без ераниц Ч
Глава 2, § 4	245
нение (7), предварительно разложив функцию g(x, у) в ряд Фурье
по ортогональной системе собственных функций {ХЛ(х)}:
g(x,r/) = Sa* Xk(x).
h
Коэффициенты аЛ, вообще говоря, зависят от у\ поэтому мы
обозначим их ik (у). После подстановки ряда (8) в уравнение по-
лучим следующее равенство;*
S[ с ₽!(»)+	?*(»)]X*W=Sa*(?)X*W.	0°)
k	k
где \k — собственные числа, отвечающие функциям Xk(x). Для
того чтобы равенство (10) было тождеством, достаточно, чтобы
коэффициенты при Xk(x) в правой части равенства равнялись
соответствующим коэффициентам в левой части:
с ₽*(*/) + е Ыу) — К h(y) = ak(y)-	(И)
Из полученной системы обыкновенных линейных дифференциаль-
ных уравнений можно найти все ^у(у). Для того чтобы найти
их однозначно, надо знать начальные условия для $k(y). Они
могут быть определены из граничных или начальных условий для
искомой функции и(х, у)\ например, если задано условие
u(x,y)\y=Q = <f>(x),
то из (8) получаем:
9 (х) = S (0) Ху(х),
k
• Действительно, подстановка ряда (8) в уравнение (7) приводит к
равенству:
Е [о • ₽*	(х) ч- с • ₽; (у) Хь (х) 4- d • ₽* (rt x't (X) + е • ₽; (у) Xt (х) +
+ /-₽»(!/)Х»(х)]=2ч(»)Х4(х).	(9)
k
Так как Ху (х) удовлетворяет уравнению (1а) (см. стр. 242) при К = \у, то
aXk (x)-f-d Xk(X) + f Xk(x) + \kXk(X) = Q,
аХу (x) + d Xk (x) 4- f Xk (x) = - Xy Xk (x).
Учитывая это, перепишем равенство (9) следующим образом:
2 [₽Л (У> • (- Ч Xk (х)) + с ₽” (у) Xk (х) + е ₽; (у) Xk (х)] =
=	(у) Xk (х),
k
откуда и вытекает равенство (10).
246
Часть III
откуда следует, что рЛ (0) равны коэффициентам ряда Фурье функ-
ции <р(х) по ортогональной системе {ХА(х)|. Аналогично— из дру-
гих условий на функцию и (х, у) — могут быть найдены, например,
₽л(0). Зная ₽А(0) и р* (0), можно однозначно определить (из
уравнений (11)) все функции $k(y).
Для того чтобы найти искомую функцию и(х,у), остается
подставить все найденные рЛ (у) в равенство (8).
§ 5. Решение уравнения колебания струны
при наличии внешних сил
(вынужденные колебания)
• Задача о вынужденных колебаниях струны сводится к на-
хождению того решения и (х, t) уравнения
u'tt = a2uxx + f(x,t)	(1)
(где / (х, t) 0), которое удовлетворяет заданным начальным
условиям
u(x, 0) = <p(x), uj(x, 0) = ф(х)	(2)
и граничным условиям
п(0, 0 = 0, u(l,i) = 0.	(3)
Здесь, в общем случае, неоднородными являются как урав-
нение (1), так и начальные условия (2) (если хотя бы одна из
функций <р (х) или ф (х) отлична от тождественного нуля), и лишь
граничные условия являются однородными.
Рассмотрим сначала соответствующее однородное уравнение
и'^—а2ихх и заданные граничные условия (3). Эта задача при-
водит к собственным функциям | sin } (см. § 1).
Вернемся теперь к нашему неоднородному уравнению. По-
ступая согласно общей теории (см. § 4), заменим функцию / (х, t)
ее разложением в ряд Фурье по собственным функциям соответ-
ствующей однородной задачи, т. е. в ряд по функциям	j:
оо
«« = С + S bt sin	(1 а)
Л=1
I
где = — J/(x, t) sin k*x dx. Очевидно, что bk являются функ-
^lataHausi^i
знание без границ Ч»
Глава 2, § 5	 247
циями от t\ поэтому, в дальнейшем, вместо убудем писать bk(t).
Будем искать решение уравнения (1а) в виде суммы тригоно-
метрического ряда по синусам (по переменной х):
не
w(x,0 = Sc*(0sin-^p-.	(4)
й=1
Допуская возможность почленного дифференцирования ряда,
получим:
06
«л (*. O = Wsin ^Г~'
С(х.о = - £ ck(t) -^-sin-^.
k=i
Подставляя это в уравнение (1а), получим тождество:
V1 "	• kltX	„V1	. knx , Vi. . knx
2j ck (0 sin ~T~ = - a Lck ~ir Sln ~T~ + 2j bk sin ~7~-
k	k	k
Это тождество будет наверняка выполнено, если для любо-
го k коэффициенты при sin в левой части равенства равны
соответствующим коэффициентам в правой части. Таким образом,
для определения ck(t) мы получаем следующие уравнения:
<(«) =—^^-с*(0 + М0.	(5)
где k = 1, 2, 3...
Каждое из этих уравнений является обыкновенным линей-
ным дифференциальным уравнением второго порядка; для того
чтобы эти уравнения однозначно определили функции ck (t), долж-
ны быть заданы, для любого номера k, числа сЛ(0) и сЛ(0) (т. е.
должны быть заданы начальные условия для Числа ck(0)
и c'k (0) легко найти из условий (2). Действительно, так как
«(^.o = S sin-^p->
k
ut (x, t) = ^ck (/) sin
k
248
Часть И!
то условия (2) равносильны следующим:
S^(0)sin-^- =<р(х),
k
£cft(0)sin-^L = <Hx).
k
(6)
Равенства (6) можно рассматривать, как разложения функций
<р(х) и <р(х) в ряд Фурье по синусам; поэтому числа сЛ(0) ис'Л(0)
являются соответствующими коэффициентами Фурье:
(0) = -7- J ? W sin dx’
о
I
СИ°)= J Ф (х)sin dx-
о
Это и будут начальные условия для функций ck(t)\ если функции
(/) удовлетворяют условиям (7), то для функции двух перемен-
ных и (х, t) — ck (t) sin выполняются заданные начальные
k
условия (2).
Найдя все ck(t) из уравнений (5) и начальных условий (7)
и затем подставив эти ck(t) в равенство (4), получим искомое
решение уравнения колебания струны. Это решение удовлетворяет
дифференциальному уравнению (1) и начальным условиям (2);
кроме того, так как каждая функция вида ck (f) sin ~ * -- обращается в
нуль в точках х = 0 и х = /, то и их сумма (т. е. функция и (х, /))
также обращается в нуль в этих точках. Следовательно, найден-
ное решение удовлетворяет и заданным граничным условиям. В
силу теоремы о единственности решения (см. § 3), можно утвер-
ждать, что никаких других решений, кроме найденного, эта
задача не имеет.
Пример. Найти закон колебания однородной струны длиной
I = 1 м, закрепленной на концах, если известно, что ее натяже-
ние Т и линейная плотность Г таковы, что а = 1/ 21 = 100—’
\ Г	сек,
В начальный момент струна оттянута в середине на h — 0,01 м
и затем отпущена без начальной скорости. На струну действует
сила, которая, в расчете на единицу массы струны, задается
^ialaHauA
знание без границ Ч *
Глава 2, § 5 249
следующей формулой: f(x, t) — psin sin <о/ (здесь р и ш —
заданные числа; для определенности примем р = 0,01 м!сек*).
Задача сводится к решению неоднородного уравнения
ut't = с?ихх + psin sinа>/
при неоднородных начальных условиях:
и (х, 0) =
2/1 Л / I
— при 0< х< -у,
2 Л-------при ~ < х < /,
I	л»
u't (х, 0) = 0,
(8)
(9)
и при граничных условиях:
u(O,t) = O; u(l,t) = O.
Согласно теории, ищем решение в виде суммы ряда по синусам
« (*. 0 = Yck sin	0°)
k
Представим, кроме того, функцию f(x, t) = psin sin о/ в
виде суммы ряда по синусам:
/(x,n = Sfc»(')s'n2rL-
/г
В данном случае при k = 1, b} (/) = рsin<«/, а при k 1,	(/) = 0.
Подставим теперь выражение (10) для и(х, /) в уравнение (8),
предварительно заменив в этом уравнении функцию psin sinwt
соответствующим тригонометрическим рядом:
S., ,,, . knx	2v k2n* . knx . V »	• knx
Ck (f)sin—— = — a^cM—Jjj-sin—j----------i-^jMOsin—
k	k	k
Приравняем коэффициенты при sin в левой и правой
частях равенства:
£>8
< (0 +	= ^(0-	(И)
250
Часть III
Для того чтобы найти начальные условия для функций сЛ(/),
разложим в ряд Фурье по синусам функции и (х, 0) и ut (х, 0)
(эти функции заданы формулами (9)):
о. . kn
viBnsin а • knx
ц (Х, 0) =2j	sin——т—
к
8h . nx 8h
о sin , —*
я1 /
. Зя x
no Sin ,
3я я1 I
8h .	5 я x
-j—г Sin---7—
» яя I
ut(x, 0) =	• sin
k
п, . kn
_	z_. oh sin -Q-
Поэтому ck (0) =------------£. (в частности,
ft1 Я1
c, (0) = - ct (0) = 0, c„ (0) = 8h
knx
I
c,(0) = -g-, c,(0> = 0,
25^f, c.(0) = 0,...); сЛ(0) = 0.
Решим уравнения (И) при этих начальных условиях. При
Л = 1 уравнение (11) запишется так:
с\ (0 2я
ci (0 = P sin
а начальные условия: q (0) =	, c\ (0) = 0. Искомое решение
имеет вид:
... 8h ant
^1(0 = -^-cos
ы I n	. ant
,	. S-»2 3---r- Sin--r-
I a1 it*	, \ I
a n I —is— — w1 I
или
P
a*n*
—я— — w
sin co/,
an
W8/i	ant	, I* p	ant	It p	ant
= -S— COS -7-H о » » Sin-7-COS-
к’	I	1 2a* n* I	2a n	I
(an \
при u> = —-— I.
При k=^ 1 уравнение (11) приводится к виду:
Ck (0 “1 т» ck (0 0,
Ч\а1аНаи$Ж
знание без ераниц * «Ь
Глава 2, § 5 251
8Л sin —
2	,
а начальные условия: ck (0) — —fea--, ;	(0) = 0. Искомое реше-
ние таково:
8ft sin ~
ck (0 =
cos
kant
г~
(в частности, при k четном ck (/) = 0).
Подставляя все найденные ck(t) (k ~ 1,2,3,...) в формулу
(10), найдем окончательное выражение для и(х, t) (при о> ™]:
u(x,t) = -^~cos
Sin
—»  --------sin со/
а ’я1	.
8A
7ГТ cos
51 я’
5a n t
~~T~
sm
8ft
3^C0S
Зап t . Зпх
-----Sin---;-
или, учитывая числовые значения: а — 10а м!сек, I м, h=-
= 0,01 м, р = 0,01 м!сек\
/ Л	о,01	. .	. г 0,08	.
и (х, t) =	,----=- sin и/ sin nx 4- —=— cos 100 nt —
'	'	104я’--to1	' I Я1
10<я(ю"я«-ш^) sin ЮОя/j sin ях — cos 300 nt sin3z% +
+ cos 500 nt sin 5 nx — ...
1 5a я1
Итак, колебание струны естественным образом разлагается
на два составляющих колебания: первый из выписанных членов
ряда "Гоч _'а>а sin s,n дает колебание с периодом — (и ча-
стотой а сумма всех остальных членов ряда — колебание с
2/1	„ а гл колеб г-, „	2/	1
периодом — = -Бк и частотой ттг = 50------. Период — = тл и
г	а 50	2/	сек	а 50
частота ~ 50 К^~—это собственные период и частота дан-
„	2я	w
нои струны, а период — и частота — это период и частота
252
Часть HI
внешней силы. Если эти периоды соизмеримы, то сложение коле-
баний (собственного и вынужденного) даст колебание большего
периода (период суммарного колебания равен общему наимень-
шему кратному этих периодов). Если же периоды несоизмеримы,
то суммарное колебание будет уже непериодическим (хотя и
близким к периодическому: это будет так называемое почти
периодическое колебание).
Мы рассмотрели тот случай, когда <о	т. е. когда
2/
период собственных колебаний струны —~ не совпадает с перио-
„	2п
дом внешней силы ——, Если же эти периоды совпадают, т. е.
если <о = —j-, то закон колебания будет иметь вид:
8h	ant
COS---7—
тг1	I
8h Зап t . 3nx
ne 9 COS , SIH 7
З’те1 I	I
P p . ant	It p	ant
2a2 л2 I	2a n	I
8h 5a n t .	5 n x
52 л"	I	I
ПХ
sin—----
или, учитывая числовые значения a, h, I, р:
и (х, t) =--— cos 100 nt sin nx + ( —cos 100 nt +
'	'	2-104тг	I «2
4—о » sin 100 к Л sin nx 0— cos 300 nt sin 3 nx +
1 2 • 10е я*	]	3ini	1
, 0.08	. . c
4- - т-А-у cos 500 nt sin 5 nx — ...
Здесь снова получена сумма двух движений: первый член ряда
t	21	1
---»——cos 100 nt sin юг дает колебание с периодом 	~-пп
2 • 104 п	*	г	а 5о
у а	с г\ кол еб
и частотой -рр = 50-----, но со все более и более увеличиваю-
щейся амплитудой (благодаря сомножителю /); сумма всех ос-
тальных членов ряда дает периодическое колебание с тем же
21	1
периодом — =
В данном случае говорят, что внешняя возмущающая сила
попадает в резонанс с собственными колебаниями струны, что
приводит к быстрому усилению размаха колебаний. Конечно,
^lalalfaus^i
знание без границ Ч *
Глава 2, §6 253
при этом надо иметь в виду, что выведенный закон колебания
струны сохраняется в силе только до тех пор, пока амплитуда
достаточно мала; как только амплитуда, в результате резонанса,
станет достаточно большой, закон колебания уже не будет удов-
летворять линейному уравнению (1), которое было выведено
только для того случая, когда отклонения точек струны от по-
ложения равновесия очень малы. Здесь уже вступают в действие
другие закономерности, описываемые другими, более сложными,
нелинейными, дифференциальными уравнениями.
$ 6. Решение задана о колебании конечной
струны в случае неоднородных граничных
условий
До сих пор мы решали задачу о колебании конечной струны
в предположении, что концы струны закреплены; это приводило
нас к однородным граничным условиям: u(O;f) = O, u(Z,/) = 0.
На концы струны могут быть наложены условия и другого
вида; так, например, можно потребовать, чтобы струна в одном
или обоих концах имела горизонтальную касательную; это при-
водит снова к однородным граничным условиям: п(0; Z) = О,
их Z) = 0 (если струна закреплена в левом конце, а в правом
имеет горизонтальную касательную); и'х (0; t) — 0, и (1\ Z) = 0
(аналогично); и'х (0; /) = 0, и'х (I; t) — 0 (если концы струны не
закреплены, но в обоих концах струна имеет горизонтальную
касательную).
Решение задачи о колебании струны во всех этих случаях почти
ничем не отличается от случая закрепленной струны, рассмотрен-
ного нами в § 1 и 5.
Однако, наряду с однородными граничными условиями, на
практике могут возникнуть и задачи с неоднородными условиями
на концах струны. Так, например, если один из концов натяну-
той струны закреплен, но не в точке с ординатой 0, а в точке
с ординатой и0 0; или если концы натянутой струны движутся
в плоскости Охи в направлении оси Ои по тому или иному задан-
ному закону; или если угловой коэффициент на каком-либо конце
струны изменяется по заданному закону и т. д. Во всех этих
случаях имеют место неоднородные граничные условия. В каж-
дом из этих случаев можно с помощью замены переменной све-
сти задачу с неоднородными граничными условиями к задаче с
однородными граничными условиями.
Не рассматривая этой задачи во всей общности, ограничим-
ся тем случаем, когда граничные условия в обоих концах на-
254
Часть Ill
кладываются на само отклонение и (х, t) (а не на угловой коэффи-
циент); пусть
—аХх = /(х>0	(О
— заданное уравнение колебания струны,
и (х; 0) = <р (х); и\ (х; 0) = ф (х)	(2)
— начальные условия, а
Ы(О;0-а(0; «(/, 0 = Р(/)	(3)
— граничные условия (они неоднородны, т. е. хотя бы одна из
функций а (0 или р (0 отлична от тождественного нуля).
Для того чтобы свести эту задачу к задаче с однородными
краевыми условиями, сделаем следующую замену переменной:
v (х, t) = u (х, t) — U (х, t),	(4)
где U (х, 0 — какая угодно, но по возможности более простая
функция двух переменных, удовлетворяющая условиям (3). Проще
всего в качестве такой функции взять функцию U (х, t), линейную
относительно х:*
и(х, t) = а(0 + Р(0~а*-)-х.	(5)
Если функция U (х, t) выбрана таким способом, то функция
о (х, t) — и (х, 0 — U (х, t) удовлетворяет нулевым граничным ус-
ловиям; действительно,
о(О,0 = u(O,t) — U (0,0 = а(0-«(0 = О;
v(1,0 =	- и=	₽(0 = 0.
• Если неоднородные краевые условия (3) были другого вида, то функ-
цию U (х, I), удовлетворяющую этим краевым условиям, надо выбирать
иным способом.
Так, например, если заданы условия иж(0, 0 = а (0, их ([,!) = Р(0, то
р (0 — а (0 х» „
в качестве U(x,t) можно взять U(x,t)=*a(t) х-р-]---- “jF* Тог-
да функция v (х, 0 = и (х, t) — U (х, 0 будет удовлетворять однородным
краевым условиям: vx (0, t) = 0, vx (I, t) s 0.
Если краевое условие на одном конце относится к отклонению:
н(О,0 = а(/), а на другом конце—к угловому коэффициенту касательной:
(/,/) = Р(0, то к аналогичному результату приведет замена переменной
р (0 х«
V (х, 0 = и (х, 0 — и (х, 0, где U (х ,0 = a (t) + —-'	•
^alaHausA
знание без границ Ч
Г лава 2, § б	255
Пусть искомая функция и(х, I) удовлетворяет уравнению (1)
и начальным условиям (2); тогда функция v(x,t) должна удов-
летворять следующему уравнению*:
v'tt —a* vxx = f (х, 0 — Uh (х, t),	(la)
и следующим начальным условиям:
v (х, 0) — и (х, 0) — U (х, 0) = <р (х) — a (0) —- —х,
(х, 0) - u'i (х, 0) - u't (х, 0) = ф (х) - «' (0) -	(0) X.	2а
Кроме того, функция v(x, i) удовлетворяет нулевым граничным
условиям v (0,0 = 0, о (/,0 = 0.
Для того чтобы найти функцию v(x, 0, удовлетворяющую
уравнению (1а), начальным условиям (2а) и нулевым граничным
условиям, достаточно применить метод Фурье, рассмотренный в
§ 1 (если правая часть уравнения (1а), т. е. f(x,t) — Utt(x,t),
равна нулю) или в § 5 (если правая часть уравнения (1а) отлич-
на от нуля).
Зная v(x,t), можно из формулы (4) найти и(х, 0. В силу
теоремы единственности решения (которая для случая неодно-
родных граничных условий также имеет место), заключаем, что
других решений наша задача не имеет.
Пример. Пусть однородная струна, заданная на отрезке
(0; 0, закреплена в левом конце, а правый конец колеблется
ио закону: и(/, 0 = msinwf. Найти закон движения струны, счи-
тая, что начальное отклонение и начальная скорость в каждой
внутренней точке струны равны нулю и что на внутренние точ-
ки струны не действует никакая внешняя возмущающая сила.
Дифференциальное уравнение, которому удовлетворяет от-
клонение струны и(х, 0, имеет вид:
Utt — а* ихх = 0,	(6)
где а* — заданное число, зависящее от линейной плотности Г и
(Т \
а* — — 1. Начальные условия:
и (х, 0) = 0; ut (х, 0) = 0 ;	(7)
граничные условия:
a(0,0 = 0, и(1,0 = msinw/.	(8)
Мы учли, что и = V 4- и, ихх = vxx + ихх , и„ = v„ + U'tt
PF
256 Часть 111
Согласно теории, сделаем замену переменной v(x, t) = и(х, t)—
— U(x,t), где U(х, I) —какая-либо функция, удовлетворяющая
условиям (8), например U(x,t)~ -^-/nsino)/. Тогда функция
v(x,t) = u(x,t)--j-tn sin vt	(9)
будет удовлетворять нулевым граничным условиям:
v(0,/)=0, и(/,/) = 0,	(8а)
уравнению
vtt — a*vxx = -^-т i»® sin w t	(6a)
и начальным условиям:
v(x, 0) = 0; v't(x, 0) = — ~~.	(7a)
Итак, для того чтобы найти функцию v(x,t), надо решить
неоднородное уравнение (6а) при неоднородных начальных
условиях (7а), но с однородными граничными условия-
ми (8а).
Решая эту задачу методом, рассмотренным в § 5, находим
v(x, t):
v(x, t) =
oo
2tn ш V,	(—D* [kan .kant .	.\ . knx
= —  > ,-------*-------- ------Sin-------<0 Sin CO t Sin-
n " /Л2а8л2	\\ /	I	I I
*-i * --T.--— '°2
\ »a	/
(при условии, что (о не равно k-~ ни при каком натураль-
ном k).
Учитывая теперь замену переменной (9), найдем окончатель-
но u(x,t):
оо ... 2пг ш V	(—0*	1 ban .kant tl(x,t)-	2j	/М a 2	\	~7~S,n	/	“ я *“*	fk2a2n2	\	\ I	I Л-1 * 	7Z— — Ш2 \ I2	/ 	^-/nsinw/.	.\ . knx -W Sin (Of ]sin	 / I
NataHauswk
знание без ераниц Ч »»
Глава 2, § 7
257
(1)
(2)
(3)
§ 7. Решение уравнения теплопроводности для
конечного стержня
Пусть на отрезке [0; /] оси Ох расположен весьма тонкий
однородный стержень, изолированный в тепловом отношении от
окружающей среды. Только на концах этого стержня поддержи-
вается некоторая определенная температура, постоянная или ме-
няющаяся с течением времени по какому-либо заданному закону.
Если начальное распределение температуры в стержне известно,
то для того, чтобы узнать закон распределения температуры и
в любой точке стержня х в любой момент времени t, надо най-
ти решение дифференциального уравнения
dt дх* и
при начальном условии
и (х, 0) = (х)
и при граничных условиях:
«(0, 0=а(0, и(1, 0 — р(О
(где a(t) — закон, по которому изменяется температура в левом
конце стержня, а Р(/)— в правом). В случае, если внутри стерж-
ня имеются источники тепла или поглотители тепла, причем функ-
ция A(x,t) дает плотность распределения тепловых источников,
то уравнение (1) заменится следующим:
ди а д*и . /	..	...
Тй---=	(4)
Для того, чтобы найти решение уравнения (1) или (4) при
начальных условиях (2) и граничных условиях (3), надо сделать
замену переменных с таким расчетом, чтобы новая неизвестная
функция удовлетворяла однородным граничным условиям*. Для
этого введем функцию v(x, t), связанную с искомой функцией
н(х, I) соотношением:
v (х, /) = и (х, t) — U (х, t),
где U(x,t)—какая угодно, но по возможности более простая
Функция, удовлетворяющая граничным условиям (3). Примем в
качестве U (х, t) функцию, линейную относительно х:
и (х. t) = а (/) 4- l^-^L х
* Подобная замена переменных применялась в предыдущем параграфе,
когда мы решали уравнение колебания струны с неоднородными граничными
условиями.
9 ю. С. Очан
258
Часть 111
Тогда функция v(xt t) удовлетворяет однородным граничным
условиям:
о(0, /) = О, ц(/,/) = 0,	(За)
начальному условию
ч(х, 0) = и (х, 0) - U (х, 0) = <р (х) - а (0) - 11 (П) ~ *(0) х (4a)
и дифференциальному уравнению
(la)
(или уравнению
^r-<‘l^-A(x.l)-U,(x,t).	(4а)
если исходным уравнением было уравнение (4)).
Для того чтобы решить уравнение (1а) или (4а) при одно-
родных граничных условиях, поступают так же, как и при ре-
шении уравнения колебания струны: если правая часть уравнения
равна нулю, то его решают методом разделения переменных,
как в § Г, если же правая часть отлична от нуля, то применяют
метод, рассмотренный в § 5.
Приведем пример на решение уравнения теплопроводности.
Пусть однородный стержень расположен на отрезке [0; /],
причем на концах стержня поддерживается постоянная темпера-
тура: в точке х — 0 — температура А, в точке х = /— температу-
ра В. Начальное распределение температуры в стержне задается
функцией <р(х). Найти закон распределения температуры u(x,t)
в любой момент времени, предполагая, что внутри стержня про-
исходит свободный теплообмен (т. е. отсутствуют источники и
поглотители тепла).
Уравнение, которому удовлетворяет искомая функция, таково:
начальное условие
и (х, 0) = р (х)
и граничные условия:
ц(0,/)=Л;	=
^lataHaus^i
знание без границ ч **
Глава 2, §7 259
Сделаем замену переменных:
V (х, t) == и (х, t) — [ А -ь	X J .
Функция v (х, t) удовлетворяет уравнению
до - d3v п	Z1XV
-ёГ~а ^=0'	(,б>
начальному условию
v (х, 0) — и (х, 0) — [ А -4- — ~Л. х J = <р (х) — £ Л 4- х j (26)
и однородным граничным условиям:
у(0,/)=0, v(l,t) = O.	(36)
Однородное уравнение (16) при однородных граничных ус-
ловиях (36) и неоднородных начальных (26) мы можем решить
дословно так же, как решали в свое время уравнение свободных
колебаний струны (см. § 1). Проделав все действия, предписыва-
емые методом Фурье, найдем функцию v(x,t) в виде суммы сле-
дующего ряда:
оо	Л*п’а* J
~ sin-4^,
где коэффициенты Ск вычисляются по формулам:
i
откуда
/
С, = 4 f f (*)sin - т- 'л + <—1 )*+1 BJ 	(6)
I J	I	kit	I
Учитывая теперь замену переменной (5), получим искомое
распределение температуры внутри стержня:
и (х, t) = v(х, i) -f- pl 4- xj =
co
» , В—A	. V r p . kitx
= л 4-----—x \ LiCke sin-r-,
где коэффициенты С* определяются по формулам (6).
9*
260
Часть 111
Исследуя полученное решение, заметим, что при t -> -|- оо
распределение температуры внутри стержня стремится к линей-
ному распределению
л I В—А
и = А 4 ——
Это — предельное распределение температуры (при I 4- °°)- Для
больших значений t температура внутри стержня в каждой точ-
д________________________________д
не х будет близка к числу А |----— х .
§ 8. Двойные ряды Фурье
Решая уравнение колебания струны, нам удалось представить
искомую функцию двух переменных u(x,t) в виде суммы неко-
торого ряда. Однако в более сложных задачах, когда искомая
функция зависит не от двух, а от большего числа перемен-
ных, не всегда удается представить эту функцию в виде суммы
обычного ряда; для ее аналитической записи часто приходится
прибегать к двойным и даже к тройным рядам.
Пусть дана таблица чисел, занумерованных двумя натураль-
ными индексами:
«н «it «13 . . . «ifc . . •
«21 «22 «23 • • • a2k • • •
ап ап а13 • • ' alk • • •
Возьмем члены, стоящие в какой-либо (i-той) строке этой
таблицы, и сложим их: «д-Ьо^-Н • - + а/л4-- • • ; если этот
ряд сходится, то мы обозначим его сумму через Ь,:
Л
(1)
Пусть ряд ^aik сходится для любой строки (т. е. для любого но-
мера I) и ряд из bt тоже сходится; тогда сумму этого последнего
ряда (S Ь^} называют суммой двойного ряда:
i
I k
(2)
а сам этот двойной ряд называют сходящимся.
^atatlauswk
знание без границ “ w
Глава 2, $ 8 261
Двойной ряд принято обозначать символом если этот
ряд сходится, то символу S ahk приписывают определенное число-
вое значение — сумму двойного ряда.
Для того чтобы все ряды (1) абсолютно сходились и чтобы
ряд также абсолютно сходился, достаточно, чтобы абсолют-
но сходился обычный ряд, который получится из данного двой-
ного, если все его члены выписать в виде простой последователь-
ности*. Превратить двойной ряд в обычный можно многими раз-
личными способами; чаще всего поступают следующим образом:
па первом месте в последовательности выписывают член ап; за-
тем два члена, у которых сумма индексов равна 3; потом три
члена, у которых сумма индексов равна 4, и т. д.:
~ «11 4' «12 4 «21 I «13 + а22 !' «31 4 «|4 } «23 4' «32 4
Л*
4 «4.4--..	(3)
Для удобства обычно объединяют вместе все те члены этого
ряда, у которых сумма индексов равна данному числу; тогда,
если обозначить
«1,л 4 «2,л—1 4 «З.л-2 4 • • • Г «л,! == сп ,
ТО
| сг |- . . . | сп -I . . .	(4)
Сумму Ci + . . . ч- сп называют п-ой частной суммой двойно-
го ряда (и обозначают S„). Если двойной ряд абсолютно схо-
дится, то его сумма S равна lim S„.
П-СО
Как сказано выше, абсолютная сходимость ряда (3) влечет
за собой абсолютную сходимость рядов (1) и (2) (а значит, и
данного двойного ряда). Однако нередко может случиться так,
что даже при условной сходимости рядов (1), (2) и (3) — сумма
ряда (3) совпадает с суммой двойного ряда.
Введем теперь понятие двойного ряда Фурье. Пусть функция
f(x,y) определена и непрерывна в прямоугольнике о:
будем считать, что на границах прямоугольника эта
Функция равна нулю. Зафиксируем какое-либо значение у, за-
* В этом случае говорят, что двойной ряд абсолютно сходится.
262
Часть 1П
ключенное между 0 и т, и разложим функцию f(x,y) (как функ-
цию от х) в ряд Фурье по синусам:
00
1(х,У)= SM'/Mn-y5-.	(5)
А-1
Коэффициенты этого ряда мы обозначили через bk(y), так как
они зависят от того, чему равно зафиксированное вначале зна-
чение у:
bt(y)=-^ff(X,y)Sin^dx.	(6)
Функция bk(y) обладает следующими свойствами:
1) ^*(0)=0; bk(m) = 0; это следует из того, что f(x, у)=0
на границах прямоугольника и, в частности, при у = 0 и при
у = т (каково бы ни было х, О^х^.1);
2) bk (у) — непрерывная функция от у; это следует из общей
теоремы (которую мы не доказываем), утверждающей, что если
подинтегральная функция есть непрерывная функция двух пере-
менных в замкнутом прямоугольнике а, то определенный интег-
рал по одному из этих переменных есть непрерывная функция
от другого переменного.
Разложим функцию bk(y) в ряд по синусам:
т
i
где
С*. / = —f b„(y)sin^-dy,
т J	т
о
или, учитывая значение bk(y) (см. (6)),
т 1
Ck,i = — {[-у f f(xty)sin-$~dx] sin — dy.
т J [ I J	I J m
о 0
Это можно записать с помощью двойного интеграла
Си = -yJJ/ (*. У)sin sinda;	(8
а
в знаменателе перед интегралом стоит площадь области интег-
рирования (а = т I).
^alallaus^k
знание Вез границ “ **
Глава 2, § 8	263
Если теперь подставить в ряд (5) выражение для Ьк(У) (см.
формулу (7)), то мы получим разложение функции f(x, у) в двойной
ряд Фурье:
/<*.
k L i
„	. tnyl . knx
Ck i sin —— sin--------
’ tn J I
пли
f(x, у) = У Cfcjsin-^- sin---- .	(9)
rn I
i,k
Коэффициенты этого двойного ряда Фурье вычисляются по фор-
мулам (8).
Можно доказать, что для любой функции f (х, у), непрерыв-
ной в замкнутом прямоугольнике а: 0<х</; 0<//</п, ряд
(9) сходится в среднем квадратичном к функции f(x,y); это зна-
чит, что среднее квадратичное расстояние между функцией f(xty)
и /i-ой частной суммой* двойного ряда Фурье
'\/ ^[f(x,y) — Sn(x,y)]zdx
СТ|Х'МИТСЯ К нулю при /I —> оо .
Более того, двойной ряд Фурье сходится в среднем квадра-
тичном к функции /(х, у) даже в том случае, когда эта функция
кусочно-непрерывна ** и ограничена в области о. Доказательство
этой теоремы значительно сложнее, чем доказательство анало-
гичной теоремы для функций одного переменного (см. часть II,
§ 13).
Имеет ли место равенство (9) в каждой точке области а?
Иначе говоря, будет ли двойной ряд Фурье сходиться к функции
/(.г,у) не в среднем, а в смысле обычной сходимости? Ответ на
этот вопрос более труден, чем для функций одного переменного.
Однако практически можно считать, что для всех тех кусочно-
непрерывных, ограниченных в области а, функций, с которыми
нам придется встречаться, это имеет место (всюду, кроме точек,
лежащих на линиях разрыва функции f(x,y), и точек, лежащих
на границе области о).
* Здесь, как и раньше (см. стр. 261), под л-ой частной суммой двойного
ряда подразумевается сумма всех таких членов ряда, у которых сумма индек-
сов i не превосходит числа л 4-1.
** Функция f(x,y) называется кусочно-непрерывной в области о, если
"У область можно разбить простыми дугами на конечное число областей,
"нутри каждой из которых функция f(x,y) непрерывна.
264
Часть III
Нами был рассмотрен вопрос о разложении функции двух
переменных в двойной ряд Фурье по синусам. Совершенно ана-
логично можно было (ы говорить о двойных рядах Фурье по
другим ортогональным системам функций (например, по функци-
ям Бесселя или по полиномам Лежандра). С такими двойными
рядами Фурье нам придется встречаться впоследствии.
$ 9. Решение уравнения колебания прямоугольной
мембраны
Пусть мембрана имеет прямоугольную форму. Будем считать,
что она расположена на плоскости Оху, занимает область о:
о < х О /п, и закреплена на границе этой области. До-
пустим, что на нее не действуют никакие внешние силы и что
в начальный момент ей приданы начальное отклонение
и (х, у, t)/t. о = <? (х, у)	(1а)
начальная скорость
Ui(x,y,t)/t„0 = ty(x,y).	(16)
Тогда отклонение мембраны и(х, у, t) в любой точке (х, у) в
любой момент времени t удовлетворяет уравнению
д*и	. / д*и , dau \	/оЧ
--- = «------------,	(2)
др \дх* ду*)
начальным условиям (1а) и (16) и граничным условиям:
и (0, у, 0 = 0; « G. У, 0 = °»
и(х, 0,0 = 0; и(х, tn,t) = 0.	(3)
Можно доказать (примерно так, как это мы делали для уравне-
ния колебания струны), что эти начальные и граничные условия
определяют единственный закон колебания мембраны; можно
также доказать устойчивость этого решения. Найдем это реше-
ние методом Фурье.
Действуя в соответствии с общим планом, попытаемся най-
ти такие решения, которые представимы в виде произведения
трех функций одного переменного
м(х,1/,0=Х(х)Г(7/)Т(/),	(4)
ftalaHauswk
знание без границ Ч *
Глава 2, §9 265
и удовлетворяют заданным граничным условиям. Граничные ус-
ловия (3) сводятся к следующим условиям на Х(х) и У (у):
Х(0)=0; Х(/)=0;
У (0) = 0; Г(т) = 0.
Подставляя решение(4) в уравнение (2), мы получим тож-
дество:
Т"Х У = а'(ТХ" У + ТХ У")
(5)
(для краткости записи мы опускаем обозначение независимого
переменного; штрихи около функции обозначают дифференциро-
вание по тому переменному, от которого эта функция зависит;
например, X" обозначает вторую производную от Х(х) по х и
т. д.)
Разделим теперь в равенстве (5) переменные, т. е. оставим
в одной части равенства выражение, зависящее только от одно-
го из независимых переменных, а в другой части равенства —
выражение, зависящее от двух остальных переменных; при этом
мы изолируем то независимое переменное, для которого у нас
заданы граничные условия (например, у). Это можно сделать
следующим образом:
Г' ХУ — агТХ"У^а*ТХУ”,
откуда
Т"Х—а*ТХ" Y"
а2ТХ
Так как левая часть этого тождества не зависит от у, то и
правая не зависит от у; аналогично убеждаемся в том, что ни
левая, ни правая части этого тождества не зависят от х и t;
следовательно, они равны постоянной величине; обозначим ее —р:*
Т"Х—а2ТХ" __ Y"
а*ТХ	Y “• И *
Следовательно,
Г"4-Иу = 0,
Т'Х — а*ТХ" + ?.а2ТХ = 0.
(6)
(7)
* См. сноску на стр. 220,
266
Часть HI
Уравнение (6) вместе с граничными условиями, налагаемыми
на Y(y), позволяет найти все допустимые значения р. и все со-
ответствующие решения Y (у):
__ я8 _____ 2ала _	_ k2n2
; р-2	—-г;	; р* - —а-; • • •
ri(«/) = sin^; r2(4') = sin^.;...;F1(y)^sin=^; ... (8)
^2^2
Подставляя теперь р. = р.Л = —а— в равенство (7) и разделяя в
нем переменные, получим:
Т"Х— агТХ"+ ~г~а2ТХ = 0,
1 tn2
k2n2a2
m2
a2T
X"
X *
Повторяя обычные рассуждения, убеждаемся в том, что обе
части этого равенства не зависят ни от t, ни от х. Приравнивая
их константе —X, получим
Л2п8а8
т2 
а2Т
откуда
Х"4-ХХ = 0;	(9)
| /2!^ ц. = 0 .	(10)
\ П12	/
Функция Х(х) должна быть нетривиальным решением уравнения
(9) и должна удовлетворять граничным условиям: X (0) = 0,
X (/) = 0. Это позволяет нам найти все допустимые значения X:
. _ я2 . _ 22л2 .	_ (2я8
/2 ’	/2 • ’  * ’ I I* » • • •
и соответствующие им решения уравнения:
X1(x)=sin“; X2(*) = sin^;...; Х,(л) = sin-Sp ; ... (11)
• 2 7^2
Подставляя, наконец, в (10) X = X/=-ya-, получим уравне-
ние для определения Т (/):
Глава 2, § 9	267
Обозначим для краткости
Ть* =
ia . Л®
/а + та‘
(12)
Каждой паре номеров i, k соответствует свое решение Т (/);
обозначим то решение, которое отвечает номерам I и k, через
Tik(t). Тогда уравнение для определения Tlk (/) примет вид:
Г;* (0 + т?*а»Т„(0 = 0.
Следовательно,
Tik (0 = Aik cos a t + Blk sin a ylk t,
где Alk и Bik — произвольные постоянные.
Подставляя найденные Xt(x), Yk(y) и Tlk(x, у) в равенство
(4), получим всевозможные нетривиальные решения уравнения
(2), удовлетворяющие заданным граничным условиям и предста-
вимые в виде произведения функций одного переменного:
«/л (*. О = sin sin (Alk cos a ylk t + Blk sin a t),
где i и k пробегают все натуральные числа от 1 до оо, а оп-
ределяется из формулы (12).
Перейдем теперь ко второму этапу решения задачи. Возьмем
сумму всех ulk(x, у, t) (i = 1, 2, 3,...; k = 1, 2,3,...). При любых
значениях коэффициентов А1к и Blk эта сумма удовлетворяет как
данному уравнению (2), так и граничным условиям*. Остается
подобрать эти коэффициенты так, чтобы сумма S ulk (х, yt t)
удовлетворяла также и начальным условиям.
Итак, пусть искомая функция и(х, у, t) является суммой
двойного ряда S ulk(x, у, t):
и (X, y,t) = S (Atk cos ayik t + Blk sin а	t) sin sin ^.(13)
i,k
Если в этом равенстве положить t = 0 и учесть начальное ус-
ловие, то мы получим следующее тождество:
/	\	V1 л • i*x	. kitu
? (х> У) = 21 А» sin — Sin
* При условии, что этот двойной ряд сходится и что его можно дважды
почленно дифференцировать по каждой переменной.
268
Часть 111
Это — разложение функции <p(x,z/) в двойной ряд Фурье (по си-
нусам); находим его коэффициенты:
А* = 1^г У) sin Т sin ТгГ da‘ (14)
а
Аналогично найдем и Blk. Для этого продифференцируем почлен-
но равенство (13) по t (допуская, что такое дифференцирование
двойного ряда возможно):
ut(x,ytt)=lL(~Aik a yik sin a yik t + Bik a llk cos a iik t)sin^ sin^,
i.k	1 m
и подставим сюда t = 0. Тогда, учитывая второе начальное ус-
ловие, получим тождество:
ф (х, у) = Е Blk a llk sin l~ sin .
i.k
Это — разложение функции ф(х, у) в двойной ряд Фурье по
синусам; следовательно, коэффициенты этого ряда можно прирав-
нять коэффициентам двойного ряда Фурье:
Bik а i/л = 4; JJ * у) sin т
<3
sin — da,
откуда
В« = jj * <*• У)sin ‘-T sin %d°-	<15>
a
Подставляя Alk и Blk из (14) и (15) в формулу (13), получим ис-
комое решение дифференциального уравнения, удовлетворяющее
заданным начальным и граничным условиям. Учитывая единст-
венность решения, удовлетворяющего этим условиям, заключаем,
что никаких других решений, кроме найденного, наша задача о
коле ании прямоугольной мембраны иметь не может.
Мы получили решение, записанное в форме двойного ряда.
Его главный член
«п (*. t) = (Au cos a 7U t sin a 7n t) sin ™ sin (13n)
называется основным тоном колебания мембраны. Если бы все
остальные члены ряда (13) отсутствовали и колебание происхо-
дило бы по закону (13ц), то мембрана в любой момент времени
WalattausiBil
знание без границ * *•
Глава 2, § 9
269
имела бы форму поверхности и = Ki sin sin ~ , где коэффи-
циент (равный выражению в скобках в формуле (13ц)) зависит от
времени; его максимальное значение равно Лц-}- B2lt (амплиту-
да основного тона). При этом каждая точка мембраны колеба-
лась бы с частотой /1 =
Yu = у
(т = /), то
J____В
/п*
или Л - -j- j/X _L , так как
частности, если мембрана квадратная
/,=
°	12
Заметим, кроме того, что если бы мембрана колебалась в
соответствии с законом (13ц), то ни одна точка мембраны не
находилась бы в покое (кроме точек, лежащих на границе); ины-
ми словами, мембрана не имела бы узлов (одно из положений
мембраны, колеблющейся по закону (13п), изображено на рис.
76 а).
Рассмотрим теперь два следующие члена ряда (13) (те чле-
ны, сумма индексов которых равна трем):
«и (х, у, t) = (Л12 cos а Ьа #12 sin a '(12 Qsin sin (1312)
(х, у, t) = (Л21 cos а ;21/ + В21 sin а ?21 /) sin ~ sin	. (13^)
Оба эти колебания в сумме дают первый обертон колебания
270
Часть HI
мембраны. При этом функция н12 (х, у, t) задает колебательный
процесс с частотой , а функция «21(х, у, t) — колебатель-
ный процесс с частотой если / т, то эти частоты, вооб-
ще говоря, не равны друг другу; если же I — т, то 721 = 7ia =
= и частота обоих колебательных процессов (а следов а-
-	\ а V5
тельно, и частота первого обертона) равна -у-	.
Заметим далее, что если бы закон колебания мембраны за-
давался формулой (13х2), то в процессе колебания мембраны точ-
ки, лежащие на прямой у — ^-, оставались бы все время в по-
кое (см. рис. 76 б); эта прямая называется линией узлов. Для
колебания, задаваемого формулой (1321), линией узлов является
прямая у == Для суммарного же колебания и12 4- н21 узлов
может и не быть (кроме центра мембраны — точки ; -ь-') •
\ Л»	Л» I
a	d	в	г	д	р.
ж	3	и	к	л	м
Рис. 77
Линии узлов для различных обертонов сравнительно легко
построить, если мембрана является квадратной (/ = т). Так, на-
пример, для первого обертона (т. е. для обертона н12 4- «21 с
частотой -у- линия узлов имеет форму, изображенную на
рис. 77а, если начальные условия симметричны (т. е. <р(х, у)=>
±=ср(у,х), фСм) ~^(у,х))\ эта линия имеет форму, изображен-
ную на рис. 77 б, если начальные условия антисимметричны
(т. е. <р(х,у) = — <р(у,х), ty(x,y) = — ф(^,х)); при других началь-
ных условиях линии узлов первого обертона могут иметь и дру-
гую форму (см. рис. 77 в, г, д).
^alaitauswii
знание без границ ’*
Глава 2, § 10
271
Более сложными являются линии узлов для более высоких
обертонов. При этом в один обертон мы будем объединять все
те члены ряда (13), которые имеют одинаковую частоту; напри-
х	у t а 1^8
мер, обертоном с частотой f — — является член ряда с ин-
дексом (2;2); обертоном с частотой / = -р	— сумма членов
ряда с индексами (1;3) и (3; 1) и т. д. Линии узлов для раз-
личных обертонов также зависят от задания начальных условий.
Некоторые линии узлов для обертонов с частотой у приве-
1 Л»
дены на рис. 77 ж-м, а для обертона с частотой у-Кд- — на
рис. 77 е.
Заметим, что, вообще говоря, с увеличением частоты обер-
тона его амплитуда (а следовательно, и сила звука, обусловлен-
ная этим обертоном) убывает; поэтому основной тон и несколь-
ко первых обертонов обычно достаточно точно задают закон коле-
бания мембраны.
$ 10, Решение уравнения колебания круглой
мембраны
Пусть мембрана имеет форму круга радиуса I. Будем счи-
тать, что она расположена на плоскости Оху и имеет центр в
начале координат.
Для того, чтобы найти закон колебания этой мембраны, пе-
рейдем к полярным координатам. Из общей теории мы знаем,
что отклонение и точки М от положения равновесия в момент
времени t есть функция от точки М и от момента /, удовлетво-
ряющая дифференциальному уравнению:
д2и _ 2 / д*и . д2и\
dt* ~а у dx2 + ду*)'
или
(1)
Здесь учтено, что и не зависит от г, а только от х и у, и
д2и . д2и	.	,т
поэтому ^2 + равен лапласиану функции и. Напомним теперь,
как выражается лапласиан в цилиндрических координатах:
1 Г 0 / ди\ .	1 д2и ; d2ul
----- г [ dr dr ) ' г д<ра ' dz2]’
272
Часть 111
но в данном случае и не зависит от z; поэтому
1 Г-д- (	\ д_ 1 д2"!
—л—>U	г [dr dr j * г дфа J*
Подставляя это выражение для лапласиана в уравнение (1),
получим после преобразований:
д2и __ а2 / ди
Hi2 ~ ~ [дг
д2и 1	d»u\
Г дг2 * г	d<paJ'
(2)
Решая это уравнение, мы найдем и, как функцию от t, а
также от г и <р, т. е. от полярных координат точки М, лежащей
в плоскости мембраны. Это уравнение и является уравнением
свободных колебаний мембраны в полярных координатах.
Обозначим искомую функцию через и (г, <р, t) и зададим гра-
ничные и начальные условия:
1) граничное условие
= O	(3)
означает, что все точки, где г = / (т. е. все точки, лежащие на
границе мембраны), находятся в покое: мембрана закреплена на
границе;
2) начальные условия:
«('.'P.O) = /('.?).	(4)
«/'’. <Р. 0) ф (г. <р)
означают, что отклонение точки мембраны с координатами (г, <р)
в начальный момент равно f(r, <р), а начальная скорость этой
точки равна ф(г, <р).
Приступим к решению уравнения методом Фурье. Будем ис-
кать те решения уравнения (2), которые удовлетворяют гранич-
ному условию (3) и представимые виде произведения трех функ-
ций одного переменного
«(''.'P.O =	(5)
Функция R(r) должна быть определена на участке 0<г</.
Граничные условия на R(r) вытекают из условия (3) и из есте-
ственного требования ограниченности функции и (г, у, t):
R(r) ограничена при г->-4-0.	(6)
Функция Ф (<р) не связана никакими условиями, кроме одно-
го: она должна быть периодической с периодом 2тс; действи-
тельно, с изменением угла <р на величину 2к точка мембраны не
ftalallauswi!.
знание без ераниц * *
273
Глава 2, § 10
изменит своего положения, а следовательно, и отклонение мемб-
раны и (г, <р, t) не изменится при замене ф на ф + 2к. Итак,
Ф (<р) = Ф (<р -f- 2тг) для любых ф.
(7)
Это условие играет роль граничного условия, наложенного на
(ф).
Подставляя (5) в уравнение (2), получим
г?
Ф/?' + а2ТФ/Г + угТФ^.
Здесь, как и в предыдущем параграфе, опускаются (для
краткости записи) обозначения независимого переменного; штри-
хи около функции обозначают дифференцирование по тому пе-
ременному, от которого эта функция зависит.
Разделяя в полученном равенстве переменные, перенесем в
одну часть члены, зависящие только от ф, а в другую — от tn г:
Т" R — — TR'—a'TR"
г	_ Ф"
-4- TR ф ’
г®
Проводя обычные рассуждения, убеждаемся в том, что обе
части этого тождества не зависят ни от ф, ни от t, ни от г и,
следовательно, являются постоянными. Обозначая их общее зна-
чение буквой — v (где v — константа, знак и числовое значение
которой пока нам не известны), получим:
T"R-—TR’—atTR"
-i-TR
Ф"
V = —
откуда
Ф" 4- v Ф = 0,	(8)
T"R —~ TR' — a2TR" + v ^TR = 0.	(9)
Используя граничное условие (7), заключаем, что v не может
быть отрицательным (в противном случае решение уравнения (8)
выражалось бы через показательные функции и не было бы пе-
риодическим). Поэтому v > 0.
274
Часть III
Если v = О, то уравнение (8) приводится к виду: Ф" = 0, и
его решение Ф =	-f- Са будет удовлетворять условию (7) только
при Cj = 0.
Итак, при v = О наша граничная задача имеет нетривиаль-
ное решение Ф = С2 (в частности, Ф==1). Значит, v0 = 0 яв-
ляется собственным значением, а функция Фо = 1 — соответст-
вующей собственной функцией.
Если v > 0, то линейно независимые частные решения урав-
нения (8) имеют вид:
Ф (<р) = cos <р)А; ф (ф) == sin <p)/v .
Функции Ф (<р) и Ф (<р) имеют период -7=; этот период будет
У У
равен 2к или он будет целое число раз содержаться в 2тс тогда
и только тогда, когда )/v — целое число; итак, v = р2 (где р =
= 1,2,3,...). Обозначая то значение v, которое соответствует
целому числу р, через vp, а соответствующие собственные функ-
ции через Фр(<р) и Фр (<р), получим:
= р2; Фр(?) = cosp<p; Фр(<р) = sinp«p.
Здесь каждому собственному числу vp отвечают, два линейно не-
зависимых частных решения; это кажущееся противоречие с об-
щей теорией объясняется тем, что в данном случае наша крае-
вая задача не является задачей Штурма-Лиувилля: заданные
граничные условия (7) отличны от тех, при которых доказыва-
лась основная теорема о собственных функциях.
Подставляя теперь v = р2 (р = 0,1,2...) в равенство (9), по-
лучим:
Т" fl— — TR' — a2 TR" +
TR = 0;
(101
разделим переменные:
т. _±R'+R"- ^-R
а*Т ~	R	’
проведя обычные рассуждения, убедимся, что каждый член ра-
венства здесь постоянен. Приравнивая его константе — X, полу-*
чим:
т. _ 4- R'+R" -£r
И*Т =	R	= — х.
f\afaHaus®fc
Глава 2, § 10
275
откуда
T" + Xa9T = 0,
г2/?" + г R' + (Кг2—р2) R = 0.
(И)
(12)
Уравнение (12) вместе с граничными условиями на искомую
функцию: /?(/) = 0, R(r) ограничена при г-^+0, было нами
изучено в § 5 второй части*. Там было установлено, что собст-
венными числами этой краевой задачи являются числа
. [нгг. . т»
/2	’ /а • ’ • • » р » • • •
(где 0 < |х^<ф2Р> < .. • — положительные корни бесселевой функ-
ции Jp), а собственными решениями этой задачи являются функ-
ции:
/ Ар). А	/ Ар).г \
/?,.« w =л (-4-);= Ц-V )•
/ \L(P> • г \
== Jр	j j »• • •	(13)
Здесь каждая собственная функция нумеруется двумя ин-
дексами (р и k); индекс р пробегает всевозможные целые не-
отрицательные значения 0 < р < 4- «>, индекс k — всевозможные
натуральные числа, 1 < k < 4- 00
[ v-W
Подставим в уравнение (11) Х= ь—; обозначая соот-
ветствующее решение этого уравнения через Tpk (/), получим:
*м(0 + -у0-Л* <0 = 0,
откуда
ар/^	<зр/^
Tpk(t) = cos -f-t 4- Bpk sin -f-t,	(14)
’ де Арк и Врк— произвольные постоянные.
Гюдставляя теперь найденные функции Ф(ф), /?(г) и Г (/) в
равенство (5), получим всевозможные решения уравнения (2),
* Только там были другие обозначения: неизвестная функция там обо-
значалась у, а здесь /?; независимое переменное там обозначалось х, здесь г.
276	Часть HI
представимые в виде произведения функций одного переменного
и удовлетворяющие нашим граничным условиям:
__	/__	а\№	__ affl \
upk(f • Ъ 0 -	соs — t -Ь Bpk sin-p t) cos p 9 • Jp	,
_-	/ =	— a\№ \	/ \ty-r
4pk(r,^t)= (A*cos —) sinp^-Jpy—i—
Нами учтено, что функция Ф (9) может равняться как cos р<р (в
частности, при р = 0, единице), так и sinpy. В соответствии с
этим мы получили два набора решений для u(r,9, t): решения,
содержащие cos р 9 (мы их обозначили ирк\ здесь0<р_< + °0)
и решения, содержащие sinp9 (они обозначены ирк, здесь
1 < р < -f- °0). Ясно, что и коэффициенты в каждой группе ре-
шений нам пришлось обозначить по-разному: Арк и Врк—в пер-
вой группе; Арки Врк — во второй.
Для того чтобы найти решение уравнения колебания мемб-
раны, удовлетворяющее не только граничным, но и начальным
условиям, надо взять сумму ряда, составленного из всех
ирк и ирк, и подобрать коэффициенты этого ряда так, чтобы удов-
летворить заданным начальным условиям:
V V (—	\
«(г. Ф. О == Zj Zj l/pfcCOS - у- / | BMsinjcospcp’J^-j—j-\-
p~=0 Л=1
I-2d 2j Mp*cos Bpks\n-f-t J sinp<P‘Jp 1^-7—) . (15)
р-i *-1 '
Подставляя в (15) t = 0 и учитывая при этом начальное ус-
ловие (4), получим:
ОО со
V V -	( №-г\
f(r, 9) -= Zj Zj Арк COSP4>-JP ) 1-
co 00
-h L L Apk sinp(p-Jp .	(16)
рш=1 Л=1
Зафиксируем на минуту переменную г. Тогда это равенство
дает нам разложение f (г, 9), как функции от 9, в ряд Фурье на от-
резке |—к; тг] по общей тригонометрической системе. Коэффи-
Глава 2, § 10
277
Ч\а1аНаиъЖ
знание Сез границ “ w
у 1$.Г\
цментами при косинусах являются выражения Z^ApkJp — ),
1
У -	{ №-г\
при синусах — выражения Zj ApkJpk —-—). С другой сто-
роны, коэффициенты ряда Фурье при cos рф (если р>0) равны
Я
•	| /(г, <p)cosp<pd<p и аналогично при sinp<p.
Поэтому при р > О
Если же р = 0, то соответствующее слагаемое ряда (16)
превращается в свободный член ряда Фурье (не содержащий ф).
я
В общей теории мы его обозначали где а0 = -- ( /(г, tp)d<p.
Поэтому
оо	п
£	=	(17„)
-п
Равенства (17) и (170) уже позволяют найти Apk, Apk и ^oft.
В правых частях этих равенств стоят известные функции от г
(«ни не зависят от <р: по ф мы проинтегрировали и подставили
границы интегрирования). В левых частях стоят ряды по функ-
циям Бесселя. Следовательно, каждое из этих равенств можно
рассматривать, как разложение в ряд Фурье-Бесселя функций,
стоящих в правых частях равенств. Коэффициенты этих рядов
легко вычисляются в соответствии с общей теорией (см. часть II,
§ 11 — в частности формулу (2')):
/]	... ______2_____ Г Г 1 i*	I / .Jp) .r\
/9[ Jp( #)]’ J rL 75 J f (r^ycospcpd(f> \ <4-7-)^’
278
Часть HI
или
Лр‘= ° [ •'И 1‘Р)]2 Я (-Ц-^сетрфЛ.»
Здесь р> 1. Аналогично
Л __ _____~____ | I	/ Р-Ь ’ I
р*~ °[ <( ^)1* JJ Jp \Т~/sinWdo’
А°" ‘PiflW И f<r-d J° (Л-)40'
О
Итак, все коэффициенты Apk, Apk, Aok — найдены. Для того что-
бы найти Bpk, Bpk, Bok, продифференцируем ряд (15) по t и в
продифференцированный ряд подставим t — 0. Учитывая началь-
ное условие для скорости и\ (г, <р, /), получим:
SV —	( \№-г\
L -^-Bpk jp(™r-)cosp'P +
p~Q
у у 0|^=	/ ^.Г \
“i" ~ ~ I Вр^ Jр \ I ) sin рф.
р~1 Л=Н
Рассуждая далее точно так же, как и выше, найдем:
Я" —	ll	/ \lk'r I
I j' (i.p)i2 J J Ф (r- ?) r~ I	>);
B=	2/	ff	/(//•'r'l
~ iv-'pc [ УД |^)p JJ Ф (r. ?) /Д—,-,/sinppdo, (p > 1);
Я -	'	fC	l Л0>т\
o»‘- 0:4”«[ ^ (|4°’)]г J j	M -r- )d°-
Подставляя найденные значения Apk, ApkH т. д. в формулу (15),
получим искомое решение уравнения колебания мембраны в ви-
де суммы двойного ряда. Решение, записанное в форме ряда (15)
• Мы записали двукратный интеграл в виде двойного интеграла по кру-
гу а в полярных координатах, учтя при этом, что г dr dtp есть элемент пло-
щади в полярных координатах. Числовой множитель перед интегралом «/*.
мы обозначили через з (площадь мембраны).
NataUausiM.
знание Вез границ ' **
Глава 2, § 10
279
(с найденными коэффициентами), является единственным реше-
нием, удовлетворяющим заданным граничным и начальным ус-
ловиям (единственности решения мы не доказываем).
Радиальные колебания мембраны. Решение уравнения коле-
бания круглой мембраны принимает более простой вид в случае
гак называемых радиальных колебаний.
Колебания круглой мембраны называются радиальными, если
они не зависят от полярного угла <р (т. е. отклонение точки М
от положения равновесия в момент t зависит только от этого
момента Г и от расстояния между точкой М и центром мембра-
ны). Очевидно, это будет иметь место тогда, когда начальное
отклонение и начальная скорость не зависят от <р, а являются
функциями одного только г:
и(г,%1)/^о ^- f(r),
u't (г, Cf>, 1)/^ = ф (г).
В этом случае все коэффициенты Apk, Apk,Bpk, ВрЛпри 1 рав-
ны нулю. Проверим это, например, для Apk.
~д __ _______2______ / И •г \
pk ° [ J'p 0х ?J)]2 JJ	cosP?d° =
G
I «
_	2_____ (’ (’	/ ^(p). r \
J J f^JP	cos pep-rdfpdr.
0 —л
Вынося за знак внутреннего интеграла (по <р) сомножители, не
п
зависящие от мы приводим его к интегралу J cospepdy, ко-
торый равен нулю при любом целом р, отличном от нуля.
Но тогда и весь двойной интеграл равен нулю, т. е. Арк = 0.
Аналогично проверяется, что Apk = 0, ВрЛ_= 0, Bpk = 0 (при
Р> 1). Если же р — 0, то коэффициенты AQk и ВоЛ, вообще го-
воря, не равны нулю, но формулы для их вычисления могут
быть несколько упрощены:
А°" = ’[•'»( 4“’)]8 В ИОЛ (4М* =
О
= "'*[ Л( |40,)Г fl, ИОЛ (^-'jrd^pdr.
280
Часть 111
Вынося за знак внутреннего интеграла сомножители, не со-
К
держащие <р, и учитывая, что J d 9 = 2 к, получим, после со-
—к
крагцения:
-Л____________2	Р	/|4м-г\
°* “ /• [ 4 ( И?’)]’ J /(04
Аналогично находим
~в ___ _______2_______ (’	/ |Л°)г \
°*- ЯЦ»>[	♦(г)Л Н-М-
Подставляя найденные коэффициенты в ряд (15), заметим,
что он превращается из двойного ряда в обычный: все члены во
второй строке этого ряда исчезают, а из членов первой строки
остаются только те, для которых р = 0; поэтому суммировать
надо только по k, но не по р. Окончательно формула (15) пе-
репишется следующим образом:
S/___ a<№t —	\	\
^ЛОЛсоз— j--h ВоЛ sin —— )J0 —j— ). (18)
Решение, записанное в форме ряда (18), легко поддается ис-
следованию. Заметим, что колебание мембраны раскладывается в
ряд более простых колебаний. Первый член этого ряда
/_ аМ°> t - qA°> t \	/ Л°> г
Ui (г, t) = ^Ао1 cos —j----1- В01 sin —у— ) Jо z—
изображает периодическое колебание с частотой колебаний
в единицу времени. Если бы мембрана колебалась по закону, за-
данному функцией их то в любой момент времени она име-
ла бы форму]
(“i№r \
где Ki — коэффициент, зависящий от t (его максимальное значе-
ние равно ]/	4- Boi ); изображение этой поверхности см. на
рис. 78 а; это — поверхность, образованная вращением первой
полуволны графика функции Бесселя Jo. Колебание, задаваемое
^alattausK^.
знание Вез границ ’ ш
Глава 2, § 10 281
функцией uv (r,t), не имеет узловых точек (т. е. точек, остаю-
щихся неподвижными в процессе колебания), за исключением
точек границы. Функцию (r,t) будем называть основным то-
ном колебания мембраны.
Второй член ряда
«2 (г,/) ==
Рис. 78
изображает колебательный процесс с частотой (эта частота
приблизительно вдвое больше, чем частота основного тона). Ес-
ли бы колебание подчинялось только закону иг то мембра-
на в любой момент t имела бы форму иа = Ка-/0	—), где
К2 зависит от t (причем шах К2 — )/ Ло2 -|- В02 ); изображение
этой поверхности дано на рис. 786. Колебание, задаваемое
Функцией па(г,/), имеет линию узлов: это — окружность г —
|^0)
— 0) /. Функция па (г, /) дает первый обертон колебательного
процесса.
Останавливаться на рассмотрении остальных обертонов мы
не будем; отметим только, что с возрастанием номера k оберто-
на, частота его колебания растет, а амплитуда стремится к нулю
(при k-\- со). Обертон порядка k имеет k узловых линий (не счи-
тая контура мембраны). Это — окружности радиусов —~;
(4н
282
Часть III
'	iA0)- i
--- г- ;...; • ifl— ’» центры всех этих окружностей находятся в
i4+i 14+1
центре мембраны.
Замечание. Если нам заранее известно, что колебания мемб-
раны являются радиальными (т. е. если начальные функции f и ф
не зависят от <р, а только от г), то вывести закон колебания (18)
можно непосредственно, минуя общий случай. В случае радиаль-
ных колебаний уравнение мембраны приобретает вид:
д*и _а®
dt9 ~ ~
(ди . д*и \
дг ' Г дг* )
(19)
(член, содержащий , исчезает, так как и не зависит от у). В
этом случае начальные условия запишутся следующим образом:
Ц (г, t) |/^о -= f (И; u't (г, t) |,e0 = ф (г),
а граничные условия:
п (/, t) == 0; и (г, t) ограничена в круге 0 <	/.
Решая уравнение (19) при заданных начальных и граничных
условиях методом Фурье, мы получим для искомой функции и (г, t)
в точности то же выражение, которое было получено выше (см.
формулу (18)).
Пример. Найти закон свободных колебаний однородной круг-
лой мембраны радиуса I = 1 м, если в начальный момент она была
оттянута в центре на высоту h ~ 10‘а м и затем отпущена без
начальной скорости. Натяжение Т и плотность Г мембраны та-
ковы, что а = у -р-	200
Рис. 79
Очевидно, в данном слу-
чае колебания мембраны яв-
ляются радиальными: если выб-
рать начало координат в центре
мембраны, то начальное откло-
нение задается формулой
(начальное положение мембра-
ны см. на рис. 79). Так как на-
чальное отклонение /(г,<р) и
Ш%иНаи$ж11
знание без границ * ш
Глава 2, $ 10 283
начальная скорость (всюду равная нулю) не зависят от <р, то ко-
лебания являются радиальными. Следовательно, искомая функция
u(r,t) удовлетворяет уравнению (19) (при а — 200) и началь-
ным условиям:
п(г,0|/»о = 1ббО—О*.	(G0|/-o = O.
Поэтому решение запишется в виде суммы ряда (24), коэф-
фициенты которого вычислятся по формулам:
Л*= '*• [ 4( i4”)]’ Too /° ^ r )<ir:
В‘ = ~2OO-l-|.i0,-2[ 4( j r'0 J° (	= °'
В примере, рассмотренном на стр. 169—170 (часть II), найдены
несколько первых коэффициентов ряда Фурье при разложении
функции 1—х на отрезке (0; 1) по функциям Бесселя:
Ci = 0,984. . .; са = 0,666. . .
В данном случае в ряд Фурье разлагается функция, в 100 раз
меньшая; следовательно, и коэффициенты Фурье уменьшатся в
100 раз; поэтому
Л, = ^5 = 0,00984 ..Л, =	= 0,00666...
Итак, ряд (24) в данном случае приводится к виду (выпи-
шем только два первых члена этого ряда):
и (г, /) = 0,00984 Jo (2,405 г) cos 4811 +
+ 0,00666 Jo (5,520 г) cos 11041 + ...
Первый член ряда (основной тон колебания) представляет собой
колебание с частотой
£ _ M°L 200.2.405 ___
'1 2я ~	6,28	~
Амплитуда этого колебания равна At = 0,00984 м.
Второй член ряда дает первый обертон колебательного про-
цесса. Здесь частота /а — 176 колебаний в секунду, а амплиту-
да Аа = 0,00666 м.
284
Часть Hl
§ 11. Решение задачи об остывании бесконечного
круглого цилиндра
Рассмотрим еще одну задачу, которая приводит нас к ря-
дам Фурье по функциям Бесселя.
Пусть нам задан бесконечный однородный круговой цилиндр;
будем считать, что его ось направлена по оси Ог и что радиус
его поперечного сечения равен I.
Если внутри цилиндра нет ни источников, ни поглотителей
тепла (т. е. если теплообмен свободный), то, как известно (см.
главу 1, § 3), распределение температуры и внутри цилиндра
удовлетворяет уравнению
или
ди
дГ
= а2
д2и
ду2 ‘ дг2) ’
д2и
дх2
(1)
Если при этом ни граничные, ни начальные условия не зависят
от г, то искомая функция и также не зависит от г (т. е. кар-
тина распределения температуры в произвольный момент време-
ни t будет одна и та же во всех горизонтальных сечениях ци-
линдра). В этом случае и зависит не от четырех, а только от
трех переменных: от х, у, t.
Уравнение (1), которому удовлетворяет искомая функция,
легко привести к уравнению в цилиндрических координатах:
Эи _ 2 /_1_
~дГ ~ г дг
д2и 1 д2и\
дг2 + г2 д<?)'
(2)
Слагаемое, содержащее производную по г в выражении для
лапласиана, мы опустили, так как по условию и не зависит от
г. Если обозначить искомую функцию через и (г, <р, /), то гра-
ничные и начальные условия могут быть записаны следующим
образом:
начальное условие
«('. % 0Uo = /(f’	<3)
граничное условие
и (г, 9»	О-	(4)
Это — плоская задача теплопроводности.
В общем случае здесь неоднородным является не только
начальное, но и граничное условие. Рассмотрим частный слу-
flafaMausi®!.
знание без границ '
285
Г лава 2, § 11
чай этой задачи, когда всюду на поверхности все время под-
держивается постоянная температура; выбором соответствую-
щего начала на температурной шкале можно сделать так, что-
бы эта постоянная температура равнялась нулю. Итак, заменяя
условие (4) условием (4'):
и (г, ?, /)|г==/= О,	(4')
мы придем к задаче с однородными граничными условиями.
Процесс решения этой задачи почти не отличается от процесса
решения уравнения круглой мембраны.
Итак, найдем решение уравнения (2), удовлетворяющее на-
чальному условию (3) и однородному граничному условию (4')-
Будем искать сначала решения, удовлетворяющие условию (4')
и имеющие вид:
м(г,ф,/) = ₽(г)Ф(<р)Т(/).	(5)
Подставляя в уравнение (2) и разделяя переменные (перенося в
одну часть равенства члены, зависящие только от <р, а в дру-
гую— от / и г), получим:*
а8
Т'Я-— R'T — a2R"T	ф„
Обе части равенства являются постоянными. Приравнивая их
константе — v, получим два уравнения:
TfR-~R'T~ + v =	(6)
Ф" + уф = 0.
(7)
Так как температура и (г, <р, /) в данной точке зависит толь-
ко от момента времени t и от положения точки, то она не мо-
жет измениться при замене <р на <р + 2тс. Таким образом,
и (г> ф» 0 — периодическая функция с периодом 2я. Но тогда и
Ф(ф) удовлетворяет тому же условию:
Ф (<р 4- 2тс) = Ф (<р).
(8)
• Как и в предыдущих параграфах, обозначения независимой перемен-
ной опускаются. Штрихи около функции обозначают дифференцирование по
той переменной, от которой эта функция зависит.
286
Часть III
Это условие выполняется только при v, равном квадрату целого
неотрицательного числа:
v0 = 0, Vj = Р, ....
Числу v0 = 0 соответствует (с точностью до постоянного мно-
жителя) только одно решение, удовлетворяющее условию (8)
Фо(?) = 1. Каждому из остальных чисел vp(p> 1) отвечают по
две собственные функции _
Фр (?) = cos р?; Фр (?) = sin р?.
Подставим теперь v = pa(p>0) в равенство (6) и разделим в
нем переменные:
1 ра
г /?" + — R'-'rR
а2Т = ——•
Приравняв каждый член этого равенства константе — X, мы при-
ходим к следующим двум уравнениям для определения T(t) и
/?(г):
Г + Ха2Т = 0;	(9)
r*R" + rR' + (Xr2 — р2) R = 0.	(10)
Займемся последним из этих уравнений. Так как для R (г) нам
известны граничные условия:
/? (/) = 0; R (г) ограничено при г -+ + 0*,
то мы можем легко найти собственные числа X и собственные
функции R (г). Эта краевая задача (см. часть II, § 5) имеет сле-
дующие собственные числа:
т*. ш*. . w.
р I	р »•••». р » ••• ’
и соответствующие им собственные функции:
(	\	/ i4₽)-
Rp\ (г) = J—j j ; • • •; Rpk (?) = Jр	j j; •••»
где, как и раньше, у\р}<	< — — все положительные корни
бесселевой функции Jp. Индекс р пробегает целые значения от
0 до + со; индекс k — от 1 до -{-со.
• Первое из этих условий сразу вытекает из граничного условия (4');
второе условие — требование ограниченности функции — совершенно естест-
венно.
ftalaHausllfo
знание без ераниц **
Глава 2, § И
287
I 1ХЛ I
Подставим в (9) к — !——— ; обозначая решение этого урав-
нения через Tpk(t), получим:
-от т _0
'	/2	1 pb ~
откуда
а1 £ 1*^^ 2 t
T„M=Apk.e т'
(где Apk— произвольная постоянная).
Подставляя теперь найденные функции Ф (<р), /?(г) и T(t) в
равенство (5), получим два набора решений для и (г, <р, /): пер-
вая группа решений получится, если в качестве Ф(<р) принять
cos р(р (р^ О), вторая — если в качестве Ф (<р) принять sin рср:
_ - [ у]2' )г
ир„(г, % о = Ар„ с '' cosp'f- J„ I -у— I ;
«„* (r, <p. f) = Ap„ e ''	sinptp-jJ	1 .
Вес эти решения удовлетворяют граничным условиям (4'). Для
того чтобы были удовлетворены еще и начальные условия (3),
возьмем сумму всех upk и ~йрк\
- - _	"•[ 4"’Г'	, .р)
«(г. ?. 0= S У Арке '' cosp?-a4-Ц—I +
р=0 Л=1
„ « "ОТ' ,	.
+	' sinpwJv). <“)
Р=1 k=\
в подставим сюда / = 0. Тогда получим:
СО со
р=0 Л=1	А
+ S X Лл-sinp^-^fl^LsV
р=1 Л=1	'	'
288
Часть HI
Тем же путем, как это было сделано выше (см. стр. 276—278),
найдем, что
Лр‘"	c°sp?d°- р >*>

4°t='°[X(W~V/(6¥H°(^d°- (|2)
Подставляя найденные коэффициенты Aok, Apk, Aok в двой-
ной ряд (11), получаем искомое распределение температуры
внутри цилиндра.
Легко видеть, что при t -> 4- оо температура в каждой точ-
ке внутри цилиндра стремится к постоянной величине, а имен-
но, к той температуре, которая поддерживается на поверхности
цилиндра (т. е. к нулю). Это следует из того, что при /->-фоо
каждый член ряда (11) стремится к нулю (за счет сомножителя
Радиальное распределение температуры внутри цилиндра.
Если начальное распределение температуры внутри цилиндра не
зависит от <р (а только от г), то и в любой, более поздний мо-
мент времени t это распределение не может зависеть от <р. Мы
говорим тогда, что распределение температуры внутри цилинд-
ра является радиальным. В этом случае формулы (12) для ко-
эффициентов ряда (11) сильно упрощаются:
V = 0 при р> 1; Лр4 = 0,
= (13)
Следовательно, и ряд (11) упростится. Вместо двойного ряда
здесь уже будет обычный ряд:
«('•.<) = X A°ke ‘‘	(14)
А=1
где коэффициенты Аок вычисляются по формулам (13).
5Valalfaas®fe
знание Вез границ * *
Глава 2, § 12	 289
§ 12. Стационарное распределение температуры
внутри бесконечного цилиндра. Плоская
задача Дирихле (для круга). Задача о ста»
ционарном отклонении мембраны
Рассмотрим опять бесконечный круговой однородный ци-
линдр, ось которого направлена по оси Ог, а радиус сечения
равен /. Будем считать, что температура внутри цилиндра уста-
новилась, и найдем закон распределения этой температуры, пред-
полагая, что на границе цилиндра в каждой точке поддержи-
вается определенная, не меняющаяся с течением времени темпе-
ратура. Для того чтобы задача была содержательной, надо
потребовать, чтобы в различных точках границы была различная
температура: ведь если всюду на границе поддерживается
одна и та же температура, то такая же температура, в конце
концов, установится и всюду внутри цилиндра.
Итак, пусть на границе цилиндра задана температура, зави-
сящая от положения точки на границе. Рассмотрим тот случай,
когда эта температура не зависит от г (а следовательно, зависит
только от угла (f>\, иначе говоря, рассмотрим тот случай, когда
распределение температуры на поверхности цилиндра одинаково
во всех сечениях, перпендикулярных к оси Ог. Ясно, что в этом
случае распределение температуры внутри цилиндра также не
будет зависеть от г; следовательно, здесь имеет место плоская
задача Дирихле.
Как известно (см. главу 1, § 3), эта задача сводится к то-
му, чтобы найти то решение уравнения Лапласа _л\н =0, ко-
торое принимает на поверхности цилиндра заданные значения.
Будем искать и как функцию от цилиндрических координат точ-
ки: и — и(г, tf>) (мы учли, что и от г не зависит). Тогда уравне*
ние Лапласа примет вид:
1	ди	. д2и ._1 дъи___р	...
г	dr	' дга '	г8 с<р8	’	' '
а граничное условие запишется так:
«О’» ?)|г=/= /(?),	(2)
где f (<р) — заданная функция. Кроме условия (2), очевидными.
Дополнительными условиями на функцию и (г, <р) являются сле-
дующие:
и (г, ср) ограничена внутри цилиндра;	(3)
и (г, <р) периодична относительно <р, с периодом 2тс. (4)
Ю Ю. С. Оман
290
Часть 111
Заметим, что условия (3) и (4) являются однородными, в отли-
чие от заданного условия (2), которое однородным не является.
В этой задаче нет начальных условий (искомая функция не
зависит от времени /); тем не менее, метод Фурье применим и
здесь. Мы поступим следующим образом: найдем все решения
уравнения (1), представимые в виде произведения
ы(г, $5) = /?(г)-Ф(<р)	(5)
и удовлетворяющие однородным условиям (3), (4). Затем пост-
роим ряд из решений такого вида (с неопределенными коэффи-
циентами) и подберем коэффициенты этого ряда так, чтобы вы-
полнялось также неоднородное граничное условие (2).
Подставив решение, записанное в виде (5), в уравнение (1),
получим следующее тождество:
у- Н'Ф + Я"Ф + i 7?Ф" S 0.
Разделим переменные и приравняем каждую часть полученного
равенства константе (обозначим ее—X):
— R' + R" ф„
откуда
Я" + -!-Я'--^-Я = 0;
ф”4-Хф = 0.
(6)
(7)
Однородные условия (3) и (4) на функцию и (г, <р) равносильны
следующим условиям на функции R(r) и Ф(<р):
R (г) ограничена на 0 < г < 1;
Ф(<р) ограничена и периодична с периодом 2л:
Ф (<р + 2л) = Ф (ср).
Последнее условие позволит определить коэффициент X:
уравнение (7) допускает периодические решения только при Х>0;
в этом случае решение будет периодической функцией с перио-
дом —. Если мы хотим, чтобы период укладывался целое чис-
Г*
ло раз в 2л, надо, чтобы X равнялась квадрату целого числа
(Х = /г\	Кроме этих чисел, задача имеет еще одно
собственное значение: Хв = 0.
№laHaus;lli
знание вез границ * *
Глава 2, § 12	 291
Итак, допустимыми значениями К будут числа:
Хо = О, Х1=Р, Х2 =2’, ...» ХЛ = Л>, ...
Числу Хо — 0 отвечает, с точностью до постоянного множителя,
только одно решение уравнения (7), удовлетворяющее условию
ф (<р + 2тс) == Ф (?); это—константа. Возьмем, например, Фо (<р) == 1.
Остальным собственным значениям нашей задачи отвечают
по два линейно независимых частных решения: числу \(Л>1)
соответствуют решения:
ФЛ (<р) = cos fap и ФЛ (<р) = sin Лер.
Подставим теперь	= Ла (Л > 0) в уравнение (6):

(8)
Это — уравнение Эйлера. Заменой независимой переменной
г — е* оно сводится к уравнению с постоянными коэффициентами:
R'r —	( так как $ = In г, $' =	;
«;= <*;)> (ъЦ=га; 4-+^ (- 4-)-
=/? <	= 4-/?^.
Подставляя /?' и /?’г в уравнение (8), получим, после упроще-
ний:
Я' — &R = 0.
Каждому значению k соответствует только одно (с точностью
до постоянного множителя) ограниченное решение этого урав-
нения. Действительно, при k > 1 решениями этого уравнения
являются функции R — е*5 и R — е-*6, или (если учесть, что
е£ = г):
R — rk и R ~ г~к.
Но второе частное решение неограниченно при г -> 0 и поэтому
оно не должно приниматься во внимание. Итак, остается толь-
ко решение R = гк. Обозначим его Rk (г):
^(r) = rft.
ю*
292
Часть III
Аналогично проверяется, что значению k — 0 отвечает только
одно ограниченное решение
Подставляя найденные функции Ф (?) и 7? (г) в формулу (5), по-
лучим следующие решения уравнения (1), удовлетворяющие од-
нородным условиям (3) и (4) и представимые в виде произведе-
ния функций одного переменного:
?) = 7?0-Ф0 = 1;
“л (г, ?) = Rk (г) • ФЛ (?) = rk • cos fap\
“k (г, ?) = Rk (r) - ФА (?) = rk • sin fap.
Решением уравнения (1), удовлетворяющим тем же условиям (3)
и (4), будет также сумма функций и0(г, ?), uk(r, ?), пЛ(г, ?) с
произвольными коэффициентами:
и (г, ?) = Ао • 1 + S (А* г* cos fap -I- Bk rk sin £?).	(9)
A=1
Подберем коэффициенты Ao, Bk так, чтобы удовлетворить
неоднородному граничному условию (2). Для этого в ряде (9)
положим г = /:
/ (?) = Ао + £ (Ak lk cos fap + Bk lk sin Л?).
Нами получено разложение функции /(?) в ряд Фурье по об-
щей тригонометрической системе на участке [—я, я]. Коэффи-
циенты этого ряда легко находятся по известным формулам:
4=-?-=-яр(^;
—тс
—к
Bk lk = bk^ J/(?)sin^?d?.
WataUausiisk
знание без границ
Глава 2, § 12 293
Перепишем эти формулы, обозначив (для удобства дальней-
ших выкладок) переменную интегрирования <р какой-либо дру-
гой буквой (например, т); как известно, величина определенного
интеграла не зависит от обозначения переменной интегриро-
вания:
Л = 2^
—К
7t
4 = j / (т) cos Лт dx,
— п
It
— It
sin kx dx.
(10)
Можно доказать, что ряд (9) с этими коэффициентами схо-
дится в любой точке 0 < <р < 2тс, 0 < г < /; его сумма и равна
искомой функции.
Итак, нами получен закон распределения температуры внут-
ри цилиндра; этот закон записан в форме сходящегося ряда (9).
Преобразовав этот ряд, можно найти тот же закон распределе-
ния, записанный в иной форме.
Подставим в ряд (9) коэффициенты Ло, Ak и Bk:
Tt
— it
СО г-	It	1t
+ I cos k<p • j f (x) cos kx dx -f-r* sin j f (x) sin kx dx
k—\ L	— n	—П
Будем считать числа г и <р фиксированными (мы вычисляем зна-
чение функции и (г, у) в произвольной, но фиксированной точке
внутри цилиндра; поэтому г и <р — определенные числа, причем
0<г</). Но тогда постоянная величина	может быть
294
Часть Я/
Г .. . t j	г* sin fc®
подведена под нак интеграла I f (т) cos лт ат, а величина—
—К
— под знак второго интеграла:
после преобразований получаем:
К	00 я
«(Г, ф) = 2Г J/(T)dx + £ j L-cos/e(T—<p)dx. (11)
—it	Л*»! —it
Здесь можно поменять местами знаки суммы и интеграла; это
следует из того, что ряд
X ( 7-Г cos А(т — 9)	(12)
Л=1
равномерно сходится на участке — к < т < к при фиксированных
г и <р: действительно, члены этого ряда по модулю меньше чле-
SM / г \k •
—I — 1
л=»1
А равномерно сходящийся ряд функций от т можно почленно
интегрировать на участке равномерной сходимости.
Итак,
к
\ cos k (т—ф) dz =
—« L а=1
* Здесь М — верхняя граница функции \f (т)| при — я < т < ж.
_	w-, М / г \k
Ряд 2.7 т сходится, как геометрическая прогрессия со знамена
телем -у меньшим, чем 1 (напомним, что г — фиксированное число, стро*
го меньшее, чем I)
Глава 2, § 12 295
WalifflausiSIl
знание вез ерании “ *
СО я
Учитывая это равенство, перепишем по-иному формулу (11):
или
dx.
fe=i
(13)
Сумму, стоящую в квадратных скобках, легко вычислить.
Обозначив эту сумму через S, отношение ~---через q и раз-
ность «с — ф через 6, получим
S = ~	Qk cos АО (где 0 < q < 1).
По известной формуле Эйлера имеет место равенство: eiM =
= cos ЛгО + i sin АО; следовательно, cos АО является действительной
частью функции е1М (это записывают так:cos АО = Re [etM ]). Поэтому
S = ~+ £ <?*cosA0=Re — + J] qkeiM
л=1	L
CO
Для того чтобы вычислить S, надо найти сумму ряда J д* е1М
(это — геометрическая прогрессия со знаменателем qen , по мо-
• Заметим, что, доказав это равенство, мы тем самым доказали схо-
димость ряда (9) при любых <р и г, где 0 < г < /: правая часть этого ра-
венства отличается от суммы ряда (9) только постоянным слагаемым Ло, а
левая часть равна интегралу от суммы равномерно сходящегося ряда (12),
т. е. интегралу от непрерывной функции (и, следовательно, конечному чис-
лу).
296
Часть 111 1
дулю меньшим, чем 1), а затем взять действительную часть этой
суммы:
s = Re 4- + 2‘,‘e'M
=4-+Re
де‘й(\—де ,е)
(1 — де'в)(1— де~л)
1	. р д cos Я -j- iq sin Н — q9
2	1 — 2(/cos«-|-<78
1 I Dp де1*—(?	=
2 +Ке 1-g(
1	, q cos В — q9
2“	1 —2qcosB 4-?а
1 — q9 *
- 2(1—2g cos Я 4-у») ‘
Возвращаясь к старым обозначениям (с? — -у-, 0=т—<р ) и
подставляя полученное выражение для S в формулу (13), по-
лучим, после простых преобразований:
т.
u(rt ф) = j /(т)
— п
________________________dx
I9 — 2r I cos (т — <р) -j- г9
(14)
Этот интеграл называется интегралом Пуассона. Формула (14)
позволяет нам записать искомое решение задачи Дирихле внут-
ри цилиндра в форме интеграла, зависящего от параметров г и <р.
Он существует для всех значений фиг, 0<г</, и удовлет-
воряет уравнению (1), в чем можно было бы убедиться, диф-
ференцируя интеграл (14) по параметрам ср и г и подставляя ре-
зультаты дифференцирования в уравнение (1). Этот интеграл
удовлетворяет также граничным условиям (2), в чем мы убеди-
лись еще тогда, когда наш интеграл Пуассона был записан в
форме ряда (9).
Заметим, однако, что интеграл (14) теряет смысл при г = 1
(подинтегральная функция обращается в нуль при t/ ip и в
бесконечность при т = ф, и говорить об интеграле от такой функ-
ции не имеет смысла). Поэтому когда говорят, что функция (14)
• Заметим, что из этих же преобразований вытекает также следующий
результат:
Im
q sin Я_______
1 — 2д cos Я 4- д9 »
L
где символом Im обозначена мнимая часть комплексного числа. Этот резуль-
тат понадобится нам в следующем параграфе.
4Xata tla nswl!.
знание без границ	“ *
Глава 2, § 12
297
удовлетворяет граничным условиям, то под этим подразумевают
что limn (г, <р) = /(<р) при любом постоянном ф.
г-»/—О
Интеграл Пуассона дает нам решение плоской задачи Ди-
рихле для круга. В данном случае, искомая функция не зависит
от г; поэтому решенная нами задача может быть сформулиро-
вана следующим образом: «найти гармоническую функцию и(г,ср)
внутри круга радиуса I на плоскости Оху, если на контуре кру-
га эта функция принимает значения, задаваемые функцией / (<р)».
Пример. Пусть на поверхности бесконечного кругового од-
нородного цилиндра радиуса I поддерживается следующая по-
стоянная температура:
и --- 0 при — п < <р < 0;
и — Т при 0 < <р < к
(при любых z и t). Внутри цилиндра температура установилась.
Найти распределение температуры внутри цилиндра.
Здесь дело сводится снова к плоской задаче Дирихле: надо
найти гармоническую функцию и (г, <р) внутри цилиндра, если на
поверхности цилиндра эта функция принимает следующие зна-
чения:
/ м I 0
“(г, ?)!,„, = I т
при —<р< 0,
при 0 < <р < п.
Решение дается интегралом Пуассона. Подставляя в него
/(т) = 0 при —тс<т<0 и Т при 0<т<к, получим
и (r*	2n /а — 2r I cos (т — <р) га
о
(15)
Вычислим этот интеграл для положительных значений <р
(0 < < к); для этого сделаем замену переменной: tg —= С.
Заметим, что при изменении т от 0 до я величина пробе-
гает значения от----до ; на этом участке тангенс не-
прерывен и монотонен (напомним, что — фиксированное число,
заключенное между нулем и я); следовательно, такая замена пе-
ременных в интеграле допустима.
298
Часть III
Проделав эту замену переменной, получим
u(r, <р) =
(P-r«)2dC
(/ - г)‘ 4- С» (/ 4- г)а
"4
откуда, после интегрирования, подстановки границ интеграции и
упрощений, окончательно получим
ц(г,
По этой формуле мы можем найти температуру в любой
точке внутри цилиндра при 0 < ф < я. Например в точке
г = 4"’ <Р = "Г бУдем иметь:
и
4) = 4-2arct«3
-•2-1,25^0,87.
п
Убедимся в том, что при г -> / температура стремится к Т
(при 0 < <р < я); действительно, при г -* / — 0 и при любом по-
ложительном ф оба выражения под знаками арктангенсов стре-
мятся к + °о; следовательно, каждое слагаемое в квадратных
скобках стремится к —, и поэтому
л
lim и (г, ф) = Т (при 0<ф<я).
Г-1—о
Напомним, что интеграл (15) вычислен нами только при
0 < ф < я. Читателю предлагается самостоятельно вычислить
этот интеграл при — я < ф < 0 и найти при этих значениях ф
аналитическое выражение для функции и (г, ф).
Задача о стационарном отклонении мембраны. Изучая урав-
нение колебания мембраны, мы заметили, что поверхность
и = и (х, у), по которой располагается мембрана, находящаяся в
покое, удовлетворяет уравнению
(см. главу 1, § 2). Для того чтобы найти функцию и(х, у), на-
до знать, чему равно отклонение мембраны от плоскости Оху в
точках контура. Иными словами, отыскание функции и(х, у)
сводится к решению плоской задачи Дирихле.
^ataittaus^i
знание без границ ч *
Глава 2, § 12
299
Выше было показано, как решается эта задача для круга.
Применяя полученный результат к стационарному уравнению
мембраны, можно найти ее форму, если контуром мембраны яв-
ляется замкнутая кривая, проектирующаяся на плоскость Оху в
окружность радиуса /. Пусть уравнение этой кривой имеет вид
и = / (?) (здесь для каждого угла ф указано, чему равна аппли-
ката соответствующей точки на контуре). Тогда аппликату лю-
бой внутренней точки мембраны можно найти по формуле ин-
теграла Пуассона
/ ч 1 С г/ ч /’ — г»	.
«('. <Р) - 2к J /4-2r/cos (т-ф)4-г» dx’
— к
(14)
где 0 < г < /, — я < ф < я.
Пример. Тонкая пленка натянута на проволочный каркас,
проектирующийся на плоскость Оху в окружность радиуса I с
центром в начале координат; уравнение контура пленки в цилин-
дрических координатах имеет вид: и = hcos2<p(— я< ф< я), г—1.
Найти форму поверхности и = и (г, ф), по которой расположится
пленка.
Решение. В данном случае можно сразу написать реше-
ние в форме интеграла Пуассона:
к
—к
Для вычисления этого интеграла сделаем замену переменной
т— <р = С (при этом границы интегрирования останутся неизмен-
ными: так как подинтегральная функция периодична с периодом
2я, то интеграл от этой функции в границах от —к — ф до
я — ф равен тому же интегралу в границах от — я до я).
Итак,
u(f, т)
/• — 2г/cos С 4-г»
= ^cos2f
— К
—к
f cos 2C__________	__
/’— 2r/cosC4-r*
h(l'— г«) . о
- 2i Sln2?
sin 2С_______jr
2r/cos С 4- г*
—It
Часть 1П
300
Второй из этих интегралов равен нулю как интеграл от не-
четной функции на участке (—л; к).
Следовательно,
Мр— г»)	_
«(л <?) = -а-о7— cos2<p
cos 2С________jr
— 2г/ cos С + г*
—п
Вычисляя этот интеграл (например, с помощью замены пе
ременных tg — = о), получим окончательно:
*
/ ч /:(/» —г9) о 2пг*
и <Г’	= 2к ~ C0S 2?' /9 (/9-?9Г ’
откуда
h г*
и (г> <Р) = -jr cos 2<р.
Таким образом, нами найдено отклонение каждой точки
(г, ф) мембраны от плоскости Оху. Функция -^-racos2y являет-
ся той гармонической внутри круга функцией, которая на кон-
туре круга принимает значения hcos2y. Заметим, что поверх-
ftatattauswili
знание без границ ' *
Глава 2, § 13
301
ность и — г* cos 2ф является гиперболическим параболоидом;
следовательно, пленка, натянутая на заданный в этом примере
контур, примет форму гиперболического параболоида («седла»;
см. рис. 80).
§ 13. Понятие о математическом
моделировании для решения физических
задач
Очень часто две совершенно различные физические задачи
приводят к одной и той же математической проблеме. Мы имели
возможность убедиться в этом на многих примерах; такими фи-
зическими задачами, приводящими к одной и той же математи-
ческой схеме, являются, например, задача о плоскопараллельном
стационарном распределении температуры внутри бесконечного
цилиндра и задача о форме упругой пленки, натянутой на про-
волочный каркас. Ленин говорил: «Единство природы обнаружи-
вается в «поразительной аналогичности» дифференциальных урав-
нений, относящихся к различным областям явлений» (В. И. Ле-
пин. Сочинения, изд. 4, т. 14, стр. 274).
Эта аналогичность дифференциальных уравнений привела
математиков к важному методу решения физических задач —
методу математического моделирования. Суть этого метода за-
ключается в следующем.
Пусть решение интересующей нас физической задачи сводит-
ся к решению некоторого дифференциального уравнения (при
определенных граничных и начальных условиях). Пусть к тому
же уравнению (с теми же граничными и начальными условия-
ми) сводится также другая физическая задача. Допустим, кроме
того, что решение второй физической задачи может быть най-
дено непосредственно — с помощью эксперимента. Тогда найден-
ное решение будет служить решением и для первой физической
задачи (если начальные и граничные условия для этих задач
выбраны так, что они гарантируют единственность решения).
В этом случае говорят, что вторая физическая задача служит
моделью для первой.
Для того чтобы этот метод стал яснее, рассмотрим его на
конкретном примере. Пусть нам надо найти распределение тем-
пературы внутри однородного и изотропного бесконечного ци-
линдра, ось которого направлена вдоль оси Oz, а сечение плос-
костью Оху ограничено кривой X (рис. 81, /). Будем считать,
что распределение температуры является установившимся и плоско-
параллельным, и что на поверхности цилиндра поддерживается
постоянная (не зависящая от времени) температура u—f(xt у).
Часть III
Рассмотрим теперь другую задачу: найти форму упругой
пленки, натянутой на контур /, если известно, что контур I
проектируется на плоскость Оху в кривую К и что для всех то-
чек (х, у) кривой X аппликаты соответствующих точек контура I
находятся по формуле u=f(x, у) (рис. 81, 2).
Обе эти задачи приводят к одному и тому же уравнению
при одном и том же граничном условии
и(х, у) |иа X = /(*, у).	(2)
Только физический смысл величины и в этих задачах различен: в
первой задаче это — температура, во второй — отклонение точки от
плоскости Оху.
Решение второй задачи можно найти непосредственно: для
этого достаточно сделать проволочный каркас, имеющий форму
кривой /, и на него натянуть пленку S. Зная форму пленки S,
мы можем найти температуру в любой точке (х, у, г) внутри
цилиндра; для этого надо измерить аппликату той точки пленки,
которая проектируется на плоскость Оху в точку (х, у). Эта ап-
пликата численно равна искомой температуре точки (х, у, z),
лежащей внутри цилиндра (при любом г). Таким образом, плен-
ка, натянутая на каркас, является моделью для решения задачи
о стационарном плоскопараллельном распределении температуры
внутри бесконечного цилиндра.
Совпадение решений обеих задач вытекает из того, что
уравнение (1) при граничном условии (2) имеет единственное
решение.
NalaHausIM.
знание без границ Ч *
Глава 2, § 14
303
£ 14. Решение уравнения гидродинамики для
плоскопараллельного движения жидкости
внутри цилиндра. Плоская задача Неймана
Пусть внутри бесконечного кругового цилиндра радиуса а,
ось которого направлена по оси Ог, происходит безвихревое
движение несжимаемой жидкости. В этом случае, как известно,
скорость v является градиентом некоторой скалярной функции
и (называемой потенциалом), которая удовлетворяет уравнению:
/л\ц = 0.
Для того, чтобы эта функция могла быть однозначно (с точ-
ностью до постоянного слагаемого) определена, на поверхности
S цилиндра должно быть дано граничное условие
ди
дп
на S
где / — функция, заданная во всех точках поверхности S (это —
проекция скорости и на внешнюю нормаль к поверхности ци-
линдра).
Будем рассматривать только случай плоскопараллельного
движения жидкости, т. е. считать, что f не зависит от апплика-
ты г. Тогда от г не будут зависеть ни скорость и, ни ее потен-
циал и, и уравнение Лапласа запишется в цилиндрических ко-
ординатах следующим образом:
1	t	. 1 д*и _ 0	m
~ 77 + 7? + Тг -ф ~ °-	<*>
а граничное условие на искомую функцию и (г, <р) запишется так:
ди
= /(<?),
(2)
где /(?) — заданная кусочно-непрерывная, ограниченная функ-
ция от <р(—п<9’<к). Известно, что эта задача может иметь
решение только тогда, когда функция / (<р) удовлетворяет сле-
дующему дополнительному условию (см. главу 1, § 4):
/(ф) dl = 0,
304
Часть Hl
где интеграл берется по контуру / того круга, по которому ци-
линдр пересекает плоскость Оху. Так как элемент дуги круга dl
легко выражается через
dl — а • d<p,
то последнее условие может быть записано следующим образом:
j / a d<f> = 0, или
—к
к
р(?)^ = 0.	(3)
—л
Далее, если учесть, что искомое решение и (г, <р) должно
быть 1) ограниченной функцией; 2) периодической функцией от <р:
и (г, <р + 2к) = и (г, <р),
то ясно, что тем же путем, как и в предыдущем параграфе,
можно получить решение уравнения (1) в виде суммы следую-
щего ряда:
и (г, <р) = Ао 4- 2 (Л rk cos + Bkrk sin kq>).	(4)
Л=1
Остается подобрать коэффициенты Ло, Ал, Bk так, чтобы удов-
летворить граничному условию (2). Для этого найдем нормальную
производную Легко видеть, что в каждой точке на поверх-
дп
ности цилиндра внешняя нормаль направлена по координатной
r-линии в сторону возрастания г. Поэтому производная по на-
правлению п во всех точках этой поверхности равна частной
производной Учитывая это, продифференцируем по г обе
части равенства (4):
= J (At k г"-' cos k<f 4- В„ k г"-' sin *?),
дп Hr Д
и подставим г — а:
f (<р) = 2 cos k(f 4- Bkkak~x sin k<p).
A=«l
^alatiaustl^
знание Вез ераниц “
Глава 2, § 14	305
Мы получили разложение функции /(<р) в ряд Фурье по об-
щей тригонометрической системе на участке (—я; nJ. В этом
разложении отсутствует свободный член; это следовало ожи-
дать, так как свободный член ряда Фурье вычисляется по фор-
муле — = 2^- J f (<р) d<f>, а последний интеграл равен нулю в си-
— К
лу условия (3). Остальные коэффициенты легко найти по фор-
мулам Фурье:
Ak k а *"* = 7- J f (ср) cos kydy,
— к
Bk kak~l = — j / (<p) sin kcf>d<f>,
—It
откуда получаем (заменяя обозначение переменной интегрирова-
ния на т):
Аь ~kna^ J	C°S kxdx'
(5)
kna" 1 J
—к
Подставляя коэффициенты Ak и Bk(k> 1) в равенство (4),
получим решение в форме суммы ряда. Постоянное слагаемое Ао
нами не определено; это объясняется самим существом задачи:
потенциал и (г, ср) может быть найден только с точностью до
постоянного слагаемого.
Ряд (4) дает нам решение плоской задачи Неймана для кру-
га (так как плоскопараллельное течение внутри кругового цилинд-
ра вполне определится, если знать закон этого течения в каком-
либо горизонтальном сечении цилиндра, т. е. в круге радиуса а).
Решение задачи Неймана для круга также может быть за-
писано с помощью интеграла, аналогичного интегралу Пуассона.
Для этого надо подставить Ak и Вк (из формул (5)) в ряд (4):
"(г, 9)=Л0+У 4^C/(,)cosfcdl+4^(7(t)sin^
1	—к	—it
306
Часть 1!Г
и проделать здесь те же преобразования, что и при решении
задачи Дирихле в § 9. В результате этих преобразований получим

* Г 00 1
pw 24-
—к L*—i
— cos£(t —<р)
dr.
(6)
Обозначим сумму ряда, стоящего в квадратных скобках, через S,
отношение —через q, разность т — <р — через 0. Тогда
S = ^~qkcoskQ.
(7>
Для того чтобы вычислить сумму этого ряда, предваритель-
но продифференцируем его почленно по 6 (считая число q по-
стоянным, 0< q< I). Это дифференцирование допустимо, так
как ряд, получившийся после почленного дифференцирования,
равномерно сходится на любом участке изменения 0 (все его
члены по модулю не превосходят членов числового сходящегося
00
ряда 2^*
Л-1
Итак,
• Л • sin Л0 = — 2<7* ,s‘n
Л-1	Л-1
Чтобы вычислить сумму последнего ряда, достаточно заметить,
что qk • sin 60 =	и что поэтому £qk sin 60=Im
Мнимая часть ряда ^qkelk* была уже найдена; она равн!
Г-2 geos 04-9* (СМ> сноску на стр- 296>’ ПоэтомУ
__	_____gsinO
-	1 — 2qcosH + q* *
Беря неопределенные интегралы от обеих частей этого равенства
получим
S = — f-i—£-1п01в.- +с=—1- 1п(1 — 2? cos в+ <?>) +С
J 1 — 2 <7 cos 04- q1	2	'	’	•	•
где С — величина, не зависящая от 0.
r\atallaus^!.
знание без ераниц	’ *•
Глава 2, $ 14 307
Возвращаясь к старым обозначениям	, 0 = т —
найдем S:
S =--Lin [1-2-^ cos(t-ф) + £]+С,
или
S =-------g- 1п [а’ — 2га cos (т — ф) 4- г1] 4- 1па + С.
Подставив найденное значение S вместо выражения, стоящего в
квадратных скобках в равенстве (6), найдем функцию и (г, ф),
выраженную в виде интеграла:
1С
и(г, Ф) = ЛО— J/(т)In (а1 — 2racos(т — ф) 4-r’j dx 4-
—к
+ v j/W(C + lna)<ft.
—К
г
Последнее слагаемое-^-J/(т) (С 4-In а) dx равно нулю (так как, по
—1С
к
условию, J f (т) dt — 0); поэтому окончательно
—К
к
«(г, ф) = Л0 —J/(T)ln[a‘ —2racos(r —ф)4-г‘1</т.
—к
(8)
Формула (8) дает нам решение плоско&Ъадачи Неймана в форме
интеграла, зависящего от параметров г и ф. Этот интеграл яв-
ляется аналогом интеграла Пуассона.
Взяв градиент найденного скалярного поля ы (г, ф), мы по-
лучим вектор скорости о частиц жидкости в каждой точке. Ис-
пользуем формулу для grad и в цилиндрических координатах:
, ои - .
gradu = -j?e,+
1 ди - ! ди -
г ~д? ev + ~дг е*'
Производные и — найдутся дифференцированием интеграла
ОГ Оф
(8) по параметру г или ф (легко проверить, что это дифференци-
рование в данном случае допустимо; см. § 2):
308
Часть Ilf
ди __ а f г/ ч — 2г | 2а cos (х — у)
dr ~~ 2п j аа — 2ra cos (х — у) -|- га
ди_ __ о f £ / \ _______2ra sin (х — <р)
ду 2п J ' ' ' аа — 2 races (х — 9) г9
—л
Так как, кроме того, -^- = 0, то окончательно получаем:
~	« Г г / \ — 2r h 2а cos (х — ср)	,	- .
V = grad и = w j / (г) a, _2raC05(;"/.R А • е, 4
—к
I 1 . ° С f(-\ 2ra sin (х — <р)	.	-
+ г 2« J '' ' а» - 2га cos (х - ср)	ra “	'
—к
или, подводя (для сокращения записи) под один знак интеграла:
к
—к
«Г [—г 4~а cos (т—ср)] 4- е<р • a sin (х — ср)
аа — 2га cos (х — ср) -|- ra
dr.
§ 15. Решение уравнения теплопроводности для
шара методом Фурье (стационарный
случай). Пространственная задача Дирихле
для шара
Рассмотрим однородный материальный шар V радиуса / (бу-
дем считать, что его центр находится в начале координат). Счи-
тая, что внутри шара температура установилась, найдем закон
распределения этой температуры; при этом должно быть задано
распределение температуры на поверхности сферы S (предпола-
гается, что в каждой точке поверхности сферы поддерживается
определенная температура, не меняющаяся с течением времени).
Будем искать температуру и в каждой точке как функцию
от сферических координат этой точки: ц(р, 0, у). Тогда уравне-
ние Лапласа /л \ и — 0, которому подчиняется стационарное
распределение температуры, запишется следующим образом:
д*и . 2 ди 1 etg ft ди 1 д*и .	1 д*и _ ~
Ip- "р~ dp + ра dft ' ра d«a pasina« ду* ~ У’
Граничное условие здесь должно быть таким:
и(р, в, ?),_, = /(©, 9),
(2)
^alatfaustik
знание без араниц Ч
Глава 2, § 15 309
где /(0, ф)—заданная ограниченная, кусочно-непрерывная функ-
ция, определенная всюду на поверхности сферы.
Кроме этого условия, естественно наложить на п(р, в,
следующие ограничения:
1) ц(р, 0, <р) ограничена всюду на V;	(3)
2) н(р, 0, <р) периодична относительно <р с периодом 2л:
«(р» в, -j- 2л) = и (р, 0. <р).	(4).
Условия (3) и (4) являются однородными (в отличие от неоднород-
ного граничного условия(2)).
Будем искать, как обычно, искомую функцию и(р, 0, <р) в
виде произведения трех функций одного переменного:
и (р, 0, <?) = /? (р) Т (0) Ф (<f).	(5)
Найдем все решения уравнения (1), представимые в таком
виде и удовлетворяющие однородным условиям (3) и (4). При
этом очевидно, что условия (3) и (4) на функцию и (р, 0, 9) рав-
носильны совокупности следующих условий на функции Z? (р),
7(0). Ф(Ф):
R (р) ограничена на участке 0 < р < /;	(6)
Т (0) ограничена на участке 0 < 0 < л;	(7)
Ф(<р) ограничена и периодична с периодом 2л:
Ф (ф + 2л) - Ф (<р).	(8)
Подставляя м(р, 0, 9) в уравнение (1), получим следующее
тождество:
ЯТФ + — ЯТФ-1- ЯГФ + 4 ЯТ"Ф+  аЪ /?ТФ"=0.
Р	Р	Р	Р sin
Разделим в этом тождестве переменные, перенеся в одну
часть равенства члены, зависящие только от <р, а в другую — от
Р и О:
2 etc н 1
R"T^ — R'T\-—^-RT'-\-^RT"	ф„
- pasinae RT
Приравняв каждую часть этого равенства константе (обозначим
ее — К), получим:
Ф" 4. Хф = 0;
(9)
X
Раsin*в
ят = о.
(Ю)
310
Часть 111
Уравнение (9) вместе с граничными условиями (8) позволяет
найти все собственные числа и собственные функции этой кра-
евой задачи: X = k*, где k = 0, 1,2,...; при этом числу X => 0
отвечает единственное (с точностью до постоянного множителя)
собственное решение Ф0(<р)=1; каждому же числу Х = Л®(Л>1)
отвечает по два линейно независимых частных решения с пери-
одом 2я:
фА (<р) = cos /?<р; ФА (<р) = sin k<?.
Подставим теперь X = Л* (Л = 0, 1, 2...) в равенство (10) и раз-
делим в нем переменные:
R"T + -у R'T +
ЛГ + -Jf RT" -	= 0;
p«R" + 2pR' _ Т’ + T' c,g 8 ~ sin* в
/?	“	— T
Приравняв каждый член этого отношения постоянной величине
{обозначим ее ц), получим:
r+rctg0 + (|x--7i^-)T = O;	(И)
p’R" + 2pR' - pR = 0.
(12)
Уравнение (11) вместе с дополнительным требованием огра-
ниченности функции Т(0) (см. условие (7)) позволит найти р и
Т(0). Сделаем в уравнении (11) замену переменной 0 = arc cost.
Очевидно, что когда 0 пробегает значения от 0 до я, новая пе-
ременная т пробегает значения от 1 до —1. Поэтому требование
ограниченности функции Т(0) на участке 0 < 0 < я равносильно
требованию ограниченности функции T(arccost) на участке
— 1<Т< 1.
Для того чтобы преобразовать уравнение (11) к новой неза-
висимой переменной, выразим Т'е и Т”ве через Т’ и Тхх:
Т'е = Т'х •	= Т'х ’ (— sin 0) (так как т = cos0 и = —sin О);
гвв= [re]e=[-r;-sine]e=-r;.cos0-sine.[r;]; =
= — Г cos0 — sin0-T" -т' = — T’cos0H TL sin“0.
Подставляя найденные выражения для и Т'9 в уравнение
(11) и учитывая, что на участке 0 < 0 < я имеет место:
^alaHausi^ii
знание без ераниц -
Глава 2, § 15
зн
cos0 = т, sin 0 = 4- )/1 — т’, ctg0 == —-т - —, получим:
[- т; • т+< 1 -1*) • л,] + [- г; vt=?] • —-+
V 1 — Т*
+ [|*-т^?]г = о,
или
2< +^_TiLi)r = o.
Это — уравнение Лежандра порядка k. Известно, что оно допус-
кает нетривиальные граничные решения только при jx = m(m4-l),
где т — целые числа, такие, что т > k. При этом каждому соб-
ственному числу p. = m(m-f-l) отвечает собственное решение
РтЬ), где Pkm — присоединенная функция Лежандра (или, в част-
ном случае, при k = 0, полином Лежандра). Возвращаясь теперь-
к старой переменной G (учитывая, что t = cosG). получим все-
возможные нетривиальные решения уравнения (11):
Тk,m (G) ~ Рт (COS G)
(мы обозначили частное решение уравнения (И), соответствую-
щее данному значению параметра k и данному значению числа
P = /n(m-f-l), через Tk.m\ следует помнить, что параметр k про-
бегает всевозможные целые значения от 0 до со, а параметр
т — все целые значения, такие, что т > k).
Вернемся теперь к последнему, оставшемуся нерешенным,
уравнению (12). Подставим сюда (ж = т(т-Ь 1):
р’Я" + 2рЯ' — т (т + 1) Я = 0.
Это — уравнение Эйлера. Решая его обычным путем (с помощью
замены независимой переменной р = е* оно приводится к уравне-
нию с постоянными коэффициентами), получим два линейно не-
зависимых частных решения:
Я = рт и Я = р“т-1.
Второе решение неограниченно при р-+ 0 и поэтому мы его
не принимаем во внимание; итак, каждому значению т отве-
чает только одно (с точностью до постоянного множителя) ог-
раниченное решение уравнения (12):
Rm = f"-
у:
312	Часть III
Подставляя теперь найденные функции Ф (<р), Т (0) и R (р) в
равенство (5), мы получим всевозможные решения уравнения
(11), удовлетворяющие однородным условиям (3) и (4) и пред-
ставимые в виде произведения функций одного переменного;
«л.т(р, 0, ?) = Pm Рт (COS 0) COS Л?;
ЙА.т(р, 0, ф) = ртРт (COS 0) sin6<jp.
(13)
Здесь учтено, что функция Ф (<р) может равняться как cos k ср
(в частности, при k ~ 0, единице), так и sin k ср. В соответствии
с этим нами получены два набора решений для и (р, 0, сру ре-
шения, содержащие cos k ср (они обозначены Uk.m", здесь
k = 0,1,2, т > k), и решения, содержащие sin k ср (они обозначе-
ны Uk.m’, здесь k = 1, 2, 3, т> k).
Для того чтобы найти решение, удовлетворяющее не толь-
ко условиям (3) и (4), но и заданному граничному условию (2),
надо взять сумму всевозможных решений вида (13), предвари-
тельно умножив их на произвольные коэффициенты, и затем
так подобрать эти коэффициенты, чтобы сумма удовлетворяла
граничному условию (2). Обозначив коэффициенты при Uk.m че-
рез dk,m, а при Uk.m — через bk.m, получим:
СО 00
п(р, 0, ср) = Е £ ak m ^ркт(со&&) cos kcp +
Л=0 т==Л
00	00
+ S Еб».и рт Рт (COS 0) Sin k Ср.
k=*l m^k
(14)
Чтобы найти неизвестные коэффициенты, подставим в этот ряд
р = /; при этом левая часть равенства превратится в f (0, ср) (в
силу граничного условия):
00	00
f (0,<Р) = Е Е nft,m/mPi»(cosO) COS kcp +
А=0 m=k
оо оо
+ Е Е bk.m lm Pm (COS 0) Sin k <p.
m=k
^alatlauslii!.
знание Без границ * *
Глава 2, § 15
313
Здесь суммирование производится сначала по т (при постоян-
ном k), а затем по k. Вынесем за знак внутренней суммы со-
множитель cos k или sin k ф, не зависящий от nr.
ОО
/(<=».<₽) = £
Л-0
оо
£ аь,т1тРт (cos 0)
m=k
ОО
— Ьц,т lm Рт (cos 0)
m=k
sin Лф.
COS k ф +
(15)
Зафиксируем теперь временно 0. Тогда равенство дает нам раз-
ложение f (0, ф), как функции от ф, в ряд Фурье по общей три-
гонометрической системе на участке —«<ф<к. Коэффициен-
со
тами при косинусах являются выражения ак,т1тРкт (cos 0), а
m=^k
со
при синусах — выражения bk,m lm Рт (cos 0). С другой сто-
лп—л
ропы, коэффициенты ряда Фурье при совЛф(^>1) для функции
К
/(0, ф) равны ---- J/(0, ф)cos Лф^ф, и аналогично коэффици-
—к
енты при sin k ф. Поэтому при k > О
СО	1С
ak,mlmPm (cos 0) = f (0, ф) COS k(f>d Ф, (15')
— iz
co	n
L bk,mlm Pm (COS	j /(©, ф)в1П k (? d ф. (15")
m=A	—к
Если же k == 0, то соответствующее слагаемое ряда (15) превра-
щается в свободный член ряда Фурье (не содержащий ф). В об-
•	к
Щеп теории мы его обозначили где Qo ~ ~ f f (в, ф) t/ф.
Поэтому
К
(cos О) = -2- J	(15°)
—к
Теперь легко найти все коэффициенты а^т и bk.m- Рассмотрим,
Щщример, равенство (15')« Оно представляет собой разложение
Функции от 0, стоящей в правой части равенства, в ряд Фурье
314
Часть III
по ортогональной системе функций Pj, (cos 0) (где k> 1, фикси-
ровано) на участке О<0<к (см. часть II, § 12). Коэффициен-
ты этого ряда равны с другой стороны, коэффициенты
этого ряда могут быть вычислены по общим формулам для ко-
эффициентов ряда Фурье. Приравнивая их, получаем следующее
равенство:
ак,т 1т =
= (2/2~рп'?М)1'"J РC0Sk*d<p] Р"^C0SSin0d0’
0	—it
откуда
d*.m =	J/(e.9)₽m(cos0)cos^ sin0dfd0 (16')
{здесь k > 1). Аналогично
«’*" =	Р(в’ (cos в) sin sin в df de. (16")
O0,m —
J J f (e,v)P°, (cos 6) sin в dfde.
(16°)
Эти формулы для коэффициентов можно было бы записать с по-
мощью интегралов по поверхности сферы S, если учесть, что
произведение Psin0d<f>d& является элементом поверхности сфе-
ры. Тогда, например, формула (16°) перепишется следующим
образом:
во.™ = И /(e.f)P°m (cos 0)dS.
Подставляя коэффициенты, вычисленные по формулам (16°), (16'),
{16"). в ряд (14), получим решение нашей задачи, записанное в
виде суммы двойного ряда. Члены этого ряда, т. е. функции
РтРт (COS 0) COS k (р И pwPm(COS0)sin k<p,
являются гармоническими функциями, определенными и ограни-
ченными внутри нашей сферы. Эти функции называются сфери-
ческими функциями-, формула (14) дает нам представление иско-
'Nalatiauswii
знание Вез границ “ *
Глава 2, § 15	315
мой гармонической функции в виде суммы ряда, членами кото-
рого являются сферические функции (это выражают словами:
«гармоническая функция разложена в ряд по сферическим функ-
циям»).
В главе 4 будет дано другое решение задачи Дирихле для
сферы; там мы представим искомую функцию в форме интегра-
ла, аналогичного интегралу Пуассона. Однако в силу теоремы
единственности решения задачи Дирихле (эта теорема будет до-
казана также в главе 4), оба решения (то, которое только что
получено в виде ряда по сферическим функциям, и то, которое
будет получено в виде интеграла) различаются только по форме;
по существу же они изображают одну и ту же функцию.
Случай, когда распределение температуры в шаре не зависит
от долготы. Рассмотрим тот случай, когда заданное распределе-
ние температуры на поверхности сферы не зависит от долготы
точки на поверхности, а зависит только от широты 0. Иными
словами, положим, что температура на поверхности сферы не-
изменна вдоль каждой параллели 0 — const. Тогда, как мы уви-
дим, и внутри сферы температура не зависит от ф, причем ряд
(14), служащий для вычисления этой температуры, очень упрос-
тится. Действительно, в этом случае все коэффициенты ak,m (при
/г > 1) и bk,m равны нулю; убедимся в этом. Подставляя в фор-
мулу (16) для ah,m вместо /(0, ф) функцию f (0), зависящую
только от 0, получим
г *
(2m -F l)(m — Л)I
2 (m + A)l nlm
J / (0)Р* (cos 0) cos k ф sin 0d ф d0 =
У+W	(cos0)sine
0
cos ktp dtp dQ — 0.
Аналогично проверяется, что Ьц,т = 0.
Коэффициенты ао.т, вообще говоря, отличны от нуля, но и
для них выражение упрощается:
Г *
2m-F 1
а°’т “ 4п 1т
J/ (0)Pm (cos 0) sin 0 dtp dQ =
J/ (e) Pm (cos 0) sin 0
dQ =
Г *
-—к
) f (tyPm (COS 0) Sin 0 dG,
316
Часть 1П
или, учитывая, что функция Р°т—это /тг-й полином Лежандра Рт,
получим
ао.т — -2Ъ/^I / (в) Рт (cos 0) sin 8d0.
b
(17)
Подставляя bk,m и flo.m в ряд (14), получим решение зада-
чи Дирихле уже в форме простого (а не двойного) ряда:
00
и — ^Яо.тр'” Pm(COS&) ,
m=0
(18)
где коэффициенты ао.т вычислены по формулам (17). Заметим,
что найденное распределение температуры и внутри шара дей-
ствительно не зависит от долготы <р.
Пример. Найти стационарное распределение температуры
внутри единичного шара радиуса 1—1, если на поверхности
сферы поддерживается следующая постоянная (т. е. не изменя-
ющаяся с течением времени) температура:
юо° при о < 8 < 4-;
и
0° при < 8 < к.
Здесь распределение температуры на поверхности сферы не
зависит от долготы ф. Следовательно, распределение температу-
ры внутри сферы также не зависит от <р; закон этого распреде-
ления можно представить в виде суммы ряда (18). Вычислим
коэффициенты этого ряда (по формулам (17)):
ao.m = -^4^J/(e)Pm(cos0)sinede =
О
к
"2
= 2т + 1 f 100 •₽„ (cos в) sine de.
о
Сделаем в интеграле замену переменных cos0 = t:
о	1
«О.т = 50 . (2/71 + 1) f Pm(T)(-dT) = 50(2/77 + 1) f PMdx.
f\alal/aus7cii
знание без границ	“ *
Глава 3, § 1 317
1
В частности, 00.0 = 50 fid? =50;
*	1 „ .
(•	г Зтш — 1
Oo.i = 50-3- ) xdx = 75;	ao.2 = 50«5* \---2----=	0;
____С 5т8 - 3? ,	175 л	275
Оо.з = 50-7- )	2 dr	— 4 » аол ~ 0;	ao,s =	8	» •••	•
6
Подставляя эти коэффициенты в ряд (18), получим несколько
первых членов разложения искомой функции в ряд:
н (р, 0) — 50 р° Ро (cos 0) + 75 р Pt (cos 0) —
- -ф- ₽* Р’ <C0S + “Г* ₽’ Рь(со5в) + - =
— 50-4-75 р cos 0 4—4— р8 •
3 cos’ Н—1
2
8
275 б 63cosbH— 70 cos8H15 cos 0
~8~ Р ' "
В частности, в центре сферы (при р = 0) температура равна
50°; в точке на оси 0z, отстоящей от центра на расстоянии
р — -у- (при 0 = 0), температура приблизительно равна
и (о] » 83,1°, и т. д.
ГЛАВА 3
ИНТЕГРАЛ ФУРЬЕ И ЕГО ПРИЛОЖЕНИЯ
§ 7. Интеграл Фурье
Основным методом решения однородных уравнений у нас
был метод Фурье: мы находили всевозможные решения, пред-
ставимые в виде произведения функций одного переменного и
удовлетворяющие однородным граничным условиям; затем стро-
318
Часть III
или из этих решений ряд с произвольными коэффициентами и
подбирали коэффициенты так, чтобы удовлетворить также и не-
однородным (граничным или начальным) условиям. При этом
для определения коэффициентов мы пользовались разложением
функций в ряд Фурье.
Этот метод действовал безотказно в тех случаях, когда всех
существенно различных решений, представимых в виде произве-
дения функций одного переменного и удовлетворяющих одно-
родным условиям, имеется счетное множество *. Если же окажется,
что таких решений несчетное множество, то построить из них
ряд уже невозможно. В таком случае, процесс суммирования
этих решений приводит нас уже не к ряду, а к интегралу. Для
того чтобы построенный интеграл удовлетворял бы не только
однородным, но и неоднородным условиям, надо определить
входящие в него неизвестные величины. А для этого надо иметь
формулу, аналогичную ряду Фурье; формулу, которая давала бы
представление произвольной функции в форме интеграла.
Настоящий параграф посвящен выводу этой формулы — ин-
тегральной формулы Фурье.
Пусть ограниченная функция /(х), заданная на всей число»
вой прямой, кусочно-непрерывна и кусочно-монотонна на любом
конечном интервале. Пусть она, кроме того, абсолютно интегри*
руема на всей числовой прямой; это значит, что несобственный
интеграл J |/ (х)| dx равен конечному числу. Напомним, что иэ
—со
теории несобственных интегралов отсюда вытекает существование
конечного интеграла от /(х):
J /W dx-
—со
Рассмотрим конечный участок оси Ох (например, отрезок
(—/; /)). Так как на этом участке функция /(х) удовлетворяет
условиям теоремы Дирихле, то она разложима в ряд Фурье по
общей тригонометрической системе:
fix) = -£-+£ /о, cos + bk sin -yi-j,
(1)
* Иначе говоря, если все эти решения могут быть занумерованы кату*
ральными числами. При этом два решения называются существенно разлиЧ*
ными, если их отношение не постоянно.
Глава 3, § 1 319
ШайаиА
знание без «раниц ’ ш
где
1 р	Аят
“*= TjfW COS —dt,
-I
(2)
1 Ь	Аят
bk = T J f (x) Sin —dx.
-i
Равенство (1) справедливо для любой точки непрерывности
функции /(х) на интервале (—/; /) ♦. Зафиксировав точку х из
(—/; /), перепишем равенство (1), подставив в него значения ко-
эффициентов Фурье из формул (2):
/
=4- J ix +
-7
ОО	I
V Г 1 Ьк* f £ / \ Лях .	. 1 Аях С -. ч .	Аят .
2j I —cos ~— J f (т) cos —j— dx -|—j- sin —j— ) / (x) sin —j— dx
*=1	-7	_/
Так как точка x зафиксирована, то выражения cos -^-Hsin^—
можно рассматривать, как постоянные числа (для данного х).
Поднеся их под знак интеграла, перепишем последнее равенство
следующим образом:
/
/(*) = f fb)dx +
-7
или
* Напомним, что равенство (1) сохраняется и в точках разрыва, но в
9том случае в левой части равенства вместо f (х) следует написать
/(х + 0) + /(х~0)
2
320
Часть III
l	co l
f(*)==7/“ J /(T)dx + I7- j/^cos-^- (T —x)tft. (3)
-/	*=l -I
Найдем предел, к которому стремится правая часть равенства
(3) при /-► оо
Заметим, прежде всего, что первое слагаемое в сумме, т. е.
i
Jстремится к нулю при /->оо; это следует из
того, что J / (т) dx стремится к конечному числу (к несобствен-
-I
4-СО
ному интегралу ( f (x)dx), а стремится к нулю,
v	XI
— СЮ
Заметим, кстати, что каждое из остальных слагаемых в на-
шей сумме также стремится к нулю при I -> оо *. Однако сум-
ма (3) имеет бесконечное число слагаемых; поэтому выяснение
вопроса о пределе этой суммы требует дополнительного иссле-
дования.
Не проводя подробного исследования, ограничимся лишь не-
которыми наводящими соображениями.
Прежде всего заменим в сумме (3) интегралы в границах от
— / до I несобственными интегралами в границах от — оо до
+ оо. Каждое слагаемое при этом изменится на величину, стре-
мящуюся к нулю при /^-оо. Примем без доказательства, что
при этом и вся сумма (3) изменится на бесконечно малую вели-
чину; обозначим ее р. Тогда равенство (3) перепишется следую-
щим о. разом:
СО	4-00
f(x) = S-у-	—X)dx4-P,	(4)
А=1 —со
где р О при / -> оо.
• Действительно, для
/
любого k > 0 имеют место следующие неравенства:
(х—х )dx
cos	(х—х) dx <
I
последнее выражение стремится к нулю при
-I
1
I
/ -+ оо ; но тогда и
Ьп
т) cos —L_ (т — х) dx также стремится к нулю
^alafiausi^
знание без границ ’
Г лава 3, § 1	321
Запишем теперь сумму (4) в форме, напоминающей интег-
ральную сумму. Для этого рассмотрим вспомогательную ось ОХ
и разобьем ее положительную полуось точками
1	п 1 2я Ai — ~у ; Л2 -- -у »	. \	Ля ...; лА 		—; ...
At Л2 Л3	Лл Лю
° Я" 2Я зя i i t	Kfi' дл„ 1
Рис. 82
на отрезки длины ДХА - ~ (рис. 82). Тогда равенство (4) мож-
но будет переписать следующим образом:
СЮ	4-0°
/(*) =	/(t)cosXa(t —x)dx-f-p.	(5>
А==1	—оо
4 00
Обозначим выражение -у j /(t)cosX (т — х) dx через Ф (X):
— 00
4-со
ф (х) = -у j f (*) cos X (х — х) dx.
— 00
Это позволит нам так записать равенство (5):
оо
/(х) -	ф(Х*)ДХА-|-₽.
*=!
Полученная сумма напоминает по форме интегральную сум-
му функции Ф(Х). Однако от интегральной суммы она отличает-
ся тем, что: 1) она построена не для конечного отрезка, а для
бесконечного луча О <Х < -|- оо; 2) число слагаемых в этой сум-
ме не конечно, а бесконечно. Тем не менее, ее предел (при
Д ХА -> 0 и, следовательно, при I -> оо) равен интегралу от Ф(Х) в
границах от 0 до оо. Этого факта мы не доказываем.
Итак, переходя в последнем равенстве к пределу при ДХА->0,
пли, что то же самое, при /-> оо, получим (учитывая при этом,
00
/(*) = f <I>Q.)dk;
ь
11 Ю. С. Очан
322
Часть HI
вспоминая
иметь:
теперь определение функции Ф(Х) (см. (6)), будем
СО	4" 00
/(*)= /(t)cosX(t —х) dxjdk.
О —со
или
(7)
со 4"00
Р | Г
f(*) = — /(r)(cosX т cos \х Ь sin Хт sin Хх) сМХ.
О —оо
Разбивая внутренний интеграл на два и вынося за знак внут-
реннего интеграла cosXx и sinXjc (они не зависят от переменной
интегрирования т), получим:
/(*) =
СО	-{-00	-{-00
= Jfcos Хх • — J /(т)совХт^т + sinXz • J /(T)sinXxdT jdX.
О	—со	—со
Введем теперь следующие обозначения:
-|-00	4-00
““ У fWcoslxdx = А (X);	j/(?) siпХт^т = В (X).	(8)
— 00	—00
Тогда предыдущая формула примет вид:
f (х) ~ f [А (X) • cos X х В (X) • sin X х] dX.	(9)
Формула (9) (или равносильная ей формула (7)) называется ин-
тегральной формулой Фурье, а интеграл, стоящий в правой час-
ти этой формулы, интегралом Фурье.
Интегральная формула Фурье является естественным обоб-
щением ряда Фурье: если последний давал возможность пред-
ставить любую ограниченную кусочно-монотонную на (—/; /)
функцию в виде суммы тригонометрических функций aAcos
bk sin	то интеграл Фурье также позволяет представить про-
извольную абсолютно интегрируемую на (—оо; + со) функцию
--- - СлачийЛьиоОля
^atattausf^
знание без границ	’
Глава 3, §2 323
в виде «суммы» тригонометрических функций 4(X)cosXx,
В(X)sink*. Но в случае ряда Фурье круговые частоты* слагае-
мых образуют «дискретный спектр»:
я 2я Зя kn
~Г' ~Г...... / •
В случае же интеграла Фурье круговые частоты образуют «не-
прерывный спектр»: частота X пробегает всевозможные значения
от 0 до -(-со. Говорят, что в первом случае мы имеем сумму
счетного множества слагаемых (их можно занумеровать с по-
мощью натуральных чисел); во втором случае этих слагаемых
несчетное множество; здесь уже приходится процесс суммиро-
вания с помощью ряда заменить процессом интегрирования (это
как бы суммирование несчетного множества слагаемых).
Коэффициенты при «слагаемых» cosXx и sinХлг, т. е. функ-
ции Д(Х) и В(Х), вычисляются по формулам (8). Эти коэффици-
енты играют здесь ту же роль, что и коэффициенты ап и Ьп в
ряде Фурье.
В следующем параграфе будут даны приложения интеграль-
ной формулы Фурье к решению одной задачи математической
физики.
2.	Распространение тепла в бесконечном
стержне
Рассмотрим одномерную задачу теплопроводности: найти за-
кон распределения температуры в однородном стержне, если
известно начальное распределение температуры (при t — 0).
Вудем считать данный стержень бесконечным (т. е. столь длин-
ным, что влиянием температурного режима на концах стержня
можно пренебречь). Кроме того, будем считать, что функция от х,
дающая начальное распределение температуры, абсолютно интег-
рируема (т. е. интеграл от модуля этой функции существует, ес-
ли этот интеграл рассматривать в границах от — оо до 4- со).
Итак, сформулируем нашу задачу.
Требуется найти функцию двух переменных и(х, /), опреде-
ленную для — оо < х < оо, / >0, удовлетворяющую уравнению
ди а д*и
~дГ “ а ~дх*~
* Круговой частотой периодической функции называется отношение чис-
•’1.1 2 я к периоду функции (это отношение показывает, сколько раз период
укладывается в числе 2я). Таким образом, например, круговая частота функ-
ций cos X х и sin К х равна X.
И*
324
Часть III
и начальному условию
и(х, O) = f(x),	(2)
где f(x)— заданная абсолютно интегрируемая на (—оо; -f-оо)
функция.
Будем решать эту задачу методом Фурье. Представим и(х, 1)
в виде произведения двух функций одного переменного:
и(х, t) = X(x)-T(t).	(3)
Подставляя и(х, t) в уравнение и разделяя переменные, получим:
Т' (О = Х"(х)
а» Т (/)	’ Х(х)' •
Приравняем каждое из полученных выражений константе — щ
тогда мы придем к следующим уравнениям для определения X (х)
и Т(0:
Г (0 4- |л а*Т (0 = 0;	(4)
Х"(х)4-Ц Х(х)-.О.	(5)
Из уравнения (4) находим:
Т (t) =Се~^1‘.
Отсюда сразу видно, что р не может быть отрицательным: если
р. < 0, то -* оо при t -> оо, а это не имеет физического
смысла (температура в точке не может неограниченно возрастать
в результате свободного теплообмена).
Таким образом, р > 0. Обозначим для удобства дальнейших
выкладок р = Хя (гдеХ>0). Тогда с точностью до постоянного
множителя
7'(0 = е-х*а,/ .
Кроме того, из уравнения (5) находим:
X (х) = cos X х или sin X х.
Итак, для каждого X > 0 получаем следующие нетривиаль-
ные решения уравнения (1):
(х, t) — е~У'аЧ cosXx;
(х, 0 = е~у*аЧ sin Хх.	(6)
^lalattaus№V
знание Вез границ * *
Глава 3, $ 2
325
Так как уравнение (1) является однородным, то любая ли-
нейная комбинация этих функций также является решением; обо-
значая коэффициент при пх через А (X), а при пх — через В (X),
получим решение, соответствующее числу X, в виде:
нх (х, I) — А (X) е~х’0,/ cos Хх |- В (X) e~**a*1 sin X х.
Никаких граничных условий на функции X (х) и Т (/) не на-
ложено. Поэтому на Х">0 также не накладывается никаких ог-
раничений: X может быть любым неотрицательным числом.
Сумма функций нх(х, t) при различных X и при различных
числах Л (X) и В(Х) также является решением уравнения. Если
бы различных функций пх(х /) было конечное число, то здесь
шла бы речь о конечной сумме; если бы их было счетное мно-
жество (т. е. их можно было бы занумеровать натуральными
числами), — речь шла бы о сумме бесконечного ряда; однако
в данном случае X пробегает всевозможные значения от 0 до-|-°°,
и поэтому здесь процесс суммирования сведется к интегрирова-
нию по X в границах от 0 до 4-°°:
ОО
и (х, i) J [Л (Х)с“х,н,/ cos X X 4 В (к)е~^аЧ sin X х] dX. (7)
о
Конечно, приведенных рассуждений еще не достаточно для
того, чтобы быть уверенным, что функция (7) является решением
уравнения. Для того чтобы убедиться в этом, надо продифферен-
цировать (7) по х и по t и результаты дифференцирования под-
ставить в уравнение:
оо
«; (х, О = J [ А (X) (- Х2«2) см/ cos X X 4-
0
4- В (X) (— Х2«2) е~*аЧ sin X X ] d X;
ОО
<х(х, 0 = f [Д(Х)(—Х2)^~Мв,/ cos X X 4- В (X) (—X») е-и,>ч sin X х] dX.
о
Здесь мы применили дифференцирование по параметру (в первом
случае — по параметру t, во втором случае — по параметру х);
из общих теорем о дифференцировании интеграла по параметру
вытекает допустимость этого дифференцирования (при условии,
что Л (X) и В (К) абсолютно интегрируемы в границах О <Х < 4-со).
Подставляя найденные и( и utt в уравнение (1), получим, что
ut а2“хх-
326	4acTb Jn
Значит, интеграл (7) является решением данного уравнения при
любых абсолютно интегрируемых функциях Л(Х) и В (к). Подбе-
рем эти функции так, чтобы интеграл (7) удовлетворял задан-
ному начальному условию. Для этого подставим в этот интеграл
t — 0 и приравняем его f (х):
f (х) = J [Л (X) cos X х 4- В (X) sin X х] d X.
Согласно интегральной формуле Фурье, заключаем, что по-
следнее равенство будет выполняться, если в качестве А (X) и В (X)
взять коэффициенты Фурье:
+ °°
Л (X) = — J f (т) cos X т d т;
(в)
В G) — J f (t) sin X т d т.
— со
Теперь можно считать нашу задачу уже решенной: вычислив
коэффициенты Л(Х) и В(Х) по формулам (8) и подставив их в (7),
получим искомое решение уравнения. В силу теоремы единствен-
ности решения (мы ее не доказываем) заключаем, что других ре-
шений, кроме найденного, наша задача не имеет.
Преобразуем найденное решение, подставив выражения для
Л(Х) и В(Х) в равенство (7):
00	4" 00
и(х, 0 = j*ё~х*аН[cosXх • ~ j /(т) cosXтdт 4-
0	— со
-f- со
4- sin X х-J /(T)sinXrdi:]dX.
— 00
Внося cosXx и sinXx под знак внутренних интегралов и произ-
водя очевидные преобразования, получим:
со	+ 00
и (х, t) = ~ У е~г'аЧ f f (т) cos X (т — х) d х d X.
О	— оо
Изменим в этом двойном интеграле порядок интегрирования:
и (х, /) =
vf JfW«-X,“‘'cosX(x
— оо О
— х) d X d х.
flataUausllk
знание без границ ’ *
Г лава 3, § 2
327
Функцию f (?) можно вынести за знак внутреннего интеграла (по X);
после этого внутренний интеграл можно будет вычислить (он не
содержит функции /(?)):
+ °°
0 = V J fb)
— 00
е x’"v cos X (т — х) d X
d t =
4 co
— ©о
е d х.
Здесь применена формула
Je ах* cosfixdx =е 4“ (где а > 0),
о
выведенная в
Итак,
§ 2, главы 2 (стр. 234—237).
и (х, 0 =
1
2а У п t
(1-ху
/(т)е dt.
(9)
Заметим, что этот интеграл, вообще говоря, довольно труден
для вычисления: даже в тех случаях, когда /(х)— кусочно-по-
стоянная функция, он не берется в элементарных функциях. Од-
нако мы будем считать задачу решенной, если нам удастся вы-
разить этот интеграл через функцию Erf.
Пример. Найти закон распределения температуры внутри бес-
конечного стержня, если в начальный момент температура на участ-
ке— /^х<;/ была 1030°, а в остальных точках стержня 30°.
Задача сводится к решению уравнения
ди
dt
д*и
— а
дх*
с начальным условием
и(х,
1030 при — I < х < Г,
30 при | х | >/.
Функция, задающая начальное распределение температуры, не
является абсолютно интегрируемой на (—оо; -f-co). Для того
чтобы исправить положение, сделаем замену переменной и = и —30
328
Часть III
(где и — новая неизвестная функция); тогда и удовлетворяет урав-
нению	_
ди 2 д»и
dt и дх»
и начальному условию
и (х, 0) =
1000 при — I х • /;
0 при | х | > /.
Здесь уже функция /(х), задающая начальное условие, аб-
солютно интегрируема. Поэтому для нахождения и (х, t) можно
применить формулу (9):
и (х, 0 =
1 г _ <х~х>*
—77=7- 1000-е	4«''dx.
2а У nt ,)
-/
Для того чтобы выразить и (х, t) через функцию Erf (через одни
только элементарные функции ее выразить нельзя), заменим пе-
ременную интегрирования т переменной г, связанной с х соотно-
шением:  т ~~L  = z\ тогда х - x-|~z-2al// , -—— dz.
2а ft	r 2а ft
Следовательно,
1-х
2а УГ
•ООО	С ~	—
и (х, /) - 2а	J е • 2а \ t dz —
-l-x
2а VT
l-x
2a V Г
2	.
- 500-77=	e~* dz F)OO
1 Tt J
-l-x
2a VT
Для того, чтобы найти и(х, t), достаточно вспомнить, что
и = и -}- 30:
/ — х ~ г —1—X
---- =--Erf-----
2а^ t	2а ft
и (х, 0 = 500fErf - '~i- -Erf ~(7- 1 + 30.
L 2а Vt	2а Vt J
На рис. 83 изображен график распределения температуры
и (х, /) внутри стержня в начальный момент времени (/0 = 0), а
ftalattauswii
знание без границ Ч *
329
Глава 3, § 2
также графики распределения температуры в некоторые последую-
щие моменты времени (/х < /2 < /з)-
Импульсная функция. Пусть начальное распределение темпе-
ратуры в стержне задано следующим образом: температура равна
пулю всюду вне весьма малого участка [х0, х0 4- е], а на этом
участке температура равна и0. Иными словами, можно считать,
что стержню, температура которого всюду была равна нулю, пе-
редано на участке [х0, х0 4- е] количество тепла ф = есГи0*,
вызвавшее мгновенное повышение температуры на этом участке
па величину и0.
Функцию, задающую начальное распределение температуры
в этом примере, можно выразить через импульсную функцию.
Импульсная функция &Хо(л), введенная Дираком, определяется
следующим образом: она равна 4- оо в точке х0 и нулю всюду вне
этой точки; интеграл от этой функции по любому отрезку, содержа-
щему внутри себя точку х0» равен единице.
Эта «функция» не является функцией в точном математиче-
ском смысле слова (потому что интеграл от функции, которая
всюду, кроме одной точки, равна нулю, не может равняться еди-
нице). Однако импульсную функцию Дирака можно приближенно
заменить настоящей функцией, свойства которой очень близки
к функции Дирака, а именно функцией, равной нулю вне очень
малого участка [х0, х0 4~ £] и равной на этом участке (график
этой функции см. на рис. 84). Очевидно, что интеграл от такой
функции (как и интеграл от функции Дирака) равен единице на
любом участке, включающем отрезок [л0, х0 4- е].
• Где с — коэффициент теплоемкости, Г — линейная плотность массы
стержня.
330
Часть III
В дальнейшем под импульсной функцией 6Х# (х) мы будем под-
разумевать как саму функцию Дирака, так и ее приближенное зна-
чение:

1	г
—	на (х0, х0 + е],
О	вне [х0, х0	е].
В этих обозначениях функция, дающая первоначальное рас-
пределение температуры в рассматриваемом примере, может быть
выражена через импульсную функцию следующим образом:
" о = ~7F <*>•
где Q — количество тепла, сообщенного в начальный момент ма-
лому участку стержня [х0, х0 + е). Начальная температура и0 этого
Q
участка равна
Найдем закон, по которому будет изменяться температура
стержня с течением времени. Согласно формуле (9),
1 > 0
— 00
Так как подинтегральная функция равна нулю всюду вне отрез-
ка [х0; х0 + е], а на нем В (т) = —, то
1 с 0
u(x,t)~ 2аУ^Г J "с1Т * е 4аЧ dx‘
ХО
WaiaUauswk
знание без границ “ w
Глава 3, § 2 331
Наконец, в силу малости участка [х0, х0 + е] можно считать, что
непрерывная функция е *и*1 всюду на этом отрезке равна зна-
чению этой функции при t - х0. Поэтому
и (х, I)
I _ Q
2а V nt с Г в
(хо—х)*
е
или
1	_ <х»—*)*
и (х, t) за-------иое *а*‘ е.
'	' 2а У nt	0
(10)
На'рис. 85 представлены графики распределения температуры для
некоторых моментов времени t.
Рис. 85
Вернемся теперь к общей задаче распространения температу-
ры в бесконечном стержне. Пусть нам задано какое-то перво-
начальное распределение температуры /(х). Будем рассматривать
эту начальную температуру как результат одновременного воз-
действия множества тепловых импульсов: разбив мысленно весь
стержень точками хД—оо < i < оо) на элементарные участки Дхр
мы можем считать, что на каждом таком малом участке задан тепло-
вой импульс, поднявший температуру на этом участке до f(x,)
(см. рис. 86).
Тогда, согласно формуле (10), закон распределения темпера-
туры, вызванной тепловым импульсом на участке Дхр таков:
1	(x<~x)8
и,(х,/) = ’^7;Г/(х')е Лх‘
332
Часть III
(здесь роль х0 играет xt, роль и0 — начальная температура f (xt),
роль е — длина элементарного участка Дх,).
С другой стороны, воздействие всей начальной температуры
f (х), как известно, задается интегралом:
и t) =
(т-Х)«
dt.
Заменяя этот интеграл интегральной суммой, соответствующей
разбиению всей прямой на участки bxit получим:
«U 0 = 1	,а" йх‘-
I- —00
т. е.
-I 00
V*
U (х, t)= 2j Щ (х> О-
I---со
Итак, общее воздействие, обусловленное всей начальной тем-
пературой, может быть получено суммированием тех элементарных
воздействий, которые произошли от каждого теплового импульса
в отдельности. Точнее говоря, температура в какой-либо точке X
в некоторый момент времени t может быть получена суммирова-
нием температур, которые получились бы в этой точке в момент
времени t в результате воздействия каждого начального импульса
в отдельности.
^alatiaus^i
Глава 4, § 1	333
ГЛАВА 4
ОБЩИЕ СВОЙСТВА ГАРМОНИЧЕСКИХ ФУНКЦИЙ.
ФУНКЦИЯ ГРИНА
$ /. Общие свойства гармонических функций.
Формулы Грина. Метод сеток
Целью настоящей главы является изучение общих свойств
гармонических функций; это изучение приведет нас к доказатель-
ству теоремы о единственности решения задачи Дирихле (конец
§ 1); затем мы познакомимся с одним общим методом решения
задачи Дирихле (метод функций Грина) и, используя этод метод,
выведем формулу для решения задачи Дирихле в случае сферы;
при этом нам удастся записать гармоническую функцию в форме
интеграла, зависящего от параметров, аналогичного интегралу
Пуассона.
Предварительно выведем некоторые формулы, связывающие
тройные и поверхностные интегралы.
Пусть р и q — две скалярные функции, заданные и непрерыв-
ные всюду в области V и на ее границе. Будем считать, что эти
функции имеют непрерывные частные производные до второго
порядка включительно; будем считать, кроме того, что поверх-
ность S области V является гладкой или кусочно-гладкой.
Рассмотрим поверхностный интеграл
?ldS,
где п—еди-
S
ничный вектор внешней нормали к поверхности S. Сведем этот
интеграл к тройному. Так как производная функции в каком-либо
направлении равна проекции градиента на это направление, то
~ — gradq-nt и поэтому
П p~LdS = jjp-gradq-ri’dS.
*s	's
Применив к этому интегралу формулу Гаусса-Остроградского,
получим:
JJ p^LdS = j'Jpgradtz-ndS = Jj Jdiv(pgrad^)dV.
s	*s	V17
(1)
334
Часть lit
Под знаком интеграла стоит дивергенция произведения скалярной
функции р на векторную grad q. Применим формулу для вычисле-
ния дивергенции произведения (см. часть I, § 13):
div (р grad q) = р • div grad q -|- (grad p • grad q) ~
= P' Q + (gradp-gradq).
Подставляя это в равенство (1), получим окончательно:
• /л\ qdV + J J J (grad р • grad q) dV.
s
(2)
Эта формула называется первой формулой Грина.
Поменяв ролями р и q, вычислим теперь
^dS:
s
Щ (grad grad p)dV.
(3)
Вычитая почленно из равенства (2) равенство (3), получим вто-
рую формулу Грина:
Применим теперь эту формулу к тому случаю, когда одна из
функций (например, q) является гармонической всюду внутри об-
ласти V, а другая (р) равна где г — расстояние от перемен-
ной точки М области V до некоторой фиксированной точки Мо,
лежащей внутри этой области. Не-
посредственно применить вторую
формулу Грина к этим функциям
мы не можем, так как функция
р -у- терпит разрыв внутри V
(она стремится к бесконечности
при М -> Мо). Поэтому мы приме-
ним эту формулу, взяв в ней
вместо области V область Vt, ко-
торая получится, если исключить
из V шар радиуса е с центром
в точке Мо (рис. 87). Но тогда и
Яа1аНаи$Ж
знание без границ * w
Глава 4, § 1
335
граница области изменится; граница области Ув составится из
двух поверхностей: поверхности S, которая ограничивала
область V, и сферической поверхности Se. В связи с этим вместо
интеграла по поверхности S нам придется написать сумму двух
интегралов: по S и по St.
Тройной интеграл, стоящий в правой части равенства, равен ну-
лю; это вытекает из того, что функции q и -у- являются гармо-
ническими всюду в области Vt, и, следовательно, лапласианы
этих функций тождественно равны нулю *. Поэтому последнее
равенство может быть переписано следующим образом:
О	«Sg
Это равенство справедливо при любом е > 0. Перейдем в этом
равенстве к пределу (при е -> 0). Для этого оценим интегралы
по поверхности St и посмотрим, к чему они стремятся при е -> 0:
JJ г дп
так как ~ ВСЮДУ на $,•
Далее — = (grad^-n) и, следовательно,
дд
дп
= | (grad «7-п)|
< I grad q |; последнее выражение ограничено в шаре достаточно
* Функция q гармонична по условию; что же касается функции —, то
ее гармоничность легко проверяется, если записать эту функцию в виде:
___________________1________________
Р	V (х — хв)« + (У — '/о)’ 4- (г — ?о)’ ’
д9р д*р д9р
найтн ее вторые производные -^а~,	и подставить их в выражение
для лапласиана.
Часть III
336
, а
малого радиуса, так как | grad q | =
да да да
частные производные	по условию, непрерывны и,
значит, ограничены в этом шаре. Пусть |grad^|< А.
Тогда
--4-S
£
— • А -4 к е1 = 4 it еД.
е
Произведение
довательно, и
s.
4 « е А стремится
к нулю при е -> 0; сле-
2) Рассмотрим интеграл
Д=— dS. Поскольку нормаль
дп
к сфере St направлена но радиусу, то производная по нормали
равна частной производной по г, взятой с обратным знаком (нор-
маль п, внешняя по отношению к области Vt, направлена внутрь
сферы; поэтому в направлении этой нормали величина г убывает).
Итак,
2 •
дп “ дг
На поверхности St имеет место г ~ г. Поэтому

S,
5,
5.
=	• 4 к е2 = 4 к • q (/Иср).
Здесь мы применили теорему о среднем к интегралу ^qdS\ точка
Л1ср— какая-то точка, лежащая па поверхности сферы радиуса е
(с центром в точке Л40); при е -> 0 эта точка стремится к Мо, а
значение функции q в точке Мср стремится к q(M0) (в силу не-
прерывности этой функции).
Итак,
lim ]
-°
dS = lim 4 к g(Mcp) —4 ~ q (Mo).
«•♦о
Г лава 4, § 1
337
^alallau^!.
знание без границ ’ w
Перейдем теперь к пределу (при е -> 0) в равенстве (5); учи-
тывая пределы, к которым стремятся интегралы по S, , а также
учитывая, что интегралы по S (в равенстве (5)) не зависят от е,
получим:
откуда
-q- - q	dS — 4nq (Мо) - О,
дп	дп /
Эта формула дает значение гармонической функции q в любой
внутренней точке Мо области V. Однако эта формула не реша-
ет еще ни задачи Дирихле, ни задачи Неймана: для вычисле-
ния функции q(M) по формуле (6) надо знать и значения самой
функции, и значения ее нормальной производной всюду на по-
верхности S. В случае же задач Дирихле или Неймана нам за-
дана на поверхности S только одна из этих величин (только q—
п	да
в случае задачи Дирихле или только ~ — в случае задачи
дп
11еймана).
Итак, непосредственно эта формула не решает указанных
задач. Однако после некоторых преобразований она сможет
быть приспособлена для решения задачи Дирихле в тех
случаях, когда поверхность 5 имеет сравнительно простой вид
(см. § 2).
В настоящем параграфе будут рассмотрены некоторые при-
ложения формул Грина и формулы (6) к исследованию свойств
гармонических функций и к доказательству единственности ре-
шения задачи Дирихле.
1. Если во вторую формулу Грина подставить р~\, а в
качестве q взять произвольную гармоническую функцию, то мы
получим
*-^dS-O.	(7)
дп
Таким образом, мы снова установили, что интеграл по поверх-
ности S от нормальной производной гармонической функции ра-
вен нулю.
2. Пусть S — сфера радиуса а, внутри которой задана гар-
моническая функция q. С помощью формулы (6) легко вычис-
338
Часть Ш
лить значение этой функции в центре сферы, если известны ее
значения на поверхности сферы. Действительно, если Мо — центр
сферы S, то внешняя нормаль к поверхности сферы направлена по
радиусу, в сторону возрастания радиуса. Поэтому производная по
нормали равна производной по радиусу:
Итак,
а»
<S
Всюду на поверхности сферы имеет место равенство г = а. Поэтому
S	v>
Но С f	dS = 0 (см. (7)). Поэтому
J J дп
S
(8)
Этот результат может быть сформулирован следующим образом:-
означение гармонической функции в центре сферы равно сред-
нему арифметическому ее значений на поверхности сферы».
Покажем, что выражение, стоящее в правой части равенст-
ва (8), действительно можно принять за среднее арифметичес-
кое значений функции на поверхности S. Разобьем S на п ма-
лых по диаметру, равных друг другу по площади, элементар-
ных площадок Д5Л. Выберем внутри каждой из этих площадок
произвольную точку Mk и рассмотрим среднее арифметическое
значений функции в этих точках. Оно равно
л
4 S ч w.
А=1
Неограниченно уменьшая диаметры этих площадок (но сох-
раняя каждый раз все элементарные площадки одинаковыми по
площади), получим в пределе при л-> оо число, которое естест-
^iataUaus^i
знание Сезграниц '*
Глава 4, § 1
339
пенно назвать «средним арифметическим значений функции на
.S». Вычислим, чему оно равно:
л
среднее арифметическое равно lim — У ?(Ч)=
л - оо п
А«=1
А=1
Выражение, стоящее под знаком предела, мы умножили и раз-
делили на Д5, т. е. на площадь элементарной площадки при
л
числе делений, равном л. При л -► оо сумма У Д5 стре-
мится к интегралу
jj q(M)dS (эта сумма является интегральной);
s
выражение же л-Д5, стоящее в знаменателе, при любом л рав-
но площади всей сферы S (т. е. 4тша).
Итак,
среднее арифметическое равно

Замечание. Приведенные рассуждения приложимы не толь-
ко к поверхностным интегралам, но и к двойным, тройным и т. д.
Так, например, средним арифметическим для функции f(x, у, г)
трех переменных в области V называется число
ТгЩЛ*. у’ dV<
средним арифметическим функции f(x) одного переменного на
отрезке [л; Ь] — число
ь
b=-a^fMdx
И т. д.
3. Теорема о наибольшем и наименьшем значениях гармо-
нической функции. Если функция q(M) является гармонической
внутри связной * замкнутой ограниченной области V и непре-
рывной на ее границе, то наибольшее и наименьшее значения
этой функции могут достигаться только на границе области
* Напомним, что область V называется связной, если любые две внут-
ренние точки этой области можно соединить непрерывной линией, целиком
лежащей внутри области.
340
Часть 111
V (за исключением того случая, когда q (/И) постоянна всюду
в V).
Поясним смысл этой теоремы. Так как функция q(M), по
условию, является непрерывной в замкнутой ограниченной об-
ласти V, то она ограничена в этой области и достигает в ней
наибольшего и наименьшего значений. Где же находится та
точка /Ио, в которой функция дости-
гает, например, наибольшего значе-
ния? Докажем, что она не может
находиться внутри области; следо-
вательно, она находится на ее гра-
нице.
Докажем это от противного.
Пусть функция q(M) достигает своего
наибольшего значения в точке
лежащей внутри области V (рис. 88).
Если Мо является внутренней точкой
области, то вокруг Мо можно опи-
сать шар (с центром в ЛЕ), целиком
принадлежащий области V. Обозна*
чим радиус этого шара через р, Д
его поверхность — через Sp . Тогда
по ранее доказанному свойству гар-
монических функций, имеет месте
равенство
sp
С другой стороны, имеет место очевидное равенство:
vW=-^^<i(M0)dS.*
sp
Вычитая почленно из второго равенства первое, получим:
sp
или
И[<7(Ч)-?(Л1)Н5 = 0.
sp
* Для вычисления этого интеграла достаточно вынести постоянный
множитель q (Л10) за знак интеграла и затем учесть, что jj dS — Sp = 4«ра
s₽
ftataHausisk
знание без границ “ w
Г лава 4, § 1	341
Подинтегральная функция здесь непрерывна и неотрицательна
(так как q (Мо), по условию, является наибольшим значением
функции в области V); но интеграл от непрерывной неотрицатель-
ной функции может быть равен пулю в том и только в том слу-
чае, когда эта функция тождественно равна нулю в области
интегрирования.
Итак,
q(M0) — q(M) = 0, или q(M) — q(M0)
всюду на Sp- А так как все эти вычисления можно применить
и к сфере любого радиуса, меньшего чем р, то,
q(M) — q(M0)
всюду внутри шара радиуса р, т. е. в этом шаре функция по-
стоянна.
Докажем теперь, что если внутренняя точка Мо является
точкой наибольшего значения в области V, то функция будет
постоянной не только в окрестности точки Мо, но и всюду вну-
три области V. Возьмем для этого произвольную точку
внутри V и соединим ее с точкой Мо непрерывной кривой /, ле-
жащей внутри этой области (что можно сделать в силу связности
области V; рис. 89). Пусть а>0 — наименьшее расстояние между
точками этой кривой и точками границы области V. Опишем во-
круг Л40 шар радиуса р, где р — какое-либо число, меньшее, чем а;
он лежит внутри V; по доказанному, внутри этого шара функция
постоянна. Сместим теперь центр шара вдоль по кривой I так,
чтобы новый центр MQ не вышел за пределы ранее построенного
шара. Тогда и внутри нового шара функция всюду прини-
мает постоянное значение, равное /(Мо) (это следует из
того, что в точке М'о функция принимает наибольшее в об-
ласти V значение, так как f (.М') = /(Мо)). Перемещая таким
образом центр шара все дальше и дальше, совместим его, в кон-
це концов, с точкой Mt. Рассуждая так же, как и при переходе
от точки Мо к точке Мо, убеждаемся, что значение функции во
всех точках кривой / одно и то же; в частности, f (Mt) — f (М).
Итак, если бы гармоническая функция достигала наибольше-
го значения внутри области V, то эта функция принимала бы
во всех внутренних точках области одно и то же значение;
в силу непрерывности, она должна была бы принимать это же
значение и на границе области; иными словами, эта функция
была бы постоянной в области V.
342
Часть Itf
Следовательно, если гармоническая функция не постоянна,
то она не может достигать наибольшего значения внутри об-
ласти V. Значит, точка, в которой функция достигает своего наи-
большего в области V значения, находится на границе этой
области.
Рис. 89
Аналогично доказывается, что для непостоянной гармони-
ческой функции точка, где функция достигает своего наимень-
шего значения, также находится на границе области V.
Замечание. Частным случаем гармонической функции
является линейная функция q = Ах 4- By + Cz + D. Для нее до-
казанное свойство совершенно очевидно: поверхностями уровня
для такой функции являются параллельные плоскости Ах-\-Ву +
+ Cz + D~ const; если точка Л10 является внутренней точкой обла-
сти V, то на плоскостях уровня, лежащих по одну сторону от точ-
ки Мо, функция принимает значения, меньшие, чем q(M0)t
а на плоскостях, лежащих по другую сторону, — большие, чем
7(М0) (рис. 90). Но это означает, что точка MQ не является ни
точкой наибольшего, ни точкой наименьшего значения функ-
ции q(M).
Из доказанной теоремы следует, что это свойство выпол-
няется не только для линейных, но и для любых функций, гар-
монических в связной области.
4. Теорема о единственности решения задачи Дирихле. Если
две функции, гармонические внутри замкнутой ограниченной
связной области V и непрерывные на ее границе, равны dpyi
другу всюду на границе области V, то они равны друг другу и
всюду внутри V. Иными словами, гармоническая внутри обла*
WalaHausA
знание без границ ' ш
Глава 4, § 1 343
emu V функция однозначно определяется своими значениями на
границе области.
Доказательство. Пусть qi(M) и qt(M)— две гармони-
ческие функции, принимающие одинаковые значения на границе
области V. Обозначим через q (Л4) разность этих функций
qtM^q^Mj-q^M).
Тогда q(M) — гармоническая внутри V функция, равная нулю
всюду на границе области V. Докажем, что она равна нулю также
всюду внутри V. Допустим, что внутри V найдутся точки, в ко-
торых функция отлична от нуля, например положительна. Тогда
и наибольшее значение функции должно быть положительным.
Но на границе функция равна нулю; следовательно, наибольшее
значение функции достигается во внутренней точке области V.
К это невозможно, так как q(M) — гармоническая функция. Ана-
логичное противоречие мы получили бы, если бы внутри области
V оказалась точка, где функция отрицательна.
Итак, во всех точках области V функция q(M) должна рав-
няться нулю:
q(M)^0,
откуда
qt(M) — q2(M) = 0,
что и требовалось доказать.
Приведем пример, который на первый взгляд опровергает
эту теорему.
Пример. Рассмотрим две функции: qt(M)^l и q2(M)—
= —"" •	; легко подсчитать лапласиан для каждой из
Ул1 4- |/а 4- z4
этих функций и убедиться, что /	= 0, Ул xga == 0. На гра-
нице шара единичного радиуса с центром в начале координат эти
функции принимают одинаковые значения (и та, и другая функ-
ция равны единице всюду на поверхности единичной сферы). И
вместе с тем эти функции не равны друг другу внутри сферы.
Чем объясняется кажущееся противоречие с доказанной теоремой
единственности? Это противоречие раскрывается просто: 0Й(М) не
является гармонической внутри единичного шара (хотя ее лапла-
сиан и равен нулю); дело в том, что она терпит разрыв внутри
шара, в точке (0; 0; 0). Единственной же гармонической функцией,
равной единице всюду на поверхности шара, является функ-
ция ^(М)^ 1.
344
Часть Hi
Замечание. Теорема единственности решения задачи Ди-
рихле доказана нами для того случая, когда на поверхности S
(где S — граница области V) задана непрерывная функция. Одна-
ко можно доказать, что эта теорема остается в силе и для бо-
лее общего случая, когда функция, заданная на поверхности S,
кусочно-непрерывна и ограничена на этой поверхности.
Метод сеток для приближенного решения задачи Дирихле.
Теорема о том, что значение гармонической функции в центре
сферы равно среднему арифметическому ее значений на поверх-
ности, может быть применена к приближенному решению задачи
Дирихле.
Для простоты изложения ограничимся плоской задачей Ди-
рихле. Заметим, что теорема о среднем арифметическом справед-
лива и для гармонических функций от двух переменных; только
в этом случае она формулируется следующим образом: значение
гармонической функции в центре круга равно среднему арифме-
тическому ее значений на контуре круга.
Пусть нам задана область а на плоскости, ограниченная
прямоугольником /, стороны которого соизмеримы. Требуется
найти гармоническую функцию, определенную в области о и
принимающую заданные значения на контуре I. Для того, чтобы
решить эту задачу, разобьем каждую из сторон прямоугольника /
на несколько малых, равных друг другу, отрезков (это можно
сделать, так как стороны прямоугольника, по условию, соизме-
римы). Проведя через точки деления прямые, параллельные сто-
ронам прямоугольника, мы разобьем область а на несколько
квадратов (рис. 91). Будем считать нашу задачу решенной, если
WalaUaustlk
знание без границ * ш
Г лава 4, § 1
345
нам удастся вычислить значения искомой гармонической функции
во всех узлах построенной сетки (т. е. во всех вершинах постро-
енных малых квадратиков).
Обозначим через М/, k точку пересечения i-ой горизонтальной
прямой с Л-ой вертикальной (i — О, 1, 2, ... т\ k — 0, 1, 2,... л),
а через а{ Л — значение искомой гармонической функции в точке
Mi, k • Проведем для каждой точки Mi, *, лежащей внутри пря-
моугольника, окружность с центром в этой точке и с радиусом,
равным стороне малых квадратиков. Тогда, согласно теореме о
среднем арифметическом, можно написать:
/(М/,л) =
I ( M/-I, а) + I ( MI, *-l)+ f (^/4-1. л) + f (М/, A4-I)
4
ИЛИ
а1. k ” ~4 (ai~l, k I а1, Л-1 1 а/+!,Л '1 а1, Л+1)-
Это равенство можно рассматривать как уравнение с неизвест-
ными числами а/л, a{_t л и т. д. Число этих уравнений равно
числу неизвестных (и уравнений, и неизвестных будет ровно
столько, сколько имеется, узлов сетки, лежащих внутри прямо-
угольника, т. е. (т—1)(л—1)). Эта система всегда разрешима.
Практическое ее решение сопряжено с известными трудностями;
однако эти трудности легко преодолимы, если пользоваться для
вычислений счетной машиной. Решив эту систему, найдем зна-
чения искомой гармонической функции во всех узлах построен-
ной сетки (т. е. во всех точках M/t k )•
Совершенно ясно, что чем более мелкими будут квадраты,
на которые делят основной прямоугольник, тем с большей точ-
ностью получится результат.
Следует отметить, что метод сеток применяется не только
тогда, когда область ограничена прямоугольным контуром, но и
тогда, когда контур области имеет произвольную форму.
Метод сеток применяется также для решения пространствен-
ной задачи Дирихле. В этом случае область, в которой ищется
гармоническая функция, разбивается на элементарные кубы,
после чего система уравнений для вычисления значений функции
в вершинах этих кубов составляется и решается так же, как и
в случае плоской задачи Дирихле.
346
Часть III
§ 2.	Функция Грина.
Решение задачи Дирихле для шара
В настоящем параграфе будет изложен один важный метод
решения задачи Дирихле. Суть его заключается в том, что мы
строим внутри области V некоторую фиксированную гармониче-
скую функцию Glt а затем с ее помощью решаем задачу Дирих-
ле в той же области И при любых заданных граничных условиях.
Иначе говоря, построение любой гармонической внутри V функции
сводится к построению некоторой, вполне определенной, гармо-
нической функции внутри V.
Определим эту функцию.
Пусть V — связная замкнутая ограниченная область, а Мо—
какая-либо фиксированная точка внутри V. Обозначим через
Gi(M, Мо) следующую функцию от точки М:
a)	Gi (М, Мо) является гармонической функцией от М всюду
внутри области V;
б)	Gi(M, Мо) непрерывна (как функция от М) во всей зам-
кнутой области V',
в)	Gj (М, Мо) = во всех точках М, лежащих на грани-
це области V.
Можно доказать, что для любой области V, граница которой
является гладкой или кусочно-гладкой поверхностью, такая функ-
ция Gi(M, Мо) существует. Из последней теоремы, доказанной в
предыдущем параграфе, вытекает, что такая функция единственна.
Итак, функция СХ(Л1, 7И0) определена однозначно. Если для
данной области V нам удалось построить функцию Glt то с ее
помощью можно будет найти гармоническую внутри V функцию,
удовлетворяющую на границе V любым, наперед заданным усло-
виям. Покажем, как это делается.
Пусть q (М) — какая-либо функция, гармоническая внутри V
и непрерывная во всей замкнутой области V. Применим к функ-
циям q(M) и Gi(M, Мо) вторую формулу Грина (см. § 1, форму-
лу (4))- Так как внутри V имеет место: /л х^=0. , л \Gt=0,
то в данном случае формула (4) запишется следующим образом:
n(9i-GiWds=°- (,)
Глава 4, §2 347
Ш1аНаи$Ж
знаниеВезгрании
где S-—граница области V. Далее, из формулы (6), §1, вытекает:
fj(^-«4r-)ds=^	<2>
3
где г — расстояние от переменной точки на поверхности S до
точки Мо.
Умножив обе части равенства (1) на— и сложив почленно
с равенством (2), получим:
s	J
Но на поверхности S функции Gi и ~ равны друг другу. По-
этому вторая скобка под знаком интеграла содержит выражение,
равное нулю всюду на поверхности S. У читателя может по-
явиться искушение приравнять нулю и первую скобку, но это
неверно: из того, что значения функций Gx и -J- совпадают на
поверхности S, еще не следует, что равны друг другу их нор-
мальные производные.
Итак, последнюю формулу можно переписать следующим
образом:
я (Ч) = -J- j‘J я (М) ±	-1) OS. (3)
's’
Разность ~ — Gj (М, Мо) называется функцией Грина для об-
ласти V и обозначается G(M, Мо):
G(M, Мо)= у-Gi(4 Ч)-
С помощью функции Грина равенство (3) приводится к следую-
щему виду:
я (Ч) = -	jJ я (М) Л с (М, Ч) ds. (4)
Формула (4) полностью решает задачу Дирихле: если известны
граничные значения гармонической функции q(M) на поверхно-
сти S и если известна функция Грина G(M, Мо) для области V,
348
Часть III
то с помощью формулы (4) можно вычислить значения искомой
гармонической функции q(M) в любой внутренней точке Мо.
Заметим, что функция Грина G(M, Мо) не является гармо-
нической в области V. Ее лапласиан равен нулю всюду в обла-
сти V, кроме точки Мо\ в этой точке функция G терпит разрыв.
Однако этот разрыв не мешает вычислению интеграла (4): всюду
на поверхности S функция G(M, Мо) непрерывна (ведь точка Мо
лежит строго внутри области V).
Итак, для решения задачи Дирихле в области V надо сна-
чала построить функцию Грина для этой области. Задача построе-
ния функции Грина в общем случае является очень трудной за-
дачей; однако для некоторых простых областей найти функцию
Грина сравнительно легко. Построим сейчас функцию Грина для
того случая, когда областью V является шар, и затем с помощью
этой функции решим задачу Дирихле для шара.
Функция Грина для шара. Рассмотрим шар V радиуса R с
центром О в начале координат. Пусть Мо — какая-либо фиксирован-
ная точка внутри шара. Построим
Gj (М, Мо), непрерывную в этом шаре
на его поверхности.
Если Л40 — центр шара, то такую
это константа
гармоническую функцию
и принимающую значения
функцию легко построить:
С,(М, М„) = ±.
(5)
является гармонической и непрерывной; она
точках М на поверхности S значения, равные
что Мо находится в центре шара, то M0M=R
Функция Gj = д-
принимает во всех
5Й7Г <если >'"есть’
для всех точек М на поверхности шара). В силу теоремы един-
ственности, других, гармонических внутри шара функций, удов-
летворяющих тому же граничному условию, не существует.
Если /Ио не лежит в центре шара, то для построения функ-
ции Gi(M, Мо) найдем сначала точку симметричную точке /Ио,
т. е. такую точку, которая лежит на продолжении луча ОМп и
для которой имеет место равенство: OM0-OMt = R2 (рис. 92).
Обозначим через р расстояние от центра шара до Мо, а через
гх — расстояние от до М (где М — переменная точка, лежа-
щая внутри или на поверхности шара) и рассмотрим следующую
функцию:
G1 (AJ. Af0) =-5- -
Она является гармонической внутри шара (в чем можно убедиться
(6)
TfaiaUausllk
знание без границ “ *
Г лава 4, § 2
349
непосредственным дифференцированием, если учесть, что R и р
постоянны и что — — -.....................   -	где (xlt y^,zx)
У (х — xi)a 4- («/ —i/i)a4- (* —*0*
— координаты фиксированной точки Л4>, а (х, у, г)—коорди-
наты переменной точки М в шаре); эта функция непрерывна для
всех точек М, лежащих внутри и на границе шара, причем ее
значения на границе равны . В этом можно убедиться сле-
Рис. 92	Рис. 93
дующим образом (рис. 93); пусть М—точка на поверхности сфе-
ры; соединим ее с точками О, Мо и Mt (все эти четыре точки
лежат в одной плоскости, так как точки О, Мо, Мх лежат на од-
ной прямой). Треугольники ОМ0М и ОММ} подобны: они имеют
общий угол (при вершине О) и по две пропорциональные стороны
(так как ОЛ10-ОЛ11 — R2, то	. Следовательно, и
третьи стороны пропорциональны этим двум, т. е.
мм1 ом
М0М ~ ОМ0 ’
откуда
1	R 1
М0М	Р ‘	’
(7)
R
Итак, значения функции г
Мо'м~; следовательно, функция, определяемая равенством (6),
на границе шара равны
удовлетворяет всем требованиям, предъявляемым к функции
Gi(M, Мо). В силу теоремы единственности, других гармоничес-
350
Часть III
ких функций, удовлетворяющих тем же условиям, не существует.
Теперь можно построить функциц» Грина G(M, Мо):
G(M, Мо) = y- — Gc(M, М„),
где г — расстояние от Мо до переменной точки М в замкнутом
шаре; используя равенства (5) и (6), получим:
G(M, Мо) =
7 — при Мо = 0;
1 _ А . 2_ при мо * °.
Г р '1
(8)
С помощью функции Грина можно решить задачу Дирихле для
сферы при произвольных, наперед заданных граничных условиях.
Пусть q(M)— функция, гармоническая внутри шара ра-
диуса R (с центром в точке О). Считая известными значе-
ния, принимаемые функцией q(M) на поверхности S этого шара,
найдем значение этой функции в какой-либо точке Мо, лежащей
внутри шара.
1. Пусть Мо— центр шара. Тогда
<?(Ч)=-^-Д?(Л1)Хс(Л1, M„)ds =
<s
Так как, по условию, Мо находится в центре сферы, то произ-
водная по направлению внешней нормали к поверхности сферы
равна частной производной по г:
д П \ =	=____L
дп \ r / dr \ г / г*
Во всех точках поверхности S имеем г = /?; поэтому
?(Ч) = - ^ДО Я(М) (- ^)dS = ДО, (М) dS.
S	s
Таким образом, нами получен тот же результат, который был
уже получен раньше (§ 1): значение гармонической функции в
центре сферы равно среднему арифметическому ее значений на
поверхности сферы.
yatatiauswk
знание без границ * w
Глава 4, § 2	 351
2. Пусть теперь Мо — произвольная внутренняя точка шара,
отличная от его центра. Тогда
1
Но 1 =
наты Мо,
ляя градиент, находим:
,	________*_______(где (х0, i/0, Zo) — коорди-
V(X- х0)» + (у - у0)3 + (Z - го?
а (*. z)— координаты переменной точки М). Вычис-
crrad — = _ (* —Хр)* + (У —Уо)7-Нг —Zp)fe _ _	.
® г	_3~~ г3 ’
1(х - х0)а + (У - «/«)’ + (г - г0)»] 2
следовательно, градиент направлен в сторону, 'прямо противопо-
ложную вектору М^М. Если обозначить через а угол между
векторами М0М и п (рис. 93), то угол между grad — и п равен
it — а, а косинус этого угла равен —cos а.
Далее,
grad-5- =1^1= ।
° Г	Г3	г3
Подставляя это в равенство (10), получим:
дп
1
-г cos а
d(-L)
Аналогично вычисляется ——: обозначая через 04 угол между
векторами и л, будем иметь:
1
-у cos 04.
ri
352
Часть III
Внесем полученные результаты в формулу (9):
<7(Ч) = -
1	.	1Q
-----cos а Н —z- cos а, aS.
S
В подинтегральном выражении легко исключить a, и (вы-
разив их через переменную величину г и постоянные 7? и р).
Рассматривая треугольник ОМ0М (рис. 93), мы видим, что
ра — г2 + /?а — 2г7? COS а;
следовательно,
cos а
г2 + Я9 - р9
2rR
Аналогично из треугольника получаем:
(OMJ* == г? + Яа — 2rx/? cos av
pa pa
Ho OMi	; кроме того, из подобия треугольников (см.
1	R 1	Rr
выше, равенство (7)) имеем: — = — — , откуда rt — — . Итак,
Г	р ' 1	р
COSOij —
^+«*-
R*
Р9
Внося найденные выражения для cos a, cos 04 и — у под знак
интеграла (И), получим, после преобразований:
<12>
Интеграл (12) называется интегралом Пуассона для сферы. Он
дает значение гармонической функции в любой точке Мо внутри
сферы по значениям этой функции на поверхности*. Преобразу-
ем этот интеграл, чтобы сделать его более удобным для прак-
• Заметим, что формула (12), выведенная нами в предположении, что
Af0¥=O, сохраняется в силе и при =0; в этом случае г — R, р = 0 и фор-
мула (12) переходит в ранее выведенную для центра Мо сферы формулу:
^alatlaus^
знание без границ “ *
Глава 4, §2	 353
тического пользования. Обозначим через 7 угол между вектора-
ми ОМ0 и ОМ. Тогда •
г® =ря _]_ ft2 — 2рЯ cos 7
и
s (р’4-Яа—2p/?cos?)2
Переходя к сферическим координатам (учитывая, что поверхность
S является координатной поверхностью в сферических коорди-
натах и что dS = /?а sin 0 d<pd0), получим:
2it it
Я(Ме)	f f-----------• sin	(13)
0 0 (pa 4 Яа — 2p/? COS?) 2
Этот интеграл также называется интегралом Пуассона для сфе-
ры-, для его практического вычисления надо предварительно
представить 7 (для переменной точки М на поверхности сферы)
и q(M) как функции от широты 0 и долготы ср точки М. Пока-
жем на примере, как это делается.
Пример. На верхней половине поверхности сферы поддер-
живается постоянная температура 4-100°, на нижней половине —
температура 0°. Считая, что температура внутри однородного
шара, ограниченного этой поверхностью, установилась, вычис-
лить, чему она равна в точках О (0, 0, 0) и Мо ( 0,0, j, где /?—
радиус шара, а О —его центр.
Задача сводится к вычислению значений гармонической
функции q(M), заданной на поверхности сферы. Значение этой
функции в точке О вычисляется совсем легко:
~ 4к/?а
S,
где Si —верхняя половина сферы. Но lOOdS = 100-2к/?а.
Поэтому

q(O) = ^-W0-2«R* = 5Q°.
Вычислим теперь q(M0). Применим для этого формулу (13).
12 ю. С. Очан
354
Часть III
Так как Мо лежит на оси Oz, то угол у равен широте 0 точки
р	о
М (рис. 94), р = Кроме того, на поверхности сферы
4U
q(M) =
100° при 0 < © < у,
0° при у < 0 * \ it.
Рис. 94
Поэтому формула (13), в данном случае,
щим образом:
перепишется следую-
т:
= 300_ Г Г Sin 0d0_ . = 150> Л---------и _ 82,92°.
,6л J V	л	* ’5/
0 О 5_cos0
[4	J
Напомним, что эта задача была ранее решена методом Фурье
(глава 2, § 15). Там мы получили значение температуры в точке
Мо равное 83,1°. Расхождение результатов объясняется тем, что
при решении методом Фурье мы ограничивались лишь несколь-
Mtattaus^
знание без границ * *“
Глава 5, § 1
355
кими первыми членами ряда; отбросив остальные члены, мы до-
пустили погрешность « 0,2°; результат же вычисления с по-
мощью интеграла Пуассона дает точное значение гармоничес-
кой функции в данной точке: д(М0) — 150- ( '	'

ГЛАВА 5
КЛАССИФИКАЦИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
МЕТОД ХАРАКТЕРИСТИК
§ /. Преобразование линейных уравнений второго
порядка с помощью замены переменных
До сих пор мы шли следующим путем: ставили ту или иную
физическую задачу и затем составляли дифференциальное урав-
нение; потом, решая это уравнение, мы находили решение на-
шей физической задачи. Как мы видели, все те задачи, которые
мы ставили, приводили нас к линейным уравнениям второго по-
рядка (т. е. к уравнениям, линейным относительно неизвестной
функции и ее производных, причем порядок производных, вхо-
дящих в эти уравнения, был не выше второго).
В настоящем параграфе мы пойдем другим путем: будем
исходить не из той или иной физической задачи, а непосредст-
венно из математической задачи исследования и решения ли-
нейного дифференциального уравнения второго порядка в общем
виде (независимо от того, какая физическая задача может при-
вести к этому уравнению). При этом мы ограничимся уравнениями,
в которых неизвестная функция и зависит только от двух неза-
висимых переменных х и у.
Любое линейное дифференциальное уравнение второго поряд-
ка (при двух независимых переменных) может быть записано в
следующем виде:
а-пхх + 2Ь’п^ + с-н^ + ^-<4-е-п' 4-/.п + ^ = 0,	(1)
12*
356
Часть 111
где^а, b, с, d, е, f, g — заданные непрерывные функции от х и у
(или в частном случае, постоянные).
Попытаемся упростить это уравнение с помощью замены не-
зависимых переменных:
* = <?(*, У)',
==	У)-
(2)
Здесь £ и — новые независимые переменные. Функции ? и ф,
связывающие новые переменные со старыми, будут подобраны
позднее; пока же мы будем считать их дифференцируемыми нуж-
ное число раз. Кроме того, будем считать, что система уравнений
(2) может быть однозначно разрешена относительно х и у\ это
надо понимать следующим образом: если функции (риф отобра-
жают некоторую область G плоскости Оху в область G* плоско-
сти Obj, то при этом каждой точке ($, vj области G* соответст-
вует только одна точка области G (иначе говоря, отображение
области G на G*, даваемое функциями и ф, является взаимно
однозначным). Как известно, для этого
биан преобразования (т. е. определитель
достаточно, чтобы ЯКО-
ср ' Ф' \
нигде в обла-
" к iy /
сти G не обращался в нуль.
Для того чтобы сделать требуемую замену переменных, вы-
разим частные производные от функции и по х и у через произ-
водные от и по 5 и tj:
. ди
Ux ~ 0Р
ди
(3J
> ди ег . ди
Uv~ 1%
(3s}
Это записано на основании правила дифференцирования сложно^
функции от двух переменных (здесь и зависит от £ и 7}, которые
в свою очередь, зависят от х и у).
Для того чтобы выразить и'хх через производные по £ и тд
учтем формулу (3J и применим снова правило дифференцирова
ния сложной функции:
“хх ( ^х)х
(ди . ди	(ди\ с, . ди с,,	(ди\'	. . ди ..
“	д^ ‘	/л дЕ ’	\0Ч /х	^хх
t, ! д2и	ди ( [daz£ , д2и	L ди_
~	+	\г“Г 06 * *ХХ "Г Idle’S;’'"	0VJ "Чхх
^alallaus^k
знание без границ “ *
Глава 5, § 1
357
Следовательно,
,, Гд’и / {.» V . пд*и н'  . д2и	( . \21 । ди ди	.
Uxx~ [dga ^х/ + ^д&т 'х^х + дт?	Их) J + 06 $хх+ 0Г Г(хх' (41)
Аналогично найдем:
,, Гд’и с. с. д2и { h, , . Л . даи , .1
Uxy~ [дб8 + д&ч \ сх% +	+ 0т;а Г1Х % J +
0м р.» . ди
0$Г ’Х|/+ 0? TW
(4а)
[0aM/t- \2 । Q д*и н> •	। 02м/ 'хг! . ди	ди
06*	+ 2060т(	* 07^^ J + 06"	\)У
(4з)
Правые части равенств (3,). (32), (4!), (42), (43) представляют со-
бой линейные функции относительно частных производных |р
ди д*и д*и даи	,
0V 06s’ 060? д?' Подставляя их, и*, ихх,... из этих формул в урав-
нение (1), мы получим снова линейное уравнение второго порядка с
неизвестной функцией и и независимыми переменными £ и тр
a wee + 2Ь + с и^ + F (ui и'Г1, и, Е, tq) = 0,	(5)
где
а - flU;j2 + 2 b ej; + c(^)2;
b = atx^ 4- b( Цу + ^7^) 4- с 5y Ни
с = а( Нх)2 + ЪЬцхНу + с( TJ2.
(5')
а Г — функция, линейная относительно и'ъ и^, и .
Уравнение (5) становится особенно простым, если в нем ко-
эффициенты о ис окажутся равными нулю. Для того чтобы пер-
воначально заданное уравнение (1) можно было привести к тако-
му простому виду, надо в нем сделать замену переменных
-=	У),
*1 = Ф(*. У)>
подобрав функции и ф так, чтобы они являлись решениями
уравнения:
а( z ’ )24- 2bz'x 2У +с (zy )а = 0.	(6)
Это уравнение является нелинейным уравнением в частных про-
изводных первого порядка. Следующая теорема покажет, как свя-
358
Часть III
заны его решения с общим решением некоторого обыкновенного
уравнения.
Теорема. Для того чтобы функция z ~ Дх, у) во всех точ-
ках области G удовлетворяла уравнению (6), необходимо и до-
статочно, чтобы семейство
Дх, у) = k	(7)
было общим интегралом уравнения
a(dy)* — 2b dy dx + c(dx)* = 0
(8)
в той же области G.
Доказательство. Необходимость. Пусть z = Дх, у)— ре-
шение уравнения (6). Рассмотрим семейство кривых Дх, у) = k
и докажем, что любая кривая этого семейства удовлетворяет
уравнению (7).
В любой точке, лежащей на кривой Дх, у) = k (где k —
фиксировано), выполняется следующее равенство:
fx{x, y)dx+ fy(x, y)dy = 0;
действительно вдоль данной кривой функция Дх, у) постоянна, и
поэтому ее полный дифференциал равен нулю.
Следовательно, всюду на кривой имеет место равенство:
dx dy _
обозначим каждое из этих отношений через к; тогда
dx = у-, dy = — к f'x.
Подставляя эти выражения для dx и dy в левую часть уравне-
ния (8), получим:
a(dy)* — 2bdxdy + c(dy? = к« [ а( Д)2 + 2bf'x fv +?( f J2] .
Выражение, стоящее в квадратных скобках, равно нулю, так как,
по условию, функция /(х, у) есть решение уравнения (6). Следо-
вательно, во всех точках нашей кривой имеет место равенство
a(dy)2 — 2bdxdy + c(dy)* — 0,
откуда вытекает, что она является интегральной кривой уравне-
ния (8).
Итак, любая кривая вида Дх, у) — k является интегральной
кривой уравнения (8); с другой стороны, через каждую точку об-
^alallausffll
знание без границ '*
Глава 5, § 1 359
ласти G проходит кривая такого вида; это вытекает из того, что
функция /(х, у) определена всюду в области G и поэтому, на-
пример, через точку (х0, у0) проходит кривая
f(x, у) = Дх0 у0).
Отсюда следует, что семейство Дх, у) = k является общим
интегралом уравнения (8).
Достаточность. Пусть семейство f (х, у) — k будет общим ин-
тегралом уравнения (8). Возьмем произвольную точку (х0, у0) из
G и выделим ту кривую семейства, которая проходит через эту
точку:
/(х, у) = k0.	(9)
Так же, как и при доказательстве необходимости, убеждаемся,
что всюду вдоль этой кривой выполняется равенство
dx	dy
fy	~fx
откуда
dx = l-fy-, dy = —k.	(10)
Так как кривая является интегральной кривой уравнения (8), то
при подстановке в это уравнение dx и dy из (10), получим тож-
дество:
x’[a(/;)s+26/;/; + c(/f)a] = о,
или, после сокращения на
<>(/;>2+2&/;4 + с(/,)2= о.
В частности, в точке (х0, у0) имеет место:
о(Хо, Уо)’[ fx) |(х0, ув) + 2Ь(хс,1/о)* fx |(Хо,	• /у|(х0, у0) ~!~
+ С(Х0, у0)- ( f у)2 |(х0, у0) = 0.
Но последнее равенство означает, что функция двух переменных
Дх, у) удовлетворяет в точке (х0, у0) уравнению (7). Так как точ-
ка (х0, у0) была взята произвольно в области G, то функция
/(х, у) удовлетворяет уравнению (7) во всех точках этой области,
т. е. эта функция является одним из решений уравнения (7).
Таким образом, теорема доказана.
Рассмотренная теорема открывает путь для упрощения ис-
ходного уравнения (1). Для этого сначала составляем вспомога-
тельное уравнение (8); оно называется характеристическим у рае-
360 Часть 111
нением для данного уравнения (1). Характеристическое уравне-
ние есть обыкновенное дифференциальное уравнение первого по-
рядка, но второй степени. Разрешая его относительно ух (предва-
рительно разделив все члены уравнения на dx2), получим два
уравнения:	____
у' = b + Vb*-ac ;
а
у' = b-V^i .	(10а)
а
(предполагается, что ас — Ь2<0, Ь2— ас>0 всюду в области G).
Пусть общий интеграл уравнения (10J имеет вид
?(*. y) = k,	(ПО
а общий интеграл уравнения (102)
Ф(х,У) = Л.	(112)
Интегральные кривые характеристического уравнения (т. е. все
кривые, входящие в семейства (llj и (11а)) называются харак-
теристиками заданного дифференциального уравнения (1). В
связи с этим рассматриваемый метод упрощения уравнения (1)
называется методом характеристик.
Семейства (11Х) и (112) можно рассматривать, как общие ин-
тегралы уравнения (8) (это уравнение распадается на два урав-
нения (10j) и (Ю2)).
Следовательно, согласно доказанной теореме, функции
z = <? (х, у) и z = ф (х, у)
являются решениями уравнения в частных производных (6).
Функции ср (х, у) и ф (х, у) независимы друг от друга (можно
доказать, что их якобиан отличен от нуля, если ас — Ь2<0). По-
этому, возвращаясь к уравнению (1), мы можем в нем сделать
замену переменных:
5 = ? (X, У), TQ = ф (х, у).
Так как функции и ф удовлетворяют уравнению (6), то в ре-
зультате этой замены переменных окажется а = 0 и с = 0. Сле-
довательно, уравнение (1) преобразуется к виду:
2b и^ + F(uk, и^, и, В, Tj) = 0 ,
или, после деления на 2Ь и переноса в другую часть равенства:
NataHausiiilk
знание без ераниц Ч w
Глава 5, § 1
361
где Ф — функция, линейная относительно о-,	, и (см. выше,
формула (5)).
Полученное уравнение имеет более простой вид, чем исход-
ное уравнение (1); если мы его сможем решить (т. е. найти и
как функцию от i и vj), то для того, чтобы найти решение ис-
ходного уравнения, достаточно вернуться к старым переменным
(выразив £ и через х и у).
Пример. Найти общее решение уравнения
UXx — У2 Иуу = 0.	(12)
При этом под «общим решением уравнения в частных производ-
ных» мы будем подразумевать семейство всех функций, являю-
щихся решениями этого уравнения.
В нашем уравнении а = х2, Ь = 0, с = — у2\ следовательно,
ас — Ь2 ~ — х2у2 < 0 всюду на плоскости Оху (кроме точек, рас-
положенных на осях координат). Поэтому здесь можно приме-
нить указанный прием упрощения уравнения.
Составим характеристическое уравнение:
x2dy2 — y2dx2 = 0,
или
Оно распадается на два уравнения:
у' — -У- (его общий интеграл — -- k)\
У" =----(его общий интеграл ху — k)*.
Следовательно, исходное уравнение упростится в результате
следующей замены переменных:
5 у == ху.
Выразим ихх и иуу через производные от и по $ и и затем
подставим их в уравнение (12).
* Прямые у — kx и гиперболы у = являются
уравнения (12).
ха рактеристикам и
362
Часть 111
«к = «и^)2+ 2«ё, • е; • <+<,-«+
+«е •	+«; •	=
= и.". • (-тА*	+ 2и".	 (  -v)	• У + и'„„ •	Уг +
«I	X2 I	\	/	VI	1
।	2у	,	л
+ • —f- + и -0;
1	t	х3	1 TJ
п	п	1	.	л п	1
УУ	«	Ха	1 Ц	X
X + и'т • х*-
VJ
Подставляя выражения для и” и н" в уравнение, получим
лл	уу
после упрощений:
-4</! «ц + -|^ = 0.
Заменяя, далее, -у- на 5, а у2 на Ь], приведем наше уравнение
к виду:
—	4- 25 и\ — 0,
или
2т]	= и[.
Уравнение приведено к простейшему виду. Для того чтобы его
решить, обозначим — v. Тогда уравнение (13) перепишется так:
2т]	= V.
В этом уравнении фигурирует только одна независимая перемен-
ная (другая, 5, может рассматриваться как параметр). Решая это
уравнение, как обыкновенное (с неизвестной функцией v и неза-
висимым переменным т)), получим:
dv   dy
v	2i) ’
In v = In vj + InC;
V ~ С J 7) .
Здесь С — произвольная величина, не зависящая от vj; однако
она может зависеть от 5, которое мы зафиксировали в процессе
интегрирования уравнения; поэтому обозначим эту величину че-
рез С (5):
v = С (5) V vj.
NataHauswk
знание без границ ч *•
Г лава 5, § 2
363
Вспоминая теперь, что v == и[, получим:
< = C(;)|<V
Проинтегрируем обе части этого равенства по 5 (в процессе ин-
тегрирования мы можем считать здесь tq постоянным, так как
— частная производная по £):
«=/•»! Jc©dN-C,.
Здесь — произвольная функция от тр, обозначим ее CY (tj). Кро-
ме того, неопределенный интеграл J С (Q d 5 является произволь-
ной функцией от £ (в силу произвольности подинтегральной
функции С ($)); обозначим этот интеграл С2 (?):
и = У у С2 (5) + Сх (vj).
Возвращаясь теперь к старым переменным х и у, получим:
и = к ху С, (-J-) + С, (ху).
(И)
где Сх и С2 — произвольные функции от своих аргументов. Се-
мейство (14) является общим решением данного уравнения; оно
включает все его решения. В частности, например, решениями
уравнения являются функции:
и
= Vxy +
У_
х
+ In (ху);
w = Уху sin	+ Vху
и т. д.
$ 2, Классификация линейных
дифференциальных уравнений второго
порядка. Приведение к каноническому виду
В предыдущем параграфе, когда мы упрощали уравнение
второго порядка:
аи"хх + 2КУ + с%у + du'x + еи'у + fu + g = О,
предполагалось, что выражение
Д = ас — Ь2
(1)
(2)
364
Часть 1П
(дискриминант уравнения) отрицательно всюду в области G.
В этом случае заменой независимых переменных:
& = ?(*. у),	=	у),	(3)
мы свели уравнение (1) к уравнению
% = ФЦ, и, с, Т|).	(4)
При этом функции ф и ф, с помощью которых мы осуществляли
замену, были двумя независимыми друг от друга решениями
уравнения
a(z')2 -\-2bz z + c(z')2 =_ 0.	(5)
Л	л и	у
В случае, если дискриминант уравнения отрицателен, уравнение
(1) называется уравнением гиперболического типа; простейший
вид уравнения гиперболического типа — уравнение (4), называет-
ся каноническим видом уравнения гиперболического типа.
Рассмотрим теперь те случаи, когда дискриминант не явля-
ется отрицательным.
Если Ь — ас— Ь2> 0 в точке (х0, z/0), то уравнение (1) назы-
вается уравнением эллиптического типа в точке (х0, у0). Если
Д > 0 во всех точках области G, то уравнение называется уравне-
нием эллиптического типа в области G.
Если Д = ас — Ь* ~ 0 в точке (х0, !/0), то уравнение называет-
ся уравнением параболического типа в точке (х0, yQ). Если
Д = 0 всюду в области G, то уравнение называется уравнением па-
раболического типа в области G.
Как уже указывалось выше, если Д < 0 в точке (или всюду
в области G), то уравнение называется уравнением гиперболиче-
ского типа в точке (или в области G).
Наконец, если в одних точках области G уравнение принад-
лежит к одному типу, а в других — к другому, то уравнение
называется уравнением смешанного типа в области G.
Заметим, что тип уравнения не меняется при преобразова-
нии уравнения с помощью замены переменных:
£ = ?(*, у), тг-ф(х, у),	(6)
каковы бы ни были функции «риф (лишь бы их якобиан был
отличен от нуля). Действительно, если обозначить через Д ди-
скриминант уравнения после замены переменных (т. е.
^alatiausiik
знание безераниц Ч *
Г лава 5, § 2 365
Д=ос— Ъ2, где а, Ь, с — новые коэффициенты уравнения),
то, как легко подсчитать, имеет место равенство:
Это равенство можно получить, если учесть формулы (5') из
предыдущего параграфа, выражающие а, b и с_ через _а, Ь, с,
и затем вычислить Д, подставив в Д вместо о, b и с их зна-
чения, найденные по формулам (5')- После несложных преобразо-
ваний получаем равенство (7).
Из этого равенства вытекает (в силу того, что якобиан не
равен нулю и, следовательно,
0), что
если Д < 0, то и Д < 0;
если Д -= 0, то и Д = 0;
если Д > 0, то и Д > 0.
Иными словами, преобразование (6) не меняет типа дифферен-
циального уравнения; говорят, что тип уравнения инвариантен*
относительно преобразования независимых переменных.
Рассмотрим, как можно упростить уравнение («привести его
к каноническому виду»), если оно является уравнением парабо-
лического типа. В этом случае
ас — Ь- 0.
(8)
Будем считать, что b 0 (если бы было b 0, то тогда из (8) сле-
довало бы, что по крайней мере один из коэффициентов а или с так-
же равен нулю; но тогда в уравнении фигурировал бы только один
член, содержащий производные второго порядка, т. е. уравнение
уже было бы столь простым, что не требовалось бы его даль-
нейшего упрощения).
Итак, пусть b / 0. Тогда ас > 0, откуда следует, что а и с
одного знака; всегда можно считать, что они оба положитель-
ны (если они оба отрицательны, то нужно предварительно умно-
жить все члены уравнения на —1). Обозначим а — ая, с = В2;
* Инвариантен (invariant)—неизменен.
366
Часть Ilf
тогда b2 = а2{52. Выберем знаки аир так, чтобы произведение
о$ имело бы тот же знак, что и Ь. Тогда b = ар, и уравнение (1)
перепишется следующим образом:
-I' ?’р »«+ ?г«‘ю Н- К + с% -I- /« -I- g = °-	(!')
Его характеристическое уравнение
a2 dy2 — 2ар dx dy F р2 dx2 = 0
приводится к виду
(vdy — pdx)2 = 0,
или	а dy = р dx.
Решая его, находим только одно семейство характеристик:
ф(х, y) = k.
Для того чтобы упростить уравнение (1), сделаем следующую
замену переменных:
У)>	У),
где <р(х, у) — функция, найденная нами выше (при решении ха-
рактеристического уравнения), а ф (х, у) — совершенно произволь-
ная дифференцируемая функция, удовлетворяющая единственному
требованию — чтобы она была независима с у (х, у).
Если мы сделаем указанную замену, то а обратится в нуль;
действительно, согласно основной теореме предыдущего пара-
графа, <р(х, у) является решением уравнения
а2(?;)2 + 2apz;z;H-p2(zy)2=o,
и поэтому
а =а(е;>» -I- 2«;	2«ре;	= о.
Коэффициент с отличен от нуля. Что же касается коэффициен-
та Ь, то его можно вычислить по формулам (5') из § 1:
b =~ а^х^х ~F b "I* £.«/Tix) ~F ау'Чи ~
=<л’л+«₽	-I-	=к +	-I- ч>-
NafaHausllli
знание без границ Ч
Глава 5, § 2	 367
Заметим теперь, что буквально так же, как мы доказывали ос-
новную теорему § 1, можно доказать следующее утверждение.
Для того чтобы функция z = f (х, у) во всех точках области G
удовлетворяла уравнению агх -|- $z'v ---• 0, необходимо и достаточно,
чтобы семейство f (х, у) = k было общим интегралом уравнения
ady — pdx = 0 в той же области G.
В данном случае семейство <р(х, у) --- k является общим ре-
шением уравнения ad// — pdx 0; следовательно, a<?/ -f- pq/= 0;
но	у), поэтому
b (яС -}- р?„) (от^. -|- ртр = 0.
Итак, в результате выполненного преобразования уравнение (1')
привелось к виду:
си,л -|- F(M=, z/тр и, 5, т|)	0,
или, после деления на с и переноса:
«vi -- Ф(«ь «тр и, 5, Tj),	(9)
где Ф — функция, линейная относительно щ, wTj, и. Уравнение,
записанное в форме (9), называется каноническим видом уравне-
ния параболического типа.
Пример 1. Найти общее решение уравнения:
хКх -	2x11 х -= °-	(> °)
Решая характеристическое уравнение
x2dy2 -|- 2ху dx dy -|- у2 dx2 — 0,
или, что то же самое,
xdy -F ydx --- 0,
находим одно семейство характеристик:
ху -- k.
Поэтому здесь можно произвести следующую замену переменных:
£ = *//, т\^у.
368
Честь III
Вторая функция нами выбрана произвольно — с единственным
условием, чтобы якобиан был отличен от нуля (в данном случае,
якобиан равен у; он отличен от нуля во всякой области, не со-
держащей точек оси Ох).
Для того чтобы преобразовать уравнение к новым координа-
там, выразим ихх, иху, и , и'х через производные от и по но-
вым переменным:
“х-
“ХХ Щ-'У^
“„Г ИЕ"=-Х</ I и'^-у \
Подставляя в уравнение (10), получим, после упрощений:
"v.	°-
Таким образом, уравнение приведено к каноническому виду;
в данном случае приведенное уравнение легко интегрируется:
% - (5),
и- С, 4 С2(В),
где Ci и С2 — произвольные функции от 5. Возвращаясь к старым
переменным, получим окончательно:
и - Ct (ху)-у\С2 (ху).
Это общее решение. Беря в качестве С, и С2 те или иные конк-
ретные функции от 5, получим различные частные решения; так,
например, частными решениями будут:
//	(ху)2-у +	;
и - у • sin (ху) + ху,	и т. д.
В заключение рассмотрим вопрос об упрощении уравнения
эллиптического типа. Пусть всюду в рассматриваемой области
Д ас — Ь2 > 0.
* См. формулы (4,), (4«), (43) из § 1.
^atattauswk
знание Без границ \*
Глава 5, § 2	369
Тогда характеристическое уравнение распадается на два диффе
ренциальных уравнения:
у' М-М1 —> Ь — К ft8 — ас	(И
правые части которых комплексны для всех точек из области
G, причем в каждой точке (х, у) из G числа
Ь -|- У Ь2 — ас b — у Ь2 — ас
а	а
являются сопряженными комплексными числами.
Пусть <р(х, y)~k — общий интеграл одного из полученных
уравнений (11); ясно, что <р(х, у) — функция, принимающая
комплексные значения. Можно показать, что если 9* (х, у) —
функция, комплексно сопряженная с <р(х, у), то семейство
<р* (х, у) — k будет общим интегралом другого уравнения (11).
Если теперь сделать замену переменных:
5 -= ЧР(лг, у),	-<(х, у),
то, согласно общей теории, уравнение (1) приведется к виду
пе\ = ф(пЕ-	11 •	’*!)•	02)
В этом мы убеждаемся так же, как и в случае уравнения ги-
перболического типа. Однако полученное уравнение неудобно
считать каноническим уравнением: здесь новые переменные 5 и
принимают комплексные значения в каждой точке области G.
Поэтому, рассматривая уравнение (12) как промежуточное, сде-
лаем еще одну замену переменных:
Легко проверить, что в результате этой замены уравнение (12)
приведется к уравнению следующего вида;
< Н- == Ufi. и, Ю-	(12')
Здесь а и [з являются действительными функциями действитель-
ных переменных х и у:
~ .	ф(*- у) + ф’ (*. у) . о Ф(х. у) — Ф*(х, у)
2	’ ,	-	2.
370
Часть III
Уравнение (12'). получившееся в результате этой замены пере-
менных, называется каноническим уравнением для уравнения
эллиптического типа.
Пример 2. Привести к каноническому виду уравнение
“«+K+4f=°-	<13>
Здесь Д =ас — Ь2 = 5 — 22=1 >0; значит это уравнение является
уравнением эллиптического типа.
Характеристическое уравнение
(dy)2 — 4dxdy + 5 (dx)2 --- 0
разбивается на два:
У' = 2 -I-1; у' = 2 — i.
Общими интегралами этих уравнений являются семейства:
у — (2 + 0 х = Аг, у — (2 — t) х = k.
Согласно теории, делаем замену переменных:
а =	+	+	(2-^1 =у_2х.
r = 1У-(2-НМ-1У-(2-0х] = _ у
Р	2i	х-
Выразим и" , и” и” через производные по а и В:
и’„ = 4< + 4ы^ +
=- ч. - «:₽;
fr	fr &
“уу =	
Подставляя в уравнение (13), получим, после сокращений:
«:.+ «»== о-	(и)
Итак, уравнение (13) приведено к каноническому виду. Так как
уравнение (14) является уравнением Лапласа, то его решением
будет любая гармоническая функция переменных аир:
п=/(а, р).
* Здесь снова использованы формулы (40, (42), (48) из § 1; роль новых
переменных играют а и 3 (вместо 6 и *)).
NataHausiVil
знание без границ Ч «Ь
Глава 5, § 3
371
Возвращаясь к старым переменным, получим
"=/(// — 2х; —х).
Это общее решение уравнения (13). Оно получилось в результа-
те подстановки в произвольную гармоническую функцию от
двух переменных и (а, р) вместо а — функции у — 2х, а вместо
Р — функции — X.
В частности, если в качестве и (а, р) взять гармоническую
функцию In (я8 -|- р2), то мы получим частное решение уравне-
ния (13):
In [(// — 2х)8 + х2].
§ 3, Решение уравнения колебания бесконечной
струны методом характеристик
(метод Даламбера)
Вернемся к рассмотренному ранее уравнению колебания
струны и попробуем решить его методом характеристик.
Пусть нам дана струна столь длинная, что ее практически
можно считать бесконечной. Пусть иа эту струну не действуют
никакие внешние силы. Тогда закон колебания струны будет
задаваться уравнением
- «к = <’
и начальными условиями:
м(х,/)| =<р (л),
пДх, /)| = Ф(х),
/=0
(2J
(23)
где <р(х)— начальное отклонение, а ф (х) — начальная скорость
(ясно, что 9(х) и ф(х) должны быть заданы для всех х,
— оо X -Т <х>).
Задавать граничные условия здесь не имеет смысла: струна
бесконечна и, следовательно, не имеет границ.
w
г
372 Часть III
Уравнение колебания струны является уравнением гипербо-
лического типа: здесь
Д = 1 • (—а2) — О2 - ~ а2 < 0.
Составим его характеристическое уравнение:
l-(dx)2 — a2(dt)2 - 0.
Решая его, получаем два семейства характеристик:
х — at = k; х |- at — k.
Следовательно, для приведения уравнения колебания струны
к каноническому виду, надо сделать замену переменных:
Е--х — at’, ц~х [ at.
Для того чтобы осуществить эту замену, надо выразить и и
и"„ через производные от и по Е и i):
их == ut Ex + uTJ iq.v = Uk +	;
tit = — аи^ 4- au(.;
Uxx ~~ ^EE 'f* 2//£t] 4“	•
Utt = a2 — 2a2	4- a2 .
Подставляя в уравнение (1), получим после сокращений:
и^~ 0 .
Итак, наше уравнение (1) приведено к каноническому виду.
Для того чтобы решить это каноническое уравнение, перепи-
шем его следующим образом:
(щК = 0.
Так как производная от не по равна нулю, то ui не зависит
от rf, следовательно, может зависеть только от ;:
„е - /(f) •
Г лава 5, § 3	 273
^ialdttaus^i
Интегрируя по $ полученное равенство, получим:
и- ^f(i)di + c,
где С — величина, не зависящая от «; однако С может зависеть
от ц; поэтому обозначим С — F (tq), где F — совершенно произ-
вольная функция одного переменного. С другой стороны, в силу
произвольности функции /($), ее неопределенный интеграл также
является произвольной функцией от В; обозначим его Ф(£).
Итак,
и^Ф^ + F^),
или, если вернуться к старым переменным:
и ~ Ф (х — at) 4- F (х 4- at).	(3)
Это — общее решение уравнения колебания струны. Для того что-
бы определить функции Ф и F (и тем самым найти закон коле-
бания данной струны), надо использовать начальные условия.
Из условия (2i) следует:
^Ф(х)рР(х).	(4)
Для того, чтобы применить условие (2а), продифференцируем обе
части равенства (3) по /:
ut(x, t) — Ф'(х — at) • (— а) 4 F' (х + at) - а.
Здесь под Ф' подразумевается производная от функции одного
переменного Ф (с) по своему аргументу. Чтобы найти — , нам
пришлось продифференцировать Ф по £ и результат умножить на
(т. е. на — а). Аналогичным образом мы поступили и при нахож-
dF
дении
Подставим теперь t — 0 в полученное равенство; тогда будем
иметь:
— а Ф' (х) 4- a F' (х) = ф (х).
Это равенство справедливо для всех х; интегрируя его в грани-
цах от 0 до х, получим:
-а IФ (л) - Ф (0) Ц- а | F (х) - F (0) | j 4 (х) dx,
или
— а Ф (х) 4- aF (х) -- J ф (г) dz 4- аС.
с
374
Часть 111
Здесь постоянную величину Г (0) — Ф(0) мы обозначили через С;
кроме того, переменную интегрирования под знаком интеграла
мы обозначили через z (чтобы не путать с верхней границей ин-
теграции). Решая теперь полученное уравнение совместно с ра-
нее найденным уравнением (4), найдем неизвестные функции Ф
и F:
Ф(х) + F (х) = <р(х),
1 г
—Ф(х) + F(x)~ — J ф (z) dz 4- С,
о
х
Ф(*) =	'Hz)dz — '2-’
о
х
F(x) = -L?(x)-|-±.j<|,(z)dz + -~.
(5)
Хотя здесь имеется еще некоторый элемент неопределенности (неиз-
вестная константа С), но, как мы увидим, это не помешает нам
однозначно найти функцию и(х, t).
Равенства (5) справедливы, каким бы ни было вещественное
число х. Они остаются в силе и в том случае, если вместо х
подставить, например, х — at (ведь х—at также является вещест-
венным числом при любых х и t, и поэтому равенства (5) остают-
ся в силе, если в них подставить х — at вместо х). Поэтому
х - at
Ф(х —а/) = — ф(Л_а/) _-L j ф(г)с/г —
о
(6)
Аналогично, если во второе из равенств (5) подставить вместо х
величину х 4 at, получим:
х -} at
F(x + at) =-^-<?(x + at) 4- j Ф(z)dz + -j-.	(7)
Складывая почленно равенства (6) и (7) и учитывая равенство (3),
получим окончательно искомую функцию и(х, t), дающую закон
колебания данной струны:
х + а/	х — at
и (х, /) =ф-(*	+ at} 4- JL j ty(z)dz — ± ( ty(z)dz,
о	о
Nalattausnik
знание без границ Ч *
Глава 5, § 4
375
или
х 4- at
+	+	+ J + (z)d,.
х - - at
(8)
Итак, постоянная С исключилась и закон колебания струны
u(x,t) определился однозначно.
§4. Исследование закона колебания бесконечной
струны
Функция (8) из предыдущего параграфа, дающая отклонение
любой точки струны в любой момент /, может быть представ-
лена в виде суммы двух слагаемых:
и (х, t) = Ф (х — at) + F (х + at),
(1)
где
Ф(х — at) = -~<f>(x — at) — ~ J ^(z)dz,	(2)
F(x + a/) = -l-<p(x-}-a/) + ^- j ty(z)dz	(3)
b
(см. формулы (6) и (7) из § 3; произвольное слагаемое С, фигу-
рирующее в этих формулах, можно, не ограничивая общности,
положить равным нулю).
Построим график функции Ф(л):
,v
Ф(*) =	—
6
(см., например, рис. 95). График функции Ф(х — at) при фикси-
рованном t получится из графика Ф(х) смещением вправо на ве-
личину at. Таким образом, для того чтобы получить график
Ф(х — at) из графика Ф(л), надо последний перемещать вправо
со скоростью, равной а.
Если же построен график F (х), то для построения графика
F (х 4- at) достаточно передвинуть его влево на величину at; ины-
ми словами, график F (х -f- at) получится из графика F (х) в ре-
зультате перемещения влево со скоростью, равной а.
376
Часть III
Из этих рассуждений ясно, что если нами построены гра-
фики функций Ф(х) и F(x), то нетрудно построить линию, даю-
щую форму струны в любой момент t\ для этого достаточно
сдвинуть кривую Ф(х) вправо на величину at, кривую F (х)—
влево на ту же величину и затем для каждого х сложить гра-
фически ординаты полученных кривых. Полученная в результате
сложения кривая даст нам форму струны в момент t (или, как
говорят, профиль струны) (рис. 96).
Функция Ф(х — at) называется прямой волной, а функция
F(x + af) — обратной волной. Профиль струны получится в ре-
зультате сложения прямой и обратной волн.
Величина а дает нам скорость распространения поперечных
колебаний. Как известно (см. вывод уравнения колебаний стру-
ны в главе 1, § 1), она имеет размерность скорости и равна
। / т
У —; таким образом, скорость распространения колебаний про-
порциональна квадратному корню из силы натяжения струны и
обратно пропорциональна квадратному корню из ее линейной
плотности.
NalaHausliM.
знание без ераниц **
Г лава 5, § 4
377
Рассмотрим геометрический смысл формулы
и (х, t) = Ф (х — at) + F (х -J- at).
Функция Ф(х — at), рассматриваемая как функция двух пере-
менных хи/, имеет в качестве линий уровня на плоскости Oxt
прямые линии х — at const; иными словами, линиями уровня
являются характеристики данного уравнения. Для того чтобы
найти значение функции Ф в точке (х0, /0), достаточно провести
линию уровня х — at — const через эту точку и найти пересече-
ние этой линии с осью t 0; пусть это будет точка (xlt 0)
(рис. 97). Тогда
Ф (х0 — atQ) - Ф (xi — a • 0) - Ф (х,),
т. е. значение функции Ф в точке (х0, t0) равно Ф(Х1).
Аналогичные рассуждения применимы и к функции F (х+а/):
ее линиями уровня служат характеристики уравнения — прямые
х + at — const. Значение функции F в точке (х0, L) равно зна-
чению этой же функции в точке (х2, 0) (где (х2, 0) — точка пе-
ресечения линии уровня, проходящей через точку (х0, Q, с осью
Ох). Поэтому
F (х0 + at0) = F (х2 + a • 0) = F (х2).
Теперь для того, чтобы найти значение функции и(х, t) в
точке (х0, tQ) (т. е. для того, чтобы найти величину отклонения
струны в точке х0 в момент t0), достаточно провести через точ-
ку (хй, t0) на плоскости Oxt две характеристики: х — at = const
и х + о/= const; если они пересекают ось Ох соответственно в
точках xt и х2, то значение и (х0, t0) равно сумме значений функ-
ции Ф в точке Ху и функции F в точке х2 (см. рис. 97).
378
Часть III
Пример 1. Пусть начальная скорость равна нулю, а началь-
ное отклонение задается следующим условием: струна, закреп-
ленная в начальный момент в точках х = а и х ~ р, оттянута в
середине отрезка [а; р] на высоту h (рис. 98 а).
Если обозначить через <р(х) функцию, дающую начальное от-
клонение, то отклонение в любой момент выразится по формуле:
и(х,
<?(x — al) , ср (х -р- at)
2 "Г 2
Первое 'слагаемое дает прямую волну, второе — обратную. На
рис. 98 б, 98 в изображен профиль струны в различные момен-
ты времени.
t Плоскостью Oxt можно воспользоваться для того, чтобы
найти отклонение струны в произвольной точке х0 в любой мо-
мент времени /0. Для этого надо через точку (х0, /0) на плоскос-
ти Oxt провести две характеристики. Если они пересекут ось Ох
в точках Xi и хг, то отклонение в точке х0 в момент /0 равно
сумме значений функции -у <?(*) в точках xt и х2.
Проведем две характеристики через точку а на оси Ох и еще
две характеристики через точку 3. Эти четыре прямые разобьют
^atallausX
знание без араниц W *
Г лава 5, § 4
379
верхнюю полуплоскость (/ > 0) на 6 областей (рис. 99). Отклоне-
ние будет отлично от нуля только в тех точках плоскости Oxt,
для которых хотя бы одна из характеристик, проходящих через
эти точки, пересекает ось абсцисс на участке (а, р). Таким об-
разом, положению покоя соответствуют точки, лежащие в об-
ластях 4, 5, 6; отклонение будет положительно всюду в облас-
тях 1, 2, 3. Для того чтобы сказанное стало яснее, проследим,
как с течением времени t изменяется отклонение точки струны с
абсциссой X (рис. 99): в моменты времени от 1 = 0 до t =xi
точка пребывает в состоянии покоя; колебание до нее еще не
дошло (в этом случае точка (X, t) находится в области 5). В мо-
менты от t = Ti до t = та точка будет находиться в состоянии
движения: до этой точки дошла прямая волна. Во все моменты
времени, более поздние, чем т2, мы попадаем снова в область по-
коя (область 6); значит, при t > т2 точка с абсциссой X будет
снова пребывать в покое (отклонение равно нулю).
Пример 2. Рассмотрим бесконечную струну, у которой на-
чальное отклонение равно нулю, а начальная скорость равна о0
на участке а < х < р и нулю — вне этого участка.
Тогда решение запишется следующим образом:
1
х - at
где
? (?) = I
I о
при а < z < Р,
при z < а или
Z>p.
380
Часть HI
Если через Ф (г) обозначить какую-либо первообразную от функ-
ции то отклонение и(х, t) можно представить следующим
образом:
и (х, t) ~ Ч; (х |- at) — \Г(х — at).
Ясно, что в данном случае верхняя полуплоскость плоскости Oxt
снова естественным образом разбивается на 6 областей (см. выше,
рис. 99). При этом четвертая и пятая области соответствуют точ-
кам, для которых отклонение равно нулю; в шестой области от-
клонение также постоянно, но оно уже отлично от нуля (оно
равно j v„dt == — 2— •
в	/
Если проследить, чему равно отклонение в различные мо-
менты времени, например, в точке X (рис. 99), то можно заме-
тить, что на участке 0 < t < -q отклонение в точке X равно ну-
лю, за период времени от до та отклонение будет нарастать,
и начиная с момента т2 отклонение в точке X остается неизмен-
ным (равным -° Это — так называемая остаточная дефор-
мация струны в точке X.
ОГЛАВЛЕНИЕ
Часть I.
Векторный анализ (Математическая теория поля)
Стр.
§ 1.	Скалярные и векторные поля....................................................................... 3
§ 2.	Скалярное поле. Поверхности уровня. Производная по
дуге .......................................................... 7
§	3.	Градиент скалярного поля.................... 12
§	4.	Интеграл по поверхности............................................................... 17
§	5.	Формула1 Гаусса-Остроградского ........................................................... 22
§	6.	Векторное поле. Векторные линии. Векторные трубки	. .	25
§	7.	Поток векторного поля через поверхность............................................... 29
§	8.	Дивергенция векторного поля........................................................... 33
§	9.	Соленоидальные поля................................................................... 40
§	10.	Циркуляция векторного поля по контуру..................................................... 41
§	11.	Формула Грина-Остроградского и теорема Стокса .	.	45
§	12.	Плотность циркуляции векторного поля. Ротор	....	52
§	13.	Правила действий над дивергенцией и ротором	....	60
§	14.	Безвихревое поле...............................................................   61
§	15.	Потенциальное поле.......................................................................... 66
§	16.	Криволинейные координаты.................................................................... 74
§ 17.	Скалярные и векторные поля в криволинейных координа-
тах. Вычисление градиента с помощью криволинейных
координат..................................................... 82
§ 18.	Интегральные и дифференциальные операции над вектор-
ным полем в криволинейных	координатах.................. 85
§ 19.	Дифференциальные операции	второго порядка...................................................... 100
Часть II.
Краевые задачи. Ортогональные системы функций
§ 1.	Краевые задачи для обыкновенных дифференциальных урав-
нений второго порядка. Собственные решения................... 105
§	2.	Самосопряженное уравнение второго порядка......... 108
§	3.	Собственные числа и собственные функции........... 114
§	4.	Уравнение Бесселя................................. 123
§ 5.	Краевая задача, приводящая к функциям Бесселя. Орто-
гональность функций Бесселя........................... 129
§	6.	Уравнение Лежандра нулевого порядка. Полиномы	Лежандра	134
§	7.	Уравнение Лежандра n-го порядка................... 143
§	8.	Краевые задачи, приводящие к тригонометрическим	функциям	146
§	9.	Ряды по ортогональным системам функций............ 149
§	10.	Тригонометрические ряды Фурье..................... 159
3S2
Стр.
§ 11.	Ряды Фурье-Бесселя .................................... 168
§ 12.	Ряды Фурье-Лежандра.................................... 170
§ 13.	О замкнутости системы тригонометрических функции и
системы полиномов Лежандра................................... 174
Часть III.
УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Глава 1. Вывод некоторых уравнений математической физики
§ 1.	Уравнение колебания струны.............................. 185
§ 2.	Уравнение колебания мембраны............................ 193
§ 3.	Вывод уравнения теплопроводности........................ 203
§ 4.	Вывод основного уравнения гидродинамики................. 214
Глава 2. Решение уравнений методом Фурье (метод разделения
переменных)
§ 1.	Решение уравнения свободных колебании струны методом
Фурье........................................................ 219
§ 2.	Интегралы, зависящие от параметра, и их приложения 228
§ 3.	Доказательство единственности решения задачи о колеба-
нии струны............................................... .	237
§ 4.	Общие замечания о методе Фурье......................... 241
§ 5.	Решение уравнения колебания струны при наличии внешних
сил (вынужденные колебания).................................. 246
§ 6.	Решение задачи о колебании конечной струны в случае не-
однородных граничных условий ................................ 253
§ 7.	Решение уравнения теплопроводности для конечного стержня 257
§ 8.	Двойные ряды Фурье..................................... 260
§ 9.	Решение уравнения колебания прямоугольной мембраны 264
§ 10.	Решение уравнения колебания круглой мембраны . . .	271
§ 11.	Решение задачи об остывании бесконечного круглого ци-
линдра ...................................................... 284
§ 12.	Стационарное распределение температуры внутри беско-
нечного цилиндра. Плоская задача Дирихле (для круга).
Задача о стационарном отклонении мембраны ................... 289
§ 13.	Понятие о математическом моделировании для решения
физических задач ............................................ 301
§ 14.	Решение уравнения гидродинамики для плоскопараллель-
ного движения жидкости внутри цилиндра. Плоская зада-
ча Неймана................................................... 303
§ 15.	Решение уравнения теплопроводности для шара методом
Фурье (стационарный случай). Пространственная задача
Дирихле для шара............................................. 308
Глава 3. Интеграл Фурье и его приложення
§ 1.	Интеграл Фурье......................................... 317
§ 2.	Распространение тепла в бесконечном стержне ....	323
Глава 4. Общие свойства гармонических функций. Функция
Грина
§ 1. Общие свойства гармонических функций. Формулы Грина.
Метод сеток............................................ ;;33
§ 2. Функция Грина. Решение задачи Дирихле для шара . .	346
_____________________________________________________________383
Глава 5. Классификация линейных дифференциальных урав-
нений. Метод характеристик
Стр.
§ 1.	Преобразование линейных уравнений второго порядка с
помощью замены переменных................................... 355
§ 2.	Классификация линейных дифференциальных уравнений
второго порядка. Приведение к каноническому виду . .	363
§ 3.	Решение уравнения колебания бесконечной струны мето-
дом характеристик (метод Даламбера)......................... 371
§ 4.	Исследование закона колебания бесконечной струны . . Ъ75
Юрий Семенович Очан
МЕТОДЫ МАТЕМАТИЧЕСКОЙ
ФИЗИКИ
Редактор Д. А. Тальский
Художник Л/. Шнейдер
Технический редактор
И, И. Коробкова
Корректор С. Н. Юровец
Т —04738. Сдано, в набор 8/Х—64 г.
Подп. к печати 30/III—65 г. Формат
60x90’/i«. Объем 24 печ. л. Уч.-над.
л. 18,08. Изд. М ФМ—181. Тираж
18000 акз. Цена 64 коп.
Тип. зак. 728
Сводный тематический план 1965 г,
учебников для вузов и техникумов.
Позициям 271.
Москва. И-51, Неглииная ул.,
Д. 29/14
Издательство «Высшая школа»
Ярославский полиграфкомбинат
«Главполнграфпрома»
Государственного комитета
Совета Министров СССР по гечтаи.
Ярославль, ул. Свободы, 97.