Автор: Краснов М.Л. Киселев А.И. Макаренко Г.И.
Теги: анализ высшая математика учебное пособие
Год: 1978
Текст
ЛА.Л.КРАСНОВ
А.И.КИСЕЛЕВ
Г. И.МАКАРЕНКО
ВЕКТОРНЫЙ
АНАЛИЗ
ИЗБРАННЫЕ ГЛАВЫ .
ВЫСШЕЙ МАТЕМАТИКИ
ДЛЯ ИНЖЕНЕРОВ
И СТУДЕНТОВ ВТУЗОВ
ЗАДАЧИ И УПРАЖНЕНИЯ
МЛ. КРАСНОВ
А.И. КИСЕЛЕВ
Г. И.МАКАРЕНКО
ВЕКТОРНЫЙ
АНАЛИЗ
Допущено Министерством высшвво
и среднего специального образования СССР
в качестве учебного пособия для студентов
высших технических учебных заведений
МОСКВА кНАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
19 7 8
517.1
К 78
УДК 517
Векторный анализ. М. Л. К р а с н о в, А. И.* К п -
с е л е в, Г. И. Макаренко. Главная редакция
физико-математической литературы издательства «Нау-
ка», М., 1978,160 стр.
Как и другие книги авторов, вышедшие в серии
«Избранные главы высшей математики для инженеров
и студентов втузов», книга «Векторный анализ» пред-
назначается в основном для студентов технических
вузов, а также для инженеров, решивших освежить
в памяти такой важный раздел высшей математики,
каким является векторный анализ.
В начале каждого параграфа приводится сводка
основных теоретических положений, определений и фор-
мул, а также дается подробное решение примеров и
задач.
В книге содержится около 300 задач и примеров
для самостоятельного решения. Все они снабжены
ответами или указаниями к решению. Многочислен-
ные чертежи должны способствовать усвоению ма-
териала.
Илл. 42. Библ. 12.
20203—138
053(02)-78
21-78
Главная редакция
физико-математической литературы
издательства «Наука», 1978
ОГЛАВЛЕНИЕ
Предисловие .............................................................................................. 5
Глава I. Вектор-функция скалярного аргумента ... 7
§ 1. Годограф вектор-функции....................................................... 7
§ 2. Предел и непрерывность вектор-функции скалярного
аргумента.............................................. 9
§ 3. Производная вектор-функции по скалярному аргу-
менту ......................................... .... 11
§ 4. Интегрирование вектор-функции скалярного аргумента 15
§ 5. Первая и вторая производные вектора по длине дуги
кривой. Кривизна кривой. Главная нормаль............. 23
§ 6. Соприкасающаяся плоскость. Бинормаль. Кручение.
Формулы Френе.......................................... 26
Глава II. Скалярное ноле................................................................................. 30
§ 7. Примеры скалярных полей. Поверхности и линии уровня 30
| 8. Производная по направлению ......................................................................... 33
| 9. Градиент скалярного поля............................................................................ 37
Глава III. Векторное поле........................... . 45
| 10. Векторные линии. Дифференциальный уравнения век-
торных линий....................................... 45
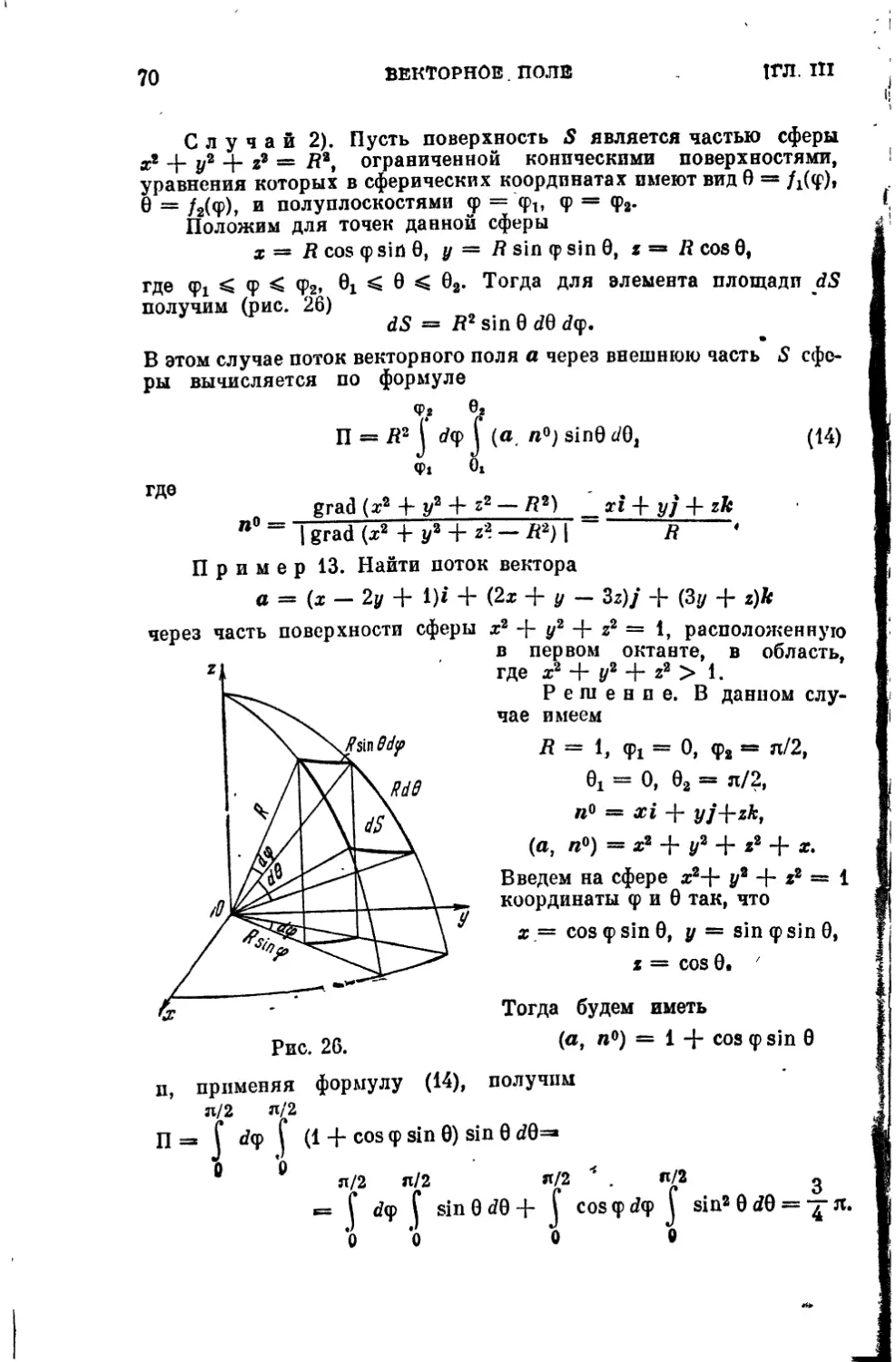
| И. Поток векторного поля. Способы вычисления потока 50
5 12. Поток вектора через замкнутую поверхность. Теорема
Гаусса — Остроградского............................ 71
5 13. Дивергенция векторного поля. Солеиоидальное поле 74
$ 14. Линейный интеграл в векторном поле. Циркуляция
векторного поля......................................... 81
§15 . Ротор (вихрь) векторного поля................... 91
§ 16. Теорема Стокса.................................*. 93
§17 . Независимость линейного интеграла от пути интегри-
рования. Формула Грина........................«... 97
Глава IV. Потенциальное поле........................... 102
§ 18. Признаки потенциальности поля................... 102
§19 . Вычисление линейного интеграла в потенциальном
поле.................................................. 104
ОГЛАВЛЕНИЕ
Глава V. Оператор Гамильтона. Дифференциальные
операции второго порядка. Оператор Лапласа
§ 20. Оператор Гамильтона «наб л а»................... 110
$ 21 . Дифференциальные операции второго порядка. Опера-
тор Лапласа......................................... 114
§ 22. Векторный потенциал............................... 123
Глава VI. Криволинейные координаты. Основные опе-
рации векторного анализа в криволинейных
координатах......................................... 128
§ 23. Криволинейные координаты.......................... 128
§ 24. Основные операции векторного анализа в криволи-
нейных координатах.................................. 131
§ 25. Оператор Лапласа в ортогональных координатах . . . 148
Ответы.................................................. 151
Приложение I........................................... 157
Приложение II........................................... 158
Литература.............................................. 160
ПРЕДИСЛОВИЕ
Хорошая математическая подготовка современного ин-
женера безусловно способствует новым достижениям тех-
ники в различных ее направлениях. Одной из математи-
ческих дисциплин, имеющих большое значение в матема-
тическом образовании инженера, является векторный
анализ, который в настоящее время включен в обязатель-
ную втузовскую программу курса зысшей математики.
Предлагаемый сборник задач по векторному анализу
содержит необходимый минимум задач и упражнений по
курсу векторного анализа в объеме втузовской программы.
В начале каждого параграфа приводятся основные
теоретические сведения и даются подробные решения до-
статочно большого числа типовых задач. В тексте разо-
брано 100 примеров, и для самостоятельного решения
дается 314 задач. В книге имеется некоторое количество
задач прикладного характера, которые выбраны так»
чтобы их разбор не требовал от читателя дополнительных
сведений из специальных дисциплин. Материал шестой
главы, посвященный криволинейным координатам и ос-
новным операциям векторного анализа в криволинейных
координатах, внесен в книгу из тех соображений, чтобы
дать читателю хотя бы минимальное количество задач
для приобретения необходимых навыков.
Методика изложения материала в сборнике близка
к той, которая принята на кафедре высшей математики
Московского энергетического института.
Книгу можно рассматривать как краткий курс век-
торного анализа, в котором сообщаются без доказатель-
ства основные факты с иллюстрацией их на конкретных
примерах. Поэтому предлагаемый задачник может быть
использован, с одной стороны, для повторения основ
векторного анализа, а с другой — как учебное пособие
6
ПРЕДИСЛОВИЕ
для лиц, которые, не вдаваясь в доказательства тех или
иных предложений и теорем* хотят овладеть техникой
операций векторного анализа.
При составлении задачника авторы использовали ма-
териал, содержащийся в имеющихся курсах векторного
исчисления и сборниках задач. Значительная часть за-
дач составлена самими авторами.
Сборник задач рассчитан на студентов дневных и ве-
черних отделений технических вузов, а также для сту-
дентов-заочников, знакомых с векторной алгеброй и ма-
тематическим анализом в объеме первых двух курсов
втуза.
Мы выражаем нашу искреннюю благодарность про-
фессору В. П. Громову (МПИ им. Н. К. Крупской), про-
фессору А. В. Ефимову и доцентам И. М. Петрову,
Б. И. Фридлендеруг В. Н. Земскову (МИЭТ) за их тща-
тельный просмотр рукописи книги и за ценные и полез-
ные советы и замечания, которые нами были учтены при
окончательном редактировании.
Все замечания и пожелания, направленные на улуч-
шение книги* будут приняты нами с благодарностью.
Москва — Дубна, 1977 г.
М. Л. Краснов
А. И. Киселев
Г. И. Макаренко
ГЛАВА I
ВЕКТОР-ФУНКЦИЯ
СКАЛЯРНОГО А?ГУМ^ЙТА
§ 1. Годограф вектор-функцни
Определение 1. Вектор г называется ее шпор-функцией
скалярного аргумента t, если каждому значению скаляра из облас-
ти допустимых значений соответствует определенное значение век-
тора г. Будем это записывать так:
Г =» r(t).
Если вектор г является функцией скалярного аргумента t
г ° г(0,
то координаты х, у, z вектора г также будут функциями аргумента /:
х =® ж(0, у у(0, z “ г(0.
Обратно, если координаты вектора г являются функциями /,
то функцией t будет и сам вектор г:
r= x(t)i + у(0/ + »(<)*•
Таким образом, задание вектор-функции r(t) равносильно заданию
трех скалярных функций «(/), y(t), «(/).
Определение 2. Годографом вектор-функции r(t) ска-
лярного аргумента называется геометрическое место точек, кото-
рое описывает конец вектора r(t) при -----__
изменении скаляра t, когда начало век-
тора г(0 помещено в фиксированную
точку О пространства (рис. 1). /
Годографом радиуса-вектора г~r(t) 1
движущейся точки будет сама траекто-
рия L этой точки. Годографом скорости /
г = п(0 этой точки будет некоторая /
другая линия Lx (рис. 2). Так, если ';
материальная точка движется по ок- ° •
^>ужности с постоянной скоростью
t?|= const, то ее годограф скорое- Рис.
тей также представляет собой окруж-
ность с центром в точке О* и с радиусом, равным |п|.
Пример 1. Построить годограф вектора ti + tj +
8
ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
(ГЛ. I
Решение. 1°. Это построение можно вести по точкам, со-
ставляя таблицу:
t 0 1 1 3 4
г 0 2/4-2/+4Л 3t+3/+9fc «+4/+16*
2®. Можно поступить и так. Обозначив через х, у, г координаты
вектора г, будем иметь
х = t, у =* t, z ~
Исключая из этих уравнений параметр е, получим уравнения
поверхностей у = х, z = х2, линия пересечения L которых и оп-
ределит годограф вектора r(t) (рис. 3).
t 2]
ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ВЕКТОР-ФУНКЦИИ
9
1. Построить годографы векторов;
а) г = 2i + t2j — 1гк.
'«’ + 1 t , 2t
б) г (г + 1)8 1 + (t + 1)2 J'
в) г = cos t • i 4- sin t • j + k.
r) r = ti + у + -J- tsk.
nx „ _ 2ti + 2t/+(t2-2)fc
r ““ Й + 2
§ 2. Предел и непрерывность вектор-функции
скалярного аргумента
а(Л называется бесконечно
Пусть вектор-функция r~r(t) скалярного аргумента t опре-
делена в некоторой окрестности значения аргумента tf кроме,
быть может, самого значения tQ.
Определение 1. Постоянный вектор А называется пре*
делом вектора г(Д) при t tQ, если для любого е > 0 существует
б > О такое, что для всех
t tQf удовлетворяющих условию
Н — М < выполняется нера-
венство
|г(0 — А] < е.
Как и в обычном анализе, пи-
шут lim г ($) » А.
t-*t9 *
Геометрически это означает, **
что вектор r(t) при t -► f0 стре- *
мится к вектору А как по длине,
так и по направлению (рис. 4).
Определение 2. Вектор
малым при t -> tQl если a(t) имеет предел при / и этот предел
равен нулю:
Пт а («) =0,
t~*ie
или, что то же, для любого 8 > 0 существует б *> 0 такое, что для
всех t =И= ;0, удовлетворяющих условию |f — f0| < б, выполняется
неравенство |а(/)1 < е.
Пример 1. Показать, что вектор = ti+ sin tj есть
бесконечно малый вектор при t -> 0.
Решение. Имеем
1«(01 =1 ti + sin f/| < h| + |sin d
10
ВИКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
1ГЛ. I
откуда видно, что если для всякого • > 0 взять в = в/2, то при
|< — 0|< б = е/2 будем им ть |a(t)| < ». Согласно определению
вто означает, что a(t) есть бесконечно малый вектор при t -► 0.
2. Показать, что предел модуля вектора равен моду-
лю его предела, если последний предел существует.
3. Доказать, что для того, чтобы вектор-функция
г(1) имела при t -> 10 предел А, необходимо и достаточно,
чтобы г(1) можно было представить в виде
г(1) *=» А + a(t),
где7 a(t) — бесконечно малый при 1-»- tt вектор.
4. Показать, что если вектор-функции а(1) и 6(1) име-
ют при t -► tt пределы:
lim а (1) = A, lim Ь (1) = В,
t-t.
то их сумма a(t) + 6(1) и разность «(1) — 6(1) также имеют
пределы при 1 -*• 10, причем
lim [а (1) ± 6 (1)] = Л ± В.
б. Пусть
lima(i) = 4, lim 6(1) = В.
t-и, t-t,
Доказать, что
lim(a(i), 6(1)) = (4, В),
где (а(0> Ь(0) — скалярное произведение вектор-функ*
ций a(t) и b(t).
6. Пусть
r(£) « x(t)i + y(t)j + z(t)k, А = axi + aj + a3k.
Показать, что если lim г (t) «= Л, то
t-t,
lim х (t) » limi/(Z) = a2, limz(£) = a8B
t—*to
Найти следующие пределы:
m /sin t . . cost — 1 . , лл,\
7. lim —1 + —j +
s- й(т^г-‘ + гт1' + 4
§-3)
ПРОИЗВОДНАЯ ВЕКТОР-ФУНКЦИИ
11
9.
10.
11.
/sin t . , . . , к \
Inn I —— i 4- cos t • j 4 —7— I.
i-лк * ' ^t + n)
... {sin t . , 14 cost . . t
lim I - i 4—4 j 4—
lim ( e ~ e i 4 j 4 2&\
. \ t — 1 ' 1 — t J 1 /
Определение 3. Вектор-функция г = r(t), определен-
ная в некоторой окрестности значения называется непре-
рывной при t = £0, если
limr(i) = r(z0).
Иными словами, г r(t) непрерывна при t~~t^ если для всякого
е > 0 существует 6 > 0 такое, что для всех t, удовлетворяющих
условию |£ — /0| < 6, верно неравенство |г(£) —- r(i0)| < е.
Годографом непрерывной вектор-функции скалярного аргу-
мента является непрерывная кривая.
12. Исходя из известного неравенства \а — Ь|
11^1 — |&||, показать, что непрерывность векторной
функции влечет за собой непрерывность ее модуля. Верно
ли обратное предложение?
13. Показать, что если a(t) и b(t) непрерывны при
t == f0, то вектор-функция a(t) Ч- 6(f) также непрерывна
при t = tQ.
*14. Вектор-функция а(0 + b(t) непрерывна при t = tQ.
Следует ли отсюда, что векторы a(t) и b(t) дакже непре-
рывны при t — f0?
15. Доказать, что если a(t) и &(£)—непрерывные век-
тор-фупкции, тег их скалярное произведение (а(0, 6(0)
и векторное произведение [«(t), *6(01 также непрерывны.
§ 3. Производная вектор-функции
по скалярному аргументу
Пусть всктор-фупкцпя г = г(0 определена для всех t из интер-
вала (f0, tj). Возьмем некоторое значение t е (f0, ГД дадим t прира-
щение Аг такое, чтобы t + Аг е (г0, *i), и найдем соответствующее
приращение Ar == r(t + &t) — r(t) вектор-функции r(t). Рассмот-
рим далее отношение
Определение. Если при А/ 0 отношение -- имеет
предел, то этот предел называется производной вектор-функ-
ции г = r(t) по скалярному аргументу t при данном значении t
г
12 ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА [ГЛ. I
аргумента и обозначается (а также г '(t) или г(/)). Таким
dt
образом,
/г (0 „ Ит Ar = lim г (1 + At) — г (0 ,
dt Д/->0 &t д/->0 &t
В этом случае вектор-функция г = r(t) называется дифференци-
руемой»
16. Показать, что если вектор-функция г = r(t) имеет
производную при некотором
значении t аргумента, то
она непрерывна при этом
значении t.
Производная вектор-функ-
ции r(t) скалярного аргумен-
та t есть вектор, направлен-
ный по касательной к годо-
графу исходного вектора в
рассматриваемой точке (рис.5).
dr
При этом вектор -g- направ-
лен в ту сторону, куда пере-
мещается конец вектора r(t) по
годографу, когда параметр t
растет.
Пусть г = r(t) есть радиус-вектор движущейся точки. Тогда
вектор v = есть вектор скорости этой точки.
Пусть
r(i) = x(l)i + y(t)j + z(t)k,
где функции x(t), y(t), z(t) дифференцируемы в точке t. Тогда су-
dr
ществует — при этом значении t и
dt
dr dx dy dz
dt ** dt * ' dt J ' dt
(1)
i &г
[Пример 1. Найти если г = ia cos t + jb sin t (точка'
движется по эллипсу).
Решение. По формуле (1)
— = — ia sin t + jb cos t.
dt
По аналогии с дифференциалом скалярной функции Зиффе-
ренциал вектор-функции г — r(t) есть вектор dr, определяемый
f 31
ПРОИЗВОДНАЯ ВЕКТОР-ФУНКЦИИ
13
равенством*
_ dr J»
“—ЗГ**
где dt»» Дг — приращение скалярного аргумента t.
Как и для скалярных функций,
Дг= dr + a-Af,
где а » a(f, Д0 -> 0 при Д$ -> 0.
Основные правила дифференцирования,
вектор-функции
Предположим, что все рассматриваемые функции (как ска-
лярные, так и векторные) непрерывны и дифференцируемы.
1°. Если с — постоянный вектор, то
2*. Производная суммы вектор-функции равна сумме произ-
водных слагаемых
d (а (0 + b(t)) __ da db
dt at + dt *
3°. Пусть вектор-функция a(t) умножается на скалярную функ-
цию m(t) того же скалярного аргумента. Тогда
d (та) da dm
~~di = m~dt +”5Г “
4’
d(g, b) f db^\ / da \
dt ~ dt j + \ dt ' j*
5%
d [a, &] [da
dt = [ dt ’ b
d&l
dt J*
+ «,
(В этой формуле в правой части надо соблюдать тот же порядок
множителей ап Ь, что и в левой части.)
Докажем, например, формулу 4°. Положим <р(0=(а(0, &(*))•
Дадим t приращение Дг; будем иметь в силу распределительного
свойства для скалярного произведения
Дф = <р(г + Д£) — ф(г) = (а + Да, b + Д&) — (а, Ь) =»
= (Да, Ь) + (а, Дд) + (Да, Дб).
Отсюда
Дф /Да \ / Д&\ f \а \
дГ = ^"дГ1 + (“• "at) + 1 д Y ‘(2)
По условию функции a(t) и b(t) имеют производные при значении
t аргумента и, значит, непрерывны при этом значении t. Поэтому
, Да da , ДЬ db л
lim -тт «-тг» “а7“ =а lim До «0.
At->0 М dt Д*-0 dt АЬ>0
14
ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
[ГЛ I
Переходя в (2) к пределу при Д* -► 0, получим
d (a, b) ^fda Л , / db\
е dt \ dt ' ) \ dt J
17. Дано г «« r(t). Найти производные
х d / о\ d / dr \ \ d Г dr |
а) б> ф’ -2Г)’ в) dTp "dTj’
18. Доказать, что если модуль |г| вектор-функции
г = r(f) остается постоянным для всех значений t, то
4^-1 г. Каков геометрический смысл этого факта?
at
19. Доказать, что если е единичный вектор направ-
ления вектора Е, то
r , . [Е, dE]
[е, de] |^|2 .
20. Пусть
и = и^х, у, z, t)i + и.^х, у, z, t)j + и3(х, у, z, t)k9
где ulf u2, и3 — непрерывно дифференцируемые функции
своих аргументов, а х} у9 z — непрерывно дифференци-
руемые функции от L Показать что
du ____ \ dx J dy Ou dz
dt dt дх dt * ду dt 1 dz dt
21. Найти траекторию движения, для которого ради-
ус-вектор r(t) движущейся точки удовлетворяет условию
« [а, г], где а — постоянный вектор.
dr
Производная — вектор-функции r(t) скалярного аргумента
dt
является всктор-функцией того же аргумента. Если существует
dr
производная от------ то опа называется производной второго порядка
dt
и обозначается -^4-. Вообще
dt2
dvr _ d
dln ~ dt
d/”-1
n 5= 1, 2, ...
t4]
ИНТЕГРИРОВАНИИ ВЕКТОР-ФУНКЦИИ
15
22. Дан радиус-вектор движущейся в пространстве
точки
r{a sin tt —a cos t, bt*}
(t — время, а и b — постоянные). Найти годографы ско-
рости и ускорения.
23. Дано: r=a cos col 4- b sin col, где a, b — по-
стоянные. Доказать что
1)
2)
С?2Г I Л
-лг + “’г = 0-
24. Показать, что если г == аей< 4- be~(at, где а и
Ь — постоянные векторы4 то —----<о2г = 0.
25. Показать, что модуль дифференциала радиуса-
вектора точки равен дифференциалу длины дуги4 описы-
ваемой этой точкой.
26. Пусть а = а(и) есть вектор-функция скаляра и,
где и в свою очередь есть некоторая скалярная функция
от основного скаляра i. Предполагая а(и) и и ==
дифференцируемыми нужное число раз, найти выражение
« • da d2a
для производных сложной функции
§ 4. Интегрирование вектор-функции
скалярного аргумента *
Определение 1. Будем называть вектор-функцию Л(0
первообразной функцией для вектор-функции a(t) при t0 < t < *1»
если A(t) дифференцируема и
~ = О. (t), t s (te. <1).
at
Определение 2. Неопределенным интегралом от век-
тор-функции скалярного аргумента а == a(t) называется совокуп-
ность всех первообразных для a(t). Неопределенный интеграл от
вектор-функции, как и в интегральном исчислении, обозначается
знаком^ J. Имеем
Р(0«-л(1) + с,
16
ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
(ГЛ 1
J (c, a (Z)) dt = (c, J
f [c, a (Z)] dt — [c, f
где A(t) — какая-нибудь из первообразных для а(/), С — произ-
вольный постоянный вектор.
Для интегралов от вектор-функций справедливы следующие
свойства:
Г. j a a (t) dt ~ a J a (t) dt (а — числовая постоянная).
2“. j (a (t) ± Ь (t)) dt - f a (t) dt ± f b (t) dt.
27. Показать, что если с — постоянный вектор, a(t) —
переменный вектор, то
a(Z) dt^
а
Если
а(0 = а^}1 + a2(f)j + ajj к,
то
J a (t) dt « i J ax (i) dt +'] J aa (*) dt + к J a3 (t) dt, (1)
т. e. интегрирование векторной функции сводится к трем обычным
интегрированиям.
Пример 1. Найти неопределенный интеграл для вектор-
ной функции a(t) == i cos t + je—t + к.
Решение. Согласно формуле (1)
J a (t) dt = i J* cos t dt+ j J dt-\- к ^dt = i sin f — je^ + kt + c,
где с—произвольный постоянный вектор.
Найти интегралы от следующих вектор-функциш
ь
28. a(Z) = te4 4-sin21 j —
29. a (Z) = + te1'j -|-cos t k.
30. a (Z) = cos Zesln 1 • i — t cos Z2 / +fc.
31. a(Z) = -x-Z2i — ZsinZ-y 4-2*fc.
Пусть вектор-функция a{t) определена и непрерывна на неко-
тором отрезке Uo, Г] изменения аргумента L
Определение 3. Определенным интегралом от вектор-
функции a(t) на отрезке [£0, Г] называется предел векторных ин-
тегральных сумм
п— 1
2 в(тйЖ. тл65 [fft- ‘h+ii.
&=Q
$ 4)
ИНТЕГРИРОВАНИЕ ВЕКТОР-ФУНКЦИИ
17
у
t
при стремлении к нулю длины М наибольшего из отрезков
гА+1 ] (/с= 0, 1, п — 1), на которые разбит отрезок [f0, Т]:
/ п^‘
Справедлива формула
Т
\a(t)dt = A (Г) - A (i0), (2)
h
где A(t) —какая-нибудь первообразная для функции a(t) на Ro, Г].
Если
а(0 = ax(/)i + а2(0/ + as(t)kf
то
т т т г
С a (t) dt ~ i J аг (t) dt + j j* a2 (/) dt + к a3 (t) dt. (3)
t9 t9 '
n!?
Пример 2. Вычислить j a (t) dt, где cos f—/ sin2f.
о
Решение. В силу формулы (3) •
Я/2 91/2 91/2
j a (t) dt ~i J cos t dt— j sin21 dt^
0 0 0
, |*V2 ft sin2f\|n/2 t n л
= isint|o -7^--T-j|o
Вычислить следующие интегралы:
м
Л
32. j a(t) dt, где a=sin2t cos t • i + cos21 • sin t • /4-fc.
b
C fc-’/2 ie^2
33. I a (t) dt, где a = —s-1- ^—r—|- fee*.
0
1
34. ^a(t)dt, где a = 3л cos nt -i — + 2tk.
Л
35. [ a (t) dt, где a = (2t + л) i 4-1 sin t • j j лЛ.
b
2 M. Л. Краснов и др.
18
ВЕКТОР-ФУЯКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
[ГЛ. I
Пример 3. Электрический ток силы I течет снизу вверх по
бесконечному проводу, совпадающему с осью Oz. Найти вектор Н
напряженности магнитного поля, создаваемого этим током в про-
извольной точке M(xt у, z) пространства (рис. 6).
Решение. Рассмотрим достаточно малый элемент РРг =
в dt, оси Oz. По закону Био — Савара напряжение dH магнитного
поля, создаваемого в точке М током, протекающим по элементу
провода совпадает по направлению с векторным произведением
[dg, где dg « РРЬ |dg| = dg, rt «в PM (см. рис. 6). По этому
же закону модуль вектора dll равен
| dH | == -4 S'11 (4/\) '<&
•л
где (dg,~rj — угол, образованный векторами dg и rv Поскольку
|[dg, г, 1| == rxdg sin (dg,'^),
можно написать
rf// = 4(4. (4)
Г1
Чтобы получить искомый вектор Н в точке М, нужно просуммиро-
вать все векторы dH, относящиеся к различным элементам РР^
провода, т. е. проинтегрировать выражение (4) по всей оси Ozt
+°о
я= f 4[«.rxJ. (5)
г 1
§ 4] ИНТЕГРИРОВАНИЕ ВЕКТОР-ФУНКЦИИ ‘19
Имеем
Г1 = дм — др.
Но
ОМ = xi + yj + zk, OP =
поэтому
Ч = xi + yj + (z — Qk,
так что
ri = I ri I = = 1/ра4-(»-02.
где р = Ухг + уг — расстояние точки М до оси провода.
Для векторного произведения [dt>, rj имеем
i
О
х
] к
О
У z—
— i'j
и формула (5) принимает вид (точка М(х, у, z) фиксирована, Z=
®= const)
4-00
С
иj ——
— ОО
(6)
Для вычисления интеграла в правой части (6) сделаем подстановку
р dt
i-z = ptgi, ^=^^27.
Будем иметь
4-эо Я/2
С dt. Г pdt_________
J 1Р2 + (г-О213/2== J cos3 t lp« + р2 tg« t]3^ ~
•—•CO •~Л/Л
л/2
1 ‘ 2
•=^r J cos —
—л/2
Итак, вектор напряженности Н магнитного поля в нашем слу-
чае определяется формулой
/у = у/ 4- ,/)
2*
г
20 ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА [ГЛ. I
ИЛИ
В —Д-(/, И,
где I — I-к — вектор тока, г — радиус-вектор точки M(xt yt z)
поля, р — расстояние точки М до оси провода.
Пример 4. Движение электрона в однородном магнит-
ном поле.
Г Пусть в какой-либо области пространства создано магнитное
поле Я, постоянное по величине и направлению (однородное поле).
Пусть в момент времени t =«
=£0 в это поле попадает элект-
рон с начальной скоростью г0.
Определить траекторию элект-
рона.
Решение. Предполо-
жим сначала, что вектор <?0
перпендикулярен к Я и что
начальное положение элект-
рона — в точке Мо. Выберем
начало О в произвольной точ-
ке плоскости Р, проходящей
через точку Мо перпендику-
лярно вектору Я (рис. 7).
Начальный радиус-вектор ОМ0
пусть будет г0 и пусть г — ра-
диус-вектор электрона в те-
кущий момент времени t,
a v — мгновенная скорость
в этот момент. Основное дифференциальное уравнение движения
d2r „
т dt2 ~ F'
Сила F, действующая в момент t на электрон со стороны магнитного
поля, как известно, равна
f = —е0[//, с],
где ел — абсолютная величина заряда электрона. Таким образом,
d2r
та^ = е®1р> И>'
(7)
Сила F в каждый момент t перпендикулярна к направлению скоро-
сти и к направлению поля Я; она будет заставлять электрон в каж-
дый момент уклоняться от прямолинейного пути и описывать неко-
торую криволинейную траекторию.
Перепишем уравнение (7) в виде
dv „1
т dt ~ е° Л ’ й
§ 4] ИНТЕГРИРОВАНИЕ ВЕКТОР-ФУНКЦИИ 21
и проинтегрируем его по t от f0 до t. Получим
mv — mPp = ee[rt Я] — е0[г0, Я]
или
mv = eQ[rt Я] + (mvQ — <?0[r0, Я]). (8)
Выберем теперь начало координат О' так, чтсбы обратилось в нуль
слагаемое, стоящее в круглых скобках в правой части (8), т. е. чтобы
eoko, Н] = mv0. (9)
Из (9) следует, что начальный вектор г0 должен быть перпендику-
лярен к вектору 1?0 и лежать на прямой М0К, перпендикулярной к
плоскости векторов и Я. Модуль вектора г0 в силу (9) должен
удовлетворять соотношению
«oZol • |Я| = пфо|.
откуда
' . т I I
' г°1 = е01 И Г (10)
Этим положение нового начала О' определено. Относительно него
уравнение (8) перепишется так:
mv = е0[г, Я] (11)
или
dr
т1й = ео 1г’Я!. (12)
Из уравнения (11) вытекает, что траекторией электрона будет пло-
ская кривая, лежащая в плоскости Р, так как вектор v в каждый
момент времени перпендикулярен к Я^ Умножим теперь обе части
уравнения (12) скалярно на г:
/ dr \
w|r,-^J=e0(r, [г,Я]). (13)
Смешанное произведение в правой части (13) равно нулю, так что
Отсюда
d d
(г2) = 0 или -jj- (г2) = 0, т. е. г2 = const.
Это — уравнение окружности, лежащей в плоскости Р, с центром в
выбранной нами точке О'. Радиус этой окружности определяется
формулой (10), поскольку начальная точка Мо также должна лежать
22
ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
(ГЛ. I
на этой окружности. Итак, окончательно
т | I
= <10>
Таким образом, если электрон попадает в однородное магнитное
поле Н с начальной скоростью г0, перпендикулярной к Я, то он
будет описывать в этом поле круговую траекторию, лежащую в
плоскости Р, перпендикулярной к Я и проходящей через начальную
точку. Радиус этой окружности определяется формулой (10), а ее
центр О' лежит на прямой, перпендикулярной к плоскости векторов
гои Я, причем из точки О\ поворот от v0 к Я должен быть виден
против часовой стрелки.
Из формулы (10) видно, что радиус г0 окружности обратно про*
порционален )Я[. Таким образом, чем сильнее напряженность маг-
нитного поля, тем больше кривизна траектории.
Из формулы (11)
mv = £0[г, Я]
видно, что если г постоянен по модулю п все время перпендикулярен
к Я, то и скорость v точки будет постоянна по величин?:
|н| — г0 — const,
так что электрон движется по орбите равномерно. Период обраще-
ния Т равен
2лг0 л т
г=“1=211 мйт
s (14)
В эту формулу не входит начальная скорость г0. Таким образом,
с какой бы начальной скоростью г0, перпендикулярной к Я, ни по-
пал электрон в однородное магнит-
ное поле Я, он будет совершать
один оборот по орбите • всегда в
одно и то же время Г, незави-
симо от величины р0.
2®. Пусть теперь электрон
попадает в однородное магнит-
ное поле Я с какой-либо началь-
ной скоростью V, которая не пер-
пендикулярна вектору Я. Тогда
эту скорость V можно разложить
на две составляющие: вектор г0,
направленный перпендикулярно
полю, и вектор направленный
вдоль магнитного поля.
Из формулы
F = e[V, ЯГ = е0[г0, Н]
видно, что «закручивающая» сила F будет определяться только пер-
пендикулярной составляющей ноп она сообщит электрону вра-
<51
ПЕРВАЯ И ВТОРАЯ ПРОИЗВОДНЫЕ ВЕКТОРА
23
щательное движение по кругу (с центром в Ол, рассмотренному
выше. Что касается второй составляющей vlt то электрон со-
хранит ее по инерции и будет, кроме кругового равномерного
движения, перемещаться еще прямолинейно и равномерно вдоль
направления Я со скоростью = |V| cos а. Сочетание этих дви-
жений даст винтовую линию с осью, параллельной вектору Н
и проходящей через точку О' (рис. 8).
§ 5. Первая и вторая производные вектора
по длине дуги кривой. Кривизна кривой.
Главная нормаль
Рассмотрим в пространстве некоторую линию £. Выберем на
ней какую-либо точку Л/о в качестве начала отсчета и выберем также
какое-либо направление вдоль линии L, которое будем считать по-
ложительным. В качестве параметра возьмем длину дуги 5, от-
считываемую от точки Мо кривой (]Упс. 9). Тогда радиус-вектор
точки М кривой будет
г = г($).
При таком выборе параметра
где т° — единичный вектор, направленный по касательной к ли-
нии L в сторону возрастания параметра s.
Если вектор г задан координатами.
г == xl + У] +
то
^-/4- J4-- к
ds ’ di * ’ ds 9
24
ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
(ГЛ. I
причем
Так как
|т°| = то вектор — ортогонален вектору т°.
ds
Модуль вектора
ds
Здесь К — кривизна линии L в точке М.
Йт^
Прямая, имеющая направление вектора — и проходящая
через точку М кривой, называется главной нормалью кривой
в точке М. Обозначая единичный вектор этого направления
через я0, будем иметь
„ л
— = /ОЛ
ds
(1)
Величина, обратная кривизне кривой в данной точке, называет-
ся радиусом кривизны кривой в этой точке и обозначается через R:
Поэтому формулу (1) можно переписать так:
d*r dr0 n°
ds2 ~ ds ~~ R *
Отсюда
J________________________________ifri
K ~ R ~ \ ds2 I
или
Формула (2) позволяет вычислить кривизну линии в любой точке,
если эта линия вадана параметрическими уравнениями, в которых ,
параметром является длина дуги s.
В частном случае плоской кривой — окружности радиуса а
8
х— a cos ,
а 9
y = «sin-£-
I 51
ПЕРВАЯ И ВТОРАЯ ПРОИЗВОДНЫЕ ВЕКТОРА
25
имеем
(Рх 1 8 (Ру
d$’ ~ a cos а ’ di*
и формула (2) дает
1 8
— sin — j
a a J
„ 5 , 1 . о s 1
COS’— 2 —= — (
т. e. что кривизна окружности радиуса а постоянна и равна величине
обратной радиусу окружности.
Если линия L определяется векторно-параметрическим урав-
нением г = г (t), где параметр t — произвольный, то
| [ dr
dt 1 dt2
1 dr |з
"=4
(3)
Формула (3) дает возможность вычислить кривизну кривой в
любой ее точке при произвольном параметрическом задании этой
кривой.
Пример 1. Вычислить кривизну винтовой линии
г = a cos t-i + a sin t> j + htk.
Решение. Так как
dr
— == — a sin t« i + a cos t* j + hk}
d2r ...
— = — a cost-i — a sin
то векторное произведение
dr cftrl __
dt ’ dt2 |
i
— a sin t
— a cos t
a cost
— a sin t
к
h
0
= ah sin t.i — ah cos t* j +
Следовательно,
It £fl| = a ТДГРР,
[Л ’ dt2 J I v
I —I = Д/а’ + Л’.
I dt ।
В силу формулы (3)
a
или
1
Я “ a? + №
a2 + &2
r _ —_— = const.
Таким образом, винтов я линия имеет постоянный радиус кривизны.
26
ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА > ТТЛ. I
Найти радиус кривизны данных линий:
36. г = In cos t • i + In sin t • j + У21 • k.
37. r = t2i + 2^j.
88. r = 3t2i + (3i -t3) j + 2Ar при t =* 1.
39. r = a (cos t~\-t sin t) i+a (sin t—t cos t) j при i = л/2.
40. r = a ch t • i + a sh t • j -(- atk в любой точке t.
§ в. Соприкасающаяся плоскость* Бинормаль*
Кручение* Формулы Френе
Плоскость, проходящая через касательную прямую и главную
нормаль к данной кривой L в точке Mt называется соприкасающейся
плоскостью в точке М.
Для плоской кривой соприкасающаяся плоскость совпадает с
плоскостью кривой.
Если вектор г = r{t) имеет непрерывную производную —
dt
в окрестности точки f0 и, кроме того, вторую производную
(<о)
d&
такую, что
ад ад] 0
L dt ’ J
то в точке существует соприкасающаяся плоскость к кривой
r= г(/), векторное уравнение которой
/ (р — Г (t0), = о,
/ \ L dt dt* J/
т \м где р = р(0 — радиус-вектор текущей
точки плоскости.
X. -Нормаль к кривой в точке М, пер-
\ А пендикулярная к соприкасающейся
X/ J плоскости кривой в этой точке, назы-
/ вается бинормалью кривой в дайной
точке М.
Рис. 10. Обозначим через 6° единичный век-
- тор бинормали, ориентированный так,
чтобы векторы г°, 6° образовывали правую тройку (рис. 10).
Тогда
60* = 1( &0 [То( „0J,
•Ml
СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ
27
Для производной получаем
ds
__ Го
(Й L ’ds J
Вектор — перпендикулярен и вектору т°, и вектору &°, т. е.
ds
он коллинеарен вектору д°. Положим
| d№ I
I ds I “ Т '
тогда будем иметь
2
Т
dbQ
ds
/г°.
4
Величина называется кручением данной кривой, а величину
Т называют радиусом кручения кривой.
Кручение кривой определяется формулой
Л = Л2 d3f*\
Т dsl’ ds3/
где символ (а, 5, с) обозначает смешанное произведение векторов
a, b, с, т. е. (а, 6,с) = (а, [6, с]).
В случае, когда кривая задана векторно-параметрическим
уравнением г =» r(t)t имеем
/Jr d2r d3r
1 \dt ’ dt2 ’ dt3 ,
T 11 I г
11 dt' dt2 J
Пример 1. Найти кручение винтовой линии
г = a cos t i 4- a sin Г/ + htk.
Решение. Находим производные данного вектора
dr . . . . , , >
~ == —. a sin t • i + а cos t • ] -f- hk,
d^r
™ = — а cos t • i — a sin t • /»
d3r
« a sin t • I — a cos t •
2Я
ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
[ГЛ. I
Смешанное произведение этих векторов
dr d*r d^r
dt ’ dt2. 1 dt3 4
— a sin t
— a cos t
a sin t
a cost
— a si n t
— a cos t
h
О ==а2Л,
О
В примере 1, § 5 найдено, что
1^’£-1Гвв*(“*+м)-
I Lat at* j |
Применяя формулу (1), получим для кручения
1 h
Т a2 + h2'
кручение винтовой линии во всех ее точках
Таким образом,
одно и то же.
Пример 2.
кости в точке t == О
Написать уравнение соприкасающейся плос-
винтовой линии
г « a cos t-i + a sin t-j + htk.
Решение. Находим значения производных данного векто-
dr d2r Л л
ра и его производных----и -— в точке t = 0:
dt dt2
г (0) = ai, =aj + hk, --Ц?! = —al.
dt dt-
Следовательно (см. пример 1, § 5),
pr(0) d2r(0)1 t>i „
\~dT’~d^~aht
Векторное уравнение соприкасающейся плоскости
dr (0) <Pr (0)\
dt ’ dt3 Г0
1ИЛИ
(р — —ahj + а2к) = 0.
Так как радиус-вектор текущей точки соприкасающейся плоскости
р = xi + у] + zk, то, переходя к координатной записи, получим
уравнение искомой плоскости в виде hy — az~ 0.
Формулы, выражающие производные векторов т°, fc°, на-
зываются формулами Френех
rft° = _Ln» £1° =____Lt0 — —6°
R ’ di Т ’ dt R Т
$ 6]
СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ
41. Написать уравнение соприкасающейся плоскости
в точке t == 2 кривой
г = и — tj
42. Написать уравнение соприкасающейся плоскости
в точке t = 0 кривой
г = + e~*j + Д/2/fc.
43. Найти кручение в точке t = 0 кривой
г = е* cos t-i + sin t* j + е*к.
!А. Найти кручение в любой точке t кривой z
г = a ch t'i + a sh t>j + at-к.
Г Л А В A II
СКАЛЯРНОЕ ПОЛЕ
Г§ 7. Примеры скалярных полей. Поверхности
и линии уровня
Определение. Если в каждой точке пространства или
части пространства определено значение некоторой величины, то
говорят, что задано ноле данной величины.
Поле называется если рассматриваемая величина
(л\ скалярна, т. е. вполне харакгерйзуется своим числовым значением,
(•у Пример скалярных полей дает поле температур, влектростати-
ческов поле.
Им» V Задание скалярного поля осуществляется заданием скалярной
’ функции точки М
и « КМ).
Если в пространстве введена декартова система координат
xyz} то
u == /(а?, у, з);
Геометрической характеристикой скалярного поля служат
[ поверхности уровня — геометрическое место точек, в которых ска-
и । ляР1,ая функция поля принимает одно и то же значение. Поверхность ?
J уровня данного поля определяется уравнением
Г f(x, р, z) => С, где С = const.
В случае поля температур, создаваемого в однородной и изо-
тропной среде точечным источником тепла, поверхности уровня
.будут сферами с центром в источнике (центрально-симметрич-
ное поле).
В случае бесконечной равномерно нагретой нити поверхностя-
р ми уровня (изотермическими поверхностями) будут круговые ци-
I л и ндры, ось которых совпадает с нитью.
( Пример 1. Построить поверхности уровня скалярного
1 поля
I и » х + 2у + 3z«
\ Решение. Поверхности уровня определяются уравнением
I < + 2у + 3z = С. где С « const.
§7J
ПРИМЕРЫ СКАЛЯРНЫХ ПОЛЕЙ
31
Это есть однопараметрическое семейство параллельных плос- 1
костей.
Пример 2. Найти поверхности уровня скалярного поля
ц= х1 + у2 — z2.
Решение. Поверхности уровня определяются уравнением
я2 + у2 — z2 = С, где С = const.
При С =» 0 получаем круговой конус. При любом С > 0 получаем
однополостные гиперболоиды вращения с осью, совпадающей с . -
осью Oz. При С < 0 получаем двуподостный гиперболоид вращения. ,
Пример 3. Найти поверхности уровня скалярного поля I
Z
и arcsin 77=====.
V + у*
Решение. Область определения данного скалярного поля
находится из неравенства
Z Z2
< 1, т. е. О -Tn—2 С 1»
откуда 0 < z2 < х2 + У2- Это двойное неравенство показывает,
что поле определено вне кругового конуса z2 = х2 + У2 и на нем
самом, кроме его вершины О (0, 0, 0). j
Поверхности уровня определяются уравнением I
z ~ я' л л I
arrs,n где —г < с « I
Z
т. е. *7 == sin С пли z2 = (я2 +у2) sin2 С, Это есть семейство
V х2 + у2
круговых конусов, расположенных вне конуса z2 =» ж3 + у2 с об-
щей осью симметрии Oz и общей вершиной 0(0,0,0),в которой данное
поле не определено, причем сам кон$с z2 =» х2+ у2 также входит
в это семейство. ]
Пример 4. Найти поверхности уровня скалярного поля I
и = I
где а — постоянный вектор, г — радиус-вектор точки, I
Решен и,е. Здесь J /
г ={*, У> 2} =» xl + yj + zkt ’
п пусть
Л = {а^, a2i fl3) aji 4" т
Тогда скалярное произведение
(а, г) =» ахх 4- а^у +
32
СКАЛЯРНОЕ ПОЛЕ
(ГЛ. и
I Уравнение поверхностей уровня будет
/а,г) e с, С > 0.
Отсюда
(а, г) = In С
или
вхх + а2у + a3z == In С.
к^Это есть семейство параллельных плоскостей.
Найти поверхности уровня следующих скалярных
полей:
ГК
г к S8 . Ъ8 . Z8
45. u = — + v + —.
46. и — х* + уг — z.
х"- 4- у*
47. и «
48. и — 2у* + 9z2.
49. и = 3х +2« ~г.
50. и = (®. Ь — постоянные векторы).
51. и = In |г|.
52. и = e(a'b'r> (а, Ъ — постоянные векторы).
мм ] / Скалярное поле называется плоским, если существует некото-
t \$/ / рая плоскость такая, что во всех плоскостях, параллельных указан-
Г* х | ной, скалярное поле будет одним и тем же.
Au \ Если эту плоскость принять за плоскость хОу, то скалярное
' Л) поле определится скалярной функцией
I u = f(x„y),
I т. е. не будет зависеть от г.
I Примером плоского скалярного поля может служить поле тем-
/ ператур бесконечной равномерно нагретой нити.
I Геометрической характеристикой плоских скалярных полей
\ служат линии уровня — геометрические места точек, в которых
| скалярная функция имеет одно и то же значение.
I Пример 5. Найти линии уровня скалярного поля
\ и = х8 — у8.
\ Решение. Линии уровня определяются уравнениями
1 \ х8 — у1 = С, С — const.
§8]
ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ
33
При С = 0 получаем пару прямых
У = х, у == ~—х.
При С 0 получаем семейство гипербол (рис, 11).
Найти линии уровня следующих плоских полей:
53. и — 2<х у»
54. и = In 1Z
г 2х
55. и = —.
X
56. u=ex’~v*.
57. Найти линии уровня скалярного поля их заданно-
го неявно уравнением
и + х In и 4- у = 0.
§ 8. Производная по направлению X
Пусть имеем скалярное поле, определяемое скалярной функ-
цией
и = f(M). {
Возьмем в поле точку Мо и выберем некоторое направление,
определяемое вектором I, Возьмем в поле другую тЬчку М так,
3 м. Л. Краснов и др.
34
СКАЛЯРНОЕ ПОЛЕ
(ГЛ. п
чтобы вектор MqM был параллелен вектору Z.
Ди разность
ди = fW _
Обозначим через
а через &1 — длину вектора М0М. Отношение-—^-определяет сред-
нюю скорость изменения скалярного поля на единицу длины по дан-
ному направлению. Будем стремить точку Л/ к точке Л/о так, чтобы
вектор MqM оставался все время коллинеарен вектору I. При этом
Д/-^0.
Определение. Если существует при AZ —> О предел
отнес ения то его называют производной функции и = /(Л/).
Д/ ’
в данной точке Мо по направлению I и обозначают символом
oi
так что по определению
— = lim — = lim / (М') ~ f ^Мп\, ЩМ НI.
dl дг—о М д/-о Д/ °
Это определение производной по направлению носит инвариантный
характер, т. е. не связано с выбором системы координат.
Пусть в пространстве введена декартова система координат
и пусть функция f(M) = Д(х, у, z) дифференцируема в точке
М0(х0, уь z0). Тогда
ди I ди I ~ । дм I а । ди \
--- =----- cos a -------- cos р Cos у,
dl |Д10 дх \М0 ду |А10 dz |м0
(1)
где cos a, cos р, cos у — направляющие косинусы вектора
I г= (Zjl “J" Ч” Я3А?
— находятся по формулам
cos а = cos Р
COS у «
*
р| = )/ а? + аг + аз>
ди I ди | ди I
символы }означают, что частные произ-
дх \м0 ду |м0 dz |м0
водные берутся в точке Л/о.
Для плоского поля и = /(я, у) производная по направлению I
в точке М0(х0, уо) будет равна
ди I ди I . ди |
—- = -— cosa+—— sma;
c'l |мв дх |МО ду |м0
где a — угод, образованный вектором I с осью Ох.
(2)
§8]
ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ
35
л _ ди ди ди
Замечание. Сами частные производные -gjp "TtyT* "дТ"
являются производными функции и по направлению координатных
осей Ox, Оу, Oz соответственно.
Формула (1) для вычисления производной по направлению в
данной точке остается в силе и в том случае, когда точка М стремит-
ся к точке Мо по кривой, для которой вектор I является касатель-
ным в точке Мо.
Пример 1. Найти производную скалярного поля
и =» хуз
в точкеМ0(1,—1, 1) по направлению от точки Л/о к точке Mi (2, 3, 1).
Решение. Находим направляющие косинусы вектора
Af0Mi= {1, 4» 0), длина которого равна |М0М1|= Имеем
cos а « Cos ₽ “ cos Y я 0-
Значения частных производных функции точке Мо(1,—1,1)
равны
di I . Sk
--- as —-
дх I Mo
-i( ±L|-----------1.
ду 1м. dz Im.
Используя формулу (1), получим
ди I_______1 4
dl Im. “ + —
О
Рис. 12.
Тот факт, что > 0, означа-
ем |мв
ет, что скалярное поле в точке Л/о
в данном направлении возрастает.
Пример 2. Вычислить производную скалярного поля
и ® arctg ху
в точке Мо (1, 1), принадлежащей параболе у « х2, по направле-
нию этой кривой (в направлении возрастания абсциссы).
Решение. Направлением I параболы х2 в точке
считается направление касательной к параболе в этой точке
(рис. 12).
Пусть касательная I к кривой J Точке М$ образует с осью Ох
угол а. Имеем
у' = 2х; tg а => р7)^ — 2.
откуда направляющие косинусы касательной
1 1 о . tg а 2
cos а = —т=== = —=, cos В = sin а = —тт======== = т=г.
"К 1 + tg? а У 5 }' 1 + tg? а у 5
86
СКАЛЯРНОЕ ПОЛЕ
[ГЛ. II
Значения частных производных данной функции и (х, у) в точке
Mod, 1):
ди I _ у | __ 1 ди I __ х | __
дх |мо 1+®2У2Шо 2> дУ ш0 1 + «V |М0 ~2~*
Подставляя найденные величины в формулу (2), получим
au 1 1 1 2_____L_
dl ~ 2 ’ /5 + 2 ‘ /5 ~ 2 /Г
Пример 3. Найти производную скалярного поля
•= xz* + 2уз в точке Мо(1, 0, 2) вдоль окружности
1 = 1 + COS 11 '
y = sinf —1,
f* « 2.
Решение. Векторное уравнение окружности имеет вид
r(z) = (1 + cos t)i + (sin t — 1)7 + 2k.
Находим вектор т, касательный к ней в любой точке М. Имеем
•
т = —- = — sin t . i + cos t • у,
dt
Данная точка M0(l, 0, 2) находится в плоскости xOz в первом октан-
те, и ей соответствует значение параметра t = j. В этой точке бу-
дем иметь
т I = — sin -А • i + cos JL . j = — i.
IMo 2 2
Отсюда получаем, что направляющие косинусы касательной к ок-
ружности равны cos а = —1, cos р = 0, cos у = 0. Значения ча-
стных производных данного скалярного поля в точке Мо(1, 0, 2)
равны
2Л| = 2?| = 4, 211 = 2.1 = 4, Л-1 = ;
дх IM® 1М0 ду |м0 |М0 dz 1м0 |
Следовательно, искомая производная ,
Л.1 =211 =4. (-1)4-4.04-4.0 =-4. 1
dl |Мв дх |м0
В следующих задачах найти для данных функций
производную в точке М0(л:01 yQ z0) по направлению к точ-
ке М^хи уп ?х).
j
1
5 9]
ГРАДИЕНТ СКАЛЯРНОГО ПОЛЯ
37
58. и = ]/х2 + У24-з2, Мо(1, 1, 1), АГх(3, 2, 1).
59. и = хъу + zz2 - 2, Af0(l, lt -1), М,(2, -1, 3).
60. u = уе* - z\ M0(3t 0, 2), 1,3).
61. «= » м0(1,1), ад, 5).
У *
62. Найти производную скалярного поля
и = In (х2 + у2)
в точке Мо(1, 2) параболы у2 = 4х по направлению этой
кривой.
63. Найти производную скалярного поля u»arctg —
в точке Мо (2, —2) окружности я2 + р2 — 4з =« 0 вдоль
дуги этой окружности.
64. Найти производную скалярного поля и = х2 +
+ у2 в точке Mq (xQi у0) окружности х2 + у2 == R2 по
направлению этой окружности.
65. Найти производную скалярного поля и == 2ху +
+ У2 в точке (V2, 1) эллипса 1 по направле-
нию внешней нормали к эллипсу в этой точке
66. Найти производную скалярного поля и =» х2 —
— у2 в точке (5, 4) гиперболы х2 — у2 » 9 по направле-
нию этой кривой.
67. Найти производную скалярного поля
и » In (ху + уъ + xz)
в точке Мо(О,1,1) по направлению окружности х = cos
у = sin tt z = 1.
68. Найти производную скалярного поля и ~ х2 +
+ У2 + z2 в точке М01 соответствующей значению пара-
метра t = -у- по направлению винтовой линии х =9
₽= R cos у = R sin t, z = at.
§ 9. Градиент скалярного поля (
Пусть имеем скалярное поле, определяемое скалярной функ-
цией
и = f(x, у, z),
где функция / предполагается дифференцируемой.
88
СКАЛЯРНОЕ ПОЛЕ
(ГЛ. п
Определение. Градиентом скалярного поля и в данной
точке М называется вектор, обозначаемый символом grad и и опре-
деляемый равенством
gradu-^Li + ^L(1)
ОХ оу 02
Используя формулу (1) из § 8 для производной по направле-
нию, имеем
-§L-(gradtt, ?»), (2)
ol
где 1° — единичный вектор в направлении Z, т. е.
Z° =
— Z cos а + j* cos Р + & cos у.
Свойства градиента.
1. Градиент направлен по нормали к поверхности уровня (или
к линии уровня, если поле плоское).
2. Градиент направлен в сторону возрастания функции поля.
3. Модуль градиента равен наибольшей производной по направ-
лению в данной точке поля:
max = | grad и |
Эти свойства дают инвариантную характеристику градиента.
Они говорят о том, что вектор grad и указывает направление и ве-
личину наибольшего изменения скалярного поля в данной точке.
Пример 1. Найти градиент скалярного поля
и == х — 2у + 3z.
Решение. Согласно формуле (1) имеем
grad и = 14 -2/ + 3fc.
Поверхностями уровня данного скалярного поля являются плоско-
сти х — 2у + 3z = С; вектор grad и = {1,-2, 3} есть нормальный
вектор плоскостей этого семейства.
Пример 2. Найти наибольшую крутизну подъема поверх-
ности и «» ху в точке 7И(2, 2, 4).
Решение. Имеем
grad и = уху~Ч + ху Inx'j, grad и\^ = 4i + 4 In2/*,
(ди \ г_________
~лГ) = I grad и | = 4 + (In 2)?.
/max
Пример 3. Найти единичный вектор нормали к поверх-
ности уровня скалярного поля и х2 + у2 + «а.
8 9]
ГРАДИЕНТ СКАЛЯРНОГО ПОЛЯ
39
РеЙ’ение. Поверхности уровня данного скалярного поля —
сферы &
s’ + у1 + * •* С (С> 0).
Градиент направлен по нормали к поверхности уровня, так что
g’ad и =* 2x4 + 2у j + 2z-k определяет вектор нормали к поверх-
ности уровня в точке М(х, у, z). Для единичного вектора нормали
получаем выражение
о — 8га<* а _ xi + yj + zk_____r__
n ~ | grad uj~~ yx2 + ya + z2 ~|r|*
Пример 4. Найти градиент поля и = (а, &, г), где а и
Ъ — постоянные векторы, г — радиус-вектор точки.
Решение. Пусть
а»= {«j, a2i а3}, Ъ » {bt, b2, b3}t г = {х, у, 0.
Тогда
ai
u«= bi
X
По правилу дифференцирования
ди
дх
ai <4
bi bt
1 0
«з
Ьз
0
I л.
,1
о
аз аз
Ьз Ьз .
V *
определителя *) получаем
«2 «8
Ь2 &з
1 О
ди___
' dz ~~
«^ «2 «3
^2
О 0 1
♦) Пусть дан определитель Z)(0, элементами а^ которого явля*
ются дифференцируемые функции от t
au(t) «12(0
«21 (0 «22(0
D(t)
ain (0
а2п (0
«nl(0 «п2(0 •••• «пп(0
Тогда производная определителя D'(t) находится по формуле
ац (0 ai2 W • • • й1пМ
«21 (0 «22 (0 ... «2п (0 -р
ТУ (0 =
Qnl (t) ап2 (0
Япп (t)
«и (О «12(0 . . «1п (0
+ а21 «22 (0 . . «2п(^
«п! (0 аП2 (0 . . . «пп (0
«11(0 «12 (0
«21 (0 «22(0
am(t)
&2п (0
anl (0 вп2 (<) • • • °пп У)
40
СКАЛЯРНОЕ ПОЛЕ
(ГЛ. И
Следовательно,
Пример 5. Найти градиент
расстояния
к
«з
^8
= [а,
г = V (х — ®0)? + (у — у0)а + (г — z0)a,
где Р(х, у, 1) — изучаемая точка поля, Р0(х0) у0, z0) — некоторая
фиксированная точка.
Решение. Имеем
, 8г . дг . 8г ь * + (У — Уо) j + (2 —z0) к
gra г— дх i + ду] 4- bz У (х — ж0)2-j- (у— !/(Sv + (z —z^)2 ~ '
— единичный вектор направления Р^Р.
Пример 6. Рассмотрим скалярную функцию
и == Г1 +г2,
где гх, г2 — расстояния некоторой точки Р(х, у) плоскости до двух
фиксированных точек Fr и F2 плоскости.
Линии уровня этой функции — эллипсы. Имеем(см. пример 5)
grad (rx + r2) = + г®.
Эго показывает, что градиент равен диагонали ромба, построенного
на ортах радиусов-векторов, проведенных к точке Р из фокусов
Fi и Р2 (рис. 13). Следовательно, нормаль к эллипсу в какой-либо
его точке делит пополам угол между радиусами-векторами, про-
веденными в эту точку.
§91
ГРАДИЕНТ СКАЛЯРНОГО ПОЛЯ
41
Физическая интерпретация: луч света, вышедший из одного
фокуса, попадает в другой фокус.
Пример 7. Найти угол 0 между градиентами функций
и ® У + у? и г = а? + у + 2 Ужу
в точке ЛГ0<1, 1).
Решение. Находим градиенты данных функций в точке
Afo(l, !)• Имеем
, I + у) I i + /
8'ad“r-VH+7k"W
«”4 ф,. - [(1 + I + (1 + /Z) /] |м> - 2i + 2/.
Угол 0 между grad и и grad v в точке MQ определяется из равенства
2 2
(grad u, grad р)|м> = Vf + yf = J
|gradu|M,-|gradr|Mt l«21/2
Отсюда
0 = 0.
Пример 8. Найти производную по направлению радиуса-
вектора г для функции и =» sin г, где г = |г|.
Решение. По формуле (2) производная данной функ-
ции по направлению радиуса-вектора г равна
® (grad sin г, г°).
(3)
Находим градиент этой функции:
д (sin г) . d (sin г) д (sin г)
gradsinr = —»+ —] + дг « =.
d (sin г) dr . ,
= —~—* т- г +
dr ох
d (sin г) dr . *
dr dy^ *
d (sin r) dr ,
dr dz
I dr . . dr . , dr > \ _ ...
= Hr I + r- ] + -r- «I cos r -» r° cos r. (4)
\dx dy' dz J v '
Подставляя (4) в (3), получим
du
~ s (rO cos r, r°) = (r°, r°) cos r = cos r<
Пример 9. Найти производную скалярного поля и =
= /(ж, у, z) в точке Л/о(^о, Уо> z0) линии I, заданной системой
42
СКАЛЯРНОЕ ПОЛЕ
(ГЛ. II
уравнений
/(х, yt z) = а,
ф(а?» У. z) = О
а = const
по направлению этой линии.
Решение. Направление линии I определяется направлением
ее касательного вектора т, который, по определению, есть вектор,
касательный к поверхности /(ж, yf z) « а. Поверхность /(х, у, z) —
= а есть поверхность уровня данного скалярного поля и =*
= /(*, У, г)- Поскольку
— «а (grad u, lQ) = (grad и, т°)
dl
и вектор grad и перпендикулярен к поверхности уровня f(xt у, z) =»
= а, то grad и перпендикулярен и орту т°, и потому
-S|M,-=(grad“- =
Пример 10. Найти в точке M0(l, 1,1) направление наиболь-
шего изменения скалярного поля и ~ ху + yz + xz и величину это-
го наибольшего изменения в этой точке.
Решение. Направление наибольшего изменения поля ука-
зывается вектором grad и(М). Находим его:
grad и(М) = (у + z)i + (х + z)j + (у + х)к
и, значит, grad и (Мо) == 2(1 + / + к). Этот вектор определяет
направление наибольшего возрастания данного поля в точке
7И0(1» 1> 1)* Величина наибольшего изменения поля в этой точке
равна
max | grad и (Л/в) I = 2/X
о!
69. Найти градиент скалярного поля
и = In (х2 + у8 + х2)
в точке Мо(1, 1, —1).
70. Найти градиент скалярного поля и = zex'+v*+z'
в точке О (0, 0. 0).
71. Найти угол <р между градиентами функции и —
= arctg-^- в точках М/1, 1) и Л/2(—1, —1).
72. Найти угол <р между градиентами функции и =
= (х + уХ'+и в точках 0) и М2(1, 1).
73. Найти угол <р между градиентами функций
и = Ух2 + у2 + z8- и и = In (х2 + у2 + «2) в точке
0, 1).
5 9]
ГРАДИЕНТ СКАЛЯРНОГО ПОЛЯ
43
74. Найти точки, в которых градиент скалярного
поля и = sin (х + у) равен i + /.
75. Найти точки, в которых модуль градиента ска.
лярного поля и = In + у2 + z2 равен единице.
76. Пусть и у, z) и р= i?(x, у, z) — дифферен-
цируемые в точке ЛЦх, у г z) функции. Показать^ чго
a) grad (ku) = X grad и, X = const;
6) grad(u±p)= grad и ± grad p;
в) grad (uv) == v grad и + и grad v\
v л / w\ vgradu—wgradv , n
r) grad (j-j = , V ф 0.
77. Показатьj что
grad и (<p) = -^ grad <p,
где <p = ф(ж, у, z) — дифференцируемая функция, а и —
— и(ф) имеет производную по ф.
Найти градиенты следующих скалярных нолей, если
г = xi + yj 4- zk, г = | г [ = jAc2 + у2 4- z2,
а и b — постоянные векторы.
78. и = In г.
79. и =» (a, г).
80. и (a, г)-(Ь, г).
81. и = | la, г 112.
82. Показать, что
(grad u(r), г) = u'(r)-r.
83. Показать, что
[grad u(r), г J = 0.
84. Пусть w =» /(u, v)t где u=u(x,y,z)t v = v(x,y,z).
Доказать, что
л Л , df ,
grad w = grad и 4- grad v,
если /, и, v — дифференцируемые функции.
85. Пусть G — выпуклая область в пространстве
(т. е. такая область, что если две точки .V и N принадле-
жат области G, то и весь отрезок MN принадлежит этой
44
СКАЛЯРНОЕ ПОЛЕ
[ГЛ. II
области). Пусть в области G задано скалярное поле и(М)г
имеющее во всех точках градиент, непрерывный и огра-
ниченный в G:
|grad и(М) | 4, М^G, А = const.
Доказать, что для любых точек М и N области G имеет
место неравенство
\u(N) - и(М)|<Я|Й|.
86. Найти производную функции и ®
в произвольной точке М(х* yt z) в направлении радиуса-
вектора г этой точки.
87. Найти производную функции и——, гдег=|г|,
в направлении вектора I » cos ai + cos fi-j + cos y-fc.
При каком условии эта производная равна нулю?
88. Найти производную функции и=—* где г = |г|,
в направлении ее градиента.
89. Найти производную функции и = yzex в точке
Мо(0, 0, 1) по направлению ее градиента.
90. Найти производную скалярного поля
и = и(х, у, z)
по направлению градиента скалярного поля
у = и(х, у, z).
При каком условии она равна нулю?
91. Для следующих скалярных полей найти направ-
ление и величину наибольшего изменения в данных точ-
ках Мо:
а) и(М) = х2у + y2z + z2x; М0(1г 0х 0).
б) u(M) = xyz- М0(2х 12 -1).
ГЛАВА III
ВЕКТОРНОЕ ПОЛЕ
§ 10. Векторные линии.
Дифференциальные уравнения
векторных линий
Определение 1. Если в каждой точке М пространства
пли части пространства определена векторная величина а = а(М),
то говорят, что задано векторное поле.
Если в пространстве введена декартова система координат, то
задание векторного поля а = а(М) равносильно заданию трех ска-
лярных функций точки P(Af), Q(M) R(M), так что
а(М) » Р(х, у, z)i + Q(x, у, z)j + R(x, у, z')kj
Определение 2. Векторной линией векторного поля а
называется кривая, в каждой точке М которой вектор а направлен
по касательной к этой кривой.
Пусть векторное поле определяется вектором
а =* Pi + Qj + Rkt
где
Р = Р(х, у, z), Q = Q(xt у, z), R « R(x, у, z)
— непрерывные функции от x у, zt имеющие частные производные
первого порядка. *
Тогда дифференциальные уравнения векторных линий имеют
вид
и]
Р Q ~ R * 1 ''
Интегрирование системы двух дифференциальных уравнений
(1) дает систему двух конечных уравнений
У, z) = (р2(х, у, z) = С2,
которые, рассматриваемые в совокупности, определяют двухпара-
метрическое семейство векторных линий
(pt (х, у, z) = Ср 1 ^2]
У» г) = @2* J
46
ВЕКТОРНОЕ ПОЛИ
{ГЛ. III
Если в некоторой области G ддя системы (1) выполнены условия j
теоремы существования и единственности решения, то через каждую )
точку MQ(xQ, yQ, zQ) е G проходит единственная векторная линия /
Ф1 (*» У» «) Ф1 (*о» Уо» zo)>
Фа У» в Фа (*о> Уо» *о)-
Пример 1. Найти векторные линии векторного поля
а = [с, rj,
где с — постоянней вектор.
Решение. Имеем
с=« qi + c2j + с3к, г = xi + yj + zkf
так что
Дифференциальные уравнения векторных линий
dx dy dz х
C3X — CjZ Cjl/—c2z*
Домножим числитель и знаменатель первой дроби на х, второй —
на у, третьей — на z и сложим почленно. Используя свойство про-
порций, получим
dx dy . dz x dx у dyz’dz
c2z ~ сзУ ~ сзх ^ciz ** С1У — C2X ** 6 *
Отсюда
x dx + y* dy + z dz « 0,
а значит,
я2 + у2 + z2 = Л1, const > 0.
Домножив теперь числитель и знаменатель первой дроби (3) на сь
второй — на с2, третьей — на с3 и сложив почленно, получим
dx
c2z — с3у
dy dz c±dx + c2dy 4~ c8dz
откуда
cxdx + c2dy + c3dz = 0
п, следовательно,
4х + CiM + c8z = A 2, A 8 = const.
§ 101
ВЕКТОРНЫЕ линии
47
Искомые уравнения векторных линий
+ У2 + z- = А, |
Схх + с3у + c3z = Л2. /
Эти уравнения показывают, что векторные линии получаются в ре-
зультате пересечения сфер, имеющих
общий центр в начале координат, с
плоскостями, . перпендикулярными
вектору с = с2/ + с3к. Отсюда
следует, что векторные линии явля-
ются окружностями, центры которых
находятся на прямой, проходящей
через начало координат в направле-
нии вектора с. Плоскости окружнос-
тей перпендикулярны указанной
прямо!! (рис. 14).
Пример 2. Найти вектор-
ную ЛИНИЮ ПОЛЯ;
а = —yi -j- х] + bkt
проходящую через точку (1, 0, 0).
Решение. Дифференциальные уравнения векторных линий
dx dy dz
~-у а? ~ ‘
Отсюда находим
*а + У2 = Cit Сг > О,
или, если ввести параметр t, то будем иметь
г = cos у = 3*п
В этом случае уравнение
dy 3z
х Ъ
принимает вид
"\/С1 cos t dt dz
V^icosi b
или dz —b dtt
откуда находим
z ~ bt +
Итак, параметрические уравнения векторных линий будут
х = cos
У = sin*»
в ® bt 4-
(4)
48
ВЕКТОРНОЕ ПОЛИ
[ГЛ. III
Точке (1, 0, 0) соответствует значение параметра t, равное
нулю. Полагая f = 0 в системе (4), получим
1 = ус\,
0х=/С1-0,
0 = С»» /
откуда находим (\ = 1, С2 = 0, и значит, параметрические уравне/
ния векторной линии, проходящей через точку (1, 0, 0), будут
w = cos f]
у = sin Г, I
s = bt. J
Это — винтовая линия.
Найти векторные линии следующих векторных полей;
92. г « xi + yj + zk.
93. а = ati + a2j + где аи а2} а> — постоянные.
94. а = (z — y)i + (х — z)/ + (у — х)к.
95. Найти векторную линию поля t
а = хЧ — y*j + z2&8
/ 1 1 А
проходящую через точку 1-у,---------1 1.-
Векторное поле называется плоским, если все векторы а рас-
положены в параллельных плоскостях и поле одно и то же в каж-
дой из этих плоскостей.
Если в какой-либо из этих плоскостей ввести декартову систе-
му координат хОу, то векторы поля не будут содержать компоненты
по оси Oz и координаты вектора не будут зависеть от zt т. е.
а= Р(х, y)i + Q(x, y)j.
Дифференциальные уравнения векторных линий плоского поля
будут иметь вид
dx dy dz
у) ~ Q(x, у) ~ 0
или
<*У (x> &
dx P (х,"у)' ►
• z = const.
Отсюда видно, что векторные линии плоского поля являются пло-
скими кривыми, лежащими в плоскостях, параллельных плоско-
сти хОу.
Пример 3. Найти векторные линии магнитного поля бес-
конечного проводника тока.
(
§ 101
ВЕКТОРНЫЕ ЛИНИИ
49
(
Решение. Будем считать, что проводник направлен по оси
Oz и в этом же направлении течет ток I. Вектор напряженности Н
магнитного поля, создаваемого током, равен
<5>
гдеГ = Z-& есть нектор тока, г — радиус-вектор точки М (я, у,з),
р — расстояние от оси провода до
точки М. Раскрывая векторное про-
изведение (5), получим
21 у . , 21х .
р2 р2 /•
Дифференциальные уравнения век-
торных линий:
dx dy dz
— у ~~ х = 0 ’
откуда
в? + у2 = Я2, 1
«“С, J
т. е. векторные линии являются ок-
ружностями с центрами на оси Oz
(рис. 15).
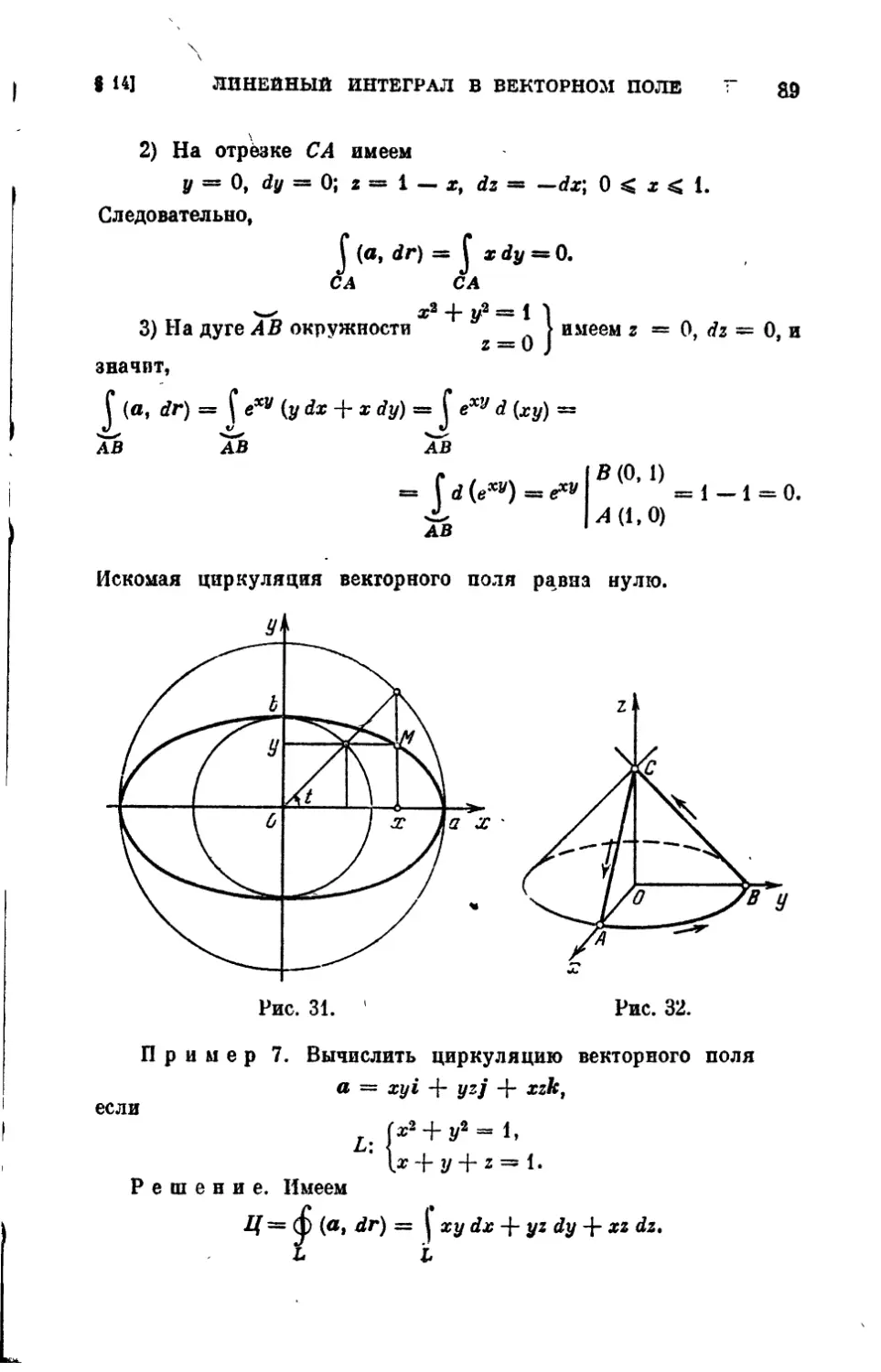
, Найти векторные линии следующих плоских вектор-
‘ ных полей:
96. а == xi + 2yj.
97. а = xi + zk. ш
I 98. а = xi — yj.:
99. а = 2zj + 4ук.
100. а = хЧ + У2]*
101. а = zj — ук.
Дифференциальные уравнения векторных линий
dx dy dz
Р
могут быть записаны так:
или в векторной форме:
4 м Л. Краснов и др.
(6)
50
ВЕКТОРНОЕ ПОЛЕ
[ГЛ. П1
Эта форма уравнений векторных линий оказывается удобной при
решении ряда задач.
Пример 4. Найти векторные линии поля а = [с, г], где
с— постоянный вектор.
Решение. Применяя соотношение (6), получим
dr
. (7)
Умножая обе части (7) скалярно на с и используя свойства смешан-
ного произведения, находим
( dr \ d
ir]=:'dt<c’ г)с=0- <8)
Аналогично, умножая обе части (7) скалярно на г, получим
/ dr\ d
= 7Г<Г’Г) = °- (9)
Из уравнения (8) следует, что
(с, г) = const,
а из уравнения (9) следует, что
(г, г) a const.
Векторные линии являются линиями пересечения плоскостей
(<?, г) == const со сферами г2 = const.
Найти векторные линии следующих векторных полей:
102 а=/(г).г.
103. а == (а0, г)60, где а0, Ьо — постоянные векторы.
§ И. Поток векторного ноля.
Способы вычисления потока
I. Поток векторного поля. Пусть имеем векторное поле
а(М) = Р(х, у, z)i + Q(xt у, z)j + R(xt у, z)k,
где координаты P(x, yt z), Q(xt у, z), R(x, y, z) вектора a(M) непре-
рывны (поле a(M) непрерывно) в некоторой области б?. Пусть S —
некоторая гладкая или кусочно гладкая двусторонняя поверхность,
у которой выбрана определенная сторона (ориентированная поверх-
ность).
Определение. Потоком П векторного поля а(М) через
ориентированную поверхность S называется поверхностный интег-
рал первого рода по поверхности 5 от проекции вектора а(М) на
нормаль п(М) к этой поверхности:
п = J J прпа dS—У У (а, в0) dSt
JaJ s
$ 11]
ПОТОК ВЕКТОРНОГО ПОЛЯ
51
где п° — единичный вектор (орт) нормали п к выбранной стороне
поверхности S; dS — элемент площади поверхности S.
В случае замкнутой поверхности будем всегда выбирать внеш-
нюю нормаль п, которая направлена вовне области, ограниченной
поверхностью S.
Если а, 0, у — углы, которые образует с осями координат
Ох, Оу, Oz нормаль п к поверхности S, то поток можно выразить
через поверхностный интеграл второго рода
у, i) cos a +
8 8 „
+ Q (®» У» 2) Cos Р + R (х, у, z) COS у] dS
ИЛИ
n = j J («.»’) d<S== j J P (х» У) z) dy dz^
8 8
+ Q (%, z) dxdz-{- R (х, у, z) dxdy,
где
cos a dS =* dy dz, cos 0 dS =« dx dz, cos у dS » dx dy»,
Основные свойства потока векторного
поля
а) Поток меняет знак на обратный с изменением ориентации
поверхности (т. е. с изменением ориентации нормали п к поверх-
ности 5):
У (a, n°) dS= — J J (a, »’) dS,
8—
где 5+ — сторона поверхности S, на которой выбрана нормаль п,
а 5" - сторона поверхности S, на которой берется нормаль — п
(см. (6J).
б) Свойство линейности: *
j J (la + Ц&, »°) dS= 1J j (a, n«) Ц J j (&, »°) dS,
8 8 8
где 1 и p, — постоянные числа.
в) Свойство аддитивности: если поверхность S состоит из не-
скольких гладких частей S2, . . ., Sm, то поток векторного поля
а(М) через S равен сумме потоков вектора а(М) через поверхности
*?1, ^2> • • •>
m л л
и = 2 j J <«• »’)
k=l 4
Это свойство позволяет распространить понятие потока на ку-
сочно гладкие поверхности.
4*
52
ВЕКТОРНОЕ ПОЛЕ
(ГЛ. П1
Пример 1. Найти поток вектора а = I через площадку,
перпендикулярную оси Ох, имеющую форму прямоугольника со
сторонами, равными 1 и 2 (рис. 16), в положительном направлении
оси Ох,
Решение. Согласно определению потока вектора через по-
верхность S, будем иметь
п = j j (a, n°) dS,
В нашем случае a—i, = i, так что (a, n°) « (i, i) =1. Учитывая
то, что площадь прямоугольника равна 2, получим
П-у1И-2.
Замечание. Выбрав единичный вектор (орт) нормали
к площадке S так, что л°= — i, получили бы П = —2.
Пример 2. Вычислить поток векторного поля а = г, где
г — радиус-вектор, через прямой круговой цилиндр с высотой h,
радиусом основания R и осью Oz.
Решение. Поверхность S состоит из боковой поверхнсс-
ти ох, верхнего основания о2 u нижнего основания о3 цилиндра.
Искомый поток П в силу свойства аддитивности будет равен П =
= Пх + П2 + П3, где П1} П2, П3 — потоки данного поля через оь
о2, о3 соответственно.
На боковой поверхности цилиндра внешняя нормаль п°
параллельна плоскости хОу, и поэтому
(а, л°) = (г, п°) = прп’Г = R
(см. рис. 17). Следовательно,
Пх = J J (а, л°) dS= Я J J <1S — R-2nRh = 2лЯ%
Gt а*
§ 11]
ПОТОК ВЕКТОРНОГО ПОЛЯ
53
На верхнем основании о2 нормаль л° параллельна оси Qzt и по-
этому можно положить л° = к (рис. 17). Тогда
(а, в0) = (г, к) = прОг г = h,
и значит,
dS= h- лЯ2 = nR*h.
at at
На нижнем основании о3 вектор а —г перпендикулярен к нор-
мали «° = — к. Поэтому (а, и0) — (г, —/с) = 0 и
п3 = J J (а, в0) dS= 0.
а*
Искомый поток будет равен
Н = (а, в°) dS = Злй2Л.
S
Пример 3. Найти поток векторного поля
через сферу радиуса R с центром в начале координат.
Решение. Так как нормаль п к сфере коллинеарна радиусу-
вектору г, то можно взять п° » г° 8= .—_ Поэтому
(а, п°) =
1
1
Но на сфере S имеем |r| = R, поэтому (а, п°) = —.
л?
Искомый поток П будет равен
п = $ (а, в») d5= JL g 4л,
8 8
так как площадь всей сферы S равна ^dS— 4лЯ2.
S
104. Вычислить поток вектора а == 3/ через площадку,
имеющую форму треугольника с вершинами в точках
Mt(l, 2, 0), М3(0, 2, 0), М3(0, 2, 2)л в сторону, где распо-
ложено начало координат.
105. Найти поток вектора
а = ai + Pj + yfcj
54
ВЕКТОРНОЕ ПОЛЕ
(ГЛ. П1
где а, Р, ? — постоянные, через площадку, перпендику-
лярную оси Oz и имеющую форму круга радиуса R, в по-
ложительном направлении оси Oz.
106. Найти поток вектора а « г через внешнюю сто-
рону кругового конуса, вершина которого находится
в начале координат, радиус основания равен R и высота
равна h (ось конуса идет по оси Oz).
107. Найти поток вектора а = f(\r\)r через сферу ра-
диуса R с центром в начале координат.
II. Способы вычисления потока вектора.
1°. Метод проектирования на одну из
координатных плоскостей. Пусть незамкнутая по-
верхность S проектируется взаимно однозначно на плоскость хОу
в область Dxy. В этом случае поверхность S можно задать уравне-
нием z =» /(х, у), и так как элемент площади dS этой поверхности
равеп
то вычисление потока П через выбранную сторону поверхности S
сводится к вычислению двойного интеграла по формуле
И(«, *°)
I cosvl
S Dxy
(а, n°) dS
dxdy.
(1)
Здесь орт n° нормали к выбранной стороне поверхности S находится
по формуле
в0 =. + grad у)1 = + дх * dz 1 +
| grad [z — f (х, j/)] | Г(df_\2 (df_\2 ’
V +w +1
(2)
a cos у равен коэффициенту при орте к в формуле (2):
(3)
Если угол у между осью Oz и нормалью п° острый, то в формулах
(2) и (3) берется знак «+», если же угол у тупой, то берется знак
Символ "1
in
ПОТОК ВЕКТОРНОГО ПОЛЯ
означает, что в подынтегральной функции вместо z надо подставить
Л®, у)-
Если оказывается удобным проектировать поверхность 5 на
координатные плоскости yOz или xOz, то для вычисления потока П
пользуются соответственно формулами:
пли
1/х
П
dy di
2)
г)
dxdz.
(4)
(5)
Формула (4) применяется в случае, когда поверхность S про-
ектируется взаимно однозначно в область Dyt плоскости yOz, а зна-
чит, ее можно задать уравнением х = <р(у, z)> cos а находится как
коэффициент при орте I в формуле
„О = ± gredfc —<р(у, z)} = +____________ду dz
| grad [х - <р (у. z)l | (ару’
Знак «+» берется в случае, если угол а между осью Ох и нормалью
п° острый, если же а — тупой угол, то берут знак «—».
Формула (5) применяется при взаимно однозначном проектиро-
вании поверхности S на плоскость xOz\ в этом случае S можно задать
уравнением у == ф(х, z) и тогда
no= + grad [у —1|> (д?, z)J
| grad [у —1|) (х, z)] |
cos Р есть коэффициент при орте / в последней формуле, т. е.
Если угол р между осью Оу и нормалью п° острый, то берут знак
если же угол р тупой, то берут знак
Замечание. В случае, когда поверхность S задана неявно
уравнением Ф(х у, z) = 0, единичный вектор нормали
л° = i cos а + j cos р + к cos у
находится по формуле
. ЭФ ЭФ ь
no = + grad Ф (а?, у, z) == дх ду dz_________________
- | grad Ф (х, у, z) | /I 0Ф\3 ,( дФ\г , 1дФ\*
V w +bj + v&J
где знак в правой части определяется выбором нормали к поверх-
ности S.
Для вычисления потока П векторного'поля а через поверхность
$ надо ее спроектировать взаимно однозначно на какую-либо из
координатных плоскостей хОу, xOz, yOz, что возможно сделать, если
уравнение Ф(х, у, z) = 0 однозначно разрешимо соответственно
относительно z(z = f(x, у)), у (у = ф(х, z)) или х(х — <р(у, z)), после
чего можно воспользоваться одной из формул (1), (4), (5).
Пример 4. Найти поток векторного поля
л = (х — 2z)i -|- (х + Зу 4* z)j 4- (5# 4" у№
через верхнюю сторону треугольника АВС с вершинами в точках
А(1, 0, 0), В(0, 1, 0), С(0, 0, 1).
Решение. Уравнение плоскости, в которой лежит тре-
угольник АВС, имеет вид х + у + z = 1, откуда z = 1 — х — у.
Треугольник АВС проектируется взаимно однозначно на пло-
скость хОу в область Dxy, которой является треугольник О АВ
(рис. 18).
По условию нормаль п° к плоскости, в которой лежит треуголь-
ник АВС, образует острый угол у с осью Oz, поэтому в формуле (2)
берем знак плюс и получаем
grad (я? 4- у 4- z — 1)_1 ._____1 , ____1 , /т
"° = | grad (х + у + z — 1) ] — у % уз 1 + у$ '
Находим скалярное произведение
1 1 1
(а, п°) = (х — 2z) 4~ (я + Зу 4~ г) 4- (5я 4" у) «•
_ 7а? 4~ 4у — z
/3
1
Из формулы (6) получаем, что cos у = у=- > 0 и, значит,
dS = faJlL =У 3dx dy.
cos у
§ ill
ПОТОК ВЕКТОРНОГО ПОЛЯ
57
Применяя формулу (1), вычисляем искомый поток:
П
j (7а? + 4у —z)
}ху
dxdy^
z—1—х—у
1 1—х
(8х + 5у — 1) dx dy— J dx J (8a? + 5y — 1) dy = -L,
Dxy 0 0
Пример 5. Найти поток вектора а — y2j + zk через часть
поверхности z = х2 + у2, отсеченной плоскостью z = 2. Нормаль
берется внешняя по отношению к области, ограниченной пара-
болоидом.
Решение. Данная поверхность (параболоид врапспия)
проектируется взаимно однозначно на плоскость хОу в круг Dxy
(рис. 19). Находим орт нормали п%к поверхности 5:
0 _ , grad (z — х2 —у2)______— 2xi — 2у/ + к
” ± I grad (z — ж2 — у2) | ~ - -j/^z 4.4у« -|_ 1 ‘
По условию задачи нормаль п° образует тупой угол у с осью
Oz, поэтому перед дробью следует взять знак минус. Таким об-
разом,
по = 2xi + 2у7‘ ~~ *
П ул4а?2 + 4у2 + 1
Отсюда
1
COS V — — "г ..... < о
У 4а?2 + 4у2 + 1
ВЕКТОРНОЕ ПОЛЕ
[ГЛ. ш
58
и, значит, э w
dS = -JU1L = /4х? + 4у» + 1 dx dy,
I cos YI
Находим скалярное произведение
2y8 — z
(•. n°> = i77"a j=7‘
У 4sa + 4ya + 1
Искомый поток в силу формулы (1) равен
п = Jf (a, n*)dS = JJ (2у»-г) dxdy =
s Dxy z—x^y*
= f f (2y8 — у2 — x2) dxdy.
Область интегрирования Dxy есть круг с центром в начале коорди-
нат радиуса R = 1^2. Вводя полярные координаты х = р cos <р,
у » р sin ф, будем иметь
П = j* J (2р3 sin3 ф—р2) р dp аф=»
^ху _
2Л - /2
= I dtp f (2р4 sin3 ф —• р8) dp = —- 2л 1 ^ = — 2л.
•' J 4 о
0 0 1
Пример 6. Найти поток векторного поля а = i — / + zyzk
через круг S, полученный сечением
шара я2 + уа + z2 < 7?а плоскостью
у х. Взять сторону круга, обра-
щенную к положительной части
оси Ох.
Решение. Так как плос-
кость у = х перпендикулярна ко-
ординатной плоскости хОу, то круг
5, лежащий на этой плоскости, про-
ектируется на плоскость хОу в отре-
зок ЛрДа и, значит, нарушается
взаимная однозначность проектиро-
вания. На другие координатные
плоскости круг 5 проектируется вза-
имно однозначно. Проектируя круг,
например, на плоскость xOz, полу-
чим область Dxz, ограниченную эл-
липсом (рис. 20). Уравнение эллипса
найдем, исключив у из системы уравнений
а;2 + у2 -р z2 = R2,
у = х, J
$ Н1
ПОТОК ВЕКТОРНОГО ПОЛЯ
59
Отсюда
2x2 -j- z2 = Я2 или + X - 1.
Д Л
2
По условию нормаль к кругу S образует тупой угол Р с осью
Оу (рис. 20), поэтому берем
п = —grad (у — г) = i — /,
. » 1 . 1 .
П “l»l “ У 2 1 Y2J'
Из последнего равенства имеем cos £ « —. —= < 0. Элемент площа-
г “
ди dS круга равен
as = , - х «У?dx dz.
| COS Р I
Находим скалярное произведение: (а, п°) =*
Искомый поток по формуле (5) равен
П = J J 2 dx dz=2 f j dx dz= 2 . = УГй2л,
DXz Кг
так как площадь Q области ограниченной эллипсом с полуося-
r
ми а = и Ь = Rt равна
Q == С f dx dz~ nab ==
£ /2
xz
Пример 7. Вычислить поток вектора а = xl + у} + zk
через внешнюю сторону боковой поверхности кругового цилиндра
#2 ^2 — д2, ограниченной плоскостями z = 0 и z *=Н (Я > 0).
Решение. Данный цилиндр проект гоуется на плоскость
хОу в линию, а именно, в окружность (рис. 21)
х2 + у2 = Я2, |
2 = 0. J
Поэтому будем проектировать цилиндр на другие координатные
плоскости, например, на плоскость yOz. Так как цилиндр проекти-
руется на плоскость yOz не взаимно однозначно, то воспользуемся
свойством аддитивности потока вектора и представим искомый
поток П в виде суммы потоков П = Щ + П2, где Щ — поток
поля через часть St цилиндра, расположенную в области, где
у > 0, а Щ - поток этого же поля через часть S2 цилиндра,
60
ВЕКТОРНОЕ ПОЛЕ
[ГЛ. III
расположенную в области, где у < 0. На Si имеем
„0 = 21+^., (а> И0) = *?.+ у!-я.
R R
Следовательно,
Si Si
где S — площадь части 5^ цилиндра. Так как S = itRH, то Hi
=« nR^Hv
На 52 опять имеем
„О = **+у/ (а, «’) = = R
R R
и, значит,
П2 = j j RdS=-RS = nR^H.
Искомый поток равен П = 2л/?2Я.
Замечание.
Рис. 21.
Задача решается проще, если на цилиндре
ввести криволинейные координаты х =»
«=Я cos ф, y~R sin ф, z=z. (См. далее п. 3°).
Для нахождения потока векторного
поля а == Р(х, у, z)i + Q(x, у, z)j +
+Л(я, y,z)k через поверхность 5, заданную
уравнением z = /(х, у) методом проекти-
рования на координатную
обязательно находить орт
можно брать вектор
» « ± grad [z — / (х, у)] =
df •
— \ дх 1'
плоскость, не
п° нормали, а
ду J 1 /
Тогда формула (1) для вычисления потока
П примет вид
П = (а, л°) dS =
в
О'
Dxy
Аналогично получаются формулы
через поверхности, заданные уравнениями х = ф(у, z) или у
= z).
Формула (7) в координатной форме записывается так:
п = ± И (— р[хг у, f(x, — Q[x, у, !&, у)]-^- +
для вычисления потоков
4- У1 f&> y)]}dxdy.
§ И]
ПОТОК ВЕКТОРНОГО ПОЛЯ
61
Пример 8. Вычислить поток векторного поля
а == xi + yj + ТА* + у* — 1 &
через внешнюю сторону однополостного гиперболоида z «=»
= ух2 + У2—1, ограниченного плос-
костями z = 0, z ~ У$.
Решение. Данная поверх-
ность проектируется взаимно од-
нозначно на плоскость хОу в область
£>хУ, ограниченную окружностями
а?? + у2 «= 1, ) х2 + у2 == 4, |
z — Q J И z = 0. J
Находим внешнюю нормаль п:
п = ± grad (z — У х2 у2 — 1) =
в + ( -«-у/
Так как п образует с осью Oz тупой
угол у (рис.22), то берем знак минус
и, значит,
н + у/ _
II — у—............. , — ц,.
Находим скалярное произведение
/р2
(в’ п) = К®? + у2 —i ~ -1 = уxi + yi_ f
Применяя формулу (7), получим
1
U (a, nO)dS
S
* С dx dy
J Vxi + у2 - Г
*XV
Переходя к полярным координатам х=р cos <р, p = psin<p, будем
иметь
2л 2
ЧУЖ-УЧиЙ-2”^-2^
0 1 •
Пример 9. Вычислить поток векторного поля
* а = yi + zj + хк
через замкнутую поверхность, ограниченную цилиндром х2 + у2 =
= R2 и плоскостями z = xf z — 0 (z > 0).
Решение. Поверхность 5 кусочно гладкая, поэтому вос-
пользуемся свойством аддитивности потока, представляя искомый
поток П в виде суммы потоков Пх, П2гП3 через гладкие куски,
62
ВЕКТОРНОЕ ПОЛЕ
(ГЛ. ш
соответственно, Sf (полукруг х2 + у2 < Я2, 0 < х < Я, z = 0),
S2 (часть плоскости z—x) и 53 (часть цилиндра х2+у2 — Я2): П =
= Щ + П2 + П3. Так как S замкнута, то берем внешнюю нормаль
к ней (рис. 23).
1) На Sit где z « 0, имеем л° = —If, поэтому
(а, п°) = ~-х
и, значит, поток Пх будет равен
Щ = ** J J я? dS ® —J J х dx dy.
Si Si
Переходя к полярным координатам х = р cos ф, у = р sin ф, найдем
л/2 Я
п>—и р cos ф р dp j cos ф dtp J p2dp = — Я3.
Si *-л/2 О
2) Ha Sa, где z «= х, имеем
п « ± gradfz — х) =» ± (—f + к),
и так как нормаль п к S2 образует с осью Oz острый угол, то в пра-
вой части берем знак плюс. Таким
образом, п “ — i + к и, значит,
(а, п) = х — у.
Проектируя Sa на плоскость
хОу, получим полукруг
DxV: O^x^VW-y*.
Тогда по формуле (6) будем иметь
dxdy,
z=x
и снова переходя к полярным коор-
динатам, найдем
П2 =?
л/2 я
» j (Cos ф sin ф) б/ф I p2dp =
~я/2 о
2
в 3
3) На £3, где х2 + у2 » Я2, т. е. на боковой поверхности ци-
линдра, имеем
о 4. (^а + У8 Д2) _ , + У7 __ , + vi
n e ± I grad (Х2 + у2 _ Д2) | ~ 1/'а,2 _[_ ^2 — Я
хг*уг
8,
И
Рис. 23,
щ-
В этом случае нормаль п образует с осью Oz прямой угол и, значит,
§ И]
ПОТОК ВЕКТОРНОГО ПОЛЯ
63
cos V « о, поэтому выбор знака в правой части произволен; возь-
мем, например, знак плюс, тогда
„о = ?* + У7, (в, по} « (*+,?) У,
R R
и, следовательно,
Пз = JL|J(® + z)y AS.
Проектировать поверхность 53 (прямой цилиндр) на плоскость
хОу нельзя, так как она спроектируется в линию — полуокруж-
ность (будет нарушена взаимная однозначность проектирования).
То же самое имеет место и в случае проектирования на плоскость
xOz. Поэтому будем проектировать поверхность $3 на плоскость
yOz, на которую она проектируется взаимно однозначно в область
Dyz, ограниченную линией
а;2 + у? «
2=1.
Исключая отсюда х, получим уравнение проекции этой линии на
плоскость zOy. z2 + уа = R2 — окружность. Так как
|cosa|=|cos(np)| = l(n’, £)| = 1 *1 = 4 (ж>0),
I -П I л
то будем иметь
П-7Г.И^
Dyz x—z »yz x—z
dy dz~ 2 (* С у dy dz.
Dyz Dyz
Используя полярные координаты: у = р cos ф, z = р sin (р, найдем
л R
П3 = 2 J J р cos ф р dp <7ф= 2 j* cos ф <7ф J р2 dp = 0.
Dyz * 0 0
Итак,
п=—а лдз + 4-пЛ’+°=°*
3 3
108. Вычислить поток векторного поля а = yi +
4- zy + хк через верхнюю сторону треугольника,
64
ВЕКТОРНОЕ ПОЛЕ
I ГЛ. III
ограниченного плоскостями
S + У + 2 = Я, я? — О, у = Of Z = О,
109. Вычислить поток векторного поля а » xzi через
внешнюю сторону параболоида z = 1 — ж2 — y2t огра-
ничейного плоскостью z = 0 (z 0).
110. Вычислить поток векторного поля а == xi + zk
через боковую поверхность кругового цилиндра у ==»
= )АН2 — х\ ограниченную плоскостями z =? 0а z-S
(й>0).
Hi. Вычислить поток векторного поля а » xi +
+ У] + через верхнюю сторону круга, вырезаемого
конусом z = ]/ я2 + у2 на плоскости z = h (Л > 0).
112. Вычислить поток векторного поля а =*
= Зя:/ — yj — zk через внешнюю сторону параболоида
х2 + у2 = 9 — 2, расположенную в перво.м октанте.
ИЗ. Вычислить поток векторного поля
а = (х2 + y2}i + (у2 + z2)] + (z2 + х2)к
через часть плоскости z = 0Л ограниченную окружностью
х2 4- у2 = 1, в направлении орта к.
114. Вычислить поток векторного поля а =* yzi —
— xj —- ук через полную поверхность конуса х2 + у2 =*
— z2, ограниченную плоскостью z = 1 (0 z 1).
115. Вычислить поток векторного поля а = 2xi +
+ (1 — 2y)j + 2zk через замкнутую поверхность, огра-
ниченную параболоидом х2 + z2 = 1 —- 2у (у 0) и
плоскостью z = 0.
116. Вычислить поток векторного поля а = x2i +
+ У2] + 22Л через полную поверхность пирамиды, огра*
ниченной плоскостями х + У + 2 = 1г х = 0А у = 0,
2 = 0.
117. Вычислить поток векторного поля а = xi +
+ У] + 2fc через сферу х2 + у2 + z2 = R2.
2°. Метод проектирования на все три коор-
динатные плоскости. Пусть поверхность S взаимно
однозначно проектируется на все три координатные плоскости.
Обозначим через Dxyt Dxz, Dyz проекции S соответственно на
плоскости xOyt xOzt yOz.
В этом случае уравнение F(xt у, я) = 0 поверхности S однознач-
но разрешимо относительно каждого из аргументов х, у, z, так что
х = х(у, z), у = у(х, z), z = z(x, у).
| 11] ПОТОК ВЕКТОРНОГО поля 65
Тогда поток вектора
а = Р(х, у, z)< + Q(x, у, z)j + Я(*, У, z)k
через поверхность 5, единичный вектор нормали к которой равен
«° = cos a-i + cos р«/ + ccs у*к
можно записать так:
П = J J (а, п”) dS =
8
= J J [P (r, y, z) cos a+Q (*, y, z) cos p+R (r, y, z) cos y] dS.(%)
8
Известно, что
dScosa = + dy dz,
dS cos P = + dx dz, (9)
dS cos у = ± dx dy,
причем знак в каждой из формул 9) выбирается таким, каков знак
< os a, cos р и cos у на поверхности S. Подставляя (9) в (8), будем
иметь
П = ± J Р [я (у, z), у, z] dy dz ± j* j Q [*, У (x, z), z] dx dz ±
bvz *DXZ
± j* J Pfs, y, z(x, y)]dxdy. (19)
&xy .
Пример 10. Найти поток вектора
а = xyi + yzj + xzk
через часть внешней стороны сферы z2 + У2 + — 1, заключенной
в первом октанте.
Р е ш е н и ел Имеем
п grad (*2 + yg + za — 1) xi + yj + zk
П ~ Fgrad (X* + у2 4- za — 1 )l | ~ -Х1 + У^ +
откуда, учитывая, что данная поверхность S находится" в первом
октанте, получим
cos а = х > 0, cos р = у > 0, cos у = z > 0.
Поэтому в формуле (10) берем перед всеми интегралами знак плюс
и, полагая в ней
Р == ху, Q = yz, R = xz,
5 М. Л. Краснов и др.
66
ВЕКТОРНОЙ ПОЛЕ
(ГЛ. III
получим
(И)
П =» j J ху dy dz + ] j У2 dx dz + j J xz dx dy.
DyZ I*xz . DXy
Из уравнения сферы ж3 + у2 + z3 == 1, находим
z = Z (х, у) « 1/1 — *2 ~ У2, у = у (*, 2) » V1 — а?2 — Z2,
г~х(у, z) = y’l — у* — Z*.
Подставляя эти выражения для ж, у, z соответственно в третий,
второй и первый интегралы правой части (И), получим
П ® J J х рЧ — ж? — у3 dx dy -{- f f z /I — ж3 — z2 dx dz
Dxy
D
z2 dy dz. (12)
Dyz
Вычислим первый интеграл, стоящий в правой части, переходя к
полярным координатам ж = р cos ф, у — р sin (р, где 0 < <р < л/2,
О < р < 1. Тогда получим'
= J J ж ]^1 — ж3 — у2 dx dy = У р2 У1 — р2 cos ф rfq) dp =»
®ху Dxy
п/2 1 1
«= у cos ф б?ф р2 1/1 — р2 dp = j* р2 /1 —р2 dp.
ob о
Полагая в последнем интеграле р = sin t, dp » cos t dt, будем иметь
л/2 я/2
Г,® I sin3 t cos21 dt = -L 1 sin22fdf = —.
.1 4 .1 16
0 0
Второй и третий интегралы в формуле (12) вычисляются аналогично;
при этом получим *
I2 = f С z 1/1 — ж2 — z2 dx dz
^xz
я
яГ
Ц = f f У 1/1 — у2 — *а dy dz
п
16
Искомый поток будет равен
п-Л-1- /2 1 '3=-£Н
16
4 Hl
ftotdk BfeKfoPHOfo йоЯй
65
118 Применяя метод проектирования на все три коор-
динатные плоскости» вычислить поток векторного поля
а = zi — xj + ук
через верхнюю сторону треугольника, получаемого пере-
сечением плоскости Зя + 6р — 2z — 6 ® 0 с координат-
ными плоскостями.
3°. Метод введения криволинейных коор-
динат на поверхности. В некоторых случаях про вы-
числении потока векторного поля через данную поверхность S
возможно выбрать на самой поверхности простую систему координат,
в которой удобно вычислять поток, не применяя проектирования
на координатные плоскости.
Рассмотрим частные случаи.
Случай!). Пусть поверхность S является частью кру-
гового цилиндра х4 + у* = Я2, ограниченного поверхностями
2 = /1(А у) И 2 = у),
причем Л(х, у) < /2(х, у).
Полагая
х=Ясозф, y—R sin ф,
будем иметь для данной по*
верх пости
О < ф < 2л,
ДСЯсоэф, Я sin ф)^
< z < /4(Я cos ф, R sin ф),
а для элемента площади dS
получаем следующее выра-
жение (рис. 24):
dS « R <7ф dz»
Тогда поток векторного поля а через внешнюю сторону, поверх-
ности 5 вычисляется по формуле
2 л (Н cos ф, R sin ф)
П = В J б/ф j (a, n°) dz, (13)
О h (R cos ф, R sin ф)
где
Ло = grad (** 'I- У1 — Я*) = - VJ
| grad (х2Ч- у* — R'2) Г В ’
Пример 11. Найти поток вектора г = xi -Ь yj + zk
через внешнюю сторону боковой поверхности кругового цилиндра
х2 + у2 = Я2, ограниченного плоскостями z = 0 и z = Н(Н > 0).
5*
68
ВЕКТОРНОЕ ПОЛЕ
тт*п Ш
Решение. В данном случае имеем:
О < <р < 2л; /Х(Я cos ф,, R sin ф) = 0, f2(R cos ф, R sin ф) = Я-
Введем на цилиндре криволинейные координаты
х = R cos ф, у = R sin ф, z = z.
Тогда искомый поток вектора г будет равен
2л Н
П = R J с?ф ( (г, л°) dz.
О о
Но так как
г = xi + yj + zk ® R cos ф- i + R sin ф- / + zk,
а нормаль л° на цилиндре
П0 ~ + У] в ЯС08ф • /?81Пф • ]
R R
— совф • i + sin ф • j,
то скалярное произведение на цилиндре будет равно
Рис. 25.
Переходя к координатам на
(г, п") = R cos2 ф + R sin2 ф == R.
Окончательно находим
2л И
п = я2 J Лр у dz = 2nR2ff.
О V
Пример 12. Вычислить по-
ток радиуса-вектора
г = xi + yj + zk
через боковую поверхность кругово-
го цилиндра х2 + у2 =1, ограничен-
ного снизу плоскостью я+у-Н=1,
а сверху — плоскостью x+y+z=2.
Решение. В данном случае
(рис. 25) имеем
R = 1, /1(*, У) =*
= 1 — х — у, fi(x, у) = 2 — х — у.
цилиндре
х == cos ф, у = sin ф, z = z,
будем иметь
/1(^» Й = 1 — cos ф — sin ф, /а(я, у) = 2 — cos ф — sin ф.
§ Hl
ПОТОК ВЕКТОРНОГО ПОЛЯ
69
Согласно формуле (13) поток вектора г будет равен
2л 2 — cos — sin <р
П = j d<p J (г, n°) dz.
О 1 — cos ф — sin ф
Но так как на цилиндре х2 + у2 = 1
л° = xi + yj = cos + sin ф-/,
то
(г, п°) = х2 + у2 = cos 2ф + sin2 ф = 1
и, следовательно,
2л 2 — cos ф — sin ф 2л
П = | fihp j dz =» j* dy = 2л.
О 1 — cos ф — sin ф О
119. Найти поток вектора
а = yi + xj — exv*k
через внешнюю сторону боковой поверхности цилиндра
я2 + У2 == 4, ограниченной плоскостями z = 0 и х +
4- у + z = 4.
120. Найти поток вектора
а = xi — xyj 4~ zk
через внешнюю сторону цилиндрической поверхности
+ z2 = /?2, ограниченной плоскостями у = 1 и х +'
+ У =
121. Найти поток вектора
а = x3i — у3] + xz3k
через внешнюю сторону цилиндрической поверхности
я2 у2 ~ д? ограниченной сферой х2 + у2 + z2 =• 25.
122. Найти поток векторного поля
а = xi — yj — xyz3k
через внешнюю сторону боковой поверхности цилиндра
я2 + У2 = 1» ограниченной плоскостью z = 0 и гипербо-
лическим параболоидом z == х2 — у2.
123. Найти поток векторного поля
а = (ху — y2)i + (2х — х2 + xy}j + zk
через внешнюю сторону боковой поверхности цилиндра
я2 + У2 — I, ограниченной эллиптическим конусом z2 =
п
= + У •
70
ВЕКТОРНОЕ . ПОЛЕ
ТТЛ. III
Случай 2). Пусть поверхность S является частью сферы
ж2 + у2 + z2 = R2t ограниченной коническими поверхностями,
уравнения которых в сферических координатах имеют вид 0 = Д(ф),
0 = /2(ф), и полуплоскостями <р = Фъ Ф = ф2.
Положим для точек данной сферы
х = R cos ф sin 0, у — R sin ф sin 0, z « R cos 0,
где фх ф < Фг, 0i 0 < 02- Тогда для элемента площади dS
получим (рис. 26)
dS = R2 sin 0 d0 t/ф.
В этом случае поток векторного поля а через внешнюю часть 5 сфе-
ры вычисляется по формуле
%
П = R2 j (/ф J (а. л°) sin0 с/0, (14)
Ф1 01
где
о _ grad (х2 у2 + z2 —- 7?2) __ xi + yj + zk
п в | grad (х2 + У3 + z2 — R2) | R *
Пример 13. Найти поток вектора
а = (х — 2у + l)i + (2х + у —. 3z)j + (Зу + z)k
через часть поверхности сферы х2 + у2 + z2 = 1, расположенную
в первом октанте, в область,
где х2 + у2 + z2 > 1.
Решение. В данном слу-
чае имеем
R = ф1 = о, ф2 =® л/2,
01 = 0, 02 = л/2,
«о = xi + yj+zk,
(a, п*) = х2 + у2 + z2 + х»
Введем на сфере ж2+ у2 + х2 =* 1
координаты ф и 0 так, что
х = cos ф sin 0, у == sin ф sin 0,
Z = cos 0, z
Тогда будем иметь
(а, п°) = 1 -j- cos ф sin О
п, применяя формулу (14), получим
л/2 л/2
П = J <?ф j* (1 + cos ф sin 0) sin 0 d0=»
0 0 ' i
п/2 n/2 я/2 ' . я/2 3
= sin 0 d0 + J cos <p d<f J sin2 0 dQ = л.
0 0 0 0
| 12] ПОТОК ВЕКТОРА ЧЕРЕЗ ЗАМКНУТУЮ ПОВЕРХНОСТЬ
71
124. Найти поток векторного поля
а = x3i — y3j + zk
через внешнюю сторону части сферы х2 + у2 + z2 = 1,
вырезаемой конической поверхностью z2 = х2 + у\
125. Найти поток векторного поля
а == yzi + xzj + хук
через внешнюю сторону части сферы х2 + у2 + z2 =
расположенную в первом октанте.
126. Найти поток радиуса-вектора
г = xi + yj + zk
через внешнюю сгорону части сферы х2 + у2 + z2 = 2,
ограниченной плоскостями z = О и z = у.
127. Найти поток вектора
а = xzi + УЧ + z2&
через внешнюю часть сферы х2 + у2 + z2 = 9, отсеченной
плоскостью z w 2 (z > 2).
§ 12. Поток вектора через замкнутую поверхность.
Теорема Гаусса — Остроградского
коор-
дй
dz ’
Теорема. Если в некоторой области G пространства
Оинаты вектора
а ® Р(х, у, z)i + Q(x, у, z)j + Я(х, у, z)k
dP dQ
непрерывны и имеют непрерывные частные производные
то поток вектора а через любую замкнутую кусочно гладкую поверх-
ность S, расположенную в области G, равен тройному интегралу от
ЭР dQ dR
dx 'dy "dz по °°ласти ограниченной по ерхностъю 2:
(формула Гаусса—Остроградского).
Нормаль п к поверхности 2 берется внешняя.
Пример 1. Вычислить поток вектора
9 = хЧ +
72
ВЕКТОРНОЕ ПОЛЕ
(ГЛ. ш
через замкнутую поверхность
х* + F* + ? “ Я', « = о (г > 0).
Решение. По формуле (1)
П = j (2г + 2у + 2z) Л. (2)
JyJ
Интеграл (2) удобно вычислять в сферических координатах г, 0, ф.
Имеем
х = г sin 0 cos ф, у = г sin 0 sin ф, z = г cos 0
в элемент объема
dv = г3 sin 0 dr dQ </ф,
так что
П = 2 [ j J (г sin 0 cos ф + г sin 0 sin ф + г cos 0) г2 sin 0 dr dQ атф =i
v v
2-j л/2 R
= 2 j б?ф | sin 0 (sin 0 cos ф + sin 0 sin ф + cos 0) d0 j r3dr =
0 0 b
2л л/2
2Я4С С Л л л лЯ4
е= ) (?ф j cos 0 sin 0 с?0—
о о
Пример 2. Вычислить поток вектора а = 4xi — yj + zk
через поверхность тора.
Решение. Воспользовавшись теоремой Гаусса—Остроград-
ского, получим, что искомый
2 1 поток П равен
П = (а, л°) do =
*6
ff(7ap , dQ , ,
+ ^+e7jdv=iV>
где V — объем тора. Чтобы
вычислить объем V, восполь-
*ЕС- 27. зуемся теоремой Гюльдена
об объеме тела вращения,» силу
которой этот объем равен произведению площади вращающейся
фигуры на путь, описываемый центром масс этой фигуры при
вращении.
Пусть 2?! и R2 — внутренний и внешний радиусы тора (рис.27).
Площадь S круга, который при вращении образует тор, равна
5 = л
I 2 г
$ 121 ПОТОК ВЕКТОРА ЧЕРЕЗ ЗАМКНУТУЮ ПОВЕРХНОСТЬ
73
Длина пути, описываемого центром масс — центром этого круга,—
+ Я2
есть длина I окружности радиуса —т,—, т. е.
1 = 2л^Ц-^а = n(^ +Л2).
Таким образом, объем V тора равен
V - л Л (Я2 + /?!)= -£ № - Ях)» (Ла + Ях).
Искомый поток
П = л2(Я2 - + Ях).
Пример 3. Используя теорему Гаусса—Остроградского,
вычислить поток векторного поля
. _ + ( + 2, к
через внешнюю сторону части поверхности z = 1 — z2 — у®, рас-
положенной над плоскостью
хОу.
Решение. Для того
чтобы можно было применить
теорему Гаусса — Остроградс-
кого, замкнем снизу данную
поверхность куском плоскости
хОу, который ограничен ок-
ружностью
х2 + у® = 1, )
z = 0. j
Рис. 28.
Пусть v — объем полученного
тела, ограниченного замкну-
той кусочно гладкой поверх-
ностью о, состоящей из части
ог параболоида вращения z —
и 1 — х2 — у2 и части о2
плоскости z = 0 (рис. 28).
Поток данного вектора через поверхность а по теореме
са—Остроградского равен
Гаус.
а V
Находим сумму
ЭР , dQ dR 2ху , 2х 2х(1+у)
дх ‘ ду *" dz 1 + у2 "г 1 + У® 1 + у2 S 1
74
ВЕКТОРНОЕ ПОЛЕ
[ГЛ. III
Следовательно, поток
П = (a, n°) da = 0.
о
В силу аддитивности потока будем иметь
П = J J (a, nQ) da + J J (а, л°) da = 0.
at <Ji
Отсюда искомый поток
Щ = И (а,
а, п?) da.
ai 0»
Поток П2 вектора а через круг х2 + у2 < 1, z = 0 равен
- - - - П2 У У (а, «°) da.
01
Так как на плоскости z = 0 имеем
х^у
а = Г+V1 + 2a?arcts W — п" = — к,
и следовательпо, (а, п°) = 1, то поток 112 через круг о2 будет равен
площади круга о2:
ML
01
Искомый поток Пх = —П2 =» —л.
Используя теорему Гаусса — Осгроградского, вычис-
лить потоки векторных полей через указанные замкнутые
поверхности S.
128. ‘ ‘ ‘ ~ *
z>0.
129.
130.
Я.
a ~ (1 + 2x)i + yj + zfe; 5: x2 + y2 = z\ z ~ 4f
а = xi + xzj + ук\ 5: х2 + г/2==4—z, z=0, z^O.
а = (У2 + z2)i — y2j + 2yzk-t S: x2 + z2 s= y2s
§13. Дивергенция векторного поля.
Соленоидальное поле
Понятие потока вектора через замкнутую поверхность приводит
к понятию о дивергенции или расходимости поля. Это понятие дает
некоторую количественную характеристику поля в каждой его
точке.
( § 13]
ДИВЕРГЕНЦИЯ ВЕКТОРНОГО ПОЛЯ
75
Пусть М—изучаемая точка поля. Окружим ее поверхностью S
произвольной формы, например, сферой достаточно малого радиуса.
Область, ограниченная поверхностью S, пусть будет (7), а ее объем
V. Рассмотрим отношение
(а, л°) da
2----V-----• (1)
Определение 1. Если отношение (1) име т конечный пре-
дел, когда область (V) стягивается к точке М, то этот предел назы-
вают дивергенцией векторного поля (дивергенцией вектора а) в
точке М и обозначают символом div а (М). Так что
(а, л°) da
div а (А/) = lim -----т;----• (2)
(V)->AI v
Формула (2) дает инвариантное определение дивергенции. Это
определение означает, что дивергенция поля а в точке М есть
объемная плотность потока вектора а в этой точке.
Точки М векторного поля а(М), в которых div а>0, называют-
ся источниками, а точки, в которых div а < 0, называются стоками
векторного поля.
Дивергенция векторного поля есть скалярная функция точек
поля.
Если координаты вектора
а(М) = Р(х, у, z)i -|- Q(x, у, z)j + Щх, у, z)k
дР dQ dR
имеют непрерывные частные производные — — — в окрестности
дх’ ду* dz
точки М(х, у, z), то, пользуясь инвариантным определепием дивер-
генции, из теоремы Гаусса — Остроградского получаем, что
дР dQ dR
diva = ai + % + az-
(3)
Все величины в формуле (3) рассматриваются в одной и той же точ-
ке Af(z, у, z).
Используя формулу (3) для дивергенции, можно теорему Гаус-
са — Остроградского (см. § 12) записать в векторной форме
(a, a0) da = f J J div a du.
s VJ
(4)
I Пример!. Пользуясь инвариантным определением, вычис-
лить дивергенцию вектора а = xi в точке 0(0, 0, 0), выбрав в ка-
честве поверхностей о, окружающих точку О, сферы ое радиуса 8
’ с центром в этой точке.
76
ВЕКТОРНОЕ ПОЛЕ
1ГЛ. Ill
Решение. По определению дивергенции в данной точке
имеем
(а, п°) da
og
div а (0) ® lim --------------,
(пе)-*0
где t?e — объем шара, ограниченного сферой og, или
(а, п°) do
0g
div a (0) « lim------------.
E->0
4
Но так как объем шара равен vs = -g- ле3, то
(а, и0) do
°s
div а (0) = lim----т------.
е-*° -о- ле3
о
Вычислим поток (а, «°)do данного вектора через сферу <те. Орт
с*е
нормали /1° к сфере ое направлен по радиусу сферы, поэтому мож-
но положить:
л г г
где г0 — орт радиуса-вектора г = xi + yj + zk, или
я" _ xi + + zk
Искомый поток будет равен
Sec ж2
(a,n")da= $—da.
<Jg Og
Переходя к координатам на сфере Ог
х = е cos <р sin 9, у = 8 sin ф sin 0, z — е cos 0,
получим
§ (a, «•) da = J J =
a® o8
2л я
f 4
«= e3 j cos2 ф dtp j sin3 ф (?ф= Л83.
Q 0
$ 13]
ДИВЕРГЕНЦИЯ ВЕКТОРНОГО ПОЛЯ
77
Следовательно,
div а (0) ==lim
е-*0
Пример 2. Вычислить div г.
Решение. Имеем г = xi + yj + zkt так что Р—х, Q—y,
R « z и, значит, по формуле (3)
дх ду . dz _
dlvr= с7+а7+а7=3-
Пример 3. Вычислить div (и-в),. где и(М) — скалярная
функция, а(М) == Р(х, у, z)i + Q(xt у, z)j + R(x, y, z)k —вектор-
ная функция.
Решение. Используя формулу (3), находим
div (иа) =
сх ду Oz сх дх 1 ду * ду *
dR , ди (ЭР 8Q , dR\ . п ди . .ди ди
+ “а? + R + dl) + R~di -
« и-div а + (a, grad и).
Итак,
div (иа) «= u-div а + (л, grad и). (5)
Пример 4. Найти дивергенцию вектора
а = ф(г)г«=^г,
где г == |г| — расстояние от па<!ала координат до переменной
точки М(х, yt z).
Решение. Используя формулу (5), получим.
div а = div г + (г, grad —-j.
Далее,
о /Ф(Н\' , . гф'(г) —Ф(г) л
div г = 3, grad —у ® I —у I grad г «в---у—• г°#
Поэтому
,. Ф(Н а . /ГФ' И —Ф(Н л \
diva= -у-3+ I--------ji-----г°,г| =□
Ф(г) гфл(Н—ф(г) Ф(г)
— 3 +--------------« 2 —- + ф (г).
78
ВЕКТОРНОЕ ПОЛЕ
(ГЛ. Ш
131. При какой функции ф(г) будет div ф(г)г=2ф(г)?
132. Найти div(r4r).
133. Найти дивергенцию векторного поля
а =* 1с, г|,
где с — постоянный вектор.
134. Найхи
div(r[w, г])я
где w — постоянный вектор.
135. При какой функции \|?(z) дивергенция .поля
а = xzi + yj + ф(г)к
будет равна zt
136. Найтп поток радиуса вектора г через поверхность
сферы.
137. Электростатическое поле точечного заряда q равно
Е == —
4ле0 гЗ *
Вычислить div Е. '
138. Показать, что
4 (Г, я0) da V,
О v
где V — объем, ограниченный замкнутой поверхностью S.
139. Доказать, что если S — замкнутая кусочно глад-
кая поверхность и с — ненулевой постоянный вектор, то
cos (n, с) da == О,
2
где п — вектор, нормальный к поверхности S.
140. Доказать формулу
(<ра, п°) da = J И (ф div а + (a, grad ср)) dvt
х V
где ср == ф(х, у, z), а 2 - поверхность, ограничивающая
объем У, Установить условия применимости формулы.
i 13) \ дивергенция векторного йоля ft
141. Доказать, что если функция z) удовлетворя-
ет уравнению Лапласа
д2и t fl2 u t д2и _ fl
дх* ду* dz* “ U’
то ' $ -|£- do = О,
X 0л
где — производная по направлению внешней норма-
ли к кусочно гладкой замкнутой поверхности 2.
142. Доказать, что если,функция и(х, у, z) является
многочленом второй степени и 2 - кусочно гладкая замк-
нутая поверхность, то интеграл
пропорционален объему, ограниченному поверхностью 2.
Найти поток векторного ноля через указанные замк-
нутые поверхности: 1) непосредственно, 2) до теореме
Гаусса — Остроградского.
( z = х1 4- д’,
143. a = xi + zi; S: { .
I г = 4.
( Р = ? + у2,
144. a^2xi + 2yj — zfc; s-[ tssjj h>q
f Z ~ 6' — x2 — y2,
145, {z»-x24-y2, «>0.
( x2 4- z2 = y2,
146. а-IKiS: | y_t
( z* = x2 4- y*,
147. a~xi + 2yj -zk-, S: \ t .
( Z — X "Г if •
•'s'.y» • . ( x* 4- y* = 4,
148. e = 2xi-(z-l)fc; 5: I n .
( z = 0, z » 1.
( x2 4- У® 4- s2 = 4,
М». а = 2х<-р/4-^; s-[3z=sx* + y*'
80
ВЕКТОРНОЕ ПОЛЕ
[ГЛ. Ш
150. а — yxi + 2yj г- zk; S: х2 4- у2 yz2 = 4.
./ [ х2 4- Р2 =2?2,
151. a = (x+z)i+(y+x) j + (z+y)fc; St | z =s z^0
| 9 — z = x2 + y2,
152. a — 3xi — yj—zk; y = Oj 2 = 0
153. a = (y—x) 14- (z—y) j 4- (x—z) k; St
*+₽+«=1»
x—у 4-2=1»
x=0, z=0.
[ 1 — z = x2 4- y2,
154. a — xi — 2yj — zk; St j n
Солевопдальное (трубчатое) поле
Определение. Если во всех точках М некоторой области G
дивергенция векторного поля (заданного в области G) равна нулю
div а (М) ® 0,
то говорят, что поле соленоидально в этой области.
Таким образом, по определению, соленопдальное поле не имеет
источников и стоков.
Из теоремы Гаусса—Остроградского следует, что в соленой*
дальном поле поток вектора а = а(М) через любую замкнутую по-
верхность а, лежащую в этом поле, равен нулю
(а, л°) do = 0.
а
В соленоидальном поле G векторные линии не могут ни начинаться,
ни кончаться. Они могут быть либо замкнутыми кривыми, либо
иметь концы на границе поля.
Уравнение
div а(М) == 0
называете! в гидродинамике уравнением неразрывности несжимае-
мой жидкости.
В этом случае количество жидкости, выходящей через какую-
нибудь замкнутую поверхность о, всегда равняется количеству
входящей жидкости, и полный поток равен нулю.
Какие из следующих векторных полей являются соло-
ней дельными?
155. а — x(z2 — y2)i 4- у(х2 — z2)/ 4- z(y2 — x2)k,
156. a — y2i — (x2 4- y3)j 4- z(3j/2 4- i)k. |
157. a = (1 4* 2xy)i — y2zj 4- (z2y — 2zy + l)k. 1
J
к
$ 14]
[НЕЙНЫЙ ИНТЕГРАЛ В ВЕКТОРНОМ ПОЛЕ
81
1ть, что поле вектора
является соленоида^гьным во всякой области, не содержа-
щей начала координат 0(0, 0, 0).
159. При каком условии век-
торное поле а = (р(г)г будет со-
леноидальным?
Пусть име м поле вектора а(М) (не
обязательно соленоидальное). Рассмот-
рим в поле замкнутый ориентированный
контур L. Поверхность 2, имеющую
линию L своим краем, назовем поверх-
ностью, натянутой на контур L. Нор-
маль п к поверхности 2 условимся
Рис. 29.
ориентировать так, чтобы пз конца нор-
мали выбранный обход контура L был виден совершающимся про-
тив часовой стрелки (рис. 29).
160. Показать, что в соленоида льном поле поток векто-
ра а(М) не зависит от вида поверхности 2, натянутой на
данный контур L, а зависит только от самого контура.
§14. Линейный интеграл в векторном поле.
Циркуляция векторного поля
Пусть даны непрерывное векторное поле a=a(J/) и кусочно
гладкая кривая L, на которой выбрано положительное направле-
ние (ориентированная кривая).
। Определение!. Линейным интегралом от вектора а =
г =а(Л£) вдоль ориентированной кривой L называется криволинейный
интеграл первого рода (интеграл по длине дуги кривой) от скаляр-
ного произведения (а, т°)
f (а, т°) ds,
где т° «= т° (М) — орт вектора, касательного к линии L, ориента-
ция которого совпадает с ориентацией L\ ds — дифференциал длины
дуги $ кривой L.
) Если г = г(М) есть радиус-вектор произвольной точки М ли-
] нии L, то линейный интеграл в поле а(М) можно записать в виде
J (а, т°) ds = j* (а, dr). (1)
| 1 L
6 M. л. Краснов и др.
82
ВЕКТОРНОЕ ПОЛЯ
(ГЛ. Itl
Если в векторном поле введена прямоугольная система коорди-
нат Oxyz, то г “ xi yj 4- zk, /
а=Р(х, у, z}i+Q(x, у, z)/+B(X у, z)k
п линейный интеграл (1) выразится через х«риволинейный интеграл
второго рода /
j (a, dr) =* j Р (х, у, z) dx + Q (xt yt z) dy 4» R (xt у, z) dz,
L L
В случае, когда a = a(M) является силовым полем, линейный
интеграл (1) дает величину работы этого поля вдоль линии L,
Свойства линейного интеграла.
а) Линейность:
J (Хе, + ца2, dr) = к («!, dr) + J* f (а„ dr),
L L L
где К, p — постоянные числа.
б) Аддитивность:
; [ (a, dr) = j* (a, dr) + f (а, dr).
Lx-I-L, Lt 1,
в) При изменении ориентации линии L интеграл меняет знак
С (а, dr) == — f (а, dr),
ВА АВ
где А — начальная, а В — конечная точки линии L.
Вычисление линейного интеграла в век-
торном поле. Пусть линия L задана параметрическими урав-
нениями
« = ф(0. v =* Ф(0, * - х(0> t, < t < tu
при этом в начальной точке А линии L параметр t принимает зна-
чение t = t0, а в конечной точке В линии L — значение t » t^
(направление на линии L соответствует возрастанию параметра t
от to до tj); функции ф(/), ф(7), */(/) имеют непрерывные производные
на отрезке [£0, /J. Тогда
f (a, Jr) = J (Я1 = j { P[<p (О, ф (0, x (01 ф' (0 +
L AB t,
+ Q [ф (0, (0. X (01Ф' (t) + л [<P (t), Ф (0.X (01X' (0) dt.
Если линия L задана системой уравнений у = ф(х), z = х(х),
а х < Ь, то
ъ
[ (a, dr) = f {Р [z, ф (х), х (х)J -{• (J [.г, t (-). X (x)l Ч>' (х) +
АВ а
+ Л [х, (х), X (X)! х' СО) dx
9
{ 141 ЛИТЕЙНЫЙ ИНТЕГРАЛ В ВЕКТОРНОМ ПОЛВ 83
А|«алогичные\ррмулы можно написать и для случаев, когда
линия задается одной из следующих систем уравнений:
* в ф(у), « « Х(^) (Уо < У < Ух)
или
«« ф(з), у » ф(з) (z0 < Z < zx).
Пример 1. Найти линейный интеграл от вектора а
где г — радиус-вектор, вдоль отрезка прямой от точки Л(гд) до
точки В(гв).
Решение. Искомым линейным интегралом будет
С Г (г, dr)
j («. dr)= J -дтр- (1)
АВ АВ
Из равенства
d(r, г) ® (dr, г) + (г, dr) = 2(r, dr)
находим
(г, dr)=.ld(r, r)=l-d(|r|«)»-L.2|r|d|r| = ]r|d|r|.
Отсюда
2£^ = d|r|. (2)
Подставляя (2) в интеграл (1), будем иметь
гв
j* (a, dr)» J d|r| = J d | r | = | rB | - | rA |.
AB AB r
A
Следует обратить внимание на то* что
|dr| d|r|.
Найти линейный интеграл вдоль отрезка прямой,
ограниченного точками 4(гх) и В(г2), для следующих век-
торных полей:
161. а = г.
162. . -jL,.
lfi3- « — г;р' г° — °РТ-
164. Вычислить линейный интеграл вдоль прямой,
проходящей через точки 0(0, 0, 0) и 1х 1) в направ-
в*
84
ВЕКТОРНОЕ ПОЛЕ
(ГЛ. Ш
лении от точки О к точке А/х, если а =з ty, г
тоянный вектор. /
165. Доказать, что
[ (grad u, dr) = и (В) и (А).
АВ
Пример 2. Найти линейный интеграл от вектора
а = zi 4" XJ 4" ук
L винтовой линии
, где Ь — пос-
вдоль дуги
от точки А
t
x — Rcost, y=Rsint, z=z~2n
линии с плоскостью z = 0 до точки В пе-
ресечения с плоскостью z=l (рис. 30).
Решение. Линейный интеграл в
данном примере имеет вид
пересечения
z Сх 4- х dy + у dz.
Рис. 30.
то интеграл будет равен
2л
Винтовая линия расположена на круговом
цилиндре х2 4* У* = Я2. В точке А имеем
t0 = 0, в точке В имеем = 2л. Так как
dx == — R sin t dt, dy — R cos t dt,
dt
dz~ 2л’
/? \
+ R2 cos2t4" "2п s*n
pa, dr) = J +
L 0 '
2л 2л
- R2 i cos2 tdt — — I t sin t dt ** nR? J- R,
J 2л J 1
0 0
так как
2л
j* cos2t dt = л;
b
2л
p sin t dt = — 2л.
0
$ 14] ЛИНЕЙНЫЙ ИНТЕГРАЛ В ВЕКТОРНОМ ПОЛЕ 85
Пример Найти линейный интеграл от вектора (см. при-
мер 2)
а = zi + xj + ук
вдоль прямой А В (см. рис. 30) в направлении от точки А к точке В.
Решение. Так как прямая АВ (образующая цилиндра
х2 + у2 =R2) расположена на плоскости xOz и проходит через точ-
ку A(R, 0, 0), то у == 0, х = Я, dx = 0 и для радиуса-вектора г
точек прямой АВ будем иметь г = Ri + zkt dr— dz-k. Поэтому
скалярное произведение
(a, dr) = z dx -f- х dy + у dz = 0.
Следовательно, искомый линейный интеграл
J (a, dr) = J (а, dr)
L АВ
на прямой АВ будет равен нулю.
Из примеров 2 и 3 следует, что в общем случае линейный интег-
рал в векторном поле зависит не только от начальной и конечной
точек пути интегрирования, но и от формы этого пути.
Пример 4. Вычислить работу силового поля
F = yi -j- xj + (х + у + z)k
вдоль отрезка АВ прямой, проходящей через точки МЛ2. 3, 4) и
Л/2(3, 4, 5).
Решение. Работа данного силового поля будет равна линей-
ному интегралу вдоль отрезка М1Л/2:
А = J (F, dr) = J у dx 4 х dy 4 (х 4 у 4 z) dz.
м
Находим канонические уравнения прямой Имеем
х — 2 у — 3 z — 4
~Г ==“2“Т— = “
Отсюда
У = *4 Ъ j
z = х 4 2, J
dy = dx, dz dx.
Здесь x изменяется в пределах от 2 до 3 (так как абсцисса точки Мг
равна 2, а абсцисса точки М2 равна 3). Искомая работа будет равна
з з
Л = f (х+1 + ® + ® + х + 1 + «4-2)<?® = С(5г-Н)<?*==д
.ВЕКТОРНОЕ ПОЛИ
(ГЛ. III
86
/
166. Вычислить линейный интеграл в плоском вектор*
ном поле
вдоль полуокружности
® “ R cos tt у — R sin t (0 < t < л).
167. Вычислить линейный интеграл в плоском вектор-
ном поле
''в = (ж’ 4- у2)/ + (х2 — y)j
вдоль линии у => |а:| от точки (—1, 1) до точки (2, 2).
168. Вычислить линейный интеграл в плоском вектор-
ном поле.
а = (а:2 — 2ху)1 + (у’ — 2ху)}
а) вдоль параболы у = х2 от точки (—1, 1) до точ-
ки (I, 1);
б) вдоль отрезка прямой2 соединяющей точки (—1, 1)
и (1, 1).
169. Вычислить работу силового поля F — 2xyi 4* ж2/
вдоль дуги окружности X2 + у2 = 1 от точки (12 0) до
точки (0, 1).
170. Вычислить работу силового поля
F (х2 + 2xy)i + (х* + у2,/
вдоль параболы у =* х2 от точки (0, 0) до точки (1,1).
171. Вычислить линейный интеграл в векторном поле
; _ xi + yj 4- zk
а “ '-/j:1-..1;_11 """гт--=s
У х2 + у2 + z2- — х — I/ +
вдоль отрезка прямой от точки (lt 1, 1) до точки (4, 4, 4).
172, Вычислить линейный интеграл в векторном поле
а = (у2 — z2)i 4- 2yzj — х2к
вдоль Линии
X = t
y — t2
z — t2
(0<f<l)
в направлении возрастания параметра L
I it] Линейный интеграл в векторном поле 8Т
\
173. Вычислить линейный интеграл в векторном поле
а « yi + zj 4- хк
вдоль витка винтовой линии
х ® а соя tf
у ® a sin t,
я ® Ы
(0<*<2л)
в направлении возрастания параметра I.
174. Вычислить линейный интеграл в векторном поле
а = хЧ + У2} + z2k
в направлении от точки (0f 0г 0) до точки (1, 1х 1) вдоль
отрезка прямой^ проходящей через эти точки.
Циркуляция векторного ноля
и ее вычисление
Определение 2. Циркуляцией Ц векторного поля
а = а(М) называется линейный интеграл, взятый вдоль замкнутой
ориентированной кривой L. Таким образом, по определению
dr)9
где символ $ означает интеграл по замкнутой кривой L.
L
Если векторное поле а = а(М) задано в координатной форме
а == Р(х, у, z)i + Q(x, уч z)j + R(xt у, z)k,
то циркуляция векторного поля будет равна
За положительное направление обхода замкнутой кривой L
будем считать направление, при котором область, ограниченная
этой кривой, будет оставаться слева.
Пример 5. Вычислить циркуляцию векторного поля
а = — y*i + x*j вдоль эллипса Lt
Решение. По определению циркуляции имеем
Ц— (£ {a,dr) = j) — y*dx + x*dy. (3)
L L
88
ВЕКТОРНОЕ ПОЛЕ
[ГЛ. Ш
Параметрические уравнения данного эллипса имедо вид (рис. 31)
х = о cos t,
у = b sin t,
О < t < 2л.
(4)
Отсюда
dx == —a sin t dt, dy = 6.cos t dt. (5)
Подставляя (4) n (5) в (3), получим
г? 3
Z(— ab J (b2 sin41 + a2 cos4 t) dt — ~£nab (a2 + fc2),
0
так как
2л . 2л . 2л . . , , .
fir 1 (* [ 1 + cos 4и
sin4t dt=-^\ (1- cos 2t)2 4 j 11 -2 cos 2*+ ---j dt =«
0 *0 o' '
2л 2л
1 f /3 n o , 1 \ 1 f 3 j 3
s T ] IT “~2 cos 2*+ ^cos 4/ I dt = -% 1 у dt « yn.
o' 0
Аналогично находим, что
2л
I cos4t dt— ~т л.
О
Пример 6. Вычислить циркуляцию векторного иотч
a== yexyi + xexyj + xyzk
вдоль линии L, получаемой пересечением конуса z2 + у2 = (z —-I)3
с координатными плоскостями (рис. 32).
Решение. Линия L состоит из двух отрезков ВС и CAt
расположенных на координатных плоскостях у Oz п xOz соответст-
—* а;2 “Ь у2 53 1 ] „
венно и дуги АВ окружности >. Поэтому циркуляция
z = О J
данного векторного поля будет равна
Ц= ф(а, dr) = J (a, dr) 4- (a, dr) + J (a, dr).
1 ВС CA
1) На отрезке ВС имеем
x = 0, dx = 0; z — 1 — у, dz — —dy] 1 > у > 0.
Следовательно,
(a, dr) = у dx — 0.
BC
§ 14] ЛИНЕЙНЫЙ ИНТЕГРАЛ В ВЕКТОРНОМ ПОЛЕ Г 39
2) На отрезке СА имеем
у ~ 0, dy = 0; 2=1 — х, dz = — dx\ 0 < х < 1.
Следовательно,
J (a, dr) = J х dy = 0.
ел СА
ж2 + У2 = 1 1
3) На дуге АВ окружности л } имеем z = 0, dz = 0. и
2 = О J
значит,
У (а, dr) == f exv (у dx + х dy) = У еху d (Ху) —
АВ АВ АВ
=
АВ
В (0, 1)
= 1—1 = 0.
/1(1,0)
Пример 7. Вычислить циркуляцию векторного поля
а = xyi + yzj + xzkt
если
£. ^2 + у2=1,
+ 2/ + 2 = 1.
Решение. Имеем
Ц~ ф (a, dr) = ху dx + yz dy + xz dz.
I I
ft)
ВЕКТОРНОЕ ПОЛЕ
(ГЛ. Ш
Линия L есть эллипс, получающийся в результате сечения цилиндра
х2 + у2 ® 1 плоскостью х + у + z « 1. Найдем параметрические
уравнения этой линии. Проекция любой точки этой линии на плос-
кость хОу находится на окружности ж2 + у2 « 1. Отсюда получаем
х » cos t, у sin L Но эллипс лежит на плоскости х + у + z « 1,
откуда z = 1 — х — у или z =1 — cos t — sin t Следовательно,
параметрические уравнения линии Li
v «= cos t,
у OB sin f,
I « 1 «» COS t — sin t,
Отсюда находим
dx » —sin t dt, dy ™ cos t dt, dz =» (sin t — cos t)dt,
и, вначит, циркуляция будет равна
2л
ц з» J cos t sin11 + sin t (1 ** cos t — sin t) cos t +
0
+ cos t (1 -* cos t sin t) (sin t — COS 01 dt =B
2л
J (— 3 sin81 cos t + sin 2t ** cos *t sin t —
0
2л
cos11 + cos11) dt = — cos8t dt = — я.
v ‘0
Вычислить циркуляцию Ц вектора а вдоль данной
линии L:
175. а = (xz + y)i + (yz — x)j — (x2 + y2)k\
(x2 + y2 = l,
L: I z ~ 3.
176. a = y2i 4- z2j + x2k;
(x2 + y2 + z2 я» Л2,
L I X2 + y2 =x Rx (z^ 0).
177. a= (2x + z)i + (2z/ — z)j + xyzk-,
L — линия пересечения параболоида вращения х2 + у2 **
х= 1 — 2 с координатными плоскостями.
178. Показать, что если в векторном поле циркуляция
вектора по любому замкнутому контуру равна нулю то
в таком поле не мощет быть замкнутых векторных линий.
I 15]
РОТОР (ВИХРЬ) ВЕКТОРНОГО ПОЛЯ
91
§15. Ротор (вихрь) векторного поля
Пусть имеем поле вектора
а (М) == Р(х, у, «)< + Q(x, yt z)j + R(x, у, z)k.
Будем предполагать, что координаты Р, Q, R вектора а (Л/) непре-
рывны и имеют непрерывные частные производные первого порядка
по всем своим аргументам.
Определение 1. Ротором вектора а(М) называется век-
тор, обозначаемый символом rot а(М) и определяемый равенством
дх) \дх ду /
i +
rot а =
(1)
или в символической,, удобной для запоминания, форме
I ] к
д д д
rat а — dz 9
Р Q R
(2)
Этот определитель обычно раскрывается по элементам первой
строки, при этом операции умножения элементов второй строки на
элементы третьей строки понимаются как операции дифферен-
д Л дО
цирования, например, — • О = —С
дх дх
Определение 2. Если в некоторой области G имеем
rot a=0, то поле вектора а в области G называется безвихревым.
Пример 1. Найти ротор вектора
а = (х + i)i + (у + t)j + (х* + »)fc.
Решение. Используя формулу. (2), им гем
i j к
д д д
rota = &
X Z У 4" z X2 + z
Раскрывая определитель по элементам первой строки и понимая
операцию умножения, скажем, д!ду на я2 + я, как операцию част-
ного дифференцирования, найдем
rot а = — i — (2х — 1)/.
П р и м е р 2. Найти ротор вектора II напряженности магнитного
поля в условиях примера 3 § 10.
Решение. Вектор Н напряженности магнитного поля
или
р-
i ь
о I
У 2
i
0
х
21 •.27 1
-py* + pixi>
92
ВЕКТОРНОЕ ПОЛЕ
[ГЛ. Ш
где р2 = х2 + у2. Отсюда в силу (2)
rot Н =
дх ду
2Ту 21х
х2 + у* х2 + у*
к
д
ft
О
а / 2Тх \
дх \х2 + у2/
4- д ( 21 у YI к = 21 Г+ У2 ~ 2ж* 4 ** + У* — 2у21 fc = о
^dy\«» + y»/J L С₽34-3/Ъа (*2 + y2)2 J
(хг + у* Ф 0).
Таким образом, rot Л = 0 везде, кроме оси Oz, в точках которой
последние формулы теряют смысл (знаменатель обращается в нуль)
т. е. поле вектора Я является безвихревым всюду вне точек оси Oz9
Найти ротор следующих векторов:
179. а = (х* + y*)i + (у* + z2)j + (z2 + х*)к.
180. а = z3i + у3] + х3к.
181. а = -| (—уЧ + а-2/).
182. Показать, что если координаты вектора а(М)
имеют непрерывные частные производные вюрого поряд-
ка, то
div rot а — 0,
т. е. что поле вектора rot а(М) есть соленоидальное поле
183. Показать, чго
a) rot (а ± Ь) = rot а ± rot Ь,
б) rot ().а) = X rot а
(X — числовая постоянная).
184. Показать, что если и = и (Л/)— скалярная функ-
ция, а — а(М)— вектор, то
rot (иа) = urota + [gradи, а].
185. Показать, что если а и Ъ — постоянные векторы,
г— радиус-вектор точки М(х, у, г), то
rot (г, a)b — 1а, Ы,
186. Показать, что
rot (га) = — [г, а],
где а — постоянный вектор, г = |г| = ]/Д2 4- у2 + г2.
TEOPFMa стокса
93
1 I16)
I 187. Показать, что rot (/(r)a) = a], где /(r)—
I произвольная дифференцируемая функция своего аргу-
I мента, а—постоянный вектор.
188. Показать, что векторное поле а = /(г)г является
безвихревым, т. е. roto — O.
189. Показать, что
div la, Ы = (Ь, rota) — (a, rot 6).
190. Показать, что ротор пиля линейных скоростей v
вращающегося твердого тела есть постоянный вектор,
направленный параллельно оси вращения, модуль которо-
; го равен удвоенной угловой скорости вращения: rot v — 2а>.
I 191. Определить угловую скорость <о, с которой вра-
щается твердое тело около неподвижной оси, проходящей
через некоторую его точку, если его линейная скорость
v ==• 2xi + y*j + xzk.
192. Показать, что поле ротора вектора а(М) свободно
от источников и стоков.
193 Какова должна быть функция f(x1 z), чтобы ротор
векторного поля
a = yzi + f(x. z)j + хук
совпадал с вектором к — i?
§ 16. Теорема Стокса
Пусть координаты вектора ш
а(М) = Р(х, у, z)i + Q(x, у z)j + R(xt у, z)k
непрерывны и имеют непрерывные частные производные.
Теорема. Циркуляция вектора а по замкнутому контуру
L равна потоку ротора этого вектора через любую поверхность
2, натянутую на контур L:
(j) xa, dr) = J J (rot a, n°) da*
(1)
Предполагается, что ориентация нормали я0 к поверхности
S согласована с ориентацией контура L так, чтобы из конца нор-
мали обход контура в выбранном направлении был виден совершаю-
щимся против часовой стрелки.
94
бёкторноё пола
(Fit tti
Пример 1. Вычислить циркуляцию вектора а ==
+ х2/ — zk по контуру L:
теореме Стокса.
Решение. 1) Контур L — окружность радиуса R = 2,
лежащая в плоскости z == 3 (рис.^33). Выберем ориентацию на ней
как указано на рисунке. Параметри-
• 1 ческие уравнения линии Lx
^ + у2±=4, л
_ 1) непосредственно, 2) по
Z-— О,
х == 2 cos t,
у = 2 sin
z = 3,
так что
О < t < 2л,
dx — —2 sin t dt, dy — 2 cos t dt, dz == 0.
Для циркуляции вектора а 'имеем
2л
Ц » J [2 sin t (— 2 sin t) +
0
4- 4 cos2 12 cos t — 3 • 0] dt = — 4л.
Рис. 33. 2 )Для вычисления циркуляции по
теореме Стокса выберем какую-нибудь
поверхность 2, натянутую на контур L. Естественно в качестве 2
взять круг, имеющий'линию L своей границей. Согласно выбранной
ориентации контура нормаль //° к кругу необходимо взять равной
к'. л°= к. Далее
i i
д д
дх ду
у ж2.
к
д
dz
~ (2х »» 1) ki
Поэтому, в силу теоремы Стокса,
Ц = J j (rot а, п9) da = f J (2х — 1) da
2Л 2
С С Р2 Р
= I dtp I (2р cos tp — 1) р dp = — 2л "2 L в 4л,
0 0
194. Показать, что поток ротора через незамкнутую
поверхность, натянутую на данный контур, не зависит ст
формы поверхности.
I и]
ТЕ0РЕД1А СТОКСА
95
Найти циркуляцию векторов по указанным контурам
непосредственно и по теореме Стокса.
(ж2 + i/2 = 4,
195. а «== zi + xj + ук\ L: | 2 == о '
[я2 + У2 + z2 = 4,
196. a ~yi- х/ + zk', L: _
t У —— а , 2 V.
197. а « 2xzi — yj + zk по контуру, образованному
пересечением плоскости х + У + 2z = 2с координатными
плоскостями.
198.
199.
[ Z = X2 + у2,
а = у1—х]' + (х + у) к; L: | = *
[ х2 + у2 + z2 = 16,
а =* zH; L: \ Л _ Л
(х — 0, у — 0, z = 0.
200. а — zy2i + xz2j + х2ук; L: < о
(Я = У.
(х2 + у2 = 9,
2О1. « = «!‘-+’"Л ^{3j+4z = 5;
г ( X2 + у2 + Z2 = 1,
202. а == yi — xj zk\ L: j __
203. Дано векторное поле скоростей v точек твердого
тела, вращающегося с постоянной угловой скоростью <о
вокруг оси Oz. Вычислить циркуляцию этого поля по
окружности *
х = a cost,
Lx у = a sin t, 0^^<2л,
lz=0,
непосредственно и по теореме Стокса.
Из теоремы Стокса получаем: проекция вектора rot а на любое
направление п не зависит от, выбора системы координат и равна
поверхностной плотности циркуляции вектора а по контуру пло-
щадки, перпендикулярной этому направлению:
(л, dr)
пр/| rot а |м = (rot а, «°) |м - lim -. (2)
96
ВЕКТОРНОЕ ПОЛЕ
1ГЛ. Ш
Здесь (S) — плоская площадка, перпендикулярная вектору п\
S — площадь этой площадки; L — контур площадки, ориентиро-
ванный так, чтобы обход контура был виден из конца вектора п
против часовой стрелки; запись (S) —> М означает, что площадка
(S) стягивается к точке М, в которой рассматривается вектор rot а,
причем направление нормали п к этой площадке остается все время
одним и тем же.
Пример 2. Вычислить плотность циркуляции вектора а =
» yi ио окружности
{х = а cost,
у » a sin 0 < t < 2л,
2 = 0,
в центре этой окружности 0, 0) в положительном направлении
оси Oz.
Решение. Здесь (S) — круг радиуса а с центром в точке
М, тяж что S — па4.
Искомая плотность циркуляции равна
L L
2л
= lim С (— a2) sin2t dt = — 1.
<н0 «« J
о
С другой стороны,
» /
д д
rota = -о!
у о
и, значит,
(rot а, п*)\м = (—к, к) = —1,
что, в силу (2), подтверждает верность результата.
•
204. Вычислить плотность циркуляции вектора а =
= zi + х/ + ук по окружности L: {у= a cost, z=a sin t,
х = 0; 0 t < 2л} в центре этой окружнссти С(0, 0, 0)
в положительном направлении оси Ох.
205. Вычислить плотность циркуляции вектора а =
= 2yi + 5xzj по эллипсу L: {х =асоя£, у = &sin£, 2=1;
0 t < 2л} в центре эллипса С(0, 0, 1) в положительном
направлении оси Oz.
f 17)
ФОРМУЛА ГРИНА
97
§ 17. Независимость линейного интеграла
от пути интегрирования. Формула Грина
Определение. Область G трехмерного пространства
называется односвязной (точнее, поверхностно односвязной), если
на любой замкнутый контур, лежащий в этой области, можно натя-
нуть поверхность, целиком лежащую в области G. Например, все
трехмерное пространство, внутренность сферы являются односвяз-
ными областями; внутренность тора, трехмерное пространство, из
которого выброшена прямая, не являются односвязными областями.
Теорема. Для того чтобы линейный интеграл
j* (a, dr) =» J Р (х, у, z) dx + Q (х, у, z) dy + R (x, у, z) dz
L L
не зависел от формы пути интегрирования L, необходимо и доста-
точно, чтобы векторное поле
а Р(х, у, z)i + Q(x, у, z)j + R(x, у, z)k
было безвихревым, т. е.
rot а(М) = 0.
Здесь предполагается, что координаты Р(х, у, z), Q(x, у, z)9
Н(х, у, z) вектора а имеют непрерывные частные производные пер-
вого порядка и область определения вектора а(М) односвязна.
В этом случае линейный интеграл J (a, dr) будет зависеть толь-
L ‘
ко от положения начальной и концевой точек пути интегрирова-
ния £.
При выполнении условий теоремы циркуляция вектора а{М)
по любому замкнутому контуру С, расположенному в полб вектора
а(М), равна нулю: (a, dr) ® 0.
с
Пример 1. Показать, что в поле вектора
а = xy*zl + x*yzj + "2 хгу2к
линейный интеграл J (л, dr) не зависит от формы пути интегриро-
вания L,
Р е ш е н и е. Координаты вектора а являются всюду непре-
рывными функциями, так что область определения G вектора а
есть все пространство — односвязная область. В этой области
имеем
rot а =»
i i ь
д д д
дх ду dz
xy2z x*yz
7 М. Л, Краснов и др.
98
ВЕКТОРНОЕ ПОЛЕ
[ГЛ. Ш
Следовательно, линейный интеграл
I (a, dr) = I xy2z dx~\~x2yz dy-\- — x2y2dz
L L
не зависит от формы пути интегрирования L.
В частности, для плоского векторного поля
а(М) = Р(х, y)i + CU У)1 (1)
имеем
rot а (Л/) =
i
д
дх
Р
J
д
ду
Q
к
д
dz
О
dQ dP\
dx dy j ’
Поэтому для плоского векторного поля (1), определенного в одно-
связной области О, условие rot а(М) = 0 в координатной форме
дР dQ
записывается так: = -gj-.
Таким образом, для того чтобы в плоском поле, определенном
в односвязной области G, линейный интеграл
Р (х, y)dx + Q (х, у) dy
L
не зависел от формы пути интегрирования, необходимо и достаток-
но, чтобы выполнялось соотношение
дР __ dQ
dy ~ dx *
Замечание. Требование, чтобы область G, где опреде-
лен вектор а=а(М), была односвязной, существенно. Если область
G неодносвязна, то при условии rot а(М) = 0 линейный интеграл
может зависеть от формы пути, интегрирования.
Пример 2. Рассмотрим линейный интеграл
— у dx х dy
У2 я2 + У2 *
L
Р е in е п и е. Подынтегральное выражение теряет смысл
в точке 0(0, 0); поэтому исключим эту точку. В оставшейся части
плоскости (это будет уже неодносвязная область) коэффициенты
при dx и dy непрерывны, имеют непрерывные частные производные,
и выполняется тождество
д / х \ д / у \
дх х2 + у2 j ~ ду у х2 -|- у2 j
С другой стороны, если вычислить этот интеграл вдоль окружности
§ <71
ФОРМУЛА ГРИНА
99
L: х2 + у1 = Я2, то параметризируя уравнение этой окружности,
будем иметь
2л 2л
Г — у dx-rx dy f* R2 sin2 t + R2 cos2 t (*
dp Д.2 _|_ = J ДЗ = j dt = 2jl>
L 0 0
т. e. линейный интеграл зависит от пути интегрирования.
Определить, в каких из указанных ниже векторных
полей интеграл не зависит от формы пути интегрирования:
206. а — z2i + х2] + У2к.
207. а =
Vi + x^ + y^ + zi-
208. а =
xt + у2. + z-
Формула Грина
Пусть в области D с границей L задано плоское векторное поле
а = Р(х, y)i + Q(x, y)j,
где координаты P(xt у), Q(x, у) непрерывны и имеют непрерывные
дР dQ
частные производные и
Тогда справедлива формула Грина
§Pdx+Qf:y= $$(11
L D
При этом граница L проходится так,*что область D остается слева.
dx dy.
(2)
Рис. 34
Область D может быть и неодносвязной, так что граница
ее может состоять из нескольких компонент (см, рис. 34).В этом
7*
г
100
ВЕКТОРНОЕ ПОЛЕ
[ГЛ. III
случае под интегралом
Р dx + Q dy
понимается сумма интегралов по всем компонентам границы об-
ласти D.
Формула Грина (2) представляет собой частный случай теоре-
мы Стокса (см. § 16).
Формула Грина дает возможность в некоторых случаях упрос-
тить вычисление циркуляции векторного поля.
Пример 3. Вычислить циркуляцию вектора
а = У 1 + х2 + уЧ + у [ху + In (а? + уЧ + а:2 + 3/2)] j
по окружности X2 + у2 = R2.
Рете н и е. Циркуляция данного вектора равна
Ц = Ф (a, dr) = (j) Yi + х^ + уЧх +
L L
+р \ху + In (х 4- dy.
Здесь
Р = “1/1 + аг2 + Р2» Q = ®Р- +р In (я -f- ДА + я2 + Р2)»
Находим частные производные
дР_________У QQ _ 2 .________________У
ду у 1 + X2 + у*’ дх у + +
Применяя формулу Грина, получим
Д - Ш’’ + У - )'! + ’> + ,>) л М Р’"* 4’-
D D
Переходя к полярным координатам
х = р cos ф, у = р sin ф,
будем иметь
Ц » J J р2 sin2 фр dp с?ф— [ Jp3 sin2 ф dp dф.
Так как 0 < ф < 2л, 0 < р < R, то
2л я
Ц = J sin2 Ф dq> J р3<?р =
0 0
। 17] ФОРМУЛА ГРИНА 101
Вычислить циркуляцию следующих векторов по дан-
ным контурам, применяя формулу Грина:
209. а « {у + х)1 + (у — x)j; L: х + у = 1,
х = 0. у = 0.
210. а — (х — y2)l + 2xyj; Lt у » х, у = х2.
211. а^х}п(Д + у2)1-}-^^]'; L: х2 4- у2 = 2х.
212. а = y2i — х2]'’, L: х + у — —1, х = 0, у — 0.
213 а = (Зх — у3 V1 + Д2 4~ ^у5) i + (18у34-х3 V 1+ж2+4у^)/;
3 У 1 + х'2 -J- 4у3
L: х2 4- у2 *=* 1.
214. С помощью формулы Грина вычислить разность
между интегралами
/j ° J (х 4- у)2 dx — (x — у)2 dy
П АтВ
J (х 4- У? dx — (х — у)2 dy,
АпВ
где АтВ — отрезок прямой, соединяющей точки Л(0, 0)
и 5(1,1), а АпВ дуга параболы у = х2.
215. Доказать, что величина интеграла
(£ (2х — y)dx х* dy,
L
где L — замкнутый контур, дает площадь области, ог-
раниченной этим контуром.
216. Пользуясь формулой Грина, вычислить линей-
ный интеграл J (a, dr) в векторном поле
а « (ех sin у — у) i + (ех cos у — 1) j,
где линия L есть верхняя полуокружность я2 + р* = 2х,
проходимая в направлении от точки А (2,0) до точки 0(0, 0).
ГЛАВА IV
ПОТЕНЦИАЛЬНОЕ ПОЛЕ
§ 18. Признаки потенциальности поля
Определепие. Векторное поле а(М) = Р(х, у, z)i +
+ 2Л s)j +.v, заданное в пространственной области
V, называется потенциальным, если существует такая скаляр-
ная функция ф(М), что во всех точках области V выполняется
равенство
а(М) = grad ф(М). (1)
Функция ф(7И) = ф(я, у, z), удовлетворяющая в области V ра-
венству (1), называется потенциалом (или потенциальной функци-
ей) векторного поля а.
Соотношение (1) равносильно следующим трем скалярным ра-
венствам:
$<р с1© дер
р (X, у, 2) = Q (X, у, 2) = R(x,y,z)=-^. (2)
Потенциал поля определяется неоднозначно, с точностью до
постоянного слагаемого.
Замечание. Для силовых полей функция ф(М) обычно
называется силовой функцией, а потенциалом называется функция
-ф(М).
Пример 1. (Электростатическое поле точечного заряда.)
Показать, что поле электрической напряженности Е, создаваемое
точечным зарядом q, помещенным в начале координат:
а „ .-----------
Е 33 “jT г» г = У я2 + у2 + 22,
является потенциальным полем.
Решение. Задача ставится так: показать, что существует
функция Ц)(х, у, z) такая, что выполняются соотношения (2).
В нашем случае имеем
Р(Х, у, z) = Q (х,у, z) R(x, у, z) =
Так как
д f 1 \ _ 1 дг в х
дх I г ) ~ г2 дх ~~ г3
I 181
ПРИЗНАКИ ПОТЕНЦИАЛЬНОСТИ ПОЛЯ
103
п аналогично
dL/JL\ = _.JL АЦЗ_______________г
ду I г j = г3 9 dz I г 1 г3 9
то функция
g q
ф (®, у, z) = —— = — l/j.2-1- у2 +jr
является потенциалом данного поля:
В данном примере начало координат, где сосредоточен заряд
д, является особой точкой поля Е.
Критерий потенциальности
векторного поля
Теорема!. Для того, чтобы векторное поле а(М), заданное
в односвязной области V, было потенциальным, необходимо и доста-
точно, чтобы в каждой точке области V выполнялось условие
rot а = 0. (3)
Иными словами, для того чтобы векторное поле, заданное
в односвязной области, было потенциальным, необходимо и доста-
точно, чтобы оно было безвихревым.
Потенциал (р(я, у, z) векторного доля
а = Р(х, у, z)i + Q(x, у, z)j + R(x. ц, z)k
определяется формулой «
ф (я, У» z) « J Р dx+Q dy-\-R clz, (4)
где (x0, y0, z0) — некоторая фиксированная точка поля, a (xt yt z) —
произвольная текущая точка.
Пример 2. Показать, что поле вектора
а = хЧ + У2] + z2k
является потенциальным.
Решение. Координаты Р — х2, Q = у2, R = z2 вектора
а являются бесконечно дифференцируемыми функциями во всем
пространстве, так что а есть бесконечно дифференцируемый вектор,
104
ПОТЕНЦИАЛЬНОЕ ПОЛИ
(ГЛ. IV
определенный во
i i
д о
rot а =» -тг— -г-
дх ду
** у2
всем' трехмерном пространстве. Имеем
к
д
dz
12
а А
/ д 9 \ . f 9 9 \.
+ I “Т" х* — 22 1 7 + I У2 —* Т“ х2 ) к = 0.
1 I dz дх Н 1 \дх ” ду j
В силу теоремы 1 поле вектора а потенциально. Легко видеть, что
функция
Ф У,*) =
а?8 + у8 + **
3
С,
где С — произвольная постоянная, является потенциалом данного
поля.
т
Проверить, будут ли следующие векторные поля по-
тенциальными:
217. а = xzi + 2у/ + хук.
218. а = (2ху + z2)i + (2yz + x2)j + (2xz + p2)fc.
219. a = -у (xH + p3/ + xz2k).
220. a = yz cos xy*i + xz cos xy^j + sin xy-k.
221. a = ln(l + z2)i + In (1 + x2)j + xzk.
222. a = (4 + —V + (4^ + J_k- +7x +l]fc.
X2 ‘ у J \y* I22 1 X j
223. Я= (— yi + xj), r2 = x* 4- j/2, r =# 0.
224. Доказать, что поле a = /(r)-r# где /(г)—диффе-
ренцируемая функция, является потенциальным.
225. Показать, что в потенциальном поле а =» grad ф
векторные линии перпендикулярны к поверхности уровня
функции ф.
§ 19. Вычисление линейного интеграла
в потенциальном поле
Теорема. Линейный интеграл в потенциальном поле а(М)
равен разности значений потенциала ф(М) поля е конечной и началь-
ной точках пути интегрирования*.
М9
[ (a, dr) = <р (М2) — <р (4/J. (1)
М.
§ 19]
ВЫЧИСЛЕНИЕ ЛИНЕЙНОГО ИНТЕГРАЛА
105
Пример 1. Вычислить линейный интеграл в поле вектора
г xi + yj + zk
вдоль отрезка прямой, ограниченного точками Мг (— 1, 0, 3) и
М2(2, -1, 0).
Решение. Покажем, что поле данного вектора потенци-
ально. В самом деле,
rot а —
i i
д д
дх ду
* У
к
z
Легко убедиться, что потенциал этого поля
. x’ + p’ + z»
ф(х, у, «)—-------2-------^С*
Применяя формулу (1), получим
м,
( (а,4г)-ф(2,-1,0)-ф(-1,0,3)=-1-5 = - *
iii
Отметим, что несущественно, какой линией соединены точки Мх
и Л/8; в любом случае при фиксированных Мг и М2 интеграл
J (a, dr) я J х dx + у dy + z dz
Mi
имеет одно и то же значение.
Вычисление потенциала поля
в декартовых координатах
Формулой
Ф (х, yf z) —
(хф*)
» J Р (х, у, z) dx-}- Q (х> у, z) dy + R (х, у, z) dz (2)
(х«,!/•,«•)
можно пользоваться для нахождения потенциальной функции
Ф(М) = <р(я, у, i) заданного потенциального поля
а(ж, у, i) -= Р(х, у, z)i + Q(x> у, z)j + R(x, у, z)k.
Для этого зафиксируем начальную точку ЛГ0(х0, Уо, го) и соединим
ее с текущей точкой М(х, yt z) ломаной MqABM, звенья которой
параллельны координатным осям, а именно, MqA^Ox, АВ^Ру,
106
ПОТЕНЦИАЛЬНОЕ ПОЛЕ
[ГЛ. IV
BM\\Oz (рис. 35). Тогда формула (2) примет вид
X у Z
ф (я, у, z) « J Р (х, у0, Zo) dx + J Q (x, у, z0) dy 4~ J R {x, y, z) dz, (3)
Ул *л
где x, у, z — координаты текущей точки на звеньях ломаной, вдоль
которых ведется интегрирование.
Пример 2. Доказать, что векторное поле
а == (у + z)i + (х + z)j + (х + у)к
является потенциальным, и найти его потенциал.
Решение. 1-й способ. Необходимым и достаточным усло-
вием потенциальности поля а(М) является равенство нулю rot a(Af).
В нашем случае
rot а —
i
д
дх
у 4-2
7
д
ду
х + z
к
д
dz
* + У
= (! — !)£ + (1-1) у + (1 — 1) * = 6,
Потенциал этого поля найдем
с помощью формулы (3). За
начальную фиксированную
точку примем начало коорди-
нат 0(0, 0, 0). Тогда получим
х
Ф (а?, 1/, z) = I (0 + 0) dx +
о
у Z
+ J (х + 0) dy + J(s + у) dz
О
О
= ху + XZ + yz»
Итак,
ф (я, у, z) = ху + яг+ yz + С,
где С — произвольная посто-
янная.
потенциал ф(я, у, z) есть такая
Рис. 35.
2-й способ. По определению
скалярная функция, для которой grad ф = а, Это векторное ра-
венство равносильно трем скалярным равенствам:
дф
дх
у 4-2,
(4)
дф
ду
= X 4“ Z,
дд
OZ
= *4- У-
(5)
(6)
$ 19] ВЫЧИСЛЕНИЕ ЛИНЕЙНОГО ИНТЕГРАЛА Ю7
Интегрируя (4) по х, получим
X
Ф (х, у, z) = J (у + z) dx = ху 4- xz + / (у, z), (7)
О
где /(у, z) — произвольная дифференцируемая функция от у и z.
Дифференцируя по у обе части (7) и учитывая (5), получим соот-
ношение для нахождения пока неопределенной функции /(у, z).
Имеем
,£ф_ । 2L
ду х'ду
или
откуда
Of
2 “ ду* (8)
Проинтегрировав (8) по у, будем иметь "
у
/ (у> 2) = J Z dy = zy + F (z), (9)
где F(z) — пока неопределенная функция от z. Подставив (9) в (7)>
получим
ф(я, у, г) — ху + xz + zy + F(z).
Продифференцировав последнее равенство по z и учитывая соот-
ношение (6), получим уравнение для нахождения F(z):
dF
ж + 2/=х + г/ + —
dF
Отсюда = О, так что F(z) = С = const.
Итак,
ф(лг, у, z) = ху + yz + ZX + С.
3-й способ. По определению полного дифференциала функции
ф(х, у, z) имеем
дф дф ' ф
dq^^+^dy + ^dz.
,. дф дф дф
Подставляя сюда вместо частных производных их выра-
жения из (4), (5), (6), получим
d<f=* (у + z)dx -J- (х + z)dy + (х + y)dz
108
ПОТЕНЦИАЛЬНОЕ ПОЛЕ
(ГЛ.. IV
или, после несложных преобразований,
йф = (у dx + я dy) + (z dx + х dz) + (у dz + 2 dy) “
« d(xy) + d(xz) 4“ d (yz) = d(xy + xz + yz).
Итак,
dtp «и d(xy + yz + zx).
Отсюда следует, что
q(x, у, z) » xy + yz + zx + C.
В следующих задачах установить потенциальность
данных векторных полей а(М) и найти их потенциалы
226. а = 2xyzi + x2zj 4- хгук.
227. а = (yz + 1)4 4- xzj + хук.
228. а = (2ху 4- z)i 4- (хг — ty)j 4- хк.
229. а = + + \
230. а =
1 + x2y2z*
231. а = —.
г
232. а = 4.
Г?
233. а = г г.
В тохм случае, когда область Q является звездной с центром
в начале координат 0(0, 0, 0) *), потенциал ф(М) векторного поля
а = а(М) в точке М(х, у, z) можно находить по формуле
1
ф (М) » [ (а (Л/')» г (М)) dt-\-C, const, (10)
О
где r(M) = xi + yj + zk —радиус-вектор точки М(х, yt z), а точ-
ка M'(tx, ty, tz) при 0 < t < 1 пробегает отрезок ОМ прямой, про-
ходящей через точки О и М.
Пример 3. Найти потенциал векторного поля
а =» yzi + xzj + хук.
*) Область Q называется звездной относительно точки О, при-
надлежащей Q, если любой луч, выходящий из этой точки, пере-
секает границу этой области не более чем в одной точке. Например,
па плоскости звездными областями будут сама плоскость, парал-
лелограмм, круг; в трехмерном пространстве само пространство,
параллелепипед, шар.
। 19] ВЫЧИСЛЕНИЕ ЛИНЕЙНОГО ИНТЕГРАЛА Ю9
Решение. Легко видеть, что rot а г 0, т. е. данное вектор-
ное поле потенциально. Это поле определено во всем трехмерном
пространстве, которое является звездным с центром в начале коор-
динат 0(0, 0, 0), поэтому для нахождения его потенциала восполь-
зуемся формулой (10). Так как в данном случае
а(М') « a(tx, tyt tz) «= t2yzi + t*xzj + t2xykt
то скалярное произведение векторов a(M') и г(М) равно
(а(М'), r(M)) = t2(xyz + xyz 4- xyz) « 3>t2xyz.
Искомый потенциал
1 1
ф (Л/) = j* (а (Л/'), г (М)) dt == xyz J + C s XVZ + С.
Q О
Итай,
ф(М) « xyz + С.
Используя формулу (10)* найти потенциалы следую-
щих векторных полей:
234. а = са + Р/ + yfc, где а» у—постоянные.
235. а = (у + z)i + (х + z)j + (у + х)к.
236. а ® yi + xj + е*к.
237. а = ех sin y-i + ех cos y j + к.
t-
ГЛАВА V
ОПЕРАТОР ГАМИЛЬТОНА.
ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ
ВТОРОГО ПОРЯДКА.
ОПЕРАТОР ЛАПЛАСА £
§ 20. Оператор Гамильтона «набла» |
Многие операции векторного анализа могут быть записаны f
в сокращенной и удобной для расчетов форме с помощью символа- |
ческого оператора Гамильтона «набла»: J
. д . д д ъ
В этом операторе соединены дифференциальные и векторные свой- 1
г di
тва. Будем понимать формальное умножение на функцию Tf
df
f(x, у, z) как частное дифференцирование -gj. 4 #
В рамках векторной алгебры формальные операции над one- 1
ратором «набла» будем проводить так, как если бы он был векгором. В
Используя этот формализм, получим следующее. Т
1. Если и = и(х, у, z) — скалярная дифференцируемая функ- 1
ция, то по правилу умножения вектора на скаляр имеем ‘ f
Vu = (z 5+/5+& =/|u+y3u + fc^=gradM> . j
\ дх ду dz / дх ду dz Л
2. Если а = Р(х, у, z)i + Q(x, у, z)j-\- R(x, у, z)kt где Р, Qt
R — дифференцируемые функции, то по известной формуле для <
скалярного произведения имеем ;
(у, а) = (* + i-=г- + Pi + Qi +*ялА=
\ дх ду dz /
_w + s2 + afl = aiv„, (3) ;
дх ду dz
в частности, (у, с) = 0 (с — постоянный вектор).
3. Если a =P(x,y,z)i + Q (x,y,z)j + R(x,y,z)k, то
i ] к
д д д
[V. «] — дх ду dz — rot а,
Р Q R
в частности, (у, с) «= 0 (с — постоянный вектор).
(4)
§ 20]
ОПЕРАТОР ГАМИЛЬТОНА «НАБЛА»
111
Продолжая формализм действий с у как с вектором, из распре-
делительного свойства для скалярного и векторного произведений
получаем
(v, а + b) = (v, а) + (V, Ь), (5)
т. е. div (а + Ь) = div а + div Ъ,
[V, а + &] = [у, а] + (у- И (6)
т. е. rot (а + b) = rot а + rot Ь.
Формулы (5) и (6) можно, трактовать также как проявление диф-
ференциальных свойств опёраТОра «набла» (у — линейный диф-
ференциальный оператор).
Используя формализм действий с оператором у как с вектором,
следует помнить, что у не является вектором — он не име°т ни
величины, ни направления, так что, цапример, вектор [у, а] не
будет, вообще говоря, перпендикуляре^ вектору а (однако для плос-
кого поля а = Р(х, y)i + Q(x, y)j вектор
tV> а] = rot а = — df'j k
\dx dy /
будет перпендикулярен плоскости хОу, а значит, и вектору а)
Точно так же по отношению
к символическому вектору
у понятие коллинеарности
не имеет смысла. Напри-
мер, выражение [у<р, уф],
где (р и ф — скалярные
функции, формально напо-
минает векторное произ-
ведение двух коллинеар-
ных векторов, которое все-
гда равно нулю. Но в об-
щем случае это не имеет
места. В самом деле, вектор
УФ — grad ф направлен по
нормали к поверхности
уровня ф s= const, а вектор
уф s=s grad ф определяет
нормаль к поверхности
уровня ф — const, и эти ™ис- 36.
нормали в общем случае не
обязаны быть коллинеарными (рис. 35). С другой стороны, в лю-
бом дифференцируемом скалярном поле ф имеем [уф, уф] =» 0.
Эти примеры показывают, что с ое зратором у нужно обращаться
с осторожностью.
Наряду с векторной природой, оператор Гамильтона «набла»
имеет дифференциальную природу. Учитывая дифференциальный
характер у, условимся считать, что оператор у действует на все
величины, написанные за ним. В этом смысле, скажем, (у, а)
(а, у). В самом деле,
(у, а) — div а,
115 ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ ВТОРОГО ПОРЯДКА [ГЛ. V
в то время как
(а, ?) = р2. + <?± + Я±
дх ду dz
есть скалярный дифференциальный оператор.
Применяя оператор у к произведению каких-либо величин,
надо иметь в виду правило дифференцирования произведения
Отсюда следует, что оператор «набла» надо применять поочередно
к каждому множителю, оставляя остальные множители неизмен-
ными, и затем брать сумму полученных выражений. При этом бу-
дем руководствоваться следующими правилами.
1°. Если оператор у действует на какое-либо произведение, то
в первую очередь учитывается его дифференциальный характер,
а затем уже векторные свойства.
2°. Чтобы отметить тот факт, что «набла> не воздействует на
какую-либо величину, входящую в состав сложной формулы, эту
величину отмечают индексом с (const), который в окончательном
результате может быть снят.
3°. Все величины, на которые оператор «набла» не воздейству-
ет, в окончательном результате ставятся впереди «набла», т. е.
слева от него.
Пример 1. Показать, что
div (иа) « и div а + (a, grad и).
Вдесь и — скалярная функция, а — векторная функция.
Решение. В символической записи
div (иа) =» (у, иа).
Учитывая сначала дифференциальный характер у, мы должны
написать
(у, иа) «в (у, иса) + (у, иас).
Рассматривая выражение (у, и<а) мы можем постоянный множи-
тель ис вынести за знак «набла» и, как скаляр, за знак скалярного
произведения, что дает
(у, иса) = (ису, а) « ис(у, а) « и(у, а)
(на последнем шаге мы опустили индекс с).
В выражении (у, иас) оператор у действует только на скаляр-
ную функцию и; поэтому мы можем написать, что
(у, иас) * (у и, а() =» (ас, у и) = (а, у и).
6 результате получаем формулу
(у, иа) « и(у, а) + (а, у и)
ИЛИ
div (иа) «= и div a -j- (a, grad и).
6 20]
ОПЕРАТОР ГАМИЛЬТОНА «ПАВЛА»
113
Пример 2. Показать, что
rot (иа) — и rot а — [a, grad и].
Решение. В символической записи
rot (иа) — [у, иа].
Учитывая дифференциальные свойства у, сначала питием
[у, иа] — [у, иса] + [у, иас]. (7)
Затем в первом слагаемом справа выносим скалярный множитель
ис за знак у и за знак векторного произведения, что дает
[у, и а] » ис[у, а] = и[у, а].
Во втором слагаемом в (7) относим и к оператору у и изменяем
порядок множителей для того, чтобы вектор ас, на который «набла»
не действует, оказался впереди у. Это дает
[у, иа<] = [у и, ас] = —[а, уи].
Таким образом,
[у, иа] » и[у, а] — [а, уи]
или
rot (иа) — и rot а — [а, grad и].
Пример 3. Пользуясь символическим методом, найти
div [а, Ь].
Решение. Имеем
div [а, д] = (у, [а, &]) = (у, [а, Ьс]) + (у, [ас, Ъ]). (8)
Пользуясь свойством циклической перестановки множителей в сме-
шанном произведении, преобразуем выражения в правой части (8)
так, чтобы все постоянные величины оказались перед оператором
у, а переменные — позади него. Получим
div [а, Ь] « ([у, а], Ъс) — (у, [Ь, ас]) «= ([у, а], Ьс) —
— ([у, Ь], ас) = (Ь, [у, а]) — (а, [у, Ь]),
т. е. div [а, Ь] = (Ъ, rot а) — (а, rot Ъ).
Замечание. Применяя символический метод, мы избе-
гаем весьма сложных аналитических преобразований и быстро по-
лучаем окончательный результат. Но, с другой стороны, различны >
формальные преобразования с оператором «набла» надо произво-
дить очень внимательно, в противном случае возможны, как мы
ридели, грубые ошибки. Поэтому при отсутствии уверенности в по-
лученном результате его следует проверить аналитическим методом.
238. Показать, что
(и \ uyu — иуу
б) vftu) =
8 М. Л. Краснов и др.
114 ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ ВТОРОГО ПОРЯДКА (ГЛ. V
239. Доказать, что вектор [у и, ур] соленоидален,
если и и и — дифференцируемые скалярные функции.
Используя оператор Гамильтона у, доказать следую-
щие равенства:
240. a) grad (up) = р grad и + и grad р;
б) rot [а, д] — (6, у)а — (а, у)& + а div Ь—Ь div а.
241. rot 1а, г] = 2а, а — постоянный вектор.
242. Доказать, что вектор а — и grad р ортогонален
к rot а.
§ 2L Дифференциальные операции второго порядка.
Оператор Лапласа
Дифференциальные операции второго порядка получаются
в результате двукратного примеПения к полям оператора у.
Пусть имеем скалярное поле и = и(М). В ЗтОм поле оператор
V порождает векторное пбле уц=з grad и.
В векторном поле у и оператор у, примененный повторно
к у и, дает скалярное поле
(у, — div grad и (1)
и векторное поле
[у, у и] = rot grad и. (2)
Если задано векторное поле а = а(М),то оператор у порожда-
ет в нем скалярное поле (у, а) = div а. В скалярном поле div а
оператор V порождает векторное поле
у (у, а) = grad div а. (3)
В векторном поле а — а(М) оператор у порождает также векторное
поле [у, а] — rot а. Применяя К этому полю снова оператор у,
получим скалярное поле
(у,[у, a])=divrota (4)
и векторное поле
[у, [у, а]] = rot rot а. (5)
Формулы (1) — (5) определяют так называемые дифференци-
альные операции второго порядка.
Пример 1 Пусть функция и == и(х, у, z) имеет непрерывные
частные производные до второго порядка включительно. Доказать,
что
rot grad и = 0.
Решение. 1-й способ. Действуя формально, получим
rot grad и = [у, у и] = [у, у ] и = 0,
§21] ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ ВТОРОГО ПОРЯДКА 115
так как [у, vl * 0 как векторное произведение двух одинаковых
«векторов».
2-й способ. Используя выражения градиента и ротора в декар-
товых координатах и учитывая данные условия, будем иметь
rot grad u =
i j к
d d d
dx dy dz
du du du
dx dy dz
d (du\ d / du ]1; ,
-- [ - I - -- | - I I fr-U
dy \dz / dz \dyjj
* I d2u — / d2u — d2u \ f d2u __ d2u _ q
\dydz dzdy) \dzdx dx dz) \dx dy dy dx) ~~ 9
так как смешанные производные в этом случае равны
д2и __ д2и d2u d2u д2и d2u
dy dz dz dy' dz dx dx dz' dxdy dy dx*
Аналогично доказывается, что для векторного поля
а =» Р(х, у, z)i + Q(xt у, z)j + R(xt у, z)kt
координаты P, Q, R которого имеют непрерывные частные произ-
водные второго порядка, получим div rot а = 0.
Обратим особое внимание на дифференциальную операцию вто-
рого порядка div grad и « (у, у и). Предполагая, что функция
и(х, у, z) имеет вторые частные проиводные по х, у и z, получим
(V, VU) = (* Z + Я fc) du i+^/ + du Л
\dx dy dz dx dy dz /
д /ди\ d fdu\ d fdu\ __ 02u d2u d2u _ .
dx {dx'J dy \dy / ' dz \dz ] dx2 ’ dy/2 dz2 U'
. . A A __d2u ! d2u d2u
Итак, (у, yu)« Au, где символ ^'dy^^’dz2 называет-
ся оператором Лапласа. Его можно представить как скалярное
произведение оператора Гамильтона у на самого себя, т. е.
d2 , d2 , d2
A-(V, V)“V* = ^2 + ^2+372.
Этот оператор играет важную роль в математической физике.
Рассмотрим еще одну операцию второго порядка rot rot а: Имеем
rot rot а « [у, [у, а]]. Воспользуемся формулой для двойного
векторного произведения, записанной в виде [Л, [В, С]] =
«= B(At С) — (А, В)С. Заменяя в этой формуле Л па у, В на у,
С на а, получим
[у, [у, «11 = v(y> л) ~ (V* у)« = у(у, а) — Аа (6)
116 ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ ВТОРОГО ПОРЯДКА [ГЛ. V
rot (rot а) =« grad div а — Да, где Да » ДР 4 + Дф./ -|~ ДЯ
Дифференциальные операции второго порядка можно для на-
глядности записать в виде следующей таблицы:
Скалярное поле и Векторное поле a
grad div rot
grad — grad div a •— , ,, .
— —
div div grad и~ Au — div rot a=0
rot rot grad u—0 — rot rot a» —grad div a—Да
(8)
Пример 2. Законы классической теории электромагнетизма
постулируются в виде системы уравнений Максвелла.
В простейшем случае непроводящей однородной и изотропной
среды при отсутствии зарядов и токов эта система имеет вид
= (7)
(V, Е)=0, (9)
(V, Я)=0. (Ю)
Здесь Е и Я — векторы напряженности электрического и магнит-
ного полей; е и р — коэффициенты электрической и магнитной про-
ницаемости (в наших предположениях е, р ® const); с — скорость
света в пустоте.
Поскольку пространственная и временная производные ком-
мутируют, т. е.
4-[?.Я]= [v. 2?],
dt L J
то дифференцируя (7) по t, получим
дЭЧ? Г дН]
с dt2. ~~ Р * dt J
ЭЯ к d2E с
Заменяя из (8), найдем ==_[V, £]] плн
^ = [V,[V,EJ]. (11)
В силу формулы (6) [у, [V, Е]] = у (у, Е) — ДЕ. Так как
(у, Е) = 0, то из (11) имеем ДЕ.
|21] ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ ВТОРОГО ПОРЯДКА Ц7
Итак, для векторного поля Е получаем уравнение
dt1 2 ер
Это — одно из основных уравнений математической физики, назы*
ваемое волновым уравнением.
Нетрудно убедиться (проверьте это!), что векторное поле Н
удовлетворяет точно такому же волновому уравнению
dt2 ер *
Таким образом, каждая из координат Ех, Еу, Ez
Нг векторов Е и Н удовлетворяет в наших условиях
д2и = а2[ д2и д2и d2u\
и Ях,
уравнению
В вакууме
с
Здесь Д/~ц— СК0Р0СТЬ распространения процесса.
при е =» р 1 имеем а = с, т. е. в пустоте электромагнитные про-
цессы распространяются со скоростью света.
243. Показать, что любое решение уравнения
IV» IV» Л]] — Bl-О, удовлетворяющее условию со-
леноидальности, удовлетворяет векторному уравнению
Гельмгольца у2 А + к2 А = 0.
Определение. Скалярное поле и ** и(х, у, z), удовлетво-
ряющее условию Ди = 0, называется лапласовым или гармониче-
ским полем,
ПримерЗ. Важным примером гармонического поля является
скалярное поле и » к/г, к = const, г = ~l/x2 +уа +*?• Эта функ-
ция представляет собой потенциал поля тяготения, создаваемого
точечной массой, помещенной в начале координат. Нетрудно
проверить, что функция и = к!г — гармоническая всюду, кроме
начала координат, где она не определена. В самом деле,
(v. v — ) = *( v, v —) = 4vq-—*(v,—./••)-
= —r°') — fc4(v>r°) = —*(— 4vnr°') — 4(v. f*) =
\ r2 j r2 \ / \ r3 Jr2
= 2? <r«, r°) — — (у, r°) = — —- . — = 0
r3 r2 r9 r2 r
для всех r =^= 0, так как
(V> rft) = f V. —) = (v — 4-1 (V, г) = г) 4- — =
\ г / \ г / г \ Н ] г
1 3 1 3 1,32
--р-4-7 =-7 (г% г») 4-7 = -74-7 = 7-
118 ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ ВТОРОГО ПОРЯДКА [ГЛ. V
Пример 4. Доказать, что в потенциальном поле вектора а
его потенциальная функция и(х, у, z) удовлетворяет уравнению
Пуассона
А __д2и . д2и t д2и
= + + =P(®.2/.Z). (>2)
где р(я, у, z) —- дивергенция вектора а.
Решение. По условию
div а = р (13)
Так как поле вектора а потенциальное, то а = grad и, где и —
потенциал поля. Подставляя в (13) а = grad и, получим
div grad и == р или, так как div grad и = Ди, то Ди » р.
В частном случае, в точках поля, где дивергенция равна нулю,
уравнение (12) обращается в уравнение Лапласа Ди = 0. Уравне-
ние Лапласа — Пуассона дает возможность найти потен-
циальную функцию и с помощью интегрирования дифференциаль-
ного уравнения в частных производных. В некоторых задачах это
оказывается более удобным.
В электростатике нередко предпочитают вместо функции и
брать противоположную ей по знаку функцию v = —и. Тогда
а =• —gra<i v- Сообразно с этим в теории электростатического поля
уравнение Пуассона имеет вид
д2и , д2и I 4лр 04)
дх2. ду* dz2 е
Рассмотрим элементарный пример на применение уравнения
Пуассона.
Пример 5. Пусть две бесконечные разноименно заряженные
параллельные пластины А А} и ВВг имеют потенциалы vr и г2,
причем, для определенности, > v2. Найти поле Е между ними
(рис. 37).
Решение. Направим ось Ох перпендикулярно к пластинам
в направлении убывания потенциала, а плоскость yOz совместим с
Рис. 37.
положительно заряженной пластиной ААГ Будем искать потен-
циальную функцию из уравнения Пуассона. В силу симметрии за-
дачи относительно оси Ох и бесконечности пластин, можно заклю-
чить, что эквипотенциальными поверхностями будут плоскости,
§ 21] ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ ВТОРОГО ПОРЯДКА 119
(16)
параллельные пластинам, а функция и будет зависеть лишь от од-
ной переменной z. Уравнение (14) примет вид
^=о, (15)
dx2
поскольку объемные заряды во всем пространстве между пластина-
ми отсутствуют. Интегрируя (15), найдем
v = Cjz + С2
(Съ С2 — произвольные постоянные).
Потребуем, чтобы при х = 0 функция и принимала значение vlt
а при х == d, где d — расстояние между пластинами, она принимала
значение v2. Это дает С2 = vu v2 = Cxd + С2, откуда С2 = vlf
Подставляя эти значения Cl9 С2 в (16), получим
d
Ро ----------- Р, । , Pi — v9
v » -2--L х =® р, — -1——1 х.
d
d
Вектор E определится по формуле Е == —grad р, что дает
Е = ElZZJk L
d
так что поле будет однородным и направлено по оси Ох. Величина Е
в любой точке равна | Е | = Я-ZL^l, т. е. равна падению потенци-
ей
ала на единицу длины кратчайшего пути между пластинами.
244. Пусть скалярная функция <р(М) удовлетворяет
уравнению Лапласа. Показать, что вектор — соле-
нои дальний и безвихревой.
245. Показать, что Д(#и) — «Др + гДи + 2(уи} уи).
246. Доказать, что если г — радиус-вектор, то
2
— в пространстве,
— на плоскости.
г
247. Проверить, являются ли следующие скалярные
поля гармоническими:
а) и = х2 + 2ху — у2,
б) и = х2у + y2z + z2xt
в) и = х2 — у2.
248. Показать, что скалярное поле
и = In где г = Ух2 + у2 (г Ф 0),
является гармоническим.^
j20 ДИФФЕРЕНЦИАЛЬНЫЙ ОПЕРАЦИИ ВТОРОГО ПОРЯДКА (ГЛ. V
249. Найти все гармонические поля, зависящие толь-
ко от х.
250. Найти общий вид однородного гармонического
многочлена второй степени от х и у.
251. Найти все решения уравнения Пуассона Ди=яп~2,
зависящие только от ж.
Пример 6. Формулы Грина. Пусть ф, ф — две ска-
лярные функции точки. Составим вектор а » ф grad ф. Тогда
div а « div (ф grad ф) = ф div grad ф + (grad ф, grad ф) «
«= ф • Аф + (grad ф, grad ф).
(17)
Применим теперь формулу Гаусса — Остроградского
(а, я0) do » J J J div a dv,
Заметим, что в нашем случае
(а, я0) «а (ф grad ф, яа) = ф (grad ф, я0) = ф
on
В результате получаем первую формулу Грина
J J [фАф + (grad ф, grad ф)] dv =» ф -~L do,
которая при ф = ф превращается в формулу
JJ J [q-A<P+|gi,ad<p|s]rfp = ^q>-|2-da.
Если в формуле (17) положить ф = 1, то получим
V
Поменяем в формуле (17) местами ф и ф и вычтем получившуюся в
результате формулу
J j* J [фАф + (grad ф, grad ф)] dv = ф -|!L do
(18)
из формулы (17). Мы получим тогда вторую формулу Грина
J j У (ф • —1|> • Дф)
J v J s
Здесь предполагается, что все функции, с которыми приходится
иметь дело, так же как и их производные, встречающиеся в форму-
лах, непрерывны в рассматриваемой области.
121J ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ ВТОРОГО ПОРЯДКА 121
Пример 7. Найти поверхностный интеграл
I = й) ф дф da,
f дп
взятый по сфере S: х9 Ц- у2 + z2 « 1 для ф ==» х9 + У2 и ф=® у9 4~z2.
Решение. В силу первой формулы Грина искомый интеграл
равен
I =» J J J [фДф + (grad ф, grad ф)] du,
где область интегрирования V — шар: х9 + у* + z9 < 1.
Имеем Дф = 4, grad ф = 2xi + 2yjt grad ф «=» 2yj + 2zk\
(grad ф, grad ф),= 4y2, поэтому
/ = J f j(4x»4-4^+4yS) dp-4 +
v J у J
Переходя к сферическим координатам х— г cos ф sin 0,
!/=r sin ф sin 0, z = г cos 0, получим
I а» 4 J j* J (г2 cos2 ф sin2 0 + 2r? sin2 ф sin2 0) г2 sin 0 dr dQ с?ф ==
J v v
2л л 1
«=4^ (cos? ф + 2 sin2 ф) </ф j*sin3 0d0j* r*dr ='
О bo
2л л
' ^Ф J (1 — cos? 0) sin 0 d0=s
О
12 / 1 16
-g- Л ( — CQS 0 + -у СОЗ3 0 I == “У л.
О
Пример 8. Найти поверхностный» интеграл
взятый по поверхности S: х2 + у9 =« Я2, z «• 0, z = Я, Я > О,
если ф = ж2 + у2 + х + z, ф =х2 + у2 + 2z + х.
Решение. Искомый интеграл по второй формуле Грина равен
I =» J J J (фДф — фДф) dv.
Для данных функций ф и ф имеем Дф = 4, Дф = 4 и, значит,
122 ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ ВТОРОГО ПОРЯДКА (ГЛ. V
<1
Переходя к цилиндрическим координатам х = р cos ф, у =* р sin ф,
z=i, получим
2л R Н
I «я — 4 J J f zp dp dtp dz=—4 J dcp j* p dp j* z dz = — 2лЯ2№.
J v о b b
Пример 9. Найти поверхностный интеграл I = эд ф de
по замкнутой поверхности S, ограниченной плоскостями: я4~У+
4-х =1, х = 0, у = 0, z = 0, если ф = е* sin у + 1.
Решение. Данная функция является гармонической, так
как Дф = ех sin у — ех sin у = 0 Поэтому по формуле (18) будем
иметь
I = J f J | grad ф |2 dv.
J v J
Находим модуль градиента функции ф:
grad ф = ех sin yd + ех cos y-j, [grad ф| = ex.
Искомый интеграл равен
Z = f j* J e2xdp = j* e2xds j* dy dz~ — (e* — §). if
J V bob 8 I
«252. Вычислить поверхностный интеграл I — Ф de I
s j
по замкнутой поверхности 2: {x2 4- у2 + z2—1, y=0t *
У 0}, если <p = z2, г|) = x2 + i/2 —- z2.
253. Вычислить поверхностный интеграл «
— взятыя по всея поверхности замкнутого Я
цилиндра 2: {х2 4- у2 = z = 0t z == 1}, если <р (
s= 2х2, яр = х2 4- z2.
254. Вычислить поверхностный интеграл I = <р |“dorf
если ср= х — -z, а 2 есть сфера: х24- у2 +z2 = R2. ;
уз -1
$ 221
ВЕКТОРНЫЙ ПОТЕНЦИАЛ
123
255. Найти поверхностный интеграл
если ф =® ех sin у + еу sin х + а 2 — трехосный эл-
zp2 1/^ z%
ЛИНСОИД -Р4-Х- + — = 1.
§ 22. Векторный потенциал
Пусть векторное поле
а = а(М) = Р(х, yt z)i + Q(x, у, z)j + R(x, у, z)k
является соленоида л ьпым в области G, т. е. div а(М) = О в G.
Определение. Векторным потенциалом векторного поля
а = а(М) называется вектор Ь(М) = Р^х, у9 z)i + Q^x, y,z)j-f-
+ У, z)k, удовлетворяющий в области G условию
rot Ъ(М) = а(М) (1)
или в координатной форме
2^1-221 = Р, ~ Q, - д. (2)
ду dz * dz дх * - дх ду *
Для соленоидального векторного поля а(М) векторный потен-
циал Ь(М) определяется неоднозначно; условию (1) удовлетворя-
ет также вектор В(М) — Ь(М) + grad f(M), где f(M) — произ-
вольная дифференцируемая скалярная функция, так как
rot (grad / (М)) = 0.
Таким образом, два векторных потенциала соленоидального
поля а(М) отличаются друг от друга на градиент скалярного поля.
Нахождение векторного потенциала Ь(М) соленоидального поля
с(М) сводится к нахождению какого-фтбо частного р'ешения систе-
мы (2) трех дифференциальных уравнений в частных производных
относительно трех неизвестных функций Pi(x, у, z), Q^x, yt z),
#i(z, у, z).
Векторный потенциал b(M) можно построить следующим
образом. Пользуясь произволом в выборе вектора Ь(М), для упро-
щения положим, например, Pv(xt у, z) = 0, т. е. вектор Ь(М) бумы
искать в виде Ь(М) = Qi(xt у, z)j + yt z)k. В этом случае
система дифференциальных уравнений (2) для нахождения неиз-
вестных функций Qt(xt у, z) и R^x, yt z) примет вид
dRj__= р
ду dz
^21 = R.
дх
124 ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ ВТОРОГО ПОРЯДКА [ГЛ. V
Из второго и третьего уравнений этой системы находим
-Ri (*, у, ж) “ — J Q (х, у, ж) dx + Ci (у, ж),
Qi (»» У> «) — J R (х, у, z) dx 4- Ct (у, ж),
где С^у, z) и C2(y,z) — любые дифференцируемые функции у и z.
Положим для упрощения С2(у, г) = 0 и выберем функцию Сг(у^)
так, чтобы удовлетворялось и первое уравнение системы (3). Для
этого подставляем в первое уравнение найденные выражения для Qi
и
д С dCi д С
“~~ду \ + R^x> У’ г) dx Р (х, у, г).
(Ухскщь найдем
дсх д г t ар
~0у ~~ду W (*> V» ») + &М R (х> V> z)dx + P (х, у, ж).
Легко проверить, что правая часть этого уравнения не зависит
от х в силу того, что div а(М) «= 0 в G.
Интегрируя последнее равенство по у, найдем
Cl (у. 2) =•
“ J J Q (х> V> 2) dx + У R(x, у, ж) dx + Р (ж, у, ж)j <7y+Cs (z).
(4)
Полагая в (4) C3(z) ~ 0' и подставляя (4) в выражение для
Ях(х, у, z), получим частное решение системы (3):
Рх = 0, (5)
Q1 = У R (х, у, г) dx, (fi)
Ri = У У <2 (х, у, z) dx + У R (х, у, г) dx +
+ Р (х, у, z)J dy — J Q (x, у, ж) dx. (7)
Вектор Ь(М), координаты Pt (x,y, z), Q^x, y, z) и Яг(х, у, z) ко-
торого определяются формулами (5), (6), (7), является векторным
потенциалом, так как он удовлетворяет условию rot Ь » а.
Пример!. Найти векторный потенциал Ь = b(xt yt z) для со-
леноидального поля, задаваемого вектором
а « 2yi — zj+ 2хк.
Решение. Потенциал Ь ищем в виде
Ь = b(xt у, z) « Q^x, у, z)j + Я^х, у, z)kt
где <?i(x, у, z) и Rt(xt yt z) находим по формулам (7) и (8). Так как в
§ 22]
ВЕКТОРНЫЙ ПОТЕНЦИАЛ
125
данном случае Р « 2у, Q *= —z, R 2х, то будем иметь
Qi (*> У» z) e J 2xdx=* я1,
У, 2) =у z'_dz + j*2y dy = xz + {/2.
Итак,
Ъ(х, у, z) = x2j + (xz + y-)k.
Непосредственной проверкой убеждаемся, что rot ft =.а, и, значит,
этот вектор является векторным потенциалом данного поля.
Замечание. В виду произвола, допустимого при выборе
вектора ft, вместо условия Р^х, у, z) = О можно потребовать,
чтобы Qi(x,y,z) = 0 или Рг(х,у,г) = 0. Система уравнений (2) и
формулы (5), (6), (7) соответственно изменятся.
Найти векторные потенциалы соленоидальных полей:
256. а = i + ] + к.
257. а = 2yi + 2zj.
258. а « (ех — е*)к.
259. а « буЧ + 6zj 4- бхк.
260. а = ЗуЧ — Зя2/ — (У* + 2х)к,
26L а = уехЧ + 2yzj — (2xyzex* + z2) к. i
i
Если векторное поле а =а(М) соленоидально в области G, ко-
торая является звездной (см. § 19, гл. IV) с центром в начале коор-
динат 0(0, 0, 0) (поле а(М) может быть не определено в точке 0),
то один из векторных потенциалов ft = Ь(М) можно найти по фор-
муле
1
ft (М) =» С[а (АГ), г (Л/)] t dt, (8)
где r(M) == xi + yj + zk есть радиус-вектор точки М(х, у, z), а точ-
ка ty, tz) при изменении параметра t от 0 до 1 пробегает от-
резок ОМ,
П р и м е р 2. Пользуясь формулой (8), найти векторный потен-
циал соленоидального поля а « 2yi — zj + 2хк.
Решение. Данное векторное поле определено во всем трех-
мерном пространстве, которое является звездной областью о цент-
ром в начале координат, поэтому для нахождения векторного по-
тенциала можно применить формулу (8). В точке M*(tx, ty, tz) имеем
а(М') = 2tyi — tzj + 2txk,
Находим векторное произведение
i 4 i
2ty — tz
x у
[a(Af')» г (А/)] =
к
2tx
z
= I- (2xy + x«) i + (2x« - 2yz) j + (2y« + xz) fcj t.
126 ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ ВТОРОГО ПОРЯДКА [ГЛ. V
По формуле (8) находим
1
Ъ (Л/) = У [- (2*У + z2) i + (2х« - 2yz) j + (2у2 -|- xz) Л] t*dt =
О
=- 4 (2хУ+г») i+4- +y^i -I- 4 м*+к‘
о О о
Легко установить, что rot Ъ(М) == а(М).
Замечание. В примерах 1 и 2 для одного и того же соле-
ноидального поля а == 2yi — zj + 2хк получены разные векторные
потенциалы:
Ьг (М) = x2j+(xz+y2)k9
bt (М) - - 4- (2жУ + г2)» + 4- <»• - Уг) i + 4- (2У2 + ®г)-
и о О
Они отличаются друг от друга слагаемым, равным градиенту
некоторого скалярного поля f(M). Это слагаемое играет роль про-
извольной постоянной (при действии на нее ротора). Оно предста-
вимо как градиент некоторой скалярной функции f(M). Найдем эту
функцию в нашем случае. Имеем
grad / (Л/) = (Л/) - Ъ2 (Л/) =
= 4 (2®У + г2) i + 4 + 2Уг> / + "Г (2жг + *•
Для нахождения скалярного поля f(M) применим формулу
(3) из § 19, в которой за точку (я0, j/0, z0) возьмем начало координат
О (0, 0, 0). Тогда получим
х у *
4*4/+ f4(^+y’)^+c=
О J О
0 0 о
=4^2у+y2z +с'
где С — произвольная постоянная. Так как grad С = 0, то можно
положить С = 0 и, значит, / (Л7) =-4- (х2у + y2z + z2x).
о
Пример °. Найти векторный потенциал Ь магнитного поля
Я, создаваемого электрическим зарядом е, движущимся с постоян-
ной скоростью г.
Решение. Согласно закону Био—Сава ра напряженность ма-
гнитного поля равна
Я (Л/) = [£41, (9)
4лг8
где г — расстояние точки М до заряда е.
/(Л/)
§ 22]
ВЕКТОРНЫЙ ПОТЕНЦИАЛ
127
Так как Н является соленоидальным вектором, т. е. div Я=0,
то для него существует векторный потенциал Ь такой, что #=rot Й
пли, учитывая формулу (9),
-nt h lev’ Н - е [°’ и.
4лг3 4л г3
Перепишем последнюю формулу в виде
Применяя легко проверяемое равенство
[, с) а "1 Г с'л 1 с) a 1
l> "to ] + р ”аГ] + |*’
получим
rot Ь — Л- rot —,
4л г;
откуда
&=*•—•
4л г
Пользуясь формулой (8), найти векторные потенци-
алы соленоидальных полей, определенных в звездных
областях:
262. а = г. *
263. а = 6xi — 15у/ + Qzk.
264. а == 5x2yi — lOxyzk.
265. a = 2cosxz-J.
266. а = х2 + у2 > 0.
х3 + yi
ГЛАВА VI
КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ*
ОСНОВНЫЕ ОПЕРАЦИИ
ВЕКТОРНОГО АНАЛИЗА
В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
$ 23. Криволинейные координаты
Во многих задачах удобнее определять положение точки М
пространства не тремя декартовыми координатами (ж, у, г), а тремя
другими числами (glt д2> <7з)> более отвечающими рассматриваемой
частной задаче.
Пусть каждой точке М отвечает определенная тройка чисел
(gi, g2, д3) и, обратно, каждой такой тройке чисел отвечает единствен-
ная точка М. В этом случае величины g2, g3 называют криволи-
нейными координатами точки М.
Координатными поверхностями в системе криволинейных ко-
ординат q^ qif qs называются поверхности
<zi - Ct; (U
5, = С2, (2)
<?3 = ^з> (3)
на которых
одна пз координат сохраняет постоянное значение.
Линии пересечения двух ко-
ординатных поверхностей называ-
ются координатными линиями.
Вдоль линии пересечения ко-
ординатных поверхностей (2) и (3)
координаты д2 и Яз сохраняют
постоянные значения; изменяется
только координата qt. Аналогич-
но на линиях пересечения повер-
хностей (1) и (3) или (1) и (2)
меняются соответственно только
ffa и Яз-
В едем единичные векторы
еъ е2, ез> направленные по ка-
сательным к координатным лини-
ям (<7i)> (Qa)> (Яз) в точке М в сто-
рону возрастания переменных qt,
q2, Яз соответственно (рис. 38). Условимся брать орты е2, е3 всег-
да в таком порядке, чтобы их совокупность составляла правую
тройку.
Подчеркнем коренное отличие криволинейных координат от
обычных декартовых координат. В декартовой системе векторы
§23]
КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
129
eh е2, ез постоянны для всех точек пространства и равны соответ-
ственно i, j, к. Во всякой другой системе они будут, вообще говоря,
изменять свои направления при переходе от одной точки М к другой.
В качестве примеров криволинейных координат рассмотрим
цилиндрические и сферические координаты.
1°. Цилиндрические координаты. В цилиндри-
ческих координатах положение точки М пространства определяется
тремя координатами^
Я1 = Р, 0 р < + со,
§2~ <р, 0 < <р < 2л, (4)
д3 = z, —со < z < + оо.
Координатными поверхностями
являются:
р = const — круговые цилин-
дры с осью Oz;
ф » const — полуплоскости,
примыкающие к оси Oz;
z = const — плоскости, пер-
пендикулярные оси Oz.
Координатными линиями явля-
ются: линии (р) —лучи, перпенди-
кулярные оси Oz и имеющие
начало на этой оси; линии (ф)
— окружности с центром иа оси
Oz, лежащие в плоскостях, пер-
пендикулярных этой оси; линии
(z)— прямые, параллельные оси
Oz (рис. 39).
Связь декартовых координат с цилиндрическими определяет-
ся формулами
® = р cos ф,
у р sin ф, (5)
Z = Z. *
2°. Сферические координаты. В сферических
координатах положение точки М пространства опр деляет я сле-
дующими координатами:
91 = г, 0 < г < + со,
& = 0, 0 < 0 < Л, (6)
д3 = ф, 0 < ф < 2п.
Координатными поверхностями являются:
г = const — сферы с центром в точке О;
0 ® const — круговые полуконусы с осью Oz;
ф = const — полуплоскости, примыкающие к оси Oz.
Координатными линиями являются:
линии (г) — лучи, выходящие из точки О;
линии (0) — меридианы на сфере;
линии (ф) — параллели на сфере (рис. 40).
9 м. Л, Краснов и др.
130
КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
[ГЛ. VI
Связь декартовых координат со сферическими определяется
формулами:
в 33 г cos <р sin 0,
у = г sin ф sin 0,
X = г cos 0.
(7)
Система криволинейных координат называется ортогональной^
если в каждой точке М орты е1У е2, е3 попарно ортогональны. Коор-
динатные линии и координатные поверхности в такой системе будут
Рис. 40.
также ортогональны. Системы цилиндрических и сферических ко-
ординат служат примером ортогональных криволинейных систем
координат. В дальнейшем будут рассматриваться только ортого-
нальные системы координат.
Пусть г =* r(qlt q3i q3) — радиус-вектор точки М. Тогда
dr = H^dq^ + H3dq2e3 + H3dq3e3. (8)
Здесь
П. = 1 /+ i = 1. 2, 3,
* |/ \9Ь/ \d4i)
— коэффициенты Ламэ данной криволинейной системы координат.
6 цилиндрических координатах
J 24]
ОСНОВНЫЕ ОПЕРАЦИИ ВЕКТОРНОГО АНАЛИЗА
131
в силу (5) имеем
В сферических координатах
Qi = П = G, 7з = ф
в силу (7) имеем
Величины'
, dlt = H.dq^ t « 1, 2, 3,
фигурирующие в формуле (8), являются дифференциалами длин
дуг координатных линий. Это соображение в ряде случаев позволя-
ет более просто вычислять коэффициенты Ламэ. Так, в случае ци-
линдрических координат (4) (см. рис.*38) дифференциалы длин дуг
координатных линий (р), (<p), (z) буд*ут
d(p) = 1 - dp, откуда *= 1;
й(ф) == р.Жр, откуда Н2 « р;
d(z) =« 1-dz, откуда Н3 ® 1.
Так же просто получаются выражения для коэффициентов Ламэ
в случае сферических координат (6).
§ 24. Основные операции векторного анализа
в криволинейных координатах
1°. Дифференциальные уравнения век-
торных линий. Пусть имеем поле вектора
® " «х(9х. 91> 91)«х + «g(9x, 91. 9а)«1 + в»(9Х. 9s, 91)в|.
в»
132
КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
(ГЛ. Vt
Уравнения векторных линий в криволинейных координатах
glf ?2, q3 имеют вид
#2^02 _ H3dq3
ai (01» 0з» 0з) аа (01» 0а» 0з) а9 (01* 0а» 0а)*
В частности, в цилиндрических координатах (дх = р, д2 = <р,
0з = г):
dp = Р^Ф dz
«1 (Р, Ф, г) а2 (р, ф, z) а3 (р, ф, zy W
в сферических координатах (qt =» г, q2 = 0, q3 = ф):
dr rd& г sin 0 dq>
fli (г, 6, Ф) = «2 (r, 0, Ф) = a3 (r, 0, ф) •
Пример 1. Векторное поле задано в цилиндрических
координатах
a(Af) = ер + феф.
Найти векторные линии этого поля.
Решение. По условию задачи =1, аа = ф, а3 = 0.
В силу формулы (1) имеем
dp р dq> dz
“= ф
Отсюда
« == Of, "I
р = С2ф; J
это — спирали Архимеда, лежащие в плоскостях, параллельных
плоскости хОу,
2°. Градиент в ортогональных коорди-
натах. Пусть имеем скалярное поле
w = а(0ь 02> 0з)*
Тогда
1 ди 1 ди 1 ди
gradu= Bi дд1«1 + -Щ Н3 ~д^е*‘
В частности, в цилиндрических координатах (дх = р, д2 = ф,
Чз == г):
ди t 1 ди ди
ггааи=-^ер + --^-еф + -^-ег; (2)
в сферических координатах = г, q2 = 0, q3 = ф):
ди 1 ди 1 ди
gradu=-^er + 7Wee + 755¥-^v (3)
Основйьга ОПЕРАЦИИ ёёкТоРноГо АЙАЛЙЗА
ш
Пример 2. Вычислить градиент скалярного поля, задан-
ного в цилиндрических координатах (р, ф, z): и = р + z cos <р.
Решение. Пользуясь формулой (2), получаем
1
grad u « 1 • ер — — z sin <р • еф + cos ф • ez.
Пример 3. Найти градиент скалярного поля, заданного
в сферических координатах (г, 0, ф)
, sin 0 , л
и =х г + —— — sin 0 cos ф.
Решение. Пользуясь формулой (3), будем иметь
grad м —
sin 0\ , cos 0/1 \ , sin ф
1 - —) ег + ~Г~ (7 - cos *) ее + ~ *9-
3°. Ротор в ортогональных координатах.
Пусть
• “ Л. 9»)«i + ?2,?з)е» + в»(?1, 4i, 9э)е«-
Тогда
rota =
1__
д
«Л
В частности, в цилиндрических координатах (qx = р, да — ф,
9» - *):
rota =
1 1
р еФ р
д d d
dp дф * dz
ai Раа as
в сферических координатах (дх = г, q2 — 0, q2 = <pj:
1
r?sin0 er
d
dr
ai
rot a =
i 2.
rsinO г вФ
d d
d0 dф
ra2 r sin 0 • a*
Пример
в цилиндрических координатах
4. Вычислить ротор векторного поля, заданного
. cos ф
а = 8Шф. ер-|—
<34
КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
(ГЛ. vt
Решение. Воспользовавшись формулой (4), будем иметь
rot а =
£
р еР е<₽ р е*
д д д
др dtp dz
sin ф cos ф — pz
= 1»р(0-0)-«ф |-г-0) +
1 COS Ф
+ -р е, (0 - cos ф) = геф------— ее
4°. Дивергенция в ортогональных коор-
динатах. Пусть задано векторное поле
а “ aitai, да» gs)*i + «а(дх» да, дз)ег +°з(дп да» дз)*з-
Тогда
1 г^вд а^Яз) ,
<nve- вд1 + dqt + ддз j.
В частности, в цилиндрических координатах (gx = р, q* * ф,
9» - *):
1 д (pa,) 1 6д2 да3
div а = р + р ар + :
В сферических координатах (qY » г, д2 — 0, q3 « ф):
„ 1 д , 1 д (sin 6 • а2) , 1 да3
а и г* dr ' г sin 0 60 'г sin 0 бф ’
Пример 5. Показать, что поле вектора
i cos 6 sin 0
в ~ ~ er + r3
соленоидально.
Решение. Пользуясь формулой (5), будем иметь
_ 1 Э / 2cos0
dlve = -?-07 г‘“75-
1 й sin 0 \ л
TsinT 60 (аи0~?-) + ?
1/ 2cos0\ 1 _
75- (- —тг I + угиЕе 1 2 sin 0 cos 0 = °
всюду, где г ф 0. Это и означает, что поле вектора а соленоидально
всюду, кроме точки г = 0.
267. Наити уравнение векторных линий поля, задан-
ного в сферических координатах
2a’cos0 . asin0
a =* -75— ет.+ -j- е0, ' a = const.
$ 24] ОСНОВНЫЕ ОПЕРАЦИИ ВЕКТОРНОГО АНАЛИЗА 135
Найти градиенты скалярных полей:
а) В цилиндрических координатах
268. и = р2 + 2р cos <р — е* sin ф.
269. и = р cos ф + z sin2 ф — Зр.
б) В сферических координатах
270. и = г2 cos 0.
271. и = Зг2 sin 0 + er cos ф — г.
cos 0 .
272. u = у-, р = const.
Вычислить дивергенцию векторов:
а) В цилиндрических координатах
273. а = рер + z sin феф + еч cos zez.
274. а = ф arctg рер -j- 2еф — z2ezez.
б) В сферических координатах
275. а = г2ег — 2 соз2фве + еф.
Вычислить ротор следующих векторных полей:
276. а = (2r4~acosф)ег—аsincost)еф1а=const.
277 а = г2ег+ 2 cos 0ее — феф.
278. а = cos ф efi — еф + р2 ez.
279. Показать, что векторное поле
является потенциальным.
280. Показать, что векторное»поле
« = f(r)e„
где / — любая дифференцируемая функция, является по-
тенциалтным.
5°. Вычисление потока в криволинейны»
координатах. Пусть S — часть координатной поверхности
= С, где С == const, ограниченная координатными линиями
Qi e ai> Qi *** аа (а1 < аа)»
Яз ~ ₽ь Яз Pa (Pi < Pa)*
Тогда поток вектора
d Q^)e{ + q* q9)e9
КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ [ГЛ. VI
через поверхность S в направлении вектора вычисляется по фор-
муле
П — J j ej (С, дз) Нъ (С> да» дз) #з (£, q3i q3) dqzdqv (6)
Аналогично вычисляется поток через часть поверхности д2 == С
или через часть поверхности q3 = С, где С == const.
Прим р 6. Найти поток векторного поля, заданного в
сферических координатах:
• л в + ге^с^
через внешнюю сторону верхней полусферы S радиуса R с цент-
ром в начале координат.
Решение. Полусфера S является часть координатной по-
верхности г = const, именно г ® R, На поверхности $ имеем
л
дх « г = Я; да « 0, 0 < 0 <
д3 — Ф, 0 < ф < 2л.
Учитывая, что в сферических координатах
= Нт = 1, Яа = Яо = г,
Я8 = Яф = г sin 0,
по формуле (6) найдем
л/2 2я л/2 .
П = j dO | R*Q sin Gt/ф = 2лЯ4 j* 0 sin 0 d0 = 2 л Z?4.
об b -
Пример 7. Вычислить поток векторного поля, заданного
в цилиндрических координатах:
« = Р«р + геф
через замкнутую поверхность, образованную плоскостями z =« О
и z = 1 и цилиндром р = 1. Поток вычислить непосредственно и
с помощью теоремы Гаусса—Остроградского.
Решение. 1) Непосредственное вычисление. Рассмотрим
систему прямоугольных координат р, ф, я. Цилиндру в этой
системе будет отвечать прямоугольный параллелепипед, ограни-
ченный плоскостями р = 0, р = 1, ф « 0, ф = 2л, z = 0, z = 1.
Тогда в координатах р, ф, z поток надо вычислить через полную
поверхность этого параллелепипеда. Для этого вычисляем поток
через каждую из граней и берем сумму потоков. На координатных
поверхностях р = С = const имеем
2я 1
П = § C*dz скр^лС*,
откуда для поверхности р — 0 получаем П; = 0; при р « I имеем
И8 == 2л.
1
<241
ОСНОВНЫЕ ОПЕРАЦИЙ ВЕКТОРНОГО АНАЛИЗА
137
На координатных поверхностях <р =» const имеем в случае
ф « О
1 1
П3 = — J J z dz dp = — -|*
О О
(знак минус определяется выбором нормали); в случае <р » 2л
1 1
п« = + — Ач
о о
На координатных поверхностях в = const в случаях « = 0 и
z = 1 имеем П5 = П8 = 0, так как в нашем случае в3(р, Ф’ z)
тождественно равно нулю.
Искомый поток *
П=2ПП = 2«.
п=1
2) Вычисление по теореме Гаусса—Остроградского
n = J fpivadp.
По формуле для дивергенции вектора а в цилиндрических коорди-
натах
1 д 1 да% да3
dive = 7 ^(Ра1) + 7-ёф +~дГ
в нашем случае получим
Id i dz
diva = ?-^(P»)+?^=2.
Поэтому искомый поток
П = J J §2dv = 2a.
Вычислить поток векторного поля, заданного в ци-
линдрических координатах, че^ез данную поверхность S
непосредственно и с помощью теоремы Гаусса—Остро-
градского.
281 а = рер — cos <реф 4- zet,
S — замкнутая поверхность, образованная цилиндром
р = 2 и плоскостями z = 0 и » = 2.
282. a = рер + рфвф — 2zez,
S — замкнутая поверхность, образованная цилиндром
р = 1, полуплоскостями ф = О И ф = л/2 и плоскостями
z = —1, г = 1.
283. Найти поток векторного поля, заданного в сфе-
рических координатах:
a =
188
КРИПбЛЙНЁЙНЁТЁ ЙбОРДЙЙАТЫ
(ГЛ. vt
через замкнутую поверхность, окружающую начало коор-
динат.
284. Найти поток вектора, заданного в сферических
координатах:
а = гег + т sin 0 ее — Злр sin 0 еф
через замкнутую поверхность S, ограниченную верхней
полусферой радиуса R и плоскостью © = у-
285. Найти поток вектора, заданного в сферических
координатах:
а = r2er + R2 cos <реф
через сферу г «= R.
286. Найти поток вектора, заданного в сферических
координатах:
а = гег
через замкнутую поверхность S, ограниченную верхней
полусферой радиуса R и плоскостью 0 — 2, непосредствен-
но и с помощью теоремы Гаусса — Остроградского.
287. Найти поток вектора, заданного в сферических
координатах:
а = r2er + R2 rsin0 cos <реф
через замкнутую поверхность, ограниченную координат-
ными поверхностями г = Я, <р == 0, <р = у, 0 = у,
непосредственно и с помощью теоремы Гаусса—Остро-
градского.
6°. Нахождение потенциала в криволи-
нейных координатах. Пусть в криволинейных коорди-
натах qlt q2t q3 задано векторное поле
а(М) — at(qlt q3t q3)et + a2(qlt qit q3)e3 + a3(qlt q3, q3)e3,
которое является потенциальным в некоторой области Q изменения
переменных ql9 q2, q3t т. е. rot а = 0 в Q.
Для нахождения потенциала и = u(qly q2, q3) этого поля равен-
ство а(М) grad и (М) записывается в виде
1 ди 1 ди 1 ди
“Л + М» + “А = ei + е2 + «8 •
j 24] ОСНОВНЫЕ ОПЕРАЦИИ ВЕКТОРНОГО АНАЛИЗА 139
Отсюда следует, что
ди _ ди ди
Это есть система дифференциальных уравнений с частными произ-
водными, интегрируя которую найдем искомый потенциал и »
e w(^i> ^2» Яз) + где С произвольная постоянная.
Система дифференциальных уравнений (7) решается так же,
как при нахождении потенциала в декартовых координатах.
Система дифференциальных уравнений (7) имеет вид:
1) в цилиндрических координатах (gx = р, да « ф, q9 » х)
ди ди ди
др ~~ ар9 дф в Ра9* дз в %* ( '
2) в сферических координатах (qt == г, ga = 0, Чз =* ф)
ди ди ди . л
a7 = V 30-ree> ^> = rs,n0 V
Пример 8. Найти потенциал векторного поля, заданного
в цилиндрических координатах:
/arctg 1 \ . In р
« = I—+ cos <р I ер — sin фвф + ppp е.
Решение. По формуле (4) находим
1 1
— « — е
Р * ф Р «
д д д
rot а = др дф dz = 0
arctg ъ , . In р
—рГ~ + С08Ф *~Р8Шф jqyjs
(Р> 0),
т. е. данное поле потенциально. Искомый потенциал и=» u(p, <р, z)
является решением следующей системы дифференциальных урав-
нений:
ди arctg z
др р +
cos ф,
ди
^ = -81Пф.Р<
ди In р
dz 1 4- за*
Из первого уравнения интегрированием по р находим, что
и — In р -arctg х + р cos ф + С(ф, х). (8)
140
КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
П‘Л. VI
Дифференцируя (8) по ф, получим
ди , дС
рапф + ^
ди дС
и так как — р sin ф, то = 0, т. е. С » Cx(z). Таким об-
разом,
и == In р. arctg z + р cos ф + Сх(г).
Отсюда
. с н
dz +
В силу третьего уравнения системы имеем
1пр 1пр ,
l + z2=al+s«+Cl(2)*
т. е. С\ (г) = 0, откуда C1(z) ~ С ~ const.
Итак, потенциал данного поля
и(р, ф, z) » In р • arctg z + р cos ф 4- С.
В следующих задачах убедиться в томт что векторные
поля, заданные в цилиндрических координатах^ являются
потенциальными, и найти их потенциалы.
288. а = 4*
289. а ® рер + ~ еФ +
290. а ® ф2вр + геф + p<pez.
291. а ® ер81Пфвр +~ epcos<pe<p + 2zez.
292. а = ф cos zeQ + cos z еф — рф sin z et.
Пример 9. Найти потенциал векторного поля, заданного
в сферических координатах:
1 G In г а™ . In г
а я—е Ч + г*ете Ч+“ ч-
Решение. По формуле (4') получаем, что
1 rota~r*sin0 ег ге6 д д дг с/0 rsin0«ev д д(р «0.
-у-«вф ^Inr-e6” 0 In r-ee<f
I 24]
ОСНОВНЫЕ ОПЕРАЦИИ ВЕКТОРНОГО АНАЛИЗА
141
(9)
Данное поде потенциально в области, где г > 0, 0 =/= ля (л = 0,
±1, . . .).
Система дифференциальных уравнений (7) для нахождения по-
тенциала и — w(r, 0, ф) имеет вид
-т- = — е0ф.
дг г 9
==. фе0ф In г,
^ = 0.веч>1п г.
Оф
Интегрируя первое уравнение системы (9), получим
и = «0Ф In г + С(ф, 0)
(Ю)
Дифференцируя (10) по 0 и учитывая второе уравнение системы,
будем иметь
фе0ф In г = фе0ф In г +
дС
т. е. -gg- = 0, откуда С(<р, 0) ее ^(ф), и значит,
?ф1пг+ Сх(ф). (И)
Дифференцируя (И) по ф и принимая во внимание третье уравне-
ние системы (9), найдем
Ое0ф In г = 0е0ф 1пг + С; (ф)
или С\ (ф) = 0, откуда б\(ф) = С = const. Искомый потенциал
равен
u(r, 0, ф) =» е0ф In г + С.
ч
Установить потенциальность следующих векторных
полей, заданных в сферических координатах, и найти их
потенциалы.
293. а = 0ег +
294. а = 2гег + еф +1 ев.
295. «ЦфЧ+^ + уво.
296. а = cos <р sin 0-er + cos ф cos О-ве — sin ф-еф.
297. а = г sin 0. вг+1 е, cos 0. ев+ еф.
142
КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
(ГЛ. VI
7°. Вычисление линейного интеграла и
циркуляции векторного поля в криволиней-
ных координатах. Пусть векторное поле
а(М) = g2, qa)ei + a2(g1( qt, qa)et + aa(qlt qt, qa)ea
определено и непрерывно в области Q изменения ортогональных
криволинейных координат qlt q2t q3.
Дифференциал dr радиуса-вектора г любой точки
Qi» Яз) е как известно, равен (см. § 23, (8))
dr ® H\d<hci + H2dq2e2 + H3dq3e3.
Поэтому линейный интеграл вектора а(М) по ориентированной
гладкой или кусочно гладкой кривой L С й будет равен
J (Л, dr) =К У + ^2^2^Q1 4“ ^З^З^З* (12)
В частности, для цилиндрических координат qr == р, q2 = ф,
g3 = z будем имзть
« = «р(Р, Ф, «)вр + вф (Р, ф. г)еф+ at (р, Ф, z)et,
dr = dpep + р йфеф + dzez>
поэтому
J (a, dr) = f apdp + афр d(p + azdz; (13)
LJ L
для сферических координат qt » г, q2 = 0, q3 ® ф будем иметь
a « ar(r, 0, ф)ег + aQ (r, 0, ф)е0 + аф(г, 0, ф)еф,
dr «= dr-er + r d0-e0 + r sin 0 ^Ф*еф,
и следовательно,
f (a, dr) ® j* a^dr + raQdQ + гдф sin 0 d(p. (14)
L L
Циркуляция Ц векторного поля a(M) в криволинейных коорди-
натах qlt q2, q3 вычисляется в общем случае по формуле (12), а в слу-
чае цилиндрических или сферических координат она вычисляется
по формуле (13) или (14) соответственно.
Пример 10. Вычислить линейный интеграл в векторном
поле, заданном в цилиндрических координатах
a = 4р sin ф-ер + ^Р-еф + (р + ф)-е2,
вдоль прямой
L
п
Ф="Г
ъ = 0
I л \ • / зь
от точки 010, -j-, 01 до точки А II, 0
$ 241 0СЙОВНЫЁ ОПЕРАЦИЙ ВЕКТОРНОГО АЙАЛЙЗА 143
Решение. В данном примере
в( = 4р sin ф, вф = zeP, at = р + ф.
По формуле (13) искомый линейный интеграл
f (a, dr/ = J 4р sin ф dp + рзЛф + (р + ф) dz«
L L
На прямой L имеем:
Ф » dф = 0; s = 0, dz = 0; 0 < р < 1.
Поэтому
L L О
Пример 11. Вычислить линейный ингеграл в векторном
поле, заданном в сферических координатах
er sin 0-er+ 302 sin ф-ев + гф0-еф>
а
вдоль линии
L:
я о<0<-5-,
Ф = ~2~, 2
в направлении
от точки Мо
Л я я
до точки Mt 11, -тр -у
(рис. 41).
Решение. Линия L есть дуга окружности с центром в нача-
ле координат и радиусом й = 1, расположенная в плоскости yOz.
Координаты данного вектора равны ш
ат « ersin 0, aQ = 302 sin ф, аф « гф0.
В силу формулы (14) линейный интеграл имеет вид
f (a, dr) == f er sin 0 dr + 30яг sin ф d0 + гаф0 sin 0 dy.
Учитывая, что на линии L выполняются условия:
г » 1, d? sa 0; ф = ~2“, dф = 0, 0 < 0 <
получим
(a, dr) =» 302^0 = I 302d0 =
<44
КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
(ГЛ. VI
Пример 12. Вычислить циркуляцию векторного поля, за-
данного в цилиндрических координатах
в = р sin <р.ер 4- ргеф р3^,
по кривой
у f P = sinq),
X: | * 0С<рСл,
непосредственно и по теореме Стокса.
Решение. Координаты данного вектора
«р = р Sin ф, аф = pz, аг = р3.
Контур L представляет собой замкнутую кривую, расположенную
в плоскости z = 0 (рис. 42).
1) Непосредственное вычисление циркуляции.
Подставляя координаты данного вектора в формулу (13), по-
лучим
Ц = (j) р sin <р dp + p2z б?ф + p3dz. *
На кривой L имеем:
х « 0, dz а* 0; р = sin ф, dp = cos ф dф, 0 < ф < я.
Поэтому искомая циркуляция будет равна
л
Ц = (£ р sin ф dp » j* sin2 ф cos ф dф-= 0.
1 О
§24] Л ОСЙОВЙЫЕ ОПЕРАЦИИ ВЕКТОРНОГО АНАЛИЗА 145
2) Вычисление циркуляции с помощью теоремы Стокса,
По теореме Стокса искомая циркуляция равна
(a, dr) = J J (rot
a, n°) dS,
Где S — поверхность, натянутая на контур L.
Находим ротор данного поля
ер Р-% ег -
1 rot а = — Р д д д с’р с?ф dz = — рер — Зргеф + (2z — cos <р) «а.
р sin ф p2z р3
В точках, где р = 0, значение rot а доопределяем по непрерывности,
полагая
rot а(0, ф, z) = (2z — cos ф)ех>
Таким образом, rot а определен во всем трехмерном пространстве.
Так как кривая L лежит в плоскости z = 0, то в качестве поверх-
ности S, натянутой на эту кривую, возьмем часть плоскости z = О,
ограниченной кривой L. Тогда за орт нормали л° к поверхности S
можно взять орт т.е. Находим скалярное произведение:
j (rot а, л°) = (—рер—Зр2еф + (2z —• cos ф>2, ej = 2z - cos ф,
так как в силу ортонормированности базиса ер,еф, е* имеем
. (ер’ “ (еф-“ °’ <««’ ер =
Искомая циркуляция равна
Ц = J J (2z — cos ф) dS*.
s
Учитывая, что z = 0 на S и элемент площади dS координатной по-
верхности z = 0 равен *
dS ~ р dp £ф,
окончательно получим
Ц аж — у у CQS Ф = — У У cos ФР dp dф =»
S
п В1пф п
8= —. J cos ф dф j* р dp =«= — j sin8 ф cos ф dф в О,
о о о
Пример 13. Вычислить циркуляцию вектора, заданного
в сферических координатах
а = гег + (Я + г) sin 0- еф,
Ю м. Л, Краснов и др.
148
КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
(ГЛ. vt
по окружности
( r=R,
L: I fl- —
I 0e 2
в направлении возрастания угла ф непосредственно и по теореме
Стокса.
Решение. В данном примере
•г в г> а» = °’ лф = (Л + г) sin 0‘
1) Непосредственное вычисление циркуляции.
По формуле (14) искомая циркуляция равна
Ц =» ф г dr + (R + т) sin 0 г sin 0 dqp= ф г dr + г (R + г) sin2 0 dy.
На данной окружности L, центр которой находится в начале коор-
динат, имеем:
г = Я, dr = 0; 0 = 0 ф < 2л,
и, следовательно,
2л
Ц = 2Я« dj d<f = 2R* j dq> = 4лЯ».
1 О
2) Вычисление циркуляции по теореме Стокса.
Искомая циркуляция по теореме Стокса равна
(a, dr) « J j* (rot а, п°) dS,
где 5 — поверхность, натянутая на окружность L.
Находим ротор данного вектора
1 ет д г-е0 д г sin 0«еф д
f ЗСЕ а . .
1 г® sin U дг 00 0ф
V 0 (Яг 4- г2) sin2 0
2 1
е= — (Я + г) cos “ (Я + 2r) sin 0»eQ
В качестве поверхности S, натянутой на окружность L, возь*
мем, например, верхнюю полусферу радиуса R: г “ R, 0< 0 <
0 < ф < 2л. Орт п° нормали к внешней стороне полусферы S на-
правлен по вектору ег, поэтому берем л° ж ег. Находим скалярное
\
$ 24] i ОСНОВНЫЕ ОПЕРАЦИИ ВЕКТОРНОГО АНАЛИЗА J47
произведение
/2(Л + г)
(rot а, л°) = I------cos 0- ет
sin 0*ев,
2(Д + г) л
---------COS0,
так как (ег, ег) = 1, (ег, ее) = 0.
Учитывая, что г == R на поверхности S. для искомого потока
получим выражение
cos 0 dS = 4
J J cos0 dS.
В сферических координатах элемент площади dS координатной по-
верхности г = Я, т. е. полусферы S, будет равен
dS = R2 sin 0 d0 dtp
и, следовательно,
л/2 2rt
П = 4 J J cos 0Я2 sin 0 dQ dtp = 4Я2 j* cos 0 sin 0 d0 J dtp = 4лЯ*.
S 0 0
В силу теоремы Стокса получаем Ц = 4лЯ2.
В качестве поверхности 5, натянутой на окружность L, можно
было взять нижнюю полусферу, орт нормали которой л° » —ег;
результат будет тот же: Ц = 4лЛа.
Заметим, что за поверхность 5, натянутую на окружность Л,
не следует брать круг, ограниченный этой окружностью, так как
в этом круге имеется точка г — 0 (центр круга), в которой ротор
данного вектора имеет разрыв. *
Вычислить линейный интеграл по данным линиям L
в векторных полях^ заданных в цилиндрических коор-
динатах.
298. а = zep + рф-еф + cos
L — отрезок прямой: {р = at <р = 0, O^z^l}.
299. а = рер + 2рфеф + zeIt
L — полуокружность: {р = z = 0, 0 ф л}.
300. а — е<> cos ф>ер + р sin ф«еф + pez,
L — виток винтовой линии: {р = Rz z = q>,
0 < <p < 2л}.
Вычислить линейный интеграл по данной линии L
в векторных полях* заданных в сферических координатах.
10*
148
КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
ГГЛ. VI
301. а — ercos 0-е, + 20 cos ф-е0 4- ф-еф,
L — полуокружность: {г = 1, ф = 0, 0 <1 0 л}.
302. a=4ratg у ег + 0-ф«еэ+со82 ф-вф,
L — отрезок прямой: |ф = у, 0 = —, 0 г 1 j.
303. а = sin2 0-е, 4- sin О-е0 4* гф0-еф,
L — отрезок прямой: |ф = у, г =8-|уд, y^O^yj.
Вычислить циркуляцию векторных полей, заданных
в цилиндрических координатах, по данным контурам
непосредственно и с помощью теоремы Стокса.
304. а = zep 4- ргеф + рег.
L — окружность: {р = 1, z = 0).
305. а — рмпф-вр — р2геф 4- рге2,
L — окружность: {р = R, z = R}.
306. а = z cos ф‘вр 4- реф 4- ф2ег,
L — петля: {р = sin ф, z = 1}.
Вычислить циркуляцию векторов, заданных в сфери-
ческих координатах, по данным контурам L непосредст-
венно и с помощью теоремы Стокса.
307. а = гОе, 4- г sin 0-еф,
L — окружность: {г » 1, 0 = у}.
308. а — г sin 0-е, 4- 0ее е0,
L — петля: |r = sin ф, 0 = у, 0 ф п}.
309. а — пр0-еф,
L — контур, ограниченный полуокружностью {г =
— R, ф = у, 0-^0^л|_ и ее вертикальным диаметром:
{<Н- 0 = о).
§ 25. Оператор Лапласа
в ортогональных координатах
Если и = u(qlt qs, q3) — скалярная функция, то
„ . . 1 ди 1 ди 1 ди ...
grad и — — г— е1 + — — ег + 7ГЗ—е9. (1)
: RiVqi 1 . Н, dq9 х Я, dq9 •’ ' '
I 28]
ОПЕРАТОР ЛАПЛАСА
149
Если
« - «1(?ь 9s, 9з)в1 + ®s(9i, 9s, 9s)«s + «s(9i, 9s, 9а)е»,
то
®’ — н^Г, + К + £ Р)
Используя формулы (1) и (2), для оператора Лапласа Ап получим
следующее выражение:
д д- д 1 Г д (Н2Н3ди\ .
Дu = div grad u - [dgi H1 dqi) +
4. d . JL *»Y|.
\ H2 d^l \ H3 dgrj/J
В цилиндрических координатах
1 F_d / du\ . d /_1_ du\ . d / du\l
u = p [dp V dp/ ’ d<p \ p d<p/ dz V dz /J
1 d f diA । 1 d2u d2/t
в P dp V dp/ p2 dtp2 ’ dz2 ’
В сферических координатах
. 1 fd ( a . Adu\ . d ( . ьди\ d ( 1 du\l
“ r2 sin 0 [dr V SID dr/”^d0\in d0/ dtp' sin 0d<p/j
1 1 d'( • Adw1_u 1 d2lt
e r2 dr V dr/ “г r2 sin 0 d0 Vin W d0/ ф r2 sin2 0 dtp2’
Прим е р. Найти все решения уравнения Лапласа Au = О,
зависящие только от расстояния г.
Решение. Записывая уравнение Лапласа в сферических
координатах и учитывая сферическую симметрию решения (оно не
должно зависеть от 0 и <р), будем иметь
Отсюда
так что
. Id/, diA л / / u
Дм~~2— г2— 1 = 0 (u= u(r)).
r2 dr \ or ]
Г dr “ C1’
w = + C2i
где Clt C2 — постоянные.
150
КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
[ГЛ. VI
310. Дано скалярное поле и » и(М) в цилиндриче-
ских координатах
(;;, и(р» Ф> г) = Р*Ф + г*ф’ - РФг>
Найти Au.
311. Дано скалярное поле и = и(М) в сферических
координатах
u(r, 0, ф) = г2ф0 + г?фа + ф + О2.
Найти Au.
312. Являются ли гармоническими следующие функ-
ции:
1) и == р1 cos 2ф,
2) и =» г cos 20.
313. Найти всевозможные гармонические функции
1) зависящие только от 0,
2) зависящие только от ф
(в сферической системе координат).
314. Найти все решения уравнения Пуассона
Дц =з
в сферической системе координат если и = u(r).
ОТВЕТЫ
<• a) —Q— ~^ = ~р б) ® + у = 1; в) х* + у* = 1,
t = 1;
Г)У = У> z = y! Д) ®* + уя + «* — 1» « —у = 0.
7. » + *. 8. i + k. 9.—i + ^k.
10. —i+k. 11. ei-j + 2k. 12. Нет. 14. Нет.
17. a) 2
21. Окружности, лежащие в плоскостях, перпендикулярных к
вектору а.
22. Годограф скорости — винтовая линия: х=а cos tt у »
«аsin/, я “ 2bt; годограф ускорения—окружность: х « —asin/,
у e a cos /, « == 2b.
da d*u
du dt1 *
26.
28. (t-l)e'i +
da ~dadu, d2a __ d*a
dt ““ du dt'^dt2 ^di?
- -± sin 2/1 / — arctg t • к + c.
2 /
29. у In (1 + /*) • i + у e** j + sin t • к 4- c.
80. e»ln U —A-sin j 4- tk + c.
at
/8 2f
31. g- i + (/ cos / — sin /) j + -Z- к + c.
u in z
/ _ n / 1 \
32.*j+nk. ЗЗД1-» 2/i + \«a-l//+(e-l)fc.
3
84. -In 2 • j + к. 85.2я» I + nj + n*k. 36. Д= , .
# 7 I sin 2/1
37. R = |t(l + 9t’)s/«. 88. R= 6. 39. R =1 an.
Q 2
152
ОТВЕТЫ
40. R = 2а ch1/. 41. х 4- у = 0. 42. х — у — }/2 1 = 0.
,, 1 1 .. _1=_J____________
43. у- 3. 44. т 2ach»f
х1 уа za
45. “4" + “дГ + Тб" “ семейство трехосных эллипсоидов.
46. х1 + уа — z — С — семейство параболоидов.
47. ? + = Cz - семейство параболоидов.
48. 2уа + 9z2= С — семейство эллиптических цилиндров.
49. х+ 2у — z— С — семейство параллельных плоскостей.
50. axx + а2у + a3z ® С(6хх + b2y + b3z) — пучок плоскостей,
проходящих через прямую
а1^ + агУ + azz == 0» 1
&1Х 4-Ь2у + 68z ® 0. J
Здесь л2, а3 — координаты вектора а; b2t Ъ3— координаты
вектора Ъ.
51. х1 + У2 + я2 == С2 — семейство концентрических сфер.
52. (а, Ъ, г) = С или
лельных плоскостей.
х
а1
bi
У
«2
&2
й3
^8
= С —семейство
парал-
53. 2х — у = С — семейство параллельных прямых.
54. у == Сх, С > 0 — пучок прямых.
55. уа == Сх—сем 'йство парабол.
56. ха — у2 = С — семейство гипербол.
57. у=—х In С — С, С>0—семейство прямых.
58. 13?. 59. - X?-1- 60. XIА 61. —2.62. 2 1/2.
5 7 3 5 5
63. JL. 64. 0. 65. -ХИ? (1/2 + 3). 66. 0. 67. - 2.
4 3
70. к. 71. <р == л. 72. ф = 0.
73. ф == 0. 74. у = —х + 2пя п = 0, +1, ±2,...
75. я? + у* + г3 = 1. 78.1. 79. а. 80. а(Ъ, г) + Ъ(а, г).
Л 2и
81. 21 a |3г - 2 (а. г) а. 86.-^=
ди cos (г? 1} . ,
87• д1----г* ’ д1 прн r-L^’
ди 1 ди
д1 = г3 * 89, д1 “
ОТВЕТЫ
153
направлении вектора а —— i — 2; + 2к,
У e_L. 9з, * _ У—<71 — * — Сг
ai в» в»
99.
101.
103.
104.
107.
110.
ЛЛ (grad u, grad v) 8и
®°- = —fgFSdTl—; ~Э1 “ °’ всли в 1 v'
91 а) 1 в направлении оси Оу\
б) 3 в направлении вектора
92. х —_________
Ct ct
94. х’ + р’ + а» = Cl 1 £ £ 1 1
. + » + 7+V-1'
96. х1 » Схр, I = С* 97.1 = Схх, у—С* 98. ху « Сх, х » Сг
1 1
х « Ct, 2у* - х’ = С2. 100. - — — = Сй х = Са.
си х = С2. 102. х =» Сгу, х = Сах.
i'-'£+Ct- •
п - —3. 105. П = лй2у. 100. П = яЯ’А.
П = 4яЯ»/(Я). 108- П=£. 109. П-i.
2 6
П=.1лЯ»Л. Ш. П=лЛ’.
2
П = ^-я. 113. П=”
8 4
114. П = 0. 115. П = у. 116. П - j. 117. П “ 4яЯ».
/ 7
118. П => — уг. Ц9. П = 0. 120. П = 6лЯ. 121. П = 0.
и
2 / 3
122. П = я. 123. П = 0. 124. П = у л (1~V L125. П =g Я*.
126. П => /2я. 127. П = 45л. 128. П=»-^?я. 129. П=8л.
С
130. П-0. 131. ф(г) 132. 7г*. 133. 0. 134. 0.
135. Ф(а) “ С — а, С « const. 136. П 4лЯ*.
137. aivE “ 0 (г =)Ь 0).
32 я
143. 16л. 144. лЯ8. 145. — л. 146. 0. 147. .
148. 4л. 149. -у я. 150. -у л. 151. 2Я».
152. у- я. 153, - 1. 154.- л.
112.
154
ОТВЕТЫ
155. Силеноидальное
156. Несоленоидальное.
157. Соленоидальное.
С
159. ф (г) «= , г О, С = const.
2 2 /
161. -Г2. Г-« 162. 1п-^. 163. -НЛ-тЛ 164' °*
Z 1\ А \г1ж Fja/
4 41 14 2
166. — уЛ». 167.-у. 168. а) —б) у. 169.0.
5 г- 1
170. у. 171. 3/3. 172.
173. — ла’. 174. 1.'
лЛ8 4
175. -2л. 176. — -у-. 177. -у. 179. — 2(zi + xj + ук).
1 Z
180. 3(z2 — ж2)/. 181. (х + у)к. 191. <в = у rot г? = — у /.
193. f(xt z) =» xz + х + z + C, C “ const.
195. 4л. 196.—4л. 197. 4-. 198. —2я. 199.
О о
200. 729л. 201. 0. 202. — /2л.
203. 2шлаа. Указание, v = [<o,rJ.
204. цс » 1. 205. цс — 3. 206. Зависит.
4
207. Не зависит. 208. Зависит. 209.—1. 210.
2 л 1
211, 0. 212. у. 213е -у 214. у.
л
216. у. Указание. Дополнить путь интегрирования L
отрезком О А оси Ох.
217. Нет. 218. Да. 219. Нет. 220. Да. 221. Нет.
222. Нет. 223. Да. 226. ф =» x*yz. 227. ф = х + xyz.
. 228. ф = х*у — у2 + xz. 229. ф = In |х + у + z|.
230. ф = arctg(xyz). 231. ф = г. 232. ф = In г.
233. ф = у г8« 234. ф == ах + Ру + yz + С, С » const.
235. ф == ху + yz + zx + С. 236. ф = ху + + С.
237. ф «= e*sin у + а + С. 247. а) Да; б) нет; в) да.
249. и « Сгх +
250. и = 4х2 + Вху — Ау\ А и В — любые.
{*п
—-------+ Сгх + С», если п 1,
(п — 1) П т 1 !
®ln [xj + Сгх + С, если в — 1 (х 0).
ОТВЕТЫ
155
252. /==гАя. 253. / = -” 254. I = A nR»,
15 3 3
255. I = 0.
256. b » xj + (у - х)к. 257. Ъ = (у* - 2xz)k
258. Ь « (е* - х#)]. 259. Ь = Зя2/ + (2ы3 - 6«)Л>
260. Ь ««—«(л + y2)j + (ж3 + р3)&.
261. Ъ = — (xz1 + yzex*) j — 2xyzk,
262. & “ 4 (—z; +
263 b = — 8yzi + xzj + Ixyk.'
264. b » 2xy*zi — 3x2yzj + x2y*k.
265. b » — sin»z4 — — sina?2*&.
x z
266. b^^ + y/ g-fe.
x2- + y3
267. <p = Clt r » C8sin20.
(1 \
2 sin ф 4- — ez cos ф 1 еф
*-ef зГиф-ег.
269. grad и = (cos ф 3P in 3) ep + sin 2ф — sin ф^ еф +
+ 81П2ф-е2.
270. grad u=2rcos9 er — rsinO«ee.
271. grad u = (6r sin 0 + ет созф — 1) eT + 3r Cos8’e0-*
_^er sin ф *
rsinO ф*
, /2 cos 0 . , sin 0 '
272. grad и = — ц I ..er + -p—eQ
r3
273. div a = 2 + — cos ф — еф sin z.
P
274. div a = -!L arctg p + - —
P 1 + P*
(z« + 2z)
2 4
275. diva = 4r — — cos* <f ctg 0 + —L_i=_.
Г r(r*+ 1)8100
276. rot a - e-(2cos0 + _«^n0
6in0 T I rsine/’ г ф
15в‘
OtBEtbi
Ф • . . ф , 2 cos 0
277. rota = —— ctg0 • сг+ у е0-j-----—еф.
_ „ sin ф
278. rot а = — 2реф + —— ег.
281. 24л. 282.1л. 283. 4л. 284. -|.лАа. Указание. При во-
посредственном вычислении потока надо рассматривать потоки
через все координатные поверхности г = О, г = В,
в — О, 9 =
ф « 0, ф = 2л. 285. 4лВ4. 286. 2лВ3.
1 В®
287. -2 лЯ‘—j-.
288. и®р-|-ф4"24-С.
289. и = у (р1 + ф’ + z2) + С. 290. и = р<р» + С.
291. и “ epsin ф + г* + С. 292. и — рф cos z + С.
293. и - г0 + С. 294. и - г2 + ф + 0+ С.
295. i» = y (гф* + 02) + С. 290. и = гсозфз1п04* С.
297. и - ersin 0 + 1п(1 + ф’) + С.
298. 1. 299. л8. 300. 2лЯ. 301. л2. 302. 1.
303. f+^-1.
304. 0. 305. —2лЯ4. 300. я.
307. л. 308. 0. 3Q9. 0.
310. Ди = 4ф — + 2ф\
Г К
311. Ди -= 6ф0 4- 12гф2 + -Д +фС1?0 + ^з-с1?0 + ^^.
312. 1) Да; 2) нет.
I 0 I
313. 1) и (0) = Cj, In tg у + Ct. 2) и (ф) = Схф + С,.
314. и (г) =
_ZZL_4-£1+C
(п + 1) (п + 2) + г
In г + + Сг,
„111 . +с
г + г +t«‘ -
n — 1, — 2,
—1. (г¥«0)
л = -2.
ПРИЛОЖЕНИЕ 1
ОСНОВНЫЕ ОПЕРАЦИИ ВЕКТОРНОГО АНАЛИЗА В
ОРТОГОНАЛЬНЫХ криволинейных координатах
I. Скалярное ноле задано в ортогональных криволинейных
координатах и = u(qlt q2, gs). Тогда
1 ди 1 ди 1 ди
grad u = е, +es.
Оператор Лапласа
1 Г а f Н*Нз ди У > д (
Н1Н3Н3 [ dqx 001/ ’ 002/”^"
д f нгн2 ац\1
+ 00з \ Из 003 /|
Частные случаи, а) Скалярное поле задано в цилиндри-
ческих координатах и = u(p, ф, z). Тогда
ди 1 ди ди
grad и = ер + - еф + ег
Оператор Лапласа
1 д ( ди \ . 1 д*и « a2u
Ди “ р др др ) + рг с'<₽а + dz* ‘
б) Скалярное поле задано в сферических координата? и »
= u(r, 0, <р). Тогда
ди 1 ди 1 ди
grad и = ет + т ее + “ТИгПГ дф еФ’
Оператор Лапласа
ди = L_lfl“SineV_______1___
r»dr\ drj r г4 sin е de \40 Mr«sin»0d<p«
II. Векторное поле задано в ортогональных” криволинейных
координатах
« = 9s. 9»)ei + 9г> 9з)еа + “s(9i> 9s. 9s)«s-
Тогда
1 1 div а д (ахН2Н3) д {атН9Н^
и и и 1 ZZ^/Z^AZs 1 091 1 я2я,ei 002 1 1 Яхя3 е* нгн3 8 0д» J
rot а « д 091 в1ям д д 002 003 в3Яв в«#з •
158
ПРИЛОЖЕНИЕ I It
Частные случаи, а) Векторное поле задано в цилинд*
рических координатах
а = ajp, <p, z)efi + в2(р, ф, з)еф + а8(р, ф, z)ez.
Тогда
div а =. 1 д (ря,) , £д^
Р др Г Р дф ~ dz ’
1 1
еФ Р
rot а = 2 2 £ •
др дф dz
а1 Ра2 аз
б) Векторное поле задано в сферических координатах
a = ajr, 0, ф)ег +a2 (г, 0, ф)е0 + а3(г, 0, ф)еф.
Тогда
diva = 4^ Г2 ( 21Га) . 1 д (а2 sin 0) 1 да3 Эг г sin 0 д0 г sin 0 дф* 1 1
rot а == г2 sin 0 Cr г sin 0 е® г d_ £ £ dr д0 дф «1 ra3 a3r sin 0
ПРИЛОЖЕНИЕ II
ЭЛЕМЕНТЫ ПЛОЩАДЕЙ КООРДИНАТНЫХ ПОВЕРХНОСТЕЙ
Координаты Координат- ные поверх- ности Элементы площадей
Общие Qu Qa Яз 71=С—const 72=С= const g3=(7—const dSy=H2(C, q2, q3) H3(Cf g2, q3)dq2dq3 dS^H^q^ C, q3) H3{q^ C, q^dqx dq3 ^5.3=7/1(71,72» ^2»/^)^7i dq2
Цилиндрические «1=Р> «а=Ф, p=C=const Ф=С= const z—C= const Co Co Co II II II а» a a s- •o §- -e -в н
Сферические 91=г 98=0 9з“ф r=C= const 0=C== const Ф==С= const dS^=C2 sin 0 d0 дф dS~r sin C dr дф dS—rdr d0.
ЛИТЕРАТУРА
1. Гольдфайн И. А., Векторный анализ и теория поля.
ГИФМЛ, 1962.
2. Демидович Б. П., Сборник задач и упражнений по мате-
матическому анализу, ГИФМЛ, 1962.
3. Кальницкий Л. А., Добротин Д. А., Ж е в е р-
ж е е в В. Ф., Специальный курс высшей математики, «Выс-
шая школа», 1976.
4. Кочин Н. Б., Векторное исчисление и начала тензорного
исчисления, Изд-во АН СССР, 1951.
5. Кручкович Г. И., Мордасова Г. М., Подольс-
кий В. А., Римский-Корсаков Б. С., Сулей-
ман о в а X. Р., Ч е г и с И. А., Сборник задачи упражнений
по специальным главам высшей математики, «Высшая школа»,
1970.
6. К у д р я в ц е в Л. Д., Математический анализ, том II, «Выс-
шая школа»; 1973.
7. Ладон И. Ф., Основы векторного исчисления е'приложени-
ями к теории электромагнитного поля. — Издание ВЭТА, Ле-
нинград, 1938.
8. Лаптев Г. Ф., Элементы векторного исчисления, «Наука»,
1975.
9. МисюркеевИ. В., Сборник задач и упражнений по мето-
дам математической физики, «Просвещение», 1975.
10. Н и к о л ь с к и й С. М., Курс математического анализа^
том II, «Наука», 1973.
И. О ч а н Ю. С., Сборник задач по методам математической фи-
зики, «Высшая школа», 1967.
12. ПчелинБ. К., Векторный анализ для инженеров-электри-
ков и радистов, «Энергия», 1968,
Михаил Леонтьевич
Краснов
Александр Иванович
Киселев
Григорий Иванович
Макаренко
ВЕКТОРНЫЙ АНАЛИЗ
(Серия: «Избранные главы
высшей математики для инженеров
и студентов втузов»)
М., 1978 г.| 160 стр., с илл.
Редакторы В. В. Абзарян,
А. С. Чистопольский
Техн, редактор Е. В. Морозова
Корректор Л. С. Сомова
ИВ N 2221
Сдано в набор 05.04.78.
Подписано к печати 21.08.78.
Бумага 84хЮ81/»г» тип. М« 1.
Обыкновенная гарнитура.
Высокая печать.
Условн. печ. л. 8,4. Уч.-изд. л. 8,41.
Тираж 60 000 экз. Заказ Mi НО,
Цена книги 35 коп. *
Издательство «Наука»
Главная редакция
физико-математической литературы
117071,Москва,В-71, Ленинский проспект, 15
Типография № 4 издательства «Наука»
630077, Новосибирск, 77,
Станиславского, 25
Цена 35 кол.